
IAHR
CIC
XX SEMINARIO NACIONAL DE HIDRÁULICA E HIDROLOGÍA-
BARRANQUILLA, COLOMBIA, 8 AL 10 DE AGOSTO DE 2012
EFECTO DEL USO DE LA ECUACIÓN DE DARCY-WEISBACH VS LA
ECUACIÓN DE HAZEN-WILLIAMS EN EL DISEÑO DE REDES
MATRICES
Rafael A. Flechas
Investigador, Centro de Investigación en Acueductos y Alcantarillados de la Universidad de Los Andes –CIACUA–,
Departamento de Ingeniería Civil y Ambiental, Bogotá, Colombia, rafalflechas@gmail.com
RESUMEN:
En el diseño y análisis de redes de distribución de agua potable (RDAP), las ecuaciones más
empleadas para calcular las pérdidas por fricción son: la ecuación de Darcy-Weisbach y la ecuación
de Hazen-Williams. El uso de esta última ecuación empírica se ha popularizado alrededor del
mundo por su facilidad de manejo. Sin embargo, el uso de ésta en el diseño de redes matrices, parte
fundamental de RDAP, muchas veces se hace sin tener en cuenta sus límites de aplicabilidad. Por
ello, en este artículo se analizó el efecto del uso de la ecuación de Darcy-Weisbach vs la Ecuación
de Hazen-Williams en redes matrices, las cuales presentan tuberías de gran diámetro que
transportan altos caudales. Con base en ello, se encontró que la ecuación de Hazen-Williams no
cumple con los requisitos de diseño de estas redes, dado que no tiene en cuenta el efecto de la
variación de la rugosidad relativa para números de Reynolds de gran magnitud.
PALABRAS CLAVES: Ecuación de Darcy-Weisbach, Ecuación de Hazen-Williams, redes
matrices.

INTRODUCCIÓN
El creciente aumento de la demanda de agua en las ciudades, y la limitada oferta de agua que
existe alrededor del mundo exige, por parte de los ingenieros, el diseño optimizado de las redes
matrices, las cuales se encargan de transportar, con tuberías de gran diámetro, el agua desde las
fuentes de abastecimiento hasta los tanques de almacenamiento, que posteriormente distribuyen este
recurso vital a una población especifica.
Para llevar a cabo dicho propósito, es necesario establecer con certeza la magnitud de las
pérdidas por fricción que se generan en las tuberías. En este sentido, las ecuaciones más empleadas
por los ingenieros para calcular dichas pérdidas son: la ecuación de Darcy-Weisbach [1] en
conjunto con la ecuación de Colebrook-White [2], ecuaciones físicamente basadas, y la ecuación de
Hazen-Williams [3], ecuación de origen experimental que es válida solamente en los rangos
investigados para su formulación.
donde hf son las pérdidas por fricción, L es la longitud de la tubería, V la velocidad de flujo, g
es la aceleración de la gravedad, f es el factor de fricción, Re el número de Reynolds y ks la
rugosidad absoluta de la tubería.
donde C
HW
es el coeficiente de la ecuación de Hazen-Williams, R es el radio hidráulico y S es
la pendiente de la línea del gradiente hidráulico.
En relación con la ecuación de Darcy-Weisbach, se puede decir que ésta se puede aplicar para
cualquier temperatura, rango de velocidades, diámetros y longitudes de tubería. Sin embargo, el
cálculo de las pérdidas por fricción por medio de ésta se dificulta, dado que el factor de fricción es
un parámetro difícil de cuantificar analíticamente, lo cual se refleja en la ecuación de Colebrook-
White ya que no explícita para f. Este problema ocasionó la aparición de ecuaciones empíricas más
sencillas de utilizar como la ecuación de Hazen-Williams [3], la cual es ampliamente utilizada en la
actualidad por muchos ingenieros, debido a que presenta la ventaja de ser explícita para el cálculo
de la velocidad. Sin embargo, el uso de esta ecuación empírica muchas veces se hace sin tener en
cuenta las limitaciones inherentes que presenta desde el punto de vista hidráulico (Bombardelli &
García, 2003), dado que esta ecuación utiliza un coeficiente de rugosidad que no depende solamente
de la rugosidad absoluta de la tubería (ks), sino de la velocidad, magnitud del diámetro y viscosidad
del fluido (Vennard 1958, Diskin 1960; Liou 1998).
Teniendo en cuenta estas limitaciones, algunos investigadores (Diskin 1960, Barlow y
Markland 1975, Jain et al 1978, Kamand 1988; Liou 1998) han propuesto metodologías para la
aplicación adecuada de esta ecuación restringiendo su uso para un rango específico del número de
Reynolds (Re) y diámetros. A pesar de todos estos esfuerzos, en la actualidad muchos de los
ingenieros no consideran las implicaciones hidráulicas que puede tener el uso de dicha ecuación
empírica en el diseño de redes matrices, las cuales presentan tuberías de gran diámetro que
transportan altos caudales.

Por esta razón, en este artículo se pretende analizar el efecto del uso de la ecuación de Hazen-
Williams vs. la ecuación de Darcy-Weisbach en el diseño de redes matrices. Para ello, se diseñaron
distintas redes matrices hipotéticas utilizando las ecuaciones de Darcy-Weisbach y Hazen-Williams,
bajo parámetros de presión mínima, temperatura y diferentes tipos de materiales, según la
normativa colombiana. Luego, con base en estos diseños se establecieron las implicaciones
hidráulicas en el diseño de éstas redes por el uso de una ecuación respecto al uso de la otra. Luego,
teniendo en cuenta las implicaciones de la ecuación de Hazen-Williams en el diseño de las redes
matrices, se propone la corrección de los coeficientes de Hazen-Williams, sugeridos en la normativa
colombiana, a fin de minimizar el error en el cálculo de las pérdidas por fricción. Finalmente, se
muestran algunas conclusiones con base en este análisis.
BASE TEORICA
Teniendo en cuenta las limitaciones inherentes que presenta la ecuación de Hazen-Williams, a
lo largo del Siglo XX se han realizado diversos estudios para establecer cuáles son los efectos de
utilizar esta ecuación en el cálculo de flujo de tuberías en comparación con la ecuación de Darcy-
Weisbach. Vennard (1958) fue el primer investigador en establecer que la ecuación de Hazen-
Williams no se podía aplicar en tuberías que presentaban flujo turbulento hidráulicamente rugoso
(FTHR), dado que el coeficiente de ésta depende de las condiciones de flujo y la rugosidad relativa.
Luego, a diferencia de este investigador, Diskin (1960) logró establecer los límites de aplicabilidad
de esta ecuación para los diferentes tipos de flujo. Para ello, reorganizó la ecuación de Hazen-
Williams en la forma de la ecuación de Darcy-Weisbach para obtener una relación potencial que
relacionara el factor de fricción y el coeficiente de la ecuación de Hazen-Williams (Ecuación [4]):
Graficando la Ecuación [4] en el diagrama de Moody, Diskin (1960) concluyó que la ecuación
de Hazen-Williams es aplicable en una parte de la zona de transición de este diagrama, para un
rango de números de Reynolds y coeficientes de Hazen-Williams (100 y 160), donde las líneas de
este diagrama son paralelas a las líneas dibujadas a partir de la Ecuación [4].
Teniendo en cuenta las limitaciones que presentaba la ecuación de Hazen-Williams, expuestas
por Vennard (1958) y Diskin (1960), diversos investigadores (Barlow y Markland 1975, Jain et al
1978; Kamand 1988) intentaron corregir dicha ecuación a fin de obtener una mayor exactitud en el
cálculo de las pérdidas por fricción en tuberías en comparación con la ecuación de Darcy-Weisbach.
A pesar de estos esfuerzos, en la actualidad esta ecuación se sigue utilizando alrededor del mundo
sin tener en cuenta los efectos que podría tener su uso en las redes de distribución de agua potable
(RDAP) y específicamente en las redes con tuberías de gran diámetro. Por esta razón, recientemente
los investigadores Liou (1998), Bombardelli y García (2003) realizaron algunos estudios para
analizar dicho efecto.
Liou (1998) mostró cuantitativamente los efectos y las limitaciones que presenta la utilización
de la ecuación de Hazen-Williams en tuberías. Para ello, este investigador, primero dedujo la
relación que existe entre el coeficiente de esta ecuación empírica, el número de Reynolds y la
rugosidad relativa, con base en la ecuación de Darcy-Weisbach [1], la ecuación de Colebrook-
White [2] y la ecuación de Hazen-Williams [3], tal como se ilustra a continuación:
[5]
donde ν es la viscosidad cinemática del fluido.
Graficando los datos utilizados por Hazen & Williams (1905) para la formulación de su
ecuación, a partir de la Ecuación [5], para un ks = 0.0003 m y ν = 1.133x10
-6
m
2
/s (viscosidad
cinemática del agua a una temperatura de 15.56
o
C), Liou (1998) coincide con Diskin en afirmar que
estos datos se encuentran en la zona de transición del diagrama de Moody. Adicionalmente, este
investigador logró establecer que por fuera de este rango de validez se pueden presentar errores de
hasta el 40% en el cálculo de las pérdidas por fricción cuando se utiliza la Ecuación de Hazen-
Williams en comparación a la Ecuación de Darcy-Weisbach. Por lo anterior, Liou recomienda
evitar la utilización de la ecuación de Hazen-Williams para el cálculo de flujo de tuberías.
Luego, Bombardelli y García (2003), analizaron los efectos que tiene el uso de la ecuación de
Hazen-Williams posteriormente al diseño de redes matrices con esta ecuación. Para ello, estos
investigadores partieron del problema que se presentaba en una red matriz de una ciudad después de
5 años de operación, el cual era la disminución significativa de los coeficientes de Hazen-Williams
calculados por firmas de ingeniería (entre 85 y 95 para tuberías de 2.29 m de diámetro) en
comparación a los coeficientes utilizados inicialmente en el diseño de las tuberías del sistema (C
HW
=120, tuberías de concreto). Después de verificar que las mediciones hechas por estas firmas no
presentaban error alguno, Bombardelli y García establecieron las causas de dichas mediciones.
Estas estaban relacionadas con el tipo de flujo que se presentaba en la operación del sistema, ya que
el aumento de la demanda y la continua operación del sistema generaban flujos que se ubicaban en
el régimen de FTHR, régimen donde no es posible aplicar la ecuación de Hazen-Williams. Por lo
anterior, estos investigadores recomiendan utilizar la ecuación de Darcy-Weisbach en el diseño de
RDAP y redes matrices debido a que esta incluye todos los tipos de flujo.
METODOLOGIA
Para llevar a cabo los objetivos propuestos, se diseñaron y analizaron dos redes matrices
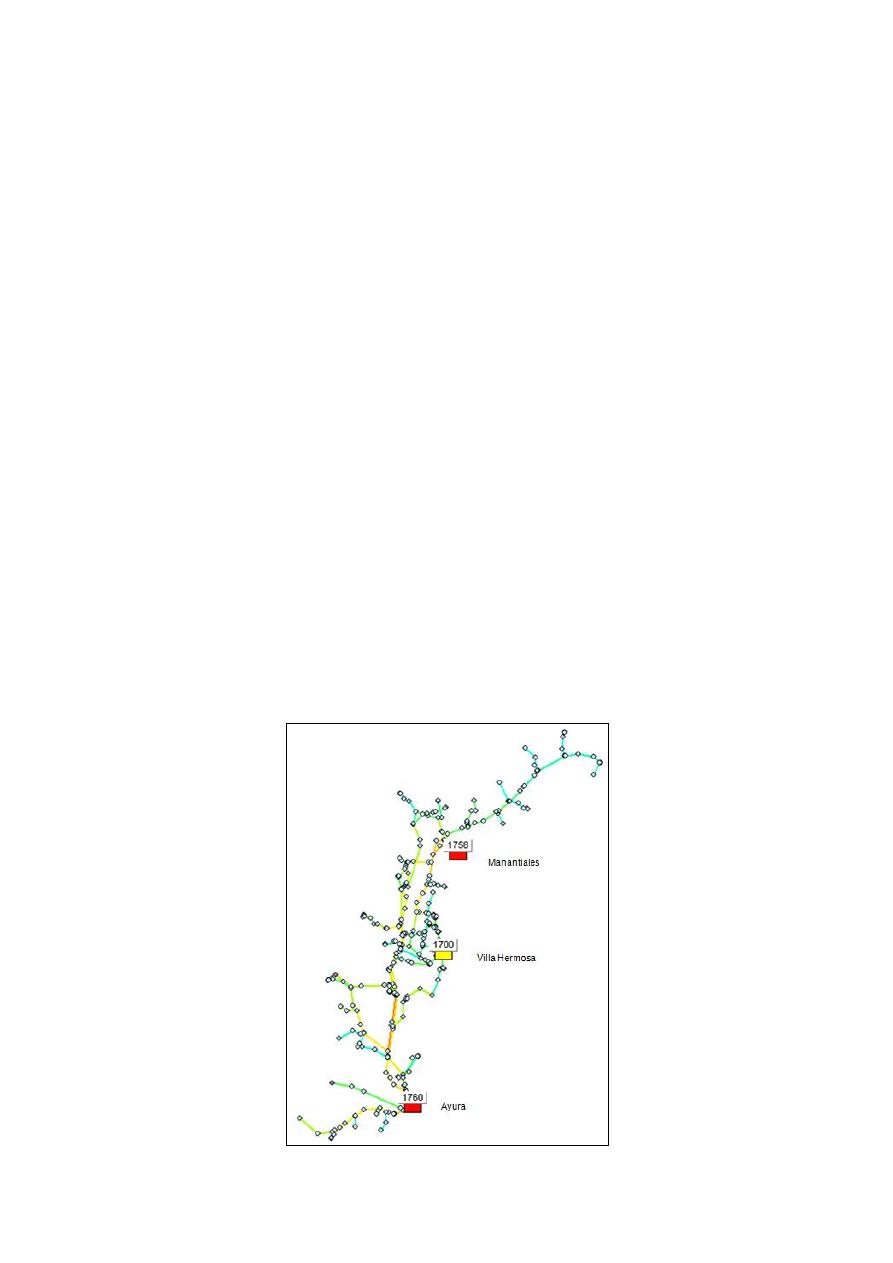
utilizando las ecuaciones de Darcy-Weisbach y Hazen-Williams: una red matriz hipotética de la
ciudad de Medellín, la cual consta de 685 nudos y 768 tuberías y está conformada por 3 embalses
(Ver Figura 1), cuya oferta de agua es igual a 8 m
3
/s y se distribuye de la siguiente manera: Ayurá
(5 m
3
/s) y Manantiales (3 m
3
/s). Adicionalmente, se escogió la red matriz Hanoi, red hipotética que
consta de 34 tuberías y 31 nudos, los cuales presentan una demanda igual a 830 m
3
/h.
Figura 1.- Topología Red matriz hipotética de Medellín.

Para diseñar estas redes, se utilizó el programa REDES, programa creado en la Universidad
de los Andes, Bogotá, Colombia (1988), teniendo en cuenta los siguientes parámetros de diseño en
común para estas redes:
Método de diseño: Superficie Óptima del Gradiente Hidráulico.
Presión mínima: 20 metros de columna de agua (mca).
Materiales: CCP, GRP y Acero (Ver tabla 1).
Temperatura: 15°C (solo aplica para los diseños con la ecuación de Darcy-Weisbach).
Tabla 1.- Valores de k
s
y C
HW
materiales seleccionados.
Material
ks
[mm]
C
HW
[ - ]
CCP
0.12
120
GRP
0.03
150
Acero
0.45
120
Con base en lo anterior, se procedió a analizar estas redes, para cada uno de estos materiales,
realizando comprobaciones de diseño mediante las herramientas computacionales EPANET (2000)
y REDES (1988), a fin de obtener las pérdidas por fricción, caudales y presión de los nudos tanto
para la ecuación de Hazen-Williams y Darcy-Weisbach. Con base en estos resultados, se procedió a
calcular la variación del coeficiente de Hazen-Williams a partir de la ecuación [5] propuesta por
Liou (1998) y su efecto en los errores en las pérdidas por fricción y distribución de presiones en las
redes de estudio cuando se utiliza dicha ecuación empírica.
Luego, dependiendo si el error en las pérdidas por fricción, para cada material, en algunas
tuberías de estas redes es mayor al 5%, se desarrolló un programa en Visual Basic para corregir los
coeficientes de Hazen-Williams sugeridos en la normativa colombiana (Ver Tabla 1), para un rango
de número de Reynolds y velocidades asociado a un diámetro mínimo, situación crítica en el diseño
de redes matrices, dado que así se subestiman las pérdidas por fricción; se correría el riesgo de no
cumplir con las presiones de operación en estas redes.
Posteriormente, se validaron los diseños obtenidos a partir de estos coeficientes corregidos,
realizando comprobaciones de diseño utilizando la ecuación de Darcy-Weisbach para establecer la
precisión de los mismos en cuanto a la distribución de presiones y cumplimiento de la presión
mínima. Igualmente, se compararon los resultados de estos diseños con los obtenidos a partir de los
coeficientes de Hazen-Williams sugeridos en la normativa colombiana.
Finalmente, teniendo en cuenta los límites de aplicabilidad de la ecuación de Hazen-Williams,
los cuales están definidos por la zona de transición del diagrama de Moody (Diskin, 1960), y los
establecidos para los coeficientes de Hazen-Williams corregidos, se analizaron los diseños
obtenidos en el diagrama de Moody.
RESULTADOS
En el presente capítulo se presentan los resultados obtenidos en relación con los efectos del
uso de la ecuación de Hazen-Williams vs la Ecuación de Darcy-Weisbach en redes matrices,
específicamente para la red matriz hipotética de Medellín, dado que para la red Hanoi se
encontraron resultados similares a esta. Para ello, este capítulo se dividirá en cuatro partes. En la
primera, se analizará el efecto del uso de la ecuación de Hazen-Williams cuando se utiliza un
coeficiente de rugosidad constante, sugerido en la normativa colombiana, en la estimación de las
pérdidas por fricción y distribución de presiones. Luego, se ilustrarán los coeficientes de Hazen-
Williams corregidos para los materiales de estudio. Posteriormente, en la tercera parte se mostrarán
los resultados obtenidos en relación con el diseño de las redes matrices de estudio, utilizando tanto
los coeficientes de Hazen-Williams corregidos y sugeridos en la normativa colombiana. En la
última parte, se expondrá la comparación de estos diseños y su respectiva validación, utilizando la
ecuación de Darcy-Weisbach.
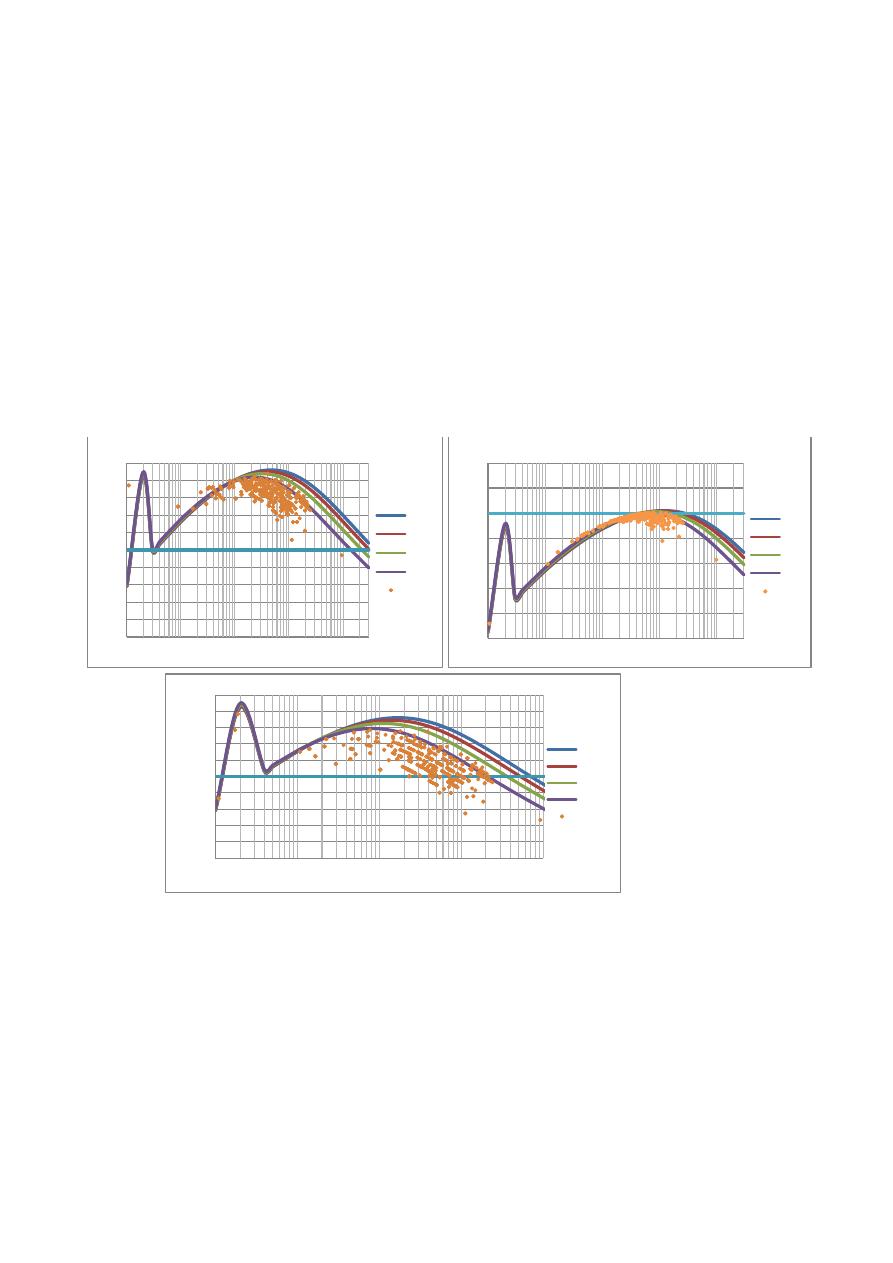
Error pérdidas por Fricción
Con base en la metodología propuesta, se calcularon los errores en la estimación de las
pérdidas por fricción utilizando la ecuación de Hazen-Williams, acorde a los coeficientes de esta
ecuación sugeridos en la normativa colombiana para el Acero, CCP y GRP (Tabla 1). A partir de lo
anterior, se obtuvo que los valores sugeridos de este coeficiente en la normativa colombiana para el
Acero y CCP, sobreestiman las pérdidas por fricción hasta en un 40% y 20% respectivamente (ver
Figura 2). Adicionalmente, en la Figura 2 se puede apreciar que estos coeficientes son válidos para
un rango de número de Reynolds superior a 200.000 para el Acero y superior a 1.000.000 para
CCP, dado que en estos rangos los errores en las pérdidas por fricción en la red matriz de Medellín
no superan el 10%. Por su parte, para el material GRP, se puede ver en esta misma figura que el
valor sugerido en la normativa colombiana es adecuado dado que los errores en las pérdidas por
fricción no superan el 10% en la subestimación en las pérdidas por fricción. Pese a ello, se corre el
riesgo de que para números de Reynolds inferiores a 10.000 o superiores a 1.000.000 se subestimen
las pérdidas por fricción en la red y por lo tanto no se pueda cumplir con las presiones mínimas
exigidas en la red de estudio.
Figura 2.- Errores en las pérdidas por fricción en la red matriz hipotética de Medellín, utilizando la
ecuación de Darcy-Weisbach y Hazen-Williams para el CCP, GRP y Acero.
Errores presiones de los nudos
Con base en la metodología propuesta, se obtuvo (Ver Figura 3) que los valores sugeridos del
coeficiente de Hazen-Williams, acorde a la normativa colombiana, para el CCP, GRP y Acero
sobreestiman las presiones en los nudos hasta en un 10%, 17% y 70% respectivamente, cerca al
embalse de Ayurá, el cual suministra el mayor caudal a esta red (5 m
3
/s). Lo anterior, es consistente
con los resultados obtenidos en cuanto a los errores en las pérdidas por fricción para estos
materiales, dado que en este sector de la red matriz hipotética de Medellín se presentan números de
Reynolds superiores a 9.000.000, rango en el cual los coeficientes de Hazen-Williams para estos
materiales, tiende a subestimar las pérdidas por fricción por encima del 10%.
-50%
-40%
-30%
-20%
-10%
0%
10%
20%
30%
40%
50%
1,00E+03
1,00E+04
1,00E+05
1,00E+06
1,00E+07
(S
h
w
-S
d
w
)/
Sd
w
Número de Reynolds
Errores pérdidas por fricción (CCP, ks: 0.12 mm, CHw:120 )
d=2.5 m
d=2.0 m
d=1.5 m
d=1.0 m
Errores
Red
-50%
-40%
-30%
-20%
-10%
0%
10%
20%
1,00E+03
1,00E+04
1,00E+05
1,00E+06
1,00E+07
(S
h
w
-S
d
w
)/
Sd
w
Número de Reynolds
Errores pérdidas por Fricción (GRP, ks:0.03 mm, CHw:150 )
d=2.5 m
d=2.0 m
d=1.5 m
d=1.0 m
Error
Red
-50%
-40%
-30%
-20%
-10%
0%
10%
20%
30%
40%
50%
1,00E+03
1,00E+04
1,00E+05
1,00E+06
1,00E+07
(S
h
w
-S
d
w
)/
Sd
w
Número de Reynolds
Errores pérdidas por Fricción (Acero, ks:0.45 mm, CHw:120)
d=2.5 m
d=2.0 m
d=1.5 m
d=1.0 m
Error Red
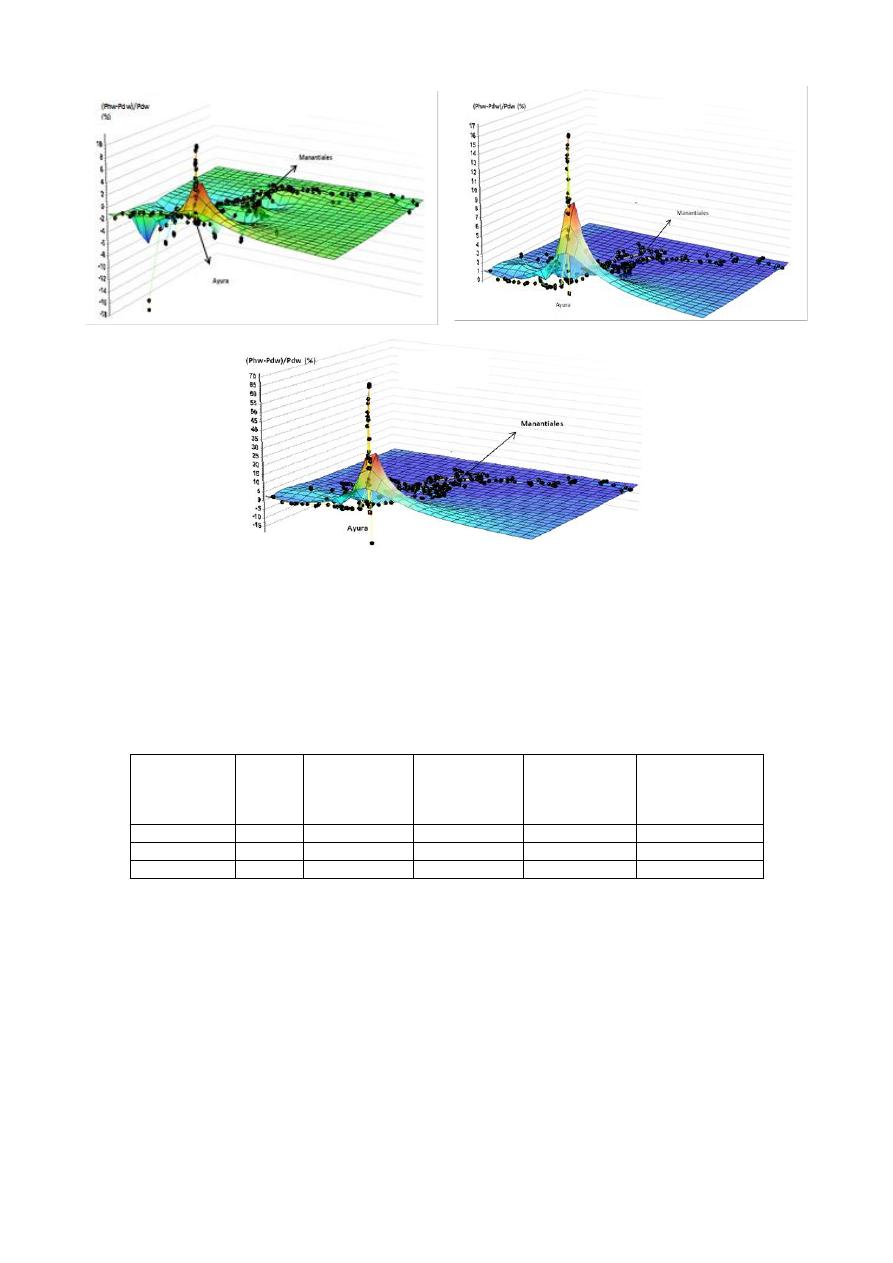
Figuras 3.- Errores en las presiones en los nudos de la red matriz hipotética de Medellín, utilizando la
ecuación de Darcy-Weisbach y Hazen-Williams para el Acero, GRP y CCP
Corrección Coeficientes de Hazen-Williams
Teniendo en cuenta los anteriores resultados, se sugirió modificar los coeficientes de Hazen-
Williams sugeridos en la normativa colombiana para el Acero, CCP y GRP (Ver Tabla 2), a fin de
controlar el error en las pérdidas por fricción hasta en un 5%.
Tabla 2.- Corrección del Coeficiente de Hazen-Williams para los materiales de estudio.
Material
[ - ]
CHw
[ - ]
Re mínimo
[ - ]
Re máximo
[ - ]
Diámetro
mínimo
[mm]
Velocidad límite
máxima
[m/s]
CCP
144
4.50E+04
4.15E+05
500
0.95
GRP
147
7.00E+04
2.48E+06
500
5.6
Acero
139
2.50E+04
2.55E+05
1000
0.3
Validación y Análisis Diseños
Con base en los resultados obtenidos en los errores en las presiones en los nudos, se puede ver
que el sector donde se presentan mayores errores en la estimación de la distribución de presiones de
la red matriz hipotética de Medellín, es el sector delimitado por el Embalse de Ayurá. Por ello se
decidió diseñar solamente el sector comprendido por este embalse, para los coeficientes de Hazen-
Williams sugeridos en la normativa colombiana y los corregidos en este artículo. Luego de haber
obtenido los diseños de esta red para dicho sector, se procedió a validar estos diseños a fin de
verificar si en realidad cumplen con la presión mínima establecida (20 mca).
Posteriormente, se analizaron los factores de fricción obtenidos mediante estos diseños en la
zona de transición del diagrama de Moody, zona que va desde la línea límite máxima donde se
puede presentar flujo turbulento hidráulicamente liso (FTHL) hasta la línea límite mínima donde se
puede presentar flujo turbulento hidráulicamente rugoso (FTHR). A continuación se ilustran las
CCP
GRP
ACERO
ecuaciones que se utilizaron para delimitar el límite inferior y superior de la zona de transición,
incluyendo las nuevas ecuaciones propuestas por el autor para estos límites con base en la ecuación
de Colebrook-White y los límites establecidos por estos dos investigadores para esta zona (Flechas,
2010).
Límite inferior zona de transición (Límite FTHL)
Límite superior zona de transición (Límite FTHR)
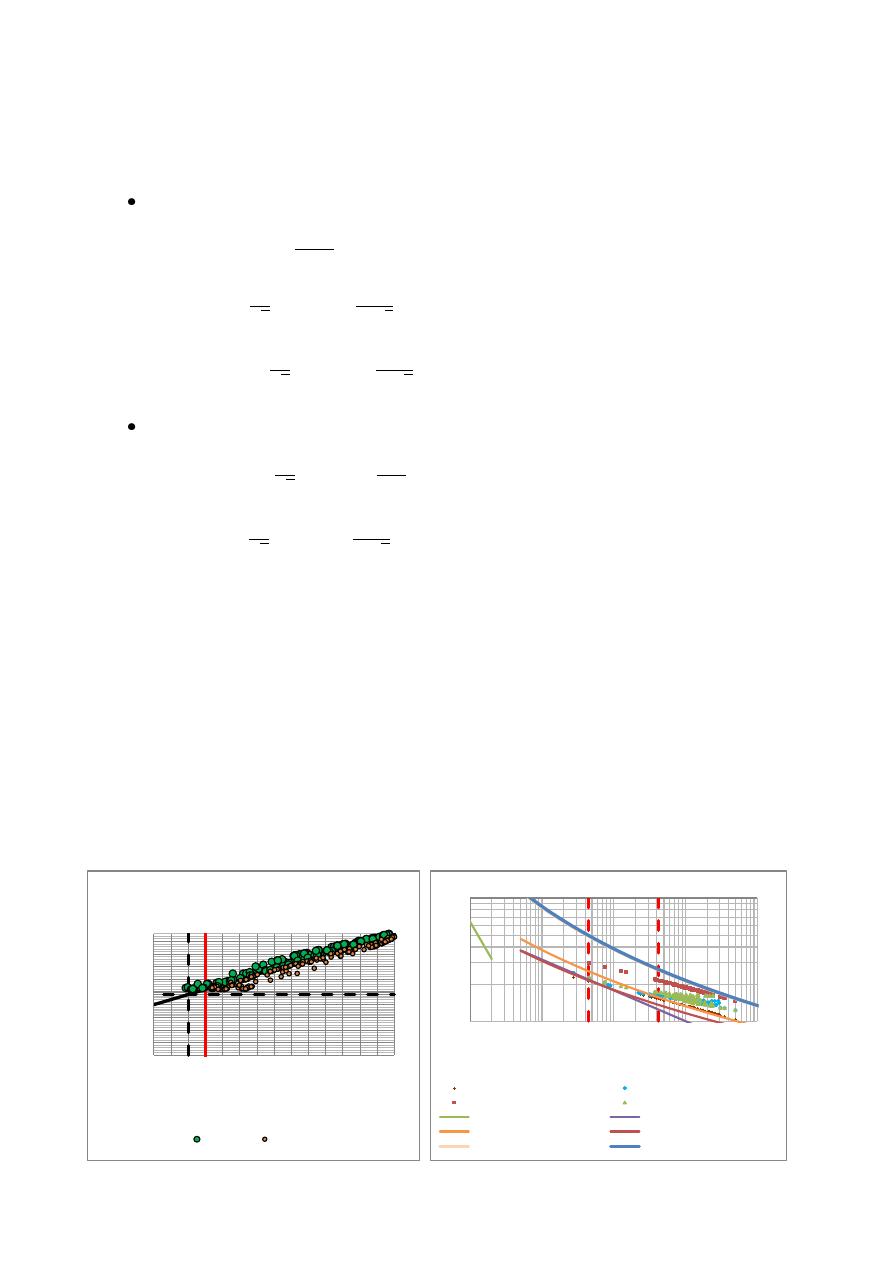
A partir de lo anterior, se puede apreciar en la Figura 4 que el diseño obtenido a partir del
coeficiente de Hazen-Williams corregido para el material CCP (CHw: 144) tiende a sobreestimar
las presiones en la red matriz hipotética de Medellín. Así mismo, se puede ver en esta misma figura
que este diseño no cumple con la presión mínima de diseño de esta red (20 mca). Por otro lado, el
diseño obtenido a partir del coeficiente de Hazen-Williams sugerido en la normativa colombiana
(CHw: 120) subestima las presiones en esta red, pero se encuentran por encima de la presión
mínima de diseño. Lo anterior se explica ya que el coeficiente de Hazen-Williams corregido para
este material subestima las pérdidas por fricción, dado que dicho coeficiente obliga a que el flujo en
las tuberías en esta red sea FTHL, cuando en la realidad, para la rugosidad absoluta dada para el
CCP, el flujo es turbulento transicional (Ver Figura 4) para los diámetros obtenidos en este diseño.
Adicionalmente, los factores de fricción obtenidos a partir del coeficiente de Hazen-Williams
corregido para el material CCP no se ubican en el rango de número de Reynolds establecido en la
Tabla 2, lo cual no permite cumplir con la presión mínima de diseño (Ver Figura 4).
-240
-190
-140
-90
-40
10
60
110
160
210
-40 -20 0 20 40 60 80 100 120 140 160 180 200 220 240
P
re
si
o
n
e
s
H
az
e
n
-W
ill
ia
m
s
(
m
.c
.a
)
Comprobación Presiones diseño Darcy-Weisbach
(m.c.a)
Diagrama dispersión de presiones diseño Red
Medellín (CCP, ks: 0.12 mm)
CHw: 144
CHw: 120
0,01
0,1
1,00E+03
1,00E+04
1,00E+05
1,00E+06
1,00E+07
Fa
ct
o
r
d
e
f
ri
cc
ió
n
Número de Reynolds
Diagrama de Moody (Red Medellín, CCP, ks: 0.12 mm)
Hazen-Williams (CHW: 144)
Validación (CHW: 144)
Hazen-Williams (CHW:120)
Validación (CHW: 120)
Flujo laminar
FTHL (Blasius)
Límite FTHL (Colebrook-White)
Límite FTHL (Prandtl-Von Kármán)
Límite FTHR (Colebrook-White)
Límite FTHR (Prandtl-Von Kármán)
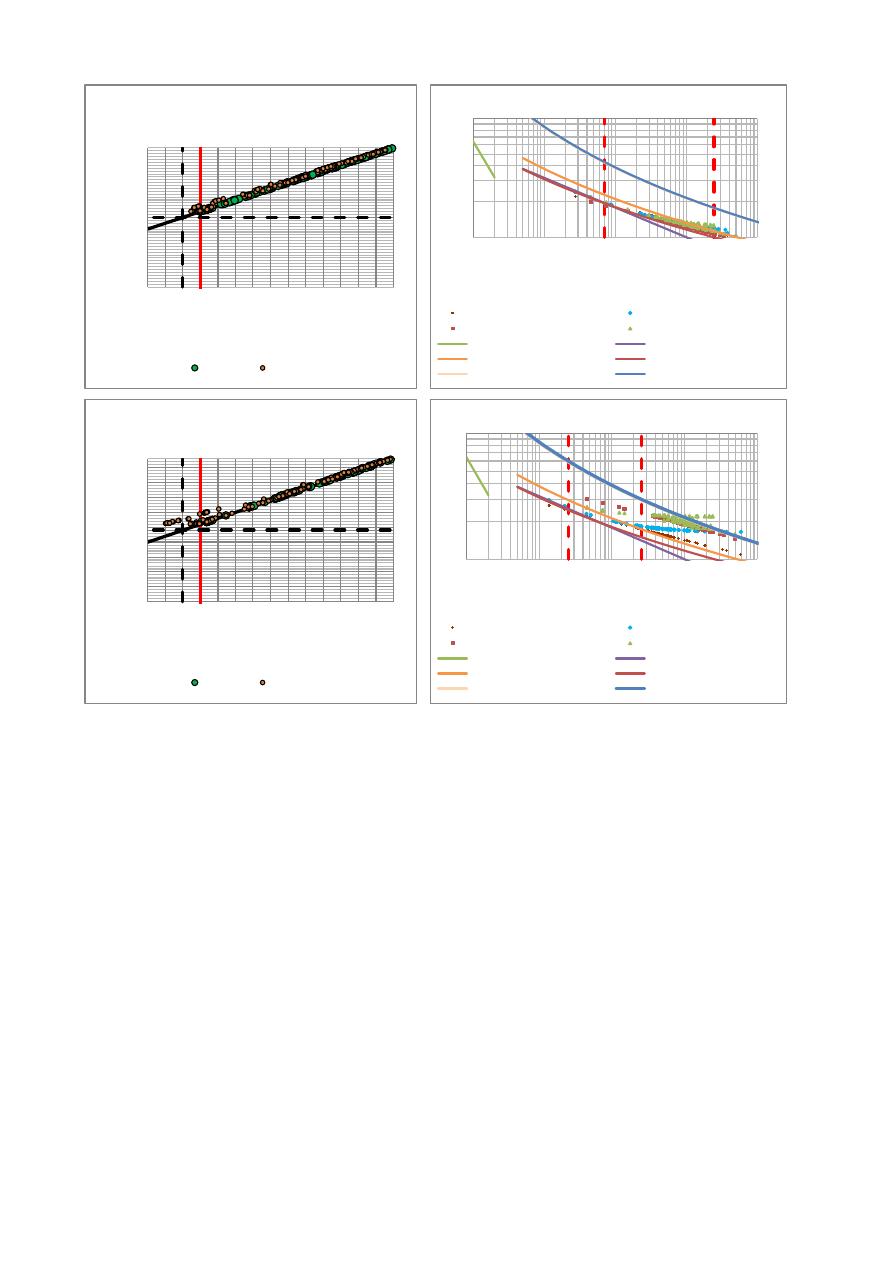
Figura 4.- Validación y análisis de los diseños obtenidos mediante los coeficientes de Hazen-Williams
sugeridos en la normativa colombiana y los corregidos para los materiales Acero, CCP y GRP.
Por otro lado, para el material GRP, se puede ver en la Figura 4 que el diseño obtenido a partir
del coeficiente de Hazen-Williams corregido (CHw: 147) tiende a igualar las presiones en la red
matriz hipotética de Medellín, cumpliendo con la presión mínima de diseño de esta red (20 mca).
Entre tanto, el diseño obtenido a partir del coeficiente de Hazen-Williams sugerido en la normativa
colombiana (CHw: 150) para este material, subestima las presiones en esta red y en algunos nudos
no se logra cumplir con la presión mínima de diseño. Lo anterior se explica dado que los factores de
fricción obtenidos mediante el coeficiente de Hazen-Williams corregido para este material se
localizan en el FTHL, según los límites de la zona de transición definidos por el autor (2010), donde
es posible utilizar dicho coeficiente con buena precisión, con respecto a la ecuación de Darcy-
Weisbach, según el rango de número de Reynolds definido para dicho coeficiente (Ver Tabla 2).
Por su parte, para el coeficiente de Hazen-Williams sugerido en la normativa colombiana, los
factores de fricción tienden subestimar las pérdidas por fricción para números de Reynolds
superiores a 1.000.000.
Finalmente, con respecto a los diseños obtenidos para el Acero, se puede apreciar en la Figura
4 que los factores hidráulicos obtenidos a partir del diseño de esta red, utilizando la ecuación de
Hazen-Williams y el coeficiente corregido para este material (CHw: 139), se localizan en la zona
del flujo turbulento transicional, para números de Reynolds superiores a 200.000. De otro lado, para
este mismo rango de números de Reynolds, los factores de fricción obtenidos en la validación de
este diseño, se localizan en la zona de transición y tienden a ubicarse en el FTHR. Pese a lo anterior,
-240
-190
-140
-90
-40
10
60
110
160
210
-40 -20 0 20 40 60 80 100 120 140 160 180 200 220 240
P
re
si
o
n
e
s
H
az
e
n
-W
ill
ia
m
s
(
m
.c
.a
)
Comprobación Presiones diseño Darcy-Weisbach
(m.c.a)
Diagrama dispersión de presiones Diseño Red
Medellín (GRP, ks: 0.03 mm)
CHw: 147
CHw: 150
0,01
0,1
1,00E+03
1,00E+04
1,00E+05
1,00E+06
1,00E+07
Fa
ct
o
r
d
e
f
ri
cc
ió
n
Número de Reynolds
Diagrama de Moody (Red Medellín, GRP, ks: 0.03 mm)
Hazen-Williams (CHw: 147)
Validación (CHW: 147)
Hazen-Williams (CHw:150)
Validación (CHw: 150)
Flujo laminar
FTHL (Blasius)
Límite FTHL (Colebrook-White)
Límite FTHL (Prandtl-Von Kármán)
Límite FTHR (Colebrook-White)
Límite FTHR (Prandtl-Von Kármán)
-240
-190
-140
-90
-40
10
60
110
160
210
-40 -20 0 20 40 60 80 100 120 140 160 180 200 220 240
P
re
si
o
n
e
s
H
az
e
n
-W
ill
ia
m
s
(m
.c
.a
)
Comprobación Presiones diseño Darcy-Weisbach
(m.c.a)
Diagrama dispersión de presiones en la Red
Medellín (Acero, ks: 0.45 mm)
CHw: 139
CHw: 120
0,01
0,1
1,00E+03
1,00E+04
1,00E+05
1,00E+06
1,00E+07
Fa
ct
o
r
d
e
f
ri
cc
ió
n
Número de Reynolds
Diagrama de Moody (Red Medellín, Acero, ks: 0.45 mm)
Hazen-Williams (CHw: 139)
Validación (CHW: 139)
Hazen-Williams (CHw:120)
Validación (CHw: 120)
Flujo laminar
FTHL (Blasius)
Límite FTHL (Colebrook-White)
Límite FTHL (Prandtl-Von Kármán)
Límite FTHR (Colebrook-White)
Límite FTHR (Prandtl-Von Kármán)

es importante resaltar que, en el rango de número de Reynolds definido para utilizar dicho
coeficiente, los factores de fricción tanto del diseño como la validación del mismo, tienden a
igualarse en el FTHL en el diagrama de Moody según el límite definido por el autor (2010) para
este tipo de flujo (Ver Figura 4). Lo anterior, explica por qué el coeficiente de Hazen-Williams
sugerido en este trabajo para este material permite cumplir con la presión mínima de diseño.
CONCLUSIONES
Los coeficientes de Hazen-Williams sugeridos en la normativa colombiana no son correctos
para el Acero y CCP, dado que estos valores tienden a sobrestimar las pérdidas por fricción y
no tienen en cuenta la variabilidad que presenta dicho coeficiente en el comportamiento
hidráulico de estas redes.
A partir de los resultados obtenidos en la corrección de los coeficientes de Hazen-Williams,
en especial para el Acero, CCP y GRP, se puede concluir que se logró tener en cuenta la
variabilidad de estos y controlar hasta en un 5% las pérdidas por fricción para un rango
específico de números de Reynolds y velocidades.
Si se desea utilizar la ecuación de Hazen-Williams para el diseño de redes matrices para
materiales como el Acero, CCP y GRP, se sugiere verificar si los factores de fricción
obtenidos después de realizar la comprobación de diseño mediante la ecuación de Darcy-
Weisbach se ubican en el FTHL en el diagrama de Moody, según el límite definido por el
autor, a diferencia de lo establecido por Diskin y Liou.
Teniendo en cuenta los efectos que tiene la variabilidad del coeficiente de Hazen-Williams en
la estimación de las pérdidas por fricción en las redes de estudio, se sugiere utilizar en el
diseño de las redes matrices la ecuación de Darcy-Weisbach, dado que ésta es físicamente
basada, la cual se puede utilizar para cualquier fluido, rango de velocidades, diámetros y
longitudes de tubería.
REFERENCIAS
Barlow, J.F., and Markland, E. (1975). "Converting the Hazen-Williams equation to the Colebrook
function". Water Power Dam Construction , 331-334.
Bombardelli & García M.(2003). "Hydraulic Design of Large-Diameter Pipes". Recuperado 13 Marzo,
2010, de ascelibrary: http//: www.ascelibrary.com
Brown, G. O. (2004). "The History of the Darcy-Weisbach equation for pipe flow resistance". Recuperado
Marzo 4, 2010, de ascelibrary: http://www.ascelibrary.org
Colebrook C.F. (1939). "Turbulent Flow in pipes with particular reference to the transition region between
the smooth and rough pipes laws". Proc. Institution Civil Engrs , 393-422.
Diskin, M. (1960). The limits of applicability of the Hazen-Williams formula. Houille Blanche , 720-723.
Flechas R.A. (2010). Efecto del uso de la Ecuación de Darcy-Weisbach vs la Ecuación de Hazen-Williams
sobre los costos de diseños optimizados en acueductos, teniendo en cuenta la rugosidad de las tuberías,
linea del gradiente hidráulico y temperatura. Bogotá: Trabajo de Grado: Universidad de los Andes.
Gardner Williams, A. H. (1905). Hydraulic tables: showing the loss of head due to the friction of water
flowing in pipes, aqueducts, sewers, etc (primera edicion ed.). New York: Jhon Wiley & Sons.
Jain, A. K., Mohan, D.M, and Khanna, P. (1978). "Modified Hazen-Williams formula". J. Environ. Eng.
Div (ASCE) , 137-146.
Kamand, F. Z. (1988). "Hidraulic Friction Factors for Pipe Flow". ASCE , 311-323.
Liou, C. P. (1998, septiembre). Limitations and proper use of the Hazen-Williams equation. Retrieved
Marzo 5, 2010, from ascelibrary: http://www.ascelibrary.com
Moody, L. (1944). Friction factors for pipe flow. Trans. ASME. 671-684.
Saldarriaga Valderrama, J. G. (2007). Hidráulica de tuberías: abastecimiento de agua, redes, riegos .
Bogotá, D.C.: Alfaomega: Uniandes.
Vennard, J. K. (1958). Elementary Fluid Mechanics (3rd ed.). New York: Wiley.
