
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Proyecto de Grado
Pregrado en Ingeniería Ambiental
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del
Flujo Turbulento Hidráulicamente Liso
Presentado por:
Gloria Patricia Moscote Ordóñez
Asesor:
Juan Guillermo Saldarriaga Valderrama
Bogotá D.C., Colombia
Julio de 2012

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
i
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Agradecimientos
A Dios y a mi familia por darme la vida y la oportunidad de ingresar a la Universidad de
los Andes, lugar donde alcanzo uno de mis sueños, el de ser Ingeniera Ambiental; además
sin su apoyo y entrega no habría llegado a este punto. De igual forma, quiero hacer
extensivo el agradecimiento a mis amigos por su interés y colaboración en el desarrollo de
este proyecto.
Así mismo, agradezco a mi asesor Juan Saldarriaga por todo el apoyo y guía brindada
durante esta investigación.
Al laboratorista del laboratorio de Alcantarillados perteneciente al grupo de investigación
CIACUA (Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de
los Andes), John Calvo, quien me apoyó y asesoró en las actividades relacionadas en la
construcción del montaje.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
ii
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Tabla de Contenido
Agradecimientos ...................................................................................................................... i
Índice de Ecuaciones ............................................................................................................. iv
Índice de Figuras .................................................................................................................... v
Índice de Tablas ................................................................................................................... viii
1
Introducción .................................................................................................................... 1
1.1
Objetivos .................................................................................................................. 2
1.1.1
Objetivo General............................................................................................... 2
1.1.2
Objetivos Específicos ....................................................................................... 3
1.2
Antecedentes ............................................................................................................ 3
2
Marco Teórico ................................................................................................................. 5
2.1
Hidráulica del Flujo en Tuberías ............................................................................. 5
2.1.1
Capa Límite y Subcapa Laminar Viscosa......................................................... 5
2.1.2
Número de Reynolds ........................................................................................ 7
2.1.3
Ecuación de Bernoulli ...................................................................................... 8
2.1.4
Pérdidas Menores en Sistemas de Tuberías .................................................... 10
2.2
Flujo Turbulento Hidráulicamente Liso ................................................................ 13
2.2.1
Definición ....................................................................................................... 13
2.2.2
Ecuaciones Características ............................................................................. 13
2.2.3
Diagrama de Moody ....................................................................................... 22
2.3
Últimos Estudios Sobre el Flujo Turbulento Hidráulicamente Liso ...................... 25
2.3.1
Estudios de Brkic ............................................................................................ 25
2.3.2
Estudios en la Universidad de los Andes........................................................ 27
3
Diseño del Modelo ........................................................................................................ 43
3.1
Diseño del Montaje ................................................................................................ 43
3.2
Instrumentación del Montaje ................................................................................. 43
3.2.1
Medición de Caudal ........................................................................................ 43
3.2.2
Medición de Presión ....................................................................................... 45
3.2.3
Medición de la Temperatura ........................................................................... 47
4
Construcción del Montaje ............................................................................................. 48

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
iii
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
4.1
Instalación de Soportes .......................................................................................... 48
4.2
Adquisición de la Tubería Principal ...................................................................... 52
4.3
Instalación de las Rejillas Uniformadoras de Flujo ............................................... 62
4.4
Acoplamiento de la Estructura ............................................................................... 65
4.5
Instalación de los Manómetros Diferenciales ........................................................ 73
5
Costos ............................................................................................................................ 76
6
Metodología .................................................................................................................. 77
6.1
Medición de Diámetro Externo .............................................................................. 77
6.2
Determinación de la Viscosidad ............................................................................ 78
6.3
Comprobación de Diseño ....................................................................................... 79
6.3.1
Ecuaciones Para el Cálculo de Tuberías Simples ........................................... 81
6.4
Descripción de las Pruebas .................................................................................... 82
6.4.1
Calibración de Tuberías Simples .................................................................... 83
6.4.2
Verificación del Régimen de Flujo ................................................................. 86
7
Conclusiones y Recomendaciones ................................................................................ 89
7.1
Conclusiones .......................................................................................................... 89
7.2
Recomendaciones .................................................................................................. 89
8
Bibliografía.................................................................................................................... 91
9
Anexos ........................................................................................................................... 92
9.1
Planilla para el Registro de Datos .......................................................................... 92
9.2
Planos del Montaje ................................................................................................. 93
9.3
Manuales de Usuario ............................................................................................. 93

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
iv
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Índice de Ecuaciones
Ecuación 1. Esfuerzo cortante. ............................................................................................... 5
Ecuación 2. Número de Reynolds. ......................................................................................... 8
Ecuación 3. Energía total de una partícula del líquido. .......................................................... 9
Ecuación 4. Altura piezométrica de líquido en el punto U. .................................................. 10
Ecuación 5. Altura piezométrica de líquido en el punto D. .................................................. 10
Ecuación 6. Ecuación de Bernoulli. ..................................................................................... 10
Ecuación 7. Ecuación de Bernoulli Modificada. .................................................................. 10
Ecuación 8. Coeficiente de pérdidas menores. ..................................................................... 11
Ecuación 9. Cálculo de pérdidas menores. ........................................................................... 11
Ecuación 10. Sumatoria de pérdidas dentro de una tubería. ................................................. 11
Ecuación 11. Ecuación de Darcy-Weisbach. ........................................................................ 14
Ecuación 12. Ecuación de Blasius. ....................................................................................... 14
Ecuación 13. Espesor de la subcapa laminar viscosa. .......................................................... 16
Ecuación 14. Relación entre el factor de fricción y el esfuerzo cortante. ............................ 16
Ecuación 15. Velocidad de corte. ......................................................................................... 16
Ecuación 16. Flujo turbulento hidráulicamente liso. ............................................................ 16
Ecuación 17. Flujo turbulento hidráulicamente rugoso. ....................................................... 16
Ecuación 18. Comparación entre la rugosidad absoluta y el espesor de la subcapa laminar
viscosa. ................................................................................................................................. 17
Ecuación 25. Relación entre la rugosidad y la subcapa laminar viscosa para el flujo
turbulento hidráulicamente liso. ........................................................................................... 18
Ecuación 26. Relación entre la rugosidad y la subcapa laminar viscosa para el flujo
turbulento hidráulicamente rugoso. ...................................................................................... 19
Ecuación 27. Ecuación de Colebrook-White. ....................................................................... 19
Ecuación 32. Relación de Buzzelli para el Régimen Hidráulicamente Liso con Presencia de
Rugosidad. Tomada de (Brkic1, 2011). ................................................................................ 26
Ecuación 37. Límite inferior de la zona de transición. ......................................................... 28
Ecuación 42. Límite superior de la zona de transición. ........................................................ 30
Ecuación 43. Presión en el punto A. ..................................................................................... 45
Ecuación 44. Presión en el punto B. ..................................................................................... 45
Ecuación 46. Caída de presión. ............................................................................................ 45
Ecuación 47. Cálculo de la altura piezométrica. .................................................................. 45
Ecuación 49. Altura del nivel del agua en una tubería simple. ............................................ 81
Ecuación 50. Evaluación de las pérdidas por fricción. ......................................................... 81
Ecuación 51. Pérdidas por fricción a partir de la ecuación de Darcy-Weisbach. ................. 81
Ecuación 55. Cálculo de la velocidad. .................................................................................. 82
Ecuación 56. Rugosidad absoluta obtenida a partir de la ecuación de Colebrook-White. ... 84

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
v
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Índice de Figuras
Figura 1. Distribución de velocidad sobre una placa plana (Akan, 2006). ............................. 5
Figura 2. Capa límite (Saldarriaga, 2007). ............................................................................. 6
Figura 3. Capa límite laminar y turbulenta (http://es.scribd.com/doc/46682434/tema4-
Conveccion). ........................................................................................................................... 6
Figura 4. Flujo cerca a la pared rugosa y lisa
(http://www.itcmp.pwr.wroc.pl/~znmp/dydaktyka/fundam_FM/Lecture11_12.pdf). ........... 7
Figura 5. Flujo laminar vs. Flujo turbulento
(http://www.manualvuelo.com/PBV/PBV18.html). ............................................................... 8
Figura 6. Principio de energía para el flujo de agua en tuberías (Akan, 2006). ..................... 9
Figura 7. Tipos de válvulas: de compuerta, de globo y angular, respectivamente (Crane). . 12
Figura 8. Tipos de codos: 45°, 90° y 180°, respectivamente (Crane). ................................. 12
Figura 9. Tee (Crane)............................................................................................................ 12
Figura 10. Entrada y salida de la tubería, respectivamente (Crane). .................................... 12
Figura 11. Regímenes hidráulicos: A) hidráulicamente liso, B) parcialmente turbulento, C)
turbulento (Brkic
3
, 2010) ...................................................................................................... 13
Figura 12. Diagrama de Nikuradse (Saldarriaga, 2007). ...................................................... 15
Figura 13. Rugosidad relativa como función del factor de fricción y el número de Reynolds
en la zona transicional (Saldarriaga, 2007). ......................................................................... 18
Figura 14. Diagrama de flujo para el cálculo del factor de fricción f por medio de Newton-
Raphson (Saldarriaga, 2007). ............................................................................................... 21
Figura 15. Diagrama de Moody (White, 2008). ................................................................... 22
Figura 16. Diagrama de rugosidades relativas como función del diámetro de la tubería y
material del tubo (Beltrán, 2005). ......................................................................................... 24
Figura 17. Precisión de algunas aproximaciones a la ecuación de Prandtl (Brkic
2
, 2011). 26
Figura 18. Delimitación de la zona de transición en el diagrama de Moody (Flechas, 2010).
.............................................................................................................................................. 30
Figura 19. Factores hidráulicos obtenidos para la red San Vicente (Flechas, 2010). ........... 32
Figura 20. Factores hidráulicos obtenidos para la red Bogotá-Cazucá (Flechas, 2010). ..... 32
Figura 21. Factores hidráulicos obtenidos para la red La Cumbre (Flechas, 2010). ............ 33
Figura 22. Vista general del montaje de Laura Nieto en PAVCO S.A. ............................... 35
Figura 23. Tanque de alimentación en PAVCO S.A (Nieto, 2011). .................................... 36
Figura 24. Tanque de almacenamiento en PAVCO S.A (Nieto, 2011). ............................... 36
Figura 25. Vertedero de cresta delgada para la medición del caudal en PAVCO S.A (Nieto,
2011). .................................................................................................................................... 37
Figura 26. Medidores (diferencia de presión, caudalímetro y válvula de regulación de
caudal) en PAVCO S.A (Nieto, 2011). ................................................................................ 37
Figura 27. Medidor electrónico de presión en PAVCO S.A (Nieto, 2011). ......................... 38
Figura 28. Sistema de bombeo en PAVCO S.A (Nieto, 2011). ........................................... 38
Figura 29.Sistema eléctrico del montaje en PAVCO S.A (Nieto, 2011). ............................ 39

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
vi
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 30. Metodología empleada (Nieto, 2011). ................................................................ 40
Figura 31. Cálculo de k
s
usando la ecuación de Colebrook-White (Nieto, 2011). ............... 40
Figura 32. Cálculo de k
s
usando el método gráfico (Nieto, 2011). ...................................... 41
Figura 33. Cálculo de k
s
usando el método estadístico (Nieto, 2011). ................................. 42
Figura 34. Caudalímetro a emplear en las mediciones. ........................................................ 44
Figura 35. Principio de diferencia de tiempo de tránsito de ondas ultrasónicas (Ultraflux). 44
Figura 36. Manómetro diferencial. ....................................................................................... 45
Figura 37. Tablero manométrico. ......................................................................................... 46
Figura 38. Ubicación de las Mangueras en la Tubería Principal. ......................................... 46
Figura 39. Dimensiones del manómetro diferencial. ............................................................ 47
Figura 40. Termómetro digital (Dwyer Instruments, 2012). ................................................ 47
Figura 41. Sitio de ubicación del montaje. ........................................................................... 48
Figura 42. Vista de los soportes............................................................................................ 49
Figura 43. Instalación de los soportes. ................................................................................. 49
Figura 44. Soportes instalados. ............................................................................................. 50
Figura 45. Vista de los soportes instalados en el sitio de ubicación del montaje. ................ 50
Figura 46. Soportes recortados. ............................................................................................ 51
Figura 47. Cuerda instalada para nivelación de soportes. .................................................... 51
Figura 48. Nivelación de soportes. ....................................................................................... 52
Figura 49. Transporte de la tubería principal (I). ................................................................. 52
Figura 50. Transporte de la tubería principal (II). ................................................................ 53
Figura 51. Transporte de la tubería principal (III). ............................................................... 53
Figura 52. Desplazamiento de la tubería (I). ........................................................................ 54
Figura 53. Desplazamiento de la tubería (II). ....................................................................... 54
Figura 54. Desplazamiento de la tubería (III). ..................................................................... 54
Figura 55. Desplazamiento de la tubería (IV). ..................................................................... 55
Figura 56. Desplazamiento de la tubería (V). ....................................................................... 55
Figura 57. Desplazamiento de la tubería (VI). ..................................................................... 55
Figura 58. Desplazamiento de la tubería (VII). .................................................................... 56
Figura 59. Desplazamiento de la tubería (VIII). ................................................................... 56
Figura 60. Desplazamiento de la tubería (IX). ..................................................................... 56
Figura 61. Ubicación de la tubería en el laboratorio (I). ...................................................... 57
Figura 62. Ubicación de la tubería en el laboratorio (II). ..................................................... 57
Figura 63. Ubicación de la tubería en el laboratorio (III). .................................................... 58
Figura 64. Ubicación de la tubería en el laboratorio (IV). ................................................... 58
Figura 65. Ubicación de la tubería en el laboratorio (V). ..................................................... 58
Figura 66. Ubicación de la tubería en el laboratorio (VI). ................................................... 59
Figura 67. Ubicación de la tubería en el laboratorio (VII). .................................................. 59
Figura 68. Ubicación de la tubería en el laboratorio (VIII). ................................................. 59
Figura 69. Ubicación de la tubería en el laboratorio (IX). ................................................... 60
Figura 70. Ubicación de la tubería en el laboratorio (X). ..................................................... 60
Figura 71. Ubicación de la tubería en el laboratorio (XI). ................................................... 60
Figura 72. Ubicación de la tubería en el laboratorio (XII). .................................................. 61
Figura 73. Ubicación de la tubería en el laboratorio (XIII). ................................................. 61

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
vii
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 74. Ubicación de la tubería en el laboratorio (XIV). ................................................. 61
Figura 75. Ubicación de la tubería en el laboratorio (XV). .................................................. 62
Figura 76. Ubicación preliminar de la tubería. ..................................................................... 62
Figura 77. Rejillas Uniformadoras de Flujo. ........................................................................ 63
Figura 78. Soporte para las rejillas uniformadoras de flujo. ................................................ 63
Figura 79. Instalación del soporte de la primera rejilla uniformadora de flujo. ................... 64
Figura 80. Instalación de la primera rejilla uniformadora de flujo. ...................................... 64
Figura 81. Instalación del segundo soporte de las rejillas uniformadoras de flujo. ............. 64
Figura 82. Instalación del tercer soporte y la segunda rejilla uniformadora de flujo ........... 65
Figura 83. Amarre empleado para el acoplamiento de codos (vista inferior). ..................... 65
Figura 84. Amarre empleado para el acoplamiento de codos (vista superior). .................... 66
Figura 85. Acoplamiento de codos (I). ................................................................................. 66
Figura 86. Acoplamiento de codos (II). ................................................................................ 66
Figura 87. Acoplamiento inicial de la estructura de desagüe. .............................................. 67
Figura 88. Tubería principal y primer tubo de desagüe acoplado (I). .................................. 67
Figura 89. Tubería principal y primer tubo de desagüe acoplado (II). ................................. 68
Figura 90. Tubería principal soportada................................................................................. 68
Figura 91. Acoplamiento de la unión en la estructura de desagüe. ...................................... 69
Figura 92. Tubería de desagüe fraccionada. ......................................................................... 69
Figura 93. Instalación de estructura de desagüe (I). ............................................................. 70
Figura 94. Instalación de estructura de desagüe (II). ............................................................ 70
Figura 95. Instalación de estructura de desagüe (III). .......................................................... 70
Figura 96. Tubería de desagüe acoplada. ............................................................................. 71
Figura 97. Vista frontal del acople. ...................................................................................... 71
Figura 98. Detalle del acople. ............................................................................................... 72
Figura 99. Vista posterior del acople. ................................................................................... 72
Figura 100. Sección final del acople. ................................................................................... 73
Figura 101. Localización de las mangueras para los manómetros diferenciales. ................. 74
Figura 102. Instalación de los manómetros. ......................................................................... 74
Figura 103. Tablero Manométrico. ....................................................................................... 75
Figura 104. Mercurio metálico. ............................................................................................ 75
Figura 105. Medición de diámetro externo de la tubería. ..................................................... 77
Figura 106. Regresión polinomial para la viscosidad como función de la temperatura. ...... 78
Figura 107. Diagrama de flujo para la comprobación de diseño de tuberías simples
(Saldarriaga, 2007). .............................................................................................................. 80
Figura 108. Metodología para las pruebas a realizar. ........................................................... 83
Figura 109. Diagrama de flujo para la calibración de una tubería simple. Adaptado de
(Saldarriaga, 2007). .............................................................................................................. 85
Figura 110. Termómetro infrarrojo de la marca Erasmus. Tomado de (Erasmus, 2009). .... 90

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
viii
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Índice de Tablas
Tabla 1. Coeficientes de pérdidas K para válvulas abiertas, codos y tees (White, 2008). ... 11
Tabla 2. Valores recomendados de rugosidad para tubos comerciales (White, 2008). ........ 23
Tabla 3. Ecuaciones para el flujo turbulento hidráulicamente liso en usencia de rugosidad
(Brkic2, 2011). ...................................................................................................................... 25
Tabla 4. Resultados método gráfico (Nieto, 2011). .............................................................. 41
Tabla 5. Resultados método estadístico (Nieto, 2011). ........................................................ 42
Tabla 6. Detalles de los Costos Generados por el Proyecto. ................................................ 76
Tabla 7. Solicitud de material a PAVCO S.A. ..................................................................... 76
Tabla 8. Diferencia entre valores teóricos y experimentales del diámetro interno y externo
de la tubería principal. .......................................................................................................... 78
Tabla 9. Propiedades físicas del agua (Saldarriaga, 2007). .................................................. 78
Tabla 10. Condiciones estándar para el cálculo del espesor de la subcapa límite. ............... 86
Tabla 11. Cálculo del espesor de la subcapa laminar viscosa y determinación del tipo de
flujo. ...................................................................................................................................... 87
Tabla 12. Formato de registro de datos y cálculos para la calibración de la tubería. ........... 92
Tabla 13. Formato de registro de datos y cálculos para la determinación del grosor de la
subcapa laminar viscosa. ...................................................................................................... 93

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
1
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
1 Introducción
El crecimiento de la población mundial acarrea una gran necesidad de incrementar la
capacidad de los sistemas de abastecimiento de agua y de drenaje. Comúnmente, se
encuentran tuberías de diámetros grandes en sistemas de distribución de agua potable
(Bombardelli & García, 2003). Consecuentemente, el mal uso de las ecuaciones para
estimar la resistencia del flujo en tuberías largas puede tener varios inconvenientes.
Específicamente, en esos sistemas, puede que no se conozca la demanda para la que fueron
diseñados, reduciendo así, su vida útil.
La resistencia al flujo de un fluido en un sistema de tuberías a presión es producida por la
rugosidad del material de la tubería, y por la cantidad y tipos de accesorios con que cuente
este sistema. Para que el diseño del sistema sea eficiente es necesario conocer varios
detalles de la tubería de abastecimiento como el material, la rugosidad, el diámetro, el
caudal de abastecimiento, entre otros. Así como contar con herramientas (por ejemplo,
computacionales) que permitan el cálculo de las pérdidas del sistema (sean ocasionadas por
la fricción del fluido o por la instalación de accesorios) que se van a tener durante el
funcionamiento de la red.
Numerosos estudios se han realizado respecto al diseño apropiado de tuberías; se tienen los
aportes de Colebrook y White, Blasius y Prandtl y von Kármán, para el caso del flujo
turbulento hidráulicamente liso. La importancia de este tipo de flujo radica en que,
actualmente, en las tuberías de distribución que cuentan con superficies lisas, se alcanzan
velocidades tan altas que permiten su desarrollo. Sin embargo, es importante tener en
cuenta que no hay una superficie perfectamente lisa. En general, todas las paredes de las
tuberías presentan una rugosidad, la cual depende, entre otras, del proceso de manufactura,
tipo de material, edad y condiciones de operación.
La dificultad para resolver problemas en flujo turbulento en tuberías recae en el hecho de
que el factor de fricción es una función compleja de la rugosidad relativa de la superficie y
el número de Reynolds (Brkic
3
, 2010). El diseño de tuberías usualmente se lleva a cabo
utilizando fórmulas empíricas como la de Hazen-Williams dejando de lado ecuaciones
basadas en un desarrollo físico y científico mucho más coherentes como las ecuaciones de
Darcy-Weisbach y Colebrook-White, debido a la sencillez matemática de las primeras
(Camacho & Saldarriaga, 1990).
El desarrollo del presente proyecto de grado consiste en la descripción y entendimiento del
comportamiento del flujo turbulento hidráulicamente liso en sistemas que fluyen a presión,
siendo esta una herramienta importante para que, por ejemplo, empresas fabricantes de
tuberías de abastecimiento que emplean materiales lisos, puedan garantizar a las empresas

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
2
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
de acueducto este tipo de flujo con el fin de minimizar pérdidas de energía que se presentan
en la distribución.
Para lograr lo anterior se proponen dos etapas. La primera consiste en la revisión de las
ecuaciones de cálculo del factor de fricción y, la segunda corresponde al diseño y
construcción de un montaje que permita determinar el factor de fricción, el cual se conoce
que tiene una gran influencia del número de Reynolds y no depende de la rugosidad
absoluta de la tubería y así modificar el diagrama de Moody en la zona de transición,
específicamente el límite del flujo turbulento hidráulicamente liso.
El documento se encuentra estructurado de la siguiente manera:
El Capítulo 1 corresponde a una introducción a la temática del proyecto, junto con
los objetivos y un breve resumen de antecedentes.
El Capítulo 2 contiene la base teórica para el flujo turbulento hidráulicamente liso,
específicamente. Se parte de definiciones básicas como los conceptos de capa límite
y subcapa laminar viscosa que tienen una utilidad significativa para entender la
definición de este tipo de flujo. Se detallan las ecuaciones características del mismo.
Finalmente se realiza una breve descripción de algunos precedentes en el tema.
El Capítulo 3 muestra una descripción del montaje construido que cumple con los
objetivos planteados en el Capítulo 1
El Capítulo 4 contiene fotografías que muestran detalladamente el proceso de
construcción del montaje.
El Capítulo 5 muestra los costos en los que se incurrió para el desarrollo del
presente trabajo.
El Capítulo 6 muestra el planteamiento de una metodología para lograr los objetivos
planteados en la Parte 2.
El Capítulo 7 muestra las conclusiones de este documento y las recomendaciones
para futuros trabajos.
1.1 Objetivos
1.1.1 Objetivo General
Diseño y construcción de un montaje a escala de laboratorio para estudiar el caso del Flujo
Turbulento Hidráulicamente Liso en un sistema de flujo a presión en una tubería lisa
(PVC), con el fin de presentar una nueva metodología que permita determinar el factor de
fricción en sistemas de distribución modernos.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
3
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
1.1.2 Objetivos Específicos
Estudiar los principios que rigen el movimiento del agua en sistemas a presión en
tuberías lisas considerando un régimen de flujo turbulento hidráulicamente liso.
Realizar una revisión bibliográfica de las ecuaciones que permiten obtener el factor
de fricción para el caso del flujo turbulento hidráulicamente liso, estableciendo su
relación con el número de Reynolds y el valor de la rugosidad absoluta.
Definir los parámetros geométricos (dimensiones) e hidráulicos para el diseño del
montaje.
Construir el montaje (soporte, estructura, conexiones pertinentes) que permita
realizar medidas de pérdidas por fricción y velocidad de flujo para la determinación
del factor de fricción.
1.2 Antecedentes
De acuerdo con los estudios realizados por (Brkic, 2011), el régimen hidráulicamente liso
no solo ocurre en ausencia de rugosidad (k
s
/d = 0). Esto significa que el régimen liso puede
ocurrir incluso cuando la rugosidad relativa existe (k
s
/d → 0). Lo anterior invalidaría
algunas ecuaciones propuestas, hace varios años en la hidráulica clásica; este problema se
muestra a la luz de algunas nuevas ecuaciones desarrolladas para el cálculo del factor de
fricción.
La ecuación de Colebrook es válida para todo el rango de régimen turbulento el cual
incluye el régimen hidráulicamente liso, el transciente y el completamente turbulento. El
efecto de la rugosidad es la principal razón por la cual la ecuación de Colebrook es tan
ampliamente utilizada incluso para la zona lisa de la turbulencia. El efecto de la rugosidad
puede ser mínimo, pero con un ligero incremento en el valor del número de Reynolds,
aparecerá inevitablemente (Brkic
1
, 2011).
Investigaciones previas han encontrado que para tuberías lisas se presenta una invalidación
del diagrama de Moody en los límites del flujo turbulento hidráulicamente liso. Diferentes
estudios realizados en el CIACUA han demostrado que las ecuaciones utilizadas
actualmente para la determinación del factor de fricción, cuando se presenta este tipo de
flujo, han empezado a presentar cierta incertidumbre debido a que en la época de su
aparición las rugosidades estudiadas eran considerablemente mayores a aquellas que se
encuentran hoy en día (Nieto, 2011). Algunos de los estudios realizados en el CIACUA
corresponden a la determinación de la rugosidad absoluta de tuberías, tanto plásticas como
de otros materiales. El resultado principal de estas investigaciones afirma que las tuberías
plásticas operan bajo condiciones de flujo turbulento hidráulicamente liso y por lo tanto su
rugosidad no afecta a las pérdidas de energía.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
4
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Considerando lo anterior, se presenta un estudio sobre el efecto de la variación de
parámetros hidráulicos en las ecuaciones definidas para el flujo turbulento hidráulicamente
liso en una tubería de PVC con rugosidad constante de 0.0015 mm. Se tiene como
referencia el montaje realizado por la estudiante (Nieto, 2011) para la empresa PAVCO
S.A, como una ayuda preliminar para el cumplimiento de los objetivos del presente trabajo
de grado.
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
5
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
2 Marco Teórico
2.1 Hidráulica del Flujo en Tuberías
2.1.1 Capa Límite y Subcapa Laminar Viscosa
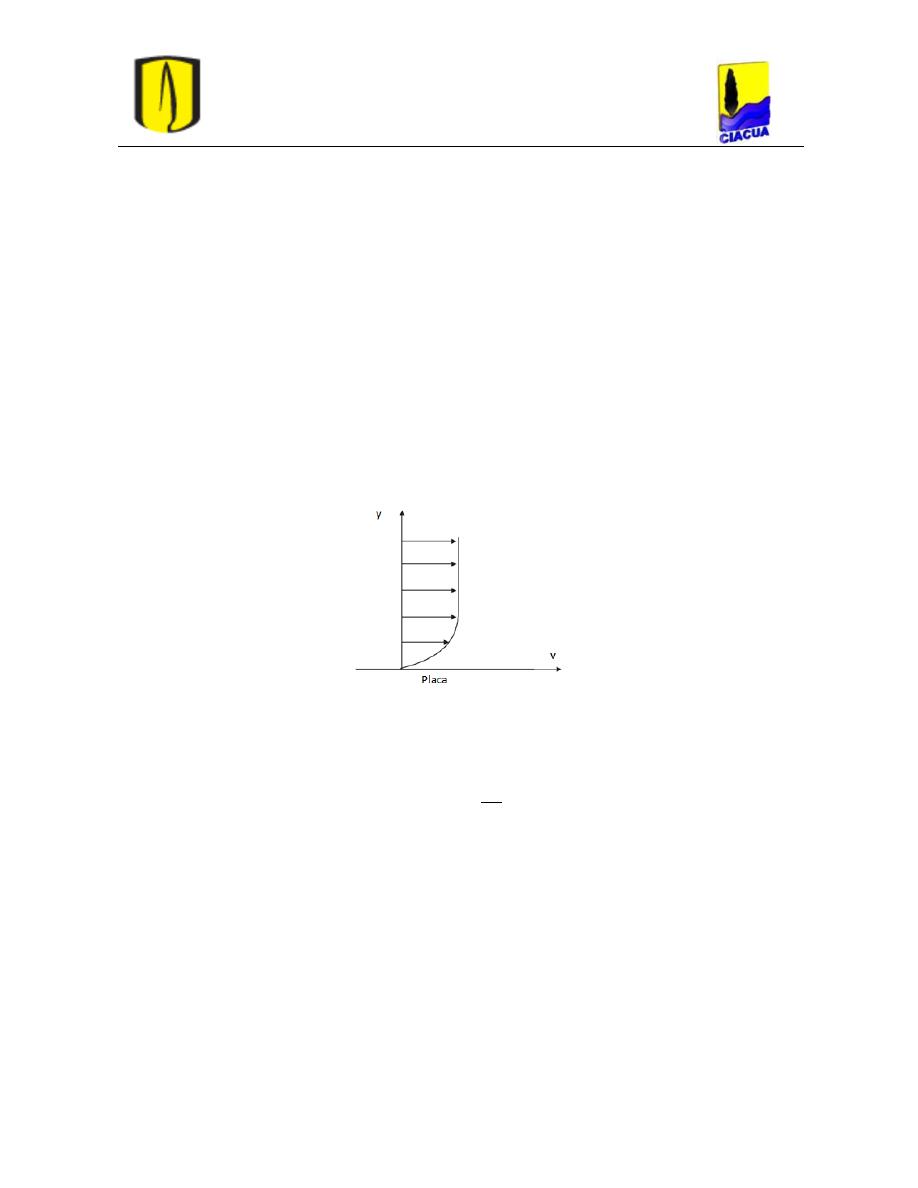
Cuando un fluido fluye sobre una placa plana y sólida las partículas en contacto con la
placa se mantienen en reposo mientras las partículas por encima de la placa tienen una
velocidad finita paralela a ésta. De acuerdo con lo anterior, la superficie sólida crea un
gradiente de velocidad transversal con el flujo como se muestra en la Figura 1 (Akan,
2006).
Figura 1. Distribución de velocidad sobre una placa plana (Akan, 2006).
Se tiene que el esfuerzo cortante, τ
w
, es proporcional al gradiente de la velocidad en la
superficie y puede ser evaluada como (Akan, 2006):
𝜏
𝑤
= 𝜇
𝑑𝑣
𝑑𝑦
Ecuación 1. Esfuerzo cortante.
donde μ es la viscosidad del fluido, v es la velocidad paralela a la placa, y la distancia desde
la placa. El grosor de esta capa depende de la viscosidad del agua y la velocidad fuera de la
capa límite, y crece con la distancia a través de la superficie (Akan, 2006). Ésta ecuación
también se conoce como la Ecuación de Viscosidad de Newton.
Las características más sobresalientes de la capa límite se pueden describir mediante el
flujo sobre una superficie plana paralela a una corriente uniforme de velocidad v, como se
muestra en la Figura 2 (Beltrán, 2005).
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
6
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
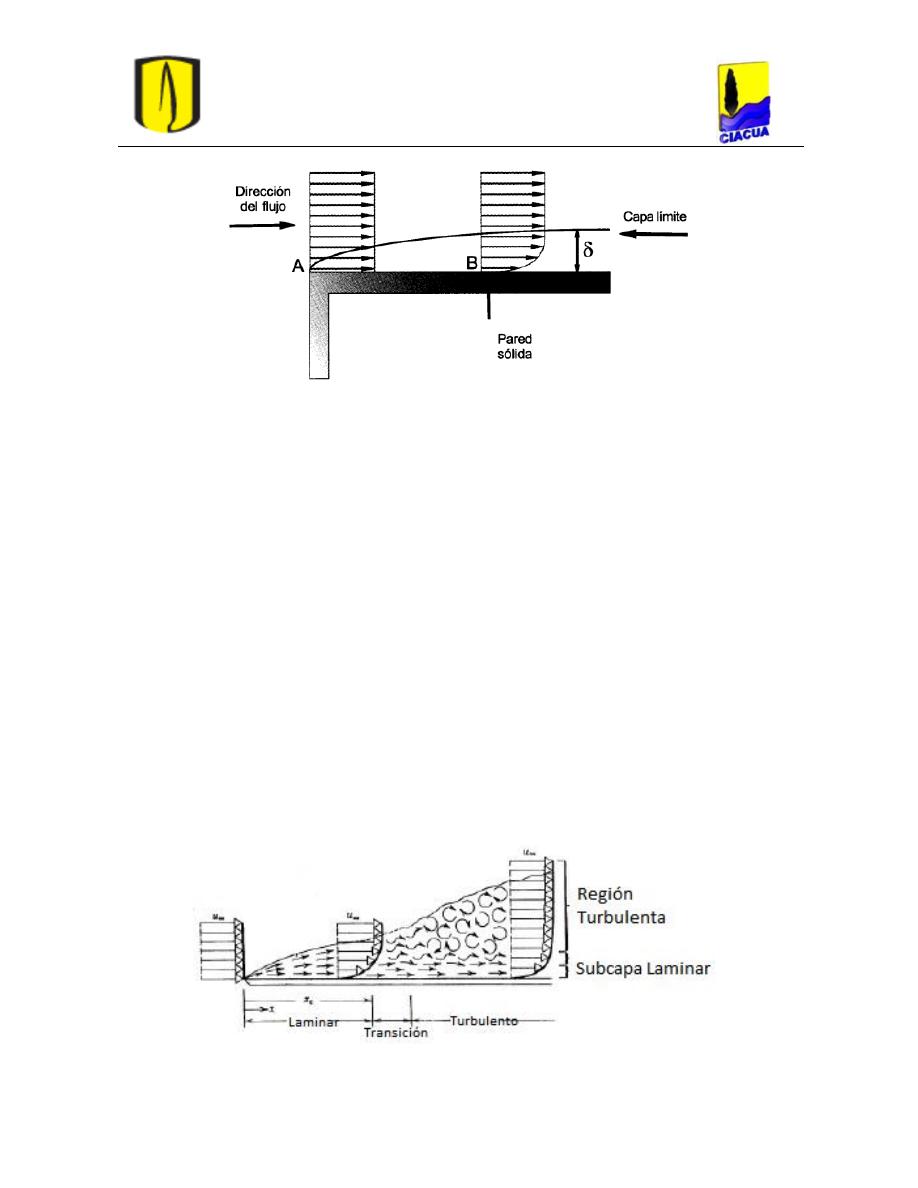
Figura 2. Capa límite (Saldarriaga, 2007).
Por efecto de la viscosidad, el fluido que está en contacto con la pared o superficie tiene
velocidad cero. En el borde delantero, A, de la placa hay una discontinuidad de la velocidad
en una distancia extremadamente pequeña. Aguas debajo de este punto, para la posición B,
la velocidad cambia en forma un poco más gradual desde la velocidad v hasta velocidad
cero en la pared. La distancia en que esto ocurre es δ. En la parte más alejada de la
superficie se observa que dv/dy=0 (ver Ecuación 1). Según la ley de Newton de la
viscosidad, no habría más esfuerzos de corte más allá de la distancia δ (Beltrán, 2005).
Si el flujo sobre la placa es laminar, el efecto de la placa en la velocidad de flujo es limitada
a una capa llamada capa límite laminar (Akan, 2006).
Si el flujo sobre la placa es turbulento, la capa límite puede ser al comienzo laminar cerca a
la superficie de la placa pero tan pronto como ocurre la transición, la capa límite se vuelve
turbulenta como se muestra en la Figura 3 (Akan, 2006). A medida que se avanza en la
dirección B (ver Figura 2) más y más partículas son retardadas y por tanto el espesor δ de la
zona de influencia viscosa va aumentando hasta un cierto punto donde el flujo comienza a
mostrar los efectos notables de la turbulencia, lo que ocasiona un aumento más rápido de la
capa límite (Beltrán, 2005). Aunque la velocidad aumenta con la distancia desde la
superficie a través de la capa límite turbulenta, el gradiente de velocidad es más marcado en
una delgada capa llamada subcapa viscosa cerca a la pared (Akan, 2006).
Figura 3. Capa límite laminar y turbulenta (http://es.scribd.com/doc/46682434/tema4-Conveccion).
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
7
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
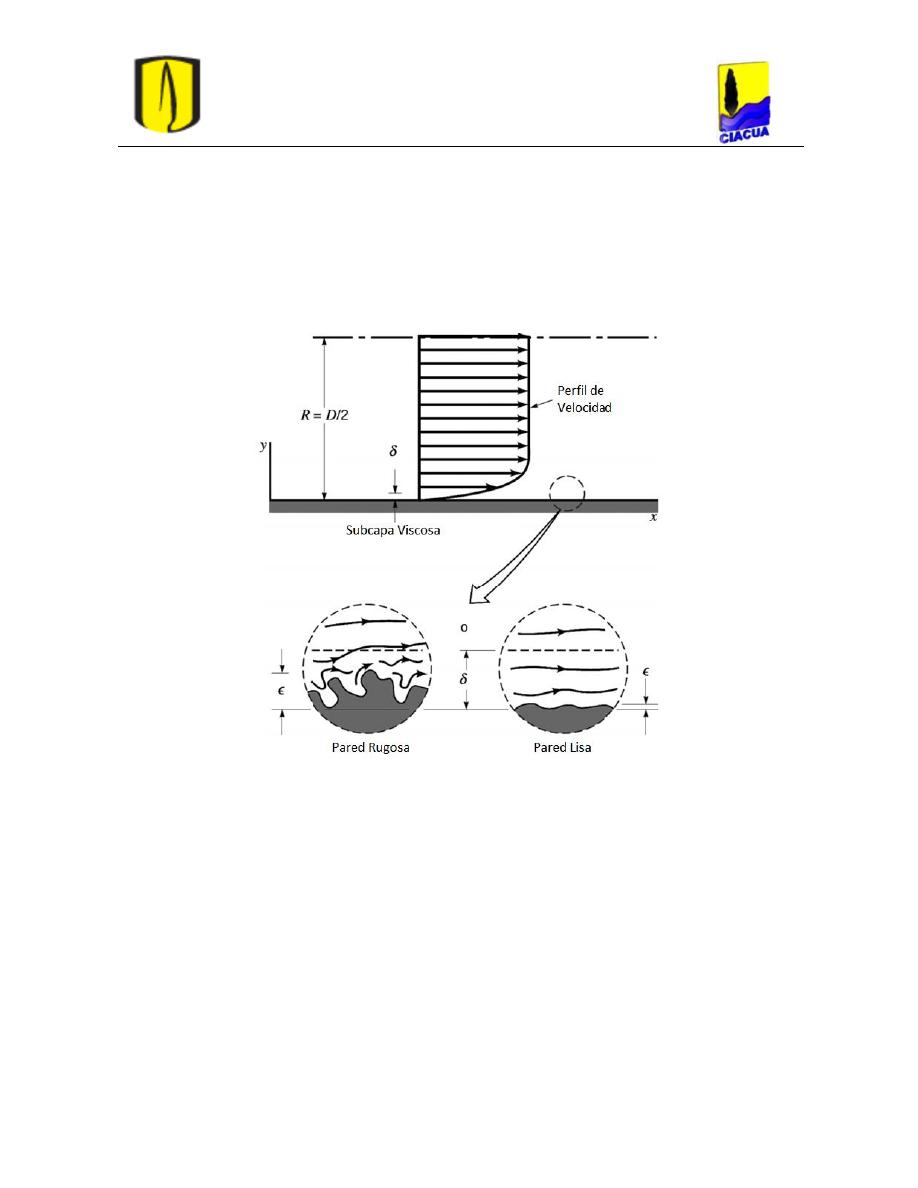
El espesor de la subcapa laminar viscosa es mucho menor que el de la capa límite. La
relación existente entre el espesor de la subcapa laminar viscosa y el tamaño medio de la
rugosidad de las paredes establece la diferencia entre los flujos hidráulicamente lisos y los
hidráulicamente rugosos. Cuando el espesor de la subcapa laminar viscosa es mayor que el
tamaño medio de la rugosidad, el flujo se comporta como si la rugosidad de la tubería no
existiera, es decir, como flujo hidráulicamente liso. En el caso contrario el flujo sería
hidráulicamente rugoso (Saldarriaga, 2007).
Figura 4. Flujo cerca a la pared rugosa y lisa
(http://www.itcmp.pwr.wroc.pl/~znmp/dydaktyka/fundam_FM/Lecture11_12.pdf).
2.1.2 Número de Reynolds
La magnitud relativa de las fuerzas inerciales y viscosas determinan si el flujo es laminar o
turbulento: el flujo es laminar si las fuerzas viscosas predominan, y el flujo es turbulento si
las fuerzas inerciales dominan (Chaudhry, 2008).
La relación de fuerzas viscosas e inerciales se define como el número de Reynolds
(Chaudhry, 2008):

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
8
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
𝑅𝑒 =
𝑣 𝑑
𝜐
Ecuación 2. Número de Reynolds.
donde v es la velocidad media, d el diámetro de la tubería y υ la viscosidad cinemática del
fluido dependiente de la temperatura (Chaudhry, 2008). Se pueden establecer los siguientes
límites para cada tipo de flujo:
Flujo laminar: Re < 2200
Flujo transicional: 2200 ≤ Re ≤ 5000
Flujo turbulento: Re > 5000
El flujo es llamado laminar cuando las partículas del líquido parecen moverse en caminos
suaves y el flujo parece tener un movimiento de capas delgadas, una encima de la otra. En
el flujo turbulento, las partículas del líquido se mueven en caminos irregulares que no son
fijos con respecto a tiempo o espacio (Chaudhry, 2008).
Figura 5. Flujo laminar vs. Flujo turbulento (http://www.manualvuelo.com/PBV/PBV18.html).
2.1.3 Ecuación de Bernoulli
Mientras el agua fluye a través de una tubería hay fricción entre las moléculas de agua y la
pared de la tubería. Ésta fricción causa que la energía se pierda, siendo convertida de
energía de presión y energía cinética a calor. La presión continuamente disminuye aguas
abajo de la tubería. La cantidad de presión perdida debido a la fricción, también conocida
como altura de pérdida debido a la fricción, depende del flujo, las propiedades del agua
(densidad relativa y viscosidad), diámetro, longitud y rugosidad de la tubería. La ecuación
de Bernoulli es una forma de ecuación de energía para un líquido fluyendo a través de una
tubería (Menon, 2005).
En cada punto a lo largo de una tubería, la energía total del líquido se calcula considerando
la energía del líquido debida a la presión, velocidad y elevación. La energía total del líquido
contenido en la tubería en cualquier punto es constante. Esto también es conocido como el
principio de conservación de energía (Menon, 2005).
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
9
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
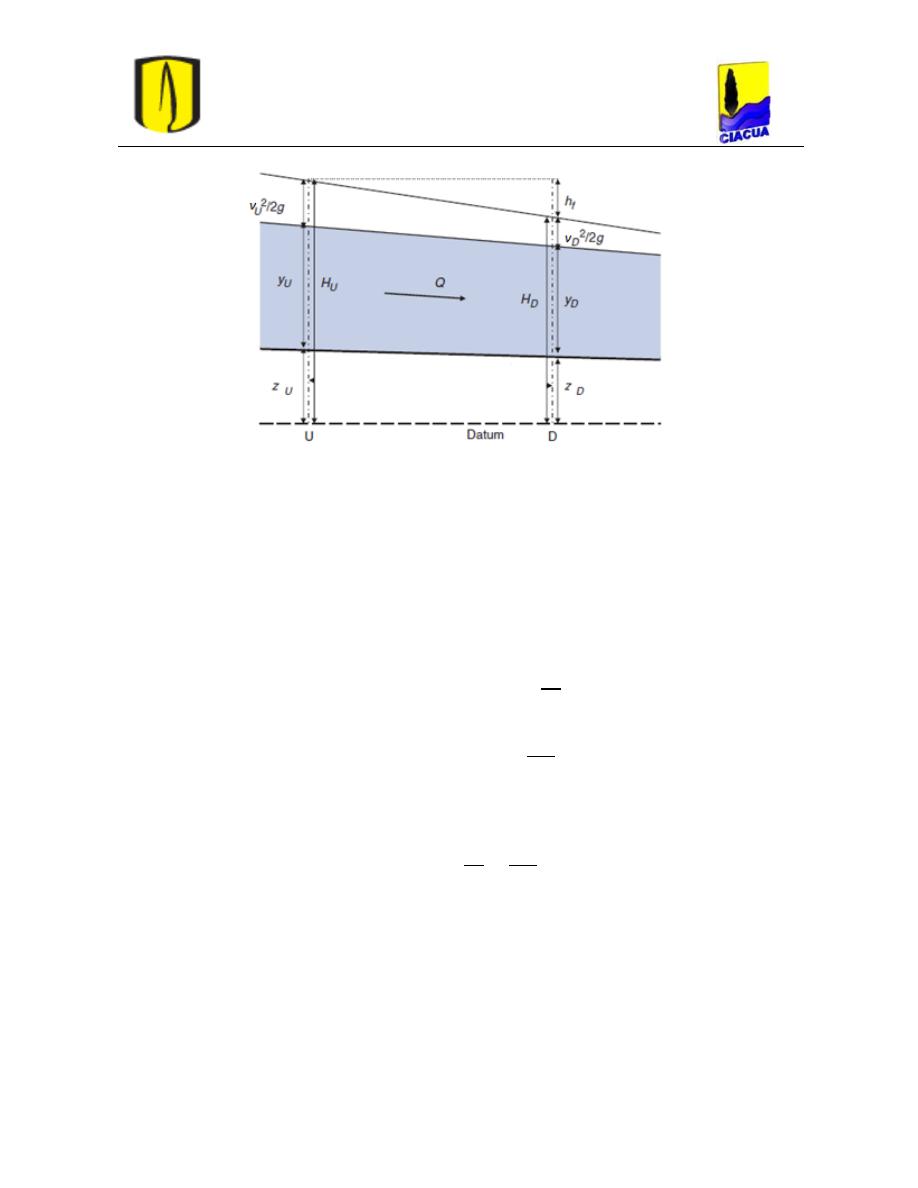
Figura 6. Principio de energía para el flujo de agua en tuberías (Akan, 2006).
Se considera el líquido fluyendo por una tubería desde el punto U hasta el punto D como se
muestra en la Figura 6. La elevación del punto U es z
U
y la elevación en el punto D es z
D
.
La presión en el punto U es P
U
y en el punto D es P
D
. Se supone que el diámetro de la
tubería en U y D es diferente (y
U
y y
D
), por lo tanto la velocidad de flujo en U y D es
diferente y se representa por v
U
y v
D
, respectivamente. Una partícula del líquido en el punto
U de la tubería posee una energía total E que consiste de tres componentes (Menon, 2005):
𝐸𝑛𝑒𝑟𝑔í𝑎 𝑃𝑜𝑡𝑒𝑛𝑐𝑖𝑎𝑙 = 𝑧
𝑈
𝐸𝑛𝑒𝑟𝑔í𝑎 𝑑𝑒 𝑃𝑟𝑒𝑠𝑖ó𝑛 =
𝑃
𝑈
𝛾
𝐸𝑛𝑒𝑟𝑔í𝑎 𝐶𝑖𝑛é𝑡𝑖𝑐𝑎 =
𝑣
𝑈
2
2𝑔
donde γ es el peso específico del líquido. La energía total E es (Menon, 2005):
𝐸 = 𝑧
𝑈
+
𝑃
𝑈
𝛾
+
𝑣
𝑈
2
2𝑔
Ecuación 3. Energía total de una partícula del líquido.
Dado que cada término en la Ecuación 3 tiene dimensiones de longitud, se refiere a la
energía total en el punto U como H
U
en metros (en el Sistema Internacional de Unidades,
SI) de altura piezométrica de líquido. Por lo tanto, rescribiendo la energía total en metros de
altura piezométrica de líquido en el punto U, se obtiene (Menon, 2005):

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
10
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
𝐻
𝑈
= 𝑧
𝑈
+
𝑃
𝑈
𝛾
+
𝑣
𝑈
2
2𝑔
Ecuación 4. Altura piezométrica de líquido en el punto U.
De manera similar se obtiene la altura piezométrca de líquido para el punto D (Menon,
2005).
𝐻
𝐷
= 𝑧
𝐷
+
𝑃
𝐷
𝛾
+
𝑣
𝐷
2
2𝑔
Ecuación 5. Altura piezométrica de líquido en el punto D.
Por el principio de conservación de energía: H
U
=H
D
. Por lo tanto (Menon, 2005):
𝑧
𝑈
+
𝑃
𝑈
𝛾
+
𝑣
𝑈
2
2𝑔
= 𝑧
𝐷
+
𝑃
𝐷
𝛾
+
𝑣
𝐷
2
2𝑔
Ecuación 6. Ecuación de Bernoulli.
La Ecuación 6 se conoce como la Ecuación de Bernoulli. Sin embargo, no se ha
considerado energía suministrada (por ejemplo, por una bomba ubicada en el punto U, que
se denotará como H
p
) o removida al líquido, o las pérdidas de energía debido a la fricción
(h
f
). Al modificar esta ecuación se obtiene una forma más común de la Ecuación de
Bernoulli (Menon, 2005).
𝑧
𝑈
+
𝑃
𝑈
𝛾
+
𝑣
𝑈
2
2𝑔
+ 𝐻
𝑝
= 𝑧
𝐷
+
𝑃
𝐷
𝛾
+
𝑣
𝐷
2
2𝑔
+ ℎ
𝑓
Ecuación 7. Ecuación de Bernoulli Modificada.
En la Sección 2.2.2 se mostrará como se calcula la altura de pérdida debido a la fricción (h
f
)
en la ecuación de Bernoulli para la condición de flujo hidráulicamente liso.
2.1.4 Pérdidas Menores en Sistemas de Tuberías
Para cualquier sistema de tuberías, en adición al cálculo de las pérdidas de fricción para la
longitud de la tubería, se deben adicionar las pérdidas menores debidas a (White, 2008):
1. Entrada y salida de la tubería.
2. Expansiones o contracciones repentinas.
3. Expansiones o contracciones graduales.
4. Curvas, codos, tees y otros acoples.
5. Válvulas, abiertas o parcialmente cerradas.
La medida de las pérdidas menores se da usualmente como la relación entre la altura
piezométrica perdida a través del dispositivo y la altura piezométrica de velocidad asociada
con el sistema de tuberías (White, 2008).
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
11
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
𝐶𝑜𝑒𝑓𝑖𝑐𝑖𝑒𝑛𝑡𝑒 𝑑𝑒 𝑃é𝑟𝑑𝑖𝑑𝑎𝑠 (𝐾) =
ℎ
𝑚
𝑣
2
2𝑔
⁄
=
∆𝑝
1
2 𝜌𝑣
2
Ecuación 8. Coeficiente de pérdidas menores.
ℎ
𝑚
= 𝐾
𝑣
2
2𝑔
Ecuación 9. Cálculo de pérdidas menores.
Una sola tubería puede tener varias pérdidas menores. Debido a que los términos de
pérdidas se relacionan con el término de altura de velocidad, se pueden sumar en un solo
término de pérdidas siempre y cuando la tubería tenga un diámetro constante (White,
2008):
∆ℎ
𝑡𝑜𝑡𝑎𝑙
= ℎ
𝑓
+ ∑ ℎ
𝑚
Ecuación 10. Sumatoria de pérdidas dentro de una tubería.
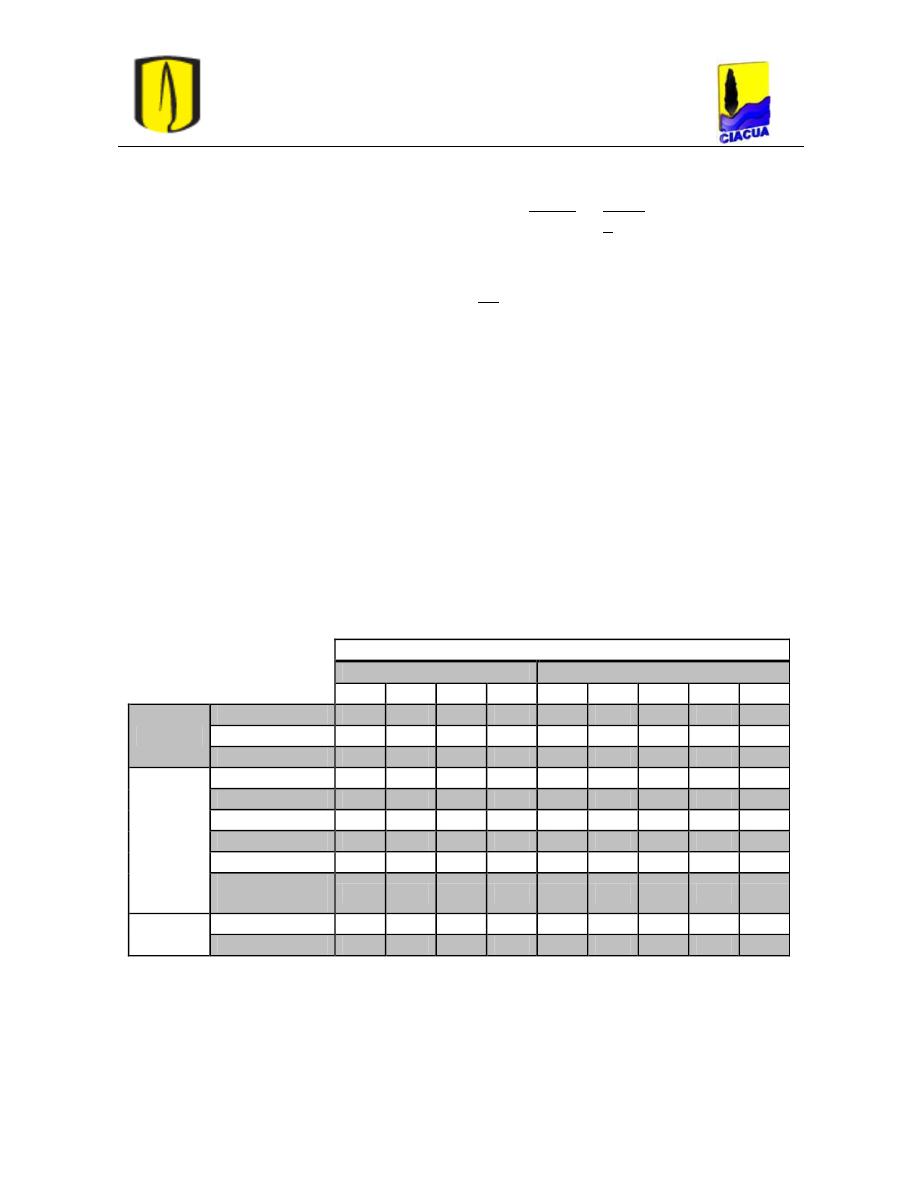
La Tabla 1 lista los coeficientes de pérdidas K para distintos tipos de válvulas, ángulos de
codos y conexiones de tees; cabe destacar que el valor de K tiende a disminuir con el
aumento de tamaño de la tubería (White, 2008).
Tabla 1. Coeficientes de pérdidas K para válvulas abiertas, codos y tees (White, 2008).
Diámetro Nominal (in)
Roscado
Con Brida
1/2
1
2
4
1
2
4
8
20
Válvulas
Globo
14
8.2
6.9
5.7
13
8.5
6.0
5.8
5.5
Compuerta
0.30
0.24
0.16
0.11
0.80
0.35
0.16
0.07
0.03
Angular
9.0
4.7
2.0
1.0
4.5
2.4
2.0
2.0
2.0
Codos
45° regular
0.39
0.32
0.30
0.29
45° radio largo
0.21
0.20
0.19
0.16
0.14
90° regular
2.0
1.5
0.95
0.64
0.50
0.39
0.30
0.26
0.21
90° radio largo
1.0
0.72
0.41
0.23
0.40
0.30
0.19
0.15
0.10
180° regular
2.0
1.5
0.95
0.64
0.41
0.35
0.30
0.25
0.20
180° radio
largo
0.40
0.30
0.21
0.15
0.10
Tees
Línea de flujo
0.90
0.90
0.90
0.90
0.24
0.19
0.14
0.10
0.07
Derivación
2.4
1.8
1.4
1.1
1.0
0.8
0.64
0.58
0.41
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
12
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
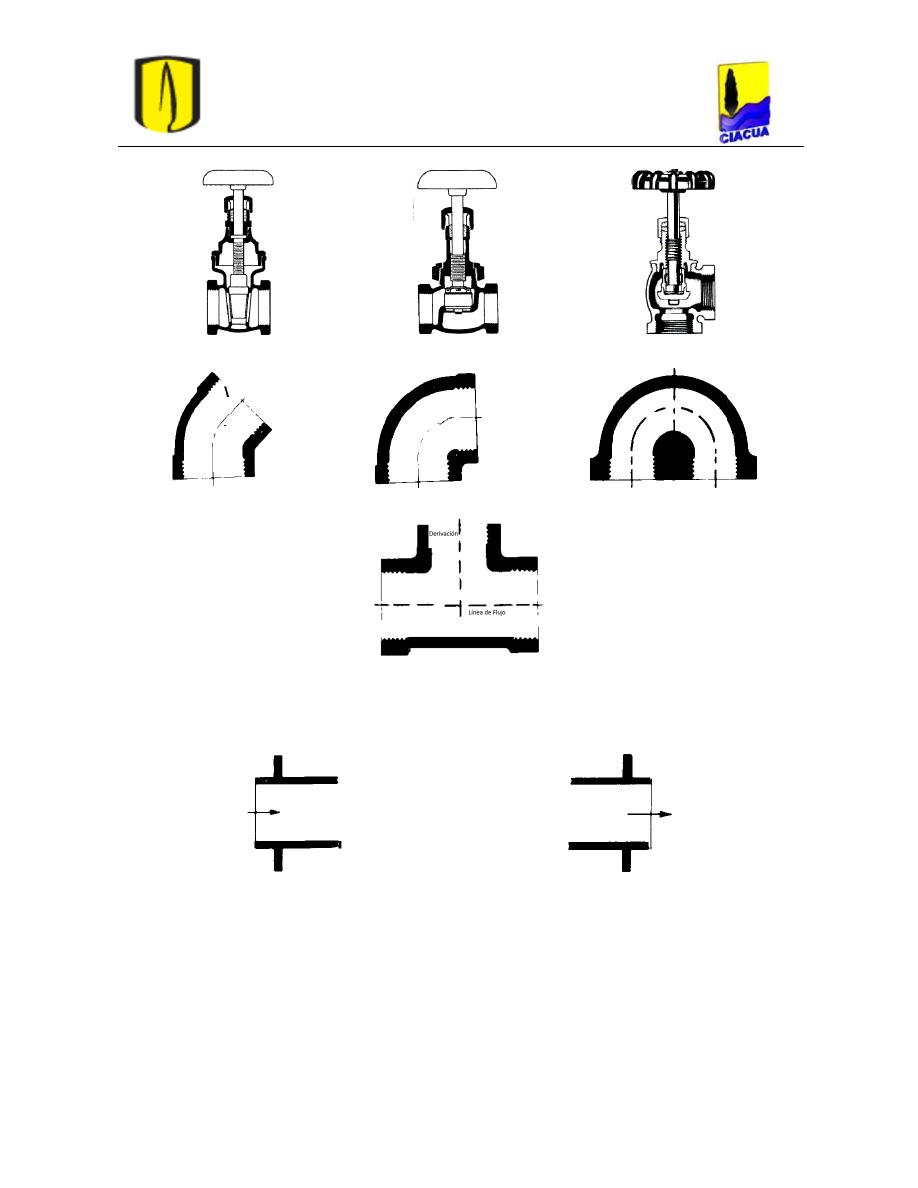
Figura 7. Tipos de válvulas: de compuerta, de globo y angular, respectivamente (Crane).
Figura 8. Tipos de codos: 45°, 90° y 180°, respectivamente (Crane).
Figura 9. Tee (Crane).
En cuanto a las pérdidas por la entrada y salida de la tubería se pueden suponer valores
constantes de 0.78 y 1.0, respectivamente (Crane).
Figura 10. Entrada y salida de la tubería, respectivamente (Crane).
Es necesario destacar que el cálculo de las pérdidas menores no se realizará para la tubería
principal debido a que esta no presenta ningún tipo de accesorio; sin embargo, estas se
calculan para realizar la comprobación de diseño de todo el sistema.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
13
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
2.2 Flujo Turbulento Hidráulicamente Liso
2.2.1 Definición
El flujo turbulento hidráulicamente liso se define como el flujo turbulento en una tubería en
el cual el espesor de la subcapa laminar viscosa es mayor que el tamaño de la rugosidad
absoluta del material que conforma la pared interna de la tubería. En este tipo de flujo las
pérdidas de energía y, por consiguiente, el factor de fricción, únicamente dependen de las
propiedades del fluido y de las características del flujo (Saldarriaga, 2007).
Figura 11. Regímenes hidráulicos: A) hidráulicamente liso, B) parcialmente turbulento, C) turbulento (Brkic
3
,
2010)
2.2.2 Ecuaciones Características
2.2.2.1 Ecuación de Darcy-Weisbach
La ecuación de Darcy-Weisbach es la ecuación de resistencia fluida más general para el
caso de tuberías circulares fluyendo a presión la cual es el resultado de aplicar las leyes
físicas del movimiento de Newton. Fue establecida por Henry Darcy (1803-1858) ingeniero
francés, quién llevó a cabo numerosos experimentos en tuberías con flujo de agua, y Julius
Weisbach (1806-1871), ingeniero sajón de la misma época que propuso el uso del factor de
fricción (Saldarriaga, 2007).
La ecuación de Darcy-Weisbach es una fórmula racional que se deduce a través de análisis
dimensional, y por consiguiente es una ecuación basada en la física clásica (Saldarriaga,
2007). Mientras el agua fluye a través de la tubería desde el punto U al D (ver Figura 6) la

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
14
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
presión disminuye debido a la fricción entre el agua y la pared de la tubería. Esta ecuación
puede ser usada para calcular la caída de presión en las tuberías que transporten cualquier
tipo de fluido, sea líquido o gas (Menon, 2005).
ℎ
𝑓
= 𝑓
𝐿
𝑑
𝑣
2
2𝑔
Ecuación 11. Ecuación de Darcy-Weisbach.
donde: h
f
= pérdida de presión por fricción
f = factor de fricción de Darcy
L = longitud de la tubería
d = diámetro de la tubería
v = velocidad media
g = aceleración de la gravedad (9.81 m/s
2
en el Sistema Internacional de Unidades)
El término v
2
/2g en la Ecuación 11 se llama altura de velocidad, y representa la energía
cinética del agua. El factor de fricción, f, es un valor adimensional que depende de la
rugosidad interna de la tubería y el número de Reynolds (Menon, 2005).
2.2.2.2 Ecuación de Blasius
Para el caso de flujos hidráulicamente lisos se sabía que el factor de fricción sólo era
función del número de Reynolds. P.R.H Blasius, en 1911, encontró empíricamente que para
números de Reynolds situados entre 5,000 y 100,000, el factor de fricción se podría
calcular con base en la siguiente ecuación (Saldarriaga, 2007):
𝑓 =
0.316
𝑅𝑒
0.25
Ecuación 12. Ecuación de Blasius.
2.2.2.3 Diagrama de Nikuradse
A fin de estudiar la naturaleza del factor de fricción f, el ingeniero alemán Johann
Nikuradse, en 1933 hizo una serie de experimentos en los cuales utilizó tubos de diferentes
diámetros en cuyo interior pegó arenas de granulometría uniforme, de tal manera que
obtuvo varias rugosidades relativas. En cada tubo varió el caudal, de modo que cubrió un
amplio rango de números de Reynolds, con flujos que cubrían el intervalo desde laminar
hasta hidráulicamente rugoso. Sus resultados se observan en la Figura 12 (Saldarriaga,
2007).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
15
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 12. Diagrama de Nikuradse (Saldarriaga, 2007).
En la Figura 12 se observa que si el flujo es laminar (Re <2000), el factor de fricción f varía
en forma lineal con respecto al número de Reynolds, independiente de la rugosidad relativa
(k
s
/d) (Saldarriaga, 2007).
Cuando el flujo es turbulento, el comportamiento de f se vuelve más complejo. Cerca al Re
crítico (2200) todas las curvas coinciden (Saldarriaga, 2007).
Existe una curva límite desde la cual se separan poco a poco las curvas
correspondientes a diferentes valores de k
s
/d (Saldarriaga, 2007).
Los tubos con mayor rugosidad relativa se separan más rápidamente de la curva lisa,
lo cual se debe a que a medida que aumenta Re, disminuye el espesor de la subcapa
laminar viscosa, pasando así los flujos en forma gradual de hidráulicamente lisos a
rugosos (Saldarriaga, 2007).
Una vez que el flujo se separa de la curva lisa, el factor de fricción empieza a ser
una función compleja de Re y de k
s
/d. Esta zona se conoce como flujo transicional.
A medida que Re sigue aumentando, las curvas individuales correspondientes a cada
k
s
/d se vuelven horizontales, lo cual implica que el factor f deja de ser función de Re
y pasa a ser función de k
s
/d (Saldarriaga, 2007).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
16
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
2.2.2.4 Ecuación de Prandtl-von Kármán
Con base en los experimentos de Nikuradse, Prandtl y su estudiante von Kármán plantearon
las ecuaciones para calcular el factor de fricción para el flujo hidráulicamente liso y el flujo
hidráulicamente rugoso (Saldarriaga, 2007).
Las ecuaciones deducidas por Prandtl y von Kármán para el flujo turbulento
hidráulicamente liso son (Saldarriaga, 2007):
𝛿
′
=
11.6 𝜈
𝑣
∗
Ecuación 13. Espesor de la subcapa laminar viscosa.
𝑓 =
8 𝜏
0
𝜌𝑣
2
Ecuación 14. Relación entre el factor de fricción y el esfuerzo cortante.
𝑣
∗
= √
𝑓
8
𝑣̅
Ecuación 15. Velocidad de corte.
Al realizar un desarrollo matemático combinando las ecuaciones anteriores con los perfiles
de velocidad de flujo para los casos hidráulicamente liso y rugoso, la forma final para el
cálculo del factor de fricción, para ambos casos, es:
1
√𝑓
= 2 log
10
(𝑅𝑒 √𝑓) − 0.8
Ecuación 16. Flujo turbulento hidráulicamente liso.
1
√𝑓
= 2 log
10
(
𝑑
𝑘
𝑠
) + 1.14
Ecuación 17. Flujo turbulento hidráulicamente rugoso.
Sin embargo, estas ecuaciones no resultaron de mayor aplicabilidad para el diseño de
tuberías, ya que en la mayoría de tuberías se ubicaban en la zona del régimen de transición,
zona delimitada entre el flujo turbulento hidráulicamente liso y el flujo hidráulicamente
rugoso (Saldarriaga, 2007).
2.2.2.5 Ecuación de Colebrook-White
Colebrook y White hicieron una clasificación de las rugosidades relativas a fin de entender
el flujo transicional y establecer una ecuación que permitiera el cálculo del factor de

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
17
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
fricción para este tipo de flujo. Los pasos seguidos por los investigadores fueron
(Saldarriaga, 2007):
1. Comparación de la rugosidad absoluta con el espesor de la subcapa laminar viscosa
(Saldarriaga, 2007):
𝑘
𝑠
𝛿′
=
𝑘
𝑠
𝑑
𝛿′
𝑑
Ecuación 18. Comparación entre la rugosidad absoluta y el espesor de la subcapa laminar viscosa.
Esta ecuación se remplaza por el valor del espesor de la subcapa laminar viscosa (Ecuación
13) obteniendo el siguiente resultado:
𝛿′
𝑑
=
11.6 𝜈
𝑣
∗
𝑑
Ecuación 19.
Combinando las Ecuaciones 15 y 19 se tiene
𝛿′
𝑑
=
11.6 𝜈
𝑣̅ 𝑑
√
𝑓
8
=
32.81
𝑅𝑒 √𝑓
𝑘
𝑠
𝑑
𝑅𝑒 √𝑓 = 32.81
𝑘
𝑠
𝛿′
Ecuación 20.
2. De la ecuación de Prandtl-von Kármán (Ecuación 16) se tiene la siguiente
transformación restando 2 log
10
(d/k
s
) a ambos lados (Saldarriaga, 2007):
1
√𝑓
− 2 log
10
(
𝑑
𝑘
𝑠
) = 2 log (
𝑘
𝑠
𝑑
𝑅𝑒 √𝑓) − 0.8
Ecuación 21.
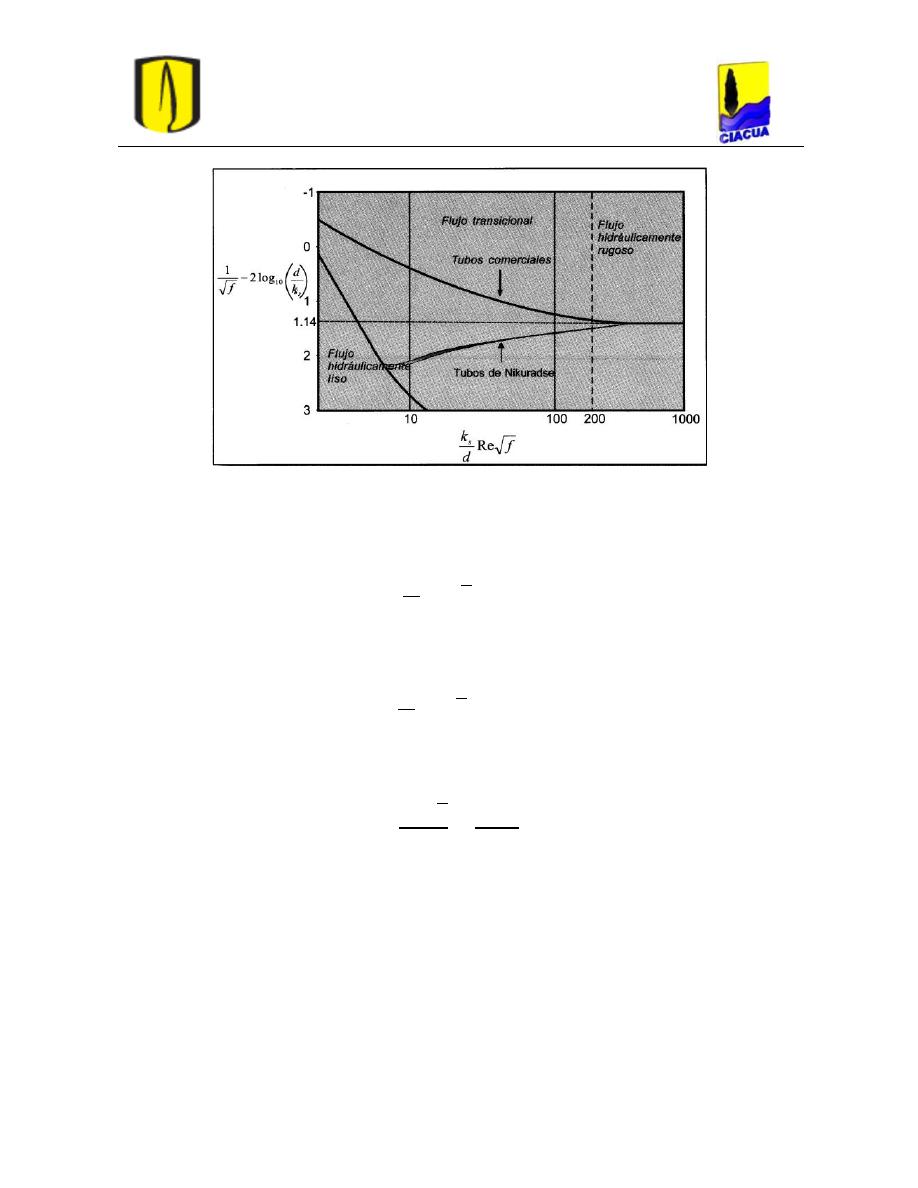
3. Colebrook y White compararon los términos de las Ecuaciones 20 y 21 y produjeron la
gráfica que aparece en la Figura 13, para tubos comerciales y tubos con rugosidad artificial
(Saldarriaga, 2007):
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
18
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 13. Rugosidad relativa como función del factor de fricción y el número de Reynolds en la zona transicional
(Saldarriaga, 2007).
4. A partir de los resultados de la Figura 13 obtuvieron las siguientes relaciones para el caso
del flujo turbulento hidráulicamente liso (Saldarriaga, 2007):
𝑘
𝑠
𝑑
𝑅𝑒 √𝑓 ≤ 10
Ecuación 22.
Y para el caso del flujo turbulento hidráulicamente rugoso se obtuvo (Saldarriaga, 2007):
𝑘
𝑠
𝑑
𝑅𝑒 √𝑓 > 200
Ecuación 23.
5. De la Ecuación 20 obtuvo (Saldarriaga, 2007)
𝑅𝑒 √𝑓
𝑑
=
32.81
𝛿′
Ecuación 24.
y remplazando este resultado en la Ecuación 22:
𝑘
𝑠
≤ 0.305 𝛿′
Ecuación 25. Relación entre la rugosidad y la subcapa laminar viscosa para el flujo turbulento hidráulicamente
liso.
Este resultado indica que para que el flujo sea hidráulicamente liso, el tamaño de la
rugosidad tiene que ser inferior al 30%, aproximadamente, del espesor de la subcapa
laminar viscosa (Saldarriaga, 2007).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
19
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Para flujos hidráulicamente rugosos se tiene que combinando las Ecuaciones 20 y 23:
𝑘
𝑠
≥ 6.10 𝛿′
Ecuación 26. Relación entre la rugosidad y la subcapa laminar viscosa para el flujo turbulento hidráulicamente
rugoso.
Para que el flujo sea hidráulicamente rugoso, el tamaño de la rugosidad debe ser superior a
6 veces el espedos de la subcapa laminar viscosa (Saldarriaga, 2007).
6. A partir de los resultados obtenidos por Prandtl y von Kármán, Colebrook y White
establecieron que el comportamiento de las tuberías reales en la zona de transición debería
estar descrito por una ecuación única que incluyera los extremos establecidos por el flujo
turbulento hidráulicamente liso y rugoso (Saldarriaga, 2007).
1
√𝑓
= −2 log
10
(
𝑘
𝑠
3.7 𝑑
+
2.51
𝑅𝑒 √𝑓
)
Ecuación 27. Ecuación de Colebrook-White.
La Ecuación 27 probó ser válida para todo tipo de flujo turbulento en tuberías. Sin
embargo, tiene el problema de que no es una ecuación explícita para el factor de fricción, lo
cual implica la necesidad de utilizar algún método numérico para calcularlo una vez se
conozcan las otras variables (Saldarriaga, 2007).
Este problema matemático ocasionó la aparición de Ecuaciones empíricas más sencillas de
utilizar; entre éstas la más famosa es la ecuación de Hazen-Williams. Sin embargo, esta
ecuación y otras ecuaciones empíricas tienen límites de aplicación claros; algunas de ellas
sólo se pueden utilizar para agua, o tienen límites para las velocidades máximas o mínimas,
o sólo pueden utilizarse para rangos limitados de diámetros y materiales de tuberías
(Saldarriaga, 2007).
El método más apropiado para el cálculo de f es iterativo y sigue la metodología de
Newton-Raphson. El método converge para una precisión muy buena en un orden de 3 a 4
iteraciones (Camacho & Saldarriaga, 1990). A continuación se hace una explicación
general del método:
El método parte de la Ecuación 28:
𝑥 = 𝑔(𝑥)
Ecuación 28.
El valor de la aproximación a la raíz de la ecuación en la iteración i+1 se calcula con base
en la aproximación de la iteración i de acuerdo a la siguiente ecuación (Saldarriaga, 2007):

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
20
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
𝑥
𝑖+1
= 𝑥
𝑖
−
𝑔(𝑥
𝑖
) − 𝑥
𝑖
𝑔′(𝑥
𝑖
) − 1
Ecuación 29.
donde g’(x) es la derivada de la función. Para el caso de la función de Colebrook-White la
variable x es el inverso de la raíz cuadrada del factor de fricción (Saldarriaga, 2007):
𝑥 =
1
√𝑓
Por consiguiente (Saldarriaga, 2007):
𝑔(𝑥) = −2 log
10
(
𝑘
𝑠
3.7 𝑑
+
2.51 𝑥
𝑖
𝑅𝑒
)
Ecuación 30.
La derivada de la función anterior es (Saldarriaga, 2007):
𝑔
′
(𝑥) = −
2
ln 10
(
2.51
𝑅𝑒
𝑘
𝑠
3.7 𝑑 +
2.51 𝑥
𝑖
𝑅𝑒
)
Ecuación 31.
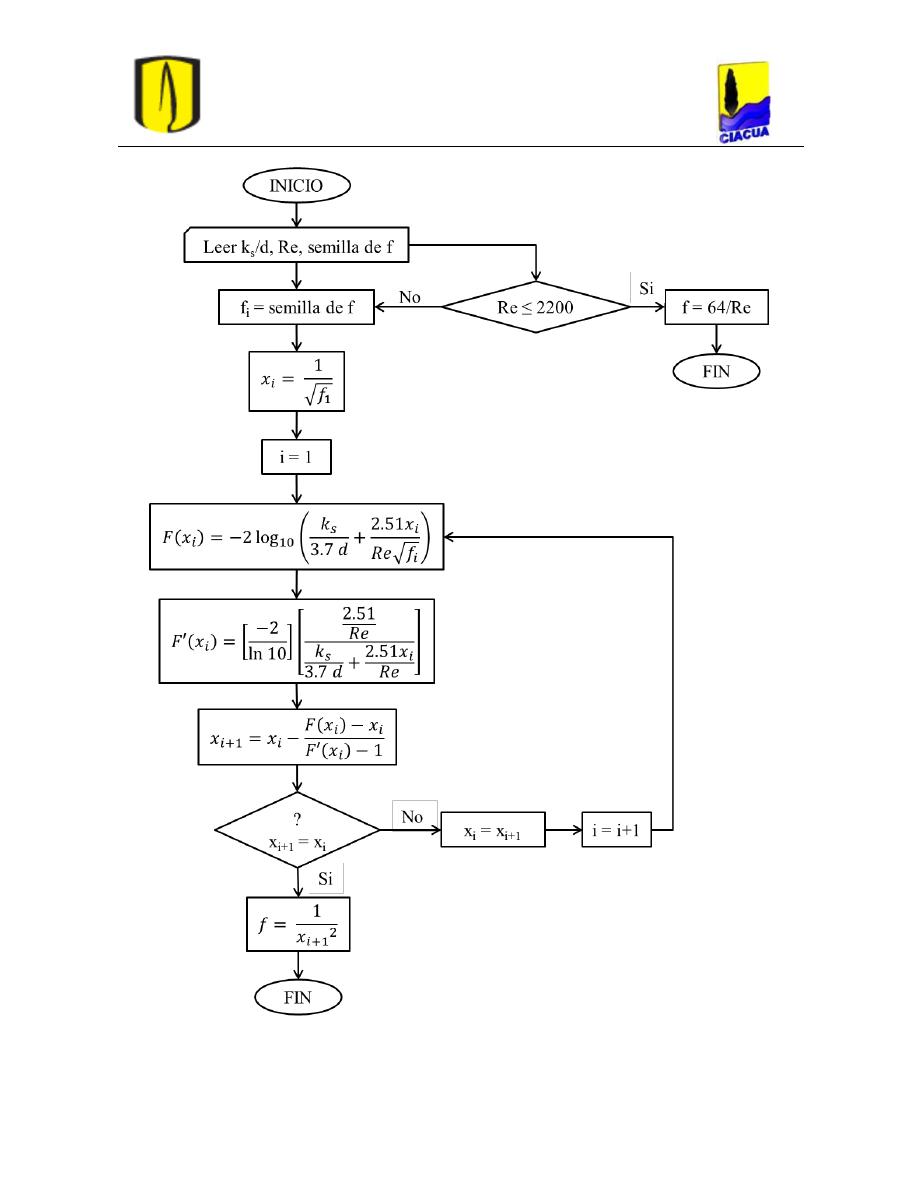
En el diagrama de flujo mostrado en la Figura 14 se puede observar el algoritmo utilizado
por este método.
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
21
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 14. Diagrama de flujo para el cálculo del factor de fricción f por medio de Newton-Raphson (Saldarriaga,
2007).
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
22
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
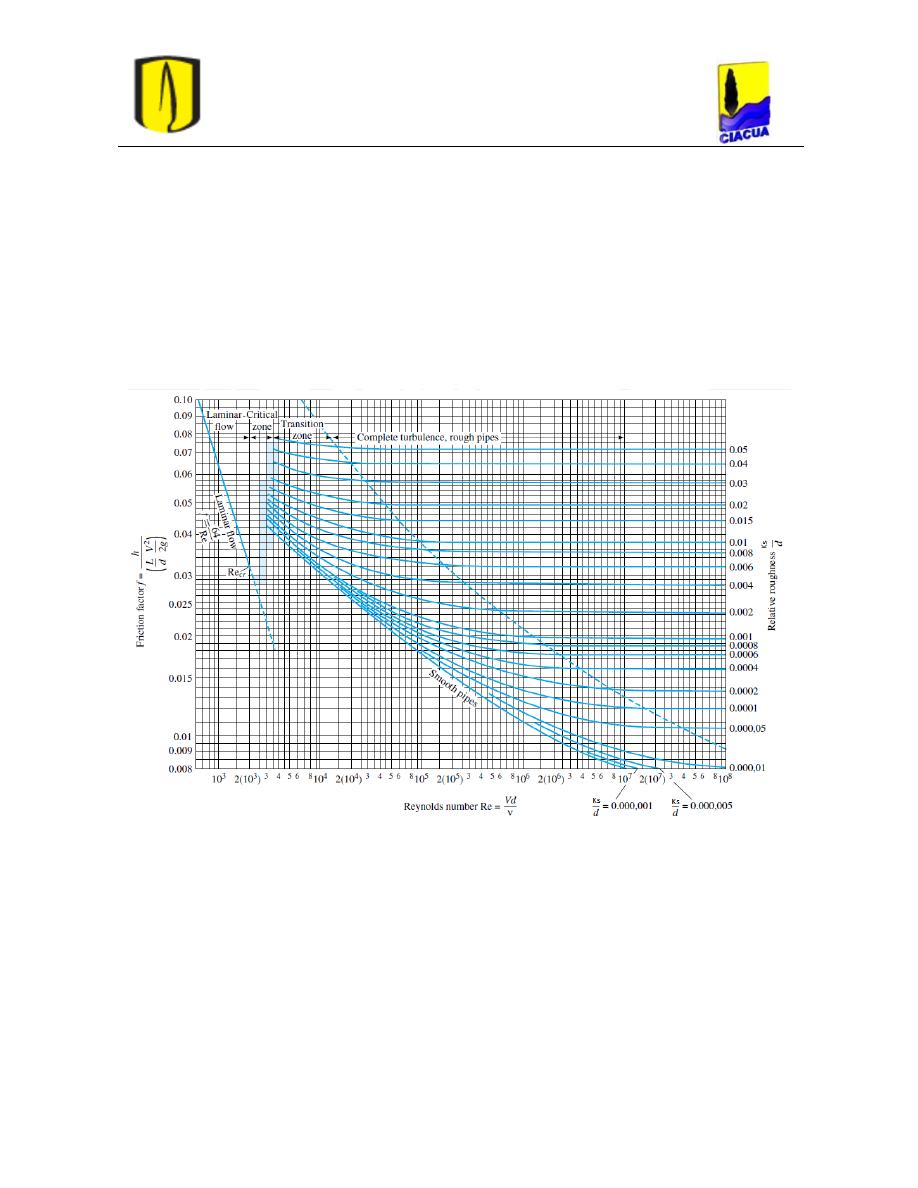
2.2.3 Diagrama de Moody
Moody se basó en los resultados de Nikuradse y Colebrook a fin de investigar las pérdidas
por fricción en tuberías con rugosidades reales y no artificiales. El diagrama de Moody es
una gráfica del factor de fricción para todos los regímenes de flujo contra el número de
Reynolds a varios valores de la rugosidad relativa de la tubería (Menon, 2005). La Figura
15 muestra el diagrama de Moody el cual se delimita en cinco zonas: flujo laminar, zona
crítica, zona lisa, zona de transición y turbulencia completa.
Figura 15. Diagrama de Moody (White, 2008).
En principio, el diagrama de Moody es usado para la solución de tres tipos de problemas:
en el que la altura de pérdida es desconocida, la tasa de flujo volumétrico es desconocida o
el diámetro es desconocido (Brkic
3
, 2010). El método para determinar el factor de fricción
gráficamente es: para un número de Reynolds dado en el eje horizontal, se dibuja una línea
vertical hacia la curva que represente la rugosidad relativa k
s
/d. el factor de fricción es el
que se lee siguiendo horizontalmente al eje vertical de la izquierda (Menon, 2005).
Se puede ver en el diagrama de Moody que la región turbulenta está dividida en dos
regiones: la zona de transición y la zona de completa turbulencia. El límite inferior está
designado como tuberías lisas y la zona de transición se extiende hasta la línea punteada.
Más allá de la línea punteada está la zona de turbulencia completa en tuberías rugosas. En

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
23
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
esta zona el factor de fricción depende muy poco del número de Reynolds y más de la
rugosidad relativa. Esto es evidente de la ecuación de Colebrook-White (Ecuación 27)
donde a grandes número de Reynolds, el segundo término se empieza a acercar a cero. El
factor de fricción, entonces, depende únicamente del primer término el cual es proporcional
a la rugosidad relativa k
s
/d. En contraste con la zona de transición, ambos, Re y k
s
/d
influencian el valor del factor de fricción (Menon, 2005).
La Tabla 2 muestra los valores de rugosidad recomendados para ductos comerciales. Con el
uso, los tubos se vuelven más rugosos debido a la corrosión, incrustaciones y depositación
de material en las paredes (Camacho & Saldarriaga, 1990).
Tabla 2. Valores recomendados de rugosidad para tubos comerciales (White, 2008).
Material
Condición
k
s
(mm)
Acero
Lámina de metal, nuevo
0.05
Inoxidable, nuevo
0.002
Comercial, nuevo
0.046
Remachado
3.0
Oxidado
2.0
Hierro
Fundido, nuevo
0.26
Forjado, nuevo
0.046
Galvanizado, nuevo
0.15
Asfaltado, nuevo
0.12
Plástico
0.0015
Concreto
Liso
0.04
Rugoso
2.0
Caucho
Liso
0.01
Madera
0.5
Con los resultados anteriores se produjo el diagrama de rugosidades relativas ampliamente
usado para diseño de tuberías.
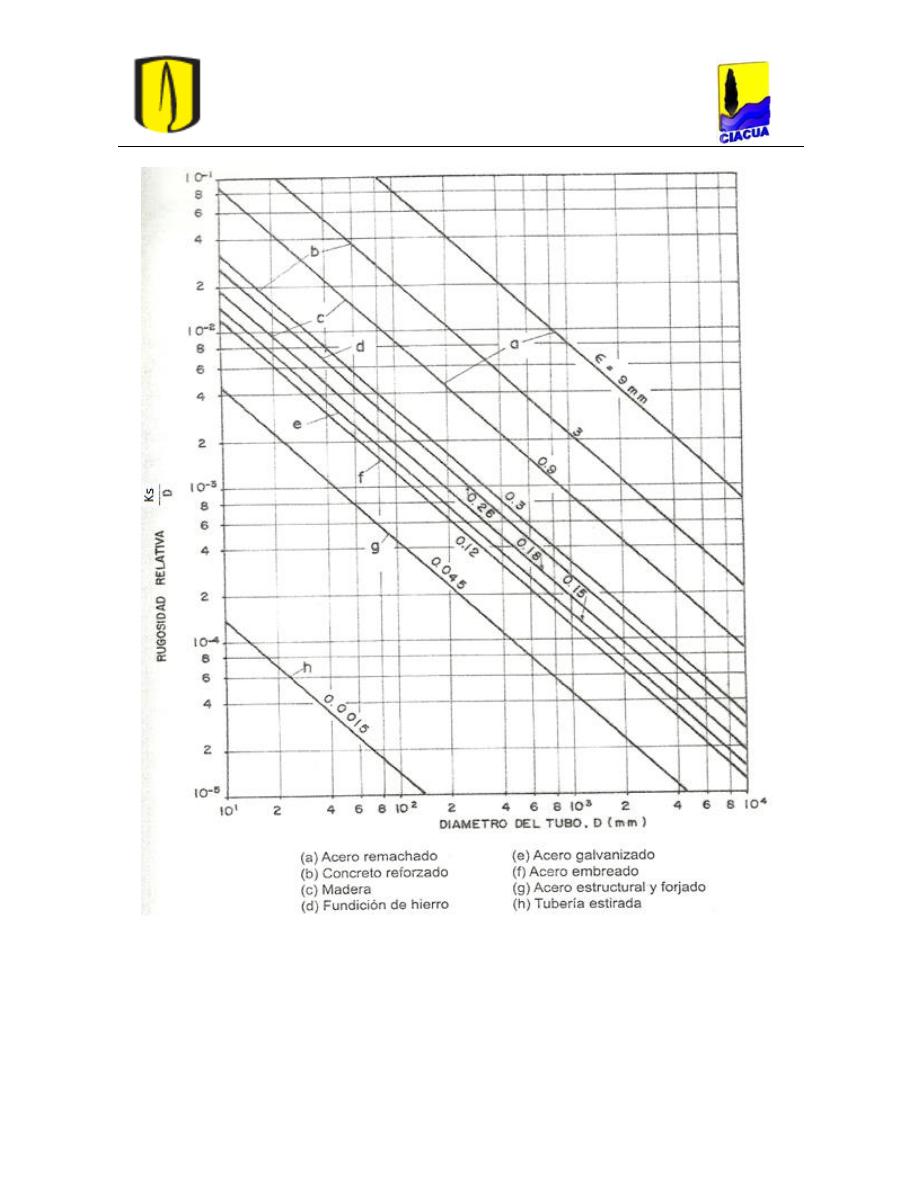
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
24
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 16. Diagrama de rugosidades relativas como función del diámetro de la tubería y material del tubo
(Beltrán, 2005).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
25
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
2.3 Últimos Estudios Sobre el Flujo Turbulento Hidráulicamente Liso
2.3.1 Estudios de Brkic
Actualmente se busca obtener nuevas relaciones del factor de fricción para el flujo
turbulento hidráulicamente liso, tal y como lo muestran los estudios realizados por Brkic,
quien recopila nuevas expresiones para la determinación del factor de fricción, haciendo
una marcada distinción entre las relaciones cuando se asume la ausencia total de rugosidad
y cuando hay presencia de ésta.
Régimen Liso en Ausencia de Rugosidad: corresponde a la Ecuación de Colebrook en
ausencia total de rugosidad relativa (Ecuación de Prandtl-von Kármán).
Tabla 3. Ecuaciones para el flujo turbulento hidráulicamente liso en usencia de rugosidad (Brkic2, 2011).
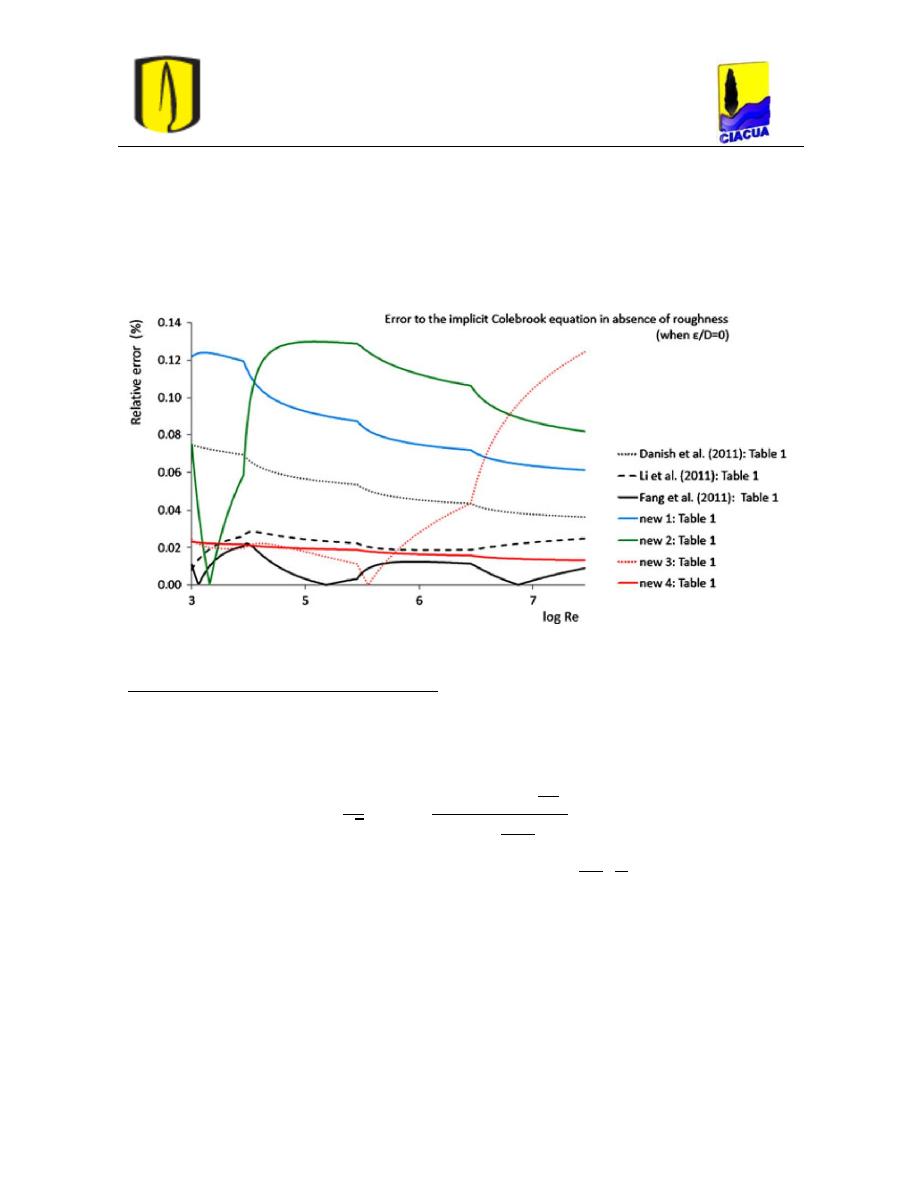
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
26
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Para las relaciones propuestas en la Tabla 3, la variable λ corresponde a f (factor de
fricción); adicionalmente, los parámetros S
1
, S
2
y S
3
corresponden a variables de la
Ecuación denominada como New 4.
La comparación de estas aproximaciones de la relación de Prandtl (Tabla 3) se muestra en
la Figura 17. El error relativo a la Ecuación de Prandtl es de 0,15%.
Figura 17. Precisión de algunas aproximaciones a la ecuación de Prandtl (Brkic
2
, 2011).
Régimen Liso con Presencia de Rugosidad: toma como referencia la relación propuesta por
Buzzelli (2008) desarrollada especialmente para las condiciones “lisas”. Éste enfoque es
bueno porque usa la rugosidad relativa incluso para el régimen “liso” de la turbulencia
(Brkic
1
, 2011).
1
√𝜆
= 𝐴 − [
𝐴 + 2 ∙ log
10
(
𝐵
𝑅𝑒)
1 +
2.18
𝐵
]
𝐴 = [0.774 ∙ ln(𝑅𝑒)] − 1.41 𝐵 = (
𝑅𝑒
3.7
∙
𝜀
𝐷
) + 2.51 ∙ 𝐴
Ecuación 32. Relación de Buzzelli para el Régimen Hidráulicamente Liso con Presencia de Rugosidad. Tomada de
(Brkic1, 2011).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
27
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
2.3.2 Estudios en la Universidad de los Andes
2.3.2.1 Estudios Realizados por Rafael Flechas
Los límites actuales (del diagrama de Moody) se basan en las ecuaciones propuestas por
Prandtl y von Kármán (Ecuación 16 y 17). Sin embargo, para delimitar esta zona, Moody
nunca se basó en la ecuación de Colebrook-White (Ecuación 27) y los límites definidos
claramente por este investigador para la zona de transición en función de la rugosidad y el
espesor de la subcapa laminar viscosa (Flechas, 2010).
En la investigación realizada por Rafael Flechas, se presenta la delimitación de la zona de
transición en el diagrama de Moody con base en la Ecuación de Colebrook-White y los
efectos que puede tener esta nueva zona para entender el comportamiento de las redes de
distribución de agua potable (RDAP). A continuación se muestra el procedimiento
empleado para determinar las nuevas ecuaciones de los límites de la zona de transición.
Límite Inferior de la Zona de Transición:
El límite inferior de la zona de transición está definido por los flujos que pueden
clasificarse como turbulentos hidráulicamente lisos. Según Colebrook-White, esto se
presenta cuando la rugosidad es igual al 30% del espesor de la subcapa laminar viscosa. Por
ello, si el tamaño de la rugosidad de la tubería es inferior a dicho valor, el flujo es
hidráulicamente liso. Teniendo en cuenta lo anterior, a continuación se ilustra el proceso
deductivo de la ecuación que describe el límite inferior de la zona de transición basado en
la ecuación de Colebrook-White (Flechas, 2010).
Primero, se remplaza en la ecuación de Colebrook-White (Ecuación 27) la rugosidad (k
s
)
por el 30% de la subcapa laminar viscosa (δ’) (Flechas, 2010):
1
√𝑓
= −2 log
10
(
0.305 𝛿′
3.7 𝑑
+
2.51
𝑅𝑒√𝑓
)
Ecuación 33.
Teniendo en cuenta que el espesor de la subcapa laminar viscosa se define como en la
Ecuación 13 y la velocidad de corte se calcula como en la Ecuación 15, se procede a
remplazar estas Ecuaciones en la ecuación anterior (Flechas, 2010).
1
√𝑓
= −2 log
10
[
0.305
3.7
(
11.6 𝑣
√
𝜏
0
𝜌 )
+
2.51
𝑅𝑒√𝑓
]
Ecuación 34.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
28
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Considerando la relación entre el factor de fricción (f) y el esfuerzo cortante (τ
0
) (Ecuación
14) se remplaza esta ecuación en la ecuación anterior; el resultado se muestra a
continuación (Flechas, 2010):
1
√𝑓
= −2 log
10
[
0.305
3.7
(
11.6 𝜈
√
𝑓 𝜌𝑣
2
8
𝜌 )
+
2.51
𝑅𝑒√𝑓
]
1
√𝑓
= −2 log
10
(
2.7 𝜈
𝑣 𝑑 √𝑓
+
2.51
𝑅𝑒√𝑓
)
Ecuación 35.
Posteriormente en la Ecuación 35 se expresa la velocidad media de flujo en términos del
número de Reynolds, la viscosidad cinemática del fluido y el diámetro de la tubería, tal y
como se ilustra a continuación (Flechas, 2010):
1
√𝑓
= −2 log
10
[
2.7 𝜈
(
𝑅𝑒 𝜈
𝑑 ) 𝑑 √𝑓
+
2.51
𝑅𝑒√𝑓
]
1
√𝑓
= −2 log
10
(
2.7
𝑅𝑒√𝑓
+
2.51
𝑅𝑒√𝑓
)
Ecuación 36.
Finalmente, si se suman los factores en común de la Ecuación 36, se obtiene la siguiente
ecuación que define el límite inferior de la zona de transición basado en la ecuación de
Colebrook-White y los límites claramente definidos por estos investigadores para la zona
de transición (Flechas, 2010).
1
√𝑓
= −2 log
10
(
5.21
𝑅𝑒√𝑓
)
Ecuación 37. Límite inferior de la zona de transición.
Límite Superior de la Zona de Transición:
El límite superior de la zona de transición está definido por los flujos que pueden mínimo
clasificarse como flujo turbulento hidráulicamente rugoso. Según Colebrook-White, estos
se presentan cuando la rugosidad absoluta de la tubería es igual a 6.1 veces el espesor de la
subcapa laminar viscosa. Por ello, si la rugosidad de la tubería es superior a dicho valor, el
flujo es hidráulicamente rugoso. Teniendo en cuenta lo anterior, a continuación se ilustra el

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
29
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
proceso deductivo de la ecuación que describe el límite superior de la zona de transición
basado en la ecuación de Colebrook-White (Flechas, 2010).
Primero, se remplaza en la ecuación de Colebrook-White la rugosidad (k
s
) por 6.1 veces el
espesor de la subcapa laminar viscosa (Flechas, 2010):
1
√𝑓
= −2 log
10
(
6.1 𝛿′
3.7 𝑑
+
2.51
𝑅𝑒√𝑓
)
Ecuación 38.
Posteriormente, se procede a remplazar en la Ecuación 38 el espesor de la subcapa laminar
viscosa por las Ecuaciones 13 y 15, como se muestra a continuación (Flechas, 2010):
1
√𝑓
= −2 log
10
[
6.1
3.7
(
11.6 𝑣
√
𝜏
0
𝜌 )
+
2.51
𝑅𝑒√𝑓
]
Ecuación 39.
A partir de la Ecuación 39 se remplaza en la Ecuación 14 el esfuerzo cortante por el factor
de fricción, la densidad del fluido y la velocidad media de flujo, como se muestra a
continuación (Flechas, 2010):
1
√𝑓
= −2 log
10
[
6.1
3.7
(
11.6 𝜈
√
𝑓 𝜌𝑣
2
8
𝜌 )
+
2.51
𝑅𝑒√𝑓
]
1
√𝑓
= −2 log
10
(
54.09 𝜈
𝑣 𝑑 √𝑓
+
2.51
𝑅𝑒√𝑓
)
Ecuación 40.
Posteriormente, en la Ecuación 40, se expresa la velocidad media de flujo en términos del
número de Reynolds, la viscosidad cinemática del fluido y el diámetro de la tubería, con
base en la definición de este número adimensional, tal y como se ilustra a continuación
(Flechas, 2010):
1
√𝑓
= −2 log
10
[
54.09 𝜈
(
𝑅𝑒 𝜈
𝑑 ) 𝑑 √𝑓
+
2.51
𝑅𝑒√𝑓
]
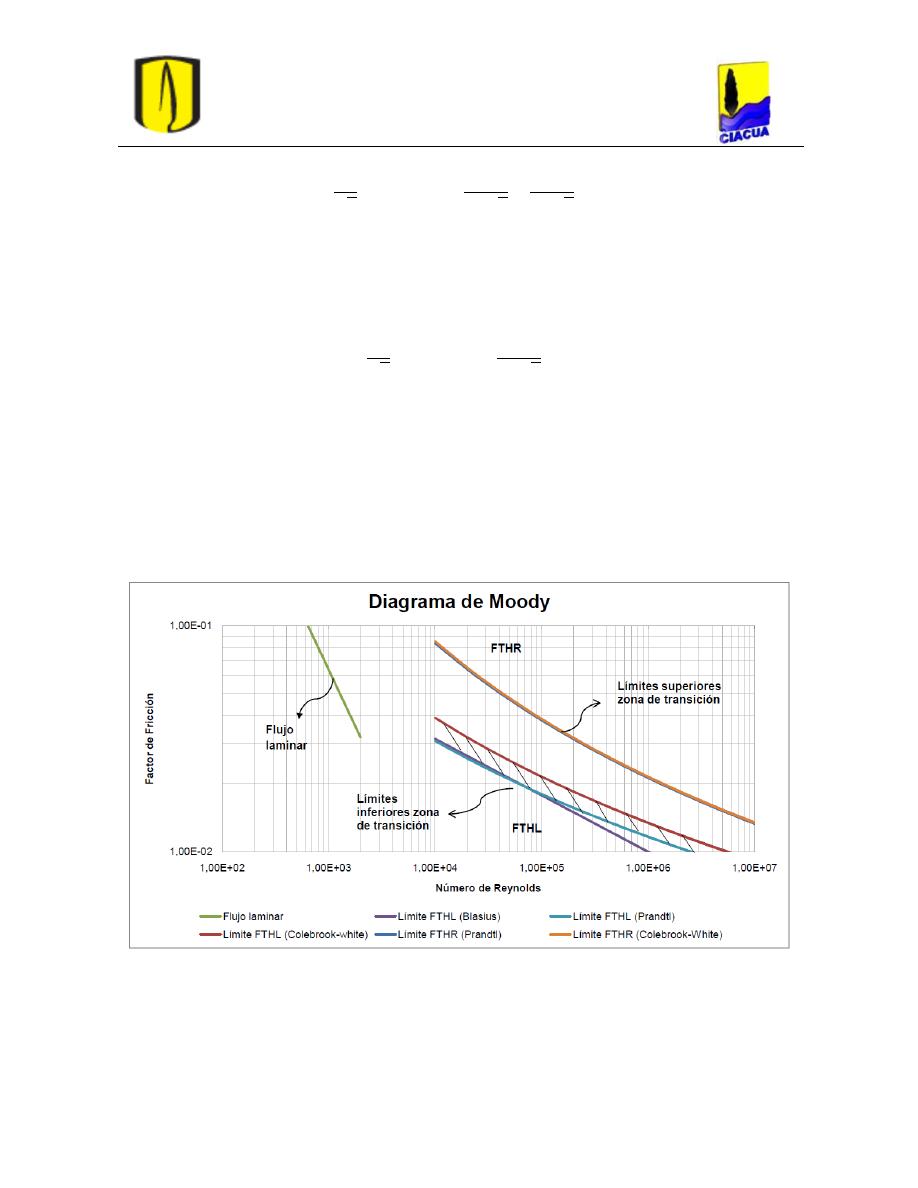
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
30
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
1
√𝑓
= −2 log
10
(
54.09
𝑅𝑒√𝑓
+
2.51
𝑅𝑒√𝑓
)
Ecuación 41.
Finalmente, si se suman los factores en común de la Ecuación 41 se obtiene la siguiente
ecuación que describe el límite superior de la zona de transición con base en la ecuación de
Colebrook-White (Flechas, 2010):
1
√𝑓
= −2 log
10
(
56.6
𝑅𝑒√𝑓
)
Ecuación 42. Límite superior de la zona de transición.
Para entender el efecto que puede tener estos nuevos límites de la zona de transición en el
diagrama de Moody, se dibujó el límite inferior y superior de la zona de transición en el
diagrama de Moody con base en las Ecuaciones 37 y 42 respectivamente. Luego se
demarcaron los límites de esta zona en dicho diagrama a partir de las Ecuaciones de Blasius
(Ecuación 12) y Prandtl-von Kármán (Ecuación 16 y 17), para luego compararlos con los
límites obtenidos a partir de la Ecuación de Colebrook-White, tal y como se muestra en la
Figura 18 (Flechas, 2010).
Figura 18. Delimitación de la zona de transición en el diagrama de Moody (Flechas, 2010).
Si se compara el límite superior de la zona de transición obtenido a partir de la ecuación de
Colebrook-White vs la ecuación de Prandtl-von Kármán, se puede ver que estos coinciden
en toda la extensión del diagrama de Moody. Lo anterior se debe a que el segundo sumando
del paréntesis de la ecuación de Colebrook-White se puede considerar despreciable en

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
31
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
comparación con el orden de magnitud del primer sumando como se puede observar
detalladamente en el proceso deductivo de la Ecuación 42 (Flechas, 2010).
En relación con el límite inferior de la zona de transición, se puede ver que el límite
descrito por la ecuación de Blasius coincide con el definido por la ecuación de Prandtl-von
Kármán en el rango de validez que fue deducida esta primera ecuación. Sin embargo, el
límite inferior de esta zona demarcado a partir de estas dos Ecuaciones difiere del dibujado
en el diagrama de Moody con base en la Ecuación de Colebrook-White y la Ecuación 37 ya
que el obtenido a partir de estas dos últimas Ecuaciones hace más estrecha esta zona en el
diagrama de Moody, lo cual facilita que se representen flujos turbulentos hidráulicamente
lisos en el diseño de tuberías en comparación con la ecuación de Prandtl-von Kármán y
Blasius. Esto se refleja claramente en la región sombreada de la Figura 18 y se presenta
debido a que el orden de magnitud del primer sumando del paréntesis de la ecuación de
Colebrook-White es igual al orden de magnitud del segundo sumando como se puede ver
en el proceso deductivo de la Ecuación 37 ilustrado anteriormente (Flechas, 2010).
Teniendo en cuenta lo anterior, es necesario analizar el efecto que pueden tener estos
nuevos límites de la zona de transición del diagrama de Moody en el diseño de redes de
distribución de agua potable (RDAP). Para ello, se diseñaron diversas RDAP de Colombia,
tales como La Cumbre, Red Bogotá-Cazucá y Red San Vicente utilizando las ecuaciones de
Darcy-Weisbach y Hazen Williams. Para diseñar estas redes se utilizó el programa REDES
creado en la Universidad de los Andes para realizar el análisis y diseño optimizado de
RDAP (Flechas, 2010).
Se localizaron los factores hidráulicos obtenidos a partir de cada uno de los diseños de la
Red San Vicente, Red Bogotá-Cazucá y La Cumbre en el diagrama de Moody de la Figura
18, como se pueden ver en las Figuras 19, 20 y 30 respectivamente (Flechas, 2010).
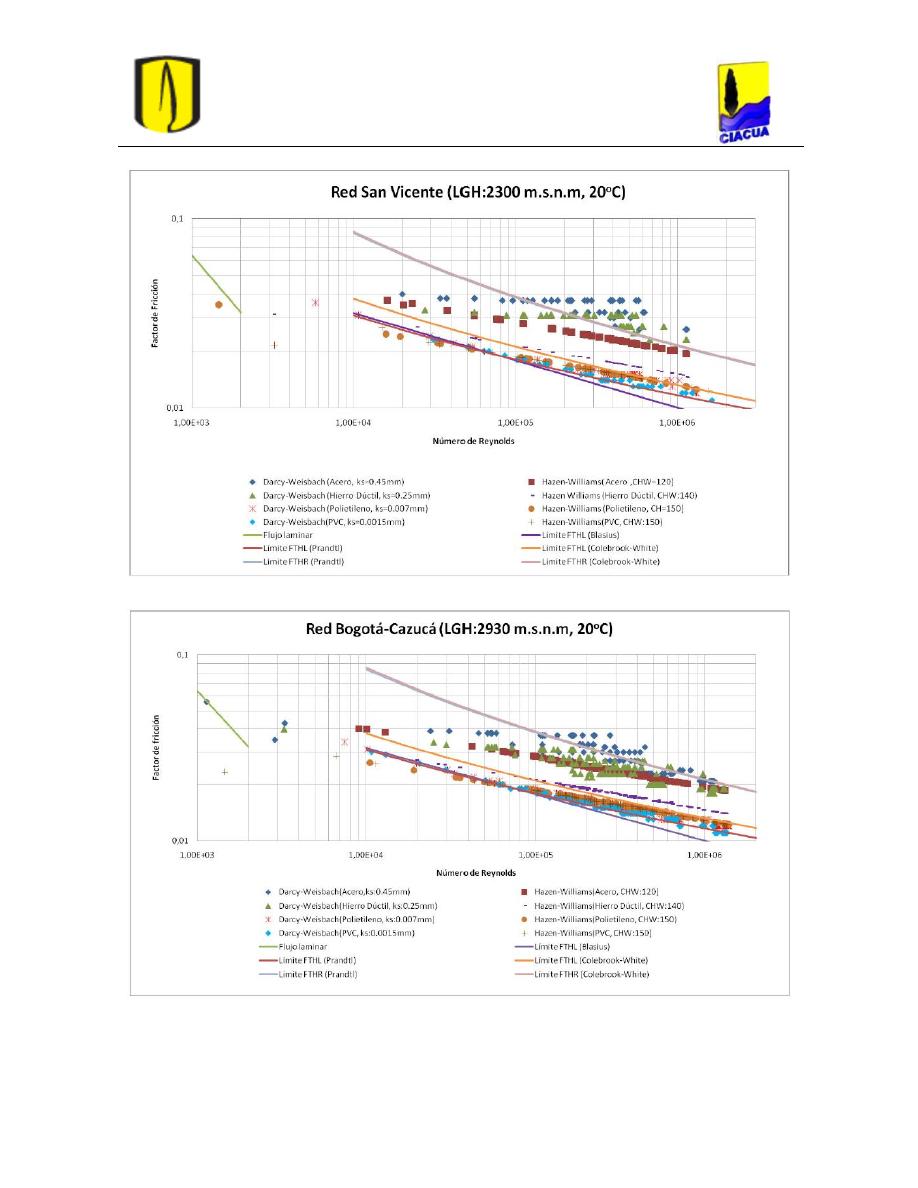
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
32
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 19. Factores hidráulicos obtenidos para la red San Vicente (Flechas, 2010).
Figura 20. Factores hidráulicos obtenidos para la red Bogotá-Cazucá (Flechas, 2010).
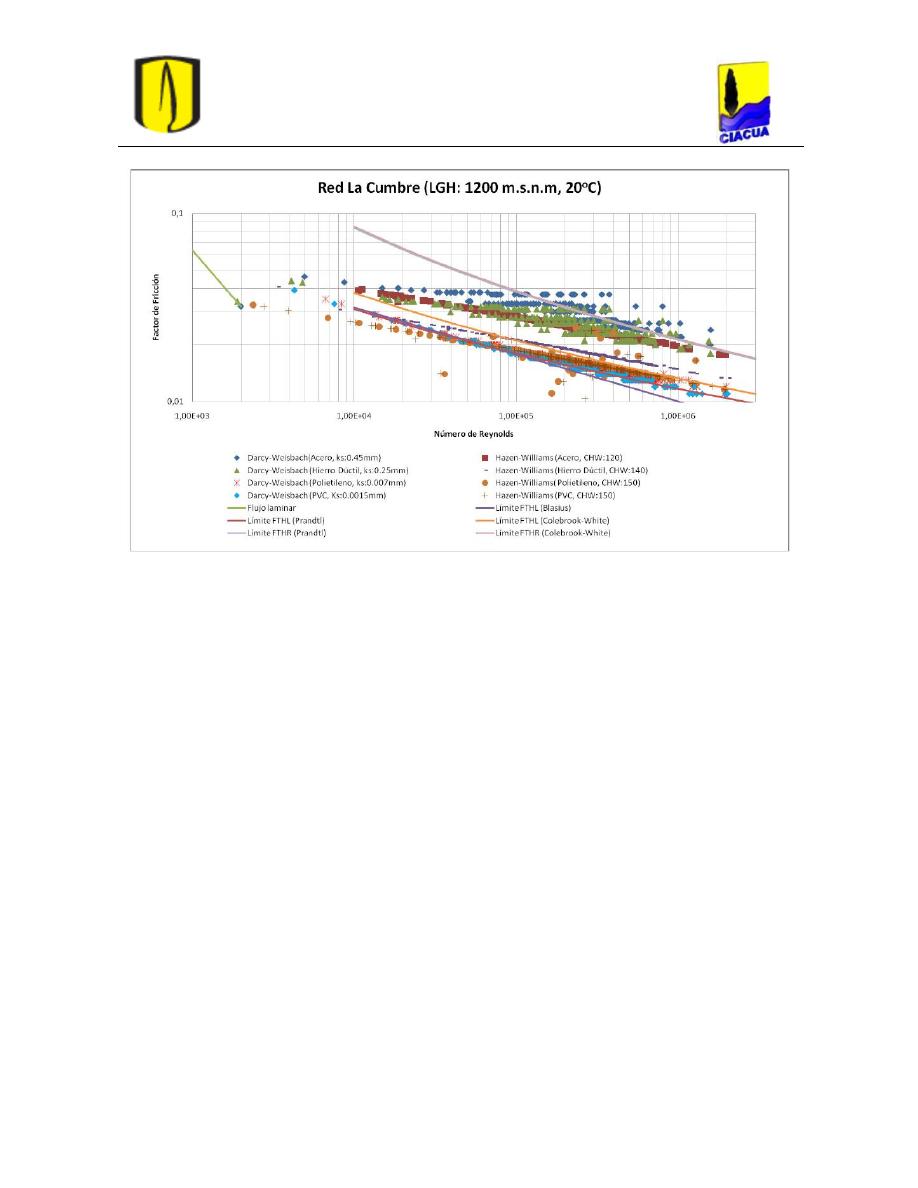
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
33
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 21. Factores hidráulicos obtenidos para la red La Cumbre (Flechas, 2010).
En relación con el diseño de la red San Vicente, en la Figura 19 se puede observar que los
factores hidráulicos obtenidos para el diseño de esta red con el Acero y el Hierro dúctil, se
localizan en su mayoría en la zona de flujo turbulento hidráulicamente rugoso cuando se
utiliza en el diseño la ecuación de fricción de Darcy-Weisbach. Sin embargo, se puede
observar que los factores hidráulicos obtenidos por medio de la ecuación de Hazen-
Williams se ubican en su mayoría en la zona de transición definida a partir de las
Ecuaciones de Prandtl-von Kármán y Colebrook-White, pero se distingue claramente que
para números de Reynolds inferiores a 100,000 los factores hidráulicos calculados para el
hierro dúctil con esta última ecuación se localizan dentro de la zona de FTHL definida a
partir de la ecuación de Colebrook-White. Igualmente, en esta figura se puede observar que
la tendencia que se presenta para el Acero y Hierro Dúctil no sucede de igual forma para el
PVC y el Polietileno, debido a que los factores de fricción obtenidos por medio de la
ecuación de Darcy-Weisbach tienden a igualarse con los computados en la ecuación de
Hazen-Williams, los cuales se ubican en su mayoría en la región sombreada de la Figura
18, definido a partir de la ecuación de Colebrook-White y la zona de transición demarcada
con base en la ecuación de Prandtl-von Kármán. Lo anterior, significa que el uso de la
ecuación Hazen-Williams para la Red San Vicente no se limita exclusivamente para la zona
de transición con base en el nuevo límite inferior de esta zona deducido a partir de la
ecuación de Colebrook-White (Flechas, 2010).
A partir de la Figura 20, se puede observar que los factores hidráulicos obtenidos para el
diseño de la Red Bogotá-Cazucá con el Acero y Hierro Dúctil, se localizan en su mayoría
en la zona de transición cuando se utiliza en el diseño la ecuación de fricción de Darcy-
Weisbach. Por otro lado, se puede ver que los factores hidráulicos obtenidos por medio de

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
34
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
la ecuación de Hazen-Williams se ubican por debajo de los calculados por esta ecuación o
se alejan del límite de la zona de transición dibujado a partir de la ecuación de Prandtl-von
Kármán o la ecuación de Colebrook-White. En esta misma figura; se puede observar que la
tendencia que se presenta para el Acero y Hierro Dúctil no ocurre de igual forma para el
Polietileno y PVC, ya que los factores de fricción obtenidos por la ecuación de Darcy-
Weisbach tienden a igualarse con los computados en la ecuación de Hazen-Williams y se
ubican en su mayoría en la región sombreada de la Figura 18, pero después de dicho
número esta similitud no se cumplen ya que se ubican en la región sombreada de la Figura
18 (Flechas, 2010).
Finalmente, con base en la Figura 21, se puede observar que, los factores hidráulicos
obtenidos en el diseño de la Red La Cumbre con el Acero y el Hierro Dúctil, se localizan en
su mayoría cerca al límite superior de la zona de transición cuando se utiliza en el diseño la
ecuación de fricción de Darcy-Weisbach. Por otro lado, se puede ver que los factores
hidráulicos obtenidos por medio de la ecuación de Hazen-Williams para estos materiales se
alejan de este límite descrito por la ecuación de Prandtl-von Kármán y la ecuación de
Colebrook-White. Adicionalmente, de esta misma figura se puede observar que la
tendencia que presenta para el Acero y Hierro Dúctil ocurre de igual forma para el
Polietileno y el PVC para números de Reynolds inferiores a 100,000 ya que los factores de
fricción obtenidos por la ecuación de Darcy-Weisbach tienden a ser mayores comparados
con los calculados con la ecuación de Hazen-Williams. Sin embargo, es importante
mencionar que los factores de fricción por estas Ecuaciones tienden a igualarse para estos
dos materiales, los cuales se ubican en su mayoría en la región sombreada de la Figura 18,
y específicamente en el FTHL con base en el nuevo límite inferior de la zona de transición
definido a partir de la ecuación de Colebrook-White y la zona de transición demarcada con
base en la ecuación de Prandtl-von Kármán. Por último, en esta figura se puede ver que en
comparación al diseño de la Red San Vicente, para números de Reynolds inferiores a
100,000, se obtienen de igual forma factores hidráulicos dentro del FTHL para materiales
rugosos como el Hierro Dúctil cuando se diseña esta red con la ecuación de Hazen-
Williams a partir del nuevo límite inferior de la zona de transición con base en la ecuación
de Colebrook-White (Flechas, 2010).
Para materiales que presentan rugosidades absolutas inferiores a 0.007 mm o coeficientes
de Hazen-Williams superiores a 140, los factores hidráulicos obtenidos a partir del diseño
de las redes analizadas utilizando las Ecuaciones de Darcy-Weisbach y Hazen-Williams, se
localizan en la región sombreada de la Figura 18. Por lo anterior, se puede concluir que el
nuevo límite de la zona de transición definido a partir de la Ecuación de Colebrook-White y
los límites establecidos claramente por estos dos investigadores para esta zona pueden
contribuir a entender mejor el comportamiento hidráulico de las RDAP en el FTHL, ya que
este nuevo límite hace más estrecha la zona de transición y permite identificar este tipo de
flujo con mayor exactitud (Flechas, 2010).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
35
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
2.3.2.2 Estudio Realizado por Launa Nieto
Otro estudio realizado en la Universidad de los Andes fue elaborado por Laura Nieto, quien
construyó un montaje (similar al propuesto en el presente proyecto de grado) en las
instalaciones de la empresa PAVO S.A. (ver Figura 22), a fin de determinar el valor de la
rugosidad absoluta en la tubería empleada.
Figura 22. Vista general del montaje de Laura Nieto en PAVCO S.A.
Descripción del modelo físico: la tubería principal es de 78 m de longitud sin uniones, un
tanque de alimentación de 54 pulgadas de diámetro y 6 m de longitud ubicado sobre una
estructura de concreto a 0.9 m del suelo (ver Figura 23), llega a otro tanque (ver Figura 24)
que cumple dos funciones: medir el caudal transportado con un vertedero de pared delgada
(ver Figura 25), y almacenar agua en el sistema con el fin de que el mismo se alimente
continuamente; el nivel mínimo de este debe permanecer a 0.7 m debido a la sumergencia
de la bomba. La instrumentación del sistema está conformada por medidores electrónicos
de presión y caudal, medición diferencial de la presión (ver Figuras 26 y 27) y un sistema
de bombeo (ver Figura 28).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
36
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 23. Tanque de alimentación en PAVCO S.A (Nieto, 2011).
Figura 24. Tanque de almacenamiento en PAVCO S.A (Nieto, 2011).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
37
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 25. Vertedero de cresta delgada para la medición del caudal en PAVCO S.A (Nieto, 2011).
Figura 26. Medidores (diferencia de presión, caudalímetro y válvula de regulación de caudal) en PAVCO S.A
(Nieto, 2011).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
38
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 27. Medidor electrónico de presión en PAVCO S.A (Nieto, 2011).
Figura 28. Sistema de bombeo en PAVCO S.A (Nieto, 2011).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
39
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 29.Sistema eléctrico del montaje en PAVCO S.A (Nieto, 2011).
Para el diseño del montaje se ejecutan pruebas de comprobación de diseño (de manera
similar se mostrará este procedimiento en la Sección 6.3) y la calibración del vertedero.
Las pruebas experimentales incluyen el cálculo de la viscosidad cinemática y la
determinación de la rugosidad absoluta considerando la velocidad de flujo y las pérdidas
por fricción. La Figura 30 muestra la metodología ejecutada para la toma de mediciones.
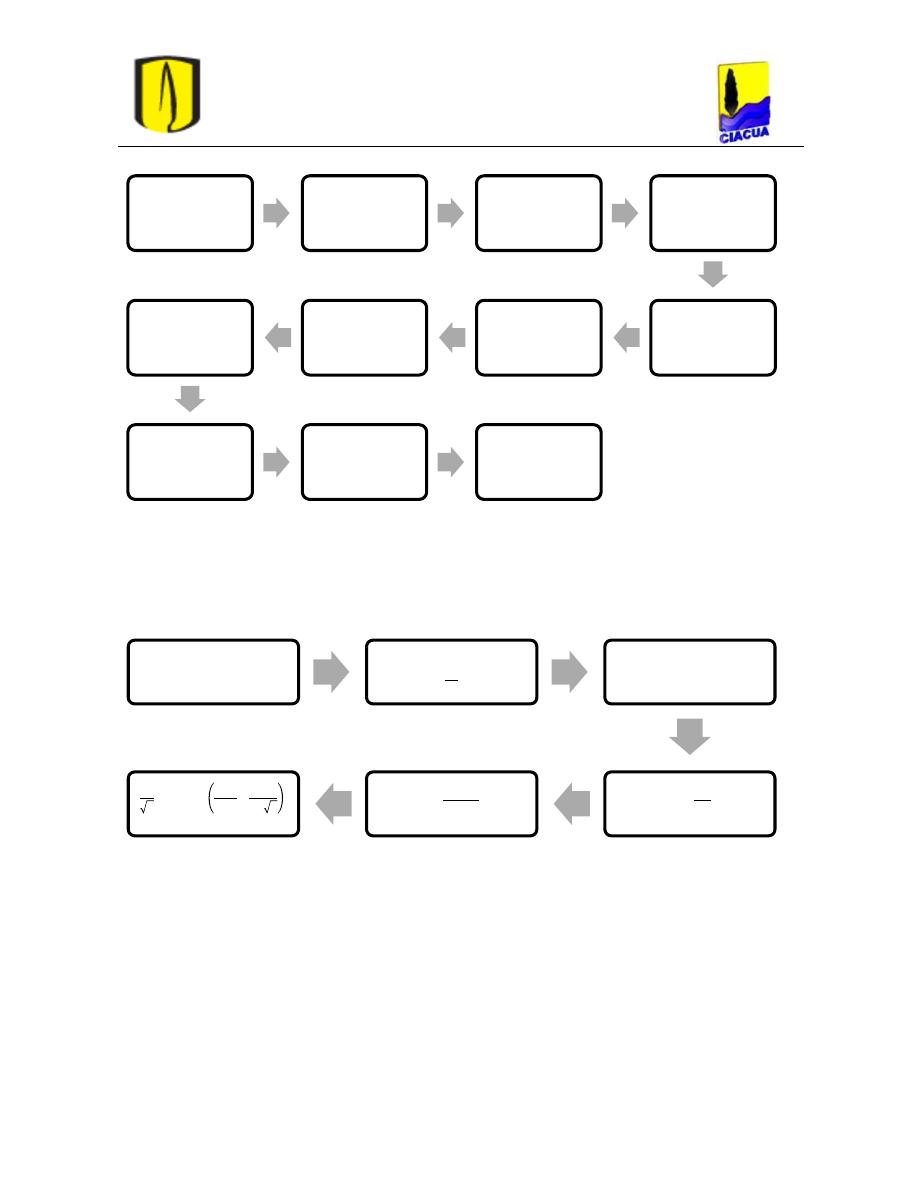
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
40
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 30. Metodología empleada (Nieto, 2011).
Para determinar la rugosidad absoluta se emplean tres métodos diferentes: cálculo mediante
la ecuación de Colebrook-White, método gráfico y método estadístico. A continuación, se
muestran las tres metodologías en las Figuras 31, 32 y 33.
Figura 31. Cálculo de k
s
usando la ecuación de Colebrook-White (Nieto, 2011).
PASO1:
Encender el sistema
eléctrico y de bombeo
PASO 2:
Llenar el tanque de
alimentación
PASO 3:
Purgar mangueras y
manómetros
PASO 4:
Abrir válvula de
regulación
PASO 5:
Medir la temperatura
del agua
PASO 6:
Ingresar datos en el
software de
adquisición de datos
PASO 7:
Registro de datos en el
software
PASO 8:
Medir la lámina de
agua en el vertedero y
altura piezométrica de
los maómetros
PASO 9:
Guardar datos
PASO 10:
Variar caudal
PASO 11:
Repetir desde el paso 5
Leer P
1
, P
2
, T y Q
Determinar
ℎ
𝑓
=
∆𝑃
𝜌𝑔
+ ∆𝑧
Determinar
v = Q/A
𝑅𝑒 =
𝑣 𝑑
ν
𝑓 =
2 𝑔 𝑑 ℎ
𝑓
𝐿 𝑣
2
1
𝑓
= −2 log
10
𝑘
𝑠
3.7 𝑑
+
2.51
𝑅𝑒 𝑓
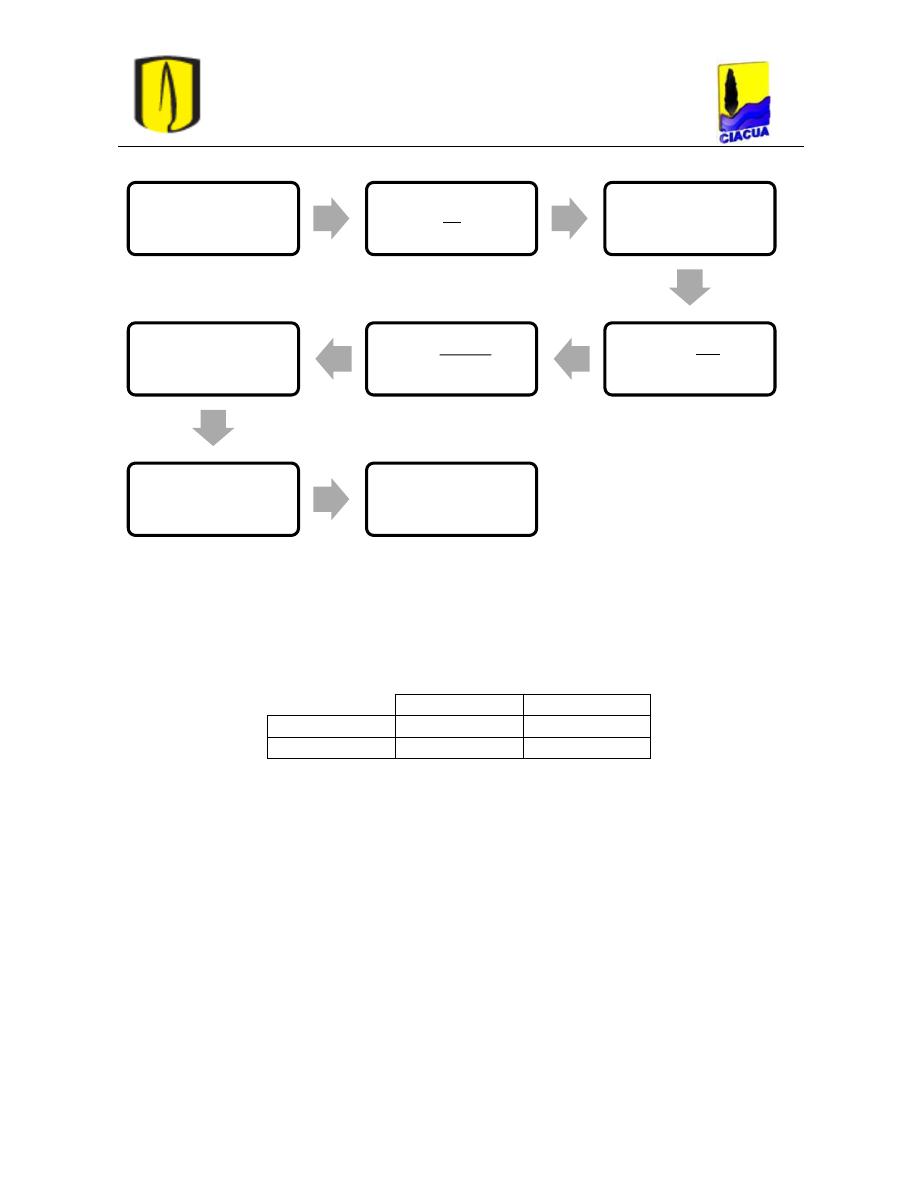
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
41
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 32. Cálculo de k
s
usando el método gráfico (Nieto, 2011).
Es necesario destacar que los cálculos se realizaron tanto para las mediciones por sensores,
como para la medición con los manómetros diferenciales de forma independiente. La Tabla
4 muestra los resultados obtenidos aplicando la metodología anterior.
Tabla 4. Resultados método gráfico (Nieto, 2011).
k
s
/d
k
s
[mm]
Sensores
0.000075
0.012065
Manómetros
0.00013
0.020912
Leer P
1
, P
2
, T y Q
Determinar
ℎ
𝑓
=
𝑃
𝜌𝑔
+ ∆𝑧
Determinar
v = Q/A
𝑅𝑒 =
𝑣 𝑑
ν
𝑓 =
2 𝑔 𝑑 ℎ
𝑓
𝐿 𝑣
2
Graficar f vs Re en el
Diagrama de Moody
Determinar la curva de
k
s
/d
Determinar k
s
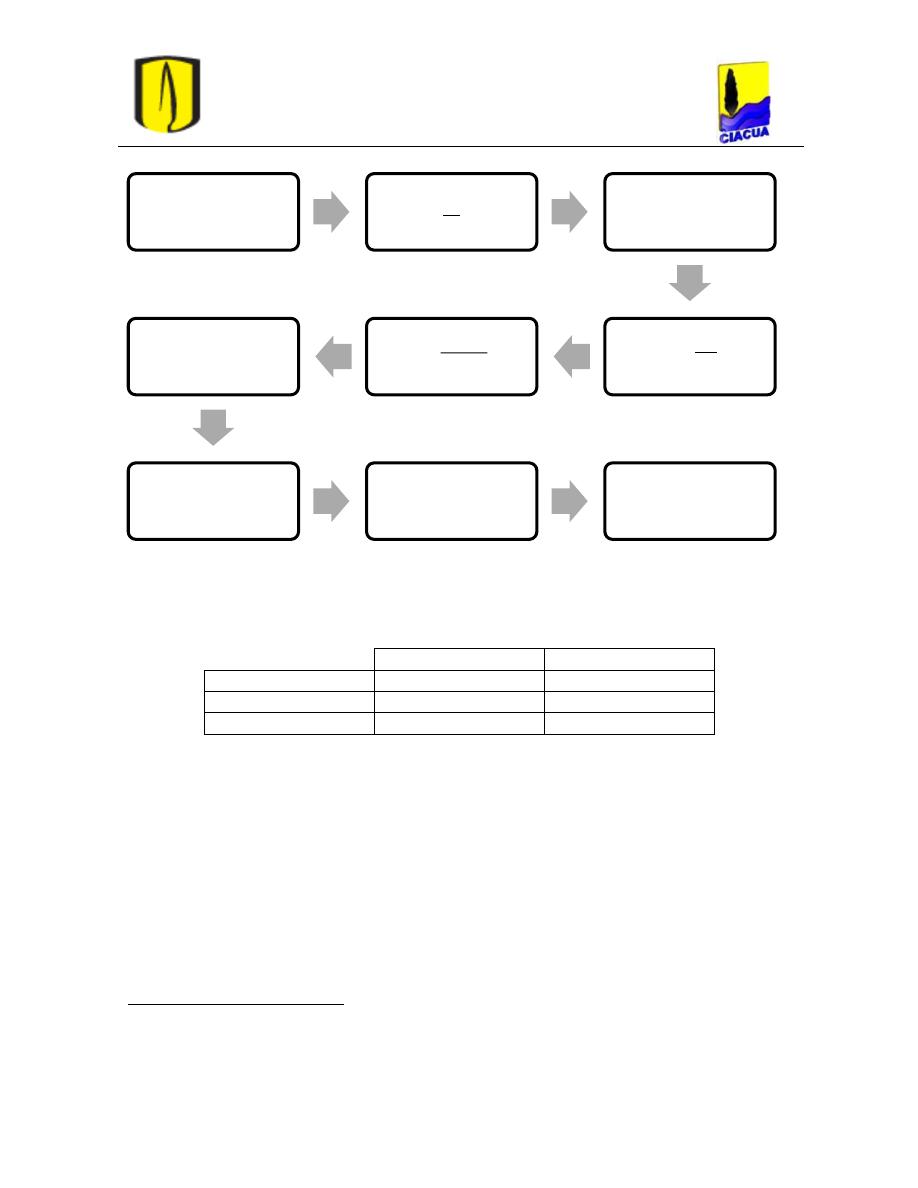
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
42
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 33. Cálculo de k
s
usando el método estadístico
1
(Nieto, 2011).
Los resultados aplicando el método anterior se muestran en la Tabla 5.
Tabla 5. Resultados método estadístico (Nieto, 2011).
Sensores
Manómetros
k
s
óptimo [mm]
0.0114
0.0208
ECM mínimo
2.89E-4
2.38E-4
R
2
máximo
0.78
0.92
Se encontró que todas las pruebas corresponden al caso del flujo turbulento hidráulicamente
liso, lo que indica que las pérdidas de energía del sistema dependieron del número de
Reynolds, por lo tanto requiere que se usen caudales altos. La rugosidad absoluta obtenida
es 0.0114 mm con el método estadístico y 0.0120 mm con el método gráfico
2
. Debido a que
el método estadístico es una metodología más robusta y confiable se adopta este como valor
final de la rugosidad absoluta. Este valor se encuentra alejado del valor teórico (0.0150
mm), estos resultados se pueden explicar debido a un posible desarrollo de biopelículas y/o
adhesión de sedimentos en las paredes de la tubería (Nieto, 2011).
1
Para éste método se usa el coeficiente de determinación (R
2
) y el error cuadrático medio (ECM).
2
Éstos resultados corresponden a los obtenidos por los sensores, se seleccionan estos debido a que tienen
mayor aproximación al valor teórico reportado, en comparación con los resultados obtenidos mediante los
manómetros diferenciales.
Leer P
1
, P
2
, T y Q
Determinar
ℎ
𝑓
=
∆𝑃
𝜌𝑔
+ ∆𝑧
Determinar
v = Q/A
𝑅𝑒 =
𝑣 𝑑
ν
𝑓 =
2 𝑔 𝑑 ℎ
𝑓
𝐿 𝑣
2
Determinar valores
promedio por grupo de
datos
Calcular f teórica con la
ecuación de Colebrook-
White para diferentes
valores de k
s
y Re
Graficar ECM y R
2
para
cada k
s
Seleccionar el k
s
con menor
ECM y mayor R
2

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
43
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
3 Diseño del Modelo
3.1 Diseño del Montaje
Como primer paso se definieron las condiciones generales del montaje. La tubería principal
se compone de un tubo de PVC de 12 m de largo, sin uniones, con 6 pulgadas de diámetro
nominal. Una brida fabricada en acero inoxidable ubicada en la alimentación del montaje
de 12 pulgadas de diámetro con salida de 6 pulgadas para adaptarla a las condiciones del
tubo principal. Se incluye una válvula de compuerta de 6 pulgadas de diámetro fabricada en
acero inoxidable para regular la entrada de agua a la tubería principal. La tubería se
encuentra sostenida en unos soportes especialmente diseñados a las condiciones del
laboratorio y ubicados de tal manera que permita mantener la tubería completamente
horizontal, para así eliminar efectos de la pendiente del terreno. El desagüe del montaje va
acoplado a una estructura previamente instalada en el laboratorio y soportado en los
cimientos del mismo.
Adicionalmente, se emplearon rejillas (2) uniformadoras de flujo, fabricadas en acrílico,
ubicadas a la entrada del tubo principal, esto con el fin de garantizar las condiciones de
flujo uniforme a lo largo de la tubería. Las dimensiones de las rejillas son 6 pulgadas de
diámetro y aproximadamente 1 cm de espesor.
Las estructuras de soporte tienen dimensiones de 20 cm x 13 cm en la base, en donde se
encuentra un tubo (conocido generalmente como tubo ‘ruana’) de 20 cm de largo en donde
se encuentra un pequeño orificio que contiene un tornillo el cual ejerce presión sobre un
tubo más delgado ubicado dentro del tubo ‘ruana’ con una longitud de 25 cm; sobre este se
soporta un semicírculo de 6 pulgadas de diámetro donde irá sujetada la tubería principal. Se
diseñaron un total de 20 soportes a lo largo de la tubería con el fin de brindar mayor
estabilidad y evitar vibraciones.
Para mayor detalle referirse a la sección de planos de los anexos, al final del documento.
3.2 Instrumentación del Montaje
3.2.1 Medición de Caudal
La Figura 34 muestra el caudalímetro disponible en el Laboratorio de Hidráulica y de
Sistemas de Alcantarillado de la marca Ultraflux (referencia UF 801-P). Este caudalímetro
se ubicará aproximadamente 10-50 cm antes del final de la tubería.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
44
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 34. Caudalímetro a emplear en las mediciones.
Este caudalímetro es un medidor portátil ultrasónico que puede ser empleado en todos los
tipos de tuberías (distintos materiales) y con todo tipo de líquidos (agua, químicos,
derivados del petróleo, entre otros). Tiene un rango de medición entre 1 mm/s y 45 m/s,
para diámetros entre 10 mm y 10 m (Ultraflux).
La medición de flujo en un trayecto se da por la instalación de dos sondas, donde ambas
transmiten y reciben alternadamente una señal. Esta señal va a través del líquido y es
recibida por la sonda opuesta. Las mediciones de los tiempos de propagación en las
direcciones ascendente y descendente se miden con precisión (típicamente 0.2 ns). La
velocidad media se puede calcular a partir de estos tiempos y de la posición geométrica de
las sondas (Ultraflux).
Figura 35. Principio de diferencia de tiempo de tránsito de ondas ultrasónicas (Ultraflux).
La ventaja del principio de medición empleado es que es aplicable tanto a líquidos como a
gases y solo depende de la longitud y el diámetro de la tubería (Ultraflux).
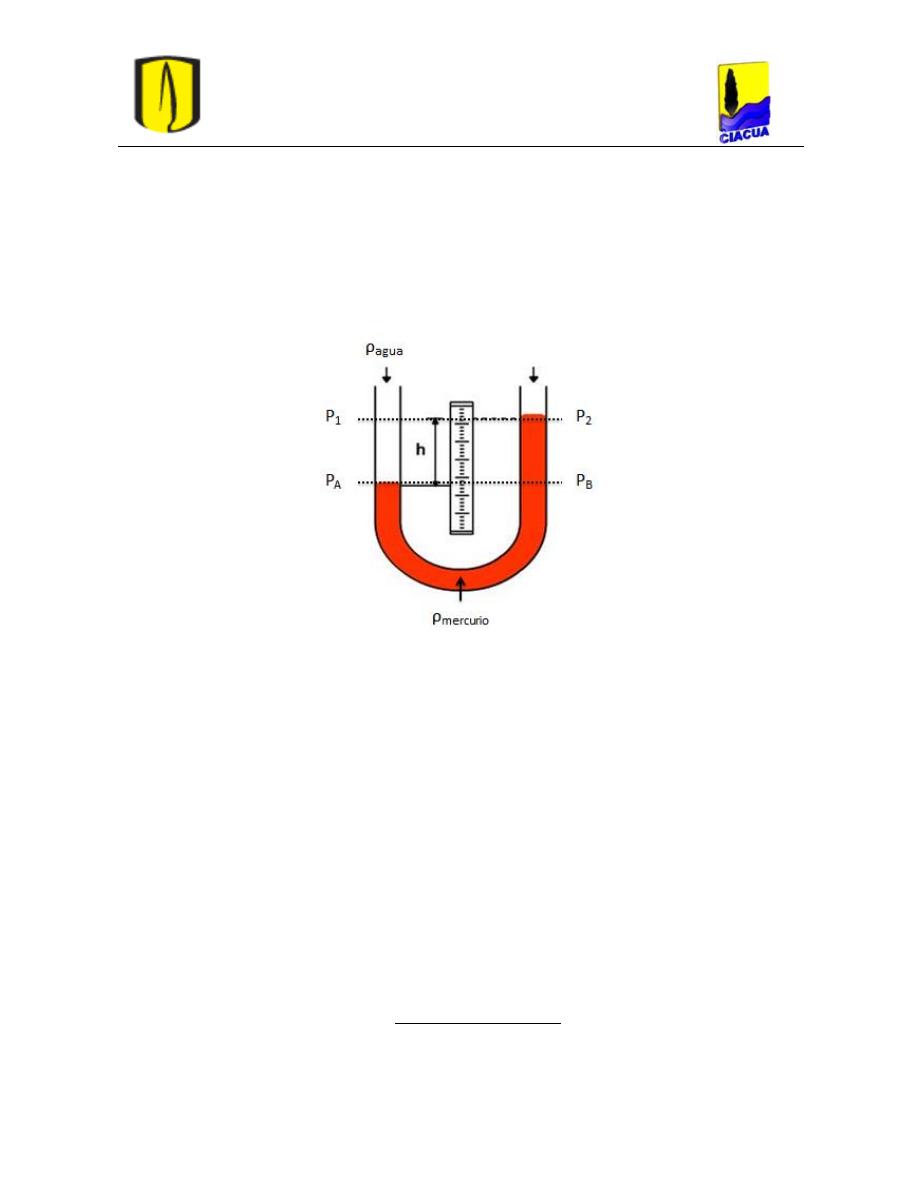
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
45
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
3.2.2 Medición de Presión
Se propone implementar un manómetro diferencial para medir las pérdidas por fricción a lo
largo de la tubería principal, a través de la determinación de la altura piezométrica. El
fluido manométrico por excelencia es el mercurio (ρ
mercurio
= 13,600 kg/m
3
) y es el que se
empleará en el presente proyecto. Las Ecuaciones se describen a continuación teniendo
como referencia la Figura 36.
Figura 36. Manómetro diferencial.
𝑃
𝐴
= 𝑃
1
+ 𝜌
𝑎𝑔𝑢𝑎
𝑔ℎ
Ecuación 43. Presión en el punto A.
𝑃
𝐵
= 𝑃
2
+ 𝜌
𝑚𝑒𝑟𝑐𝑢𝑟𝑖𝑜
𝑔ℎ
Ecuación 44. Presión en el punto B.
𝑃
𝐴
= 𝑃
𝐵
Ecuación 45.
𝑃
1
+ 𝜌
𝑎𝑔𝑢𝑎
𝑔ℎ = 𝑃
2
+ 𝜌
𝑚𝑒𝑟𝑐𝑢𝑟𝑖𝑜
𝑔ℎ
𝑃
1
− 𝑃
2
= ∆𝑃 = 𝜌
𝑚𝑒𝑟𝑐𝑢𝑟𝑖𝑜
𝑔ℎ − 𝜌
𝑎𝑔𝑢𝑎
𝑔ℎ = (𝜌
𝑚𝑒𝑟𝑐𝑢𝑟𝑖𝑜
− 𝜌
𝑎𝑔𝑢𝑎
)𝑔ℎ
Ecuación 46. Caída de presión.
ℎ =
∆𝑃
(𝜌
𝑚𝑒𝑟𝑐𝑢𝑟𝑖𝑜
− 𝜌
𝑎𝑔𝑢𝑎
)𝑔
Ecuación 47. Cálculo de la altura piezométrica.
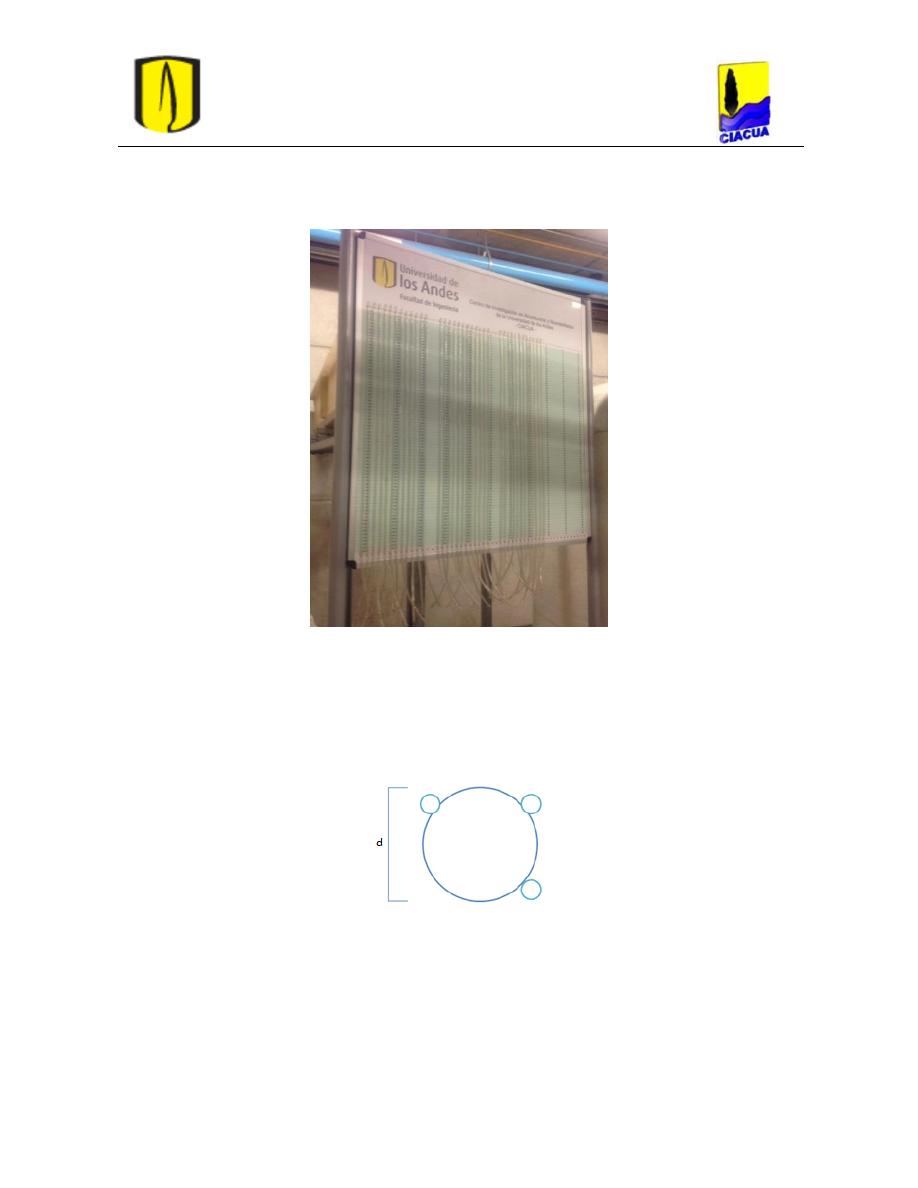
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
46
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
En el Laboratorio de Hidráulica y de Sistemas de Alcantarillado se encuentra disponible el
tablero manométrico que se muestra en la Figura 37.
Figura 37. Tablero manométrico.
En total se emplearán tres manómetros los cuales se acoplaran a tres orificios de la tubería
principal por medio de mangueras de plástico, la ubicación de estos orificios será 1.38 m
desde el comienzo de la tubería, y 20 cm antes del final de la misma. En la Figura 38 se
muestran las posiciones de las tres perforaciones, se harán a 45° aproximadamente desde el
eje vertical (d es el diámetro exterior de la tubería).
Figura 38. Ubicación de las Mangueras en la Tubería Principal.
Cada uno de los manómetros tiene una longitud de 70 cm y diámetro de 0.6 cm
(aproximadamente ¼ pulgadas), la separación entre los dos brazos del manómetro es de 5
cm (ver Figura 39).
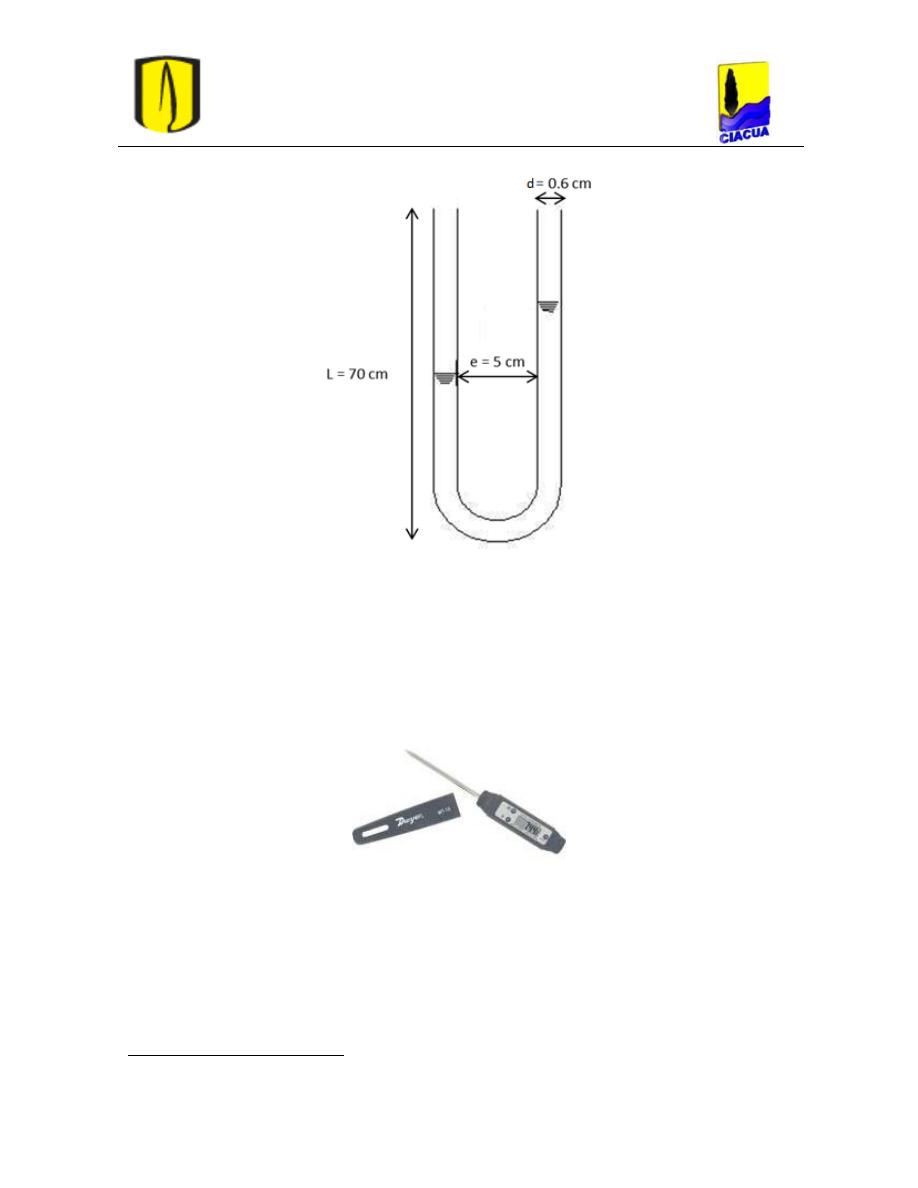
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
47
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 39. Dimensiones del manómetro diferencial
3
.
3.2.3 Medición de la Temperatura
Se conoce que la densidad y viscosidad del agua cambian con la variación de la
temperatura, por lo tanto se debe realizar un ajuste para la misma. La medición de la
temperatura se realizará con un termómetro digital (ver Figura 40).
Figura 40. Termómetro digital (Dwyer Instruments, 2012).
El termómetro es de la marca Dwyer, modelo WT-10. La unidad presenta mediciones de
temperatura desde -40 a 200 °C con una precisión de 0.1 °C (Dwyer Instruments, 2012).
3
La imagen no está a escala.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
48
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
4 Construcción del Montaje
La Figura 41 muestra el sitio seleccionado para la ubicación del montaje del presente
proyecto de grado.
Figura 41. Sitio de ubicación del montaje.
A continuación se muestran fotografías tomadas durante el proceso de instalación del
montaje en el laboratorio de Hidráulica y de Sistemas de Alcantarillado.
4.1 Instalación de Soportes
Las estructuras de soporte fueron fabricadas por Hernando Pérez en un plazo de 15 días en
su taller y posteriormente fueron trasladados a las instalaciones del laboratorio para su
acoplamiento. La Figura 42 muestra una vista general de los mismos.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
49
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 42. Vista de los soportes.
Posteriormente, se procedió a su instalación. Tal y como se puede observar en la Figura 43,
se demarcó la referencia de los tornillos de la base para perforar el muro y fijarlos.
Figura 43. Instalación de los soportes.
Una vez demarcados, se atornillaron al muro y se fijaron a lo largo del canal (ver Figuras
44 y 45).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
50
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 44. Soportes instalados.
Figura 45. Vista de los soportes instalados en el sitio de ubicación del montaje.
Una vez instalados todos los soportes se debieron recortar debido a la válvula localizada en
el centro del montaje. La ubicación de la válvula y la altitud que proporcionaba el tubo
interno del soporte dejaba un espacio limitado, inferior al diámetro externo de la tubería
principal, por lo tanto el espacio era insuficiente. Se decidió recortar 5 cm de este tubo (ver
Figura 46).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
51
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 46. Soportes recortados.
A seguir, se instaló una cuerda, fija al primer y último soporte, esto con el fin de nivelarlos
para dejar la tubería principal en posición completamente horizontal (ver Figura 47).
Figura 47. Cuerda instalada para nivelación de soportes.
Una vez sujeta la cuerda entre los dos soportes se definió, una altura de 22 cm, con respecto
al muro de soporte.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
52
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 48. Nivelación de soportes.
4.2 Adquisición de la Tubería Principal
La tubería principal consta de una tubería de 12 m de largo, sin uniones, adquirida por la
empresa PAVCO S.A, fabricada especialmente para el cumplimiento de los objetivos del
presente trabajo. La tubería fue transportada en un vehículo de carga convencional que
arribó por el costado sur del edificio Mario Laserna. Las Figuras 49, 50 y 51 muestran al
vehículo de carga con la tubería principal en su interior.
Figura 49. Transporte de la tubería principal (I).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
53
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 50. Transporte de la tubería principal (II).
Figura 51. Transporte de la tubería principal (III).
Se contó con la colaboración de los estudiantes Juan Ossa, Juan Pablo Duarte y Santiago
Botía del CIACUA y el laboratorista John Calvo para el transporte de la tubería desde el
vehículo de carga hasta las instalaciones del laboratorio. Las Figuras 52-60 muestran el
desplazamiento de la tubería desde el vehículo hasta las instalaciones del laboratorio.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
54
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 52. Desplazamiento de la tubería (I).
Figura 53. Desplazamiento de la tubería (II).
Figura 54. Desplazamiento de la tubería (III).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
55
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 55. Desplazamiento de la tubería (IV).
Figura 56. Desplazamiento de la tubería (V).
Figura 57. Desplazamiento de la tubería (VI).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
56
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 58. Desplazamiento de la tubería (VII).
Figura 59. Desplazamiento de la tubería (VIII).
Figura 60. Desplazamiento de la tubería (IX).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
57
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Una vez se logró ingresar la tubería se procedió a ubicarla en el sitio designado para la
construcción del montaje. Fue necesario, debido a su gran longitud, ubicar la tubería por
encima de otros montajes y el canal de pendiente variable, las Figuras 61-75 muestran el
proceso.
Figura 61. Ubicación de la tubería en el laboratorio (I).
Figura 62. Ubicación de la tubería en el laboratorio (II).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
58
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 63. Ubicación de la tubería en el laboratorio (III).
Figura 64. Ubicación de la tubería en el laboratorio (IV).
Figura 65. Ubicación de la tubería en el laboratorio (V).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
59
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 66. Ubicación de la tubería en el laboratorio (VI).
Figura 67. Ubicación de la tubería en el laboratorio (VII).
Figura 68. Ubicación de la tubería en el laboratorio (VIII).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
60
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 69. Ubicación de la tubería en el laboratorio (IX).
Figura 70. Ubicación de la tubería en el laboratorio (X).
Figura 71. Ubicación de la tubería en el laboratorio (XI).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
61
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 72. Ubicación de la tubería en el laboratorio (XII).
Figura 73. Ubicación de la tubería en el laboratorio (XIII).
Figura 74. Ubicación de la tubería en el laboratorio (XIV).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
62
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 75. Ubicación de la tubería en el laboratorio (XV).
Originalmente, en el momento en el que arribó la tubería principal, no se encontraban
instalados los soportes, por lo que fue necesario dejarla en el suelo para posteriormente
ubicarla en su sitio definitivo.
Figura 76. Ubicación preliminar de la tubería.
4.3 Instalación de las Rejillas Uniformadoras de Flujo
Las rejillas se fabricaron por John Calvo con material existente en el laboratorio. A partir
de una lámina de acrílico se obtuvieron dos modelos que se ubican al comienzo de la
tubería principal.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
63
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 77. Rejillas Uniformadoras de Flujo.
Para cada una de las rejillas fue necesario recortar un soporte (ver Figura 78), empleando
una tubería de PVC del mismo diámetro de estas (6 pulgadas), a fin de fijar las rejillas a la
tubería y evitar su arrastre por la fuerza del agua.
Figura 78. Soporte para las rejillas uniformadoras de flujo.
Las rejillas se fijaron en serie a aproximadamente 15 cm desde el inicio de la tubería. Para
fijar cada uno de los soportes se usó una soldadura líquida para tubería de PVC llamada
“Soldamax – PVC” proporcionada por la empresa PAVCO S.A.
El procedimiento de instalación consistió en la instalación de un soporte (ver Figura 79),
seguido por la primera rejilla (ver Figura 80), después, nuevamente un soporte (ver Figura
81), la segunda rejilla y un soporte final (ver Figura 82).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
64
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 79. Instalación del soporte de la primera rejilla uniformadora de flujo.
Figura 80. Instalación de la primera rejilla uniformadora de flujo.
Figura 81. Instalación del segundo soporte de las rejillas uniformadoras de flujo.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
65
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 82. Instalación del tercer soporte y la segunda rejilla uniformadora de flujo
4.4 Acoplamiento de la Estructura
Para el acoplamiento de los codos de la estructura se hizo necesaria la ayuda de un amarre
conformado por una tabla de madera y un tornillo flexible, tal y como se muestra en las
Figuras 83 y 84. Este amarre permitía inmovilizar los codos y facilitar el ajuste de estos con
la tubería.
Figura 83. Amarre empleado para el acoplamiento de codos (vista inferior).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
66
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 84. Amarre empleado para el acoplamiento de codos (vista superior).
Figura 85. Acoplamiento de codos (I).
Figura 86. Acoplamiento de codos (II).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
67
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Primero, se acoplaron un par de codos a la tubería principal (uno en cada extremo) y
posteriormente se procedió a realizar el acople para la estructura de desagüe (ver Figura
87).
Figura 87. Acoplamiento inicial de la estructura de desagüe.
Una vez acoplados estos dos tubos se procedió a ubicar la estructura sobre los soportes,
previamente instalados, tal y como se muestra en las Figuras 88 y 89. Se decidió realizar un
amarre con cuerda de manera provisional, mientras se instalaba la estructura restante.
Figura 88. Tubería principal y primer tubo de desagüe acoplado (I).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
68
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 89. Tubería principal y primer tubo de desagüe acoplado (II).
Figura 90. Tubería principal soportada.
Para la tubería de desagüe fue necesario acoplar una unión (ver Figura 91). El tubo, que
originalmente, era de 6 m de longitud se dividió en exactamente 3 m para poder
manipularlo más fácilmente.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
69
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 91. Acoplamiento de la unión en la estructura de desagüe.
Figura 92. Tubería de desagüe fraccionada.
Una vez se fracciona la tubería se elevaron cada una de las partes de manera independiente.
En la Figura 94 se observa únicamente la tubería de la Figura 92 apoyada en los perfiles del
laboratorio. En la Figura 95 se observa la pieza restante, aún sin acoplar al primero.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
70
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 93. Instalación de estructura de desagüe (I).
Figura 94. Instalación de estructura de desagüe (II).
Figura 95. Instalación de estructura de desagüe (III).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
71
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
La Figura 96 muestra las piezas acopladas; esto se logró gracias a la colaboración del
laboratorista John Calvo y personal de apoyo del Laboratorio de Estructuras del
Departamento de Ingeniería Civil.
Figura 96. Tubería de desagüe acoplada.
Seguidamente, se dispone a acoplar una última tubería de 6 m de longitud con el fin de
dirigir el agua dentro de la pileta ubicada en el laboratorio. La Figura 97 muestra una vista
frontal de este acople.
Figura 97. Vista frontal del acople.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
72
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 98. Detalle del acople.
Figura 99. Vista posterior del acople.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
73
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 100. Sección final del acople.
Es necesario agregar que en los dos codos que se encuentran sujetos la tubería de 6 m con
unión hay un amarre a fin de evitar el movimiento hacia arriba y hacia adentro ocasionado
por la presión que ejerce el agua. Estos amarres son indispensables, pues son por la
seguridad de quienes trabajan en las instalaciones del laboratorio.
No se tienen especificaciones del acoplamiento de la estructura de alimentación, debido a
que ésta, en el momento de presentar el presente informe, no se encontraba disponible en el
laboratorio.
4.5 Instalación de los Manómetros Diferenciales
Como se indicó en la Sección 3.2.2, las distancias a las cuales se instalarán las mangueras
para la medición de la altura piezométrica son 1.38 m aguas debajo de las rejillas
uniformadoras de flujo y 20 cm antes de que se curve la tubería. En la Figura 101 se
muestra la referencia para perforar la tubería (se muestra un solo lado).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
74
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 101. Localización de las mangueras para los manómetros diferenciales.
No se muestra la ubicación de las mangueras, debido a que en el momento de elaboración
del presente documento no se contaban con las mismas en el laboratorio. La instalación de
los manómetros se puede observar en la Figura 102.
Figura 102. Instalación de los manómetros.
La Figura 103 muestra el tablero manométrico y la Figura 104 muestra la presentación del
mercurio metálico, cuyo frasco contiene en su interior 767 gramos del mismo (es necesario

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
75
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
considerar que este valor incluye el peso del frasco contenedor). La cantidad de mercurio a
verter en cada uno de los manómetros debe ser la misma, por lo que se toma como
referencia una altura de 20-30 cm (en los brazos del manómetro) con este líquido, y el
espacio restante (40-50 cm) se deja como espacio libre para el desplazamiento del agua.
Figura 103. Tablero Manométrico.
Figura 104. Mercurio metálico.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
76
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
5 Costos
A continuación se realiza un resumen de los costos generados por el presente proyecto. Es
importante mencionar que los accesorios en PVC empleados, que no se incluyen en la
Tabla 6, fueron proporcionados por PAVCO S.A sin ningún costo; la Tabla 7 muestra un
resumen del material proporcionado por esta empresa.
Tabla 6. Detalles de los Costos Generados por el Proyecto.
ÍTEM
DESCRIPCIÓN
ENCARGADO
VALOR
TOTAL
(COP)
Brida
Brida en acero inoxidable de 12 pulgadas
con salida en 6 pulgadas
EHR S.A
$ 5.776.800
Manómetro
5 manómetros de Vidrio "U" de 70 cm
Rodaquímicos
LTDA
$ 100.000
Mercurio
Metálico
1/2 Libra de Mercurio Metálico
Químicos Campota
y CIA LTDA.
$ 89.500
Soportes
20 soportes en platina y tubo col roll.
Según modelo de plano
Hernando
Pérez Mateus
$ 900.000
Termómetro
WT10 Termómetro digital de mínimos y
máximos de 40°C a +200°C Dwyer
Ferricentro
S.A
$ 94.100
Válvula
de
Compuerta
Válvula de compuerta de 6'' en acero
inoxidable. REF: Walworth F.5202F
Ferretería Reina
S.A
$ 1.260.000
VALOR TOTAL
$ 8.220.400
Tabla 7. Solicitud de material a PAVCO S.A.
TUBERÍAS
Descripción
Diámetro (pulgadas)
Longitud (m)
Cantidad
Vía axial Espigo-Espigo
6
12
1
CONEXIONES
Descripción
Diámetro (pulgadas)
Cantidad
Codos 90°
6
9
Unión campana por espigo
6
1
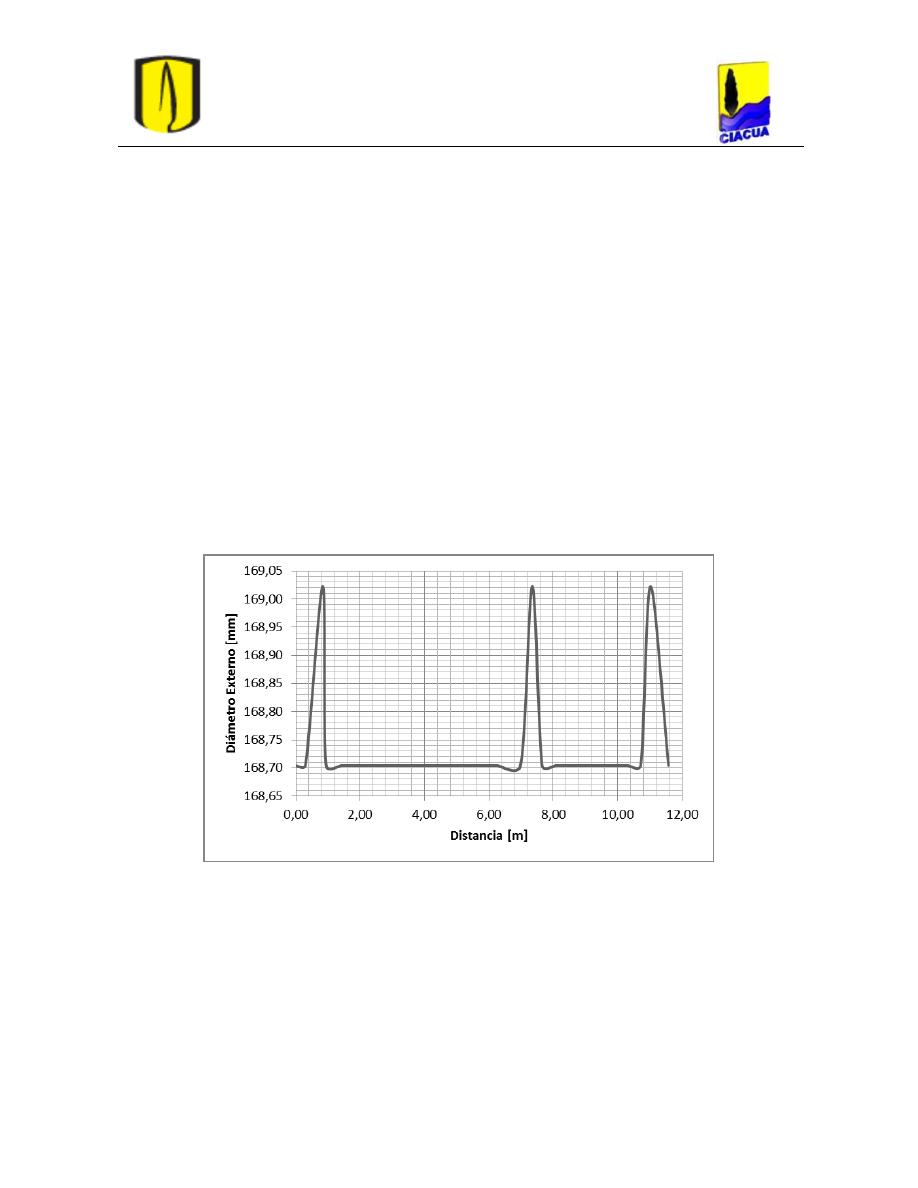
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
77
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
6 Metodología
Una vez finalizada la construcción del montaje se ejecutaron algunas pruebas, así mismo,
se proponen pruebas para la comprobación de diseño y la determinación de la rugosidad
absoluta una vez se encuentre terminado el montaje.
6.1 Medición de Diámetro Externo
De acuerdo al “Manual Técnico de Turbosistemas para Acueducto Biaxial, PVC
Biorientado Dúctil” de PAVCO (Ver sección de Anexos) la tubería principal de diámetro
nominal de 6 pulgadas, cuenta con un diámetro exterior de 168.28 mm, un espesor de pared
de 3.71 mm y diámetro interior de 160.86 mm. A fin de corroborar esta información se
realizó una medición de la circunferencia de la tubería mediante una cinta métrica. Los
resultados se muestran a continuación.
Figura 105. Medición de diámetro externo de la tubería.
De acuerdo con la Figura 105, se observan tres variaciones del diámetro en la tubería, una
al comienzo, la segunda aproximadamente en la mitad y la tercera al final de la misma. La
mayoría de datos corresponden al valor de 168.70 mm, por lo tanto se supondrá este valor
como el diámetro externo de la tubería. Suponiendo que el espesor de la tubería es el
mismo reportado por PAVCO, el diámetro interno es 161.28 mm. La Tabla 8 muestra una
comparación de los valores obtenidos y la diferencia con respecto al reportado por el
manual, de lo que se puede concluir que no existe una diferencia considerable entre ellos.
Para cálculos posteriores, se empleará el valor obtenido experimentalmente.
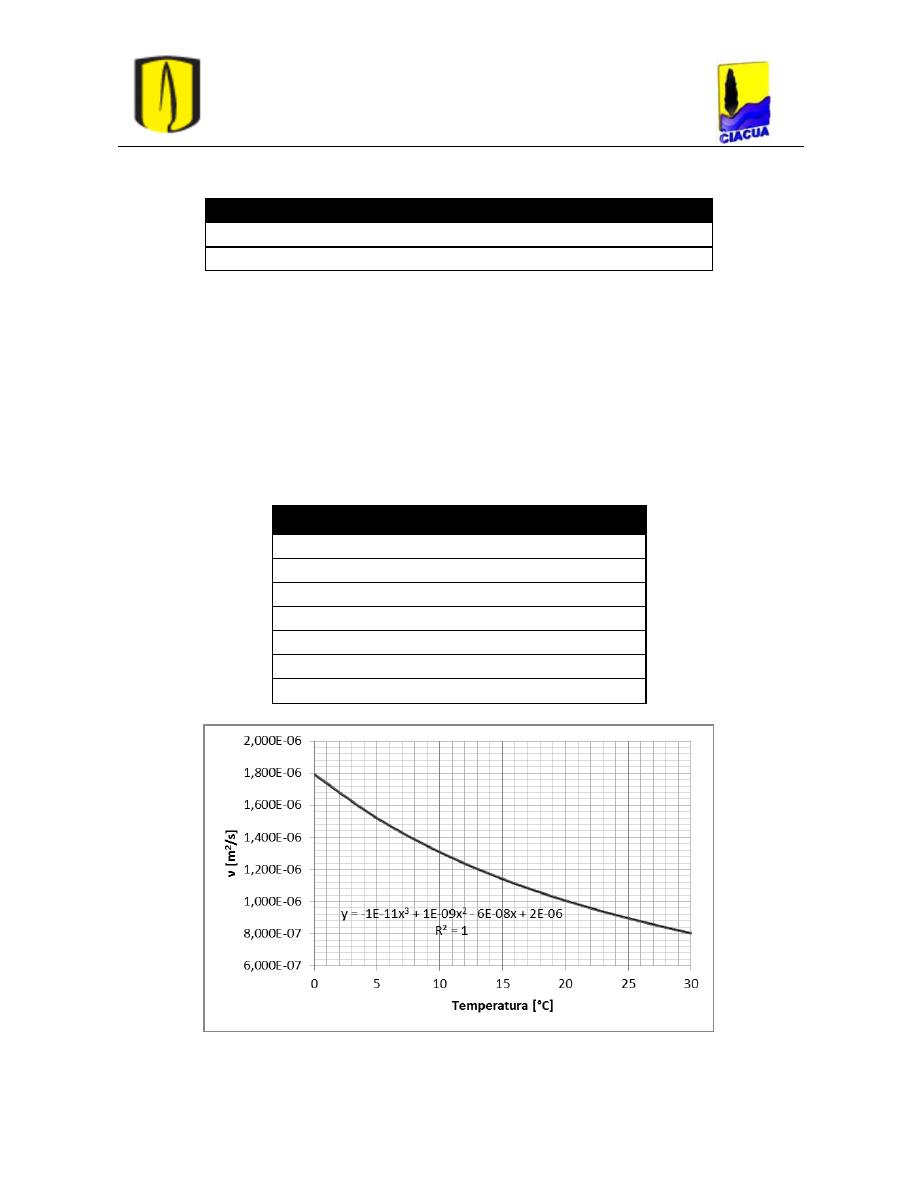
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
78
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Tabla 8. Diferencia entre valores teóricos y experimentales del diámetro interno y externo de la tubería principal.
Teórico (mm)
Experimental (mm)
Diferencia (%)
D
externo
168,28
168,70
0,25
D
interno
160,86
161,28
0,26
6.2 Determinación de la Viscosidad
Como se indicó en la Sección 3.2.3 es necesario determinar la viscosidad de acuerdo con la
temperatura reportada para cada medición. Para esto, se toma como referencia los datos
reportados por (Saldarriaga, 2007). Se realiza una regresión de los datos y se obtiene una
ecuación que relaciona el valor de la viscosidad con la temperatura. Los resultados de la
regresión se muestran a continuación.
Tabla 9. Propiedades físicas del agua (Saldarriaga, 2007).
T [°C]
ρ [kg/m
3
]
μ [N s/m
2
]
υ [m
2
/s]
0
999,9
1,792E-03
1,792E-06
5
1000
1,519E-03
1,519E-06
10
999,7
1,308E-03
1,308E-06
15
999,1
1,140E-03
1,141E-06
20
998,2
1,005E-03
1,007E-06
25
997,1
8,940E-04
8,970E-07
30
995,7
8,010E-04
8,040E-07
Figura 106. Regresión polinomial para la viscosidad como función de la temperatura.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
79
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Es necesario destacar que la interpolación de los datos re realizó hasta una temperatura de
30 °C, debido a que la temperatura del agua en las pruebas no alcanzará temperaturas
mayores a esta, ya que se trabajará a condiciones ambiente.
6.3 Comprobación de Diseño
El montaje elaborado consta de una tubería simple, debido a que presenta un diámetro
constante y está hecha de un solo material a lo largo de toda su longitud, además contiene
un cierto número de accesorios que producen pérdidas menores, incluyendo una válvula
para el control de caudal.
Se plantea una metodología para la comprobación del diseño de la tubería. Para esto se
utilizarán las Ecuaciones planteadas en las Secciones 2.1 y 2.2 del Marco Teórico, basadas
en los estudios de Prandtl-von Kármán sobre interacción fluido – pared sólida y en la
ecuación de Darcy-Weisbach, considerada la ecuación físicamente fundamentada para
pérdidas por fricción en ductos (Saldarriaga, 2007).
Los problemas de comprobación de diseño implican que son conocidos la longitud, el
diámetro y la rugosidad absoluta de la tubería (valor teórico reportado), al igual que todos
los accesorios y sus coeficientes de pérdidas menores, y las propiedades del fluido
(densidad y viscosidad cinemática). La incógnita es el caudal que pasa por la tubería. Este
problema es típico en el diseño de redes de distribución de agua potable o redes de riego, en
las cuales se hace un pre dimensionamiento de los diámetros para luego comprobar si se
cumple o no con restricciones hidráulicas de caudal y presión en los nodos (Saldarriaga,
2007).
Para resolver este problema se debe seguir el procedimiento indicado en el diagrama de
flujo de la Figura 107. En el diagrama, el término E representa el error de aproximación, el
cual debe ser definido por el diseñador o por la persona encargada de los cálculos.
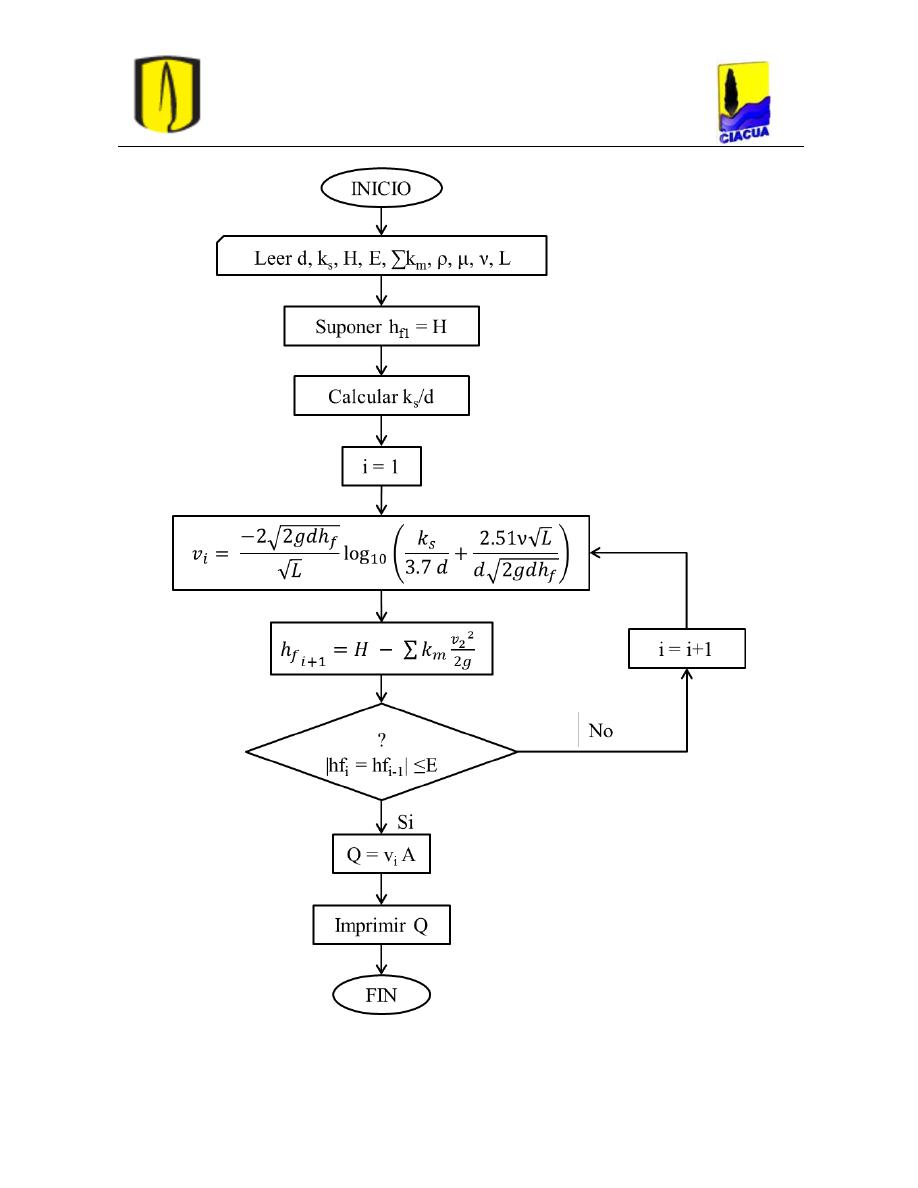
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
80
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 107. Diagrama de flujo para la comprobación de diseño de tuberías simples (Saldarriaga, 2007).

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
81
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
6.3.1 Ecuaciones Para el Cálculo de Tuberías Simples
Mediante el uso de la ecuación de Colebrook-White (Ecuación 27) conjuntamente con la
ecuación de Darcy-Weisbach (Ecuación 11) se puede desarrollar el siguiente procedimiento
a fin de obtener las Ecuaciones necesarias para llevar a cabo los cálculos en tuberías
simples. Se inicia con una ecuación de conservación de energía empleando la ecuación de
Bernoulli (Saldarriaga, 2007).
𝑃
1
𝜌𝑔
+
𝑣
1
2
2𝑔
+ 𝑧
1
=
𝑃
2
𝜌𝑔
+
𝑣
2
2
2𝑔
+ 𝑧
2
+ ℎ
𝑓
+ ∑ ℎ
𝑚
Ecuación 48.
De acuerdo con el sistema ubicado en el laboratorio, no hay una variación de nivel entre la
entrada y el punto final de la tubería principal, por lo que z
1
=z
2
=0; además, se considera que
la velocidad es constante a lo largo de la tubería por lo que v
1
=v
2
. Tendiendo en cuenta lo
anterior la ecuación de Bernoulli se puede expresar de la siguiente forma:
𝑃
1
𝜌𝑔
=
𝑃
2
𝜌𝑔
+ ℎ
𝑓
+ ∑ ℎ
𝑚
𝐻 =
∆𝑃
𝜌𝑔
=
𝑃
1
𝜌𝑔
−
𝑃
2
𝜌𝑔
= ℎ
𝑓
+ ∑ ℎ
𝑚
Ecuación 49. Altura del nivel del agua en una tubería simple.
El término ΔP se puede encontrar a partir de la ecuación del manómetro diferencial
(Ecuación 46). H corresponde a la altura del nivel del agua con respecto al nivel de
referencia en la superficie. De esta última ecuación se puede obtener la siguiente ecuación,
la cual describe las pérdidas por fricción en función de las otras variables:
ℎ
𝑓
= 𝐻 +
𝑣
2
2𝑔
∑ 𝑘
𝑚
=
∆𝑃
𝜌𝑔
+
𝑣
2
2𝑔
∑ 𝑘
𝑚
Ecuación 50. Evaluación de las pérdidas por fricción.
Mediante la ecuación de Darcy-Weisbach (Ecuación 11), que también predice las pérdidas
por fricción, se puede despejar el factor de fricción f:
𝑓 =
2 𝑔 𝑑 ℎ
𝑓
𝐿 𝑣
2
Ecuación 51. Pérdidas por fricción a partir de la ecuación de Darcy-Weisbach.
Lo que implica que:
√𝑓 =
√2 𝑔 𝑑 ℎ
𝑓
𝑣√𝐿

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
82
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
y que:
1
√𝑓
=
𝑣√𝐿
√2 𝑔 𝑑 ℎ
𝑓
Ecuación 52.
Al remplazar la Ecuación 52 en la Ecuación 27 se obtiene:
𝑣√𝐿
√2 𝑔 𝑑 ℎ
𝑓
= −2 log
10
(
𝑘
𝑠
3.7 𝑑
+
2.51
𝑅𝑒
𝑣√𝐿
√2 𝑔 𝑑 ℎ
𝑓
)
Ecuación 53.
El número de Reynolds puede remplazarse en esta última ecuación:
𝑣√𝐿
√2 𝑔 𝑑 ℎ
𝑓
= −2 log
10
(
𝑘
𝑠
3.7 𝑑
+
2.51 𝜈
𝑣 𝑑
𝑣√𝐿
√2 𝑔 𝑑 ℎ
𝑓
)
𝑣√𝐿
√2 𝑔 𝑑 ℎ
𝑓
= −2 log
10
(
𝑘
𝑠
3.7 𝑑
+
2.51 𝜈
𝑑
√𝐿
√2 𝑔 𝑑 ℎ
𝑓
)
Ecuación 54.
Finalmente, si se despeja la velocidad se encuentra una ecuación explícita para esa variable:
𝑣 = −
2√2 𝑔 𝑑 ℎ
𝑓
√𝐿
log
10
(
𝑘
𝑠
3.7 𝑑
+
2.51 𝜈
𝑑
√𝐿
√2 𝑔 𝑑 ℎ
𝑓
)
Ecuación 55. Cálculo de la velocidad.
6.4 Descripción de las Pruebas
Para evaluar la rugosidad absoluta de la tubería se propone realizar pruebas experimentales
en un periodo de tiempo prolongado (mínimo dos meses), esto a fin de tomar réplicas. Se
propone registrar alrededor de 20 caudales diferentes entre 5 y 60 L/s.
A continuación, se presenta la metodología a emplear para las pruebas:
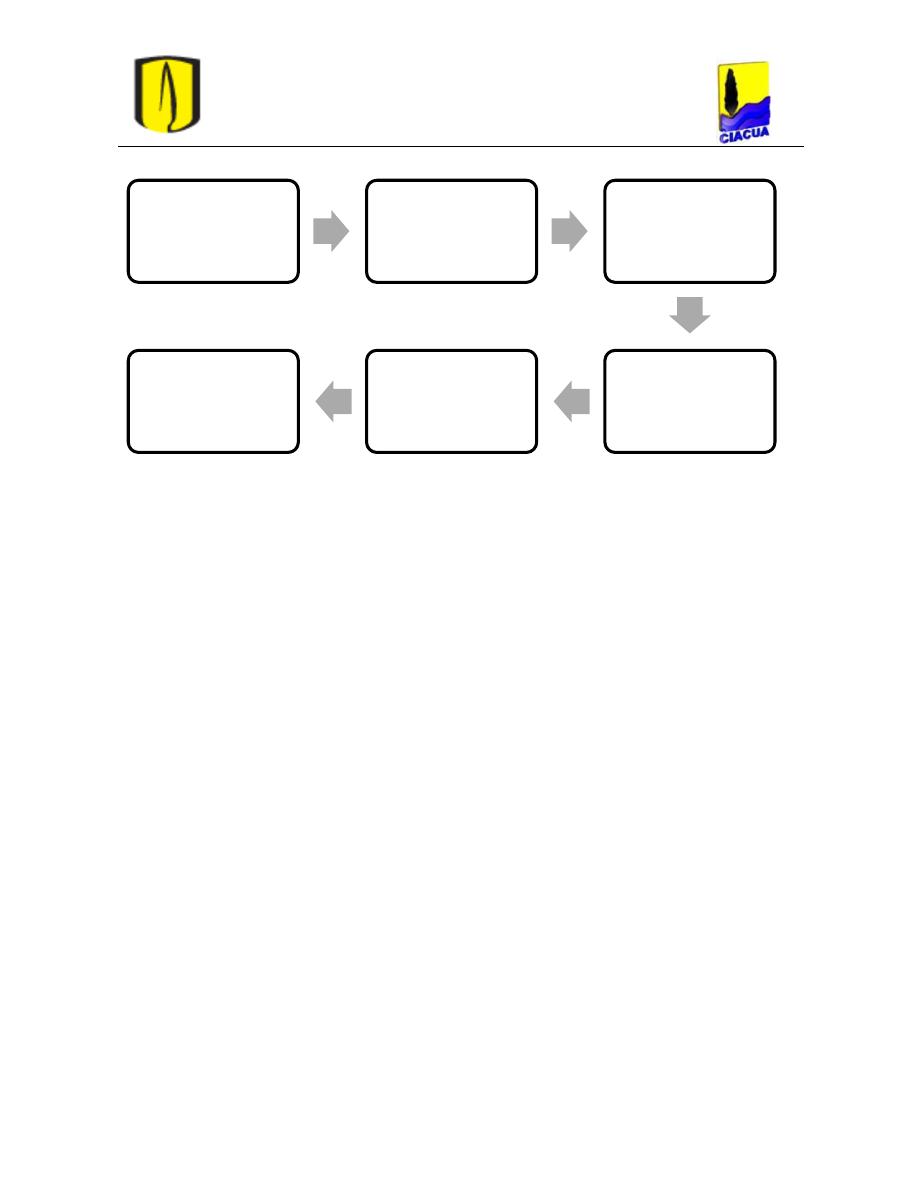
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
83
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 108. Metodología para las pruebas a realizar.
La toma de datos y el cálculo de la rugosidad absoluta se registra mediante el formato de la
Tabla 12 que se encuentra en la sección de Anexos.
6.4.1 Calibración de Tuberías Simples
Uno de los problemas más comunes que deben enfrentar los ingenieros encargados del
movimiento de fluidos a través de tuberías es calcular el factor de fricción de una tubería
que puede llevar varios años operando. Usualmente es sencillo conocer la rugosidad
absoluta teórica de la tubería cuando ésta es nueva y éste valor, de todas maneras, presenta
cierta incertidumbre. Sin embargo, a medida que transcurre el tiempo la rugosidad de la
tubería tiende a incrementarse en la gran mayoría de los materiales. Por consiguiente, para
poder llevar a cabo acciones de operación y/o mantenimiento de sistemas de tuberías, un
paso necesario es establecer las rugosidades absolutas reales presentes en dichos sistemas
(Saldarriaga, 2007).
En el caso de la calibración de la tubería se conoce el caudal demandado, la caída en la
altura piezométrica que ocurre entre la entrada y la salida de la tubería, algunas de las
características de la tubería (longitud, diámetro y accesorios necesarios con sus
correspondientes coeficientes de pérdidas menores) y las propiedades del fluido (densidad y
viscosidad dinámica o cinemática). Se desconoce la rugosidad absoluta de la tubería que
produce esa caída en la presión piezométrica para el caudal medido (Saldarriaga, 2007).
El cálculo de la rugosidad absoluta o calibración de la tubería se hace mediante las
siguientes Ecuaciones:
Poner en marcha el sistema
para purgar las mangueras
del tablero de medición, esto
a fin de asegurar el
desplazamiento total del aire
dentro del sistema
Definir un caudal de
medición (empezar con el
máximo y disminuir
paulatinamente) y tomar
registro del mismo
Medir la temperatura del
agua
Para cada caudal tomar el
registro de la altura en el
tablero de medición
Variar el caudal
Repetir el procedimiento
para distintos caudales

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
84
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Utilizando la ecuación de Darcy-Weisbach (Ecuación 11) se puede despejar el factor de
fricción y utilizando la ecuación de Colebrook-White (Ecuación 27) se puede despejar la
rugosidad absoluta de la tubería tal como se muestra en las siguientes Ecuaciones:
−
1
2√𝑓
= log
10
(
𝑘
𝑠
3.7 𝑑
+
2.51
𝑅𝑒√𝑓
)
10
−
1
2√𝑓
=
𝑘
𝑠
3.7 𝑑
+
2.51
𝑅𝑒√𝑓
𝑘
𝑠
= 3.7 𝑑 (10
−
1
2√𝑓
−
2.51
𝑅𝑒√𝑓
)
Ecuación 56. Rugosidad absoluta obtenida a partir de la ecuación de Colebrook-White.
Debido a que esta última ecuación es explícita para la rugosidad relativa, una vez se
conozca el factor de fricción de Darcy, resolver el problema de calibración de una tubería
es un trabajo sencillo. El diagrama de flujo de la Figura 109 explica los cálculos necesarios.
Es preciso tener en cuenta que los cálculos están basados en la ecuación de Colebrook-
White la cual puede llegar a dar una rugosidad absoluta negativa para la tubería.
Obviamente este es un resultado equivocado y su significado físico es que la tubería se
encuentra en un estado de flujo turbulento hidráulicamente liso (Saldarriaga, 2007).
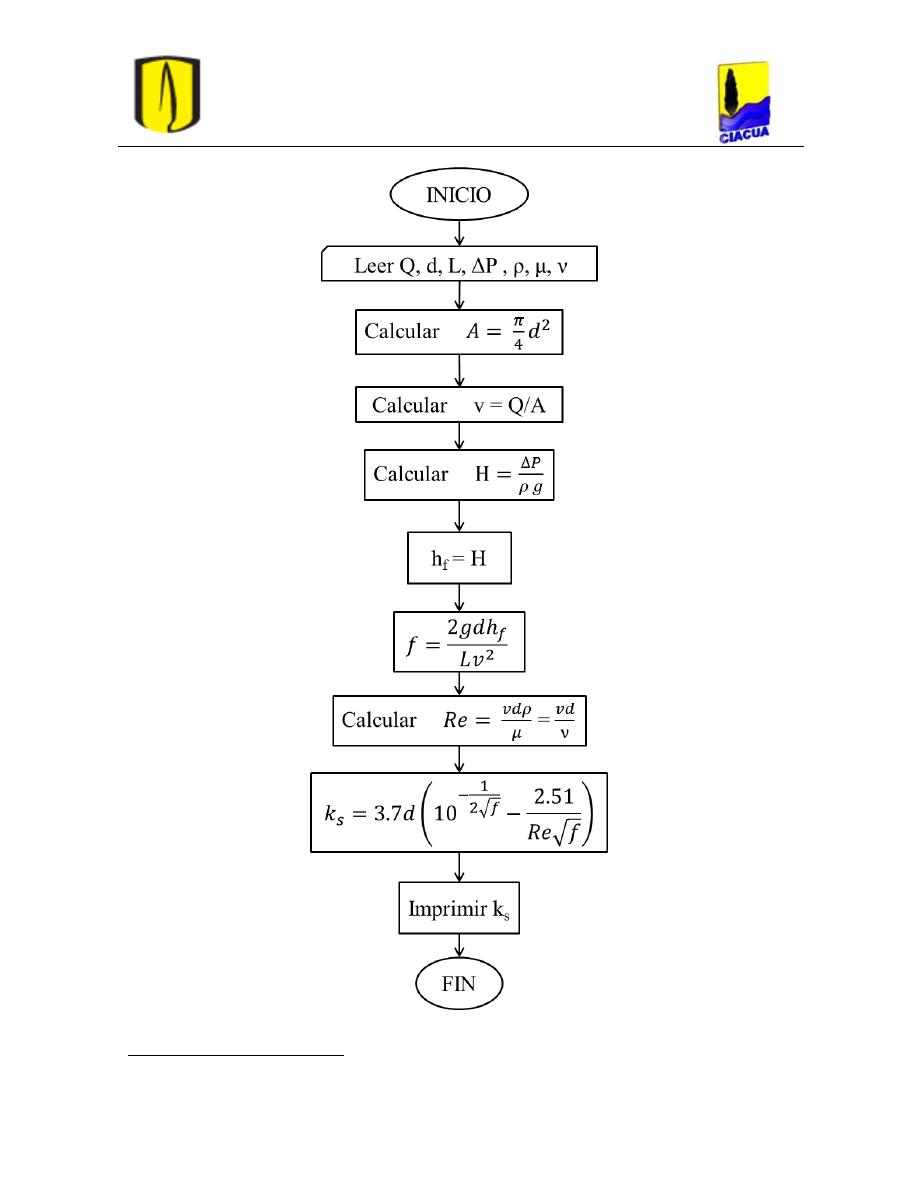
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
85
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 109. Diagrama de flujo para la calibración de una tubería simple. Adaptado de (Saldarriaga, 2007)
4
.
4
En la metodología presentada se omitieron los cálculos correspondientes a las pérdidas menores.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
86
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Considerando el factor de fricción calculado para cada número de Reynolds se procede a
superponer estos resultados en un diagrama de Moody. De esta manera se corrobora el
valor de rugosidad absoluta calculado mediante la ecuación de Colebrook-White.
6.4.2 Verificación del Régimen de Flujo
Para verificar que los resultados obtenidos se encuentran en el régimen de flujo turbulento
hidráulicamente liso se determina el valor de la subcapa laminar viscosa. A manera de
demostración, se presenta a continuación el cálculo realzado considerando la rugosidad
absoluta reportada (1.5E-6 m) y una viscosidad del agua constante (a 15°C). En la Tabla 10
se encuentran los parámetros constantes para el cálculo y el la Tabla 11 se encuentran los
resultados obtenidos.
Tabla 10. Condiciones estándar para el cálculo del espesor de la subcapa límite.
Diámetro (mm)
Área (m
2
)
k
s
(m)
T (°C)
ν (m
2
/s)
160,86
0,020
1,50E-06
15
1,14E-06

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
87
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Tabla 11. Cálculo del espesor de la subcapa laminar viscosa y determinación del tipo de flujo.
Q
[L/s]
v
[m/s]
Re
[-]
f
[-]
v*
[m/s]
δ'
[m]
0.305 δ'
[m]
6.1 δ'
[m]
TIPO DE
FLUJO
1
0,049
6,94E+03
3,41E-02
0,003
4,12E-03
1,26E-03
2,51E-02
FTHL
2
0,098
1,39E+04
2,84E-02
0,006
2,26E-03
6,88E-04
1,38E-02
FTHL
3
0,148
2,08E+04
2,57E-02
0,008
1,58E-03
4,83E-04
9,65E-03
FTHL
4
0,197
2,78E+04
2,39E-02
0,011
1,23E-03
3,75E-04
7,49E-03
FTHL
5
0,246
3,47E+04
2,27E-02
0,013
1,01E-03
3,08E-04
6,15E-03
FTHL
10
0,492
6,94E+04
1,95E-02
0,024
5,45E-04
1,66E-04
3,32E-03
FTHL
20
0,984
1,39E+05
1,69E-02
0,045
2,93E-04
8,92E-05
1,78E-03
FTHL
30
1,476
2,08E+05
1,56E-02
0,065
2,03E-04
6,19E-05
1,24E-03
FTHL
40
1,968
2,78E+05
1,48E-02
0,085
1,56E-04
4,77E-05
9,54E-04
FTHL
50
2,460
3,47E+05
1,42E-02
0,104
1,28E-04
3,89E-05
7,79E-04
FTHL
100
4,921
6,94E+05
1,26E-02
0,195
6,78E-05
2,07E-05
4,13E-04
FTHL
200
9,841
1,39E+06
1,13E-02
0,370
3,58E-05
1,09E-05
2,18E-04
FTHL
300
14,762
2,08E+06
1,06E-02
0,538
2,46E-05
7,49E-06
1,50E-04
FTHL
400
19,682
2,78E+06
1,02E-02
0,704
1,88E-05
5,73E-06
1,15E-04
FTHL
500
24,603
3,47E+06
9,96E-03
0,868
1,52E-05
4,65E-06
9,29E-05
FTHL
1000
49,206
6,94E+06
9,24E-03
1,672
7,91E-06
2,41E-06
4,82E-05
FTHL
1100
54,126
7,64E+06
9,16E-03
1,831
7,22E-06
2,20E-06
4,40E-05
FTHL
1200
59,047
8,33E+06
9,09E-03
1,990
6,65E-06
2,03E-06
4,05E-05
FTHL
1300
63,967
9,03E+06
9,02E-03
2,148
6,16E-06
1,88E-06
3,75E-05
FTHL
1400
68,888
9,72E+06
8,97E-03
2,306
5,73E-06
1,75E-06
3,50E-05
FTHL
1500
73,808
1,04E+07
8,92E-03
2,464
5,37E-06
1,64E-06
3,27E-05
FTHL
1600
78,729
1,11E+07
8,87E-03
2,622
5,04E-06
1,54E-06
3,08E-05
FTHL
1620
79,713
1,12E+07
8,87E-03
2,654
4,98E-06
1,52E-06
3,04E-05
FTHL
1640
80,697
1,14E+07
8,86E-03
2,685
4,93E-06
1,50E-06
3,00E-05
FTHL
1642
80,795
1,14E+07
8,86E-03
2,688
4,92E-06
1,50E-06
3,00E-05
FTHL
1643
80,845
1,14E+07
8,86E-03
2,690
4,92E-06
1,50E-06
3,00E-05
FT
De la Tabla 11 se tiene que dado un caudal (Q) y el área constante (ver Tabla 10) se
encuentra la velocidad (v). Con el valor de la viscosidad cinemática y el diámetro
constantes, se encuentra el número de Reynolds (Re) para cada caso. El cálculo del factor

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
88
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
de fricción (f) se hace de acuerdo con la ecuación de Colebrook-White (Ecuación 27). La
velocidad de corte (v*) se calcula con la Ecuación 15 y el espesor de la subcapa laminar
(δ’) se calcula empleando la Ecuación 13. Se procede a calcular los valores límites de
acuerdo a las Ecuaciones 25 y 26, el límite inferior se compara con el valor de la rugosidad
y se determina que para un caudal de 1,643 L/s el flujo deja de ser hidráulicamente liso.
Éste caudal es considerablemente grande y poco factible en una tubería de distribución, por
lo tanto, es certero afirmar que para una tubería de 6 pulgadas de diámetro nominal se
satisface la condición de hidráulicamente liso, luego la rugosidad de la tubería no va a
afectar el cálculo de las pérdidas de energía.
De acuerdo con los resultados presentados en la Tabla 11 es importante destacar que el
espesor de la subcapa laminar (δ’) disminuye a medida que aumenta el número de
Reynolds, al igual que se observa que se hace más estrecho el límite de la rugosidad entre
hidráulicamente liso e hidráulicamente rugoso.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
89
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
7 Conclusiones y Recomendaciones
7.1 Conclusiones
Se conoce que existe una correlación entre el número de Reynolds y el factor de
fricción, para el caso del flujo turbulento hidráulicamente liso, la cual no depende
de la rugosidad relativa de la tubería.
El montaje de laboratorio fue diseñado de acuerdo con el espacio disponible, por
consiguiente fue posible la implementación de la tubería de 12 m sin uniones la
cual, se espera, cumpla con los requerimientos para determinar el coeficiente de
rugosidad absoluta (k
s
) y comparar este valor con el reportado.
De acuerdo con la revisión realizada en el Marco Teórico, se afirma que las
rugosidades estudiadas con las que se obtuvieron las fórmulas de Blasius, Prandtl-
von Kármán y Colebrook-White son mayores a las que se pueden encontrar hoy en
día. Esto se deduce a partir de los estudios recientes del flujo hidráulicamente liso
en los que la propuesta de nuevas formas de calcular el valor del factor de fricción
se acercan más a la realidad, en comparación con la aplicación de las Ecuaciones
clásicas.
En general, se cumplieron con los objetivos propuestos al inicio del presente
documento, se diseñó el sistema, se ensambló parcialmente; sin embargo no se puso
a prueba, es necesario destacar que este documento es solo el comienzo de una
investigación más amplia que se ejecutará en un futuro. Actualmente, se encuentra
en trámite los materiales necesarios para la culminación del montaje. Una vez
finalizado y puesto en marcha, se deben hacer cuidadosas observaciones al fin de
corregir imperfecciones.
7.2 Recomendaciones
El uso de un termómetro de mayor precisión y menor rango de medición que
permita mayor exactitud en la toma de mediciones para determinar la viscosidad del
agua. Existen diferentes productos en el mercado que cumplen con estas
características; sin embargo son considerablemente costosos. Por ejemplo, se tiene
el termómetro de la Figura 110 de la marca Erasmus, referencia EIR-750, cuyo
rango de medición varía entre 0-50 °C, resolución de 0.1 °C y su valor oscila
alrededor de los $534,300 (Erasmus, 2009).
Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
90
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Figura 110. Termómetro infrarrojo de la marca Erasmus. Tomado de (Erasmus, 2009).
La investigación realizada no permite obtener conclusiones del valor de la
rugosidad absoluta para la tubería empleada, por lo tanto se recomienda la
implementación de las pruebas descritas en la sección de Metodología; sin embargo,
es necesario considerar que esta investigación solo proveerá resultados
significativos para tuberías como la empleada (material de PVC y diámetro nominal
de 6 pulgadas). Para obtener resultados variados es necesario realizar esta misma
investigación variando el diámetro y el material de la tubería.
La presente investigación se efectuará inicialmente con manómetros diferenciales y
se espera obtener resultados concluyentes. Posteriormente, se recomienda
implementar la misma metodología con sensores de presión para corroborar los
resultados obtenidos previamente.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
91
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
8 Bibliografía
Akan, O. (2006). Open Channel Hydraulics. Canadá: ELSEVIER.
Beltrán, R. (2005). Fundamentos de mecánica de fluídos. Bogotá: Ediciones Uniandes.
Bombardelli, F., & García, M. (2003). Hydraulic Design of Large-Diameter Pipes. Journal
of Hydraulic Engineering, 839-846.
Brkic
1
, D. (2011). Can pipes be actually really that smooth? International Journal of
Refrigeration, 209-215.
Brkic
2
, D. (2011). New Explicit Correlations for Turbulent Flow Friction Factor. Nuclear
Engineering Design, 4055-4059.
Brkic
3
, D. (2010). Review of explicit approximations to the Colebrook relation for flow
friction. Journal of Petroleum Science and Engineering, 34-48.
Camacho, L. A., & Saldarriaga, J. (1990). Efectos comparativos en el diseño de tuberías
utilizando las ecuaciones de Colebrook-White y Hazen-Williams. IX Seminario
Nacional de Hidráulica e Hidrología (págs. 33-44). Manizales: Sociedad
Colombiana de Ingenieros.
Chaudhry, H. (2008). Open-Channel Flow. Columbia: Springer.
Crane. (s.f.). Flujo de fluidos en válvulas, accesorios y tuberías. McGraw-Hill.
Dwyer Instruments. (2012). Modelo WT-10. Recuperado el 6 de Junio de 2012, de
http://www.dwyer-
inst.com/Products/Product.cfm?Group_ID=419&Product_ID=761&sPageName=Sp
ecs
Erasmus. (2009). Termómetro Infrarrojo. Recuperado el 19 de Junio de 2012, de
http://www.erasmus.com.co/tienda/index.php?act=viewProd&productId=29
Flechas, R. (2010). Efecto del uso de la ecuación de Darcy-Weisbach vs la ecuación de
Hazen-Williams sobre los costos de diseños optimizados en acueductos, teniendo en
cuenta la rugosidad de las tuberías, línea del gradiente hidráulico y temperatura.
Bogotá: Universidad de los Andes.
(2005). Water Systems Piping. En E. S. Menon, Piping calculations manual (pág. Capítulo
1). New York ; Chicago: McGraw-Hill.
Nieto, L. (2011). Estudio de las Ecuaciones que Describen el Flujo Turbulento
Hidráulicamente Liso: Revisión del Diagrama de Moody y las Ecuaciones de
Colebrook-White. Bogotá: Universidad de los Andes.
Saldarriaga, J. (2007). Hidráulica de Tuberías. Bogotá, D.C: Alfaomega.
Ultraflux. (s.f.). UF 801- P. Recuperado el 6 de Junio de 2012, de Productos:
http://www.ultraflux.net/product/uf-801-p-21/
White, F. M. (2008). Fluid mechanics . New York: McGraw-Hill.

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
92
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
9 Anexos
9.1 Planilla para el Registro de Datos
Tabla 12. Formato de registro de datos y cálculos para la calibración de la tubería.
Fecha
ID
Prueba
T
[°C]
ν
[m
2
/s]
Q
[L/s]
V
[m/s]
h manómetro
[m]
ΔP
[Pa]
h
f
[m]
f
[-]
Re
[-]
K
s
[mm]
FORMATO:
[1] CALIBRACIÓN DE LA TUBERÍA
PROYECTO DE GRADO
PREGRADO INGENIERÍA AMBIENTAL (IAMB 201210 19)
DIÁMETRO INTERNO [mm]
ÁREA [m
2
]
ING. JUAN SALDARRIAGA VALDERRAMA
REVISIÓN DE LAS ECUACIONES DE RESISTENCIA FLUIDA PARA EL CASO DEL FTHL
0,020
161,28
NOMBRE DEL PROYECTO:
ASESOR:
FECHA DE ENTREGA:
22 DE JUNIO DE 2012

Universidad de Los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Revisión de las Ecuaciones de Resistencia Fluida Para el Caso del Flujo
Turbulento Hidráulicamente Liso
IAMB 201210 19
93
Gloria Patricia Moscote Ordóñez
Proyecto de Grado Ingeniería Ambiental
Tabla 13. Formato de registro de datos y cálculos para la determinación del grosor de la subcapa laminar viscosa.
9.2 Planos del Montaje
Se anexan los planos desarrollados en Autocad® para el proyecto:
Vista en planta del montaje.
Vista de perfil del montaje (incluido sistema de alimentación y desagüe).
Vista de la estructura de soporte.
9.3 Manuales de Usuario
Ultraflux UF 801-P: User Guide.
“Manual Técnico de Turbosistemas para Acueducto Biaxial, PVC Biorientado Dúctil” de
PAVCO.
ID
Prueba
T
[°C]
ν
[m
2
/s]
Q
L/s]
V
[m/s]
Re
[-]
K
s
[mm]
f
[-]
v*
[m/s]
δ'
[m]
0.305 δ'
[m]
6.1 δ'
[m]
TIPO DE
FLUJO
PROYECTO DE GRADO
PREGRADO INGENIERÍA AMBIENTAL (IAMB 201210 19)
161,28
0,020
REVISIÓN DE LAS ECUACIONES DE RESISTENCIA FLUIDA PARA EL CASO DEL FTHL
ING. JUAN SALDARRIAGA VALDERRAMA
[2] DETERMINACIÓN DEL GROSOR DE LA SUBCAPA LAMINAR Y TIPO DE RÉGIMEN DEL FLUJO
DIÁMETRO INTERNO [mm]
FECHA DE ENTREGA:
22 DE JUNIO DE 2012
ÁREA [m
2
]
NOMBRE DEL PROYECTO:
ASESOR:
FORMATO:
