
Universidad de los Andes
Facultad De Ingeniería
Departamento de Ingeniería Civil y Ambiental
Proyecto de grado de Ingeniería Civil
Resaltos hidráulicos en tuberías lisas de sección circular
fluyendo parcialmente llenas, con números de Froude inferiores a
4.0
Preparado por:
Ing. Juan Camilo Franco Agudelo
Asesor:
Ing. Juan Saldarriaga
Informe Final Proyecto de grado
Bogotá, Julio 2014

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
II
“La disciplina es la parte más importante del éxito.
Usted tiene que tener una actitud de constancia,
disciplina, esfuerzo y perseverancia inalterables,
para llegar al éxito y que éste perdure”
Truman Streckfus Persons
Agradecimientos
Hoy doy gracias a Dios por haberme permitido este logro profesional, a la Universidad de
los Andes que me formó como ingeniero civil, a mi papá Jorge Orlando Franco y a mi mama
Juliett Agudelo por su apoyo incondicional en todo momento, al ingeniero Juan Guillermo
Saldarriaga por ser mi asesor y guiarme semana a semana en este proceso tan arduo,
mostrándome el camino adecuado y la información necesaria para culminar de manera
exitosa mi proyecto de grado, a John Calvo y a Gloria Moscote que siempre estuvieron muy
pendientes de todo mi proceso, al excelente grupo de personas que me acompañaron en
este camino, que me ayudaron a desarrollar este proyecto que con esfuerzo y dedicación
se logró sacar adelante, y por último a cada uno de los amigos y compañeros que
compartieron esta gran experiencia y que seguirán siendo apoyo incondicional en el
desarrollo profesional y en el logro de nuevos e importantes proyectos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
I
Tabla de contenido
Agradecimientos ................................................................................................................ II
Índice de Tablas ............................................................................................................... III
Índice de gráficas .............................................................................................................. IV
Índice de Ecuaciones ....................................................................................................... VII
1.
Introducción .............................................................................................................. 11
2.
Antecedentes de modelos realizados a través del tiempo sobre el fenómeno del
resalto hidráulico .............................................................................................................. 14
Kindsvater y Lane (1938) ............................................................................................. 14
Kalinske y Robertson (1943) ........................................................................................ 15
Richard Silvester (1964) ............................................................................................... 17
Estudio de canales cerrados (tuberías) ..................................................................... 18
Rajaratnam (1965) ....................................................................................................... 21
C. Smith y W. Chen (1989) ........................................................................................... 23
Willi H. Hager y Helmut Stahl (1999) ............................................................................ 28
Steven Michell (2002) ................................................................................................... 32
2.1 Canales rectangulares ........................................................................................ 33
2.2 Canales trapezoidales ........................................................................................ 33
2.3 Canales circulares .............................................................................................. 35
2.4 Resultados obtenidos de todas las secciones ..................................................... 36
Journal of Hydraulic Research (2006) .......................................................................... 40
2.1 Estructura del resalto hidráulico .......................................................................... 40
2.2 Ecuaciones recomendadas en resaltos hidráulicos ............................................. 41
2.3 Condiciones del resalto ....................................................................................... 42
2.4 Ecuación del resalto hidráulico en canales circulares y en forma de U. .............. 45
2.4.1 Ecuación del resalto hidráulico en canales circulares ...................................... 46
2.4.2 Ecuación del resalto hidráulico en canales en forma de U ............................... 48
2.5
Resultados y conclusiones ............................................................................. 48
3.
Marco Teórico ........................................................................................................... 53
Resalto hidráulico ......................................................................................................... 53
3.1 Tipos de resaltos hidráulicos ............................................................................... 54

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
II
3.2 Características básicas del resalto ...................................................................... 56
4.
Diseño y Construcción de un Modelo para Estudiar el Comportamiento de Resaltos
Hidráulicos en Tuberías Parcialmente Llenas de Sección Circular, con Números de
Froude menores a 4 ........................................................................................................ 59
Diseño del modelo........................................................................................................ 59
Resultados obtenidos ................................................................................................... 61
5.
Modelo físico ............................................................................................................ 66
Fotos del modelo .......................................................................................................... 66
Precisión de los instrumentos ....................................................................................... 73
5.1 Caudalímetro ...................................................................................................... 73
5.2 Sensores de profundidades ................................................................................ 74
6.
Resultados Experimentales ...................................................................................... 76
7.
Conclusiones ............................................................................................................ 97
8.
Glosario .................................................................................................................... 98
9.
Bibliografía ................................................................................................................ 99
10.
Anexos ................................................................................................................ 101
Anexo I ....................................................................................................................... 101
Anexo II ...................................................................................................................... 113
Anexo III ..................................................................................................................... 116
Anexo IV .................................................................................................................... 117

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
III
Índice de Tablas
Tabla 1. Datos típicos para los ensayos (Kalinske, 1943). ............................................... 16
Tabla 2. Resultados de números de Froude aguas arriba para diferentes relaciones de
llenado (Chen, 1989). ...................................................................................................... 28
Tabla 3. Diámetros seleccionados que superen el caudal de diseño y no superen los 48
cm de altura con relaciones de llenado del 50 % (Montaño, 2012). ................................. 60
Tabla 4. Diámetros seleccionados que superen el caudal de diseño y no superen los 48
cm de altura con relaciones de llenado del 85 % (Montaño, 2012). ................................. 60
Tabla 5. Diámetros seleccionados que superen el caudal de diseño y no superen los 48
cm de altura con relaciones de llenado del 92.9 % (Montaño, 2012). .............................. 61
Tabla 6. Mediciones realizadas en el laboratorio. ............................................................ 66
Tabla 7. Incertidumbre del sensor de profundidades U-GAGE T30 (BANNER, 2013). ..... 75
Para la toma de datos de este informe se hace referencia a la Tabla 8. Mediciones
realizadas en el laboratorio, donde se muestra que se utilizaron cuatro pendientes
distintas: 0,011- 0,016- 0,018 y 0,025. En cada una de estas pendientes se trabajó con 35
caudales diferentes, ocasionando el fenómeno del resalto hidráulico mediante la
compuerta ubicada aguas abajo. Para ver las tablas de los resultados obtenidos ver
ANEXO I. La obtención de los resultados se obtuvo de las siguientes ecuaciones: ......... 76
Tabla 9. Caudales máximos que resiste cada pendiente hasta su presurización y hasta
una relación de llenado del 86%. ..................................................................................... 88
Tabla 10. Resultados obtenidos para la pendiente 0,011. .............................................. 101
Tabla 11. Resultados obtenidos para la pendiente 0,016. .............................................. 104
Tabla 12. Resultados obtenidos para la pendiente 0,018. .............................................. 107
Tabla 13. Resultados obtenidos para la pendiente 0,025. .............................................. 110
Tabla 14. Datos de Entrada para calcular ecuación de Darcy Weisbach. ...................... 113
Tabla 15. Ecuaciones teóricas utilizando ley de Darcy Weisbach. ................................. 113
Tabla 16. Ecuaciones teóricas utilizando ley de Darcy Weisbach. ................................. 114
Tabla 17. Datos de Entrada para calcular ecuación de Darcy Weisbach. ...................... 114
Tabla 18. Ecuaciones teóricas utilizando ley de Darcy Weisbach. ................................. 115
Tabla 19. Comparación de resultados teóricos con resultados experimentales en
profundidades de flujo aguas abajo para todas las pendientes. ..................................... 116

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
IV
Índice de gráficas
Gráfica 1. Montaje realizado por Kindsvater y Lane (Kindsvater, 1938). .......................... 14
Gráfica 2. Alturas versus Caudales (Kindsvater, 1938). ................................................... 15
Grafica 3. Montaje de Kalinske y Robertson (Kalinske, 1943). ......................................... 15
Gráfica 4. Valores críticos experimentales del número de Froude contra la relación de
llenado (Kalinske, 1943). ................................................................................................. 16
Gráfica 5. Datos obtenidos para los diferentes tipos de secciones (Silvester, HYDRAULIC
JUMP IN ALL SHAPES OF HORIZONTAL CHANNELS., 1964). ..................................... 20
Gráfica 6. Resultados obtenidos de la variación de alturas versus la longitud del resalto
(Silvester, HYDRAULIC JUMP IN ALL SHAPES OF HORIZONTAL CHANNELS., 1964). 21
Gráfica 7. Relación de llenado versus número de Froude aguas arriba (Rajaratnamn,
1965). .............................................................................................................................. 22
Gráfica 8. Comportamiento del resalto hidráulico dentro de la tubería (Chen, 1989)........ 23
Gráfica 9. Longitud del resalto hidráulico versus el número de Froude aguas arriba (Chen,
1989). .............................................................................................................................. 27
Gráfica 10. Profundidades subsecuentes según el número de Froude (Hager, 1999). ..... 30
Gráfica 11.Tipo de resalto ondular con números de Froude< 1.5 (Hager, 1999). ............. 31
Gráfica 12. Tipo de resalto ondular con números de Froude entre (1.5-2) (Hager, 1999). 31
Gráfica 13. Tipo de resalto ondular con números de Froude entre (2-4.1) (Hager, 1999). 31
Gráfica 14. Tipo de resalto ondular con números de Froude>6.5 (Hager, 1999). ............. 32
Gráfica 15. Grafica de elevación del resalto hidráulico (Michell, 2008) ............................ 33
Gráfica 16. Definición de secciones para canal trapezoidal (Michell, 2008). .................... 34
Gráfica 17. Definición de ángulo para tuberías circulares parcialmente llenas (Michell,
2008). .............................................................................................................................. 35
Gráfica 18. Relación de alturas VS Froude 1 del canal trapezoidal (Michell, 2008). ......... 37
Gráfica 19. Relación de alturas VS Froude 1 de la tubería circular (Michell, 2008). ......... 37
Gráfica 20. Comparación de datos teóricos y experimentales del canal trapezoidal
(Michell, 2008). ................................................................................................................ 38
Gráfica 21. Pérdidas de energía contra el número de Froude 1 en canales trapezoidales.
........................................................................................................................................ 39
Gráfica 22.Pérdidas de energía contra el número de Froude 1 en tuberías circulares. .... 40
Gráfica 23. Partes que componen un resalto hidráulico (Francis, 2006). ......................... 41
Gráfica 24. Sección circular y en forma de U que se van a trabajar en el experimento
(Francis, 2006). ................................................................................................................ 41
Gráfica 25. Profundidades subsecuentes versus en número de Froude aguas arriba en
canales circulares (Francis, 2006). .................................................................................. 49
Gráfica 26. Longitud del resalto versus en número de Froude aguas arriba en canales
circulares (Francis, 2006). ............................................................................................... 50
Gráfica 27. Profundidades subsecuentes versus en número de Froude aguas arriba en
canales con sección en forma de U (Francis, 2006)......................................................... 51

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
V
Gráfica 28. Longitud del resalto versus en número de Froude aguas arriba en canales con
sección en forma de U (Francis, 2006). ........................................................................... 52
Gráfica 29. Tipos de resaltos en tuberías circulares (Ead, 2002). .................................... 53
Gráfica 30. Tipos de resaltos en tuberías circulares (Ead, 2002). .................................... 54
Gráfica 31. Resalto ondular (Rodríguez, 1992). ............................................................... 54
Gráfica 32. Resalto débil (Rodríguez, 1992). ................................................................... 55
Gráfica 33. Resalto oscilante (Rodríguez, 1992). ............................................................. 55
Gráfica 34. Resalto permanente (Rodríguez, 1992). ........................................................ 55
Gráfica 35. Resalto fuerte (Rodríguez, 1992). .................................................................. 56
Gráfica 36. Caso A de la ubicación del resalto hidráulico (Rodríguez, 1992). .................. 57
Gráfica 37. Caso B de la ubicación del resalto hidráulico (Rodríguez, 1992). .................. 57
Gráfica 38. Caso C de la ubicación del resalto hidráulico (Rodríguez, 1992). .................. 58
Gráfica 39. Variación del caudal respecto a la relación de llenado (Montaño, 2012). ....... 62
Gráfica 40. . Variación del número de Froude respecto a la relación de llenado para
diferentes pendientes (Montaño, 2012). ........................................................................... 63
Gráfica 41. Variación del número de Froude para diversos caudales (Montaño, 2012). ... 64
Gráfica 42. Comparación número de Froude respecto a diferentes relaciones de llenado
(Montaño, 2012). ............................................................................................................. 65
Gráfica 43. Foto del montaje listo para ser utilizado. ........................................................ 67
Gráfica 44. Ensayo de prueba para la verificación de los instrumentos y la tubería. ........ 67
Gráfica 45. Ensayo de prueba aguas arriba para la verificación de los instrumentos y la
tubería. ............................................................................................................................ 68
Gráfica 46. Compuerta aguas abajo de la tubería para controlar el fenómeno del resalto
hidráulico. ........................................................................................................................ 69
Gráfica 47. Gatos mecánicos para controlar la variación de la pendiente. ....................... 69
Gráfica 48. Fenómeno del resalto hidráulico. ................................................................... 70
Gráfica 49. Alturas piezómetricas del resalto hidráulico. .................................................. 70
Gráfica 50. Sensor IQ Plus. ............................................................................................. 71
Gráfica 51. Procedimiento de instalación del sensor IQ Plus. .......................................... 72
Gráfica 52. Estructura del sensor IQ Plus para obtener un funcionamiento adecuado de
los rayos emitidos por este. ............................................................................................. 72
Gráfica 53. Caudalímetro electromagnético WaterMaster (ABB)...................................... 73
Gráfica 54. Rangos de error del caudalímetro electromagnético clase 2 según OIML R49
(WaterMaster, 2013). ....................................................................................................... 74
Gráfica 55. Sensor U-GAGE T30 Series (BANNER, 2013). ............................................. 75
Gráfica 56. Comparación de las pendientes con respecto a su relación de llenado aguas
arriba. .............................................................................................................................. 79
Gráfica 57. Comparación de la pendiente 0,011 con la ecuación de Darcy Weisbach. .... 80
Gráfica 58. Comparación de la pendiente 0,018 con la ecuación de Darcy Weisbach. .... 81
Gráfica 59.Comparación de la relación de llenado aguas abajo con respecto a las
pendientes trabajadas. ..................................................................................................... 82
Gráfica 60. Comparación de la pendiente 0,011 con la ecuación de Darcy Weisbach. .... 83

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
VI
Gráfica 61. Comparación de resultados teóricos contra los resultados experimentales de
la pendiente 0,011. .......................................................................................................... 84
Gráfica 62. Comparación de resultados teóricos contra los resultados experimentales de
la pendiente 0,016. .......................................................................................................... 85
Gráfica 63. Comparación de resultados teóricos contra los resultados experimentales de
la pendiente 0,018. .......................................................................................................... 85
Gráfica 64. Pérdidas de energía experimentales en la tubería. ........................................ 86
Gráfica 65. Eficiencia experimental de la tubería. ............................................................ 87
Gráfica 66. Relación de llenado óptima para las cuatro pendientes trabajadas................ 88
Grafica 67. Comportamiento experimental del número de Froude aguas arriba. .............. 89
Gráfica 68. Ecuación del resalto hidráulico mediante el método de regresión para la
pendiente de 0,011. ......................................................................................................... 90
Gráfica 69. Comparación de alturas con respecto al caudal de entrada para la pendiente
de 0,011. .......................................................................................................................... 92
Gráfica 70. Solución de relación de llenado para pendiente 0,011 mediante programa de
VBA. ................................................................................................................................ 93
Gráfica 71.Comparación de alturas con respecto al caudal de entrada para la pendiente
de 0,016. .......................................................................................................................... 93
Gráfica 72.Solución de relación de llenado para pendiente 0,016 mediante programa de
VBA. ................................................................................................................................ 94
Gráfica 73. Comparación de alturas con respecto al caudal de entrada para la pendiente
de 0,018. .......................................................................................................................... 94
Gráfica 74. Solución de relación de llenado para pendiente 0,018 mediante programa de
VBA. ................................................................................................................................ 95
Gráfica 75. Solución de relación de llenado para pendiente 0,025 mediante programa de
VBA. ................................................................................................................................ 95

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
VII
Índice de Ecuaciones
Ecuación 1. Fuerza del resalto en secciones horizontales. .............................................. 17
Ecuación 2.Fuerza del resalto en secciones horizontales. ............................................... 17
Ecuación 3. Calculo del número de Froude. .................................................................... 17
Ecuación 4. Cálculo de profundidades subsecuentes. ..................................................... 17
Ecuación 5. Relación del número de Froude aguas arribas y aguas abajo de la tubería. . 18
Ecuación 6. Número de Froude aguas arriba del resalto. ................................................ 18
Ecuación 7. Procedimiento para el cálculo de alturas subsecuentes en el resalto. .......... 18
Ecuación 8. Ecuación final de alturas subsecuentes en el resalto.................................... 18
Ecuación 9. Diámetro de flujo con respecto al centro de gravedad para tuberías fluyendo
parcialmente llenas. ......................................................................................................... 19
Ecuación 10. Profundidades subsecuentes para tuberías fluyendo parcialmente llenas. . 19
Ecuación 11.Diámetro de flujo con respecto al centro de gravedad para tuberías fluyendo
totalmente llenas. ............................................................................................................. 19
Ecuación 12. Expresión para el cálculo de la longitud del resalto en cualquier tipo de
sección. ........................................................................................................................... 20
Ecuación 13. Momentum en un Resalto hidráulico. ......................................................... 21
Ecuación 14. Conservación de momentum en un resalto hidráulico. ............................... 22
Ecuación 15. Cálculo del número de Froude según Rajaratnam. ..................................... 22
Ecuación 16. Calculo de Momentum para tuberías. ......................................................... 23
Ecuación 17. Cálculo de momentum corregido para tuberías. ......................................... 24
Ecuación 18. Profundidades aguas arriba y aguas abajo de la tubería. ........................... 24
Ecuación 19. Cálculo de profundidades subsecuentes aguas abajo de la tubería. .......... 24
Ecuación 20.Cálculo de ecuación factorizada de profundidades subsecuentes aguas abajo
de la tubería. .................................................................................................................... 24
Ecuación 21.Cálculo del número de Froude para tuberías. .............................................. 25
Ecuación 22. Sustitución trigonométrica. ......................................................................... 25
Ecuación 23. Cálculo simplificado de profundidades subsecuentes aguas abajo de la
tubería. ............................................................................................................................ 25
Ecuación 24. Cálculo del resalto hidráulico en tuberías. .................................................. 25
Ecuación 25. Cálculo del resalto hidráulico reemplazado en términos conocidos. ........... 25
Ecuación 26. Ecuación factorizada de la longitud del resalto reemplazada en términos
conocidos. ....................................................................................................................... 26
Ecuación 27. Supuestos realizados por Smith y Chen para el cálculo de la longitud del
resalto. ............................................................................................................................. 26
Ecuación 28. Expresión final para el cálculo de la longitud del resalto hidráulico ............. 26
Ecuación 29. Cálculo de Froude para profundidad crítica. ............................................... 27
Ecuación 30. Supuesto final para cálculo de la profundidad crítica. ................................. 27
Ecuación 31. Profundidades subsecuentes. .................................................................... 28
Ecuación 32. Fuerza de presión del agua en una tubería. ............................................... 28

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
VIII
Ecuación 33. Ecuación de momentum en tuberías. ......................................................... 28
Ecuación 34. Número de Froude para conductos circulares. ........................................... 29
Ecuación 35. Ecuación 33 reorganizada. ......................................................................... 29
Ecuación 36. Relación de alturas aguas arriba y aguas abajo de una tubería parcialmente
llena. ................................................................................................................................ 29
Ecuación 37. Ecuación de momentum en una tubería fluyendo parcialmente llena. ........ 29
Ecuación 38. Ecuación final de momentum en una tubería fluyendo parcialmente llena. . 29
Ecuación 39. Cálculo de profundidades subsecuentes para números de Froude aguas
arriba mayores a 2. .......................................................................................................... 30
Ecuación 40. Nuevo cálculo de profundidades subsecuentes para números de Froude
aguas arriba mayores a 2. ............................................................................................... 30
Ecuación 41. Ecuación de Momentum. ............................................................................ 32
Ecuación 42. Relación entre alturas para canales rectangulares. .................................... 33
Ecuación 43. Expresión para calcular pérdidas de energía en canales rectangulares. .... 33
Ecuación 44. Centroide aguas arriba del área transversal de un canal de sección
trapezoidal. ...................................................................................................................... 34
Ecuación 45. Centroide aguas abajo del área transversal de un canal de sección
trapezoidal. ...................................................................................................................... 34
Ecuación 46. Ecuación de momentum en un canal trapezoidal. ...................................... 34
Ecuación 47. Ecuación de momentum reemplazada en un canal trapezoidal. ................. 34
Ecuación 48. Cálculo de Profundidades subsecuentes en un canal trapezoidal. ............. 35
Ecuación 49. Método iterativo te Newton-Raphson. ......................................................... 35
Ecuación 50. Centroide del área transversal de una tubería de sección circular. ............ 35
Ecuación 51. Derivada del centroide del área transversal de una tubería de sección
circular. ............................................................................................................................ 36
Ecuación 52. Alturas obtenidas por método de Newton en términos de
𝛉. ....................... 36
Ecuación 53.Área obtenida por método de Newton en términos de
𝛉. ............................. 36
Ecuación 54. Función para el cálculo de profundidades subsecuentes en una tuberia
circular. ............................................................................................................................ 36
Ecuación 55. Derivada de la función para el cálculo de profundidades subsecuentes en
una tubería circular. ......................................................................................................... 36
Ecuación 56. Gradiente de presiones. ............................................................................. 41
Ecuación 57. Ecuación de la continuidad. ........................................................................ 41
Ecuación 58. Ecuación de Reynolds. ............................................................................... 42
Ecuación 59. Esfuerzos cortantes de Reynolds. .............................................................. 42
Ecuación 60.Condiciones de frontera de la velocidad de desplazamiento. ...................... 42
Ecuación 61. Condiciones de la superficie libre aerodinámica. ........................................ 42
Ecuación 62. Ecuación de momentum para canales circulares y en forma de U. ............. 42
Ecuación 63. Ecuación de momentum para canales circulares y en forma de U. ............. 43
Ecuación 64. Cálculo del número de Froude aguas arriba del canal. ............................... 43
Ecuación 65. Velocidades subsecuentes en el resalto hidráulico. .................................... 43
Ecuación 66. Ecuación de profundidad de Reynolds en el resalto hidráulico. .................. 43

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
IX
Ecuación 67. Viscosidad de remolino. ............................................................................. 43
Ecuación 68. Gradiente promedio de la velocidad axial. .................................................. 43
Ecuación 69. Ecuación simplificada del resalto hidráulico. ............................................... 44
Ecuación 70. Constantes para el cálculo del resalto hidráulico. ....................................... 44
Ecuación 71. Condiciones de frontera para el cálculo del resalto hidráulico aguas arriba y
aguas abajo del canal. ..................................................................................................... 44
Ecuación 72. Calculo del resalto hidráulico dentro de las condiciones de frontera. .......... 44
Ecuación 73. Cálculo de la longitud del resalto a través de la pendiente y las
profundidades aguas arriba y aguas abajo. ..................................................................... 44
Ecuación 74. Cálculo de la longitud del resalto teniendo en cuenta la profundidad media.
........................................................................................................................................ 45
Ecuación 75. Términos importantes para el cálculo del resalto hidráulico en canales
circulares y en forma de U. .............................................................................................. 45
Ecuación 76. Cálculo del Resalto hidráulico en términos de Ψ y Φ. ................................. 45
E
cuación 77. Cálculo del número de Froude en términos de Ψ y Φ. ................................ 46
Ecuación 78. Integral para el cálculo del resalto hidráulico. ............................................. 46
Ecuación 79. Definición de variables. .............................................................................. 46
Ecuación 80.Cálculo de la longitud del resalto en términos de
𝚽 𝐲 𝚿, teniendo en cuenta
la profundidad media. ...................................................................................................... 46
Ecuación 81. Relación entre profundidad de flujo y diámetro en canales de sección
circular. ............................................................................................................................ 46
Ecuación 82. Cálculo del área y de la fuerza de presión por unidad de peso en canales
circulares. ........................................................................................................................ 47
Ecuación 83. Número de Froude para canales circulares. ............................................... 47
Ecuación 84. Cálculo de la profundidad crítica en canales de sección circular. ............... 47
Ecuación 85.Simplificación de ecuaciones para canales circulares fluyendo parcialmente
llenos. .............................................................................................................................. 47
Ecuación 86. Número de Froude simplificado para canales circulares fluyendo
parcialmente llenos. ......................................................................................................... 47
Ecuación 87. Longitud del resalto simplificado para canales circulares fluyendo
parcialmente llenos. ......................................................................................................... 48
Ecuación 88. Cálculo del área y la fuerza de presión por unidad de peso para canales en
forma de U. ...................................................................................................................... 48
Ecuación 89. Simplificación del modelo de Hager para canales en forma de U. .............. 48
Ecuación 90. Cálculo de pérdidas de energía en canal rectangular horizontal. ................ 56
Ecuación 91. Cálculo de la eficiencia en un canal rectangular horizontal (Rodríguez,
1992). .............................................................................................................................. 56
Ecuación 92. Curva que describe el número de Froude máximo (Montaño, 2012). ......... 65
Ecuación 93. Cálculo del área mojada en secciones circulares. ...................................... 76
Ecuación 94. Cálculo de la velocidad de flujo en secciones circulares. ............................ 76
Ecuación 95. Cálculo del ancho de la superficie de agua en secciones circulares. .......... 77
Ecuación 96. Cálculo del perímetro mojado en secciones circulares. .............................. 77

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
X
Ecuación 97. Cálculo de la profundidad hidráulica en secciones circulares. .................... 77
Ecuación 98. Cálculo del número de Froude en secciones circulares. ............................. 77
Ecuación 99. Cálculo de la relación de llenado en secciones circulares. ......................... 77
Ecuación 100. Cálculo de la energía especifica en secciones circulares. ........................ 78
Ecuación 101. Cálculo de las pérdidas de energía del resalto hidráulico en secciones
circulares. ........................................................................................................................ 78
Ecuación 102. Cálculo de la eficiencia del resalto hidráulico en secciones circulares. ..... 78
Ecuación 103. Cálculo del momentum específico en secciones circulares. ..................... 78
Ecuación 104. Momentum en un resalto hidráulico. ......................................................... 83
Ecuación 105. Ecuación del resalto hidráulico para una pendiente de 0,011. .................. 90
Ecuación 106. Definición de variables dependientes e independientes. .......................... 90
Ecuación 107. Ecuación para encontrar el número de Froude. ........................................ 90
Ecuación 108. Velocidad de flujo. .................................................................................... 91
Ecuación 109. Número de Froude reemplazado. ............................................................. 91
Ecuación 110. Ecuación del resalto hidráulico para la pendiente de 0,011. ..................... 91
Ecuación 111. Ecuación del resalto hidráulico reemplazada para la pendiente de 0,011. 91
Ecuación 112. Ecuación del resalto hidráulico reemplazada para la pendiente de 0,016. 91
Ecuación 113. Ecuación del resalto hidráulico reemplazada para la pendiente de 0,018. 91
Ecuación 114. Ecuación del resalto hidráulico reemplazada para la pendiente de 0,025. 92
Ecuación 115. Método de regresión para pendiente de 0,018. ........................................ 94
Ecuación 116. Método de regresión para pendiente de 0,025. ........................................ 95

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
11
1.
Introducción
El resalto hidráulico es un fenómeno que se presenta cuando un flujo genera una transición de
un estado supercrítico a un estado subcrítico. Es decir, cuando se muestra un conflicto entre
las profundidades de flujo aguas arriba y aguas abajo, lo cual hace que la altura de flujo cambie
rápidamente de menor a mayor. Este tipo de fenómeno se puede presentar tanto en canales
abiertos como canales cerrados y se produce por variaciones en las pendientes o por
obstáculos en el canal como compuertas. Este tipo de fenómeno hidráulico se produce
principalmente con el fin de obtener grandes pérdidas de energía, las cuales se presentan por
la turbulencia y sirven para controlar de una mejor forma el comportamiento del flujo. Otras de
sus funciones principales son: la eficiencia, puesto que es la relación de la energía específica
antes y después del resalto, dependiendo del número de Froude aguas arriba; y por último, se
encuentra que el resalto hidráulico es un excelente mezclador de fluidos. Para obtener un
análisis detallado de este fenómeno se deben tener en cuentas algunas características
principales del resalto como:
La longitud del resalto: Esta distancia está medida desde donde comienza la
turbulencia del fluido aguas abajo formando el resalto, hasta donde se estabiliza el fluido
aguas arriba.
Número de Froude: El número de Froude se calcula para determinar si el
comportamiento del flujo es supercrítico, subcrítico o crítico. Su cálculo puede variar
según la forma geométrica del canal; ya sea rectangular, triangular, trapezoidal o
circular.
Ubicación del resalto: Esta característica es muy importante para el entendimiento de
las condiciones óptimas del canal, reduciendo los daños y las sobrecargas. En el resalto
puede variar su ubicación según el canal de entrada a la tubería, el control de una
compuerta aguas abajo o la pendiente que este tenga.
El desarrollo de este proyecto se va a enfocar en la toma de datos y análisis de resultados del
modelo construido anteriormente para el desarrollo y estudio de resaltos hidráulicos en tuberías
parcialmente llenas de sección circular, con números de Froude menores a 4, con el fin de
minimizar los fenómenos de sobrecarga en los sistemas de drenaje urbano en Colombia.
Por un lado, este trabajo contará con un estudio previo de los modelos de resaltos hidráulicos
que se han realizado a través del tiempo en canales abiertos y cerrados para tener un mejor
entendimiento y manejo del tema a estudiar. Se comenzará analizando los ensayos realizados
por Kindsvater y Lane en canales rectangulares, seguido de los ensayos de Kalinske y
Robertson enfocados en la variación de pendientes para producir el resalto, y por último Hager
que ha sido el principal autor junto con sus ecuaciones empíricas para el cálculo del resalto
hidráulico en tuberías circulares, entre otros.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
12
Por otro lado, se contará con la prueba del montaje en el Laboratorio de Hidráulica en la
Universidad de los Andes, donde se trabajará el fenómeno de resaltos hidráulicos en tuberías
circulares, con la variación de diferentes pendientes y con el manejo de una compuerta aguas
abajo para garantizar: la generación del resalto, la obtención de profundidades subsecuentes,
la ubicación del resalto entre los dos sensores aguas arriba y aguas abajo, y el cálculo del
número de Froude.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
13
Objetivos
Objetivo General
Entender el fenómeno del resalto hidráulico en tuberías lisas de sección circular, fluyendo
parcialmente llenas con número de Froude inferiores a 4. De esta forma, determinar el
comportamiento del resalto en la tubería con diferentes pendientes y bajo condiciones de llenado
menores al 85%, generando una mayor aireación y pérdidas de energía.
Objetivos Específicos
Conocer los instrumentos con los cuales se va a trabajar en el desarrollo de este
proyecto de grado para entender la precisión de estos y su incertidumbre a la hora de
presentar los resultados. Los instrumentos con los cuales que se trabajará son: dos
sensores que medirán las profundidades de flujo aguas arriba y aguas abajo del resalto,
mostrando el comportamiento de este; un caudalímetro electromagnético que informará
cuanto caudal está pasando en el modelo; y un nivel de precisión que presentará las
pendientes en las que se está trabajando.
Desarrollar un estudio previo de los modelos realizados a través del tiempo acerca del
fenómeno del resalto hidráulico en tuberías circulares, identificando los instrumentos y
métodos utilizados en estos, para obtener información suficiente en el análisis de
resultados obtenidos en este proyecto de grado.
Calcular los posibles caudales críticos que causen desbordamiento en el canal,
mostrando cierta relación de llenado. Y además, encontrar la relación de llenado óptima
para los números de Froude más críticos.
Desarrollar una ecuación empírica para encontrar la pendiente óptima de la tubería, para
un caudal de diseño, evitando el fenómeno de sobrecarga y relaciones de llenado
superiores al 85%.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
14
2. Antecedentes de modelos realizados a través del tiempo sobre el
fenómeno del resalto hidráulico
Para entender y estudiar el comportamiento de la tubería frente a los resaltos hidráulicos,
primero se debe encontrar los estudios previos que se han ido realizando a través del tiempo,
con sus principales autores y finalmente con las conclusiones de cada uno de estos. De esta
forma, se logrará entender las ecuaciones demostradas por cada uno de ellos y el
procedimiento de cómo se llegó a ellas, si de forma experimental o teórica. A continuación se
mostrarán los principales estudios que se realizaron con sus respectivos autores.
Kindsvater y Lane (1938)
Los primeros experimentos que aparecen a través de la historia en cuanto al tema de resaltos
hidráulicos en tuberías circulares fueron los realizados por Kindsvater y Lane en 1938. Este
montaje se realizó en la Universidad de lowa, con una tubería de 150 mm de diámetro y 6 m de
longitud totalmente horizontal. Se realizaron tres tipos de pruebas con diferentes porcentajes
de obstrucción: el primero era del 40% del diámetro, el segundo era del 60% del diámetro y el
tercero ocupaba el 80% de diámetro (Kindsvater E. W., 1938). A continuación se mostrará el
ensayo que se realizó para la segunda prueba:
Gráfica 1. Montaje realizado por Kindsvater y Lane (Kindsvater, 1938).
Al realizar las pruebas en la tubería circular Kindsvater y Lane, estudiaron la variación de alturas
medidas para diferentes caudales, y pudieron concluir, como se puede observar en la Gráfica
2, que al tener caudales muy bajos la tubería no alcanzaba su presurización; en cambio a
caudales grandes la tubería se presurizaba completamente. Por otro lado, encontraron que, al
analizar el resalto por medio de la variación de momentum aguas arriba y aguas abajo, se
generaba un mayor momentum aguas arriba de la tubería, lo cual demostraba que este no se
estaba conservando antes y después del resalto, estas diferencias entre los dos momentum lo
asimilaban a tres posibles causas: la fricción causada por la tubería, la omisión de burbujas en
los cálculos y la uniformidad del resalto aguas abajo (Kindsvater E. W., 1938).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
15
Gráfica 2. Alturas versus Caudales (Kindsvater, 1938).
Kalinske y Robertson (1943)
Los experimentos de Kalinske y Robertson se basaron en varias pruebas a sistemas cerrados
en tuberías circulares, para encontrar el fenómeno del resalto hidráulico por medio de la
aireación de esta. Estos tipos de experimentos consistían en colocar varias tuberías circulares
a diferentes pendientes para verificar cuál era el comportamiento del resalto hidráulico y cuáles
eran las causas que lo generaban. Durante sus estudios encontraron que la cantidad de
aireación dependía del número de Froude aguas arriba del resalto hidráulico, de la pendiente
de esta y de la relación de llenado (Mortensen, 2009). A continuación se mostrará en la Gráfica
3 uno de los resultados que ellos obtuvieron:
Grafica 3. Montaje de Kalinske y Robertson (Kalinske, 1943).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
16
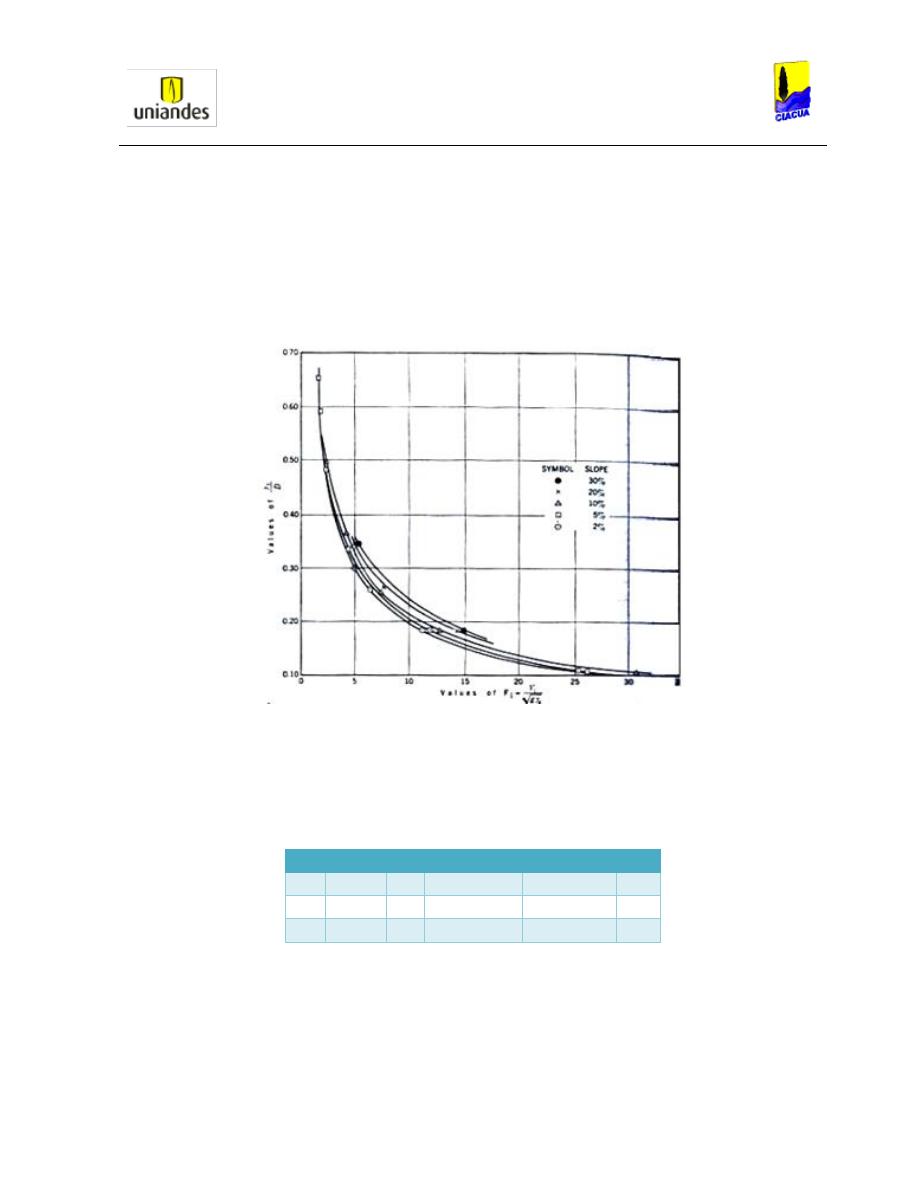
Como se puede observar en la Gráfica 3, encontraron que efectivamente para un cambio de
pendiente en la tubería y para cambios de números de Froude, la intensidad del resalto
hidráulico sería diferente. Esta prueba se demostró en una tubería de 10 m de largo y de 150
mm de diámetro que se sometió a seis pendientes diferentes (0.2%, 2%, 5%, 10%, 20% y 30%).
Por otro lado, en su experimento obtuvieron resultados para los valores críticos que
presentaban las tuberías, graficando el número de Froude contra las diferentes relaciones de
llenado.
Gráfica 4. Valores críticos experimentales del número de Froude contra la relación de llenado (Kalinske,
1943).
Como se puede observar en la Gráfica 4, para las diferentes pendientes que se estudiaron, se
encontró que la pendiente era directamente proporcional a la relación de llenado, es decir, a
mayores pendientes en la tubería, se presentaron mayores relaciones de llenado.
Tabla 1. Datos típicos para los ensayos (Kalinske, 1943).
Fig. Y1 (m) Fr1 Qw (m^3/s) Qd (m^3/s) S (-)
(a)
0,147 8,2
0,720
0,060
2%
(b)
0,127 7,5
0,482
0,039
5%
(c)
0,290 2,6
0,848
0,014
10%
Por otro lado, para cada una de las pruebas que realizaron con diferentes pendientes Robertson
y Kalinske, descubrieron que los resaltos en la tubería se comportaban de forma diferente a
medida que cambiaban la pendiente. De esta forma concluyeron que la cantidad de aireación
y presión de aire que producía el resalto a medida que se inclinaba la tubería, eran directamente
proporcionales, siempre y cuando el número de Froude y la profundidad subsecuente se
mantuvieran constantes (Kalinske, 1943).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
17
Richard Silvester (1964)
Para el desarrollo de su experimento, Richard Silvester se enfocó en estudiar el
comportamiento de los resaltos hidráulicos a través de varios tipos de tuberías, entre ellas las
circulares, triangulares y rectangulares. En su publicación en 1964 descubrió que para
encontrar las propiedades de un resalto hidráulico en tuberías circulares debía estudiar las dos
situaciones que se podían presentar (fluyendo parcialmente llenas y fluyendo totalmente
llenas). Por otro lado, descubrió que para obtener el comportamiento del flujo aguas arriba y
aguas abajo del resalto, debía tener en cuenta ciertas variables de entrada como la relación de
llenado aguas arriba y aguas abajo, el caudal de entrada a los canales y a las tuberías, la
disipación de energía, el radio de profundidades subsecuentes y la longitud del resalto.
Así mismo, comenzó su análisis introduciendo la ecuación de fuerza del resalto de un flujo a
través de una sección horizontal como se muestra a continuación:
𝐴
1
𝑘
1
´
𝑑
1
− 𝐴
2
𝑘
2
´
𝑑
2
= (
𝑄
2
𝑔
) ∗ (
1
𝐴
2
−
1
𝐴
1
)
Ecuación 1. Fuerza del resalto en secciones horizontales.
donde
𝐴 es el área mojada, 𝑘 es la distancia al centro de gravedad, 𝑑 el diámetro de la tubería,
𝑔 es la gravedad y 𝑄 es el caudal de entrada, los subíndices (1 y 2) se utilizan para la
diferenciación entre aguas arriba y aguas abajo respectivamente. La Ecuación 1 se puede
describir de una mejor forma así:
𝐴
1
𝑘
1
´
𝑑
1
− 𝐴
2
𝑘
2
´
𝑑
2
= (
𝑄
2
𝑔𝐴
2
−
𝑄
2
𝑔𝐴
1
)
Ecuación 2.Fuerza del resalto en secciones horizontales.
Además, se conoce que la ecuación del número de Froude se expresa de la siguiente forma:
𝐹
2
=
𝑄
2
𝐴
2
𝑔𝐷
Ecuación 3. Calculo del número de Froude.
donde
𝐹 es el número de Froude; ahora al reemplazar la Ecuación 2 en la Ecuación 3, y
multiplicando por menos 1 se obtiene la siguiente expresión
𝐴
2
𝑘
2
´
𝐷
2
− 𝐴
1
𝑘
1
′
𝐷
1
= 𝐹
1
2
𝐴
1
𝐷
1
− 𝐹
2
2
𝐴
2
𝐷
2
Ecuación 4. Cálculo de profundidades subsecuentes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
18
Por otro lado, se tiene que la relación entre el número de Froude aguas arriba y el número de
Froude aguas abajo se expresa de la siguiente forma:
𝐹
2
2
𝐹
1
2
=
𝐴
1
2
𝐷
1
𝐴
2
2
𝐷
2
Ecuación 5. Relación del número de Froude aguas arribas y aguas abajo de la tubería.
Despejando el número de Froude aguas abajo, se puede despejar una incógnita de la Ecuación
5 y expresar todo en términos del número de Froude aguas arriba
𝐹
2
2
=
𝐴
1
2
𝐷
1
𝐹
1
2
𝐴
2
2
𝐷
2
Ecuación 6. Número de Froude aguas arriba del resalto.
Y reemplazando queda:
𝐴
2
𝑘
2
´
𝐷
2
− 𝐴
1
𝑘
1
′
𝐷
1
= 𝐹
1
2
𝐴
1
𝐷
1
−
𝐴
1
2
𝐷
1
𝐹
1
2
𝐴
2
𝐷
2
𝐴
2
2
𝐷
2
𝐴
2
𝑘
2
´
𝐷
2
− 𝐴
1
𝑘
1
′
𝐷
1
= 𝐹
1
2
𝐴
1
𝐷
1
−
𝐴
1
2
𝐷
1
𝐹
1
2
𝐴
2
𝐷
2
𝐴
2
𝑘
2
´
𝐷
2
− 𝐴
1
𝑘
1
′
𝐷
1
= 𝐹
1
2
𝐴
1
𝐷
1
(1 −
𝐴
1
𝐴
2
)
Ecuación 7. Procedimiento para el cálculo de alturas subsecuentes en el resalto.
Finalmente, se divide la Ecuación 7 por
𝐴
1
∗ 𝐷
1
𝑘
2
′
(𝐴
2
𝐷
2
)
𝐴
1
𝐷
1
− 𝑘
1
′
= 𝐹
1
2
[1 −
𝐴
1
𝐴
2
]
Ecuación 8. Ecuación final de alturas subsecuentes en el resalto.
Estudio de canales cerrados (tuberías)
El desarrollo de este documento se va a enfocar principalmente en el estudio que Richard
Silvester realizó para las tuberías circulares, fluyendo parcialmente llenas y totalmente llenas.
2.1 Tubería parcialmente llena
En este tipo de tuberías no se presenta un
𝑘 (distancia al centro de gravedad) constante, por
lo cual Silvester planteó la siguiente ecuación:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
19
𝑘
′
= 1 −
1
2
𝑑
𝐷
+
(2 (1 −
𝐷
𝑑
)
3
2
∗ (
𝐷
𝑑
)
1
2
)
3𝑚
Ecuación 9. Diámetro de flujo con respecto al centro de gravedad para tuberías fluyendo parcialmente
llenas.
donde
𝐷 es la profundidad de sección, 𝑑 es el diámetro de la tubería, 𝑘
′
es el diámetro de la
profundidad de flujo con respecto al centro de gravedad y
𝑚 es el área de los segmentos del
agua. Finalmente, para tuberías fluyendo parcialmente llenas, se puede expresar la ecuación
de profundidades subsecuentes reemplazando la Ecuación 9 en la Ecuación 8 obteniendo:
𝑘
2
′
𝑑
2
𝑑
1
𝑚
2
𝑚
1
− 𝑘
1
´
= 𝐹
1
2
[1 −
𝑚
1
𝑚
2
]
Ecuación 10. Profundidades subsecuentes para tuberías fluyendo parcialmente llenas.
2.2 Tubería totalmente llena
Para este tipo de tuberías, el flujo se presuriza aguas abajo de la tubería lo cual hace que
𝑘
(distancia al centro de gravedad) se exprese con función de la relación de llenado como se
observa en la Ecuación 11.
𝑘
2
′
=
(𝑑
2
−
𝐷
2)
𝑑
2
Ecuación 11.Diámetro de flujo con respecto al centro de gravedad para tuberías fluyendo totalmente llenas.
Por otro lado, reemplazando la Ecuación 11 en la Ecuación 8 se obtiene:
𝑚
2
𝑚
1
𝑑
2
𝑑
1
−
1
2
𝑚
2
𝑚
1
𝐷
𝑑
1
− 𝑘
1
′
= 𝐹
1
2
[1 −
𝑚
1
𝑚
2
]
2.3 Resultados finales
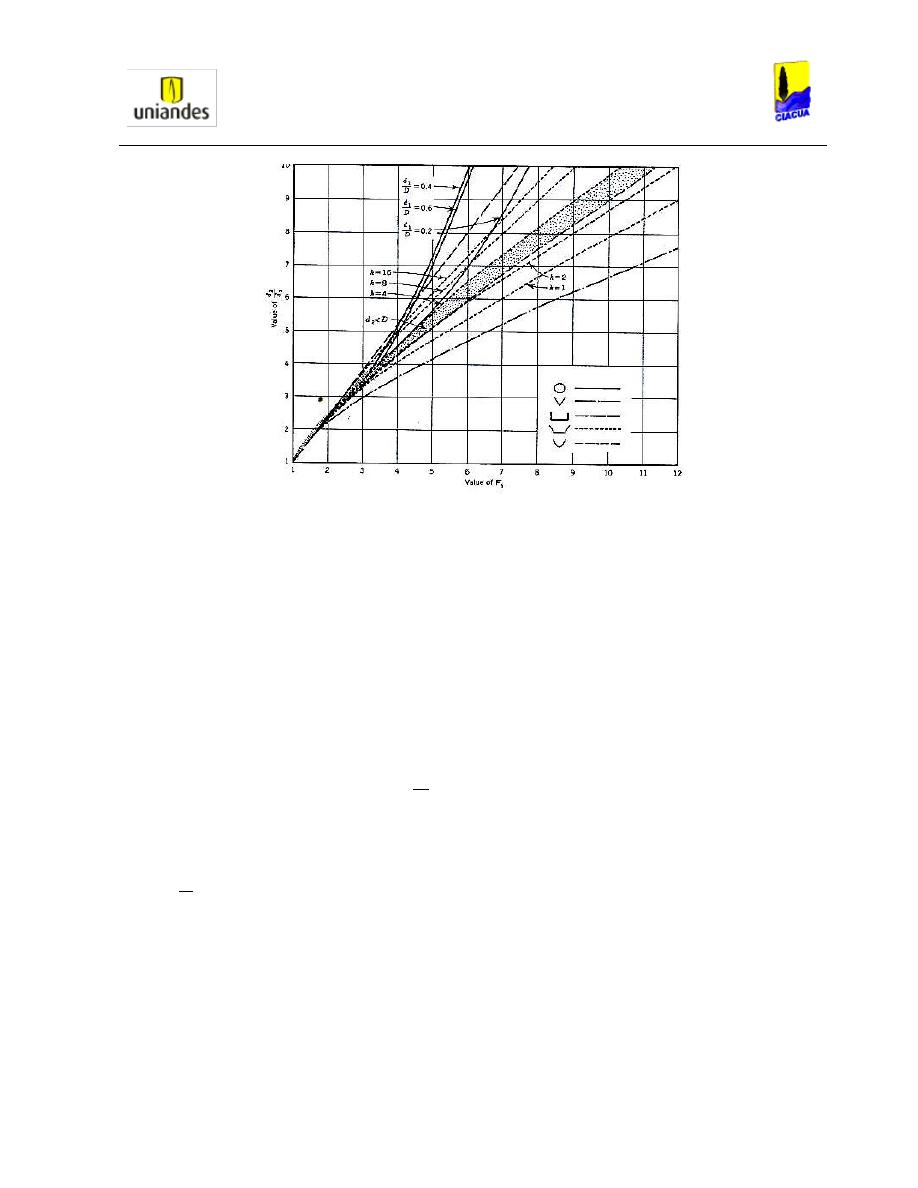
Luego de que Richard Silvester estudiara el comportamiento de cada una de las secciones
horizontales, realizó un diagrama de las relaciones de llenado contra el número de Froude
aguas arriba, encontrando que las tuberías con sección circular presentan números de Froude
menores con mayores relaciones de llenado que las demás secciones estudiadas. Además, la
sección rectangular es la que presenta el mejor comportamiento, soportando números de
Froude mayores y presentando relaciones de llenado más bajas con respecto a las demás
secciones, tal como se observa en la Gráfica 5 que presenta los resultados finales de todas las
secciones trabajadas.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
20
Gráfica 5. Datos obtenidos para los diferentes tipos de secciones (Silvester, HYDRAULIC JUMP IN ALL
SHAPES OF HORIZONTAL CHANNELS., 1964).
Por otro lado, Silvester fue el primero en encontrar una ecuación de forma experimental para
determinar la longitud del resalto que se producía en una tubería circular. Sin embargo, para
esto se basó en las relaciones de llenado obtenidas aguas abajo y aguas arriba de la tubería y
en los experimentos realizados anteriormente por Kindsvater y Lane en 1934. Lo anterior para
obtener como resultado una ecuación en función del número de Froude y de las pérdidas por
fricción las cuales supuso como constantes a través de toda la tubería (Silvester, HYDRAULIC
JUMP IN ALL SHAPES OF HORIZONTAL CHANNELS., 1964). La expresión se muestra a
continuación:
𝐿
𝑑
1
= 𝐾 (𝐹
1
− 1)
𝛼
Ecuación 12. Expresión para el cálculo de la longitud del resalto en cualquier tipo de sección.
donde
𝐿
𝑑
1
es la relación entre la longitud del resalto y la profundidad de flujo aguas arriba del
resalto,
𝐾 es la constante de pérdidas por fricción, 𝐹
1
es el número de Froude aguas arriba y
𝛼 se determina por las relaciones de llenado y el número de Froude aguas arriba.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
21
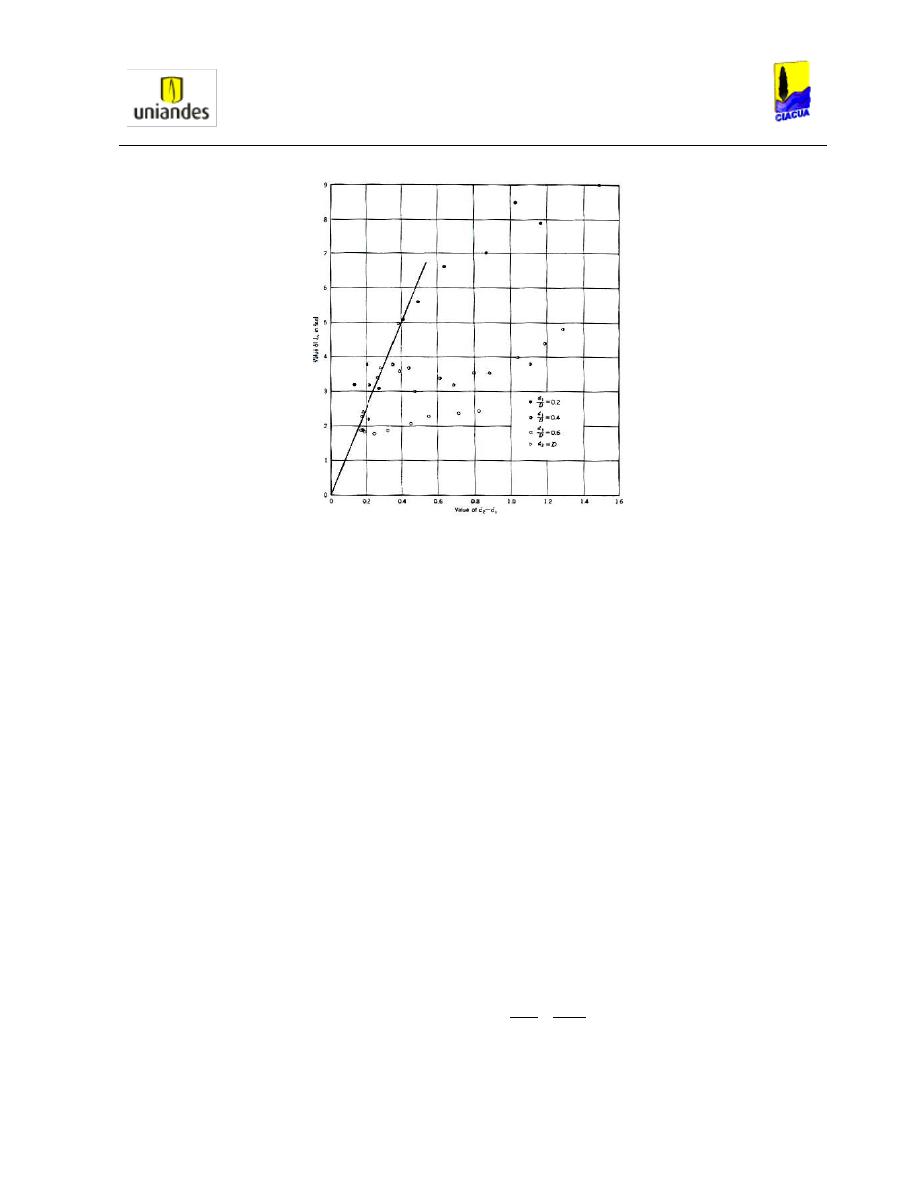
Gráfica 6. Resultados obtenidos de la variación de alturas versus la longitud del resalto (Silvester,
HYDRAULIC JUMP IN ALL SHAPES OF HORIZONTAL CHANNELS., 1964).
Como se puede observar en la gráfica anterior, al utilizar variaciones de alturas bajas, la longitud
del resalto aumenta, lo cual hace que este comportamiento sea inversamente proporcional.
Esto afirma lo explicado anteriormente en la Gráfica 5, donde se presentaba que a menores
relaciones de llenado, menores números de Froude, lo cual hace que el flujo sea menor y se
comporte de forma más lenta, presentando una menor aireación y por lo tanto una menor
longitud de resalto.
Rajaratnam (1965)
El análisis que realizó Rajaratnam se basó principalmente en los estudios anteriormente
realizados sobre el fenómeno de resaltos hidráulicos de Kindsvater (1938) sobre tuberías
horizontales y de Kalinske (1943) sobre canales abiertos y cerrados presentando variaciones
en su pendiente.
En su montaje trabajó las diferentes relaciones de llenado en una tubería para establecer la
cantidad de aireación que estas producían en un resalto hidráulico. Su experimento lo basó
partiendo principalmente de la ecuación de momentum en un resalto hidráulico (Rajaratnamn,
1965), expresada a continuación:
𝑃 + 𝑀 = 𝛾𝛹𝐷
2
𝜆𝑦 +
𝛾𝑄
2
𝑔
∗
1
𝛹𝐷
2
Ecuación 13. Momentum en un Resalto hidráulico.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
22
donde
𝑃 es la presión del agua, 𝑀 es el momentum, 𝛾 es función de la relación de llenado
aguas arriba,
𝐷 es el diámetro de la tubería, 𝑄 es el caudal de entrada, 𝛹 es función de la
relación de llenado,
𝑦 es la altura de la superficie de agua y 𝑔 es la gravedad. De esta forma,
se conoció anteriormente que en un resalto hidráulico la energía no se conserva pero el
momentum sí. Entonces la Ecuación 13 queda de la siguiente forma:
𝑃
1
+ 𝑀
1
= 𝑃
2
+ 𝑀
2
Ecuación 14. Conservación de momentum en un resalto hidráulico.
Ahora, se procede a combinar la Ecuación 13 y la Ecuación 14 para obtener finalmente:
1 −
𝛹
1
𝛹
2
𝜆
1
𝜆
2
𝑦
2
𝑦
1
= 𝐹
1
2
𝜂
1
𝜆
1
(
𝛹
1
𝛹
2
− 1)
Como se ha explicado anteriormente se conoce que la ecuación del número de Froude es:
𝐹
1
2
=
𝑄
2
𝑔𝐷
5
𝛤
1
Ecuación 15. Cálculo del número de Froude según Rajaratnam.
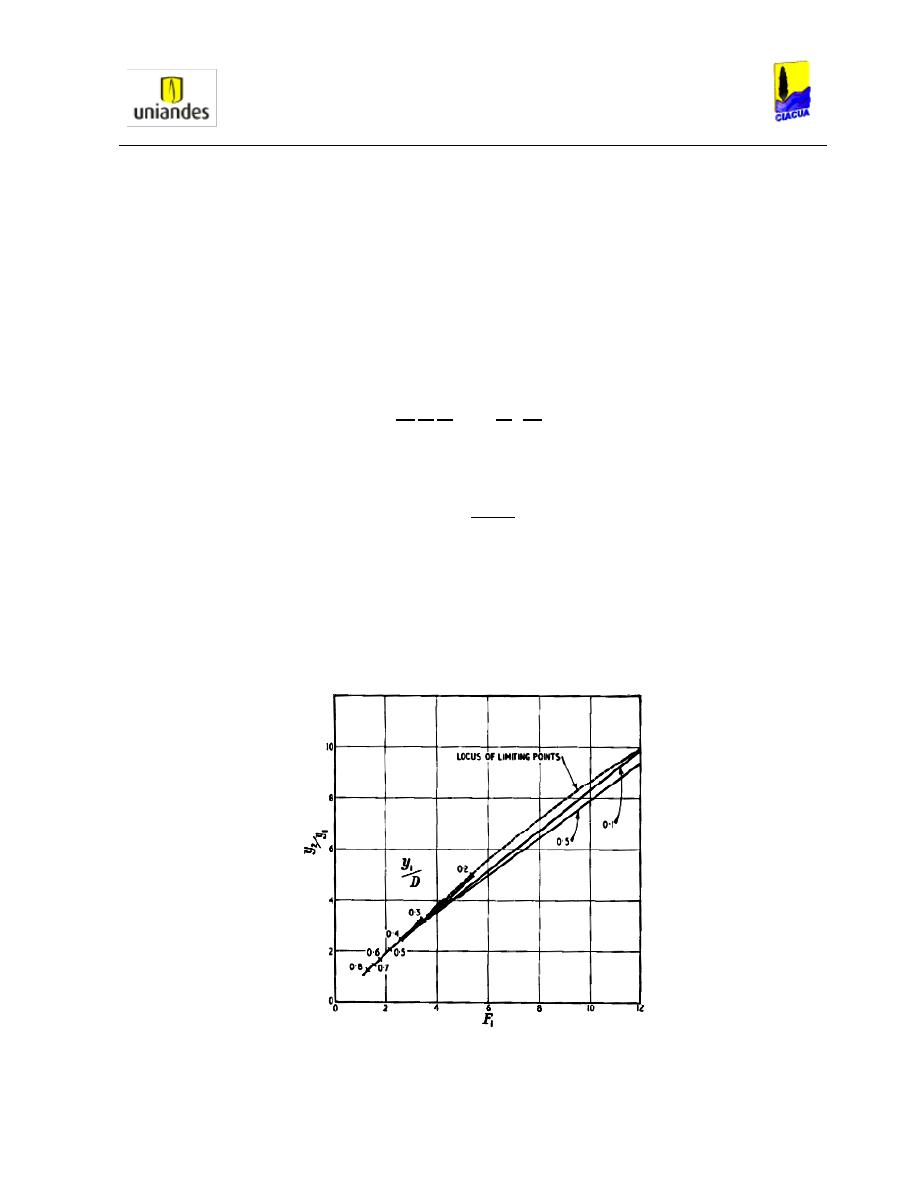
Luego de obtener las ecuaciones anteriores, Rajaratnam procedió al cálculo de las relaciones
de llenado en las tuberías y a estudiar el comportamiento de estas con respecto al número de
Froude aguas arriba obteniendo los resultados presentados en la Gráfica 7.
Gráfica 7. Relación de llenado versus número de Froude aguas arriba (Rajaratnamn, 1965).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
23
Cuando analizó los datos obtenidos, Rajaratnam encontró que para relaciones de llenado
superiores a 1.0, el estudio de estas no iba a ser válido por el comportamiento del flujo. Por lo
cual, no se permitía realizar ningún análisis o algún estudio adecuado del fenómeno del resalto
hidráulico. Por otro lado, al analizar la Gráfica 7, encontró que cuando el número de Froude
comienza a divergir, sus límites de relaciones de llenado se mantienen entre 0.2 y 0.5.
C. Smith y W. Chen (1989)
Las publicaciones hechas por C. Smith y W. Chen en 1989 acerca del fenómeno del resalto
hidráulico, se originaron a través de tuberías rectangulares sometidas a grandes pendientes,
para determinar los coeficientes más importantes que generan dicho fenómeno, y de esta
forma, obtener las variables de entrada necesarias para el cálculo de las profundidades
subsecuentes. Este artículo explica que la formación de un resalto hidráulico ocurre cuando hay
un cambio abrupto entre la altura de la superficie del flujo aguas arriba y la altura de la superficie
del flujo aguas abajo. Por esto, se necesita que la línea de gradiente hidráulico aguas abajo sea
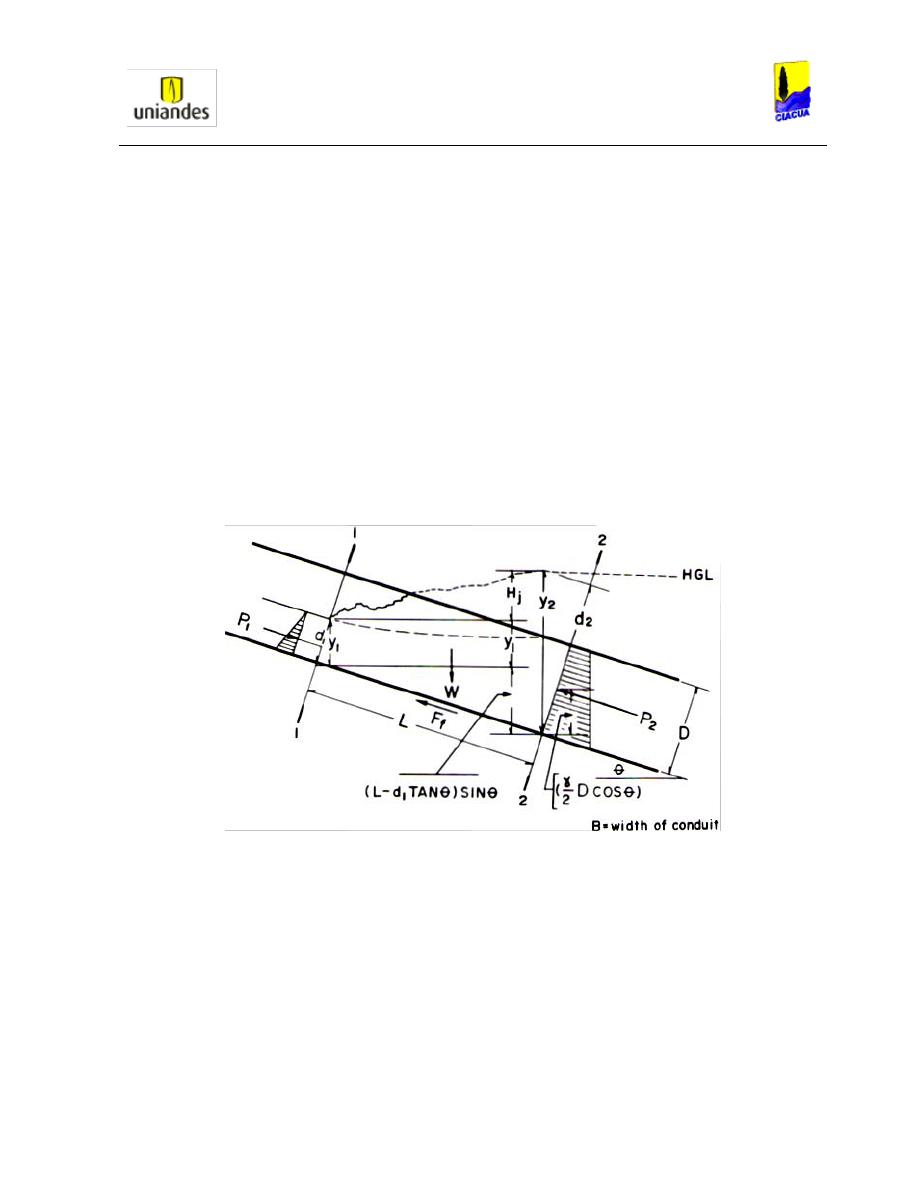
mayor que la cota clave de la tubería (Chen, 1989). A continuación se presenta una imagen del
procedimiento que desarrollaron con su respectiva explicación:
Gráfica 8. Comportamiento del resalto hidráulico dentro de la tubería (Chen, 1989).
Como se puede observar en la Gráfica 8, se estudió el comportamiento del resalto hidráulico
con su respectivo diagrama de fuerzas, perfiles de velocidades y líneas de gradiente hidráulico.
Luego se procedió al cálculo teórico de las ecuaciones para determinar el comportamiento de
este fenómeno. Primero se planteó la ecuación de conservación de momentum en la tubería
según la Gráfica 8 de la siguiente forma:
𝑃
1
− 𝑃
2
+ 𝑊 𝑠𝑒𝑛𝜃 − 𝐹
𝑓
= 𝑀
2
− 𝑀
1
Ecuación 16. Calculo de Momentum para tuberías.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
24
donde
𝑀 es el momentum, 𝑃 es la presión del agua, 𝑊es el peso del agua y 𝜃 es el ángulo de
la pendiente. Siguiendo con su análisis C. Smith y W. Chen encontraron que además de las
fuerzas mostradas en la Gráfica 8, esta tubería presentaba presiones de aire que no habían
sido mencionadas, por lo cual presentaron la siguiente corrección para la Ecuación 16
𝛾
2
𝐵 𝑑
1
2
𝑐𝑜𝑠𝜃 − [(
𝛾
𝑐𝑜𝑠𝜃
𝑑
2
−
𝛾
2
𝐷 𝑐𝑜𝑠𝜃) 𝐵𝐷] +
𝛾𝐾𝐵𝐷𝐿
1 + 𝛽
𝑗
𝑠𝑒𝑛𝜃 − 𝐹
𝑓
=
𝛽
2
𝛾𝑄
2
(1 + 𝛽
𝑎
)
𝑔𝐵𝐷
−
𝛽
1
𝛾𝑄
2
𝑔𝐵𝑑
1
Ecuación 17. Cálculo de momentum corregido para tuberías.
donde
𝛽 es el factor de corrección del Momentum, 𝛾 es el peso específico del agua, 𝑄 es el
caudal de entrada,
𝛽
𝑎
es la relación del aire con el agua debido a la entrada de aire aguas
abajo del resalto,
𝐵 es el ancho del canal, 𝐷 es el diámetro del canal, 𝐿 la longitud del resalto,
𝐾 es el factor de corrección menor a uno, 𝑔 es la gravedad, 𝜃 es el ángulo de la pendiente y 𝐹
𝑓
es la fuerza de fricción a lo largo del resalto. De esta forma, de la Gráfica 8 se puede deducir
que:
𝑦
1
=
𝑑
1
𝑐𝑜𝑠𝜃
; 𝑦
2
=
𝑑
2
𝑐𝑜𝑠𝜃
Ecuación 18. Profundidades aguas arriba y aguas abajo de la tubería.
Ahora se procede a reemplazar y a despejar la profundidad subsecuente aguas abajo en
términos de la profundidad subsecuente aguas arriba. Por lo tanto, se obtiene la siguiente
ecuación:
𝑑
2
= (
(𝛽
2
𝛾𝑄
2
(1 + 𝛽
𝑎
)
𝑔𝐵𝐷
−
𝛽
1
𝛾𝑄
2
𝑔𝐵𝑑
1
−
𝛾
2
𝐵𝑑
1
2
𝑐𝑜𝑠𝜃 + 𝐹
𝑓
−
𝛾𝐾𝐵𝐷𝐿
1 + 𝛽
𝑗
𝑠𝑒𝑛𝜃 −
𝛾𝐷𝐵𝐷
2
𝑐𝑜𝑠𝜃)
𝑐𝑜𝑠𝜃
𝛾𝐵𝐷
Ecuación 19. Cálculo de profundidades subsecuentes aguas abajo de la tubería.
Ahora, se procede a factorizar D obteniendo:
𝑑
2
= 𝐷 {(
(𝛽
2
𝛾𝑄
2
(1 + 𝛽
𝑎
)
𝑔𝐵𝐷
2
−
𝛽
1
𝛾𝑄
2
𝑔𝐵𝑑
1
𝐷
−
𝛾
2𝐷
𝐵𝑑
1
2
𝑐𝑜𝑠𝜃 +
𝐹
𝑓
𝐷
−
𝛾𝐾𝐵𝐿
1 + 𝛽
𝑗
𝑠𝑒𝑛𝜃 −
𝛾𝐷𝐵
2
𝑐𝑜𝑠𝜃)
𝑐𝑜𝑠𝜃
𝛾𝐵𝐷
2
}
Ecuación 20.Cálculo de ecuación factorizada de profundidades subsecuentes aguas abajo de la tubería.
Y sabiendo que el número de Froude se expresa de la siguiente forma

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
25
𝐹𝑟
1
2
=
𝑄
2
𝐵
2
𝑑
1
2
𝑔𝑑
1
Ecuación 21.Cálculo del número de Froude para tuberías.
Y realizando una sustitución trigonométrica
𝑐𝑜𝑠𝜃𝑠𝑒𝑛𝜃 = 𝑡𝑎𝑛𝜃 cos
2
𝜃
Ecuación 22. Sustitución trigonométrica.
Se pueden reemplazar la Ecuación 21 y la Ecuación 22 en la Ecuación 20:
𝑦
2
= 𝐷 {[𝛽
1
𝐹𝑟
1
2
(
𝑑
1
𝐷
)
2
− 𝛽
2
𝐹𝑟
1
2
(
𝑑
1
𝐷
)
3
(1 + 𝛽
𝑎
)] +
1
2
[(
𝑑
1
𝐷
)
2
+ 1] 𝑐𝑜𝑠𝜃 + 𝐾 (
𝐿
𝐷
)
𝑡𝑎𝑛𝜃𝑐𝑜𝑠𝜃
(1 + 𝛽
𝑗
)
−
𝐹
𝑓
𝛾𝐵𝐷
2
}
Ecuación 23. Cálculo simplificado de profundidades subsecuentes aguas abajo de la tubería.
Ahora, para el cálculo de la longitud del resalto hidráulico se tiene la siguiente ecuación
𝐻
𝑗
𝐷
=
1
𝐷
[𝑦
2
− 𝑦
1
− (𝐿 − 𝑑
1
𝑡𝑎𝑛𝜃)𝑠𝑒𝑛𝜃]
Ecuación 24. Cálculo del resalto hidráulico en tuberías.
Reemplazando en la Ecuación 23 se obtiene:
𝐻
𝑗
𝐷
=
1
𝐷
[𝐷 {[𝛽
1
𝐹𝑟
1
2
(
𝑑
1
𝐷
)
2
− 𝛽
2
𝐹𝑟
1
2
(
𝑑
1
𝐷
)
3
(1 + 𝛽
𝑎
)] +
1
2
[(
𝑑
1
𝐷
)
2
+ 1] 𝑐𝑜𝑠𝜃 + 𝐾 (
𝐿
𝐷
)
𝑡𝑎𝑛𝜃𝑐𝑜𝑠𝜃
(1 + 𝛽
𝑗
)
−
𝐹
𝑓
𝛾𝐵𝐷
2
} −
𝑑
1
𝑐𝑜𝑠𝜃
− ((𝐿 − 𝑑
1
𝑡𝑎𝑛𝜃)𝑠𝑒𝑛𝜃)]
Ecuación 25. Cálculo del resalto hidráulico reemplazado en términos conocidos.
Finalmente, factorizando
𝐹𝑟
1
2
,
(
𝑑
1
𝐷
) y reorganizando la ecuación, la expresión de la longitud del
resalto queda de la siguiente forma:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
26
𝐻
𝑗
𝐷
= 𝐹𝑟
1
2
(
𝑑
1
𝐷
)
2
[𝛽
1
− 𝛽
2
𝑑
1
𝐷
(1 + 𝛽
𝑎
) ] +
1
2
𝑑
1
𝐷
[(
𝑑
1
𝐷
) +
1
𝑑
1
𝐷
− 2 (
1
cos
2
𝜃
− tan
2
𝜃) ] 𝑐𝑜𝑠𝜃
+
𝐿
𝐷
(
𝐾
1 + 𝛽
𝑗
− 1) 𝑠𝑒𝑛𝜃 −
𝐹
𝑓
𝛾𝐵𝐷
2
Ecuación 26. Ecuación factorizada de la longitud del resalto reemplazada en términos conocidos.
Como se puede observar, a pesar de que la Ecuación 26 se reemplazó por términos conocidos,
se sigue teniendo cinco incógnitas en la ecuación por lo cual C. Smith y W. Chen realizaron los
siguientes supuestos:
𝛽
1
= 1
𝛽
2
= 1
𝛽
𝑎
= 0
𝛽
𝑗
= 0
𝑐𝑜𝑠𝜃 = 1
𝑠𝑒𝑛𝜃 = 0
1
cos
2
𝜃
− tan
2
𝜃 = 1
Ecuación 27. Supuestos realizados por Smith y Chen para el cálculo de la longitud del resalto.
Posteriormente, se simplifica la Ecuación 26 y se obtiene la expresión necesaria para el cálculo
de la longitud del resalto en tuberías:
𝐻
𝑗
𝐷
= 𝐹𝑟
1
2
(
𝑑
1
𝐷
)
2
[1 −
𝑑
1
𝐷
] +
1
2
𝑑
1
𝐷
[(
𝑑
1
𝐷
) +
1
𝑑
1
𝐷
− 2]
Ecuación 28. Expresión final para el cálculo de la longitud del resalto hidráulico
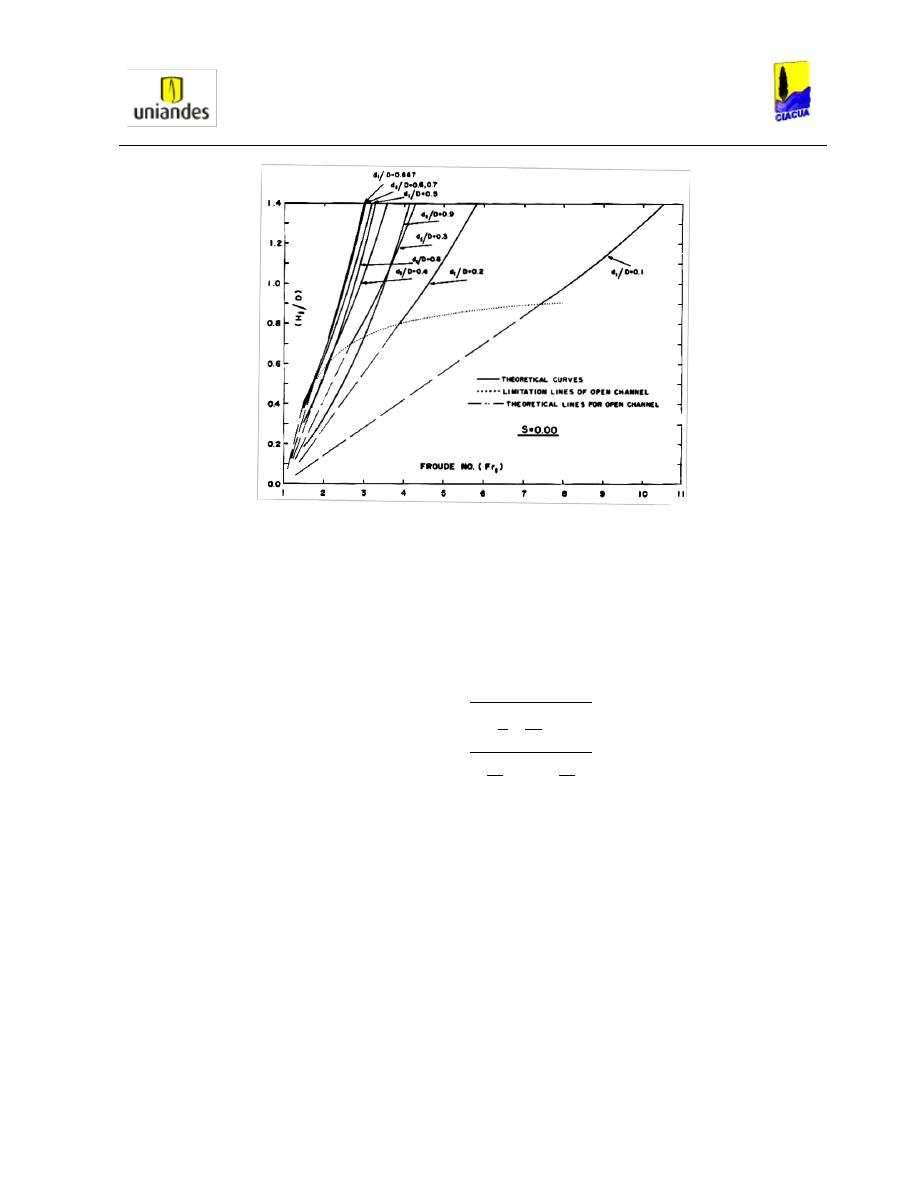
Finalmente, se utilizó la Ecuación 28 para comparar la longitud del resalto con el número de
Froude aguas arriba de la tubería obteniendo los resultados mostrados en la Gráfica 9:
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
27
Gráfica 9. Longitud del resalto hidráulico versus el número de Froude aguas arriba (Chen, 1989).
Como se puede observar en la Gráfica 9, Smith y Chen concluyeron que para este ensayo en
tuberías cuadradas con pendiente horizontal, la profundidad subsecuente del resalto era mayor
al diámetro de la tubería, por lo cual esta se iba a presurizar aguas abajo. Por otro lado, para
encontrar la profundidad critica de la tubería y encontrar el sitio donde se forma el resalto
hidráulico aguas arriba, ellos despejaron la siguiente ecuación:
𝐹𝑟
1
= √
1 −
1
2 [(
𝑑
1
𝐷 )
2
+ 1]
(
𝑑
1
𝐷 )
2
(1 −
𝑑
1
𝐷 )
Ecuación 29. Cálculo de Froude para profundidad crítica.
Y suponiendo que
𝑑
2
= 𝐷
Ecuación 30. Supuesto final para cálculo de la profundidad crítica.
Se obtuvieron los siguientes números de Froude aguas arriba
(𝐹𝑟
1
) para diferentes relaciones
de llenado
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
28
Tabla 2. Resultados de números de Froude aguas arriba para diferentes relaciones de llenado (Chen, 1989).
d
1
/D (-)
0.1
0.2
0.3
0.4
0.5
0.6
Fr
1
7.42
3.87
2.69
2.09
1.73
1.49
En conclusión se encontró que mientras el flujo sea más supercrítico, o sea, con menor
profundidad de flujo aguas arriba, el resalto se va comportar de forma más violenta. Por último,
si la profundidad aguas arriba del resalto es cercana al diámetro de la tubería, se formaría un
resalto hidráulico y la ecuación de profundidades subsecuentes tendería a cero.
Willi H. Hager y Helmut Stahl (1999)
El experimento de Hager y Stahl trató de los resaltos hidráulicos en tuberías circulares,
enfocándose en la demostración experimental, entre el comportamiento de la tubería en la
variación del número de Froude y la variación del momentum. Tal demostración partió del
supuesto inicial de la profundidad subsecuente para calcular el área y de esta forma llegar a la
presión que ejerce el agua en la tubería circular de la siguiente forma (Hager S. H., 1999):
𝐴
𝐷
= 𝑦
1
5
Ecuación 31. Profundidades subsecuentes.
donde
𝐴 es el área mojada, 𝐷 es el diámetro de la tubería y 𝑦 la relación de llenado. Por otro
lado, se utilizó la Ecuación 32 para obtener una aproximación a la presión del agua en la tubería:
𝑃
𝜌 ∗ 𝑔 ∗ 𝐷
3
=
1
2
∗ 𝑦
2.5
Ecuación 32. Fuerza de presión del agua en una tubería.
donde
𝑃 es la Fuerza de presión, 𝜌 es la densidad y 𝑔 es la gravedad.
Por lo tanto, la ecuación del momentum quedaría de la siguiente forma:
1
2
∗ 𝑦1
2.5
+
𝑄
2
𝑔 ∗ 𝐷
5
∗ 𝑦1
1.5
=
1
2
∗ 𝑦2
2.5
+
𝑄
2
𝑔 ∗ 𝐷
5
∗ 𝑦2
1.5
Ecuación 33. Ecuación de momentum en tuberías.
En esta ecuación (Ecuación 33) Hager y Stahl determinaron que existía un error de un 20%
estando en un rango entre 0.2 <
𝑦 < 0.9; esta desventaja fue aceptable para ellos porque se

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
29
ajustaría empíricamente. Por otro lado, se introdujo la ecuación del número de Froude que
había planteado Hager en 1990 en su libro
“Froude number in Circular Conduits”.
𝐹 =
𝑄
√𝑔 ∗ 𝐷 ∗ ℎ
4
Ecuación 34. Número de Froude para conductos circulares.
donde
𝐹 es el número de Froude, ℎ es la altura del flujo, 𝐷 es el diámetro de la tubería y 𝑔 es
la gravedad. Ahora se procede a dividir la Ecuación 33 en
1/2 ∗ 𝑦1
1 +
2𝑄
2
𝑔 ∗ 𝐷
5
∗ (
ℎ1
𝐷 )
3.75
=
𝑦2
2.5
𝑦1
2.5
+
2 ∗ 𝑄
2
𝑔 ∗ 𝐷
5
∗ 𝑦2
1.5
∗ 𝑦1
2.5
Ecuación 35. Ecuación 33 reorganizada.
Luego, sabiendo que
𝑌 =
𝑌1
𝑌2
Ecuación 36. Relación de alturas aguas arriba y aguas abajo de una tubería parcialmente llena.
Y aproximando 3.75 a 4, la Ecuación 35 queda de la siguiente forma:
1 +
2𝑄
2
𝑔 ∗ 𝐷
5
∗ (
ℎ1
𝐷 )
4
= 𝑌
2.5
+
2 ∗ 𝑄
2
∗ 𝑦
1.5
𝑔 ∗ 𝐷
5
∗ 𝑦2
1.5
∗ (
ℎ1
𝐷 )
4
Ecuación 37. Ecuación de momentum en una tubería fluyendo parcialmente llena.
Y reemplazando la Ecuación 34 en la Ecuación 37, quedaría de la siguiente forma:
1 + 2 ∗ 𝐹1
2
= 𝑌
2.5
+ 2 ∗ 𝐹1
2
∗ 𝑌
−1.5
Ecuación 38. Ecuación final de momentum en una tubería fluyendo parcialmente llena.
Para números de Froude mayores a 2 (F
1
>2), una aproximación sería:
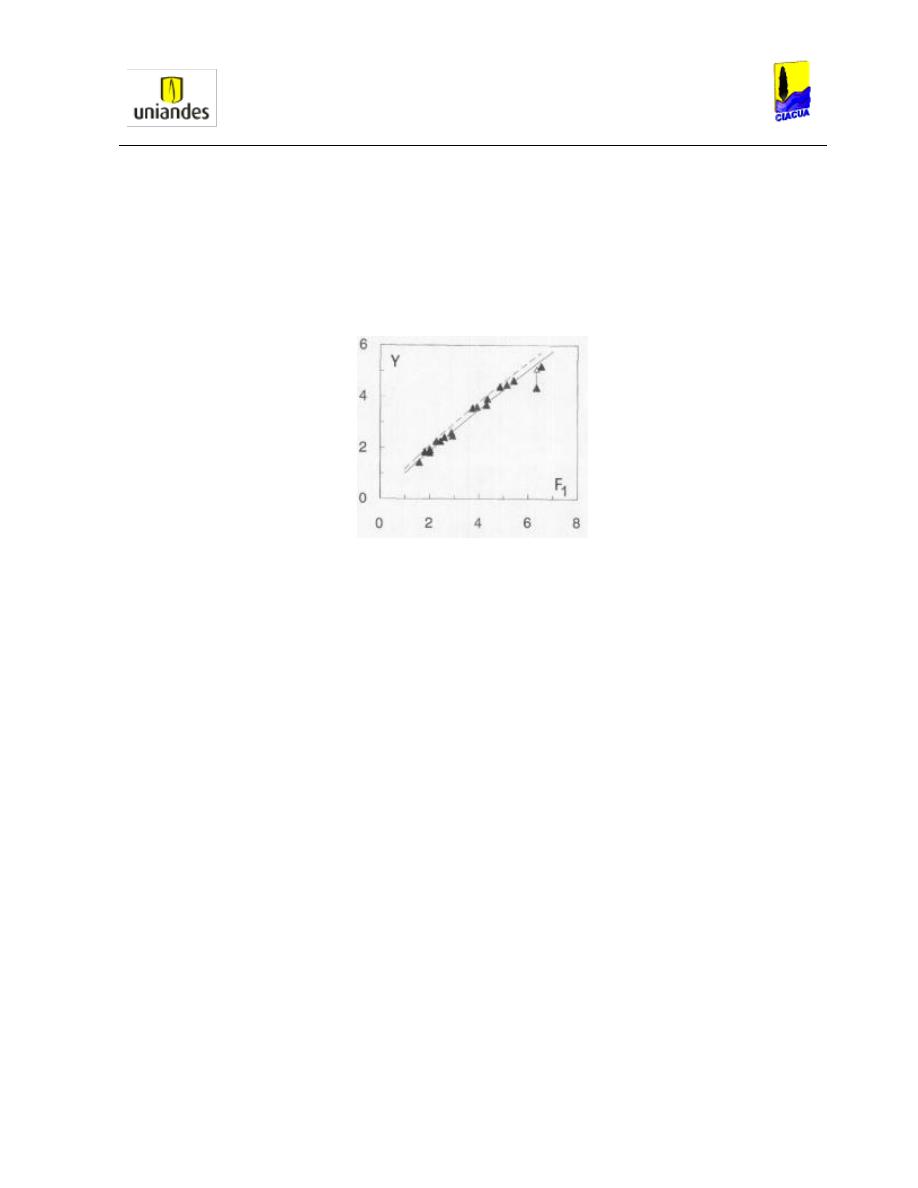
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
30
𝑌 = 1.16 ∗ 𝐹𝑟
1
0,85
Ecuación 39. Cálculo de profundidades subsecuentes para números de Froude aguas arriba mayores a 2.
Este experimento fue realizado con una tubería circular en acrílico con un diámetro de 240 mm,
una pendiente del 0,5% y una longitud de 6 m. Stahl y Hager realizaron el experimento y los
primeros resultados que obtuvieron fueron los siguientes:
Gráfica 10. Profundidades subsecuentes según el número de Froude (Hager, 1999).
Como se puede observar en la Gráfica 10, los resultados obtenidos en el experimento
mostraron un número de Froude entre los rangos de {1,5 y 6,5}, lo cual presenta que el flujo se
va a mantener en estado supercrítico. Por esta razón, Hager y Stahl se dieron cuenta que
habían sobrestimado la Ecuación 39 a causa de la viscosidad, por lo cual para satisfacer la
condición
𝑌(𝐹1 = 1) = 1 plantearon la siguiente ecuación:
𝑌 = 1.16 ∗ 𝐹1
0.90
Ecuación 40. Nuevo cálculo de profundidades subsecuentes para números de Froude aguas arriba
mayores a 2.
En conclusión, se pudo determinar que para secciones circulares en tuberías fluyendo
parcialmente llenas, existen cuatro diferentes tipos de resaltos: ondular, normal, flujo
recirculante y con turbulencia presurizada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
31
Gráfica 11.Tipo de resalto ondular con números de Froude< 1.5 (Hager, 1999).
El resalto hidráulico ondular se presenta cuando el número de Froude es 1.5; se
reconoce por presentar un comportamiento ondular y permanente durante todo el
trayecto.
Gráfica 12. Tipo de resalto ondular con números de Froude entre (1.5-2) (Hager, 1999).
El resalto hidráulico normal se presenta cuando el número de Froude se encuentra entre
un rango de {1,5 y 2}; se reconoce porque la tubería se presuriza y las ondas que genera
se pierden aguas abajo.
Gráfica 13. Tipo de resalto ondular con números de Froude entre (2-4.1) (Hager, 1999).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
32
El resalto hidráulico de flujo recirculante se presenta cuando el número de Froude se
encuentra entre un rango de {2 y 4,1}; se reconoce por formar remolinos laterales que
recirculan a través de toda la tubería aguas abajo.
Gráfica 14. Tipo de resalto ondular con números de Froude>6.5 (Hager, 1999).
El último tipo y más fuerte de resalto hidráulico es con la tubería presurizada. Este se
presenta con números de Froude superiores a 6,5 y se caracteriza por tener una
profundidad de flujo aguas abajo mayor al diámetro de la tubería, lo cual hace que la
tubería en esta sección se presurice.
Steven Michell (2002)
Este conocido ingeniero civil de la Universidad de Bank, al sur de Londres, trabajó sobre los
resaltos hidráulicos en canales abiertos con diferentes tipos de tuberías, entre las cuales
estaban las secciones trapezoidales, circulares, rectangulares y triangulares. Steven Michell se
encargó de encontrar las diferencias entre secciones y estudiar el comportamiento del flujo a
través de cada una de estas. Además, encontró que los resaltos hidráulicos son fundamentales
en la hidráulica de canales abiertos, y por medio de unos algoritmos estimó la relación de alturas
en un resalto hidráulico y el número de Froude para tuberías parcialmente llenas. El desarrollo
de estos algoritmos se basó en la conservación del momentum y usó valores estimados para
obtener un radio adecuado para la tubería por medio del proceso iterativo de Newton-Raphson
(Michell, 2008).
El desarrollo de su estudio comenzó con un modelo de sección rectangular en un canal
horizontal en el que supuso que la respectiva ecuación de momentum se podía expresar de la
siguiente forma:
𝑍̅
1
∗ 𝐴
1
+
𝑄
2
𝑔 ∗ 𝐴
1
= 𝑍̅
2
∗ 𝐴
2
+
𝑄
2
𝑔 ∗ 𝐴
2
Ecuación 41. Ecuación de Momentum.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
33
donde
𝑍̅ es la distancia vertical entre el centroide del área del flujo y la superficie del agua, 𝐴
es el área transversal del canal,
𝑄 es el caudal de entrada y 𝑔 es la aceleración de la gravedad.
La notación que se presenta como subíndices 1 y 2 hace referencia a la diferencia de alturas
luego que ocurre el resalto, como se observa en la Gráfica 15:
Gráfica 15. Grafica de elevación del resalto hidráulico (Michell, 2008)
2.1 Canales rectangulares
Para un canal rectangular
𝑍̅ =
𝑦
2
y
𝑄 = 𝑞 ∗ 𝐵, donde 𝑦 es la altura del flujo, 𝑞 es el caudal por
unidad de área y
𝐵 es el ancho del canal. Obteniendo una mejor expresión:
𝑦
2
𝑦
1
=
1
2
∗ (√1 + 8 ∗ 𝐹
1
2
− 1)
Ecuación 42. Relación entre alturas para canales rectangulares.
donde F es el número de Froude dado por
𝐹 =
𝑣
√𝑔∗𝑦
, y
𝑣 es la velocidad del flujo dada por 𝑣 =
𝑄
𝐴
. En la Ecuación 42 es posible obtener una aproximación para la relación entre alturas aguas
arriba y aguas abajo. Por otro lado, en un canal horizontal se pueden calcular las pérdidas de
energía que se presentan por el resalto hidráulico por medio de la siguiente expresión:
∆𝐸 = (𝑦
1
+
𝑣
1
2
2 ∗ 𝑔
) − (𝑦
2
+
𝑣
2
2
2 ∗ 𝑔
)
Ecuación 43. Expresión para calcular pérdidas de energía en canales rectangulares.
2.2 Canales trapezoidales
Para el caso de un canal con sección trapezoidal fluyendo parcialmente lleno, estas ecuaciones
no son equivalentes. Por esta razón se debe realizar el siguiente análisis:
Para calcular el área del canal se tomó la siguiente expresión
𝐴 = (𝐵 + 𝑠 ∗ 𝑦) ∗ 𝑦 , como se
observa en la siguiente gráfica:
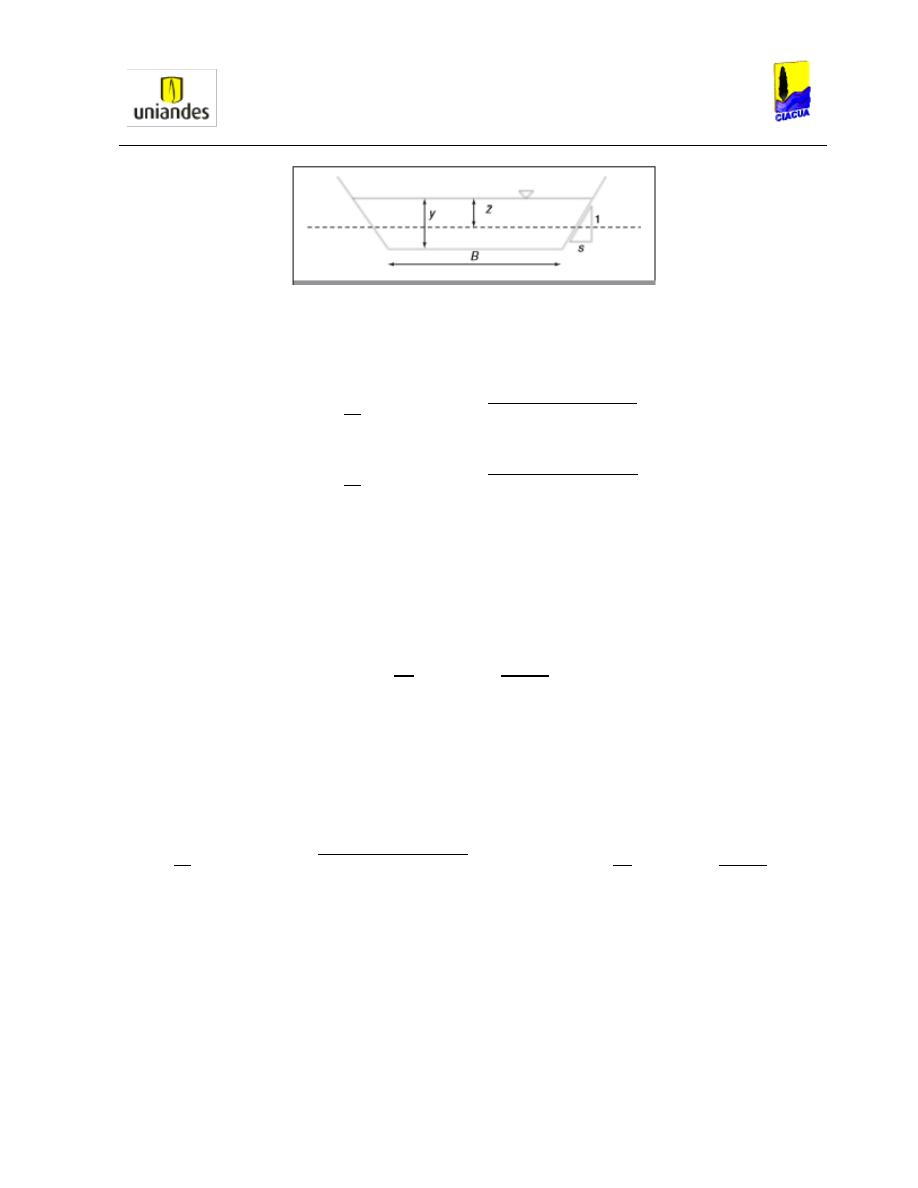
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
34
Gráfica 16. Definición de secciones para canal trapezoidal (Michell, 2008).
Por lo tanto para encontrar el centroide del área transversal,
𝑍̅ se expresa de la siguiente forma
𝑍̅
1
=
1
4𝑠
∗ (4𝑠𝑦
1
+ 2𝐵 − √4𝐵
2
+ 8𝑠(𝐵 + 𝑠𝑦
1
)𝑦
1
)
Ecuación 44. Centroide aguas arriba del área transversal de un canal de sección trapezoidal.
𝑍̅
2
=
1
4𝑠
∗ (4𝑠𝑦
2
+ 2𝐵 − √4𝐵
2
+ 8𝑠(𝐵 + 𝑠𝑦
2
)𝑦
2
)
Ecuación 45. Centroide aguas abajo del área transversal de un canal de sección trapezoidal.
La notación que se presenta como subíndices de 1 y 2, hace referencia a la diferencia de alturas
luego de que ocurre el resalto. La fórmula del área puede ser reemplazada con la Ecuación 41
de momentum, para obtener
𝑍̅
1
∗ (𝐵 + 𝑠𝑦
1
)
2
𝑦
1
2
+
𝑄
2
𝑔
− (𝑍̅
2
𝐴
2
+
𝑄
2
𝑔 ∗ 𝐴
2
) ∗ ((𝐵 + 𝑠𝑦
1
)𝑦
1
) = 0
Ecuación 46. Ecuación de momentum en un canal trapezoidal.
Reemplazando
𝑍̅
1
1
4𝑠
∗ (4𝑠𝑦
1
+ 2𝐵 − √4𝐵
2
+ 8𝑠(𝐵 + 𝑠𝑦
1
)𝑦
1
) ∗ (𝐵 + 𝑠𝑦
1
)
2
𝑦
1
2
+
𝑄
2
𝑔
− (𝑍̅
2
𝐴
2
+
𝑄
2
𝑔 ∗ 𝐴
2
)
∗ ((𝐵 + 𝑠𝑦
1
)𝑦
1
) = 0
Ecuación 47. Ecuación de momentum reemplazada en un canal trapezoidal.
Suponiendo que el valor de
𝑦
2
se conoce, se puede concluir que para calcular
𝑦
1
se utiliza la
siguiente ecuación:
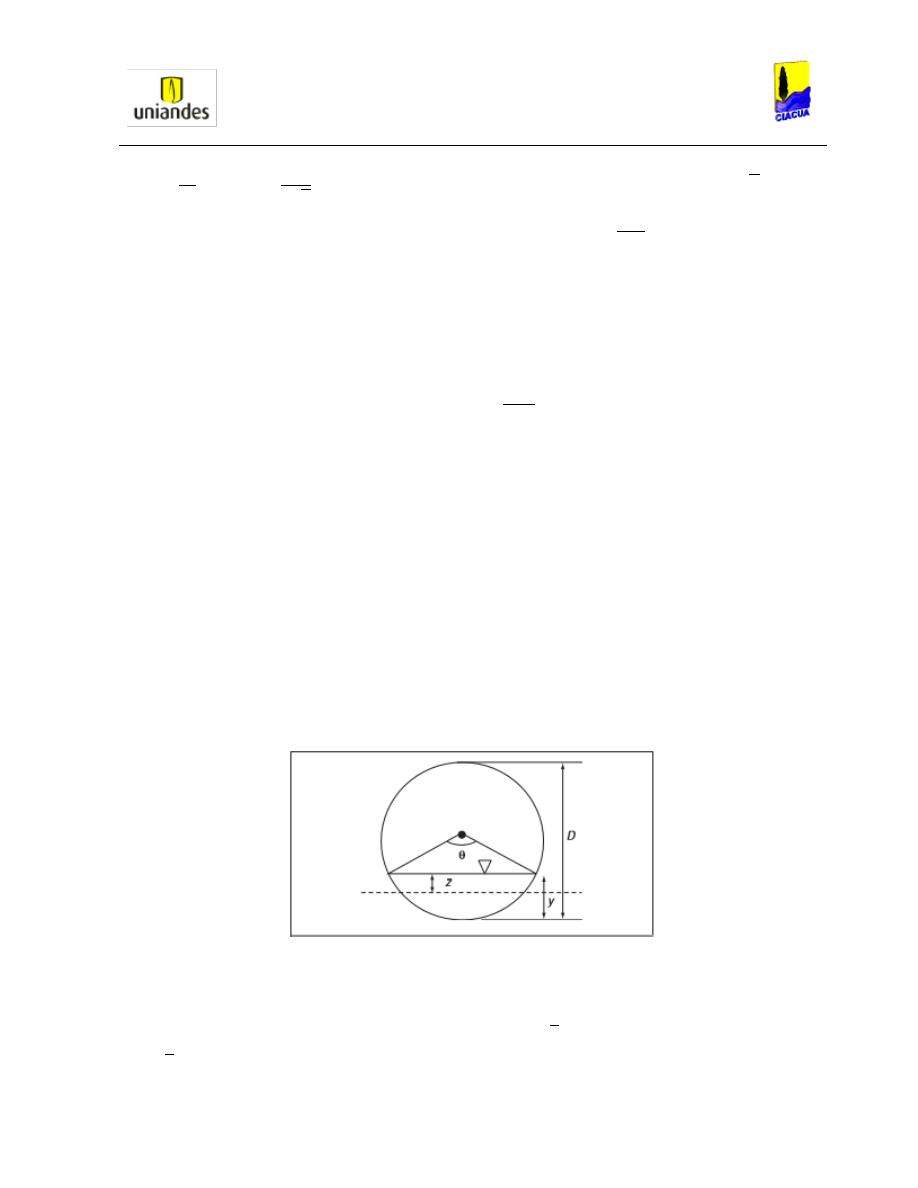
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
35
1
4𝑠
∗ {𝐴
1
[4𝑠 −
1
2√∅
∗ (8𝑠(4𝑠𝑦
1
+ 2𝐵) − (8𝑠(𝐵 + 𝑠𝑦
1
) + 8𝑠
2
𝑦
1
] + (4𝑠𝑦
1
+ 2𝐵 − √∅)
∗ (2𝑠𝑦
1
2
(𝑏 + 𝑠𝑦
1
) + 𝑠𝑦
1
(𝐵 + 𝑠𝑦
1
2
))} − [𝑍̅
2
𝐴
2
+
𝑄
2
𝑔𝐴
2
] (2𝑦
1
𝑠 + 𝐵)
Ecuación 48. Cálculo de Profundidades subsecuentes en un canal trapezoidal.
Con
∅ = (4𝑠𝑦
1
+ 2𝐵) − 8𝑠𝑦
1
(𝐵 + 𝑠𝑦
1
) y usando el método iterativo con la ecuación de Newton
Raphson
𝑦
𝑛
= 𝑦
𝑛−1
−
𝑓
(𝑥)
𝑓`
(𝑥)
Ecuación 49. Método iterativo te Newton-Raphson.
2.3 Canales circulares
Para el caso de una tubería de sección circular fluyendo parcialmente llena se debe tener en
cuenta el diámetro. Para este tipo de tuberías calcular
𝑍 de forma analítica no es posible, por
lo cual se procede a realizar una optimización numérica de aproximación polinómica de orden
cinco para D=1, llegando a la siguiente ecuación:
𝑍̅ = −0.000075𝜃
5
+ 0.000743𝜃
4
− 0.004636𝜃
3
+ 0.03232𝜃
2
− 0.00798𝜃 + 0.00232
Ecuación 50. Centroide del área transversal de una tubería de sección circular.
donde
𝜃 es el ángulo en el centro de la tubería conectando las líneas de la superficie de agua
como se muestra en la Gráfica 17.
Gráfica 17. Definición de ángulo para tuberías circulares parcialmente llenas (Michell, 2008).
De esta forma es posible obtener otra aproximación para
𝑍̅
𝐷
de forma polinómica, con un rango
para
𝑦
𝐷
entre 0.02-0.98. Luego se deriva la Ecuación 50 con respecto a
𝜃 y se obtiene

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
36
𝑑𝑍̅
𝑑𝜃
= −0.000376𝜃
4
+ 0.00297𝜃
3
− 0.0139𝜃
2
+ 0.0646𝜃 − 0.00798
Ecuación 51. Derivada del centroide del área transversal de una tubería de sección circular.
Con las expresiones ya obtenidas, se realiza el proceso iterativo de Newton Raphson para
obtener una aproximación de
𝜃. Los resultados que se obtuvieron para 𝑦 y para 𝐴 en términos
del ángulo
𝜃 son:
𝑦 =
𝐷
2
(1 − cos (
𝜃
2
))
Ecuación 52. Alturas obtenidas por método de Newton en términos de
𝛉.
𝐴 =
𝐷
2
8
(𝜃 − sin 𝜃)
Ecuación 53.Área obtenida por método de Newton en términos de
𝛉.
Usando la ecuación de momentum y utilizando el valor obtenido de
𝑍 calculado anteriormente
se puede obtener la siguiente ecuación:
𝑓
(𝜃1)
= 𝑍̅
1
𝐷
4
64
(𝜃
1
− sin 𝜃
1
)
2
+
𝑄
2
𝑔
− (𝑍̅
2
𝐴
2
+
𝑄
2
𝑔𝐴
2
)
𝐷
2
8
(𝜃
1
− sin 𝜃
1
)
Ecuación 54. Función para el cálculo de profundidades subsecuentes en una tuberia circular.
Ahora, se procede a volver a derivar la ecuación con respecto a
𝜃
1
𝑓`
(𝜃1)
=
𝐷
4
64
(𝜃
1
− sin 𝜃
1
)
2
𝑑𝑍
1
𝑑𝜃
1
+ 2𝑍̅
1
(𝜃
1
− sin 𝜃
1
) (1 − cos 𝜃
1
) − (𝑍̅
2
𝐴
2
+
𝑄
2
𝑔𝐴
2
)
𝐷
2
8
(1 − cos 𝜃
1
)
Ecuación 55. Derivada de la función para el cálculo de profundidades subsecuentes en una tubería
circular.
Usando las expresiones de la Ecuación 54 y la Ecuación 55 es posible aplicar el método de
Newton Raphson aplicado en el método de la sección trapezoidal para encontrar los valores de
𝜃
1
y 𝑦
1
.
2.4 Resultados obtenidos de todas las secciones
Finalmente, los resultados que se obtuvieron de estos tres ensayos para encontrar ciertas
similitudes y diferencias en cada una de estas secciones fueron los siguientes:
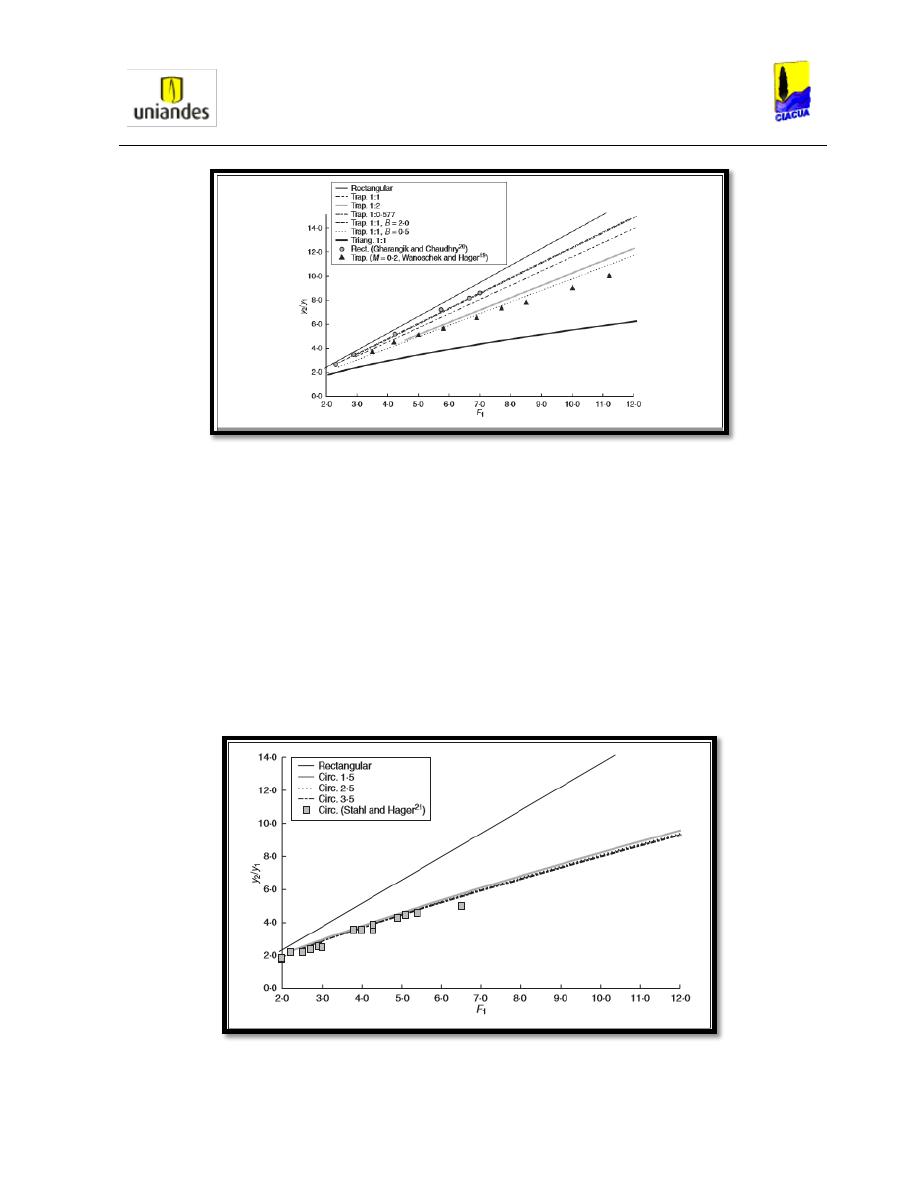
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
37
Gráfica 18. Relación de alturas VS Froude 1 del canal trapezoidal (Michell, 2008
)
.
Como se puede observar en la Gráfica 18, se trabajaron los canales trapezoidales con
diferentes pendientes y diferentes anchos para estudiar el comportamiento de estas. Steven
Michell analizó que, al variar el ancho del canal, la relación de alturas aumentaba de forma
proporcional al ancho. Además, encontró que los valores de Y2/Y1 decrecían para un Y1 dado
al aumentar la pendiente del canal. En el caso de los datos obtenidos por Wanoschek y Hager
se puede analizar que ellos presentaron sus resultados en términos del parámetro M
(𝑠𝑦_1)/𝑏 =
0.2 por lo cual concluyó que no era posible generar una comparación directa con los resultados
de este estudio. Por esta razón recurrieron a un ajuste en la gráfica y calcularon los coeficientes
mediante una recta más ajustada utilizando la binomial como se muestra en la Gráfica 19.
Gráfica 19. Relación de alturas VS Froude 1 de la tubería circular (Michell, 2008).
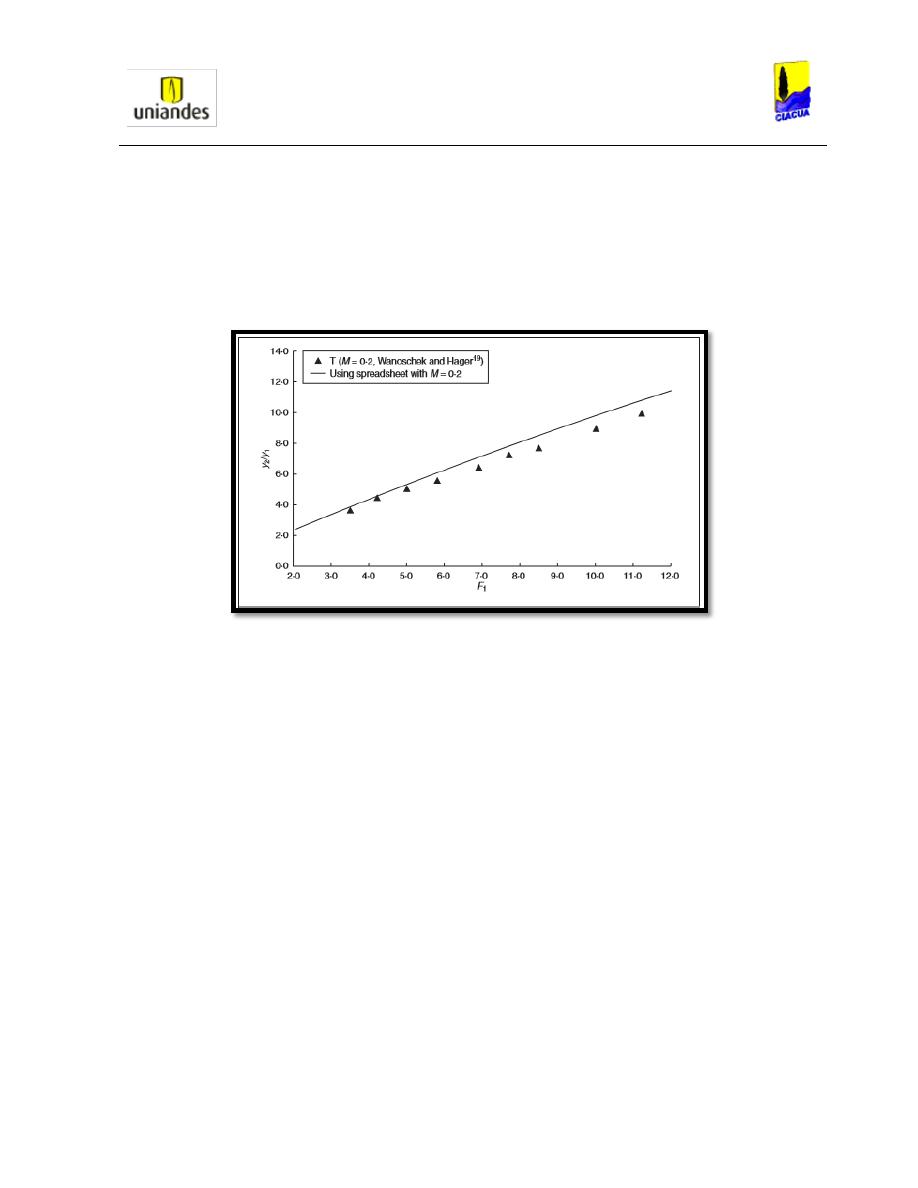
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
38
Para la tubería circular se observó en la Gráfica 19 que el comportamiento de esta a diferentes
diámetros presentó un Y2/Y1 de forma constante para un Y1 dado, por lo cual se descartó que
los cambios dependieran del diámetro de la tubería. Además se analizó que todos los
resultados presentados por el laboratorio coinciden con los datos teóricos calculados
anteriormente por Stahl y Hager en 1999.
Gráfica 20. Comparación de datos teóricos y experimentales del canal trapezoidal (Michell, 2008).
Como se observa en la Gráfica 20, al realizar el ajuste para un M=0.2 se encontró que el
comportamiento de la recta era de forma similar a lo propuesto por Wanoschek y Hager. Pero
al analizar todas las tuberías se encontró que para Fr
1
>6.0 las tuberías circulares presentaban
un mejor ajuste y comportamiento que los canales trapezoidales o rectangulares, basándose
en los resultados teóricos. Asimismo, se encontró que al comenzar la turbulencia en el inicio
del resalto, el perfil hidrostático no es tan válido y que las fuerzas de momentum verticales son
importantes.
Finalmente, se desarrolló un algoritmo en el experimento para encontrar las pérdidas de energía
que causaba cada tipo de resalto en cada una de las tuberías en las que se realizaron las
pruebas. De esta forma se encontró que un moderado incremento en pérdidas de energía era
muy variable para el canal trapezoidal en comparación de los demás y que la tubería circular
era la que presentaba un comportamiento más estable. A continuación se mostrarán los
resultados obtenidos en cada una de las secciones.
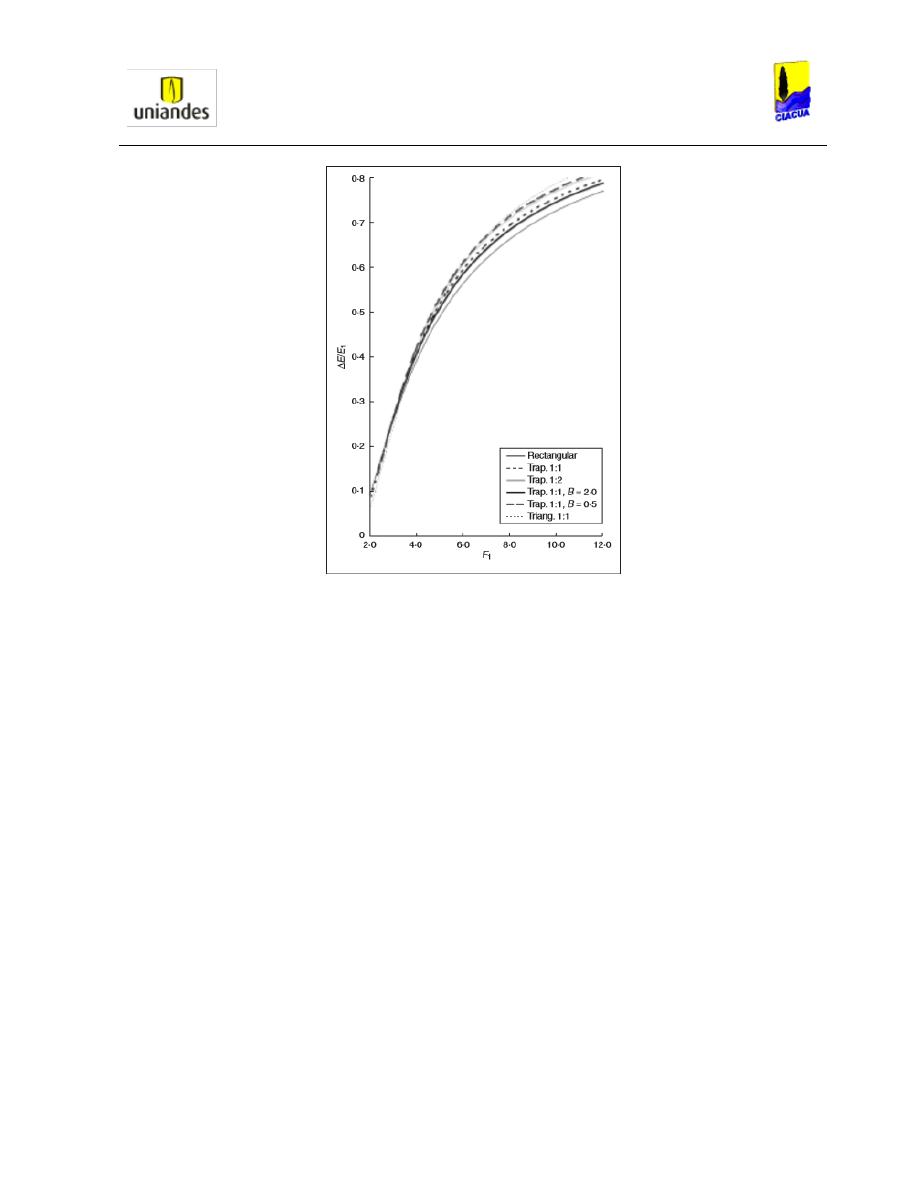
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
39
Gráfica 21. Pérdidas de energía contra el número de Froude 1 en canales trapezoidales.
Como se había dicho anteriormente, en canales trapezoidales se presentan cambios
constantes en cada una de las pendientes trabajadas y se puede observar que el canal de
mayor pendiente que se trabajó encontraba su estabilidad de forma más rápida que los demás.
Por otro lado, en las tuberías circulares que se trabajaron, se encontró que no había cambios
importantes en los cambios de pendientes y que la única pendiente que se comportó de manera
irregular con respecto a los demás ensayos, fue la de mayor pendiente, comportándose de
forma similar a las demás secciones que se trabajaron. A continuación se presentan los
resultados obtenidos en la tubería circular:
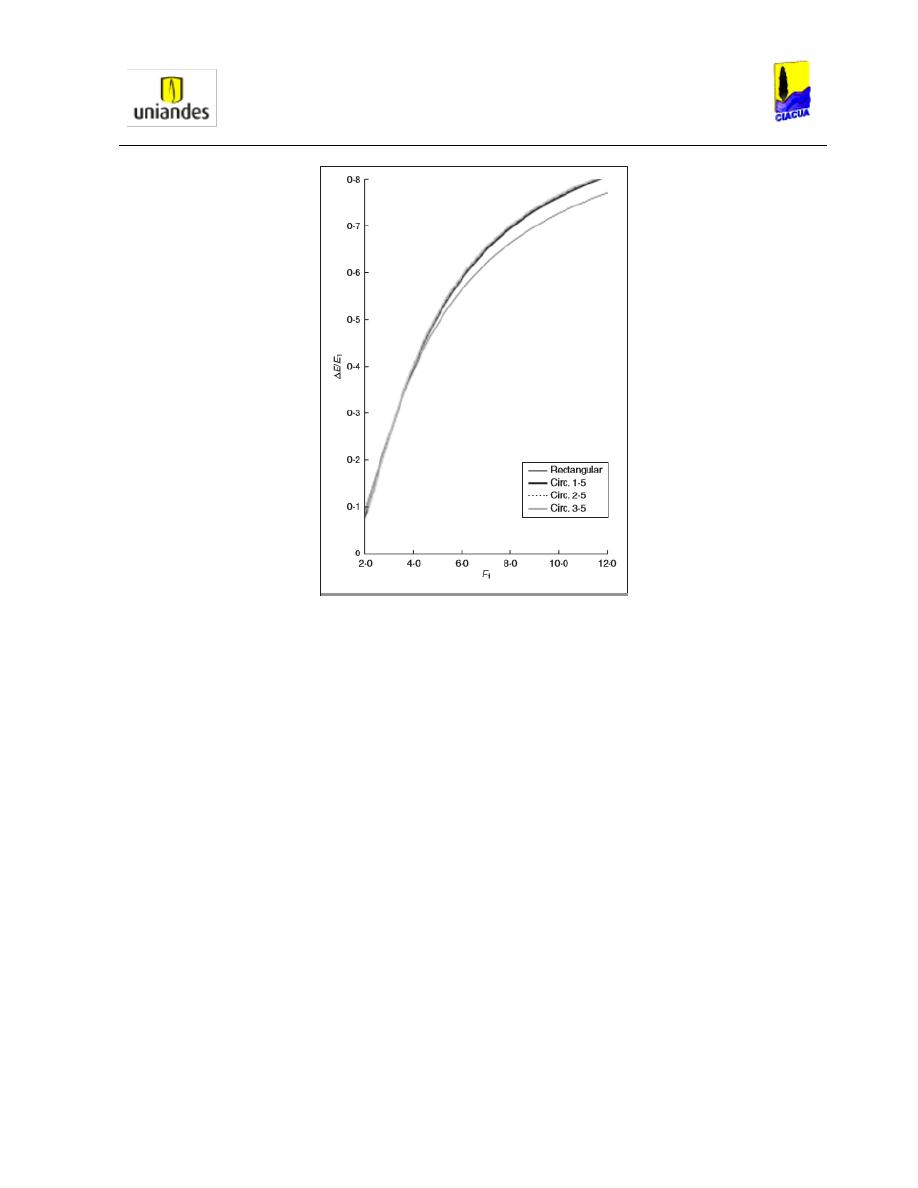
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
40
Gráfica 22.Pérdidas de energía contra el número de Froude 1 en tuberías circulares.
Journal of Hydraulic Research (2006)
La revista internacional de ingeniería “International Association of Hydraulic Engineering and
Research”, publicada por Taylor & Francis, publicó un análisis del comportamiento de los
resaltos hidráulicos en canales circulares y en forma de u, por el poco estudio y alta complejidad
que estos generan en ingeniería civil. Este estudio comenzó basándose en los experimentos
anteriores enfocados en modelos matemáticos y analíticos como el de Rajaratnam (1967) o el
de Hager (1992). Estos estudios fueron mostrados en canales rectangulares o con números de
Froude superiores a 4 para encontrar diferentes enfoques hidráulicos como: el comportamiento
del resalto hidráulico, la distribución hidrostática de presiones, las pérdidas de energías a lo
largo del canal, entre otras (Francis, 2006).
2.1 Estructura del resalto hidráulico
Primero que todo se comienza con la explicación de todas las partes que contiene un resalto
hidráulico y de las secciones que se trabajaron en este ensayo para entender mejor las
dimensiones y los términos que se utilizaron, tal como se muestra en las Gráfica 23 y en la
Gráfica 24.
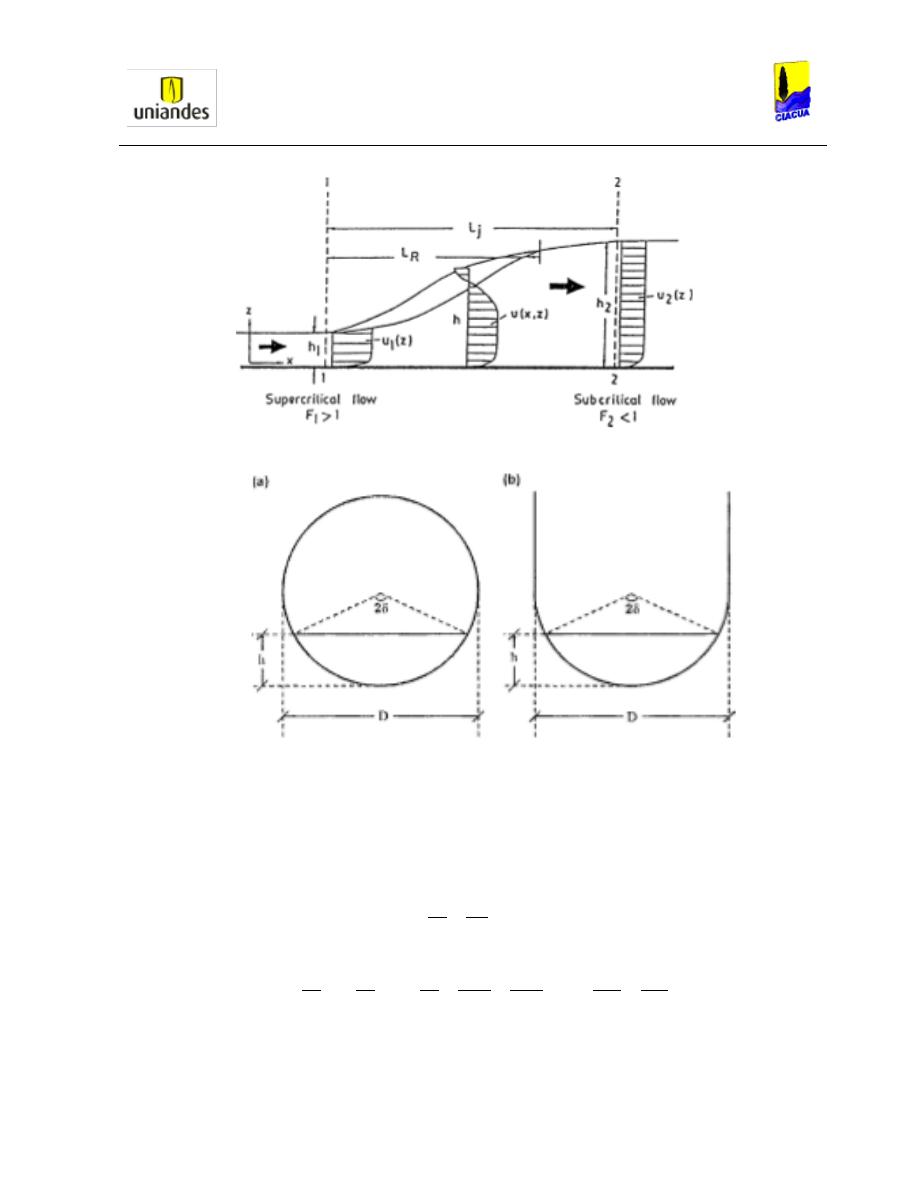
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
41
Gráfica 23. Partes que componen un resalto hidráulico (Francis, 2006).
Gráfica 24. Sección circular y en forma de U que se van a trabajar en el experimento (Francis, 2006).
2.2 Ecuaciones recomendadas en resaltos hidráulicos
En un flujo turbulento el flujo se somete a diferentes gradientes de presiones. Es por esto que
en este caso se trabajó con la ecuación de continuidad y la ecuación de Reynolds en el sentido
x del flujo, expresándolas a continuación:
𝜕𝑢
𝜕𝑥
+
𝜕𝑤
𝜕𝑧
= 0
Ecuación 56. Gradiente de presiones.
𝜌 (𝑢
𝜕𝑢
𝜕𝑥
+ 𝑤
𝜕𝑢
𝜕𝑧
) = −
𝜕𝑝
𝜕𝑥
+
𝜕𝜏
𝑥𝑥
𝜕𝑥
+
𝜕𝜏
𝑥𝑥
𝜕𝑧
+ 𝜌𝑣 (
𝜕
2
𝑢
𝜕
2
𝑥
+
𝜕
2
𝑢
𝜕
2
𝑧
)
Ecuación 57. Ecuación de la continuidad.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
42
𝜌 (𝑢
𝜕𝑤
𝜕𝑥
+ 𝑤
𝜕𝑤
𝜕𝑧
) = −𝜌𝑔 −
𝜕𝑝
𝜕𝑧
+
𝜕𝜏
𝑥𝑧
𝜕𝑥
+
𝜕𝜏
𝑧𝑧
𝜕𝑧
+ 𝜌𝑣 (
𝜕
2
𝑤
𝜕𝑥
2
+
𝜕
2
𝑤
𝜕𝑧
2
)
Ecuación 58. Ecuación de Reynolds.
donde
𝑢 es la velocidad en el sentido x del flujo, 𝑤 es la velocidad normal en el sentido z, 𝑝 es
la presión del agua,
𝜌 es la densidad del flujo y 𝑔 es la gravedad. Además, se conocen los
esfuerzos cortantes de Reynolds como:
𝜏
𝑥𝑥
= −𝜌𝑢`𝑢`
̅̅̅̅̅
𝜏
𝑧𝑥
= −𝜌𝑢`𝑤`
̅̅̅̅̅̅
𝜏
𝑧𝑧
= −𝜌𝑤`𝑤`
̅̅̅̅̅̅
Ecuación 59. Esfuerzos cortantes de Reynolds.
En el fondo del canal, las condiciones de fronteras de la velocidad de desplazamiento se toman
como:
𝑧 = 0 , 𝑢 = 𝑤 = 0 , 𝜏
𝑖𝑗
= 0
Ecuación 60.Condiciones de frontera de la velocidad de desplazamiento.
Como la superficie libre
𝑧 = ℎ
(𝑥)
es una línea de corriente donde las tensiones y las presiones
son constantes a lo largo de la tubería, se encuentra que los esfuerzos cortantes se desprecian.
Del mismo modo las condiciones de la superficie libre aerodinámica son:
𝑧 = ℎ
(𝑥)
,
𝑢 = 𝑢
ℎ(𝑥)
,
𝑤 = 𝑢
ℎ
𝜕ℎ
𝜕𝑥
,
𝜏
𝑖𝑖
≝ 𝑜
Ecuación 61. Condiciones de la superficie libre aerodinámica.
2.3 Condiciones del resalto
Para que se consigan las condiciones adecuadas en el resalto es necesario expresar dos
ecuaciones fundamentales: la primera es la ecuación de equilibrio de momentum aguas arriba
y aguas abajo de la tubería, y la segunda ecuación es la del número de Froude aguas arriba.
𝑤 +
𝑄
2
𝑔𝐴
1
= 𝑤 +
𝑄
2
𝑔𝐴
2
Ecuación 62. Ecuación de momentum para canales circulares y en forma de U.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
43
Reescribiendo la Ecuación 62, quedaría de la siguiente forma:
𝐴
1
𝐴
2
𝐴
2
− 𝐴
1
(𝑊
2
− 𝑊
1
) =
𝑄
2
𝑔
Ecuación 63. Ecuación de momentum para canales circulares y en forma de U.
Y sabiendo que el número de Froude aguas arriba se expresa como:
𝐹𝑟
1
2
=
𝑄
2
𝑔𝐴
1
3
𝑑𝐴
1
𝑑ℎ
1
Ecuación 64. Cálculo del número de Froude aguas arriba del canal.
donde
𝐹𝑟 es el número de Froude aguas arriba del canal. La segunda ecuación muestra que el
producto de las velocidades subsecuentes en el resalto permanece constante.
𝑈
1
𝑈
2
= 𝑈
𝑐
2
= 𝑔ℎ
𝑐
,
ℎ
𝑐
=
𝑊
2
− 𝑊
1
𝐴
2
− 𝐴
1
Ecuación 65. Velocidades subsecuentes en el resalto hidráulico.
donde
𝑈
𝑐
= √𝑔ℎ
𝑐
es la velocidad crítica. Además, la ecuación de profundidad de Reynolds en
el resalto hidráulico, basada en la Ecuación 61 se puede expresar de la siguiente forma:
𝑇
𝑥𝑥
𝐴
2
(𝐴
2
− 𝐴
1
)
𝜌𝑔
= 𝑊𝐴(𝐴
2
− 𝐴
1
) − 𝐴(𝑊
2
𝐴
2
− 𝑊
1
𝐴
1
) + 𝐴
2
𝐴
1
(𝑊
2
− 𝑊
1
)
Ecuación 66. Ecuación de profundidad de Reynolds en el resalto hidráulico.
Para seguir con la demostración y simplificación de la ecuación de momentum, es necesario
conocer que:
𝜏
𝑛𝑛
= 𝜌𝑣
𝑡
𝜕𝑈
𝜕𝑥
Ecuación 67. Viscosidad de remolino.
donde
𝑣
𝑡
= ∈ (𝑈
1
− 𝑈
2
)(ℎ
2
− ℎ
1
)
Ecuación 68. Gradiente promedio de la velocidad axial.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
44
En el resalto hidráulico, para la viscosidad cinemática en el remolino, la velocidad es asociada
con
∆𝑈 = 𝑈
1
− 𝑈
2
y la longitud con
∆ℎ = ℎ
1
− ℎ
2
y
∈ a una variable independiente asociada con
la geometría del canal. De esta forma, la ecuación del resalto hidráulico puede ser simplificada
de la siguiente forma:
∈ (1 − 𝛼)
𝜕𝐴
𝜕𝑥
+ (𝛾
1
𝑊
𝑊
2
− 𝛾
3
) 𝐴 + 𝛾
2
𝐴 = 0 , 𝑋 =
𝑥
ℎ
2
Ecuación 69. Ecuación simplificada del resalto hidráulico
.
donde las constantes
𝛾
1
,
𝛾
2
y
𝛾
3
son:
𝛾
1
=
𝑊
2
𝑊
2
− 𝑊
1
,
𝛾
2
=
𝐴
2
𝐴
2
− 𝐴
1
, 𝛾
3
=
𝑊
2
𝐴
2
(𝑊
2
− 𝑊
1
)(𝐴
2
− 𝐴
1
)
Ecuación 70. Constantes para el cálculo del resalto hidráulico.
Ahora se procede a obtener las condiciones de frontera para que se cumpla la Ecuación 69:
𝑥 → −∝ ,
𝐴 → 𝐴
1
, 𝑊 → 𝑊
1
;
𝑥 → +∝ ,
𝐴 → 𝐴
2
, 𝑊 → 𝑊
2
Ecuación 71. Condiciones de frontera para el cálculo del resalto hidráulico aguas arriba y aguas abajo del
canal.
Y para obtener el cálculo del resalto hidráulico aguas arriba y aguas abajo en el canal es
necesario expresar la Ecuación 69 como:
∫ [(𝛾
1
𝑊
𝑊
2
− 𝛾
3
) 𝐴 + 𝛾
2
𝐴]
−1
𝑑𝐴 = −
𝑋 + 𝐿
∈ (1 − 𝛼)
Ecuación 72. Calculo del resalto hidráulico dentro de las condiciones de frontera
.
En la solución anterior, aparece una constante L la cual hace referencia a la longitud del resalto.
Por lo cual es necesario calcular esta constante en la dirección axial del fluido, expresándose
de la siguiente forma:
𝐿
𝑗
=
ℎ
2
− ℎ
1
(𝜕ℎ 𝜕𝑥
⁄
)
∗
Ecuación 73. Cálculo de la longitud del resalto a través de la pendiente y las profundidades aguas arriba y
aguas abajo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
45
donde
(𝜕ℎ 𝜕𝑥
⁄
)
∗
es la pendiente de la superficie en
ℎ = ℎ
∗
, donde
ℎ
∗
= (ℎ
2
+ ℎ
1
)/2 es la
profundidad media. Basada en la Ecuación 72 del resalto hidráulico, la ecuación de la longitud
del resalto está dada por:
𝐿𝑗
ℎ2
= ∈ (1 − 𝛼)Ʌ , 𝛼 =
ℎ2
ℎ1
Ʌ =
(1 − 𝛼)
(𝛾
1
(
𝑊
∗
𝑊
2
) − 𝛾
3
) 𝐴
∗
+ 𝛾
2
𝐴
1
ℎ
2
(
𝜕𝐴
𝜕ℎ
)
∗
Ecuación 74. Cálculo de la longitud del resalto teniendo en cuenta la profundidad media.
donde
𝐴
∗
y
(
𝜕𝐴
𝜕ℎ
)
∗
dependen del calculo de
ℎ
∗
.
2.4 Ecuación del resalto hidráulico en canales circulares y en forma de U.
En canales circulares y en forma de U la profundidad axial (h), el área del canal (A) y la presión
por unidad de peso (W), pueden ser adimensionales mediantes las características de la escala
(D) del canal:
ℎ
𝐷
= 𝑌,
𝐴
𝐷
2
= 𝛷(𝑌),
𝑊
𝐷
3
= 𝛹(𝑌)
Ecuación 75. Términos importantes para el cálculo del resalto hidráulico en canales circulares y en forma
de U.
La Ecuación 62 y la Ecuación 63 mostradas anteriormente para la formación del resalto
hidráulico, se convierten en términos de
𝛷 𝑦 𝛹.
𝛷
2
𝛷
1
𝛷
2
− 𝛷
1
(𝛹
2
− 𝛹
1
) =
𝑄
2
𝑔 ∗ 𝐷
5
𝑈
2
𝑈
1
= 𝑔𝐷
𝛹
2
− 𝛹
1
𝛷
2
− 𝛷
1
Ecuación 76. Cá
lculo del Resalto hidráulico en términos de Ψ y Φ.
También se expresa la Ecuación 64 del número de Froude en términos de
𝛷 𝑦 𝛹.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
46
𝐹𝑟
1
2
=
𝑄
2
𝑔𝐷
5
(
1
𝛷
1
3
)
𝑑𝛷
1
𝑑𝑌
1
Ecuación 77. Cá
lculo del número de Froude en términos de Ψ y Φ.
La integral que relaciona la Ecuación 72 en términos de la Ecuación 75 es:
∫ [(𝛾
1
𝛹
(𝑑)
𝛹
2
− 𝛾
3
) 𝛷
(𝑑)
+ 𝛾
2
𝛷
(1)
]
−1
𝑥
𝑑𝛷
(𝑑)
𝑑𝛿
𝑑𝛿 = −
𝑋 + 𝐿
∈ (1 − 𝛼)
,
𝑋 =
𝑥
ℎ
2
Ecuación 78. Integral para el cálculo del resalto hidráulico
.
donde,
𝛾
1
𝑦 𝛾
2
son expresados como
𝛾
1
=
𝛹
2
𝛹
2
− 𝛹
1
, 𝛾
2
=
𝛷
2
𝛷
2
− 𝛷
1
, 𝛾
3
=
𝛹
2
𝛷
2
− 𝛹
1
𝛷
1
(𝛹
2
− 𝛹
1
)(𝛷
2
− 𝛷
1
)
Ecuación 79. Definición de variables.
Basada en la Ecuación 72 del resalto hidráulico, la ecuación de la longitud del resalto en
términos de
𝛷 𝑦 𝛹 está dada por:
𝐿𝑗
ℎ2
= ∈ (1 − 𝛼)Ʌ , 𝛼 =
𝑌
1
𝑌
2
Ʌ =
(1 − 𝛼)𝑌
2
𝛺
∗
(𝛾
1
(
𝛹
∗
𝛹
2
) − 𝛾
3
) 𝛷
∗
+ 𝛾
2
𝛷
1
,
𝛺
∗
= (
𝜕𝛷
𝜕𝑌
)
∗
Ecuación 80.Cálculo de la longitud del resalto en términos de
𝚽 𝐲 𝚿, teniendo en cuenta la profundidad
media.
2.4.1 Ecuación del resalto hidráulico en canales circulares
La profundidad de flujo axial (h), está relacionada con el diámetro del canal circular como:
ℎ
𝐷
= 𝑌 =
1
2
(1 − 𝑐𝑜𝑠𝛿)
Ecuación 81. Relación entre profundidad de flujo y diámetro en canales de sección circular.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
47
donde
𝛿 es el ángulo del centro de la tubería como se observó en la Gráfica 24; para el cálculo
del área (A) y de la fuerza de presión por unidad de peso (W) se expresan las siguientes
ecuaciones:
𝐴
𝐷
2
= 𝛷
(𝛿)
=
1
4
(𝛿 − sin
3
𝛿 cos 𝛿),
𝑊
𝐷
3
= 𝛹
(𝛿)
=
1
8
(sin 𝛿 −
1
3
sin
3
𝛿 − 𝛿 cos 𝛿)
Ecuación 82. Cálculo del área y de la fuerza de presión por unidad de peso en canales circulares.
Reemplazando en la ecuación del número de Froude quedaría:
𝐹𝑟
1
2
=
𝑄
2
𝑔𝐷
5
64 sin 𝛿
1
(𝛿
1
− sin 𝛿
1
cos 𝛿
1
)^3
Ecuación 83. Número de Froude para canales circulares.
La profundidad crítica en estas tuberías se presenta cuando
𝐹𝑟 = 1 (Hager S. H., 1999).
ℎ
𝑐𝑟
𝐷
= (
𝑄
2
𝑔𝐷
5
)
1
4
Ecuación 84. Cálculo de la profundidad crítica en canales de sección circular.
Debido al complicado cálculo en tuberías circulares fluyendo parcialmente llenas, Hager en
1999 planteó las siguientes ecuaciones simplificadas:
𝛷
(𝑌)
=
𝐴
𝐷
2
= 𝑌
3/2
, 𝛹
(𝑌)
=
𝑊
𝐷
3
=
1
2
𝑌
5
2
Ecuación 85.Simplificación de ecuaciones para canales circulares fluyendo parcialmente llenos.
Esto es válido para un rango entre
0.2 < 𝑌 < 0.9 para un error máximo del 20%. Para el caso
del número de Froude y el resalto hidráulico las ecuaciones se expresan de la siguiente forma:
𝐻
2
4
− (1 + 2𝐹
1
2
)𝐻
2
3
2
+ 2𝐹
1
2
= 0 , 𝐹
1
=
𝑄
√𝑔𝐷
5
1
𝑌
1
2
Ecuación 86. Número de Froude simplificado para canales circulares fluyendo parcialmente llenos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
48
Y para el resalto hidráulico
𝐿
𝑗
ℎ
2
=∈
12√2
4√2 − 1
Ecuación 87. Longitud del resalto simplificado para canales circulares fluyendo parcialmente llenos.
2.4.2 Ecuación del resalto hidráulico en canales en forma de U
Los canales en forma de U constan de una parte inferior semi-circular con diámetro D y en la
parte superior constan de un diámetro constante como se observa en la Gráfica 24. El área (A)
y la fuerza de presión por unidad de peso (W) están dados por las siguientes ecuaciones:
𝐴
𝐷
2
= 𝛷(𝑌) = 𝑌 −
1
2
+
𝜋
8
,
𝑊
𝐷
3
= 𝛹(𝑌) =
1
2
(𝑌 −
1
2
)
2
+
𝜋
8
(𝑌 −
1
2
) +
1
12
Ecuación 88. Cálculo del área y la fuerza de presión por unidad de peso para canales en forma de U.
De esta forma, despejando
𝛷 𝑦 𝛹 y utilizando las simplificaciones de Hager, las ecuaciones
quedan de la siguiente forma:
𝛷(𝑌) =
𝐴
𝐷
2
=
3
4
𝑦
3
2
(1 −
1
3
𝑌)
𝛹(𝑌) =
𝑊
𝐷
3
=
8
15
𝑦
5
2
(1 −
1
4
𝑌)
Ecuación 89. Simplificación del modelo de Hager para canales en forma de U.
2.5 Resultados y conclusiones
Luego de realizar la toma de los datos, se procedió a verificar los resultados obtenidos con los
propuestos por Stahl y Hager en 1999. Para esto graficaron dos tipos de curvas en cada uno
de los canales: la relación entre alturas subsecuentes Y1/Y2 contra en número de Froude aguas
arriba y la relación entre la longitud del resalto y la altura aguas abajo contra el número de
Froude aguas arriba. Los primeros resultados mostrados fueron los del canal circular
presentando las siguientes tendencias:
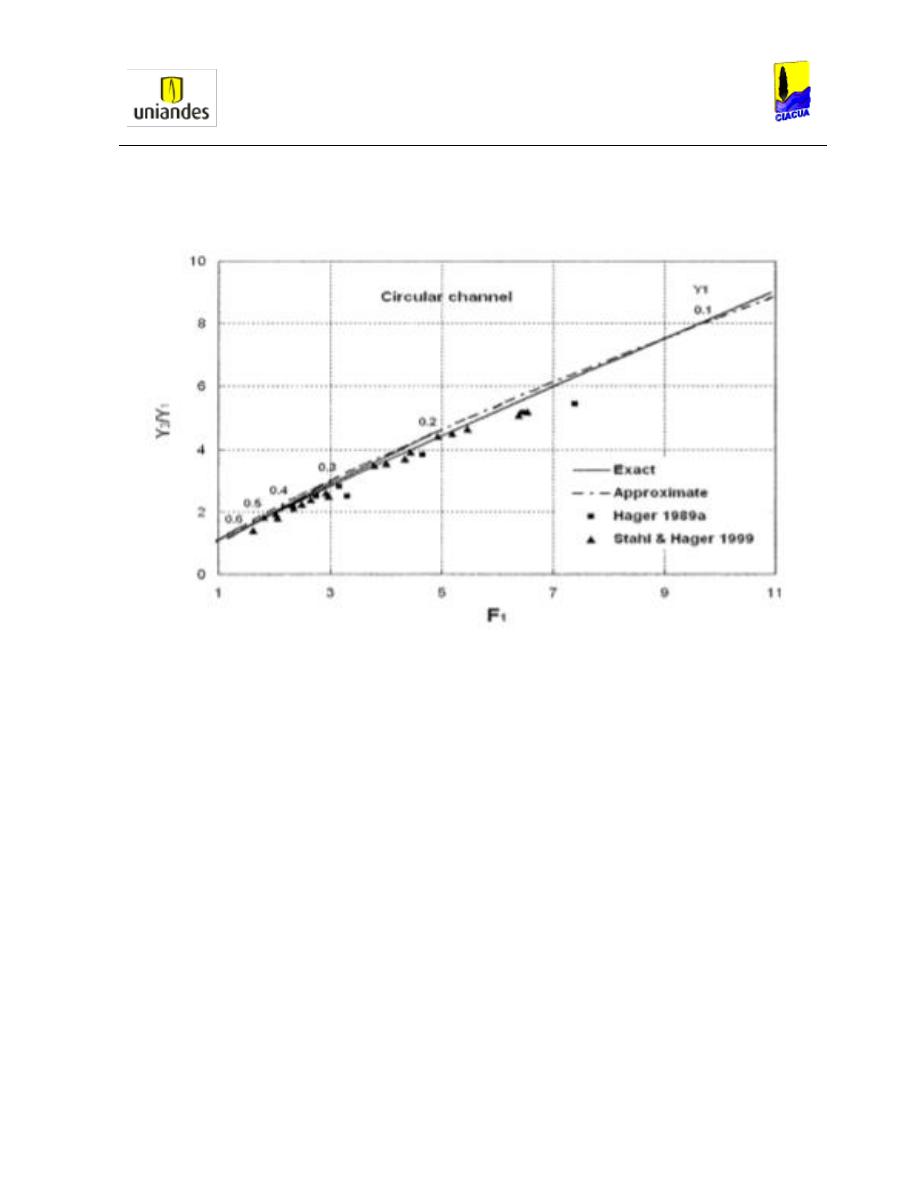
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
49
Gráfica 25. Profundidades subsecuentes versus en número de Froude aguas arriba en canales circulares
(Francis, 2006).
Como se observa en la gráfica anterior, los resultados obtenidos de la relación de profundidades
o profundidades subsecuentes versus el número de Froude aguas arriba en el canal circular
fueron bastante similares en cuanto al comportamiento del experimento realizado por Stahl y
Hager en 1999, donde se muestra que el flujo se comporta de manera lineal. Además, se puede
observar que para las diferentes profundidades de Y1 el flujo va variando, para alturas mayores
el número de Froude va disminuyendo notablemente por pérdidas de energía cinética.
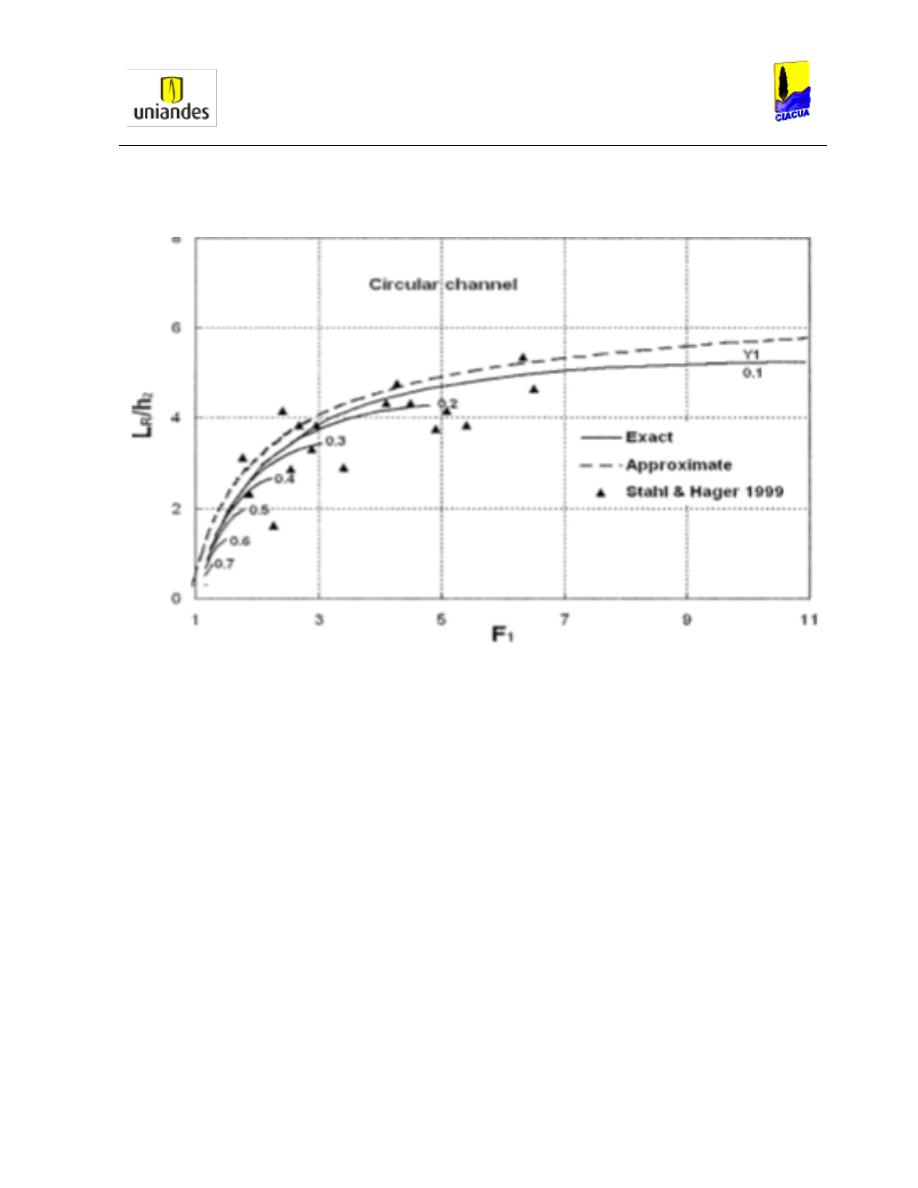
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
50
Gráfica 26. Longitud del resalto versus en número de Froude aguas arriba en canales circulares (Francis,
2006).
Para la longitud del resalto se encontró que el comportamiento era muy similar al expuesto
anteriormente por Stahl y Hager en 1999. De esta forma, en los resultados teóricos se encontró
que la longitud del resalto es independiente del número de Froude aguas arriba, pero al
graficarlos se encontró cierta similitud entre ellos. Por otro lado, se encontró que en la altura
superior de la parte derecha, es la altura aguas abajo del canal donde se presenta Y
2
=1, lo cual
demuestra que la tubería en esta sección se encuentra totalmente presurizada como se observa
en la Gráfica 26. Para los canales en forma de U el comportamiento fue similar como se observa
a continuación:
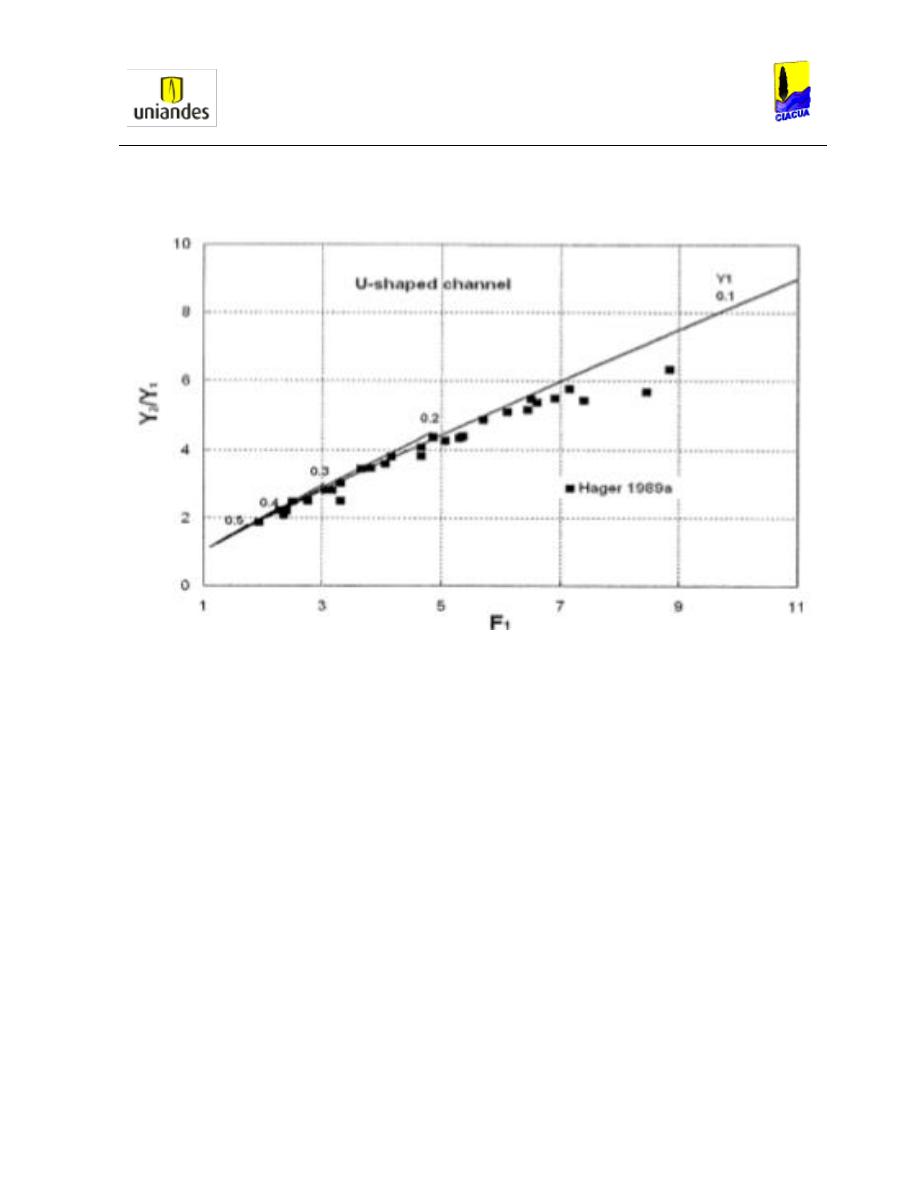
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
51
Gráfica 27. Profundidades subsecuentes versus en número de Froude aguas arriba en canales con sección
en forma de U (Francis, 2006).
En la Gráfica 27, el comportamiento del canal en forma de U, fue de tendencia muy similar al
canal con sección circular y a los resultados obtenidos por Hager en 1989. En este se expone
que las alturas subsecuentes son directamente proporcionales al número de Froude. Esto
quiere decir que, a medida que aumenta el número de Froude, las profundidades subsecuentes
también aumentan y este se genera de forma lineal. Por otro lado, en la Gráfica 28 se dedujo
que el comportamiento del canal en forma de U era semejante al de la tubería circular, como
se muestra a continuación:
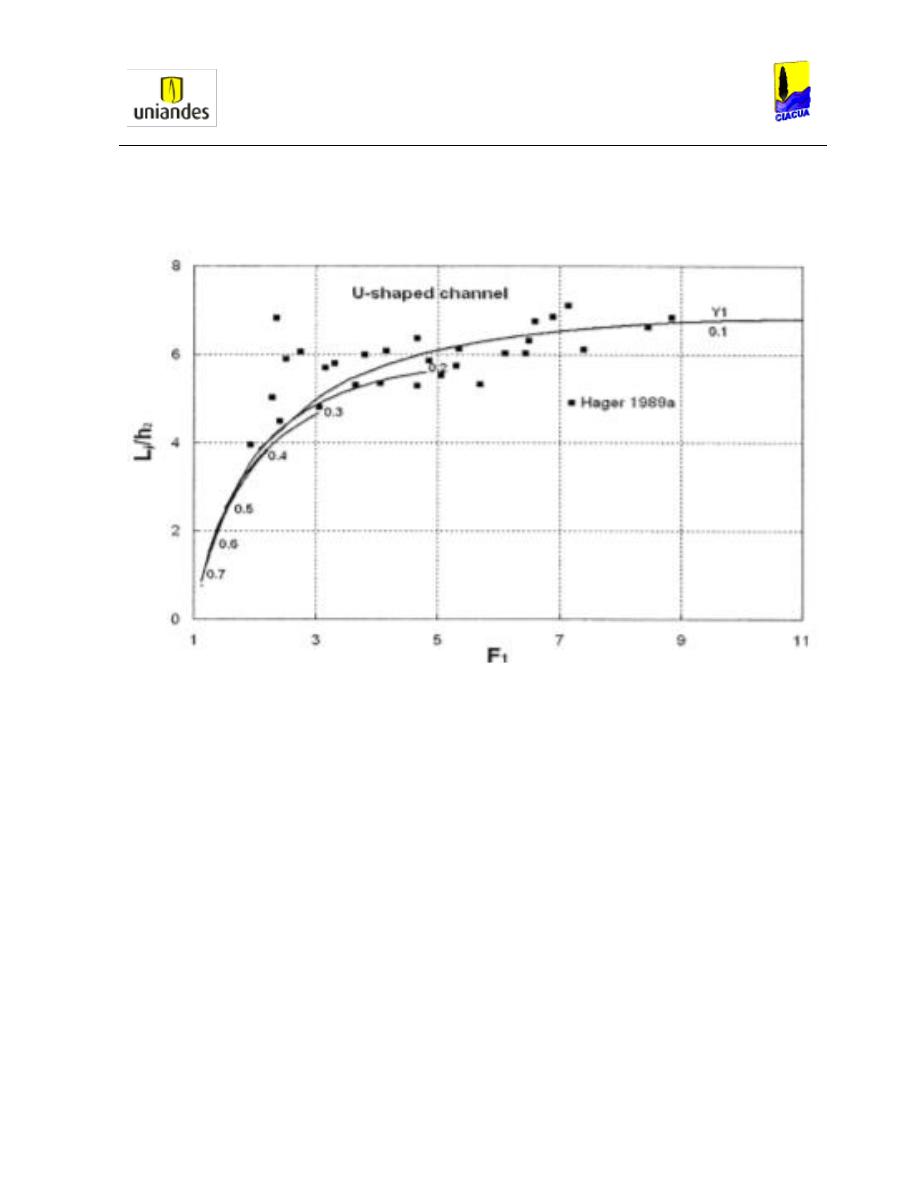
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
52
Gráfica 28. Longitud del resalto versus en número de Froude aguas arriba en canales con sección en forma
de U (Francis, 2006).
Todos los resultados teóricos mostrados anteriormente se generaron solo para canales
circulares y en forma de U, de los cuales se pudo concluir que las alturas subsecuentes aguas
arriba y aguas abajo del canal (Y
2
/Y
1
), y que la longitud del resalto (L
_j
/ h
_2
) dependían del
número de Froude aguas arriba (Fr
1
) y de la profundidad de flujo aguas arriba (Y
1
), estas
predicciones son apoyadas de los textos de Stahl y Hager en 1999 (Francis, 2006).
Finalmente, se postuló que la longitud de remolino (Lr) es del orden de la misma escala de la
longitud del resalto total
(𝐿
𝑗𝑡
), por lo cual se planteó que 𝑅 = 𝑛1, donde n1 era una constante
universal que no dependía de la geometría del canal (Francis, 2006).
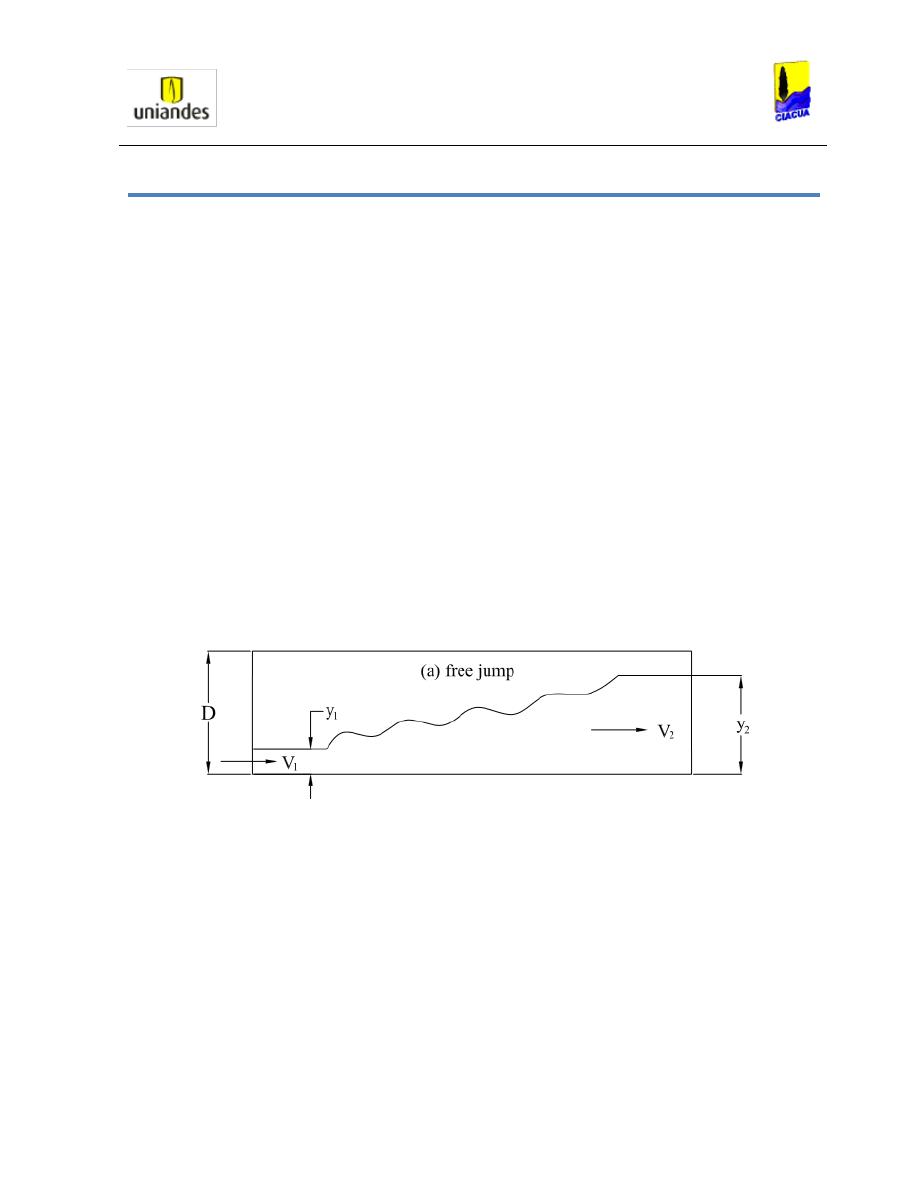
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
53
3. Marco Teórico
Resalto hidráulico
Loa resaltos hidráulicos son fenómenos generados cuando se presenta una transición de un
flujo subcrítico a un flujo supercrítico. Es decir, cuando se genera un cambio abrupto entre las
alturas aguas arriba y aguas abajo de un canal abierto o cerrado. Este fenómeno hidráulico se
puede generar por obstrucciones en el flujo aguas abajo como compuertas o por cambios de
pendientes a lo largo del canal.
Las principales funciones de un resalto hidráulico son:
Disipación de energía.
Excelente aireador
Excelente mezclador
Estos tipos de fenómenos se pueden ocasionar tanto en canales abiertos como en canales
cerrados. Para el desarrollo de este proyecto de grado se van a trabajar tuberías circulares
(canales cerrados). En este tipo de tuberías se presentan dos tipos de resaltos:
El primer tipo de resalto en una tubería circular se genera cuando la profundidad aguas
abajo del resalto es menor al diámetro (Y
2
<D). Esto genera que el resalto se comporte
de forma libre, como se observa en la siguiente gráfica.
Gráfica 29. Tipos de resaltos en tuberías circulares (Ead, 2002).
El segundo tipo de resalto en una tubería circular se genera cuando la profundidad
aguas abajo del resalto es mayor al diámetro de la tubería (Y
2
>D). Esto genera que la
tubería se presurice aguas abajo, como se observa en la siguiente gráfica.
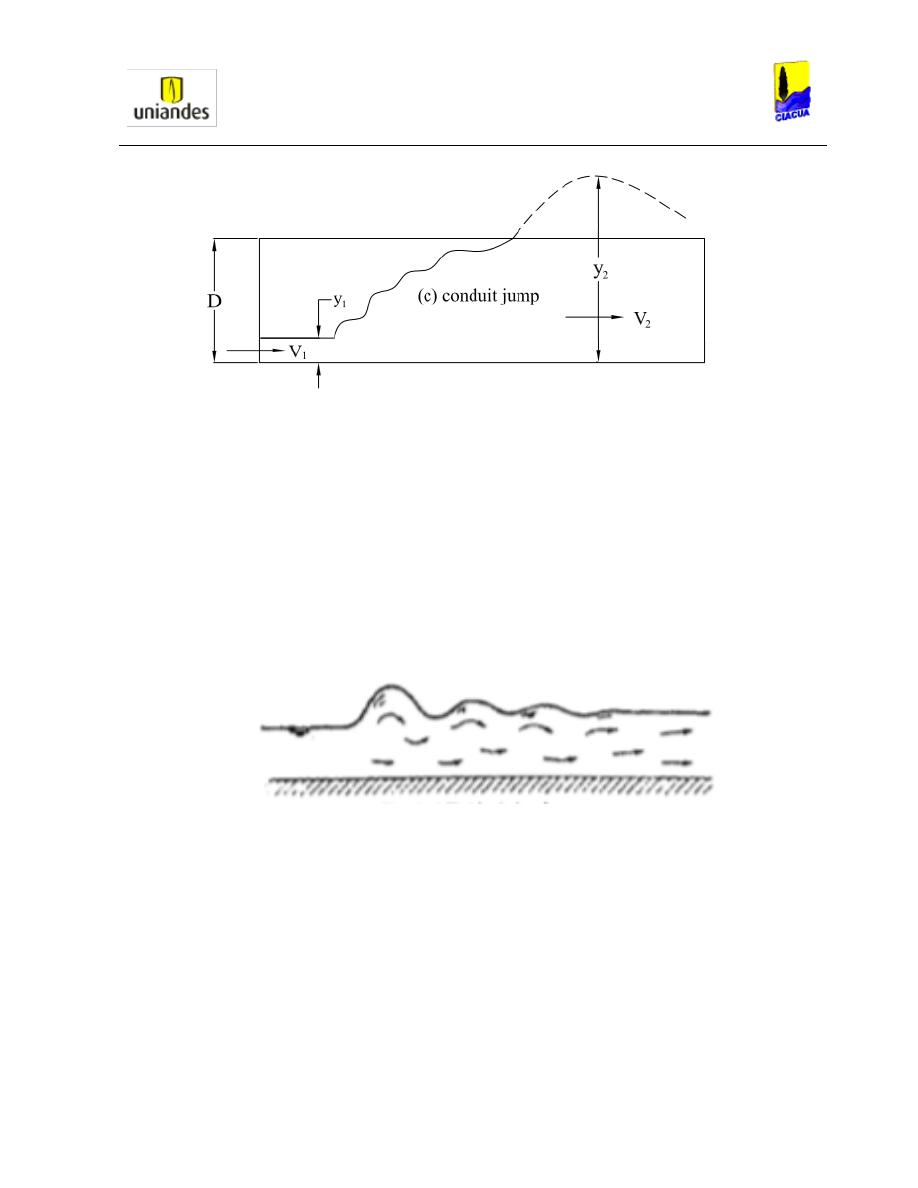
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
54
Gráfica 30. Tipos de resaltos en tuberías circulares (Ead, 2002).
3.1 Tipos de resaltos hidráulicos
En la hidráulica existen cinco tipos de resaltos: resalto ondular, resalto débil, resalto oscilante,
resalto permanente o estable y resalto fuerte. Estos varían según el incremento o disminución
del número de Froude de aguas arriba que se puede modificar según la pendiente de la tubería
o del canal, la altura del flujo y la velocidad del mismo.
Resalto Ondular: se genera entre un rango de 1.0 < Fr < 1.7; se caracteriza por generar
una baja disipación de energía y por mantener la superficie de agua lisa aguas abajo.
Gráfica 31. Resalto ondular (Rodríguez, 1992).
Resalto Débil: se genera entre un rango de 1.7 < Fr < 2.5; se caracteriza por generar
una serie de pequeños remolinos sobre la superficie del resalto, pero en la superficie
aguas abajo de la tubería, el flujo sigue siendo liso.
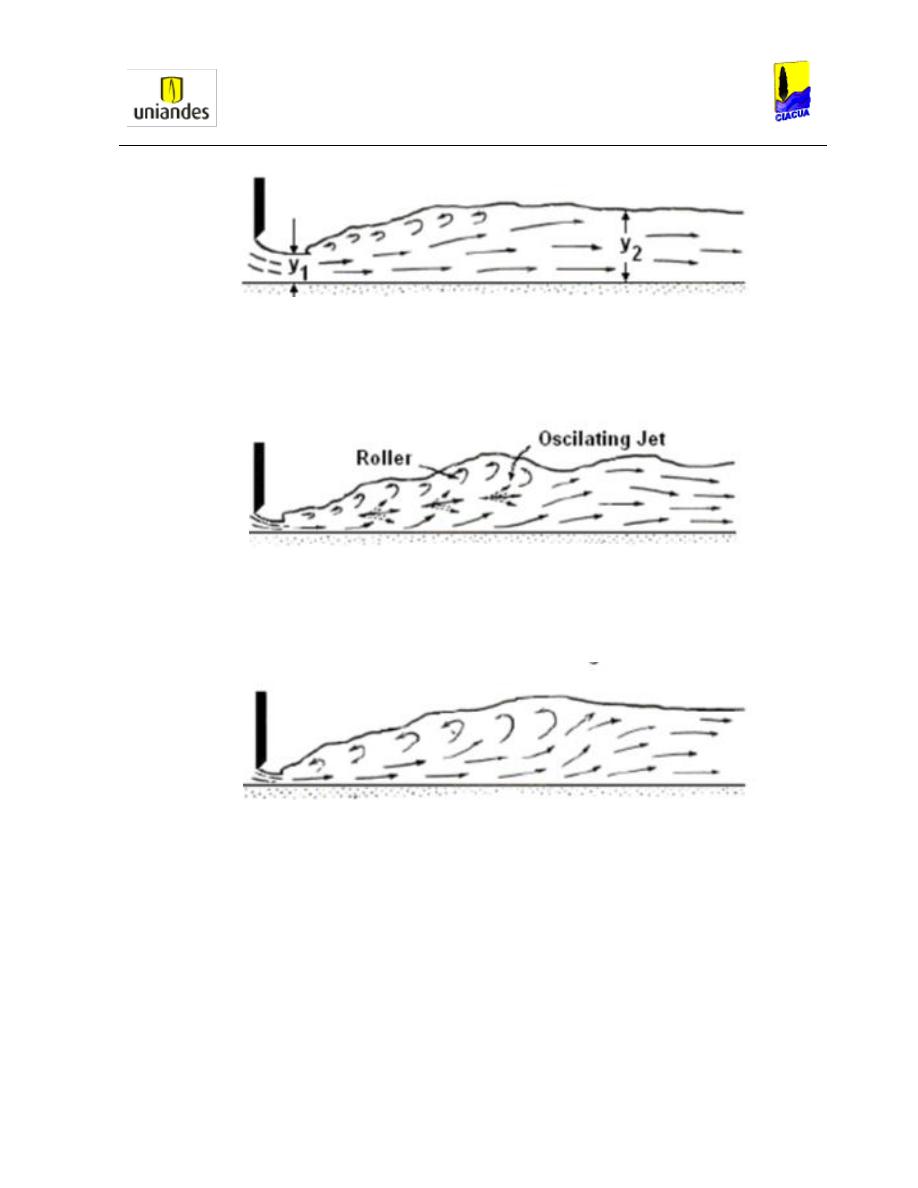
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
55
Gráfica 32. Resalto débil (Rodríguez, 1992).
Resalto Oscilante: se genera entre un rango de 2.5 < Fr < 4.5; se caracteriza porque
en cada oscilación genera una larga ola con períodos irregulares. Es muy común en
canales abiertos y puede causar ilimitados daños en bancos de tierra.
Gráfica 33. Resalto oscilante (Rodríguez, 1992).
Resalto Permanente o Estable: se genera entre un rango de 4.5 < Fr < 9.0, se
caracteriza por genera un resalto muy balanceado y ser el de mejor rendimiento. Puede
tener unos rangos de disipación de energía entre el 45% y el 70%.
Gráfica 34. Resalto permanente (Rodríguez, 1992).
Resalto Fuerte: se genera cuando Fr > 9.0; se caracteriza por formarse con grandes
cambios de pendientes y por generar un resalto muy fuerte con grandes remolinos
aguas abajo. Se pueden obtener pérdidas de energías de hasta un 85%.
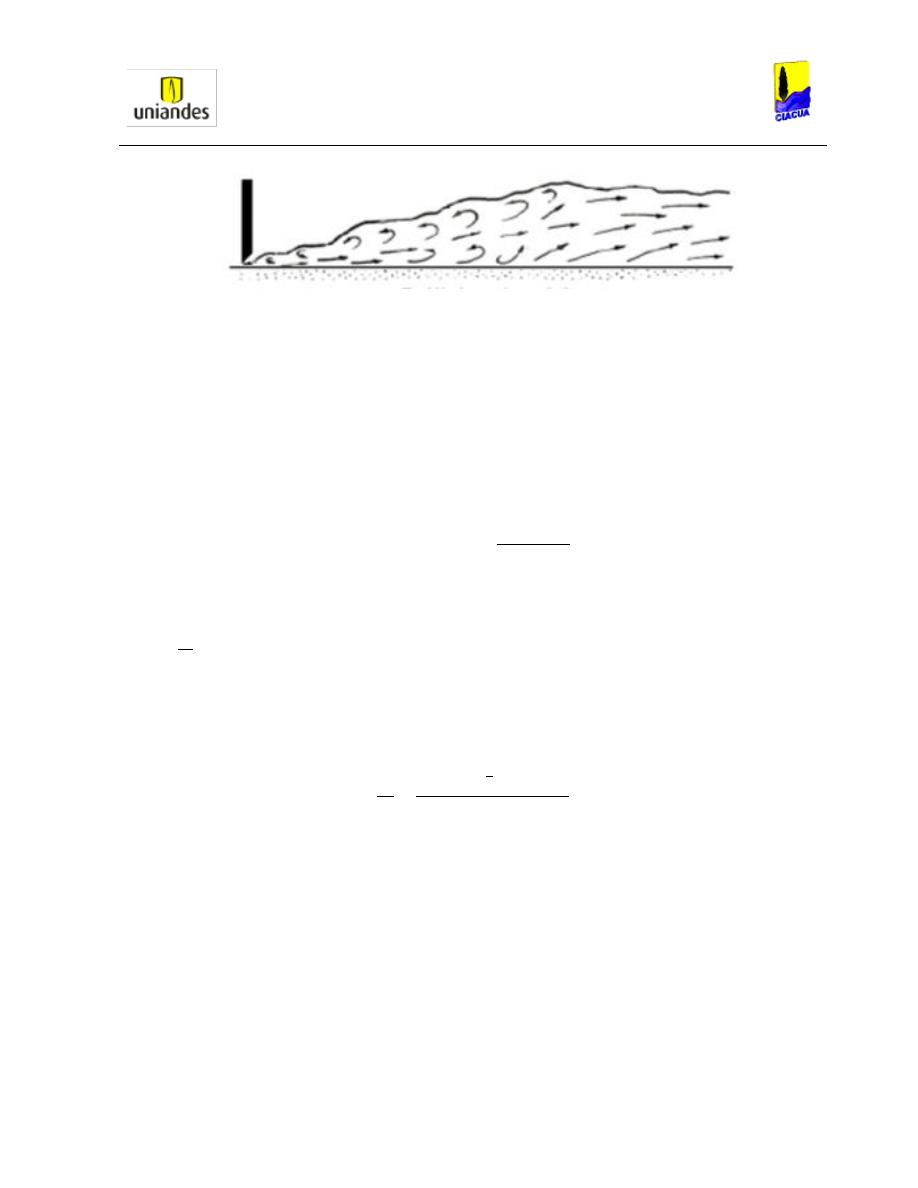
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
56
Gráfica 35. Resalto fuerte (Rodríguez, 1992).
3.2 Características básicas del resalto
Las principales características del fenómeno de un resalto hidráulico en canales horizontales
rectangulares abiertos son:
3.2.1 Pérdidas de energía
Las pérdidas de energía en un resalto hidráulico hacen referencia a las pérdidas que genera el
flujo antes y después del resalto. La ecuación se conoce como:
∆𝐸 = 𝐸
1
− 𝐸
2
=
(𝑦
2
− 𝑦
1
)
3
4𝑦
2
𝑦
1
Ecuación 90. Cálculo de pérdidas de energía en canal rectangular horizontal.
donde
∆𝐸
𝐸
1
se conoce como la pérdida relativa de energía.
3.2.2 Eficiencia
La eficiencia de un resalto hidráulico es definida como el radio de la energía especifica antes y
después de que ocurre el fenómeno hidráulico, se puede expresar de la siguiente forma:
𝐸
2
𝐸
1
=
(8𝐹
1
2
+ 1)
3
2
− 4𝐹
1
2
+ 1
8𝐹
1
2
(2 + 𝐹
1
2
)
Ecuación 91. Cálculo de la eficiencia en un canal rectangular horizontal (Rodríguez, 1992)
.
Esta ecuación indica que la eficiencia de un resalto es una variable adimensional y depende
solo del número de Froude.
3.2.3 Ubicación del resalto
Un resalto hidráulico ocurre cuando se ejerce un cambio abrupto entre profundidades de un
flujo supercrítico a un flujo subcrítico; a continuación se mostrará las ubicaciones del resalto
hidráulico en sus tres principales casos:
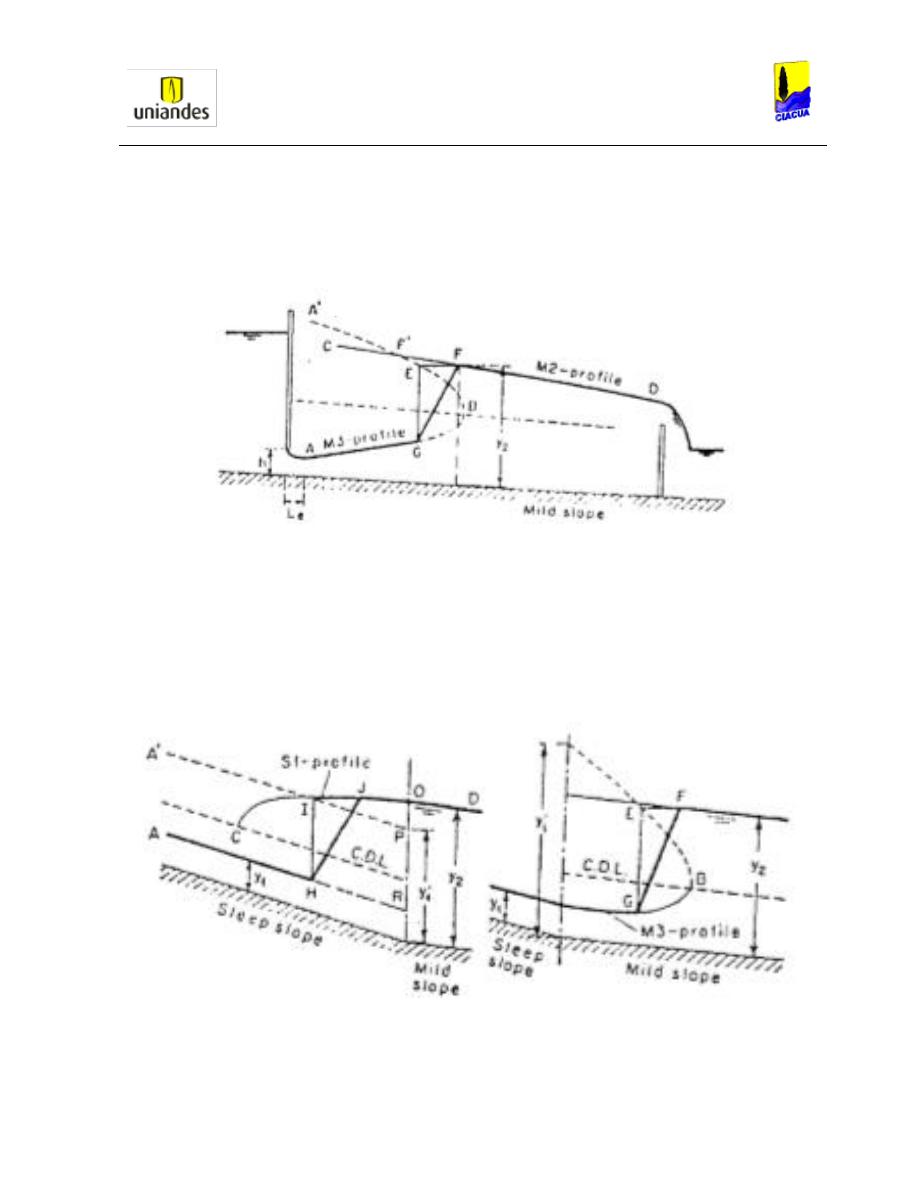
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
57
Caso A: se muestra el comportamiento del resalto regulándolo por medio de una compuerta en
el canal. Los perfiles AB y CD pueden ser fácilmente identificados como resaltos tipos
𝑀
3
y
𝑀
2
respectivamente, para F’ la posición del resalto puede ser estimada por prueba y error. Por otro
lado, la distancia horizontal EF es igual a la longitud del resalto correspondiente a la profundidad
entre y
2
y F (Rodríguez, 1992). Esto se observa en la Gráfica 38:
Gráfica 36. Caso A de la ubicación del resalto hidráulico (Rodríguez, 1992).
Caso B: en este caso se muestra que el resalto hidráulico se forma en el momento que se
produce un cambio de pendiente en el canal que cambia de empinada a leve. Por simplicidad,
se supone que el flujo es uniforme en el canal excepto cuando ocurre el resalto en el cambio
de pendiente. El resalto que se puede ocurrir puede ser leve o empinado dependiendo del
comportamiento del
𝑦
2
aguas abajo si es mayor o menor a la profundidad subsecuente
𝑦
1
(Rodríguez, 1992). A continuación se presenta la gráfica que ejemplifica lo anterior:
Gráfica 37. Caso B de la ubicación del resalto hidráulico (Rodríguez, 1992).
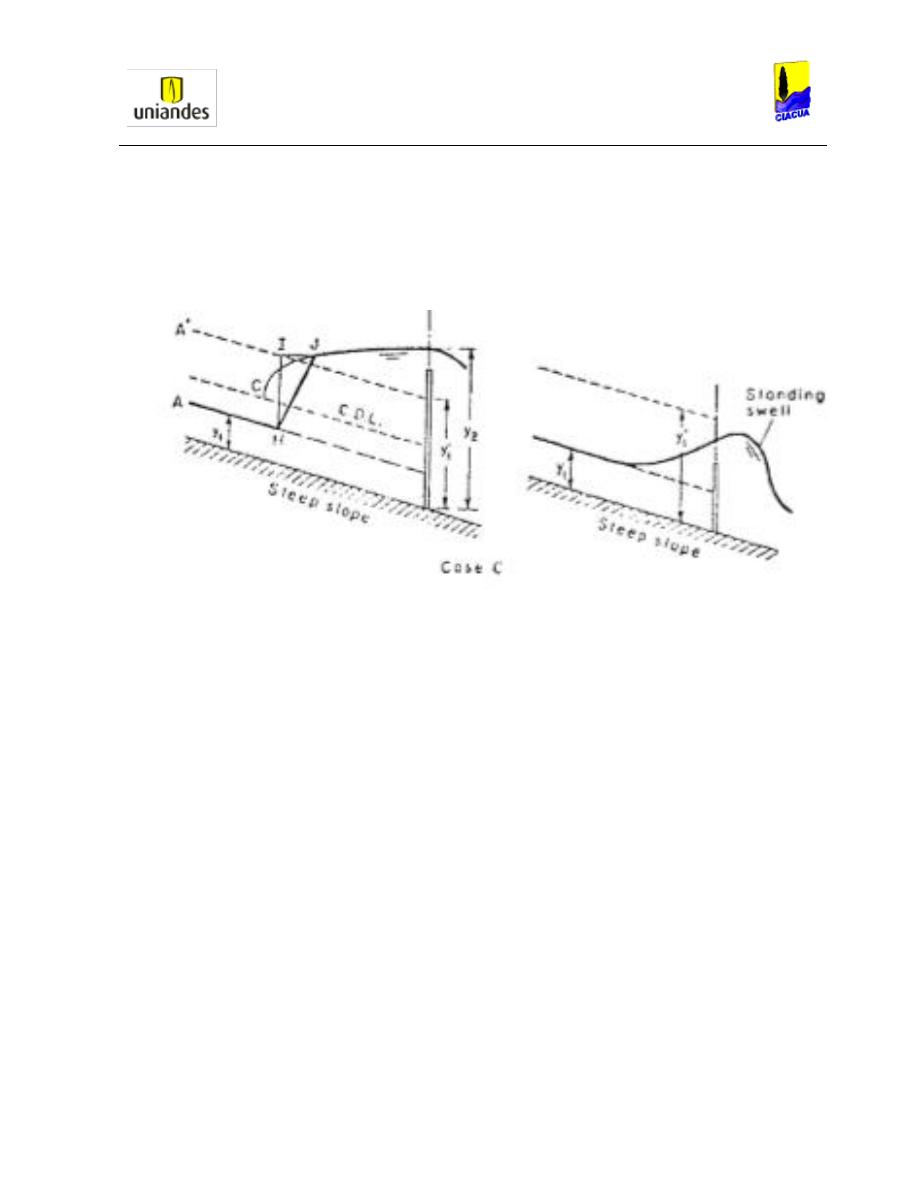
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
58
Caso C: en el caso C se puede observar en la Gráfica 40; que el resalto comienza detrás de
una barrera de desbordamiento, el resalto se puede formar si la altura de desbordamiento es
mayor que la altura subsecuente aguas arriba
(𝑦
1
), la cual se encuentra en flujo supercrítico.
En cambio, al incrementar la altura del desbordamiento, el resalto se puede mover aguas arriba
y cuando la altura de desbordamiento es más pequeña que la altura subsecuente, la barrera
puede ser cruzada por el oleaje pero no será seguido por otras ondulaciones (Rodríguez, 1992).
Gráfica 38. Caso C de la ubicación del resalto hidráulico (Rodríguez, 1992).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
59
4. Diseño y Construcción de un Modelo para Estudiar el
Comportamiento de Resaltos Hidráulicos en Tuberías
Parcialmente Llenas de Sección Circular, con Números de Froude
menores a 4
Para el desarrollo de este documento, fue necesario tomar como guía la tesis de la Ingeniera
Laura Elizabeth Montaño,
acerca de “Diseño y Construcción de un Modelo para Estudiar el
Comportamiento de Resaltos Hidráulicos en Tuberías Parcialmente Llenas de Sección Circular,
con Números
de Froude Supercríticos Menores a 4”. Esta tesis desarrolló una investigación
acerca de los experimentos realizados por investigadores a través del tiempo en resaltos
hidráulicos en tuberías de sección circular y canales de secciones rectangulares, trapezoidales
y triangulares.
Dado que la tesis de Laura Montaño se basó específicamente en el modelo constructivo, se
debe realizar una tesis posterior que analice el modelo del resalto hidráulico mediante una toma
de datos y elección de condiciones que permitan la formación del resalto. Lo anterior con el fin
de realizar un análisis y determinar la importancia de los resaltos hidráulicos sobre el fenómeno
de sobrecarga (Montaño, 2012).
Diseño del modelo
El diseño del modelo de la tubería se planteó en un material de acrílico transparente por sus
facilidades a la hora de observar el fenómeno del resalto hidráulico. Este montaje se realizó en
el Laboratorio de Hidráulica de la Universidad de los Andes, con una pendiente de 1,88% inicial
y con una longitud total de 13,00 metros separado por siete secciones: 6 de dos metros y 1 de
un metro. Estas secciones se unieron mediante bridas para su fácil transporte y mantenimiento.
Además, la tubería tiene un diámetro final de 0,25 metros, diseñado para soportar un caudal
mínimo de 6,1 L/s y un caudal máximo de 77,6 L/s. Para la elección del diámetro final de la
tubería se tuvo en cuenta que cumpliera con las condiciones de relación de llenado propuesta
para los caudales y las pendientes mencionados anteriormente, tal como se puede observar en
la Tabla 3 (Montaño, 2012).
De esta forma, se realizaron tres pruebas para la verificación del diámetro óptimo para el diseño
de la tubería. El primer ensayo se realizó con una relación de llenado del 50%, la segunda con
una relación de llenado del 85% y la última prueba se realizó con una relación de llenado del
92,9% y todas se trabajaron con una pendiente del 1,88%.
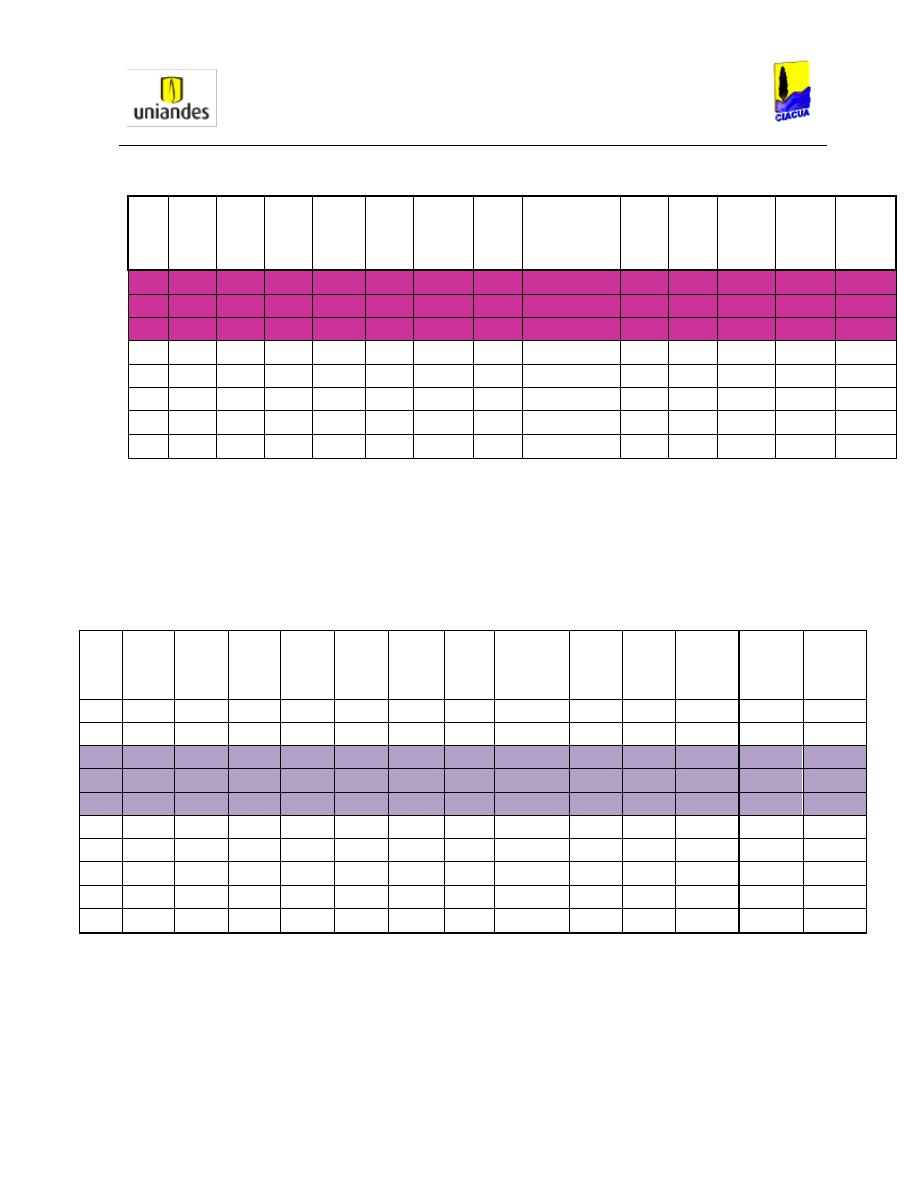
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
60
Tabla 3. Diámetros seleccionados que superen el caudal de diseño y no superen los 48 cm de altura con
relaciones de llenado del 50 % (Montaño, 2012).
d
(m)
yn
(m)
𝜃
(-)
Á
(m²)
P
(m)
R
(m)
V
(m)
Q
(m³/s)
Re
(-)
T
(m)
D
(m)
Froude
(-)
h
soporte
(m)
d +
soporte
(m)
0,2
0,1
3,142 0,016 0,314 0,050 2,315 0,036 406173,515 0,200 0,079 2,638
0,100
0,300
0,25 0,125 3,142 0,025 0,393 0,063 2,676 0,066 586753,110 0,250 0,098 2,726
0,100
0,350
0,3
0,15 3,142 0,035 0,471 0,075 3,009 0,106 791802,752 0,300 0,118 2,799
0,100
0,400
0,35 0,175 3,142 0,048 0,550 0,088 3,321 0,160 1019595,837 0,350 0,137 2,860
0,100
0,450
0,4
0,2
3,142 0,063 0,628 0,100 3,616 0,227 1268764,140 0,400 0,157 2,913
0,100
0,500
0,45 0,225 3,142 0,080 0,707 0,113 3,897 0,310 1538186,062 0,450 0,177 2,960
0,100
0,550
0,5
0,25 3,142 0,098 0,785 0,125 4,165 0,409 1826918,772 0,500 0,196 3,001
0,100
0,600
0,55 0,275 3,142 0,119 0,864 0,138 4,424 0,525 2134154,161 0,550 0,216 3,039
0,100
0,650
Como se observa en la Tabla 3, el diámetro óptimo para el diseño de la tubería con una relación
de llenado del 50% es la de diámetro de 0,25 metros. Además, se puede observar que los
diámetros de 0,2 y 0,3 metros transportan un caudal menor que el caudal máximo, lo cual indica
que se puede trabajar para mayores relaciones de llenado.
Tabla 4. Diámetros seleccionados que superen el caudal de diseño y no superen los 48 cm de altura con
relaciones de llenado del 85 % (Montaño, 2012).
d
(m)
yn
(m)
𝜃
(-)
Á
(m²)
P
(m)
R
(m)
V
(m)
Q
(m³/s)
Re
(-)
T
(m)
D
(m)
Froude
(-)
h
soporte
(m)
d +
soporte
(m)
0.1
0.085 4.692 0.007 0.235 0.030 2.158 0.015 229631.7 0.071 0.100
2.183
0.1
0.200
0.15 0.128 4.692 0.016 0.352 0.045 2.814 0.045 449084.9 0.107 0.149
2.324
0.1
0.250
0.2
0.17
4.692 0.028 0.469 0.061 3.388 0.096 721077.9 0.143 0.199
2.423
0.1
0.300
0.25 0.213 4.692 0.044 0.587 0.076 3.909 0.174 103982.9 0.179 0.249
2.501
0.1
0.350
0.3
0.255 4.692 0.064 0.704 0.091 4.390 0.281 140129.7 0.214 0.299
2.563
0.1
0.400
0.35 0.298 4.692 0.087 0.821 0.106 4.840 0.422 180243.3 0.250 0.349
2.617
0.1
0.450
0.4
0.34
4.692 0.114 0.938 0.121 5.265 0.599 224082.5 0.286 0.399
2.663
0.1
0.500
0.45 0.383 4.692 0.144 1.056 0.136 5.669 0.817 271449.7 0.321 0.448
2.703
0.1
0.550
0.5
0.425 4.692 0.178 1.173 0.152 6.055 1.077 322178.7 0.357 0.498
2.739
0.1
0.600
0.55 0.468 4.692 0.215 1.290 0.167 6.427 1.383 376127.4 0.393 0.548
2.772
0.1
0.650
Como se observa en la Tabla 4, para la relación de llenado del 85% máximo estipulado por el
RAS (Reglamento Técnico del Sector de Agua Potable y Saneamiento Básico) los diámetros
con la capacidad de soportar el caudal máximo con esta relación son el de 0,20-0,25 y 0,3
metros. Sin embargo, al igual que la tabla anterior, los diámetros de 0,2 y 0,3 metros permiten
un mejor desarrollo de la tubería por no alcanzar su máximo caudal permitido.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
61
Tabla 5. Diámetros seleccionados que superen el caudal de diseño y no superen los 48 cm de altura con
relaciones de llenado del 92.9 % (Montaño, 2012).
d
(m)
yn
(m)
(-)
A
(m²)
P
(m)
R
(m)
V
(m/s)
Q
(m³/s)
Re
(-)
h
(m)
d +
soporte
(m)
0,1 0,093 5,204 0,008 0,260 0,029 1,627 0,012 166855,528
0,100
0,200
0,15 0,139 5,204 0,017 0,390 0,044 2,125 0,036 326990,425
0,100
0,250
0,2 0,186 5,204 0,030 0,520 0,058 2,563 0,078 525738,360
0,100
0,300
0,25 0,232 5,204 0,048 0,651 0,073 2,959 0,141 758879,656
0,100
0,350
0,3 0,279 5,204 0,068 0,781 0,088 3,326 0,228 1023461,122 0,100
0,400
0,35 0,325 5,204 0,093 0,911 0,102 3,669 0,342 1317254,232 0,100
0,450
0,4 0,372 5,204 0,122 1,041 0,117 3,993 0,486 1638493,834 0,100
0,500
0,45 0,418 5,204 0,154 1,171 0,132 4,302 0,663 1985733,499 0,100
0,550
0,5 0,465 5,204 0,190 1,301 0,146 4,597 0,874 2357757,724 0,100
0,600
0,55 0,511 5,204 0,230 1,431 0,161 4,881 1,123 2753524,982 0,100
0,650
Finalmente, para la relación de llenado del 92,9%, el único diámetro que soporta esta cantidad
es el de 0,2 metros. No obstante, como se estipula en el RAS (Reglamento Técnico del Sector
de Agua Potable y Saneamiento Básico), la máxima relación de llenado permitida es del 85%
para que no ocurra el fenómeno de sobrecarga, pero para este ejemplo la única tubería que
serviría sería la de 0,20 metros. Con el fin de que se cumpla con la norma y se observe de una
mejor forma el fenómeno del resalto hidráulico, se utilizó el diámetro de 0,25 metros el cual
cumplía la relación de llenado del 85%, como se mostró en la Tabla 4.
Resultados obtenidos
Para obtener los resultados cabe resaltar que en la tesis “Diseño y Construcción de un Modelo
para Estudiar el Comportamiento de Resaltos Hidráulicos en Tuberías Parcialmente Llenas de
Sec
ción Circular, con Número de Froude Supercríticos Menores a 4” de la Ingeniera Laura
Montaño, se trabajaron resultados teóricos para probar el funcionamiento de la tubería
diseñada. Además, se trabajó como un flujo uniforme utilizando la ecuación de Darcy Weisbach
suponiendo
𝑆
𝑓
= 𝑆
0
El primer análisis que se realizó se enfocó en el valor máximo del número de Froude que podía
soportar la tubería a diferentes pendiente. De esta forma, se sometió cada pendiente a
diferentes caudales variándolos desde el más pequeño, que podía soportar la tubería, hasta el
mayor que esta resistía para analizar el comportamiento del caudal respecto a la relación de
llenado.
Como se puede observar en la Gráfica 41, a menor pendiente de la tubería, esta resistirá
mayores caudales y llegará a sus relaciones de llenado máximas después que las de mayores
pendientes. Además, se puede observar que para obtener un mejor comportamiento de la
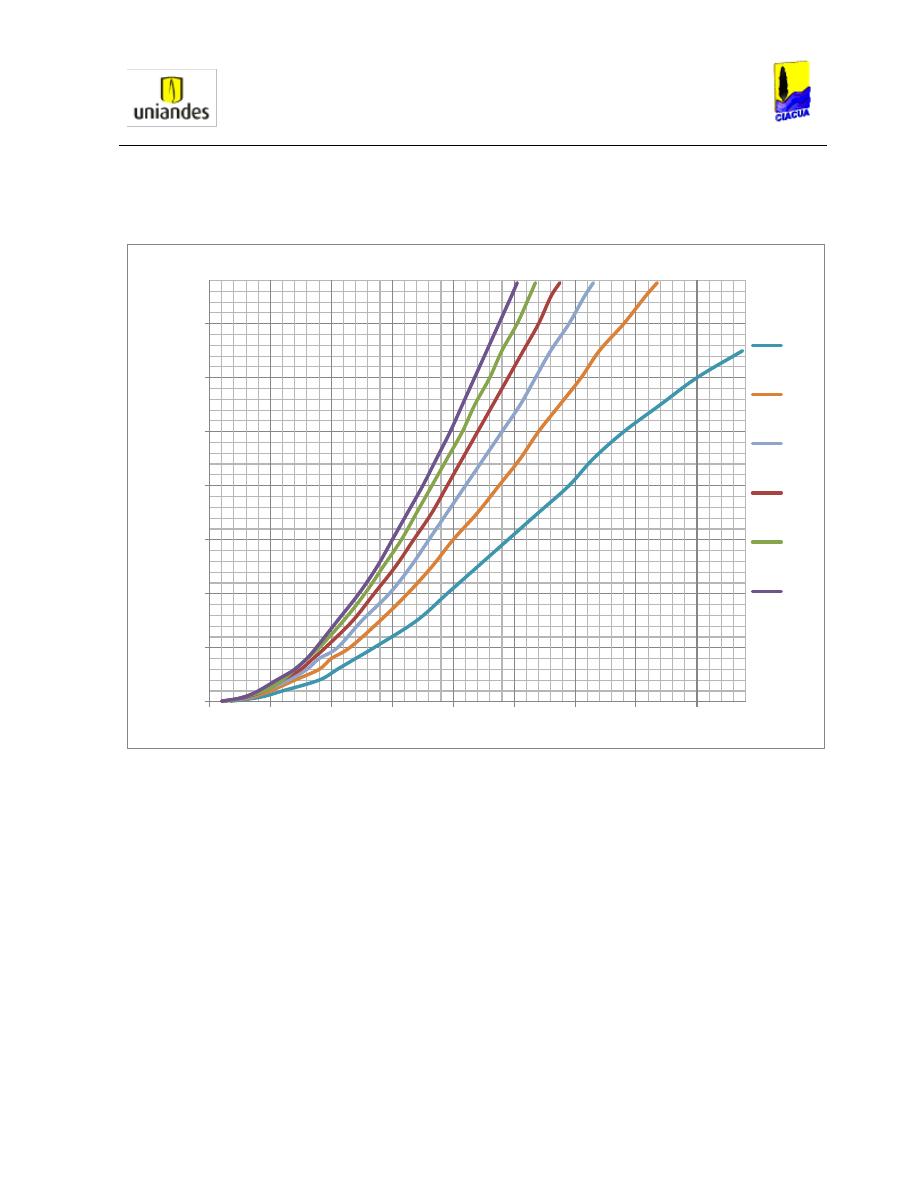
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
62
tubería, sería necesario utilizar la pendiente más baja, puesto que resistirá mayores caudales
y tardaría mayor tiempo en alcanzar sus relaciones de llenado máximas evitando
presurizaciones, sobre cargas en la tubería y posteriormente daños en la misma.
Gráfica 39. Variación del caudal respecto a la relación de llenado (Montaño, 2012).
Por otro lado, se quiso analizar el comportamiento teórico que tendría la tubería en los caudales
más altos y por ende en las relaciones de llenado más altas. Para esto se verificó que la tubería
cumpliera con el requisito de modelo y que no sobrepasara el número de Froude > 4. De esta
forma, se procedió a calcular el número de Froude para todas las relaciones de llenado posibles
en la tubería, estudiando el comportamiento del fluido, suponiendo la ecuación de Darcy
Weisbach
(𝑆
𝑓
= 𝑆
0
) para flujos uniformes. A continuación se presentará el resultado obtenido
para las pendientes de 0,019 y 0,031.
0
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
Q
(m
³/
s)
y/d (-)
Comparación Pendientes
S =
0.005
S = 0.01
S =
0.015
S = 0.02
S =
0.025
S = 0.03
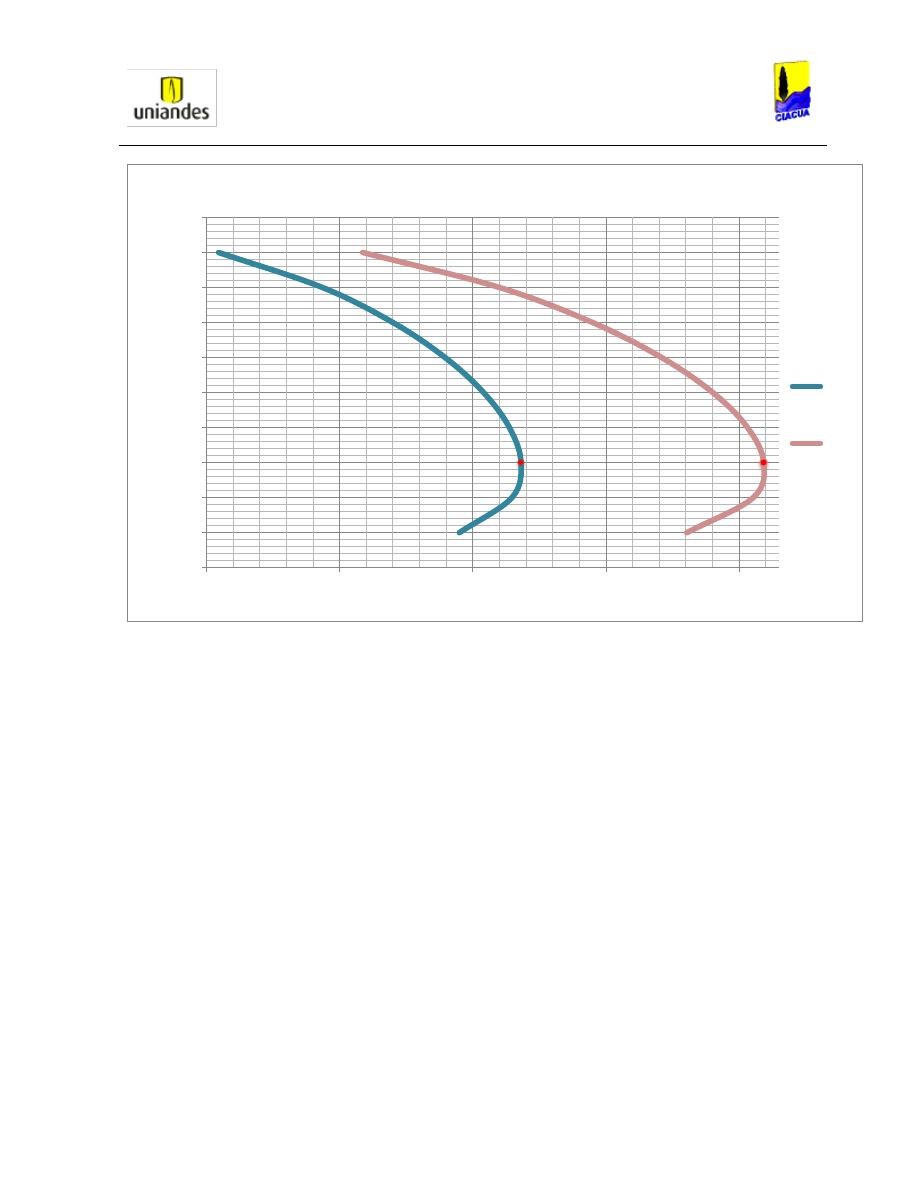
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
63
Gráfica 40. . Variación del número de Froude respecto a la relación de llenado para diferentes pendientes
(Montaño, 2012).
Se puede evidenciar que los mayores números de Froude se presentan en las zonas donde las
relaciones de llenado son más bajas (Flujo supercrítico). Sin embargo, se evidencia que en las
dos pendientes este comportamiento no es lineal, sino que cuando se obtienen las relaciones
de llenado más bajas el número tiende a aumentar hasta llegar a su máximo punto. De esta
forma comienza a hacer su transición de flujo supercrítico a flujo a subcrítico, como se observa
desde la relación de llenado del 30% en adelante. Finalmente, se puede observar en la Gráfica
42 que la mayor pendiente que se puede analizar es la de 0,031 puesto que esta ya está
alcanzando el rango máximo de número de Froude para el cual fue diseñada la tubería.
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,650
2,150
2,650
3,150
3,650
y/
d
(
-)
Froude (-)
Variación Froude vs y/d
So =
0.019
So =
0.031
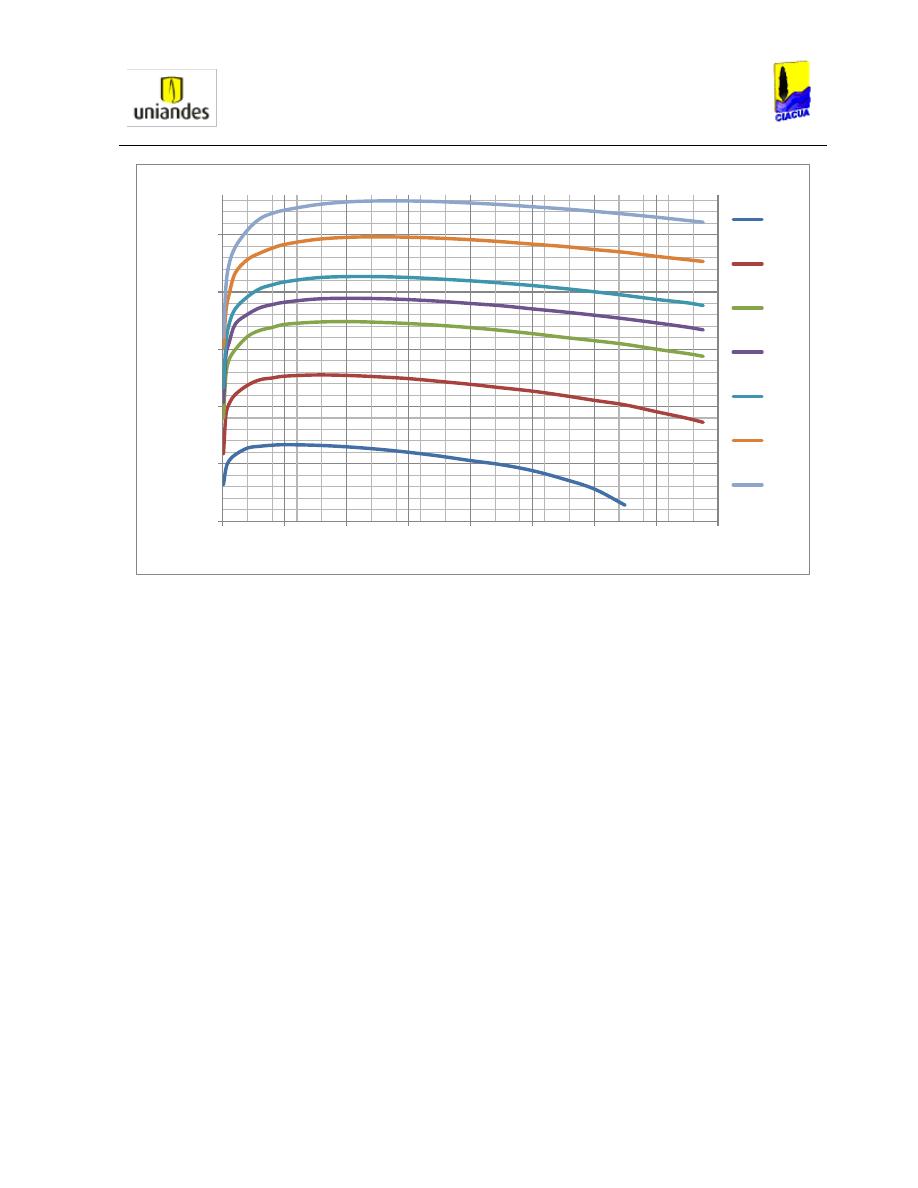
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
64
Gráfica 41. Variación del número de Froude para diversos caudales (Montaño, 2012).
Para el análisis del número de Froude y el caudal para cada pendiente estudiada se analizó
que para las pendientes más bajas el flujo no iba a ser tan crítico. Entonces, se observa en la
Gráfica 43 que las pendientes siguen cierta tendencia, y que al aumentar la pendiente y
trabajando con los mismos caudales este va a presentar mayores números de Froude. Por otro
lado, se observa que este crecimiento como se evidencia en la Gráfica 42 tiene un límite en el
cual el flujo pasa a ser de supercrítico y se convierte a subcrítico. Por esto la tendencia del
número de Froude es a disminuir, como se presentó en la gráfica anterior.
Finalmente, la relación que cabe resaltar para estudiar todo el comportamiento de la tubería
sería la relación de llenado de esta, contra el caudal que va a pasar. Para este análisis se
concluye que el comportamiento que va a presentar esta gráfica va a tender a ser el mismo de
las presentadas anteriormente, mostrando cuales van a hacer las relaciones de llenado más
críticas, donde el flujo va a ser más supercrítico y más fuerte de controlar. Esto con el fin de
que, al realizar un experimento en el Laboratorio de Hidráulica de la Universidad de los Andes
sobre el fenómeno del resalto hidráulico, se tenga en cuenta cuando se van a tener las
condiciones más críticas.
0,800
1,300
1,800
2,300
2,800
3,300
0
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
N
ú
m
e
ro
d
e
Fr
o
u
d
e
(
-)
Q (m
3
/s)
Comparación de Pendientes
S =
0.005
S =
0.01
S =
0.015
S =
0.0175
S =
0.02
S =
0.025
S =
0.03
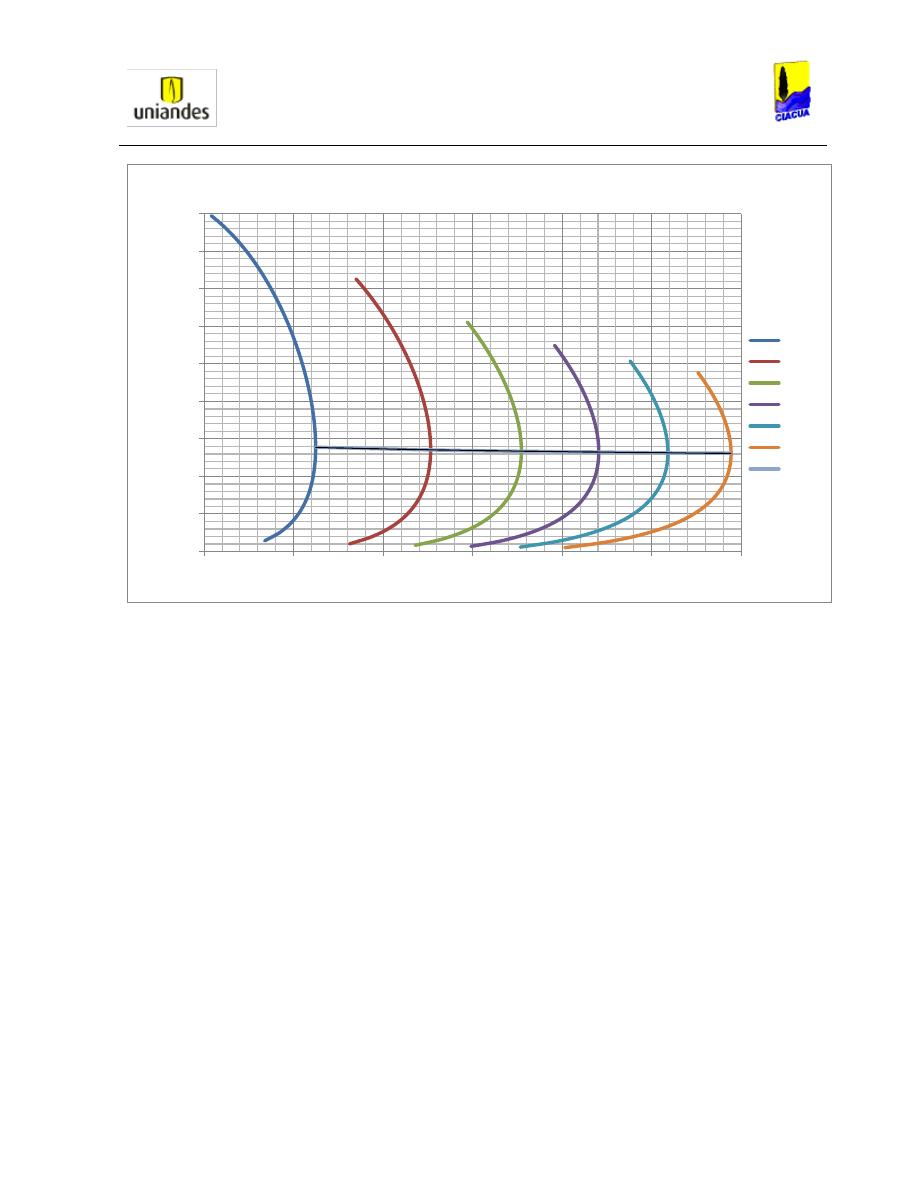
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
65
Gráfica 42. Comparación número de Froude respecto a diferentes relaciones de llenado (Montaño, 2012).
Efectivamente, como se mencionaba anteriormente, la Gráfica 44 presenta un comportamiento
muy similar a las presentadas anteriormente, por lo cual se puede obtener que generalmente
donde se va a generar el mayor flujo supercrítico y por ende el resalto hidráulico más fuerte va
a ser en la relación de llenado del 30%.
Finalmente, se puede demostrar que la curva que describe mejor en qué relación de llenado se
encuentran los números de Froude máximos se ajusta a una curva potencial, la cual se calculó
mediante la Ecuación 92 (Montaño, 2012):
𝑦 = 0.3026𝑥
−0.055
Ecuación 92. Curva que describe el número de Froude máximo (Montaño, 2012).
Por esta razón, en el montaje que se realizó, los números de Froude máximos se encuentran
entre las relaciones de llenado del 20% y 30%, es decir, que el resalto hidráulico más fuerte se
presentará cuando la profundidad aguas arriba del resalto se encuentre entre 0,28 a 0,30 veces
el diámetro (Montaño, 2012).
0,020
0,120
0,220
0,320
0,420
0,520
0,620
0,720
0,820
0,920
0,750
1,250
1,750
2,250
2,750
3,250
3,750
y/
d
(
-)
Froude (-)
Comparación de Número de Froude vs y/d
S =0.005
S = 0.01
S = 0.015
S = 0.02
S = 0.025
S = 0.03
MAX

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
66
5. Modelo físico
Para el estudio del fenómeno del resalto hidráulico, se va a realizar una tesis de pregrado
acerca de “Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4
”, con el fin de estudiar el comportamiento del
fenómeno de resalto hidráulico en diferentes pendientes variando 35 veces su caudal en cada
una. A continuación se presenta una tabla de mediciones:
Tabla 6. Mediciones realizadas en el laboratorio.
El modelo que se dispuso para la toma de datos fue realizado por una tesis anterior y consta
con las siguientes características de diseño y materiales para su funcionamiento:
Diámetro = 0,25 m
Longitud = 13,0 m (consta de 6 secciones de 2 m y de una sección de 1 m)
Material = acrílico transparente (para observar mejor el fenómeno del resalto)
Gatos mecánicos (para obtener la variación de pendientes)
Una diferencial (para ayudar a que el cambio de pendiente sea más preciso)
Un soporte metálico (para sostener el peso de la tubería)
Bridas (para unir las secciones de la tubería)
Un caudalímetro electromagnético (para tener información de la cantidad de caudal que
está pasando a lo largo de la tubería)
Dos sensores de precisión (para medir profundidades de flujo aguas arriba y aguas
abajo del fenómeno del resalto hidráulico)
15 Piezómetros (para obtener profundidades de flujo)
Una compuerta aguas abajo
Fotos del modelo
Primero, se realizó un reconocimiento del modelo ubicando todos los materiales que lo
componían y se procedió a limpiar todo el montaje para obtener un ensayo más limpio y apto
para el inicio de la toma de datos. Luego, se realizó un ensayo de este para verificar el
comportamiento de la tubería verificando los datos del caudalímetro, de los sensores de
precisión y de los piezómetros. A continuación se presentará la foto del montaje limpio y
adecuado para comenzar con la toma de datos pertinentes:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
67
Gráfica 43. Foto del montaje listo para ser utilizado.
De esta forma, se procedió a corregir pequeños detalles que tenía la tubería como fugas, por
medio de un autopolimerizable (VERACRIL) el cual consta de un resina acrílica y de un líquido
acrílico que al juntar activa sus funciones de sellante para cualquier tipo de acrílico. Luego de
tener el modelo listo, se continúa con un ensayo de prueba para verificar la consistencia de los
datos y el funcionamiento de la tubería como se muestra a continuación:
Gráfica 44. Ensayo de prueba para la verificación de los instrumentos y la tubería.
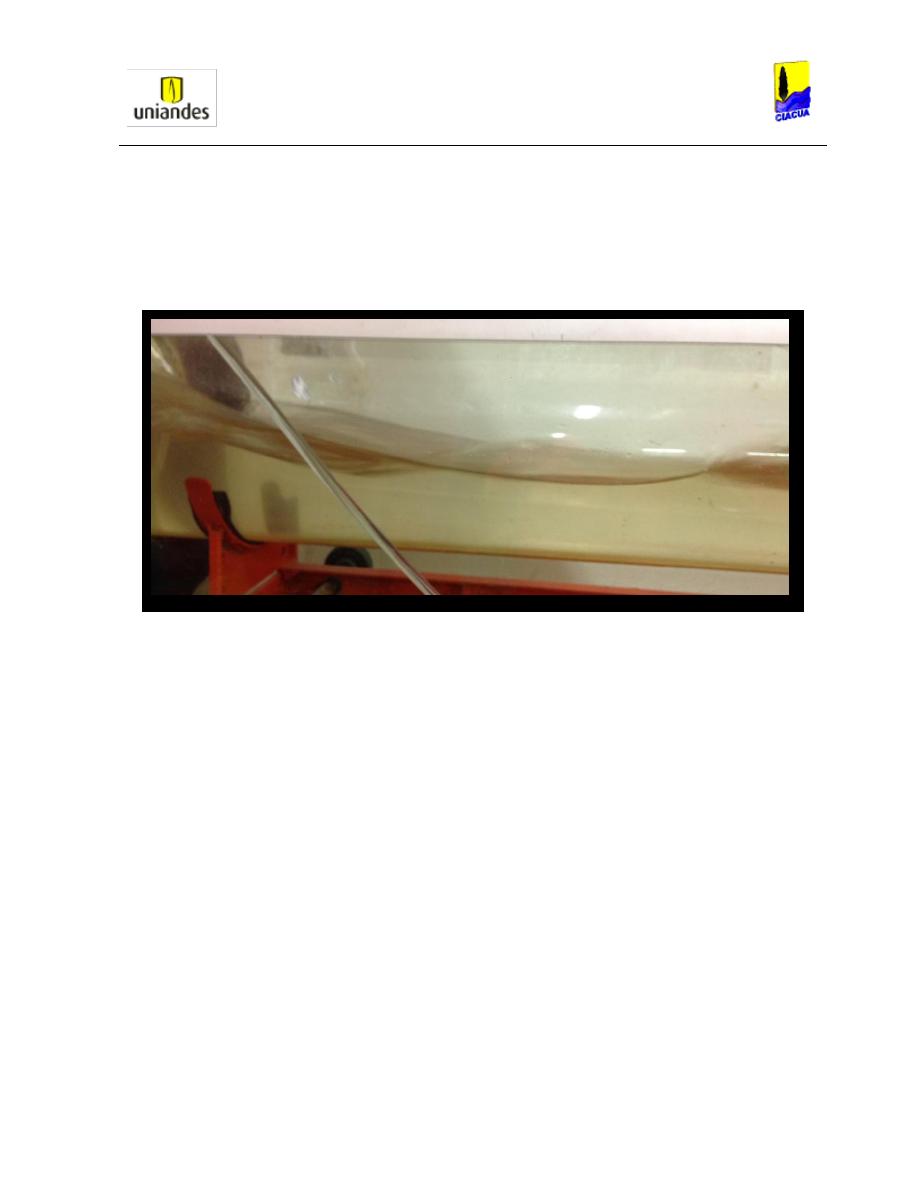
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
68
El modelo funcionó de manera óptima, sin ninguna fuga. El flujo, como se observa en la Gráfica
46, se comporta de manera ondular por ser de sección circular lo cual puede ser un motivo de
error a la hora de tomar los datos experimentales. Por esto el flujo no se comporta del todo
uniforme y esto puede afectar las medidas aguas arriba o aguas abajo con los sensores de
profundidades. A continuación se mostrará una foto del flujo aguas arriba comenzando en la
sección de la tubería:
Gráfica 45. Ensayo de prueba aguas arriba para la verificación de los instrumentos y la tubería.
Como se mencionó anteriormente, se puede evidenciar que a lo largo de toda la tubería el flujo
se comporta de forma ondular desde su inicio hasta el final en sus ensayos de prueba. Ahora
se procede a mostrar las imágenes de un ensayo tipo para la realización del informe, generando
el fenómeno del resalto hidráulico por medio de la compuerta aguas abajo, ubicándolo entre los
dos sensores y verificando el fenómeno de sobrecarga (Presurización aguas abajo de la
tubería) o como lo estipula la RAS (Reglamento Técnico del Sector de Agua Potable y
Saneamiento Básico), que se encuentre menor a una relación de llenado del 85%.
Para presentar el comportamiento de la tubería en los primeros ensayos de prueba, es
necesario describir los instrumentos que se utilizaron para generar el fenómeno del resalto
hidráulico y la variación de pendiente en la tubería.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
69
Gráfica 46. Compuerta aguas abajo de la tubería para controlar el fenómeno del resalto hidráulico.
Como se puede observar en la Gráfica 48, la compuerta con la que contaba el modelo tenía
como función generar un estancamiento de agua para generar el cambio de flujo supercrítico a
subcrítico por medio del resalto hidráulico. Para generar la variación de las pendientes se
utilizaron cuatro gatos mecánicos con la función de generar cambios de alturas en las secciones
de la tubería como se observa a continuación.
Gráfica 47. Gatos mecánicos para controlar la variación de la pendiente.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
70
A continuación se presentarán las imágenes del resalto que se produjo para un ensayo de
prueba:
Gráfica 48. Fenómeno del resalto hidráulico.
Se generó el fenómeno del resalto hidráulico debido al estancamiento de aguas mediante la
compuerta aguas abajo. Luego, se procedió a realizar la toma de datos experimentales para
verificar el comportamiento de la tubería y evitar el fenómeno de sobrecarga para no generar
daños ni inundaciones. A continuación se va a presentar las medidas tomadas por los
piezómetros donde efectivamente se puede observar el comportamiento del resalto y su
transición de flujo supercrítico a flujo subcrítico, mostrando la variación de alturas.
Gráfica 49. Alturas piezómetricas del resalto hidráulico.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
71
Por otro lado, para la ejecución de la tesis experimental se contaba con el sensor IQ Plus para
la toma de datos más efectiva reduciendo el rango de error y obteniendo datos más concretos
del comportamiento de la tubería. No obstante, debido a que este sensor está diseñado
especialmente para canales abiertos, se tuvo complicaciones y no generaba ninguna clase de
resultado.
Gráfica 50. Sensor IQ Plus.
Para su instalación se desmontó una sección del montaje, se limpió toda la tubería por dentro
y se procedió a instalar el sensor por medio de tornillos que aseguraran este a la estructura en
acrílico de la tubería. A continuación se presenta la imagen del procedimiento de instalación del
sensor IQ Plus.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
72
Gráfica 51. Procedimiento de instalación del sensor IQ Plus.
Debido a que los rayos del sensor chocaban con una parte de la tubería, se procedió a realizar
una estructura en acrílico para ubicar de mejor forma y elevar el sensor para que los rayos
trabajaran adecuadamente.
Gráfica 52. Estructura del sensor IQ Plus para obtener un funcionamiento adecuado de los rayos emitidos
por este.
Debido a las complicaciones con respecto al cambio de sección con la que se estaba
trabajando, no se pudo realizar ninguna medición con este instrumento. Por esta razón, solo se
trabajó con los sensores de profundidades y caudalímetro electromagnético, lo cual generó
mayor incertidumbre a la hora de medir el caudal por su constante variación y su alto grado de
error. A continuación se va a explicar cuál es la incertidumbre de cada uno de los instrumentos
que se utilizaron para realizar la toma de datos y de esta forma encontrar otras posibles causas
de error.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
73
Precisión de los instrumentos
La incertidumbre de los instrumentos con los cuales se va a trabajar resulta ser un tema muy
importante para la ejecución de estos ensayos experimentales, puesto que se debe tener en
cuenta los rangos de variación que se trabajan en cada uno de los instrumentos para encontrar
las posibles causas de la diferencia entre los errores teóricos con los resultados obtenidos en
el laboratorio.
5.1 Caudalímetro
Para la toma de las medidas de todos los caudales de entrada al modelo que se estaba
trabajando se utilizó un caudalímetro magnético WaterMaster (ABB) diseñado especialmente
para diversas aplicaciones que se encuentran en la industria del agua potable y aguas
residuales. Este modelo tiene rendimiento de flujo con un rango de caudal de operación con
una precisión estándar de
±0,4%en ambos sentidos de flujo.
Las principales características de este modelo son:
Flujo bidireccional
Único transmisor autocalibrable que ofrece la máxima estabilidad y repetibilidad
El cumplimiento con OIML, la continua auto verificación con alarmas aseguran la
precisión tanto el sensor como el transmisor
Amplio modo de simulación
Gráfica 53. Caudalímetro electromagnético WaterMaster (ABB).
La OIML (Organization Internationale de Métrologie Légale) es una organización
intergubernamental creada en 1955. Su principal objetivo es la armonización internacional
de la metrología legal, proporcionando una referencia importante para la credibilidad de las
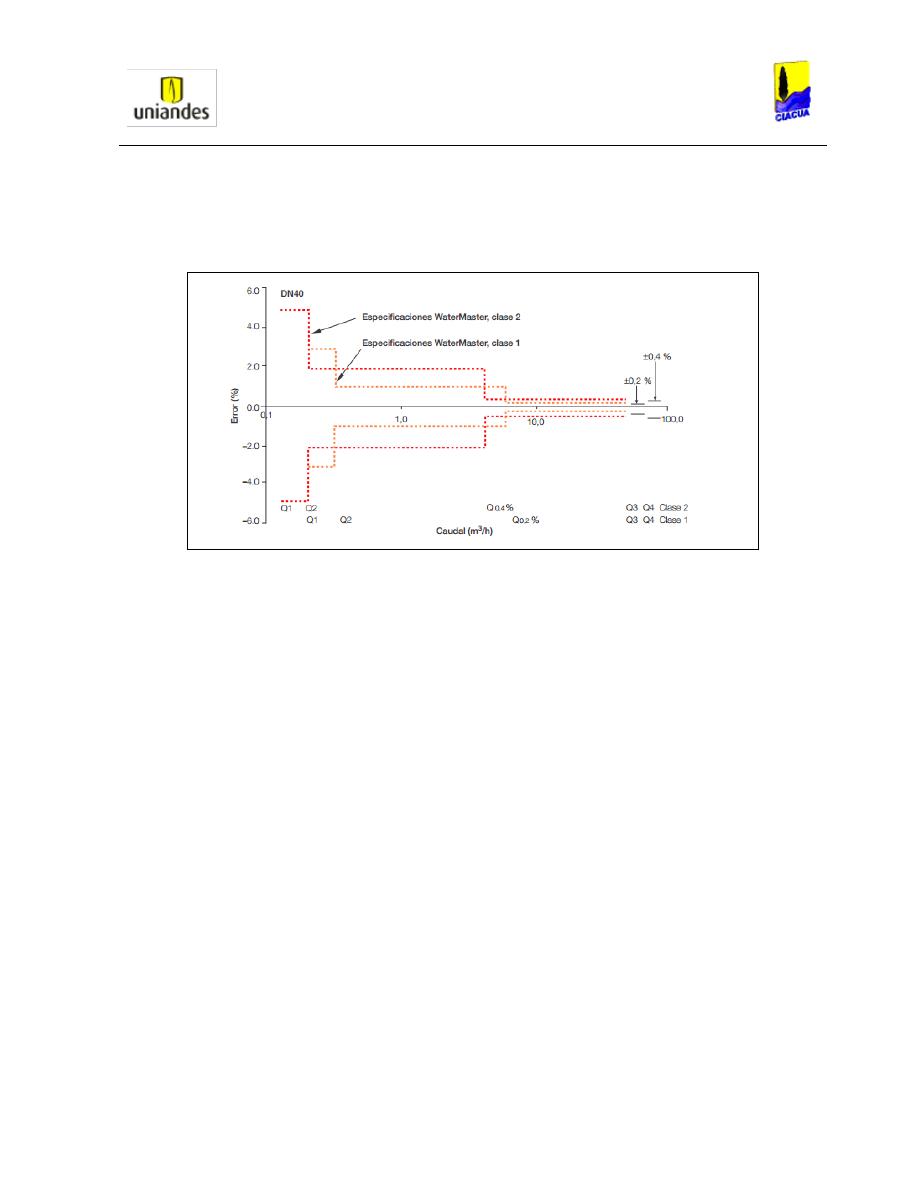
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
74
mediciones. La OIML R49 consiste en modelos fundamentados técnicamente para controlar
legalmente los instrumentos de medición, especialmente está diseñada para controlar
mediciones de agua potable fría y caliente. A continuación se presenta la incertidumbre del
sensor basándose en la OIML R49 (WaterMaster, 2013):
Gráfica 54. Rangos de error del caudalímetro electromagnético clase 2 según OIML R49 (WaterMaster,
2013).
Además, como se observa en la Gráfica 56, para la clase 2 que es el caudalímetro del
Laboratorio de Hidráulica el rango de error aumenta a medida que se toman caudales más
bajos, es por esto que al trabajarse con caudales bajos la variación va a ser mayor y el rango
de error y de incertidumbre que se va a trabajar va a ser mucho más grande que con los
caudales más grandes.
5.2 Sensores de profundidades
En el modelo se utilizaron dos sensores de precisión encargados de mostrar los resultados de
las profundidades de flujo aguas arriba y aguas abajo del resalto hidráulico separados por una
distancia de 4,05 metros de distancia entre sí. A continuación se muestra la imagen del sensor
puesto en el modelo que se desarrolló el ensayo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
75
Gráfica 55. Sensor U-GAGE T30 Series (BANNER, 2013).
El sensor U-GAGE T30 Series es un sensor ultrasónico fácil de utilizar y rápido, excelente para
aplicaciones de mediciones como niveles de profundidades de flujo en un tanque. Cada sensor
incluye un análogo y una salida discreta, que puede ser programado independientemente con
diferentes límites y cada salida tiene la opción de ser fijado con un punto de ajuste de la
distancia de detección centrado con una ventana de 10 mm (BANNER, 2013).
Tabla 7. Incertidumbre del sensor de profundidades U-GAGE T30 (BANNER, 2013).
La incertidumbre del sensor varía según la medición que se va a analizar: resolución análoga
del sensor es
±0,25% de la distancia medida, la linealidad análoga es ±0,5% del rango total de
la escala de sensibilidad y la sensibilidad de repetitividad es
±0,25% de la distancia.
Por otro lado, cabe resaltar que al realizar las mediciones de prueba y de los ensayos de toma
de datos, se encontró que el sensor que estaba puesto aguas abajo se comportaba de una
forma muy variable por problemas técnicos propios del sensor y que para solicitar un cambio
de sensor las fechas estipuladas de llegada de este con las fechas estipuladas del cronograma
del proyecto que se iba a realizar no concordaban y se saldría del tiempo estipulado. Por lo
tanto, se decidió realizar la toma de mediciones con este sensor y trabajar un margen de error
más alto para las medidas que se tomaran aguas abajo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
76
6. Resultados Experimentales
Para la toma de datos de este informe se hace referencia a la Tabla 8. Mediciones realizadas
en el laboratorio, donde se muestra que se utilizaron cuatro pendientes distintas: 0,011- 0,016-
0,018 y 0,025. En cada una de estas pendientes se trabajó con 35 caudales diferentes,
ocasionando el fenómeno del resalto hidráulico mediante la compuerta ubicada aguas abajo.
Para ver las tablas de los resultados obtenidos ver ANEXO I. La obtención de los resultados se
obtuvo de las siguientes ecuaciones:
Datos de Entrada
• Caudal (Q)
• Profundidades aguas arriba y aguas abajo (Yn)
• Diámetro (d)
• Pendiente (S)
Fórmulas
Área mojada
(𝒎
𝟐
)
𝑨 = (
𝟏
𝟖
∗ ( 𝜽 − 𝐬𝐢𝐧 𝜽)) ∗ 𝒅
𝟐
Ecuación 93. Cálculo del área mojada en secciones circulares.
Expresando
ϴ como:
𝜃 = 𝜋 + 2 ∗ arcsin (
𝑦
𝑛
− (
𝑑
2)
𝑑
2
)
donde
𝑑 es el diámetro de la tubería que es constante en este informe experimental,
𝑦
𝑛
es la profundidad de flujo ya sea aguas arriba o aguas abajo.
Velocidad de fuljo
(
𝒎
𝒔
𝟐
)
𝑣 =
𝑄
𝐴
Ecuación 94. Cálculo de la velocidad de flujo en secciones circulares.
donde
𝐴 es el área mojada y 𝑄 el caudal de entrada a la tubería.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
77
Ancho de la superficie de agua
(𝒎)
𝑇 = 𝑑 ∗ cos
(
arcsin
(𝑦
𝑛
− (
𝑑
2))
𝑑
2
)
Ecuación 95. Cálculo del ancho de la superficie de agua en secciones circulares.
Perímetro mojado
(𝒎)
𝑃 =
𝜃 ∗ 𝑑
2
Ecuación 96. Cálculo del perímetro mojado en secciones circulares.
Profundidad hidráulica
(𝒎)
𝐷 =
𝐴
𝑇
Ecuación 97. Cálculo de la profundidad hidráulica en secciones circulares.
Número de Froude
𝐹𝑟 =
𝑣
√9,81 ∗ 𝐷
Ecuación 98. Cálculo del número de Froude en secciones circulares.
Relación de llenado
𝑦
𝑑
=
𝑦
𝑛
𝑑
Ecuación 99. Cálculo de la relación de llenado en secciones circulares.
donde
𝑦
𝑛
es la altura dada por el sensor aguas arriba o aguas abajo y
𝑑 es el diámetro de la
tubería.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
78
Energía específica
𝐸 = 𝑦
𝑛
+ (
𝑣
2
2 ∗ 9,81
)
Ecuación 100. Cálculo de la energía especifica en secciones circulares.
Pérdidas de energía en el resalto hidráulico
∆𝐸 = 𝐸
1
− 𝐸
2
Ecuación 101. Cálculo de las pérdidas de energía del resalto hidráulico en secciones circulares.
Eficiencia del resalto hidráulico (%)
𝐸𝑓𝑖𝑐𝑖𝑒𝑛𝑐𝑖𝑎 =
∆𝐸
𝐸
1
∗ 100
Ecuación 102. Cálculo de la eficiencia del resalto hidráulico en secciones circulares.
Momentum
𝑍
1
∗ 𝐴
1
+
𝑄
2
𝑔 ∗ 𝐴
1
= 𝑍
2
∗ 𝐴
2
+
𝑄
2
𝑔 ∗ 𝐴
2
Ecuación 103. Cálculo del momentum específico en secciones circulares.
donde
𝑍 es el centroide mojado, 𝐴 es el área mojada, 𝑔 es la gravedad y 𝑄 es el caudal de
entrada a la tubería.
Luego de obtener todos los resultados por los ensayos, se procedió a realizar un análisis de los
resultados, verificando el comportamiento de cada una de las pendientes que se estudiaron. Lo
primero que se estudió fue el comportamiento de la relación de llenado aguas arriba de la
tubería contra los caudales que se trabajaron en cada una de las cuatro pendientes, obteniendo
los siguientes resultados:
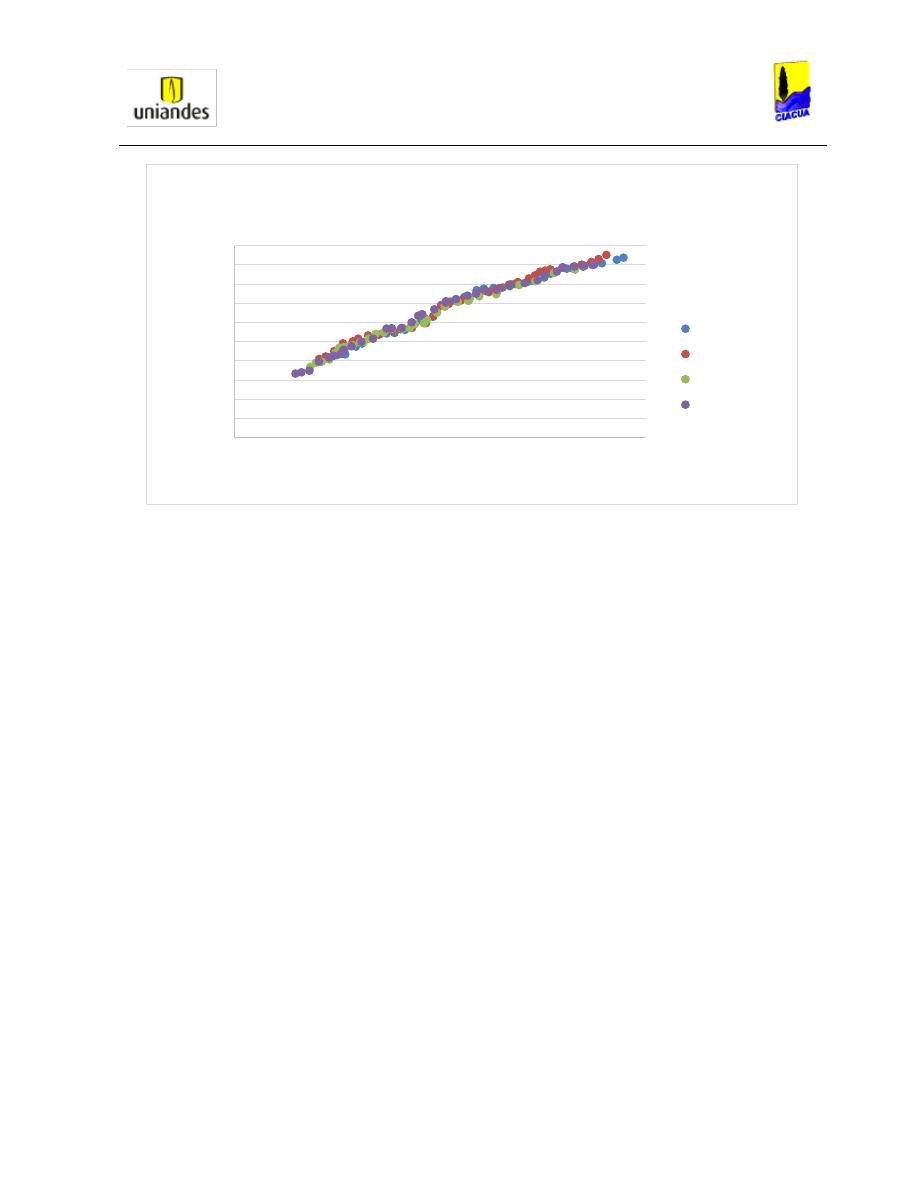
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
79
Gráfica 56. Comparación de las pendientes con respecto a su relación de llenado aguas arriba.
En la Gráfica 58 se puede observar que en todas las pendientes trabajadas no hubo cambios
significativos en las relaciones de llenado aguas arriba con respecto a los caudales trabajados,
por lo cual se puede llegar a la conclusión, que en este tipo de experimentos acerca del
fenómeno de resalto hidráulico, la pendiente no es función de la relación de llenado aguas
arriba: Esto se debe al trabajo que realiza la compuerta aguas abajo de la tubería para
ocasionar el resalto hidráulico, lo cual hace que el flujo aguas arriba no genere ningún cambio
abrupto en su profundidad de flujo mediante diferentes caudales. Lo otro que se puede analizar
de la Grafica 58 es que presenta un comportamiento lineal y directamente proporcional a los
caudales trabajados; a mayor caudal mayor relación de llenado aguas arriba de la tubería.
Ahora se procede a verificar si este flujo aguas arriba se puede suponer como un flujo de
comportamiento uniforme utilizando la ecuación de Darcy Weisbach para comparar los datos
experimentales con estos datos teóricos. Para ver la tabla de resultados teóricos ver ANEXO
II.
0,0%
5,0%
10,0%
15,0%
20,0%
25,0%
30,0%
35,0%
40,0%
45,0%
50,0%
0
0,01
0,02
0,03
0,04
0,05
Y
1
/d
(
-)
Caudal (m
3
/s)
Relación de llenado aguas arriba de la tubería vs caudal de
entrada
Pendiente 0,011
Pendiente 0,016
Pendiente 0,018
Pendiente 0,025
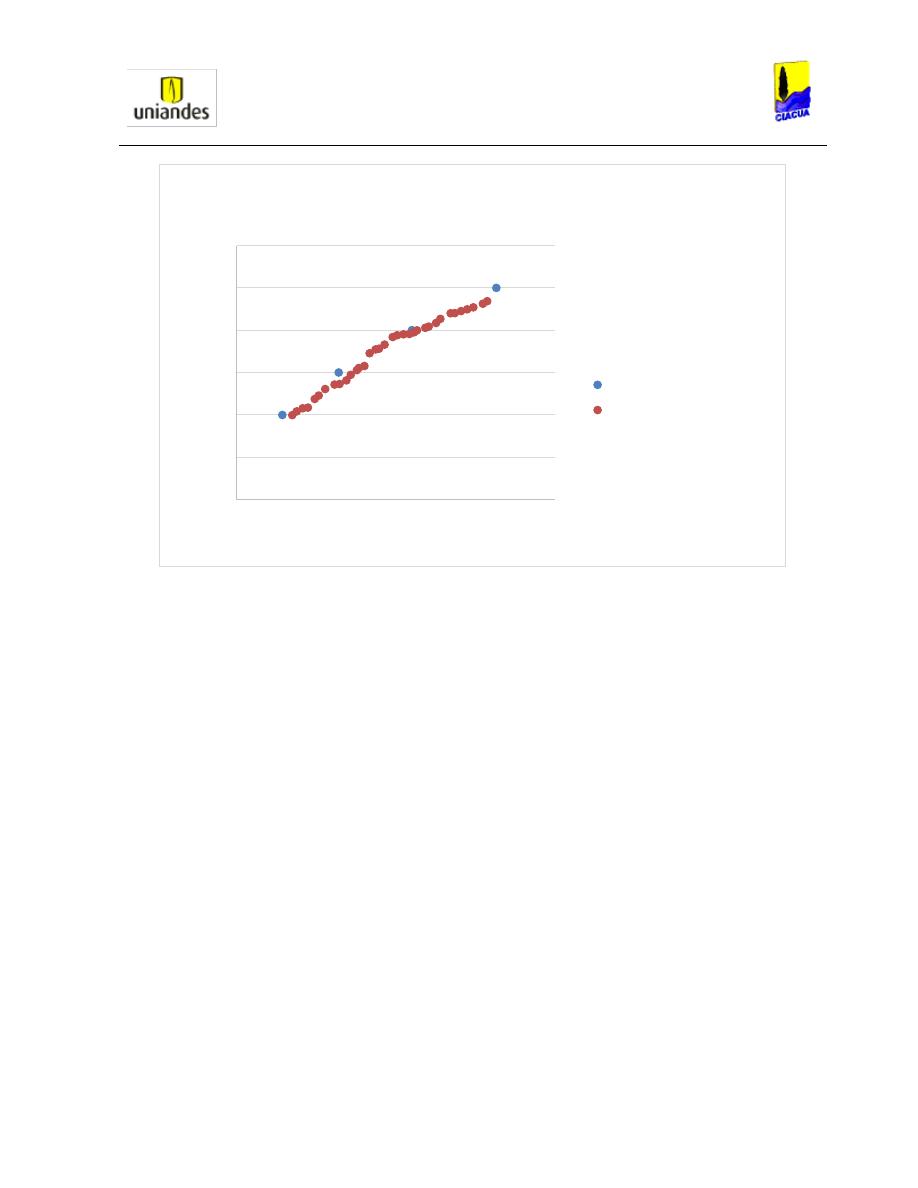
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
80
Gráfica 57. Comparación de la pendiente 0,011 con la ecuación de Darcy Weisbach.
Para analizar la ecuación de Darcy Weisbach se debe realizar la siguiente suposición para usar
un flujo uniforme
𝑆
𝑓
= 𝑆
𝑜
donde
𝑆
𝑓
es la pendiente de fricción y
𝑆
𝑜
es la pendiente del canal.
Por otro lado, este análisis solo se realizó para la pendiente 0,011 y muestra una muy buena
relación con la ecuación de Darcy, por lo cual se puede suponer que en los ensayos que se
realizaron aguas arriba por la longitud de la tubería y por no tener ninguna obstrucción el flujo
es uniforme tal como se observa en la Gráfica 59. Ahora se procede a desarrollar el mismo
proceso para otra pendiente para verificar lo dicho anteriormente.
0%
10%
20%
30%
40%
50%
60%
0,000
0,010
0,020
0,030
0,040
0,050
0,060
y1/d
(
-)
Caudal (m^3/s)
Relación de llenado aguas arriba de la tubería
suponiendo un flujo uniforme
Ecuación de Darcy
Datos Experimentales S=0,011
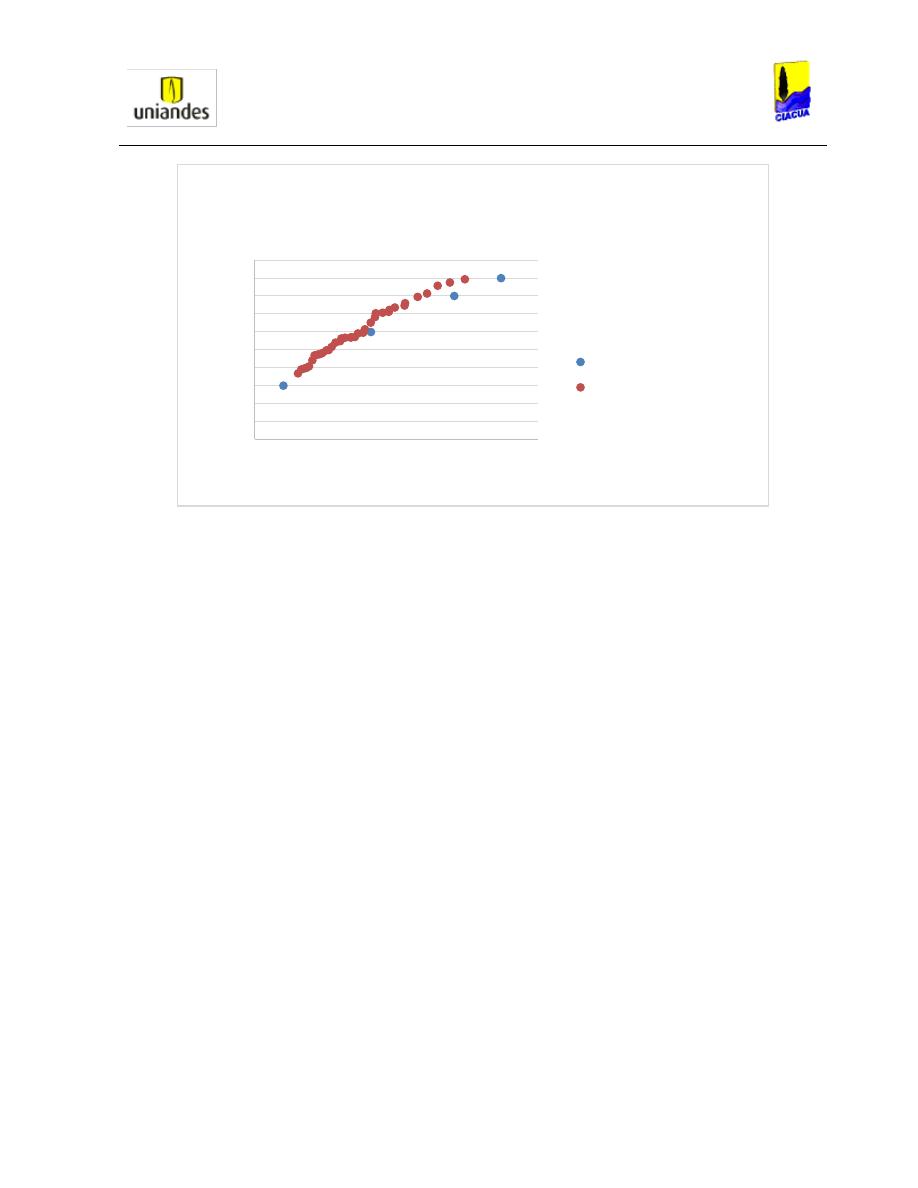
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
81
Gráfica 58. Comparación de la pendiente 0,018 con la ecuación de Darcy Weisbach.
Como se había dicho anteriormente de la pendiente de 0,011, en la Gráfica 60 de la
comparación de la pendiente 0,018 y la ecuación teórica de Darcy Weisbach se observa cierta
similitud con los resultados teóricos. Por lo cual, se puede suponer que aguas arriba de la
tubería siempre se va a trabajar con un flujo uniforme. Estos pequeños desfases que se pueden
observar se suponen a la variación de dato en la toma de profundidades por tener un
comportamiento de oleaje como se mostraba en las Gráfica 46 y Gráfica 47.
Cabe resaltar que no se tomaron relaciones de llenado experimentales menores al 16% y
caudales menores a 8 L/s, por lo que al tener estos caudales tan bajos las posibilidades de
aumentar la incertidumbre en el caudalímetro electromagnético eran mayores, y además por
tener tan poco caudal en el momento que se controlaba la compuerta no se alcanzaba a generar
el fenómeno del resalto hidráulico o era muy difícil de observar y analizar.
0%
5%
10%
15%
20%
25%
30%
35%
40%
45%
50%
0,000
0,010
0,020
0,030
0,040
0,050
0,060
y
1
/d
(
-)
Caudal (m
3
/s)
Relación de llenado aguas arriba de la
tubería suponiendo un flujo uniforme
Ecuación de Darcy
Datos Experimentales S=0,018
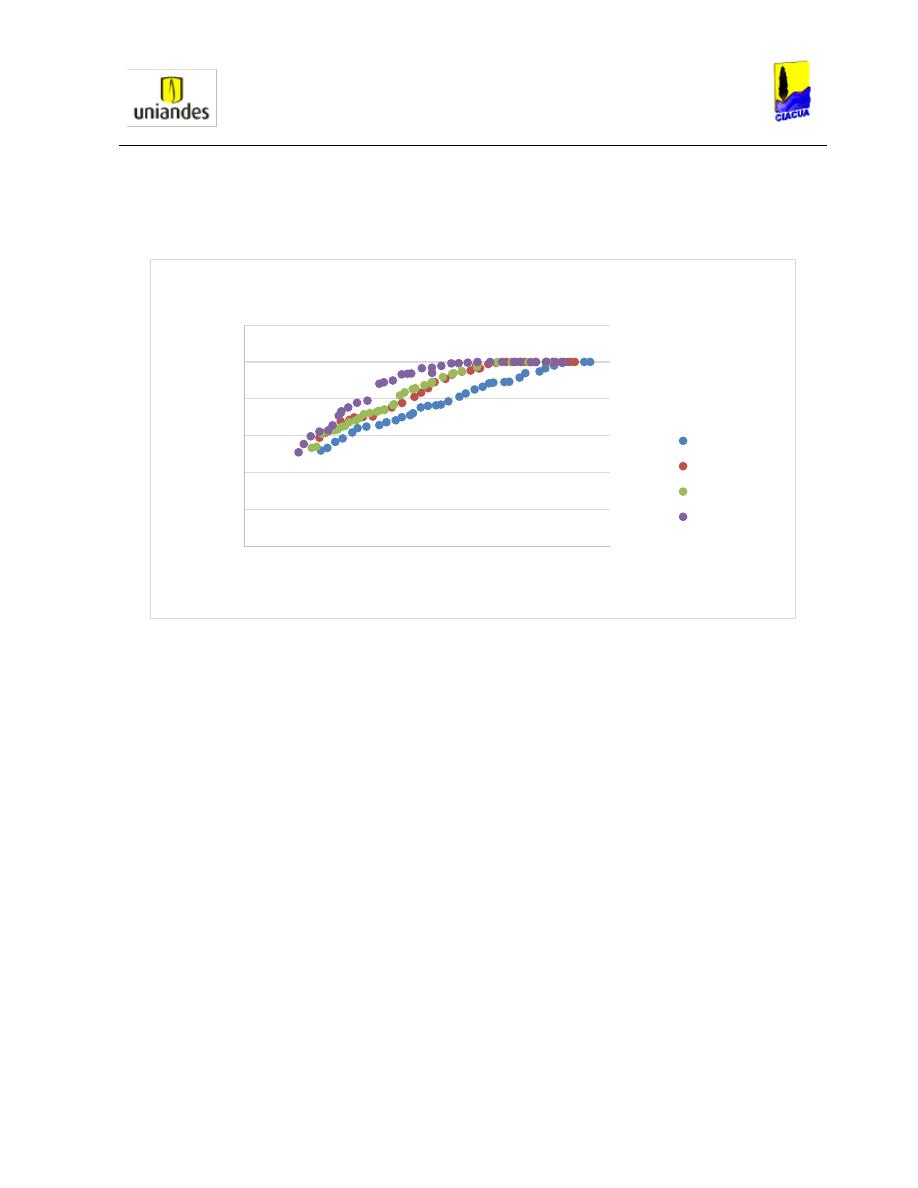
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
82
Luego se procedió a encontrar el comportamiento que tiene la tubería aguas abajo, calculando
las relaciones de llenado de esta parte de la tubería contra los caudales que se trabajaron.
Gráfica 59.Comparación de la relación de llenado aguas abajo con respecto a las pendientes trabajadas.
Como se esperaba tras el fenómeno del resalto hidráulico, se puede observar en la Gráfica 61
que la pendiente que más rápido llegó a su presurización aguas abajo fue la mayor, y que la
que tarda más en llegar a su presurización es el ensayo realizado con la pendiente menor. De
esta gráfica se puede llegar a la conclusión que, para diseñar una tubería para el alcantarillado
de drenaje urbano (que es el objetivo de esta tesis) para ciudades donde se tenga altas
presurizaciones promedios anuales, es mejor diseñar con tuberías de bajas pendientes y de
esta forma no causar sobrecargas en el sistema y evitar daños en estas e inundaciones en las
ciudades.
Por otro lado, se va analizar si también se puede realizar la suposición de flujo uniforme aguas
abajo y asegurar que
𝑆
𝑓
= 𝑆
𝑜
utilizando la ecuación de Darcy Weisbach para las relaciones de
llenado que se presentan aguas abajo.
0,0%
20,0%
40,0%
60,0%
80,0%
100,0%
120,0%
0
0,01
0,02
0,03
0,04
0,05
Y
2
/d
(
-)
Caudal (m
3
/s)
Relación de llenado aguas abajo de la tubería
vs caudal de entrada
Pendiente 0,011
Pendiente 0,016
Pendiente o,o18
Pendiente 0,025
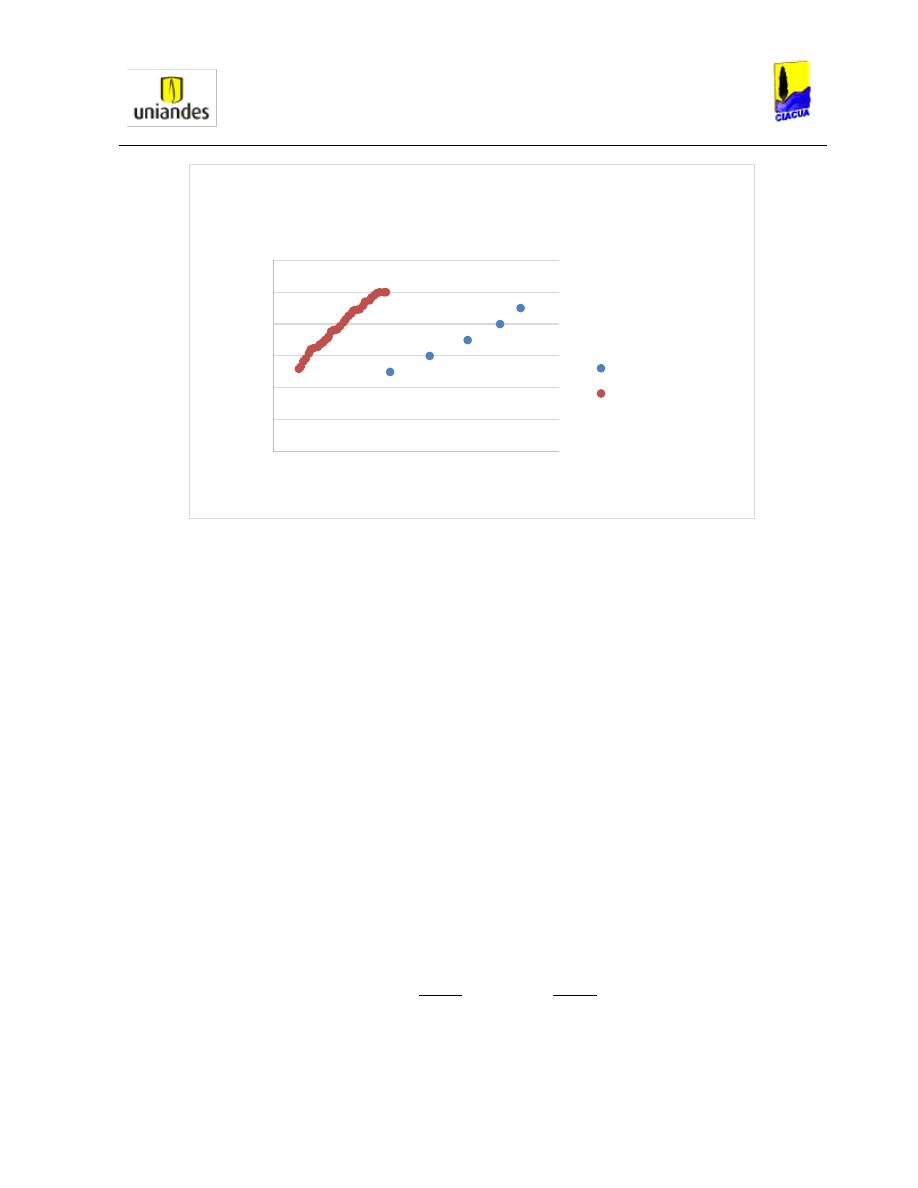
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
83
Gráfica 60. Comparación de la pendiente 0,011 con la ecuación de Darcy Weisbach.
Como se observa en la gráfica anterior, no se puede utilizar la ecuación de Darcy Weisbach
aguas abajo de la tubería, puesto que no se posee ninguna relación entre sí. Esto se debe a
que la relación de llenado aguas abajo en el proyecto realizado en el Laboratorio de Hidráulica
de la Universidad de los Andes, no es de forma uniforme puesto que se está generando el
fenómeno del resalto hidráulico, causando así que el flujo llegue a su presurización de forma
más rápida con caudales menores; alcanzando su máxima capacidad en 45 L/s. Por otro lado,
lo que se puede evidenciar en los resultados teóricos obtenidos mediante la ecuación de Darcy,
es que el flujo presenta un comportamiento lineal a medida que se aumentan los caudales
alcanzando un máximo caudal de 105 L/s.
No cabe mostrar el comportamiento de las demás pendientes puesto que se sabe que ninguno
va a cumplir con los datos teóricos de la ecuación de Darcy Weisbach. Por lo tanto, aguas abajo
se descarta que
𝑆
𝑓
= 𝑆
𝑜
, entonces se llega a la conclusión que el flujo aguas abajo no es
uniforme sino gradualmente variado. Para poder observar el comportamiento de la tubería
aguas abajo es necesario hacer referencia a la ecuación de momentum específico, puesto que
en un resalto hidráulico la energía no se conserva pero el momentum sí. Se supone la ecuación
de momentum como:
𝑍
1
∗ 𝐴
1
+
𝑄
2
𝑔 ∗ 𝐴
1
= 𝑍
2
∗ 𝐴
2
+
𝑄
2
𝑔 ∗ 𝐴
2
Ecuación 104. Momentum en un resalto hidráulico.
0%
20%
40%
60%
80%
100%
120%
0,000
0,020
0,040
0,060
0,080
0,100
0,120
y/d
(
-)
Caudal (m^3/s)
Relación de llenado aguas abajo de la
tubería suponiendo un flujo uniforme
Darcy
Experimentales S=0,011
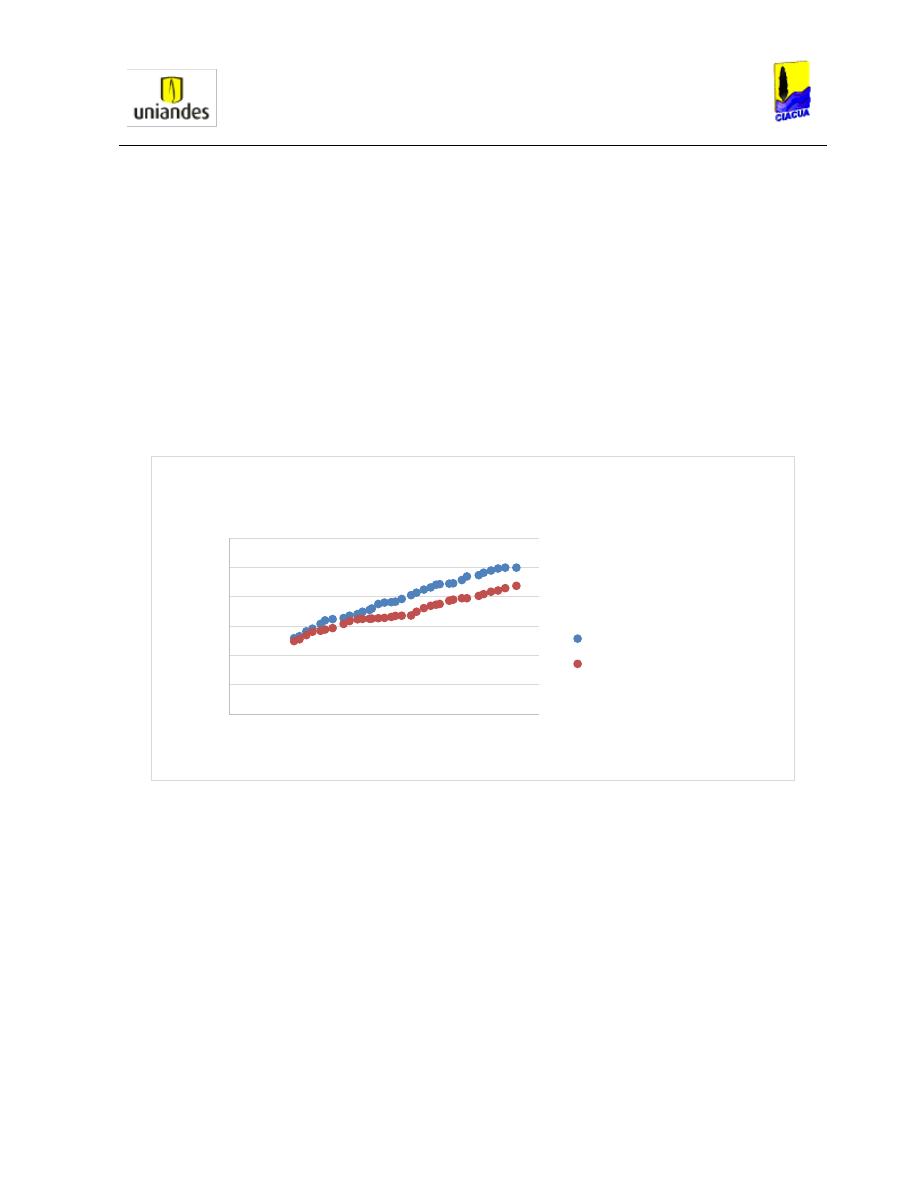
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
84
donde
𝑍 es el centroide mojado, 𝐴 es el área mojada, 𝑔 es la gravedad y 𝑄 es el caudal de
entrada a la tubería. De esta forma, se pueden encontrar los resultados teóricos para
𝑦
2
y
realizar una verificación de datos para determinar qué tan variables fueron los resultados dados
por el sensor de profundidades aguas abajo, teniendo en cuenta otra posible causa de error
como: para que el momentum en un resalto hidráulico se conserve es necesario tomar las
mediciones exactamente cuándo comienza el resalto y cuando este termina. Debido a que los
sensores de profundidades se encuentran a una distancia de 4,05 metros entre sí, no se pudo
generar esta medida con seguridad. Sin embargo, debido a que anteriormente se asumió que
el comportamiento aguas arriba era uniforme, los resultados obtenidos por el sensor aguas
arriba se consideran de forma válida. Por lo tanto, se van a analizar las medidas obtenidas por
el sensor aguas abajo contra los resultados teóricos aguas abajo igualando momentum:
Gráfica 61. Comparación de resultados teóricos contra los resultados experimentales de la pendiente
0,011.
Como era de esperarse los resultados experimentales cuentan con un cierto grado de error con
respecto a los resultados teóricos con respecto a la pendiente de 0,011. A continuación, se
procede para el análisis de este comportamiento en las demás pendiente que se trabajaron en
este proyecto.
0
0,05
0,1
0,15
0,2
0,25
0,3
0
0,01
0,02
0,03
0,04
0,05
Altu
ra
s a
gu
as
ab
aj
o
(m
)
Caudal (m
3
/s)
Comparión de alturas aguas abajo experimentales vs
teóricas igualando M1=M2 para S=0,011
Alturas aguas abajo experimentales
Alturas aguas abajo teóricas
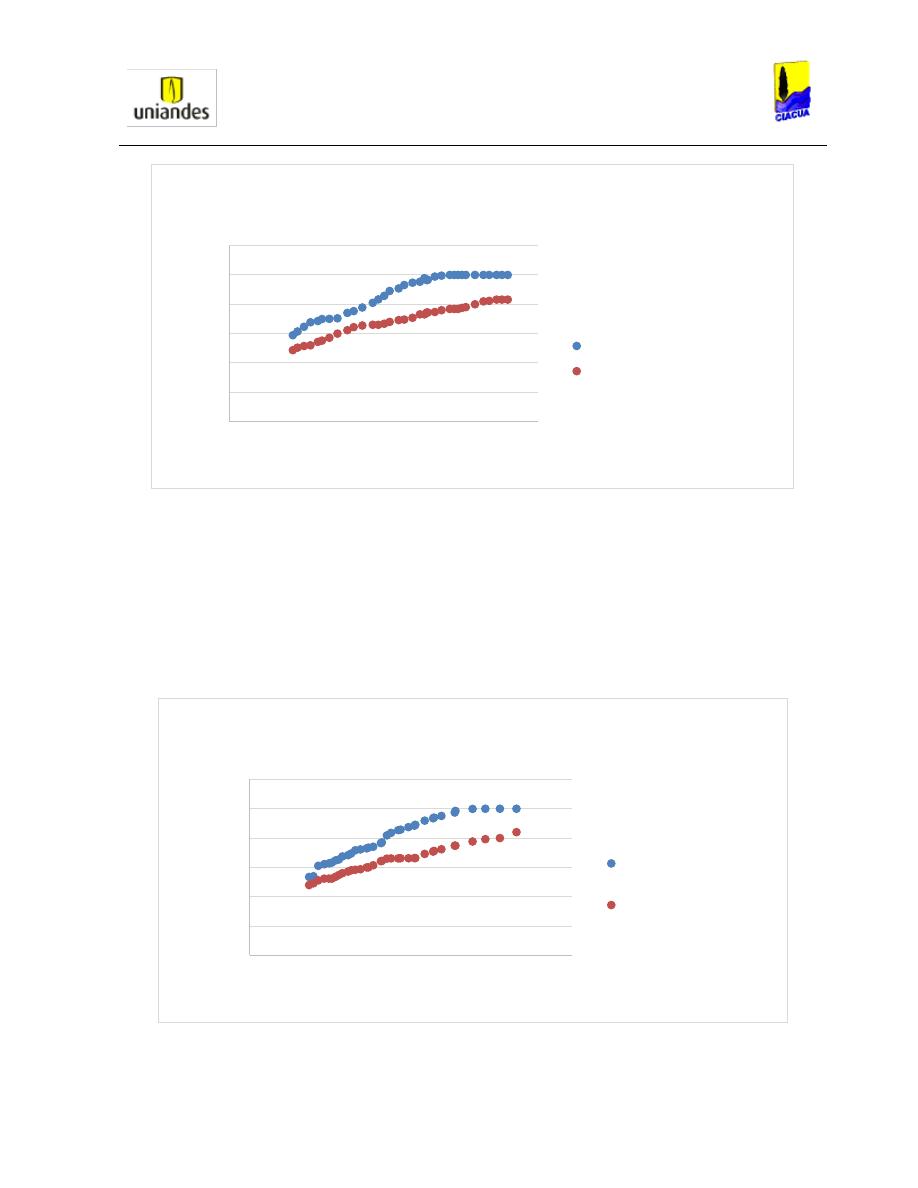
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
85
Gráfica 62. Comparación de resultados teóricos contra los resultados experimentales de la pendiente
0,016.
Al igual que la Gráfica 63, la Gráfica 64 presenta un comportamiento similar demostrando que
para los caudales trabajados existe cierto margen de error lo cual pudo deberse a que no se
tomaron las mediciones aguas abajo exactamente donde se acababa el resalto o por las
constantes variaciones del sensor aguas abajo, lo que pudo ocasionar un incremento en las
medidas.
Gráfica 63. Comparación de resultados teóricos contra los resultados experimentales de la pendiente
0,018.
0
0,05
0,1
0,15
0,2
0,25
0,3
0
0,01
0,02
0,03
0,04
0,05
Altu
ra
s a
gu
as
ab
aj
o
(m
)
Caudal (m
3
/s)
Comparión de alturas aguas abajo experimentales vs
teóricas igualando M1=M2 para S=0,016
Alturas aguas abajo experimentales
Alturas aguas abajo teóricas
0,0000
0,0500
0,1000
0,1500
0,2000
0,2500
0,3000
0
0,01
0,02
0,03
0,04
0,05
Altu
ra
s a
gu
as
ab
aj
o
(m
)
Caudal (m
3
/s)
Comparión de alturas aguas abajo experimentales vs
teóricas igualando M1=M2 para S=0,016
Alturas aguas abajo
experimentales
Alturas aguas abajo teóricas
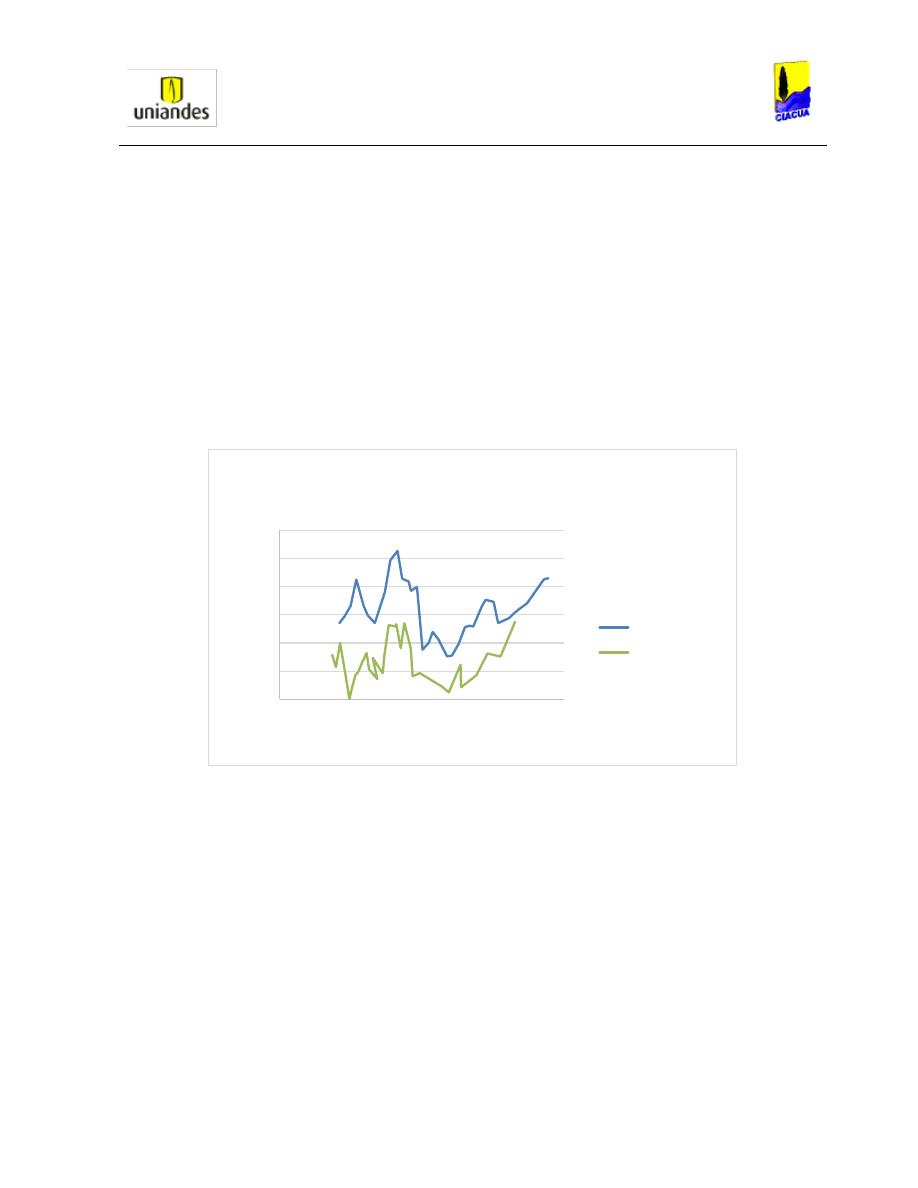
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
86
Finalmente, para la pendiente de 0,018 se muestra que el comportamiento sigue estable y
muestra cierta tendencia con respecto a las demás pendientes analizadas anteriormente. Como
el fin de este experimento es encontrar el verdadero comportamiento de la tubería y entender
el fenómeno del resalto hidráulico, se van a estudiar las alturas aguas abajo dadas por el sensor
y se va a trabajar para obtener una ecuación empírica de este experimento que demuestre los
caudales más críticos con los cuales se debe trabajar en cada una de las pendientes. Para este
proceso se va a necesitar un análisis de regresión lineal.
Antes de mostrar el proceso para la obtención de la ecuación empírica se va a mostrar el
comportamiento de la tubería en cuanto a las pérdidas de energía teniendo en cuenta ya los
errores de las mediciones mostrados anteriormente.
Gráfica 64. Pérdidas de energía experimentales en la tubería.
De la Gráfica 66 se puede concluir que en los caudales más pequeños el comportamiento es
más inestable en la tubería, en cambio en los caudales más altos se puede mostrar que la
gráfica sigue cierta tendencia a disipar mayor energía a mayores a caudales, lo cual debería
ocurrir normalmente en un resalto hidráulico.
Los motivos por los cuales el comportamiento de la tubería en caudales mayores es tan
inestable se puede asimilar a posibles errores de medición que ya fueron mencionados
anteriormente y a posibles errores de los instrumentos (Caudalímetro) como se presentaba en
la Gráfica 56 (Rangos de error del caudalímetro electromagnético clase 2 según OIML R49
(WaterMaster, 2013). La cual presentaba que a menores caudales se iban a generar mayores
incertidumbres. Por otro lado, otra muy posible causa de error en esta sección de la gráfica se
0,0
1,0
2,0
3,0
4,0
5,0
6,0
0
0,01
0,02
0,03
0,04
0,05
∆E
(%
)
Caudal (m
3
/s)
Pérdidas de energía experimentales en la
tubería contra el caudal
Pendiente 0,011
Pendiente 0,018
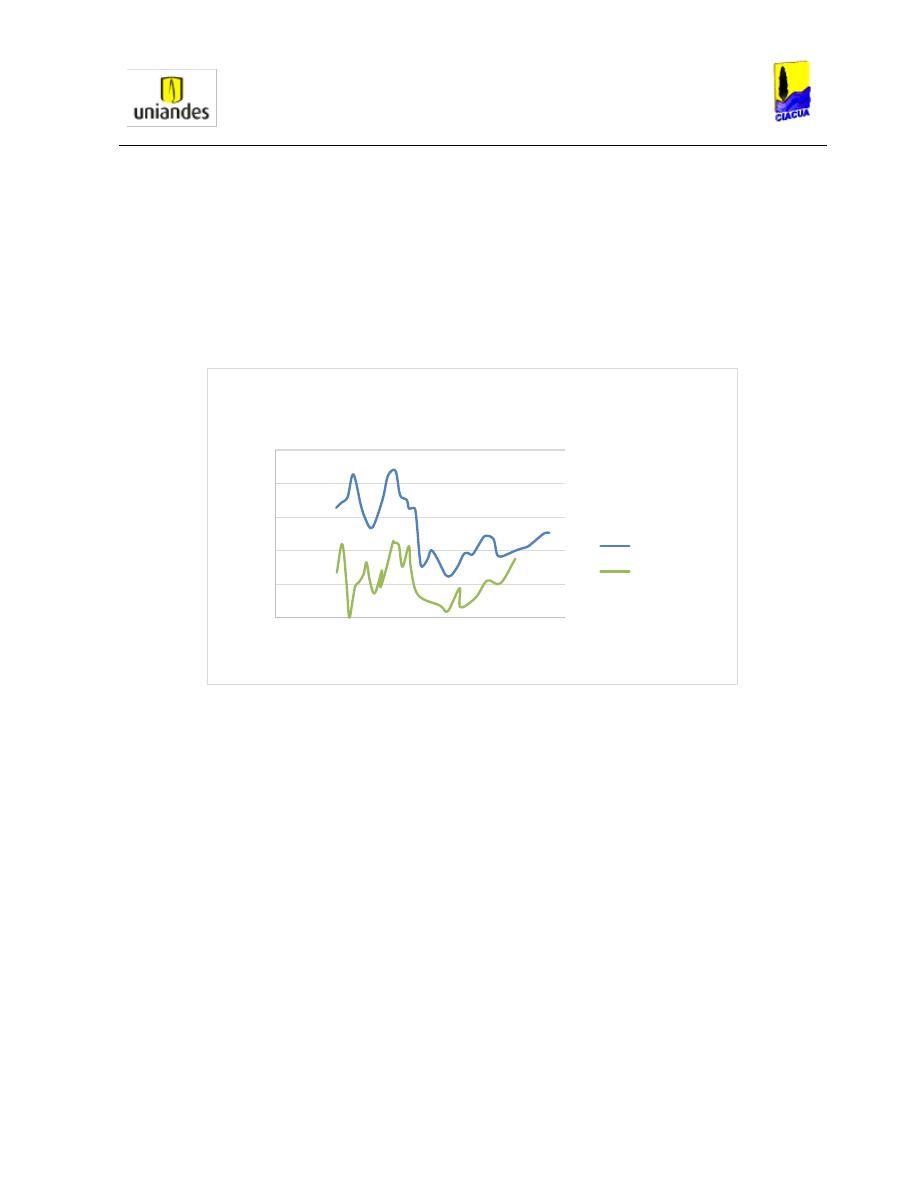
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
87
pudo generar porque al presentar el fenómeno del resalto hidráulico esta altura subsecuente
aguas abajo se presentara muy cercana a la altura crítica. Esto puede generar que el flujo sea
cuasi-crítico y presente bastantes variaciones en estas zonas de los resultados.
En cambio, en el rango de los caudales más altos (> 30 L/s) se puede analizar cierta tendencia
de los resultados, mostrando un incremento directamente proporcional al caudal, lo que infiere
que a mayor caudal, mayor disipación de energía. Esto es cierto puesto que a mayores
caudales se van a presentar flujos más supercríticos aguas arriba generando un resalto mucho
más fuerte, disipando mayor energía.
Gráfica 65. Eficiencia experimental de la tubería.
Como se explicaba anteriormente, el comportamiento tan inestable para los caudales menores
puede deberse a que las profundidades subsecuentes estén muy cercanas a las profundidades
críticas, por lo que genera que el comportamiento sea muy inestable. Otra causa de este
comportamiento puede ser ocasionada por errores en las mediciones o por errores de los
instrumentos. Además también se puede observar que en el rango de los caudales más altos
(> 30 L/s) se comienza a generar una tendencia directamente proporcional que al aumentar el
caudal se aumenta la eficiencia.
Ahora se procede a encontrar cuál es el caudal máximo que se necesita para alcanzar la
presurización en cada uno de los ensayos que se realizaron con las cuatro pendientes
diferentes, y por otro lado de cuanto caudal se necesita para encontrar la relación de llenado
estipulada por la RAS (Reglamento Técnico del Sector de Agua Potable y Saneamiento Básico).
0
5
10
15
20
25
0
0,01
0,02
0,03
0,04
0,05
∆E
/E
1 (%
)
Caudal (m^3/s)
Eficiencia experimental de la tubería versus el
caudal
Pendiente 0,011
Pendiente 0,018
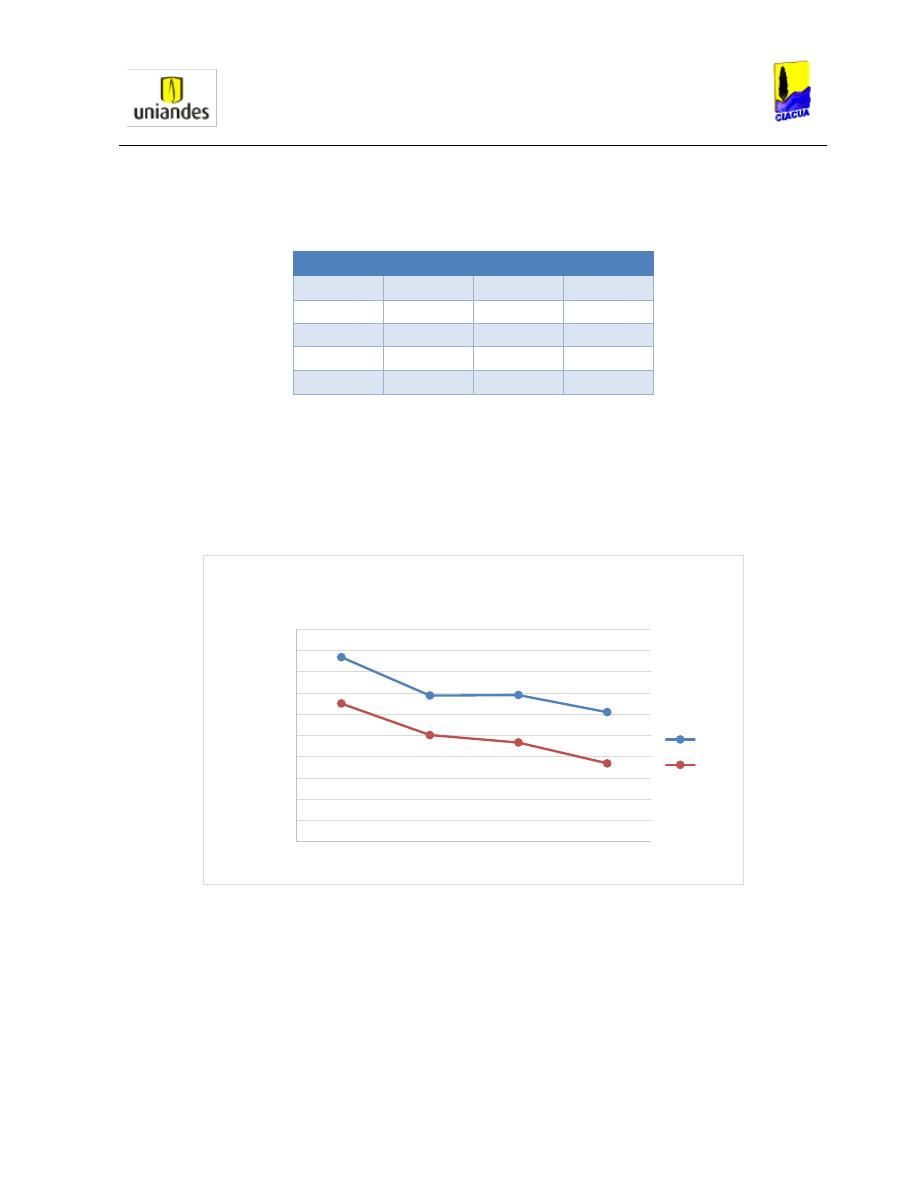
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
88
Tabla 9. Caudales máximos que resiste cada pendiente hasta su presurización y hasta una relación de
llenado del 86%.
100%
86%
S (-)
Q (m
3
/s)
S(-)
Q (m
3
/s)
0,011
0,043
0,011
0,033
0,016
0,034
0,016
0,025
0,018
0,035
0,018
0,023
0,025
0,031
0,025
0,018
Como se esperaba, el ensayo que resiste mayores caudales hasta llegar a su presurización o
hasta llegar a una relación de llenado del 85%, es el experimento realizado con la pendiente
más baja (S=0,011) y esto se puede observar de manera sucesiva (a menor pendiente, se
resiste mayores caudales). Esto se puede evidenciar de una mejor forma en la gráfica
presentada a continuación:
Gráfica 66. Relación de llenado óptima para las cuatro pendientes trabajadas.
Ahora, se procede a verificar el comportamiento de la tubería en las diferentes pendientes
graficando el número de Froude aguas arriba para los diferentes caudales trabajados en este
proyecto.
0,000
0,005
0,010
0,015
0,020
0,025
0,030
0,035
0,040
0,045
0,050
0,011
0,016
0,018
0,025
Cau
d
al
(m
3
/s
)
Relación de llenado óptima para las cuatro
pendientes trabajadas en laboratorio
100%
85%
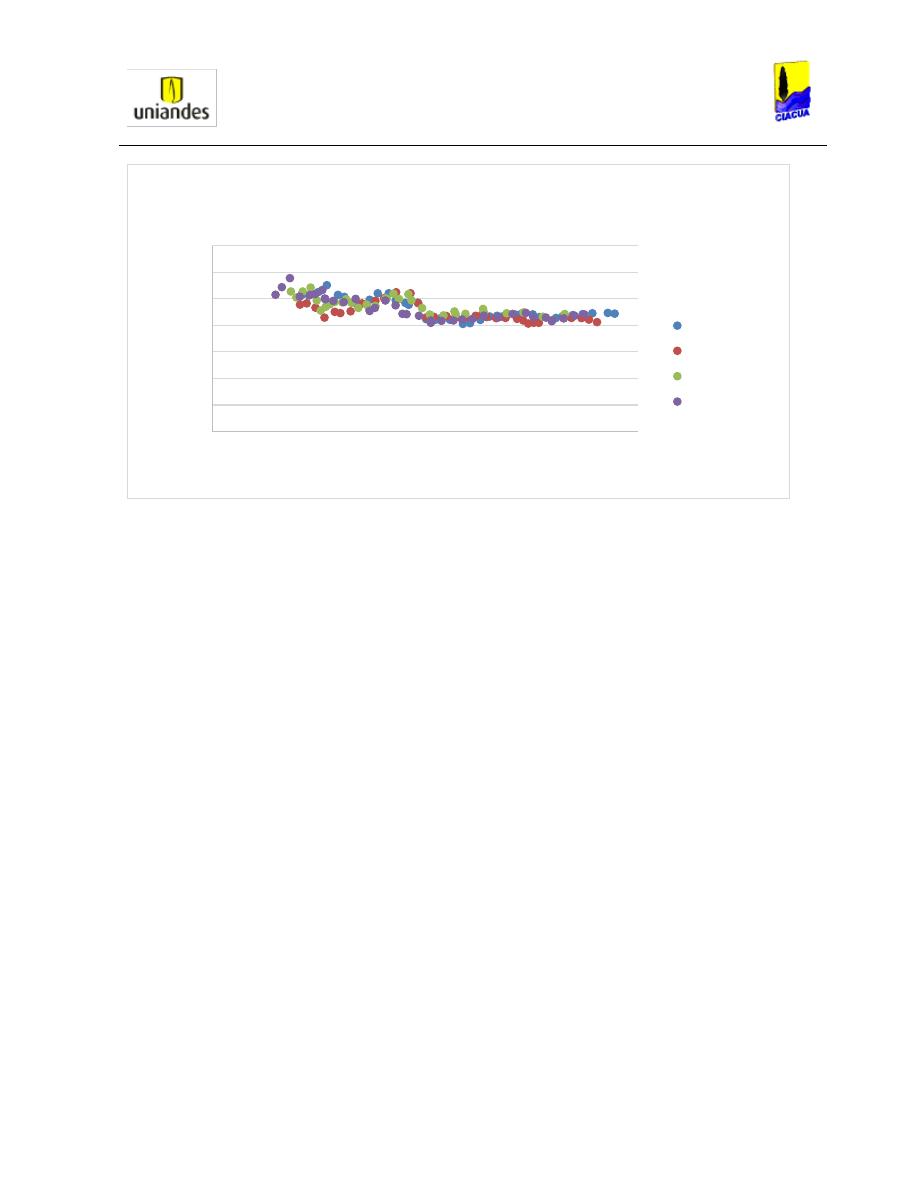
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
89
Grafica 67. Comportamiento experimental del número de Froude aguas arriba.
El número de Froude aguas arriba de la tubería se comporta de forma inversamente
proporcional al caudal como se puede observar en la Gráfica 67, es decir, mientras el caudal
es mayor y la profundidad de flujo es mayor; el número de Froude tiende a disminuir y a
comportarse de forma más estable y más subcrítico. En cambio, cuando se procede a disminuir
el caudal; este tiene a comportarse de forma más crítica, teniendo un comportamiento inestable
hasta pasar a una forma más supercrítica y más difícil de controlar.
Finalmente, se procede a explicar el procedimiento que se tuvo en cuenta para la obtención de
una ecuación empírica para encontrar la pendiente óptima para un caudal dado, evitando la
presurización de esta o una relación de llenado superior al 85% como lo estipula la RAS
(Reglamento Técnico del Sector de Agua Potable y Saneamiento Básico).
Primero, se realizó una comparación entre pendientes mediante el método de regresión, entre
las alturas aguas arriba, las alturas aguas abajo y el caudal del entrada que se utilizó, para
encontrar una ecuación empírica que demuestre el comportamiento de la tubería en cada una
de las pendientes trabajadas. A continuación se mostrará cada una de las regresiones que se
realizaron
0,000
0,500
1,000
1,500
2,000
2,500
3,000
3,500
0
0,01
0,02
0,03
0,04
0,05
Froud
e a
gua
s a
rriba
(
-)
Caudal (m
3
/s)
Comportamiento experimental del número de Froude aguas
arriba vs caudal
Pendiente 0,011
Pendiente 0,016
Pendiente 0,018
Pendiente 0,025
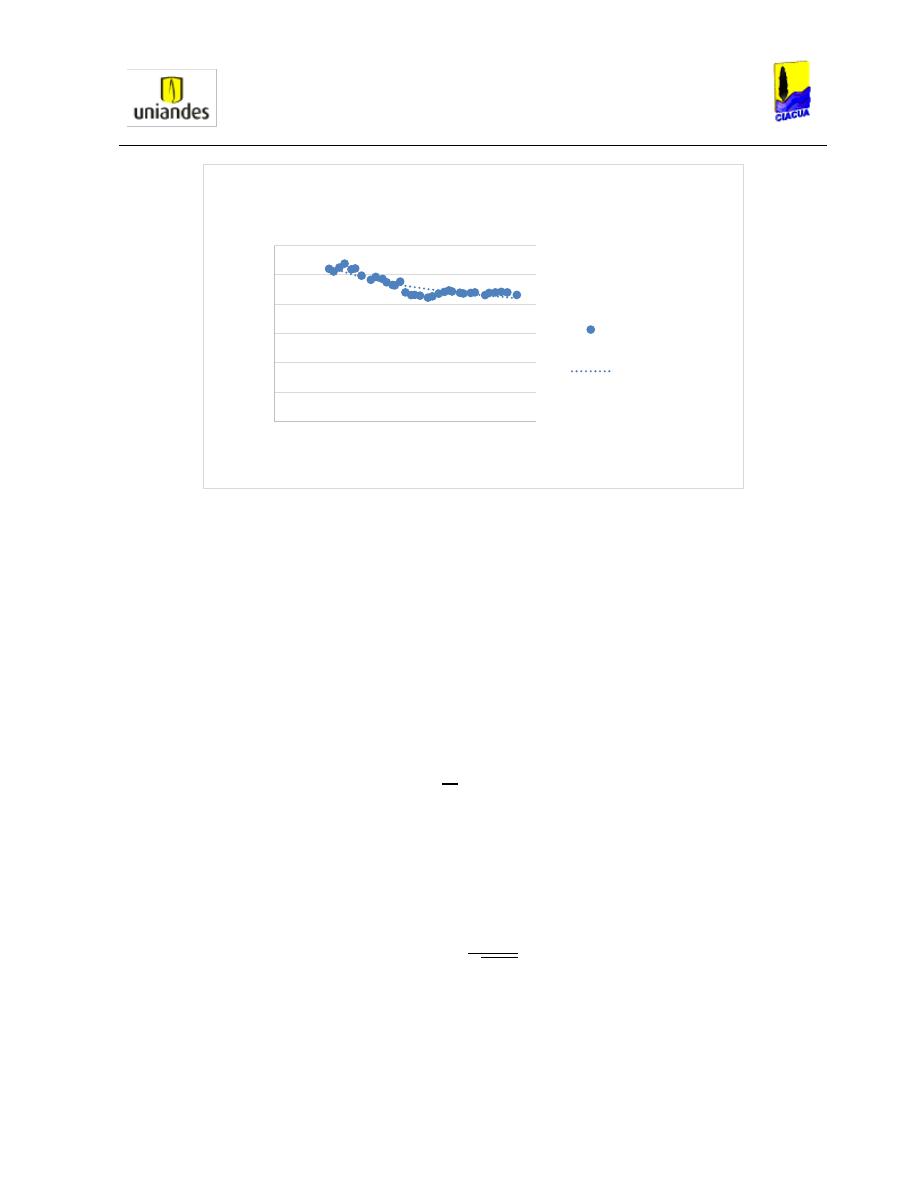
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
90
Gráfica 68. Ecuación del resalto hidráulico mediante el método de regresión para la pendiente de 0,011.
Para la pendiente más pequeña (0,011), se puede encontrar un factor de correlación del 0,7982
lo cual puede mostrar que se encuentra una muy buena relación de los datos con un ajuste
potencial que se expresa de la siguiente forma:
𝑦 = 1,3091𝑥
−0,155
Ecuación 105. Ecuación del resalto hidráulico para una pendiente de 0,011.
Por lo tanto, se puede expresar la variable dependiente e independiente como
𝑦 =
𝑦
2
𝑦
1
; 𝑥 = 𝑄
Ecuación 106. Definición de variables dependientes e independientes.
donde
𝑦
2
es la altura aguas abajo del resalto,
𝑦
1
es la profundidad de flujo aguas arriba y
𝑄 es
el caudal de entrada a la tubería. Ahora, conociendo la ecuación del número de Froude como:
𝐹𝑟 =
𝑉
√𝑔 ∗ 𝐷
Ecuación 107. Ecuación para encontrar el número de Froude.
La velocidad se puede expresar como
y = 1,3091x
-0,155
R² = 0,7983
0
0,5
1
1,5
2
2,5
3
0
0,01
0,02
0,03
0,04
0,05
Y
2
/Y
1
(-
)
Caudal (m
3
/s)
Ecuación del resalto hidráulico mediante el
método de regresión
Pendiente 0,011
Potencial (Pendiente
0,011)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
91
𝑉 =
𝑄
𝐴
Ecuación 108. Velocidad de flujo.
Reemplazando la Ecuación 97 en la Ecuación 96:
𝐹𝑟 =
𝑄
𝐴 ∗ √𝑔 ∗ 𝐷
Ecuación 109. Número de Froude reemplazado.
Y reemplazando y despejando en la Ecuación 94 obtenemos como resultado
𝑦
2
𝑦
1
= 1,3091(𝐹𝑟 ∗ 𝐴 ∗ √𝑔 ∗ 𝐷)
−0,155
Ecuación 110. Ecuación del resalto hidráulico para la pendiente de 0,011.
Para una sección circular se tiene que:
𝑦
2
𝑦
1
= 1,3091 (𝐹𝑟 ∗
1
8
∗ (𝛳 − sin 𝛳) ∗ 𝑑
2
∗ √𝑔 ∗ 𝐷)
−0,155
Ecuación 111. Ecuación del resalto hidráulico reemplazada para la pendiente de 0,011.
Se realiza el mismo procedimiento para cada pendiente y se obtienen las siguientes
ecuaciones empíricas para el resalto hidráulico según la pendiente:
𝑦
2
𝑦
1
= 1,2927 (𝐹𝑟 ∗
1
8
∗ (𝛳 − sin 𝛳) ∗ 𝑑
2
∗ √𝑔 ∗ 𝐷)
−0,181
Ecuación 112. Ecuación del resalto hidráulico reemplazada para la pendiente de 0,016.
𝑦
2
𝑦
1
= 1,6684 (𝐹𝑟 ∗
1
8
∗ (𝛳 − sin 𝛳) ∗ 𝑑
2
∗ √𝑔 ∗ 𝐷)
−0,122
Ecuación 113. Ecuación del resalto hidráulico reemplazada para la pendiente de 0,018.
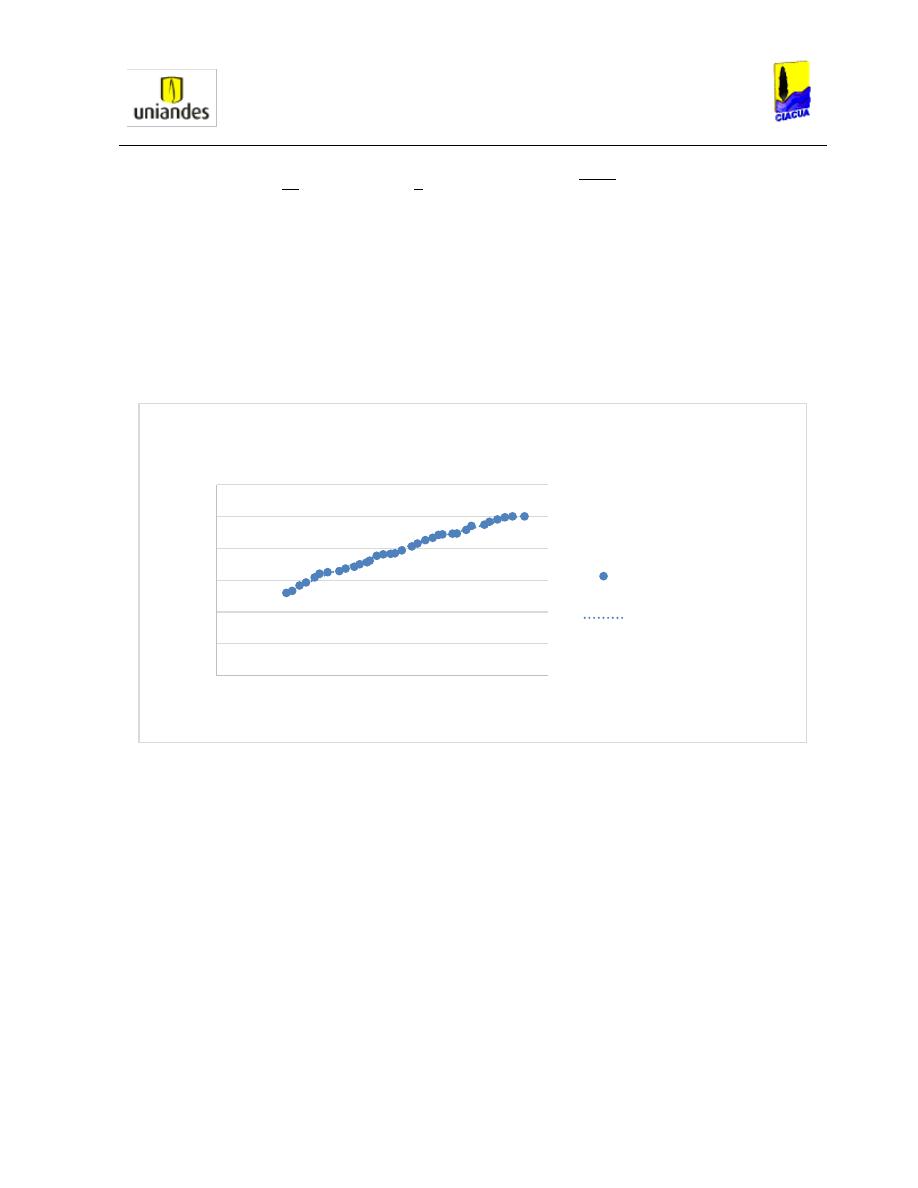
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
92
𝑦
2
𝑦
1
= 1,1785 (𝐹𝑟 ∗
1
8
∗ (𝛳 − sin 𝛳) ∗ 𝑑
2
∗ √𝑔 ∗ 𝐷)
−0,225
Ecuación 114. Ecuación del resalto hidráulico reemplazada para la pendiente de 0,025.
Además, se realizó la programación de una macro en Excel (VBA VER ANEXO IV), para
encontrar cuál es la pendiente óptima entre las cuatro trabajadas en este documento para un
caudal de diseño dado. De esta forma, se procedió a realizar las siguientes regresiones y
encontrar una ecuación que describa las profundidades de flujo aguas abajo de la tubería
evitando las sobrecargas (Y/d > 85%).
Gráfica 69. Comparación de alturas con respecto al caudal de entrada para la pendiente de 0,011.
Mediante una regresión se puede encontrar que la ecuación que mejor se ajusta a los datos
experimentales es una potencial mostrando un factor de correlación bastante alto. Ahora, a
manera de ejemplo, se procede a mostrar el funcionamiento del programa para esta pendiente
con un caudal de diseño de 31 L/s (0,031 m^3/s), donde alcanzaría su relación de llenado
máxima del 85%, sin causar daños ni sobrecargas.
y = 0,9946x
0,4475
R² = 0,9928
0
0,05
0,1
0,15
0,2
0,25
0,3
0
0,01
0,02
0,03
0,04
0,05
Altu
ra
s a
gu
as
ab
aj
o
(m
)
Caudal (m
3
/s)
Comparación de alturas aguas abajo contra caudal para la
S=0,011
Alturas aguas abajo
experimentales
Potencial (Alturas aguas abajo
experimentales )
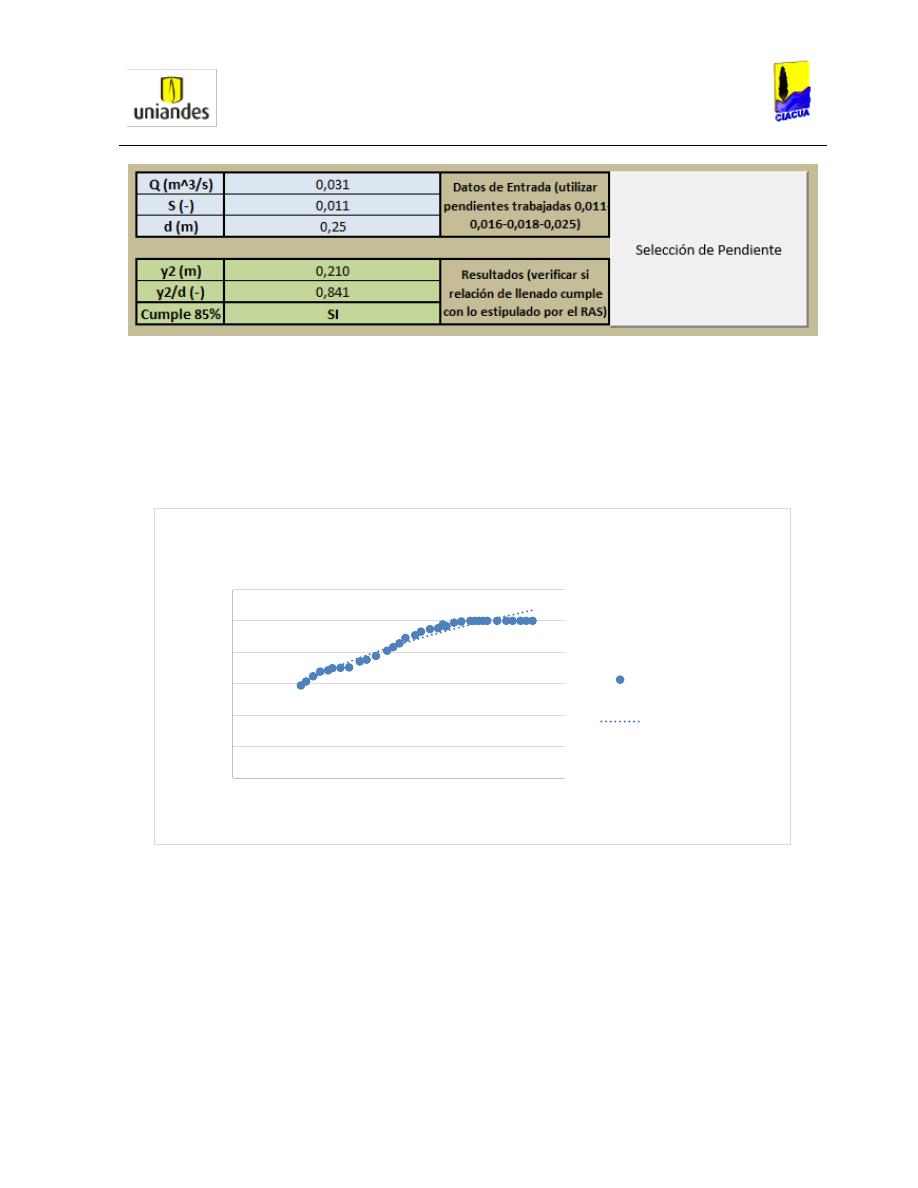
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
93
Gráfica 70. Solución de relación de llenado para pendiente 0,011 mediante programa de VBA.
Como se puede observar en la gráfica anterior, efectivamente con este caudal de diseño está
pendiente (S=0,011) alcanza su mayor relación de llenado permitida sin exceder el 85%, tal
como se podía observar en la Gráfica 68. Ahora, se procede a verificar el comportamiento de
las demás pendientes estudiadas en este proyecto de grado.
Gráfica 71.Comparación de alturas con respecto al caudal de entrada para la pendiente de 0,016.
Para encontrar la ecuación de la pendiente 0,016 se realizó una regresión de orden potencial
al igual que la pendiente anterior, obteniendo un factor de correlación bastante positivo, lo cual
demuestra que los resultados se ajustan muy bien a la ecuación. De esta forma, se verifica que
se cumpla el caudal necesario requerido para una relación de llenado del 85% como se muestra
en la Gráfica 68 (Relación de llenado más crítica para las cuatro pendientes trabajadas).
y = 0,8892x
0,3884
R² = 0,9635
0
0,05
0,1
0,15
0,2
0,25
0,3
0
0,01
0,02
0,03
0,04
0,05
Altu
ra
s a
gu
as
ab
aj
o
(m
)
Caudal (m
3
/s)
Comparación de alturas aguas abajo contra caudal para
S=0,016
Alturas aguas abajo
experimentales
Potencial (Alturas aguas
abajo experimentales)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
94
Gráfica 72.Solución de relación de llenado para pendiente 0,016 mediante programa de VBA.
Como se puede observar en la gráfica anterior, el máximo caudal que puede resistir esta tubería
de 25 centímetros de diámetro es de 25 L/s (0,025 m
3
/s) para que se cumpla una relación de
llenado del 85%. Para la pendiente de 0,018 se realiza el mismo procedimiento de regresión y
se encuentra que también se acerca a una ecuación potencial con un factor de correlación
bastante alto
(𝑅
2
= 0,9635), y generando un buen ajuste. Por esta razón se va a calcular un
caudal de diseño que mediante esta ecuación resista la tubería, cumpliendo la relación de
llenado del 85%, para luego comparar con los datos experimentales mostrados en la Gráfica
68 (Relación de llenado óptima para las cuatro pendientes trabajadas).
Gráfica 73. Comparación de alturas con respecto al caudal de entrada para la pendiente de 0,018.
Se presenta la gráfica de la cual se realizó la regresión y se obtuvo la siguiente ecuación:
𝑦 = 0,8892𝑥
0,3884
Ecuación 115. Método de regresión para pendiente de 0,018.
y = 1,1367x
0,4509
R² = 0,9789
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0
0,01
0,02
0,03
0,04
0,05
Pro
fu
n
d
id
ad
agu
as
ab
aj
o
(m
)
Caudal (m
3
/s)
Comparación de alturas aguas abajo contra caudal para
S=0,018
Alturas aguas abajo
experimentales
Potencial (Alturas aguas abajo
experimentales)
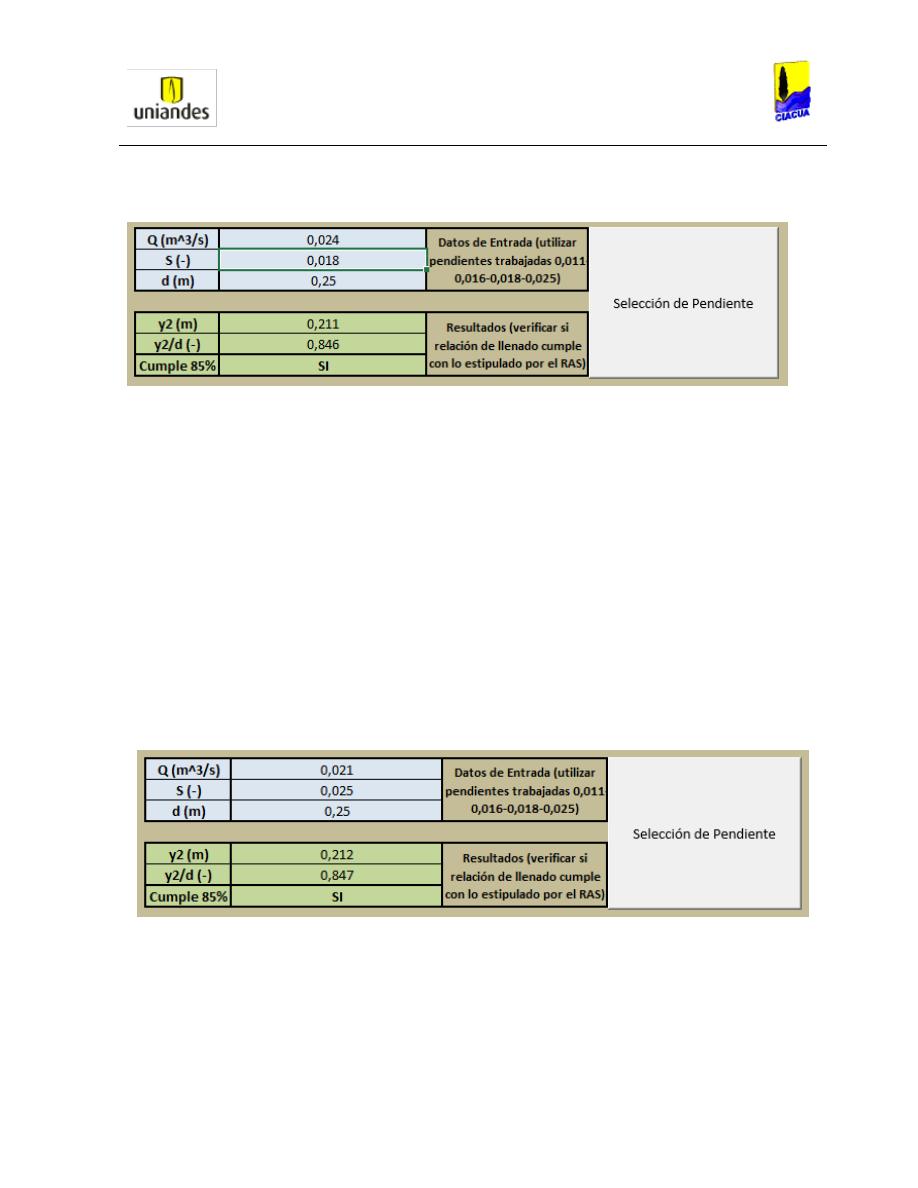
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
95
Para encontrar el caudal máximo permitido por esta pendiente, se procede a verificar en el
programa de VBA, mostrando los siguientes resultados:
Gráfica 74. Solución de relación de llenado para pendiente 0,018 mediante programa de VBA.
Como era de esperarse, y como se había visto en los resultados experimentales, la pendiente
de 0,018 se comporta de una forma muy similar a la pendiente anterior (S=0,016) pero está
alcanzando su nivel máximo de 85% un poco antes (24L/s-0,024m
3
/s), tal como se mostraba
anteriormente en la Gráfica 68 (Relación de llenado más crítica para las cuatro pendientes
trabajadas). En definitiva, para la última pendiente y la más crítica (S=0,025) se realizó una
regresión y se obtuvo la siguiente ecuación que más se ajustaba a los datos:
𝑦 = 0,8893𝑥
0,3715
Ecuación 116. Método de regresión para pendiente de 0,025.
Luego, utilizando esta ecuación se puede obtener la capacidad máxima que posee la tubería
con esta pendiente si exceder el 85% de relación de llenado aguas abajo.
Gráfica 75. Solución de relación de llenado para pendiente 0,025 mediante programa de VBA.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
96
Finalmente, se puede encontrar que está pendiente trabaja caudales mucho más bajos que las
demás por tener una mayor inclinación soportando un caudal máximo de 21 L/s (0,021m
3
/s).
Pero esta ecuación de aproximación sí demuestra mucha coherencia con los resultados
obtenidos experimentalmente.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
97
7. Conclusiones
Se determinó que las condiciones más adecuadas de la tubería para soportar una mayor
cantidad de caudal se desarrollaban en la pendiente más pequeña (S=0,011), llegando
alcanzar un caudal máximo de 31 L/s (0,031 m
3
/s), manteniendo una relación de llenado menor
al 85% aguas abajo de la tubería. También se pudo concluir que el comportamiento de todas
las pendientes siguió una tendencia y por ende la pendiente más crítica que se encontró fue la
de 0,025 resistiendo tan solo un caudal de 21 L/s (0,021m
3
/s).
Por otro lado, se encontró que en la tubería el flujo aguas arriba no representaba ninguna
dependencia de la pendiente y se comportaba de una forma uniforme, lo cual concluyó que el
flujo aguas arriba solo dependía del caudal de entrada. Por otro lado, se pudo encontrar que el
comportamiento aguas abajo de la tubería después del resalto se presentaba como un flujo
gradualmente variado y por ende iba alcanzar la presurización mucho antes que lo concluido
en la ecuación teórica de Darcy Weisbach. Es por esta razón que para poder entender el
comportamiento aguas abajo se trabajó la ecuación de momentum específico, el cual se
conserva en un resalto hidráulico.
Al realizar la comparación de estos resultados experimentales con los teóricos se encontró un
rango ciertamente grande de error, especialmente cuando se trabajó en los caudales más
pequeños. Este tipo de error se puede asociar con dos diferentes causas: la primera, a la
incertidumbre generada por el caudalímetro electromagnético el cual presenta una mayor
variación en los datos a medida que se disminuía el caudal; la segunda, a la alta variación que
presentó el sensor aguas abajo, lo cual pudo producir error en las medidas.
Al analizar los resultados teóricos aguas abajo con los experimentales, se descubrió que el
momentum de los datos experimentales no se alcanzaba a conservar por lo cual se adjudicó
que teóricamente el momentum en un resalto hidráulico se conserva exactamente en el punto
donde comienza y el punto donde termina el resalto hidráulico. Lo anterior debido a que en el
modelo que se trabajó este proyecto de grado, los sensores se encontraban separados a 4,05
metros entre sí, y por tanto no se pudo tomar la medición exacta del punto final del resalto, esta
pudo haber sido una causa de desequilibrio en los datos.
Finalmente, se puede llegar a la conclusión que, para obtener un máximo funcionamiento de la
tubería resistiendo mayores caudales a través de esta, luego de que ocurra el fenómeno del
resalto hidráulico, la pendiente más adecuada a trabajar sería la pendiente más pequeña
(S=0,011) porque demostró un mejor comportamiento en todo el experimento y mostró unos
resultados muchos más claros y concisos, como una mayor eficacia, generó mayores pérdidas
de energía y tardó más en llegar a la presurización de la tubería, resistiendo caudales mayores
sin generar daños ni sobrecargas en el sistema.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
98
8. Glosario
Altura aguas arriba: Es la profundidad de flujo que se genera antes de que se ocasione el
fenómeno del resalto hidráulico.
Altura aguas abajo: Es la profundidad de flujo que se genera después de que se ocasione el
fenómeno del resalto hidráulico.
Número de Froude: El número de Froude se calcula para denominar si el comportamiento
del flujo es supercrítico, subcrítico o crítico
Longitud del resalto: Esta distancia está medida desde donde comienza la turbulencia del
fluido aguas abajo formando el resalto, hasta donde se estabiliza el fluido aguas arriba.
Pérdidas de energía: Es la energía que se disipa y pierde el flujo al producirse el fenómeno
del resalto hidráulico.
Eficiencia: Es el porcentaje de energía que se pierde tras ocurrir el fenómeno del resalto
hidráulico.
Flujo crítico: Este tipo de flujo se evidencia por ser el momento en el cual es más difícil de
controlar el flujo, se diferencia por ser la zona de transición donde el flujo puede pasar de
subcrítico a supercrítico o viceversa, generalmente es representado por tener un número de
Froude igual a 1.
Relación de llenado: Se conoce como el porcentaje de llenado que tiene la tubería con
respecto al flujo que transporta.
Resalto hidráulico: Es un fenómeno que se presenta cuando un flujo genera una transición
de un estado supercrítico a un estado subcrítico
Tubería presurizada: Este término se utiliza para describir cuando la tubería se encuentra
totalmente llena o soportando cargas de presión por que el flujo que contiene tiende a salir de
allí.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
99
9. Bibliografía
Akan, A. O. (2006). OPEN CHANNEL HYDRAULICS. Canada: ELSEVIER.
BANNER. (2013). U-
GAGE™ T30 Series with Analog and Discrete Outputs. USA: Banner
Engineering Corp.
Chen, C. S. (1989). The hydraulic jump in a steeply sloping square conduit. JOURNAL OF
HYDRAULIC RESEARCH, 385-399.
CIVIL ENGINEERING PORTAL. (2011). What are the effects of Hydraulic Jump? Recuperado
el 28 de Noviembre de 2011, de http://www.engineeringcivil.com/what-are-the-effects-
of-hydraulic-jump.html
Ead, S. A. (2002). HYDRAULIC JUMPS IN CIRCULAR CONDUITS. Annual conference of the
Canadian Society for Civil Engineeing, 6.
FHWA. (2006). Hydraulic Design of Energy Dissipators for Culverts and Channels. Hydraulic
Engineering Circular, 6-1 a 6-14.
Francis, T. a. (2006). Hydraulic jump in circular and U-shaped channels. Journal of Hydraulic
Research vol. 44, 567-576.
French, R. H. (2007). The Momentum Principle. En R. H. French, Open Channel Hydraulics
(págs. 93 - 111). Colorado, USA: Copyright.
Gargano, R., & Hager, W. H. (2002). Undular Hydraulic Jump in Circular Conduits. JOURNAL
OF HYDRAULIC ENGINEERING, 1008-1013.
Ghamry, H. K., Shames, A., & Branch, F. (2002). Hydraulic Jumps in Circular Conduits .
Québec: CSCE.
Gonzales Rodríguez, M. (1992). Estudio Experimental de Flujos Disipativos: I. Resalto
Hidráulico. Cantabria: Universidad de Cantabria.
Hager, S. H. (1999). HYDRAULIC JUMP IN CIRCULAR PIPES. Canada: ProQuest Science
Journals.
Hager, W. H. (1990). CRITICAL FLOW. En W. Hager, Wastewater Hydraulics (págs. 137 -
172). Berlin: Springer.
Kalinske, J. M. (1943). Closed Conduits Flow. Transactions of the American Society of Civil
Engineers, 1435-1447.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
100
Kindsvater, E. W. (1938). Hydraulic Jump in Enclosed Conduits. Engineering News Record ,
815-817.
Kindsvater, E. W. (1938). Hydraulic Jump In Enclosed Conduits. Engineering News Record,
815 - 817.
Michell, S. B. (2008). Hydraulic jumps in trapezoidal and circular channels. ICE (Institution of
Civil Engineers), 161-167.
Montaño, L. E. (2012). Diseño y construcción de un modelo para estudiar el comportamiento
de resaltos hidráulicos en tuberías parcialmente llenas de seccion circular, con número
de Froude supercríticos menores a 4. Bogotá D.C.: Universidad de los Andes.
Mortensen, J. D. (2009). Factors Affecting Air Entrainment of Hydraulic Jumps within Closed
Conduits. utah: utah state university.
Rajaratnam, N. (1965). Hydraulic Jump in Horizontal Conduits. WATER POWER, 80 - 83.
Rajaratnamn, N. (1965). Hydraulic Jump in Horizontal Conduits. En Water Power (págs. 80-
85).
Robertson, J. M., & Kalinske, A. A. (1943). Closed Conduit Flow. Transactions of the American
Society of Civil Engineers, 1435-1447.
Rodríguez, M. G. (1992). The Hydraulic Jump. Cantabria: Universidad de Cantabria.
Silvester, R. (1964). HYDRAULIC JUMP IN ALL SHAPES OF HORIZONTAL CHANNELS.
Proceedings of the American Society of Civil Engineers, 23 - 55.
Silvester, R. (1964). HYDRAULIC JUMP IN ALL SHAPES OF HORIZONTAL CHANNELS.
Proceedings of the American Society of Civil Engineers, 23-55.
SMITH, C. D., & CHEN, W. (1989). The hydraulic jump in a steeply sloping square conduit.
JOURNAL OF HYDRAULIC RESEARCH, 385 - 399.
Stahl, H., & Hager, W. H. (1999). Hydraulic jump in circular pipes. Canadian Journal of Civil
Engineering, 368 -373.
WaterMaster. (2013). Caudalímetro electromagnético (Ficha técnica). Reino Unido: DS/WM-E
Edición 5.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
101
10. Anexos
Anexo I
Tabla 10. Resultados obtenidos para la pendiente 0,011.
Pendiente 0,011
Ensayo
Alturas
Q
[L/s]
Yn
[m]
Ѳ
[Rad]
A
[m
2
]
D [m]
T
P
R
V
(m/s)
Fr
Relación de
llenado
Tipo de
Resalto
Tipo de
Resalto
E
∆E
∆E/E1
(%)
E2/E1
1
Aguas arriba 47,240 0,117 3,016 0,023 0,091 0,250 0,377 0,060 2,092 2,220
46,9%
Supercrítico
Y<d
0,340
0,043 12,643
0,874
Aguas abajo 47,240 0,250 6,275 0,049 49,087 0,001 0,784 0,063 0,962 0,044
100,0%
Subcrítico
Y>d
0,297
1,138
2
Aguas arriba 46,430 0,116 2,993 0,022 0,089 0,249 0,374 0,059 2,090 2,235
46,3%
Supercrítico
Y<d
0,338
0,043 12,606
0,874
Aguas abajo 46,430 0,250 6,275 0,049 49,087 0,001 0,784 0,063 0,946 0,043
100,0%
Subcrítico
Y>d
0,296
1,114
3
Aguas arriba 44,610 0,114 2,957 0,022 0,087 0,249 0,370 0,059 2,058 2,227
45,4%
Supercrítico
Y<d
0,329
0,037 11,328
0,887
Aguas abajo 44,610 0,250 6,275 0,049 49,087 0,001 0,784 0,063 0,909 0,041
100,0%
Subcrítico
Y>d
0,292
1,105
4
Aguas arriba 43,460 0,112 2,939 0,021 0,086 0,249 0,367 0,058 2,031 2,211
45,0%
Supercrítico
Y<d
0,323
0,034 10,555
0,894
Aguas abajo 43,460 0,249 5,987 0,049 1,330 0,037 0,748 0,066 0,886 0,245
99,5%
Subcrítico
Y>d
0,289
1,094
5
Aguas arriba 42,320 0,111 2,922 0,021 0,085 0,248 0,365 0,058 2,003 2,193
44,5%
Supercrítico
Y<d
0,316
0,032 10,270
0,897
Aguas abajo 42,320 0,245 5,724 0,049 0,708 0,069 0,715 0,068 0,866 0,329
98,1%
Subcrítico
Y>d
0,283
1,089
6
Aguas arriba 41,120 0,110 2,904 0,021 0,084 0,248 0,363 0,057 1,973 2,174
44,1%
Supercrítico
Y<d
0,309
0,031
9,887
0,901
Aguas abajo 41,120 0,242 5,542 0,049 0,536 0,091 0,693 0,070 0,847 0,369
96,6%
Subcrítico
Y>d
0,278
1,086
7
Aguas arriba 40,350 0,110 2,901 0,021 0,084 0,248 0,363 0,057 1,940 2,140
44,0%
Supercrítico
Y<d
0,302
0,029
9,577
0,904
Aguas abajo 40,350 0,237 5,367 0,048 0,435 0,111 0,671 0,072 0,838 0,406
94,8%
Subcrítico
Y>d
0,273
1,080
8
Aguas arriba 38,410 0,107 2,848 0,020 0,081 0,247 0,356 0,056 1,921 2,157
42,7%
Supercrítico
Y<d
0,295
0,027
9,184
0,908
Aguas abajo 38,410 0,235 5,292 0,048 0,403 0,119 0,661 0,072 0,802 0,404
94,0%
Subcrítico
Y>d
0,268
1,105
9
Aguas arriba 37,620 0,104 2,809 0,019 0,079 0,247 0,351 0,055 1,939 2,207
41,7%
Supercrítico
Y<d
0,296 0,035 11,717 0,883
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
102
Aguas abajo 37,620 0,229 5,100 0,047 0,338 0,139 0,638 0,074 0,799 0,439
91,5%
Subcrítico
Y<d
0,261
1,109
10
Aguas arriba 36,200 0,102 2,774 0,019 0,077 0,246 0,347 0,054 1,919 2,211
40,9%
Supercrítico
Y<d
0,290
0,035 12,199
0,878
Aguas abajo 36,200 0,223 4,951 0,046 0,300 0,154 0,619 0,075 0,782 0,456
89,3%
Subcrítico
Y<d
0,254
1,124
11
Aguas arriba 35,560 0,101 2,762 0,019 0,076 0,246 0,345 0,054 1,904 2,203
40,6%
Supercrítico
Y<d
0,286
0,033 11,565
0,884
Aguas abajo 35,560 0,223 4,939 0,046 0,297 0,156 0,617 0,075 0,770 0,451
89,1%
Subcrítico
Y<d
0,253
1,089
12
Aguas arriba 34,020 0,100 2,738 0,018 0,075 0,245 0,342 0,054 1,856 2,166
40,0%
Supercrítico
Y<d
0,276
0,026
9,390
0,906
Aguas abajo 34,020 0,222 4,915 0,046 0,291 0,158 0,614 0,075 0,739 0,437
88,7%
Subcrítico
Y<d
0,250
1,098
13
Aguas arriba 33,430 0,099 2,718 0,018 0,074 0,244 0,340 0,053 1,855 2,181
39,5%
Supercrítico
Y<d
0,274
0,026
9,539
0,905
Aguas abajo 33,430 0,221 4,890 0,046 0,286 0,160 0,611 0,075 0,728 0,435
88,4%
Subcrítico
Y<d
0,248
1,083
14
Aguas arriba 32,570 0,098 2,702 0,018 0,073 0,244 0,338 0,053 1,831 2,165
39,1%
Supercrítico
Y<d
0,269
0,026
9,573
0,904
Aguas abajo 32,570 0,216 4,781 0,045 0,265 0,171 0,598 0,076 0,721 0,448
86,6%
Subcrítico
Y<d
0,243
1,062
15
Aguas arriba 31,460 0,098 2,699 0,018 0,073 0,244 0,337 0,053 1,774 2,101
39,0%
Supercrítico
Y<d
0,258
0,020
7,656
0,923
Aguas abajo 31,460 0,213 4,698 0,045 0,250 0,178 0,587 0,076 0,707 0,451
85,1%
Subcrítico
Y<d
0,238
1,039
16
Aguas arriba 30,270 0,097 2,691 0,018 0,072 0,244 0,336 0,052 1,718 2,040
38,8%
Supercrítico
Y<d
0,248
0,016
6,268
0,937
Aguas abajo 30,270 0,207 4,580 0,044 0,231 0,188 0,572 0,076 0,695 0,462
82,9%
Subcrítico
Y<d
0,232
1,045
17
Aguas arriba 29,410 0,096 2,673 0,017 0,071 0,243 0,334 0,052 1,695 2,026
38,4%
Supercrítico
Y<d
0,242
0,015
6,297
0,937
Aguas abajo 29,410 0,203 4,489 0,043 0,218 0,195 0,561 0,076 0,689 0,471
81,2%
Subcrítico
Y<d
0,227
1,061
18
Aguas arriba 27,890 0,092 2,600 0,016 0,068 0,241 0,325 0,050 1,713 2,104
36,6%
Supercrítico
Y<d
0,241
0,021
8,842
0,912
Aguas abajo 27,890 0,197 4,363 0,041 0,202 0,205 0,545 0,076 0,673 0,478
78,7%
Subcrítico
Y<d
0,220
1,086
19
Aguas arriba 26,860 0,089 2,558 0,016 0,065 0,239 0,320 0,049 1,713 2,137
35,6%
Supercrítico
Y<d
0,239
0,024 10,052
0,899
Aguas abajo 26,860 0,192 4,277 0,040 0,192 0,211 0,535 0,076 0,663 0,483
76,9%
Subcrítico
Y<d
0,215
1,085
20
Aguas arriba 26,210 0,089 2,551 0,016 0,065 0,239 0,319 0,049 1,683 2,105
35,4%
Supercrítico
Y<d
0,233
0,020
8,637
0,914
Aguas abajo 26,210 0,191 4,259 0,040 0,190 0,212 0,532 0,076 0,651 0,476
76,5%
Subcrítico
Y<d
0,213
1,072
21
Aguas arriba 25,100 0,086 2,514 0,015 0,063 0,238 0,314 0,048 1,667 2,115
34,6%
Supercrítico
Y<d
0,228
0,018
7,728
0,923
Aguas abajo 25,100 0,191 4,245 0,040 0,189 0,213 0,531 0,076 0,625 0,460
76,2%
Subcrítico
Y<d
0,210
1,174
22
Aguas arriba 24,110 0,079 2,385 0,013 0,057 0,232 0,298 0,045 1,816 2,426
31,5%
Supercrítico
Y<d
0,247 0,040 16,189 0,838
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
103
Aguas abajo 24,110 0,188 4,201 0,040 0,184 0,216 0,525 0,075 0,608 0,453
75,3%
Subcrítico
Y<d
0,207
1,149
23
Aguas arriba 23,060 0,078 2,366 0,013 0,056 0,231 0,296 0,044 1,772 2,387
31,1%
Supercrítico
Y<d
0,238
0,039 16,219
0,838
Aguas abajo 23,060 0,180 4,060 0,038 0,169 0,224 0,508 0,075 0,608 0,472
72,2%
Subcrítico
Y<d
0,199
1,197
24
Aguas arriba 22,660 0,076 2,343 0,013 0,055 0,230 0,293 0,043 1,784 2,425
30,6%
Supercrítico
Y<d
0,239
0,042 17,570
0,824
Aguas abajo 22,660 0,178 4,015 0,037 0,165 0,227 0,502 0,074 0,607 0,477
71,1%
Subcrítico
Y<d
0,197
1,197
25
Aguas arriba 21,530 0,074 2,296 0,012 0,053 0,228 0,287 0,042 1,781 2,469
29,5%
Supercrítico
Y<d
0,235
0,043 18,198
0,818
Aguas abajo 21,530 0,175 3,964 0,037 0,160 0,229 0,496 0,074 0,587 0,468
70,0%
Subcrítico
Y<d
0,193
1,251
26
Aguas arriba 20,710 0,070 2,236 0,011 0,050 0,225 0,280 0,041 1,829 2,602
28,1%
Supercrítico
Y<d
0,241
0,053 21,914
0,781
Aguas abajo 20,710 0,171 3,895 0,036 0,154 0,232 0,487 0,073 0,579 0,471
68,4%
Subcrítico
Y<d
0,188
1,240
27
Aguas arriba 19,530 0,068 2,199 0,011 0,049 0,223 0,275 0,039 1,799 2,602
27,3%
Supercrítico
Y<d
0,233
0,049 21,195
0,788
Aguas abajo 19,430 0,168 3,848 0,035 0,150 0,235 0,481 0,073 0,553 0,456
67,3%
Subcrítico
Y<d
0,184
1,182
28
Aguas arriba 18,470 0,068 2,194 0,011 0,049 0,222 0,274 0,039 1,711 2,481
27,2%
Supercrítico
Y<d
0,217
0,038 17,562
0,824
Aguas abajo 18,470 0,164 3,780 0,034 0,144 0,237 0,472 0,072 0,540 0,455
65,7%
Subcrítico
Y<d
0,179
1,127
29
Aguas arriba 16,700 0,065 2,145 0,010 0,046 0,220 0,268 0,038 1,637 2,426
26,1%
Supercrítico
Y<d
0,202
0,027 13,410
0,866
Aguas abajo 16,700 0,162 3,748 0,034 0,141 0,239 0,469 0,072 0,495 0,420
64,9%
Subcrítico
Y<d
0,175
1,150
30
Aguas arriba 15,490 0,061 2,074 0,009 0,043 0,215 0,259 0,036 1,655 2,534
24,6%
Supercrítico
Y<d
0,201
0,030 14,802
0,852
Aguas abajo 15,490 0,160 3,713 0,033 0,139 0,240 0,464 0,072 0,466 0,400
64,1%
Subcrítico
Y<d
0,171
1,158
31
Aguas arriba 14,750 0,059 2,037 0,009 0,042 0,213 0,255 0,035 1,651 2,573
23,8%
Supercrítico
Y<d
0,198
0,033 16,741
0,833
Aguas abajo 14,750 0,154 3,613 0,032 0,131 0,243 0,452 0,070 0,464 0,410
61,7%
Subcrítico
Y<d
0,165
1,206
32
Aguas arriba 13,440 0,054 1,940 0,008 0,038 0,206 0,242 0,032 1,686 2,756
21,7%
Supercrítico
Y<d
0,199
0,043 21,375
0,786
Aguas abajo 13,440 0,146 3,483 0,030 0,121 0,246 0,435 0,069 0,451 0,414
58,5%
Subcrítico
Y<d
0,157
1,177
33
Aguas arriba 12,450 0,054 1,932 0,008 0,038 0,206 0,241 0,032 1,600 2,625
21,6%
Supercrítico
Y<d
0,184
0,033 17,957
0,820
Aguas abajo 12,450 0,142 3,408 0,029 0,116 0,248 0,426 0,067 0,434 0,407
56,6%
Subcrítico
Y<d
0,151
1,137
34
Aguas arriba 11,350 0,052 1,895 0,007 0,036 0,203 0,237 0,031 1,533 2,564
20,8%
Supercrítico
Y<d
0,172
0,029 17,116
0,829
Aguas abajo 11,350 0,133 3,272 0,027 0,107 0,249 0,409 0,065 0,427 0,418
53,3%
Subcrítico
Y<d
0,142
1,161
35
Aguas arriba 10,480 0,050 1,852 0,007 0,035 0,200 0,231 0,030 1,505 2,575
19,9%
Supercrítico
Y<d
0,165 0,027 16,377 0,836
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
104
Aguas abajo 10,480 0,130 3,219 0,026 0,103 0,250 0,402 0,064 0,407 0,405
51,9%
Subcrítico
Y<d
0,138
Tabla 11. Resultados obtenidos para la pendiente 0,016.
Pendiente 0,016
Ensayo
Alturas
Q
[L/s]
Yn
[m]
Ѳ
[Rad]
A
[m
2
]
D [m]
T
P
R
V
(m/s)
Fr
Relación de
llenado
Tipo de
Resalto
Tipo de
Resalto
E
∆E
∆E/E1
(%)
E2/E1
1
Aguas arriba 45,160 0,119 3,044 0,023
0,092
0,250 1,961 5,931 1,961 2,062
47,6%
Supercrítico
Y<d
0,315
0,022 6,940
0,931
Aguas abajo 45,160 0,250 6,275 0,049 49,087 0,001 0,920 0,121 0,920 0,042
100,0%
Subcrítico
Y>d
0,293
1,077
2
Aguas arriba 44,220 0,116 3,001 0,022
0,090
0,249 1,978 5,926 1,978 2,109
46,5%
Supercrítico
Y<d
0,316
0,024 7,696
0,923
Aguas abajo 44,220 0,250 6,275 0,049 49,087 0,001 0,901 0,121 0,901 0,041
100,0%
Subcrítico
Y>d
0,291
1,079
3
Aguas arriba 43,340 0,114 2,970 0,022
0,088
0,249 1,981 5,922 1,981 2,135
45,7%
Supercrítico
Y<d
0,314
0,025 7,842
0,922
Aguas abajo 43,340 0,250 6,275 0,049 49,087 0,001 0,883 0,121 0,883 0,040
100,0%
Subcrítico
Y>d
0,290
1,068
4
Aguas arriba 42,160 0,113 2,943 0,021
0,086
0,249 1,966 5,917 1,966 2,138
45,0%
Supercrítico
Y<d
0,310
0,022 7,093
0,929
Aguas abajo 42,160 0,250 6,275 0,049 49,087 0,001 0,859 0,121 0,859 0,039
100,0%
Subcrítico
Y>d
0,288
1,061
5
Aguas arriba 41,210 0,111 2,922 0,021
0,085
0,248 1,951 5,913 1,951 2,136
44,5%
Supercrítico
Y<d
0,305
0,019 6,331
0,937
Aguas abajo 41,210 0,250 6,275 0,049 49,087 0,001 0,840 0,121 0,840 0,038
100,0%
Subcrítico
Y>d
0,286
1,031
6
Aguas arriba 39,830 0,111 2,910 0,021
0,084
0,248 1,902 5,911 1,902 2,091
44,2%
Supercrítico
Y<d
0,295
0,011 3,843
0,962
Aguas abajo 39,830 0,250 6,275 0,049 49,087 0,001 0,811 0,121 0,811 0,037
100,0%
Subcrítico
Y>d
0,284
1,003
7
Aguas arriba 38,340 0,110 2,895 0,021
0,083
0,248 1,852 5,907 1,852 2,047
43,8%
Supercrítico
Y<d
0,284
0,003 1,153
0,988
Aguas abajo 38,340 0,250 6,275 0,049 49,087 0,001 0,781 0,121 0,781 0,036
100,0%
Subcrítico
Y>d
0,281
1,002
8
Aguas arriba 37,740 0,109 2,880 0,020
0,083
0,248 1,842 5,904 1,842 2,046
43,5%
Supercrítico
Y<d
0,282
0,002 0,560
0,994
Aguas abajo 37,740 0,250 6,275 0,049 49,087 0,001 0,769 0,121 0,769 0,035
100,0%
Subcrítico
Y>d
0,280
0,994
9
Aguas arriba 37,090 0,108 2,866 0,020
0,082
0,248 1,830 5,900 1,830 2,043
43,1%
Supercrítico
Y<d
0,279
0,001 0,185
1,002
Aguas abajo 37,090 0,250 6,281 0,049 155,228 0,000 0,756 0,038 0,756 0,019
100,0%
Subcrítico
Y>d
0,279
1,004
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
105
10
Aguas arriba 36,490 0,106 2,829 0,020
0,080
0,247 1,852 5,891 1,852 2,093
42,2%
Supercrítico
Y<d
0,280
0,002 0,774
0,992
Aguas abajo 36,490 0,250 6,275 0,049 49,087 0,001 0,743 0,121 0,743 0,034
100,0%
Subcrítico
Y>d
0,278
1,005
11
Aguas arriba 35,770 0,104 2,800 0,019
0,078
0,246 1,858 5,882 1,858 2,122
41,5%
Supercrítico
Y<d
0,280
0,003 0,931
0,991
Aguas abajo 35,770 0,250 6,275 0,049 49,087 0,001 0,729 0,121 0,729 0,033
100,0%
Subcrítico
Y>d
0,277
0,993
12
Aguas arriba 34,420 0,101 2,759 0,019
0,076
0,245 1,847 5,868 1,847 2,139
40,5%
Supercrítico
Y<d
0,275
0,001 0,418
0,996
Aguas abajo 34,420 0,249 6,006 0,049
1,423
0,034 0,702 1,673 0,702 0,188
99,5%
Subcrítico
Y>d
0,274
0,985
13
Aguas arriba 33,330 0,100 2,733 0,018
0,075
0,245 1,827 5,858 1,827 2,137
39,8%
Supercrítico
Y<d
0,270
0,001 0,389
1,004
Aguas abajo 33,330 0,247 5,861 0,049
0,935
0,052 0,680 2,201 0,680 0,225
98,9%
Subcrítico
Y>d
0,271
0,982
14
Aguas arriba 32,200 0,097 2,697 0,018
0,073
0,244 1,819 5,844 1,819 2,155
39,0%
Supercrítico
Y<d
0,266
0,002 0,847
0,992
Aguas abajo 32,030 0,242 5,546 0,049
0,539
0,090 0,659 3,122 0,659 0,287
96,6%
Subcrítico
Y>d
0,264
1,012
15
Aguas arriba 32,030 0,097 2,684 0,018
0,072
0,243 1,828 5,839 1,828 2,176
38,7%
Supercrítico
Y<d
0,267
0,004 1,555
0,984
Aguas abajo 31,630 0,241 5,529 0,049
0,527
0,092 0,652 3,165 0,652 0,287
96,5%
Subcrítico
Y>d
0,263
1,015
16
Aguas arriba 31,630 0,096 2,666 0,017
0,071
0,243 1,833 5,831 1,833 2,197
38,2%
Supercrítico
Y<d
0,267
0,000 0,116
0,999
Aguas abajo 32,200 0,244 5,681 0,049
0,659
0,074 0,660 2,754 0,660 0,260
97,8%
Subcrítico
Y>d
0,267
0,982
17
Aguas arriba 30,920 0,095 2,654 0,017
0,070
0,243 1,810 5,826 1,810 2,178
37,9%
Supercrítico
Y<d
0,262
0,003 0,995
0,990
Aguas abajo 30,920 0,238 5,412 0,048
0,458
0,105 0,641 3,452 0,641 0,302
95,3%
Subcrítico
Y>d
0,259
0,977
18
Aguas arriba 29,710 0,094 2,635 0,017
0,069
0,242 1,769 5,817 1,769 2,144
37,5%
Supercrítico
Y<d
0,253
0,003 1,248
1,012
Aguas abajo 29,710 0,237 5,360 0,048
0,432
0,111 0,618 3,572 0,618 0,300
94,8%
Subcrítico
Y>d
0,256
0,954
19
Aguas arriba 28,360 0,092 2,607 0,016
0,068
0,241 1,730 5,804 1,730 2,119
36,8%
Supercrítico
Y<d
0,245
0,006 2,578
1,026
Aguas abajo 28,360 0,233 5,222 0,048
0,376
0,127 0,596 3,874 0,596 0,310
93,1%
Subcrítico
Y>d
0,251
0,975
20
Aguas arriba 27,480 0,089 2,562 0,016
0,066
0,240 1,746 5,781 1,746 2,175
35,7%
Supercrítico
Y<d
0,245
0,000 0,033
1,000
Aguas abajo 27,480 0,227 5,052 0,047
0,324
0,144 0,587 4,210 0,587 0,329
90,8%
Subcrítico
Y<d
0,245
0,965
21
Aguas arriba 26,010 0,087 2,526 0,015
0,064
0,238 1,709 5,761 1,709 2,158
34,8%
Supercrítico
Y<d
0,236
0,003 1,269
1,013
Aguas abajo 26,010 0,223 4,938 0,046
0,297
0,156 0,563 4,416 0,563 0,330
89,1%
Subcrítico
Y<d
0,239
0,966
22
Aguas arriba 25,130 0,086 2,503 0,015
0,063
0,237 1,687 5,747 1,687 2,150
34,3%
Supercrítico
Y<d
0,231
0,000 0,140
0,999
Aguas abajo 25,130 0,214 4,736 0,045
0,257
0,175 0,561 4,746 0,561 0,354
85,8%
Subcrítico
Y<d
0,230
1,070
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
106
23
Aguas arriba 24,170 0,079 2,390 0,013
0,057
0,233 1,813 5,674 1,813 2,417
31,6%
Supercrítico
Y<d
0,247
0,023 9,193
0,908
Aguas abajo 24,170 0,208 4,601 0,044
0,235
0,186 0,553 4,942 0,553 0,364
83,3%
Subcrítico
Y<d
0,224
1,147
24
Aguas arriba 23,260 0,075 2,312 0,012
0,054
0,229 1,891 5,617 1,891 2,604
29,9%
Supercrítico
Y<d
0,257
0,039 15,223
0,848
Aguas abajo 23,260 0,203 4,481 0,043
0,217
0,196 0,546 5,101 0,546 0,374
81,0%
Subcrítico
Y<d
0,218
1,139
25
Aguas arriba 21,570 0,072 2,257 0,012
0,051
0,226 1,860 5,574 1,860 2,622
28,6%
Supercrítico
Y<d
0,248
0,039 15,894
0,841
Aguas abajo 21,570 0,194 4,319 0,041
0,197
0,208 0,527 5,292 0,527 0,379
77,8%
Subcrítico
Y<d
0,209
1,104
26
Aguas arriba 20,170 0,071 2,242 0,011
0,051
0,225 1,769 5,561 1,769 2,511
28,3%
Supercrítico
Y<d
0,230
0,029 12,513
0,875
Aguas abajo 20,170 0,188 4,203 0,040
0,184
0,216 0,509 5,414 0,509 0,379
75,3%
Subcrítico
Y<d
0,201
1,092
27
Aguas arriba 19,140 0,069 2,221 0,011
0,050
0,224 1,718 5,544 1,718 2,460
27,8%
Supercrítico
Y<d
0,220
0,022 10,171
0,898
Aguas abajo 19,140 0,185 4,149 0,039
0,178
0,219 0,490 5,465 0,490 0,371
74,1%
Subcrítico
Y<d
0,198
1,045
28
Aguas arriba 17,554 0,067 2,179 0,011
0,048
0,222 1,653 5,507 1,653 2,412
26,9%
Supercrítico
Y<d
0,206
0,019 9,182
0,908
Aguas abajo 17,540 0,176 3,983 0,037
0,162
0,228 0,475 5,609 0,475 0,377
70,4%
Subcrítico
Y<d
0,188
1,004
29
Aguas arriba 16,230 0,067 2,170 0,011
0,048
0,221 1,545 5,499 1,545 2,263
26,7%
Supercrítico
Y<d
0,188
0,003 1,654
0,983
Aguas abajo 16,230 0,175 3,969 0,037
0,161
0,229 0,441 5,619 0,441 0,352
70,1%
Subcrítico
Y<d
0,185
0,964
30
Aguas arriba 15,020 0,065 2,132 0,010
0,046
0,219 1,496 5,464 1,496 2,229
25,8%
Supercrítico
Y<d
0,179
0,005 2,697
1,027
Aguas abajo 15,020 0,175 3,962 0,037
0,160
0,229 0,410 5,625 0,410 0,327
69,9%
Subcrítico
Y<d
0,183
0,958
31
Aguas arriba 14,370 0,063 2,099 0,010
0,045
0,217 1,489 5,432 1,489 2,252
25,1%
Supercrítico
Y<d
0,176
0,004 2,202
1,022
Aguas abajo 14,370 0,171 3,902 0,036
0,155
0,232 0,401 5,668 0,401 0,325
68,6%
Subcrítico
Y<d
0,180
0,901
32
Aguas arriba 13,170 0,062 2,077 0,009
0,044
0,215 1,403 5,410 1,403 2,145
24,6%
Supercrítico
Y<d
0,162
0,015 9,029
1,090
Aguas abajo 13,170 0,169 3,868 0,035
0,151
0,234 0,372 5,692 0,372 0,305
67,8%
Subcrítico
Y<d
0,176
0,933
33
Aguas arriba 12,110 0,056 1,981 0,008
0,040
0,209 1,457 5,311 1,457 2,333
22,6%
Supercrítico
Y<d
0,165
0,004 2,305
1,023
Aguas abajo 12,110 0,162 3,740 0,034
0,141
0,239 0,360 5,770 0,360 0,307
64,7%
Subcrítico
Y<d
0,168
0,958
34
Aguas arriba 11,070 0,053 1,914 0,008
0,037
0,204 1,458 5,235 1,458 2,414
21,2%
Supercrítico
Y<d
0,161
0,001 0,824
0,992
Aguas abajo 11,070 0,154 3,605 0,032
0,130
0,243 0,350 5,836 0,350 0,309
61,5%
Subcrítico
Y<d
0,160
0,961
35
Aguas arriba 10,290 0,051 1,881 0,007
0,036
0,202 1,418 5,197 1,418 2,388
20,5%
Supercrítico
Y<d
0,154
0,001 0,376
0,996
Aguas abajo 10,290 0,147 3,499 0,030
0,122
0,246 0,342 5,876 0,342 0,312
58,9%
Subcrítico
Y<d
0,153
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
107
Tabla 12. Resultados obtenidos para la pendiente 0,018.
Pendiente 0,018
Ensayo
Alturas
Q
[L/s]
Yn
[m]
Ѳ
[Rad]
A
[m
2
]
D [m]
T
P
R
V
(m/s)
Fr
Relación de
llenado
Tipo de
Resalto
Tipo de
Resalto
E
∆E
∆E/E1
(%)
E2/E1
1
Aguas arriba 41,370 0,109 2,892 0,021 0,083 0,248 2,002 6,251 2,002 2,215
43,8%
Supercrítico
Y<d
0,314
0,028
8,779
0,912
Aguas abajo 41,370 0,250 6,275 0,049 49,087 0,001 0,843 0,129 0,843 0,038
100,0%
Subcrítico
Y>d
0,286
1,038
2
Aguas arriba 38,800 0,107 2,856 0,020 0,081 0,247 1,930 6,242 1,930 2,162
42,9%
Supercrítico
Y<d
0,297
0,015
5,107
0,949
Aguas abajo 38,800 0,250 6,275 0,049 49,087 0,001 0,790 0,129 0,790 0,036
100,0%
Subcrítico
Y>d
0,282
1,045
3
Aguas arriba 36,530 0,102 2,769 0,019 0,076 0,246 1,944 6,214 1,944 2,245
40,7%
Supercrítico
Y<d
0,295
0,016
5,535
0,945
Aguas abajo 36,530 0,250 6,275 0,049 49,087 0,001 0,744 0,129 0,744 0,034
100,0%
Subcrítico
Y>d
0,278
1,019
4
Aguas arriba 34,560 0,099 2,729 0,018 0,074 0,245 1,901 6,198 1,901 2,227
39,7%
Supercrítico
Y<d
0,284
0,009
3,011
0,970
Aguas abajo 34,560 0,250 6,153 0,049 3,016 0,016 0,704 1,071 0,704 0,129
99,9%
Subcrítico
Y>d
0,275
0,989
5
Aguas arriba 31,890 0,095 2,657 0,017 0,071 0,243 1,864 6,167 1,864 2,241
38,0%
Supercrítico
Y<d
0,272
0,004
1,555
0,984
Aguas abajo 31,890 0,246 5,782 0,049 0,789 0,062 0,652 2,600 0,652 0,234
98,4%
Subcrítico
Y>d
0,268
1,036
6
Aguas arriba 31,790 0,093 2,630 0,017 0,069 0,242 1,900 6,154 1,900 2,307
37,4%
Supercrítico
Y<d
0,277
0,012
4,430
0,956
Aguas abajo 31,790 0,244 5,635 0,049 0,613 0,080 0,652 3,053 0,652 0,266
97,4%
Subcrítico
Y>d
0,265
0,978
7
Aguas arriba 29,720 0,092 2,608 0,016 0,068 0,241 1,812 6,143 1,812 2,218
36,8%
Supercrítico
Y<d
0,259
0,002
0,950
0,990
Aguas abajo 29,720 0,238 5,382 0,048 0,442 0,109 0,617 3,731 0,617 0,296
95,0%
Subcrítico
Y>d
0,257
0,984
8
Aguas arriba 28,580 0,090 2,581 0,016 0,067 0,240 1,785 6,128 1,785 2,208
36,2%
Supercrítico
Y<d
0,253
0,000
0,091
1,001
Aguas abajo 28,580 0,235 5,292 0,048 0,403 0,119 0,597 3,945 0,597 0,300
94,0%
Subcrítico
Y>d
0,253
1,013
9
Aguas arriba 28,420 0,089 2,558 0,016 0,065 0,239 1,812 6,116 1,812 2,261
35,6%
Supercrítico
Y<d
0,256 0,005
1,806
0,982
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
108
Aguas abajo 28,420 0,234 5,252 0,048 0,387 0,123 0,595 4,035 0,595 0,305
93,5%
Subcrítico
Y>d
0,252
0,969
10
Aguas arriba 27,130 0,088 2,548 0,016 0,065 0,239 1,747 6,110 1,747 2,188
35,4%
Supercrítico
Y<d
0,244
0,003
1,032
1,010
Aguas abajo 27,130 0,230 5,125 0,047 0,345 0,137 0,575 4,310 0,575 0,313
91,8%
Subcrítico
Y<d
0,246
0,930
11
Aguas arriba 25,660 0,088 2,540 0,015 0,065 0,239 1,664 6,105 1,664 2,091
35,2%
Supercrítico
Y<d
0,229
0,009
4,060
1,041
Aguas abajo 25,660 0,223 4,935 0,046 0,296 0,156 0,556 4,681 0,556 0,326
89,1%
Subcrítico
Y<d
0,238
0,993
12
Aguas arriba 25,530 0,085 2,497 0,015 0,062 0,237 1,724 6,079 1,724 2,202
34,2%
Supercrítico
Y<d
0,237
0,000
0,012
1,000
Aguas abajo 25,530 0,221 4,896 0,046 0,287 0,160 0,556 4,752 0,556 0,331
88,4%
Subcrítico
Y<d
0,237
1,020
13
Aguas arriba 24,610 0,081 2,430 0,014 0,059 0,234 1,773 6,035 1,773 2,325
32,6%
Supercrítico
Y<d
0,242
0,008
3,384
0,966
Aguas abajo 24,610 0,219 4,832 0,046 0,274 0,166 0,541 4,864 0,541 0,330
87,4%
Subcrítico
Y<d
0,233
1,056
14
Aguas arriba 23,370 0,077 2,351 0,013 0,056 0,231 1,824 5,976 1,824 2,472
30,7%
Supercrítico
Y<d
0,246
0,018
7,409
0,926
Aguas abajo 23,370 0,214 4,734 0,045 0,256 0,175 0,522 5,027 0,522 0,329
85,7%
Subcrítico
Y<d
0,228
1,113
15
Aguas arriba 23,020 0,074 2,309 0,012 0,054 0,229 1,877 5,943 1,877 2,587
29,8%
Supercrítico
Y<d
0,254
0,027 10,678
0,893
Aguas abajo 23,020 0,213 4,710 0,045 0,252 0,177 0,516 5,065 0,516 0,328
85,3%
Subcrítico
Y<d
0,227
1,056
16
Aguas arriba 21,910 0,074 2,301 0,012 0,053 0,228 1,802 5,936 1,802 2,494
29,6%
Supercrítico
Y<d
0,240
0,018
7,572
0,924
Aguas abajo 21,910 0,209 4,608 0,044 0,236 0,186 0,501 5,221 0,501 0,329
83,5%
Subcrítico
Y<d
0,221
1,101
17
Aguas arriba 21,270 0,071 2,255 0,012 0,051 0,226 1,839 5,897 1,839 2,595
28,6%
Supercrítico
Y<d
0,244
0,027 10,963
0,890
Aguas abajo 21,270 0,205 4,523 0,043 0,223 0,193 0,495 5,342 0,495 0,334
81,9%
Subcrítico
Y<d
0,217
1,066
18
Aguas arriba 20,480 0,071 2,254 0,012 0,051 0,226 1,773 5,897 1,773 2,502
28,5%
Supercrítico
Y<d
0,232
0,026 11,173
0,888
Aguas abajo 20,480 0,193 4,286 0,041 0,193 0,210 0,505 5,640 0,505 0,367
77,1%
Subcrítico
Y<d
0,206
1,122
19
Aguas arriba 20,330 0,071 2,249 0,011 0,051 0,226 1,770 5,892 1,770 2,504
28,4%
Supercrítico
Y<d
0,231
0,026 11,447
0,886
Aguas abajo 20,330 0,191 4,260 0,040 0,190 0,212 0,504 5,668 0,504 0,369
76,5%
Subcrítico
Y<d
0,204
1,043
20
Aguas arriba 19,140 0,071 2,247 0,011 0,051 0,225 1,670 5,890 1,670 2,364
28,4%
Supercrítico
Y<d
0,213
0,016
7,342
0,927
Aguas abajo 19,140 0,185 4,145 0,039 0,178 0,219 0,491 5,789 0,491 0,372
74,0%
Subcrítico
Y<d
0,197
1,036
21
Aguas arriba 18,390 0,070 2,237 0,011 0,050 0,225 1,622 5,882 1,622 2,307
28,2%
Supercrítico
Y<d
0,205
0,009
4,527
0,955
Aguas abajo 18,390 0,184 4,120 0,039 0,175 0,221 0,476 5,814 0,476 0,363
73,5%
Subcrítico
Y<d
0,195
1,068
22
Aguas arriba 18,120 0,069 2,205 0,011 0,049 0,223 1,657 5,853 1,657 2,390
27,4%
Supercrítico
Y<d
0,209 0,015
7,076
0,929
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
109
Aguas abajo 18,120 0,182 4,096 0,038 0,173 0,222 0,472 5,836 0,472 0,363
73,0%
Subcrítico
Y<d
0,194
1,023
23
Aguas arriba 17,150 0,068 2,187 0,011 0,048 0,222 1,601 5,836 1,601 2,328
27,0%
Supercrítico
Y<d
0,198
0,007
3,625
0,964
Aguas abajo 17,150 0,181 4,065 0,038 0,170 0,224 0,451 5,864 0,451 0,350
72,3%
Subcrítico
Y<d
0,191
1,043
24
Aguas arriba 16,340 0,065 2,132 0,010 0,046 0,219 1,626 5,783 1,626 2,423
25,8%
Supercrítico
Y<d
0,199
0,011
5,340
0,947
Aguas abajo 16,340 0,179 4,037 0,038 0,167 0,225 0,434 5,890 0,434 0,339
71,6%
Subcrítico
Y<d
0,189
1,058
25
Aguas arriba 15,710 0,062 2,093 0,010 0,044 0,216 1,640 5,743 1,640 2,490
25,0%
Supercrítico
Y<d
0,200
0,017
8,271
0,917
Aguas abajo 15,710 0,174 3,939 0,036 0,158 0,230 0,432 5,971 0,432 0,347
69,4%
Subcrítico
Y<d
0,183
1,052
26
Aguas arriba 15,240 0,062 2,088 0,010 0,044 0,216 1,600 5,738 1,600 2,433
24,9%
Supercrítico
Y<d
0,193
0,013
6,517
0,935
Aguas abajo 15,240 0,171 3,892 0,036 0,154 0,233 0,427 6,007 0,427 0,348
68,3%
Subcrítico
Y<d
0,180
1,037
27
Aguas arriba 14,360 0,060 2,053 0,009 0,043 0,214 1,576 5,701 1,576 2,437
24,1%
Supercrítico
Y<d
0,187
0,010
5,240
0,948
Aguas abajo 14,360 0,169 3,853 0,035 0,150 0,234 0,408 6,035 0,408 0,336
67,4%
Subcrítico
Y<d
0,177
1,019
28
Aguas arriba 13,800 0,060 2,039 0,009 0,042 0,213 1,540 5,686 1,540 2,397
23,8%
Supercrítico
Y<d
0,180
0,009
4,795
0,952
Aguas abajo 13,800 0,163 3,765 0,034 0,143 0,238 0,406 6,092 0,406 0,343
65,3%
Subcrítico
Y<d
0,172
1,014
29
Aguas arriba 13,310 0,059 2,030 0,009 0,042 0,212 1,503 5,676 1,503 2,349
23,6%
Supercrítico
Y<d
0,174
0,004
2,511
0,975
Aguas abajo 13,310 0,162 3,739 0,034 0,141 0,239 0,396 6,108 0,396 0,337
64,7%
Subcrítico
Y<d
0,170
0,978
30
Aguas arriba 12,730 0,059 2,022 0,009 0,041 0,212 1,452 5,667 1,452 2,279
23,5%
Supercrítico
Y<d
0,166
0,000
0,039
1,000
Aguas abajo 12,730 0,158 3,681 0,033 0,136 0,241 0,388 6,140 0,388 0,336
63,3%
Subcrítico
Y<d
0,166
1,045
31
Aguas arriba 12,260 0,055 1,957 0,008 0,039 0,207 1,523 5,593 1,523 2,469
22,1%
Supercrítico
Y<d
0,173
0,009
5,233
0,948
Aguas abajo 12,260 0,157 3,661 0,032 0,134 0,242 0,377 6,150 0,377 0,329
62,8%
Subcrítico
Y<d
0,164
1,108
32
Aguas arriba 11,530 0,051 1,874 0,007 0,036 0,201 1,604 5,493 1,604 2,711
20,4%
Supercrítico
Y<d
0,182
0,020 10,980
0,890
Aguas abajo 11,530 0,156 3,635 0,032 0,132 0,242 0,359 6,163 0,359 0,315
62,2%
Subcrítico
Y<d
0,162
1,049
33
Aguas arriba 10,610 0,050 1,846 0,007 0,035 0,199 1,537 5,456 1,537 2,638
19,8%
Supercrítico
Y<d
0,170
0,011
6,736
0,933
Aguas abajo 10,610 0,153 3,590 0,031 0,129 0,244 0,338 6,184 0,338 0,300
61,1%
Subcrítico
Y<d
0,159
0,994
34
Aguas arriba 9,880 0,049 1,832 0,007 0,034 0,198 1,461 5,438 1,461 2,525
19,5%
Supercrítico
Y<d
0,158
0,016 10,010
0,900
Aguas abajo 9,880 0,135 3,302 0,027 0,109 0,249 0,365 6,269 0,365 0,354
54,0%
Subcrítico
Y<d
0,142
1,112
35
Aguas arriba 9,210 0,046 1,776 0,006 0,032 0,194 1,480 5,364 1,480 2,637
18,4%
Supercrítico
Y<d
0,158 0,018 11,462 0,885
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
110
Aguas abajo 9,210 0,134 3,279 0,027 0,107 0,249 0,345 6,272 0,345 0,337
53,4%
Subcrítico
Y<d
0,140
Tabla 13. Resultados obtenidos para la pendiente 0,025.
Pendiente 0,025
Ensayo
Alturas
Q
[L/s]
Yn
[m]
Ѳ
[Rad]
A
[m
2
]
D [m]
T
P
R
V
(m/s)
Fr
Relación de
llenado
Tipo de
Resalto
Tipo de
Resalto
E
∆E
∆E/E1
(%)
E2/E1
1
Aguas arriba 43,670 0,113 2,945 0,021 0,086 0,249 2,032 6,260 2,032 2,208
45,1%
Supercrítico
Y<d
0,323
0,033 10,181
0,898
Aguas abajo 43,670 0,250 6,275 0,049 49,087 0,001 0,890 0,129 0,890 0,041
100,0%
Subcrítico
Y>d
0,290
1,086
2
Aguas arriba 42,510 0,112 2,932 0,021 0,086 0,249 1,997 6,257 1,997 2,179
44,8%
Supercrítico
Y<d
0,315
0,027
8,570
0,914
Aguas abajo 42,510 0,250 6,275 0,049 49,087 0,001 0,866 0,129 0,866 0,039
100,0%
Subcrítico
Y>d
0,288
1,059
3
Aguas arriba 41,270 0,111 2,924 0,021 0,085 0,249 1,950 6,255 1,950 2,134
44,6%
Supercrítico
Y<d
0,305
0,019
6,308
0,937
Aguas abajo 41,270 0,250 6,275 0,049 49,087 0,001 0,841 0,129 0,841 0,038
100,0%
Subcrítico
Y>d
0,286
1,027
4
Aguas arriba 39,860 0,111 2,917 0,021 0,085 0,248 1,894 6,254 1,894 2,078
44,4%
Supercrítico
Y<d
0,294
0,010
3,490
0,965
Aguas abajo 39,860 0,250 6,275 0,049 49,087 0,001 0,812 0,129 0,812 0,037
100,0%
Subcrítico
Y>d
0,284
1,047
5
Aguas arriba 39,150 0,108 2,870 0,020 0,082 0,248 1,925 6,242 1,925 2,146
43,2%
Supercrítico
Y<d
0,297
0,015
4,928
0,951
Aguas abajo 39,150 0,250 6,275 0,049 49,087 0,001 0,798 0,129 0,798 0,036
100,0%
Subcrítico
Y>d
0,282
1,032
6
Aguas arriba 37,680 0,106 2,832 0,020 0,080 0,247 1,909 6,231 1,909 2,156
42,3%
Supercrítico
Y<d
0,291
0,011
3,916
0,961
Aguas abajo 37,680 0,250 6,275 0,049 49,087 0,001 0,768 0,129 0,768 0,035
100,0%
Subcrítico
Y>d
0,280
1,053
7
Aguas arriba 36,820 0,103 2,780 0,019 0,077 0,246 1,942 6,215 1,942 2,233
41,0%
Supercrítico
Y<d
0,295
0,016
5,451
0,945
Aguas abajo 36,820 0,250 6,275 0,049 49,087 0,001 0,750 0,129 0,750 0,034
100,0%
Subcrítico
Y>d
0,279
1,025
8
Aguas arriba 35,240 0,101 2,750 0,019 0,075 0,245 1,904 6,204 1,904 2,213
40,3%
Supercrítico
Y<d
0,286 0,009
3,247
0,968
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
111
Aguas abajo 35,240 0,250 6,275 0,049 49,087 0,001 0,718 0,129 0,718 0,033
100,0%
Subcrítico
Y>d
0,276
0,984
9
Aguas arriba 33,580 0,100 2,735 0,018 0,075 0,245 1,838 6,198 1,838 2,148
39,9%
Supercrítico
Y<d
0,272
0,002
0,724
1,007
Aguas abajo 33,580 0,250 6,275 0,049 49,087 0,001 0,684 0,129 0,684 0,031
100,0%
Subcrítico
Y>d
0,274
0,975
10
Aguas arriba 31,860 0,096 2,677 0,017 0,072 0,243 1,830 6,173 1,830 2,184
38,5%
Supercrítico
Y<d
0,267
0,005
1,706
1,017
Aguas abajo 31,860 0,250 6,275 0,049 49,087 0,001 0,649 0,129 0,649 0,030
100,0%
Subcrítico
Y>d
0,271
0,941
11
Aguas arriba 30,530 0,095 2,665 0,017 0,071 0,243 1,771 6,168 1,771 2,123
38,2%
Supercrítico
Y<d
0,255
0,013
5,266
1,053
Aguas abajo 30,530 0,249 6,044 0,049 1,642 0,030 0,622 1,611 0,622 0,155
99,6%
Subcrítico
Y>d
0,269
0,925
12
Aguas arriba 29,310 0,094 2,636 0,017 0,069 0,242 1,743 6,154 1,743 2,111
37,5%
Supercrítico
Y<d
0,249
0,018
7,250
1,072
Aguas abajo 29,310 0,248 5,966 0,049 1,243 0,039 0,598 1,936 0,598 0,171
99,4%
Subcrítico
Y>d
0,267
0,908
13
Aguas arriba 28,300 0,093 2,616 0,017 0,068 0,241 1,714 6,143 1,714 2,092
37,0%
Supercrítico
Y<d
0,242
0,023
9,455
1,095
Aguas abajo 28,300 0,248 5,938 0,049 1,142 0,043 0,577 2,047 0,577 0,172
99,3%
Subcrítico
Y>d
0,265
0,886
14
Aguas arriba 26,910 0,090 2,579 0,016 0,067 0,240 1,684 6,124 1,684 2,085
36,1%
Supercrítico
Y<d
0,235
0,025 10,820
1,108
Aguas abajo 26,910 0,245 5,704 0,049 0,684 0,071 0,551 2,846 0,551 0,213
97,9%
Subcrítico
Y>d
0,260
0,868
15
Aguas arriba 25,660 0,089 2,556 0,016 0,065 0,239 1,640 6,111 1,640 2,047
35,6%
Supercrítico
Y<d
0,226
0,024 10,557
1,106
Aguas abajo 25,660 0,235 5,299 0,048 0,406 0,118 0,536 3,924 0,536 0,268
94,1%
Subcrítico
Y>d
0,250
0,917
16
Aguas arriba 25,650 0,088 2,540 0,015 0,065 0,239 1,664 6,102 1,664 2,090
35,2%
Supercrítico
Y<d
0,229
0,026 11,513
1,115
Aguas abajo 24,650 0,242 5,577 0,049 0,563 0,086 0,507 3,218 0,507 0,216
96,9%
Subcrítico
Y>d
0,255
0,895
17
Aguas arriba 24,260 0,084 2,466 0,014 0,061 0,236 1,686 6,056 1,686 2,180
33,4%
Supercrítico
Y<d
0,229
0,026 11,280
1,113
Aguas abajo 24,260 0,242 5,547 0,049 0,540 0,090 0,499 3,301 0,499 0,217
96,7%
Subcrítico
Y>d
0,254
0,877
18
Aguas arriba 22,810 0,080 2,412 0,014 0,058 0,234 1,672 6,019 1,672 2,209
32,2%
Supercrítico
Y<d
0,223
0,023 10,344
1,103
Aguas abajo 22,810 0,234 5,273 0,048 0,395 0,121 0,477 3,984 0,477 0,242
93,8%
Subcrítico
Y>d
0,246
0,897
19
Aguas arriba 22,310 0,079 2,395 0,013 0,058 0,233 1,665 6,006 1,665 2,216
31,8%
Supercrítico
Y<d
0,221
0,024 11,016
1,110
Aguas abajo 22,310 0,234 5,256 0,048 0,389 0,123 0,467 4,023 0,467 0,239
93,6%
Subcrítico
Y>d
0,245
0,930
20
Aguas arriba 21,510 0,075 2,321 0,012 0,054 0,229 1,731 5,950 1,731 2,375
30,1%
Supercrítico
Y<d
0,228
0,016
6,888
1,069
Aguas abajo 21,510 0,233 5,237 0,048 0,382 0,125 0,451 4,067 0,451 0,233
93,3%
Subcrítico
Y>d
0,244
0,935
21
Aguas arriba 20,310 0,072 2,258 0,012 0,051 0,226 1,751 5,897 1,751 2,467
28,6%
Supercrítico
Y<d
0,228 0,007
2,993
1,030
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
112
Aguas abajo 20,310 0,225 4,993 0,047 0,309 0,150 0,437 4,571 0,437 0,251
89,9%
Subcrítico
Y<d
0,235
0,896
22
Aguas arriba 19,080 0,071 2,255 0,012 0,051 0,226 1,651 5,894 1,651 2,329
28,5%
Supercrítico
Y<d
0,210
0,021
9,930
1,099
Aguas abajo 19,080 0,222 4,928 0,046 0,294 0,157 0,414 4,691 0,414 0,243
89,0%
Subcrítico
Y<d
0,231
0,876
23
Aguas arriba 18,470 0,071 2,250 0,012 0,051 0,226 1,605 5,890 1,605 2,270
28,5%
Supercrítico
Y<d
0,202
0,026 12,964
1,130
Aguas abajo 18,470 0,220 4,880 0,046 0,284 0,161 0,403 4,779 0,403 0,242
88,2%
Subcrítico
Y<d
0,229
0,908
24
Aguas arriba 16,830 0,065 2,132 0,010 0,046 0,219 1,675 5,780 1,675 2,497
25,8%
Supercrítico
Y<d
0,208
0,002
0,878
0,991
Aguas abajo 16,830 0,197 4,378 0,042 0,204 0,204 0,405 5,528 0,405 0,286
79,0%
Subcrítico
Y<d
0,206
0,943
25
Aguas arriba 15,420 0,062 2,094 0,010 0,044 0,216 1,607 5,741 1,607 2,438
25,0%
Supercrítico
Y<d
0,194
0,008
4,004
1,040
Aguas abajo 15,420 0,195 4,325 0,041 0,198 0,207 0,376 5,591 0,376 0,270
77,9%
Subcrítico
Y<d
0,202
0,927
26
Aguas arriba 14,210 0,060 2,041 0,009 0,042 0,213 1,582 5,685 1,582 2,460
23,9%
Supercrítico
Y<d
0,187
0,008
4,036
1,040
Aguas abajo 14,210 0,188 4,201 0,040 0,184 0,216 0,359 5,729 0,359 0,267
75,3%
Subcrítico
Y<d
0,195
0,937
27
Aguas arriba 13,280 0,057 1,996 0,008 0,040 0,210 1,568 5,635 1,568 2,492
22,9%
Supercrítico
Y<d
0,182
0,007
3,737
1,037
Aguas abajo 13,280 0,183 4,111 0,039 0,174 0,221 0,344 5,819 0,344 0,263
73,3%
Subcrítico
Y<d
0,189
0,965
28
Aguas arriba 13,210 0,057 1,990 0,008 0,040 0,210 1,571 5,628 1,571 2,504
22,8%
Supercrítico
Y<d
0,183
0,004
2,398
1,024
Aguas abajo 13,210 0,181 4,069 0,038 0,170 0,224 0,347 5,857 0,347 0,269
72,4%
Subcrítico
Y<d
0,187
1,018
29
Aguas arriba 12,920 0,055 1,944 0,008 0,038 0,207 1,633 5,575 1,633 2,663
21,8%
Supercrítico
Y<d
0,190
0,007
3,754
0,962
Aguas abajo 12,920 0,177 4,002 0,037 0,164 0,227 0,347 5,917 0,347 0,274
70,9%
Subcrítico
Y<d
0,183
0,977
30
Aguas arriba 12,070 0,053 1,923 0,008 0,037 0,205 1,570 5,549 1,570 2,589
21,4%
Supercrítico
Y<d
0,179
0,009
4,831
0,952
Aguas abajo 12,070 0,164 3,778 0,034 0,144 0,237 0,353 6,081 0,353 0,297
65,6%
Subcrítico
Y<d
0,170
1,018
31
Aguas arriba 11,480 0,052 1,899 0,007 0,037 0,203 1,542 5,521 1,542 2,573
20,9%
Supercrítico
Y<d
0,173
0,010
5,707
0,943
Aguas abajo 11,480 0,157 3,663 0,033 0,135 0,242 0,353 6,146 0,353 0,307
62,9%
Subcrítico
Y<d
0,164
0,988
32
Aguas arriba 10,270 0,050 1,849 0,007 0,035 0,200 1,481 5,457 1,481 2,538
19,9%
Supercrítico
Y<d
0,162
0,001
0,502
0,995
Aguas abajo 10,270 0,156 3,635 0,032 0,132 0,242 0,320 6,159 0,320 0,281
62,2%
Subcrítico
Y<d
0,161
1,060
33
Aguas arriba 9,100 0,044 1,727 0,006 0,030 0,190 1,577 5,292 1,577 2,889
17,5%
Supercrítico
Y<d
0,170
0,017
9,887
0,901
Aguas abajo 9,100 0,149 3,530 0,031 0,124 0,245 0,298 6,205 0,298 0,270
59,6%
Subcrítico
Y<d
0,154
0,989
34
Aguas arriba 8,150 0,043 1,704 0,006 0,030 0,188 1,464 5,260 1,464 2,717
17,1%
Supercrítico
Y<d
0,152 0,009
5,786
0,942
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
113
Aguas abajo 8,150 0,139 3,362 0,028 0,113 0,248 0,291 6,255 0,291 0,277
55,5%
Subcrítico
Y<d
0,143
0,963
35
Aguas arriba 7,420 0,042 1,686 0,005 0,029 0,187 1,372 5,234 1,372 2,574
16,7%
Supercrítico
Y<d
0,138
0,006
4,372
0,956
Aguas abajo 7,420 0,127 3,179 0,025 0,101 0,250 0,295 6,278 0,295 0,297
50,9%
Subcrítico
Y<d
0,132
Anexo II
Datos para pendiente de 0,011 aguas arriba
Tabla 14. Datos de Entrada para calcular ecuación de Darcy Weisbach.
Datos de Entrada
ks
1,50E-06
S
0,011
Viscosidad
1,14E-06
Tabla 15. Ecuaciones teóricas utilizando ley de Darcy Weisbach.
AGUAS ARRIBA
d
(m)
y/d
(-)
yn
(m)
teta
(-)
Área
(m
2
)
Perímetro
(m)
Radio
(m)
Velocidad
(Darcy)
(m/s)
Velocidad
(Manning)
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
0,25 10% 0,025 1,287 0,003
0,161
0,016
0,798
4417,461
0,002
44462,929 0,150 0,017
1,952
0,25 20% 0,050 1,855 0,007
0,232
0,030
1,233
6772,920
0,009 130468,977 0,200 0,035
2,107
0,25 30% 0,075 2,319 0,012
0,290
0,043
1,555
8546,649
0,019 233178,698 0,229 0,054
2,135
0,25 40% 0,100 2,739 0,018
0,342
0,054
1,803
9934,523
0,033 338908,322 0,245 0,075
2,105
0,25 50% 0,125 3,142 0,025
0,393
0,063
1,995
11011,803
0,049 437394,924 0,250 0,098
2,032

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
114
Datos para pendiente de 0,011 aguas abajo
Tabla 16. Ecuaciones teóricas utilizando ley de Darcy Weisbach.
AGUAS ABAJO
d
(m)
y/d
(-)
yn
(m)
teta
(-)
Área
(m
2
)
Perímetro
(m)
Radio
(m)
Velocidad
(Darcy)
(m/s)
Velocidad
(Manning)
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
0,25 50% 0,125 3,142 0,025
0,393
0,063
1,995
11011,803 0,049 437394,924 0,250 0,098
2,032
0,25 60% 0,150 3,544 0,031
0,443
0,069
2,135
11809,300 0,066 519971,306 0,245 0,126
1,924
0,25 70% 0,175 3,965 0,037
0,496
0,074
2,226
12330,735 0,082 578545,352 0,229 0,160
1,776
0,25 80% 0,200 4,429 0,042
0,554
0,076
2,265
12550,609 0,095 604350,218 0,200 0,210
1,576
0,25 90% 0,225 4,996 0,047
0,625
0,075
2,235
12380,691 0,104 584350,313 0,150 0,310
1,281
0,25 100% 0,238 5,381 0,048
0,673
0,072
2,179
12057,738 0,105 547421,382 0,109 0,442
1,046
Datos de entrada para pendiente de 0,018 aguas arriba
Tabla 17. Datos de Entrada para calcular ecuación de Darcy Weisbach.
Datos de Entrada
ks
1,50E-06
S
0,018
Viscosidad
1,14E-06
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
115
Tabla 18. Ecuaciones teóricas utilizando ley de Darcy Weisbach.
AGUAS ARRIBA
d
(m)
y/d
(-)
yn
(m)
teta
(-)
Área
(m
2
)
Perímetro
(m)
Radio
(m)
Velocidad
(Darcy)
(m/s)
Velocidad
(Manning)
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
0,25 15% 0,038 1,591 0,005
0,199
0,023
1,323
5690,787
0,006 107822,902 0,179 0,026
2,628
0,25 20% 0,050 1,855 0,007
0,232
0,030
1,578
6772,920
0,011 166896,476 0,200 0,035
2,695
0,25 30% 0,075 2,319 0,012
0,290
0,043
1,989
8546,649
0,025 298283,193 0,229 0,054
2,732
0,25 40% 0,100 2,739 0,018
0,342
0,054
2,307
9934,523
0,042 433532,982 0,245 0,075
2,692
0,25 45% 0,113 2,941 0,021
0,368
0,058
2,438
10509,341
0,052 498407,561 0,249 0,086
2,652

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
116
Anexo III
Tabla 19. Comparación de resultados teóricos con resultados experimentales en profundidades de flujo
aguas abajo para todas las pendientes.
S=0,011
S=0,016
S0,018
S=0,025
Y2
Y2 Teóricos
Y2
Y2 Teórico
Y2
Y2 Teórico
Y2
Y2 Teóricos
0,250
0,219
0,250
0,208
0,250
0,210
0,250
0,215
0,250
0,215
0,250
0,208
0,250
0,200
0,250
0,210
0,249
0,211
0,250
0,208
0,250
0,198
0,250
0,206
0,245
0,209
0,250
0,206
0,250
0,194
0,250
0,200
0,242
0,205
0,250
0,205
0,246
0,187
0,250
0,200
0,237
0,202
0,250
0,200
0,244
0,187
0,250
0,198
0,235
0,198
0,250
0,195
0,238
0,181
0,250
0,197
0,229
0,198
0,250
0,194
0,235
0,178
0,250
0,195
0,223
0,196
0,250
0,192
0,234
0,177
0,250
0,188
0,223
0,194
0,250
0,192
0,230
0,173
0,250
0,186
0,222
0,188
0,250
0,192
0,223
0,166
0,249
0,180
0,221
0,187
0,249
0,190
0,221
0,166
0,248
0,177
0,216
0,185
0,247
0,187
0,219
0,166
0,248
0,167
0,213
0,181
0,242
0,186
0,214
0,166
0,245
0,167
0,207
0,175
0,241
0,186
0,213
0,165
0,235
0,165
0,203
0,169
0,244
0,183
0,209
0,165
0,242
0,165
0,197
0,168
0,238
0,183
0,205
0,165
0,242
0,165
0,192
0,168
0,237
0,177
0,193
0,161
0,234
0,162
0,191
0,166
0,233
0,174
0,191
0,161
0,234
0,160
0,191
0,165
0,227
0,173
0,185
0,154
0,233
0,160
0,188
0,164
0,223
0,170
0,184
0,150
0,225
0,160
0,180
0,163
0,214
0,167
0,182
0,150
0,222
0,153
0,178
0,163
0,208
0,165
0,181
0,147
0,220
0,150
0,175
0,163
0,203
0,165
0,179
0,146
0,197
0,149
0,171
0,162
0,194
0,164
0,174
0,145
0,195
0,143
0,168
0,159
0,188
0,161
0,171
0,143
0,188
0,139
0,164
0,154
0,185
0,156
0,169
0,140
0,183
0,137
0,162
0,147
0,176
0,150
0,163
0,137
0,181
0,137
0,160
0,145
0,175
0,143
0,162
0,134
0,177
0,136
0,154
0,143
0,175
0,138
0,158
0,131
0,164
0,133
0,146
0,141
0,171
0,136
0,157
0,131
0,157
0,131
0,142
0,135
0,169
0,130
0,156
0,131
0,156
0,125
0,133
0,128
0,162
0,129
0,153
0,128
0,149
0,123

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
117
0,130
0,125
0,154
0,126
0,135
0,123
0,139
0,114
0,123
0,120
0,147
0,122
0,134
0,120
0,127
0,100
Anexo IV
Function y2()
Q = Cells(2, 3)
s = Cells(3, 3)
d = Cells(4, 3)
If s = 0.025 Then
y2 = 0.8893 * Q ^ 0.3715
Cells(6, 3) = y2
rel = y2 / d
Cells(7, 3) = rel
If rel <= 0.85 Then
Cells(8, 3) = "SI"
Else
Cells(8, 3) = "NO"
End If

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
118
ElseIf s = 0.018 Then
y2 = 1.1367 * Q ^ 0.4509
Cells(6, 3) = y2
rel = y2 / d
Cells(7, 3) = rel
If rel <= 0.85 Then
Cells(8, 3) = "SI"
Else
Cells(8, 3) = "NO"
End If
ElseIf s = 0.016 Then
y2 = 0.8892 * Q ^ 0.3884
Cells(6, 3) = y2
rel = y2 / d
Cells(7, 3) = rel
if rel <= 0.85 Then
Cells(8, 3) = "SI"
Else
Cells(8, 3) = "NO"

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Resaltos hidráulicos en tuberías lisas de sección circular fluyendo parcialmente
llenas, con números de Froude inferiores a 4.0
119
End If
ElseIf s = 0.011 Then
y2 = 0.9946 * Q ^ 0.4475
Cells(6, 3) = y2
rel = y2 / d
Cells(7, 3) = rel
If rel <= 0.85 Then
Cells(8, 3) = "SI"
Else
Cells(8, 3) = "NO"
End If
Else
y2 = "No Registrado en Laboratorio"
Cells(6, 3) = y2
End If
End Function
