
PROYECTO DE GRADO
INGENIERÍA CIVIL
METODOLOGÍA PARA LA OPTIMIZACIÓN DEL DISEÑO DE TUBERÍAS EN SERIE EN
SISTEMAS DE ALCANTARILLADO
PRESENTADO POR:
NATALIA DUQUE VILLARREAL
a
ASESOR:
JUAN GUILLERMO SALDARRIAGA VALDERRAMA
a
a
Centro de Investigación en Acueductos y Alcantarillados (CIACUA), Departamento de Ingeniería
Civil y Ambiental, Universidad de los Andes, Bogotá, Colombia
CO-ASESOR:
DANIEL DUQUE VILLARREAL
b
b
Centro para la Optimización y Probabilidad Aplicada (COPA), Departamento de Ingeniería
Industrial, Universidad de los Andes, Bogotá, Colombia
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
BOGOTÁ D.C
DICIEMBRE DE 2013

EL presente trabajo corresponde al Proyecto de Grado con el cual se culminan los estudios
de pregrado del programa de Ingeniería Civil de la Universidad de los Andes.

AGRADECIMIENTOS
A mi familia, por su apoyo incondicional y sus enseñanzas a lo largo de toda mi vida,
a mi hermano y co-asesor, por enseñarme nuevas cosas, tenerme paciencia y exigirme al máximo
en este Proyecto de Grado, lo cual me hizo crecer no solo a nivel académico pero también a nivel
personal,
a mi asesor Juan Saldarriaga por su apoyo para lograr el desarrollo de este Proyecto de Grado y
por su contribución en mi formación profesional y personal,
al grupo CIE-AGUA por su colaboración y paciencia durante el semestre.
¡Gracias!

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
i
TABLA DE CONTENIDO
1
INTRODUCCIÓN Y OBJETIVOS ..................................................................................................... 1
1.1
Introducción ........................................................................................................................ 1
1.2
Objetivos ............................................................................................................................. 2
1.2.1
Objetivo general .......................................................................................................... 2
1.2.2
Objetivos específicos ................................................................................................... 2
2
MARCO TEÓRICO ......................................................................................................................... 3
2.1
Redes de drenaje urbano .................................................................................................... 3
2.1.1
Efectos de la urbanización ........................................................................................... 3
2.1.2
Componentes de las redes de drenaje urbano ........................................................... 5
2.1.3
Fallas en redes de drenaje urbano .............................................................................. 7
2.2
Sistema integrado de drenaje urbano ................................................................................. 8
2.3
Diseño de redes de drenaje urbano .................................................................................. 10
2.3.1
Definición del problema ............................................................................................ 10
2.3.2
Supuestos del diseño ................................................................................................. 11
2.3.3
Ecuaciones de diseño ................................................................................................ 12
2.4
Restricciones de diseño ..................................................................................................... 18
2.4.1
Restricciones hidráulicas ........................................................................................... 18
2.4.2
Restricciones comerciales ......................................................................................... 21
2.5
Función de costos .............................................................................................................. 21
2.6
Pendientes Propias e Intermedias .................................................................................... 24
2.7
Potencia Específica ............................................................................................................ 28
3
METODOLOGÍA PARA EL DISEÑO OPTIMIZADO DE SISTEMAS DE ALCANTARILLADO .............. 30
3.1
Problemas de flujo en redes ............................................................................................. 30
3.1.1
Problema de la ruta más corta .................................................................................. 31
3.1.2
Algoritmo de Bellman-Ford ....................................................................................... 32
3.2
Planteamiento del problema ............................................................................................ 34

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
ii
3.2.1
Datos de entrada ....................................................................................................... 34
3.2.2
Modelaje del grafo .................................................................................................... 34
3.2.3
Variables de decisión ................................................................................................. 37
3.2.4
Función objetivo ........................................................................................................ 38
3.2.5
Representación una serie de tuberías de la red de alcantarillado en un grafo ........ 39
3.2.6
Diseño óptimo de series de tuberías de alcantarillado ............................................. 43
3.2.7
Dimensionamiento del problema ............................................................................. 47
4
RESULTADOS Y ANÁLISIS DE RESULTADOS ................................................................................ 49
4.1
Diseño de un tramo de alcantarillado ............................................................................... 49
4.2
Diseño de series de tuberías de alcantarillado ................................................................. 54
4.3
Análisis de costos y tiempos .............................................................................................. 60
5
CONCLUSIONES ......................................................................................................................... 69
6
BIBLIOGRAFÍA ............................................................................................................................ 71
7
ANEXOS ..................................................................................................................................... 73

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
iii
ÍNDICE DE TABLAS
Tabla 2.1 Tipos de flujo ..................................................................................................................... 11
Tabla 2.2 Resumen de propiedades geométricas del alcantarillado ................................................ 13
Tabla 2.3 Límites de la profundidad a cota clave de la tubería......................................................... 20
Tabla 2.4 Resumen de restricciones hidráulicas de diseño............................................................... 20
Tabla 2.5 Lista de diámetros comerciales ......................................................................................... 21
Tabla 4.1 Resultados de diseños de un tramo – comparación de costos y PE. ................................. 50
Tabla 4.2 Resultados de diseño de un tramo – comparación de diámetros y pendientes de
diseño ................................................................................................................................................ 52
Tabla 4.3 Datos de entrada de serie 10 tramos ................................................................................ 54
Tabla 4.4 Resultados en tiempos y costos ........................................................................................ 55
Tabla 4.5 Resultados para el diseño de serie de 10 tramos –Metodología 1. .................................. 55
Tabla 4.6 Resultados para el diseño de serie de 10 tramos –Metodología 2. .................................. 55
Tabla 4.7 Datos de entrada de serie 50 tramos. ............................................................................... 57
Tabla 4.8 Resultado del diseño. ........................................................................................................ 58
Tabla 4.9 Resultados para el diseño de serie de 50 tramos –Metodología 2. .................................. 58
Tabla 4.10 Datos de entrada de serie 12 tramos. ............................................................................. 61
Tabla 4.11 Diseño de series de tuberías con costos totales y una variación de la pendiente de
1/1000. .............................................................................................................................................. 61
Tabla 4.12 Diseño de series de tuberías solo con costos tuberías y una variación de la pendiente de
1/1000. .............................................................................................................................................. 62
Tabla 4.13 Diseño de series de tubería solo con costos de excavación y una variación de la
pendiente de 1/1000. ........................................................................................................................ 62
Tabla 4.14 Diseño de series de tuberías con costos totales y una variación de la pendiente de
1/10000. ............................................................................................................................................ 65
Tabla 4.15 Diseño de series de tuberías solo con costos de tuberías y una variación de la pendiente
de 1/10000. ....................................................................................................................................... 65
Tabla 4.16 Diseño de series de tuberías solo con costos de excavación y una variación de la
pendiente de 1/10000. ...................................................................................................................... 66
Tabla 7.1 Cálculo de la hidráulica Ejemplo 1 – Metodología 1 ......................................................... 73
Tabla 7.2 Cálculo de la hidráulica Ejemplo 1 – Metodología 2 ......................................................... 74
Tabla 7.3 Cálculo de la hidráulica Ejemplo 2 – Metodología 2 ......................................................... 74

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
iv
ÍNDICE DE FIGURAS
Figura 2.1 Interacciones del Sistema de Drenaje Urbano ................................................................... 3
Figura 2.2 Efectos de la urbanización .................................................................................................. 4
Figura 2.3 Fallas en redes de drenaje urbano. .................................................................................... 8
Figura 2.4 Sistema Integrado de Drenaje Urbano. .............................................................................. 9
Figura 2.5 Flujo uniforme en canales abiertos. ................................................................................. 12
Figura 2.6 Sección transversal de tubería fluyendo parcialmente llena ........................................... 13
Figura 2.7 Proyección del trapecio que produce el área excavada para una tubería de
alcantarillado ..................................................................................................................................... 23
Figura 2.8 Búsqueda de la pendiente de diseño. .............................................................................. 25
Figura 3.1. Grafo. ............................................................................................................................... 31
Figura 3.2. Algorito de Bellman-Ford ................................................................................................ 33
Figura 3.3. Conjunto de nodos que pertenecen a un mismo pozo de inspección. ........................... 35
Figura 3.4. Representación de un arco . ...................................................................... 36
Figura 3.5. Representación de un tramo de alcantarillado. .............................................................. 37
Figura 3.6. Representación de una tubería en un grafo ................................................................... 40
Figura 3.7. Grafo de un tramo. .......................................................................................................... 40
Figura 3.8. Grafo de una serie de 2 tramos ...................................................................................... 41
Figura 3.9. Solución del grafo. ........................................................................................................... 42
Figura 3.10 proceso de compilación de la JVM ................................................................................. 46
Figura 4.1 Relación entre la Potencia Específica el costo. ................................................................ 51
Figura 4.2 Relación ente la Potencia Específica y el caudal. ............................................................. 51
Figura 4.3 Efectos del aumento del caudal en los costos. ................................................................ 52
Figura 4.4 Pendiente de diseño. ........................................................................................................ 53
Figura 4.5 Perfil del diseño óptimo para una serie de 10 tramos para costos totales. .................... 56
Figura 4.6 Perfil del diseño óptimo para una serie de 50 tramos para costos totales. .................... 60
Figura 4.7 Mejoras en costos computacionales utilizando la nueva metodología (variando la cota
cada dm). ........................................................................................................................................... 63
Figura 4.8 Mejoras en costos de construcción utilizando la nueva metodología (variando la cota
cada dm). ........................................................................................................................................... 64
Figura 4.9 Mejoras en costos computacionales utilizando la nueva metodología (variando la cota
cada cm). ........................................................................................................................................... 66
Figura 4.10 Mejoras en costos de construcción utilizando la nueva metodología (variando la cota
cada cm). ........................................................................................................................................... 67

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
v
TABLA DE ECUACIONES
Ecuación 2.1 Ángulo theta .......................................................................................................... 14
Ecuación 2.2 Área mojada ........................................................................................................... 14
Ecuación 2.3 Perímetro mojado .................................................................................................. 14
Ecuación 2.4 Radio hidráulico ..................................................................................................... 14
Ecuación 2.5 Ancho en la suericie ............................................................................................... 15
Ecuación 2.6 Profundidad hidráulica........................................................................................... 15
Ecuación 2.7 Número de Froude ................................................................................................. 15
Ecuación 2.8 Número de Reynolds ............................................................................................. 15
Ecuación 2.9 Esfuerzo cortante en la pared ................................................................................ 15
Ecuación 2.10 Ecuación de Manning ........................................................................................... 16
Ecuación 2.11 Echuación de Chézy ............................................................................................. 16
Ecuación 2.12 Ecuación de Darcy para las pérdidas por fricción ................................................ 17
Ecuación 2.13 Relación entre el C de Chézy y las pérdidas por fricción ..................................... 17
Ecuación 2.14 Ecuación de Colebrook-White para el factor de fricción ..................................... 17
Ecuación 2.15 Ecuación de Darcy-Weisbach en conjunto con Colebrook-White para la
velocidad .................................................................................................................................... 17
Ecuación 2.16 Función de costos De Oro Vergara (2008) ........................................................... 21
Ecuación 2.17 Costo de una tubería ........................................................................................... 22
Ecuación 2.18 Costo de excavación ............................................................................................ 22
Ecuación 2.19 Volumen de excavación ....................................................................................... 23
Ecuación 2.20 Función de costos ............................................................................................... 24
Ecuación 2.21 Número total de alternativas de diseño .............................................................. 25
Ecuación 2.22 Pendiente Intemedia .......................................................................................... 26
Ecuación 2.23 Variación de la pendiente cuando
..................................................... 26
Ecuación 2.24 Variación de la pendiente cuando
..................................................... 26
Ecuación 2.25 Potencia Específica (PE) ....................................................................................... 28
Ecuación 3.1 Función Objetivo del problema de la ruta más corta ............................................ 32
Ecuación 3.2 Restricción del problema de la ruta más corta ...................................................... 32
Ecuación 3.3 Variable de decisión de natualeza binaria
....................................................... 32
Ecuación 3.4 Diámetro del arco (
) ....................................................................... 37
Ecuación 3.5 Pendiente del arco (
) .................................................................... 37
Ecuación 3.6 Función objetivo del problema de diseño ............................................................ 38
Ecuación 3.7 Función de costos asociados a un arco
....................................... 38
Ecuación 3.8 Volumen de excavación asociado al arco
.................................... 38

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
vi
Ecuación 3.9 Profundidad de excavación aguas arriba en
........................................ 39
Ecuación 3.10 Profundidad de excavación aguas abajo en
................................... 39
Ecuación 3.11 Número total de alternativas para un grafo de tramos y cantidad de
diámetros .................................................................................................................................... 47
Ecuación 3.12 Número total de alternativas de diseño .............................................................. 48

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
vii
GLOSARIO
• Relación de Llenado: Relación entre la profundidad del flujo en la tubería con respecto al
Escorrentía: Lámina de agua que corre por la superficie de una cuenca de drenaje. En este
caso la escorrentía se da sobre zonas impermeables.
• Corrosión: cualquier proceso, involuntario, que sea químico, físico, biológico o eléctrico
cómo la oxidación de los metales, agentes electroquímicos, descargas industriales, agua
subterránea con alto contenido de sulfato, erosión y agentes microbiológicos, que
implique deterioro, degradación o destrucción de los componentes del sistema de
recolección de agua y que sea debido a la operación natural del mismo (ASCE, 2007).
• Capacidad Hidráulica: Caudal máximo que puede transportar una tubería.
• diámetro interno de la misma.
• Autodepuración: es el proceso de recuperación de un curso de agua después de un
episodio de contaminación orgánica (Branco, 1984).
• Cavitación: Fenómeno en el cual el agua en estado líquido pasa a estado gaseoso (vapor
de agua) a raíz de una disminución de la presión y posterior mente estas burbujas de
vapor vuelven a pasar a estado líquido repentinamente y con presiones muy altas que
generan daños en la infraestructura de la red (Saldarriaga, Clase de Hidráulica, 2012).
• Ciclo negativo: Se refiere a ciclos de un grafo en los que la suma del valor asociado con sus
arcos es negativa.
• Alternativa de diseño: se refiere una combinación de tuberías factibles (una de cada
tramo), que conforman una serie.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
1
1 INTRODUCCIÓN Y OBJETIVOS
1.1 Introducción
Las redes de drenaje urbano ayudan a evacuar grandes volúmenes de agua residual. Para esto,
las ciudades cuentan con redes de alcantarillado compuestos por tuberías y pozos de inspección,
además de otros elementos complementarios que ayudan al funcionamiento integral de las
mismas. Hasta el momento, el Centro de Investigaciones en Acueductos y Alcantarillados de la
Universidad de los Andes (CIACUA) ha desarrollado e implementado una metodología de diseño
que intenta encontrar el diseño de mínimo costo. Para esto se busca aprovechar al máximo las
tuberías asegurando una relación de llenado máxima, sin infringir las normas de diseño y
construcción establecidas por el RAS (2000), por medio de los conceptos de Pendiente Propia y
Pendiente Intermedia.
Este proyecto busca entonces, encontrar el diseño óptimo de una serie de tramos de un
sistema de drenaje urbano por medio de una nueva metodología. La metodología propuesta
pretende modelar el problema de diseño como un problema de optimización conocido como el
problema de ruta más corta (Ahuja & et Al., 1993). Para el modelaje, se hace uso de un grafo en el
que se representan las diferentes decisiones concernientes al diseño de la serie de tramos, i.e., el
diámetro y pendiente de cada tubería en cada tramo.
EL presente documento presenta un amplio marco teórico en el Capítulo 2, donde se
establecen los componentes de un sistema integrado de drenaje urbano y más específicamente de
los sistemas de alcantarillado. Se definen también conceptos importantes relacionados con la
hidráulica en sistemas de alcantarillado, que son la base para evaluar la factibilidad hidráulica del
diseño de tuberías de alcantarillado. Así mismo, el Capítulo 3 presenta en detalle la nueva
metodología propuesta. Se definen los diferentes conceptos relacionados con los problemas de
optimización, además de la aplicación de estos en el diseño de series de tuberías de alcantarillado.
Se explica además, la forma en que un grafo puede representar una serie de tuberías de
alcantarillado, con la ayuda de un ejemplo.
En el Capítulo 4 se presentan los resultados obtenidos con la nueva metodología, para el
diseño un tramo y posteriormente para el diseño de series de tramos de tuberías en sistemas de
alcantarillado. Además, se presenta el análisis de resultados que incluye las comparaciones de
costos computacionales y costos constructivos con respecto a los resultados obtenidos con la
metodología basada en el uso de Pendientes Propias e Intermedias. Finalmente en el Capítulo 5 se
presentan las conclusiones de este proyecto de grado.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
2
1.2 Objetivos
1.2.1 Objetivo general
Desarrollar una metodología para el diseño costo-óptimo de las tuberías en serie para un
sistema de alcantarillado, que tenga en cuenta los aspectos hidráulicos que aseguran el
funcionamiento adecuado del sistema de drenaje urbano, siguiendo las normas colombianas:
Reglamento Técnico del Sector de Agua Potable y Saneamiento Básico – RAS (2000).
1.2.2 Objetivos específicos
Diseñar tramos de redes de drenaje urbano para caudales de diseño dados, que cumplan
con las restricciones hidráulicas, comerciales y técnicas establecidas por las normas
colombianas: Reglamento Técnico del Sector de Agua Potable y Saneamiento Básico – RAS
(2000).
Determinar el diseño óptimo de tuberías en series en redes de drenaje urbano para
caudales de diseño dados, que cumplan con el RAS (2000).
Diseñar para tres tipos de costos: los costos totales de construcción, únicamente costos de
tuberías y únicamente costos de excavación.
Establecer la relación entre el diseño de mínimo costo y el índice de confiabilidad, la
Potencia Específica.
Analizar el tiempo computacional de solución con respecto al número de tramos evaluado
en cada serie y a la precisión con la que se decide diseñar.
Entregar una herramienta de apoyo que permita realizar el diseño óptimo de series de
tuberías a partir de un conjunto de datos de entrada dados.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
3
2 MARCO TEÓRICO
2.1 Redes de drenaje urbano
Las redes de drenaje urbano son obras civiles necesarias dentro del desarrollo de zonas
urbanas debido a la constante interacción entre el hombre y el ciclo natural del agua. Dicha
interacción se presenta por la necesidad del hombre de abastecerse de agua para su consumo y
por el proceso de urbanización que desvía los sistemas de drenaje naturales originales. De estas
dos actividades se producen aguas residuales y pluviales que deben ser canalizadas y tratadas. EL
propósito de las redes de drenaje urbano es minimizar posibles problemas causados a seres
humanos o al ambiente (Butler & Davies, 2011).
La Figura 2.1 muestra las interacciones del sistema de drenaje urbano con la población y el
medio ambiente. En este sentido, el propósito de las redes de drenaje urbano se traduce en evitar
problemas de inundación y reducir los problemas de contaminación que se generan al no evacuar
las aguas residuales y pluviales de una población.
Figura 2.1 Interacciones del Sistema de Drenaje Urbano. Tomado y Modificado de Butler & Davies (2011).
2.1.1 Efectos de la urbanización
El crecimiento poblacional acelerado, que se ha venido experimentando en el mundo desde
principios del siglo XX, ha generado un aumento significativo en la densidad de viviendas y el
movimiento de la gente de zonas rurales a zonas urbanas. La afluencia de personas en las zonas
urbanas exige la realización de obras civiles para facilitar las actividades que allí se desenvuelven y
suplir las necesidades de la gente. La pavimentación de las vías y la construcción de edificios hacen
parte de dicho proceso de urbanización, donde la impermeabilización del suelo impide la
infiltración del agua lluvia (Muth, Brinson, & Bernhar, 2010).
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
4
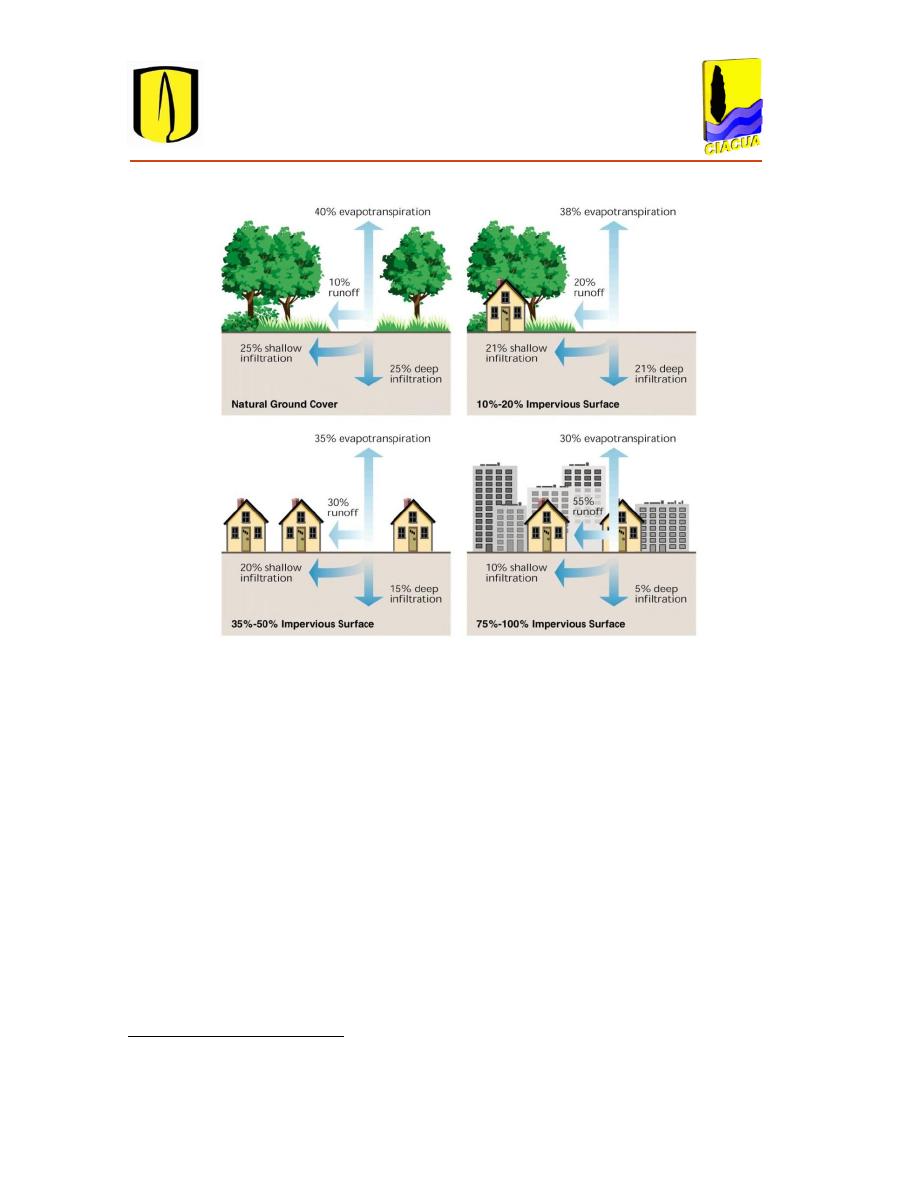
Figura 2.2 Efectos de la urbanización. Tomado de Muth, Brinson, & Bernhar (2010).
La Figura 2.2 presenta la relación entre la impermeabilización del suelo y la escorrentía
1
superficial. Como se observa, la impermeabilización del suelo aumenta la escorrentía superficial y
disminuye las infiltraciones y la evaporación del agua, lo que afecta el ciclo hidrológico normal.
Esto genera acumulación de aguas lluvias que pueden generar problemas de control de
inundaciones. Además, existe la necesidad de evacuar las aguas residuales domésticas,
comerciales o industriales para prevenir problemas de salud pública y contaminación ambiental.
1
Escorrentía: Lámina de agua que corre por la superficie de una cuenca de drenaje. En este caso la
escorrentía se da sobre zonas impermeables.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
5
2.1.2 Componentes de las redes de drenaje urbano
Para recolectar y transportar las aguas residuales y pluviales, desde donde se origina la
descarga hasta el sitio donde se va a depositar y tratar el agua, se necesita un sistema
completamente artificial de alcantarillado. Esto quiere decir que las redes están compuestas por
componentes de captación, de conducción, de inspección y conexión, de regulación y alivio y de
bombeo (Saldarriaga, Clase de Sistemas Integrados de Drenaje Urbano, 2013).
2.1.2.1 Estructuras de captación
El principal componente de captación de agua lluvia es el agua superficial que cae en zonas
impermeables. Las estructuras que recolectan las aguas pluviales y residuales son:
Sumideros: estructuras para la captación de la escorrentía superficial que se drena a
través de las calles. Estas pueden ser diseñadas en forma lateral o transversal al sentido
del flujo, y se localizan en las vías vehiculares o peatonales del proyecto (RAS, 2000).
Canaletas y bajantes: Estructuras complementarias de captación que ayudan a drenar el
agua desde los techos hasta el sistema de alcantarillado o a la calle, donde se colocan
sumideros.
En el caso de las aguas residuales la captación se realiza directamente. Las aguas residuales se
clasifican de acuerdo con su procedencia: domésticas o no domésticas (comerciales o industriales)
(Butler & Davies, 2011). En ambos casos el agua es conducida directamente desde el punto de
descarga hasta la red de alcantarillado, por medio de tuberías.
2.1.2.2 Estructuras de conducción
Los componentes de conducción corresponden a las tuberías que se encargan de transportar
el agua a lo largo y ancho de la red de drenaje urbano. Estas conforman el mayor porcentaje de
área de la red y son su componente principal.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
6
2.1.2.3 Estructuras de inspección y conexión
Los componentes de inspección y conexión de colectores corresponden a:
Pozos de inspección: Estructuras hidráulicas con tapa removible, que permiten el acceso a
la red de alcantarillado, para el mantenimiento e inspección de la misma. Estas estructuras
son utilizadas cuando se debe cambiar la dirección del flujo, cambiar la pendiente, cambiar
el diámetro de las tuberías, realizar conexiones con otras redes, asegurar aireación al
alcantarillado o cada 90 m.
Pozos de caída: Estructuras diseñadas para dirigir el flujo que entra a un pozo de
inspección con mucha energía, de forma que se pueda disipar gran cantidad de su energía
para proteger la infraestructura de la red contra impactos del flujo sobre las paredes.
2.1.2.4 Estructuras de regulación y alivio
Para el buen funcionamiento del sistema se necesitan los componentes de regulación y alivio,
que corresponden a:
Sifones invertidos: Estructuras en forma de U dispuestas entre dos pozos en caso que el
sistema de alcantarillado requiera atravesar un cuerpo de agua o se quiera evitar la
interferencia del trazado de la red con otros servicios públicos. Estos sifones trabajan
como tuberías a presión.
Sistemas de almacenamiento temporal: Tanques subterráneos para retener el agua con el
objetivo de disminuir los picos de caudal a fin de evitar la evacuación rápida de los
contaminantes desde el sistema hacia al cuerpo receptor, en un evento de precipitación.
Sin embargo, el tiempo de retención no debe ser muy grande puesto que puede ocasionar
problemas de olores.
Aliviaderos: Estructuras que permiten la salida de cierto volumen del agua que viaja por el
alcantarillado, cuando se presenta un evento extremo de precipitación.
Canales abiertos: Estructuras de conducción de escorrentía pluvial, diseñados para
manejar velocidades mínimas que eviten la sedimentación de sólidos arrastrados por el

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
7
agua lluvia y velocidades máximas que evitan daños en la estructura por erosión, cuyo
valor depende del material de la misma.
Estructuras de disipación de energía: Estructuras que reducen la velocidad del flujo
generando un cambio de régimen de supercrítico a subcrítico, permitiendo entregar el
agua con un nivel de energía bajo. Esto ayuda a minimizar el riesgo de socavación o
erosión en los puntos de descarga del sistema de alcantarillado (Planta de tratamiento o
cuerpo receptor).
2.1.2.5 Estructuras de bombeo
Finalmente, los componentes de bombeo son necesarios cuando la energía hidráulica en una
zona es demasiado baja para que las aguas residuales sean evacuadas por gravedad y necesite
bombearse. En otras palabras, se requiere bombeo cuando se deba elevar la línea de gradiente
hidráulico para vencer una diferencia de alturas topográficas y el flujo por gravedad no lo permita.
2.1.3 Fallas en redes de drenaje urbano
El diseño de las redes de drenaje urbano debe cumplir con ciertos requerimientos de forma
que se tenga una buena operación del sistema y se eviten fallas que puedan llegar a generar
problemas de salud pública, problemas ambientales o daños en la infraestructura de la misma. Los
tipos de fallas más comunes son (López, 2012):
Fallas estructurales: Se pueden presentar por problemas de corrosión
2
o cargas aplicadas
que pueden agrietar o ahuecar las tuberías, causando una pérdida en la capacidad
hidráulica
3
y el aumento de infiltraciones y exfiltraciones. Este tipo de falla se puede
observar en la Figura 2.3 (a).
2
Corrosión: cualquier proceso, involuntario, que sea químico, físico, biológico o eléctrico cómo la oxidación
de los metales, agentes electroquímicos, descargas industriales, agua subterránea con alto contenido de
sulfato, erosión y agentes microbiológicos, que implique deterioro, degradación o destrucción de los
componentes del sistema de recolección de agua y que sea debido a la operación natural del mismo (ASCE,
2007).
3
Capacidad Hidráulica: Caudal máximo que puede transportar una tubería.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
8
Sedimentación de partículas sólidas: La sedimentación se refiere a la acumulación de
partículas en el fondo de las tuberías, causando pérdidas en la capacidad hidráulica de la
red. Pueden ser de tipo sanitario, superficial o de alcantarillado. Los sanitarios
corresponden a las partículas finas de materia orgánica o fecal, papel y material vegetal,
que recoge la red; la sedimentación superficial se refiere a las partículas que entran a la
red arrastradas por aguas superficiales, como material vegetal o basura en general y
finalmente la sedimentación de alcantarillado hace referencia a la sedimentación de las
partículas propias del sistema o sus áreas circundantes. Este tipo de falla se puede
observar en la Figura 2.3 (b).
Sobrecargas: Se da al sobrepasar una relación de llenado
4
del 80% que genera una
desaceleración del flujo y aumento de la profundidad hasta alcanzar una relación de
llenado del 94% donde la tubería lleva el máximo caudal posible. De seguir aumentando la
profundidad del agua la tubería se presuriza, a lo que se denomina sobrecarga. Este tipo
de falla es el más importante de controlar para prevenir inundaciones, ya que el agua está
altamente contaminada y puede generar grandes problemas de salud pública y ambiental.
Este tipo de falla se puede observar en la Figura 2.3 (c).
(a)
(b)
(c)
Figura 2.3 Fallas en redes de drenaje urbano.
2.2 Sistema integrado de drenaje urbano
Actualmente se sabe que el crecimiento de las zonas urbanas y la densidad poblacional es
inevitable. Por lo mismo, se deben diseñar las ciudades para que estén en la capacidad de resistir
4
Relación de Llenado: Relación entre la profundidad del flujo en la tubería con respecto al diámetro interno
de la misma.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
9
la demanda del futuro. Esto sin duda aumenta la cantidad y la contaminación del agua a tratar, lo
que se traduce en la necesidad de construir plantas de tratamiento de aguas residuales (PTAR). Las
PTAR, tienen como fin descontaminar el agua, captada y transportada por las redes de
alcantarillado, antes de depositarla en el cuerpo receptor. Esto se requiere cuando la capacidad de
autodepuración
5
del cuerpo receptor es muy baja o los niveles de contaminación del agua son muy
altos (Saldarriaga, Clase de Sistemas Integrados de Drenaje Urbano, 2013).
Se entiende entonces, como Sistema Integrado de Drenaje Urbano al conjunto conformado
por las redes de drenaje urbano (alcantarillado), la planta de tratamiento de aguas residuales
(PTAR) y el cuerpo receptor, como una unidad. Este concepto tiene en cuenta la cantidad y calidad
del agua en cada uno de los componentes del sistema. El papel del alcantarillado es recolectar las
aguas residuales y lluvias, y transportarlas hacia la PTAR. La red de alcantarillado debe asegurar
hermeticidad en las redes, minimizando infiltraciones y exfiltraciones, además de lograr algún
tratamiento preliminar, controlando la cantidad y la calidad del agua residual que llega al tramo
(interceptor) aguas arriba de dichas plantas (RAS, 2000). A continuación se muestra un esquema
del sistema integrado de drenaje urbano en la Figura 2.4.
Figura 2.4 Sistema Integrado de Drenaje Urbano.
La PTAR es necesaria, como se había mencionado, siempre que la capacidad de
autodepuración del cuerpo receptor no sea lo suficientemente alta para que este se recupere de la
contaminación de la descarga que recibe. La PTAR se encarga de entregar una descarga que
5
Autodepuración: es el proceso de recuperación de un curso de agua después de un episodio de
contaminación orgánica (Branco, 1984).

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
10
cumpla con ciertos parámetros de calidad que se establecen de acuerdo con la capacidad de
autodepuración del cuerpo receptor y al uso que se le dará al agua aguas abajo.
2.3 Diseño de redes de drenaje urbano
2.3.1 Definición del problema
El diseño de las redes de alcantarillado es un problema complejo que tiene dos componentes
fundamentales: la topología de la red y el diseño hidráulico. La topología de la red se refiere a la
forma en que se deben poner las tuberías, de manera que se tenga un diseño hidráulico que
cumpla con una serie de requisitos y restricciones hidráulicas, teniendo en cuenta el Plan de
Saneamiento y Manejo de Vertimientos PSMV regional. Simultáneamente el diseño debe ser
económicamente factible, lo que quiere decir que se deben minimizar los costos. Esto es posible
gracias a las nuevas tecnologías que permiten realizar modelos matemáticos de un problema para
que, por medio de procesos de optimización, se encuentre el diseño óptimo desde el punto de
vista económico, dentro de millones de alternativas de diseño posibles, para una red de drenaje
urbano.
Para buscar el punto de operación óptimo de una red de drenaje urbano se debe intervenir
alguno de sus componentes y minimizar los costos de construcción del mismo. Sin embargo,
intervenir el cuerpo receptor implica cambiar las características del río para aumentar su
capacidad de autodepuración, lo cual resulta muy costoso. De acuerdo con esto, es importante
resaltar que el diseño de un sistema integrado de drenaje gira en torno a las condiciones naturales
del cuerpo receptor (río), ya que se busca causar el menor impacto posible sobre los cuerpos de
agua naturales.
Así mismo, la intervención en las PTAR también resulta en altos costos. Si el diseño original de
la planta no tiene la eficiencia requerida se requeriría la ampliación de la misma, generando muy
altos costos. Finalmente, la intervención de la red de alcantarillado es una opción muy viable, ya
que con pocos cambios en zonas específicas de la red se puede mejorar mucho el funcionamiento
de la misma, ofreciendo la mayor relación beneficio-costo (B/C) (López, 2012).
Este proyecto busca encontrar el diseño óptimo de series de tramos de tuberías en sistemas
de alcantarillado, diseñando para todos los posibles diámetros de tuberías combinados con todas
las posibles pendientes a las que se pueden instalar las tuberías. Para el diseño de sistemas de
alcantarillados en general se debe considerar unos supuestos de diseño, como se definirá en el

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
11
Numeral 2.3.2. Un diseño factible también debe cumplir un mínimo de condiciones, como que los
tramos deben estar interconectados para formar la serie y no pueden haber pendientes adversas
que desaceleren el flujo; además de un conjunto de restricciones hidráulicas y comerciales que se
mencionarán en el Numeral 2.4. Siendo así, cada diseño factible tiene un costo asociado, que
corresponde a la suma del costo asociado al diseño de cada tramo. El óptimo se encuentra con el
diseño más económico por medio de un proceso de optimización que se explicará en el Capítulo 3.
2.3.2 Supuestos del diseño
A la hora de diseñar se debe suponer un tipo de flujo que describa la hidráulica. Es decir, que
establezca cómo es el comportamiento hidráulico de un flujo en espacio y tiempo. En este caso se
está tratando con agua, por lo que el primer supuesto de diseño considera un fluido
incompresible, lo que quiere decir que su densidad es constante. También, se tiene una suposición
del tipo de flujo.
Las condiciones de flujo se clasifican según su variación en espacio y tiempo. La variación del
flujo en el espacio puede ser uniforme o variable. Así mismo, las características del flujo pueden
ser constantes en el tiempo formando un flujo permanente o pueden ser variables (no
permanente). Se forman entonces, cuatro tipos de flujo como se muestra en la Tabla 2.1. Sin
embargo, es imposible que el flujo variado no permanente se de en la naturaleza, dejando sólo
tres tipos de flujo (Saldarriaga, Clase de Sistemas Integrados de Drenaje Urbano, 2013).
Tabla 2.1 Tipos de flujo
Flujo Permanente
Flujo No-Permanente
Flujo Uniforme
Flujo Uniforme
Flujo Uniforme- No Permanente
Flujo Variable
Flujo Variado-Permanente
Flujo Variado- No permanente
En el caso del flujo en tuberías de alcantarillado se considera que el flujo mantiene sus
características en tiempo y espacio, es decir que se considera un Flujo Uniforme (Flujo Uniforme -
Permanente).
Este tipo de flujo se da gracias a que las fuerzas gravitacionales, las fuerzas de presión y las
fuerzas viscosas están en equilibrio; las gravitacionales aceleran el flujo y las viscosas le oponen
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
12
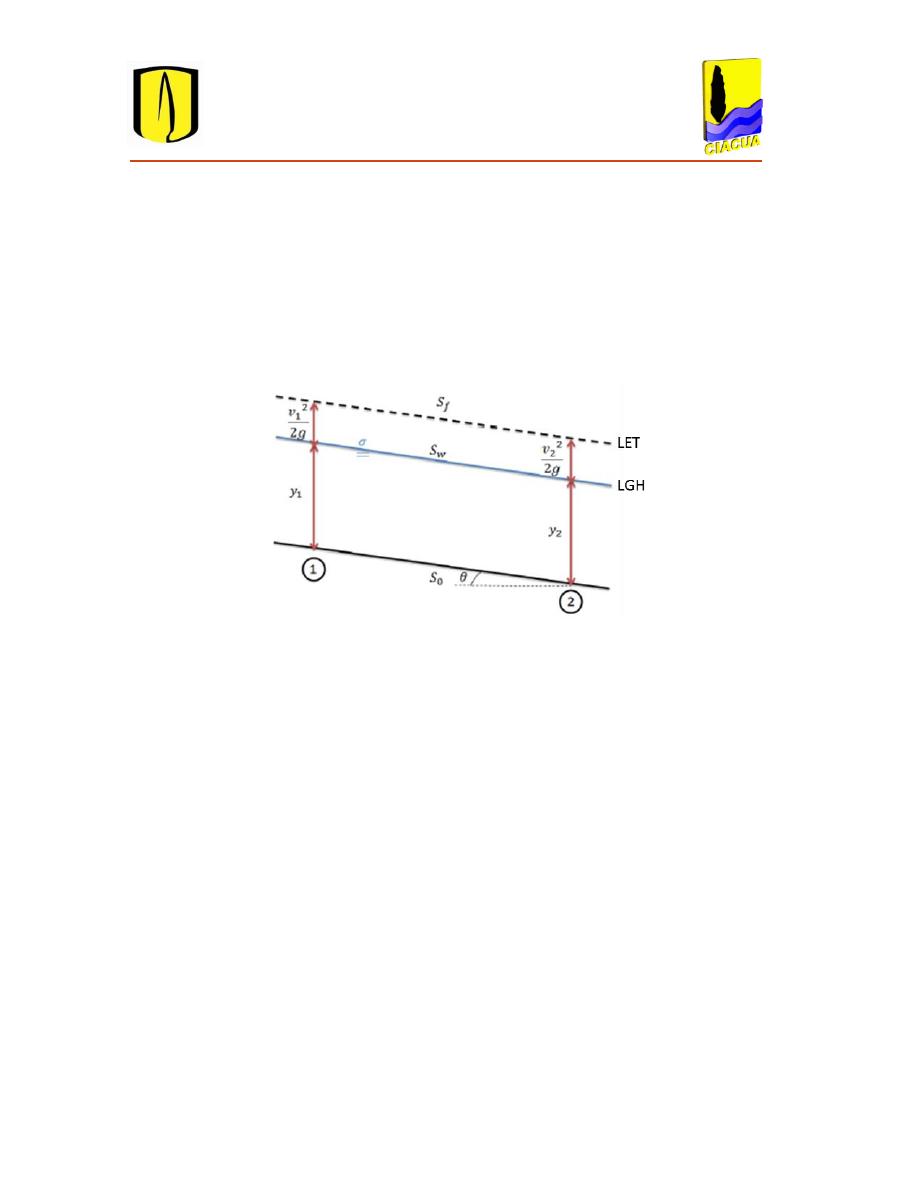
resistencia. Analizando un canal abierto en dos puntos, se puede observar cómo la altura de la
lámina de agua (altura por presión hidrostática) , la altura por velocidad
y demás
propiedades geométricas e hidráulicas permanecen constantes a lo largo del canal. De ahí que, la
pendiente
de Línea de Energía Total (LET), la pendiente
de Línea de Gradiente Hidráulico
agua (LGH) y pendiente
del fondo del canal son la misma
, es decir que son
paralelas. Por lo tanto, las pérdidas por fricción serán constantes en toda la longitud de la tubería
(Saldarriaga, Hidráulica de tuberías: abastecimiento de agua, redes, riegos, 2007).
Figura 2.5 Flujo uniforme en canales abiertos. Tomado y modificado de Salcedo (2012).
2.3.3 Ecuaciones de diseño
En sistemas de alcantarillado las tuberías trabajan bajo la condición de flujo libre por
gravedad, debido a que las tuberías deben ir fluyendo parcialmente llenas. Este tipo de flujo es un
caso especial del flujo en canales abiertos, por lo cual aplican las mismas teorías (Butler & Davies,
2011). En este caso se manejan secciones transversales circulares como la que se muestra en la
Figura 2.6.
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
13
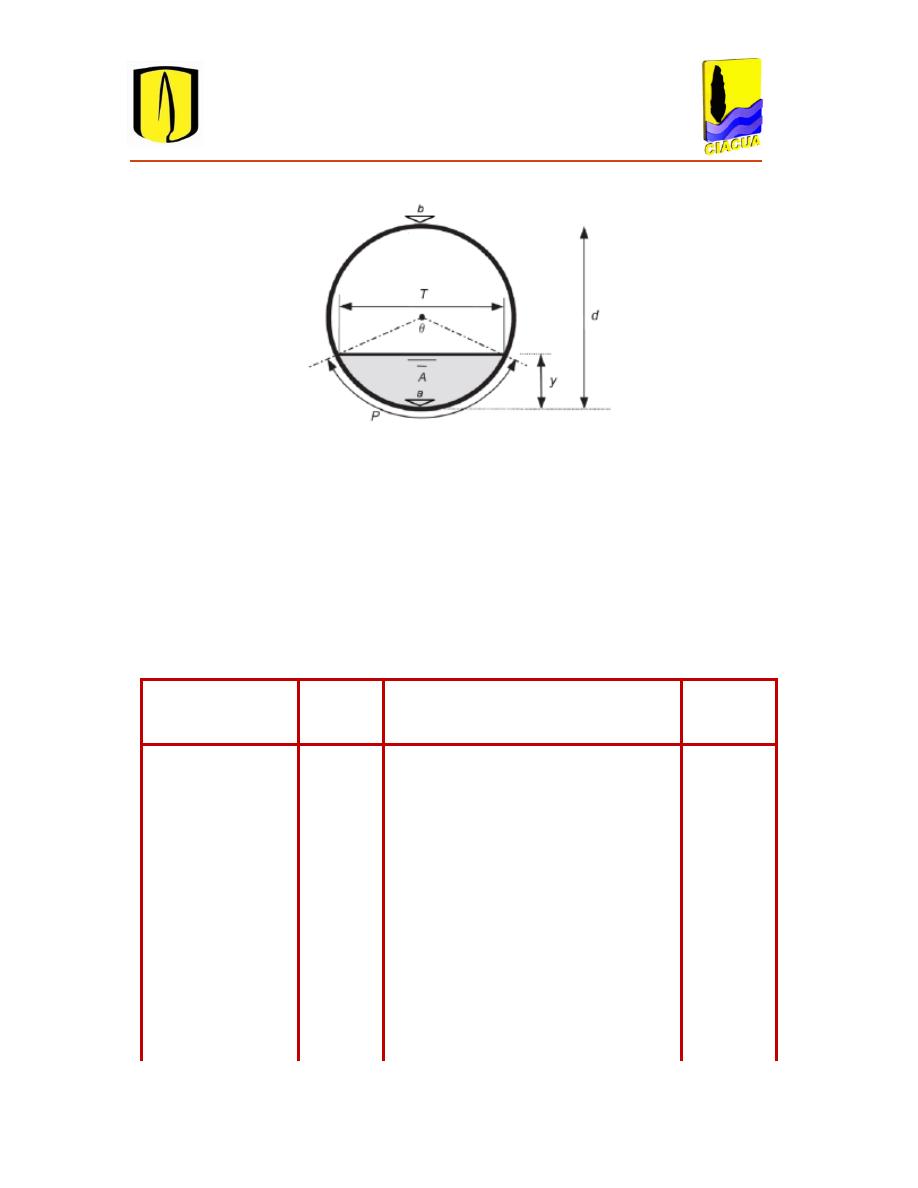
Figura 2.6 Sección transversal de tubería fluyendo parcialmente llena. Tomada de Salcedo (2012).
En este caso las ecuaciones de diseño se modifican en función de la profundidad de llenado
y el diámetro de la tubería , que forman un ángulo a partir del cual se calcula el resto de las
propiedades geométricas descritas en la Tabla 2.2.
Tabla 2.2 Resumen de propiedades geométricas del alcantarillado. Tomado y adaptado de Butler & Davies (2011) y
Salcedo (2012).
Propiedad
Geométrica
Símbolo
Descripción
Unidades
(SI)
Profundidad de flujo
Altura del agua por encima de la cota de
batea.
[m]
Ángulo
Ángulo formado en el centro de la tubería
por la superficie libre.
[rad]
Área Mojada
Área mojada de la sección transversal.
[m
2
]
Perímetro Mojado
Porción del perímetro del flujo que está
en contacto con el canal.
[m]
Radio Hidráulico
Área por unidad de perímetro.
[m]
Ancho de la
Ancho del flujo en la superficie libre del
[m]
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
14
Superficie
agua.
Profundidad
Hidráulica
Área por unidad de ancho en la
superficie.
[m]
Cota de Batea
El punto más bajo de la sección
transversal de la tubería.
[m]
Cota Clave
El punto más alto de la sección
transversal de la tubería.
[m]
Las expresiones que describen los elementos geométricos para una tubería fluyendo
parcialmente llena, se exponen a continuación (Saldarriaga, Clase de Sistemas Integrados de
Drenaje Urbano, 2013).
Ángulo
(
)
Ecuación 2.1
Área Mojada
Ecuación 2.2
Perímetro Mojado
Ecuación 2.3
Radio Hidráulico
Ecuación 2.4

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
15
Ancho de la Superficie
(
(
))
Ecuación 2.5
Profundidad Hidráulica
(
(
))
Ecuación 2.6
A continuación se presentan algunas propiedades hidráulicas relacionadas con las propiedades
geométricas.
Número de Froude
√
Ecuación 2.7
Número de Reynolds
Ecuación 2.8
Esfuerzo cortante en la pared
Ecuación 2.9
donde:
Densidad del fluido que en este caso corresponde al agua.
La aceleración de la gravedad.
Radio hidráulico.
pendiente de diseño.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
16
Además de estas propiedades hidráulicas también se debe calcular la velocidad del flujo que si
bien es función del radio hidráulico y la pendiente , se puede calcular de dos formas. La
primera es la Ecuación de Manning, propuesta en 1889 por Robert Manning. Esta ecuación es
empírica y fue deducida a partir de los experimentos realizados por Darcy y Bazin en 1865 sobre
canales reales abiertos fluyendo bajo la condición de flujo uniforme. Estás condiciones implican
que la Ecuación de Manning sólo es aplicable para el caso de flujo uniforme turbulento
hidráulicamente rugoso (Saldarriaga, Clase de Sistemas Integrados de Drenaje Urbano, 2013). La
Ecuación de Manning para el cálculo de la velocidad entonces es:
Ecuación 2.10
donde es una constante que se calcula en función a la rugosidad absoluta (conocida como de
Manning) y se supone uniforme a lo largo del canal. Estudios posteriores de la Asociación
Americana de Ingenieros Civiles (ASCE por sus siglas en inglés) establecieron valores constantes
del de Manning para diferentes materiales de la tubería, encontrando así un rango de valores de
partiendo de un caudal y una sección transversal dados. Sin embargo, el uso de esta ecuación en
la actualidad es inapropiado ya que los materiales modernos, como el PVC o el GRP, son muy lisos
e invalidan la suposición de Flujo Turbulento Hidráulicamente Rugoso (Saldarriaga, Clase de
Sistemas Integrados de Drenaje Urbano, 2013).
La segunda forma de calcular la velocidad es a partir de una ecuación físicamente basada. La
Ecuación de Chézy describe la velocidad bajo la condición de flujo uniforme y está dada por:
√
Ecuación 2.11
donde es el radio hidráulico de la tubería, la pendiente de la misma y es el coeficiente de
Chézy
6
. Dicho coeficiente es un factor que describe la rugosidad del canal por el cual fluye el agua.
Ahora bien, se deben tener en cuenta las pérdidas de energía por fricción que representan las
pérdidas de presión por unidad de longitud. Estás, según los experimentos de Reynolds (1884),
varían linealmente con respecto a la velocidad del flujo cuando el flujo es laminar o turbulento
(Saldarriaga, Hidráulica de tuberías: abastecimiento de agua, redes, riegos, 2007). Las pérdidas por
fricción se calculan según la ecuación físicamente basada, planteada por Darcy-Weisbach,
mostrada a continuación.
6
Saldarriaga, J. (2007). Hidráulica de tuberías: abastecimiento de agua, redes, riegos. Bogotá: Alfaomega.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
17
Pérdidas por Fricción (Darcy-Weisbach)
Ecuación 2.12
Combinando la Ecuación de Chézy con la Ecuación físicamente basada de Darcy-Weisbach, se
obtiene la siguiente relación (Salcedo, 2012):
Relación entre el de Chézy y las pérdidas por fricción
√
Ecuación 2.13
donde es el factor de fricción descrito por la Ecuación de Colebrook-White.
Factor de fricción (Colebrook-White)
√
(
√
)
Ecuación 2.14
Reemplazando la Ecuación 2.13 en la Ecuación 2.14, se obtiene coeficiente en términos del
rádio hidráulico de la tubería , la rugosidad absoluta de la tubería
y el número de Reynolds
descrito en la Ecuación 2.8. Posteriormente, se reemplaza la ecuación de velocidad de Chézy
(Ecuación 2.11), en esta última para obtener así la velocidad en función de las propiedades
mencionadas, como se muestra en la Ecuación 2.15.
Ecuación de Darcy-Weisbach en conjunto con Colebrook-White
√
(
√
)
Ecuación 2.15
Las ventajas de utilizar la Ecuación 2.15 para el cálculo de la velocidad son: primero, que es
una ecuación explícita por lo cual su cálculo no requiere de métodos numéricos; en segundo lugar,
que es físicamente basada y por lo mismo es la que mejor describe la resistencia fluida (Salcedo,

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
18
2012). Además, esta ecuación es válida esta ecuación es válida para cualquier tipo de flujo,
abarcando desde el Flujo Turbulento Hidráulicamente Liso FTHL hasta el Flujo Turbulento
Hidráulicamente Rugoso FTHR. Gracias a que funciona para cualquier valor de
, cualquier fluido
newtoniano y en cualquier planeta, esta ecuación tiene mayor aplicación hoy en día que la
Ecuación de Manning (Saldarriaga, Clase de Sistemas Integrados de Drenaje Urbano, 2013).
2.4 Restricciones de diseño
2.4.1 Restricciones hidráulicas
Las restricciones hidráulicas buscan garantizar que el diseño de las redes de alcantarillado
cumpla con la capacidad de demanda y aseguren un proceso de auto-limpieza de la red. A
continuación se mencionan las restricciones hidráulicas para redes de drenaje urbano de aguas
residuales y para redes de drenaje urbano pluvial y combinado (residual y pluvial) (RAS, 2000).
1. Diámetro mínimo
En sistemas de alcantarillado de aguas residuales el diámetro interno mínimo de las
tuberías debe ser de 170 mm, para evitar la obstrucción del sistema por objetos de gran
tamaño que logren entrar al sistema. En el caso de las redes de aguas lluvias el diámetro
mínimo es de 250 mm puesto que se corre mayor riesgo de que entren objetos al sistema
arrastrados por el agua superficial (Saldarriaga, Clase de Sistemas Integrados de Drenaje
Urbano, 2013). Para este proyecto se utilizó un diámetro mínimo de 200 mm establecido
por el RAS (2000).
2. Relación de llenado máxima
Esta relación de llenado máxima se establece con el fin de evitar problemas de sobrecarga
del sistema y asegurar la aireación del mismo para evitar problemas ambientales. A partir
de esta se establecen las profundidades máximas del flujo de acuerdo al diámetro interno
de la tubería. La máxima relación de llenado entonces corresponde al 85%. Sin embargo,
para las tuberías con diámetros menores a 600 mm la relación de llenado máxima es del
70%. Adicionalmente, se recomienda establecer una relación de llenado máxima del 80%
siempre que se presente flujo cuasi-crítico i.e, que el número de Froude esté entre 0.7
y 1.5 una pequeña alteración en la energía específica del flujo causa variaciones

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
19
bruscas en la profundidad de la lámina de agua, lo que puede generar problemas de
sobrecarga (Copete, 2012).
Para el caso de este proyecto, se manejaron relaciones de llenado máximas del 70% para
tuberías de diámetros menores a 500 mm o para cuando se presente flujo cuasi-crítico,
80% para tuberías con diámetros entre 500 y 1000 mm y 85% para tuberías con diámetros
mayores a 1000 mm. Esto, con el fin de hacer comparable los resultados de este proyecto
con los resultados obtenidos utilizando la metodología propuesta por el CIACUA.
3. Velocidad mínima
La velocidad mínima busca evitar problemas de sedimentación y/o acumulación de
partículas sólidas dentro de las tuberías. De esta forma se evita la obstrucción de las
tuberías, lo que podría causar problemas de sobrecarga de la misma. Para tuberías de
alcantarillado el RAS (2000) sugiere una velocidad mínima de 0.75 m/s para diámetros
menores a 450 mm.
4. Esfuerzo cortante mínimo
El esfuerzo cortante en el fondo de una tubería de alcantarillado de aguas residuales debe
ser igual o mayor que en tuberías de diámetros mayores o iguales a 450 mm, para
asegurar un proceso de auto-limpieza. En el caso de alcantarillados de aguas lluvias el
esfuerzo cortante debe ser mayor o igual a en tuberías de diámetros mayores o
iguales a 450 mm (RAS, 2000).
5. Velocidad máxima
La velocidad máxima se establece con el fin de evitar problemas de erosión en las tuberías,
problemas de cavitación
7
, entrapamiento de aire, generación de resaltos hidráulicos
dentro de la red, entre otros. El RAS 2000 recomienda que la velocidad máxima sea de 5
m/s y para tuberías termoplásticas (PVC) de 10 m/s.
6. Pendiente máxima y mínima
Las pendientes pueden variar en un rango en el cual se cumplen las restricciones de
velocidad mínima y máxima. En este sentido, el valor mínimo para la pendiente debe ser
aquel para el cual el flujo alcanza la velocidad mínima y cumple con la restricción del
7
Cavitación: Fenómeno en el cual el agua en estado líquido pasa a estado gaseoso (vapor de agua) a raíz de
una disminución de la presión y posterior mente estas burbujas de vapor vuelven a pasar a estado líquido
repentinamente y con presiones muy altas que generan daños en la infraestructura de la red (Saldarriaga,
Clase de Hidráulica, 2012).

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
20
esfuerzo cortante mínimo. Así mismo, la pendiente máxima será aquella para la cual el
flujo alcanza la velocidad máxima.
7. Profundidad a cota clave de la tubería.
La profundidad mínima a cota clave de la tubería debe ser tal se asegure la protección de
las tuberías y que las descargas domiciliarias sin sótano puedan ser drenadas por
gravedad. Así mismo, se establece una profundidad máxima por razones constructivas y
para limitar las cargas que deberá soportar la tubería. Estos límites de excavación se
presentan a continuación.
Tabla 2.3 Límites de la profundidad a cota clave de la tubería.
Tipo de Vía
Peatonal o Zona Verde
0.7
5.0
Vehicular
1.2
5.0
La Tabla 2.4 resumen las restricciones hidráulicas utilizadas para el diseño de series de
tuberías en sistemas de alcantarillado.
Tabla 2.4 Resumen de restricciones hidráulicas de diseño. Tomado y modificado de Butler & Davies (2011).
Restricción
Aguas residuales
Aguas lluvias
1
Diámetro nominal mínimo
170 mm
200 mm
2
Relación máxima entre la profundidad
y el diámetro de la tubería
85%
85%
3
Velocidad mínima
0.6 m/s
0.75 m/s
4
Velocidad máxima
5 m/s
5 m/s
5
Esfuerzo de cortante mínimo
> 2 Pa
> 3 Pa
6
Pendiente mínima
Aquella que cumple la velocidad mínima y el
esfuerzo de cortante mínimo.
7
Pendiente máxima
Aquella para la que se obtiene la velocidad
máxima real.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
21
2.4.2 Restricciones comerciales
El diámetro asignado a cada tubería del sistema de alcantarillado, sólo puede tomar valores
discretos que pertenecen al conjunto de diámetros comercialmente disponibles (PAVCO, 2013).
Para este proyecto se utilizó la siguiente lista de diámetros comerciales.
Tabla 2.5 Lista de diámetros comerciales
Diámetros
Pequeños (m)
0.200
0.250
0.300
0.350
0.400
0.450
0.500
Diámetros
Grandes (m)
0.600
0.675
0.750
0.825
0.900
1.000
1.100
2.5 Función de costos
Con base en un estudio realizado por el Trenchless Technology Center de Louisiana Tech
University, De Oro Vergara (2008) propuso una ecuación para analizar los costos asociados con
sistemas de alcantarillado. Dicha ecuación presenta los costos como una función del diámetro de
la tubería y la profundidad a la que se instale la misma.
Ecuación 2.16
donde:
Costo por metro lineal de tubería [COP/m].
Diámetro de la tubería en milímetros [mm].
Profundidad de la Instalación en metros [m].
Posteriormente, esta ecuación fue ajustada de acuerdo con información de las bases de datos
del Ministerio de Medio Ambiente, Vivienda y Desarrollo Territorial (MAVDT), del Fondo Financiero
de Proyectos de Desarrollo (FONADE) y de empresas encargadas de prestar el servicio, por medio
de un estudio análisis de inversiones en acueducto y alcantarillado, desarrollado por la Comisión
de Regulación de Agua Potable y Saneamiento Básico (CRA) (Navarro, 2009).
Se encontró entonces que los costos de las tuberías, son función del diámetro de la misma y se
pueden la calcular de acuerdo con la Ecuación 2.17.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
22
Ecuación 2.17
donde:
Costo por metro lineal de tubería a Mayo de 2009 [COP/m].
Diámetro de la tubería en milímetros [mm].
Factor de conversión de pesos de Diciembre de 2007 a Mayo de 2009. Este fue
calculado como:
.
Análogamente, los costos de excavación son función del volumen de excavación necesario
para la instalación de la tubería, como plantea la Ecuación 2.18.
Ecuación 2.18
donde:
Costo por metro lineal de tubería a Mayo de 2009 [COP/m].
Volumen de excavación por tubería [m
3
].
Factor de conversión de pesos de Diciembre de 2007 a Mayo de 2009. Este fue
calculado como:
.
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
23
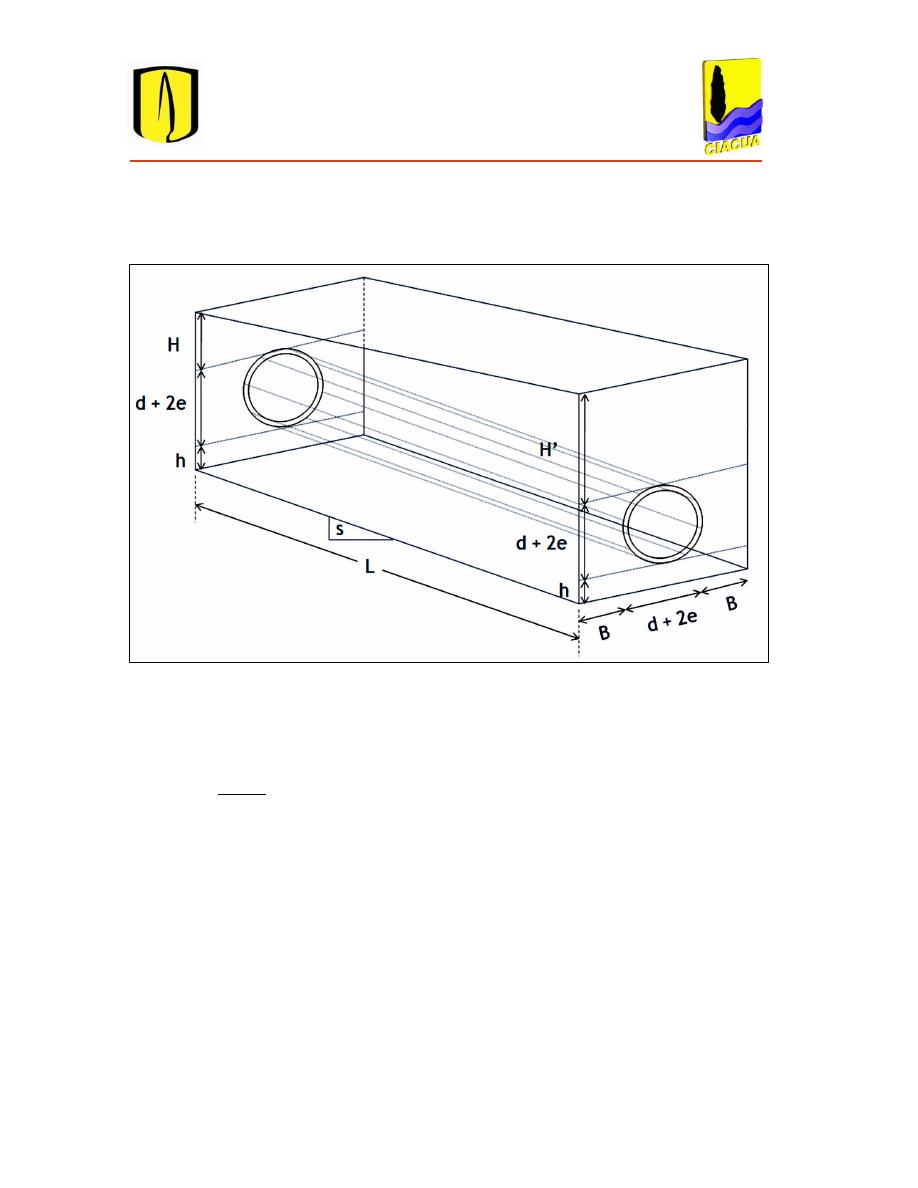
A continuación se presenta la ecuación para el cálculo del volumen de excavación necesario
para la instalación de una tubería, de acuerdo al análisis de la Figura 2.7 (CIACUA, 2013).
Figura 2.7
Proyección del trapecio que produce el área excavada para una tubería de alcantarillado.
Tomada de (CIACUA, 2013)
([
] ) [
]
Ecuación 2.19
donde:
Volumen excavado para poner la tubería.
Profundidad de excavación hasta la cota clave aguas arriba de la tubería.
Profundidad de excavación hasta la cota clave aguas abajo de la tubería.
Diámetro interno de la tubería
Espesor de la pared de la tubería.
Relleno que debe disponerse bajo la tubería. Depende de la reglamentación del
lugar donde se lleve a cabo el diseño. Para los ejemplos se siguieron las
recomendaciones del RAS (2000): .

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
24
Espacio lateral que debe dejarse a ambos lados de la tubería para ponerla.
Pendiente en la que se dispone la tubería.
Longitud de la tubería.
De acuerdo con lo anterior, los costos asociados con la construcción de sistemas de
alcantarillado se calculan como la suma entre los costos de las tuberías como tal (Ecuación 2.17) y
los costos de la excavación (Ecuación 2.18), tal como plantea la Ecuación 2.20.
Ecuación 2.20
Para este proyecto se utilizó la Ecuación 2.20 como función de costos; así como fue utilizada
por López (2012) y Copete (2012) en sus proyectos de grado, con el fin de hacer comparables las
diferentes metodologías propuestas: El diseño optimizado utilizando el concepto de Pendientes
Propias (Ver Numeral 2.6) y el diseño optimizado utilizando el problema de la ruta más corta (Ver
Capítulo 3).
2.6 Pendientes Propias e Intermedias
La metodología de diseño de redes de alcantarillado propuesta por López (2012) plantea que
se puede encontrar una pendiente específica para la cual se pueda aprovechar al máximo la
tubería. Esto se logra teniendo en cuenta que al aumentar la pendiente de una tubería se reduce
el nivel de agua dentro de la misma, llevándola a fluir parcialmente libre en muchos casos. Por lo
tanto se busca maximizar la relación de llenado para una tubería de diámetro conocido, con una
pendiente específica. Según esto, a medida que se aumenta la pendiente, el diámetro de la tubería
disminuye de forma que se mantenga la condición de llenado máxima posible (López, 2012).
Se entiende entonces como Pendiente Propia, aquella pendiente que para un diámetro
conocido y un caudal de diseño dado, lleva la máxima relación de llenado posible. Teniendo que
entre mayor sea la pendiente el diámetro disminuye, se sabe que pueden haber varias Pendientes
Propias para cada tramo de la serie, lo que aumenta la magnitud del problema como describe la
Ecuación 2.21 (López, 2012).
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
25
∏
Ecuación 2.21
donde:
Número total de alternativas [-].
Número de tramos [-].
Número de Pendientes Propias en el tramo [-].
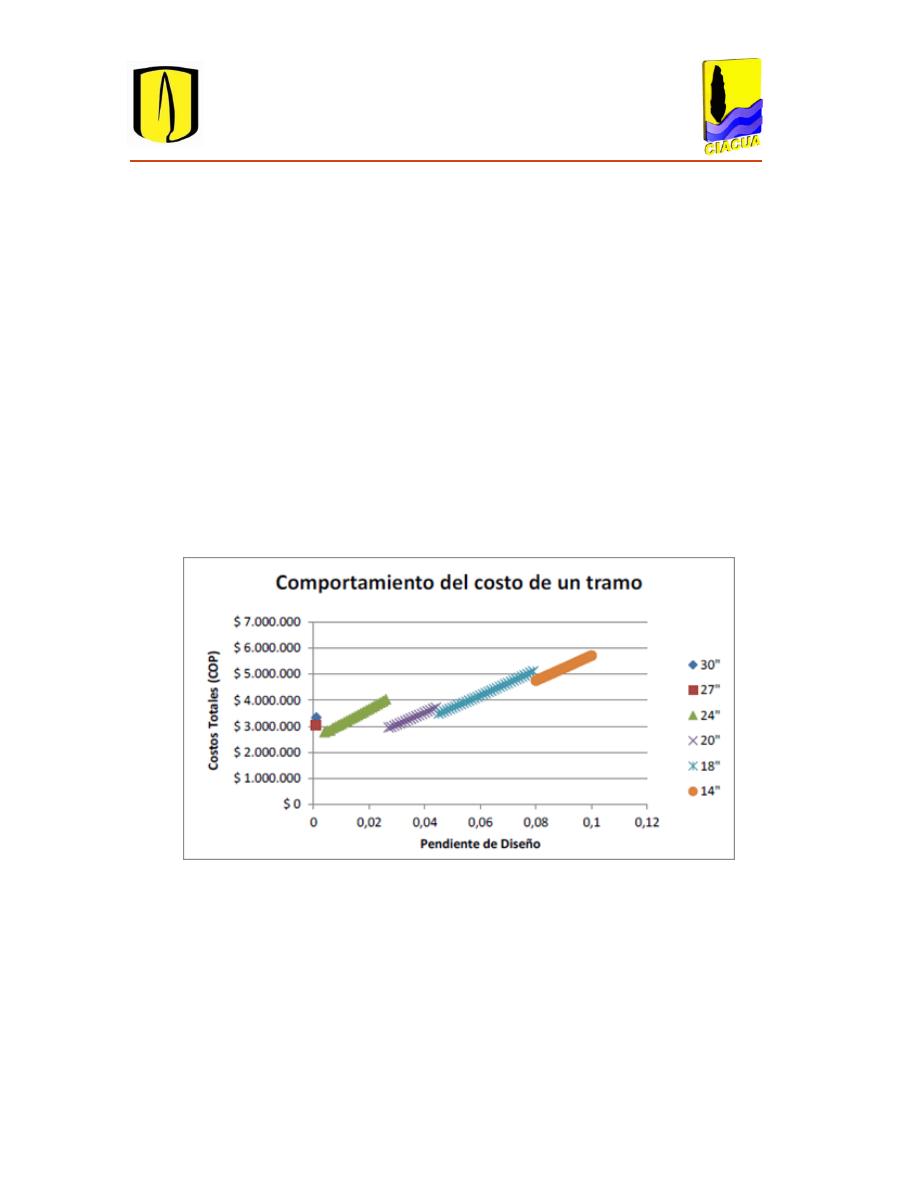
Es claro que los costos de las tuberías serán menores al aumentar las pendientes. Sin
embargo, los costos totales presentan un aumento importante, como se observa en la Figura 2.8.
Esto se debe a que el volumen de excavación aumenta a medida que la pendiente de diseño
también lo hace, causando un incremento importante en los costos de excavación, que son más
representativos que los costos de las tuberías.
Figura 2.8 Búsqueda de la pendiente de diseño. Tomado de López (2012).
Posteriormente, el Centro de Investigaciones en Acueductos y Alcantarillados CIACUA de la
Universidad de los Andes en Bogotá, Colombia estableció que “después de llevar a cabo una gran
cantidad de diseños para series de tramos, fue claro que el concepto de Pendiente Propia no era
suficiente para garantizar que los costos se reducirían en todos los casos” (CIACUA, 2013). Esto
surge como consecuencia de que el concepto de Pendientes Propias, como se mencionó, es muy

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
26
efectivo disminuyendo el costo de las tuberías pero descuida el costo de excavación. Las
posibilidades de instalación de una tubería se limitan a una pendiente por diámetro para cada
tramo. La limitación del diseño de la red genera sobrecostos sobre todo cuando la Pendiente
Propia es mucho mayor que la del terreno.
Para amortiguar los sobrecostos, se desarrolló el concepto de Pendiente Intermedia
) que
se refiere al promedio ponderado entre dos Pendientes Propias consecutivas
(Ecuación
2.22). El diseño con Pendientes Intermedias permite utilizar pendientes menos empinadas que
llevan una relación de llenado buena (no máxima) y reduzcan significativamente los costos de
excavación.
Ecuación 2.22
donde:
Pendiente Intermedia.
Pendientes Propias consecutivas.
Coeficiente de variación de la pendiente.
El coeficiente se calcula como:
cuando
Ecuación 2.23
cuando
Ecuación 2.24
donde:
Pendiente del terreno.
Coeficiente de variación de la pendiente.
El coeficiente permite la variación leve entre pendientes y varía entre valores mayores o
iguales a 0 y menores a 0.5 [0; 0.5). Sin embargo, la mayor reducción de costos se encuentra
utilizando un coeficiente (CIACUA, 2013).
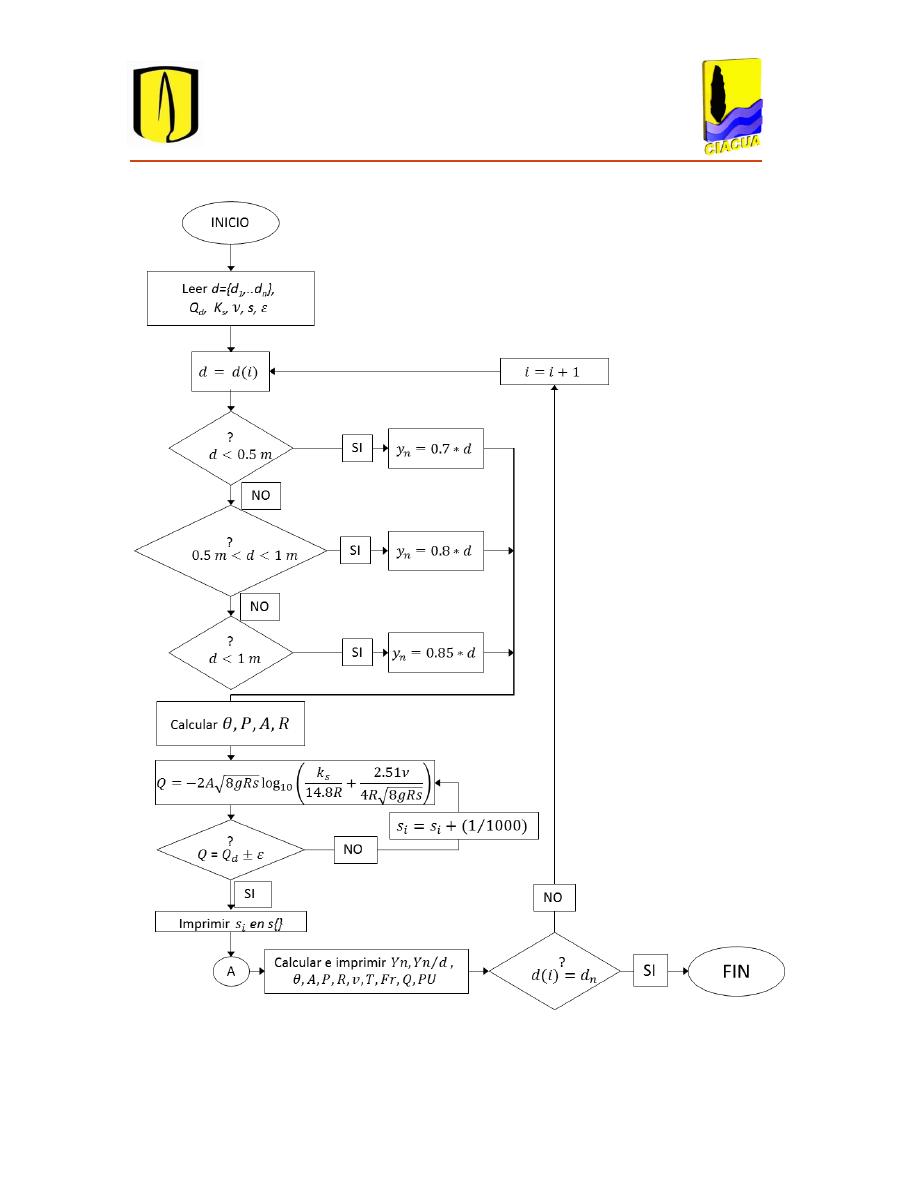
Esta metodología de diseño se describe a continuación en el Diagrama de Flujo 2.1 (a) Diseño
de series de alcantarillado utilizando el concepto de Pendientes Propias e Intermedias: cálculo de
Pendientes Propias.
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
27
Diagrama de Flujo 2.1 (a) Diseño de series de alcantarillado utilizando el concepto de Pendientes Propias e
Intermedias: cálculo de Pendientes Propias.
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
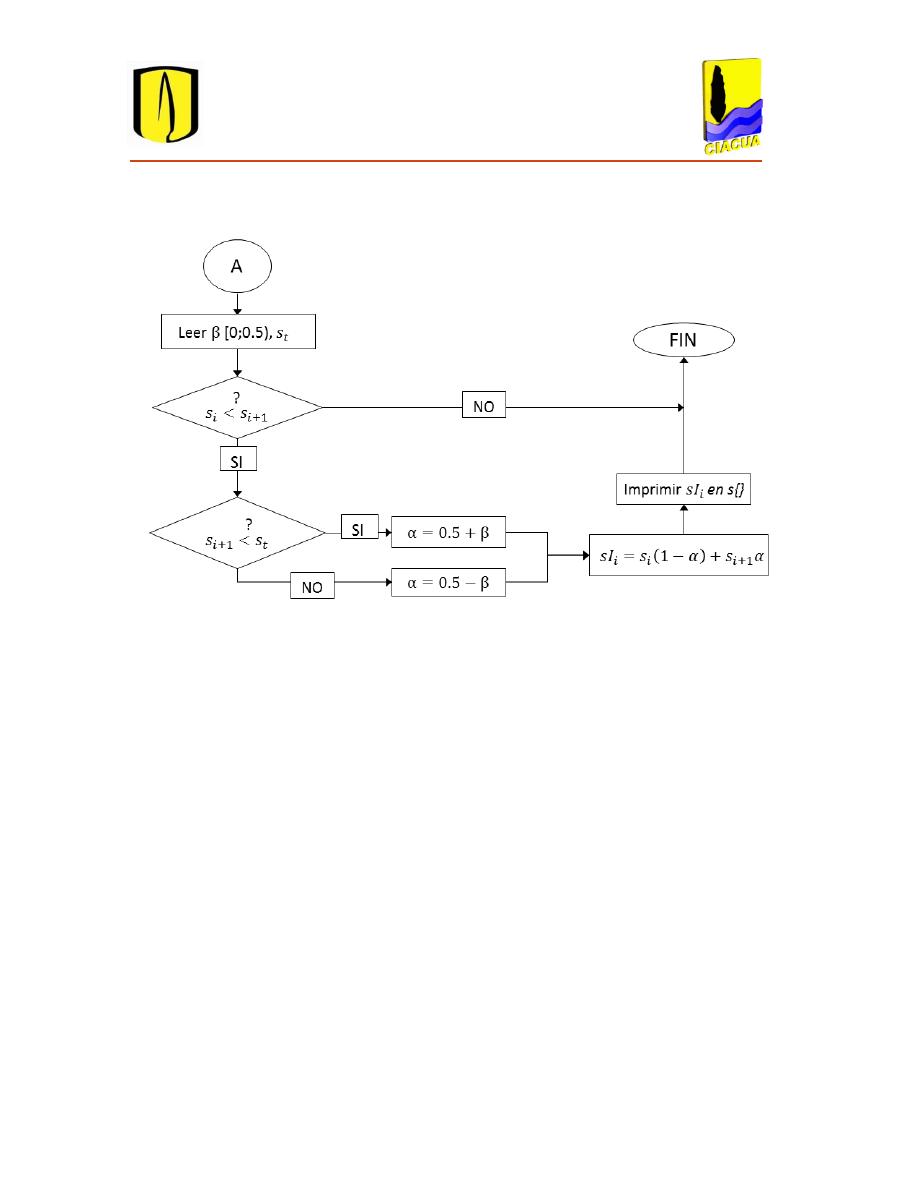
28
Diagrama de Flujo 2.1 (b) Diseño de series de alcantarillado utilizando el concepto de Pendientes Propias e
Intermedias: cálculo de Pendientes Intermedias.
2.7 Potencia Específica
La Potencia Específica (PE) es un criterio de confiabilidad en la etapa del diseño de una red que
reduce la probabilidad de que durante la operación de la misma se presenten problemas que
puedan afectar la infraestructura de la red o las áreas circundantes a ésta.
Este concepto fue desarrollado como un indicador del comportamiento hidráulico en redes de
distribución de agua potable RDAP por Saldarriaga, Romero, Ochoa, Moreno & Cortés (2007). La
Potencia Específica se entiende entonces, como la energía que pierde el flujo como consecuencia
de su paso a través de un tramo (López, 2012). Esta se describe según la Ecuación 2.25.
Ecuación 2.25

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
29
donde:
Potencia Específica [m
4
/s].
Altura piezométrica en el pozo aguas arriba del tramo [m].
Altura piezométrica en el pozo aguas abajo del tramo [m].

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
30
3 METODOLOGÍA PARA EL DISEÑO OPTIMIZADO DE SISTEMAS DE
ALCANTARILLADO
En general los procesos de optimización buscan encontrar la mejor forma de realizar una
actividad. En el caso del diseño de sistemas de alcantarillado, un diseño óptimo es aquel que
cumple con todos los aspectos hidráulicos de diseño y cuyo costo de construcción es mínimo. Al
igual que otros problemas de optimización, en este problema existen cuatro componentes
importantes para el modelaje y solución: los parámetros, las variables de decisión, las restricciones
y la función objetivo. Los parámetros proporcionan la información necesaria (o conocida) que se
tiene de los problemas. Las variables de decisiones son los aspectos del problema sobre los cuales
el decisor tiene injerencia. Las restricciones limitan el problema estableciendo las reglas que se
deben cumplir en una solución de mismo. Finalmente, la función objetivo guía la búsqueda de la
solución que se quiere encontrar.
Dada la complejidad del problema, este es considerado NP-duro, es decir que no es
determinista en un tiempo polinómico y por lo tanto no existen algoritmos que puedan resolverlos
de manera práctica. La ejecución de este tipo de problemas tomaría demasiado tiempo
computacional sin encontrar la solución, volviendo impráctico el algoritmo (Corrales & et Al,
2013). La forma de abordar este tipo de problemas es por medio de métodos heurísticos que dan
soluciones muy buenas o incluso óptimas. En este caso el problema será abordado como un
problema de optimización conocido como el problema de ruta más corta.
3.1 Problemas de flujo en redes
Los problemas de flujo en redes buscan encontrar la solución a un problema que se modela a
través de un grafo como por ejemplo, encontrar un camino óptimo (según el caso, podría ser el
más económico, más corto, con mayor capacidad, etc.). Un grafo se representa a partir de un
conjunto de Nodos y un conjunto de Arcos . Cada arco, es un elemento que conecta pares de
nodos diferentes (Ahuja & et Al., 1993), como los que se muestran en la Figura 3.1.
Cada grafo, puede tener múltiples caminos para ir de un nodo inicial a uno final dados. Cada
elemento del grafo tiene atributos. Por ejemplo, los nodos tienen atributos que determinan cuál
es el nodo de inicio y cuál el nodo final, mientras los arcos tienen como atributo un costo asociado,
una distancia, una capacidad, entre otros.
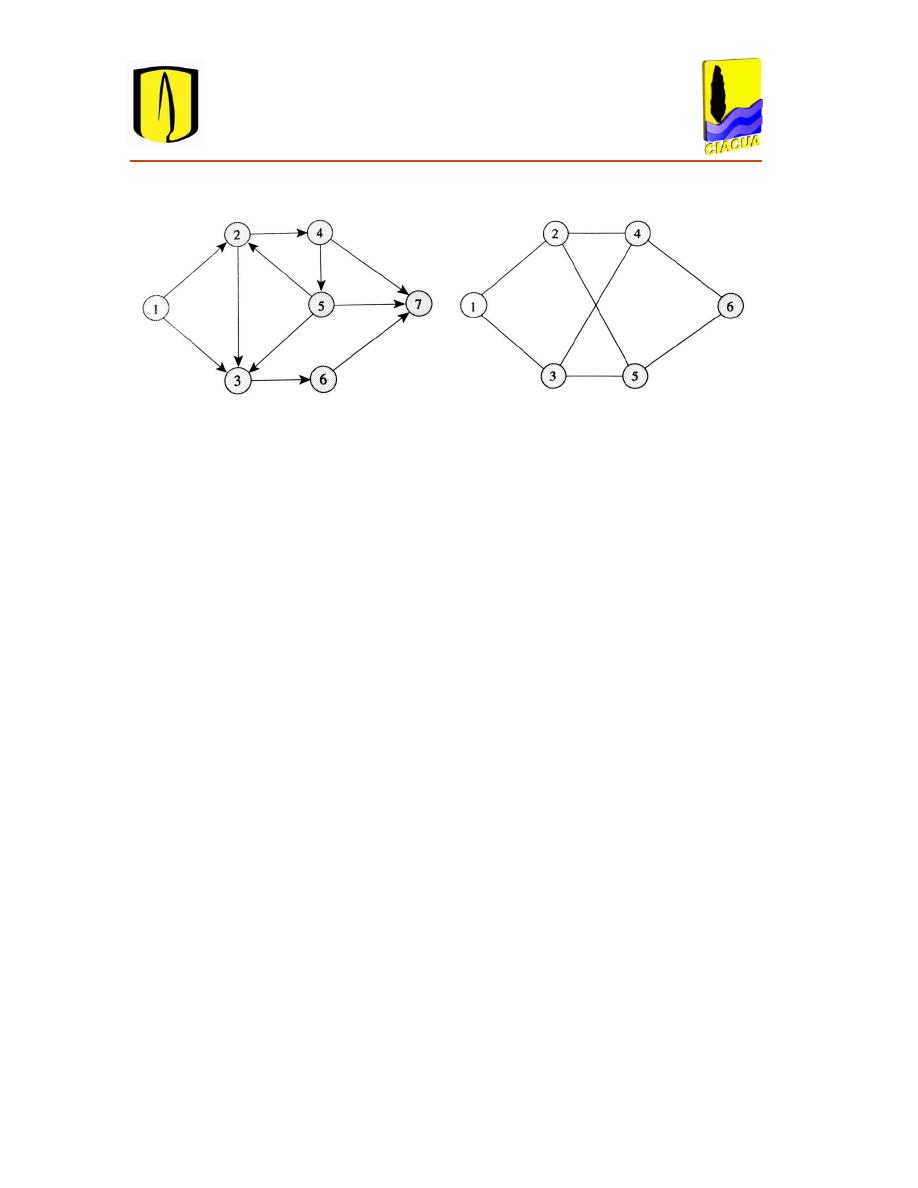
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
31
(a) Grafo Dirigido
(b) Grafo No-Dirigido
Figura 3.1. Grafo. Tomado de Ahuja & et Al (1993).
En la Figura 3.1 (a) se muestra un grafo dado por un conjunto de nodos
y arcos , para los cuales se conoce su dirección. Por otro
lado la Figura 3.1 (b) presenta otro grafo dado por el conjunto de nodos y con
arcos no dirigidos que pueden ser definidos en ambos sentidos, por ejemplo ó
.
De acuerdo con la Figura 3.1 un camino para el grafo dirigido, entre los nodos y podría
estar definido de diferentes maneras. Por ejemplo, un camino puede ser el comprendido por los
arcos y . Otro camino puede ser y , entre otras posibles
combinaciones de arcos. Así mismo, también se pueden dar ciclos como el comprendido por los
arcos y .
3.1.1 Problema de la ruta más corta
El problema de la ruta más corta pertenece a la rama de la optimización que estudia los
problemas de flujo en redes. En un grafo dado, este problema busca encontrar el camino de
mínimo costo (distancia o tiempo de recorrido) desde un nodo específico inicial hasta un nodo
final. Las principales aplicaciones de estos modelos de optimización se encuentran en problemas
de transporte, donde se busca minimizar tiempos de recorrido de un punto a otro (Ahuja & et Al,
Network Flows: Theory, Algorithms, and Applications, 1993).
Matemáticamente, un problema de ruta más corta se define como:

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
32
∑
(
)
Ecuación 3.1
∑
{ |(
) }
∑
{ |(
) }
{
Ecuación 3.2
Ecuación 3.3
donde,
, es una variable binaria que toma el valor de uno si el arco está en la solución
del problema (el camino) o toma el valor de cero de lo contrario.
es el costo de utilizar el arco
en el camino,
es el nodo inicial del cual parte el camino y
es el nodo final del
camino. La Ecuación 3.1 determina la función objetivo del problema, que en este caso es la
minimización de los costos del camino. La Ecuación 3.2 determina las restricciones que garantizan
que un camino parta del nodo
y llegue al nodo
y finalmente la Ecuación 3.3 establece la
naturaleza binaria de las variables.
3.1.2 Algoritmo de Bellman-Ford
El Algoritmo de Bellman-Ford nace por la necesidad de conocer el camino que representa el
mínimo tiempo de viaje entre dos ciudades que hacen parte de un conjunto de ciudades, donde
cada par de ciudades están interconectadas entre sí por una vía que tiene un tiempo de viaje
asociado. Estos tiempos no son directamente proporcionales a las distancias, debido a la cantidad
de rutas que existen para viajar de una ciudad a otra y la variación del tráfico en cada una de ellas
(Bellman, 1956).
Este es un algoritmo clásico de ruta más corta que resuelve el problema de ruta más corta
para grafos dirigidos, que no presentan ciclos negativos
8
. De lo contrario el algoritmo puede
quedar en un ciclo infinito, sin dar solución alguna. Sin embargo, el algoritmo permite resolver, en
un tiempo polinomial, problemas NP-duros, ya que converge en un número de pasos finito si los
ciclos del grafo son positivos y los costos de cada arco son fijos (Hutson, Schlosser, & Shier, 2011).
8
Ciclo negativo: Se refiere a ciclos de un grafo en los que la suma del valor asociado con sus arcos es
negativa.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
33
3.1.2.1 Definición y notación
Los parámetros de entrada para este problema de ruta más corta son
: donde
es un grafo dirigido, es la función de costo o distancia asociada a cada arco
(e.g., distancia, costo) y el nodo inicial
que pertenece al conjunto de nodos . El
objetivo es encontrar la ruta más corta desde el nodo
a todos los otros nodos del grafo .
Este algoritmo se basa en un método de corrección de etiquetas, para resolver el problema de
la ruta más corta. La corrección de etiquetas actualiza para cada nodo
, su costo
acumulado
,
el
nodo
predecesor
y
el
estado
del
nodo
. Inicialmente para cada nodo tiene que
,
y
. Posteriormente, se comienza por el nodo inicial
con
y
, para después escanear el resto de nodos y
actualizar sus etiquetas hasta que no existan más nodos por etiquetar en el grafo (Goldberg &
Radzik, 1993). En este momento ya se tienen todas las rutas más cortas desde un nodo inicial a
todos los demás nodos del grafo. El algoritmo de Bellman-Ford se describe entonces, como se
muestra en el algoritmo presentado en la Figura 3.2.
Figura 3.2. Algorito de Bellman-Ford. Tomado y modificado de Goldberg & Radzik (1993).
Como se observa, el método empieza asignarle a cada nodo un costo acumulado, de forma
que si el costo acumulado
del nodo
más el costo del arco
es menor
que el costo acumulado (
) del nodo
, entonces se actualiza el costo acumulado (
).
De lo contrario se mantiene el costo acumulado (
), obtenido por otro camino y se relaja
(elimina) el nodo
que no hace parte de la ruta más corta (MIT: Massachusetts Institute of
Technology, 2011). Para encontrar una ruta más corta en particular, entre un nodo inicial y uno
final establecidos, se comienza en el nodo final y se van evaluando sus nodos predecesores. El
camino conformado por estos nodos forma entonces la ruta más corta.
procedure
for all
if
then
(
)
(
)
(
)
(
)
EndIf
EndFor

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
34
3.2 Planteamiento del problema
3.2.1 Datos de entrada
Se reciben como datos de entrada la topografía de la zona donde se planea construir o
reemplazar una serie de tramos de una red de alcantarillado, además de las características de las
tuberías como: la rugosidad absoluta
, la longitud de la tubería y los posibles diámetros que se
podrían utilizar en el diseño (según las restricciones comerciales). Específicamente, los parámetros
de entrada son los siguientes:
•
Conjunto de diámetros comerciales disponibles.
•
Conjunto de pozos de inspección que conforman una serie de tramos de una red
de alcantarillado.
El Pozo representa el pozo inicial y el pozo el punto de descarga del sistema de
alcantarillado.
•
Caudal del pozo .
•
Cota del terreno en el pozo .
•
Rugosidad absoluta de las tuberías.
•
Longitud de tramos.
•
Viscosidad cinemática del agua.
3.2.2 Modelaje del grafo
En el caso del diseño de series de tramos de una red de alcantarillado lo que se quiere es
minimizar los costos de construcción. Para esto se puede modelar la red como un grafo dirigido,
donde:
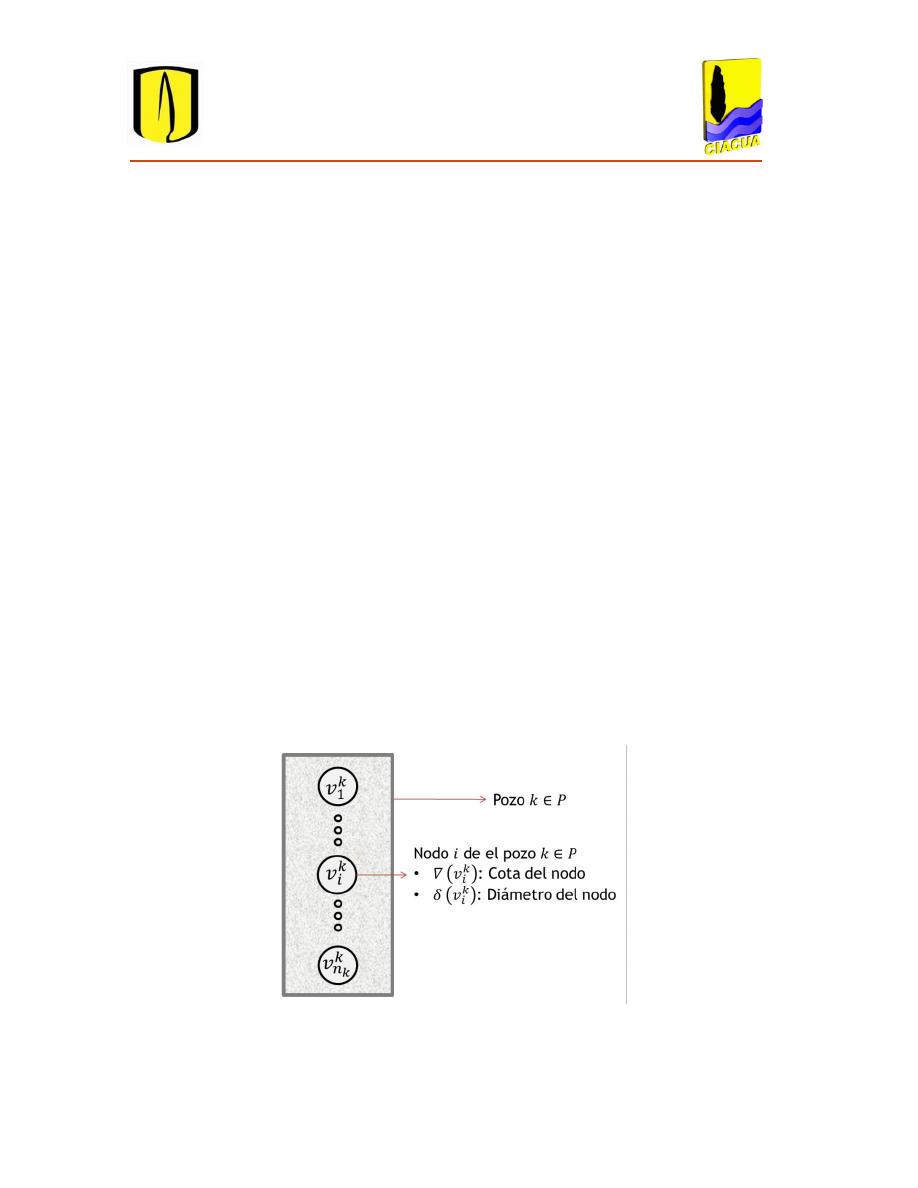
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
35
Los nodos representan profundidades a las cuales se podría instalar la tubería a cota de
batea.
Los arcos representan las tuberías como tal, desde un nodo en un primer pozo de
inspección hasta un nodo en el pozo de inspección sucesivo .
Se quiere modelar un grafo que represente la una serie de tuberías, de tal forma que hayan
tantos arcos como tuberías posibles, para cada tramo. Para esto, los pozos de inspección serán
representados imaginariamente como grupos de nodos. Cada nodo representa una profundidad a
la cual se puede instalar la tubería a cota de batea y un diámetro. En general se tiene un conjunto
global de nodos , que le otorga una identificación distinta a cada nodo. Cada nodo, además,
pertenece a un conjunto
que contiene los nodos de un pozo que pertenece al conjunto de
pozos , como se observa en la Figura 3.3. Esto permite conocer cuántos nodos hay por pozo.
La notación que se utiliza se muestra a continuación:
•
Conjunto de nodos.
•
Conjunto de nodos que pertenecen a el pozo .
Figura 3.3. Conjunto de nodos que pertenecen a un mismo pozo de inspección.
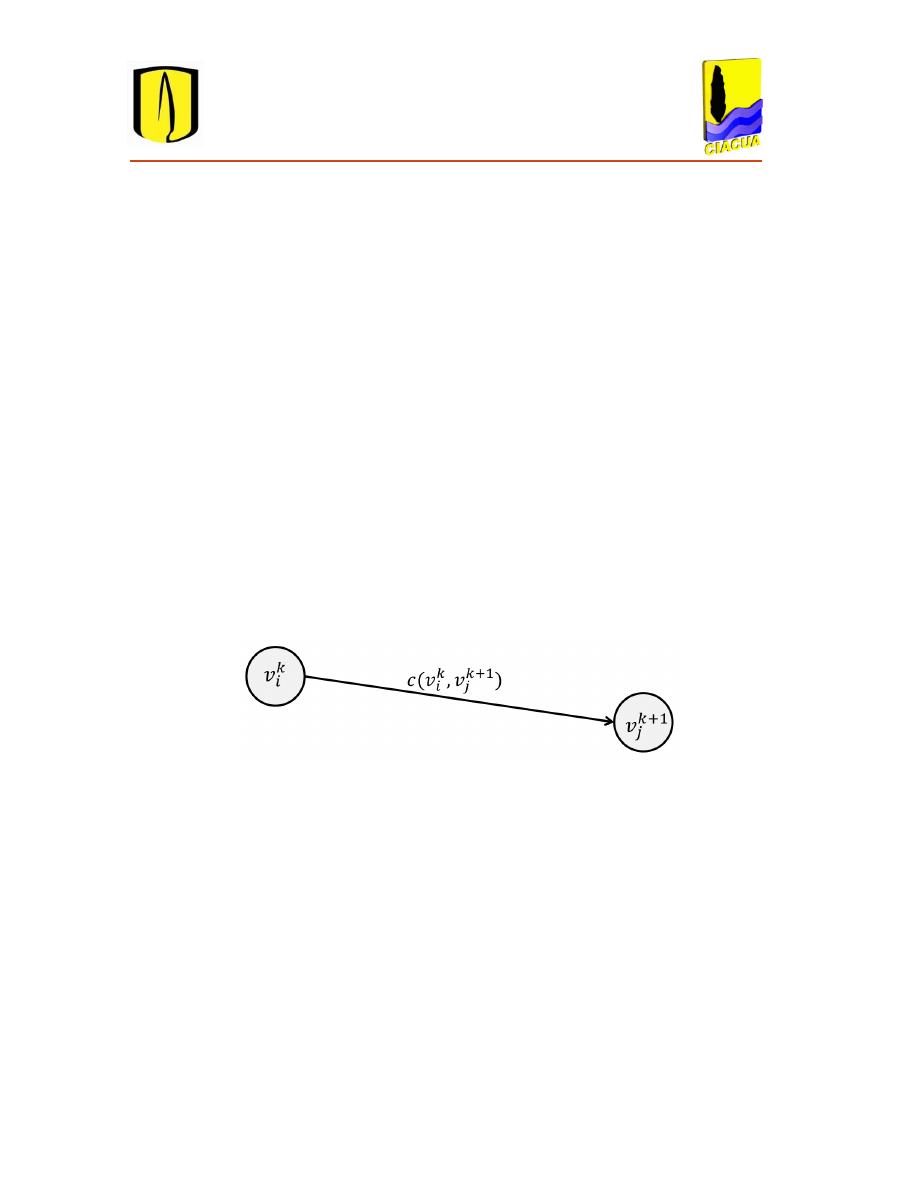
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
36
Para efectos del modelaje del problema, cada nodo
va a tener dos atributos. El
primero, es la cota en metros sobre un nivel de referencia
y el segundo es el diámetro
. El primer atributo representa la cota batea de una tubería y el segundo representa el
diámetro de una tubería asociada con el tramo entre el pozo y .
EL grafo también está conformado por arcos (
) que se definen entre dos nodos
y
, donde
es el i-ésimo nodo del pozo y
es el j-ésimo nodo
del pozo estrictamente siguiente . Además, cada arco tiene un costo asociado que
representa el costo total de construcción, es decir la suma entre el costo de la tubería y los costos
de excavación, según la función de costos presentada en el Numeral 2.5. A continuación se
muestra la notación y una representación de un arco.
•
Conjunto de arcos.
{ (
)|
}
•
Costo del arco
.
Figura 3.4. Representación de un arco (
).
Teniendo en cuenta que, como se mencionó, quien carga la información del diámetro es el
nodo, el diámetro de un arco
adopta el valor del nodo
. Así mismo, el
nodo carga la información de la cota batea donde se instalaría la tubería.
•
(
)
Cota de cada nodo en el pozo .
•
(
) Diámetro del arco
, representado como un atributo del
nodo
.
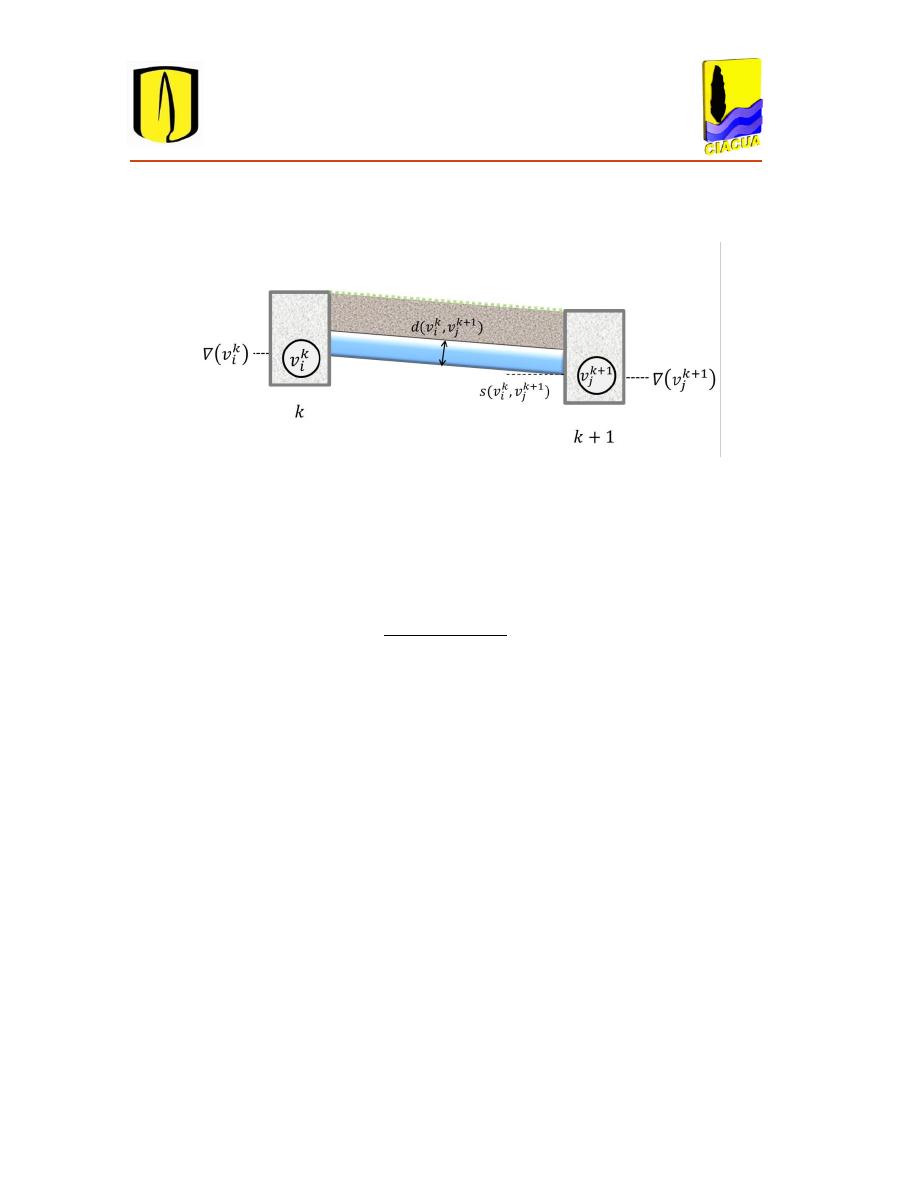
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
37
(
)
Ecuación 3.4
Figura 3.5. Representación de un tramo de alcantarillado.
La pendiente asociada con el arco
, es función de las cotas de los nodos que lo
componen. Esta se calcula como:
(
) (
)
Ecuación 3.5
3.2.3 Variables de decisión
En este caso las variables de decisión son los arcos
.
, es una variable binaria
que toma el valor de uno si el arco
pertenece al camino que forma la ruta más
corta o toma el valor de cero de lo contrario, como se plantea en la Ecuación 3.3 (b).
Ecuación 3.3 (b)
La escogencia de un arco
implica escoger un diámetro
y una
pendiente de diseño
.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
38
3.2.4 Función objetivo
En este caso la función objetivo es la planteada en la Ecuación 3.1, donde
corresponde a la
función de costos planteada en la Ecuación 2.20, en función del diámetro del arco
y
las cotas de los nodos que lo componen (
) y (
). Se busca entonces, minimizar la
función de costos para encontrar el diseño que, cumpliendo con todas las restricciones, sea el más
económico. De acuerdo con esto, la función objetivo sería:
∑
(
)
Ecuación 3.6
(
)
Ecuación 3.7
Recordando la Ecuación 2.21, el volumen se calcula en términos del diámetro de la tubería y la
profundidad a la que se instale. Dicha profundidad se calcula de acuerdo con las cotas de batea del
nodo
y el nodo
de cada arco, como se explica a continuación:
([
]
) (
)
[
]
Ecuación 3.8
donde:
Volumen excavado para poner la tubería.
Profundidad de excavación hasta la cota clave aguas arriba de la tubería.
Profundidad de excavación hasta la cota clave aguas abajo de la tubería.
Diámetro del arco
Espesor de la pared de la tubería.
Relleno que debe disponerse bajo la tubería. Depende de la reglamentación del
lugar donde se lleve a cabo el diseño. Para los ejemplos se siguieron las
recomendaciones del RAS: .
Espacio lateral que debe dejarse a ambos lados de la tubería para colocarla.
Pendiente asociada al arco
(Ecuación 3.5).
Longitud de la tubería.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
39
La profundidad de excavación, se refiere a la diferencia entre la cota del terreno y la cota clave
de la tubería. La Ecuación 3.9 y la Ecuación 3.10 describen la profundidad de excavación aguas
arriba y aguas abajo de la tubería, respectivamente.
(
)
Ecuación 3.9
donde:
Profundidad de excavación hasta la cota clave aguas arriba de la tubería.
Cota del terreno del pozo .
(
)
Cota del nodo de salida
.
(
) Diámetro interno de la tubería.
(
)
Ecuación 3.10
donde:
Profundidad de excavación hasta la cota clave aguas abajo de la tubería.
Cota del terreno del pozo .
(
)
Cota del nodo de llegada
.
(
) Diámetro interno de la tubería.
3.2.5 Representación una serie de tuberías de la red de alcantarillado en un grafo
En la Figura 3.6 se presenta la representación de tres tuberías de diferentes diámetros en un
grafo. Los tres arcos salen del mismo nodo y tienen la misma pendiente, pero cada uno llega a un
nodo diferente, debido a que cada uno representa un diámetro distinto. Como se puede observar,
cada arco (flecha) representa una tubería de cierto diámetro que está ubicada con una pendiente
específica. El arco entonces tiene un diámetro asociado
y una pendiente asociada
. Con base en esto, se calcula el costo asociado
de cada arco como se
observa.
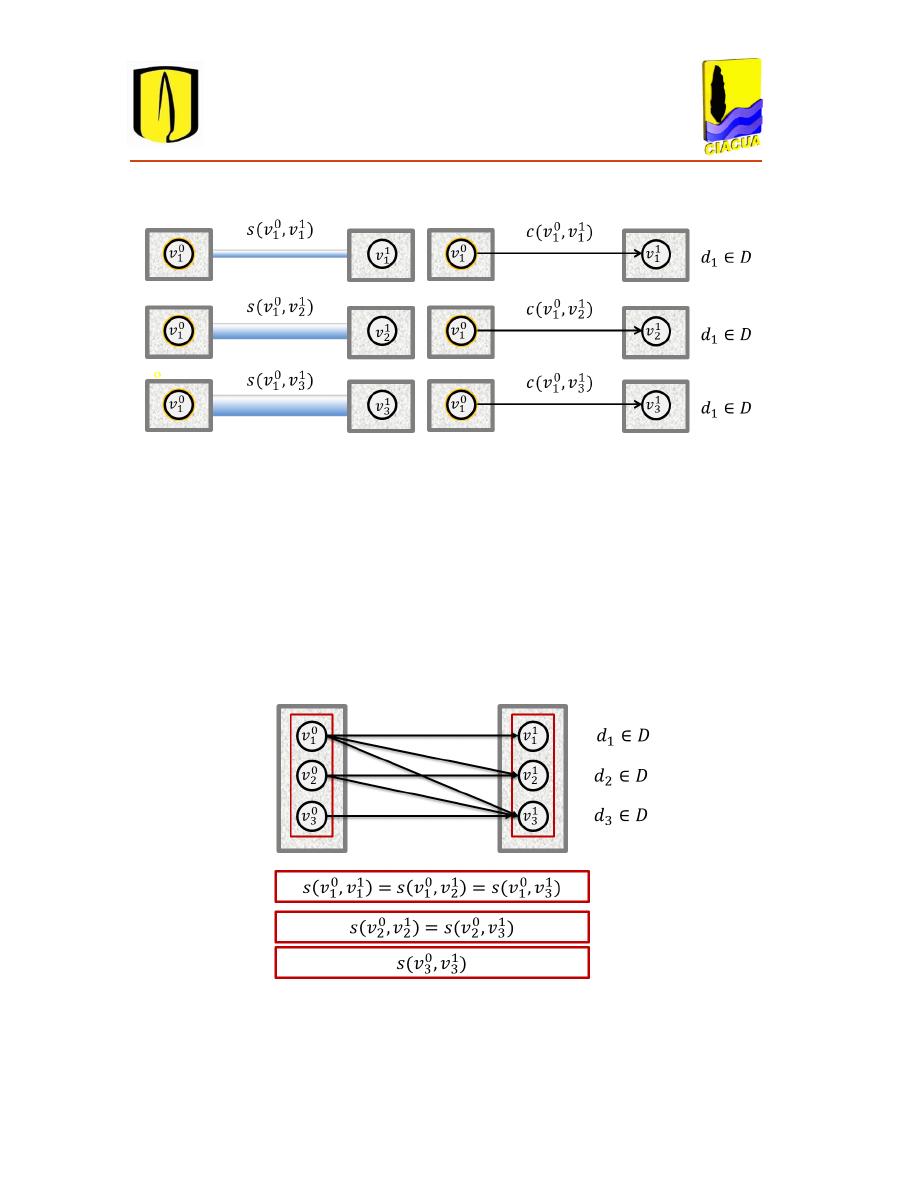
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
40
Figura 3.6. Representación de una tubería en un grafo.
A continuación, se presenta el primer tramo de un ejemplo de una serie de 2 tramos con 3
diámetros disponibles para el diseño y 1 sola profundidad posible de instalación. Como muestra la
Figura 3.7, todos los arcos tienen la misma pendiente. Es importante resaltar que nos nodos que
están agrupados en rectángulos rojos están ubicados a una misma profundidad, pero cada uno
tiene un diámetro diferente, ordenados de forma ascendente. Además, de cada nodo salen arcos
hacia los nodos del pozo siguiente que tengan diámetros y profundidades mayores o iguales. De
esta forma se cumple la restricción hidráulica de diámetros y se evitan pendientes adversas.
Figura 3.7. Grafo de un tramo.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
41
Además, se puede observar que para nodos con diámetros mayores y a mayores
profundidades existen menos alternativas de diseño. Esto también se puede observar en el
siguiente ejemplo, Figura 3.8, donde se extiende el mismo problema a una serie de dos tramos;
también con 3 diámetros comerciales disponibles y 3 posibles profundidades.
Figura 3.8. Grafo de una serie de 2 tramos.
Al ampliar el problema se observa mejor la complejidad del mismo, dado el aumento de
alternativas de diseño
9
que se presenta. Para encontrar cuál de todas las alternativas de diseño es
la óptima se debe conocer el costo total de cada una de ellas y buscar la más económica. El costo
total de una alternativa es entonces la suma del costo de cada una de las tuberías que componen
la serie. De este modo, a cada nodo se le va atribuir un nuevo valor que corresponde a un costo
acumulado, proceso que se explicará más adelante. La solución se encuentra entonces, al
encontrar el nodo cuyo costo acumulado es el mínimo. Una vez encontrado el nodo de mínimo
costo, se busca el nodo anterior o predecesor. EL nodo predecesor va ser aquel nodo del pozo
anterior que condujo a que la suma de los costos fuera mínima. La búsqueda se continúa hasta
9
Alternativa de diseño: se refiere una combinación de tuberías factibles (una de cada tramo), que
conforman una serie.
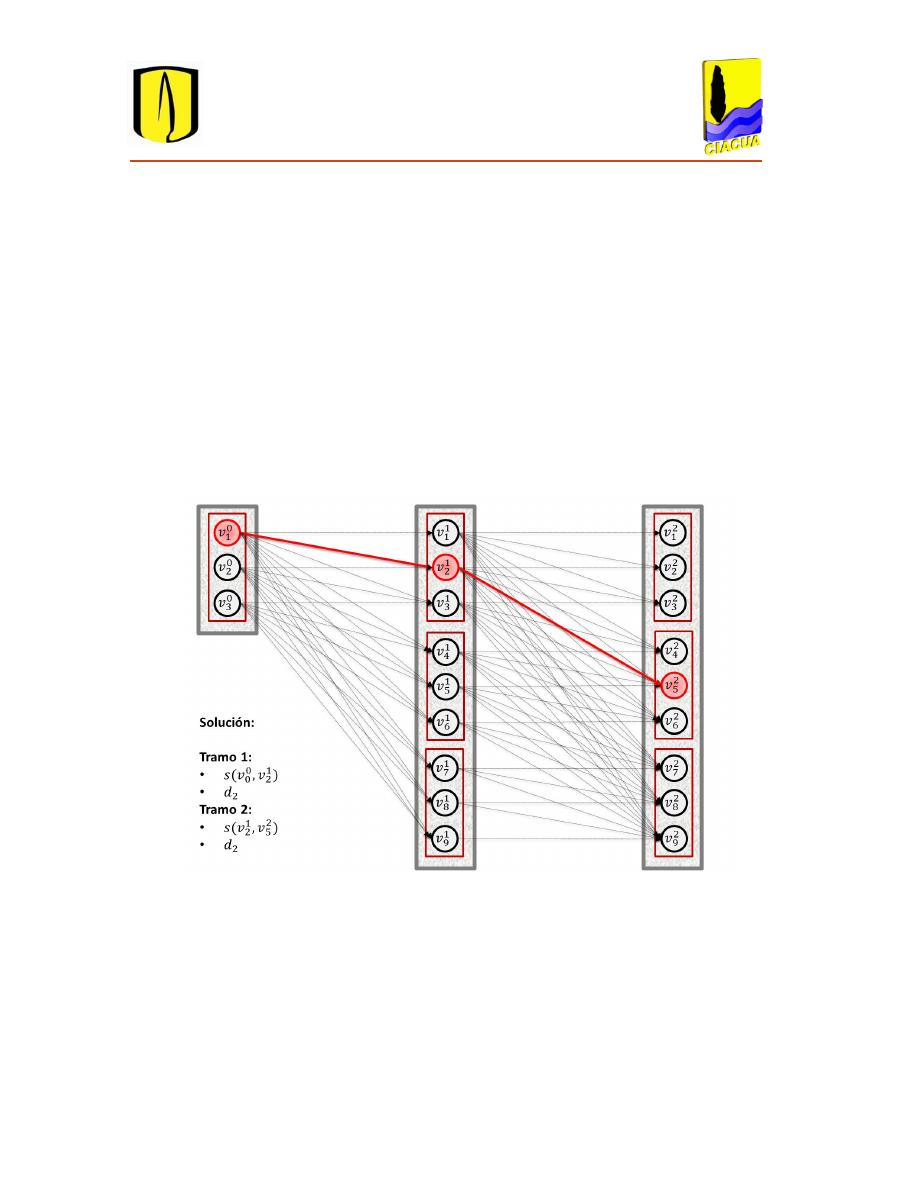
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
42
llegar al primer pozo. De esta forma traza un camino en el grafo que es el que representa la ruta
más corta y por lo tanto el diseño óptimo.
La Figura 3.9 muestra la solución del grafo donde la suma acumulada de los costos fue mínima
para el Nodo 5 del Pozo 2 (
). Este nodo corresponde al segundo diámetro de la lista de
diámetros comerciales disponibles y se encuentra ubicado en la segunda profundidad posible. En
seguida, se busca el nodo predecesor, que según las restricciones debe tener un diámetro y una
profundidad menores o iguales. Para el ejemplo, el nodo que llevó al camino de la ruta más corta
fue el Nodo 2 del Pozo 1
, que también representa el segundo diámetro de la lista y está
ubicado en la primera profundidad. Finalmente se busca el nodo predecesor de
, llegando al
Nodo 1 del Pozo 0
, que representa el primer diámetro disponible en la única posición posible
en el Pozo 0.
Figura 3.9. Solución del grafo.
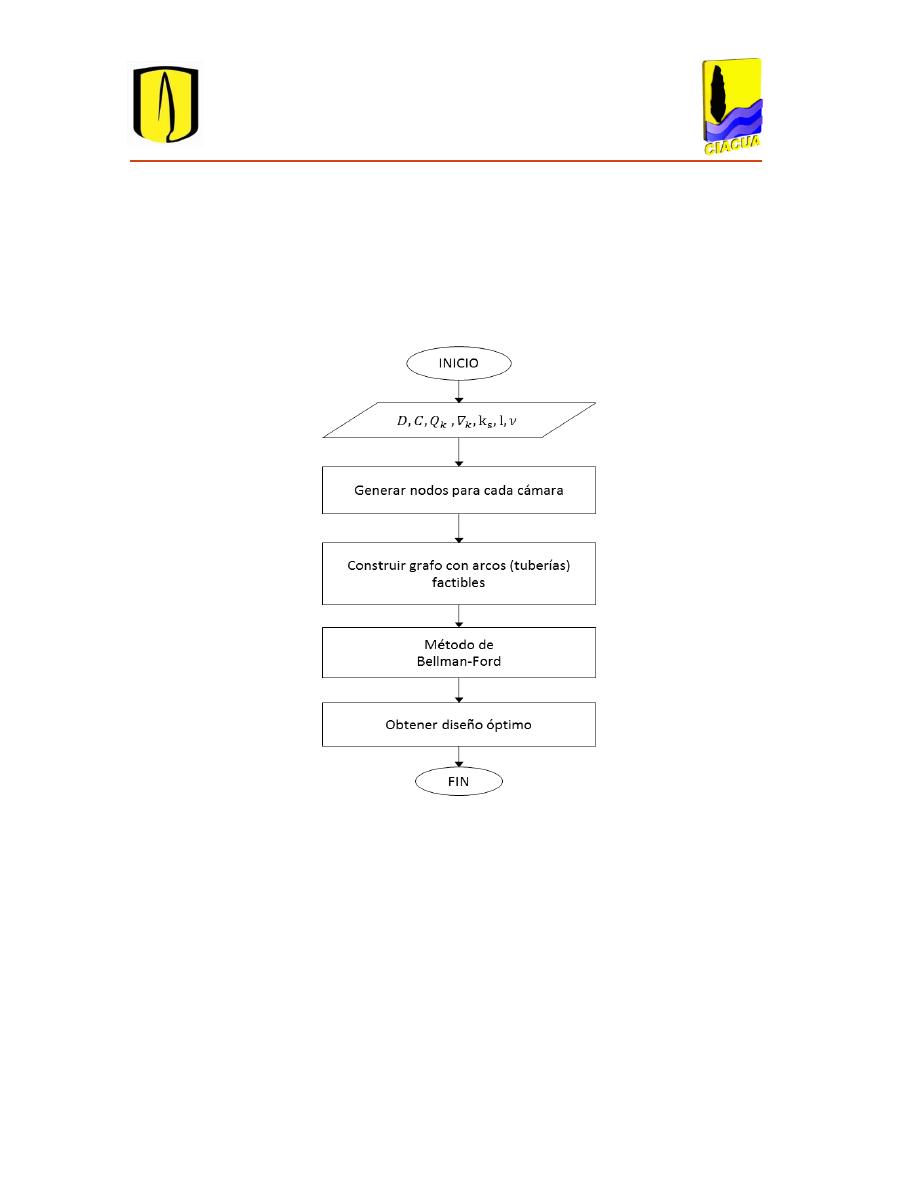
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
43
3.2.6 Diseño óptimo de series de tuberías de alcantarillado
Una vez explicado el proceso de representación de una serie de tuberías como un grafo y el
proceso de selección del diseño óptimo, se describe entonces la metodología de diseño de una
serie de tramos de alcantarillado, por medio del Diagrama de Flujo 3.1.
Diagrama de Flujo 3.1 Metodología para el diseño optimizado se series de tramos de alcantarillado.
Como se observa, se reciben los datos de entrada mencionados en el Numeral 3.2.1, según los
cuales se empiezan a generar los nodos de cada pozo. Esto quiere decir que se crean un nodo para
cada combinación de diámetro (
) y cota (
). Este proceso se describe en el Algoritmo 1,
mostrado a continuación.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
44
Después de creados todos los nodos se pasa a generar el grafo con los arcos factibles. Esto
quiere decir que solo se crean aquellos arcos
que cumplan con todas las
condiciones y restricciones hidráulicas. El siguiente pseudocódigo, presenta este proceso. Además,
se puede observar que el Algoritmo 2 contiene dos procesos del Diagrama de Flujo 3.1. Este evalúa
si el arco
es factible y en caso de que lo sea, se actualizan las etiquetas de los
nodos, siguiendo el Algoritmo de Bellman-Ford, como se mencionó en el Numeral 3.1.2.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
45
Finalmente para solucionar el grafo como se presentó en el ejemplo, se busca el nodo de
mínimo costo acumulado en el último pozo de la serie
. Se empieza por establecer el
mínimo costo como infinito y posteriormente se va actualizando este valor, guardando costos que
sean cada vez menores, hasta encontrar el mínimo. Posteriormente se buscan los nodos
predecesores que conforman la ruta más corta, tal como se muestra en el Algoritmo 3.
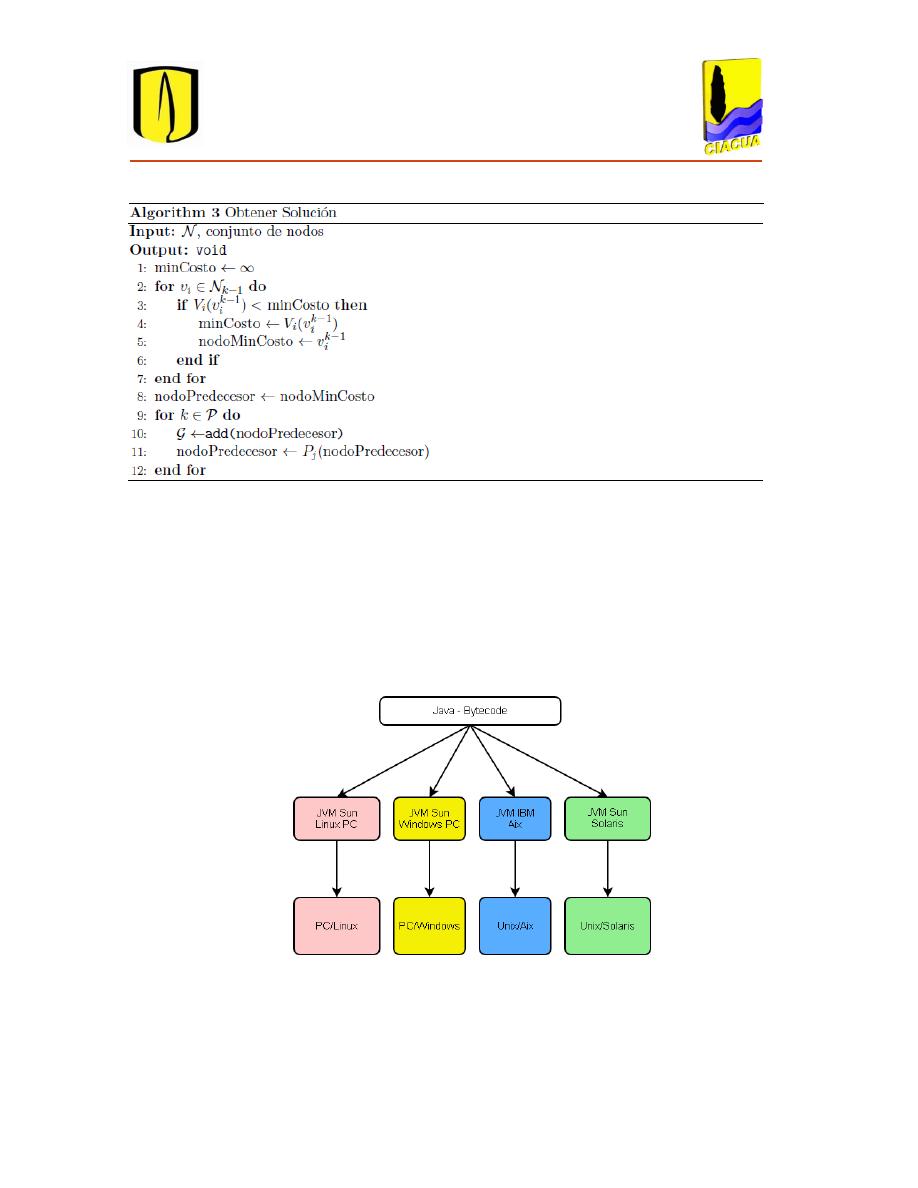
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
46
El algoritmo fue desarrollado en Java que es uno de los lenguajes de programación más
eficientes hoy en día, después de C y C++. A pesar de no ser un lenguaje nativo del sistema
operativo, como sí lo es Visual Basic, el lenguaje usado para el diseño con la metodología de
Pendientes Propias e Intermedias, Java es el tercer lenguaje de programación más eficiente con
respecto a la programación orientada a objetos (Jiménez, 2010). Este lenguaje de programación
tiene la ventaja de funcionar para cualquier sistema operativo (multiplataforma) utilizando una
máquina virtual JAVA (JVM, por sus siglas en inglés) que compilan la información (Java (lenguaje
de programación), 2013). La Figura 3.10 muestra este proceso.
Figura 3.10 proceso de compilación de la JVM. Tomado de Máquina virtual Java (2013).

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
47
3.2.7 Dimensionamiento del problema
Tras observar la Figura 3.9, se puede apreciar que el pozo inicial (Pozo 0) tiene una única
posición posible, que va a ser la profundidad mínima a la que se pueda poner una tubería. Es decir
que los nodos de las primeras pozos van a tener siempre una cota
correspondiente a la
diferencia entre la cota del terreno de dicha pozo
y la mínima profundidad de excavación según
el RAS (2000) que corresponde a 1.2 m más el diámetro asociado al arco (tubería)
.
Además, el número de nodos
va a ser igual al número de diámetros comerciales
disponibles.
Para el resto de pozos el número de profundidades disponibles puede variar de a centímetro
(cm) o de a decímetro (dm) en un rango de 3.8 m. Esto debido a que según los límites de
excavación establecidos por el RAS (2000) hay una distancia de 3.8 m para realizar la construcción
de la red de drenaje urbano. En ese orden de ideas, el número de nodos
será igual al
producto entre el número de profundidades disponibles por el número de diámetros comerciales
disponibles.
El número total de alternativas de diseño para un grafo de tramos y cantidad de
diámetros comerciales disponibles que pertenecen a , corresponde al producto del número de
arcos existentes en cada tramo. Teniendo en cuenta el número de nodos de cada pozo, el número
de alternativas de la serie se podría plantear de la siguiente forma:
Ecuación 3.11
donde:
la precisión con que se varíen las cotas:
•
si se varían las cotas cata decímetro.
•
si se varían las cotas cata centímetro.
Sin embargo, este número de alternativas se reduce mucho teniendo en cuenta que no existen
arcos que conecten dos nodos, de forma que el nodo de llegada tenga un diámetro menor o se
encuentre a una cota más elevada (no se permiten pendientes adversas).

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
48
∑
( ∑
)
Ecuación 3.12
donde:
la precisión con que se varíen las cotas:
•
si se varían las cotas cata decímetro.
•
si se varían las cotas cata centímetro.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
49
4 RESULTADOS Y ANÁLISIS DE RESULTADOS
En esta sección se presentaran los resultados de diferentes diseños realizados bajo el
concepto de Pendientes Propias e Intermedias, en comparación con los resultados utilizando la
metodología de optimización del problema de la ruta más corta. En todos los casos se analizan tres
tipos de costos: los costos totales de la construcción CT, los costos de tuberías CT y los costos de
excavación CE. Los últimos dos tienen como fin establecer un parámetro de diseño en caso de que
sólo se deba responder por uno de los dos costos, si el otro es subsidiado por una entidad del
estado o una empresa privada.
Más adelante también se presentarán los resultados acerca del tiempo computacional en cada
método, teniendo en cuenta que el uso de Pendientes Propias elimina una gran cantidad de
alternativas y por ende sería intuitivo pensar que el tiempo de simulación es menor para este
método. Sin embargo, al utilizar también Pendientes Intermedias el número de alternativas se
eleva, ya que cada tramo tiene casi el doble de pendientes factibles, lo que representa un leve
aumento en el tiempo computacional.
En primer lugar se presentan los resultados del diseño de un solo tramo, para después pasar al
diseño de series de tuberías de alcantarillado. En el caso de los diseños de tramos de alcantarillado
se busca ratificar, por medio de esta nueva metodología, que el comportamiento de los costos se
da tal como se concluyó de los diseños basados en el método de Pendientes Propias e
Intermedias, referirse a Corrales & et Al (2013).
4.1 Diseño de un tramo de alcantarillado
A continuación se muestran los resultados del diseño óptimo de 20 tramos independientes,
por medio del método de la ruta más corta. Cada uno tiene un caudal diferente; sin embargo
comparten la misma topografía, material (PVC:
) y longitud de 100 m. Todos los
tramos se dan entre dos pozos: el pozo de salida se encuentra a una cota de 1000 m y el de
entrada está a 999 m. Es decir que para cada caso la pendiente del terreno es de 0.010 y la
pendiente máxima a la que se podrías instalar la tubería es de 0.048, según los límites de
excavación.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
50
Tabla 4.1 Resultados de diseños de un tramo – comparación de costos y PE.
Diseño
Q
(m
3
/s)
Costo Total
Costo de Tuberías
Costo de Excavación
Costo
(COP)
PE
(m
2
/s)
Costo
(COP)
PE
(m
2
/s)
Costo
(COP)
PE
(m
2
/s)
1
0.15 $ 1,568,306
0.21 $ 570,829
0.50 $ 934,534
0.21
2
0.19 $ 1,634,368
0.20 $ 633,771
0.39 $ 941,995
0.20
3
0.34 $ 2,005,765
0.36 $ 692,373
1.04 $ 1,206,012
0.36
4
0.45 $ 2,179,380
0.45 $ 747,498
1.17 $ 1,329,794
0.45
5
0.59 $ 2,179,380
0.59 $ 747,498
2.54 $ 1,329,794
0.59
6
0.79 $ 2,501,958
1.34 $ 799,754
3.28 $ 1,652,373
1.34
7
0.99 $ 2,697,129
1.18 $ 849,586
2.56 $ 1,753,864
1.18
8
1.02 $ 2,750,557
1.33 $ 849,586
2.86 $ 1,807,293
1.33
9
1.17 $ 2,913,079
1.87 $ 849,586
4.08 $ 1,928,209
1.20
10
1.35 $ 3,055,306
1.65 $ 943,265
2.83 $ 2,046,100
1.65
11
1.42 $ 3,114,866
1.89 $ 943,265
3.27 $ 2,105,660
1.89
12
1.56 $ 3,235,184
2.37 $ 943,265
4.20 $ 2,225,978
2.37
13
1.67 $ 3,307,132
1.76 $ 943,265
5.19 $ 2,235,043
1.76
14
1.75 $ 3,372,193
2.02 $ 943,265
5.96 $ 2,300,104
2.02
15
1.84 $ 3,437,692
2.30 $ 943,265
6.82 $ 2,365,603
2.30
16
2.01 $ 3,636,758
3.12 $ 1,009,206
5.08 $ 2,564,669
3.12
17
2.35 $ 3,845,592
2.99 $ 1,009,206
7.80 $ 2,713,249
2.99
18
2.62 $ 4,044,982
2.62 $ 1,009,206 10.55 $ 2,854,681
2.62
19
2.84 $ 4,201,306
3.41 $ 1,072,089
8.10 $ 3,011,004
3.41
20
3.00 $ 4,280,200
3.90 $ 1,072,089
9.45 $ 3,089,899
3.90
En la Tabla 4.1 se observa una vez más que en el diseño de redes de alcantarillado los costos
de excavación (CE) son mucho mayores y por lo mismo más representativos que los costos de
tuberías (CT), sobre los costos totales (CTT). Además se observa que para todos los casos la
Potencia Específica para los CTT y los CE es la misma y siempre es menor que la Potencia Específica
relacionada con los CT. Esto comprueba cómo el diseño óptimo siempre toma el camino que le
tenga los mínimos CE.
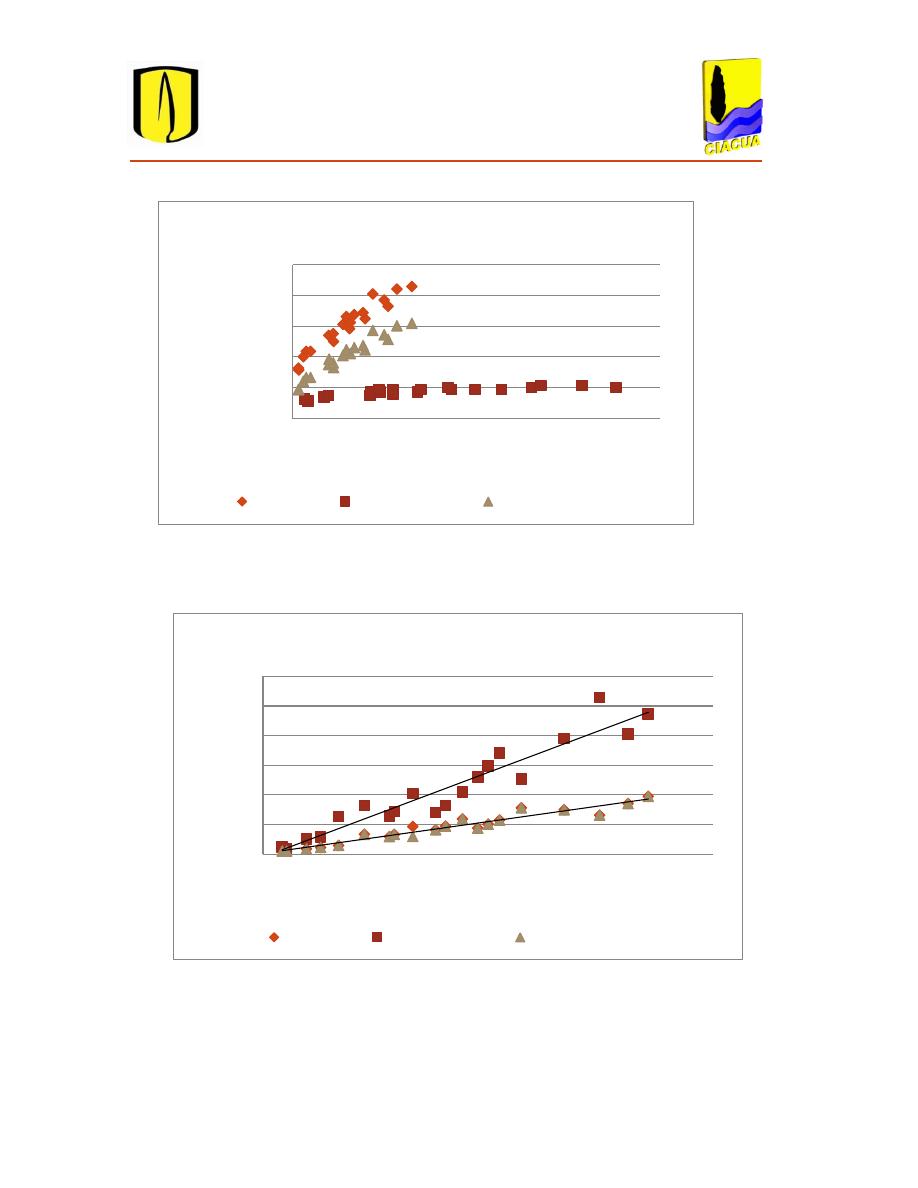
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
51
Figura 4.1 Relación entre la Potencia Específica el costo.
Figura 4.2 Relación ente la Potencia Específica y el caudal.
La Figura 4.1 permite apreciar cómo para los CT la Potencia Específica tiene a aumentar para
mantener bajos los CT. En todos los casos se presenta la PU máxima para los CT; sin embargo tiene
a aumentar linealmente con respecto al caudal, como se observa en la Figura 4.2. En promedio la
$-
$1000000.0
$2000000.0
$3000000.0
$4000000.0
$5000000.0
0.00
2.00
4.00
6.00
8.00
10.00
12.00
Co
sto
(
COP)
PE (m
2
/s)
Costos vs Potencia Específica
Costo Total
Costo de Tuberías
Costo de Excavación
y = 1.2205x + 0.0629
R² = 0.9343
y = 3.2494x - 0.1812
R² = 0.9122
0.00
2.00
4.00
6.00
8.00
10.00
12.00
0.00
0.50
1.00
1.50
2.00
2.50
3.00
3.50
PE
(m
2/s)
Q (m
3
/s)
Potencia Específica vs Caudal
Costo Total
Costo de Tuberías
Costo de Excavación
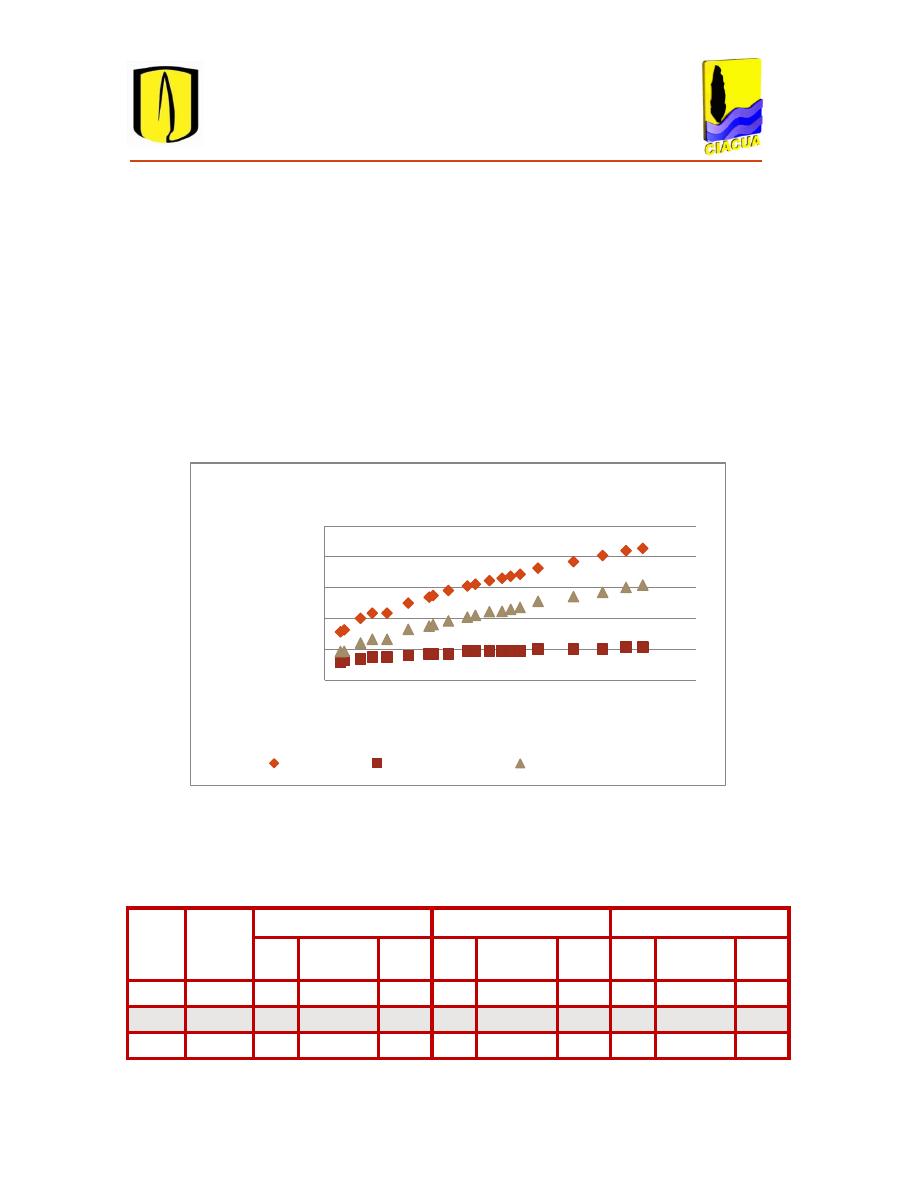
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
52
Potencia Específica relacionada a los CT es 2.5 veces mayor que la de los CE, que a su vez
corresponde a la razón entre las pendientes que describen las relaciones PU-caudal. Esto se debe a
que los mínimos CE buscan minimizar también la pendiente. Por el contrario, el mínimo CT se
obtiene maximizando la pendiente de diseño para minimizar el diámetro de la tubería.
El que la Potencia Específica, para un caudal dado, tienda a ser la misma para CTT y CE,
también ayuda a entender por qué el comportamiento de la función de costos tiende a seguir
mejor el comportamiento de la ecuación de CE, como se observa en la Figura 4.3. En todos los
casos son directamente proporcionales al caudal de diseño que se requiere transportar, que
incurre en el aumento del diámetro de la tubería y por ende, del volumen de excavación. Como se
ve, el aumento del caudal no eleva en gran medida los CT, mas si los de excavación.
Figura 4.3 Efectos del aumento del caudal en los costos.
Tabla 4.2 Resultados de diseño de un tramo – comparación de diámetros y pendientes de diseño.
Diseño Q (m
3
/s)
Costo Total
Costo de Tuberías
Costo de Excavación
d
(m)
Pendiente
(-)
PE
(m
2
/s)
d
(m)
Pendiente
(-)
PE
(m
2
/s)
d
(m)
Pendiente
(-)
PE
(m
2
/s)
1
0.15 0.300
0.014
0.21 0.250
0.0335
0.50 0.300
0.014
0.21
2
0.19 0.350
0.011
0.20 0.300
0.0210
0.39 0.350
0.011
0.20
3
0.34 0.450
0.011
0.36 0.350
0.0305
1.04 0.450
0.011
0.36
$-
$1000000.0
$2000000.0
$3000000.0
$4000000.0
$5000000.0
0.00
0.50
1.00
1.50
2.00
2.50
3.00
3.50
Co
sto
(
COP)
Q (m
3
/s)
Caudal vs Costos
Costo Total
Costo de Tuberías
Costo de Excavación
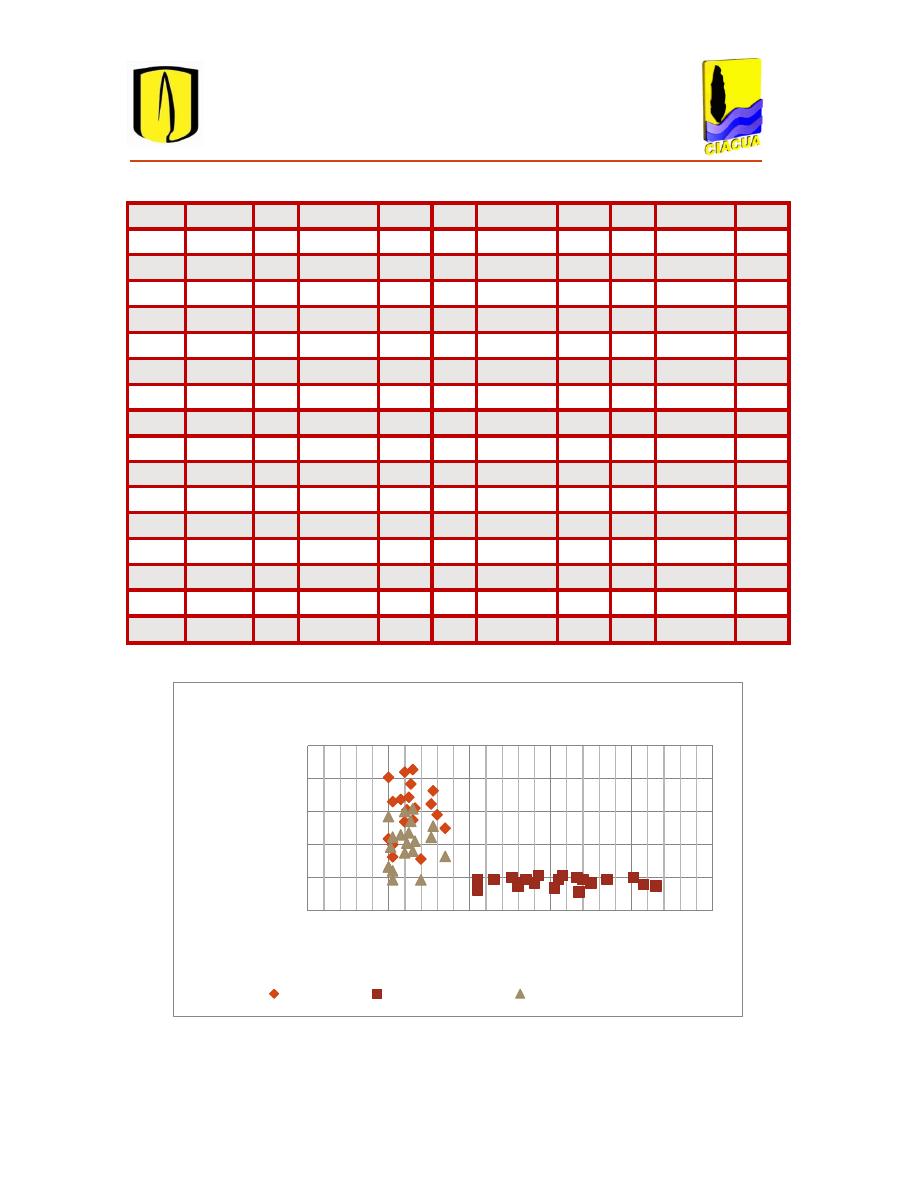
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
53
4
0.45 0.500
0.010
0.45 0.400
0.0260
1.17 0.500
0.010
0.45
5
0.59 0.500
0.010
0.59 0.400
0.0430
2.54 0.500
0.010
0.59
6
0.79 0.500
0.017
1.34 0.450
0.0415
3.28 0.500
0.017
1.34
7
0.99 0.600
0.012
1.18 0.500
0.0260
2.56 0.600
0.012
1.18
8
1.02 0.600
0.013
1.33 0.500
0.0280
2.86 0.600
0.013
1.33
9
1.17 0.600
0.016
1.87 0.500
0.0350
4.08 0.675
0.010
1.20
10
1.35 0.675
0.012
1.65 0.600
0.0210
2.83 0.675
0.012
1.65
11
1.42 0.675
0.013
1.89 0.600
0.0230
3.27 0.675
0.013
1.89
12
1.56 0.675
0.015
2.37 0.600
0.0270
4.20 0.675
0.015
2.37
13
1.67 0.750
0.011
1.76 0.600
0.0310
5.19 0.750
0.011
1.76
14
1.75 0.750
0.012
2.02 0.600
0.0340
5.96 0.750
0.012
2.02
15
1.84 0.750
0.013
2.30 0.600
0.0370
6.82 0.750
0.013
2.30
16
2.01 0.750
0.016
3.12 0.675
0.0253
5.08 0.750
0.016
3.12
17
2.35 0.825
0.013
2.99 0.675
0.0333
7.80 0.825
0.013
2.99
18
2.62 0.900
0.010
2.62 0.675
0.0403
10.55 0.900
0.010
2.62
19
2.84 0.900
0.012
3.41 0.750
0.0285
8.10 0.900
0.012
3.41
20
3.00 0.900
0.013
3.90 0.750
0.0315
9.45 0.900
0.013
3.90
Figura 4.4 Pendiente de diseño.
$-
$1000000.0
$2000000.0
$3000000.0
$4000000.0
$5000000.0
0.00
0.01
0.02
0.03
0.04
0.05
Co
sto
(
COP)
Pendiente (-)
Pendiente de diseño
Costo Total
Costo de Tuberías
Costo de Excavación

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
54
Con la Tabla 4.2 y la Figura 4.4 se pretende demostrar que los diseños óptimos son aquellos
cuya pendiente de diseño se asemeja más a la pendiente del terreno. En el caso de que la
excavación sea subsidiada y solo se tengan los CT, sucede lo contrario, el diseño óptimo es aquel
cuya pendiente tiende a ser la máxima pendiente permitida según los límites de excavación.
4.2 Diseño de series de tuberías de alcantarillado
Ejemplo 1
A continuación se presenta un diseño óptimo para una serie de tramos de un sistema de
alcantarillado, que consta de 12 tramos de 100 m de longitud cada uno y los caudales y cotas de
terreno que se muestran en la Tabla 4.10. Las tuberías son de concreto
. A
continuación se evalúa el diseño obtenido con las dos metodologías mencionadas: el diseño
utilizando los conceptos de Pendientes Propias e Intermedias (1) y el diseño utilizando el problema
de la ruta más corta (2).
Tabla 4.3 Datos de entrada de serie 10 tramos.
Pozo
k
Caudal de diseño
Q
k
(m3/s)
Cota del terreno
k
(m)
0
0.058
100.00
1
0.128
99.70
2
0.137
99.99
3
0.181
99.62
4
0.277
99.92
5
0.351
99.55
6
0.451
99.88
7
0.543
99.47
8
0.637
99.87
9
0.689
99.39
10
0.000
99.86

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
55
Tabla 4.4 Resultados en tiempos y costos.
Metodología
Costo de Construcción
(COP)
Costos Computacionales
(s)
PE
(m
2
/s)
1
$ 40,642,817
35.06
0.095
2
$ 32,796,110
11.70
0.090
En la Tabla 4.4 se puede observar que para este diseño se obtiene un ahorro del 19.3% sobre
los costos totales, con un tiempo de ejecución del algoritmo casi 3 veces más rápido que el del
método 1. En la sección de Anexos se pueden encontrar los resultados para el cálculo de la
hidráulica de cada ejemplo.
Tabla 4.5 Resultados para el diseño de serie de 10 tramos –Metodología 1.
Pozo
Cota Clave
(m)
Cota Batea
(m)
Tramo
Costo Tramo
(COP)
Pendiente
(-)
Diámetro
(m)
Caudal
(m
3
/s)
PE
(m
2
/s)
0
98.8
98.4
-
-
-
-
-
1
98.72
98.32
1
$ 1,850,882
0.0008
0.400 0.058 0.0046
2
98.35
97.95
2
$ 1,993,066
0.0037
0.400 0.127 0.0471
3
98.17
97.72
3
$ 2,367,559
0.0023
0.450 0.137 0.0315
4
97.77
97.32
4
$ 2,629,029
0.0040
0.450 0.181 0.0724
5
96.86
96.41
5
$ 3,240,601
0.0091
0.450 0.276 0.2516
6
96.915
96.24
6
$ 4,999,219
0.0017
0.675 0.351 0.0597
7
96.695
96.02
7
$ 5,100,758
0.0022
0.675 0.450 0.0991
8
96.58
95.83
8
$ 5,758,277
0.0019
0.750 0.543 0.1032
9
96.33
95.58
9
$ 5,986,000
0.0025
0.750 0.636 0.1591
10
96.225
95.40
10
$ 6,717,426
0.0018
0.825 0.688 0.1239
Tabla 4.6 Resultados para el diseño de serie de 10 tramos –Metodología 2.
Pozo
Cota Clave
(m)
Cota Batea
(m)
Tramo
Costo Tramo
(COP)
Pendiente
(-)
Diámetro
(m)
Caudal
(m
3
/s)
PE
(m
2
/s)
0
98.80
98.40
-
-
-
-
-
1
98.71
98.31
1 $ 1,853,700
0.0009
0.4 0.058 0.0050
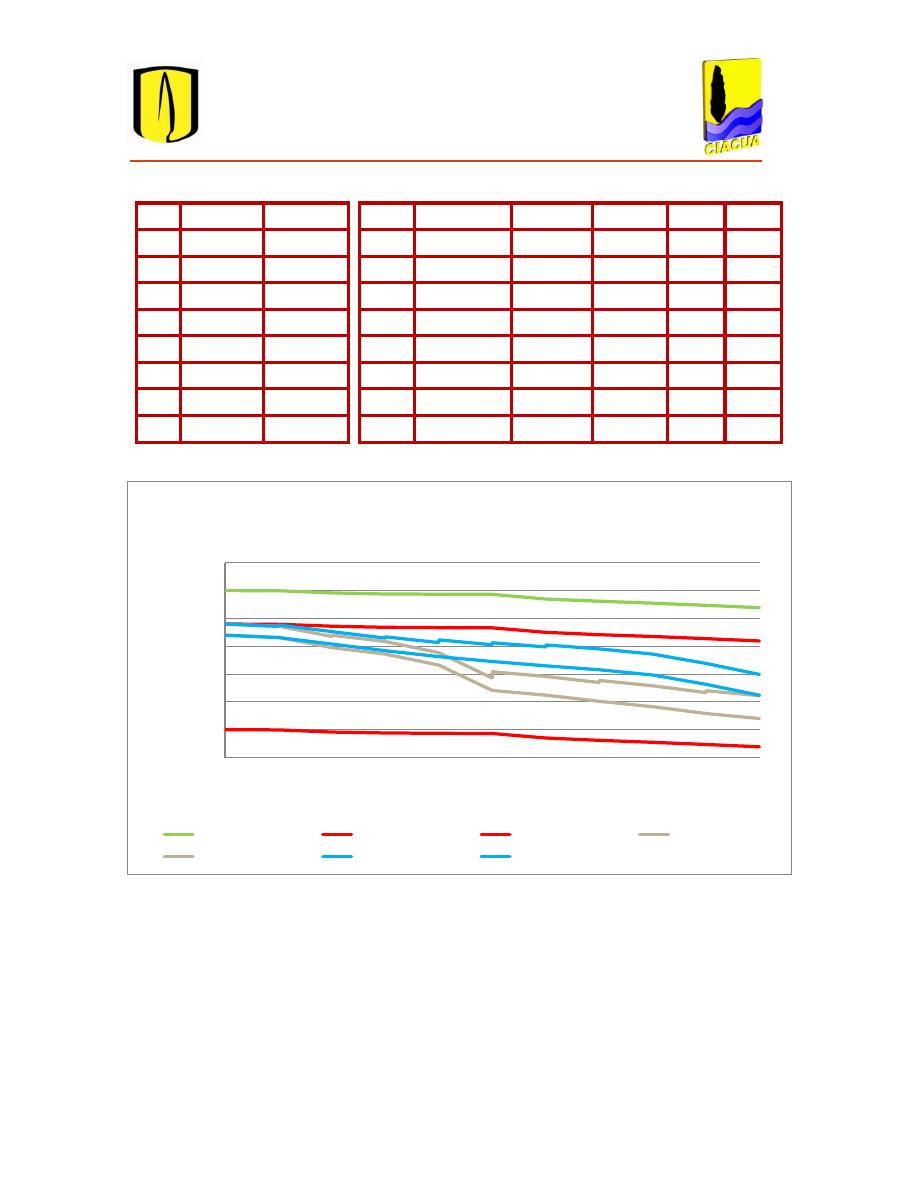
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
56
2
98.53
98.08
2 $ 2,105,125
0.0024
0.45 0.136 0.0321
3
98.29
97.84
3 $ 2,259,089
0.0024
0.45 0.137 0.0324
4
98.13
97.63
4 $ 2,620,025
0.0021
0.5 0.207 0.0439
5
98.05
97.45
5 $ 3,200,693
0.0018
0.6 0.293 0.0520
6
97.97
97.30
6 $ 3,605,630
0.0015
0.675 0.351 0.0534
7
97.91
97.16
7 $ 3,958,344
0.0014
0.75 0.450 0.0640
8
97.72
96.97
8 $ 4,082,960
0.0019
0.75 0.543 0.1024
9
97.38
96.63
9 $ 4,350,057
0.0034
0.75 0.729 0.2469
10
96.99
96.24
10 $ 4,760,487
0.0039
0.75 0.688 0.2713
Figura 4.5 Perfil del diseño óptimo para una serie de 10 tramos para costos totales.
La Figura 4.5 permite observar de forma gráfica, el punto donde se empieza a dar la diferencia
en costos de excavación entre ambas alternativas de diseño. El diseño azul es el óptimo, calculado
utilizando la metodología 2 y el gris es una alternativa muy cercana al diseño óptimo, calculado
utilizando los conceptos de Pendientes Propias e Intermedias.
94.00
95.00
96.00
97.00
98.00
99.00
100.00
101.00
0
200
400
600
800
1000
Co
ta
(m
)
Abcisa (m)
Perfil del diseño óptimo
serie de 10 tramos
Terreno
Límite superior
Límite inferior
Cota Clave (1)
Cota Batea (1)
Cota Clave (2)
Cota Batea (2)

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
57
Ejemplo 2
A continuación se presenta un diseño óptimo para una serie de tramos de un sistema de
alcantarillado, que consta de 50 tramos de 100 m de longitud cada uno y los caudales y cotas de
terreno que se muestran en la Tabla 4.7. Las tuberías son de PVC
. A
continuación se evalúa el diseño obtenido la Metodología 2 que utiliza el problema de la ruta más
corta.
En efecto hay ocasiones en que no existen diseños que cumplan con todas las restricciones,
sobre todo a medida que se aumenta el número de tramos a diseñar. Sin embargo, en caso de que
exista se puede calcular con la nueva metodología, a diferencia de la Metodología 1 que hasta el
momento tiene la capacidad de diseñar series de hasta 20 tramos.
Tabla 4.7 Datos de entrada de serie 50 tramos.
Pozo
Caudal
(m
3
/s)
Cota Terreno
(m)
Pozo
Caudal
(m
3
/s)
Cota Terreno
(m)
Pozo
Caudal
(m
3
/s)
Cota Terreno
(m)
0 0.025
1000.00
17 0.492
987.57
34 0.910
971.77
1 0.048
999.05
18 0.524
986.53
35 0.925
969.89
2 0.072
998.47
19 0.556
985.21
36 0.962
969.78
3 0.107
996.51
20 0.566
983.25
37 0.978
969.74
4 0.136
996.19
21 0.609
983.07
38 0.987
968.33
5 0.173
995.54
22 0.613
981.89
39 1.020
967.11
6 0.184
994.56
23 0.625
981.49
40 1.063
965.44
7 0.227
993.81
24 0.651
980.55
41 1.090
964.03
8 0.252
993.12
25 0.671
980.33
42 1.126
963.40
9 0.274
992.80
26 0.690
979.37
43 1.159
963.12
10 0.294
992.70
27 0.726
978.61
44 1.173
961.91
11 0.324
992.32
28 0.758
977.28
45 1.219
961.17
12 0.341
990.84
29 0.771
976.69
46 1.240
960.85
13 0.371
990.22
30 0.782
975.74
47 1.274
960.10
14 0.401
990.22
31 0.803
973.79
48 1.287
959.04
15 0.406
988.75
32 0.840
973.13
49 1.312
958.07
16 0.444
988.00
33 0.881
971.91
50
1000
957.00

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
58
Tabla 4.8 Resultado del diseño.
Metodología
Costo de Construcción
(COP)
Costos Computacionales
(s)
2
$ 137,430,516
0.907
Tabla 4.9 Resultados para el diseño de serie de 50 tramos –Metodología 2.
Pozo
Cota Clave
(m)
Cota Batea
(m)
Tramo
Costo Tramo
(COP)
Pendiente
(-)
Diámetro
(m)
Caudal
(m
3
/s)
0
998.80
998.60
1
997.75
997.55 $ 626,291
0.0105
0.200
0.025 0.026
2
997.22
996.97 $ 728,491
0.0058
0.250
0.048 0.027
3
995.26
995.01 $ 728,491
0.0196
0.250
0.072 0.141
4
994.94
994.59 $ 924,800
0.0042
0.350
0.107 0.045
5
994.29
993.94 $ 959,266
0.0065
0.350
0.135 0.088
6
993.31
992.96 $ 959,266
0.0098
0.350
0.173 0.169
7
992.51
992.11 $ 1,088,309
0.0085
0.400
0.184 0.157
8
991.87
991.42 $ 1,226,761
0.0069
0.450
0.227 0.156
9
991.60
991.10 $ 1,329,794
0.0033
0.500
0.308 0.101
10
991.20
990.70 $ 1,466,009
0.0040
0.500
0.274 0.110
11
990.72
990.22 $ 1,652,373
0.0047
0.500
0.294 0.139
12
989.64
989.14 $ 1,512,103
0.0109
0.500
0.324 0.352
13
988.92
988.42 $ 1,374,849
0.0071
0.500
0.341 0.243
14
988.22
987.72 $ 1,747,493
0.0071
0.500
0.371 0.262
15
987.45
986.95 $ 1,747,493
0.0077
0.500
0.401 0.308
16
986.70
986.20 $ 1,420,256
0.0075
0.500
0.406 0.303
17
985.87
985.37 $ 1,605,290
0.0084
0.500
0.444 0.371
18
985.03
984.53 $ 1,699,775
0.0084
0.500
0.492 0.415
19
984.01
983.51 $ 1,466,009
0.0101
0.500
0.524 0.531
20
981.95
981.45 $ 1,374,849
0.0206
0.500
0.556 1.145
21
981.47
980.87 $ 1,861,098
0.0058
0.600
0.566 0.331
22
980.59
979.99 $ 1,915,274
0.0087
0.600
0.609 0.532
23
979.89
979.29 $ 1,915,274
0.0070
0.600
0.613 0.429
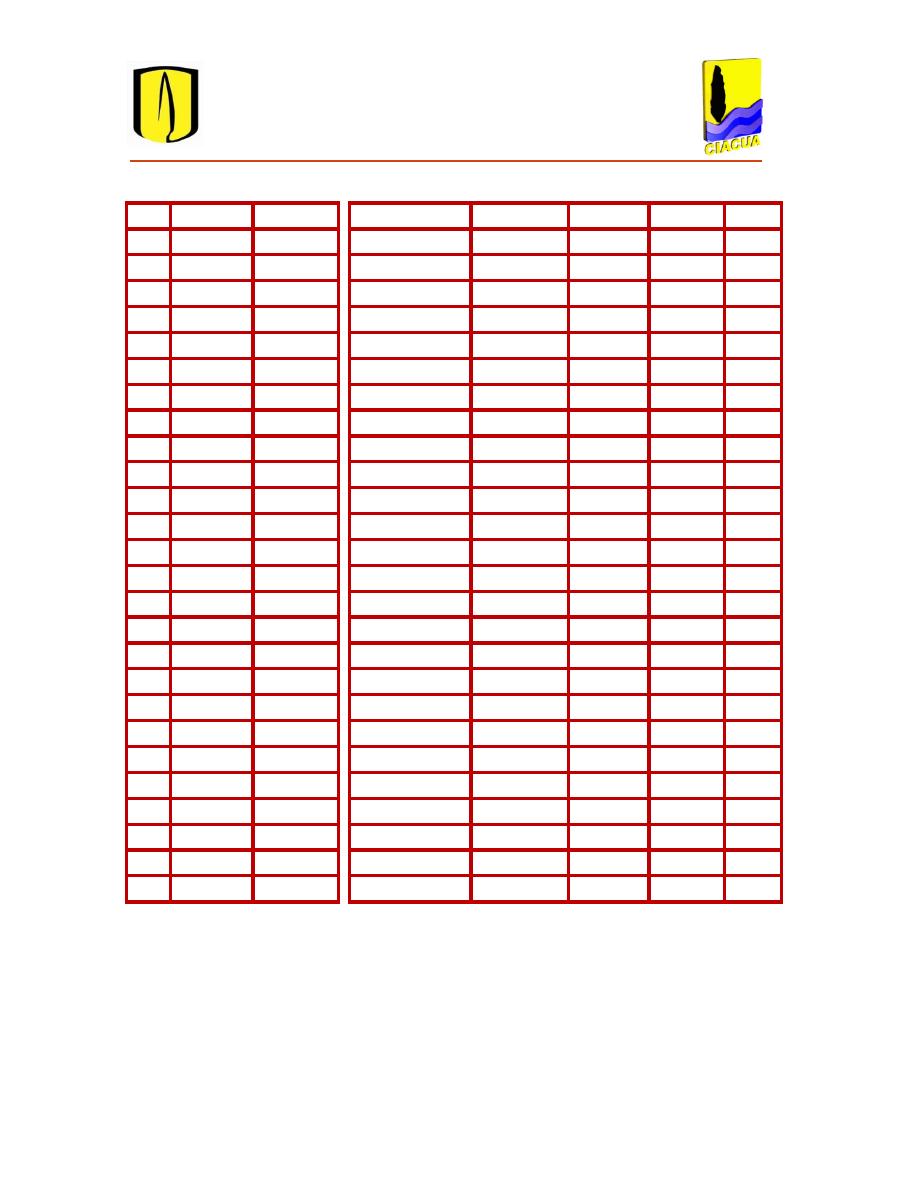
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
59
24
979.15
978.55 $ 1,969,815
0.0074
0.600
0.625 0.465
25
978.43
977.83 $ 2,135,575
0.0072
0.600
0.651 0.470
26
977.67
977.07 $ 2,304,440
0.0076
0.600
0.671 0.507
27
976.91
976.31 $ 2,191,525
0.0077
0.600
0.690 0.529
28
976.08
975.48 $ 1,915,274
0.0083
0.600
0.726 0.600
29
975.29
974.69 $ 1,753,864
0.0079
0.600
0.758 0.598
30
974.44
973.84 $ 1,807,293
0.0085
0.600
0.771 0.653
31
972.59
971.99 $ 1,700,818
0.0185
0.600
0.782 1.447
32
971.73
971.13 $ 1,753,864
0.0086
0.600
0.803 0.694
33
970.71
970.11 $ 1,753,864
0.0102
0.600
0.840 0.854
34
969.67
969.07 $ 2,135,576
0.0104
0.600
0.881 0.917
35
968.59
967.99 $ 2,191,525
0.0108
0.600
0.910 0.987
36
968.23
967.48 $ 2,398,515
0.0050
0.750
0.925 0.467
37
967.69
966.94 $ 3,008,571
0.0054
0.750
0.962 0.522
38
967.08
966.33 $ 2,801,613
0.0061
0.750
0.978 0.596
39
965.86
965.11 $ 2,267,518
0.0122
0.750
0.987 1.204
40
964.19
963.44 $ 2,267,518
0.0167
0.750
1.020 1.702
41
962.78
962.03 $ 2,267,518
0.0141
0.750
1.063 1.499
42
962.15
961.40 $ 2,267,518
0.0064
0.750
1.090 0.693
43
961.47
960.72 $ 2,531,228
0.0068
0.750
1.227 0.834
44
960.66
959.91 $ 2,531,228
0.0081
0.750
1.159 0.936
45
959.92
959.17 $ 2,267,518
0.0074
0.750
1.173 0.870
46
959.20
958.45 $ 2,531,228
0.0072
0.750
1.219 0.872
47
958.45
957.70 $ 2,801,613
0.0075
0.750
1.240 0.926
48
957.69
956.94 $ 2,598,213
0.0076
0.750
1.274 0.974
49
956.82
956.07 $ 2,332,799
0.0087
0.750
1.287 1.114
50
955.75
955.00 $ 2,267,518
0.0107
0.750
1.312 1.409
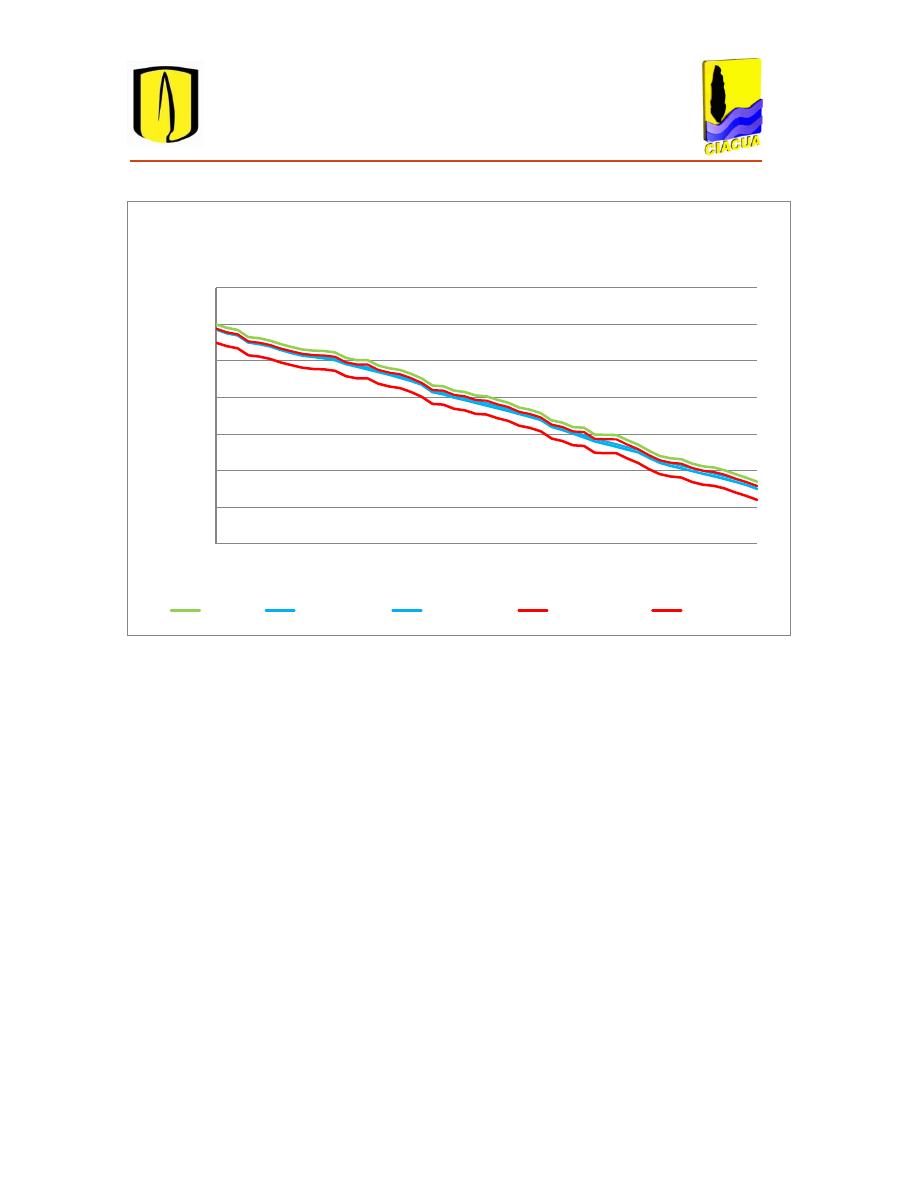
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
60
Figura 4.6 Perfil del diseño óptimo para una serie de 50 tramos para costos totales.
Como se observa en la Figura 4.6, corresponde a aquel que esté más cerca de la superficie,
para lo cual debe tener pendientes similares a las del terreno y en lo posible evitar pendientes
altas que incurran en altos costos de excavación.
4.3 Análisis de costos y tiempos
A continuación se presenta un diseño óptimo para una serie de tramos de un sistema de
alcantarillado, que consta de 12 tramos de 100 m de longitud cada uno y los caudales y cotas de
terreno que se muestran en la Tabla 4.10. Esta serie se evaluará para los dos materiales más
utilizado de tuberías: PVC
y concreto
. Además con estos
mismos datos de entrada, se evaluarán los resultados para series más cortas de 10 y 5 tramos y
para un solo tramo. Esto con el fin de observar la eficiencia del diseño, en cuanto a tiempo y
costos, por medio de las dos metodologías propuestas, en función del número de tramos.
940.00
950.00
960.00
970.00
980.00
990.00
1000.00
1010.00
0.00
500.00 1000.00 1500.00 2000.00 2500.00 3000.00 3500.00 4000.00 4500.00 5000.00
Co
ta
(m
)
Abcisa (m)
Perfil del diseño óptimo
serie de 50 tramos
Terreno
Cota Clave (2)
Cota Batea(2)
Límite superior
Límite inferior

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
61
Tabla 4.10 Datos de entrada de serie 12 tramos.
Pozo
k
Caudal de diseño
Q
k
(m
3
/s)
Cota del terreno
k
(m)
0
0.052
100
1
0.081
99
2
0.117
98
3
0.139
97
4
0.148
95
5
0.155
94
6
0.164
92
7
0.170
92
8
0.180
92
9
0.200
91
10
0.220
91
11
0.240
91
12
0.000
90
Cabe aclarar que el diseño utilizando la metodología de Pendientes Propias (2) se basa en la
variación de las pendientes de diseño, mientras que en el caso de la metodología que aplica el
problema de la ruta más corta (1) se varía la profundidad a la que podría ser instalada la tubería
(cota de batea). De esta forma y para hacer comparables ambos métodos se diseña en primera
medida, variando la cota cada decímetro (dm) que equivale a la variación de la pendiente que
utiliza actualmente el primer método (1/1000), para tramos de 100 m de longitud.
4.2.1 Variación de la pendiente de 1/1000
Tabla 4.11 Diseño de series de tuberías con costos totales y una variación de la pendiente de 1/1000.
Costos Totales - cotas cada dm
No. de
Tramos
Material
Pendientes Propias e
Intermedias
Problema de la ruta más corta
Aceleración en
tiempo
computacional
Ahorro
en costos
(%)
Costo (COP)
Tiempo (s)
Costo (COP)
Tiempo (s)
1
Concreto
$ 1,316,494
0.105
$ 1,302,340
0.008
13.18
1%

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
62
PVC
$ 1,230,613
0.102
$ 1,230,513
0.009
11.28
0%
5
Concreto
$ 7,936,029
0.137
$ 7,752,766
0.203
0.67
2%
PVC
$ 7,508,520
0.121
$ 7,096,347
0.222
0.55
5%
10
Concreto
$ 19,172,687
5.758
$ 18,808,976
0.343
16.79
2%
PVC
$ 18,192,759
3.406
$ 17,279,135
0.376
9.06
5%
12
Concreto
$ 25,123,534
43.785
$ 24,195,077
0.384
114.02
4%
PVC
$ 23,245,550
18.027
$ 22,330,050
0.430
41.92
4%
Tabla 4.12 Diseño de series de tuberías solo con costos tuberías y una variación de la pendiente de 1/1000.
Costos Tuberías - cotas cada dm
No. de
Tramos
Material
Pendientes Propias e
Intermedias
Problema de la ruta más corta Aceleración en
tiempo
computacional
Ahorro
en costos
(%)
Costo (COP)
Tiempo (s)
Costo (COP)
Tiempo (s)
1
Concreto
$ 502,370
0.106
$ 502,237
0.007
15.07
0.03%
PVC
$ 502,294
0.106
$ 502,237
0.008
13.18
0.01%
5
Concreto
$ 3,033,421
0.148
$ 3,032,982
0.237
0.63
0.01%
PVC
$ 2,849,045
0.129
$ 2,848,497
0.206
0.63
0.02%
10
Concreto
$ 6,674,233
44.688
$ 6,673,689
0.478
93.49
0.01%
PVC
$ 6,370,341
13.977
$ 6,369,827
0.466
29.99
0.01%
12
Concreto
$ 8,321,732
314.211
$ 8,321,200
0.613
512.58
0.01%
PVC
$ 7,920,485
75.609
$ 7,919,948
0.591
127.93
0.01%
Tabla 4.13 Diseño de series de tubería solo con costos de excavación y una variación de la pendiente de 1/1000.
Costos Excavación - cotas cada dm
No. de
Tramos
Material
Pendientes Propias e
Intermedias
Problema de la ruta más corta Aceleración en
tiempo
computacional
Ahorro
en
costos
(%)
Costo (COP)
Tiempo (s)
Costo (COP)
Tiempo (s)
1
Concreto
$ 745,689
0.113
$ 731,511
0.008
14.16
1.90%
PVC
$ 728,426
0.156
$ 714,469
0.008
19.53
1.92%
5
Concreto
$ 4,654,539
0.168
$ 4,471,047
0.159
1.06
3.94%
PVC
$ 4,464,190
0.141
$ 4,043,639
0.170
0.83
9.42%

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
63
10
Concreto
$ 11,999,989
5.246
$ 11,630,700
0.260
20.18
3.08%
PVC
$ 11,375,304
3.273
$ 10,403,377
0.285
11.49
8.54%
12
Concreto
$ 16,351,416
42.164
$ 15,191,106
0.293
143.90
7.10%
PVC
$ 14,828,617
17.430
$ 13,826,470
0.323
53.96
6.76%
Figura 4.7 Mejoras en costos computacionales utilizando la nueva metodología (variando la cota cada dm).
La Figura 4.7 presenta las mejoras en costos computacionales utilizando la metodología de la
ruta más corta, teniendo en cuenta que se evalúan más alternativas de diseño. Esto se debe al
lenguaje de programación utilizado (Java) y al orden en que se pide evaluar cada arco. Se encontró
que el costo computacional se reducía drásticamente si se evalúa primero la factibilidad
económica, antes de la hidráulica que requiere más iteraciones. Dicho proceso se presenta en el
Algoritmo 2. Entonces, se encontró que para series de 5 tramos se obtiene un tiempo menor a 1
segundo para obtener el diseño con ambos lenguajes de programación (Visual Basic y Java). Sin
embargo no hay mejoría con la Metodología 2, en este caso. En el caso de las series con mayor
número de tramos se observa un crecimiento exponencial de la aceleración en tiempo, llegando a
ser hasta 93 veces más rápido para la serie de 10 tramos y 512 veces más rápido para la serie de
12 tramos.
Aunque en términos generales ambos programas presentaban tiempos de ejecución muy
buenos, en comparación con programas antiguos que demoraban días obteniendo un diseño que
0.00
100.00
200.00
300.00
400.00
500.00
600.00
0
2
4
6
8
10
12
14
A
ce
le
rac
ió
n
e
n
t
ie
m
p
o
c
o
m
p
u
tac
io
n
al
(M
e
to
d
o
lo
gí
a 1
(s)
/M
e
to
d
o
lo
gí
a 2
(s))
No. De Tramos
Mejoramiento en Costos Computacionales
Cambio de profundidad de a decímetro
Costos de Tuberías-Concreto
Costos de Excavación-Concreto
Costos Totales-Concreto
Costos de Tuberías-PVC
Costos de Excavación-PVC
Costos Totales-PVC

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
64
no llega a ser el óptimo. Sin embargo, esta mejora en tiempo se hace importante para el diseño de
series de más de 10 tramos, donde la Metodología 1 empieza a tomar minutos para obtener un
diseño cercano al óptimo versus un tiempo en milisegundos obteniendo el óptimo global con la
Metodología 2.
Figura 4.8 Mejoras en costos de construcción utilizando la nueva metodología (variando la cota cada dm).
Ahora bien, con respecto a la mejoría en costos de construcción, se puede observar en las
tablas y en la Figura 4.8 que para todos los casos se presenta una disminución en los costos, ya
que como se mencionó el problema de la ruta más corta, asegura encontrar el óptimo realizando
una búsqueda exhaustiva desde un nodo inicial hasta cada uno de los nodos del grafo. En general
se ha encontrado que el ahorro en costos de tuberías es casi nulo, lo cual demuestra que el uso de
Pendientes Propias lleva a los mínimos costos de tuberías. De forma que, el ahorro se presenta por
la reducción de los costos de excavación que llegan a estar entre un 8% a 10%, representando
ahorros hasta del 4% y 5% sobre los costos totales.
Es evidente que un 4% y 5% no son representativos con respecto a los costos totales de este
tipo de proyectos. Esto quiere decir que los diseños realizados bajo los conceptos de Pendientes
Propias e Intermedias son muy buenos, pues están muy cerca al óptimo. Esto se da gracias al uso
de Pendientes Intermedias que buscar asemejarse más a la pendiente del terreno, más que al uso
de Pendientes Propias únicamente.
0.00%
1.00%
2.00%
3.00%
4.00%
5.00%
6.00%
7.00%
8.00%
9.00%
10.00%
0
2
4
6
8
10
12
14
D
ism
in
u
ci
ó
n
e
n
c
o
sto
s (%
)
No. De Tramos
Mejoramiento en Costos
Cambio de profundidad de a decímetro
Costos de Tuberías-Concreto
Costos de Excavación-Concreto
Costos Totales-Concreto
Costos de Tuberías-PVC
Costos de Excavación-PVC
Costos Totales-PVC

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
65
4.2.2 Variación de la pendiente de 1/10,000
En seguida se presentan los resultados para la misma serie de tuberías de alcantarillado, pero
esta vez evaluando los costos constructivos y computacionales variando la profundidad de
instalación (a cota de batea) cada centímetro (cm). Esto amplia el rango de estudio, pues
encuentra una mayor cantidad de alternativas factibles. Esta variación de cota corresponde a una
variación de 1/10,000 de las pendientes en tramos de 100 m, por lo que se evaluará el programa
del CIACUA (Metodología 2) bajo esta condición.
Tabla 4.14 Diseño de series de tuberías con costos totales y una variación de la pendiente de 1/10000.
Costos Totales - cotas cada cm
No. de
Tramos
Material
Pendientes Propias e
Intermedias
Problema de la ruta más corta
Aceleración en
tiempo
computacional
Ahorro
en costos
(%)
Costo (COP)
Tiempo (s)
Costo (COP)
Tiempo (s)
1
Concreto
$ 1,299,575
0.098
$ 1,288,304
0.075
1.30
1%
PVC
$ 1,215,076
0.105
$ 1,214,985
0.078
1.35
0%
5
Concreto
$ 8,278,046
0.133
$ 7,636,621
17.921
0.01
8%
PVC
$ 7,377,751
0.129
$ 7,010,671
19.370
0.01
5%
10
Concreto
$ 19,470,952
6.652
$ 18,178,205
29.930
0.22
7%
PVC
$ 18,311,065
7.258
$ 16,922,310
33.103
0.22
8%
12
Concreto
$ 24,888,892
46.438
$ 23,073,815
32.961
1.41
7%
PVC
$ 23,137,311
38.238
$ 21,745,206
36.513
1.05
6%
Tabla 4.15 Diseño de series de tuberías solo con costos de tuberías y una variación de la pendiente de 1/10000.
Costos Tuberías - cotas cada cm
No. de
Tramos
Material
Pendientes Propias e
Intermedias
Problema de la ruta más corta Aceleración en
tiempo
computacional
Ahorro
en costos
(%)
Costo (COP)
Tiempo (s)
Costo (COP)
Tiempo (s)
1
Concreto
$ 502,369
0.105
$ 502,237
0.072
1.46
0.03%
PVC
$ 502,289
0.090
$ 502,237
0.077
1.17
0.01%
5
Concreto
$ 2,974,917
0.141
$ 2,974,381
12.981
0.01
0.02%
PVC
$ 2,849,013
0.129
$ 2,848,497
13.529
0.01
0.02%
10
Concreto
$ 6,664,222
34.938
$ 6,663,698
23.151
1.51
0.01%
PVC
$ 6,315,207
39.434
$ 6,314,702
25.251
1.56
0.01%
12
Concreto
$ 8,269,494
267.781
$ 8,268,944
26.444
10.13
0.01%

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
66
PVC
$ 7,865,341
327.805
$ 7,864,822
29.337
11.17
0.01%
Tabla 4.16 Diseño de series de tuberías solo con costos de excavación y una variación de la pendiente de 1/10000.
Costos Excavación - cotas cada cm
No. de
Tramos
Material
Pendientes Propias e
Intermedias
Problema de la ruta más corta Aceleración en
tiempo
computacional
Ahorro
en
costos
(%)
Costo (COP)
Tiempo (s)
Costo (COP)
Tiempo (s)
1
Concreto
$ 728,766
0.105
$ 717,475
0.076
1.39
1.55%
PVC
$ 712,883
0.105
$ 700,511
0.078
1.35
1.74%
5
Concreto
$ 5,055,227
0.133
$ 4,354,901
13.086
0.01
13.85%
PVC
$ 4,335,031
0.133
$ 3,956,863
14.276
0.01
8.72%
10
Concreto
$ 12,361,258
6.230
$ 10,999,107
22.219
0.28
11.02%
PVC
$ 11,377,132
6.871
$ 10,046,552
24.604
0.28
11.70%
12
Concreto
$ 16,080,035
43.027
$ 13,201,304
27.380
1.57
17.90%
PVC
$ 14,620,125
47.441
$ 14,151,705
24.359
1.95
3.20%
Figura 4.9 Mejoras en costos computacionales utilizando la nueva metodología (variando la cota cada cm).
0.00
2.00
4.00
6.00
8.00
10.00
12.00
0
2
4
6
8
10
12
14
A
ce
le
rac
ió
n
e
n
t
ie
m
p
o
c
o
m
p
u
tac
io
n
al
(M
e
to
d
o
lo
gí
a 1(
s) /
M
e
to
d
o
lo
gí
a 2(
s))
No. De Tramos
Mejoramiento en Costos Computacionales
Cambio de profundidad de a centímetro
Costos de Tuberías-Concreto
Costos de Excavación-Concreto
Costos Totales-Concreto
Costos de Tuberías-PVC
Costos de Excavación-PVC
Costos Totales-PVC
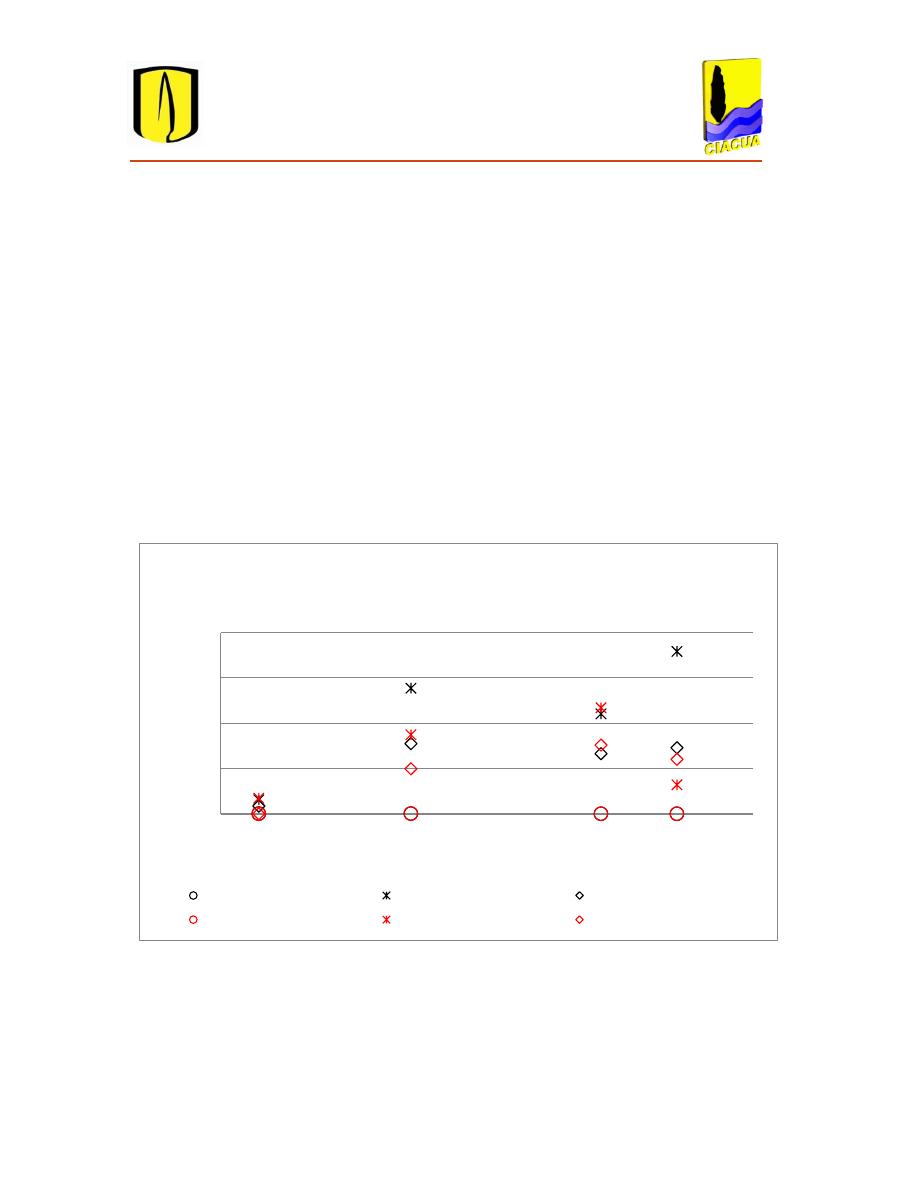
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
67
Con los últimos resultados se observa que se tienen los mismos resultados que antes, con un
orden de magnitud menor. Es decir que, a pesar que se siguen obteniendo tiempos de ejecución
menores para tramos individuales y series de más de 5 tramos, ya no se hace tan notoria la
diferencia en costos computacionales. La aceleración en costos computacionales llega a ser de
hasta 11 veces más rápido si se evalúan solo costos de tuberías en series de 12 tramos, mientras
que cuando se evalúan los costos totales o los de excavación solo se alcanzan aceleraciones del
tiempo de 1 y 2 veces más rápido, respectivamente.
Comparando las mejoras en costos computacionales, diseñando cada centímetro (cm) versus
cada decímetro (dm), se observa que con la Metodología 1 el cambio de pendientes no afecta el
tiempo de ejecución, para cada número de tramos evaluados y tipos de costos analizados se
obtienen los mismos tiempos aproximadamente. Incluso llegan a ser un poco mayores diseñando
cada dm en ciertos casos. Con la Metodología 2 si se puede apreciar una diferencia en el tiempo
que pasa de arrojar el resultado en milisegundos (diseñando cada dm) a durar aproximadamente
30 segundos (diseñando cada cm).
Figura 4.10 Mejoras en costos de construcción utilizando la nueva metodología (variando la cota cada cm).
Con respecto al ahorro en costos sucede lo contrario, al evaluar profundidades cada
centímetro es más probable encontrar mayor ahorro. En este caso se alcanza un ahorro en costos
de excavación entre 13% y 17% lo que se traduce en un ahorro de hasta el 8% sobre los costos
0%
5%
10%
15%
20%
0
2
4
6
8
10
12
14
D
ism
in
u
ci
ó
n
e
n
c
o
sto
s (%
)
No. De Tramos
Mejoramiento en Costos
Cambio de profundidad de a centímetro
Costos de Tuberías-Concreto
Costos de Excavación-Concreto
Costos Totales-Concreto
Costos de Tuberías-PVC
Costos de Excavación-PVC
Costos Totales-PVC

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
68
totales. En cuanto a los costos de tuberías se sigue manteniendo el hecho de que el ahorro es casi
nulo.
Tras el análisis de todas las series se hace evidente que el número de arcos factibles se va
reduciendo después del primer tramo, ya que se da un proceso de poda que evita que salgan arcos
de nodos a los cuales no les llega al menos un arco factible. Como se ha mencionado, los arcos no
se consideran factibles si no cumplen con absolutamente todas las restricciones.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
69
5 CONCLUSIONES
La metodología de diseño de series de tuberías en sistemas de alcantarillado cumple con
el objetivo general, pues asegura el óptimo global desde el punto de vista económico,
teniendo en cuenta los aspectos hidráulicos que aseguren el adecuado funcionamiento del
sistema, con base en las normas colombianas: Reglamento Técnico del Sector de Agua
Potable y Saneamiento Básico – RAS (2000).
Los problemas de ruta más corta ayudan a resolver problemas de tipo NP-duros en un
tiempo polinómico.
El uso del algoritmo de Bellman-Ford para etiquetar los nodos, permite establecer la ruta
más cota mientras se genera el grafo que representa la serie de tuberías de un sistema de
alcantarillado.
El grafo que representa la serie de tuberías está conformado por nodos
, que
representan una combinación diámetro
-cota
y arcos
que
representan las tuberías y tienen asociado un diámetro
, una pendiente
y un costo
.
La solución del grafo se busca desde el nodo final que es el nodo de mínimo costo del
último pozo de inspección, hacia aguas arriba, buscando los nodos predecesores que
conforman la ruta más corta (la serie de mínimo costo), hasta llegar al pozo de inspección
inicial.
Al evaluar los diseños con los tres tipos de costos, se rectificó que la mayor influencia
sobre los costos totales se da por los costos de construcción. Además para ambos casos las
pendientes de diseño tienden a ser las mismas y buscan asemejarse a las pendientes del
terreno.
La Potencia Específica para un diseño evaluado solo para costos de tuberías puede es en
promedio 2.5 veces, la Potencia Específica para diseños evaluados solo con costos de
excavación o con costos totales.
El diseño óptimo de series de tuberías de alcantarillado se encuentra con la mínima
Potencia Específica posible en cada tramo. Por el contrario, el diseño óptimo evaluando
solo costos de tuberías, tiende a maximizar la Potencia Específica.
El diseño de series de tuberías de alcantarillado utilizando el concepto de Pendientes
Propias elimina muchas alternativas de diseño factibles y no minimiza los costos de
excavación, por la que no conduce al diseño óptimo. Sin embargo, la implementación de
las Pendientes Intermedias y de terreno en el diseño ayudan a reducir dichos costos de
excavación, lo que genera un diseño muy cercano al óptimo.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
70
El porcentaje de ahorro en costos depende de una serie de factores, de los cuales el que
más puede influir es la topografía del terreno que afecta los volúmenes de excavación.
Con la nueva metodología se reducen en mayor porcentaje los costos de excavación,
mientras que la disminución de costos de tuberías es casi nula. Esto representa una
disminución en cotos totales, cuya función de costos tiene el mismo comportamiento que
los costos de excavación. Esto comprueba lo mencionado anteriormente, que la
metodología de Pendientes Propias e Intermedias minimiza los costos de tuberías,
descuidando un poco los de excavación, pero dando un resultado muy cercano al óptimo.
Los costos computacionales se reducen de forma importante para series de tuberías de
más de 12 tramos aproximadamente, donde el tiempo de ejecución del algoritmo empieza
a crecer exponencialmente.
La precisión del diseño afecta tanto los costos como los tiempos de ejecución del
algoritmo; sin embargo para la primera metodología estos tiempos no parecen variar en
función de la precisión del diseño. A veces incluso, se presentan mayores tiempos para
menores precisiones lo que no tiene mucho sentido, ya que se están evaluando menos
pendientes por tramo y por lo tanto el número de alternativas debe ser menor según la
Ecuación 2.21. Por el contrario con la segunda metodología si se presenta un aumento
significativo al aumentar la precisión de decímetros a centímetros, pues se pasa de un
tiempo en milisegundos a casi medio minuto.
Se encontró que el costo computacional se reduce drásticamente si se evalúa primero la
factibilidad económica, antes de la hidráulica que consume más tiempo de ejecución, por
el número de iteraciones que realiza.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
71
6 BIBLIOGRAFÍA
Java (lenguaje de programación). (15 de 12 de 2013). Obtenido de Wikipedia:
http://es.wikipedia.org/wiki/Java_(lenguaje_de_programaci%C3%B3n)
Máquina
virtual
Java.
(11
de
10
de
2013).
Obtenido
de
Wikipedia:
http://es.wikipedia.org/wiki/M%C3%A1quina_virtual_Java
Ahuja, R. K., & et Al. (1993). Network Flows: Theory, Algorithms, and Applications. New Jersey:
Prentice-Hall.
ASCE, A. S. (2007). Gravity Sanitary Sewer: Design and Construction. Reston.
Bellman, R. (20 de Diciembre de 1956). On a Routing Problem.
Branco, S. (1984). Limnología sanitaria, estudio de la polución de aguas continentales. (OEA, Ed.)
Butler, D., & Davies, J. (2011). Urban Drainage (Third Edition ed.). New York: Spon Press.
CIACUA. (2013). Diseño Optimizado en Redes de Alcantarillado: Desarrollo de Técnicas
Computacionales Exhaustivas para el Diseño Optimizado de Redes de Drenaje Urbano.
Bogotá: Universidad de Los Andes.
Copete, D. (2012). Diseño Hidráulico Optimizado de Redes de Alcantarillado Usando los Conceptos
de de Potencia Unitaria y Pendiente Lógica. Bogotá: Universidad de los Andes.
Corrales, E., Cuero, P., & et al. (2013). Metodología de Diseño Optimizado de Series de Tramos de
Alcantarillado Utilizando los Conceptos de Pendiente Propia y Pendiente Intermedia.
Bogotá: Universidad de los Andes.
Engineers, A. S. (2007). Gravity Sanitary Sewer: Design and Construction. Reston.
Goldberg, A., & Radzik, T. (1993). A Heuristic improvement of the Bellman-Ford Algorithm. Gran
betaña.
Hutson, K., Schlosser, T., & Shier, D. (2011). On the Distributed Bellman-Ford Algorithm and the
Looping Problem. INFORMS Journal on Computing ISSN 1091-9856, 19, 542–551.
Jiménez, C. (2010). Clase de algorítmica y programación orientada a objetos I. Bogotá, Colombia:
Universidad de los Andes.

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
72
López, A. (2012). Diseño Optimizado de Redes de Drenaje Urbano Usando el Concepto de Potencia
Unitaria. Bogotá: Universidad de los Andes.
MIT: Massachusetts Institute of Technology. (2011). Introduction to Algorithms: Bellman-Ford
Algorithm. MIT Open Courses. Massachusetts.
Muth, C., Brinson, L., & Bernhar, E. (2010). Inquiry-based exploration of human impacts on stream
ecosystems: The Mud Creek case study. LEARN NC. Chapel Hill, North Carolina, United
States:
University
of
North
Carolina
at
Chapel
Hill
.
Obtenido
de
http://www.learnnc.org/lp/editions/mudcreek/6394
Navarro, I. (2009). Diseño Optimizado de Redes de Drenaje Urbano. Bogotá: Uniersidad de los
Andes.
PAVCO. (2013). Lista de referencia de precios Tubosistemas. Recuperado el 05 de 12 de 2013, de
http://pavco.com.co/files/data/20130926115937_s.pdf
RAS. (2000). Reglamento Técnico del Sector de Agua Potable y Saneamineto Básico. Ministerio de
Desarrollo Económico: Dirección de Agua Potable y Saneamineto Básico.
Salcedo, C. (2012). Diseño optimizado de sistemas de alcantarillado utilizando los conceptos de
resiliencia y potencia unitaria. Bogotá: Universidad de Los Andes.
Saldarriaga, J. (2007). Hidráulica de tuberías: abastecimiento de agua, redes, riegos. Bogotá:
Alfaomega.
Saldarriaga, J. (2012). Clase de Hidráulica. Bogotá, Colombia: Universidad de los Andes.
Saldarriaga, J. (2013). Clase de Sistemas Integrados de Drenaje Urbano. Bogotá, Colombia:
Universidad de los Andes.
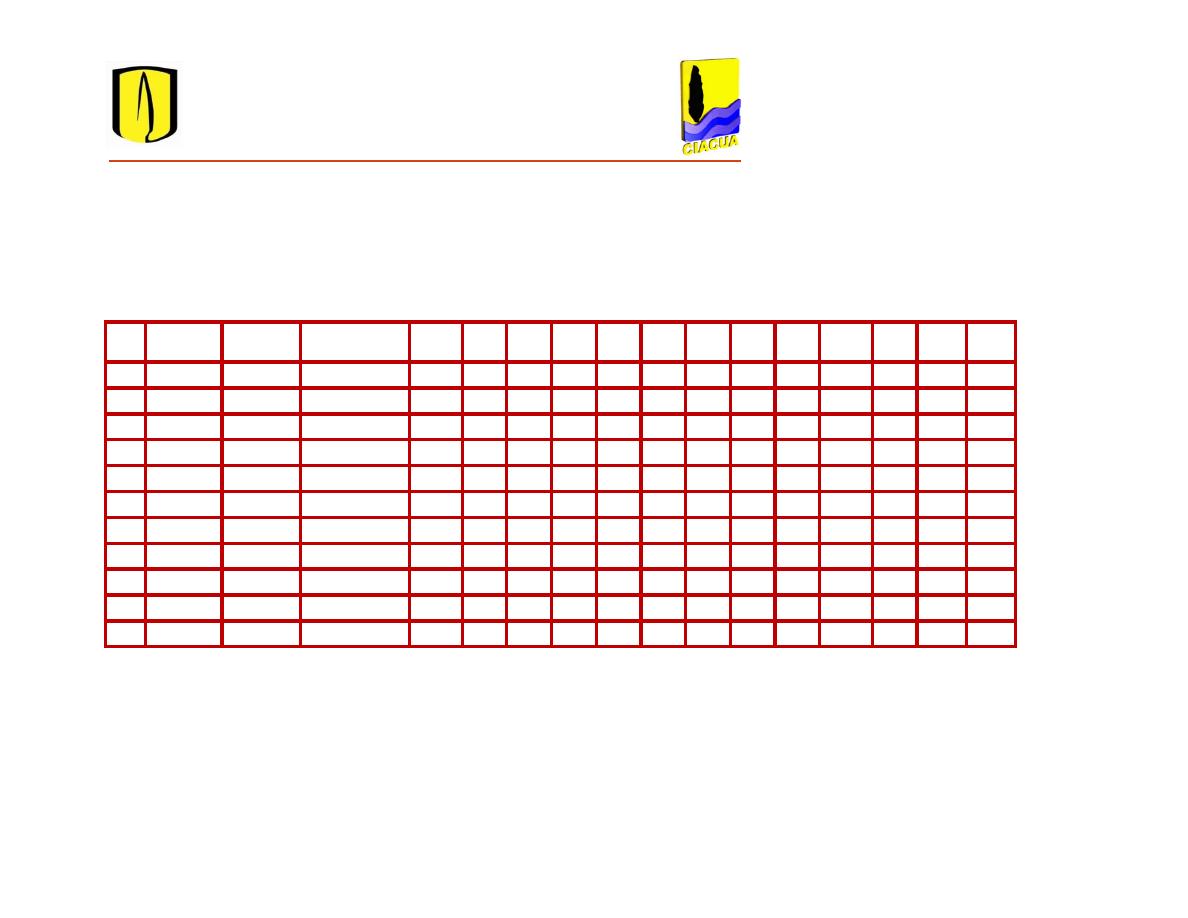
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
73
7 ANEXOS
Tabla 7.1 Cálculo de la hidráulica Ejemplo 1 – Metodología 1
Pozo
Cota Clave
(m)
Cota Batea
(m)
Costo Tramo
(COP)
(-)
(m)
(-)
(m)
(-)
(m
2
)
(m)
(m)
(m/s)
(Pa)
(-)
(m
3
/s)
(m
2
/s)
0
98.80
98.40
1
98.72
98.32 $ 1,850,882 0.0008 0.400 0.694 0.278 3.939 0.093 0.788 0.118 0.623 0.927 0.396 0.058 0.005
2
98.35
97.95 $ 1,993,066 0.0037 0.400 0.695 0.278 3.943 0.093 0.789 0.118 1.367 4.291 0.868 0.128 0.047
3
98.17
97.72 $ 2,367,559 0.0023 0.450 0.699 0.315 3.960 0.119 0.891 0.133 1.157 3.006 0.689 0.137 0.032
4
97.77
97.32 $ 2,629,029 0.0040 0.450 0.696 0.313 3.948 0.118 0.888 0.133 1.532 5.222 0.915 0.181 0.072
5
96.86
96.41 $ 3,240,601 0.0091 0.450 0.700 0.315 3.963 0.119 0.892 0.133 2.327 11.898 1.384 0.277 0.252
6
96.92
96.24 $ 4,999,219 0.0017 0.675 0.715 0.483 4.032 0.274 1.361 0.201 1.282 3.357 0.611 0.351 0.060
7
96.70
96.02 $ 5,100,758 0.0022 0.675 0.794 0.536 4.397 0.305 1.484 0.205 1.480 4.429 0.633 0.451 0.099
8
96.58
95.83 $ 5,758,277 0.0019 0.750 0.782 0.587 4.342 0.371 1.628 0.228 1.465 4.245 0.604 0.543 0.103
9
96.33
95.58 $ 5,986,000 0.0025 0.750 0.797 0.598 4.415 0.378 1.656 0.228 1.686 5.594 0.680 0.637 0.159
10
96.23
95.40 $ 6,717,426 0.0018 0.825 0.794 0.655 4.400 0.455 1.815 0.251 1.513 4.430 0.585 0.689 0.124
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
74
Tabla 7.2 Cálculo de la hidráulica Ejemplo 1 – Metodología 2
Pozo
Cota Clave
(m)
Cota Batea
(m)
Costo Tramo
(COP)
(-)
(m)
(-)
(m)
(-)
(m
2
)
(m)
(m)
(m/s)
(Pa)
(-)
(m
3
/s)
(m
2
/s)
0
98.80
98.40
1
98.71
98.31 $ 1,853,700 0.0009 0.400 0.671 0.268 3.839 0.090 0.768 0.117 0.647 1.001 0.423 0.058 0.005
2
98.53
98.08 $ 2,105,125 0.0024 0.450 0.690 0.311 3.922 0.117 0.882 0.133 1.167 3.065 0.703 0.137 0.032
3
98.29
97.84 $ 2,259,089 0.0024 0.450 0.692 0.311 3.930 0.117 0.884 0.133 1.169 3.074 0.702 0.137 0.032
4
98.13
97.63 $ 2,620,025 0.0021 0.500 0.821 0.411 4.538 0.173 1.135 0.152 1.204 3.158 0.573 0.208 0.044
5
98.05
97.45 $ 3,200,693 0.0018 0.600 0.787 0.472 4.364 0.239 1.309 0.182 1.231 3.169 0.564 0.294 0.052
6
97.98
97.30 $ 3,605,630 0.0015 0.675 0.749 0.506 4.186 0.288 1.413 0.204 1.221 3.042 0.556 0.351 0.053
7
97.91
97.16 $ 3,958,344 0.0014 0.750 0.755 0.566 4.212 0.358 1.580 0.227 1.259 3.158 0.540 0.451 0.064
8
97.72
96.97 $ 4,082,960 0.0019 0.750 0.785 0.589 4.356 0.372 1.634 0.228 1.460 4.215 0.600 0.543 0.102
9
97.38
96.63 $ 4,350,057 0.0034 0.750 0.784 0.588 4.351 0.372 1.632 0.228 1.964 7.560 0.808 0.730 0.247
10
96.99
96.24 $ 4,760,487 0.0039 0.750 0.699 0.524 3.960 0.330 1.485 0.222 2.088 8.583 0.963 0.689 0.271
Tabla 7.3 Cálculo de la hidráulica Ejemplo 2 – Metodología 2
Pozo
Cota Clave
(m)
Cota Batea
(m)
Costo Tramo
(COP)
(-)
(m)
(-)
(m)
(-)
(m
2
)
(m)
(m)
(m/s)
(Pa)
(-)
(m
3
/s)
(m
2
/s)
0
998.80
998.60
1
997.75
997.55 $ 1,128,529 0.0105 0.20 0.482 0.096 3.070 0.015 0.307 0.049 1.654 5.027 1.928 0.025 0.026
2
997.22
996.97 $ 1,299,320 0.0058 0.25 0.613 0.153 3.600 0.032 0.450 0.070 1.507 3.966 1.337 0.048 0.027
3
995.26
995.01 $ 1,299,321 0.0196 0.25 0.521 0.130 3.225 0.026 0.403 0.064 2.786 12.350 2.765 0.072 0.141
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
75
Pozo
Cota Clave
(m)
Cota Batea
(m)
Costo Tramo
(COP)
(-)
(m)
(-)
(m)
(-)
(m
2
)
(m)
(m)
(m/s)
(Pa)
(-)
(m
3
/s)
(m
2
/s)
4
994.94
994.59 $ 1,617,172 0.0042 0.35 0.651 0.228 3.757 0.066 0.657 0.101 1.606 4.164 1.150 0.107 0.045
5
994.29
993.94 $ 1,651,639 0.0065 0.35 0.652 0.228 3.761 0.066 0.658 0.101 2.038 6.435 1.457 0.135 0.088
6
993.31
992.96 $ 1,651,639 0.0098 0.35 0.663 0.232 3.807 0.068 0.666 0.102 2.560 9.751 1.806 0.173 0.169
7
992.51
992.11 $ 1,835,807 0.0085 0.40 0.572 0.229 3.432 0.074 0.686 0.108 2.472 9.049 1.821 0.184 0.157
8
991.87
991.42 $ 2,026,515 0.0069 0.45 0.577 0.260 3.452 0.095 0.777 0.122 2.382 8.276 1.644 0.227 0.156
9
991.60
991.10 $ 2,179,380 0.0033 0.50 0.803 0.401 4.442 0.169 1.110 0.152 1.823 4.886 0.894 0.308 0.101
10
991.20
990.70 $ 2,315,595 0.0040 0.50 0.665 0.332 3.813 0.139 0.953 0.145 1.976 5.707 1.165 0.274 0.110
11
990.72
990.22 $ 2,501,958 0.0047 0.50 0.656 0.328 3.774 0.136 0.944 0.145 2.156 6.699 1.285 0.294 0.139
12
989.64
989.14 $ 2,361,689 0.0109 0.50 0.520 0.260 3.222 0.103 0.806 0.128 3.142 13.660 2.207 0.324 0.352
13
988.92
988.42 $ 2,224,435 0.0071 0.50 0.622 0.311 3.634 0.128 0.909 0.141 2.656 9.863 1.648 0.341 0.243
14
988.22
987.72 $ 2,597,078 0.0071 0.50 0.661 0.331 3.799 0.138 0.950 0.145 2.692 10.067 1.593 0.371 0.262
15
987.45
986.95 $ 2,597,078 0.0077 0.50 0.678 0.339 3.869 0.142 0.967 0.146 2.832 11.031 1.642 0.401 0.308
16
986.70
986.20 $ 2,269,842 0.0075 0.50 0.692 0.346 3.931 0.145 0.983 0.148 2.802 10.808 1.596 0.406 0.303
17
985.87
985.37 $ 2,454,876 0.0084 0.50 0.707 0.353 3.993 0.148 0.998 0.149 2.992 12.177 1.674 0.444 0.371
18
985.03
984.53 $ 2,549,361 0.0084 0.50 0.768 0.384 4.273 0.162 1.068 0.151 3.043 12.519 1.569 0.492 0.415
19
984.01
983.51 $ 2,315,595 0.0101 0.50 0.743 0.371 4.156 0.156 1.039 0.151 3.350 14.966 1.788 0.524 0.531
20
981.95
981.45 $ 2,224,435 0.0206 0.50 0.586 0.293 3.489 0.120 0.872 0.137 4.642 27.732 3.007 0.556 1.145
21
981.47
980.87 $ 2,804,362 0.0058 0.60 0.684 0.410 3.893 0.206 1.168 0.176 2.747 10.111 1.444 0.566 0.331
22
980.59
979.99 $ 2,858,538 0.0087 0.60 0.617 0.370 3.614 0.183 1.084 0.169 3.324 14.473 1.894 0.609 0.532

Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
76
Pozo
Cota Clave
(m)
Cota Batea
(m)
Costo Tramo
(COP)
(-)
(m)
(-)
(m)
(-)
(m
2
)
(m)
(m)
(m/s)
(Pa)
(-)
(m
3
/s)
(m
2
/s)
23
979.89
979.29 $ 2,858,538 0.0070 0.60 0.675 0.405 3.858 0.203 1.157 0.176 3.018 12.039 1.603 0.613 0.429
24
979.15
978.55 $ 2,913,079 0.0074 0.60 0.668 0.401 3.827 0.201 1.148 0.175 3.114 12.763 1.668 0.625 0.465
25
978.43
977.83 $ 3,078,840 0.0072 0.60 0.697 0.418 3.950 0.210 1.185 0.177 3.094 12.577 1.600 0.651 0.470
26
977.67
977.07 $ 3,247,705 0.0076 0.60 0.700 0.420 3.963 0.211 1.189 0.178 3.174 13.180 1.635 0.671 0.507
27
976.91
976.31 $ 3,134,790 0.0077 0.60 0.712 0.427 4.015 0.215 1.205 0.179 3.207 13.424 1.628 0.690 0.529
28
976.08
975.48 $ 2,858,539 0.0083 0.60 0.717 0.430 4.038 0.217 1.211 0.179 3.347 14.516 1.687 0.726 0.600
29
975.29
974.69 $ 2,697,129 0.0079 0.60 0.760 0.456 4.233 0.230 1.270 0.181 3.291 14.042 1.567 0.758 0.598
30
974.44
973.84 $ 2,750,557 0.0085 0.60 0.745 0.447 4.165 0.226 1.249 0.181 3.413 15.028 1.659 0.771 0.653
31
972.59
971.99 $ 2,644,082 0.0185 0.60 0.557 0.334 3.372 0.162 1.012 0.160 4.827 29.073 2.956 0.782 1.447
32
971.73
971.13 $ 2,697,129 0.0086 0.60 0.765 0.459 4.258 0.232 1.277 0.182 3.460 15.395 1.636 0.803 0.694
33
970.71
970.11 $ 2,697,129 0.0102 0.60 0.737 0.442 4.129 0.223 1.239 0.180 3.760 17.978 1.846 0.840 0.854
34
969.67
969.07 $ 3,078,840 0.0104 0.60 0.760 0.456 4.234 0.230 1.270 0.181 3.824 18.523 1.821 0.881 0.917
35
968.59
967.99 $ 3,134,789 0.0108 0.60 0.766 0.460 4.265 0.232 1.279 0.182 3.914 19.332 1.847 0.910 0.987
36
967.96
967.28 $ 3,311,177 0.0070 0.68 0.728 0.492 4.089 0.279 1.380 0.202 3.315 13.983 1.552 0.925 0.652
37
967.21
966.54 $ 4,135,233 0.0074 0.68 0.735 0.496 4.119 0.282 1.390 0.203 3.415 14.765 1.586 0.962 0.714
38
966.41
965.73 $ 4,201,014 0.0081 0.68 0.717 0.484 4.039 0.275 1.363 0.201 3.563 15.985 1.693 0.978 0.791
39
965.69
965.01 $ 3,495,984 0.0072 0.68 0.762 0.514 4.245 0.293 1.433 0.204 3.374 14.426 1.510 0.987 0.711
40
964.22
963.54 $ 3,070,158 0.0147 0.68 0.587 0.396 3.493 0.218 1.179 0.185 4.668 26.698 2.600 1.020 1.498
41
962.81
962.13 $ 2,952,061 0.0141 0.68 0.612 0.413 3.594 0.230 1.213 0.189 4.629 26.191 2.502 1.063 1.499
42
961.97
961.30 $ 3,070,158 0.0084 0.68 0.774 0.523 4.304 0.297 1.453 0.205 3.664 16.792 1.611 1.090 0.911
43
961.37
960.62 $ 3,737,698 0.0068 0.75 0.694 0.520 3.937 0.327 1.476 0.222 3.442 14.772 1.598 1.126 0.765
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados-CIACUA
“
Diseño optimizado de series de tuberías en sistemas de alcantarillado
”
77
Pozo
Cota Clave
(m)
Cota Batea
(m)
Costo Tramo
(COP)
(-)
(m)
(-)
(m)
(-)
(m
2
)
(m)
(m)
(m/s)
(Pa)
(-)
(m
3
/s)
(m
2
/s)
44
960.66
959.91 $ 3,670,302 0.0071 0.75 0.698 0.523 3.954 0.329 1.483 0.222 3.521 15.401 1.627 1.159 0.820
45
959.92
959.17 $ 3,339,607 0.0074 0.75 0.691 0.518 3.925 0.326 1.472 0.221 3.604 16.084 1.679 1.173 0.870
46
959.20
958.45 $ 3,603,317 0.0072 0.75 0.722 0.542 4.063 0.342 1.524 0.224 3.566 15.741 1.597 1.219 0.872
47
958.45
957.70 $ 3,873,702 0.0075 0.75 0.719 0.539 4.047 0.340 1.518 0.224 3.648 16.414 1.640 1.240 0.926
48
957.69
956.94 $ 3,670,302 0.0076 0.75 0.728 0.546 4.086 0.344 1.532 0.225 3.701 16.853 1.646 1.274 0.974
49
956.82
956.07 $ 3,404,888 0.0087 0.75 0.695 0.521 3.944 0.328 1.479 0.222 3.925 18.826 1.819 1.287 1.114
50
955.75
955.00 $ 3,339,607 0.0107 0.75 0.647 0.485 3.739 0.302 1.402 0.216 4.336 22.738 2.131 1.312 1.409
