
UNIVERSIDAD DE LOS ANDES
FACULT AD DE INGENIERÍA
DEPART AMENTO DE INGENIERÍA CIVIL Y AMBIENT AL
PROYECTO DE GRADO
MAESTRÍA EN INGENIERÍA CIVIL
RECURSOS HÍDRICOS E HIDROINFORMÁTICA
OPTIMIZACIÓN DEL DISEÑO DE LOS TRAZADOS DE SISTEMAS DE DRENAJE URBANO
BASADO EN CRITERIO ECONÓMICO
PRESENTADO POR:
DANIEL ANDRÉS LÓPEZ SABOGAL
ASESOR:
JUAN SALDARRIAGA
BOGOTÁ D.C, JUNIO 2014

El presente trabajo corresponde al Proyecto de Grado con el cual se culmina el ciclo de estudios de
la Maestría en Ingeniería Civil, en el área de Recursos Hídricos e Hidroinformática, en la
Universidad de los Andes, Bogotá, Colombia.

A Juan Saldarriaga un agradecimiento especial por haberme guiado,
no solo en el presente trabajo, si no a lo largo de toda la Maestria.
Gracias por inculcar en mi el amor hacia la academia.
A Diego Páez, gracias por su asesoría y consejos
para el desarrollo del presente trabajo.
A Daniel Luna, gracias por su amistad y su apoyo, vital para la
consecución de la finalización tanto de la Maestría como del
presente trabajo.
A mis Padres y Hermanos, por ser los pilares de mi vida, porque
sin ellos nada de lo que he conseguido hubiera sido posible.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
i
Contenido
Lista de Figuras........................................................................................................................ iii
Lista de Tablas ......................................................................................................................... iv
1.
INTRODUCCIÓN ............................................................................................................. 1
1.1.
Objetivos ................................................................................................................... 2
1.1.1.
Objetivo general.................................................................................................. 2
1.1.2.
Objetivos específicos ........................................................................................... 2
2.
MARCO TEÓRICO........................................................................................................... 3
2.1.
Sistema Integrado de Drenaje Urbano .......................................................................... 3
2.1.1.
Drenaje Urbano................................................................................................... 3
2.1.2.
Historia .............................................................................................................. 3
2.1.3.
Actualidad .......................................................................................................... 4
2.2.
Componentes de los Sistemas Integrados de Drenaje Urbano ......................................... 6
2.2.1.
Redes de drenaje ................................................................................................. 6
2.2.2.
Plantas de Tratamiento de Aguas Residuales (PTAR) ............................................ 7
2.2.3.
Cuerpo receptor .................................................................................................. 8
2.3.
Tipos de redes en los Sistemas Integrados de Drenaje Urbano ........................................ 8
2.4.
Fallas de los Sistemas Integrados de Drenaje Urbano .................................................... 9
2.4.1.
Fallas en las redes de drenaje urbano .................................................................... 9
2.4.2.
Fallas en la PTAR ..............................................................................................11
2.5.
Normatividad Colombiana sobre Sistemas de Drenaje Urbano ......................................11
2.5.1.
Redes de drenaje urbano sanitario........................................................................12
2.5.2.
Redes de drenaje urbano pluvial ..........................................................................17
2.5.3.
Redes de drenaje urbano combinado ....................................................................18
2.6.
Diseño hidráulico de los tramos de las redes de los Sistemas Integrados de Drenaje
Urbano18
2.6.1.
Geometría hidráulica ..........................................................................................19
2.6.2.
Cálculo de la velocidad de flujo ..........................................................................20
2.6.3.
Obtención de diámetros y pendientes ...................................................................21
2.6.4.
Suposición de flujo uniforme ..............................................................................21
2.7.
Aproximaciones a la optimización del diseño hidráulico de las redes de los Sistemas
Integrados de Drenaje Urbano ...............................................................................................22
2.8.
Aproximaciones a la optimización de un trazado dado de una red del Sistema Integrado de
Drenaje Urbano ....................................................................................................................24
2.9.
Metodología del ‘camino más corto’ ...........................................................................25
2.9.1.
Metodología de Bellman Ford .............................................................................26
2.9.2.
Metodología de Dijkstra .....................................................................................26
3.
METODOLOGÍA .............................................................................................................28
3.1.
Implementación de Dijkstra........................................................................................28
3.2.
Generación del ‘árbol cerrado’....................................................................................29
3.2.1.
Definición del ‘árbol cerrado’ .............................................................................29

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
ii
3.2.2.
Descripción del proceso operativo .......................................................................30
3.2.3.
Tipos de frentes de avance ..................................................................................32
3.2.4.
Diseño ...............................................................................................................33
3.2.5.
Verificación de las cotas de batea ........................................................................34
3.3.
Parámetros de optimización........................................................................................34
3.3.1.
Función objetivo ................................................................................................34
3.3.2.
Variables de decisión..........................................................................................36
3.3.3.
Restricciones .....................................................................................................37
4.
RESULTADOS ................................................................................................................38
4.1.
Red tipo 3x3..............................................................................................................39
4.1.1.
Terreno plano.....................................................................................................39
4.1.2.
Terreno a favor del drenaje .................................................................................40
4.1.3.
Terreno con topografía variable...........................................................................41
4.2.
Red tipo 4x4..............................................................................................................42
4.2.1.
Terreno plano.....................................................................................................43
4.2.2.
Terreno a favor del drenaje .................................................................................45
4.2.3.
Terreno con topografía variable...........................................................................46
4.3.
Red tipo 5x5..............................................................................................................48
4.3.1.
Terreno plano.....................................................................................................48
4.3.2.
Terreno a favor del drenaje .................................................................................50
4.3.3.
Terreno con topografía variable...........................................................................52
4.4.
Gasto computacional..................................................................................................54
5.
CONCLUSIONES Y RECOMENDACIONES ...................................................................56
6.
BIBLIOGRAFÍA ..............................................................................................................57

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
iii
Lista de Figuras
Figura 1. Pérdida de la capacidad hidráulica como consecuencia de los sedimentos. .....................10
Figura 2. Relaciones hidráulicas para una sección circular. Tomado de (López Sabogal, 2012). .....10
Figura 3. Características de una sección circular fluyendo parcia lmente llena. ..............................19
Figura 4. Ejemplo de un grafo. ..................................................................................................25
Figura 5. Representación de una red como un grafo. ...................................................................28
Figura 6. Detalle del grafo.........................................................................................................29
Figura 7. Ejemplo de árbol y 'árbol cerrado'. ..............................................................................29
Figura 8. Ejemplo del proceso operativo de la metodología. ........................................................31
Figura 9. Tipos de frente de avance. ..........................................................................................32
Figura 10. Profundidad mínima y máxima..................................................................................34
Figura 11. Proyección del trapecio que produce el área excavada para una tubería. Tomado de
(Saldarriaga, y otros, Desarrollo de Técnicas Computacionales Exhaustivas para el Diseño
Optimizado de Redes de Drenaje Urbano, 2013) ........................................................................36
Figura 12. Relación de costos en un proyecto de drenaje urbano. Tomado de (Saldarriaga, y otros,
Desarrollo de Técnicas Computacionales Exhaustivas para el Diseño Optimizado de Redes de
Drenaje Urbano, 2013). ............................................................................................................37
Figura 13. Convenciones de los resultados. ................................................................................38
Figura 14. Esquema de la red tipo 3x3. ......................................................................................39
Figura 15. Red para terreno plano. 3x3. .....................................................................................40
Figura 16. Red para terreno a favor del drenaje. 3x3. ..................................................................41
Figura 17. Red para terreno con topografía variable. 3x3. ............................................................42
Figura 18. Esquema de la red tipo 4x4. ......................................................................................43
Figura 19. Red para terreno plano. 4x4. .....................................................................................44
Figura 20. Red para terreno a favor de drenaje. 4x4. ...................................................................45
Figura 21. Red para terreno con topografía variable. 4x4 .............................................................47
Figura 22. Esquema de la red tipo 5x5. ......................................................................................48
Figura 23. Red para terreno plano. 5x5. .....................................................................................49
Figura 24. Red para terreno a favor del drenaje. 5x5. ..................................................................51
Figura 25. Red para terreno con topografía variable. 5x5.............................................................53

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
iv
Lista de Tablas
Tabla 1. Asignación del nivel de complejidad (RAS, 2000). ........................................................12
Tabla 2. Valores recomendados para el consumo diario per cápita y el coeficiente de retorno (RAS,
2000). ......................................................................................................................................12
Tabla 3. Aporte de industrias pequeñas, en zonas residenciales (RAS, 2000). ...............................13
Tabla 4. Aportes de conexiones erradas (RAS, 2000). .................................................................13
Tabla 5. Tasas de infiltración dependiendo las variables que la afectan (RAS, 2000). ....................14
Tabla 6. Velocidades mínimas como función de la DBO (RAS, 2000). ........................................15
Tabla 7. Velocidades máximas (RAS, 2000). .............................................................................17
Tabla 8. Metodología de diseño de los sistemas de drenaje urbano. Tomado de (Burian & Edwards,
Historical Perspectives of Urban Drainage, 2002). ......................................................................22
Tabla 9. Información de las cámaras. 3x3. ..................................................................................39
Tabla 10. Resultado diseño terreno plano. 3x3. ...........................................................................40
Tabla 11. Información de las cámaras. 3x3. ................................................................................40
Tabla 12. Resultado diseño terreno a favor del drenaje. 3x3. .......................................................41
Tabla 13. Información de las cámaras. 3x3. ................................................................................41
Tabla 14. Resultado diseño terreno con topografía variable. 3x3. .................................................42
Tabla 15. Información de las cámaras. 4x4. ................................................................................43
Tabla 16. Resultado diseño terreno plano. 4x4. ...........................................................................44
Tabla 17. Información de las cámaras. 4x4. ................................................................................45
Tabla 18. Resultado diseño terreno a favor de drenaje. 4x4. ........................................................46
Tabla 19. Información de las cámaras. 4x4. ................................................................................46
Tabla 20. Resultado diseño terreno con topografía variable. 4x4. .................................................47
Tabla 21. Información de las cámaras. 5x5. ................................................................................48
Tabla 22. Resultado diseño terreno plano. 5x5. ...........................................................................49
Tabla 23. Información de las cámaras. 5x5. ................................................................................50
Tabla 24. Resultado diseño terreno a favor del drenaje. 5x5. .......................................................51
Tabla 25. Información de las cámaras. 5x5. ................................................................................52
Tabla 26. Resultado diseño terreno con topografía variable. 5x5. .................................................53

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
1
1. INTRODUCCIÓN
El agua, como recurso o amenaza, es un factor decisivo para el desarrollo de la sociedad. Como
recurso está presente en varias de las actividades del día a día, además de ser el pilar fundamental
de varias industrias y servicios. Como amenaza puede representar la inestabilidad de un entorno y
un consecuente riesgo para las diferentes formas de vida de este.
Debido a las dos facetas que presenta el agua, y a su variabilidad espacial y temporal el hombre ha
erigido diferentes estructuras y soluciones que le permitan hacer frente a las condiciones inherentes
del agua. De esta manera, se construyen Plantas de Tratamiento de Agua Potable (PTAP), distritos
de riego, pozos de extracción, presas, entre otros, para el aprovechamiento del recurso. Por otro
lado, las Plantas de Tratamiento de Agua Residual (PTAR), los diques, alcantarillas, redes de
drenaje urbano, entre otras, son obras para hacer frente al agua como amenaza.
Las redes de drenaje urbano, por ejemplo, permiten la evacuación, y el control, de las aguas
residuales. Éstas, son las estructuras más extensas de un sistema de drenaje urbano, el cual, según
Butler & Davies, se define como la infraestructura necesaria para controlar la interacción entre la
actividad humana y el ciclo del agua. La interacción consta de dos partes: la abstracción del recurso
del medio ambiente para beneficio del ser humano y la alteración del entorno que conlleva a la
modificación de los procesos del ciclo hidrológico. Como consecuencia de la interacción se generan
dos tipos de aguas: aguas residuales y aguas pluviales. Las residuales son los desechos de los
diferentes usos que le da el ser humano; si no se disponen correctamente se pueden generar
problemas de salubridad. Las pluviales son consecuencia de la imposibilidad de infiltrarse de las
aguas lluvias; si no se evacúan pueden generar daños materiales, principalmente (Butler & Davies,
2011). Así pues, el sistema de drenaje urbano provee una solución común para estos dos tipos de
aguas: transportarlas, tratarlas (si es necesario) y disponerlas.
En Colombia, las cifras de cobertura de acueducto y drenaje urbano (alcantarillado) fueron de
41.4% y 51%, respectivamente para la zona rural y de 94.6% y 81.8%, respectivamente para la zona
urbana, para el año de 1993. Dichas coberturas se lograron gracias a préstamos concedidos por la
banca internacional y a la consolidación de un esquema institucional bajo la dirección del Instituto
de Fomento Municipal –INSFOPAL–. Para el año 2008 dichas coberturas aumentaron a 72% y 69%
(acueducto y alcantarillado rural) y 97.6% y 92.9% (acueducto y alcantarillado urbano). Para el año
2015 se espera que en las zonas rurales se alcancen coberturas de 81.6% y 75.5% de acueducto y
alcantarillado, y en las zonas urbanas coberturas de 99.4% y 97.6%, respectivamente (estadísticas
Departamento Nacional de Planeación –DNP–)
1
(Superintendencia de Servicios Públicos
Domiciliarios, 2007).
1
Tomado de https://www.dnp.gov.co/LinkClick.aspx?fileticket=Yt%2FHYNFDhkg%3D&tabid=238.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
2
En pro de cumplir los objetivos propuestos para el año 2015, se necesita, además de voluntad
política y transparencia en las ejecuciones, diseños que sean superiores al mínimo exigido en la
normatividad. Según Argaman, Shamir, & Spivak el problema de optimización de diseño de
drenaje urbano se puede descomponer en dos: optimización del trazado y optimización del diseño
para un trazado dado. El principal objetivo sería abordar el problema de manera unificada, pero
debido a la complejidad de la formulación resultante, la optimización se hace en los dos
componentes enunciados (Argaman, Shamir, & Spivak, 1973).
Este trabajo tiene como objetivo desarrollar una metodología que permita optimizar el segundo de
los dos componentes descritos por Argaman, Shamir, & Spivak (optimización del diseño para un
trazado dado). La optimización de éste se enfoca en dos objetivos. El primero de ellos es optimizar
la operación de la red, lo cual se logra maximizando la capacidad hidráulica de la misma; el
segundo de ellos se enfoca en minimizar el costo de la misma, para lo cual se desarrolla una
metodología, explícita, que evalúa las posibilidades para una ruta de una red y escoge la más
económica; a partir de las
1.1. Objetivos
1.1.1. Objetivo general
Desarrollar una metodología mediante la cual se establezca el costo óptimo del diseño de una red de
drenaje urbano, para una topología dada, siendo la función objetivo de ésta, la minimización del
costo de cada una de las series que componen la red; lo anterior sin afectar su comportamiento
hidráulico.
1.1.2. Objetivos específicos
Verificar la posibilidad de implementar el algoritmo de Dijkstra como metodología de
solución.
Establecer relaciones entre los resultados obtenidos y las variables topológicas de entrada.
Establecer la sensibilidad de la metodología a los modelos de costos.
Validar la metodología desarrollada, contrastando los resultados obtenidos con resultados
conseguidos haciendo uso de metodologías desarrolladas por el CIACUA.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
3
2. MARCO TEÓRICO
2.1. Sistema Integrado de Drenaje Urbano
2.1.1. Drenaje Urbano
El drenaje urbano es una de las consecuencias de la acción antrópica sobre el medio ambiente, la
cual se da en dos formas. La primera es la utilización de los recursos hídricos por parte del hombre
para su bienestar y calidad de vida; de esta manera, no toda el agua que es extraída del ambiente es
consumida, por lo que se genera lo que se denominan aguas residuales. Por otro lado, la generación
y expansión de nuevas urbanizaciones conlleva la impermeabilización del suelo, lo que causa un
aumento de la escorrentía. El volumen de agua que no se infiltra naturalmente, y que por lo tanto no
entra de nuevo en el ciclo hidrológico, se denomina aguas lluvia (Butler & Davies, 2011).
Si las aguas residuales y las aguas lluvia no se evacuan y disponen de manera correcta, se generan
unos impactos cuyas consecuencias abarcan desde daños materiales a riesgos mortales. La gravedad
de dichas consecuencias depende de factores como la calidad del agua y el volumen acumulado,
entre otros. El drenaje urbano es la solución concebida para dicha problemática. De manera general,
el funcionamiento del drenaje urbano es como sigue: las aguas lluvias se recolectan en un sistema
de canales y canaletas, posiblemente tuberías también, y se vierten en cuerpos de agua. Las aguas
residuales se recolectan en un sistema de tuberías y se conducen a una PTAR, idealmente, o
directamente a un cuerpo receptor.
2.1.2. Historia
Debido a la composición biológica del ser humano, hay una alta dependencia entre éste y los
recursos hídricos. No en vano los primeros asentamientos humanos se desarrollaron en torno a los
cuerpos de agua. Esta relación de dependencia conllevó a que el ser humano desarrollara sistemas
de manejo del agua, como sistema de drenaje y de acueducto. Aunque hay algunas discrepancias, la
mayoría de autores establece que el inicio de los sistemas de drenaje se remonta al año 3000 A.C,
en la civilización Hindú (ciudades de Harappa y Moheno -Daro). Las ruinas sugieren que los
sistemas eran construidos con gran cuidado y que su principal función era evacuar aguas lluvias y
aguas residuales. Para ello, las casas estaban conectadas a los canales de drenaje, que estaban en el
centro de las calles. Sin embargo, no estaba permitido que se vertieran sólidos en éstos, por lo cual
cada casa tenía un sistema donde sedimentaban los sólidos en pozos y el agua llegaba a los canales
(Burian & Edwards, Historical Perspectives of Urban Drainage, 2002).
Adicional a las ruinas hindús, se encuentran las persas y mesopotámicas, las cuales demuestran un
ligero avance en la construcción y planeación de estos sistemas. Por otra parte, las ruinas de la
civilización Minoica resaltan el gran avance de estos sistemas, los cuales contaban con canales

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
4
separados para aguas residuales y aguas lluvias, además de sistemas de almacenamiento de estas
últimas. Los canales llegaban a grandes colectores que se encargaban de drenar y disponer el agua
lejos de la civilización (Burian, y otros, 1999).
Las grandes y complejas obras de la civilización Minoica fueron superadas por las Romanas. Son
éstas las más conocidas. Aunque el sistema de drenaje romano fue construido iterativamente, por
prueba y error, fue el más grande de las civilizaciones antiguas. Este sistema estaba compuesto de
una vasta red de canales superficiales y alcantarillas subterráneas. Éste tenía como fin evacuar la
escorrentía, las aguas residuales y el agua del acueducto que no era utilizada. Al igual que la
civilización Minoica, el sistema de drenaje Romano contaba con un gran colector que transportaba
las aguas hasta el río Tiber, éste se llama Cloaca Maxima (Burian & Edwards, Historical
Perspectives of Urban Drainage, 2002).
Con la caída del Imperio Romano los sistemas de drenaje sufrieron un retroceso. Las
urbanizaciones estaban establecidas en torno a cuerpos de agua, por lo que los sistemas de drenaje
no eran una necesidad. Conforme crecían dichas civilizaciones, se construían canales abiertos, que
no solo eran usados para evacuar las aguas lluvias sino que en éstos se depositaban desechos de las
casas (de las cocinas, principalmente). En época seca, se acumulaban las basuras y se generaban
problemas de olores, para lo cual la solución fue cubrir los canales. Con el paso del tiempo, la falta
de mantenimiento de dichas estructuras de conducción conllevó a que los problemas fueran peores.
El problema se trató de solucionar con pagos por la limpieza de los canales, lo cual ocasionó un
problema peor pues los habitantes, al estar pagando, se atribuían el derecho a disponer todo tipo de
residuo en ellos (Burian, y otros, 1999).
Los ingenieros se percataron de la ineficiencia constructiva de los canales, por lo que variaron la
forma, materiales y pendientes de éstos, disminuyendo así los problemas que se presentaban. Con la
experiencia que se tenía por las construcciones y sus deficiencias, y apoyados en estudios, se
elaboraron normas que limitaban la velocidad mínima del flujo para evitar problemas de
sedimentación y acumulación de residuos. Lo que siguió fue la mejora de los diseños, con base en
los aciertos y equivocaciones de los diferentes sistemas que ya se encontraban en funcionamiento
(Burian, y otros, 1999).
2.1.3. Actualidad
Nueve factores fueron decisivos para la evolución de los sistemas de drenaje; dichos factores son
(Burian & Edwards, Historical Perspectives of Urban Drainage, 2002) :
Mejoramiento de la calidad de los materiales de las tuberías, en los métodos de
construcción y en las prácticas de mantenimiento.
Permitir que los desechos sanitarios fueran evacuados mediante los sistemas de drenaje.
Mayor comprensión de los sistemas.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
5
Debate entre sistemas separados y combinados.
Correlación entre infecciones y problemas de salubridad y calidad de los sistemas de
drenaje y las aguas.
Tratamiento de las aguas residuales.
Avances en hidrología urbana.
Avances en computación.
Preocupación por el impacto medio ambiental.
De los anteriores factores es importante destacar algunos de ellos: el avance en la hidrología urbana,
el cual se fundamenta en el cambio de método para calcular los caudales de aguas lluvia para un
evento dado. El método más utilizado y conocido era el Método Racional, mediante el cual se hacía
el cálculo de los caudales con los cuales se diseñaban los sistemas de drenaje. Varios estudios que
se llevaron a cabo para validar dicho método llegaron a la conclusión que la utilización de éste
introduce un error (sobrestimación) de los diseños resultantes. En respuesta, se plantearon diferentes
métodos alternativos para realizar las estimaciones necesarias para el diseño.
Respecto a los avances en computación, los programas desarrollados (modelos) y la velocidad de
cálculo han permitido validar y mejorar los diseños bajo varios escenarios. De esta manera se
pueden lograr diseños óptimos para las condiciones dadas de cada lugar. Adicionalmente se han
podido incluir un mayor número de variables en los análisis de los sistemas, como los son la calidad
del agua y los costos asociados con la construcción y operación del sistema.
El tercer factor a destacar es la preocupación por el impacto sobre el medio ambiente. Este factor se
da, de cierta manera, gracias a los avances y descubrimientos en los demás factores. Es así como se
ha planteado el concepto de Sistema Integrado de Drenaje Urbano, el cual pretende que no se
evalúen las redes por separado, sino que se tenga en cuenta todo el sistema desde que el agua es
servida desde las unidades residenciales (o industriales, públicas, etc) hasta que se entrega al cuerpo
receptor. El diseño de los sistemas que sigan estos lineamientos optimizará los costos, el tratamiento
de las aguas y mejorará la calidad aguas abajo del punto de entrega. En el marco de este concepto se
ha desarrollado el de Sistemas Urbanos de Drenaje Sostenible (SUDS), el cual tiene como fin
“mitigar tanto los problemas de cantidad como de calidad de las escorrentías urbanas,
minimizando los impactos del desarrollo urbanístico y maximizando la integración paisajística y
los valores sociales y ambientales de las actuaciones programadas” (Secretaria Distrital de
Ambiente, 2011, pág. 11).
Las políticas de drenaje urbano han cambiado de ‘evacuar el agua lo más rápido y lejos posible’ a
‘proveer un sistema que esté interconectado desde el diseño hasta la operación, es decir que cada
uno de sus componentes sea diseñado con base en la optimización de los demás. Se cambia el
enfoque de evacuación, el cual debe ser regulado y, de ser posible, con pre-tratamiento a lo largo de
la red’ (Saldarriaga, Clase Sistema Integrado de Drenaje Urbano, 2011).

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
6
2.2. Componentes de los Sistemas Integrados de Drenaje Urbano
Para cumplir con el propósito de los Sistemas Integrados de Drenaje Urbano, recoger las aguas y
tratarlas para entregarlas al cuerpo receptor con una mínima calidad que no afecten los usos aguas
abajo, éstos se componen de: redes de drenaje, PTAR y cuerpo receptor.
2.2.1. Redes de drenaje
Son las encargadas de transportar las aguas desde los puntos de recolección hasta la PTAR. Son el
elemento de mayor extensión dentro de los Sistemas Integrados de Drenaje Urbano. Éstas están
compuestas por (Saldarriaga, Clase Sistema Integrado de Drenaje Urbano, 2011) :
Tuberías: Es el componente más común de la red, su función es transportar el agua de un
punto a otro.
Cámaras de inspección: Permiten el acceso a la red para mantenimiento y verificación de la
operación, adicionalmente posibilitan los cambios de dirección.
Canaletas, sumideros y bajantes: La finalidad de estas estructuras es recolectar el agua
lluvia de las superficies impermeables (techos, calles) y conducirlas a las redes de drenaje.
Aliviaderos: Son estructuras que permiten la salida del agua de la red cuando la
profundidad de ésta sobrepasa cierto nivel. Gracias a estas estructuras se pueden disminuir
los costos de la red, pues el caudal que circulará será men or al que se presentaría si éstas no
existieran.
Canales abiertos: Tienen como función el transporte de aguas lluvias.
Cámaras de caída: Su función es disipar energía con el fin de proteger la infraestructura. El
exceso de energía puede estar dado por la presencia de flujo supercrítico o por una
diferencia de cotas entre la tubería de entrada y la tubería de salida.
Estructuras de disipación de energía: Estas estructuras se encuentran en los puntos de
entrega. Se diseñan para que el flujo que es entregado al cuerpo receptor no genere
problemas en el lecho natural de este (erosión o socavación).
Tanques de almacenamiento temporal: Los tanques entran en funcionamiento en eventos de
precipitación, con lo cual disminuyen el pico de caudal y de contaminación de las aguas
entregadas a la PTAR (o al cuerpo receptor). Para su diseño se debe tener en cuenta que los
tiempos de retención no pueden ser muy altos debido a posibles problemas con las aguas
residuales (olores).
Sifones invertidos: Estas estructuras se utilizan cuando el trazado de la red debe pasar por
algún obstáculo. El mecanismo de acción es presurizar la tubería para que gane la energía
suficiente para sobrepasar el obstáculo.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
7
2.2.2. Plantas de Tratamiento de Aguas Residuales (PTAR)
Las PTAR son un conjunto de varias estructuras que funcionan de manera articulada con el fin de
mejorar la calidad del agua que será entregada al cuerpo receptor. Las estructuras que componen las
PTAR dependen del tipo de tratamiento, el contaminante a remover y la eficiencia de remoción que
se pretende lograr. De manera general, una PTAR está compuesta por los siguientes procesos
(Empresa de Acueducto de Bogotá, 2013):
Cribado o remoción de sólidos: Mediante rejillas de diferente tamaño que se ubican a la
entrada de la planta, se remueven sólidos suspendidos cuyo tamaño sea mayor al de la
rejilla más fina. Este proceso es necesario pues los sólidos podrían dañar o generar un mal
funcionamiento de los equipos de la planta.
Desarenado y desengrasado: En este proceso se retiran las grasas, mediante flotación, y las
arenas, por medio de decantación. En pro de agilizar y aumentar la eficiencia del proceso se
inyecta aire al agua.
Floculación y coagulación: El fin de este proceso es que las partículas de sólidos
suspendidos se adhieran, unas a otras, con el fin de que, por su peso, se sedimenten. Para
esto se suministra una especie química al agua, la cual cambia la carga eléctrica de las
partículas suspendidas, favoreciendo así su cohesión. Para acelerar el proceso se agita el
agua, de manera que la probabilidad de que una partícula colisione con otra y se unan sea
mayor. Las velocidades de agitación tienen que disminuir a medida que las partículas
aumentan su tamaño para evitar fraccionarlas.
Sedimentación: En este proceso el agua se pasa a tanques, en los cuales el tiempo de
retención es alto para que las partículas se sedimenten.
Dependiendo de la calidad del agua al culminar los procesos descritos se implementan otros que
aumentan la eficiencia. Los diversos procesos de tratamiento se agrupan en diferentes grupos,
dependiendo del mecanismo de acción o de su objet ivo a remover. Estos grupos, denominandos
trenes de tratamiento, son:
Pre-tratamiento: Se dispone el agua para el tratamiento; esto consiste en retirar sólidos,
arenas y grasas.
Tratamiento primario: Se busca retirar los sólidos suspendidos del agua. Actualmente, los
procesos más comunes son procesos físicos (sedimentación por gravedad) y químico-
asistidos (coagulación y sedimentación). Se espera que los procesos sean sólo físicos
(filtración por membranas).
Tratamiento secundario: El objetivo es eliminar la materia orgánica existente en el agua.
Esto se realiza a través de procesos microbiológicos, que pueden ser aerobios o anaerobios.
Tratamiento terciario: Con estos procedimientos se pretende eliminar contaminantes que los
procesos predecesores no tenían la capacidad de hacer. Estos procedimientos varían
ampliamente, dependiendo del contaminante que se quiera disminuir o eliminar.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
8
Los diferentes procesos existentes en una PTAR generan unos desechos que son responsabilidad de
la planta. Así, los procesos más básicos producen como desechos los diferentes sólidos que se
encontraban suspendidos en el agua. Para procesos más avanzados se producen lodos con contenido
de materia orgánica, metales, entre otras diversas especies químicas, dependiendo de la fuente del
agua resuidual.
2.2.3. Cuerpo receptor
El cuerpo receptor es aquel sobre el cual se descargan las aguas (tratadas si provienen de la PTAR o
sin tratar si provienen directamente de la red). Debido a las nuevas perspectivas que se tienen sobre
los Sistemas Integrados de Drenaje Urbano, el cuerpo receptor tiene un papel fundamental y
determinante, en la medida que su capacidad de autodepuración determina si es necesaria la
construcción de una PTAR o si se pueden verter las aguas residuales directamente.
2.3. Tipos de redes en los Sistemas Integrados de Drenaje Urbano
Las redes de los Sistemas Integrados de Drenaje Urbano pueden ser de dos tipos: separadas o
combinadas. Las separadas tienen tuberías que son exclusivas para aguas lluvias y tuberías que son
únicamente para aguas residuales. De manera contraria, en las redes combinadas, las tuberías
transportan aguas lluvias y aguas residuales.
En las redes separadas se tiene un mayor costo constructivo dado que se tienen que instalar tuberías
para aguas residuales y tuberías para aguas lluvias; sin embargo, el costo de tratamiento se reduce,
pues los picos de caudales y de contaminación tienden a ser uniformes a pesar de que, en esta
modalidad, se hace necesario tratar ‘el primer lavado’ debido a su alta carga contaminante.
En contraparte, las redes combinadas tienen un costo constructivo más bajo pues solo es necesario
instalar una tubería por donde fluirán tanto las aguas residuales como las aguas lluvias; no obstante
la eficiencia de la PTAR a la que son conducidas las aguas se reducirá como consecuencia de
caudales y concentraciones de contaminantes variables. Debido a la probabilidad de que sucedan
eventos de precipitación superiores al evento de diseño, estas redes cuentan con unas estructuras
denominadas aliviaderos (ver Sección 2.2.1). Las aguas que son evacuadas a través de estas
estructuras son una combinación de ‘el primer lavado’ y de la resuspensión de los sedimentos de las
tuberías, lo que conlleva a que generen un fuerte impacto sobre el cuerpo de agua receptor, y por
ende sobre el medio circundante (Giraldo Gómez, 2000).

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
9
2.4. Fallas de los Sistemas Integrados de Drenaje Urbano
2.4.1. Fallas en las redes de drenaje urbano
Las redes de drenaje urbano están compuestas, en su mayoría, por tuberías. Esta característica,
aunada con su gran longitud, conlleva a que el mantenimiento, reparación o cambio presente una
mayor dificultad que otros elementos de la red. Por lo anterior, son propensas a varias fallas, de las
cuales las más comunes son (López Sabogal, 2012):
Fallas estructurales: Este tipo de fallas tiene dos causas: el desgaste de la tubería y el exceso
de carga. La primera de estas es una consecuencia directa de la naturaleza del flujo que
circula por las tuberías. Las aguas residuales, por su composición química, generan ácidos
(sulfúrico y sulfhídrico), que corroen las tuberías. Adicionalmente los sólidos presentes en
este tipo de agua, y los que, eventualmente, aportan las aguas lluvias, generan abrasión en
la tubería. La corrosión y la abrasión conllevan a que se disminuya el grosor de la tubería y
que por ende sea más probable que falle.
Por otro lado, el exceso de carga (ya sea que se supera la carga de diseño o que es una
tubería frágil por haber cumplido con su vida útil) puede generar que la tubería se deforme
o se fragmente. Las fallas de las tuberías favorecen las exfiltraciones e infiltraciones y
ocasionan disminución de la capacidad hidráulica de las mismas.
Sedimentos: Los sedimentos que se pueden encontrar en las tuberías se clasifican en tres
(Saldarriaga, Clase Sistema Integrado de Drenaje Urbano, 2011): Sanitarios, superficiales y
vegetales. Los primeros son los inherentes a las aguas residuales; los segundos son los que
entran a la red por los sumideros y los terceros son las partículas de la estructura del
sistema, es decir fragmentos de tubería. Los sedimentos disminuyen el área mojada lo que
resulta en un aumento de la velocidad, lo que a su vez, genera reacomodación de los
sedimentos y por ende cambio de la rugosidad. La consecuencia final de los cambios es la
disminución de la capacidad hidráulica del conducto, tal como se muestra en la Figura 1.
Sobrecarga: Las sobrecargas se presentan como una consecuencia de la disminución de la
capacidad hidráulica de la tubería causada por las fallas estructurales y/o los sedimentos, o
por las características hidráulicas de una tubería, las cuales determinan que una vez la
profundidad sobrepase una relación de llenado del 80% la velocidad disminuye, lo que
aumenta las probabilidades de un represamiento del flujo y finalmente la sobrecarga de la
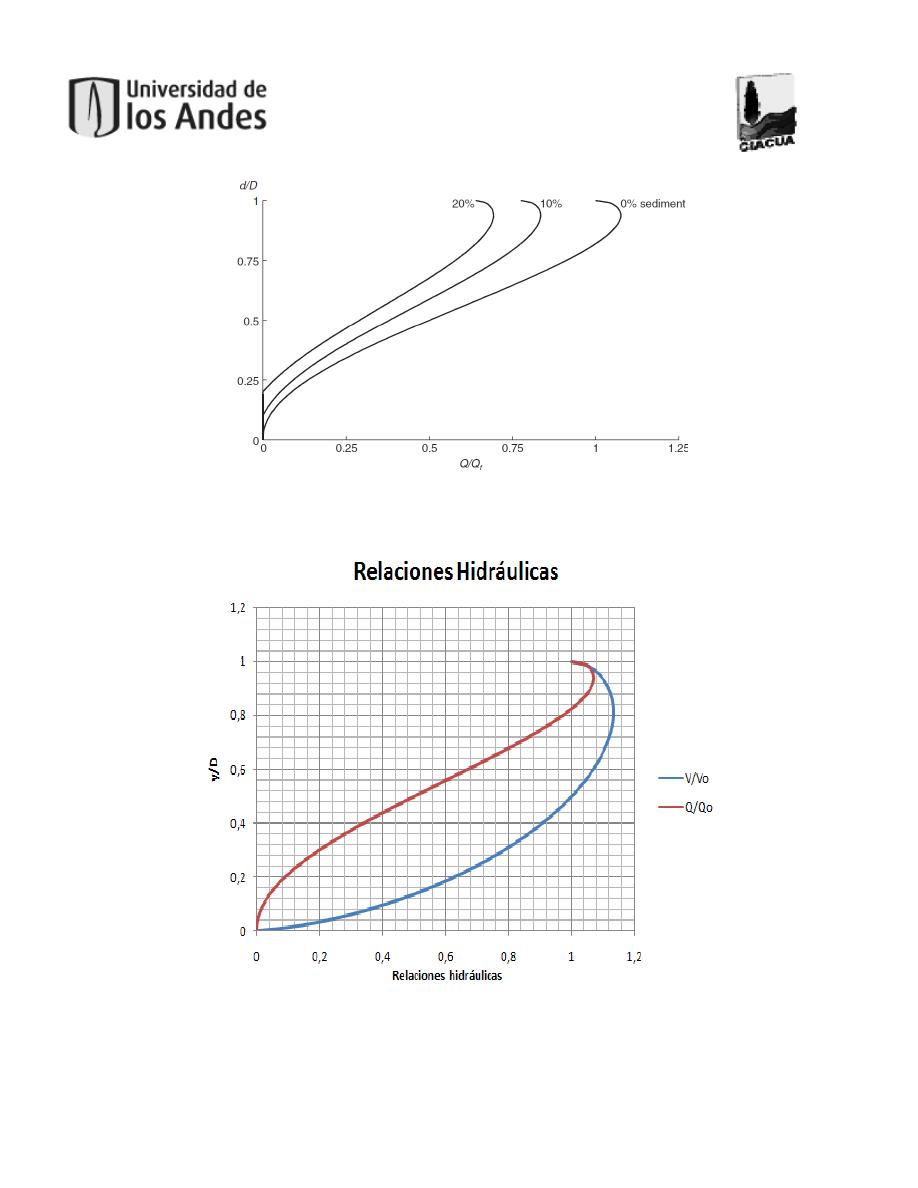
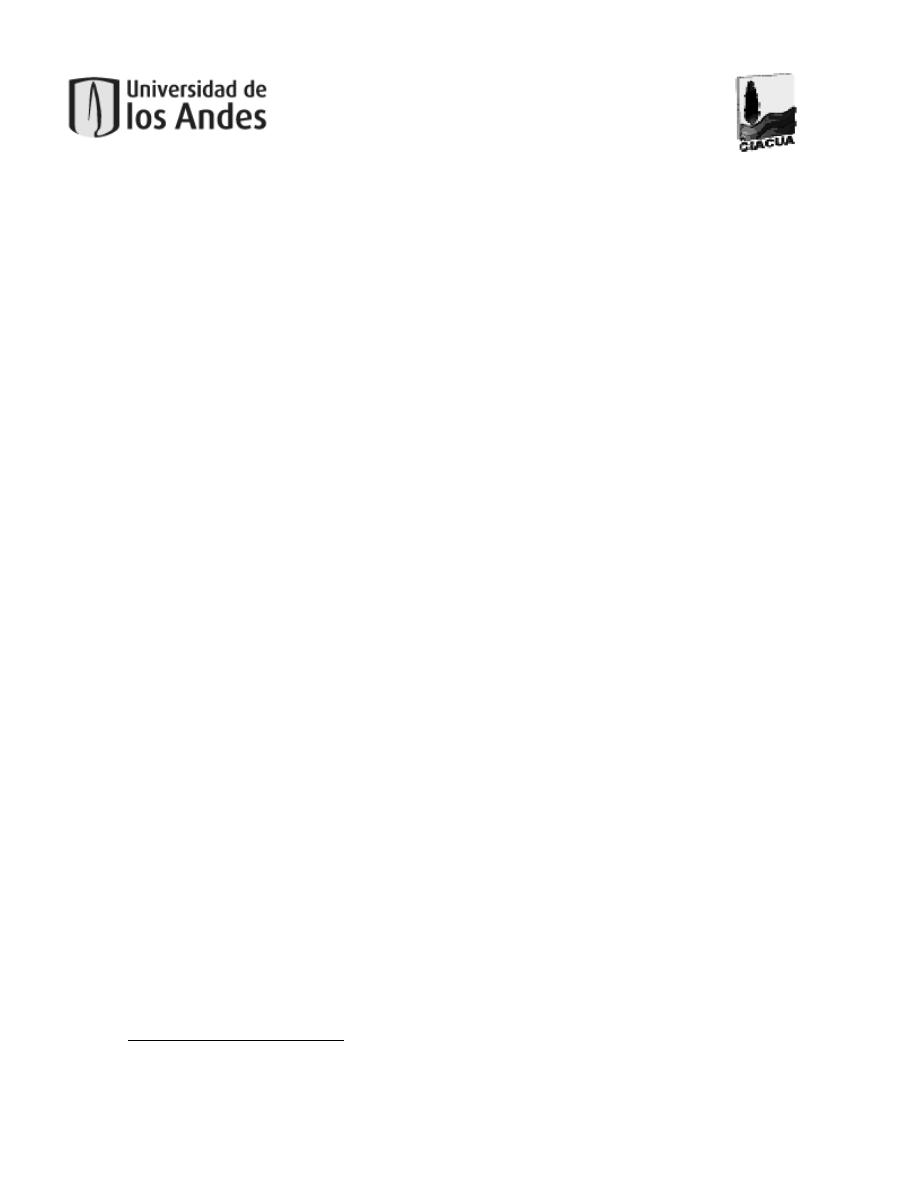
tubería. La Figura 2 muestra el comportamiento del caudal y de la velocidad con respecto a
la relación de llenado.
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
10
Figura 1. Pérdida de la capacidad hidráulica como consecuencia de los sedimentos.
Tomado de (Butler & Davies, 2011).
Figura 2. Relaciones hidráulicas para una sección circular. Tomado de (López Sabogal, 2012).
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
11
En la Figura 1 y en la Figura 2 el eje de las ordenadas representa el porcentaje de la tubería que está
lleno. El eje de las abscisas muestra la relación entre la variable en un punto específico y el valor de
la variable en tubo fluyendo lleno (para la Figura 1 la variable es el caudal y para la Figura 2 las
variables son el caudal y la velocidad).
2.4.2. Fallas en la PTAR
En las PTAR se pueden presentar fallas en el diseño o en la operación de ésta. Dicho de otra
manera, se pueden presentar fallas hidráulicas o fallas operacionales. Las fallas hidráulicas se
derivan de un diseño que no cumple con la premisa de que la planta funcione por acción de la
gravedad, es decir sin la necesidad de bombeo. Por lo anterior, es imprescindible que el cálculo de
la Elevación de la Línea de la Superficie del Agua (ELSA) esté muy detallado, y que en este se
contemple que la PTAR debe operar por gravedad en todo momento, inclusive cuando se tienen
caudales superiores al caudal de diseño, para no incurrir en costos adicionales de energía eléctrica y
evitar el represamiento del agua, y una eventual inundación, en alguno de los procesos.
Por su parte, las fallas operacionales corresponden a las fallas de los equipos y/o de las estructuras,
las cuales son previsibles mas no inevitables. Por lo anterior este tipo de fallas se deben contemplar
desde el diseño mediante la inclusión de medidas de contingencia, tales como la redundancia de los
procesos o el ‘bypass’ para eventos más severos. El mantenimiento preventivo de los diferentes
equipos y la rotación de los mismos son medidas que aumentan la confiabilidad de la PTAR, y por
ende disminuyen la probabilidad de falla en la operación.
2.5. Normatividad Colombiana sobre Sistemas de Drenaje Urbano
Aunque en Colombia algunas empresas tienen lineamientos propios basados en estudios y
experiencia propia, para el cálculo de caudales de redes de drenaje (de aguas residuales y aguas
pluviales), a nivel nacional existe un reglamento técnico, que si bien no es obligatorio su
seguimiento, sí establece unos estándares que deben ser cumplidos. Este reglamento se llama
Reglamento Técnico del sector de Agua Potable y Saneamiento Básico (RAS); está compuesto por
títulos, de los cuales seis establecen estándares para diferentes actividades. El título D concierne a
los alcantarillados, por esto cada vez que se haga referencia al RAS
2
, será al título D de éste, si no
se indica lo contrario.
Varios de los parámetros de diseño que serán mostrados dependen del ‘nivel de complejidad del
sistema’; la asignación de la complejidad se muestra en la Tabla 1.
2
La versión oficial del título D del RAS es la del 2000, por ello se trabajará con esta, a pesar de existir
versiones más recientes, pero que son no oficiales.
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
12
Tabla 1. Asignación del nivel de complejidad (RAS, 2000).
Nivel de
Complejidad
Población
(Hab)
Capacidad económica
de los usuarios
Bajo
<2500
Baja
Medio
2501 a 12500
Baja
Medio Alto
12501 a 60000
Media
Alto
>60000
Alta
2.5.1. Redes de drenaje urbano sanitario
De manera general, los parámetros y las restricciones de diseño de las redes de drenaje urbano
sanitario se muestran a continuación. Si se quiere un mayor detalle de stos se recomienda consultar
el literal D.3 del RAS 2000. Para todos los caudales se debe calcular la condición inicial y la
condición final.
Caudal de aguas residuales domésticas (Q
D
): El caudal aportado por las viviendas se puede
calcular de cualquiera de las dos formas de la Ecuación 2.1, dependiendo de las variables
que se conozcan.
2.1
De las ecuaciones anteriores se tiene:
Q
D
: Caudal de aguas residuales domésticas [L/s]
C: Consumo diario per cápita [L/Hab-día]
D: Densidad de población [Hab/Ha]
A
rb
: Área residencial bruta [Ha]
R: coeficiente de retorno [-]
La estimación del consumo diario per cápita y del coeficiente de retorno debe hacerse con base en
la Tabla 2.
Tabla 2. Valores recomendados para el consumo diario per cápita y el coeficiente de retorno (RAS, 2000).
Nivel de
Complejidad
Dotación per cápita.
Clima cálido
Dotación per cápita.
Clima frio o templado
Coeficiente
de reto rno
Bajo
100 L/Hab-día
90 L/Hab-día
0.7-0.8
Medio
125 L/Hab-día
115 L/Hab-día
0.7-0.8
Medio Alto
135 L/Hab-día
125 L/Hab-día
0.8-0.85
Alto
150 L/Hab-día
140 L/Hab-día
0.8-0.85
Caudal de aguas residuales industriales (Q
I
): Debido a la variedad de los tipos de industrias
y las condiciones de operación propias de cada una (consumo y recirculación de agua), el
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
13
caudal de aguas industriales debe obtenerse como resultado de un censo de las mismas. Sin
embargo, si la zona es residencial con pocas industrias (pequeñas) el aporte de estás puede
estimarse tomando como referencia la
Tabla 3.
Tabla 3. Aporte de industrias pequeñas, en zonas residenciales (RAS, 2000).
Nivel de complejidad del sistema
Contribución industrial (L/s-ha ind)
Bajo
0.4
Medio
0.6
Medio Alto
0.8
Alto
1.0-1.5
Caudal de aguas residuales comerciales (Q
C
): Si la zona es netamente comercial, el aporte
de ésta debe estar justificado con la densidad de población y el consumo diario por persona.
Por otro lado si la zona es mixta comercial los aportes pueden ser calculados con un factor
de 0.4 – 0.5 L/s·ha comercial.
Caudal de aguas residuales institucionales (Q
IN
): Las instituciones tienen consumos
diferentes, los cuales dependen del tipo de institución. Debido a esto, el aporte de las
instituciones debe calcularse de manera individual con base en información pre-existente.
Si las instituciones se encuentran en zonas residenciales y son de tamaño pequeño, el aporte
de éstas se puede calcular con un factor de 0.4 – 0.5 L/s·ha institucional.
Caudal medio de aguas residuales (Q
M D
): Este es la suma de los aportes domésticos,
industriales, comerciales e institucionales (Ecuación 2.2).
2.2
Caudal de conexiones erradas (Q
CE
): Los aportes de caudal como consecuencia de
conexiones erradas varían dependiendo del control que se ejerza sobre dicha práctica y de la
existencia de sistemas de aguas lluvia. La Tabla 4 muestra valores guía (máximos) para
aportes por conexiones erradas. En caso de obtener valores muy altos de aport es por
conexiones erradas para Niveles de Complejidad del Sistema Medio Alto y Alto, se debe
desarrollar un proyecto de sistema de recolección de aguas lluvias; por lo tanto el diseño
debe ser consistente con el nuevo proyecto. Para Niveles de Complejidad del Sistema Bajo
y Medio, si bien no es necesario la proyección de sistemas de recolección de aguas lluvias,
es recomendable establecer medidas de control.
Tabla 4. Aportes de conexiones erradas (RAS, 2000).
Nivel de
complejidad
Aporte (Con
sistema pluvial)
Aporte (Sin
sistema pluvial)
Bajo y Medio
0.2 L/s-Ha
2 L/s-Ha
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
14
Medio Alto y Alto
0.1 L/s-Ha
2 L/s-Ha
Caudal de infiltración (Q
INF
): Debido a deficiencias constructivas y a fallas en las tuberías
de las redes, es inevitable la infiltración de agua subsuperficial al sistema. Para contabilizar
el aporte de la infiltración es recomendable adelantar un estudio en horas de poco consumo,
en el cual se tenga en cuenta la topografía, variables hidrológicas y geológicas. En caso de
imposibilidad de desarrollar el estudio, la Tabla 5 muestra unos valores guías para el aporte
por infiltración. En ésta, ‘infiltración alta’ corresponde a altas deficiencias constructivas y,
consecuentemente, ‘infiltración baja’ atañe a circunstancias en las que la probabilidad de
infiltración es la menor.
Tabla 5. Tasas de infiltración dependiendo las variables que la afectan (RAS, 2000).
Nivel de
complejidad
Infiltración
alta (L/s-Ha)
Infiltración
media (L/s-Ha)
Infiltración
baja (L/s-Ha)
Bajo y Medio
0.15-0.4
0.1-0.3
0.05-0.2
Medio Alto y Alto
0.15-0.4
0.1-0.3
0.05-0.2
Caudal Máximo Horario (Q
M H
): Es el caudal que representa la máxima demanda que tendrá
la red en el periodo de diseño, por ende es el caudal de diseño. Se halla haciendo uso de la
Ecuación 2.3. En esta, F se denomina factor de mayoración
2.3
Factor de Mayoración: Es un factor mediante el cual se calcula el caudal máximo horario a
partir del caudal medio diario en las condiciones finales del sistema. Este factor incluye,
implícitamente, la relación entre la variación de caudales y el tamaño de la población. A
continuación se presenta de la Ecuación 2.4 a la Ecuación 2.8, las cuales representan
diferentes metodologías para obtener el factor de mayoración. Se recomienda investigar
acerca de las limitaciones de cada una antes de implementarlas. De manera general F no
puede superar el valor de 1.4. Este factor debe calcularse para cada uno de los tramos de la
red de drenaje urbano, debido al incremento del caudal que se espera hacia aguas abajo
(debido a la población aferente) (RAS, 2000).
2.4
2.5
2.6

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
15
2.7
2.8
De la Ecuación 2.4 a la Ecuación 2.6, P representa el número de habitantes. Por otro lado en
la Ecuación 2.7 y en la Ecuación 2.8, Q
MD
representa el caudal medio diario.
Caudal de diseño (Q
DT
): Es el caudal que debe transportar cada uno de los tramos de la red.
Es la suma del caudal medio horario (Q
M H
), el aporte de la infiltración (Q
INF
) y de las
conexiones erradas (Q
CE
). Si el valor calculado es inferior a 1.5 L/s se debe adoptar esta
valor. Todos los caudales deben ser los correspondientes al final del periodo de operación.
2.9
Diámetro interno real mínimo: Se establece un valor mínimo con el fin de evitar
obstrucciones del sistema; este valor es 8” (200 mm). Si el nivel de complejidad es bajo, y
mediante una justificación adecuada, este valor puede ser 6” (150 mm).
Velocidad mínima: Se establece un valor mínimo de velocidad para favorecer condiciones
de autolimpieza en las tuberías y que la sedimentación no se convierta en un problema de
las redes. Así, el valor mínimo para la velocidad es de 0.45 m/s. Sin embargo, si las tuberías
han de transportar aguas industriales, el criterio de velocidad mínima está sujeto a la calidad
del agua (DBO
5
). En la Tabla 6, se presentan las relaciones enunciadas.
Tabla 6. Velocidades mínimas como función de la DBO (RAS, 2000).
DBO efectiva
(mg / L)
Velocidad mínima
real (m / s)
Hasta 225
0.5
De 226 a 350
0.65
De 351 a 500
0.75
De 501 a 690
0.9
De 691 a 900
1
Velocidad máxima: El valor del límite superior de la velocidad está dado por las
condiciones de la tubería (material y empotramiento) y las del agua (características
abrasivas y turbulencia). Por ende se insta a justificar los valores establecidos como límite
para la velocidad. A manera de recomendación se sugiere un valor de 5 m/s.
Esfuerzo cortante mínimo: Al igual que para la velocidad, el valor del esfuerzo cortante
mínimo obedece a razones de autolimpieza. El esfuerzo cortante se calcula mediante la

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
16
Ecuación 2.11, en la cual el caudal a utilizar está dado por la Ecuación 2.10, para
condiciones iniciales. El valor de caudal medio horario para las condiciones iniciales (Q
M Hi
)
mínimo es 1.5 L/s. En caso de obtener un valor menor se debe adoptar 1.5 L/s. Si, por las
condiciones topográficas, no es posible asegurar una velocidad mayor o igual a la mínima,
debe verificarse que el valor del esfuerzo cortante sea mayor o igual a 1.2 N/m
2
.
2.10
donde,
Q
Di
: Caudal doméstico para el inicio del periodo de operación (L/s).
Q
Ii
: Caudal industrial para el inicio del periodo de operación (L/s).
Q
Ci
: Caudal comercial para el inicio del periodo de operación (L/s).
Q
INi
: Caudal de infiltración para el inicio del periodo de operación (L/s).
Q
CEi
: Caudal de conexiones erradas para el inicio del periodo de operación (L/s).
K
1
: Relación entre el caudal máximo diario y el caudal medio diario, varía entre 1.2 y 1.5.
2.11
donde,
τ : Esfuerzo cortante (Pa)
γ : Peso específico (N/m
3
).
S
f
: Pendiente de fricción (-).
Pendiente mínima: Se establece el valor mínimo de la pendiente como aquel que cumple
con las restricciones de velocidad y esfuerzo cortante mínimo.
Pendiente máxima. Se establece el valor máximo de la pendiente como aquel que cumple
con las restricciones de velocidad máxima.
Profundidad hidráulica máxima: Este valor debe estar entre el 70 - 85% del diámetro
interno de la tubería, con el fin de favorecer la aireación del flujo.
Profundidad mínima a la cota clave: La profundidad mínima a la que se encuentra la cota
clave de la tubería se establece con el fin de proteger la tubería de fractur as ocasionadas por
las cargas vivas. Ésta depende del tipo de servidumbre que se encuentra por encima de la
tubería. De esta manera, si la servidumbre es vías peatonales o zonas verdes, el valor de la
profundidad debe ser, mínimo, 0.75 m. Por otro lado, si la servidumbre corresponde a vías
vehiculares, la profundidad debe tener como valor mínimo 1.20 m.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
17
Profundidad máxima a la cota clave: Por razones de seguridad durante la construcción, el
valor máximo de la profundidad a la cota clave es 5 m. Sin embargo, el valor puede ser
mayor si se garantizan requerimientos geotécnicos de las cimentaciones y estructurales de
los materiales durante la construcción de estos.
2.5.2. Redes de drenaje urbano pluvial
A continuación se muestran los parámetros de diseño y restricc iones que fueron designadas para las
redes de drenaje urbano pluvial. Si se quiere un mayor detalle sobre la información presentada se
recomienda consultar el literal D.4 del RAS 2000.
Áreas de drenaje: Las áreas aferentes a los tramos de las redes deben definirse de acuerdo
con las redes de drenaje natural y estar debidamente delimitadas, para lo cual se aconseja
elaborar una medición directa en planos.
Caudal de diseño: Es el caudal que se estima que circulará por el tramo objeto del diseño,
en un evento de precipitación, dada la probabilidad de ocurrencia de este. Para ha llar el
caudal se hace uso del Método Racional, Ecuación 2.12. En esta, C es el coeficiente de
escorrentía, i es la intensidad del evento y A es el área aferente. Se recomienda revisar los
condicionamientos del modelo, antes de su implementación.
2.12
Diámetro mínimo: El diámetro mínimo debe ser de 10” (250 mm). En casos justificados
puede llegar a ser 8” (200 mm).
Velocidad mínima: Debido a que los sólidos transportados por el agua lluvia pueden
sedimentarse se debe tener una velocidad mínima de 0.75 m/s para garantizar condiciones
de autolimpieza. Adicionalmente, se debe verificar que el esfuerzo cortante para el 10% de
la capacidad de tubo lleno sea mínimo 1.5 Pa.
Velocidad máxima: Los valores máximos de la velocidad dependen de la resistencia de la
tubería a la abrasión. Por ende, influye el material de la tubería y los sedimentos que
transporte el agua. En la Tabla 7 se muestran algunos valores recomendados de velocidad
máxima para diferentes materiales.
Tabla 7. Velocidades máximas (RAS, 2000).
Tipo de material
v (m/s)
Ladrillo común
3
Ladrillo vitrificado y gres
5
Concreto
5
PVC
10

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
18
Pendiente mínima: El límite inferior del valor de la pendiente es para el cual se obtiene la
velocidad mínima.
Pendiente máxima: La pendiente máxima debe ser aquella con la cual se obtiene la
velocidad máxima.
Profundidad hidráulica máxima: El flujo puede fluir a tubo lleno.
Profundidad mínima y máxima a la cota clave: Se deben seguir las mismas indicaciones que
para redes de drenaje urbano sanitario.
2.5.3. Redes de drenaje urbano combinado
Los parámetros de diseño de las redes de drenaje combinadas son similares a las de las redes de
drenaje urbano pluvial. Los máximos y mínimos corresponden a los de drenaje urbano pluvial y de
manera excepcional, cuando el caudal de aguas residuales supera el 5% del caudal de aguas lluvia.
En este caso el caudal de diseño debe ser igual a la suma de los dos caudales. Para hallar el caudal
de aguas residuales es necesario tener en cuenta los aportes domésticos, industriales, comerciales,
institucionales, y de infiltración. Las conexiones erradas no se tienen en cuenta.
2.6. Diseño hidráulico de los tramos de las redes de los Sistemas
Integrados de Drenaje Urbano
El diseño de una red de drenaje urbano se puede escindir en dos procesos: diseño del trazado de la
red y el diseño hidráulico del trazado seleccionado. El primero de estos procesos, de manera
general, consiste en la construcción de un trazado: escoger los puntos donde se ubicarán las cámaras
de inspección y, por ende, determinar la longitud de los tramos y las cámaras de inicio y final para
cada uno. Como resultado de este proceso se obtiene lo que se denomina la topología de la red.
El segundo proceso consiste en, basado en el trazado, hallar el conjunto de diámetros y pendientes
que pueden transportar el flujo por gravedad y que cumplan con las restricciones hidráulicas. Este
proceso se puede hacer siguiendo alguna metodología, por prueba y error o por experiencia. A
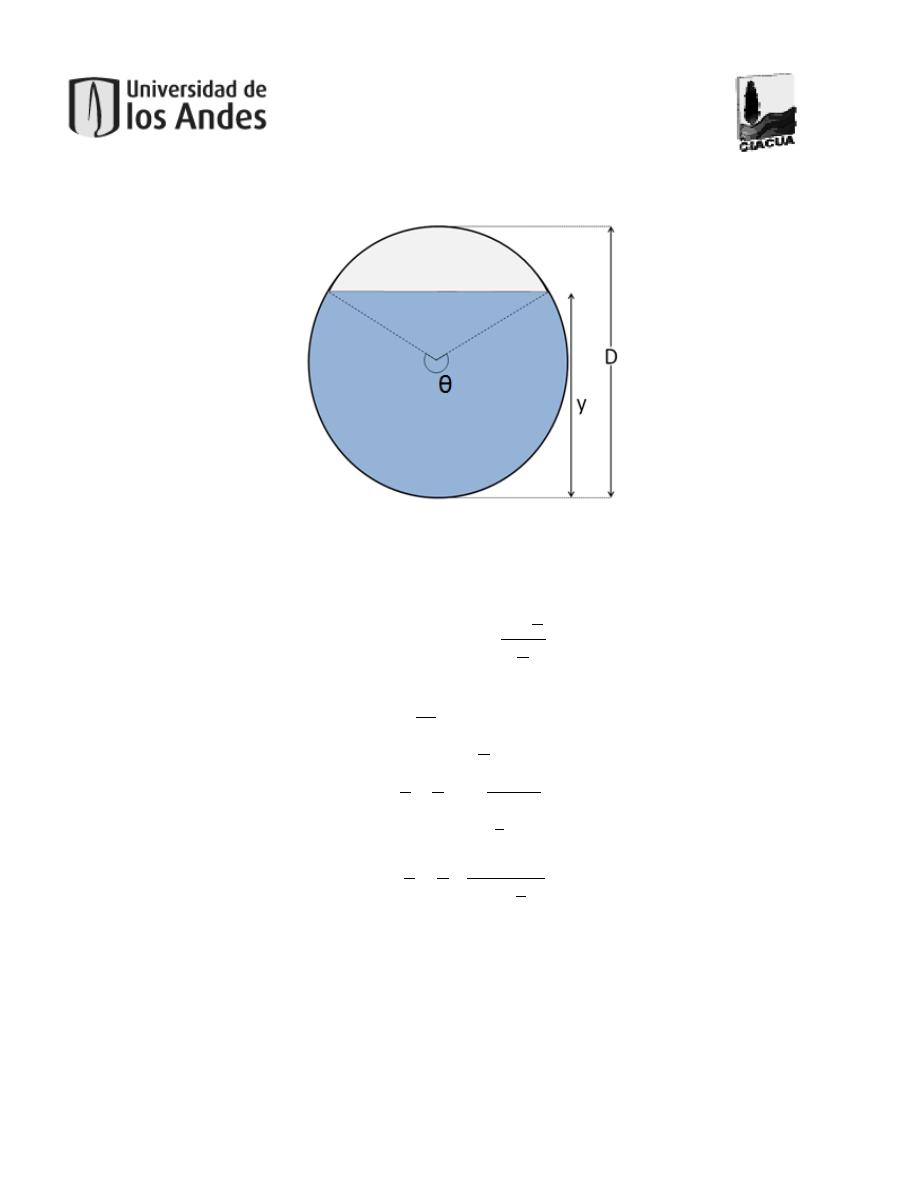
continuación se enuncian las ecuaciones utilizadas para el diseño. La Figura 3 muestra las variables
de una sección circular fluyendo parcialmente llena.
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
19
2.6.1. Geometría hidráulica
Figura 3. Características de una sección circular fluyendo parcialmente llena.
Tomado de (López Sabogal, 2012).
Con base en la Figura 3 se obtienen las características geométricas (Ecuación 2.13 a Ecuación 2.18).
2.13
( )
2.14
2.15
( )
2.16
2.17
( )
2.18
En las anteriores ecuaciones,
θ: Ángulo entre el centro de la tubería y el nivel del agua (rad).
D: Diámetro de la tubería (m).
A: Área mojada (m
2
).
P: Perímetro mojado (m).
R: Radio hidráulico (m).

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
20
B: Ancho en la superficie (m).
D
h
: Profundidad hidráulica (m).
Con las ecuaciones de la geometría hidráulica definidas, se halla el caudal que puede transportar
una tubería; para ello se hace uso de la ecuación de conservación de la masa (Ecuación 2.19):
2.19
donde,
Q: Caudal que fluye por la tubería (m
3
/s).
v: Velocidad del flujo (m/s).
2.6.2. Cálculo de la velocidad de flujo
Para hallar la velocidad del flujo existen varias ecuaciones empíricas, de las cuales las más
utilizadas son la ecuación de Manning (Ecuación 2.20) y la de Chézy (Ecuación 2.21). Estas dos
ecuaciones, aunque fueron deducidas para canales, tienen una amplia difusión debido a la facilidad
de cálculo. Actualmente, con los materiales lisos de las tuberías se insta a utilizar otras expresiones
para el cálculo de la velocidad, pues la implementación de estas ecuaciones conlleva a errores en el
diseño.
2.20
donde,
n: Coeficiente que describe la rugosidad del conducto (s/m
3
).
2.21
donde,
C: Coeficiente que describe la rugosidad del conducto (m
1/2
/s).
En contraparte a las ecuaciones presentadas, las ecuaciones de Colebrook – White (Ecuación 2.22)
y Darcy – Weisbach (Ecuación 2.23), son físicamente basadas, por lo cual tienen una mayor
precisión y exactitud. Al despejar el factor de fricción, f, de la Ecuación y reemplazarlo en la
Ecuación, se llega a la Ecuación 2.24.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
21
2.22
2.23
o
2.24
donde,
f: Factor de fricción (-).
ν: Viscosidad cinemática (m
2
/s).
K
s
: Rugosidad interna de la tubería (m).
g: Aceleración de la gravedad (m/s
2
).
Re: Número de Reynolds (-).
2.6.3. Obtención de diámetros y pendientes
El proceso para la obtención de los conjuntos de pendientes y diámetros es un proceso iterativo, en
el cual se parte de unos valores iniciales de pendiente y relación de llenado (escogidos por
experiencia). Con base en estos se calculan los valores de área, perímetro y radio hidráulico, con los
cuales se halla la velocidad y el caudal. Si el caudal calculado es mayor o igual al caudal de diseño,
se verifica el cumplimiento de las diferentes restricciones, en caso contrario se aumenta el diámetro
hasta que el caudal calculado sea igual o mayor al de diseño. Si se llega a un diseño satisfactorio, es
decir que se cumplan las restricciones, existen dos alternativas: se culmina el proceso de diseño o se
cambian los valores iniciales en pro de un mejor diseño.
2.6.4. Suposición de flujo uniforme
El flujo puede variar en el espacio o en el tiempo. Si varía en el espacio se denomina flujo no
uniforme, de manera contraria, flujo uniforme. Si la variación es en el tie mpo, será flujo no
permanente, y si es constante, se llama permanente. Las variaciones del flujo dependen de las
características del conducto y de las de éste: rugosidad, geometría, caudal y pendiente. La
modelación más sencilla se da cuando el flujo es permanente y uniforme (no cambia ni en el tiempo
ni en el espacio), estas condiciones se cumplen cuando se igualan las fuerzas inerciales y las
gravitatorias, es decir las fuerzas que aceleran el flujo son iguales a las que resisten el movimiento.
La Ecuación 2.25, muestra la consecuencia del flujo uniforme - permanente
3
.
3
Aunque no varía ni en el tiempo, ni en el espacio se denomina flujo uniforme únicamente, debido a que la
existencia de un flujo uniforme – no permanente es muy poco probable.
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
22
2.25
donde,
S
0
: Pendiente del fondo del canal (-).
S
f
: Pendiente de fricción (-).
S
w
: Pendiente de la superficie de agua (-).
Dado que el flujo uniforme permanece constante a lo largo del conducto mientras no se cambien las
condiciones, los diseños se hacen basados en la suposición de que se presentará este tipo de flujo.
Una vez se tiene el diseño se debe verificar la operación del sistema con el flujo que se espera que
se presente para varias condiciones.
2.7. Aproximaciones a la optimización del diseño hidráulico de las
redes de los Sistemas Integrados de Drenaje Urbano
Como se describe en la Sección 2.1.2 los sistemas de drenaje tenían el único propósito de evacuar
las aguas (pluviales y/o residuales), sin importar el costo asociado con las estructuras. La evolución
de estos representó un cambio, el cual consistió en que la concepción no era solo evacuar aguas
eficientemente sino también hacerlo a un bajo costo. Londres y París fueron dos ciudades
determinantes dado que mediante los sistemas de drenaje de estas se adquirió experiencia y se
establecieron algunos criterios para el diseño, con los cuales se cumplían los requerimientos.
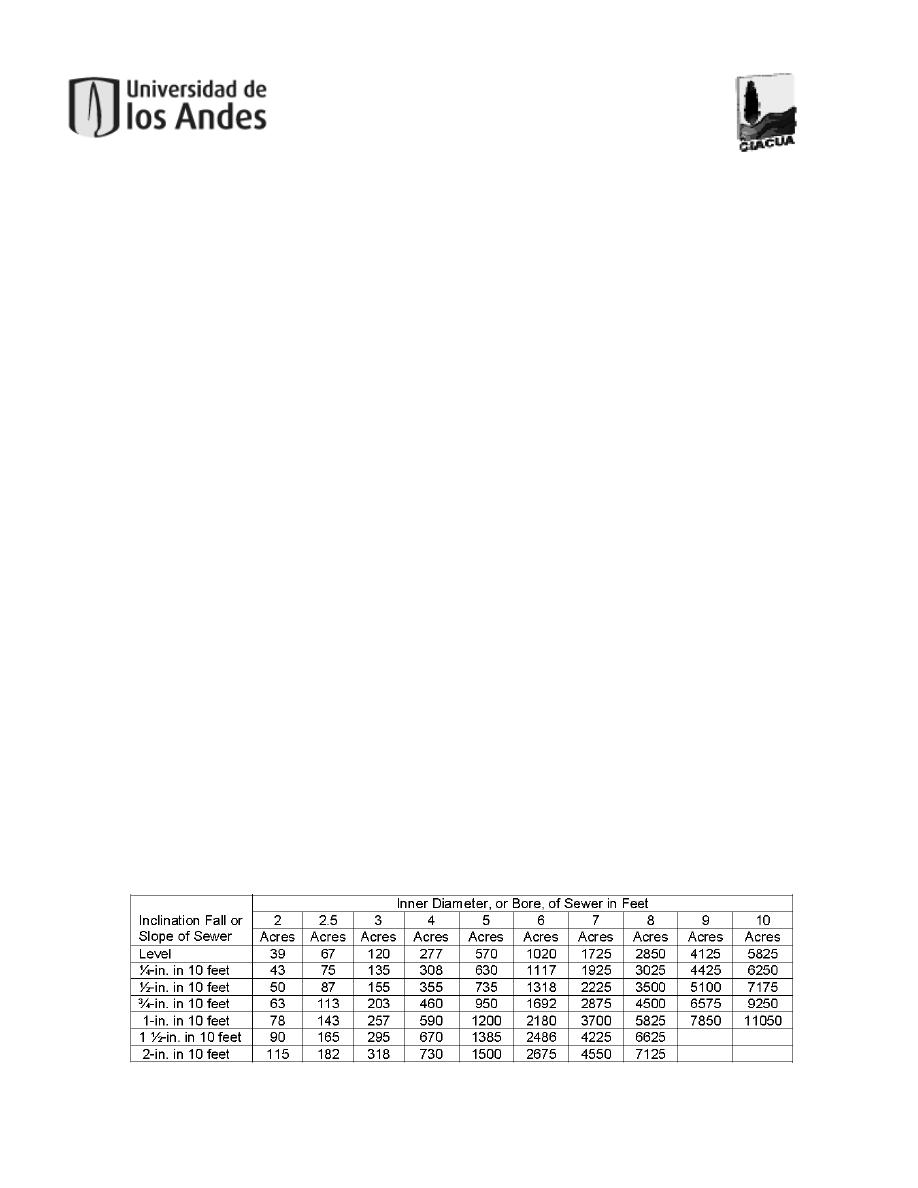
Así, se crearon diferentes tablas en las cuales se reportaban los diámetros como función de la
pendiente del terreno y el área aferente. La Tabla 8 muestra un ejemplo. La experiencia que se
obtenía de los sistemas en funcionamientos mejoró el criterio de selección del diámetro y el
desarrollo de la tecnología ejerció un papel determinante en la evolución del proceso de diseño. A
pesar de esto, “el estudio de procesos de optimización de sistemas de drenaje urbano es criticado
por los ingenieros de campo, quienes afirman que los métodos son muy complicados para ser
aplicados a los diseños actuales” (Holland, 1968).
Tabla 8. Metodología de diseño de los sistemas de drenaje urbano. Tomado de (Burian & Edwards, Historical
Perspectives of Urban Drainage, 2002).

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
23
Los grandes avances en el campo de la computación cambiaron la metodología tradicional de
diseño, lo cual, como se muestra en el párrafo anterior, no fue un proceso inmediato. Dado que los
diversos cálculos eran hechos por las máquinas, el nuevo objetivo era optimizar los diseños. De esta
manera surgieron soluciones mediante la Programación Lineal (LP) y Programación No Lineal
(NLP) (Guo, Walters, & Savic, 2008).
Como consecuencia de las restricciones de los métodos enunciados y de la naturaleza del problema,
éstos fueron descartados. La Programación Lineal, aunque está en capacidad de operar con
diferentes variables de decisión, requiere que sean lineales lo cual no corresponde al problema de
los sistemas de drenaje. En contraparte, la Programación No Lineal no presenta restricciones en
cuanto al grado de las ecuaciones del problema; sin embargo debido a la complejidad de este
(clasificado como NP) los costos computacionales son muy elevados y no siempre se tiene una
solución factible (Guo, Walters, & Savic, 2008).
La Programación Dinámica (DP) y la Programación Dinámica Discreta Diferencial (DDDP), una
versión modificada de la primera, es una metodología cuyas restricciones cumplen las
características del problema por lo cual ha sido ampliamente utilizada para diferentes estudios de
optimización de diseño de redes de drenaje urbano. Cuatro características de la metodología que la
hacen exitosa para el problema de drenaje urbano son: el problema debe ser representado de forma
secuencial y dividido en partes, en cada una de ellas se tiene un conjunto de variables y decisiones,
es flexible con respecto a la función objetivo y los resultados se presentan de manera discreta (Guo,
Walters, & Savic, 2008).
Sin embargo, la Programación Dinámica, a pesar de ser una metodología que ha demostrado
buenos resultados, tiene limitaciones que conllevan a que sea una solución básica y no pueda ser
implementada en problemas con espacios de solución amplios y complejos. Entre estas limitaciones
se tiene: si el sistema tiene más de un punto de descarga el modelo no funciona correctamente; dado
que se diseña un tramo a la vez, las simplificaciones necesarias pueden llevar a obtener resultados
lejos del óptimo o que no sean factibles; cuando el flujo es subcrítico el diseño de un tramo se ve
afectado por el tramo aguas abajo, lo cual impide que el diseño global se lleve a cabo de manera
individual (como lo requiere la Programación Dinámica); por definición, solo se maneja una
variable de decisión, la cual se adopta como la cota de batea de la tubería, por lo cual el diámetro
queda fuera de la optimización; y, por último, dado que en cada una de las etapas el proceso de
optimización se enfoca en una variable, si el problema se complejiza, la metodología es obsoleta
(Guo, Walters, & Savic, 2008).
El vertiginoso ritmo de la evolución de la computación y la preocupación creciente por un sistema
integrado de drenaje urbano (descrito en la Sección 2.1.3) impulsaron el desarrollo de nuevas
técnicas de optimización del diseño de redes de drenaje urbano. La meta heurística se convierte en
un recurso importante a la hora de abordar el problema, siendo los Algoritmos Genéticos (GA) la
metodología más destacada y difundida (Guo, Walters, & Savic, 2008).

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
24
Gracias a que en el proceso de optimización basado en Algoritmos Genéticos se toma toda la
hidráulica de la red, y no por tramos como los métodos antecesores, las r epercusiones de un evento
en cualquier punto de ésta estarán contempladas en la solución que se obtenga. Adicionalmente, los
Algoritmos Genéticos son independientes del tipo y la forma de la función objetivo, por lo cual no
es necesario realizar simplificaciones ni suposiciones que alteren el funcionamiento modelado de la
red (Guo, Walters, & Savic, 2008).
Los Algoritmos Genéticos, en combinación con otras técnicas, han sido utilizados en diversos
estudios de optimización del diseño de redes de drenaje urbano. Algunos de ellos son: (Haghighi &
Bakhshipour, Optimization of Sewer Networks Using an Adaptive Genetic Algorithm, 2012), (Pan
& Kao, 2009) y (Navarro, 2009). A pesar de la eficacia y eficiencia del método, se tienen algunas
advertencias en la aplicación de este. Como consecuencia de su naturaleza estocástica, el uso de
diferentes semillas y parámetros conlleva a diferentes soluciones, por lo que se recomienda realizar
un análisis de sensibilidad frente a éstos con el fin de obtener los mejores resultados (aún así, no se
garantiza la consecución del óptimo global).
Hay otras metodologías reportadas para la optimización del diseño de redes de drenaje urbano
(Algoritmos tipo Colonias de Hormigas y Recocido Simulado); sin embargo éstas no difieren
mucho de Algoritmos Genéticos y la implementación de ésta ha probado ser efectiva en redes
pequeñas, por lo cual no son muy usadas (Guo, Walters, & Savic, 2008).
La combinación de las mejores características de cada uno de los métodos converge en resultados
cercanos al óptimo global y con un costo computacional menor que sus predecesores originales. El
siguiente paso será la implementación de técnicas de optimización en diferentes programas de
diseño con lo cual se permita una migración de la técnica actual de diseño (experiencia) hacia una
técnica optimizada de diseño.
2.8. Aproximaciones a la optimización de un trazado dado de una red
del Sistema Integrado de Drenaje Urbano
“Los diseños de mínimo costo de un sistema de drenaje se pueden dividir en dos: (1) optimización
del trazado del sistema; y (2) optimización de los parámetros de diseño de las tuberías
(profundidades, pendientes, diámetros, y profundidades de las cámaras de inspección) para un
trazado dado. Los dos aspectos en conjunto constituyen la totalidad del problema de diseño”
(Mays, Wenzel, & Liebman, 1976).
De esta manera, la optimización del diseño total de las redes de drenaje se puede afrontar de manera
conjunta (trazado y diseño hidráulico en el mismo modelo) o seccionada (trazado en un modelo y
diseño hidráulico en otro). De esta última, (Liebman, 1967), (Tekeli & Belkaya, 1986), (Weng &
Liaw, 2005), (Haghighi, Loop by Loop Cutting Algorithm to Generate Urban Drainage Systems
Layout, 2012), entre otros, han desarrollado modelos que optimizan el diseño del trazado de la red.
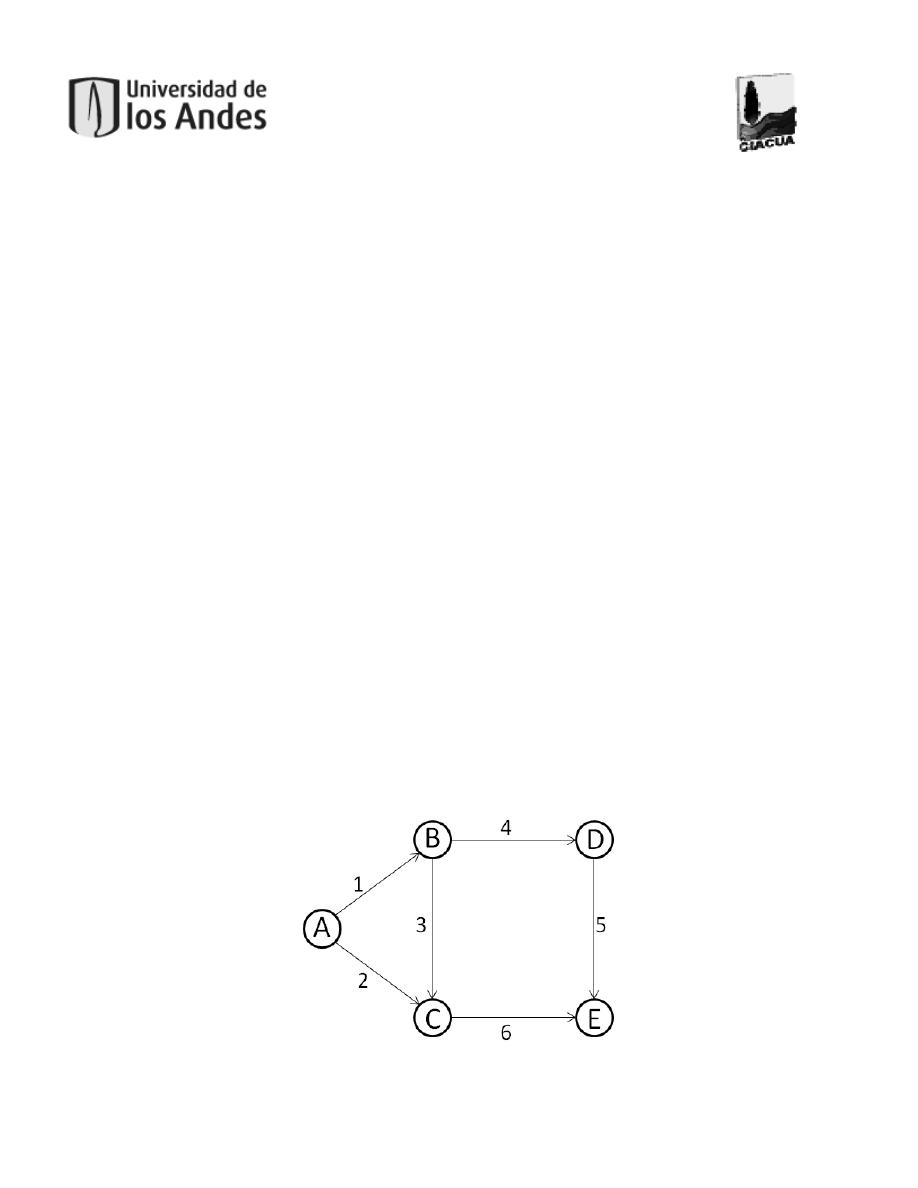
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
25
Con el trazado diseñado, solo resta hallar el conjunto de diámetros y pendientes (diseño hidráulico);
dado que, como se describe en la Sección 2.7, la optimización del diseño hidráulico es un problema
ampliamente estudiado, los investigadores se enfocan o en la optimización del trazado o en la
optimización de la red completa (trazado y diseño hidráulico).
Esta última forma de afrontar el problema de diseño de redes ha sido abordada, entre otros por
(Dajani & Gemmell, 1971), (Argaman, Shamir, & Spivak, 1973), (Mays, Wenzel, & Liebman,
1976) y (Li & Matthew, 1990). En estos estudios, aunque aseguran la obtención de muy buenos
resultados, advierten que no está garantizado el óptimo global. Igualmente sugieren que los
resultados obtenidos aunando las dos partes del problema son mejores que aquellos que se han
obtenido mientras sólo se ha tenido en cuenta una de la partes.
2.9. Metodología del ‘camino más corto’
De acuerdo con lo descrito en la Sección 2.8, los mejores resultados de la optimización de las redes
de drenaje urbano se obtienen cuando se aborda el problema integralmente, es decir teniendo en
cuenta tanto el trazado como el diseño hidráulico. Lo anterior conlleva a que el problema se centre
en encontrar la mejor manera de conectar una serie de puntos (cámaras) y de hallar la mejor
conexión entre los puntos (la mejor tubería entre dos cámaras cualesquiera). Así, los algoritmos que
resuelven el problema de camino más corto (Shortest Path), se convierten en una alternativa factible
para la solución del problema puesto que permiten modelar la red como varios caminos que van de
un punto a otro (de una cámara inicial a un punto de descarga), siendo cada uno de los caminos una
posibilidad de tubería entre una cámara y otra.
La abstracción de la realidad que hacen estos algoritmos se da a través de grafos, los cuales se
definen como unas estructuras de datos que contienen un conjunto de nodos y de arcos, siendo los
arcos las conexiones entre los nodos. En la Figura 4, los círculos denotados con una letra son los
nodos o vértices del grafo y las líneas que conectan dichos nodos son los arcos del grafo.
Figura 4. Ejemplo de un grafo.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
26
2.9.1. Metodología de Bellman Ford
Esta metodología fue desarrollada en 1956 con el propósito de solucionar un problema de tiempo de
viaje entre diferentes ciudades (Bellman, 1956). En la actualidad es uno de los algoritmos con más
uso en los problemas de camino más corto con un único origen
4
(Goldberg & Radzik, 1993).
Aunque el tiempo de solución de este algoritmo es mayor que el tiempo de solución del algoritmo
de Dijkstra, Bellman-Ford aventaja a Dijkstra en cuanto a que este último no puede manejar ciclos
negativos, es decir no puede manejar arcos con valores negativos.
Descontando las diferencias mencionadas en el párrafo anterior, los dos algoritmos trabajan de
manera similar:
Cada uno de los nodos tiene una etiqueta la cual se determina como la suma de la etiqueta del nodo
anterior más el valor (costo) del arco que une al nodo y al nodo anterior. Así, se empieza desde el
nodo inicial (cuyo valor de la etiqueta es cero) y se buscan todos los nodos que están directamente
conectados; el valor de la etiqueta de cada nodo se actualiza, según lo descrito anteriormente.
Cuando todos los nodos adyacentes al nodo inicial estén etiquetados se realiza el mismo
procedimiento para cada uno de los nodos, con la diferencia que el valor de la etiqueta de un nodo
siguiente se actualiza sí y solo sí el valor obtenido para ese nodo es menor al valor existente
(siempre y cuando al nodo llegue más de un arco). Una vez se han etiquetado todos los nodos, la
etiqueta del nodo final será el valor del camino más corto (de menos costo); de esta manera se parte
del nodo final al nodo predecesor, de este al predecesor; así, continuando hasta el nodo inicial.
2.9.2. Metodología de Dijkstra
Debido a la similitud entre el algoritmo de Dijkstra y el de Bellman-Ford, el hecho de que en los
problemas reales no se requiera la evaluación de ciclos negativos y a la rapidez del primer método,
se ha optado por esta metodología como la predilecta para resolver los problemas de camino más
corto. Esto ha conllevado a diferentes estudios en los que se pretenden introducir algunas mejoras al
método, ya sea para aplicaciones específicas o para corregir algunas deficiencias consideradas por
algunos autores.
De esta manera (Wang, 2012), plantea un algoritmo modificado, en el cual da solución a tres
inconvenientes que presenta la metodología: el mecanismo de finalización del método puede
conllevar a ciclos infinitos, se presentan problemas con la priorización de los vértices adyacentes al
momento de generar nuevas etiquetas y más de un nodo puede ser etiquetado al mismo tiempo.
Por otro lado, (Ahuja, Magnanti, & Orlin, 1993) plantean dos modificaciones: la primera consiste
en una metodología inversa, en la cual la gran diferencia radica en que en cada paso se parte del
nodo de etiqueta de menor valor. La segunda plantea un cambio para la situación específica en que
4
Un único origen implica que se calculará la ruta de un solo nodo hacia los demás nodos del grafo.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
27
no sea necesario hallar la distancia desde el nodo de inicio a todos los nodos de la red, así la
transformación implica que el cómputo del algoritmo finalice tan pronto todas las etiquetas del nodo
sean evaluadas.
Dado que en el presente trabajo se pretende modelar una red de drenaj e urbano, se plantea la
implementación de la metodología de Dijkstra dado que en las redes de drenaje urbano no se
esperan ni arcos ni ciclos negativos. En la Sección 3.1 se describe la adaptación de la metodología
para poder acoplarla a una red de drenaje urbano. Mediante dicha adaptación se espera obtener el
diseño de mínimo costo, partiendo de una topología dada.
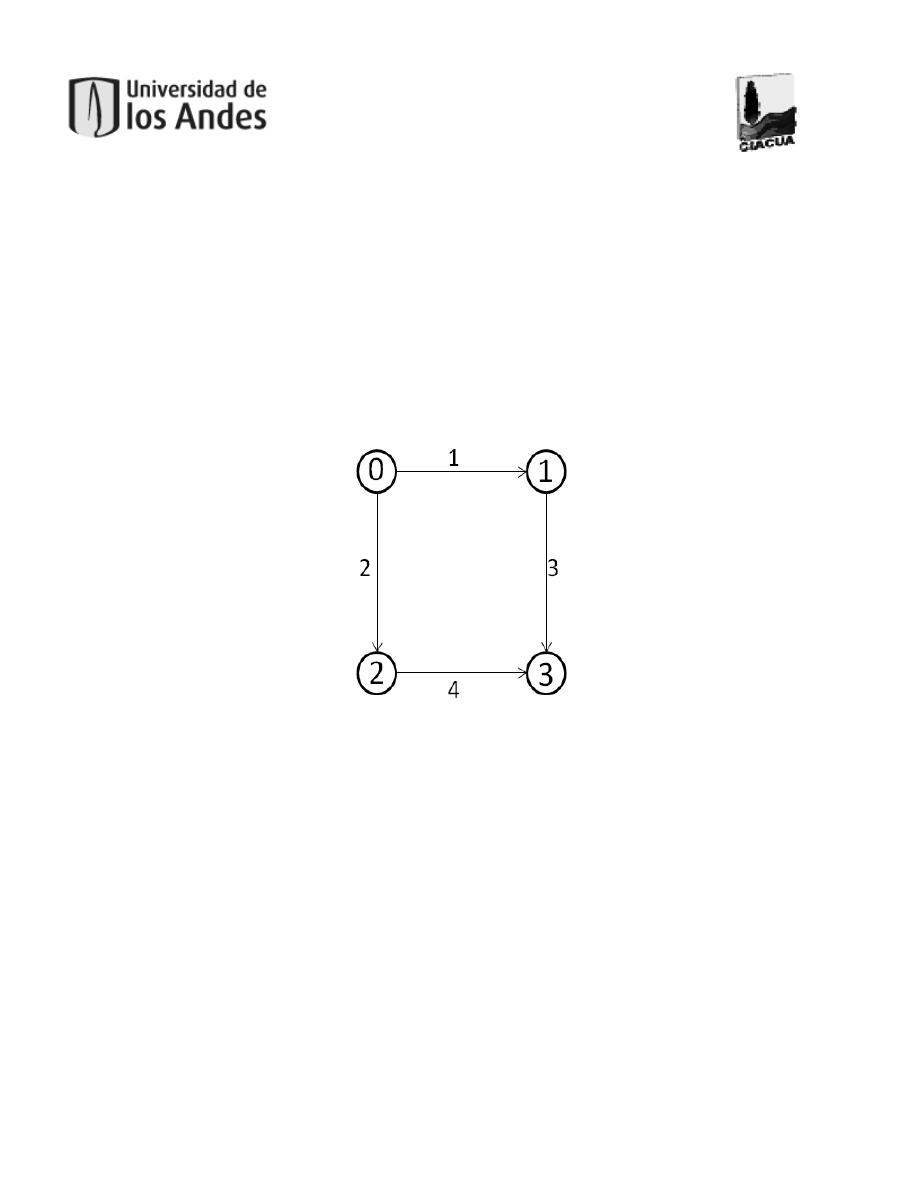
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
28
3. METODOLOGÍA
3.1. Implementación de Dijkstra
La implementación del algoritmo de Dijkstra requiere que se maneje una estructura de datos tipo
grafo (ver Sección 2.9). La analogía completa entre las redes de drenaje y el grafo sería: el grafo
estaría representado por toda la red, los nodos por las cámaras y los arcos por las diferentes
opciones de tubería entre una cámara y otra. Las posibilidades de tubería resultan de una
combinación entre diámetro y pendiente. Como ejemplo, se ilustra en la Figura 5 la representación
de una red de 4 cámaras y 4 tuberías.
Figura 5. Representación de una red como un grafo.
En la Figura 5, cada una de las 4 líneas representa un conjunto de arcos entre los dos nodos, como
también cada uno de los 4 círculos representa un conjunto de nodos. Cada uno de los arcos es una
posibilidad de poner una tubería entre dos cámaras. En la Figura 6 se muestra el detalle del grafo,
suponiendo que sólo hay dos diámetros disponibles para hacer el diseño al igual que dos
profundidades. El Diámetro 1 es menor que el Diámetro 2 y la Profundidad 2 es mayor que la
Profundidad 1. De la Figura 6 es importante aclarar que:
El número de nodos en la Cámara 1 es 2 y en la Cámara 2 y Cámara 3 es 4.
Los arcos que salen de un nodo a otro nodo con la misma profundidad y el mismo diámetro
existen sí y solo sí la cota de la cámara aguas abajo es inferior que la cota de la cámara
aguas arriba.
No existen arcos que conecten un diámetro, aguas abajo, con un diámetro menor, aguas
arriba.
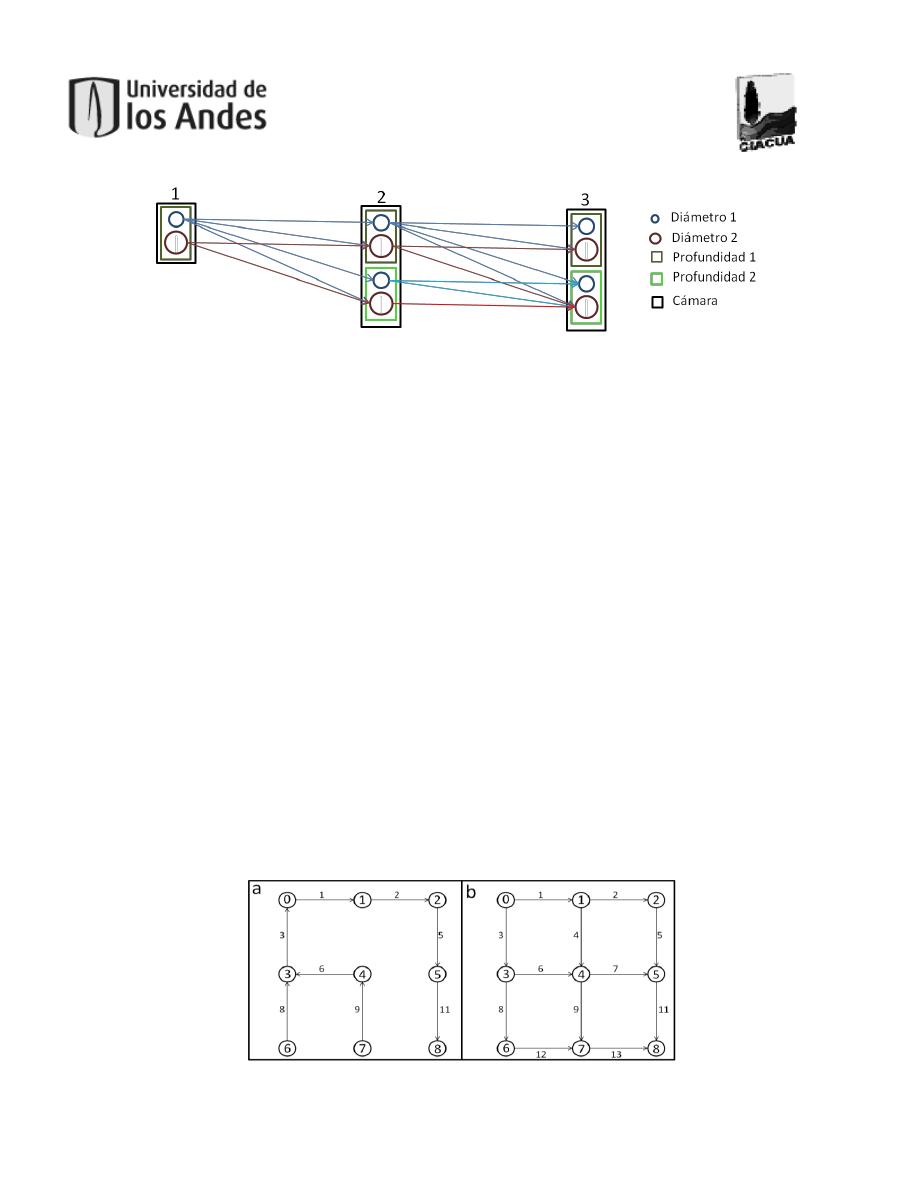
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
29
Figura 6. Detalle del grafo.
Dado que el algoritmo de Dijkstra tiene como objetivo conectar un nodo, nodo inicial, con el resto
del grafo, se debe tener en cuenta que en una red de drenaje urbano el nodo inicial sería el punto de
descarga pues es éste el que debe estar conectado con el resto de la red. Adicionalmente e l resultado
final de la metodología de Dijkstra es un árbol, es decir, para cada nodo existe un camino que lo
conecta con el punto de descarga, pero no todos los nodos están conectados con todos. Lo anterior
implica que habría que crear una nueva metodología para agregar las tuberías que hacen parte de la
red, pero no fueron incluidas en el árbol.
Debido al problema descrito se trabajó en una metodología con la cual se obtuviera, como
resultado final, un ‘árbol cerrado’, es decir que todas las tuberías de la red sean agregadas.
3.2. Generación del ‘árbol cerrado’
3.2.1. Definición del ‘árbol cerrado’
Un árbol se denomina a un grafo que tiene, para todos los nodos (ramas), un camino para llegar
hasta el nodo inicial (raíz). En el caso de una red de drenaje urbano se ría que cada una de las
cámaras tiene una ruta de drenaje hacia el punto de descarga. A pesar de la veracidad de lo anterior,
la disposición de las tuberías de las redes de drenaje urbano (topología) no sigue la forma de un
árbol. En la Figura 7 se observan dos configuraciones; en (a) se puede observar una red en árbol y
en (b) se muestra una red en ‘árbol cerrado’, el cual representa el trazado de una red real de drenaje
urbano.
Figura 7. Ejemplo de árbol y 'árbol cerrado'.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
30
La metodología desarrollada para la creación del ‘árbol cerrado’ tiene gran influencia de la
metodología de Dijkstra; así las características más importantes son:
Recorrido de los nodos: La diferencia con la metodología de Dijkstra radica en que una vez
se encuentra el camino más corto hacia el nodo i-ésimo (el tubo de menor costo que parte
de uno de los nodos adyacentes) se vuelven a evaluar las demás tuberías que llegan a éste,
en iteraciones posteriores. De esta manera se asegura que todas las tuberías hagan parte del
resultado final.
Temporalidad del camino más corto: Esta metodología evalúa en cada iteración cuáles son
los frentes de avance (ver Sección 2.9.1), de éstos evalúa todas las posibilidades. A medida
que calcula dichas posibilidades genera camino más corto de las posibilidades evaluadas.
Éste, es un camino más corto temporal, pues no se han computado todas las posibilidades.
El algoritmo de Dijkstra denomina la temporalidad del resultado como etiqueta-t (t-label),
etiqueta temporal, y etiqueta-p (p-label), etiqueta permanente.
3.2.2. Descripción del proceso operativo
En la Figura 8 se muestra un ejemplo del proceso operativo de la metodología. Como se explicó en
la Sección 3.1, es necesario empezar desde el punto de descarga. De esta manera, todos los nodos
adyacentes conforman los denominados frentes de avance. Éstos se definen como las nuevas
tuberías que pueden ser agregadas al ‘árbol cerrado’ en cada una de las iteraciones. Así los frentes
de avance tienen tres posibilidades (ver Sección 3.2.3): una tubería que llega al nodo de descarga,
una tubería que crea una nueva serie o una tubería que se pega a una serie existente.
En el literal a de la Figura 8 se muestran los dos frentes de avance que tiene el punto de descarga,
éstos son: la tuberías de la cámara 1 a la cámara 3 y la tubería de la cámara 2 a la cámara 3. En los
literales b y c se muestra la evaluación individual de cada uno de los frentes de avance. En el literal
d se ha agregado al árbol el resultado del camino más corto (la tubería de menor precio). Una vez el
árbol cuenta con un nuevo elemento se buscan los nuevos frentes de avance y se evalúa cada uno de
ellos.
En el literal g se observa que el valor de la tubería que conecta las cámaras 2 y 3 cambia de $100 a
$130; esto se da porque se está agregando una tubería aguas arriba de esta, por lo que deberá
transportar un mayor caudal. En el literal h se ha agregado la tubería que va de la cámara 1 a la
cámara 3, a pesar de que el costo de esta es de $ 150 y el costo de la otra tubería evaluada (de la
cámara 0 a la cámara 2) es de $70. Esto es porque se debe tener en cuenta el costo total de la serie,
ya que el diseño de la tubería que va de la cámara 2 a la cámara 3 cambió.
El proceso se repite iterativamente hasta que los todos los nodos estén conectados entre sí.
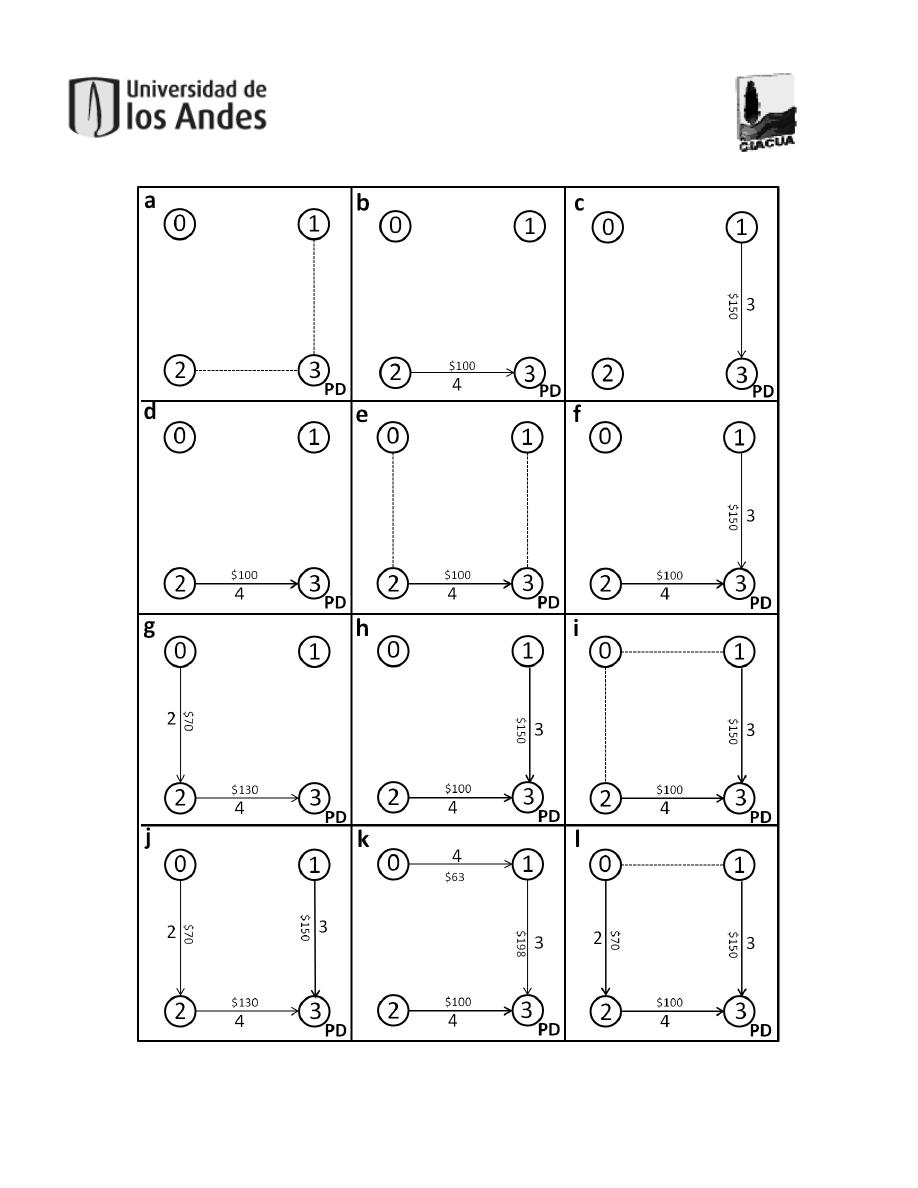
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
31
Figura 8. Ejemplo del proceso operativo de la metodología.
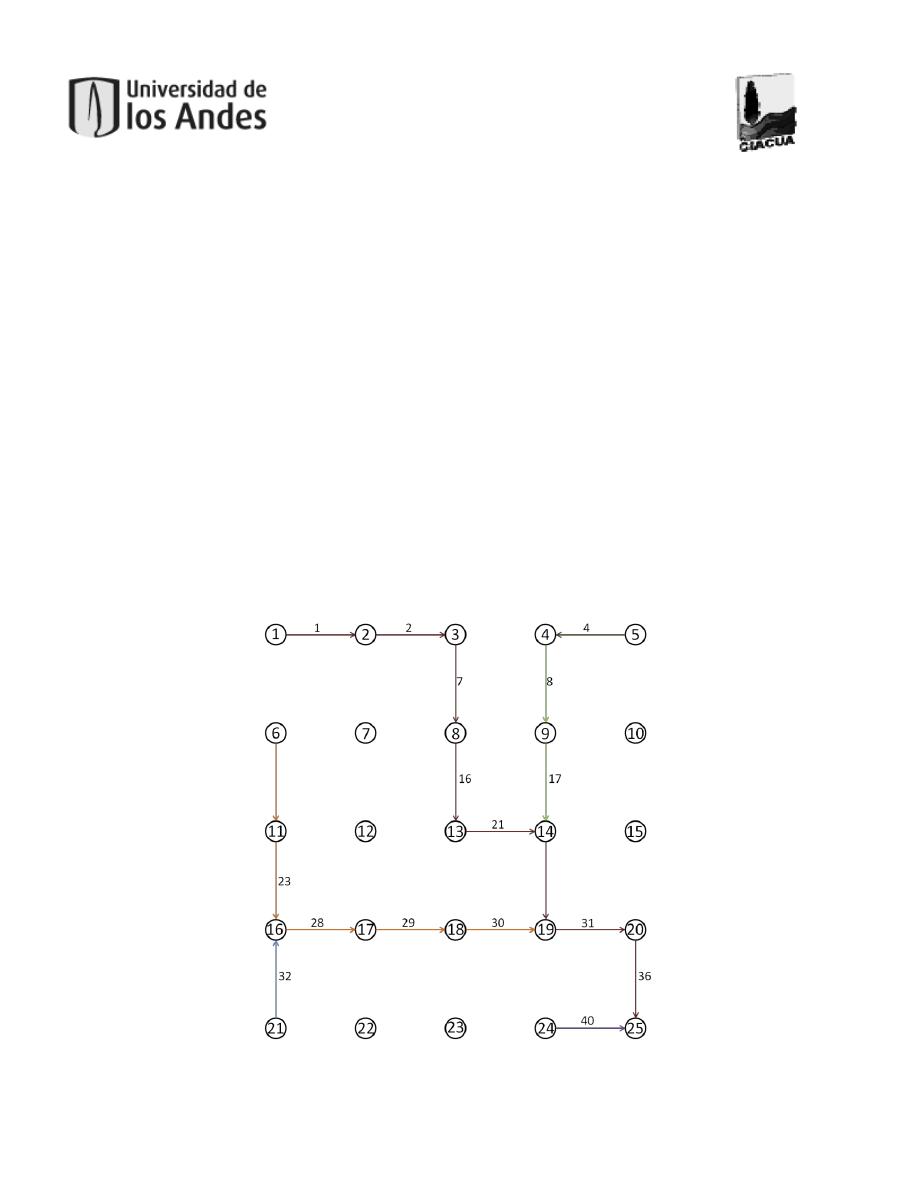
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
32
3.2.3. Tipos de frentes de avance
Cuando se agrega un nuevo tubo al ‘árbol cerrado’ es necesario revaluar los frentes de avance, si se
agregan, se suprimen o se mantienen. La importancia de los frentes de avance, en la metodología,
radica en que el proceso a seguir depende en qué tipo de frente de avance se trate. Se han
clasificado en tres los frentes de avance, esta clasificación depende del efecto que genere el nuevo
tubo sobre el ‘árbol cerrado’ existente:
La tubería a agregar llega a una cámara perteneciente al ‘árbol cerrado’; dicha cámara es el
punto de descarga. En esta situación es necesario diseñar únicamente la tubería; para esto,
el caudal de diseño equivale al caudal de aportes.
La tubería a agregar llega a una cámara que se encuentra en el ‘árbol cerrado’, pero que no
es el punto de descarga: en este caso se estaría diseñando una tubería y una serie. Los
caudales de diseño de la serie cambian desde aguas abajo de la tubería.
La tubería a agregar llega a una cámara que es la cámara inicial del tubo más aguas arriba
de una serie: este escenario implicaría el rediseño de una serie, todos los caudales cambian.
Los nuevos caudales serían igual a los antiguos más el caudal de la nueva tubería.
Figura 9. Tipos de frente de avance.
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
33
En la Figura 9 se observan los diferentes tipos de frentes de avance. La serie roja es la serie
principal. El primer tipo de frente de avance está representado por la línea morada que une los
nodos 24 y 25. El segundo tipo se representa con la línea azul que va del nodo 21 al 16, en este caso
se tiene la serie naranja (inicia en el nodo 6 y termina en el nodo 19) y llega la tubería en mención.
Para la evaluación de este frente de avance es necesario rediseñar la serie naranja (los caudales de
las tuberías 28, 29 y 30 se incrementan en el caudal aportado por la tubería azul). Por lo anterior, en
este tipo de frente de avance se realiza tanto el diseño de una serie como de una tubería. Por último,
la línea café entre los nodos 5 y 4 representa el tercer tipo de avance, en el cual la tubería para
agregar al ‘árbol cerrado’ se adiciona a una serie existente. Se hace el diseño de la serie completa.
3.2.4. Diseño
El orden de diseño viene dado por los frentes de avance. Una vez se escogen cada uno de los frentes
de avance, se diseña y evalúa cada uno de ellos. El diseño se hace con la metodología desarrollada
por Natalia Duque en su trabajo de grado “Metodología para la optimización del diseño de tuberías
en serie en sistemas de alcantarillado”. Esta metodología parte de un grafo dirigido, es decir, los
arcos tienen una dirección definida, de una función de costos y de un nodo de inicio. Dado que se
trata de una serie de tuberías (a cada una de las cámara s entra solo una tubería y de cada una de
ellas sale una sola tubería, exceptuando las cámaras inicial y final), no es necesario considerar
bidireccionalidad (Duque, 2013).
Cada una de las cámaras de la serie tiene un conjunto de nodos cuyo tamaño depende de la
precisión con la que se trabaje el diseño y el número de diámetros disponibles para el diseño. La
precisión se define como el inverso de la distancia vertical entre nodos. Así, el tamaño del conjunto
de nodos de la cámara i-ésima estará dado por:
(
)
3.1
donde,
NPC
i
: Número de nodos de la cámara i-ésima
5
.
h
min
: Profundidad mínima a la que se debe encontrar la cota clave de la tubería.
h
max
: Profundidad máxima a la que se debe encontrar la cota batea de la tubería.
p: precisión.
ND: número de diámetros disponibles para el diseño.
En la Figura 10 se muestra la descripción de las variables de profundidad. El espacio entre la línea
roja y la línea vinotinto se denomina espacio de factibilidad y es en el cual se pueden posicionar las
tuberías. Entre mayor sea la precisión, una mayor cantidad de nodos se pueden ubicar en el espacio
5
Si la cámara es la primera el número de nodos en esa cámara será únicamente el número de diámetros
disponibles, pues el tubo se ubica en la mínima profundidad posible.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
34
de factibilidad. De manera general, la precisión con la que se trabajó fue de centímetros, es decir, la
distancia vertical entre un nodo y otro, para cada diámetro, es de un centímetro. Así mismo, la
profundidad mínima es de 1.2 m y la máxima es de 5 m, según lo establecido en el Reglamento de
Agua Potable y Saneamiento Básico (RAS, 2000).
Figura 10. Profundidad mínima y máxima.
Una vez se crean la totalidad de los nodos se procede a generar los arcos que conecten a los nodos
de una cámara con la siguiente. Para esto se verifica que la pendiente del tubo sea diferente de cero
y que el diámetro aguas abajo sea igual o mayor que el diámetro aguas arriba. Una vez se arma el
grafo (para un ejemplo de un grafo, ver la Figura 6) se inicia la búsqueda del camino más corto,
partiendo desde el nodo inicial (ver Sección 2.9.1).
3.2.5. Verificación de las cotas de batea
Dado que el diseño de la red se lleva a cabo en series independientes, es necesario verificar que
cuando se intersequen dos series la cota de batea de la serie que se va a diseñar sea superior a la
cota de batea de la serie que está diseñada. Este procedimiento supone que las series que fueron
incluidas primero que otras (dado que tenían un menor costo) son principales sobre las últimas.
De esta manera, la verificación de las cotas de batea se lleva a cabo modificando el espacio de
factibilidad antes de realizar el diseño en cada una de las iteraciones. Así, cuando se va a diseñar un
frente de avance que llega al punto de descarga, se limita h
max
de dicha cámara. Si el frente de
avance es una serie completa, se modifica h
max
de la cámara a la cual llega la serie. Por último, si el
frente de avance se compone de dos series (una serie y una tubería), se limita el h
max
de la cámara
donde llega la serie y con el diseño de la serie se modifica el h
max
del nodo final de la tubería (el
cual pertenece a la serie diseñada).
3.3. Parámetros de optimización
3.3.1. Función objetivo
Dada la característica del método de solución, y según lo enunciado en la Sección 3.2.4, es
necesario plantear una función objetivo, la cual será la que le asigna el valor a cada uno de los

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
35
arcos, es decir, es la directriz de la optimización. Por la naturaleza del problema se requiere hallar
un diseño que tenga el menor costo posible, sin sacrificar el buen funcionamiento de la red. Así
pues, la función objetivo es el costo total de la red. La mecánica de la metodología trabajada busca
un mínimo global partiendo de la minimización de los componentes, es decir que para el caso
trabajado, se consigue el mínimo costo de la red, partiendo del mínimo costo de las tuberías.
En el Centro de Investigaciones en Acueductos y Alcatarillados (CIACUA) se estableció una
fórmula para hallar los costos de las tuberías (instaladas) de una red de drenaje urbano. Ésta se
encuentra dividida en dos criterios: costo de tubería y costo de excavación. Para los costos de
tubería se halla una relación entre el costo por unidad de longitud y el diámetro de ésta; para los
costos de excavación se halla el volumen excavado y los costos asociados con la mano de obra
requerida para tal fin (Saldarriaga, y otros, Trazado Óptimo de la red, 2013).
(
)
3.2
donde,
CT: Costo de la tubería (COP $).
k: Coeficiente que determina el aumento del costo de la tubería, de acuerdo con la inflación (1.32).
A
1
: Coeficiente que determina el aumento del costo de la tubería, de acuerdo con la inflación
(9579.31).
L: Longitud de la tubería (m).
D: Diámetro de la tubería (m).
3.3
donde,
CE: Costo de excavación (COP $).
A
2
: Coeficiente que determina el aumento del costo de excavación, de acuerdo con la inflación
(1163.77).
V: Volumen de excavación, definido en la Ecuación 3.5 (m
3
).
El costo total está dado por la suma del costo de la tubería más el costo de excavación. Así, la
función objetivo cuando se quiere minimizar el costo total, será :
3.4
En la Figura se muestran las diferentes variables utilizadas para calcular el volumen de excavación,
(Ecuación 3.5).
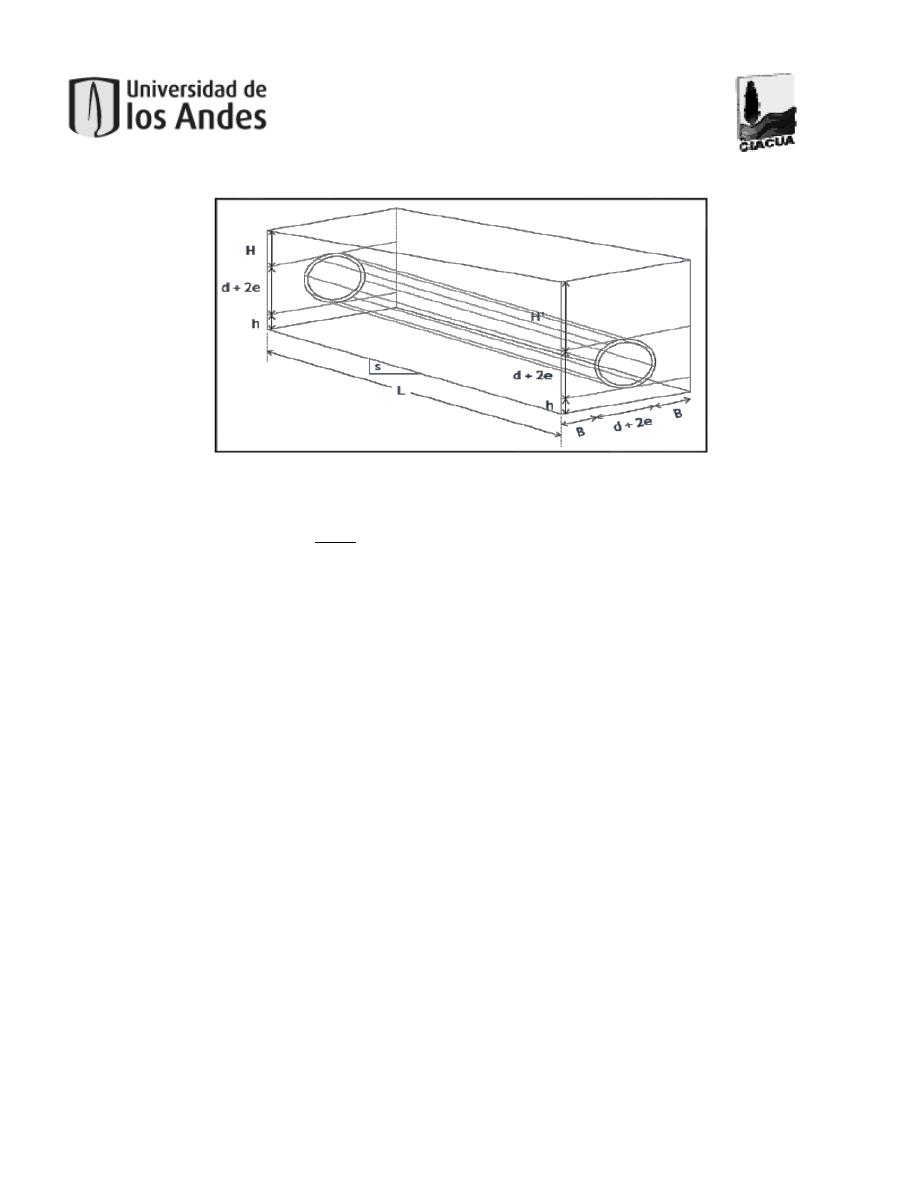
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
36
Figura 11. Proyección del trapecio que produce el área excavada para una tubería. Tomado de (Saldarriaga, y otros,
Desarrollo de Técnicas Computacionales Exhaustivas para el Diseño Optimizado de Redes de Drenaje Urbano,
2013)
( ) (tan
)
3.5
donde,
H: Profundidad de excavación hasta la cota clave de aguas arriba de la tubería (m).
H’: Profundidad de excavación hasta la cota clave de aguas abajo de la tubería (m).
e: Espesor de la tubería (m).
h: Relleno que debe disponerse bajo la tubería. Depende de la normatividad. (0.15 m).
B: Espacio lateral a cada uno de los lados de la tubería para facilidad de la instalación (m).
3.3.2. Variables de decisión
De manera general, la solución del problema, mediante la metodología planteada, consiste en
cambiar el valor de las variables de decisión y encontrar un valor específico para cada una de ellas
tal que resuelva de manera satisfactoria la función objetivo, cumpliendo todas las restricciones
estipuladas. En el caso de este proyecto, las variables de decisión son la pendiente y el diámetro de
cada una de las tuberías de la red.
Adicionalmente, el tipo de costo se puede considerar una variable de decisión puesto que, como se
ve en la Figura 12, en una red normal los costos de excavación representan cerca del 70 % del costo
total de la red. De esta manera, la función objetivo estaría definida como la función de costos, sin
especificar a qué tipo de costos se hace referencia. Así, para cada diseño en específico se puede
establecer qué tipo de costo prevalece, si el costo total o el costo de excavación.
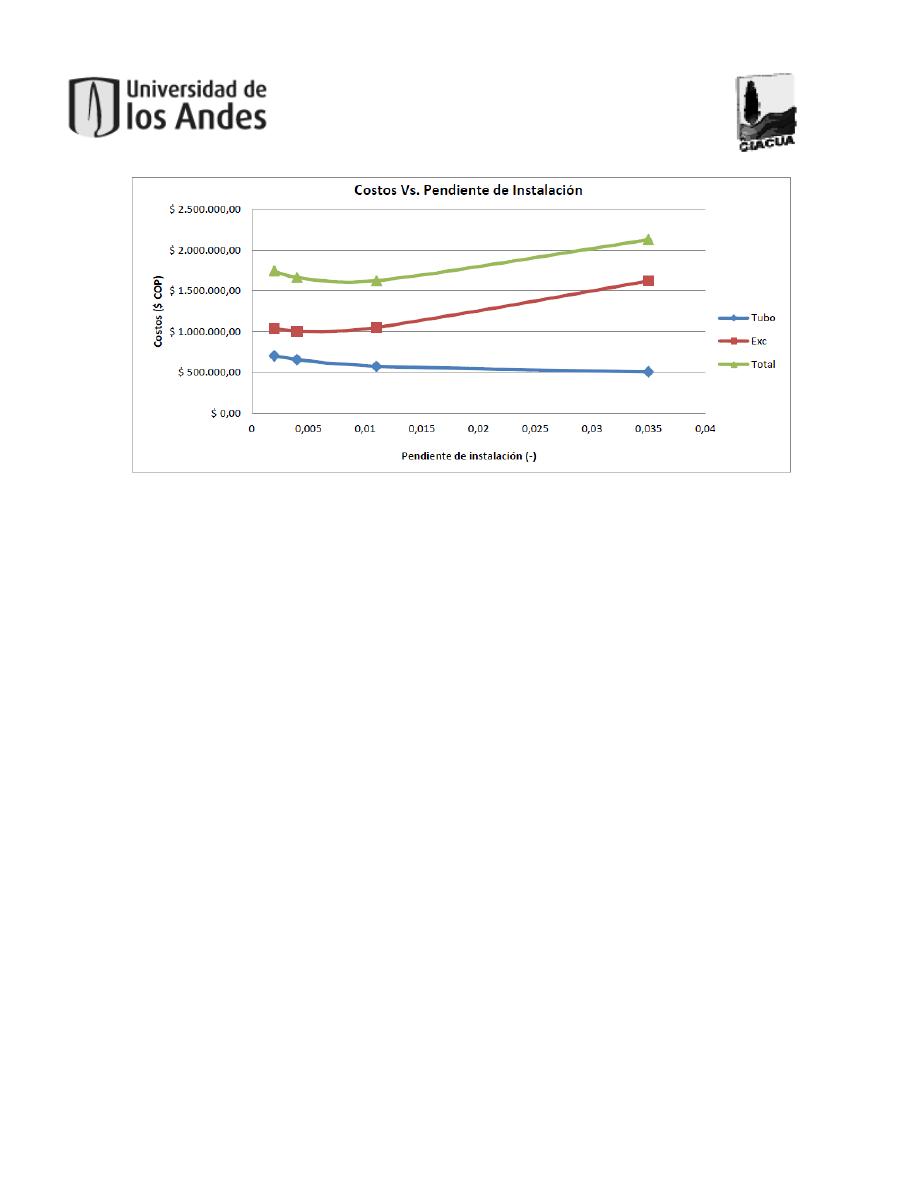
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
37
Figura 12. Relación de costos en un proyecto de drenaje urbano. Tomado de (Saldarriaga, y otros, Desarrollo de
Técnicas Computacionales Exhaustivas para el Diseño Optimizado de Redes de Drenaje Urbano, 2013).
3.3.3. Restricciones
La solución óptima debe ceñirse a un espacio de solución definido por ciertas restricciones, para
este proyecto éstas son:
El diámetro de aguas abajo tiene que ser mayor o igual al diámetro de aguas arriba.
La pendiente del tubo tiene que ser mayor a cero,
La máxima relación de llenado es función del diámetro: diámetros menores a 0.5 m,
relación de llenado máxima es de 70 %; diámetro entre 0.5 m y 1 m, relación de llenado
máxima de 80 %; para diámetros mayores a 1 m, relación de llenado máxima de 80 %.
La velocidad tiene que ser menor a 10 m/s si el material es PVC, 5 m/s si el material es
concreto.
Si la relación de llenado es menor o igual al 10 %, el esfuerzo cortante tiene que ser mayor
a 2 Pa.
Si el diámetro es mayor o igual a 0.45 m el esfuerzo cortante tiene que ser mayor a 3 Pa; si
el diámetro es menor a 0.45 m, la velocidad debe ser mayor a 0.6 m/s.
Si la relación de llenado es mayor al 70 % el número de Froude no puede estar en un rango
entre 0.7 y 1.5.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
38
4.
RESULTADOS
En esta Sección se muestran 3 tamaños de redes: 3x3, 4x4 y 5x5. El tamaño de las redes está dado
por el número de cámaras que hacen parte de la red, así, la red de 3x3 está compuesta por 9
cámaras. Cada uno de los tipos de redes se calculó para tres configuraciones diferentes:
Terreno plano: Las cotas de las cámaras (100 m), los caudales aferentes a cada tubo (0.02
m
3
/s) y las longitudes son iguales (100 m).
Terreno a favor del drenaje: Las cotas de las cámaras disminuyen hacia el punto de
descarga, las longitudes varían aleatoriamente y los caudales aferentes (0.02 m
3
/s) a cada
tubo son iguales.
Terreno con topografía variable: Las cotas de las cámaras varían de manera aleatoria al
igual que las longitudes. La diferencia entre el punto más alto y el más bajo de toda la red
es de 1.5 m. Los caudales aferentes (0.02 m
3
/s) a cada tubo son iguales.
Las convenciones que se utilizarán en los resultados se muestran en la Figura 13. Se aclara que
serie secundaria es cualquier serie (de más de una tubería) diferente a la principal, el inicio es una
tubería que se adiciona a una serie existente. Las tuberías sin diseñar están en los esquemas de las
redes y no tienen sentido de flujo pues esa decisión está incluida en la respuesta.
Figura 13. Convenciones de los resultados.
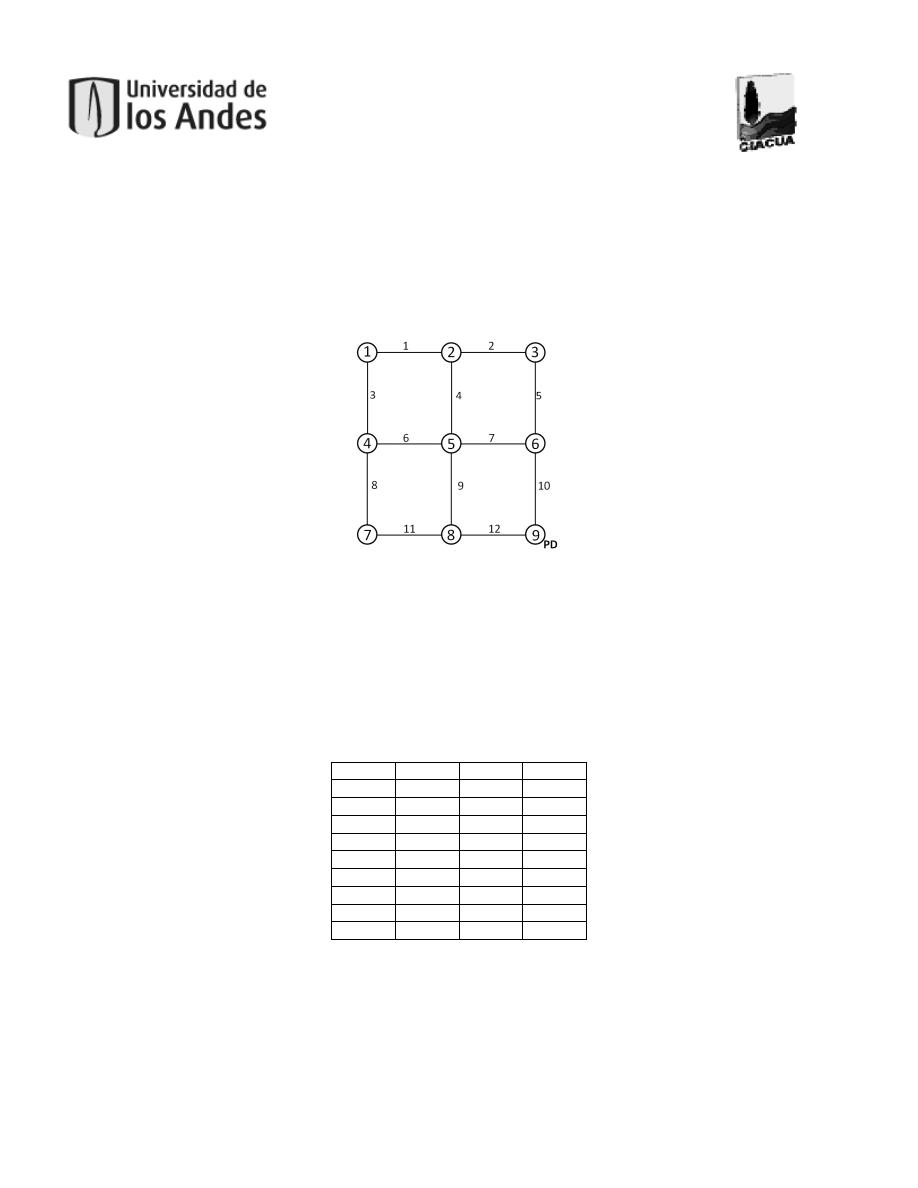
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
39
4.1. Red tipo 3x3
En la Figura 14 se muestra la red de tipo 3x3. No es un modelo a escala y se muestra para tener una
referencia de las numeraciones de las cámaras y los tubos. Los círculos representan las cámaras y
los números al interior de cada círculo son el ID de cada cámara. Las líneas son las tuberías y los
números al lado de cada línea el ID de la tubería.
Figura 14. Esquema de la red tipo 3x3.
4.1.1. Terreno plano
Las características topológicas de cada una de las cámaras se muestran en la
Tabla 9
. En la Figura 15 se muestra el resultado de diseño de la red y en la Tabla 10 se muestra el
diseño obtenido.
Tabla 9. Información de las cámaras. 3x3.
ID
X (m)
Y (m)
Cota (m)
1
0.0
0.0
100.0
2
100.0
0.0
100.0
3
200.0
0.0
100.0
4
0.0
100.0
100.0
5
100.0
100.0
100.0
6
200.0
100.0
100.0
7
0.0
200.0
100.0
8
100.0
200.0
100.0
9
200.0
200.0
100.0
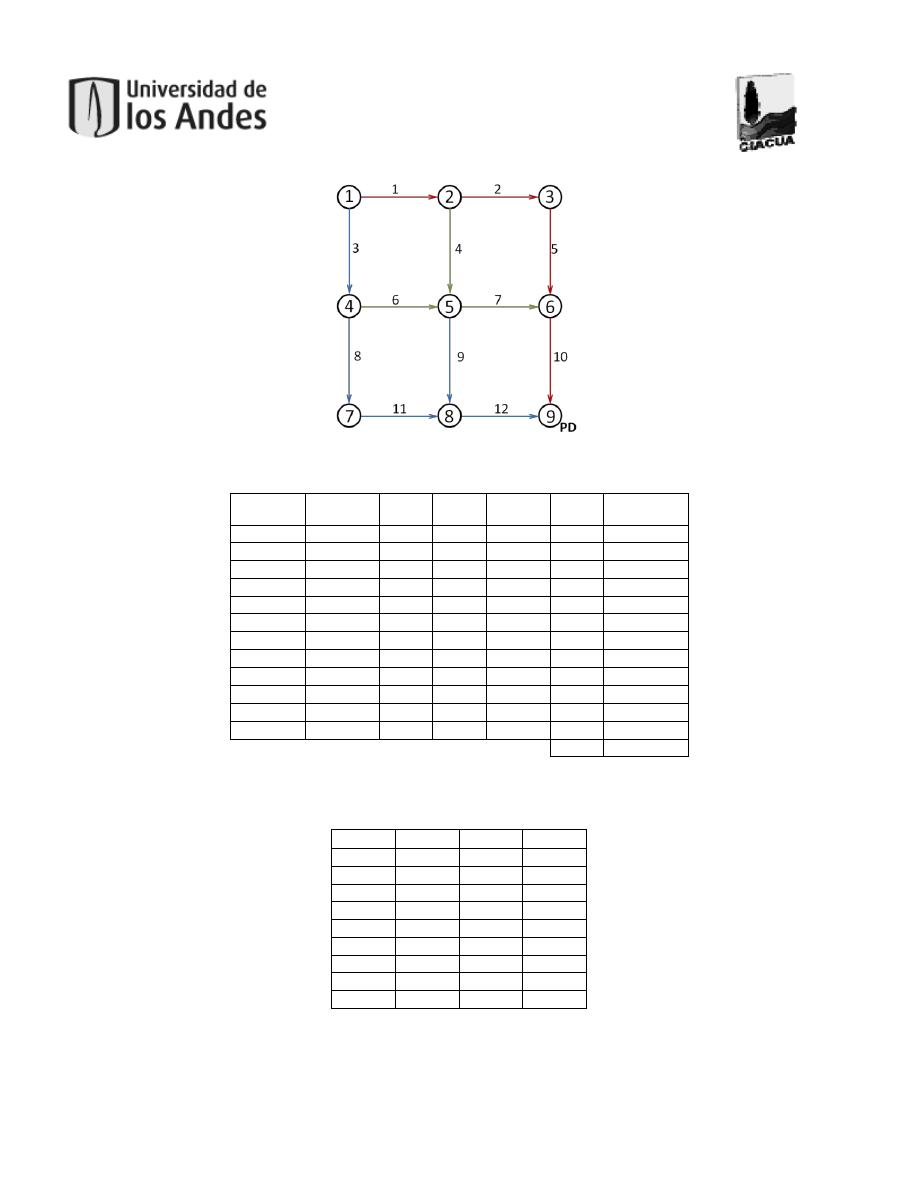
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
40
Figura 15. Red para terreno plano. 3x3.
Tabla 10. Resultado diseño terreno plano. 3x3.
ID cámara
inicial
ID cámara
final
D (m)
y
n
(m)
S (-)
L (m)
Costo (COP)
1
2
0.25
0.161
0.00106
100.0
$ 1,301,126
2
3
0.3
0.206
0.00130
100.0
$ 1,518,169
3
6
0.3
0.210
0.00260
100.0
$ 1,643,772
6
9
0.35
0.245
0.00580
100.0
$ 2,114,544
5
8
0.2
0.138
0.00260
100.0
$ 1,168,889
8
9
0.3
0.201
0.00660
100.0
$ 2,420,443
2
5
0.2
0.138
0.00260
100.0
$ 1,168,889
5
6
0.3
0.210
0.00260
100.0
$ 1,626,528
1
4
0.2
0.138
0.00260
100.0
$ 1,168,889
4
7
0.25
0.175
0.00300
100.0
$ 1,478,345
7
8
0.25
0.175
0.00630
100.0
$ 1,763,154
4
5
0.2
0.138
0.00260
100.0
$ 1,168,889
Total
$ 18,541,639
4.1.2. Terreno a favor del drenaje
Tabla 11. Información de las cámaras. 3x3.
ID
X (m)
Y (m)
Cota (m)
1
0.0
0.0
101.3
2
75.0
0.0
100.9
3
160.0
0.0
101.5
4
5.0
98.0
101.0
5
100.0
100.0
100.9
6
169.0
91.0
100.4
7
15.0
135.0
100.3
8
100.0
200.0
100.3
9
150.0
184.0
100.0
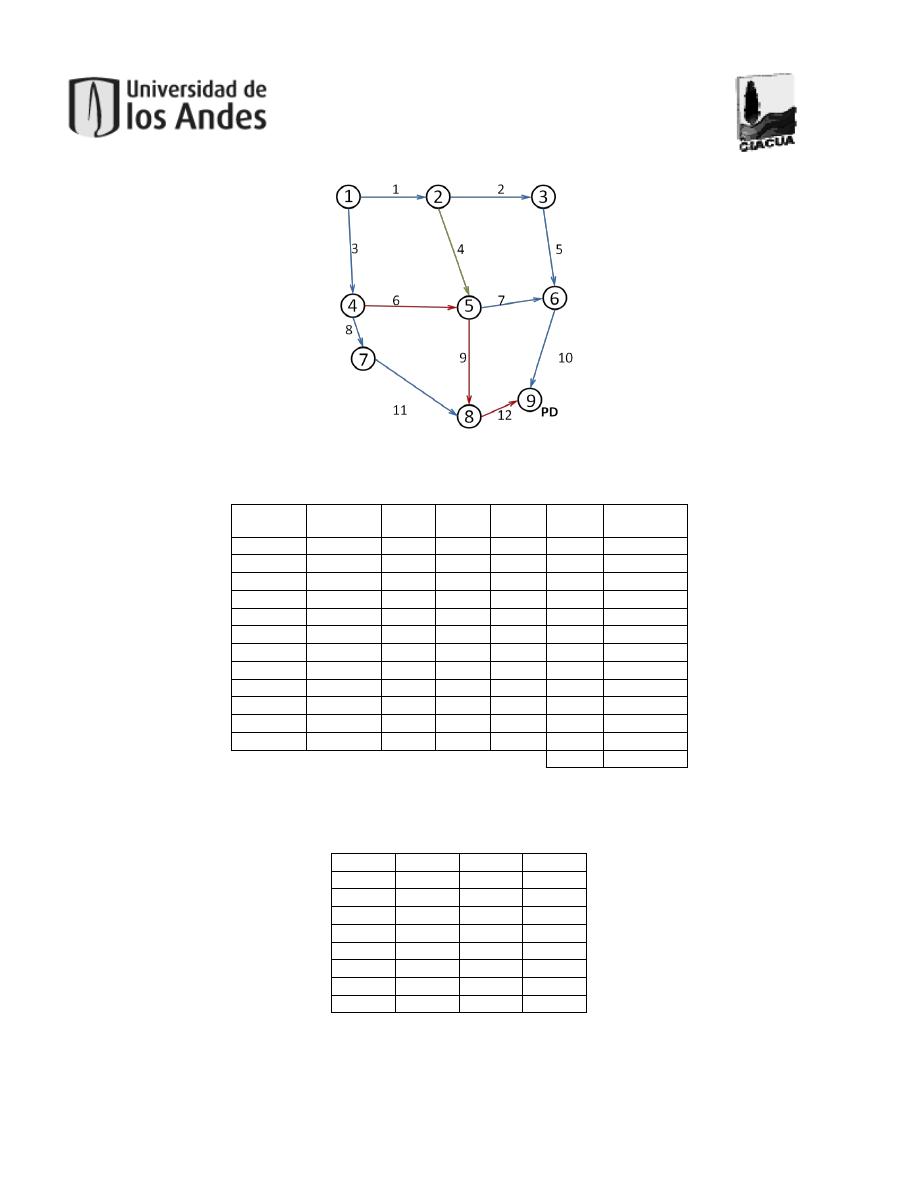
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
41
Figura 16. Red para terreno a favor del drenaje. 3x3.
Tabla 12. Resultado diseño terreno a favor del drenaje. 3x3.
ID cámara
inicial
ID cámara
final
D (m)
y
n
(m)
S (-)
L (m)
Costo (COP)
4
5
0.2
0.138
0.0026
95.0
$ 1,074,039
5
8
0.25
0.175
0.0063
100.0
$ 1,840,052
8
9
0.3
0.210
0.0122
52.5
$ 993,696
5
6
0.15
0.105
0.0100
69.6
$ 640,756
6
9
0.3
0.210
0.0066
94.9
$ 1,658,259
1
2
0.2
0.095
0.0074
75.0
$ 815,819
2
3
0.25
0.175
0.0030
85.0
$ 1,302,341
3
6
0.25
0.175
0.0063
91.5
$ 1,511,735
1
4
0.15
0.105
0.0100
98.1
$ 1,066,133
4
7
0.2
0.140
0.0088
38.3
$ 429,889
7
8
0.25
0.175
0.0063
107.0
$ 1,731,029
2
5
0.15
0.105
0.0100
103.1
$ 1,216,223
Total
$ 14,279,971
4.1.3. Terreno con topografía variable
Tabla 13. Información de las cámaras. 3x3.
ID
X (m)
Y (m)
Cota (m)
1
0.0
0.0
100.9
2
75.0
0.0
100.8
3
160.0
0.0
101.5
4
5.0
98.0
101.0
5
100.0
100.0
101.0
6
169.0
91.0
100.4
7
15.0
135.0
100.2
8
100.0
200.0
100.3
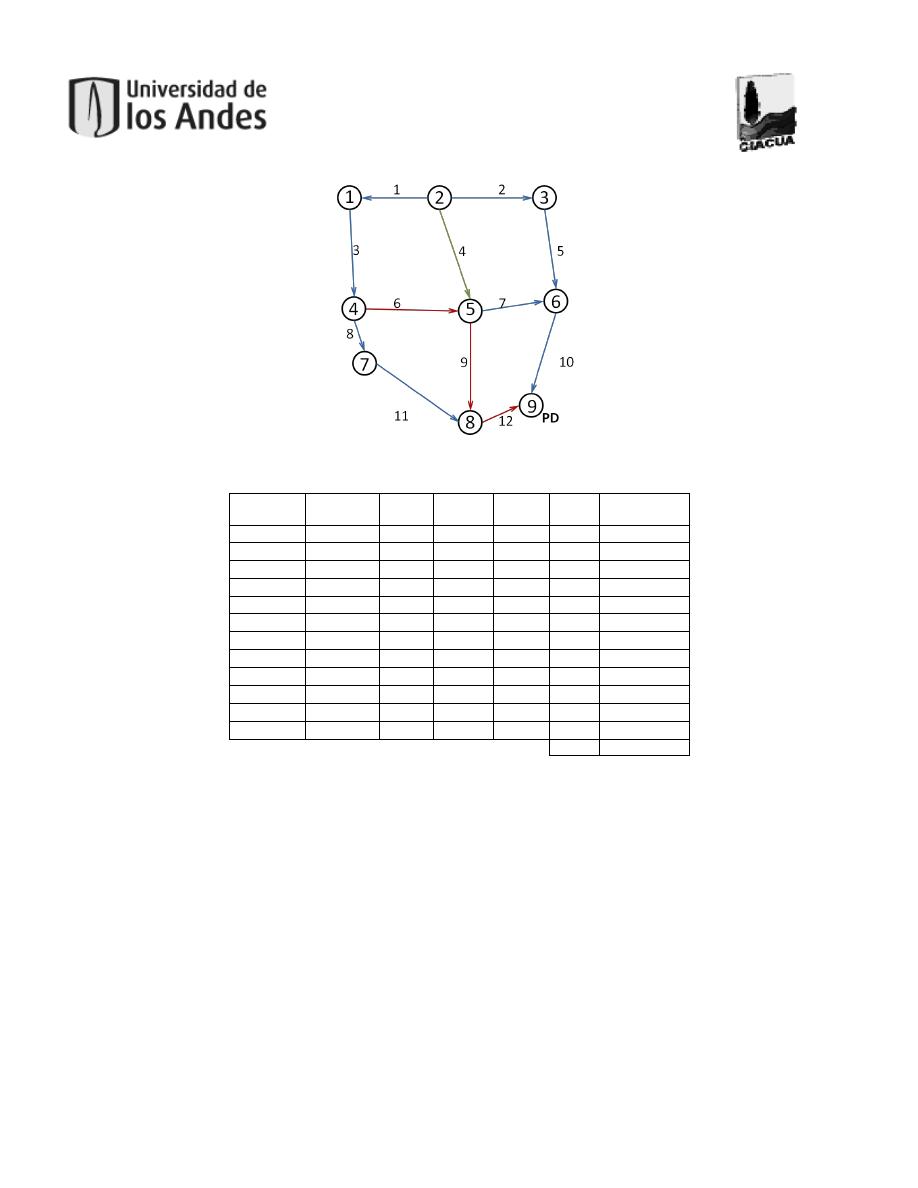
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
42
Figura 17. Red para terreno con topografía variable. 3x3.
Tabla 14. Resultado diseño terreno con topografía variable. 3x3.
ID cámara
inicial
ID cámara
final
D (m)
y
n
(m)
S (-)
L (m)
Costo (COP)
4
5
0.2
0.138
0.0026
95.0
$ 1,097,666
5
8
0.25
0.175
0.0063
100.0
$ 1,937,071
8
9
0.3
0.210
0.0156
52.5
$ 1,133,428
5
6
0.15
0.099
0.0115
69.6
$ 641,377
6
9
0.3
0.210
0.0044
94.9
$ 1,540,463
2
3
0.2
0.138
0.0026
85.0
$ 1,105,335
3
6
0.25
0.175
0.0030
91.4
$ 1,381,255
2
1
0.2
0.135
0.0026
75.0
$ 840,118
1
4
0.25
0.175
0.0030
98.1
$ 1,493,239
4
7
0.25
0.175
0.0063
38.3
$ 477,190
7
8
0.3
0.210
0.0044
107.0
$ 1,781,738
2
5
0.15
0.105
0.0100
103.1
$ 1,266,390
Total
$ 14,695,270
4.2. Red tipo 4x4
En la Figura 18 se muestra la red de tipo 4x4. No es un modelo a escala y se muestra para tener una
referencia de las numeraciones de las cámaras y los tubos.
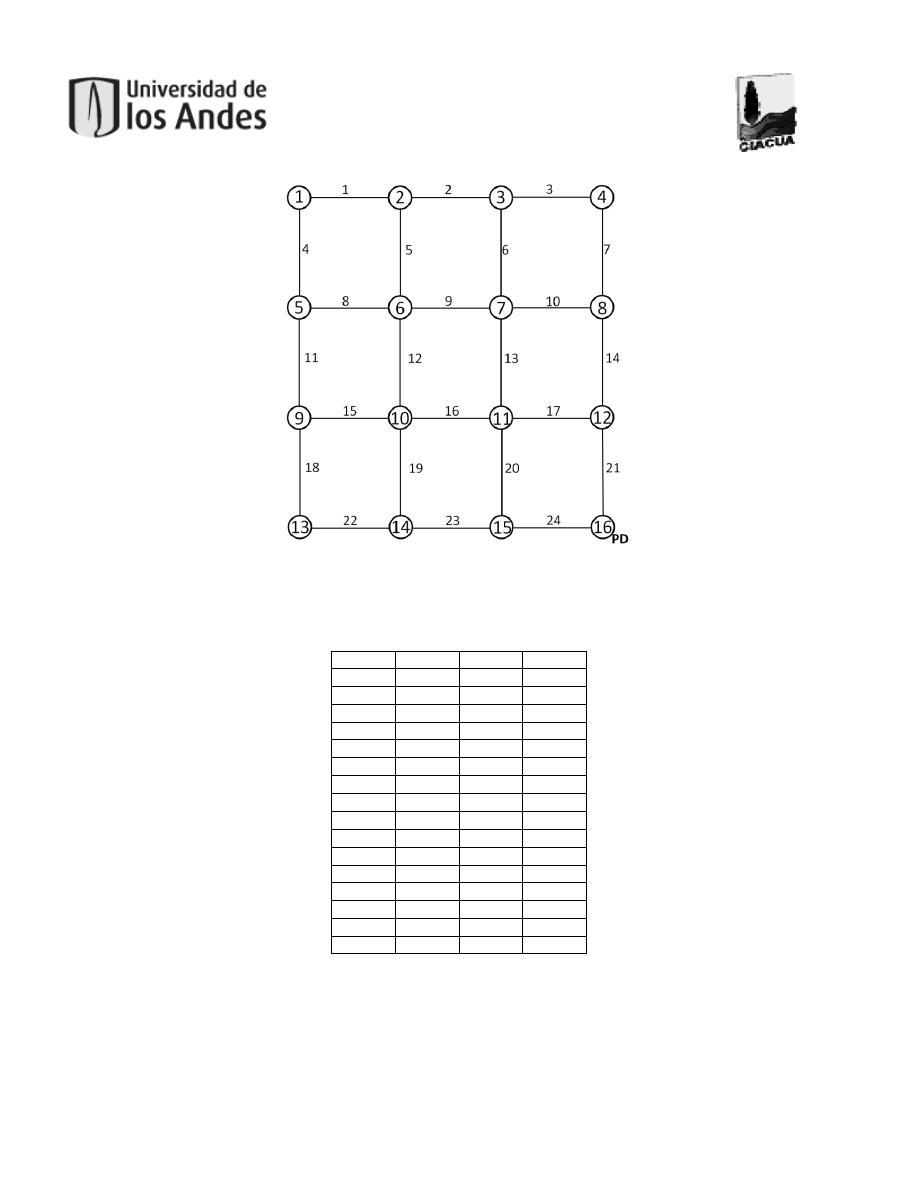
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
43
Figura 18. Esquema de la red tipo 4x4.
4.2.1. Terreno plano
Tabla 15. Información de las cámaras. 4x4.
ID
X (m)
Y (m)
Cota (m)
1
0.0
0.0
100.0
2
100.0
0.0
100.0
3
200.0
0.0
100.0
4
300.0
0.0
100.0
5
0.0
100.0
100.0
6
100.0
100.0
100.0
7
200.0
100.0
100.0
8
300.0
100.0
100.0
9
0.0
200.0
100.0
10
100.0
200.0
100.0
11
200.0
200.0
100.0
12
300.0
200.0
100.0
13
0.0
300.0
100.0
14
100.0
300.0
100.0
15
200.0
300.0
100.0
16
300.0
300.0
100.0
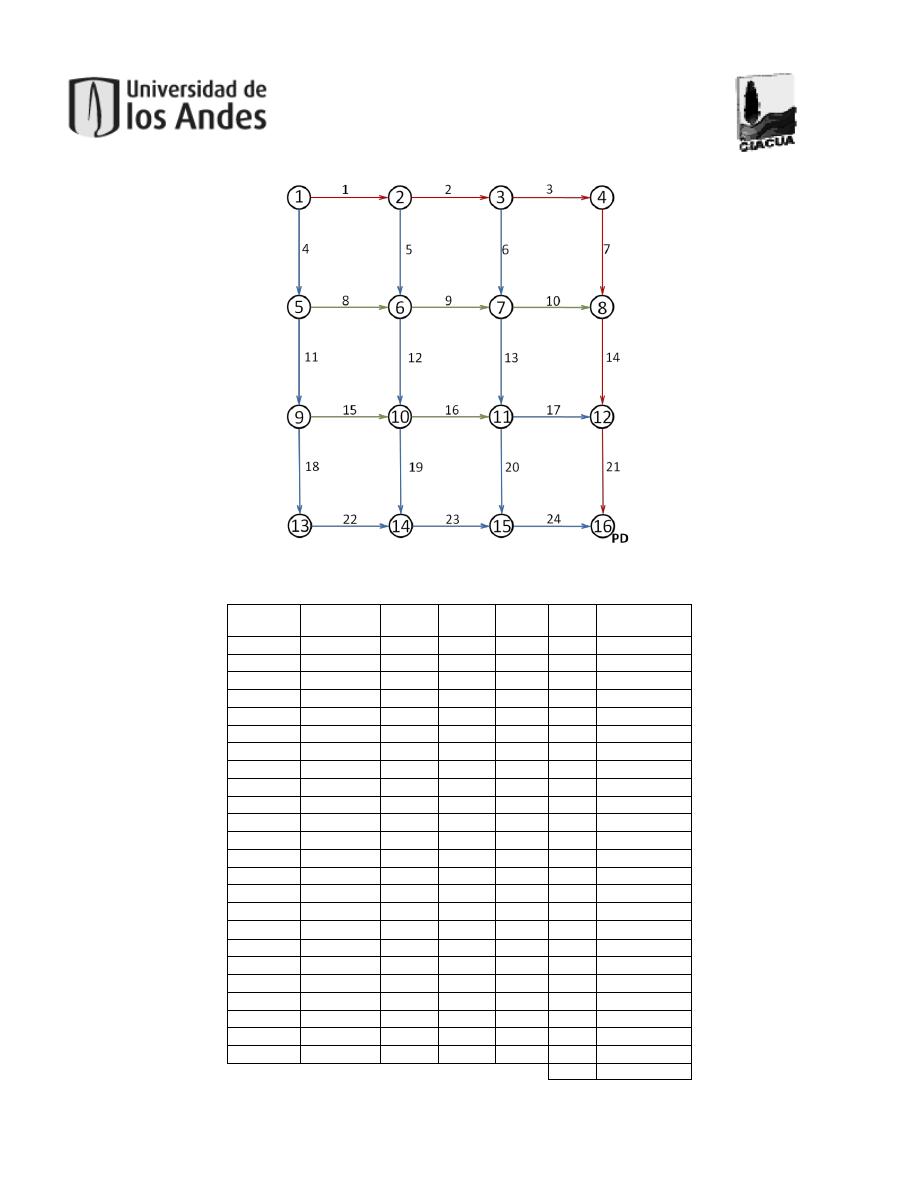
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
44
Figura 19. Red para terreno plano. 4x4.
Tabla 16. Resultado diseño terreno plano. 4x4.
ID cámara
inicial
ID cámara
final
D (m)
y
n
(m)
S (-)
L (m)
Costo (COP)
1
2
0.25
0.161
0.0011
100.0
$ 1,301,126
2
3
0.35
0.229
0.0007
100.0
$ 1,645,879
3
4
0.4
0.272
0.0007
100.0
$ 1,844,893
4
8
0.4
0.280
0.0011
100.0
$ 1,914,008
8
12
0.4
0.280
0.0023
100.0
$ 2,494,206
12
16
0.4
0.279
0.0082
100.0
$ 3,154,001
11
15
0.2
0.138
0.0026
100.0
$ 1,168,889
15
16
0.4
0.279
0.0082
100.0
$ 3,565,755
3
7
0.25
0.161
0.0010
100.0
$ 1,301,126
7
11
0.35
0.240
0.0013
100.0
$ ,251,753
11
12
0.35
0.243
0.0032
100.0
$ 2,428,791
2
6
0.25
0.161
0.0011
100.0
$ 1,301,126
6
10
0.35
0.240
0.0013
100.0
$ 2,251,753
10
14
0.4
0.276
0.0017
100.0
$ 2,579,788
14
15
0.4
0.279
0.0059
100.0
$ 2,913,611
10
11
0.2
0.138
0.0026
100.0
$ 1,168,889
1
5
0.25
0.161
0.0011
100.0
$ 1,301,126
5
9
0.35
0.229
0.0007
100.0
$ 1,645,879
9
13
0.4
0.272
0.0007
100.0
$ 1,844,893
13
14
0.4
0.280
0.0011
100.0
$ 1,914,008
7
8
0.15
0.105
0.0100
100.0
$ 1,165,501
6
7
0.15
0.105
0.0100
100.0
$ 1,165,501
9
10
0.15
0.105
0.0100
100.0
$ 1,165,501
5
6
0.15
0.105
0.0100
100.0
$ 1,165,501
Total
$ 44,653,507
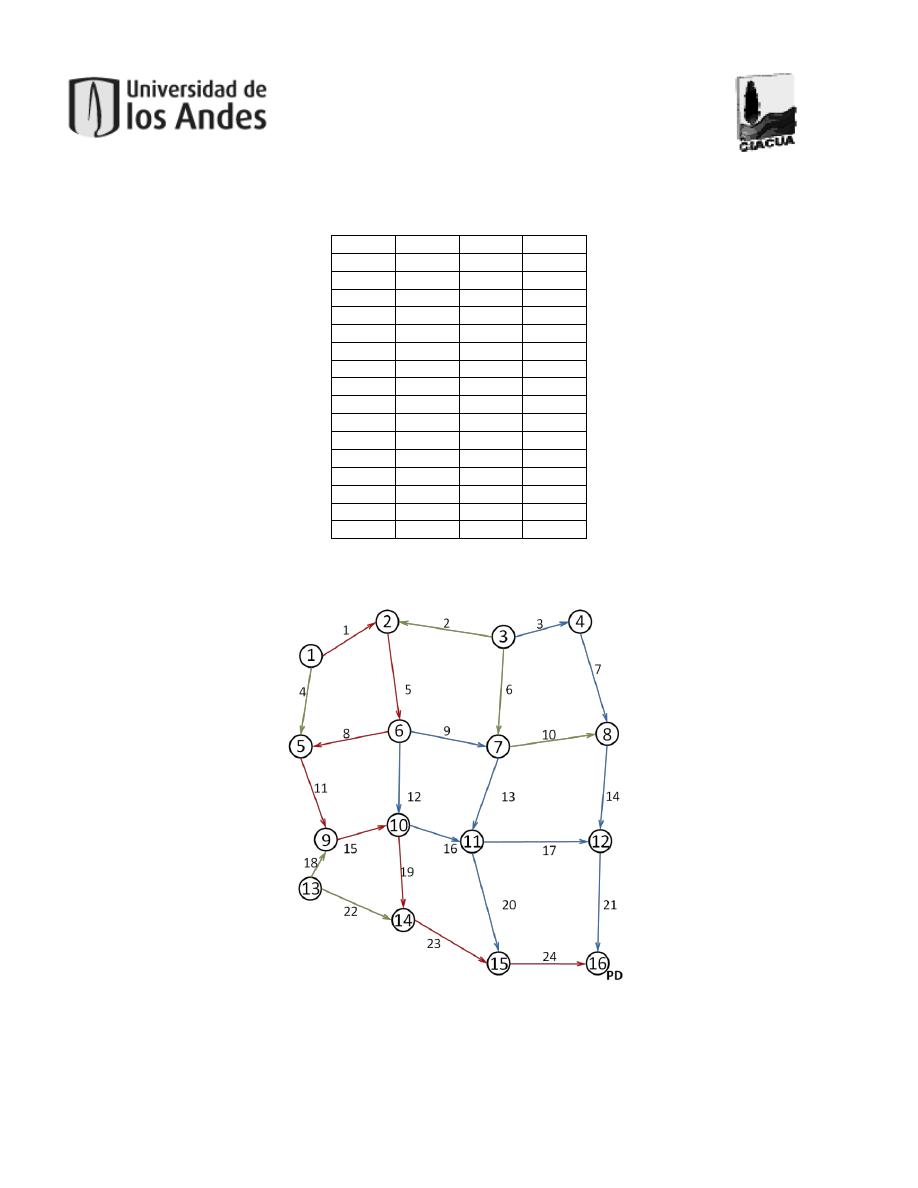
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
45
4.2.2. Terreno a favor del drenaje
Tabla 17. Información de las cámaras. 4x4.
ID
X (m)
Y (m)
Cota (m)
1
0.0
30.0
100.9
2
76.0
0.0
100.4
3
194.0
12.0
100.5
4
269.0
0.0
100.2
5
20.0
153.0
100.0
6
99.0
99.0
100.3
7
210.0
130.0
100.2
8
300.0
100.0
100.1
9
17.0
197.0
100.0
10
88.0
184.0
100.0
11
164.0
200.0
100.0
12
293.0
200.0
100.1
13
3.0
243.0
100.3
14
96.0
271.0
100.3
15
197.0
305.0
100.2
16
283.0
310.0
100.0
Figura 20. Red para terreno a favor de drenaje. 4x4.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
46
Tabla 18. Resultado diseño terreno a favor de drenaje. 4x4.
ID cámara
inicial
ID cámara
final
D (m) y
n
(m)
S (-)
L (m)
Costo (COP)
10
14
0.25
0.160 0.0011
87.4
$ 1,178,986
14
15
0.30
0.210 0.0026 106.6
$ 2,213,102
15
16
0.45
0.315 0.0097
86.1
$ 2,966,721
7
8
0.20
0.138 0.0026
94.9
$ 1,071,923
8
12
0.30
0.210 0.0044 100.2
$ 2,085,581
12
16
0.35
0.244 0.0044 110.5
$ 2,951,049
6
5
0.20
0.106 0.0053
95.7
$ 1,097,262
5
9
0.40
0.272 0.0007
44.1
$ 718,182
9
10
0.40
0.276 0.0017
72.2
$ 1,319,082
10
11
0.45
0.315 0.0033
77.7
$ 1,708,395
11
15
0.45
0.313 0.0062 110.1
$ 3,182,035
6
7
0.20
0.138 0.0026 115.2
$ 1,363,253
7
11
0.25
0.175 0.0063
83.8
$ 1,175,922
11
12
0.20
0.138 0.0026 129.0
$ 1,641,202
3
4
0.20
0.116 0.0041
76.0
$ 802,889
4
8
0.20
0.140 0.0088 104.7
$ 1,395,444
13
9
0.15
0.105 0.0100
48.1
$ 415,718
13
14
0.15
0.105 0.0100
97.1
$ 1,118,905
1
2
0.15
0.105 0.0100
81.7
$ 793,886
2
6
0.30
0.210 0.0026 101.6
$ 1,631,198
6
10
0.30
0.210 0.0044
85.7
$ 1,397,170
3
7
0.20
0.138 0.0026 119.1
$ 1,357,016
1
5
0.15
0.105 0.0100 124.6
$ 1,314,644
3
2
0.20
0.138 0.0026 118.6
$ 1,412,999
Total
$36,312,564
4.2.3. Terreno con topografía variable
Tabla 19. Información de las cámaras. 4x4.
ID
X (m)
Y (m)
Cota (m)
1
0.0
30.0
100.0
2
76.0
0.0
100.4
3
194.0
12.0
100.5
4
269.0
0.0
100.2
5
20.0
153.0
100.4
6
99.0
99.0
101.5
7
210.0
130.0
101.0
8
300.0
100.0
100.9
9
17.0
197.0
100.9
10
88.0
184.0
100.5
11
164.0
200.0
100.0
12
293.0
200.0
100.1
13
3.0
243.0
100.3
14
96.0
271.0
100.3
15
197.0
305.0
100.2
16
283.0
310.0
100.0
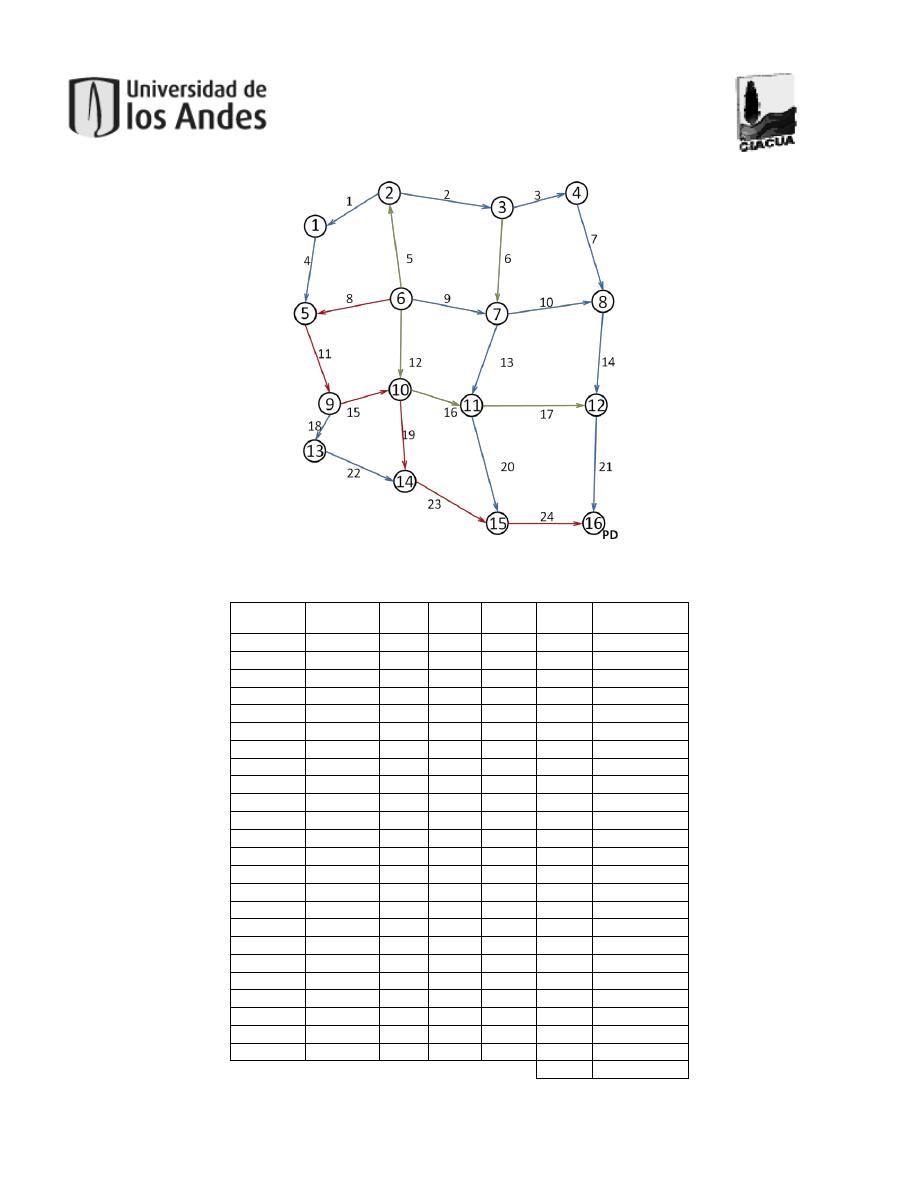
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
47
Figura 21. Red para terreno con topografía variable. 4x4
Tabla 20. Resultado diseño terreno con topografía variable. 4x4.
ID cámara
inicial
ID cámara
final
D (m)
y
n
(m)
S (-)
L (m)
Costo (COP)
10
14
0.20
0.116
0.0041
87.4
$ 975,780
14
15
0.35
0.244
0.0021
106.6
$ 2,479,083
15
16
0.45
0.313
0.0079
86.1
$ 3,160,380
7
8
0.20
0.138
0.0026
94.9
$ 1,071,923
8
12
0.30
0.210
0.0092
100.2
$ 2,431,174
12
16
0.35
0.245
0.0074
110.5
$ 3,405,181
6
7
0.15
0.105
0.0100
115.3
$ 1,282,997
7
11
0.25
0.154
0.0087
83.8
$ 1,324,105
11
15
0.40
0.279
0.0070
110.1
$ 3,203,654
6
5
0.15
0.092
0.0142
95.7
$ 943,705
5
9
0.35
0.244
0.0021
44.1
$ 895,611
9
10
0.40
0.276
0.0017
72.2
$ 1,859,065
10
11
0.40
0.278
0.0031
77.7
$ 1,865,635
6
10
0.15
0.093
0.0135
85.7
$ 810,551
11
12
0.20
0.138
0.0026
129.0
$ 1,641,202
9
13
0.15
0.086
0.0167
48.1
$ 417,660
13
14
0.20
0.140
0.0088
97.1
$ 1,358,276
3
7
0.20
0.138
0.0026
119.1
$ 1,615,806
6
2
0.15
0.095
0.0128
101.6
$ 999,814
2
3
0.30
0.206
0.0013
118.6
$ 1,902,852
3
4
0.30
0.210
0.0026
76.0
$ 1,157,467
4
8
0.30
0.210
0.0044
104.7
$ 2,071,266
2
1
0.20
0.098
0.0068
81.7
$ 901,757
1
5
0.25
0.175
0.0030
124.6
$ 2,027,857
Total
$ 39,802,803
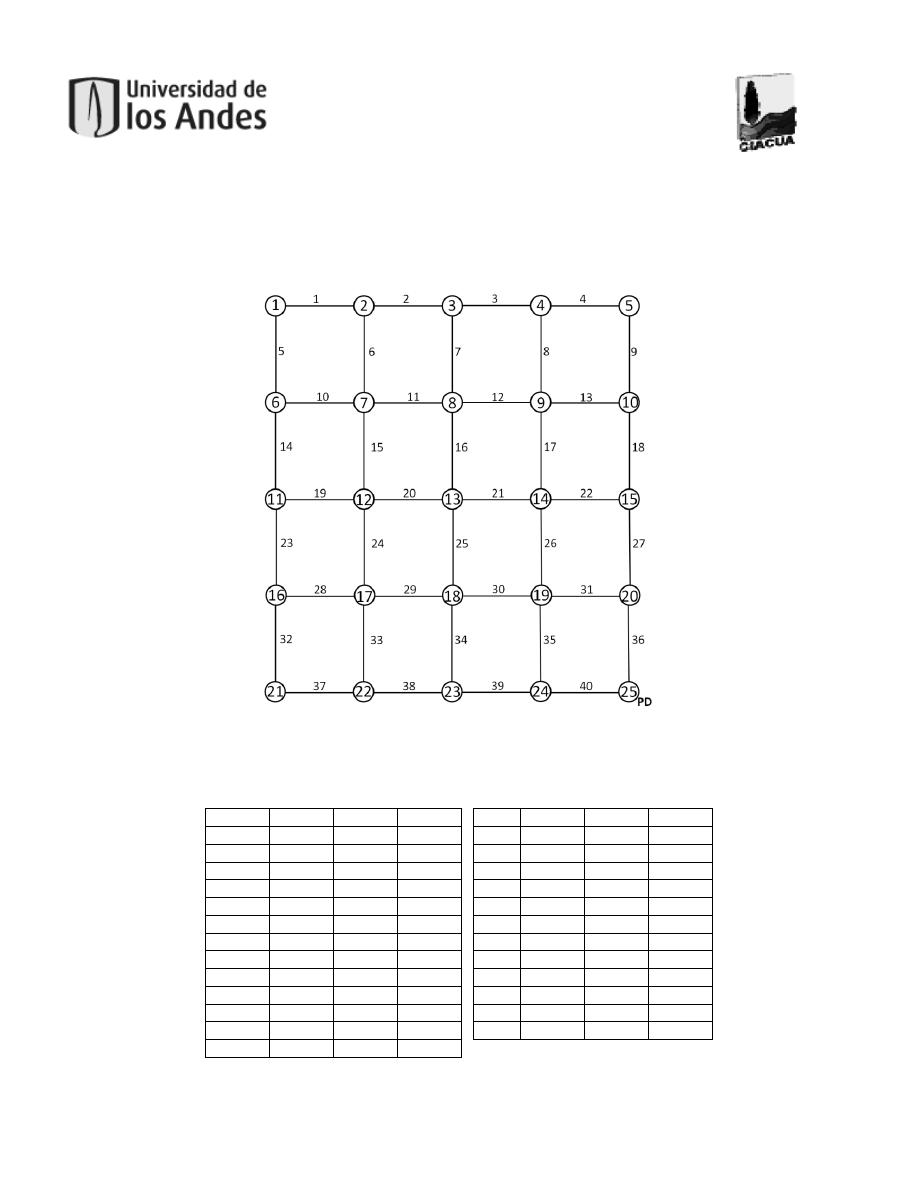
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
48
4.3. Red tipo 5x5
En la Figura 22 se muestra la red de tipo 5x5. No es un modelo a escala y se muestra para tener una
referencia de las numeraciones de las cámaras y los tubos.
Figura 22. Esquema de la red tipo 5x5.
4.3.1. Terreno plano
Tabla 21. Información de las cámaras. 5x5.
ID
X (m)
Y (m)
Cota (m)
ID
X (m)
Y (m)
Cota (m)
1
0.0
0.0
100.0
14
300.0
200.0
100.0
2
100.0
0.0
100.0
15
400.0
200.0
100.0
3
200.0
0.0
100.0
16
0.0
300.0
100.0
4
300.0
0.0
100.0
17
100.0
300.0
100.0
5
400.0
0.0
100.0
18
200.0
300.0
100.0
6
0.0
100.0
100.0
19
300.0
300.0
100.0
7
100.0
100.0
100.0
20
400.0
300.0
100.0
8
200.0
100.0
100.0
21
0.0
400.0
100.0
9
300.0
100.0
100.0
22
100.0
400.0
100.0
10
400.0
100.0
100.0
23
200.0
400.0
100.0
11
0.0
200.0
100.0
24
300.0
400.0
100.0
12
100.0
200.0
100.0
25
400.0
400.0
100.0
13
200.0
200.0
100.0
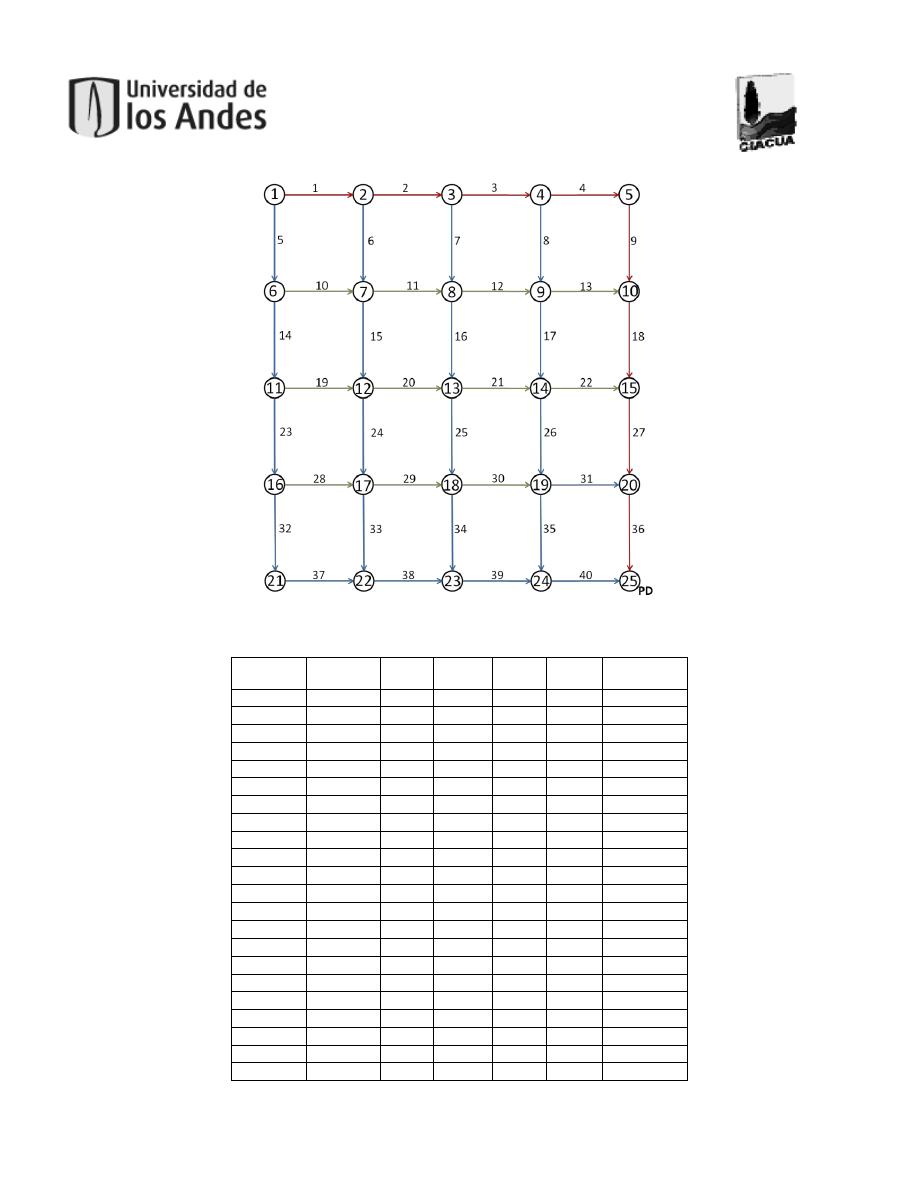
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
49
Figura 23. Red para terreno plano. 5x5.
Tabla 22. Resultado diseño terreno plano. 5x5.
ID cámara
inicial
ID cámara
final
D (m)
y
n
(m)
S (-)
L (m)
Costo (COP)
1
2
0.25
0.160
0.0011
100.0
$ 1,301,126
2
3
0.35
0.229
0.0007
100.0
$ 1,645,879
3
4
0.40
0.272
0.0007
100.0
$ 1,844,893
4
5
0.40
0.280
0.0011
100.0
$ 1,914,008
5
10
0.40
0.276
0.0017
100.0
$ 2,023,464
10
15
0.40
0.278
0.0031
100.0
$ 2,528,331
15
20
0.45
0.311
0.0028
100.0
$ 3,013,503
20
25
0.45
0.314
0.0088
100.0
$ 3,604,332
19
24
0.20
0.138
0.0026
100.0
$ 1,168,889
24
25
0.45
0.314
0.0153
100.0
$ 6,447,468
4
9
0.25
0.160
0.0011
100.0
$ 1,301,126
9
14
0.35
0.240
0.0013
100.0
$ 2,251,753
14
19
0.40
0.276
0.0017
100.0
$ 2,579,788
19
20
0.40
0.278
0.0031
100.0
$ 2,789,067
3
8
0.25
0.160
0.0011
100.0
$ 1,301,126
8
13
0.35
0.240
0.0013
100.0
$ 2,251,753
13
18
0.40
0.276
0.0017
100.0
$ 2,579,788
18
23
0.40
0.278
0.0031
100.0
$ 2,789,067
23
24
0.45
0.315
0.0129
100.0
$ 4,826,737
18
19
0.20
0.138
0.0026
100.0
$ 1,168,889
2
7
0.25
0.160
0.0011
100.0
$ 1,301,126
7
12
0.35
0.240
0.0013
100.0
$ 2,251,753

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
50
ID cámara
inicial
ID cámara
final
D (m)
y
n
(m)
S (-)
L (m)
Costo (COP)
12
17
0.40
0.276
0.0017
100.0
$ 2,579,788
17
22
0.40
0.278
0.0031
100.0
$ 2,789,067
22
23
0.40
0.279
0.0095
100.0
$ 3,362,687
14
15
0.15
0.105
0.0100
100.0
$ 1,165,501
1
6
0.25
0.160
0.0011
100.0
$ 1,301,126
6
11
0.35
0.229
0.0007
100.0
$ 1,645,879
11
16
0.35
0.240
0.0013
100.0
$ 1,715,778
16
21
0.35
0.244
0.0021
100.0
$ 1,836,910
21
22
0.40
0.276
0.0017
100.0
$ 2,151,329
9
10
0.15
0.105
0.0100
100.0
$ 1,165,501
13
14
0.15
0.105
0.0100
100.0
$ 1,165,501
8
9
0.15
0.105
0.0100
100.0
$ 1,165,501
17
18
0.15
0.105
0.0100
100.0
$ 1,165,501
12
13
0.15
0.105
0.0100
100.0
$ 1,165,501
7
8
0.15
0.105
0.0100
100.0
$ 1,165,501
16
17
0.15
0.105
0.0100
100.0
$ 1,165,501
11
12
0.15
0.105
0.0100
100.0
$ 1,165,501
6
7
0.15
0.105
0.0100
100.0
$ 1,165,501
Total
$ 81,921,444
4.3.2. Terreno a favor del drenaje
Tabla 23. Información de las cámaras. 5x5.
ID
X (m)
Y (m)
Cota (m)
ID
X (m)
Y (m)
Cota (m)
1
50.0
50.0
100.8
14
312.0
215.0
100.1
2
86.0
0.0
100.5
15
429.0
265.0
100.1
3
184.0
12.0
100.4
16
2.0
350.0
100.3
4
267.0
12.0
100.4
17
106.0
312.0
100.3
5
388.0
20.0
100.3
18
189.0
297.0
100.2
6
5.0
88.0
100.4
19
299.0
314.0
100.1
7
98.0
94.0
100.3
20
391.0
320.0
100.1
8
167.0
102.0
100.2
21
3.0
459.0
100.2
9
269.0
95.0
100.2
22
91.0
412.0
100.2
10
335.0
100.0
100.2
23
167.0
399.0
100.1
11
0.0
200.0
100.3
24
305.0
389.0
100.1
12
100.0
254.0
100.2
25
428.0
421.0
100.0
13
200.0
239.0
100.1
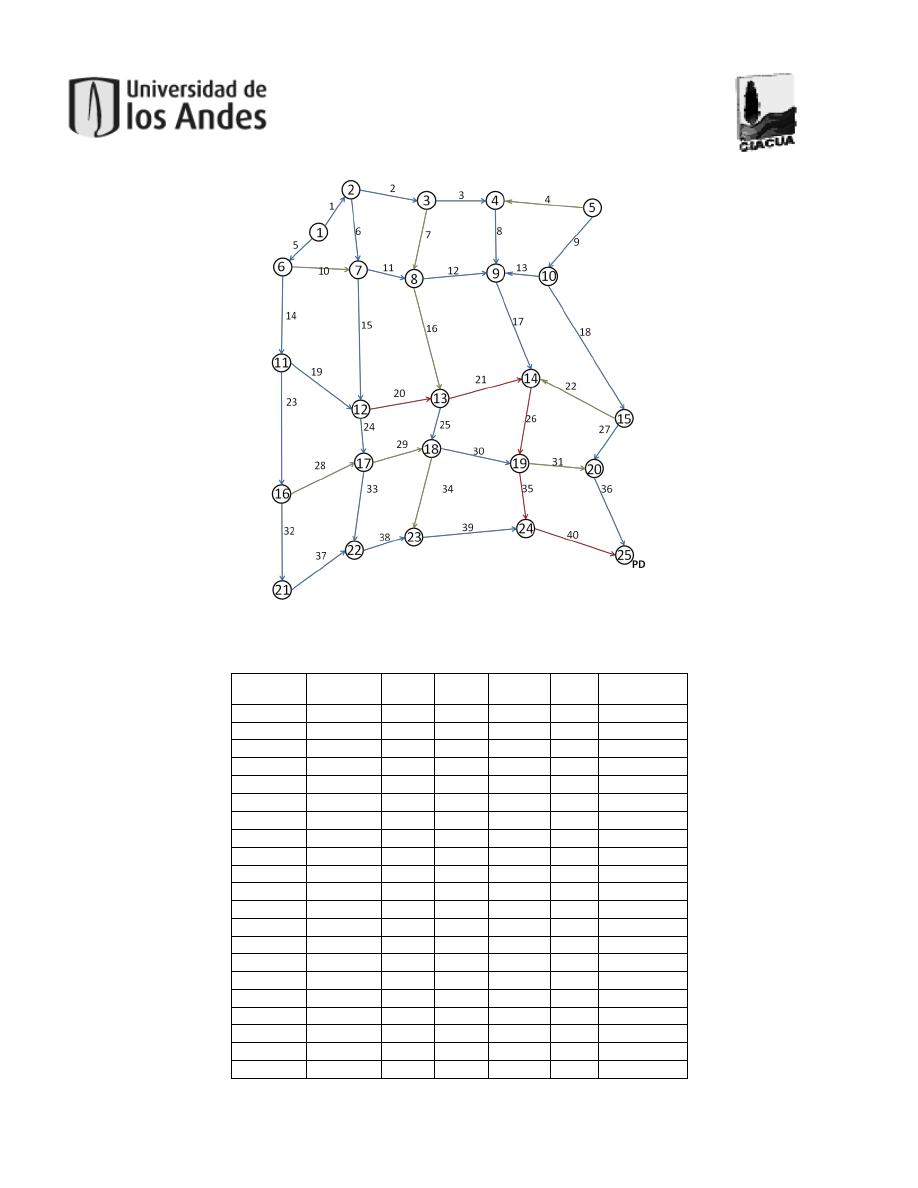
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
51
Figura 24. Red para terreno a favor del drenaje. 5x5.
Tabla 24. Resultado diseño terreno a favor del drenaje. 5x5.
ID cámara
inicial
ID cámara
final
D (m)
y
n
(m)
S (-)
L (m) Costo (COP)
10
15
0.25
0.160
0.0011
189.9
$ 2,773,006
15
20
0.30
0.206
0.0013
66.9
$ 935,860
20
25
0.30
0.210
0.0044
107.6
$ 1,799,593
12
13
0.20
0.138
0.0026
101.1
$ 1,159,375
13
14
0.35
0.240
0.0013
114.5
$ 2,056,932
14
19
0.45
0.313
0.0079
99.9
$ 4,109,339
19
24
0.45
0.315
0.0118
75.2
$ 3,513,247
24
25
0.60
0.422
0.0085
127.1
$ 10,220,646
19
20
0.25
0.160
0.0011
92.2
$ 1,180,731
13
18
0.20
0.138
0.0026
59.0
$ 629,889
18
19
0.25
0.175
0.0063
111.3
$ 2,094,509
1
6
0.15
0.105
0.0100
58.9
$ 526,903
6
11
0.30
0.206
0.0013
112.1
$ 1,694,203
11
12
0.35
0.240
0.0013
113.6
$ 1,928,243
12
17
0.40
0.278
0.0031
58.3
$ 1,110,548
17
22
0.45
0.311
0.0028
101.1
$ 2,814,402
22
23
0.45
0.313
0.0054
77.1
$ 2,190,396
23
24
0.45
0.314
0.0070
138.4
$ 5,461,437
18
23
0.20
0.138
0.0026
104.3
$ 1,205,186
5
10
0.20
0.138
0.0026
96.0
$ 1,087,123
10
9
0.30
0.206
0.0013
66.2
$ 923,933

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
52
ID cámara
inicial
ID cámara
final
D (m)
y
n
(m)
S (-)
L (m) Costo (COP)
9
14
0.40
0.279
0.0070
127.5
$ 4,129,758
15
14
0.20
0.138
0.0026
127.2
$ 1,577,756
17
18
0.15
0.105
0.0100
84.3
$ 902,449
1
2
0.20
0.095
0.0074
61.6
$ 648,977
2
3
0.30
0.206
0.0013
98.7
$ 1,463,631
3
4
0.35
0.240
0.0013
83.0
$ 1,346,983
4
9
0.40
0.276
0.0017
83.0
$ 1,481,146
7
8
0.20
0.138
0.0026
69.5
$ 734,426
8
9
0.25
0.175
0.0063
102.2
$ 1,885,056
11
16
0.25
0.160
0.0011
150.0
$ 2,124,154
16
21
0.25
0.175
0.0030
109.0
$ 1,581,068
21
22
0.25
0.175
0.0063
99.8
$ 1,680,608
8
13
0.20
0.138
0.0026
140.9
$ 1,755,123
16
17
0.15
0.105
0.0100
110.7
$ 1,346,156
5
4
0.25
0.160
0.0011
121.3
$ 1,676,990
2
7
0.20
0.120
0.0037
94.8
$ 1,071,460
7
12
0.30
0.210
0.0026
160.0
$ 2,754,368
6
7
0.20
0.138
0.0026
93.2
$ 1,048,777
3
8
0.15
0.105
0.0100
91.6
$ 989,524
Total
$ 79,613,911
4.3.3. Terreno con topografía variable
Tabla 25. Información de las cámaras. 5x5.
ID
X (m)
Y (m)
Cota (m)
ID
X (m)
Y (m)
Cota (m)
1
50.0
50.0
100.8
14
312.0
215.0
100.1
2
86.0
0.0
100.3
15
429.0
265.0
100.1
3
184.0
12.0
100.4
16
2.0
350.0
100.2
4
267.0
12.0
100.4
17
106.0
312.0
100.3
5
388.0
20.0
100.5
18
189.0
297.0
100.5
6
5.0
88.0
100.4
19
299.0
314.0
100.1
7
98.0
94.0
101.0
20
391.0
320.0
100.1
8
167.0
102.0
100.0
21
3.0
459.0
100.3
9
269.0
95.0
100.2
22
91.0
412.0
100.2
10
335.0
100.0
100.2
23
167.0
399.0
100.1
11
0.0
200.0
100.0
24
305.0
389.0
100.2
12
100.0
254.0
100.2
25
428.0
421.0
100.0
13
200.0
239.0
101.5
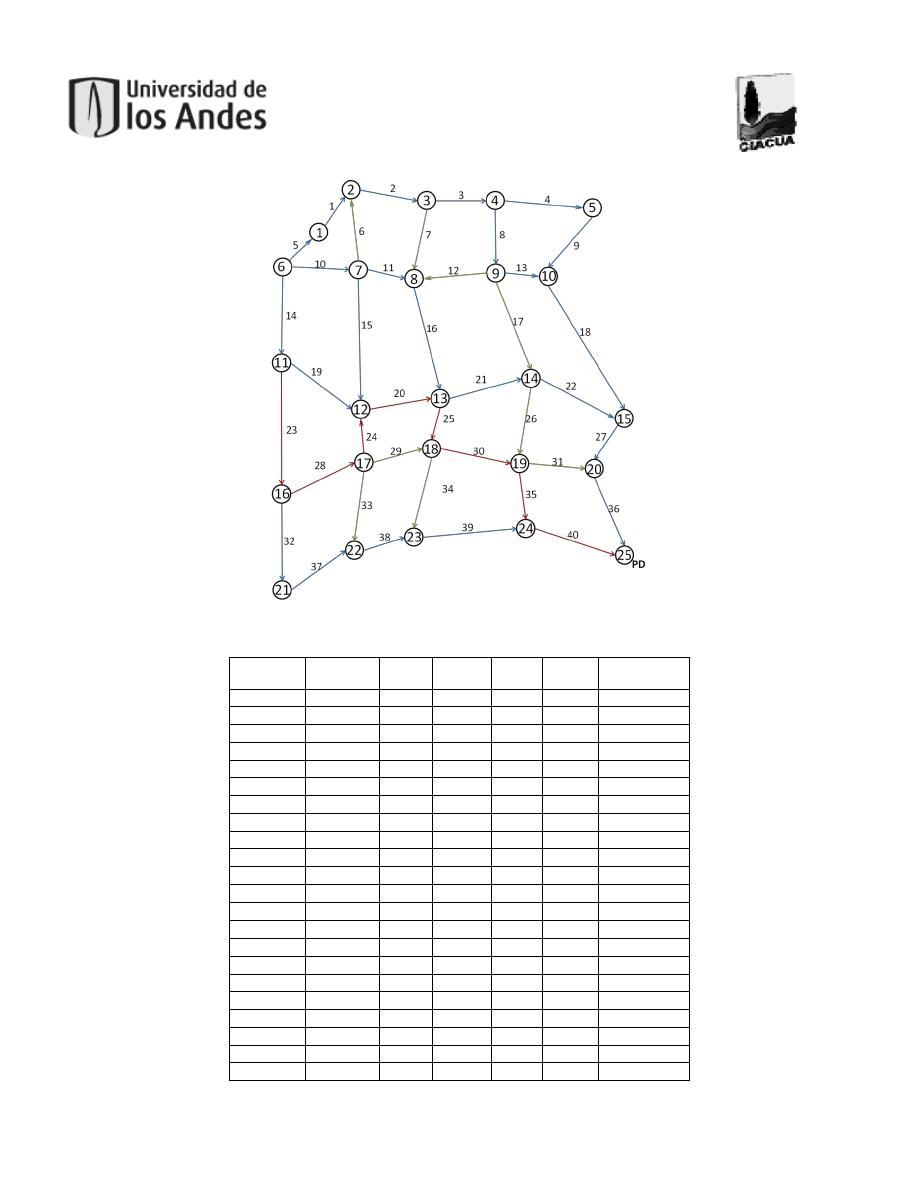
|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
53
Figura 25. Red para terreno con topografía variable. 5x5.
Tabla 26. Resultado diseño terreno con topografía variable. 5x5.
ID cámara
inicial
ID cámara
final
D (m)
y
n
(m)
S (-)
L (m)
Costo (COP)
13
14
0.15
0.091
0.0145
114.6
$ 1,166,957
14
15
0.35
0.240
0.0013
127.2
$ 3,226,059
15
20
0.45
0.313
0.0062
66.9
$ 1,907,692
20
25
0.45
0.313
0.0079
107.6
$ 4,057,402
11
16
0.25
0.160
0.0011
150.0
$ 2,221,156
16
17
0.35
0.229
0.0007
110.7
$ 2,104,973
17
12
0.40
0.272
0.0007
58.3
$ 1,091,228
12
13
0.40
0.279
0.0039
101.1
$ 2,865,788
13
18
0.50
0.424
0.0022
59.0
$ 2,104,561
18
19
0.50
0.339
0.0045
111.3
$ 4,143,725
19
24
0.60
0.470
0.0017
75.2
$ 3,062,189
24
25
0.60
0.397
0.0047
127.1
$ 6,414,582
19
20
0.20
0.138
0.0026
92.2
$ 1,057,743
16
21
0.25
0.160
0.0011
109.0
$ 1,474,528
21
22
0.30
0.206
0.0013
99.8
$ 1,551,695
22
23
0.35
0.244
0.0021
77.1
$ 1,279,238
23
24
0.35
0.244
0.0044
138.4
$ 3,264,610
14
19
0.15
0.105
0.0100
99.9
$ 1,163,050
18
23
0.15
0.105
0.0100
104.4
$1,137,656
17
22
0.20
0.138
0.0026
101.1
$ 1,159,375
17
18
0.15
0.105
0.0100
84.3
$ 959,273
6
1
0.20
0.138
0.0026
58.9
$ 666,741

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
54
ID cámara
inicial
ID cámara
final
D (m)
y
n
(m)
S (-)
L (m)
Costo (COP)
1
2
0.25
0.175
0.0030
61.6
$ 828,352
2
3
0.40
0.280
0.0011
98.7
$ 1,877,852
3
4
0.40
0.276
0.0017
83.0
$ 1,635,660
4
9
0.40
0.280
0.0023
83.0
$ 1,677,456
9
10
0.40
0.278
0.0031
66.2
$ 1,326,192
10
15
0.45
0.315
0.0033
189.9
$ 5,879,852
6
11
0.20
0.116
0.0041
112.1
$ 1,278,847
11
12
0.25
0.175
0.0030
113.6
$ 1,666,268
7
8
0.15
0.084
0.0180
69.5
$ 647,104
8
13
0.30
0.210
0.0044
140.9
$ 3,700,263
4
5
0.20
0.138
0.0026
121.3
$ 1,518,378
5
10
0.25
0.175
0.0030
96.0
$ 1,407,188
9
14
0.15
0.105
0.0100
127.5
$ 1,617,067
6
7
0.20
0.138
0.0026
93.2
$ 1,214,210
7
12
0.25
0.175
0.0030
160.0
$ 2,897,962
7
2
0.15
0.105
0.0100
94.8
$ 930,521
9
8
0.20
0.138
0.0026
102.2
$ 1,149,430
3
8
0.15
0.105
0.0100
91.6
$ 948,263
Total
$ 80,281,086
4.4. Gasto computacional
Debido a la naturaleza explícita de la metodología implementada, el tiempo computacional es uno
de los factores determinantes en el rendimiento de esta. Las variables que conllevan a un mayor
gasto computacional son:
Tamaño de la red (número de nodos).
Precisión.
Tamaño del espacio de factibilidad.
Tamaño del vector de diámetros
De acuerdo con lo anterior se sugieren dos estrategias para reducir el gasto de recursos
informáticos, y por ende el tiempo de cálculo. Dado que el tamaño de la red es una variable
inmodificable (dato de entrada) y el tamaño del espacio de factibilidad está definido por la
reglamentación (profundidades máxima y mínima), la primera estrategia consiste en limitar el
número de diámetros para el diseño. La forma en que se pueden limitar es a partir de una
estimación del máximo caudal que puede circular por el último tramo y estimar el diámetro
necesario, utilizando la pendiente del terreno. De esta manera, para las redes más grandes trabajadas
(5 x 5) el número de diámetros disponibles para el diseño se puede reducir hasta en un 50 %, lo cual
implica la reducción del espacio solución en una proporción similar, dado que el número de nodos
por cámara es proporcional al número de diámetros disponibles para el diseño. Así, el tiempo se
reduce a un 30 %.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
55
La segunda consiste en trabajar con precisiones no tan altas, siendo suficiente para un esquema del
problema, una precisión de decímetro y para la solución definitiva de este una precisión de
centímetro. De esta manera, para un diseño dado el tiempo necesario para obtener una solución, con
una precisión de decímetros equivale a un 2 % del tiempo requerido para encontrar la solución con
una precisión de centímetros. Así mismo, contrastando los tiempos empleados en la solución del
problema utilizando precisiones de centímetros y milímetros, se obtiene que en el primer caso el
tiempo es un 1 % del tiempo para el segundo caso. Por otro lado, comparando los costos obtenidos
para las soluciones con cada una de las precisiones se tiene que, en promedio, este es un 4 % más
bajo si se pasa de una precisión de decímetros a una de centímetros y entre precisiones de
centímetros y milímetros este se reduce un 0.8 %, aproximadamente.
En esta Sección no se hace referencia, explícita, a los tiempos computacionales dado que la
máquina virtual de Java (lenguaje en el que fue implementada la metodología) tiene
configuraciones propias en cada uno de los computadores donde se corrió el programa. Lo anterior
impide que las comparaciones entre diferentes computadores puedan ser llevadas a cabo. A manera
de ejemplo se ilustra la siguiente situación: una red de 2 x 2 tardó 4 horas y 33 minutos con una
precisión de milímetros, 2 minutos y 51 segundos con una precisión de centímetros y 2 segundos
con una precisión de decímetros; los tiempos mencionados fueron obtenidos en un computador con
un procesador Intel® Core™ i7-2600 @ 3.4 GHz, con una memoria Ram de 8 GB. Por otro lado, la
misma red tardó 43 minutos y 51 segundos con una precisión de milímetros, 27 segundos con una
precisión de centímetros y 0.6 segundos con una precisión de decímetros; estos tiempos fueron
obtenidos en un computador con un procesador Intel® Core™ 2 Duo E7500 @ 2.93 GHz, con una
Ram de 4 GB.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
56
5. CONCLUSIONES Y RECOMENDACIONES
El algoritmo de Dijkstra se pudo implementar, haciendo a lgunas modificaciones, y se
pudieron modelar diferentes redes de drenaje urbano.
Aunque la metodología trabajada encamina el resultado al óptimo global (camino más
corto), no se puede afirmar que los resultados sean los óptimos globales del problema, dado
que los resultados se pueden mejorar manipulando la precisión.
De acuerdo a lo anterior, se afirma que los resultados obtenidos son óptimos globales
dentro del espacio solución configurado para la solución determinada del problema.
En general, la variable topológica más importante es la pendien te del terreno. Para terrenos
a favor del drenaje se obtuvieron las redes de menor costo.
El tiempo de cálculo puede aumentarse hasta 1500 % si se aumenta la precisión del
problema en un orden de magnitud.
Con base en los resultados se sugiere trabajar con precisiones de centímetro. Precisiones
superiores requieren un gran tiempo de cálculo y con precisiones inferiores se obtienen
mayores costos.
Se sugiere limitar la lista de diámetros para disminuir los tiempos de cálculo.
El costo de un diseño, en promedio, disminuye 4 % comparando precisiones de decímetro y
centímetro.
El costo de un diseño, en promedio, disminuye 0.8 % comparando precisiones de
centímetro y milímetro.
No se observan grandes diferencias, en cuanto a los costos, entre los resultados obtenidos
con la metodología trabajada y la metodología desarrollada por el CIACUA. En promedio
la diferencia es del 3 %.
Hay grandes diferencias, en cuanto al tiempo computacional, entre los resultados obtenidos
con la metodología trabajada y la metodología desarrollada por el CIACUA. Se llegan a
obtener resultados con un tiempo mayor hasta en un 10000 %.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
57
6. BIBLIOGRAFÍA
Ahuja, R. K., Magnanti, T. L., & Orlin, J. B. (1993). Network flows: theory, algorithm and
applications. New Jersey: Prentice Hall.
Argaman, Y., Shamir, U., & Spivak, E. (1973). Design of Optimal Sewerage Systems. Journal of the
Environmental Engineering Division.
Bellman, R. (1956). Ona routing problem.
Burian, S., & Edwards, F. (2002). Historical Perspectives of Urban Drainage. Obtenido de
http://rpitt.eng.ua.edu/Class/International%20urban%20water%20systems/M1%20Burian%
20paper.pdf
Burian, S., & Edwards, F. (s.f.). Historical Perspectives of Urban Drainage. Obtenido de
http://rpitt.eng.ua.edu/Class/International%20urban%20water%20systems/M1%20Burian%
20paper.pdf
Burian, S., Nix, S., Durrans, R., Pitt, R., Fan, C.-Y., & Field, R. (1999). The Historical
Development of Wet-Weather Flow Management. Environmental Protection Agency.
Butler, D., & Davies, J. (2011). Urban Drainage. Abingdon: Spon Press.
Dajani, J., & Gemmell, R. (1971). Economics of Wastewater Collection Systems. Evanston:
University of Illinois.
Duque, N. (2013). Metodología para la optimización del diseño de tuberías en serie en sistemas de
alcantarillado. Bogotá: Universidad de los Andes.
Giraldo Gómez, E. (2000). ¿Combinar o separar? Una discusión con un siglo de antigüedad y de
gran actualidad para los bogotanos. Revista de Ingeniería, 17-20.
Goldberg, A. V., & Radzik, T. (1993). A heuristic improvement of the Bellman-Ford algorithm.
Pergamon Press Ltd.
Guo, Y., Walters, G., & Savic, D. (2008). Optimal design of storm sewer networks: Past, Present
and Future. 11th International Conference on Urban Drainage , (págs. 1-10). Edinburgh.
Haghighi, A. (2012). Loop by Loop Cutting Algorithm to Generate Urban Drainage Systems
Layout. Journal of Water Resources Planning and Management, 693-703.
Haghighi, A., & Bakhshipour, A. (2012). Optimization of Sewer Networks Using an Adaptive
Genetic Algorithm. Water Resources Management, 3441-3456.
Holland, M. (1968). Discusion of Heuristic aid for the design of sewer networks. Journal of the
Sanitary Engineering Division, 437-438.
Li, G., & Matthew, R. (1990). New Approach for Optimization of Urban Drainage Systems.
Journal of Environmental Enggineering, 927-944.
Liebman, J. (1967). A Heuristic Aid for the Design of Sewer Networks. Journal f the Sanitary
Engineering Division, 81-90.
López Sabogal, D. A. (Enero de 2012). Diseño Optimizado De Redes De Drenaje Urbano Usando
El Concepto De Potencia Unitaria. Trabajo de proyecto de grado. Bogotá: Universidad de
los Andes.
Mays, L., Wenzel, H., & Liebman, J. (1976). Model for Layout and Design of Sewer Sytems.
Journal of the Water Resources Planning and Management Division, 385-40.

|Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueducto y Alcantarillado-CIACUA-
Optimización del Diseño de los Trazados de Sistemas de Drenaje Urbano
Basado en Criterio Económico
58
Navarro, I. (2009). Diseño Optimizado de Redes de Drenaje Urbano. Bogotá: Universidad de los
Andes.
Ovalle, F. (2011). Criterio de tuberías fluyendo parcialmente llenas: Velocidad mínima, esfuerzo
cortante mínimo y número de Froude cuasicrítico. Bogotá: Universidad de los Andes.
Pan, T.-C., & Kao, J.-J. (2009). GA-QP Model to Optimize Sewer System Design. Journal of
Environmental Engineering, 17-24.
Saldarriaga, J. (2007). Hidráulica de Tuberías. Bogotá: Alfaomega.
Saldarriaga, J. (2011). Clase Sistema Integrado de Drenaje Urbano. Bogotá, Colombia: Universidad
de los Andes.
Saldarriaga, J., Corrales, E., Cuero, P., Luna, D., Montaño, D., & Ardila, A. (2013). Trazado
Óptimo de la red. Bogotá: Centro de Investigaciones en Acueductos y Alcantarillados.
Saldarriaga, J., Corrales, E., Cuero, P., Luna, D., Montaño, L., & Ardila, A. (2013). Desarrollo de
Técnicas Computacionales Exhaustivas para el Diseño Optimizado de Redes de Drenaje
Urbano. Bogotá: Centro de Investigaciones en Acueductos y Alcantarillados.
Secretaria Distrital de Ambiente. (2011). Sistemas Urbanos de Drenaje Sostenible SUDS Para el
Plan de Ordenamiento Zonal Norte POZN. Bogotá.
Superintendencia de Servicios Públicos Domiciliarios. (2007). Estudio Sectorial Acueducto y
Alcantarillado 2002 - 2005. Bogotá.
Tekeli, S., & Belkaya, H. (1986). Computerized Layput Generation for Sanitary Sewers. Journal of
Water Resources Planning and Management, 500-515.
Wang, S.-X. (2012). The improved Dijkstra's shortest path algorithm and its application. Procedia
Engineering, 1186-1190.
Weng, H., & Liaw, S. (2005). Establishing an Optimization Model for Sewer System Layout wit
Applied Genetic Algorithm. Journal of Environmental Informatics , 26-35.
