
PROYECTO DE GRADO INGENIERÍA CIVIL
CONTRUCCIÓN DE UN MODELO FÍSICO PARA LA MEDICIÓN DE MEZCLA
EN NUDOS DE REDES DE DISTRIBUCIÓN DE AGUA POTABLE
PRESENTADO POR:
LAURA NATALIA COTES GÓMEZ
ASESOR:
JUAN GUILLERMO SALDARRIAGA VALDERRAMA
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
BOGOTÁ D.C
JUNIO DE 2013

A Dios,
A mis papás, por su apoyo y amor incondicional.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
iii
Laura Natalia Cotes Gómez
Tabla de contenido
1.
INTRODUCCIÓN ..................................................................................................................... 1
1.1 . OBJETIVOS .......................................................................................................................... 5
1.1.1.
Objetivo general .............................................................................................................. 5
1.1.2.
Objetivos específicos ....................................................................................................... 5
2.
ANTECEDENTES .................................................................................................................... 6
3.
MARCO TEÓRICO ............................................................................................................... 18
3.1.
Modelación hidráulica ....................................................................................................... 18
3.1.1.
Ecuaciones de modelación hidráulica ....................................................................... 18
3.1.2.
Método del gradiente ................................................................................................. 20
3.1.3.
Ejemplo de aplicación de modelación hidráulica ...................................................... 23
3.2.
Modelación de calidad del agua ........................................................................................ 33
3.2.1.
Modelos estáticos ...................................................................................................... 33
3.2.2.
Modelos dinámicos ................................................................................................... 35
3.2.3.
Ejemplo de aplicación de modelación de la calidad del agua ................................... 36
3.3.
Relación entre la modelación hidráulica y de calidad del agua ......................................... 37
3.4.
Difusión ............................................................................................................................. 37
3.4.1.
Definición .................................................................................................................. 38
3.4.2.
Ecuación de la difusión ............................................................................................. 39
3.4.3.
Ley de Fick ................................................................................................................ 40
3.4.4.
Tipos de difusión ....................................................................................................... 42
3.4.5.
Concentración............................................................................................................ 43
4.
DISEÑO Y CONSTRUCCIÓN DEL MODELO ................................................................. 46
4.1.
Alimentación del modelo .................................................................................................. 46
4.2.
Plataforma ......................................................................................................................... 49
4.3.
Modelo .............................................................................................................................. 52
5.
COSTOS DEL PROYECTO .................................................................................................. 58

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
iv
Laura Natalia Cotes Gómez
6.
PRUEBAS Y RESULTADOS ................................................................................................ 60
7.
CONCLUSIONES Y RECOMENDACIONES .................................................................... 71
8.
AGRADECIMIENTOS .......................................................................................................... 73
9.
BIBLIOGRAFÍA ..................................................................................................................... 74
10. ANEXOS .................................................................................................................................. 76

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
v
Laura Natalia Cotes Gómez
Índice de ilustraciones
Ilustración 1.Comportamiento del cloro residual de acuerdo con la dosis agregada………………...3
Ilustración 2. Bifurcación de los flujos en la simulación en CFD……………………………………9
Ilustración 3. Flujos con diferentes patrones.. ................................................................................... 12
Ilustración 4.Resultados de simulaciones de los modelos de mezcla. ............................................... 17
Ilustración 5. Longitud y diámetros de las tuberías de la red. .......................................................... 24
Ilustración 6. Caudales en las tuberías de la red. .............................................................................. 24
Ilustración 7. Resultado de caudales. ................................................................................................ 32
Ilustración 8. Resultado de alturas piezométricas. ............................................................................ 32
Ilustración 9. Esquema de conservación de masa en el nudo j. ......................................................... 33
Ilustración 10. Proceso de difusión. .................................................................................................. 38
Ilustración 11. Proceso de difusión gráficamente. ............................................................................ 39
Ilustración 12. Flujo de materia ......................................................................................................... 40
Ilustración 13. Difusión convectiva .................................................................................................. 42
Ilustración 14. Difusión turbulenta. ................................................................................................... 43
Ilustración 15. Esquema de balance de masa en la unión de tuberías ............................................... 44
Ilustración 16. Fuente de agua potable. ............................................................................................. 47
Ilustración 17. Extensión de tubería de agua potable. ....................................................................... 47
Ilustración 18. División de tuberías de alimentación. ....................................................................... 48
Ilustración 19. Tuberías de alimentación en tanques. ....................................................................... 49
Ilustración 20 a. Plataforma preliminar. ............................................................................................ 50
Ilustración 21. Plataforma terminada. ............................................................................................... 51
Ilustración 22. Válvulas de entrada. .................................................................................................. 53
Ilustración 23. Vista en planta del modelo. ....................................................................................... 54
Ilustración 24. Válvulas de salida. .................................................................................................... 55
Ilustración 25. Dimensiones del tanque. ........................................................................................... 56
Ilustración 26. Tanques almacenamiento. ......................................................................................... 57
Ilustración 27. Vista en planta prueba 1. ........................................................................................... 60
Ilustración 28.Vista en perfil prueba 1. ............................................................................................. 61

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
vi
Laura Natalia Cotes Gómez
Ilustración 29. Vista en planta prueba 2. ........................................................................................... 62
Ilustración 30. Acercamiento al nodo prueba 2. ................................................................................ 62
Ilustración 31. Vista en perfil prueba 2. ............................................................................................ 63
Ilustración 32. Vista en planta prueba 3. ........................................................................................... 64
Ilustración 33. Acercamiento al nodo prueba 3. ................................................................................ 64
Ilustración 34. Vista en perfil prueba 3. ............................................................................................ 65
Ilustración 35. Vista en planta prueba 4. ........................................................................................... 65
Ilustración 36. Vista en planta prueba 5. ........................................................................................... 66
Ilustración 37.Vista en perfil prueba 5. ............................................................................................. 66
Ilustración 38. Vista en planta prueba 6. ........................................................................................... 67
Ilustración 39. Vista en perfil prueba 6. ............................................................................................ 67
Ilustración 40. Vista en planta prueba 7. ........................................................................................... 68
Ilustración 41. Vista en perfil prueba 7. ............................................................................................ 68
Ilustración 42. Vista en planta mezcla completa. .............................................................................. 69
Ilustración 43. Acercamiento al nodo de mezcla completa. .............................................................. 69
Ilustración 44. Vista en perfil de mezcla completa. .......................................................................... 70

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
vii
Laura Natalia Cotes Gómez
Índice de ecuaciones
Ecuación 1. Ecuación bidimensional de advección-difusión………………………...........................6
Ecuación 2. Ecuación unidimensional de advección- difusión………………………………….…..7
Ecuación 3. Balance de masa del soluto………………………………………………………….....10
Ecuación 4. Impulso del flujo………………………………………………………………………12
Ecuación 5. Criterio de impulso en las tuberías…………………………………………………….13
Ecuación 6. Relación caudal-concentración en las tuberías 1 y 4…………………………………..13
Ecuación 7. Relación de concentraciones en tuberías 1 y 4…………………………………….......13
Ecuación 8. Balance de masa del soluto en la unión………………………………………………..13
Ecuación 9. Concentración en la tubería 3………………………………………………………….14
Ecuación 10. Relaciones entre los caudales de entrada y salida……………………………………14
Ecuación 11. Conservación de masa en la unión…………………………………………………...14
Ecuación 12. Concentración de la tubería 3 en términos de x y y………………………………….14
Ecuación 13. Número de Reynolds……………………………………………………………...….15
Ecuación 14. Concentración en la tubería 3 en términos del número de Reynolds………………...15
Ecuación 15. Concentración combinada……………………………………………………………15
Ecuación 16. Conservación de masa en las redes……………………………………………….......18
Ecuación 17. Caudal utilizando la ecuación de Darcy-Weisbach en conjunto con la ecuación de
Colebrook-White………………………………………………………………………………........18
Ecuación 18. Altura piezométrica………………………………………………………………......19
Ecuación 19. Altura piezométrica teniendo en cuanta pérdidas menores causadas por accesorios..19
Ecuación 20. Definición del valor de α…………………………………………………………......20
Ecuación 21. Pérdida de altura piezométrica en cada tramo………………………………….........21
Ecuación 22. Ecuación de continuidad para todos los nodos……………………………………....21
Ecuación 23. Desbalance de energía por unidad de peso…………………………………………..22
Ecuación 24. Desbalance de caudal en cada nodo………………………………………………....22

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
viii
Laura Natalia Cotes Gómez
Ecuación 25. Cálculo de alturas piezométricas…………………………………………………….23
Ecuación 26. Cálculo de caudales………………………………………………………………......23
Ecuación 27. Ecuación de continuidad para la modelación de la calidad del agua………………..34
Ecuación 28. Concentración en el nudo j…………………………………………………………...34
Ecuación 29. Tiempo de permanencia medio para el nudo j………………………………………..34
Ecuación 30. Transporte de sustancias conservativas………………………………………………35
Ecuación 31. Transporte de sustancias no conservativas…………………………………………...36
Ecuación 32. Ecuación general de la difusión…………………………………………………..…..39
Ecuación 33. Ecuación de difusión cuando el coeficiente de difusión es constante…………….....40
Ecuación 34. Ecuación de Fick………………………………………………………………...........41
Ecuación 35. Fenómeno de difusión…………………………………………………………….......41
Ecuación 36. Concentración a partir de la conservación de masa……………………………….....43
Ecuación 37. Aporte de masa a la unión i……………………………………………………..........45
Ecuación 38. Masa de salida del nudo i…………………………………………………………......45
Ecuación 39. Concentración de la mezcla…………………………………………………………..45
Ecuación 40. Ecuación de continuidad…………………………………………………………......61

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
ix
Laura Natalia Cotes Gómez
Índice de tablas
Tabla 1. Enfermedades relacionadas con el agua…………………………………………………...2
Tabla 2. Cálculo de coeficientes α………………………………………………..…………………28
Tabla 3. Costos del proyecto……………………………………………………………………......59

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
1
Laura Natalia Cotes Gómez
1. Introducción
Las redes de abastecimiento de agua potable surgieron con la necesidad del hombre de trasladar y
distribuir agua en condiciones adecuadas de cantidad y calidad a los lugares más apartados o a sus
propias viviendas. La idea surgió en Europa aproximadamente desde el año 312 A.C. cuando fue
construido el primer acueducto de Roma, el Aqua Appia; el cual medía 16 km de largo y la mayor
parte de su recorrido era subterráneo. (Sedna, 2012)
A partir de esa época, y con la creciente necesidad de obtener el recurso hídrico, las estructuras de
abastecimiento de agua fueron cambiando continuamente para suplir la demanda que se presentaba
por el crecimiento poblacional. Dicho crecimiento fue más notorio después de la Revolución
Industrial, en donde ya se tenían los suficientes avances tecnológicos para poder abastecer de agua a
una ciudad entera.
Es importante mencionar, que las redes de abastecimiento tienen como principal objetivo llevar
agua a los usuarios en óptimas condiciones de cantidad y calidad para su consumo. Sin embargo,
para este proyecto, se va a enfatizar en el aspecto de la calidad del agua.
La calidad del agua potable es uno de los factores más relevantes a la hora de hablar de salud
pública, ya que muchas de las enfermedades que se presentan en niños menores de 5 años, se deben
a bacterias que se encuentran en el agua que consumen. Estudios que ha realizado la Organización
Mundial de la Salud (OMS), encuentran que alrededor del 80% de las enfermedades y más de la
tercera parte de todas las muertes en los países en desarrollo, están relacionadas con la calidad del
agua que utilizan.
Los patógenos que se encuentran con mayor frecuencia en el agua pueden generar enfermedades
como cólera, fiebre tifoidea, disenterías, poliomielitis, hepatitis y salmonelosis. A continuación se
muestra una tabla en donde se muestran las enfermedades relacionadas con el uso de agua
contaminada:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
2
Laura Natalia Cotes Gómez
ENFERMEDADES RELACIONADOS CON EL AGUA
Enfermedades
Casos registrados
por año
Decesos por año
Cólera
384000
11000
Tifoidea
500000
25000
Giardiasis
500000
30000
Amoebiasis
48000000
110000
Diarrea
1500000000
4000000
Ascaiasis
1000000
20000
Tabla 1. Enfermedades relacionadas con el Agua. Fuente: (Organización Mundial de la Salud (OMS) ,2009)
Por ejemplo, se ha estimado que 500000 personas en Asia, África y América Latina sufren de
Giardiasis, la cual es una infección intestinal que se transmite por el consumo de agua contaminada
con estos patógenos. Así mismo, en los países en vías de desarrollo, cada año se registran 15
millones de casos de cólera, donde el 80% se origina por el consumo de agua de baja calidad.
Debido a lo anterior, es de vital importancia que antes de que el agua sea transportada por las redes
del acueducto, se realice un tratamiento de las mismas, en donde se dé un proceso de purificación
del agua. Entre estos procesos está la desinfección, el cual es el último paso para producir agua pura
después de hacerla pasar por unidades de sedimentación, aireación, coagulación-floculación,
decantación y filtración. La desinfección es uno de los pasos más importantes de la potabilización
del agua, ya que allí se lleva a cabo la remoción de los organismos patógenos como protozoarios y
bacterias que generan las enfermedades anteriormente mencionadas.
El Cloro (Cl
2
) es el desinfectante más utilizado a nivel mundial para el agua de consumo humano ya
que tiene un carácter fuertemente oxidante, lo cual le permite destruir una gran cantidad de agentes
patógenos en su mayoría bacterias; es de fácil manejo y tiene un bajo costo (Agbar Agua, 2003).
Éste compuesto además de eliminar los agentes patógenos del agua reduce malos olores y sabores,
pues está en capacidad de oxidar compuestos que le aportan al agua estas características (como por
ejemplo el Hierro y el Manganeso). A su vez este, a una concentración excesiva no es perjudicial
para la salud, sino que genera mal sabor en el agua cuando se encuentra en concentraciones
superiores a 0,5 ppm (Revista Ambientum, 2002).
La cantidad de cloro que se agrega depende de los estándares de calidad que se tengan en el país
para obtener una concentración adecuada de cloro residual. Es importante resaltar, que el cloro
residual es indicativo de que en una determinada cantidad de agua hay suficiente cantidad de cloro
para inactivar los microorganismos presentes; a su vez, protege el agua de posibles re
contaminaciones microbiológicas durante su almacenamiento y transporte en sistemas de
distribución. Para esto, es importante conocer cuál es la cantidad de cloro que se debe aplicar a una
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
3
Laura Natalia Cotes Gómez
muestra de agua para producir una determinada cantidad de cloro residual disponible después de
cierto tiempo de contacto, lo cual es denominado la demanda de cloro. Esta demanda, es
cuantificada a partir de la diferencia entre la cantidad de cloro aplicada a la muestra y la cantidad de
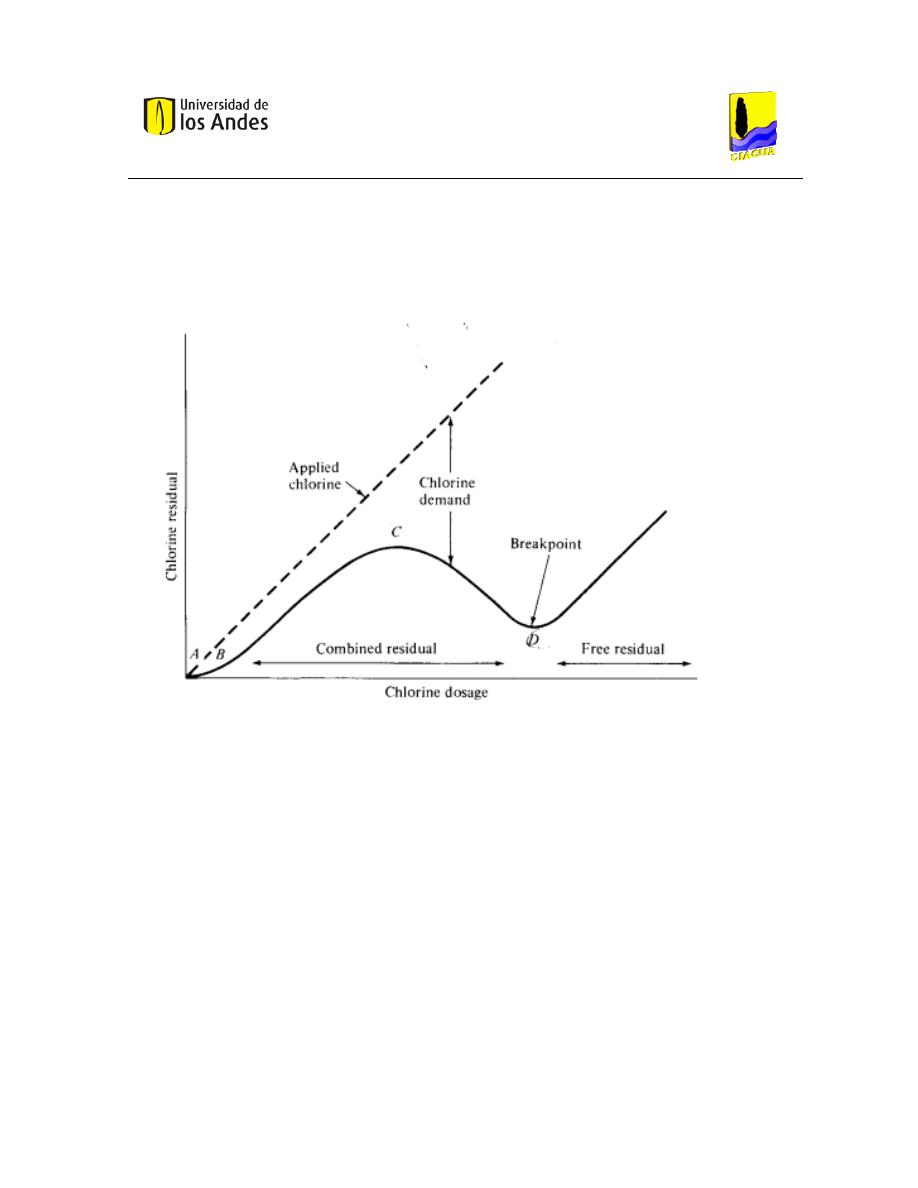
cloro remanente al final del periodo de contacto. La siguiente gráfica muestra el comportamiento
del cloro residual dependiendo de la dosis agregada a la muestra de agua:
Ilustración 1.Comportamiento del cloro residual de acuerdo con la dosis agregada.
Fuente: (Ocasio & Manuel, 2007)
De la gráfica se puede concluir que el punto A representa la cantidad requerida para satisfacer la
demanda de agentes reductores; si se realiza la adición de cloro de manera excesiva se va a dar la
formación de cloraminas. Una vez, los agentes reductores reaccionan, se genera un aumento en el
cloro residual (A-B) el cual oxida las cloraminas antes formadas, generando una disminución en el
cloro residual de nuevo. Cuando se eliminan todas las cloraminas (punto C) el agua ha salido ya de
la planta y tiene cloro residual (Ocasio & Manuel, 2007).
Estos cálculos se realizan basados en la mezcla que se supone que hay en los nudos de las redes de
abastecimiento. Es decir, en un tanque de almacenamiento se agrega una determinada cantidad de
cloro y en otro tanque no se agrega nada. El agua de estos dos tanques se envía al mismo tiempo,
por lo tanto al llegar al primer cruce, el agua con cloro y el agua sin cloro se mezclan. Dicha mezcla
se supone que es completa e instantánea así como lo plantea la teoría y los modelos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
4
Laura Natalia Cotes Gómez
computacionales de calidad del agua; por lo tanto se tendría la misma concentración en las tuberías
de salida, la cual es la necesaria para suplir los estándares de calidad del agua, en términos de cloro
residual, que llega a los puntos de consumo. Pero, ¿qué pasa si dicha mezcla no es completa? ¿Qué
pasa si las concentraciones de cloro en las tuberías de salida son diferentes y en una de las salidas,
no se cumple con los estándares para la calidad del agua de consumo? Estudios previos, han
demostrado que la mezcla en las uniones no es completa y este proyecto busca confirmar estos
resultados, los cuales pueden llegar a tener implicaciones importantes en la salud pública.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
5
Laura Natalia Cotes Gómez
1.1 . Objetivos
1.1.1. Objetivo general
El objetivo de este proyecto, es desarrollar el diseño y la construcción de un modelo en el
Laboratorio de Hidráulica de la Universidad de los Andes, en donde se pueda estudiar los procesos
de mezcla que se llevan a cabo en las uniones de las redes de abastecimiento de agua potable.
1.1.2. Objetivos específicos
A partir del objetivo general, se espera que se pueda realizar un estudio de manera cualitativa de los
procesos de mezcla que se presentan en los nodos de las redes de abastecimiento de agua potable.
Para esto, se van a utilizar tuberías de vidrio, en donde se puede apreciar visualmente lo que ocurre
con un trazador, en la unión de las tuberías.
A partir de los resultados obtenidos, se espera determinar algunos de los factores más importantes
que influyen en el proceso de mezcla que afectan la proporción de la misma y las concentraciones
de salida del trazador.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
6
Laura Natalia Cotes Gómez
2.
Antecedentes
Para llevar a cabo este proyecto, se realizó una investigación acerca de los estudios realizados
anteriormente con respecto a los procesos de mezcla en las uniones de las redes de abastecimiento
de agua potable. Se encontró principalmente, que en la Universidad de Tucson, Arizona, se
realizaron pruebas similares a cargo de Pedro Romero-Gómez (Tzatchkov, Buchberger, Li,
Romero-Gómez, & Choi, 2009).
En primer lugar, debido a los procesos físicos, químicos y biológicos que se pueden presentar en las
tuberías, la calidad del agua se puede deteriorar en los sistemas de distribución de agua potable
durante el transporte del recurso entre los puntos de tratamiento y el consumo. Para tener un mayor
entendimiento de los procesos que ocurren mientras el agua es transportada por las redes, se
realizaron varias simulaciones en donde se hace una variación de las condiciones del flujo.
Teniendo en cuenta que la dispersión axial o longitudinal de un fluido a través de un tubo, se define
como un proceso de transporte de masa en el que un soluto se extiende en la dirección axial
mientras el solvente se mueve aguas abajo; en este caso, el soluto es el trazador, y el solvente es el
agua. Se identificó que en la presencia de flujo laminar, la dispersión axial puede ser un factor
importante cuando se está hablando de la predicción de la calidad del agua.
El transporte de un trazador químico de tipo conservador que se mueve bajo flujo laminar constante
a través de un tubo, se describe por la ecuación bidimensional de advección-difusión:
(
) (
)
Ecuación 1- Ecuación bidimensional de advección-difusión. Fuente: (Tzatchkov, Buchberger, Li, Romero-Gómez,
& Choi, 2009).
donde,
, es la concentración del soluto en cualquier punto en la sección transversal.
D, es el coeficiente de difusión molecular del soluto en el agua (difusividad).
U, es la velocidad media en la dirección axial.
K, es la velocidad constante de reacción de primer orden.
a, es el radio de la tubería.
r, es la posición radial.
x, es la posición axial.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
7
Laura Natalia Cotes Gómez
t, es el tiempo.
De acuerdo con la teoría clásica de Taylor para la dispersión, la Ecuación 1 se puede simplificar a la
ecuación de advección-dispersión unidimensional, siempre y cuando una cierta inicialización del
proceso de difusión ha transcurrido:
Ecuación 2- Ecuación unidimensional de adveccion-difusión. Fuente: (Tzatchkov, Buchberger, Li, Romero-Gómez,
& Choi, 2009).
donde,
C, ahora es la concentración media en la sección transversal.
E, es el coeficiente axial de dispersión, el cual es constante.
Al utilizar esta ecuación con un coeficiente de dispersión constante, se tiene como consecuencia un
proceso de difusión estable. Sin embargo, debido al pequeño valor de la difusividad del agua
(
y el constante cambio del flujo en las redes de distribución, el proceso de
dispersión es inestable y la teoría de Taylor, descrita anteriormente, no tiene validez. Lo que quiere
decir que es importante medir la concentración del soluto de manera independiente espacialmente y
no se puede tomar una concentración media. A partir de lo anterior, los científicos llegaron a la
conclusión de que este último modelo, subestima significativamente las concentraciones en los
nodos obtenidas mediante la resolución de la ecuación de advección-dispersión a baja velocidad de
flujo (Tzatchkov, Buchberger, Li, Romero-Gómez, & Choi, 2009).
Así pues, Romero-Gómez (2009) llevó a cabo una serie de experimentos con el fin de comparar los
resultados empíricos de una dispersión axial de un trazador no reactivo en un tubo bajo condiciones
de flujo laminar y transicional, con los resultados obtenidos con simulaciones realizadas en
EPANET, Computational Fluid Dynamics (CFD), y Advection Dispersion (AD) del modelo. El
montaje experimental se construyó en el Laboratorio de Redes de Distribución, en una instalación
experimental en la Universidad de Tucson, Arizona, EE.UU. El modelo consistía en un tubo de
PVC de 10 m de longitud, con un diámetro interior de 15,3 mm (diámetro nominal de 1/2 pulgada),
montado en andamios de metal. El agua potable se bombeó desde un tanque de almacenamiento,
mientras que una micro-bomba inyectaba agua que contenía un trazador (cloruro de sodio). La
velocidad de flujo fue controlada por medio de sensores tipo caudal de turbina y válvulas de aguja
ubicadas en el extremo aguas abajo de las tuberías. La concentración de los trazadores se controló
con sensores de conductividad eléctrica y transmisores que fueron colocados en sitios de monitoreo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
8
Laura Natalia Cotes Gómez
aguas arriba y aguas abajo, para medir el indicador de concentraciones. Las tasas de flujo y las
concentraciones se observaron en tiempo real y se registraron cada segundo.
Los resultados de la simulación CFD para flujos laminares fueron acordes con los datos
experimentales. Se observaron dos características distintas: (i) la concentración máxima encontrada
experimentalmente y simulada en CFD aguas abajo de la unión es menor que las basadas en las
simulaciones de mezcla completa realizadas en EPANET, y (ii) el avance aguas abajo del flujo,
siempre se retrasa en comparación con el grupo experimental y simulado en CFD; esta diferencia se
hace más pequeña con un mayor número de Reynolds. Por lo tanto, la dispersión axial de un soluto
puede ser un proceso de transporte importante en regímenes de flujo laminar y transitorio. La
magnitud del coeficiente de dispersión se redujo rápidamente cuando el flujo sale del régimen
laminar y entra en el régimen de transición.
Además de lo anterior, se determinó que la difusión de solutos o contaminantes a través de redes de
tuberías de distribución de agua, está controlada en gran parte, por la mezcla en las uniones del
tubo y la variación de caudales y concentraciones que puede entrar en la unión. Es por esto que
existen modelos de mezcla completa y modelos computaciones de la dinámica de fluidos basados
en las ecuaciones de Navier-Stokes, que ayudan a determinar los procesos de mezcla en las redes de
abastecimiento de agua.
Dentro de dichos modelos se encuentran los realizados por el software EPANET, el cual es un
estándar para la modelación hidráulica y el comportamiento de la calidad del agua en sistemas de
distribución de agua. Sin embargo, el programa supone que la mezcla de solutos en las uniones de
tuberías es completa e instantánea, contrariamente a estudios que mostraron que la mezcla en las
uniones de tubos individuales era incompleta. Los flujos que inciden en un cruce tienden a
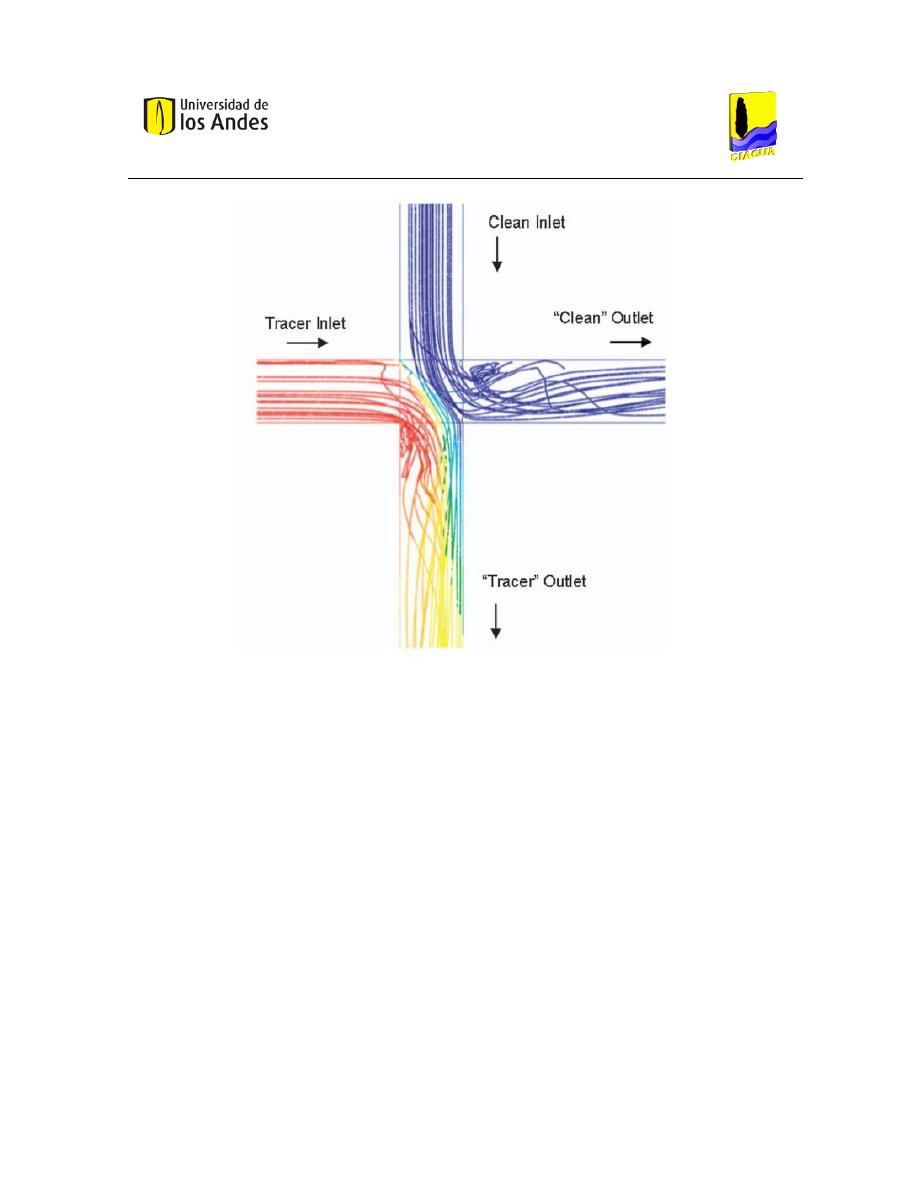
bifurcarse en lugar de mezclarse completamente (ver Ilustración 2).
También se simuló una red de 3 x 3 tuberías a pequeña escala de para evaluar la validez de los
modelos de mezcla completa e incompleta para sistemas de distribución de agua bajo diferentes
tasas de flujo y condiciones de contorno. Simulaciones en CFD mostraron que las predicciones de
las concentraciones del trazador a lo largo de la red podrían alcanzarse si se compara con los datos
experimentales. Por el contrario, un modelo de EPANET que supone la mezcla completa dentro de
las uniones, produjo concentraciones uniformes en toda la red, que fue significativamente diferente
de las concentraciones espacialmente variables observadas en la red experimental (Ho, Choi, &
McKenna, 2007).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
9
Laura Natalia Cotes Gómez
Ilustración 2. Bifurcación de los flujos en la simulación en CFD.
Fuente: (Ho C. K., 2008).
Como se puede ver, la mezcla de solutos dentro de la unión se limita a la incidencia de la interfaz
donde los flujos convergen (Ilustración 2). Se evidenció que un factor dominante que controla el
comportamiento y las concentraciones de mezcla son las tasas de entrada y salida de las uniones; las
corrientes de flujo entrantes se bifurcan en diversos grados a través de los tubos de salida en función
de las velocidades de flujo relativas.
Por lo tanto, la cantidad de mezcla que se produce dentro de la unión depende de la relación de
impulso que lleva un flujo de corriente. Los resultados de los estudios mostraron que la mezcla en
uniones en cruz es incompleta y dependiente de las inestabilidades transitorias en la interfaz
incidente y las tasas de flujo relativas que entran y salen la unión.
La mezcla de solutos dentro de la unión se supone que es conservativa y no reacciona. Sin embargo,
existen procesos que implican reacciones de pared y reacciones de flujo que no se han incorporado
en los modelos de flujo y transporte dentro de las tuberías.
La Ilustración 2 muestra un ejemplo de flujo simulado y el transporte de solutos en una unión
transversal utilizando un modelo de CFD. Un resultado notable de esta simulación es que el flujo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
10
Laura Natalia Cotes Gómez
entrante se refleja en los otros, como si fueran cuerpos rígidos. La mezcla se limita a la interfaz
incidente en donde los dos flujos se encuentran, y la mezcla no es completa. También, en esta
simulación, el flujo en el tubo vertical es mayor que el flujo en el tubo horizontal, el agua "limpia"
cruza la intersección, desviando la mayor parte del "trazador" del agua. Estos fenómenos simulados,
han sido confirmados experimentalmente.
Aunque los modelos CFD se han utilizado recientemente para obtener una perspectiva de los
procesos de mezcla en uniones de tubos individuales, los modelos más simples son los de mezcla
completa, por lo tanto sigue siendo necesario que se pueda incorporar en los modelos de la red de
agua, los que se basan en la mezcla incompleta.
Como investigación, se han realizado modelos analíticos utilizados para limitar el comportamiento
de la mezcla en las uniones de las tuberías. Estos modelos son el de mezcla completa y mezcla
incompleta.
Modelo de mezcla completa
El modelo de mezcla completa es empleado por EPANET y otros modelos de redes de distribución
de agua que suponen una mezcla completa e instantánea dentro de las uniones de tuberías. La
formulación se puede implementar fácilmente con una ecuación analítica en los modelos de red para
cálculos rápidos y eficientes.
En el modelo de mezcla completa, se supone que la concentración en el fluido que sale de la unión
es uniforme e igual en todas las tuberías de salida. Y depende de las concentraciones de flujo
ponderadas que entran en el tubo.
En un balance de masa del soluto, se obtiene la siguiente ecuación para la concentración:
∑
∑
∑
Ecuación 3- Balance de masa del soluto. Fuente: (Ho C. K., 2008).
donde:
, es el caudal de entrada a la unión desde la tubería i.
, es la concentración en cada tubería de entrada a la unión.
n, es el número de tuberías que llegan a la unión.
Se supone que no se presenta ningún almacenamiento en la unión, por lo tanto, el caudal de salida
es igual al caudal de entrada en la unión.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
11
Laura Natalia Cotes Gómez
La desventaja del modelo de mezcla completa es que no tiene en cuenta los procesos físicos de
mezcla que se han observado en experimentos y simulaciones utilizando modelos CFD para muchas
configuraciones de flujo. El modelo de mezcla completa predice la mayor mezcla posible que puede
ocurrir físicamente dentro de un cruce. Esta suposición puede dar concentraciones que son
significativamente diferentes de las concentraciones reales para muchas configuraciones de
conexiones.
Modelo de mezcla incompleta
El modelo de mezcla incompleta pretende complementar el modelo de mezcla completa
proporcionando un límite inferior para la mezcla en las uniones. El modelo de mezcla incompleta se
basa en el conocimiento de las velocidades de flujo relativas y las concentraciones que entran y
salen de una unión.
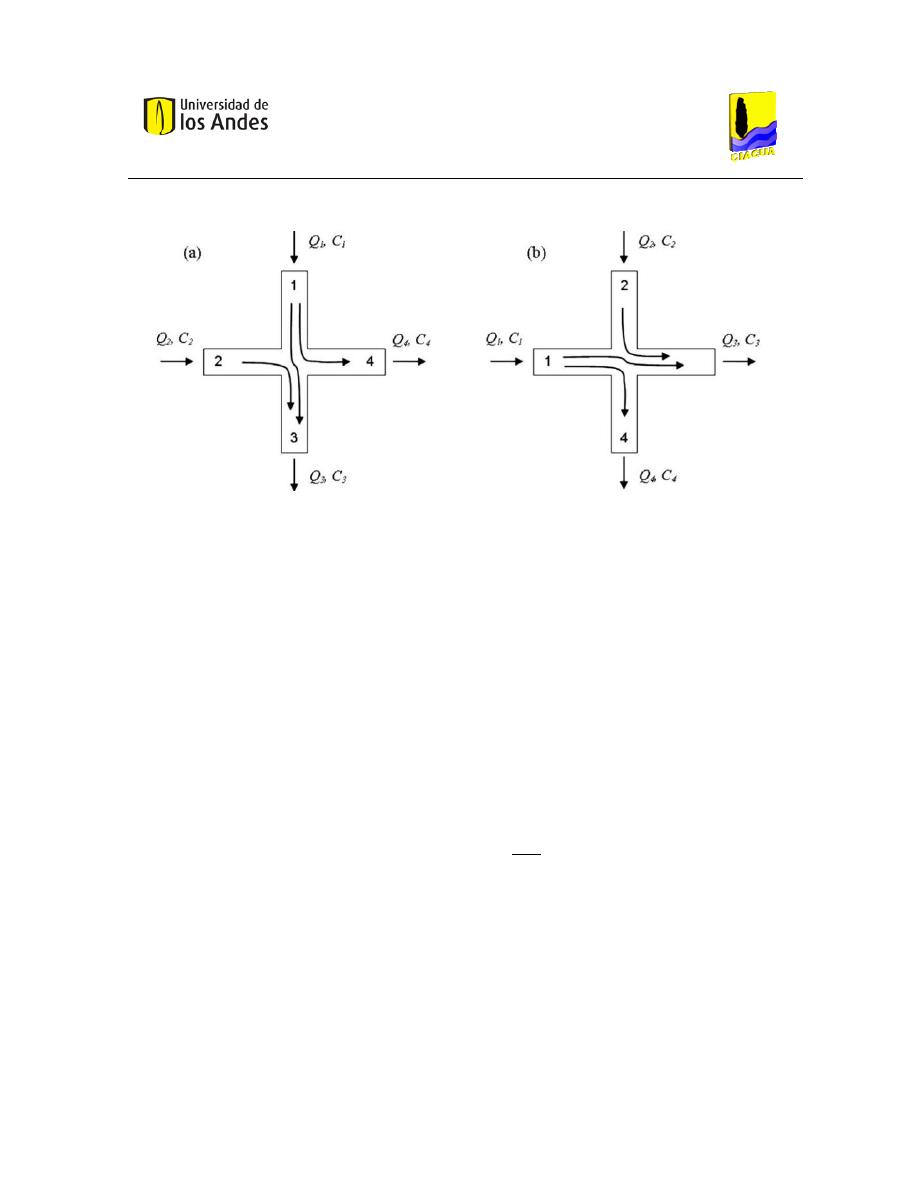
Como se muestra en la Ilustración 3, el impulso desigual de diferentes flujos provocará una
transferencia masiva de los fluidos y componentes entre los flujos entrantes y salientes. Con
caudales diferentes, los modelos CFD muestran que el impulso adicional realizado por una corriente
puede ser suficiente para cruzar la unión en la corriente opuesta. La Ilustración 2, muestra esta
situación en la que la velocidad de flujo de entrada de agua limpia es 80% mayor que la velocidad
de flujo del agua con trazador y las tasas de flujo de salida son iguales. Como resultado, el impulso
adicional del agua limpia hace que una parte de esta agua empuje la otra a través de la unión. Este
comportamiento de mezcla de fluido, va a diluir la concentración del trazador en la tubería de salida
al tiempo que reduce la cantidad de trazador que puede migrar en la salida de agua limpia. Similar
pero opuesto, se producirá el comportamiento si la velocidad de flujo en la entrada de trazador es
mayor que la velocidad de flujo en la entrada de agua limpia, con tasas de flujo de salida iguales.
Los flujos de diferentes patrones se muestran en la Ilustración 3 (Ho C. K., 2008).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
12
Laura Natalia Cotes Gómez
Ilustración 3. Flujos con diferentes patrones. Fuente: (Ho C. K., 2008).
El modelo de mezcla incompleta supone que la mezcla se produce sólo a través de la interacción del
fluido a granel. Si todas las velocidades de flujo son iguales, o si las velocidades de flujo en tuberías
de entrada y salida adyacentes son iguales, se supone que el flujo se bifurca completamente y no
hay mezcla. Por lo tanto, el modelo de mezcla incompleta proporciona un límite inferior,
físicamente basado, de la cantidad de mezcla que puede ocurrir dentro de las uniones.
El modelo de mezcla incompleta se obtiene suponiendo que se conocen las tasas de entrada del
flujo, o que se pueden calcular. En primer lugar, los tubos están numerados de modo que la
nomenclatura utilizada en la solución es consistente para todas las configuraciones del flujo, luego
se siguen los siguientes pasos:
1. Calcular la tasa de impulso total del fluido en pares de tubos opuestos, es decir, entradas y
salidas situados a 180° entre ellos.
Ecuación 4- Impulso del flujo. Fuente: (Ho C. K., 2008).
donde
, es al área transversal de cada tubería.
2. Para el par de tubos que tiene el mayor impulso del fluido, asignar “1” para la tubería de
entrada y “3” para la de salida.
3. Asignar “2” para la entrada restante y “4” para la salida restante
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
13
Laura Natalia Cotes Gómez
Suponiendo que la densidad del agua es constante, el criterio de impulso es el siguiente:
Ecuación 5- Criterio de impulso en las tuberías. Fuente: (Ho C. K., 2008).
Para este caso, se va a considerar que las áreas transversales de todas las tuberías son iguales. En los
ejemplos presentados en la Ilustración 3, se encuentran diferentes velocidades de flujo en los tubos
individuales que causan un impulso dominante en uno de los pares de tubos opuestos. En la
Ilustración 3(a), el impulso dominante es de arriba a abajo, mientras que en la Ilustración 3 (b), el
impulso dominante es de izquierda a derecha. Los tubos 1 y 3 siempre corresponden a la entrada y
la salida, respectivamente, de la tubería con el impulso más grande. Por lo tanto, con este esquema
de numeración, la mayor parte del modelo de mezcla supone que todo el flujo de entrada de la
tubería 2 fluye hacia el tubo de salida 3. Por lo tanto, la concentración en la tubería de salida 3 es
una mezcla de las concentraciones de las tuberías de entrada 1 y 2. La concentración en la tubería
de salida 4 es la misma que la concentración en la tubería de entrada 1, que es la única fuente de
flujo de la tubería de salida 4.
Suponiendo que la velocidad de flujo en cada tubería es conocida junto con las concentraciones de
entrada C1 y C2, se identifica que:
Ecuación 6- Relación caudal concentración en tuberías 1 y 4. Fuente: (Ho C. K., 2008).
donde:
, es la porción del flujo de la tubería de entrada 1 que fluye hacia el tubo de salida 4.
Como se supone que el flujo de la tubería 2 no sale por la tubería 4, todo el flujo que sale de la
tubería 4 es del tubo de entrada 1, es decir,
entonces se establece que la concentración
en la tubería de salida 4 es igual a la concentración en la tubería de entrada 1:
Ecuación 7- Relación de concentraciones en tuberías 1 y 4. Fuente: (Ho C. K., 2008).
La concentración en la tubería de salida 3 se deriva mediante la realización de un balance de masa
del soluto en la unión:
Ecuación 8- Balance de masa del soluto en la unión. Fuente: (Ho C. K., 2008).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
14
Laura Natalia Cotes Gómez
Despejando la concentración de la tubería 3 se tiene que:
Ecuación 9- Concentración en la tubería 3. Fuente: (Ho C. K., 2008).
Las Ecuaciones 7 y 9 describen las soluciones analíticas de la mezcla incompleta. En un modelo de
red, estas soluciones pueden ser aplicadas secuencialmente a cada unión aguas abajo a partir de la
unión aguas arriba donde se prescriben las condiciones límite de concentración. La velocidad de
flujo en cada tubería es típicamente calculado de antemano en los modelos CFD de red o sobre las
condiciones prescritas de límite de presión y / o las tasas de flujo. En las simulaciones transitorias,
la solución del modelo de mezcla incompleta se puede aplicar en cada paso de tiempo con
velocidades de flujo actualizadas en cada unión.
La solución para la concentración en la tubería de salida 3 puede ser también reescrita en términos
de las relaciones entre los caudales de entrada y salida si se realiza la siguiente definición:
Ecuación 10- Relación entre los caudales de entrada y salida. Fuente: (Ho C. K., 2008).
Los caudales expresados en la Ecuación 9 pueden ser derivados utilizando la Ecuación 10 y
utilizando la conservación de masa en la unión se tiene lo siguiente:
Ecuación 11- Conservación de masa en la unión. Fuente: (Ho C. K., 2008).
Remplazando:
Utilizando las dos últimas ecuaciones en la Ecuación 9, se puede determinar la concentración en la
tubería 3:
(
)
(
)
Ecuación 12- Concentración de la tubería 3 en términos de x y y. Fuente: (Ho C. K., 2008).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
15
Laura Natalia Cotes Gómez
Las relaciones de flujo también son equivalentes si se expresan en términos del número de
Reynolds para cada tubo:
Ecuación 13- Número de Reynolds.
donde:
, es la velocidad media del flujo en cada tubería.
, es el diámetro de cada tubería.
, es la densidad del agua.
, es la viscosidad dinámica del agua.
De esta manera, la concentración en la tubería 3 sería:
Ecuación 14- Concentración en la tubería 3 en términos del número de Reynolds. Fuente: (Ho C. K., 2008).
Combinación de los modelos de mezcla completa y modelos de mezcla incompleta
Debido a que el modelo de mezcla completa y el modelo de mezcla incompleta proporcionan los
límites superior e inferior, respectivamente, la cantidad real de la mezcla estará entre estos dos
límites. Por lo tanto, se puede definir un parámetro de escala 0<S<1 para estimar la combinación de
concentración en un tubo de salida:
Ecuación 15- Concentración combinada. Fuente: (Ho C. K., 2008).
El valor del parámetro de escala, s, puede depender de las propiedades del fluido, las condiciones de
flujo, y la configuración geométrica de la conexión de tubos, lo que puede contribuir a
inestabilidades locales en la interfaz incidente y la mezcla turbulenta dentro de la unión.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
16
Laura Natalia Cotes Gómez
Comparación con los experimentos
Se han realizado experimentos en los estudios anteriores para investigar el comportamiento de
mezcla en las articulaciones cruzadas bajo diferentes configuraciones de flujo.
Realizando nuevamente la prueba, donde, se controló la velocidad de flujo en las entradas y salidas
de las tuberías por medio de válvulas y medidores de flujo. Los tubos de entrada y de salida se
construyeron de PVC, y las longitudes de tubería fueron lo suficientemente largas para asegurar que
el agua se mezcló bien dentro de cada tubo antes de entrar a la unión y antes de ser supervisado
aguas abajo de la confluencia. El agua que entra al sistema fue bombeada a partir de dos tanques de
suministro, un tanque de alimentación de agua con trazador y un depósito de suministro de agua
limpia. En todos los experimentos, el NaCl fue continuamente mezclado con agua en el tanque de
suministro de trazador. El trazador de NaCl fue monitoreado en las tuberías utilizando sensores de
conductividad eléctrica. El diámetro de la tubería utilizada en la prueba de Romero-Gómez (2006)
era 1.905 cm, y los números de Reynolds oscilaron entre aproximadamente 5.000 a 50.000 en los
diferentes experimentos. El diámetro de la tubería utilizada en la prueba de McKenna (2007) fue de
2.54 cm, y los números de Reynolds variaron entre aproximadamente 500 a 40.000 en los diferentes
experimentos para obtener las relaciones de flujo deseadas (Ho C. K., 2008). A partir de estas
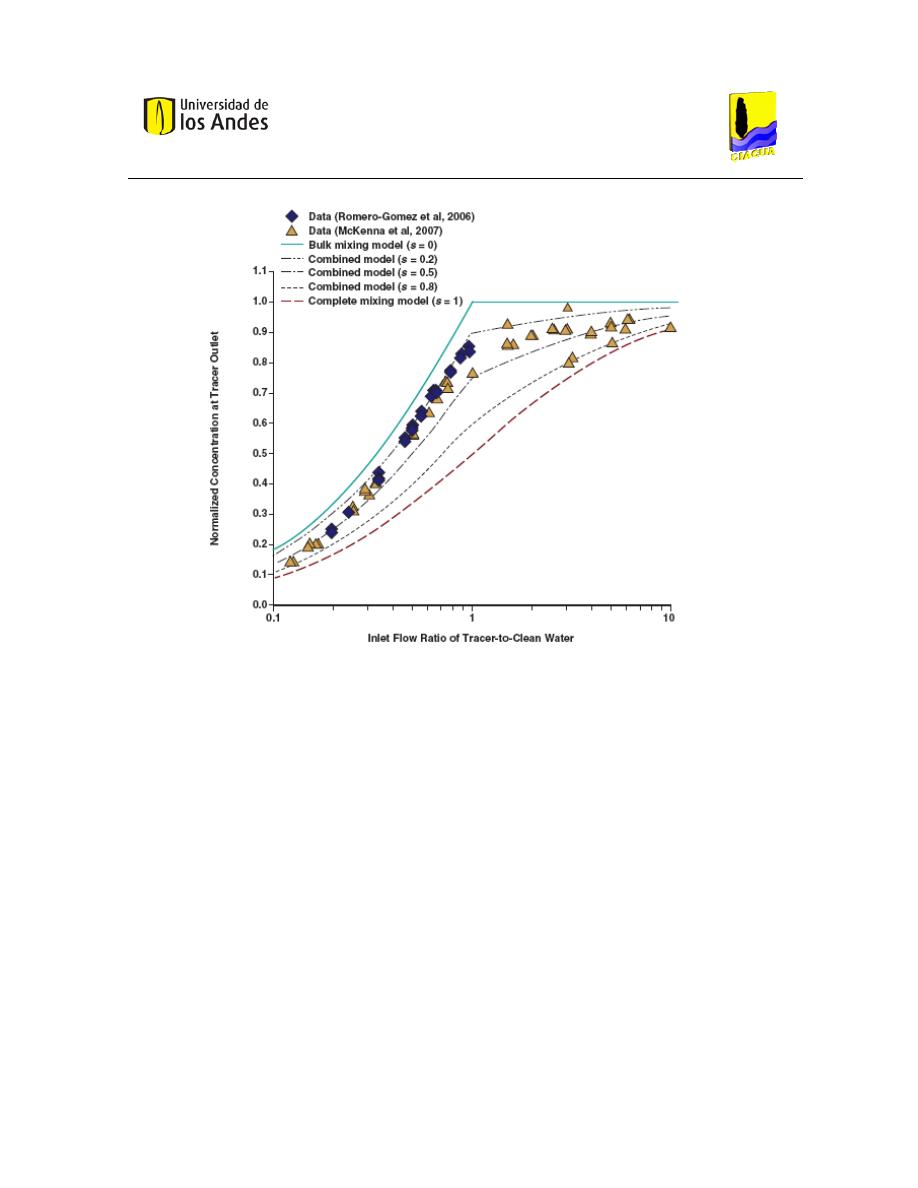
condiciones y variando el parámetro S, se obtuvieron los siguientes resultados:
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
17
Laura Natalia Cotes Gómez
Ilustración 4.Resultados de simulaciones de los modelos de mezcla. Fuente: (Clifford & Leslie, 2009).
Se muestra una comparación de la concentración del trazador, medida en la salida de diferentes
experimentos con diferentes combinaciones de velocidades de flujo. Las concentraciones medidas
están limitadas por los modelos de mezcla incompleta y modelos de mezcla completa, y la mayoría
de los datos se dividen entre las concentraciones predichas utilizando un parámetro de mezcla S
entre 0,2 y 0,5 (Clifford & Leslie, 2009).
Se puede ver que cuando el parámetro s es igual a cero, se presenta una mezcla totalmente
incompleta. Y cuando el parámetro s es igual a 1 la mezcla es incompleta. De esta manera se
ilustran los límites de mezcla descritos anteriormente.
Finalmente se puede decir que la dispersión de los solutos es un componente importante en la
simulación de la calidad del agua de la red, y que debe ser incorporado en la modelación de las
redes de distribución de agua en modelos de calidad. Para esto es importante la comprensión de
cómo los solutos se mueven y se mezclan a través de la red y es fundamental para el diseño de una
red de tuberías y sus uniones.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
18
Laura Natalia Cotes Gómez
3.
Marco teórico
Los modelos para la calidad del agua se componen de la modelación hidráulica y la modelación de
la calidad del agua. La modelación hidráulica está basada en el cálculo de caudales y presiones de
las redes y la modelación de la calidad del agua estudia de manera espacial y temporal los procesos
que afectan la calidad del agua.
3.1.
Modelación hidráulica
3.1.1. Ecuaciones de modelación hidráulica
Como se mencionó anteriormente, la modelación hidráulica está basada en el cálculo de caudales y
presiones, por lo tanto, se debe cumplir la conservación de la masa en las redes. De acuerdo con
esto, la ecuación de continuidad es la siguiente:
∑
Ecuación 16- Conservación de masa en las redes.
donde:
, es el número de tuberías.
, es el caudal demandado en la unión i.
, es el caudal de entrada al nudo i.
, es el caudal de la tubería.
Para el cálculo de caudales se utiliza la ecuación de Darcy-Weisbach en conjunto con la ecuación
de Colebrook-White. La ecuación se describe la de siguiente manera:
√
√
(
√
√
)
Ecuación 17- Caudal utilizando la ecuación de Darcy-Weisbach en conjunto con la ecuación de Colebrook-White.
Fuente: (Saldarriaga, 2007).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
19
Laura Natalia Cotes Gómez
donde:
, es la aceleración de la gravedad.
, es el diámetro de la tubería.
, es la altura por pérdidas por fricción.
, es la longitud de la tubería.
, es la rugosidad relativa de la tubería, la cual depende del material.
es la viscosidad cinemática del fluido.
Por otro lado, para calcular las alturas piezométricas, se supone que en cada tubo la energía total
disponible se gasta en pérdidas por fricción y en pérdidas menores:
∑
Ecuación 18- Altura piezométrica. Fuente: (Saldarriaga, 2007).
Si se tienen en cuenta las pérdidas menores causadas por cualquier tipo de accesorios y/o bombas en
alguno de los tubos de la red, la anterior ecuación se ve modificada de la siguiente manera:
Ecuación 19- Altura piezométrica teniendo en cuenta pérdidas menores causadas por accesorios. Fuente:
(Saldarriaga, 2007).
donde:
, es un exponente que depende de la ecuación de fricción utilizada, la cual es 2 si se utiliza la
ecuación de Darcy-Weisbach, ó 0.85 para la ecuación de Hazen-Williams.
, son parámetros característicos del tubo, las válvulas y las bombas.
Generalmente, en las tuberías sólo ocurren pérdidas por fricción y pérdidas menores, las cuales son
función únicamente de la altura de velocidad; en este caso, se puede utilizar la anterior ecuación
para definir el valor de
∑

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
20
Laura Natalia Cotes Gómez
Utilizando la ecuación de Darcy-Weisbach:
(
∑
)
Despejando
:
(
∑
)
Ecuación 20- Definición del valor de
. Fuente: (Saldarriaga, 2007).
3.1.2. Método del gradiente
Para este método se planteó, que las ecuaciones de energía individuales para cada tubo se combinan
con las ecuaciones de masa individuales en cada unión con el fin de obtener una solución
simultánea tanto de los caudales en las tuberías como de las alturas piezométricas de los nodos. En
este método, las ecuaciones se resuelven utilizando un esquema imaginativo que se basa en la
inversión de la matriz de coeficientes originales.
Por otro lado, este método se basa en el hecho de que al tener un flujo permanente se garantiza que
se cumplan las ecuaciones de conservación de la masa en cada uno de los nodos de la red y la
ecuación de conservación de energía en los circuitos de la misma (Saldarriaga, 2007).
Para aplicar este método se deben cumplir tres condiciones:
-
En cada nodo se debe cumplir la ecuación de continuidad.
-
Debe haber una relación no lineal entre las pérdidas por fricción y el caudal para cada uno
de los tubos.
-
En cada tubo la energía total se gasta en pérdidas por fricción y en pérdidas menores.
Estas tres condiciones se basan en las ecuaciones presentadas anteriormente.
Para el método del gradiente hidráulico se deben tener en cuenta las siguientes definiciones, con el
fin de describir la topología de la red en forma matricial.
NT= número de tuberías de la red.
NN=número de nodos con alturas piezométricas desconocidas.
[ ]= matriz de conectividad asociada a cada uno de los nodos de la red. Su dimensión es -1 en la
columna correspondiente al nodo inicial del tramo i, y es 1 en la columna correspondiente al nodo
final del tramo i.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
21
Laura Natalia Cotes Gómez
NS= número de nodos de altura piezométrica conocida.
[ ]= matriz topológica tramo a nodo para los NS nodos de altura piezométrica fija. Su dimensión
es NT x NS con un valor de -1 en las filas correspondientes a los tramos conectados a los nodos de
altura piezométrica fija.
De esta manera, la pérdida de altura piezométrica en cada tramo de tubería que conecte dos nodos
de la red es:
[ ][ ] [ ][ ] [ ][
]
Ecuación 21- Pérdida de altura piezométrica en cada tramo. Fuente: (Saldarriaga, 2007).
donde:
[ ], es la matriz diagonal de NT x NT definida se la siguiente forma:
[ ]
[
]
[ ]= vector de caudales con dimensiones NT X 1.
[ ]= vector de alturas piezométricas desconocidas con dimensión NN x 1.
[
]= vector de altura piezométricas fijas con dimensión NS x 1.
La ecuación de continuidad para todos los nodos de la red es:
[ ][ ] [ ]
Ecuación 22- Ecuación de continuidad para todos los nodos. Fuente: (Saldarriaga, 2007).
donde:
[ ]= matriz transpuesta de [ ].
[ ]= vector de consumo o de entrada en cada nodo de la red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
22
Laura Natalia Cotes Gómez
En forma compacta, las anteriores ecuaciones se pueden expresar en términos matriciales:
[
[ ]
[ ] [ ]
] [
[ ]
[ ]
] [
[ ][
]
[ ]
]
Esta ecuación no puede resolverse en forma directa ya que la parte superior no es lineal, por lo tanto
es necesario utilizar algún método iterativo. En el método de gradiente se utiliza una expansión
truncada de Taylor, en donde al operar simultáneamente sobre el campo y aplicar el operador
gradiente se obtiene:
[
[ ][ ] [ ]
[ ] [ ]
] [
[ ]
[ ]
] [
[ ]
[ ]]
donde:
[ ]=matriz diagonal con dimensiones NT x NT
[ ] =matriz con dimensión NT x NT definida como:
[ ]
[
]
Fuente: (Saldarriaga, 2007).
En cualquier iteración i, [
] representa el desbalance de energía por unidad de peso en cada tubo y
[ ] representa el desbalance de caudal en cada nodo. Estos desbalances se definen,
respectivamente, por las siguientes ecuaciones:
[ ] [ ][
] [ ][
] [ ][
]
Ecuación 23- Desbalance de energía por unidad de peso. Fuente: (Saldarriaga, 2007).
[ ] [ ][
] [ ]
Ecuación 24- Desbalance de caudal en cada nodo. Fuente: (Saldarriaga, 2007).
Se debe tener en cuenta que para cada iteración:
[ ] [
] [
]
[ ] [
][
]

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
23
Laura Natalia Cotes Gómez
La solución, puede calcularse resolviendo el siguiente sistema:
[
[ ]
[ ]
] [
[ ][ ]
[ ]
[ ] [ ]
]
[
[ ]
[ ]]
Utilizando el álgebra matricial, es posible calcular de forma explícita los caudales y las alturas de la
siguiente manera:
[
] {[ ] [ ][ ]
[ ]}
{[ ] [ ][ ]
[ ][
] [ ][
] [ ][
] [ ] }
Ecuación 25- Cálculo de alturas piezométricas. Fuente: (Saldarriaga, 2007).
[
] {[ ] [
][ ] [ ]}[
] {([ ][ ]
[ ][
] [ ][
])}
Ecuación 26-Cálculo de caudales. Fuente: (Saldarriaga, 2007).
Para solucionar un problema con el Método del Gradiente se deben seguir los siguientes pasos
iterativamente:
-
Se suponen unos caudales iniciales en cada uno de los tubos de la red.
-
Se resuelve el sistema representado por las anteriores ecuaciones utilizando un método
estándar para la solución de ecuaciones lineales simultáneas.
-
Con [
] calculado se utiliza la ecuación 26 para terminar [
].
-
Con este [
] se vuelve a ensamblar en el sistema para encontrar un nuevo [
].
-
El proceso se repite hasta que en dos iteraciones sucesivas se cumpla que [
] [
].
3.1.3. Ejemplo de aplicación de modelación hidráulica
El ejemplo que se va a mostrar a continuación es tomado del libro Hidráulica de Tuberías
(Saldarriaga, 2007).
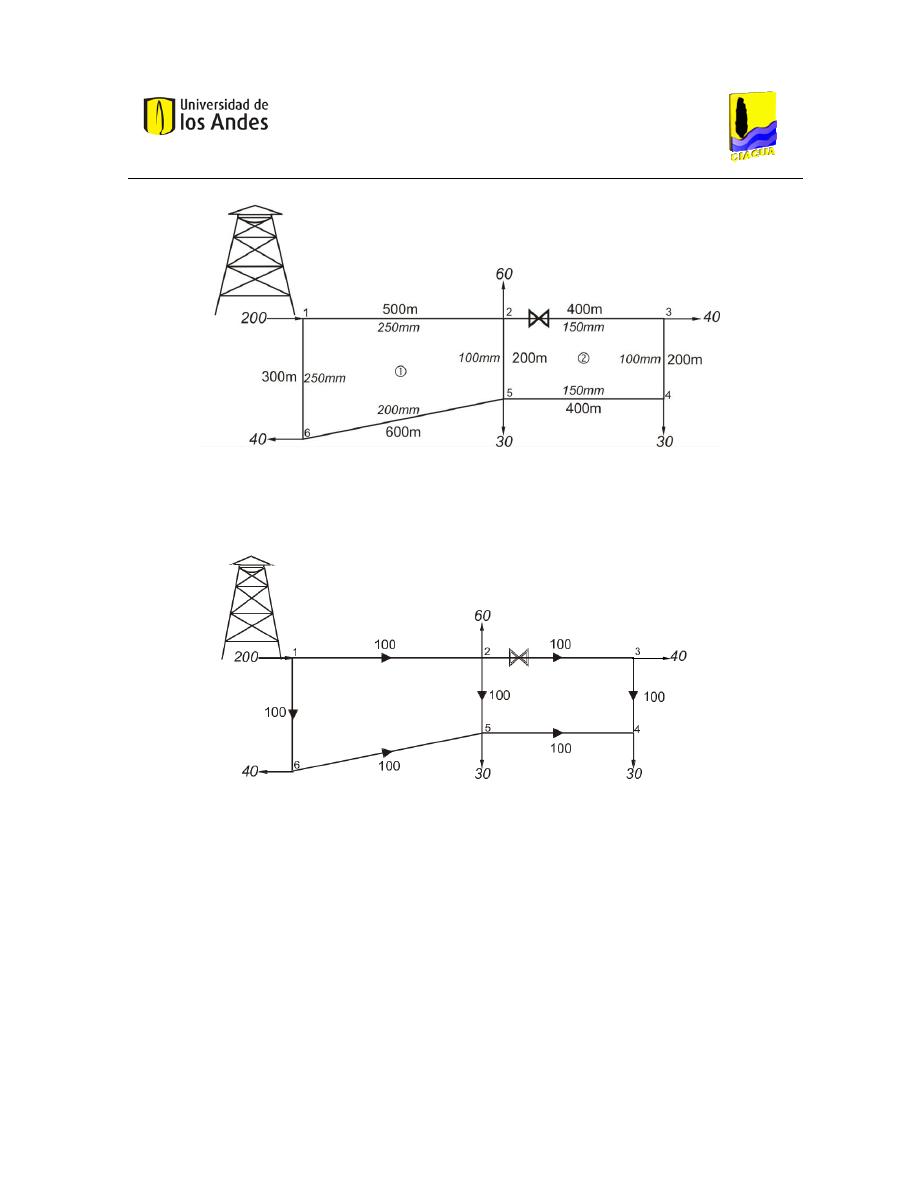
La red mostrada en la siguiente figura tiene una válvula en la tubería 2-3 la cual se encuentra
parcialmente cerrada y produce una pérdida menor local de
. Las pérdidas menores son
despreciables en las otras tuberías. Analizar los caudales y presiones en la red. Los caudales están
dados en L/s. la viscosidad cinemática es de
y la rugosidad relativa de las tuberías
es de 0.00006 m.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
24
Laura Natalia Cotes Gómez
Ilustración 5. Longitud y diámetros de las tuberías de la red.
Para todos los tramos de tuberías se ha supuesto un caudal inicial de 100 L/s con las direcciones
mostradas en la figura las cuales fueron supuestas de forma arbitraria.
Ilustración 6. Caudales en las tuberías de la red.
Para realizar el cálculo de las presiones y caudales en la red es necesario efectuar los siguientes
planteamientos matrices y vectores, teniendo en cuenta que:
NT=7
NN=5
NS=1

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
25
Laura Natalia Cotes Gómez
[ ] = Matriz de conectividad, donde su dimensión es (7x5)
[ ] = matriz transpuesta de [ ]
1
-1
0
0
-1
0
0
0
1
1
0
0
0
0
0
0
-1
1
0
0
0
0
0
0
-1
1
1
0
0
0
0
0
0
-1
1
[A10] = Matriz topológica tramo a nudo. Dimensión (7 x 1).
[Q] = Vector de caudales. Dimensión (7 x 1).
1
0
0
0
0
-1
1
0
0
0
0
1
-1
0
0
0
0
1
-1
0
-1
0
0
1
0
0
0
0
1
-1
0
0
0
0
1

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
26
Laura Natalia Cotes Gómez
[H] = Vector de alturas piezométricas desconocidas. Dimensión (5 x 1).
[H
o
] = Vector de alturas piezométricas fijas. Dimensión (1 x 1).
[q] = Vector de consumo. Dimensión (5 x 1).
[A10]
[H]
[q]
-1
H
2
0,06
0
H
3
0,04
0
H
4
0,03
0
H
5
0,03
0
H
6
0,04
0
0
-1
[N] = Matriz Diagonal. Dimensión (7 x 7). Con el valor 2 en la diagonal ya que se utiliza la
ecuación de Darcy- Weisbach como la ecuación de fricción.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
27
Laura Natalia Cotes Gómez
2
0
0
0
0
0
0
0
2
0
0
0
0
0
0
0
2
0
0
0
0
0
0
0
2
0
0
0
0
0
0
0
2
0
0
0
0
0
0
0
2
0
0
0
0
0
0
0
2
[I] = Matriz Identidad. Dimensión (7 x 7).
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
28
Laura Natalia Cotes Gómez
Primera iteración
Las matrices anteriormente definidas son válidas para todas las iteraciones necesarias en el cálculo
de la red. Las expuestas a continuación varían de iteración en iteración.
[A11] = Matriz diagonal de dimensiones (7 x 7).
Con el valor
en la diagonal. Los coeficientes β y γ son ceros al no existir bombas
en la red. La siguiente tabla resume el cálculo de los coeficientes α:
Tubería
No.
Q (m3/s)
f
v (m/s)
h
f
(m)
h
f
+ h
m
(m)
α
1 2
0,10
0,0159
2,037
6,73
6,73
672,65
2 3
0,10
0,0166
5,659
72,25
88,57
8857,01
3 4
0,10
0,0178
12,732
294,15
294,15
29415,0
4 5
0,10
0,0166
5,659
72,25
72,25
7224,89
2 5
0,10
0,0178
12,732
294,15
294,15
29415,0
5 6
0,10
0,0161
3,183
24,94
24,94
2494,29
1 6
0,10
0,0159
2,037
4,04
4,04
403,59
Tabla 2. Cálculo de coeficientes α.
Por la tanto:
Matriz [A11]:
67,265
0,000
0,000
0,000
0,000
0,000
0,000
0,000
885,701
0,000
0,000
0,000
0,000
0,000
0,000
0,000
2941,50
0,000
0,000
0,000
0,000
0,000
0,000
0,000
722,489
0,000
0,000
0,000
0,000
0,000
0,000
0,000
2941,50
0,000
0,000
0,000
0,000
0,000
0,000
0,000
249,429
0,000
0,000
0,000
0,000
0,000
0,000
0,000
40,359
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
29
Laura Natalia Cotes Gómez
[A11]' = Matriz diagonal de dimensiones (7 x 7). Con el valor
en la diagonal. Para esta
red la matriz [A11'] resulta ser igual a la matriz [A11].
67,265
0,000
0,000
0,000
0,000
0,000
0,000
0,000
885,701
0,000
0,000
0,000
0,000
0,000
0,000
0,000
2941,50
0,000
0,000
0,000
0,000
0,000
0,000
0,000
722,489
0,000
0,000
0,000
0,000
0,000
0,000
0,000
2941,50
0,000
0,000
0,000
0,000
0,000
0,000
0,000
249,429
0,000
0,000
0,000
0,000
0,000
0,000
0,000
40,359
Cálculo de H
i+1
[
] {[ ] [ ][ ]
[ ]}
{[ ] [ ][ ]
[ ][
] [ ][
] [ ][
] [ ] }
Resolviendo las operaciones entre las matrices, se obtiene el siguiente resultado
Nodo
Altura (m)
H
2
91,36
H
3
170,04
H
4
=
78,39
H
5
99,23
H
6
97,11

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
30
Laura Natalia Cotes Gómez
Cálculo de Q
i+1
[
] {[ ] [ ][ ] [ ]} [
] { [ ][ ]
[ ][
] [ ][
] }
Resolviendo las operaciones entre las matrices, se obtiene el siguiente resultado:
Tubería No.
Caudal (m³/s)
1 2
0,1142
1 6
0,0056
2 3
0,0344
3 4
=
0,0644
4 5
0,0487
2 5
0,0458
5 6
0,0858
De esta manera se realizan las iteraciones hasta conseguir la similitud de las respuestas en dos
iteraciones continuas.
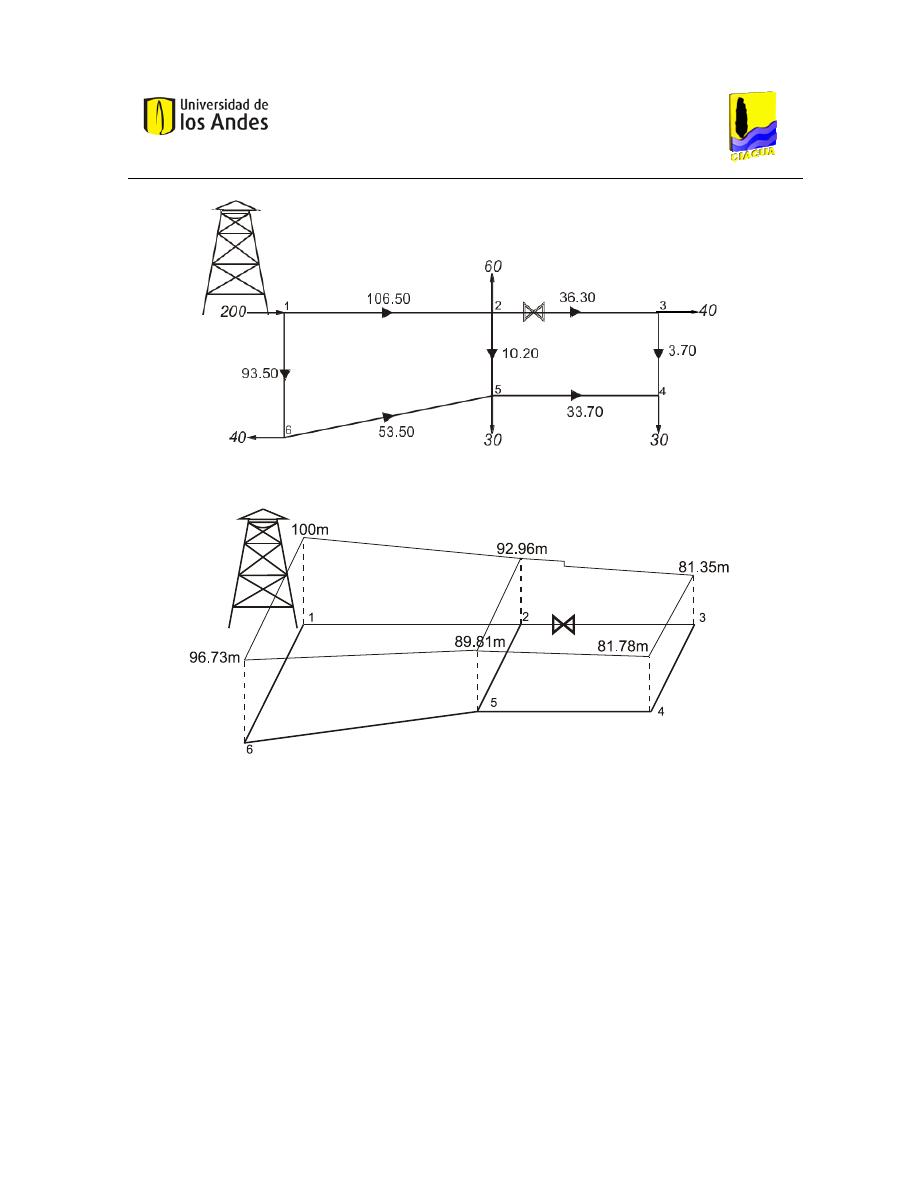
Luego de la quinta iteración. Se obtuvieron los siguientes resultados:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
31
Laura Natalia Cotes Gómez
Nodo
Altura (m)
H
2
92,37
H
3
80,71
H
4
=
81,11
H
5
89,32
H
6
96,47
Tubería No.
Caudal (m³/s)
1 2
0,1065
1 6
0,0363
2 3
0,0037
3 4
=
0,0337
4 5
0,0102
2 5
0,0535
5 6
0,0935
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
32
Laura Natalia Cotes Gómez
Ilustración 7. Resultado de caudales.
Ilustración 8. Resultado de alturas piezométricas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
33
Laura Natalia Cotes Gómez
3.2.
Modelación de calidad del agua
La modelación de la calidad del agua está basada en la variación temporal y espacial de un
parámetro de calidad del agua; existen dos modelos de cálculo: los estáticos y los dinámicos. En los
modelos estáticos se supone que los caudales demandados e inyectados a la red permanecen
constantes, y no varían las condiciones de operación de la red, definidas por el estado de las
válvulas o bombas presentes. Por otra parte, los modelos dinámicos permiten la variación temporal
en los caudales demandados e inyectados así como las condiciones de operación de la red.
3.2.1. Modelos estáticos
Estos modelos se aplican al estudio del transporte de contaminantes conservativos en las redes de
distribución de agua potable determinando sus rutas de procedencia y tiempos de permanencia en
las mismas condiciones estáticas de operación. Los planteamientos básicos para la resolución de
estos modelos son la conservación de masa en los nudos, la concentración de mezclas y los tiempos
de permanencia (Vidal, Martínez, & Ayza, 1994).
La conservación de masa para cada nudo de la red se describe con la ecuación de continuidad, en
donde se define el porcentaje de la demanda en un nudo j procedente de la fuente i como C(i,j) y
se puede expresar de la siguiente manera:
Ilustración 9. Esquema de conservación de masa en el nudo j. Fuente: (Vidal, Martínez, & Ayza, 1994).
𝒍
𝟏
𝒍
𝟐

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
34
Laura Natalia Cotes Gómez
∑
∑
Ecuación 27- Ecuación de continuidad para modelación de calidad del agua. Fuente: (Vidal, Martínez, & Ayza,
1994).
donde,
, es el conjunto de nudos adyacentes al nudo j desde los que fluye caudal.
, son los factores de contribución de la fuente i en los nudos .
, es el caudal que fluye del nudo k al j.
, es el caudal que alimenta directamente al nudo j desde la fuente i.
, es el caudal total que abandona el nudo j.
, son los nudos alimentados por el nudo j.
La concentración de mezclas se trata de determinar las concentraciones de determinadas sustancias
en cada uno de los nudos de la red, considerando la mezcla de aguas procedentes de fuentes de
distinta calidad. Por lo tanto, la concentración de un cierto contaminante no reactivo en el nudo j
suponiendo mezcla completa, se describe de la siguiente manera:
∑
(
) ∑ (
)
∑
(
) ∑ (
)
Ecuación 28- Concentración en el nudo j. Fuente: (Vidal, Martínez, & Ayza, 1994).
donde:
, es la concentración de la sustancia en los nudos aguas arriba adyacentes al j.
, es la concentración de dicha sustancia de la fuente i que alimenta el nudo j.
Finalmente, el tiempo de permanencia es uno de los planteamientos más importantes debido a que
el caudal desde el punto de alimentación hasta el nudo determinado puede seguir distintas rutas y el
tiempo de permanencia del agua en la red desde que se inyecta en i hasta que llega al nudo j puede
ser muy variable. Se define el tiempo de permanencia medio para un nudo j como:
∑
∑
Ecuación 29- Tiempo de permanencia medio para el nudo j. Fuente: (Vidal, Martínez, & Ayza, 1994).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
35
Laura Natalia Cotes Gómez
donde,
, es el caudal que llega al nudo en estudio por el camino i.
, es la edad del agua en el punto de alimentación.
3.2.2. Modelos dinámicos
Estos modelos consideran el movimiento y reacción de los contaminantes bajo condiciones
variables en el tiempo, como sucede en la realidad con las demandas, en cambios de nivel en los
depósitos, cierre y apertura de válvulas, arranque y detención de bombas, etc. En los modelos
dinámicos están implicados tres procesos: el transporte por convección en las tuberías, el
decaimiento o crecimiento de las concentraciones en el tiempo por reacción, y los procesos de
mezcla en los nudos de la red (Vidal, Martínez, & Ayza, 1994).
El trasporte de las sustancias por las tuberías está causado principalmente por el flujo del agua bajo
la acción del gradiente de presiones; es importante tener en cuenta que el transporte es diferente
para sustancias conservativas y no conservativas.
-
Sustancias conservativas: se caracterizan por que su concentración no cambia en el tiempo
debido a reacciones biológicas o químicas. Para estas sustancias, el proceso de transporte a
lo largo de una línea i esta descrito por la siguiente ecuación:
Ecuación 30- Transporte se sustancias conservativas. Fuente: (Vidal, Martínez, & Ayza, 1994).
donde,
, es la concentración de la sustancia en la sección de cálculo x y el instante t.
, es la velocidad media del agua en la línea, la cual puede ser variable en el tiempo si
cambian las condiciones hidráulicas.
-
Sustancias no conservativas: estas sustancias pueden tener reacciones químicas o biológicas
a lo largo del tiempo mientras recorren las tuberías, modificando así su concentración. Para
este caso, la ecuación de transporte debe incluir el término de reacción:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
36
Laura Natalia Cotes Gómez
( )
Ecuación 31- Transporte de sustancias no conservativas. Fuente: (Vidal, Martínez, & Ayza, 1994).
Para resolver esta última ecuación, se debe dividir cada línea de corriente en segmentos, dentro de
los cuales se producen las reacciones, mientras que las mezclas tienen lugar en los nudos.
3.2.3. Ejemplo de aplicación de modelación de la calidad del agua
El siguiente ejemplo fue realizado por elaboración propia.
En un tramo de tubería que tiene 20 m de longitud, se agrega, al comienzo del mismo 0,5 mg/L de
cloro. Calcular la concentración del cloro al final del tramo después de 15 segundos, teniendo en
cuenta que la tubería tiene un diámetro de 300 mm y por ella fluye un caudal de 0,212 m³/s, además
el término de reacción del cloro es 0,05/s.
Como el cloro es una sustancia no conservativa es necesario hacer uso de la Ecuación 31. En primer
lugar se va a calcular la velocidad haciendo uso de la ecuación de continuidad:
(
)
Ahora reemplazando en la Ecuación 31, se tiene lo siguiente:
(
)
(
(
)
) (
)
Despejando el valor correspondiente a c, se tiene que:
Como resultado, se obtiene que después de 15 segundos al final del tramo de tubería, la
concentración del cloro es de 0,406 mg/L.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
37
Laura Natalia Cotes Gómez
3.3.
Relación entre la modelación hidráulica y de calidad del agua
Los modelos hidráulicos y de calidad del agua se han desarrollado y utilizado durante décadas para
los sistemas de distribución de agua potable. Estos modelos han demostrado ser herramientas de
gran alcance para ganar una comprensión sistemática de las condiciones del sistema. En particular,
los modelos de calidad del agua se han convertido en una práctica cada vez más importante. Los
modelos no sólo son una alternativa prometedora para la predicción de concentraciones residuales
de desinfectantes en una forma rentable, sino también es un medio de proporcionar una enorme
comprensión de ingeniería en la dinámica de la variación de la calidad del agua y el sofisticado
proceso de reacciones constituyentes que ocurren en los sistemas de distribución de agua (Yi Wu &
Elsayed, 2013) .
Para obtener resultados completos en cuanto a la calidad del agua, se requiere que la modelación
hidráulica y la modelación de la calidad del agua estén relacionadas. Esto se debe a que existen
algunos fenómenos que son calculados en la modelación hidráulica, que influyen de manera
significativa en la calidad del agua. En las simulaciones realizadas por Yi Wu y Elsayed, se
utilizaron modelos de redes de distribución con gran cantidad de tuberías, las cuales tenían bombas
y válvulas. Este tipo de accesorios generan pérdidas menores, las cuales son calculadas por la
modelación hidráulica, y que pueden influir de alguna manera en la modelación de la calidad del
agua. A partir de lo anterior, se realizó una paralelización entre los dos tipos de modelación; los
modelos de calidad del agua toman lo datos de la modelación hidráulica, los cuales son guardados
en una matriz de memoria dinámica, que permite el acceso directo y eficiente para el cálculo la
calidad del agua. Aplicando este método, se obtuvieron resultados en un menor tiempo, mejorando
el análisis de los sistemas de distribución de agua y teniendo en cuenta los fenómenos hidráulicos y
de calidad de agua que se presentan en las redes.
3.4.
Difusión
Entre los años 1828 y 1833, Graham descubrió la difusión por medio de experimentos realizados en
líquidos y gases (Mompremier, 2009). El investigador, demostró que el flujo de difusión de un gas a
través de un tapón poroso es inversamente proporcional a la raíz cuadrada de las densidades de los
gases empleados.
Tiempo después, el fisiólogo alemán Adolf Eugen Fick, quien participaba activamente en el círculo
científico de la época y buscada relacionar las matemáticas con la medicina, comenzó sus estudios
sobre la difusión en 1855 basado en los estudios realizados previamente por Graham. Se planteó
que existe una relación lineal entre el flujo de difusión y la diferencia de concentraciones que
produce dicho flujo (Mompremier, 2009).
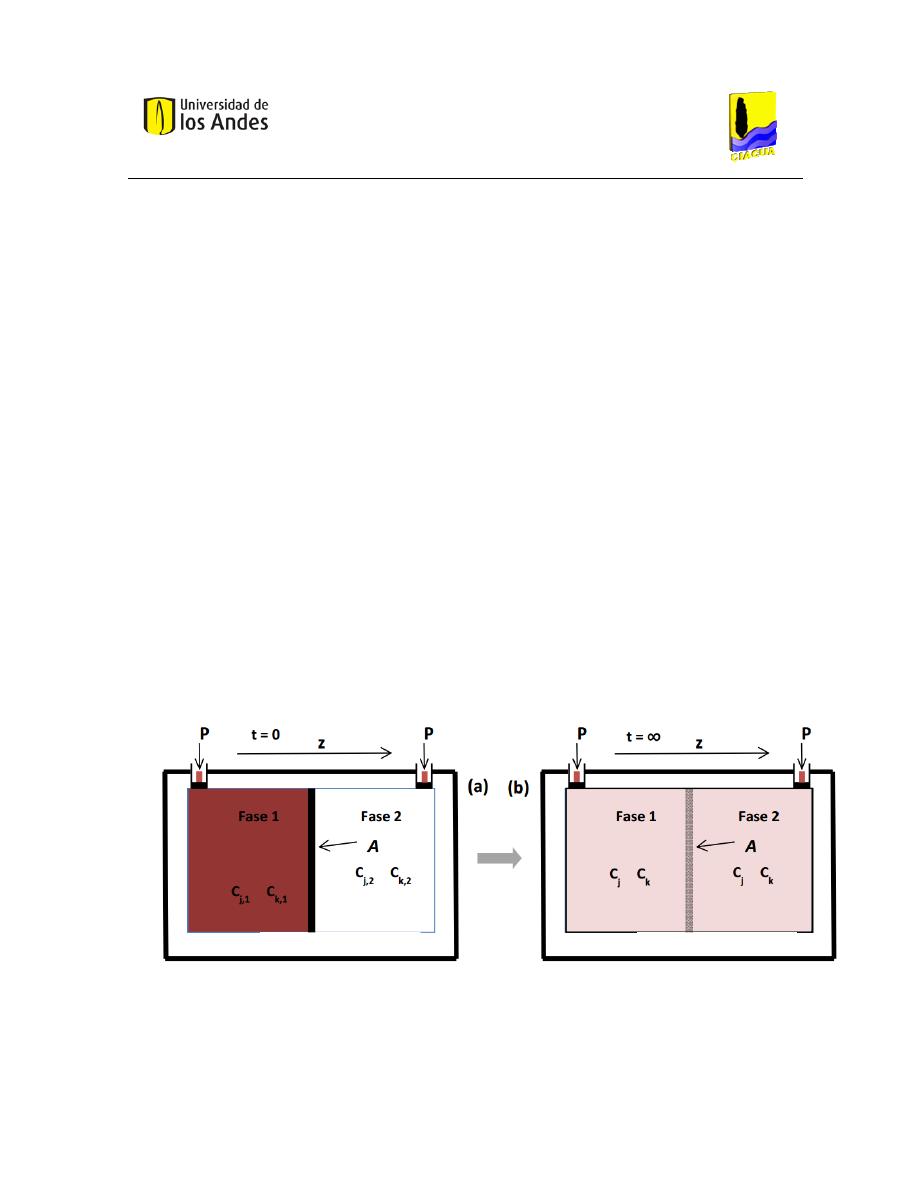
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
38
Laura Natalia Cotes Gómez
3.4.1. Definición
La difusión es el proceso por el cual una substancia se distribuye en el espacio que la encierra o en
el medio en que se encuentra. Por ejemplo, si se conectan dos tanques conteniendo el mismo gas a
diferentes presiones, en corto tiempo la presión es igual en ambos tanques. Esto demuestra, que la
difusión es consecuencia del movimiento continuo y elástico de las moléculas. (Biblioteca Digital
de la Universidad de Chile, 2005)
La difusión de solutos en líquidos es muy importante en muchos procesos industriales , en especial
en las operaciones de separación, como extracción líquido-líquido o extracción con disolventes. Así
mismo, la difusión es muy frecuente en la naturaleza, como la difusión se sales en la sangre.
La velocidad de difusión molecular en los líquidos es mucho menor que en los gases. Esto se debe a
que las moléculas de un líquido están muy cercanas entre sí en comparación con las de un gas. Por
lo tanto las moléculas de un soluto A que se difunden, chocarán contra las moléculas de un líquido
B con más frecuencia y se difundirán con mayor lentitud que en los gases (Universidad de Valencia,
2006).
Por lo anterior, el coeficiente de difusión de un gas es de un orden de magnitud 100 veces mayor
que en un líquido.
El proceso de difusión se puede observar en la siguiente imagen:
Ilustración 10. Proceso de difusión. Fuente: (Universidad de Valencia, 2006).
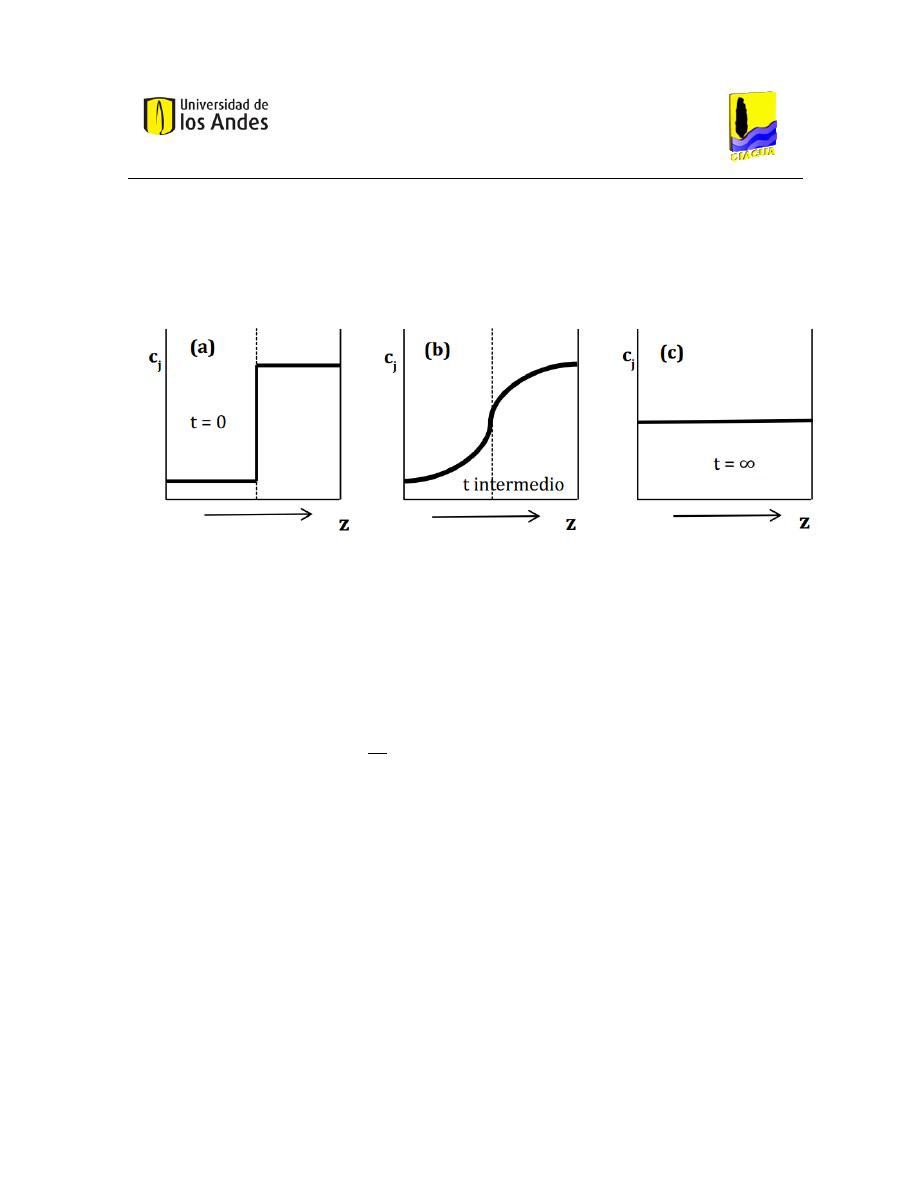
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
39
Laura Natalia Cotes Gómez
Así mismo, se puede describir gráficamente este proceso:
Ilustración 11. Proceso de difusión gráficamente. Fuente: (Universidad de Valencia, 2006).
3.4.2. Ecuación de la difusión
La ecuación de difusión describe las fluctuaciones de densidad de un material que se difunde.
También es usada para describir procesos exhibiendo un comportamiento de difusión. La ecuación
general es la siguiente:
( ⃗ ⃗ )
Ecuación 32- Ecuación general de la difusión. Fuente: (Mompremier, 2009).
donde,
, es la densidad del material que se difunde.
t, es el tiempo de difusión.
D, es el coeficiente de difusión colectivo.
⃗, es la coordenada espacial.
, es el vector operador diferencial nabla.
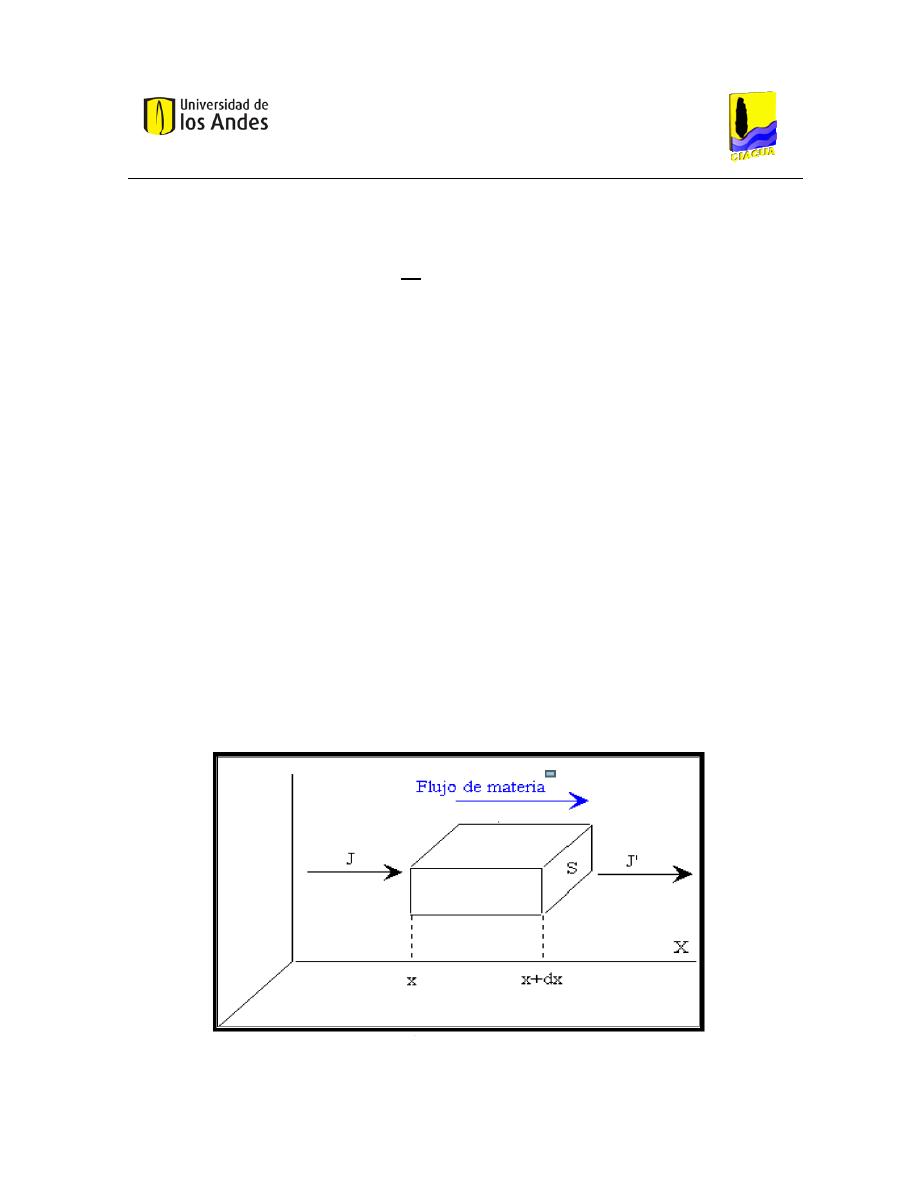
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
40
Laura Natalia Cotes Gómez
Si el coeficiente de difusión depende de la densidad, entonces la ecuación no es lineal. Si D es
constante, entonces la ecuación se reduce a:
⃗
Ecuación 33- Ecuación de difusión cuando el coeficiente de difusión es constante. Fuente: (Mompremier, 2009).
Cuando D es una matriz simétrica definida y positiva, la ecuación describe una difusión anisótropa.
3.4.3. Ley de Fick
La ley de Fick es una ley cuantitativa en forma de ecuación diferencial que describe diversos casos
de difusión de materia o energía en un medio en que inicialmente no existe equilibrio químico o
térmico. En situaciones en las que existe gradiente de concentración de una sustancia, o de
temperatura, se produce un flujo de partículas o de calor que tiende a homogenizar la disolución y
uniformizar la concentración o la temperatura. Esto es consecuencia del movimiento azaroso de las
partículas. Es importante mencionar, que para que se lleve a cabo el proceso de difusión, debe haber
un gradiente de concentración entre los fluidos que se estén analizando; las moléculas siempre se
van a mover de una zona de mayor concentración a una con menor, para después llegar a un
equilibrio.
Si se supone que la concentración de algún fluido, varía con la posición a lo largo del eje X, se
puede tener el siguiente esquema del flujo de materia:
Ilustración 12. Flujo de materia. Fuente: (Mompremier, 2009).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
41
Laura Natalia Cotes Gómez
Sea J la densidad de corriente de partículas, es decir, el número efectivo de partículas que atraviesan
en la unidad de tiempo un área unitaria perpendicular a la dirección en la que tiene lugar la difusión
(Mompremier, 2009). La ley de Fick afirma que la densidad de corriente de partículas es
proporcional al gradiente de concentración.
Ecuación 34- Ecuación de Fick. Fuente: (Mompremier, 2009).
La constante de proporcionalidad se denomina coeficiente de difusión D y es característico tanto del
soluto como del medio en el que se disuelve.
La acumulación de partículas en la unidad de tiempo que se produce en el elemento de volumen
S(dx) es igual a la diferencia entre el flujo entrante JS, menos el flujo saliente J’S.
La acumulación de partículas en la unidad de tiempo es:
Igualando estas expresiones y utilizando la ley de Fick, se obtiene lo siguiente:
(
)
Esta ecuación diferencial en derivadas parciales, describe el fenómeno de la difusión. Por otro lado,
so el coeficiente de difusión D no depende de la concentración, se tiene la siguiente ecuación:
Ecuación 35- Fenómeno de difusión. Fuente: (Mompremier, 2009).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
42
Laura Natalia Cotes Gómez
3.4.4. Tipos de difusión
En la naturaleza existen varios procesos de difusión, en donde existen factores determinantes que
permiten que se puedan clasificar en los siguientes tipos de difusión.
3.4.4.1.
Difusión por reacción
Toda sustancia contenida en el agua puede entrar en reacción con otras sustancias, con las paredes
del tubo, con la propia agua o con microorganismos que allí se encuentren y como resultado se
pueden tener variaciones de concentración debido a diferentes procesos químicos o bioquímicos que
se pueden llevar a cabo. Según la forma de reacción, las sustancias en el agua se pueden dividir en
tres grupos:
-
Conservativas: no reaccionan con el agua ni con las paredes de los tubos.
-
No conservativas y decrecientes: su concentración decrece con el tiempo de permanencia
en el agua. Dentro de este grupo se encuentra el cloro utilizado como desinfectante.
-
No conservativas y crecientes: son compuestos químicos que se forman en el agua y su
concentración crece con el tiempo de permanencia en el agua. Dentro de esta clasificación,
se encuentran los trihalometanos, los cuales se forman debido al contacto entre el cloro y la
materia orgánica.
3.4.4.2.
Difusión convectiva
También es conocida como difusión por advección; considera los cambios de concentración
generados por la velocidad del flujo. La agitación no es un proceso molecular, pero es un proceso
microscópico que cambia porciones de fluidos sobre distancias largas, tal como lo muestra la
siguiente figura.
Ilustración 13. Difusión convectiva. Fuente: (Mompremier, 2009).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
43
Laura Natalia Cotes Gómez
3.4.4.3.
Difusión molecular
La difusión molecular es la mezcla de químicos disueltos debido al movimiento aleatorio de las
moléculas dentro del fluido. Esta difusión es causada por el movimiento molecular vibratorio,
rotacional y transversal de las partículas. En el movimiento de sustancias disueltas se mueven de
regiones de altas concentraciones, a regiones de bajas concentraciones. La ecuación de Fick
presentada anteriormente, es la que describe este tipo de procesos.
3.4.4.4.
Difusión turbulenta
La difusión turbulenta es la mezcla de sustancias finas debido a la turbulencia en pequeña escala
causada por el rozamiento dentro del cuerpo del agua.
Ilustración 14. Difusión turbulenta. Fuente: (Mompremier, 2009).
3.4.5. Concentración
El cálculo de la difusión en fluidos heterogéneos se hace con base en la ecuación de conservación
de masa, que debe verificar cada componente o especie. Para la mezcla entre dos componentes
diferentes (A y B), se entiende por concentración a la cantidad relativa de una sustancia en un cierto
punto y en un tiempo dado. Se puede expresar en unidades de masa, peso, volumen, número de
partículas por unidad de volumen (Mompremier, 2009). De esta manera, la concentración de
determinada sustancia se puede calcular de la siguiente manera:
Ecuación 36- Concentración a partir de la conservación de masa. Fuente: (Mompremier, 2009).
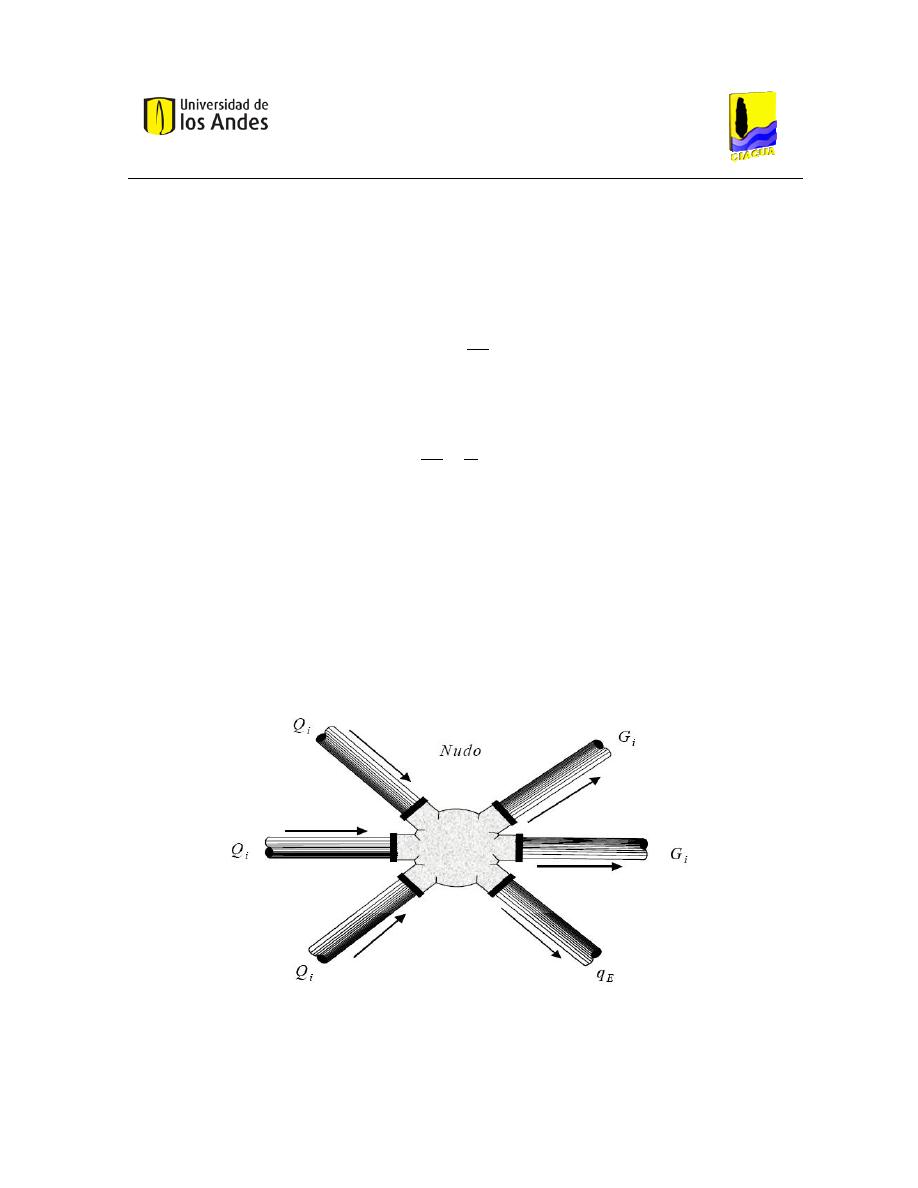
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
44
Laura Natalia Cotes Gómez
Además, se tiene que cumplir que:
En el caso en que una de las sustancias tenga una masa mucho menor que la otra (en este caso se va
a tomar la sustancia B como despreciable) se tiene el siguiente planteamiento:
Si se realiza un arreglo de términos, para obtener la concentración en términos de la densidad de la
sustancia se tiene lo siguiente:
3.4.5.1.
Balance de masa en la unión de varias tuberías.
Dentro de las tuberías que se juntan en un nudo existen dos tipos de estas; el primero está
conformado por las tuberías que tienen un caudal de entrada al nudo y, el segundo son las tuberías
por las que sale el caudal proveniente de la unión. Esto se esquematiza de la siguiente manera:
Ilustración 15. Esquema de balance de masa en la unión de tuberías. Fuente: (Mompremier, 2009).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
45
Laura Natalia Cotes Gómez
Se considera que el aporte de masa de cada una de las tuberías del primer grupo a una unión en
particular se define como:
∑
Ecuación 37- Aporte de masa a la unión i. Fuente: (Mompremier, 2009).
donde,
, es el caudal de entrada al nudo i desde una tubería de entrada.
N, es el número de tuberías de entrada.
, es la concentración de algún componente en las tuberías de entrada.
Así mismo, por las tuberías de salida, egresará desde el nudo, un fluido que contiene una mezcla
uniforme de concentración
, por lo que la masa que sale se describe como:
(∑
)
Ecuación 38- Masa de salida del nudo i. Fuente: (Mompremier, 2009).
donde,
, es el caudal de salida por cada tubería de salida.
M, es el número de tuberías de salida.
, es el caudal de concesión que se les suministra a los usuarios de la red.
Por lo tanto, debido al concepto de conservación de masa, lo que entra es igual a lo que sale,
entonces:
Si se reemplazan las correspondientes ecuaciones, se puede despejar la concentración de la mezcla,
la cual sería completa y uniforme, de la siguiente manera:
∑
∑
Ecuación 39- Concentración de la mezcla. Fuente: (Mompremier, 2009).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
46
Laura Natalia Cotes Gómez
4.
Diseño y construcción del modelo
Para poder comenzar con el proceso de diseño primero se identificó, en el Laboratorio de Hidráulica
de la Universidad de los Andes, el espacio disponible para el modelo. Para esto se tuvo en cuenta
que cualquiera de las tuberías del modelo, no interfirieran con otros modelos ni con los espacios
libres para trasladarse y así evitar el riesgo de que ocurra algún accidente con las personas o con el
mismo modelo. Luego se tomaron las medidas pertinentes para poder realizar los diseños
preliminares en AutoCAD (Ver Anexos 1 y 2).
4.1.
Alimentación del modelo
En primera instancia, se concretó la utilización de tanques de almacenamiento del agua que va a ser
usada en el modelo. Como recurso existente, se tomó el canal que hace parte del Modelo 8, el cual
ya estaba construido, pero no se encontraba en uso y se modificó para que sirviera como tanques
para el actual proyecto. En dicho canal existe una compuerta, la cual sirvió para dividir los dos
tanques de alimentación. Además, se compró una lámina de madera de 20 mm de espesor con las
dimensiones transversales del canal, para poder sellar la salida del mismo y tener un
almacenamiento adecuado del agua. Como resultado, las dimensiones de cada tanque son: 1,25 m.
de largo, 0,39 m. de ancho y 0,59 m. de alto. Esto corresponde a un almacenamiento máximo en
cada tanque de 287 litros, pero como factor de seguridad se va a llenar cada uno de los tanques a
una altura de 0,52 m., lo que proporciona un almacenamiento de 254 litros. Finalmente, se
realizaron modificaciones a los tanques, como retirar los piezómetros que tenía anteriormente y
sellar los agujeros.
Por otro lado, se diseñó la alimentación de dichos tanques (ver Anexo 3). Para esto, se identificó el
punto más cercano de abastecimiento de agua potable. A partir de éste, se extendió la tubería
existente con una de PVC con diámetro de 1 ½ pulgadas, la cual se colocó por el piso, teniendo
cuidado con que no interfiriera con el paso de las personas ni con otro modelo. Para la distribución
del agua hacia los dos tanques, se dividió la tubería, y se utilizaron válvulas de bola, esto con el fin
de independizar el llenado de los tanques.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
47
Laura Natalia Cotes Gómez
Ilustración 16. Fuente de agua potable.
Ilustración 17. Extensión de tubería de agua potable.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
48
Laura Natalia Cotes Gómez
Ilustración 18. División de tuberías de alimentación.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
49
Laura Natalia Cotes Gómez
Ilustración 19. Tuberías de alimentación en tanques.
4.2.
Plataforma
En el lugar donde se ubicó el modelo se encuentra una serie de vertederos, por lo tanto la
colocación de las tuberías era difícil. Por este motivo, se diseñó una plataforma en madera de pino,
la cual cubriera todos los vertederos para permitir que las pruebas que se realicen en el modelo, se
hagan de una manera más cómoda y también, para que el modelo en conjunto, se viera mucho
mejor desde el punto de vista estético. Para el diseño de la plataforma se tuvo en cuenta la altura de
un perfil que se encontraba para sostener los limnímetros que miden la altura del agua de los
vertederos que se encuentran allí. De acuerdo con lo anterior, las dimensiones de la plataforma
fueron: 2,15 m. de ancho; 1,62 m. de largo y 5 cm. de altura. Para la construcción de la plataforma
se tomaron 5 listones de madera de 2 cm. de altura, 10 cm. de ancho y 1,52 m. de largo; y se
colocaron encima de las divisiones que ya se encontraban. La longitud se dividió en dos tramos, uno
de 1,14 m. y otro de 0,38 m. Uno de los tramos se ubicó antes del perfil, y el otro se colocó después
del perfil.
Luego, se ubicaron 8 listones de madera, perpendicularmente a los que se colocaron previamente.
Estos listones tenían 3 cm. de altura, 19 cm. de ancho y 2,15 m. de largo. Se unieron los listones con
tornillos distanciados 5 cm (ver Anexo 4). De esta manera, la plataforma se veía así:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
50
Laura Natalia Cotes Gómez
Ilustración 20 a. Plataforma preliminar.
Ilustración 20 b. Plataforma preliminar.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
51
Laura Natalia Cotes Gómez
Ilustración 20 c. Plataforma preliminar.
Por cuestiones estéticas, se decidió cambiar el perfil metálico por uno de pino. Para esto se utilizó
un listón de 3 cm. de altura, 12 cm. de ancho y 2,15 m. de largo y se realizaron unas ranuras
longitudinales para que pudieran soportar los limnímetros. Así mismo, se abrieron agujeros al listón
en donde quedaban las agujas del limnímetro, para que se pudieran realizar las mediciones
necesarias en las prácticas de Mecánica de Fluidos. Con estas modificaciones la plataforma se veía
así:
Ilustración 21. Plataforma terminada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
52
Laura Natalia Cotes Gómez
4.3.
Modelo
Por otro lado, se abrieron los agujeros correspondientes a las salidas de los tanques de
almacenamiento, en donde van ubicadas las tuberías de entrada al modelo. Se definió que estas
tuberías tendrían un diámetro de 1 pulgada, esto quiere decir 24 mm. de diámetro; sin embargo, las
tuberías comerciales de PVC de este tamaño, tienen un diámetro externo de 33 mm., por lo tanto la
unión que se utilizó tiene un diámetro interno de 33,8 mm. A partir de esta dimensión, se mandaron
a fabricar las tuberías de vidrio las cuales incluían la intersección de las tuberías con un ángulo de
90°. Por lo tanto, el diámetro externo de las tuberías de vidrio es de 34 mm.; por cuestiones de
seguridad, el espesor es de 2 mm.; de esta manera, el diámetro interno es de 30 mm. Además, las
tuberías de vidrio tienen una longitud, cada una, de 40 cm. antes y después de la intersección (ver
Anexo 5). Como se puede ver, el diámetro externo de la tubería de vidrio, es mayor al diámetro
interno de la unión de PVC, por lo tanto, en el Laboratorio de Mecánica, se pulió el interior de la
unión para permitir que la tubería de vidrio pueda entrar adecuadamente. Cuando se realizó el
ensamblaje de las tuberías de vidrio con las de PVC se rodeó la tubería de vidrio con caucho para
generar mayor ajuste entre la unión de PVC y la tubería de vidrio; luego se rellenó el espacio
sobrante con silicona fría. De esta manera se puede garantizar que no existan fugas en las uniones.
Simultáneamente a lo anterior, se ensamblaron las válvulas en las tuberías de entrada. Estas
válvulas están hechas de cobre y son tipo cortina; se escogió esta clase de válvula por su facilidad
de uso. Para colocar las válvulas, se utilizaron uniones de rosca en un extremo y lisas por el otro.
Para asegurar impermeabilidad entre la unión y la válvula, se forró la rosca de la válvula con teflón,
para cubrir cualquier ranura que se genere a la hora de unir el dispositivo. Es importante mencionar
que las válvulas no están pegadas; únicamente están roscadas. Es por esto que se utilizó una prensa
para asegurar que hayan quedado bien ajustadas. En el extremo liso de la unión, se utilizó soldadura
de PVC y se colocó en el extremo de la tubería de entrada. Del mismo modo se realizó el proceso
para colocar la tubería de salida de la válvula.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
53
Laura Natalia Cotes Gómez
Ilustración 22. Válvulas de entrada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
54
Laura Natalia Cotes Gómez
Se identificó, que las tuberías del modelo, debían ir elevadas con respecto a la plataforma una
distancia de 5,5 cm. Esta dimensión corresponde al radio de la brida del caudalímetro que se
colocará posteriormente. Esta elevación, implica el sostenimiento de todo el modelo debido a la
deflexión que se puede generar en las tuberías de PVC y el riesgo de que las tuberías de vidrio se
facturen, a causa del peso de las tuberías y del agua a través de ellas. Se pueden generar deflexiones
excesivas que pueden dañar la tubería, y por ende el modelo. Es por esto, que se determinó la
utilización de soportes; en primer lugar se eligieron soportes de metal para que pudieran soportar el
peso de las tuberías y los caudalímetros; sin embargo, en la definición inicial del modelo, se
determinó que éste debería ser estéticamente perfecto. Se cambiaron los soportes, por una canaleta
hecha en pino, para que combinara con el material de la plataforma; la longitud de este nuevo
soporte, es equivalente a la longitud de las tuberías de PVC que se encuentran sobre la plataforma.
Esta canaleta se mandó a fabricar con las medidas correspondientes a la elevación y al diámetro
externo de las tuberías de PVC. Así mismo, los soportes para las tuberías de vidrio, se realizaron en
acrílico, pero estos tienen una longitud de 10 cm y van ubicados en la mitad de cada tubería de
vidrio. Se decidió utilizar acrílico para no afectar la transparencia del vidrio, y así poder apreciar de
una manera más adecuada, el proceso de mezcla que se lleva a cabo en la unión.
Ilustración 23. Vista en planta del modelo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
55
Laura Natalia Cotes Gómez
Por otro lado, también se colocaron válvulas en las tuberías de PVC de salida del modelo. Estas
válvulas son del mismo tipo de las que se colocaron en las tuberías de entrada. Estos dispositivos, se
van a utilizar en proyectos futuros para generar pérdidas menores en la salida y poder realizar un
análisis de su influencia en los procesos de mezcla en la unión.
Ilustración 24. Válvulas de salida.
Por último, se determinó que debían existir tanques para almacenar el agua que sale del modelo,
para que en futuros proyectos, se puedan tomar muestras de trazadores químicos y así poder realizar
un análisis cuantitativo de los procesos de mezcla. Estos tanques se compraron en Ajover con las
dimensiones adecuadas para que se pudieran ubicar en el canal que se encuentra actualmente. Para
esto de determinó que la altura máxima de los tanques debía ser de 1 metro ya que arriba del canal
se encuentra una plataforma. Así mismo, el diámetro máximo de los tanques debía ser de 80 cm.
Para estas restricciones se encontró el siguiente tanque:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
56
Laura Natalia Cotes Gómez
en donde las dimensiones correspondientes son:
A: 94,5 cm
B: 57,9 cm
C: 71,8 cm
Con estas dimensiones se cumplen las restricciones de espacio anteriormente descritas y se
consigue una capacidad de 255 litros, lo cual es acorde con la capacidad de los tanques de
almacenamiento de entrada. Además, para evitar que el agua proveniente del modelo se salga
accidentalmente de los tanques, se utilizaron las tapas de los mismos con un agujero en donde se
encuentra la tubería de salida del agua. Es importante mantener aislada el agua del modelo, del agua
del canal ya que, la primera contiene trazadores que contaminan el agua que es reutilizable en el
laboratorio.
Para facilitar el proceso de desagüe de los dos tanques, se colocó una válvula de bola que une los
tanques; entonces, cuando el modelo está en funcionamiento, la válvula está cerrada y cuando la
prueba finaliza, se abre la válvula y en uno de los dos tanques se encuentra un bomba sumergible
que transporta el agua desde el tanque hasta el sifón por una manguera. De esta manera se extrae el
agua de los dos tanques de una manera más eficiente. Pero como se mencionó anteriormente que los
C
A
B
Ilustración 25. Dimensiones del tanque.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
57
Laura Natalia Cotes Gómez
tanques van a estar con sus respectivas tapas, la bomba se va a quedar fija adentro del tanque y se
adecuaron unas tuberías que conectan la bomba con una manguera que se encuentra afuera del
tanque. Estas tuberías se conocen comercialmente como universales y tienen la característica que
pueden desarmarse en cualquier momento. Esto facilita en gran medida el desagüe de los tanques,
ya que por un dispositivo electrónico se enciende y se apaga la bomba.
Ilustración 26. Tanques almacenamiento.
Es importante mencionar, que dentro de la construcción del modelo debe incluirse la instalación de
los caudalímetros, pero para este proyecto no fue posible la implementación de estos dispositivos
debido que estos son instrumentos importados y traerlos a Colombia requiere de un tiempo que
supera el tiempo del semestre académico.
Finalmente, después de tener el modelo totalmente construido, se realizó una prueba para verificar
el diseño. En esta etapa, surgieron pequeños inconvenientes, debido a que se generaron fugas en los
tanques de almacenamiento de entrada y en una de las uniones entre las tuberías de vidrio y PVC.
Para solucionar estas fugas, se identificó el punto exacto del problema, y se cubrió con silicona fría.
De esta manera se solucionaron estas dificultades y se procedió a realizar pruebas preliminares en el
modelo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
58
Laura Natalia Cotes Gómez
5.
Costos del proyecto
A continuación se muestra un análisis detallado de la cantidad y los costos de los materiales que se
utilizaron en el proyecto. Cabe resaltar que los elementos que son de PVC, no tuvieron ningún costo
ya que estos materiales son proporcionados por PAVCO a través del convenio de esta empresa con
el laboratorio en los proyectos de cátedra PAVCO-UNIANDES. Al final se muestra el costo total
que se invirtió en el modelo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
59
Laura Natalia Cotes Gómez
Tabla 3. Costos del proyecto.
ITEM
Unidad
Cantidad
Precio unitario
Total
Tuberías 1 1/2 pulgadas
Un
3
-
$
-
$
Tuberías 1 pulgada
Un
4
-
$
-
$
Tee
Un
1
-
$
-
$
Codos 1 1/2 pulgadas
Un
12
-
$
-
$
Codos 1 pulgada
Un
12
-
$
-
$
Uniones 1 pulgada
Un
4
-
$
-
$
Válvulas de Bola
Un
3
-
$
-
$
Uniones válvulas
Un
8
-
$
-
$
Otras uniones
Un
3
-
$
-
$
SUMA
-
$
Válvulas de cobre
Un
4
26.726,40
$
106.905,60
$
Bridas PVC
Un
6
11.020,00
$
66.120,00
$
Tornillos, Tuercas y Arandelas
Un
24
1.898,92
$
45.574,08
$
SUMA
218.599,68
$
Listones de madera 182 X 2 X 10
Un
5
9.500,00
$
47.500,00
$
Listones de madera 215 X 3 X 19
Un
8
25.300,00
$
202.400,00
$
Listón 5 X 7 X100
Un
4
4.500,00
$
18.000,00
$
Fabricación de canaleta
m
4
60.000,00
$
240.000,00
$
Lámina de madera
Un
1
9.500,00
$
9.500,00
$
Acarreos madera
2
30.000,00
$
60.000,00
$
SUMA
577.400,00
$
Tanques
Un
2
167.040,00
$
334.080,00
$
Acarreo tanques
1
25.000,00
$
25.000,00
$
SUMA
359.080,00
$
Caudalímetros
Un
3
8.261.520,00
$
24.784.560,00
$
SUMA
24.784.560,00
$
Tuberías de vidrio
Un
2
80.000,00
$
160.000,00
$
Trazador (permanganato de potasio)
Un
1
17.000,00
$
17.000,00
$
SUMA
177.000,00
$
26.116.639,68
$
Costo total proyecto
Accesorios PVC
Accesorios
Elementos de madera
Tanques
Sensores
Elementos de Rodaquímicos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
60
Laura Natalia Cotes Gómez
6.
Pruebas y resultados
Para realizar las pruebas cualitativas se utilizó Permanganato de Potasio como trazador. Al ser este,
un químico controlado es necesario llevar una planilla de uso. Para cada prueba se utiliza 10 gramos
de Permanganato de Potasio, el cual va disuelto en uno de los tanques de almacenamiento de
entrada.
Como se mencionó anteriormente, los tanques se llenan a 0,53 metros de altura. Luego se agrega el
trazador a uno de los tanques y luego se abren las válvulas. Para realizar los análisis cualitativos, se
realizaron 7 pruebas, en las cuales se realizó una variación de la apertura de las válvulas de entrada
al modelo. Para poder identificar las diferentes pruebas se utilizó la siguiente nomenclatura:
Válvula 1: Válvula de la tubería de entrada que no tiene trazador.
Válvula 2: Válvula de la tubería de entrada que tiene trazador.
Esta nomenclatura también corresponde a la que se va a usar en las tuberías.
A continuación se muestran las diferentes pruebas.
Prueba 1: Válvula 1 y 2 abiertas al 100%
Teniendo las dos válvulas completamente abiertas se observaron los siguientes resultados:
Ilustración 27. Vista en planta prueba 1.
2
1
3
4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
61
Laura Natalia Cotes Gómez
Ilustración 28.Vista en perfil prueba 1.
Para esta prueba se calculó de una manera aproximada la velocidad de flujo. En primer lugar se
calculó el caudal a partir del conocimiento del volumen de entrada y la duración de la prueba. El
volumen almacenado en cada tanque fue de 0,25 m³ y el tiempo de duración de la prueba fue de 193
segundos; a partir de esto, el caudal es:
Por otra parte, se calculó el área transversal de la tubería:
(
)
Utilizando la ecuación de continuidad se puede calcular la velocidad:
Ecuación 40- Ecuación de continuidad.
A partir de la velocidad se puede calcular el número de Reynolds, usando la viscosidad cinemática
en condiciones de temperatura ambiente (20º)
Este valor indica que el régimen de flujo era turbulento
2
1
3
4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
62
Laura Natalia Cotes Gómez
Prueba 2: Válvula 1 y 2 abiertas al 50%
Ilustración 29. Vista en planta prueba 2.
Ilustración 30. Acercamiento al nodo prueba 2.
2
1
3
4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
63
Laura Natalia Cotes Gómez
Ilustración 31. Vista en perfil prueba 2.
En esta prueba, al disminuir en un 50% la apertura de las dos válvulas, se considera que el caudal
también disminuye un 50%. A partir de esto la velocidad seria de:
Y el número de Reynolds seria:
Este régimen el flujo continuó siendo turbulento, a pesar de la disminución del caudal.
2
1
3
4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
64
Laura Natalia Cotes Gómez
Prueba 3: Válvula 1 abierta al 100% y válvula 2 abierta al 50%
Ilustración 32. Vista en planta prueba 3.
Ilustración 33. Acercamiento al nodo prueba 3.
2
1
3
4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
65
Laura Natalia Cotes Gómez
Ilustración 34. Vista en perfil prueba 3.
Prueba 4: Válvula 1 abierta al 50% y válvula 2 abierta al 100%
Ilustración 35. Vista en planta prueba 4.
2
1
3
4
2
1
3
4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
66
Laura Natalia Cotes Gómez
Prueba 5: Válvula 1 abierta al 100% y válvula 2 cerrada
Esta prueba se realizó como control del modelo.
Ilustración 36. Vista en planta prueba 5.
Ilustración 37.Vista en perfil prueba 5.
2
1
3
4
2
1
3
4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
67
Laura Natalia Cotes Gómez
Prueba 6: Válvula 1 cerrada y válvula 2 abierta al 100%
Esta prueba se realizó como control del modelo.
Ilustración 38. Vista en planta prueba 6.
Ilustración 39. Vista en perfil prueba 6.
2
1
3
4
2
1
3
4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
68
Laura Natalia Cotes Gómez
Prueba 7: Válvula 1 y 2 abiertas al 75%
Ilustración 40. Vista en planta prueba 7.
Ilustración 41. Vista en perfil prueba 7.
2
1
3
4
2
1
3
4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
69
Laura Natalia Cotes Gómez
Además de las anteriores pruebas, donde se tenía fijada una apertura determinada de cada válvula,
se decidió variar la apertura de la válvula 1 con el fin de lograr un equilibrio de las concentraciones
de salida. A pesar de que no se sabe con certeza si se presentó una mezcla completa, se llegó a
observar lo siguiente:
Ilustración 42. Vista en planta mezcla completa.
Ilustración 43. Acercamiento al nodo de mezcla completa.
2
1
3
4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
70
Laura Natalia Cotes Gómez
Ilustración 44. Vista en perfil de mezcla completa.
Esta situación se logró cuando la apertura de la válvula 1 era del 7% y la apertura de la válvula 2 era
el 75%.
Por lo tanto, las velocidades de las respectivas tuberías son:
El número de Reynolds para tubería es:
Se puede ver que en la tubería 1 se presentó un régimen de flujo transicional, esto coincide con la
afirmación realizada por estudios anteriores acerca de la influencia del régimen de flujo en los
procesos de mezcla.
2
1
3
4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
71
Laura Natalia Cotes Gómez
7.
Conclusiones y recomendaciones
Al realizar las pruebas se puede concluir, que efectivamente no se presenta una mezcla completa en
la unión. Cuando los caudales de entrada por las dos tuberías es el mismo, se puede ver que existe el
mismo patrón de mezcla, el cual es que por la tubería de salida 3 se va la mayor parte del trazador; y
por la tubería de salida 4 existe una pequeña mezcla. Esto mismo sucedió cuando las aperturas de
ambas válvulas fueron de 100%, 50% y 75%.
En la prueba en donde la válvula 1 estaba abierta el 50% y la 2 el 100%, se puede ver que existe una
mayor mezcla en la unión; por lo tanto, en la tubería 4 la concentración del trazador es mucho
mayor que en las demás pruebas (sin tener en cuenta los controles).
Por otro lado, cuando la válvula 1 estaba abierta al 100% y la válvula 2 al 50%, se puede ver que la
concentración del trazador en la tubería 4 era muy pequeño en comparación con las demás pruebas
(sin contar los controles); esto quiere decir que, debe existir un punto en donde no se presenta
ningún tipo de mezcla en la unión. Este punto seguramente se presentará cuando la apertura de la
válvula 2 sea mucho más pequeña que la apertura de la válvula 1.
Así mismo, al tener una apertura en la válvula 2 mucho mayor a la válvula 1, se pudo determinar
cualitativamente que existe una mezcla completa y uniforme; sin embargo la diferencia de caudales
es significativa. La válvula 1 estaba abierta, aproximadamente, un 10% de lo que estaba abierta la
válvula 2. Esta situación es muy difícil reproducirla en la realidad debido a que la mayoría de las
tuberías son subterráneas y el manejo de válvulas en cada intersección sería muy complicado.
A partir de los resultados obtenidos en estas pruebas, se puede decir que un factor que influye
significativamente en los procesos de mezcla, es la velocidad en las tuberías de entrada y por ende
el régimen de flujo en las mismas.
Este proyecto permitió corroborar los estudios que se habían hecho, y se puede determinar que estos
procesos de mezcla que se llevan a cabo en las intersecciones de las tuberías, representan un grave
problema de salud pública. Si por una de las tuberías de salida, no existe la concentración adecuada
de cloro para que éste desinfecte el agua que se puede contaminar en las redes, los usuarios pueden
consumir agua contaminada lo que puede generar graves enfermedades. Como solución se propone
la implementación de un sistema de inyección de cloro a lo largo de las redes de abastecimiento de
agua potable.
Como recomendaciones para futuras pruebas que se realicen en el modelo se encuentran las
siguientes:
-
Se deben perfeccionar algunos aspectos en el modelo. En primer lugar se debe nivelar la
plataforma, ya que existe un desnivel que genera que la canaleta de pino, y por ende las

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
72
Laura Natalia Cotes Gómez
tuberías de PVC, queden levantadas, y esta es la causa de que en la unión entre la tubería de
vidrio y de PVC 4, exista una imperfección y por esto se presenta la fuga de agua.
-
Se debe terminar la instalación adecuada de la bomba sumergible para que pueda quedar
fija en el tanque y de esta manera sea más fácil el desagüe de los tanques de salida.
-
Para realizar otras pruebas y que la utilización de las válvulas de entrada al modelo sean
más fáciles de usar y no se desperdicie agua mientras se hace la variación de apertura de las
válvulas, se recomienda implementar un sistema en el agujero de salida de los tanques para
que cuando se finalice una prueba se obstruyan mientras que se cambia la apertura de las
válvulas.
-
Es muy importante la instalación de los caudalímetros. En este documento se realizó una
aproximación del caudal que atraviesa las tuberías; sin embargo para obtener resultados
más exactos y confiables se requiere de un sensor con la precisión de los caudalímetros que
ya se compraron, pero están en proceso de traslado. Una vez instalado el dispositivo, las
pruebas se facilitan mucho y los resultados serían más certeros.
-
Al análisis cualitativo da una buena aproximación de los procesos de mezcla, además que
es muy fácil de ver; sin embargo se quiere llegar a resultados numéricos, los cuales generan
un mayor impacto al análisis ya que se cuantifican las concentraciones de salida. Es por
esto que se deben usar, en un futuro, trazadores químicos. Para esto se recomienda utilizar
sal, ya que es un trazador que se puede medir fácilmente, además es una sustancia no
conservativa, por lo tanto se garantiza que en las tuberías no existe ningún fenómeno de
reacción. De esta manera se puede saber con precisión cuál fue el porcentaje de mezcla en
la intersección.
-
Se recomienda realizar pruebas en donde el régimen del flujo sea laminar para poder
corroborar los resultados de otros experimentos que se mencionaron en la sección de
antecedentes. Esta prueba es más fácil de realizar una vez se hayan instalado los
caudalímetros.
-
Finalmente, se deben ultimar detalles en cuanto al aspecto físico del modelo, como pintar
las válvulas, pulir algunas partes de la plataforma y organizar la zona para que el modelo se
vea bien desde el punto estético y quede uniforme con los demás modelos del laboratorio.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
73
Laura Natalia Cotes Gómez
8.
Agradecimientos
La realización de este proyecto no pudo haber llegado a mejor término sin la guía y asesoría de Juan
Saldarriaga, quien siempre me corrigió y apoyó para llevar a cabo el diseño y la construcción
exitosa del modelo.
También, un especial agradecimiento, por su ayuda incondicional, al técnico del Laboratorio de
Hidráulica Jhon Calvo.
Por último, pero no menos importante, agradezco a mis papás por su apoyo y confianza en mí, a mi
novio: Iván Cárdenas, a mis amigos y a los integrantes del CIACUA quienes fueron de gran ayuda
en alguna de las diferentes etapas de mi proyecto.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
74
Laura Natalia Cotes Gómez
9.
Bibliografía
Agbar Agua. (2003). Cloro residual. Recuperado el 14 de Noviembre de 2012, de Aguagest-
Región de Murcia: http://www.aquagest-regiondemurcia.es/img/contenidos/1/ficha-sobre-
calidad-del-agua.pdf
Biblioteca Digital de la Universidad de Chile. (2005). Ley de disfusión de Graham. Recuperado el
27 de mayo de 2013, de Ciencias químicas y farmaceúticas:
http://mazinger.sisib.uchile.cl/repositorio/ap/ciencias_quimicas_y_farmaceuticas/ap-
quimgral-6/c4.2.html
Clifford, H. K., & Leslie, O. (Septiembre de 2009). Journal AWWA. Recuperado el 27 de mayo de
2013, de Evaluation of solute mixing in Water distribution pipe junctions:
http://www.sandia.gov/EPANET-BAM/download/J_AWWA_2009_101_9_Ho.pdf
Ho, C. K. (2008). Solute Mixing Model for Water-Distribution Pipe Networks. Recuperado el 10 de
Marzo de 2013, de ASCE:
http://gsgc.gzhu.edu.cn/gpsgd/UploadFile/200942623229730.pdf
Ho, C. K., Choi, C. Y., & McKenna, S. A. (2007). Evaluation of complete and incomplete mixing
models in water distribution pipe network simulations. Recuperado el 3 de Junio de 2013,
de World Environmental and Water Resources congress (ASCE):
http://ascelibrary.org.biblioteca.uniandes.edu.co:8080/doi/abs/10.1061/40927%28243%294
86?prevSearch=%28evaluation+of+complete+and+incomplete+mixing+models%29+and+
%5BFulltext%3A+evaluation+of+complete+and+incomplete+mixing+models%5D&search
HistoryKey=
Mompremier, R. (2009). Difusión de sustancias en redes de tuberías presión. México D.F: Intituto
politécnico Nacional.
Ocasio, N., & Manuel, L. (2007). El uso del Cloro en la Desinfección del Agua. Recuperado el 15
de Noviembre de 2012, de Hispagua: Sistema Español de Información sobre el Agua:
http://hispagua.cedex.es/sites/default/files/uso_cloro.pdf
Revista Ambientum. (Febrero de 2002). Cloro Residual en Agua de Consumo. Recuperado el 15 de
Noviembre de 2012, de Revista Ambientum:
http://www.ambientum.com/revista/2002_05/CLORES2.asp
Saldarriaga V., J. G. (2011). Clase de Hidráulica. Bogotá D.C, Colombia: Universidad de los
Andes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
75
Laura Natalia Cotes Gómez
Saldarriaga, J. G. (2007). Hidráulica de Tuberías: Abastecimiento de Aguas, Redes, Riegos. Bogotá
D.C.: Alfaomega.
Sedna, P. P. (Diciembre de 2012). Los acueductos romanos. Recuperado el 25 de Mayo de 2013, de
http://www.portalplanetasedna.com.ar/acueductos.htm
Tzatchkov, V. G., Buchberger, S. G., Li, Z., Romero-Gómez, P., & Choi, C. (5 de Septiembre de
2009). Axial Dispersion in Pressurized Water Ditribution Networks-A Review. Recuperado
el 10 de Marzo de 2013, de International Symposium on Water Management and Hydraulic
Engineering: http://wmhe.gf.ukim.edu.mk/downloads/paperstopic2/a104-tzatchkov-
buchberger-li-romero-gomez-choi.pdf
Universidad de Valencia. (2006). Fenómenos de transporte y conductividad electrolítica.
Recuperado el 27 de mayo de 2013, de Departamento de Química Física:
http://www.uv.es/tunon/QFIII/tema_4.pdf
Vidal, R., Martínez, F., & Ayza, M. (1994). Aplicaciones de los modelos de calidad en la
simulación de las redes de distribución de agua potable. Recuperado el 15 de Octubre de
2012, de http://upcommons.upc.edu/revistes/bitstream/2099/4203/1/article5.pdf
Yi Wu, Z., & Elsayed, S. M. (2013). Parallelized hydraulic and water quality simulation for water
ditribution system analysis. World Environmental and Water Resources Congress , (pág.
11). ASCE.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable”
76
Laura Natalia Cotes Gómez
10. Anexos
A continuación se presentan todos los planos desarrollados para el proyecto.
1. Planta del modelo.
2. Perfil del modelo.
3. Alimentación.
4. Plataforma.
5. Tuberías de vidrio.
