
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y
Alcantarillados
CIACUA
Modelación Física de Cambios Operativos en Redes de
Distribución de Agua Potable: Modelaciones en Período
Extendido y Modelación de Flujo No Permanente
Proyecto de Grado
Ingeniería Ambiental
Iván Camilo Viveros Góngora
Bogotá, Julio de 2013

A mis padres, yo también los amo.

Contenido
1
I
NTRODUCCIÓN
....................................................................................................................................... 1
2
Montaje de Laboratorio ...................................................................................................................... 9
2.1
Antecedentes .................................................................................................................................... 9
2.2
Accesorios de la Red Elevada ............................................................................................................ 9
2.3
Sistema de Medición ....................................................................................................................... 12
2.4
Medición de presión ........................................................................................................................ 12
2.5
Medición de Demandas de Puntos de Extracción de Caudal .......................................................... 15
2.6
Escenarios ....................................................................................................................................... 17
2.6.1
Escenario 5 Inicial ....................................................................................................................... 18
2.6.2
Escenario 5 Final ......................................................................................................................... 20
2.6.3
Escenario 6 Inicial ....................................................................................................................... 21
2.6.4
Escenario 6 Final ......................................................................................................................... 22
2.7
Resultados de mediciones de presión y demandas ......................................................................... 23
3
Modelo Computacional ..................................................................................................................... 26
3.1
EPANET ............................................................................................................................................ 26
3.2
REDES .............................................................................................................................................. 26
3.2.1
Método del Gradiente ................................................................................................................ 27
3.2.2
Método de Gauss o Factorización de Cholesky .......................................................................... 30
3.2.3
Descomposición de Cholesky ..................................................................................................... 33
3.3
Modelo Hidráulico ........................................................................................................................... 34
3.3.1
Energía de Entrada ..................................................................................................................... 35
3.3.2
Demandas en Nudos de Extracción de Caudal ........................................................................... 35
3.3.3
Diámetros Reales ........................................................................................................................ 36
3.3.4
Coeficientes de Pérdidas Menores ............................................................................................. 36
3.3.5
Representatividad del Modelo ................................................................................................... 37
3.3.6
Coeficiente de Determinación .................................................................................................... 37
3.3.7
Error Cuadrático Medio .............................................................................................................. 38
3.3.8
Indicadores de Representatividad .............................................................................................. 39
4
Resultados ......................................................................................................................................... 41
4.1
Procedimiento ................................................................................................................................. 41
4.2
Ubicaciones ..................................................................................................................................... 41
4.2.1
Ubicación 1 ................................................................................................................................. 41
4.2.2
Ubicación 2 ................................................................................................................................. 55

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
iv
Iván Camilo Viveros Góngora
4.2.3
Ubicación 3 ................................................................................................................................. 71
4.3
Comparación con Magnitudes de la Ecuación de Joukowsky ......................................................... 86
4.4
Comparación entre Escenarios en Estado Estable y Escenarios Sometidos a Variaciones Súbitas . 88
5
Modelación en Período Extendido ..................................................................................................... 91
5.1
Características del Modelo .............................................................................................................. 91
5.2
Energía de Entrada.......................................................................................................................... 91
5.3
Demandas ....................................................................................................................................... 91
5.4
Patrones de Altura de Presión y de Demanda de Caudal ................................................................ 92
Patrones de la Variación del Escenario 5 ................................................................................................. 93
5.4.1
Patrones de Variación del Escenario 6 ....................................................................................... 95
5.5
Resultados y Representatividad del Modelo ................................................................................... 96
5.5.1
Representatividad....................................................................................................................... 96
6
Conclusiones ..................................................................................................................................... 98
7
Agradecimientos ............................................................................................................................. 100
8
Bibliografía ...................................................................................................................................... 101
9
Anexos ............................................................................................................................................ 103
9.1
Escenario 5 .................................................................................................................................... 103
9.2
Escenario 6 .................................................................................................................................... 104

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
v
Iván Camilo Viveros Góngora
Índice de Ilustraciones
Ilustración 1 Caída de Altura de Presión ............................................................................................. 3
Ilustración 2 Fluctuaciones de Presión ................................................................................................ 4
Ilustración 3 Válvula de Bola de 2 Pulgadas. ..................................................................................... 10
Ilustración 4 Válvula de 3 Pulgadas. .................................................................................................. 10
Ilustración 5 Transductor de Presión Vegabar 52. ............................................................................ 10
Ilustración 6 Válvula de 2 Pulgadas. .................................................................................................. 10
Ilustración 7 Diámetros de Tuberías en la Red Elevada .................................................................... 11
Ilustración 8 FieldPoint FP-1601 y Extensión FP-AI-111. ................................................................... 12
Ilustración 9 Vegabar 52.................................................................................................................... 13
Ilustración 10 MAN LD3S (Kobold). ................................................................................................... 13
Ilustración 11 Mapa de Transductores de Presión............................................................................ 14
Ilustración 12 Puntos de Extracción de Caudal. ................................................................................ 16
Ilustración 13 Gráfica Comparativa de Diferentes Válvulas. ............................................................. 17
Ilustración 14 Escenario 5 Inicial. ...................................................................................................... 19
Ilustración 15 Escenario 5 Final. ........................................................................................................ 20
Ilustración 16 Escenario 6 Inicial. ...................................................................................................... 21
Ilustración 17 Escenario 6 Final. ........................................................................................................ 22
Ilustración 18 Modelo Computacional Epanet. ................................................................................. 36
Ilustración 19 Modelo Computacional Redes (vista 3D). .................................................................. 37
Ilustración 20 Ubicación 1. ................................................................................................................ 42
Ilustración 21 Ubicación 2 del Caudalímetro. ................................................................................... 55
Ilustración 22 Ubicación 3. ................................................................................................................ 71

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
vi
Iván Camilo Viveros Góngora
Índice de Ecuaciones
Ecuación 1 de Joukowsky .................................................................................................................... 2
Ecuación 2 Velocidad de Propagación de la Onda .............................................................................. 2
Ecuación 3 Período de la Tubería ........................................................................................................ 4
Ecuación 4 Presión Máxima en Tuberías de Conducción y Aducción ................................................. 6
Ecuación 5 Presión de Diseño para Tuberías de Aducción y Conducción ........................................... 6
Ecuación 6 Ecuación de Continuidad. .............................................................................................. 27
Ecuación 7 Ecuación de Darcy Weisbach. ......................................................................................... 27
Ecuación 8 Ecuación de Colebrook-White. ....................................................................................... 28
Ecuación 9 Ecuación Explícita para el Cálculo del Caudal a partir de las Ecuaciones de Darcy-
Weisbach y Colebrook-White. ........................................................................................................... 28
Ecuación 10 Energía Total Disponible. .............................................................................................. 28
Ecuación 11 Pérdidas Totales. ........................................................................................................... 29
Ecuación 12 Constante de Pérdidas Totales. .................................................................................... 29
Ecuación 13 Conservación de Energía. .............................................................................................. 29
Ecuación 14 Ecuación de Continuidad. ............................................................................................. 30
Ecuación 15 Expresión Ensamblada de Continuidad y Energía. ........................................................ 30
Ecuación 16 Expresión Iterativa de Alturas. ...................................................................................... 30
Ecuación 17 Ecuación Iterativa de Caudales. .................................................................................... 30
Ecuación 18 Ecuación de Cholesky .................................................................................................... 33
Ecuación 19 Ecuación de Cholesky .................................................................................................... 34
Ecuación 20 Coeficiente de Determinación ...................................................................................... 38
Ecuación 21 Suma de Cuadrados del Error ....................................................................................... 38
Ecuación 22 Suma Total de Cuadrados ............................................................................................. 38
Ecuación 23 Variación de Laboratorio. ............................................................................................. 86
Ecuación 24 Diferencia de Velocidades. ........................................................................................... 86
Ecuación 25 Diferencia Entre Variaciones. ........................................................................................ 87
Ecuación 26 Factores de Multiplicación. ........................................................................................... 92

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
vii
Iván Camilo Viveros Góngora
Índice de Tablas
Tabla 1 Promedios de Demandas de Caudal. .................................................................................... 23
Tabla 2 Desviaciones Estándar de las Demandas de los Escenarios. ................................................ 23
Tabla 3 Mediana de las Demandas de los Escenarios. ...................................................................... 24
Tabla 4 Medias de Presión. ............................................................................................................... 24
Tabla 5 Desviación Estándar de Presiones de Escenarios. ................................................................ 25
Tabla 6 Mediana de Presiones de Escenarios. .................................................................................. 25
Tabla 7 Indicadores Estadísticos. ...................................................................................................... 39
Tabla 8 Tabla Valores Máximos de Presión. ...................................................................................... 54
Tabla 9 Valores Máximos del Escenario 6 Ubicación 2. .................................................................... 69
Tabla 10 Valores Mínimos del Escenario 6 Ubicación 2. ................................................................... 70
Tabla 11 Valores Máximos del Escenario 6 en la Ubicación 3. ......................................................... 84
Tabla 12 Valores Mínimos de Presión del Escenario 6 en la Ubicación 3. ........................................ 85
Tabla 13 Escenario 5 Inicial Estable y Escenario 5 Sometido a Variación ......................................... 89
Tabla 14 Escenario 5 Final Estable y Escenario 5 Sometido a Variación .......................................... 89
Tabla 15 Escenario 6 Inicial Estable y Escenario 6 Sometido a Variación ........................................ 90
Tabla 16 Escenario 6 Final Estable y Escenario 6 Sometido a Variación .......................................... 90
Tabla 17 Representatividad de Modelación en Período Extendido. ................................................. 97

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
1
Iván Camilo Viveros Góngora
1 I
NTRODUCCIÓN
El presente proyecto de grado tiene como finalidad analizar el perfil de caudal y presión
en estado de flujo no permanente. Otro de sus objetivos consiste en determinar la
representatividad de los modelos EPANET y REDES a partir de configuraciones hidráulicas
en estado estable. Finalmente, con los perfiles de variación de caudal y presión se busca
determinar la representatividad de los modelos computacionales en período extendido.
Cuando se hace referencia a las diferentes clasificaciones de flujo es necesario tener en
cuenta la variación de las características hidráulicasen relación con el espacio y con el
tiempo. El flujo variado no permanente presenta fluctuaciones tanto en espacio como en
tiempo; un ejemplo de éste es el golpe de ariete (Saldarriaga, 2007). Cuando se hace
referencia a flujo inestable o flujo variado, la suposición acerca de la incompresibilidad del
fluido no es adecuada y en transientes rápidos es engañosa (Thorley, 1991). Los
transientes o rápidos tránsitos de presión ocurren en cortos períodos de tiempo cuando el
estado estable del flujo es alterado (Bosserman II & Hunt, 2006). Desde hace poco más de
un siglo la literatura científica ha presentado estudios relativosa las particularidades que
se observan en la presión y en el caudal después de un cambio operativo súbito. Es
importante mencionar que la literatura científica ha abordado extensamente el fenómeno
del golpe de ariete.
Los transientes son causados por cierres súbitos de válvulas, saltos de línea, fallas del
sistema de control, pérdida de potencia, pérdida de telemetría, interacción de servicios
múltiples o una inadecuada selección del equipo (Stone, 2006). Cambios en la demanda,
intrusión de aire, fallas en los sistemas de regulación de presión y ruptura de tubos
también pueden originar el fenómeno (Bosserman II & Hunt, 2006). La energía del agua en
un punto se distribuye entre cinética y potencial (el agua tiende a fluir de un punto de
mayor energía a un punto de menor energía); un cambio súbito provoca un intercambio
de energía entre el flujo y la presión (LeChevallier, Gullick, Karim, Friedman, & Funk,
2003).
Los fenómenos de presión no ocurren en todos los lugares del sistema al mismo tiempo,
sin embargo su propagación sucede de manera inmediata. El intervalo en el cual la señal
se distribuye en el sistema depende de la distancia desde el punto analizado al punto

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
2
Iván Camilo Viveros Góngora
donde se produce el cambio en el flujo. Otro factor que influye en la duración del proceso
de dispersión de la señal es la velocidad de propagación de ondas del transiente, cuya
magnitudes cercana o igual a la de la velocidad del sonido.
La magnitud del cambio de presión fue descrita hace más de un siglo por Joukowsky. El
término ∆𝐻 representa la variación en la altura de presión esperada, 𝑎 la velocidad de
propagación de la onda y ∆𝑉 los cambios de velocidad con respecto a los escenarios en
estado estable antes y después del cambio súbito que tuvo lugar en el sistema (Thorley,
1991). En algunos artículos es denominado ley de golpe de ariete instantáneo (Bergant,
Simpsom, & Tijsseling, 2006) (Joukowsky, 1900).
∆𝐻 =
𝑎 ∗ ∆𝑉
𝑔
Ecuación 1 (Joukowsky, 1900)
Los términos relativos a la gravedad y a la velocidad del flujo pueden ser extraídos de
textos o directamente de montajes de laboratorio. La velocidad de propagación “𝑎" de la
onda fue descrita por Kortweg quien la relaciona con“𝑒” el espesor, “𝐾” el módulo de
compresibilidad, “D” el diámetro de la tubería, “𝜌" la densidad del fluido y “E” el módulo
de elasticidad del material (Korteweg, 1878).
𝑎 =
𝐾
𝜌
1 +
𝐾
𝐸
∗
𝐷
𝑒
Ecuación 2 Velocidad de Propagación de la Onda (Korteweg, 1878)
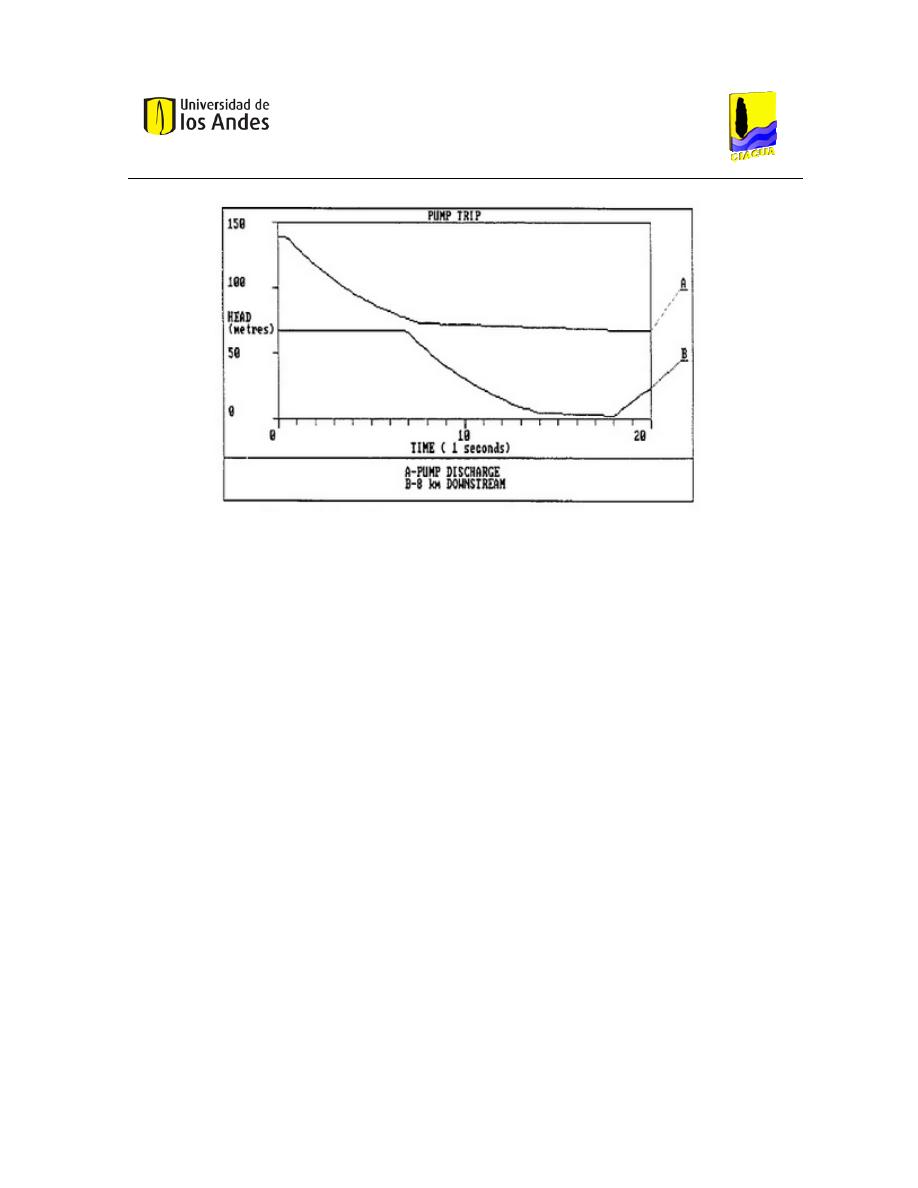
Una manera clara de exponer el comportamiento de los transientes es a través del
ejemplo que brinda Thorley en su libro “Fluid Transients in Pipelines”(Thorley, 1991).
Supóngase hay una bomba que impulsa agua desde el punto A al punto B el cual se
encuentra a una altura superior. Si la bomba cesa su actividad de manera súbita la
fracción de agua en puntos distantes conserva el momentum y tiende a mantener el
movimiento. Por el contrario, el volumen del fluido en las vecindades de la bomba se
detiene. Si se divide el flujo en varios anillos, el más cercano al punto donde se efectuó el
cambio “hala” al segundo y así sucesivamente hasta que la altura de presión disminuye en
una magnitud similar a la que se plantea en la ecuación de Joukowsky.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
3
Iván Camilo Viveros Góngora
Ilustración 1 Caída de Altura de Presión (Thorley, 1991)
En la ilustración se ven dos líneas que disminuyen de manera significativa con respecto a
la altura inicial. Como se mencionó anteriormente, el efecto del transiente no ocurre al
mismo tiempo en todo el sistema, sin embargo cuenta con una enorme velocidad de
propagación. La línea A representa el perfil de presión en la descarga de la bomba
mientras que la B un punto situado a ocho kilómetros aguas abajo. Como regla general se
supone que por cada 0.3 m/s de velocidad que sea forzada a detenerse de manera súbita,
la presión del agua aumenta de 345 a 414 kPa (Kirmeyer, y otros, 2001).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
4
Iván Camilo Viveros Góngora
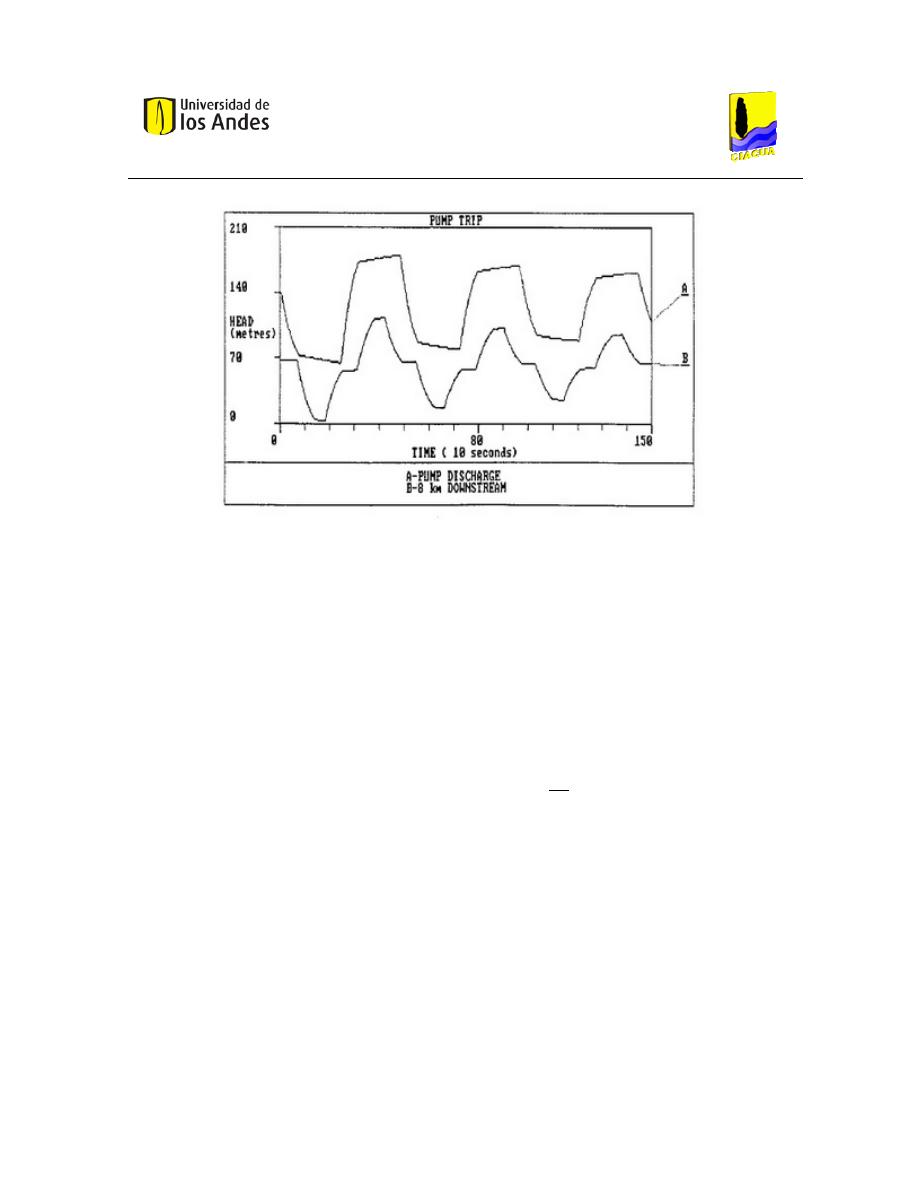
Ilustración 2 Fluctuaciones de Presión (Thorley, 1991)
La disminución súbita en la presión insta al sistema a buscar el equilibrio por lo cual la
sustancia en la tubería tiende a fluir,suceso que causa fluctuaciones de presión. La onda
viaja constantemente desde el punto donde se originó el cambio hacia aguas abajo y
viceversa. El tiempo que requiere la onda para recorrer la tubería y volver al punto inicial
es llamado “período de la tubería” y hace parte de los términos de la ecuación de
Joukowsky. “L” representa la longitud de la tubería y “a” la velocidad de propagación de la
onda.
𝑃𝑒𝑟í𝑜𝑑𝑜 𝑑𝑒 𝑙𝑎 𝑇𝑢𝑏𝑒𝑟í𝑎 =
2𝐿
𝑎
Ecuación 3 Período de la Tubería (Thorley, 1991)
En algunos experimentos la configuración de un sistema de embalse, tubería y válvula
permite identificar los patrones de variación de la presión. En algunos casos, debido a la
superposición de ondas (producto de la reflexión relacionada con el cierre súbito de una
válvula) se puede llegar a inducir cambios de presión superiores a los pronosticados en la
ecuación de Joukowsky (Simpson & Wylie, 1991). La fricción también puede modificar la
magnitud de variación, especialmente en tuberías largas.
Durante el proceso de disminución de la altura de presión la presencia de gases y/o aire
son factores modificadores de la onda y del perfil de altura de presión del transiente. Una

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
5
Iván Camilo Viveros Góngora
vez se transmite la señal existe la posibilidad de alcanzar la presión de vapor, lo cual
conlleva al cambio de fase del fluido. La presencia de múltiples fases conlleva a cambios
en la magnitud de la aceleración de la onda. La diferencia entre los segmentos del
volumen del fluido implica en algunos casos un choque el cual produce un aumento en la
presión (Thorley, 1991).
Las ondas de tensión que se propagan en las paredes modifican las predicciones basadas
en Joukowsky. Se debe considerar que aumentos en la presión modifican ligeramente el
diámetro de la tubería; las ondas producto de las alteraciones viajan más rápido en el
material de la tubería que en el fluido, lo cual genera pequeñas fluctuaciones de presión;
por este motivo la tubería debe estar protegida con soportes (Thorley, 1991).
El efecto de los gases y/o el aire no sólo se reduce a un aumento de presión. Aquellas
zonas que cuentan con una gran cantidad de éstos, sirven como punto de reflexión del
transiente. Los lugares que cuentan con cantidades pequeñas y dispersas disminuyen la
velocidad de transmisión del fenómeno.
Hay consecuencias en ámbitos esenciales como la calidad del agua e infraestructura
debido a las variaciones de presión. Se puede presentar resuspensión de partículas
sedimentadas, así como desprendimiento de biopelículas, ruptura de tuberías (por ende
intrusión de elementos externos) y como resultado un desmejoramiento en términos de
calidad (Wood, 2005). Vibraciones, desplazamientos de tuberías, deformación y cavitación
también hacen parte de los posibles efectos asociados con el fenómeno (Bosserman II &
Hunt, 2006).
La producción de transientes negativos de presión crea circunstancias aptas para una
contrapresión de agua no potable de origen doméstico, industrial o institucional
(LeChevallier, Gullick, Karim, Friedman, & Funk, 2003). En el suelo y el agua al exterior del
sistema de distribución de agua potable hay presencia de indicadores fecales y virus
humanos; sin embargo no hay suficiente información para afirmar que los transientes
representan un riesgo significativo para la calidad del agua, en parte porque los sistemas
de monitoreo no consideran las zonas vulnerables a presiones bajas y no cuentan con
equipos de medición de alta frecuencia (LeChevallier, Gullick, Karim, Friedman, & Funk,
2003).
Puesto que en algunos casos el transiente se considera un fenómeno indeseable hay
disponible una amplia variedad demétodos para suprimirlos agrupados en dos categorías:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
6
Iván Camilo Viveros Góngora
acciones directas y tácticas de distracción. Las acciones directas tienen como objetivo
influenciar o modificar las causas primarias que inducen el cambio de flujo. Modificar el
patrón de apertura de una válvula es una solución perteneciente a la primera categoría.
Las tácticas de distracción se enfocan en expulsar o modificar el flujo; algunos ejemplos
son las válvulas de control, las vesículas de aire y los tanques de alimentación.
Dentro de los documentos técnicos o recomendaciones impulsadas por el Ministerio de
Ministerio de Vivienda, Ciudad y Territorio se destaca el Reglamento Técnico del Sector de
Agua Potable y Saneamiento Básico (RAS). En el Título B abarca amplitud de lineamientos
relacionados con el diseño y operación del sistema de acueducto. En lo relacionado con el
golpe de ariete, cuenta con especificaciones para el proceso de diseño y operación de las
tuberías de aducción, conducción y red de distribución.
Relativo a las tuberías de aducción y conducción establece criterios que guardan
conexidad con el fenómeno de golpe de ariete para la selección del material, los rangos de
presión y el análisis hidráulico. En el proceso de selección del material de las tuberías, se
debe tener en cuenta las condiciones hidráulicas del proyecto, incluidas las fluctuaciones
de presión producto del golpe de ariete. La presión de diseño debe tener en cuenta la
diferencia entre las condiciones estáticas y el máximo valor producto de un golpe de
ariete, además se debe multiplicar dicho rango por un factor de seguridad estipulado en el
documento. El análisis de golpe de ariete debe realizarse en condiciones normales y
excepcionales de operación.
𝑃𝑚𝑎𝑥 = max 𝑃𝑒𝑠𝑡á𝑡𝑖𝑐𝑎, 𝑃𝑡𝑟𝑎𝑛𝑠𝑖𝑒𝑛𝑡𝑒
Ecuación 4 Presión Máxima en Tuberías de Conducción y Aducción
𝑃𝑑𝑖𝑠𝑒ñ𝑜 = 𝑘 ∗ 𝑃𝑚𝑎𝑥
Ecuación 5 Presión de Diseño para Tuberías de Aducción y Conducción
En los sistemas por bombeo y gravedad el análisis de golpe de ariete debe ser realizado a
través del método de las características o algún método de elementos finitos, bajo la
consideración del agua como columna elástica para condiciones específicas de operación.
Una vez se haya construido el proyecto se deben realizar pruebas de golpe de ariete con el
escenario de operación normal que presente las mayores sobrepresiones o las menores
subpresiones.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
7
Iván Camilo Viveros Góngora
Las redes de distribución, en el RAS Título B, también cuentan con la ocurrencia del golpe
de ariete como criterio para la selección de material, el análisis hidráulico y proceso de
verificación. Además de consideraciones de toxicidad, resistencia mecánica y aspectos
económicos, en el proceso de selección de materiales de la red deben considerarse las
condiciones hidráulicas especialmente las presiones normales de trabajo, las presiones
estáticas y aquéllas producto de un golpe de ariete. Una vez se ha implementado en su
totalidad la red de distribución debe hacerse una prueba de golpe de ariete con el fin de
verificar que ningún segmento posea presiones que superen el máximo admitido, hecho
que podría conducir a estallidos. Se debe verificar que no se produzcan durante el
fenómeno, presiones negativas que induzcan la intrusión de agua desde el exterior de la
red.
El diseño de estaciones de bombeo debe considerar la pérdida de suministro eléctrico y la
consecuente interrupción del flujo de agua. Se debe enfatizar en los efectos relacionados
con la sobre elevación de presiones, las subpresiones y la velocidad de la onda de
compresión. Las condiciones de operación deben ser verificadas durante toda la vida útil
en condiciones estáticas y de flujo no permanente. Finalmente, se debe realizar pruebas
en condiciones normales que produzcan las mayores sobrepresiones y las menores
subpresiones; los datos tomados en campo deben ser conservados por la Persona
Prestadora del Servicio con el fin de someterlos a comparación con aquéllos durante los
períodos de operación normal.
Se puede afirmar que el transiente de presión ocurre durante eventos de flujo variado no
permanente, inducido por cambios súbitos como el cierre de una válvula de control,
cambios en la demanda o suspensión de la actividad de una bomba, entre otros. La
suposición acerca de la compresibilidad no es fiel a las características del fenómeno,
especialmente en aquéllos de corta duración. El tiempo de propagación es bastante corto,
inclusive puede durar menos de un segundo, motivo por el cual se deben considerar
equipos de medición de alta frecuencia. Durante las fluctuaciones de presión existen
períodos positivos y negativos que pueden afectar las características de la hidráulica de
una red o la calidad del agua. Aún se requiere más documentación científica para declarar
el fenómeno un riesgo para la salud pública. La magnitud del tránsito súbito de presiones
ha sido explicada a través de la ecuación de Joukowsky; sin embargo, puede haber
variaciones no pronosticadas debido a la presencia de gases o aire, y a la propagación de
la onda en el material de la tubería. Existen dos categorías de métodos de supresión del

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
8
Iván Camilo Viveros Góngora
transiente: métodos directos y tácticas de distracción. Las recomendaciones técnicas
locales están enfocadas a la selección del material, modelación hidráulica, rangos de
presión y pruebas de operación en los sistemas de aducción, de conducción, de la red de
distribución y de las estaciones de bombeo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
9
Iván Camilo Viveros Góngora
2
Montaje de Laboratorio
El montaje de laboratorio propuesto en este proyecto de grado tuvo como escenario la
red elevada del Laboratorio de Hidráulica de la Universidad de los Andes, ubicado en el
edificio Mario Laserna (Carrera 1 # 18ª-10).
Dos escenarios cuyas características fueronmedidas en estado estable (presión y caudal)
son sometidos a transiciones en períodos de tiempo cortos, en este caso a un cierre súbito
de una válvula. Se contaba con cuatro Escenarios: 5 Inicial, 5 Final, 6 Inicial y 6 Final. Sus
nombres obedecen a la recopilación de información en trabajos previos.
2.1 Antecedentes
En la tesis de César Mauricio Prieto Gamboa “Modelación física y calibración de sustancias
en redes de distribución de agua potable”(Prieto Gamboa, 2011) se hizo un levantamiento
topológico y topográfico a la red elevada del Laboratorio de Hidráulica de la Universidad
de Los Andes,se crearon escenarios hidráulicos, seestimaron las demandas, se midieronlas
presiones, se determinaronlas pérdidas menores y se analizó el comportamiento de
sustancias. Además se llevó a cabo un proceso de calibración y validación en EPANET y
Redes.
El proyecto de grado presente,retomó el modelocalibrado y validadoen el proyecto de
grado de César Prieto. La nomenclatura relativa a nodos de extracción y transmisores de
presión, se conserva con el fin de permitir comparaciones.
El trabajo de grado previo creó seis escenarios. Con base en los promedios de las
mediciones de presión, se llevó a cabo para cada uno, un proceso de calibración de las
pérdidas menores. El resultado más satisfactorio fue el del Escenario 5 Inicial, el cual fue
validado en todos los escenariosy arrojó mejores resultados que los modelos previos.
Dos escenarios fueron retomados de los estudios previos: el 5 y el 6; para evitar
confusiones son llamados5 Inicial y 6 Inicial, puesto que fueron el punto de partida para
evolucionar a los Escenarios 5 Final y 6 Final.
2.2 Accesorios de la Red Elevada

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
10
Iván Camilo Viveros Góngora
La red elevada cuenta con 31 puntos de extracción de caudal dotados de válvulas de bola
de 2 pulgadas; en más de siete hay tuberías disponibles para dirigir el flujo a unas zonas
de descarga. También posee 23 válvulas de 2, 3 y 4 pulgadas las cuales permiten modificar
la dirección del flujo. Los tubos son de PVC de 2, 3 y 4 pulgadas, en algunas zonas unidos
por reducciones y tesIlustración 7 Diámetros de Tuberías en la Red Elevada). En nueve
puntos de la red hay transductores de presión instalados los cuales permiten mediciones
en tiempo real.
Ilustración 3 Válvula de Bola de 2
Pulgadas.
Ilustración 4 Válvula de 3 Pulgadas.
Ilustración 5 Transductor de Presión
Vegabar 52.
Ilustración 6 Válvula de 2 Pulgadas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
11
Iván Camilo Viveros Góngora

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
12
Iván Camilo Viveros Góngora
Ilustración 7 Diámetros de Tuberías en la Red Elevada

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
13
Iván Camilo Viveros Góngora
2.3 Sistema de Medición
La red elevada cuenta con diferentes puntos en los cuales hay instalados sensores que
miden la presión. Éstos están conectados a una compleja red que direcciona la señal a un
“fieldpoint”de National Instruments cuya referencia es FP-1601 y cuenta con una
extensión FP-AI-111 (National Instruments, 2003). Usualmente este tipo de instrumentos
alberga máximo nueve conexiones pero la presencia de una extensión, amplía su rango.
Esta configuración de la red permite recibir en tiempo real la información de los nueve
puntos de presión en un “software”diseñado para el Centro de Investigaciones en
Acueductos y Alcantarillados (CIACUA) de la Universidad de Los Andes.
Ilustración 8FieldPoint FP-1601 y Extensión FP-AI-111.
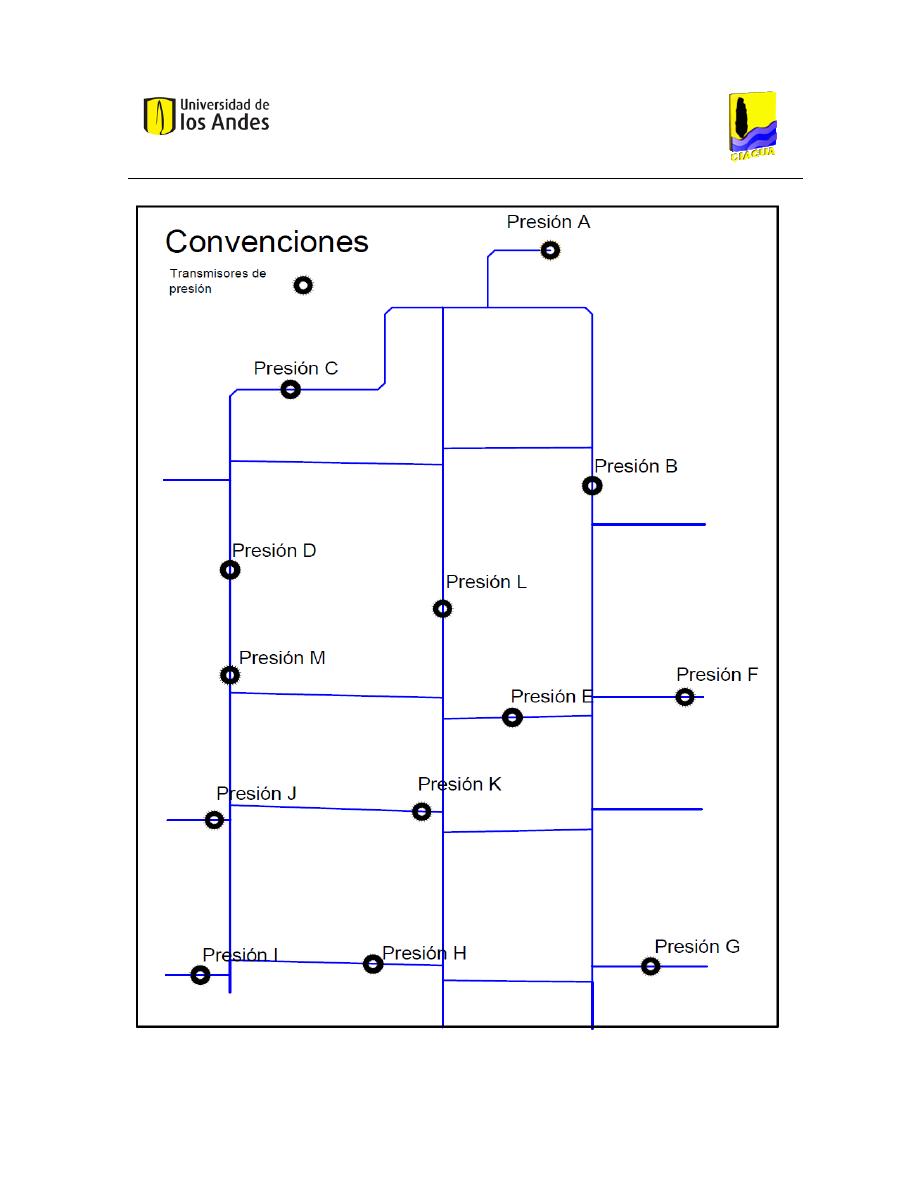
2.4 Medición de presión
La red elevada cuenta con 12 puntos en los cuales pueden ser instalados transductores de
presión. Sin embargo, no todos pueden ser utilizados debido a que algunos no cuentan
con la instalación y conducción de cables, algo indispensable para la transmisión de la
señal. “El punto A es esencial para los modelos computacionales puesto que con base en
éste se determina la altura del primer nodo”. La Ilustración 11 Mapa de Transductores de
Presión” es un esquema de los medidores en la red, la ubicación de los puntos y su
nomenclatura.
Inicialmente se contaba con transmisores de dos modelos MAN-SD2S B2 (Kobold) y
Vegabar 52. Dado que el rango de medición de éstos abarcaba de 0 a 1 bar, se decidió
adquirir 4 nuevos transmisores de presión los cuales estuvieran en capacidad de detectar

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
14
Iván Camilo Viveros Góngora
presiones de -1 a 5bar, su referencia es MAN LD3S (Kobold). Éstos fueron instalados en los
puntos de mayor variabilidad de presión.
Ilustración 9Vegabar 52.
Ilustración 10 MAN LD3S (Kobold).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
15
Iván Camilo Viveros Góngora
Ilustración 11 Mapa de Transductores de Presión.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
16
Iván Camilo Viveros Góngora
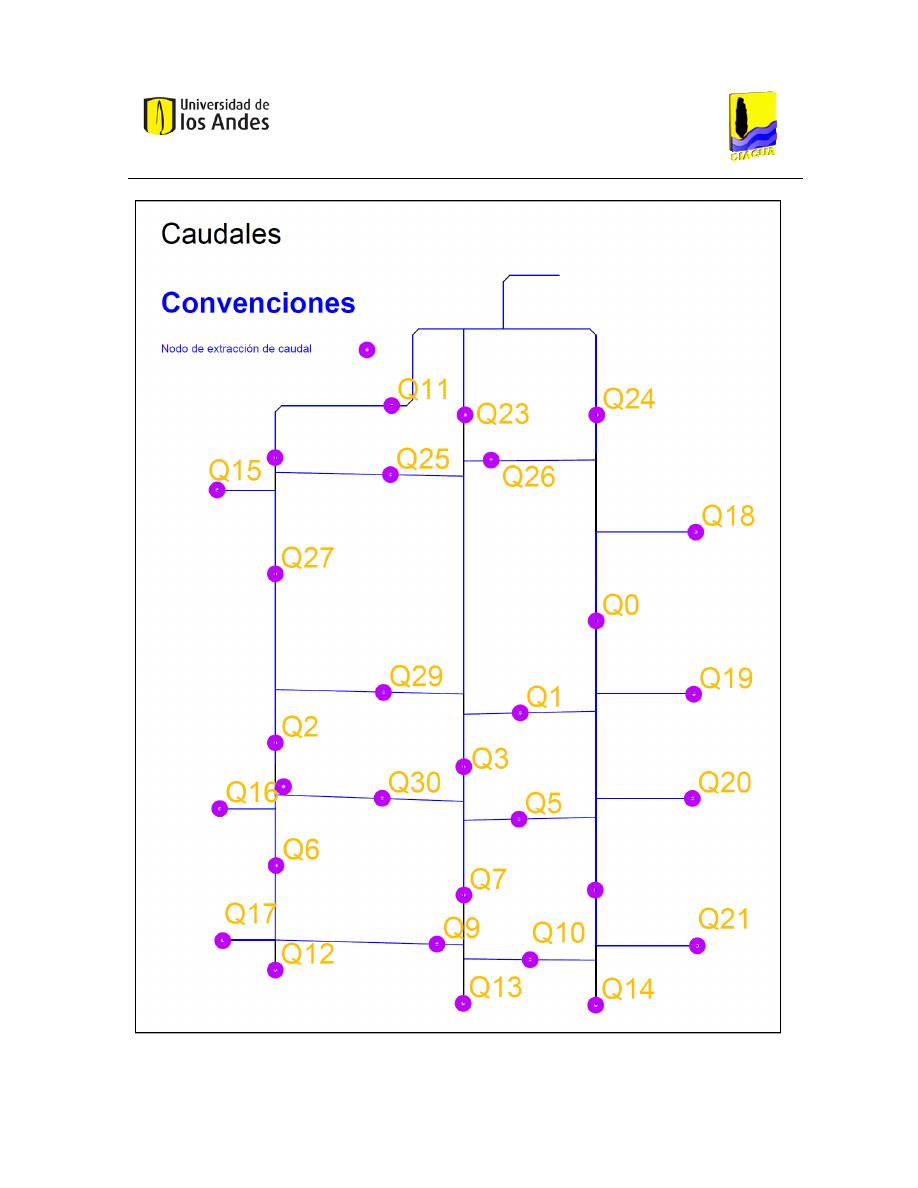
2.5 Medición de Demandas de Puntos de Extracción de Caudal
Determinar el caudal en los nodos de extracción es esencial para cuantificar las demandas
e implementarlas en los diferentes modelos computacionales. Se debe considerar que a la
entrada de la red hay un caudalímetro electrónico WATERMASTER FEV. En total hay 31
puntos desde los cuales se puede extraer agua por medio de válvulas de bola de 2
pulgadas. En estos puntos se instalaron mangueras las cuales transportaban el fluido a
baldes de volumen conocido. La ubicación de los nodos y su nomenclatura puede ser
consultada en el esquema de la Ilustración 12 Puntos de Extracción de Caudal”.
Para la medición de caudal se retomó la metodología usada en estudios previos. Los
baldes de 10.90L y 10.94L se llenaron y con un cronómetro se determinó el tiempo que
esta actividad requirió. Después de diez intentos se calculó el promedio y la desviación
estándar.
Lasmangueras utilizadas para la extracción de caudal no son parte de la red y no están
presurizadas. Éstas se instalan a alguna de las válvulas de bola y se permite el flujo de
agua. En el interior del balde, producto de la acumulación delfluido hay turbulencia.
Factores como la dirección de la manguera y la fricción del material, en conjunto con las
situaciones mencionadas anteriormente son fuentes de incertidumbre.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
17
Iván Camilo Viveros Góngora
Ilustración 12 Puntos de Extracción de Caudal.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
18
Iván Camilo Viveros Góngora
2.6 Escenarios
A continuación se presentan los esquemas de los escenarios implementados. Los cambios
súbitos fueron del Escenario 5 Inicial al Escenario 5 Final y del Escenario 6 Inicial al
Escenario 6 Final. Se tenía conocimiento de los caudales demandados para el 5 Inicial y el
6 Inicial, debido a estudios previos. En el caso de los montajes 5 Final y 6 Final, fue
necesario seguir el procedimiento planteado para la determinación de los caudales
demandados en los nodos de extracción.
Ladiferencia básica entre uno y otro escenario, radica en el cierre súbito de una válvula.
Para decidir qué puntos eran idóneos para dicho cambio se consideraron los cambios en
presión y demanda. En relación con los transientes, se puede afirmar que las válvulas de
bola incumplen con los tres componentes recomendados para evitar el fenómeno:
componentes móviles ligeros, corto desplazamiento para cierre y movimiento asistido por
resortes(Thorley, 1991).
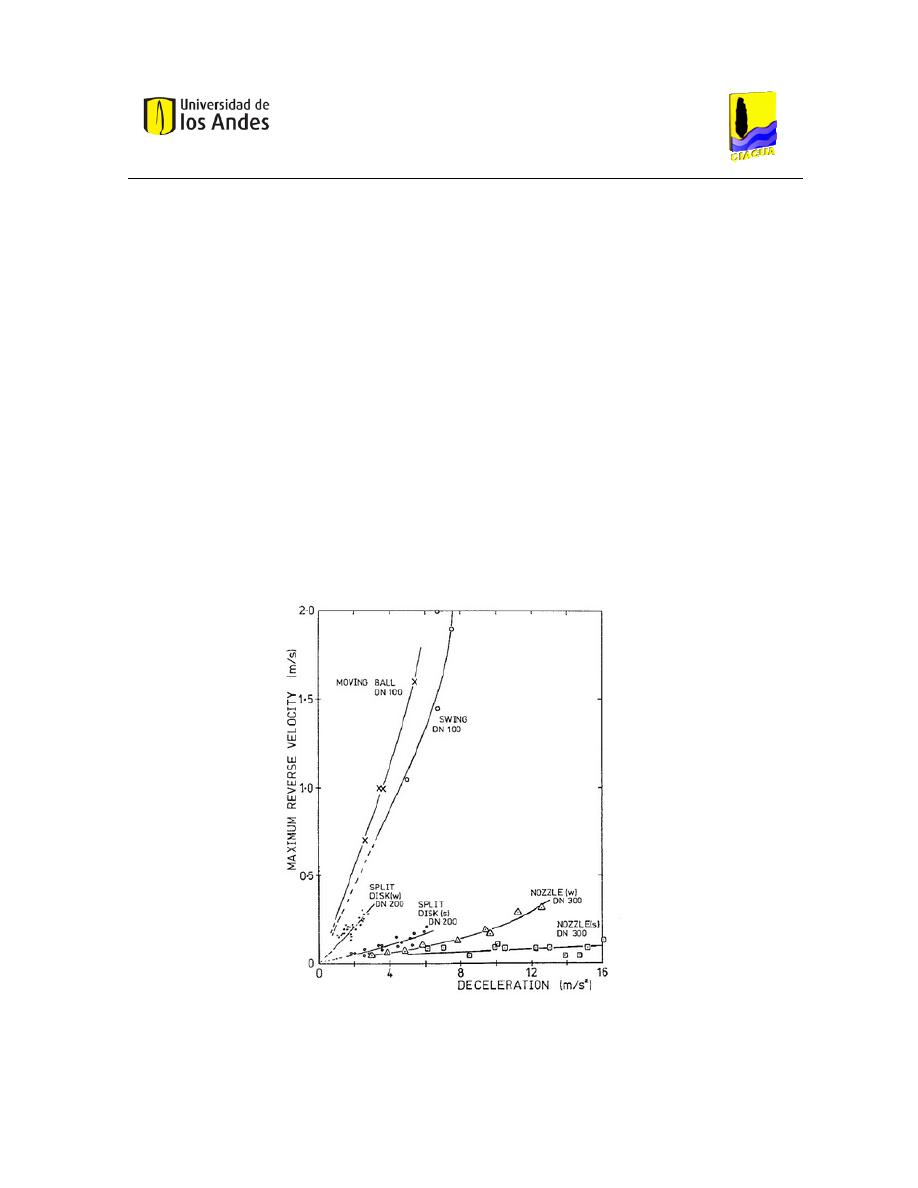
Ilustración 13 Gráfica Comparativa de Diferentes Válvulas(Thorley, 1991).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
19
Iván Camilo Viveros Góngora
En la gráfica se puede apreciar que las válvulas ideales son las de boquilla porque tienen
una excelente relación entre deceleración y máxima velocidad reversa. Al contrario, las
válvulas de bola pueden inducir fácilmente un transiente. Éstas para pequeñas
magnitudes de deceleración del flujo tienen enormes aumentos en lo que respecta a la
máxima velocidad reversa. Si se analiza la ecuación de Joukowsky, es evidente que esto
repercute en los cambios de presión que sean observados durante y después del evento.
2.6.1 Escenario 5 Inicial
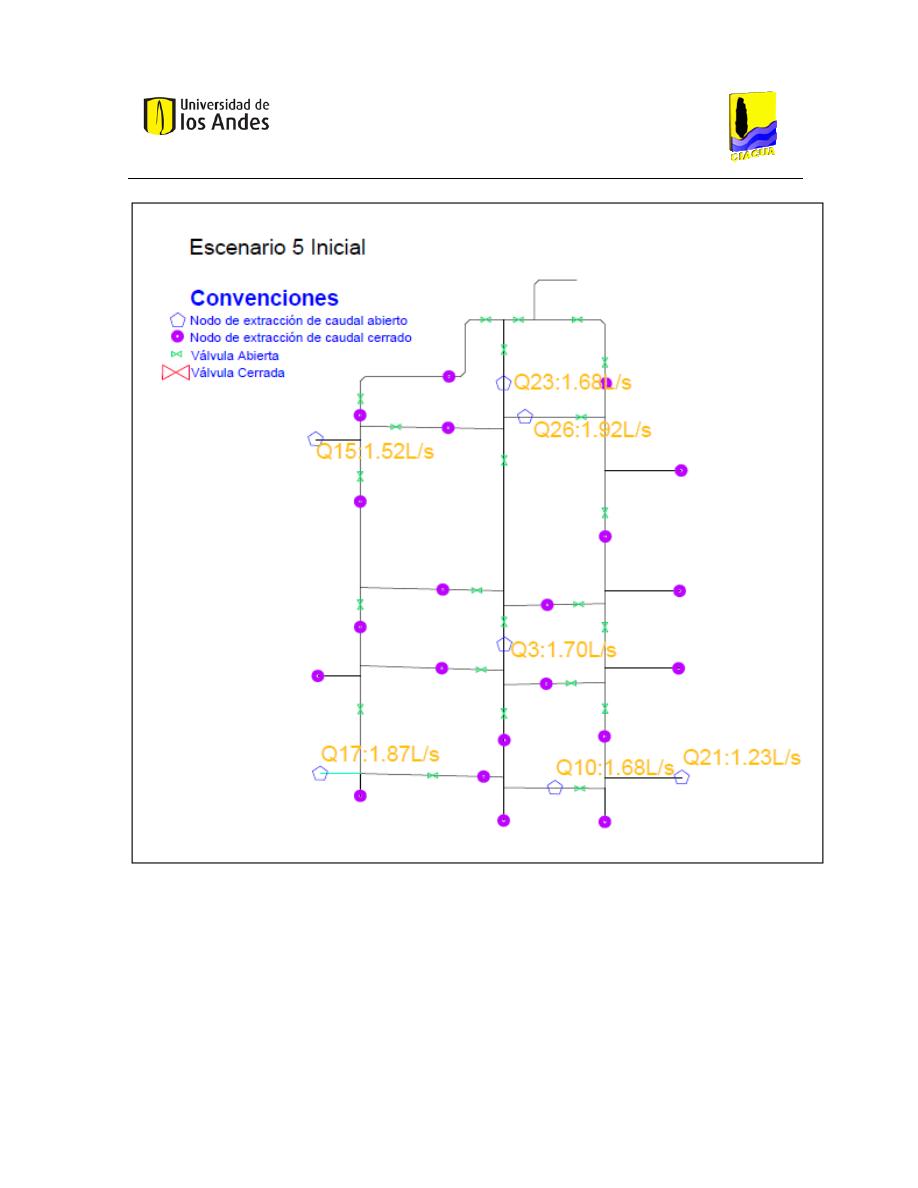
El Escenario 5 Inicial (ver Ilustración 14 Escenario 5 Inicial.”) es el que mejor se adecúa a
los programas validados (Prieto Gamboa, 2011). Esta configuración del sistema se
caracteriza por tener todas las válvulas abiertas y siete puntos de extracción de caudal.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
20
Iván Camilo Viveros Góngora
Ilustración 14 Escenario 5 Inicial.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
21
Iván Camilo Viveros Góngora
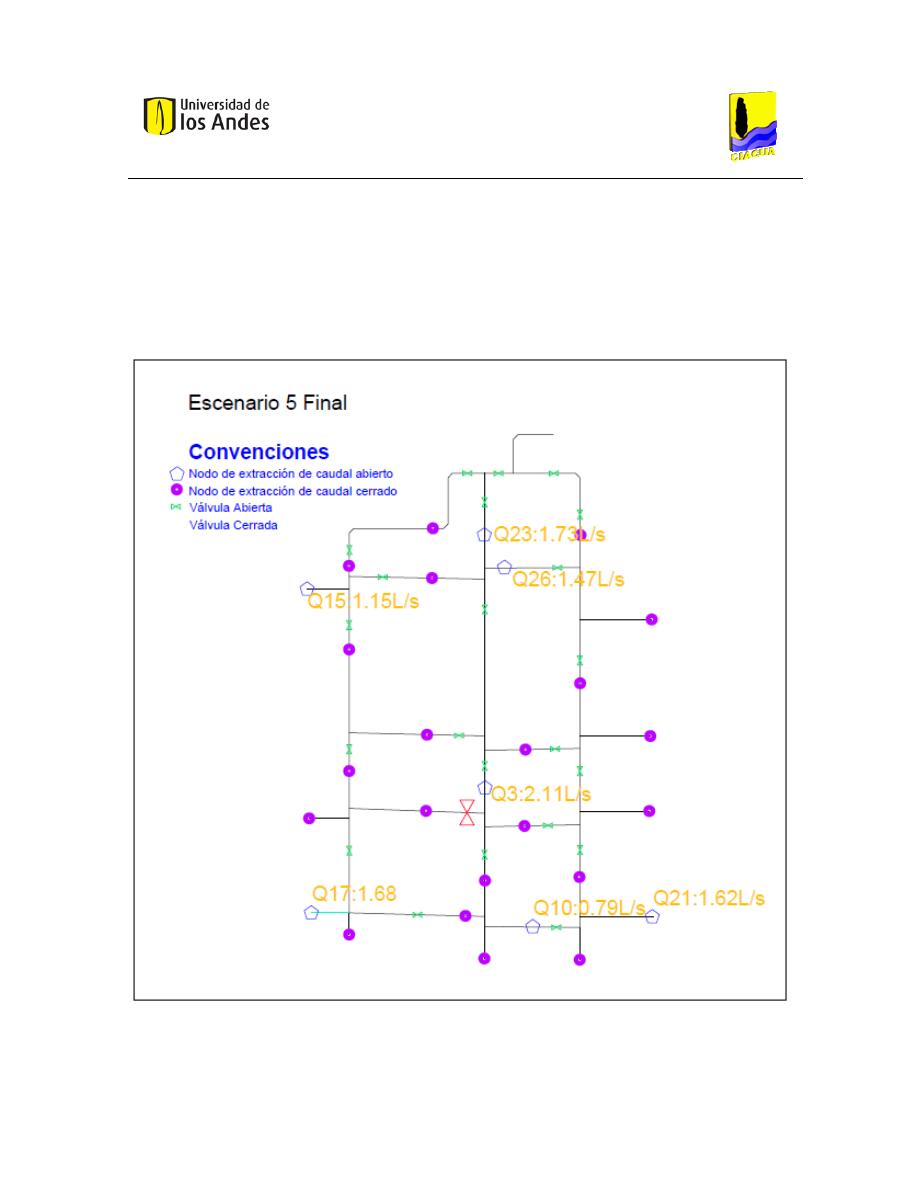
2.6.2 Escenario 5 Final
El Escenario 5 Final (Ilustración 15), al igual que el inicial tiene únicamente una de las
válvulas cerradas. Ésta se encuentra cerca a uno de los puntos de mayor presión
reportados por el Escenario 5 Inicial.
Ilustración 15 Escenario 5 Final.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
22
Iván Camilo Viveros Góngora
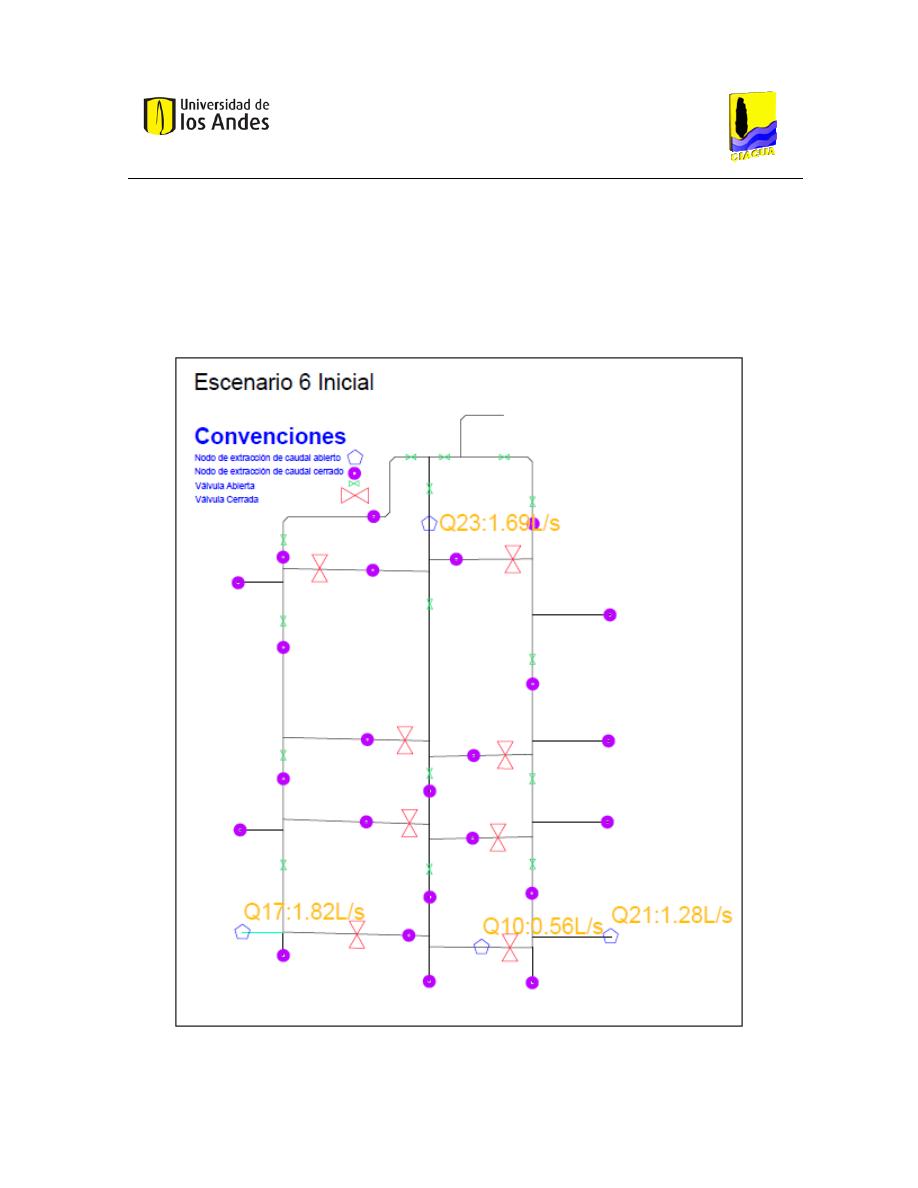
2.6.3 Escenario 6 Inicial
El Escenario 6 Inicial (Ilustración 16) cuenta con 8 válvulas cerradas, las cuales permiten el
flujo a través de tres líneas. Hay 4 puntos de extracción de caudal. La válvula al inicio de la
red se encuentra completamente abierta.
Ilustración 16 Escenario 6 Inicial.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
23
Iván Camilo Viveros Góngora
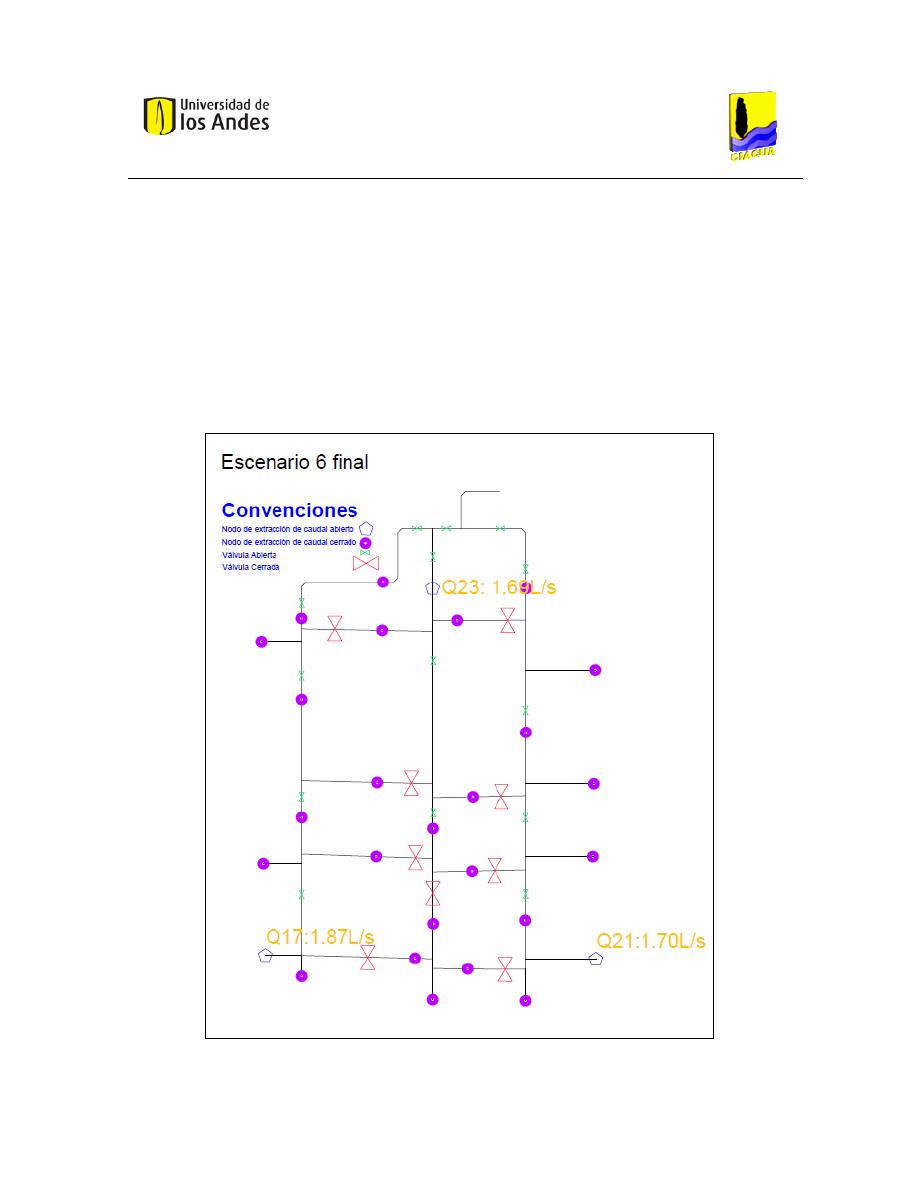
2.6.4 Escenario 6 Final
En el Escenario 6 Final (Ilustración 17) únicamente se extrae caudal desde tres puntos. Se
permite el flujo a través de las tres principales ramificaciones de la red elevada, para lo
cual se deben cerrar las válvulas en las interconexiones. La diferencia con el Escenario 6
Inicial radica en el cierre de una de las válvulas en la línea central, está se encuentra en las
vecindades de uno de los puntos que registraron mayor presión para las condiciones
iniciales. En total las válvulas cerradas son nueve.
Ilustración 17 Escenario 6 Final.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
24
Iván Camilo Viveros Góngora
2.7 Resultados de mediciones de presión y demandas
A continuación se presentan los promedios de las demandas o caudales medidos para
cada uno de los puntos (Tabla 1). El Escenario 5 Final reportó el mayor caudal total en
promedio. En contraparte, el Escenario 6 Final cuenta con la demanda total de menor
magnitud.
Tabla 1 Promedios de Demandas de Caudal.
Las siguientes dos tablas (Tabla 2 y Tabla 3) resumen la información referente a dos
importantes indicadores estadísticos: desviación estándar y mediana. El motivo de
presentarlos es analizar la variabilidad de los datos (y por ende su confiabilidad). Se puede
analizar que las diferencias entre los promedios y las medianas poseen magnitudes bajas.
Adicionalmente, la desviación estándar no tienen valores que puedan sugerir variaciones
significativas.
Al lector le pueden llamar la atención los datos reportados del Escenario 5 Final, en el
nudo de extracción Q10. Una desviación estándar y una varianza igual a cero puede ser
motivo de sospecha; sin embargo al analizar la configuración del montaje es evidente que
las válvulas restringen por completo el paso de agua por el nudo (a pesar de que esté
abierto) lo cual explica los valores presentados.
Tabla 2 Desviaciones Estándar de las Demandas de los Escenarios.
Caudal [L/s]
Q15
Q23
Q26
Q3
Q21
Q10
Q17
Total
Escenario 5 Inicial
1.52
1.68
1.92
1.70
1.23
0.56
1.87
10.48
Escenario 5 Final
1.15
1.73
1.47
2.11
1.62
0.79
1.68
10.55
Escenario 6 Inicial
-
1.69
-
-
1.28
0.56
1.82
5.35
Escenario 6 Final
-
1.69
-
-
1.70
0.00
1.87
5.26
Promedios de las Demandas de los Escenarios
Caudal [L/s]
Q15
Q23
Q26
Q3
Q21
Q10
Q17
Escenario 5 Final
0.07
0.08
0.02
0.07
0.04
0.02
0.05
Escenario 6 Final
-
0.04
-
-
0.05
0.00
0.06
Desviación Estándar de las Demandas de los Escenarios

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
25
Iván Camilo Viveros Góngora
Tabla 3 Mediana de las Demandas de los Escenarios.
Tabla 4 Medias de Presión.
En la tabla “medias de presión” (Tabla 4) se presentan los resultados de presión
relacionados con cada uno de los escenarios, medidos en metros de columna de agua. La
presión A es esencial para la construcción de los modelos, puesto que corresponde a la
altura del embalse al inicio de la red. La mayor presión a la entrada de la red la reportó el
Escenario 6 Final, el cual también cuenta con el mayor promedio de presiones.
Caudal [L/s]
Q15
Q23
Q26
Q3
Q21
Q10
Q17
Escenario 5 Final
1.12
1.72
1.46
2.14
1.62
0.79
1.68
Escenario 6 Final
-
1.69
-
-
1.69
0.00
1.85
Mediana de Las Demandas de los Escenarios
[M.C.A]
Escenario 5 Inicial
Escenario 5 final
Escenario 6 Inicial
Escenario 6 Final
Presión A
4.0455
4.0460
4.3844
4.4110
Presión B
3.8905
3.8913
4.3020
3.3316
Presión C
4.0312
4.0270
4.4275
4.4782
Presión D
3.4626
3.4619
3.9169
3.9517
Presión E
3.8555
3.8543
4.2527
4.2893
Presión F
3.4133
3.4125
3.8541
3.9093
Presión G
3.2986
3.2964
3.7434
3.7801
Presión H
3.3488
3.3493
3.8084
3.8873
Presión I
3.2807
3.2770
3.6483
3.6980
Medias de Presiones

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
26
Iván Camilo Viveros Góngora
Tabla 5 Desviación Estándar de Presiones de Escenarios.
Tabla 6 Mediana de Presiones de Escenarios.
Es importante analizar si los datos son precisos, o se encuentran dentro de un rango
adecuado de precisión; por este motivo se presentan dos indicadores estadísticos: la
mediana y la desviación estándar. Se puede inferir de las magnitudes de las desviaciones
estándar que la dispersión en el proceso de medición no fue considerablemente alta (del
orden de milímetros). Por otro lado, las medianas son bastante cercanas a las medias lo
cual indica que no hay un sesgo considerable en la toma de datos.
[M.C.A]
Escenario 5 Inicial
Escenario 5 Final
Escenario 6 Inicial
Escenario 6 Final
Presión A
0.0031
0.0032
0.0009
0.0011
Presión B
0.0022
0.0025
0.0010
0.0009
Presión C
0.0070
0.0070
0.0080
0.0080
Presión D
0.0065
0.0063
0.0059
0.0054
Presión E
0.0064
0.0060
0.0063
0.0064
Presión F
0.0052
0.0052
0.0068
0.0073
Presión G
0.0042
0.0045
0.0035
0.0072
Presión H
0.0022
0.0019
0.0010
0.0009
Presión I
0.0059
0.0053
0.0047
0.0048
Desviación Estándar de Presiones
[M.C.A]
Escenario 5 Inicial
Escenario 5 Final
Escenario 6 Inicial
Escenario 6 Final
Presión A
4.0453
4.0461
4.3845
4.4108
Presión B
3.8911
3.8913
4.3024
4.3318
Presión C
4.0347
4.0265
4.4311
4.4819
Presión D
3.4588
3.4586
3.9176
3.9481
Presión E
3.8568
3.8566
4.2548
4.2855
Presión F
3.4112
3.4112
3.8554
3.905
Presión G
3.2995
3.2991
3.7436
3.7867
Presión H
3.3485
3.3491
3.8088
3.8872
Presión I
3.2794
3.2794
3.6448
3.6961
Mediana de Presiones

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
27
Iván Camilo Viveros Góngora
3
Modelo Computacional
El presente proyecto de grado consideró la modelación estática y en período extendido de
los escenarios, en los programas REDES y EPANET. Éstos son ampliamente utilizados en el
campo profesional y cuentan con una base teórica sujeta a revisión y actualizada.
3.1 EPANET
EPANET es un programa que simula el comportamiento del agua en período extendido y
en estado estático en sistemas de tuberías presurizadas (United States Environmental
Protection Agency, 2013); además permite introducir diferentes accesorios como válvulas
y tanques. Se puede descargar de manera gratuita desde el sitio web de la Agencia de
Protección Ambiental de los Estados Unidos de América.
“Soluciona matemáticamente la red con el método del gradiente” y permite manejar tres
tipos de ecuaciones relativas a las pérdidas por fricción: Darcy-Wesibach, Hazen-Williams
y Chézy-Manning, así como la simulación del comportamiento de solutos en redes de
distribución (Saldarriaga, 2007).
3.2 REDES
El programa redes fue desarrollado en el Centro de Investigaciones en Acueductos y
Alcantarillados (CIACUA) del Departamento de Ingeniería Civil y Ambiental de la
Universidad de Los Andes (Saldarriaga, 2007). Se trata de un “software”que modela
sistemas de tuberías de flujo a presión. Está basado en investigaciones de diferentes
universidades; una de las más relevantes está relacionada con los criterios análogos de
optimización económica y diámetros de tuberías en redes de distribución de agua, cuyos
autores son Ronald Featherstone y Karim El-Jumaily (quiénes a su vez retoman el criterio
de Wu) (Saldarriaga, 2007).
Nacido en 1998 en un proyecto especial y desarrollado a través de diferentes proyectos de
grado, en el año 2001 se unificó (Saldarriaga, 2007). Está programado bajo el paradigma
orientado por objetos, su lenguaje computacional es Delphi, es compatible con el sistema
operativo Windows, utiliza dos ecuaciones de fricción (la unificación Colebrook-White y

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
28
Iván Camilo Viveros Góngora
Darcy-Weisbach, y Hazen-Williams), su método de cálculo es el del gradiente y el sistema
matricial es resuelto a través del método de Gauss o Factorización de Cholesky
(Saldarriaga, 2007).
3.2.1 Método del Gradiente
El método del gradiente fue desarrollado por EzioTodini , E.P.O Connell y R. Salgado
(Saldarriaga, 2007). Este método soluciona las ecuaciones de energía y masa
simultáneamente. Esto permite un grado mayor de precisión en períodos más cortos de
tiempo. Juan Saldarriaga explica el método en su libro “Hidráulica de Tuberías” con base
en el cual se basa ésta elucidación(Saldarriaga, 2007). Para entender el método se
presenta la ecuación de continuidad la cual es aplicable en flujo permanente.
𝑄𝑖𝑗 − 𝑄𝐷𝑖 + 𝑄𝑒𝑖 = 0
𝑁𝑇𝑖
𝑗 =1
Ecuación 6 Ecuación de Continuidad.
La nomenclatura “Q” representa un caudal de una tubería, “i” la nomenclatura del nodo,
“j” el rótulo de la tubería, “QD” el caudal demandado y “Qe” el caudal que es introducido
a ese punto de la tubería. Esta ecuación expresa la relación entre los caudales de las
tuberías y un determinado nodo: la suma de los caudales de los tubos asociados con un
determinado nudo, menos el caudal demandado, más el caudal que le es aportado,
resulta en cero.
El texto presenta la relación entre la ecuación de Darcy-Wesibach para pérdidas por
fricción y la de Colebrook-White.
𝑓 = 𝑓 ∗
𝑙
𝑑
∗
𝑣
2
2 ∗ 𝑔
Ecuación 7 Ecuación deDarcyWeisbach.
“Hf” representa las pérdidas por fricción, “f” el factor de fricción, “l” la longitud de la
tubería, “d” el diámetro, “v” la velocidad y “g” la gravedad. Las pérdidas por fricción son
directamente proporcionales a un factor, a la longitud y al cuadrado de la velocidad; éstas
son inversamente proporcionales al diámetro y a la gravedad.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
29
Iván Camilo Viveros Góngora
El lector puede preguntarse por el factor de fricción y la manera de calcularlo. Existen
diferentes ecuaciones, en este trabajo se utiliza Colebrook-White debido a que es
físicamente basada.
1
𝑓
= −2 ∗ 𝑙𝑜𝑔
10
𝑘𝑠
3.7 ∗ 𝑑
+
2.51
𝑅𝑒 ∗ 𝑓
Ecuación 8Ecuación de Colebrook-White.
“F” es el factor de fricción, “ks” la rugosidad de la tubería, “d” el diámetro y “Re” el
número de Reynolds. En términos de cálculo, esta ecuación se resuelve de manera no
explícita, es decir, a través de métodos numéricos. La unión de las ecuaciones de
DarcyWeisbach y Colebrook White resulta en una nueva que comprende una relación
entre caudal y pérdidas por fricción.
𝑄 = −2 ∗
2 ∗ 𝑔 ∗ 𝑑 ∗ 𝑓
𝑙
∗ 𝐴 ∗ 𝑙𝑜𝑔
10
𝑘𝑠
3.7 ∗ 𝑑
+
2.51 ∗ ѵ ∗ 𝑙
2 ∗ 𝑔 ∗ 𝑑
3
∗ 𝑓
Ecuación 9Ecuación Explícita para el Cálculo del Caudal a partir de las Ecuaciones de
Darcy-Weisbach y Colebrook-White.
Las letras conocidas como por ejemplo“g”, conservan la repsentación asignada
anteriormente, en este caso gravedad. “A” representa el área perpendicular al sentido del
flujo (en ocasiones denominada área mojada) y “ѵ" la viscosidad cinemática.
Se sabe que las pérdidas en un sistema están asociadas tanto con las pérdidas por fricción,
como con las pérdidas menores.
𝐻𝑖 = 𝑓 + 𝑘𝑚 ∗
𝑣
2
2 ∗ 𝑔
Ecuación 10 Energía Total Disponible.
En la ecuación que explica este concepto “H”representa pérdidas totales, “hf” pérdidas
por fricción, “km” factor de pérdidas menores, “v” velocidad y “g” gravedad.
Considérese cualquier tipo de pérdida asociada con diferentes accesorios. Las pérdidas
totales pueden ser modeladas a través de una ecuación con exponentes y constantes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
30
Iván Camilo Viveros Góngora
𝐻𝑡 = 𝛼 ∗ 𝑄
𝑛
+ 𝛽 ∗ 𝑄 + 𝛾
Ecuación 11 Pérdidas Totales.
Los factores "𝛼", "𝛽" 𝑦 "𝛾" son constantes. El exponente n depende de la ecuación de
pérdidas por fricción seleccionada, en este caso se utiliza DarcyWeisbach, por ende su
valor es 2. El segundo y el tercer término son necesarios únicamente cuando hay pérdidas
menores atípicas. De las dos ecuaciones de pérdidas totales se puede deducir una
expresión para 𝛼.
𝛼 =
𝑓 ∗
𝑙
𝑑
+ 𝑘𝑚
2 ∗ 𝑔 ∗ 𝐴
2
Ecuación 12 Constante de Pérdidas Totales.
Para cada una de las tuberías la pérdida de altura piezométrica puede ser expresada de
manera matricial, en cada uno de los tramos constituidos por dos nodos.
𝐴11 ∗ 𝑄 + 𝐴12 ∗ 𝐻 = − 𝐴10 ∗ [𝐻
0
]
Ecuación 13 Conservación de Energía.
A11 representa una matriz cuya diagonal contiene la ecuación de pérdidas totales, sus
dimensiones son NT*NT, donde NT es el número de tuberías.
Q es un vector de caudales con dimensión NT*1.
A12 es la matriz de conectividad cuyas dimensiones son NT*NN, donde NN es el número
de nudos. Indica de qué nudo parte la tubería y hacia qué nudo se dirige: -1 para el punto
inicial y 1 para el punto final.
H es el vector de alturas piezométricas desconocidas cuyas dimensiones son NN*1.
A10 es la matriz que contiene la información de los nudos con altura piezométrica
conocida. Su dimensión es NT*NS, con valores de -1 para aquellas filas conectadas a
alguno de estos nudos conocidos.
En un inicio se habló de la simultaneidad entre la ecuación de energía y la ecuación de
continuidad para el método del gradiente. Ésta última puede ser expresada a través de
matrices.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
31
Iván Camilo Viveros Góngora
𝐴21 ∗ 𝑄 = [𝑞]
Ecuación 14 Ecuación de Continuidad.
A21 es la matriz transpuesta de A12.
Q es el vector de caudales.
q es el vector de consumo u oferta de cada nodo cuyas dimensiones son NN*1.
Dado que se desea que las dos ecuaciones mencionadas estén en sinergia, pueden ser
representadas a través de matrices en una sola expresión.
𝐴11 𝐴12
𝐴21
0
𝑄
𝐻
=
− 𝐴10
∗
𝐻
0
𝑞
Ecuación 15 Expresión Ensamblada de Continuidad y Energía.
La parte superior de la matriz relaciona caudal y altura piezométrica, mientras que la parte
inferior representa la conservación de la masa en cada uno de los puntos; dado que no se
puede resolver el sistema matricial de manera directa, debe aplicarse un algoritmo
iterativo; el método del gradiente realiza una expansión truncada de una serie de Taylor
(Saldarriaga, 2007).
𝐻
𝑖+1
= − 𝐴21 𝑁 𝐴11
′
−1
𝐴12
−1
𝑥 𝐴21 𝑁 𝐴11
′
−1
𝐴11 𝑄𝑖
+ 𝐴10 𝐻
0
− 𝐴21 𝑄𝑖 − 𝑞
Ecuación 16 Expresión Iterativa de Alturas.
𝑄
𝑖+1
= 𝑙 − 𝑁
−1
𝐴11
′
− 𝐴11 𝑄
𝑖
− { 𝑁 𝐴11
′
−1
( 𝐴12 𝐻
𝑖+1
+ [𝐴10][𝐻
0
])}
Ecuación 17 Ecuación Iterativa de Caudales.
Con las dos ecuaciones de iteración, se establece el nivel de error o tolerancia deseado y
se calculan alturas y caudales.
3.2.2 Método de Gauss o Factorización de Cholesky

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
32
Iván Camilo Viveros Góngora
3.2.2.1 Factorización LU
La factorización LU permite expresar una matriz A como el producto de una matriz
triangular inferior L y una matriz triangular superior U. Si A es cuadrada (n*n) puede ser
reducida por reglones a una matriz triangular superior U; si U tiene pivotes, es decir, es
invertible, la factorización es única (Grossman, 2008).
A través del Método de Gauss A es transformada en una matriz triangular superior; sin
embargo los números en la diagonal no son llevados a 1 (aun cuando es posible); dicha
matriz corresponde a U.
A la derecha de las matrices se puede ver paso a paso las modificaciones que se realizan.
Las primera operación consisten en restar dos veces la fila 1 (R1) a la fila 3 (R3).
Posteriormente se le resta la fila 1 (R1) a la fila 4 (R4). Tanto a la fila 3 (R3) como a la fila 4
(R4) se les resta la fila 2 (R2). Finalmente se le resta 4 veces la fila 3 (R3) a la fila 4 (R4). A
través de este proceso se logra obtener una matriz triangular superior.
𝐴 =
𝑅3 → 𝑅3 − 2𝑅1
𝑅4 → 𝑅4 − 𝑅1
→
𝑅3 → 𝑅3 − 𝑅2
𝑅4 → 𝑅4 − 𝑅2
→
𝑅4 → 𝑅4 − 4𝑅3
→
= 𝑈
Para determinar cuál es la matriz U se expresa el procedimiento para llegar a la matriz
1
2
-1
4
0
-1
5
8
2
3
1
4
1
-1
6
4
1
2
-1
4
0
-1
5
8
0
-1
3
-4
0
-3
7
0
1
2
-1
4
0
-1
5
8
0
0
-2
-12
0
0
-8
-24
1
2
-1
4
0
-1
5
8
0
0
-2
-12
0
0
0
24

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
33
Iván Camilo Viveros Góngora
triangular superior en matrices elementales. La multiplicación de tales matrices permite
determinar L. Es necesario aclarar que para matrices cuadradas singulares, se puede hallar
A=LU; sin embargo su solución no es única.
𝐴 =
𝑈
→ 𝐿 =
Si A es una matriz que para ser triangular superior requiere alguna permutación, es
necesario aplicar una matriz de permutación P (Grossman, 2008). Se requiere modificar la
expresión general P*A=L’U’, donde la factorización corresponde a la matriz permutada.
Si la matriz A (m*n) es no cuadrada, se deben plantear sistemas de ecuaciones que
permitan su solución. Una matriz no cuadrada (m*n) puede ser factorizada en una matriz
triangular superior (m*m) con unos en la mitad y otra matriz triangular superior (m*n)
cuya primera fila corresponda a la primera fila de A. De la relación entre las incógnitas y el
producto esperado se pueden inferir los números correspondientes a las matrices.
1
0
0
0
0
1
0
0
2
0
1
0
0
0
0
1
1
0
0
0
0
1
0
0
2
0
1
0
0
0
0
1
1
0
0
0
0
1
0
0
0
1
1
0
0
0
0
1
1
0
0
0
0
1
0
0
0
0
1
0
0
3
0
1
1
0
0
0
0
1
0
0
0
0
1
0
0
0
4
1
1
0
0
0
0
1
0
0
2
1
1
0
1
3
4
1
0
2
4
4
1
5
4
1
5
A=
0
3
7
0
3
7
0
3
7
4
1
5
0
2
4
0
0
- 2/3
R1<->R3
R3->R3-(2/3)R2
0
0
1
4
1
5
1
0
0
P=
0
1
0
U=
0
3
7
L=
0
1
0
1
0
0
0
0
- 2/3
0
2/3
1
2
1
1
0
0
2
1
A=
-1
4
L=
a
1
0
U=
0
d
6
0
b
c
1
0
0

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
34
Iván Camilo Viveros Góngora
2𝑎 = −1 → 𝑎 = −
1
2
𝑎 + 𝑑 + 0 = 4 → 𝑑 = 4 +
1
2
=
9
2
2𝑏 = 6 → 𝑏 = 3
𝑏 + 𝑐 ∗ 𝑑 + 0 = 0 → 𝑐 = −
𝑏
𝑑
= −
3
1
9
2
= −
6
9
= −
2
3
Para resolver el sistema es importante plantear dos sistemas de ecuaciones. Sea Ax=b
entonces Ly=b. Una vez se halla “y” se procede a determinar los valores de “x”, Ux=y
(Grossman, 2008).
3.2.3 Descomposición de Cholesky
Las matrices simétricas son aquéllas para las cuales se cumple aij=aji es decir [𝐴] = 𝐴
𝑡
(Chapra & Canale, 2007). Éstas presentan grandes ventajas ya que requieren la mitad de
espacio de almacenamiento y de tiempo de resolución (Chapra & Canale, 2007). La
descomposición de Cholesky permite expresar una matriz como el producto de una matriz
triangular inferior y su transpuesta. Las ecuaciones son presentadas a continuación.
𝐴 = 𝐿 𝐿
𝑇
𝑙
𝑘𝑖
= (𝑎
𝑘𝑖
− 𝑙
𝑖𝑗
𝑙
𝑘𝑗
𝑖−1
𝑗 =1
)/(𝑙
𝑖𝑖
) 𝑝𝑎𝑟𝑎 𝑖 = 1,2, … , 𝑘 − 1
Ecuación 18 Ecuación de Cholesky (Chapra & Canale, 2007).
2
1
1
0
0
2
1
A=
-1
4
L=
- 1/2
1
0
U=
0
9/2
6
0
3
- 2/3
1
0
0

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
35
Iván Camilo Viveros Góngora
𝑙
𝑘𝑘
= 𝑎
𝑘𝑘
− (𝑙
𝑘𝑗
𝑘−1
𝑗 =1
)^2
Ecuación 19 Ecuación de Cholesky (Chapra & Canale, 2007).
A continuación se desarrolla la descomposición de Cholesky en una matriz, con base los
pasos propuestos en la literatura (Chapra & Canale, 2007).
𝐴 =
𝐿11 = 𝑎11
1
2
= 10.00
1
2
= 3.16
𝐿21 =
𝑎21
𝐿11
=
20.00
3.16
= 6.32
𝐿22 = 𝑎22 − 𝐿21
2
1
2
= 67.00 − 6.32
2
1
2
= 5.20
𝐿31 =
𝑎31
𝐿11
=
67.00
3.16
= 21.19
𝐿32 =
𝑎32 − 𝐿21 ∗ 𝐿31
𝐿22
=
245.00 − 6.32 ∗ 21.19
5.20
= 21.36
𝐿33 = 𝑎33 − 𝐿31
2
∗ 𝐿32
2
1
2
= 979.00 − 21.19
2
∗ 21.36
2
1
2
= 8.59
3.3 Modelo Hidráulico
Este proyecto de grado retomó el modelo calibrado y validado de la red elevada (Prieto
Gamboa, 2011), cuyo autor es César Mauricio Prieto Gamboa. Éste está disponible en
REDES y EPANET, los dos softwaresexplicados anteriormente. Su realización se basó en el
Escenario 5 Inicial. Puesto que se llevaron a cabo levantamientos topológicos y
10.00
20.00
67.00
20.00
67.00
245.00
67.00
245.00
979.00
3.16
0.00
0.00
3.16
6.32
21.19
10.00
20.00
67.00
6.32
5.20
0.00
0.00
5.20
21.36
=
20.00
67.00
245.00
21.19
21.36
8.59
0.00
0.00
8.59
67.00
245.00
979.00

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
36
Iván Camilo Viveros Góngora
topográficos, se contaba con las longitudes de los segmentos y sus coordenadas. La
información relativa a diámetros, rugosidades, tipo de fluido, altura inicial disponible y
demanda de nodos de extracción de caudal, también estaba disponible.
El análisis de sensibilidad de la rugosidad absoluta demostró que variaciones de 1000ks
comparadas con 100ks, 10ks, 1ks y 0.1ks no tenían efectos en la presión de entrada
(presión A); poseían una ligera influencia sobre la presión B (menos de 0.2 m.c.a) y sobre
la presión H (menos de 0.2m.c.a) (Prieto Gamboa, 2011). Esto explica los motivos por los
cuales las rugosidades absolutas no fueron consideradas como una variable relevante para
ser calibrada en el modelo.
La variable comparativa de calibraciónfue la presión debido a la alta complejidad del
sistema, a las condiciones de campo y objetivos del estudio; dentro de las variables
analizadas de la red se incluyeron: asignación de demandas, diámetros reales y
coeficientes de pérdidas menores, éstas últimas la incógnita del proceso.
3.3.1 Energía de Entrada
La energía de entrada, o energía inicial corresponde a la altura registrada en el primer
sensor de presión antes de que se ramifique la red. Se debe considerar que el modelo
inicia en este punto (presiónA) y además, se dispone de mediciones en condiciones
aproximadamente constantes. El valor que se introduce en el elemento embalse de los
diferentes programas es el promedio de los datos recogidos en campo, previa verificación
de una dispersión adecuada de datos.
3.3.2 Demandas en Nudos de Extracción de Caudal
Las demandas en los nudos de extracción de caudal cuentan con poca incertidumbre
debido a que fueron medidas directamente para cada uno de los escenarios en
condiciones hidráulicas aproximadamente estables. Los valores son insertados en los
puntos del modelo que los representan. Como se mencionó en la sección dedicada a la
medición de demandas, se utilizaron los métodos de recolección de datos de estudios
previos para hacer las medidas comparables; adicionalmente, se presentaron indicadores
estadísticos que permitieran juzgar la precisión como satisfactoria.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
37
Iván Camilo Viveros Góngora
3.3.3 Diámetros Reales
El diámetro en algunos casos es aproximado a los valores reportados por el distribuidor.
Esta suposición es inexacta, debido a que los diámetros reales son los que tienen una
influencia relevante en las condiciones hidráulicas y sus variaciones. Para cada diámetro
comercial se tomó el valor del diámetro real: 4” comprende el rango de diámetros de
101.6mm a 103.42, 3” se relaciona con el rango que va de 76.2mm a 80.42 y 2” abarca de
50.8mm a 54.58mm (Prieto Gamboa, 2011).
3.3.4 Coeficientes de Pérdidas Menores
La red elevada se caracteriza por tener tuberías cortas y una enorme cantidad de
accesorios (Prieto Gamboa, 2011) lo cual hizo relevante las pérdidas menores en el
proceso de calibración, al punto de ser la variable calibrada para cumplir con una buena
representación de los escenarios analizados. Para calificar la representatividad del modelo
se utilizaron 2 indicadores de bondad de ajuste: el coeficiente de determinación y el error
cuadrático medio aplicados a los promedios de las presiones.
Ilustración 18 Modelo Computacional Epanet.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
38
Iván Camilo Viveros Góngora
Ilustración 19 Modelo Computacional Redes (vista 3D).
3.3.5 Representatividad del Modelo
Una vez se posee un modelo que simula una situación de la realidad, se debe formular la
pregunta acerca de su fidelidad con respecto a los datos recogidos en campo. Dentro de la
literatura existe amplia diversidad de indicadores; sin embargo en este proyecto de grado
se seleccionaron el coeficiente de determinación (identificado con la notación 𝑟
2
) y el
error cuadrático medio.
3.3.6 Coeficiente de Determinación
El coeficiente de determinación es la proporción de variación de un parámetro medido en
campo con respecto a un modelo. Es decir, indica qué tan adecuadamente se representa
la variabilidad medida con respecto a la modelada. Sus valores oscilan entre 0 y 1: 0 indica
que no hay representatividad y 1 que hay una excelente representatividad de la variación.
Retoma los conceptos de suma de cuadrados del error y suma total de cuadrados.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
39
Iván Camilo Viveros Góngora
𝑅
2
= 1 −
𝑆𝑆𝐸
𝑆𝑆𝑇
Ecuación 20 Coeficiente de Determinación (Devore, 2005).
La suma de cuadrados del error o del residuo, relaciona los datos medidos y los datos
obtenidos en el proceso de simulación. Es útil utilizar el cuadrado de éstos, debido a que
una dispersión positiva o negativa podría alterar el estimativo. La SSE o suma de
cuadrados del error consiste en restar por cada uno de los valores tomados en campo, el
valor de la predicción modelada. Esta diferencia se eleva al cuadrado y se realiza una suma
con todos los datos reales disponibles. Finalmente se divide por el número de valores.
𝑆𝑆𝐸 =
𝑦𝑖 − 𝑦
2
𝑛
Ecuación 21 Suma de Cuadrados del Error (Devore, 2005).
La suma total de cuadrados es una suma cuantitativa de la cantidad total de variación de
los valores observados: corresponde a la suma de desviaciones cuadradas con respecto a
la media de la muestra observada en campo (Devore, 2005).
𝑆𝑆𝑇 = 𝑦𝑖 − 𝑦
2
Ecuación 22 Suma Total de Cuadrados (Devore, 2005).
Para el cálculo de los indicadores de bondad se utilizaron los promedios de las presiones
en cada uno de los puntos y fueron comparados con las que reportó el modelo de Epanet
y Redes para cada uno de los escenarios. Para garantizar que no hubiera variaciones, se
construyeron los escenarios en la red elevada y se concedieron quince minutos para que
las condiciones hidráulicas se mantuvieran relativamente constantes. Se tomaron los
datos durante diez minutos y con base en éstos se calcularon los indicadores.
3.3.7 Error Cuadrático Medio
El coeficiente de determinación permite al analista concluir acerca de la variación del
modelo con respecto a la dispersión de los datos. El error cuadrático medio, como su
definición lo indica, es un promedio del cuadrado del error; esto significa que de acuerdo
con su magnitud se puede inferir cuánto se puede esperar que un valor varíe con respecto

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
40
Iván Camilo Viveros Góngora
a una predicción de un modelo. Se debe resaltar que este indicador es siempre positivo
por lo cual la magnitud de la variación aplica para valores positivos y negativos.
𝑅𝑀𝑆 =
1
𝑛
∗ (𝑚𝑜𝑑𝑒𝑙𝑎𝑑𝑜𝑖 − 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑑𝑜𝑖
𝑛
𝑖=1
)
2
3.3.8 Indicadores de Representatividad
Los escenarios fueron construidos y a cada uno de ellos se le dieron más de 15 minutos
inicialmente para que las condiciones hidráulicas estuvieran relativamente constantes.
Posteriormente,se tomaron datos durante 10 minutos y con base en los promedios de
presión se reportaron los indicadores explicados anteriormente. La tabla precedente
contiene los valores de los coeficientes de correlación y de los errores cuadráticos medios
para cada uno de los escenarios.
Tabla 7 Indicadores Estadísticos.
Los indicadores estadísticos fueron satisfactorios. Si se considera que todos estuvieron por
encima de 0.93, se puede concluir que para todos los escenarios sobre los cuales se
basaron las mediciones, los datos tenían representada su variabilidad por lo menos en un
90%. El error cuadrático medio presentó valores ligeramente más altos que los reportados
por César Prieto. El escenario cuyo coeficiente de correlación era más cercano a 1 fue el 6
Inicial. Por el contrario, el escenario que reportó el menor 𝑟
2
fue el 6 Final. Estos
resultados eran de esperarse puesto que los escenarios iniciales (5 Inicial y 6 Inicial)
habían reportado ajustes satisfactorios en estudios anteriores. El RMS indica que la
variabilidad con respecto a la predicción, en promedio no supera los 0.11 m.c.a, lo cual no
representa ni siquiera el 3% de la magnitud de algunas de las mediciones.
[M.C.A]
R2
R.M.S
Escenario 5 Inicial
0.96
0.11
Escenario 5 Final
0.96
0.11
Escenario 6 Inicial
0.97
0.07
Escenario 6 Final
0.94
0.08
Indicadores Estadísticos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
41
Iván Camilo Viveros Góngora
Se puede afirmar que el modelo computacional planteado en estudios previos se ajusta
satisfactoriamente para todos los escenarios de este proyecto de grado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
42
Iván Camilo Viveros Góngora
4
Resultados
4.1 Procedimiento
Inicialmente se cerraron las válvulas y se abrieron los nudos de acuerdo con el escenario
que se deseara construir. Se esperaba quince minutos para garantizar que las condiciones
hidráulicas fueran relativamente constantes. Los programas computacionales de los
sensores de presión y el caudalímetro estaban en sincronía con los relojes de los
computadores.
Una vez se hacía la variación se anotaba y reportaba el tiempo exacto en el que sucedía y
se permitía en otra ventana de tiempo la estabilización del escenario final.
4.2 Ubicaciones
Los resultados se dividen de acuerdo con las ubicaciones del caudalímetro. Se intentó
encontrar lugares de alta variabilidad de caudal; sin embargo existen restricciones
importantes relacionadas con la distancia que debe tener el equipo de los diferentes
accesorios. No todos los segmentos de la red eran aptos para la medición. Se buscaron
espacios donde fuera posible instalar el caudalímetro y apreciar las tendencias en cada
uno de los escenarios.
4.2.1 Ubicación 1
El caudalímetro fue instalado en el tubo que conduce el agua a ser descargada en el nodo
Q17. En el siguiente esquema (Ilustración 1) puede ser apreciada su localización,
representada por un círculo rojo.
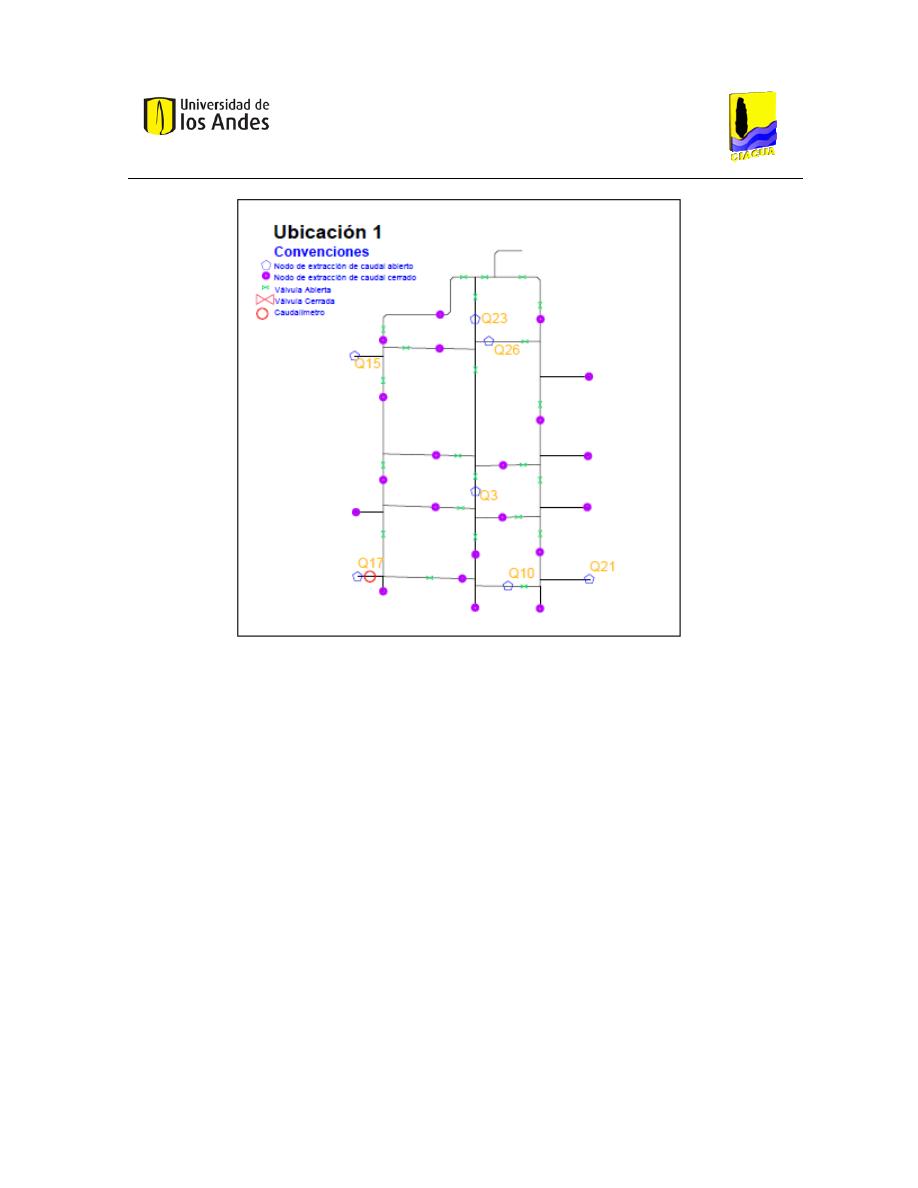
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
43
Iván Camilo Viveros Góngora
Ilustración 20 Ubicación 1.
4.2.1.1 Variación del Escenario 5 Inicial al Escenario 5 Final
Las mediciones iniciaron a la hora 9:03’28’’AM y terminaron a las 9:48’27’’AM. El cierre
súbito de la válvula se realizó a las 9:22’07’’. Los gráficos presentan la serie datos, la
media del escenario inicial y la media del escenario final, señalizadas con dos asíntotas
horizontales. La asíntota vertical representa el momento del cierre súbito de la válvula
para generar la transición de un escenario a otro.
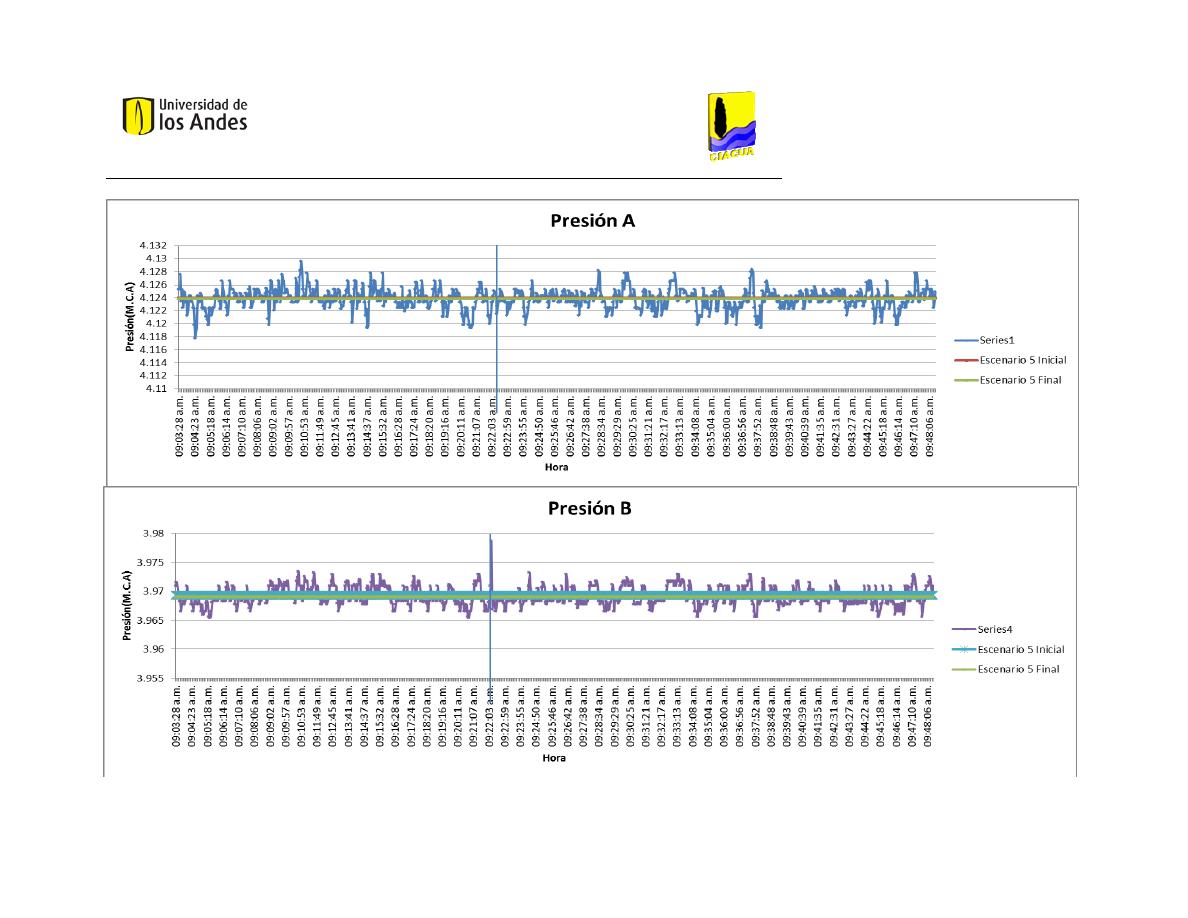
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
44
Iván Camilo Viveros Góngora
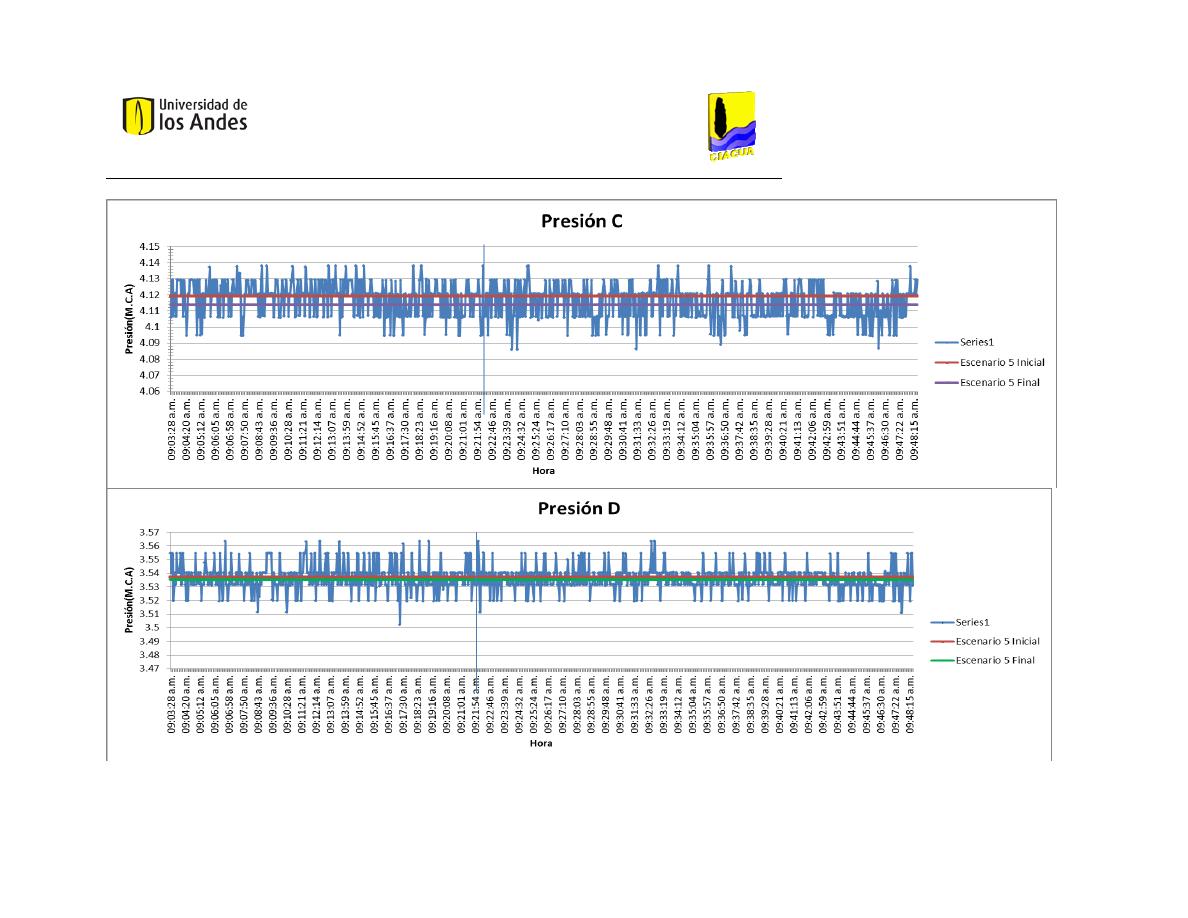
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
45
Iván Camilo Viveros Góngora
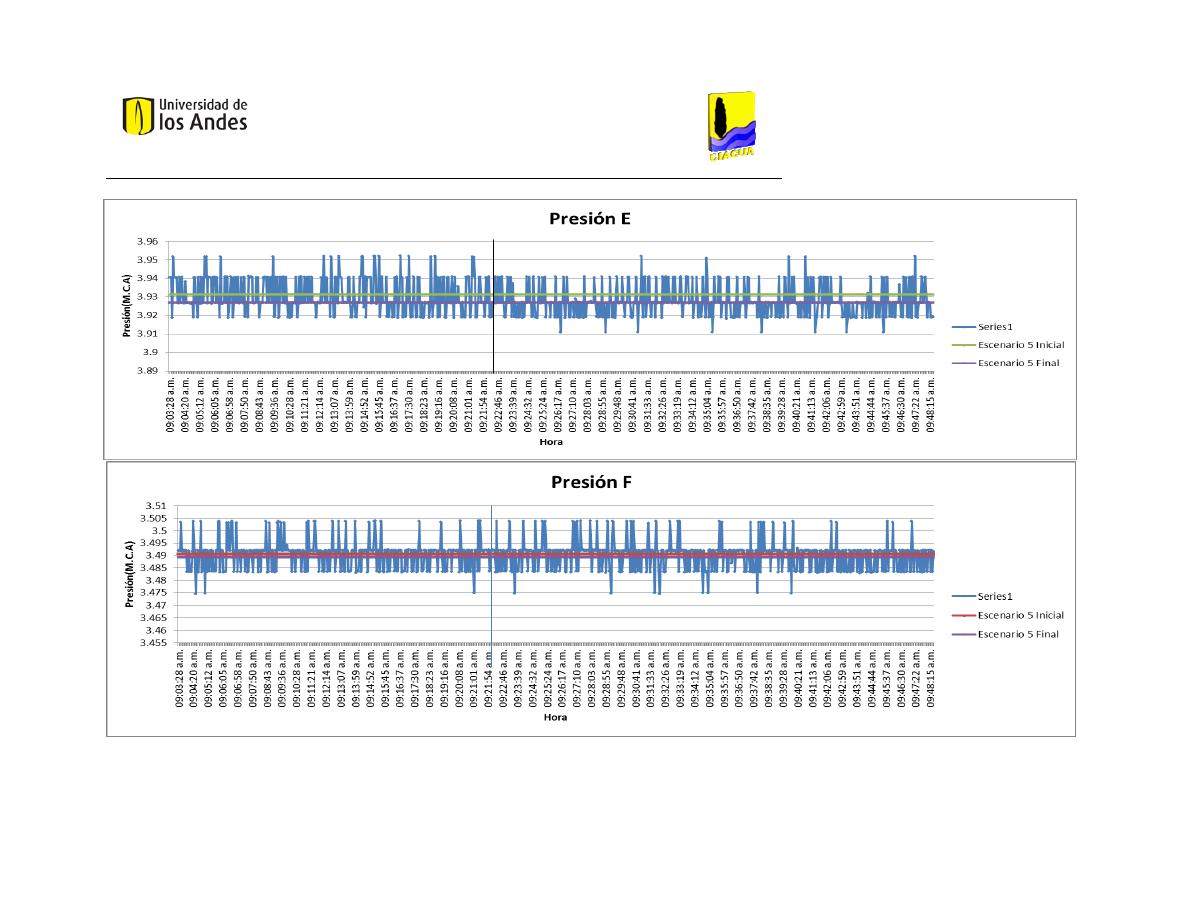
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
46
Iván Camilo Viveros Góngora
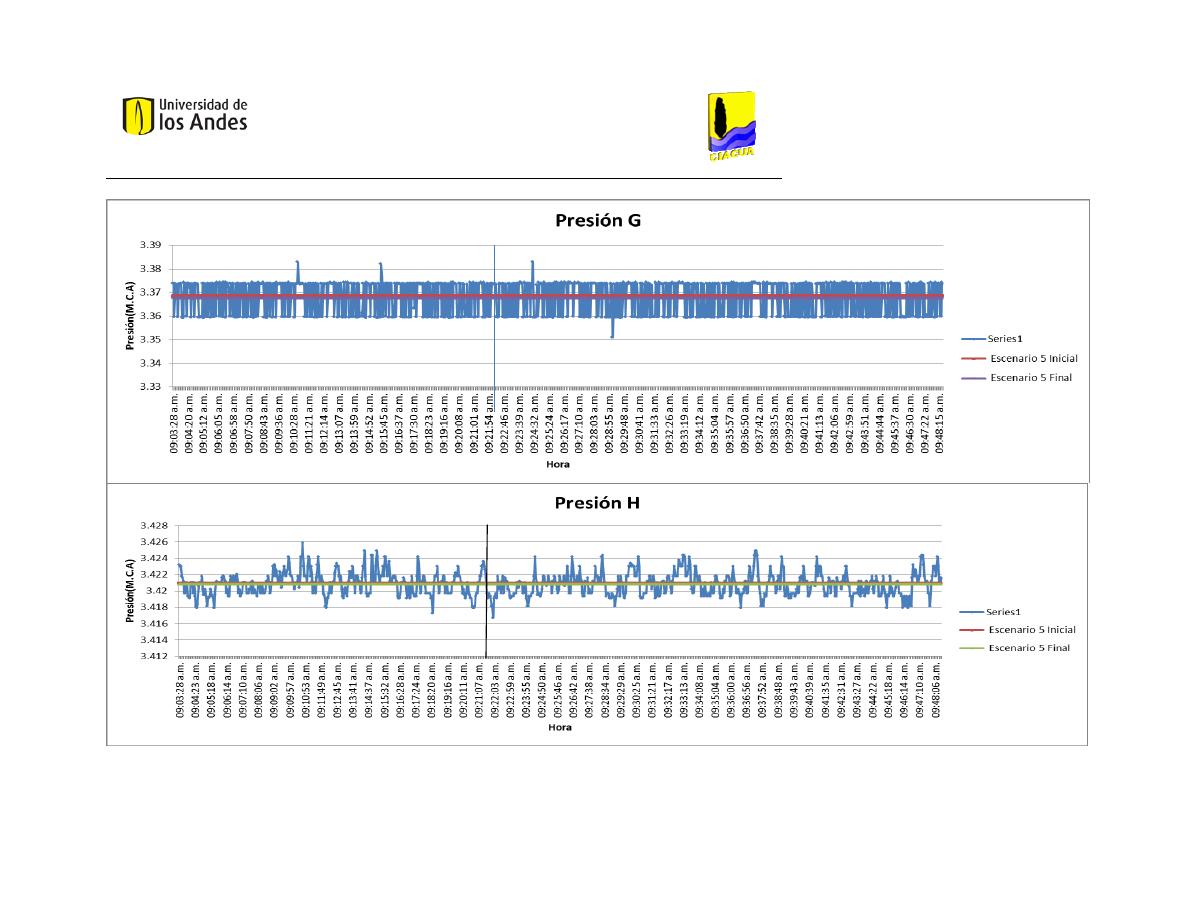
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
47
Iván Camilo Viveros Góngora
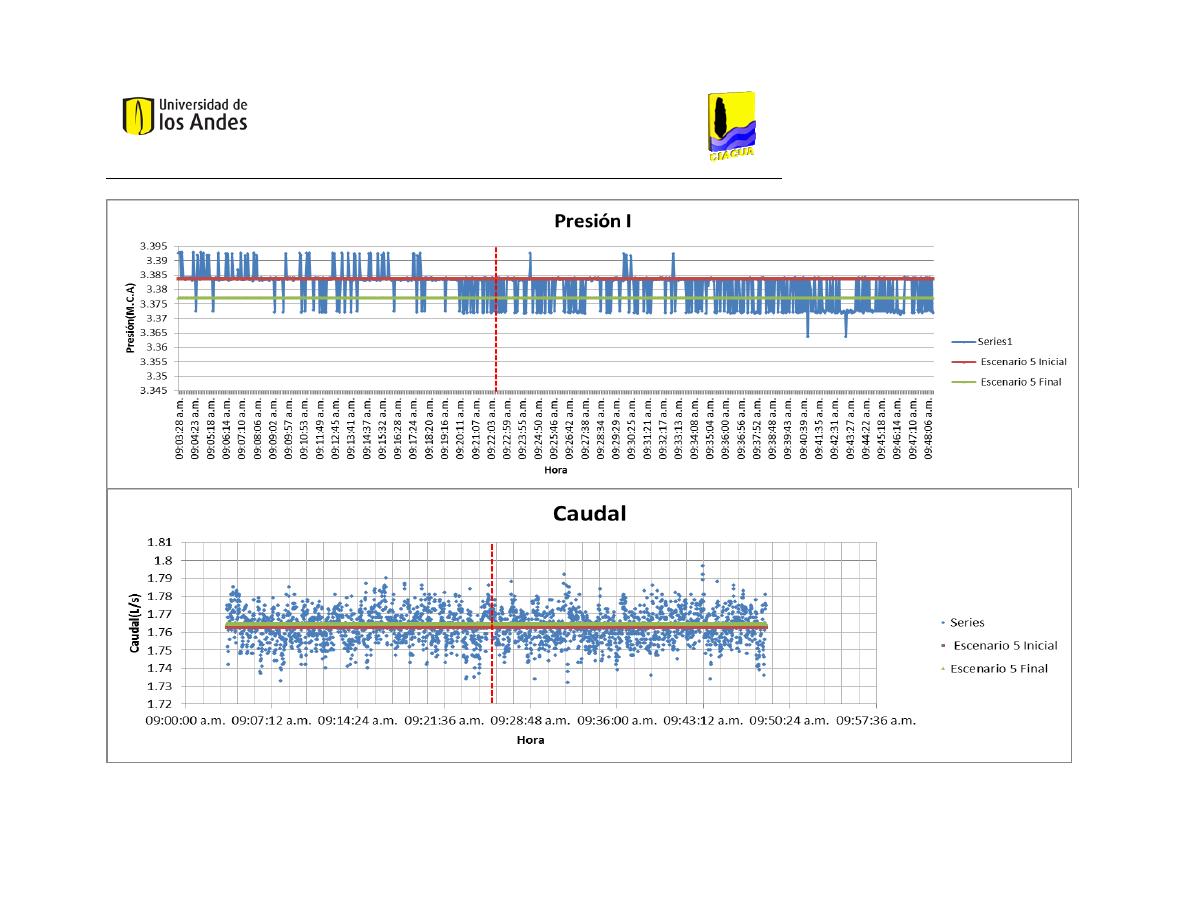
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
48
Iván Camilo Viveros Góngora

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
49
Iván Camilo Viveros Góngora
4.2.1.1.1 Descripción de Resultados
Se puede apreciar que entre la media del escenario inicial y la media del escenario final la
diferencia es poca (del orden de milímetros); esto se puede contemplar entre las asíntotas
horizontales de los gráficos. Una vez se realiza el cierre súbito de la válvula, la dispersión
de presiones no presente tendencias anómalas a excepción de la presión B, la cual en
sincronía con el evento, alcanza un valor máximo en el tiempo 9:22’12’’.
Para los Escenarios 5 Inicial y 5 Final las desviaciones estándares de la presión B son
0.0025 y 0.0022, respectivamente. La diferencia absoluta entre la media del Escenario 5
Final para la presión B y el valor máximo es de 0.0097, lo cual equivale a una variación
significativa si se considera que tiene una magnitud mucho mayor a la desviación
estándar.
A excepción de la presión B la variación entre las medias del Escenario 5 Final y el
Escenario 5 Inicial se encuentran dentro del rango de la varianza, lo cual dificulta ver
tendencias significativas posteriores al evento súbito de cambio de escenario.
Los datos tienden a centrarse en la media correspondiente a los escenarios estáticos. En
un principio, los valores de presión se dispersan en un rango alrededor del Escenario
Inicial en estado estable. Una vez se realiza el cierre de la válvula, el rango se centra en la
media del Escenario final.
4.2.1.2 Variación del Escenario 6 Inicial al Escenario 6 Final
A continuación se presentan los datos de la variación del Escenario 6 Inicial al Escenario 6
Final. Las mediciones iniciaron a las 9:10’31’’ AM y terminaron a las 10:00’30’’AM. El
caudalímetro estaba localizado en la Ubicación 1, descrita anteriormente. El cierre súbito
de la válvula se hizo a las 9:26’57’’. Las características relacionadas con representación de
datos, promedios y hora de variación se mantienen en las gráficas expuestas.
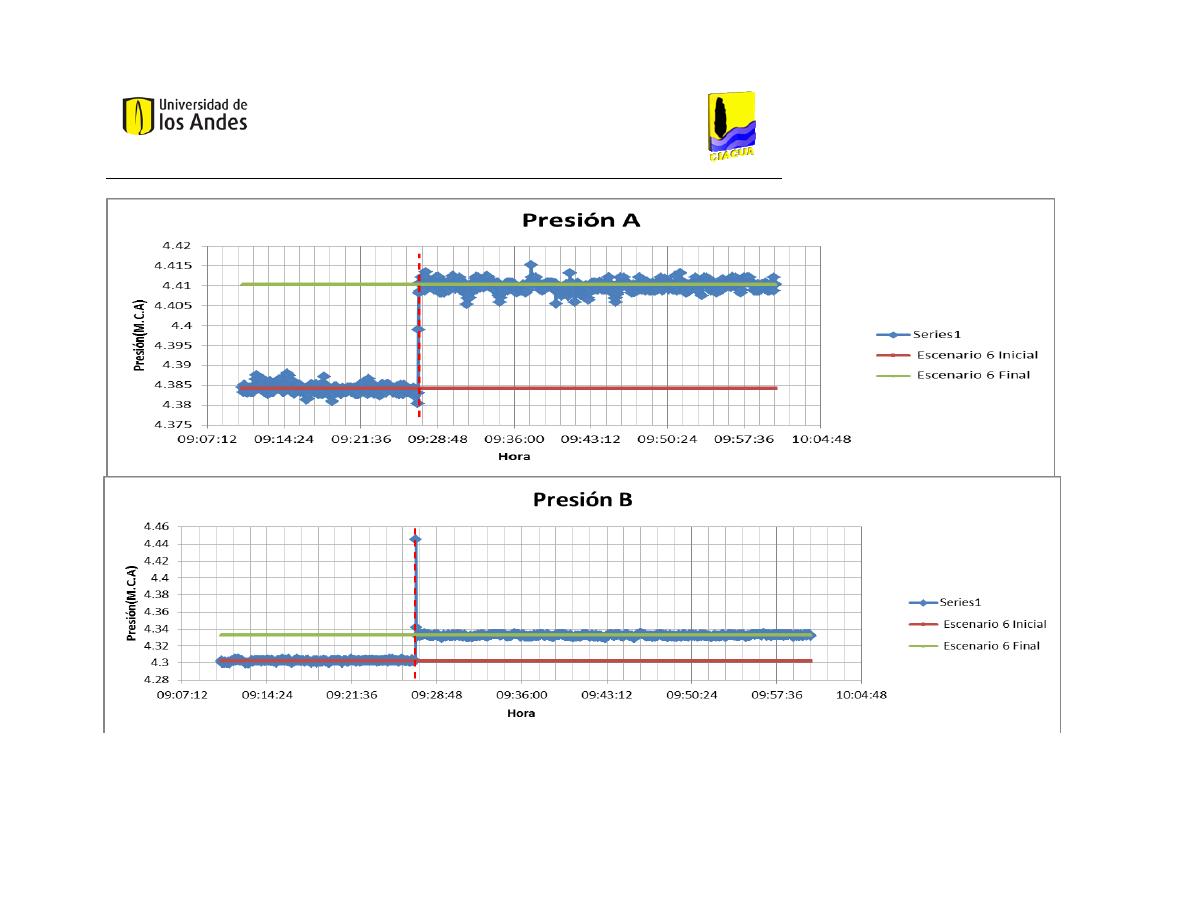
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
50
Iván Camilo Viveros Góngora
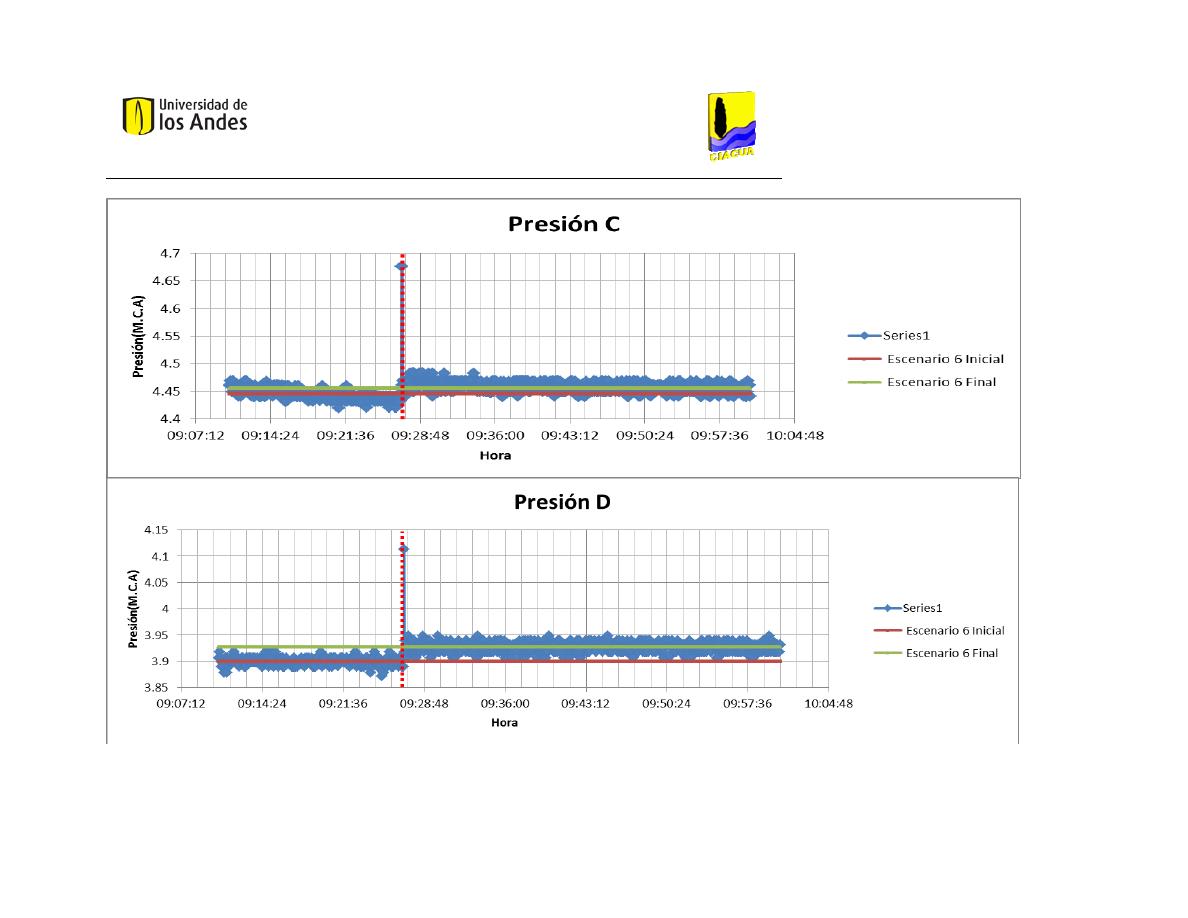
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
51
Iván Camilo Viveros Góngora
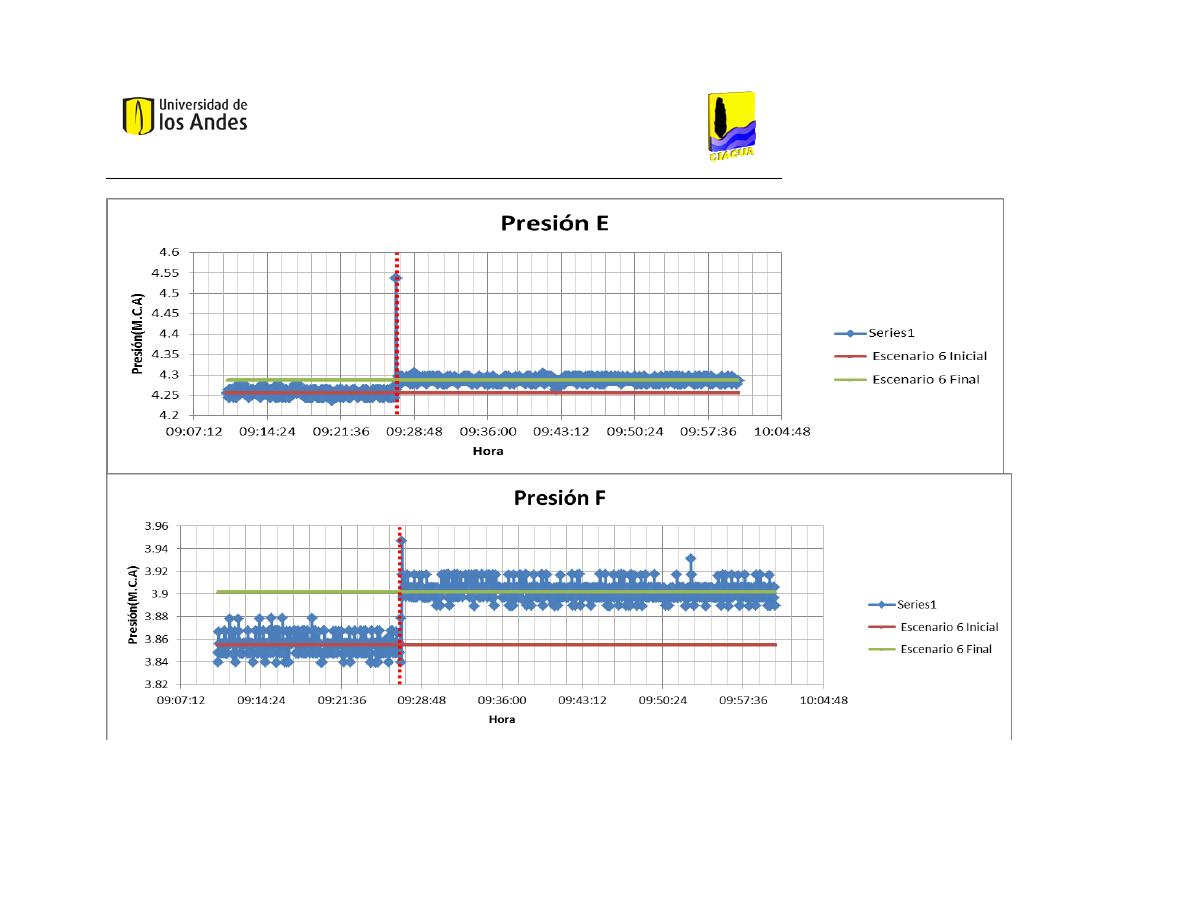
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
52
Iván Camilo Viveros Góngora
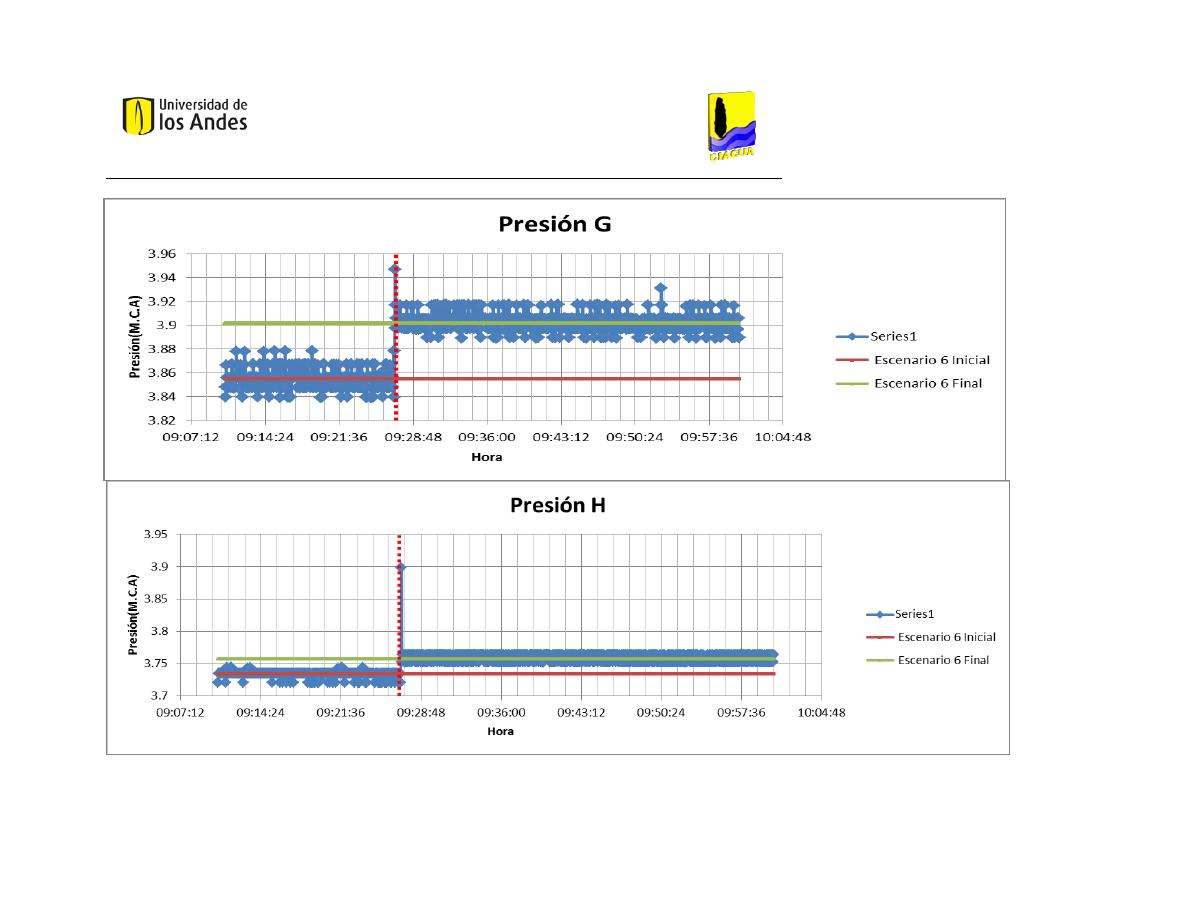
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
53
Iván Camilo Viveros Góngora
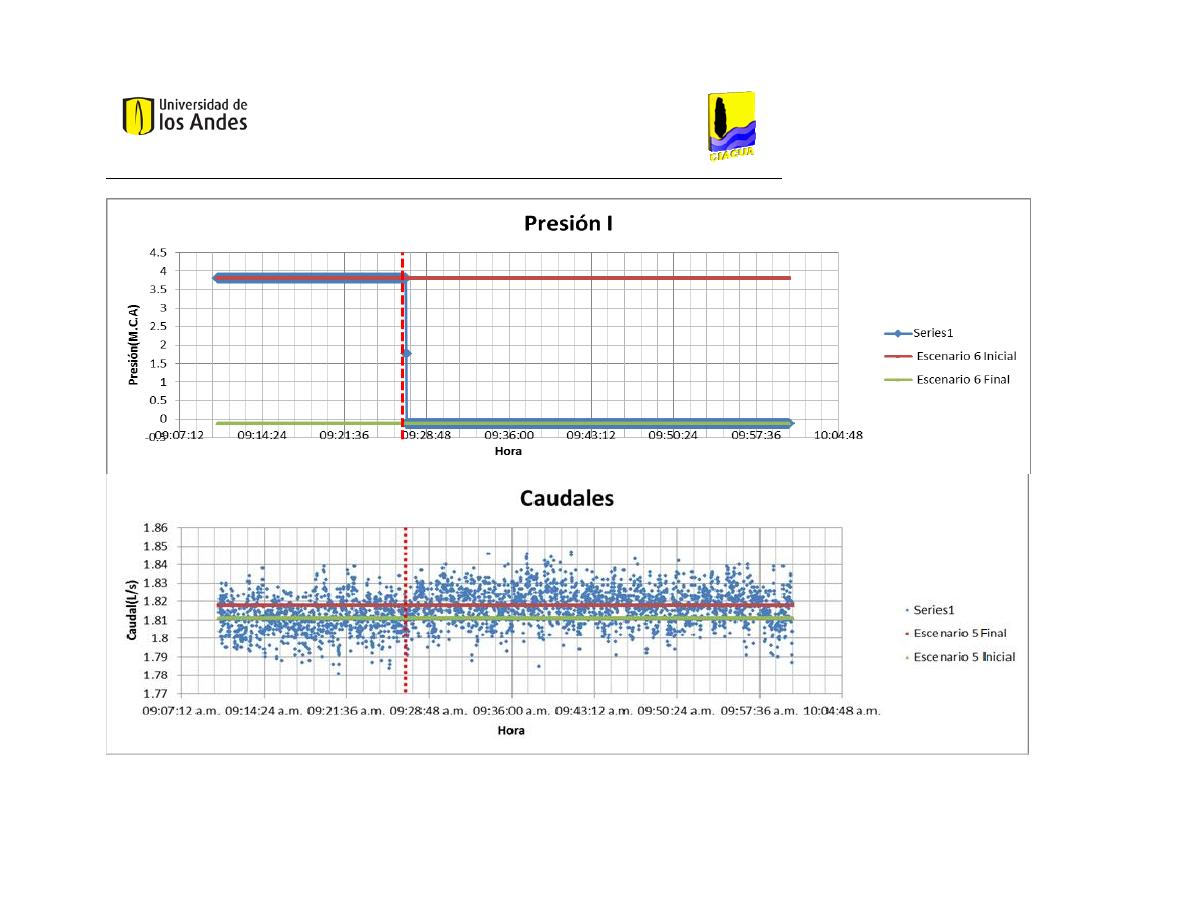
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
54
Iván Camilo Viveros Góngora

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
55
Iván Camilo Viveros Góngora
4.2.1.2.1 Descripción de Resultados
A diferencia del Escenario 5, el Escenario 6 presenta cambios abruptos en todos los puntos
donde se midió presión. En todos los sitios, a excepción de A y B, se aprecian variaciones
positivas de presión con desviaciones considerables con respecto a la varianza del
Escenario 6 Final. Se considera oportuno analizar los valores máximos y mínimos en
relación con el tiempo, con el fin de profundizar en las observaciones obtenidas.
Tabla 8 Tabla Valores Máximos de Presión.
Los valores máximos de presión en su mayoría ocurren en un lapso de tiempo menor o
igual a tres segundos con excepción de la presión A (presión de entrada a la red), sin
importar la distancia. Es posible afirmar con base en las gráficas que los picos que se
obtienen posteriores al cambio súbito entre escenarios, están considerablemente por
fuera del rango de variación aleatoria de los datos y en relación temporal con el cierre de
la válvula.
En lo relativo al caudal, los promedios no tienen una magnitud considerable por ende no
es evidente la variación. Sin embargo, se puede ver un leve cambio antes y después de la
variación de la válvula. Inclusive se puede identificar una zona de transición la cual
permite que los datos se centren en la media correspondiente a cada escenario. El tiempo
aproximado de estabilización para el punto medido es de 6 minutos, cuando los datos se
concentran en la tendencia del escenario final.
Valores
máximos
(M.C.A)
Hora
Tiempo después
del cambio
súbito(s)
Presión A
4.4153
09:37:37 a.m.
636
Presión B
4.4456
09:27:01 a.m.
3
Presión C
4.6761
09:27:01 a.m.
3
Presión D
4.1131
09:27:01 a.m.
3
Presión E
4.5371
09:27:01 a.m.
3
Presión F
3.9468
09:27:01 a.m.
3
Presión G
3.8982
09:27:01 a.m.
3
Presión H
3.8072
09:26:58 a.m.
1
Presión I
3.8184
09:27:01 a.m.
3

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
56
Iván Camilo Viveros Góngora
Aun cuando los datos de presión presentan cambios evidentes durante el cierre súbito e la
válvula, es claro que antes de dicho suceso se centran en la media del Escenario Inicial.
Una vez se ha configurado el Escenario Final, los datos tienden a centrarse en la media el
Escenario estático; esto implica un desplazamiento del rango en el cual se dispersan los
datos.
4.2.2 Ubicación 2
El caudalímetro fue localizado en la tubería que alimentaba el nudo de extracción de
caudal Q21 y se procedió a hacer las variaciones en los diferentes escenarios.
Ilustración 21 Ubicación 2 del Caudalímetro.
4.2.2.1 Variación del Escenario 5 Inicial al Escenario 5 Final

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
57
Iván Camilo Viveros Góngora
La variación del Escenario 5 Inicial al Escenario 5 Final se realizó a las 9:34’58’’29AM, con
el cierre de la válvula correspondiente. Los resultados de presión y caudal se presentan a
continuación. Los relojes de los diferentes computadores fueron sincronizados al inicio de
la medición. Las mediciones iniciaron a las 9:20’41’’AM y finalizaron a las 10:05’01’’ AM
con una duración de 44’14’’.
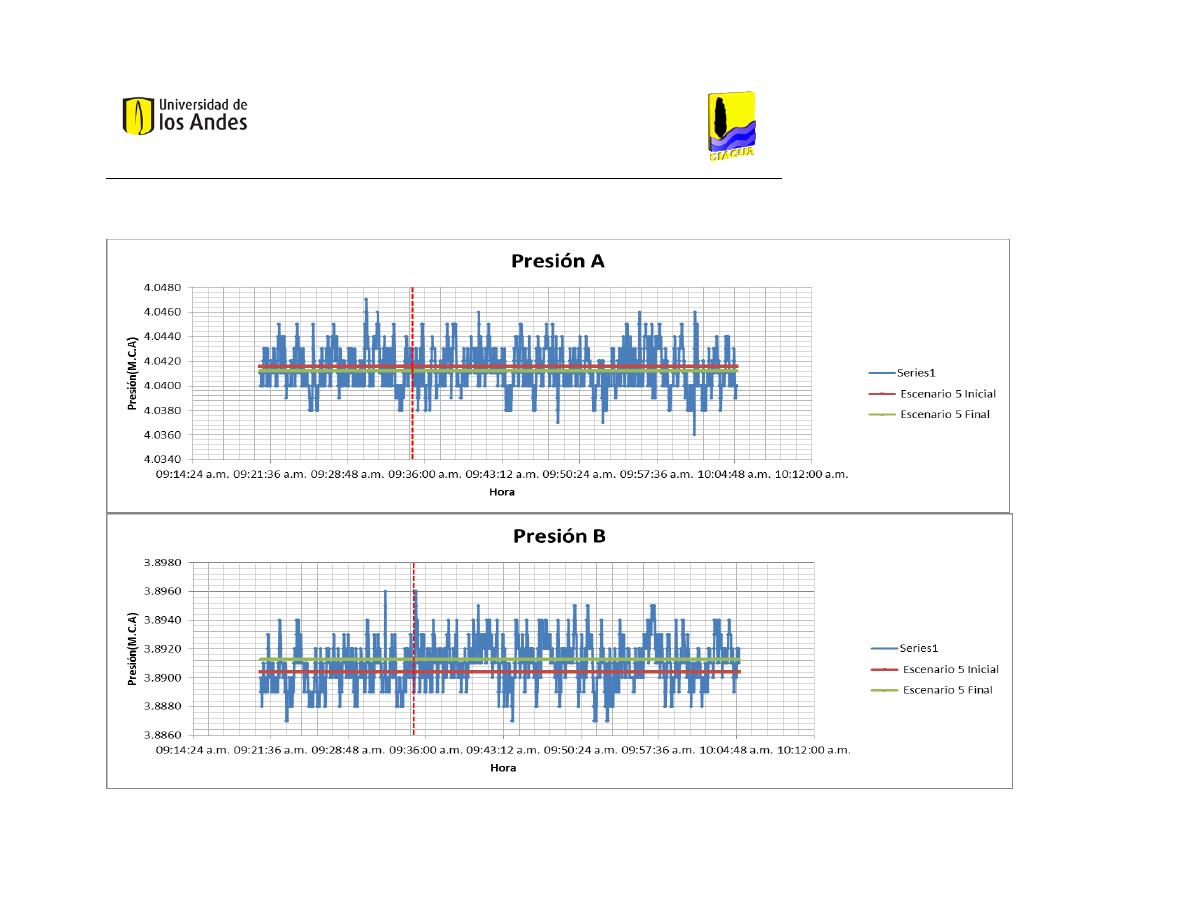
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
58
Iván Camilo Viveros Góngora
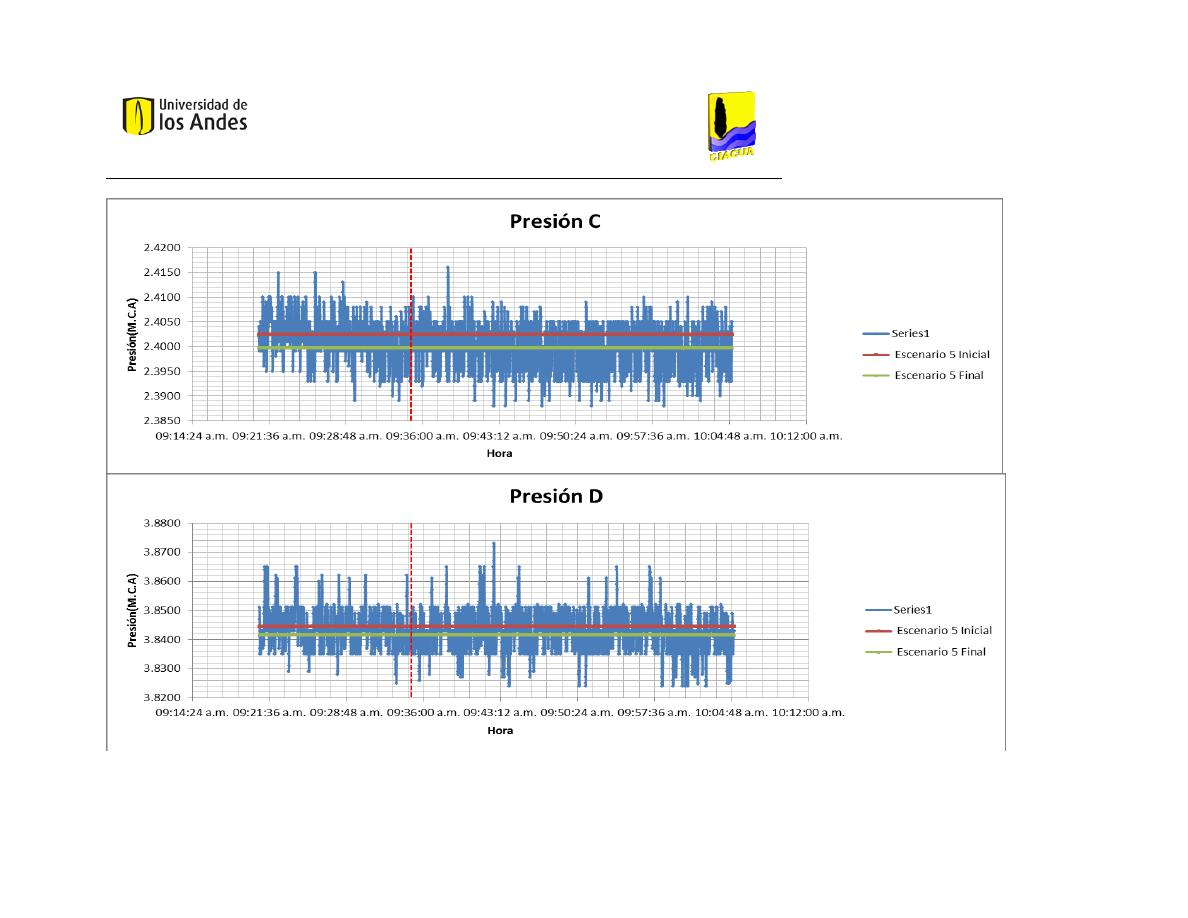
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
59
Iván Camilo Viveros Góngora
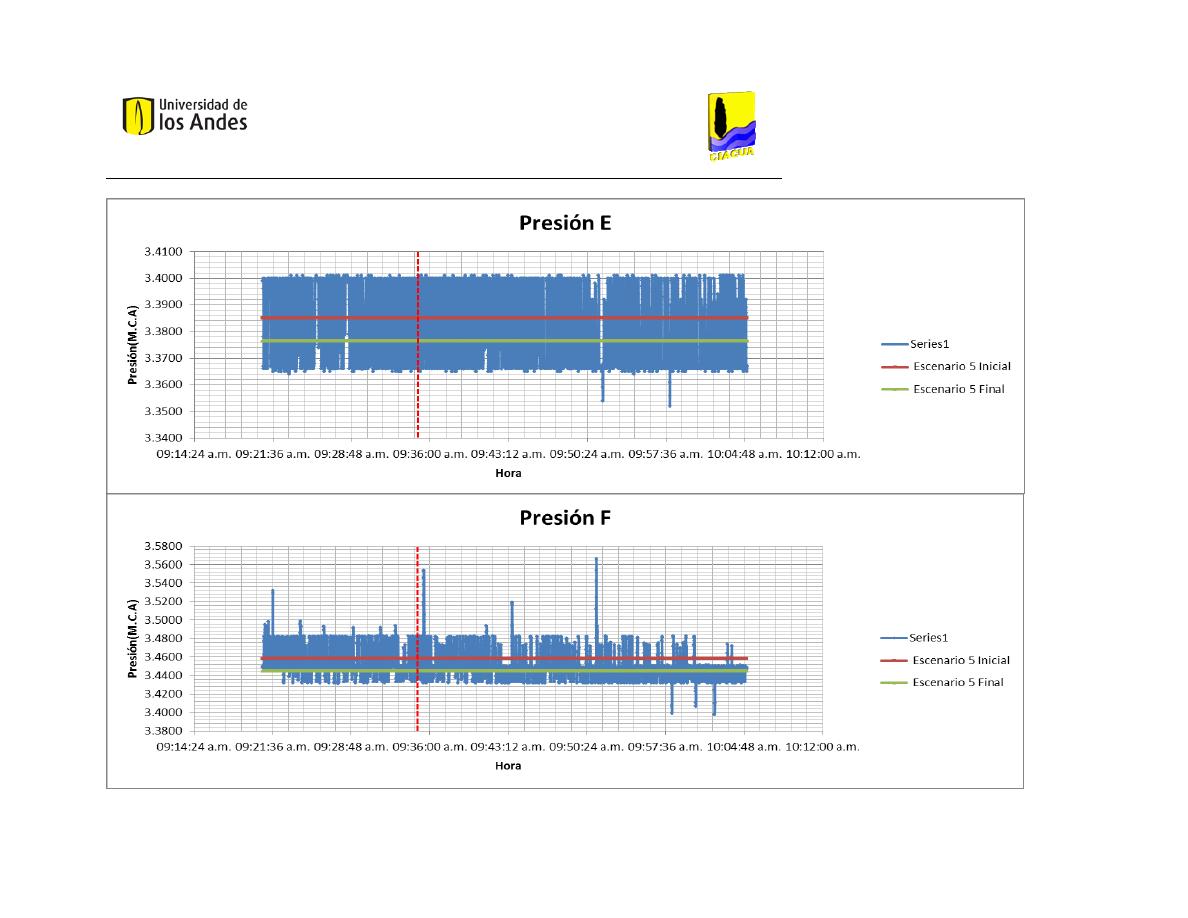
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
60
Iván Camilo Viveros Góngora
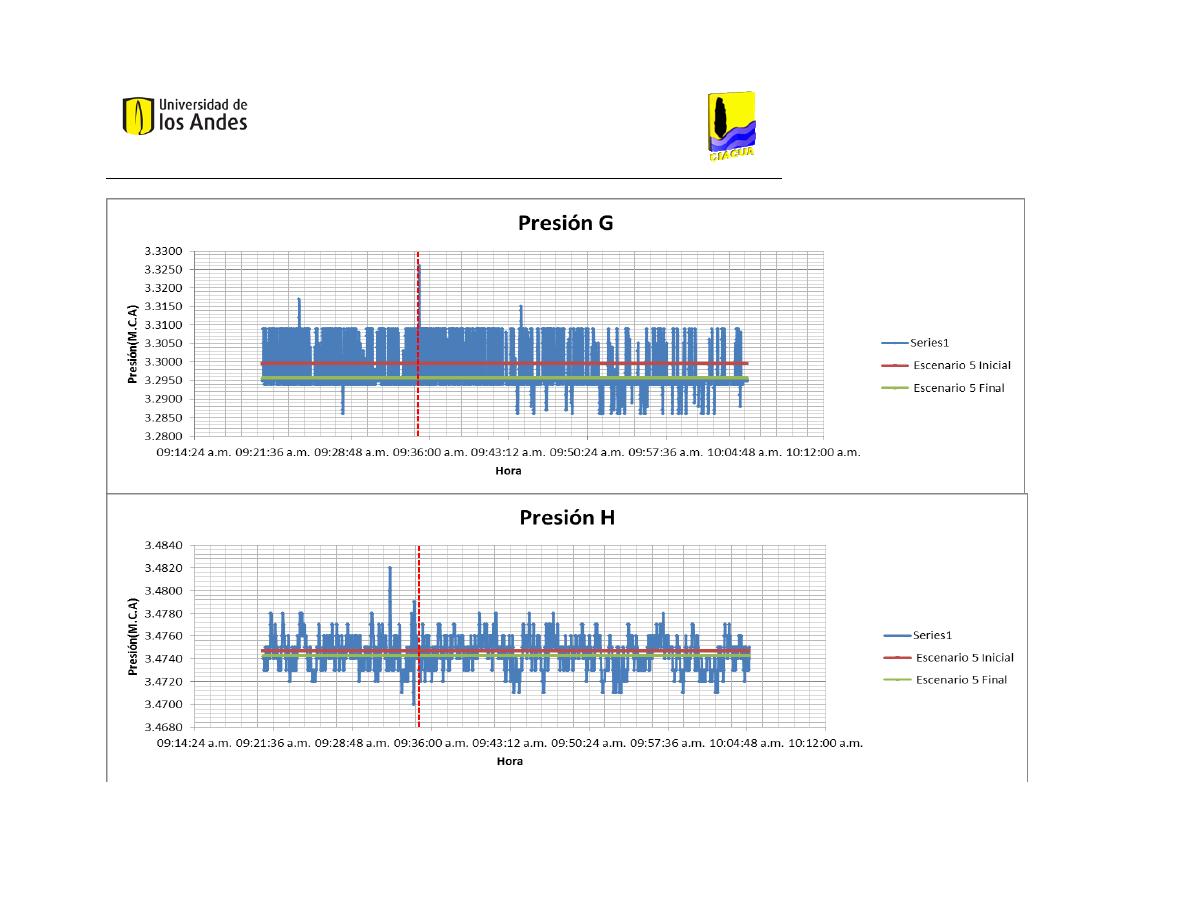
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
61
Iván Camilo Viveros Góngora
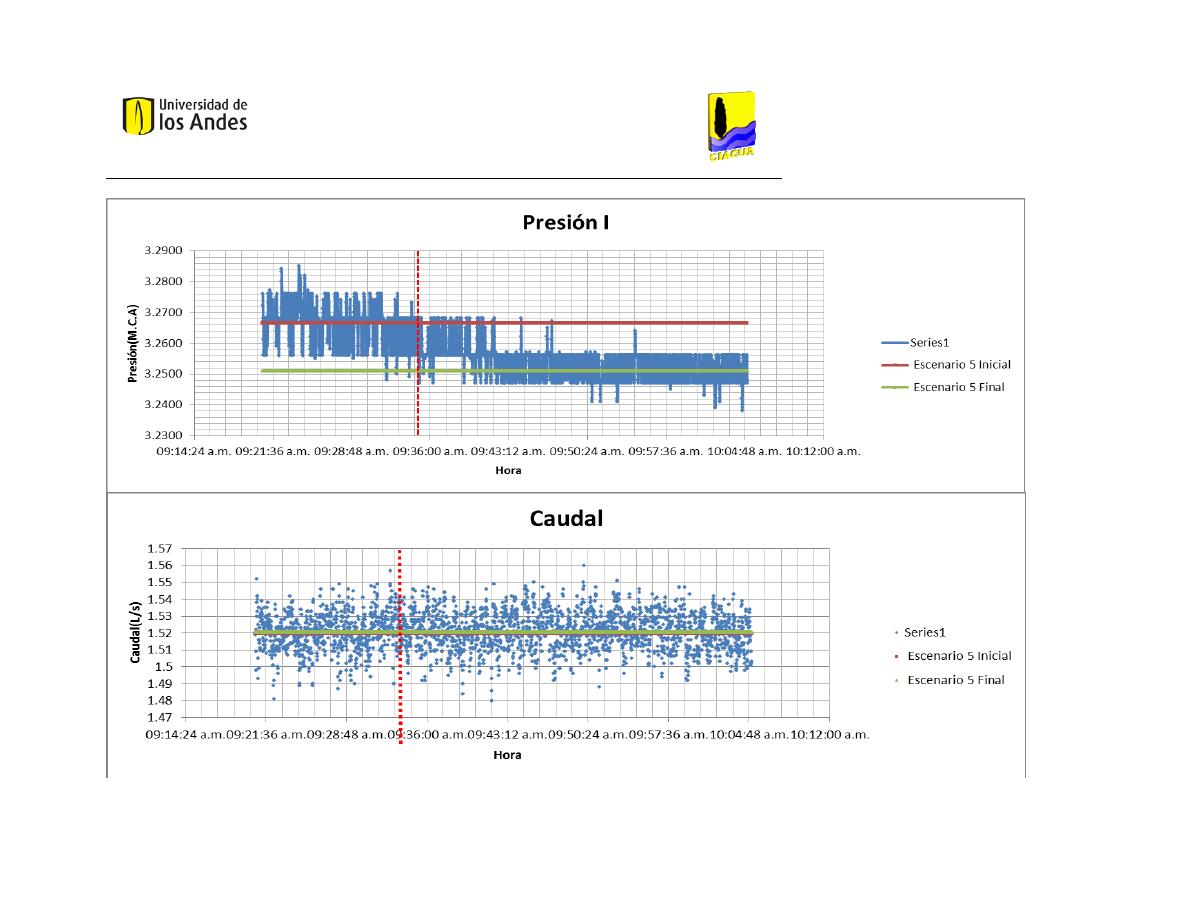
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
62
Iván Camilo Viveros Góngora

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
63
Iván Camilo Viveros Góngora
4.2.2.1.1 Descripción de Resultados
A diferencia de la Ubicación 1, en la Ubicación 2 se pueden apreciar máximos, o
tendencias fuera de la desviación aleatoria en respuesta al cierre súbito de la válvula. El
perfil de los datos del sensor de presión G se asemeja a las distribuciones de presión a lo
largo del tiempo que se evidenciaron en el Escenario 6 en la Ubicación 1. Los datos del
sensor de presión B también alcanzan un máximo después del evento de variación, sin
embargo su magnitud no permite inferir que se trate de un evento extraordinario si se
considera que en lapsos de tiempo previos al cierre de la válvula hubo sucesos similares.
Otra característica de los datos que llama la atención son los valores mínimos: algunos de
éstos se desvían considerablemente de la tendencia, inclusive de los rangos de variación
que pueden ser apreciados; sin embargo, están distantes temporalmente del cambio
súbito del escenario. Por ejemplo, el punto de medición de presiones E reportó dos
mínimos considerablemente fuera de la tendencia más de quince minutos después del
momento de cambio súbito, algo similar ocurre con el punto de medición de presiones F.
Los datos de presión, a excepción de aquéllos relacionados con los segmentos temporales
cercanos al cierre súbito de la válvula, se centran en la media de los Escenarios en estado
estático. Si bien existe una dispersión de los registros de presión, éstos en un principio
están centrados en el Escenario Inicial. Después del cambio súbito del Escenario Inicial al
Escenario Final, se observa una transición que puede durar algunos minutos y finalmente
el rango de variación se ubica en el Escenario Final.
En lo respectivo al punto de medición de caudal, las medias tienen una diferencia bastante
pequeña y se encuentran dentro del rango de variación de los datos lo cual dificulta
identificar el período de transición y el momento en el cual se alcanza una relativa
estabilidad hidráulica. Se puede afirmar que el caudal en el punto de extracción de caudal
Q21 en este escenario es menos susceptible a los cambios que fueron propuestos en el
presente estudio.
4.2.2.2 Variación del Escenario 6 Inicial al Escenario 6 Final

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
64
Iván Camilo Viveros Góngora
Las mediciones iniciaron a las 8:44’55’’AM y terminaron a las 9:20’03’’AM. El cierre súbito
de la válvula se realizó a las 8:58’24’’25 AM. Los programas para la obtención de los datos
se encontraban sincronizados con los relojes de los respectivos computadores.
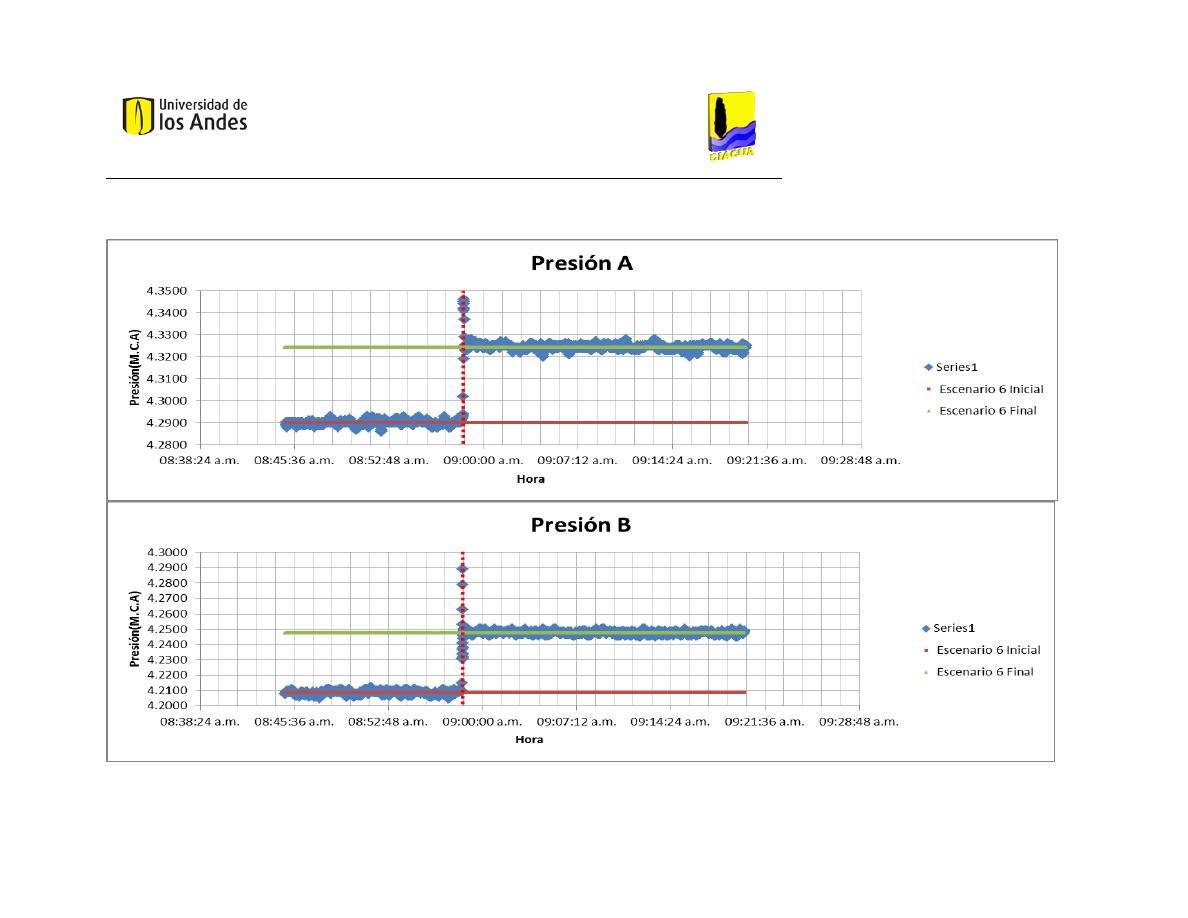
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
65
Iván Camilo Viveros Góngora
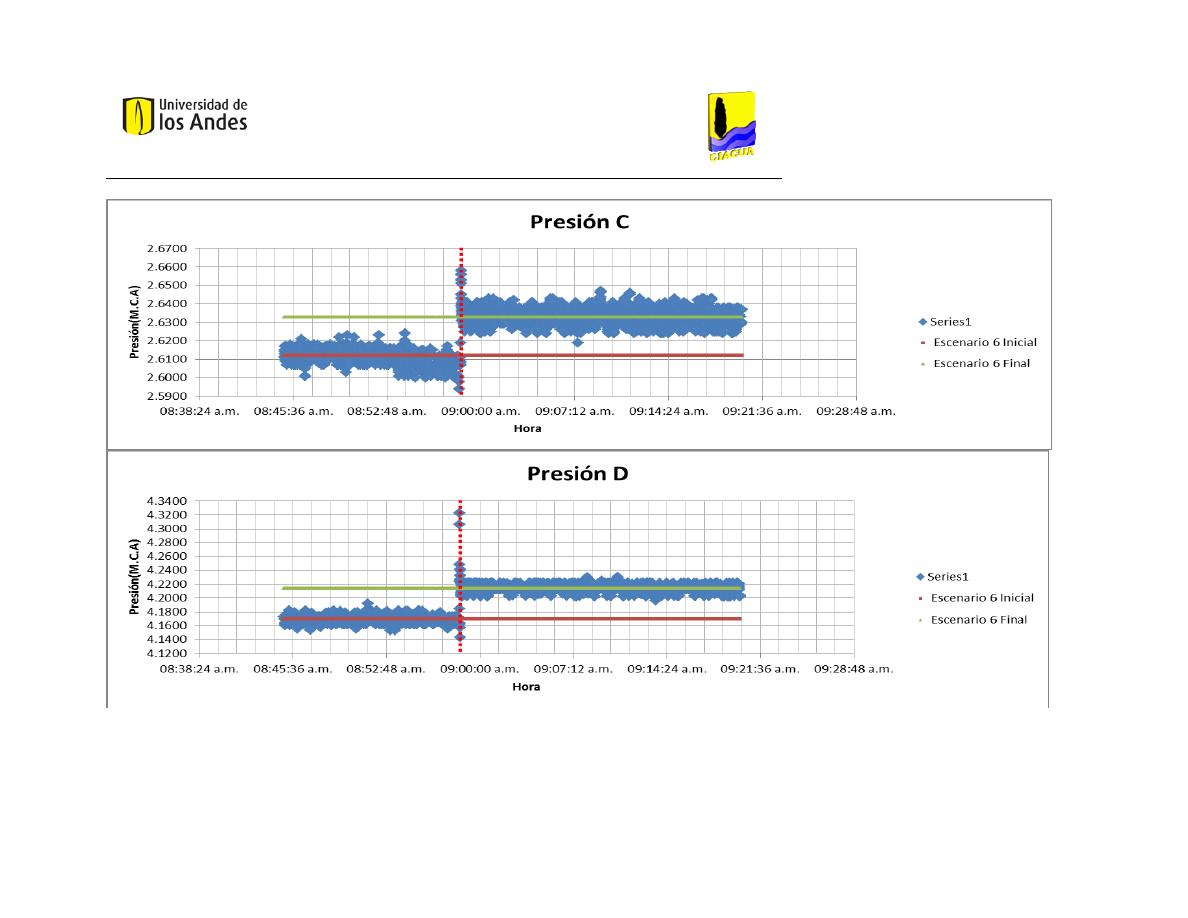
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
66
Iván Camilo Viveros Góngora
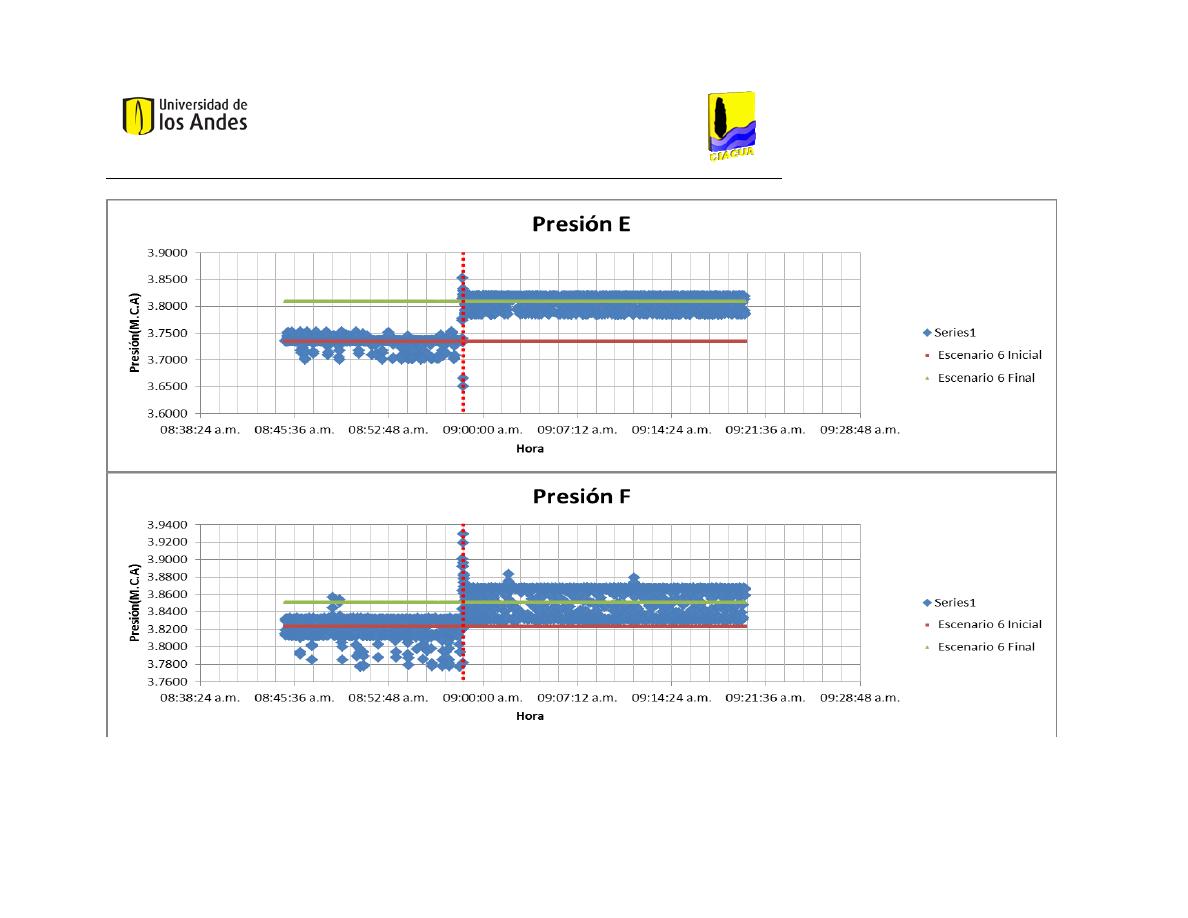
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
67
Iván Camilo Viveros Góngora
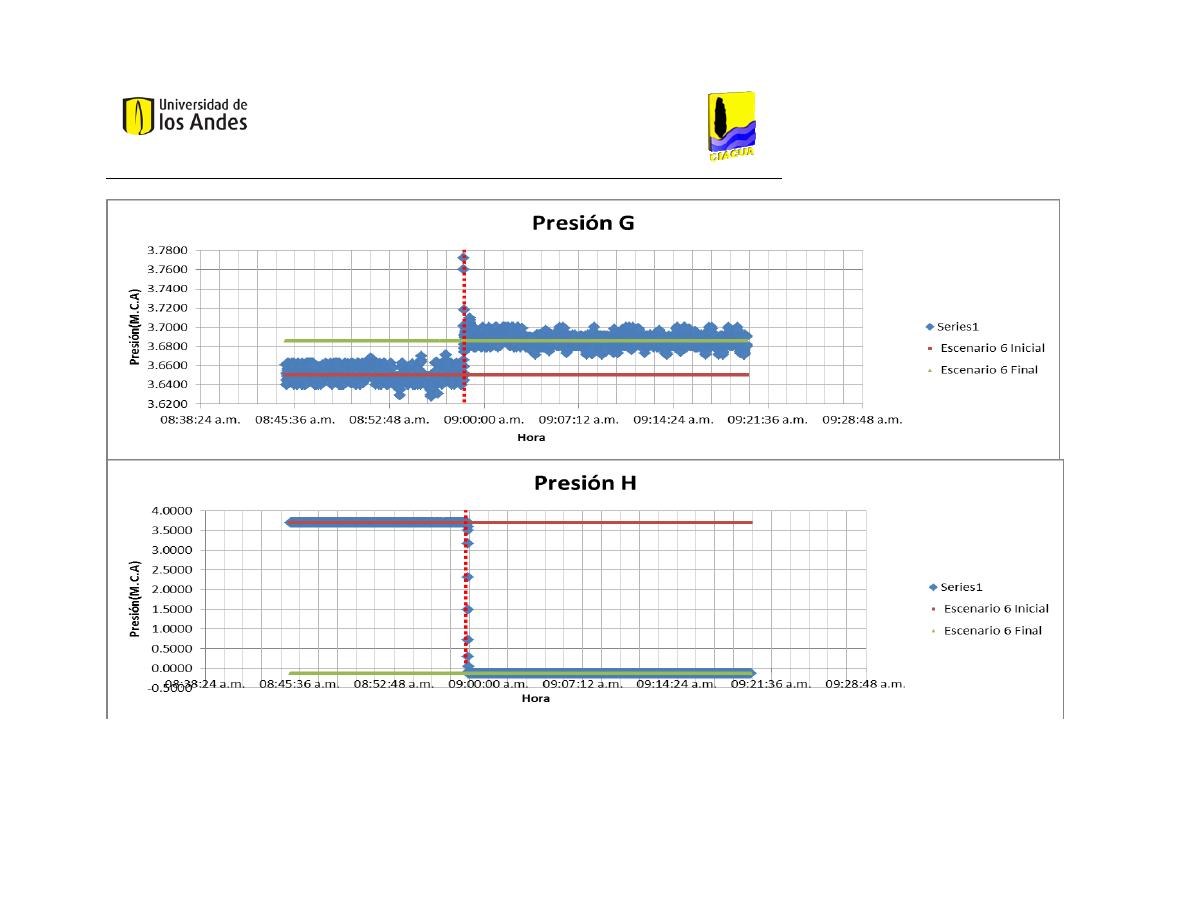
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
68
Iván Camilo Viveros Góngora
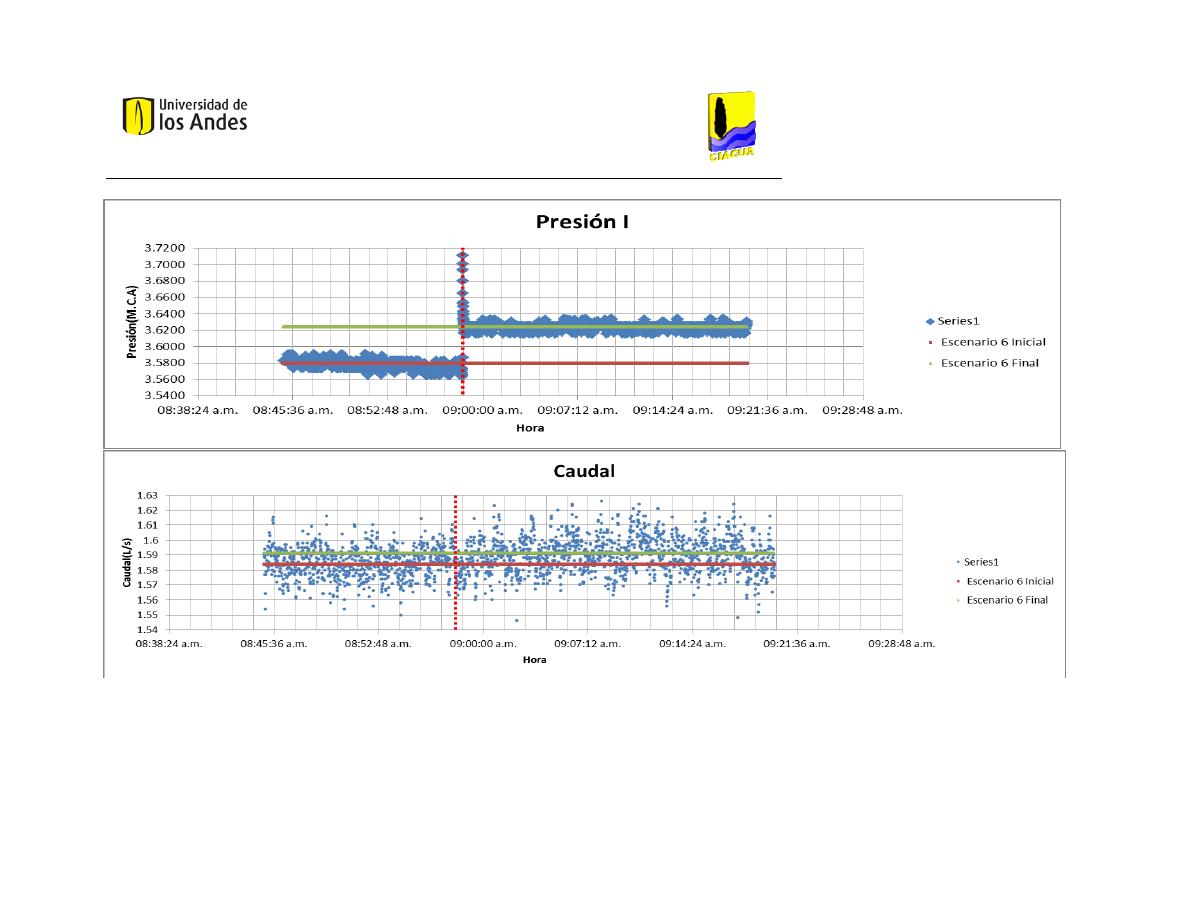
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
69
Iván Camilo Viveros Góngora

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
70
Iván Camilo Viveros Góngora
4.2.2.2.1 Descripción de Resultados
Una vez se realizó la variación de la válvula, dado que los datos de presión de los
escenarios en estado estático se concentraron en grupos distantes, la diferencia entre el
estado inicial y el estado final fue evidente. Justo después del cierre súbito de la válvula en
la mayoría de los casos hay aumentos significativos de presión que superan la varianza de
los escenarios iniciales y finales. Se considera conveniente analizar los valores máximos y
mínimos con el fin de determinar si existe una relación significativa entre el evento de
variación y la ocurrencia de los datos extremos.
Tabla 9 Valores Máximos del Escenario 6 Ubicación 2.
La tabla presenta los valores máximos para cada una de las presiones con los momentos
en los que éstos ocurrieron. También se puede leer la diferencia “absoluta” con respecto
al evento de variación: independientemente si el máximo ocurrió antes o después el valor
se reporta positivo. Similar a la tabla anterior, los máximos ocurren de 3, 4, 5 y 6 segundos
posteriores al cierre súbito de válvula.
¿Qué hace al punto H singular con respecto a los demás? Éste se localiza en una zona en la
cual el flujo es cero después de la variación, lo cual explica por qué tanto en las gráficas
como en el análisis de datos sus valores pueden estar por fuera de la tendencia. Sin
Valor Máximo(M.C.A)
Hora
Diferencia
absoluta con
el tiempo de
variación (s)
Presión A
4.346
08:58:28 a.m.
4
Presión B
4.289
08:58:28 a.m.
4
Presión C
2.658
08:58:28 a.m.
4
Presión D
4.323
08:58:27 a.m.
3
Presión E
3.853
08:58:27 a.m.
3
Presión F
3.929
08:58:30 a.m.
6
Presión G
3.772
08:58:28 a.m.
4
Presión H
08:51:08 a.m.
412
08:51:28 a.m.
392
08:51:29 a.m.
391
08:52:02 a.m.
358
Presión I
3.711
08:58:29 a.m.
5
3.700

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
71
Iván Camilo Viveros Góngora
embargo, todos los demás sensores reportaron un valor máximo unos segundos después
de la variación súbita, lo cual permite interrelacionarlos por lo menos un nivel temporal.
Tabla 10 Valores Mínimos del Escenario 6 Ubicación 2.
En los puntos A, C, F y G los valores mínimos ocurrieron inclusive antes de la variación,
con distancias temporales del orden de minutos. En aquéllas zonas donde se reportaron
dichos mínimos después del cierre de la válvula (D, E e I), tales eventos ocurrieron unos
cuántos segundos después de la variación.
El punto H debe ser analizado desde sus condiciones dado que queda desabastecido, el
valor mínimo corresponde al valor mínimo del equipo.
Es evidente la presencia de valores extremos de presión asociados al cambio súbito de
Escenario; sin embargo, se debe destacar las tendencias antes y después de éste. El rango
de dispersión de los datos de presión se ubica en el promedio de los Escenarios estáticos.
Inicialmente el rango se encuentra centrado en la media del Escenario Inicial. Una vez
ocurre el cambio súbito, se presentan datos extremos en la mayoría de los casos.
Valor Mínimo(M.C.A)
Hora
Diferencia
absoluta con el
tiempo de
variación (s)
Presión A
4.29
08:52:10 a.m.
374
08:52:11 a.m.
373
Presión B
4.21
08:47:30 a.m.
54
08:47:31 a.m.
53
08:57:24 a.m.
60
08:57:25 a.m.
59
08:57:26 a.m.
58
Presión C
4.14
08:58:19 a.m.
5
Presión D
2.59
08:58:28 a.m.
4
Presión E
3.65
08:58:28 a.m.
4
Presión F
3.65
08:50:37 a.m.
467
08:58:15 a.m.
9
Presión G
3.78
08:56:00 a.m.
180
Presión H
3.63
1513 registros 1513 registros
Presión I
-0.13
08:58:27 a.m.
3
08:58:28 a.m.
4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
72
Iván Camilo Viveros Góngora
Finalmente, tras un período de normalización, el rango de dispersión se centra en la media
del Escenario Final.
En el nudo de extracción de caudal Q21, la diferencia entre las tendencias del escenario
inicial y final puede verse claramente, lo cual no significa que las medias no se encuentren
aún dentro del rango de dispersión. El período de estabilización aún es difuso. Los valores
máximo y mínimo, ocurren minutos después de la variación: el caudal máximo sucede diez
minutos después de la variación de escenarios y posee una magnitud de 1.629 𝐿/𝑠
mientras que el caudal mínimo se presenta 4 minutos después del cierre de la válvula y
reporta un valor de 1.546L/s. El tiempo de estabilización es de aproximadamente 6
minutos.
4.2.3 Ubicación 3
El caudalímetro fue instalado en uno de los tubos de alimentación del nodo Q10.
Ilustración 22 Ubicación 3.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
73
Iván Camilo Viveros Góngora
4.2.3.1 Variación del Escenario 5 Inicial al Escenario 5 Final
La medición del Escenario 5 en el punto 3, inició a las 8:59’24’’AM y finalizó a las
9:46’53’’AM. El cierre súbito de la válvula fue llevado a cabo a las 9:16’07’’43AM. Los
relojes de los computadores se encontraban sincronizados.
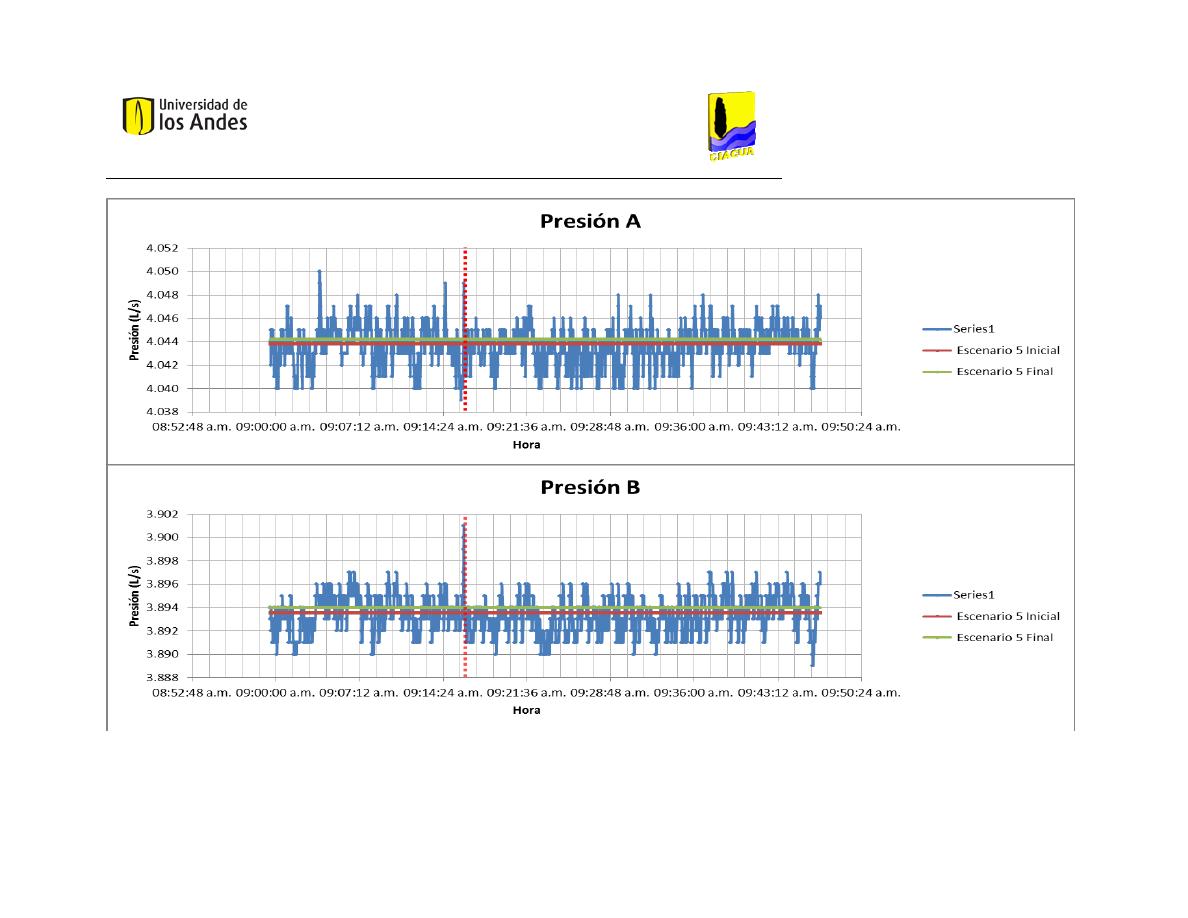
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
74
Iván Camilo Viveros Góngora
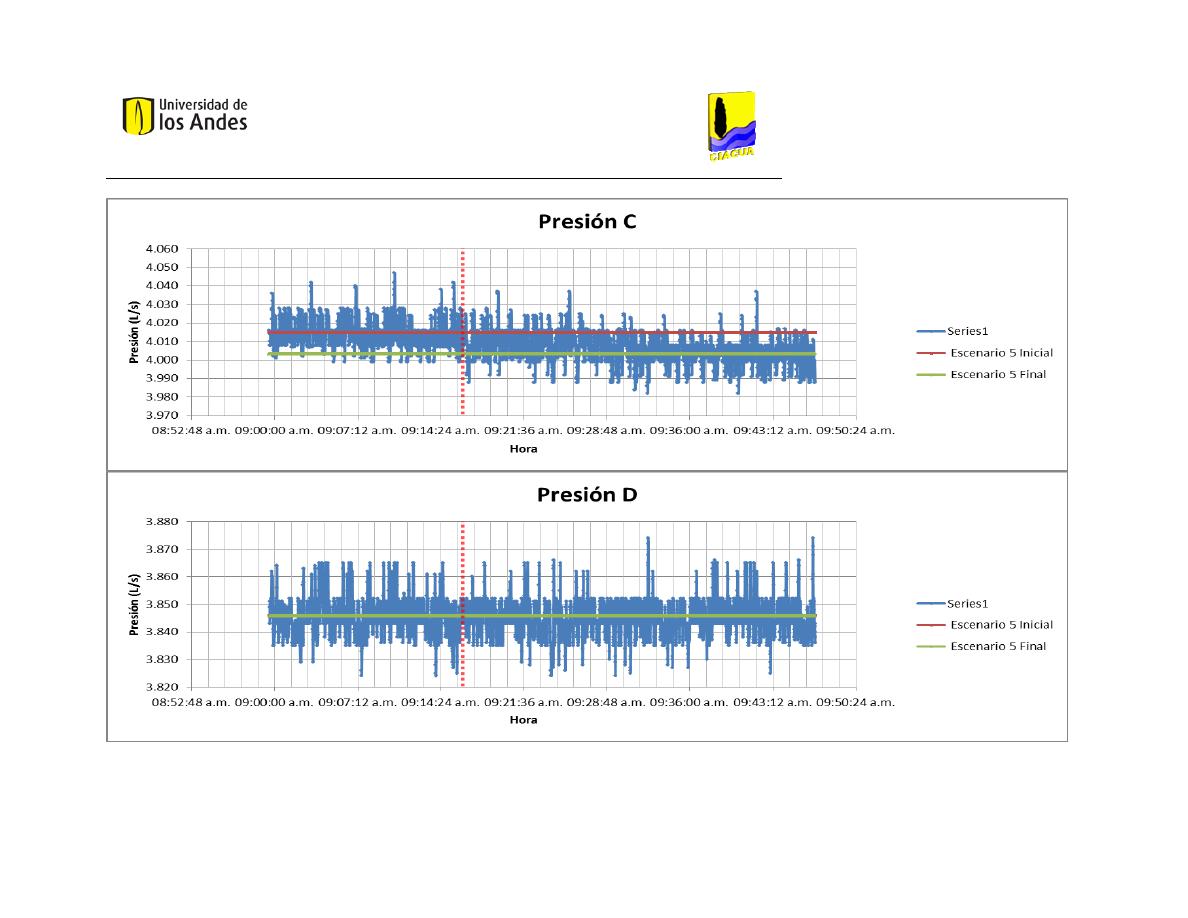
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
75
Iván Camilo Viveros Góngora
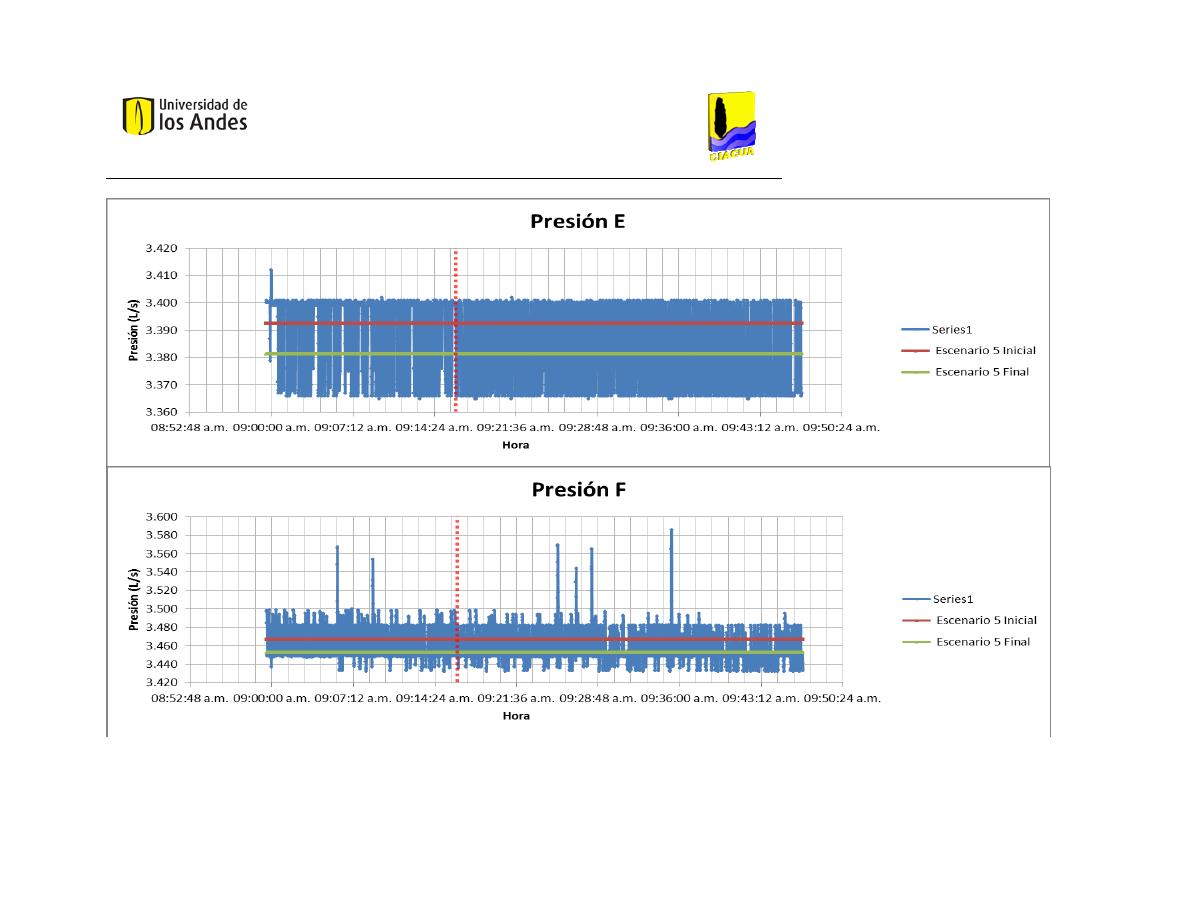
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
76
Iván Camilo Viveros Góngora
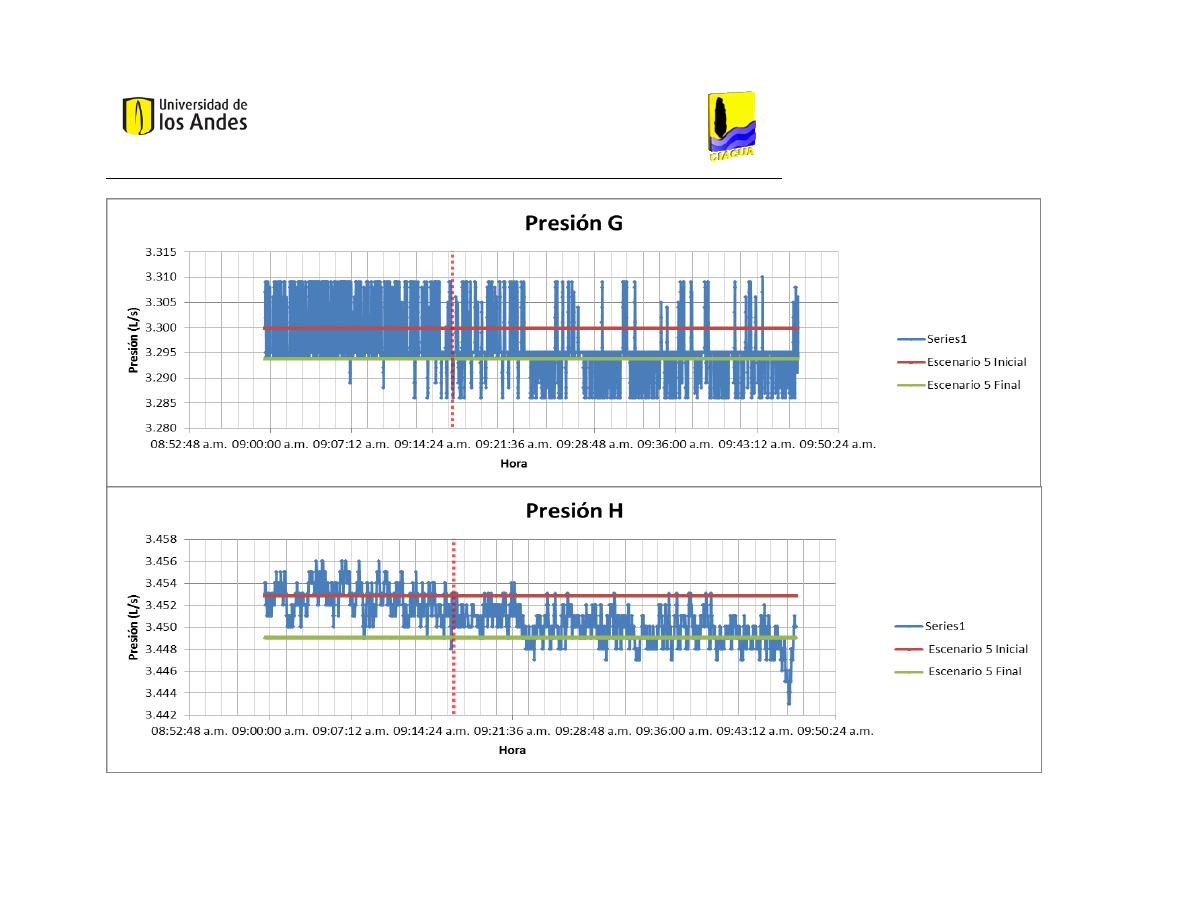
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
77
Iván Camilo Viveros Góngora
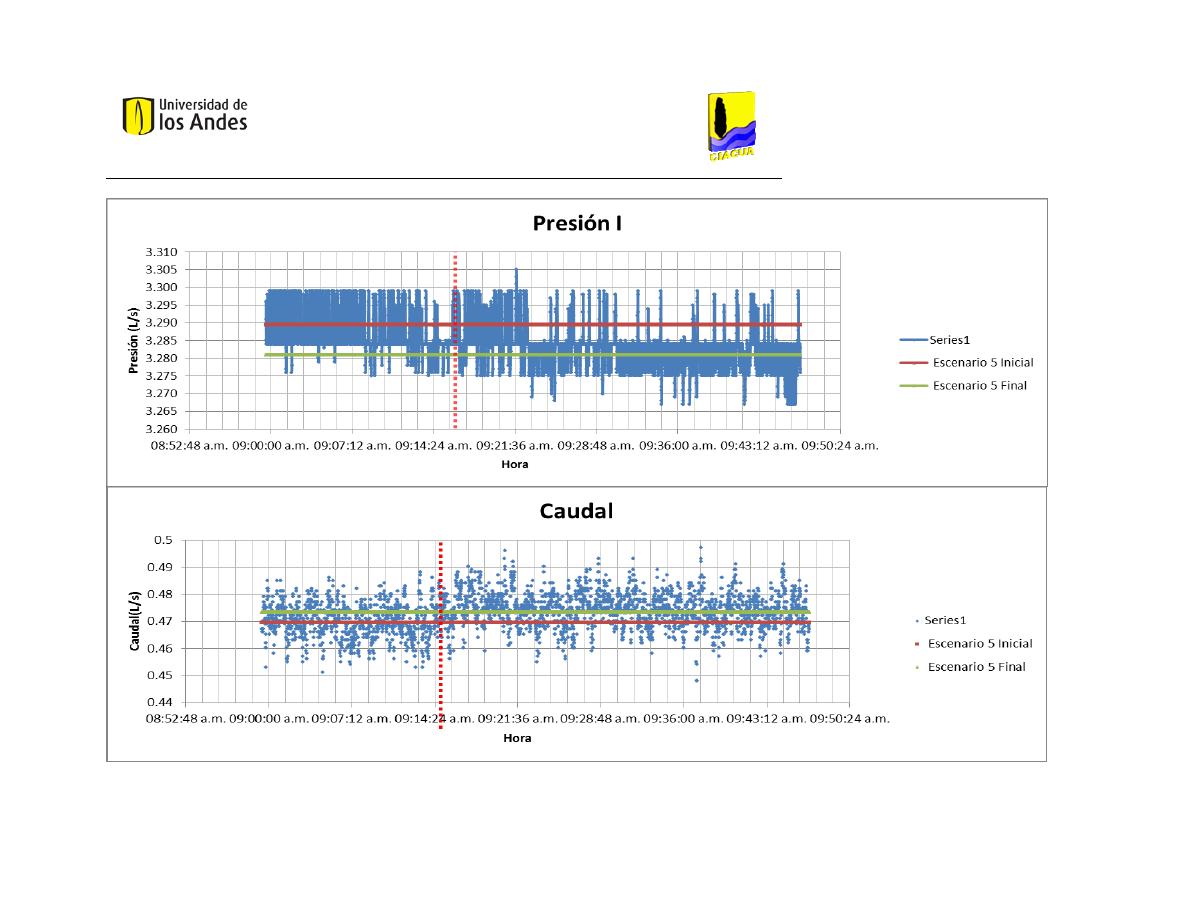
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
78
Iván Camilo Viveros Góngora

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
79
Iván Camilo Viveros Góngora
4.2.3.1.1 Descripción de Resultados
En concordancia con los reportes anteriores las presiones no muestran cambios
significativos después de la variación de escenario, salvo una rápida transición de los datos
para centrarse en la nueva media. Sin embargo, en el punto B se alcanza a apreciar un
máximo atípico el cual con una magnitud de 3.901 M.C.A ocurre en el segundo 9:16:11,
tan sólo 4 segundos después de la variación de escenario. Este punto requiere atención,
puesto que es el único que en las tres sesiones de laboratorio permitió apreciar reacciones
inmediatamente después del cierre súbito de la válvula.
Los datos de presión, en la mayoría de los casos, no presentan variaciones significativas
tras el cierre súbito de la válvula; sin embargo, el rango dispersión se centra en la media
de los Escenarios estáticos. El rango de dispersión en un principio se ubica alrededor de la
media de los datos de presión del Escenario Inicial. Tras un período de transición el cual
dura alrededor de 4 minutos, el rango se centra en el Escenario Final.
Los datos de caudal también concuerdan con las observaciones pasadas: las medias antes
y después del escenario tienen poca diferencia, inclusive menor que la dispersión
aleatoria. El proceso de estabilización de unas condiciones a otras, requiere por lo menos
de algunos minutos.
4.2.3.2 Variación del Escenario 6 Inicial al Escenario 6 Final
Las mediciones iniciaron a las 8:19’35’’ AM y finalizaron a las 9:09’16’’AM. El cierre súbito
de la válvula se realizó a las 8:34’19’’69 AM. Los relojes de los diferentes computadores se
encontraban sincronizados.
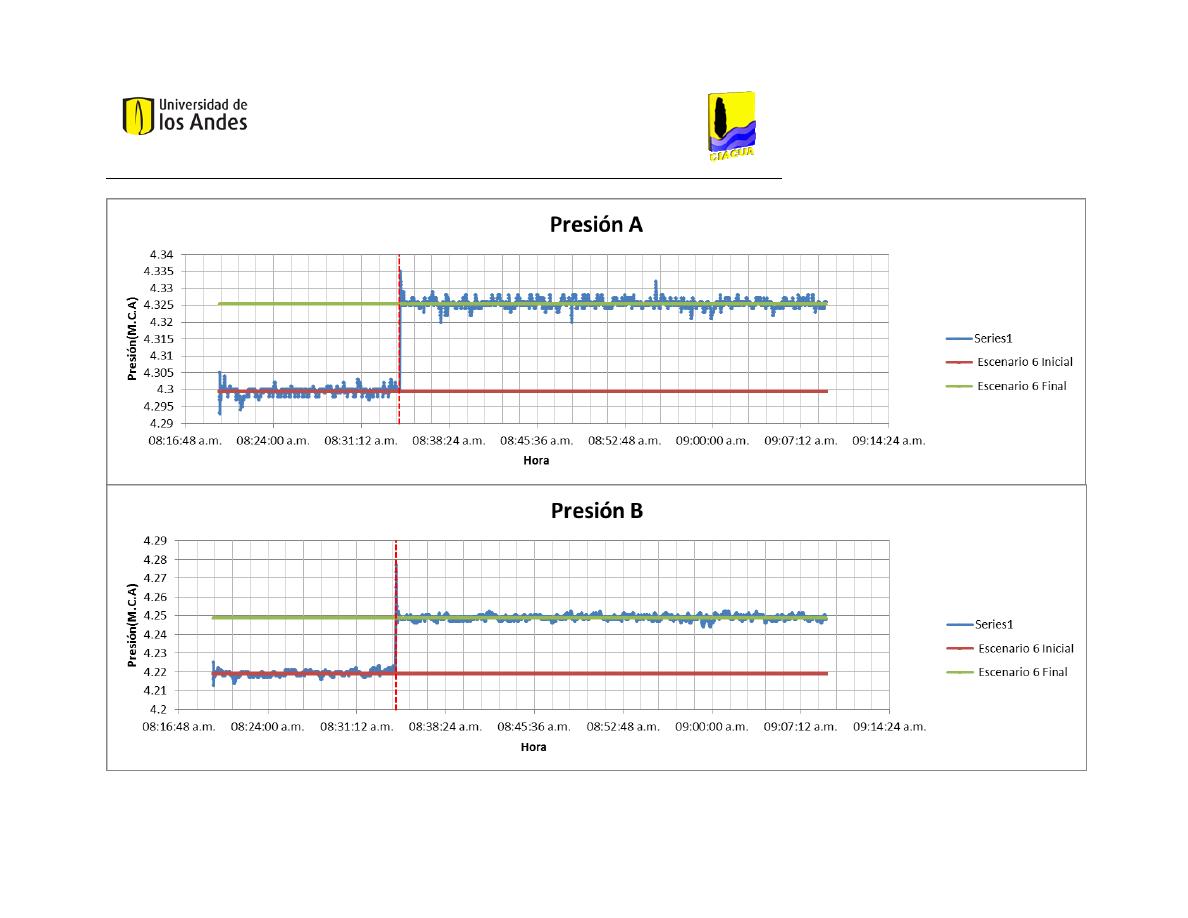
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
80
Iván Camilo Viveros Góngora
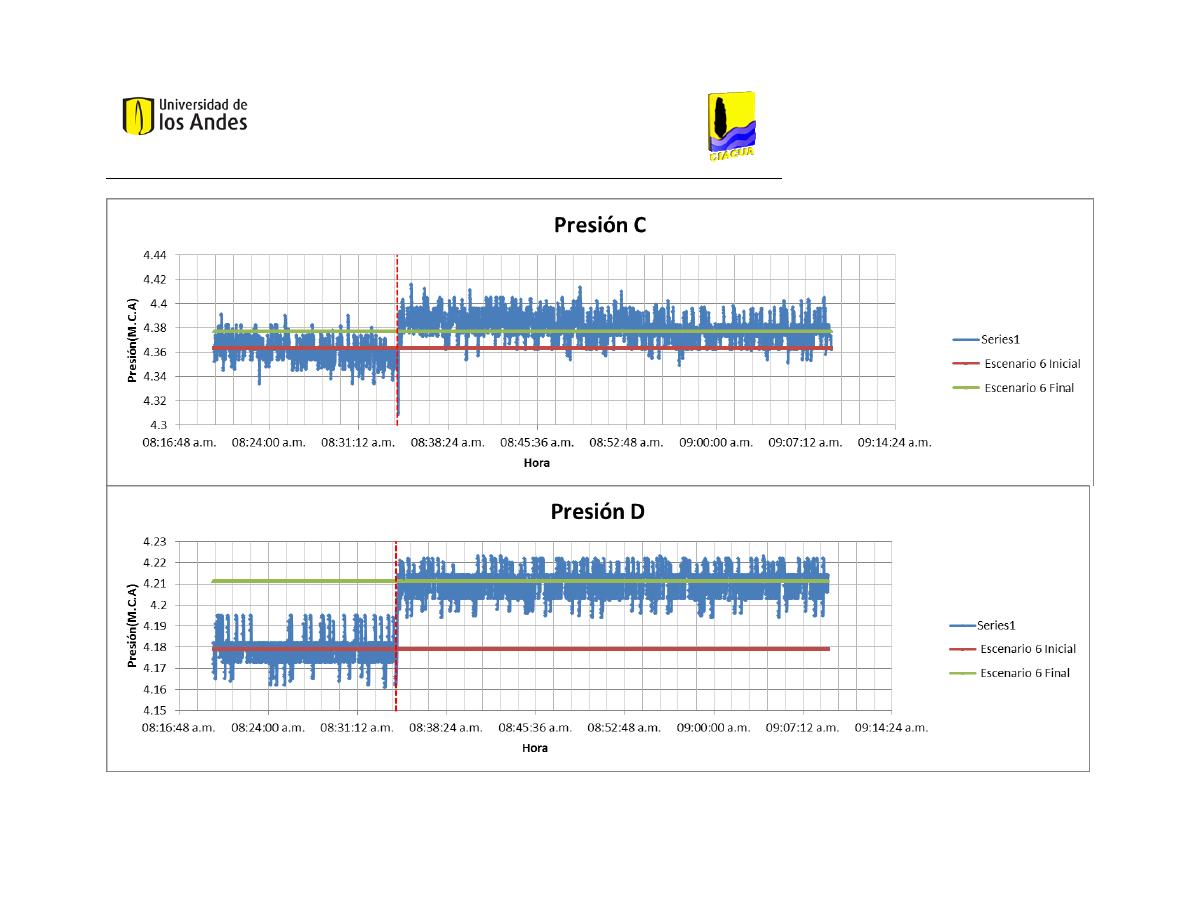
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
81
Iván Camilo Viveros Góngora
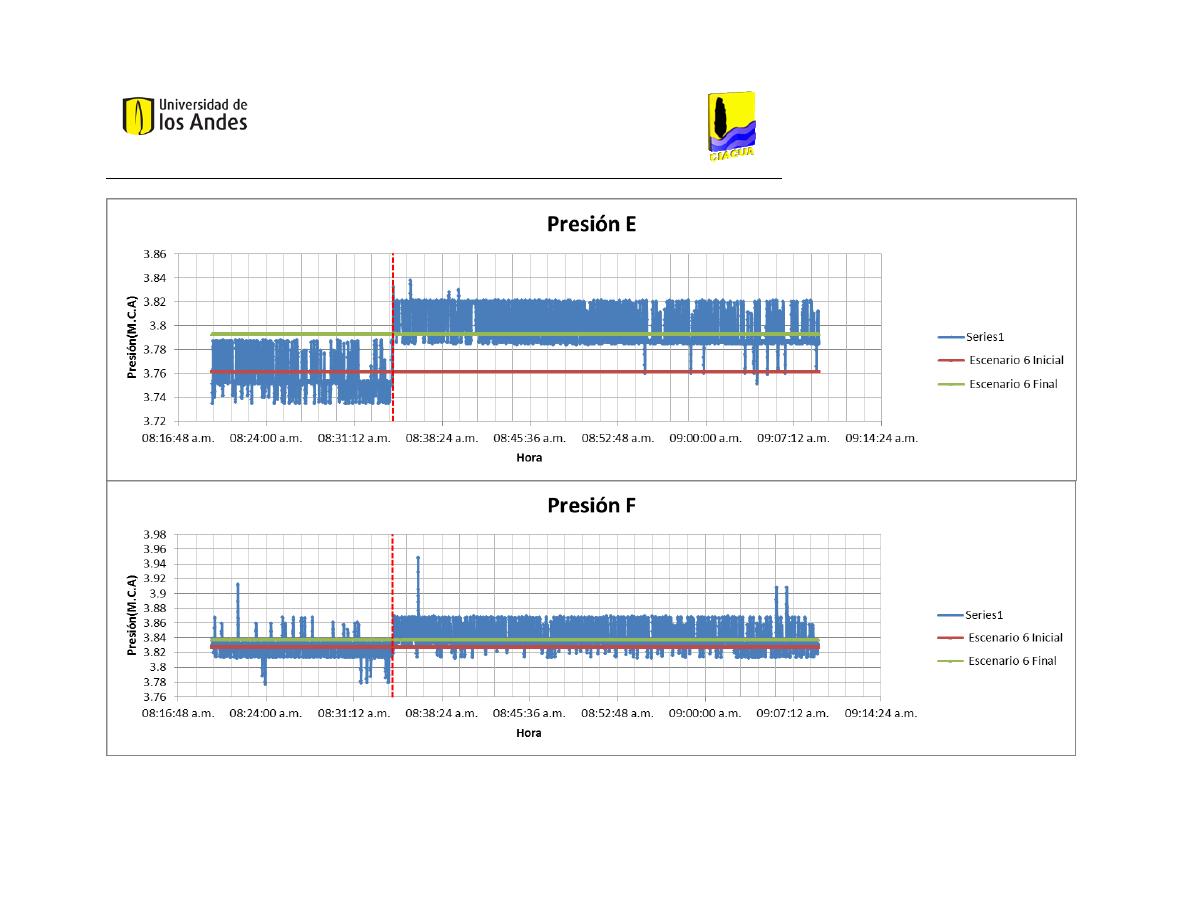
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
82
Iván Camilo Viveros Góngora
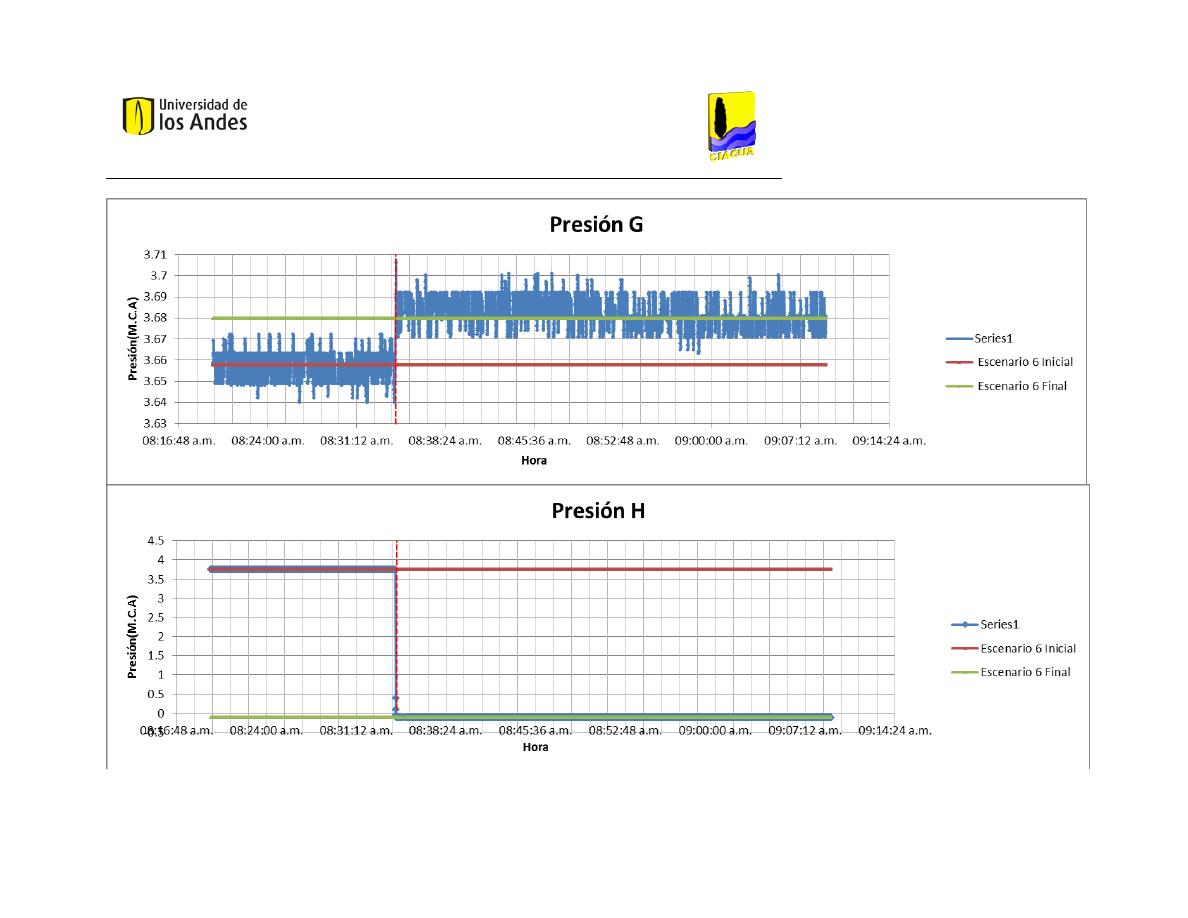
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
83
Iván Camilo Viveros Góngora
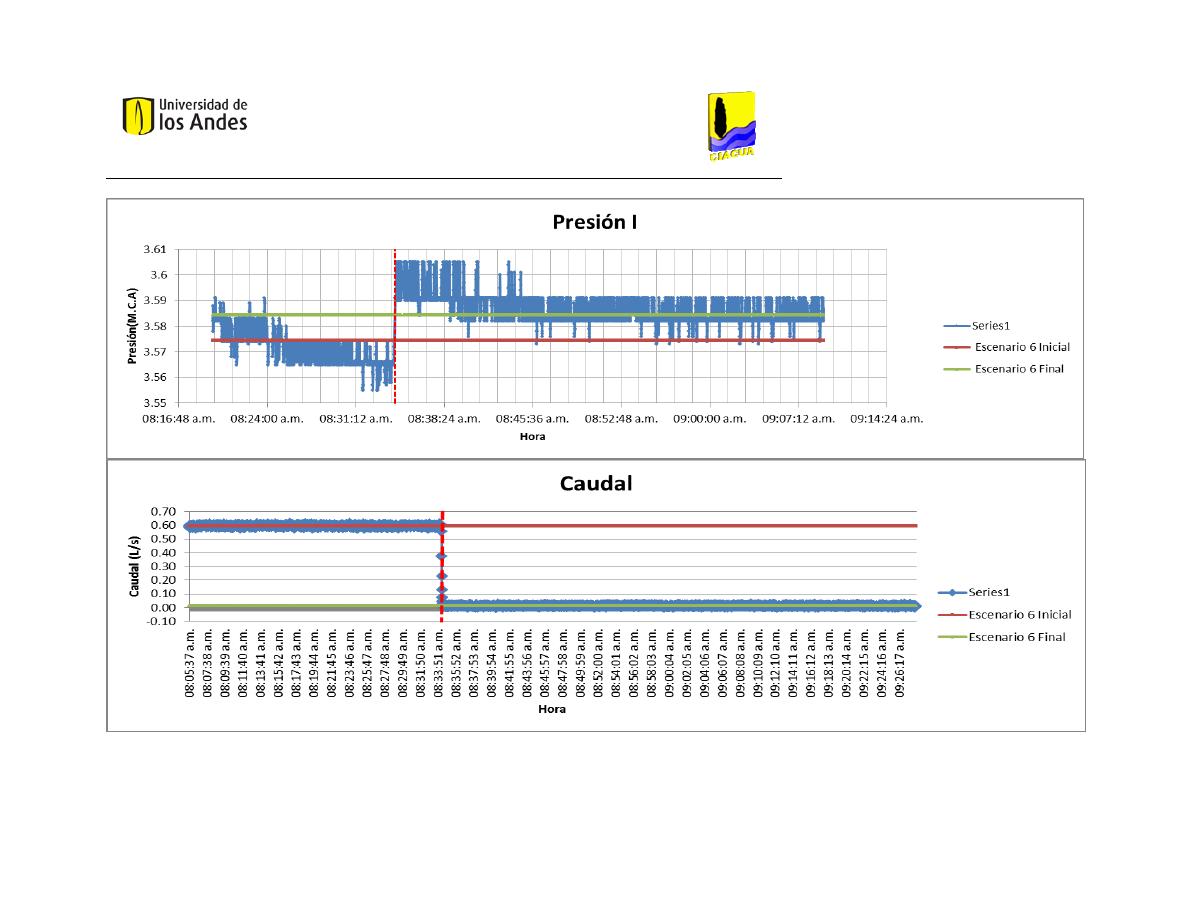
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
84
Iván Camilo Viveros Góngora

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
85
Iván Camilo Viveros Góngora
4.2.3.2.1 Descripción de Resultados
La tendencia en los perfiles de presión a reportar máximos, o por lo menos máximos
locales después de una variación se mantienen. Dado que la media de los escenarios
inicial y final es distante, es factible el análisis del período de transición entre un escenario
y otro. Dado que el cierre fue manual en todos los casos, existe una incertidumbre
asociada con los tiempos y métodos de cierre de válvula. Cada una de las transiciones es
diferente, lo cual conlleva a obtener resultados diferentes.
Los datos de presión presentan valores extremos en segmentos de tiempo relacionados
con el cambio súbito de los Escenarios; sin embargo, antes y después del cierre de la
válvula se puede afirmar que los rangos de dispersión se centran en la media de los
Escenarios en estado estático. Inicialmente el rango de dispersión se localiza en el
Escenario Inicial, después del cambio de Escenario hay un período de transición.
Finalmente, el rango de dispersión de los datos se centra en la media del Escenario Final.
Tabla 11 Valores Máximos del Escenario 6 en la Ubicación 3.
Valores
Máximos
(M.C.A)
Hora
Diferencia
Absoluta con
el Tiempo de
Variación (s)
Presión A
4.335
08:34:24 a.m.
5
Presión B
4.277
08:34:24 a.m.
5
Presión C
4.416
08:35:27 a.m.
68
Presión D
4.223
08:40:58 a.m.
399
08:41:26 a.m.
427
08:42:05 a.m.
456
08:42:49 a.m.
500
08:42:50 a.m.
501
08:55:44 a.m.
1275
09:04:03 a.m.
1774
Presión E
3.838
08:35:49 a.m.
90
Presión F
3.949
08:36:28 a.m.
129
Presión G
3.706
08:34:24 a.m.
5
Presión H
3.749
08:19:36 a.m.
883
Presión I
3.605
>40 registros
-

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
86
Iván Camilo Viveros Góngora
A diferencia de las otras ubicaciones, la cercanía temporal de los máximos de presión y el
cierre súbito de la válvula, sólo es evidente en los puntos A, B y G. En los demás puntos de
medición los máximos de presión se alcanzaron en lapsos de tiempo de más de un minuto.
En el caso de la presión I, se obtuvieron más de 40 registros; sin embargo el primero
ocurrió a las 8:34:31 AM, es decir 12 segundos después del cambio de escenario.
Tabla 12 Valores Mínimos de Presión del Escenario 6 en la Ubicación 3.
Valores
Mínimos
(M.C.A)
Hora
Diferencia
Absoluta con
el Tiempo de
Variación (s)
Presión A
4.293
08:19:36 a.m.
883
Presión B
4.213
08:19:36 a.m.
883
Presión C
4.310
08:34:24 a.m.
5
Presión D
4.161
08:33:28 a.m.
51
Presión E
08:34:41 a.m.
22
08:35:11 a.m.
52
08:35:12 a.m.
53
08:38:49 a.m.
270
08:38:50 a.m.
271
08:39:09 a.m.
290
08:39:38 a.m.
319
Presión F
0.350
08:23:56 a.m.
623
Presión G
3.640
08:26:35 a.m.
464
08:32:05 a.m.
134
08:34:16 a.m.
3
Presión H
-0.125
08:39:29 a.m.
310
08:41:05 a.m.
466
08:41:06 a.m.
467
08:43:38 a.m.
619
Presión I
3.555
08:31:46 a.m.
213
08:31:47 a.m.
212
08:32:35 a.m.
164
08:32:56 a.m.
143
08:32:57 a.m.
142
08:32:58 a.m.
141

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
87
Iván Camilo Viveros Góngora
En general los mínimos valores de presión no presentan cercanía temporal con respecto al
momento del cierre súbito de la válvula. Algunos inclusive ocurren antes de la variación
del escenario. Para que éstos ocurran en algunos puntos toma algo más de diez minutos.
4.3 Comparación con Magnitudes de la Ecuación de Joukowsky
La Ecuación 1 propuesta por Joukowsky en 1900 es una herramienta útil para decribir las
variaciones de magnitud en un transiente. Como se ha explicado al inicio del documento,
factores como el material o la presencia de gases pueden alterar esta predicción.
A continuación se presentan unas tablas con las variaciones de presión en cada uno de los
escenarios. La variación de presión es la diferencia entre el promedio del escenario inicial
y el valor máximo. Se debe aclarar que no todos los máximos están relacionados
temporalmente con el cierre súbito de la válvula, motivo por el cual la variación de
laboratorio puede estar relacionada con diferencias en las condiciones hidráulicas.
𝑉𝑎𝑟𝑖𝑎𝑐𝑖ó𝑛 𝑑𝑒 𝑙𝑎𝑏𝑜𝑟𝑎𝑡𝑜𝑟𝑖𝑜 𝑛
= 𝑃𝑟𝑜𝑚𝑒𝑑𝑖𝑜 𝑑𝑒 𝑃𝑟𝑒𝑠𝑖ó𝑛 𝑛 𝐸𝑠𝑐𝑒𝑛𝑎𝑟𝑖𝑜 𝑖𝑛𝑖𝑐𝑖𝑎𝑙 − 𝑀á𝑥𝑖𝑚𝑜 𝑑𝑒 𝑃𝑟𝑒𝑠𝑖ó𝑛 𝑛
Ecuación 23 Variación de Laboratorio.
Para el cálculo de la variación de presión de la ecuación de Joukowsky, se aplicó
laEcuación 1. La diferencia de velocidad es la diferencia entre el promedio de velocidades
del escenario inicial y el promedio de velocidades del escenario final en la ubicación
correspondiente.
∆𝑉 𝑢𝑏𝑖𝑐𝑎𝑐𝑖ó𝑛 𝑛
= 𝑃𝑟𝑜𝑚𝑒𝑑𝑖𝑜 𝑑𝑒 𝑣𝑒𝑙𝑜𝑐𝑖𝑑𝑎𝑑𝑒𝑠 𝑒𝑠𝑐𝑒𝑛𝑎𝑟𝑖𝑜 𝑖𝑛𝑖𝑐𝑖𝑎𝑙
− 𝑃𝑟𝑜𝑚𝑒𝑑𝑖𝑜 𝑑𝑒 𝑣𝑒𝑙𝑜𝑐𝑖𝑑𝑎𝑑𝑒𝑠 𝑒𝑠𝑐𝑒𝑛𝑎𝑟𝑖𝑜 𝑓𝑖𝑛𝑎𝑙
Ecuación 24 Diferencia de Velocidades.
La diferencia entre las variaciones es con la finalidad de establecer la distancia entre los
valores de variación pronosticados y los valores recogidos en laboratorio.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
88
Iván Camilo Viveros Góngora
𝐷𝑖𝑓𝑒𝑟𝑒𝑛𝑐𝑖𝑎 = 𝑉𝑎𝑟𝑖𝑎𝑐𝑖ó𝑛 𝑒𝑛 𝐿𝑎𝑏𝑜𝑟𝑎𝑡𝑜𝑟𝑖𝑜 − 𝑉𝑎𝑟𝑖𝑎𝑐𝑖ó𝑛 𝑑𝑒 𝐸𝑐𝑢𝑎𝑐𝑖ó𝑛 𝑑𝑒 𝐽𝑜𝑢𝑘𝑜𝑤𝑠𝑘𝑦
Ecuación 25 Diferencia Entre Variaciones.
Variación en
Laboratorio
(M.C.A)
Variación de
Ecuación de
Joukowsky
(M.C.A)
Diferencia
Variación en
Laboratorio
(M.C.A)
Variación de
Ecuación de
Joukowsky
(M.C.A)
Diferencia
Presión A
0.0057
0.0053
Presión A
0.0312
0.0286
Presión B
0.0094
0.0090
Presión B
0.1434
0.1409
Presión C
0.0191
0.0187
Presión C
0.2309
0.2284
Presión D
0.0264
0.0259
Presión D
0.2135
0.2109
Presión E
0.0210
0.0206
Presión E
0.2808
0.2783
Presión F
0.0135
0.0131
Presión F
0.0917
0.0892
Presión G
0.0142
0.0138
Presión G
0.1647
0.1621
Presión H
0.0050
0.0046
Presión H
0.0046
0.0020
Presión I
0.0091
0.0087
Presión I
0.1614
0.1589
Variación en
Laboratorio
(M.C.A)
Variación de
Ecuación de
Joukowsky
(M.C.A)
Diferencia
Variación en
Laboratorio
(M.C.A)
Variación de
Ecuación de
Joukowsky
(M.C.A)
Diferencia
Presión A
0.0054
0.0037
Presión A
0.0560
0.0529
Presión B
0.0056
0.0039
Presión B
0.0803
0.0771
Presión C
0.0136
0.0119
Presión C
0.0460
0.0428
Presión D
0.0286
0.0269
Presión D
0.1528
0.1497
Presión E
0.0159
0.0142
Presión E
0.1186
0.1155
Presión F
0.1075
0.1057
Presión F
0.1059
0.1028
Presión G
0.0265
0.0248
Presión G
0.1218
0.1187
Presión H
0.0073
0.0056
Presión H
0.0034
0.0003
Presión I
0.0183
0.0166
Presión I
0.1316
0.1285
Variación en
Laboratorio
(M.C.A)
Variación de
Ecuación de
Joukowsky
(M.C.A)
Diferencia
Variación en
Laboratorio
(M.C.A)
Variación de
Ecuación de
Joukowsky
(M.C.A)
Diferencia
Presión A
0.0062
0.0047
Presión A
0.0356
0.2152
Presión B
0.0074
0.0059
Presión B
0.0581
0.1928
Presión C
0.0322
0.0307
Presión C
0.0527
0.1981
Presión D
0.0282
0.0267
Presión D
0.0441
0.2068
Presión E
0.0195
0.0179
Presión E
0.0770
0.1739
Presión F
0.1190
0.1175
Presión F
0.1219
0.1290
Presión G
0.0102
0.0087
Presión G
0.0483
0.2026
Presión H
0.0032
0.0016
Presión H
0.0049
0.2460
Presión I
0.0156
0.0141
Presión I
0.0306
0.2203
Escenario 5
Escenario 6
0.0004
0.0025
Ubicación 1
Ubicación 2
Escenario 5
Escenario 6
0.0017
0.0031
Ubicación 3
Escenario 5
Escenario 6
0.0015
0.2509

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
89
Iván Camilo Viveros Góngora
En todos los casos las variaciones fueron superiores a las pronosticadas por la ecuación de
Joukowsky. Si bien no todos los máximos estaban temporalmente relacionados con el
cambio súbito y esta variación pudo obedecer a condiciones hidráulicas, inclusive en
aquellos casos donde era clara la relación entre el cambio súbito y el pico de presión, la
magnitud del transiente superó el valor pronosticado.
Llama la atención que en las tres ubicaciones del caudalímetros las diferencias para cada
una de las presiones tienen aproximadamente el mismo orden de magnitud en cada uno
de las 3 mediciones.
4.4 Comparación entre Escenarios en Estado Estable y Escenarios
Sometidos a Variaciones Súbitas
El presente proyecto de grado ha presentado Escenarios en estado estable y Escenarios
sometidos a una variación súbita ¿Los Escenarios sometidos al cierre de la válvula vuelven
a las condiciones del estado estable? Lo más apropiado es analizar las presiones antes y
después del cierre de válvula, en conjunto con los Escenarios Iniciales y Finales.
Los promedios de presión de los Escenarios Iniciales en estado estable son comparados
con los promedios de los primeros diez minutos de medición en los Escenarios sometidos
a variaciones súbitas. Los promedios de presión de los Escenarios Finales son comparados
con los promedios de los últimos diez minutos de los Escenarios sometidos al cierre de la
válvula.
En la Tabla 13 la mayor diferencia porcentual relativa la presenta la ubicación (40.4044%),
en la presión C. A excepción del punto mencionado, los valores oscilan entre variaciones
del 2% al 3% y en algunos casos del 12%. En contraste con la Tabla 13, la Tabla 14 presenta
una diferencia porcentual relativa máximo de 0.4041 en la Ubicación 2, Presión C.
En la Tabla 14 la Ubicación 2, en la Presión C nuevamente se reporta la mayor diferencia
porcentual relativa (41.0037%); si se ignora ese punto, los datos resultan cercanos al
Escenario en estado estable con valores entre 0.0186% y 11.5716%. En la Tabla 16 las
mayores variaciones se presentan en todas las Ubicaciones, en el Punto H. La presión C, en
la Ubicación 2 también reporta gran variación.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
90
Iván Camilo Viveros Góngora
En general, se puede afirmar que la mayoría de los puntos de los Escenarios sometidos a
variaciones logran alcanzar las condiciones del estado estable; sin embargo, la Presión C
en la Ubicación 2 presente una gran variación. Por otro lado, el punto H, en el Escenario 6
Final la distancia entre el estado estable y el Escenario sometido a una variación súbita, es
significativa.
Tabla 13 Escenario 5 Inicial Estable y Escenario 5 Sometido a Variación
Tabla 14 Escenario 5 Final Estable y Escenario 5 Sometido a Variación
Escenario en Estado Estable
Promedios de Presión
Escenario 5 Inicial
Ubicación 1
Ubicación 2
Ubicación 3
Presión A
4.0455
4.1239
4.0416
4.0438
Presión B
3.8905
3.9693
3.8904
3.8936
Presión C
4.0312
4.1189
2.4024
4.0148
Presión D
3.4626
3.5371
3.8444
3.8458
Presión E
3.8555
3.9314
3.3851
3.3925
Presión F
3.4133
3.4904
3.4585
3.4670
Presión G
3.2986
3.3686
3.2995
3.2998
Presión H
3.3488
3.4209
3.4747
3.4528
Presión I
3.2807
3.3837
3.2667
3.2894
Promedios de Presión Antes del Cierre Súbito
Escenario Sometido a Variación
[M.C.A]
Escenario en Estado Estable
Promedios de Presión
Escenario 5 Final
Ubicación 1
Ubicación 2
Ubicación 3
Presión A
4.0460
4.1239
4.0412
4.0442
Presión B
3.8913
3.9690
3.8913
3.8940
Presión C
4.0270
4.1136
2.3997
4.0033
Presión D
3.4619
3.5351
3.8416
3.8457
Presión E
3.8543
3.9270
3.3765
3.3813
Presión F
3.4125
3.4892
3.4450
3.4525
Presión G
3.2964
3.3675
3.2958
3.2937
Presión H
3.3493
3.4208
3.4743
3.4490
Presión I
3.2770
3.3770
3.2509
3.2809
[M.C.A]
Escenario Sometido a Variación
Promedios de Presión Después del Cierre Súbito

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
91
Iván Camilo Viveros Góngora
Tabla 15 Escenario 6 Inicial Estable y Escenario 6 Sometido a Variación
Tabla 16 Escenario 6 Final Estable y Escenario 6 Sometido a Variación
Escenario en Estado Estable
Promedios de Presión
Escenario 6 Inicial
Ubicación 1
Ubicación 2
Ubicación 3
Presión A
4.3844
4.3841
4.2900
4.2994
Presión B
4.3021
4.3022
4.2087
4.2189
Presión C
4.4275
4.4452
2.6120
4.3633
Presión D
3.9169
3.8996
4.1702
4.1789
Presión E
4.2527
4.2563
3.7344
3.7610
Presión F
3.8541
3.8551
3.8231
3.8271
Presión G
3.7434
3.7335
3.6502
3.6577
Presión H
3.8084
3.8026
3.6966
3.7441
Presión I
3.6483
3.6570
3.5794
3.5744
[M.C.A]
Escenario Sometido a Variación
Promedios de Presión Antes del Cierre Súbito
Escenario en Estado Estable
Promedios de Presión
Escenario 6 Final
Ubicación 1
Ubicación 2
Ubicación 3
Presión A
4.4110
4.4102
4.3242
4.3253
Presión B
4.3316
4.3326
4.2475
4.2489
Presión C
4.4782
4.4557
2.6328
4.3767
Presión D
3.9517
3.9264
4.2138
4.2111
Presión E
4.2893
4.2862
3.8085
3.7929
Presión F
3.9093
3.9015
3.8511
3.8371
Presión G
3.7801
3.7574
3.6855
3.6797
Presión H
3.8873
-0.1270
-0.1250
-0.1250
Presión I
3.6980
3.6556
3.6234
3.5842
[M.C.A]
Escenario Sometido a Variación
Promedios de Presión Después del Cierre Súbito

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
92
Iván Camilo Viveros Góngora
5
Modelación en Período Extendido
“La modelación en período extendido es esencialmente una secuencia de simulaciones en
estado estable cuyas condiciones de frontera son cargadas para reflejar cambios en las
demandas de los nodos, los niveles de los tanques y las operaciones de las bombas”
(Giustolizi, Kapelan, & Savic, 2008).
La modelación en período extendido, a diferencia de la modelación en condiciones
constantes puede incluir variaciones en la altura del nivel de tanques, embalses, entre
otros. En los nodos también es factible incluir cambios de la demanda en función del
tiempo. El resultado del modelo permite analizar las diferentes condiciones hidráulicas a
lo largo del tiempo.
5.1 Características del Modelo
En lo relacionado a diámetros, coeficientes de pérdidas menores, rugosidad, coordenadas
de nodos y tuberías, la información es exactamente igual al modelo calibrado y validado
en condiciones hidráulicasestables.
5.2 Energía de Entrada
La energía de entrada, inicialmente (en los modelos sin variación) usó la presión A como
base. Dado que de las 3 variaciones la que más se asemeja a lo reportado en la literatura
fue la de la Ubicación 1, se considera la más adecuada para la formación de un patrón de
variación.
5.3 Demandas
Se cuenta con información de calidad acerca de la variación de las demandas en tres
nudos. Sin embargo, dado que se cuenta con valores de variación los nudos Q23, Q26 y
Q15, éstos conservan su demanda base pero adoptan alguno de los tres patrones. Los
puntos de extracción de caudal Q17, Q10 y Q21, además de modificar su demanda base
de acuerdo con los promedios obtenidos en las mediciones, adoptan alguno de los
patrones de demanda.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
93
Iván Camilo Viveros Góngora
5.4 Patrones de Altura de Presión y de Demanda de Caudal
En secciones anteriores se expuso de manera detallada las mediciones de cada uno de los
escenarios, en alguna de las 3 ubicaciones del caudalímetro. Eso significa que para cada
variación se pueden determinar 3 patrones de altura de presión (energía de entrada), sin
embargo se seleccionó el de la Ubicación 1 debido a su similaridad a los casos prácticos y
teóricos expuestos en la literatura científica.
El procedimiento consiste en tomar un promedio el cual es introducido en los programas
como altura o demanda base. La división entre los valores calculados (numerador) y el
promedio (denominador) resulta en los factores de multiplicación (patrones de altura de
presión) los cuales varían en el tiempo. El intervalo temporal de los programas es de
minutos, por este motivo se calculan los promedios minuto a minuto y con base en esto se
establece un patrón de variación temporal.
𝐹𝑎𝑐𝑡𝑜𝑟 𝑑𝑒 𝑀𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑎𝑐𝑖ó𝑛 𝑖 =
𝑉𝑎𝑙𝑜𝑟 𝑖
𝑝𝑟𝑜𝑚𝑒𝑑𝑖𝑜 𝑑𝑒 𝑣𝑎𝑙𝑜𝑟𝑒𝑠
Ecuación 26 Factores de Multiplicación.
Como resultado de las mediciones que se hicieron en los tres escenarios, hay tres nudos
de extracción de caudal que tienen poca incertidumbre. Se puede calcular la media y con
la división mencionada determinar los factores de multiplicación en el tiempo. Por otro
lado, hay nudos de extracción de caudal que no fueron medidos; por lo tanto es necesario
hacer suposiciones.
Debido a que hubo tres mediciones por cada uno de los escenarios, hay disponibles tres
patrones los cuales incluyen demandas y alturas de presión A. Lo único que varía de uno a
otros es la extensión de tiempo y la presión A. Dado que las mediciones de presión más
adecuadas debido a su ausencia de datos sospechosos y consistencia, son las de la
primera ubicación; en consecuencia, estas presiones son tomadas para la generación de
patrones de energía de entrada y evaluación del modelo.
La suposiciones hechas para la modelación computacional se listan a continuación:
1. Los patrones de demanda relacionados con las mediciones en el nudo Q17
(ubicación 1), se aplican a Q15 y Q23.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
94
Iván Camilo Viveros Góngora
2. Los patrones de demanda relacionados con las mediciones del nudo Q21
(ubicación 2), se aplican a Q3 y a Q26.
3. El patrón de demanda calculado para Q10, únicamente aplica para este nudo
puesto que tiene la particularidad de quedar completamente desabastecido
después de la variación.
4. Los patrones de energía de entrada o altura del embalse son extraídos de las
presiones registradas en el punto A en la primera ubicación.
Patrones de la Variación del Escenario 5
Los valores de los factores multiplicadores concuerdan con los análisis alrededor de los
resultados de las mediciones. Si se considera que los factores oscilan entre 0.96 y 1.02, la
variación a lo largo del tiempo no presenta cambios bruscos, ni tendencias determinadas
por el cambio súbito del Escenario 5 Inicial al Escenario 5 Final. Los factores
multiplicadores y los valores base se encuentran en la sección de anexos.
0.9990
0.9992
0.9994
0.9996
0.9998
1.0000
1.0002
1.0004
1
3
5
7
9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39
Fact
o
r
M
u
ltipli
cad
o
r
Tiempo(min)
Patrones de Energía de Entrada Escenario 5
Ряд1
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
95
Iván Camilo Viveros Góngora
0.9920
0.9940
0.9960
0.9980
1.0000
1.0020
1.0040
1.0060
1
3
5
7
9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39
Fact
o
r
M
u
ltipli
cad
o
r
Tiempo(min)
Patrón de Variación de Demanda (Q15-Q17-
Q23)
Ряд1
0.9900
0.9950
1.0000
1.0050
1
3
5
7
9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39
Fact
o
r
M
u
ltipli
cad
o
r
Tiempo(min)
Patrón de Variación de Demanda (Q21-Q3-
Q26)
Ряд1
0.9600
0.9700
0.9800
0.9900
1.0000
1.0100
1.0200
1
3
5
7
9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39
Fact
o
r
M
u
ltipli
cad
o
r
Tiempo (min)
Patrón de Variación de Demanda (Q10)
Ряд1
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
96
Iván Camilo Viveros Góngora
5.4.1 Patrones de Variación del Escenario 6
En la sección Anexos están disponibles los valores numéricos de los patrones de variación
del Escenario 6. En los patrones se refleja la alta variabilidad del escenario durante los
cambios bruscos. La presión A, o energía de entrada tiene dos tendencias segmentadas por
el cierre súbito de la válvula. Los patrones Q17-Q23 y Q21 reflejan un ligero aumento de
caudal una vez se ha cambiado de escenario. El nodo de extracción de caudal que se ve
afectado por el desabastecimiento producto del cambio súbito, tiene un perfil de factores
multiplicadores coherentes con esta situación.
0.9920
0.9940
0.9960
0.9980
1.0000
1.0020
1.0040
1
3
5
7
9
11 13 15 17 19 21 23 25 27 29 31 33 35
Fact
o
r
M
u
ltipli
cad
o
r
Tiempo (min)
Patrones de Energía de Entrada Escenario 6
Ряд1
0.9900
0.9920
0.9940
0.9960
0.9980
1.0000
1.0020
1.0040
1.0060
1
3
5
7
9
11 13 15 17 19 21 23 25 27 29 31 33 35
Fact
o
r
M
u
ltipli
cad
o
r
Tiempo (min)
Patrones de Variación de Demanda(Q17-Q23)
Ряд1

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
97
Iván Camilo Viveros Góngora
5.5 Resultados y Representatividad del Modelo
Una vez los valores base de demanda y de energía de entrada, así como los patrones de
variaciónfueron introducidos al programa computacional, éste calculó las variables
hidráulicas para la red minuto a minuto.
5.5.1 Representatividad
La representatividad de los modelos en estado estable fue evaluada por medio del error
0.9850
0.9900
0.9950
1.0000
1.0050
1.0100
1
3
5
7
9
11 13 15 17 19 21 23 25 27 29 31 33 35
Fact
o
r
M
u
ltipli
cad
o
r
Tiempo (min)
Patrones de Variación de Demanda(Q21)
Ряд1
0.0000
0.5000
1.0000
1.5000
2.0000
2.5000
3.0000
1
3
5
7
9
11 13 15 17 19 21 23 25 27 29 31 33 35
Fact
o
r
M
u
ltipli
cad
o
r
Tiempo (min)
Patrones de Variación de Demanda(Q10)
Ряд1

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
98
Iván Camilo Viveros Góngora
cuadrático medio y el coeficiente de representatividad, éstos fueron retomados de la
modelación de los escenarios propuestos en estado estable.
R
2
RMS
Escenario 5
0.95
0.07
Escenario 6
0.15
1.09
Escenario 6
1
0.95
0.08
Tabla 17 Representatividad de Modelación en Período Extendido.
El Escenario 5 presenta un índices satisfactorios de representatividad, es factible afirmar
que su variabilidad (R
2
=0.95) y exactitud (RMS=0.07) son fieles a los datos recogidos en
campo. En el caso del Escenario 6, a pesar de que la mayoría de los perfiles se asemejan
bastante los índices de representatividad son poco satisfactorios. Inicialmente se puede
afirmar que el modelo no representa la variabilidad (R
2
=0.15) y se desvía
significativamente (RMS=1.09) de los datos de campo. Sin embargo, se debe tener en
cuenta que las mediciones de presión del punto H estaban sometidas a un proceso de
desabastecimiento súbito (aislamiento) por lo cual se decidió analizar el modelo sin la
influencia de este segmento de datos.
Una vez se elimina la influencia de los valores del punto H, el modelo del Escenario 6
cobra una significancia similar a la del Escenario 5. Sin los datos de la presión H en el
tiempo, se puede afirmar que hay alta representatividad de la variabilidad (R
2
=0.95) y una
desviación del orden de centímetros (RMS=0.08) con respecto a los datos tomados en el
laboratorio.
Un análisis en retrospectiva permite concluir que el Escenario 5 y el Escenario 6 (a
excepción del punto H) en período extendido, bajo las especificaciones y suposiciones
asumidas, representan de manera satisfactoria la variabilidad y cuentan con un grado
aceptable de exactitud si se toma como referencia el grupo de valores medidos
directamente.
1
Éstos indicadores fueron calculados sin tener en cuenta el efecto de la presión H

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
99
Iván Camilo Viveros Góngora
6
Conclusiones
En los perfiles de presión del Escenario 5 (del Inicial al Final) no fue factible apreciar
máximos o mínimos después de la transición de corta duración. Por otro lado, el Escenario
6 (del Inicial al Final) presentó en sus registros de presión, en la mayoría de los puntos y
ensayos, máximos considerablemente fuera de la tendencia y temporalmente
relacionados con el cambio súbito (cierre de válvula).En futuros proyectos de
investigación podría evaluarse la relación entre ramificación, cantidad de nudos
afectados por el cambio súbito, aislamiento de segmentos de la red y magnitud del
transiente de presión.
Los rangos de dispersión de los datos de presión se localizaron en los Escenarios estáticos.
Al inicio, el rango de dispersión se centró en la media del Escenario Inicial. Durante el
cambio súbito, en algunos casos era factible observar datos extremos. Posteriormente, los
perfiles de presión tenían un período de normalización hacia la media del Escenario Final
el cual duraba algunos minutos. Una vez las condiciones del Escenario Final se
estabilizaban, los datos se dispersaban alrededor del promedio de presión del Escenario
Final.
Los cambios notorios estaban relacionados con aumentos súbitos de la presión; no hubo
una tendencia considerable de presiones bajas como se ha reportado en estudios
relacionados con suspensión del funcionamiento de alguna bomba.En todos los casos, la
diferencia entre el promedio de presiones del escenario inicial y el máximo valor,
reportaron magnitudes superiores a laspronosticadas en la ecuación de Joukowsky.
Los perfiles de caudal no presentaron máximos o mínimos, o eventos atípicos durante el
cambio de escenario. Sin embargo es factible analizar transiciones que duran algunos
minutos. En las zonas aisladas en las cuales hay desabastecimiento después del cambio de
escenario, las variaciones están temporalmente relacionadas con la transición del estado
inicial al estado final.
Los Escenarios 5 Inicial, 5 Final, 6 Inicial y 6 Final en los modelos estáticos de EPANET y
REDES cuentan con una satisfactoria representación de la variabilidad y desviación, con
respecto a los datos de laboratorio.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
100
Iván Camilo Viveros Góngora
En la modelación en período extendido los valores simulados del Escenario 5 representan
la variabilidad y magnitud de manera satisfactoria con respecto a los datos de laboratorio
producto de un cierre súbito de una válvula.
En el caso del Escenario 6 los indicadores estadísticos (coeficiente de determinación y
error cuadrático medio) son poco satisfactorios. “Si se considera que una región de la red
elevada es aislada”, al ignorar los valores del punto de presión localizado en la zona en
estado de desabastecimiento (presión H), la variabilidad y la magnitud de los datos
modelados alcanzan niveles de fidelidad casi iguales a los del Escenario 5.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
101
Iván Camilo Viveros Góngora
7 Agradecimientos
Agradezco a John Calvo, miembro del Laboratorio de Hidráulica de la Universidad de Los
Andes, quién colaboró intensivamente en el proceso de medición e instalación de
equipos. A Juan Saldarriaga, asesor de tesis por el tiempo dedicado y el apoyo brindado en
el proyecto. A aquellos miembros del CIACUA que estuvieron dispuestos a ayudarme con
los posibles contratiempos en el proceso.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
102
Iván Camilo Viveros Góngora
8
Bibliografía
Bergant, A., Simpsom, A., & Tijsseling, A. (2006). Water hammer with column separation:
A historical review. Journal of Fluids and Structures, 135-171.
Bosserman II, B., & Hunt, W. (2006). Pumping Station Design. (G. Jones, Ed.) Estados
Unidos de América: Elsevier Inc.
Chapra, S., & Canale, R. (2007). Métodos Numéricos para Ingenieros. México D.F:
McGrawHill.
Devore, J. L. (2005). Probabilidad y Estadística para Ingeniería y Ciencias.México:
International Thomson Editores S.A.
Giustolizi, O., Kapelan, Z., & Savic, D. (2008). Extended Period Simulation Analysis
Considering Valve Shutdowns. Journal of Water Resources Planning and
Management, 527-537.
Grossman, S. (2008). Álgebra Lineal. México: McGrawHill.
Joukowsky, N. (1900). Über den hydraulischen Stoss in Wasserleitungsröhren. Mémoires
de l’Académie Impé riale des Sciences de St.-Pétersbourg, 9(5).
Kirmeyer, G. J., Friedman, M., Martel, K., Howie, D., LeChevallier, M., Abbaszadegan, M., y
otros. (2001). Pathogen Intrusion into the Distribution System. Estados Unidos de
América: AWWA Research Foundation and American Water Works Association.
Korteweg, D. (1878). Ueber die Fortpflanzungsgeschwindigkeit des Schalles in elastischen
Röhren. Annalen der Physik und Chemie, 525–542.
LeChevallier, M. W., Gullick, R. W., Karim, M. R., Friedman, M., & Funk, J. E. (2003). The
Potential Risk from Intrusion of Contaminants into the Distribution System from
Pressure Transients. Journal of Water Health, 3-14.
Ministerio de Vivienda, Ciudad y Territorio. (2012). Reglamento Técnico del Sector de Agua
Potable y Saneamiento Básico. Recuperado el 7 de Junio de 2013, de
http://www.minvivienda.gov.co/Agua/Temas%20de%20inter%C3%A9s/Document
s/240512_sistemas_acueducto_b-.pdf

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
103
Iván Camilo Viveros Góngora
National Instruments. (Abril de 2003). National Instruments. Recuperado el 8 de Junio de
2013, de FieldPoint FP-1601 User Manual:
http://www.ni.com/pdf/manuals/370707a.pdf
Prieto Gamboa, C. M. (2011). Modelación física y calibración de sustancias en redes de
distribución de agua potable. Bogotá: Universidad de Los Andes.
Saldarriaga, J. (2007). Hidráulica de Tuberías.(L. J. Buitrago, Ed.) Colombia: Alfaomega-
Uniandes.
Simpson, A., & Wylie, B. (1991). Large Water-Hammer Pressure for Column Separation in
Pipelines. Journal of Hydraulic Engineering, 1310-1316.
Stone, G. (2006). Contractual and physical risks from waterhammer. World Pumps, 34,
37.38.
Thorley, A. (1991). Fluid Transients in Pipeline Systems. Inglaterra: D. & L. George.
United States Environmental Protection Agency. (28 de Enero de 2013). EPA. Recuperado
el 6 de Febrero de 2013, de http://www.epa.gov/NRMRL/wswrd/dw/epanet.html
Universidad de Harvard. (Enero de 2013). Harvard University The Graduate School of Arts
and Science.Recuperado el 8 de Junio de 2013, de Dissertation Guidelines:
http://www.gsas.harvard.edu/images/stories/pdfs/form%20of%20dissertation.pdf
Wood, D. (2005). Waterhammer Analysis—Essential and Easy (and Efficient). Journal of
Environmental Engineery, 1123–1131.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
104
Iván Camilo Viveros Góngora
9
Anexos
9.1 Escenario 5
Escenario 5
Q15-Q17-Q23
Q21-Q3-Q26
Q10
Presión A
Demanda base(L/s)
Demanda base(L/s)
Demanda base(L/s) Altura Base(m) 1
1.763044583
1.521305
0.472922917
4.123879947
Minuto
Factores Multiplicadores
1
0.9989
1.0009
0.9925
1.0001
2
0.9998
1.0011
0.9978
1.0003
3
0.9993
0.9956
0.9914
1.0003
4
0.9986
1.0007
1.0010
1.0002
5
1.0010
0.9950
0.9888
1.0000
6
0.9983
0.9971
0.9829
1.0001
7
0.9994
1.0002
0.9916
1.0000
8
1.0010
1.0029
0.9950
1.0002
9
1.0042
0.9994
0.9952
0.9999
10
0.9997
0.9968
0.9952
1.0001
11
1.0003
0.9964
0.9855
1.0000
12
1.0021
1.0033
0.9902
1.0000
13
1.0003
1.0035
1.0006
0.9995
14
1.0002
1.0018
0.9968
1.0000
15
1.0013
1.0006
1.0093
0.9999
16
0.9982
0.9985
1.0130
1.0000
17
0.9972
1.0025
1.0068
0.9999
18
1.0031
1.0005
1.0076
1.0001
19
0.9978
0.9970
1.0058
1.0001
20
1.0020
0.9975
1.0071
0.9999
21
0.9992
0.9984
1.0044
1.0001
22
1.0002
0.9986
0.9957
1.0000
23
0.9985
0.9999
1.0059
1.0001
24
1.0003
1.0019
0.9938
0.9999
25
1.0020
1.0006
1.0010
1.0002
26
0.9980
0.9997
1.0124
1.0002
27
0.9979
1.0041
1.0050
0.9997
28
0.9981
0.9979
1.0072
1.0000
29
1.0002
0.9993
1.0006
0.9996
30
0.9987
1.0000
1.0116
1.0000

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
105
Iván Camilo Viveros Góngora
31
0.9994
1.0021
0.9955
1.0001
32
0.9999
0.9999
1.0017
0.9998
33
1.0006
1.0024
1.0078
1.0000
34
1.0018
1.0006
0.9992
1.0001
35
1.0014
1.0010
1.0026
1.0001
36
1.0000
0.9998
1.0019
0.9999
37
0.9998
1.0033
0.9965
1.0000
38
1.0012
0.9993
0.9985
0.9999
39
1.0015
1.0018
1.0087
0.9997
40
0.9987
0.9980
0.9962
1.0003
9.2 Escenario 6
Escenario 6
Q17-Q23
Q21
Q10
Presión A
Demanda base(L/s) Demanda base(L/s) Demanda base(L/s)
Altura Base(m)
1.8155
1.5881
0.2427
4.3991
Minuto
Factores Multiplicadores
1
0.9957
1.0010
2.4535
0.9966
2
0.9991
0.9986
2.4428
0.9968
3
0.9973
0.9958
2.4465
0.9968
4
0.9977
0.9991
2.4506
0.9966
5
0.9980
0.9995
2.4393
0.9965
6
0.9953
0.9952
2.4504
0.9966
7
0.9967
0.9973
2.4417
0.9964
8
0.9987
0.9964
2.4488
0.9965
9
0.9959
0.9971
2.4412
0.9965
10
1.0004
0.9971
2.4388
0.9966
11
0.9987
0.9956
2.4535
0.9965
12
0.9976
0.9989
2.4547
0.9965
13
0.9978
1.0014
2.4437
0.9966
14
0.9985
0.9979
2.4408
0.9966
15
0.9967
0.9983
0.7882
0.9964
16
0.9997
0.9989
0.0475
1.0025
17
1.0016
1.0030
0.0507
1.0027
18
0.9996
0.9969
0.0424
1.0024
19
1.0039
1.0037
0.0394
1.0026
20
1.0013
0.9989
0.0406
1.0022

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
“Modelación Física de Cambios Operativos en Redes de Distribución
de Agua Potable: Modelaciones en Período Extendido y Modelación
de Flujo No Permanente
”
106
Iván Camilo Viveros Góngora
21
1.0014
1.0019
0.0456
1.0026
22
1.0015
1.0050
0.0466
1.0028
23
1.0005
1.0002
0.0453
1.0023
24
0.9998
1.0032
0.0468
1.0026
25
1.0035
1.0007
0.0460
1.0022
26
1.0040
1.0024
0.0423
1.0026
27
1.0014
1.0073
0.0474
1.0025
28
1.0045
1.0041
0.0424
1.0025
29
1.0016
0.9995
0.0419
1.0023
30
1.0011
1.0000
0.0503
1.0023
31
1.0028
1.0037
0.0488
1.0022
32
1.0026
1.0007
0.0411
1.0025
33
1.0008
1.0047
0.0460
1.0026
34
1.0023
0.9982
0.0523
1.0022
35
1.0008
0.9981
0.0440
1.0026
36
1.0013
0.9996
0.0580
1.0024
