
PROYECTO DE GRADO INGENIERÍA AMBIENTAL
MODELACIÓN FÍSICA DE LOS PROCESOS DE MEZCLA DE SUSTANCIAS EN REDES DE
DISTRIBUCIÓN DE AGUA POTABLE
PRESENTADO POR:
NICOLÁS EDUARDO PÁEZ RINCÓN
ASESOR:
JUAN GUILLERMO SALDARRIAGA VALDERRAMA
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
BOGOTÁ D.C.
JUNIO DE 2014

A Dios,
A mis papás, a mi familia y a mis amigos,
por su apoyo y amor incondicional.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
i
Nicolás Eduardo Páez Rincón
Tabla de Contenido
1. Introducción ........................................................................................................................................................ 1
1.1. Objetivos ........................................................................................................................................................... 5
1.1.1.
Objetivo general .................................................................................................................................... 5
1.1.2.
Objetivos específicos ........................................................................................................................... 5
2. Antecedentes ...................................................................................................................................................... 6
2.1.
Aproximaciones iniciales al fenómeno de mezcla completa ................................................... 6
2.1.1.
Flujo laminar ...................................................................................................................................... 6
2.1.2.
Flujo turbulento ................................................................................................................................ 8
2.2.
Modelo de mezcla completa ............................................................................................................... 11
2.3.
Modelo de mezcla incompleta ........................................................................................................... 12
2.4.
Combinación de los modelos ............................................................................................................. 16
2.5.
Comparación entre los modelos teóricos y los experimentos realizados ....................... 17
2.6.
Modelación del cloro residual ........................................................................................................... 21
2.6.1.
Antecentes ....................................................................................................................................... 21
2.6.2.
Modelo de cloro residual ........................................................................................................... 22
3. Tesis anteriores .............................................................................................................................................. 26
3.1.
Construcción de un modelo físico para la medición de mezcla en nudos de redes de
distribución de agua potable ............................................................................................................................ 26
3.1.1.
Diseño y construcción del modelo físico ............................................................................. 26
3.1.2.
Pruebas cualitativas ..................................................................................................................... 26
3.1.3.
Conclusiones ................................................................................................................................... 30
3.2.
Efectos de una mezcla no completa ni homogénea en los nudos sobre el contenido
residual de cloro en redes de distribución de agua potable................................................................ 31
3.2.1.
Adecuación del modelo físico .................................................................................................. 31
3.2.2.
Pruebas cuantitativas .................................................................................................................. 32
3.2.3.
Conclusiones ................................................................................................................................... 34

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
ii
Nicolás Eduardo Páez Rincón
3.3.
Análisis de la dilución de concentraciones de NaCl en una unión tipo cruz .................. 34
3.3.1.
Modelo físico ................................................................................................................................... 34
3.3.2.
Resultados ........................................................................................................................................ 35
3.3.3.
Conclusiones ................................................................................................................................... 39
4. Marco Teórico ................................................................................................................................................. 40
5.1.
Modelación hidráulica .......................................................................................................................... 40
5.1.1.
Método del gradiente .................................................................................................................. 42
5.1.2.
Ejemplo de aplicación ................................................................................................................. 46
5.2.
Modelación de la calidad del agua ................................................................................................... 59
5.2.1.
Modelos estáticos .......................................................................................................................... 60
5.2.2.
Modelos dinámicos....................................................................................................................... 62
5.3.
Procesos difusivos .................................................................................................................................. 63
5.3.1.
Definición ......................................................................................................................................... 63
5.3.2.
Ley de Fick ....................................................................................................................................... 65
5.3.3.
Tipos de difusión ........................................................................................................................... 67
5.3.4.
Concentración ................................................................................................................................ 68
6. Modelo físico .................................................................................................................................................... 72
6.1.
Descripción del modelo físico ........................................................................................................... 72
6.1.1.
Sistema de alimentación ............................................................................................................ 72
6.1.2.
Modelo físico ................................................................................................................................... 78
6.1.3.
Sistema de recirculación ............................................................................................................ 79
6.1.4.
Instrumentos de medición ........................................................................................................ 80
7. Resultados ......................................................................................................................................................... 88
7.1.
Casos de análisis ..................................................................................................................................... 88
7.2.
Resultados ................................................................................................................................................. 89
7.2.1.
Caso 1: Todas las válvulas al 25% .......................................................................................... 90
7.2.2.
Caso 2: Todas las válvulas al 50% .......................................................................................... 91
7.2.3.
Caso 3: Todas las válvulas al 75% .......................................................................................... 92
7.2.4.
Caso 4: Todas las válvulas al 100% ....................................................................................... 93
7.2.5.
Caso 5: Válvula 1 al 25%; válvulas 2, 3 y 4 al 100% ....................................................... 94
7.2.6.
Caso 6: Válvula 2 al 25%; válvulas 1, 3 y 4 al 100% ....................................................... 95
7.2.7.
Caso 7: Válvula 3 al 25%; válvulas 1, 2 y 4 al 100% ....................................................... 96
7.2.8.
Caso 8: Válvula 4 al 25%; válvulas 1, 2 y 3 al 100% ....................................................... 97

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
iii
Nicolás Eduardo Páez Rincón
7.2.9.
Caso 9: Válvula 1 al 50%; válvulas 2, 3 y 4 al 100% ....................................................... 98
7.2.10. Caso 10: Válvula 2 al 50%; válvulas 1, 3 y 4 al 100% .................................................... 99
7.2.11. Caso 11: Válvula 3 al 50%; válvulas 1, 2 y 4 al 100% ................................................. 100
7.2.12. Caso 12: Válvula 4 al 50%; válvulas 1, 2 y 3 al 100% ................................................. 101
7.2.13. Caso 13: Válvula 1 al 75%; válvulas 2, 3 y 4 al 100% ................................................. 102
7.2.14. Caso 14: Válvula 2 al 75%; válvulas 1, 3 y 4 al 100% ................................................. 103
7.2.15. Caso 15: Válvula 3 al 75%; válvulas 1, 2 y 4 al 100% ................................................. 104
7.2.16. Caso 16: Válvula 4 al 75%; válvulas 1, 2 y 3 al 100% ................................................. 105
7.3.
Análisis de resultados ........................................................................................................................ 106
8. Conclusiones y recomendaciones ..................................................................................................... 107
9. Agradecimientos ......................................................................................................................................... 110
10.
Bibliografía ............................................................................................................................................... 111

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
iv
Nicolás Eduardo Páez Rincón
Índice de Figuras
Figura 1. Comportamiento de cloro residual de acuerdo a la dosis agregada (Ocasio & López Díez,
2007). ........................................................................................................................................................ 4
Figura 2. Simulación de flujo en CFD. ............................................................................................................ 10
Figura 3. Flujos con diferentes impulsos (Ho, 2008). .................................................................................. 12
Figura 4. Concentraciones normalizadas, medidas y predichas para la salida con trazador para
diferentes caudales de entrada e iguales caudales de salida (Ho, 2008). .......................................... 18
Figura 5. Concentraciones normalizadas, medidas y predichas para la salida con trazador para
diferentes caudales de salida e iguales caudales de entrada (Ho, 2008). .......................................... 20
Figura 6. Concentración normalizada en la tubería 3 (Cotes Gómez, 2013). ............................................. 33
Figura 7. Concentración normalizada en la tubería 4 (Cotes Gómez, 2013). ............................................. 33
Figura 8. Resultados obtenidos para la concentración en la tubería 4 (Buitrago, 2013). ......................... 38
Figura 9. Resultados obtenidos para la concentración en la tubería 3 (Buitrago, 2013). ......................... 39
Figura 10. Red del ejemplo. ............................................................................................................................ 47
Figura 11. Convergencia de las alturas en los nudos con el método del gradiente. ................................... 58
Figura 12. Convergencia de los caudales en las tuberías con el método del gradiente. ............................ 58
Figura 13. Esquema de conservación de masa en el nudo j (Vidal, Martínez, & Ayza, 1994). .................. 60
Figura 14. Proceso de difusión (Universidad de Valencia, 2006). ............................................................... 64
Figura 15. Proceso de difusión en función del tiempo (Mompremier, 2009). ........................................... 64
Figura 16. Flujo de materia (Mompremier, 2009). ....................................................................................... 66
Figura 17. Ecuación de Fick (Mompremier, 2009). ...................................................................................... 66
Figura 18. Fenómeno de difusión (Mompremier, 2009). ............................................................................. 67
Figura 19. Difusión convectiva (Mompremier, 2009). ................................................................................. 68
Figura 20. Difusión turbulenta (Mompremier, 2009). ................................................................................. 68
Figura 21. Esquema de balance de masa en la unión de tuberías (Mompremier, 2009)........................... 69
Figura 22. Modo de operación del caudalímetro (Kobold, 2009). .............................................................. 81
Figura 23. Precisión del caudalímetro (Kobold, 2009). ............................................................................... 82
Figura 24. Esquema del sensor de cloro (Endress - Hauser, 2007). ........................................................... 84
Figura 25. Esquemas del portaelectrodos (Endress Hauser, 2009). ........................................................... 85
Figura 26. Esquema del montaje a realizar (Endress Hauser, 2009). ......................................................... 86

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
v
Nicolás Eduardo Páez Rincón
Índice de ecuaciones
Ecuación 1. Ecuación bidimensional de advección-difusión (Tzatchkov, Buchberger, Li, Romero -
Gómez, & Choi, 2009). .............................................................................................................................. 7
Ecuación 2. Ecuación unidimensional de advección-difusión (Tzatchkov, Buchberger, Li, Romero -
Gómez, & Choi, 2009). .............................................................................................................................. 7
Ecuación 3. Balance de masa del soluto (Ho, 2008). .................................................................................... 11
Ecuación 4. Balance de masa del soluto (Ho, 2008). .................................................................................... 11
Ecuación 5. Impulso del flujo (Ho, 2008). ..................................................................................................... 13
Ecuación 6. Criterio de impulso en tuberías (Ho, 2008). ............................................................................. 13
Ecuación 7. Relación entre los caudales y las concentraciones en las tuberías 1 y 4 (Ho, 2008). ............ 14
Ecuación 8. Relación entre los caudales y las concentraciones en las tuberías 1 y 4 (Ho, 2008). ............ 14
Ecuación 9. Balance de masa del soluto en el nudo (Ho, 2008). .................................................................. 14
Ecuación 10. Concentración de soluto en la tubería 3 (Ho, 2008). ............................................................. 14
Ecuación 11. Relación entre los caudales de entrada (Ho, 2008). .............................................................. 15
Ecuación 12. Relación entre los caudales de salida (Ho, 2008). .................................................................. 15
Ecuación 13. Conservación de masa en la unión (Ho, 2008). ...................................................................... 15
Ecuación 14. Relación entre los caudales en las tuberías 2 y 3 (Ho, 2008). ............................................... 15
Ecuación 15. Relación entre los caudales en las tuberías 1 y 4 (Ho, 2008). ............................................... 15
Ecuación 16. Concentración de soluto en la tubería 3, en términos de las variables "x" y "y" (Ho, 2008).
................................................................................................................................................................. 16
Ecuación 17. Número de Reynolds. ............................................................................................................... 16
Ecuación 18. Concentración en la tubería 3, en términos del número de Reynolds (Ho, 2008). .............. 16
Ecuación 19. Concentración combinada en un tubo de salida (Ho, 2008). ................................................ 16
Ecuación 20. Ecuación de conservación de la masa para el cloro libre (Rossman, Clark, & Grayman ,
1994).. ..................................................................................................................................................... 22
Ecuación 21. Balance de masa para el cloro en la pared de la tubería (Rossman, Clark, & Grayman ,
1994). ...................................................................................................................................................... 23
Ecuación 22. Balance de masa del cloro con reacción en la pared de la tubería (Rossman, Clark, &
Grayman , 1994). .................................................................................................................................... 23
Ecuación 23. Coeficiente de transferencia de masa (Rossman, Clark, & Grayman , 1994). ...................... 23
Ecuación 24. Número de Sherwood (Rossman, Clark, & Grayman , 1994). ................................................ 24
Ecuación 25. Número de Schmidt (Rossman, Clark, & Grayman , 1994). ................................................... 24
Ecuación 26. Conservación de masa del cloro en el tubo i-ésimo (Rossman, Clark, & Grayman , 1994). 24
Ecuación 27. Constante total de decaimiento del cloro (Rossman, Clark, & Grayman , 1994). ................ 25
Ecuación 28. Ecuación de conservación de masa del cloro con condición de contorno (Rossman, Clark, &
Grayman , 1994). .................................................................................................................................... 25
Ecuación 29. Ecuación estándar (Buitrago, 2013). ...................................................................................... 36
Ecuación 30. Ecuación para el cálculo de la concentración C
3
planteada por Buitrago León (Buitrago,
2013). ...................................................................................................................................................... 37

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
vi
Nicolás Eduardo Páez Rincón
Ecuación 31. Ecuación para el cálculo de la concentración C4 planteada por Buitrago León (Buitrago,
2013). ...................................................................................................................................................... 37
Ecuación 32. Conservación de masa en los nudos de la red (Saldarriaga, 2007)....................................... 40
Ecuación 33. Caudal en una tubería (Saldarriaga, 2007). ............................................................................ 40
Ecuación 34. Conservación de la energía (Saldarriaga, 2007). ................................................................... 41
Ecuación 35. Altura piezométrica teniendo en cuenta pérdidas menores causadas por accesorios
(Saldarriaga, 2007). ............................................................................................................................... 41
Ecuación 36. Parámetro α (Saldarriaga, 2007). ............................................................................................ 42
Ecuación 37. Ecuación de conservación de la energía (Saldarriaga, 2007). ............................................... 43
Ecuación 38. Matriz A11 (Saldarriaga, 2007). .............................................................................................. 44
Ecuación 39. Ecuación de continuidad para todos los nudos (Saldarriaga, 2007). ................................... 44
Ecuación 40. Combinación de las ecuaciones de conservación de energía y continuidad (Saldarriaga,
2007). ...................................................................................................................................................... 44
Ecuación 41. Ecuación obtenida al aplicar el operador gradiente (Saldarriaga, 2007). ............................ 45
Ecuación 42. Matriz A11' (Saldarriaga, 2007). ............................................................................................. 45
Ecuación 43. Desbalance de energía en cada tubería (Saldarriaga, 2007). ................................................ 45
Ecuación 44. Desbalance de caudal en cada nudo (Saldarriaga, 2007). ..................................................... 45
Ecuación 45. Diferencia de caudal para cada tubería en dos iteraciones sucesivas (Saldarriaga, 2007). 45
Ecuación 46. Diferencia de altura piezométrica para cada nudo en dos iteraciones sucesivas
(Saldarriaga, 2007). ............................................................................................................................... 45
Ecuación 47. Sistema solucionado con el método del gradiente. ................................................................ 46
Ecuación 48. Cálculo de alturas piezométricas (Saldarriaga, 2007). .......................................................... 46
Ecuación 49. Cálculo de caudales (Saldarriaga, 2007). ................................................................................ 46
Ecuación 50. Ecuación de continuidad para la modelación de calidad del agua (Vidal, Martínez, & Ayza,
1994). ...................................................................................................................................................... 60
Ecuación 51. Concentración de soluto en el nudo j (Vidal, Martínez, & Ayza, 1994). ................................ 61
Ecuación 52. Tiempo de permanencia medio para el nudo j (Vidal, Martínez, & Ayza, 1994). ................. 61
Ecuación 53. Transporte de sustancias conservativas (Vidal, Martínez, & Ayza, 1994). .......................... 62
Ecuación 54. Transporte de sustancias no conservativas (Vidal, Martínez, & Ayza, 1994). ..................... 62
Ecuación 55. Ecuación general de difusión (Mompremier, 2009). ............................................................. 64
Ecuación 56. Ecuación de difusión con coeficiente de difusión constante (Mompremier, 2009)............. 65
Ecuación 57. Cálculo de concentración (Mompremier, 2009)..................................................................... 68
Ecuación 58. Aporte de masa a la unión i (Mompremier, 2009). ................................................................ 70
Ecuación 59. Salida de masa del nudo i (Mompremier, 2009). ................................................................... 70
Ecuación 60. Concentración de la mezcla (Mompremier, 2009). ................................................................ 71
Ecuación 61. Definición de campo eléctrico (Kobold, 2009). ...................................................................... 81

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
vii
Nicolás Eduardo Páez Rincón
Índice de Tablas
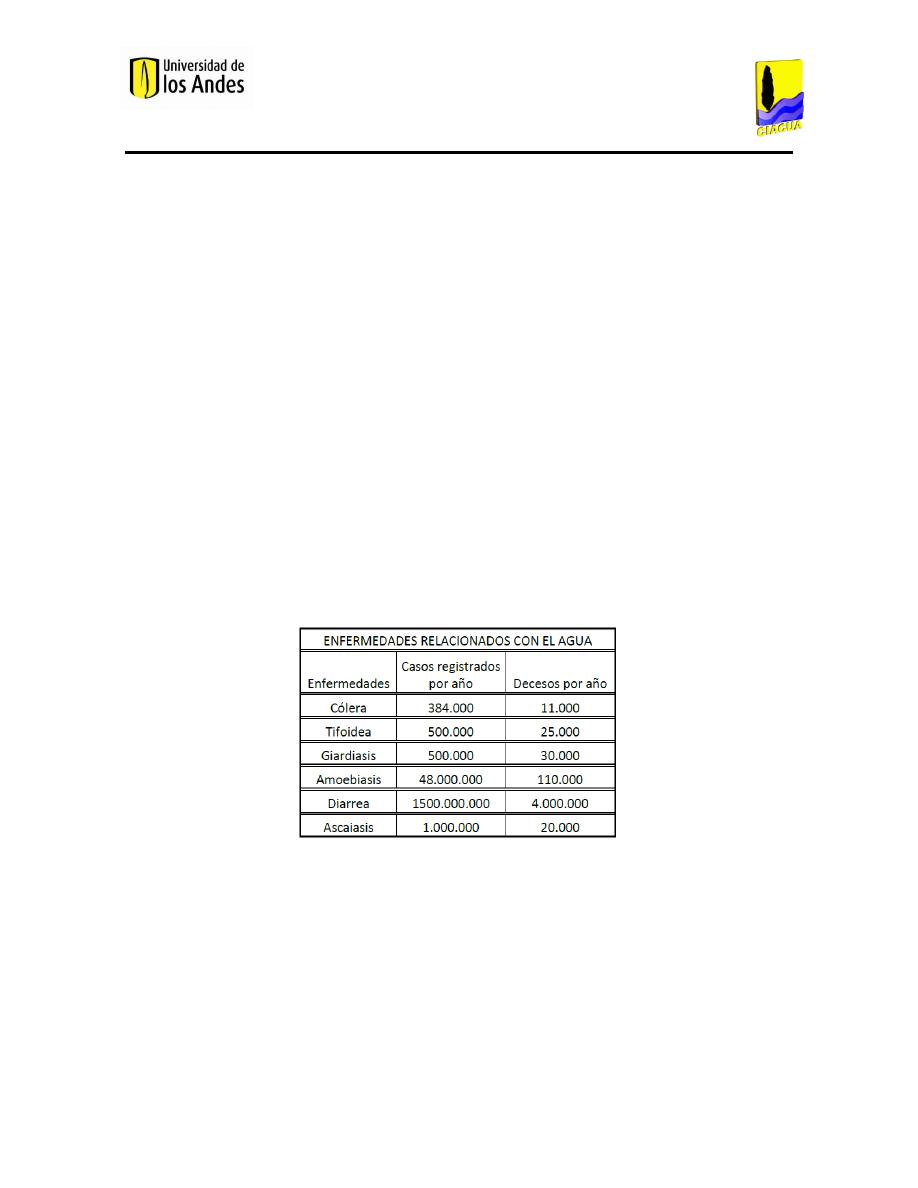
Tabla 1. Enfermedades relacionadas con el agua (Organización Mundial de la Salud, 2009). ................... 2
Tabla 2. Casos de análisis planteados por Cotes Gómez (Cotes Gómez, 2013). ......................................... 27
Tabla 3. Casos de análisis planteados por Cotes Gómez (Cotes Gómez, 2013). ......................................... 32
Tabla 4. Casos de análisis planteados por Buitrago León (Buitrago, 2013). .............................................. 35
Tabla 5. Ecuaciones para el cálculo de las concentraciones C
3
y C
4
de acuerdo a la relación de los
caudales Q
1
y Q
2
, según las restricciones planteadas por Ho (Buitrago, 2013). ................................ 36
Tabla 6. Ecuaciones para el cálculo de las concentraciones C
3
y C
4
de acuerdo a la relación de los
caudales Q
1
y Q
2
, según las restricciones planteadas por Pedro Romero-Gómez (Buitrago, 2013). 37
Tabla 7. Características de las tuberías. ........................................................................................................ 47
Tabla 8. Caudal de demanda en cada nudo. .................................................................................................. 47
Tabla 9. Escenarios planteados para el presente proyecto. ......................................................................... 88
Tabla 10. Velocidades y números de Reynolds para cada porcentaje de abertura de las válvulas. ......... 88

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
viii
Nicolás Eduardo Páez Rincón
Índice de Ilustraciones
Ilustración 1. Acueducto romano (France monthly, s.f.). ............................................................................... 1
Ilustración 2. Vista en planta de la prueba 1 (Cotes Gómez, 2013). ............................................................ 27
Ilustración 3. Vista en planta de la prueba 2 (Cotes Gómez, 2013). ............................................................ 28
Ilustración 4. Vista en planta de la prueba 3 (Cotes Gómez, 2013). ............................................................ 28
Ilustración 5. Vista en planta de la prueba 4 (Cotes Gómez, 2013). ............................................................ 29
Ilustración 6. Vista en planta de la prueba 5 (Cotes Gómez, 2013). ............................................................ 29
Ilustración 7. Vista en planta de la prueba 6 (Cotes Gómez, 2013). ............................................................ 30
Ilustración 8. Vista en planta de la prueba 7 (Cotes Gómez, 2013). ............................................................ 30
Ilustración 9. Modelo físico realizado (Buitrago, 2013). .............................................................................. 35
Ilustración 10. Tubería del laboratorio que alimenta el modelo. ................................................................ 72
Ilustración 11. Válvula que permite el paso de agua al modelo. ................................................................. 73
Ilustración 12. Tubería de alimentación al modelo. ..................................................................................... 73
Ilustración 13. Bifurcación de la tubería de alimentación y válvulas reguladoras de caudal a los tanques.
................................................................................................................................................................. 74
Ilustración 14. Tuberías de alimentación a los tanques. .............................................................................. 74
Ilustración 15. Tanque de agua limpia. ......................................................................................................... 75
Ilustración 16. Tubería de rebose del tanque de agua limpia. ..................................................................... 75
Ilustración 17. Tanque de agua clorada, previo a las modificaciones. ........................................................ 76
Ilustración 18. Tanque modificado en funcionamiento. .............................................................................. 77
Ilustración 19. Fugas en el tanque modificado. ............................................................................................ 77
Ilustración 20. Tuberías de entrada al modelo físico. .................................................................................. 78
Ilustración 21. Válvulas de entrada. .............................................................................................................. 78
Ilustración 22. Modelo físico. ......................................................................................................................... 79
Ilustración 23. Especificaciones de los dos tanques comprados para el sistema de recirculación (PAVCO,
2013). ...................................................................................................................................................... 79
Ilustración 24. Caudalímetro magnético. ...................................................................................................... 83
Ilustración 25. Sensor de cloro. ..................................................................................................................... 84
Ilustración 26. Portaelectrodos para cloro libre. .......................................................................................... 87
Ilustración 27. Nomenclatura para las vistas en planta. .............................................................................. 89
Ilustración 28. Nomenclatura para las vistas en perfil. ................................................................................ 89
Ilustración 29. Vista en planta........................................................................................................................ 90
Ilustración 30. Vista en perfil. ........................................................................................................................ 90
Ilustración 31. Vista en planta........................................................................................................................ 91
Ilustración 32. Vista en perfil. ........................................................................................................................ 91
Ilustración 33. Vista en planta........................................................................................................................ 92
Ilustración 34. Vista en perfil. ........................................................................................................................ 92

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
ix
Nicolás Eduardo Páez Rincón
Ilustración 35. Vista en planta........................................................................................................................ 93
Ilustración 36. Vista en perfil. ........................................................................................................................ 93
Ilustración 37. Vista en planta........................................................................................................................ 94
Ilustración 38. Vista en perfil. ........................................................................................................................ 94
Ilustración 39. Vista en planta........................................................................................................................ 95
Ilustración 40. Vista en perfil. ........................................................................................................................ 95
Ilustración 41. Vista en planta........................................................................................................................ 96
Ilustración 42. Vista en perfil. ........................................................................................................................ 96
Ilustración 43. Vista en planta........................................................................................................................ 97
Ilustración 44. Vista en perfil. ........................................................................................................................ 97
Ilustración 45. Vista en planta........................................................................................................................ 98
Ilustración 46. Vista en perfil. ........................................................................................................................ 98
Ilustración 47. Vista en planta........................................................................................................................ 99
Ilustración 48. Vista en perfil. ........................................................................................................................ 99
Ilustración 49. Vista en planta...................................................................................................................... 100
Ilustración 50. Vista en perfil. ...................................................................................................................... 100
Ilustración 51. Vista en planta...................................................................................................................... 101
Ilustración 52. Vista en perfil. ...................................................................................................................... 101
Ilustración 53. Vista en planta...................................................................................................................... 102
Ilustración 54. Vista en perfil. ...................................................................................................................... 102
Ilustración 55. Vista en planta...................................................................................................................... 103
Ilustración 56. Vista en perfil. ...................................................................................................................... 103
Ilustración 57. Vista en planta...................................................................................................................... 104
Ilustración 58. Vista en perfil. ...................................................................................................................... 104
Ilustración 59. Vista en planta...................................................................................................................... 105
Ilustración 60. Vista en perfil. ...................................................................................................................... 105

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
1
Nicolás Eduardo Páez Rincón
1. Introducción
El acueducto fue inventado en Roma en el año 313 A.C. Inicialmente, los romanos contaban
con el río Tiber y los pozos de la ciudad; sin embargo, el agua obtenida no era de la mejor
calidad y mostró ser insuficiente ante el rápido crecimiento de la ciudad, así como por su uso
en los juegos navales y baños públicos. Ante tal necesidad, se inventó el acueducto como un
modo de transporte de agua desde las colinas que rodeaban la ciudad (Pontificia Universidad
Javeriana Cali, 2014).
Con el paso de los años, el número de acueductos aumentó paulatinamente, hasta que en
tiempos de Procopio existían 14. Tal era su nivel de complejidad, que Plinio expresó su
admiración en el siguiente pasaje: “Pero si alguien calcula cuidadosamente la cantidad de agua
suministrada al público, para baños, reservorios, casas, canales, jardines y casas de campo; y
la distancia que recorre, los arcos construidos, las montañas perforadas, los valles nivelados;
confesará que nunca antes hubo algo más maravilloso en el mundo entero”.
Ilustración 1. Acueducto romano (France monthly, s.f.).
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
2
Nicolás Eduardo Páez Rincón
En dicha época, se contaba con un equipo de 460 esclavos bajo la orden de los curatores
aquarum para atender los acueductos. Entre ellos se encontraban los Villici, encargados de las
tuberías; los castellari, que supervisaban las castellas; los circuitores que vigilaban a los
obreros; los silicarii, que removían el pavimento cuando se requería intervenir las tuberías; y
los tectores, encargados de la construcción de los acueductos.
Si bien con el paso de los años se ha mantenido el uso de los acueductos como sistema de
transporte y distribución de agua, nuevas necesidades han surgido; tales que han contribuido
al desarrollo y cambio continuo de dichos sistemas, mientras suple de agua a la población. En
particular, la Revolución Industrial conllevó al aumento en la cantidad de agua distribuida; así
como el inicio de los procesos modernos de potabilización en la década de 1930 mostraron la
importancia en la calidad del agua distribuida.
Actualmente, la calidad del agua distribuida se ha convertido en tema de interés global. Se
estima que 5 millones de personas mueren al año debido a enfermedades transmitidas por el
agua (Water Treatment Solutions LENNTECH, 2014). Las más importantes de dichas
enfermedades se muestran a continuación:
Tabla 1. Enfermedades relacionadas con el agua (Organización Mundial de la Salud, 2009).
Debido a lo anterior, se hace prioritaria la potabilización del agua. Dicho tratamiento se
encuentra a su vez compuesto por varios procesos, como lo son la coagulación, la
sedimentación, la filtración, y por último el proceso de desinfección. De entre los procesos
anteriormente mencionados, el proceso de desinfección de agua cobra una especial
importancia para propósitos del presente trabajo. En dicho proceso, se remueven los

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
3
Nicolás Eduardo Páez Rincón
organismos patógenos presentes en el agua, y que pueden encontrarse asociados con las
enfermedades descritas anteriormente.
El cloro es el desinfectante más utilizado a nivel mundial para la potabilización del agua. Al
entrar en contacto con el agua, reacciona para producir ácido hipocloroso, el cual con su
capacidad oxidante, penetra en la célula y destruye las enzimas, ocasionando eventualmente
la muerte celular. Adicionalmente es de fácil manejo y bajo costo (Water Treatment Solutions
LENNTECH, Desinfectantes, 2014).
En el proceso de desinfección no sólo se añade el cloro suficiente para eliminar los patógenos
presentes en el agua en dicho momento. Adicionalmente, se añade una cantidad extra bajo el
supuesto que a lo largo de la red de distribución, pueden ocurrir eventos de contaminación
del agua. Dicha cantidad extra recibe el nombre de cloro residual. Se espera que con dicha
cantidad, el agua tenga una capacidad de autodepuración suficiente en casos de
contaminación microbiológica durante su transporte y almacenaje en la red.
La cantidad de cloro que se añade depende de los estándares de calidad, y varían de acuerdo
con el país. Por ejemplo, la EPA ha establecido que la concentración de cloro residual no
puede ser inferior a 0,1 mg/l ni superior a 0,3 mg/l (Ocasio & López Díez, 2007). Sin embargo,
se coincide en que depende de la demanda de cloro, es decir, de la cantidad de cloro que se
debe aplicar a una muestra de agua para producir una determinada cantidad de cloro residual
disponible después de cierto tiempo de contacto. De esta forma la demanda de cloro es la
diferencia entre la cantidad de cloro aplicada inicialmente, y la cantidad de cloro remanente
después del período de contacto (Cotes Gómez, 2013).
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
4
Nicolás Eduardo Páez Rincón
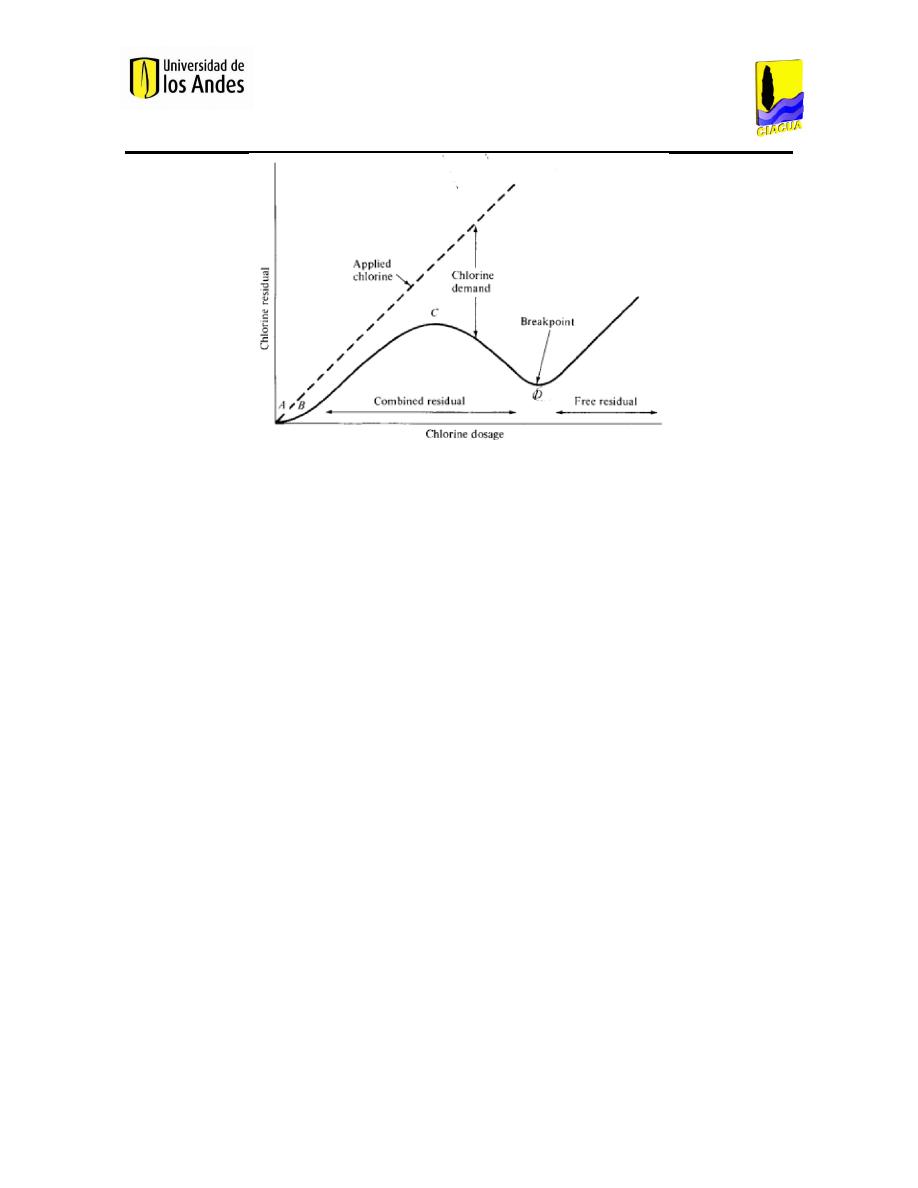
Figura 1. Comportamiento de cloro residual de acuerdo a la dosis agregada (Ocasio & López Díez, 2007).
En la Figura 1 se muestra el comportamiento de cloro residual de acuerdo con la dosis
agregada a la muestra de agua. El punto A muestra la cantidad de cloro requerida para
satisfacer la demanda de los agentes reductores, y su adición en exceso conlleva a la
formación de cloraminas, las cuales son desinfectantes efectivos contra las bacterias
presentes. Una vez los agentes reductores han reaccionado, el cloro residual aumenta (curva
A-B). Dicho cloro residual oxida las cloraminas previamente formadas, por lo que disminuye
de nuevo (Curva B-C). Una vez las cloraminas han sido eliminados (Punto C), el agua sale de la
planta de tratamiento y hacia la red (Ocasio & López Díez, 2007).
La dosis de cloro a añadir depende de la red, en cuanto a que debe asegurar que el agua
cuente con la capacidad de autodepuración a lo largo del tiempo de viaje. Adicionalmente,
supone que en los nudos de la red existe un proceso de mezcla completo y homogéneo, de tal
manera que las concentraciones de salida en las tuberías de salida de una unión tengan una
concentración igual. Sin embargo, estudios recientes han demostrado que dichos procesos de
mezcla en los nudos de la red no son completos ni homogéneos.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
5
Nicolás Eduardo Páez Rincón
1.1. Objetivos
1.1.1.
Objetivo general
El objetivo del presente proyecto, es la cuantificación de los porcentajes de mezcla de cloro
residual en los nudos de redes de distribución de agua potable. Para lo anterior se hará uso
del modelo físico de mezcla completa construido en el Laboratorio de Hidráulica de la
Universidad de Los Andes.
1.1.2.
Objetivos específicos
Se espera poder realizar un estudio cualitativo de los procesos de mezcla que se presentan en
los nudos de las redes de distribución de agua potable. Para esto, se van a utilizar tuberías de
vidrio y trazadores, con los cuales se pueda apreciar visualmente lo que ocurre en la unión de
las tuberías.
Adicionalmente, se cuantificarán las concentraciones de cloro en las entradas y salidas de la
unión en cruz, junto con los caudales en dichas tuberías. De esta forma se espera obtener
resultados sobre los porcentajes de mezcla de sustancias en las uniones de tuberías mediante
el uso de trazadores no conservativos.
A partir de los resultados obtenidos, se espera determinar los parámetros con mayor
influencia en el proceso de mezcla, y corroborar los resultados obtenidos en estudios
anteriores.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
6
Nicolás Eduardo Páez Rincón
2.
Antecedentes
2.1. Aproximaciones iniciales al fenómeno de mezcla completa
A medida que las empresas prestadoras del servicio de agua potable evolucionan, tienen la
obligación de no sólo entregar agua de alta calidad, sino de asegurar la seguridad de la misma.
Para esto, los modelos computacionales han evolucionado para simular de una mejor forma el
transporte de químicos y agentes biológicos. Dichos modelos se conforman típicamente por
dos modelos: Uno hidráulico, y otro de calidad del agua.
Entre los fenómenos caracterizados por los modelos de calidad del agua, se encuentra el de la
mezcla de agua en los nudos de las redes de distribución. Mays (2004) declaró que en todos
los nudos de la red se presenta una mezcla perfecta e instantánea del agua que llega a dichos
nudos. Sin embargo, ya en 1991, Fowler y Jones cuestionaban la ocurrencia de una mezcla
perfecta en los nudos de las redes. Debido a lo anterior, una de las preocupaciones sobre la
modelación de calidad del agua radica en que la suposición de mezcla perfecta es considerada
como una causa potencialmente significativa en las discrepancias entre las predicciones de los
modelos y los valores reales (Romero Gómez, Ho, & Choi, 2008).
2.1.1.
Flujo laminar
En redes de distribución de agua potable es común encontrar zonas con condiciones de bajo
caudal. Dependiendo de la hora del día, dichas condiciones pueden predominar en
aproximadamente el 20% a 50% de la red, según los patrones de demanda. Bajo la presencia
de flujo laminar, la dispersión axial puede ser un factor importante al predecir la calidad del
agua. Por ejemplo, el tiempo de viaje del agua a través de un sistema de distribución se supone
normalmente como el tiempo de residencia hidráulico nominal, o estimado como el tiempo de
residencia mediante el uso de programas de modelación hidráulica como EPANET. En ambos
casos, no se tiene en cuenta el proceso de dispersión que se pueda presentar. Sin embargo, es
posible que un soluto en la red viaje bajo condiciones de Advección – Dispersión, en lugar que
bajo advección pura. De forma similar, bajo condiciones de transporte A – D, una parte del
soluto no se moverá tanto como lo esperado bajo condiciones de advección pura (Tzatchkov,
Buchberger, Li, Romero - Gómez, & Choi, 2009).
El transporte de un trazador conservativo que se mueve bajo flujo laminar constante a través
de una tubería, se describe por la ecuación bidimensional de advección – difusión:

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
7
Nicolás Eduardo Páez Rincón
𝜕𝐶
𝜕𝑡
= 𝐷 (
𝜕
2
𝐶
𝜕𝑟
2
+
1
𝑟
𝜕𝐶
𝜕𝑟
+
𝜕
2
𝐶
𝜕𝑥
2
) − 2𝑈 (1 −
𝑟
2
𝑎
2
)
𝜕𝐶
𝜕𝑥
− 𝐾𝐶
Ecuación 1. Ecuación bidimensional de advección-difusión (Tzatchkov, Buchberger, Li, Romero - Gómez, & Choi, 2009).
donde,
𝐶(𝑟, 𝑥, 𝑡), es la concentración del soluto en cualquier punto de la sección transversal.
𝐷, es el coeficiente de difusión molecular del soluto en el agua (difusividad).
𝑈, es la velocidad media en la dirección axial.
𝐾, es la velocidad constante de reacción de primer orden.
𝑎, es el radio de la tubería.
𝑟, es la posición radial.
𝑥, es la posición axial.
𝑡, es el tiempo.
De acuerdo con la teoría clásica de Taylor para dispersión, la Ecuación 1 se puede simplificar a
la ecuación unidimensional de advección – dispersión, siempre y cuando una cierta
inicialización del proceso de difusión ha transcurrido:
𝜕𝐶
𝜕𝑡
+ 𝑈
𝜕𝐶
𝜕𝑥
= 𝐸
𝜕
2
𝐶
𝜕𝑥
2
− 𝐾𝐶
Ecuación 2. Ecuación unidimensional de advección-difusión (Tzatchkov, Buchberger, Li, Romero - Gómez, & Choi,
2009).
donde,
𝐶, es la concentración media en la sección transversal.
𝐸, es el coeficiente axial de dispersión, el cual es constante.
Al utilizar esta ecuación con un coeficiente de dispersión constante, se tiene como
consecuencia un proceso de difusión estable. Sin embargo, debido al pequeño valor de la
difusividad del agua (𝐷 = 10
−5
𝑐𝑚
2
𝑠
⁄ ) y el constante cambio del flujo en las redes de

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
8
Nicolás Eduardo Páez Rincón
distribución, el proceso de dispersión es inestable y la teoría de Taylor, descrita
anteriormente, no tiene validez. Lo que quiere decir que es importante medir la concentración
del soluto de manera independiente espacialmente y no se puede tomar una concentración
media. A partir de lo anterior, los científicos llegaron a la conclusión de que este último
modelo, subestima significativamente las concentraciones en los nodos obtenidas mediante la
resolución de la ecuación de advección-dispersión a baja velocidad de flujo (Tzatchkov,
Buchberger, Li, Romero - Gómez, & Choi, 2009).
2.1.2.
Flujo turbulento
El régimen de flujo más común en redes de distribución de agua potable es el de flujo
turbulento, por lo que el número de estudios que se han realizado es mayor en comparación
con el régimen laminar. En primer lugar, Ashgriz (2001) examinó dos corrientes en chorro e
indicó que en su intersección, los flujos se bifurcan en lugar de mezclarse si las velocidades del
flujo son bajas. Para velocidades altas (mayores a 10 m/s), los flujos se atomizan y se logran
condiciones de mezcla adecuadas. Resultados experimentales y analíticos indican que para
tuberías, es poco probable que los flujos entrantes atraviesen a través del otro bajo
condiciones típicas (Orear 2005). Sin embargo, si las velocidades de entrada eran diferentes,
podría ocurrir mezcla si la corriente con mayor momentum empujaba a la corriente con
menor momentum a través de la unión (Austin, van Bloemen Waanders, McKenna, & Choi,
2008).
Van Bloemen Waanders (2005) estudió el transporte de químicos en modelos de redes para
flujos presurizados que convergen en un nudo. En dicho estudio, dos flujos de entrada
adyacentes con igual número de Reynolds (Re = 44000) se mezclaron en un nudo, y fueron
descargados por dos tuberías de salida adyacentes con los mismos números de Reynolds. Se
utilizó cloruro de sodio como trazador en una de las tuberías de entrada, y adicionalmente se
realizaron simulaciones mediante CFD. Si ocurriera mezcla completa, el flujo en cada tubería
de salida debería cargar el 50% de la masa de cloruro de sodio añadida. Sin embargo, tanto
experimental como computacionalmente se demostró que dicha mezcla completa no ocurrió,
sino que las concentraciones de salida en las tuberías de salida adyacente y opuesta a la
tubería de entrada del trazador, fue del 85% y 15%, respectivamente. De ahí se concluyó que
el suponer mezcla completa en los nudos de la red puede conllevar a discrepancias
significativas (Romero Gómez, Ho, & Choi, 2008).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
9
Nicolás Eduardo Páez Rincón
Ho (2006) investigó diversas geometrías en los nudos (como por ejemplo uniones en cruz y en
doble tee), así como redes de 3 x 3 nudos con dos fuentes de agua con diferentes
concentraciones de NaCl. Se simuló mediante CFD, con números de Reynolds entre 5000 y
80000. Adicionalmente, se modificó el número turbulento de Schmidt para determinar si
difusividad turbulenta se podía usar para representar la mezcla en los nudos. En el
experimento se utilizaron números de Schmidt entre 0,001 y 0,1 para simular la mezcla
producida por inestabilidades en la interfaz entre los dos flujos. Los resultados observados
sugirieron que el ajuste de dicho parámetro podrían mejorar los resultados obtenidos
mediante modelos computacionales.
Romero Gómez (2006) estudió un gran rango de números de Reynolds para generalizar los
hallazgos anteriores. Los radios entre los números de Reynolds fueron definidos como los
parámetros adimensionales significativos para determinar el porcentaje de mezcla en nudos
bajo condiciones de flujo turbulento (Re>10000), e integró los resultados obtenidos mediante
las simulaciones CFD en EPANET. Las curvas de contorno obtenidas muestran que los
patrones espaciales de concentración cambiaron significativamente al ingresar los resultados
obtenidos con CFD.
Adicionalmente, van Bloemen Waanders (2005) investigó la precisión de los modelos de
mezcla para configuraciones de bajo número de nudos, mediante el uso del modelo de Navier
Stokes combinado con una formulación de convección – difusión. Dicho estudio predijo que
sólo una pequeña fracción de los dos flujos entrantes se mezcla. Romero Gómez (2008) aplicó
un modelo CFD (Dinámica de Fluidos Computacional) utilizando un modelo bajo condiciones
de estado estable para estudiar los mecanismos de mezcla en uniones de tuberías. Webb y van
Bloemen Waanders (2006) utilizaron un modelo LES para describir el comportamiento
espacial y temporal de los fenómenos de mezcla, y encontraron que el comportamiento de la
mezcla era altamente transiente debido a las fluctuaciones de velocidad de los flujos
entrantes. Webb (2007) también aplicó un modelo LES para el caso de flujos con velocidades
de entrada muy diferentes entrando en una unión. Ellos encontraron que la interfaz de mezcla
se formaba en cercanías a la pared en lugar del eje de la unión debido a la diferencia entre los
momentos de las corrientes de flujo (Song, Romero - Gómez, & Choi, 2009).
Austin (2008) caracterizó más detalladamente el comportamiento de los procesos de mezcla
para uniones en cruz bajo diversas condiciones hidráulicas para flujos turbulentos. Él
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
10
Nicolás Eduardo Páez Rincón
correlacionó los porcentajes de mezcla con los radios del número de Reynolds entre los dos
flujos entrantes, y los dos flujos salientes en una unión, e incorporó dichos resultados en un
modelo de calidad del agua para una red. Por ende, primero se determinaron los caudales en
la red mediante un modelo hidráulico, y posteriormente, se calcularon las concentraciones de
soluto de acuerdo con los radios de número de Reynolds calculados para cada una de las
uniones de la red.
Por último, Plesniak y Cusano (2005) investigaron la mezcla de flujos en uniones tipo T en la
que los dos flujos convergen (típicamente a 90°) en una única tubería. Los resultados
mostraron que el porcentaje de mezcla se incrementaba si había estructuras que promovieran
la turbulencia en la interfaz de los dos flujos. También encontraron el porcentaje de mezcla en
uniones tipo Tee dependía del ángulo de intersección de los dos flujos entrantes, así como de
la distancia aguas abajo donde se medía, debido a la presencia de vórtices aguas debajo de la
unión (Ho, 2008).
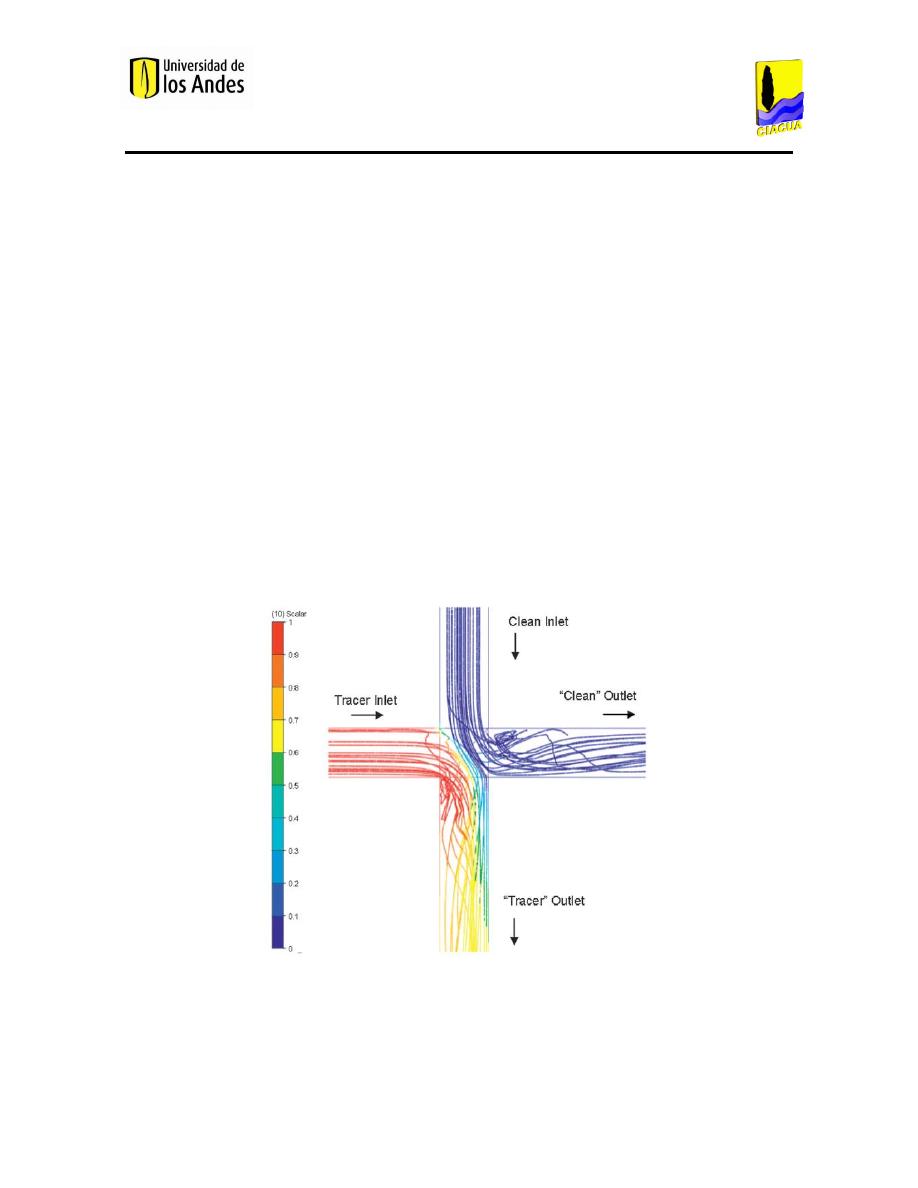
Los resultados obtenidos mediante modelos CFD muestran el siguiente comportamiento:
Figura 2. Simulación de flujo en CFD.
La Figura 2 muestra como los flujos entrantes actúan como cuerpos rígidos, tal que chocan
entre sí y se redirigen hacia las tuberías de salida adyacentes. La mezcla se limita a la

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
11
Nicolás Eduardo Páez Rincón
superficie de contacto entre los dos flujos. Adicionalmente, el modelo muestra como una
porción de la corriente de mayor caudal (la corriente azul) cruza la unión y sale por la tubería
opuesta, deflectando al flujo de menor caudal (la corriente roja).
2.2. Modelo de mezcla completa
El modelo de mezcla completa es el que actualmente utilizan los programas que modelan
redes de distribución de agua potable, entre ellos EPANET. Este modelo supone que el
proceso de mezcla al interior de los nudos de la red es completo e instantáneo. Por ende, la
concentración en el fluido inmediatamente después que sale del nudo es uniforme e igual en
todas las tuberías de salida, y depende de las concentraciones de flujo ponderadas que entran
al nudo.
Al realizar el balance de masa del soluto se obtiene la siguiente ecuación:
𝑐
𝑜𝑢𝑡
=
∑
𝑄
𝑖
𝑛
𝑖=1
𝐶
𝑖
𝑄
𝑜𝑢𝑡
Ecuación 3. Balance de masa del soluto (Ho, 2008).
Dado que no hay acumulación de masa en el nudo, se obtiene la siguiente ecuación:
𝑐
𝑜𝑢𝑡
=
∑
𝑄
𝑖
𝑛
𝑖=1
𝐶
𝑖
∑
𝑄
𝑖
𝑛
𝑖=1
Ecuación 4. Balance de masa del soluto (Ho, 2008).
donde,
𝑄
𝑖
, es el caudal de entrada al nudo desde la tubería i.
𝐶
𝑖
, es la concentración de soluto en la tubería de entrada i.
𝑛, es el número de tuberías que llegan a la unión.
El modelo de mezcla completa predice la mayor mezcla posible que puede ocurrir físicamente
al interior de un nudo. Sin embargo, no tiene en cuenta los procesos físicos de mezcla que se
han observado en experimentos y simulaciones, mediante el uso de modelos CFD para muchas
configuraciones de flujo. Por ende, la no inclusión de dichos fenómenos puede producir
concentraciones significativamente diferentes a las reales para muchos tipos de nudos.
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
12
Nicolás Eduardo Páez Rincón
2.3. Modelo de mezcla incompleta
El modelo de mezcla incompleta ha sido desarrollado como un complemento al modelo de
mezcla completa, mediante la inclusión de un límite inferior para la determinación de mezcla
de sustancias en los nudos de la red. Para esto, el modelo usa como base el conocimiento de
las velocidades de flujo relativas, así como las concentraciones de entrada y salida del nudo.
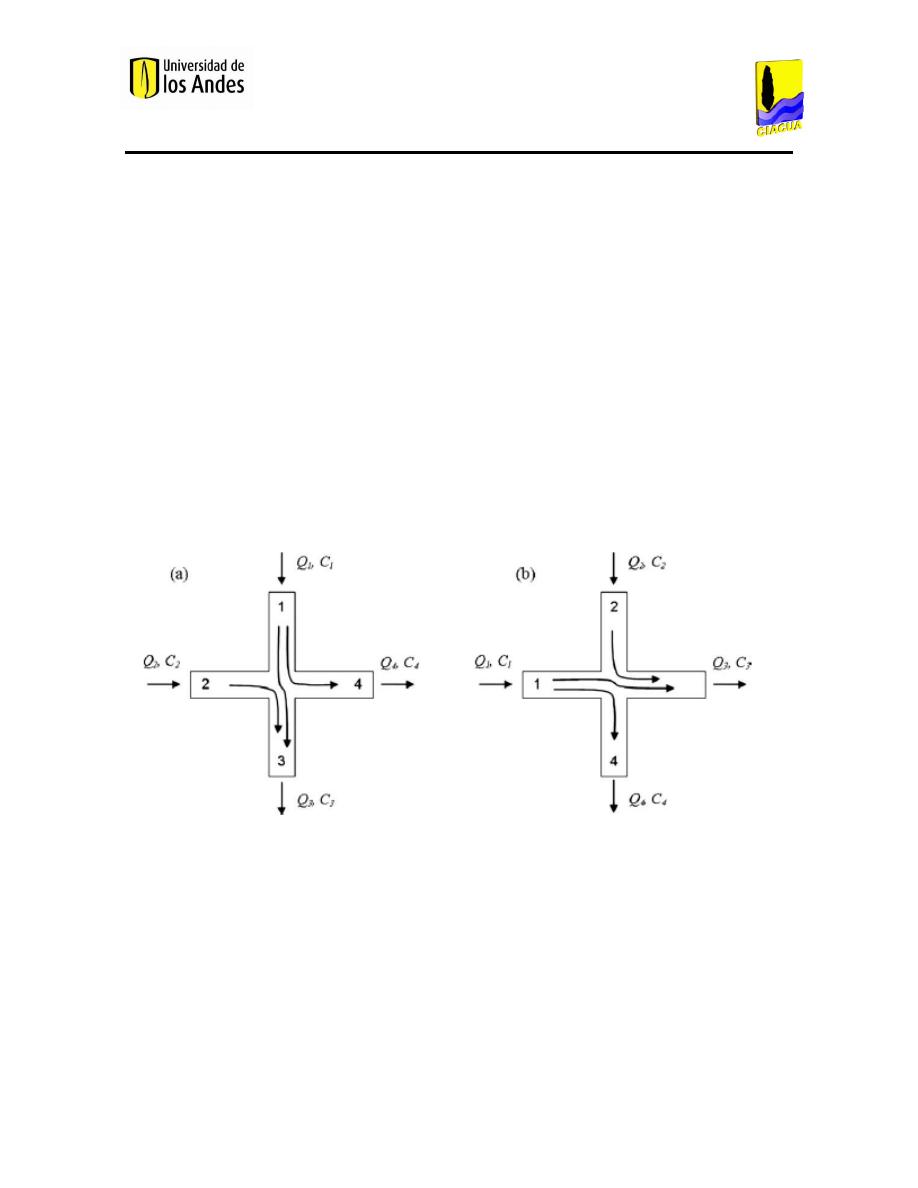
El impulso desigual de diferentes flujos que convergen en un nudo de la red provocará una
transferencia masiva de fluidos, así como de los solutos allí presentes entre los flujos
entrantes y salientes, tal y como se muestra en la Figura 3. Para caudales diferentes, los
modelos CFD realizados muestran que el impulso adicional realizado por una corriente, puede
llegar a ser suficiente para que este flujo cruce la cruz y salga por la tubería opuesta. Como
resultado de este fenómeno, el impulso adicional del flujo con mayor impulso causa que el
flujo con mayor impulso empuje el otro flujo a través del nudo.
Figura 3. Flujos con diferentes impulsos (Ho, 2008).
Las situaciones anteriormente descritas se muestran en la Figura 2. En este caso, la velocidad
del flujo de entrada de agua limpia es un 80% mayor con respecto a la velocidad del flujo de
entrada del agua con trazador, mientras las velocidades del flujo de salida son iguales. Como
resultado, el impulso adicional en el flujo de agua limpia causa que este flujo empuje al de
agua con trazador, de tal forma que por la tubería de salida adyacente a la del agua limpia
únicamente sale agua limpia, mientras que por la otra tubería de salida sale una mezcla entre
agua limpia y agua con trazador, lo cual diluye la concentración del trazador en dicha tubería

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
13
Nicolás Eduardo Páez Rincón
de salida. Similar pero opuesto será el comportamiento de los flujos si la velocidad de entrada
del agua con trazador fuese superior a la velocidad de entrada del agua limpia, manteniendo
iguales las velocidades de los flujos de salida.
El modelo de mezcla incompleta supone que la mezcla sólo se produce por la interacción del
fluido a granel. Si las velocidades de todos los flujos fuesen iguales, el flujo se bifurcaría por
completo de tal forma que no se presentaría mezcla. Por ende, este modelo proporciona el
límite inferior, físicamente basado, del porcentaje de mezcla que puede ocurrir en el nudo.
El modelo de mezcla incompleta se obtiene suponiendo que se conocen las tasas de entrada
del flujo, o que se pueden calcular. El procedimiento es el siguiente:
1. Calcular la tasa de impulso total del fluido en pares de tubos opuestos, es decir,
entradas y salidas situados a 180° entre ellos, mediante la siguiente ecuación:
𝐼𝑚𝑝𝑢𝑙𝑠𝑜 =
𝜌𝑄
𝑖
2
𝐴
𝑖
Ecuación 5. Impulso del flujo (Ho, 2008).
donde 𝐴
𝑖
, es el área transversal de la tubería 𝑖.
2. Para el par de tubos con el mayor impulso, asignar “1” para la tubería de entrada y “3”
para la tubería de salida.
3. Asignar “2” para la tubería de entrada restante y “4” para la tubería de salida restante.
Suponiendo que la densidad del agua es constante, el criterio de impulso es el siguiente:
𝑄
1
2
𝐴
1
+
𝑄
3
2
𝐴
3
>
𝑄
2
2
𝐴
2
+
𝑄
4
2
𝐴
4
Ecuación 6. Criterio de impulso en tuberías (Ho, 2008).
En este caso se considera que todas las tuberías tienen igual sección transversal. En los
ejemplos presentados en la Figura 3, se encuentran diferentes velocidades de flujo en los
tubos individuales que causan un impulso dominante en unos de los pares de tubos opuestos.
En la Figura 3a, el impulso dominante es de arriba abajo, mientras que en la Figura 3b, el
impulso dominante es de izquierda a derecha.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
14
Nicolás Eduardo Páez Rincón
Dado que las tuberías 1 y 3 corresponden a la entrada y la salida, respectivamente, de la
tubería con el mayor impulso; la totalidad del flujo que entra por la tubería 2 fluye hacia la
tubería 3, junto con parte del flujo que entra por la tubería 1. Por ende, la concentración en la
tubería de salida “3” corresponderá a la mezcla de los flujos provenientes de las tuberías 1 y 2.
Por otro lado, la concentración en la tubería de salida 4 será igual a la concentración de la
tubería de entrada 1, dado que es la única fuente que le proporciona flujo a dicha tubería.
Suponiendo que la velocidad del flujo en cada tubería es conocida junto con las
concentraciones de entrada C
1
y C
2
:
𝑄
4
𝐶
4
= 𝑄
1→4
𝐶
1
Ecuación 7. Relación entre los caudales y las concentraciones en las tuberías 1 y 4 (Ho, 2008).
donde,
𝑄
1→4
, es la porción del flujo de la tubería de entrada 1 que fluye hacia la tubería de salida 4.
Como se supone que el flujo de la tubería 2 no sale por la tubería 4, todo el flujo que sale de la
tubería 4 proviene del tubo de entrada 1, es decir, 𝑄
1→4
= 𝑄
4
. Es entonces que se establece
que la concentración en la tubería de salida 4 es igual a la concentración en la tubería de
entrada 1, 𝐶
4
= 𝐶
1
.
𝑄
4
𝐶
4
= 𝑄
1→4
𝐶
1
= 𝑄
4
𝐶
1
Ecuación 8. Relación entre los caudales y las concentraciones en las tuberías 1 y 4 (Ho, 2008).
La concentración en la tubería de salida se calcula mediante la realización del balance de masa
del soluto en el nudo:
𝑄
1
𝐶
1
+ 𝑄
2
𝐶
2
= 𝑄
3
𝐶
3
+ 𝑄
4
𝐶
4
Ecuación 9. Balance de masa del soluto en el nudo (Ho, 2008).
Despejando la concentración de la tubería 3, se obtiene:
𝐶
3
=
𝑄
2
𝐶
2
+ (𝑄
1
−𝑄
4
)𝐶
1
𝑄
3
Ecuación 10. Concentración de soluto en la tubería 3 (Ho, 2008).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
15
Nicolás Eduardo Páez Rincón
Las Ecuaciones 8 y 10 describen las soluciones analíticas del modelo de mezcla incompleta. En
una red, estas soluciones pueden aplicarse secuencialmente a cada unión aguas abajo a partir
de la unión aguas arriba donde se conocen las concentraciones de entrada. La velocidad de
flujo en cada tubería es típicamente calculada de antemano en los modelos CFD de red o sobre
las condiciones prescritas de límite de presión y/o las tasas de flujo. En las simulaciones
transitorias, la solución del modelo de mezcla incompleta se puede aplicar en cada paso de
tiempo con velocidades de flujo actualizadas en cada unión.
La solución para la concentración en la tubería de salida 3 puede reescribirse en términos de
las relaciones entre los caudales de entrada y salida, mediante la siguiente definición:
𝑥 =
𝑄
1
𝑄
2
Ecuación 11. Relación entre los caudales de entrada (Ho, 2008).
𝑦 =
𝑄
4
𝑄
3
Ecuación 12. Relación entre los caudales de salida (Ho, 2008).
Los caudales expresados en la Ecuación 10 pueden ser derivados utilizando las Ecuaciones 11
y 12, y utilizando la conservación de masa en la unión se tiene lo siguiente:
𝑄
1
+ 𝑄
2
= 𝑄
3
+ 𝑄
4
Ecuación 13. Conservación de masa en la unión (Ho, 2008).
Reemplazando:
𝑄
2
𝑄
3
=
𝑦 + 1
𝑥 + 1
Ecuación 14. Relación entre los caudales en las tuberías 2 y 3 (Ho, 2008).
𝑄
1
𝑄
4
=
𝑦 + 1
1
𝑥 + 1
Ecuación 15. Relación entre los caudales en las tuberías 1 y 4 (Ho, 2008).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
16
Nicolás Eduardo Páez Rincón
Utilizando las 2 últimas ecuaciones en la Ecuación 10, se puede determinar la concentración
en la tubería 3:
𝐶
3
= (
𝑦 + 1
𝑥 + 1
) 𝐶
2
+ (
𝑥 − 𝑦
𝑥 + 1
) 𝐶
1
Ecuación 16. Concentración de soluto en la tubería 3, en términos de las variables "x" y "y" (Ho, 2008).
Las relaciones de flujo también son equivalentes si se expresan en términos del número de
Reynolds para cada tubería, en lugar de los caudales medios en las tuberías:
𝑅𝑒
𝑖
=
𝑣
𝑖
𝑑
𝑖
𝜈
Ecuación 17. Número de Reynolds.
donde,
𝑣
𝑖
, es la velocidad media del flujo en cada tubería.
𝑑
𝑖
, es el diámetro de cada tubería.
𝜈, es la viscosidad cinemática del agua.
Finalmente, la concentración en la tubería 3 sería:
𝐶
3
=
𝑅𝑒
2
𝐶
2
+ (𝑅𝑒
1
−𝑅𝑒
4
)𝐶
1
𝑅𝑒
3
Ecuación 18. Concentración en la tubería 3, en términos del número de Reynolds (Ho, 2008).
2.4. Combinación de los modelos
Dado que los modelos de mezcla completa e incompleta proporcionan los límites superior e
inferior, respectivamente, del proceso de mezcla, la cantidad real de la mezcla se encontrará
entre estos dos límites. Por lo tanto, es posible definir un parámetro de escala 0 < 𝑆 < 1
para estimar la concentración en un tubo de salida.
𝐶
𝑐𝑜𝑚𝑏𝑖𝑛𝑎𝑑𝑎
= 𝐶
𝑖𝑛𝑐𝑜𝑚𝑝𝑙𝑒𝑡𝑎
+ 𝑆(𝐶
𝑐𝑜𝑚𝑝𝑙𝑒𝑡𝑎
− 𝐶
𝑖𝑛𝑐𝑜𝑚𝑝𝑙𝑒𝑡𝑎
)
Ecuación 19. Concentración combinada en un tubo de salida (Ho, 2008).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
17
Nicolás Eduardo Páez Rincón
El valor del parámetro de escala 𝑆, depende de las propiedades del fluido, las condiciones del
flujo y la configuración geométrica de la conexión de tubos. Lo anterior puede contribuir a la
presencia de inestabilidades locales en la interfaz incidente, y la mezcla turbulenta dentro de
la unión.
2.5. Comparación entre los modelos teóricos y los experimentos realizados
Los resultados de los modelos de mezcla completa e incompleta han sido comparados con los
resultados obtenidos por diversos investigadores, entre ellos, Romero Gómez (2006) y
McKenna (2007). En los experimentos realizados por Romero Gómez, se investigó el efecto de
diferentes radios entre los caudales de entrada y salida de la unión. En un primer conjunto de
experimentos, los caudales en la entrada de la unión variaron, mientras los caudales de salida
de la unión permanecieron constantes. En un segundo conjunto de experimentos, los caudales
de entrada permanecieron constantes mientras se variaron los de salida. En los experimentos
realizados por McKenna, sólo se variaron los caudales de entrada a la unión, mientras los
caudales de salida permanecieron constantes.
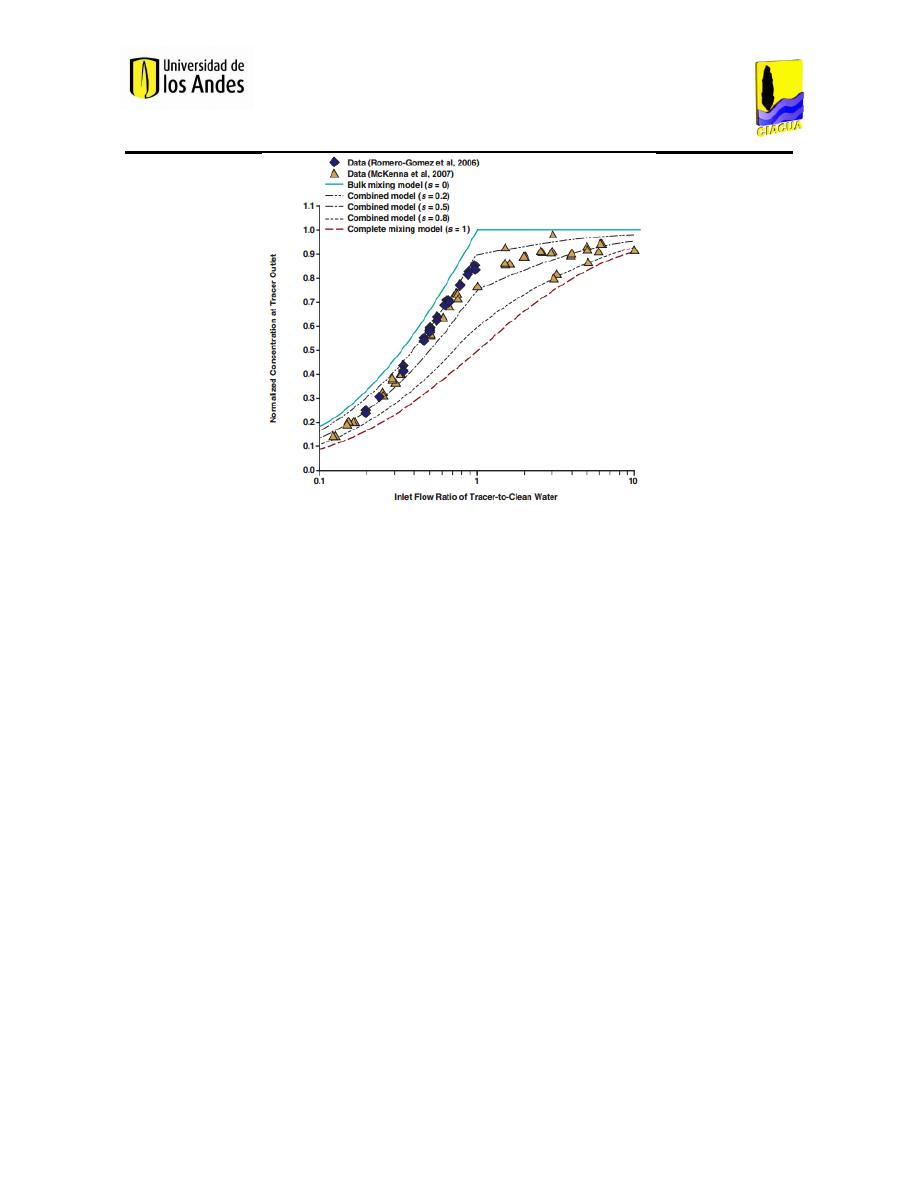
Las Figuras 4 y 5 muestran las concentraciones de trazador normalizadas, analíticas y
experimentales para la salida con mayor concentración de trazador para diferentes
configuraciones de caudal. En la Figura 4, se muestran los resultados obtenidos cuando los
caudales de salida permanecen constantes mientras se varían los de entrada. En la Figura 5, se
muestran los resultados para el caso contrario.
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
18
Nicolás Eduardo Páez Rincón
Figura 4. Concentraciones normalizadas, medidas y predichas para la salida con trazador para diferentes caudales de
entrada e iguales caudales de salida (Ho, 2008).
Los resultados obtenidos confirman que los modelos de mezcla completa e incompleta
proporcionan los límites para cualquier combinación de radios en los caudales de entrada y
salida de la unión. Mayores porcentajes de mezcla se ven indicados por menores valores en la
concentración normalizada en la salida de trazador.
Como se ha discutido previamente, el modelo de mezcla completa supone que las
concentraciones en las tuberías de salida son iguales, y son causadas por la mezcla completa e
instantánea dentro de la unión. Por ende, este modelo proporciona el límite inferior para las
concentraciones normalizadas en la tubería por la que sale la mayor parte del trazador para
todos los casos. El modelo de mezcla incompleta predice concentraciones normalizadas
mayores en la tubería de salida del trazador para cualquier radio de caudales de entrada
porque la mezcla del trazador es causada por la mezcla de los flujos, y no por difusión o
mezcla turbulenta.
En la Figura 4, radios de entrada (trazador/limpio) menores a uno indican que un mayor
caudal de agua limpia llega a la unión en comparación con el caudal de agua con trazador.
Para radios mayores a uno, el caudal de agua con trazador que llega a la unión es mayor que el
caudal de agua limpia. Adicionalmente, los resultados experimentales se encuentran

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
19
Nicolás Eduardo Páez Rincón
delimitados por los valores analíticos obtenidos mediante los modelos de mezcla completa e
incompleta, y se observa que la tendencia de los datos experimentales es similar a la de los
modelos.
A medida que un mayor caudal de agua con trazador se introduce en el modelo en
comparación con el caudal de agua limpia, el porcentaje de dilución disminuye y la
concentración normalizada se incrementa hasta un valor cercano a 1. Sin embargo, debido a
las inestabilidades transitorias causadas por el flujo turbulento, se presenta un pequeño
porcentaje de dilución, aun cuando el radio de los caudales de entrada es superior a 1. Para
radios de caudales de entrada entre 0,3 y 3, los valores experimentales pueden ser predichos
por el modelo combinado con un parámetro de mezcla S entre 0,2 y 0,5. Para radios inferiores
a 0,3 y superiores a 3, los datos experimentales son más precisamente predichos por un
modelo combinado con parámetro de mezcla entre 0,5 y 0,8. Esto implica que la mezcla
aumenta cuando existe una discrepancia significativa entre los caudales de entrada, mayor a
un factor de 3.
Como se mencionó previamente, los diámetros de las tuberías utilizadas en los dos conjuntos
de experimentos realizados por Romero – Gómez y McKenna son diferentes. Además, las
uniones en PVC utilizadas en ambos conjuntos de experimentos fueron construidas por
diferentes empresas. Los accesorios utilizados por Romero Gómez en 2006 crearon una
conexión más al ras entre el diámetro interno de las tuberías y el diámetro interno de la
unión, en comparación con los accesorios utilizados por McKenna en 2007. Estos últimos
accesorios permitieron una mayor expansión del fluido cuando entró a la unión, por lo que se
esperarían mayores porcentajes de mezcla asociados con este fenómeno. Este
comportamiento se ve reflejado en cierta medida en los datos obtenidos por McKenna, aunque
las tendencias son bastante comparables para el rango de relaciones de flujo de entrada que
se superponen en los dos conjuntos de datos.
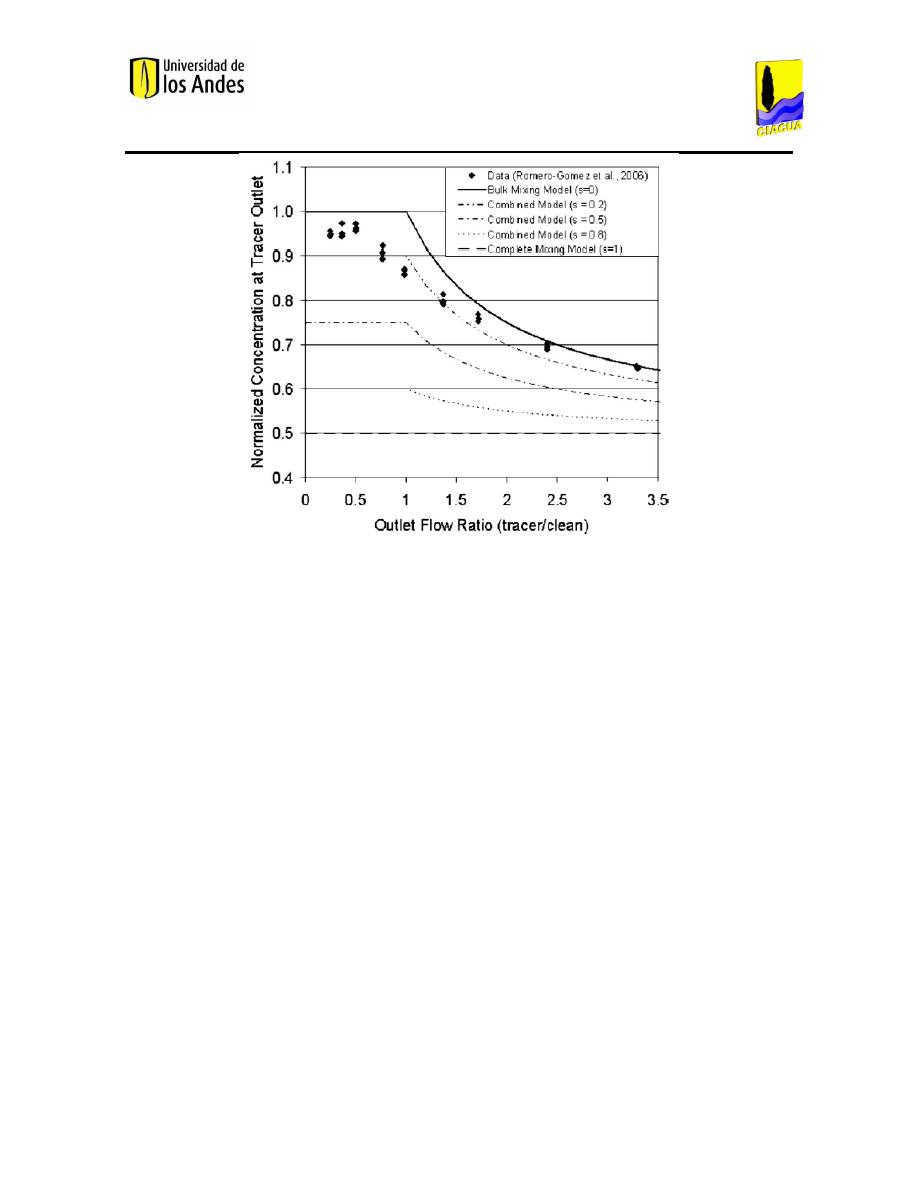
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
20
Nicolás Eduardo Páez Rincón
Figura 5. Concentraciones normalizadas, medidas y predichas para la salida con trazador para diferentes caudales de
salida e iguales caudales de entrada (Ho, 2008).
La Figura 5 muestra los resultados obtenidos para diferentes relaciones de flujos de salida y
relaciones iguales de flujos de entrada. Sólo se considera el trabajo realizado por Romero –
Gómez, dado que McKenna no analizó esta configuración de caudales. Cuando la relación de
los flujos de salida (trazador/limpia) es menor a 1, un mayor caudal de agua sale por la
tubería limpia en comparación con la tubería del trazador. Cuando la relación es mayor a 1, un
mayor caudal de agua sale por la tubería del trazador, en comparación con la tubería limpia.
Dado que la relación entre los caudales de entrada es igual, el modelo de mezcla completa
predice que las concentraciones de salida serán la mitad de las concentraciones normalizadas
en la tubería de entrada de trazador, aun cuando los caudales de salida son diferentes. Sin
embargo, los datos experimentales y el modelo de mezcla incompleta muestran desviaciones
significativas del modelo de mezcla completa. En los casos en que las relaciones en los flujos
de salida son mayores a 1, el mayor flujo a través de la salida del trazador se complementa por
el agua de la entrada limpia, lo que diluye la concentración de trazador. A muy altas relaciones
en los caudales de salida, casi toda el agua que entran por las dos tuberías de entrada sale por
la tubería de trazador, por lo que la concentración de trazador en dicha tubería se acerca de
forma asintótica a 0,5.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
21
Nicolás Eduardo Páez Rincón
Para relaciones menores a 1, la Figura 5 muestra que las concentraciones normalizadas
experimentales tienden a 1 ya que el agua que sale a través de la tubería de trazador, se
compone principalmente del agua que entra a la unión a través de la tubería de entrada de
agua con trazador. El modelo de mezcla incompleta predice concentraciones normalizadas de
1 para estas condiciones porque supone que el flujo predominante que viene de la tubería de
entrada de agua con trazador previene que el agua limpia cruce a través de la unión para
diluir el agua que sale a través de la tubería de salida de trazador. En general, las tendencias
en los datos experimentales están bien acompañadas por las predicciones del modelo de
mezcla incompleta, especialmente para relaciones de flujo de salida mayores que un factor de
2 o 3. Para relaciones menores a 2, el modelo de mezcla combinado con un parámetro de
mezcla de aproximadamente 0,1 o 0,2 predice el comportamiento de los datos
experimentales.
2.6. Modelación del cloro residual
2.6.1.
Antecentes
El cloro es ampliamente utilizado como desinfectante en las redes de distribución de agua
potable a través del mundo. La mayoría de proveedores de agua tratan de mantener una
concentración detectable de cloro residual en la red de distribución para minimizar el
potencial de crecimiento microbiano.
Sin embargo, a medida que el cloro viaja por las tuberías de la red de distribución, reacciona
con una variedad de materiales, tanto en el agua como en las paredes de la tubería. Estas
reacciones disminuyen la concentración de cloro, dependiendo del tiempo de viaje a través de
la red y del tiempo de residencia en los tanques de almacenamiento.
Clark et al. (1993) demostró que el cloro residual varía durante el día en diferentes lugares de
la red de distribución dependiendo del camino del flujo y el tiempo de residencia del agua que
llega a cierto lugar de la red. Los estudios demuestran que la tasa de decaimiento en la tubería
es muchas veces más grandes que la tasa de decaimiento para una misma masa de agua, en un
frasco (Wable et al 1991). Lo anterior demuestra que la pared de la tubería de alguna forma
contribuye a la demanda de cloro en las redes de distribución. Hunt y Kroon (1991)
describieron un modelo de red para cloro residual en el que utilizaron una reacción de
decaimiento de primer orden con una única tasa constante para cada tubería y tanque de

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
22
Nicolás Eduardo Páez Rincón
almacenamiento. Al calibrar el modelo, notaron que tuberías de menor diámetro requerían
mayores constantes de decaimiento para coincidir con los datos observados. Lo anterior es
consistente en cuanto a que tuberías de menor diámetro tienen una mayor área superficial
por unidad de volumen para la reacción. Biswas et al. (1993) desarrolló un modelo de
decaimiento de cloro bajo condiciones de flujo estable que incluían las reacciones dentro del
flujo, difusión radial y la reacción en las paredes de la tubería (Rossman, Clark, & Grayman ,
1994).
2.6.2.
Modelo de cloro residual
Basados en los trabajos previos, parece razonable suponer que el decaimiento de cloro
residual obedece a una cinética de primer orden. Se supone que este decaimiento se da por
reacciones dentro de flujo, y en las paredes de la tubería (o en cercanías a ésta). Las tasas de
estas reacciones pueden ser diferentes, con la tasa de reacción en la pared siendo afectada por
la tasa con la cual el cloro es transportado desde el flujo hacia la pared.
La ecuación unidimensional de conservación de la masa para una concentración diluida de
cloro en agua que fluye a través de una sección de tubería es:
𝜕𝐶
𝜕𝑡
= −𝑢
𝜕𝐶
𝜕𝑥
− 𝑘
𝑏
𝐶 −
𝑘
𝑓
𝑟
ℎ
(𝐶 − 𝐶
𝑤
)
Ecuación 20. Ecuación de conservación de la masa para el cloro libre (Rossman, Clark, & Grayman , 1994)..
donde,
𝐶, es la concentración de cloro en el flujo global.
𝑡, es el tiempo.
𝑢, es la velocidad del flujo en la tubería.
𝑥, es la distancia a lo largo de la tubería.
𝑘
𝑏
, es la constante de descomposición del cloro en el flujo.
𝑘
𝑓
, es el coeficiente de transferencia de masa.
𝑟
ℎ
, es el radio hidráulico de la tubería.
𝐶
𝑤
, es la concentración de cloro en la pared de la tubería.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
23
Nicolás Eduardo Páez Rincón
El término del lado izquierdo de la Ecuación 20 representa la tasa de cambio de la
concentración de cloro dentro de una sección diferencial del tubo. El primer término del lado
derecho de la ecuación representa la advección del cloro en el flujo a través de la sección. El
segundo término representa la descomposición del cloro en el flujo; y el tercer término
representa el transporte de cloro a partir del flujo y hacia la pared de la tubería, así como su
posterior reacción. La inversa del radio hidráulico representa el área de superficie específica,
es decir, el área de la pared de la tubería por unidad de volumen, disponible para la reacción.
Suponiendo que la reacción del cloro en la pared de la tubería es de primer orden con
respecto a la concentración 𝐶
𝑤
de la pared, y que tiene la misma velocidad que la tasa de
transporte de cloro a la pared, de tal modo que no se presente acumulación de cloro en las
paredes, se tiene como resultado el siguiente balance de masa para el cloro en la pared:
𝑘
𝑓
(𝐶 − 𝐶
𝑤
) = 𝑘
𝑤
𝐶
𝑤
Ecuación 21. Balance de masa para el cloro en la pared de la tubería (Rossman, Clark, & Grayman , 1994).
donde,
𝑘
𝑤
, es una constante de decaimiento con unidades de longitud sobre tiempo.
Resolviendo la Ecuación 21 para 𝐶
𝑤
y sustituyendo en la Ecuación 20, se obtiene:
𝜕𝐶
𝜕𝑡
= −𝑢
𝜕𝐶
𝜕𝑥
− 𝑘
𝑏
𝐶 −
𝑘
𝑤
𝑘
𝑓
𝐶
𝑟
ℎ
(𝑘
𝑤
+ 𝑘
𝑓
)
Ecuación 22. Balance de masa del cloro con reacción en la pared de la tubería (Rossman, Clark, & Grayman , 1994).
En la literatura se pueden encontrar coeficientes de transferencia de masa 𝑘
𝑓
como los
siguientes (Edwards et al. 1976):
𝑘
𝑓
= 𝑆ℎ
𝐷
𝑑
Ecuación 23. Coeficiente de transferencia de masa (Rossman, Clark, & Grayman , 1994).
𝑆ℎ = 0,023𝑅𝑒
0,83
𝑆𝑐
0,333
para Re > 2300

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
24
Nicolás Eduardo Páez Rincón
𝑆ℎ = 3,65 +
0,0668 (
𝑑
𝐿) (𝑅𝑒𝑆𝑐)
1 + 0,04 [(
𝑑
𝐿) (𝑅𝑒𝑆𝑐)]
2
3
⁄
para Re < 2300
Ecuación 24. Número de Sherwood (Rossman, Clark, & Grayman , 1994).
𝑅𝑒 =
𝑣𝑑
𝜈
𝑆𝑐 =
𝜈
𝑑
Ecuación 25. Número de Schmidt (Rossman, Clark, & Grayman , 1994).
donde,
𝑆ℎ, es el número de Sherwood.
𝑅𝑒, es el número de Reynolds.
𝑆𝑐, es el número de Schmidt.
𝐷, es la difusividad molecular del cloro en el agua.
𝜈, es la viscosidad cinemática del agua.
𝑑, es el diámetro de la tubería.
𝐿, es la longitud de la tubería.
Para una determinada especie química, 𝑘
𝑓
es función del diámetro de la tubería, la velocidad
del flujo, y la temperatura, que a su vez afecta la difusividad y la viscosidad del fluido.
La Ecuación 22 describe la variación en el tiempo del cloro a lo largo de un solo tubo. Para un
sistema de distribución, la ecuación de conservación de masa para el tubo i-ésimo se puede
expresar como:
𝜕𝐶
𝑖
𝜕𝑡
= −𝑢
𝑖
𝜕𝐶
𝑖
𝜕𝑥
𝑖
− 𝑘
𝑖
𝐶
𝑖
Ecuación 26. Conservación de masa del cloro en el tubo i-ésimo (Rossman, Clark, & Grayman , 1994).
donde,

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
25
Nicolás Eduardo Páez Rincón
𝑘
𝑖
, es una constante total de decaimiento que tiene en cuenta la constante de decaimiento del
cloro, el radio hidráulico, el coeficiente de transferencia de masa y la constante de
decaimiento de la pared:
𝑘
𝑖
= 𝑘
𝑏
+
𝑘
𝑤
𝑘
𝑓
𝑟
ℎ𝑖
(𝑘
𝑤
+𝑘
𝑓
)
Ecuación 27. Constante total de decaimiento del cloro (Rossman, Clark, & Grayman , 1994).
Para sistemas hidráulicos conocidos que pueden cambiar en el tiempo, la Ecuación 26 puede
ser resuelta con una condición inicial para el cloro a través de la red en el tiempo 0, y una
condición de frontera en el cruce de tuberías. Suponiendo que se produce mezcla completa e
instantánea en los nudos, esta condición de contorno se puede expresar con la siguiente
ecuación de conservación de masa:
𝐶
𝑖|𝑥=0
=
∑ 𝑞
𝑘
𝐶
𝑘|𝑥=𝐿
+ 𝑀
𝑖
∑ 𝑞
𝑘
+ 𝑆
𝑖
Ecuación 28. Ecuación de conservación de masa del cloro con condición de contorno (Rossman, Clark, & Grayman ,
1994).
donde,
𝑞
𝑘
, es el caudal aguas arriba de la unión de la tubería.
𝑀
𝑖
, es cualquier flujo de masa de cloro externo introducido en la tubería principal i.
𝑆
𝑖
, es cualquier flujo externo de agua introducida en la tubería principal i.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
26
Nicolás Eduardo Páez Rincón
3.
Tesis anteriores
3.1. Construcción de un modelo físico para la medición de mezcla en nudos
de redes de distribución de agua potable
3.1.1.
Diseño y construcción del modelo físico
Esta tesis, realizada durante el periodo 2013 – 10 por la estudiante Laura Natalia Cotes
Gómez, es la primera en tratar el fenómeno de mezcla completa en los nudos de la red de
distribución de agua potable. Durante este periodo, Cotes Gómez, en conjunto con el técnico
del Laboratorio de Hidráulica, Jhon Adalberto Calvo, diseñaron y construyeron el modelo
físico que se utiliza en la actualidad para cuantificar los porcentajes de mezcla en uniones.
Las tuberías que comprenden el modelo se ubicaron encima de una serie de vertederos, por lo
que se diseñó una plataforma en madera de pino que cubriese los vertederos y que además,
permitiese una toma de pruebas más cómoda y sencilla, así como fuese estéticamente
agradable a la vista.
Posteriormente, se definieron los diámetros de las tuberías que conformarían el modelo y a
partir de éstos, se mandaron a fabricar las tuberías de vidrio, las cuales incluyen la
intersección de las tuberías. En la unión entre las tuberías de vidrio y PVC se utilizaron
cauchos y silicona fría para evitar las fugas. Adicionalmente, se instalaron las válvulas que
regulan los caudales de entrada y salida del modelo.
Por otro lado, el sistema de alimentación del modelo se construyó a partir de parte del modelo
8, el cual ya se encontraba construido, mas no en funcionamiento. El canal que hace parte de
dicho modelo se adecuó y dividió de tal forma que allí funcionasen los tanques de
alimentación del modelo. Las tuberías que suplen agua a dichos tanques se instalaron a partir
del punto de abastecimiento más cercano de agua potable.
3.1.2.
Pruebas cualitativas
Al final del proceso de construcción se realizaron las primeras pruebas cualitativas en el
modelo recientemente construido. Para lo anterior, se utilizó permanganato de potasio como
trazador, el cual se disolvió en uno de los dos tanques de alimentación al modelo.
Las válvulas se nombraron de la siguiente forma:

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
27
Nicolás Eduardo Páez Rincón
Válvula 1: Válvula de la tubería de entrada de agua limpia.
Válvula 2: Válvula de la tubería de entrada de agua con trazador.
Para las pruebas, se identificaron 7 diferentes casos de análisis como se muestra a
continuación:
Apertura de Válvulas
Prueba Válvula 1 Válvula 2
1
100%
100%
2
50%
50%
3
100%
50%
4
50%
100%
5
100%
0%
6
0%
100%
7
75%
75%
Tabla 2. Casos de análisis planteados por Cotes Gómez (Cotes Gómez, 2013).
Los resultados se muestran a continuación:
Prueba 1:
Ilustración 2. Vista en planta de la prueba 1 (Cotes Gómez, 2013).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
28
Nicolás Eduardo Páez Rincón
Prueba 2:
Ilustración 3. Vista en planta de la prueba 2 (Cotes Gómez, 2013).
Prueba 3:
Ilustración 4. Vista en planta de la prueba 3 (Cotes Gómez, 2013).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
29
Nicolás Eduardo Páez Rincón
Prueba 4:
Ilustración 5. Vista en planta de la prueba 4 (Cotes Gómez, 2013).
Prueba 5:
Ilustración 6. Vista en planta de la prueba 5 (Cotes Gómez, 2013).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
30
Nicolás Eduardo Páez Rincón
Prueba 6:
Ilustración 7. Vista en planta de la prueba 6 (Cotes Gómez, 2013).
Prueba 7:
Ilustración 8. Vista en planta de la prueba 7 (Cotes Gómez, 2013).
3.1.3.
Conclusiones
Al finalizar la tesis, Cotes Gómez concluyó que efectivamente, no se presenta una mezcla
completa en la unión de las tuberías. Más específicamente, cuando el caudal por las dos
tuberías de entrada es el mismo, el porcentaje de mezcla es pequeño. Sin embargo, si se
aumenta el caudal de agua con trazador, en comparación con el caudal de agua limpia, parece

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
31
Nicolás Eduardo Páez Rincón
aumentar el porcentaje de mezcla en la unión. A medida que aumenta dicha diferencia de
caudales, el proceso de mezcla en la unión es cada vez más completo.
Si por el contrario, se aumenta el caudal de entrada de agua limpia en comparación con el
caudal de agua con trazador, también se fomenta el proceso de mezcla, pero las
concentraciones aguas abajo de la unión son muy pequeñas dada la pequeña masa de trazador
que llega a la unión debido al bajo caudal por dicha tubería.
3.2. Efectos de una mezcla no completa ni homogénea en los nudos sobre el
contenido residual de cloro en redes de distribución de agua potable
Esta tesis, realizada durante el período 2013 – 20 por la estudiante Laura Natalia Cotes
Gómez, es la continuación de la tesis previamente realizada por ella misma, con el objetivo de
cuantificar más detalladamente los porcentajes de mezcla en uniones de las redes de
distribución de agua potable.
3.2.1.
Adecuación del modelo físico
Durante el periodo de la tesis se diseñaron los sistemas de rebose en los dos tanques de
alimentación. Para el tanque de agua limpia, se decidió evacuar el agua por encima del nivel
del rebose, hasta el sifón más cercano. Por otro lado, para el tanque de agua con trazador se
decidió modificar la estructura de caída del modelo 8 para que funcionase como un tanque.
Para esto, se retiraron las placas inclinadas de dicha estructura, se realizó una limpieza de
material oxidado y silicona, y se colocó una plataforma en triplex de pino en el fondo de dicha
cámara. Para evitar el pandeo de la plataforma debido al peso del agua se colocó un refuerzo.
Los sistemas de rebose se diseñaron con el fin de tener una altura constante en los dos
tanques de alimentación y por ende, asegurar un caudal constante durante las pruebas. Dado
que era necesario conservar la misma concentración de trazador en el agua de dicho tanque,
se decidió que el agua rebosara al tanque modificado y, una vez llenos los dos tanques a la
misma altura, se inyectara el trazador. Posteriormente, mediante una bomba se recirculaba el
agua del tanque modificado al tanque de agua con trazador, con el fin de tener un sistema
cerrado en el que se conservara la altura del nivel del agua.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
32
Nicolás Eduardo Páez Rincón
3.2.2.
Pruebas cuantitativas
Una vez modificado el modelo físico, se realizaron pruebas cuantitativas con trazadores
conservativos (Cloruro de sodio) y no conservativos (Cloro). Los casos de análisis definidos se
muestran a continuación:
Apertura de Válvulas
Prueba Válvula 1 Válvula 2 Válvula 3 Válvula 4
1
100%
100%
100%
100%
2
50%
50%
100%
100%
3
100%
50%
100%
100%
4
50%
100%
100%
100%
5
75%
75%
100%
100%
6
100%
100%
50%
100%
7
100%
100%
100%
50%
Tabla 3. Casos de análisis planteados por Cotes Gómez (Cotes Gómez, 2013).
donde,
Válvula 1: Válvula de la tubería de entrada de agua limpia.
Válvula 2: Válvula de la tubería de entrada de agua con trazador.
Válvula 3: Válvula de la tubería de salida de agua con trazador.
Válvula 4: Válvula de la tubería de salida de agua limpia.
Los resultados obtenidos se condensan en las siguientes 2 figuras:
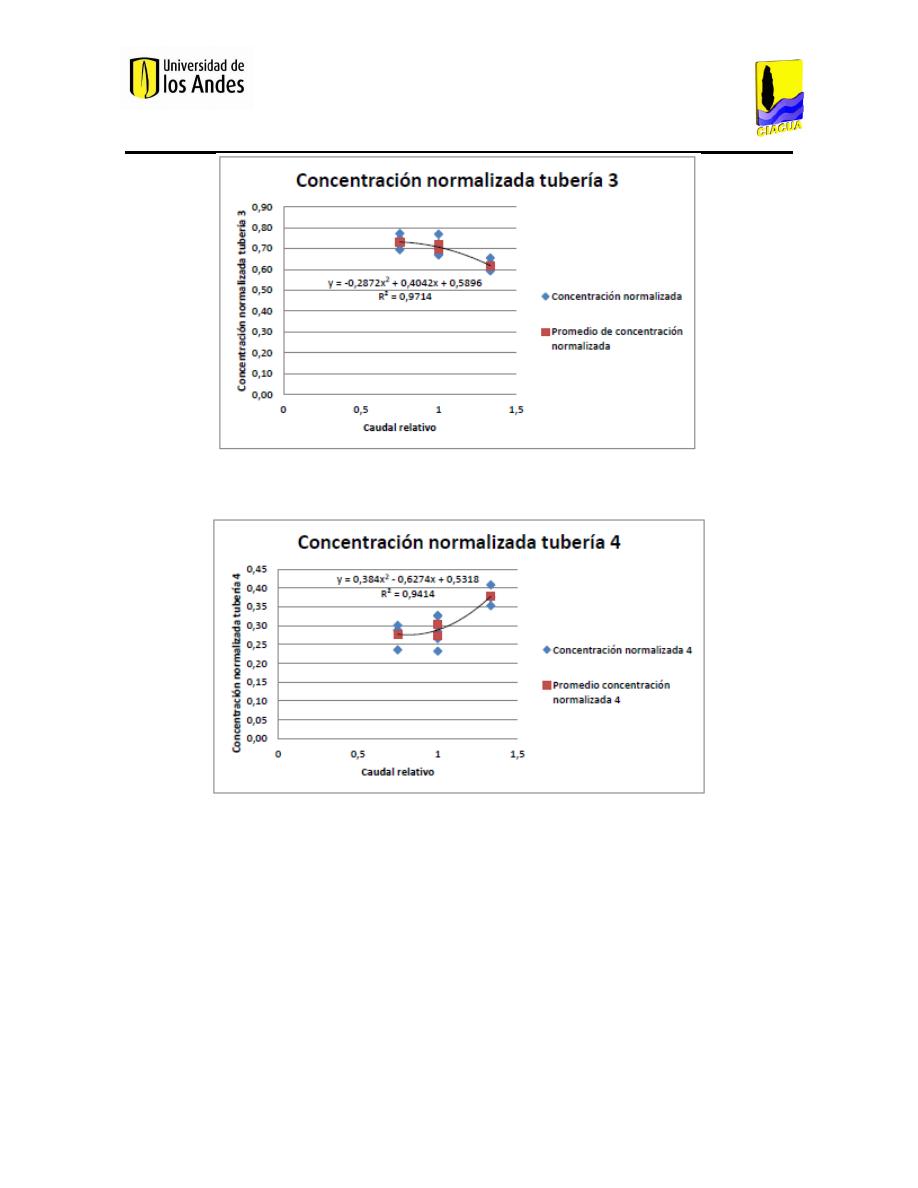
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
33
Nicolás Eduardo Páez Rincón
Figura 6. Concentración normalizada en la tubería 3 (Cotes Gómez, 2013).
Figura 7. Concentración normalizada en la tubería 4 (Cotes Gómez, 2013).
La Figura 6 muestra como a medida que aumenta el caudal relativo, disminuye la
concentración adimensional de cloro en la tubería 3. Lo anterior se debe a que a medida que
aumenta el caudal de la tubería 1 con respecto al caudal de la tubería 2, la masa de trazador
que se desvía hacia la tubería 3 es menor.
Por otra parte, la Figura 7 muestra el aumento de la concentración adimensional de cloro en la
tubería 4 al aumentar el caudal relativo. Lo anterior se debe a que a medida que aumenta el

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
34
Nicolás Eduardo Páez Rincón
caudal de la tubería 1 con respecto al caudal de la tubería 2, la masa de trazador que se desvía
hacia la tubería 4 es mayor.
De esta forma se puede observar que los resultados de las concentraciones adimensionales de
las tuberías 3 y 4 son complementarios, lo que es consistente con la conservación de masa que
se debe presentar en cualquier sistema cerrado.
3.2.3.
Conclusiones
Al finalizar la tesis, se corroboró que el proceso de mezcla en la unión no es completo, por lo
que en una de las dos tuberías de salida siempre sale una mayor parte del trazador inyectado.
En particular, se determinó que el porcentaje de trazador que sale por dicha tubería se
encuentra entre el 60% y el 75% del total, dependiendo del caso que se esté analizando. Por
otro lado, para la tubería por la que sale la menor parte del trazador, el porcentaje de trazador
en dicha tubería se encuentra entre el 25% y el 40% del total.
Para las pruebas con cloro, no se tuvo en cuenta los procesos de reacción de este trazador, ya
que se consideró que su tiempo de permanencia dentro de las tuberías del modelo es muy
pequeño, por lo que no se alcanza a presentar una degradación significativa de dicho trazador.
Por ende, los resultados obtenidos mediante el uso de dicho trazador fueron similares a los
obtenidos mediante el uso de cloruro de sodio.
A partir de los resultados obtenidos, se concluyó que uno de los factores que influye
significativamente en los procesos de mezcla, es la velocidad en las tuberías de entrada y por
ende, el régimen de flujo en las mismas.
3.3. Análisis de la dilución de concentraciones de NaCl en una unión tipo cruz
Esta tesis, realizada en el periodo 2013 – 20 por el ingeniero Iván Alexander Buitrago León,
pretendió cuantificar el porcentaje de mezcla obtenido en tuberías, y más específicamente
uniones en PVC, en comparación con Cotes Gómez, quien utilizó tuberías de vidrio.
3.3.1.
Modelo físico
El modelo físico realizado por Buitrago en su tesis se muestra a continuación:

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
35
Nicolás Eduardo Páez Rincón
Ilustración 9. Modelo físico realizado (Buitrago, 2013).
3.3.2.
Resultados
Los casos planteados por Buitrago León se muestran a continuación:
Caso Válvula 1
Válvula 2
Válvula 3
Válvula 4
1 Abierta
Abierta
Abierta
Abierta
2 Abierta
Cerrada 25° Abierta
Abierta
3 Abierta
Cerrada 45° Abierta
Abierta
4 Abierta
Cerrada 65° Abierta
Abierta
5 Cerrada 25° Abierta
Abierta
Abierta
6 Cerrada 45° Abierta
Abierta
Abierta
7 Cerrada 65° Abierta
Abierta
Abierta
8 Abierta
Abierta
Cerrada 25° Abierta
9 Abierta
Abierta
Cerrada 45° Abierta
10 Abierta
Abierta
Cerrada 65° Abierta
11 Cerrada 45° Abierta
Abierta
Cerrada 45°
12 Cerrada 45° Abierta
Cerrada 45° Abierta
Tabla 4. Casos de análisis planteados por Buitrago León (Buitrago, 2013).
3.3.2.1.
Metodologías utilizadas para el cálculo de las concentraciones
Buitrago León calculó las concentraciones de salida, C
3
y C
4
, mediante 4 diferentes
metodologías. Posteriormente comparó los resultados obtenidos con el promedio de los
valores medidos con el fin de confirmar que la propuesta metodológica para determinar una

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
36
Nicolás Eduardo Páez Rincón
ecuación que relacionaba las concentraciones de salida en función de las variables conocidas,
se aproximara a los valores obtenidos en las mediciones realizadas sobre el modelo físico del
experimento.
3.3.2.1.1.
Ecuación estándar
La ecuación estándar corresponde al balance de masa para el soluto en la unión de las
tuberías, es decir:
𝑄
1
𝐶
1
+ 𝑄
2
𝐶
2
= 𝑄
3
𝐶
3
+ 𝑄
4
𝐶
4
Ecuación 29. Ecuación estándar (Buitrago, 2013).
3.3.2.1.2.
Formulación para el cálculo de la concentración a partir de la ecuación de
Clifford K. Ho
En el planteamiento realizado por Ho, el cálculo de las concentraciones C
3
y C
4
depende de la
relación entre los caudales de entrada a la cruz Q
1
y Q
2
. En la Tabla 5 se encuentran las
ecuaciones obtenidas mediante el planteamiento realizado por Ho:
Tabla 5. Ecuaciones para el cálculo de las concentraciones C
3
y C
4
de acuerdo a la relación de los caudales Q
1
y Q
2
,
según las restricciones planteadas por Ho (Buitrago, 2013).
3.3.2.1.3.
Formulación para el cálculo de la concentración a partir de la ecuación de
Pedro Romero-Gómez
En el planteamiento realizado por Romero-Gómez, el cálculo de las concentraciones C
3
y C
4
depende de la relación entre los caudales de entrada a la cruz Q
1
y Q
2
. En la Tabla 6 se
encuentran las ecuaciones obtenidas mediante el planteamiento realizado por Romero-
Gómez:

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
37
Nicolás Eduardo Páez Rincón
Tabla 6. Ecuaciones para el cálculo de las concentraciones C
3
y C
4
de acuerdo a la relación de los caudales Q
1
y Q
2
,
según las restricciones planteadas por Pedro Romero-Gómez (Buitrago, 2013).
3.3.2.1.4.
Formulación para el cálculo de la concentración planteado por Buitrago León
Buitrago León creó 2 ecuaciones para el cálculo de las concentraciones C
3
y C
4
a partir de
regresiones realizadas a los resultados obtenidos en sus experimentos. En este caso, las
ecuaciones no varían dependiendo de la relación entre los caudales Q
1
y Q
2
. A continuación se
muestran las ecuaciones obtenidas por Buitrago León:
𝐶
3
=
𝑄
1
𝐶
1
+ 𝑄
2
𝐶
2
𝑄
3
[
1
0,3580 ln (
𝑄
1
𝐶
1
𝑄
2
𝐶
2
) − 2,0724
+ 1]
Ecuación 30. Ecuación para el cálculo de la concentración C
3
planteada por Buitrago León (Buitrago, 2013).
𝐶
4
=
𝑄
1
𝐶
1
+ 𝑄
2
𝐶
2
𝑄
4
[
1
0,3580 ln (
𝑄
1
𝐶
1
𝑄
2
𝐶
2
) − 1,0724
]
Ecuación 31. Ecuación para el cálculo de la concentración C4 planteada por Buitrago León (Buitrago, 2013).
3.3.2.2.
Resultados obtenidos
Dichos resultados se ilustran a continuación:
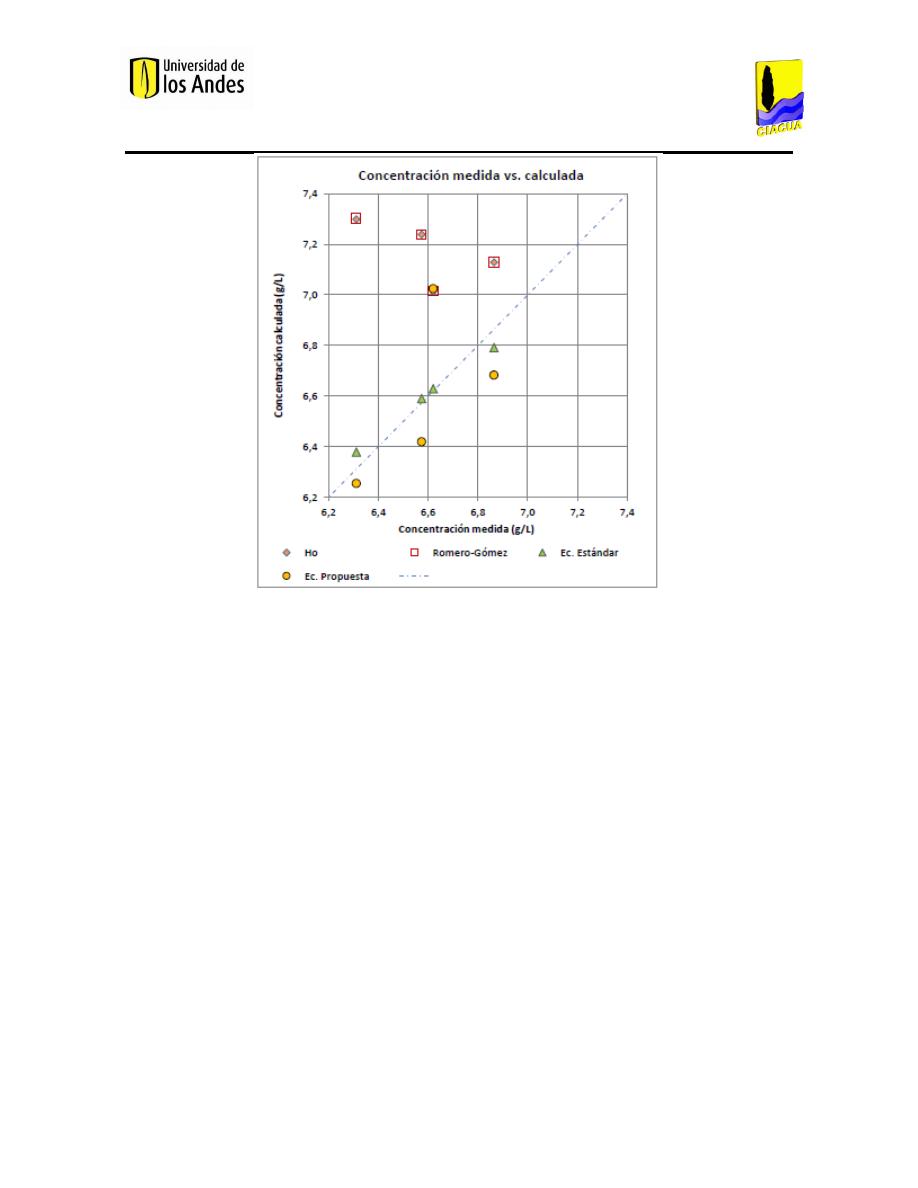
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
38
Nicolás Eduardo Páez Rincón
Figura 8. Resultados obtenidos para la concentración en la tubería 4 (Buitrago, 2013).
Como se puede observar, la ecuación estándar es de las cuatro evaluadas la que más se ajusta
a las mediciones realizadas; sin embargo es importante tener en cuenta que su uso se
restringe al conocimiento de las concentraciones de tres de las tuberías que componen la cruz,
situación que no es real debido a que en los modelos hidráulicos de redes de distribución de
agua a presión las concentraciones de salida son de por sí las incógnitas. Entre las ecuaciones
explícitas para el cálculo de C
4
, se puede observar que la propuesta en el presente estudio es la
que más se ajusta a los valores medidos, incluso más que las ecuaciones de Ho y Romero-
Gómez debido a las diferencias notables en el modelo físico de los experimentos realizados
por los diferentes autores.
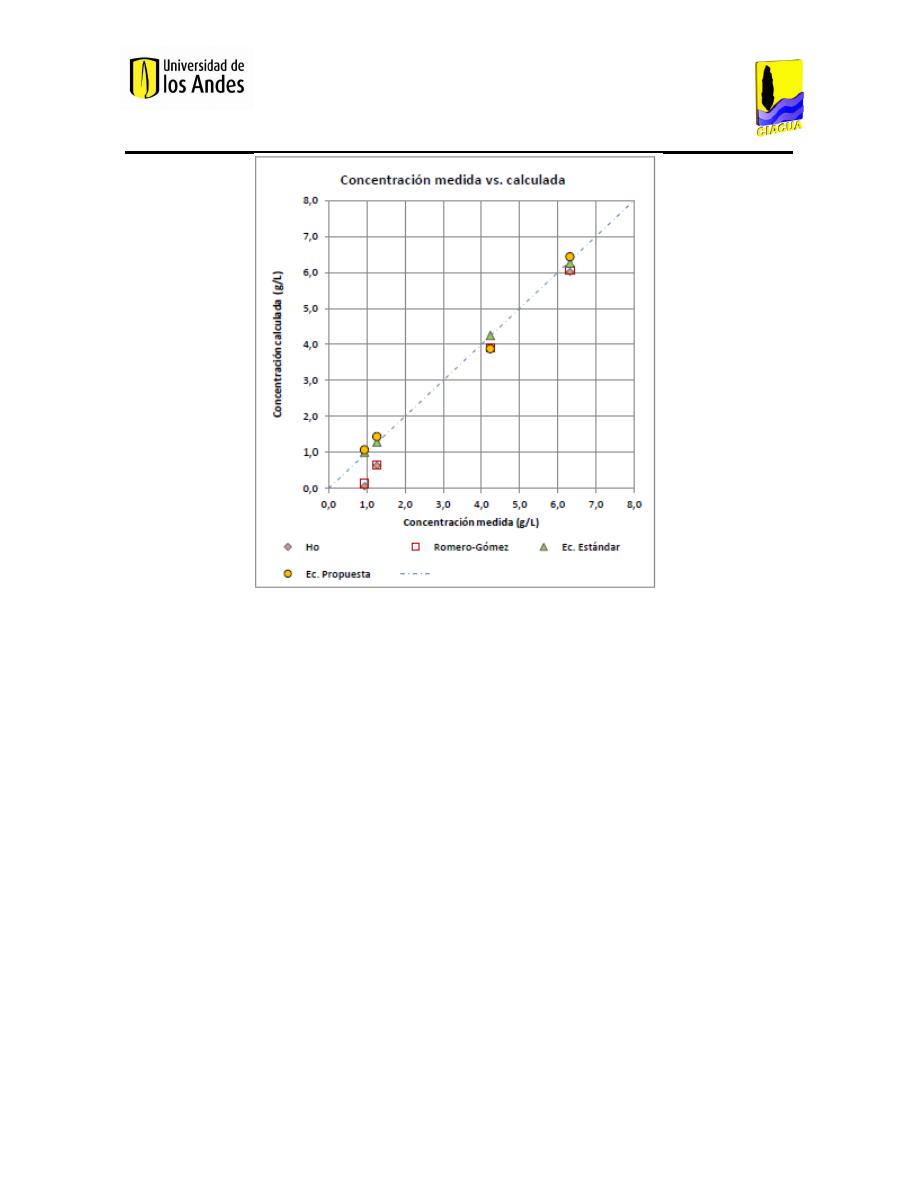
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
39
Nicolás Eduardo Páez Rincón
Figura 9. Resultados obtenidos para la concentración en la tubería 3 (Buitrago, 2013).
En este caso se puede observar que tal como ocurrió en el caso anterior, la ecuación propuesta
muestra un alto nivel de ajuste a las mediciones realizadas en las pruebas del experimento.
Adicionalmente, confirma que el choque de dos flujos genera una redirección de éstos, tal que
las concentraciones de salida son similares a las concentraciones de entrada. Sin embargo, si
la diferencia de velocidades es importante, el flujo con mayor velocidad logra salir por la
tubería opuesta a aquella por la que entró. En esta tubería se presentará mezcla de los dos
flujos, mientras en la otra tubería de salida saldrá un flujo con las mismas características que
las del flujo de entrada de mayor velocidad.
3.3.3.
Conclusiones
Al finalizar la tesis, se concluyó que algunas de las ecuaciones para determinar las
concentraciones en las tuberías de salida se ajustan más a los resultados obtenidos
experimentalmente, en comparación con otras. En particular, las dos mejores ecuaciones son
la propuesta por Buitrago León y la ecuación estándar.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
40
Nicolás Eduardo Páez Rincón
4.
Marco Teórico
5.1. Modelación hidráulica
En la modelación hidráulica se realiza el cálculo de los caudales en las tuberías, y las presiones
en los nudos de la red; por ende, se debe cumplir la ecuación de conservación en cada uno de
los nudos de la red. De acuerdo con esto, la ecuación de continuidad es la siguiente:
∑ 𝑄
𝑖𝑗
− 𝑄
𝐷𝑖
+ 𝑄
𝑒𝑖
= 0
𝑁𝑇
𝑖
𝑗=𝑖
Ecuación 32. Conservación de masa en los nudos de la red (Saldarriaga, 2007).
donde,
𝑁𝑇
𝑖
, es el número de tuberías.
𝑄
𝐷𝑖
, es el caudal demandado en la unión i.
𝑄
𝑒𝑖
, es el caudal de entrada al nudo i.
𝑄
𝑖𝑗
, es el caudal de la tubería.
Para el cálculo de los caudales se hace uso de la ecuación de Darcy – Weisbach en conjunto
con la ecuación de Colebrook – White. De esta forma se obtiene una ecuación explícita para el
caudal, en la que se observa claramente como la relación entre las pérdidas por fricción y el
caudal para cada uno de las tuberías que conforman la red, no es lineal:
𝑄 = 2
√2𝑔𝑑ℎ
𝑓
√𝑙
𝐴𝑙𝑜𝑔
10
(
𝑘
𝑠
3,7𝑑
+
2,51𝜈√𝑙
𝑑√2𝑔𝑑ℎ
𝑓
)
Ecuación 33. Caudal en una tubería (Saldarriaga, 2007).
donde,
𝑔, es la aceleración de la gravedad.
𝑑, es el diámetro de la tubería.
ℎ
𝑓
, es la altura por pérdidas de fricción.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
41
Nicolás Eduardo Páez Rincón
𝑙, es la longitud de la tubería.
𝑘
𝑠
, es la rugosidad absoluta de la tubería.
𝜈, es la viscosidad cinemática del fluido.
Por otro lado, para el cálculo de las alturas piezométricas se supone que en cada tubo, la
energía total disponible se gasta en pérdidas por fricción y en pérdidas menores:
𝐻
𝑇
= ℎ
𝑓
+ ∑ ℎ
𝑚
Ecuación 34. Conservación de la energía (Saldarriaga, 2007).
Al tener en cuenta las pérdidas menores causadas por cualquier tipo de accesorios y/o
bombas en algunos de los tubos de la red, la ecuación anterior se modifica de la siguiente
manera:
𝐻
𝑇
= 𝛼𝑄
𝑛
+ 𝛽𝑄 + 𝛾
Ecuación 35. Altura piezométrica teniendo en cuenta pérdidas menores causadas por accesorios (Saldarriaga, 2007).
donde,
𝑛, es un exponente que depende de la ecuación de fricción utilizada. Para la ecuación de Darcy
– Weisbach es 2, mientras para la ecuación de Hazen – Williams es 0,85.
𝛼, 𝛽, 𝛾, son los parámetros característicos del tubo, las válvulas y las bombas.
Por lo general, en las tuberías sólo se presentan pérdidas por fricción y pérdidas menores, las
cuales son función únicamente de la altura de velocidad. Esta situación se presenta ya que en
la red es rara la presencia de bombas u otros accesorios diferentes a los típicamente utilizados
(Saldarriaga, 2014). En este caso, se puede utilizar la ecuación anterior para definir el valor de
𝛼:
𝐻
𝑇
= 𝛼𝑄
𝑛
ℎ
𝑓
+ ∑ ℎ
𝑚
= 𝛼𝑄
𝑛

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
42
Nicolás Eduardo Páez Rincón
Utilizando la ecuación de Darcy – Weisbach, esta última ecuación se transforma en:
(𝑓
𝐿
𝑑
+ ∑ 𝑘
𝑚
)
𝑄
2
2𝑔𝐴
2
= 𝛼𝑄
𝑛
Despejando 𝛼:
𝛼 =
(𝑓
𝐿
𝑑 + ∑ 𝑘
𝑚
)
2𝑔𝐴
2
Ecuación 36. Parámetro α (Saldarriaga, 2007).
El parámetro 𝛼 es un parámetro característico de la tubería que incluye los factores de
pérdidas por fricción y pérdidas menores. Por otro lado, en el caso de accesorios especiales en
la tubería, como algunos tipos de válvulas, el parámetro 𝛼 establece su relación con 𝑄
𝑛
adicional a las relaciones para las pérdidas antes mencionadas. Para bombas colocadas en las
tuberías se requieren los tres parámetros 𝛼, 𝛽, 𝛾 ya que la relación entre la altura
piezométrica suministrada por la bomba y el canal es polinomial (Saldarriaga, 2007).
5.1.1. Método del gradiente
El método del gradiente fue desarrollado por los profesores E. Todini y E. P. O’Connell en la
Universidad de Newcastle upon Tyne y por R. Salgado, como parte de su tesis doctoral en
1982-1983. El método plantea que las ecuaciones de energía individuales para cada tubería se
combinan con las ecuaciones de masa individuales en cada unión, con el fin de obtener una
solución simultánea tanto de los caudales en las tuberías como de las alturas piezométricas en
los nudos (Saldarriaga, 2007).
El método del gradiente linealiza las ecuaciones de energía mediante el uso de expansiones en
series de Taylor, y las ecuaciones se resuelven utilizando un esquema imaginativo que se basa
en la inversión de la matriz de coeficientes originales.
El método se basa en el hecho de que al tener un flujo permanente, se garantiza que se
cumplan las ecuaciones de conservación de la masa en cada uno de los nudos de la red, al
tiempo que se cumple la ecuación de conservación de la energía en los circuitos de la misma.
Para utilizar este método se deben cumplir 3 condiciones, basadas en las ecuaciones
previamente presentadas:

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
43
Nicolás Eduardo Páez Rincón
1. En cada nudo se debe cumplir la ecuación de continuidad.
2. Debe haber una relación no lineal entre las pérdidas por fricción y el caudal para cada
uno de los tubos.
3. En cada tubo, la energía total se gasta en pérdidas por fricción y en pérdidas menores.
El método de gradiente hidráulico describe la topología de la red en forma matricial. Para
esto, hace uso de las siguientes definiciones:
𝑁𝑇, es el número de tuberías en la red.
𝑁𝑁, es el número de nudos con alturas piezométricas desconocidas.
[𝐴12], es la “matriz de conectividad” asociada con cada uno de los nudos de la red. Su
dimensión es 𝑁𝑇 𝑥 𝑁𝑁 con sólo dos elementos diferentes de cero en la i-ésima fila: Es -1 en la
columna correspondiente al nudo inicial al tramo i, y es 1 en la columna correspondiente al
nudo final del tramo i.
𝑁𝑆, es el número de nudos de altura piezométrica conocida.
[𝐴10], es la matriz topológica tramo a nudo para los NS nudos de altura piezométrica fija. Su
dimensión es 𝑁𝑇 𝑥 𝑁𝑆 con un valor de -1 en las filas correspondientes a los tramos
conectados a los nudos de altura piezométrica fija.
De esta manera, la pérdida de altura piezométrica en cada tramo de tubería que conecte dos
nudos de la red es:
[𝐴11][𝑄] + [𝐴12][𝐻] = −[𝐴10][𝐻
0
]
Ecuación 37. Ecuación de conservación de la energía (Saldarriaga, 2007).
donde,
[𝐴11], es la matriz diagonal de 𝑁𝑇 𝑥 𝑁𝑇 definida de la siguiente forma:

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
44
Nicolás Eduardo Páez Rincón
[𝐴11] =
[
𝛼
1
𝑄
1
(𝑛
1
−1)
+ 𝛽
1
+
𝛾
1
𝑄
1
0
0
𝛼
2
𝑄
2
(𝑛
2
−1)
+ 𝛽
2
+
𝛾
2
𝑄
2
0 0
0 0
0 0
0 0
⋱
0
0 𝛼
𝑛
𝑄
𝑛
(𝑛
𝑛
−1)
+ 𝛽
𝑛
+
𝛾
𝑛
𝑄
𝑛
]
Ecuación 38. Matriz A11 (Saldarriaga, 2007).
[𝑄], es el vector de caudales con dimensiones 𝑁𝑇 𝑥 1.
[𝐻], es el vector de alturas piezométricas desconocidas con dimensiones 𝑁𝑁 𝑥 1.
[𝐻
0
], es el vector de alturas piezométricas fijas con dimensiones 𝑁𝑆 𝑥 1.
La ecuación de continuidad para todos los nudos de la red es:
[𝐴21][𝑄] = [𝑞]
Ecuación 39. Ecuación de continuidad para todos los nudos (Saldarriaga, 2007).
donde,
[𝐴21], es la matriz transpuesta de [𝐴12].
[𝑞], es el vector de consumo o de entrada en cada nudo de la red, con dimensiones 𝑁𝑁 𝑥 1.
En forma compacta, las ecuaciones de conservación de energía y continuidad para los nudos
se pueden expresar en términos matriciales:
[
[𝐴11] [𝐴12]
[𝐴21]
[0]
] [
[𝑄]
[𝐻]
] = [
−[𝐴10] [𝐻
0
]
[𝑞]
]
Ecuación 40. Combinación de las ecuaciones de conservación de energía y continuidad (Saldarriaga, 2007).
Esta ecuación no puede resolverse en forma directa, ya que la parte superior no es lineal. Por
ende, es necesario utilizar algún método iterativo. En el método del gradiente se utiliza una
expansión truncada de Taylor, en donde al operar simultáneamente sobre el campo ([𝑄], [𝐻])
y aplicar el operador gradiente se obtiene:

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
45
Nicolás Eduardo Páez Rincón
[
[𝑁][𝐴11]′ [𝐴12]
[𝐴21]
[0]
] [
[𝑑𝑄]
[𝑑𝐻]
] = [
[𝑑𝐸]
[𝑑𝑞]]
Ecuación 41. Ecuación obtenida al aplicar el operador gradiente (Saldarriaga, 2007).
donde,
[𝑁], es la matriz diagonal (𝑛1, 𝑛2, … , 𝑛𝑁𝑇) con dimensiones 𝑁𝑇 𝑥 𝑁𝑇.
[𝐴11]′, es la matriz con dimensión 𝑁𝑇 𝑥 𝑁𝑇 definida como:
[𝐴11]
′
=
[
𝛼
1
𝑄
1
(𝑛
1
−1)
0
0
𝛼
2
𝑄
2
(𝑛
2
−1)
0 0
0 0
0 0
0 0
⋱
0
0 𝛼
𝑛
𝑄
𝑛
(𝑛
𝑛
−1)
]
Ecuación 42. Matriz A11' (Saldarriaga, 2007).
En cualquier iteración i, [𝑑𝐸] representa el desbalance de energía por unidad de peso (altura
piezométrica) en cada tubería y [𝑑𝑞] representa el desbalance de caudal en cada nudo. Esos
desbalances se definen, respectivamente, por las siguientes ecuaciones:
[𝑑𝐸] = [𝐴11][𝑄
𝑖
] + [𝐴12][𝐻
𝑖
] + [𝐴10][𝐻
0
]
Ecuación 43. Desbalance de energía en cada tubería (Saldarriaga, 2007).
[𝑑𝑞] = [𝐴21][𝑄
𝑖
] − [𝑞]
Ecuación 44. Desbalance de caudal en cada nudo (Saldarriaga, 2007).
El método del gradiente soluciona el sistema descrito mediante la Ecuación 41, teniendo en
cuenta para cada iteración que:
[𝑑𝑄] = [𝑄
𝑖+1
] − [𝑄
𝑖
]
Ecuación 45. Diferencia de caudal para cada tubería en dos iteraciones sucesivas (Saldarriaga, 2007).
[𝑑𝐻] = [𝐻
𝑖+1
] − [𝐻
𝑖
]
Ecuación 46. Diferencia de altura piezométrica para cada nudo en dos iteraciones sucesivas (Saldarriaga, 2007).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
46
Nicolás Eduardo Páez Rincón
La solución puede calcularse resolviendo el siguiente sistema:
[
[𝑑𝑄]
[𝑑𝐻]
] = [
[𝑁][𝐴11]′ [𝐴12]
[𝐴21]
[0]
]
−1
[
[𝑑𝐸]
[𝑑𝑞]]
Ecuación 47. Sistema solucionado con el método del gradiente.
Utilizando el álgebra matricial, es posible calcular de forma explícita los caudales y las alturas
de la siguiente manera:
𝐻
𝑖+1
= −([𝐴21]([𝑁][𝐴11]′)
−1
[𝐴12])
−1
([𝐴21]([𝑁][𝐴11]′)
−1
([𝐴11][𝑄] + [𝐴10][𝐻
𝑜
])
− ([𝐴21][𝑄] − [𝑞]))
Ecuación 48. Cálculo de alturas piezométricas (Saldarriaga, 2007).
𝑄
𝑖+1
= {([𝐼] − ([𝑁][𝐴11]′)
−1
[𝐴11])[𝑄] − (([𝑁][𝐴11]′)
−1
([𝐴12][𝐻
𝑖+1
] + [𝐴10][𝐻
𝑜
]))}
Ecuación 49. Cálculo de caudales (Saldarriaga, 2007).
Para solucionar cualquier problema con el método del gradiente se deben seguir los
siguientes pasos iterativamente:
1. Se suponen unos caudales iniciales en cada uno de los tubos de la red (no
necesariamente balanceados, lo cual implica ahorro de tiempo).
2. Se resuelve el sistema representado por la Ecuación 48 utilizando un método estándar
para la solución de ecuaciones lineales simultáneas.
3. Con [𝐻
𝑖+1
] calculado se utiliza la Ecuación 49 para determinar [𝑄
𝑖+1
].
4. Con el [𝑄
𝑖+1
] se vuelve a ensamblar el sistema 48 para encontrar un nuevo [𝐻
𝑖+1
].
5. El proceso se repite hasta que en dos iteraciones sucesivas se cumpla que [𝐻
𝑖+1
] ≈
[𝐻
𝑖
].
5.1.2. Ejemplo de aplicación
El ejemplo que se muestra a continuación es realizado por el autor:
La red mostrada en la Figura 10 tiene accesorios en todas sus tuberías, tal que producen unas
pérdidas menores locales. Analizar los caudales y presiones en la red. Los caudales están
dados en L/s. La viscosidad cinemática del agua es de 1,14 x 10
-6
m
2
/s.
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
47
Nicolás Eduardo Páez Rincón
Figura 10. Red del ejemplo.
Tubería Diámetro (mm) Σk
m
Longitud (m)
k
s
(m)
1-2
300
10,1
1000
0,0000015
1-3
300
11,7
1486,6
0,0000015
2-3
250
8,4
1100
0,0000015
2-4
300
7,3
1200
0,0000015
3-5
300
12
1200
0,0000015
4-5
250
5,7
1100
0,0000015
4-6
250
8,4
1300
0,0000015
5-7
250
5,7
1300
0,0000015
6-7
200
3,8
1100
0,0000015
Tabla 7. Características de las tuberías.
Nudo
Q
demanda
(L/s)
2
78
3
45
4
55
5
50
6
24
7
33
Tabla 8. Caudal de demanda en cada nudo.
Para todos los tramos de tuberías se ha supuesto un caudal inicial de 100 L/s con las
direcciones mostradas en la figura, las cuales fueron supuestas de forma arbitraria.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
48
Nicolás Eduardo Páez Rincón
Para realizar el cálculo de las presiones y caudales en la red es necesario efectuar el siguiente
planteamiento de matrices y vectores, teniendo en cuenta que:
NT = 9
NN = 6
NS = 1
[𝐴12] = Matriz de conectividad, cuya dimensión es (9x6).
1
0
0
0
0
0
0
1
0
0
0
0
1
-1
0
0
0
0
-1
0
1
0
0
0
0
-1
0
1
0
0
0
0
1
-1
0
0
0
0
-1
0
1
0
0
0
0
-1
0
1
0
0
0
0
-1
1
[𝐴21] = Matriz transpuesta de [𝐴12], cuya dimensión es (6x9).
1
0
1
-1
0
0
0
0
0
0
1
-1
0
-1
0
0
0
0
0
0
0
1
0
1
-1
0
0
0
0
0
0
1
-1
0
-1
0
0
0
0
0
0
0
1
0
-1
0
0
0
0
0
0
0
1
1
[𝐴10] = Matriz topológica tramo a nodo, cuya dimensión es (9x1).
[𝑄] = Vector de caudales, cuya dimensión es (9x1).
[𝐻] = Vector de alturas piezométricas desconocidas, cuya dimensión es (6x1).
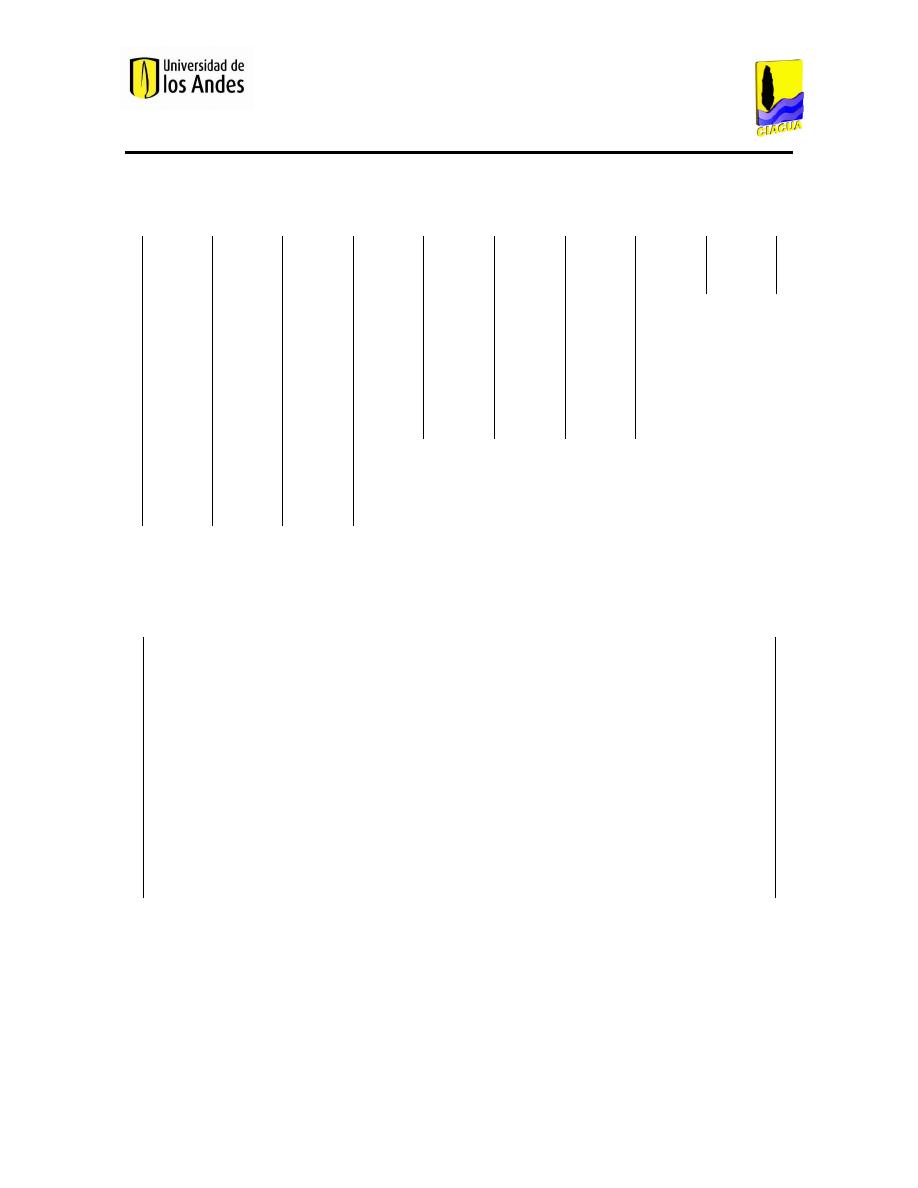
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
49
Nicolás Eduardo Páez Rincón
[𝐻
0
] = Vector de alturas piezométricas fijas, cuya dimensión es (1x1).
[𝑞] = Vector de consumo, cuya dimensión es (6x1).
A10
Q
H
q
H
o
-1
0,1
H
2
0,078
30
-1
0,1
H
3
0,045
0
0,1
H
4
0,055
0
0,1
H
5
0,05
0
0,1
H
6
0,024
0
0,1
H
7
0,033
0
0,1
0
0,1
0
0,1
[𝑁] = Matriz diagonal, cuya dimensión es (9x9). Presenta el valor de 2 en la diagonal, ya que se
utiliza la ecuación de Darcy – Weisbach como la ecuación de fricción.
2
0
0
0
0
0
0
0
0
0
2
0
0
0
0
0
0
0
0
0
2
0
0
0
0
0
0
0
0
0
2
0
0
0
0
0
0
0
0
0
2
0
0
0
0
0
0
0
0
0
2
0
0
0
0
0
0
0
0
0
2
0
0
0
0
0
0
0
0
0
2
0
0
0
0
0
0
0
0
0
2

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
50
Nicolás Eduardo Páez Rincón
[𝐼] = Matriz identidad, cuya dimensión es (9x9).
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
Primera iteración
Las matrices anteriormente definidas son válidas para todas las iteraciones necesarias en el
cálculo de la red. Las expuestas a continuación varían de una iteración a otra.
[𝐴11] = Matriz diagonal cuya dimensión es (9x9). Presenta el valor 𝛼
𝑖
𝑄
𝑖
(𝑛
𝑖
−1)
+ 𝛽
𝑖
+
𝛾
𝑖
𝑄
𝑖
en la
diagonal, los coeficientes 𝛽 y 𝛾 son ceros, ya que no existen bombas en la red.
La siguiente tabla resume el cálculo de los coeficientes 𝛼.
Tubería Q (m
3
/s) v (m/s) N. Reynolds
f
𝛼
1-2
0,100
1,415 372292,265 0,014
577,368
1-3
0,100
1,415 372292,265 0,014
824,503
2-3
0,100
2,037 446750,717 0,014
1435,246
2-4
0,100
1,415 372292,265 0,014
643,674
3-5
0,100
1,415 372292,265 0,014
691,618
4-5
0,100
2,037 446750,717 0,014
1378,134
4-6
0,100
2,037 446750,717 0,014
1663,894
5-7
0,100
2,037 446750,717 0,014
1606,783
6-7
0,100
3,183 558438,397 0,013
3892,929

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
51
Nicolás Eduardo Páez Rincón
Matriz [𝐴11]:
57,736
0,0000
0,0000
0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
0,0000
82,450
0,0000
0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
0,0000
0,0000 143,524 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
0,0000
0,0000
0,0000
64,367 0,0000 0,0000 0,0000 0,0000 0,0000
0,0000
0,0000
0,0000
0,0000 69,161 0,0000 0,0000 0,0000 0,0000
0,0000
0,0000
0,0000
0,0000 0,0000 137,813 0,0000 0,0000 0,0000
0,0000
0,0000
0,0000
0,0000 0,0000 0,0000 166,389 0,0000 0,0000
0,0000
0,0000
0,0000
0,0000 0,0000 0,0000 0,0000 160,678 0,0000
0,0000
0,0000
0,0000
0,0000 0,0000 0,0000 0,0000 0,0000 389,292
[𝐴11]′ = Matriz diagonal cuya dimensión es (9x9). Presenta el valor 𝛼
𝑖
𝑄
𝑖
(𝑛
𝑖
−1)
en la diagonal.
Para esta red, la matriz [𝐴11]′ resulta ser igual a la matriz [𝐴11].
57,736
0,0000
0,0000
0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
0,0000
82,450
0,0000
0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
0,0000
0,0000 143,524 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
0,0000
0,0000
0,0000
64,367 0,0000 0,0000 0,0000 0,0000 0,0000
0,0000
0,0000
0,0000
0,0000 69,161 0,0000 0,0000 0,0000 0,0000
0,0000
0,0000
0,0000
0,0000 0,0000 137,813 0,0000 0,0000 0,0000
0,0000
0,0000
0,0000
0,0000 0,0000 0,0000 166,389 0,0000 0,0000
0,0000
0,0000
0,0000
0,0000 0,0000 0,0000 0,0000 160,678 0,0000
0,0000
0,0000
0,0000
0,0000 0,0000 0,0000 0,0000 0,0000 389,292
Cálculo de H
i
+1
Para el cálculo de H
i+1
se utiliza la ecuación:
𝐻
𝑖+1
= −([𝐴21]([𝑁][𝐴11]′)
−1
[𝐴12])
−1
([𝐴21]([𝑁][𝐴11]′)
−1
([𝐴11][𝑄] + [𝐴10][𝐻
𝑜
])
− ([𝐴21][𝑄] − [𝑞]))
De la solución sistemática de esta ecuación resultan las siguientes matrices:

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
52
Nicolás Eduardo Páez Rincón
([𝑁][𝐴11]′)
115,473 0,0000
0,0000
0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
0,0000 164,900
0,0000
0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
0,0000 0,0000
287,049
0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
0,0000 0,0000
0,0000
128,734 0,0000 0,0000 0,0000 0,0000 0,0000
0,0000 0,0000
0,0000
0,0000 138,323 0,0000 0,0000 0,0000 0,0000
0,0000 0,0000
0,0000
0,0000 0,0000 275,626 0,0000 0,0000 0,0000
0,0000 0,0000
0,0000
0,0000 0,0000 0,0000 332,778 0,0000 0,0000
0,0000 0,0000
0,0000
0,0000 0,0000 0,0000 0,0000 321,356 0,0000
0,0000 0,0000
0,0000
0,0000 0,0000 0,0000 0,0000 0,0000 778,585
([𝑁][𝐴11]′)
−1
0,0087
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0061
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0035
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0078
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0072
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0036
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0030
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0031
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0000
0,0013
[𝐴21]([𝑁][𝐴11]′)
−1
0,0087 0,0000 0,0035 -0,0078
0,0000
0,0000
0,0000
0,0000 0,0000
0,0000 0,0061 -0,0035 0,0000
-0,0072
0,0000
0,0000
0,0000 0,0000
0,0000 0,0000 0,0000 0,0078
0,0000
0,0036
-0,0030
0,0000 0,0000
0,0000 0,0000 0,0000 0,0000
0,0072
-0,0036
0,0000
-0,0031 0,0000
0,0000 0,0000 0,0000 0,0000
0,0000
0,0000
0,0030
0,0000 -0,0013
0,0000 0,0000 0,0000 0,0000
0,0000
0,0000
0,0000
0,0031 0,0013
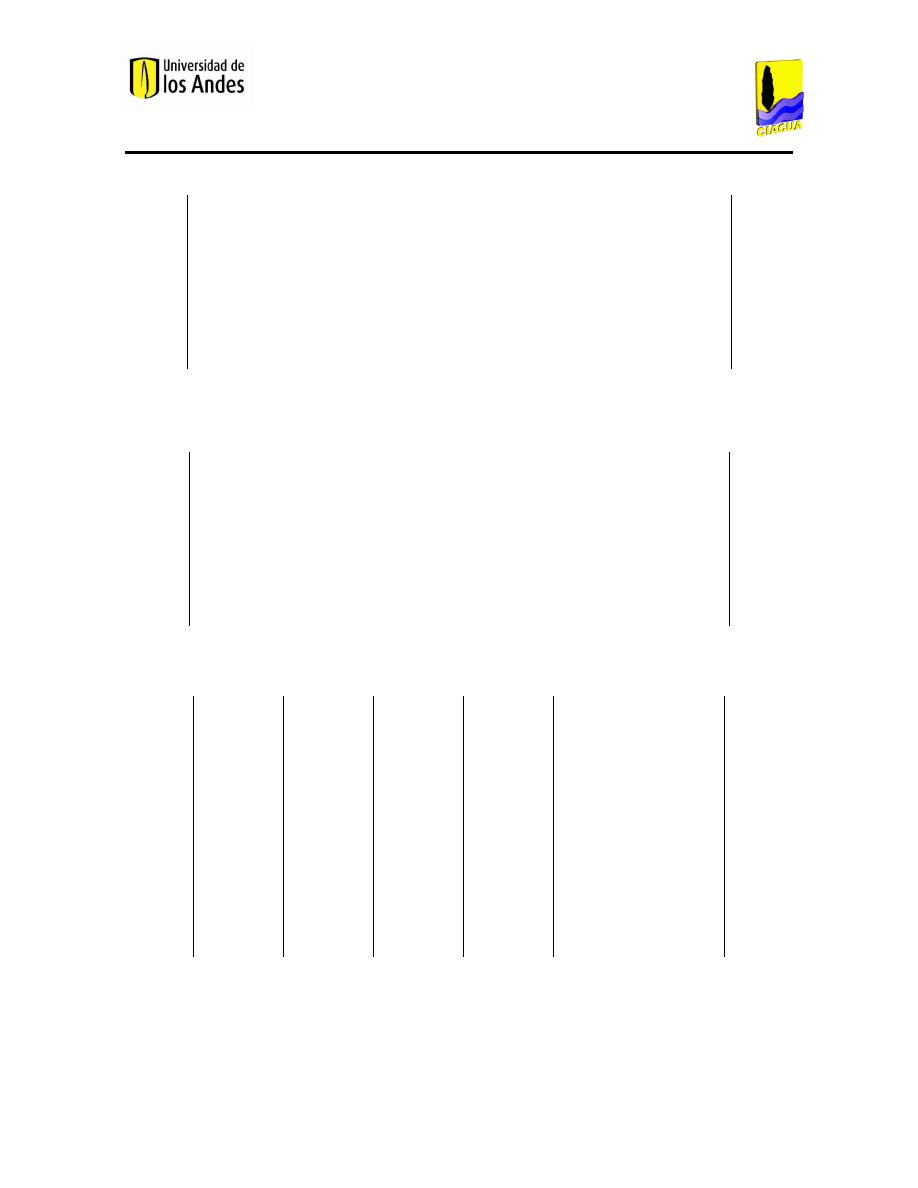
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
53
Nicolás Eduardo Páez Rincón
[𝐴21]([𝑁][𝐴11]′)
−1
[𝐴12]
0,0199
-0,0035
-0,0078
0,0000
0,0000
0,0000
-0,0035
0,0168
0,0000
-0,0072
0,0000
0,0000
-0,0078
0,0000
0,0144
-0,0036
-0,0030
0,0000
0,0000
-0,0072
-0,0036
0,0140
0,0000
-0,0031
0,0000
0,0000
-0,0030
0,0000
0,0043
-0,0013
0,0000
0,0000
0,0000
-0,0031
-0,0013
0,0044
([𝐴21]([𝑁][𝐴11]′)
−1
[𝐴12])
−1
-86,6427
-41,1717
-74,8933
-53,7962
-69,9931
-58,5282
-41,1717 -106,1059 -57,9502
-88,0777
-64,9479
-81,3202
-74,8933
-57,9502 -165,9861 -98,3959 -150,2869 -113,5563
-53,7962
-88,0777
-98,3959 -178,4795 -116,9970 -160,5169
-69,9931
-64,9479 -150,2869 -116,9970 -398,0388 -199,1055
-58,5282
-81,3202 -113,5563 -160,5169 -199,1055 -399,2606
[𝐴11][𝑄]
[𝐴10][𝐻
𝑜
]
[𝐴11][𝑄] + [𝐴10][𝐻
𝑜
]
5,7737
-30,0000
-24,2263
8,2450
-30,0000
-21,7550
14,3525
0,0000
14,3525
6,4367
0,0000
6,4367
6,9162
0,0000
6,9162
13,7813
0,0000
13,7813
16,6389
0,0000
16,6389
16,0678
0,0000
16,0678
38,9293
0,0000
38,9293

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
54
Nicolás Eduardo Páez Rincón
[𝐴21]([𝑁][𝐴11]′)
−1
([𝐴11][𝑄]
+ [𝐴10][𝐻
𝑜
])
[𝐴21][𝑄]
([𝐴21]([𝑁][𝐴11]′)
−1
([𝐴11][𝑄]
+ [𝐴10][𝐻
𝑜
])
− ([𝐴21][𝑄] − [𝑞]))
-0,2098
0,1000
-0,2318
-0,2319
-0,1000
-0,0869
0,0500
0,1000
0,0050
-0,0500
-0,1000
0,1000
0,0000
0,0000
0,0240
0,1000
0,2000
-0,0670
Luego,
Nudo
Altura (m)
2
20,150
3
13,559
4
=
15,730
5
9,733
6
13,206
7
25,988
Cálculo de Q
i
+1
Para el cálculo de Q
i+1
se utilizará la ecuación:
𝑄
𝑖+1
= {([𝐼] − ([𝑁][𝐴11]′)
−1
[𝐴11])[𝑄] − (([𝑁][𝐴11]′)
−1
([𝐴12][𝐻
𝑖+1
] + [𝐴10][𝐻
𝑜
]))}
De la solución sistemática de esta ecuación resultan las siguientes matrices:
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
55
Nicolás Eduardo Páez Rincón
[𝐴12][𝐻
𝑖+1
]
[𝐴12][𝐻
𝑖+1
]
+ [𝐴10][𝐻
𝑜
]
([𝑁][𝐴11]′)
−1
([𝐴12][𝐻
𝑖+1
]
+ [𝐴10][𝐻
𝑜
])
20,1502
-9,8498
-0,0853
13,5593
-16,4407
-0,0997
6,5909
6,5909
0,0230
-4,4206
-4,4206
-0,0343
-3,8262
-3,8262
-0,0277
5,9965
5,9965
0,0218
-2,5234
-2,5234
-0,0076
16,2552
16,2552
0,0506
12,7821
12,7821
0,0164
([𝑁][𝐴11]′)
−1
[𝐴11]
0,5
0
0
0
0
0
0
0
0
0
0,5
0
0
0
0
0
0
0
0
0
0,5
0
0
0
0
0
0
0
0
0
0,5
0
0
0
0
0
0
0
0
0
0,5
0
0
0
0
0
0
0
0
0
0,5
0
0
0
0
0
0
0
0
0
0,5
0
0
0
0
0
0
0
0
0
0,5
0
0
0
0
0
0
0
0
0
0,5

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
56
Nicolás Eduardo Páez Rincón
([𝐼] − ([𝑁][𝐴11]′)
−1
[𝐴11])
0,5
0
0
0
0
0
0
0
0
0
0,5
0
0
0
0
0
0
0
0
0
0,5
0
0
0
0
0
0
0
0
0
0,5
0
0
0
0
0
0
0
0
0
0,5
0
0
0
0
0
0
0
0
0
0,5
0
0
0
0
0
0
0
0
0
0,5
0
0
0
0
0
0
0
0
0
0,5
0
0
0
0
0
0
0
0
0
0,5
([𝐼] − ([𝑁][𝐴11]′)
−1
[𝐴11])[𝑄]
0,05
0,05
0,05
0,05
0,05
0,05
0,05
0,05
0,05
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
57
Nicolás Eduardo Páez Rincón
Luego,
Tubería
Caudal (m
3
/s)
1-2
0,1353
1-3
0,1497
2-3
0,0270
2-4
0,0843
3-5
=
0,0777
4-5
0,0282
4-6
0,0576
5-7
-0,0006
6-7
0,0336
Para las siguientes iteraciones se repite el procedimiento anterior y finalmente, en la quinta
iteración se obtienen los siguientes resultados:
Nudo
Altura (m)
2
16,797
3
16,842
4
=
12,295
5
12,296
6
10,695
7
10,590
Tubería
Caudal (m
3
/s)
1-2
0,1562
1-3
0,1288
2-3
0,0041
2-4
0,0823
3-5
=
0,0797
4-5
0,0005
4-6
0,0278
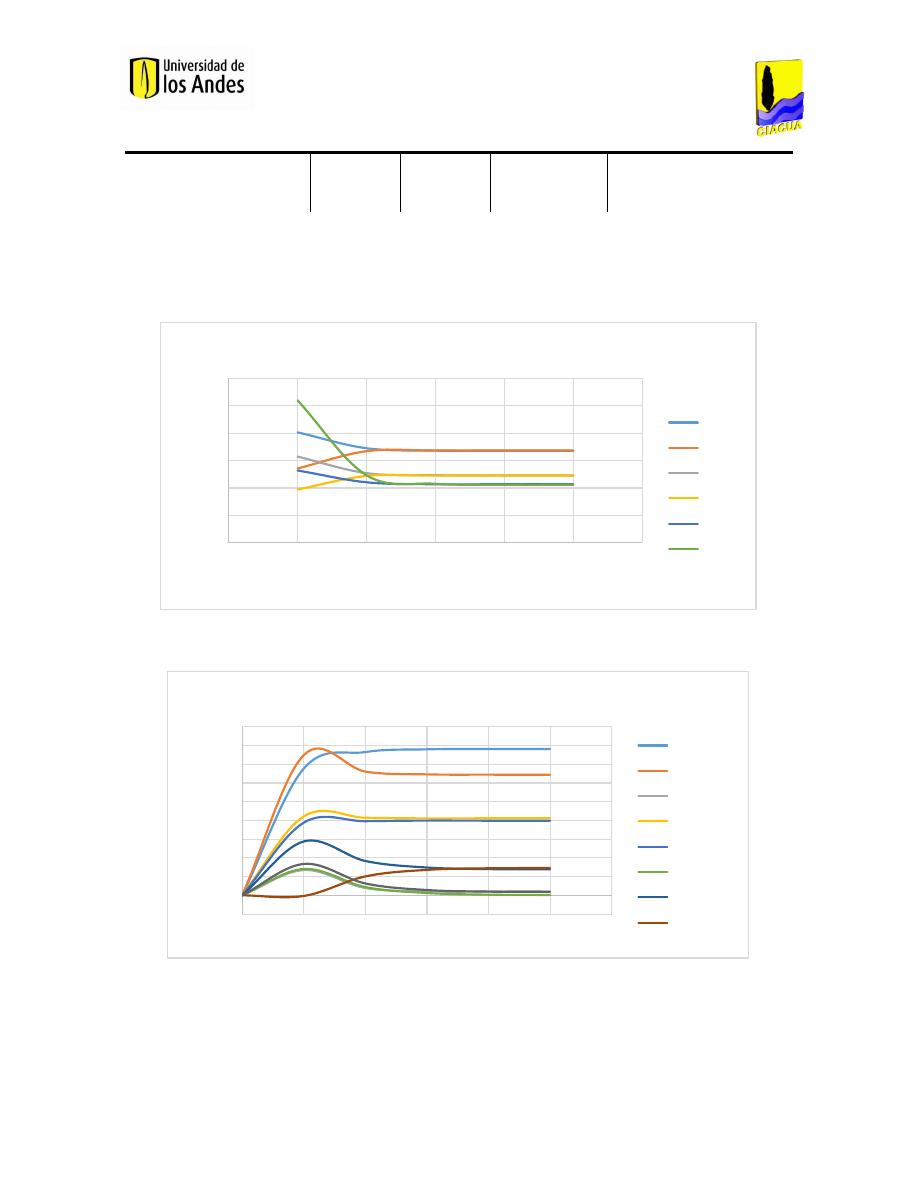
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
58
Nicolás Eduardo Páez Rincón
5-7
0,0292
6-7
0,0038
Para mostrar el proceso de convergencia del método del gradiente se encuentran las Figuras
11 y 12:
Figura 11. Convergencia de las alturas en los nudos con el método del gradiente.
Figura 12. Convergencia de los caudales en las tuberías con el método del gradiente.
En las Figuras 11 y 12 se puede apreciar la rápida velocidad de convergencia que se alcanza
mediante la implementación del método del gradiente. Para el caso particular del presente
0
5
10
15
20
25
30
0
1
2
3
4
5
6
Altu
ra
(m)
Número de Iteraciones
Convergencia de alturas - Método del Gradiente
Nudo 2
Nudo 3
Nudo 4
Nudo 5
Nudo 6
Nudo 7
-20
0
20
40
60
80
100
120
140
160
180
0
1
2
3
4
5
6
Cau
d
al
(L/s
)
Número de Iteraciones
Convergencia de caudales - Método del Gradiente
Tubería 1-2
Tubería 1-3
Tubería 2-3
Tubería 2-4
Tubería 3-5
Tubería 4-5
Tubería 4-6
Tubería 5-7

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
59
Nicolás Eduardo Páez Rincón
ejemplo, se puede concluir que con 3 iteraciones se alcanza un nivel de precisión adecuado.
Con el uso de más iteraciones no se alcanzarán cambios significativos en la precisión
alcanzada, aunque el método garantiza la solución en máximo NN iteraciones (Saldarriaga,
Hidráulica de Tuberías, 2007).
5.2. Modelación de la calidad del agua
La modelación de la calidad del agua constituye uno de los temas de mayor auge en el campo
de la hidráulica urbana durante los últimos años. La preocupación por la calidad del agua
potable mientras permanece en la red de distribución, una vez ha abandonado la planta de
tratamiento, surgió en EE.UU. en la década de los ochenta por el endurecimiento que
estableció la EPA sobre los requisitos de calidad que debía tener el agua al llegar a los puntos
de consumo (Vidal, Martínez, & Ayza, 1994).
El control de la calidad del agua y el análisis del comportamiento hidráulico de las redes han
constituido durante mucho tiempo dos campos de estudio independientes en relación con el
suministro de agua potable a las poblaciones. Por una parte, en las plantas de tratamiento se
pretende asegurar que el agua cumpla con los requisitos de calidad establecidos, tomando
como referencia usualmente el punto de salida de la planta o el de entrada a la red. Por otra
parte, los modelos hidráulicos se han utilizado, tanto en la fase de proyecto como en la de
operación de la red, para garantizar fundamentalmente que el agua llegue a los puntos de
consumo en las condiciones de presión y caudal requeridas, sin preocuparse por la calidad del
agua en el momento de ser consumida
Durante el tiempo que el agua permanece en la red, las sustancias más reactivas contenidas en
la misma, reaccionan o se combinan con otras sustancias presentes en el agua o adheridas a
las paredes de las tuberías. En el caso de los desinfectantes, su concentración disminuye a
través de la red favoreciendo el crecimiento bacteriológico, con el consiguiente riesgo
sanitario si no se garantiza una concentración mínima.
El diseño hidráulico de una red suele realizarse para el consumo punta, buscando asegurar
unas condiciones de suministro aceptables ante cualquier situación. El resultado es el
sobredimensionamiento de la red, y como consecuencia, la presencia de tramos con
velocidades muy bajas que conducen a largos tiempos de permanencia del agua en la red,
provocando el deterioro de la calidad del agua. La situación más desfavorable corresponde a
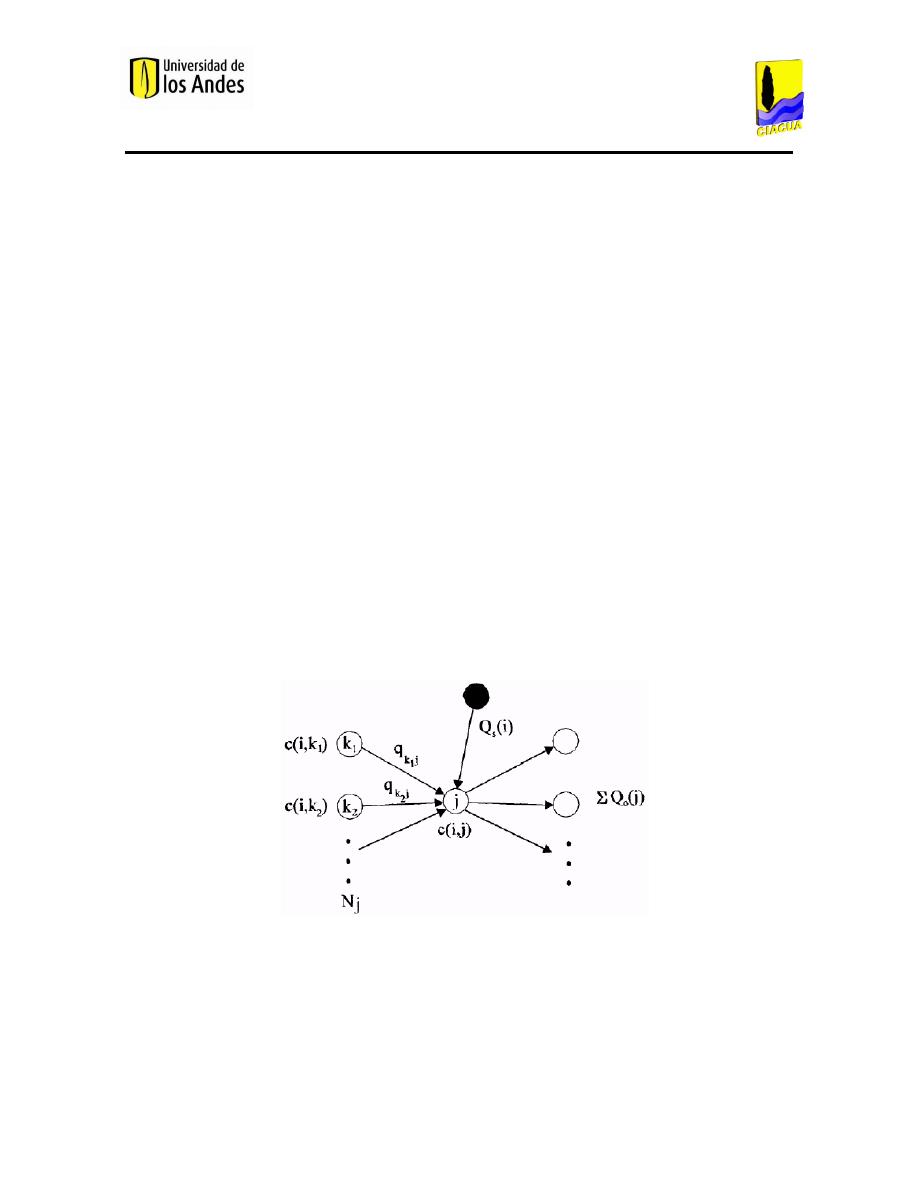
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
60
Nicolás Eduardo Páez Rincón
la de bajos consumos, período durante el cual debe procurarse que los tiempos de
permanencia del agua en la red resulten lo más cortos posibles.
En la modelación de la calidad del agua existen dos modelos de cálculo: Los modelos estáticos
y los modelos dinámicos.
5.2.1. Modelos estáticos
En los modelos estáticos se supone que los caudales demandados e inyectados a la red
permanecen constantes, y se admite que no varían las condiciones de operación de la red,
definidas por el estado de las válvulas y equipos de bombeo, y por los niveles de los depósitos
(Vidal, Martínez, & Ayza, 1994).
Estos modelos se aplican al estudio de transporte de contaminantes conservativos en las
redes de distribución de agua potable, determinando sus rutas, procedencias y tiempos de
permanencia en la misma bajo condiciones estáticas de operación.
Procedencias
La conservación de masa para cada nudo de la red se describe con la ecuación de continuidad,
en donde se define el porcentaje de la demanda en un nudo 𝑗 procedente de la fuente 𝑖
como 𝐶(𝑖, 𝑗) y se puede expresar de la siguiente manera:
Figura 13. Esquema de conservación de masa en el nudo j (Vidal, Martínez, & Ayza, 1994).
∑ 𝑐(𝑖, 𝑘)𝑞
𝑘𝑗
+ 𝑄
𝑠
(𝑖) = 𝑐(𝑖, 𝑗) ∑ 𝑄
0
(𝑗)
𝑁𝑗
𝑘=1
Ecuación 50. Ecuación de continuidad para la modelación de calidad del agua (Vidal, Martínez, & Ayza, 1994).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
61
Nicolás Eduardo Páez Rincón
donde,
𝑁𝑗, es el conjunto de nudos adyacentes al nudo j desde los que fluye caudal hacia dicho nudo.
𝑐(𝑖, 𝑘), son los factores de contribución de la fuente i en los nudos 𝑁𝑗.
𝑞
𝑘𝑗
, es el caudal que fluye del nudo 𝑘 al nudo 𝑗.
𝑄
𝑠
(𝑖), es el caudal que alimenta directamente al nudo 𝑗 desde la fuente 𝑖.
∑ 𝑄
0
(𝑗), es el caudal total que abandona el nudo 𝑗.
Concentración de mezclas
En la concentración de mezclas se determinan las concentraciones de determinadas
sustancias en cada uno de los nudos de la red, considerando la mezcla de aguas procedentes
de fuentes de distinta calidad. Por ende, la concentración de un cierto contaminante no
reactivo en el nudo 𝑗 suponiendo mezcla completa, se describe de la siguiente forma:
𝐶
𝑗
=
∑
(𝑞
𝑘𝑗
𝐶
𝑘
) + ∑ (𝑄
𝑠
(𝑖)𝐶
𝑠
(𝑖))
𝑖∈𝑆
𝐾∈𝑁𝑗
∑
(𝑞
𝑘𝑗
) + ∑ (𝑄
𝑠
(𝑖))
𝑖∈𝑆
𝐾∈𝑁𝑗
Ecuación 51. Concentración de soluto en el nudo j (Vidal, Martínez, & Ayza, 1994).
donde,
𝐶
𝑘
, es la concentración de la sustancia en los nudos aguas arriba adyacentes al nudo 𝑗.
𝐶
𝑠
(𝑖), es la concentración de dicha sustancia en la fuente 𝑖 que alimenta al nudo 𝑗.
Tiempos de permanencia
Dado que el caudal desde el punto de alimentación hasta un nudo determinado puede seguir
distintas rutas, el tiempo de permanencia del agua en la red desde que se inyecta en 𝑖 hasta
que llega a un nudo 𝑗 puede ser muy variable. Para considerar la mezcla de flujos con
diferentes antigüedades y tiempos de tránsito, se define el tiempo de permanencia medio 𝐴𝐴
𝑗
,
para un nudo 𝑗 como:
𝐴𝐴
𝑗
=
∑ 𝑞
𝑖
𝐴
𝑖
𝑞
𝑖
Ecuación 52. Tiempo de permanencia medio para el nudo j (Vidal, Martínez, & Ayza, 1994).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
62
Nicolás Eduardo Páez Rincón
donde,
𝑞
𝑖
, es el caudal que llega al nudo en estudio por el camino 𝑖.
𝐴
𝑖
, es la edad del agua en el punto de alimentación.
5.2.2. Modelos dinámicos
Los modelos dinámicos consideran el movimiento y reacción de los contaminantes bajo
condiciones variables en el tiempo, como sucede en realidad con las demandas, cambios de
nivel en los depósitos, cierre y apertura de válvulas, arranque y paro de bombas, entre otros.
En la evolución de los contaminantes a través de una red de distribución de agua potable
están implicados básicamente tres procesos: El transporte por convección en las tuberías, el
decaimiento o crecimiento de las concentraciones en el tiempo por reacción, y los procesos de
mezcla en los nudos de la red (Vidal, Martínez, & Ayza, 1994).
Sustancias conservativas
El proceso de transporte a lo largo de una línea 𝑖 está descrito por:
𝛿𝑐𝑖(𝑥, 𝑡)
𝛿𝑡
+ 𝑢
𝑖
𝛿𝑐𝑖(𝑥, 𝑡)
𝛿𝑥
= 0
Ecuación 53. Transporte de sustancias conservativas (Vidal, Martínez, & Ayza, 1994).
donde,
𝑐𝑖(𝑥, 𝑡), es la concentración de la sustancia en la sección de cálculo 𝑥 y el instante 𝑡.
𝑢
𝑖
, es la velocidad media del agua en la línea, la cual puede ser variable en el tiempo si se
cambian las condiciones hidráulicas.
𝑥, es la distancia de la sección de cálculo al extremo de la línea.
Sustancias no conservativas
El proceso de transporte a lo largo de una línea 𝑖 está descrito por:
𝛿𝑐𝑖(𝑥, 𝑡)
𝛿𝑡
+ 𝑢
𝑖
𝛿𝑐𝑖(𝑥, 𝑡)
𝛿𝑥
+ 𝜃(𝑐𝑖(𝑥, 𝑡)) = 0
Ecuación 54. Transporte de sustancias no conservativas (Vidal, Martínez, & Ayza, 1994).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
63
Nicolás Eduardo Páez Rincón
Para resolver esta última ecuación, se debe dividir cada línea de corriente en segmentos,
dentro de los cuales se producen las reacciones, mientras que las mezclas tienen lugar en los
nudos.
Tiempos de permanencia y procedencia
Se puede modelar la edad del agua mediante un modelo dinámico, sin más que interpretar la
variable 𝑐 de la Ecuación 54 como el tiempo de permanencia en la red, con lo que el término 𝜃
pasaría a ser una constante igual a 1 (Vidal, Martínez, & Ayza, 1994).
Asimismo, para determinar el porcentaje de agua que le llega a un nudo de la red desde otro
nudo de suministro mediante el modelo dinámico, basta con interpretar la variable 𝑐 de la
Ecuación 53 como el factor de contribución de la fuente de referencia al nudo deseado, no
debiendo considerar en este caso término de reacción alguno. El valor de la variable 𝑐 en los
puntos de suministro será en este caso 100, actuando como condición de retorno (Vidal,
Martínez, & Ayza, 1994).
5.3. Procesos difusivos
El descubrimiento de la difusión se dio por Graham entre los años de 1828 y 1833. Para gases,
demostró que el flujo a través de un tapón poroso es inversamente proporcional a la raíz
cuadrada de las densidades de los gases empleados. Para líquidos trató de encontrar una
relación similar, sin éxito alguno (Mompremier, 2009).
Años más tarde, Adolf Eugen Fick planteó los experimentos de Graham sobre bases
cuantitativas y descubrió la ley de difusión.
5.3.1. Definición
La difusión es el proceso por el cual las moléculas, iones u otras pequeñas partículas
espontáneamente se mezclan, moviéndose de regiones de relativamente alta concentración
hacia regiones de baja concentración, generando un gradiente de concentración
(Mompremier, 2009).
La velocidad de difusión molecular en los líquidos es mucho menor que en los gases. Esto se
da debido a que las moléculas de un líquido se encuentran muy cercanas entre sí en
comparación con las de un gas. Por lo tanto, las moléculas de un soluto A que se difunden,
chocarán contra las moléculas de un líquido B con mayor frecuencia y se difundirán con
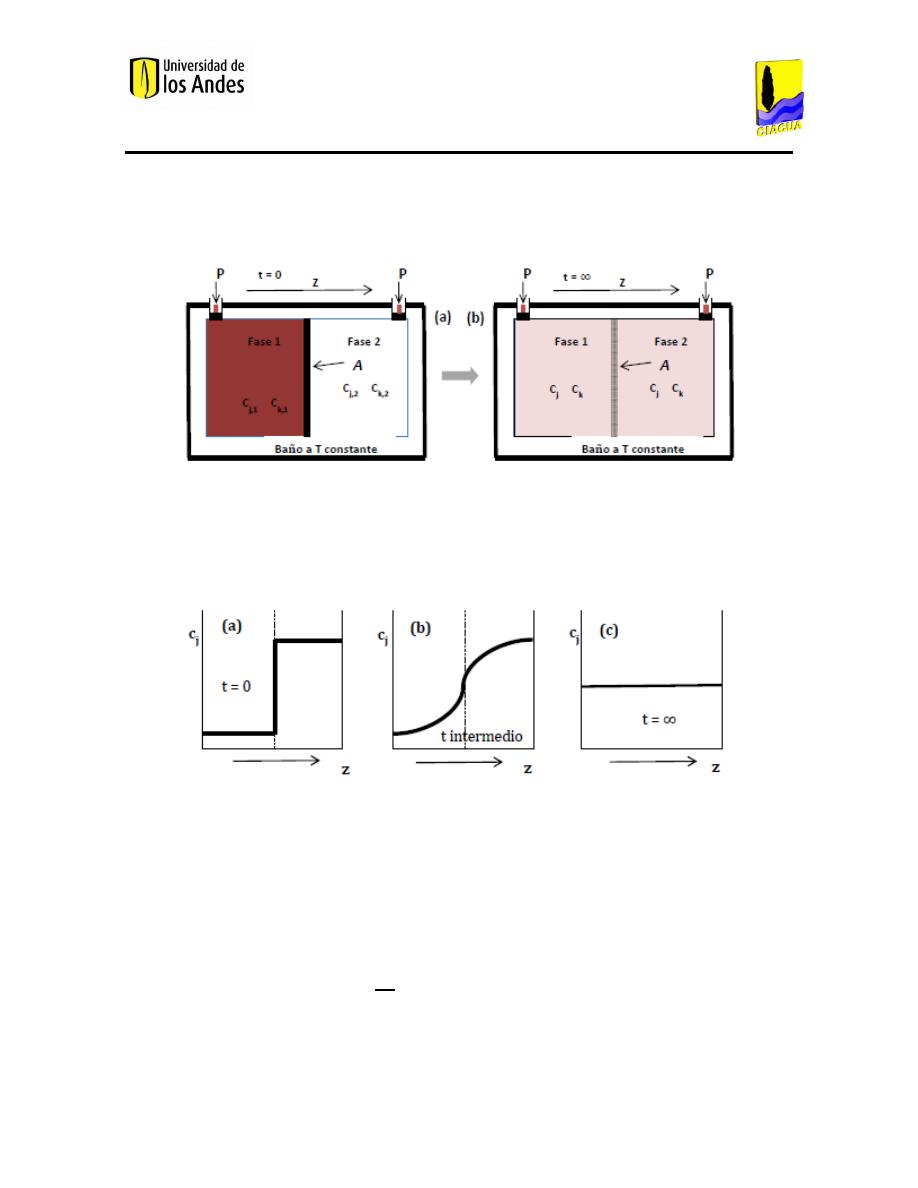
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
64
Nicolás Eduardo Páez Rincón
mayor lentitud que en los gases. Por ende, el coeficiente de difusión de un gas es de un orden
de magnitud 100 veces mayor que en un líquido.
El proceso de difusión se puede observar en la siguiente imagen:
Figura 14. Proceso de difusión (Universidad de Valencia, 2006).
El perfil de concentración de cualquiera de las sustancias que se difunde de un lado al otro
está representado por la Figura 15 a tres tiempos diferentes (inicial, intermedio e infinito).
Figura 15. Proceso de difusión en función del tiempo (Mompremier, 2009).
5.3.1.1.
Ecuación de difusión
La ecuación de difusión describe las fluctuaciones de densidad en un material que se difunde.
Es también usada para describir procesos exhibiendo un comportamiento de difusión. La
ecuación es la siguiente:
𝜕∅
𝜕𝑡
= ∇(𝐷(∅,𝑟⃗)∇∅(𝑟⃗, 𝑡))
Ecuación 55. Ecuación general de difusión (Mompremier, 2009).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
65
Nicolás Eduardo Páez Rincón
donde,
∅, es la densidad del material que se difunde.
𝑡, es el tiempo de difusión.
𝐷, es el coeficiente de difusión colectivo.
𝑟⃗, es la coordenada espacial.
∇, es el vector operador diferencial nabla.
Si el coeficiente de difusión depende de la densidad, entonces la ecuación no es lineal; de otra
forma es lineal. Si 𝐷 es constante, entonces la ecuación se reduce a la siguiente ecuación lineal:
𝜕∅
𝜕𝑡
= 𝐷∇
2
∅(𝑟⃗, 𝑡)
Ecuación 56. Ecuación de difusión con coeficiente de difusión constante (Mompremier, 2009).
Más generalmente, cuando 𝐷 es una matriz simétrica definida y positiva, la ecuación describe
una difusión anisotrópica.
5.3.1.2.
Coeficiente de difusión
El coeficiente de difusión representa la facilidad con que cada soluto en particular, se mueve
en un solvente determinado, y depende de tres factores:
Tamaño y forma del soluto.
Viscosidad del solvente.
Temperatura.
5.3.2. Ley de Fick
Lay ley de Fick describe diversos casos de difusión de materia o energía en un medio en el que
inicialmente no existe equilibrio térmico o químico. En situaciones en las que existen
gradientes de concentración de una sustancia, o de temperatura, se produce un flujo de
partículas o de calor que tiende a homogeneizar la disolución y uniformizar la concentración o
la temperatura. El flujo homogeneizador es una consecuencia del movimiento azaroso de las
partículas. Así, los procesos físicos de difusión son vistos como procesos físicos o
termodinámicos irreversibles.
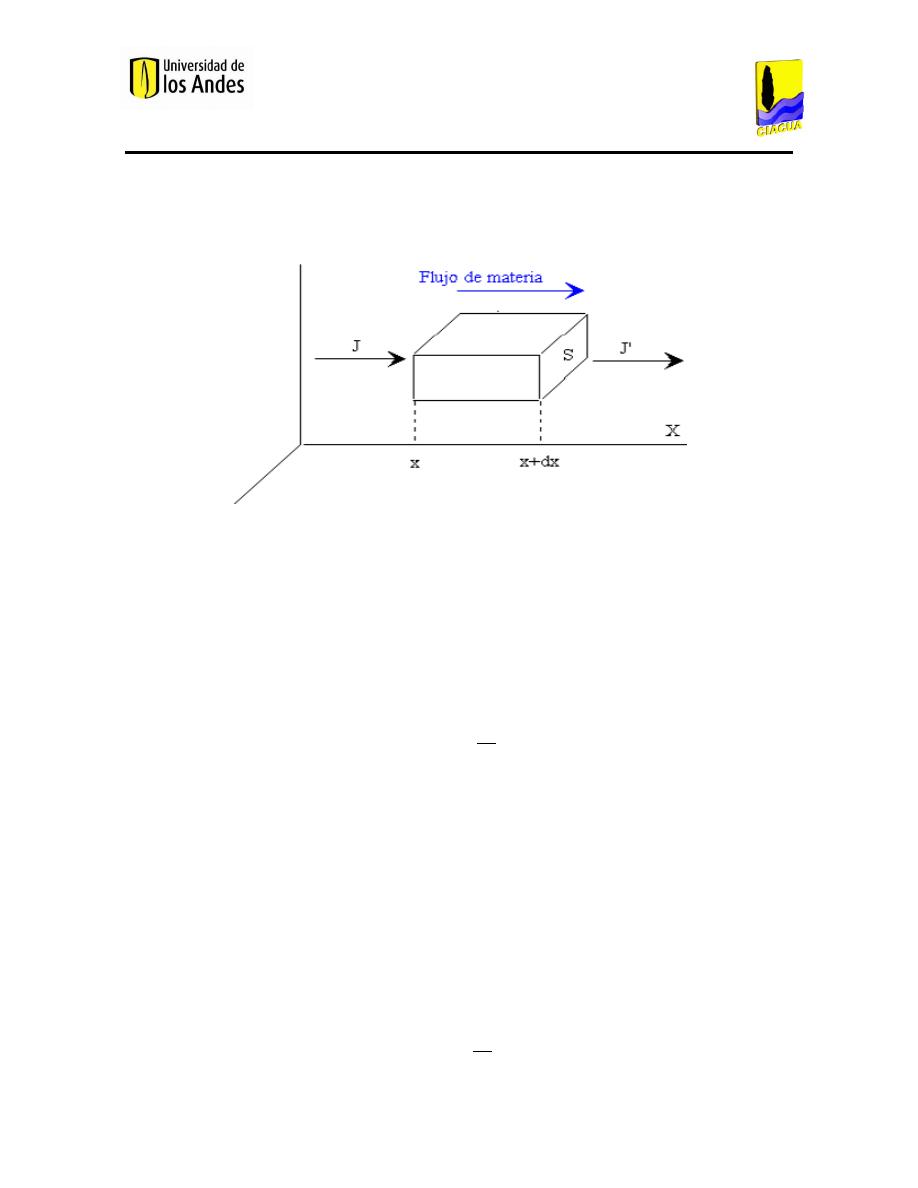
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
66
Nicolás Eduardo Páez Rincón
Para que tenga lugar el fenómeno de difusión, la distribución espacial de moléculas no debe
ser homogénea, debe existir una diferencia o gradiente de concentración entre dos puntos del
medio.
Figura 16. Flujo de materia (Mompremier, 2009).
Si se supone que la concentración varía con la posición a lo largo del eje X, sea 𝐽 la densidad de
corriente de partículas, es decir, el número efectivo de partículas que atraviesan en la unidad
de tiempo un área unitaria perpendicular a la dirección en la que tiene lugar la difusión. La ley
de Fick afirma que la densidad de corriente de partículas es proporcional al gradiente de
concentración:
𝐽 = −𝐷
𝜕𝑛
𝜕𝑥
Figura 17. Ecuación de Fick (Mompremier, 2009).
donde,
𝐷, es el coeficiente de difusión, y es característico tanto del soluto como del medio en el que se
disuelve.
La acumulación de partículas en la unidad de tiempo que se produce en el elemento de
volumen 𝑆𝑑𝑥 es igual a la diferencia entre el flujo entrante 𝐽𝑆, menos el flujo saliente 𝐽
′
𝑆, es
decir:
𝐽𝑆 − 𝐽
′
𝑆 =
𝜕𝐽
𝜕𝑥
𝑆𝑑𝑥

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
67
Nicolás Eduardo Páez Rincón
La acumulación de partículas en la unidad de tiempo es:
𝑆𝑑𝑥
𝜕𝑛
𝜕𝑡
Igualando ambas expresiones y utilizando la Ley de Fick se obtiene:
𝜕
𝜕𝑥
(𝐷
𝜕𝑛
𝜕𝑥
) =
𝜕𝑛
𝜕𝑡
La ecuación anterior describe el fenómeno de difusión. Por otro lado, si el coeficiente de
difusión D no depende de la concentración, se tiene la siguiente ecuación:
1
𝐷
𝜕𝑛
𝜕𝑡
=
𝜕
2
𝑛
𝜕𝑥
2
Figura 18. Fenómeno de difusión (Mompremier, 2009).
5.3.3. Tipos de difusión
5.3.3.1.
Difusión por reacción
Toda sustancia contenida en el agua puede entrar en reacción con otras sustancias, con las
paredes de la tubería, con el agua, o con microorganismos; y como resultado de diferentes
procesos químicos o bioquímicos puede variar su concentración. Según la forma de la
reacción, las sustancias en el agua se pueden dividir en tres grupos:
Conservativas: No reaccionan con el agua ni con las tuberías.
No conservativas y decrecientes: Su concentración decrece con el tiempo de
permanencia en el agua.
No conservativas y crecientes: Son compuestos químicos que se forman en el agua y su
concentración crece con el tiempo de permanencia.
5.3.3.2.
Difusión convectiva
Conocida también como difusión por advección, considera los cambios de concentración
generados por la velocidad del flujo. La agitación no es un proceso molecular pero es un
proceso microscópico que cambia porciones de fluidos sobre distancias largas.
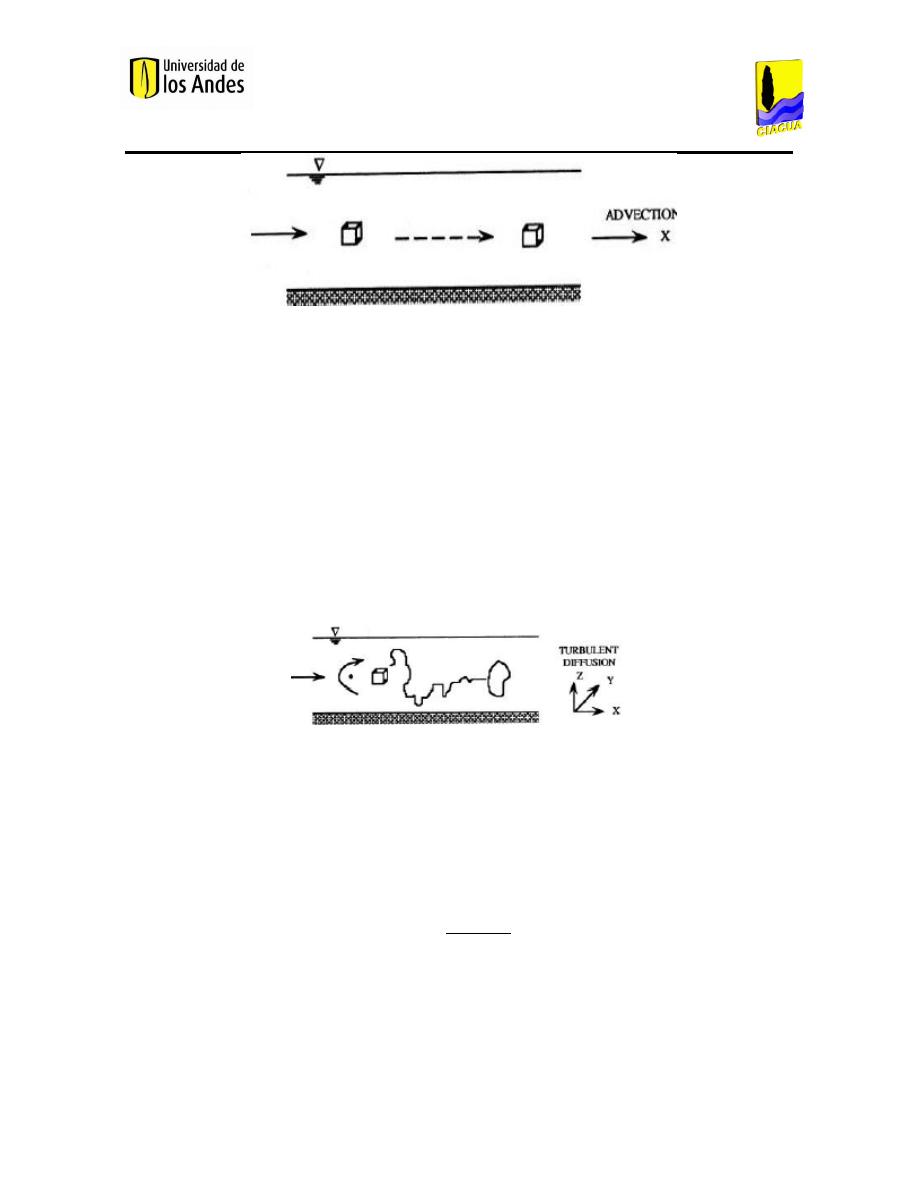
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
68
Nicolás Eduardo Páez Rincón
Figura 19. Difusión convectiva (Mompremier, 2009).
5.3.3.3.
Difusión molecular
La difusión molecular es la mezcla de químicos disueltos debido al movimiento al azar o
aleatorio de las moléculas dentro del fluido causado por movimiento molecular vibratorio,
rotacional o transversal. En el movimiento, las sustancias disueltas se mueven de regiones de
altas concentraciones a regiones de bajas concentraciones, de acuerdo a la Ley de Fick.
5.3.3.4.
Difusión turbulenta
La difusión turbulenta es la mezcla de sustancias particuladas finas debido a la turbulencia en
micro escala causada por fuerza del rozamiento dentro del cuerpo de agua.
Figura 20. Difusión turbulenta (Mompremier, 2009).
5.3.4. Concentración
Se entiende por concentración a la cantidad relativa de una sustancia en un cierto punto y
tiempo dado. Se puede expresar en unidades de masa, peso, volumen o número de partículas
por unidad de volumen.
𝐶
𝐴
=
𝑚
𝐴
𝑚
𝐴
+ 𝑚
𝐵
Ecuación 57. Cálculo de concentración (Mompremier, 2009).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
69
Nicolás Eduardo Páez Rincón
O bien,
𝐶
𝐵
=
𝑚
𝐵
𝑚
𝐴
+ 𝑚
𝐵
Por otra parte se tiene que
𝑚
𝐴
+ 𝑚
𝐵
= 𝑚
En el caso que la sustancia A tuviese mucho mayor masa en comparación con la sustancia B, se
tiene el siguiente planteamiento:
𝑚
𝐴
+ 𝑚
𝐵
= 𝑚 ≈ 𝑚
𝐴
Entonces,
𝐶
𝐴
=
𝑚
𝐴
𝑚
𝐴
O bien,
𝐶
𝐵
=
𝑚
𝐵
𝑚
𝐴
5.3.4.1.
Balance de masa en las uniones de varias tuberías
Las tuberías que confluyen en un nudo se clasifican en dos grupos: El primero, formado por
las tuberías por las que llega caudal al nudo, y el segundo, con las tuberías por las que sale
caudal del nudo, tal y como se muestra en la siguiente figura:
Figura 21. Esquema de balance de masa en la unión de tuberías (Mompremier, 2009).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
70
Nicolás Eduardo Páez Rincón
Se considera que las aportaciones de masa de cada una de las tuberías del primer grupo a un
nudo en particular es igual a:
𝑚
𝑖
= ∑ 𝑐
𝑘
𝑖
𝑄
𝑖
∆𝑡
𝑁
𝑖=1
Ecuación 58. Aporte de masa a la unión i (Mompremier, 2009).
donde,
𝑄
𝑖
, es el caudal de entrada al nudo 𝑖 desde una tubería de entrada.
𝑁, es el número de tuberías de entrada.
𝑐
𝑘
𝑖
, es la concentración de algún componente en las tuberías de entrada.
Así mismo, por las tuberías de salida, saldrá desde el nudo, un flujo con una mezcla uniforme
de concentración, por lo que la masa que sale se describe como:
𝑚
𝑠
= 𝑐
𝐸
(∑ 𝐺
𝑖
+ 𝑞
𝐸
𝑀
𝑖=1
)
Ecuación 59. Salida de masa del nudo i (Mompremier, 2009).
donde,
𝐺
𝑖
, es el caudal de salida por cada tubería de salida.
𝑀, es el número de tuberías de salida.
𝑞
𝐸
, es el caudal de concesión que se les suministra a los usuarios de la red.
Dado que se debe cumplir la conservación de la masa, entonces:
𝑚
𝑖
= 𝑚
𝑠
Al reemplazar las correspondientes ecuaciones, se despeja la concentración de la mezcla, la
cual sería completa y uniforme, de la siguiente manera:

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
71
Nicolás Eduardo Páez Rincón
𝑐
𝐸
=
∑
𝑐
𝑘
𝑖
𝑄
𝑖
𝑁
𝑖=1
∑
𝐺
𝑖
+ 𝑞
𝐸
𝑀
𝑖=1
Ecuación 60. Concentración de la mezcla (Mompremier, 2009).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
72
Nicolás Eduardo Páez Rincón
6. Modelo físico
6.1. Descripción del modelo físico
El modelo físico se encuentra ubicado en el Laboratorio de Hidráulica de la Universidad de
Los Andes. El modelo fue diseñado por la estudiante Laura Natalia Cotes Gómez, quien a su
vez lo construyó en conjunto con el técnico del laboratorio, Jhon Adalberto Calvo Ovalle.
6.1.1. Sistema de alimentación
El sistema de alimentación inicia con una válvula de cobre tipo cortina, que permite el paso
del agua desde la tubería de abastecimiento más cercana al modelo, hasta los tanques de
alimentación. Una vez el agua pasa a través de la válvula, se lleva a través de una tubería en
PVC de 1
1/2
pulgada de diámetro hasta las inmediaciones del modelo, lugar en el cual la
tubería se bifurca en dos tuberías de igual material y diámetro. Posteriormente, en cada una
de las dos tuberías se encuentra una válvula de bola con la cual se regula e independiza el
caudal de agua que entra a cada uno de los tanques de alimentación.
Ilustración 10. Tubería del laboratorio que alimenta el modelo.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
73
Nicolás Eduardo Páez Rincón
Ilustración 11. Válvula que permite el paso de agua al modelo.
Ilustración 12. Tubería de alimentación al modelo.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
74
Nicolás Eduardo Páez Rincón
Ilustración 13. Bifurcación de la tubería de alimentación y válvulas reguladoras de caudal a los tanques.
Los tanques de alimentación del modelo tienen como objetivo principal, el almacenamiento
del agua que se utilizará posteriormente durante las pruebas. Los tanques no fueron
construidos para tal función, sino la de “cámaras de paso”, es decir, actuaban como un canal
mediante el cual pasaba agua. Sin embargo, se añadieron paredes para poder almacenar el
agua, y se modificaron de tal forma que el nivel de agua en su interior permaneciese
constante.
Ilustración 14. Tuberías de alimentación a los tanques.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
75
Nicolás Eduardo Páez Rincón
El tanque de agua limpia recibe agua de manera continua a través de su respectiva tubería de
alimentación. Para impedir el rebosamiento del tanque se abrió un agujero de 2 pulgadas a
una altura de 0,40 metros, medidos desde el fondo del tanque. Al agujero se le conectó una
tubería de igual diámetro, con el fin de evacuar toda el agua que se encuentre por encima del
nivel del agujero hasta el sifón más cercano. Por último, la tubería de rebose cuenta con una
válvula de bola para regular el flujo de agua en ella.
Ilustración 15. Tanque de agua limpia.
Ilustración 16. Tubería de rebose del tanque de agua limpia.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
76
Nicolás Eduardo Páez Rincón
Al tanque de agua clorada también se le abrió un agujero de 2 pulgadas a una altura de 0,40
metros, medidos desde el fondo del tanque. Sin embargo, dicho agujero no llevaba el agua a
una tubería sino a un tercer tanque. El tercer tanque funcionaba como una estructura de
caída, pero se le insertó una plataforma en triplex de pino de 1,02 m x 0,39 m x 0,019 m, y se
colocó un refuerzo en la parte de abajo para evitar el pandeo debido al peso del agua.
Ilustración 17. Tanque de agua clorada, previo a las modificaciones.
Inicialmente, el tanque de agua clorada funcionaba de tal forma que, cuando el nivel del agua
alcanzaba el nivel del agujero, rebosaba a través de éste y llenaba el tanque modificado. Una
vez los dos tanques tuviesen la misma altura de agua, se cerraba la válvula de alimentación al
tanque de agua clorada (a diferencia de la válvula de alimentación al tanque de agua limpia); y
una vez iniciadas las pruebas, se utilizaba una bomba sumergible que llevaba el agua del
tanque modificado al tanque 2, mientras que el agua de éste seguía rebosando al tanque
modificado. De esta forma se mantenía el nivel de agua constante en el tanque 2, al igual que
la concentración de cloro inicial.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
77
Nicolás Eduardo Páez Rincón
Ilustración 18. Tanque modificado en funcionamiento.
Sin embargo, el tanque modificado no fue diseñado como un tanque sino como una estructura
de caída. Debido a esto, su llenado ocasionó un pandeo de las paredes laterales del tanque,
dado que no se diseñaron para soportar las presiones hidrostáticas de la columna de agua allí
almacenada. Como medida temporal se utilizó silicona para sellar las fugas en el tanque, pero
el pandeo generado por el agua terminaba despegando la silicona, con lo cual se volvían a
presentar dichas fugas.
Ilustración 19. Fugas en el tanque modificado.
Como solución, se compraron dos tanques botella, cada uno con una capacidad de 600 litros y
se colocaron a ambos lados del tanque modificado. Así, el agua rebosada a través del tanque
de agua clorada ahora pasa a uno de los dos tanques botella. Allí, una bomba redirige el agua

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
78
Nicolás Eduardo Páez Rincón
hacia el otro tanque; y de este último, una segunda bomba lleva el agua clorada de vuelta al
tanque de agua clorada.
6.1.2. Modelo físico
De cada uno de los 2 tanques de alimentación sale una tubería vertical en PVC de 1 in de
diámetro, cada una con una válvula de cobre tipo cortina. Posteriormente, mediante un codo
ambas tuberías pasan a ser horizontales y convergen en la cruz.
Ilustración 20. Tuberías de entrada al modelo físico.
Ilustración 21. Válvulas de entrada.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
79
Nicolás Eduardo Páez Rincón
Para el modelo, dicha cruz es en vidrio, con un diámetro interno de 30 mm y un espesor de 2
mm, longitud de las tuberías de 40 cm y ángulo de 90° entre tuberías adyacentes.
Ilustración 22. Modelo físico.
Una vez el agua pasa a través de la cruz, las dos tuberías de salida de la cruz se conectan con 2
tuberías en PVC de 1 in de diámetro. En dichas tuberías también se encuentran válvulas de
cobre tipo cortina para regular los caudales de salida de la cruz. Por último, cada una de las 2
tuberías de salida descarga el caudal a un tanque de plástico con las siguientes dimensiones:
6.1.3. Sistema de recirculación
El sistema de recirculación se encuentra conformado por dos tanques tipo botella, cada uno
de 600 litros con las siguientes especificaciones:
Ilustración 23. Especificaciones de los dos tanques comprados para el sistema de recirculación (PAVCO, 2013).
La capacidad total del sistema de recirculación, sin contar con el volumen de agua en el tanque
de alimentación de agua clorada es de 1200 litros. Para una apertura total de la válvula de la

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
80
Nicolás Eduardo Páez Rincón
tubería de entrada de agua clorada al modelo, se obtiene un caudal de aproximadamente 50
litros/min. Por ende, el sistema de recirculación permite realizar pruebas durante un tiempo
de aproximadamente 25 minutos, mientras se utiliza el agua almacenada en los dos tanques.
6.1.4. Instrumentos de medición
En la tesis realizada por Cotes Gómez, la medición de los caudales se realizaba mediante 4
caudalímetros volumétricos, los cuales registraban el cambio en el volumen acumulado de
agua que pasaba a través de ellos. La medición de las concentraciones de cloro se hacía
mediante el uso de instrumentos portátiles, otorgados por la coordinación de los laboratorios
del Departamento de Ingeniería Civil y Ambiental de la Universidad de Los Andes.
Los caudalímetros volumétricos son de tipo intrusivo, es decir, se encontraban conectados a
las tuberías del modelo para medir el caudal de agua. Por otro lado, la medición de las
concentraciones se realizaba mediante la toma de muestras en los tanques de alimentación y
de descarga del modelo. Sin embargo, dado que los datos obtenidos carecían de la precisión
deseada, se realizó la compra de 3 caudalímetros magnéticos, así como de 2 sensores de cloro
residual, los cuales fueron entregados a mitad del semestre en el que se realiza el presente
trabajo.
Los caudalímetros volumétricos fueron retirados del modelo, y dichos tramos fueron
reemplazados por tuberías en PVC del mismo diámetro que las tuberías anexas, que se
conectaron con las tuberías existentes mediante uniones universales.
6.1.4.1.
Caudalímetros magnéticos
El modelo físico cuenta con tres caudalímetros magnéticos, todos de marca Kobold. Estos
instrumentos son utilizados para medir o monitorear el caudal de fluidos con o sin
concentraciones de sólidos, lodos, pastas u otros medios conductores eléctricos, mientras
minimiza las pérdidas de energía. Adicionalmente, los cambios en presión, temperatura,
densidad y viscosidad no afectan las mediciones realizadas (Kobold, 2009).
De acuerdo con la ley de inducción electromagnética de Faraday, cuando un líquido conductor
se desplaza a una velocidad 𝑣 por un un campo magnético 𝐵, se produce un campo eléctrico 𝐸
tal que:
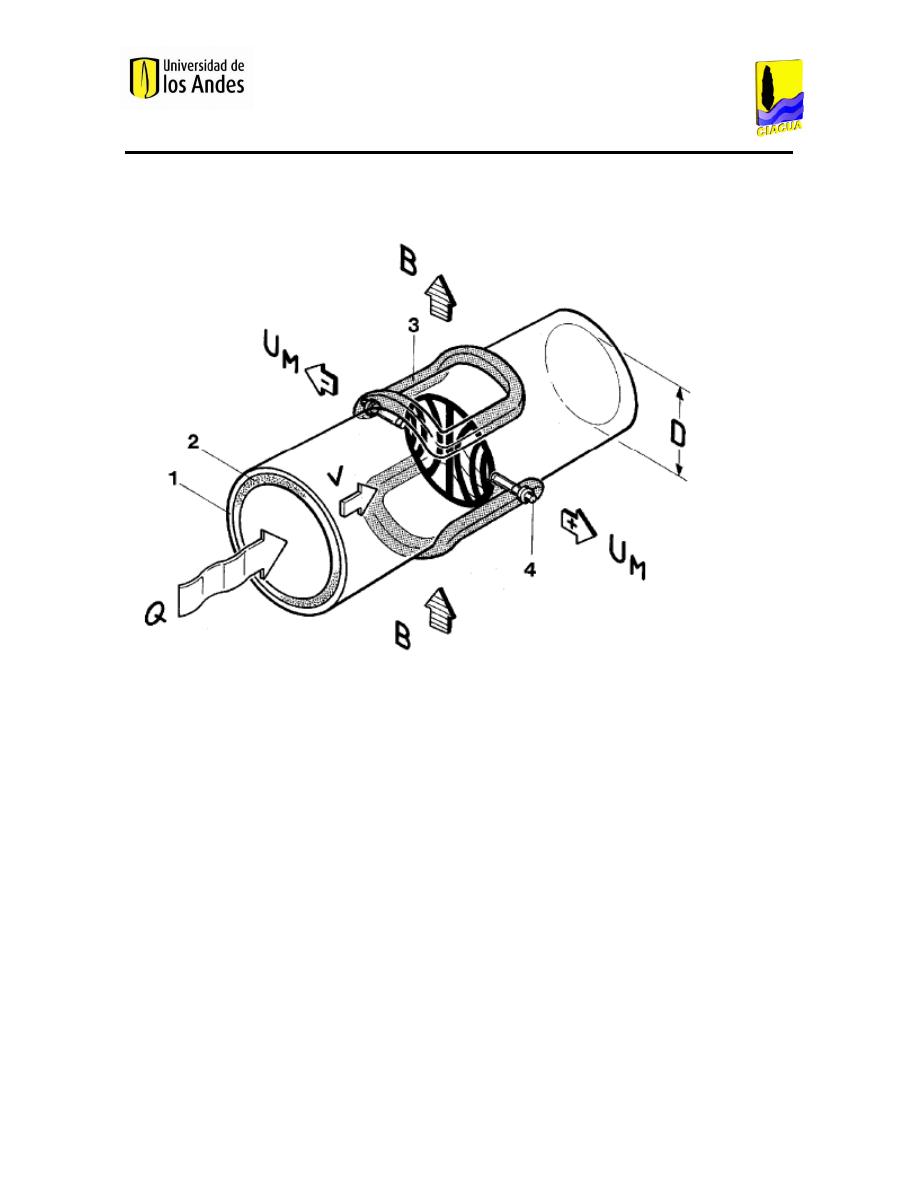
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
81
Nicolás Eduardo Páez Rincón
𝐸 = 𝑣𝐵
Ecuación 61. Definición de campo eléctrico (Kobold, 2009).
Figura 22. Modo de operación del caudalímetro (Kobold, 2009).
La Figura 22 ilustra el funcionamiento del Caudalímetro. El caudalímetro funciona de tal
forma que cuando el fluido fluye a través del tubo (1) con un revestimiento aislante (2), se
produce un circuito de medición de voltaje en los dos electrodos (4) perpendiculares a la
dirección del flujo y al campo magnético generado por las bobinas (3). La magnitud del campo
eléctrico generado es directamente proporcional a la velocidad del flujo, y por ende, al caudal.
El caudalímetro cuenta con una precisión igual a:
±[0,3% 𝑑𝑒𝑙 𝑣𝑎𝑙𝑜𝑟 𝑚𝑒𝑑𝑖𝑑𝑜 + 0,01% ∗ (𝑄 𝑝𝑎𝑟𝑎 10 𝑚/𝑠)]
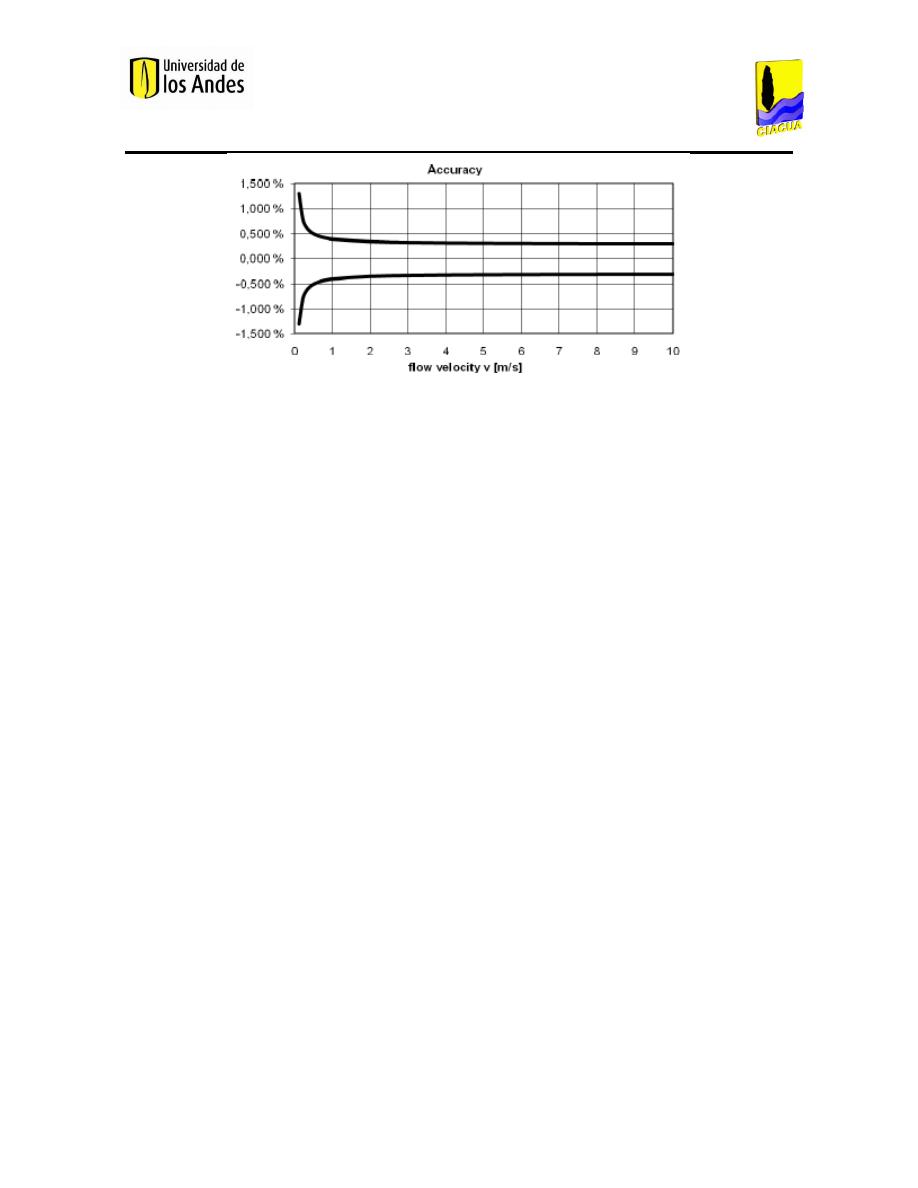
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
82
Nicolás Eduardo Páez Rincón
Figura 23. Precisión del caudalímetro (Kobold, 2009).
A medida que aumenta la velocidad del flujo, la precisión de la medición disminuye y se
estabiliza. De acuerdo a la Figura 23, se puede concluir que para velocidades de flujo entre 2,5
m/s y 10 m/s, la precisión es independiente de la velocidad, y aproximadamente igual al 0,3%
de la medición.
Entre las condiciones de operación del caudalímetro dadas por el proveedor, se encuentran:
1. Los caudalímetros deben ser instalados de tal forma que inmediatamente aguas arriba
y aguas abajo de éstos, y hasta una distancia igual a diez veces el diámetro nominal en
la sección aguas arriba, y cinco veces el diámetro nominal en la sección aguas abajo de
la tubería, no debe existir ningún accesorio que pueda perturbar el perfil del flujo.
2. El fluido debe tener una conductividad mayor a 5 μS/cm.
3. La tubería siempre debe encontrarse presurizada cuando se haga uso del
caudalímetro.
4. La velocidad mínima del flujo no puede ser inferior a 0,5 m/s.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
83
Nicolás Eduardo Páez Rincón
Ilustración 24. Caudalímetro magnético.
6.1.4.2.
Sensores de cloro
El sensor de cloro monitorea de forma continua la concentración de cloro residual en
efluentes de procesos industriales o agua potable. Para esto, analiza la corriente de agua que
pasa a través del portaelectrodos en donde debe ir instalado el sensor. Dicho conjunto
portaelectrodos – sensor debe utilizarse en conjunto para asegurar la correcta medición de las
concentraciones.
La concentración de cloro residual se determina de acuerdo con principio de medida
amperométrica. El ácido hipocloroso (HOCl) contenido en el flujo se difunde a través de la
membrana del sensor y se reduce a iones cloruro (Cl
-
) en el cátodo de oro del sensor. Por otro
lado, en el ánodo de plata, la plata se oxida a cloruro de plata. La liberación de electrones en el
cátodo y su viaje hasta el ánodo genera una corriente que es proporcional a la concentración
de cloruro en el medio (Endress - Hauser, 2007).

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
84
Nicolás Eduardo Páez Rincón
El rango de medición del sensor de cloro se encuentra entre 0,05 mg/L y 20 mg/L, y tiene una
precisión igual a ±0,5% del valor medido. Para mediciones máximas de 20 mg/L, la precisión
de la medida será de 0,1 mg/L (Endress - Hauser, 2007).
Figura 24. Esquema del sensor de cloro (Endress - Hauser, 2007).
Ilustración 25. Sensor de cloro.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
85
Nicolás Eduardo Páez Rincón
6.1.4.3.
Portaelectrodos para cloro libre
El portaelectrodos ha sido especialmente diseñado para la instalación de los sensores de
cloro, o los sensores de Dióxido de Cloro. También incluye conexiones para instalar otros dos
electrodos (uno de pH y otro de Redox). El cuerpo está fabricado en plexiglass, y dispone de
una válvula de aguja para ajustar el caudal de agua y un rotámetro para el control visual del
caudal (Endress Hauser, 2009).
Figura 25. Esquemas del portaelectrodos (Endress Hauser, 2009).
Para el correcto funcionamiento del sistema portaelectrodos – sensor, se debe instalar en la
manguera aguas arriba de la celda, una válvula y un filtro de partículas. Adicionalmente, en la
manguera aguas abajo del portaelectrodo se debe instalar otra válvula para regular el flujo de
agua.
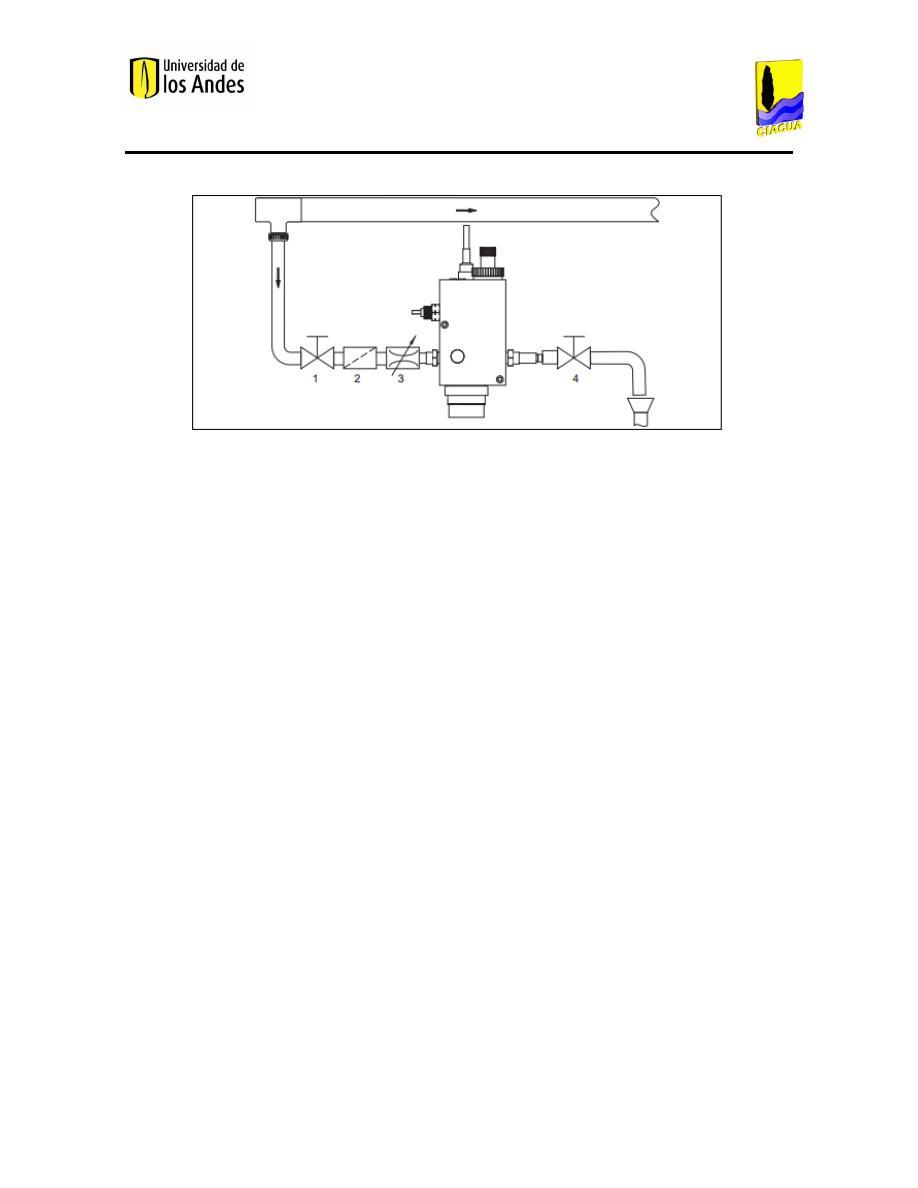
Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
86
Nicolás Eduardo Páez Rincón
Figura 26. Esquema del montaje a realizar (Endress Hauser, 2009).
El portaelectrodos se puede instalar de tal manera que la manguera aguas abajo se conecte de
nuevo con la tubería en PVC, o descargue libremente. Si se conecta de nuevo a la tubería, es
necesario que exista una diferencia de la presión en los dos puntos de conexión del by-pass
con la tubería principal. Dado que la tubería principal es en PVC, se espera que la diferencia de
presión entre ambos puntos de conexión sea mínimo, lo cual puede evitar el correcto flujo a
través del portaelectrodos (Endress Hauser, 2009).
Como solución, para el proyecto se decidió no realizar la conexión de vuelta con la tubería
principal sino que la manguera aguas abajo de cada portaelectrodos descargue a un tanque.
Para el sensor ubicado en la tubería de entrada de agua con cloro, el portaelectrodos se
encuentra aguas arriba del caudalímetro, de tal forma que el caudal registrado corresponda al
que llega a la cruz y no tenga en cuenta el caudal perdido a través del portaelectrodo. Para el
sensor ubicado en una de las tuberías de salida, el portaelectrodos se encuentra aguas abajo
del caudalímetro, y la manguera aguas debajo de éste descarga directamente al mismo tanque
donde descarga la tubería principal.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
87
Nicolás Eduardo Páez Rincón
Ilustración 26. Portaelectrodos para cloro libre.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
88
Nicolás Eduardo Páez Rincón
7. Resultados
7.1. Casos de análisis
Los casos de análisis utilizados para el presente proyecto se muestran a continuación:
Caso Válvula 1 Válvula 2 Válvula 3 Válvula 4
1
25%
25%
25%
25%
2
50%
50%
50%
50%
3
75%
75%
75%
75%
4
100%
100%
100%
100%
5
25%
100%
100%
100%
6
100%
25%
100%
100%
7
100%
100%
25%
100%
8
100%
100%
100%
25%
9
50%
100%
100%
100%
10
100%
50%
100%
100%
11
100%
100%
50%
100%
12
100%
100%
100%
50%
13
75%
100%
100%
100%
14
100%
75%
100%
100%
15
100%
100%
75%
100%
16
100%
100%
100%
75%
Tabla 9. Escenarios planteados para el presente proyecto.
Los caudales, las velocidades y los números de Reynolds que se obtienen para cada uno de los
anteriores porcentajes de abertura de las válvulas, se muestran a continuación:
Porcentaje de
Abertura
Caudal
(L/min)
Velocidad
(m/s)
Número de
Reynolds
Régimen
25%
12,5
0,294
7756,08
Turbulento
50%
25
0,589
15512,17
Turbulento
75%
37,5
0,884
23268,26
Turbulento
100%
50
1,178
31024,35
Turbulento
Tabla 10. Velocidades y números de Reynolds para cada porcentaje de abertura de las válvulas.
La definición de los escenarios se hizo tal que varíen los radios entre los caudales de entrada y
salida, para determinar la influencia de éstos en el proceso de mezcla.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
89
Nicolás Eduardo Páez Rincón
7.2. Resultados
Para los resultados que se muestran a continuación se usa la siguiente nomenclatura:
Ilustración 27. Nomenclatura para las vistas en planta.
Ilustración 28. Nomenclatura para las vistas en perfil.
1
2
3
4
1
2
3
4

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
90
Nicolás Eduardo Páez Rincón
7.2.1. Caso 1: Todas las válvulas al 25%
Ilustración 29. Vista en planta.
Ilustración 30. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
91
Nicolás Eduardo Páez Rincón
7.2.2. Caso 2: Todas las válvulas al 50%
Ilustración 31. Vista en planta.
Ilustración 32. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
92
Nicolás Eduardo Páez Rincón
7.2.3. Caso 3: Todas las válvulas al 75%
Ilustración 33. Vista en planta.
Ilustración 34. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
93
Nicolás Eduardo Páez Rincón
7.2.4. Caso 4: Todas las válvulas al 100%
Ilustración 35. Vista en planta.
Ilustración 36. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
94
Nicolás Eduardo Páez Rincón
7.2.5. Caso 5: Válvula 1 al 25%; válvulas 2, 3 y 4 al 100%
Ilustración 37. Vista en planta.
Ilustración 38. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
95
Nicolás Eduardo Páez Rincón
7.2.6. Caso 6: Válvula 2 al 25%; válvulas 1, 3 y 4 al 100%
Ilustración 39. Vista en planta.
Ilustración 40. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
96
Nicolás Eduardo Páez Rincón
7.2.7. Caso 7: Válvula 3 al 25%; válvulas 1, 2 y 4 al 100%
Ilustración 41. Vista en planta.
Ilustración 42. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
97
Nicolás Eduardo Páez Rincón
7.2.8. Caso 8: Válvula 4 al 25%; válvulas 1, 2 y 3 al 100%
Ilustración 43. Vista en planta.
Ilustración 44. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
98
Nicolás Eduardo Páez Rincón
7.2.9. Caso 9: Válvula 1 al 50%; válvulas 2, 3 y 4 al 100%
Ilustración 45. Vista en planta.
Ilustración 46. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
99
Nicolás Eduardo Páez Rincón
7.2.10. Caso 10: Válvula 2 al 50%; válvulas 1, 3 y 4 al 100%
Ilustración 47. Vista en planta.
Ilustración 48. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
100
Nicolás Eduardo Páez Rincón
7.2.11. Caso 11: Válvula 3 al 50%; válvulas 1, 2 y 4 al 100%
Ilustración 49. Vista en planta.
Ilustración 50. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
101
Nicolás Eduardo Páez Rincón
7.2.12. Caso 12: Válvula 4 al 50%; válvulas 1, 2 y 3 al 100%
Ilustración 51. Vista en planta.
Ilustración 52. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
102
Nicolás Eduardo Páez Rincón
7.2.13. Caso 13: Válvula 1 al 75%; válvulas 2, 3 y 4 al 100%
Ilustración 53. Vista en planta.
Ilustración 54. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
103
Nicolás Eduardo Páez Rincón
7.2.14. Caso 14: Válvula 2 al 75%; válvulas 1, 3 y 4 al 100%
Ilustración 55. Vista en planta.
Ilustración 56. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
104
Nicolás Eduardo Páez Rincón
7.2.15. Caso 15: Válvula 3 al 75%; válvulas 1, 2 y 4 al 100%
Ilustración 57. Vista en planta.
Ilustración 58. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
105
Nicolás Eduardo Páez Rincón
7.2.16. Caso 16: Válvula 4 al 75%; válvulas 1, 2 y 3 al 100%
Ilustración 59. Vista en planta.
Ilustración 60. Vista en perfil.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
106
Nicolás Eduardo Páez Rincón
7.3. Análisis de resultados
Los casos 1 a 4, que son aquellos en los cuales se presentan los mismos caudales de entrada y
salida, muestran resultados similares. Cuando los caudales de entrada son similares, los flujos
chocan entre sí y salen por las tuberías adyacentes a aquellas por las cuales entran. Esto se
evidencia porque, prácticamente, la coloración en las tuberías de salida es igual a la coloración
en las de entrada, lo cual muestra bajos porcentajes de mezcla entre los dos flujos.
En el resto de casos, en los cuales variaba el porcentaje de apertura de una válvula con
respecto a las otras, se observa que a medida que aumenta la diferencia de los caudales de
entrada, se observa una mayor mezcla de los dos flujos. Sin embargo, se observa que la mezcla
se presenta en una de las dos tuberías únicamente, siendo ésta la que se encuentra opuesta a
la tubería de entrada del flujo de mayor impulso, mientras que por la tubería de salida
adyacente sale una porción del flujo de mayor impulso, sin que se mezcle.
Para los casos 5, 9 y 13, en los que el flujo de entrada de agua limpia es menor al flujo de
entrada de agua con trazador, el flujo por la tubería de salida adyacente a la tubería de
entrada de agua limpia, comprende una mezcla de los dos flujos; mientras que por la tubería
de salida adyacente a la tubería de entrada de agua con trazador sale agua con trazador, sin
que se presente mezcla alguna.
Para los casos 6, 10 y 14, en los que el flujo de entrada de agua limpia es mayor al flujo de
entrada de agua con trazador, el flujo por la tubería de salida adyacente a la tubería de
entrada de agua limpia, es de agua limpia; mientras que por la tubería de salida adyacente a la
tubería de entrada de agua con trazador sale agua mezclada. Es decir, el comportamiento
obtenido es inverso al obtenido en los casos 5, 9 y 13.
Por último, para los casos 7, 8, 11, 12, 15 y 16 el comportamiento es variable. En general, se
observa que la variación de los flujos de salida no ejerce el mismo efecto sobre el porcentaje
de mezcla que ejerce la variación de los flujos de entrada. Sin embargo, dependiendo del
porcentaje de apertura de las válvulas de salida, el fenómeno de mezcla puede aproximarse
más al fenómeno de mezcla en una Tee, en lugar de al fenómeno de mezcla en una cruz.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
107
Nicolás Eduardo Páez Rincón
8. Conclusiones y recomendaciones
La mezcla de dos flujos con diferentes características en las uniones entre tuberías, no es en
ningún modo completa e instantánea, como se sugiere por algunos autores. Por el contrario,
es incompleta y altamente dependiente de diversos parámetros, como lo es el régimen de
flujo, que a su vez depende de las características físicas de la tubería y del caudal.
Para tuberías de igual diámetro y material, el parámetro decisivo que determina el porcentaje
de mezcla en los nudos es el régimen de flujo. Para flujos que tienen velocidades similares de
entrada, el impulso generado es similar y al llegar al nudo, los dos flujos chocan entre sí con
igual fuerza y el choque los redirige a las tuberías de salida adyacentes a aquellas por las
cuales entraron. Entonces, la mezcla entre los dos flujos se limita únicamente a la interfaz de
contacto entre ellos en el nudo, lo que genera bajos porcentajes de mezcla.
A medida que la diferencia de velocidades entre los dos flujos de entrada es más significativa,
el flujo con mayor velocidad genera un mayor impulso con respecto al flujo de menor
velocidad. Entonces, cuando los flujos convergen en la cruz, el flujo con mayor impulso es
capaz de salir por la tubería opuesta a aquella por la cual entra, siendo que por ésta también
sale la totalidad del otro flujo. Este fenómeno genera un mayor contacto entre los dos flujos, lo
cual incrementa el porcentaje de mezcla de éstos. Sin embargo, por la otra tubería de salida
sale únicamente una porción del flujo de mayor impulso. En esta tubería, el porcentaje de
mezcla es 0%.
Por otro lado, cuando se mantienen constantes los flujos de entrada y se varían los de salida,
el efecto sobre los procesos de mezcla parece ser menor. En estos casos, la variación de los
flujos no afecta los porcentajes de mezcla de la misma forma que sí lo afectan las variaciones
en los flujos de entrada. Sin embargo, la variación de los flujos de salida sirve como
aproximación para estudiar el fenómeno de mezcla en uniones Tee, en las cuales sólo se
presenta una salida.
Los resultados obtenidos con las pruebas cualitativas concuerdan con la teoría previamente
mencionada. En aquellos escenarios en los que los dos flujos de entrada cuentan con un
mismo caudal, independientemente del caudal, la mezcla es altamente incompleta. Esto se
muestra en los dos flujos de salida de la unión, con concentraciones similares a los flujos de
entrada. Los mayores porcentajes de mezcla se presentan para los escenarios en los que los

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
108
Nicolás Eduardo Páez Rincón
caudales en las tuberías no son iguales, y aumenta de forma proporcional con la diferencia de
caudales entre las tuberías.
Los resultados muestran como es necesario cambiar la concepción que se tiene sobre los
fenómenos de mezcla en los nudos de las redes de distribución. Es necesario modificar los
programas de modelación de calidad del agua en redes de distribución de agua potable, tal
que incluyan fenómenos de mezcla incompleta en los nudos. Lo anterior cambiará por
completo la distribución de concentraciones a lo largo de la red, e indicará sitios en los que
posiblemente la concentración de cloro residual se encuentre por debajo del mínimo
permisible.
El fenómeno estudiado puede convertirse en una problemática de salud pública si la
concentración de cloro se encuentra por debajo de los mínimos permisibles. En tal caso, ante
un evento de contaminación, la concentración de cloro residual puede no ser suficiente para
que se realice un adecuado proceso de autodepuración del agua, y el agua que reciben los
usuarios podría tener una concentración remanente de microorganismos. Por ende, se debe
contar con modelos adecuados de calidad del agua, y en caso que se presenten deficiencias en
la concentración, se puede considerar la implementación de sistemas de inyección de cloro a
lo largo de las redes de distribución.
El presente trabajo no incluye la cuantificación de los porcentajes de mezcla dadas las
dificultades presentadas durante el semestre para la implementación de los sistemas de
adquisición de datos. Por ende, el siguiente trabajo contendrá dicha cuantificación para
uniones en vidrio y PVC, así como para uniones tipo Doble Tee.
Entre las recomendaciones se encuentran:
La completa implementación de un sistema de adquisición de datos es importante
para contar con un registro preciso y agilizar el proceso de toma de datos, en
comparación a como se realizó en tesis anteriores.
Se debe realizar una limpieza continua del modelo, que comprenda principalmente, la
limpieza de las tuberías y el pulido de la base en madera. Dicha limpieza se hace
necesaria debido a la continua manipulación que se realiza sobre dichos elementos, y
tiene como fin tener un modelo bien visto desde el punto de vista estético.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
109
Nicolás Eduardo Páez Rincón
Durante el periodo intersemestral se modificará el sistema de rebose, tal que se
instalará una Tee y una tubería para que el tanque de agua clorada pueda rebosar a los
dos tanques de almacenamiento. Adicionalmente, en cada una de las dos tuberías se
instalarán válvulas tipo bola. Lo anterior con el fin de contar con un sistema de
recirculación que utilice un único tanque y una única bomba. Cuando dicho tanque se
vacíe, se volverá a llenar a partir del agua almacenada en el otro tanque.
Durante el periodo intersemestral se realizará la instalación de los portaelectrodos de
cloro, con el fin de comenzar a realizar las pruebas cuantitativas.
Es recomendable realizar pruebas para régimen laminar. Para el presente trabajo se
trató de realizar pruebas en dicho régimen, pero el caudal necesario para tener
números de Reynolds de aproximadamente 1000 es significativamente menor al
caudal mínimo que pueden registrar los caudalímetros magnéticos. Por ende, se
descartó la realización de pruebas para dicho tipo de flujo.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
110
Nicolás Eduardo Páez Rincón
9. Agradecimientos
La realización del presente proyecto no pudo haber concluido en mejor término sin la guía y
asesoría del profesor Juan Guillermo Saldarriaga, quien siempre se interesó por el estado del
proyecto, y me corrigió y apoyó para llevar a cabo las modificaciones al modelo realizado, así
como la toma de los datos experimentales.
También, deseo agradecer al técnico del Laboratorio de Hidráulica de la Universidad de Los
Andes, Jhon Adalberto Calvo, quien me ayudó con las modificaciones realizadas al modelo
físico, y me enseñó muchas cosas necesarias para ser un mejor profesional, pero sobretodo
una mejor persona.
A Jimmy Salgado, quien me colaboró con la instrumentación del modelo, y estuvo pendiente
de las gestiones asociadas con la adquisición e instalación de los equipos necesarios para la
toma de datos.
A los integrantes del CIACUA, quienes fueron de gran ayuda durante la realización del
proyecto. En especial, quiero agradecer a mis amigas Laura Natalia Cotes, quien construyó el
modelo físico y me brindó especial asesoría durante las diferentes etapas de mi proyecto; y a
Natalia Duque Villarreal y María Ximena Borrero, quienes me apoyaron incondicionalmente
durante el desarrollo de este proyecto.
Por último, pero no menos importante, agradezco a mis papás por su apoyo y confianza en mí,
a mi familia, y a mis amigos.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
111
Nicolás Eduardo Páez Rincón
10. Bibliografía
Austin, R. G., van Bloemen Waanders, B., McKenna, S., & Choi, C. Y. (2008). Mixing at Cross
Junctions in Water Distribution Systems II: Experimental Study .
Buitrago, L. I. (2013). Análisis de la dilución de concentraciones de NaCl en una unión tipo cruz.
Bogotá D.C.
Cotes Gómez, L. N. (2013). Construcción de un modelo físico para la medición de mezcla en
nudos de redes de distribución de agua potable.
Cotes Gómez, L. N. (2013). Efectos de una mezcla no completa ni homogénea en los nudos sobre
el contenido residual de cloro en redes de distribución de agua potable. Bogotá D.C.
Endress - Hauser. (2007). Operating instructions: Sensors for free chlorine.
Endress Hauser. (2009). Operating Instructions: Flow assembly for chlorine sensors.
France monthly. (s.f.). Obtenido de Like a trip to la belle France:
http://www.francemonthly.com/n/0903/
Ho, C. K. (2008). Solute Mixing Model por Water Distribution Pipe Networks. Recuperado el 22
de Febrero de 2014, de ASCE:
http://gsgc.gzhu.edu.cn/gpsgd/UploadFile/200942623229730.pdf
Kobold. (2009). Operating Instructions for Magnetic - Inductive Flowmeter.
Mompremier, R. (2009). Difusión de sustancias en redes de tuberías a presión.
Ocasio, N., & López Díez, M. E. (2007). El uso del cloro en la desinfección del agua. Recuperado
el 07 de febrero de 2014, de
http://hispagua.cedex.es/sites/default/files/uso_cloro.pdf
Organización Mundial de la Salud. (2009). Agua, saneamiento y salud (ASS). Obtenido de
Enfermedades relacionadas con el agua:
http://www.who.int/water_sanitation_health/diseases/es/
PAVCO. (2013). Línea de tanques en polietileno PAVCO. Recuperado el 29 de abril de 2014
Pontificia Universidad Javeriana Cali. (07 de febrero de 2014). El final de la República.
Obtenido de
http://pioneros.puj.edu.co/cronologias/revolucion_agricola/roma/el_final_de_la_repu
blica.html
Romero Gómez, P., Ho, C. K., & Choi, C. Y. (2008). Mixing at Cross Junctions in Water
Distribution Systems I: Numerical Study.

Universidad de Los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigación en Acueductos y Alcantarillados - CIACUA
“Modelación física de los procesos de mezcla de sustancias en redes de distribución de agua
potable”
112
Nicolás Eduardo Páez Rincón
Rossman, L., Clark, R., & Grayman , W. (1994). Modeling Chlorine Residuals in Drinking -
Water Distribution Systems . ASCE, 18.
Saldarriaga, J. G. (2007). Hidráulica de Tuberías. Bogotá D.C.: Alfaomega ISBN 978-958-682-
680-8.
Saldarriaga, J. G. (2014). Clase de Hidráulica de Tuberías.
Song, I., Romero - Gómez, P., & Choi, C. Y. (2009). Experimental Verification of Incomplete
Solute Mixing in a Pressurized Pipe Network with Multiple Cross Junctions.
Tzatchkov, V. G., Buchberger, S. G., Li, Z., Romero - Gómez, P., & Choi, C. (2009). Axial
Dispersion in Pressurized Water Distribution Networks - A Review.
Universidad de Valencia. (2006). Fenómenos de transporte y conductividad electrolítica.
Vidal, R., Martínez, F., & Ayza, M. (1994). Aplicaciones de los modelos de calidad en la
simulación de las redes de distribución de agua potable. Obtenido de
http://upcommons.upc.edu/revistes/bitstream/2099/4203/1/article5.pdf
Water Treatment Solutions LENNTECH. (07 de febrero de 2014). Desinfectantes. Obtenido de
http://www.lenntech.es/procesos/desinfeccion/quimica/desinfectantes-cloro.htm
Water Treatment Solutions LENNTECH. (07 de febrero de 2014). Enfermedades transmitidas
por el agua. Obtenido de
http://www.lenntech.es/procesos/desinfeccion/deseases/enfermedades-
transmitidas-por-el-agua.htm
