
TESIS II MAESTRÍA INGENIERÍA CIVIL
MODELACIÓN DE LA CALIDAD DEL AGUA EN REDES DE DISTRIBUCIÓN
DE AGUA POTABLE: MEZCLA COMPLETA VS. MEZCLA INCOMPLETA EN
NUDOS HACIENDO USO DE UN MODELO FÍSICO Y DINÁMICA DE FLUIDOS
COMPUTACIONAL
PRESENTADO POR:
LAURA NATALIA COTES GÓMEZ
ASESOR:
JUAN GUILLERMO SALDARRIAGA VALDERRAMA
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
BOGOTÁ D.C
DICIEMBRE DE 2015

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
El presente trabajo corresponde a la Tesis con la cual se culminan los estudios de Maestría
en Ingeniería Civil con énfasis en Recursos Hídricos e Hidroinformáticos de la Universidad
de los Andes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
i
Tabla de
contenido
1. INTRODUCCIÓN ............................................................................................................ 1
1.1. OBJETIVOS .................................................................................................................. 2
1.1.1. Objetivo general ........................................................................................................ 2
1.1.2. Objetivos específicos ................................................................................................ 2
2. ANTECEDENTES ........................................................................................................... 3
1.1.
Modelación con trazadores conservativos ............................................................. 17
3. MARCO TEÓRICO ....................................................................................................... 38
3.1 Modelación hidráulica ................................................................................................ 38
3.1.1 Ecuaciones de modelación hidráulica .................................................................. 38
3.2 Modelación de calidad del agua .................................................................................. 40
3.2.1. Modelos estáticos ................................................................................................ 40
3.2.2. Modelos dinámicos ............................................................................................. 41
3.2.3. Concentración...................................................................................................... 42
3.3. Dinámica de Fluidos Computacional ......................................................................... 45
3.3.1. Funcionamiento del código de CFD.................................................................... 45
3.3.2. Leyes de conservación del movimiento de los fluidos y las condiciones de
frontera… ...................................................................................................................... 48
3.3.3. Conservación de la masa en tres dimensiones .................................................... 49
3.3.4. Ecuación de momento en tres dimensiones......................................................... 51
3.3.5. Ecuación de Navier-Stokes para un fluido Newtoniano ..................................... 53
3.3.6. Modelación de la turbulencia .............................................................................. 54
3.3.7 Ecuaciones de Reynolds-Averaged Navier-Stokes (RANS) para fluidos
incompresibles ............................................................................................................... 56
3.3.8 Cálculos para del flujo turbulento ........................................................................ 57
3.3.9 Modelo de turbulencia K-ε ................................................................................... 58
4. MODELO FÍSICO DE LOS PROCESOS DE MEZCLA EN LOS NUDOS ........... 61
5. DEFINICIÓN DE CONFIGURACIONES DE LAS UNIONES DE TUBERÍAS .... 66
6. MODELACIÓN NUMÉRICA EN CFD ...................................................................... 69
6.1. Modelación configuración cruz con tuberías de 1” ................................................... 70

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
ii
6.2. Modelación configuración cruz con tubería de salida de 1.5’ ................................... 77
6.3. Modelación configuración cruz con tubería de entrada de 1.5” ................................ 81
6.4. Modelación configuración doble tee (L/d=14) .......................................................... 84
6.5. Modelación configuración doble tee (L/d=CFD) ...................................................... 87
7. RESULTADOS DE LA MODELACIÓN FÍSICA ...................................................... 94
7.1. Resultados con trazador Permanganato de Potasio .................................................... 94
7.1.1. Configuración cruz con tuberías de 1” ................................................................ 97
7.1.2. Configuración cruz con una tubería de salida de 1.5’ ....................................... 101
7.1.3. Configuración cruz con tubería de entrada de 1.5” ........................................... 106
7.1.4. Configuración doble tee (L/d=14) ..................................................................... 110
7.1.4. Configuración doble tee (L/d=3.7) .................................................................... 115
7.2. Resultados trazador Cloro ........................................................................................ 120
7.2.1. Configuración cruz con tuberías de 1” .............................................................. 120
7.2.2. Configuración cruz con tubería de salida de 1.5” ............................................. 125
7.2.3. Configuración cruz con tubería de entrada de 1.5” ........................................... 127
7.2.4. Configuración doble tee (L/d=14) ..................................................................... 129
7.2.5. Configuración doble tee (L/d=3.7) .................................................................... 131
8. ANÁLISIS DE RESULTADOS ................................................................................... 133
9. CONCLUSIONES Y RECOMENDACIONES ......................................................... 148
10. AGRADECIMIENTOS ............................................................................................ 150
11. BIBLIOGRAFÍA ........................................................................................................ 151

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
iii
Índice de Figuras
Figura 1. Bifurcación de los flujos en la simulación en CFD ................................................ 5
Figura 2. Flujos con diferentes patrones ................................................................................. 7
Figura 3. Interfaz EPANET BAM ........................................................................................ 10
Figura 4. Red modelada en EPANET-BAM ........................................................................ 10
Figura 5. Resultados EPANET-BAM .................................................................................. 11
Figura 6. Concentración normalizada en cada nodo de la red .............................................. 11
Figura 7. Tabla de predicción de muertes en cada vecindario suponiendo mezcla completa
(s=1)). ................................................................................................................................... 12
Figura 8. Tabla de predicción de muertes en cada vecindario suponiendo mezcla incompleta
(s=0.5). .................................................................................................................................. 12
Figura 9. Simulación de red 3x3 con unión en cruz con caudal de trazador mayor a caudal
de agua limpia. ...................................................................................................................... 13
Figura 10. Simulación de red 3x3 con unión en cruz con caudal de agua limpia mayor a
caudal con trazador. .............................................................................................................. 14
Figura 11. Simulación red 3x3 con unión doble tee con caudal de trazador mayor a caudal
de agua limpia ....................................................................................................................... 14
Figura 12. Simulación red 3x3 con unión doble tee con caudal de agua limpia mayor a
caudal de trazador. ................................................................................................................ 15
Figura 13. Resultados de simulaciones de los modelos de mezcla. ..................................... 16
Figura 14. Configuración típica en redes de distribución de agua potable. ......................... 17
Figura 15. Configuración utilizada en el modelo. ................................................................ 18
Figura 16. Interfaz incidente en la intersección de tuberías ................................................ 20
Figura 17. Relación entre la concentración adimensional de la tubería Este con el número
de Reynolds .......................................................................................................................... 21
Figura 18. Resultados obtenidos para el escenario 2 ............................................................ 22
Figura 19. Resultados obtenidos para el escenario 3 ............................................................ 23
Figura 20. Tasa de masa de NaCl en la tubería Este para el escenario 2 ............................. 25
Figura 21. Concentración normalizada en la tubería Este para el escenario 2 ..................... 25
Figura 22. Tasa de masa de NaCl en la tubería Este para el escenario 3 ............................. 26
Figura 23. Concentración normalizada en la tubería Este para el escenario 3 ..................... 26
Figura 24. (a) Concentración de NaCl (b) Vectores de velocidad en la unión, cuando el
número de Reynolds es igual en las tuberías de entrada y salida ......................................... 27
Figura 25. Esquema completo del modelo experimental usado en Arizona. ....................... 28
Figura 26. Valores de conductividad cuando Retotal=4200. ............................................... 29
Figura 27. Número de Reynolds promedio en las tuberías vs. Concentración normalizada en
la tubería Este ....................................................................................................................... 30
Figura 28. Relación del número de Reynolds S/W y la concentración normalizada en la
tubería Este para el escenario 2 ............................................................................................ 30
Figura 29. Modelo implementado en Fluent. ....................................................................... 32

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
iv
Figura 30. Enmallado de la geometría .................................................................................. 32
Figura 31. Contornos de concentración ................................................................................ 32
Figura 32. Isocontornos de la concentración. ....................................................................... 33
Figura 33. Fracción de masa de NaCl en función del tiempo............................................... 33
Figura 34. Geometría interna de las uniones en cruz. .......................................................... 34
Figura 35. Contornos de concentración después de corrección............................................ 34
Figura 36. Fracción de masa de NaCl en función del tiempo después de corrección .......... 34
Figura 37. Fracción de masa para diferentes diámetros de tuberías. .................................... 35
Figura 38. Configuraciones doble tee ................................................................................... 36
Figura 39. (a) resultados experimentales para mayor momento en tuberías adyacentes (b)
mayor momento en tuberías opuestas ................................................................................... 37
Figura 40. Esquema de conservación de masa en el nudo j. ................................................ 40
Figura 41. Esquema de balance de masa en la unión de tuberías ......................................... 43
Figura 42. Volumen de control del fluido ............................................................................ 48
Figura 43. Flujo de masa en el elemento .............................................................................. 50
Figura 44. Componentes de los esfuerzos de tensión en las tres caras del elemento ........... 51
Figura 45. Componentes de tensión en la dirección x. ......................................................... 52
Figura 46. Flujos turbulentos libres ...................................................................................... 55
Figura 47. Válvulas de entrada y salida para controlar caudal. ............................................ 62
Figura 48. Caudalímetro electromagnético, ......................................................................... 63
Figura 49. Sensor de cloro. ................................................................................................... 64
Figura 50. Modelo físico general. ......................................................................................... 65
Figura 51. Definición de configuraciones. a) cruz con tuberías de 1". b) Cruz con tubería de
salida de 1.5". c) Cruz con tubería de entrada de 1.5". d) doble tee. .................................... 67
Figura 52. Configuraciones con Permanganato de Potasio. a) cruz con tuberías de 1". b)
Cruz con tubería de salida de 1.5". c) Cruz con tubería de entrada de 1.5". d) doble tee. ... 68
Figura 53. Geometría configuración a). ............................................................................... 70
Figura 54. Comparación del tamaño de la malla. ................................................................. 71
Figura 55. Comparación de resultados de Fracción de Masa para cada tamaño de malla. .. 72
Figura 56. Refinamiento del mallado del modelo. ............................................................... 73
Figura 57. Gráfica de convergencia del modelo k-ε. ............................................................ 73
Figura 58. Gráfica de convergencia del modelo k-ω. ........................................................... 74
Figura 59. Resultados con el modelo de turbulencia k-ω. .................................................... 74
Figura 60. Resultados en CFD de la configuración a). ......................................................... 75
Figura 61. Resultados en CFD correspondientes al número de simulación para la
configuración a). ................................................................................................................... 76
Figura 62. Geometría configuración b). ............................................................................... 78
Figura 63. Malla configuración b). ....................................................................................... 78
Figura 64. Resultados en CFD de la configuración b). ........................................................ 79
Figura 65. Resultados en CFD correspondientes al número de simulación para la
configuración b). ................................................................................................................... 80
Figura 66. Geometría configuración c). ............................................................................... 81

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
v
Figura 67. Malla configuración c). ....................................................................................... 82
Figura 68. Resultados en CFD de la configuración c). ......................................................... 82
Figura 69. Resultados en CFD correspondientes al número de simulación para la
configuración c). ................................................................................................................... 83
Figura 70. Geometría configuración d). ............................................................................... 84
Figura 71. Malla de configuración d). .................................................................................. 85
Figura 72. Resultados en CFD de la configuración d). ........................................................ 85
Figura 73. Resultados en CFD correspondientes al número de simulación para la
configuración d). ................................................................................................................... 86
Figura 74. Resultados CFD configuración doble tee (L/d=2). ............................................. 88
Figura 75. Resultados CFD configuración doble tee (L/d=2.5). .......................................... 88
Figura 76. Resultados CFD configuración doble tee (L/d=3). ............................................. 89
Figura 77. Resultados CFD configuración doble tee (L/d=5). ............................................. 89
Figura 78. Resultados CFD configuración doble tee (L/d=10). ........................................... 90
Figura 79. Resultados en CFD de la configuración e). ......................................................... 91
Figura 80. Resultados en CFD correspondientes al número de simulación para la
configuración e). ................................................................................................................... 92
Figura 81. Montaje experimental análisis de imagen ........................................................... 94
Figura 82. Resultados de relación de concentración e intensidad de color rojo ................... 95
Figura 83. Interfaz y definición del umbral de color de las imágenes en ImageJ. ............... 96
Figura 84. Resultados configuración a) usando KMnO
4
. ..................................................... 98
Figura 85. Análisis de imagen configuración a). .................................................................. 99
Figura 86. Resultados configuración b) usando KMnO
4
. ................................................... 103
Figura 87. Análisis de imagen configuración b)................................................................. 104
Figura 88. Resultados configuración c) usando KMnO4. .................................................. 107
Figura 89. Análisis de imagen configuración c). ................................................................ 108
Figura 90. Resultados configuración d) usando KMnO4. .................................................. 111
Figura 91. Análisis de imagen configuración d)................................................................. 112
Figura 92. Resultados configuración e) usando KMnO4. .................................................. 116
Figura 93. Análisis de imagen configuración e). ................................................................ 117

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
vi
Índice de Gráficas
Gráfica 1. Resultados en CFD para la Fracción de masa de la configuración a). ................ 77
Gráfica 2. Resultados en CFD para la Fracción de masa de la configuración b). ................ 81
Gráfica 3. Resultados en CFD para la Fracción de masa de la configuración c). ................ 84
Gráfica 4. Resultados en CFD para la Fracción de masa de la configuración d). ................ 87
Gráfica 5. Resultados en CFD para la Fracción de masa de la configuración e). ................ 93
Gráfica 6. Caudales para configuración a) usando KMnO4. ................................................ 97
Gráfica 7. Intensidad de rojo en la tubería 3 para la configuración a). .............................. 100
Gráfica 8. Fracción de masa vs intensidad de rojo para la configuración a). ..................... 100
Gráfica 9. Fracción de masa en la tubería 3 en función de la relación del número de
Reynolds para la configuración a). ..................................................................................... 101
Gráfica 10. Caudales para configuración b) usando KMnO4. ........................................... 102
Gráfica 11. Intensidad de rojo en la tubería 3 para la configuración b). ............................ 105
Gráfica 12.Fracción de masa vs intensidad de rojo para la configuración b). .................... 105
Gráfica 13. Fracción de masa en la tubería 3 en función de la relación del número de
Reynolds para la configuración b). ..................................................................................... 106
Gráfica 14. Caudales para configuración c) usando KMnO4. ............................................ 106
Gráfica 15. Intensidad de rojo en la tubería 3 para la configuración c). ............................ 109
Gráfica 16. Fracción de masa vs intensidad de rojo para la configuración c). ................... 109
Gráfica 17. Fracción de masa en la tubería 3 en función de la relación del número de
Reynolds para la configuración c). ..................................................................................... 110
Gráfica 18. Caudales para configuración d) usando KMnO4. ........................................... 110
Gráfica 19. Intensidad de rojo en la tubería 3 para la configuración d). ............................ 113
Gráfica 20. Fracción de masa vs intensidad de rojo para la configuración d). ................... 114
Gráfica 21.Fracción de masa en la tubería 3 en función de la relación del número de
Reynolds para la configuración d). ..................................................................................... 114
Gráfica 22. Caudales para configuración e) usando KMnO4. ............................................ 115
Gráfica 23. Intensidad de rojo en la tubería 3 para la configuración e). ............................ 118
Gráfica 24. Fracción de masa vs intensidad de rojo para la configuración e). ................... 118
Gráfica 25. Fracción de masa en la tubería 3 en función de la relación del número de
Reynolds para la configuración e). ..................................................................................... 119
Gráfica 26. Caudales para configuración a) usando Cloro. ................................................ 120
Gráfica 27. Concentraciones de cloro para la configuración a). ........................................ 121
Gráfica 28. Fracción de masa de cloro para la configuración a). ....................................... 122
Gráfica 29. Concentración normalizada para la configuración a). ..................................... 122
Gráfica 30. Comparación C* entre configuración a) y bibliografía. .................................. 123
Gráfica 31. Comparación Fracción de masa entre configuración a) y bibliografía. ........... 124
Gráfica 32. Caudales para configuración b) usando Cloro. ................................................ 125
Gráfica 33. Concentraciones de cloro para la configuración b). ........................................ 125
Gráfica 34. Fracción de masa de cloro para la configuración b). ....................................... 126

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
vii
Gráfica 35. Concentración normalizada para la configuración b). ..................................... 126
Gráfica 36. Caudales para configuración c) usando Cloro. ................................................ 127
Gráfica 37. Concentraciones de cloro para la configuración c). ........................................ 127
Gráfica 38. Fracción de masa de cloro para la configuración c). ....................................... 128
Gráfica 39. Concentración normalizada para la configuración c). ..................................... 128
Gráfica 40. Caudales para configuración d) usando Cloro. ................................................ 129
Gráfica 41. Concentraciones de cloro para la configuración d). ........................................ 129
Gráfica 42. Fracción de masa de cloro para la configuración d). ....................................... 130
Gráfica 43. Concentración normalizada para la configuración d). ..................................... 130
Gráfica 44. Caudales para configuración e) usando Cloro. ................................................ 131
Gráfica 45. Concentraciones de cloro para la configuración e). ........................................ 131
Gráfica 46. Fracción de masa de cloro para la configuración e). ....................................... 132
Gráfica 47. Concentración normalizada para la configuración e). ..................................... 132
Gráfica 48. Comparación metodologías de medición en configuración a). ....................... 134
Gráfica 49. Comparación metodologías de medición en configuración b). ....................... 135
Gráfica 50. Comparación metodologías de medición en configuración c). ....................... 135
Gráfica 51. Comparación metodologías de medición en configuración d). ....................... 136
Gráfica 52. Comparación metodologías de medición en configuración e). ....................... 136
Gráfica 53. Comparación concentración normalizada entre configuraciones. ................... 138
Gráfica 54. Comparación C* entre configuraciones y bibliografía. ................................... 139

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
viii
Índice de Tablas
Tabla 1. Resultados en CFD de la configuración a). ............................................................ 75
Tabla 2. Resultados en CFD de la configuración b). ............................................................ 79
Tabla 3. Resultados en CFD de la configuración c). ............................................................ 83
Tabla 4. Resultados en CFD de la configuración d). ............................................................ 86
Tabla 5. Configuraciones doble tee modeladas en CFD. ..................................................... 87
Tabla 6. Resultados en CFD de la configuración e). ............................................................ 91
Tabla 7. Escenarios de estudio para la configuración a). ..................................................... 97
Tabla 8. Intensidad de rojo asociada con la relación de número de Reynolds para la
configuración a). ................................................................................................................... 99
Tabla 9. Escenarios de estudio para la configuración b). ................................................... 102
Tabla 10. Intensidad de rojo asociada con la relación de número de Reynolds para la
configuración b). ................................................................................................................. 104
Tabla 11. Escenarios de estudio para la configuración c). ................................................. 107
Tabla 12.Intensidad de rojo asociada con la relación de número de Reynolds para la
configuración c). ................................................................................................................. 108
Tabla 13. Escenarios de estudio para la configuración d). ................................................. 111
Tabla 14.Intensidad de rojo asociada con la relación de número de Reynolds para la
configuración d). ................................................................................................................. 113
Tabla 15. Escenarios de estudio para la configuración e). ................................................. 115
Tabla 16. Intensidad de rojo asociada con la relación de número de Reynolds para la
configuración e). ................................................................................................................. 117
Tabla 17. Errores con respecto a la bibliografía para las configuraciones a), b) y c). ....... 139
Tabla 18. Comparación de los valores de concentración normalizada entre las
configuraciones b) y c) con respecto a la configuración a). ............................................... 140
Tabla 19. Resultados Regresión polinómica y RNA para configuración a). ...................... 142
Tabla 20. Resultados Regresión polinómica y RNA para configuración b). ..................... 143
Tabla 21. Resultados Regresión polinómica y RNA para configuración c). ...................... 144
Tabla 22. Resultados Regresión polinómica y RNA para configuración d). ..................... 144
Tabla 23. Resultados Regresión polinómica y RNA para configuración e). ...................... 145
Tabla 24. Error entre resultados medidos en el laboratorio, Regresión polinómica y RNA
para configuración a). ......................................................................................................... 145
Tabla 25. Error entre resultados medidos en el laboratorio, Regresión polinómica y RNA
para configuración b). ......................................................................................................... 146
Tabla 26. Error entre resultados medidos en el laboratorio, Regresión polinómica y RNA
para configuración c). ......................................................................................................... 146
Tabla 27. Error entre resultados medidos en el laboratorio, Regresión polinómica y RNA
para configuración d). ......................................................................................................... 147
Tabla 28. Error entre resultados medidos en el laboratorio, Regresión polinómica y RNA
para configuración e). ......................................................................................................... 147

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
ix
Índice de Ecuaciones
Ecuación 1. Balance de masa del soluto ................................................................................. 6
Ecuación 2. Relación caudal concentración en tuberías 1 y 4. ............................................... 8
Ecuación 3. Relación de concentraciones en tuberías 1 y 4. .................................................. 8
Ecuación 4. Balance de masa del soluto en la unión. ............................................................. 8
Ecuación 5. Concentración en la tubería 3 ............................................................................. 8
Ecuación 6. Concentración combinada .................................................................................. 9
Ecuación 7. Concentración adimensional del trazador. ........................................................ 18
Ecuación 8. Relación de número de Reynolds para las tuberías. ......................................... 19
Ecuación 9. Porcentaje de separación de NaCl. ................................................................... 23
Ecuación 10. Número de Reynolds total en el sistema......................................................... 28
Ecuación 11. Fracción de masa de NaCl. ............................................................................. 35
Ecuación 12. Factor de distribución de flujo. ....................................................................... 36
Ecuación 13. Tasa de momento ............................................................................................ 37
Ecuación 14. Conservación de masa en las redes. ................................................................ 38
Ecuación 15. Caudal utilizando la ecuación de Darcy-Weisbach en conjunto con la
ecuación de Colebrook-White .............................................................................................. 39
Ecuación 16. Altura piezométrica ........................................................................................ 39
Ecuación 17. Altura piezométrica teniendo en cuenta pérdidas menores causadas por
accesorios.............................................................................................................................. 39
Ecuación 18. Ecuación de continuidad para modelación de calidad del agua. .................... 40
Ecuación 19. Concentración en el nudo j. ............................................................................ 41
Ecuación 20. Tiempo de permanencia medio para el nudo j ................................................ 41
Ecuación 21. Transporte se sustancias conservativas ........................................................... 42
Ecuación 22. Transporte de sustancias no conservativas. .................................................... 42
Ecuación 23. Concentración a partir de la conservación de masa ........................................ 42
Ecuación 24. Aporte de masa a la unión i ............................................................................ 44
Ecuación 25.Masa de salida del nudo i................................................................................. 44
Ecuación 26.Concentración de la mezcla ............................................................................. 44
Ecuación 27.Presión en las caras del elemento. ................................................................... 49
Ecuación 28.Tasa de incremento de masa. ........................................................................... 49
Ecuación 29.Tasa de flujo a través de las fronteras .............................................................. 49
Ecuación 30. Conservación de masa en tres dimensiones en estado inestable..................... 50
Ecuación 31.Conservación de masa para un fluido incompresible ...................................... 50
Ecuación 32. Tasas de incremento del momento en x, y y z ................................................ 51
Ecuación 33. Componente en x de la ecuación de momento ............................................... 52
Ecuación 34. Componente en y de la ecuación de momento ............................................... 52
Ecuación 35. Componente en z de la ecuación de momento................................................ 52

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
x
Ecuación 36. Velocidad de deformación lineal .................................................................... 53
Ecuación 37. Deformación volumétrica ............................................................................... 53
Ecuación 38. Ecuación de Navier-Stokes ............................................................................. 54
Ecuación 39. Ley de pared ................................................................................................... 56
Ecuación 40. Ecuación de Reynolds-Averaged Navier-Stokes ............................................ 57
Ecuación 41. Disipación en la ecuación de energía cinética turbulenta. .............................. 60

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
1
1. Introducción
Los sistemas de distribución de agua potable hacen parte de la infraestructura general de
una ciudad, por lo tanto, su diseño y modelación deben ser adecuados para los estándares
que determinan la condición del servicio en cuanto a disponibilidad y calidad del agua. Con
respecto a la calidad del agua, existen muchas formas de conocer la variación de los
parámetros que determinan cuán apta está el agua para el consumo humano. Una de estas es
la modelación del decaimiento del cloro a lo largo de la red de distribución de agua potable
teniendo en cuenta parámetros de reacción y decaimiento. Sin embargo, en el presente
estudio se va a profundizar en la modelación de la calidad del agua desde el punto de vista
de los procesos de mezcla que ocurren en las intersecciones de las redes de distribución de
agua potable.
Para realizar la modelación de la calidad del agua en las redes de distribución se usa con
mucha frecuencia programas, como EPANET, que suponen que la mezcla en los nudos es
totalmente completa. Esto quiere decir que si existen dos tuberías de entrada, cada una con
una concentración de cloro y caudal diferente, las concentraciones de las tuberías de salida
son iguales. Estos cálculos se realizan con una ecuación sencilla de balance y ponderación
de la masa del soluto.
Sin embargo, hace unos años, algunos investigadores pusieron en duda la suposición de
mezcla completa. Esto llevó a una serie de experimentos que han demostrado que la mezcla
en los nudos no es completa y que la proporción del soluto que se dirige hacia alguna de las
tuberías de salida, depende en gran parte del caudal de las tuberías de entrada.
Lo anterior podría tener una implicación en la salud pública ya que la dosis de cloro que se
agrega en las Plantas de Tratamiento de Agua Potable está basadas en los modelos que
suponen mezcla completa. Dichos modelos predicen que con esa dosis inicial, la
concentración de cloro residual dentro de toda la red es suficiente para evitar
contaminaciones que se puedan presentar durante el transporte del agua desde la planta
hasta los consumidores. Entonces, si la mezcla no es completa, es posible que en algunos
puntos de consumo la concentración de cloro no sea suficiente y el agua pueda estar
contaminada.
Se ha evidenciado que los procesos de mezcla dependen del contacto e interacción espacial
y temporal de los flujos incidentes. Esto puede variar de acuerdo con, no solo, la relación
de los flujos de entrada, sino también, con el tipo de configuración y la geometría interna de
la intersección. De esta manera, en este proyecto se va a realizar un análisis de dichos
factores que afectan la mezcla.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
2
Para esto, se van a utilizar conexiones en cruz y doble tee. Durante la revisión bibliográfica
se encontró que en todos los estudios realizados previamente, modelan configuraciones en
donde todas las tuberías tienen el mismo diámetro, por lo tanto, en este caso se va a realizar
una variación de los diámetros de las tuberías de entrada y salida. De esta manera se podrá
identificar de qué manera afecta la ampliación o disminución de los diámetros en la
concentración del soluto en las tuberías de salida.
1.1. Objetivos
1.1.1. Objetivo general
El objetivo de este proyecto es realizar un análisis de los procesos de mezcla realizando
variaciones en la configuración del nudo en términos de la forma de conexión, es decir,
intersección en cruz y doble tee y diámetros de tuberías de entrada y salida.
1.1.2. Objetivos específicos
A partir del objetivo general, se espera que se pueda realizar un estudio de manera
cualitativa de los procesos de mezcla que se presentan en los nudos de las redes de
abastecimiento de agua potable. Esto se realizará para todas las configuraciones de
conexión analizadas. Para esto, se van a utilizar tuberías de vidrio o acrílico, en donde se
puede apreciar visualmente lo que ocurre con un trazador en la unión de las tuberías.
En segundo lugar, se espera tener resultados cuantitativos acerca de los procesos de mezcla
en las uniones de las tuberías. Así como en el objetivo anterior, esto se va a realizar para
todas las configuraciones estudiadas. Para esto se van a medir las concentraciones de
entrada y salida de cloro.
Finalmente, se espera que para cada escenario se realice una comparación de los resultados
cuantitativos obtenidos experimentalmente con los resultados obtenidos por medio de una
modelación numérica en utilizando la metodología de Dinámica de Fluidos Computacional
(Por sus siglas en inglés, CFD).
A partir de los resultados obtenidos, se espera concluir sobre los efectos que tiene la
geometría de la unión sobre los procesos de mezcla de cloro que allí se generan.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
3
2. Antecedentes
Para este proyecto, se llevó a cabo una revisión bibliográfica de los estudios realizados
anteriormente con respecto a los procesos de mezcla en las uniones de las redes de
abastecimiento de agua potable. Durante muchos años se utilizó la suposición de la mezcla
completa en las uniones para modelar la calidad del agua en las redes de distribución de
agua potable, pero Fowler y Jones (1991) fueron los primeros en poner en duda esta. Desde
aquella época, una de las preocupaciones acerca de la modelación de la calidad del agua
radica en que la suposición de mezcla perfecta es considerada como una causa significativa
en las diferencias entre las predicciones de modelos en EPANET y los valores reales
(Romero-Gómez, Ho, & Choi, 2008). De esta manera, se encontró que en la Universidad de
Tucson, Arizona, se realizaron experimentos a cargo de Pedro Romero-Gómez, en los que
se demuestra que la mezcla en los nudos no es completa (Tzatchkov, Buchberger, Li,
Romero-Gómez, & Choi, 2009).
En primer lugar, debido a los procesos físicos, químicos y biológicos que se pueden
presentar en las tuberías, la calidad del agua se puede deteriorar en los sistemas de
distribución de agua potable durante el transporte del recurso entre los puntos de
tratamiento y el consumo. Para tener un mayor entendimiento de los procesos que ocurren
mientras el agua es transportada por las redes, se realizaron varias simulaciones en donde se
hizo una variación de las condiciones del flujo.
Así pues, Romero-Gómez (2009) llevó a cabo una serie de experimentos con el fin de
comparar los resultados empíricos de la dispersión axial de un trazador no reactivo en un
tubo bajo condiciones de flujo laminar y transicional, con los resultados obtenidos con
simulaciones realizadas en EPANET, Dinámica de Fluidos Computacional (CFD), y
Advección-Dispersión (AD) del modelo. El montaje experimental se construyó en el
Laboratorio de Redes de Distribución, en una instalación experimental en la Universidad de
Arizona, Arizona, EE.UU. El modelo consistía en un tubo de PVC de 10 m de longitud, con
un diámetro interior de 15,3 mm (diámetro nominal de 1/2 pulgada), montado en andamios
de metal. El agua potable se bombeó desde un tanque de almacenamiento, mientras que una
micro-bomba inyectaba agua que contenía un trazador (cloruro de sodio). La velocidad de
flujo fue controlada por medio de sensores tipo caudal de turbina y válvulas de aguja
ubicadas en el extremo aguas abajo de las tuberías. La concentración de los trazadores se
controló con sensores de conductividad eléctrica y transmisores que fueron colocados en
sitios de monitoreo aguas arriba y aguas abajo, para medir el indicador de concentraciones.
Las tasas de flujo y las concentraciones se observaron en tiempo real y se registraron cada
segundo.
Los resultados de la simulación en CFD para flujos laminares fueron acordes con los datos
experimentales. Se observó que la dispersión axial de un soluto puede ser un proceso de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
4
transporte importante en regímenes de flujo laminar y transitorio. Por consiguiente, se
determinó que la mezcla en la unión es altamente dependiente de la variación de los
caudales en las tuberías de entrada. Por lo tanto, es de gran importancia el uso de modelos
computacionales que puedan simular diferentes escenarios que permitan observar como es
la variación en la concentración dependiendo de los parámetros de entrada.
Dentro de dichos modelos se encuentran los realizados por el software EPANET, el cual es
un estándar para la modelación hidráulica y el comportamiento de la calidad del agua en
sistemas de distribución de agua. Sin embargo, el programa supone que la mezcla de
solutos en las uniones de tuberías es completa e instantánea, lo que es contrario a estudios
que demostraron que la mezcla en las uniones era incompleta.
También, se simuló una red de 3 x 3 tuberías a pequeña escala para evaluar la validez de los
modelos de mezcla completa e incompleta para sistemas de distribución de agua bajo
diferentes tasas de flujo y condiciones de contorno. Las simulaciones en CFD mostraron
que las predicciones de las concentraciones del trazador a lo largo de la red podrían
alcanzarse si se compara con los datos experimentales. Por el contrario, un modelo de
EPANET que supone la mezcla completa dentro de las uniones, produjo concentraciones
uniformes en toda la red, que fue significativamente diferente de las concentraciones
espacialmente variables observadas en la red experimental (Ho, Choi, & McKenna,
Evaluation of complete and incomplete mixing models in water distribution pipe network
simulations, 2007).
La mezcla de solutos dentro de la unión se limita a interfaz incidente donde los flujos
convergen (Figura 1). Adicionalmente, se evidenció que un factor dominante que controla
el comportamiento y las concentraciones de mezcla son las tasas de entrada y salida de las
uniones; las corrientes de flujo entrantes se bifurcan en diversos grados a través de los
tubos de salida como función de las velocidades de flujo relativas.
Por lo tanto, la cantidad de mezcla que se produce dentro de la unión depende de la relación
de impulso que lleva un flujo de corriente. Los resultados de los estudios mostraron que la
mezcla en uniones en cruz es incompleta y dependiente de las inestabilidades transitorias en
la interfaz incidente y las tasas de flujo relativas que entran y salen de la unión.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
5
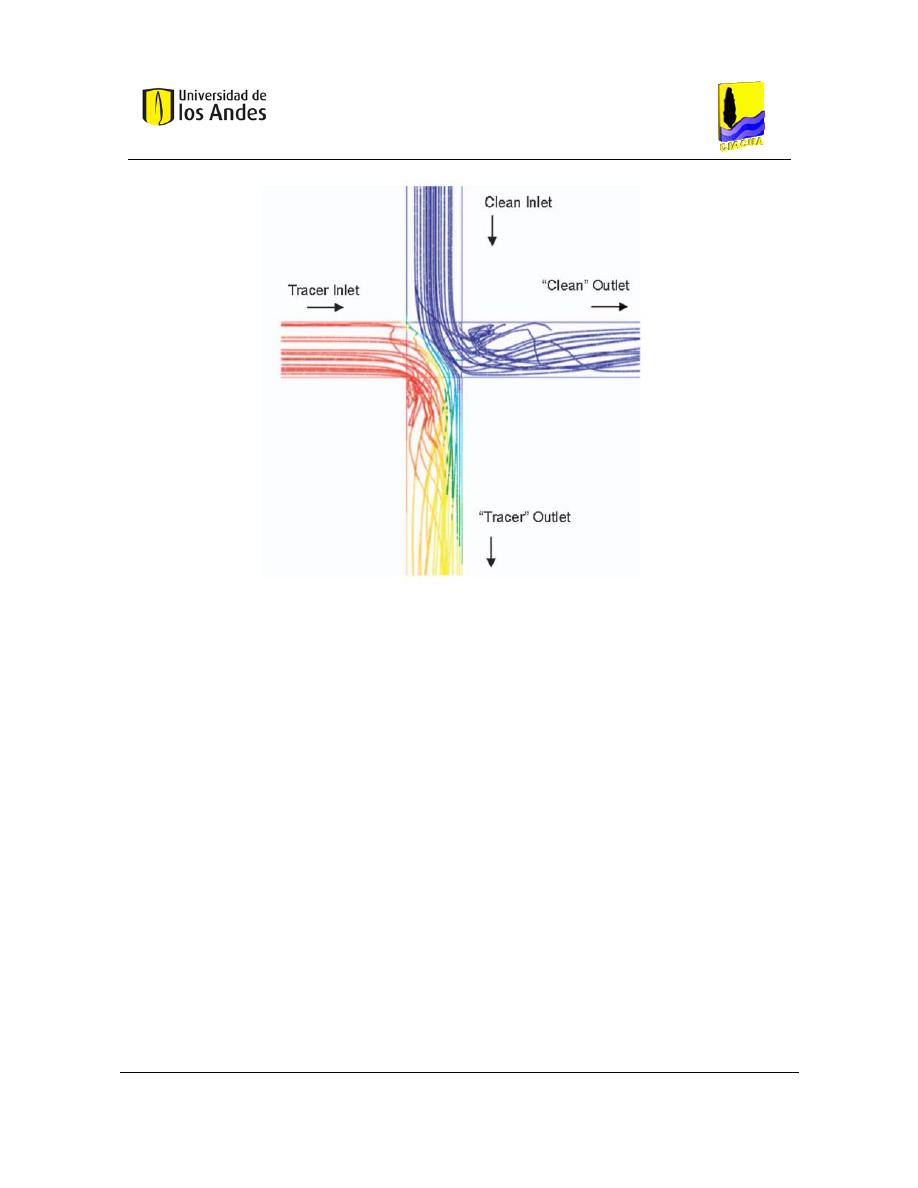
Figura 1. Bifurcación de los flujos en la simulación en CFD (Ho C. K., 2008).
La Figura 1 muestra un ejemplo de flujo simulado y el transporte de solutos en una unión
transversal utilizando un modelo de CFD. Un resultado notable de esta simulación es que el
flujo entrante se refleja en los otros, como si fueran cuerpos rígidos. La mezcla se limita a
la interfaz incidente en donde los dos flujos se encuentran, y la mezcla no es completa.
También, en esta simulación, el flujo en el tubo vertical es mayor que el flujo en el tubo
horizontal, el agua "limpia" cruza la intersección, desviando la mayor parte del "trazador"
del agua. Estos fenómenos simulados, han sido confirmados experimentalmente.
Aunque los modelos CFD se han utilizado recientemente para obtener una perspectiva de
los procesos de mezcla en uniones de tubos individuales, los modelos más simples son los
de mezcla completa; por lo tanto sigue siendo necesario que se pueda incorporar en los
modelos de la red de agua, los que se basan en la mezcla incompleta.
Como investigación, se han realizado modelos analíticos utilizados para limitar el
comportamiento de la mezcla en las uniones de las tuberías. Estos modelos son el de
mezcla completa y mezcla incompleta.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
6
Modelo de mezcla completa:
El modelo de mezcla completa es empleado por EPANET y otros modelos del
comportamiento hidráulico de redes de distribución de agua que suponen una mezcla
completa e instantánea dentro de las uniones de tuberías. La formulación se puede
implementar fácilmente con una ecuación analítica en los modelos de red para cálculos
rápidos y eficientes.
En el modelo de mezcla completa, se supone que la concentración en el fluido que sale de
la unión es uniforme e igual en todas las tuberías de salida. Y depende de las
concentraciones de flujo ponderadas que entran en el tubo.
En un balance de masa del soluto, se obtiene la siguiente ecuación para la concentración:
𝐶
𝑜𝑢𝑡
=
∑
𝑄
𝑖
𝐶
𝑖
𝑛
𝑖=1
𝑄
𝑜𝑢𝑡
=
∑
𝑄
𝑖
𝐶
𝑖
𝑛
𝑖=1
∑
𝑄
𝑖
𝑛
𝑖=1
Ecuación 1. Balance de masa del soluto (Rossman, EPANET, 1993).
donde:
𝑄
𝑖
, es el caudal de entrada a la unión desde la tubería i.
𝐶
𝑖
, es la concentración en cada tubería de entrada a la unión.
n, es el número de tuberías que llegan a la unión.
Se supone que no se presenta ningún almacenamiento en la unión, por lo tanto, el caudal de
salida es igual al caudal de entrada en la unión.
La desventaja del modelo de mezcla completa es que no tiene en cuenta los procesos físicos
de mezcla que se han observado en experimentos y simulaciones utilizando modelos CFD
para muchas configuraciones de flujo. El modelo de mezcla completa predice la mayor
mezcla posible que puede ocurrir físicamente dentro de un cruce. Esta suposición puede dar
concentraciones que son significativamente diferentes de las concentraciones reales para
muchas configuraciones de conexiones.
Modelo de mezcla incompleta:
El modelo de mezcla incompleta pretende complementar el modelo de mezcla completa
proporcionando un límite inferior para la mezcla en las uniones. El modelo de mezcla
incompleta se basa en el conocimiento de las velocidades de flujo relativas y las
concentraciones que entran y salen de una unión.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
7
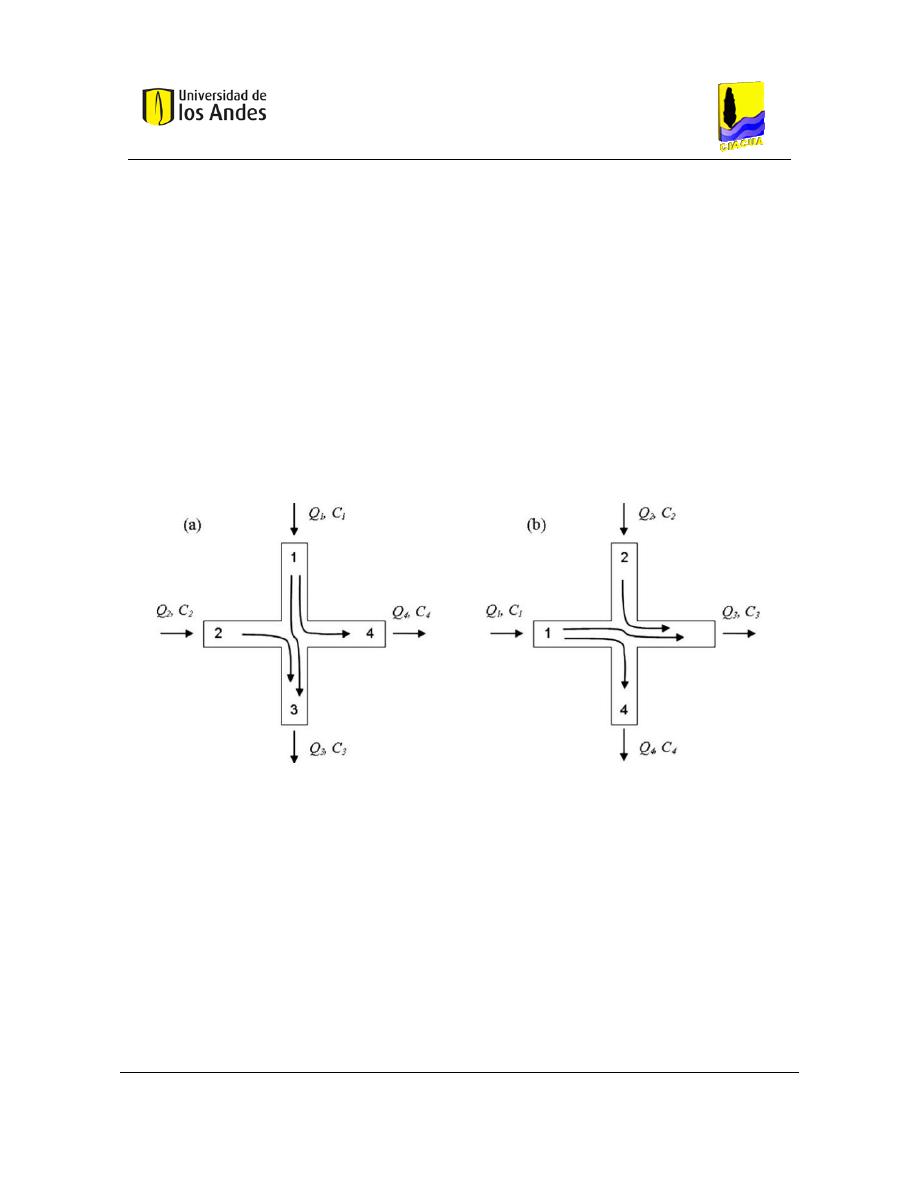
Como se muestra en la Figura 2, el impulso desigual de diferentes flujos provocará una
transferencia masiva de los fluidos y componentes entre los flujos entrantes y salientes. Con
caudales diferentes, los modelos CFD muestran que el impulso adicional realizado por una
corriente puede ser suficiente para cruzar la unión en la corriente opuesta. Por ejemplo, si
existe una configuración donde la velocidad de flujo de entrada de agua limpia es 80%
mayor que la velocidad de flujo del agua con trazador y las tasas de flujo de salida son
iguales. Como resultado, el impulso adicional del agua limpia hace que una parte de esta
agua empuje la otra a través de la unión. Este comportamiento de mezcla de fluido, va a
diluir la concentración del trazador en la tubería de salida al tiempo que reduce la cantidad
de trazador que puede migrar en la salida de agua limpia; el resultado de esta situación se
puede observar en la Figura 1. Similar pero opuesto, se producirá el comportamiento si la
velocidad de flujo en la entrada de trazador es mayor que la velocidad de flujo en la entrada
de agua limpia, con tasas de flujo de salida iguales. Los flujos de diferentes patrones se
muestran en la Figura 2 (Ho C. K., 2008).
Figura 2. Flujos con diferentes patrones (Ho C. K., 2008).
El modelo de mezcla incompleta supone que la mezcla se produce sólo a través de la
interacción del fluido a granel. Si todas las velocidades de flujo son iguales, o si las
velocidades de flujo en tuberías de entrada y salida adyacentes son iguales, se supone que el
flujo se bifurca y la mezcla es distinta a la suposición de mezcla completa. Por lo tanto, el
modelo de mezcla incompleta proporciona un límite inferior, físicamente basado, de la
cantidad de mezcla que puede ocurrir dentro de las uniones.
El modelo de mezcla incompleta se obtiene suponiendo que se conocen las tasas de entrada
del flujo, o que se pueden calcular. En primer lugar, los tubos están numerados de modo
que la nomenclatura utilizada en la solución es consistente para todas las configuraciones
del flujo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
8
Para este caso, se va a considerar que las áreas transversales de todas las tuberías son
iguales. En los ejemplos presentados en la Figura 2, se encuentran diferentes velocidades de
flujo en los tubos individuales que causan un impulso dominante en uno de los pares de
tubos opuestos. En la Figura 2(a), el impulso dominante es de arriba a abajo, mientras que
en la Figura 2(b), el impulso dominante es de izquierda a derecha. Los tubos 1 y 3 siempre
corresponden a la entrada y la salida, respectivamente, de la tubería con el impulso más
grande. Por lo tanto, con este esquema de numeración, la mayor parte del modelo de mezcla
supone que todo el flujo de entrada de la tubería 2 fluye hacia el tubo de salida 3. Por lo
tanto, la concentración en la tubería de salida 3 es una mezcla de las concentraciones de las
tuberías de entrada 1 y 2. La concentración en la tubería de salida 4 es la misma que la
concentración en la tubería de entrada 1, que es la única fuente de flujo de la tubería de
salida 4.
Suponiendo que la velocidad de flujo en cada tubería es conocida junto con las
concentraciones de entrada C1 y C2, se identifica que:
𝑄
4
𝐶
4
= 𝑄
1→4
𝐶
1
= 𝑄
4
𝐶
1
Ecuación 2. Relación caudal concentración en tuberías 1 y 4 (Ho C. K., 2008).
donde:
Q
1→4
, es la porción del flujo de la tubería de entrada 1 que fluye hacia el tubo de salida 4.
Como se supone que el flujo de la tubería 2 no sale por la tubería 4, todo el flujo que sale de
la tubería 4 es del tubo de entrada 1, es decir,
Q
1→4
= Q
4
entonces se establece que la
concentración en la tubería de salida 4 es igual a la concentración en la tubería de entrada 1:
𝐶
4
= 𝐶
1
Ecuación 3. Relación de concentraciones en tuberías 1 y 4 (Ho C. K., 2008).
La concentración en la tubería de salida 3 se deriva mediante la realización de un balance
de masa del soluto en la unión:
𝑄
1
𝐶
1
+ 𝑄
2
𝐶
2
= 𝑄
3
𝐶
3
+ 𝑄
4
𝐶
4
Ecuación 4. Balance de masa del soluto en la unión (Ho C. K., 2008).
Despejando la concentración de la tubería 3 se tiene que:
𝐶
3
=
𝑄
2
𝐶
2
+ (𝑄
1
− 𝑄
4
)𝐶
1
𝑄
3
Ecuación 5. Concentración en la tubería 3 (Ho C. K., 2008).
Las Ecuaciones 3 y 5 describen las soluciones analíticas de la mezcla incompleta. En un
modelo de red, estas soluciones pueden ser aplicadas secuencialmente a cada unión aguas

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
9
abajo a partir de la unión aguas arriba donde se prescriben las condiciones límite de
concentración. La velocidad de flujo en cada tubería es típicamente calculada de antemano
en los modelos CFD de red o sobre las condiciones prescritas de límite de presión y/o las
tasas de flujo. En las simulaciones transitorias, la solución del modelo de mezcla
incompleta se puede aplicar en cada paso de tiempo con velocidades de flujo actualizadas
en cada unión.
Combinación de los modelos de mezcla completa y modelos de mezcla incompleta:
Debido a que el modelo de mezcla completa y el modelo de mezcla incompleta
proporcionan los límites superior e inferior, respectivamente, la cantidad real de la mezcla
estará entre estos dos límites. Por lo tanto, se puede definir un parámetro de escala 0<s<1
para estimar la combinación de concentración en un tubo de salida:
𝐶
𝑐𝑜𝑚𝑏𝑖𝑛𝑎𝑑𝑎
= 𝐶
𝑖𝑛𝑐𝑜𝑚𝑝𝑙𝑒𝑡𝑎
+ 𝑠(𝐶
𝑐𝑜𝑚𝑝𝑙𝑒𝑡𝑎
− 𝐶
𝑖𝑛𝑐𝑜𝑚𝑝𝑙𝑒𝑡𝑎
)
Ecuación 6. Concentración combinada (Ho C. K., 2008).
El valor del parámetro de escala, s, puede depender de las propiedades del fluido, las
condiciones de flujo, y la configuración geométrica de la conexión de tubos, lo que puede
contribuir a inestabilidades locales en la interfaz incidente y la mezcla turbulenta dentro de
la unión.
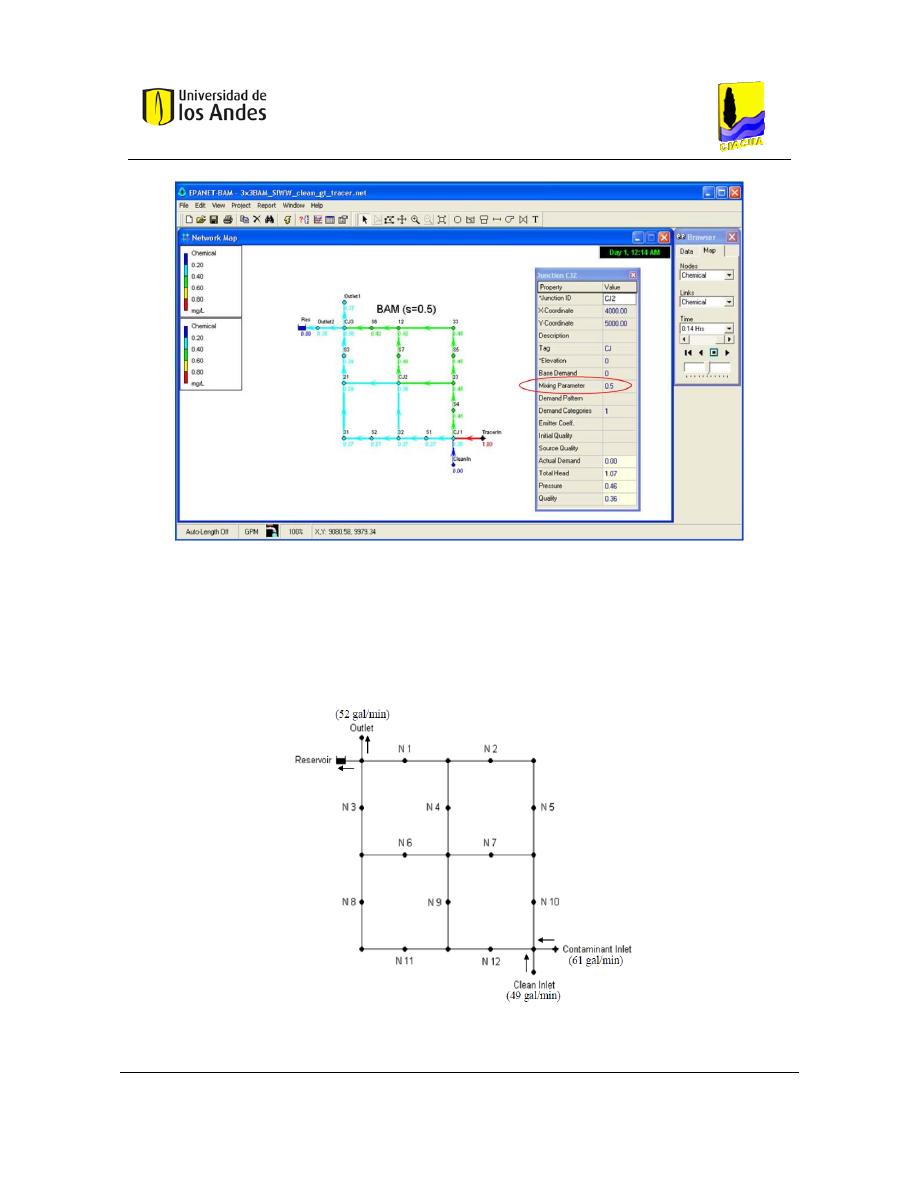
Debido a esto, se realizaron modificaciones al programa EPANET creando una nueva
versión llamada EPANET-BAM en donde se tiene en cuenta la mezcla incompleta. El
programa utiliza un parámetro de mezcla s, el cual puede ser modificado por el usuario (Ho
& Khalsa, EPANET-BAM: Water quality modeling with incomplete mixing in pipe
junctions, 2008).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
10
Figura 3. Interfaz EPANET BAM (Ho & Khalsa, EPANET-BAM: Water quality modeling with incomplete mixing
in pipe junctions, 2008).
Para demostrar la implicación que puede tener la suposición de mezcla completa, estos
investigadores realizaron simulaciones en una red sencilla en donde cada nodo representa
un vecindario en el que habitan 100 personas. Las condiciones de entrada a la red se
basaban en un caudal constante de agua limpia por una tubería y por la otra un flujo de agua
con un contaminante mortal. La red modelada fue la siguiente:
Figura 4. Red modelada en EPANET-BAM (Ho & Khalsa, EPANET-BAM: Water quality modeling with
incomplete mixing in pipe junctions, 2008).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
11
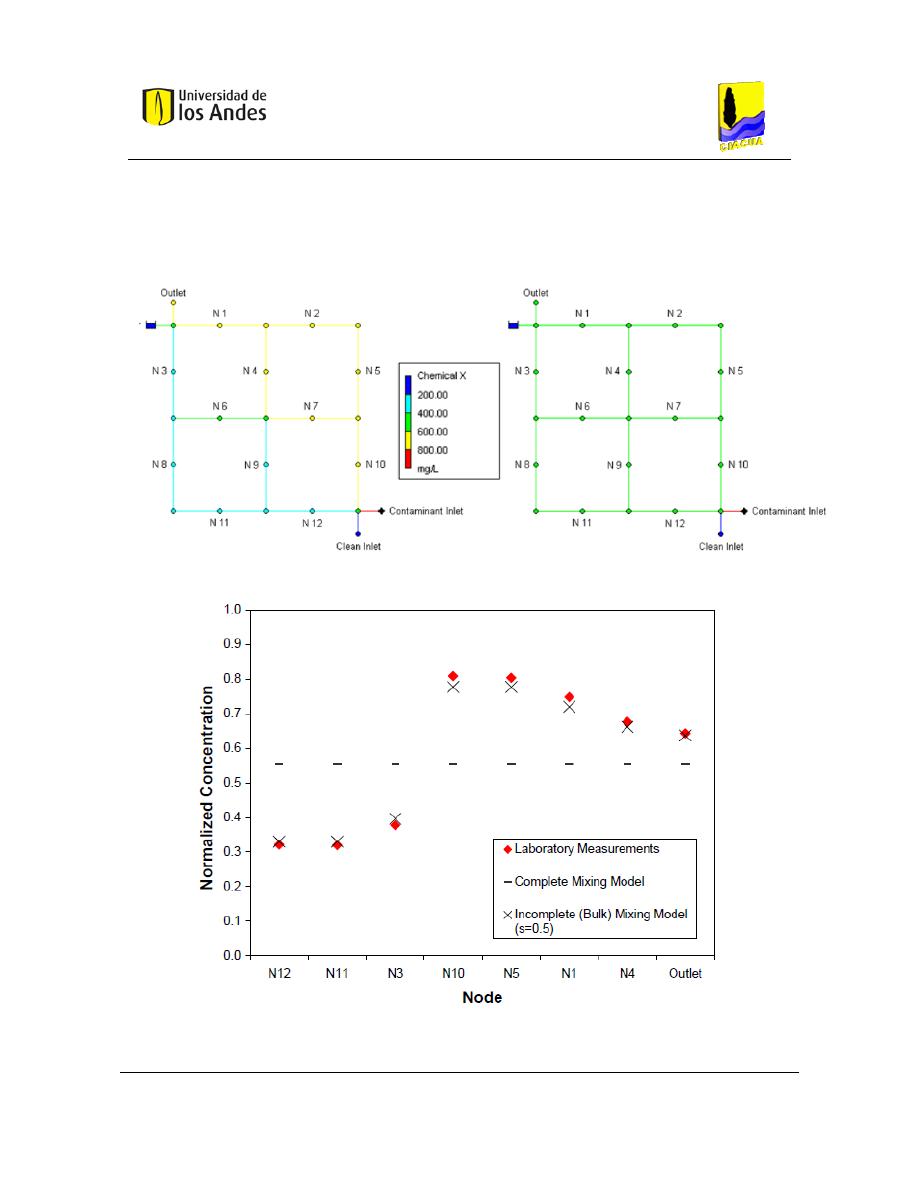
La calidad del agua se modeló en EPANET en donde se supone mezcla completa y en
EPANET-BAM en donde se ingresó un parámetro de mezcla s de 0.5. Los resultados
obtenidos se pueden observar en las siguientes figuras:
Figura 5. Resultados EPANET-BAM (Ho & Khalsa, EPANET-BAM: Water quality modeling with incomplete
mixing in pipe junctions, 2008).
Figura 6. Concentración normalizada en cada nodo de la red (Ho & Khalsa, EPANET-BAM: Water quality
modeling with incomplete mixing in pipe junctions, 2008).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
12
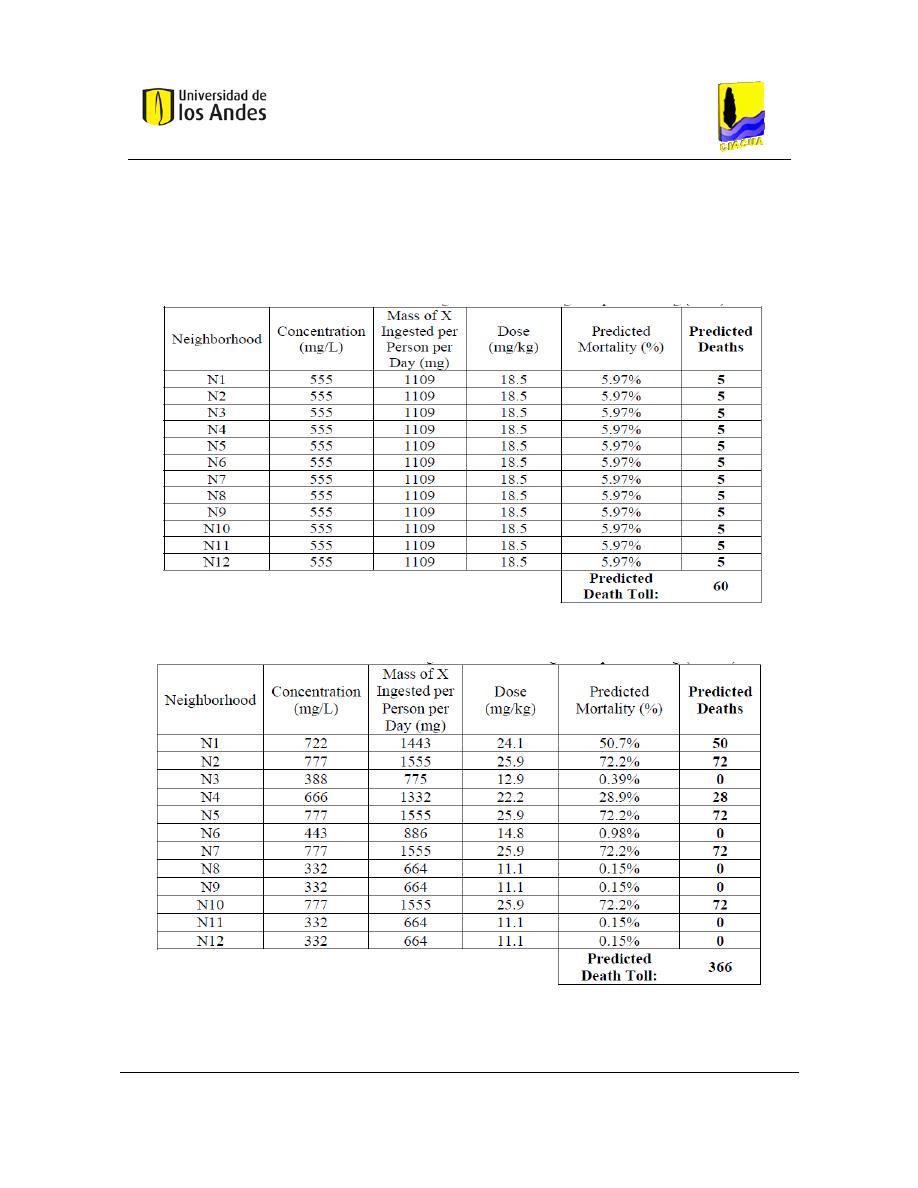
Además de los resultados gráficos, para cada vecindario se obtuvo la concentración que
llegaba al nodo, la masa del contaminante que es ingerida por persona, la dosis, el
porcentaje de predicción de mortalidad y la predicción de las personas muertas en cada
vecindario. Los valores obtenidos para la modelación suponiendo mezcla completa y
mezcla incompleta se muestran a continuación:
Figura 7. Tabla de predicción de muertes en cada vecindario suponiendo mezcla completa (s=1) (Ho & Khalsa,
EPANET-BAM: Water quality modeling with incomplete mixing in pipe junctions, 2008).
Figura 8. Tabla de predicción de muertes en cada vecindario suponiendo mezcla incompleta (s=0.5) (Ho & Khalsa,
EPANET-BAM: Water quality modeling with incomplete mixing in pipe junctions, 2008).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
13
Se puede observar que la suposición de mezcla completa subestima significativamente la
predicción de muertes totales en un 83%. Los resultados presentados muestran que, como la
mezcla es incompleta la masa del contaminante se inclina hacia un lado de la red; por lo
tanto la dosis es mayor y el número de personas que toman el agua contaminada aumenta,
por consiguiente también el número de muertes incrementa. A pesar de ser un ejemplo
hipotético, da una idea de lo importante que es tener en cuenta la mezcla incompleta a la
hora de modelar la calidad del agua.
Sabiendo de qué manera pueden influir los procesos de mezcla en la calidad del agua, se
modelaron otros escenarios en una red similar usando intersecciones en cruz y doble tee.
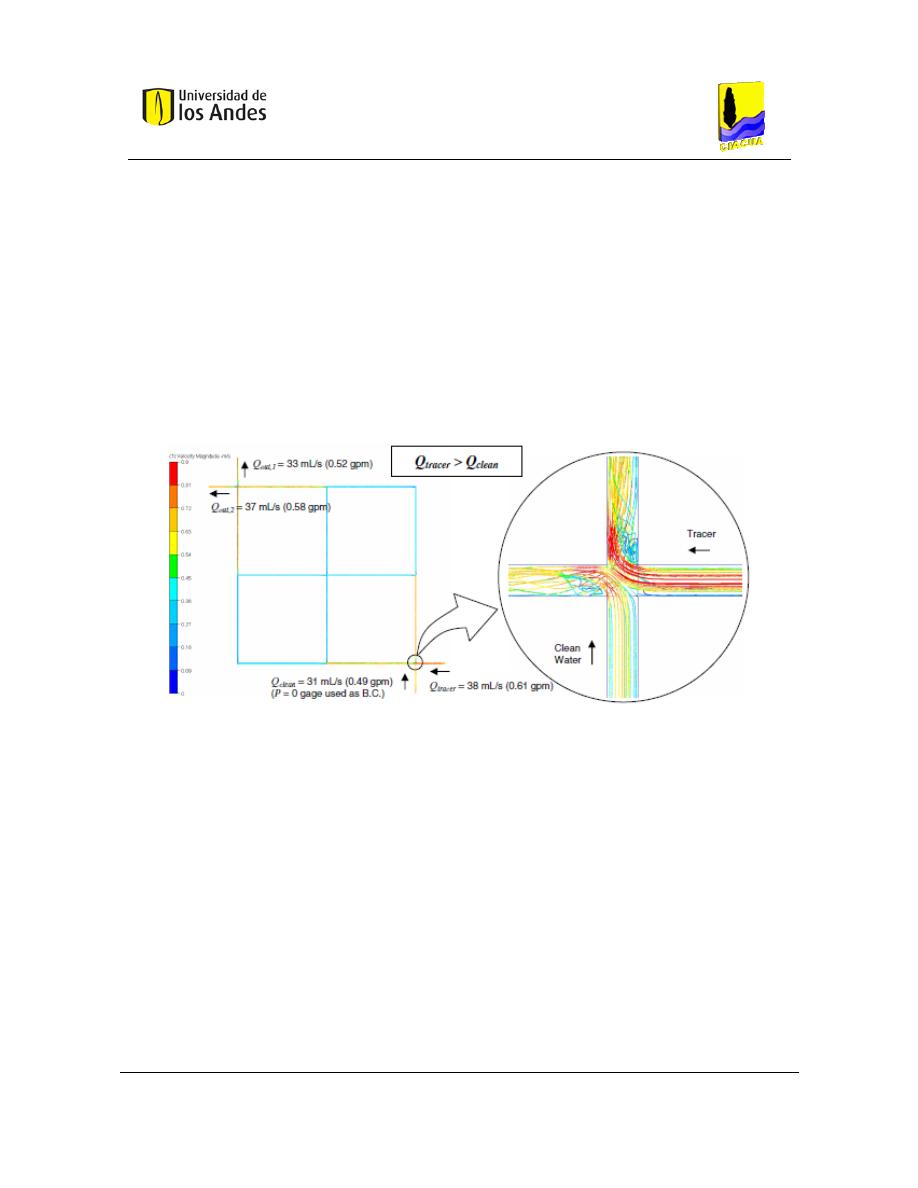
Los resultados se pueden observar a continuación:
Figura 9. Simulación de red 3x3 con unión en cruz con caudal de trazador mayor a caudal de agua limpia (Ho,
Choi, & McKenna, Evaluation of complete and incomplete mixing models in water distribution pipe network
simulations, 2007).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
14
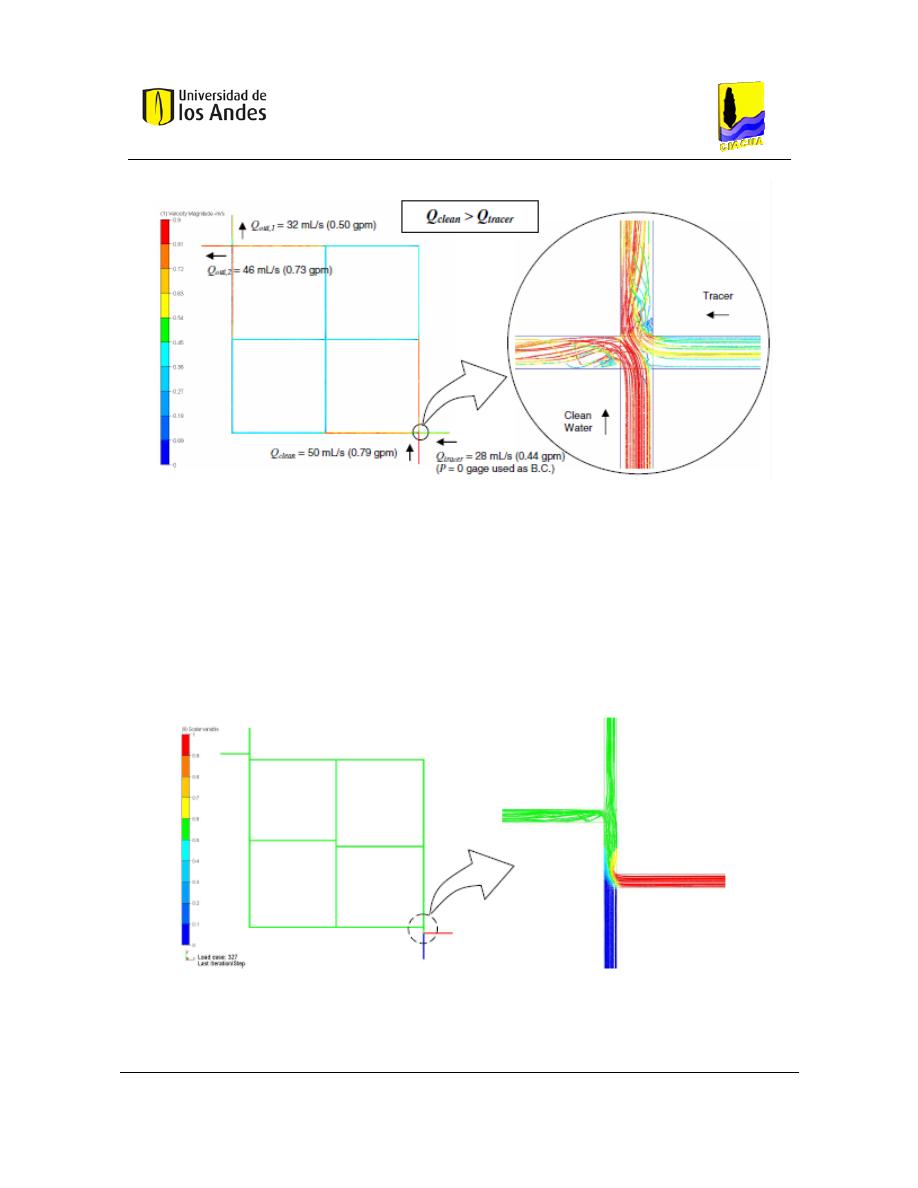
Figura 10. Simulación de red 3x3 con unión en cruz con caudal de agua limpia mayor a caudal con trazador (Ho,
Choi, & McKenna, Evaluation of complete and incomplete mixing models in water distribution pipe network
simulations, 2007).
Este mismo experimento se consideró cambiando las uniones por doble tee. En estudios
previos realizados con uniones doble tee determinaron que la distancia entre las uniones en
tee tenían un efecto significativo en el proceso de mezcla, ya que entre más separado estén,
el tiempo de contacto es mayor y el porcentaje de mezcla aumenta. Aproximadamente con
una longitud cercana a los 10 diámetros, se presenta una mezcla completa (Ho, Choi, &
McKenna, Evaluation of complete and incomplete mixing models in water distribution pipe
network simulations, 2007).
Figura 11. Simulación red 3x3 con unión doble tee con caudal de trazador mayor a caudal de agua limpia (Ho,
Choi, & McKenna, Evaluation of complete and incomplete mixing models in water distribution pipe network
simulations, 2007).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
15
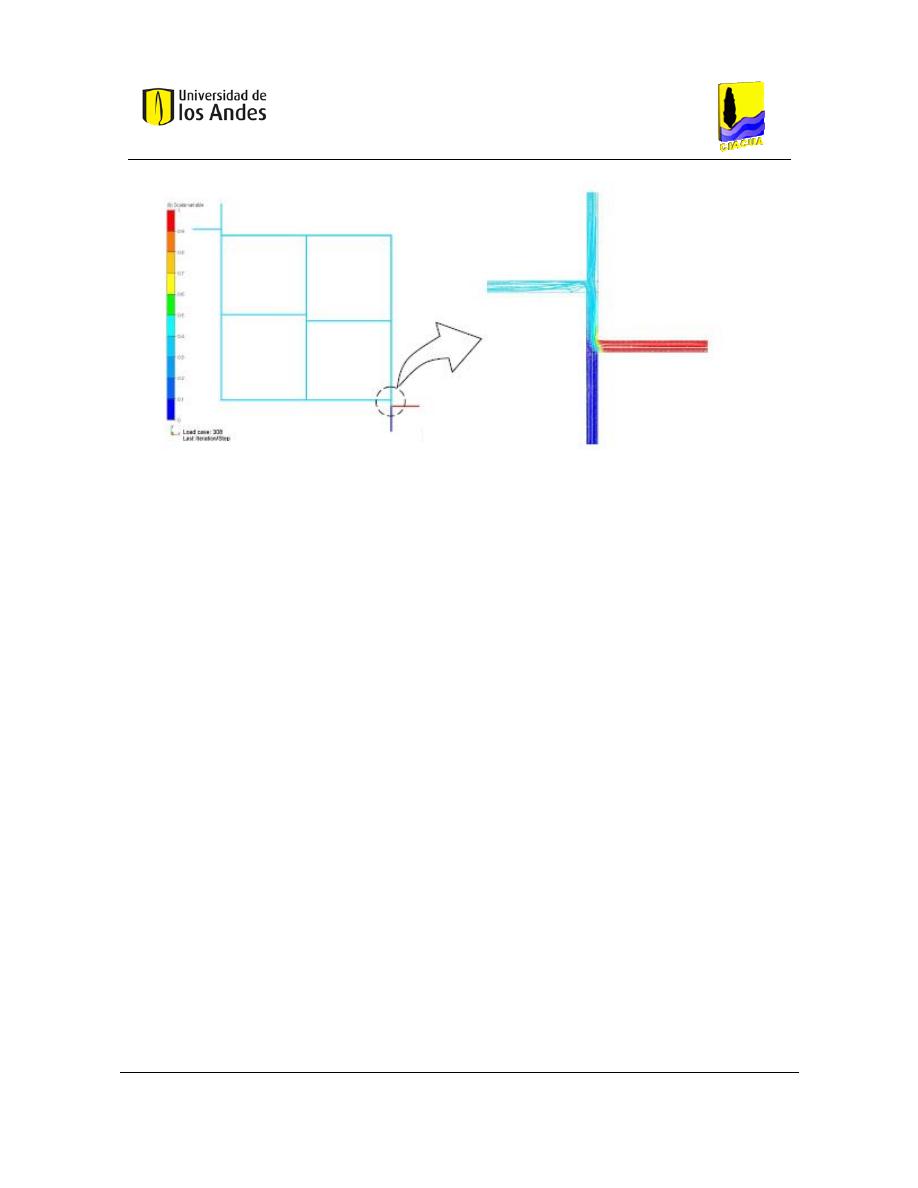
Figura 12. Simulación red 3x3 con unión doble tee con caudal de agua limpia mayor a caudal de trazador (Ho,
Choi, & McKenna, Evaluation of complete and incomplete mixing models in water distribution pipe network
simulations, 2007).
Similar al anterior, se han realizado estudios de transporte de un contaminante en una red
de tuberías. Para la simulación de este tipo de redes en CFD se utiliza un modelo de
turbulencia K-ε, el cual resuelve ecuaciones turbulentas de energía cinética y disipación de
energía al mismo tiempo haciendo uso de las ecuaciones de conservación de masa y
momento de Navier-Stokes (Ho, Orear, Wright, & McKenna, 2007).
Comparación con los experimentos
Se han realizado experimentos en los estudios anteriores para investigar el comportamiento
de mezcla en las articulaciones cruzadas bajo diferentes configuraciones de flujo.
Realizando nuevamente la prueba donde se controló la velocidad de flujo en las entradas y
salidas de las tuberías por medio de válvulas y medidores de flujo. Los tubos de entrada y
de salida se construyeron de PVC, y las longitudes de tubería fueron lo suficientemente
largas para asegurar que el agua se mezcló bien dentro de cada tubo antes de entrar a la
unión y antes de ser supervisado aguas abajo de la confluencia. El agua que entra al sistema
fue bombeada a partir de dos tanques de suministro, un tanque de alimentación de agua con
trazador y un depósito de suministro de agua limpia. En todos los experimentos, el NaCl
fue continuamente mezclado con agua en el tanque de suministro de trazador. El trazador
de NaCl fue monitoreado en las tuberías utilizando sensores de conductividad eléctrica. El
diámetro de la tubería utilizada en la prueba de Romero-Gómez (2006) era 1.905 cm, y los
números de Reynolds oscilaron entre aproximadamente 5.000 a 50.000 en los diferentes
experimentos. El diámetro de la tubería utilizada en la prueba de McKenna (2007) fue de
2.54 cm, y los números de Reynolds variaron entre aproximadamente 500 a 40.000 en los
diferentes experimentos para obtener las relaciones de flujo deseadas (Ho C. K., 2008). A
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
16
partir de estas condiciones y variando el parámetro S, se obtuvieron los siguientes
resultados:
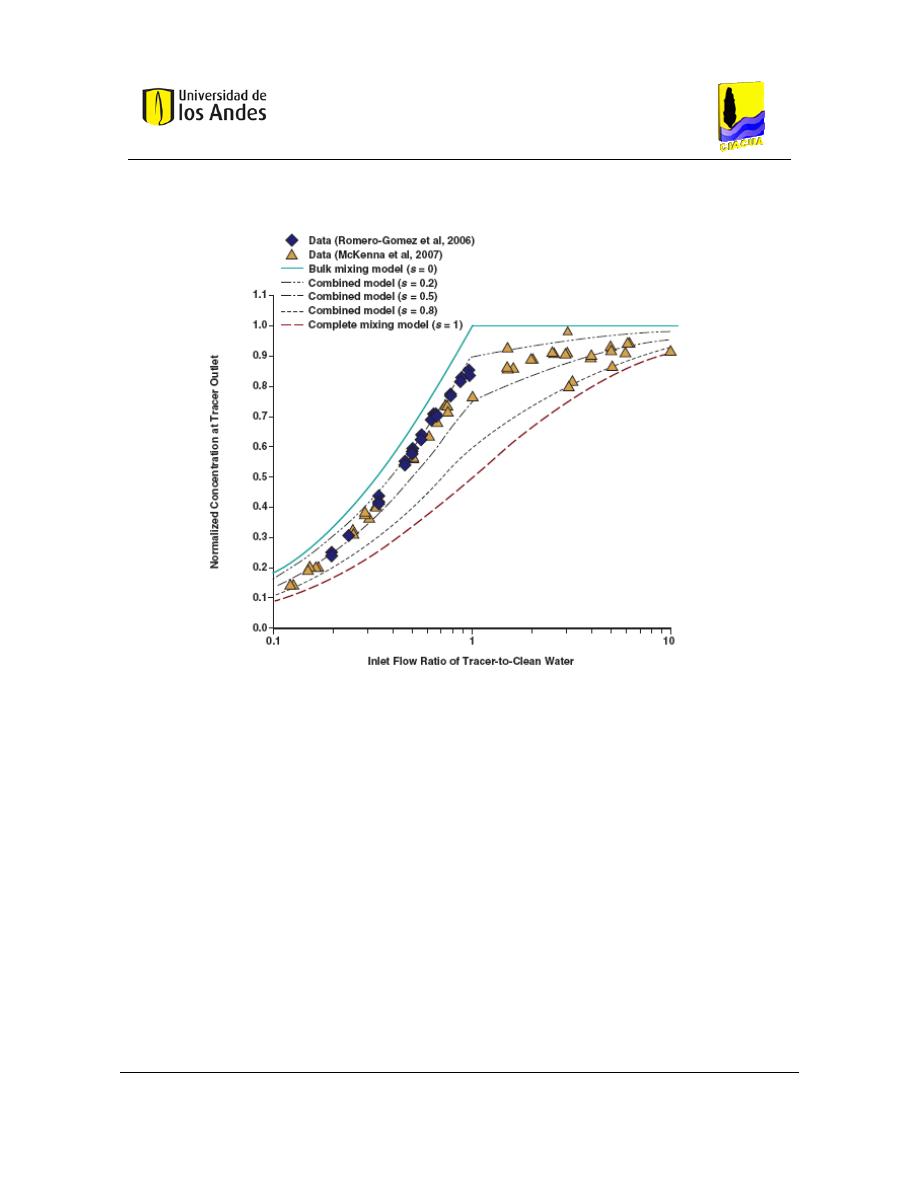
Figura 13. Resultados de simulaciones de los modelos de mezcla (Ho & Leslie, Journal AWWA, 2009).
Se muestra una comparación de la concentración del trazador, medida en la salida de
diferentes experimentos con diferentes combinaciones de velocidades de flujo. Las
concentraciones medidas están limitadas por los modelos de mezcla incompleta y modelos
de mezcla completa, y la mayoría de los datos se dividen entre las concentraciones
predichas utilizando un parámetro de mezcla S entre 0,2 y 0, 5 (Ho & Leslie, Journal
AWWA, 2009).
Se puede ver que cuando el parámetro s es igual a cero, se presenta una mezcla totalmente
incompleta. Y cuando el parámetro s es igual a 1 la mezcla es completa. De esta manera se
ilustran los límites de mezcla descritos anteriormente.
Finalmente se puede decir que la dispersión de los solutos es un componente importante en
la simulación de la calidad del agua de la red, y que debe ser incorporado en la modelación
de las redes de distribución de agua en modelos de calidad. Para esto es importante la
comprensión de cómo se mueven y se mezclan los solutos a través de la red y es
fundamental para el diseño de una red de tuberías y sus uniones.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
17
1.1.
Modelación con trazadores conservativos
Como se mencionará más adelante, los trazadores conservativos son aquellos que no
presentan reacciones en el tramo estudiado. Este es el caso del Cloruro de Sodio (NaCl), el
cual ha sido usado en diferentes modelos para estudiar los procesos de mezcla. Por ejemplo,
Van BloemenWaanders et al. (2005) realizaron modelos de redes en donde se estudió el
transporte de sustancias químicas por flujos a presión en un cruce transversal de tuberías.
En este estudio el Cloruro de Sodio fue introducido como trazador en una de las entradas,
mientras que en la otra entrada se utilizó agua limpia. Se planteó que si la mezcla completa
se llevaba a cabo, cada tubería de salida debería llevar el 50% de la masa de entrada de
NaCl. Sin embargo, experimentalmente se demostró que la mezcla completa no ocurre y
que la tasa de salida fue del 85% y del 15% de la masa total de entrada de NaCl en las
salidas adyacente y opuesta a la tubería de entrada con el trazador, respectivamente. Por lo
tanto, las conclusiones extraídas de los resultados sugirieron que la suposición de la mezcla
perfecta e instantánea puede llevar a imprecisiones significativas (Romero-Gómez, Ho, &
Choi, 2008).
De la misma manera, Romero et al. (2008) realizaron un modelo utilizando NaCl en la red
de distribución de agua de los Laboratorios de la Universidad de Tucson, Arizona, en donde
se determinó una concentración adimensional para explicar de manera detallada los
mecanismos de mezcla que inciden en la interfaz de los flujos. Los resultados obtenidos en
este estudio indican claramente que la mezcla en los cruces transversales de tuberías está
lejos de ser perfecta.
Como se muestra en la Figura 5, las uniones cruzadas son muy comunes en los sistemas de
distribución de agua potable modernos. Es por esto que en todos los casos analizados en
este estudio, la configuración del flujo consistió en dos entradas y dos salidas adyacentes,
como se presenta en la Figura 15.
Figura 14. Configuración típica en redes de distribución de agua potable (Romero-Gómez, Ho, & Choi, 2008).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
18
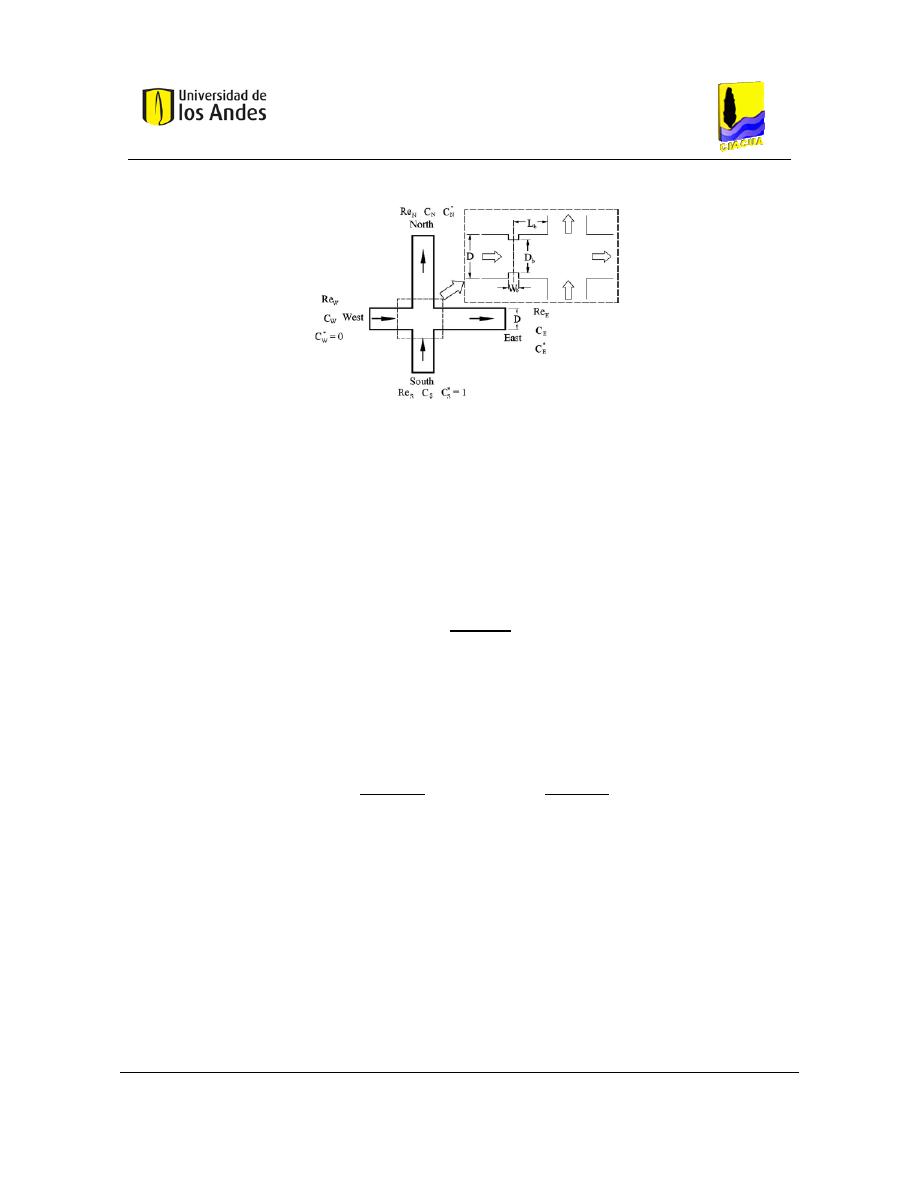
Figura 15. Configuración utilizada en el modelo (Romero-Gómez, Ho, & Choi, 2008).
Los tubos fueron etiquetados de la siguiente manera:
- W (Oeste): tubería de entrada con baja concentración de trazador.
- S (Sur): tubería de entrada con alta concentración de trazador.
- E (Este): tubería de salida opuesta a la tubería W.
- N (Norte): tubería de salida opuesta a la tubería S.
Debido a la variación implícita de la concentración del trazador, se puede expresar la
concentración en términos adimensionales:
𝐶
∗
=
𝐶 − 𝐶
𝑊
𝐶
𝑠
− 𝐶
𝑊
Ecuación 7. Concentración adimensional del trazador (Romero-Gómez, Ho, & Choi, 2008).
Esta ecuación es válida para determinar la concentración adimensional en cualquiera de las
4 tuberías, por ejemplo para las salidas Norte y Este la concentración adimensional del
trazador sería respectivamente:
𝐶
𝑁
∗
=
𝐶
𝑁
− 𝐶
𝑊
𝐶
𝑠
− 𝐶
𝑊
; 𝐶
𝐸
∗
=
𝐶
𝐸
− 𝐶
𝑊
𝐶
𝑠
− 𝐶
𝑊
Como un análisis general, si se genera una mezcla completa en la unión, la concentración
adimensional en la salida sería de 0,5. Sin embargo, bajo la premisa de esta investigación,
las concentraciones adimensionales pueden variar de 0 a 1 debido a la mezcla incompleta.
Adicionalmente, se plantea la hipótesis de que los números de Reynolds tienen una
importancia significativa en los procesos de mezcla. Es por esto que se deben tener en
cuenta en la modelación de la calidad del agua. Para describir las configuraciones del
número de Reynolds en las uniones cruzadas, su tuvieron en cuenta las siguientes
relaciones (Romero-Gómez, Ho, & Choi, 2008):

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
19
𝑅𝑒
𝑆/𝑊
=
𝑅𝑒
𝑆
𝑅𝑒
𝑊
𝑅𝑒
𝐸/𝑁
=
𝑅𝑒
𝐸
𝑅𝑒
𝑁
Ecuación 8. Relación de número de Reynolds para las tuberías (Romero-Gómez, Ho, & Choi, 2008).
De esta manera, se estudiaron tres escenarios simplificados:
- Escenario 1: caudales de entrada y salida iguales. (𝑅𝑒
𝑆
= 𝑅𝑒
𝑊
= 𝑅𝑒
𝑁
= 𝑅𝑒
𝐸
).
- Escenario 2: caudales de entrada diferente, caudal de salida iguales.
(
𝑅𝑒
𝑆
≠ 𝑅𝑒
𝑊
, 𝑅𝑒
𝑁
= 𝑅𝑒
𝐸
).
- Escenario 3: caudales de entrada igual, caudales de salida diferentes.
(𝑅𝑒
𝑆
= 𝑅𝑒
𝑊
, 𝑅𝑒
𝑁
≠ 𝑅𝑒
𝐸
).
En este estudio, el número de Reynolds (Re) se considera como el parámetro adimensional
primario. Sin embargo, el número de Reynolds no siempre es un indicador constante del
proceso de mezcla. Por ejemplo, con diámetros más grandes, la velocidad de flujo será
significativamente menor que las velocidades utilizadas en los experimentos para el mismo
número de Reynolds. Una velocidad menor y un diámetro mayor de la tubería podría
aumentar el tiempo de contacto, el área de contacto, y potencialmente la cantidad de la
mezcla en comparación con la mezcla presentada en tubos más pequeños con velocidades
más altas en el mismo número de Reynolds (Austin, Van Bloemen Waanders, McKenna, &
Choi, 2008).
Un aspecto que hay que tener en cuenta es que la relación entre la rugosidad de la pared y
el diámetro de la tubería contribuye a un aumento de la intensidad de la turbulencia,
especialmente para tubos largos. Adicionalmente, los accesorio también afectan la
turbulencia ya que crean cambios en la geometría, en la velocidad y/o dirección del flujo;
esto genera cambios en la intensidad de la turbulencia y la proporción de mezcla del
trazador (Romero-Gómez, Ho, & Choi, 2008).
En las Figuras 16a y 16b se pueden observar los vectores de velocidad y los contornos de
concentración adimensional de NaCl (C*), respectivamente, cuando el número de Reynolds
en las cuatro tuberías es de 44000. Para el escenario 1, los gradientes más grandes ocurren
cuando los dos flujos entrantes se fusiona a lo largo de la línea AB en la Figura 7b, donde
se produce la mezcla real de las dos fuentes de agua. Se puede observar que en la interfaz
incidente los chorros se reflejan y los vectores de velocidad son casi simétricos con
respecto a la línea AB (Romero-Gómez, Ho, & Choi, 2008).
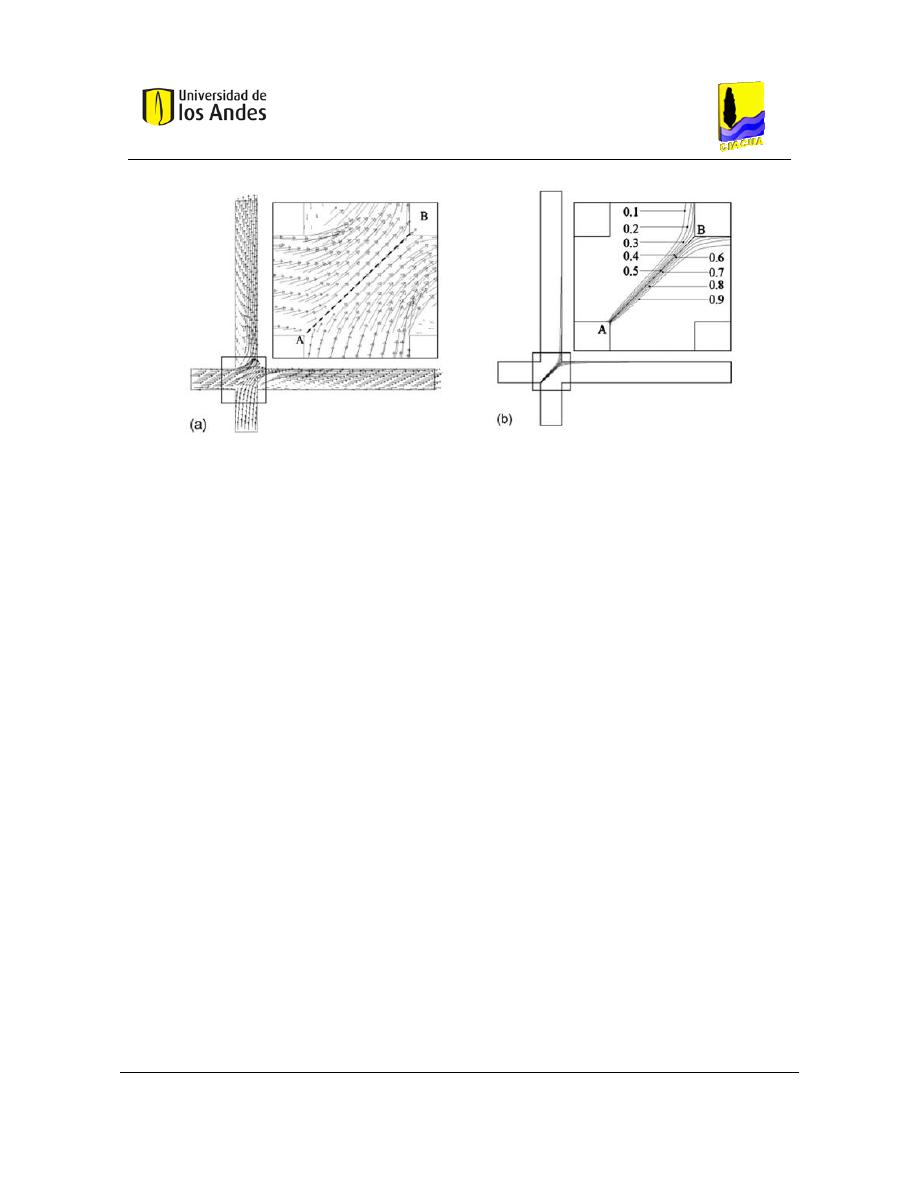
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
20
Figura 16. Interfaz incidente en la intersección de tuberías (Romero-Gómez, Ho, & Choi, 2008).
En la Figura 17 se puede ver la relación existente entre el número de Reynolds y la
concentración adimensional de la tubería Este. Estos resultados fueron obtenidos por las
simulaciones realizadas en CFD.
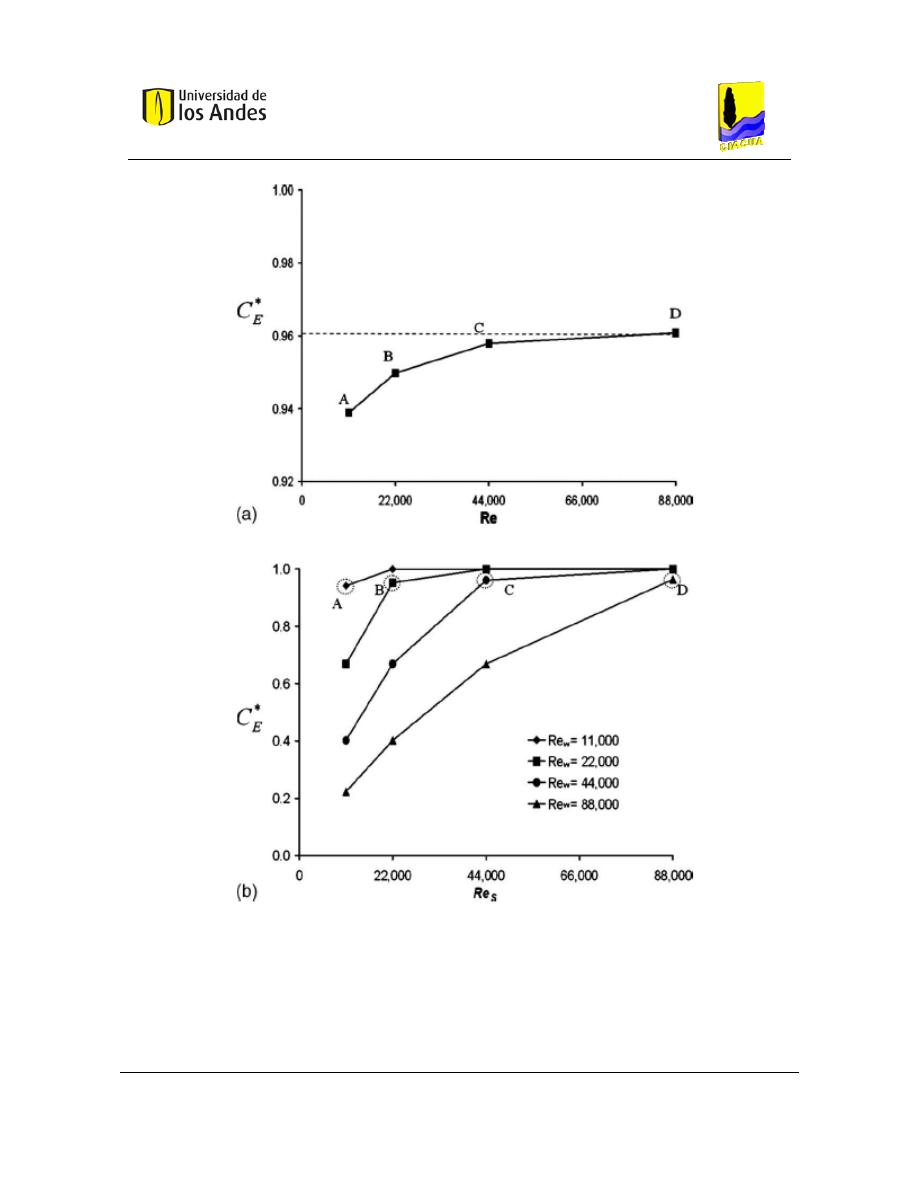
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
21
Figura 17. Relación entre la concentración adimensional de la tubería Este con el número de Reynolds (Romero-
Gómez, Ho, & Choi, 2008).
Se pudo determinar que el tiempo de interacción entre los dos flujos es más alto para
números de Reynolds mayores. Junto con las observaciones de la Figura 16, se muestra
claramente que el tiempo de interacción y el espacio de interacción, tienen un efecto
significativo en los procesos de mezcla en la unión. Por otro lado, en la Figura 17b se
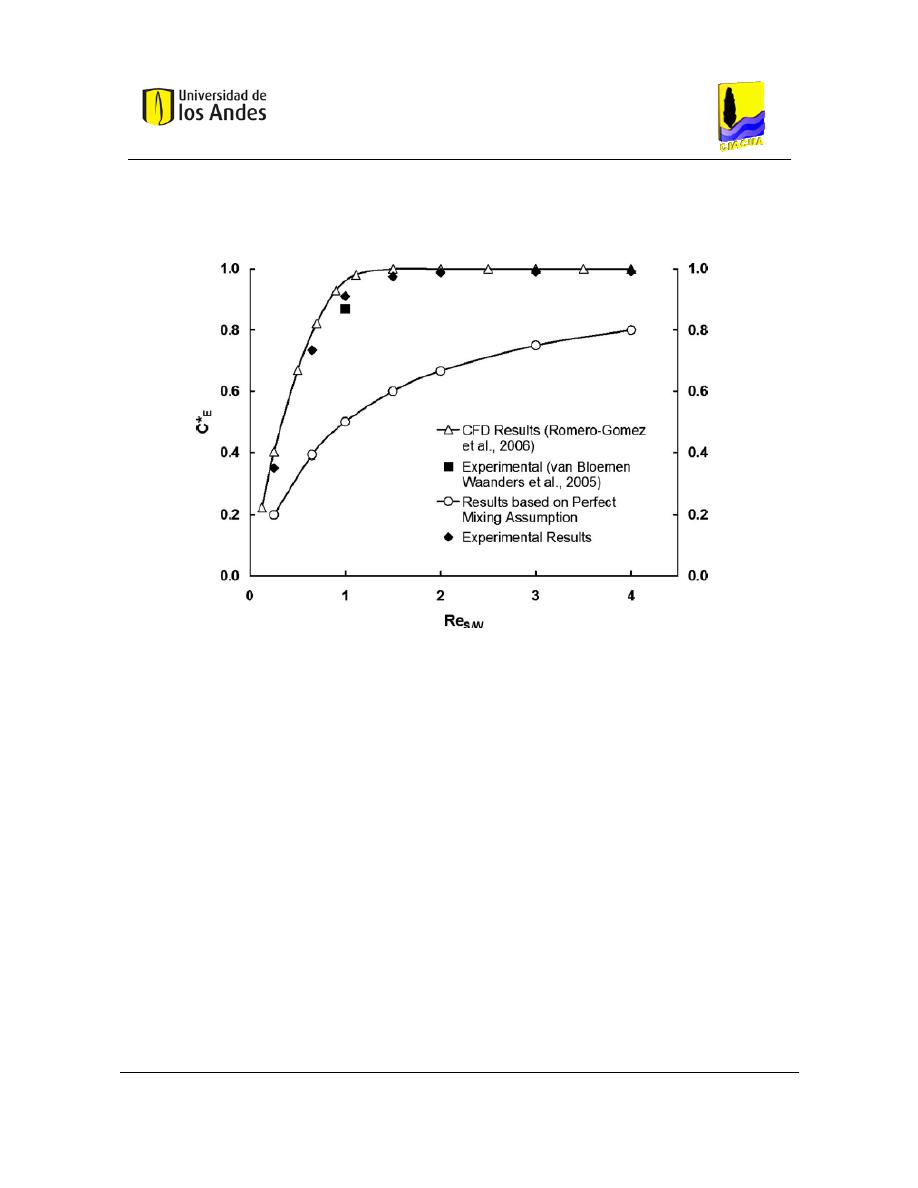
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
22
muestra la relación de la concentración adimensional de la tubería Este con respecto al
número de Reynolds de la tubería de entrada Sur (Romero-Gómez, Ho, & Choi, 2008).
Los resultados obtenidos para el escenario 2 se pueden ver en la Figura 18.
Figura 18. Resultados obtenidos para el escenario 2 (Austin, Van Bloemen Waanders, McKenna, & Choi, 2008)-
Cuando
𝑅𝑒
𝑆/𝑊
→ ∞, la concentración adimensional de la tubería Este tiende a 1. Esto quiere
decir que cuanto el número Reynolds de la tubería Sur es mucho mayor al de la tubería
Oeste, la concentración adimensional en la tubería Este tiende a 1. Cuando
𝑅𝑒
𝑆/𝑊
→ 0 la
concentración adimensional de la tubería Este tiende a 0 (Austin, Van Bloemen Waanders,
McKenna, & Choi, 2008). Se puede observar que los resultados obtenidos
experimentalmente por Romero-Gómez et al (2006) con CFD y los resultados
experimentales realizados por van Bloemen Waanders et al. (2005) son muy similares. Así
mismo, los resultados obtenidos suponiendo mezcla completa, siguen una tendencia
parecida a los demás valores, pero la diferencia de concentración adimensional es
significativa.
Por otro lado, los resultados obtenidos para el escenario 3 se muestran en la Figura 19.
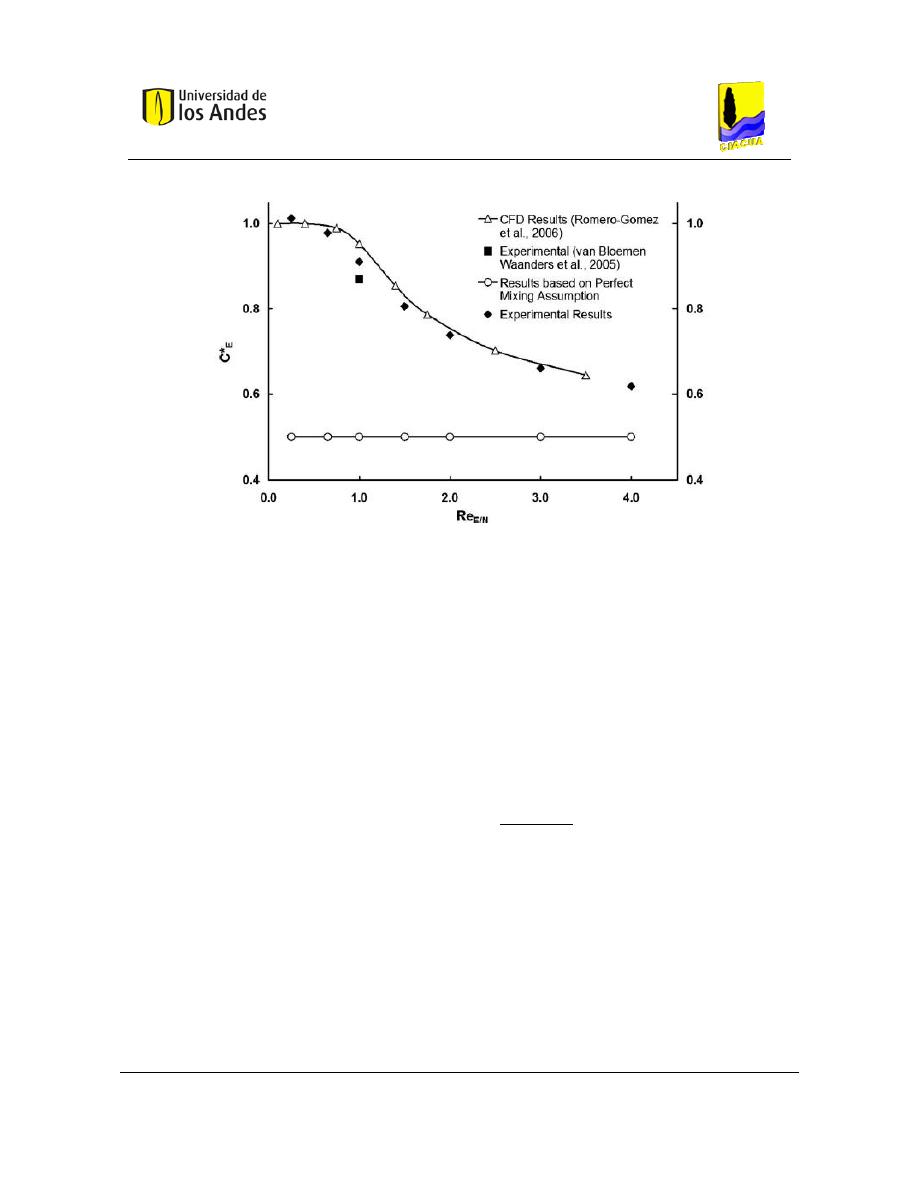
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
23
Figura 19. Resultados obtenidos para el escenario 3 (Austin, Van Bloemen Waanders, McKenna, & Choi, 2008).
En este escenario el número de Reynolds en las tuberías de entrada era el mismo, y en las
tuberías de salida era variable. En este caso se puede notar la diferencia en el
comportamiento de los procesos de mezcla. Por un lado, suponiendo mezcla completa en la
unión, la concentración adimensional de la tubería Este sería constante e igual a 0,5 para
todas las relaciones de
𝑅𝑒
𝐸/𝑁
. Sin embargo, los resultados experimentales y de CFD
muestran un comportamiento totalmente distinto, cuando
𝑅𝑒
𝐸/𝑁
→ 0 la concentración
adimensional de la tubería Este tiende a 1, lo que quiere decir que toda la masa del trazador
se encuentra en esta tubería.
La mezcla también puede ser medida en términos de la separación de masa de NaCl de
entrada entre las dos tuberías de salida:
%𝑁𝑎𝐶𝑙
𝐸 ó 𝑁
= 100 ∗
𝑚̇
𝐸 ó 𝑁
𝑚̇
𝑆
+ 𝑚̇
𝑊
Ecuación 9. Porcentaje de separación de NaCl (Romero-Gómez, Choi, van Bloemen Waanders, & McKenna,
2006).
La mezcla perfecta en la unión en una concentración adimensional seria de 0.5 o 50% NaCl
en las dos tuberías de salida. Esta simplificación puede ser alterada dependiendo de la
geometría de la intersección y de la velocidad del flujo (Romero-Gómez, Choi, van
Bloemen Waanders, & McKenna, 2006).
Simulando los tres escenarios mencionados anteriormente se obtuvieron los siguientes
resultados para cada uno.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
24
Escenario 1: Para el caso en donde las entradas y salidas tienen un número de Reynolds
igual, se encontró que la división porcentual promedio de la masa de NaCl fue de 84.6% y
16.5% para las tuberías Este y Norte, respectivamente. Este resultado está de acuerdo con
lo presentado por van Bloemen Waanders et al. (2005). Los resultados de la modelación en
CFD se pueden observar en la Figura 24.
Escenario 2: Para el caso en donde los números de Reynolds en las tuberías de salida son
iguales y en las tuberías de entrada son diferentes, la relación de concentración y el
porcentaje de división de masa son muy diferentes. Tal como se presenta en la Figura 20, el
porcentaje de división de la masa alcanza un máximo nivel cuando la relación del número
de Reynolds es de 0.7. Cuando
Re
S W
⁄
→ ∞ se puede observar que la concentración
normalizada en la tubería Este tiende a 1. Esto es lógico ya que lo que está ocurriendo, es
que el caudal con trazador es mucho mayor al caudal de agua limpia, por lo tanto, en la
unión no existe mezcla y la concentración de las dos tuberías de salida es casi igual a la
tubería Sur, la cual tiene una concentración normalizada de 1. Estos resultados se pueden
observar en las Figuras 20 y 21.
Escenario 3: Para el caso en donde el número de Reynolds en las tuberías de entrada son
iguales y en las tuberías de salida son diferentes, cuando
𝑅𝑒
𝐸 𝑁
⁄
→ 0 se puede observar que
la tasa de masa de NaCl tiende a 100. Esto es consistente con que, cuando se presenta esta
condición de flujo, el caudal que sale por la tubería Este es mucho mayor que el de la
tubería Norte; por lo tanto, casi toda la masa proveniente de la tubería Sur se desvía hacia la
tubería Este. De la misma manera, para esta condición, la concentración normalizada en la
tubería Este tiende a 0.5 ya que el agua, al solo tener una salida, se mezcla alcanzado lo que
sería una mezcla completa. Por otro lado, cuando
𝑅𝑒
𝐸 𝑁
⁄
→ ∞ el caudal por la tubería
Este es prácticamente nulo, por lo cual casi toda la masa de NaCl se dirige hacia la tubería
Norte; es por esto que el valor de la división de masa de NaCl en la tubería Este tiende a
cero. Estos resultados se pueden apreciar en las Figuras 22 y 23.
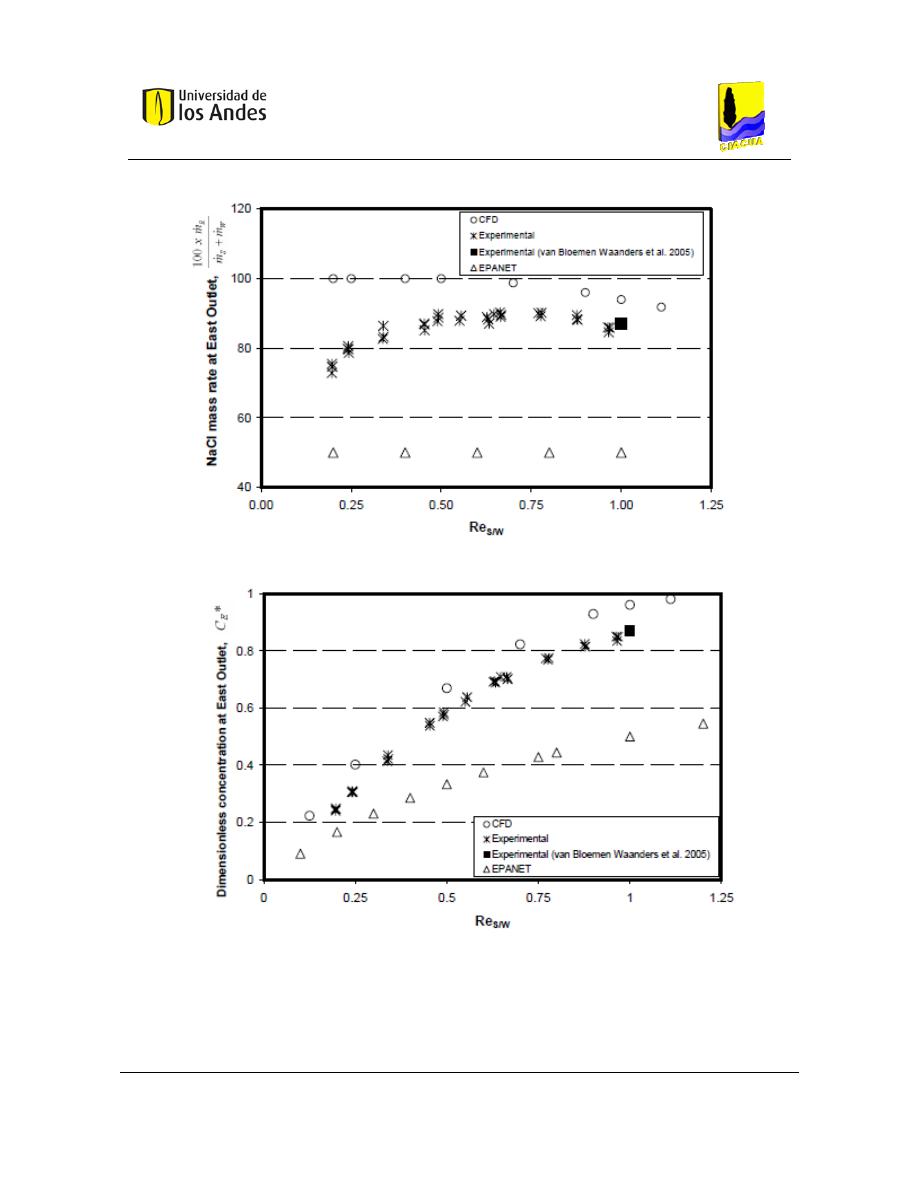
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
25
Figura 20. Tasa de masa de NaCl en la tubería Este para el escenario 2 (Romero-Gómez, Choi, van Bloemen
Waanders, & McKenna, 2006)
Figura 21. Concentración normalizada en la tubería Este para el escenario 2 (Romero-Gómez, Choi, van Bloemen
Waanders, & McKenna, 2006)
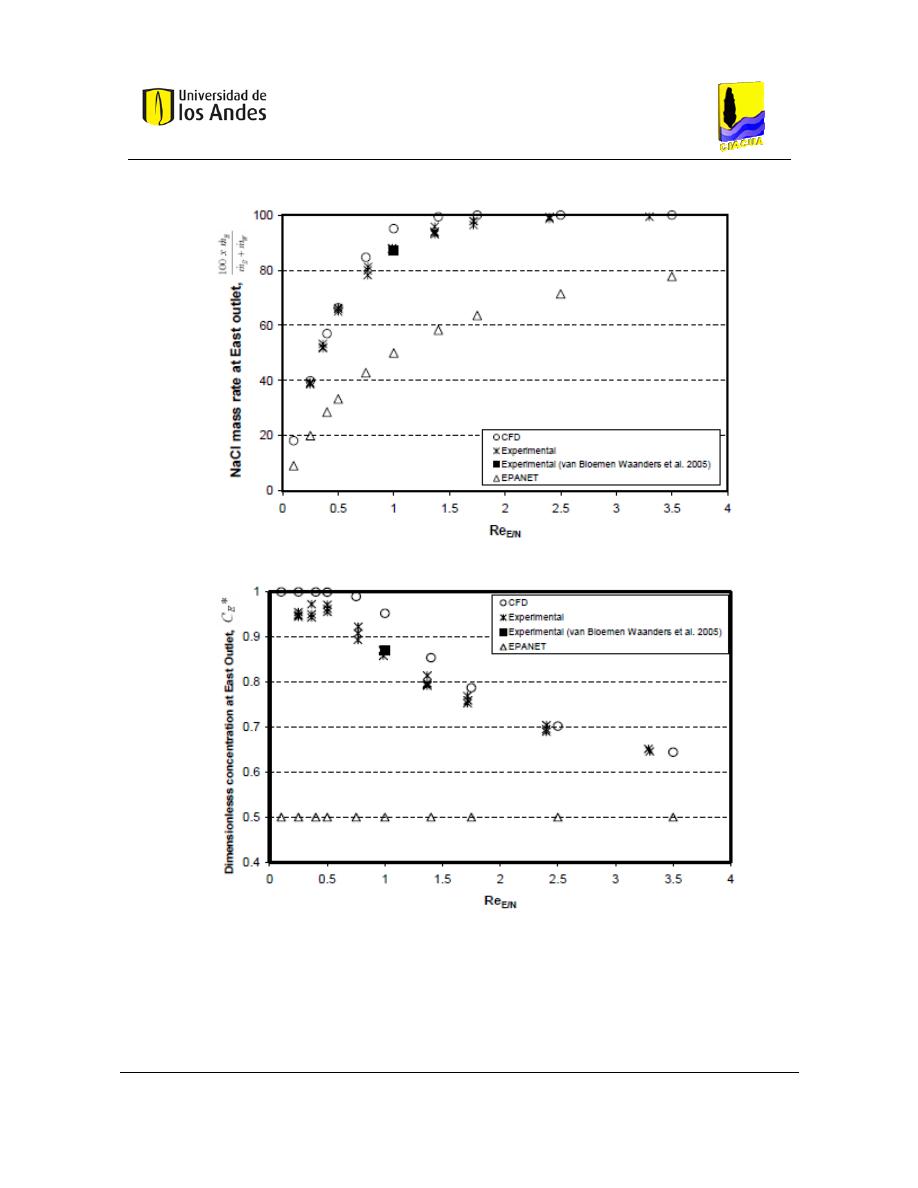
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
26
Figura 22. Tasa de masa de NaCl en la tubería Este para el escenario 3 (Romero-Gómez, Choi, van Bloemen
Waanders, & McKenna, 2006).
Figura 23. Concentración normalizada en la tubería Este para el escenario 3 (Romero-Gómez, Choi, van Bloemen
Waanders, & McKenna, 2006).
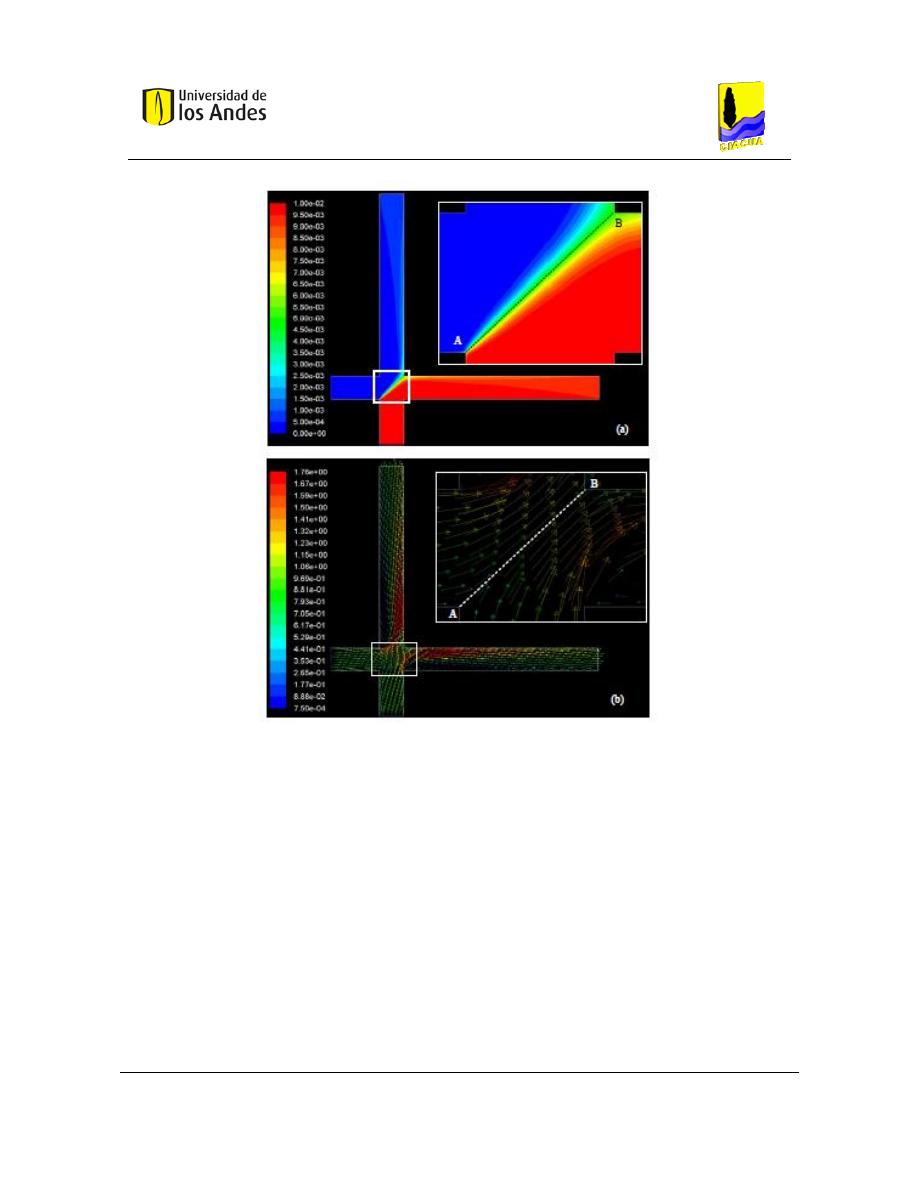
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
27
Figura 24. (a) Concentración de NaCl (b) Vectores de velocidad en la unión, cuando el número de Reynolds es igual
en las tuberías de entrada y salida (Romero-Gómez, Choi, van Bloemen Waanders, & McKenna, 2006).
En la mayoría de los estudios que se han realizado se simulan escenarios en donde el
régimen de flujo es turbulento debido a que este es el régimen que gobierna los sistemas de
distribución de agua potable. Sin embargo, el flujo laminar se puede presentar en zonas
residenciales durante los momentos de baja utilización (Buchburger y Wu, 1995), por lo
tanto estas áreas podrían tener un impacto significativo en la calidad del agua suministrada
al usuario final. Debido a esto, se realizó un estudio que se centra en los patrones de mezcla
en los regímenes de flujo laminar y transitorio (Austin, Romero-Gomez, & Choi, Transport
Phenomena at intersections at Low Reynolds Number, 2007).
Para dicho estudio se utilizó como trazador NaCl y la misma configuración presentada en la Figura
15. Sin embargo, en la Figura 25 se muestra el esquema completo del montaje experimental usado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
28
Figura 25. Esquema completo del modelo experimental usado en Arizona (Austin, Romero-Gomez, & Choi,
Transport Phenomena at intersections at Low Reynolds Number, 2007).
Adicionalmente, para el análisis de los procesos de mezcla se utilizó la Ecuación 7 de
concentración normalizada, la relación de los números de Reynolds de las tuberías sur y
Oeste y el número de Reynolds total en el sistema:
𝑅𝑒
𝑡𝑜𝑡𝑎𝑙
=
𝑅𝑒
𝑆
+ 𝑅𝑒
𝑊
+ 𝑅𝑒
𝑁
+ 𝑅𝑒
𝐸
2
Ecuación 10. Número de Reynolds total en el sistema (Austin, Romero-Gomez, & Choi, Transport Phenomena at
intersections at Low Reynolds Number, 2007).
Se probaron dos escenarios:
- Escenario 1: los flujos de todas las tuberías son iguales. El número de Reynolds
usado fue entre 700 y 26000; estas limitaciones se deben a las restricciones físicas
de la ejecución experimental.
- Escenario 2: los flujos de las tuberías de salida son iguales mientras que los flujos
de las tuberías de entrada son diferentes
Algunos de los resultados obtenidos fueron los siguientes:
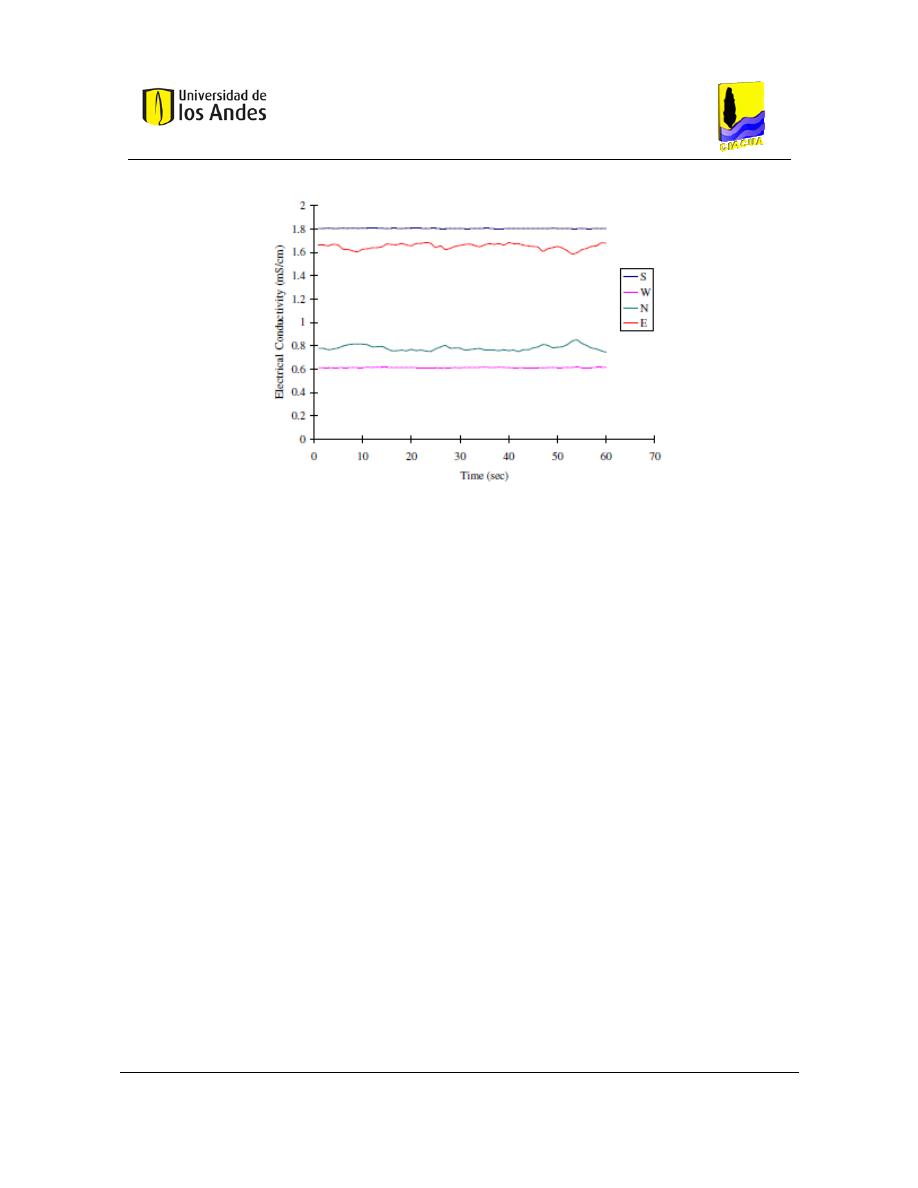
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
29
Figura 26. Valores de conductividad cuando Retotal=4200 (Austin, Romero-Gomez, & Choi, Transport
Phenomena at intersections at Low Reynolds Number, 2007).
Escenario 1: A partir de los datos obtenidos, el número de Reynolds tiene un efecto
significativo sobre la cantidad de mezcla que se produce en la unión transversal. Se puede
apreciar que en el régimen de flujo laminar,
C
E
∗
disminuye mientras ocurre la transición
entre flujo laminar y turbulento. Es lógico que en el régimen de flujo laminar se presente
una menor cantidad de mezcla debido a que el flujo se mueve en capas y no existen
remolinos turbulentos que generan un mayor porcentaje de mezcla. Cuando aumentan los
caudales y el flujo se vuelve turbulento,
C
E
∗
se eleva de forma asintótica (ver Figura 27). La
hipótesis que plantean los autores es que hay dos factores que compiten para equilibrar la
proporción de mezcla: la velocidad de flujo y el tiempo de contacto entre los flujos
incidentes. A medida que aumenta la velocidad de flujo, el porcentaje de mezcla también
aumenta. Sin embargo, el tiempo de contacto es menor, por lo que la mezcla se reduce.
También se sugiere que estos dos factores se pueden anular entre sí, dando lugar a una
estabilización de la concentración en la salida.
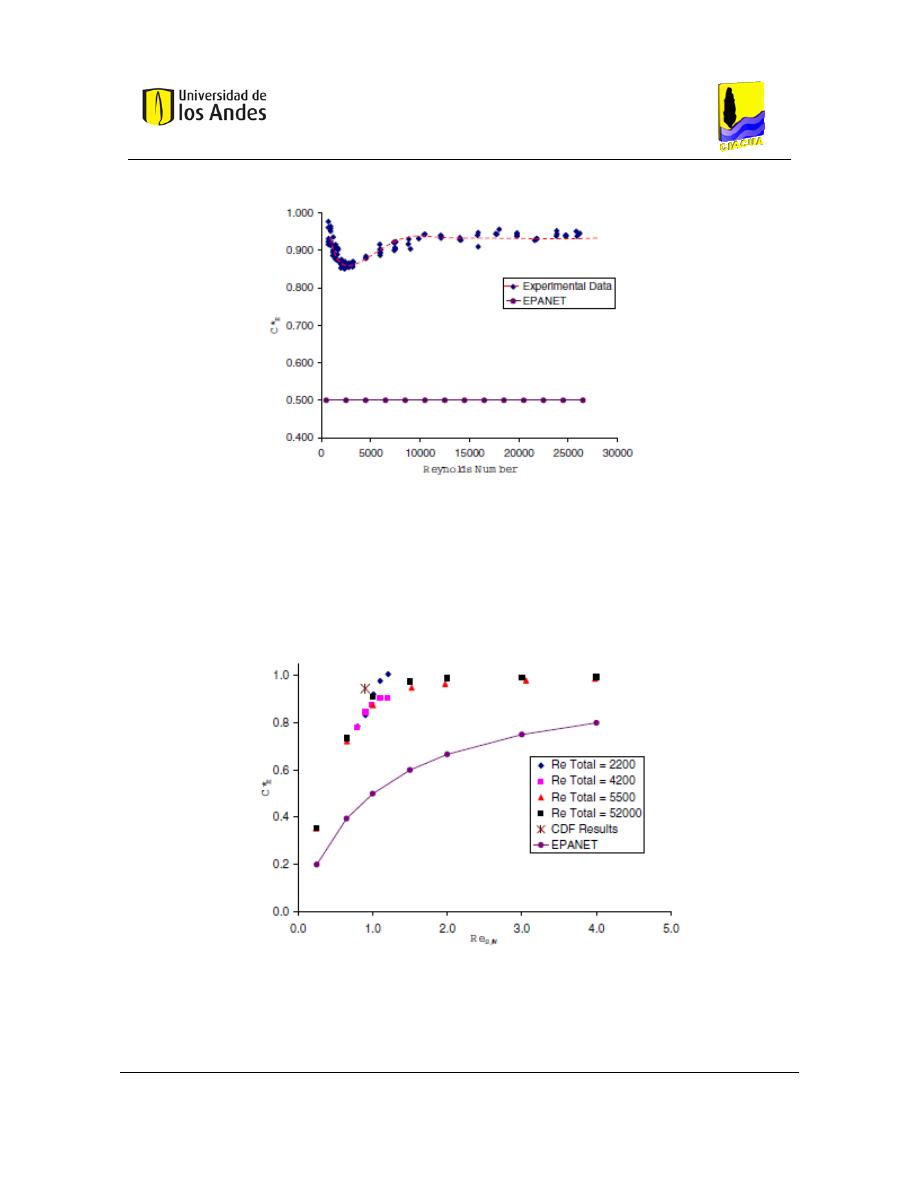
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
30
Figura 27. Número de Reynolds promedio en las tuberías vs. Concentración normalizada en la tubería Este
(Austin, Romero-Gomez, & Choi, Transport Phenomena at intersections at Low Reynolds Number, 2007).
Escenario 2: Los resultados del Escenario 2 se muestran en la Figura 28. La tendencia
parece similar a la observada en el régimen de flujo turbulento; es decir, la concentración
adimensional de la salida Este se incrementa cuando el flujo desde la salida Sur se
incrementa. También está claro que los resultados obtenidos experimentalmente
demuestran que la mezcla está lejos de la suposición de mezcla completa.
Figura 28. Relación del número de Reynolds S/W y la concentración normalizada en la tubería Este para el
escenario 2 (Austin, Romero-Gomez, & Choi, Transport Phenomena at intersections at Low Reynolds Number,
2007).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
31
Por otro lado, es importante mencionar que los estudios que se han realizado no solo han
involucrado configuraciones en cruz, si no también uniones doble tee, en donde se ha
corroborado que los modelos de mezcla dependen de las condiciones de flujo, las
condiciones de la tubería y la geometría de la intersección. En estas situaciones, el
porcentaje de mezcla puede ser mayor o menor dependiendo del impulso relativo del flujo
con respecto a las demás tuberías. Por ejemplo, si existe una intersección donde una tubería
de entrada tenga un diámetro más grande que la otra tubería de entrada, suponiendo que el
trazador se inyecta en la tubería más pequeña, el porcentaje de mezcla puede variar
dependiendo del impulso predominante. Si el impulso es predominante en la tubería grande,
el porcentaje de mezcla disminuye. En cambio, si el impulso es predominante en la tubería
pequeña el porcentaje de mezcla es mayor. Estudios experimentales y numéricos han
demostrado que ampliaciones o cambios en la geometría interna pueden causar
desviaciones en la predicción del modelo (Braun, Bernard, Ung, Piller, & Gilbert, 2013).
Un ejemplo de lo anterior, en cuanto a la influencia de la geometría interna de la
intersección, se puede encontrar en un estudio realizado por Braun et al. (2013). Allí se
puede ver que en el escenario donde las tasas de flujo de las tuberías de entrada son
diferentes y los flujos en las tuberías de salida son iguales, los resultados experimentales y
computacionales muestran resultados significativamente diferentes.
De acuerdo con los datos de McKenna et al. (2007) para este mismo escenario, el proceso
de mezcla comienza a ser más completa a medida que la relación de flujo entre la tubería
con trazador y con agua limpia, se reduce. Romero-Gómez et al. (2006) realizaron
simulaciones numéricas para este escenario utilizando el modelo de turbulencia de
Reynolds-Averaged Navier-Stokes (RANS) para predecir la mezcla en la unión de las
tuberías. En general los resultados en CFD estuvieron de acuerdo con los datos
experimentales a excepción del escenario donde los flujos de entrada son diferentes. Los
resultados numéricos muestran que la mezcla se reduce a medida que la tasa de flujo
trazador-/limpia también se reduce.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
32
Figura 29. Modelo implementado en Fluent (Braun, Bernard, Ung, Piller, & Gilbert, 2013).
Figura 30. Enmallado de la geometría (Braun, Bernard, Ung, Piller, & Gilbert, 2013).
Figura 31. Contornos de concentración (Braun, Bernard, Ung, Piller, & Gilbert, 2013).
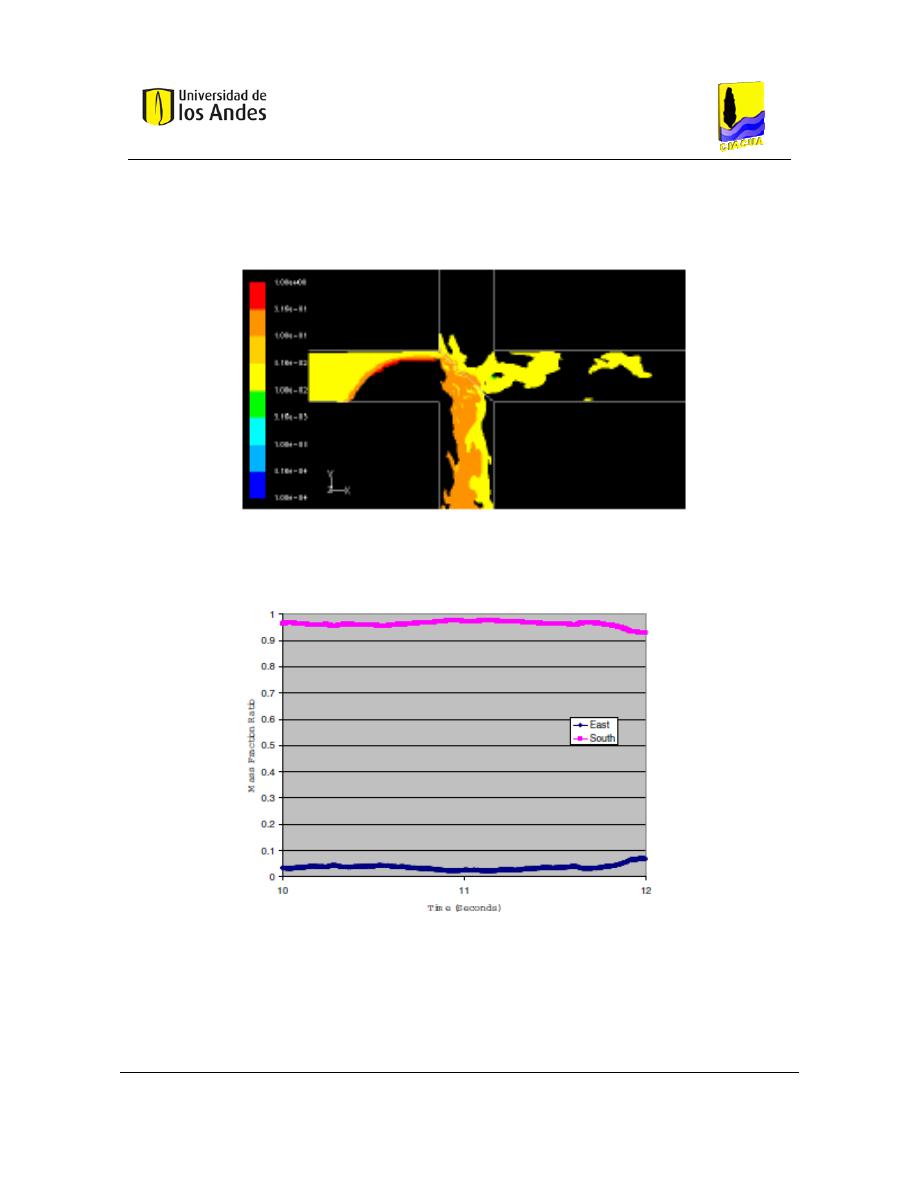
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
33
La Figura 31 (a) muestra los resultados en una escala lineal y la Figura 31(b) en una escala
logarítmica. Se puede ver el flujo de agua que tiene trazador realiza un “salto” a través de la
intersección desde la tuberías Oeste a la Este. Los isocontornos se muestran a continuación:
Figura 32. Isocontornos de la concentración (Braun, Bernard, Ung, Piller, & Gilbert, 2013).
Para una mezcla completa, la fracción de masa en las dos tuberías de salida debería ser
50%. Los resultados obtenidos en este estudio fueron de 96% por la tubería Sur y 4% en las
tuberías Este.
Figura 33. Fracción de masa de NaCl en función del tiempo (Braun, Bernard, Ung, Piller, & Gilbert, 2013).
En contraste, los resultados de McKena et al. (2007) indican que aproximadamente el 58%
de la masa del trazador se encuentra en la tubería Sur, mientras que 42% de la masa se
encuentra en la tubería Este.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
34
El estudio determinó que estas significativas diferencias se deben a la geometría interna de
las intersecciones. Por este motivo, se realizaron simulaciones con las siguientes
modificaciones:
Figura 34. Geometría interna de las uniones en cruz (Braun, Bernard, Ung, Piller, & Gilbert, 2013).
Figura 35. Contornos de concentración después de corrección (Braun, Bernard, Ung, Piller, & Gilbert, 2013).
Con estas modificaciones se encontró que la masa del trazador por tubería Sur era del 64%
y por la tubería Este fue del 34%. Estos valores se encuentran más cercanos a los
reportados por los demás estudios realizados en este tema.
Figura 36. Fracción de masa de NaCl en función del tiempo después de corrección (Braun, Bernard, Ung, Piller, &
Gilbert, 2013).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
35
Al ver las diferencias que se generan en términos de mezcla cuando se cambia la geometría
interna de la unión, se realizó un estudio detallado. En la nueva geometría se encuentran
algunos baches los cuales podrían influir en los procesos de mezcla. Cuando se presenta el
escenario en donde los flujos de entrada son diferentes, existe un mayor impulso en alguna
de las tuberías lo que genera que la interfaz incidente de los dos chorros se desplace y se
acerque a la pared de la tubería, por lo tanto la geometría de la pared puede afectar la
manera en que se distribuye la masa del trazador.
Por otro lado, también es importante analizar similitud geométrica de los procesos de
mezcla, es decir, si la cantidad de mezcla tiene alguna variación si se cambia el diámetro de
las tuberías. Para esto se diseñó un experimento para identificar los factores críticos que
pueden influir en la cantidad de mezcla en las uniones en cruz. Dentro de dichos factores se
estudió el tamaño de las tuberías; entonces se probaron 4 experimentos, cada uno con
diámetros de 0.5, 1,1.5 y 2 pulgadas. Para cada unión en cruz, las cuatro tuberías tenían el
mismo diámetro (McKenna, Orear, & Wright, 2007).
Para realizar el análisis de los resultados se utilizó el concepto de fracción de masa
normalizada:
𝑀𝐹 =
𝑄
𝑆𝑎𝑙𝑖𝑑𝑎
𝑇𝑟𝑎𝑧𝑎𝑑𝑜𝑟
∗ 𝐶
𝑆𝑎𝑙𝑖𝑑𝑎
𝑇𝑟𝑎𝑧𝑎𝑑𝑜𝑟
(𝑄
𝐸𝑛𝑡𝑟𝑎𝑑𝑎
𝑇𝑟𝑎𝑧𝑎𝑑𝑜𝑟
∗ 𝐶
𝐸𝑛𝑡𝑟𝑎𝑑𝑎
𝑇𝑟𝑎𝑧𝑎𝑑𝑜𝑟
) + (𝑄
𝐸𝑛𝑡𝑟𝑎𝑑𝑎
𝐿𝑖𝑚𝑝𝑖𝑎
∗ 𝐶
𝐸𝑛𝑡𝑟𝑎𝑑𝑎
𝐿𝑖𝑚𝑝𝑖𝑎
)
Ecuación 11. Fracción de masa de NaCl (McKenna, Orear, & Wright, 2007).
Los resultados obtenidos se pueden observar en la siguiente gráfica:
Figura 37. Fracción de masa para diferentes diámetros de tuberías (McKenna, Orear, & Wright, 2007).
En esta gráfica se puede observar los efectos que tiene, sobre el proceso de mezcla, la
variación de los diámetros de las tuberías y la variación del número de Reynolds.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
36
Los resultados muestran que no existe un cambio significativo en los valores de fracción de
masa por la tubería Este, si se incrementa el diámetro de las tuberías. Esto quiere decir que
el proceso es independiente del tamaño de las tuberías, teniendo en cuenta que todas las
tuberías que llegan y salen de la unión tienen el mismo diámetro.
Como se ha mencionado anteriormente, también se han realizado estudios que involucran
configuraciones doble tee en donde las simulaciones en CFD muestran que la mezcla de
solutos depende de la relación del impulso del flujo y la longitud entre las conexiones
(Shao, Jeffrey Yang, Jiang, Yu, & Shen, 2014). Se probaron los siguientes escenarios:
Figura 38. Configuraciones doble tee (Shao, Jeffrey Yang, Jiang, Yu, & Shen, 2014).
Se propone un factor de distribución de flujo para describir el grado de mezcla en la unión.
{
𝑓
1
=
𝑄
14
𝑄
1
𝑓
2
=
𝑄
23
𝑄
2
Ecuación 12. Factor de distribución de flujo (Shao, Jeffrey Yang, Jiang, Yu, & Shen, 2014).
Después, realizando un balance de masa se obtienen las siguientes ecuaciones:
{
𝑄
1
𝑓
1
+ 𝑄
2
(1 − 𝑓
2
) = 𝑄
4
𝑄
1
(1 − 𝑓
1
) + 𝑄
2
𝑓
2
= 𝑄
3
𝑄
1
𝑓
1
𝐶
1
+ 𝑄
2
(1 − 𝑓
2
)𝐶
2
= 𝑄
4
𝐶
4
𝑄
1
(1 − 𝑓
1
)𝐶
1
+ 𝑄
2
𝑓
2
𝐶
2
= 𝑄
3
𝐶
3
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
37
Despejando los factores se obtiene:
{
𝑓
1
=
𝑄
4
(𝐶
4
− 𝐶
2
)
𝑄
1
(𝐶
1
− 𝐶
2
)
𝑓
2
= 1 −
𝑄
4
(𝐶
1
− 𝐶
4
)
𝑄
2
(𝐶
1
− 𝐶
2
A partir de los resultados experimentales y los datos determinados por CFD se puede
obtener las siguientes gráficas:
Figura 39. (a) resultados experimentales para mayor momento en tuberías adyacentes (b) mayor momento en
tuberías opuestas (Shao, Jeffrey Yang, Jiang, Yu, & Shen, 2014).
donde el parámetro η es la tasa de momento:
{
𝐾
𝑖
=
𝑄
𝑖
2
𝐴
𝑖
𝜂 =
𝐾
1
+ 𝐾
3
𝐾
2
+ 𝐾
4
Ecuación 13. Tasa de momento (Shao, Jeffrey Yang, Jiang, Yu, & Shen, 2014).
Con los resultados presentados anteriormente se puede evidenciar, una vez más, que la
suposición de mezcla completa en las intersecciones de las tuberías no es correcta. Debido
a esto, mejorar los modelos de calidad del agua existentes teniendo en cuenta una mezcla
incompleta es importante, no sólo para predecir las concentraciones de sustancias químicas
tales como el cloro en el agua en sistemas de distribución de agua potable, sino también
para prepararse para posibles casos de contaminación.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
38
3. Marco teórico
Las simulaciones de los sistemas de redes de tuberías a presión se componen de dos
motores: la modelación hidráulica y la modelación de la calidad del agua. El análisis de
calidad del agua está siempre acompañado de los resultados de las simulaciones hidráulicas
debido a que todos los productos químicos o especies biológicas, son transportados a través
de la red por procesos de advección y difusión. Este enfoque conceptual es ampliamente
utilizado para el desarrollo de la mayoría de las herramientas de software orientadas a la
modelación y la gestión de los sistemas de agua potable (Boulos, Altman, Jarrige, &
Collevati, 1995).
Teniendo en cuenta que la modelación hidráulica está basada en el cálculo de caudales y
presiones de las redes y la modelación de la calidad del agua estudia de manera espacial y
temporal los procesos que afectan la calidad del agua, existen modelos computacionales
que pueden realizar un análisis detallado de procesos de transporte que afectan la calidad
del agua en un red de distribución de agua potable. Dentro de estos modelos, se encuentra
Dinámica de Fluidos Computacional en donde se puede evaluar con mayor profundidad los
fenómenos que afectan los procesos de mezcla en los nudos de las redes, haciendo que
dichos procesos no sean homogéneos.
3.1 Modelación hidráulica
3.1.1 Ecuaciones de modelación hidráulica
Como se mencionó anteriormente, la modelación hidráulica está basada en el cálculo de
caudales y presiones, por lo tanto, se debe cumplir la conservación de la masa en las redes.
De acuerdo con esto, la ecuación de continuidad es la siguiente:
∑ 𝑄
𝑖𝑗
− 𝑄
𝐷𝑖
+ 𝑄
𝑒𝑖
= 0
𝑁𝑇
𝑖
𝑗=𝑖
Ecuación 14. Conservación de masa en las redes.
donde:
𝑁𝑇
𝑖
, es el número de tuberías.
𝑄
𝐷𝑖
, es el caudal demandado en la unión i.
𝑄
𝑒𝑖
, es el caudal de entrada al nudo i.
𝑄
𝑖𝑗
, es el caudal de la tubería.
Para el cálculo de caudales se utiliza la ecuación de Darcy-Weisbach en conjunto con la
ecuación de Colebrook-White. La ecuación se describe de la siguiente manera:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
39
𝑄 = −2
√2𝑔𝑑ℎ
𝑓
√𝑙
𝐴 𝑙𝑜𝑔
10
(
𝑘
𝑠
3.7 𝑑
+
2.51 𝜐√𝑙
√2𝑔𝑑
3
ℎ
𝑓
)
Ecuación 15. Caudal utilizando la ecuación de Darcy-Weisbach en conjunto con la ecuación de Colebrook-White
(Saldarriaga, 2007).
donde:
𝑔, es la aceleración de la gravedad.
𝑑, es el diámetro de la tubería.
ℎ
𝑓
, es la altura por pérdidas por fricción.
𝑙, es la longitud de la tubería.
𝑘
𝑠
, es la rugosidad relativa de la tubería, la cual depende del material.
𝜐, es la viscosidad cinemática del fluido.
Por otro lado, para calcular las alturas piezométricas, se supone que en cada tubo la energía
total disponible se gasta en pérdidas por fricción y en pérdidas menores:
𝐻
𝑡
= ℎ
𝑓
+ ∑ ℎ
𝑚
Ecuación 16. Altura piezométrica (Saldarriaga, 2007).
Si se tienen en cuenta las pérdidas menores causadas por cualquier tipo de accesorios y/o
bombas en alguno de los tubos de la red, la anterior ecuación se ve modificada de la
siguiente manera:
ℎ
𝑓
+ ℎ
𝑚
= 𝛼𝑄
𝑛
+ 𝛽𝑄 + 𝛾
Ecuación 17. Altura piezométrica teniendo en cuenta pérdidas menores causadas por accesorios (Saldarriaga,
2007).
donde:
𝑛, es un exponente que depende de la ecuación de fricción utilizada, la cual es 2 si se utiliza
la ecuación de Darcy-Weisbach, ó 0.85 para la ecuación de Hazen-Williams.
𝛼, 𝛽, 𝛾, son parámetros característicos del tubo, las válvulas y las bombas.
Generalmente, en las tuberías sólo ocurren pérdidas por fricción y pérdidas menores, las
cuales son función únicamente de la altura de velocidad; en este caso, se puede utilizar la
anterior ecuación para definir el valor de
𝛼:
𝐻
𝑡
= 𝛼𝑄
𝑛
ℎ
𝑓
+ ∑ ℎ
𝑚
= 𝛼𝑄
𝑛
Utilizando la ecuación de Darcy-Weisbach:
(𝑓
𝑙
𝑑
+ ∑ 𝑘
𝑚
)
𝑄
2
2𝑔𝐴
2
= 𝛼𝑄
2
Despejando
𝛼:
𝛼 =
(𝑓
𝑙
𝑑 + ∑ 𝑘
𝑚
)
2𝑔𝐴
2

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
40
3.2 Modelación de calidad del agua
La modelación de la calidad del agua está basada en la variación temporal y espacial de un
parámetro de calidad del agua; existen dos tipos de modelo de cálculo: los estáticos y los
dinámicos. En los modelos estáticos se supone que los caudales demandados e inyectados a
la red permanecen constantes, y no varían las condiciones de operación de la red, definidas
por el estado de las válvulas o bombas presentes. Por otra parte, los modelos dinámicos
permiten la variación temporal en los caudales demandados e inyectados así como las
condiciones de operación de la red.
3.2.1. Modelos estáticos
Estos modelos se aplican al estudio del transporte de contaminantes conservativos en las
redes de distribución de agua potable determinando sus rutas de procedencia y tiempos de
permanencia en las mismas condiciones estáticas de operación. Los planteamientos básicos
para la resolución de estos modelos son la conservación de masa en los nudos, la
concentración de mezclas y los tiempos de permanencia (Vidal, Martínez, & Ayza, 1994).
La conservación de masa para cada nudo de la red se describe con la ecuación de
continuidad, en donde se define el porcentaje de la demanda en un nudo j procedente de la
fuente i como C (i,j) y se puede expresar de la siguiente manera:
Figura 40. Esquema de conservación de masa en el nudo j (Vidal, Martínez, & Ayza, 1994).
∑ 𝑐(𝑖, 𝑘)𝑞
𝑘𝑗
+ 𝑄
𝑠
(𝑖)
𝐾=𝑁𝑗
= 𝑐(𝑖, 𝑗) ∑ 𝑄
0
(𝑗)
Ecuación 18. Ecuación de continuidad para modelación de calidad del agua (Vidal, Martínez, & Ayza, 1994).
donde,
𝑁𝑗, es el conjunto de nudos adyacentes al nudo j desde los que fluye caudal.
𝑐(𝑖, 𝑘), son los factores de contribución de la fuente i en los nudos 𝑁𝑗.
𝑞
𝑘𝑗
, es el caudal que fluye del nudo k al j.
𝒍
𝟐
𝒍
𝟏

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
41
𝑄
𝑠
(𝑖), es el caudal que alimenta directamente al nudo j desde la fuente i.
𝑄
0
(𝑗), es el caudal total que abandona el nudo j.
𝑙
𝑖
, son los nudos alimentados por el nudo j.
La concentración de mezclas se trata de determinar las concentraciones de determinadas
sustancias en cada uno de los nudos de la red, considerando la mezcla de aguas procedentes
de fuentes de distinta calidad. Por lo tanto, la concentración de un cierto contaminante no
reactivo en el nudo j suponiendo mezcla completa, se describe de la siguiente manera:
𝐶
𝑗
=
∑
(𝑞
𝑘𝑗
𝐶
𝑘
) + ∑ (𝑄
𝑠
(𝑖)𝐶
𝑠
(𝑖))
𝑖∈𝑠
𝐾∈𝑁𝑗
∑
(𝑞
𝑘𝑗
) + ∑ (𝑄
𝑠
(𝑖))
𝑖∈𝑠
𝑘∈𝑁𝑗
Ecuación 19. Concentración en el nudo j (Vidal, Martínez, & Ayza, 1994).
donde:
𝐶
𝑘
, es la concentración de la sustancia en los nudos aguas arriba adyacentes al j.
𝐶
𝑠
(𝑖), es la concentración de dicha sustancia de la fuente i que alimenta el nudo j.
Finalmente, el tiempo de permanencia es uno de los planteamientos más importantes
debido a que el caudal desde el punto de alimentación hasta el nudo determinado puede
seguir distintas rutas y el tiempo de permanencia del agua en la red desde que se inyecta en
i hasta que llega al nudo j puede ser muy variable. Se define el tiempo de permanencia
medio para un nudo j como:
𝐴𝐴
𝑗
=
∑ 𝑞
𝑖
𝐴
𝑖
∑ 𝑞
𝑖
Ecuación 20. Tiempo de permanencia medio para el nudo j (Vidal, Martínez, & Ayza, 1994).
donde,
𝑞
𝑖
, es el caudal que llega al nudo en estudio por el camino i.
𝐴
𝑖
, es la edad del agua en el punto de alimentación.
3.2.2. Modelos dinámicos
Estos modelos consideran el movimiento y reacción de los contaminantes bajo condiciones
variables en el tiempo, como sucede en la realidad con las demandas, en cambios de nivel
en los depósitos, cierre y apertura de válvulas, arranque y detención de bombas, etc. En los
modelos dinámicos están implicados tres procesos: el transporte por convección en las
tuberías, el decaimiento o crecimiento de las concentraciones en el tiempo por reacción, y
los procesos de mezcla en los nudos de la red (Vidal, Martínez, & Ayza, 1994).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
42
El trasporte de las sustancias por las tuberías está causado principalmente por el flujo del
agua bajo la acción del gradiente de presiones; es importante tener en cuenta que el
transporte es diferente para sustancias conservativas y no conservativas.
- Sustancias conservativas: se caracterizan por que su concentración no cambia en el
tiempo debido a reacciones biológicas o químicas. Para estas sustancias, el proceso
de transporte a lo largo de una línea i esta descrito por la siguiente ecuación:
𝛿𝑐𝑖(𝑥, 𝑡)
𝛿𝑡
+ 𝑢
𝑖
𝛿𝑐𝑖(𝑥, 𝑡)
𝛿𝑥
= 0
Ecuación 21. Transporte se sustancias conservativas (Vidal, Martínez, & Ayza, 1994).
donde,
𝑐𝑖(𝑥, 𝑡), es la concentración de la sustancia en la sección de cálculo x y el instante t.
𝑢
𝑖
, es la velocidad media del agua en la línea, la cual puede ser variable en el
tiempo si cambian las condiciones hidráulicas.
- Sustancias no conservativas: estas sustancias pueden tener reacciones químicas o
biológicas a lo largo del tiempo mientras recorren las tuberías, modificando así su
concentración. Para este caso, la ecuación de transporte debe incluir el término de
reacción:
𝛿𝑐𝑖(𝑥, 𝑡)
𝛿𝑡
+ 𝑢
𝑖
𝛿𝑐𝑖(𝑥, 𝑡)
𝛿𝑥
+ 𝜃(𝑐𝑖(𝑥, 𝑡)) = 0
Ecuación 22. Transporte de sustancias no conservativas (Vidal, Martínez, & Ayza, 1994).
Para resolver esta última ecuación, se debe dividir cada línea de corriente en segmentos,
dentro de los cuales se producen las reacciones, mientras que las mezclas tienen lugar en
los nudos.
3.2.3. Concentración
El cálculo de la difusión en fluidos heterogéneos se hace con base en la ecuación de
conservación de masa, que debe verificar cada componente o especie. Para la mezcla entre
dos componentes diferentes (A y B), se entiende por concentración a la cantidad relativa de
una sustancia en un cierto punto y en un tiempo dado. Se puede expresar en unidades de
masa, peso, volumen, número de partículas por unidad de volumen (Mompremier, 2009).
De esta manera, la concentración de determinada sustancia se puede calcular de la siguiente
manera:
𝐶
𝐴
=
𝑚
𝐴
𝑚
𝐴
+ 𝑚
𝐵
Ecuación 23. Concentración a partir de la conservación de masa (Mompremier, 2009).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
43
Además, se tiene que cumplir que:
𝑚
𝐴
+ 𝑚
𝐵
= 𝑚
En el caso en que una de las sustancias tenga una masa mucho menor que la otra (en este
caso se va a tomar la sustancia B como despreciable) se tiene el siguiente planteamiento:
𝐶
𝐴
=
𝑚
𝐴
𝑚
Si se realiza un arreglo de términos, para obtener la concentración en términos de la
densidad de la sustancia se tiene lo siguiente:
𝑚
𝐴
𝑉
=
𝑚
𝑉
𝐶
𝐴
𝜌
𝐴
= 𝐶
𝐴
𝜌
3.2.3.1 Balance de masa en la unión de varias tuberías.
Dentro de las tuberías que se juntan en un nudo existen dos tipos de estas; el primero está
conformado por las tuberías que tienen un caudal de entrada al nudo y, el segundo son las
tuberías por las que sale el caudal proveniente de la unión. Esto se esquematiza de la
siguiente manera:
Figura 41. Esquema de balance de masa en la unión de tuberías (Mompremier, 2009).
Se considera que el aporte de masa de cada una de las tuberías del primer grupo a una unión
en particular se define como:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
44
𝑚
𝑖
= ∑ 𝐶
𝑘
𝑖
𝑄
𝑖
∆𝑡
𝑁
𝑖=1
Ecuación 24. Aporte de masa a la unión i (Mompremier, 2009).
donde,
𝑄
𝑖
, es el caudal de entrada al nudo i desde una tubería de entrada.
N, es el número de tuberías de entrada.
𝐶
𝑘
𝑖
, es la concentración de algún componente en las tuberías de entrada.
Así mismo, por las tuberías de salida, egresará desde el nudo un fluido que contiene una
mezcla uniforme de concentración
𝐶
𝐸
, por lo que la masa que sale se describe como:
𝑚
𝑠
= 𝐶
𝐸
(∑ 𝐺
𝑖
+ 𝑞
𝐸
𝑀
𝑖=1
)
Ecuación 25.Masa de salida del nudo i (Mompremier, 2009).
donde,
𝐺
𝑖
, es el caudal de salida por cada tubería de salida.
M, es el número de tuberías de salida.
𝑞
𝐸
, es el caudal de concesión que se les suministra a los usuarios de la red.
Por lo tanto, debido al concepto de conservación de masa, lo que entra es igual a lo que
sale, entonces:
𝑚
𝑖=
𝑚
𝑠
Si se reemplazan las correspondientes ecuaciones, se puede despejar la concentración de la
mezcla, la cual sería completa y uniforme, de la siguiente manera:
𝐶
𝐸
𝑘+1
=
∑ 𝐶
𝑖
𝑘
𝑄
𝑖
𝑁
𝑖
∑ 𝐺
𝑖
+ 𝑞
𝐸
𝑀
𝑖
Ecuación 26.Concentración de la mezcla (Mompremier, 2009).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
45
3.3. Dinámica de Fluidos Computacional
Dinámica de Fluidos Computacional o CFD es el análisis de sistemas que involucran el
movimiento del fluido, la transferencia de calor y fenómenos asociados, por ejemplo
reacciones químicas, por medio de una simulación computacional. Esta técnica es muy
poderosa y abarca una amplia gama de áreas de aplicación industriales y no industriales.
Para el objetivo de esta investigación, las áreas de estudio más importantes son (Versteeg &
Malalasekera, 1995):
- Ingeniería de procesos físicos: mezcla y separación de fluidos.
- Ingeniería Ambiental: distribución de los contaminantes y efluentes.
El objetivo final de los desarrollos en el campo de CFD es proporcionar la capacidad de
comparar los resultados con otras herramientas de la ingeniería, tales como modelos físicos.
3.3.1. Funcionamiento del código de CFD
Los códigos de CFD se estructuran en torno a los algoritmos numéricos que puedan hacer
frente a problemas del flujo del fluido. Con el fin de proporcionar un fácil acceso, los
paquetes comerciales de CFD incluyen interfaces sofisticadas para poder ingresar los
parámetros del problema y examinar los resultados. Por lo tanto el código contiene tres
elementos principales:
- Un pre-procesador.
- Un programa de solución.
- Un post-procesador.
Pre-procesador: Este proceso consiste en la generación de un problema de flujo con la
utilización de un programa que cuente con una interfaz de fácil manejo y posteriormente
una transformación de esta entrada en una forma adecuada para su solución. Las
actividades que el usuario debe realizar en esta etapa son:
- Definición de la geometría de la región de interés: domino computacional.
- Generación de la malla del espacio solución o la subdivisión del dominio en
subdominios más pequeños, de tal forma que se cree una red con células o
volúmenes de control.
- Selección de los fenómenos físicos y químicos que necesitan ser modelados.
- Definición de las propiedades del fluido.
- Especificación de las condiciones de frontera adecuadas para los volúmenes de
control.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
46
La solución de un problema de flujo (velocidad, presión, temperatura, etc.) se define en los
nudos dentro de cada volumen de control, por lo tanto, la precisión de una solución en CFD
se rige por el número de células que defina el usuario. En general, cuanto mayor sea el
número de células, la precisión es mejor. Tanto la exactitud de una solución y su costo en
términos de hardware del equipo y el tiempo computacional dependen del refinamiento de
la malla. Las mallas óptimas generalmente no son uniformes: existen zonas más finas en
donde se producen grandes variaciones de un punto a otro y más gruesas en las regiones
con pocos cambios.
Programa de solución: Hay varias corrientes distintas de las técnicas de solución numérica:
- Diferencias finitas.
- Elementos finitos.
- Volúmenes finitos.
- Métodos espectrales.
En este caso, el estudio se va a concentrar en el método de volúmenes finitos, lo cual es una
formulación especial de diferencias finitas que se desarrollan en CFX/ANSYS, FLUENT,
PHOENICS y STAR-CD.
En resumen, el algoritmo numérico incluye los siguientes pasos:
- Integración de las ecuaciones gobernantes del flujo de los fluidos a través de todo el
volumen de control del dominio.
- Discretización y conversión de las ecuaciones integrales resultantes en un sistema
de ecuaciones algebraicas.
- Solución de las ecuaciones algebraicas por un método iterativo.
El primer paso, la integración del volumen de control, distingue el volumen finito para el
desarrollo de las demás técnicas de CFD.
Los estados resultantes expresan la conservación de las propiedades pertinentes para cada
celda de tamaño finito. A partir de esto, se presenta una clara relación entre el algoritmo
numérico y el principio de conservación física, esto hace que los conceptos sean más fáciles
de entender por los ingenieros que los métodos de elementos finitos y métodos espectrales.
La conservación de una variable θ dentro de un volumen de control finito se puede expresar
como un equilibrio entre los diversos procesos que tienden a aumentarlo o disminuirlo. En
otras palabras se tiene (Versteeg & Malalasekera, 1995):

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
47
[
𝑇𝑎𝑠𝑎 𝑑𝑒 𝑐𝑎𝑚𝑏𝑖𝑜 𝑑𝑒 𝜃
𝑒𝑛 𝑒𝑙 𝑣𝑜𝑙𝑢𝑚𝑒𝑛 𝑑𝑒 𝑐𝑜𝑛𝑡𝑟𝑜𝑙
𝑐𝑜𝑛 𝑟𝑒𝑠𝑝𝑒𝑐𝑡𝑜 𝑎𝑙 𝑡𝑖𝑒𝑚𝑝𝑜
]
= [
𝑇𝑎𝑠𝑎 𝑑𝑒 𝑖𝑛𝑐𝑟𝑒𝑚𝑒𝑛𝑡𝑜 𝑛𝑒𝑡𝑎 𝑑𝑒 𝜃
𝑑𝑒 𝑎𝑐𝑢𝑒𝑟𝑑𝑜 𝑐𝑜𝑛 𝑙𝑎 𝑐𝑜𝑛𝑣𝑒𝑐𝑐𝑖ó𝑛
𝑑𝑒𝑛𝑡𝑟𝑜 𝑑𝑒𝑙 𝑣𝑜𝑙𝑢𝑚𝑒𝑛 𝑑𝑒 𝑐𝑜𝑛𝑡𝑟𝑜𝑙
]
+ [
𝑇𝑎𝑠𝑎 𝑑𝑒 𝑖𝑛𝑐𝑟𝑒𝑚𝑒𝑛𝑡𝑜 𝑛𝑒𝑡𝑎 𝑑𝑒 𝜃
𝑑𝑒 𝑎𝑐𝑢𝑒𝑟𝑑𝑜 𝑐𝑜𝑛 𝑙𝑎 𝑑𝑖𝑓𝑢𝑠𝑖ó𝑛
𝑑𝑒𝑛𝑡𝑟𝑜 𝑑𝑒𝑙 𝑣𝑜𝑙𝑢𝑚𝑒𝑛 𝑑𝑒 𝑐𝑜𝑛𝑡𝑟𝑜𝑙
]
+ [
𝑇𝑎𝑠𝑎 𝑑𝑒 𝑐𝑟𝑒𝑎𝑐𝑖ó𝑛
𝑛𝑒𝑡𝑎 𝑑𝑒 𝜃
𝑑𝑒𝑛𝑡𝑟𝑜 𝑑𝑒𝑙 𝑣𝑜𝑙𝑢𝑚𝑒𝑛 𝑑𝑒 𝑐𝑜𝑛𝑡𝑟𝑜𝑙
]
Los códigos de CFD contienen técnicas de discretización adecuadas para el tratamiento de
fenómenos de transporte como convección (transporte debido al flujo del fluido) y difusión
(transporte debido a las variaciones de θ de un punto a otro), así como para términos de
fuente (asociada con la creación o destrucción de θ) y la tasa de cambio con respecto al
tiempo.
El fenómeno físico subyacente es complejo y no lineal por lo tanto se requiere una solución
iterativa.
Los procedimientos de solución más populares son el TDMA (algoritmo matricial tri-
diagonal), el cual soluciona línea por línea cada una de las ecuaciones algebraicas y el
Algoritmo SIMPLE para asegurar la correcta vinculación entre la presión y la velocidad.
Post-procesador: Al igual que en el pre-procesamiento, se requiere una cantidad enorme en
el trabajo de desarrollo.
Debido a la creciente popularidad de CFD en la ingeniería, muchos paquetes tienen
capacidades gráficas sobresalientes equipados con herramientas versátiles de visualización
de. Estos incluyen:
- Geometría de dominio y visualización de la rejilla.
- Parcelas vectoriales.
- Línea y sombreadas parcelas de contorno.
- Parcelas de superficie en 2D y 3D.
- Rastreo de partículas.
- Ver la manipulación (traslación, rotación, escalado, etc.).
- Salida de color PostScript.
Las actualizaciones más recientes pueden incluir animación para resultados dinámicos de
visualización y capacidad de exportación de datos para su posterior.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
48
3.3.2. Leyes de conservación del movimiento de los fluidos y las condiciones de
frontera
Las ecuaciones gobernantes del flujo de fluidos representan afirmaciones matemáticas de
las leyes de conservación de la física:
- Conservación de la masa.
- La tasa de cambio del momento es igual a la suma de las fuerzas sobre una partícula
del fluido (la segunda ley de Newton).
- La tasa de cambio de la energía es igual a la suma de la tasa de calor más la tasa del
trabajo realizado sobre una partícula de fluido (primera ley de termodinámica).
El fluido será considerado como uno continuo. Para el análisis de los flujos de fluidos a
escalas de longitud macroscópicas, la estructura molecular de la materia y los movimientos
moleculares pueden ser ignorados. Se describe el comportamiento del fluido en términos de
propiedades macroscópicas, tales como la velocidad, la presión, densidad y temperatura, y
sus derivadas: espacio y tiempo.
Para entender las leyes de conservación, se va a considerar un volumen de control del
fluido con lados
𝛿𝑥, 𝛿𝑦 y 𝛿𝑧.
Figura 42. Volumen de control del fluido (Versteeg & Malalasekera, 1995).
Las seis caras están etiquetadas como N, S, E, W, T y B, que significan Norte, Sur, Este,
Oeste, Arriba y Abajo, respectivamente. Todas las propiedades del fluido son funciones del
espacio y el tiempo, por lo tanto, se representan como ρ (x, y, z, t), p (x, y, z, t), T (x, y, z, t)
y u (x, y, z, t) para la densidad, presión, temperatura y el vector de velocidad,
respectivamente.
Suponiendo que el volumen de control presentado en la Figura 42 es muy pequeño, las
propiedades del fluido en las caras se pueden expresar con suficiente precisión por medio

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
49
de los dos primeros términos de la serie de Taylor. Así, por ejemplo, la presión en las caras
W y E, medida desde el centro del elemento, puede ser expresada como:
𝑝 −
𝛿𝑝
𝛿𝑥
1
2
𝛿𝑥 ; 𝑝 +
𝛿𝑝
𝛿𝑥
1
2
𝛿𝑥
Ecuación 27.Presión en las caras del elemento (Versteeg & Malalasekera, 1995).
3.3.3. Conservación de la masa en tres dimensiones
El primer paso para la derivación de la ecuación de la conservación de masa es escribir el
balance de masa para un elemento del fluido:
𝑇𝑎𝑠𝑎 𝑑𝑒 𝑖𝑛𝑐𝑟𝑒𝑚𝑒𝑛𝑡𝑜 𝑑𝑒 𝑙𝑎 𝑚𝑎𝑠𝑎 𝑑𝑒𝑙 𝑒𝑙𝑒𝑚𝑒𝑛𝑡𝑜 𝑑𝑒𝑙 𝑓𝑙𝑢𝑖𝑑𝑜
= 𝑡𝑎𝑠𝑎 𝑛𝑒𝑡𝑎 𝑑𝑒 𝑓𝑙𝑢𝑗𝑜 𝑜 𝑑𝑒 𝑚𝑎𝑠𝑎 𝑑𝑒𝑛𝑡𝑟𝑜 𝑑𝑒𝑙 𝑒𝑙𝑒𝑚𝑒𝑛𝑡𝑜 𝑑𝑒𝑙 𝑓𝑙𝑢𝑖𝑑𝑜
La tasa de incremento de masa del elemento del fluido es:
𝛿
𝛿𝑡
(𝜌𝛿𝑥𝛿𝑦𝛿𝑧) =
𝛿𝜌
𝛿𝑡
𝛿𝑥𝛿𝑦𝛿𝑧
Ecuación 28.Tasa de incremento de masa (Versteeg & Malalasekera, 1995).
Lo siguiente que se necesita para tener en cuenta es la tasa de flujo de masa a través de una
cara del elemento, que viene dada por el producto de la densidad, área y la componente de
la velocidad normal a la cara. En la Figura 43 se puede observar que la tasa neta de flujo de
masa en el elemento a través de sus fronteras está dada por:
(𝜌𝑢 −
𝛿(𝜌𝑢)
𝛿𝑥
1
2
𝛿𝑥) 𝛿𝑦𝛿𝑧 − (𝜌𝑢 +
𝛿(𝜌𝑢)
𝛿𝑥
1
2
𝛿𝑥) 𝛿𝑦𝛿𝑧
+ (𝜌𝑣 −
𝛿(𝜌𝑣)
𝛿𝑦
1
2
𝛿𝑦) 𝛿𝑥𝛿𝑧 − (𝜌𝑣 +
𝛿(𝜌𝑣)
𝛿𝑦
1
2
𝛿𝑦) 𝛿𝑥𝛿𝑧
+ (𝜌𝑤 −
𝛿(𝜌𝑤)
𝛿𝑧
1
2
𝛿𝑧) 𝛿𝑥𝛿𝑦 − (𝜌𝑤 +
𝛿(𝜌𝑤)
𝛿𝑧
1
2
𝛿𝑧) 𝛿𝑥𝛿𝑦
Ecuación 29.Tasa de flujo a través de las fronteras (Versteeg & Malalasekera, 1995).
El flujo que está dirigido hacia adentro del elemento produce un incremento en la masa del
elemento y toma un signo positivo, de la misma manera, el flujo que deja el elemento se le
asigna un signo negativo.
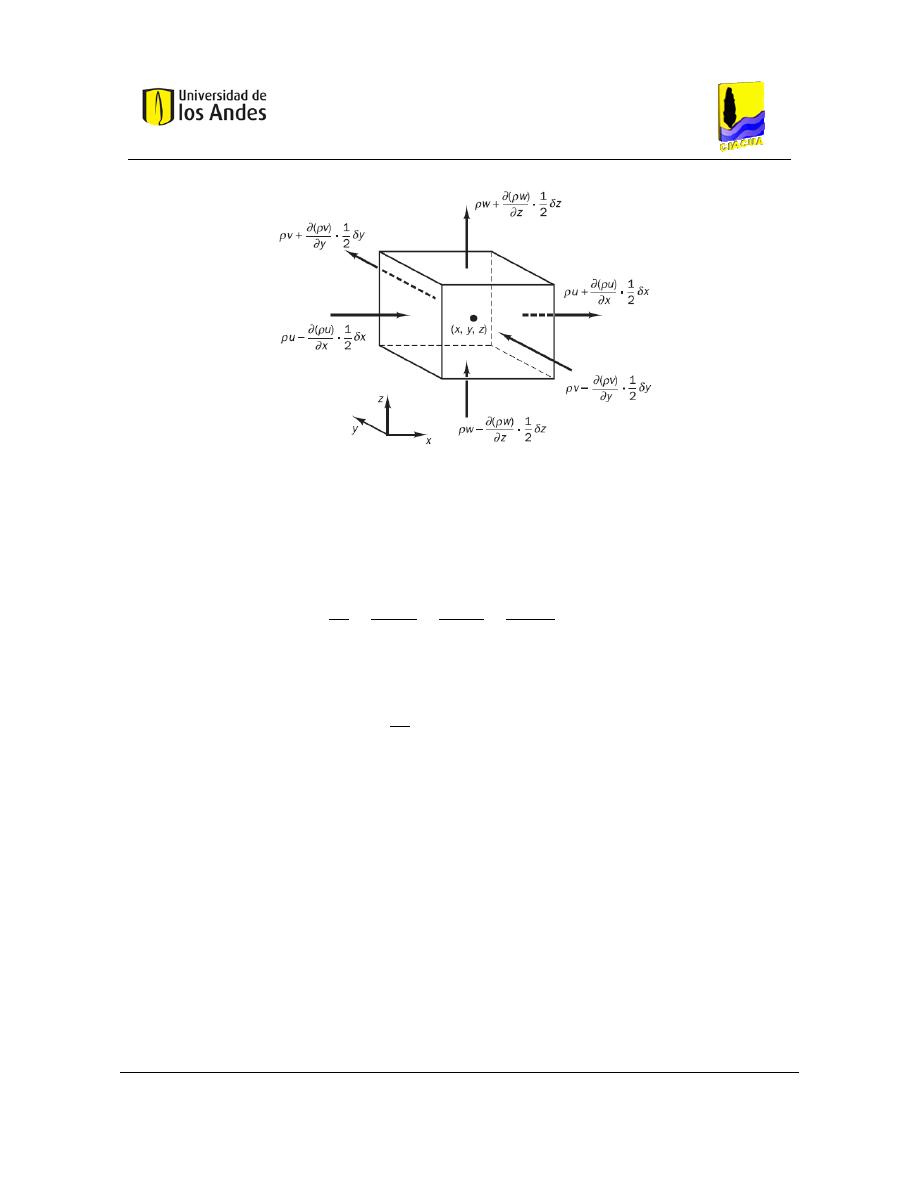
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
50
Figura 43. Flujo de masa en el elemento (Universidad de Valencia, 2006).
La tasa de incremento de la masa en el interior del elemento (Ecuación 28), ahora equivale
a la tasa neta de flujo de masa en el elemento a través de sus caras (Ecuación 29). Todos los
términos del resultante balance de masas están dispuestos en el lado izquierdo del signo
igual y la expresión se divide por el volumen δxδyδz elemento:
𝛿𝜌
𝛿𝑡
+
𝛿(𝜌𝑢)
𝛿𝑥
+
𝛿(𝜌𝑣)
𝛿𝑦
+
𝛿(𝜌𝑤)
𝛿𝑧
= 0
En notación vectorial más compacta:
𝛿𝜌
𝛿𝑡
+ 𝑑𝑖𝑣(𝜌𝒖) = 0
Ecuación 30. Conservación de masa en tres dimensiones en estado inestable (Versteeg & Malalasekera, 1995).
La Ecuación 30 es la ecuación de conservación de la masa en tres dimensiones en estado
inestable o ecuación de continuidad en un punto de un fluido compresible. El primer
término en el lado izquierdo, es la tasa de cambio de la densidad en el tiempo (masa por
unidad de volumen). El segundo término, describe el flujo neto de masa del elemento a
través de sus límites y se llama el término de aceleración convectiva.
Para un fluido incompresible (es decir, un líquido) la densidad ρ es constante y la Ecuación
30 se convierte en:
𝑑𝑖𝑣 𝒖 = 0
Ecuación 31.Conservación de masa para un fluido incompresible (Versteeg & Malalasekera, 1995).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
51
3.3.4. Ecuación de momento en tres dimensiones
La segunda ley de Newton establece que la tasa de cambio del momento de una partícula de
un fluido es igual a la suma de las fuerzas sobre la partícula. Las tasas de aumento de x, y y
z por unidad de volumen de una partícula de fluido están dadas por:
𝜌
𝐷𝑢
𝐷𝑡
; 𝜌
𝐷𝑣
𝐷𝑡
; 𝜌
𝐷𝑤
𝐷𝑡
Ecuación 32. Tasas de incremento del momento en x, y y z (Versteeg & Malalasekera, 1995).
Se distinguen dos tipos de fuerzas sobre las partículas del fluido:
• Fuerzas de superficie:
- Fuerzas de presión.
- Fuerzas viscosas.
- Fuerza de la gravedad.
• Fuerzas de cuerpo:
- Fuerza centrífuga.
- Fuerza de Coriolis.
- Fuerza electromagnética.
Es una práctica común tener en cuenta las fuerzas de superficie como términos
independientes en la ecuación de momento. El estado de tensión de un elemento de fluido
se define en términos de la presión y los nueve componentes de la tensión viscosa
mostrados en la Figura 44. La presión, la cual es una tensión normal, se denota por p y los
esfuerzos viscosos se denotan por τ.
Figura 44. Componentes de los esfuerzos de tensión en las tres caras del elemento (Versteeg & Malalasekera, 1995).
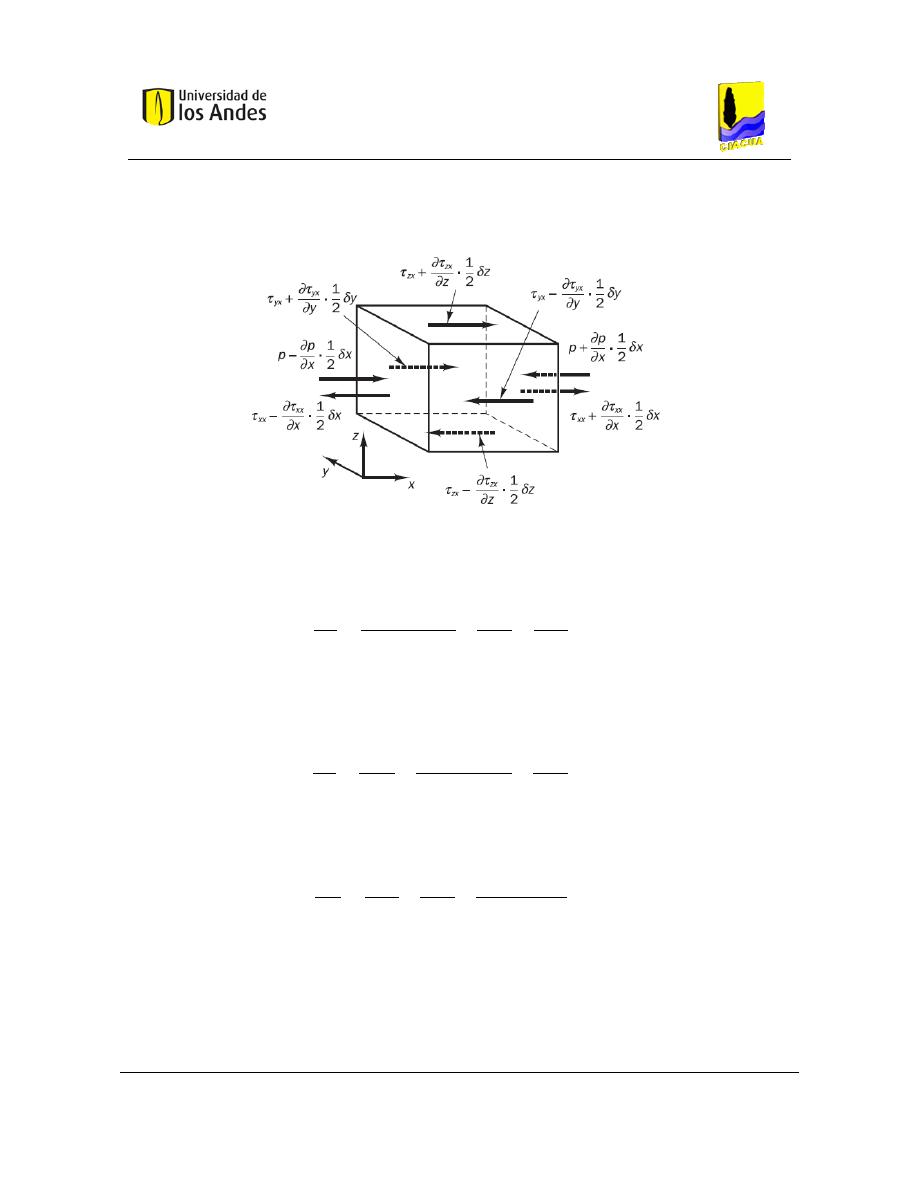
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
52
En primer lugar, se consideran las componentes de la fuerza en x debido a la presión p y a
los esfuerzos cortantes τ
xx
, τ
yx
y τ
zx
mostrados en la Figura 45. La magnitud de la fuerza
resultante de una tensión de superficie es el producto entre la tensión y el área.
Figura 45. Componentes de tensión en la dirección x (Versteeg & Malalasekera, 1995).
El componente en x de la ecuación de momento es:
𝜌
𝐷𝑢
𝐷𝑡
=
𝛿(−𝑝 + 𝜏
𝑥𝑥
)
𝛿𝑥
+
𝛿𝜏
𝑦𝑥
𝛿𝑦
+
𝛿𝜏
𝑧𝑥
𝛿𝑧
+ 𝑆
𝑀𝑥
Ecuación 33. Componente en x de la ecuación de momento (Versteeg & Malalasekera, 1995).
El componente en y de la ecuación de momento es:
𝜌
𝐷𝑣
𝐷𝑡
=
𝛿𝜏
𝑥𝑦
𝛿𝑥
+
𝛿(−𝑝 + 𝜏
𝑦𝑦
)
𝛿𝑦
+
𝛿𝜏
𝑧𝑦
𝛿𝑧
+ 𝑆
𝑀𝑦
Ecuación 34. Componente en y de la ecuación de momento (Versteeg & Malalasekera, 1995).
Y la componente en z de la ecuación de momento es:
𝜌
𝐷𝑤
𝐷𝑡
=
𝛿𝜏
𝑥𝑧
𝛿𝑥
+
𝛿𝜏
𝑦𝑧
𝛿𝑦
+
𝛿(−𝑝 + 𝜏
𝑧𝑧)
𝛿𝑧
+ 𝑆
𝑀𝑧
Ecuación 35. Componente en z de la ecuación de momento (Versteeg & Malalasekera, 1995).
El signo asociado con la presión es opuesta a la asociada con el esfuerzo viscoso normal,
porque la convención de signos generalmente representa un esfuerzo de tracción. Por lo
tanto, al ser la presión un esfuerzo normal de compresión, lleva un signo negativo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
53
3.3.5. Ecuación de Navier-Stokes para un fluido Newtoniano
Las ecuaciones que rigen el flujo de los fluidos contienen en su mayoría incógnitas de las
componentes del esfuerzo viscoso. Las formas más útiles de las ecuaciones de conservación
de flujos se obtienen mediante la introducción de un modelo adecuado para las tensiones
viscosas. En muchos fluidos los esfuerzos viscosos pueden expresarse como funciones de la
tasa de velocidad de deformación o la tensión local. En los flujos tridimensionales, la tasa
local de deformación se compone por la velocidad de deformación lineal y la tasa de
deformación volumétrica.
Teniendo en cuenta que los gases y los líquidos se pueden considerar isotrópicos, la
velocidad de deformación lineal de un elemento de fluido tiene nueve componentes en tres
dimensiones, seis de los cuales son independientes en los fluidos isotrópicos. Dichos
componentes se pueden representar mediante el símbolo
𝑆
𝑖𝑗
.
𝑆
𝑥𝑥
=
𝜕𝑢
𝜕𝑥
𝑆
𝑦𝑦
=
𝜕𝑣
𝜕𝑦
𝑆
𝑧𝑧
=
𝜕𝑤
𝜕𝑧
Ecuación 36. Velocidad de deformación lineal (Versteeg & Malalasekera, 1995).
También existen seis componentes de tensión de deformación lineal:
𝑆
𝑥𝑦
= 𝑆
𝑦𝑥
=
1
2
(
𝜕𝑢
𝜕𝑦
+
𝜕𝑣
𝜕𝑥
)
𝑆
𝑥𝑧
= 𝑆
𝑧𝑥
=
1
2
(
𝜕𝑢
𝜕𝑧
+
𝜕𝑤
𝜕𝑥
)
𝑆
𝑦𝑧
= 𝑆
𝑧𝑦
=
1
2
(
𝜕𝑣
𝜕𝑧
+
𝜕𝑤
𝜕𝑦
)
La deformación volumétrica está dada por la siguiente ecuación:
𝜕𝑢
𝜕𝑥
+
𝜕𝑣
𝜕𝑦
+
𝜕𝑤
𝜕𝑧
= 𝑑𝑖𝑣 𝒖
Ecuación 37. Deformación volumétrica (Versteeg & Malalasekera, 1995).
En un fluido Newtoniano las tensiones viscosas son proporcionales a las tasas de la
deformación. La forma tridimensional de la ley de la viscosidad de Newton para flujos
compresibles implica dos constantes de proporcionalidad: la primera es la viscosidad
(dinámica) μ, para relacionar las tensiones y las deformaciones lineales. Y la segunda, es la
viscosidad λ, para relacionar las tensiones y la deformación volumétrica.
𝜏
𝑥𝑥
= 2𝜇
𝜕𝑢
𝜕𝑥
+ 𝜆 𝑑𝑖𝑣 𝒖

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
54
𝜏
𝑦𝑦
= 2𝜇
𝜕𝑣
𝜕𝑦
+ 𝜆 𝑑𝑖𝑣 𝒖
𝜏
𝑧𝑧
= 2𝜇
𝜕𝑤
𝜕𝑧
+ 𝜆 𝑑𝑖𝑣 𝒖
𝜏
𝑥𝑦
= 𝜏
𝑦𝑥
= 𝜇 (
𝜕𝑢
𝜕𝑦
+
𝜕𝑣
𝜕𝑥
)
𝜏
𝑥𝑧
= 𝜏
𝑧𝑥
= 𝜇 (
𝜕𝑢
𝜕𝑧
+
𝜕𝑤
𝜕𝑥
)
𝜏
𝑦𝑧
= 𝜏
𝑧𝑦
= 𝜇 (
𝜕𝑣
𝜕𝑧
+
𝜕𝑤
𝜕𝑦
)
Reemplazando las anteriores ecuaciones en la Ecuación 33 para la dirección x se puede
derivar la siguiente ecuación:
𝜌
𝐷𝑢
𝐷𝑡
= −
𝜕𝑝
𝜕𝑥
+
𝜕
𝜕𝑥
(2𝜇
𝜕𝑢
𝜕𝑥
+ 𝑑𝑖𝑣 𝒖) +
𝜕
𝜕𝑦
(𝜇 (
𝜕𝑢
𝜕𝑦
+
𝜕𝑣
𝜕𝑥
)) +
𝜕
𝜕𝑧
(𝜇 (
𝜕𝑢
𝜕𝑧
+
𝜕𝑤
𝜕𝑥
)) + 𝑆
𝑀
𝑥
De una manera más simplificada:
𝜌
𝐷𝑢
𝐷𝑡
= −
𝜕𝑝
𝜕𝑥
+ 𝑑𝑖𝑣(𝜇 𝑔𝑟𝑎𝑑 𝑢) + 𝑆
𝑀
𝑥
Ecuación 38. Ecuación de Navier-Stokes (Versteeg & Malalasekera, 1995).
3.3.6. Modelación de la turbulencia
3.3.6.1 Características de flujos simples turbulentos
La mayor parte de la teoría del flujo turbulento fue desarrollada inicialmente a partir de un
cuidadoso análisis de la estructura de la turbulencia de las capas delgadas que se forman en
el fluido, dado que es en estas capas donde se presentan grandes cambios de velocidad. De
esta manera, las tasas de cambio de las variables que se encuentran en dirección del flujo,
son insignificantes en comparación con las variables transversales.
Los principales flujos que se tienen en cuenta en los modelos de turbulencia son los
siguientes:
Flujos turbulentos libres:
- Flujo en la capa de mezcla.
- Chorro.
- Estela.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
55
Capas límite cerca de paredes sólidas:
- Capa límite de placa plana.
- El flujo en la capa límite de la tubería.
3.3.6.2 Flujos turbulentos libres
Como se mencionó anteriormente, los flujos turbulentos libres se pueden clasificar en flujo
en la capa de mezcla, chorro y estela.
El flujo en la capa de mezcla se forma en la interface entre dos regiones: una con un rápido
movimiento del flujo y otra con uno lento. En un chorro, un flujo de alta velocidad está
completamente rodeado por un flujo estacionario. Por último, una estela se forma detrás de
algún objeto, por lo tanto existe una región del flujo que se mueve lentamente y está
rodeado por una región con una velocidad mayor. En la siguiente figura se muestra un
esquema de estos tres tipos de flujos turbulentos libres, junto con la distribución de
velocidades que se generan en la dirección del flujo.
3.3.6.3 Capas límite cerca de paredes sólidas
Debido a la presencia de un sólido como frontera del fluido, el comportamiento del flujo y
la estructura de la turbulencia son considerablemente diferentes a la de los flujos
turbulentos libres.
En las capas delgadas de los flujos turbulentos se puede determinar un número de Reynolds
basado en un longitud de escala L en la dirección del flujo (o radio de la tubería)
𝑅𝑒
𝐿
.
Generalmente este valor es muy grande, por ejemplo, si se tiene una velocidad de 1 m/s,
una longitud de 0,1 m y una viscosidad de
10
−6
𝑚
2
/𝑠, se puede obtener un 𝑅𝑒
𝐿
= 10
5
.
(a) Flujo en capa de
mezcla
(b) Chorro
(c) Estela
Figura 46. Flujos turbulentos libres (Versteeg & Malalasekera, 1995).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
56
Esto implica que las fuerzas de inercia son significativamente mayores a las fuerzas
viscosas en estas escalas.
Si se forma un número de Reynolds basado en una distancia y lejos de la pared (
𝑅𝑒
𝑦
=
𝑈
𝑦
/𝜐) se ve que si el valor de y es del orden de L el anterior argumento es válido y las
fuerzas dominantes en las pared son las inerciales. Por otro lado, si y tiende a cero, el
número de Reynolds también tiende a cero; pero justo antes de que y sea cero, se encontrará
una gama de valores de y en donde
𝑅𝑒
𝑦
es del orden de 1. A esta distancia de la pared la
corriente se ve influida, en su mayoría, por los esfuerzos viscosos y no dependerá de los
parámetros de corriente libre. La velocidad media del flujo solo depende de la distancia y
desde la pared, la densidad del fluido, la viscosidad y el esfuerzo cortante generado por la
pared. Por lo tanto:
𝑈 = 𝑓(𝑦, 𝜌, 𝜇, 𝜏
𝑤
)
El análisis dimensional muestra que:
𝑢
+
=
𝑈
𝑢
𝜏
= 𝑓 (
𝜌𝑢
𝜏
𝑦
𝜇
) = 𝑓(𝑦
+
)
Ecuación 39. Ley de pared (Versteeg & Malalasekera, 1995).
Esta ecuación es llamada la ley de pared y contiene la definición de
𝑢
+
y
𝑦
+
. Donde
𝑢
𝜏
es
la velocidad de corte.
Es importante conocer las condiciones y los parámetros que gobiernan los tipos de flujo
turbulento para poder comprender las ecuaciones de Reynols-Averaged Navier-Stokes.
3.3.7 Ecuaciones de Reynolds-Averaged Navier-Stokes (RANS) para fluidos
incompresibles
Este tipo de ecuaciones ayudan a entender las
consecuencias de las fluctuaciones
turbulentas medias para flujos incompresibles con viscosidad constante. El hecho de
suponer que el flujo es incompresible, ayuda de manera significativa a la simplificación del
algebra involucrada en el desarrollo de las ecuaciones de RANS.
En primer lugar, se deben tener en cuenta las ecuaciones de continuidad de Navier Stokes:
𝑑𝑖𝑣 𝒖 = 0
𝜕𝑢
𝜕𝑡
+ 𝑑𝑖𝑣(𝑢𝒖) = −
1
𝜌
𝜕𝑝
𝜕𝑥
+ 𝜐 𝑑𝑖𝑣(𝑔𝑟𝑎𝑑(𝑢))

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
57
En los sistemas de ecuaciones para todas las direcciones de flujo, se van a remplazar las
variables de velocidad y de presión por las suma de los componentes medios y fluctuantes:
𝑢 = 𝑈 + 𝑢
′
; 𝑣 = 𝑉 + 𝑣
′
; 𝑤 = 𝑊 + 𝑤
′
; 𝑝 = 𝑃 + 𝑝′
Sustituyendo estas variables en la ecuación de momento se obtiene:
𝜕𝑈
𝜕𝑡
+ 𝑑𝑖𝑣(𝑈𝑼) + 𝑑𝑖𝑣(𝑢
′
𝒖
′
̅̅̅̅̅̅) = −
1
𝜌
𝜕𝑃
𝜕𝑥
+ 𝜐 𝑑𝑖𝑣(𝑔𝑟𝑎𝑑(𝑈))
Los términos se refieren a los productos de velocidades fluctuantes y están asociados con la
transferencia de momento de convección debido a los remolinos turbulentos.
Reorganizando los términos se obtiene la ecuación de RANS
:
𝜕𝑈
𝜕𝑡
+ 𝑑𝑖𝑣(𝑈𝑼) = −
1
𝜌
+ 𝜐𝑑𝑖𝑣(𝑔𝑟𝑎𝑑(𝑈)) +
1
𝜌
[
𝜕(−𝜌𝑢
′2
̅̅̅̅)
𝜕𝑥
+
𝜕(−𝜌𝑢′𝑣′
̅̅̅̅̅)
𝜕𝑦
+
𝜕(−𝜌𝑢′𝑤′
̅̅̅̅̅̅)
𝜕𝑧
]
Ecuación 40. Ecuación de Reynolds-Averaged Navier-Stokes (Versteeg & Malalasekera, 1995).
3.3.8 Cálculos para del flujo turbulento
Dada la importancia de la turbulencia en la aplicación de la ingeniería y de la manera
dinámica y compleja en que interactúan las escalas de longitud y tiempo, se han
desarrollado métodos numéricos que permiten capturar de maneras diferentes los efectos de
la turbulencia. Estos métodos se pueden agrupar en las siguientes tres categorías (Versteeg
& Malalasekera, 1995):
•Modelos de turbulencia para las ecuaciones RANS: la atención se centra en el flujo
medio y en los efectos de la turbulencia en las propiedades medias de flujo. Existen
términos adicionales en las ecuaciones de flujo de tiempo medio que interactúan con las
fluctuaciones turbulentas. Estos términos adicionales se modelan con los modelos clásicos
de turbulencia: modelo k-ε y modelo cortante de Reynolds. Para resolver estos modelos, es
necesario contar con recursos informáticos y computacionales para que los cálculos sean
precisos y acordes con el enfoque de ingeniería.
• Large Eddy Simulation (LES): Este es un cálculo intermedio de la turbulencia el cual
realiza un seguimiento del comportamiento de los remolinos más grandes del fluido. El
método implica un refinamiento de las ecuaciones de Navier-Stokes, en donde se rechazan
los remolinos más pequeños. Este modelo es el más adecuado para resolver problemas en
donde se tenga una geometría compleja.
• Simulación Numérica Directa (DNS): Estas simulaciones calculan el flujo medio y
todas las fluctuaciones de velocidad turbulenta. Las ecuaciones de Navier-Stokes se

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
58
resuelven en redes espaciales que son lo suficientemente finas para que se puedan resolver
con las escalas de longitud de Kolmogorov en donde la energía de disipación tiene lugar y
en donde los pasos del tiempo son lo suficientemente pequeños para resolver el periodo de
las fluctuaciones más rápidas. Estos cálculos con extremadamente costosos en términos
computacionales.
3.3.9 Modelo de turbulencia K-ε
Cuando se realiza un análisis en dos dimensiones de las capas cortantes, los cambios en la
turbulencia son tan suaves que se pueden ajustar a las condiciones locales. En flujos donde
la convección y la difusión generan diferencias significativas entre la producción y
destrucción de la turbulencia, por ejemplo en flujos re circulantes, se debe realizar un
análisis algebraico para la longitud de mezcla. El modelo k-ε se enfoca en los mecanismos
que afectan la energía cinética turbulenta (Versteeg & Malalasekera, 1995).
Es necesario conocer algunas definiciones. La energía cinética instantánea de un flujo k(t)
es la suma de la energía cinética media
𝐾 =
1
2
(𝑈
2
+ 𝑉
2
+ 𝑊
2
) y la energía cinética
turbulenta
𝑘 =
1
2
(𝑢
′2
̅̅̅̅ + 𝑣
′2
̅̅̅̅ + 𝑤
′2
̅̅̅̅̅).
Por otro lado, para facilitar los cálculos, es común escribir los componentes de las tasas de
deformación
𝑆
𝑖𝑗
y esfuerzo cortantes
𝜏
𝑖𝑗
de forma matricial:
𝑆
𝑖𝑗
= [
𝑆
𝑥𝑥
𝑆
𝑥𝑦
𝑆
𝑥𝑧
𝑆
𝑦𝑥
𝑆
𝑦𝑦
𝑆
𝑦𝑧
𝑆
𝑧𝑥
𝑆
𝑧𝑦
𝑆
𝑧𝑧
] 𝜏
𝑖𝑗
= [
𝜏
𝑥𝑥
𝜏
𝑥𝑦
𝜏
𝑥𝑧
𝜏
𝑦𝑥
𝜏
𝑦𝑦
𝜏
𝑦𝑧
𝜏
𝑧𝑥
𝜏
𝑧𝑦
𝜏
𝑧𝑧
]
La descomposición de las tasas de deformación de un elemento del fluido en un flujo
turbulento se desarrolla de la siguiente manera:
𝑠
𝑥𝑥
(𝑡) = 𝑆
𝑥𝑥
+ 𝑠
𝑥𝑥
′
=
𝜕𝑈
𝜕𝑥
+
𝜕𝑢′
𝜕𝑥
; 𝑠
𝑦𝑦
(𝑡) = 𝑆
𝑦𝑦
+ 𝑠
𝑦𝑦
′
=
𝜕𝑉
𝜕𝑦
+
𝜕𝑣′
𝜕𝑦
;
𝑠
𝑧𝑧
(𝑡) = 𝑆
𝑧𝑧
+ 𝑠
𝑧𝑧
′
=
𝜕𝑊
𝜕𝑧
+
𝜕𝑤′
𝜕𝑧
𝑠
𝑥𝑦
(𝑡) = 𝑆
𝑥𝑦
+ 𝑠
𝑥𝑦
′
= 𝑠
𝑦𝑥
(𝑡) = 𝑆
𝑦𝑥
+ 𝑠
𝑦𝑥
′
=
1
2
[
𝜕𝑈
𝜕𝑦
+
𝜕𝑉
𝜕𝑥
] +
1
2
[
𝜕𝑢
′
𝜕𝑦
+
𝜕𝑣
′
𝜕𝑥
]

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
59
𝑠
𝑥𝑧
(𝑡) = 𝑆
𝑥𝑧
+ 𝑠
𝑥𝑧
′
= 𝑠
𝑧𝑥
(𝑡) = 𝑆
𝑧𝑥
+ 𝑠
𝑧𝑥
′
=
1
2
[
𝜕𝑈
𝜕𝑧
+
𝜕𝑊
𝜕𝑥
] +
1
2
[
𝜕𝑢
′
𝜕𝑧
+
𝜕𝑤
′
𝜕𝑥
]
𝑠
𝑦𝑧
(𝑡) = 𝑆
𝑦𝑧
+ 𝑠
𝑦𝑧
′
= 𝑠
𝑧𝑦
(𝑡) = 𝑆
𝑧𝑦
+ 𝑠
𝑧𝑦
′
=
1
2
[
𝜕𝑉
𝜕𝑧
+
𝜕𝑊
𝜕𝑦
] +
1
2
[
𝜕𝑣
′
𝜕𝑧
+
𝜕𝑤
′
𝜕𝑦
]
Teniendo en cuenta lo anterior, la ecuación de energía cinética media K se puede obtener
multiplicando la componente de velocidad en cada dirección por su respectiva Ecuación de
Reynolds (Ecuación 36).
𝜕(𝜌𝐾)
𝜕𝑡
+ 𝑑𝑖𝑣(𝜌𝐾𝑼) = 𝑑𝑖𝑣(−𝑃𝑼 + 2𝜇𝑼𝑆
𝑖𝑗
− 𝜌𝑼𝑢
𝑖
′
𝑢
𝑗
′
̅̅̅̅̅̅) − 2𝜇𝑆
𝑖𝑗
. 𝑆
𝑖𝑗
+ 𝜌𝑢
𝑖
′
𝑢
𝑗
′
̅̅̅̅̅̅. 𝑆
𝑖𝑗
(I) (II) (III) (IV) (V) (VI) (VII)
(I): Tasa de cambio de la energía cinética media K.
(II): Transporte de K por convección.
(III): Transporte de K por presión.
(IV): Transporte de K por esfuerzos viscosos.
(V): Transporte de K por esfuerzos de Reynolds.
(VI): Tasa de disipación viscosas de K.
(VII): Tasa de destrucción de K por la producción de turbulencia.
Por otro lado, multiplicando la ecuación de Navier-Stokes por los componentes fluctuantes
de velocidad, se puede obtener la ecuación de energía cinética turbulenta:
𝜕(𝜌𝑘)
𝜕𝑡
+ 𝑑𝑖𝑣(𝜌𝑘𝑼) = 𝑑𝑖𝑣 (−𝑝
′
𝒖
′
̅̅̅̅̅̅ + 2𝜇𝒖
′
𝑠
𝑖𝑗
′
̅̅̅̅̅̅ − 𝜌
1
2
𝑢
𝑖
′
. 𝑢
𝑖
′
𝑢
𝑗
′
̅̅̅̅̅̅̅̅̅) − 2𝜇𝑠
𝑖𝑗
′
. 𝑠
𝑖𝑗
′
̅̅̅̅̅̅̅̅ + 𝜌𝑢
𝑖
′
𝑢
𝑗
′
̅̅̅̅̅̅. 𝑆
𝑖𝑗
(I) (II) (III) (IV) (V) (VI) (VII)
(I): Tasa de cambio de la energía cinética turbulenta k.
(II): Transporte de k por convección.
(III): Transporte de k por presión.
(IV): Transporte de k por esfuerzos viscosos.
(V): Transporte de k por esfuerzos de Reynolds.
(VI): Tasa de disipación de k.
(VII): Tasa producción de k.
Teniendo en cuenta los fenómenos de disipación de energía cinética causada por los
remolinos pequeños y los esfuerzos cortantes viscosos, la tasa de disipación por unidad de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
60
volumen (VI) es normalmente escrita como el producto entre la densidad y la tasa de
disipación de la energía cinética turbulenta por unidad de masa ε:
𝜀 = 2𝜈𝑠
𝑖𝑗
′
. 𝑠
𝑖𝑗
′
̅̅̅̅̅̅̅̅
Ecuación 41. Disipación en la ecuación de energía cinética turbulenta (Versteeg & Malalasekera, 1995).
Condiciones de frontera:
Las ecuaciones del modelo para k y ε son elípticas a causa del termino de difusión de
gradiente. Su comportamiento es similar a otras ecuaciones de flujo elípticas, lo que da
lugar a la necesidad de las siguientes condiciones de frontera:
• Entrada: deben recibir distribuciones de k y ε.
• Salida: ejes simétricos, ∂k / ∂n = 0 y ∂ε / ∂n = 0.
• Corriente libre: k y ε se debe dar o ∂k / ∂n = 0 y ∂ε / ∂n = 0.
• Paredes sólidas: enfoque depende de número de Reynolds.
Como se mencionó al principio del capítulo, la metodología CFD se desarrolla utilizando
softwares especializados en donde se pueden aplicar las ecuaciones a modelos
computacionales basados en modelos físicos. De esta manera se puede analizar el
comportamiento de los fluidos y obtener conclusiones con el fin de modificar los modelos
computacionales y físicos de acuerdo con los resultados obtenidos. Para el caso de este
proyecto se utilizó ANSYS FLUENT y el desarrollo de todo el modelo computacional y
sus resultados se encuentran en el Capítulo 6. Modelación numérica en CFD.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
61
4. Modelo físico de los procesos de mezcla en los nudos
El modelo físico requerido para la parte experimental de éste proyecto se encuentra ubicado
en el Laboratorio de Hidráulica de la Universidad de los Andes y cuenta con los siguientes
componentes:
- Tanques de almacenamiento. El modelo cuenta con dos tanques elevados de
almacenamiento, los cuales son alimentados con agua proveniente directamente de la
red de distribución de agua potable de Bogotá. Los tanques tienen unas dimensiones de
1.25 m. de largo, 0.39 m. de ancho y 0.59 m. de alto. Esto corresponde a un
almacenamiento máximo en cada tanque de 287 L. Los dos tanques tienen un sistema
de rebose a una altura de 0.5 m lo que permite que el agua no pase de ese límite. El
sistema de rebose para cada tanque consiste en que, para el tanque que siempre tiene el
agua limpia, va a existir un caudal de entrada constante de tal manera que la altura
piezométrica sea la misma durante todo el ensayo. De manera similar, para el tanque
que va a contener el trazador existe un caudal de entrada constante que hace parte de
un sistema de recirculación. Este funciona a partir de un tanque a nivel del suelo, el
cual tiene una capacidad de 600 L, allí es en donde se mezcla el agua con el trazador,
luego, por medio de una bomba sumergible se envía el agua "contaminada" al tanque
elevado para comenzar con los ensayos. Al igual que el otro tanque, el sistema de
rebose se encuentra a 0.5 m, lo que permite que las alturas piezométricas de los dos
tanques sean las mismas.
- Tuberías: Originalmente el modelo fue construido para realizar ensayos con tuberías de
1 pulgada de diámetro por lo cual todos los accesorios con los que se cuenta, son para
tuberías de este tamaño. Las tuberías que salen de los tanques de almacenamiento están
construidas en PVC y se conserva este mismo material hasta una unión, en la cual se
cambia a una tubería, del mismo tamaño, construida en vidrio o en acrílico. Por
consiguiente, la intersección de las tuberías está hecha de un material transparente que
permita observar cómo son los procesos de mezcla cuando se utiliza un colorante del
agua. Para este proyecto las configuraciones presentan algunas variaciones; por lo
tanto, existe una unión en cruz donde una de las tuberías de salida es de 1.5 pulgadas.
- Control de caudal: Para controlar los caudales de entrada y salida del sistema, se
utilizan unas válvulas de cobre tipo cortina, las cuales permiten modificar el flujo que
entra y sale por cada una de las tuberías.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
62
Figura 47. Válvulas de entrada y salida para controlar caudal.
Para medir el caudal se cuenta con 3 sensores electromagnéticos de caudal. Estos
sensores son de la marca Kobold y son usados para medir y monitorear la tasa de
caudal de fluidos. Cuando una medida de conductividad eléctrica atraviesa el campo
direccional magnético, una medida de voltaje es inducida de acuerdo con la ley de
Faraday de inducción. El tamaño de la medida del voltaje es proporcional a la tasa
media de flujo, y por ende, a la tasa del flujo de volumen. Es importante mencionar que
la medición del flujo con este sensor, no es afectada por variables como la presión,
temperatura, densidad ni viscosidad.
Los caudalímetros están fabricados en acero inoxidable y los electrodos están hechos
en platino. El rango de medición se encuentra entre 0.4 y 2500 m
3
/h con una precisión
de 0.5 L/s. Para las mediciones realizadas en este proyecto se obtuvo un rango de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
63
caudal entre 0.065 L/s y 1.11 L/s, lo que corresponde a velocidades entre 0.028 m/s y
1.233 m/s.
A continuación se muestra una imagen del equipo:
Figura 48. Caudalímetro electromagnético,
- Medición de concentración: Para medir la concentración de cloro se cuenta con dos
sensores de cloro libre. Uno de los sensores está conectado a una de las tuberías de
entrada y el otro a una de las tuberías de salida. La tubería de entrada que tiene
conectado el sensor es la que contiene una mayor concentración de cloro; en la otra
tubería de entrada, se supone una concentración constante de cloro la cual es medida
antes de iniciar con la ejecución de los ensayos. Como se conocen tres valores de
concentración, se puede conocer la concentración en la tubería restante haciendo uso
del concepto de conservación de masa.
El sensor utilizado es de la marca Endress+Hauser y tiene la capacidad de medir
concentraciones dentro de un rango entre 0,05 y 20 mg/L con una precisión de ±0.5%
de la lectura. Adicionalmente, tiene una resolución de 0,01 mg/L. Para las mediciones

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
64
realizadas en este proyecto se obtuvo un rango de concentración de cloro entre 0.074
mg/L y 15.27 mg/L.
El sensor está compuesto por el medidor de cloro, el sensor de cloro y la celda de flujo.
Estas tres herramientas trabajan en conjunto para proporcionar una medida adecuada
de la concentración en el tiempo.
Figura 49. Sensor de cloro.
A continuación, se muestra el modelo físico general con todos los componentes que se
mencionaron anteriormente:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
65
Figura 50. Modelo físico general.
Tuberías de PVC
Caudalímetros
electromagnéticos
Sensor de cloro
y celda de flujo
Medidor de
cloro

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
66
5. Definición de configuraciones de las uniones de tuberías
Para lograr los objetivos propuestos en este proyecto se van a analizar 5 configuraciones de
la intersección de las tuberías. Con el fin de comparar los datos obtenidos en este proyecto
con los reportados en la literatura, se define analizar la configuración en cruz con todas las
tuberías del mismo diámetro. De esta manera se podrá comparar los resultados obtenidos en
este proyecto para dicha configuración con los resultados reportados por los autores, y
verificar que los datos son coherentes y comparables. Además, esto sirve para asegurarse de
que para las demás configuraciones los datos se están tomando de la manera adecuada. A
continuación se muestran las configuraciones que se van a estudiar:
Configuraciones
Pruebas
realizadas por
otros autores
Doble tee del mismo
diámetro (L/d=14)
NO
Cruz con salida de
1.5"
NO
Cruz con entrada de
1.5"
NO
Doble tee del mismo
diámetro
(L/d=CFD)
NO
Cruz todos
diámetros de 1”
SI
En la casilla “Doble tee del mismo diámetro (L/d=CFD)” quiere decir que se van a simular
varias configuraciones doble tee variando la relación L/d hasta encontrar una en la que se
presente el punto de cambio entre mezcla completa e incompleta. Una vez se encuentre este
valor, se realizará el montaje físico para confirmar los resultados de manera experimental.
Las configuraciones estudiadas son las siguientes:
a) Configuración en cruz con tuberías de 1”.
b) Configuración en cruz con tubería de salida de 1.5”.
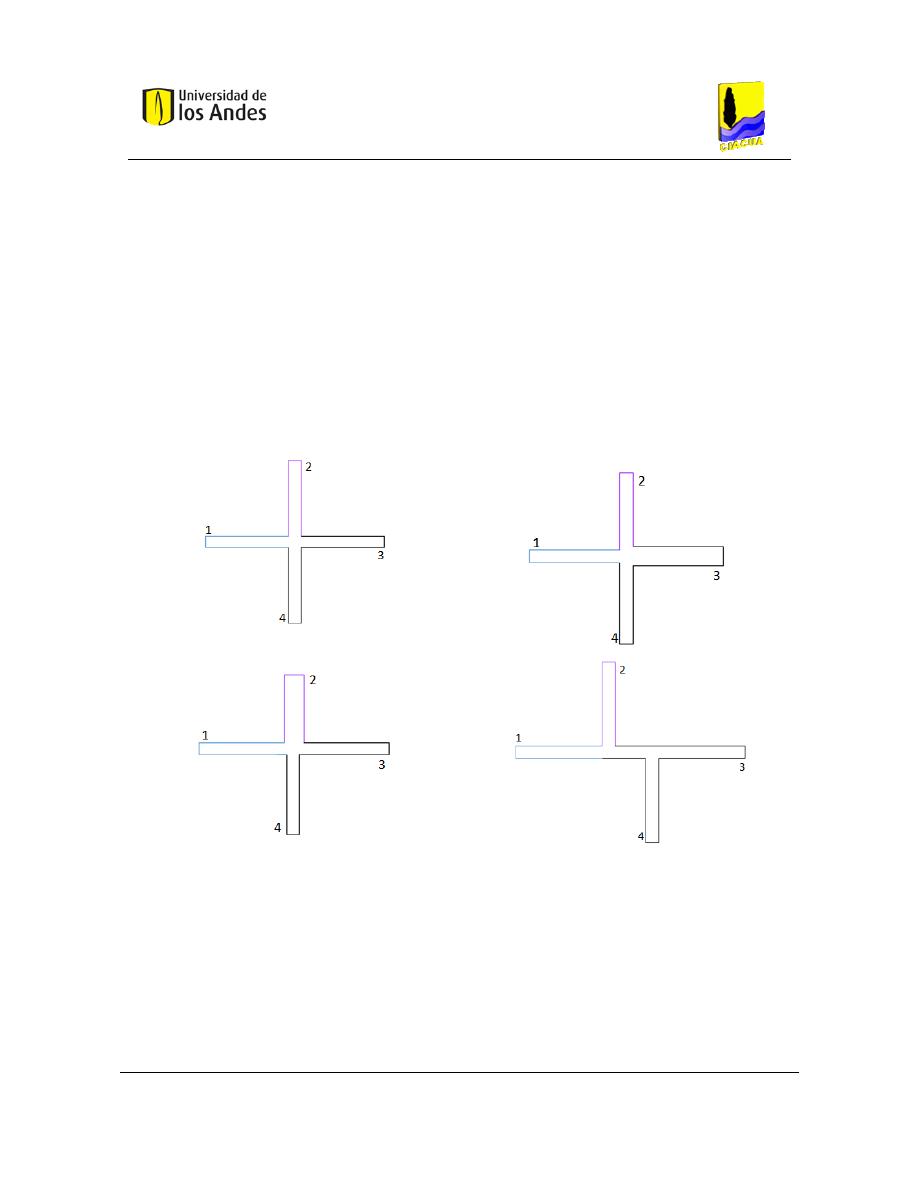
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
67
c) Configuración en cruz con tubería de entrada de 1.5”.
d) Configuración doble tee con tuberías de 1” (L/d=14).
e) Configuración doble tee con tuberías de 1” (L/d=3.7).
En la relación L/d mencionada en las configuraciones d) y e), el numerador representa la
longitud entre las uniones tee de las tuberías de entrada y las de salida, respectivamente.
Por su parte, el denominador es el diámetro de las tuberías de la configuración, que para
este caso es de 1”. Se decidió utilizar la relación L/d ya que la literatura hace uso de esta
cuando se refieren a configuraciones doble tee.
A continuación se muestran de manera esquemática las configuraciones, junto con la
nomenclatura utilizada para cada tubería:
a)
b)
c)
d)
Figura 51. Definición de configuraciones. a) cruz con tuberías de 1". b) Cruz con tubería de salida de 1.5". c) Cruz
con tubería de entrada de 1.5". d) doble tee.
En las configuraciones, la tubería 1 es la tubería de entrada que lleva agua limpia, la tubería
2 es la tubería de entrada que lleva el trazador, la tubería 3 es la tubería de salida adyacente
a la tubería con trazador y la tubería 4 es la tubería de salida opuesta a la tubería con
trazador.
Para evaluar los procesos de mezcla en las diferentes intersecciones del modelo físico se
realizaron dos tipos de experimentos. En el primero, se utilizó como trazador Permanganato

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
68
de Potasio (KMnO
4
), el cual es un colorante y se puede apreciar de manera visual la mezcla
que se presenta en la unión de las tuberías. En el segundo tipo, se utilizó cloro como
trazador; en este caso, se midieron las concentraciones de este soluto en las tuberías de
entrada y de salida de manera continua mientras se variaba la relación de los caudales de
entrada.
A continuación se pueden observar el montaje de las configuraciones definidas
anteriormente cuando se está utilizando Permanganato de Potasio como trazador.
a)
b)
c)
d)
Figura 52. Configuraciones con Permanganato de Potasio. a) cruz con tuberías de 1". b) Cruz con tubería de salida
de 1.5". c) Cruz con tubería de entrada de 1.5". d) doble tee.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
69
6. Modelación numérica en CFD
La modelación numérica y computacional se realizó haciendo uso del software ANSYS
FLUENT, el cual se basa en la ecuación de Navier-Stokes y desarrolla las ecuaciones
presentadas en el marco teórico de este documento. El programa contiene amplias
características para modelar flujos, turbulencias, transferencias de calor y reacciones para
aplicaciones industriales. ANSYS aporta claridad y conocimiento para los problemas de
diseño por medio de una simulación de ingeniería rápida, exacta y flexible. Su tecnología
permite predecir el comportamiento del flujo, para este caso, de una manera confiable. Los
modelos realizados en este proyecto son comparables con los modelos reportados en la
literatura ya que autores como Pedro Romero-Gómez (2008) y Christopher Choi (2008)
también utilizaron ANSYS FLUENT en sus análisis de mezcla completa.
Para la modelación, ANSYS cuenta con una plataforma llamada WorkBench, que conecta
los softwares encargados de la creación de la geometría y el dominio del modelo (Fluid
Flow -DesignModeler), el enmallado (Fluid Flow- Meshing), el procesamiento (Fluent) y el
postprocesamiento (Fluid Flow – CFD-Post).
Por lo tanto, lo primero que se realiza es la definición de la geometría, y dependiente de la
configuración que se quiere analizar, se cambian las longitudes de las tuberías y el tamaño
de los diámetros de las tuberías de entrada y/o salida. Después se genera la malla del
modelo; para esto se utilizaron elementos tetraédricos ya que dentro de la bibliografía se
encontró que varios autores usaron esta forma y obtuvieron buenos resultados.
Posteriormente, se procede a procesar los datos. Para esto, en Fluent se debe realizar la
definición de los modelos. En este caso, para los modelos viscosos se escoge el modelo de
turbulencia k-ε y transporte de especies, en donde se define que los materiales que se van a
transportar son agua y cloro. Se escogió el modelo k-ε debido a que es el más utilizado por
otros autores ya que es el que mejor representa las condiciones de turbulencia en sistemas
como el desarrollado en este proyecto.
Luego, se determinan las condiciones de frontera en donde se asigna para las tuberías de
entrada la velocidad, la intensidad de turbulencia, el diámetro y la fracción de masa de
cloro que entra por la tubería correspondiente.
Por otro lado, se definieron los métodos de solución que recomienda la bibliografía para
modelos de turbulencia k-ε utilizando RANS. Para el esquema de acoplamiento de la
presión con la velocidad se escoge SIMPLE y para la discretización espacial se definen los
siguientes métodos para cada parámetro, respectivamente:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
70
- Gradiente: Green- Gauss Cell Based.
- Presión: Standard.
- Momento: Second order Upwind.
- Energía cinética turbulenta: Quick.
- Tasa de disipación turbulenta: Quick.
Después de correr el modelo, se pueden visualizar los resultados obtenidos y realizar el
análisis correspondiente.
Para cada una de las configuraciones estudiadas, se siguió el procedimiento anteriormente
descrito para obtener resultados con respecto a los procesos de mezcla en las intersecciones.
6.1. Modelación configuración cruz con tuberías de 1”
La geometría de esta configuración consiste en una cruz donde las dos tuberías de entrada y
las dos de salida tienen un diámetro de 1”. La longitud de todas las tuberías en el modelo
físico es de 40 cm; sin embargo, para el modelo computacional se utilizó una longitud de
90 cm con el fin de asegurar que los perfiles de velocidades en las tuberías se desarrollen
completamente antes de llegar a la intersección. A continuación se muestra la imagen del
dominio.
Figura 53. Geometría configuración a).
Una vez teniendo la geometría y el domino definidos, se procede a crear la malla. Se realizó
un análisis de independencia de mallado con el fin de determinar si el número de elementos
tenía alguna influencia sobre los resultados de mezcla. Por lo tanto, la primera malla se creó
con 53,260 elementos, la segunda con el doble 108,353 y la tercera con 206,315 elementos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
71
Para saber si la calidad de la malla es buena, ANSYS arroja un valor entre 0 y 1, siendo 1
una malla de muy buena calidad. Si este valor es mayor a 0.01 se puede asegurar que la
calidad de la malla es buena y el modelo converge.
Nodos:
11980
Elementos:
53260
Calidad de malla:
0.247
Nodos:
24014
Elementos:
108353
Calidad de la malla:
0.273
Nodos:
44184
Elementos:
206315
Calidad de la malla:
0.251
Figura 54. Comparación del tamaño de la malla.
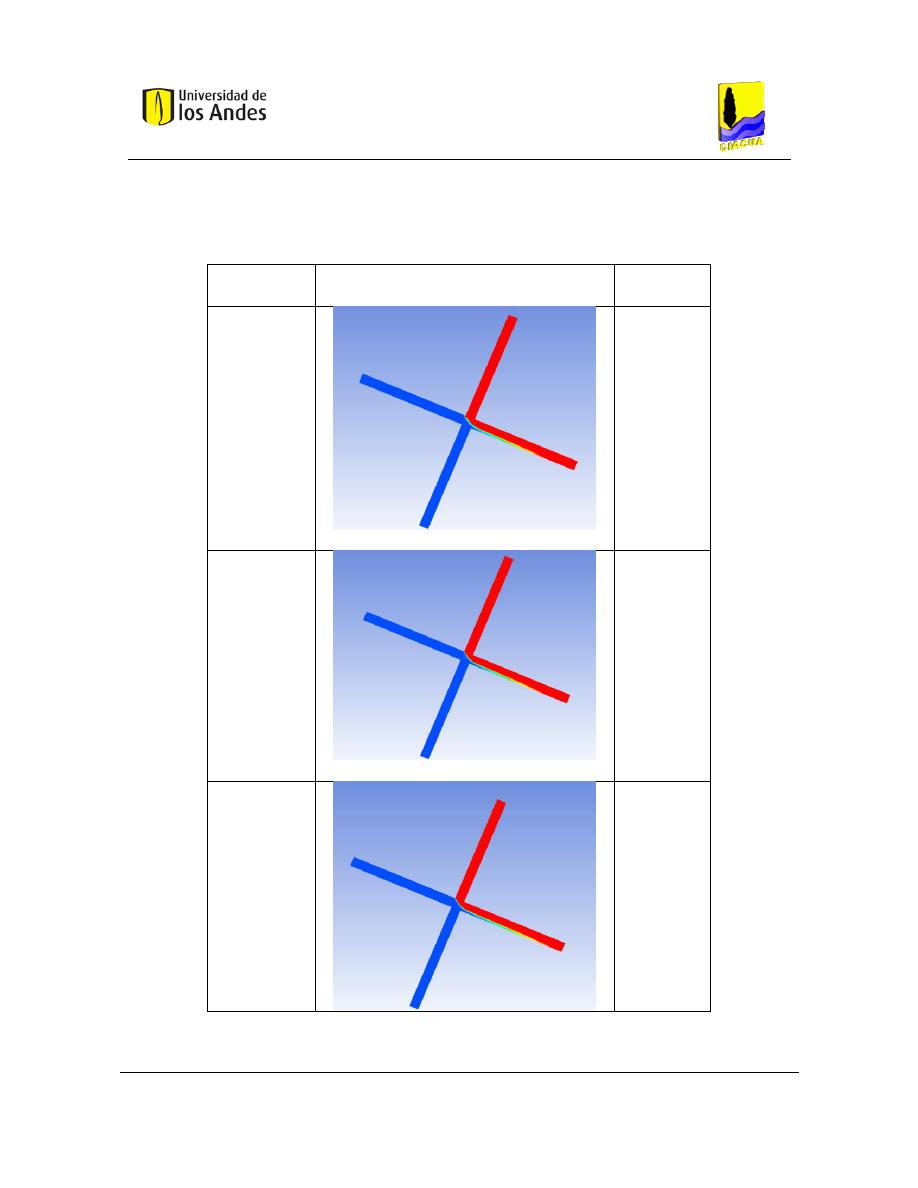
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
72
Después de realizar el procesamiento de los resultados para un mismo escenario en donde
el flujo de las tuberías de entrada es el mismo, se obtuvieron los siguientes resultados:
Elementos
de la malla
Imagen
Fracción
de Masa
53260
0.709
108353
0.705
206315
0.701
Figura 55. Comparación de resultados de Fracción de Masa para cada tamaño de malla.
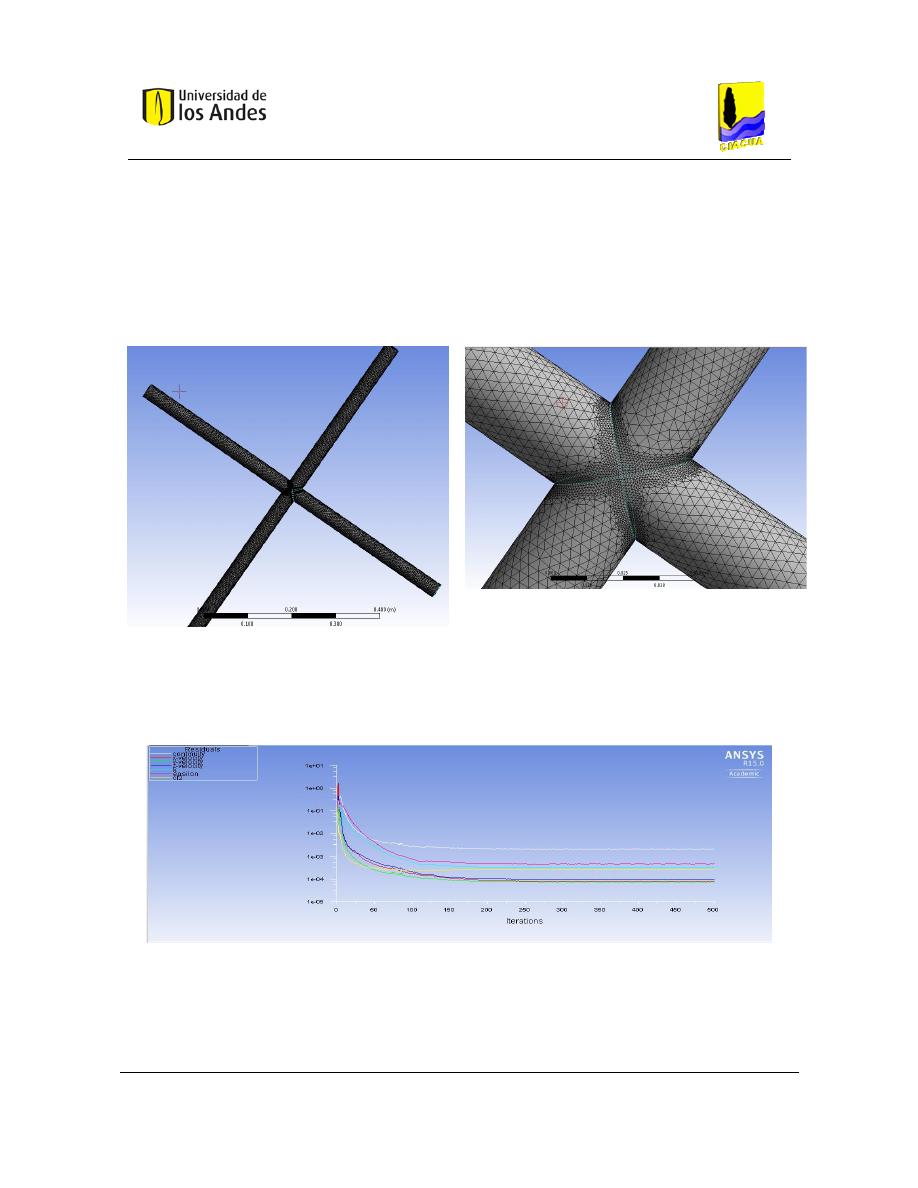
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
73
Como se puede observar, los resultados varían muy poco, esto quiere decir que para este
tipo de modelos, los resultados son independientes del número de nudos entonces no es
necesario tener una malla con tantos elementos si el resultado va a ser el mismo pero el
costo computacional sí es mucho mayor. Se puede observar que a medida que aumenta el
número de elementos, la interfaz incidente de los flujos y los contornos de concentración se
ven más delineados y suaves, por lo tanto solo se realizó el refinamiento de la malla en la
intersección:
Figura 56. Refinamiento del mallado del modelo.
Después de realizar el análisis del mallado, se procedió a realizar el procesamiento de los
datos. Para todas las simulaciones se obtuvo una gráfica de convergencia como la que se
muestra a continuación:
Figura 57. Gráfica de convergencia del modelo k-ε.
En la anterior gráfica se muestran las curvas que hacen referencia a la ecuación de
continuidad (blanca), velocidad en el eje x (roja), velocidad en el eje y (verde), velocidad en
el eje z (azul), k (azul aguamarina), épsilon (fucsia) y cloro (amarilla). Los valores en el eje
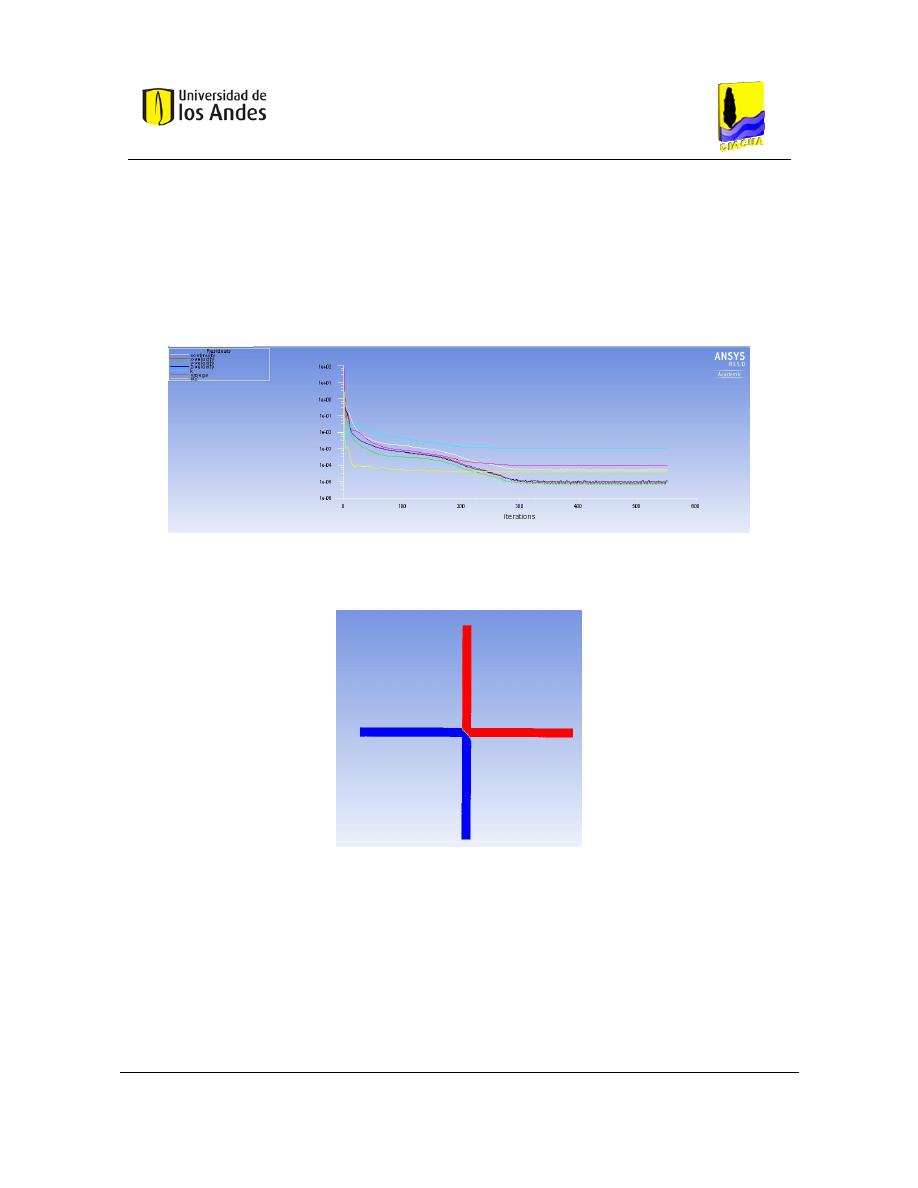
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
74
y indican el error relativo de todos los parámetros con respecto a la iteración anterior. Por
su parte, los valores del eje x corresponden al número de iteraciones realizadas. Se puede
observar en la Figura 57 que todos los parámetros convergen a partir de la iteración 150.
Adicionalmente, se realizó una simulación utilizando el modelo de turbulencia k-ω, para
comparar los resultados obtenidos con diferentes modelos y saber si vale la pena realizar un
análisis de sensibilidad. Para el modelo k-ω se obtuvo la siguiente gráfica de convergencia:
Figura 58. Gráfica de convergencia del modelo k-ω.
Para este caso, y utilizando las mismas condiciones de frontera usadas en el modelo k-ε, se
obtuvo el siguiente resultado:
Figura 59. Resultados con el modelo de turbulencia k-ω.
Se puede observar que las líneas de contorno en la intersección no son tan difusas como las
que resultan utilizando el modelo k-ε.
Se decidió comparar los resultados utilizando el modelo de turbulencia k-ω ya que, según la
bibliografía, es el que mejor representa, junto con el modelo k-ε, el movimiento de los
flujos de acuerdo con las condiciones de frontera definidas. Existen otros modelos de
turbulencia como el LES, en el cual se obtienen resultados mucho más detallados otorgando
una mayor importancia a la resolución temporal. Sin embargo, los costos computacionales
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
75
son mayores y de acuerdo con los objetivos de este trabajo, se determinó que es mejor
utilizar los modelos RANS, los cuales les brinda mayor importancia a la resolución espacial
por medio de un promedio en el tiempo.
Teniendo en cuenta que el modelo de turbulencia k-ε es el más utilizado y el que se reporta
en la bibliografía, y sabiendo que no existe una diferencia considerable con el modelo de
turbulencia k-ω, se decidió utilizar este modelo para la simulación en CFD de las demás
configuraciones. De esta manera, los resultados obtenidos con el modelo de turbulencia k-ε
son los que se muestran a continuación:
Figura 60. Resultados en CFD de la configuración a).
Se cambiaron las condiciones de frontera para la velocidad en las tuberías de entrada de tal
forma que para diferentes relaciones de números de Reynolds se tuvieran los resultados de
la fracción de masa de cloro en la tubería 3 (ver Tabla 1).
Tabla 1. Resultados en CFD de la configuración a).
CFD
Escenario
Re
2
/Re
1
Re
3
/Re
4
Fracción de
masa
tubería 3
1
0.1
1.0
0.3
2
0.3
1.0
0.77
3
0.5
1.0
0.87
4
0.7
1.0
0.92
5
1
1.0
0.94
6
1.3
1.0
0.95
7
1.5
1.0
0.96
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
76
1)
4)
2)
5)
3)
6)
Figura 61. Resultados en CFD correspondientes al número de simulación para la configuración a).
Con los valores reportados en la Tabla 1 se obtuvo la siguiente gráfica:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
77
Gráfica 1. Resultados en CFD para la Fracción de masa de la configuración a).
Como se puede observar en la gráfica, la fracción de masa de cloro que se dirige hacia la
tubería 3 aumenta a medida que aumenta la relación entre los números de Reynolds de las
tuberías de entrada. A partir de una relación cercana a 1, la fracción de masa es constante y
se aproxima a 1.
6.2. Modelación configuración cruz con tubería de salida de 1.5’
La geometría de esta configuración consiste en una cruz donde las dos tuberías de entrada y
una de las tuberías de salida tienen un diámetro de 1” y la otra tubería de salida tiene un
diámetro de 1.5”; la tubería de mayor diámetro es la adyacente a la tubería del trazador. La
longitud de todas las tuberías en el modelo físico es de 40 cm; sin embargo, para el modelo
computacional se utilizó una longitud de 90 cm con el fin de asegurar que los perfiles de
velocidades en las tuberías se desarrollen completamente antes de llegar a la intersección. A
continuación se muestra la imagen del dominio:
0
0.2
0.4
0.6
0.8
1
1.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
78
Figura 62. Geometría configuración b).
Una vez teniendo la geometría y el domino definidos, se procede a crear la malla. Para este
caso, se creó una maya con celdas de forma tetraédrica en la cual se incluyen 8600 nodos y
37631 elementos, teniendo en cuenta el refinamiento de la malla en la intersección.
Figura 63. Malla configuración b).
Después de realizar el mallado, se procedió a realizar el procesamiento de los datos en
donde se obtuvieron resultados como el siguiente:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
79
Figura 64. Resultados en CFD de la configuración b).
Se cambiaron las condiciones de frontera para la velocidad en las tuberías de entrada de tal
forma que para diferentes relaciones de números de Reynolds se tuvieran los resultados de
la fracción de masa de cloro en la tubería 3. A continuación se muestra una tabla con la
fracción de masa obtenida para diferentes relaciones de números de Reynolds. Los
resultados resaltados son los correspondientes a las imágenes.
Tabla 2. Resultados en CFD de la configuración b).
CFD
Simulación
Re
2
/Re
1
Re
3
/Re
4
Fracción de
masa 3
1
0.191
1.0
0.439
2
0.451
1.0
0.554
3
0.955
1.0
0.662
4
0.989
1.0
0.719
5
1.002
1.0
0.706
6
1.048
1.0
0.696
7
1.136
1.0
0.727
8
2.000
1.0
0.801
9
2.429
1.0
0.855
10
3.520
1.0
0.881
11
5.153
1.0
0.931
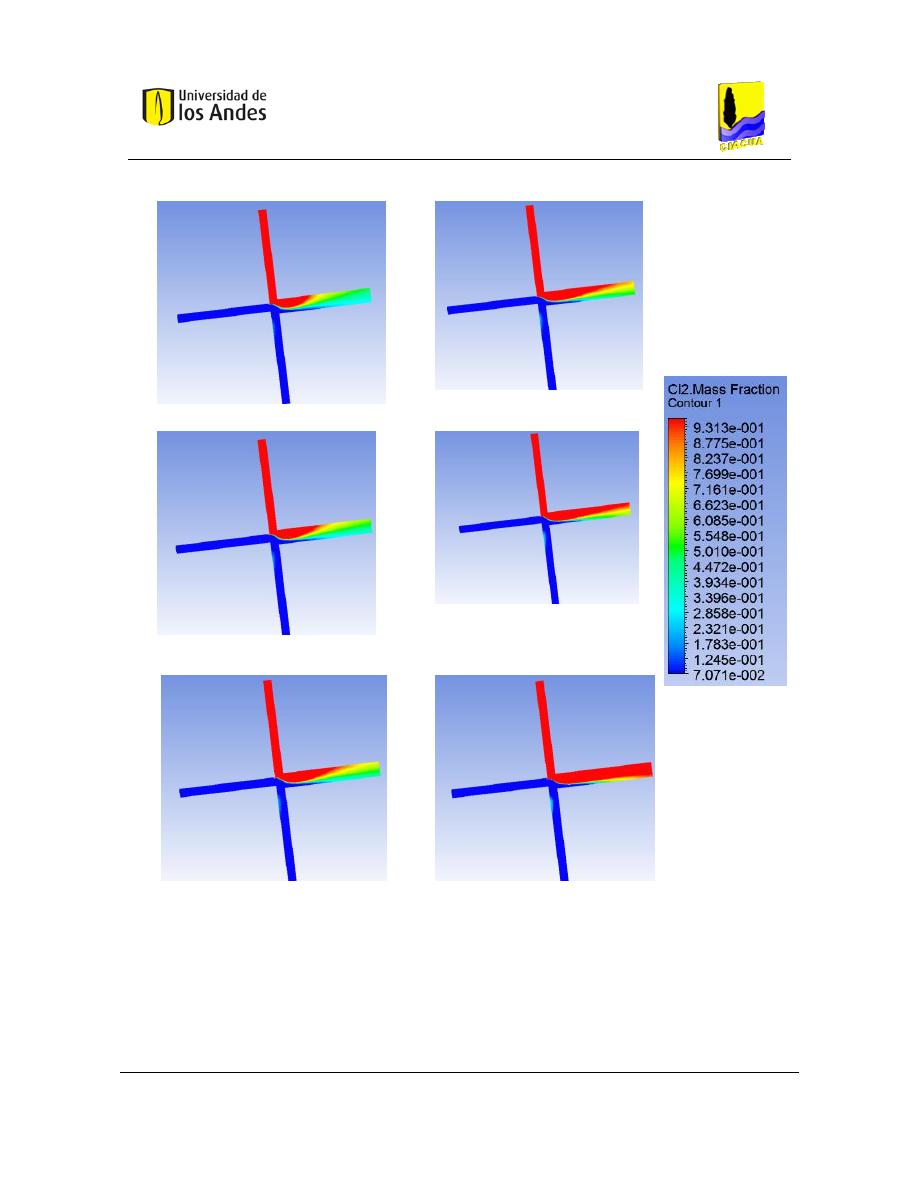
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
80
1)
4)
2)
8)
3)
11)
Figura 65. Resultados en CFD correspondientes al número de simulación para la configuración b).
Con los valores reportados en la Tabla 2 se obtuvo la siguiente gráfica:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
81
Gráfica 2. Resultados en CFD para la Fracción de masa de la configuración b).
Se puede observar que a medida que aumenta la relación del número de Reynolds, la
fracción de masa que se desvía por la tubería adyacente a la del trazador, también aumenta.
6.3. Modelación configuración cruz con tubería de entrada de 1.5”
La geometría de esta configuración consiste en una cruz donde las dos tuberías de salida y
una de las tuberías de entrada tienen un diámetro de 1” y la otra tubería de entrada tiene un
diámetro de 1.5”; la tubería de mayor diámetro es la que lleva el trazador. La longitud de
todas las tuberías en el modelo físico es de 40 cm; sin embargo, para el modelo
computacional se utilizó una longitud de 90 cm con el fin de asegurar que los perfiles de
velocidades en las tuberías se desarrollen completamente antes de llegar a la intersección. A
continuación se muestra la imagen del dominio:
Figura 66. Geometría configuración c).
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0.0
1.0
2.0
3.0
4.0
5.0
6.0
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
82
Una vez teniendo la geometría y el domino definidos, se procede a crear la malla. Para este
caso, se creó una maya con celdas de forma tetraédrica en la cual se incluyen 8600 nodos y
37631 elementos, teniendo en cuenta el refinamiento de la malla en la intersección.
Figura 67. Malla configuración c).
Después de realizar el mallado, se procedió a realizar el procesamiento de los datos en
donde se obtuvieron resultados como el siguiente:
Figura 68. Resultados en CFD de la configuración c).
Se cambiaron las condiciones de frontera para la velocidad en las tuberías de entrada de tal
forma que para diferentes relaciones de números de Reynolds se tuvieran los resultados de
la fracción de masa de cloro en la tubería 3. A continuación se muestra una tabla con la
fracción de masa obtenida para diferentes relaciones de números de Reynolds.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
83
Tabla 3. Resultados en CFD de la configuración c).
CFD
Simulación
Re
2
/Re
1
Re
3
/Re
4
Fracción de masa
tubería 3
1
0.1
1.0
0.3
2
0.3
1.0
0.5
3
0.5
1.0
0.8
4
0.7
1.0
0.82
5
1
1.0
0.85
6
1.3
1.0
0.87
7
1.5
1.0
0.89
1)
3)
2)
4)
Figura 69. Resultados en CFD correspondientes al número de simulación para la configuración c).
Con los valores reportados en la Tabla 3 se obtuvo la siguiente gráfica:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
84
Gráfica 3. Resultados en CFD para la Fracción de masa de la configuración c).
Como se puede observar en la gráfica, la fracción de masa de cloro que se dirige hacia la
tubería tres aumenta a medida que aumenta la relación entre los números de Reynolds de
las tuberías de entrada.
6.4. Modelación configuración doble tee (L/d=14)
La geometría de esta configuración consiste en una doble tee donde todas las tuberías
tienen un diámetro de 1”. La longitud entre las uniones es de 50 cm, lo que corresponde a
una relación de L/d de 14. El resto de la modelación se realizó de la misma manera que en
la configuración en cruz.
Figura 70. Geometría configuración d).
0
0.2
0.4
0.6
0.8
1
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
85
Una vez teniendo la geometría y el domino definidos, se procede a crear la malla. Para este
caso, se creó una maya con celdas de forma tetraédrica en la cual se incluyen 15830 nodos
y 70940 elementos, teniendo en cuenta el refinamiento de la malla en la intersección.
Figura 71. Malla de configuración d).
Después de realizar el mallado, se procedió a realizar el procesamiento de los datos donde
se obtuvieron resultados como el siguiente:
Figura 72. Resultados en CFD de la configuración d).
Se cambiaron las condiciones de frontera para la velocidad en las tuberías de entrada de tal
forma que para diferentes relaciones de números de Reynolds se tuvieran los resultados de
la fracción de masa de cloro en la tubería 3. A continuación se muestra una tabla con la
fracción de masa obtenida para diferentes relaciones de números de Reynolds. Los
resultados resaltados son los correspondientes a las imágenes.
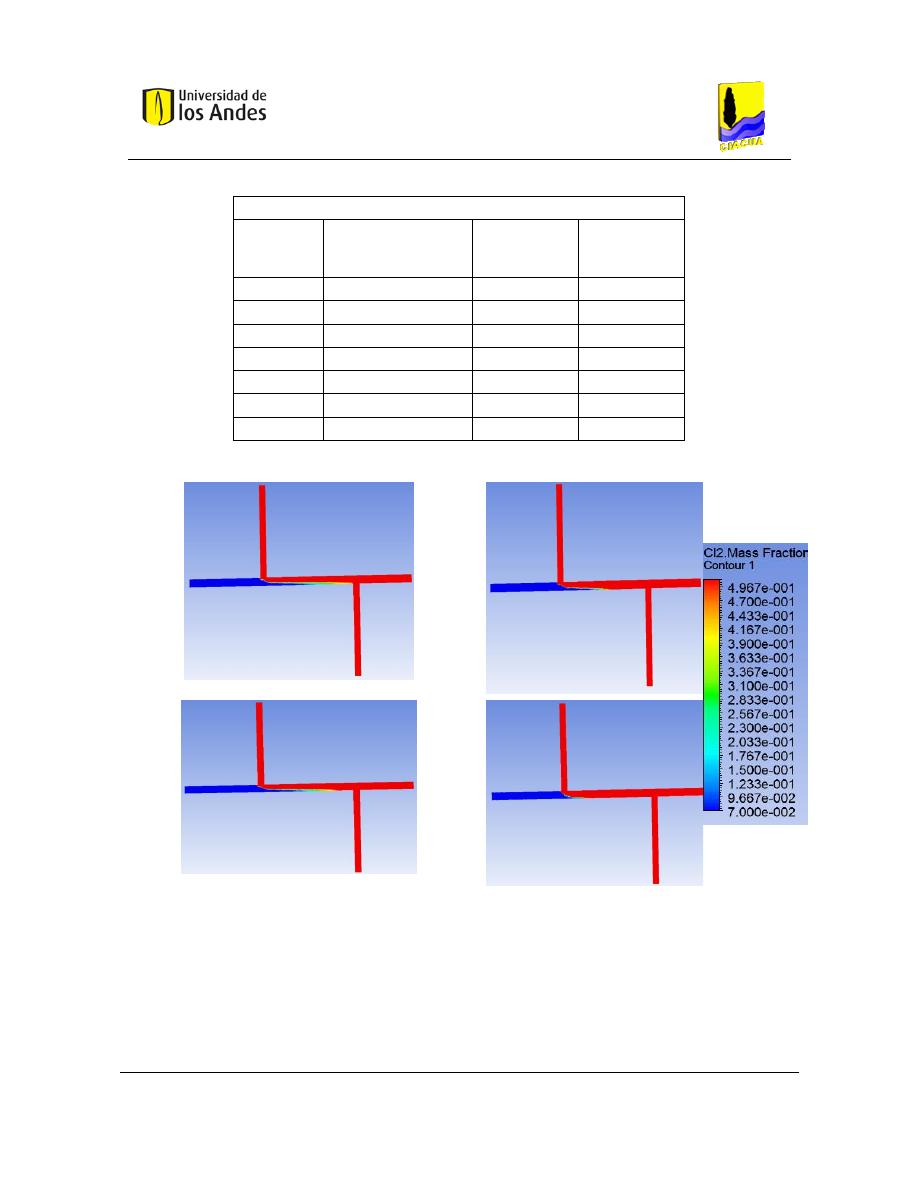
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
86
Tabla 4. Resultados en CFD de la configuración d).
CFD
Simulación
Re
2
/Re
1
Re
3
/Re
4
Fracción de
masa tubería
3
1
0.1
1.0
0.489
2
0.3
1.0
0.499
3
0.5
1.0
0.501
4
0.8
1.0
0.501
5
1
1.0
0.502
6
1.3
1.0
0.502
7
1.5
1.0
0.51
1)
5)
3)
7)
Figura 73. Resultados en CFD correspondientes al número de simulación para la configuración d).
Con los valores reportados en la Tabla 4 se obtuvo la siguiente gráfica:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
87
Gráfica 4. Resultados en CFD para la Fracción de masa de la configuración d).
Para este caso, se puede observar que la fracción de masa es prácticamente constante y se
aproxima a 0.5 independientemente de la relación del número de Reynolds de las tuberías
de entrada. Esto quiere decir que para todas las relaciones de flujo medidas se presente una
mezcla completa.
6.5. Modelación configuración doble tee (L/d=CFD)
Con el fin de determinar la relación de longitud sobre diámetro que permitiera saber cuál es
la longitud a partir de la cual la mezcla comienza a ser completa fue necesario realizar
pruebas utilizando diferentes modelos en los que se varió la relación L/d y en donde se
utilizó una relación de número de Reynolds en las tuberías de entrada de 1. Debido a que
realizar este proceso en un modelo físico resultaba costoso y los recursos temporales no
eran suficientes, se decidió realizar estas simulaciones en ANSYS. Una vez que se encontró
cuál es la relación L/d que cumple el criterio de mezcla completa se realizaron las pruebas
en el laboratorio para comprobar dichos resultados. Por lo tanto las configuraciones que se
probaron utilizando CFD consistieron en una doble tee donde todas las tuberías tienen un
diámetro de 1” y la longitud de las tuberías es de 90 cm para garantizar que el perfil de
velocidades se desarrolle completamente antes de llegar a la intersección. En cuanto a la
longitud entre las uniones tee, se simularon las siguientes relaciones L/d:
Tabla 5. Configuraciones doble tee modeladas en CFD.
Configuraciones
doble tee
L/d
L
1
2
0.068
2
2.5
0.085
3
3
0.102
4
5
0.17
5
10
0.34
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.5
1
1.5
2
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
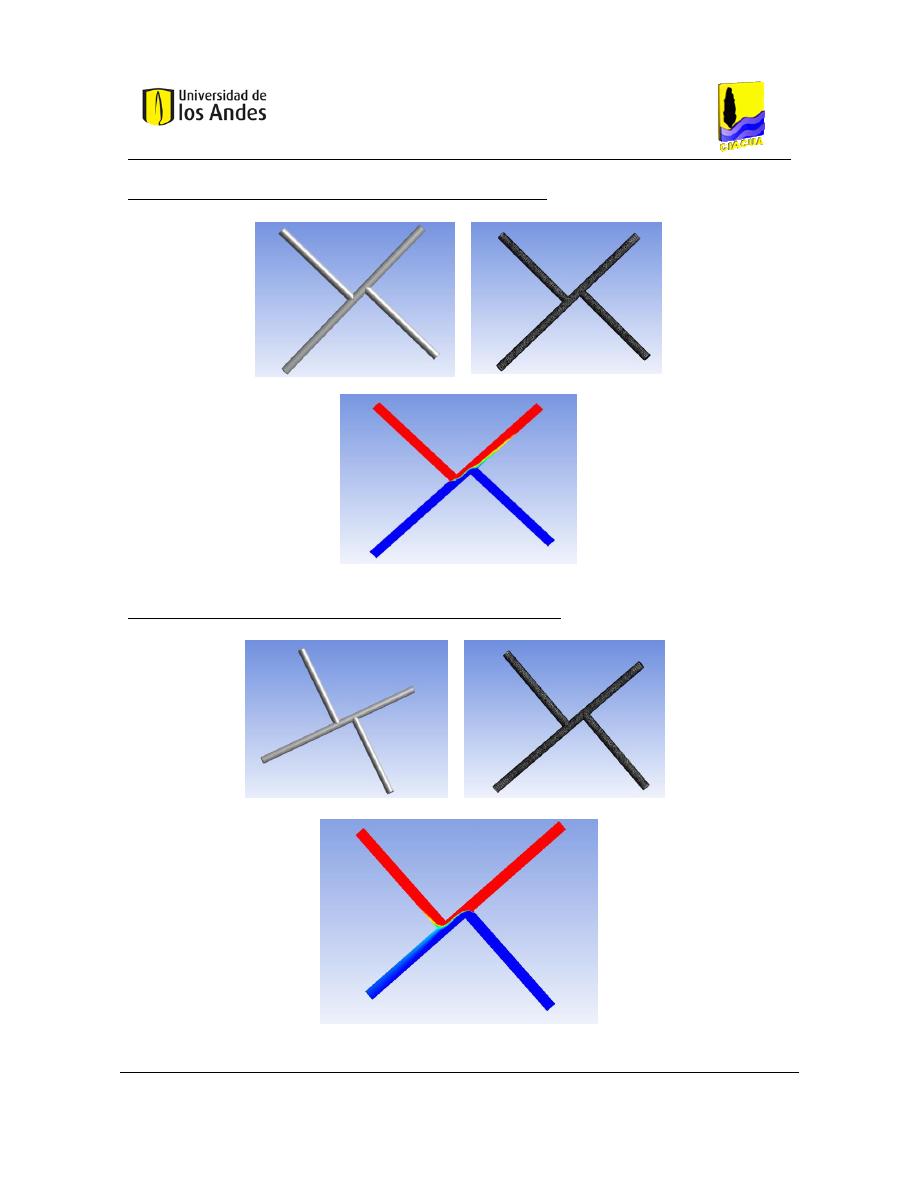
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
88
Configuración doble tee 1 (L/d=2): Fracción de masa 0.78
Figura 74. Resultados CFD configuración doble tee (L/d=2).
Configuración doble tee 2 (L/d=2.5): Fracción de masa 0.72
Figura 75. Resultados CFD configuración doble tee (L/d=2.5).
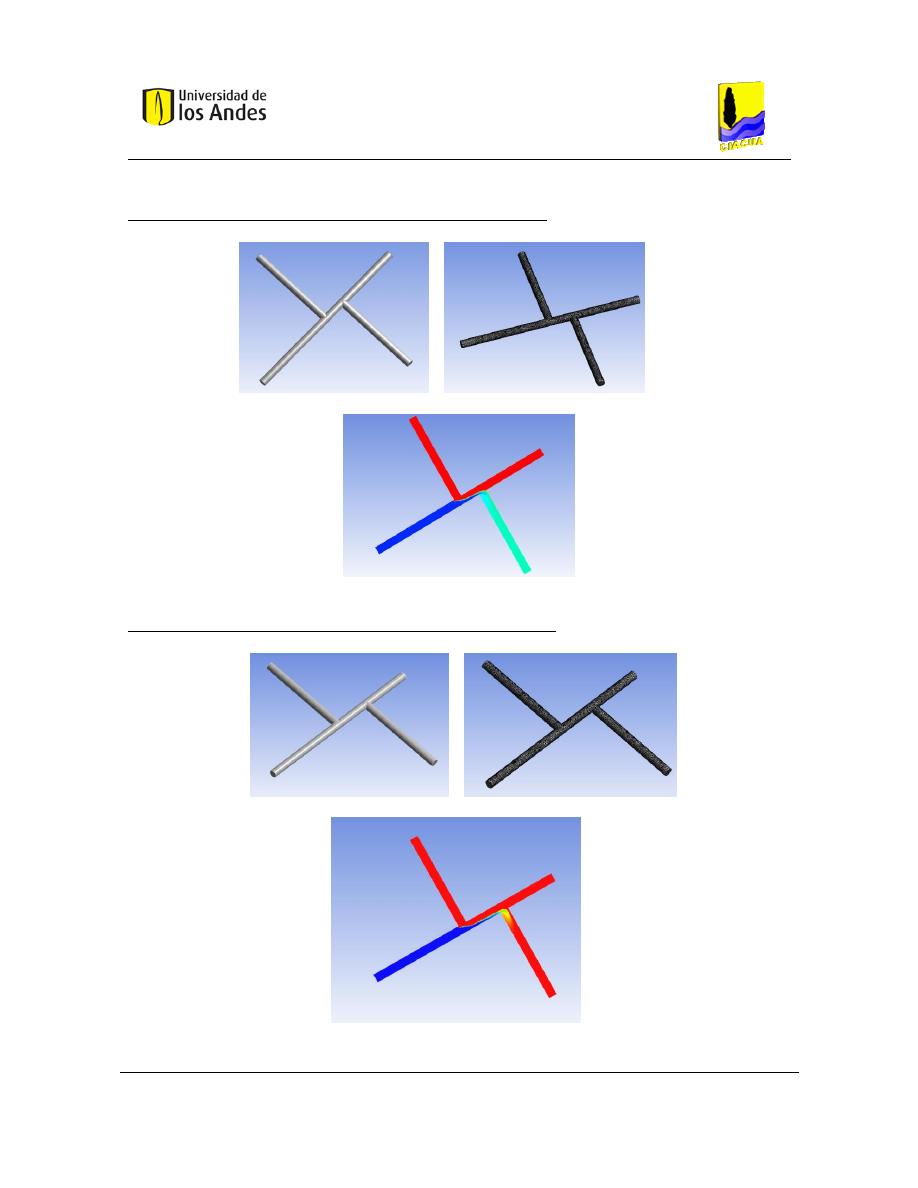
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
89
Configuración doble tee 3 (L/d=3): Fracción de masa 0.65
Figura 76. Resultados CFD configuración doble tee (L/d=3).
Configuración doble tee 4 (L/d=5): Fracción de masa 0.501
Figura 77. Resultados CFD configuración doble tee (L/d=5).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
90
Configuración doble tee 5 (L/d=10): Fracción de masa 0.503
Figura 78. Resultados CFD configuración doble tee (L/d=10).
De acuerdo con los resultados presentados anteriormente, se determinó que la relación L/d
a partir de la cual comienza la mezcla completa se encuentra entre 3 y 5. Por lo tanto, se
probaron varias configuraciones entre estas relaciones L/d y se encontró que la relación que
cumple el criterio de mezcla completa es 3.7. A continuación se muestran los resultados
obtenidos para esta longitud.
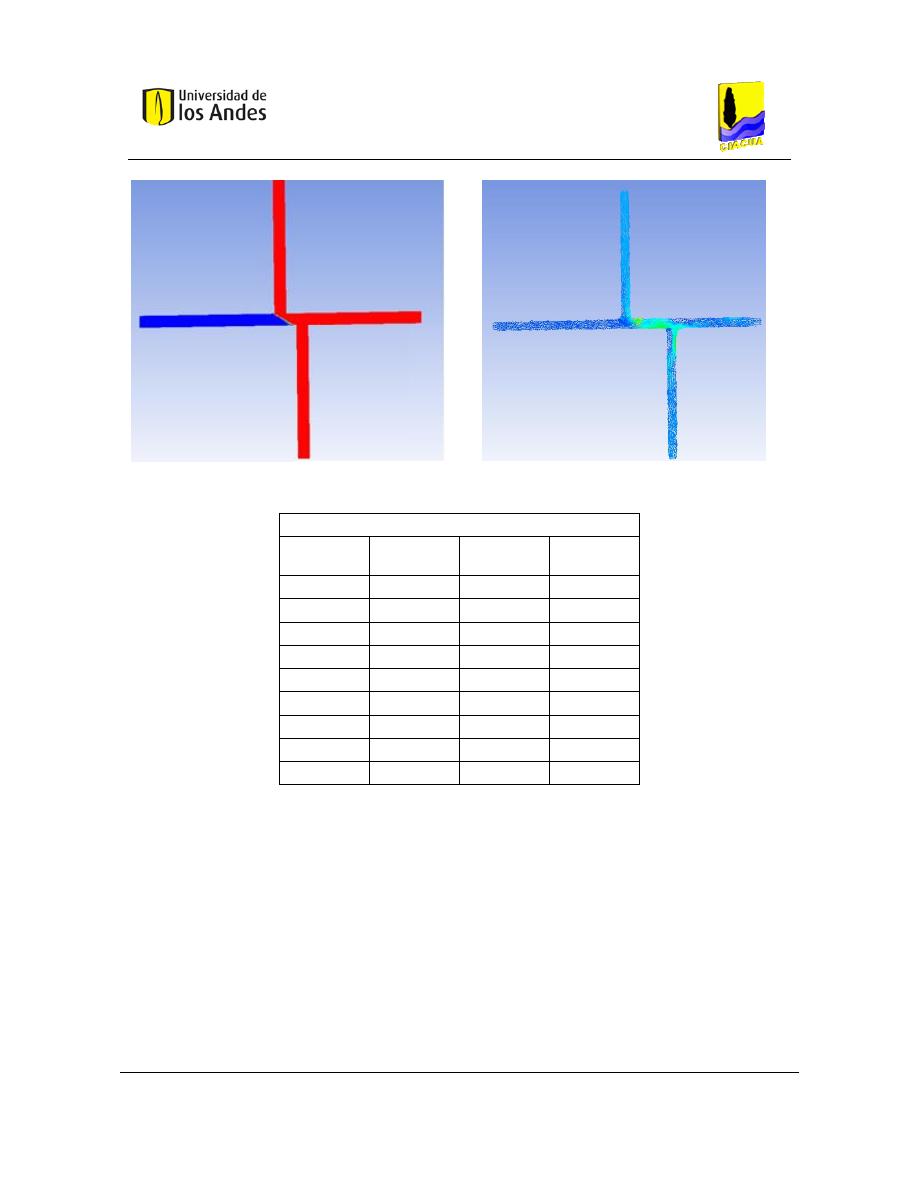
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
91
Figura 79. Resultados en CFD de la configuración e).
Tabla 6. Resultados en CFD de la configuración e).
CFD
Simulación
Re
2
/Re
1
Re
3
/Re
4
Fracción
de masa
1
0.3
1.0
0.49
2
0.5
1.0
0.501
3
0.8
1.0
0.502
4
1
1.0
0.503
5
1.3
1.0
0.504
6
1.6
1.0
0.51
7
1.8
1.0
0.511
8
2
1.0
0.513
9
2.3
1.0
0.535
A continuación se presentan los resultados obtenidos para algunas simulaciones en CFD:
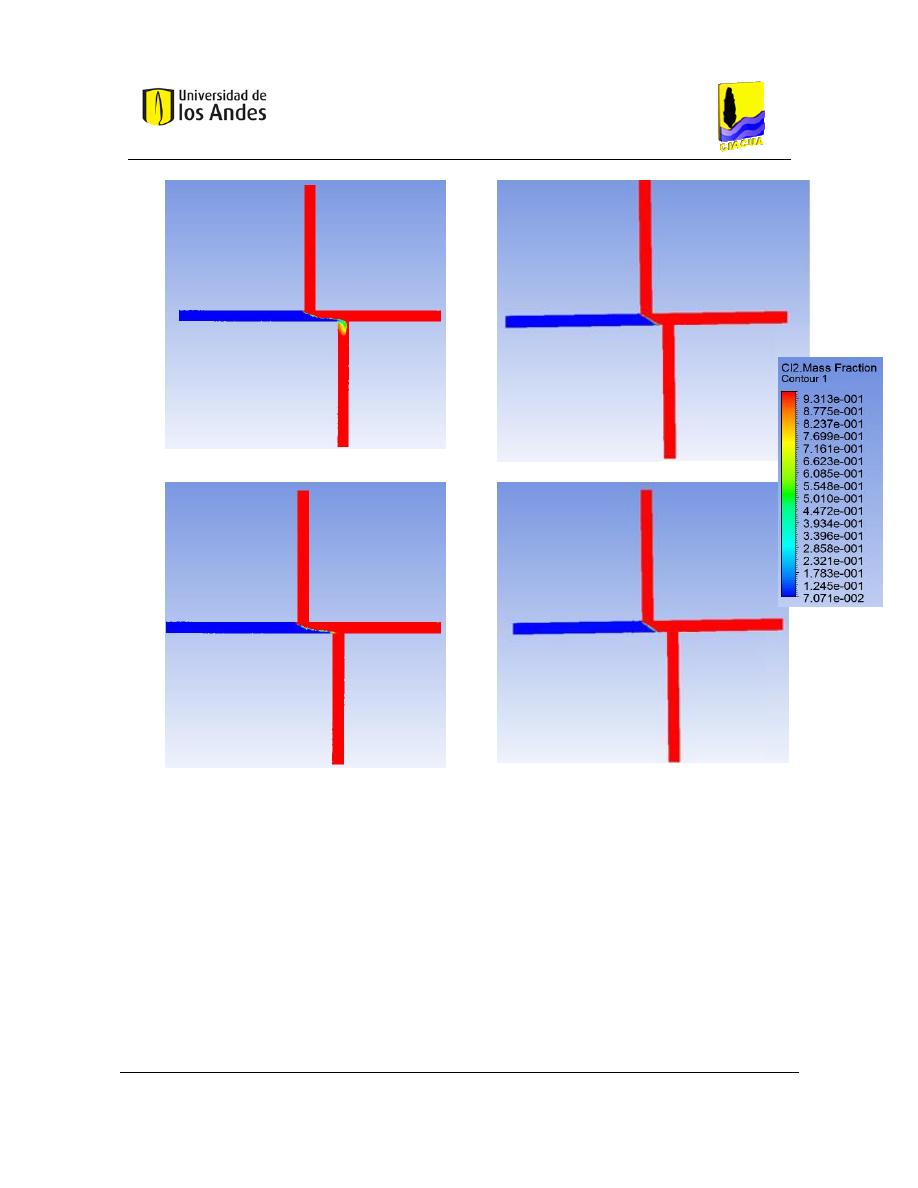
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
92
1)
6)
4)
8)
Figura 80. Resultados en CFD correspondientes al número de simulación para la configuración e).
Con los valores reportados en la Tabla 6 se obtuvo la siguiente gráfica:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
93
Gráfica 5. Resultados en CFD para la Fracción de masa de la configuración e).
Como era de esperarse, para esta configuración la fracción de masa se aproxima a 0.5 para todas las
relaciones de número de Reynolds modeladas; pero se puede ver que para las relaciones mayores
existe una tendencia mínima a aumentar. Esto quiere decir que cuando la velocidad en la tubería 2
es mucho más grande que la velocidad en la tubería 1, se puede alcanzar un valor de fracción de
masa mayor a 0.55. Sin embargo, este tipo de relación de flujo es muy difícil que se presente en una
red de distribución de agua potable real.
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0.0
0.5
1.0
1.5
2.0
2.5
Títu
lo
d
el
eje
Re
2
/Re
1
Fracción de masa tubería 3
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
94
7. Resultados de la modelación física
7.1. Resultados con trazador Permanganato de Potasio
Durante los ensayos se llevó a cabo una variación aleatoria de los caudales de entrada para
observar de qué manera se veía afectada la mezcla en la intersección de acuerdo con los
flujos de entrada. Estos procesos de mezcla se podían observar fácilmente, por lo tanto se
tomaron videos y fotografías en diferentes instantes de tiempo. Utilizando estas fotografías
se realizó un análisis de imagen el cual consiste en medir la intensidad de color rojo en las
tuberías y relacionar estos valores con la fracción de masa del trazador en las tuberías de
salida respectivas.
Para saber si era adecuado suponer que la intensidad de color es proporcional a la
concentración del trazador, se realizó una revisión bibliográfica en donde se encontró un
estudio que presenta una metodología de análisis de imagen para la determinación de la
concentración de trazadores conservativos y contaminantes en un modelo de red de vidrio
poroso en dos dimensiones. Se utilizaron trazadores de uranina y de color rojo
(Chrysikopoulos, Plega, & Katzourakis, 2011).
Figura 81. Montaje experimental análisis de imagen (Chrysikopoulos, Plega, & Katzourakis, 2011).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
95
La técnica de determinación de concentración no invasiva se utilizó para analizar la
migración y la difusión del color. Para cada experimento se capturaron fotografías
instantáneas con una cámara digital en un intervalo de tiempo preseleccionado. Para cada
imagen separaron los componentes de rojo, verde y azul. Analizando la relación entre la
intensidad de rojo y lo concentración, se determinó que ésta es proporcional.
Figura 82. Resultados de relación de concentración e intensidad de color rojo (Chrysikopoulos, Plega, &
Katzourakis, 2011).
Como lo muestra el estudio, es importante realizar una curva de calibración en la cual se
determine la constante de proporcionalidad entre la concentración y la intensidad de rojo.
A partir de lo anterior, se buscó una forma de analizar las imágenes de una manera
estandarizada con el fin de que los resultados entre las diferentes configuraciones sean
consistentes. Por consiguiente los videos y las fotografías se tomaron con una cámara
profesional en donde se configuró la apertura del lente a 5.6 f y la velocidad de captura a
1/125 de segundo. Estas imágenes se analizaron utilizando el programa ImageJ. Este es un
programa de procesamiento de imagen digital programado en Java y desarrollado en el
National Institutes of Health. ImageJ fue diseñado con una arquitectura abierta que
proporciona extensibilidad vía plugins Java y macros (ImageJ, 2011). Para este estudio, se
utilizó ImageJ para calcular el área y las estadísticas de valor de píxel y la intensidad de
objetos de umbral. Es decir, a partir de un umbral definido, el programa calcula la
intensidad de rojo en las tuberías del modelo.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
96
Figura 83. Interfaz y definición del umbral de color de las imágenes en ImageJ.
El análisis para establecer la relación entre la fracción de masa del trazador y la intensidad
de rojo y saber la fracción de masa en las tuberías de salida, se realizó una interpolación,
asignando el valor de 1 a la intensidad de rojo determinada para la tubería 2.
Los resultados para las configuraciones estudiadas se muestran a continuación.
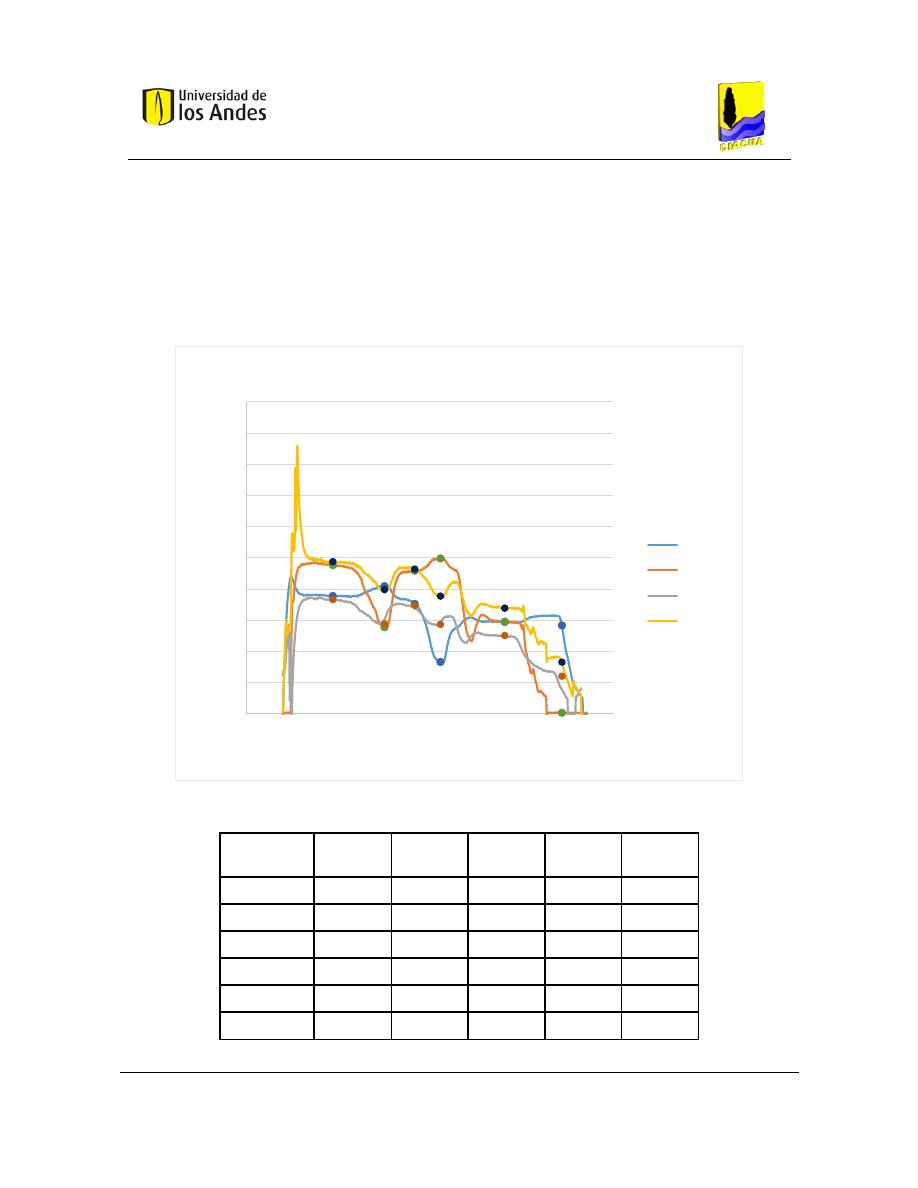
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
97
7.1.1. Configuración cruz con tuberías de 1”
A continuación se muestra la gráfica que relaciona los caudales medidos en todas las
tuberías para esta configuración. Dentro del periodo de simulación se escogieron instantes
de tiempo para analizar; en la tabla se muestran estos tiempos y la información
correspondiente. Luego se muestran las imágenes capturadas en esos tiempos y
posteriormente el análisis de umbral definido en ImageJ.
Gráfica 6. Caudales para configuración a) usando KMnO4.
Tabla 7. Escenarios de estudio para la configuración a).
Escenarios
Tiempo
(min)
Caudal 1
(L/s)
Caudal 2
(L/s)
Caudal 3
(L/s)
Caudal 4
(L/s)
1
7.067
0.755
0.953
0.733
0.976
2
11.292
0.818
0.555
0.577
0.797
3
13.775
0.705
0.917
0.695
0.928
4
15.883
0.332
0.996
0.573
0.754
5
21.142
0.589
0.589
0.502
0.677
6
25.833
0.567
0.007
0.241
0.332
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0.0
5.0
10.0
15.0
20.0
25.0
30.0
Cau
d
al
(L/s
)
Tiempo (min)
Caudales
Caudal 1
Caudal 2
Caudal 3
Caudal 4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
98
1)
4)
2)
5)
3)
6)
Figura 84. Resultados configuración a) usando KMnO
4
.
Se puede observar que las imágenes de los Escenarios 1 y 3 son muy parecidos debido a
que los flujos de las tuberías de entrada son relativamente parecidos y se puede ver que la
mezcla es muy poca. Para el caso del Escenario 2 en donde el caudal de la tubería 1 es
mayor al de la tubería 2, la interfaz incidente se inclina hacia la tubería 3 por lo tanto la
masa del trazador se desvía de manera más notable hacia esta tubería. Por el contrario, en el
Escenario 4 el caudal de la tubería 1 es menor al de la tubería 2 y la interfaz incidente se
desplaza hacia la tubería 1, lo que permite que una mayor masa del trazador se dirija hacia
la tubería 4.
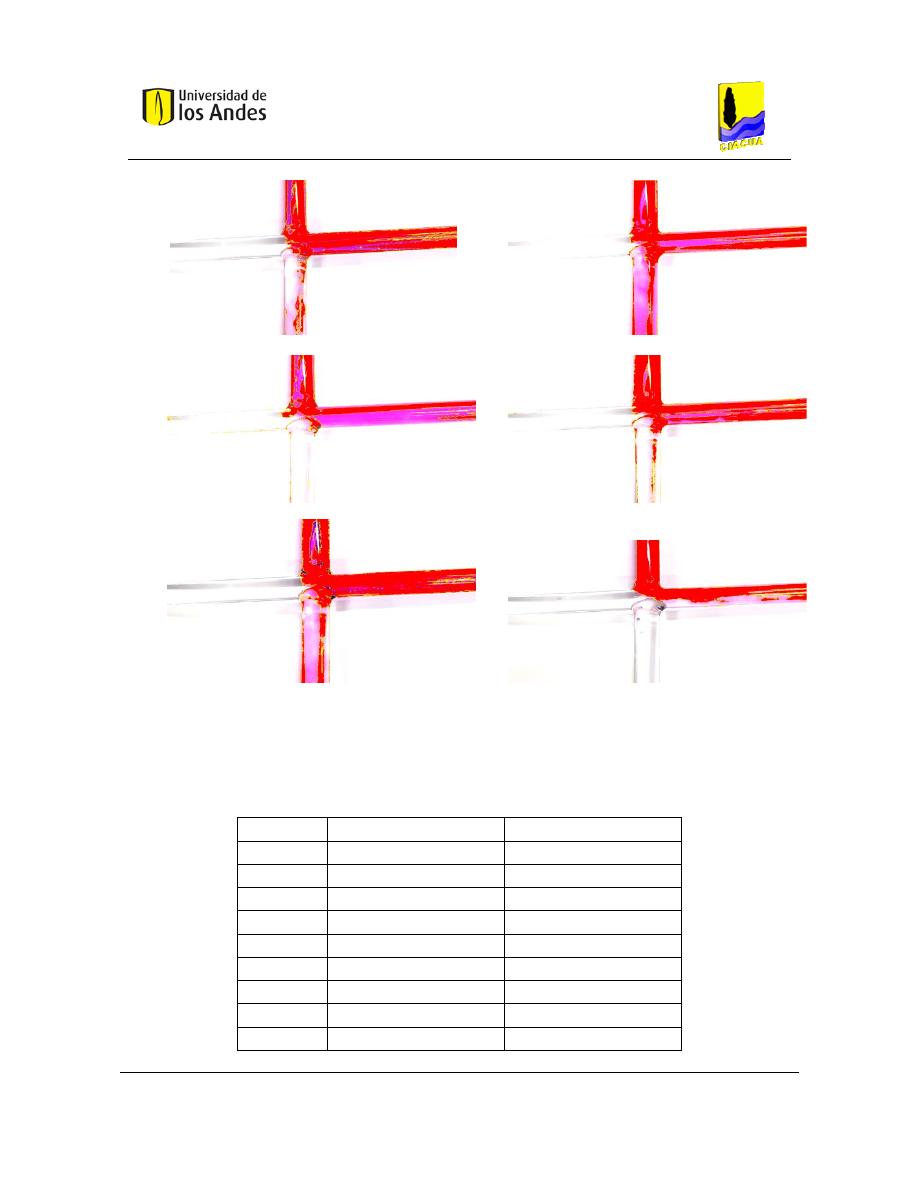
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
99
1)
4)
2)
5)
3)
6)
Figura 85. Análisis de imagen configuración a).
Con la información de los caudales se determinaron los números de Reynolds de cada
tubería y luego se calculó la relación entre las tuberías de entrada para cada instante de
tiempo, así como la intensidad de rojo obtenida en la tubería 3.
Tabla 8. Intensidad de rojo asociada con la relación de número de Reynolds para la configuración a).
Re
2
/Re
1
Re
3
/Re
4
Intensidad de Rojo
1.26
0.75
98.88
0.67
0.72
93.35
1.30
0.75
100.46
2.99
0.76
102.96
1.00
0.74
94.26
0.01
0.73
38.95
0.50
0.74
80.00
0.30
0.75
66.00
0.20
0.75
55.00
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
100
Gráfica 7. Intensidad de rojo en la tubería 3 para la configuración a).
Realizando la interpolación, se determina la relación entre la intensidad de rojo y la
fracción de masa en la tubería 3.
Gráfica 8. Fracción de masa vs intensidad de rojo para la configuración a).
De acuerdo con la información presentada en las anteriores gráficas, se determinó el valor
de la fracción de masa en la tubería 3, como función de la relación del número de Reynolds
de las tuberías de entrada.
0
20
40
60
80
100
120
0
0.5
1
1.5
2
2.5
3
3.5
In
tes
n
d
id
ad
d
e r
o
jo
Re
2
/Re
1
Intensidad de rojo tubería 3
y = 0.01x - 0.0299
R² = 0.9785
0
0.2
0.4
0.6
0.8
1
1.2
0
20
40
60
80
100
120
Fracción
d
e
m
asa
Intensidad de rojo
Fracción de masa vs intensidad de rojo
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
101
Gráfica 9. Fracción de masa en la tubería 3 en función de la relación del número de Reynolds para la configuración
a).
7.1.2. Configuración cruz con una tubería de salida de 1.5’
Para este caso se escogieron 4 escenarios en donde se puede observar claramente la forma
como influye el caudal sobre los procesos de mezcla. A continuación, se muestran las
gráficas de la variación de caudales para cada tubería en función del tiempo, con los puntos
que indican el momento en el que fueron tomadas las fotografías.
0
0.2
0.4
0.6
0.8
1
1.2
0
0.5
1
1.5
2
2.5
3
3.5
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
102
Gráfica 10. Caudales para configuración b) usando KMnO4.
Tabla 9. Escenarios de estudio para la configuración b).
Escenario
Tiempo
(min)
Caudal 1
(L/s)
Caudal 2
(L/s)
Caudal 3
(L/s)
Caudal 4
(L/s)
1
5.75
0.700
0.775
0.744
0.731
2
10.55
0.797
0.328
0.554
0.571
3
16.05
0.129
0.953
0.586
0.495
4
25
0.785
0.119
0.442
0.462
1)
3)
0
0.2
0.4
0.6
0.8
1
1.2
0.0
5.0
10.0
15.0
20.0
25.0
30.0
35.0
Cau
d
al
(L/s
)
Tiempo (min)
Caudales
Caudal 1
Caudal 2
Caudal 3
Caudal 4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
103
2)
4)
Figura 86. Resultados configuración b) usando KMnO
4
.
Se puede observar que en los Escenarios 1 y 2, no es apreciable la diferencia a pesar de que
los caudales son diferentes, en especial el caudal de la tubería 3. Sin embargo, para el
Escenario 3, donde el caudal de la tubería 1 es mucho mayor al de la tubería 2, se puede
apreciar que la concentración del trazador que se divide hacia la tubería 4, se reduce con
respecto a los escenarios anteriores y se podría decir que se acerca a la mezcla completa. Se
observa que la concentración no es tan alta debido a que el impulso predominante lo tiene
la tubería que lleva el agua limpia.
1)
3)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
104
2)
4)
Figura 87. Análisis de imagen configuración b).
Con la información de los caudales se determinaron los números de Reynolds de cada
tubería y luego se calculó la relación entre las tuberías de entrada para cada instante de
tiempo, así como la intensidad de rojo obtenida en la tubería 3.
Tabla 10. Intensidad de rojo asociada con la relación de número de Reynolds para la configuración b).
Re
2
/Re
1
Re
3
/Re
4
Intensidad
de Rojo
1.10
1.01
69.15
0.41
0.97
43.90
3.52
1.18
90.59
0.15
0.95
29.02
2.11
0.98
88.48
0.80
1.2
59.04
0.52
1.1
47.35
1.35
0.94
72.10
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
105
Gráfica 11. Intensidad de rojo en la tubería 3 para la configuración b).
Realizando la interpolación, se determina la relación entre la intensidad de rojo y la
fracción de masa en la tubería 3.
Gráfica 12.Fracción de masa vs intensidad de rojo para la configuración b).
De acuerdo con la información presentada en las anteriores gráficas, se determinó el valor
de la fracción de masa en la tubería 3, como función de la relación del número de Reynolds
de las tuberías de entrada.
y = 21.732ln(x) + 65.972
R² = 0.9663
0
10
20
30
40
50
60
70
80
90
100
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
In
ten
sid
ad
d
e r
o
jo
Re
2
/Re
1
Intensidad de rojo en tubería 3
y = 0.009x + 0.0465
R² = 0.9887
0
0.2
0.4
0.6
0.8
1
1.2
0
20
40
60
80
100
120
Fracció
n
d
e
mas
a
Intensidad de color rojo
Fracción de masa vs intensidad de rojo
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
106
Gráfica 13. Fracción de masa en la tubería 3 en función de la relación del número de Reynolds para la
configuración b).
7.1.3. Configuración cruz con tubería de entrada de 1.5”
Para este caso se escogieron 4 escenarios en donde se puede observar claramente la forma
como influye el caudal sobre los procesos de mezcla. A continuación, se muestran las
gráficas de la variación de caudales para cada tubería en función del tiempo, con los puntos
que indican el momento en el que fueron tomadas las fotografías.
Gráfica 14. Caudales para configuración c) usando KMnO4.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
0.0
5.0
10.0
15.0
20.0
25.0
30.0
35.0
40.0
Cau
d
al
(L/s
)
Tiempo (min)
Caudales
Caudal 1
Caudal 2
Caudal 3
Caudal 4
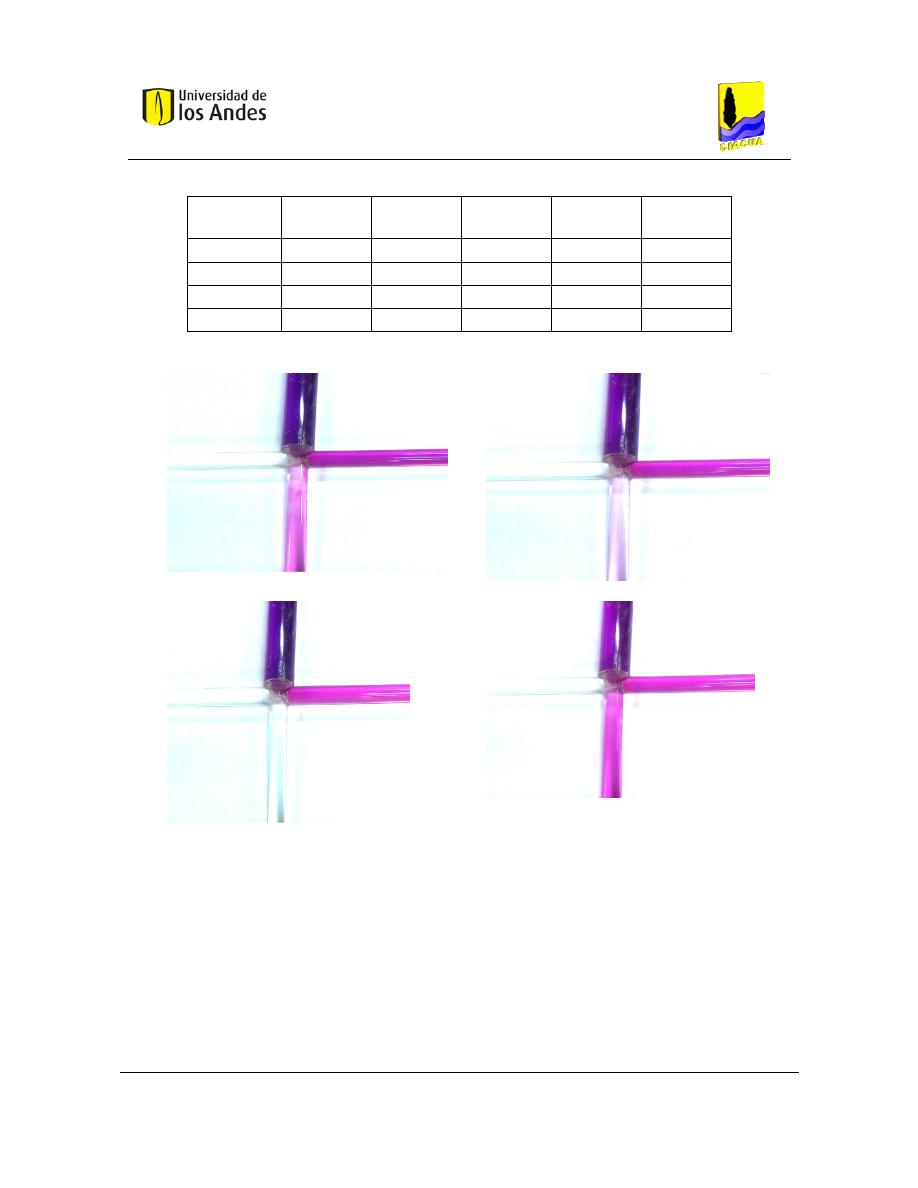
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
107
Tabla 11. Escenarios de estudio para la configuración c).
Escenarios
Tiempo
(min)
Caudal 1
(L/s)
Caudal 2
(L/s)
Caudal 3
(L/s)
Caudal 4
(L/s)
1
6.383
0.661
0.855
0.874
0.642
2
10.850
0.751
0.346
0.715
0.382
3
15.933
0.370
0.367
0.453
0.284
4
19.750
0.327
0.880
0.653
0.554
1)
3)
2)
4)
Figura 88. Resultados configuración c) usando KMnO4.
Con estas imágenes se puede clasificar el Escenario 2 como uno critico ya que la mezcla es
mínima; esto se presenta cuando el caudal de la tubería 2 es menos al de la tubería 1. Por el
contrario, en el Escenario 4, donde el caudal de la tubería 2 es mayor al de la tubería 1,
existe una mayor proporción de masa en la tubería 4.
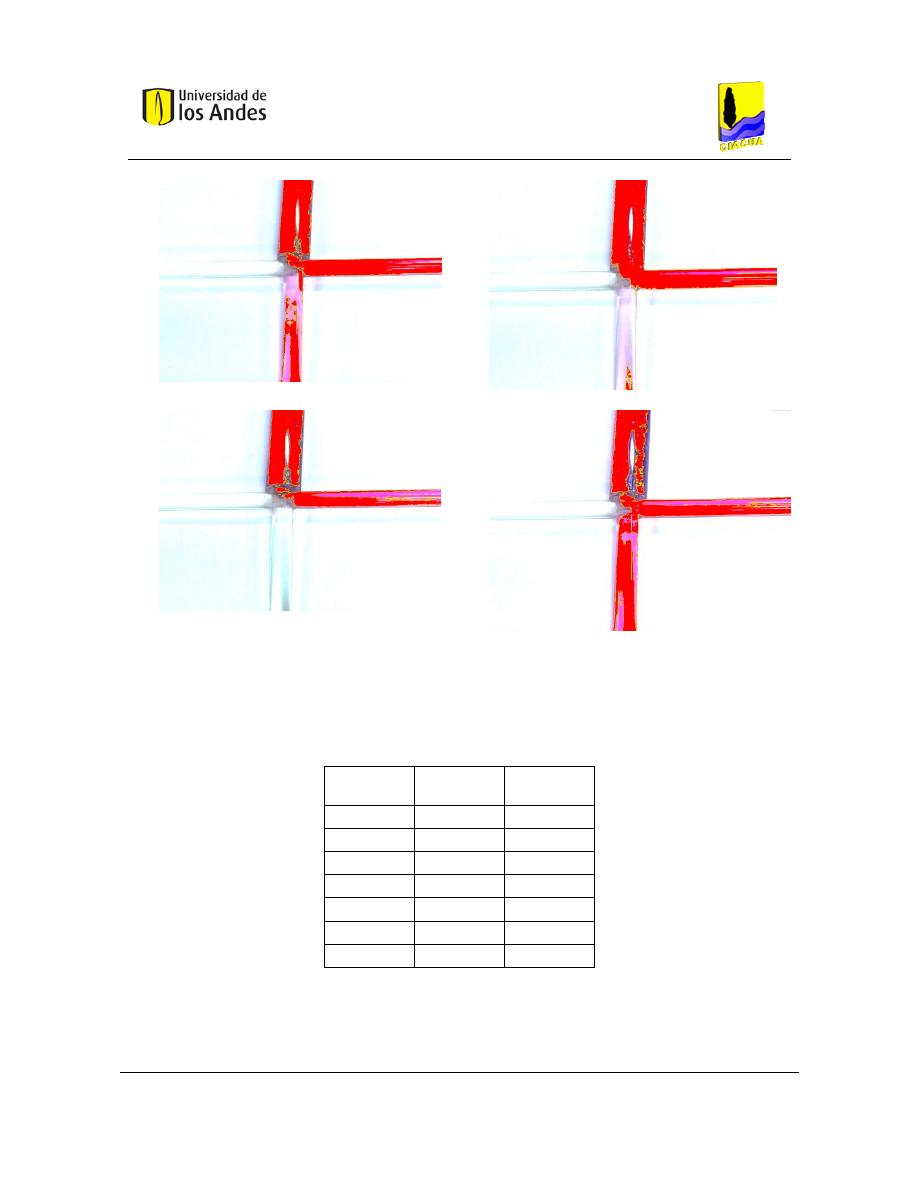
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
108
1)
3)
2)
4)
Figura 89. Análisis de imagen configuración c).
Con la información de los caudales se determinaron los números de Reynolds de cada
tubería y luego se calculó la relación entre las tuberías de entrada para cada instante de
tiempo, así como la intensidad de rojo obtenida en la tubería 3.
Tabla 12.Intensidad de rojo asociada con la relación de número de Reynolds para la configuración c).
Re
2
/Re
1
Re
3
/Re
4
Intensidad
de Rojo
0.74
1.36
73.48
0.26
1.86
31.97
0.57
1.59
66.65
1.55
1.17
78.30
0.30
1.78
41.72
0.92
1.49
74.78
0.24
1.95
21.03
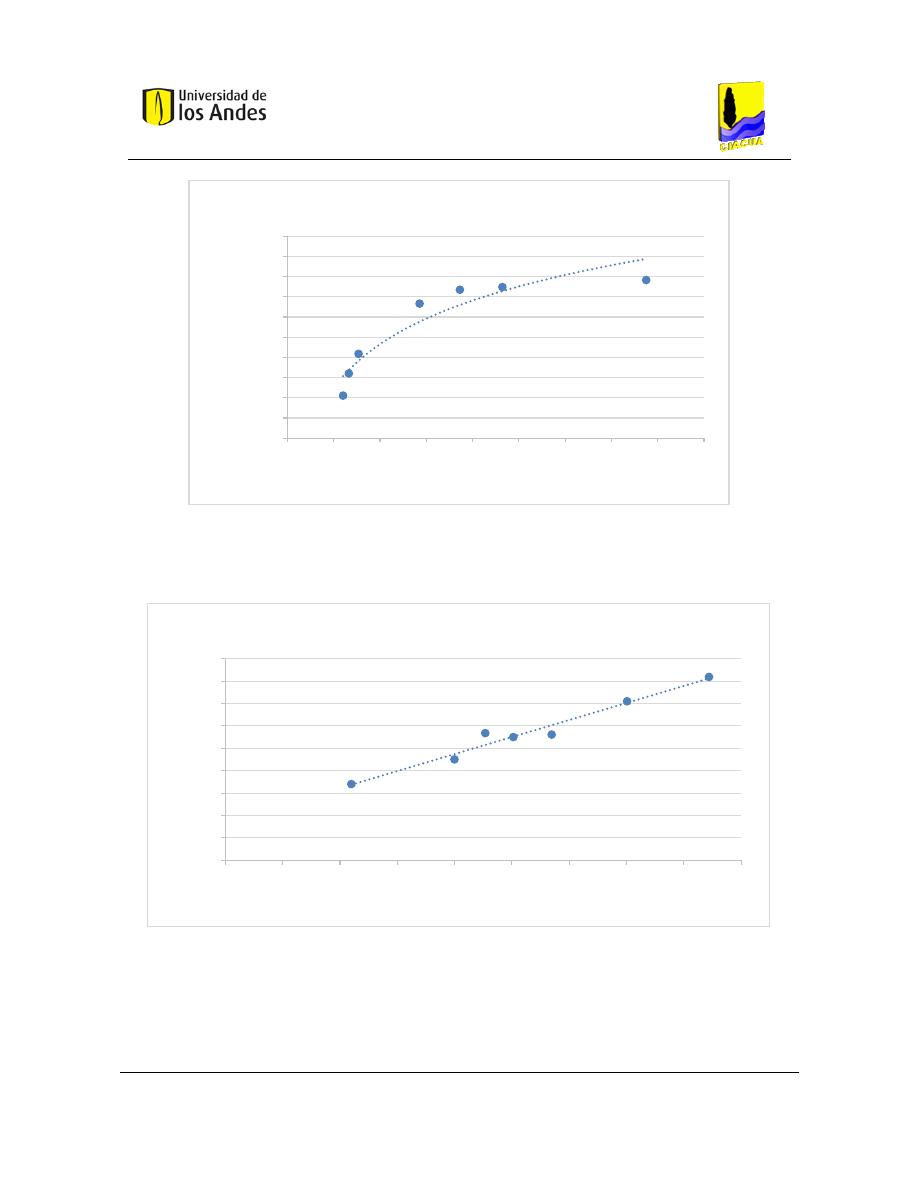
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
109
Gráfica 15. Intensidad de rojo en la tubería 3 para la configuración c).
Realizando la interpolación, se determina la relación entre la intensidad de rojo y la
fracción de masa en la tubería 3.
Gráfica 16. Fracción de masa vs intensidad de rojo para la configuración c).
De acuerdo con la información presentada en las anteriores gráficas, se determinó el valor
de la fracción de masa en la tubería 3, como función de la relación del número de Reynolds
de las tuberías de entrada.
y = 31.199ln(x) + 75.14
R² = 0.89
0.000
10.000
20.000
30.000
40.000
50.000
60.000
70.000
80.000
90.000
100.000
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
In
ten
sid
ad
d
e r
o
jo
Re
2
/Re
1
Intensidad de rojo en tubería 4
y = 0.0076x + 0.1707
R² = 0.9648
0.00
0.10
0.20
0.30
0.40
0.50
0.60
0.70
0.80
0.90
0.0
10.0
20.0
30.0
40.0
50.0
60.0
70.0
80.0
90.0
Fracció
n
d
e
mas
a
Intensidad de rojo en tubería 3
Fracción de masa vs intensidad de rojo
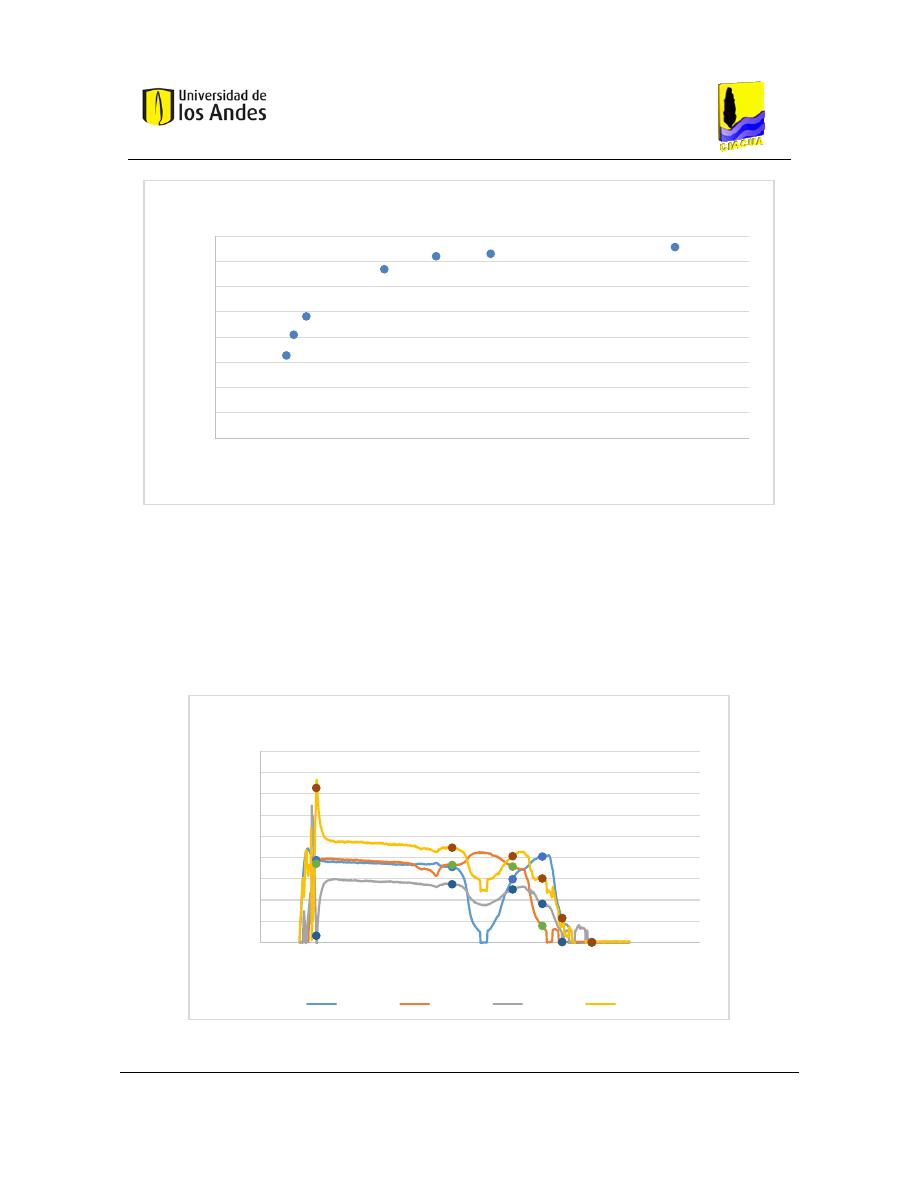
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
110
Gráfica 17. Fracción de masa en la tubería 3 en función de la relación del número de Reynolds para la
configuración c).
7.1.4. Configuración doble tee (L/d=14)
Para este caso se escogieron 5 escenarios en donde se puede observar claramente la forma
en que influye el caudal sobre los procesos de mezcla. A continuación, se muestran las
gráficas de la variación de caudales para cada tubería en función del tiempo, con los puntos
que indican el momento en el que fueron tomadas las fotografías.
Gráfica 18. Caudales para configuración d) usando KMnO4.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
Cau
d
al
(L/s
)
Tiempo (min)
Caudales
Caudal 1
Caudal 2
Caudal 3
Caudal 4
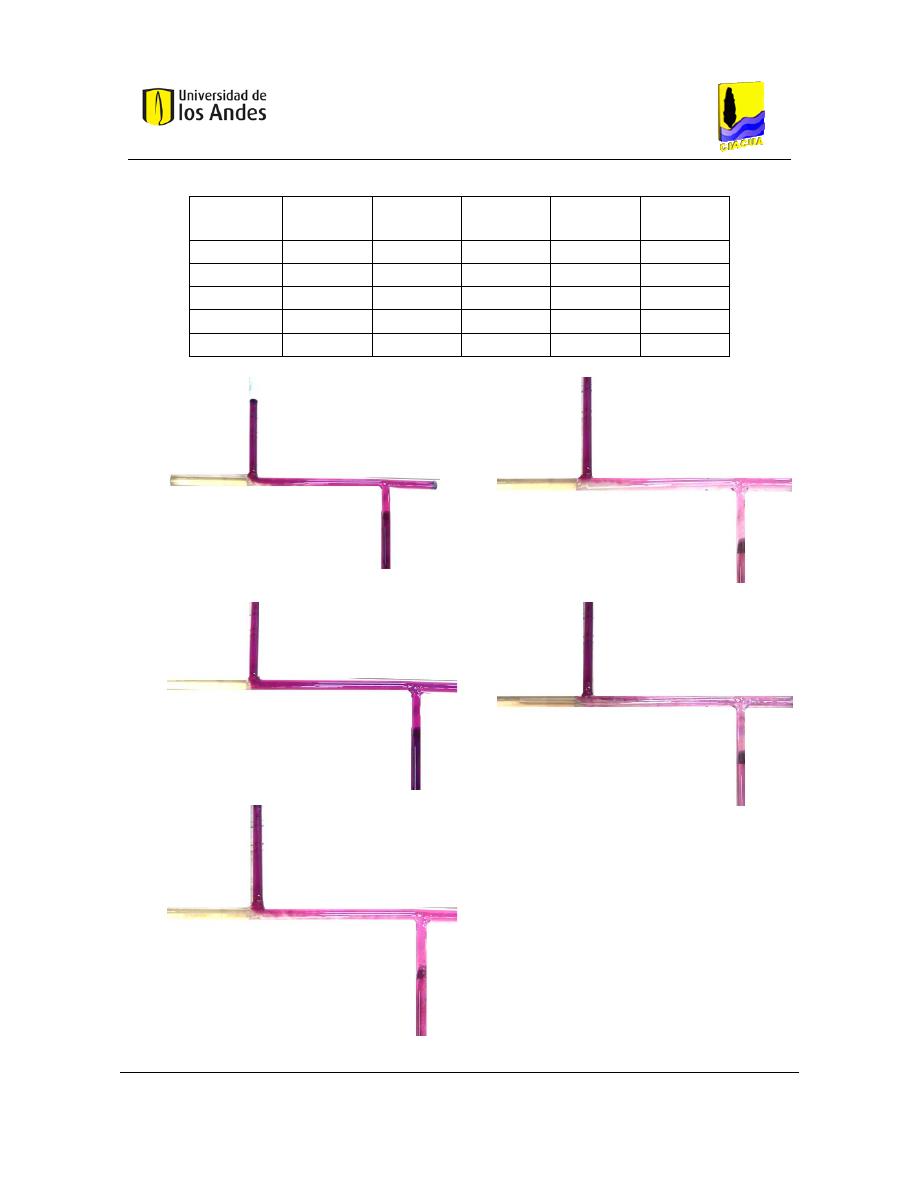
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
111
Tabla 13. Escenarios de estudio para la configuración d).
Escenarios
Tiempo
(min)
Caudal 1
(L/s)
Caudal 2
(L/s)
Caudal 3
(L/s)
Caudal 4
(L/s)
1
1,02
0,777
0,743
0,065
1,455
2
3,49
0,711
0,731
0,550
0,893
3
4,59
0,597
0,715
0,499
0,813
4
5,13
0,809
0,158
0,364
0,603
5
5,49
0,229
0,007
0,005
0,231
1)
4)
2)
5)
3)
Figura 90. Resultados configuración d) usando KMnO4.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
112
Para esta configuración se puede observar que para todos los escenarios el color del
trazador en las tuberías de salida es el mismo. Entre los diferentes escenarios cambia la
intensidad de color, pero lo importante es la comparación entre las tuberías de salida.
1)
4)
2)
5)
3)
Figura 91. Análisis de imagen configuración d).
Con la información de los caudales se determinaron los números de Reynolds de cada
tubería y luego se calculó la relación entre las tuberías de entrada para cada instante de
tiempo, así como la intensidad de rojo obtenida en la tubería 3.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
113
Tabla 14.Intensidad de rojo asociada con la relación de número de Reynolds para la configuración d).
Re
2
/Re
1
Re
3
/Re
4
Intensidad
de rojo
0.95
0.00005
52.05
1.02
0.62
51.54
1.19
0.61
49.35
0.19
0.60
51.54
0.03
0.021
50.28
0.55
0.59
50.8
0.3
0.63
50.78
0.85
0.60
51.12
0.81
0.64
51.98
0.75
0.62
51.26
Gráfica 19. Intensidad de rojo en la tubería 3 para la configuración d).
Realizando la interpolación, se determina la relación entre la intensidad de rojo y la
fracción de masa en la tubería 3.
0
10
20
30
40
50
60
70
80
90
100
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
In
ten
sid
ad
d
e r
o
jo
Re
2
/Re
1
Intensidad de rojo tubería 3
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
114
Gráfica 20. Fracción de masa vs intensidad de rojo para la configuración d).
De acuerdo con la información presentada en las anteriores gráficas, se determinó la el
valor de la fracción de masa en la tubería 3, en función de la relación del número de
Reynolds de las tuberías de entrada.
Gráfica 21.Fracción de masa en la tubería 3 en función de la relación del número de Reynolds para la
configuración d).
0
0.2
0.4
0.6
0.8
1
1.2
0
20
40
60
80
100
120
Fracción
d
e
m
asa
Intensidad color rojo
Fracción de masa vs intensidad de rojo
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Fracció
n
d
e
mas
a
Re
2
/Re
1
Fracción de masa tubería 3
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
115
7.1.4. Configuración doble tee (L/d=3.7)
Para este caso se escogieron 6 escenarios en donde se puede observar claramente la forma
en que influye el caudal sobre los procesos de mezcla. A continuación, se muestran las
gráficas de la variación de caudales para cada tubería en función del tiempo, con los puntos
que indican el momento en el que fueron tomadas las fotografías.
Gráfica 22. Caudales para configuración e) usando KMnO4.
Tabla 15. Escenarios de estudio para la configuración e).
Escenarios
Tiempo
(min)
Caudal 1
(L/s)
Caudal 2
(L/s)
Caudal 3
(L/s)
Caudal 4
(L/s)
1
5.486
0.734
0.777
0.936
0.576
2
10.587
0.853
0.173
0.655
0.370
3
13.667
0.685
0.686
0.849
0.522
4
17.225
0.354
0.734
0.677
0.412
5
19.667
0.380
0.345
0.467
0.258
6
21.775
0.329
0.781
0.683
0.427
0
0.2
0.4
0.6
0.8
1
1.2
1.4
0.0
5.0
10.0
15.0
20.0
25.0
30.0
Cau
d
al
(L/s
)
Tiempo (min)
Caudales
Caudal 1
Caudal 2
Caudal 3
Caudal 4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
116
1)
4)
2)
5)
3)
6)
Figura 92. Resultados configuración e) usando KMnO4.
Las imágenes muestran que, al igual que la configuración anterior, el color del trazador en
las tuberías de salida es el mismo, lo que implica una suposición de mezcla completa.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
117
1)
4)
2)
5)
3)
6)
Figura 93. Análisis de imagen configuración e).
Con la información de los caudales se determinaron los números de Reynolds de cada
tubería y luego se calculó la relación entre las tuberías de entrada para cada instante de
tiempo, así como la intensidad de rojo obtenida en la tubería 3.
Tabla 16. Intensidad de rojo asociada con la relación de número de Reynolds para la configuración e).
Re
2
/Re
1
Re
3
/Re
4
Intensidad de
Rojo
1.05
1.63
52.94
0.20
1.77
47.63
1.00
1.63
52.78
2.07
1.64
54.76
0.90
1.81
52.42
2.37
1.60
55.21
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
118
Gráfica 23. Intensidad de rojo en la tubería 3 para la configuración e).
Realizando la interpolación, se determina la relación entre la intensidad de rojo y la
fracción de masa en la tubería 3.
Gráfica 24. Fracción de masa vs intensidad de rojo para la configuración e).
De acuerdo con la información presentada en las anteriores gráficas, se determinó el valor
de la fracción de masa en la tubería 3, como función de la relación del número de Reynolds
de las tuberías de entrada.
0
20
40
60
80
100
0.0
0.5
1.0
1.5
2.0
2.5
In
ten
sid
ad
d
e r
o
jo
Re
2
/Re
1
Intensidad de rojo tubería 3
y = 0.0096x - 1E-13
0.45
0.46
0.47
0.48
0.49
0.5
0.51
0.52
0.53
0.54
46
48
50
52
54
56
Fracción
d
e
m
asa
Intensidad de rojo
Fracción de masa vs intensidad de rojo
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
119
Gráfica 25. Fracción de masa en la tubería 3 en función de la relación del número de Reynolds para la
configuración e).
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.5
1
1.5
2
2.5
3
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
120
7.2. Resultados trazador Cloro
Durante el ensayo se llevó a cabo una variación aleatoria de los caudales de entrada para
observar de qué manera se veía afectada la mezcla en la intersección de acuerdo con los
flujos de entrada. En adición, se midió la concentración de cloro en las tuberías de entrada y
salida como datos continuos en función del tiempo.
Los resultados para las configuraciones estudiadas se muestran a continuación.
7.2.1. Configuración cruz con tuberías de 1”
Gráfica 26. Caudales para configuración a) usando Cloro.
0.0
0.2
0.4
0.6
0.8
1.0
1.2
0.0
5.0
10.0
15.0
20.0
25.0
30.0
Cau
d
al
(L/s
)
Tiempo (min)
Caudales
Caudal 1
Caudal 2
Caudal 3
Caudal 4
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
121
Gráfica 27. Concentraciones de cloro para la configuración a).
Como se puede observar en la gráfica de caudales, existen algunos intervalos de tiempo en
los que los caudales de todas las tuberías se estabilizan. En esto puntos se tomaron los datos
tanto de caudal como de concentración para obtener valores como la fracción de masa y la
concentración normalizada en la tubería 3. Estos valores se obtuvieron utilizando la
Ecuación 7 y la Ecuación 9, respectivamente. Por otra parte, con la información de las
caudales se calculó el número de Reynolds de las tuberías y se determinó la relación para
las tuberías de entrada. A partir de lo anterior, se graficaron los datos para analizar la
relación entre la fracción de masa o la concentración normalizada y la relación del número
de Reynolds de las tuberías de entrada.
0.0
2.0
4.0
6.0
8.0
10.0
12.0
14.0
0.0
5.0
10.0
15.0
20.0
25.0
30.0
C
o
n
ce
n
tr
ac
ió
n
(m
g/
L)
Tiempo (min)
Concentraciones
Concentración 1
Concentración 2
Concentración 3
Concentración 4
Mezcla completa
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
122
Gráfica 28. Fracción de masa de cloro para la configuración a).
Gráfica 29. Concentración normalizada para la configuración a).
Es importante tener un punto de referencia, por lo tanto se compararon los resultados
obtenidos con los reportados en la literatura. Se tomó la gráfica que aparece en la Figura 7,
se digitalizaron los datos reportados por los demás autores y se colocaron los datos
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
0
0.2
0.4
0.6
0.8
1
1.2
Fracción
d
em
asa
Re
2
/Re
1
Fracción de masa
y = 0.0173x
3
- 0.1814x
2
+ 0.6026x + 0.3426
R² = 0.9871
0.0
0.2
0.4
0.6
0.8
1.0
1.2
0.0
1.0
2.0
3.0
4.0
5.0
6.0
C*
3
Re
2
/Re
1
Concentración normalizada 3
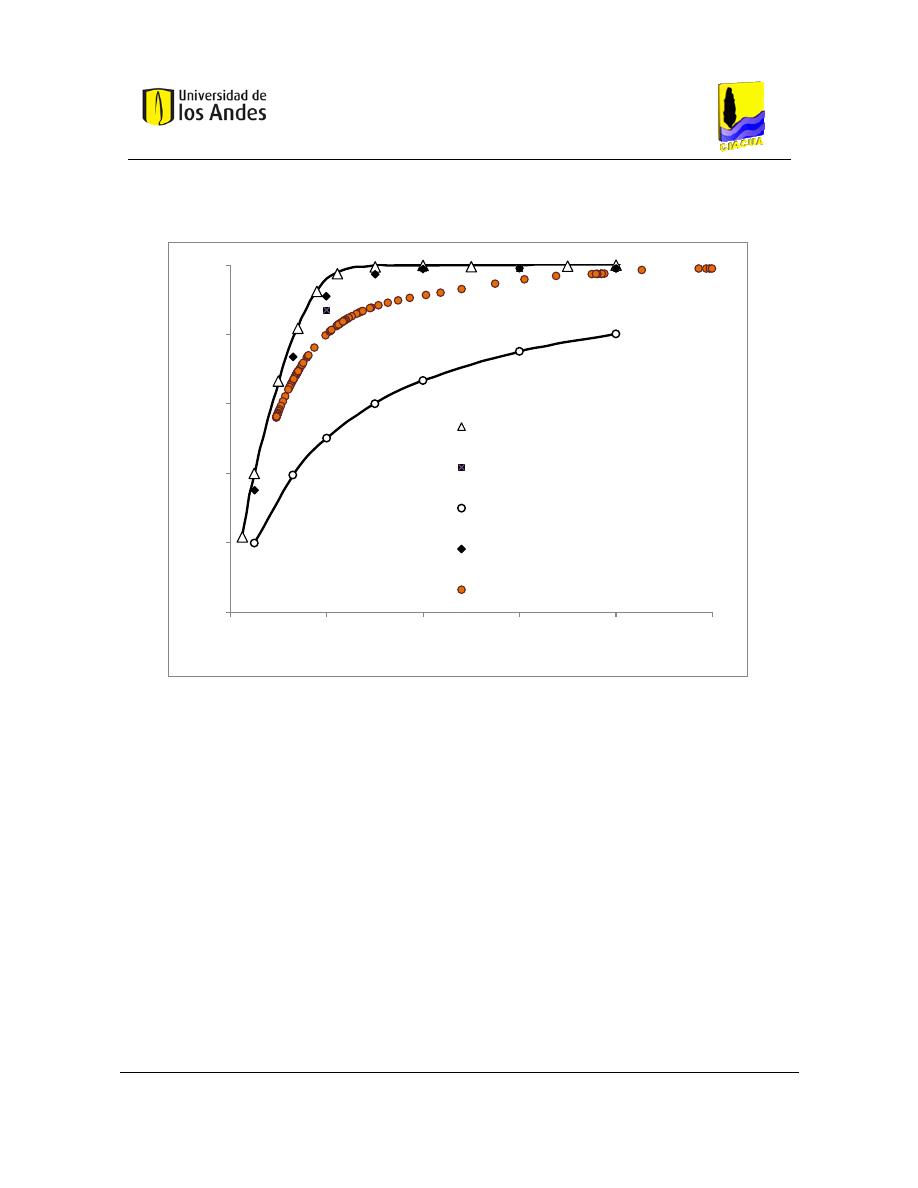
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
123
obtenidos en esta tesis, los cuales son los puntos naranjas que se muestran en la siguiente
figura:
Gráfica 30. Comparación C* entre configuración a) y bibliografía.
Como se puede observar, se compararon los valores de la concentración normalizada en la
tubería 3. Los puntos naranjas siguen la misma tendencia de mezcla que los resultados
reportados por Romero-Gómez et al., 2008. Era de esperarse alguna discrepancia entre los
resultados dado que las condiciones experimentales son diferentes. Cuando la relación del
número de Reynolds en las tuberías de entrada está entre 1 y 2, es en donde se presenta una
mayor diferencia; para los resultados de esta tesis se genera un mayor porcentaje de mezcla
y esto se debe a razones constructivas de la intersección.
De la misma manera, se tomó la gráfica de la Figura 19 para comparar los valores de
Fracción de Masa, en donde se puede ver que los resultados reportados en esta tesis
coinciden con los resultados reportados en la literatura por otros autores.
0.0
0.2
0.4
0.6
0.8
1.0
0
1
2
3
4
5
C*
3
Re
2
/Re
1
Resultados CFD (Romero Gomez et al.,2006)
Resultados experimentales (Van Bloemen
Waanders et al.,2005)
Resultados basados en mezcla completa
Resultados experimentales (Romero-Gomez et
al.,2008)
Resultados experimentales
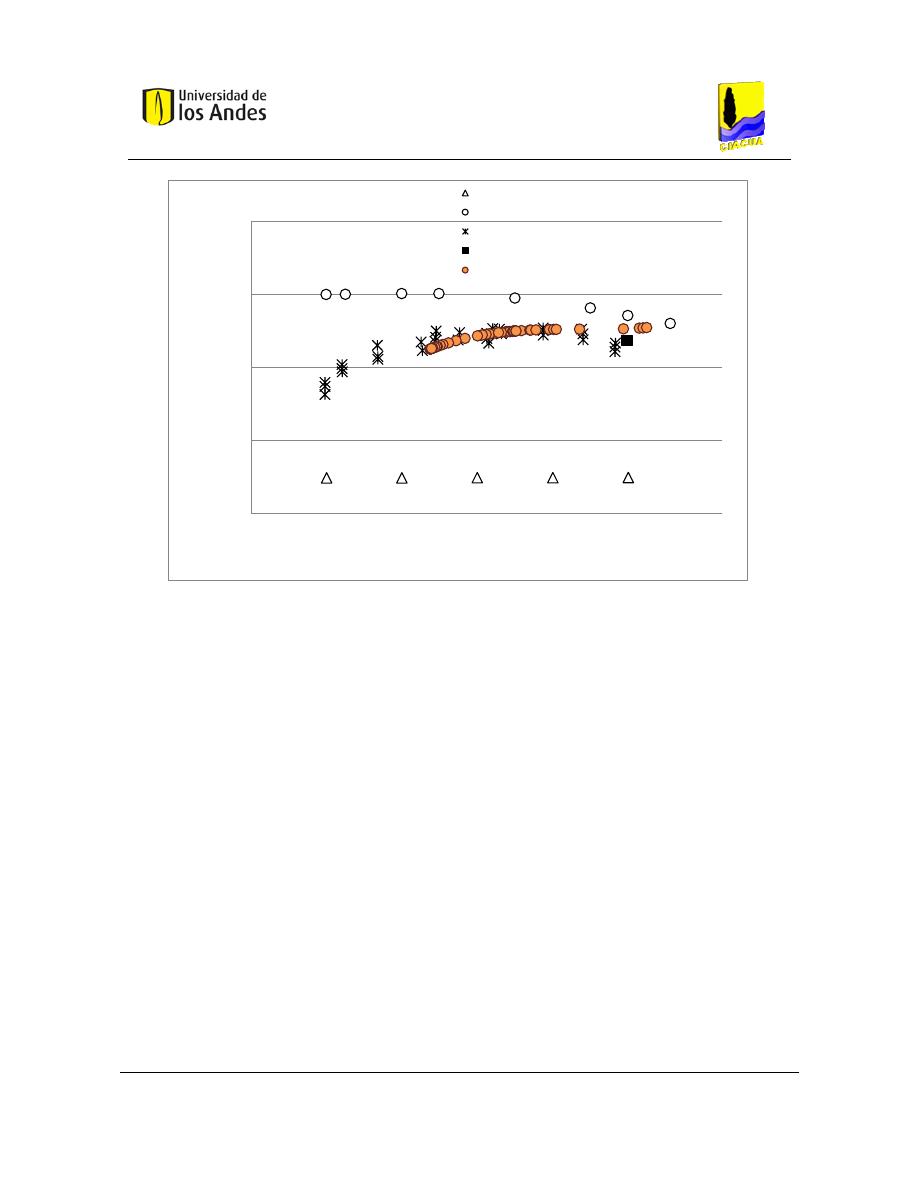
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
124
Gráfica 31. Comparación Fracción de masa entre configuración a) y bibliografía.
La comparación que se realizó para la configuración en cruz con todas las tuberías del
mismo diámetro es importante para saber si los ensayos que se estaban realizando son
coherentes con los resultados de referencia. Como los resultados están acordes con los de la
bibliografía, se puede asegurar que la metodología que se utilizó para esta configuración es
adecuada y que se puede seguir utilizando para las demás configuraciones con la confianza
de que los datos van a estar bien medidos.
40
60
80
100
120
0
0.25
0.5
0.75
1
1.25
Frac
ci
ón
d
e
m
as
a
tu
b
ería 3
Re
2
/Re
1
EPANET
CFD (Romero-Gomez et al.,2008)
Experimental (Romero-Gomez et al.,2008)
Experimental (van Bloemen Waanders et al.,2005)
Resultados experimentales
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
125
7.2.2. Configuración cruz con tubería de salida de 1.5”
Gráfica 32. Caudales para configuración b) usando Cloro.
Gráfica 33. Concentraciones de cloro para la configuración b).
0
0.2
0.4
0.6
0.8
1
1.2
0.0
5.0
10.0
15.0
20.0
25.0
30.0
35.0
Cau
d
al
(L/s
)
Tiempo (min)
Caudales
Caudal 1
Caudal 2
Caudal 3
Caudal 4
0
1
2
3
4
5
6
0.0
5.0
10.0
15.0
20.0
25.0
30.0
35.0
C
on
ce
n
tración
(m
g/
L)
Tiempo (min)
Concentraciones
Concentración 1
Concentración 2
Concentración 3
Concentración 4
Mezcla completa
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
126
Se puede observar que la concentración en la tubería 3 generalmente es mayor que en la
tubería 4, lo que corrobora una vez más que la mezcla es incompleta.
Gráfica 34. Fracción de masa de cloro para la configuración b).
Gráfica 35. Concentración normalizada para la configuración b).
0.000
0.200
0.400
0.600
0.800
1.000
1.200
0.0
1.0
2.0
3.0
4.0
5.0
6.0
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
y = 0.0242x
3
- 0.192x
2
+ 0.5622x + 0.256
R² = 0.9703
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
0.0
0.5
1.0
1.5
2.0
2.5
3.0
C*
3
Re
2
/Re
1
Concentración normalizada 3
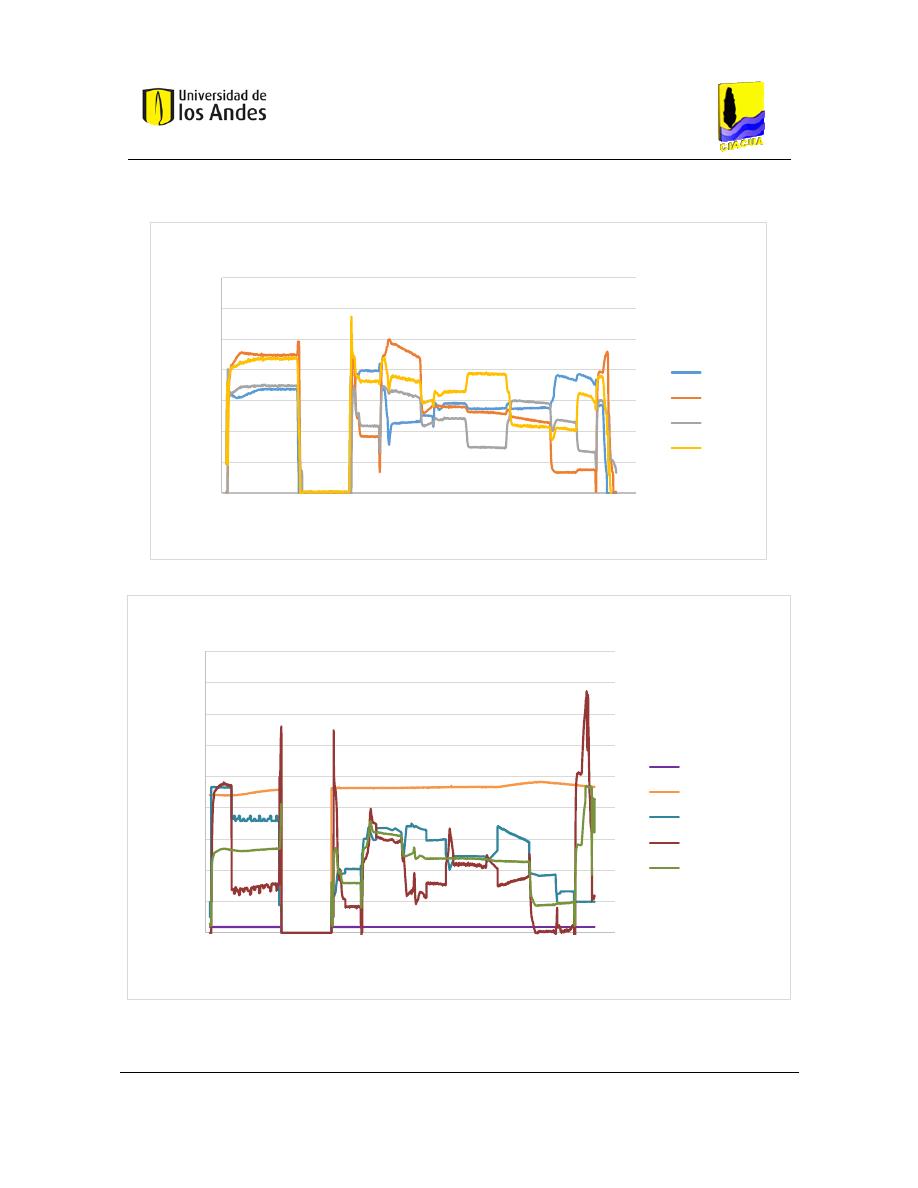
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
127
7.2.3. Configuración cruz con tubería de entrada de 1.5”
Gráfica 36. Caudales para configuración c) usando Cloro.
Gráfica 37. Concentraciones de cloro para la configuración c).
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
0.0
5.0
10.0
15.0
20.0
25.0
30.0
35.0
Cau
d
al
(L/s
)
Tiempo (min)
Caudales
Caudal 1
Caudal 2
Caudal 3
Caudal 4
0.0
2.0
4.0
6.0
8.0
10.0
12.0
14.0
16.0
18.0
0.0
5.0
10.0
15.0
20.0
25.0
30.0
35.0
Con
ce
n
tra
ción
(mg
/L)
Tiempo (min)
Concentraciones
Concentración 1
Concentración 2
Concentración 3
Concentración 4
Mezcla completa
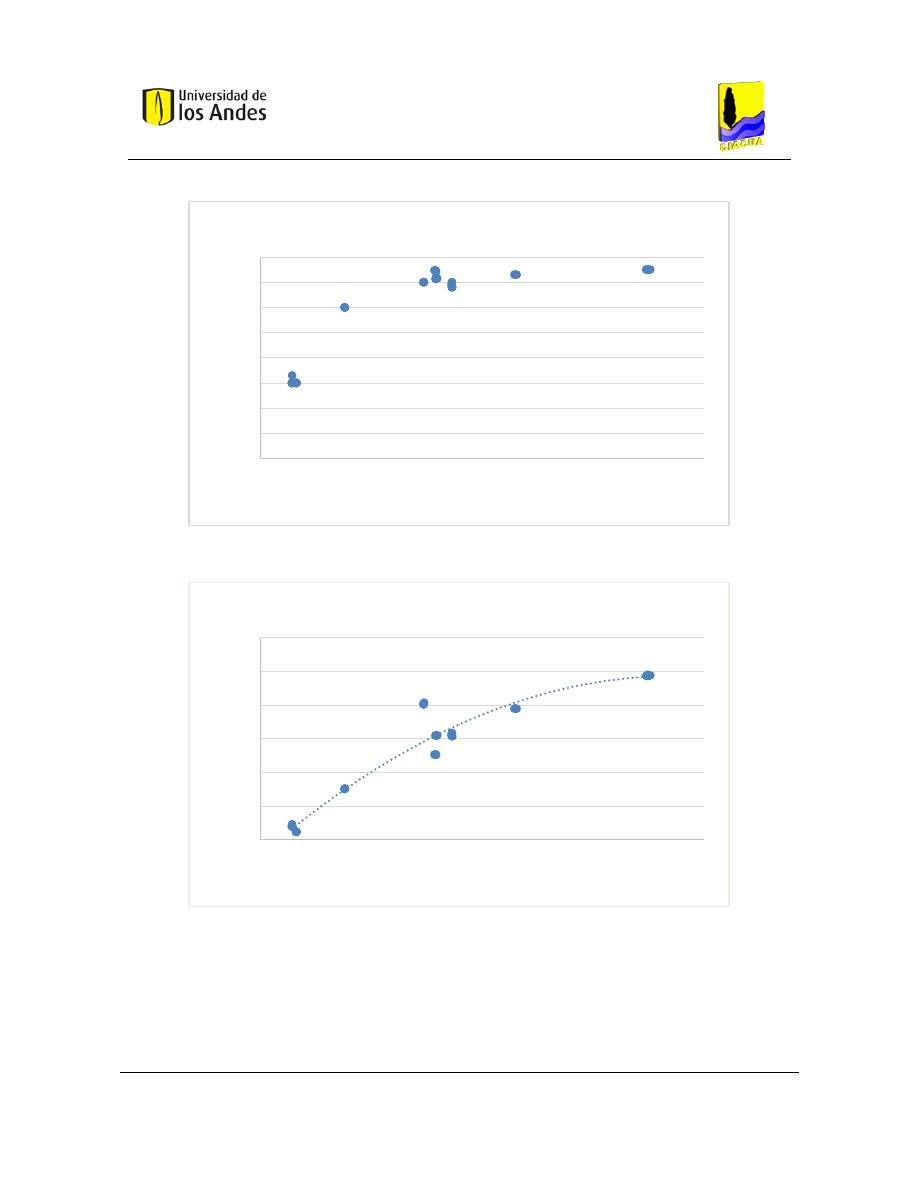
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
128
Gráfica 38. Fracción de masa de cloro para la configuración c).
Gráfica 39. Concentración normalizada para la configuración c).
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
y = 0.8982x
3
-2.3508x
2
+2.4765x-0.1782
R² = 0.9355
0.0
0.2
0.4
0.6
0.8
1.0
1.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
C*
3
Re
2
/Re
1
Concentración normalizada 3
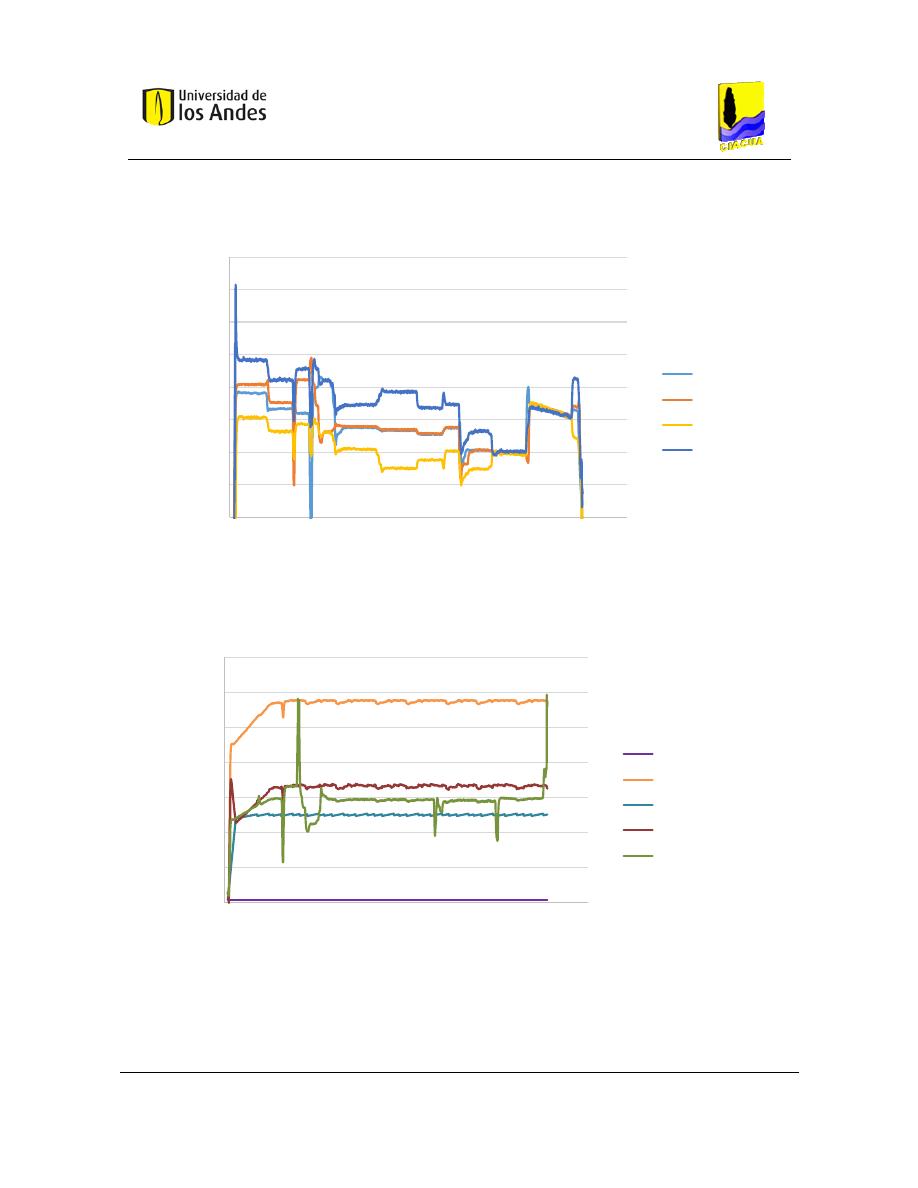
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
129
7.2.4. Configuración doble tee (L/d=14)
Gráfica 40. Caudales para configuración d) usando Cloro.
Gráfica 41. Concentraciones de cloro para la configuración d).
Los resultados de concentraciones para esta configuración son notablemente diferentes a
los de las demás configuraciones. Se puede ver que la concentración en las tuberías de
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
0.0
5.0
10.0
15.0
20.0
25.0
30.0
35.0
Cau
d
al
(L/s
)
Tiempo (min)
Caudales
Caudal 1
Caudal 2
Caudal 3
Caudal 4
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
0.0
5.0
10.0
15.0
20.0
25.0
30.0
35.0
Con
ce
n
tra
ción
(mg
/L)
Tiempo (min)
Concentración Cloro
Concentración 1
Concentración 2
Concentración 3
Concentración 4
Mezcla completa

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
130
salida es prácticamente constante durante todo el periodo de simulación y son aproximadas
a la curva que representa la mezcla completa.
Gráfica 42. Fracción de masa de cloro para la configuración d).
Gráfica 43. Concentración normalizada para la configuración d).
0.3
0.4
0.4
0.5
0.5
0.6
0.6
0.7
0.7
0.8
0.8
0.0
0.5
1.0
1.5
2.0
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería
y = 0.1119x
3
- 0.1764x
2
+ 0.0743x + 0.4977
R² = 0.9397
0.3
0.4
0.4
0.5
0.5
0.6
0.6
0.7
0.7
0.8
0.8
0.0
0.2
0.4
0.6
0.8
1.0
1.2
C*
3
Re
2
/Re
1
Concentración normalizada tubería 3
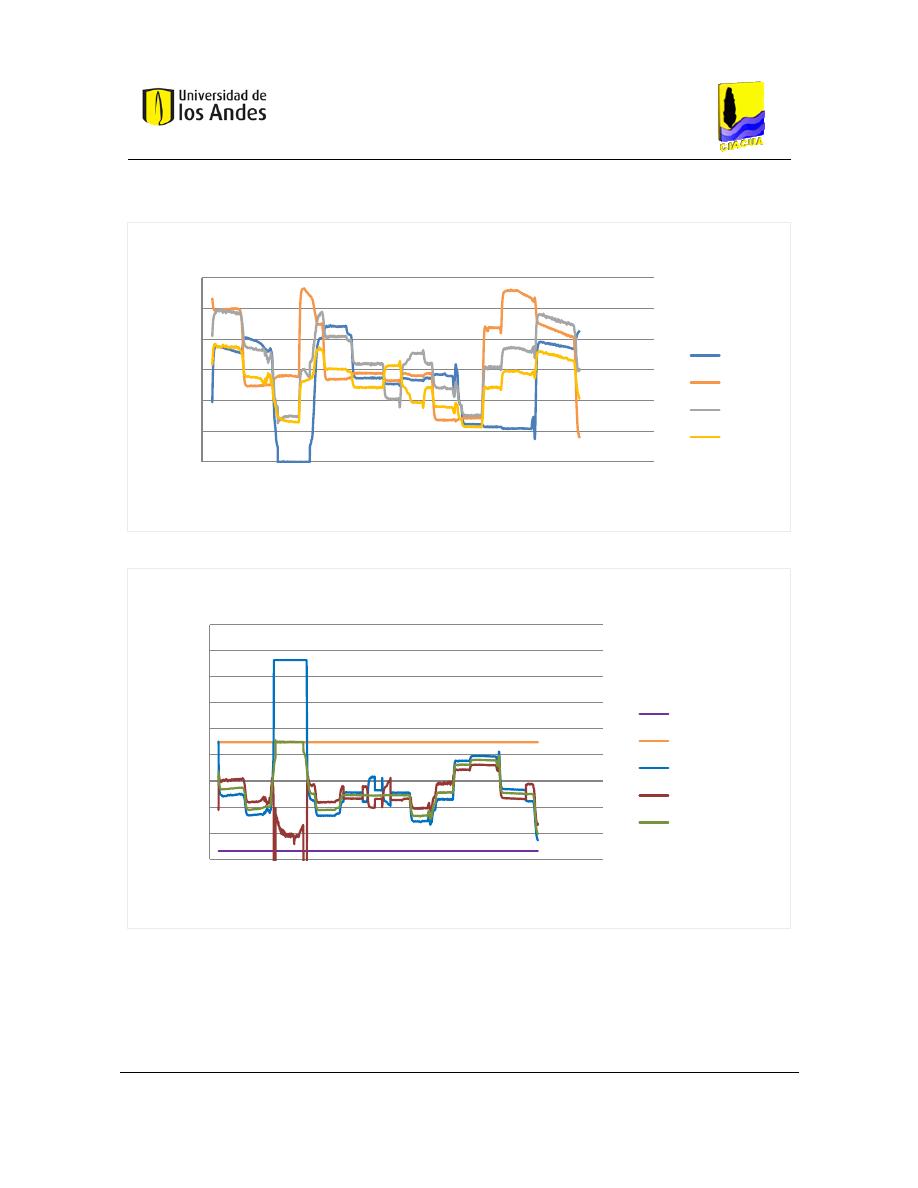
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
131
7.2.5. Configuración doble tee (L/d=3.7)
Gráfica 44. Caudales para configuración e) usando Cloro.
Gráfica 45. Concentraciones de cloro para la configuración e).
0
0.2
0.4
0.6
0.8
1
1.2
0.0
5.0
10.0
15.0
20.0
25.0
30.0
Cau
d
al
(L/s
)
Tiempo (min)
Caudales
Caudal 1
Caudal 2
Caudal 3
Caudal 4
0.0
2.0
4.0
6.0
8.0
10.0
12.0
14.0
16.0
18.0
0.0
5.0
10.0
15.0
20.0
25.0
30.0
Co
n
ce
n
tra
ció
n
(mg/L)
Tiempo (min)
Concentraciones
Concentración 1
Concentración 2
Concentración 3
Concentración 4
Mezcla completa
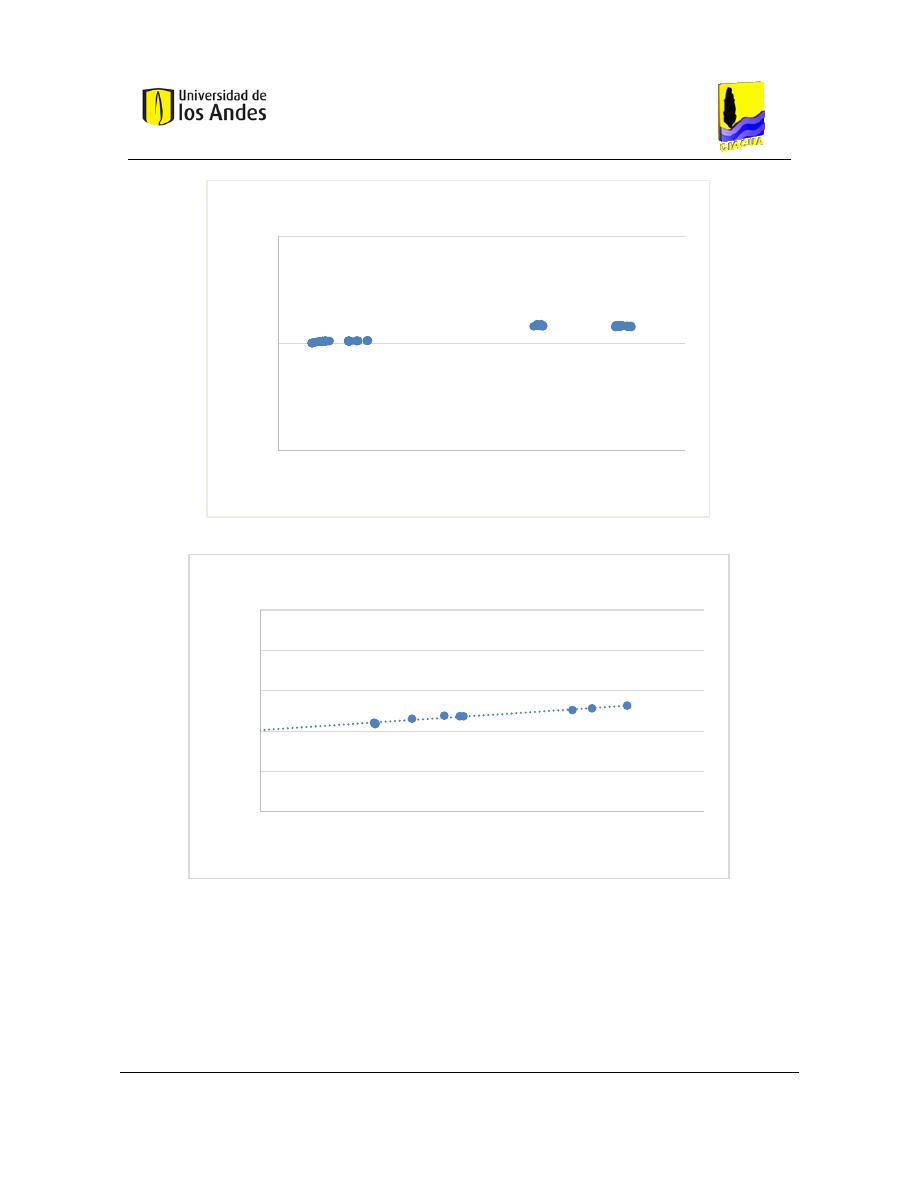
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
132
Gráfica 46. Fracción de masa de cloro para la configuración e).
Gráfica 47. Concentración normalizada para la configuración e).
0.0
0.5
1.0
0.0
1.0
2.0
3.0
4.0
5.0
6.0
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
y = 0.0887x
3
- 0.3078x
2
+ 0.596x + 0.0524
R² = 0.9955
0.0
0.2
0.4
0.6
0.8
1.0
0.9
1.0
1.1
1.2
1.3
1.4
1.5
C*
3
Re
2
/Re
1
Concetración normalizada 3

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
133
8. Análisis de resultados
De acuerdo con lo presentado anteriormente se puede evidenciar que los resultados para la
modelación computacional y física (con Permanganato de Potasio y Cloro) son consistentes
entre sí. Esto es importante de verificar ya que los datos medidos en el laboratorio pueden
servir como una medida de calibración de los modelos computaciones, los cuales se pueden
utilizar en un futuro para analizar diferentes escenarios, y los resultados obtenidos serán
confiables.
Como se mencionó anteriormente, también es importante comparar los resultados con los
reportados en la bibliografía, ya que permite obtener una medida de comparabilidad para
poder analizar los resultados de las demás configuraciones. En este caso, la configuración
que se comparó fue la cruz con todas las tuberías del mismo diámetro y como se muestra en
la Gráfica 30 los datos medidos siguen la misma tendencia a los valores reportados por
otros autores. Esto también proporciona confianza en que la metodología que se usó es la
adecuada para realizar los análisis respectivos.
Con los resultados presentados se puede determinar que cuando el caudal de la tubería 1 es
mayor que el de la tubería 2, la concentración en la tubería 4 se encuentra entre un 56% y
66% menor que en la tubería 3, para las configuraciones en cruz.
Por otro lado, se puede observar en algunas gráficas de concentración normalizada que
cuando los números de Reynolds son iguales (Re
2
/Re
1
=1) existe una dispersión mínima de
valores de C*3. Esto se debe a que la intensidad de turbulencia en cada uno de los casos es
diferente. Esto quiere decir que independientemente de que los caudales de entrada sean los
mismos, la intensidad de turbulencia tiene una influencia en los procesos de mezcla. Este
fenómeno también se puede explicar de acuerdo con lo reportado en la literatura (Austin et
al., 2008); en donde se explica que cuando se presenta una relación de número de Reynolds
de Re
2
/Re
1
=1 y Re
3
/Re
4
=1 el sistema se encuentra en una condición inestable, en la cual
cualquier variación, por mínima que sea, se multiplica y se magnifica, dando lugar a la
dispersión observada.
En general, para todas las configuraciones en cruz la Fracción de Masa y la Concentración
normalizada en la tubería 3 siempre tiende a aumentar a medida que aumenta la relación del
número de Reynolds de las tuberías de entrada
En cuanto a las configuraciones doble tee, si el análisis se enfoca en las tuberías de salida,
se logra deducir que el color es el mismo, lo que se podría traducir como una mezcla
completa. De acuerdo con la Gráfica 41, la concentración es aproximadamente constante
durante todo el tiempo de simulación y es muy cercana a lo que sería una mezcla completa,
independientemente de las variaciones de caudal de las tuberías de entrada. Esto se debe a

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
134
que, al tener una distancia tan grande entre las uniones en tee, existe un mayor contacto en
términos de espacio y tiempo, entre los flujos incidentes que permite que el agua se mezcle
en esta longitud y cuando llega a las tuberías de salida, la concentración es parecida para
ambas.
Para comparar los resultados obtenidos por las diferentes metodologías para cada una de las
configuraciones estudiadas, se presentan a continuación las gráficas que muestran los
resultados obtenidos en el modelo computacional (CFD) y en el modelo físico (laboratorio)
usando como trazador Cloro y Permanganato de Potasio, para la fracción de masa en la
tubería 3.
Cruz con todas las tuberías de 1”:
Gráfica 48. Comparación metodologías de medición en configuración a).
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
0.0
0.5
1.0
1.5
2.0
Fracción
d
em
asa
Re
2
/Re
1
Fracción de masa tubería 3
Laboratorio - Cloro
CFD
Laboratorio-KMNO4
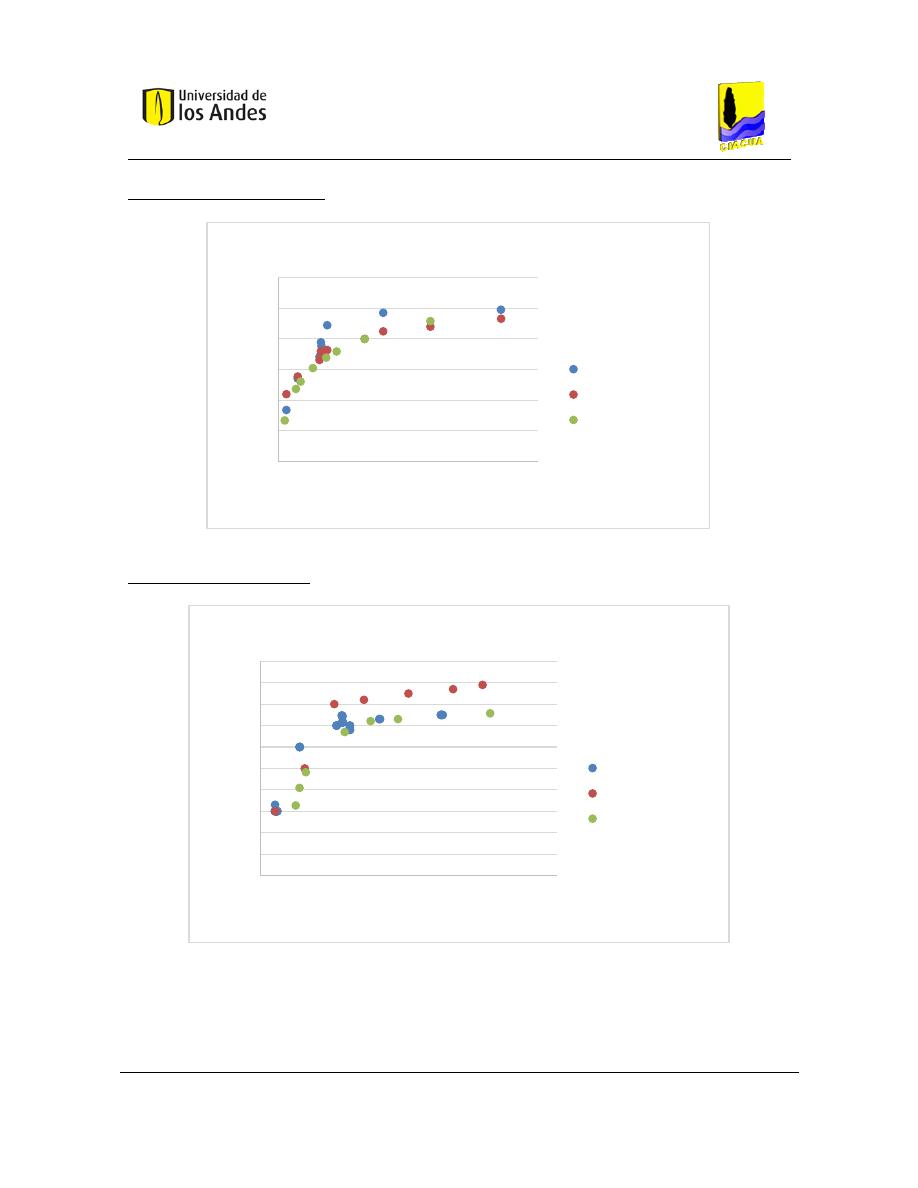
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
135
Cruz tubería de salida 1.5”:
Gráfica 49. Comparación metodologías de medición en configuración b).
Cruz tubería entrada 1.5”
Gráfica 50. Comparación metodologías de medición en configuración c).
0.0
0.2
0.4
0.6
0.8
1.0
1.2
0.0
2.0
4.0
6.0
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
Laboratorio - Cloro
CFD
Laboratorio- KMNO4
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
0.0
0.5
1.0
1.5
2.0
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
Laboratorio-Cloro
CFD
Laboratorio- KMNO4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
136
Doble tee (L/d=14):
Gráfica 51. Comparación metodologías de medición en configuración d).
Doble tee (L/d=3.7):
Gráfica 52. Comparación metodologías de medición en configuración e).
0.3
0.4
0.4
0.5
0.5
0.6
0.6
0.7
0.7
0.8
0.8
0.0
0.5
1.0
1.5
2.0
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
Laboratorio - Cloro
CFD
Laboraotrio - KMnO4
0.0
0.5
1.0
0.0
1.0
2.0
3.0
4.0
5.0
6.0
Fracción
d
e
m
asa
Re
2
/Re
1
Fracción de masa tubería 3
Laboratorio - Cloro
CFD
Laboratorio - KMNO4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
137
Se podría pensar que los procesos de mezcla son diferentes cuando se utiliza Permanganato
de Potasio y cuando se utiliza cloro ya que son especies diferentes. Sin embargo, es
importante tener en cuenta que existen varios procesos de transporte; la difusión, por su
parte se presenta cuando el soluto se transporta por el agua, estando ésta en estado estable.
En dicho caso, el trasporte entre los dos trazadores sí sería diferente. Pero para los
experimentos que se llevaron a cabo en este proyecto, los procesos predominantes fueron
los de convección-advección, en donde la naturaleza de los trazadores no afecta de manera
significativa la mezcla que se presenta en la unión. Es por esto que los resultados obtenidos
para los dos trazadores, si bien no son los mismos, siguen la misma tendencia y presentan
un error relativo de menos del 3%, el cual se debe a que las metodologías de medición
fueron diferentes.
Se puede observar que para todos los casos, los resultados obtenidos con el análisis de
imagen realizado con el Permanganato de Potasio, se encuentran con mayor dispersión con
respecto a los resultados obtenidos con las otras metodologías. Esto se debe a que el
análisis de imagen es la metodología que más presenta incertidumbre ya que la definición
del umbral de intensidad de rojo depende en gran parte de factores externos como la
incidencia de la luz sobre las imágenes, las sombras, el ángulo en el que se toman las fotos,
etc.
Por otro lado, los resultados de la modelación en CFD se acercan a los experimentales,
siguiendo la tendencia de que a medida que aumenta la relación del número de Reynolds,
también aumenta la fracción de masa. Lo anterior está de acuerdo con los resultados
presentados por Austin, et al., (2008), como se puede ver en la Gráfica 54. Sin embargo
existen discrepancias, en especial para las configuraciones en cruz con salida o entrada de
1.5”. La diferencia que existe entre los valores experimentales y los numéricos, se debe a
que el modelo computacional en muchos casos no representa algunas alteraciones
geométricas que se pueden presentar a la hora de la construcción del modelo físico. Por
ejemplo, para las configuraciones mencionadas, el cambio entre los diámetros de las
tuberías presenta una geometría interna brusca, la cual no se ve representada en la
geometría definida en ANSYS. Es por esto que los resultados demuestran una mayor
mezcla en el modelo fisco con respecto al computacional.
A pesar de lo anterior, se lograron resultados consistentes, demostrando que a medida que
aumenta la relación del número de Reynolds de las tuberías de entrada, aumenta la fracción
de masa.
Para cada una de las configuraciones se mostró la respectiva gráfica de concentración
normalizada. Sin embargo, no es muy clara la diferencia de los procesos de mezcla en las
diferentes configuraciones. Debido a esto, se presenta a continuación una gráfica que
compara los resultados de concentración normalizada en la tubería 3 para las
configuraciones estudiadas:
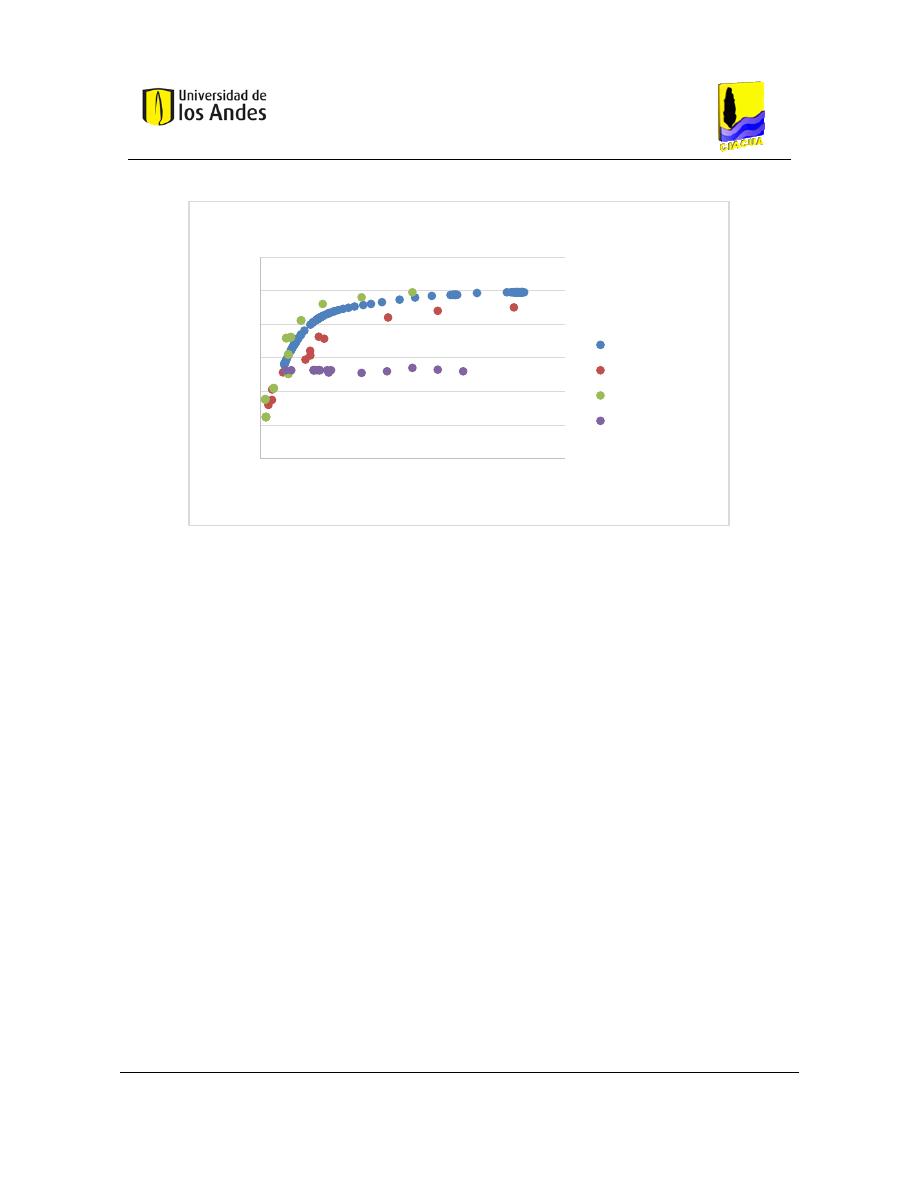
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
138
Gráfica 53. Comparación concentración normalizada entre configuraciones.
Se puede observar que la configuración en cruz con la tubería de entrada de 1.5”, es la que
presenta menor mezcla. Estos cambios se hacen más evidentes a partir de la Re2/Re1=0.5.
Con la Gráfica 53 se puede determinar que los procesos de mezcla dependen en gran
medida del tipo de configuración. Se puede observar que para la configuración en cruz con
la tubería de salida de 1.5” se presenta una mayor mezcla con respecto a las otras
configuraciones en cruz. Por su parte, la configuración en cruz con entrada de 1.5” es en
donde se presenta la menor mezcla. Esto ocurre principalmente por la forma en que la
interfaz incidente se genera en la intersección. El aumento del diámetro de una de las
tuberías genera una diferencia en la proporción de bifurcación de los flujos y por lo tanto en
la relación de velocidad. El proceso de mezcla se puede explicar usando el concepto de
continuidad: para un mismo caudal, la velocidad es menor si el área es mayor; por el
contrario, si se reduce el área, la velocidad va aumentar. Por lo tanto, para la configuración
con salida de 1.5”, la velocidad en esa tubería es menor que en las demás, lo que hace que
el impulso de los flujos incidentes se incline hacia la tubería 4, aumentando la mezcla y
reduciendo la concentración normalizada en la tubería 3. Por su parte, para la configuración
con la tubería de entrada de 1.5”, la velocidad en la tubería 2 generalmente es menor al de
la tubería 1, lo que hace que el impulso de los flujos incidentes se incline hacia la tubería 3
y enviando la mayor cantidad de agua con trazador por esta tubería.
Los valores obtenidos en esta tesis se compararon con los valores reportados por la
literatura:
0.0
0.2
0.4
0.6
0.8
1.0
1.2
0.0
1.0
2.0
3.0
4.0
5.0
6.0
C*
3
Re
2
/Re
1
Concentración normalizada tubería 3
Cruz 1"
Cruz salida 1.5"
Cruz entrada 1.5"
Doble tee (L/d=3.7)
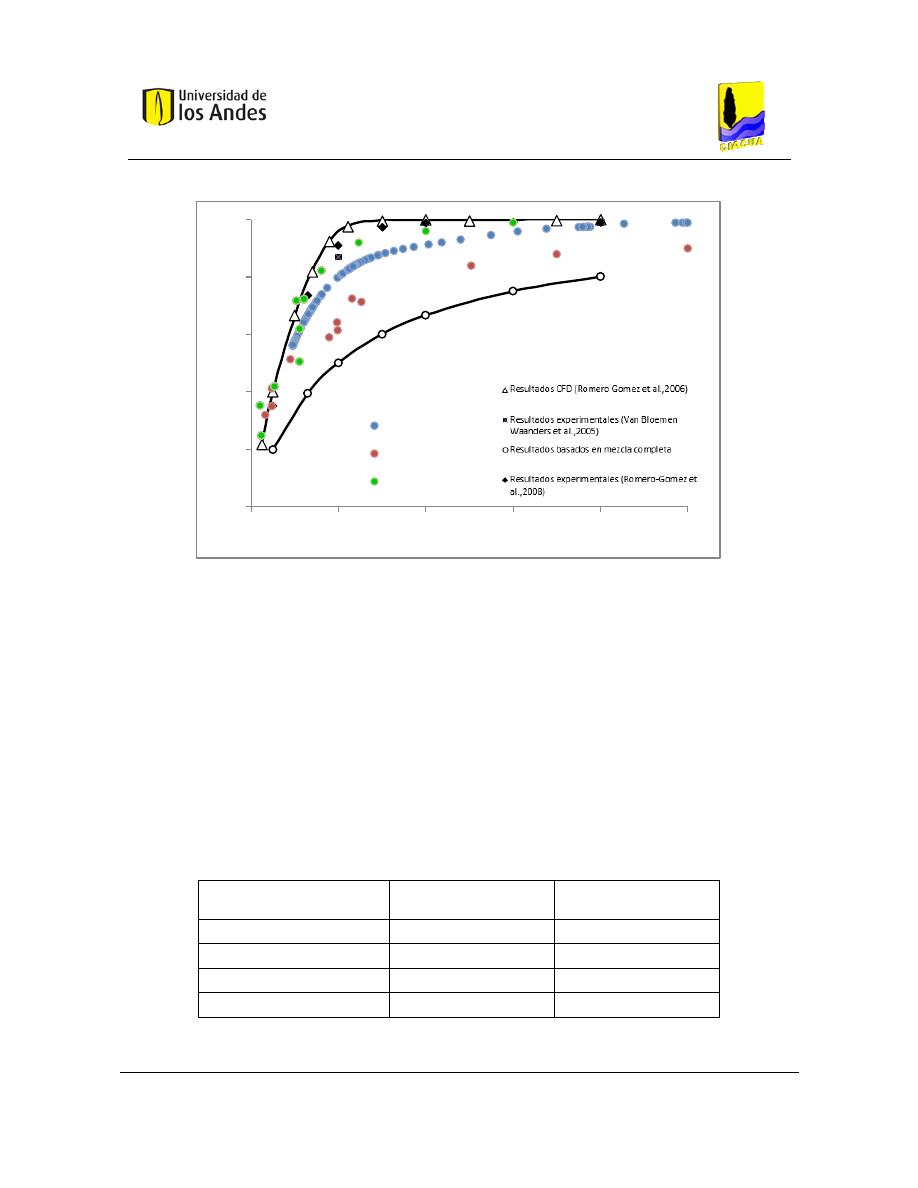
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
139
Gráfica 54. Comparación C* entre configuraciones y bibliografía.
Se puede ver en la gráfica que los valores siguen la misma tendencia, en especial hacia los
extremos. Se podría decir que los datos obtenidos con la configuración en cruz con tubería
de entrada de 1.5” son los más cercanos a los de la bibliografía; sin embargo, no son
comparables ya que la configuración es diferente. Esto podría demostrar que diferentes
configuraciones en diferentes condiciones experimentales, pueden presentar los mismos
resultados.
Es importante realizar una comparación para un escenario estándar con el fin de conocer la
magnitud del error experimental del modelo físico de este proyecto. Para esto se van a
comparar los valores de concentración normalizada, cuando la relación de los flujos de las
tuberías de entrada es la misma, para las configuraciones a), b) y c) con los reportados en la
literatura:
Tabla 17. Errores con respecto a la bibliografía para las configuraciones a), b) y c).
Configuración
C*3
Error con respecto a
la bibliografía
a)
0.82
9.9%
b)
0.614
32.5%
c)
0.89
2.2%
Literatura
0.91
-
0.0
0.2
0.4
0.6
0.8
1.0
0
1
2
3
4
5
C
*3
Re
2
/Re
1
Cruz 1"
Cruz salida 1.5"
Cruz entrada 1.5"

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
140
Se puede observar que la menor diferencia porcentual se encuentra en la configuración c);
sin embargo, estos resultados no son comparables debido a que la configuración es
diferente. En este caso, la diferencia porcentual de la configuración a) es la única
comparable ya que tiene todas las tuberías del mismo diámetro, así como las
configuraciones de los experimentos reportados en la literatura. Por lo tanto, el error
experimental es del 10% con respecto a los valores obtenidos por otros autores. Este error
se puede presentar por dos motivos, el principal es que en el modelo físico se produce una
mayor mezcla a causa de diferencias en la geometría interna generadas en el momento de
construcción de la unión. El segundo, se debe a errores aleatorios en cuanto a la precisión o
tipo de instrumento utilizado para medir las concentraciones de cloro.
También se realizó una comparación de los valores de concentración normalizada entre las
configuraciones b) y c) con respecto a la configuración a). Se encontró que para la
configuración b) existe una diferencia del 25% y para la configuración c) del 8.5%. Para
estas diferencias porcentuales se debe tener en cuenta que en la configuración b) se presenta
una mayor mezcla y en la configuración c) una menor mezcla con respecto a la
configuración a). Estos valores se muestran a continuación:
Tabla 18. Comparación de los valores de concentración normalizada entre las configuraciones b) y c) con respecto
a la configuración a).
Configuración
C*3
Error con respecto a la
configuración a)
a)
0.82
-
b)
0.614
25.1%
c)
0.89
8.5%
Por otro lado, para los resultados de concentración normalizada de cada una de las
configuraciones se obtuvo una ecuación por regresión polinómica de los datos. Esto se
realizó con el fin de caracterizar los procesos de mezcla en cada una de las configuraciones.
A continuación de muestran las ecuaciones obtenidas:
Configuración cruz con tuberías de 1”
0.0173𝑥
3
− 0.1814𝑥
2
+ 0.6026𝑥 + 0.3426
Configuración cruz con tubería de salida de 1.5”
0.0242𝑥
3
− 0.192𝑥
2
+ 0.5622𝑥 + 0.256
Configuración cruz con tubería de entrada de 1.5”
0.8982𝑥
3
− 2.3508𝑥
2
+ 2.4765𝑥 − 0.1782

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
141
Configuración doble tee (L/d=14)
0.1119𝑥
3
− 0.1764𝑥
2
+ 0.0743𝑥 + 0.4977
Configuración doble tee (L/d=3.7)
0.0887𝑥
3
− 0.3078𝑥
2
+ 0.569𝑥 + 0.0524
Se decidió realizar el análisis para la concentración normalizada ya que este valor depende
de menos parámetros, únicamente de las concentraciones. Por el contrario, la Fracción de
Masa, también depende de los caudales de las tuberías.
Para todas las configuraciones se encontró que una función polinómica de orden tres es la
que representa de mejor manera los datos medidos en el laboratorio.
Para comprobar lo anterior, se utilizó la ecuación correspondiente para calcular la
concentración normalizada asociada con diferentes relaciones de número de Reynolds. Por
otro lado, se quiso utilizar otro método matemático de cálculo para poder realizar
comparaciones. Por lo tanto se utilizaron Redes Neuronales Artificiales.
Las Redes Neuronales Artificiales están inspiradas en las redes neuronales biológicas del
cerebro humano. Estas redes aprenden de la experiencia, generalizan de ejemplos previos a
ejemplos nuevos y abstraen las características principales de una serie de datos (Basogain,
2014). El funcionamiento general de las redes Neuronales Artificiales se basa en ingresar
una serie de datos medidos, junto con sus resultados; luego la red aprende de dichos valores
y finalmente, en el momento en que el usuario quiera obtener un resultado para un dato de
entrada cualquiera, obtendrá un valor de acuerdo con lo aprendido previamente.
En este caso, se utilizó un código en Matlab y se ingresaron los datos obtenidos en el
laboratorio. Dichos datos corresponden a la relación del número de Reynolds de las tuberías
de entrada y la concentración normalizada obtenida en la tubería 3. Después de que la red
procesó los datos y aprendió de los valores de entrada, se pudo obtener la concentración
normalizada para cualquier relación de número de Reynolds. Los resultados Para casa una
de las configuraciones se muestra a continuación:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
142
Configuración cruz con tuberías de 1”
Tabla 19. Resultados Regresión polinómica y RNA para configuración a).
Re
2
/Re
1
Regresión
polinómica
Redes
Neuronales
Error
0.1
0.177
0.143
19.1%
0.3
0.412
0.434
5.3%
0.5
0.578
0.583
0.8%
0.7
0.694
0.675
2.6%
1
0.801
0.788
1.6%
1.3
0.859
0.923
7.4%
1.5
0.882
0.861
2.4%
1.7
0.899
0.825
8.2%
2
0.918
0.991
8.0%
2.3
0.936
0.881
5.9%
2.5
0.950
0.876
7.8%
2.7
0.966
0.950
1.7%
3
0.995
0.919
7.7%
Promedio
6.0%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
143
Configuración cruz con tubería de salida de 1.5”
Tabla 20. Resultados Regresión polinómica y RNA para configuración b).
Re
2
/Re
1
Regresión
polinómica
Redes
Neuronales
Error
0.2
0.361
0.319
11.734%
0.3
0.408
0.443
8.619%
0.4
0.452
0.495
9.650%
0.5
0.492
0.572
16.231%
0.6
0.529
0.522
1.403%
0.7
0.564
0.589
4.441%
0.8
0.595
0.563
5.421%
0.9
0.624
0.577
7.547%
1
0.650
0.634
2.522%
1.1
0.674
0.700
3.810%
1.2
0.696
0.733
5.377%
1.3
0.716
0.725
1.251%
1.4
0.733
0.688
6.119%
1.5
0.749
0.725
3.241%
1.6
0.763
0.718
5.952%
1.7
0.776
0.777
0.186%
1.8
0.787
0.800
1.586%
1.9
0.797
0.789
1.047%
2
0.806
0.851
5.533%
2.1
0.814
0.807
0.899%
2.2
0.821
0.871
6.095%
2.3
0.828
0.712
13.991%
2.4
0.834
0.827
0.875%
2.5
0.840
0.852
1.450%
Promedio
8.450%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
144
Configuración cruz con tubería de entrada de 1.5”
Tabla 21. Resultados Regresión polinómica y RNA para configuración c).
Re
2
/Re
1
Regresión
polinómica
Redes
Neuronales
Error
0.1
0.064
0.057
11.09%
0.2
0.208
0.207
0.64%
0.3
0.340
0.345
1.47%
0.4
0.460
0.641
39.36%
0.5
0.567
0.700
23.63%
0.6
0.661
0.714
7.94%
0.7
0.743
0.737
0.76%
0.8
0.813
0.835
2.81%
0.9
0.870
0.856
1.56%
1
0.914
0.918
0.35%
1.1
0.946
0.950
0.34%
1.2
0.966
0.956
1.03%
1.3
0.973
0.970
0.37%
Promedio
7.03%
Configuración doble tee (L/d=14)
Tabla 22. Resultados Regresión polinómica y RNA para configuración d).
Re
2
/Re
1
Regresión
polinómica
Redes
Neuronales
Error
0.1
0.5034779
0.4986
0.97%
0.2
0.5063992
0.4986
1.54%
0.3
0.5071353
0.5106
0.68%
0.4
0.5063576
0.5255
3.78%
0.5
0.5047375
0.5074
0.53%
0.6
0.5029464
0.5043
0.27%
0.7
0.5016557
0.5019
0.05%
0.8
0.5015368
0.5049
0.67%
0.9
0.5032611
0.5017
0.31%
1
0.5075
0.5061
0.28%
1.1
0.5149249
0.5082
1.31%
1.2
0.5262072
0.5082
3.42%
1.3
0.5420183
0.5082
6.24%
Promedio
1.54%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
145
Configuración doble tee (L/d=3.7)
Tabla 23. Resultados Regresión polinómica y RNA para configuración e).
Re
2
/Re
1
Regresión
polinómica
Redes
Neuronales
Error
0.2
0.189
0.196
3.59%
0.3
0.222
0.216
2.90%
0.4
0.254
0.245
3.46%
0.5
0.286
0.285
0.05%
0.6
0.316
0.295
6.70%
0.7
0.345
0.345
0.07%
0.8
0.374
0.378
1.18%
1
0.428
0.448
4.53%
1.1
0.454
0.461
1.55%
1.2
0.479
0.433
9.66%
1.3
0.503
0.519
3.29%
1.4
0.526
0.514
2.23%
1.5
0.548
0.570
4.10%
Promedio
4.79%
Sin embargo, es importante realizar las comparaciones de los resultados con los datos
obtenidos en el laboratorio. Para esto se escogieron algunos datos medidos en laboratorio y
para esa misma relación de número de Reynolds se calculó la concentración normalizada
utilizando la ecuación polinómica y Redes Neuronales Artificiales:
Configuración cruz con tuberías de 1”
Tabla 24. Error entre resultados medidos en el laboratorio, Regresión polinómica y RNA para configuración a).
Re
2
/Re
1
Laboratorio
Regresión
polinómica
Error
Redes
Neuronales
Error
0.502
0.580
0.579
0.035%
0.577
0.46%
0.609
0.646
0.646
0.035%
0.6494
0.52%
0.702
0.694
0.694
0.040%
0.694
0.00%
1.030
0.808
0.808
0.014%
0.8116
0.40%
1.100
0.824
0.824
0.014%
0.825
0.09%
1.211
0.845
0.844
0.004%
0.846
0.12%
1.367
0.867
0.867
0.063%
0.8656
0.16%
1.448
0.876
0.876
0.108%
0.875
0.09%
1.462
0.877
0.878
0.117%
0.8771
0.01%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
146
Configuración cruz con tubería de salida de 1.5”
Tabla 25. Error entre resultados medidos en el laboratorio, Regresión polinómica y RNA para configuración b).
Re
2
/Re
1
Laboratorio
Regresión
polinómica
Error
Redes
Neuronales
Error
0.162
0.320
0.342
6.40%
0.337
5.0%
0.234
0.350
0.378
7.31%
0.347
1.0%
0.235
0.412
0.378
9.01%
0.347
18.8%
0.449
0.514
0.472
8.95%
0.508
1.2%
0.892
0.590
0.622
5.15%
0.583
1.3%
0.984
0.642
0.646
0.68%
0.583
10.2%
0.990
0.614
0.648
5.15%
0.606
1.4%
1.155
0.725
0.687
5.61%
0.734
1.2%
1.263
0.714
0.708
0.78%
0.709
0.7%
2.521
0.840
0.841
0.09%
0.837
0.4%
Configuración cruz con tubería de entrada de 1.5”
Tabla 26. Error entre resultados medidos en el laboratorio, Regresión polinómica y RNA para configuración c).
Re
2
/Re
1
Laboratorio
Regresión
polinómica
Error
Redes
Neuronales
Error
0.100
0.079
0.063
25.5%
0.0813
2.23%
0.101
0.093
0.065
41.6%
0.0984
5.98%
0.115
0.047
0.087
45.4%
0.0442
7.14%
0.266
0.302
0.297
1.6%
0.2987
1.08%
0.517
0.815
0.583
39.6%
0.7997
1.86%
0.559
0.619
0.623
0.6%
0.637
2.75%
0.603
0.623
0.664
6.2%
0.6296
1.08%
0.809
0.780
0.818
4.7%
0.7798
0.02%
1.218
0.975
0.968
0.6%
0.9792
0.47%
1.226
0.976
0.969
0.7%
0.9779
0.23%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
147
Configuración doble tee (L/d=14)
Tabla 27. Error entre resultados medidos en el laboratorio, Regresión polinómica y RNA para configuración d).
Re
2
/Re
1
Laboratorio
Regresión
polinómica
Error
Redes
Neuronales
Error
0.259
0.509
0.507
0.37%
0.504
1.08%
0.344
0.501
0.507
1.17%
0.506
0.91%
0.427
0.505
0.506
0.19%
0.520
2.92%
0.508
0.504
0.505
0.12%
0.506
0.30%
0.613
0.508
0.503
1.05%
0.506
0.47%
0.713
0.501
0.502
0.11%
0.500
0.16%
0.854
0.506
0.502
0.66%
0.504
0.32%
0.905
0.503
0.503
0.08%
0.502
0.20%
0.918
0.507
0.504
0.63%
0.506
0.30%
0.995
0.509
0.507
0.35%
0.505
0.81%
1.000
0.506
0.508
0.30%
0.506
0.02%
Configuración doble tee (L/d=3.7)
Tabla 28. Error entre resultados medidos en el laboratorio, Regresión polinómica y RNA para configuración e).
Re
2
/Re
1
Laboratorio
Regresión
polinómica
Error
Redes
Neuronales
Error
0.496
0.279
0.284
1.72%
0.2755
1.45%
0.500
0.285
0.286
0.19%
0.2834
0.57%
0.613
0.329
0.320
2.73%
0.3285
0.00%
1.055
0.437
0.443
1.30%
0.4334
0.77%
1.105
0.461
0.455
1.24%
0.4756
3.06%
1.149
0.476
0.466
2.13%
0.4762
0.01%
1.170
0.474
0.471
0.44%
0.474
0.09%
1.175
0.474
0.473
0.28%
0.4736
0.09%
1.322
0.504
0.508
0.73%
0.5041
0.03%
1.349
0.513
0.514
0.28%
0.5126
0.01%
Con estos resultados se confirma que se pueden utilizar las ecuaciones polinómicas para
describir los procesos de mezcla en las intersecciones de las diferentes configuraciones.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
148
9. Conclusiones y recomendaciones
Al realizar las pruebas se puede concluir, que efectivamente no se presenta una mezcla
completa en la unión y que efectivamente, el porcentaje de trazador que se bifurca depende
de las relaciones de flujo entre las tuberías de entrada y el tipo de configuración.
En cuanto a la metodología de medición usando análisis de imagen, se puede evidenciar de
manera visible los procesos de mezcla en cada una de las configuraciones. Generalmente,
cuando los caudales de las dos tuberías de entrada es el mismo, se puede ver que existe el
mismo patrón de mezcla, el cual es que por la tubería de salida 3 se va la mayor parte del
trazador; y por la tubería de salida 4 existe una pequeña mezcla. La tendencia de
concentración normalizada y fracción de masa es de aumentar a medida que aumenta la
relación del número de Reynolds de las tuberías de entrada.
En cuanto a los resultados obtenidos utilizando Cloro como trazador, se puede confirmar
que los procesos de mezcla son incompletos, lo que es consistente con los resultados
obtenidos utilizando Permanganato de Potasio. Además, dichos procesos dependen
directamente de la relación del flujo de las tuberías de entrada y de la configuración de la
intersección. Para la configuración en cruz con todas las tuberías de 1” el patrón de mezcla
presenta la misma tendencia que los reportados en la literatura, pero se puede calcular una
diferencia del 5% en el punto donde los datos son más alejados.
Los resultados reportados utilizando CFD son consistentes con los valores obtenidos en el
modelo físico. Se sabe que el tamaño de la malla siempre es importante y crítico en
cualquier problema resuelto con CFD. Sin embargo, para este caso se utilizaron tamaños de
malla relativamente pequeños y los resultados parecen ser independientes al número de
celdas. Lo anterior se debe a que se está utilizando un método RANS para modelar la
turbulencia, el cual solo demanda mallas de pequeño tamaño para producir aproximaciones
satisfactorias de problemas físicos. Además, incrementar el tamaño de la malla repercute en
un incremento de los recursos computacionales, que para este caso no valdrían la pena. Por
lo tanto, el refinamiento de la malla en la zona de la intersección es suficiente para tener
buenos resultados. No obstante, existen variaciones que se deben principalmente por la
representación adecuada de la geometría interna de las tuberías del modelo físico.
En este proyecto se confirmó la utilidad de utilizar modelos computacionales. En este caso
CFD fue de gran ayuda en el momento de definir cuál era la relación L/d que permite una
mezcla completa, ya que se pueden simular varios modelos cambiando dicha relación y los
costos, tanto temporales como de recursos físicos, son mucho menores en comparación si
se cambia el montaje en el laboratorio para cada relación L/d propuestas. Esto también
aplica para otras configuraciones que se quieran comprobar en un futuro, si se sabe que
para este proyecto la diferencia máxima entre lo medido en el laboratorio y lo simulado en

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
149
CFD fue de 10.5%, Se puede usar esta diferencia porcentual para comparar resultados
numéricos de otras configuraciones y estimar resultados para modelos físicos.
Se encontró que cuando existe una configuración en donde la tubería de salida tiene un
diámetro mayor, la mezcla en la tubería 3 es un 25% mayor a lo que se presentaría en una
configuración con todas las tuberías del mismo diámetro. De la misma manera, para la
configuración en donde la tubería de entrada tiene mayor diámetro, la mezcla en la tubería
3 es 8.5% menor con respecto a la configuración con todas las tuberías del mismo diámetro.
Como se mencionó anteriormente, los procesos de mezcla dependen de la configuración de
la intersección y esto se observó de manera muy clara cuando se realizaron los
experimentos con la configuración doble tee. Al tener una distancia grande entre las dos
uniones, los flujos incidentes tenían mayor tiempo y espacio de contacto en el que se
desarrolla la mezcla, por lo tanto las concentraciones en las tuberías de salida se acercan
mucho a la mezcla completa. Debido a lo anterior, se encontró que la relación L/d a partir
del cual se comienza a presentar una mezcla completa es 3.7. Con esta geometría se
lograron resultados consistentes para las tres metodologías utilizadas. Sin embargo, es
conveniente realizar una modelación física con una relación L/d un poco menor para
corroborar estos resultados.
El análisis de este trabajo se enfocó en los procesos de mezcla en función de la relación de
número de Reynolds de las tuberías de entrada. Sin embargo, es recomendable realizar los
mismos análisis pero teniendo en cuenta la relación del número de Reynolds de las tuberías
de salida.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
150
10. Agradecimientos
La realización de este proyecto no pudo haber llegado a mejor término sin la guía y asesoría
de Juan Saldarriaga, quien siempre me corrigió y apoyó para llevar a cabo este trabajo.
También, agradezco a mis jurados de tesis quienes estuvieron dispuestos a proporcionar su
ayuda: Pedro Romero-Gómez, que gracias a su gran conocimiento en el tema, pude
solucionar todas las dudas que surgieron durante el desarrollo de la investigación. Pedro
Iglesias, que gracias a sus recomendaciones con respecto a las metodologías de medición
pude obtener resultados más consistentes. Y a Andres González, que gracias a sus
explicaciones pude entender las bases y el funcionamiento de CFD.
Un especial agradecimiento, por su ayuda incondicional, al técnico del Laboratorio de
Hidráulica Jhon Calvo.
Por último, pero no menos importante, agradezco a mis papás por su apoyo y confianza en
mí, y a mis amigos por siempre alentarme a seguir adelante en esta investigación.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
151
11. Bibliografía
Agbar Agua. (2003). Cloro residual. Recuperado el 14 de Noviembre de 2012, de
Aguagest- Región de Murcia: http://www.aquagest-
regiondemurcia.es/img/contenidos/1/ficha-sobre-calidad-del-agua.pdf
Austin, R., Romero-Gomez, P., & Choi, C. (2007). Transport Phenomena at intersections
at Low Reynolds Number. Obtenido de ASCE.
Austin, R., Van Bloemen Waanders, S., McKenna, S., & Choi, Y. (2008). Mixing at croos
Juctions in Water Dsitribution System II. ASCE, (pág. 8).
Biblioteca Digital de la Universidad de Chile. (2005). Ley de disfusión de Graham.
Recuperado el 27 de mayo de 2013, de Ciencias químicas y farmaceúticas:
http://mazinger.sisib.uchile.cl/repositorio/ap/ciencias_quimicas_y_farmaceuticas/ap
-quimgral-6/c4.2.html
Boulos, P. F., Altman, T., Jarrige, P.-A., & Collevati, F. (1995). Discrete Simulation
Approach For Network-WaterQuality Models. ASCE, (pág. 12).
Braun, M., Bernard, T., Ung, H., Piller, O., & Gilbert, D. (2013). Model based investigation
of transport phenomena in water distribution networks for contamination scenarios.
Obtenido de 12 th International Conference on computing and Control for Water
Industry.
Chrysikopoulos, C., Plega, C., & Katzourakis, V. (2011). Non-invasive in istu
concentration determinantion of fluorescent or color tracers and pollutants in a glass
pore network model. Journal of Hazardous materials, 299-306.
Ho, C. K. (2008). Solute Mixing Model for Water-Distribution Pipe Networks. Recuperado
el 10 de Marzo de 2013, de ASCE:
http://gsgc.gzhu.edu.cn/gpsgd/UploadFile/200942623229730.pdf
Ho, C. K., & Leslie, O. (Septiembre de 2009). Journal AWWA. Recuperado el 27 de mayo
de 2013, de Evaluation of solute mixing in Water distribution pipe junctions:
http://www.sandia.gov/EPANET-BAM/download/J_AWWA_2009_101_9_Ho.pdf
Ho, C. K., Choi, C. Y., & McKenna, S. A. (2007). Evaluation of complete and incomplete
mixing models in water distribution pipe network simulations. Recuperado el 3 de
Junio de 2013, de World Environmental and Water Resources congress (ASCE):
http://ascelibrary.org.biblioteca.uniandes.edu.co:8080/doi/abs/10.1061/40927%282
43%29486?prevSearch=%28evaluation+of+complete+and+incomplete+mixing+mo
dels%29+and+%5BFulltext%3A+evaluation+of+complete+and+incomplete+mixin
g+models%5D&searchHistoryKey=
Ho, C., & Khalsa, S. (2008). EPANET-BAM: Water quality modeling with incomplete
mixing in pipe junctions. Obtenido de 10 th Annual Water Distribution Systems
Analysis Conference, WDSA.
Ho, C., Orear, L., Wright, J., & McKenna, S. (2007). Contaminant mixing at pipe joints:
Comparison between laboratory flow experiments and Computational Fluid

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
152
Dynamics models. Obtenido de 8th Annual Water Distribution Systems Analysis
Symposium.
ImageJ. (2011). Recuperado el 12 de Noviembre de 2015, de http://imagej.nih.gov/ij/
McKenna, S., Orear, L., & Wright, J. (2007). Experimental Determination of Solute Mixing
in Pipe Joints. Obtenido de World Environmental and Water Resources Congress.
Mompremier, R. (2009). Difusión de sustancias en redes de tuberías presión. México D.F:
Intituto politécnico Nacional.
Ocasio, N., & Manuel, L. (2007). El uso del Cloro en la Desinfección del Agua.
Recuperado el 15 de Noviembre de 2012, de Hispagua: Sistema Español de
Información sobre el Agua: http://hispagua.cedex.es/sites/default/files/uso_cloro.pdf
Revista Ambientum. (Febrero de 2002). Cloro Residual en Agua de Consumo. Recuperado
el 15 de Noviembre de 2012, de Revista Ambientum:
http://www.ambientum.com/revista/2002_05/CLORES2.asp
Romero-Gomez, P., Choi, C., van Bloemen Waanders, B., & McKenna, S. (2006).
Transport Phenomena at Intersections of Pressurized Pipe Systems. 8th Annual
Water Distribution Systems Analysis Symposium, (pág. 20). Cincinnati, Ohio, USA.
Romero-Gómez, P., Ho, C., & Choi, Y. (2008). Mixing at cross junctions in water
dsitribution system. ASCE, (pág. 10).
Rossman, L. (1993). EPANET. Cincinnati.
Rossman, L., Clark, R., & Grayman, W. (1994). Modeling Chlorine Residuals in Drinking-
Water Distribution Systems. ASCE, (pág. 18).
Saldarriaga V., J. G. (2011). Clase de Hidráulica. Bogotá D.C, Colombia: Universidad de
los Andes.
Saldarriaga, J. G. (2007). Hidráulica de Tuberías: Abastecimiento de Aguas, Redes, Riegos.
Bogotá D.C.: Alfaomega.
Sedna, P. P. (Diciembre de 2012). Los acueductos romanos. Recuperado el 25 de Mayo de
2013, de http://www.portalplanetasedna.com.ar/acueductos.htm
Shao, Y., Jeffrey Yang, Y., Jiang, L., Yu, T., & Shen, C. (2014). Experimental testing and
modeling analysis of solute mixing at water distribution pipe junctions. Obtenido de
Water Research.
Tzatchkov, V. G., Buchberger, S. G., Li, Z., Romero-Gómez, P., & Choi, C. (5 de
Septiembre de 2009). Axial Dispersion in Pressurized Water Ditribution Networks-
A Review. Recuperado el 10 de Marzo de 2013, de International Symposium on
Water Management and Hydraulic Engineering:
http://wmhe.gf.ukim.edu.mk/downloads/paperstopic2/a104-tzatchkov-buchberger-
li-romero-gomez-choi.pdf
Universidad de Valencia. (2006). Fenómenos de transporte y conductividad electrolítica.
Recuperado el 27 de mayo de 2013, de Departamento de Química Física:
http://www.uv.es/tunon/QFIII/tema_4.pdf
Versteeg, H., & Malalasekera, W. (1995). An introduction to Computational Fluid
Dynamics. Edinburgo: Pearson.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelación de la calidad del agua en redes de distribución de agua
potable: Mezcla completa vs. Mezcla incompleta.
MIC 201520
Laura Natalia Cotes
Tesis II
153
Vidal, R., Martínez, F., & Ayza, M. (1994). Aplicaciones de los modelos de calidad en la
simulación de las redes de distribución de agua potable. Recuperado el 15 de
Octubre de 2012, de
http://upcommons.upc.edu/revistes/bitstream/2099/4203/1/article5.pdf
Yi Wu, Z., & Elsayed, S. M. (2013). Parallelized hydraulic and water quality simulation for
water ditribution system analysis. World Environmental and Water Resources
Congress , (pág. 11). ASCE.
