
TESIS DE MAESTRÍA
INGENIERÍA CIVIL
METODOLOGÍA PARA EL DISEÑO OPTIMIZADO DE REDES DE ALCANTARILLADO
PRESENTADO POR:
NATALIA DUQUE VILLARREAL
a
ASESOR:
JUAN GUILLERMO SALDARRIAGA VALDERRAMA
a
a
Centro de Investigación en Acueductos y Alcantarillados (CIACUA), Departamento de Ingeniería
Civil y Ambiental, Universidad de los Andes, Bogotá, Colombia
CO-ASESOR:
DANIEL DUQUE VILLARREAL
b
b
Centro para la Optimización y Probabilidad Aplicada (COPA), Departamento de Ingeniería
Industrial, Universidad de los Andes, Bogotá, Colombia
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
BOGOTÁ D.C
JUNIO 2015

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
MIC 201510-00
Natalia Duque Villarreal
Tesis I
i
TABLA DE CONTENIDO
1
Introducción ................................................................................................................................ 1
1.1
Objetivos ............................................................................................................................. 2
1.1.1
Objetivo General ......................................................................................................... 2
1.1.2
Objetivos Específicos ................................................................................................... 2
1.2
Antecedentes ...................................................................................................................... 3
2
Marco teórico .............................................................................................................................. 6
2.1
Redes de drenaje urbano .................................................................................................... 6
2.1.1
Efectos de la urbanización ........................................................................................... 6
2.1.2
Componentes de las redes de drenaje urbano ........................................................... 7
2.1.3
Fallas en redes de drenaje urbano ............................................................................ 10
2.2
Sistema integrado de drenaje urbano ............................................................................... 11
2.3
Generalidades sobre el diseño hidráulico de los sistemas de alcantarillado .................... 12
2.3.1
Supuestos del diseño ................................................................................................. 12
2.3.2
Ecuaciones de diseño ................................................................................................ 14
2.3.3
Restricciones de diseño ............................................................................................. 19
2.3.4
Función de costos ...................................................................................................... 22
3
Definición del problema ............................................................................................................ 25
3.1
Problemas de flujo en redes ............................................................................................. 25
3.2
Componentes la red de alcantarillado .............................................................................. 26
3.3
Selección del trazado de la red ......................................................................................... 27
3.3.1
Datos de entrada para la selección del trazado ........................................................ 30
3.4
Diseño hidráulico de la red ................................................................................................ 30
3.4.1
Datos de entrada para el diseño hidráulico .............................................................. 31
4
Metodología para el diseño optimizado de redes de alcantarillado ........................................ 33
4.1
Metodología para la selección del trazado de redes de alcantarillado ............................ 33
4.1.1
Definición del grafo para la selección del trazado .................................................... 33

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
MIC 201510-00
Natalia Duque Villarreal
Tesis I
ii
4.1.2
Modelaje matemático para la selección del trazado ................................................ 37
4.2
Metodología para el diseño hidráulico de redes de alcantarillado ................................... 42
4.2.1
Definición del grafo para el diseño hidráulico .......................................................... 42
4.2.2
Método de optimización ........................................................................................... 55
4.2.3
Modelaje matemático para el diseño hidráulico ...................................................... 58
4.2.4
Implementación ........................................................................................................ 60
4.3
Estimación de la función de costos para la selección del trazado .................................... 70
4.3.1
Generación de trazados aleatorios ........................................................................... 71
4.4
Metodología para el diseño de redes de alcantarillado .................................................... 71
5
Resultados y análisis de resultados ........................................................................................... 74
5.1
Diseño de una red de alcantarillado ................................................................................. 74
5.2
Convergencia del diseño de redes de alcantarillado ........................................................ 80
6
Conclusiones y Recomendaciones ............................................................................................ 82
6.1
Problema de selección del trazado ................................................................................... 82
6.2
Problema de diseño hidráulico ......................................................................................... 83
7
Referencias ................................................................................................................................ 84
8
Anexos ....................................................................................................................................... 87

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
MIC 201510-00
Natalia Duque Villarreal
Tesis I
iii
ÍNDICE DE FIGURAS
Figura 2.1 Interacciones del Sistema de Drenaje Urbano. Tomado y Modificado de Butler & Davies (2011). .. 6
Figura 2.2 Efectos de la urbanización. Tomado de Muth, Brinson, & Bernhar (2010). ...................................... 7
Figura 2.3 Fallas en redes de drenaje urbano. ................................................................................................. 11
Figura 2.4 Sistema Integrado de Drenaje Urbano. ........................................................................................... 12
Figura 2.5 Flujo uniforme en canales abiertos. Tomado y modificado de Salcedo (2012). .............................. 14
Figura 2.6 Sección transversal de tubería fluyendo parcialmente llena. Tomada de Salcedo (2012). ............. 14
Figura 2.7 Proyección del trapecio que produce el área excavada para una tubería de alcantarillado. Tomada
de (CIACUA, 2013) ................................................................................................................................... 23
Figura 3.1 Grafo. Tomado de Ahuja & et Al (1993). ......................................................................................... 26
Figura 3.2. Topología de una red de alcantarillado. ......................................................................................... 27
Figura 3.3 Red de alcantarillado. ...................................................................................................................... 28
Figura 3.4 Trazado de una red de alcantarillado. ............................................................................................. 29
Figura 3.5. Diseño hidráulico de una tubería (diámetro-pendiente). ............................................................... 31
Figura 4.1 Tipos de tuberías para cada tramo de una red de alcantarillado. ................................................... 34
Figura 4.2 Grafo para la selección del trazado de una red de alcantarillado. .................................................. 35
Figura 4.3 Posibles variables de decisión por tramo. ....................................................................................... 35
Figura 4.4 Oferta/Demanda en cada nodo del grafo. ....................................................................................... 37
Figura 4.5 Conjunto de nodos que pertenecen a un mismo pozo de inspección. ............................................ 44
Figura 4.6 Representación de un arco (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
). ............................................................................................. 45
Figura 4.7 Representación de un tramo de alcantarillado. .............................................................................. 45
Figura 4.8 Representación de una tubería en el grafo auxiliar para el diseño hidráulico. ............................... 46
Figura 4.9 Grafo auxiliar para el diseño hidráulico de un tramo. ..................................................................... 47
Figura 4.10. Series de tuberías de una red de alcantarillado. .......................................................................... 48
Figura 4.11 Grafo auxiliar para el diseño hidráulico de una serie de 2 tramos. .............................................. 49
Figura 4.12 Solución del grafo auxiliar 𝒢
𝐷
para el diseño hidráulico de una serie de 2 tramos. ..................... 50
Figura 4.13. Representación del trazado de la red como un árbol. ................................................................. 51
Figura 4.14. Configuración de diámetros en el grafo para el diseño 𝒢
𝐷
. ......................................................... 53
Figura 4.15. Grafo auxiliar 𝒢
𝐷
para el diseño hidráulico de una red de alcantarillado. ................................... 54

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
MIC 201510-00
Natalia Duque Villarreal
Tesis I
iv
Figura 4.16. Conexión entre los diferentes grafos. .......................................................................................... 55
Figura 4.17. Metodología para el diseño hidráulico optimizado de redes de alcantarillado. .......................... 61
Figura 4.18. Grafo de diseño 𝒢
𝐷
reversado. ..................................................................................................... 64
Figura 4.19. Solución para el diseño hidráulico de la red. ................................................................................ 67
Figura 4.20. Pozos de caída .............................................................................................................................. 68
Figura 4.21. Función de costos para un tramo de una red de alcantarillado ................................................... 70
Figura 4.22 Diagrama de flujo para el diseño de redes de alcantarillado. ....................................................... 72
Figura 5.1 Red 4x4 ............................................................................................................................................ 74
Figura 5.2. Primer trazado aleatorio obtenido utilizando Xpress-MP. ............................................................. 75
Figura 5.3 Representación de la solución del mejor trazado de la red tras 100 iteraciones ............................ 78
Figura 9.1. Trazado del mejor diseño encontrado al utilizar ∇= 10 𝑐𝑚. ......................................................... 90
ÍNDICE DE GRÁFICAS
Gráfica 5.1.Convergencia al mejor trazado de la red de alcantarillado (∇= 1 𝑐𝑚). ........................................ 80
Gráfica 5.2. Convergencia al mejor trazado de la red de alcantarillado (∇= 10 𝑐𝑚). ..................................... 81

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
MIC 201510-00
Natalia Duque Villarreal
Tesis I
v
ÍNDICE DE TABLAS
Tabla 2.1 Tipos de flujo..................................................................................................................................... 13
Tabla 2.2 Resumen de propiedades geométricas del alcantarillado. Tomado y adaptado de Butler & Davies
(2011) y Salcedo (2012). .......................................................................................................................... 15
Tabla 2.3 Límites de la profundidad a cota clave de la tubería. ....................................................................... 21
Tabla 2.4 Resumen de restricciones hidráulicas de diseño. Tomado y modificado de Butler & Davies (2011).
................................................................................................................................................................. 21
Tabla 2.5 Lista de diámetros comerciales ........................................................................................................ 21
Tabla 5.1 Datos de entrada para la selección del trazado de una red de alcantarillado .................................. 74
Tabla 5.2. Resultado del primer trazado aleatorio en la iteración. ................................................................. 76
Tabla 5.3. Diseño hidráulico de la red 𝑡 = 1 .................................................................................................... 77
Tabla 5.4. Mejor diseño hidráulico de la red tras 100 iteraciones. .................................................................. 78
Tabla 9.1 Coeficientes aleatorios para la función de costos de cada tubería. ................................................. 87
Tabla 9.2. Diseño hidráulico del primer trazado aleatorio. .............................................................................. 88
Tabla 9.3. Mejor diseño hidráulico de la red tras 100 iteraciones (∇= 1 𝑐𝑚). ............................................... 89
Tabla 9.4. Mejor diseño hidráulico de la red tras 100 iteraciones (∇= 10 𝑐𝑚). ............................................. 91

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
MIC 201510-00
Natalia Duque Villarreal
Tesis I
vi
ÍNDICE DE ECUACIONES
Ecuación 2.1 ..................................................................................................................................................... 15
Ecuación 2.2 ..................................................................................................................................................... 15
Ecuación 2.3 ..................................................................................................................................................... 15
Ecuación 2.4 ..................................................................................................................................................... 16
Ecuación 2.5 ..................................................................................................................................................... 16
Ecuación 2.6 ..................................................................................................................................................... 16
Ecuación 2.7 ..................................................................................................................................................... 16
Ecuación 2.8 ..................................................................................................................................................... 16
Ecuación 2.9 ..................................................................................................................................................... 16
Ecuación 2.10 ................................................................................................................................................... 17
Ecuación 2.11 ................................................................................................................................................... 17
Ecuación 2.12 ................................................................................................................................................... 17
Ecuación 2.13 ................................................................................................................................................... 18
Ecuación 2.14 ................................................................................................................................................... 18
Ecuación 2.15 ................................................................................................................................................... 18
Ecuación 2.16 ................................................................................................................................................... 22
Ecuación 2.17 ................................................................................................................................................... 22
Ecuación 2.18 ................................................................................................................................................... 23
Ecuación 2.19 ................................................................................................................................................... 23
Ecuación 2.20 ................................................................................................................................................... 24
Ecuación 4.1 ..................................................................................................................................................... 36
Ecuación 4.2 ..................................................................................................................................................... 36
Ecuación 4.3 ..................................................................................................................................................... 36
Ecuación 4.4 ..................................................................................................................................................... 36
Ecuación 4.5 ..................................................................................................................................................... 38
Ecuación 4.6 ..................................................................................................................................................... 39
Ecuación 4.7 ..................................................................................................................................................... 39
Ecuación 4.8 ..................................................................................................................................................... 39

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
MIC 201510-00
Natalia Duque Villarreal
Tesis I
vii
Ecuación 4.9 ..................................................................................................................................................... 39
Ecuación 4.10 ................................................................................................................................................... 39
Ecuación 4.11 ................................................................................................................................................... 39
Ecuación 4.12 ................................................................................................................................................... 39
Ecuación 4.13 ................................................................................................................................................... 40
Ecuación 4.14 ................................................................................................................................................... 40
Ecuación 4.15 ................................................................................................................................................... 40
Ecuación 4.16 ................................................................................................................................................... 40
Ecuación 4.17 ................................................................................................................................................... 45
Ecuación 4.18 ................................................................................................................................................... 46
Ecuación 4.19 ................................................................................................................................................... 56
Ecuación 4.20 ................................................................................................................................................... 56
Ecuación 4.21 ................................................................................................................................................... 56
Ecuación 4.22 ................................................................................................................................................... 59
Ecuación 4.23 ................................................................................................................................................... 59
Ecuación 4.24 ................................................................................................................................................... 59
Ecuación 4.25 ................................................................................................................................................... 60
Ecuación 4.26 ................................................................................................................................................... 60

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
1
1 INTRODUCCIÓN
El diseño de las redes de alcantarillado es un problema complejo que tiene dos componentes
fundamentales: la topología de la red y el diseño hidráulico. El primer componente define el trazado
de la red, es decir, el recorrido del agua a través de un camino sobre la red de alcantarillado. Una
vez definido el trazado de la red, se puede pasar a realizar el diseño hidráulico, en donde se debe
determinar el tamaño y posición de cada tubería de forma que cumplan con una serie de
restricciones hidráulicas establecidas por las normas de construcción de cada país.
El diseño de este tipo de sistemas urbanos, es de vital importancia para la preservación de la
salud pública en zonas urbanas. Sin embargo, dados los altos costos de construcción, un gran
número de ciudades en el mundo, sobre todo en países en vía de desarrollo, todavía no cuentan con
un sistema de drenaje urbano (redes de alcantarillado) adecuado ya que cuentan con bajos
presupuestos. Se sabe además, que la diferencia en costos de construcción de una red de
alcantarillado, entre dos posibles trazados puede llegar a ser de hasta un 85% (Saldarriaga, et al.,
2014). De acuerdo con lo anterior, es relevante hacer una buena selección tanto del trazado como
del diseño hidráulico para reducir los costos de construcción de estos sistemas y hacerlos asequibles
a más ciudades.
De acuerdo con lo anterior, varios autores han implementado diferentes metodologías en
donde se involucran componentes de optimización para resolver este problema. Algunos ejemplos
son: Programación Lineal (LP) (Elimam, et al., 1989), Programación No Lineal (NLP) (Dajani, et al.,
1972) y Programación Dinámica (DP) (Kulkarni & Khanna, 1985). Otros autores implementaron
aproximaciones heurísticas para el diseño hidráulico de la red, que ofrecían buenos resultados en
un tiempo computacional mucho menor. Entre las metodologías utilizadas se encuentran Particle
Swarm Optimization (PSO) (Izquierdo, et al., 2008), Cellular Automata (CA) (Afshar, et al., 2011),
Genetic Algorithms (GA) (Afshar, 2012), Ant Collony Optimization Algorithms (ACOA) (Moeini &
Afshar, 2012), entre otros.
Se pretende desarrollar una nueva metodología de diseño de redes de alcantarillado, en donde
la selección del trazado de la red está basada en un modelo de optimización entera mixto conocido
en la literatura como Network Design Problem (NDP). En este modelo, el costo del diseño total se
aproxima utilizando herramientas estadísticas, en donde se ajustan diferentes funciones (lineales)
para modelar el costo de las diferentes tuberías en la red. Una vez definido el trazado de la red que
podría representar el diseño de menor costo, se pasa a realizar el diseño hidráulico de la red
mediante una extensión de la metodología propuesta por Duque et al. (2013). En esta segunda
etapa, se utiliza una adaptación de un algoritmo de ruta más corta (Ahuja, et al., 1993) sobre un
grafo que representa el tamaño y posición de cada tubería en la red de alcantarillado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
2
El resto del documento está organizado de la siguiente manera: la Sección 2 presenta la
descripción de los sistemas de alcantarillado, la Sección 3 define formalmente los dos problemas
que componen el diseño de redes de alcantarillado: la selección del trazado y el diseño hidráulico
de la red. Posteriormente, la metodología para el diseño optimizado de redes de alcantarillado en
la Sección 4, especificando el modelo matemático para la selección del trazado. Finalmente, en la
Sección 5, se presentan los resultados de la implementación de esta metodología sobre una red de
17 pozos de inspección.
1.1 Objetivos
1.1.1 Objetivo General
Desarrollar una metodología para la selección del trazado y el diseño hidráulico costo-óptimo
de redes de alcantarillado, teniendo en cuenta los aspectos hidráulicos que aseguran el
funcionamiento adecuado del sistema de drenaje urbano, siguiendo las normas colombianas:
Reglamento Técnico del Sector de Agua Potable y Saneamiento Básico – RAS (2000).
1.1.2 Objetivos Específicos
Realizar una búsqueda bibliográfica sobre las metodologías que se han utilizado para el
diseño de redes de alcantarillado a nivel mundial.
Modelar la red de alcantarillado como un grafo dirigido, sobre el cual se definirá el sentido
de flujo y tipo de cada arco, definiendo así el trazado de la red.
Determinar el trazado óptimo de la red de alcantarillado a partir de los datos de entrada.
Establecer una función de costos en función del caudal por tubería, según la cual se defina
el trazado óptimo.
Una vez definido el trazado se modelará la red de alcantarillado como un grafo auxiliar
dirigido, que representará todas las posibles alternativas de diseño hidráulico.
Establecer la metodología de optimización que se utilizará sobre los grafos, de forma que
se obtenga una solución exacta, para garantizar el óptimo global.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
3
Determinar el diseño hidráulico óptimo de la red de alcantarillado para caudales de diseño
dados, definiendo el diámetro y la pendiente de las tuberías. Estos diseños deben cumplir
con las normas establecidas por el RAS (2000).
Analizar el tiempo computacional evaluando la influencia de la precisión con la que se
decide diseñar.
Entregar una herramienta de apoyo que permita realizar el diseño de redes de alcantarillado
a partir de un conjunto de datos de entrada dados.
1.2 Antecedentes
Teniendo en cuenta que el diseño redes de alcantarillado involucra dos problemas diferentes,
la definición del trazado y el diseño hidráulico de la red, no es común encontrar metodologías que
los resuelvan simultáneamente debido a la complejidad del problema. De hecho, las estrategias de
solución disponibles en la literatura proponen resolver ambos problemas secuencialmente, sin
embargo, el problema del diseño hidráulico ha recibido más atención a través de métodos exactos
y heurísticos.
Diferentes autores han propuesto metodologías exactas para resolver el problema del diseño
hidráulico de las redes. Haith (1966) utilizó Programación Dinámica (PD) para obtener el diseño
óptimo de una serie de tuberías considerando una sola línea (tubería) dividida en diferentes
secciones, cada una con un caudal de entrada y parámetros de costos constantes. Se toman como
variables de decisión la cota batea al final de cada sección y su diámetro. Sin embargo, esta
metodología tuvo limitaciones computacionales debido a la tecnología en aquel momento. Kulkarni
y Khanna (1985) también utilizaron una aproximación basada en Programación Dinámica (PD) para
diseñar la red de alcantarillado con bombeo por gravedad de mínimo costo, utilizando una
modificación de la Ecuación de Hazen-Williams. Dada la complejidad y dimensionamiento del
problema, los autores dividieron el problema de diseño óptimo utilizando el concepto de
agrupaciones factibles en las uniones por rentabilidad y eficiencia; en consecuencia, esta
metodología no puede asegurar el óptimo global. Esta metodología de PD fue dividida en dos partes:
la primera define las variables de control asociadas con cada enlace y las almacena, y la segunda
calcula la hidráulica y los costos. La mayoría de las metodologías de PD sufre del problema de
dimensionalidad, que las hace difíciles de aplicar en los casos a gran escala. Li y Matthew (1990)
utilizan el modelo de programación no lineal (PNL) para establecer los factores topográficos e
hidráulicos tales como flujo, tamaños y pendientes de tuberías. En esta metodología los autores
dividen el problema en dos etapas. La primera corresponde a la optimización de los tamaños y
pendientes de tuberías y la ubicación de las estaciones de bombeo de un diseño. El segundo deja

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
4
todas las variables constantes excepto la tasa de flujo, buscando tuberías donde el flujo necesita ser
modificado para disminuir el valor de función objetivo que depende de la velocidad del flujo, la cota
corona de las tuberías y la ubicación de las estaciones de bombeo; por medio de una búsqueda
dirigida utilizando el algoritmo de ruta más corta de Dijkstra. Más recientemente Swamee y Sharma
(2013) utilizan programación lineal (LP) para obtener el diseño óptimo de una serie de tuberías, sin
necesidad de linealizar la función objetivo ni las restricciones, ya que se fijan las longitudes y
diámetros de cada sección, a partir de los diámetros comerciales disponibles. Este problema se
resuelve utilizando el método Simplex.
Así mismo, algunos enfoques heurísticos han sido aplicados a este problema de diseño
hidráulico. Holland (1966) utiliza una rutina de optimización general para el diseño de una red de
alcantarillado con un trazado dado. Esta rutina de optimización realiza una búsqueda al azar que
funciona con diámetros continuos que se redondean al siguiente diámetro comercial, poniendo en
peligro la optimalidad de la solución del problema. Elimam et al (1989) utiliza una aproximación
heurística basada en Programación Lineal (PL) para el diseño de redes de alcantarillado utilizando
una linealización a trozos de los términos no lineales tales como el costo y algunas restricciones
hidráulicas. Como resultado, se obtienen diámetros continuos que son redondeados al diámetro
comercial más cercano disponible, que satisface todas las restricciones hidráulicas. El método más
popular utilizado por varios autores son los Algoritmos Genéticos (AG). Haghighi A. y Bakhshipuor
A.E. (2012) y Palumbo A. et al (2014) utilizan un AG estándar para el diseño de redes de drenaje
urbano, decidiendo sobre el tamaño de las tuberías y las cotas del terreno. También se han
combinado diferentes metodologías con los AG como Cisty M. (2010) que propone un híbrido entre
AG y PL; Pan y Kao (2009) combinan los AG con Programación Cuadrática (PC) y Haghighi A., Samani
H. y Samani Z. (2011) usa AG con Programación Entero (PE) aplicada en redes de distribución de
agua. AFSHAR (2012) desarrolló un AG de renacimiento que lleva a cabo un primer diseño rápido
usando un AG estándar, posteriormente reduce el espacio de solución alrededor de las mejores
soluciones obtenidas y luego crea una nueva población que se evalúa en el nuevo espacio de
solución, obteniendo soluciones cercanas a la óptima en un menor tiempo. Esta metodología reduce
la sensibilidad de los AG al número de individuos de la población. Sanchez A., Medina N., Vojinovic
Z. y Price R. (2014) utilizan el algoritmo evolucionario, Algoritmo Genético de Clasificación No
Ordenada-II (NSGA II) junto con el programa SWWM para el diseño de las tuberías para futuras
expansiones de una red de alcantarillado existente. Este algoritmo multiobjetivo elige como la mejor
solución, aquella con el diseño más barato y que no genera inundaciones. Se han utilizado otras
metodologías heurísticas para el diseño de sistemas de alcantarillado como el Algoritmo de la
Colonia de Hormigas (ACOA) (Afshar, 2010; Moeini y Afshar, 2012); Recocido Simulado (SA) (Sousa
J., A. Ribeiro, Cunha M. C. y A. Antunes, 2002; Yen y Chu, 2011); Búsqueda Tabú (TS) (Yen y Chu,
2011; Haghighi y Bakhshipour, 2014).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
5
En este trabajo se propone una metodología exacta para encontrar el diseño de costo óptimo
de una red de alcantarillado utilizando un método basado en Programación Dinámica DP y
Programación Entera Mixta (PEM). Los problemas del trazado y el diseño hidráulico son resueltos
secuencialmente, utilizando un grafo que representa el problema de la selección del trazado y un
grafo auxiliar sobre el cual se resuelve el problema del diseño hidráulico de la red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
6
2 MARCO TEÓRICO
2.1 Redes de drenaje urbano
Las redes de drenaje urbano son obras civiles necesarias dentro del desarrollo de zonas urbanas
debido a la constante interacción entre el hombre y el ciclo natural del agua. Dicha interacción se
presenta por la necesidad del hombre de abastecerse de agua para su consumo y por el proceso de
urbanización que desvía los sistemas de drenaje naturales originales. De estas dos actividades se
producen aguas residuales y pluviales que deben ser canalizadas y tratadas. EL propósito de las
redes de drenaje urbano es minimizar posibles problemas causados a seres humanos o al ambiente
(Butler & Davies, 2011).
La Figura 2.1 muestra las interacciones del sistema de drenaje urbano con la población y el
medio ambiente. En este sentido, el propósito de las redes de drenaje urbano se traduce en evitar
problemas de inundación y reducir los problemas de contaminación que se generan al no evacuar
las aguas residuales y pluviales de una población.
Figura 2.1 Interacciones del Sistema de Drenaje Urbano. Tomado y Modificado de Butler & Davies (2011).
2.1.1 Efectos de la urbanización
El crecimiento poblacional acelerado, que se ha venido experimentando en el mundo desde
principios del siglo XX, ha generado un aumento significativo en la densidad de viviendas y el
movimiento de la gente de zonas rurales a zonas urbanas. La afluencia de personas en las zonas
urbanas exige la realización de obras civiles para facilitar las actividades que allí se desenvuelven y
suplir las necesidades de la gente. La pavimentación de las vías y la construcción de edificios hacen
parte de dicho proceso de urbanización, donde la impermeabilización del suelo impide la infiltración
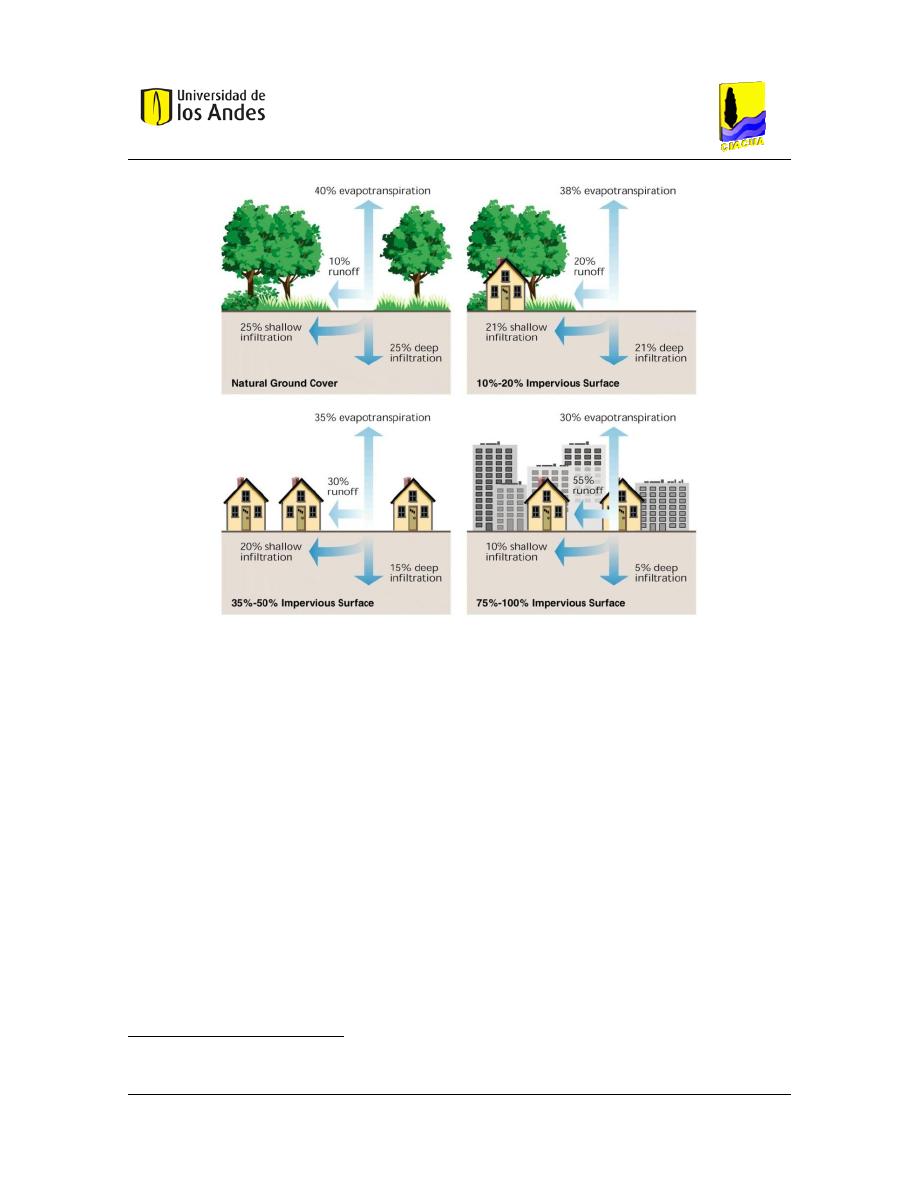
del agua lluvia (Muth, et al., 2010).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
7
Figura 2.2 Efectos de la urbanización. Tomado de Muth, Brinson, & Bernhar (2010).
La Figura 2.2 presenta la relación entre la impermeabilización del suelo y la escorrentía
1
superficial. Como se observa, la impermeabilización del suelo aumenta la escorrentía superficial y
disminuye las infiltraciones y la evaporación del agua, lo que afecta el ciclo hidrológico normal. Esto
genera acumulación de aguas lluvias que pueden generar problemas de control de inundaciones.
Además, existe la necesidad de evacuar las aguas residuales domésticas, comerciales o industriales
para prevenir problemas de salud pública y contaminación ambiental.
2.1.2 Componentes de las redes de drenaje urbano
Para recolectar y transportar las aguas residuales y pluviales, desde donde se origina la descarga
hasta el sitio donde se va a depositar y tratar el agua, se necesita un sistema completamente
1
Escorrentía: Lámina de agua que corre por la superficie de una cuenca de drenaje. En áreas urbanas la
escorrentía se da sobre zonas impermeables.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
8
artificial de alcantarillado. Esto quiere decir que las redes están compuestas por componentes de
captación, de conducción, de inspección y conexión, de regulación y alivio y de bombeo (Saldarriaga,
2013).
2.1.2.1 Estructuras de captación
El principal componente de captación de agua lluvia es el agua superficial que cae en zonas
impermeables. Las estructuras que recolectan las aguas pluviales y residuales son:
Sumideros: estructuras para la captación de la escorrentía superficial que se drena a través
de las calles. Estas pueden ser diseñadas en forma lateral o transversal al sentido del flujo,
y se localizan en las vías vehiculares o peatonales del proyecto (RAS, 2000).
Canaletas y bajantes: Estructuras complementarias de captación que ayudan a drenar el
agua desde los techos hasta el sistema de alcantarillado o a la calle, donde se colocan
sumideros.
En el caso de las aguas residuales la captación se realiza directamente. Las aguas residuales se
clasifican de acuerdo con su procedencia: domésticas o no domésticas (comerciales o industriales)
(Butler & Davies, 2011). En ambos casos el agua es conducida directamente desde el punto de
descarga hasta la red de alcantarillado, por medio de tuberías.
2.1.2.2 Estructuras de conducción
Los componentes de conducción corresponden a las tuberías que se encargan de transportar el
agua a lo largo y ancho de la red de drenaje urbano. Estas conforman el mayor porcentaje de área
de la red y son su componente principal.
2.1.2.3 Estructuras de inspección y conexión
Los componentes de inspección y conexión de colectores corresponden a:
Pozos de inspección: Estructuras hidráulicas con tapa removible, que permiten el acceso a
la red de alcantarillado, para el mantenimiento e inspección de la misma. Estas estructuras
son utilizadas cuando se debe cambiar la dirección del flujo, cambiar la pendiente, cambiar

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
9
el diámetro de las tuberías, realizar conexiones con otros ramales, asegurar aireación al
alcantarillado o cada 90 m.
Pozos de caída: Estructuras diseñadas para dirigir el flujo que entra a un pozo de inspección
con mucha energía, de forma que se pueda disipar gran cantidad de su energía para
proteger la infraestructura de la red contra impactos del flujo sobre las paredes.
2.1.2.4 Estructuras de regulación y alivio
Para el buen funcionamiento del sistema se necesitan los componentes de regulación y alivio,
que corresponden a:
Sifones invertidos: Estructuras en forma de U dispuestas entre dos pozos en caso que el
sistema de alcantarillado requiera atravesar un cuerpo de agua o se quiera evitar la
interferencia del trazado de la red con otros servicios públicos. Estos sifones trabajan como
tuberías a presión.
Sistemas de almacenamiento temporal: Tanques subterráneos para retener el agua con el
objetivo de disminuir los picos de caudal a fin de evitar la evacuación rápida de los
contaminantes desde el sistema hacia al cuerpo receptor, en un evento de precipitación.
Sin embargo, el tiempo de retención no debe ser muy grande puesto que puede ocasionar
problemas de olores.
Aliviaderos: Estructuras que permiten la salida de cierto volumen del agua que viaja por el
alcantarillado, cuando se presenta un evento extremo de precipitación.
Canales abiertos: Estructuras de conducción de escorrentía pluvial, diseñados para manejar
velocidades mínimas que eviten la sedimentación de sólidos arrastrados por el agua lluvia y
velocidades máximas que evitan daños en la estructura por erosión, cuyo valor depende del
material de la misma.
Estructuras de disipación de energía: Estructuras que reducen la velocidad del flujo
generando un cambio de régimen de supercrítico a subcrítico, permitiendo entregar el agua
con un nivel de energía bajo. Esto ayuda a minimizar el riesgo de socavación o erosión en
los puntos de descarga del sistema de alcantarillado (Planta de tratamiento o cuerpo
receptor).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
10
2.1.2.5 Estructuras de bombeo
Finalmente, los componentes de bombeo son necesarios cuando la energía hidráulica en una
zona es demasiado baja para que las aguas residuales sean evacuadas por gravedad y necesite
bombearse. En otras palabras, se requiere bombeo cuando se deba elevar la línea de gradiente
hidráulico para vencer una diferencia de alturas topográficas y el flujo por gravedad no lo permita.
2.1.3 Fallas en redes de drenaje urbano
El diseño de las redes de drenaje urbano debe cumplir con ciertos requerimientos de forma que
se tenga una buena operación del sistema y se eviten fallas que puedan llegar a generar problemas
de salud pública, problemas ambientales o daños en la infraestructura de la misma. Los tipos de
fallas más comunes son (López, 2012):
Fallas estructurales: Se pueden presentar por problemas de corrosión
2
o cargas aplicadas
que pueden agrietar o ahuecar las tuberías, causando una pérdida en la capacidad
hidráulica
3
y el aumento de infiltraciones y exfiltraciones. Este tipo de falla se puede
observar en la Figura 2.3 (a).
Sedimentación de partículas sólidas: La sedimentación se refiere a la acumulación de
partículas en el fondo de las tuberías, causando pérdidas en la capacidad hidráulica de la
red. Pueden ser de tipo sanitario, superficial o de alcantarillado. Las sanitarias corresponden
a las partículas finas de materia orgánica o fecal, papel y material vegetal, que recoge la red;
la sedimentación superficial se refiere a las partículas que entran a la red arrastradas por
aguas superficiales, como material vegetal o basura en general y finalmente la
sedimentación de alcantarillado hace referencia a la sedimentación de las partículas propias
del sistema o sus áreas circundantes. Este tipo de falla se puede observar en la Figura 2.3
(b).
2
Corrosión: cualquier proceso, involuntario, que sea químico, físico, biológico o eléctrico cómo la oxidación
de los metales, agentes electroquímicos, descargas industriales, agua subterránea con alto contenido de
sulfato, erosión y agentes microbiológicos, que implique deterioro, degradación o destrucción de los
componentes del sistema de recolección de agua y que sea debido a la operación natural del mismo (ASCE,
2007).
3
Capacidad Hidráulica: Caudal máximo que puede transportar una tubería.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
11
Sobrecargas: Se da al sobrepasar una relación de llenado
4
del 80% que genera una
desaceleración del flujo y aumento de la profundidad hasta alcanzar una relación de llenado
del 94% donde la tubería lleva el máximo caudal posible. De seguir aumentando la
profundidad del agua la tubería se presuriza, a lo que se denomina sobrecarga. Este tipo de
falla es el más importante de controlar para prevenir inundaciones, ya que el agua está
altamente contaminada y puede generar grandes problemas de salud pública y ambiental.
Este tipo de falla se puede observar en la Figura 2.3 (c).
(a)
(b)
(c)
Figura 2.3 Fallas en redes de drenaje urbano.
2.2 Sistema integrado de drenaje urbano
Actualmente se sabe que el crecimiento de las zonas urbanas y la densidad poblacional es
inevitable. Por lo mismo, se deben diseñar las ciudades para que estén en la capacidad de resistir la
demanda del futuro. Esto sin duda aumenta la cantidad y la contaminación del agua a tratar, lo que
se traduce en la necesidad de construir plantas de tratamiento de aguas residuales (PTAR). Las PTAR,
tienen como fin descontaminar el agua, captada y transportada por las redes de alcantarillado, antes
de depositarla en el cuerpo receptor. Esto se requiere cuando la capacidad de autodepuración
5
del
cuerpo receptor es muy baja o los niveles de contaminación del agua son muy altos (Saldarriaga,
2013).
Se entiende entonces, como Sistema Integrado de Drenaje Urbano al conjunto conformado por
las redes de drenaje urbano (alcantarillado), la planta de tratamiento de aguas residuales (PTAR) y
el cuerpo receptor, como una unidad. Este concepto tiene en cuenta la cantidad y calidad del agua
4
Relación de Llenado: Relación entre la profundidad del flujo en la tubería con respecto al diámetro interno
de la misma.
5
Autodepuración: es el proceso de recuperación de un curso de agua después de un episodio de
contaminación orgánica.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
12
en cada uno de los componentes del sistema. El papel del alcantarillado es recolectar las aguas
residuales y lluvias, y transportarlas hacia la PTAR. La red de alcantarillado debe asegurar
hermeticidad en las redes, minimizando infiltraciones y exfiltraciones, además de lograr algún
tratamiento preliminar, controlando la cantidad y la calidad del agua residual que llega al tramo
(interceptor) aguas arriba de dichas plantas (RAS, 2000). A continuación se muestra un esquema del
sistema integrado de drenaje urbano en la Figura 2.4.
Figura 2.4 Sistema Integrado de Drenaje Urbano.
La PTAR es necesaria, siempre que la capacidad de autodepuración del cuerpo receptor no sea
lo suficientemente alta para que este se recupere de la contaminación de la descarga que recibe. La
PTAR se encarga de entregar una descarga que cumpla con ciertos parámetros de calidad que se
establecen de acuerdo con la capacidad de autodepuración del cuerpo receptor y al uso que se le
dará al agua aguas abajo.
2.3 Generalidades sobre el diseño hidráulico de los sistemas de
alcantarillado
2.3.1 Supuestos del diseño
A la hora de diseñar se debe suponer un tipo de flujo que describa la hidráulica. Es decir, que
establezca cómo es el comportamiento hidráulico de un flujo en espacio y tiempo. Dado que se está

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
13
tratando con agua, por lo que el primer supuesto de diseño considera un fluido incompresible, lo
que quiere decir que su densidad es constante. También, se tiene una suposición del tipo de flujo.
Las condiciones de flujo se clasifican según su variación en espacio y tiempo. La variación del
flujo en el espacio puede ser uniforme o variable. Así mismo, las características del flujo pueden ser
constantes en el tiempo formando un flujo permanente o pueden ser variables (no permanente).
Se forman entonces, cuatro tipos de flujo como se muestra en la Tabla 2.1. Sin embargo, es
imposible que el flujo variado no permanente se de en la naturaleza, dejando sólo tres tipos de flujo
(Saldarriaga, 2013).
Tabla 2.1 Tipos de flujo
Espacio\Tiempo Flujo Permanente
Flujo No-Permanente
Flujo Uniforme
Flujo Uniforme
Flujo Uniforme- No Permanente
Flujo Variable
Flujo Variado-Permanente
Flujo Variado- No Permanente
En el caso del flujo en tuberías de alcantarillado se considera que el flujo mantiene sus
características en tiempo y espacio, es decir que se considera un Flujo Uniforme (Flujo Uniforme -
Permanente).
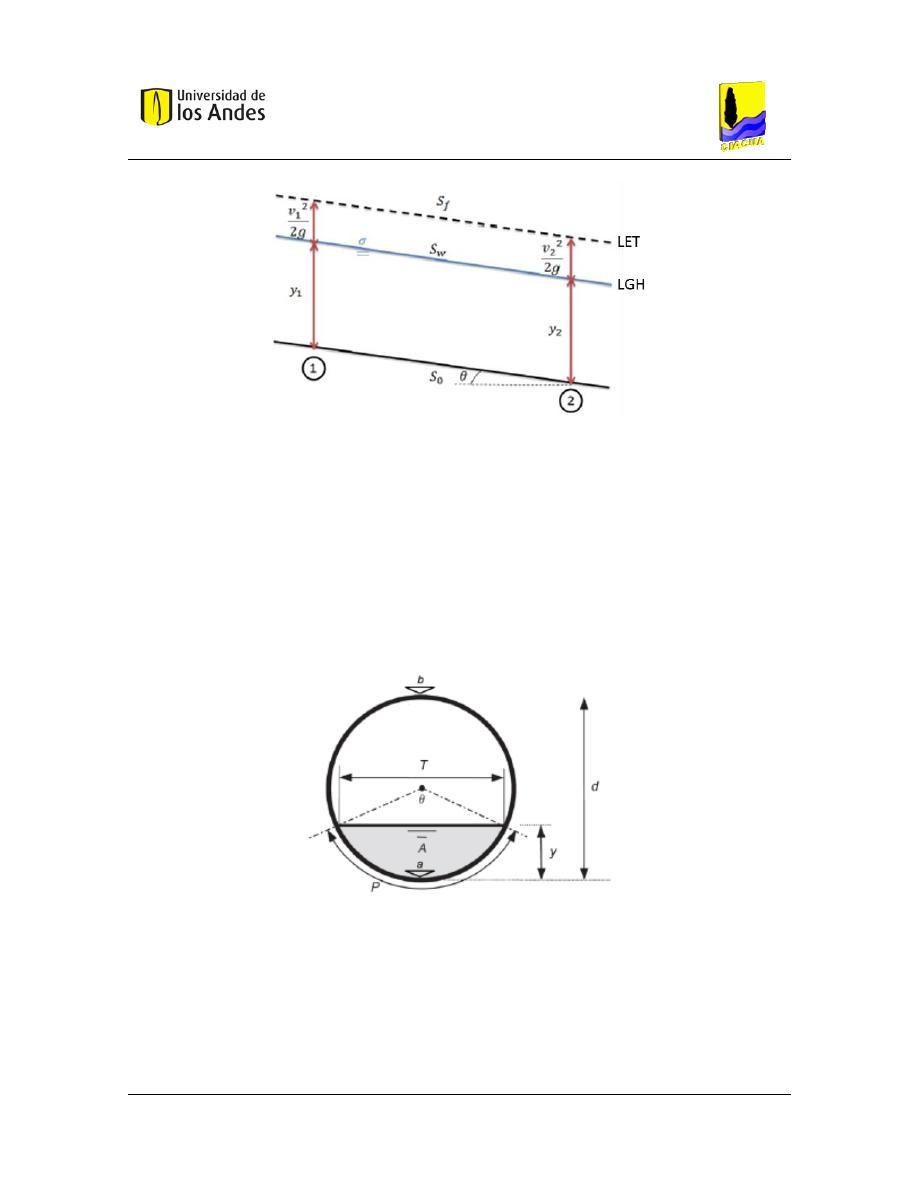
Este tipo de flujo se da gracias a que las fuerzas gravitacionales, las fuerzas de presión y las
fuerzas viscosas están en equilibrio; las gravitacionales aceleran el flujo y las viscosas le oponen
resistencia. Analizando un canal abierto en dos puntos, se puede observar cómo la altura de la
lámina de agua (altura por presión hidrostática) 𝑦, la altura por velocidad v
2
/2𝑔 y demás
propiedades geométricas e hidráulicas permanecen constantes a lo largo del canal. De ahí que, la
pendiente 𝑠
𝑓
de Línea de Energía Total (LET), la pendiente 𝑠
𝑤
de Línea de Gradiente Hidráulico agua
(LGH) y pendiente 𝑠
𝑜
del fondo del canal son la misma (𝑠 = 𝑠
𝑓
= 𝑠
𝑤
= 𝑠
0
), es decir que son
paralelas. Por lo tanto, las pérdidas por fricción serán constantes en toda la longitud de la tubería
(Saldarriaga, 2007).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
14
Figura 2.5 Flujo uniforme en canales abiertos. Tomado y modificado de Salcedo (2012).
2.3.2 Ecuaciones de diseño
En sistemas de alcantarillado las tuberías trabajan bajo la condición de flujo libre por gravedad,
debido a que las tuberías deben ir fluyendo parcialmente llenas. Este tipo de flujo es un caso especial
del flujo en canales abiertos, por lo cual aplican las mismas teorías (Butler & Davies, 2011). En este
caso se manejan secciones transversales circulares como la que se muestra en la Figura 2.6.
Figura 2.6 Sección transversal de tubería fluyendo parcialmente llena. Tomada de Salcedo (2012).
De acuerdo con lo anterior, las ecuaciones de diseño se modifican en función de la profundidad
de llenado 𝑦 y el diámetro de la tubería 𝑑, que forman un ángulo 𝜃 a partir del cual se calcula el
resto de las propiedades geométricas descritas en la Tabla 2.2.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
15
Tabla 2.2 Resumen de propiedades geométricas del alcantarillado. Tomado y adaptado de Butler & Davies (2011) y
Salcedo (2012).
Propiedad
Geométrica
Símbolo
Descripción
Unidades
(SI)
Profundidad de flujo
𝑦
𝑛
Altura del agua por encima de la cota de
batea.
[m]
Ángulo
𝜃
Ángulo formado en el centro de la tubería
por la superficie libre.
[rad]
Área Mojada
𝐴
Área mojada de la sección transversal.
[m
2
]
Perímetro Mojado
𝑃
Porción del perímetro del flujo que está
en contacto con el canal.
[m]
Radio Hidráulico
𝑅
Área por unidad de perímetro.
[m]
Ancho de la
Superficie
𝑇
Ancho del flujo en la superficie libre del
agua.
[m]
Profundidad
Hidráulica
𝐷
Área por unidad de ancho en la
superficie.
[m]
Cota de Batea
𝑎
El punto más bajo de la sección
transversal de la tubería.
[m]
Cota Clave
𝑏
El punto más alto de la sección
transversal de la tubería.
[m]
Las expresiones que describen los elementos geométricos para una tubería fluyendo
parcialmente llena, se exponen a continuación (Saldarriaga, 2013).
Ángulo
𝜃 = 𝜋 + 2 sin
−1
(
𝑦
𝑛
− 𝑑/2
𝑑/2
)
Ecuación 2.1
Área Mojada
𝐴 =
1
8
(𝜃 − sin 𝜃)𝑑
2
Ecuación 2.2
Perímetro Mojado
𝑃 =
𝑑
2
𝜃
Ecuación 2.3

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
16
Radio Hidráulico
𝑅 =
𝐴
𝑃
=
1
4
(𝜃 − sin 𝜃)𝑑
Ecuación 2.4
Ancho de la Superficie
𝑇 = 𝑑 cos (sin
−1
(
𝑦
𝑛
− 𝑑/2
𝑑/2
))
Ecuación 2.5
Profundidad Hidráulica
𝐷 =
𝐴
𝑇
=
(𝜃 − sin 𝜃)𝑑
8 cos (sin
−1
(
𝑦
𝑛
− 𝑑/2
𝑑/2 ))
Ecuación 2.6
A continuación se presentan algunas propiedades hidráulicas relacionadas con las propiedades
geométricas.
Número de Froude
𝐹𝑟 =
v
√𝑔𝐷
Ecuación 2.7
Número de Reynolds
𝑅𝑒 =
4𝑄𝜌
𝜋𝑑𝜇
Ecuación 2.8
Esfuerzo cortante en la pared
𝜏
0
= 𝜌𝑔𝑅𝑠
Ecuación 2.9
donde:
𝜌:
Densidad del fluido (agua).
𝑔 ∶
La aceleración de la gravedad.
𝑅 ∶
Radio hidráulico.
𝑠 ∶
Pendiente de diseño.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
17
Además de estas propiedades hidráulicas también se debe calcular la velocidad del flujo que si
bien es función del radio hidráulico 𝑅 y la pendiente 𝑠, se puede calcular de dos formas. La primera
es la Ecuación de Manning, propuesta en 1889 por Robert Manning. Esta ecuación es empírica y fue
deducida a partir de los experimentos realizados por Darcy y Bazin en 1865 sobre canales reales
abiertos fluyendo bajo la condición de flujo uniforme. Estás condiciones implican que la Ecuación
de Manning sólo es aplicable para el caso de flujo uniforme turbulento hidráulicamente rugoso
(Saldarriaga, 2013). La Ecuación de Manning para el cálculo de la velocidad entonces es:
v =
1
𝑛
𝑅
2/3
𝑠
1/2
Ecuación 2.10
donde 𝑛 es una constante que se calcula en función a la rugosidad absoluta (conocida como 𝑛 de
Manning) y se supone uniforme a lo largo del canal. Estudios posteriores de la Asociación Americana
de Ingenieros Civiles (ASCE por sus siglas en inglés) establecieron valores constantes del 𝑛 de
Manning para diferentes materiales de la tubería, encontrando así un rango de valores de 𝑛
partiendo de un caudal y una sección transversal dados. Sin embargo, el uso de esta ecuación en la
actualidad es inapropiado ya que los materiales modernos, como el PVC o el GRP, son muy lisos e
invalidan la suposición de Flujo Turbulento Hidráulicamente Rugoso (Saldarriaga, 2013).
La segunda forma de calcular la velocidad es a partir de una ecuación físicamente basada. La
Ecuación de Chézy describe la velocidad bajo la condición de flujo uniforme y está dada por:
v = 𝐶√𝑅𝑠
Ecuación 2.11
donde 𝑅 es el radio hidráulico de la tubería, 𝑠 la pendiente de la misma y 𝐶 es el coeficiente de
Chézy
6
. Dicho coeficiente es un factor que describe la rugosidad del canal por el cual fluye el agua.
Ahora bien, se deben tener en cuenta las pérdidas de energía por fricción que representan las
pérdidas de presión por unidad de longitud. Estás, según los experimentos de Reynolds (1884),
varían linealmente con respecto a la velocidad del flujo cuando el flujo es laminar o turbulento
(Saldarriaga, 2007). Las pérdidas por fricción se calculan según la ecuación físicamente basada,
planteada por Darcy-Weisbach, mostrada a continuación.
Pérdidas por Fricción (Darcy-Weisbach)
ℎ
𝑓
= 𝑓
𝑙
𝑑
v
2
2𝑔
Ecuación 2.12
6
Saldarriaga, J. (2007). Hidráulica de tuberías: abastecimiento de agua, redes, riegos. Bogotá: Alfaomega.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
18
Combinando la Ecuación de Chézy con la Ecuación físicamente basada de Darcy-Weisbach, se
obtiene la siguiente relación (Salcedo, 2012):
Relación entre el 𝐶 de Chézy y las pérdidas por fricción
𝐶 = √
8𝑔
𝑓
Ecuación 2.13
donde 𝑓 es el factor de fricción descrito por la Ecuación de Colebrook-White.
Factor de fricción (Colebrook-White)
1
√𝑓
= −2 log
10
(
𝑘
𝑠
14.8𝑅
+
2.51
𝑅𝑒√𝑓
)
Ecuación 2.14
Reemplazando la Ecuación 2.13 en la Ecuación 2.14, se obtiene coeficiente 𝐶 en términos del
rádio hidráulico de la tubería 𝑅, la rugosidad absoluta de la tubería 𝑘
𝑠
y el número de Reynolds
descrito en la Ecuación 2.8. Posteriormente, se reemplaza la ecuación de velocidad de Chézy
(Ecuación 2.11), en esta última para obtener así la velocidad en función de las propiedades
mencionadas, como se muestra en la Ecuación 2.15.
Ecuación de Darcy-Weisbach en conjunto con Colebrook-White
v = −2 √8𝑔𝑅𝑠 log
10
(
𝑘
𝑠
14.8𝑅
+
2.51𝜈
4𝑅√8𝑔𝑅𝑠
)
Ecuación 2.15
Las ventajas de utilizar la Ecuación 2.15 para el cálculo de la velocidad son: primero, que es una
ecuación explícita por lo cual su cálculo no requiere de métodos numéricos; en segundo lugar, que
es físicamente basada y por lo mismo es la que mejor describe la resistencia fluida (Salcedo, 2012).
Además, esta ecuación es válida para cualquier tipo de flujo, abarcando desde el Flujo Turbulento
Hidráulicamente Liso FTHL hasta el Flujo Turbulento Hidráulicamente Rugoso FTHR. Gracias a que
funciona para cualquier valor de 𝑘
𝑠
y cualquier fluido newtoniano, esta ecuación tiene mayor
aplicación hoy en día que la Ecuación de Manning (Saldarriaga, 2013).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
19
2.3.3 Restricciones de diseño
2.3.3.1 Restricciones hidráulicas
Las restricciones hidráulicas buscan garantizar que el diseño de las redes de alcantarillado
cumpla con la capacidad de demanda y aseguren un proceso de auto-limpieza de la red. A
continuación se mencionan las restricciones hidráulicas para redes de drenaje urbano de aguas
residuales y para redes de drenaje urbano pluvial y combinado (residual y pluvial) (RAS, 2000).
1. Diámetro mínimo
En sistemas de alcantarillado de aguas residuales el diámetro interno mínimo de las tuberías
debe ser de 170 mm, para evitar la obstrucción del sistema por objetos de gran tamaño que
logren entrar al sistema. En el caso de las redes de aguas lluvias el diámetro mínimo es de
250 mm puesto que se corre mayor riesgo de que entren objetos al sistema arrastrados por
el agua superficial (Saldarriaga, 2013). Para este proyecto se utilizó un diámetro mínimo de
200 mm establecido por el RAS (2000).
2. Relación de llenado máxima
Esta relación de llenado máxima se establece con el fin de evitar problemas de sobrecarga
del sistema y asegurar la aireación del mismo para evitar problemas ambientales. A partir
de esta se establecen las profundidades máximas del flujo de acuerdo con el diámetro
interno de la tubería. La máxima relación de llenado entonces corresponde al 85%. Sin
embargo, para las tuberías con diámetros menores a 600 mm la relación de llenado máxima
es del 70%. Adicionalmente, se recomienda establecer una relación de llenado máxima del
80% siempre que se presente flujo cuasi-crítico, i.e, que el número de Froude 𝐹𝑟 esté entre
0.7 y 1.5, donde una pequeña alteración en la energía específica del flujo causa variaciones
bruscas en la profundidad de la lámina de agua, lo que puede generar problemas de
sobrecarga (Copete, 2012).
Para el caso de este proyecto, se manejaron relaciones de llenado máximas del 70% para
tuberías de diámetros menores a 500 mm o para cuando se presente flujo cuasi-crítico, 80%
para tuberías con diámetros entre 500 y 1000 mm y 85% para tuberías con diámetros
mayores a 1000 mm. Esto, con el fin de hacer comparable los resultados de este proyecto
con los resultados obtenidos utilizando la metodología propuesta por el CIACUA.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
20
3. Velocidad mínima
La velocidad mínima busca evitar problemas de sedimentación y/o acumulación de
partículas sólidas dentro de las tuberías. De esta forma se evita la obstrucción de las
tuberías, lo que podría causar problemas de sobrecarga de la misma. Para tuberías de
alcantarillado el RAS (2000) sugiere una velocidad mínima de 0.75 m/s para diámetros
menores a 450 mm.
4. Esfuerzo cortante mínimo
El esfuerzo cortante en el fondo de una tubería de alcantarillado de aguas residuales debe
ser igual o mayor que 2 Pa en tuberías de diámetros mayores o iguales a 450 mm, para
asegurar un proceso de auto-limpieza. En el caso de alcantarillados de aguas lluvias el
esfuerzo cortante debe ser mayor o igual a 3 Pa en tuberías de diámetros mayores o iguales
a 450 mm (RAS, 2000).
5. Velocidad máxima
La velocidad máxima se establece con el fin de evitar problemas de erosión en las tuberías,
problemas de cavitación
7
, entrampamiento de aire, generación de resaltos hidráulicos
dentro de la red, entre otros. El RAS 2000 recomienda que la velocidad máxima sea de 5
m/s y para tuberías termoplásticas (PVC) de 10 m/s.
6. Pendiente máxima y mínima
Las pendientes pueden variar en un rango en el cual se cumplen las restricciones de
velocidad mínima y máxima. En este sentido, el valor mínimo para la pendiente debe ser
aquel para el cual el flujo alcanza la velocidad mínima y cumple con la restricción del
esfuerzo cortante mínimo. Así mismo, la pendiente máxima será aquella para la cual el flujo
alcanza la velocidad máxima.
7. Profundidad a cota clave de la tubería.
La profundidad mínima a cota clave de la tubería debe ser tal se asegure la protección de
las tuberías y que las descargas domiciliarias sin sótano puedan ser drenadas por gravedad.
Así mismo, se establece una profundidad máxima por razones constructivas y para limitar
7
Cavitación: Fenómeno en el cual el agua en estado líquido pasa a estado gaseoso (vapor de agua) a raíz de
una disminución de la presión y posterior mente estas burbujas de vapor vuelven a pasar a estado líquido
repentinamente y con presiones muy altas que generan daños en la infraestructura de la red (Saldarriaga,
2011)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
21
las cargas que deberá soportar la tubería. Estos límites de excavación se presentan en la
Tabla 2.3.
Tabla 2.3 Límites de la profundidad a cota clave de la tubería.
Tipo de Vía
𝒉
𝒎𝒊𝒏
(𝒎)
𝒉
𝒎𝒂𝒙
(𝒎)
Peatonal o Zona Verde
0.7
5.0
Vehicular
1.2
5.0
La Tabla 2.4 resume las restricciones hidráulicas utilizadas para el diseño de tuberías en
sistemas de alcantarillado.
Tabla 2.4 Resumen de restricciones hidráulicas de diseño. Tomado y modificado de Butler & Davies (2011).
Restricción
Valor
Condición
1
Diámetro nominal mínimo
200 mm
Siempre
2
Relación de llenado máxima
0.7
𝑑 ≤ 600 mm
0.8
0.7 ≤ 𝐹𝑟 ≤ 1.5
0.85
Siempre
3
Velocidad mínima
0.75 m/s
𝑑 < 450 mm
4
Velocidad máxima
5 m/s
𝑘
𝑠
> 0.0001
10 m/s
𝑘
𝑠
< 0.0001
5
Mínimo esfuerzo de cortante
2 Pa
𝑑 ≥ 450 mm
6
Pendiente mínima
Aquella que cumple la velocidad mínima y el esfuerzo
de cortante mínimo.
7
Pendiente máxima
Aquella para la que se obtiene la velocidad máxima
real.
2.3.3.2 Restricciones comerciales
El diámetro asignado a cada tubería del sistema de alcantarillado, sólo puede tomar valores
discretos que pertenecen al conjunto de diámetros comercialmente disponibles (PAVCO, 2013).
Para este proyecto se utilizó la siguiente lista de diámetros comerciales.
Tabla 2.5 Lista de diámetros comerciales
Diámetros
Pequeños (m)
0.200
0.250
0.300
0.350
0.400
0.450
0.500
Diámetros
Grandes (m)
0.600
0.675
0.750
0.825
0.900
1.000
1.100

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
22
2.3.4 Función de costos
Con base en un estudio realizado por el Trenchless Technology Center de Louisiana Tech
University, De Oro Vergara (2008) propuso una ecuación para analizar los costos asociados con
sistemas de alcantarillado. Dicha ecuación presenta los costos como una función del diámetro de
la tubería y la profundidad a la que se instale la misma.
𝐶 = 693.62 ∗ 𝑑
1.088
∗ 𝐻
0.303
Ecuación 2.16
donde:
𝐶:
Costo por metro lineal de tubería [COP/m].
𝑑:
Diámetro de la tubería en milímetros [mm].
𝐻:
Profundidad de la Instalación en metros [m].
Posteriormente, esta ecuación fue ajustada de acuerdo con información de las bases de datos
del Ministerio de Medio Ambiente, Vivienda y Desarrollo Territorial (MAVDT), del Fondo Financiero
de Proyectos de Desarrollo (FONADE) y de empresas encargadas de prestar el servicio, por medio de
un estudio análisis de inversiones en acueducto y alcantarillado, desarrollado por la Comisión de
Regulación de Agua Potable y Saneamiento Básico (CRA) (Navarro, 2009).
Se encontró entonces que los costos de las tuberías, son función del diámetro de la misma y se
pueden la calcular de acuerdo con la Ecuación 2.17.
𝐶 = 9579.31 ∗ 𝑎 ∗ 𝑑
0.5737
∗ 𝑙
Ecuación 2.17
donde:
𝐶:
Costo por metro lineal de tubería a Mayo de 2009 [COP/m].
𝑑:
Diámetro de la tubería en milímetros [mm].
𝑎:
Factor de conversión de pesos de Diciembre de 2007 a Mayo de 2009. Este fue
calculado como: (1 + 𝐼𝑃𝐶
2008
) ∗ (1 + 𝐼𝑃𝐶
06/2009
) = 1.32.
𝑙:
Longitud de la tubería.
Análogamente, los costos de excavación son función del volumen de excavación necesario para
la instalación de la tubería, como plantea la Ecuación 2.18.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
23
𝐶 = 1163.77 ∗ 𝑎 ∗ V
1.31
Ecuación 2.18
donde:
𝐶:
Costo por metro lineal de tubería a Mayo de 2009 [COP/m].
V:
Volumen de excavación por tubería [m
3
].
𝑎:
Factor de conversión de pesos de Diciembre de 2007 a Mayo de 2009. Este fue
calculado como: (1 + 𝐼𝑃𝐶
2008
) ∗ (1 + 𝐼𝑃𝐶
06/2009
) = 1.32.
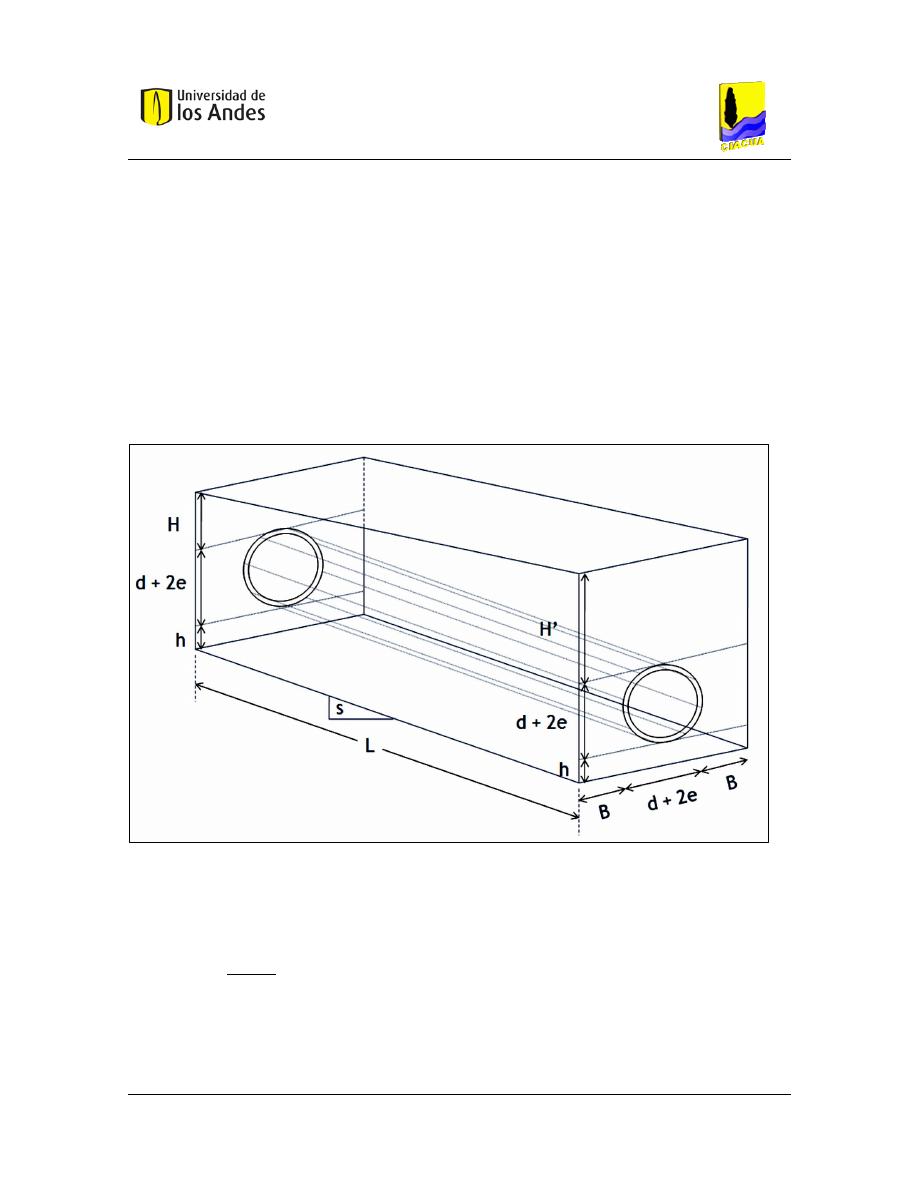
A continuación se presenta la ecuación para el cálculo del volumen de excavación necesario
para la instalación de una tubería, de acuerdo con el análisis de la Figura 2.7 (CIACUA, 2013).
Figura 2.7
Proyección del trapecio que produce el área excavada para una tubería de alcantarillado. Tomada
de (CIACUA, 2013)
𝑉 = ([
𝐻 + 𝐻′
2
] + 𝑑 + 2𝑒 + ℎ) ∗ (2𝐵 + 2𝑒 + 𝑑) ∗ (𝑙 cos[tan
−1
𝑠])
Ecuación 2.19
donde:
𝑉:
Volumen excavado para poner la tubería.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
24
𝐻:
Profundidad de excavación hasta la cota clave aguas arriba de la tubería.
𝐻 ’:
Profundidad de excavación hasta la cota clave aguas abajo de la tubería.
𝑑:
Diámetro interno de la tubería
𝑒:
Espesor de la pared de la tubería.
ℎ:
Relleno que debe disponerse bajo la tubería. Depende de la reglamentación del
lugar donde se lleve a cabo el diseño. Para los ejemplos se siguieron las
recomendaciones del RAS (2000): ℎ = 15 𝑐𝑚.
𝐵:
Espacio lateral que debe dejarse a ambos lados de la tubería para ponerla.
𝑠:
Pendiente en la que se dispone la tubería.
𝑙:
Longitud de la tubería.
De acuerdo con lo anterior, los costos asociados con la construcción de sistemas de
alcantarillado se calculan como la suma entre los costos de las tuberías como tal (Ecuación 2.17) y
los costos de la excavación (Ecuación 2.18), tal como plantea Navarro I. (2009) en la Ecuación 2.20.
𝐶 = 𝑎 ∗ (9579.31 ∗ 𝑑
0.5737
∗ 𝑙 + 1163.77 ∗ 𝑉
1.31
)
Ecuación 2.20
Esta será entonces la ecuación que se utilizará para analizar los costos de construcción de los
tramos de las redes de alcantarillado diseñadas; teniendo en cuenta que, aunque simplifica todos
los costos reales asociados a la construcción de un tramo (entibado, mano de obra, relleno, etc.), es
una buena aproximación a los costos de construcción reales puesto que los costos de excavación y
de tuberías son los más relevantes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
25
3 DEFINICIÓN DEL PROBLEMA
El diseño de las redes de alcantarillado es un problema complejo que tiene dos componentes
fundamentales: la definición del trazado de la red y el diseño hidráulico. El trazado, se refiere a la
forma en que se deben poner las tuberías, de forma que se define el sentido de flujo en cada tubería
y el tipo de tubería. A esto se le conoce como el trazado de la red. Simultáneamente, el diseño
hidráulico se refiere a la selección del diámetro y la pendiente de cada tubería de manera que se
tenga un diseño hidráulico que cumpla con una serie de requisitos y restricciones hidráulicas, según
el Plan de Saneamiento y Manejo de Vertimientos PSMV regional. Adicionalmente, durante el
diseño de la red se hace una evaluación económica para encontrar aquel diseño que tiene el mínimo
costo de construcción. Esto teniendo en cuenta que el uso de técnicas de optimización, hardware y
software moderno; permite encontrar un diseño optimizado en costos dentro de millones de
alternativas.
En este trabajo, el problema se divide en dos partes: en primer lugar, se buscará encontrar el
mejor trazado para la red siguiendo criterios de selección presentados en la Sección 4.1; en segundo
lugar, se busca encontrar el diseño hidráulico de la red partiendo de un trazado ya definido. Ambos
problemas se abordan como problemas de optimización de flujo en redes.
3.1 Problemas de flujo en redes
Los problemas de flujo en redes buscan encontrar la solución a un problema que se modela a
través de un grafo como por ejemplo, encontrar un camino óptimo (según el caso, podría ser el más
económico, más corto, con mayor capacidad, etc.). Un grafo se representa a partir de un conjunto
de Nodos 𝒩 y un conjunto de Arcos 𝒜. Cada arco, es un elemento que conecta pares de nodos
diferentes (Ahuja, et al., 1993), como los que se muestran en la Figura 3.1.
Cada grafo, puede tener múltiples caminos para ir de un nodo inicial a uno final dados. Cada
elemento del grafo tiene atributos. Por ejemplo, los nodos tienen atributos que determinan cuál es
el nodo de inicio y cuál el nodo final, mientras los arcos tienen como atributo un costo asociado, una
distancia, una capacidad, entre otros.
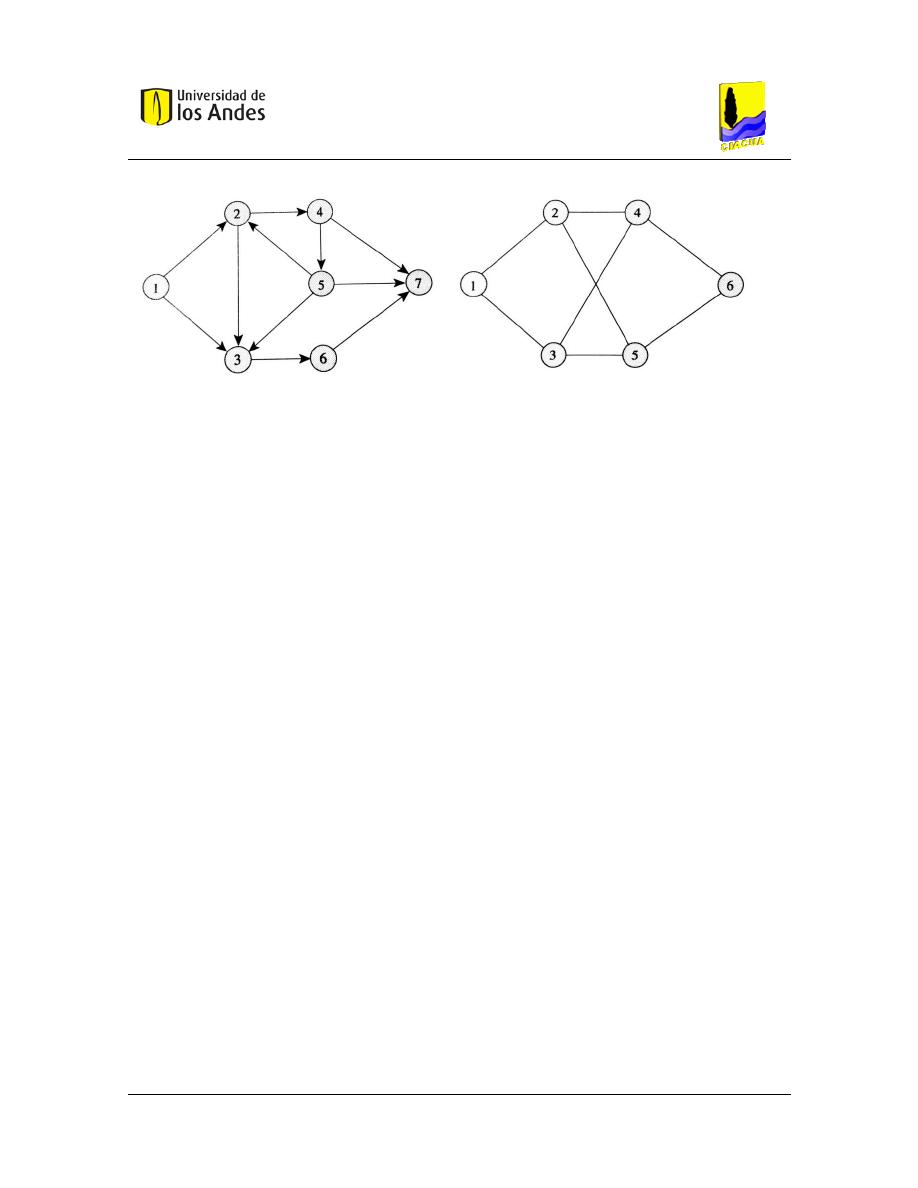
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
26
(a) Grafo Dirigido
(b) Grafo No-Dirigido
Figura 3.1 Grafo. Tomado de Ahuja & et Al (1993).
En la Figura 3.1 (a) se muestra un grafo dado por un conjunto de nodos 𝒩 = {1, 2, 3, 4, 5, 6, 7}
y arcos 𝒜 = {(1, 2), (1, 3), (2,3), (2,4), (5,2), … }, para los cuales se conoce su dirección. Por otro
lado la Figura 3.1 (b) presenta otro grafo dado por el conjunto de nodos 𝒩 = {1, 2, 3, 4, 5, 6} y con
arcos no dirigidos que pueden ser definidos en ambos sentidos, por ejemplo (1,2) ∈ 𝒜 ó (2,1) ∈
𝒜.
De acuerdo con la Figura 3.1 un camino para el grafo dirigido, entre los Nodos 1 y 7 podría estar
definido de diferentes maneras. Por ejemplo, un camino puede ser el comprendido por los Arcos
(1, 2), (2,4) y (4,7). Otro camino puede ser (1, 2), (2,3), (3,6) y (6,7), entre otras posibles
combinaciones de arcos. Así mismo, también se pueden dar ciclos como el comprendido por los
Arcos (2, 4), (4,5) y (5,2).
3.2 Componentes la red de alcantarillado
Para recolectar y transportar las aguas residuales y pluviales, desde donde se origina la descarga
hasta el sitio donde se va a depositar y tratar el agua, se necesita un sistema artificial de
alcantarillado. Los principales componentes de la red son los pozos de inspección y las tuberías entre
estos. Los pozos de inspección son estructuras de la red diseñadas para permitir el acceso a la
misma, para realizar cierto tipo de mantenimiento al sistema y además son las estructuras que
permiten la conexión entre dos o más tuberías contiguas.
Por otro lado las tuberías, son los principales elementos de conducción del sistema, a través de
los cuales se transporta el agua residual y las aguas lluvias que genera una ciudad o zona urbana. De
acuerdo con lo anterior, y por simplicidad de los modelos de estas redes, solo se van a tener en
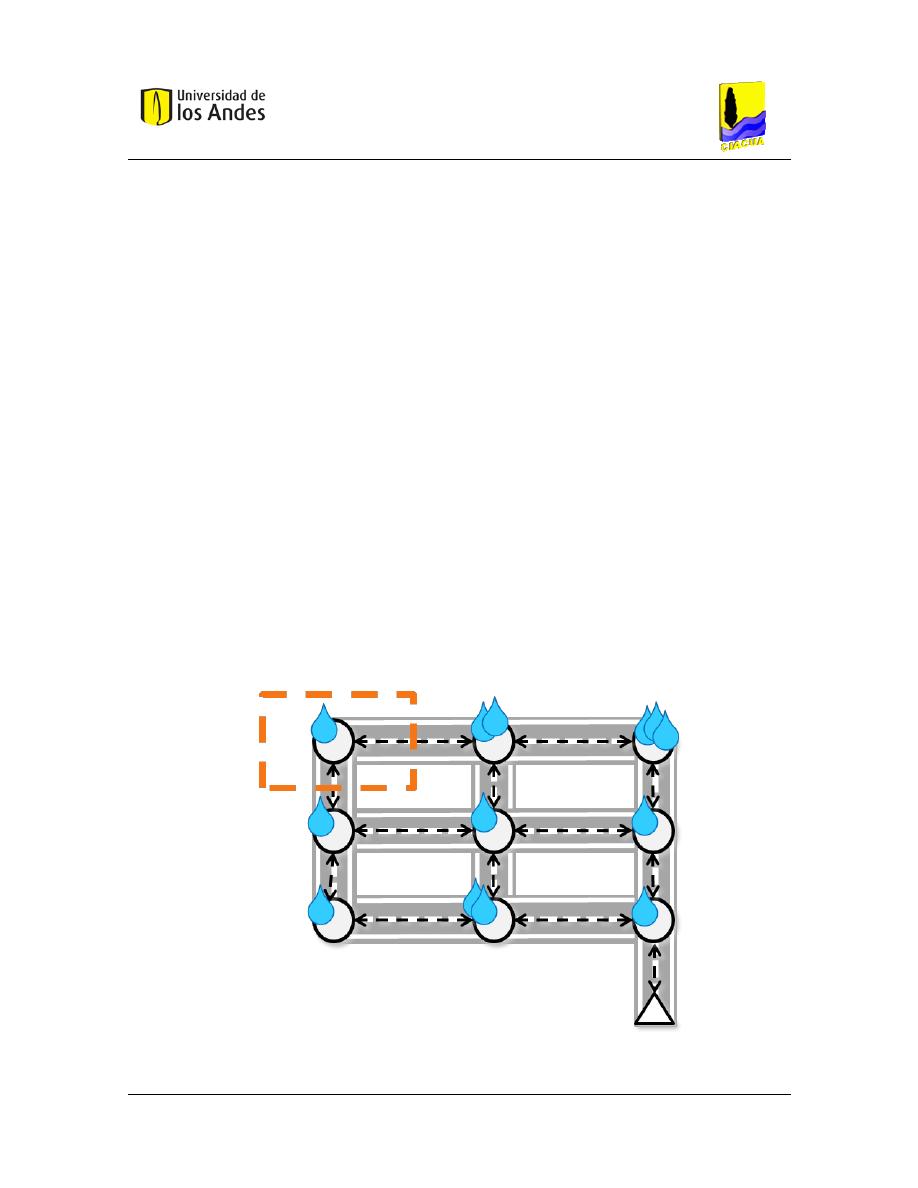
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
27
cuenta estos dos componentes principales para la modelación. Además, se sabe que los costos de
construcción más importantes son aquellos relacionados a dichos componentes.
3.3 Selección del trazado de la red
La selección del trazado de una red de drenaje urbano consiste en indicar hacia dónde fluye el
agua desde cada pozo de inspección, cómo se conectan las tuberías entre sí y qué tipo de tubería se
tiene en cada tramo. Sin embargo, para definir esto es necesario conocer la topología y topografía
de la red, que establece dónde están ubicados los pozos de inspección (coordenadas) y cómo se
deben conectar entre sí. Se debe tener en cuenta que en cada calle de la ciudad debe haber una
tubería, en cada intersección entre calles debe existir un pozo de inspección, cada pozo de
inspección sólo puede drenar hacia una tubería y la ubicación del punto de descarga debe estar
definida previamente. Además, cada pozo de inspección recibe un caudal de entrada que contempla
un caudal sanitario asociado con un área aferente al pozo (ver Figura 3.2) y un caudal que recibe de
las tuberías que llegan a éste. De acuerdo con lo anterior se define la topología de la red, i.e., cómo
están los pozos conectados entre sí, de acuerdo con la planeación de la malla vial y la ubicación del
punto de descarga, como presenta la Figura 3.2.
Figura 3.2. Topología de una red de alcantarillado.
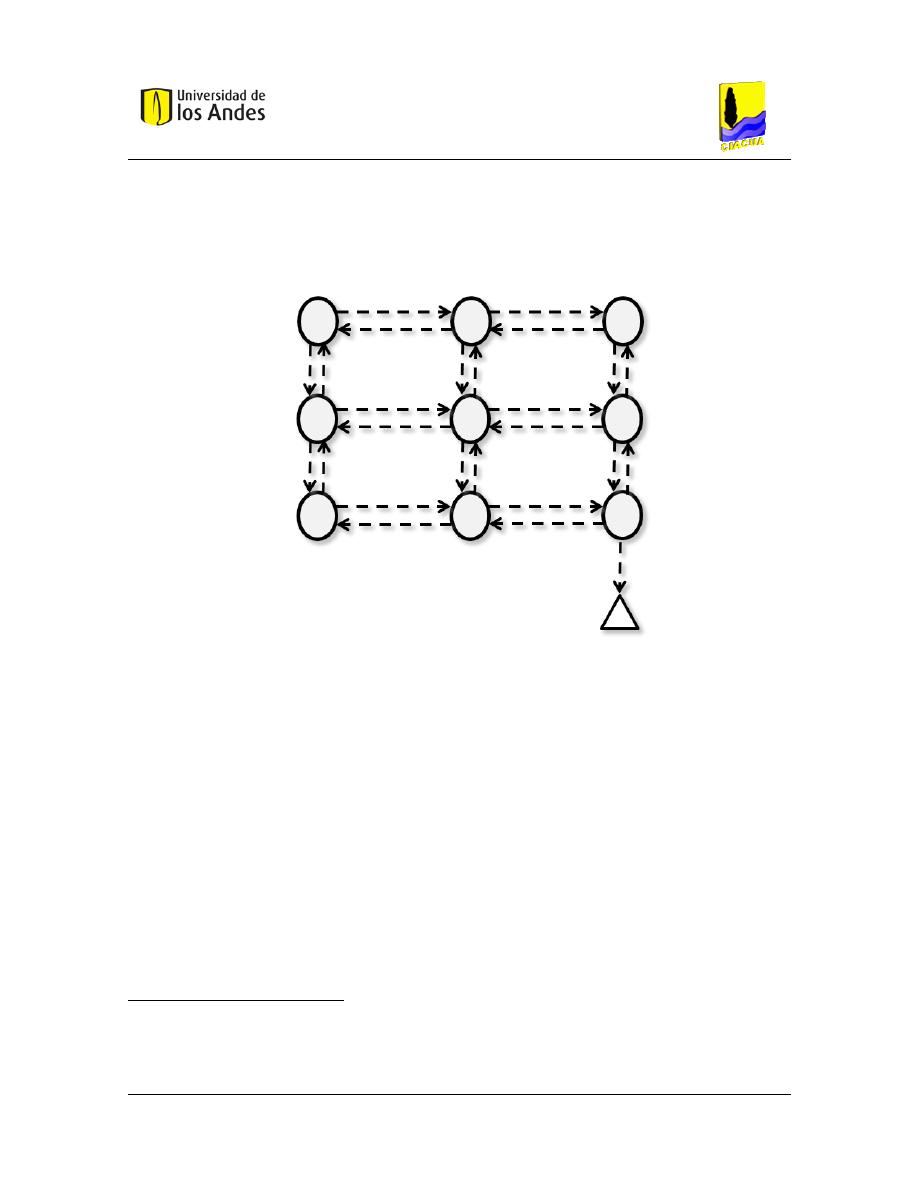
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
28
En una red de alcantarillado, como la que se muestra en la Figura 3.3, los círculos representan
los pozos de inspección; las flechas punteadas, los tramos de tuberías entre ellos y el triángulo, el
punto de descarga. Como se puede observar, para cada tramo existen dos posibles sentidos de flujo
excepto para los tramos que estén directamente conectados al punto de descarga.
Figura 3.3 Red de alcantarillado.
Adicionalmente, las redes de alcantarillado son redes abiertas (i.e., tiene estructura de árbol), a
pesar de que deben tener tuberías en todos los tramos. Al ser redes abiertas, este tipo de sistemas
no debe tener ciclos buscando evitar que el agua residual recircule por el mismo sitio. En este orden
de ideas, se tienen dos tipos de tuberías: tuberías de inicio y tuberías continuas. Las tuberías de
inicio son aquellas que están no tienen tuberías conectadas aguas arriba, es decir, están en los
extremos de cada una de las ramas del árbol. Este tipo de tuberías únicamente recibe como caudal
de entrada el aportado como caudal sanitario asociado con un área aferente al pozo aguas arriba
8
.
Por el contrario, las tuberías continuas se encuentran en los tramos de la red que reciben el caudal
de las tuberías que llegan desde aguas arriba, más el caudal aportado por el área aferente del pozo
aguas arriba. La Figura 3.4 muestra un ejemplo de estos dos tipos de tuberías, y permite ver cómo
todos los inicios están conectados a la descarga siguiendo una ruta específica.
8
Con relación a sistemas hídricos, se dice que un punto está aguas arriba si se encuentra antes del punto que
se está considerando, avanzando en dirección contraria a la corriente; en cambio los puntos que se
encuentran después del punto considerado, avanzando en el sentido de la corriente, se dice que están aguas
abajo.
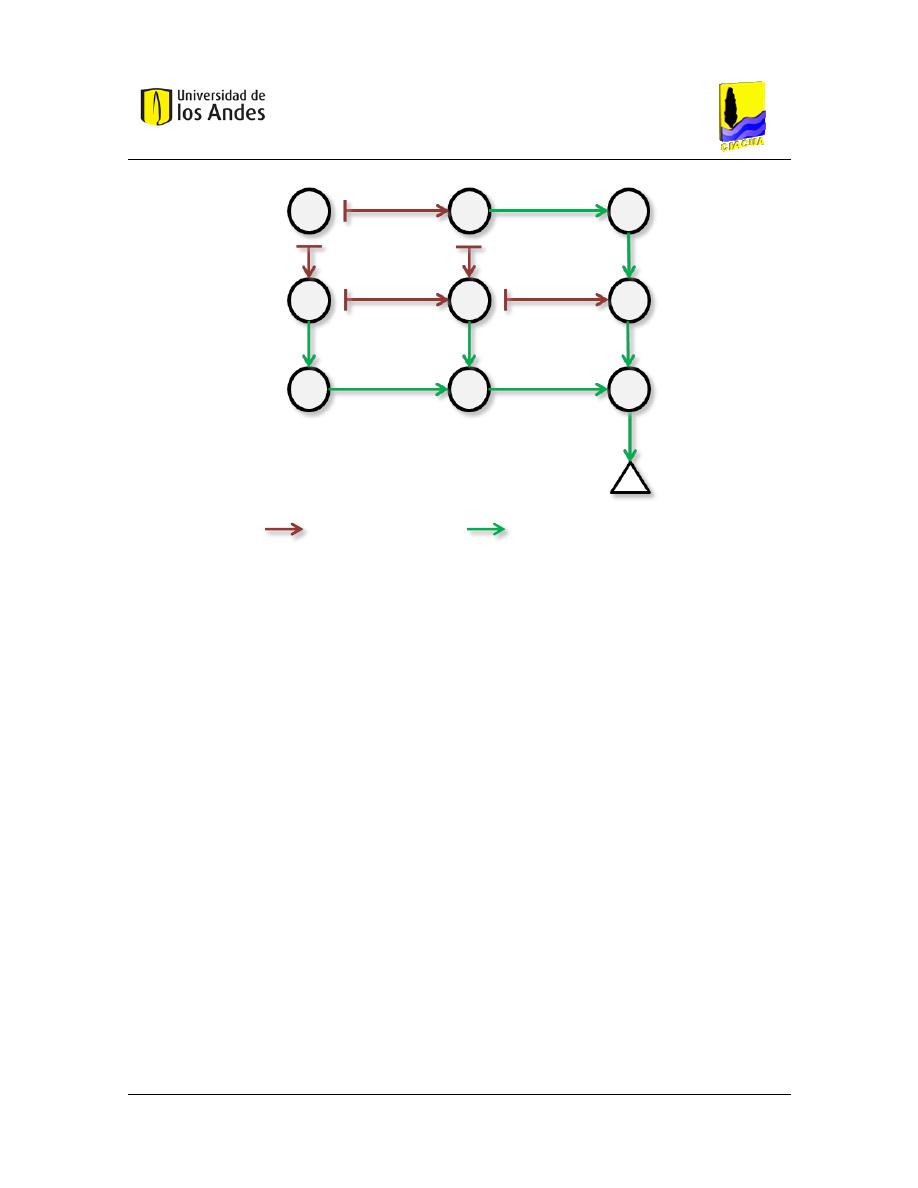
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
29
Tubería de inicio
Tubería continua
Figura 3.4 Trazado de una red de alcantarillado.
Adicionalmente, se puede observar que de cada pozo de inspección puede salir máximo una
tubería continua o tantas tuberías de inicio como pozos adyacentes tenga dicho pozo. En el ejemplo
anterior se observa cómo del pozo superior izquierdo salen dos tuberías de inicio y del resto de
nodos sale solo una tubería continua. Esto se debe a que las tuberías continuas deben ir acumulando
los caudales de las tuberías que llegan a estas más el caudal que aporte el pozo aguas arriba de esta;
mientras que las tuberías iniciales solo operan como entradas del caudal al sistema. Cuando de un
pozo sale más de una tubería de inicio, el caudal aportado por este pozo se debe distribuir entre
dichas tuberías. Lo mismo sucede si salen una tubería continua y una o más tuberías de inicio, el
caudal se divide entre éstas (no necesariamente de forma proporcional).
Por otro lado, todos los pozos de inspección aportan un caudal de entrada al sistema que sólo
puede salir por el punto de descarga, i.e., no se puede perder ni almacenar agua dentro del sistema
de alcantarillado. Por consiguiente, la suma de los caudales de entrada debe ser igual al caudal que
llega al punto de descarga.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
30
3.3.1 Datos de entrada para la selección del trazado
Se reciben como datos de entrada la topografía de la zona donde se planea construir o
reemplazar la red de alcantarillado, además de las características de la red. Específicamente, los
parámetros de entrada son los siguientes:
•
ℳ :
Conjunto de pozos de inspección que conforman la red de alcantarillado.
ℳ = { 𝑚
1
, 𝑚
2
, 𝑚
3
, 𝑚
4
, … , 𝑚
|ℳ|
}
donde el pozo 𝑚
|ℳ|
será el punto de descarga del sistema de alcantarillado.
•
𝑄
𝑘
:
Caudal de entrada del pozo 𝑚
𝑘
∈ ℳ .
•
𝑃𝑜𝑠𝑋
𝑘
: Posición en 𝑥 del pozo 𝑚
𝑘
∈ ℳ.
•
𝑃𝑜𝑠𝑌
𝑘
: Posición en 𝑦 del pozo 𝑚
𝑘
∈ ℳ.
•
𝛻
𝑘
:
Cota del terreno (Posición en 𝑧) del pozo 𝑚
𝑘
∈ ℳ.
•
𝑐:
Costo por unidad de flujo transportado para cada tubería.
3.4 Diseño hidráulico de la red
En cuanto al diseño hidráulico de la red, una vez definido el trazado, se busca encontrar la
combinación diámetro-pendiente para cada tubería que conforma la red, teniendo en cuanta que
se quiere minimizar el costo total de construcción de la red y asegurar el funcionamiento de la
misma. El diseño debe cumplir con las restricciones de diseño (hidráulicas y constructivas)
establecidas por las normas de cada país, que en caso colombiano hacen referencia a las normas
presentadas en la Sección 2.3.3.
Partiendo de una red y un trazado establecido como por ejemplo el que se muestra en la Figura
3.4, se conoce el caudal de diseño 𝑄
𝑑
, el sentido del flujo y el tipo de tubería para cada tramo. Según
el caudal de diseño de cada tramo, se debe seleccionar el tamaño (diámetro 𝑑) y posición (pendiente
𝑠) de la tubería a instalar para que el caudal pueda ser transportado (ver Figura 3.5).
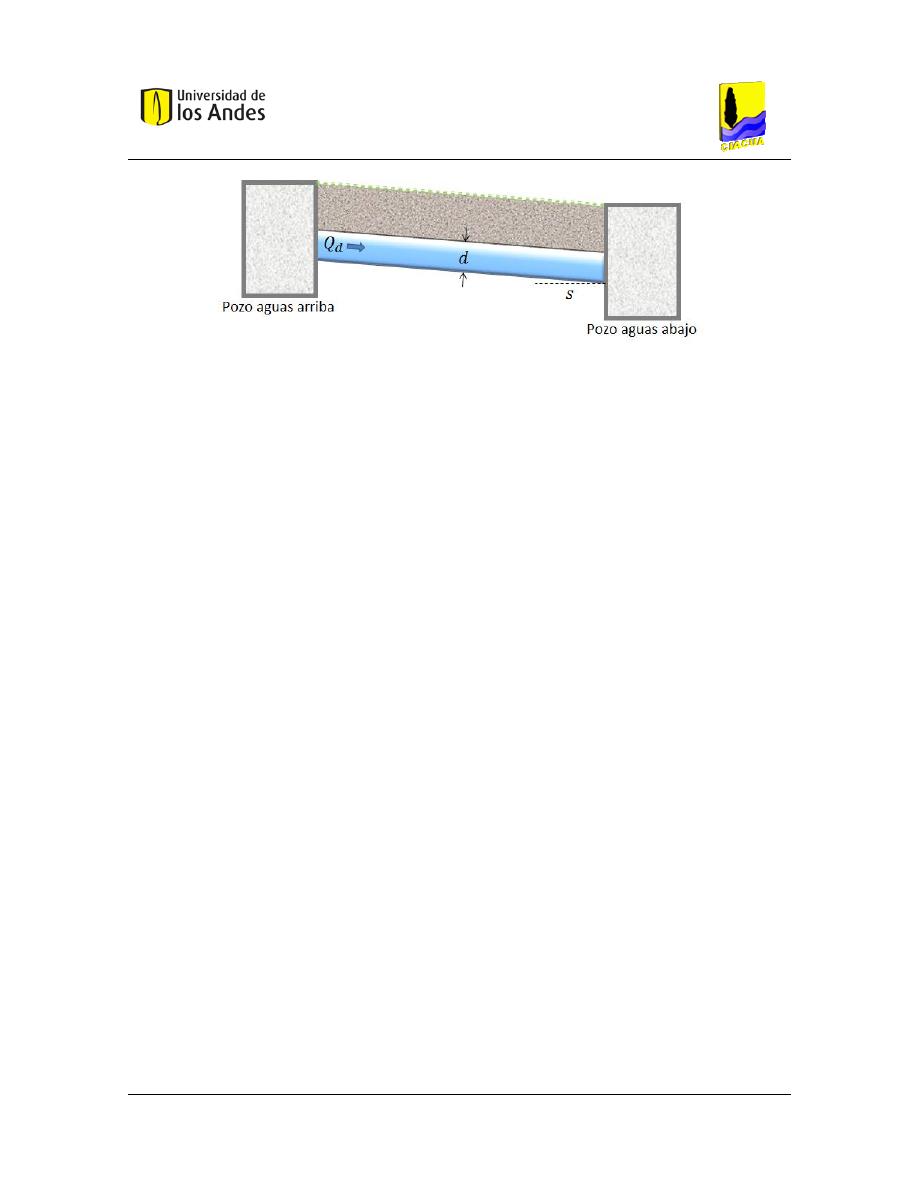
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
31
Figura 3.5. Diseño hidráulico de una tubería (diámetro-pendiente).
Ahora bien, en el caso del diseño hidráulico de toda la red de alcantarillado se debe asegurar
que la conexión entre sus tuberías sea consistente. Es decir, que se tenga siempre un flujo a favor
de la gravedad, que las tuberías estén conectadas a altura de sus cotas de batea y que todas las
tuberías de inicio estén conectadas a la descarga. Una vez se cumplen estas condiciones el diseño
hidráulico se considera factible. Sin embargo, dada la cantidad de alternativas de diseño hidráulico
que puede tener una red, se debe buscar aquella que representa el menos costo de construcción.
Este último será entonces el diseño hidráulico óptimo de la red, para el trazado dado.
3.4.1 Datos de entrada para el diseño hidráulico
Para el diseño hidráulico, es necesario conocer el trazado de la red, i.e, sentidos de flujo, tipos
de tuberías; además de la topografía y topología de la misma. También es necesario conocer las
propiedades del fluido con el que se va a trabajar (agua residual) y las características de las tuberías
que se van a utilizar. En ese orden de ideas, del fluido se debe conocer su viscosidad cinemática 𝜈;
y de las tuberías se debe conocer la rugosidad absoluta 𝑘
𝑠
del material y los posibles diámetros que
se podrían utilizar en el diseño (según la disponibilidad comercial). Específicamente, los parámetros
de entrada son los siguientes:
•
ℳ :
Conjunto de pozos de inspección que conforman la red de alcantarillado.
ℳ = { 𝑚
1
, 𝑚
2
, 𝑚
3
, 𝑚
4
, … , 𝑚
|ℳ|
}
donde el pozo 𝑚
𝑚
será el punto de descarga del sistema de alcantarillado.
•
𝑃𝑜𝑠𝑋
𝑘
: Posición en 𝑥 del pozo 𝑚
𝑘
∈ ℳ.
•
𝑃𝑜𝑠𝑌
𝑘
: Posición en 𝑦 del pozo 𝑚
𝑘
∈ ℳ.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
32
•
𝛻
𝑘
:
Cota del terreno (Posición en 𝑧) del pozo 𝑚
𝑘
∈ ℳ.
•
𝒯:
Tipos de tuberías.
𝒯 = {𝐼𝑛𝑖𝑐𝑖𝑜, 𝐶𝑜𝑛𝑡𝑖𝑛𝑢𝑎}
•
𝒫:
Conjunto de tramos que conforman la red de alcantarillado.
𝒫 = {(𝑘, 𝑘
′
)|𝑚
𝑘
∈ ℳ, 𝑚
𝑘
′
∈ ℳ}
•
𝑡
𝑘,𝑘
′
: Tipo de tubería del tramo (𝑘, 𝑘
′
) ∈ 𝒫, donde 𝑡
𝑘,𝑘
′
∈ 𝒯.
•
𝑄
𝑑
(𝑘, 𝑘
′
): Caudal de diseño de cada tubería (𝑘, 𝑘’) ∈ 𝒫.
•
𝐷:
Conjunto de diámetros comerciales disponibles.
𝐷 = { 𝑑
1
, 𝑑
2
, 𝑑
3
, 𝑑
4
, … , 𝑑
|𝐷|
}
•
𝑘
𝑠
:
Rugosidad absoluta de las tuberías.
•
𝜈 :
Viscosidad cinemática del agua.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
33
4 METODOLOGÍA PARA EL DISEÑO OPTIMIZADO DE REDES DE
ALCANTARILLADO
En general los procesos de optimización buscan encontrar la mejor solución dentro de un
conjunto de soluciones que respetan una serie de restricciones y persiguen uno o varios criterios de
selección (e.g., costos, beneficio, tiempo, etc.). En el caso del diseño de sistemas de alcantarillado,
un diseño óptimo es aquel que cumple con todos los aspectos hidráulicos de diseño y cuyo costo de
construcción es mínimo. Al igual que otros problemas de optimización, en este problema existen
cuatro componentes importantes para el modelaje y solución: los parámetros, las variables de
decisión, las restricciones y la función objetivo. Los parámetros proporcionan la información
necesaria (o conocida) que se tiene de los problemas. Las variables de decisiones son los aspectos
del problema sobre los cuales el decisor tiene injerencia. Las restricciones limitan las decisiones del
problema estableciendo las reglas que se deben cumplir en una solución. Finalmente, la función
objetivo guía la búsqueda de la solución que se quiere encontrar.
En este trabajo, el problema se divide en dos partes: en primer lugar, se buscará encontrar el
mejor trazado para la red siguiendo criterios de selección presentados en la Sección 4.1; en segundo
lugar, se busca encontrar el diseño hidráulico de la red partiendo de un trazado ya definido. Ambos
problemas se abordan como problemas de optimización de flujo en redes.
4.1 Metodología para la selección del trazado de redes de alcantarillado
De acuerdo con la definición del problema que se planteó en la Sección 3.3, se estableció una
metodología para la selección del trazado de la red en la que se hace un modelaje matemático
basado en el problema de Diseño de Redes (Network Design Problem) (Guy, et al., 2005). Este es un
problema de Programación Entera Mixta en el que se involucran variables de decisión que modelan
el flujo y variables de decisión que modelan la elección de un sentido de flujo.
4.1.1 Definición del grafo para la selección del trazado
Para resolver este problema, se puede modelar la red de alcantarillado como un grafo
dirigido 𝒢
𝐿
= (𝒩
𝐿
, 𝒜
𝐿
, 𝒯), donde:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
34
𝒩
𝐿
= { 𝑣
1
, 𝑣
2
, 𝑣
3
, 𝑣
4
, … … , 𝑣
|ℳ|
} es el conjunto de nodos que representa los pozos de
inspección que componen la red de alcantarillado. Cada nodo 𝑣
𝑖
∈ 𝒩
𝐿
va a tener una
oferta/demanda 𝑏
𝑖
(𝑏
𝑖
> 0 oferta y 𝑏
𝑖
< 0 demanda), que representarán los caudales de
entrada en cada pozo y el caudal de salida en el punto de descarga. Teniendo en cuenta
que no hay pérdidas ni almacenamiento de agua en la red, la suma de los caudales de
entrada debe ser igual al caudal de salida desde cada pozo.
𝒯 = { 𝐼, 𝐶} es el conjunto tipos de tuberías posibles, donde 𝐼 es una tubería de inicio y 𝐶
es una tubería continua.
𝒜
𝐿
=
{(
𝑖, 𝑗, 𝑡
)
| 𝑣
𝑖
∈ 𝒩
𝐿
, 𝑣
𝑗
∈ 𝒩
𝐿
, 𝑡 ∈ 𝒯
} el conjunto de arcos que representa las
tuberías entre los pozos (nodos) adyacentes
𝑣
𝑖
∈ 𝒩
𝐿
y 𝑣
𝑗
∈ 𝒩
𝐿
del tipo 𝑡 ∈ 𝒯. Cada arco
tiene atributos que definen un costo por unidad caudal transportada, una capacidad de
transporte y el tipo de tubería.
o
𝑐
𝑖𝑗
:
Costo por unidad de flujo transportado del arco (𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
.
o
𝑢
𝑖𝑗𝑡
: Capacidad de transporte del arco (𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
o
𝑡
𝑖𝑗
:
Tipo de tubería del arco (𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
.
En la definición del grafo se establecieron los arcos que representan los dos sentidos de flujo y
los dos tipos de tuberías en la red (de inicio o continuas), como se observa en la Figura 4.1. Las
tuberías de inicio (líneas punteadas rojas) son aquellos tramos donde la red se va a abrir para formar
un árbol y reciben un caudal de entrada aportado por el pozo aguas arriba. Análogamente, las
tuberías continuas (líneas punteadas verdes), son aquellas que llevan el caudal de las tuberías aguas
arriba de estas además de los caudales de entrada en el pozo aguas arriba.
Tubería de inicio
Tubería continua
Figura 4.1 Tipos de tuberías para cada tramo de una red de alcantarillado.
En este sentido, el grafo que modela el trazado de una la red de alcantarillado tiene cuatro
posibles arcos por tramo, como se muestra en la Figura 4.2.
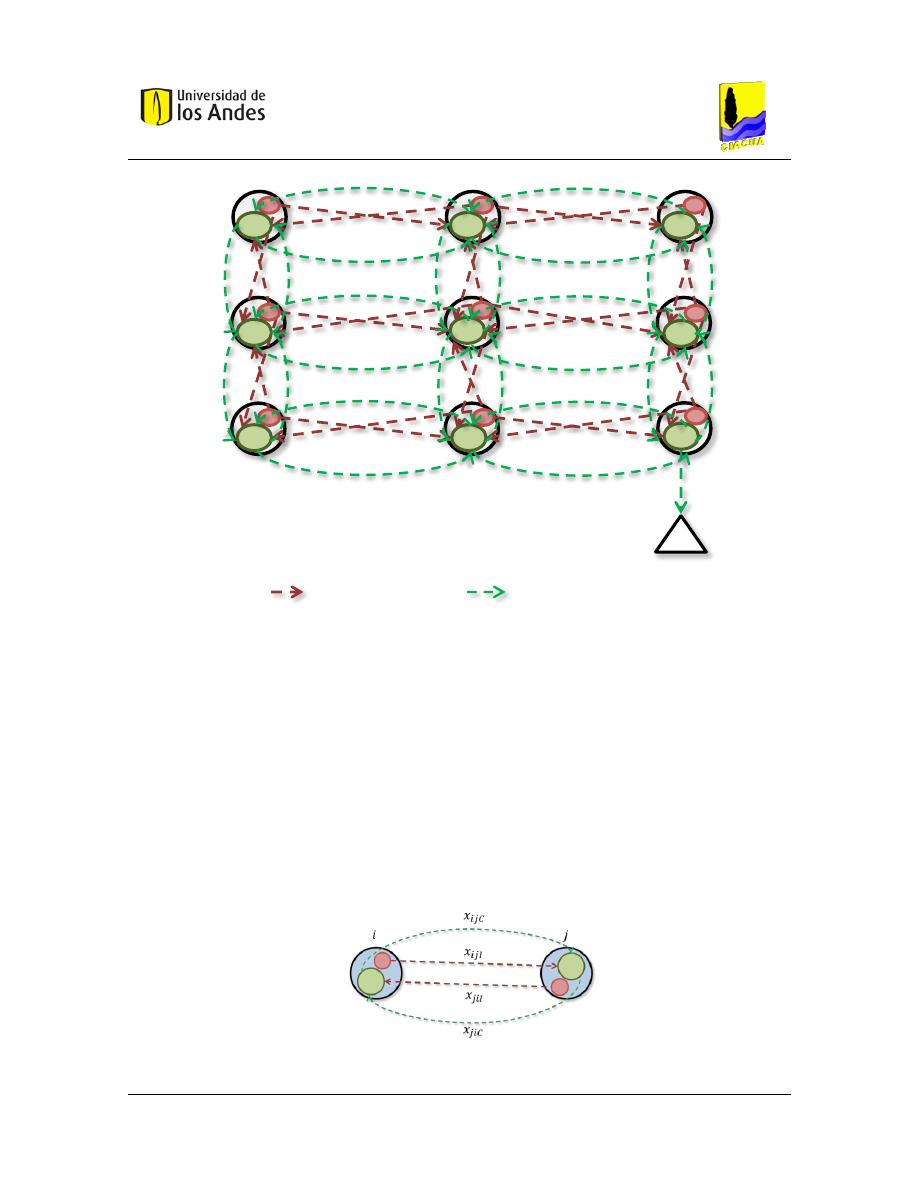
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
35
Tubería de inicio
Tubería continua
Figura 4.2 Grafo para la selección del trazado de una red de alcantarillado.
Según esto, se tiene una variable de decisión 𝑥
𝑖𝑗𝑡
que va a determinar si el arco (𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
define o no el trazado de la red, tal como se establece en la Ecuación 4.1. De acuerdo con lo anterior,
para cada tramo se debe seleccionar un sentido de flujo y el tipo de tubería, de forma que se conozca
la trayectoria del agua desde cada pozo de inspección hasta el punto de descarga. Se debe tener en
cuenta que la conexión entre los dos tipos de tuberías solo se puede dar de una tubería de inicio a
una continua o entre dos continuas para llegar a un trazado como el que presenta la Figura 3.4. En
este sentido, la Figura 4.3 presenta las posibles variables de decisión por tramo con cuatro arcos
que hacen referencia a las posibles combinaciones entre los sentidos de flujo y el tipo de las tuberías.
De estos cuatro posibles arcos se debe escoger sólo uno por tramo.
Figura 4.3 Posibles variables de decisión por tramo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
36
𝑥
𝑖𝑗𝑡
{ 1 si el arco (𝑖, 𝑗, 𝑡) define el trazado de la red
0 𝑑. 𝑙. 𝑐
∀ 𝑣
𝑖
, 𝑣
𝑗
∈ 𝒩
𝐿
, 𝑡 ∈ 𝒯
Ecuación 4.1
Por otro lado, el problema de Flujo de Costo Mínimo, busca la forma más económica de enviar
cierta cantidad de flujo a través de una red (Karger, 2006). Entonces, se quiere modelar el flujo para
conocer cuánto caudal pasaría por cada tubería, de acuerdo con el trazado evaluado. Para este
modelo la función objetivo se deberá dejar en términos del flujo (caudal), por lo cual se define 𝑦
𝑖𝑗𝑡
como el flujo que pasa por el arco (𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
y se evalúan los costos por unidad de flujo
transportado, desde los nodos que ofertan hasta los nodos que demandan. Según lo anterior,
matemáticamente este problema se define de la siguiente manera:
min ∑
∑
𝑐
𝑖𝑗
𝑦
𝑖𝑗𝑡
(𝑖,𝑗,𝑡)∈𝒜
𝐿
𝑡 ∈𝒯
Ecuación 4.2
∑
∑
𝑦
𝑖𝑗𝑡
{
𝑗
|
(𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿}
𝑡 ∈𝒯
− ∑
∑
𝑦
𝑗𝑖𝑡
{
𝑗
|
(𝑗, 𝑖, 𝑡) ∈ 𝒜
𝐿}
𝑡 ∈𝒯
= 𝑏
𝑖
∀ 𝑣
𝑖
∈ 𝒩
𝐿
Ecuación 4.3
0 ≤ 𝑦
𝑖𝑗𝑡
≤ 𝑢
𝑖𝑗𝑡
∀(𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
Ecuación 4.4
Finalmente, la Figura 4.4 muestra el grafo que representa todas las posibles conexiones entre
pozos de inspección y por ende, todos los posibles trazados. Además se muestra la oferta/demanda
en cada pozo. El Pozo 10 es el último y por ende se establece como el punto de descarga, con una
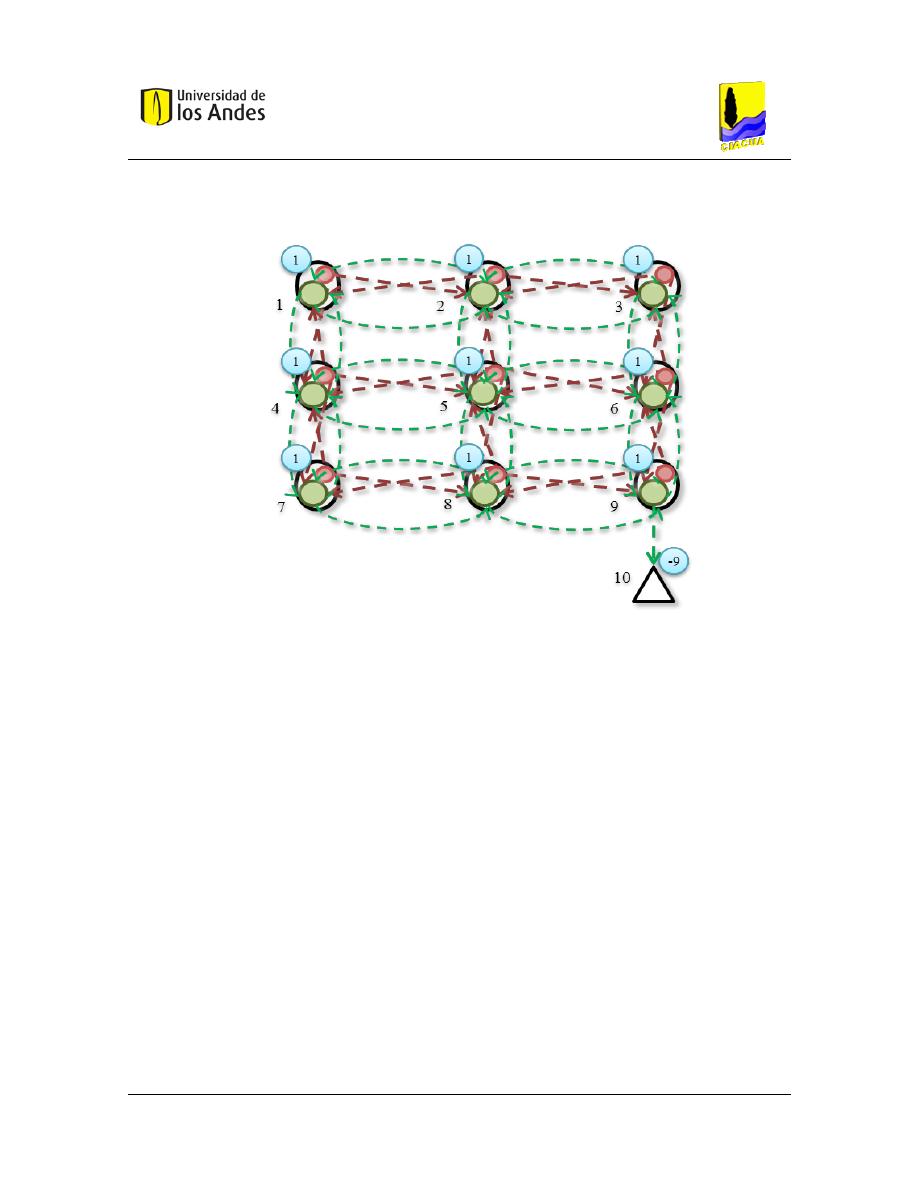
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
37
demanda de 𝑏
10
= −9 que es igual a la suma de las ofertas del resto de nodos de la red, pues cada
pozo oferta 1 unidad de agua.
Figura 4.4 Oferta/Demanda en cada nodo del grafo.
Ahora bien, la metodología para la selección del trazado de redes de alcantarillado involucra los
dos tipos de problemas mencionados; se tienen variables de decisión que modelan el flujo y
variables de decisión que modelan la elección de un sentido de flujo. La combinación de dichas
variables de decisión hacen que el problema deje de ser un Problema de Flujo de Costo Mínimo
únicamente, para pasar a ser un problema denominado Network Design Problem (NDP), que es un
problema de Programación Entera Mixta (MIP) (Larry, 2005).
4.1.2 Modelaje matemático para la selección del trazado
4.1.2.1 Variables de decisión
Para el problema de selección del trazado se tienen dos variables de decisión: 𝑥
𝑖𝑗𝑡
, es una
variable binaria que toma el valor de uno (1) si el arco (𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
define el trazado de la red o
toma el valor de cero (0) de lo contrario, como se plantea en la Ecuación 4.1 (a).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
38
𝑥
𝑖𝑗𝑡
∈ {0,1} ∀ 𝑣
𝑖
∈ 𝒩
𝐿
, 𝑣
𝑗
∈ 𝒩
𝐿
, 𝑡 ∈ 𝒯
Ecuación 4.1(a)
La segunda variable de decisión es el flujo 𝑦
𝑖𝑗𝑡
que pasa por cada arco (𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
. Esta es una
variable de decisión real que toma un valor entre 0 y la capacidad máxima de cada arco 𝑢
𝑖𝑗𝑡
, como
se muestra en la Ecuación 4.4.
0 ≤ 𝑦
𝑖𝑗𝑡
≤ 𝑢
𝑖𝑗𝑡
∀(𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
Ecuación 4.4
4.1.2.2 Función Objetivo 𝒇. 𝒐.
La función objetivo es la planteada en la Ecuación 4.2 donde 𝑐
𝑖𝑗
corresponde a un costo por
unidad de flujo transportado que se estima de acuerdo con la función de costos de construcción por
tramo, planteada en la Ecuación 2.20. Esta última depende del diámetro 𝑑 de la tubería y el volumen
de excavación 𝑉 necesario para su instalación, de acuerdo con las cotas de batea de la tubería en
los pozos aguas arriba y aguas abajo del tramo correspondiente.
𝐶 = 𝑘 ∗ (9579.31 ∗ 𝑑
0.5737
+ 1163.77 ∗ 𝑉
1.31
)
Ecuación 2.20
Se debe recordar que hasta este punto no se conoce el diseño hidráulico (diámetros y
pendientes) asociado con una tubería, sino que apenas se está definiendo la el trazado. En
consecuencia, el costo de construcción de la red se debe estimar utilizando una función de costos
en términos del caudal (flujo) que pasa por cada tubería y su sentido correspondiente. Este proceso
específico se explica en la Sección 4.3.
De forma general la función objetivo sería entonces la planteada en la Ecuación 4.5.
min ∑
∑
𝑐
𝑖𝑗
𝑦
𝑖𝑗𝑡
(𝑖,𝑗,𝑡)∈𝒜
𝐿
𝑡 ∈𝒯
+ ∑
∑
𝑎
𝑖𝑗
𝑥
𝑖𝑗𝑡
(𝑖,𝑗,𝑡)∈𝒜
𝐿
𝑡 ∈𝒯
Ecuación 4.5

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
39
4.1.2.3 Modelo Matemático
El modelo matemático que describe este problema de selección del trazado de la red, se
muestra a continuación.
min ∑
∑
𝑐
𝑖𝑗
𝑦
𝑖𝑗𝑡
(𝑖,𝑗,𝑡)∈𝒜
𝐿
𝑡 ∈𝒯
+ ∑
∑
𝑎
𝑖𝑗
𝑥
𝑖𝑗𝑡
(𝑖,𝑗,𝑡)∈𝒜
𝐿
𝑡 ∈𝒯
Ecuación 4.5
𝑠. 𝑎.
∑
∑
𝑦
𝑖𝑗𝑡
{
𝑗
|
(𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿}
𝑡 ∈𝒯
− ∑
∑
𝑦
𝑗𝑖𝑡
{
𝑗
|
(𝑗, 𝑖, 𝑡) ∈ 𝒜
𝐿}
𝑡 ∈𝒯
= 𝑏
𝑖
∀ 𝑣
𝑖
∈ 𝒩
𝐿
Ecuación 4.6
𝑥
𝑖𝑗𝑡
∗
𝑏
𝑖
𝑛
≤ 𝑦
𝑖𝑗𝑡
∀ 𝑣
𝑖
, 𝑣
𝑗
∈ 𝒩
𝐿
, 𝑡 ∈ 𝒯
Ecuación 4.7
𝑦
𝑖𝑗𝑡
≤ M ∗ 𝑥
𝑖𝑗𝑡
∀ 𝑣
𝑖
, 𝑣
𝑗
∈ 𝒩
𝐿
, 𝑡 ∈ 𝒯
Ecuación 4.8
∑
𝑥
𝑖𝑗𝑡
𝑡 ∈𝒯 | (𝑖,𝑗,𝑡)∈𝒜
𝐿
+
∑
𝑥
𝑖𝑗𝑖𝑡
𝑡 ∈𝒯 | (𝑗,𝑖,𝑡)∈𝒜
𝐿
= 1 ∀ 𝑣
𝑖
, 𝑣
𝑗
∈ 𝒩
𝐿
Ecuación 4.9
∑ 𝑥
𝑖𝑗𝐶
𝑣
𝑗
∈𝒩
𝐿
= 1 ∀ 𝑣
𝑖
∈ 𝒩
𝐿
Ecuación 4.10
∑ ∑ 𝑥
𝑗𝑖𝑡
𝑡 ∈𝒯
𝑣
𝑗
∈𝒩
𝐿
≤ M ∗ ∑ 𝑥
𝑖𝑗𝐶
𝑣
𝑗
∈𝒩
𝐿
∀ 𝑣
𝑖
∈ 𝒩
𝐿
| 𝑣
𝑖
≠ 𝑣
𝐿
Ecuación 4.11
∑ ∑ 𝑥
𝑗𝑖𝑡
𝑡 ∈𝒯
𝑣
𝑗
∈𝒩
𝐿
≥ ∑ 𝑥
𝑖𝑗𝐶
𝑣
𝑗
∈𝒩
𝐿
∀ 𝑣
𝑖
∈ 𝒩
𝐿
| 𝑣
𝑖
≠ 𝑣
𝐿
Ecuación 4.12

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
40
Para encontrar la solución óptima a este problema, se implementó el modelo matemático en
Xpress-MP que es un software de optimización que cuenta con un solver de optimización entera
mixta.
4.1.2.4 Restricciones para la selección del trazado
Las restricciones para la selección del trazado incluyen aquellas definidas dentro del Problema de
Flujo de Costo Mínimo y otras que se aseguran de que no se creen conexiones infactibles entre las
tuberías adyacentes. Entre las restricciones del problema, se encuentran las siguientes:
Restricción de Balance:
Esta se asegura de que la diferencia entre el flujo que sale de cada nodo 𝑣
𝑖
∈ 𝒩
𝐿
y el flujo
que entra a dicho nodo, sea igual a la oferta/demanda en el mismo 𝑏
𝑖
. En el caso de este
problema también ayuda a verificar que todos los caudales de entrada en los pozos lleguen
al punto de descarga, de forma que no haya almacenamientos o pérdidas de agua en la red.
Esta restricción se expresa matemáticamente con la Ecuación 4.6.
Límite inferior para el flujo:
En caso de que el arco (𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
exista, es decir que 𝑥
𝑖𝑗𝑡
= 1, entonces el flujo mínimo
por el arco (𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
será mayor o igual a la oferta del Nodo 𝑣
𝑖
∈ 𝒩
𝐿
dividida en los 𝑛
∑ 𝑦
𝑖𝑗𝐼
𝑣
𝑗
∈𝒩
𝐿
≤ 𝑏
𝑖
∀ 𝑣
𝑖
∈ 𝒩
𝐿
| 𝑣
𝑖
≠ 𝑣
𝐿
Ecuación 4.13
𝑥
𝑣
𝐿
−1,𝑣
𝐿
,𝐶
= 1
Ecuación 4.14
𝑦
𝑣
𝐿
−1,𝑣
𝐿
,𝐶
= ∑ 𝑏
𝑖
𝑣
𝐿
−1
𝑖=1
Ecuación 4.15
𝑦
𝑖𝑗𝑡
≥ 0 ∀ 𝑣
𝑖
, 𝑣
𝑗
∈ 𝒩
𝐿
, 𝑡 ∈ 𝒯
Ecuación 4.16
𝑥
𝑖𝑗𝑡
{1,0} ∀ 𝑣
𝑖
, 𝑣
𝑗
∈ 𝒩
𝐿
, 𝑡 ∈ 𝒯
Ecuación 4.1(a)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
41
nodos adyacentes, como se muestra en la Ecuación 4.7. Esto debido a que el caudal de
entrada en el nodo 𝑣
𝑖
∈ 𝒩
𝐿
se debe repartir entre todas las tuberías de salida, que pueden
ser varias tuberías de inicio y/o máximo una tubería continua.
Límite superior para el flujo:
En caso de que el arco (𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
exista, es decir que 𝑥
𝑖𝑗𝑡
= 1, entonces el flujo del arco
(𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
puede tomar cualquier valor, ya que debe ser menor a M, donde M es un
número muy grande. Así mismo, si el arco (𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
no existe, es decir que 𝑥
𝑖𝑗𝑡
= 0,
entonces el flujo máximo será de 0. La Ecuación 4.8 muestra la expresión matemática que
representa esta restricción.
Restricción de tuberías por tramo:
Esta restricción se asegura que sólo se escoja uno de los cuatro arcos posibles (Ver Figura
4.3), teniendo en cuenta que sólo puede existir una tubería por tramo, tal como se muestra
en la Ecuación 4.9.
Restricción de tuberías salida por pozo:
En una red de alcantarillado, únicamente se permite una tubería de salida de cada pozo de
inspección, por lo cual se debe restringir en número de tuberías de tipo continuo 𝐶 ∈ 𝒯
de cada nodo 𝑣
𝑖
∈ 𝒩
𝐿
, como se muestra en la Ecuación 4.10. En el caso de las tuberías de
inicio 𝐼 ∈ 𝒯 si se permite más de una saliendo de cada pozo de inspección, ya que en la
construcción éstas no están conectadas con dicho pozo.
Restricción de conexiones entre tuberías adyacentes:
Teniendo en cuenta que la conexión entre las tuberías sólo se puede dar de una tubería de
inicio a una continua y entre dos tuberías continuas, se formuló la Ecuación 4.11 y la
Ecuación 4.12 para restringir las conexiones incorrectas entre dos tuberías de inicio
contiguas o una tubería continua seguida por una de inicio, ya que esto interrumpiría el flujo
de agua a través de la red.
Restricción de flujo para las tuberías de inicio:
Teniendo en cuenta que las tuberías de inicio, no están conectadas a otras tuberías aguas
arriba, estas sólo pueden tener un flujo menor o igual al caudal de entrada en el pozo aguas
arriba de la misma, como se plantea en la Ecuación 4.13. En caso de que el flujo no sea igual
al caudal de entrada, el resto del caudal se transportará por otras tuberías salientes del
mismo pozo, sea continua o no.
Restricción de sentido de flujo y tipo de tubería en la descarga:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
42
La tubería que está directamente conectada al punto de descarga, que siempre se definirá
como el último nodo de la red ( 𝑣
𝐿
∈ 𝒩
𝐿
), deberá ir dirigida hacia dicho nodo y deberá ser
de tipo continuo 𝐶 ∈ 𝒯. Para esto se estableció la Ecuación 4.14.
Restricción de flujo de tubería en la descarga:
El flujo transportado por la tubería conectada directamente al punto de descarga debe ser
igual a la suma de todos los caudales de entrada (Oferta/demanda de cada Nodo 𝑣
𝑖
∈
𝒩
𝐿
|𝑣
𝑖
≠ 𝑣
𝐿
), como se muestra en la Ecuación 4.15.
Restricción de no negatividad:
Estas restricciones indican que las variables de decisión no pueden tomar valores negativos,
como se indica en la Ecuación 4.16 para 𝑦
𝑖𝑗𝑡
.
Naturaleza de la variable:
Teniendo en cuenta que una de las variables de decisión es binaria, esto se debe especificar
en las restricciones tal como plantea la Ecuación 4.1(a) para la variable 𝑥
𝑖𝑗𝑡
.
4.2 Metodología para el diseño hidráulico de redes de alcantarillado
Para encontrar el diseño hidráulico de una red de alcantarillado se propone extender la
metodología planteada en Duque N. et al. (2015). En este trabajo, se modela el problema del diseño
hidráulico de una serie de tuberías como un Problema de Ruta Más Corta (RMC). El problema de
RMC se resuelve sobre grafo que representa diámetros y pendientes de cada tramo de la serie. Para
extender esta metodología al caso de las redes, se parte del mismo modelaje del grafo haciendo
algunas modificaciones que permiten modelar las tuberías de inicio y la unión de las mismas hasta
la descarga.
4.2.1 Definición del grafo para el diseño hidráulico
Dado un trazado, el diseño hidráulico se realiza a partir de un grafo auxiliar 𝒢
𝐷
que va a
representar todas las posibles combinaciones de diseño hidráulico en la red. Este grafo, ya no
representará direcciones de flujo y tipos de tuberías como en el caso del problema de selección de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
43
trazado, sino los posibles diámetros y pendientes que pueden tener las tuberías de tal forma que se
pueda transportar el caudal de diseño requerido.
Este proceso comienza recibiendo un trazado con el sentido de flujo de cada tubería, el tipo de
tubería (Inicio, Continua) y el flujo que pasa por cada tubería (caudal de diseño). Con esta
información y los datos de entrada descritos en la Sección 3.4.1, se construye el grafo auxiliar 𝒢
𝐷
=
(𝒩
𝐷
, 𝒜
𝐷
), donde:
𝒩
𝐷
es el conjunto de nodos y representan una combinación entre una profundidad a la cual
se podría instalar la tubería a cota de batea y un diámetro comercial.
𝒜
𝐷
es el conjunto de arcos en donde cada arco representa una posible tubería con cierto
diámetro y cierta pendiente que depende los nodos en 𝒩
𝐷
que conecte.
De acuerdo con esto, a continuación se explicará cómo se representan en el grafo para el diseño
hidráulico 𝒢
𝐷
un pozo de inspección, una tubería, tuberías en serie y por último toda la red.
4.2.1.1 Representación de una tubería
La representación de cada tramo requiere que los pozos de inspección sean representados
como grupos de nodos (Duque, et al., 2015). Cada nodo representa una profundidad a la cual se
puede instalar la tubería a cota de batea y un diámetro comercial disponible. En general se tiene un
conjunto global de nodos para el diseño hidráulico 𝒩
𝐷
, que se agrupan en subconjuntos 𝒩
𝐷
𝑘
que
contienen los nodos que pertenecen a un pozo 𝑚
𝑘
∈ ℳ, como se observa en la Figura 4.5. Esto
permite conocer cuántos nodos hay por pozo.
La notación que se utiliza se muestra a continuación:
•
𝒩
𝐷
:
Conjunto de nodos de diseño hidráulico.
𝒩
𝐷
= { 𝑣
0
, 𝑣
1
, 𝑣
2
, 𝑣
3
, … , 𝑣
𝐷
}
•
𝒩
𝐷
𝑘
: Conjunto de nodos que pertenecen al pozo 𝑚
𝑘
∈ ℳ.
𝒩
𝐷
𝑘
= {𝑣
1
𝑘
, 𝑣
2
𝑘
, 𝑣
3
𝑘
, … , 𝑣
|𝒩
𝐷
𝑘
|
𝑘
}
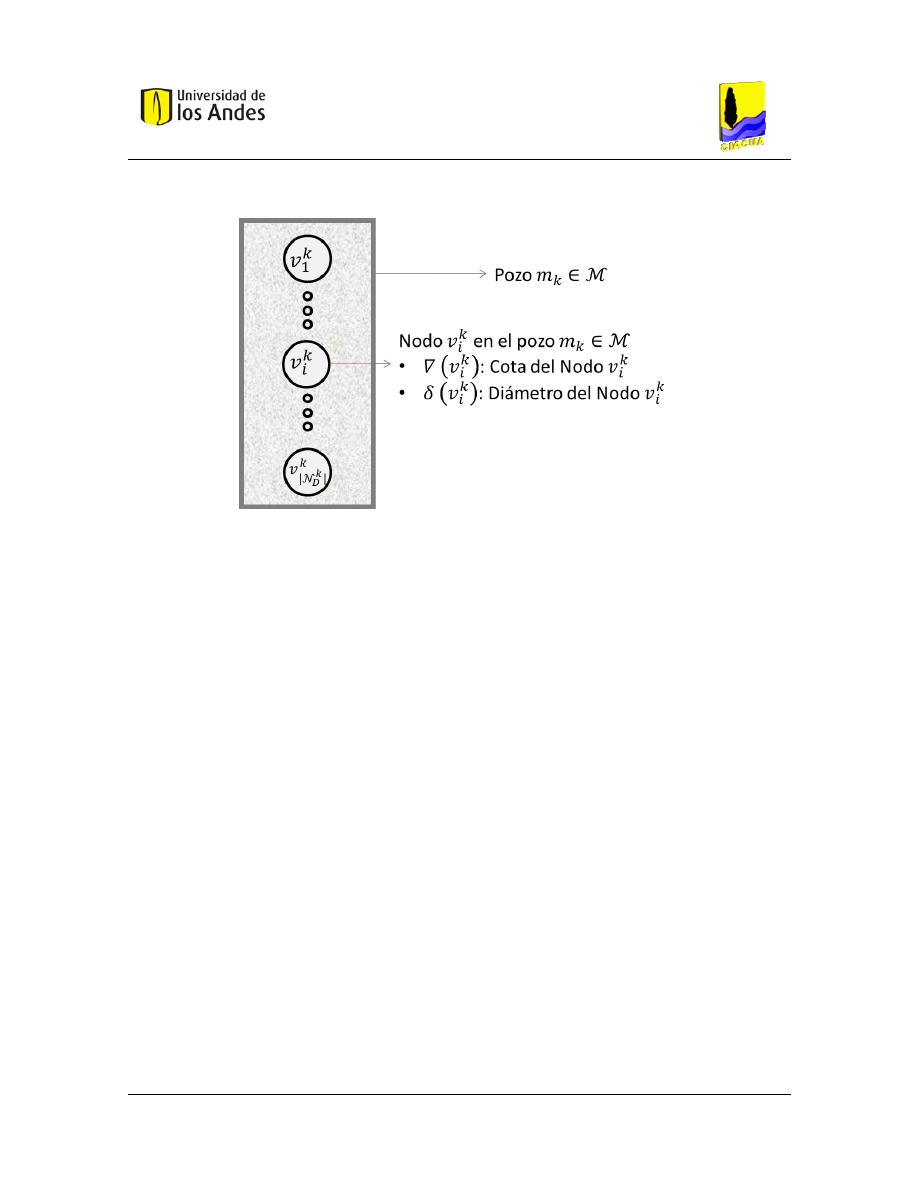
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
44
Figura 4.5 Conjunto de nodos que pertenecen a un mismo pozo de inspección.
Para efectos del modelaje del problema, cada nodo 𝑣
𝑖
𝑘
∈ 𝒩
𝑘
va a tener dos atributos. El
primero, es la cota en metros sobre un nivel de referencia ∇(𝑣
𝑖
𝑘
) y el segundo es el diámetro δ(𝑣
𝑖
𝑘
).
El primer atributo representa la cota batea de una tubería y el segundo representa el diámetro de
una tubería asociada con el tramo aguas arriba del pozo 𝑚
𝑘
∈ ℳ.
EL grafo también está conformado por arcos (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) que se definen entre dos nodos 𝑣
𝑖
𝑘
∈
𝒩
𝐷
𝑘
y 𝑣
𝑗
𝑘
′
∈ 𝒩
𝐷
𝑘
′
, donde 𝑣
𝑖
𝑘
es el i-ésimo nodo del pozo 𝑚
𝑘
∈ ℳ y 𝑣
𝑗
𝑘
′
es el j-ésimo nodo del pozo
estrictamente siguiente 𝑚
𝑘
′
∈ ℳ (ver Figura 4.6). Además, cada arco tiene un costo asociado que
representa el costo total de construcción, es decir la suma entre el costo de la tubería y los costos
de excavación, según la función de costos presentada en la Sección 2.3.4 (Ecuación 2.20). A
continuación se muestra la notación y una representación de un arco.
•
𝒜
𝐷
: Conjunto de arcos.
𝒜
𝐷
= { (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) |𝑣
𝑖
𝑘
∈ 𝒩
𝐷
𝑘
, 𝑣
𝑗
𝑘
′
∈ 𝒩
𝐷
𝑘
′
, (𝑘, 𝑘
′
) ∈ 𝒫}
•
𝑐(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
):
Costo del arco (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) ∈ 𝒜
𝐷
.
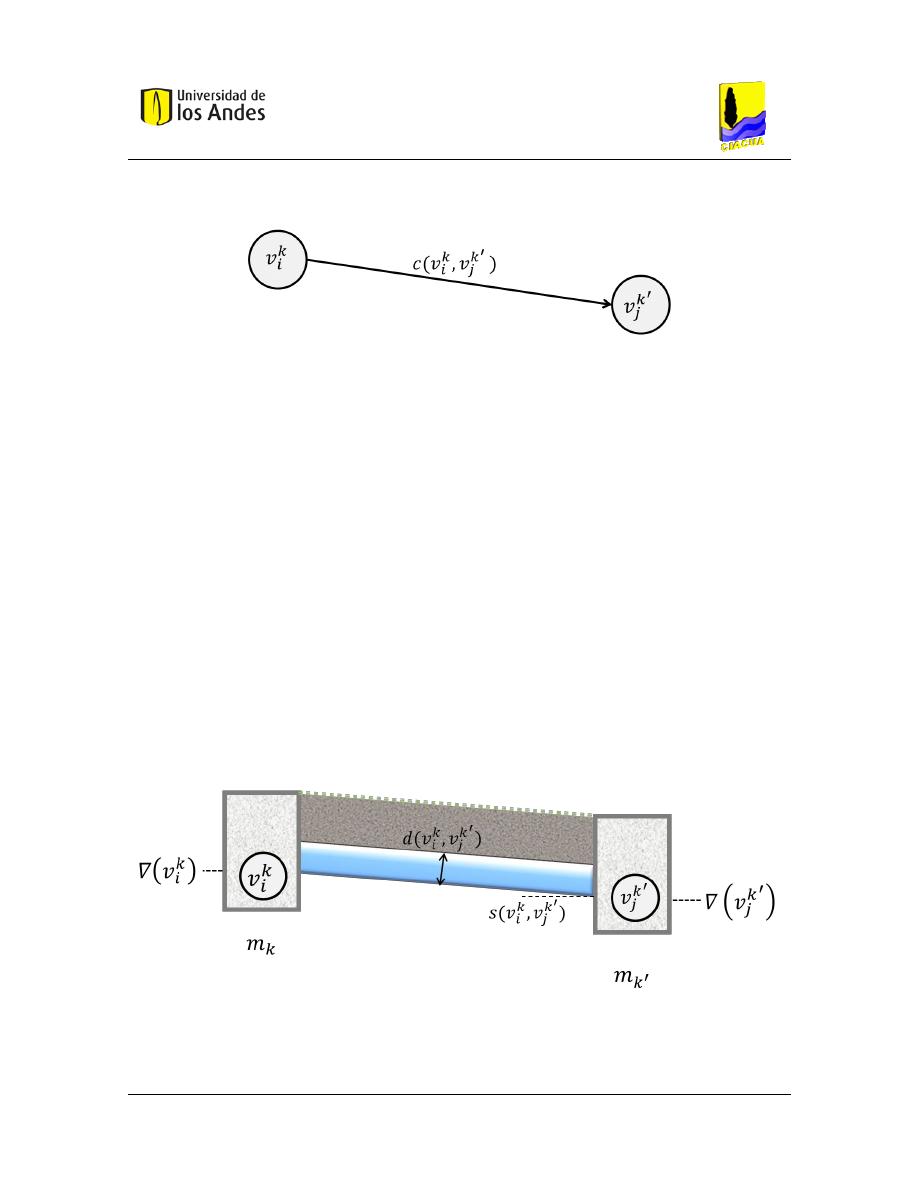
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
45
Figura 4.6 Representación de un arco (𝒗
𝒊
𝒌
, 𝒗
𝒋
𝒌
′
).
Teniendo en cuenta que quienes cargan la información de los diámetros de las tuberías son los
nodos, el diámetro de un arco (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) adopta el valor del nodo 𝑣
𝑗
𝑘
′
∈ 𝒩
𝐷
𝑘
′
. Así mismo, los nodos
cargan la información de la cota batea donde se instalaría cada tubería.
•
𝛻(𝑣
𝑖
𝑘
):
Cota de cada nodo 𝑖 en el pozo 𝑚
𝑘
∈ ℳ.
•
𝑑 (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
):
Diámetro del arco (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) ∈ 𝒜
𝐷
, representado como un atributo del
nodo 𝑣
𝑗
𝑘
′
∈ 𝒩
𝑘
′
.
𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) = 𝛿 (𝑣
𝑗
𝑘
′
)
Ecuación 4.17
Figura 4.7 Representación de un tramo de alcantarillado.
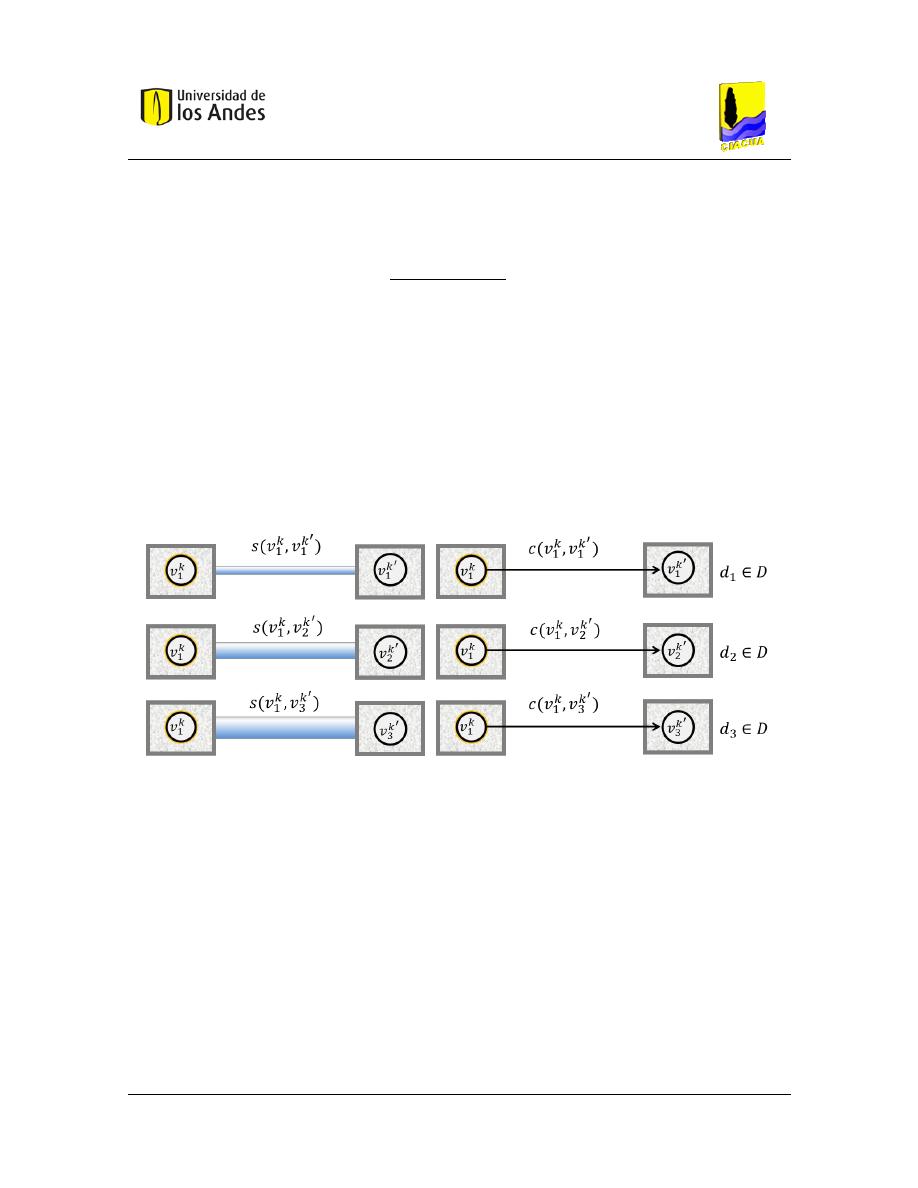
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
46
La pendiente de cada arco 𝑠(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
), es función de las cotas de los nodos que lo componen y
la longitud del tramo 𝑙. Esta se calcula como:
𝑠(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) =
𝛻(𝑣
𝑖
𝑘
) − 𝛻 (𝑣
𝑗
𝑘
′
)
𝑙
Ecuación 4.18
En la Figura 4.8 se presenta la representación de tres tuberías de diferentes diámetros en un
grafo. Los tres arcos salen del mismo nodo y tienen la misma pendiente, pero cada uno llega a un
nodo diferente, debido a que cada uno representa un diámetro distinto. Como se puede observar,
cada arco (flecha) representa una tubería de cierto diámetro que está ubicada con una pendiente 𝑠
específica. El arco entonces tiene un diámetro asociado 𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) y una pendiente asociada
𝑠(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
). Con base en esto, se calcula el costo asociado 𝑐(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) de cada arco como se observa.
Figura 4.8 Representación de una tubería en el grafo auxiliar para el diseño hidráulico.
Siguiendo con el ejemplo, la Figura 4.9 presenta el grafo 𝒢
𝐷
de un tramo con dos nuevos nodos
de diseño en el pozo 𝑚
𝑘
∈ ℳ, 𝑣
2
𝑘
y 𝑣
3
𝑘
, tal que 𝛻(𝑣
1
𝑘
) = 𝛻(𝑣
2
𝑘
) = 𝛻(𝑣
3
𝑘
) y 𝛿(𝑣
1
𝑘
) < 𝛿(𝑣
2
𝑘
) <
𝛿(𝑣
3
𝑘
). Así mismo, considera tres nodos de diseño más en el pozo 𝑚
𝑘
′
∈ ℳ, tal que 𝛻(𝑣
4
𝑘
′
) =
𝛻(𝑣
5
𝑘
′
) = 𝛻(𝑣
6
𝑘
′
); sin embargo, 𝛻(𝑣
1
𝑘
′
) = 𝛻(𝑣
2
𝑘
′
) = 𝛻(𝑣
3
𝑘
′
) > 𝛻(𝑣
4
𝑘
′
) = 𝛻(𝑣
5
𝑘
′
) = 𝛻(𝑣
6
𝑘
′
), i.e.,
los nodos de diseño 𝑣
4
𝑘
′
, 𝑣
5
𝑘
′
, y 𝑣
6
𝑘
′
representan los tres diámetros iniciales, pero están ubicados a
una profundidad mayor que los primero tres nodos. La diferencia entre ambas profundidades está
dada por el cambio entre cotas ∇
̃.
Además, de cada nodo salen arcos hacia los nodos del pozo
siguiente que tengan diámetros y profundidades mayores o iguales. De esta forma se cumple la
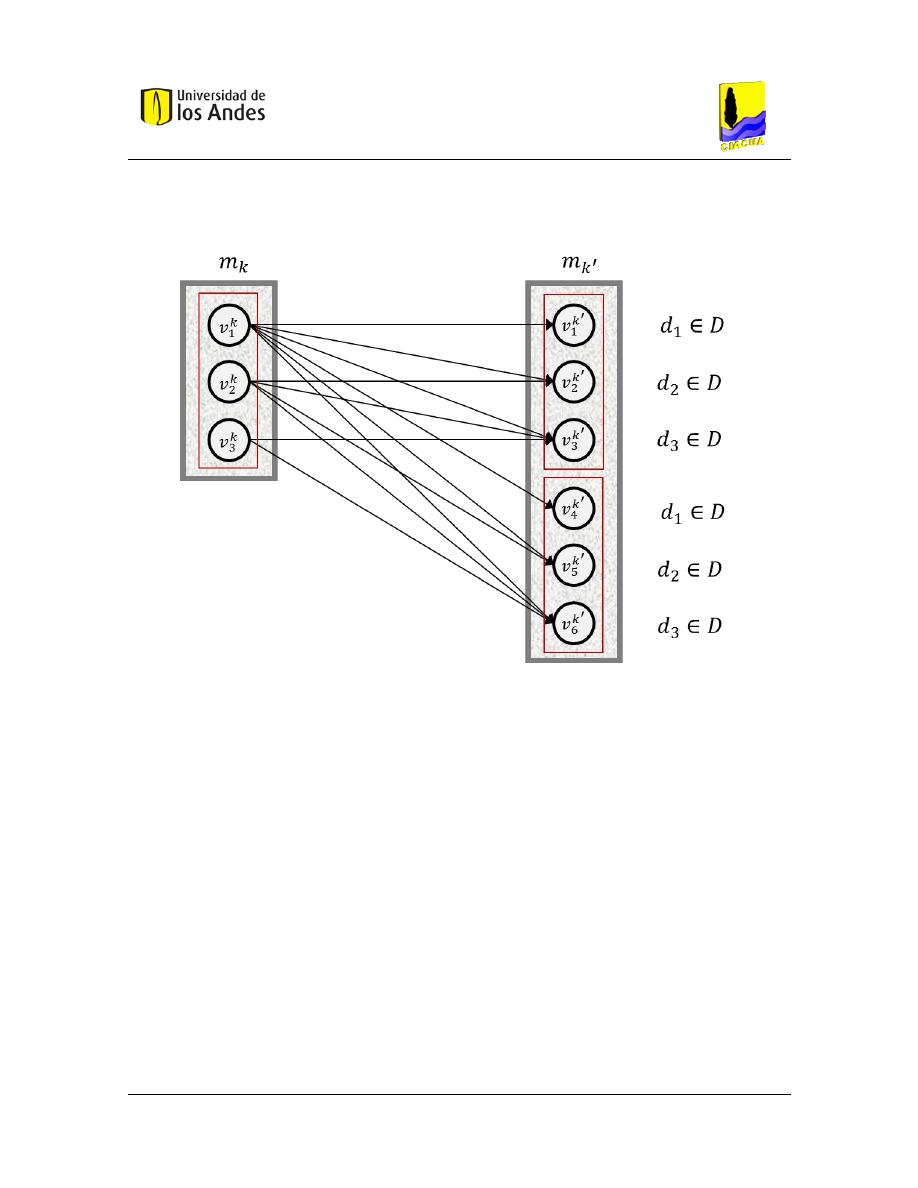
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
47
restricción hidráulica de diámetros y se evitan pendientes adversas. Según esto, para nodos con
diámetros mayores y a mayores profundidades existen menos alternativas de diseño.
Figura 4.9 Grafo auxiliar para el diseño hidráulico de un tramo.
4.2.1.2 Representación de tuberías en serie
Una vez creados los conjuntos de nodos para cada pozo 𝒩
𝐷
𝑘
, y los arcos (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) ∈ 𝒜
𝐷
de cada
tramo, se deben conectar dichos arcos para formar caminos. La conexión de los arcos entre
diferentes tramos debe seguir el trazado de la red, de forma que se formen las series de tuberías
que describen la red. Es decir que los arcos de un tramo se deben conectar directamente con los
arcos de los tramos adyacentes, de acuerdo con el trazado. A modo de ejemplo, la Figura 4.10
presenta la vista en planta de una red de alcantarillado, donde se observa una serie de tuberías
(azules) desde un nodo inicial hasta la descarga. Como se observa, la conexión entre arcos debe
seguir esta serie de tuberías, conectando los diferentes tramos que la conforman.
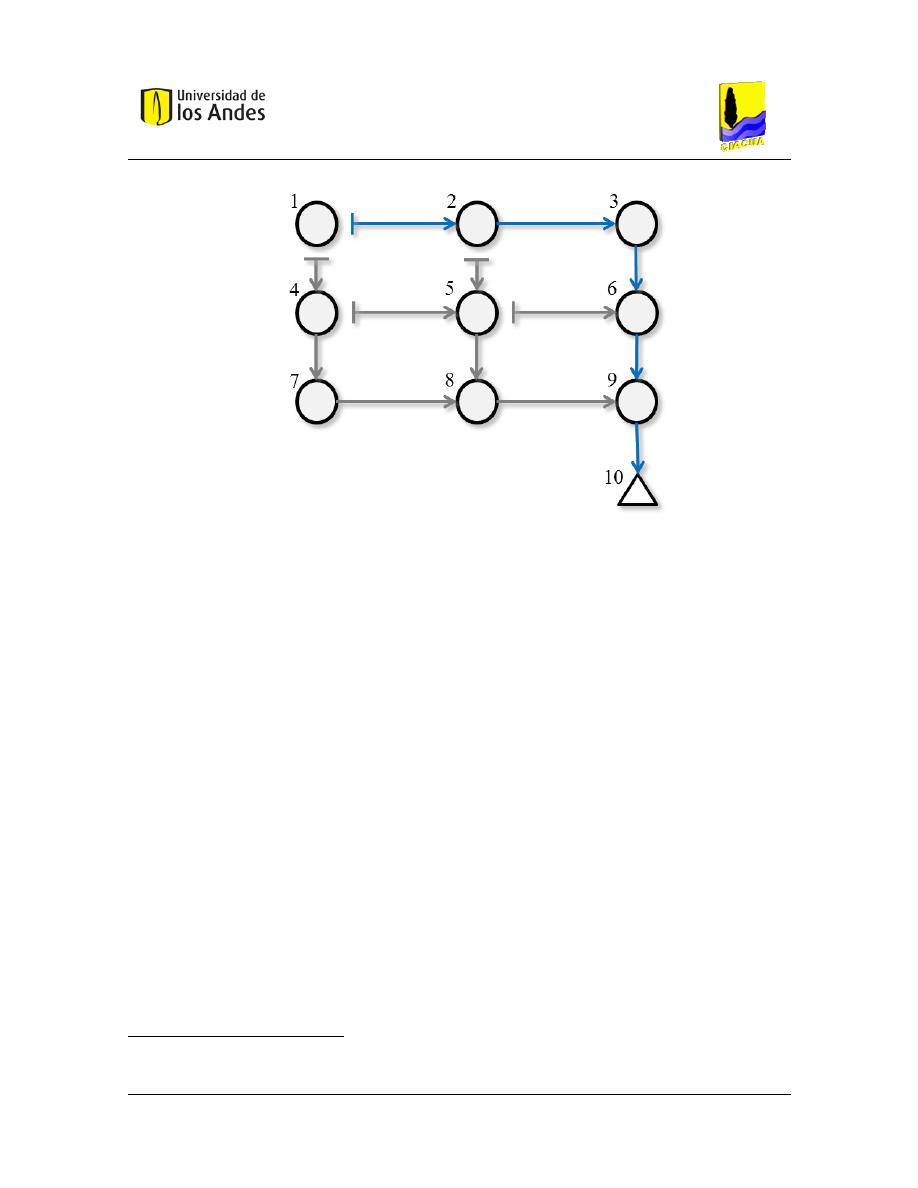
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
48
Figura 4.10. Series de tuberías de una red de alcantarillado.
Ahora bien, el grafo 𝒢
𝐷
para la representación de tuberías en serie desde una vista de perfil se
presenta en la Figura 4.11, donde se tiene una serie de 2 tramos, desde el Pozo 𝑚
1
∈ ℳ hasta el
Pozo 𝑚
3
∈ ℳ de acuerdo con la Figura 4.10. Se utilizaron 3 diámetros comerciales disponibles y 3
posibles cotas a las cuales se pueden ubicar las tuberías. Al ampliar el problema se observa mejor la
complejidad del mismo, dado el aumento de alternativas de diseño
9
que se presenta. Así como en
el caso de un solo tramo, se puede observar que de cada nodo salen arcos hacia los nodos del pozo
siguiente que tengan diámetros y profundidades mayores o iguales, evitando obstrucciones en el
sistema y pendientes adversas, respectivamente.
9
Alternativa de diseño: se refiere una combinación de tuberías factibles (una de cada tramo), que conforman
una serie.
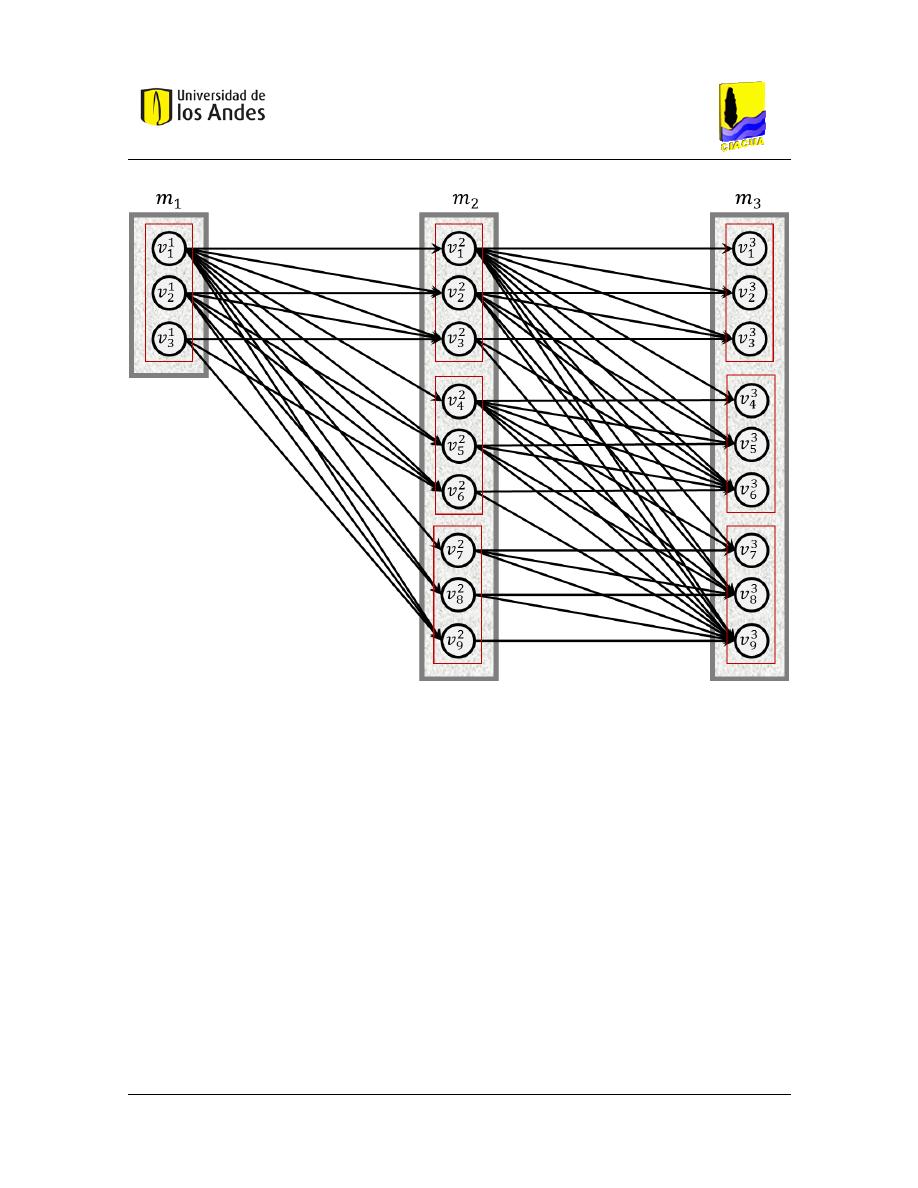
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
49
Figura 4.11 Grafo auxiliar para el diseño hidráulico de una serie de 2 tramos.
Para encontrar cuál de todas las alternativas de diseño es la óptima se debe conocer el costo
total de cada una de ellas y buscar la más económica. El costo total de una alternativa es entonces
la suma del costo de cada una de las tuberías que componen la serie. La solución se encuentra
resolviendo un problema de RMC sobre este grafo, en donde el camino resultante representa las
diferentes tuberías que serán utilizadas a lo largo de la serie. El nodo inicial del problema de RMC
se supone como un nodo ficticio que se conecta a los nodos de la primera cámara de la serie a un
costo de cero.
La Figura 4.12 muestra un ejemplo de la solución sobre el grafo. El camino involucra los nodos
{𝑣
1
2
, 𝑣
2
2
, 𝑣
5
3
} lo cual representa que una serie de tuberías en donde los dos tramos tienen tuberías
del mismo diámetro (el segundo diámetro comercial), pero la pendiente de cada tramo varía según
las cotas de cada nodo siguiendo la Ecuación 4.18.
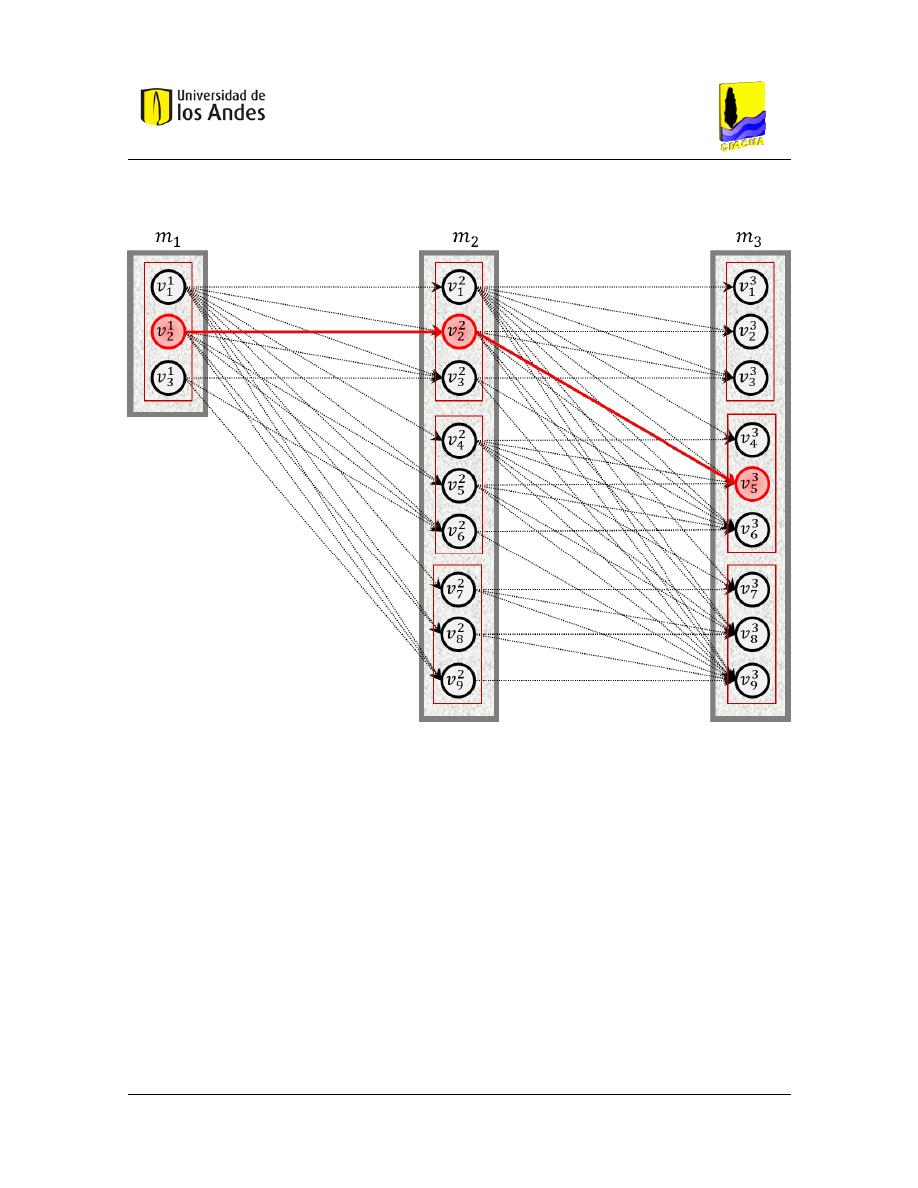
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
50
Figura 4.12 Solución del grafo auxiliar 𝓖
𝑫
para el diseño hidráulico de una serie de 2 tramos.
4.2.1.3 Representación de la red de alcantarillado
El modelaje del grafo auxiliar para el diseño hidráulico de una red de alcantarillado es una
extensión del modelaje propuesto para representar el diseño hidráulico en series de tuberías
(Duque, et al., 2015), teniendo en cuenta que en el caso de las redes se puede tener más de un
tramo adyacente. Esto es relevante debido a que, en caso de tener inicios (tramos iniciales), se
deben crear pozos imaginarios con las mismas características del original, de forma que construya
la red de alcantarillado como una red abierta, i.e., con una estructura de árbol. Esto además asegura
que todos los inicios se conecten a la descarga por un único camino (serie de tuberías).
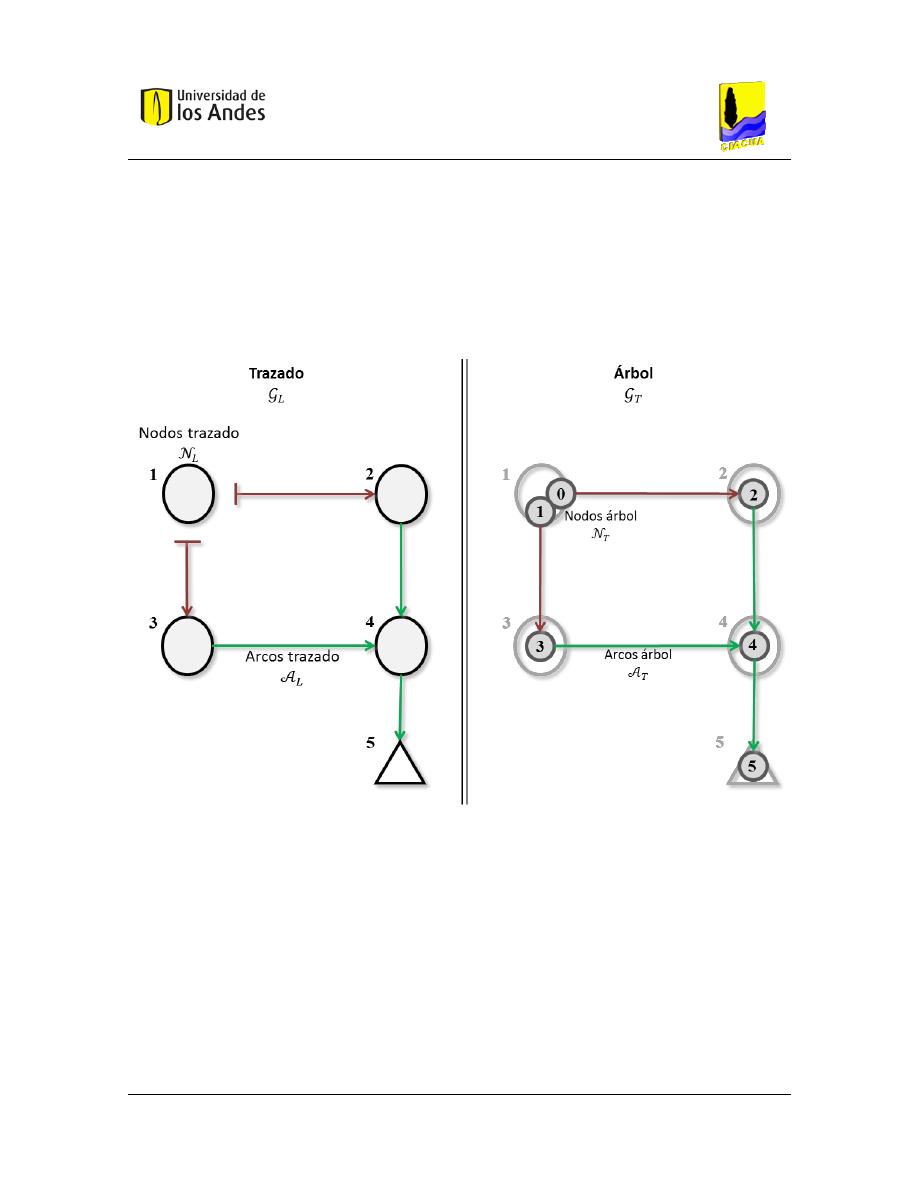
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
51
Para representar la red de alcantarillado como un red abierta, primero se hace una abstracción
del grafo que representa el trazado (𝒢
𝐿
) a un grafo que represente un árbol o red abierta (𝒢
𝑇
). La
Figura 4.13 muestra el grafo 𝒢
𝑇
que modela la red abierta para un trazado particular 𝒢
𝐿
de una red
con 5 pozos y 5 tramos. Ambos grafos representan el trazado de la red; sin embargo, el Grafo 𝒢
𝐿
describe los sentidos de flujo y los tipos de tuberías (sección 3.3), mientras que en el Grafo 𝒢
𝑇
tiene
nodos adicionales para lograr la estructura de árbol. Puntualmente, el grafo 𝒢
𝑇
tiene un nodo por
cada tubería de inicio, y tanto arcos como tramos originales.
Figura 4.13. Representación del trazado de la red como un árbol.
En este ejemplo, del nodo del trazado 𝑣
1
∈ 𝒩
𝐿
salen dos tuberías de inicio que se representan
en el grafo 𝒢
𝑇
con los nodos de árbol 𝑣
0
∈ 𝒩
𝑇
y 𝑣
1
∈ 𝒩
𝑇
. Estos nodos en 𝒩
𝑇
conservan las
características topográficas y topológicas del nodo del trazado 𝑣
1
∈ 𝒩
𝐿
. De esta forma se tienen dos
series de tuberías desde cada nodo de inicio (Nodos del árbol 𝑣
0
y 𝑣
1
) hasta la descarga (𝑣
5
∈ 𝒩
𝐿
≡
𝑣
5
∈ 𝒩
𝑇
). De esta manera, la red de alcantarillado se representa a partir de múltiples series de
tuberías que se modelan en a partir de los nodos de árbol 𝒩
𝑇
.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
52
La notación para el grafo que modela el trazado de la red como una red abierta (árbol) es la
siguiente:
•
𝒢
𝑇
= (𝒜
𝑇
, 𝒩
𝑇
) es el grafo que representa el trazado de la red como una red abierta.
•
𝒩
𝑇
= { 𝑣
1
, 𝑣
2
, 𝑣
3
, 𝑣
4
, 𝑣
5
… … , 𝑣
𝑇
} es el conjunto de nodos del árbol.
•
𝒩
𝑇
𝑖
= 𝒩
𝑇𝐼
𝑖
∪ 𝒩
𝑇𝐶
𝑖
= {𝑣
1
𝑖
, 𝑣
2
𝑖
, 𝑣
3
𝑖
, … , 𝑣
𝑇
𝑖
}: es el subconjunto de nodos del árbol asociados con
el nodo del trazado 𝑣
𝑖
∈ 𝒩
𝐿
; 𝒩
𝑇𝐼
𝑖
es el subconjunto de nodos del árbol que modelan inicios
en el nodo de trazado 𝑣
𝑖
∈ 𝒩
𝐿
; y 𝒩
𝑇𝐶
𝑖
es el subconjunto de nodos de árbol que modelan
uniones de series de tuberías (comienzo de una tubería continua) en el nodo de trazado
𝑣
𝑖
∈ 𝒩
𝐿
.
•
𝒜
𝑇
es el conjunto de arcos del árbol que se definen de acuerdo con la siguiente
función.
𝒜
𝑇
= {
{(𝑘, 𝑘
′
)| 𝑣
𝑘
∈
𝒩
𝑇𝐼
𝑖
, 𝑣
𝑘
′
∈
𝒩
𝑇𝐶
𝑗
,
(
𝑖, 𝑗, 𝑡
)
∈
𝒜
𝐿
}
𝑠𝑖 𝑡
𝑘,𝑘
′
= 𝐼
{(𝑘, 𝑘
′
)| 𝑣
𝑘
∈
𝒩
𝑇𝐶
𝑖
, 𝑣
𝑘
′
∈
𝒩
𝑇𝐶
𝑗
,
(
𝑖, 𝑗, 𝑡
)
∈
𝒜
𝐿
} 𝑠𝑖 𝑡
𝑘,𝑘
′
= 𝐶
De acuerdo con lo anterior y teniendo en cuenta que se dijo que los nodos de diseño 𝒩
𝐷
están
agrupados en subconjuntos 𝒩
𝐷
𝑘
para cada pozo 𝑚
𝑘
∈ ℳ, se puede decir ahora que esos mismos
conjuntos 𝒩
𝐷
𝑘
representan los nodos de diseño para cada nodo del árbol 𝑣
𝑘
∈ 𝒩
𝑇
. Entonces, para
el diseño hidráulico se tiene:
•
𝒢
𝐷
= (𝒜
𝐷
, 𝒩
𝐷
) es el grafo que representa el diseño hidráulico de la red.
•
𝒩
𝐷
= { 𝑣
1
, 𝑣
2
, 𝑣
3
, 𝑣
4
, 𝑣
5
… … , 𝑣
𝐷
} es el conjunto de nodos del grafo del diseño hidráulico.
•
𝒩
𝐷
𝑘
= {𝑣
1
𝑘
, 𝑣
2
𝑘
, 𝑣
3
𝑘
, … , 𝑣
𝐷
𝑘
} es el subconjunto de nodos del diseño hidráulico asociados con
el nodo del árbol 𝑣
𝑘
∈ 𝒩
𝑇
.
•
𝒜
𝐷
=
{(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
)
|
𝑣
𝑖
𝑘
∈
𝒩
𝐷
𝑘
,
𝑣
𝑗
𝑘
′
∈
𝒩
𝐷
𝑘
′
,
(𝑘, 𝑘
′
) ∈ 𝒜
𝑇
} es el conjunto de arcos de diseño
hidráulico.
Al igual que se explicó para la representación de series de tuberías, los nodos de diseño que
representan los diferentes diámetros se agrupan dentro de los recuadros rojos que representan una
misma cota. Esto se observa en la Figura 4.14, donde se presenta un ejemplo con 4 diámetros
disponibles y 3 profundidades (cotas) a las cuales se pueden ubicar las tuberías. Como se observa,
los diámetros están dispuestos de forma ascendente y se tienen tantas cotas como se pueda dentro
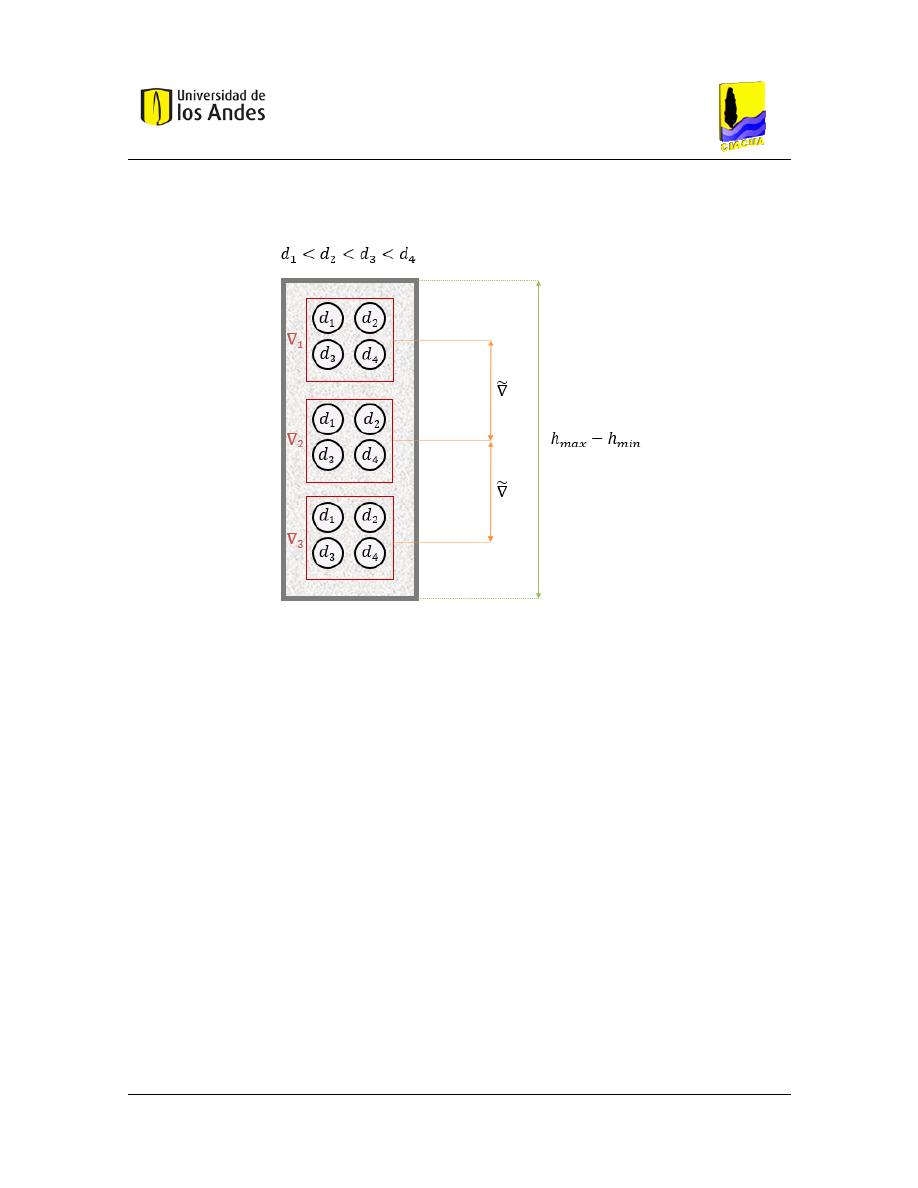
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
53
de los límites de excavación ℎ
𝑚𝑖𝑛
y ℎ
𝑚𝑎𝑥
establecidos (ver Tabla 2.3), teniendo en cuenta la
variación entre cotas ∇
̃ establecida según la precisión que se quiera en el diseño.
Figura 4.14. Configuración de diámetros en el grafo para el diseño 𝓖
𝑫
.
Según esto, la Figura 4.15 presenta el grafo para el diseño 𝒢
𝐷
hidráulico de una red de
alcantarillado, siguiendo el trazado de la Figura 4.13. En la figura se simplifica el grafo 𝒢
𝐷
representando los arcos entre diferentes cotas, que tienen diámetros diferentes, como un solo arco;
sin embargo, la modelación real de este grafo 𝒢
𝐷
sigue los mismos lineamientos que se plantearon
para la representación de tuberías en serie. Es decir que también se cumple que, si el nodo de diseño
𝑣
𝑖
𝑘
∈ 𝒩
𝐷
𝑘
está aguas arriba del nodo de diseño 𝑣
𝑗
𝑘
′
∈ 𝒩
𝐷
𝑘
′
,
el diámetro aguas arriba debe ser
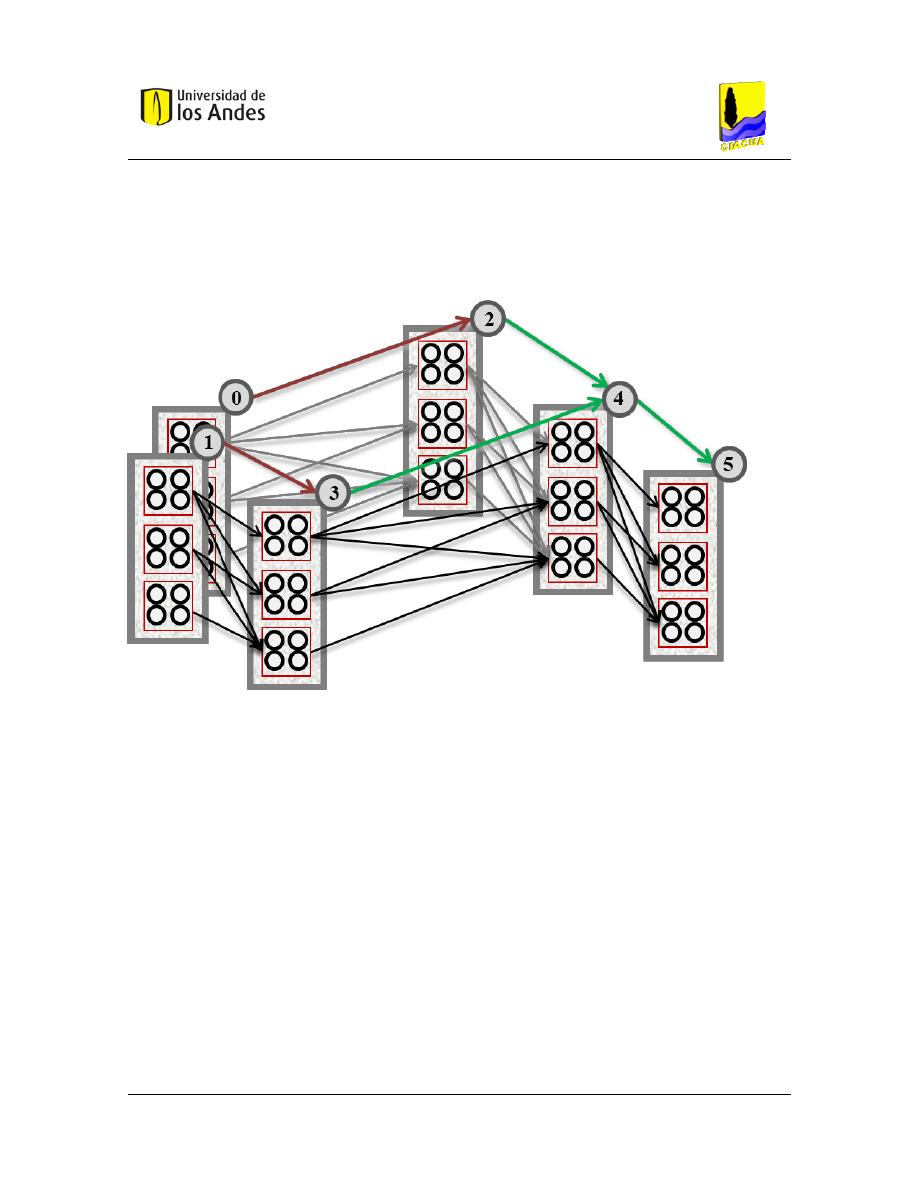
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
54
menor o igual al diámetro aguas abajo
𝛿(𝑣
𝑖
𝑘
) ≤ 𝛿(𝑣
𝑗
k
′
)
y las pendientes deben ser positivas (a
favor de la gravedad) 𝑠 (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) > 0 ≡
𝛻
(
𝑣
𝑖
𝑘
)
> 𝛻
(
𝑣
𝑗
𝑘
′
).
Figura 4.15. Grafo auxiliar 𝓖
𝑫
para el diseño hidráulico de una red de alcantarillado.
La Figura 4.16 presenta entonces la representación de todo el problema de diseño de redes de
alcantarillado, realizando la conexión entre los tres grafos involucrados para la representación de la
solución al problema de selección del trazado de la red, su traducción a una estructura tipo árbol y
la posterior representación del grafo con todas las alternativas de diseño hidráulico para dicho
trazado. Notese que representar la red como un árbol permite que dos tuberías salgan de un mismo
pozo desde cotas diferentes. Esto es válido cuando son tuberías de inicio, ya que permite evaluar
más alternativas que si se considera empezar las dos tuberías desde la misma cota.
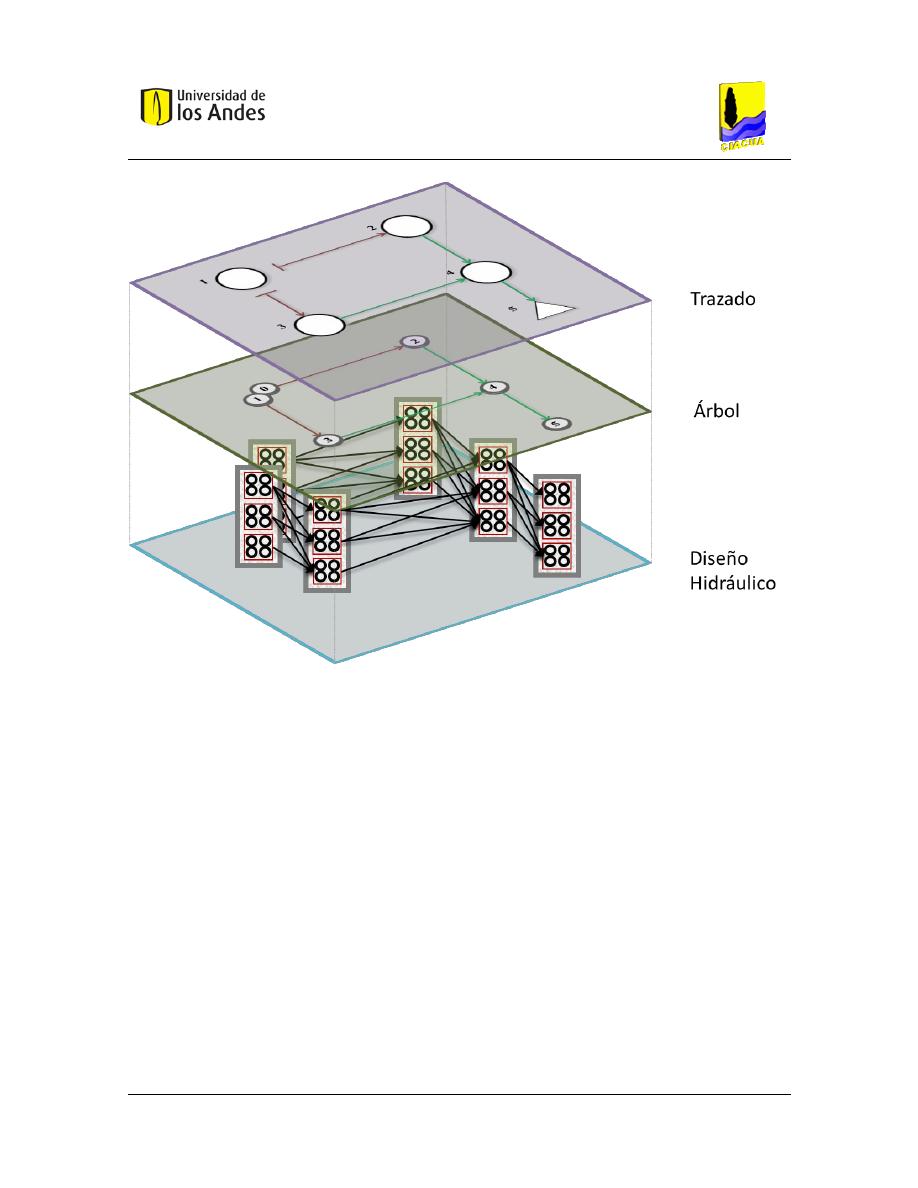
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
55
Figura 4.16. Conexión entre los diferentes grafos.
Sobre este grafo de diseño hidráulico 𝒢
𝐷
se corre un método de optimización para conocer la
solución óptima del mismo. Esta solución será el diseño hidráulico óptimo de la red, para el trazado
dado. El método de optimización que se utilizó se presenta a continuación en la Sección 4.2.2.
4.2.2 Método de optimización
Teniendo en cuenta la representación del problema de diseño hidráulico en un grafo, se plantea
resolver este problema como un Problema de Ruta Más Corta (RMC) en donde se quiere la ruta más
corta desde todos los inicios hasta el punto de descarga. De acuerdo con lo anterior, se utiliza el
Algoritmo de Bellman-Ford que encuentra la ruta más corta desde un punto de partida a todos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
56
nodos del grafo, y es particularmente eficiente sobre grafos acíclicos; teniendo en cuenta la
estructura particular del grafo presentado en la Sección 4.2.1.3, i.e., un grafo dirigido y acíclico.
4.2.2.1 Problema de la ruta más corta (RMC)
El problema de la ruta más corta pertenece a la rama de la optimización que estudia los
problemas de flujo en redes. En un grafo dado, este problema busca encontrar el camino de mínimo
costo (distancia o tiempo de recorrido) desde un nodo específico inicial hasta un nodo final. Las
principales aplicaciones de estos modelos de optimización se encuentran en problemas de
transporte, donde se busca minimizar tiempos de recorrido de un punto a otro (Ahuja & et Al,
Network Flows: Theory, Algorithms, and Applications, 1993).
Matemáticamente, un problema de ruta más corta se define como:
min ∑ 𝑐
𝑖𝑗
𝑥
𝑖𝑗
(𝑣
𝑖
,𝑣
𝑗
)∈𝒜
Ecuación 4.19
∑
𝑥
𝑖𝑗
{
𝑗
|
(𝑣
𝑖,
𝑣
𝑗
) ∈ 𝒜
}
−
∑
𝑥
𝑗𝑖
{
𝑗
|
(𝑣
𝑗
, 𝑣
𝑖
) ∈ 𝒜
}
= {
1
𝑣
𝑖
= 𝑣
𝑠
0
𝑣
𝑖
≠ 𝑣
𝑠
, 𝑣
𝑡
−1
𝑣
𝑖
= 𝑣
𝑡
∀ 𝑣
𝑖
∈ 𝒩
Ecuación 4.20
𝑥
𝑖𝑗
∈ {0,1} ∀ 𝑣
𝑖
∈ 𝒩, 𝑣
𝑗
∈ 𝒩
Ecuación 4.21
donde, 𝑥
𝑖𝑗
, es una variable binaria que toma el valor de uno si el arco (𝑖, 𝑗) ∈ 𝒜 está en la solución
del problema (el camino) o toma el valor de cero de lo contrario. 𝑐
𝑖𝑗
es el costo de utilizar el arco
(𝑖, 𝑗) ∈ 𝒜 en el camino, 𝑣
𝑠
es el nodo inicial del cual parte el camino y 𝑣
𝑡
es el nodo final del camino.
La Ecuación 4.2 determina la función objetivo del problema, que busca la minimización de los costos
del camino. La Ecuación 4.3 determina las restricciones que garantizan que un camino parta del
nodo 𝑣
𝑠
y llegue al nodo 𝑣
𝑡
y finalmente la Ecuación 4.4 establece la naturaleza binaria de las
variables.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
57
4.2.2.2 Algoritmo de Bellman-Ford
El Algoritmo de Bellman-Ford nace por la necesidad de conocer el camino que representa el
mínimo tiempo de viaje entre dos ciudades que hacen parte de un conjunto de 𝒩 ciudades, donde
cada par de ciudades están interconectadas entre sí por una vía que tiene un tiempo de viaje
asociado. Estos tiempos no son directamente proporcionales a las distancias, debido a la cantidad
de rutas que existen para viajar de una ciudad a otra y la variación del tráfico en cada una de ellas
(Bellman, 1956).
Definición y notación
Los parámetros de entrada para este problema de ruta más corta son (𝐺, 𝑣
𝑠
, 𝑐): donde 𝐺 =
(𝒩, 𝒜) es un grafo dirigido, 𝑐 es la función de costo o distancia asociada a cada arco (𝑣
𝑖
, 𝑣
𝑗
) ∈ 𝒜
(e.g., distancia, costo) y el nodo inicial 𝑣
𝑠
que pertenece al conjunto de nodos 𝒩 del grafo. El
objetivo es encontrar la ruta más corta desde el nodo 𝑣
𝑠
∈ 𝒩 a todos los otros nodos del grafo 𝐺.
Este método de corrección de etiquetas comienza estableciendo un costo acumulado 𝑉(𝑣
𝑠
) =
0 para el nodo inicial 𝑣
𝑠
∈ 𝒩 y 𝑉(𝑣
𝑘
) = ∞ para el resto de nodos del grafo. Posteriormente, cada
nodo 𝑣
𝑖
∈ 𝒩 se evalúa en orden topológico, evaluando cada arco (𝑖, 𝑗) ∈ 𝒜. Si 𝑉(𝑣
𝑗
) > 𝑉(𝑣
𝑖
) +
𝑐
𝑖𝑗
; entonces la etiqueta para el nodo 𝑣
𝑗
∈ 𝒩 se actualiza con el nuevo costo mínimo acumulado
𝑉(𝑣
𝑗
) = 𝑉(𝑣
𝑖
) + 𝑐
𝑖𝑗
así como su nodo predecesor 𝑝(𝑣
𝑗
) = 𝑣
𝑖
. Cuando todos los nodos han sido
evaluados, el costo de las etiquetas es óptimo (Ahuja M.H, et al., 1993). El algoritmo de Bellman-
Ford se describe entonces, como se muestra en el algoritmo presentado en el Algoritmo 4.1.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
58
Algoritmo 4.1. Algoritmo de Bellman-Ford. Tomado y modificado de Goldberg & Radzik (1993).
Como se observa, el método empieza asignarle a cada nodo un costo acumulado, de forma que si el
costo acumulado 𝑉(𝑣
𝑖
) del nodo 𝑣
𝑖
∈ 𝒩 más el costo del arco (𝑣
𝑖
, 𝑣
𝑗
) ∈ 𝒜 es menor que el costo
acumulado 𝑉(𝑣
𝑗
) del nodo 𝑣
𝑗
∈ 𝒩, entonces se actualiza el costo acumulado 𝑉(𝑣
𝑗
). De lo contrario
se mantiene el costo acumulado 𝑉(𝑣
𝑗
), obtenido por otro camino y se relaja (elimina) el nodo 𝑣
𝑖
∈
𝒩 que no hace parte de la ruta más corta (Introduction to Algorithms: Bellman-Ford Algorithm,
2011). Para encontrar una ruta más corta en particular, entre un nodo inicial y uno final, se comienza
en el nodo final y se van evaluando sus nodos predecesores. El camino conformado por estos nodos
forma entonces la ruta más corta.
4.2.3 Modelaje matemático para el diseño hidráulico
4.2.3.1 Variables de decisión
La variable de decisión es una variable binaria que toma el valor de uno (1) si el arco (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) ∈
𝒜
𝐷
pertenece al camino que forma la ruta más corta o toma el valor de cero (0) de lo contrario,
como se plantea en la Ecuación 4.21 (b).
𝑥
𝑖𝑗
∈ {0,1} ∀ 𝑣
𝑖
𝑘
∈ 𝒩
𝐷
𝑘
, 𝑣
𝑗
𝑘
′
∈ 𝒩
𝐷
𝑘
′
Ecuación 4.21 (b)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
59
La escogencia de un arco (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) ∈ 𝒜
𝐷
implica escoger un diámetro 𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) y una
pendiente de diseño 𝑠(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
).
4.2.3.2 Función objetivo 𝒇. 𝒐.
La función objetivo para el problema de diseño hidráulico se presenta en la Ecuación 4.2; sin
embargo, al ser planteada para cada arco (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) ∈ 𝒜
𝐷
, queda como la que se muestra en la
Ecuación 4.22 (Duque, et al., 2015). La Ecuación 4.23 presenta el costo 𝑐(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) para cada arco
(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) ∈ 𝒜
𝐷
según la función de costos planteada en la Ecuación 2.20 (Navarro, 2009), en
función del diámetro del arco 𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) y las cotas de los nodos que lo componen 𝛻(𝑣
𝑖
𝑘
) y 𝛻 (𝑣
𝑗
𝑘
′
).
El objetivo es minimizar la función de costos para encontrar el diseño que, cumpliendo con todas
las restricciones, sea el más económico. De acuerdo con esto, la función objetivo sería:
min
∑
𝑐(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
)𝑥
𝑖𝑗
(𝑣
𝑖
𝑘
,𝑣
𝑗
𝑘′
)∈𝒜
𝐷
Ecuación 4.22
𝑐(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) = 𝑎 ∗ (9579.31 ∗ 𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
)
0.5737
∗ 𝑙 + 1163.77 ∗ 𝑉(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
)
1.31
)
Ecuación 4.23
Recordando la Ecuación 2.19, el volumen se calcula en términos del diámetro de la tubería y la
profundidad a la que se instale. Dicha profundidad se calcula de acuerdo con las cotas de batea del
nodo 𝑣
𝑖
𝑘
∈ 𝒩
𝐷
𝑘
y el nodo 𝑣
𝑗
𝑘
′
∈ 𝒩
𝐷
𝑘
′
de cada arco, como se explica a continuación:
𝑉(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) = ([
𝐻 + 𝐻′
2
] + 𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) + 2𝑒 + ℎ) ∗ (2𝐵 + 2𝑒 + 𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
))
∗ (𝑙 cos [tan
−1
𝑠(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
)])
Ecuación 4.24
donde:
𝑉(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
):
Volumen excavado para poner la tubería.
𝐻:
Profundidad de excavación hasta la cota clave aguas arriba de la tubería.
𝐻
′
:
Profundidad de excavación hasta la cota clave aguas abajo de la tubería.
𝑑 (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
): Diámetro del arco (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) ∈ 𝒜
𝐷
.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
60
𝑒:
Espesor de la pared de la tubería.
ℎ:
Relleno que debe disponerse bajo la tubería. Depende de la reglamentación
del lugar donde se lleve a cabo el diseño. Para los ejemplos se siguieron las
recomendaciones del RAS: ℎ = 15 𝑐𝑚.
𝐵:
Espacio lateral que debe dejarse a ambos lados de la tubería para
colocarla.
𝑠 (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
):
Pendiente asociada con el arco (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) ∈ 𝒜
𝐷
(Ecuación 4.18).
𝑙:
Longitud de la tubería.
La profundidad de excavación, se refiere a la diferencia entre la cota del terreno y la cota clave
de la tubería. La Ecuación 4.25 y la Ecuación 4.26 describen la profundidad de excavación aguas
arriba y aguas abajo de la tubería, respectivamente.
𝐻 = ∇
𝑘
− 𝛻(𝑣
𝑖
𝑘
) + 𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
)
Ecuación 4.25
donde:
𝐻:
Profundidad de excavación hasta la cota clave aguas arriba de la tubería.
∇
𝑘
:
Cota del terreno del pozo 𝑚
𝑘
∈ ℳ.
𝛻(𝑣
𝑖
𝑘
):
Cota del nodo de salida 𝑣
𝑖
𝑘
∈ 𝒩
𝐷
𝑘
.
𝑑 (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
): Diámetro interno de la tubería.
𝐻′ = ∇
𝑘
′
− 𝛻 (𝑣
𝑗
𝑘
′
) + 𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
)
Ecuación 4.26
donde:
𝐻
′
:
Profundidad de excavación hasta la cota clave aguas abajo de la tubería.
∇
𝑘
′
:
Cota del terreno del pozo 𝑚
𝑘
′
∈ ℳ.
𝛻 (𝑣
𝑗
𝑘
′
):
Cota del nodo de llegada 𝑣
𝑗
𝑘
′
∈ 𝒩
𝐷
𝑘
′
.
𝑑 (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
):
Diámetro interno de la tubería.
4.2.4 Implementación
Con la representación de la red de alcantarillado a partir de los grafos 𝒢
𝐿
, 𝒢
𝑇
y 𝒢
𝐷
, esta sección
describe la metodología de diseño hidráulico de redes de alcantarillado. El diagrama de flujo de la
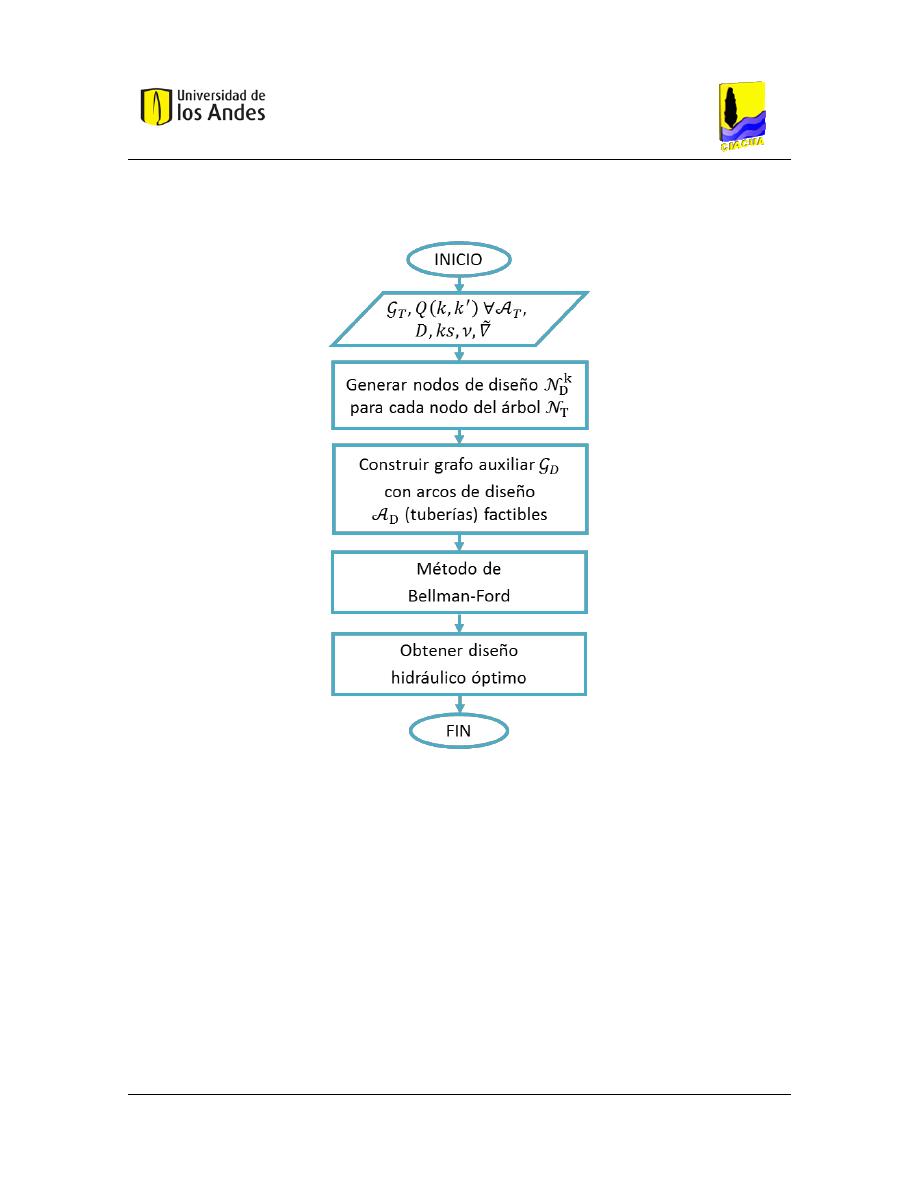
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
61
Figura 4.17 muestra los pasos para obtener el diseño hidráulico dado un trazado y parámetros de
entrada adicionales.
Figura 4.17. Metodología para el diseño hidráulico optimizado de redes de alcantarillado.
El diagrama anterior recibe los datos de entrada mencionados en la Sección 3.4.1. Con el grafo
𝒢
𝑇
se conocen los nodos 𝒩
𝑇
que representan cada uno de los pozos ℳ que conforman la red,
teniendo en cuenta la creación de nodos individuales para los inicios. Dado que cada nodo 𝑣
𝐾
∈ 𝒩
𝑇
guarda la misma información de su pozo padre 𝑚
𝑘
∈ ℳ, se conocen las coordenadas 𝑥, 𝑦 y 𝑧 de
cada uno. Adicionalmente, se tiene el conjunto de arcos 𝒜
𝑇
que representan cada uno de los tramos
que conforman el trazado de la red 𝒫. Los sentidos de flujo de cada tramo están descritos por cada
uno de los arcos (𝑘, 𝑘
′
) ∈ 𝒜
𝑇
y el tipo de tubería se deduce a partir de los nodos que componen
cada arco. Se sabe que si el nodo aguas arriba del tramo 𝑣
𝑘
∈ 𝒩
𝑇
no recibe al menos un tramo
desde aguas arriba, entonces este corresponde a uno de los extremos del árbol y por ende el arco
(𝑘, 𝑘
′
) ∈ 𝒜
𝑇
representa una tubería de inicio.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
62
Por otro lado de la solución del tazado también se conoce el flujo 𝑦
𝑖𝑗𝑡
que pasa por cada arco
(𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
. Este flujo lo que representa es el caudal que debe ser transportado en cada tramo,
denominado 𝑄
𝑑
(𝑘, 𝑘
′
) para cada arco (𝑘, 𝑘
′
) ∈ 𝒜
𝑇
. Este es entonces el caudal de diseño para cada
arco (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) ∈ 𝒜
𝐷
, que se utiliza para definir el diseño hidráulico de dicho tramo. Finalmente, se
recibe el conjunto de diámetros comerciales disponibles 𝐷, la viscosidad cinemática del fluido (agua)
𝜈, la rugosidad absoluta de las tuberías denominado 𝑘
𝑠
y el cambio entre cotas ∇
̃ que define una
mayor o menor precisión del diseño hidráulico. Con estos últimos datos de entrada se realizan los
cálculos hidráulicos y se define cuáles combinaciones diámetro-pendiente tienen la capacidad de
transportar el caudal de diseño 𝑄
𝑑
(𝑘, 𝑘
′
), solución que se conoce como el diseño hidráulico de la
red.
De acuerdo con dichos datos de entrada el proceso de diseño comienza con la generación los
nodos de diseño 𝒩
𝐷
para cada nodo del árbol 𝒩
𝑇
. Esto quiere decir que se crea un nodo para cada
combinación de diámetro 𝛿(𝑣
𝑖
𝑘
) y cota ∇(𝑣
𝑖
𝑘
) como describe el Algoritmo 4.2, mostrado a
continuación. Como se observa, de los datos de entrada para el diseño hidráulico sólo se utiliza el
grafo 𝒢
𝑇
, teniendo en cuenta toda la información que carga; el conjunto de diámetros comerciales
disponibles 𝐷 y la variación entre cotas ∇
̃ que se va a utilizar, para este proceso en particular. La
Línea 1 recorre cada uno de los nodos del árbol 𝒩
𝑇
, de acuerdo con el grafo 𝒢
𝑇
. Las Líneas 2 y 3
establecen los límites de excavación superior e inferior, de acuerdo con la restricción de
profundidades que muestra la Tabla 2.3. Estos límites establecen el espacio de solución para el
diseño hidráulico. De la Línea 4 a la Línea 10 se realiza el proceso de creación de nodos de diseño
para cada nodo del árbol 𝑣
𝑘
∈ 𝒩
𝑇
. Se comienza con un recorrido por la lista de diámetros 𝐷 en la
Línea 4, se establece la cota inicial en el límite superior en la Línea 5 y continúa con el recorrido por
las cotas batea a las cuales se podría instalar la tubería dentro de los límites de excavación en la
Línea 6. La Línea 7 crea el nuevo nodo de diseño con el diámetro 𝑑 y cota ∇
𝑖
𝑘
evaluados, como
atributos del nodo 𝛿(𝑣
𝑖
𝑘
) y ∇(𝑣
𝑖
𝑘
), respectivamente. Este nodo se guarda dentro del conjunto de
nodos de diseño 𝒩
𝐷
del nodo del árbol 𝒩
𝑇
correspondiente, en la Línea 8. Finalmente, en la Línea
9 se realiza la variación a una cota inferior de acuerdo con el cambio de cota ∇
̃ establecido, para
continuar con la evaluación de las demás cotas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
63
Algoritmo 4.2
.
Generación de nodos de diseño
Después de creados todos los nodos se pasa a generar el grafo para el diseño hidráulico 𝒢
𝐷
con
los arcos factibles. Esto quiere decir que solo se crean aquellos arcos (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) ∈ 𝒜
𝐷
que cumplan
con todas las condiciones y restricciones hidráulicas. Ahora bien, teniendo en cuenta que el
Algoritmo de Bellman- Ford busca es encontrar la ruta más corta desde un nodo inicial 𝑣
𝑠
∈ 𝒩, en
este caso la descarga 𝑣
𝑇
∈ 𝒩
T
, a todos los otros nodos de un grafo; se realizó la construcción del
grafo de diseño hidráulico 𝒢
𝐷
hacia atrás (desde la descarga hasta cada uno de los inicios). Es decir,
que el proceso de modelaje de un grafo para el diseño hidráulico de una red de alcantarillado
expuesto en la Sección 4.2.2.2, se reversó de forma que se obtuviera un grafo como el que presenta
la Figura 4.16, sobre el cual se puede correr el Algoritmo de Bellman-Ford desde un nodo a todos
los demás nodos de la red. Como se puede observar, la estructura del grafo es la misma y se
mantienen las todas las restricciones, pues solo se debe precisar que el arco de diseño para el tramo
(𝑘, 𝑘
′
) ∈ 𝒜
𝑇
ahora se define en sentido contrario como (𝑣
𝑖
𝑘
′
, 𝑣
𝑗
𝑘
) ∈ 𝒜
𝐷
. La Figura 4.16 también
presenta un nodo imaginario que se conecta, con líneas punteadas, a los nodos de diseño 𝒩
i
T
del
nodo de la descarga 𝑣
𝑇
∈ 𝒩
T
. Este nodo no posee ningún atributo, simplemente representa el nodo
inicial 𝑣
𝑠
∈ 𝒩 que describe el Algoritmo de Bellman-Ford (ver Sección 4.2.2.2), desde donde se
empieza el proceso de etiquetas hasta cada uno de los inicios del árbol.
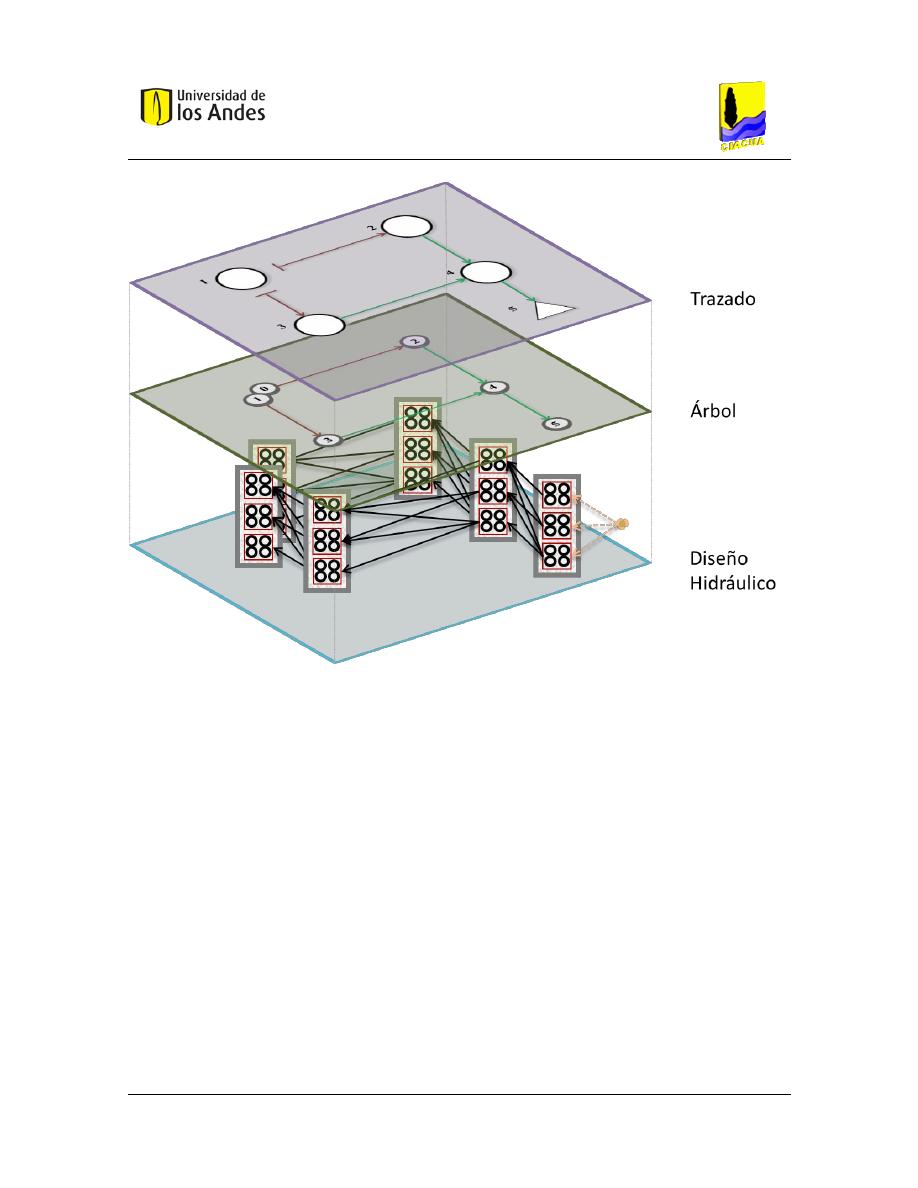
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
64
Figura 4.18. Grafo de diseño 𝓖
𝑫
reversado.
De acuerdo con lo anterior, el Algoritmo 4.3 presenta este proceso de creación del grafo de
diseño 𝒢
𝐷
que involucra también el proceso de etiquetas con el que se calcula la Ruta Más Corta.
Durante la creación del grafo auxiliar se evalúa si el arco (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) ∈ 𝒜 es factible hidráulica y
económicamente; de ser factible, se actualizan las etiquetas de los nodos de diseño 𝒩
𝐷
, siguiendo
el Algoritmo de Bellman-Ford, como se mencionó en la Sección 4.2.2.2.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
65
Algoritmo 4.3
.
Construcción del grafo auxiliar para el diseño hidráulico.
Para la generación de los arcos entre los nodos de diseño 𝒩
𝐷
de los correspondientes nodos del
árbol 𝒩
𝑇
, se utiliza un arreglo de nodos de árbol que almacena los nodos que están 𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒𝑠 por
analizar. La Línea 1 muestra que este arreglo empieza almacenando el último nodo del árbol 𝑣
𝑇
∈
𝒩
𝑇
que representa la descarga, ya que la construcción del grafo se realiza de atrás hacia adelante,
desde la descarga hacia cada uno de los inicios. La Línea 2 evalúa si el arreglo de 𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒𝑠 tiene
al menos un nodo que todavía no haya sido evaluado para que los demás nodos del árbol 𝑣
𝑘
∈ 𝒩
𝑇

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
66
que están en la lista de 𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒𝑠 sean evaluados en el orden en que fueron agregados. La Línea
3 comienza la evaluación de los 𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒𝑠 tomando como el nodo aguas abajo del tramo (a la
salida) 𝑣
𝑑𝑜𝑤𝑛
∈ 𝒩
𝑇
aquel que esté en la primera posición del arreglo de 𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒𝑠 y sacándolo
una vez haya sido evaluado. La Línea 4 realiza un recorrido entre los arcos del árbol 𝒜
𝑇
. Se toma el
nodo 𝑣
𝑘
del arco y se guarda como el nodo aguas arriba del tramo (a la entrada) 𝑣
𝑢𝑝
∈ 𝒩
𝑇
en la
Línea 5. Además, 𝑣
𝑢𝑝
se agrega al arreglo de 𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒𝑠 en la Línea 6, para que sea evaluado en la
siguiente iteración. Una vez definido el par de nodos de layout adyacentes entre los cuales se van a
generar los arcos de diseño (𝑣
𝑢𝑝
, 𝑣
𝑑𝑜𝑤𝑛
) ∈ 𝒜
𝑇
, las Líneas 7 y 8 recorren sus respectivos nodos de
diseño 𝑣
𝑖
𝑑𝑜𝑤𝑛
∈ 𝒩
𝐷
𝑑𝑜𝑤𝑛
y 𝑣
𝑗
𝑢𝑝
∈ 𝒩
𝐷
𝑢𝑝
, evaluando si los diámetros crecen o se mantienen hacía
aguas abajo 𝛿(𝑣
𝑑𝑜𝑤𝑛
) ≥ 𝛿(𝑣
𝑢𝑝
) en la Línea 9. En caso de que la restricción de diámetros se cumpla,
la Línea 10 calcula la longitud entre los nodos del árbol 𝑣
𝑢𝑝
y 𝑣
𝑑𝑜𝑤𝑛
para calcular en la Línea 11 la
pendiente entre sus nodos de diseño 𝒩
𝐷
𝑢𝑝
y 𝒩
𝐷
𝑑𝑜𝑤𝑛
, respectivamente. Posteriormente, la Línea 12
evalúa que la pendiente sea positiva, es decir que ∇(𝑣
𝑗
𝑢𝑝
) ≥ ∇(𝑣
𝑖
𝑑𝑜𝑤𝑛
) para que vaya a favor de la
gravedad. Si la pendiente es positiva, se calcula el costo 𝐶
𝑖𝑗
del arco (𝑣
𝑖
𝑑𝑜𝑤𝑛
, 𝑣
𝑗
𝑢𝑝
) en la Línea 13.
La Línea 14 muestra la implementación del Algoritmo de Bellman-Ford, evaluando si el costo
acumulado del nodo de diseño aguas arriba V(𝑣
𝑗
𝑢𝑝
) es mayor que la suma entre el costo acumulado
del nodo de diseño aguas abajo V(𝑣
𝑖
𝑑𝑜𝑤𝑛
) más el costo del arco 𝐶
𝑖𝑗
. En ese caso, se debe reescribir
el costo acumulado del nodo de diseño aguas arriba V(𝑣
𝑗
𝑢𝑝
) con el nuevo costo mínimo para ese
nodo; sin embargo, se deben evaluar las restricciones hidráulicas antes, para saber si el arco de
diseño (tubería) (𝑣
𝑗
𝑢𝑝
, 𝑣
𝑖
𝑑𝑜𝑤𝑛
) ∈ 𝒜
𝐷
es factible hidráulicamente. Para esto se calcula el caudal que
transporta el arco 𝑄(𝑣
𝑗
𝑢𝑝
, 𝑣
𝑖
𝑑𝑜𝑤𝑛
) en la Línea 15 y se evalúan las restricciones hidráulicas en las Línea
16 y 17. La Línea 16 se asegura que el caudal que puede transportar dicho arco sea mayor o igual al
caudal de diseño 𝑄
𝑑
(𝑢𝑝, 𝑑𝑜𝑤𝑛) para el arco (𝑣
𝑢𝑝
, 𝑣
𝑑𝑜𝑤𝑛
) ∈ 𝒜
𝑇
. La Línea 17 se asegura que se estén
cumpliendo las restricciones hidráulicas descritas en la Tabla 2.4. Una vez estas restricciones
hidráulicas se cumplen, se tiene un arco factible y se pasa a terminar el proceso de etiquetado del
Algoritmo de Bellman-Ford en las Líneas 18 y 19. El finalizar este proceso ya se tiene construido,
diseñado y etiquetado cada arco 𝒜
𝐷
y cada nodo 𝒩
𝐷
del grafo de diseño hidráulico 𝒢
𝐷
.
Para encontrar la solución del grafo 𝒢
𝐷
se debe seguir el procedimiento planteado por el
Algoritmo 4.4. La solución para el diseño hidráulico óptimo se está compuesta por las rutas más
cortas desde cada nodo inicial del árbol hasta la descarga. A modo de ejemplo, la Figura 4.19
muestra la solución del grafo 𝒢
𝐷
para el diseño hidráulico, donde se observa un diseño para cada
serie de tuberías. El primero recorre los nodos del árbol 𝑣
0
, 𝑣
2
, 𝑣
4
, 𝑣
5
∈ 𝒩
𝑇
con un diseño que
selecciona las siguientes combinaciones de diametrós y cotas: 𝑣
0
: (
𝑑
2
, ∇
1
)
;
𝑣
2
:
(𝑑
2
, ∇
2
);
𝑣
4
:
(𝑑
3
, ∇
2
);
𝑣
5
:
(𝑑
4
, ∇
3
). El segundo
recorre los nodos del árbol 𝑣
1
, 𝑣
3
, 𝑣
4
, 𝑣
5
∈ 𝒩
𝑇
con un diseño
que selecciona las siguientes combinaciones de diámetros y cotas: 𝑣
1
: (
𝑑
1
, ∇
1
)
;
𝑣
3
: (
𝑑
1
, ∇
2
)
;
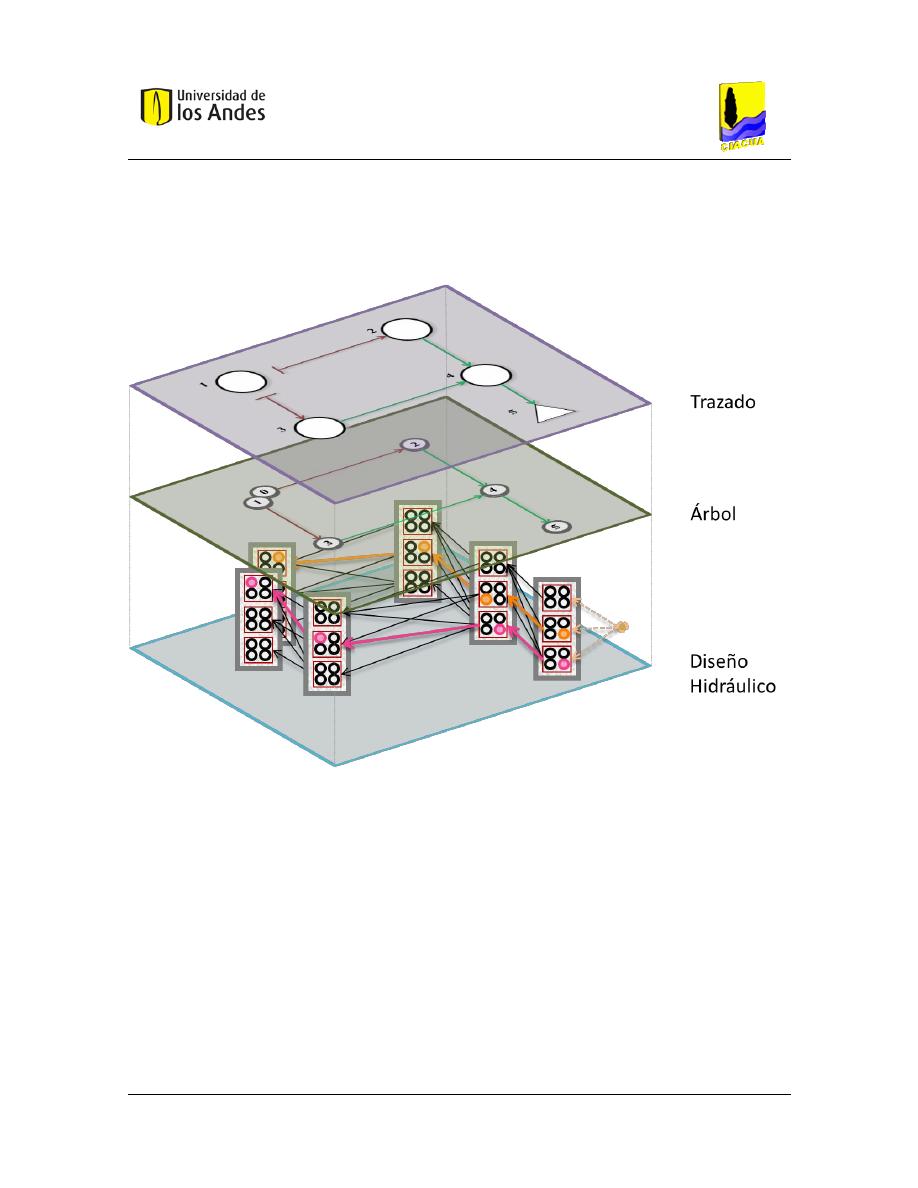
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
67
𝑣
4
: (
𝑑
4
, ∇
3
)
;
𝑣
5
:
(𝑑
4
, ∇
3
). Nótese que en ambos casos los diámetros van en aumento hacia
aguas abajo y la serie de tuberías se va profundizando.
Figura 4.19. Solución para el diseño hidráulico de la red.
El diseño de tramos por líneas independientes no garantiza el empalme adecuado de las
tuberías, por lo que se deben corregir los diseños. En el anterior ejemplo se observa cómo en el
Nodo 𝑣
4
confluyen dos ramas del árbol (dos series de tuberías). En estos casos, se puede dar que
todas las series de tuberías lleguen a un mismo nodo de diseño, lo que quiere decir que todas las
tuberías llegan a una misma cota y el flujo continúa por la misma tubería (diámetro-pendiente) en
el tramo aguas abajo. Este es el caso en el que se tienen pozos de inspección comunes con varias
entradas y una única salida. Sin embargo, cuando las tuberías que llegan a un mismo nodo del árbol,
llegan a nodos de diseño diferentes (con cotas diferentes), quiere decir que existen dos arcos de
diseño 𝒜
𝐷
diferentes en el tramo aguas abajo. Dado que por cada tramo solo debe existir una
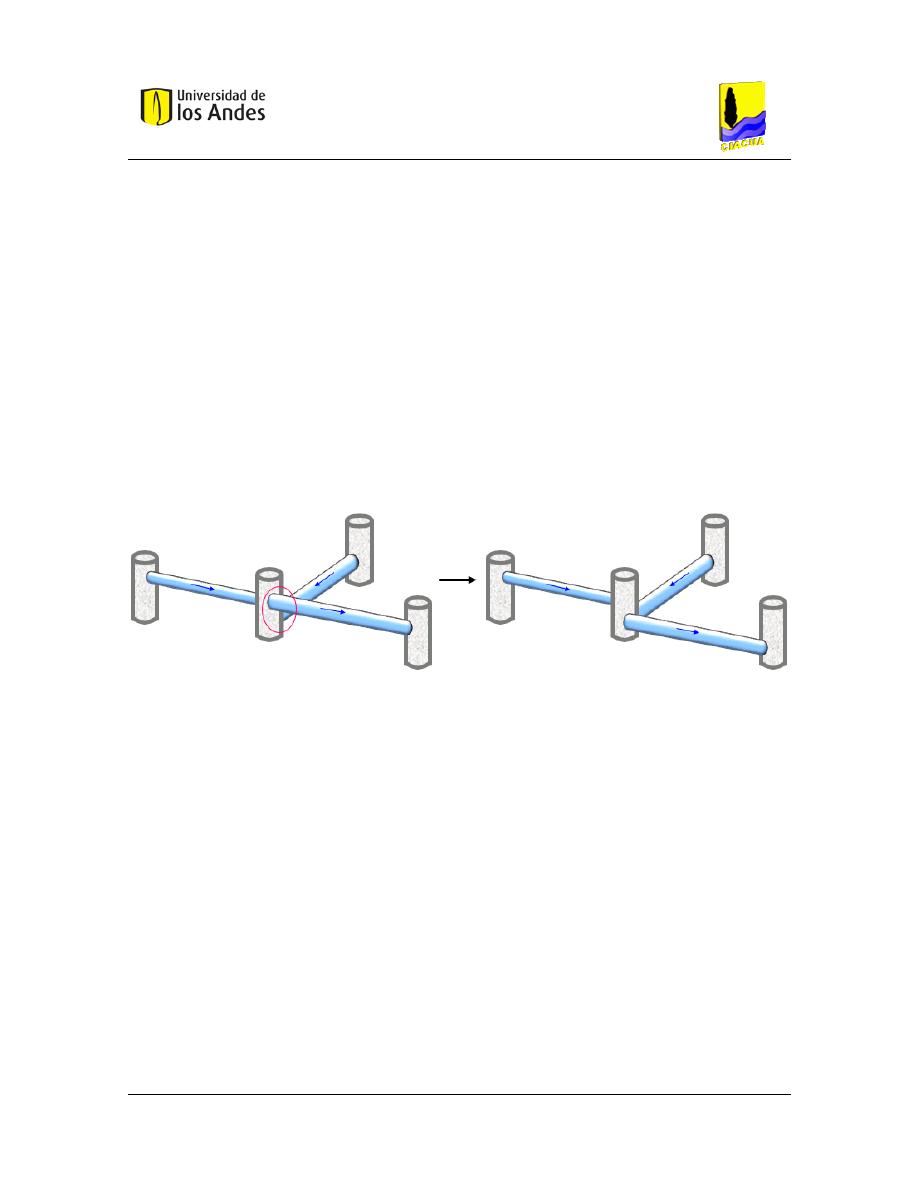
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
68
tubería, se debe escoger para el diseño hidráulico, el arco (𝑣
𝑗
𝑘
, 𝑣
𝑖
𝑘
′
) ∈ 𝒜
𝐷
que represente la tubería
más profunda. Esto debido a que se deben evitar bombeos dentro del sistema de alcantarillado,
teniendo en cuenta que el agua debe fluir por gravedad. En estos casos se requiere construir un
pozo de caída, en el cual las tuberías de entrada están por encima de la tubería de salida, como se
muestra en la Figura 4.20. En el caso de los diámetros no se tiene este problema ya que las tuberías
son diseñadas para un caudal de diseño que ya contempla el caudal proveniente de todas las
tuberías de entrada, más el caudal sanitario aportado por el pozo aguas arriba. A pesar de que los
nodos de diseño a los que llega cada tramo en el Nodo 𝑣
4
tienen diferentes diámetros, esto no
afecta el tramo aguas abajo cuyo diámetro está representado por el nodo de diseño del Nodo 𝑣
5
que
resulta ser el mismo (𝑑
4
, según la Figura 4.14) pues las tuberías se diseñan para el mismo caudal de
diseño 𝑄
𝑑
(4,5) (flujo en 𝑦
45𝐶
definido por el trazado).
Figura 4.20. Pozos de caída
El Algoritmo 4.4 muestra entonces, el procedimiento anterior de forma detallada. Se reciben los
grafos del árbol 𝒢
𝑇
y del diseño hidráulico 𝒢
𝐷
, que se recorren hacia adelante (en el sentido
contrario al que fue creado el grafo 𝒢
𝐷
), desde cada uno de los inicios hasta la descarga. La Línea 1
plantea un recorrido entre todos los nodos del árbol 𝒩
𝑇
que son Inicios, en los cuales se debe buscar
cuál de sus nodos de diseño 𝑣
𝑖
𝑘
∈ 𝒩
𝐷
𝑘
que tiene el menor costo de construcción acumulado. La Línea
2 establece una variable temporal 𝑚𝑖𝑛
𝑐𝑜𝑠𝑡𝑜
= 𝑖𝑛𝑓𝑖𝑛𝑖𝑡𝑜 que almacena el valor del costo mínimo que
se ha encontrado entre los nodos de diseño. Este valor se va actualizando a medida que se vayan
encontrando valores menores, hasta encontrar el mínimo (Líneas 3- 8). Una vez encontrado el nodo
de diseño que tiene el mínimo costo para el nodo del árbol de inicio que está siendo evaluado, se
buscan sus nodos de diseño predecesores para conformar la ruta más corta, tal como se muestra
entre las Líneas 9 a 15, guardando cada nodo y arco de diseño que pertenece a la ruta más corta en
un grafo que representa la solución del problema 𝒢
𝑠𝑜𝑙
= (𝒩
𝑠𝑜𝑙
, 𝒜
𝑠𝑜𝑙
). Finalmente, se debe revisar
si en algún tramo pasa más de una serie de tuberías y por ende existe más de una tubería. En estos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
69
casos se selecciona la tubería más profunda para que el agua caida por gravedad, como se observa
entre las Líneas 16 y 26.
Algoritmo 4.4. Obtención de la solución óptima para el diseño hidráulico

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
70
4.3 Estimación de la función de costos para la selección del trazado
Teniendo en cuenta las metodologías planteadas para los dos problemas involucrados en el
diseño de redes de alcantarillado, es claro que se tienen funciones de costos diferentes para cada
uno, como se observa en la Figura 4.21. Esto se debe a que la función objetivo en ambos problemas
busca minimizar los costos y por ende las funciones de costos deben estar en términos de las
variables de decisión que son diferentes para cada problema. En el caso del problema de selección
del trazado, dado que no se conocen los diámetros y pendientes de cada tubería, se debe estimar
una función de costos aproximada en función del flujo 𝑦
𝑖𝑗𝑡
en el arco (𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
y la variable
binaria 𝑥
𝑖𝑗𝑡
que define si el arco (𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
hace parte o no del trazado, para cada tramo de la
red de alcantarillado. Para el problema del diseño hidráulico, dado que ya se conoce el diámetro, la
longitud y las cotas a las que está instalada cada tubería, se utiliza la ecuación de costos real
planteada por Navarro, I. (2009).
Figura 4.21. Función de costos para un tramo de una red de alcantarillado
En este sentido, para tener una buena aproximación a una función de costos para el problema
de selección del trazado, se deben estimar los coeficientes 𝑐
𝑖𝑗
y 𝑎
𝑖𝑗
. Para calcular cuánto debería
ser el costo por unidad de flujo 𝑐
𝑖𝑗
para cada tramo, se debe hacer una estimación con base en
costos reales, que tengan en cuenta los costos de las tuberías y los costos de la excavación. Lo
anterior requiere conocer el costo real de un tramo ya diseñado y su caudal de diseño, para realizar
una regresión lineal y obtener una función de costos para cada tubería de la forma 𝑦 = 𝛽
𝑜
+ 𝛽
1
∗
𝑥
1
+ 𝛽
2
∗ 𝑥
2
+ ⋯ + 𝛽
𝑛
∗ 𝑥
𝑛
, donde 𝛽
1
se toma como el costo por unidad de flujo 𝑐
𝑖𝑗
dado por la

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
71
pendiente de la regresión, y 𝛽
0
como el intercepto 𝑎
𝑖𝑗
, que representa un costo asociado con cada
tubería (arco) en caso de usarla en el trazado. De esta forma se llega a la función objetivo, planteada
en la Ecuación 4.5, para el problema de selección del trazado.
min ∑
∑
𝑐
𝑖𝑗
𝑦
𝑖𝑗𝑡
(𝑖,𝑗,𝑡)∈𝒜
𝐿
𝑡 ∈𝒯
+ ∑
∑
𝑎
𝑖𝑗
𝑥
𝑖𝑗𝑡
(𝑖,𝑗,𝑡)∈𝒜
𝐿
𝑡 ∈𝒯
Ecuación 4.5
4.3.1 Generación de trazados aleatorios
La generación de trazados aleatorios se propone como un proceso de inicialización al problema,
de forma que se pueda realizar la estimación de la función de costos para la selección del trazado a
partir de los resultados del diseño hidráulico de cada trazado aleatorio.
Cada trazado aleatorio se genera por medio de la asignación de números aleatorios para los
coeficientes 𝑐
𝑖𝑗
de cada tramo. De esta forma se resuelve el problema de selección del trazado a
partir de dichos coeficientes aleatorios como parte de la función objetivo planteada por la Ecuación
4.5. Este trazado entonces, se contempla como trazado aleatorio por la naturaleza de sus
coeficientes, dado que al resolver el problema con coeficientes aleatorios se pueden obtener
diferentes trazados con el modelo.
4.4 Metodología para el diseño de redes de alcantarillado
Como se mencionó anteriormente, el diseño de una red de alcantarillado es la unión de dos
problemas: la selección del trazado y el diseño hidráulico de la red. Ahora bien, tras haber explicado
cómo se modeló el problema de la selección del trazado de una red de alcantarillado sobre un grafo
𝒢
𝐿
, cómo se representó dicho árbol en con una estructura de árbol en un grafo 𝒢
𝑇
y posteriormente
cómo se modeló el problema del diseño hidráulico sobre un grafo auxiliar 𝒢
𝐷
, se pretende explicar
la metodología global para el diseño de redes de alcantarillado en la Figura 4.22.
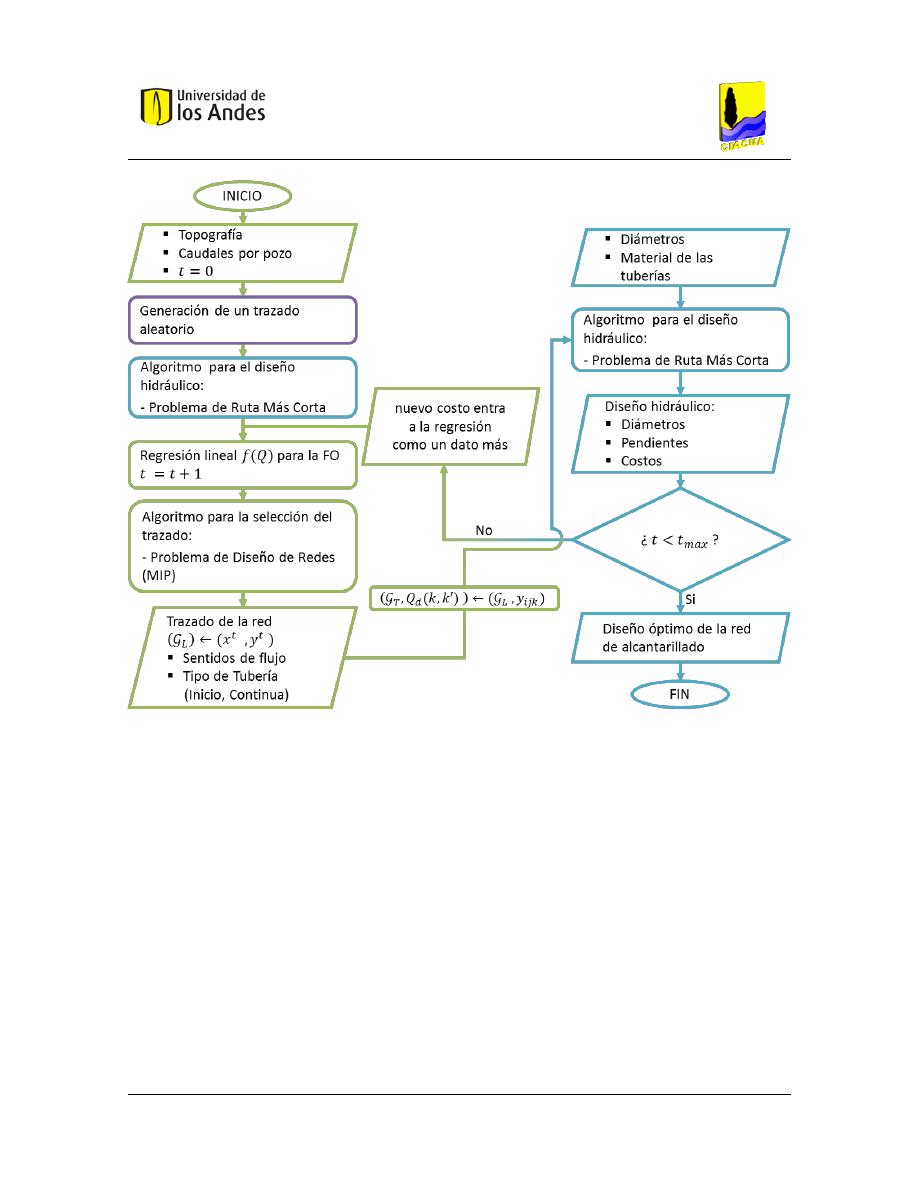
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
72
Figura 4.22 Diagrama de flujo para el diseño de redes de alcantarillado.
En la Figura 4.22 se puede observar que el diseño de redes de alcantarillado se plantea como un
proceso iterativo, donde para cada iteración se selecciona un trazado (recuadros verdes) y de
acuerdo con este se realiza el diseño hidráulico optimizado de la red (recuadros azules).
Adicionalmente, con cada iteración se espera mejorar función de costos para la selección del
trazado, de forma que se puedan encontrar trazados mejores.
El proceso comienza recibiendo los datos de entrada necesarios para resolver el problema de la
selección del trazado. Se recibe la topografía del terreno (Coordenadas 𝑥, 𝑦 y 𝑧 de cada pozo de
inspección), los caudales de entrada por pozo 𝑄
𝑘
y un contador 𝑡 que lleva la cuenta del número de
iteraciones realizadas hasta llegar al número de máximo de iteraciones 𝑡
𝑚𝑎𝑥
que definen el criterio
de parada del problema. Posteriormente, se debe realizar una primera estimación de la función de
costos en términos del caudal, como se explica en la Sección 4.3; según la cual se encuentra el mejor
trazado de la red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
73
Sin embargo, la estimación de dicha función objetivo requiere de datos verdaderos de costos
de construcción y caudales de diseño de tramos de tuberías ya diseñadas. En consecuencia, se debe
realizar una inicialización al problema por medio de la generación de un trazado aleatorio, como se
explica en la Sección 4.3.1. Posteriormente, se realiza el diseño hidráulico de dicho trazado aleatorio,
de forma que se pueda estimar una buena función de costos en términos del caudal a partir de los
costos reales de construcción y los caudales obtenidos.
Siguiendo el diagrama de flujo presentado en la Figura 4.22, una vez definida la función de
costos para la selección del trazado, se corre un algoritmo que resuelve el Problema de Diseño de
Redes, de acuerdo con el modelo matemático planteado en la Sección 4.1.2, obteniendo como
resultado el mejor trazado de la red de alcantarillado, para la función de costos dada.
A partir del trazado obtenido y con información adicional sobre el material de las tuberías y los
diámetros comerciales disponibles, se procede a realizar el diseño hidráulico de la red. Para esto se
genera el grafo para el diseño hidráulico 𝒢
𝐷
, sobre el cual se corre un algoritmo que resuelve el
problema de Ruta Más Corta (ver Sección 4.2.4). De este proceso se obtiene como resultado el
diseño hidráulico optimizado de la red, para el trazado dado. Es decir que se obtiene el diámetro de
cada tubería, su ubicación en el terreno (pendiente y profundidad) y los costos reales de
construcción de cada tramo de la red.
Ahora bien, a pesar de que ya se tiene un diseño completo de la red, donde el diseño hidráulico
es óptimo para el trazado dado, no se puede asegurar que el diseño de la red sea óptimo. Esto se
debe a que no se sabe si la función de costos para la selección del trazado representa bien los costos
reales de construcción para cada tramo de la red de alcantarillado. A raíz de lo anterior se plantea
el proceso iterativo que propone el Diagrama de Flujo de la Figura 4.22, en el cual con cada diseño
hidráulico se va mejorando la estimación de la función de costos para la selección del trazado, hasta
que se encuentre el mejor trazado para la red, tras un número de iteraciones establecido 𝑡
𝑚𝑎𝑥
. De
esta forma se va mejorando el ajuste de la función objetivo para la selección del trazado y al final
del proceso se puede asegurar que, para el número máximo de iteraciones establecidas, se obtuvo
el mejor trazado para la red y por ende un diseño optimizado de la red de alcantarillado.
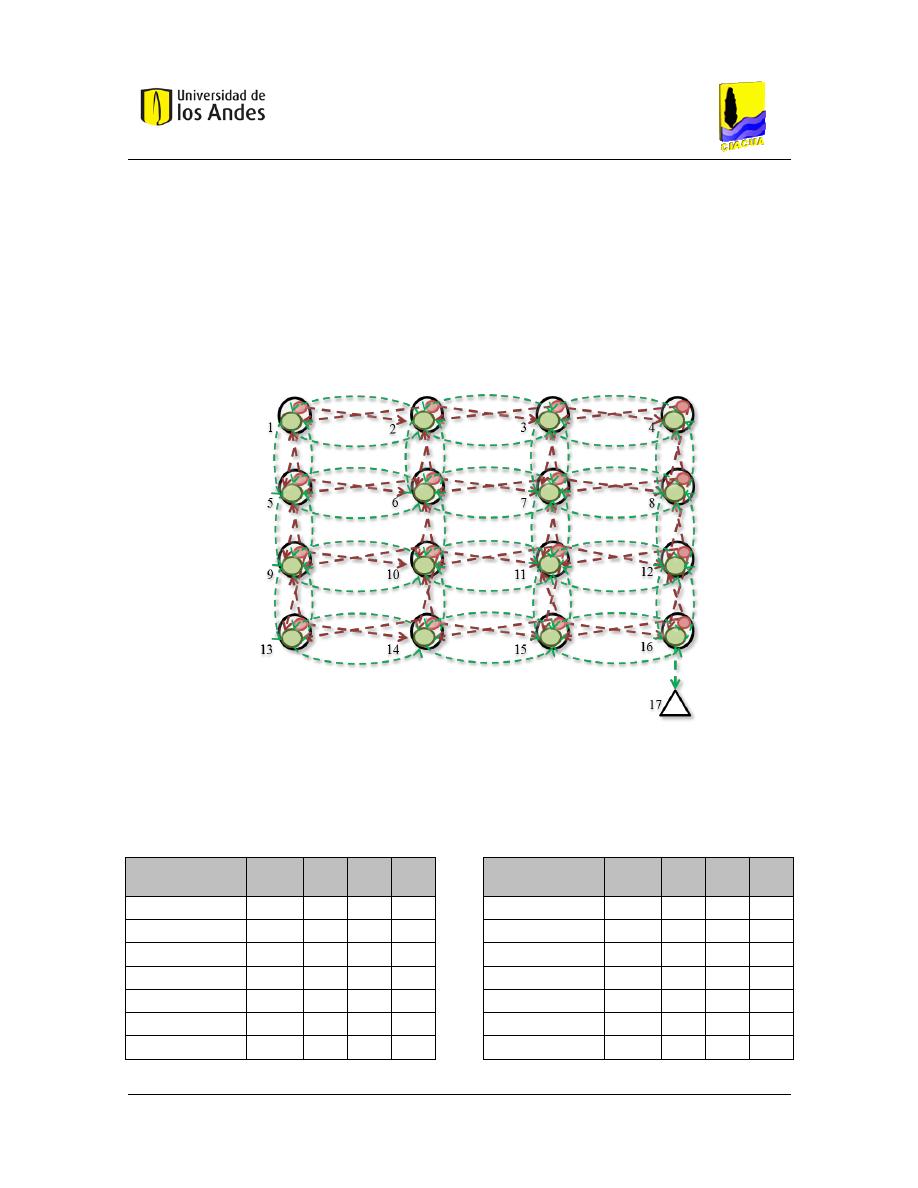
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
74
5 RESULTADOS Y ANÁLISIS DE RESULTADOS
5.1 Diseño de una red de alcantarillado
En esta sección se presentarán los resultados del diseño de redes de alcantarillado, siguiendo la
metodología planteada en la Sección4.3. Se utilizó una red de 17 nodos y 25 tramos, como la que se
muestra en la Figura 5.1.
Figura 5.1 Red 4x4
Esta red tiene una topografía plana y cuenta con la información concerniente a los caudales de
entrada en cada pozo de inspección 𝑄
𝑑
y la topografía del terreno, es decir, las coordenadas 𝑥,𝑦 y
𝑧 de cada pozo. Estos datos de entrada se presentan a continuación en la Tabla 5.1.
Tabla 5.1 Datos de entrada para la selección del trazado de una red de alcantarillado
Nodo
𝑸
𝒑
(m
3
/s)
𝑿
(m)
𝒀
(m)
𝒁
(m)
1
0.328 100 500 100
2
0.328 200 500 100
3
0.328 300 500 100
4
0.328 400 500 100
5
0.328 100 400 100
6
0.328 200 400 100
7
0.328 300 400 100
Nodo
𝑸
𝒑
(m
3
/s)
𝑿
(m)
𝒀
(m)
𝒁
(m)
8
0.328 400 400 100
9
0.328 100 300 100
10
0.328 200 300 100
11
0.328 300 300 100
12
0.328 400 300 100
13
0.328 100 200 100
14
0.328 200 200 100
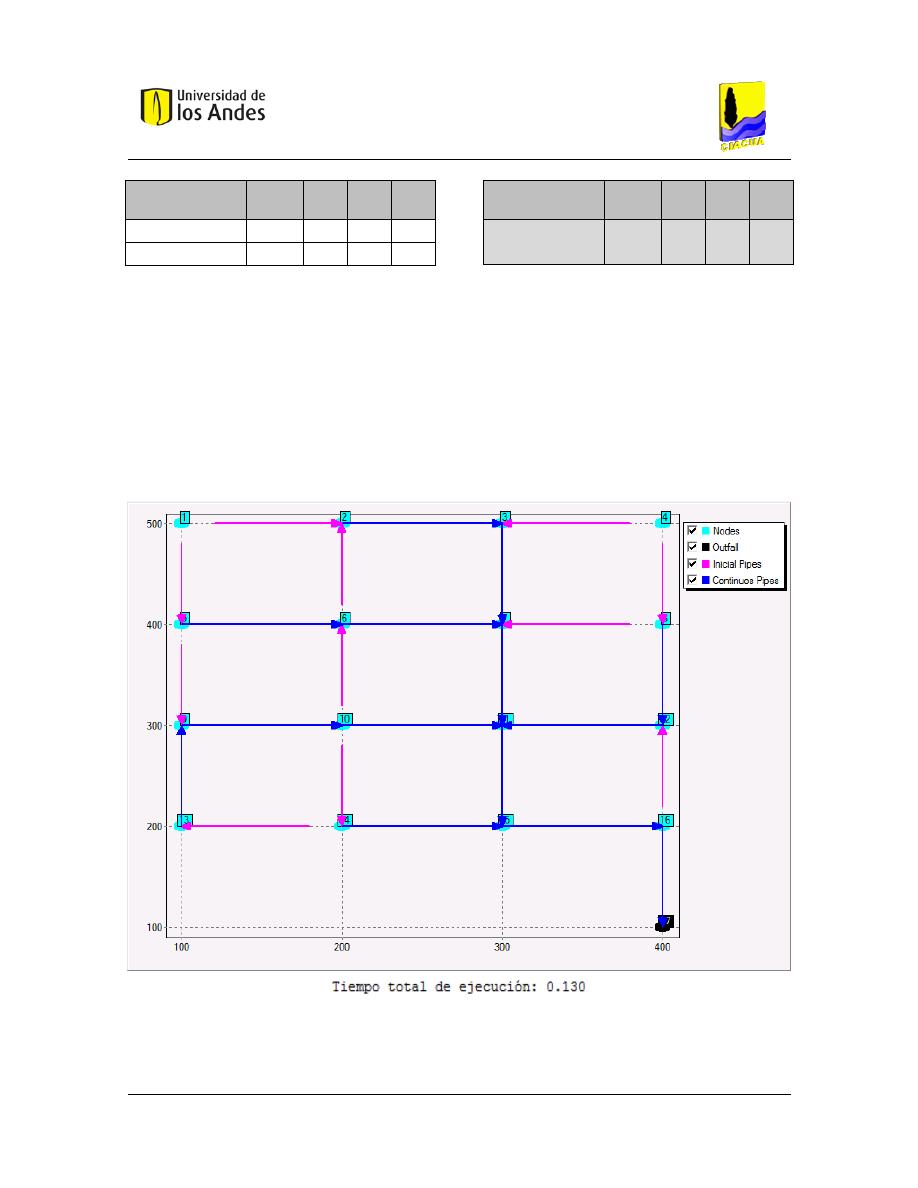
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
75
Nodo
𝑸
𝒑
(m
3
/s)
𝑿
(m)
𝒀
(m)
𝒁
(m)
15
0.328 300 200 100
16
0.328 400 200 100
Nodo
𝑸
𝒑
(m
3
/s)
𝑿
(m)
𝒀
(m)
𝒁
(m)
17
(Descarga)
0.000 400 100 100
Para definir la función de costos en términos del caudal de diseño de cada tubería, necesaria
para el problema de selección del trazado, se realizó el proceso de inicialización planteado en la
Sección 4.3.1,
donde se
generaron coeficientes 𝑐
𝑖𝑗
y 𝑎
𝑖𝑗
aleatorios positivos para cada arco del
trazado
(𝑖, 𝑗, 𝑡)
∈ 𝒜
𝐿
(ver Tabla 8.1), según los cuales se generó una función de costos para cada
arco, de la forma que plantea la Ecuación 4.17 y se obtuvo el trazado que presenta la Figura 5.2.
𝑓(𝑦
𝑖𝑗𝑡
) = 𝑐
𝑖𝑗
𝑦
𝑖𝑗𝑡
+ 𝑎
𝑖𝑗
Ecuación 4.17
Figura 5.2. Primer trazado aleatorio obtenido utilizando Xpress-MP.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
76
La Figura 5.2, también destaca que el proceso de selección de trazado es muy rápido, tomando
menos de 1 segundo para obtener el mejor trazado, de acuerdo con los coeficientes 𝑐
𝑖𝑗
y 𝑎
𝑖𝑗
dados
para cada arco del trazado
(𝑖, 𝑗, 𝑡)
∈ 𝒜
𝐿
.
Tabla 5.2. Resultado del primer trazado aleatorio en la iteración.
Tramo
ID Nodo
Tipo
𝑸
𝒅
(m
3
/s)
𝒊
𝒋
1
1
2
I
0.246
2
1
5
I
0.082
3
2
3
C
0.656
4
3
7
C
1.066
5
4
3
I
0.082
6
4
8
I
0.246
7
5
6
C
0.328
8
5
9
I
0.082
9
6
2
I
0.082
10
6
7
C
0.656
11
7
11
C
2.133
12
8
7
I
0.082
13
8
12
C
0.492
Tramo
ID Nodo
Tipo
𝑸
𝒅
(m
3
/s)
𝒊
𝒋
14
9
10
C
0.820
15
10
6
I
0.082
16
10
11
C
0.984
17
10
14
I
0.082
18
11
15
C
4.348
19
12
11
C
0.902
20
13
9
C
0.410
21
14
13
I
0.082
22
14
15
C
0.328
23
15
16
C
5.004
24
16
12
I
0.082
25
16
17
C
5.250
La Tabla 5.2 presenta el trazado obtenido, especificando el tipo de tubería (𝐼: inicio; 𝐶:
continuo), el caudal de diseño y el sentido de flujo en cada tramo. De acuerdo con este trazado
aleatorio, se realizó el diseño hidráulico de la red con cambio entre cotas de 1 cm (∇
̃= 1 𝑐𝑚) y
utilizando los siguientes diámetros comerciales disponibles en metros.
𝐷 = { 0.2 , 0.38 , 0.4 , 0.5 , 0.65 , 0.80 , 0.9 , 1.05 , 1.20 , 1.3 , 1.55 , 1.6 , 1.8 , 2.2}
La Tabla 5.3 presenta el resultado para el diseño hidráulico optimizado del trazado aleatorio
generado en la primera iteración. Esta solución al problema del diseño hidráulico se resolvió en un
tiempo computacional de 250.21 s (4.17 min). Se presenta el diámetro y las pendientes para cada
tramo, de acuerdo con las cotas batea de los nodos de diseño 𝑣
𝑖
𝑘
y 𝑣
𝑗
𝑘
′
que componen el tramo
(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) ∈ 𝒜
𝐷
≡ (𝑖, 𝑗, 𝑡) ∈ 𝒜
𝐿
. Adicionalmente, se presenta el costo de construcción de cada
tramo y el costo total de la red. El cálculo de todas las variables hidráulicas se presenta en la Tabla
8.2 en la sección de Anexos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
77
Tabla 5.3. Diseño hidráulico de la red 𝒕 = 𝟏
Tramo
ID Nodo
Tipo
𝑸
𝒅
(m
3
/s)
𝒅
(m)
Cota
𝒔
(-)
Costo
($COP)
𝒊
𝒋
𝒊
𝒋
1
1
2
I
0.246
0.65
98.14
98.03 0.0011
$ 2 921 502
2
1
5
I
0.082
0.38
98.42
98.22 0.0020
$ 1 822 855
3
2
3
C
0.656
0.80
98.03
97.85 0.0018
$ 3 647 217
4
3
7
C
1.066
1.05
97.85
97.74 0.0011
$ 4 873 219
5
4
3
I
0.082
0.38
98.42
98.22 0.0020
$ 1 822 855
6
4
8
I
0.246
0.65
98.14
98.03 0.0011
$ 2 921 502
7
5
6
C
0.328
0.65
98.22
98.09 0.0013
$ 2 841 806
8
5
9
I
0.082
0.40
98.39
98.23 0.0016
$ 1 892 045
9
6
2
I
0.082
0.38
98.42
98.22 0.0020
$ 1 822 855
10
6
7
C
0.656
0.80
98.09
97.91 0.0018
$ 3 563 901
11
7
11
C
2.133
1.20
97.74
97.52 0.0022
$ 5 856 544
12
8
7
I
0.082
0.40
98.39
98.23 0.0016
$ 1 892 045
13
8
12
C
0.492
0.80
98.03
97.93 0.0010
$ 3 591 600
14
9
10
C
0.820
0.90
98.02
97.87 0.0015
$ 4 019 655
15
10
6
I
0.082
0.38
98.42
98.22 0.0020
$ 1 822 855
16
10
11
C
0.984
1.05
97.87
97.75 0.0012
$ 4 845 838
17
10
14
I
0.082
0.38
98.42
98.22 0.0020
$ 1 822 855
18
11
15
C
4.348
1.55
97.52
97.25 0.0027
$ 8 201 123
19
12
11
C
0.902
0.90
97.93
97.75 0.0018
$ 4 183 507
20
13
9
C
0.410
0.65
98.22
98.02 0.0020
$ 2 881 555
21
14
13
I
0.082
0.38
98.42
98.22 0.0020
$ 1 822 855
22
14
15
C
0.328
0.65
98.22
98.09 0.0013
$ 2 841 806
23
15
16
C
5.004
1.30
97.10
96.24 0.0086
$ 8 641 151
24
16
12
I
0.082
0.40
98.39
98.23 0.0016
$ 1 892 045
25
16
17
C
5.250
1.30
96.24
95.29 0.0095
$ 11 009 027
Costo Total
$ 93 454 222
El costo de construcción total de la red fue de $ 93 454 222 COP. Ahora bien, para mejorar el
trazado se procede a realizar el proceso iterativo en el cual se modifica la función objetivo
calculando los coeficientes 𝑐
𝑖𝑗
y 𝑎
𝑖𝑗
para cada arco del trazado
(𝑖, 𝑗, 𝑡)
∈ 𝒜
𝐿
, como se explica en la
Sección 4.3. Para esto se realizó una regresión lineal entre los caudales de diseño de cada tramo y
su costo de construcción. En el caso de esta primera iteración, dado que solo se tiene 1 dato de
caudal y costo para cada tramo, se realizó la regresión lineal para toda la red y no para cada tramo
de forma individual. Para el resto de las regresiones se realizaron las regresiones lineales para cada
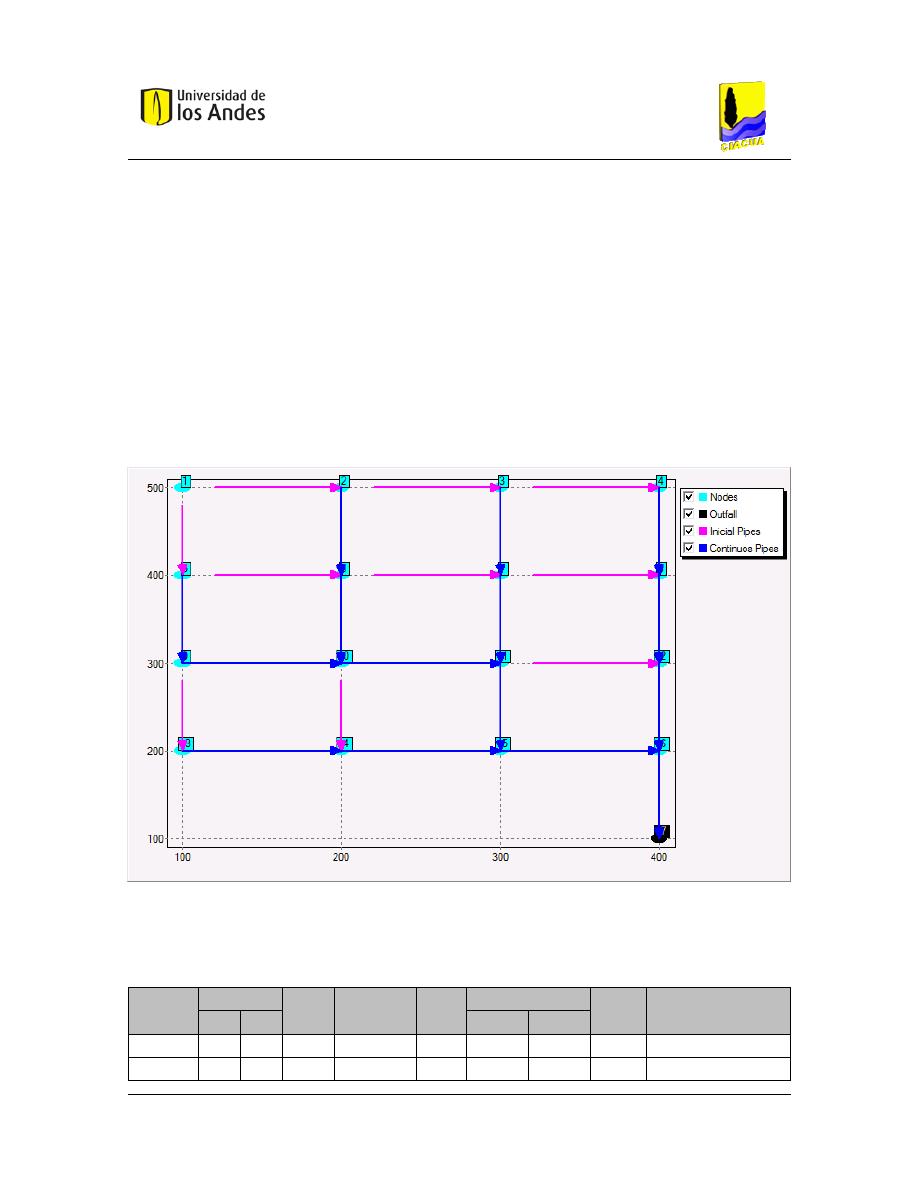
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
78
tramo, de forma que cada arco tuviera asociado un costo por unidad de flujo 𝑐
𝑖𝑗
y un costo asociado
con el uso de la tubería como tal 𝑎
𝑖𝑗
independientes. Esto permite que el análisis una mejor
aproximación de una función de costos en función del caudal (flujo) para cada tubería.
Se realizaron en total 1000 iteraciones (𝑡
𝑚𝑎𝑥
= 100), generando un trazado aleatorio inicial y
entre cada trazado obtenido a partir de la estimación de la función objetivo para la selección del
trazado. Es decir que se realizaron 50 diseños con trazados aleatorios y 50 diseños con trazados
calculados, para un total de 100 diseños de la red ejemplo. Como resultado se obtuvo entonces que
el trazado para el cual se obtuvo el diseño hidráulico más económico fue el que se presenta en la
Figura 5.3, y el diseño hidráulico óptimo para dicho trazado es el presentado en la Tabla 5.4, con el
mejor costo encontrado de $ 87 414 034 COP. El cálculo del resto de variables hidráulicas se
presentan en la Tabla 8.3.
Figura 5.3 Representación de la solución del mejor trazado de la red tras 100 iteraciones
(obtenido utilizando Xpress-MP).
Tabla 5.4. Mejor diseño hidráulico de la red tras 100 iteraciones.
Tramo
ID Nodo
Tipo
𝑸
𝒅
(m
3
/s)
𝒅
(m)
Cota
𝒔
(-)
Costo
($COP)
𝒊
𝒋
𝒊
𝒋
1
1
2
I
0.0820313 0.4
98.39
98.23 0.0016
$ 1 892 045
2
1
5
I
0.246094
0.65
98.14
98.03 0.0011
$ 2 921 502

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
79
Tramo
ID Nodo
Tipo
𝑸
𝒅
(m
3
/s)
𝒅
(m)
Cota
𝒔
(-)
Costo
($COP)
𝒊
𝒋
𝒊
𝒋
3
2
3
I
0.082
0.4
98.39
98.23 0.0016
$ 1 892 045
4
2
6
C
0.328
0.65
98.23
98.1
0.0013
$ 2 830 486
5
3
4
I
0.082
0.38
98.42
98.22 0.0020
$ 1 822 855
6
3
7
C
0.328
0.65
98.23
98.1
0.0013
$ 2 830 486
7
4
8
C
0.410
0.65
98.22
98.02 0.0020
$ 2 881 555
8
5
6
I
0.082
0.38
98.42
98.22 0.0020
$ 1 822 855
9
5
9
C
0.492
0.8
98.03
97.93 0.0010
$ 3 591 600
10
6
7
I
0.082
0.38
98.42
98.22 0.0020
$ 1 822 855
11
6
10
C
0.656
0.8
98.1
97.92 0.0018
$ 3 550 080
12
7
8
I
0.082
0.38
98.42
98.22 0.0020
$ 1 822 855
13
7
11
C
0.656
0.8
98.1
97.92 0.0018
$ 3 550 080
14
8
12
C
0.820
0.9
98.02
97.87 0.0015
$ 4 019 655
15
9
10
C
0.738
0.9
97.93
97.81 0.0012
$ 4 136 470
16
9
13
I
0.082
0.4
98.39
98.23 0.0016
$ 1 892 045
17
10
11
C
1.640
1.05
97.81
97.55 0.0026
$ 5 084 777
18
10
14
I
0.082
0.38
98.42
98.22 0.0020
$ 1 822 855
19
11
12
I
0.082
0.38
98.42
98.22 0.0020
$ 1 822 855
20
11
15
C
2.542
1.3
97.55
97.34 0.0021
$ 6 750 058
21
12
16
C
1.230
1.05
97.87
97.72 0.0015
$ 4 873 219
22
13
14
C
0.410
0.65
98.23
98.03 0.0020
$ 2 870 178
23
14
15
C
0.820
0.9
98.03
97.88 0.0015
$ 4 004 164
24
15
16
C
3.691
1.3
97.34
96.87 0.0047
$ 7 562 822
25
16
17
C
5.250
1.3
96.87
95.92 0.0095
$ 9 343 633
COSTO TOTAL
$ 87 414 034
La solución a este problema se obtuvo en un tiempo computacional de 10143.30 s (2.82 h), lo
cual se considera un muy buen tiempo, teniendo en cuenta la cantidad de alternativas evaluadas
durante las 100 iteraciones. Para esto se utilizó un servidor con 64 GB de memoria RAM, dado que
en un computador normal de 8 GB solo llegó hasta 75 iteraciones. Una vez finalizado este proceso
de diseño de toda la red de alcantarillado, se puede decir que se obtuvo un excelente costo en un
tiempo considerablemente bajo, asegurando siempre diseños hidráulicos optimizados, para los
trazados calculados. Sin embargo, no se puede asegurar que el trazado sea el óptimo, dado que la
aproximación de la función de costos en función del caudal o flujo que pasa por cada tubería no
representa muy bien los costos reales de la red.
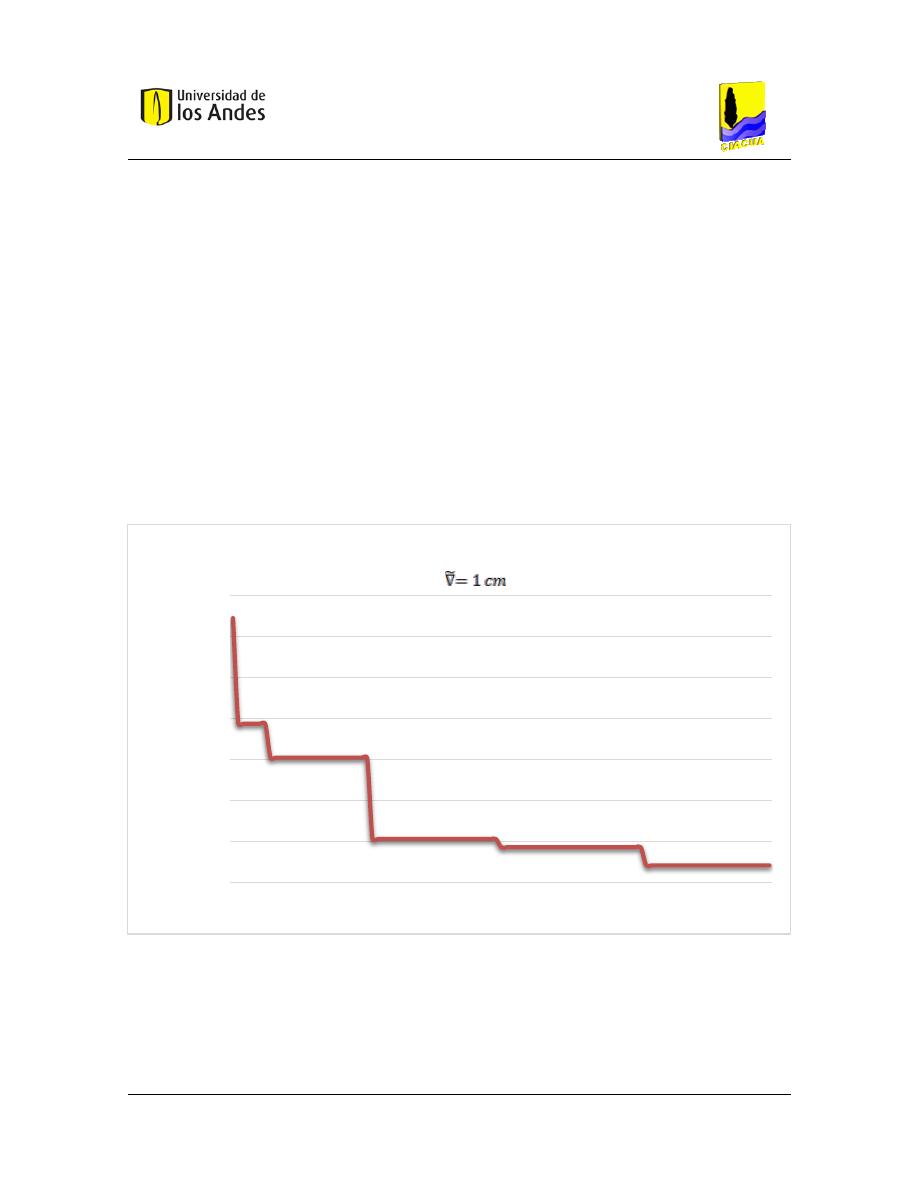
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
80
5.2 Convergencia del diseño de redes de alcantarillado
La Gráfica 5.1 presenta la convergencia al mejor diseño de la red encontrado durante este
proceso iterativo. Como se puede observar existe una tendencia a mejorar los trazados, según los
cuales se encuentran diseños con menores costos de construcción, a medida que se aumenta el
número de iteraciones. Esto se debe a que al agregar más datos a la regresión lineal, según la cual
se establecen los coeficientes 𝑐
𝑖𝑗
y 𝑎
𝑖𝑗
, se mejora la función objetivo para el problema de la selección
del trazado. Sin embargo, no se podría asegurar que tras 100 iteraciones se encontró el trazado
óptimo, por lo cual no se puede asegurar que para 100 iteraciones del problema de diseño de redes
de alcantarillado se haya encontrado el diseño óptimo, pero sí uno muy cercano al óptimo. Esto
teniendo en cuenta que la gráfica de convergencia presenta unas disminuciones en costos
importantes durante las primeras 25 iteraciones, pero de ahí en adelante las reducciones en costos
son menores al 1%.
Gráfica 5.1.Convergencia al mejor trazado de la red de alcantarillado (𝛁
̃ = 𝟏 𝒄𝒎).
Por otro lado, se realizó el diseño de esta misma red, ahora con una variación entre cotas de 10
cm (∇
̃= 10 𝑐𝑚), lo que le da al diseño una menor precisión pero permite obtener el resultado
$87 000 000
$88 000 000
$89 000 000
$90 000 000
$91 000 000
$92 000 000
$93 000 000
$94 000 000
0
5
10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100
Co
sto
(
$CO
P)
No. Iteración
Convergencia del diseño de redes de alcantarillado
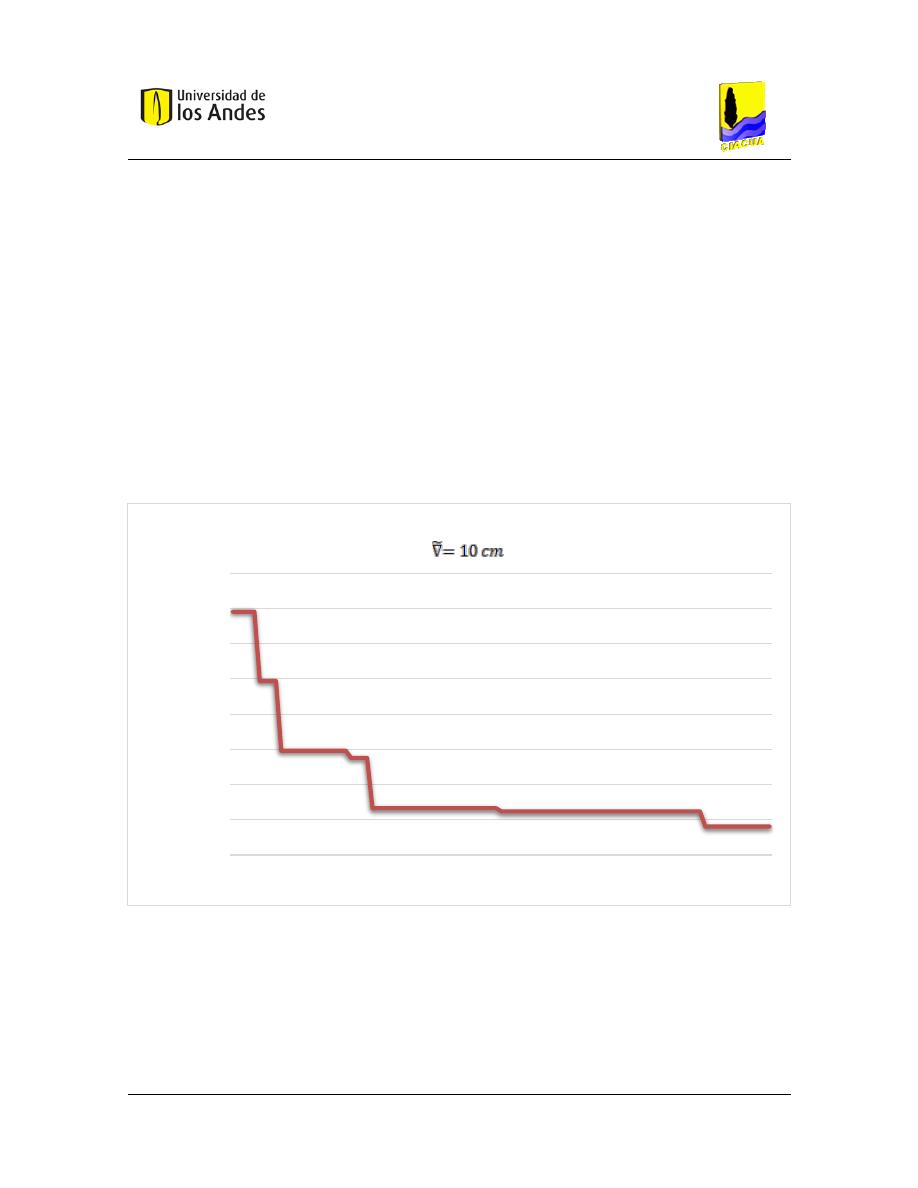
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
81
mucho más rápido. Para esto se siguió el mismo procedimiento que se ha venido explicando.
Después de 100 iteraciones, se encontró un diseño con un costo de $ 90 815 559 COP en 334.19 s
(5.57 min). De acuerdo con lo anterior, se comprueba que al bajar la precisión del diseño se
incrementa el costo de construcción, pues no se están teniendo en cuenta muchas pendientes que
podrían ser utilizadas en el diseño. Sin embargo, si lo que se necesita es tener un buen diseño en
muy poco tiempo, utilizando un computador normal de 8GB de memoria RAM, esta puede ser una
buena aproximación, teniendo en cuenta que la diferencia en costos no supera el 4%. Para este caso
se encuentra que la gráfica de convergencia tiene la misma tendencia, como se observa en la Gráfica
5.2. El Trazado y el diseño hidráulico para este caso se muestran en la Figura 8.1 y la Tabla 8.4 de la
sección de Anexos.
Gráfica 5.2. Convergencia al mejor trazado de la red de alcantarillado (𝛁
̃ = 𝟏𝟎 𝒄𝒎).
$90 000 000
$91 000 000
$92 000 000
$93 000 000
$94 000 000
$95 000 000
$96 000 000
$97 000 000
$98 000 000
0
5
10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100
Co
sto
(
$CO
P)
No. Iteración
Convergencia del diseño de redes de alcantarillado

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
82
6 CONCLUSIONES Y RECOMENDACIONES
6.1 Problema de selección del trazado
La metodología para la selección del trazado de sistemas de alcantarillado cumple con el
objetivo general, pues asegura el óptimo global desde el punto de vista económico, de
acuerdo con la función objetivo establecida para este análisis.
La determinación de la función objetivo, como una función de costos en términos del caudal
de diseño, es una muy buena primera aproximación para seleccionar el trazado, que
posteriormente será diseñado hidráulicamente.
Al comparar el diseño hidráulico de la red con el trazado óptimo, obtenido con la
metodología propuesta, se corroboró que la función de costos utilizada es una buena
aproximación a los costos reales que tendría la red en caso de tener ese trazado
seleccionado.
Gracias a la forma como se modeló el problema, y la representación de la red utilizando
cuatro arcos para representar los sentidos de flujo y el tipo de cada tubería, se logró correr
algoritmos de optimización sobre este grafo para obtener una solución óptima.
Al modelar el problema como un problema de optimización entera mixta (Problema de
diseño de redes), donde se buscar de forma simultánea el diseño de la topología de la red y
la solución al problema de Flujo de Costo Mínimo, se obtiene la selección del trazado óptimo
de una red de alcantarillado, sujeto a la función de costos que se estime.
Los tiempos computacionales para resolver este problema, son de menos de un segundo,
gracias al software utilizado que está diseñado para resolver este tipo de problemas de
optimización. Según esto, se puede decir que gracias a los avances tecnológicos y los
diferentes programas que ayudan a solucionar este tipo de problemas, hoy en día se puede
resolver de forma exacta este tipo de problema de diseño de redes de alcantarillado, lo que
antiguamente era inimaginable.
Se recomienda buscar otras funciones de costos que no sólo estén en función del caudal,
sino también del tipo de tubería (de inicio o continua), teniendo en cuenta que las tuberías
de inicio son más baratas que las continuas, ya que estas segundas llevan un mayor caudal
y están ubicadas a una mayor profundidad. De esta forma se podría encontrar una función
de costos que de una mejor aproximación a los costos reales y así poder tener mayor certeza
de que se está obteniendo el trazado óptimo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
83
6.2 Problema de diseño hidráulico
La metodología de diseño de redes de alcantarillado cumple con el objetivo general, pues
asegura el diseño hidráulico óptimo desde el punto de vista económico, teniendo en cuenta
los aspectos hidráulicos que aseguren el adecuado funcionamiento del sistema, con base en
las normas colombianas: Reglamento Técnico del Sector de Agua Potable y Saneamiento
Básico – RAS (2000).
El uso del algoritmo de Bellman-Ford para etiquetar los nodos, permite establecer la ruta
más cota mientras se genera el grafo desde la descarga hacia todos los inicios de un sistema
de alcantarillado.
El grafo que representa la red está conformado por nodos 𝑣
𝑖
𝑘
∈ 𝒩
𝐷
, que representan una
combinación diámetro 𝛿(𝑣
𝑖
𝑘
)-cota ∇(𝑣
𝑖
𝑘
) y arcos (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) ∈ 𝒜
𝐷
que representan las
tuberías y tienen asociado un diámetro 𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
), una pendiente 𝑠(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
) y un costo
𝑐(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘
′
).
La solución del grafo se busca desde cada inicio hacia aguas abajo, buscando los nodos
predecesores que conforman la ruta más corta (la serie de mínimo costo), hasta llegar a la
descarga.
La precisión del diseño afecta tanto los costos como los tiempos de ejecución del algoritmo,
ya que un diseño más preciso toma un tiempo mucho mayor, pero lleva a costos menores.
Se encontró que en el diseño hidráulico el costo computacional se reduce drásticamente si
se evalúa primero la factibilidad económica antes que la hidráulica, ya que la segunda
consume más tiempo de ejecución por el número de iteraciones que realiza.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
84
7 REFERENCIAS
Afshar, M., 2012. Rebirthing genetic algorithms for storm water networ design. Scientia Iranica,
Transactions A: Civil Engineering 19, pp. 11-19.
Afshar, M. H., Shahidi, M., Rohani, M. & Sargolzaei, M., 2011. Application of cellular automata to sewer
network optimization problems. Scientia Iranica, Transzactions A:Civil Engineering 18, pp. 304-3012.
Ahuja, R. K., Magnanti, T. L. & Orlin, J. B., 1993. Network Flows: Theory, Algorithms, and Applications.
New Jersey: Prentice-Hall.
Anon.,
2013.
Java
(lenguaje
de
programación).
[En
línea]
Available at: http://es.wikipedia.org/wiki/Java_(lenguaje_de_programaci%C3%B3n)
ASCE, A. S. o. C. E., 2007. Gravity Sanitary Sewer: Design and Construction, s.l.: Reston.
Bellman, R., 1956. On a Routing Problem. 20 Diciembre.
Butler, D. & Davies, J. W., 2011. Urban Drainage. Third Edition ed. New York: Spon Press.
CIACUA, 2013. Diseño Optimizado en Redes de Alcantarillado: Desarrollo de Técnicas Computacionales
Exhaustivas para el Diseño Optimizado de Redes de Drenaje Urbano, Bogotá: Universidad de Los
Andes.
Copete, D., 2012. Diseño Hidráulico Optimizado de Redes de Alcantarillado Usando los Conceptos de de
Potencia Unitaria y Pendiente Lógica, Bogotá: Universidad de los Andes.
Dajani, J., Gemmell, R. & Morlok, E., 1972. Optimal design of urban wastewater collection networks.
Journal of the Sanitary Engineering Division 98(6), pp. 853-867.
Duque, N., Duque, D. & Saldarriaga, J., 2015. A new methodology for the optimal design of series of
pipes on sewer systems. Journal of Hydroinformatics, Volumen (Working paper).
Elimam, A., Charalambous, C. & Ghobrial, F., 1989. Optimum design of large sewer networks. Journal
of Environmental Engineering 115(6), pp. 1171-1190.
Goldberg, A. V. & Radzik, T., 1993. A Heuristic improvement of the Bellman-Ford Algorithm. En: Gran
betaña: s.n., pp. 3-6.
Guy, E., Guy, K. & Wolfgang, S., 2005. On network design problems: fixed cost flows and the covering
steiner problem. ACM Transactions on Algorithms, 1(1), pp. 74-101.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
85
Hutson, K. R., Schlosser, T. L. & Shier, D. R., 2011. On the Distributed Bellman-Ford Algorithm and the
Looping Problem. INFORMS Journal on Computing ISSN 1091-9856, Volumen 19, p. 542–551.
Izquierdo, J., Montalvo, I., Pérez, R. & Fuertes, V. S., 2008. Design optimization of wastewater collection
networks by PSO. Computers and Mathematics with Applications, pp. 777-784.
Jiménez, C., 2010. Clase de algorítmica y programación orientada a objetos I. Bogotá, Colombia,
Universidad de los Andes.
Karger, D., 2006. Minimum cost maximum flow, Minimum cost circulation, Cost/Capacity scaling. s.l.,
s.n.
Kulkarni, V. & Khanna, P., 1985. Pumped wastewater collection systems optimization. Journal of
Environmental Engineering 111(5), pp. 589-601.
Larry, J., 2005. An algortihm for the discrete network design problem. Transportation Research Part B,
39(6), pp. 183-199.
López, A., 2012. Diseño Optimizado de Redes de Drenaje Urbano Usando el Concepto de Potencia
Unitaria, Bogotá: Universidad de los Andes.
M. M. I. o. T., 2011. Introduction to Algorithms: Bellman-Ford Algorithm. Massachusetts, s.n.
Moeini, R. & Afshar, M., 2012. Layout and size optimization of sanitary sewer network using intelligent
ants. Advances in Engineering Software 51, pp. 49-62.
Muth, C., Brinson, L. & Bernhar, E., 2010. Inquiry-based exploration of human impacts on stream
ecosystems: The Mud Creek case study, Chapel Hill: University of North Carolina at Chapel Hill .
Navarro, I., 2009. Diseño Optimizado de Redes de Drenaje Urbano, Bogotá: Uniersidad de los Andes.
PAVCO,
2013.
Lista
de
referencia
de
precios
Tubosistemas.
[En
línea]
Available
at:
http://pavco.com.co/files/data/20130926115937_s.pdf
[Último acceso: 05 12 2013].
RAS, 2000. Reglamento Técnico del Sector de Agua Potable y Saneamineto Básico. s.l.:Ministerio de
Desarrollo Económico: Dirección de Agua Potable y Saneamineto Básico.
Salcedo, C., 2012. Diseño optimizado de sistemas de alcantarillado utilizando los conceptos de
resiliencia y potencia unitaria, Bogotá: Universidad de Los Andes.
Saldarriaga, J., 2007. Hidráulica de tuberías: abastecimiento de agua, redes, riegos. Bogotá: Alfaomega.
Saldarriaga, J., 2011. Clase de hidráulica. Bogotá, Universidad de los Andes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
86
Saldarriaga, J., 2013. Clase de Sistemas Integrados de Drenaje Urbano. Bogotá, Colombia, Universidad
de los Andes.
Saldarriaga, J. et al., 2014. Metodología de selección del trazado de una red de drenaje urbano
optimizada,usando el concepto de mínima masa-longitud transportada. SANTIAGO, CHILE,, s.n.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
87
8 ANEXOS
Tabla 8.1 Coeficientes aleatorios para la función de costos de cada tubería.
No. Tubería
(arcos de trazado)
ID Nodo
Coeficientes
𝒊
𝒋
𝒄
𝒊𝒋
𝒂
𝒊𝒋
1
1
2 0.410 0.463
2
1
5 0.964 0.630
3
2
1 0.731 0.375
4
2
3 0.208 0.334
5
2
6 0.947 0.508
6
3
2 0.333 0.443
7
3
4 0.006 0.999
8
3
7 0.397 0.429
9
4
3 0.968 0.504
10
4
8 0.294 0.717
11
5
1 0.940 0.910
12
5
6 0.116 0.209
13
5
9 0.805 0.205
14
6
2 0.937 0.491
15
6
5 0.771 0.173
16
6
7 0.660 0.549
17
6 10 0.523 0.778
18
7
3 0.348 0.308
19
7
6 0.157 0.555
20
7
8 0.140 0.789
21
7 11 0.744 0.225
22
8
4 0.506 0.962
23
8
7 0.378 0.588
24
8 12 0.545 0.836
25
9
5 0.695 0.699
No. Tubería
(arcos de trazado)
ID Nodo
Coeficientes
𝒊
𝒋
𝒄
𝒊𝒋
𝒂
𝒊𝒋
26
9 10 0.205 0.637
27
9 13 0.540 0.723
28
10
6 0.005 0.255
29
10
9 0.577 0.163
30
10 11 0.623 0.009
31
10 14 0.974 0.509
32
11
7 0.142 0.983
33
11 10 0.185 0.631
34
11 12 0.161 0.880
35
11 15 0.395 0.153
36
12
8 0.482 0.804
37
12 11 0.011 0.208
38
12 16 0.432 0.824
39
13
9 0.178 0.707
40
13 14 0.890 0.617
41
14 10 0.245 0.987
42
14 13 0.038 0.482
43
14 15 0.592 0.100
44
15 11 0.218 0.711
45
15 14 0.655 0.617
46
15 16 0.120 0.028
47
16 12 0.233 0.124
48
16 15 0.652 0.591
49
16 17 0.984 0.073
50
17 16 0.207 0.074

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
88
Tabla 8.2. Diseño hidráulico del primer trazado aleatorio.
Tamo
ID Nodo
ID Nodo
Tipo
𝑸
𝒅
𝒅
cota
Cota
𝒔
Costo
($COP)
𝒍
𝒚𝒏/𝒅
𝒚𝒏
𝜽
𝑹
𝑨
𝒗
𝝉
𝑭𝒓
𝒊
𝒋
𝒊
𝒋
1
1
2
I
0.246
0.65
98.14
98.03
0.0011
$ 2 921 502
100
0.696
0.453
3.949
0.192
0.247
0.998
2.074
0.496
2
1
5
I
0.082
0.38
98.42
98.22
0.002
$ 1 822 855
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
3
2
3
C
0.656
0.80
98.03
97.85
0.0018
$ 3 647 217
100
0.822
0.657
4.540
0.243
0.442
1.485
4.298
0.558
4
3
7
C
1.066
1.05
97.85
97.74
0.0011
$ 4 873 219
100
0.847
0.889
4.673
0.319
0.782
1.364
3.438
0.429
5
4
3
I
0.082
0.38
98.42
98.22
0.002
$ 1 822 855
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
6
4
8
I
0.246
0.65
98.14
98.03
0.0011
$ 2 921 502
100
0.696
0.453
3.949
0.192
0.247
0.998
2.074
0.496
7
5
6
C
0.328
0.65
98.22
98.09
0.0013
$ 2 841 806
100
0.838
0.545
4.626
0.197
0.297
1.105
2.519
0.448
8
5
9
I
0.082
0.40
98.39
98.23
0.0016
$ 1 892 045
100
0.689
0.275
3.915
0.118
0.092
0.889
1.850
0.569
9
6
2
I
0.082
0.38
98.42
98.22
0.002
$ 1 822 855
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
10
6
7
C
0.656
0.80
98.09
97.91
0.0018
$ 3 563 901
100
0.822
0.657
4.540
0.243
0.442
1.485
4.298
0.558
11
7
11
C
2.133
1.20
97.74
97.52
0.0022
$ 5 856 544
100
0.838
1.006
4.629
0.365
1.013
2.106
7.868
0.628
12
8
7
I
0.082
0.40
98.39
98.23
0.0016
$ 1 892 045
100
0.689
0.275
3.915
0.118
0.092
0.889
1.850
0.569
13
8
12
C
0.492
0.80
98.03
97.93
0.001
$ 3 591 600
100
0.833
0.667
4.600
0.243
0.448
1.100
2.386
0.405
14
9
10
C
0.820
0.90
98.02
97.87
0.0015
$ 4 019 655
100
0.829
0.746
4.578
0.274
0.564
1.455
4.028
0.509
15
10
6
I
0.082
0.38
98.42
98.22
0.002
$ 1 822 855
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
16
10
11
C
0.984
1.05
97.87
97.75
0.0012
$ 4 845 838
100
0.746
0.784
4.172
0.316
0.693
1.420
3.725
0.520
17
10
14
I
0.082
0.38
98.42
98.22
0.002
$ 1 822 855
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
18
11
15
C
4.348
1.55
97.52
97.25
0.0027
$ 8 201 123
100
0.787
1.220
4.364
0.471
1.593
2.729
12.474
0.778
19
12
11
C
0.902
0.90
97.93
97.75
0.0018
$ 4 183 507
100
0.832
0.748
4.591
0.274
0.565
1.596
4.832
0.556
20
13
9
C
0.410
0.65
98.22
98.02
0.002
$ 2 881 555
100
0.842
0.547
4.646
0.197
0.298
1.376
3.873
0.555
21
14
13
I
0.082
0.38
98.42
98.22
0.002
$ 1 822 855
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
22
14
15
C
0.328
0.65
98.22
98.09
0.0013
$ 2 841 806
100
0.838
0.545
4.626
0.197
0.297
1.105
2.519
0.448
23
15
16
C
5.004
1.30
97.10
96.24
0.0086
$ 8 641 151
100
0.799
1.038
4.422
0.395
1.136
4.403
33.360
1.347
24
16
12
I
0.082
0.40
98.39
98.23
0.0016
$ 1 892 045
100
0.689
0.275
3.915
0.118
0.092
0.889
1.850
0.569
25
16
17
C
5.250
1.30
96.24
95.29
0.0095
$ 11 009 027
100
0.797
1.036
4.413
0.395
1.134
4.629
36.847
1.419
COSTO TOTAL
$ 93 454 222

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
89
Tabla 8.3. Mejor diseño hidráulico de la red tras 100 iteraciones (𝛁
̃ = 𝟏 𝒄𝒎).
Tamo
ID Nodo
ID Nodo
Tipo
𝑸
𝒅
𝒅
cota
Cota
𝒔
Costo
($COP)
𝒍
𝒚𝒏/𝒅
𝒚𝒏
𝜽
𝑹
𝑨
𝒗
𝝉
𝑭𝒓
𝒊
𝒋
𝒊
𝒋
1
1
2
I
0.0820313
0.4
98.39
98.23
0.0016
$ 1 892 045
100
0.689
0.275
3.915
0.118
0.092
0.889
1.850
0.569
2
1
5
I
0.246094
0.65
98.14
98.03
0.0011
$ 2 921 502
100
0.838
0.545
4.626
0.197
0.297
1.105
2.519
0.448
3
2
3
I
0.0820313
0.4
98.39
98.23
0.0016
$ 1 892 045
100
0.822
0.657
4.540
0.243
0.442
1.485
4.298
0.558
4
2
6
C
0.328125
0.65
98.23
98.1
0.0013
$ 2 830 486
100
0.696
0.453
3.949
0.192
0.247
0.998
2.074
0.496
5
3
4
I
0.0820313
0.38
98.42
98.22
0.0020
$ 1 822 855
100
0.833
0.667
4.600
0.243
0.448
1.100
2.386
0.405
6
3
7
C
0.328125
0.65
98.23
98.1
0.0013
$ 2 830 486
100
0.837
0.754
4.622
0.273
0.569
1.298
3.219
0.448
7
4
8
C
0.410156
0.65
98.22
98.02
0.0020
$ 2 881 555
100
0.840
0.882
4.638
0.319
0.777
2.113
8.135
0.671
8
5
6
I
0.0820313
0.38
98.42
98.22
0.0020
$ 1 822 855
100
0.829
1.078
4.578
0.395
1.177
2.161
8.145
0.629
9
5
9
C
0.492188
0.8
98.03
97.93
0.0010
$ 3 591 600
100
0.799
1.038
4.422
0.395
1.137
3.248
18.232
0.993
10
6
7
I
0.0820313
0.38
98.42
98.22
0.0020
$ 1 822 855
100
0.797
1.036
4.413
0.395
1.134
4.629
36.847
1.419
11
6
10
C
0.65625
0.8
98.1
97.92
0.0018
$ 3 550 080
100
0.689
0.275
3.915
0.118
0.092
0.889
1.850
0.569
12
7
8
I
0.0820313
0.38
98.42
98.22
0.0020
$ 1 822 855
100
0.838
0.545
4.626
0.197
0.297
1.105
2.519
0.448
13
7
11
C
0.65625
0.8
98.1
97.92
0.0018
$ 3 550 080
100
0.822
0.657
4.540
0.243
0.442
1.485
4.298
0.558
14
8
12
C
0.820313
0.9
98.02
97.87
0.0015
$ 4 019 655
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
15
9
10
C
0.738281
0.9
97.93
97.81
0.0012
$ 4 136 470
100
0.842
0.547
4.646
0.197
0.298
1.376
3.873
0.555
16
9
13
I
0.0820313
0.4
98.39
98.23
0.0016
$ 1 892 045
100
0.829
0.746
4.578
0.274
0.564
1.455
4.028
0.509
17
10
11
C
1.64062
1.05
97.81
97.55
0.0026
$ 5 084 777
100
0.831
0.873
4.590
0.319
0.769
1.599
4.698
0.516
18
10
14
I
0.0820313
0.38
98.42
98.22
0.0020
$ 1 822 855
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
19
11
12
I
0.0820313
0.38
98.42
98.22
0.0020
$ 1 822 855
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
20
11
15
C
2.54297
1.3
97.55
97.34
0.0021
$ 6 750 058
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
21
12
16
C
1.23047
1.05
97.87
97.72
0.0015
$ 4 873 219
100
0.689
0.275
3.915
0.118
0.092
0.889
1.850
0.569
22
13
14
C
0.410156
0.65
98.23
98.03
0.0020
$ 2 870 178
100
0.842
0.547
4.646
0.197
0.298
1.376
3.873
0.555
23
14
15
C
0.820313
0.9
98.03
97.88
0.0015
$ 4 004 164
100
0.829
0.746
4.578
0.274
0.564
1.455
4.028
0.509
24
15
16
C
3.69141
1.3
97.34
96.87
0.0047
$ 7 562 822
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
25
16
17
C
5.25
1.3
96.87
95.92
0.0095
$ 9 343 633
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
COSTO TOTAL
$ 87 414 034

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
90
Figura 8.1. Trazado del mejor diseño encontrado al utilizar 𝛁
̃ = 𝟏𝟎 𝒄𝒎.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Metodología para el Diseño Optimizado de Redes de Alcantarillado
ICYA4202-201510
Natalia Duque Villarreal
Tesis II
91
Tabla 8.4. Mejor diseño hidráulico de la red tras 100 iteraciones (𝛁
̃ = 𝟏𝟎 𝒄𝒎).
Tamo
ID Nodo
ID Nodo
Tipo
𝑸
𝒅
𝒅
cota
Cota
𝒔
Costo
($COP)
𝒍
𝒚𝒏/𝒅
𝒚𝒏
𝜽
𝑹
𝑨
𝒗
𝝉
𝑭𝒓
𝒊
𝒋
𝒊
𝒋
1
1
5
C
0.410
0.65
98.2
98.0
0.002
$ 2 904 358
100
0.842
0.547
4.646
0.197
0.298
1.376
3.873
0.555
2
2
1
I
0.082
0.38
98.4
98.2
0.002
$ 1 837 744
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
3
2
3
C
0.328
0.65
98.2
98.0
0.002
$ 2 904 358
100
0.687
0.447
3.909
0.191
0.243
1.350
3.754
0.679
4
3
7
C
1.066
0.90
98.0
97.7
0.003
$ 4 167 809
100
0.758
0.682
4.227
0.272
0.517
2.061
8.007
0.803
5
4
3
C
0.410
0.65
98.2
98.0
0.002
$ 2 904 358
100
0.842
0.547
4.646
0.197
0.298
1.376
3.873
0.555
6
5
6
C
0.820
0.90
98.0
97.8
0.002
$ 4 089 610
100
0.723
0.650
4.064
0.269
0.492
1.667
5.280
0.681
7
6
2
I
0.082
0.38
98.4
98.2
0.002
$ 1 837 744
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
8
6
7
C
0.984
1.05
97.8
97.7
0.001
$ 4 955 659
100
0.816
0.856
4.508
0.320
0.756
1.302
3.134
0.431
9
6
10
I
0.082
0.38
98.4
98.2
0.002
$ 1 837 744
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
10
7
11
C
2.461
1.30
97.7
97.5
0.002
$ 6 388 895
100
0.821
1.068
4.538
0.396
1.167
2.109
7.760
0.622
11
8
4
I
0.082
0.38
98.4
98.2
0.002
$ 1 837 744
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
12
8
7
I
0.082
0.38
98.4
98.2
0.002
$ 1 837 744
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
13
8
12
I
0.164
0.50
98.3
98.1
0.002
$ 2 300 851
100
0.685
0.342
3.898
0.147
0.143
1.145
2.884
0.659
14
9
5
I
0.082
0.38
98.4
98.2
0.002
$ 1 837 744
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
15
9
13
C
0.328
0.65
98.2
98.0
0.002
$ 2 904 358
100
0.687
0.447
3.909
0.191
0.243
1.350
3.754
0.679
16
10
9
I
0.082
0.38
98.4
98.2
0.002
$ 1 837 744
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
17
10
11
C
0.410
0.65
98.2
98.0
0.002
$ 2 904 358
100
0.842
0.547
4.646
0.197
0.298
1.376
3.873
0.555
18
11
12
I
0.082
0.38
98.4
98.2
0.002
$ 1 837 744
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
19
11
15
C
3.117
1.30
97.5
97.1
0.004
$ 7 093 306
100
0.737
0.958
4.130
0.391
1.049
2.972
15.332
0.991
20
12
16
C
0.574
0.80
98.1
97.9
0.002
$ 3 563 901
100
0.695
0.556
3.945
0.236
0.373
1.539
4.640
0.690
21
13
14
C
0.656
0.80
98.0
97.8
0.002
$ 3 703 124
100
0.778
0.622
4.320
0.243
0.420
1.564
4.763
0.629
22
14
10
I
0.082
0.38
98.4
98.2
0.002
$ 1 837 744
100
0.699
0.266
3.962
0.113
0.085
0.968
2.208
0.627
23
14
15
C
0.902
0.90
97.8
97.6
0.002
$ 4 405 313
100
0.786
0.707
4.358
0.273
0.536
1.683
5.365
0.631
24
15
16
C
4.348
1.30
97.1
96.4
0.007
$ 8 439 747
100
0.771
1.002
4.285
0.394
1.098
3.961
27.058
1.262
25
16
17
C
5.250
1.30
96.4
95.4
0.010
$ 10 645 858
100
0.777
1.010
4.317
0.394
1.107
4.743
38.698
1.497
COSTO TOTAL
$ 90 815 559

AGRADECIMIENTOS
A mi familia, por su apoyo incondicional y sus enseñanzas a lo largo de toda mi vida,
a mi hermano y co-asesor, por enseñarme nuevas cosas, tenerme paciencia y exigirme al máximo
en la vida y en durante la realización de esta Tesis de Maestría, lo cual me hizo crecer no solo a
nivel académico pero también a nivel personal,
a mi asesor Juan Saldarriaga por su apoyo para lograr el desarrollo de esta Tesis de Maestría y por
su contribución en mi formación profesional y personal,
a Diego Páez y Jorge Huertas por compartir su conocimiento y amistad conmigo, pues sus
sugerencias fueron muy importantes para la realización de este proyecto,
al grupo CIE-AGUA por su colaboración durante este año de investigación.
¡Gracias!
