Diseño y construcción de un modelo para estudiar el comportamiento de resaltos hidráulicos en tuberías

 

 

Universidad de los Andes 

Facultad De Ingeniería 

Departamento de Ingeniería Civil y Ambiental 

 
 
 

 

 

Proyecto de grado de Ingeniería Ambiental  

 
 

Diseño y construcción de un modelo para estudiar el 

comportamiento de resaltos hidráulicos en tuberías parcialmente 

llenas de sección circular, con números de Froude supercríticos 

menores a 4 

 
 

Preparado por: 

Ing. Laura Elizabeth Montaño Luna 

 
 
 

Asesor: 

Ing. Juan Saldarriaga 

 
 

Informe Final Proyecto de grado 

 
 
 
 

Bogotá, Enero 2012 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

I 

 

Tabla de contenido 

Índice de Tablas ............................................................................................................. II

 

Índice de Ilustraciones ................................................................................................... III

 

Índice de Ecuaciones ...................................................................................................... V

 

1.

  Introducción ............................................................................................................. 1 

2.

  Antecedentes........................................................................................................... 4 

3.

  Marco Teórico ........................................................................................................ 35 

3.1.

 

Resaltos Hidráulicos ....................................................................................... 35

 

3.1.1.

 

Definición ................................................................................................ 35

 

3.1.2.

 

Tipos de Resaltos Hidráulicos ................................................................. 37

 

3.1.3.

 

Cálculo de profundidades subsecuentes en el Resalto Hidráulico ......... 38

 

4.

  Diseño del modelo ................................................................................................. 44 

4.1.

 

Ubicación ........................................................................................................ 44

 

4.2.

 

Condiciones Iniciales. ..................................................................................... 44

 

4.3.

 

Elección Tubería ............................................................................................ 45

 

4.3.1.

 

Tubería en acrílico de 400mm ................................................................ 45

 

4.3.2.

 

Selección diámetro de la tubería ............................................................. 48

 

4.3.3.

 

Tubería con diámetro de 250 mm ........................................................... 49

 

5.

  Pruebas de verificación de los parámetros hidráulicos de la tubería .................... 51 

5.1.

 

Comprobación de Diseño ............................................................................... 51

 

5.2.

 

Análisis caudales máximos para diferentes pendientes ................................. 53

 

5.3.

 

Análisis del valor máximo del Número de Froude .......................................... 54

 

6.

  Costos del Proyecto .............................................................................................. 59 

7.

  Construcción y Resultados .................................................................................... 60 

8.

  Conclusiones y Recomendaciones ....................................................................... 68 

9.

  Agradecimientos .................................................................................................... 69 

10.

 

Glosario .............................................................................................................. 70

 

11.

 

Bibliografía ......................................................................................................... 71

 

12.

 

Anexos ............................................................................................................... 72

 

12.1

  Macro realizada en VBA ................................................................................. 73 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

II 

 

Índice de Tablas

 

 

Tabla 1. Valores de k' dependiendo de la relación de llenado (Silvester, 1964). ......... 11

 

Tabla 2. Resultados de números de Froude para diferentes relaciones de llenado cuando 
d

2

 = D (SMITH & CHEN, 1989). .................................................................................... 21

 

Tabla 3. Coeficientes para tuberías circulares horizontales (FHWA, 2006). ................ 34

 

Tabla 4. Tipos de Resaltos Hidráulicos en fondos sin pendiente (Gonzales Rodríguez, 
1992)............................................................................................................................. 37

 

Tabla 5. Medidas del canal. .......................................................................................... 45

 

Tabla 6. Diámetros seleccionados que superen el caudal de diseño y no superen los 48 
cm de altura con relaciones de llenado del 50 %. ........................................................ 51

 

Tabla 7. Diámetros seleccionados que superen el caudal de diseño y no superen los 48 
cm de altura con relaciones de llenado del 85 %. ........................................................ 52

 

Tabla 8.  Diámetros seleccionados que superen el caudal de diseño y no superen los 48 
cm de altura con relaciones de llenado del 92.9 %. ..................................................... 52

 

Tabla 9. Costos del proyecto. ....................................................................................... 59

 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

III 

 

Índice de Ilustraciones 

 

Ilustración 1. Montaje realizado por Kindsvater y Lane (Kindsvater, 1938). ................... 4

 

Ilustración 2. Alturas medidas con caudal variable (Kindsvater, 1938). ......................... 5

 

Ilustración 3. Montaje de Kalinske y Robertson (Robertson & Kalinske, 1943). ............. 6

 

Ilustración 4. Valores críticos experimentales del Número Froude para diferentes 
relaciones de llenado (Robertson & Kalinske, 1943). ..................................................... 7

 

Ilustración 5. Datos típicos de profundidades y presiones en un Resalto Hidráulico 
(Robertson & Kalinske, 1943). ........................................................................................ 8

 

Ilustración 6. Curvas Analíticas para d

2

/d

1

 y F

1 

(Silvester, 1964)

.

 ................................. 12

 

Ilustración 7. Variación diferencia de alturas del resalto vs Longitud (Silvester, 1964).13

 

Ilustración 8. Análisis de Froude vs y2/y1 (Rajaratnam, 1965). ................................... 15

 

Ilustración 9. Diagrama de fuerzas en un Resalto Hidráulico (SMITH & CHEN, 1989).17

 

Ilustración 10. Curvas teóricas para tuberías cuadradas horizontales (SMITH & CHEN, 
1989)............................................................................................................................. 20

 

Ilustración 11. Profundidad subsecuente según el número de Froude (Stahl & Hager, 
1999)............................................................................................................................. 24

 

Ilustración 12. Vista lateral de diferentes resaltos hidráulicos (Stahl & Hager, 1999). . 25

 

Ilustración 13. Vista en perfil de los diferentes tipos de Resalto Hidráulico (Stahl & Hager, 
1999)............................................................................................................................. 26

 

Ilustración 14. Tipos de resaltos hidráulicos generados en los experimentos realizados por 
Hager y Gargano (Gargano & Hager, 2002). ................................................................ 28

 

Ilustración 15. Comparación sumergencia del resalto vs sumersión de la compuerta 
(Ghamry, Shames, & Branch, 2002). ............................................................................ 30

 

Ilustración 16. Cálculo de la longitud del Resalto Hidráulico. (FHWA, 2006). .............. 32

 

Ilustración 17. Determinación de la longitud del resalto para profundidades subsecuentes 
menores al diámetro (FHWA, 2006). ............................................................................ 34

 

Ilustración 18. Resalto Hidráulico (Akan, 2006). ........................................................... 35

 

Ilustración 19. Profundidad subsecuente menor al diámetro de la tubería. (Ghamry, 
Shames, & Branch, 2002). ............................................................................................ 35

 

Ilustración 20. Profundidad subsecuente mayor al diámetro de la tubería. (Ghamry, 
Shames, & Branch, 2002). ............................................................................................ 36

 

Ilustración 21. Tipos de Resaltos Hidráulicos  (Gonzales Rodríguez, 1992). ............... 38

 

Ilustración 22. Diagrama de Momentum en canales circulares (Akan, 2006). ............. 40

 

Ilustración 23. Canal donde su ubicará el montaje. ...................................................... 44

 

Ilustración 24. Soportes de madera para cambiar la pendiente de la tubería. ............. 45

 

Ilustración 25. Medidas tubería de 400 mm y canal. .................................................... 46

 

Ilustración 26. Maqueta con una tubería de 400 mm. .................................................. 47

 

Ilustración 27. Relación del diámetro vs caudal. .......................................................... 49

 

Ilustración 28. Maqueta con un diámetro de 250 mm. .................................................. 50

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

IV 

 

Ilustración 29. Variación del número de Froude respecto a la relación de llenado para 
diferentes pendientes. .................................................................................................. 53

 

Ilustración 30. Variación del caudal respecto a la relación de llenado. ........................ 55

 

Ilustración 31. Variación del número de Froude para diversos caudales. .................... 56

 

Ilustración 32. Variación del número de Froude para diferentes relaciones de llenado.57

 

Ilustración 33. Comparación número de Froude respecto a diferentes relaciones de 
llenado. ......................................................................................................................... 58

 

Ilustración 34. Canal antes y después. ......................................................................... 60

 

Ilustración 35. Compuerta pintada y con el neumático. ................................................ 60

 

Ilustración 36. Fijación del soporte por medio de las chumaceras. .............................. 61

 

Ilustración 37. Vista aguas abajo del soporte. .............................................................. 61

 

Ilustración 38. Vista aguas arriba del soporte. .............................................................. 62

 

Ilustración 39. Vista aguas arriba de la tubería. ........................................................... 63

 

Ilustración 40. Vista aguas abajo de la tubería. ............................................................ 63

 

Ilustración 41. Vista dentro de la tubería. ..................................................................... 64

 

Ilustración 42. Vista de la compuerta con el neumático. .............................................. 64

 

Ilustración 43. Vista de la compuerta en el montaje. .................................................... 65

 

Ilustración 44. Vista perfil de la compuerta. .................................................................. 65

 

Ilustración 45. Vista montaje con agua. ........................................................................ 66

 

Ilustración 46. Vista flujo cuasicrítico en la tubería. ...................................................... 66

 

Ilustración 47. Vista montaje aguas abajo de la tubería. .............................................. 67

 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

V 

 

Índice de Ecuaciones 

 

Ecuación 1. Ecuación para hallar la ecuación de fuerza del resalto (Silvester, 1964). .. 9

 

Ecuación 2. Ecuación para hallar la fuerza del resalto (Silvester, 1964). ....................... 9

 

Ecuación 3. Número de Froude. ..................................................................................... 9

 

Ecuación 4. Proceso para encontrar profundidades subsecuentes. ............................ 10

 

Ecuación 5. Proceso para hallar profundidades subsecuentes. ................................... 10

 

Ecuación 6. Ecuación 5 reorganizada. ......................................................................... 10

 

Ecuación 7. Relación Número de Froude (Silvester, 1964). ......................................... 10

 

Ecuación 8. Número de Froude aguas abajo del resalto. ............................................. 10

 

Ecuación 9. Proceso para encontrar las profundidades subsecuentes en cualquier forma 
de canal. ....................................................................................................................... 10

 

Ecuación 10. Profundidades subsecuentes para cualquier tipo de canal (Silvester, 1964).
 ...................................................................................................................................... 11

 

Ecuación 11.  Valor de la proporción entre la profundidad de llenado y el centro de 
gravedad para tuberías parcialmente llenas (Silvester, 1964). .................................... 11

 

Ecuación 12. Profundidades subsecuentes para tuberías parcialmente llenas (Silvester, 
1964)............................................................................................................................. 11

 

Ecuación 13. Valor de la proporción entre la profundidad de llenado y el centro de 
gravedad para tuberías llenas (Silvester, 1964). .......................................................... 12

 

Ecuación 14. Profundidades subsecuentes para tuberías llenas (Silvester, 1964). ..... 12

 

Ecuación 15. Longitud de un resalto hidráulico para cualquier tipo de sección (Silvester, 
1964)............................................................................................................................. 13

 

Ecuación 16. Cálculo del Momentum en Resaltos Hidráulicos (Rajaratnam, 1965). ... 14

 

Ecuación 17. Conservación del Momentum (Rajaratnam, 1965). ................................ 14

 

Ecuación 18. Conservación del Momentum (Rajaratnam, 1965). ................................ 14

 

Ecuación 19. Ecuación del número de Froude según Rajaratnam (Rajaratnam, 1965).14

 

Ecuación 20. Aproximación número de Froude (French, 2007). .................................. 15

 

Ecuación 21. Cálculo profundidad subsecuente para números de Froude menores a 1.7 
(French, 2007). ............................................................................................................. 16

 

Ecuación 22. Cálculo profundidad subsecuente para números de Froude mayores a 1.7 
(French, 2007). ............................................................................................................. 16

 

Ecuación 23. Ecuación del Momentum aplicada en resaltos Hidráulicos (SMITH & CHEN, 
1989)............................................................................................................................. 16

 

Ecuación 24. Corrección de la ecuación del Momentum para Resaltos Hidráulicos (SMITH 
& CHEN, 1989). ............................................................................................................ 17

 

Ecuación 25. Profundidad de sección aguas arriba del resalto (SMITH & CHEN, 1989).18

 

Ecuación 26. Ecuación aguas abajo del resalto (SMITH & CHEN, 1989). ................... 18

 

Ecuación 27. Número de Froude (SMITH & CHEN, 1989). .......................................... 18

 

Ecuación 28. Profundidad subsecuente aguas abajo del resalto hidráulico. ................ 18

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

VI 

 

Ecuación 29. Reemplazo trigonométrico. ..................................................................... 18

 

Ecuación 30. Profundidad aguas abajo del resalto. ..................................................... 19

 

Ecuación 31. Dimensiones de la altura del resalto (SMITH & CHEN, 1989). ............... 19

 

Ecuación 32. Dimensiones del Resalto Hidráulico en canales cuadrados. .................. 19

 

Ecuación 33. Dimensiones del Resalto Hidráulico en canales cuadrados reorganizada 
(SMITH & CHEN, 1989). ............................................................................................... 19

 

Ecuación 34. Ecuación básica para tuberías cuadradas horizontales (SMITH & CHEN, 
1989)............................................................................................................................. 20

 

Ecuación 35. Número de Froude cuando d

2

 = D (SMITH & CHEN, 1989). .................. 21

 

Ecuación 36. Dimensión del Resalto hidráulico en tuberías cuadradas horizontales con 
d

1

/D constante (SMITH & CHEN, 1989). ...................................................................... 21

 

Ecuación 37. Aproximación del área (Stahl & Hager, 1999). ....................................... 22

 

Ecuación 38. Aproximación Presión (Stahl & Hager, 1999). ........................................ 22

 

Ecuación 39. Ecuación del Momentum (Stahl & Hager, 1999). .................................... 22

 

Ecuación 40. Aproximación del Número de Froude (Hager, 1990). ............................. 22

 

Ecuación 41. Proceso para encontrar la profundidad subsecuente del resalto hidráulico.
 ...................................................................................................................................... 23

 

Ecuación 42. Relación entre las relaciones de llenado aguas arriba y aguas abajo del 
resalto (Stahl & Hager, 1999). ...................................................................................... 23

 

Ecuación 43. Proceso para encontrar la profundidad subsecuente en un resalto hidráulico.
 ...................................................................................................................................... 23

 

Ecuación 44. Profundidad subsecuente en el resalto hidráulico (Stahl & Hager, 1999).23

 

Ecuación 45. Profundidad subsecuente con números de Froude mayores a 2 (Stahl & 
Hager, 1999). ................................................................................................................ 23

 

Ecuación 46. Profundidad subsecuente para números de Froude mayores a 2 (Stahl & 
Hager, 1999). ................................................................................................................ 24

 

Ecuación 47. Relación entre la longitud de recirculación y la profundidad aguas abajo del 
resalto (Stahl & Hager, 1999). ...................................................................................... 27

 

Ecuación 48. Determinación de la longitud de recirculación a partir del número de Froude.
 ...................................................................................................................................... 27

 

Ecuación 49. Relación entre la longitud de aireación y la profundidad aguas abajo del 
resalto (Stahl & Hager, 1999). ...................................................................................... 27

 

Ecuación 50. Determinación de la longitud de aireación a partir del número de Froude 
(Stahl & Hager, 1999). .................................................................................................. 27

 

Ecuación 51. Estimación para resaltos Ondulares Tipo C y D (Gargano & Hager, 2002).
 ...................................................................................................................................... 28

 

Ecuación 52. Sumersión en la compuerta (Ghamry, Shames, & Branch, 2002). ......... 29

 

Ecuación 53. Sumersión (Ghamry, Shames, & Branch, 2002). .................................... 29

 

Ecuación 54. Cálculo Momentum Específico en Canales Rectangulares (Akan, 2006).30

 

Ecuación 55. Procedimiento cálculo altura subsecuente de los resaltos hidráulicos en 
canales rectangulares (Akan, 2006). ............................................................................ 30

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

VII 

 

Ecuación 56. Caudal por unidad de ancho. .................................................................. 31

 

Ecuación 57. Procedimiento cálculo profundidades subsecuentes. ............................. 31

 

Ecuación 58. Conservación de la masa. ...................................................................... 31

 

Ecuación 59. Cálculo velocidad aguas abajo a partir de los parámetros aguas arriba. 31

 

Ecuación 60. Cálculo profundidades subsecuentes en canales rectangulares. ........... 32

 

Ecuación 61. Cálculo profundidad subsecuente para profundidades subsecuentes 
menores al diámetro (FHWA, 2006). ............................................................................ 33

 

Ecuación 62. Cálculo profundidad subsecuente para profundidades subsecuentes 
mayores al diámetro (FHWA, 2006). ............................................................................ 33

 

Ecuación 63. Determinación longitud del resalto cuando la profundidad aguas abajo es 
mayor al diámetro (FHWA, 2006). ................................................................................ 34

 

Ecuación 64. Conservación del Momentum Específico. ............................................... 38

 

Ecuación 65. Profundidad subsecuente en el resalto hidráulico (Stahl & Hager, 1999).41

 

Ecuación 66. Profundidad subsecuente con números de Froude mayores a 2 (Stahl & 
Hager, 1999). ................................................................................................................ 41

 

Ecuación 67. Curva que describe el número de Froude máximo. ................................ 58

 

Ecuación 68. Cálculo disipación de Energía ................................................................ 70

 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

1 

 

1. Introducción 

 

El  resalto  hidráulico  es  un  fenómeno  generado  cuando  la  profundidad  del  flujo  varía 
rápidamente;  es  decir,  cuando  en  un  canal  (abierto  o  cerrado)  existe  un  cambio  de  flujo 
supercrítico  a  subcrítico.  Éste  fenómeno  ocurre  por  la  presencia  de  altas  pendientes  u 
obstáculos (como las compuertas) que generan un aumento importante del flujo aguas abajo, 
afectando las condiciones del flujo aguas arriba. Es importante tener en cuenta que a medida 
que  el  flujo  sea  más  supercrítico,  la  profundidad  subsecuente  del  resalto  será  mayor  y  el 
resalto  tendrá  más  fuerza;  por  el  contrario,  cuando  el  resalto  tiene  una  relación  de  llenado 
más  grande,  la  profundidad  subsecuente  será  muy  similar  y  en  algunos  casos,  no  se  forma 
resalto. 

Las  principales  características  de  un  resalto  hidráulico  son:  las  pérdidas  de  energía,  la 
longitud del resalto y su localización. Las pérdidas de energía son causadas por la turbulencia 
generada  en  el  resalto,  y  se  calculan  como  la  diferencia  de  energía  específica  entre  el  flujo 
aguas abajo del resalto y el flujo aguas arriba. La longitud del resalto se  mide desde el lugar 
donde inicia la turbulencia hasta el lugar donde finaliza: según la literatura encontrada, existen 
relaciones empíricas que permiten encontrar la longitud del resalto hidráulico dependiendo del 
número  de  Froude  y  de  la  altura  del  flujo  aguas  arriba  del  resalto  en  canales  rectangulares, 
trapezoidales,  triangulares  y  en  el  caso  de  tuberías  circulares,  se  encontró  una  ecuación 
empírica en el artículo de Silvester  con un rango de validez muy pequeño, dada la dificultad 
de medir resaltos cuando la tubería se presuriza. Por último, la localización del resalto varía 
de acuerdo al impacto que genere el obstáculo que se encuentre aguas abajo; por lo tanto, es 
una variable que puede ser modificada en el laboratorio.    

En  éste  trabajo  se  enfocará  el  diseño  y  construcción  de  un  modelo  que  permita  investigar, 
analizar  y  generar  resaltos  hidráulicos  en  tuberías  circulares  dada  su  baja  investigación  en 
Colombia y su posible impacto en el fenómeno de sobrecarga en el Sistema de Alcantarillado, 
el cual termina generando inundaciones en las ciudades, además de impactos económicos y 
sociales.  Por  lo  tanto,  el  montaje  estará  enfocado  en  analizar  posibles  parámetros  que 
generen  resaltos  hidráulicos,  razón  por  la  cual  el  diseño  se  enfocará  en  un  modelo  que 
permita la variación de la pendiente, del caudal y de la relación de llenado. Adicionalmente el 
resalto  se  generará  mediante  una  compuerta  ubicada  aguas  abajo,  generando  un  obstáculo 
en el flujo y simulando sobrecarga. 

En el trabajo se mostrarán los antecedentes experimentales que se encuentran en la literatura 
de resaltos hidráulicos en tuberías circulares, partiendo desde el primer experimento realizado 
por Kindsvater en 1938 y en el cuál se basan todas las investigaciones posteriores enfocadas 
en  resaltos  hidráulicos  en  tuberías  circulares.  Luego  se  muestran  estudios  realizados  por 
Silvester,  Hager,  Straub,  entre  otros,  hasta  el  último  análisis  presentado  por  la  Circular  de 
Ingeniería Hidráulica N° 14 del Departamento de Transporte de Estados Unidosen el 2006, en 
donde plantean ecuaciones empíricas y gráficas para determinar profundidades subsecuentes 
y longitudes del resalto. Luego, se realiza una pequeña definición de resaltos hidráulicos, sus 
causas, sus usos y un resumen de las ecuaciones empíricas o teóricas encontradas por todos 
los  investigadores  mencionados  en  los  antecedentes.  Por  último  se  muestra  el  proceso 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

2 

 

constructivo  del  modelo,  con  las  diferentes  modificaciones  que  se  tuvieron  en  cuenta  para 
lograr la construcción de un modelo preciso para el estudio de resaltos hidráulicos en tuberías 
circulares  adaptándose  a  las  condiciones  del  lugar  de  construcción,  los  costos  de 
construcción y los planos del modelo. 

Dado  que  éste  trabajo  se  basa  específicamente  en  el  modelo  constructivo,  se  debe  realizar 
una  tesis  posterior  que  analice  el  modelo  del  resalto  hidráulico  mediante  la  toma  de  datos  y 
elección de condiciones que permitan la formación del resalto, para posteriormente realizar un 
análisis y determinar la importancia de los resaltos sobre el fenómeno de sobrecarga.   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

3 

 

Objetivos 

 

Objetivo General 

 
Diseñar  y  construir  un  modelo  físico  que  genere  resaltos  hidráulicos  en  tuberías  fluyendo 
parcialmente  llenas  de  sección  circular  por  medio  de  la  variación  de  la  pendiente  y  una 
sobrecarga  aguas  abajo,  teniendo  como  restricción  números  de  Froude  menores  a  4.0  y 
relaciones de llenado superiores al 50%. 
 

Objetivos Específicos 

Para  la  construcción  del  modelo  se  requiere  recolectar  información  de  modelos  realizados 
anteriormente  para  el  estudio  de  resaltos  hidráulicos  en  tuberías  de  sección  circular, 
identificando  los  métodos,  instrumentos  y  estudios  realizados,  adquiriendo  así,  información 
suficiente  para  la  instrumentación  del  montaje.  Para  la  determinación  del  diámetro  de  la 
tubería  se  debe  determinar  el  caudal  máximo  que  puede  pasar  por  el  canal  realizando 
comprobaciones de diseño y realizando mediciones que permitan determinar que el diámetro 
de  la  tubería  cumple  con  las  características  físicas  del  canal  teniendo  en  cuenta  los 
accesorios que requiere el montaje. 

Por otra parte, se deben analizar los factores que podrían intervenir en el montaje y pueden 
afectar la construcción y mantenimiento del montaje, así mismo, para visualizar el montaje se 
debe realizar el plano que permita analizar las medidas del montaje, y facilite la construcción 
del mismo, acompañado de la construcción de una maqueta que permita visualizar el montaje 
a escala, permitiendo encontrar posibles problemas en la construcción del montaje. 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

4 

 

2. Antecedentes 

 
 
El proceso para entender la formación y el comportamiento de resaltos hidráulicos en tuberías 
ha sido estudiando experimental y teóricamente. En éste capítulo se mostrarán los diferentes 
estudios que han trabajado algunos investigadores para entender el fenómeno. 
 
Kindsvater y Lane (1938) 
 
El  primer  análisis  de  resaltos  hidráulicos  en  tuberías  circulares  fluyendo  parcialmente  llenas 
fue  realizado  por  Kindsvater  y  Lane  en  el  año  1938,  a  raíz  de  los  estudios  que  se  venían 
realizando de resaltos hidráulicos en canales rectangulares. 

 

 
Kindsvater y Lane, en la Universidad de Iowa, establecieron que la mejor forma para analizar 
el  comportamiento  de  resaltos  hidráulicos  en  tuberías  circulares,  era  mediante  análisis 
experimentales; por lo tanto, para su montaje usaron una tubería transparente de 150 mm de 
diámetro y 6 m de longitud en posición horizontal. Los resaltos hidráulicos los produjeron con 
3 obstrucciones: la primera que ocupaba el 40% del diámetro, la segunda el 60% y la tercera 
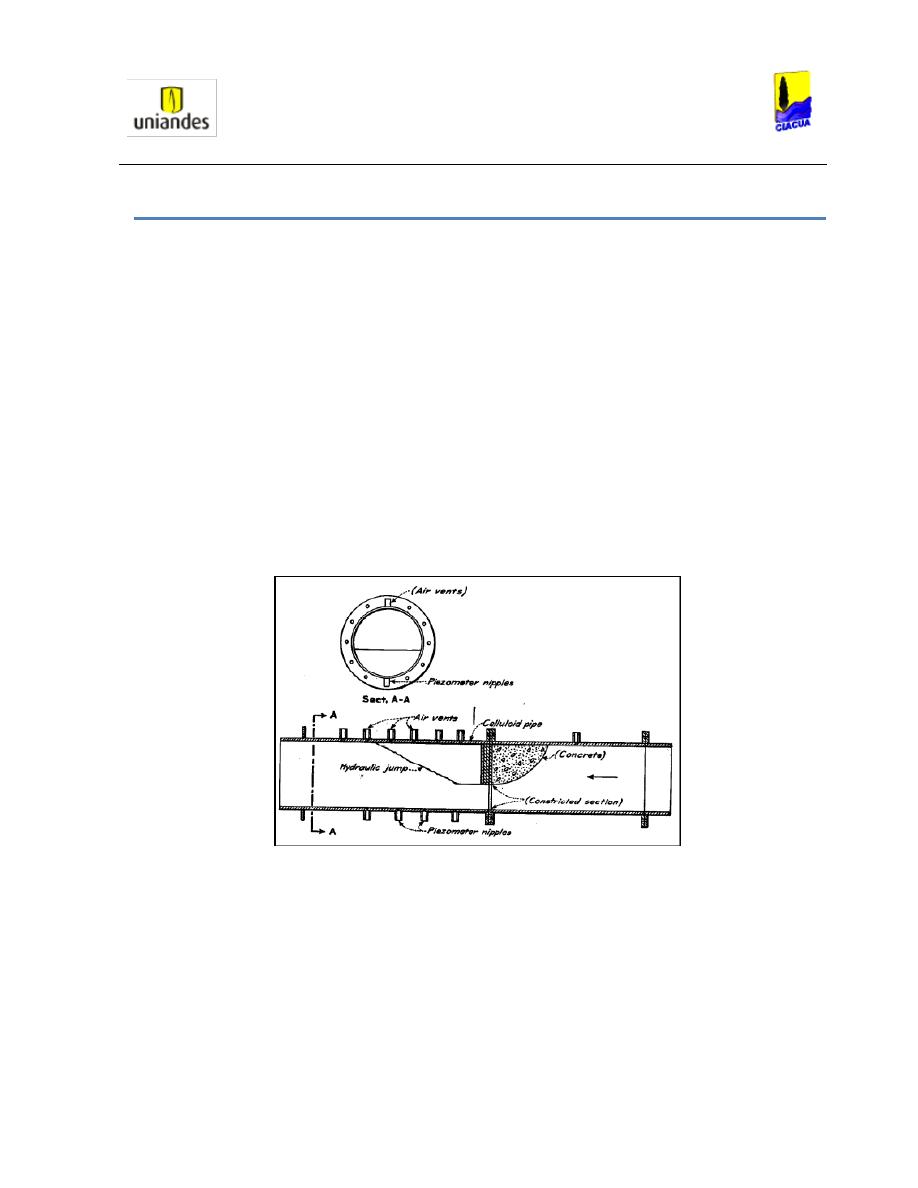
el 80% del diámetro. (Ver Ilustración 1). 
 

 

Ilustración 1. Montaje realizado por Kindsvater y Lane (Kindsvater, 1938). 

 
 
La  variación  del  nivel  del  agua  era  medida  mediante  piezómetros  aguas  abajo  de  las 
constricciones;    por  lo  tanto,  se  podía  analizar  la  variación  de  la  altura  del  resalto  a  medida 
que aumentaba o disminuía el caudal de entrada, y la longitud a la  cual ocurría tal como se 
muestra en la Ilustración 2.  
 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

5 

 

 

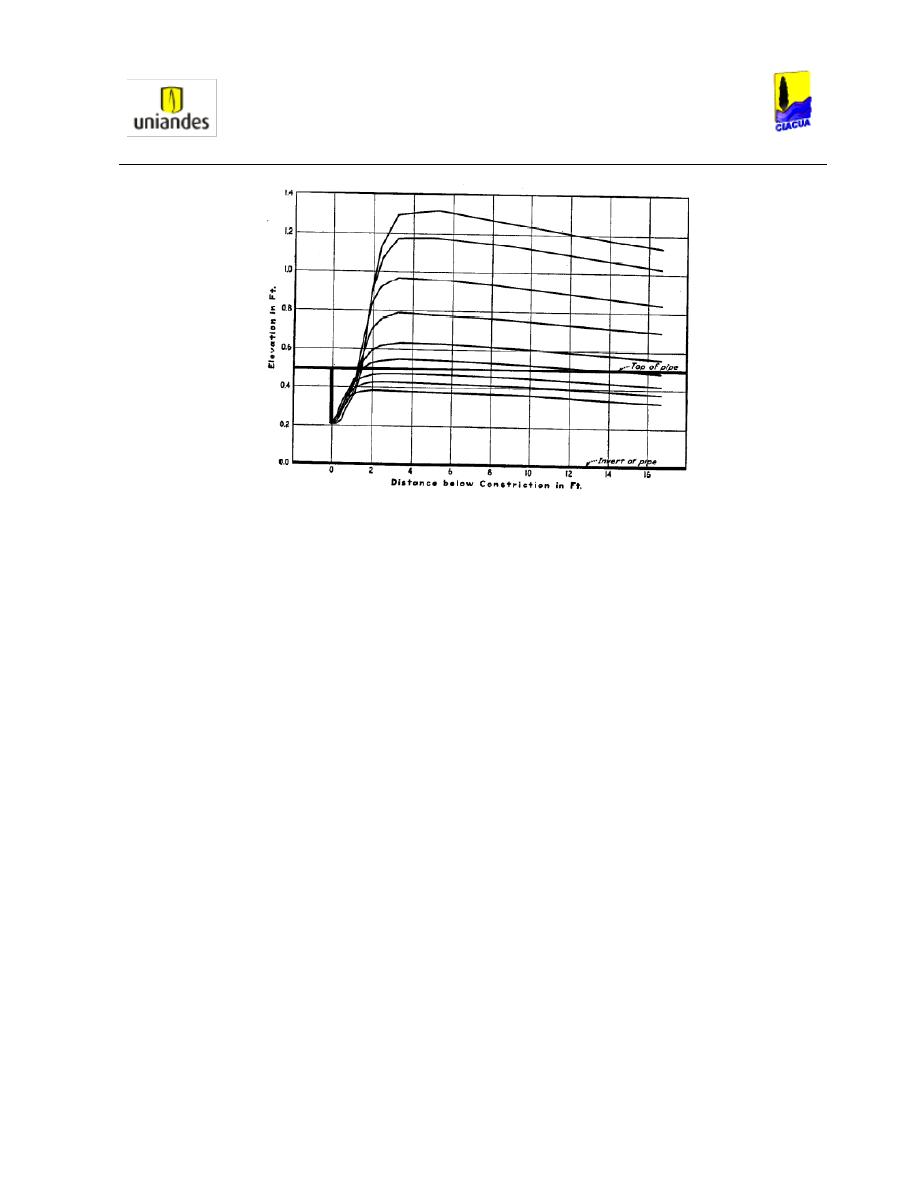
Ilustración 2. Alturas medidas con caudal variable (Kindsvater, 1938). 

 
Kindsvater  y  Lane  concluyeron  que  con  caudales  muy  bajos,  la  tubería  no  se  alcanzaba  a 
presurizar  aguas  abajo  del  resalto;  mientras  que  a  caudales  grandes,  el  resalto  presurizaba 
completamente  la  tubería.  También,  como el  montaje  tenía  ventilación,  el  aire  aumentaba  la 
presión  sobre  la  superficie  del  agua,  lo  cual  hacía  que  el  resalto  se  moviera  hacia  la 
contracción y lo terminara ahogando. 
 
Finalmente, como los análisis de resaltos hidráulicos se basan en la variación del Momentum 
aguas  arriba  y  aguas  abajo  de  la  contracción,  Kindsvater  y  Lane  observaron  que  el 
Momentum era relativamente mayor aguas arriba de la constricción que aguas abajo; a lo que 
argumentaban  la fricción causada por la tubería, la falta de uniformidad de la velocidad aguas 
abajo del resalto y la omisión de las burbujas de agua en los cálculos del Momentum.  
 
Kalinske y Robertson (1943) 
 
Posteriormente, en 1943, Kalinske y Robertson estudiaron la salida de paquetes de aire como 
consecuencia de  la  formación  de  resaltos  hidráulicos  en  tuberías  con  pendiente;  su montaje 
consistió en una tubería de diámetro de 150 mm, y aproximadamente 10 m de longitud; y las 
pendientes que estudiaron  fueron de 0.2%, 2%, 5%, 10%, 20% y 30%. En la Ilustración 3 se 
puede observar el montaje para pendientes del 2% y el 30%. 
 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

6 

 

 

Ilustración 3. Montaje de Kalinske y Robertson (Robertson & Kalinske, 1943). 

 

 
Previo  a  éste  artículo,  Kennison  había  indicado  en 

el  artículo  “The  Design  of  Pipes  Lines” 

publicado  en  la  Revista  Inglesa  N.E.W.W.A.  (New  England  Water  Works  Association)  en 
1933,  que  si  la  pendiente  de  la  tubería  es  menor  a  la  línea  de  gradiente  hidráulico,  las 
burbujas  se  moverán  a  lo  largo  de  la  tubería  sin  ninguna  dificultad.  Por  lo  tanto,  Kalinske  y 
Robertson aplicando este criterio, buscarían en su montaje el aire entrante en las tuberías. 
 
Los  resultados  de  su  estudio  arrojaron  que  la  intensidad  del  resalto  es  dependiente  del 
número de Froude aguas arriba del resalto, de la pendiente, ya que ésta determina la entrada 
de  aire  en  la  tubería  y  finalmente  de  la  relación  de  llenado,  la  cual  va  relacionada 
directamente  con  la  pendiente  de  la  tubería.  Por  lo  tanto,  para  entender  el  comportamiento, 
realizaron una relación entre el caudal de aire que entraba en la tubería (

 

 

) y el Caudal de 

agua  (

 

 

)  y  lo  graficaron  respecto  al  número  de  Froude;  se  observa  que  con  cualquier 

pendiente, mientras mayor es la relación entre los caudales, el número de Froude aumenta.  
 
También  analizaron  que  para  diferentes  relaciones  de  llenado,  existe  un  número  de  Froude 
crítico en dónde la tubería solo transporta parte del aire en el resalto (Ilustración 4): 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

7 

 

 

 

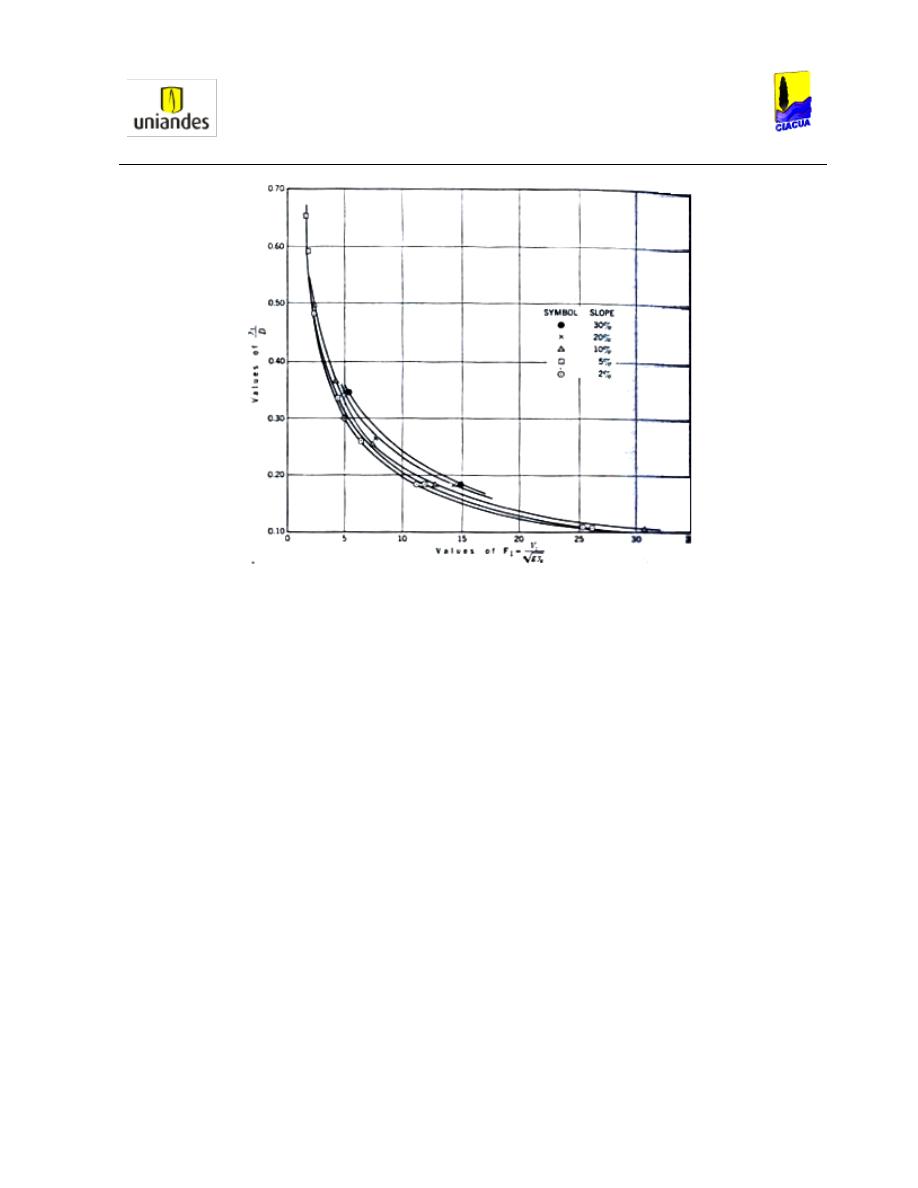
Ilustración 4. Valores críticos experimentales del Número Froude para diferentes relaciones de llenado 

(Robertson & Kalinske, 1943). 

 
En  la  Ilustración  4  se  observa  que  con  un  número  de  Froude  seleccionado,  la  relación  de 
llenado es más alta en la pendiente más alta, y más baja cuando la pendiente es más baja; 
por ejemplo, con un Froude de 10, la pendiente del 2% tiene una relación de llenado cercana 
a  0.19;  con  una  pendiente  del  5%,  la  relación  de  llenado  es  cercana  a  0.21;  con  una 
pendiente del 10%, la relación de llenado es de 0.22; con una pendiente de 20% la relación es 
de  0.24  y con  una  pendiente  del  30%,  la  relación  de  llenado  es  de  0.25.  Además  cuando  la 
pendiente  es  de  2%,  el  número  de  Froude  se  mantiene  constante  en  un  valor  cercano  a  2 
mientras la relación de llenado varía entre 0.58 y 0.68.  
 
Adicionalmente,  en  la  Ilustración  5  se  observan  diferentes  comportamientos  del  flujo  para 
diversos caudales con sus respectivos datos típicos. 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

8 

 

 

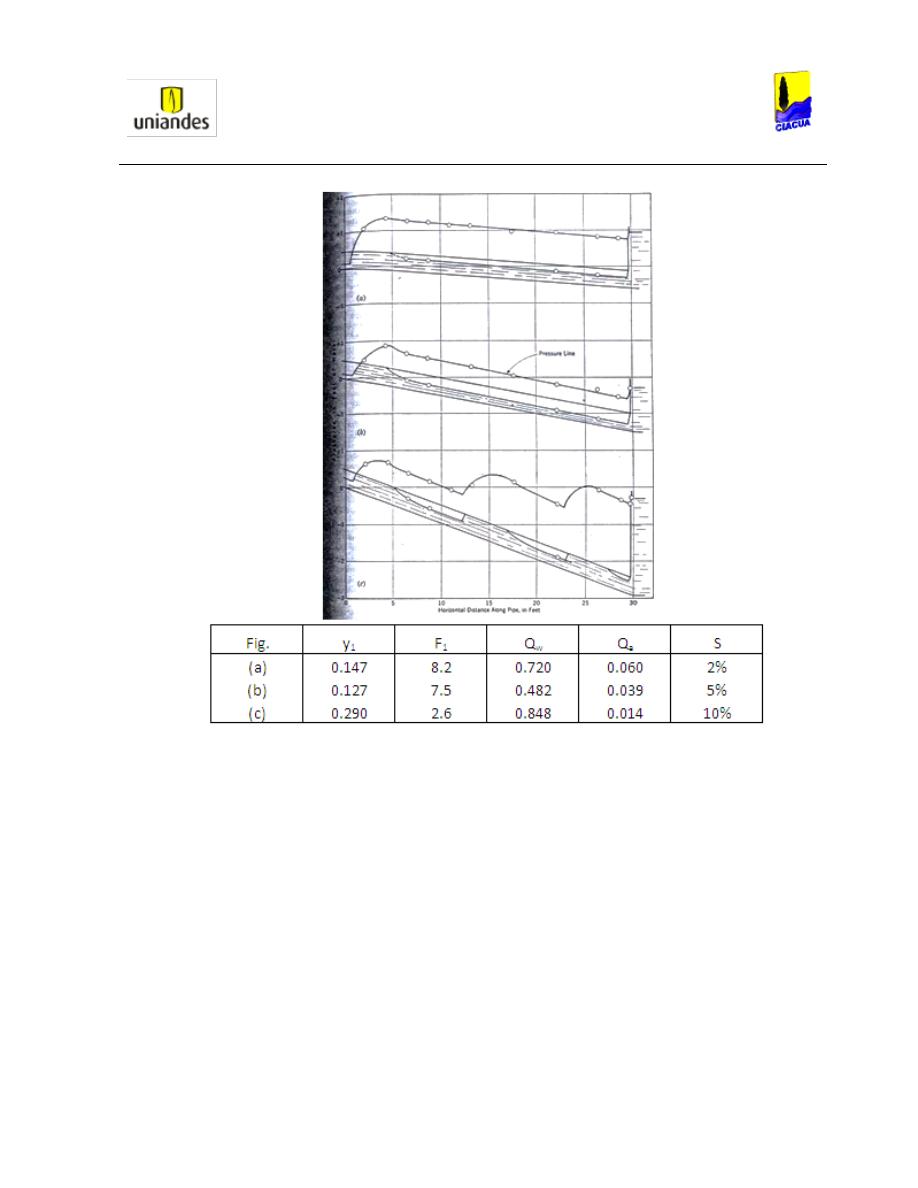
Ilustración 5. Datos típicos de profundidades y presiones en un Resalto Hidráulico (Robertson & Kalinske, 

1943). 

 
En la Ilustración 5 se puede analizar que cuando la pendiente es más alta hay más resaltos. 
Además, según Robertson y Kalinske, con cada resalto hidráulico, la cantidad de presión de 
aire  que  hay  en  la  tubería  aumenta  mientras  el  número  de  Froude  y  la  profundidad 
subsecuente se mantienen constantes, tal como se observa en la Imagen C de la Ilustración 
5,  dónde  la  altura  aguas  abajo  de  cada  uno  de  los  tres  resaltos  tiene  a  tener  un  valor 
constante.  También Robertson y Kalinske observan que cuando la profundidad aguas arriba 
del  primer  resalto  es  menor  que  la  profundidad  aguas  arriba  del  segundo  resalto,  el  primer 
resalto entregará mayor cantidad de aire a la segunda profundidad y por lo tanto la separación 
entre  estos  dos  resaltos  será  mayor.  Mientras  que  cuando  la  profundidad  aguas  arriba  del 
segundo  resalto  es  mayor  a  la  profundidad  del  primer  resalto,  el  primer  resalto  entregará 
menor cantidad de aire y se encontrarán a menor distancia. 
 
 
 
 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

9 

 

Richard Silvester (1964) 
 
En el año 1964, Richard Silvester realizó un análisis de resaltos hidráulicos que se formaban 
en  cualquier  tipo  de  canal  horizontal  (rectangular,  triangular,  parabólico,  circular  y  trapecial). 
El planteó que las características principales para cualquier disipador de energía  (incluido el 
resalto  hidráulico),  son  el  radio  de  las  profundidades  subsecuentes,  la  energía  perdida  y  la 
longitud del resalto. 
 
En  cuanto  a  las  profundidades  subsecuentes,  se  debe  tener  en  cuenta  el  radio,  la  relación 
entre  las  profundidades  (d1/d2),  el  caudal,  y  para  tuberías  circulares,  el  centro  de  gravedad 
del agua. Silvester incluye en su artículo la ecuación de fuerza del resalto para cualquier tipo 
de canal horizontal (Ver Ecuación 1): 
 

 

 

 

 

 

 

 

   

 

 

 

 

 

 

   

 

 

 

     

 

 

 

 

 

 

 

  

Ecuación 1. Ecuación para hallar la ecuación de fuerza del resalto (Silvester, 1964). 

dónde: 

 

 

= Área de la sección de agua 

 

 

= Proporción de la profundidad al centro de gravedad del canal circular 

 = Caudal 

 = Gravedad 

La Ecuación 1 puede escribirse como: 

 

 

 

 

 

 

 

   

 

 

 

 

 

 

   

 

 

  

 

 

 

 

  

 

  

Ecuación 2. Ecuación para hallar la fuerza del resalto (Silvester, 1964). 

 

También se conoce que el número de Froude es (Ver Ecuación 3): 

 

 

 

 

 

 

 

  

 

Ecuación 3. Número de Froude. 

dónde: 

 = Número de Froude 

 = Profundidad de sección 

 
 
 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

10 

 

Por lo tanto, se puede inferir que: 
 

 

 

    

  

 

   

 

 

  

 

 

 

  

 

Ecuación 4. Proceso para encontrar profundidades subsecuentes.

 

 
Luego, reemplazando la Ecuación 4 en la Ecuación 2, se tiene que: 
 

 

 

 

 

 

 

 

   

 

 

 

 

 

 

   

 

 

 

 

 

 

     

 

 

 

 

 

 

 

Ecuación 5. Proceso para hallar profundidades subsecuentes. 

 
La Ecuación 5 se puede reescribir como: 
 

 

 

 

 

 

 

 

     

 

 

 

 

 

 

   

 

 

 

 

 

 

     

 

 

 

 

 

 

 

Ecuación 6. Ecuación 5 reorganizada. 

 

Por otra parte, la relación entre el número de Froude aguas abajo del resalto sobre el número 
de Froude aguas arriba del resalto se muestra en la Ecuación 7: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ecuación 7. Relación Número de Froude (Silvester, 1964). 

 

 Y si se despeja el número de Froude aguas abajo del resalto: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ecuación 8. Número de Froude aguas abajo del resalto. 

 

Entonces, reemplazando la Ecuación 8 en la Ecuación 6: 

 

 

 

 

 

 

 

     

 

 

 

 

 

 

   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  

 

 

 

 

 

 

 

     

 

 

 

 

 

 

   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  

 

 

 

 

 

 

 

 

     

 

 

 

 

 

 

   

 

 

 

 

 

 

    

 

 

 

 

 

 

Ecuación 9. Proceso para encontrar las profundidades subsecuentes en cualquier forma de canal. 

 
 
 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

11 

 

Y  para  encontrar  las  profundidades  subsecuentes,  se  divide  la  Ecuación  9  por  el  Área  y  la 
profundidad de sección aguas arriba del resalto (

 

 

   

 

 : 

 

 

 

 

  

 

 

 

 

 

 

 

 

     

 

 

     

 

 

    

 

 

 

 

   

 

Ecuación 10. Profundidades subsecuentes para cualquier tipo de canal (Silvester, 1964). 

 
Cómo en tuberías circulares la profundidad subsecuente puede tener dos condiciones (mayor 
o menor al diámetro), el cálculo de ésta profundidad se divide en dos casos: 
 
Tubería Parcialmente Llena:   
 
Cuando la tubería está parcialmente llena, la proporción de la profundidad del agua al centro 
de gravedad (

    es variable, y se calcula con la Ecuación 11: 

 

 

 

      

 
 

 

 

 

       

 

 

 

 
 

   

 

 

 

 
 

 

  

 

 

Ecuación 11.  Valor de la proporción entre la profundidad de llenado y el centro de gravedad para tuberías 

parcialmente llenas (Silvester, 1964). 

 
dónde:  
 
 

 

= Proporción de la profundidad del flujo respecto al centro de gravedad 

  = Diámetro de la tubería 
 = Profundidad de sección 
 = Área de los segmentos del agua 
 
Y los respectivos valores de k para diferentes profundidades de llenado son: 
 

Tabla 1. Valores de k' dependiendo de la relación de llenado (Silvester, 1964). 

 

d/D 

0.1 

0.2 

0.3 

0.4 

0.5 

0.6 

0.7 

0.8 

0.9 

1 

k' 

0.41 

0.413  0.416  0.419  0.424  0.432  0.445  0.462  0.473  0.5 

 
Finalmente, reemplazando la Ecuación 11 en la Ecuación 10 se tiene que: 
 

 

 

 

 

 

 

 

 

 

 

 

     

 

 

   

 

 

    

 

 

 

 

   

Ecuación 12. Profundidades subsecuentes para tuberías parcialmente llenas (Silvester, 1964). 

 

 
 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

12 

 

Tubería Llena 
 
En aquellas tuberías que quedan presurizadas luego de un resalto hidráulico, la ecuación de 
la  proporción  entre  la  profundidad  de  llenado  y  el  centro  de  gravedad  se  calcula  con  la 
Ecuación 13

.

 

 

 

 

 

 

  

 

 

 

 

 

 

 

 

Ecuación 13. Valor de la proporción entre la profundidad de llenado y el centro de gravedad para tuberías 

llenas (Silvester, 1964). 

 
Y reemplazando la Ecuación 13 en la Ecuación 10 se tiene que: 
 

 

 

 

 

 

 

 

 

 

 
 

 

 

 

 

 

 

 

     

 

 

   

 

 

    

 

 

 

 

  

 

Ecuación 14. Profundidades subsecuentes para tuberías llenas (Silvester, 1964). 

 
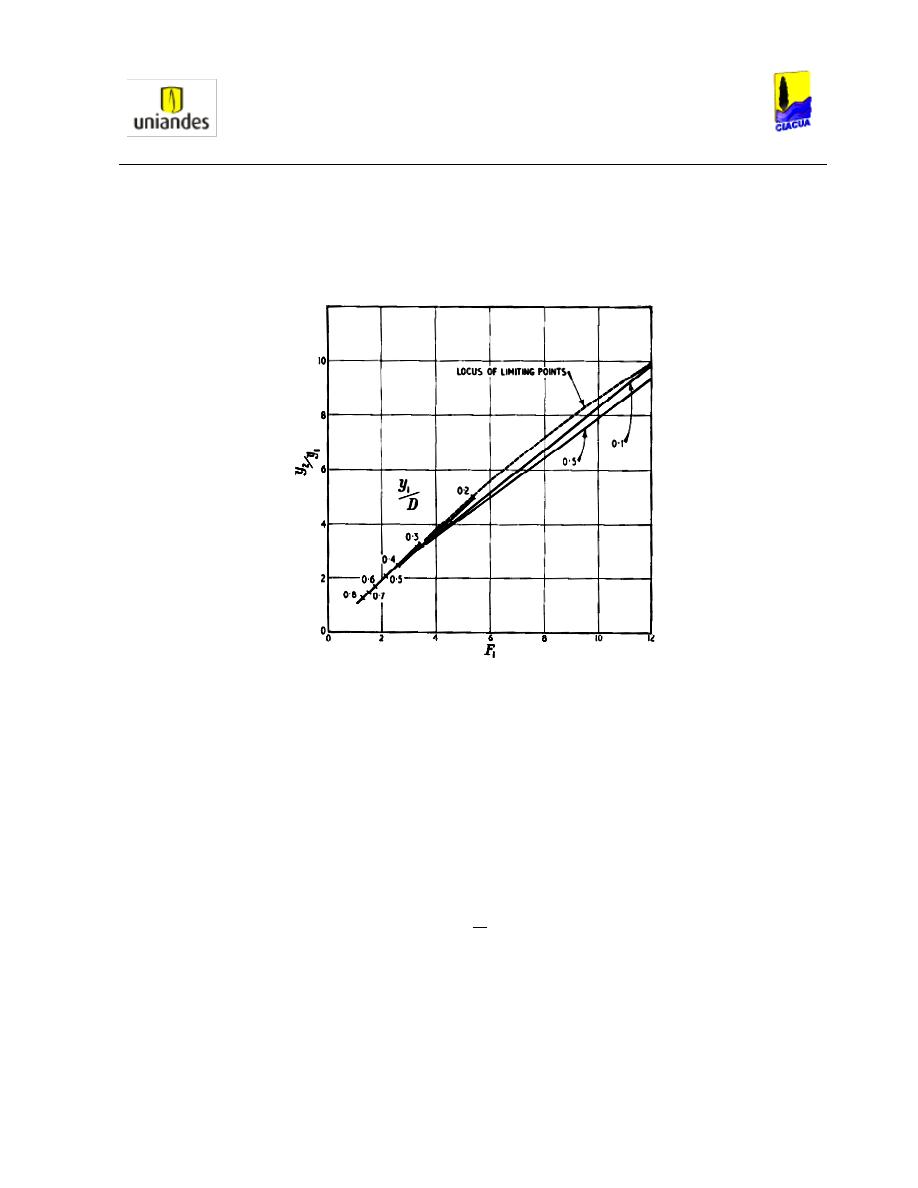
Luego, Silvester en su artículo, muestra un diagrama en el cual compara el valor del número 
de  Froude  respecto  a  la  profundidad  de  llenado  en  diferentes  tipos  de  secciones  (Ver 
Ilustración 6): 
 

 

Ilustración 6. Curvas Analíticas para d

2

/d

1

 y F

1 

(Silvester, 1964)

. 

 

En  la  Ilustración  6  se  puede  observar  que  en  tuberías  circulares,  para  relaciones de  llenado 
bajas  aguas  arriba  del  resalto  (d1/D  =  0.2),  el  número  de  Froude  es  más  alto  que  para 
relaciones  de  llenado  altas  (d1/D  =  0.6).  También  se  puede  observar  que  cuando  la  tubería 
fluye parcialmente llena luego del resalto hidráulico, existe una región válida de resultados, la 
cual se va incrementando a medida que aumenta la relación d2/d1. Otro aspecto importante 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

13 

 

que se debe considerar, es que la relación de llenado del 20% presenta el Froude más alto, el 
cual se va aproximando a  8. 
 
Adicionalmente,  Silvester  fue  el  primero  investigador  que  aproximó  una  ecuación  para hallar 
la longitud del resalto hidráulico en tuberías circulares, teniendo como parámetros L/d1, L/d2, 
y  L/(d2 

–  d1).  Por  lo  tanto,  para    comparar  las  longitudes  en  la  tubería,  Silvester  tomó  el 

experimento  realizado  por  Kindsvater  en  1934,  y  supuso  las  longitudes  como  la  distancia 
entre  el inicio  del  resalto, hasta  el punto dónde la altura  aguas abajo  alcanzaba un máximo, 
teniendo en cuenta las pérdidas por fricción. 
 
Su aproximación se basó en usar la Ecuación 15 y adaptarla para cada tipo de sección. 

 

 

 

      

 

    

 

 

 

Ecuación 15. Longitud de un resalto hidráulico para cualquier tipo de sección (Silvester, 1964). 

 
dónde: 
 
   

 

: Relación entre la longitud y la altura aguas arriba del resalto. Depende de la sección del 

canal 
 : Constante determinada experimentalmente según la sección del canal   

 : Se determina por la relación 

  
  

  

 

 

  

  

 
En  tuberías  circulares,  la  longitud  del  resalto  se  determinó  por  el  experimento  realizado  por 
Kindsvater en 1934, con el cual, Silvester adaptó las mediciones y graficó la Ilustración 7:  
 

 

Ilustración 7. Variación diferencia de alturas del resalto vs Longitud (Silvester, 1964). 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

14 

 

En la Ilustración 7 se puede observar que a medida que aumenta la relación de llenado aguas 
arriba  del  resalto,  la  longitud  del  resalto  es  menor;  esto  puede  ir  relacionado  conjuntamente 
con la disminución del número de Froude a medida que disminuye la relación de llenado (Ver 
Ilustración  6).  Esto  ocurre  porque  cuando  hay  menor  relación  de  llenado,  la  velocidad 
aumenta  por  lo  cual  el  número  de  Froude  aumenta,  haciendo  que  el  resalto  adquiera  más 
fuerza y se aumente la longitud.  

Rajaratnam (1965) 

En 1965, Rajaratnam realizó un nuevo análisis de resaltos hidráulicos en tuberías de sección 
exponencial  y  circular  para  canales  horizontales.  Su  análisis  de  basó  nuevamente  en  las 
conclusiones dadas por Kindsvater (1938), y el análisis realizado por Kalinske (1943) para las 
masas de aire que salen por la tubería luego de un resalto hidráulico.  

Por lo tanto, teniendo en cuenta el análisis de Momentum mediante la Ecuación 16: 

            

 

    

  

 

 

 

 

  

 

 

Ecuación 16. Cálculo del Momentum en Resaltos Hidráulicos (Rajaratnam, 1965). 

 

dónde: 
 
 : Peso específico del agua 
 : Presión 
   Momentum 
     : Son funciones de la relación de llenado aguas arriba (y1/D) 
 : Diámetro de la tubería 
 

 : Caudal 

 : Altura en el punto de medición 
 
Y conociendo que el Momentum se conserva (Ver Ecuación 17): 

 

 

 

     

 

   

 

     

 

 

Ecuación 17. Conservación del Momentum (Rajaratnam, 1965). 

 
Se reemplaza la Ecuación 17 en la Ecuación 16 y se simplifica: 
 

   

 

 

 

 

 

 

 

 

 

 

 

 

   

 

 

 

 

 

 

 

 

 

 

 

       

Ecuación 18. Conservación del Momentum (Rajaratnam, 1965). 

 
Tomando Froude como: 
 

 

 

 

 

 

 

  

 

 

 

  

Ecuación 19. Ecuación del número de Froude según Rajaratnam (Rajaratnam, 1965). 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

15 

 

 
Y conociendo que 

 

 

 y 

 

 

 son funciones de 

 

 

  . 

 
A  partir  de  la  Ecuación  18,  Rajaratnam  estableció  una  gráfica  con  relaciones  de  llenado 
inferiores  a  0.8  (Ver  Ilustración  8),  ya  que  en  el  análisis,  Rajaratnam  observó  que  para 
relaciones de llenado superiores a 0.8, el comportamiento del flujo no permite ningún análisis  

 

Ilustración 8. Análisis de Froude vs y2/y1 (Rajaratnam, 1965). 

 

En  la  Ilustración  8,  Rajaratnam  analiza  que  cuando  el  número  de  Froude  llega 
aproximadamente a 3, las curvas de las diferentes relaciones de llenado empiezan a diverger, 
y sus límites se encuentran entre las relaciones de llenado de 0.2 y 0.5. 
 
Straub (1978) 
 
En  1978,  Straub  planteó  las  siguientes  ecuaciones  para  determinar  las  profundidades 
subsecuentes en resaltos hidráulicos. 
 
Primero aproxima el número de Froude aguas arriba del resalto mediante la Ecuación 20: 
 

 

 

   

 

 

 

 

 

    

 

Ecuación 20. Aproximación número de Froude (French, 2007). 

 
dónde: 
 

 

: Número de Froude aguas arriba del resalto [-] 

 

 

: Profundidad crítica [m] 

 

 

: Profundidad aguas arriba del resalto [m] 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

16 

 

Luego realiza dos aproximaciones de la profundidad subsecuente con base en el número de 
Froude, dependiendo si el número de Froude es menor a 1.7 o mayor. 

Cuando el número de Froude es menor a 1.7, la profundidad subsecuente es calculada como: 

 

 

 

 

 

 

 

 

 

Ecuación 21. Cálculo profundidad subsecuente para números de Froude menores a 1.7 (French, 2007). 

 

Y cuando el número de Froude es mayor a 1.7: 

 

 

 

 

 

   

 

 

    

 

Ecuación 22. Cálculo profundidad subsecuente para números de Froude mayores a 1.7 (French, 2007). 

 
 
Smith y Chen (1989) 
 
Posteriormente, en 1989, se realizó un artículo de resaltos hidráulicos en tuberías cuadradas 
con pendientes altas, desarrollado por C. D. Smith y Wentao Chen. Su artículo destaca que la 
formación de un resalto hidráulico ocurre cuando aguas arriba la altura del agua es menor que 
la profundidad crítica en la tubería, y la línea de gradiente hidráulico aguas abajo de la tubería 
es mayor que la cota clave de la tubería. Además destacan que la velocidad del flujo aguas 
abajo de la tubería es menor a la velocidad del flujo aguas arriba.  
 
Luego, se realiza una comparación entre resaltos hidráulicos generados a superficie libre y a 
presión,  analizando  que  cuando  el  resalto  ocurre  en  tuberías  a  presión,  el  resalto  se  forma 
más violentamente y a mayor presión. Y cómo las presiones verticales del flujo siguen igual, 
el  incremento  de  las  presiones  se  observa  en  la  magnitud  horizontal  del  resalto,  lo  cual 
permite tener parámetros de seguridad al construir estructuras que puedan presentar resaltos 
hidráulicos, las cuales deben construirse más largas para evitar fallas. 
 
Tal como se ha explicado en las anteriores teorías, el análisis del resalto hidráulico inicia se 
análisis a partir de la ecuación de Momentum: 

 

 

 

   

 

            

 

   

 

   

 

 

Ecuación 23. Ecuación del Momentum aplicada en resaltos Hidráulicos (SMITH & CHEN, 1989). 

 

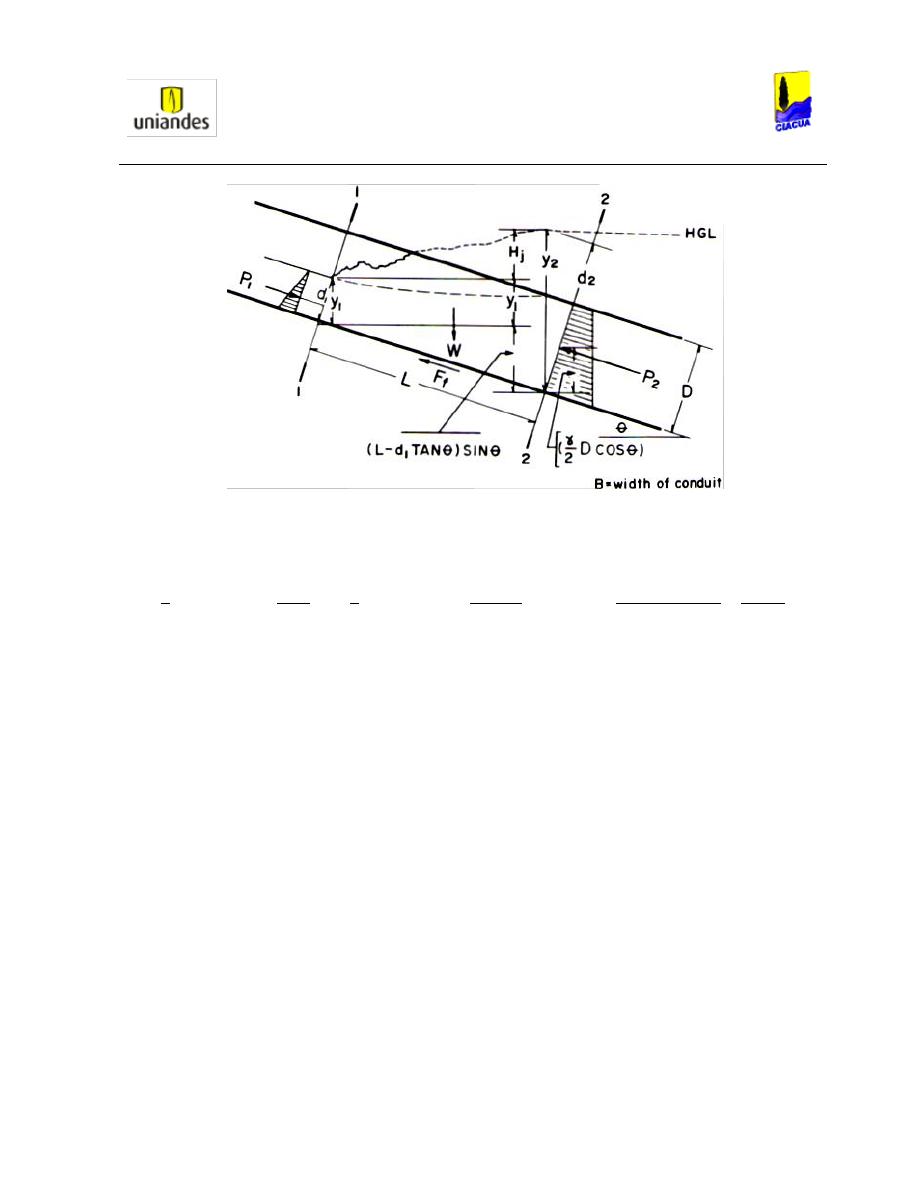
La Ecuación 23 surge de la Ilustración  9, dónde se muestran todas las fuerzas involucradas 
en  un  Resalto  Hidráulico.  Las  fuerzas  involucradas  son:  Fuerzas  de  presión,  fuerza 
gravitacional  y  fuerzas  de  fricción  (asociadas  con  el  esfuerzo  cortante).  Por  lo  tanto,  para 
analizar  la  variación  de  Momentum  en  el  resalto,  se  realiza  una  sumatoria  de  fuerzas  en  la 
parte izquierda de la igualdad. 
 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

17 

 

 

 

Ilustración 9. Diagrama de fuerzas en un Resalto Hidráulico (SMITH & CHEN, 1989). 

 
Cómo  en  el  resalto  hidráulico  existe  entrada  de  aire  y  la  distribución  de  la  velocidad  es  no 
uniforme, Smith y Chen realizan una corrección a la Ecuación 23: 
 

 
 

   

 

 

           

 

    

 

 

 

 
 

             

     

     

 

        

 

 

 

 

  

 

      

 

 

   

 

 

 

  

 

   

 

 

Ecuación 24. Corrección de la ecuación del Momentum para Resaltos Hidráulicos (SMITH & CHEN, 1989). 

 
dónde: 
 
 

 

    

 

: Factores de corrección del Momentum causados por la distribución no uniforme de la 

velocidad. 
 : Peso específico del agua 
 : Caudal de entrada 
 

 

: Relación aire 

– agua en causada por la entrada de aire aguas abajo del resalto 

 

 

: Relación aire 

– agua en el resalto 

 : Ancho del canal 
 : Alto del canal 
 : Longitud del resalto 
 

 

: Altura aguas arriba del resalto 

 

 

: Altura aguas abajo del resalto 

 : Factor de corrección menor a uno para corregir cuando el volumen del resalto es menor 
que BDL (Ancho * Alto*Longitud) 
 : Ángulo de la pendiente 
 

 

: Fuerza de fricción a lo largo del resalto 

 : Gravedad 
 
Además,  Smith  y  Chen  destacan  que  el  factor  de  corrección 

 

 

  debe  ser  mayor  al  factor  de 

corrección 

 

 

, porque el aire cuando finaliza el resalto puede escapar a la atmósfera. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

18 

 

 
Además, con la Ilustración 9 se puede observar que: 
 

 

 

 

 

 

    

 

Ecuación 25. Profundidad de sección aguas arriba del resalto (SMITH & CHEN, 1989).

 

 
y: 

 

 

 

 

 

    

 

Ecuación 26. Ecuación aguas abajo del resalto (SMITH & CHEN, 1989). 

 
Luego,  realizando  un  proceso  similar  al  realizado  por  Silvester  para  encontrar  las 
profundidades subsecuentes, despejaremos la profundidad aguas abajo del resalto: 
 

 

 

   

  

 

  

 

        

 

 

   

 

 

 

  

 

   

 

 

 
 

  

 

 

        

 

 

     

       

 

      

    

 

     

    

   

  

 
 
Factorizando D: 
 
 

 

 

      

  

 

  

 

        

 

 

   

 

 

 

 

  

 

   

 

 

 

 

  

  

 

 

      

 

 

 

 

    

       

 

      

   

 

     

    

   

 

  

 

 
Y reemplazando el número de Froude para tuberías cuadradas (Ver Ecuación 27) y dividiendo 
entre 

   

 

 se obtiene la Ecuación 28:  

 

  

 

 

 

 

 

 

 

 

 

 

  

 

 

Ecuación 27. Número de Froude (SMITH & CHEN, 1989).

 

 

 

 

       

 

  

 

 

 

 

 

 

 

 

   

 

  

 

 

 

 

 

 

 

 

        

 

         

 
 

  

 

 

 

 

 

        

 

       

 

 

 

        

 

 

        

 

 

 

 

 

   

 

   

Ecuación 28. Profundidad subsecuente aguas abajo del resalto hidráulico. 

 
 
Y reemplazando: 

                   

 

  

 

Ecuación 29. Reemplazo trigonométrico. 

 
 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

19 

 

 
Por lo tanto, reemplazando la Ecuación 28  y la Ecuación 29 en la Ecuación 26: 

 

 

 

       

 

  

 

 

 

 

 

 

 

 

   

 

  

 

 

 

 

 

 

 

 

      

 

    

 
 

  

 

 

 

 

 

               

 

 

 

        

      

 

 

 

 

 

   

 

   

Ecuación 30. Profundidad aguas abajo del resalto. 

 
Por otra parte,  la altura del resalto puede ser calculada mediante la Ecuación 31:

 

 

 

 

 

 

 

 

 

  

 

   

 

        

 

           

Ecuación 31. Dimensiones de la altura del resalto (SMITH & CHEN, 1989). 

 
Por lo tanto, reemplazando la Ecuación 25 y la Ecuación 30 en la Ecuación 31 se tiene que: 
 

 

 

 

 

 

 

      

 

  

 

 

 

 

 

 

 

 

   

 

  

 

 

 

 

 

 

 

 

      

 

    

 
 

  

 

 

 

 

 

               

 

 

 

        

      

 

 

 

 

 

   

 

       

 

 

    

         

 

             

 

Factorizando 

  

 

 

,

 

 

 

 

   y  conociendo  que                

 

        entonces  se  tiene  la 

Ecuación 32: 

 

 

 

 

 

 

 

   

 

 

 

 

 

 

  

 

   

 

 

 

 

 

          

 

            

 

       

 

    

   

 
 

 

 

      

 

 

 

 

 

 

 

 

 

 

   

 

 

       

 

      

 

 

   

 

 

Ecuación 32. Dimensiones del Resalto Hidráulico en canales cuadrados. 

 
Y reorganizando para obtener la ecuación dada por Smith y Chen: 
 

 

 

 

    

 

 

 

 

 

 

 

 

  

 

   

 

 

 

 

        

 

     

 
 

 

 

 

  

 

 

 

   

 

 

 

 

     

 

   

 

 

     

 

         

 

 

 

 

 

     

 

           

 

 

   

 

 

Ecuación 33. Dimensiones del Resalto Hidráulico en canales cuadrados reorganizada (SMITH & CHEN, 

1989). 

 
Pero,  así  se  desprecie  el  valor  de  las  fuerzas  por  fricción  (

 

 

 ,  y  tomando  los  valores  de 

corrección  de  la  distribución  de  velocidad  (

 

 

  y 

 

 

   como  uno,  no  se  puede  resolver  la 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

20 

 

Ecuación 33 porque se tienen 5 incógnitas (

 

 

   

 

   

 

       ), lo que hace que la solución de las 

dimensiones del resalto sea determinada empíricamente. 
 
Por lo tanto, la ecuación básica en tuberías cuadradas horizontales  supone que 

 

 

     

 

    

y

 

 

     

 

   ,  las  fuerzas  de  fricción  son  despreciables,  además  como  la  tubería  está 

horizontal 

     : 

 

         

         

 

   

 

 

     

 

       

 
Por lo tanto la Ecuación 33 se reduce en: 

 

 

 

 

    

 

 

 

 

 

 

 

 

    

 

 

 

   

 
 

 

 

 

  

 

 

 

   

 

 

 

 

     

Ecuación 34. Ecuación básica para tuberías cuadradas horizontales (SMITH & CHEN, 1989). 

 
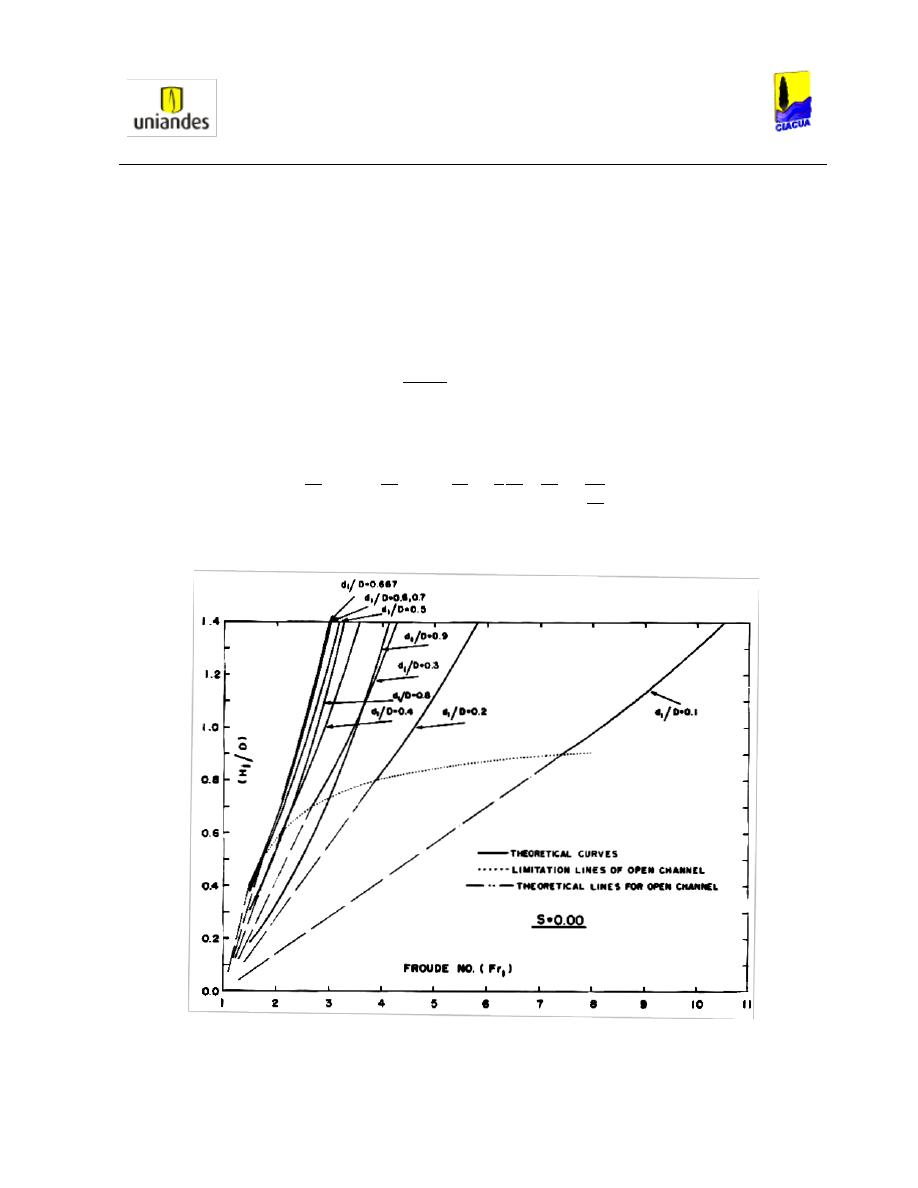
Con la Ecuación 34, Smith y Chen graficaron la Ilustración 10 y sacaron 4 conclusiones: 

 

Ilustración 10. Curvas teóricas para tuberías cuadradas horizontales (SMITH & CHEN, 1989).

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

21 

 

1.  La  ecuación  básica  asume  que  la  profundidad  subsecuente  del  resalto  es  mayor  al 

diámetro, lo que indica que la tubería queda totalmente presurizada. Por lo tanto, para 
saber  el  lugar  dónde 

 

 

       

 

  (denominado  por  Smith  y  Chen  como  el  lugar 

crítico), despejan el número de Froude de la Ecuación 34: 
 

 

  

 

     

   

 
 

  

 

 

 

 

 

    

 

 

 

 

 

 

    

 

 

 

 

 

Ecuación 35. Número de Froude cuando d

2

 = D (SMITH & CHEN, 1989). 

 

Los resultados del número de Froude crítico

1

 para relaciones de llenado entre 0.1 y 0.6 

se muestran en la Tabla 2 y en la Ilustración 10 señalados con flechas. 
 

Tabla 2. Resultados de números de Froude para diferentes relaciones de llenado cuando d

2

 = D (SMITH & 

CHEN, 1989). 

d

1

/D 

0.1 

0.2 

0.3 

0.4 

0.5 

0.6 

Fr

1

 

7.42 

3.87 

2.69 

2.09 

1.73 

1.49 

 

2.  Otra conclusión importante indica que cuando la profundidad aguas arriba del resalto 

es similar a la altura de la tubería, la Ecuación 10 tiende a 0, por lo que no se formaría 
resalto hidráulico. Además es importante tener en cuenta que mientras el flujo aguas 
arriba del resalto sea más supercrítico (menor altura), el resalto será más violento. 

3.  La  dimensión  del  resalto  varía  con  el  cuadrado  del  número  de  Froude,  lo  que  indica 

que cuando el número de Froude aumenta, el resalto es más fuerte. 

4.  La  relación 

 

 

 

  se  puede  tomar  como  una  constante  por  lo  que  la  Ecuación  34  puede 

ser representada como: 
 

 

 

 

     

 

 

    

 

Ecuación 36. Dimensión del Resalto hidráulico en tuberías cuadradas horizontales con d

1

/D constante 

(SMITH & CHEN, 1989). 

 

Hager y Stahl (1999) 

En  1999  Willi  H.  Hager  y  Helmut  Stahl  realizaron  un  nuevo  análisis  enfocado  en  tuberías 
circulares fluyendo parcialmente llenas en una sola fase (sin tener en cuenta la relación aire 

– 

agua analizada anteriormente por otros autores como Smith y Chen). 

                                                 

1

 

El número de Froude crítico se refiere en éste caso al número de Froude cuando la altura aguas abajo del resalto 

es igual a la altura de la tubería 

 

 

   .

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

22 

 

Para  calcular  la  profundidad  subsecuente,  tuvieron  en  cuenta  aproximaciones  a  las 
ecuaciones que calcular el área y la fuerza de presión en una tubería circular: 

 

 

   

   

 

Ecuación 37. Aproximación del área (Stahl & Hager, 1999).

2

 

 

 

   

 

 

 
 

 

   

 

Ecuación 38. Aproximación Presión (Stahl & Hager, 1999). 

dónde: 

   Área 

 : Diámetro de la tubería 

 : Relación de llenado 

   Fuerza de presión 

 : Densidad 

 : Gravedad 

Por lo tanto la Ecuación del Momentum resulta en: 

 
 

 

 

   

 

 

 

  

 

 

 

   

 

 
 

 

 

   

 

 

 

  

 

 

 

   

 

Ecuación 39. Ecuación del Momentum (Stahl & Hager, 1999). 

 

Por  otra  parte,  Hager  realizó  otro  análisis  en  1990  en 

el  libro  “Froudezahl  im  Kreisprofil 

(Froude number in circular conduits)” para determinar que el número de Froude en tuberías 
podía aproximarse a: 

   

 

    

 

 

Ecuación 40. Aproximación del Número de Froude (Hager, 1990). 

dónde: 

 : Número de Froude 

 : Caudal 
                                                 

2

 

Las Ecuación 37 y Ecuación 38 tienen un error máximo del 20% cuando y se encuentra entre 0.2 y 0.9, el cual es 

aceptable para Stahl y Hager porque se ajustarán empíricamente.

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

23 

 

 : Diámetro de la tubería 

 : Profundidad del flujo 

Ahora, dividiendo la Ecuación 39 entre 

 

 

 

 

: 

   

  

 

  

 

 

 

 

 

 

    

 

 

 

   

 

 

   

 

  

 

  

 

 

 

   

 

 

   

 

Ecuación 41. Proceso para encontrar la profundidad subsecuente del resalto hidráulico.

 

 

Y sabiendo que: 

   

 

 

 

 

 

Ecuación 42. Relación entre las relaciones de llenado aguas arriba y aguas abajo del resalto (Stahl & 

Hager, 1999).

 

 

Y aproximando 3.75 

  4 y remplazando las Ecuación 42 y Ecuación 40 en la Ecuación 41: 

 

 

 

   

 

 

   

 

 

 

   

 

 

   

 

 

 

 

   

  

 

  

 

 

 

 

 

 

   

   

 

  

 

 

   

  

 

 

 

   

 

 

 

 

 

 

     

Ecuación 43. Proceso para encontrar la profundidad subsecuente en un resalto hidráulico. 

 

      

 

 

   

   

     

 

 

 

    

 

Ecuación 44. Profundidad subsecuente en el resalto hidráulico (Stahl & Hager, 1999). 

 

Además, la Ecuación 44 puede modificarse a la Ecuación 45 cuando 

     : 

         

    

 

Ecuación 45. Profundidad subsecuente con números de Froude mayores a 2 (Stahl & Hager, 1999). 

 

Analizando la parte teórica, Stahl y Hager realizaron un experimento para verificar la Ecuación 
45,  determinar  un  criterio  de  choque  y  determinar  el  comportamiento  de  los  resaltos 
hidráulicos  en  tuberías  circulares.  El  diámetro  de  la  tubería  en  acrílico  que  utilizaron  fue  de 
240  mm,  la  pendiente  fue  de  0.5%  y  la  longitud  fue  de    6  m  (equivalente  a  25  veces  el 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

24 

 

diámetro).  El  resalto se formó  colocando  placas al  final de  la  tubería  y el  caudal  fue  medido 
con un vertedero en V. 

 

 

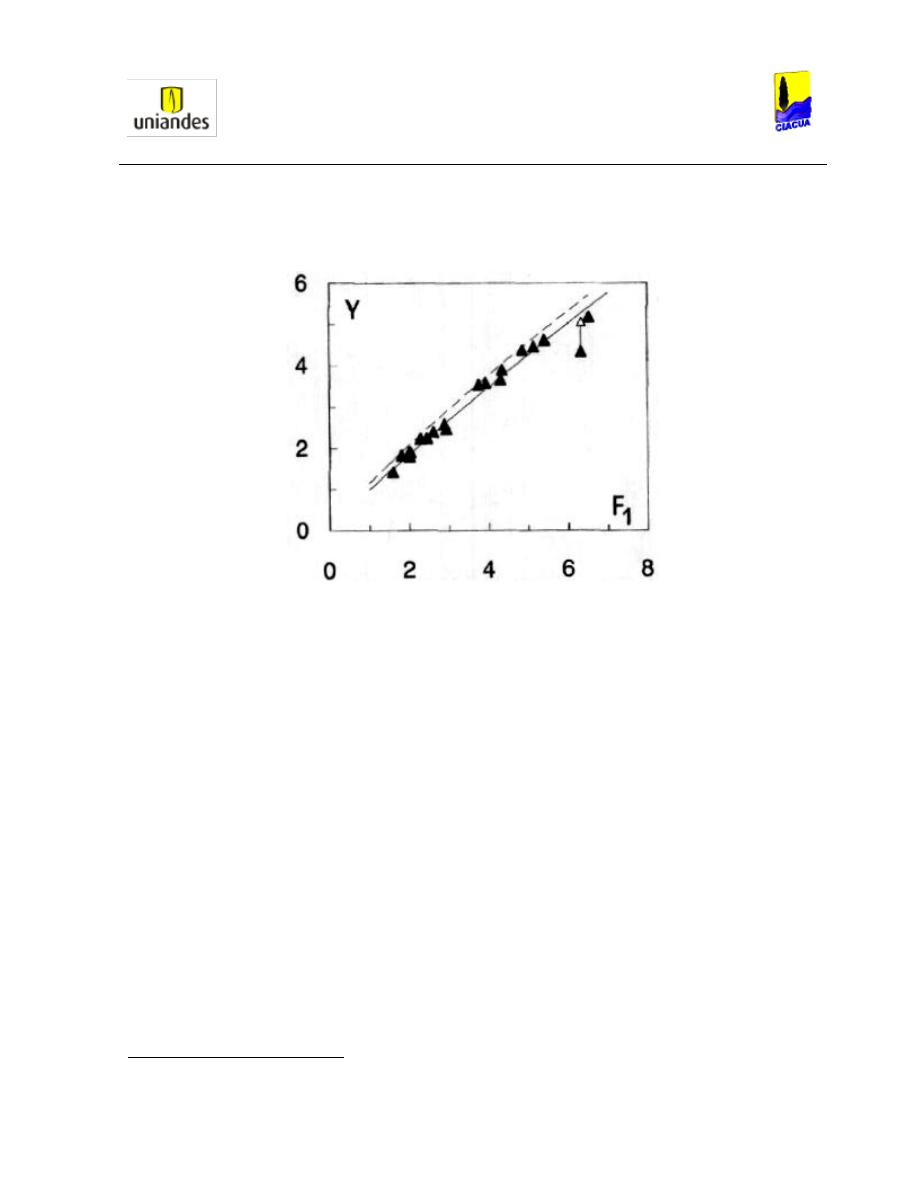
Ilustración 11. Profundidad subsecuente según el número de Froude (Stahl & Hager, 1999). 

 

En las 18 medidas realizadas, los números de Froude oscilaron entre 1.5 y 6.5 (siempre en el 
rango supercrítico), y se estableció que la Ecuación 45 había sido sobrestimada a causa de la 
viscosidad. Por lo tanto, la Ecuación 45 podía ser reemplazada por la Ecuación 46 (estimada 
con los resultados obtenidos en los experimentos y graficados en la Ilustración 11): 

         

 

    

 

Ecuación 46. Profundidad subsecuente para números de Froude mayores a 2 (Stahl & Hager, 1999). 

 

Adicionalmente,  Stahl  y  Hager  realizaron  un  análisis    para  los  tipos  de  resaltos

3

  que  se 

pueden formar: Cuando el número de Froude es 1.5, el tipo de resalto hidráulico que se forma 
es ondular y permanece a lo largo de la tubería; cuando el número de Froude oscila entre 1.5 
y  2,  las  ondas  del  resalto  hidráulico  se  pierden  aguas  abajo  porque  la  tubería  se  presuriza; 
cuando el número de Froude es mayor a 2, se producen dos tipos de resaltos hidráulicos, los 
cuales  dependen  de  la  relación  de  llenado  de  la  tubería:  cuando  la  relación  de  llenado  es 
inferior a 1/3, se forman remolinos laterales que recirculan, mientras el flujo que continua se 
concentra  en  la  superficie,  cuando  la  relación  de  llenado  es  superior  a  1/3,  el  resalto  se 
comporta normalmente, teniendo la zona de recirculación en la superficie. 

                                                 

3

 Los tipos de resaltos hidráulicos se explicarán en el Capítulo 4 (Marco Teórico).

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

25 

 

En  la  Ilustración  12  se  muestran  diferentes  tipos  de  resaltos  hidráulicos  dependiendo  el 
número de Froude:  

 

 

Ilustración 12. Vista lateral de diferentes resaltos hidráulicos (Stahl & Hager, 1999). 

 

Imagen  Número de Froude 

Tipo de Resalto 

a 

1.1 

Ondular 

b 

2.3 

Normal 

c 

4.1 

Flujo recirculante 

d 

6.5 

Con tubería 
presurizada 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

26 

 

 

En  la  Ilustración  13  se  observan  las  fluctuaciones  ocurridas  en  los  flujos,  y  las  zonas  de 
recirculación. 

 

Ilustración 13. Vista en perfil de los diferentes tipos de Resalto Hidráulico (Stahl & Hager, 1999). 

 

Imagen  Número de Froude 

Tipo de Resalto 

a 

2.3 

Normal 

b 

4.1 

Flujo recirculante 

c 

6.5 

Con tubería 
presurizada 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

27 

 

Hager  y  Stahl  analizan  las  longitudes  desde  dos  perspectivas:  longitudes  de  recirculación  y 
longitudes  de  aireación.  La  longitud  de  recirculación  (

 

 

   se  mide  desde  el  extremo  aguas 

arriba  de  los  remolinos  hasta  el  punto  de  estancamiento.  Por  lo  tanto,  para  expresar  una 
ecuación  que  determine  la  longitud  de  recirculación  del  resalto  hidráulico,  Hager  y  Stahl 
determinan una relación entre longitud y altura del flujo aguas abajo del resalto: 

 

 

 

 

 

 

 

 

Ecuación 47. Relación entre la longitud de recirculación y la profundidad aguas abajo del resalto (Stahl & 

Hager, 1999). 

 

Y 

 

 

 se calcula en función de Froude: 

 

 

    

 

   

 

Ecuación 48. Determinación de la longitud de recirculación a partir del número de Froude. 

 

La longitud de aireación se mide desde el extremo aguas arriba del resalto dónde comienzan 
los  remolinos  hasta  el  lugar  dónde  no  hay  burbujas  de  aire  (Esta  longitud  es  base  para 
encontrar  la  longitud  del    resalto).  Para  determinarla,  Hager  y  Stahl  nuevamente  calcularon 
una  relación  entre  la  longitud  del  resalto  y  la  profundidad  aguas  abajo  del  resalto    y 
encontraron una ecuación en función del número de Froude: 

 

 

 

 

 

 

 

 

Ecuación 49. 

Relación entre la longitud de aireación y la profundidad aguas abajo del resalto (Stahl & 

Hager, 1999). 

 

 

 

    

   

      

 

 

Ecuación 50. Determinación de la longitud de aireación a partir del número de Froude (Stahl & Hager, 

1999). 

 

Rudy Gargano y Willi H. Hager (2002) 

En el año 2002, el investigador Willi H. Hager realizó otro análisis en resaltos hidráulicos pero 
enfocados únicamente en los resaltos hidráulicos ondulares, analizando la longitud de las olas 
y los perfiles.  El experimento se realizó en un modelo similar al usado en 1999 (diámetro de 
240 mm y de 6 m de longitud y el material de construcción fue acrílico).  

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

28 

 

Las  relaciones  de  llenado  oscilaron  entre  0.3  y  0.8,  variándolas  cada  0.05.  Se  trabajaron  3 
pendientes:  0.001,  0.0015  y  0.003,  y  los  números  de  Froude  oscilaron  entre  1.25  y  2.0 
(Números de Froude característicos de resaltos hidráulicos ondulares). 

Como los resaltos hidráulicos ondulares son muy inestables, cualquier perturbación afecta el 
flujo  en  el  resalto;  además,  dependiendo  del  número  de  Froude  aguas  arriba  del  resalto,  se 
pueden determinar los siguientes tipos de resaltos hidráulicos ondulares: 

1.  Resalto  Ondular  Tipo  A:  Ocurre  cuando  los  números  de  Froude  aguas  arriba  del  resalto 

son bajos (F<1.20). Las ondas fluyen libremente en el flujo. 

2. 

Resalto  Ondular  Tipo  B:  Ocurre  cuando  la  pendiente  es  pronunciada  y  el  flujo  va 
aumentado de aguas arriba hacia aguas abajo sin la formación de ondas. (1.20<F<1.28)

 

3. 

Resalto Ondular Tipo C: Ocurre cuando el número de Froude oscila entre 1.28 y 1.36.

 

4. 

Resaltos Ondular Tipo D: Ocurre cuando los números de Froude  aguas arriba del resalto 
son grandes (1.28<F<1.60).

 

 

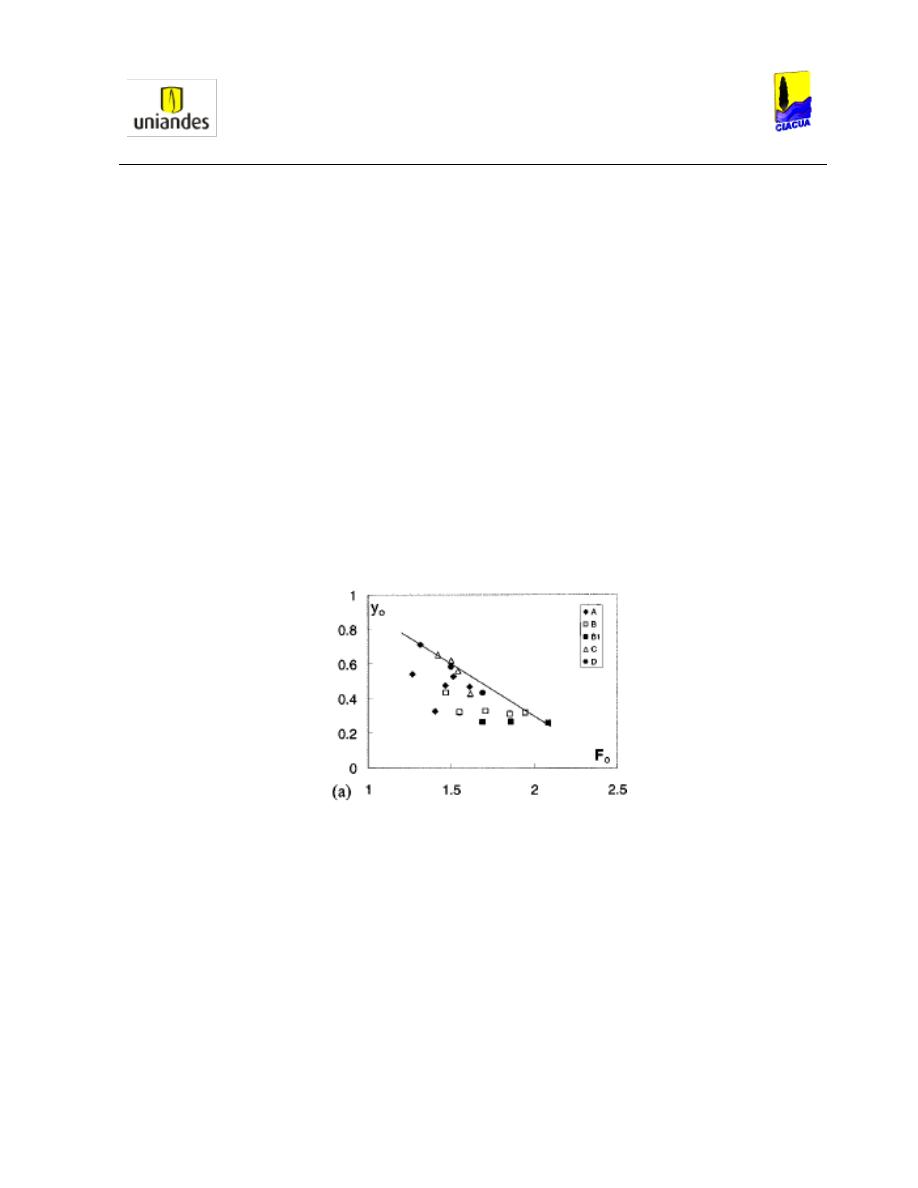
En la Ilustración 14 se muestran los diferentes tipos de resaltos hidráulicos generados en los 
experimentos realizados: 

 

Ilustración 14. Tipos de resaltos hidráulicos generados en los experimentos realizados por Hager y 

Gargano (Gargano & Hager, 2002). 

 

Por lo tanto, según la Ilustración 14, se obtienen los siguientes resultados: 

1.  Resalto Ondular Tipo A: Ocurre para números de Froude menores a 1.5 
2.  Resalto Ondular Tipo B: Ocurre para relaciones de llenado entre 0.3 y 0.45. 
3.  Resaltos Ondulares Tipo C y D: Se forman de acuerdo a la siguiente ecuación: 

 

 

 

             

 

 

Ecuación 51. Estimación para resaltos Ondulares Tipo C y D (Gargano & Hager, 2002). 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

29 

 

Como  conclusión  Gargano  y  Hager  comentan  que  el  pico  de  la  onda  ocurre  en  la  primera 

onda, además la longitud de la onda depende exclusivamente de 

 

 

 

 

  . Por último, para evitar 

problemas en las redes de alcantarillado, los números de Froude deben ser menores a 0.75 o 
mayores a 2 para evitar la inestabilidad del flujo y no producir resaltos ondulares, los cuales 
tienen las mismas características que un resalto normal. 

H.K. Ghamry, Ain Shames y Fayoum Branch (2002) 

En el año 2002 se realizó otro experimento para analizar los resaltos hidráulicos en tuberías, 
el diámetro era de 0.3 m, longitud de 1.37 m, el caudal variaba entre 7 y 35 l/s y la variación 
de los números de Froude oscilaban entre 1.29 y 6.43.  

Para calcular el resalto, introducen el término de sumersión (S): 

 

 

 

 

 

   

 

 

 

 

Ecuación 52. Sumersión en la compuerta (Ghamry, Shames, & Branch, 2002).

 

dónde: 

 

 

: Sumergencia en la compuerta 

 

 

: Altura aguas arriba de la compuerta 

 

 

: Altura en la compuerta 

   

 

 

   

 

 

 

 

Ecuación 53. Sumersión (Ghamry, Shames, & Branch, 2002). 

dónde: 

 

 

: Sumergencia  

 

 

: Altura aguas arriba del resalto 

 

 

: Altura aguas abajo del resalto 

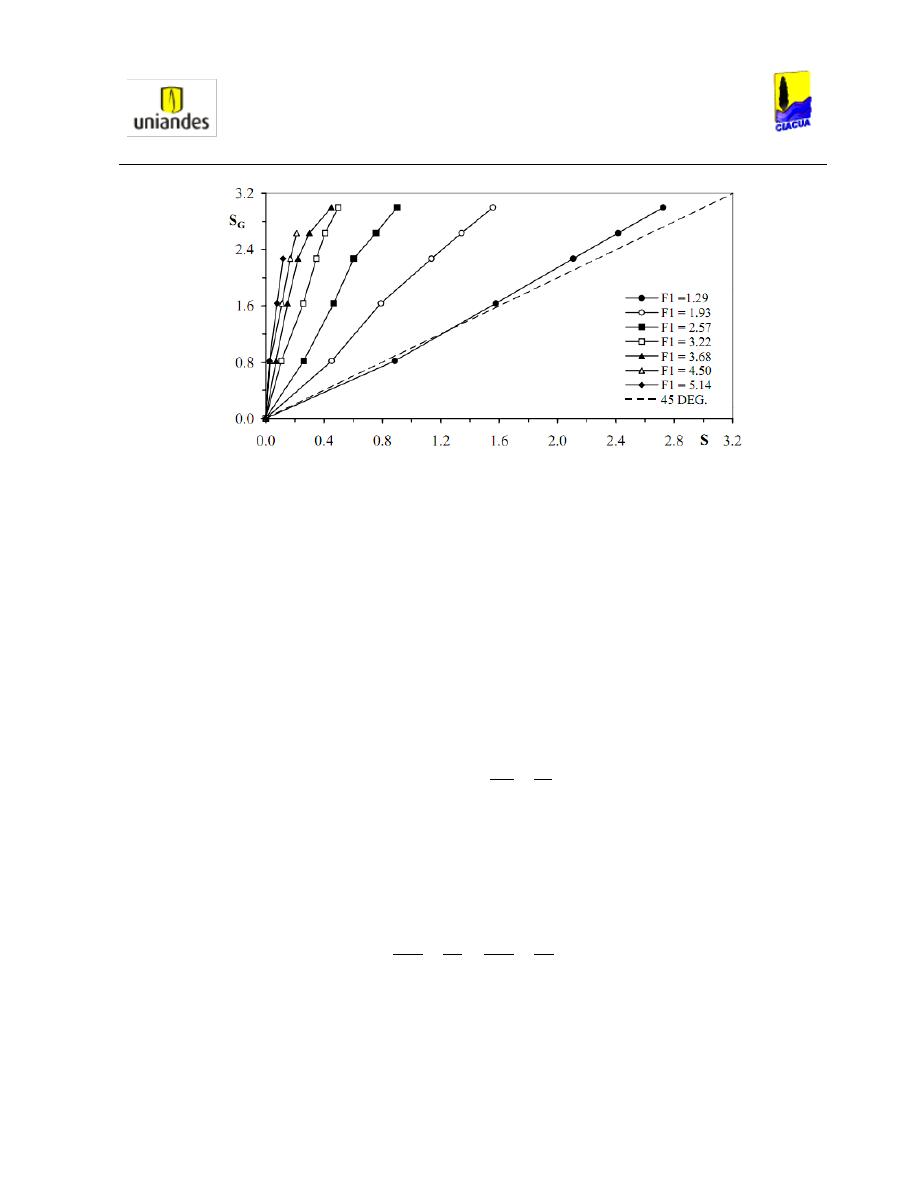
Estos  investigadores  realizaron  una comparación  entre  la  sumergencia  en  la  compuerta  y la 
sumergencia  en  el  resalto  y  concluyeron  que  la  relación  es  proporcional,  aunque  para  una 
sumergencia  del  resalto  específica,  la  sumergencia  en  la  compuerta  empieza  a  aumentar 
cuando aumenta el número de Froude (Ver Ilustración 15).  

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

30 

 

 

Ilustración 15. Comparación sumergencia del resalto vs sumersión de la compuerta (Ghamry, Shames, & 

Branch, 2002). 

 

Por  último,  para  un  número  de  Froude  específico,  se  puede  observar  que  el  resalto  pierde 
fuerza cuando la sumergencia incrementa. Además, la relación entre la energía específica en 
la  compuerta respecto a  las diferentes  energías  a lo  largo  del  resalto tiene un  leve  aumento 
cuando la sumergencia aumenta.  

Osman Akan (2006) 

La profundidad subsecuente de un resalto  hidráulico en canales rectangulares fue planteada 
por  Akan  como  la  igualdad  de  los  momentos  específicos  aguas  arriba  y  aguas  abajo  del 
resalto hidráulico: 

 

          

 

 

 

  

 

 

 

 

 

 

 

Ecuación 54. Cálculo Momentum Específico en Canales Rectangulares (Akan, 2006). 

 

Igualando  los  momentos  específicos  aguas  arriba  y  aguas  abajo  usando  la  Ecuación  54  se 
tiene que: 

 

 

  

  

 

 

  

 

 

 

 

 

  

  

 

 

  

 

 

 

Ecuación 55. Procedimiento cálculo altura subsecuente de los resaltos hidráulicos en canales 

rectangulares (Akan, 2006). 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

31 

 

Y conociendo que el caudal por unidad de ancho es igual a: 

   

 

 

 

     

 

 

         

 

        

Ecuación 56. Caudal por unidad de ancho. 

dónde: 

 : Caudal [m³/s] 

 : Caudal por unidad de ancho [m³/s*m] 

 : Ancho del canal [m] 

Y reemplazando la Ecuación 56 en la Ecuación 55: 

 

  

 

 

 

 

  

 

 

 

 

 

 

  

 

 

 

 

  

 

 

 

 

  

Ecuación 57. Procedimiento cálculo profundidades subsecuentes.  

 

Teniendo en cuenta la ecuación de conservación de la masa: 

     

 

 

 

   

 

 

 

 

Ecuación 58. Conservación de la masa. 

 

 

 

 

 

 

 

 

 

 

 

Ecuación 59. Cálculo velocidad aguas abajo a partir de los parámetros aguas arriba. 

 

Reemplazando la Ecuación 59 y la Ecuación 55 en la Ecuación 57: 

 

  

 

 

 

 

  

 

 

 

 

 

 

  

 

 

 

 

  

 

 

 

  

 

 

  

 

   

 

 

 

Y reorganizando: 

 
 

  

  

 

   

  

 

   

 

  

 

 

 

  

 

  

 

 

 

   

 

 

  

  

  

 

   

  

 

   

 

 

 

  

 

 

    

 

  

 

  

  

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

32 

 

  

  

   

  

   

  

   

  

      

  

 

  

  

 

  

  

   

  

 

 

  

  

 

  

 

 

  

 

 

 

  

 

  

     

  

 

 

 

 

  

 

  

 

 

 

 

  

 

  

     

 

 

    

 

  

 

  

 

              

 

 

 

 

Ecuación 60. Cálculo profundidades subsecuentes en canales rectangulares. 

 

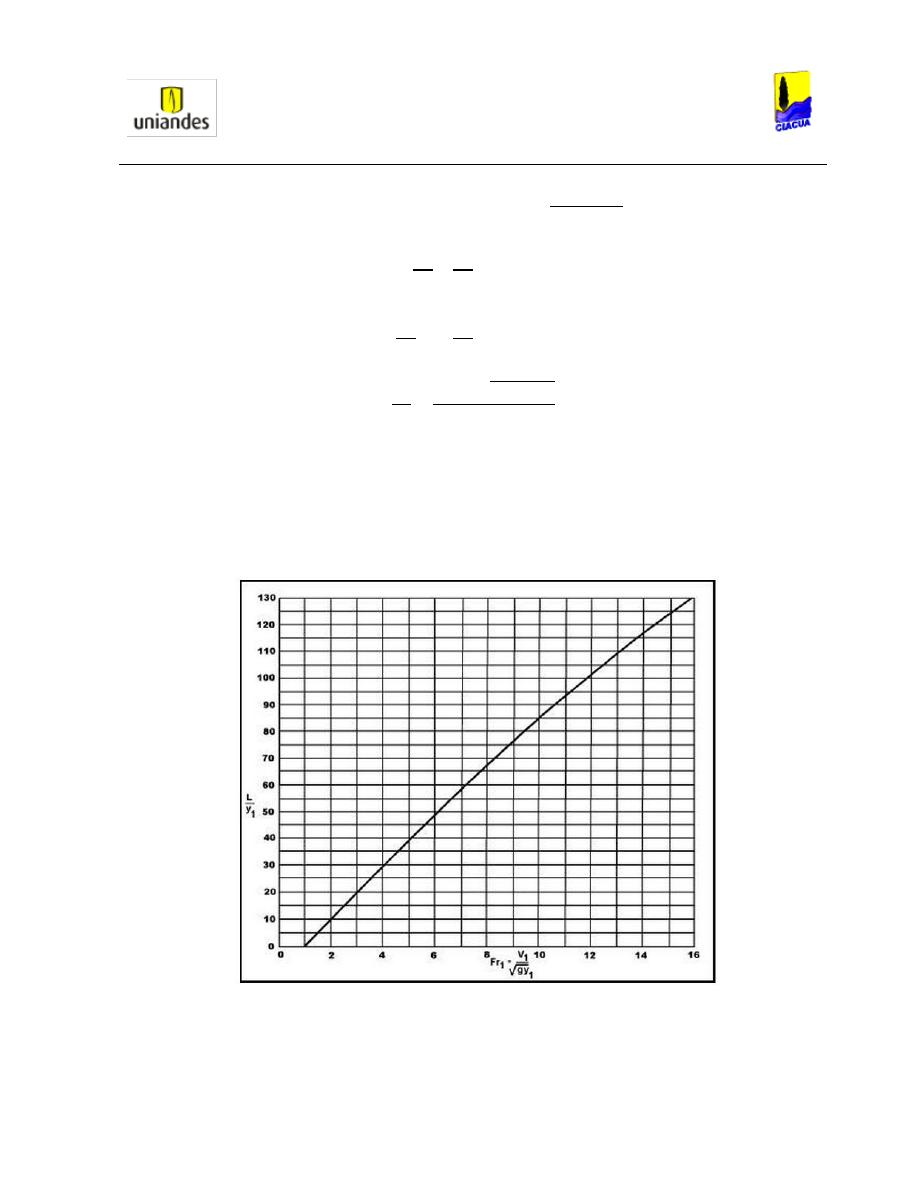
La  longitud  del  resalto  hidráulico  para  canales  rectangulares  puede  ser  medida  mediante  la 
Ilustración  16,  la  cual  puede  presentar  errores  cuando  el  resalto  hidráulico  presenta  una 
superficie muy plano. 

 

Ilustración 16. Cálculo de la longitud del Resalto Hidráulico. (FHWA, 2006). 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

33 

 

National Highway Institute (2006) 

En  el  2006  aparecen  publicadas  en  la  Circular  de  Ingeniería  Hidráulica  N°  14  del 
Departamento  de  Transporte  de  Estados  Unidos  (U.S.  Department  of  Transportation), 
ecuaciones  y  gráficas  para  determinar  resaltos  hidráulicos  en  tuberías.  Estas  ecuaciones  se 
escogen dependiente si la profundidad aguas abajo es mejor al diámetro o superior: 

Cuando la profundidad aguas abajo es menor al diámetro se tiene que: 

 

 

 

 

 

 

 

 

 

 

   

 

    

 

 

    

 

 

 

 

  

Ecuación 61. Cálculo profundidad subsecuente para profundidades subsecuentes menores al diámetro 

(FHWA, 2006). 

 

dónde: 

 

 

: Profundidad aguas abajo del resalto 

 

 

: Profundidad aguas arriba del resalto 

  

 

: Número de Froude aguas arriba del resalto 

     : Funciones de y/D, y sus valores se encuentran en la Tabla 3. 

Cuando la profundidad aguas abajo es mayor al diámetro, se realizan los cálculos con la 
Ecuación 62: 

 

 

 

 

 

 

 

 

       

 

 

 

 

 

 

 

     

 

    

 

 

    

 

 

 

 

  

Ecuación 62. Cálculo profundidad subsecuente para profundidades subsecuentes mayores al diámetro 

(FHWA, 2006). 

dónde: 

 

 

: Profundidad aguas abajo del resalto 

 

 

: Profundidad aguas arriba del resalto 

  

 

: Número de Froude aguas arriba del resalto 

     : Funciones de y/D, y sus valores se encuentran en la Tabla 3. 

 

 

 

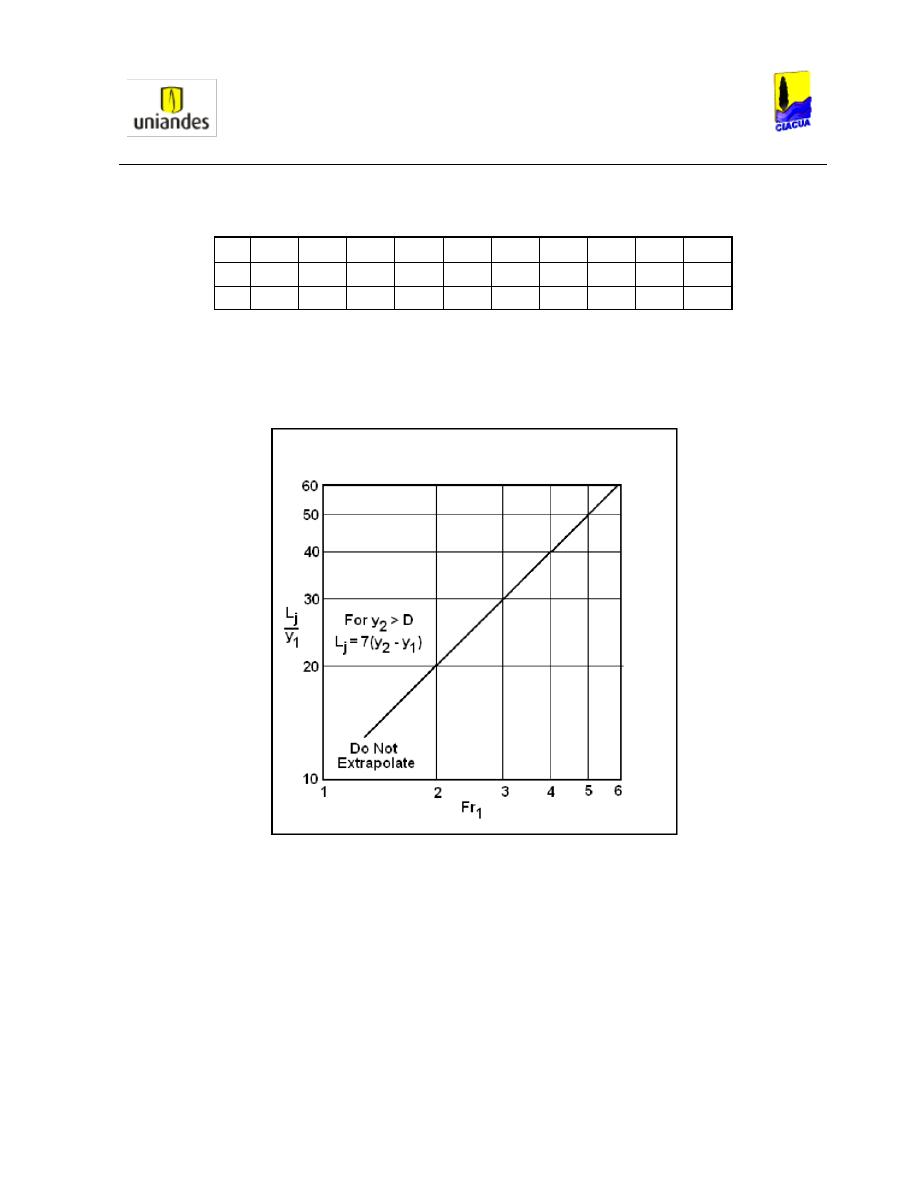
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

34 

 

 

Tabla 3. Coeficientes para tuberías circulares horizontales (FHWA, 2006). 

y/D  0.1 

0.2 

0.3 

0.4 

0.5 

0.6 

0.7 

0.8 

0.9  1,000 

K 

0.41  0.413  0.416  0.419  0.424  0.432  0.445  0.462  0.473  0.5 

C  0.041  0.112  0.198  0.293  0.393  0.494  0.587  0.674  0.745  0.748 

 

Adicionalmente,  la  longitud  del  resalto  (medida  desde  el  punto  dónde  inicia  la  turbulencia 
hasta el lugar dónde la profundidad aguas abajo alcanza el máximo)  cuando la profundidad 
aguas abajo es menor al diámetro se puede determinar mediante la Ilustración 17:  

 

Ilustración 17. Determinación de la longitud del resalto para profundidades subsecuentes menores al 

diámetro (FHWA, 2006). 

 

En la Ilustración 17 se puede observar que existe una aproximación experimental para hallar 
la longitud del resalto cuando la profundidad aguas abajo del resalto es mayor al diámetro: 

 

 

     

 

   

 

  

Ecuación 63. Determinación longitud del resalto cuando la profundidad aguas abajo es mayor al diámetro 

(FHWA, 2006). 

 

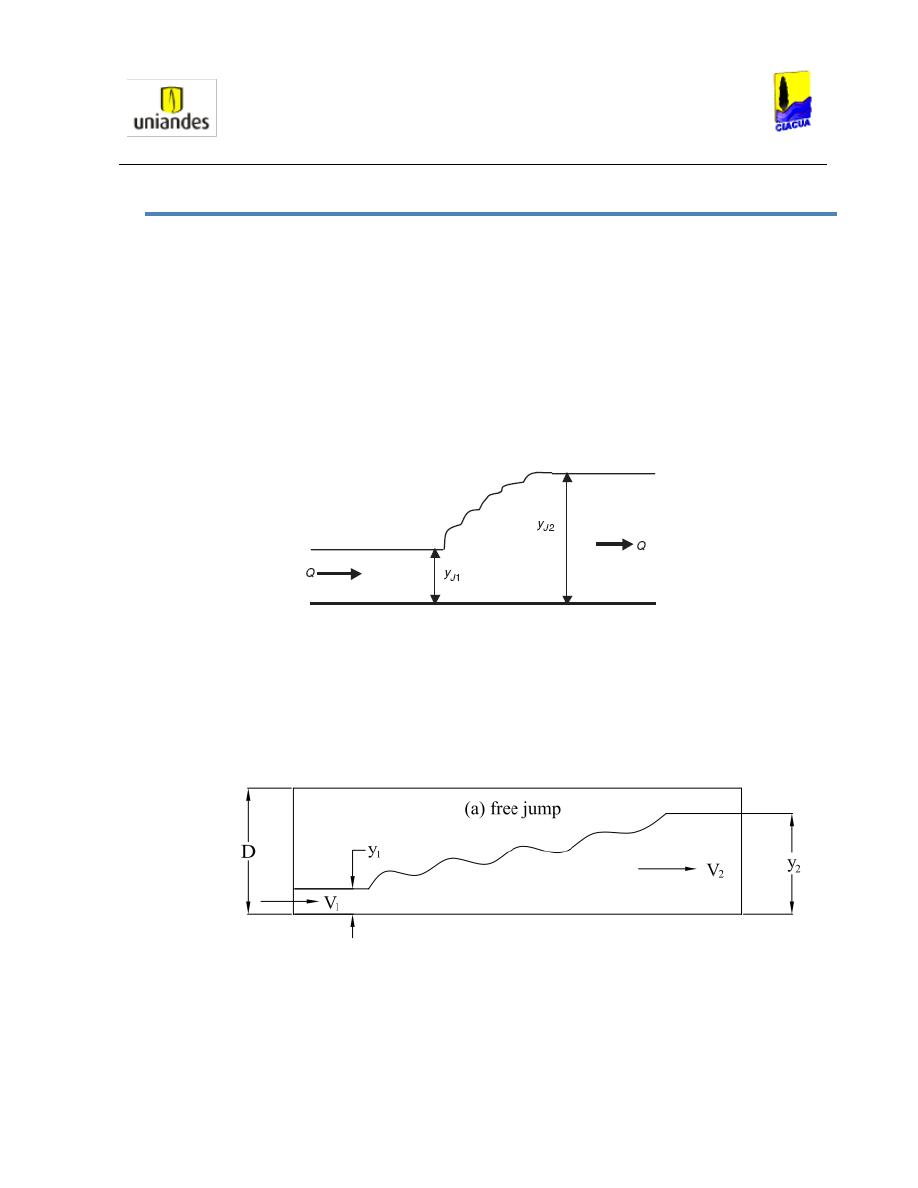
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

35 

 

3. Marco Teórico 

 

3.1. Resaltos Hidráulicos 

 

3.1.1.  Definición 

 

Los  resaltos  hidráulicos  son  fenómenos  físicos  presentados  cuando  hay  un  cambio  de  flujo 
supercrítico a flujo subcrítico, lo cual genera pérdidas de energía, turbulencia, rompimiento en 
la  superficie  del  flujo  (en  algunos  casos)  y  entrampamiento  de  aire.  Su  comportamiento  se 
puede observar en la Ilustración 18: 

 

Ilustración 18. Resalto Hidráulico (Akan, 2006). 

 

En tuberías circulares, existen dos tipos de resaltos; el primero ocurre cuando la profundidad 
subsecuente  del  resalto  es  menor  al  diámetro  de  la  tubería  (y

2

<D),  (Ver  Ilustración  19),  y  el 

segundo tipo, cuando la profundidad subsecuente supera el diámetro (y

2

>D) (Ilustración 20). 

 

Ilustración 19. Profundidad subsecuente menor al diámetro de la tubería. (Ghamry, Shames, & 

Branch, 2002). 

 

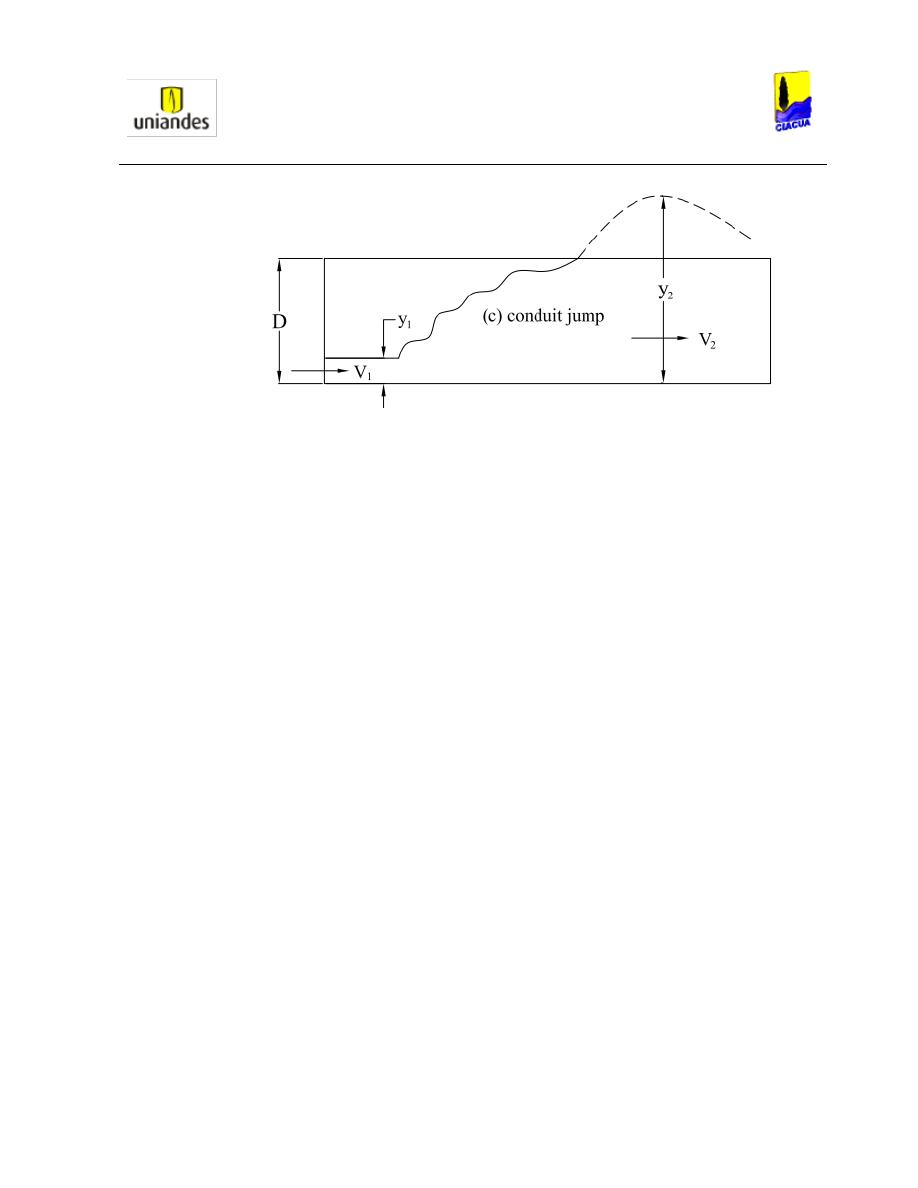
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

36 

 

 

Ilustración 20. Profundidad subsecuente mayor al diámetro de la tubería. (Ghamry, Shames, & 

Branch, 2002). 

 

Los  resaltos  hidráulicos  cumplen  la  función  de  disipar  energía  debido  a  la  turbulencia 
generada en éste fenómeno y la incorporación de aire; por lo tanto son útiles en zonas donde 
la potencia del agua puede causar daños en las estructuras y erosiones en los canales, o en 
las  Plantas  de  Tratamiento  de  Agua  Residual  o  Plantas  de  Tratamiento  de  Agua  Potable, 
dónde se usan para mezclar sustancias mientras ocurre el fenómeno.  

A continuación se mencionan otras funciones del resalto hidráulico en canales abiertos (CIVIL 
ENGINEERING PORTAL, 2011): 



  Disipación de energía en flujos sobre diques, vertederos y otras estructuras hidráulicas. 



  Condicionar  alturas  altas,  apropiadas  para  canales  usados  en  la  distribución  de  agua  o    

irrigación de cultivos. 



  Reducción de las presiones altas que se encuentran debajo de las estructuras. 



  Mezcla de sustancias químicas usadas para tratamiento de agua. 



  Airear flujos y declorinado en los procesos de tratamiento de agua. 



  Eliminación de paquetes de aire presentados en canales circulares. 



  Identificar  las  condiciones  del  flujo  mediante  mediciones,  y  así  tomar  medidas  de    

regulación. 

 

Adicionalmente,  la  formación  de  resaltos  hidráulicos  se  presenta  cuando  el  canal  tiene  altas 
pendientes, obstáculos en el canal o cambios de pendiente. 

 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

37 

 

3.1.2.  Tipos de Resaltos Hidráulicos 

 

Según la US Bureau of Reclamation, los resaltos hidráulicos se identifican de acuerdo con el 
número de Froude: 

Tabla 4. Tipos de Resaltos Hidráulicos en fondos sin pendiente (Gonzales Rodríguez, 1992). 

Número de Froude 

Características 

Froude = 1.0 

No existe formación de Resalto 

Hidráulico porque se encuentra en 

la profundidad crítica 

1.0 < Froude < 1.7 

Resalto Ondular 

1.7 < Froude < 2.5 

Resalto Débil 

2.5 < Froude < 4.5 

Resalto Oscilante 

4.5 < Froude < 9.0 

Resalto Permanente 

Froude > 9.0 

Resalto Fuerte 

 



 

Resalto  Ondular:  Cómo  se  explicó  en  los  Antecedentes,  un  resalto  hidráulico  ondular 
genera baja disipación de energía, su disipación oscila entre el 0 y el 8%. 



 

Resalto  Débil:  En  la  superficie  del  resalto  se  presenta  una  pequeña  turbulencia,  con 
disipaciones de energía entre el 10 y el 20%. 



 

Resalto  Oscilante:  Hay  una  turbulencia  no  periódica,  la  cual  va  generando  a  su  paso 
problemas  de  erosión  tanto  en  las  orillas  del  canal  como  en  el  fondo.  La  disipación  de 
energía oscila entre 20 y 45%. 



 

Resalto  Permanente:  Éste  resalto  no  tiene  en  cuenta  el  comportamiento  del  flujo  aguas 
abajo,  por  lo  tanto,  su  comportamiento  es  más  periódico.  La  disipación  de  energía  oscila 
entre 45 

– 70%. 



 

Resalto fuerte: Es un resalto violento, que alcanza disipaciones de energía del 85%. 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

38 

 

 

Ilustración 21. Tipos de Resaltos Hidráulicos  (Gonzales Rodríguez, 1992).

 

 

3.1.3.  Cálculo de profundidades subsecuentes en el Resalto Hidráulico 

 

Cómo  las  pérdidas  de  energía  son  considerables,  no  se  puede  usar  la  ecuación  de 
conservación de la energía para encontrar la relación entre las profundidades aguas arriba del 
resalto y aguas abajo, sino que se debe usar la conservación del Momentum planteada en la 
Ecuación 64. 

 

  

   

  

 

Ecuación 64. Conservación del Momentum Específico. 

 

En  canales  rectangulares  el  análisis  de  la  profundidad  subsecuente  del  resalto  hidráulico  se 
realiza mediante la demostración planteada por Akan, obteniendo como resultado la Ecuación 
60: 

 

  

 

  

 

              

 

 

 

 

Ecuación 60. Cálculo profundidades subsecuentes en canales rectangulares. 

 

 

 

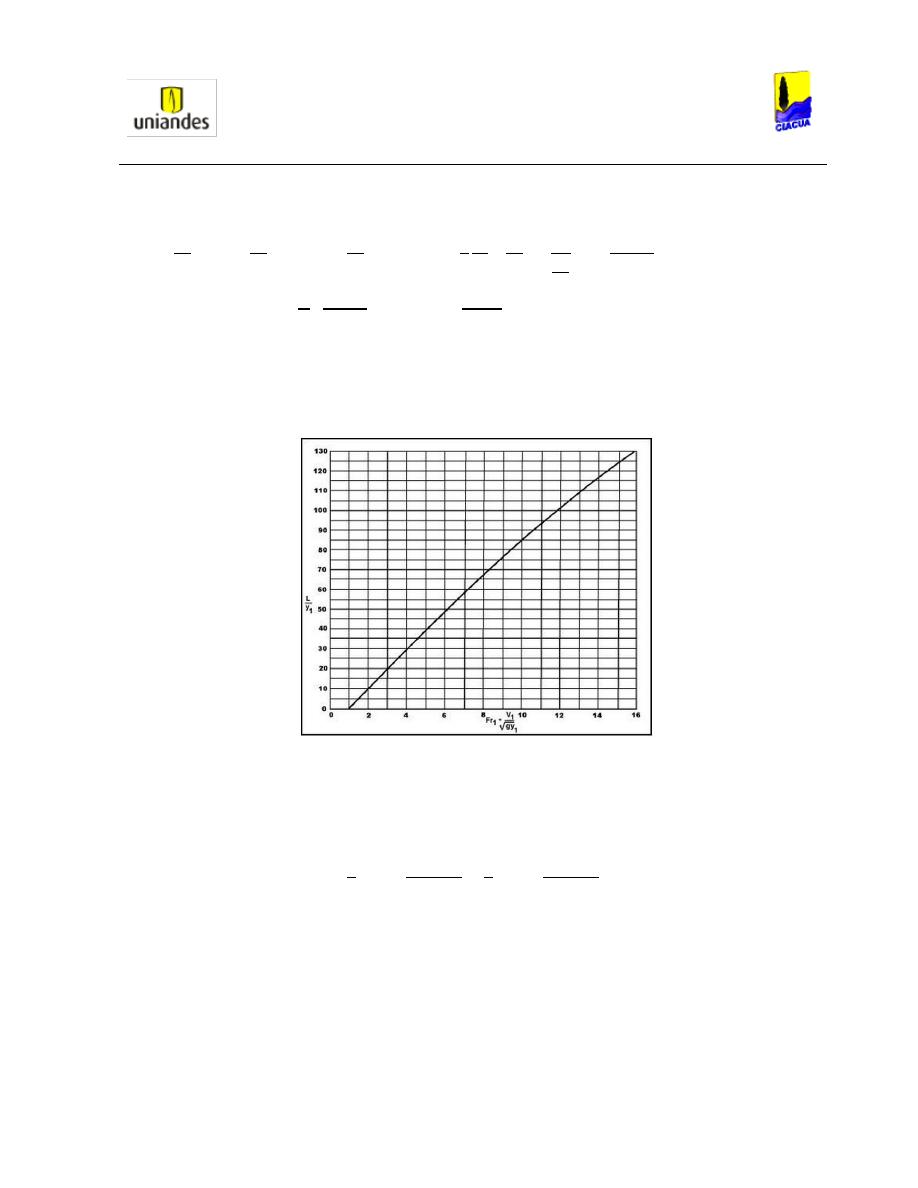
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

39 

 

O mediante la Ecuación 33 planteada por Smith y Chen: 

 

 

 

    

 

 

 

 

 

 

 

 

  

 

   

 

 

 

 

        

 

     

 
 

 

 

 

  

 

 

 

   

 

 

 

 

     

 

   

 

 

     

 

         

 

 

 

 

 

     

 

           

 

 

   

 

 

Ecuación 33. Dimensiones del Resalto Hidráulico en canales cuadrados reorganizada (SMITH & CHEN, 

1989). 

 

Además, la longitud del resalto se puede medir mediante la Ilustración 16: 

 

Ilustración 16. Cálculo de la longitud del Resalto Hidráulico. (FHWA, 2006).

 

El análisis de  Momentum para tuberías circulares se puede explicar en el análisis planteado 
por  Stahl  y  Hager  (Ver  Ecuación  39),  en  el  cual  se  obtiene  la  siguiente  ecuación  de 
conservación del Momentum: 

 
 

 

 

   

 

 

 

  

 

 

 

   

 

 
 

 

 

   

 

 

 

  

 

 

 

   

 

Ecuación 39. Ecuación del Momentum (Stahl & Hager, 1999). 

 

Adicionalmente,  en  otro  análisis,  realizado  por  Osman  Akan  en  el  libro  Open  Channel 
Hydraulics, la solución de la Ecuación 39 requiere de procedimientos de prueba y error, por lo 
tanto  se  han  graficado  diagramas  de  Momentum  para  encontrar  la  solución  en  canales 
circulares: 

 

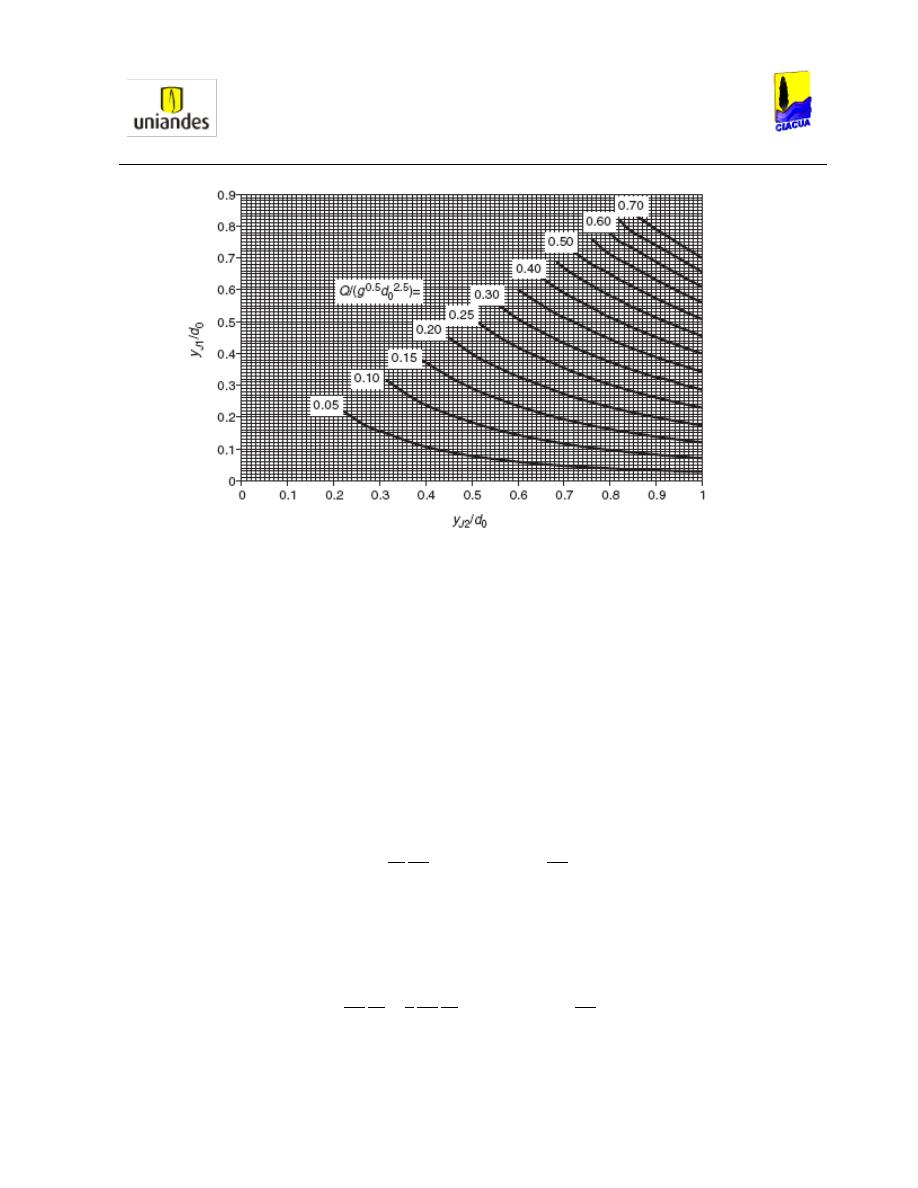
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

40 

 

 

Ilustración 22. Diagrama de Momentum en canales circulares (Akan, 2006). 

  

Como se observa en la Ilustración 22, todas las líneas tienen un límite en el inicio de la curva, 
lo que indica que en tuberías circulares, siempre se tendrá una zona supercrítica antes de la 
formación del resalto, y aguas abajo se tienen dos opciones, que el flujo siga a superficie libre 
o que la tubería se presurice. 

Por  lo  tanto,  partiendo  de  las  Ecuaciones  de  Momentum  y  diversos  experimentos,  se 
encuentran las siguientes ecuaciones para encontrar las profundidades subsecuentes: 

La primera ecuación fue calculada por Silvester en 1964 a partir de los datos obtenidos en el 
experimento  de  Kindsvater.  La  Ecuación  12  funciona  para  tuberías  fluyendo  parcialmente 
llenas: 

 

 

 

 

 

 

 

 

 

 

 

     

 

 

   

 

 

    

 

 

 

 

   

Ecuación 12. Profundidades subsecuentes para tuberías parcialmente llenas (Silvester, 1964). 

 

 

La Ecuación 14 se utiliza en tuberías presurizadas: 

 

 

 

 

 

 

 

 

 

 
 

 

 

 

 

 

 

 

     

 

 

   

 

 

    

 

 

 

 

  

 

Ecuación 14. Profundidades subsecuentes para tuberías llenas. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

41 

 

En 1978, Straub plantea ecuaciones para determinar la profundidad subsecuente del resalto 
hidráulico a partir de una aproximación en el cálculo del número de Froude: 

 

 

   

 

 

 

 

 

    

 

Ecuación 20. Aproximación número de Froude (French, 2007). 

 

Cuando el número de Froude es menor a 1.7: 

 

 

 

 

 

 

 

 

 

Ecuación 21. Cálculo profundidad subsecuente para números de Froude menores a 1.7 (French, 2007). 

 

Y cuando el número de Froude es mayor a 1.7: 

 

 

 

 

 

   

 

 

    

 

Ecuación 22. Cálculo profundidad subsecuente para números de Froude mayores a 1.7 (French, 2007). 

 

En 1999 Stahl y Hager plantearon dos ecuaciones a partir de sus resultados experimentales, 
la primera calculada para números de Froude generales: 

      

 

 

   

   

     

 

 

 

    

 

Ecuación 65. Profundidad subsecuente en el resalto hidráulico (Stahl & Hager, 1999). 

 

 

Y la siguiente para números de Froude mayores a 2: 

         

    

 

Ecuación 66. Profundidad subsecuente con números de Froude mayores a 2 (Stahl & Hager, 1999). 

 

Y  por  último,    en  la  Circular  14  de  Ingeniería  Hidráulica  del  Departamento  de  Transporte  de 
Estados  Unidos  se  establecen  las  siguientes  ecuaciones  para  encontrar  las  profundidades 
subsecuentes: 

 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

42 

 

Cuando la profundidad aguas abajo es menor al diámetro se tiene que: 

 

 

 

 

 

 

 

 

 

 

   

 

    

 

 

    

 

 

 

 

  

Ecuación 61. Cálculo profundidad subsecuente para profundidades subsecuentes menores al diámetro 

(FHWA, 2006). 

 

dónde: 

 

 

: Profundidad aguas abajo del resalto 

 

 

: Profundidad aguas arriba del resalto 

  

 

: Número de Froude aguas arriba del resalto 

     : Funciones de y/D, y sus valores se encuentran en la Tabla 3 

Cuando la profundidad aguas abajo es mayor al diámetro, se realizan los cálculos con la 
Ecuación 62: 

 

 

 

 

 

 

 

 

       

 

 

 

 

 

 

 

     

 

    

 

 

    

 

 

 

 

  

Ecuación 62. Cálculo profundidad subsecuente para profundidades subsecuentes mayores al diámetro 

(FHWA, 2006). 

dónde: 

 

 

: Profundidad aguas abajo del resalto 

 

 

: Profundidad aguas arriba del resalto 

  

 

: Número de Froude aguas arriba del resalto 

     : Funciones de y/D, y sus valores se encuentran en la Tabla 3 

Adicionalmente,  la  longitud  del  resalto  (medida  desde  el  punto  dónde  inicia  la  turbulencia 
hasta el lugar dónde la profundidad aguas abajo alcanza el máximo)  cuando la profundidad 
aguas abajo es menor al diámetro se puede determinar mediante la Ilustración 17:  

 

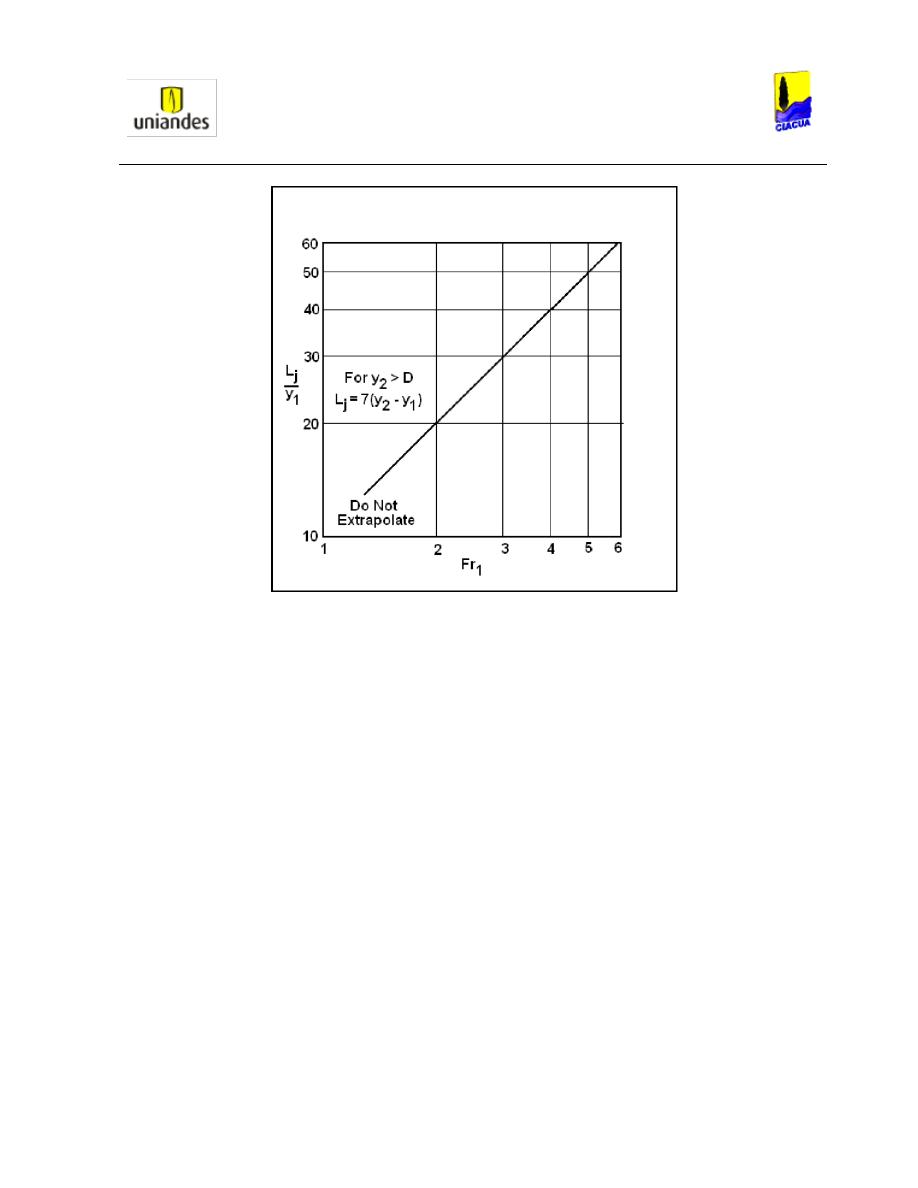
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

43 

 

 

Ilustración 17. Determinación de la longitud del resalto para profundidades subsecuentes menores al 

diámetro (FHWA, 2006). 

 

 

 

 

 

 
. 
 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

44 

 

4. Diseño del modelo 

 

4.1. 

Ubicación 

 

El montaje se realizará en el laboratorio de Hidráulica de la Universidad de los Andes, sobre 
el canal rectangular ubicado en el extremo derecho del laboratorio (Ver plano anexo). 

 

 

Ilustración 23. Canal donde su ubicará el montaje. 

 

4.2. 

Condiciones Iniciales. 

 

El canal rectangular tiene una pendiente del 1.88%, alimentado por una válvula que distribuye 
el  caudal  al  canal.  Debido  a  las  condiciones  aguas  abajo  del  canal,  el  caudal  mínimo  que 
puede transportar la tubería es de 6.1 L/s y el caudal máximo es de 77.6 L/s. 

 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

45 

 

Las medidas del canal se muestran en la Tabla 5. 

Tabla 5. Medidas del canal. 

  

Medición 

Unidades 

Aguas 

Arriba 

Altura 

0.463 

m 

Ancho 

0.628 

m 

Aguas 

Abajo 

Altura 

0.719 

m 

Ancho 

0.628 

m 

Longitud 

13.561 

m 

 

4.3. 

Elección Tubería 

4.3.1.  Tubería en acrílico de 400mm 

4.3.1.1. Hipótesis 

 

El primer diseño  del montaje se planteó con una tubería de acrílico de 400 mm de diámetro 
interno (cerca de 16 pulgadas), ya que gracias a su tamaño, permite observar detalladamente 
el comportamiento del agua. 

La  forma  de  variar  la  pendiente  de  la  tubería  sería  por  medio  de  soportes  de  madera  (Ver 
Ilustración  24)  que  dependiendo  de  su  ubicación  y  tamaño  aumentarían  o  disminuirían  la 
pendiente. 

 

Ilustración 24. Soportes de madera para cambiar la pendiente de la tubería. 

 

 

 

 

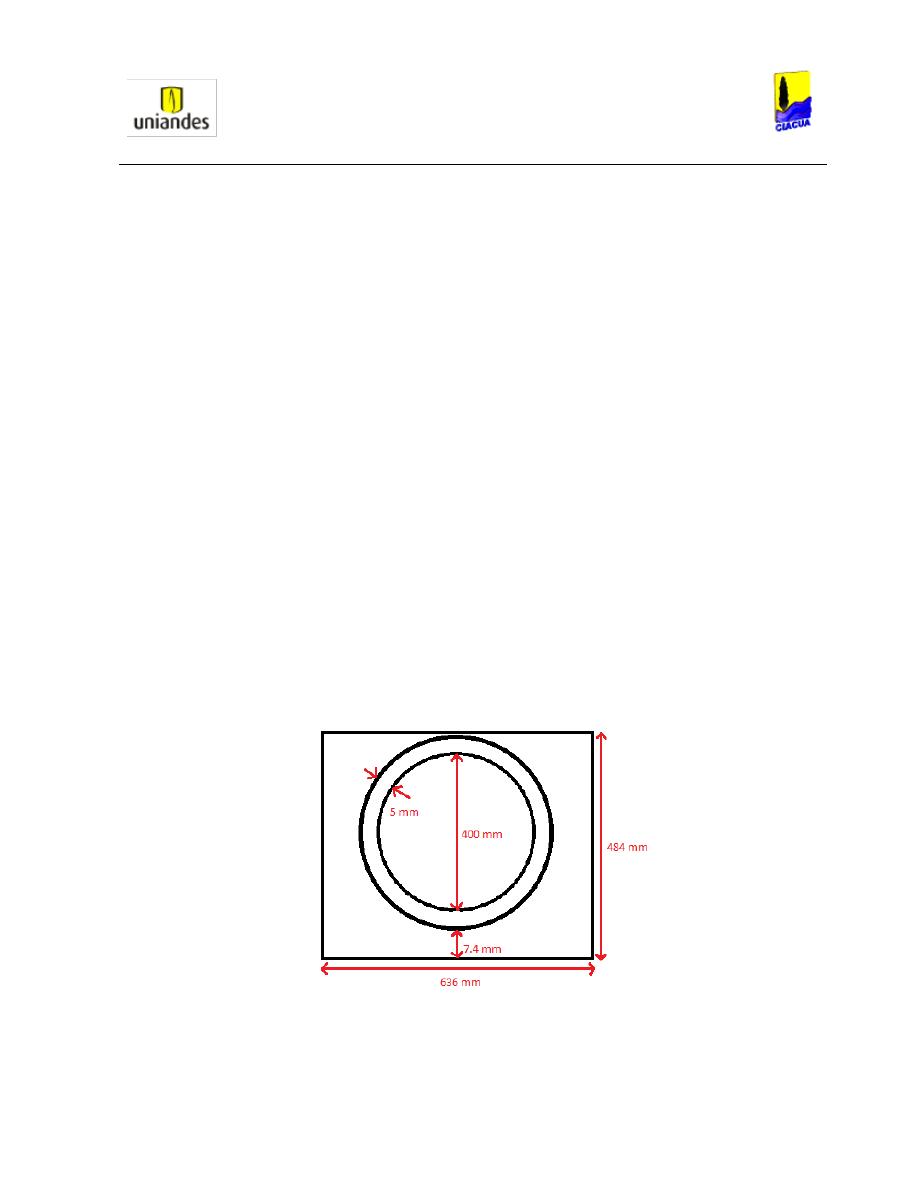
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

46 

 

4.3.1.2. Análisis 

4.3.1.2.1. 

Restricciones 

 

Los  criterios  de  selección  de  la  tubería  apropiada  para  el  montaje,  se  basaron  en  las 
siguientes restricciones: 



  El número de Froude debe ser menor a 4.0. 



  El caudal que pasa por la tubería  debe ser cercano al caudal máximo que permite la 

válvula. 



  El  espacio  que  ocupa  la  tubería  debe  estar  entre  las  condiciones  dadas  por  el  canal 

donde se realizará el montaje. 



  El  espacio  que  ocupe  la  tubería  debe  permitir  la  ubicación  de  los  elementos  que 

permitan el cambio de pendiente. 

4.3.1.2.2. 

Condiciones de la tubería 

 

Por lo tanto, para confirmar si la tubería de 400 mm era óptima para éste modelo, se inició el 
análisis  realizando  una  comprobación  de  diseño  que  tenía  como  condiciones  iniciales  una 
relación  de  llenado  del  85%,  una  pendiente  del  1.88%  (la  pendiente  original  del  canal)  y  la 
rugosidad relativa del PVC (

        

  

  ); dando como resultado un caudal de 465.3 L/s y un 

número de Froude de 2.07. 

Adicionalmente, de acuerdo com las características del canal donde se realizará el montaje, la 
tubería  tendría  aguas  arriba  un  espacio  de  movimiento  de  cerca  de  7  cm  (adicionando  el 
espesor de la tubería que es igual a 5 mm) (Ver Ilustración 25). 

 

Ilustración 25. Medidas tubería de 400 mm y canal. 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

47 

 

Para  comprobar  que  la  tubería  de  400  mm  si  podía  usarse  en  el  modelo,  se  realizó  una 
maqueta,  la  cual  mantenía  todas  las  medidas  a  escala  permitiendo  así  observar  qué  tanto 
movimiento tendría la tubería en el modelo. 

 

Ilustración 26. Maqueta con una tubería de 400 mm. 

 

Como se observa en la Ilustración 26,  la tubería con un diámetro de 400 mm  ocuparía más 
espacio  que  el  disponible  en  el  canal,  teniendo  en  cuenta  que  la  tubería  requiere  de  un 
soporte que permita la variación de pendiente.  

4.3.1.2.3. 

Conclusión 

 

La tubería permite que el flujo adquiera un número de Froude menor a 4.0, cumpliendo con la 
primera  condición;  pero  el  caudal  que  pasa  por  la  tubería  es  demasiado  grande  respecto  al 
caudal máximo que permite la válvula; es decir,  si se trabaja con la tubería de 400 mm,   la 
relación de llenado óptima para el caudal máximo que permite la válvula es menor al 35%, por 
lo tanto no se podría realizar un análisis cercano al sistema de drenaje urbano, puesto que la 
relación de llenado máxima para sistemas de drenaje es del 85%. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

48 

 

Por  otra  parte,  la  tubería  se  realizará  en  acrílico,  dividida  en  7  secciones,  6  de  2  m  y  una 
sección de 1 m. La forma de unir éstas secciones será mediante bridas, las  cuales permiten 
realizar  mantenimiento  a  la  tubería.  Pero  dado  el  peso  que  adquiere  la  tubería  cuando 
transporta  agua,  la  tubería  no  puede  sostenerse  únicamente  con  los  soportes  de  madera, 
puesto  que  podría  sufrir  algún  tipo  de  falla  en  las  uniones  de  las  secciones,  lo  que  hace 
necesario  soportar  la  tubería    con  algún  tipo  de  soporte  metálico  que  resista  el  peso  de  la 
tubería y el agua. 

Éste  soporte  tendrá  una  altura  mínima  de  10  cm,  por  lo  cual  el  diseño  de  la  tubería  de  400 
mm en el canal resulta erróneo puesto que el espacio que ocupa la tubería y el soporte sería 
mayor a 48 cm,  concluyendo que el espacio permitido por el canal es insuficiente. 

4.3.2.  Selección diámetro de la tubería 

 

La  selección  del  diámetro  de  la  tubería  se  llevó  a  cabo  analizando  el  espacio  máximo  que 
permite  el  canal,  el  caudal  máximo  posible  que  puede  permitirse  en  el  montaje,  una  tubería 
apropiada para observar los fenómenos de resalto hidráulico y cumplir que la mínima relación 
de  llenado  con  el  caudal  máximo  sea  del  50%  para  tener  la  posibilidad  de  realizar  varias 
mediciones. Por lo tanto, por medio del caudalímetro electrónico instalado en el laboratorio, se 
determinó que el máximo caudal que puede pasar por el canal es de 77.6 L/s. 

Por ende, para analizar los caudales que permitían diferentes tuberías, se realizó un proceso 
de  comprobación  de  diseño  para  diferentes  diámetros  (Ver  Ilustración  27)  en  el  cual  se 
determinó que el diámetro óptimo es de 250 mm, ya que cumple con una caudal más cercano 
al  caudal  máximo  que  recorre  el  canal,  y  su  tamaño  permite  ubicar  un  soporte  en  H  para 
sostener la tubería, permite la variación de la pendiente y en comparación con el diámetro de 
200 mm (que también cumple con las dos restricciones anteriores), la posibilidad de observar 
el fenómeno se facilita por el tamaño. 

 

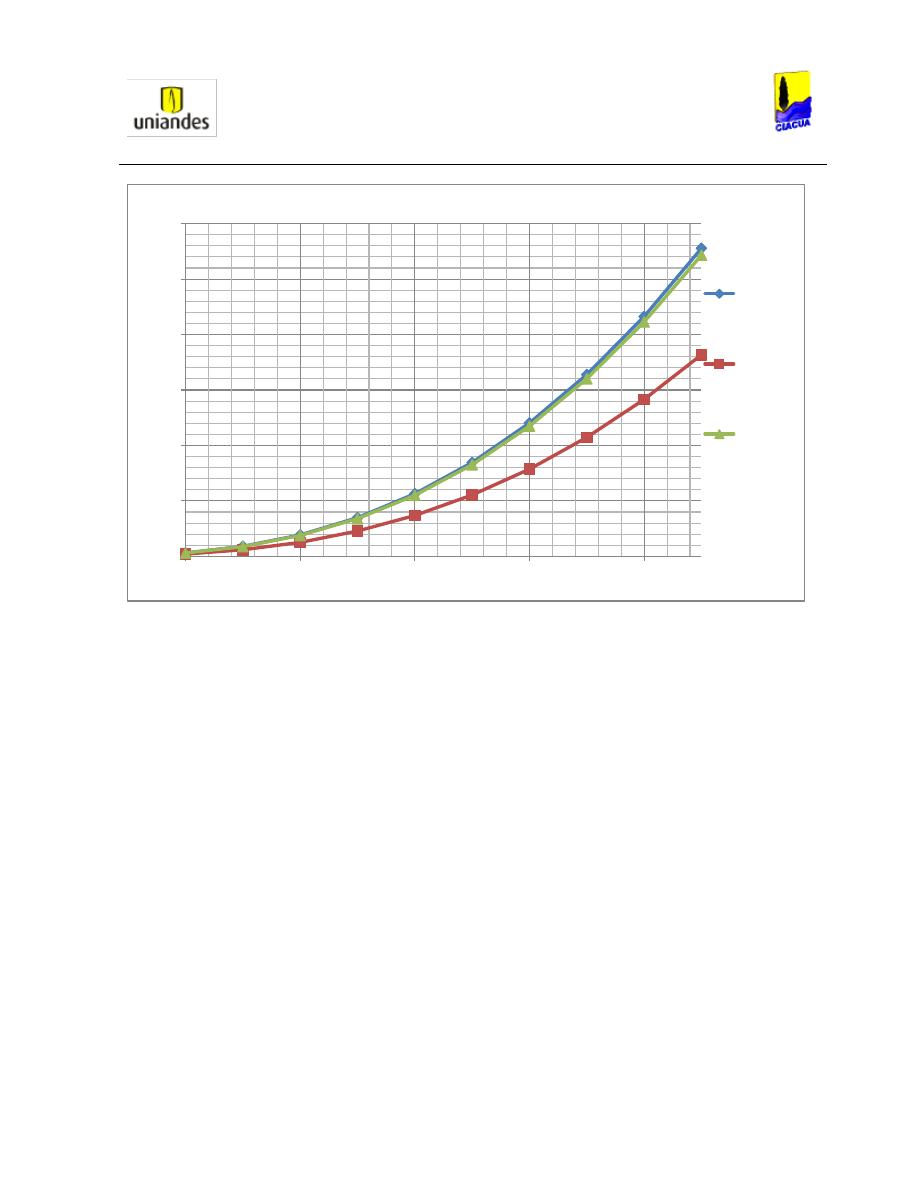
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

49 

 

 

Ilustración 27. Relación del diámetro vs caudal. 

  

4.3.3. 

Tubería con diámetro de 250 mm 

 

El diseño se realizará entonces con una tubería de 250 mm de diámetro interno, de espesor 
de  5  mm  y  dividida  en  6  secciones  de  2  m  y  una  sección  de  1  m.  La  unión  entre  sección  y 
sección  se  realizará  mediante  bridas  con  un  total  de  8  tornillos  por  unión.  La  tubería  estará 
apoyada  sobre  un  soporte  de  12  m  de  longitud,  dividido  en  secciones  de  3  m,  y  el  cuál 
conjunto a soportes de madera que se colocarán en cada unión de los soportes, se levantará 
la tubería variando la pendiente de la misma. 

Así  mismo,  el  soporte  de  la  tubería  se  fijará  mediante  soportes  de  madera  y  chumaceras  al 
inicio del canal, de tal manera que permitan la variación de la pendiente sin causar esfuerzos 
en la tubería.  

Para  comprobar  que  la  tubería  de  250  mm  es  la  óptima  para  el  montaje  se  realizó  una 
maqueta que fue construida con todos los parámetros a escala: 

 

0 

0.2 

0.4 

0.6 

0.8 

1 

1.2 

0.1 

0.2 

0.3 

0.4 

0.5 

Ca

ud

al

 (m3/

s)

 

Diámetro (m) 

Comparación Diámetro vs Caudal para diferentes relaciones de llenado 

Relación 
de 
llenado 
de 85% 
Relación 
de 
llenado 
60% 
Relación 
de 
llenado 
100% 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

50 

 

 

Ilustración 28. Maqueta con un diámetro de 250 mm. 

 

En  la  Ilustración  28  se  observar  que  la    tubería  de  250  mm  cumple  con  las  condiciones  de 
tamaño  que  requiere  el  canal,  por  lo  tanto,  es  la  tubería  óptima  para  el  montaje,  porque 
cumple  con  un  caudal  cercano  al  máximo  que  puede  pasar  por  el  canal  y  porque  tiene  el 
tamaño perfecto para realizar el análisis. 

 

  

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

51 

 

5. Pruebas de verificación de los parámetros hidráulicos de la 

tubería 

5.1. Comprobación de Diseño  

 

El proceso de comprobación de diseño se realizó para determinar cuál era el diámetro que se 
debía elegir para transportar el caudal de 77.6 L/s, evitando tener una relación de llenado muy 
baja, y alturas menores a 48 cm (altura máxima permitida por el canal en la compuerta aguas 
arriba).  

Por lo tanto, se realizó un análisis para relaciones de llenado del 50%, 85 % y 92.9% con una 
pendiente del 1.88%: 

Tabla 6. Diámetros seleccionados que superen el caudal de diseño y no superen los 48 cm de altura con 

relaciones de llenado del 50 %.

 

d 

(m) 

 

yn  

(m) 

 

  

(-) 

Á 

(m²) 

 

P 

(m) 

 

R 

(m) 

 

V 

(m) 

 

Q 

(m³/s) 

 

Re 

(-) 

 

T 

(m) 

 

D 

(m) 

 

Froude 

(-) 

 

h 

soporte 

(m) 

d + 

soporte 

(m) 

0,2 

0,1 

3,142  0,016  0,314 

0,050 

2,315 

0,036  406173,515  0,200  0,079 

2,638 

0,100 

0,300 

0,25  0,125  3,142  0,025  0,393 

0,063 

2,676 

0,066  586753,110  0,250  0,098 

2,726 

0,100 

0,350 

0,3 

0,15  3,142  0,035  0,471 

0,075 

3,009 

0,106  791802,752  0,300  0,118 

2,799 

0,100 

0,400 

0,35  0,175  3,142  0,048  0,550 

0,088 

3,321 

0,160  1019595,837  0,350  0,137 

2,860 

0,100 

0,450 

0,4 

0,2 

3,142  0,063  0,628 

0,100 

3,616 

0,227  1268764,140  0,400  0,157 

2,913 

0,100 

0,500 

0,45  0,225  3,142  0,080  0,707 

0,113 

3,897 

0,310  1538186,062  0,450  0,177 

2,960 

0,100 

0,550 

0,5 

0,25  3,142  0,098  0,785 

0,125 

4,165 

0,409  1826918,772  0,500  0,196 

3,001 

0,100 

0,600 

0,55  0,275  3,142  0,119  0,864 

0,138 

4,424 

0,525  2134154,161  0,550  0,216 

3,039 

0,100 

0,650 

 

En la Tabla 6 se resaltan los diámetros que cumplen con caudales cercanos al caudal máximo 
permitido  en  el  montaje  y  no  superan  los  48  cm  de  la  compuerta.  Cabe  destacar,  que  las 
tuberías con diámetros de 200 mm y 250 mm mueven un caudal menor que el caudal máximo 
con una relación de llenado del 50%, lo que indica que se puede realizar una variación mayor 
de las relaciones de llenado en éstos diámetros respecto a los diámetros de 300 mm. 

 

 

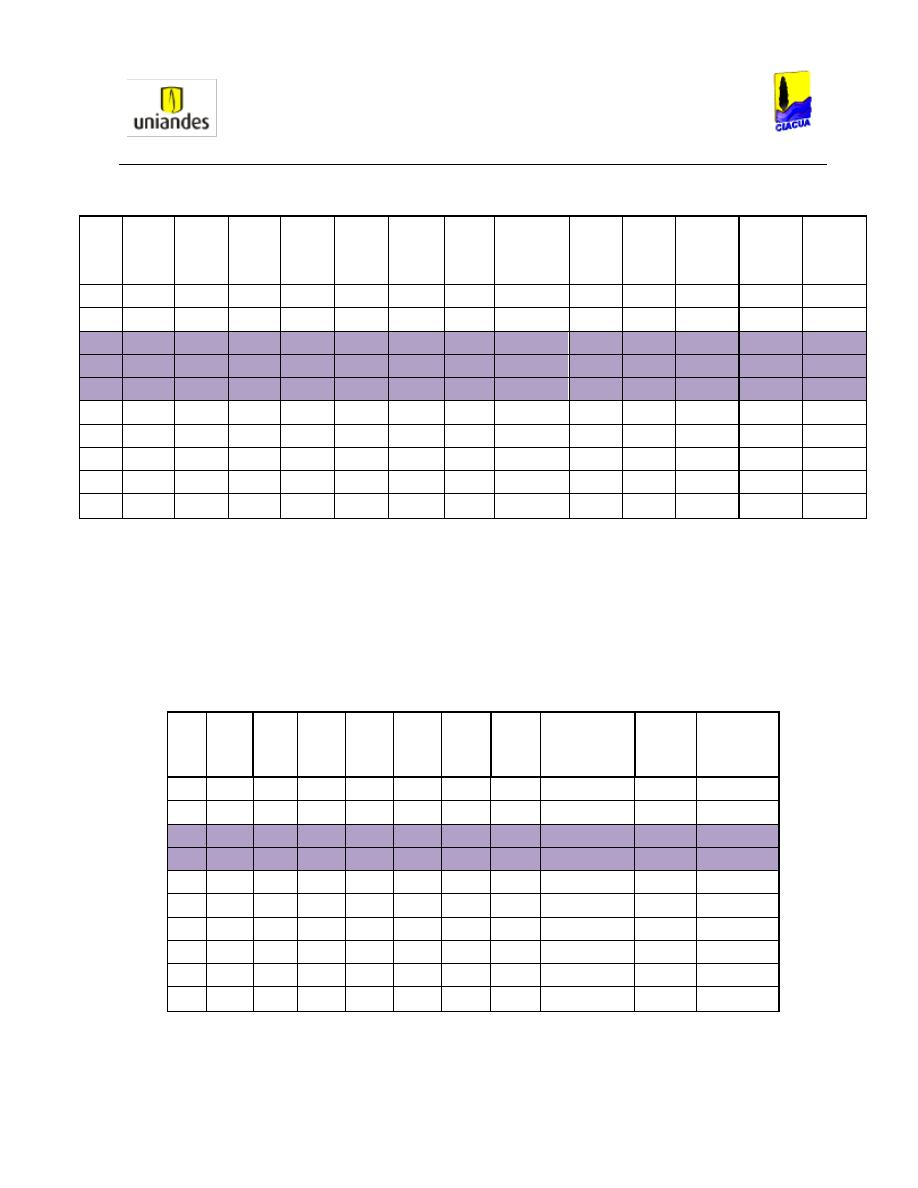
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

52 

 

Tabla 7. Diámetros seleccionados que superen el caudal de diseño y no superen los 48 cm de altura con 

relaciones de llenado del 85 %. 

d 

(m) 

yn 

(m) 

  

(-) 

Á 

(m²) 

P 

(m) 

R 

(m) 

V 

(m) 

Q 

(m³/s) 

Re 

(-) 

T 

(m) 

D 

(m) 

Froude 

(-) 

h 

soporte 

(m) 

d + 

soporte 

(m) 

0.1 

0.085 

4.692 

0.007 

0.235 

0.030 

2.158 

0.015 

229631.7 

0.071 

0.100 

2.183 

0.1 

0.200 

0.15 

0.128 

4.692 

0.016 

0.352 

0.045 

2.814 

0.045 

449084.9 

0.107 

0.149 

2.324 

0.1 

0.250 

0.2 

0.17 

4.692 

0.028 

0.469 

0.061 

3.388 

0.096 

721077.9 

0.143 

0.199 

2.423 

0.1 

0.300 

0.25 

0.213 

4.692 

0.044 

0.587 

0.076 

3.909 

0.174  1039829.5  0.179 

0.249 

2.501 

0.1 

0.350 

0.3 

0.255 

4.692 

0.064 

0.704 

0.091 

4.390 

0.281  1401297.5  0.214 

0.299 

2.563 

0.1 

0.400 

0.35 

0.298 

4.692 

0.087 

0.821 

0.106 

4.840 

0.422  1802433.9  0.250 

0.349 

2.617 

0.1 

0.450 

0.4 

0.34 

4.692 

0.114 

0.938 

0.121 

5.265 

0.599  2240825.9  0.286 

0.399 

2.663 

0.1 

0.500 

0.45 

0.383 

4.692 

0.144 

1.056 

0.136 

5.669 

0.817  2714497.0  0.321 

0.448 

2.703 

0.1 

0.550 

0.5 

0.425 

4.692 

0.178 

1.173 

0.152 

6.055 

1.077  3221787.4  0.357 

0.498 

2.739 

0.1 

0.600 

0.55 

0.468 

4.692 

0.215 

1.290 

0.167 

6.427 

1.383  3761274.8  0.393 

0.548 

2.772 

0.1 

0.650 

 

En la Tabla 7 se puede observar que con relaciones de llenado del 85 % (relación de llenado 
máxima permitida por el RAS), los diámetros cercanos al caudal máximo son los de 200 mm, 
250 mm y 300 mm; pero al igual que con la relación de llenado del 50 %, los diámetros de 200 
mm  y 250 mm permiten análisis con relaciones de llenado más altas dado que el caudal que 
transportan sigue siendo menor que el caudal máximo que puede transportar el montaje. 

Tabla 8.  Diámetros seleccionados que superen el caudal de diseño y no superen los 48 cm de altura con 

relaciones de llenado del 92.9 %.

 

d                             

(m) 

yn                           

(m) 

(-) 

A                       

(m²) 

P                       

(m) 

R                         

(m) 

V                          

(m/s) 

Q                               

(m³/s) 

Re                                   

(-) 

h                                     

(m) 

d + soporte 

(m) 

0,1 

0,093  5,204  0,008  0,260  0,029  1,627  0,012 

166855,528 

0,100 

0,200 

0,15  0,139  5,204  0,017  0,390  0,044  2,125  0,036 

326990,425 

0,100 

0,250 

0,2 

0,186  5,204  0,030  0,520  0,058  2,563  0,078 

525738,360 

0,100 

0,300 

0,25  0,232  5,204  0,048  0,651  0,073  2,959  0,141 

758879,656 

0,100 

0,350 

0,3 

0,279  5,204  0,068  0,781  0,088  3,326  0,228  1023461,122 

0,100 

0,400 

0,35  0,325  5,204  0,093  0,911  0,102  3,669  0,342  1317254,232 

0,100 

0,450 

0,4 

0,372  5,204  0,122  1,041  0,117  3,993  0,486  1638493,834 

0,100 

0,500 

0,45  0,418  5,204  0,154  1,171  0,132  4,302  0,663  1985733,499 

0,100 

0,550 

0,5 

0,465  5,204  0,190  1,301  0,146  4,597  0,874  2357757,724 

0,100 

0,600 

0,55  0,511  5,204  0,230  1,431  0,161  4,881  1,123  2753524,982 

0,100 

0,650 

 

 

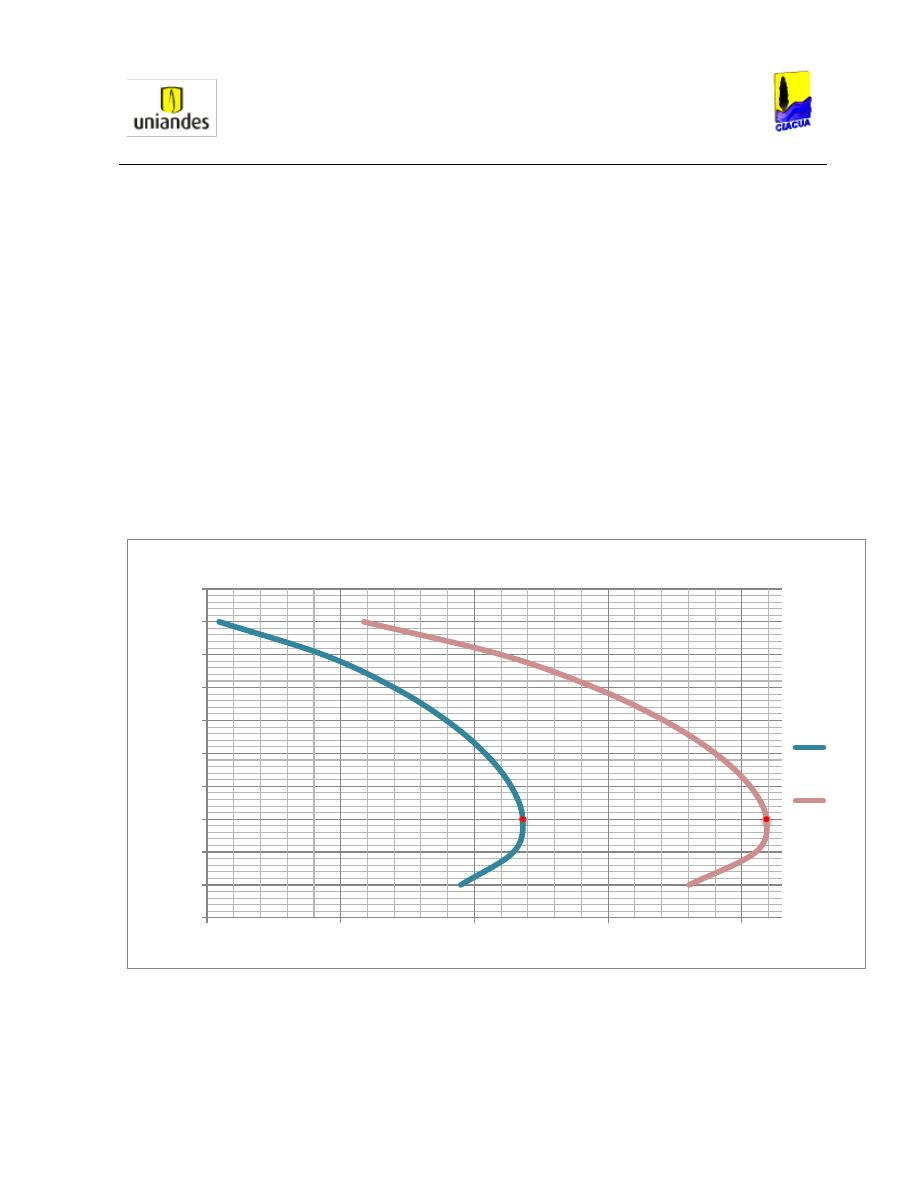
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

53 

 

En  la  Tabla  8  se  está  realizando  el  mismo  análisis  pero  con  la  relación  de  llenado  que 
produce el máximo caudal posible que puede transportar la tubería, por lo tanto, como supera 
la  normatividad,  se esperaría  que  no  se encuentren relaciones de llenado del 92.9 % en los 
alcantarillados  del  país.  Sin  embargo,  para  analizar  un  ejemplo  extremo,  se  realiza  éste 
análisis,  el  cual  muestra  que  el  único  diámetro  que  cumple  con  el  caudal  cercano  al  caudal 
máximo  que  puede  pasar  por  la  tubería  es  el  de  200  mm,  mientras  que  el  diámetro  de  250 
mm  ya se  ha  alejado  70  L/s  del  caudal  máximo,  por  lo  cual  el  único diámetro  que  permitiría 
realizar un análisis con todas las posibles relaciones de llenado sería el de 200 mm, pero con 
base en la norma y en la capacidad de visualizar el resalto, se elige el diámetro de 250 mm.  

5.2.  Análisis caudales máximos para diferentes pendientes 

 

Luego  de  elegir  el  diámetro,  se  realizó  un  análisis  con  dos  tipos  de  pendientes  y  diferentes 
relaciones  de  llenado  para  observar  la  variación  del  número  de  Froude  obteniendo  los 
siguientes resultados: 

 

Ilustración 29. Variación del número de Froude respecto a la relación de llenado para diferentes 

pendientes. 

 

0 

0.1 

0.2 

0.3 

0.4 

0.5 

0.6 

0.7 

0.8 

0.9 

1 

1.650 

2.150 

2.650 

3.150 

3.650 

y/d 

(-

) 

Froude (-) 

Variación Froude vs y/d 

So = 
0.019 

So = 
0.031 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

54 

 

La línea azul se calculó con la pendiente original del canal (1.9%), el coeficiente de rugosidad 
del  PVC,  la  viscosidad  del  agua  de 

         

  

  

 

    y  con  relaciones  de  llenado  variantes 

entre el 10% y el 100% y la línea rosada se calculó con una pendiente de 3.1 % (pendiente 
máxima que podrá tomar el montaje) y los demás valores idénticos a la línea azul. 

Por lo tanto, observando la Ilustración 29, se puede observar que para relaciones de llenado 
menores al 30%, el número de Froude aumenta a medida que aumenta la relación de llenado; 
para  relaciones  de  llenado  mayores  al  30%,    el  número  de  Froude  disminuye  a  medida  que 
aumenta la relación de llenado y cuando la relación de llenado es aproximadamente del 30%, 
se  observa  el  valor  máximo  del  número  de  Froude.  También  se  observa  que  el  rango  de 
variación  del  número  de  Froude  es  mayor  en  la  línea  rosada  que  en  la  línea  azul,  debido  a 
que el aumento de la pendiente aumenta la variación en la velocidad del flujo. 

Para corroborar el valor máximo del número de Froude, se realizó un análisis más detallado 
de  diferentes  pendientes  y  diferentes  caudales  para  encontrar  la  curva  que  representa  la 
variación del número de Froude respecto a las relaciones de llenado. 

5.3. Análisis del valor máximo del Número de Froude 

 

Para  encontrar  la  curva  que  describiría  en  qué  relaciones  de  llenado  se  encuentran  los 
valores máximos del número de Froude, se realizó un análisis con diferentes  pendientes (las 
cuales variaban entre el 0.5% al 3%)  para encontrar las relaciones de llenado qué cumplían 
con los siguientes caudales: [0.0001, 0.0005, 0.001, 0.002, 0.004, 0.006, 0.008, 0.01, 0.015, 
0.02, 0.025, 0.03, 0.035, 0.04, 0.05, 0.055, 0.06, 0.065, 0.07, 0.075 y 0.0776] m³/s. El proceso 
del análisis de describirá mediante las gráficas mostradas posteriormente. 

La primera ilustración refleja la forma como varía el caudal respecto a la relación de llenado 
(Ver Ilustración 30): 

 

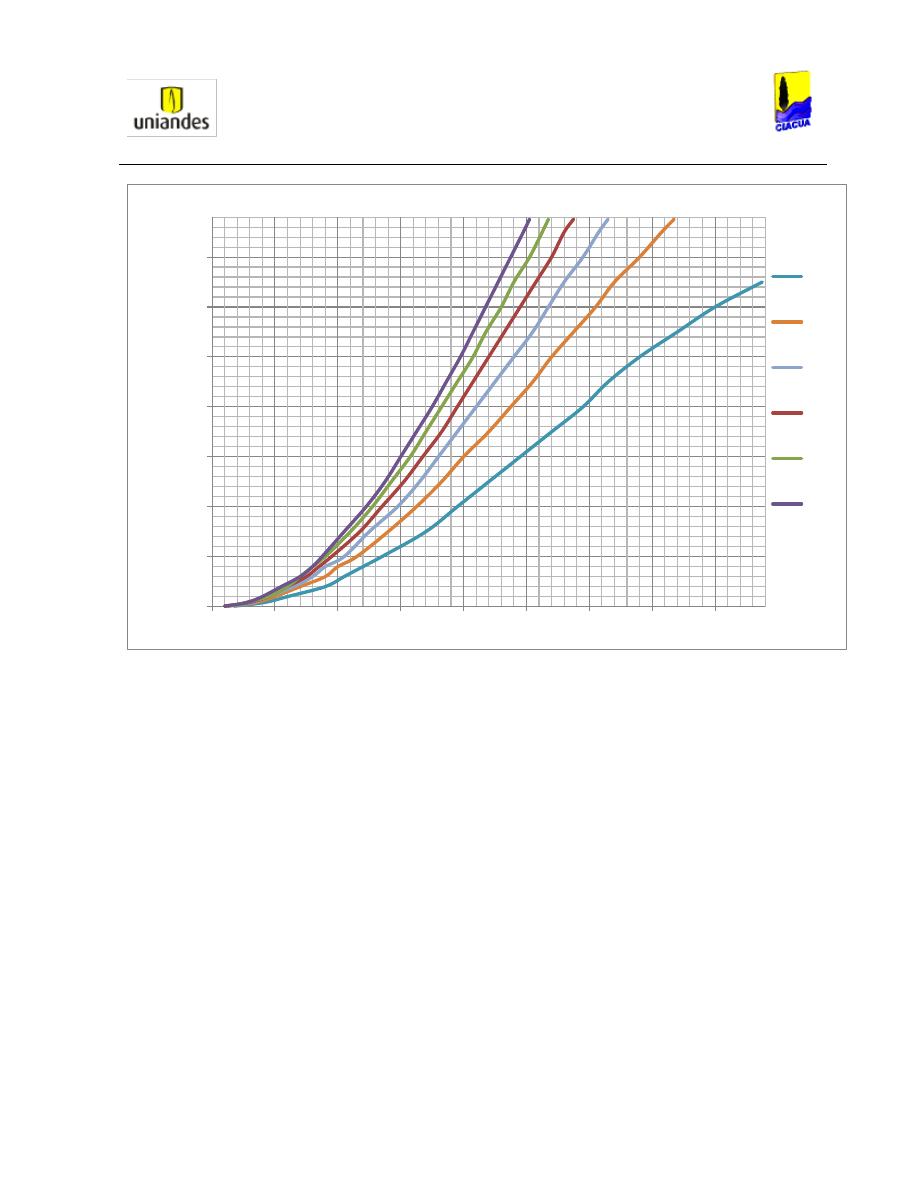
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

55 

 

 

Ilustración 30. Variación del caudal respecto a la relación de llenado. 

 

La  Ilustración  30  permite  observar  que  cuando  la  pendiente  es  más  baja,  la  variación  de  la 
relación  de  llenado    mueve  un  rango  de  caudales  más  bajo  que  las  pendientes  más  altas. 
Ésta  afirmación  se  explicaba  también  con  la  Ilustración  29,  puesto  que  en  la  pendiente  más 
alta  (3.1%),  el  número  de  Froude  tenía  mayor  rango  de  variación,  y  como  el  número  de 
Froude  y  el  caudal  son  proporcionales  a  la  velocidad,  se  concluye  que  cuando  aumenta  la 
pendiente, el rango de variación de la velocidad aumenta.  

También se observa que cuando las pendientes aumentan, las curvas se van acercando entre 
sí, lo que indica que el comportamiento del flujo empieza a ser similar. 

Posteriormente,  se  compara  la  variación  del  número  de  Froude  para  diversos  caudales  (Ver 
Ilustración 31): 

0 

0.01 

0.02 

0.03 

0.04 

0.05 

0.06 

0.07 

0 

0.1 

0.2 

0.3 

0.4 

0.5 

0.6 

0.7 

0.8 

Q 

(m³

/s)

 

y/d (-) 

Comparación Pendientes 

S = 
0.005 

S = 0.01 

S = 
0.015 

S = 0.02 

S = 
0.025 

S = 0.03 

 

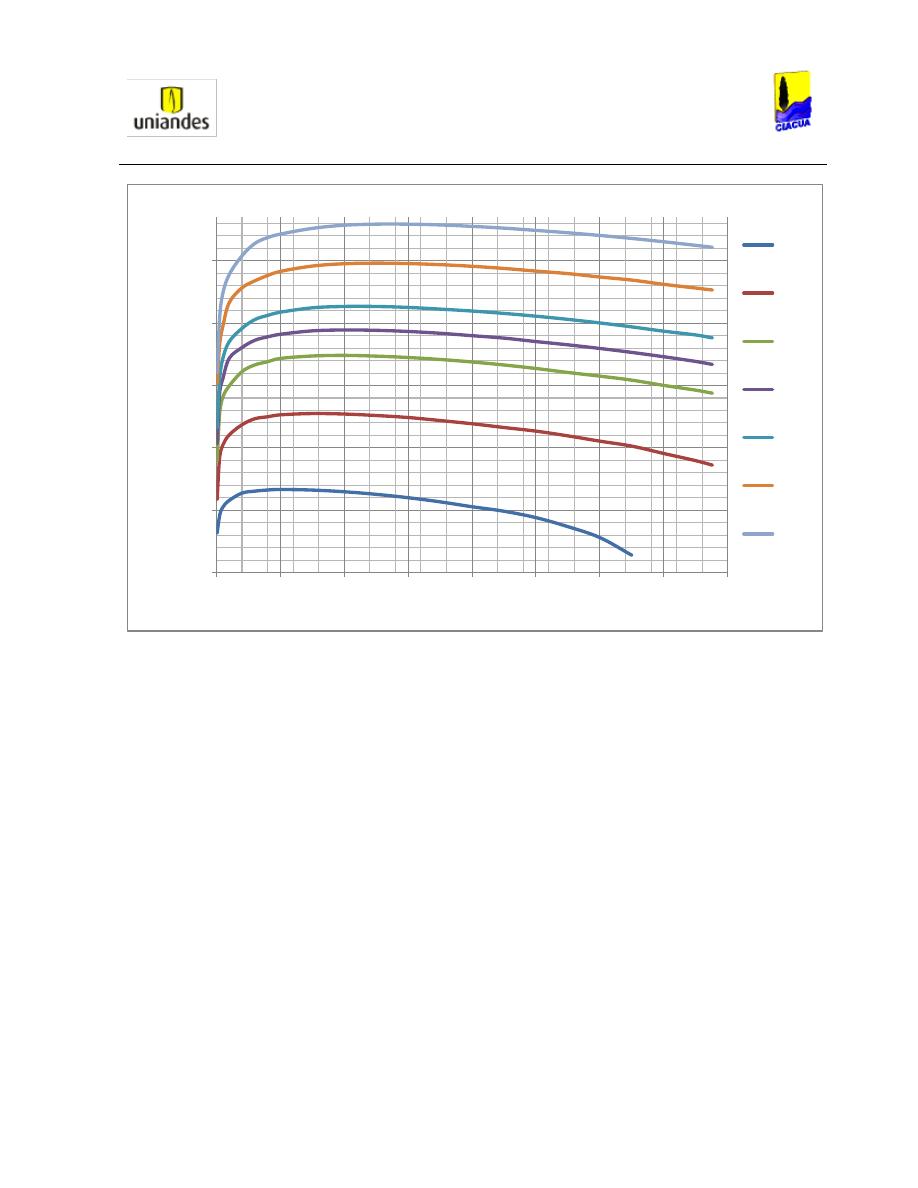
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

56 

 

 

Ilustración 31. Variación del número de Froude para diversos caudales. 

 

En  la  Ilustración  31  se  observa  un  valor  del  número  de  Froude  máximo  para  diferentes 
caudales, el cual se va desplazando hacia la derecha a medida que aumenta la pendiente, lo 
que  permite  concluir  que  a  mayor  pendiente,  el  valor  del  número  de  Froude  se  presentará 
para  caudales  más  altos.  Además  los  rangos  del  número  de  Froude  aumentan  con  el 
incremento  de  la  pendiente,  lo  que  sustenta  las  afirmaciones  expuestas  en  las  anteriores 
gráficas, dónde a mayor pendiente, mayor velocidad, es decir, mayor número de Froude. 

Luego, se realiza una gráfica similar  a la Ilustración 29 pero para los caudales expuestos en 
éste análisis, lo cual se observa en la siguiente ilustración: 

0.800 

1.300 

1.800 

2.300 

2.800 

3.300 

0 

0.01 

0.02 

0.03 

0.04 

0.05 

0.06 

0.07 

0.08 

Número 

de Froude 

(-

) 

Q (m

3

/s) 

Comparación de Pendientes 

S = 
0.005 

S = 
0.01 

S = 
0.015 

S = 
0.0175 

S = 
0.02 

S = 
0.025 

S = 
0.03 

 

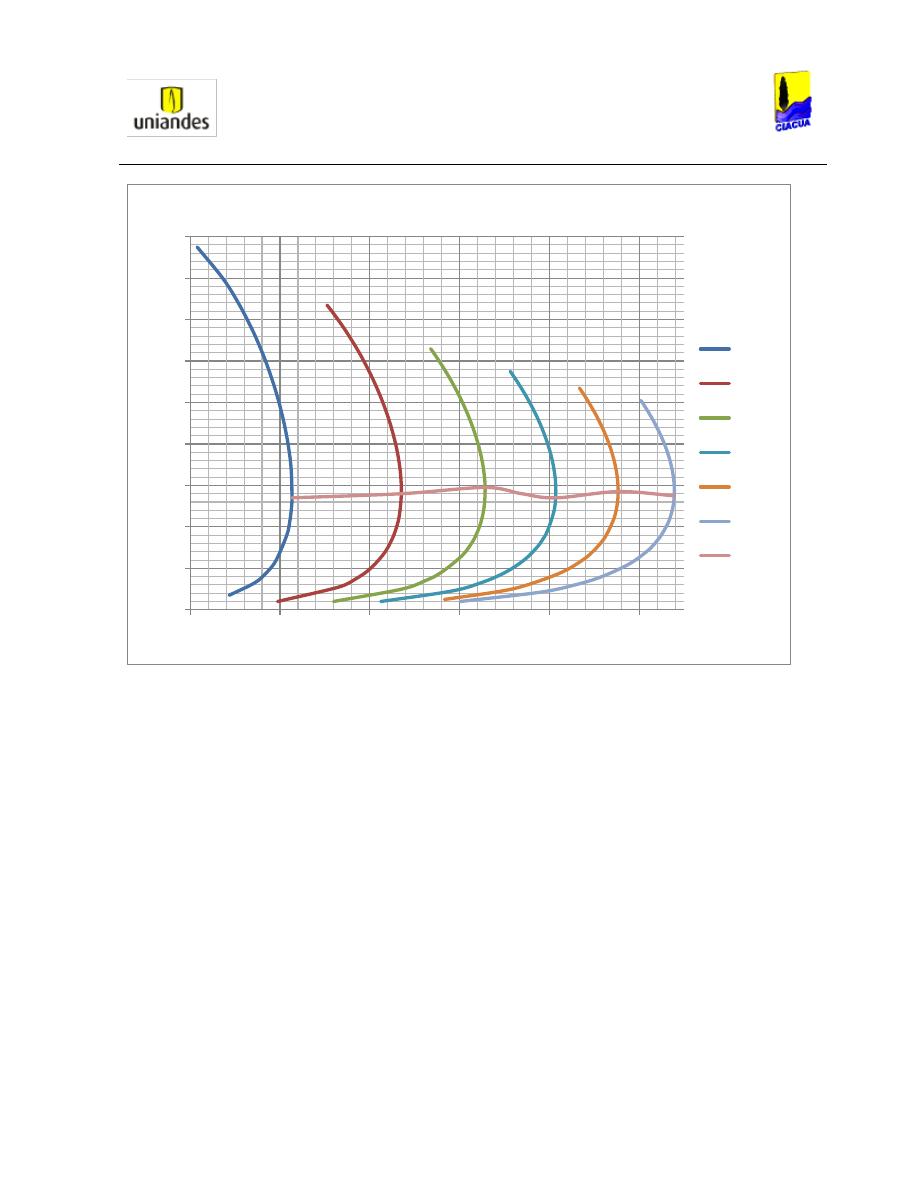
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

57 

 

 

Ilustración 32. Variación del número de Froude para diferentes relaciones de llenado. 

 

La  Ilustración  32  muestra  nuevamente  que  el  número  de  Froude  máximo  se  encuentra  con 
relaciones  de  llenado  cercanas  al  30%,  pero  la  ilustración  no  permite  obtener  una  ecuación 
coherente de la recta, por lo tanto, se requiere otro tipo de análisis para encontrar una curva 
que pueda representar el máximo en el número de Froude para el montaje. 

El análisis requiere aumentar el número de caudales elegidos para el análisis, puesto que con 
los  caudales  analizados,  se  está  parcializando  el  valor  de  las  relaciones  de  llenado,  por  lo 
tanto, para encontrar ésta curva se hizo uso de una macro en Excel con el lenguaje VBA, la 
cual  converge  mediante  el  método  de  la  bisección  (Ver  Ilustración  33),  en  la  cual  el  caudal 
aumenta cada 0.25 L/s: 

0 

0.1 

0.2 

0.3 

0.4 

0.5 

0.6 

0.7 

0.8 

0.9 

0.900 

1.400 

1.900 

2.400 

2.900 

3.400 

y/d 

(-

) 

Froude (-) 

Froude vs y/d (S total) 

S = 0.005 

S = 0.01 

S = 0.015 

S = 0.02 

S = 0.025 

S = 0.03 

Froude 
Máximo 

 

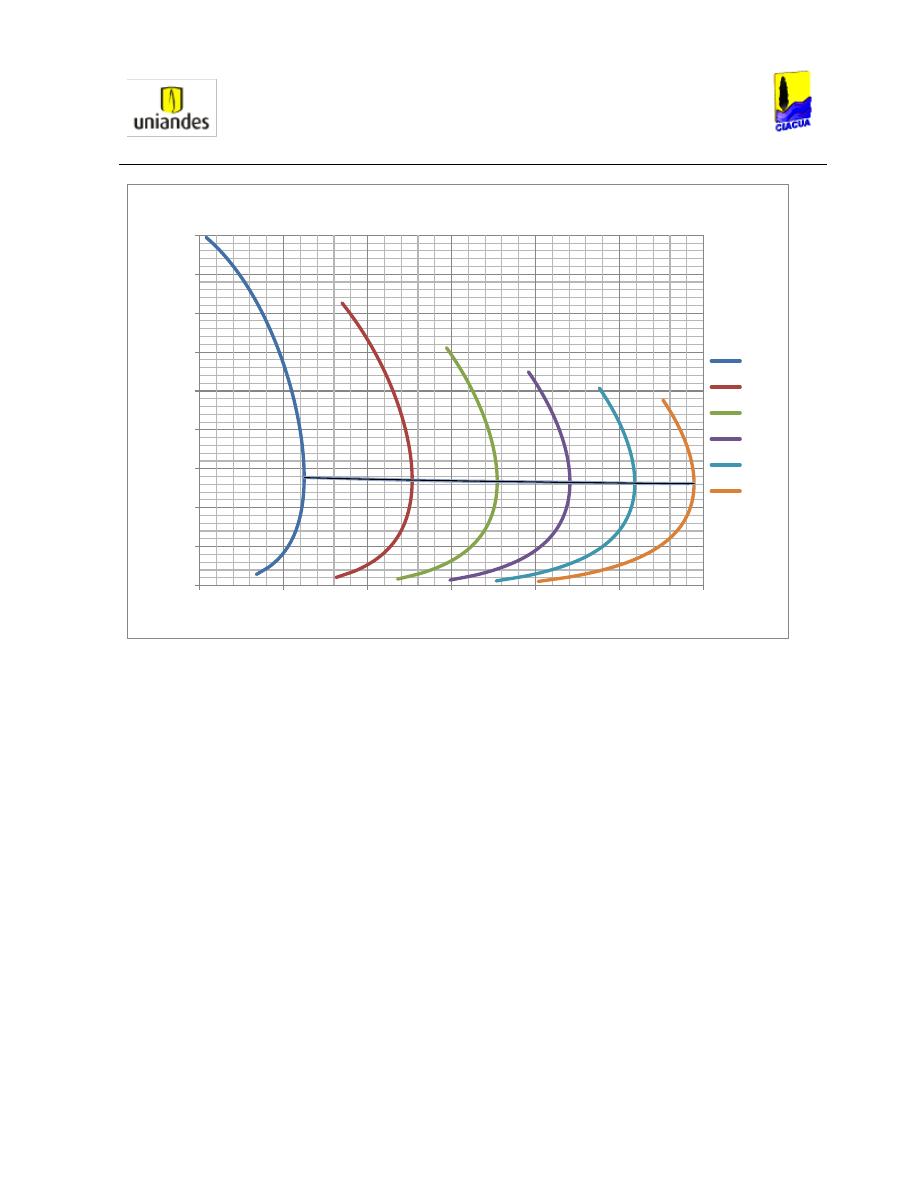
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

58 

 

 

Ilustración 33. Comparación número de Froude respecto a diferentes relaciones de llenado. 

 

La  Ilustración  33  permite  demostrar  que  la  curva  que  describe  mejor  en  qué  relación  de 
llenado  se  encuentran  los  números  de  Froude  máximos  se  ajusta  a  una  curva  potencial,  la 
cual se calcula mediante la Ecuación 67: 

           

      

 

Ecuación 67. Curva que describe el número de Froude máximo. 

 

Por lo cual, en el montaje que se realizará, los números de Froude máximos se encontrarán 
entre las relaciones de llenado de 0.28 y 0.30, es decir, que el resalto hidráulico más fuerte se 
presentará  cuando  la  profundidad  aguas  arriba  del  resalto  se  encuentre  entre  0.28  a  0.30 
veces el diámetro. 

0.020 

0.120 

0.220 

0.320 

0.420 

0.520 

0.620 

0.720 

0.820 

0.920 

0.750 

1.250 

1.750 

2.250 

2.750 

3.250 

3.750 

y/d 

(-

) 

Froude (-) 

Comparación Froude vs y/d 

S =0.005 

S = 0.01 

S = 
0.015 

S = 0.02 

S = 
0.025 

S = 0.03 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

59 

 

6. Costos del Proyecto 

 

El costo total de la construcción del modelo que permite el estudio de resaltos hidráulicos en 
tuberías circulares fue de $10.838.999, y comprende la compra de materiales como el acrílico, 
el  neopreno,  la  madera,  entre  otros;  la  mano  de  obra  en  la  construcción  de  la  tubería  y  del 
soporte, y todos los accesorios necesarios para el ensamble de la tubería.  

En  la  Tabla  9  se  observan  los  diferentes  artículos  adquiridos,  indicando  una  pequeña 
descripción de cada uno de ellos, la cantidad de elementos requeridos, y los precios unitarios 
y totales.  

Tabla 9. Costos del proyecto. 

No 

ARTÍCULO 

DESCRIPCIÓN 

CANTIDAD 

PRECIO 

UNITARIO 

PRECIO TOTAL 

1 

Tubos en acrílico 

Diámetro = 250 mm     

Longitud = 2 m 

6 

$ 900.000 

$ 5.400.000 

2 

Tubos en acrílico 

Diámetro = 250 mm     

Longitud = 0,75 m 

1 

$ 367.000 

$ 367.000 

3 

Bridas  

Diámetro = 350 mm          

8 perforaciones de 3/8               

Espesor = 1 cm 

16 

$ 69.000 

$ 1.104.000 

4 

Caja en acrílico 

 Altura = 55 cm                

Ancho = 30 cm                  

Espesor = 5 cm 

1 

$ 870.000 

$ 870.000 

5 

Tornillos 

Altura = 0,45 cm                  

Diámetro = 0,01 cm 

1 

$ 870.000 

$ 870.000 

6 

Soporte metálico 

Longitud = 3 m                    
Ancho = 25 cm              

Con 3 platinas por 

soporte cada metro 

4 

$ 487.500 

$ 1.950.000 

7 

Madera 

Longitud = 16 m               

Ancho = 15 cm                     

Altura = 3 cm 

4 

$ 23.500 

$ 94.000 

8 

Neopreno 

Largo = 1 m                   

Ancho = 1 m 

1 

$ 96.099 

$ 96.099 

9 

Pintura resistente al 

agua 

Galón 

1 

$ 37.900 

$ 37.900 

10 

Madera Mdf 

Altura = 90 cm               

Ancho = 60 cm 

1 

$ 50.000 

$ 50.000 

  

  

  

TOTAL 

 $   10.838.999  

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

60 

 

7.  Construcción y Resultados 

 

Para  iniciar  la  construcción  del  montaje,  se  limpió  y  arregló  el  canal  dónde  se  montaría  la 
tubería,  retirando  el  montaje  previo  que  existía  y  pintando  nuevamente  el  canal.  Luego  se 
adaptó la compuerta que sostendría la tubería aguas arriba,  cortando un pedazo de  madera 
(Triplex)  de  91  cm  de  largo  por  63  cm  de  ancho  y  2  cm  de  espesor,  al  cual  se  le  retiró  un 
círculo de 30 cm de diámetro (teniendo en cuenta el diámetro de la tubería y el espesor del 
neumático) para fijar la tubería en la compuerta.  

 

Ilustración 34. Canal antes y después. 

 

 

Ilustración 35. Compuerta pintada y con el neumático. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

61 

 

Luego se colocó el primer soporte para fijarlo al canal y permitir el movimiento de la tubería; 
por lo tanto, se fijaron tres soportes de madera de 40 cm de largo, 15 cm de ancho y 3 cm de 
espesor, y sobre éstos soportes, se colocaron dos chumaceras a cada extremo de las tablas 
con  un  tubo  en  acero  que  fue  fijado  en  el  inicio  del  soporte.  Éste  soporte  permite  fijar  el 
soporte  y la  tubería  aguas  arriba  e  impedir  el  movimiento  de  la  tubería  cuando  transporte  el 
agua.  Posteriormente,  se  colocaron  los  tres  soportes  adicionales,  uniéndolos  mediante 
tornillos milimétricos de 3/8. 

 

Ilustración 36. Fijación del soporte por medio de las chumaceras. 

 

 

Ilustración 37. Vista aguas abajo del soporte. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

62 

 

 

Ilustración 38. Vista aguas arriba del soporte. 

 

Luego se ubicaron los soportes horizontalmente en el canal teniendo en cuenta la pendiente 
por medio de tacos de madera (3 cm de espesor) y acrílico (0.5 cm de espesor), los cuales se 
ubicaron en cada sitio de unión de los soportes, es decir, en total se ubicaron 4 soportes de 
madera,  3  en  las  uniones  y  uno  en  la  parte  final  del  último  soporte.  Después  se    ubicó  el 
primer  tramo  de  la  tubería  retirando  los  soportes  del  canal  y  ubicándola  en  la  compuerta; 
luego  se  colocó  la  segunda  tubería  uniendo  las  bridas  de  las  tuberías  con  3  tornillos 
(colocados en X) mientras se terminaba de colocar el resto de la tubería y entre las bridas de 
acrílico se colocaba una brida de neopreno de 3 mm. Y así sucesivamente se colocaron los 6 
tramos de tubería de 2 m sobre los soportes. Fue muy importante tener en cuenta que la brida 
de la tubería no quedara encima de la unión del soporte. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

63 

 

 

 

 

Ilustración 39. Vista aguas arriba de la tubería. 

 

 

Ilustración 40. Vista aguas abajo de la tubería. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

64 

 

Posteriormente se colocaron todos los tornillos en las bridas y se colocó la última tubería en 
conjunto con la compuerta, la cual se soportó por tacos de madera. Luego de ubicar toda la 
tubería se infló el neumático y se fijó con silicona líquida a la compuerta de madera. 

 

Ilustración 41. Vista dentro de la tubería. 

 

 

Ilustración 42. Vista de la compuerta con el neumático. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

65 

 

 

Ilustración 43. Vista de la compuerta en el montaje. 

 

 

Ilustración 44. Vista perfil de la compuerta. 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

66 

 

Finalmente,  luego  de    constatar  que  todas  las  tuberías  estaban  bien  fijadas  y  que  no  había 
riesgo de que el acrílico pudiera presentar flexión, se abrió la válvula con un caudal de 20 L/s 
para probar que no existiera ninguna fuga. 

 

Ilustración 45. Vista montaje con agua. 

 

 

Ilustración 46. Vista flujo cuasicrítico en la tubería. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

67 

 

 

Ilustración 47. Vista montaje aguas abajo de la tubería. 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

68 

 

8. Conclusiones y Recomendaciones 

 

La  construcción  de  un  modelo  que  permitiera  la  formación  de  resaltos  hidráulicos  fue  un 
proceso de aprendizaje y trabajo. No solo se basó en realizar investigaciones exhaustivas en 
temas que tienen poca investigación académica y no han sido estudiados en Colombia, sino 
que  también  se  realizó  un  proceso  de  aprendizaje  en  la  interacción  del  constructor  y  el 
ingeniero.  

Al realizar éste proyecto, se investigó sobre los modelos anteriormente desarrollados para el 
estudio  de  resaltos  hidráulicos,  y  se  determinó  que  el  investigador  principal  ha  sido  Willi 
Hager,  el  cual  ha  desarrollado  varios  proyectos  para  entender  el  proceso  de  los  resaltos 
hidráulicos  en  tuberías  horizontales  y  la  formación  de  las  ondas.  Junto  con  Hager,  también 
Kindsvater (quien fue el primero en realizar la investigación), Kalinske y Ghamry han realizado 
montajes  con  diferentes  diámetros  en  las  tuberías  y  diferentes  pendientes.  Por  su  parte, 
Silvester, Rajaratnam, Straub, y la Circular de Ingeniería Hidráulica N° 14 realizaron el análisis 
teórico para sacar ecuaciones que cumplan con los resultados obtenidos en los experimentos 
realizados por los otros investigadores. 

También se encontró en este proyecto que la longitud del resalto para tuberías circulares ha 
sido  un  tema  de  baja  investigación,  y  solo  se  conocen  dos  ecuaciones  y  una  gráfica  que 
permiten  identificar  la  longitud,  la  primera  ecuación  fue  estudiada  por  Silvester,  la  segunda 
estudiada por Hager, y la gráfica que permite determinar la longitud del resalto fue hallada en 
la Circular N° 14 de Ingeniería Hidráulica del Departamento de Transporte de Estados Unidos.  

Otra  conclusión  importante  del  proyecto  se  encontró  en  la  evaluación  de  los  parámetros 
hidráulicos  del  montaje,  dónde  se  encontró  que  el  resalto  hidráulico  más  violento  que  se 
producirá  en  el  montaje,  se  formará  con  relaciones  de  llenado  de  0.3,  ya  que  bajo  éstas 
condiciones se produce el mayor número de Froude a diferentes pendientes y caudales.  

Por  lo  tanto,  para  el  siguiente  proyecto  se  recomienda  hacer  especial  énfasis  en  la  longitud 
del  resalto, realizando  varias  mediciones  para  determinar  coeficientes  y  relaciones  comunes 
para  diferentes  pendientes  y  caudales.  También  se  recomienda  mejorar  el  sistema  que 
permite  la  variación  de  la  pendiente,  ya  que  con  los  tacos  de  madera,  se  puede  presentar 
variación  en  la  pendiente  de  cada  tramo  del  soporte  y  generar  flexión  en  la  tubería;  por  lo 
tanto se recomienda el uso de gatos en cada una de las uniones de los soportes, los cuales 
permitirían un movimiento general de toda la tubería. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

69 

 

9. Agradecimientos 

 

Éste proyecto de grado se debe al  esfuerzo y dedicación de muchas personas. Primero que 
todo  quiero  darle  las  gracias  a  Dios  por  permitir  culminar  éste  proyecto,  a  mi  padre  Felix 
Humberto  Montaño,  quien  me  ayudó  en  el  proceso  de  escogencia  de  la  tubería,  en  la 
construcción de la maqueta y en elementos constructivos del montaje. También le agradezco 
a  Juan  Saldarriaga,  quien  me  otorgó  a  lo  largo  de  mi  carrera  los  conocimientos  necesarios 
para elegir ésta tesis, y además me orientó semana a semana  el tipo de avances que debía 
realizar  para  culminar  con  éxito  éste  proyecto.  Otro  agradecimiento  especial  a  John  Calvo, 
quien  me  ayudó  en  el  proceso  constructivo  del  montaje  durante  todo  el  semestre  y  a 
Hernando  Pérez,  el  constructor  de  la  tubería  y  el  soporte,  quien  cumplió  con  las  peticiones 
realizadas  y  siempre  estuvo  atento  a  cualquier  cambio  requerido  en  el  montaje.

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

70 

 

10.  Glosario 

 

Disipación de Energía: Porcentaje de energía que fue disipado a causa del resalto 
hidráulico. Su cálculo se realiza por medio de la Ecuación 68:  

   

 

 

   

 

 

 

 

Ecuación 68. Cálculo disipación de Energía 

Flujo Aguas Abajo: Profundidad del flujo que se encuentra después del resalto hidráulico. 

Flujo Aguas Arriba: Profundidad del flujo que se encuentra antes del resalto hidráulico. 

Flujo  Crítico:  El  flujo  crítico  se  presenta  cuando  las  fuerzas  inerciales  y  las  fuerzas  de 
gravedad son iguales, por lo tanto el número de Froude es igual a 1.0. Se caracteriza por ser 
un flujo inestable. 

Flujo  Subcrítico:  Flujo  caracterizado  por  tener  profundidades  altas,  velocidades  bajas, 
pérdidas  por  fricción  bajas  y  números  de  Froude  inferiores  a  1.0.  Además  las  fuerzas 
gravitacionales son mayores a las fuerzas inerciales. 

Flujo  Supercrítico:  Flujo  caracterizado  por  tener  profundidades  bajas,  velocidades  altas 
pérdidas por fricción altas y números de Froude mayores a 1.0. Además las fuerzas inerciales 
son mayores a las fuerzas gravitacionales. 

Línea de Gradiente Hidráulico: Línea que indica la altura del flujo desde el datum, es decir, 
teniendo en cuenta la energía potencial y de presión. 

Número  de  Froude:  Valor  adimensional  que  permite  determinar  a  partir  de  las  fuerzas 
gravitaciones y las fuerzas inerciales el tipo de flujo: supercrítico, crítico o subcrítico. 

Piezómetro: Instrumento para la medición de pérdidas de altura del flujo como consecuencia 
de fricción, obstrucciones, pérdidas menores, etc.  

Profundidad Subsecuente: Profundidad aguas abajo del resalto. 

Relación de llenado: Porcentaje de llenado de la tubería, es decir, la altura del flujo dividida 
entre el diámetro de la tubería. 

Resalto Hidráulico: Fenómeno generado por el cambio de flujo supercrítico a flujo subcrítico. 

Tubería presurizada: Cuando la profundidad del flujo es mayor al diámetro de la tubería. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

71 

 

11.  Bibliografía 

 

Akan, A. O. (2006). OPEN CHANNEL HYDRAULICS. Canada: ELSEVIER. 

CIVIL  ENGINEERING  PORTAL.  (2011).  What  are  the  effects  of  Hydraulic  Jump?  Retrieved 

Noviembre  28,  2011,  from  http://www.engineeringcivil.com/what-are-the-effects-of-
hydraulic-jump.html 

FHWA.  (2006).  Hydraulic  Design  of  Energy  Dissipators  for Culverts  and  Channels.  Hydraulic 

Engineering Circular, 6-1 a 6-14. 

French,  R.  H.  (2007).  The  Momentum  Principle.  In  R.  H.  French,  Open  Channel  Hydraulics 

(pp. 93 - 111). Colorado, USA: Copyright. 

Gargano, R., & Hager, W. H. (2002). Undular Hydraulic Jump in Circular Conduits. JOURNAL 

OF HYDRAULIC ENGINEERING, 1008-1013. 

Ghamry,  H.  K.,  Shames,  A.,  &  Branch,  F.  (2002).  Hydraulic  Jumps  in  Circular  Conduits  . 

Québec: CSCE. 

Gonzales  Rodriguez,  M.  (1992).  Estudio  Experimental  de  Flujos  Disipativos:  I.  Resalto 

Hidráulico. Cantabria: Universidad de Cantabria. 

Hager, W. H. (1990). CRITICAL FLOW. In W. Hager, Wastewater Hydraulics (pp. 137 - 172). 

Berlin: Springer. 

Kindsvater,  E.  W.  (1938).  Hydraulic  Jump  In  Enclosed  Conduits.  Engineering  News  Record, 

815 - 817. 

Rajaratnam, N. (1965). Hydraulic Jump in Horizontal Conduits. WATER POWER, 80 - 83. 

Robertson, J. M., & Kalinske, A. A. (1943). Closed Conduit Flow. Transactions of the American 

Society of Civil Engineers, 1435-1447. 

Silvester,  R.  (1964).  HYDRAULIC  JUMP  IN  ALL  SHAPES  OF  HORIZONTAL  CHANNELS. 

Proceedings of the American Society of Civil Engineers, 23 - 55. 

SMITH,  C.  D.,  &  CHEN,  W.  (1989).  The  hydraulic  jump  in  a  steeply  sloping  square  conduit. 

JOURNAL OF HYDRAULIC RESEARCH, 385 - 399. 

Stahl,  H.,  &  Willi  H,  H.  (1999).  Hydraulic  jump  in  circular  pipes.  Canadian  Journal  of  Civil 

Engineering, 368 -373. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

72 

 

12.  Anexos 

 

1.  Programación en VBA de Excel para calcular la profundidad normal del flujo 
2.  Mapa de la ubicación del montaje 
3.  Plano de la tubería en Perfil 
4.  Plano de la tubería en Planta 
5.  Plano en Autocad 3D de la tubería 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

73 

 

12.1  Macro realizada en VBA 

 

Sub caudal () 

d = 0.242 

ks = 0.0000015 

nu = 0.00000114 

Pi = 3.141592654 

suma = 0.01 

s = 0.005 

e = 0 

For i = 1 To 6 

For w = 1 To 308 

yd = 0.929 

yd0 = 0.01 

yp1 = 0 

    For j = 1 To 90 

    qe = Cells(e + w + 4, 6) 

    yn0 = d * yd0 

    teta0 = Pi + 2 * WorksheetFunction.Asin((yn0 - (0.5 * d)) / (0.5 * d)) 

    a0 = ((d ^ 2) / (8)) * (teta0 - Sin(teta0)) 

    p0 = (d * teta0) / 2 

 

    r0 = a0 / p0 

    vel0 = -2 * ((8 * 9.81 * r0 * s) ^ 0.5) * WorksheetFunction.Log10((ks / (14.8 * 
r0)) + ((2.51 * nu) / (4 * r0 * ((8 * 9.81 * r0 * s) ^ (0.5))))) 

    q0 = (vel0 * a0) - qe 

    re = (d * vel0) / nu 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

74 

 

    ancho = d * Cos(WorksheetFunction.Asin((yn0 - (0.5 * d)) / (0.5 * d))) 

    prof = a0 / ancho 

    froude = (vel0) / ((9.81 * prof) ^ (0.5)) 

     

    yn = d * yd 

    teta = Pi + 2 * WorksheetFunction.Asin((yn - (0.5 * d)) / (0.5 * d)) 

    a = ((d ^ 2) / (8)) * (teta - Sin(teta)) 

    p = (d * teta) / 2 

    r = a / p 

    vel = -2 * ((8 * 9.81 * r * s) ^ 0.5) * WorksheetFunction.Log10((ks / (14.8 * r)) 
+ ((2.51 * nu) / (4 * r * ((8 * 9.81 * r * s) ^ (0.5))))) 

    q = (vel * a) - qe 

                    

    ydp = (yd + yd0) / 2 

    ynp = d * ydp 

    tetap = Pi + 2 * WorksheetFunction.Asin((ynp - (0.5 * d)) / (0.5 * d)) 

    ap = ((d ^ 2) / (8)) * (tetap - Sin(tetap)) 

    pp = (d * tetap) / 2 

    rp = ap / pp 

    velp = -2 * ((8 * 9.81 * rp * s) ^ 0.5) * WorksheetFunction.Log10((ks / (14.8 * 
rp)) + ((2.51 * nu) / (4 * rp * ((8 * 9.81 * rp * s) ^ (0.5))))) 

    qp = (velp * ap) - qe 

     

    If (qp * q) < 0 Then 

        yd0 = ydp 

    Else 

        yd0 = yd0 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Diseño  y  construcción  de  un  modelo  para  estudiar  el  comportamiento  de 
resaltos  hidráulicos  en  tuberías  fluyendo  parcialmente  llenas  de  sección 
circular, con números de Froude supercríticos menores a 4

 

 

 

 

 

75 

 

    End If 

    If (qp * q0) < 0 Then 

        yd = ydp 

    Else 

        yd = yd 

    End If 

      

If (Abs((ydp - yp1) / (ydp))) < 0.0000001 Then 

        GoTo 100 

End If 

 

yp1 = ydp 

Next 

100 

Next 

s = 0.005 + s 

e = 308 + e 

Next 

End Sub