
PROYECTO DE GRADO
INGENIERÍA CIVIL
DISEÑO OPTIMIZADO DE REDES DE DRENAJE URBANO: ANÁLISIS DE
SENSIBILIDAD DE RESTRICCIONES DE DISEÑO Y VARIACIÓN TOPOGRÁFICA
PRESENTADO POR:
ANDRÉS FELIPE NORIEGA GARZÓN
ASESOR:
JUAN GUILLERMO SALDARRIAGA VALDERRAMA
Centro de Investigación en Acueductos y Alcantarillados (CIACUA), Departamento de Ingeniería
Civil y Ambiental, Universidad de los Andes, Bogotá, Colombia
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
BOGOTÁ D.C

AGRADECIMIENTOS
A mis abuelos Etelvina y Cicer
†
. Por haber materializado mis sueños hasta el día de hoy
A mi madre María Cristina y mi padre Guillermo Andrés. Por todo el amor y soporte
A mi abuelo Carlos Alberto
†
. De quien honradamente sigo sus pasos
A mi asesor y profesor, Juan Saldarriaga. Por sus enseñanzas, dedicación y orientación en el
desarrollo de esta investigación
A mis tías Victoria Eugenia Gómez y María Claudia Gómez. Por el apoyo y estar siempre
pendientes de mí
A mis amigos Nicolás Vargas y Santiago Prieto. Por todo el apoyo en momentos difíciles
A Valentina Aleg
ü
e. Por ser un soporte y ayudarme a sobrellevar estos tiempos difíciles durante
esta pandemia

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado i
TABLA DE CONTENIDO
1.
INTRODUCCIÓN ................................................................................................................................... 1
2.
OBJETIVOS ........................................................................................................................................... 3
2.1.
OBJETIVO
PRINCIPAL ......................................................................................................................... 3
2.2.
OBJETIVOS
ESPECÍFICOS .................................................................................................................... 3
3.
MARCO TEÓRICO ................................................................................................................................. 4
3.1.
VISIÓN
INTEGRAL .............................................................................................................................. 4
3.2.
EVALUACION
DE
REDES
DE
ALCANTARILLADO .................................................................................. 6
3.2.1.
FALLAS EN LOS SISTEMAS DE DRENAJE URBANO ..................................................................... 6
3.2.2.
CAUSAS DE LAS FALLAS ............................................................................................................ 6
3.2.3.
CONSECUENCIAS DE LAS FALLAS .............................................................................................. 8
3.3.
TIPOS
DE
SISTEMAS
DE
DRENAJE
URBANO........................................................................................ 9
3.4.
ELEMENTOS
DE
LAS
REDES
DE
DRENAJE
URBANO .......................................................................... 11
3.4.1.
INTRODUCCIÓN ...................................................................................................................... 11
3.4.2.
ELEMENTOS DE CAPTACIÓN ................................................................................................... 12
3.4.3.
ELEMENTOS DE CONDUCCIÓN ............................................................................................... 14
3.4.4.
ELEMENTOS DE INSPECCIÓN Y CONEXIÓN ............................................................................. 15
3.4.5.
ELEMENTOS DE ALIVIO Y REGULACIÓN .................................................................................. 17
3.4.6.
ELEMENTOS DE BOMBEO ....................................................................................................... 19
3.5.
CLASIFICACIÓN
DE
LOS
TIPOS
DE
FLUJO .......................................................................................... 19
3.5.1.
TIPOS DE FLUJO ...................................................................................................................... 19
3.5.2.
TIPOS DE FLUJO EN TUBERÍAS ................................................................................................ 20
3.6.
HIDRÁULICA
DE
TUBERÍAS
PARCIALMENTE
LLENAS
BAJO
FLUJO
UNIFORME ................................. 22
3.6.1.
FLUJO UNIFORME ................................................................................................................... 22
3.6.2.
ECUACIÓN DE MANNING ....................................................................................................... 24
3.6.3.
ECUACIÓN DE CHÉZY .............................................................................................................. 24
3.6.4.
ECUACION DE DARCY – WEISBACH CON LA ECUACIÓN DE COLEBROOK WHITE .................... 25
3.7.
PROPIEDADES
GEOMÉTRICAS
DE
LA
SECCIÓN
TRANSVERSAL
EN
TUBERÍAS
CIRCULARES .............. 26
3.8.
DISEÑO
DE
REDES
DE
DRENAJE
URBANO ........................................................................................ 28
3.8.1.
ESTIMACIÓN DE CAUDALES DE DISEÑO ................................................................................. 28
3.8.2.
DISEÑO DE UN TRAMO ........................................................................................................... 30
3.8.3.
DISEÑO DE REDES DE DRENAJE URBANO ............................................................................... 32
4.
METODOLOGÍA PARA EL DISEÑO OPTIMIZADO DE REDES DE DRENAJE URBANO .............................. 34
4.1.
INTRODUCCIÓN ............................................................................................................................... 34
4.2.
ANTECEDENTES ............................................................................................................................... 34
4.3.
METODOLOGÍA
PARA
EL
DISEÑO
OPTIMIZADO
DESARROLLADO
EN
EL
CIACUA ............................. 35
4.3.1.
DISEÑO HIDRÁULICO DE TUBERÍAS EN SERIE ......................................................................... 35
4.3.2.
INTRODUCCIÓN: REDES DE DRENAJE URBANO ...................................................................... 37

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado ii
4.3.3.
SELECCIÓN DEL TRAZADO DE REDES DE DRENAJE URBANO .................................................. 37
4.3.4.
DISEÑO HIDRÁULICO DE REDES DE DRENAJE URBANO .......................................................... 39
4.3.5.
VERSION EXTENDIDA PARA LA TOPOLOGÍA DE LA RED.......................................................... 40
5.
RESTRICCIONES DE DISEÑO EN SISTEMAS DE DRENAJE URBANO....................................................... 41
5.1.
INTRODUCCIÓN ............................................................................................................................... 41
5.2.
PROFUNDIDAD
MÁXIMA
DE
EXCAVACIÓN ...................................................................................... 41
5.3.
ESFUERZO
CORTANTE
MÍNIMO ....................................................................................................... 41
5.4.
RELACIÓN
DE
LLENADO
MÁXIMA .................................................................................................... 41
5.5.
VELOCIDAD
MÁXIMA ...................................................................................................................... 42
5.6.
VELOCIDAD
MÍNIMA ....................................................................................................................... 42
5.7.
DIÁMETRO
MÍNIMO ........................................................................................................................ 42
6.
JUSTIFICACIÓN DEL PROBLEMA Y METODOLOGÍA GENERAL ............................................................. 43
6.1.
JUSTIFICACIÓN ................................................................................................................................ 43
6.2.
METODOLOGÍA
GENERAL ............................................................................................................... 43
6.2.1.
RESTRICCIONES Y TOPOGRAFÍA .............................................................................................. 43
6.2.1.
ANÁLISIS DE MÁXIMA RELACIÓN DE LLENADO ÓPTIMA ........................................................ 46
6.2.2.
ECUACIÓN DE VELOCIDAD MEDIA DE FLUJO .......................................................................... 46
6.2.3.
ECUACIÓN DE COSTOS............................................................................................................ 46
7.
CASO DE ESTUDIO: RED CHICÓ SUR ................................................................................................... 49
8.
METODOLOGÍA PARA LA VARIACIÓN DE LAS RESTRICCIONES DE DISEÑO ......................................... 52
8.1.
INTRODUCCIÓN ............................................................................................................................... 52
8.2.
LÍMITES
E
INTERVALOS
PARA
CADA
RESTRICCIÓN
DE
DISEÑO ........................................................ 52
9.
TOPOLOGÍA Y TOPOGRÁFIA .............................................................................................................. 54
9.1.
ANÁLISIS
DE
LA
TOPOGRAFÍA
ACTUAL ............................................................................................ 54
9.2.
METODOLOGÍA
PARA
LA
VARIACIÓN
TOPOLÓGICA
DE
LA
RED ....................................................... 55
9.3.
METODOLOGÍA
PARA
LA
VARIACIÓN
TOPOGRÁFICA
DEL
TERRENO ............................................... 60
10.
RESULTADOS ................................................................................................................................. 61
10.1.
VARIACIÓN
TOPOLÓGICA
Y
TOPOGRÁFICA ..................................................................................... 61
10.1.1.
TOPOLOGÍA DE LA RED ........................................................................................................... 61
10.1.2.
TOPOGRAFÍA DEL TERRENO ................................................................................................... 62
10.2.
VARIACIÓN
DE
LAS
RESTRICCIONES
DE
DISEÑO .............................................................................. 66
10.2.1.
PROFUNDIDAD MÁXIMA DE EXCAVACIÓN ............................................................................. 66
10.2.2.
ESFUERZO CORTANTE MÍNIMO .............................................................................................. 66
10.2.3.
RELACIÓN DE LLENADO MÁXIMA ........................................................................................... 68
10.2.4.
VELOCIDAD MÁXIMA.............................................................................................................. 73
10.2.5.
VELOCIDAD MÍNIMA .............................................................................................................. 74
10.2.6.
DIÁMETRO MÍNIMO ............................................................................................................... 76
11.
ANÁLISIS DE RESULTADOS ............................................................................................................. 78

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado iii
11.1.
LIMITE
DE
VARIABILIDAD
Y
LÍMITE
SOLUCIÓN................................................................................. 78
11.2.
ANÁLISIS
DE
SENSIBILIDAD:
RESTRICCIONES
DE
DISEÑO ................................................................. 80
11.3.
EVALUACIÓN
DE
LA
FUNCIÓN
DE
COSTOS ...................................................................................... 85
11.4.
RESTRICCIONES
DE
DISEÑO:
EVALUACIÓN
DE
LA
VARIACIÓN
TOPOGRÁFICA ................................. 85
11.5.
MÁXIMA
RELACIÓN
DE
LLENADO
ÓPTIMA ...................................................................................... 87
11.5.1.
A PARTIR DE RESTRICCIONES CONSTANTES INICIALES ........................................................... 87
11.5.2.
ESFUERZO CORTANTE MÍNIMO .............................................................................................. 87
11.5.3.
VELOCIDAD MÍNIMA .............................................................................................................. 88
11.5.4.
DIÁMETROS COMERCIALES CONTINUOS ................................................................................ 88
12.
CONCLUSIONES Y RECOMENDACIONES ......................................................................................... 90
13.
REFERENCIAS ................................................................................................................................ 92
14.
ANEXOS ......................................................................................................................................... 95

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado iv
ÍNDICE DE FIGURAS
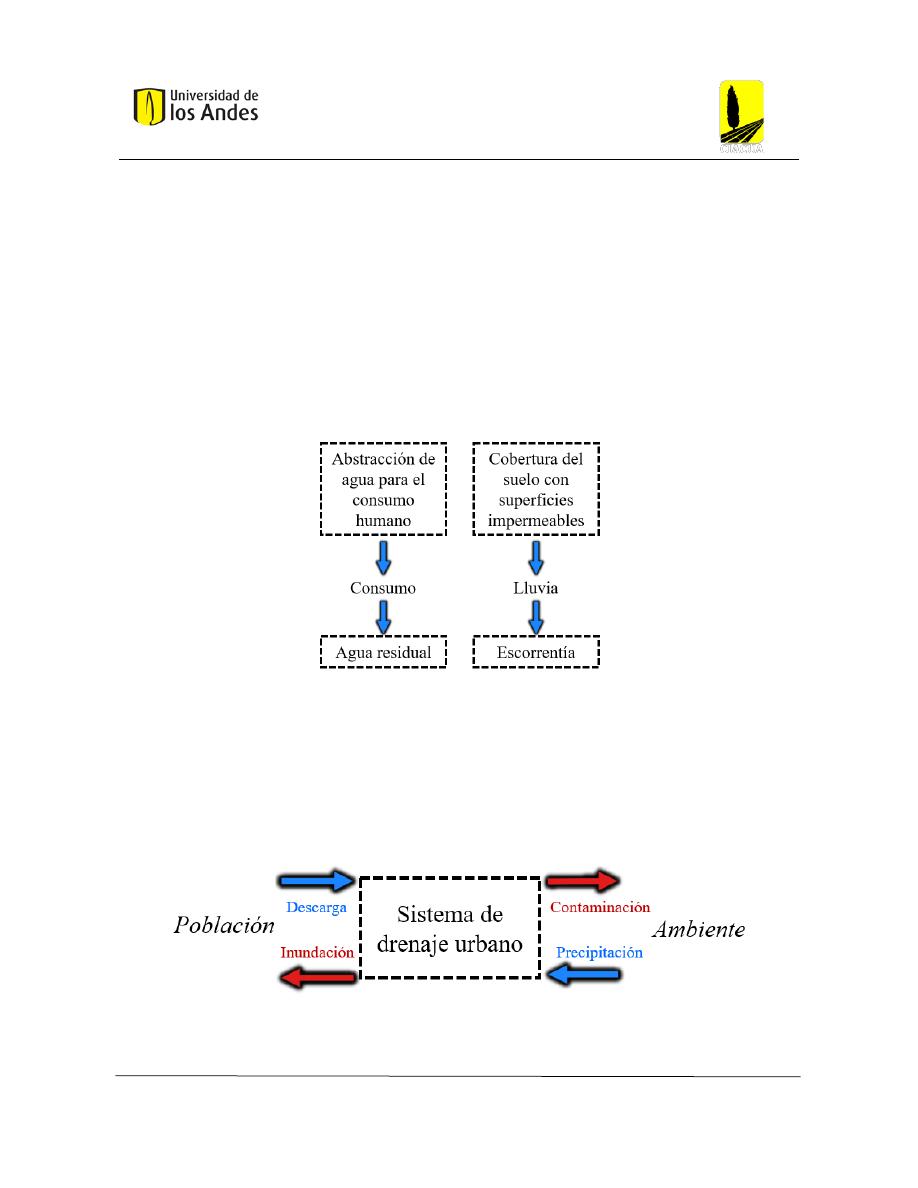
Figura 1: Fuentes de generación de agua residual y pluvial. (Butler & Davies, Urban drainage, 2011)
............................................................................................................................................................. 4
Figura 2: Interacciones del sistema de drenaje urbano. (Butler & Davies, Urban drainage, 2011) .... 4
Figura 3: Sistema integral de drenaje urbano. (Saldarriaga , Curso Sistemas de Drenaje Urbano, 2019)
............................................................................................................................................................. 5
Figura 4: Sistema integrado de drenaje con PTAR. (Saldarriaga , Curso Sistemas de Drenaje Urbano,
2019) ................................................................................................................................................... 5
Figura 5: Proceso químico de corrosión en tuberías de alcantarillado. (Park et Al. 2014) .............. 7
Figura 6: Ingreso de raíces a sistemas de alcantarillado. (Eurolimpiezas, s.f.) ................................... 8
Figura 7: Sobrecarga en los pozos. (LA CALLE Digital, 2012) ......................................................... 9
Figura 8: Formación de escorrentía. (NOTIFE, 2019) ...................................................................... 12
Figura 9: Canaletas implementadas en techos. (Benito, 2015) .......................................................... 13
Figura 10: Sumidero tipo ventana. (Saldarriaga , Curso Sistemas de Drenaje Urbano, 2019).......... 13
Figura 11: Sumidero con rejillas. (Saldarriaga , Curso Sistemas de Drenaje Urbano, 2019)............ 14
Figura 12: Sumidero mixto. (Saldarriaga , Curso Sistemas de Drenaje Urbano, 2019) .................... 14
Figura 13: Pozos de inspección. (MADERPLAST, 2016) ................................................................ 15
Figura 14: Tipos de unión en cañuelas. (López, 2003, pág. 349) ...................................................... 16
Figura 15: Cañuela vista en planta. (López, 2003, pág. 349) ............................................................ 16
Figura 16: Cámara de inspección vista en perfil. (López, 2003, pág. 350) ....................................... 17
Figura 17: Alcantarillado con estructura de alivio. (NYC Environmental Protection, s.f.). ............. 18
Figura 18: Alivio con vertedero: vista en planta y perfil. (Reglamento Técnico del Sector de Agua
Potable y Saneamiento Básico - RAS, 2016, pág. 177) .................................................................... 18
Figura 19: Resultados del segundo experimento de Reynolds. (Saldarriaga , Hidráulica de tuberías,
2019, pág. 11) .................................................................................................................................... 21
Figura 20: Perfil de flujo de una tubería parcialmente llena bajo flujo uniforme. (Saldarriaga , Curso
Sistemas de Drenaje Urbano, 2019) .................................................................................................. 22
Figura 21: Diagrama de cuerpo libre para tuberías parcialmente llenas. (Saldarriaga , Curso Sistemas
de Drenaje Urbano, 2019) ................................................................................................................. 23
Figura 22: Propiedades de la sección circular de una tubería parcialmente llena. (Saldarriaga , Curso
Sistemas de Drenaje Urbano, 2019) .................................................................................................. 27
Figura 23: Diagrama de flujo para el diseño de un tramo de alcantarillado: parte 1. (Saldarriaga ,
Curso Sistemas de Drenaje Urbano, 2019) ....................................................................................... 31
Figura 24: Diagrama de flujo para el diseño de alcantarillado: parte 2. (Saldarriaga , Curso Sistemas
de Drenaje Urbano, 2019) ................................................................................................................. 31
Figura 25: Grilla para la selección del trazado .................................................................................. 32
Figura26: Metodología desarrollada por Duque (2015) sintetizada por (Aguilar, Modelo de
Optimización Multiobjetivo para el Diseño de Redes de Drenaje Urbano , 2019, pág. 17) ............. 37
Figura 27: Tipo de tubería y posibles direcciones de flujo. (Duque, 2015, pág. 34). ........................ 38
Figura 28: Grafo para la selección del trazado. (Duque, 2015, pág. 35). .......................................... 38
Figura 29: Solución para el diseño hidráulico de una red ejemplo. (Duque, 2015, pág. 55)............. 39

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado v
Figura 30: Parte del barrio Chicó ...................................................................................................... 49
Figura 31: Delimitación de la red Chicó Sur ..................................................................................... 49
Figura 32: Red Chicó Sur .................................................................................................................. 50
Figura 33: Identificación de los pozos de la red Chicó Sur .............................................................. 51
Figura 34: Calle del barrio Chicó ...................................................................................................... 54
Figura 35: Topografía actual del terreno ........................................................................................... 55
Figura 36: Topología de una red ejemplo .......................................................................................... 58
Figura 37: Topología de la red ejemplo más plana que la topología original ................................... 58
Figura 38: Topología de la red ejemplo más inclinada que la topología original ............................. 59
Figura 39: TIN generado a partir de la topología original de la red Chicó Sur ................................. 60
Figura 40: Topografía del terreno V
1
................................................................................................ 62
Figura 41: Topografía del terreno V
2
................................................................................................ 63
Figura 42: Topografía del terreno V
3
................................................................................................ 63
Figura 43: Topografía para el terreno V
5
........................................................................................... 64
Figura 44: Topografía del terreno V
6
................................................................................................ 64
Figura 45: Serie de tuberías para exponer el perfil topográfico ........................................................ 65
Figura 46: Perfil topográfico: variación topográfica del terreno ....................................................... 65
Figura 47: Límite de variabilidad y límite solución para restricciones mínimas .............................. 78
Figura 48: Límite de variabilidad y límite solución para restricciones máximas .............................. 79
Figura 49: Costo en función de los límites para restricciones mínimas ............................................ 79
Figura 50: Costo en función de los límites para restricciones máximas............................................ 79
Figura 51: Serie de tuberías para el análisis de perfiles: velocidad mínima ...................................... 80
Figura 52: Diseño de la serie de tuberías para una velocidad mínima de 0.4 m/s (restricción baja) . 81
Figura 53: Diseño de la serie de tuberías para una velocidad mínima de 1.3 m/s (restricción
intermedia) ........................................................................................................................................ 81
Figura 54: Diseño de la serie de tuberías para una velocidad mínima de 1.7 m/s (restricción alta) . 82
Figura 55: Serie de tuberías para el análisis de perfiles: velocidad máxima ..................................... 83
Figura 56: Diseño de la serie de tuberías para una velocidad máxima de 5 m/s (restricción baja) ... 83
Figura 57: Diseño de la serie de tuberías para una velocidad máxima de 2.8 m/s (restricción
intermedia) ........................................................................................................................................ 84
Figura 58: Diseño de la serie de tuberías para una velocidad máxima de 2m/s (restricción alta) ..... 84

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado vi
ÍNDICE DE GRÁFICAS
Gráfica 1: Costo de la red ante la variación del esfuerzo cortante mínimo ....................................... 66
Gráfica 2: Costo de la red ante la variación de bajos esfuerzos cortantes mínimos .......................... 67
Gráfica 3: Profundidad máxima en la red ante variación del esfuerzo cortante mínimo................... 67
Gráfica 4: Costo de la red ante la variación de la máxima relación de llenado ................................. 68
Gráfica 5: Profundidad máxima en la red ante variación de la máxima relación de llenado ............ 69
Gráfica 6: Costo de la red para altas relaciones de llenado máximas: terreno V
1
............................. 70
Gráfica 7: Costo de la red para altas relaciones de llenado máximas: terreno V
2
............................. 70
Gráfica 8: Costo de la red para altas relaciones de llenado máximas: terreno V
3
............................. 71
Gráfica 9: Costo de la red para altas relaciones de llenado máximas: terreno V
4
............................. 71
Gráfica 10: Costo de la red para altas relaciones de llenado máximas: terreno V
5
........................... 72
Gráfica 11: Costo de la red para altas relaciones de llenado máximas: terreno V
6
........................... 72
Gráfica 12: Costo de la red ante la variación de la velocidad máxima.............................................. 73
Gráfica 13: Costo de la red ante la variación de altas velocidades máximas .................................... 73
Gráfica 14: Profundidad máxima en la red ante la variación de la velocidad máxima ..................... 74
Gráfica 15: Costo de la red ante la variación de la velocidad mínima .............................................. 75
Gráfica 16: Costo de la red ante la variación de bajas velocidades mínimas .................................... 75
Gráfica 17: Profundidad máxima en la red ante la variación de la velocidad mínima ...................... 76
Gráfica 18: Costo de la red ante la variación del diámetro mínimo .................................................. 76
Gráfica 19: Profundidad máxima en la red ante la variación del diámetro mínimo .......................... 77
Gráfica 20: Máxima relación de llenado para diámetros continuos .................................................. 89

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado vii
ÍNDICE DE TABLAS
Tabla 1: Ventajas de sistemas separados y desventajas de sistemas combinados. (Butler & Davies,
Urban Drainage, 2004) ...................................................................................................................... 10
Tabla 2: Desventajas de sistemas separados y ventajas de sistemas combinados. (Butler & Davies,
Urban Drainage, 2004) ...................................................................................................................... 11
Tabla 3: Materiales en tuberías de alcantarillado. (Saldarriaga , Curso Sistemas de Drenaje Urbano,
2019) ................................................................................................................................................. 15
Tabla 4: Clasificación de tipos de flujo. (Saldarriaga , Hidráulica de tuberías, 2019, págs. 2-3) ..... 19
Tabla 5: Características de la red de alcantarillado de análisis ......................................................... 44
Tabla 6: Lista de diámetros comerciales ........................................................................................... 45
Tabla 7: Restricciones de diseño por defecto .................................................................................... 45
Tabla 8: Abreviatura de los terrenos de análisis ................................................................................ 46
Tabla 9: Valor de los parámetros modificados por Aguilar (2017) para la ecuación de Maurer et Al.
(2012) ................................................................................................................................................ 48
Tabla 10: Límites e intervalos para la variación de restricciones de diseño ..................................... 52
Tabla 11: Límites e intervalo para la variación de altas relaciones de llenado máximas .................. 53
Tabla 12: Aplicación del parámetro V .............................................................................................. 57
Tabla 13: Valor de V y número de
∆𝑧𝑖 para llegar a los terrenos objetivo ....................................... 59
Tabla 14: Cotas del pozo 96 para todos los terrenos de análisis ....................................................... 62
Tabla 15: Relación entre el costo de la red, la topografía y restricciones altas de diseño ................. 86
Tabla 16: Relación entre el costo de la red, la topografía y restricciones bajas de diseño ................ 86
Tabla 17: Máxima relación de llenado óptima para distintos esfuerzos cortantes mínimos ............. 87
Tabla 18: Máxima relación de llenado óptima para distintas velocidades mínimas ......................... 88

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado viii
ÍNDICE DE ECUACIONES
Ecuación 1: Número de Reynolds (Saldarriaga , Hidráulica de tuberías, 2019) ............................... 20
Ecuación 2: Espesor de la subcapa laminar viscosa. (Saldarriaga , Hidráulica de tuberías, 2019) ... 21
Ecuación 3: Velocidad de corte. (Saldarriaga , Hidráulica de tuberías, 2019) .................................. 22
Ecuación 4: Pendientes en flujo uniforme ......................................................................................... 23
Ecuación 5: Manning. (Saldarriaga , Curso Sistemas de Drenaje Urbano, 2019) ............................. 24
Ecuación 6: Chézy. (Saldarriaga , Curso Sistemas de Drenaje Urbano, 2019) ................................. 24
Ecuación 7: Darcy-Weisbach. (Israelsen & Hansen, 1985, pág. 78) ................................................. 25
Ecuación 8: Darcy-Weisbach y Colebrook-White. (Saldarriaga ,2019)............................................ 25
Ecuación 9: Velocidad media en alcantarillados. (Saldarriaga , Curso Sistemas de Drenaje Urbano,
2019) ................................................................................................................................................. 26
Ecuación 10: Ángulo α ...................................................................................................................... 27
Ecuación 11: Ángulo θ ...................................................................................................................... 27
Ecuación 12: Área mojada ................................................................................................................ 28
Ecuación 13: Perímetro mojado ........................................................................................................ 28
Ecuación 14: Radio hidráulico .......................................................................................................... 28
Ecuación 15: Proyección de demanda ............................................................................................... 29
Ecuación 16: Caudal a partir de proyección de clientes .................................................................... 29
Ecuación 17: Caudal a partir de proyección de habitantes ................................................................ 29
Ecuación 18: Caudal medio diario .................................................................................................... 29
Ecuación 19: Caudal de diseño por tubería ....................................................................................... 30
Ecuación 20: Caudal de agua lluvia a partir del método racional ..................................................... 30
Ecuación 21: Número de trazados para una red de alcantarillado ..................................................... 32
Ecuación 22: Función objetivo propuesta por Safavi y Geranmehr (2016) ...................................... 35
Ecuación 23: Esfuerzo cortante en las paredes de tuberías de alcantarillado .................................... 41
Ecuación 24: Relación de llenado en tuberías de alcantarillado ....................................................... 42
Ecuación 25: Costo de un tramo por metro lineal – Ecuación de Maurer et al. (2010)..................... 47
Ecuación 26: Coeficiente α en la ecuación de Maurer et al. (2010). ................................................. 47
Ecuación 27: Coeficiente β en la ecuación de Maurer et al. (2010). ................................................. 47
Ecuación 28: Costo de un tramo – Ecuación de Maurer et al. (2012). .............................................. 47
Ecuación 29: Coeficiente α modificado en la ecuación de Maurer et al. (2012). .............................. 48
Ecuación 30: Coeficiente β modificado en la ecuación de Maurer et al. (2012). .............................. 48
Ecuación 31: Tasa de variación lineal por pozo ................................................................................ 56
Ecuación 32: Nueva cota del pozo para la variación j ....................................................................... 56
Ecuación 33: Demostración de terrenos planos para V pasos ........................................................... 57

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 1
1. INTRODUCCIÓN
Debido al aumento de la urbanización en ciudades de todo el mundo, ha sido necesario
implementar estrategias para evacuar diferentes tipos de agua generada. Dentro de estas, se
encuentra el agua lluvia como escorrentía, producida a causa de zonas impermeables como
vías, andenes, ciclo rutas entre otros. A su vez, el agua residual producida por el uso
doméstico, institucional, comercial e industrial del agua potable. En este sentido, los sistemas
de drenaje urbano convencionales se han caracterizado por ser la principal estrategia de
evacuación de aguas contaminadas en las ciudades. La principal razón consiste en que
permite condiciones de salubridad en áreas urbanas y reduce la proliferación de virus y
bacterias. Estos microrganismos pueden estar presentes en alimentos cuando se realiza el
aprovechamiento de agua lluvia o residual para riego, por ejemplo. De este modo,
representan un riesgo para la salud, puesto que son causantes de múltiples enfermedades
gastrointestinales como la diarrea.
El diseño y la construcción de redes de drenaje urbano representan un reto técnico y
económico, debido a su gran extensión espacial. Por tanto, existen normas en diferentes
países que reglamentan el diseño, la construcción, operación y mantenimiento de redes de
alcantarillado. Siendo la fase de diseño fundamental para este tipo de proyectos. El diseño
de redes de drenaje urbano depende de distintos aspectos tales como el material de las
tuberías, los diámetros comerciales, la hidrología y la topografía de la zona, y las
restricciones de diseño de la red. Con estos parámetros es posible dar solución a los dos
problemas de un diseño de red de drenaje urbano: la selección del trazado y el diseño
hidráulico. La solución a estos problemas es clave para determinar el comportamiento
hidráulico bajo distintos escenarios hidrológicos, y el costo total de la red.
A causa de la importancia del comportamiento hidráulico y los costos, se han desarrollado
distintas metodologías de optimización de redes de alcantarillado. Lo anterior, con el objetivo
de establecer un diseño óptimo que garantice una red hidráulicamente funcional al menor
costo posible. En la literatura, existen muchas metodologías sobre la optimización de las
redes de drenaje urbano. “Los ejemplos más claros están relacionados con programación
lineal y programación dinámica, que intentan darle solución a este problema. Lo anterior,
teniendo en cuenta que se deben resolver dos problemas diferentes y secuenciales, la
selección del trazado y el diseño hidráulico de la red” (Aguilar, 2019). Uno de estos ejemplos
es la metodología propuesta por Duque (2015). Esta metodología permite diseñar una red de
drenaje utilizando diferentes algoritmos de optimización: un modelo de programación entera
mixta conocido como Network Design Problem (NDP) para dar solución a la selección del
trazado y el algoritmo de Bellman–Ford para dar solución al diseño hidráulico de la red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 2
Adicionalmente, Zambrano (2019) propone una extensión a la metodología establecida por
Duque (2015). La metodología consiste en continuar empleando la programación lineal
mixta, aunque ahora variando el método de selección de trazado. Este último busca
solucionar el problema de selección de trazado teniendo en cuenta la topografía del terreno,
la topología y los caudales de entrada a la red de drenaje. De este modo, con esta extensión,
se obtienen diseños más económicos que la metodología base. Esto se logró a partir de
criterios que, para terrenos empinados, buscan reducir la profundidad de excavación a partir
de la topografía del terreno. Además, para terrenos planos, se establecieron criterios que
buscan minimizar la longitud de las series principales de la red de drenaje hasta el punto de
descarga.
A partir de los resultados de Zambrano (2019), es claro que la topografía del terreno afecta
en gran medida los costos totales de construcción de la red. En este sentido, en el presente
trabajo de investigación, se propone emplear la metodología de Zambrano (2019), para
realizar un análisis de sensibilidad de los costos de construcción de la red Chicó Sur, ubicada
en la ciudad de Bogotá. Adicionalmente, se pretende extrapolar este análisis de sensibilidad
variando las restricciones de diseño establecidas en el RAS 2016. En concreto, se pretende
entender el comportamiento de los costos de construcción ante variaciones topológicas y
variaciones en las restricciones de diseño. Esto, con el objetivo de determinar cuáles son las
condiciones topográficas y restrictivas en las que se encuentra el diseño de mínimo costo de
la red Chicó Sur.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 3
2. OBJETIVOS
2.1.
OBJETIVO PRINCIPAL
Realizar un análisis de sensibilidad de los costos de construcción de la red Chicó Sur, Bogotá.
En este, se pretende evaluar distintos escenarios de diseño, con el fin de determinar el
comportamiento de dichos costos ante la variación de las restricciones de diseño y la
topología de la red.
2.2.
OBJETIVOS ESPECÍFICOS
• Establecer un marco teórico general sobre los sistemas de drenaje urbanos y
optimización de dichas redes.
• Exponer la metodología de Duque (2015) y la extensión de Zambrano (2019) para la
optimización de redes de drenaje urbano.
• Evaluar los costos de la red Chicó Sur bajo la variación de restricciones de diseño
como: diámetro mínimo, relación de llenado máxima, velocidad mínima, velocidad
máxima y esfuerzo cortante mínimo.
• Evaluar los costos de la red Chicó Sur, bajo la variación de la topografía del terreno
y la topología de la red.
• Analizar el comportamiento y las implicaciones del uso de la ecuación de Maurer
bajo el análisis de sensibilidad.
• Establecer una metodología de variación topológica y topográfica para cualquier red
de drenaje urbano.
• Aplicar la metodología propuesta a la red Chicó Sur, para variar su topología, así
como la topografía del terreno.
• Establecer una máxima relación de llenado óptima para cada topología distinta.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 4
3. MARCO TEÓRICO
3.1.
VISIÓN INTEGRAL
Actualmente los sistemas de drenaje urbano deben tener un concepto de integralidad al
evacuar agua residual o pluvial. Es decir, evitar que el sistema actúe únicamente en función
de la recepción y evacuación del agua contaminada. Por el contrario, debe tenerse una visión
global que contemple el sistema de alcantarillado y los elementos que dependen de este. Estos
elementos son: la población y el ambiente. Es fundamental a su vez, identificar las
interacciones entre una red de drenaje y dichos elementos. Lo anterior, como afirma
Saldarriaga (2018), con el fin de minimizar posibles problemas ambientales y de salud
pública.
Figura 1: Fuentes de generación de agua residual y pluvial. (Butler & Davies, Urban drainage, 2011)
Como se puede ver en la Figura 1, el consumo humano genera agua residual, mientras que la
urbanización, escorrentía. En el escenario ideal del sistema de drenaje, este recibe descargas
o vertimientos de la población. Así como también puede recibir escorrentía, proveniente de
la precipitación. No obstante, si no cumple su función adecuada, existen riesgos asociados
que pueden generar repercusión tanto en la población y como el medio ambiente.
Figura 2: Interacciones del sistema de drenaje urbano. (Butler & Davies, Urban drainage, 2011)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 5
Dentro de estos riesgos, se encuentran las inundaciones, que implican el retorno de agua
residual y/o pluvial a la superficie urbana. Evidentemente, es un escenario indeseable, puesto
que compromete la salubridad de la población. Asimismo, si la calidad del agua que llega al
cuerpo receptor es deficiente, se tendrá repercusiones en la calidad del agua de este.
Comprometiendo así el entorno biótico y abiótico del cuerpo de agua receptor. De este modo,
es fundamental minimizar el riesgo de inundación y contaminación, garantizando al mismo
tiempo la funcionalidad del sistema sin generar sobrecostos.
Esta minimización se puede lograr a partir de la visión integral del sistema de drenaje. Para
conseguir esta integralidad, es importante evitar analizar cada componente del sistema de
manera aislada. Es decir, garantizar una gestión del agua desde su generación, hasta su punto
de entrega al cuerpo receptor. A continuación, se presenta un esquema de cómo podría ser
un sistema integral de drenaje urbano.
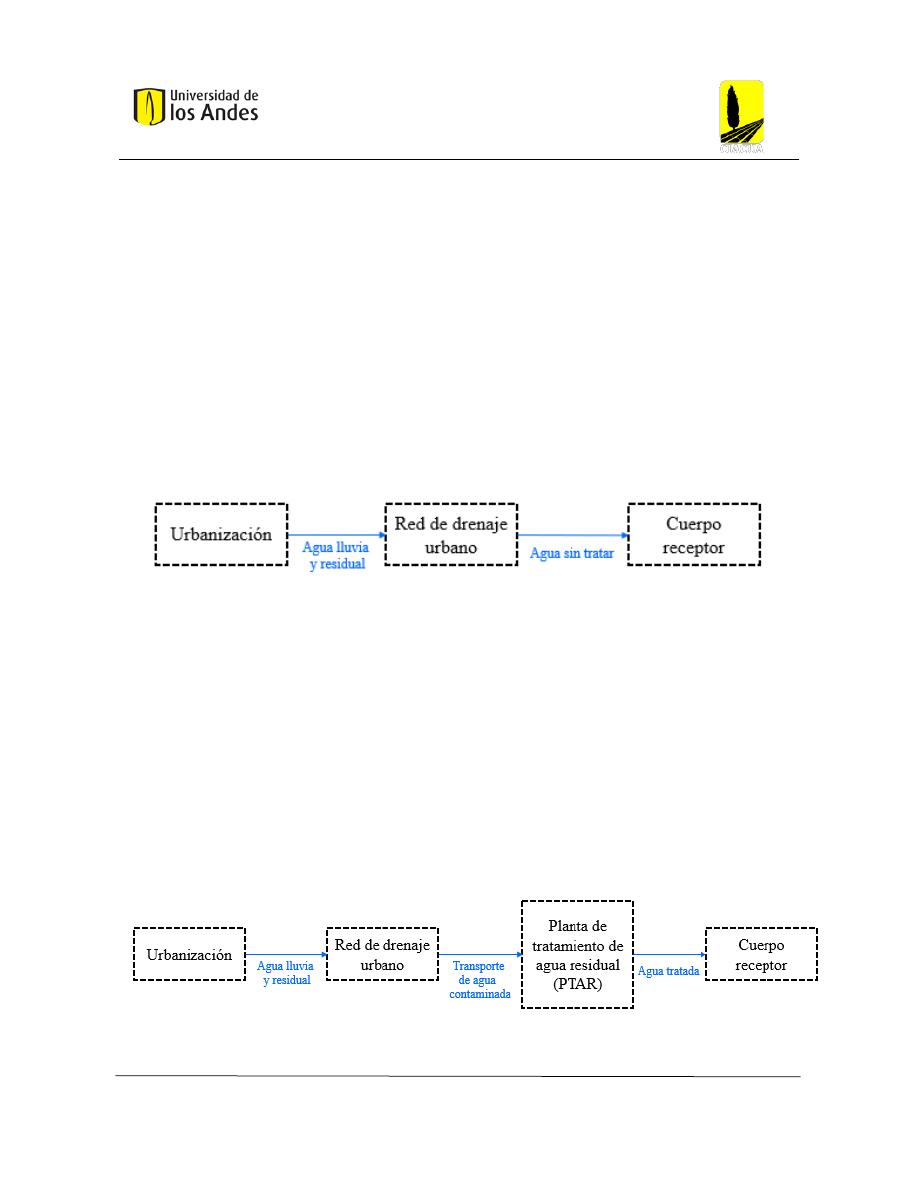
Figura 3: Sistema integral de drenaje urbano. (Saldarriaga , Curso Sistemas de Drenaje Urbano, 2019)
En este caso, cierta urbanización genera agua residual a partir del consumo de agua potable,
y escorrentía. El agua sin tratar es transportada a través de la red de drenaje hasta el cuerpo
receptor. En este sentido, para garantizar la integralidad del sistema, se debe tener en cuenta
principalmente el tamaño de la población, e identificar áreas impermeables y permeables de
la cuenca. También, evaluar la calidad del agua en la red de drenaje y la capacidad de
autodepuración del cuerpo receptor. La autodepuración se puede definir como “Proceso por
medio del cual un sistema natural puede llegar a recuperarse de los efectos o impacto de la
contaminación, ya sea natural o antropogénica” (Mata & Quevedo, 2005). No obstante, si la
carga contaminante del agua residual y/o pluvial aumenta lo suficiente, o la autodepuración
del cuerpo receptor es deficiente, es necesario implementar una planta de tratamiento de agua
residual (PTAR).
Figura 4: Sistema integrado de drenaje con PTAR. (Saldarriaga , Curso Sistemas de Drenaje Urbano, 2019)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 6
Así, analizando los componentes a partir de una gestión integral, se puede determinar las
consideraciones pertinentes en cada componente. Esta visión puede: prevenir riesgos
patogénicos en la población; evacuar de manera efectiva el agua contaminada; evaluar la
implementación de una PTAR; mitigar el riesgo de contaminación en el cuerpo receptor;
diseñar sin sobredimensionar los sistemas; evitar sobrecostos.
En concreto y, como menciona Saldarriaga (2019), es indispensable tener conocimientos en:
• La variabilidad espacial y temporal de las lluvias y vertimientos, en términos de la
cantidad y calidad del agua.
• Control de los picos de agua bajo un evento de lluvia.
• Pretratamiento o tratamiento en línea a través de la red de alcantarillado.
• Capacidad de autodepuración del cuerpo receptor
• Diseño de la red de alcantarillado y, de ser necesario, PTAR.
3.2.
EVALUACION DE REDES DE ALCANTARILLADO
3.2.1. FALLAS EN LOS SISTEMAS DE DRENAJE URBANO
Como se mencionó previamente, estos sistemas tienen una relación importante con la
población y el ambiente. Por lo tanto, cualquier falla en el sistema puede traer consecuencias
negativas para su entorno. Una falla se puede definir como un estado en el cual un sistema o
parte del sistema deja de ser funcional.
Las principales fallas estructurales son: deflexión, colapso, fisura, grieta y fractura.
(Rodríguez & Matamoros, 2017) realizan una definición para estos tipos de fallas. Dichos
autores establecen que: una deflexión se entiende como una pérdida original de la sección
transversal. Esta puede originarse tanto en las tuberías como en los pozos de inspección.
Asimismo, el colapso es la separación o destrucción de algún elemento del sistema a causa
de una carga externa. Las fisuras, por su parte, son la separación abierta del 50 % del espesor
una la tubería. Una grieta ocurre cuando se supera este 50% de separación. Una fractura se
define como una separación total en el espesor, es decir el 100%. En las redes de
alcantarillado hay muchas causas de falla, así como también distintas consecuencias
dependiendo del origen de dicha falla.
3.2.2. CAUSAS DE LAS FALLAS
Existen múltiples tipos de causas por las cuales un sistema de alcantarillado falla. Una de las
causas más comunes está relacionada a los agentes químicos presentes en el agua. Esta falla
se fundamenta en afectar, a partir de dichos agentes químicos, la tubería de la red. La
principal afección es la corrosión interna en las tuberías. Esta es causada principalmente por
la degradación anaerobia de materia orgánica presente en el agua. (López, 2003) afirma que
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 7
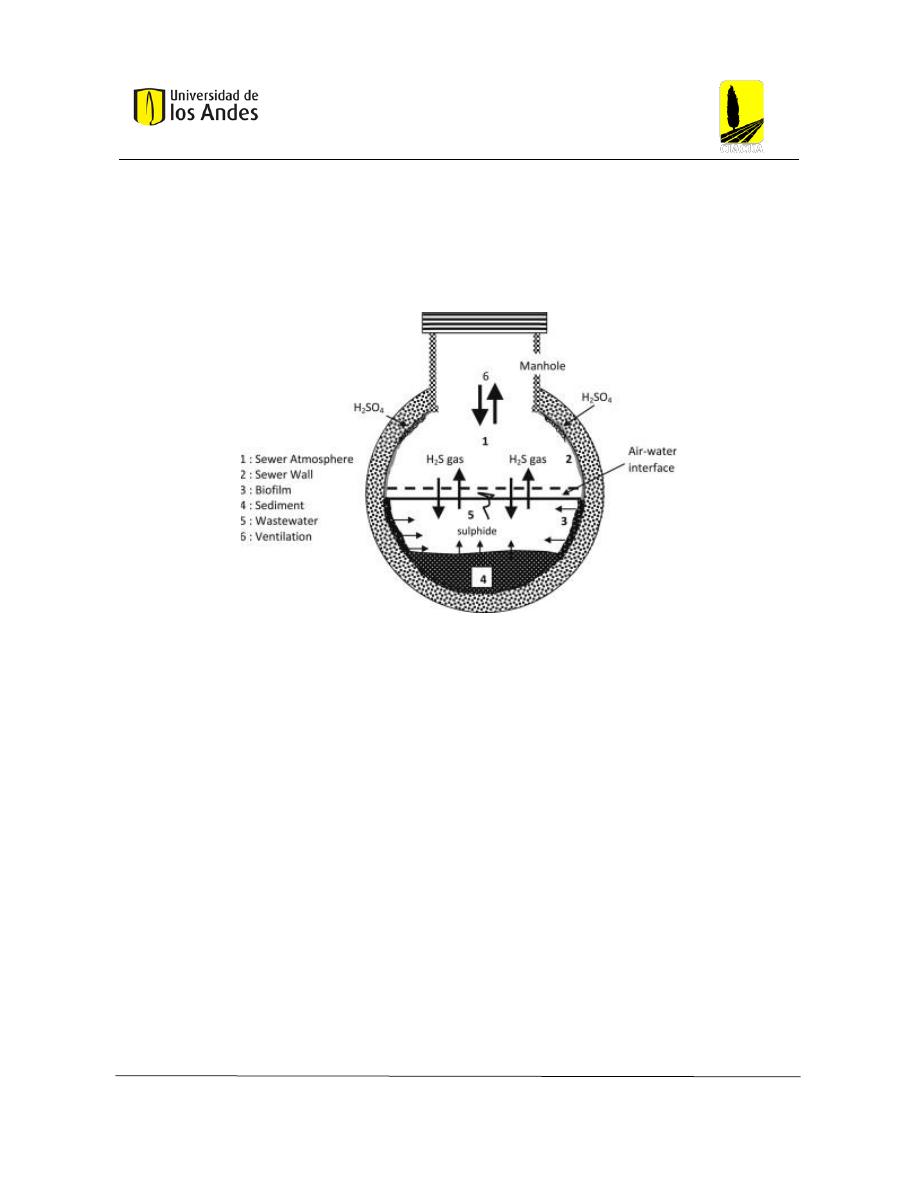
las bacterias reducen sulfatos cuando hay condiciones de pH bajo. De esta forma, se produce
ácido sulfhídrico (H
2
S). Este ácido se libera a condiciones aerobias y también vuelve a
disolverse en el agua. Sin embargo, parte del ácido sulfhídrico llega a la pared de las tuberías
y, bajo condiciones aerobias en presencia de la bacteria Thiobacillus, se genera ácido
sulfúrico (H
2
SO
4
) que es el que corroe las paredes de las tuberías.
Figura 5: Proceso químico de corrosión en tuberías de alcantarillado. (Park et Al. 2014)
Otra causa de falla se fundamenta en el comportamiento del suelo. “si bien el suelo de
contacto de las estructuras es en general material seleccionado que no debe afectar el
alcantarillado, debido a los flujos de diversas soluciones transportadas por el agua
subterránea y también a causa de los procesos de infiltración y exfiltración del agua residual
del alcantarillado, el suelo de contacto puede terminar alterado y sus características físico-
químicas pueden llegar a ser nocivas para los materiales que componen las estructuras de
alcantarillado” (Rodríguez & Matamoros, 2017, págs. 191-192). Así, la funcionalidad del
sistema de drenaje depende en gran medida del nivel freático. Si este es excesivamente alto,
predominarán las infiltraciones, y comprometerá el desempeño del sistema tanto aguas arriba
como aguas abajo. Además, la actividad física también puede causar daños estructurales la
red.
Asimismo, existen causas relacionadas a agentes externos tales como raíces de los árboles,
basuras y sedimentos. Es posible que algunas raíces cercanas al sistema perciban agua y, por
lo tanto, busquen la manera de incrustarse en las tuberías. Lo anterior se puede ver en detalle
en la Figura 6. Por otro lado, las basuras y los sedimentos pueden ingresar al sistema de
alcantarillado. Esto ocurre cuando no se implementa una estrategia de retención de sólidos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 8
como rejillas o trampa para sedimentos. Estos elementos pueden disminuir el área efectiva
de las tuberías y generar fallas en el sistema.
Figura 6: Ingreso de raíces a sistemas de alcantarillado. (Eurolimpiezas, s.f.)
Por último, está la falta de inspección y mantenimiento en las redes. A pesar de que es una
labor difícil por la complejidad de las estructuras hidráulicas, es necesaria para identificar los
riesgos más críticos en el sistema.
3.2.3. CONSECUENCIAS DE LAS FALLAS
Como se mencionó anteriormente, existen diferentes tipos de falla. Las fallas en los sistemas
de drenaje urbano pueden traer repercusiones ambientales y económicas, además de
representar un riesgo sanitario para la población.
Como menciona (Saldarriaga , Curso Sistemas de Drenaje Urbano, 2019), una de las
principales consecuencias ambientales son las exfiltraciones. Cuando el agua residual de la
tubería se filtra en el suelo, este corre el riesgo de contaminarse. Es decir, puede afectar el
medio biótico y abiótico en el subsuelo. Adicionalmente, algunos contaminantes podrían
llegar a aguas subterráneas y diluirse en estas. Esto trae dos riesgos ambientales: primero,
contaminar acuíferos. En segundo lugar, el agua subterránea podría transportar
contaminantes hasta cuerpos de agua superficiales como lagunas, ríos, quebradas, entre otros.
En ambos casos, se comprometería el uso de agua potencial para potabilizar, o que podría
ser usada en riego (tanto subterránea como superficial).
Por otra parte, están las sobrecargas. Cuando falla el sistema, existe el riesgo de que se
presente una presurización en las tuberías en parte o la totalidad del sistema. En este sentido,
el agua deja de transportarse a flujo libre por gravedad. El agua residual y/o sanitaria entonces

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 9
puede retornar a las superficies urbanas, causando así inundaciones, malos olores y
comprometiendo la salud de la población.
Figura 7: Sobrecarga en los pozos. (LA CALLE Digital, 2012)
Finalmente, las infiltraciones representan otra consecuencia común. Estas ocurren cuando se
filtra agua externa al sistema, como por ejemplo agua lluvia en alcantarillados sanitarios. A
su vez, cuando se filtra agua subterránea a las tuberías. En este sentido, aumenta
considerablemente el agua que fluye a través del alcantarillado. Como afirma Saldarriaga en
el año 2019, la cantidad de agua contaminada aumenta entre un 5% y 20%. Además, el
volumen de agua que llega a la PTAR aumenta, por lo que los costos de tratamiento terminan
siendo más elevados.
3.3.
TIPOS DE SISTEMAS DE DRENAJE URBANO
Los sistemas de drenaje urbano pueden clasificarse según el origen del agua que se esté
transportando. Según López (2013), hay cinco tipos de alcantarillados: alcantarillado
separado, alcantarillado combinado, alcantarillado simplificado, alcantarillado condominal y
alcantarillado sin arrastre de sólidos.
De este modo, López (2013) realiza las siguientes definiciones: los alcantarillados separados,
son sistemas que transportan de manera independiente agua lluvia y residual. Existen
alcantarillados sanitarios, cuya función radica en la evacuación de agua residual, sea de
origen industrial, doméstico, comercial o institucional. Por su parte, los alcantarillados
pluviales tienen el rol de evacuar escorrentía superficial, a causa de la precipitación.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 10
En contraste existen alcantarillados combinados, que conducen tanto agua residual como
agua lluvia por el mismo sistema. Los sistemas de drenaje urbano separado ofrecen múltiples
ventajas ambientales como, por ejemplo, se evita la implementación de alivios. Estos son
elementos que permiten la evacuación de agua cuando los caudales exceden la capacidad en
el sistema de alcantarillado. Son cruciales en sistemas combinados, puesto que el volumen
de agua lluvia es, considerablemente, más alto de agua residual en alcantarillados. Por lo
tanto, se debe verter agua contaminada a una fuente natural de agua externa para evitar
sobrecargas en el sistema.
Sin embargo, la conveniencia del tipo de sistema también depende de otros factores,
ambientales y económicos. De este modo, se clasificaron las ventajas y desventajas de cada
sistema, tanto económicas como ambientales. A continuación, se exponen las ventajas y
desventajas para cada sistema.
Tabla 1: Ventajas de sistemas separados y desventajas de sistemas combinados. (Butler & Davies, Urban Drainage, 2004)
SISTEMAS SEPARADOS
SISTEMAS COMBINADOS
Ventajas
Desventajas
No son necesarios alivios para sistemas sanitarios,
dado que se transporta menor caudal. No hay impacto
ambiental
Los alivios son importantes para evitar sobrecargas y
mantener funcionalidad en sistemas sanitarios. Existe
contaminación en corrientes externas de agua
Al tratar transportar menor caudal, disminuye el costo
de tratamiento en las PTAR
Al tratar transportar mayor caudal, aumenta el costo
de tratamiento en las PTAR
Si es necesario el bombeo, los costos son menores
Si es necesario el bombeo, los costos son mayores
Se diseña para una pendiente óptima según el tipo de
sistema
Se “negocia” las pendientes de las tuberías y no hay
profundidad óptima
Si se presentan, las inundaciones serían solo de agua
lluvia
Las inundaciones y sobrecargas representarían
impactos sanitarios
Los diámetros pueden son menores, hay mayor
velocidad manteniendo caudales bajos
Diámetros mayores, por lo que se presenta: velocidad
baja, acumulación de sólidos y sedimentos
Existe menor variación en los caudales de agua
residual
Existe mayor variación en caudales de agua residual:
dependen de eventos de precipitación
En sistemas sanitarios, llega menos basura y se
presenta menor acumulación de arena
Hay acumulación de basura y arena en sistemas
combinados

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 11
Tabla 2: Desventajas de sistemas separados y ventajas de sistemas combinados. (Butler & Davies, Urban Drainage, 2004)
SISTEMAS SEPARADOS
SISTEMAS COMBINADOS
Desventajas
Ventajas
Costo extra al implementar dos sistemas
separados
Menor costo al implementar un solo sistema de
evacuación de agua
Mayor riesgo de conexiones erradas (conexión
de agua lluvia a sistemas sanitarios)
Drenaje es simplificado y es más económico en
los hogares
Mayor ocupación de espacio para los sistemas
Menor ocupación de espacio para el sistema
No hay lavado de residuos sólidos en sistemas
sanitarios
Residuos sólidos lavados a causa de eventos de
precipitación
No hay tratamiento de agua lluvia
potencialmente contaminada
Hay tratamiento tanto de agua residual como de
agua lluvia
Como se puede ver, son muchas las implicaciones ambientales, económicas y funcionales en
cada sistema. Por lo tanto, es necesario un análisis profundo para determinar cuál sistema es
más conveniente en un caso específico.
El siguiente tipo de alcantarillado, a partir de López (2013) es un sistema simplificado. Este
es un sistema similar al alcantarillado sanitario. La diferencia radica en realizar esfuerzos por
reducir los diámetros y longitudes de las tuberías, con el fin de disponer de mejores equipos
de manteamiento.
A diferencia de los alcantarillados condominales, que recogen agua residual de un grupo de
viviendas (área menor a 1 hectárea), y las transportan a un sistema de alcantarillado
combinado.
Finalmente, están los alcantarillados sin arrastre de sólidos, o alcantarillados a presión. La
principal función de estos sistemas sanitarios es evacuar sólidos del sistema provenientes de
los hogares, a través de un tanque interceptor. Posteriormente, el agua es transportada al
sistema convencional de alcantarillado.
3.4.
ELEMENTOS DE LAS REDES DE DRENAJE URBANO
3.4.1. INTRODUCCIÓN
Si bien existen diferentes sistemas de drenaje, todos tienen componentes en común. Como
afirma Saldarriaga (2019), los principales componentes de estos sistemas son: captación;

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 12
conducción; inspección y conexión. Además, dependiendo del tipo de sistema, pueden ser
implementados componentes de alivio y bombeo. Cada componente mencionado cumple un
rol fundamental dentro del sistema.
3.4.2. ELEMENTOS DE CAPTACIÓN
Los componentes de captación son elementos que tienen el potencial de ingresar agua al
sistema de drenaje. Su función es recoger el agua, sea residual o lluvia, para que
posteriormente llegue a la red pública de alcantarillado.
El principal componente de captación de agua lluvia es el área superficial, principalmente el
área impermeable, que es común en áreas urbanas. Este tipo de área disminuye
considerablemente la infiltración de agua lluvia en el suelo, por lo que se genera escorrentía.
Figura 8: Formación de escorrentía. (NOTIFE, 2019)
Según Saldarriaga (2019), algunos ejemplos son: techos de las casas y edificios; canaletas y
bajantes en hogares; calles pavimentadas; parqueaderos; plazas y parques con materiales
impermeables. Luego de que se forme escorrentía en áreas impermeables, una fracción del
agua ingresa a los sistemas de drenaje.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 13
Figura 9: Canaletas implementadas en techos. (Benito, 2015)
Otro componente de captación, comúnmente implementado en vías y andenes peatonales,
son los sumideros. “Los sumideros contienen rejillas y usualmente un pozo colector
subyacente para colectar los materiales pesados arrastrados por el flujo” (Saldarriaga , Curso
Sistemas de Drenaje Urbano, 2019). Existen diferentes tipos de sumideros y se implementan
dependiendo del sitio donde se quiera construir. Los principales son sumideros de tipo
ventana, sumideros de rejillas en cunetas, sumideros mixtos y transversales.
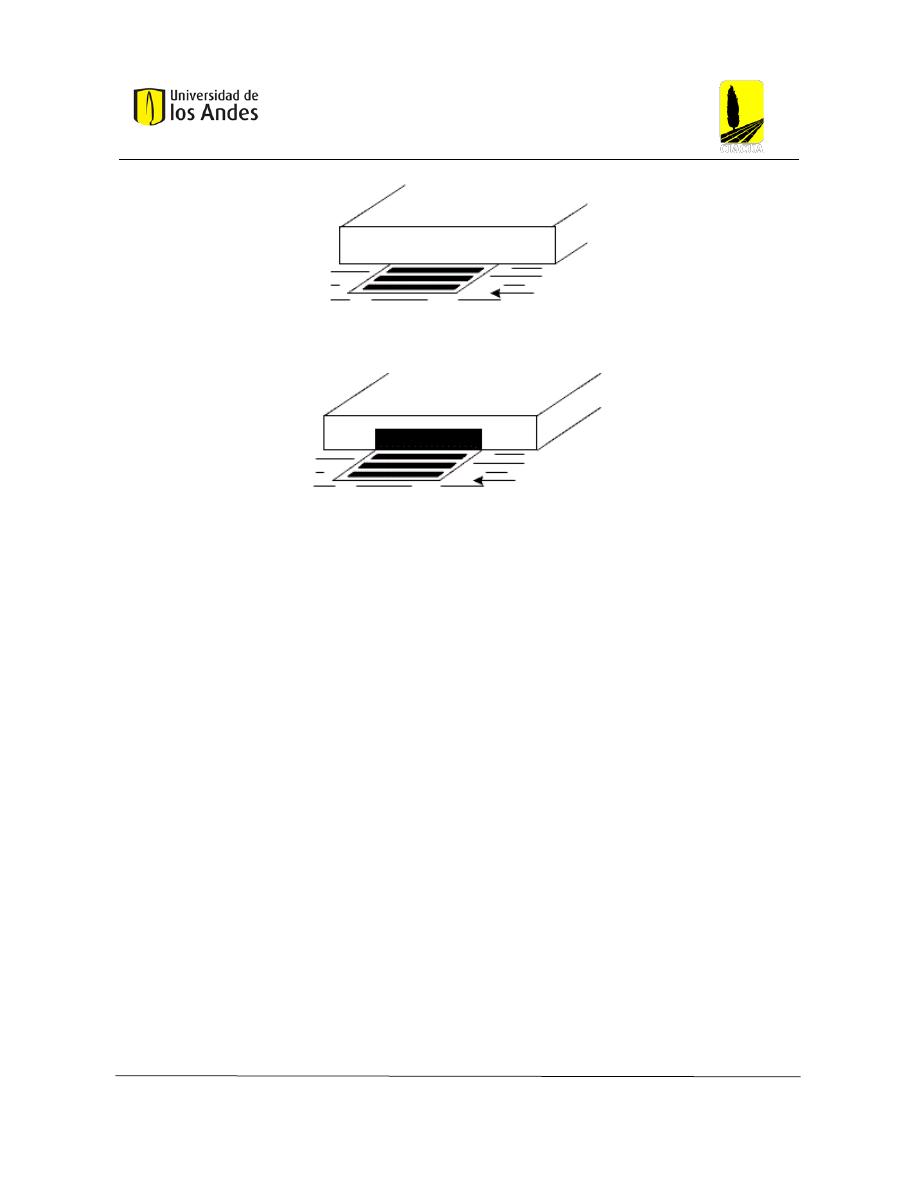
Los sumideros de tipo ventana consisten en una abertura en el andén. Además, es
perpendicular a la vía, de manera que no interfiere con el flujo de vehículos. No obstante, si
no se implementan rejillas, tiende a taponarse por basura y arena. Los sumideros de rejillas
en cunetas están ubicados sobre la vía y aprovechan las rejillas para evitar taponamiento.
Incluso, tienen un mejor desempeño bajo pendientes pronunciadas. Por su parte, los
sumideros mixtos son una combinación entre los dos anteriores, para mejorar la eficiencia de
este componente.
Figura 10: Sumidero tipo ventana. (Saldarriaga , Curso Sistemas de Drenaje Urbano, 2019)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 14
Figura 11: Sumidero con rejillas. (Saldarriaga , Curso Sistemas de Drenaje Urbano, 2019)
Figura 12: Sumidero mixto. (Saldarriaga , Curso Sistemas de Drenaje Urbano, 2019)
Finalmente, están los sumideros transversales. Estos componentes están ubicados de manera
transversal y a todo lo ancho de la vía. Además, tienen la ventaja de aumentar la capacidad
de drenaje, pero es más susceptible a daños por la carga cíclica causada por vehículos.
En cuanto a la captación de agua residual, están las conexiones domiciliaras. Su función,
como establecen Rodríguez y Matamoros en el 2017, es conectar la red interior de una
edificación o conjunto de edificaciones al sistema de alcantarillado público. (pág. 25).
3.4.3. ELEMENTOS DE CONDUCCIÓN
Los componentes de conducción son las tuberías en sistemas de drenaje. Estos son elementos
con sección transversal circular, y permiten el flujo de agua a través de estas. Los principales
materiales con los que se realizan tuberías son los siguientes.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 15
Tabla 3: Materiales en tuberías de alcantarillado. (Saldarriaga , Curso Sistemas de Drenaje Urbano, 2019)
Material
Hierro dúctil
Concreto reforzado
Arcilla vitrificada
Termoplásticos
Fibra de vidrío
Poliéster reforzado con fibra de vidrio
Acero
Mortero plástico reforzado
3.4.4. ELEMENTOS DE INSPECCIÓN Y CONEXIÓN
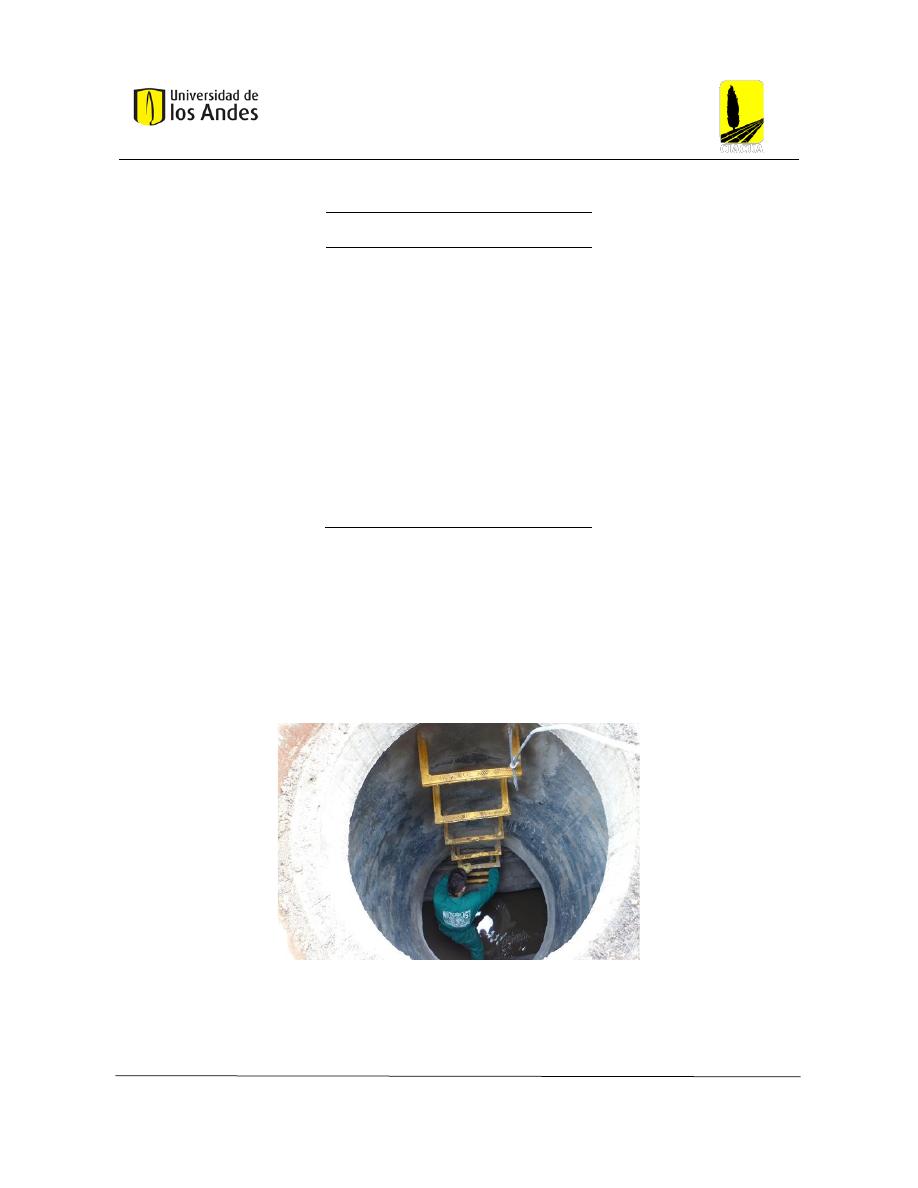
Los Manholes o cámaras son estructuras del sistema de alcantarillado, cuya principal función
es unir las tuberías para formar la red. Además, son utilizados para cambiar la dirección del
flujo, facilitar cambios en los diámetros y pendientes de las tuberías. Asimismo, las cámaras
de inspección son estructuras para determinar el estado actual de algunas secciones de la red.
Permite también realizar limpieza y mantenimiento en caso de ser pertinente.
Figura 13: Pozos de inspección. (MADERPLAST, 2016)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 16
En caso de ser necesario, las cámaras pueden ser reemplazadas por entradas de aire para
evacuación de olores y gases tóxicos. Según López (2013), los Manholes están compuestos
por los siguientes elementos: tapas de acceso, cilindro, reducción cónica y cañuela.
La tapa de acceso permite brindar ventilación al sistema y protegerlo de agentes externos.
Además, permite facilitar el acceso para labores de limpieza y mantenimiento general en las
tuberías. En segundo lugar, el cilindro es la estructura principal del pozo. Tiene una altura
variable dependiendo de la profundidad de diseño de las tuberías. Según el Reglamento
Técnico del Sector de Agua Potable y Saneamiento Básico (RAS) 2016, el diámetro mínimo
del cilindro debe ser de 1.2 metros. En tercer lugar, la reducción cónica es un elemento que
permite unificar la tapa de acceso y el cilindro, ya que tienen diámetros distintos. Por último,
está la cañuela. Este componente es la base del cilindro y, en éste, ocurre la unión de flujos
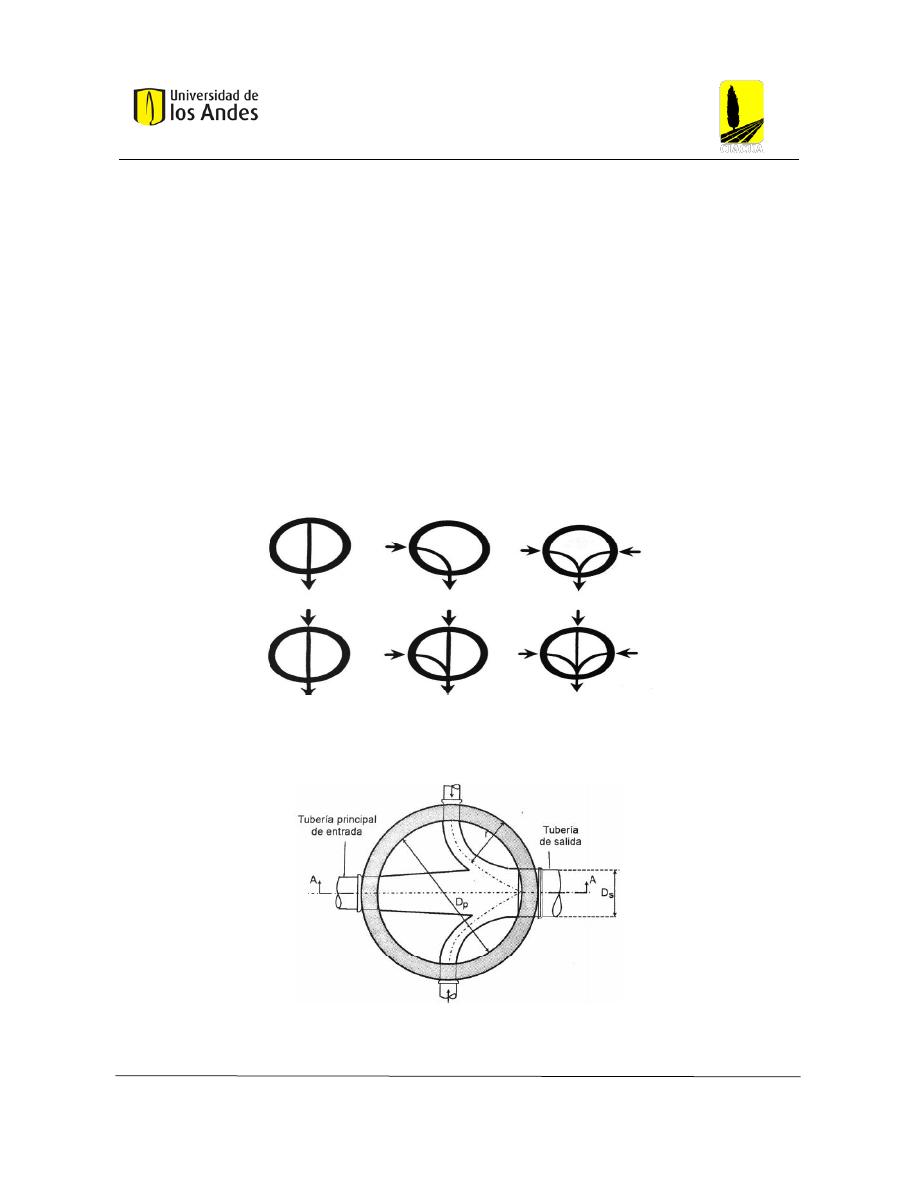
provenientes de distintas tuberías. A continuación, se presentan las posibles formas de unión
en la cañuela de las cámaras de inspección.
Figura 14: Tipos de unión en cañuelas. (López, 2003, pág. 349)
De igual forma, se presenta una cañuela en planta.
Figura 15: Cañuela vista en planta. (López, 2003, pág. 349)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 17
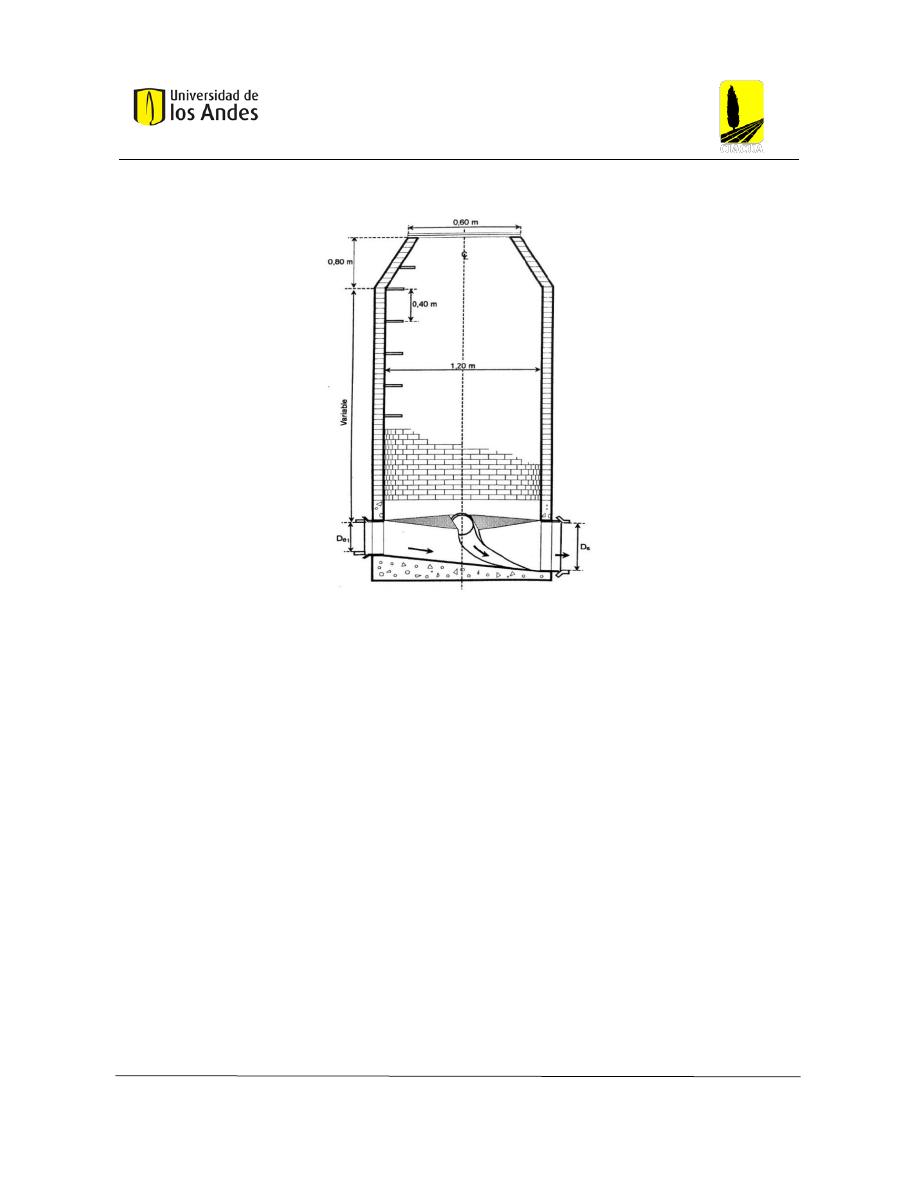
Y, finalmente, una vista en perfil de una cámara de inspección típica de alcantarillado.
Figura 16: Cámara de inspección vista en perfil. (López, 2003, pág. 350)
3.4.5. ELEMENTOS DE ALIVIO Y REGULACIÓN
Los componentes de alivio, como se mencionó anteriormente, son implementados en
sistemas de drenaje combinados. El RAS 2016 establece que “Los aliviaderos de
alcantarillados combinados tienen como objetivo disminuir los costos de conducción de los
caudales combinados de aguas residuales y aguas lluvias hasta el sitio de disposición final o
hasta la planta de tratamiento de aguas residuales, en caso de que ésta exista.” (pág. 170).
De esta forma, cuando se presenta un evento de precipitación, los aliviaderos permiten
evacuar el exceso de agua por medio de un vertedero. Así, el agua que rebosa el vertedero es
conducida a un cuerpo de agua receptor.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 18
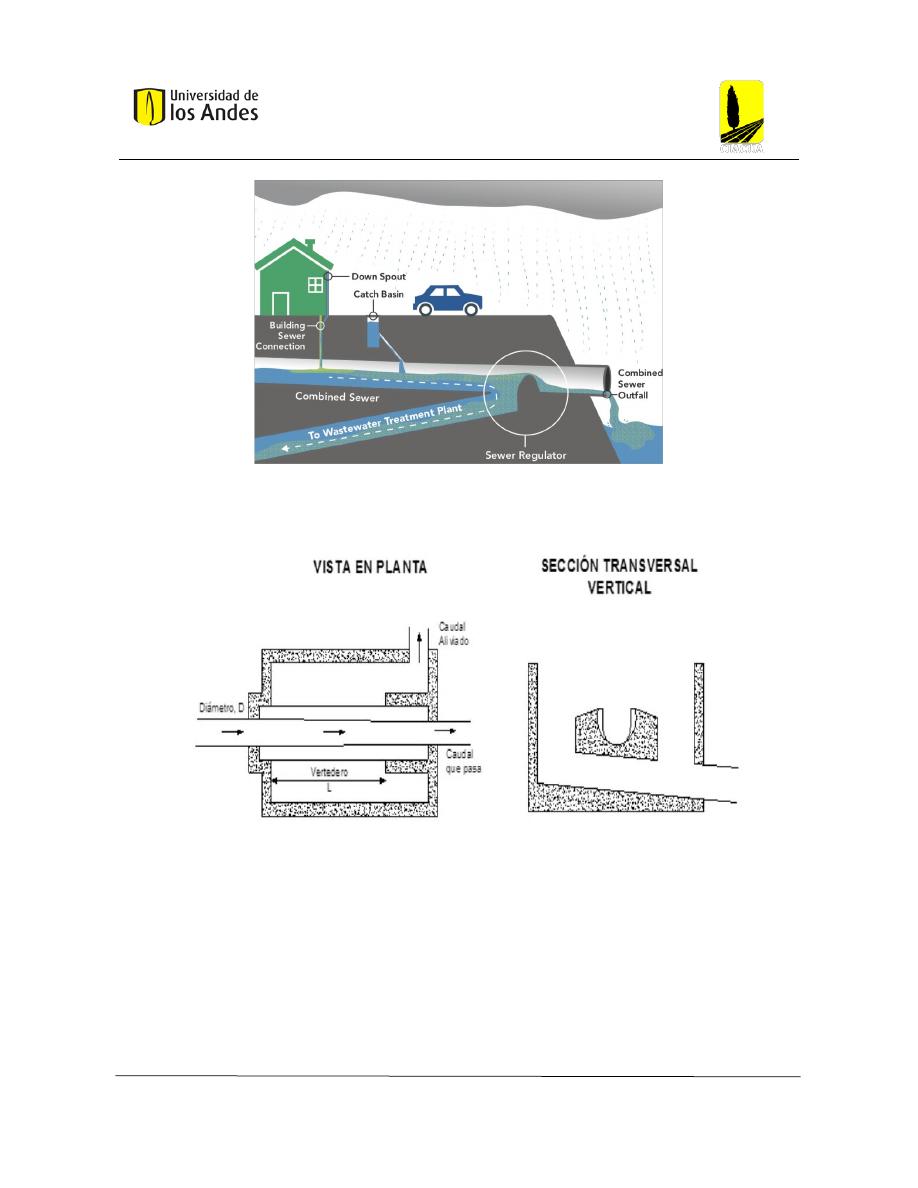
Figura 17: Alcantarillado con estructura de alivio. (NYC Environmental Protection, s.f.).
A continuación, se muestra la estructura de un aliviadero con vertedero lateral.
Figura 18: Alivio con vertedero: vista en planta y perfil. (Reglamento Técnico del Sector de Agua Potable y Saneamiento
Básico - RAS, 2016, pág. 177)
Por otro lado, los sistemas de regulación más comunes son los sistemas de almacenamiento
temporal. Estos consisten en tanques subterráneos que, durante un evento extremo de
precipitación, permiten almacenar parte del agua para retener contaminantes. Luego de
retenidos, devuelve el agua almacenada al sistema de alcantarillado. Según Saldarriaga
(2019), la práctica moderna implica que este almacenamiento esté acompañado de una
estructura de alivio como vertederos laterales.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 19
3.4.6. ELEMENTOS DE BOMBEO
Es posible que, en ciertas partes de la red de alcantarillado, la energía hidráulica sea muy baja
para continuar fluyendo por gravedad. Esto se puede dar por determinadas condiciones
topográficas o cuando se busque elevar el agua hasta una PTAR. En estos casos, es necesario
instalar una estación de bombeo. Saldarriaga (2019) establece las principales razones para
bombear agua lluvia o residual.
• Evitar excavaciones muy profundas
• Elevar el nivel de la línea piezométrica
• Elevar el agua a las corrientes naturales donde termina el drenaje
3.5.
CLASIFICACIÓN DE LOS TIPOS DE FLUJO
3.5.1. TIPOS DE FLUJO
Como aclara Saldarriaga (2019) en su obra Hidráulica de Tuberías, un flujo se puede definir
como un fluido en movimiento con respecto a un sistema de coordenadas. En este sentido,
los flujos pueden ser uniformes o no uniformes (si las cantidades físicas son constantes en el
espacio). Asimismo, los flujos pueden ser permanentes o no permanentes (si las cantidades
físicas son constantes en el tiempo). A partir de lo anterior, se pueden clasificar los tipos de
flujo como se sigue.
Tabla 4: Clasificación de tipos de flujo. (Saldarriaga , Hidráulica de tuberías, 2019, págs. 2-3)
Tipos de flujo
Permanente
No permanente
Uniforme
Flujo uniforme permanente: las
características físicas no varían en
el espacio ni en el tiempo. Se
conoce con el nombre de flujo
uniforme
Flujo uniforme no permanente:
Las características físicas no
varían en el espacio, pero sí en el
tiempo. No se puede encontrar
este tipo de flujo en la naturaleza,
ya que se tendría que presentar
cambios simultáneos a lo largo de
toda la tubería
No uniforme
Flujo variado permanente: Las
características físicas en el
espacio varían, pero permanecen
constantes en el tiempo. Los dos
subtipos son: gradualmente
variado (FGV) y rápidamente
variado (FRV)
Flujo no uniforme no permanente:
Las características varían en el
tiempo y el espacio. Dado que el
flujo uniforme no permanente no
se encuentra en la naturaleza, este
tipo de flujo se le conoce como
flujo no permanente

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 20
A su vez, es posible clasificar los tipos de flujo presentes en las tuberías.
3.5.2. TIPOS DE FLUJO EN TUBERÍAS
Como afirma Saldarriaga (2019), entre 1880 y 1884, Osborne Reynolds realizó un
experimento para evaluar el comportamiento del agua frente a variaciones en el caudal. De
este modo, inyecto una tinta para identificar los cambios en el flujo. A partir de este
experimento, clasificó tres tipos de flujo a partir de la mezcla de la tinta con el agua. Estos
son: flujo laminar, transicional y turbulento.
Saldarriaga (2019) establece que, el flujo laminar, consiste en un flujo en el cual no hay
intercambio de paquetes de fluido entre las capas. En el flujo transicional, las capas empiezan
a ser inestables. Finalmente, para el flujo turbulento, existe intercambio de paquetes de fluido
entre capas.
Para clasificar qué tipo de flujo está presente en determinada tubería, Reynolds introduce el
número de Reynolds
Re. Este parámetro es adimensional. Este se calcula de la siguiente
forma.
𝑅𝑒 =
𝑓𝑢𝑒𝑟𝑧𝑎𝑠 𝑖𝑛𝑒𝑟𝑐𝑖𝑎𝑙𝑒𝑠
𝑓𝑢𝑒𝑟𝑧𝑎𝑠 𝑣𝑖𝑠𝑐𝑜𝑠𝑎𝑠
𝑅𝑒 =
𝐷 ∙ 𝑣
𝜐
Ecuación 1: Número de Reynolds (Saldarriaga , Hidráulica de tuberías,
2019)
Donde:
𝑅𝑒: número de Reynolds
𝐷: diámetro de la tubería
𝑣: velocidad media de la tubería
𝜐: viscosidad cinemática del agua
De este modo, si Re del flujo es menor a 2200, este es de tipo laminar. En contraste con un
Re entre 2200 y 4500, que representa un flujo transicional. Finalmente, para Re mayores a
4500, flujo turbulento.
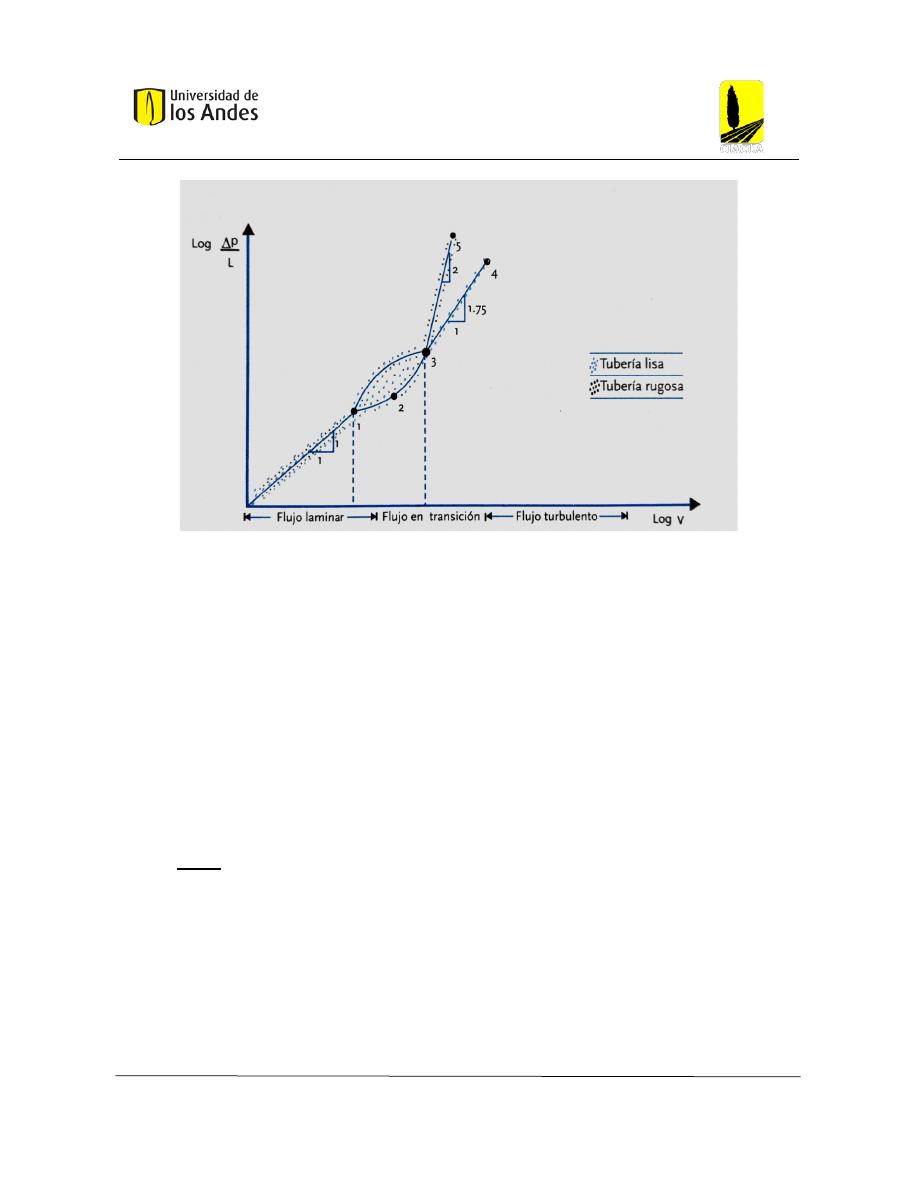
Adicionalmente, Reynolds realizó un segundo experimento. En este, evaluó la caída de
presión por unidad de longitud en función de la velocidad del flujo. Estos fueron los
resultados.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 21
Figura 19: Resultados del segundo experimento de Reynolds. (Saldarriaga , Hidráulica de tuberías, 2019, pág. 11)
Como se puede evidenciar, cuando el flujo sobre pasa la zona de transición, presenta dos
comportamientos diferentes. Esto es, si la tubería es lisa o rugosa. De modo que Reynolds
llegó a la conclusión de que el flujo turbulento se divide en dos subtipos: flujo turbulento
hidráulicamente liso y flujo turbulento hidráulicamente rugoso. El principal parámetro que
diferencia estos dos subtipos es la rugosidad de la tubería.
Reynolds determinó que, para clasificar el tipo de flujo turbulento presente en la tubería, se
debe tener en cuenta el espesor de la subcapa laminar viscosa
𝛿′. “parte de una capa límite
turbulenta localizada en la vecindad de la superficie sólida, cuya presencia atenúa las
vibraciones y el intercambio molecular típicos del flujo turbulento. Por consiguiente, el flujo
en esta zona siempre es laminar” (Saldarriaga, 2019).
𝛿
′
=
11.6𝑣
𝑣
∗
Ecuación 2: Espesor de la subcapa laminar viscosa.
(Saldarriaga , Hidráulica de tuberías, 2019)
Donde:
𝛿
′
: espesor de la subcapa laminar viscosa
𝑣: velocidad media del flujo
𝑣
∗
: velocidad de corte del flujo
Dicha velocidad de corte se calcula como se muestra a continuación.
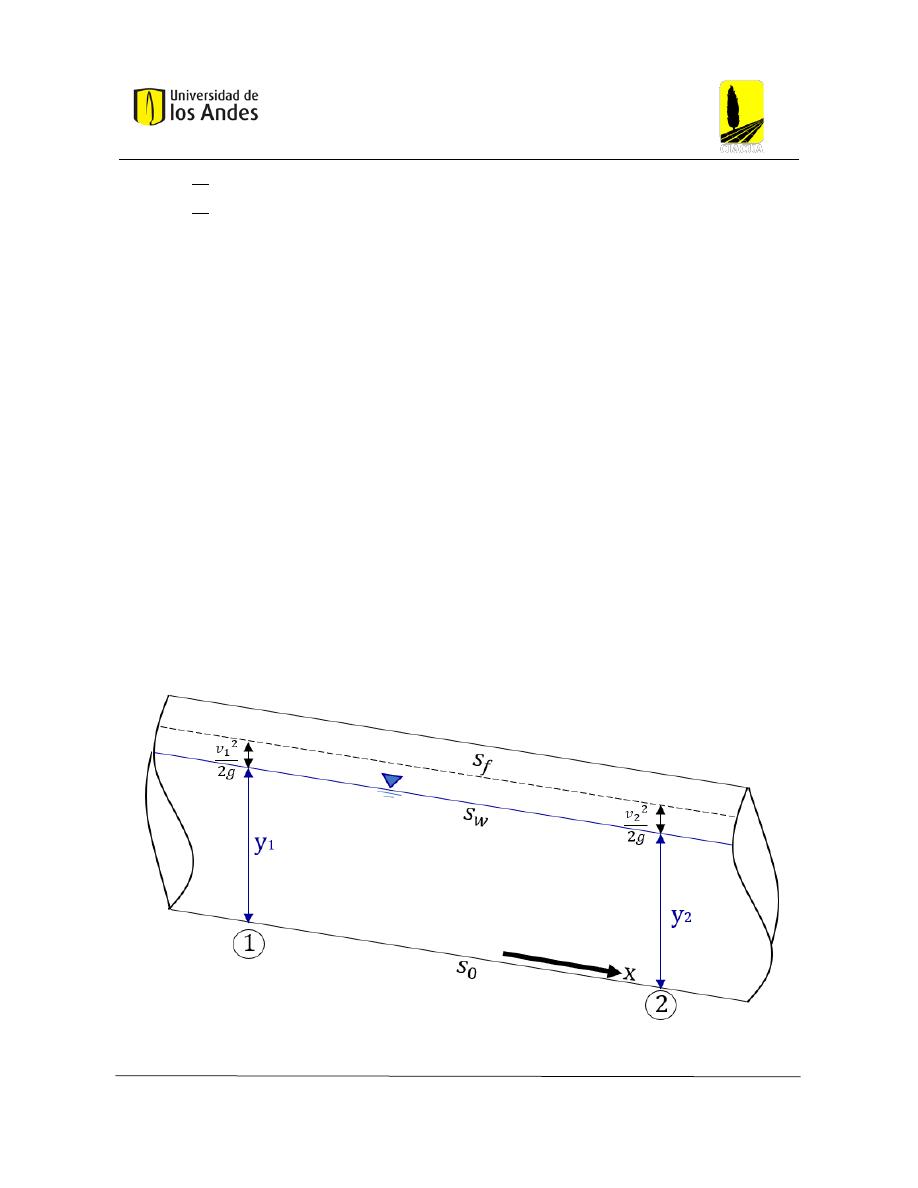
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 22
𝑣
∗
= √
𝜏
𝑜
𝜌
Ecuación 3: Velocidad de corte. (Saldarriaga , Hidráulica
de tuberías, 2019)
Donde:
𝑣
∗
: velocidad de corte
𝜏
𝑜
: esfuerzo cortante en la pared de la tubería
𝜌: densidad del fluido
Finalmente, Reynolds a partir de la rugosidad absoluta de la tubería
𝑘
𝑠
y el espesor de la
subcapa laminar viscosa, determinó las siguientes desigualdades para clasificar el flujo
turbulento.
Si
𝑘
𝑠
≤ 0.305𝛿
′
, el flujo es hidráulicamente liso. En caso de que
𝑘
𝑠
≥ 6.10𝛿
′
, el flujo es
hidráulicamente rugoso.
3.6. HIDRÁULICA DE TUBERÍAS PARCIALMENTE LLENAS BAJO FLUJO UNIFORME
3.6.1. FLUJO UNIFORME
El flujo uniforme es fundamental para la hidráulica de alcantarillados, ya que estas se diseñan
para este tipo de flujo. De este modo, se asume que en cada tubería se presenta una velocidad
y profundidad constante. El perfil de una tubería parcialmente llena se puede ver a
continuación:
Figura 20: Perfil de flujo de una tubería parcialmente llena bajo flujo uniforme. (Saldarriaga , Curso Sistemas de Drenaje
Urbano, 2019)
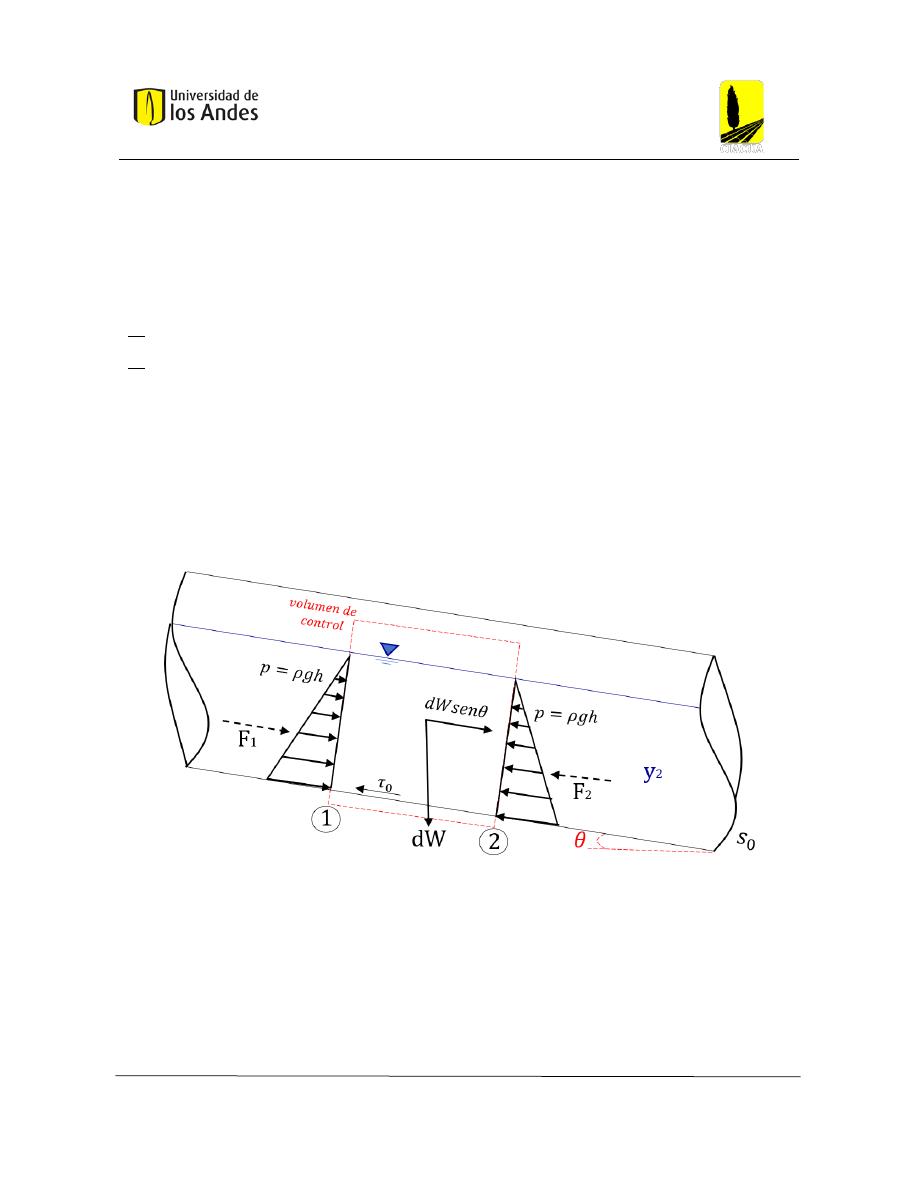
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 23
Donde:
𝑦
1
: profundidad de flujo en el punto 1
𝑦
2
: profundidad de flujo en el punto 2
𝑆
0
: endiente de fondo
𝑆
𝑤
: pendiente de la línea de gradiente hidráulico (LGH)
𝑆
𝑓
: pendiente de la línea de energía total (LET)
𝑣
1
2
2𝑔
: cabeza de velocidad en el punto 1
𝑣
2
2
2𝑔
: cabeza de velocidad en el punto 2
Dado que la profundidad y la velocidad son constantes:
𝑆
0
= 𝑆
𝑤
= 𝑆
𝑓
Ecuación 4: Pendientes en flujo uniforme
Lo cual indica que las líneas de fondo, gradiente hidráulico y energía total son paralelas.
Asimismo, a partir de un volumen de control es posible realizar el diagrama de cuerpo libre
de todas las fuerzas presentes en la tubería.
Figura 21: Diagrama de cuerpo libre para tuberías parcialmente llenas. (Saldarriaga , Curso Sistemas de Drenaje Urbano,
2019)
Donde:
𝑑𝑊𝑠𝑒𝑛𝜃: peso del flujo en la dirección del flujo
𝑑𝑊: peso del flujo
𝐹
1
: fuerza de presión en el punto 1
𝐹
2
: fuerza de presión en el punto 2
𝜏
0
: esfuerzo cortante en la pared de la tubería
𝑝: presión hidrostática

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 24
Dado que la velocidad del flujo en la tubería es constante, no hay aceleración. Por lo tanto,
las fuerzas de presión son iguales y se anulan.
3.6.2. ECUACIÓN DE MANNING
La ecuación de Robert Manning es una ecuación aplicada a los sistemas de alcantarillado, ya
que es aplicada exclusivamente para diseñar bajo flujo uniforme. Esta ecuación empírica fue
propuesta en el año 1889. Adicionalmente, fue propuesta bajo el supuesto de flujo
hidráulicamente rugoso.
𝑣 =
1
𝑛
𝑅
2/3
∙ 𝑆
1/2
Ecuación 5: Manning. (Saldarriaga , Curso Sistemas de
Drenaje Urbano, 2019)
Donde:
𝑛: coeficiente de Manning
𝑅: radio hidráulico
𝑆: pendiente de fondo de la tubería
𝑣: velocidad media del agua en la tubería
A pesar de que esta ecuación se emplea en la práctica, no es físicamente basada. Por tanto,
tiene ciertas limitaciones. Saldarriaga (2019) expone algunas.
• El empleo de nuevos materiales como el PVC y GRP en tuberías, podría invalidar la
suposición de flujo turbulento hidráulicamente rugoso.
• El n de Manning es un indicador de la rugosidad de la tubería. Sin embargo, es función
del diámetro, por lo que varía la rugosidad relativa de la tubería. En este sentido, la
rugosidad de la tubería no depende únicamente del material, sino también del
diámetro empleado.
3.6.3. ECUACIÓN DE CHÉZY
Antoine Chézy fue un ingeniero francés que propuso una ecuación físicamente basada para
determinar la velocidad media de un flujo a superficie libre. Su ecuación fue reconocida en
el año 1897.
v = 𝐶√𝑅𝑆
Ecuación 6: Chézy. (Saldarriaga , Curso Sistemas de
Drenaje Urbano, 2019)
Donde:
𝐶: factor de Chézy
𝑅: radio hidráulico
𝑆: pendiente de fondo de la tubería
𝑣: velocidad media del flujo en la tubería

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 25
3.6.4. ECUACION DE DARCY – WEISBACH CON LA ECUACIÓN DE COLEBROOK WHITE
La ecuación fundamental de Darcy – Weisbach es una ecuación físicamente basada. Como
exponen Israelsen y Hansen en el año 1985, representa la pérdida de energía cuando un fluido
cambia espacialmente de posición en un sistema. Esta pérdida de energía se conoce como
ℎ
𝑓
.
ℎ
𝑓
= 𝑓
𝑙
𝑑
𝑣
2
2𝑔
Ecuación 7: Darcy-Weisbach. (Israelsen & Hansen, 1985,
pág. 78)
Donde:
𝑑: diámetro de la tubería
𝑓: factor de fricción
ℎ
𝑓
: pérdida de energía
𝑙: longitud de la tubería
𝑣: velocidad media del flujo en la tubería
Asimismo, como afirma Saldarriaga (2019), la ecuación de Colebrook y White resulta de
experimentos en tuberías reales. En ellos, se buscó un comportamiento entre el factor de
fricción
𝑓 y la rugosidad relativa (dependiente del material y diámetro) de las tuberías.
Llegando así a una expresión que fuese aplicable para flujos turbulentos.
1
√𝑓
= −2 log
10
(
𝑘
𝑠
3.7𝑑
+
2.51
𝑅𝑒√𝑓
)
Ecuación 8: Darcy-Weisbach y Colebrook-
White. (Saldarriaga ,2019)
Donde:
𝑑: diámetro de la tubería
𝑓: factor de fricción
𝑘
𝑠
: rugosidad relativa
𝑅𝑒: número de Reynolds
A partir de la ecuación de Darcy – Weisbach y la ecuación de Colebrook y White, es posible
llegar a una nueva expresión que permita determinar la velocidad media de un flujo en
función de la rugosidad del material de la tubería, como afirma Saldarriaga (2019).
Esto, se puede hacer resolviendo la ecuación de Chézy para el factor de Chézy.
𝐶 = √
8𝑔
𝑓
Ahora, remplazando esta expresión en la ecuación de Colebrook White se obtiene la siguiente
relación.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 26
𝐶 = −2√8𝑔 log
10
(
𝑘
𝑠
14.8𝑅
+
2.51𝐶
(𝑅𝑒√8𝑔)
)
Finalmente, se remplaza la ecuación de Chézy y la ecuación de Reynolds (
𝑅𝑒) en la anterior
ecuación.
𝑣 = −2√8𝑔𝑅𝑆 log
10
(
𝑘
𝑠
14.8𝑅
+
2.51𝜐
4𝑅√8𝑔𝑅𝑆
)
Ecuación 9: Velocidad media en alcantarillados.
(Saldarriaga , Curso Sistemas de Drenaje
Urbano, 2019)
Donde:
𝑘
𝑠
: rugosidad absoluta
𝑅: radio hidráulico
𝑆: pendiente de fondo de la tubería
𝑣: velocidad media del flujo en la tubería
𝜐: viscosidad cinemática del fluido
Como se puede ver, la anterior ecuación no depende del factor de fricción (
𝑓) de Darcy, por
lo que es una ecuación explicita para la velocidad media del flujo. Esta ecuación, como
expone Saldarriaga (2019), es aplicable tanto para flujo a presión como flujo libre.
Adicionalmente, la rugosidad solo depende del material de la tubería, por lo que se conoce
como rugosidad absoluta.
3.7.
PROPIEDADES GEOMÉTRICAS DE LA SECCIÓN TRANSVERSAL EN TUBERÍAS
CIRCULARES
A continuación, se presenta la sección circular parcialmente llena de una red de
alcantarillado.
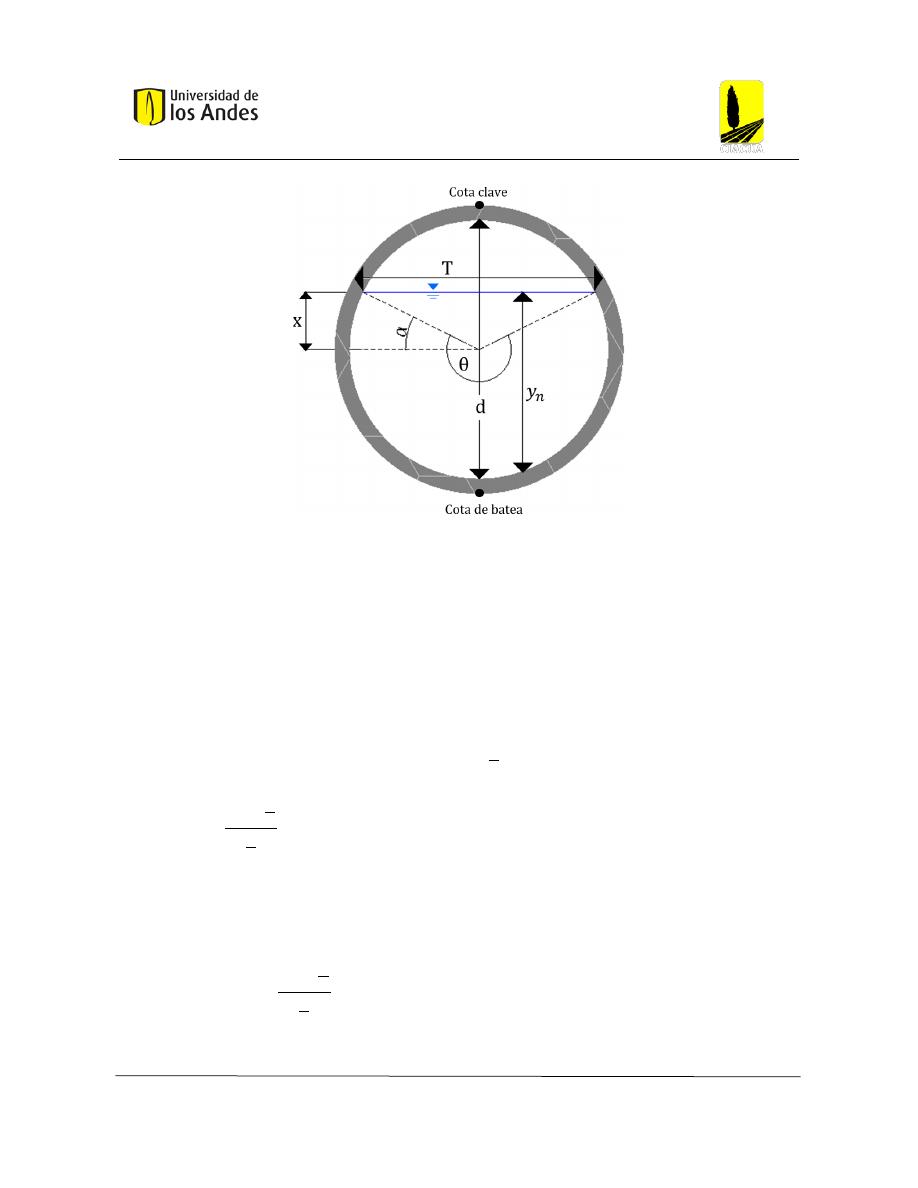
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 27
Figura 22: Propiedades de la sección circular de una tubería parcialmente llena. (Saldarriaga , Curso Sistemas de Drenaje
Urbano, 2019)
Donde:
𝑑: Diámetro de la tubería
𝑇: Ancho de la superficie
𝑦
𝑛
: Profundidad normal de flujo
𝜃, 𝛼, 𝑥: Propiedades geométricas de la tubería
A partir del anterior esquema, se pueden derivar las siguientes ecuaciones:
𝑥 = 𝑦𝑛 −
𝑑
2
𝛼 = 𝑠𝑒𝑛
−1
(
𝑦𝑛 −
𝑑
2
𝑑
2
)
Así, la ecuación para theta resulta ser:
Ecuación 10: Ángulo α
𝜃 = 𝜋 + 2𝛼
𝜃 = 𝜋 + 2 (𝑠𝑒𝑛
−1
(
𝑦𝑛 −
𝑑
2
𝑑
2
))
Ecuación 11: Ángulo θ

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 28
De este modo, el área de una tubería parcialmente llena puede calcularse como:
𝐴 =
1
8
(𝜃 − 𝑠𝑒𝑛(𝜃))𝑑
2
Ecuación 12: Área mojada
El perímetro mojado puede calcularse como:
𝑃 =
𝜃𝑑
2
Ecuación 13: Perímetro mojado
De esta forma, puede derivarse la ecuación para el radio hidráulico.
𝑅 =
𝐴
𝑃
𝑅 =
1
8
(
𝜃 − 𝑠𝑒𝑛
(
𝜃
))
𝑑
2
𝜃𝑑
2
Resolviendo:
𝑅 =
1
4
(1 −
𝑠𝑒𝑛(𝜃)
𝜃
) 𝑑
Ecuación 14: Radio hidráulico
3.8.
DISEÑO DE REDES DE DRENAJE URBANO
3.8.1. ESTIMACIÓN DE CAUDALES DE DISEÑO
Para realizar el diseño de redes de alcantarillado, es fundamental estimar los caudales
aferentes a la red. Estos caudales pueden ser de origen antropogénico (agua residual) o
causados por la escorrentía (agua lluvia).
El caudal de aguas residuales se estima considerando los aportes por:
• Agua residual doméstica
• Agua residual comercial
• Agua residual institucional
• Agua residual comercial
El RAS 2016 establece una metodología para calcular estos aportes y, además, el caudal de
diseño para agua residual. En primer lugar, se determina el caudal de agua residual
doméstica. Este puede ser estimado de tres maneras distintas: proyección de demanda,
proyección de clientes o proyección de la población. La proyección por demanda se calcula
de esta forma:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 29
𝑄
𝐷
= 𝐶
𝑅
∙ 𝐴 ∙ 𝐷
𝑁𝐸𝑇𝐴
Ecuación 15: Proyección de demanda
Donde:
𝑄
𝐷
: caudal de agua residual doméstica (L/s)
𝐶
𝑅
: coeficiente de retorno (-)
𝐴: área tributaria bruta (Ha)
𝐷
𝑁𝐸𝑇𝐴
: demanda de agua potable proyectada (L/s/Ha)
Para la proyección de clientes, se calcula como se muestra.
𝑄
𝐷
=
𝐶
𝑅
∙ 𝑃 ∙ 𝐷
𝑁𝐸𝑇𝐴
30
Ecuación 16: Caudal a partir de
proyección de clientes
Donde:
𝑄
𝐷
: caudal de agua residual doméstica (m
3
/día)
𝐶
𝑅
: coeficiente de retorno (-)
𝑃
𝑐
: número de clientes proyectados al periodo de diseño (cliente)
𝐷
𝑁𝐸𝑇𝐴
: demanda neta (m
3
/cliente/mes)
Finalmente, con la proyección de la población:
𝑄
𝐷
= 𝑄
𝐷
=
𝐶
𝑅
∙ 𝑃 ∙ 𝐷
𝑁𝐸𝑇𝐴
86400
Ecuación 17: Caudal a partir de
proyección de habitantes
Donde:
𝑄
𝐷
: caudal de agua residual doméstica (m
3
/s)
𝐶
𝑅
: coeficiente de retorno (-)
𝑃
𝑐
: número de habitantes proyectados al periodo de diseño (hab)
𝐷
𝑁𝐸𝑇𝐴
: demanda neta (m
3
/hab/día)
Por su parte, la estimación del aporte de agua industrial, comercial e institucional depende
de distintas variables como el tamaño y los procesos implementados para estos tipos. Así, el
RAS 2016 establece la siguiente ecuación para calcular el caudal medio diario de aguas
residuales:
𝑄
𝑀𝐷
= 𝑄
𝐷
+ 𝑄
𝐼
+ 𝑄
𝐶
+ 𝑄
𝐼𝑁
Ecuación 18: Caudal medio diario
Donde:
𝑄
𝑀𝐷
: caudal medio diario (m
3
/s)
𝑄
𝐷
: caudal de agua residual doméstica (m
3
/s)
𝑄
𝐼
: caudal de agua residual industrial (m
3
/s)
𝑄
𝐶
: caudal de agua residual comercial (m
3
/s)
𝑄
𝐼𝑁
: caudal de agua residual industrial (m
3
/s)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 30
Para calcular el caudal de diseño, el RAS 2016 determina que se debe considerar caudal por
infiltraciones y por conexiones erradas. El primero ocurre a causa de infiltraciones por agua
subsuperficial. El segundo, es un aporte de agua lluvia al sistema sanitario.
Finalmente, se calcula el caudal de diseño de aguas residuales.
𝑄
𝐷𝑇
= 𝑄
𝑀𝐻𝑓
+ 𝑄
𝐼𝑁𝐹𝑓
+ 𝑄
𝐶𝐸𝑓
Ecuación 19: Caudal de diseño por tubería
Q
DT
: caudal de diseño por tubería (m
3
/s)
Q
MHf
: caudal máximo horario final (m
3
/s)
Q
INFf
: caudal por infiltraciones final (m
3
/s)
Q
CEf
: caudal por conexiones erradas final (m
3
/s)
En cuanto al caudal de diseño de aguas lluvias, existen muchos modelos para estimar dicho
caudal. Uno de estos, es el método de racional. El RAS 2016 sugiere el empleo de este
modelo para diseño cuando el área de drenaje sea menor a 80 hectáreas. Este método
considera los siguientes parámetros: coeficiente de impermeabilidad, intensidad de
precipitación, y el área de drenaje.
El coeficiente de impermeabilidad, como establece el RAS 2016, es el porcentaje de agua
lluvia que se vuelve escorrentía
.
Por su parte, las curvas IDF relacionan la intensidad de
precipitación, la duración del evento y la frecuencia con que este evento sucede. “Estas
curvas permiten estimar las frecuencias de sobrepaso F de los eventos lluviosos observados
a partir de su intervalo de observación d y de su intensidad media” (Torres, 2004, pág. 42).
Dicho lo anterior, el RAS 2016 considera la siguiente ecuación.
𝑄 = 𝐶𝐼𝐴
Ecuación 20: Caudal de agua lluvia
a partir del método racional
Donde:
𝑄: caudal pico de agua lluvia (L/s)
𝐶: coeficiente de impermeabilidad
𝐼: intensidad de precipitación
𝐴: área tributaria de drenaje
3.8.2. DISEÑO DE UN TRAMO
Como afirma Saldarriaga (2019), la información necesaria para diseñar un tramo de una red
de alcantarillado es la siguiente:
• Características físicas del agua (densidad y viscosidad)
• La pendiente del terreno
• Rugosidad del material
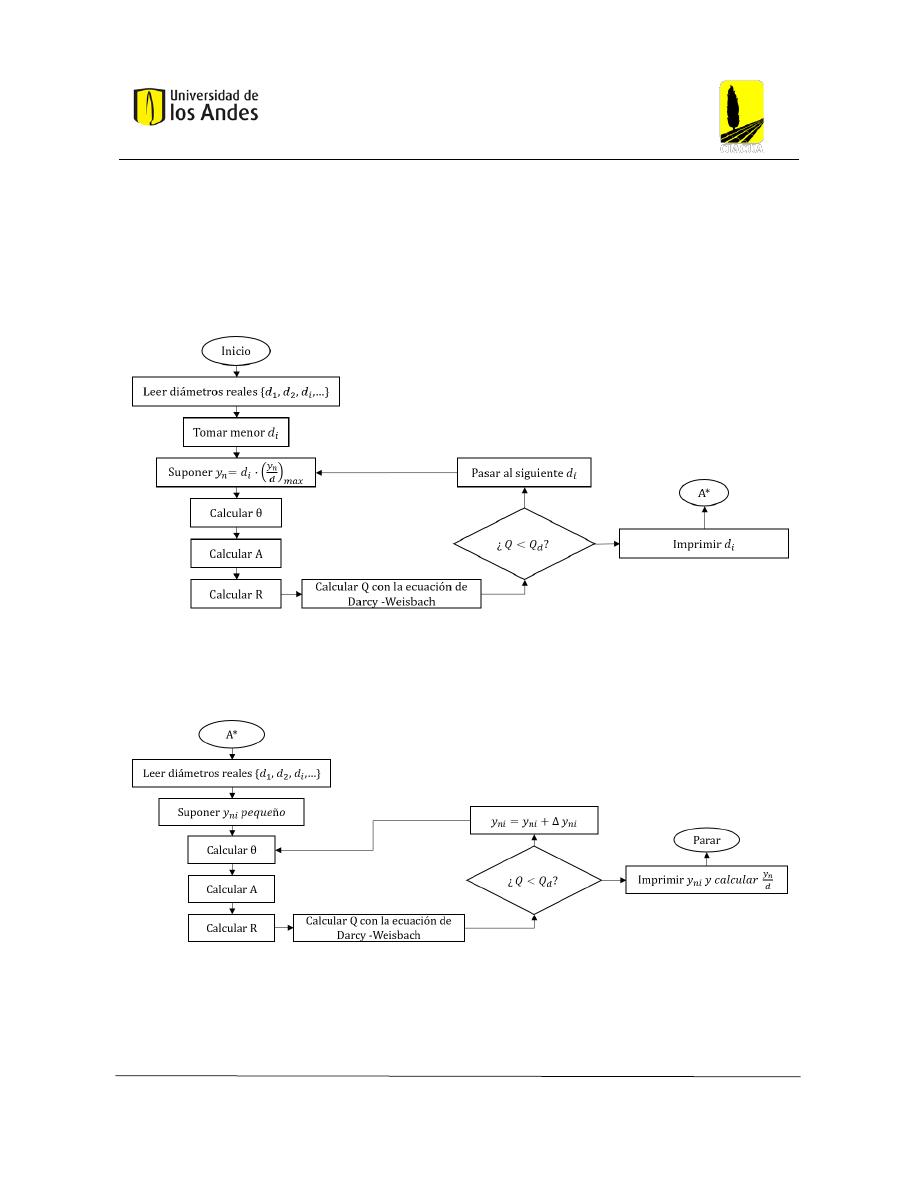
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 31
• Diámetros comerciales
• Caudal de diseño
De este modo, las incógnitas principales son el diámetro de la tubería y la relación de llenado.
Saldarriaga (2019) propone el siguiente diagrama de flujo para la resolución de este tipo de
problema.
Figura 23: Diagrama de flujo para el diseño de un tramo de alcantarillado: parte 1. (Saldarriaga , Curso Sistemas de
Drenaje Urbano, 2019)
Figura 24: Diagrama de flujo para el diseño de alcantarillado: parte 2. (Saldarriaga , Curso Sistemas de Drenaje Urbano,
2019)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 32
3.8.3. DISEÑO DE REDES DE DRENAJE URBANO
El diseño de redes de drenaje urbano tiene dos problemas fundamentales: la topología de la
red y el diseño hidráulico.
En cuanto al diseño topológico, como asegura Saldarriaga (2019), dado que existen muchas
variables ligadas al proceso de diseño, existen muchos trazados posibles para un mismo
número de cámaras de unión determinado. Entendiendo el trazado como el sentido de flujo
de agua en las tuberías.
Figura 25: Grilla para la selección del trazado
Saldarriaga (2019) establece la siguiente ecuación para determinar el número de posibles
trazados en una red de drenaje urbano.
#
𝑇𝑟𝑎𝑧𝑎𝑑𝑜𝑠
= 2
4
∙ 3
2(𝑚+𝑛−2)
∙ 4
(𝑚−1)(𝑛−1)
Ecuación 21: Número de trazados para
una red de alcantarillado
Dicha ecuación no considera el punto de descarga, ni la no-factibilidad de ciertos flujos
(conecta todos los pozos). De este modo, dado que existen muchos posibles trazados, la
topografía juega un papel determinante para seleccionar el trazado de la red.
Adicionalmente, a partir de Saldarriaga (2019), existen dos tipos de tubería para la selección
del trazado. Tuberías de inicio y tuberías continuas. La diferencia radica en que las tuberías
de inicio no están conectadas a un pozo aguas arriba.
Por otra parte, el diseño hidráulico se basa en definir el diámetro y las pendientes de las
tuberías de la red. A partir de estos parámetros se pueden calcular los demás parámetros
hidráulicos en la red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 33
A continuación, se presentan los pasos básicos para realizar un diseño de redes de
alcantarillado, como afirma Saldarriaga (2019).
1) Definir los sentidos de flujo de los tramos (Selección del trazado)
2) Definir la ubicación de puntos de inicio
3) Calcular los caudales de diseño por tramo
4) Realizar los diseños por líneas independientes
5) Agregar cámaras de caída en caso de ser necesario

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 34
4. METODOLOGÍA PARA EL DISEÑO OPTIMIZADO DE REDES DE DRENAJE
URBANO
4.1.
INTRODUCCIÓN
La optimización en diseños de drenaje urbano consiste en elegir parámetros de diseño que
garanticen funcionalidad en el sistema y, fundamentalmente, se llegue al costo mínimo.
Debido a la gran cantidad de alternativas en el diseño (tanto en la topología como en la
hidráulica), surge la necesidad de proponer nuevas metodologías para asegurar funcionalidad
y mínimo costo en el diseño de redes de alcantarillado.
En el diseño optimizado se debe hacer un procedimiento exhaustivo para evaluar todas las
posibles alternativas de diseño. El número de dichas alternativas es función del número de
tramos en la red. “Este tipo de problemas están catalogados dentro del conjunto de problemas
NP-Duros, pues no existen algoritmos que puedan resolverlos de manera práctica”
(Saldarriaga , Curso Sistemas de Drenaje Urbano, 2019).
Estos problemas de optimización por lo general son resueltos a partir de algún software. Entre
mayor sea el número de alternativas factibles, mayor será el tiempo computacional hasta
llegar a un diseño óptimo. De este modo, el diseño óptimo se elige a partir del costo total de
la red. Según Saldarriaga (2019), se debe implementar una ecuación que permita modelar los
costos de la red con base en ciertas variables de la red. Dentro de estas se encuentran: costo
de la tubería (material, diámetro, longitud, etc.), costos totales de excavación y costo de las
cámaras de inspección. En este sentido, la ecuación de costos y sus parámetros se vuelven
fundamentales para determinar el diseño óptimo de la red.
4.2.
ANTECEDENTES
Se han propuesto diversas metodologías para el diseño optimizado de redes de drenaje
urbano. Por su parte, Haghighi y Bakhshipour en el 2015 plantean una metodología para
optimizar la función de costos. Dichos autores aplican el uso de el “Tabú Search Algorithm”
(TS), propuesto por Hertz y Werra en 1987. Dicho lo anterior, la principal función de este
algoritmo, como afirman Hertz y Werra, la técnica TS es utilizada para moverse al mínimo
valor de una función paso a paso en problemas de optimización.
Así, Haghighi y Bakhshipour presentan un modelo integrado de optimización para sistemas
de drenaje urbano. En él, se propone una solución para el problema de selección de trazado
y diseño hidráulico. En este sentido, una vez solucionado dicho problema de selección de
trazado, el modelo realiza el diseño hidráulico determinando diámetros y profundidades de
excavación. Asimismo, los autores establecen que la función objetivo es la ecuación de costo
de la red de alcantarillado. De manera que, a través del método TS, se optimiza dicha
ecuación

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 35
Asimismo, Haghighi y Bakhshipour en el año 2012, adaptan algoritmos genéticos (GA) para
realizar un modelo de optimización introductorio. De modo que los GA cumplen la función
de representar cromosomas, que consisten en diámetros, pendientes e indicadores de bombeo.
En este sentido, la metodología de GA permite pasar el diseño optimizado de un problema
con restricciones complejas no lineales, a un problema de optimización sin restricciones.
Por otro lado, Safavi y Geranmehr en el 2016, proponen una metodología de optimización.
En esta, se implementa la Programación Lineal Entera Mixta (MILP). Así, dichos autores
explican que esta metodología se basa en plantear una función objetivo que considere,
simultáneamente, determinados parámetros de diseño. Estos son: costo de la tubería, costo
de instalación de la tubería y la construcción de los pozos. Asimismo, esta función tiene en
cuenta las restricciones mínimas y máximas en sistemas de alcantarillado. La función
propuesta por Safavi y Geranmehr es la siguiente.
𝐶 = 𝐶
𝑡𝑢𝑏𝑒𝑟í𝑎
+ 𝐶
𝑝𝑜𝑧𝑜
= ∑ 𝑓(𝐿
𝑖
, 𝐷
𝑖
,
𝑛𝑡
𝑖=1
ℎ
𝑖
) + ∑ 𝑔(
𝑛𝑝
𝑚=1
ℎ′
𝑚
)
Ecuación 22: Función objetivo propuesta
por Safavi y Geranmehr (2016)
Donde:
𝐶: costo total de la red
𝐶
𝑡𝑢𝑏𝑒𝑟í𝑎
: costo de las tuberías
𝐶
𝑝𝑜𝑧𝑜
: costo de los pozos
𝑛𝑡: número de tuberías
𝑛𝑝: número de pozos
𝐿
𝑖
: longitud de la tubería
𝐷
𝑖
: diámetro de la tubería
ℎ
𝑖
: profundidad de excavación de la tubería
ℎ′
𝑚
: profundidad de excavación del pozo
𝑓: función de costo para las tuberías
𝑔: función de costo para los pozos
A partir de la función objetivo, y de algunas desigualdades propuestas para cumplir las
restricciones de diseño, los autores construyen un MILP que garantiza el diseño óptimo
global. Finalmente, se propuso un método robusto método para optimizar el diseño de redes
de alcantarillado.
4.3.
METODOLOGÍA PARA EL DISEÑO OPTIMIZADO DESARROLLADO EN EL CIACUA
4.3.1. DISEÑO HIDRÁULICO DE TUBERÍAS EN SERIE
Una de las metodologías más destacadas por el CIACUA, para el diseño optimizado de
alcantarillados, fue propuesta por Duque (2013). Dicha metodología se basó, en primer

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 36
lugar, en solucionar el problema de diseño exclusivamente para series de tuberías de
alcantarillado.
En la metodología de diseño optimizado de series de tuberías, Duque (2013) emplea el
problema de ruta más corta. Dicho problema “pertenece a la rama de la optimización que
estudia los problemas de flujo en redes.” (Duque, Metodología para la optimización del
diseño de tuberías en serie en sistemas de alcantarillado, 2013, pág. 31). Para esto,
generalmente se implementan grafos. Los grafos están compuestos por elementos llamados
nodos, que están conectados mediante arcos, como mencionan Ahuja, Magnanti, y Orlin en
1993. Se afirma entonces, a partir de estos autores, que existen dos tipos de grafos: dirigidos
y no dirigidos. En los dirigidos existe una dirección entre los nodos conectados, mientras que
los no dirigidos los nodos son bidireccionales.
Uno de los tipos de problema de ruta más corta, es el algoritmo de Bellman – Ford. Como
establece Resende y Pardalos en el 2006, este algoritmo iterativo está basado en ideas
dinámicas programadas. Duque (2013) establece que dicho algoritmo surge a causa de la
necesidad de conocer los tiempos mínimos de viaje en sistemas de transporte. En el caso de
series de alcantarillado y, para modelar el grafo, Duque (2013) plantea que los nodos tengan
las siguientes propiedades: la cota del nodo y el diámetro del nodo. Asimismo, los arcos
tienen un costo y un diámetro asociados.
Para a una solución óptima, Duque (2013) plantea dos restricciones fundamentales durante
dicho proceso iterativo.
• En las tuberías no pueden existir pendientes adversas
• En un pozo k, la tubería de salida debe tener un diámetro mayor o igual al de la tubería
de entrada.
A partir de las anteriores restricciones, se reducen las alternativas. En consecuencia,
encontrar una solución óptima resulta ser más rápido cuando se emplee la función de costo.
En resumen, a partir del algoritmo de Bellman-Ford, Duque (2013), tiene en cuenta
parámetros de diseño como el diámetro de las tuberías y la profundidad de excavación, para
dar solución al diseño hidráulico (optimizado) en tuberías en serie.
Después de dar respuesta a un problema de diseño hidráulico de tuberías en serie, Duque
(2015) propone una nueva metodología. Esta, no solamente resuelve el problema de diseño
hidráulico. A su vez, realiza la selección del trazado. A este modelo de optimización se le
llamó Underground Topography for Optimal Pipeline Infrastructure Assessment (UTOPIA).
En el capítulo 4.3.3 y 4.3.4 se expondrá la metodología de Duque (2015) para la selección
del trazado y diseño hidráulico en redes de drenaje urbano.
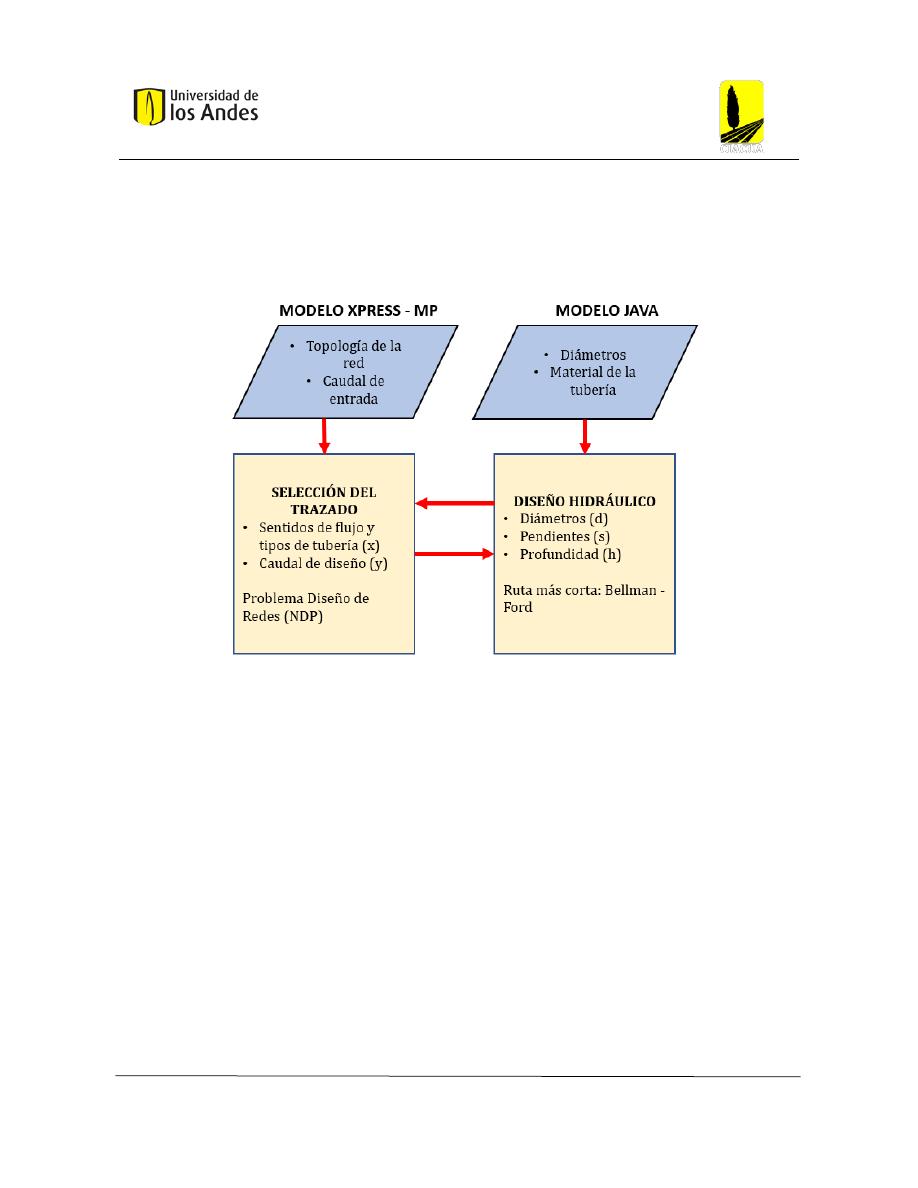
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 37
4.3.2. INTRODUCCIÓN: REDES DE DRENAJE URBANO
Duque (2015) propone una metodología que consiste en solucionar, simultáneamente, el
problema de selección de trazado y diseño hidráulico. Aguilar (2019) permite sintetizar esta
metodología a partir del siguiente esquema.
Figura26: Metodología desarrollada por Duque (2015) sintetizada por (Aguilar, Modelo de Optimización Multiobjetivo
para el Diseño de Redes de Drenaje Urbano , 2019, pág. 17)
Como se puede ver, la metodología inicia con la topología de la red (coordenada z de los
pozos) y el caudal de entrada para cada pozo. A partir de estos insumos, se selecciona el
trazado (sentido de los flujos) en la red. Esto se hace a partir del programa XPRESS – MP.
Posteriormente, a partir de un modelo en JAVA, se realiza el diseño hidráulico de la red en
la primera iteración. Con este primer diseño, se vuelve a seleccionar el trazado de la red y así
sucesivamente hasta completar determinadas iteraciones que indique el usuario.
4.3.3. SELECCIÓN DEL TRAZADO DE REDES DE DRENAJE URBANO
En primer lugar, se debe seleccionar el trazado de la red. “Al ser redes abiertas, este tipo de
sistemas no debe tener ciclos buscando evitar que el agua residual recircule por el mismo
sitio. En este orden de ideas, se tienen dos tipos de tuberías: tuberías de inicio y tuberías
continuas. Las tuberías de inicio son aquellas que están no tienen tuberías conectadas aguas
arriba, es decir, están en los extremos de cada una de las ramas del árbol.” (Duque, 2015,
pág. 28).
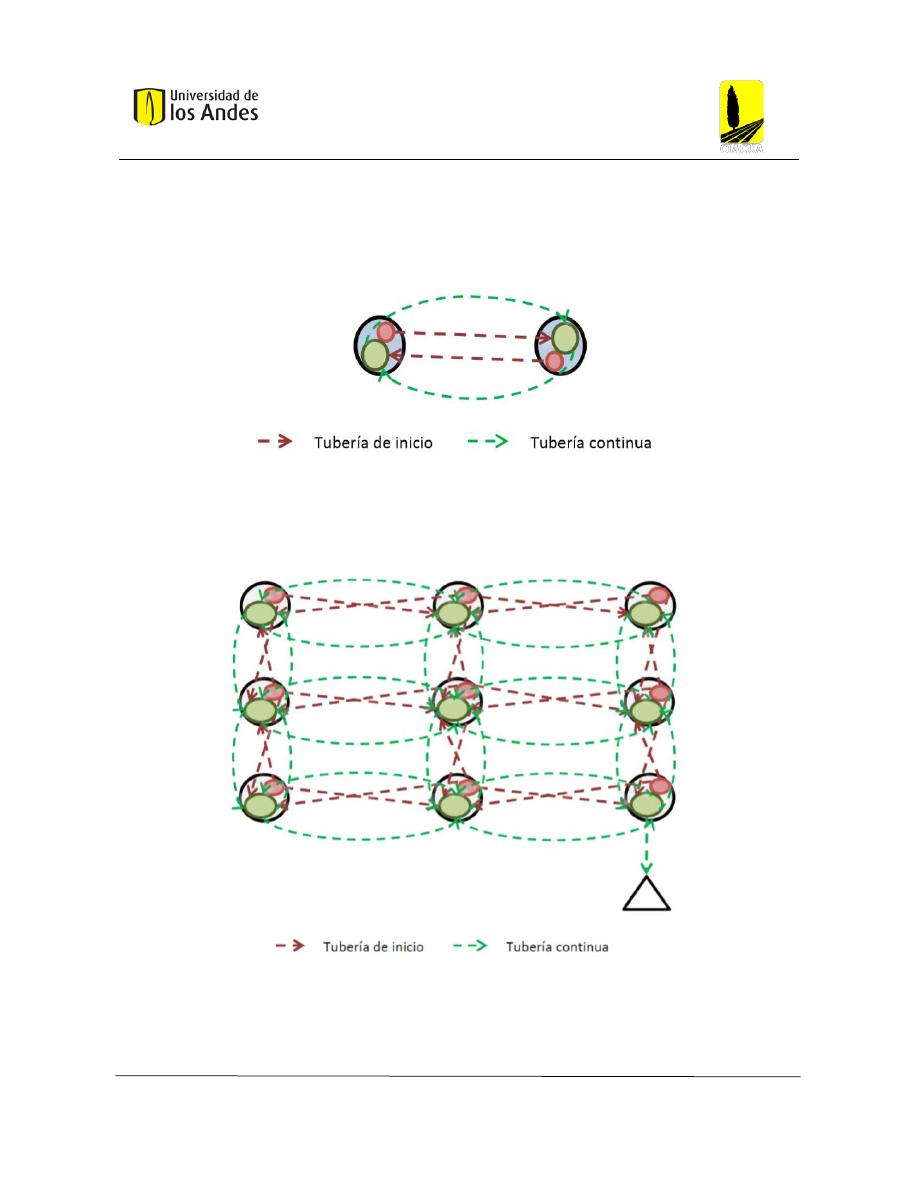
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 38
De este modo, las tuberías en el trazado tienen dos características: el sentido del flujo y el
tipo de tubería (continua o de inicio). Entre dos pozos, existen 4 diferentes configuraciones
para definir la tubería, como se muestra a continuación.
Figura 27: Tipo de tubería y posibles direcciones de flujo. (Duque, 2015, pág. 34).
Se presenta igualmente un esquema del grafo para la selección de trazado elaborado por
Duque (2015).
Figura 28: Grafo para la selección del trazado. (Duque, 2015, pág. 35).
Duque (2015) establece que, en cada pozo de inspección, debe haber máximo una tubería de
salida continua, y tantas tuberías de inicio como pozos adyacentes al pozo en cuestión.
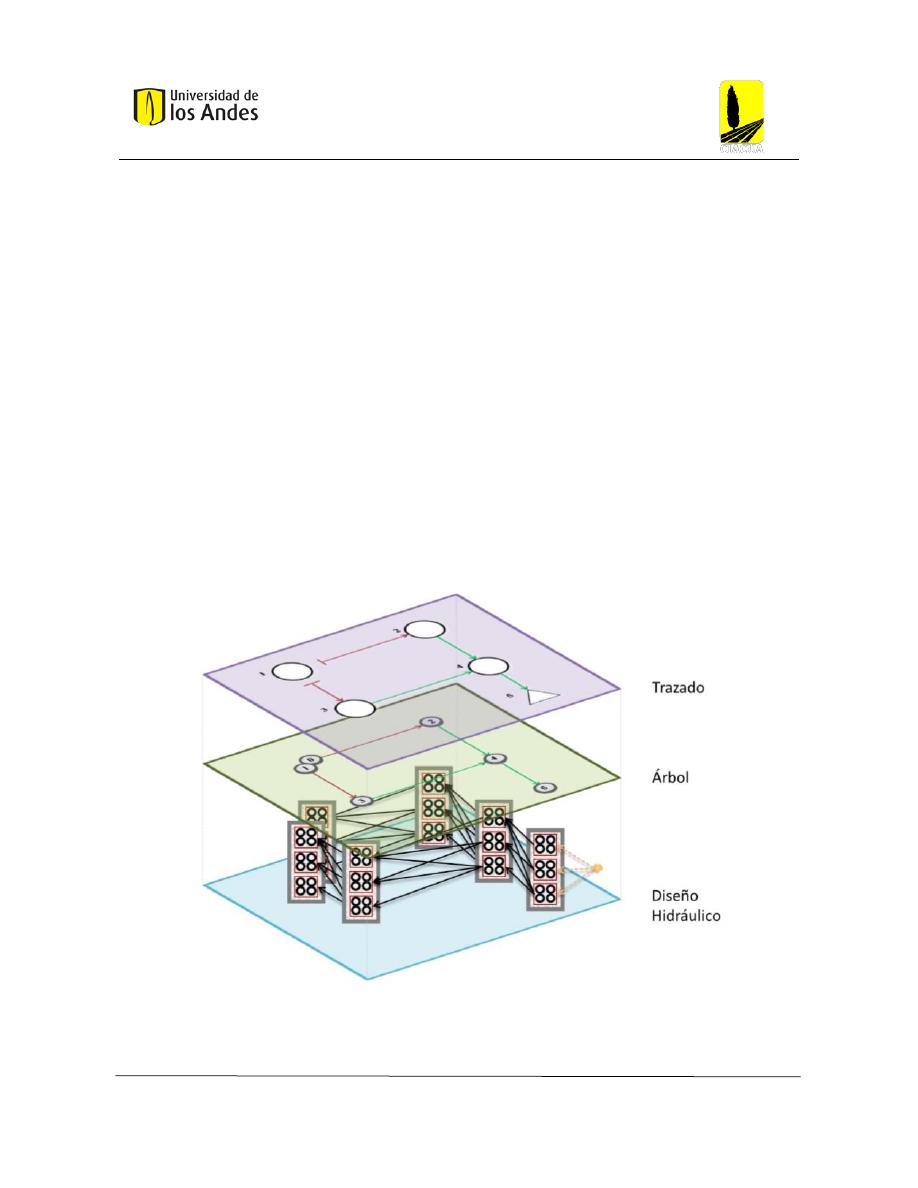
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 39
Asimismo, recalca que se debe diseñar asumiendo que no hay acumulación de agua en el
sistema, y que toda el agua llega a un y solo a un punto de descarga. Finalmente, el software
de optimización lineal XPRESS-MP soluciona este problema y determina el trazado de la
red. Como establece Aguilar (2017), el propósito en esta etapa es minimizar costos que estén
asociados al caudal y al tipo de tuberías.
4.3.4. DISEÑO HIDRÁULICO DE REDES DE DRENAJE URBANO
Una vez ha sido definido el trazado de la red, se debe solucionar la hidráulica de la red. Esto
es, determinar las pendientes de las tuberías y su respectivo caudal de diseño. En este sentido,
Duque (2015) abarca el diseño hidráulico como un Problema de Ruta Más Corta. En este, se
plantea la generación de tres diferentes grafos: grafo del trazado, el árbol y el grafo para el
diseño hidráulico. El primero es un grafo que describe el trazado seleccionado. El segundo,
denota las tuberías factibles en los pozos. Cada nodo en el árbol tiene almacenado un
conjunto de subnodos. Estos subnodos tienen información acerca de los diámetros y sus
respectivas cotas. Es con estos subnodos que, en el tercer grafo se soluciona el problema de
ruta más corta a partir de la función de costo (el camino de mínimo costo), como plantea
Duque (2015).
Figura 29: Solución para el diseño hidráulico de una red ejemplo. (Duque, 2015, pág. 55).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 40
4.3.5. VERSION EXTENDIDA PARA LA TOPOLOGÍA DE LA RED
El programa UTOPIA, cuenta con una versión desarrollada por Zambrano (2019). En ella,
se emplea la programación lineal mixta considerando anteriormente por Duque (2015).
La metodología consiste en continuar empleando la programación lineal mixta, aunque ahora
variando el método de selección de trazado. Este último busca solucionar el problema de
selección de trazado teniendo en cuenta la topografía del terreno, la topología y los caudales
de entrada a la red de drenaje. De este modo, con esta extensión, se obtienen diseños más
económicos que la metodología base. Esto se logró a partir de criterios que, para terrenos
empinados, buscan reducir la profundidad de excavación a partir de la topografía del terreno.
Además, para terrenos planos, se establecieron criterios que buscan minimizar la longitud de
las series principales de la red de drenaje hasta el punto de descarga.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 41
5. RESTRICCIONES DE DISEÑO EN SISTEMAS DE DRENAJE URBANO
5.1.
INTRODUCCIÓN
Las restricciones hidráulicas de diseño son criterios fundamentales para diseñar en redes de
drenaje urbano. El cumplimiento de estas normas puede garantizar funcionalidad hidráulica,
estructural, geotécnica y sanitaria. A continuación, se describen las restricciones de diseño
que se pretenden analizar.
5.2.
PROFUNDIDAD MÁXIMA DE EXCAVACIÓN
Este parámetro se puede entender como la distancia entre la cota en la superficie del terreno
y la cota clave de la tubería donde se va a instalar. Para la profundidad máxima a cota clave
de excavación, como establece el RAS 2016, se debe definir teniendo en cuenta el tipo de
suelo, equipos y métodos de excavación y, finalmente, métodos de entibado disponibles. Este
reglamento establece por lo general una profundidad máxima de 5 metros.
5.3.
ESFUERZO CORTANTE MÍNIMO
El esfuerzo cortante mínimo se define en el RAS 2016 como “el valor mínimo de esfuerzos
cortantes que deben actuar sobre la pared de un conducto para que se presenten condiciones
de autolimpieza.”. Esta autolimpieza es necesaria sobre todo en alcantarillados pluviales,
debido a la acumulación de arenas y sedimentos que se pueden filtrar en el sistema. El RAS
2016 propone la siguiente ecuación para el cálculo el esfuerzo cortante en tuberías de
alcantarillado.
𝜏 = 𝛾𝑅𝑆
Ecuación 23: Esfuerzo cortante en las paredes
de tuberías de alcantarillado
Donde:
𝜏: esfuerzo cortante en la pared de la tubería (Pa)
𝛾: peso específico del agua (N/m
3
)
𝑅: radio hidráulico de la tubería (m)
𝑆: pendiente de fondo de la tubería (m/m)
5.4.
RELACIÓN DE LLENADO MÁXIMA
En alcantarillados sanitarios y pluviales, debido a la gran carga contaminante presente, es
posible que se generen gases tóxicos en las tuberías. El RAS 2016 recalca sobre “la posible
generación de gases y vapores (entre ellos sulfuros) que ocasionen problemas operativos en
la red”. De este modo, se debe garantizar condiciones de flujo libre y aireación en las tuberías.
Adicionalmente, limitando la profundidad de flujo en las tuberías, se previenen sobrecargas
en el sistema.
Por las anteriores razones, el RAS 2016 establece la restricción de relación de llenado
máxima. Esta se puede definir como la relación entre la profundidad de flujo del agua y el

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 42
diámetro de la tubería. El porcentaje o relación de llenado en tuberías se calcula como se
muestra.
%
𝑑𝑒 𝑙𝑙𝑒𝑛𝑎𝑑𝑜
=
𝑦
𝑛
𝑑
Ecuación 24: Relación de llenado en
tuberías de alcantarillado
Donde:
𝑦
𝑛
: profundidad normal de flujo
𝑑: diámetro de la tubería
5.5.
VELOCIDAD MÁXIMA
Asimismo, el RAS 2016 da lineamientos acerca de la velocidad máxima a la cual puede ir el
agua en sistemas de alcantarillado. Esta restricción fue reglamentada debido al riesgo o
potencial de desgaste que tienen los sistemas de presentar erosión. Por lo general, se definió
una velocidad máxima de 5m/s en sistemas de alcantarillado. No obstante, para materiales
lisos como por ejemplo el PVC, la velocidad máxima es de 10 m/s.
5.6.
VELOCIDAD MÍNIMA
Con el fin de garantizar autolimpieza en las tuberías de alcantarillado. Se debe establecer una
velocidad mínima en el flujo. Para alcantarillados pluviales se debe tener mínimo una
velocidad de 0.75m/s para diámetros menores a 450mm. En caso de tener diámetros mayores
a 450mm, se debe garantizar un esfuerzo cortante mínimo de 2.5Pa. Por su parte, En el caso
de alcantarillados sanitarios, se debe asegurar una velocidad de 0.45m/s para diámetros
menores a 450mm. Si el diámetro es mayor a 450mm, se debe garantizar un esfuerzo cortante
de 1.5Pa.
5.7.
DIÁMETRO MÍNIMO
En redes de alcantarillado, también fue necesario reglamentar un diámetro interno mínimo
para las tuberías. Como menciona el RAS 2011, “con el fin de evitar las posibles
obstrucciones que ocurran en los tramos, causadas por objetos relativamente grandes que
puedan entrar al sistema”. El diámetro interno mínimo para sistemas sanitarios y pluviales es
de 170mm y 215mm respectivamente.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 43
6. JUSTIFICACIÓN DEL PROBLEMA Y METODOLOGÍA GENERAL
6.1.
JUSTIFICACIÓN
Como se mencionó anteriormente, las redes de drenaje urbano son necesarias para la
salubridad de la población. Sin embargo, en Colombia el costo de implementación de estas
obras hidráulicas resulta muy alto en comparación con el presupuesto de muchos municipios.
Según el Plan Director de Agua y Saneamiento Básico publicado en el 2018 por el Ministerio
de Vivienda, la cobertura de servicios de alcantarillado en zonas urbanas y rurales es de
92.4% y 70.1% respectivamente. En este sentido, aproximadamente el 30% de la población
rural no cuenta con este servicio.
A partir de lo anterior, nace la necesidad de proponer nuevas estrategias para reducir los
costos de este tipo de proyectos. Esto, con el objetivo de brindar alternativas y soluciones
económicas a entidades que busquen invertir en redes de alcantarillado. Una de las
estrategias, es implementar diseños optimizados que permitan garantizar una alta
funcionalidad al menor costo posible. Los diseños optimizados dependen de muchos
parámetros. Dentro de estos, se encuentran: las restricciones de diseño y la topografía del
terreno.
Las restricciones de diseño en alcantarillados son criterios fundamentales para el desempeño
estructural, hidráulico, geotécnico y sanitario de estos sistemas. El RAS 2016 establece los
lineamientos para diseñar considerando estos criterios. Dentro de estas restricciones se
encuentran: la profundidad máxima de excavación; el esfuerzo cortante mínimo; la relación
de llenado máxima; la velocidad mínima y máxima; el diámetro mínimo comercial.
Estas restricciones tienen repercusiones en el diseño de estas redes y, por lo tanto, en sus
costos. Por otra parte, la topografía también tiene un impacto en los costos totales de la red.
Lo anterior, debido a que a partir de la topografía se determina la selección del trazado y, por
lo tanto, del diseño hidráulico. De este modo, surge la cuestión de comprender el
comportamiento de los costos totales en función de las restricciones de diseño y la
topografía del terreno para una red de drenaje urbano específica.
6.2.
METODOLOGÍA GENERAL
6.2.1. RESTRICCIONES Y TOPOGRAFÍA
En esta investigación, se busca identificar el comportamiento de los costos totales de una red
de alcantarillado a partir de dos variables: las restricciones de diseño y la topografía del
terreno. Por lo tanto, se propone una metodología que permita analizar simultáneamente
ambos parámetros implementando el programa UTOPIA.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 44
En primer lugar, se proponen intervalos de variación para cada restricción de diseño. Dentro
de estos intervalos, se debe incluir el valor de las restricciones reglamentadas en el RAS
2016. Esto, con el fin de comparar los costos de la red a partir de las restricciones actuales
con los costos ante distintas variaciones restrictivas. Las restricciones de análisis son: la
profundidad máxima de excavación; el esfuerzo cortante mínimo; la relación de llenado
máxima; la velocidad mínima y máxima; el diámetro mínimo comercial.
Para evidenciar cambios en los costos cuando haya variación en cierta restricción específica,
es fundamental mantener los demás parámetros de diseño constantes para cada diseño. Estos
parámetros incluyen las demás restricciones de diseño, la topología de la red, los diámetros
comerciales, la ecuación de costos, material de las tuberías, entre otros. Por consiguiente, las
restricciones de diseño que permanecerán constantes adoptarán su respectivo valor
establecido por el RAS 2016.
De este modo, se debe recalcar las condiciones de la red que permanecerán constantes a lo
largo de todo el análisis.
Tabla 5: Características de la red de alcantarillado de análisis
Parámetro
Descripción
Tipo de alcantarillado
Pluvial
Material de las tuberías
PVC (
𝐾
𝑠
= 0.0015mm)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 45
Asimismo, se presenta la lista de diámetros comerciales a implementar.
Tabla 6: Lista de diámetros comerciales
Diámetro (milímetros)
182.0
227.0
452.0
595.0
670.0
747.0
824.0
977.6
1054.0
Finalmente, se establecen los valores de las restricciones de diseño por defecto para el análisis
de sensibilidad.
Tabla 7: Restricciones de diseño por defecto
Restricciones de diseño por defecto
Restricción
Valor
Unidades
Profundidad máxima de
excavación
5
Metros
Esfuerzo cortante mínimo
1.5
Pascales
Relación de llenado máxima
93
%
Velocidad máxima
10
Metros sobre segundo
Velocidad mínima
0.45
Metros sobre segundo
Diámetro mínimo
182
Milímetros
Una vez se haya determinado el comportamiento de los costos ante variaciones de las
restricciones de diseño en el terreno original, se procede a realizar el mismo análisis de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 46
variación en las restricciones, esta vez para distintas topografías del terreno. De este modo
se realizarán, a partir de una metodología de variación topológica de la red, 5 diferentes
terrenos. Algunos con mayores pendientes o más empinados, y otros con menores pendientes
o menos inclinados. Se presenta una descripción de los terrenos que se van a crear en orden
ascendente de inclinación.
Tabla 8: Abreviatura de los terrenos de análisis
Descripción
Abreviatura
Terreno totalmente plano
V
1
Terreno semiplano
V
2
Terreno parcialmente plano
V
3
Terreno original
V
4
Terreno inclinado
V
5
Terreno más inclinado
V
6
6.2.1. ANÁLISIS DE MÁXIMA RELACIÓN DE LLENADO ÓPTIMA
Adicionalmente, se realizará un análisis para identificar la máxima relación de llenado óptima
para cada terreno. Específicamente, en qué relación de llenado máxima se encuentra el diseño
optimizado de menor costo.
6.2.2. ECUACIÓN DE VELOCIDAD MEDIA DE FLUJO
La ecuación que se utilizará para determinar la velocidad media de flujo en las tuberías es la
ecuación de Darcy – Weisbach en conjunto con la ecuación de Colebrook – White. Al ser
una ecuación físicamente basada, brinda muchas ventajas en el diseño de alcantarillados
como evitar el sobredimensionamiento de estos sistemas.
6.2.3. ECUACIÓN DE COSTOS
La ecuación de costos representa un componente fundamental del análisis de sensibilidad. A
partir de esta se puede relacionar los costos de la red a ciertos parámetros de diseño como la
profundidad de excavación y el diámetro de las tuberías que componen la red.
La ecuación que será empleada para el análisis es la propuesta por Maurer et al. (2010). Esta
ecuación hace parte de un modelo de infraestructura de agua urbana. El modelo cuenta con
dos módulos: el área de la zona de captación y los costos de construcción de alcantarillados.
En el módulo de costos de construcción, Maurer et al. (2010) establecen que los parámetros

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 47
de construcción más importantes son: el diámetro de la tubería, la profundidad a la cual son
instaladas las tuberías, y la complejidad de la construcción (zona vial o zona verde). Se
explica además que, por simplicidad, no se tienen en cuenta otros parámetros como el
material de la tubería y costos en regulación constructiva y de seguridad. La ecuación
propuesta por Maurer et al. (2010) es la siguiente.
𝐶 = 𝛼 ∙ 𝐷 + 𝛽
Ecuación 25: Costo de un tramo por metro
lineal – Ecuación de Maurer et al. (2010).
Donde:
𝐶: costo específico en US$m
-1
𝐷: profundidad de excavación promedio
𝛼: coeficiente de costo asociado a la profundidad de excavación en función del diámetro US$m
-2
𝛽: coeficiente de costo asociado al diámetro y complejidad de la construcción US$m
-1
De igual forma, se pueden calcular los coeficientes de costo como se sigue.
𝛼 = 𝑚
𝛼
∙ 𝐷𝑁 + 𝑛
𝛼
Ecuación 26: Coeficiente α en la
ecuación de Maurer et al. (2010).
Donde:
𝐷𝑁: diámetro de las tuberías en metros
𝑚
𝛼,
𝑛
𝛼
: coeficientes de costo asociados a regresiones lineales del modelo de costo en US$m
-2
mm
-1
y US$m
-2
respectivamente.
Igualmente, para:
𝛽 = 𝑓
𝑆𝐹1
∙ 𝑚
𝛽
∙ 𝐷𝑁 + 𝑓
𝑆𝐹2
∙ 𝑛
𝛽
Ecuación 27: Coeficiente β en la ecuación
de Maurer et al. (2010).
Donde:
𝐷𝑁: diámetro de las tuberías en metros
𝑓
𝑆𝐹1,
𝑓
𝑆𝐹2
: factores de reducción adimensionales asociados a la complejidad de la construcción
𝑚
𝛽,
𝑛
𝛽
: coeficientes de costo asociados a regresiones lineales del modelo de costo en US$m
-1
mm
-1
y US$m
-1
respectivamente.
Es necesario recalcar que Maurer et al. (2012) emitió los factores de reducción en el
coeficiente
𝛽. Esto, con el objetivo de que las unidades sean consistentes al Sistema
Internacional (SI) y obtener los costos totales de la red, Aguilar (2017) modificó la ecuación.
De modo que la ecuación que se empleará en la presente metodología es la siguiente.
𝐶 = (𝛼 ∙ 𝐷 + 𝛽) ∙ 𝑙
Ecuación 28: Costo de un tramo – Ecuación
de Maurer et al. (2012).
Donde:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 48
𝐶: costo específico en US$
𝐷: profundidad de excavación promedio
𝑙: longitud de la tubería en metros
𝛼: coeficiente de costo asociado a la profundidad de excavación en función del diámetro US$m
-2
𝛽: coeficiente de costo asociado al diámetro y complejidad de la construcción US$m
-1
Los coeficientes se calcularán como se muestra a continuación.
𝛼 = 𝑚
𝛼
∙ 𝐷𝑁 + 𝑛
𝛼
Ecuación 29: Coeficiente α modificado
en la ecuación de Maurer et al. (2012).
Donde:
𝐷𝑁: diámetro de la tubería en metros
𝑚
𝛼,
𝑛
𝛼
: coeficientes de costo asociados a regresiones lineales del modelo en unidades de US$m
-3
y US$m
-2
respectivamente.
Igualmente, para
𝛽:
𝛽 = 𝑛
𝛼
∙ 𝐷𝑁 + 𝑛
𝛽
Ecuación 30: Coeficiente β modificado
en la ecuación de Maurer et al. (2012).
Donde
𝐷𝑁: diámetro de la tubería en metros
𝑚
𝛽,
𝑛
𝛽
: coeficientes de costo asociados a regresiones lineales del modelo de costo en US$m
-2
y US$m
-1
respectivamente. Los valores de cada constante son los siguientes.
Finalmente, se exponen los valores propuestos por Aguilar (2017) para la ecuación
modificada.
Tabla 9: Valor de los parámetros modificados por Aguilar (2017) para la ecuación de Maurer et Al. (2012)
Parámetro
Valor
𝑚
𝛼
1.02
𝑛
𝛼
127
𝑚
𝛽
0.11
𝑛
𝛽
37
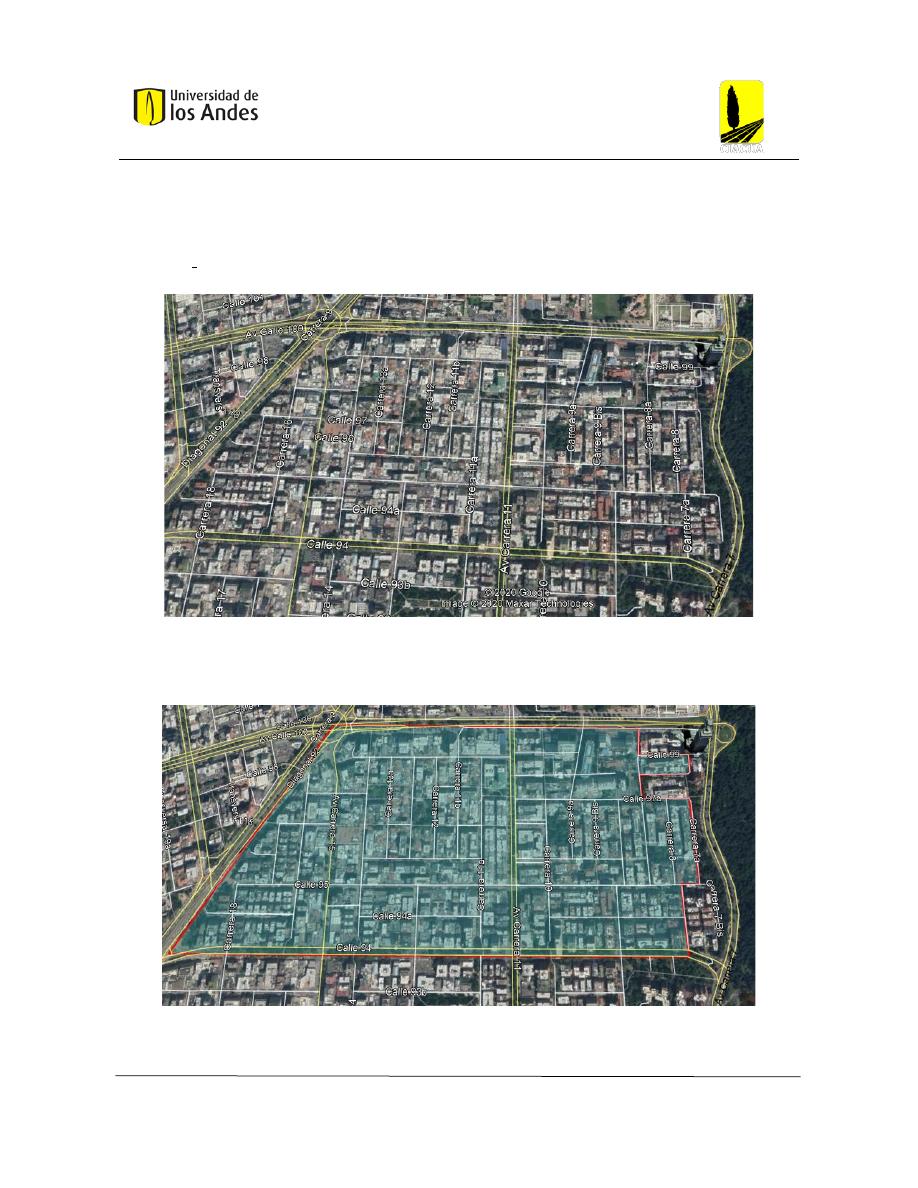
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 49
7. CASO DE ESTUDIO: RED CHICÓ SUR
La red Chicó Sur es un sistema de drenaje pluvial, ubicado en el nororiente de la ciudad de
Bogotá. Específicamente en la localidad de Usaquén: entre la calle 94 y calle 100, y entre la
carrera 7
a
y la diagonal de la calle 97. A continuación se presenta el sector de estudio.
Figura 30: Parte del barrio Chicó
Igualmente, la delimitación del área aferente a la red Chicó Sur.
Figura 31: Delimitación de la red Chicó Sur
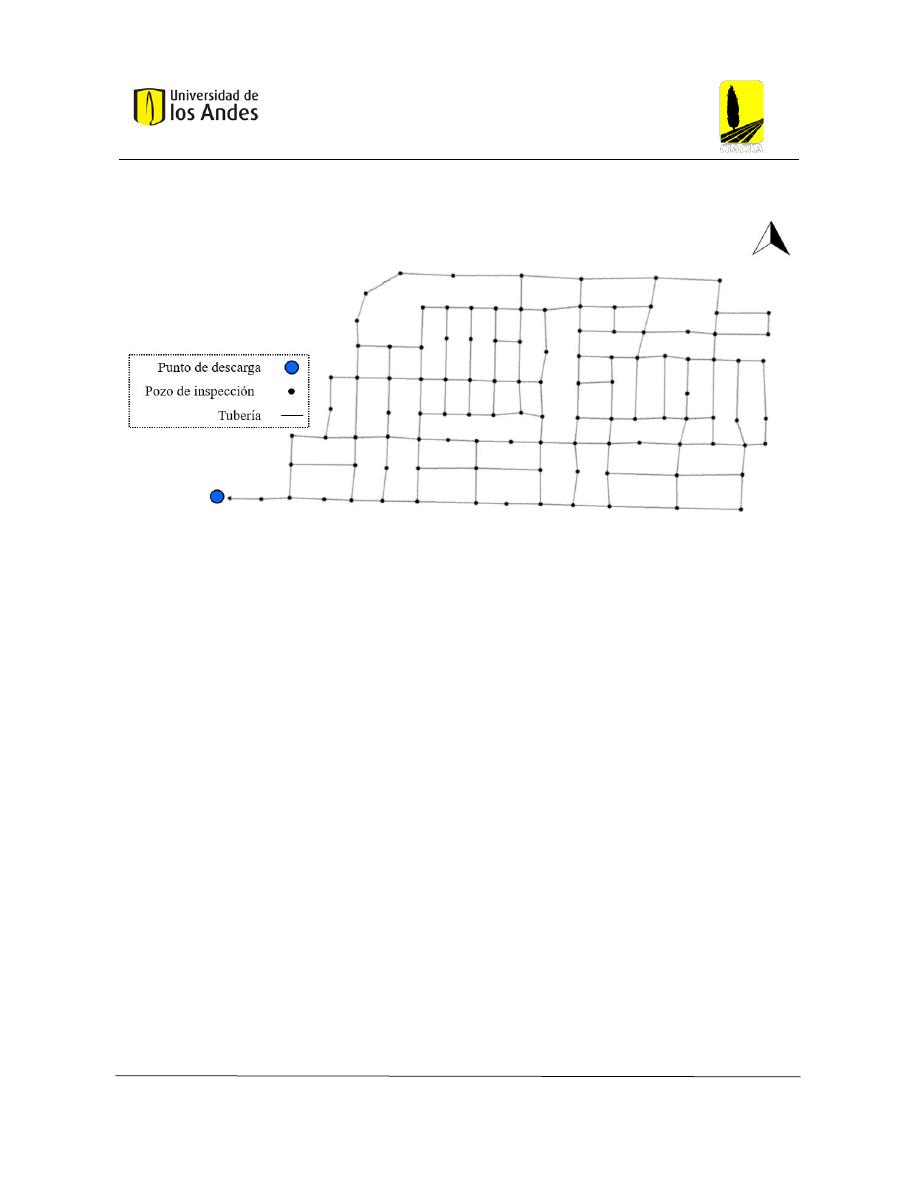
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 50
Finalmente, se expone la red Chicó Sur y su respectivo punto de descarga.
Figura 32: Red Chicó Sur
Esta red está compuesta por 109 pozos de inspección y 160 tuberías. El perímetro de la
cuenca aferente a la red es de aproximadamente 4.43 kilómetros, mientras que el área tiene
aproximadamente 86.4 hectáreas. Por otro lado, en el artículo “An exact methodology for
sewer systems design” realizado por Duque, Duque, Saldarriaga y Medaglia en el año 2016,
se establecen los caudales de diseño para cada pozo. Así como también se expone el caudal
en el punto de descarga, cuyo valor es 1.524 m
3
/s. Las coordenadas x, y ý z la de cada pozo
y sus respectivos caudales se presentan en el
Anexo A
.
Adicionalmente, se presenta el número de identificación de cada pozo para la red.
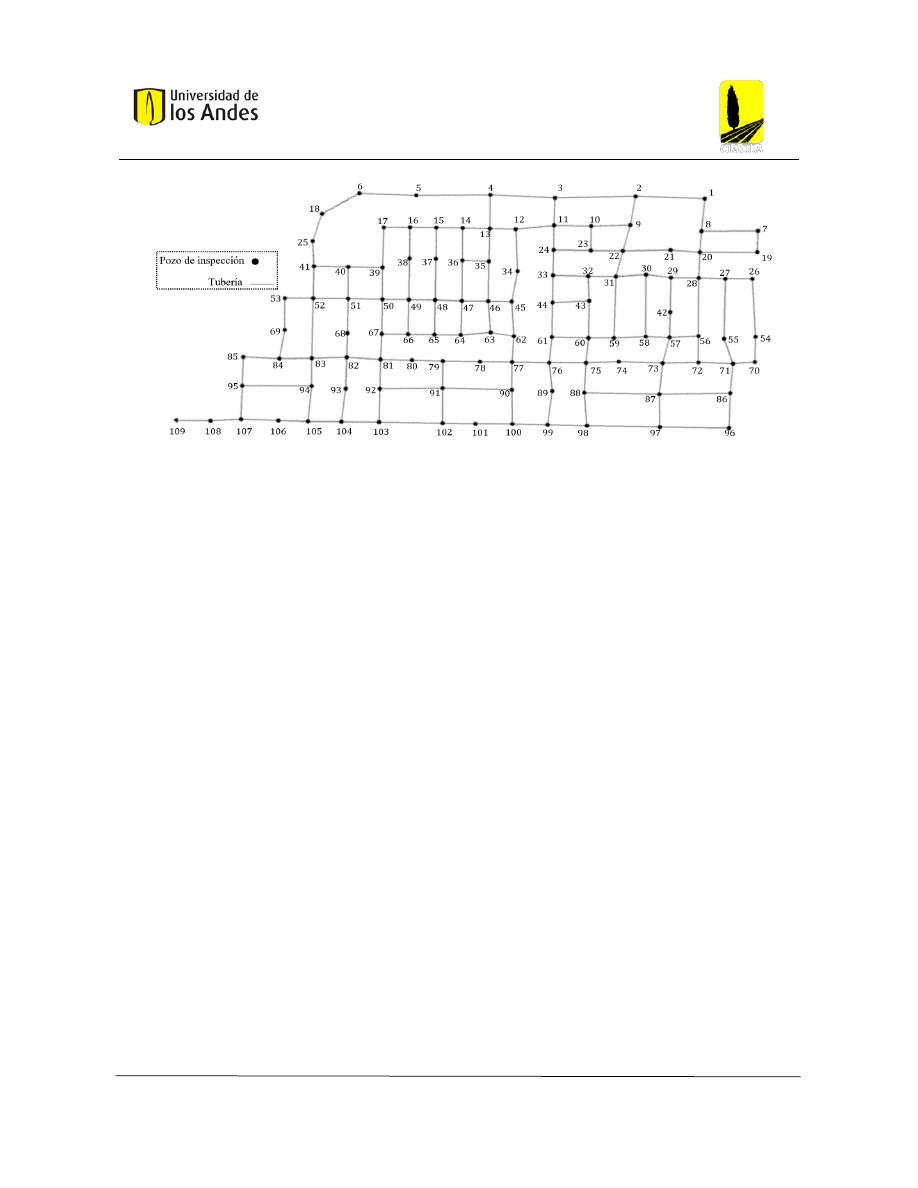
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 51
Figura 33: Identificación de los pozos de la red Chicó Sur

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 52
8. METODOLOGÍA PARA LA VARIACIÓN DE LAS RESTRICCIONES DE DISEÑO
8.1.
INTRODUCCIÓN
Como se mencionó anteriormente, con el objetivo de variar las restricciones hidráulicas de
diseño, se propone plantear intervalos de variación para cada restricción. Esto permitirá
analizar el comportamiento de los costos ante variaciones en las restricciones, para cada
topografía. De este modo, se define el límite inferior y superior como el rango de análisis
para cada restricción. Asimismo, el intervalo se entiende como el paso de variación.
8.2.
LÍMITES E INTERVALOS PARA CADA RESTRICCIÓN DE DISEÑO
A continuación, se presentan los límites, unidades e intervalos de cada restricción, para
realizar el respectivo análisis de variación.
Tabla 10: Límites e intervalos para la variación de restricciones de diseño
Restricción
Unidades
Límite inferior
Límite superior
Intervalo
Profundidad máxima
Metros
3.5
7
0.25
Esfuerzo cortante
Pascales
0
4.6
0.2
Relación de llenado
%
25
100
5
Velocidad máxima
m/s
6
2
0.2
Velocidad mínima
m/s
0
1.7
0.2 para [0,0.8] y 0.1
para [0.9,1.7]
Diámetro mínimo
mm
182
1054
Todos los diámetros
expuestos en la
Tabla 6
Del mismo modo, se debe establecer el intervalo de variación para el análisis de máxima
relación de llenado óptima. Aguilar (2017) establece que “La relación de llenado máxima
alta permite optimizar de mejor manera el flujo en las tuberías, y por lo tanto minimizar los
costos de construcción”. Teniendo en cuenta que el diseño óptimo se encuentra en valores
altos de esta restricción, se presentan los límites e inérvalo propuestos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 53
Tabla 11: Límites e intervalo para la variación de altas relaciones de llenado máximas
Restricción
Unidades
Límite inferior
Límite superior
Intervalo
Máxima relación de
llenado
óptima
%
80
100
1

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 54
9. TOPOLOGÍA Y TOPOGRÁFIA
9.1.
ANÁLISIS DE LA TOPOGRAFÍA ACTUAL
La topografía en la red Chicó Sur tiene las pendientes más altas en las zonas cercanas a la
carrera séptima. A medida que la red se acerca a la calle 97, las pendientes van disminuyendo
hasta volverse un terreno relativamente plano. Precisamente es en las zonas planas donde se
encuentra la descarga, está cerca de la calle 97. A continuación se puede ver una ilustración
de una calle perteneciente al terreno de análisis, con vista hacia la carrera séptima.
Figura 34: Calle del barrio Chicó
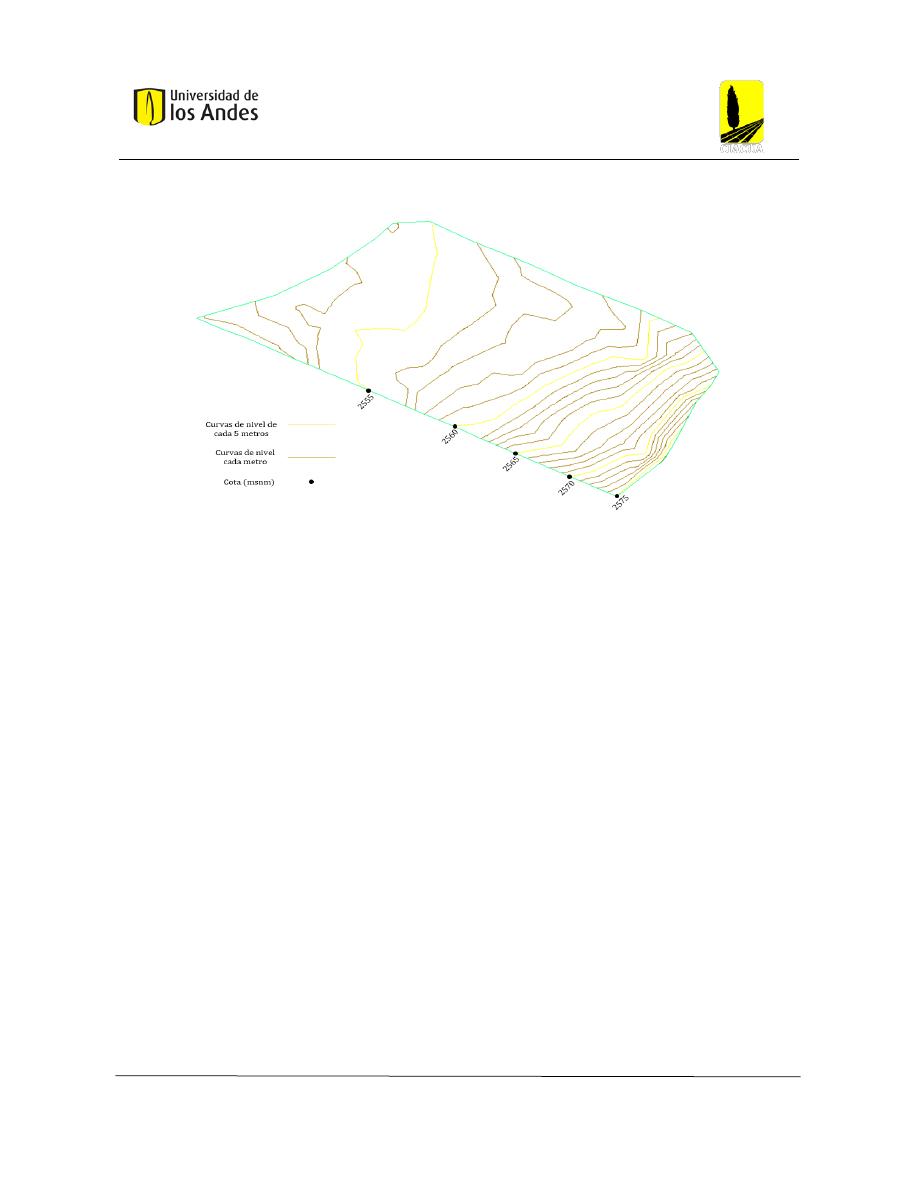
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 55
De igual forma, se presenta la topografía estimada del terreno.
Figura 35: Topografía actual del terreno
9.2.
METODOLOGÍA PARA LA VARIACIÓN TOPOLÓGICA DE LA RED
Con el objetivo de determinar el comportamiento de los costos ante la variación de la
topografía del terreno aferente a la red, es necesario plantear diferentes terrenos. Algunos
más empinados y otros más planos que el terreno original. En este sentido, se propone variar
la topología de la red, para así cambiar de manera indirecta la topografía del terreno.
Específicamente, a partir de la variación de la cota (la coordenada z) de los pozos de la red,
variar la topografía. Simultáneamente, establecer una metodología que pueda ser aplicable a
cualquier red de drenaje urbano.
Esta metodología consiste principalmente en una variación lineal de las cotas de estos pozos
a partir de un pozo de referencia. Este pozo de referencia es el pozo de menor cota en toda la
red. Establecido este pozo, se debe proponer una tasa de variación lineal independiente para
cada pozo. De manera que cada pozo de la red varíe en función del pozo de menor cota, hasta
llegar a una topología igual para todos los pozos. En otras palabras, que todos los pozos
tengan la misma cota, lo cual se traduce en un terreno totalmente plano.
De este modo, se debe definir los parámetros iniciales para poder llevar a cabo dicha
metodología.
• M: Conjunto de k pozos de inspección de la red de alcantarillado
• M = {m
1
, m
2
, m
3
, …, m
i
, …, m
k
}

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 56
• 𝛻: Conjunto de cotas de los k pozos de inspección
• 𝛻 = {𝛻
1
, 𝛻
2
, 𝛻
3
, …, 𝛻
i
, …, 𝛻
k
}
• M
m
: Pozo de menor cota
• 𝛻
m
: Cota del pozo
M
m
Ahora bien, se establece la ecuación para calcular la tasa de variación lineal independiente
para cada pozo de la red.
Δz
𝑖
=
ΔZ
i
V
=
∇
i
- ∇
m
V
Ecuación 31: Tasa de variación lineal por pozo
Donde:
Δz
i
: tasa de variación lineal para cada pozo
i
ΔZ
i
: distancia entre la cota del pozo i y
∇
m
∇
i
: cota del pozo
i
𝑉: constante arbitraría ≥ 1
El valor de V depende del cambio topológico al que se busque llegar. Entre más pequeña sea
Δz
i
, habrá más número de topologías
j antes de llegar al terreno plano. Finalmente, se calcula
las cotas por cada pozo, del nuevo terreno. Esto se logra con la siguiente ecuación.
∇
𝑖
𝑗+1
= ∇
𝑖
𝑗
− Δz
i
Ecuación 32: Nueva cota del pozo para la variación j
Donde:
∇
𝑖
𝑗+1
: cota del pozo
i para la variación j
+1
∇
𝑖
𝑗
: cota del pozo
i para la variación j
De este modo, realizados
V pasos es posible llegar a un terreno plano. Lo anterior se puede
demostrar resolviendo la Ecuación 31 para
∇
m
.
∇
i
− V ∙ Δz
i
= ∇
m

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 57
∇
i
− ∑ Δz
𝑖
𝑗
𝑉
𝑗=1
= ∇
m
Ecuación 33: Demostración de
terrenos planos para V pasos
La ecuación también es válida para generar terrenos más empinados que el terreno original.
Esto se consigue exclusivamente a partir del parámetro
V. La principal excepción es que, el
terreno no va a llegar nunca a un terreno totalmente plano. A continuación, se muestra el rol
que cumple la constante
V en dicha ecuación:
Tabla 12: Aplicación del parámetro V
Caso
Rango
Tipo de terreno
Descripción
1
V ≥ 1
Se obtienen terrenos más
planos que el original
Se llega a un terreno
plano en
V pasos
2
V ≤ -1
Se obtienen terrenos más
inclinados que el original
No se llega a un terreno
plano. M
m
siempre será
el pozo de menor cota en
la red
3
𝑉 =
∇
𝑚
∇
𝑖
− 1
Terreno original
invertido sobre el plano
xy
No se llega a un terreno
plano. M
m
se vuelve el
pozo de mayor cota en la
red.
Es importante recalcar que, para esta investigación, se hará uso de todos los casos menos el
caso 3. La metodología descrita se puede ilustrar en el ejemplo que se presenta a
continuación.
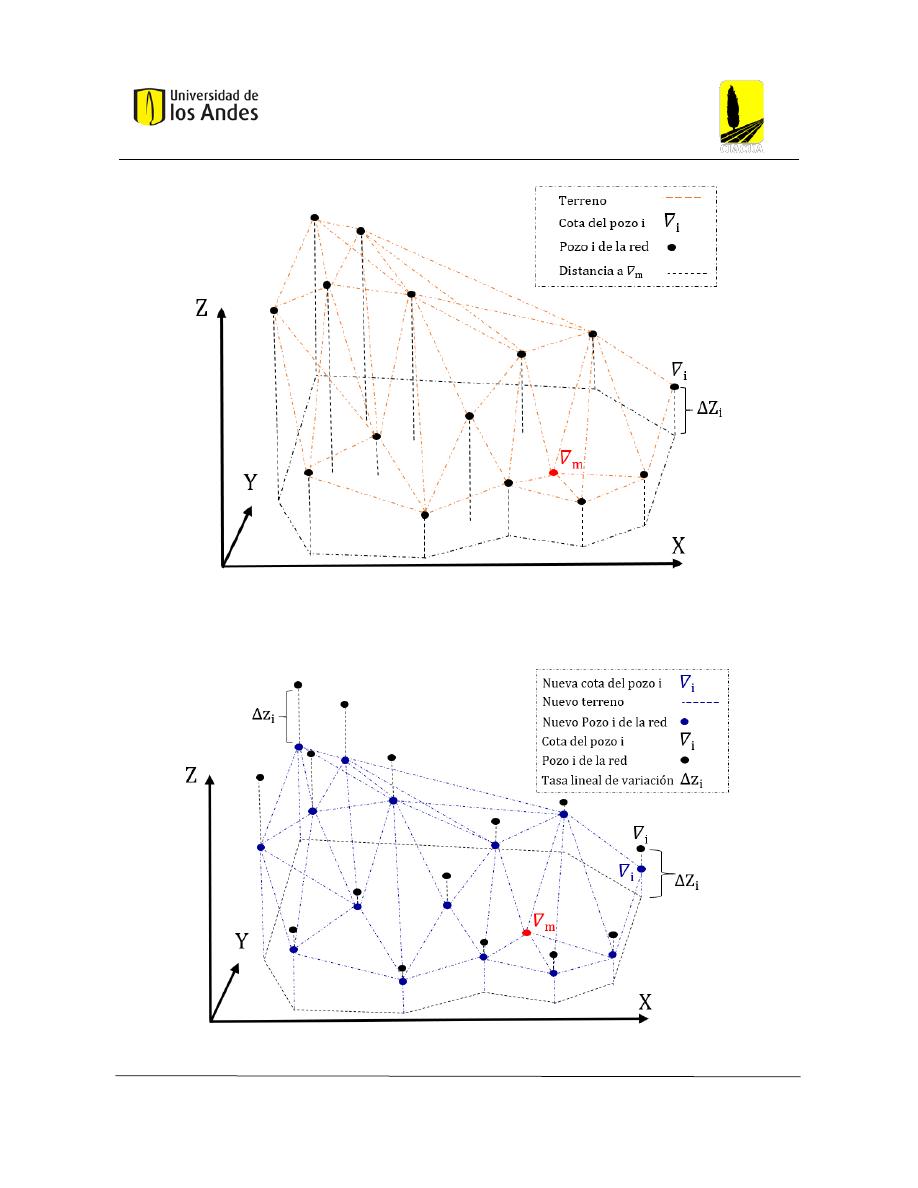
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 58
Figura 36: Topología de una red ejemplo
Así, implementando la metodología para un
V ≥ 1 se pretende llegar al siguiente resultado.
Figura 37: Topología de la red ejemplo más plana que la topología original
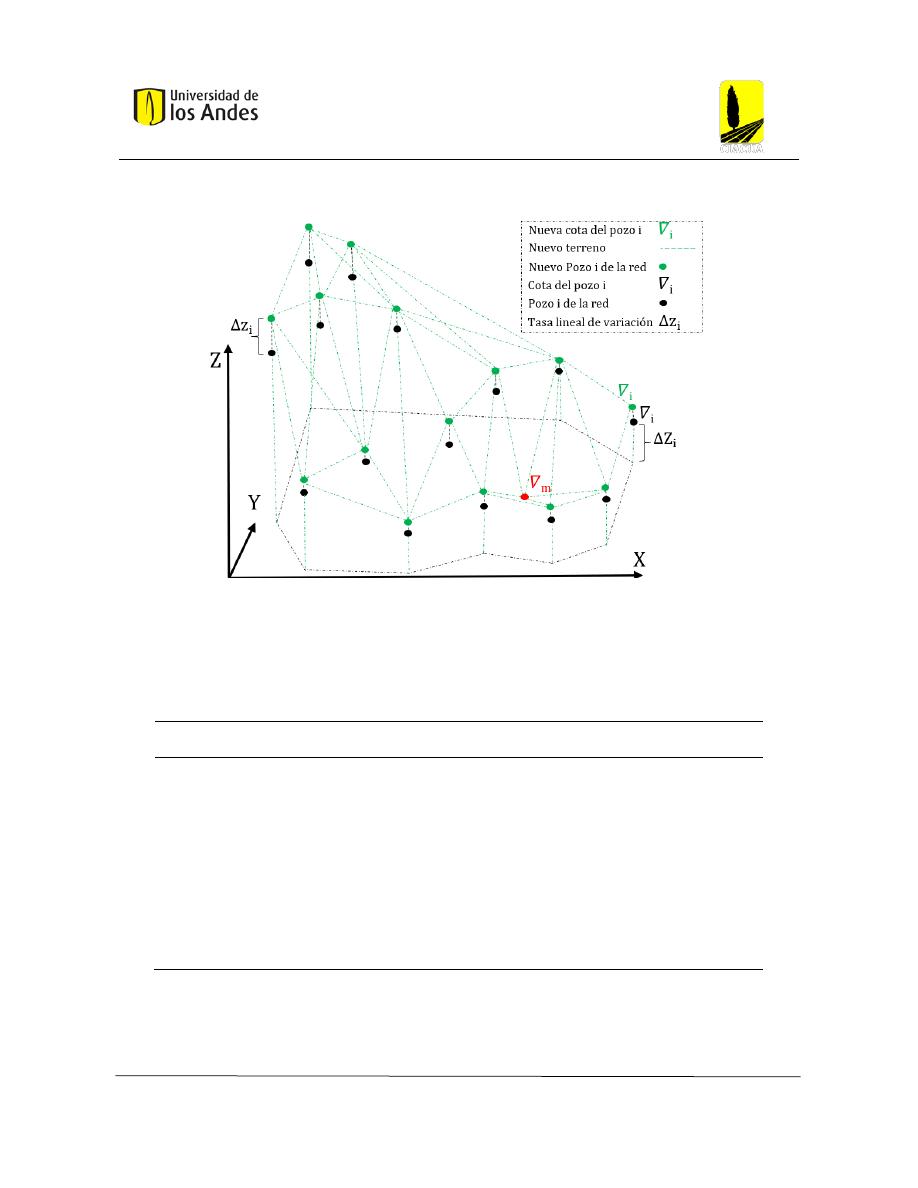
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 59
Para un
V < 1 se tiene el siguiente modelo:
Figura 38: Topología de la red ejemplo más inclinada que la topología original
Finalmente, es necesario establecer el valor de V y el número de pasos
j o ∆𝑧 para llegar a
cada terreno.
Tabla 13: Valor de V y número de ∆𝑧
𝑖
para llegar a los terrenos objetivo
Valor del parámetro V
Terreno
Número de
∆𝒛
𝒊
5
V
1
5
∆𝒛
𝒊
5
V
2
4
∆𝒛
𝒊
5
V
3
2
∆𝒛
𝒊
No aplica
V
4
No aplica
-5
V
5
2
∆𝒛
𝒊
-5
V
6
4
∆𝒛
𝒊

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 60
9.3.
METODOLOGÍA PARA LA VARIACIÓN TOPOGRÁFICA DEL TERRENO
Teniendo las coordenadas originales, y calculadas las nuevas coordenadas de los pozos para
cada terreno, a partir del programa CIVIL 3D 2020 se puede crear los nuevos terrenos y sus
respectivas curvas de nivel.
Para esto, primero se debe crear un modelo digital de elevaciones (DEM). (Peña, 2006) define
un DEM como un modelo que permite representar el relieve de un terreno. Posteriormente,
con el DEM es posible crear una superficie Triangular Irregular Networks (TIN).
Figura 39: TIN generado a partir de la topología original de la red Chicó Sur
Una TIN es importante para la generación de nuevos terrenos a partir de coordenadas.
Además, “Los TIN permiten modelar las superficies heterogéneas eficazmente incluyendo
más puntos en áreas donde la superficie es muy variable y menos en lugares donde la
superficie es relativamente constante” (Peña, 2006, pág. 204).
En este sentido, a partir de la TIN se pretende crear las curvas de nivel tanto del terreno
original como de los nuevos terrenos. De esta manera se ilustrarán los cambios en la
topografía para los nuevos terrenos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 61
10. RESULTADOS
10.1.
VARIACIÓN TOPOLÓGICA Y TOPOGRÁFICA
10.1.1. TOPOLOGÍA DE LA RED
Con la intención de exponer la metodología propuesta, se presentará el procedimiento de
variación de topología el pozo 96 para los terrenos V
1
y V
6
. En primer lugar, se determinó
que el pozo que tiene la menor cota en la red es el 108. De esta forma se calcula
∆𝑧
96
con la
Ecuación 31 para los dos terrenos.
Para
V
1
:
5Δz
96
=
5∙ΔZ
96
V
=
5∙(∇
96
- ∇
108
)
V
5Δz
96
=
5∙ΔZ
96
V
=
5∙(2575.185 -2551.463)
5
5Δz
96
=
5∙ΔZ
96
V
=
5∙(2575.185 -2551.463)
5
5Δz
96
= 23.722m
Con la Ecuación 32 se calcula la cota final del pozo 96 para el terreno
V
1
.
∇
96
−5
= ∇
96
0
− 5Δz
96
∇
96
−5
= 2575.185 − 23.722
𝛁
𝟗𝟔
−𝟓
= 2551.463
Para
V
6
:
4Δz
96
=
4∙ΔZ
96
V
=
4∙(∇
96
- ∇
108
)
V
4Δz
96
=
4∙(2575.185 -2551.463)
−5
4Δz
96
= −18.978m
Con la Ecuación 32 se calcula la cota final del pozo 96 para el terreno
V
1
.
∇
96
+4
= ∇
96
0
− 4Δz
96

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 62
∇
96
+4
= 2575.185 − (−18.978)
𝛁
𝟗𝟔
+𝟒
= 2594.163m
A continuación, se muestran las cotas del pozo 96 para los diferentes terrenos de análisis.
Tabla 14: Cotas del pozo 96 para todos los terrenos de análisis
Terreno
Cota (msnm)
V1
2551.463
V2
2556.207
V3
2565.696
V4
2575.185
V5
2584.674
V6
2594.163
Los resultados de las cotas de los distintos terrenos para los demás pozos de la red se muestran
en el
Anexo B
.
10.1.2. TOPOGRAFÍA DEL TERRENO
A continuación, se presenta los diferentes mapas topográficos obtenidos para cada terreno.
En estos, se evidencia las curvas de nivel y sus respectivas cotas.
Figura 40: Topografía del terreno V
1
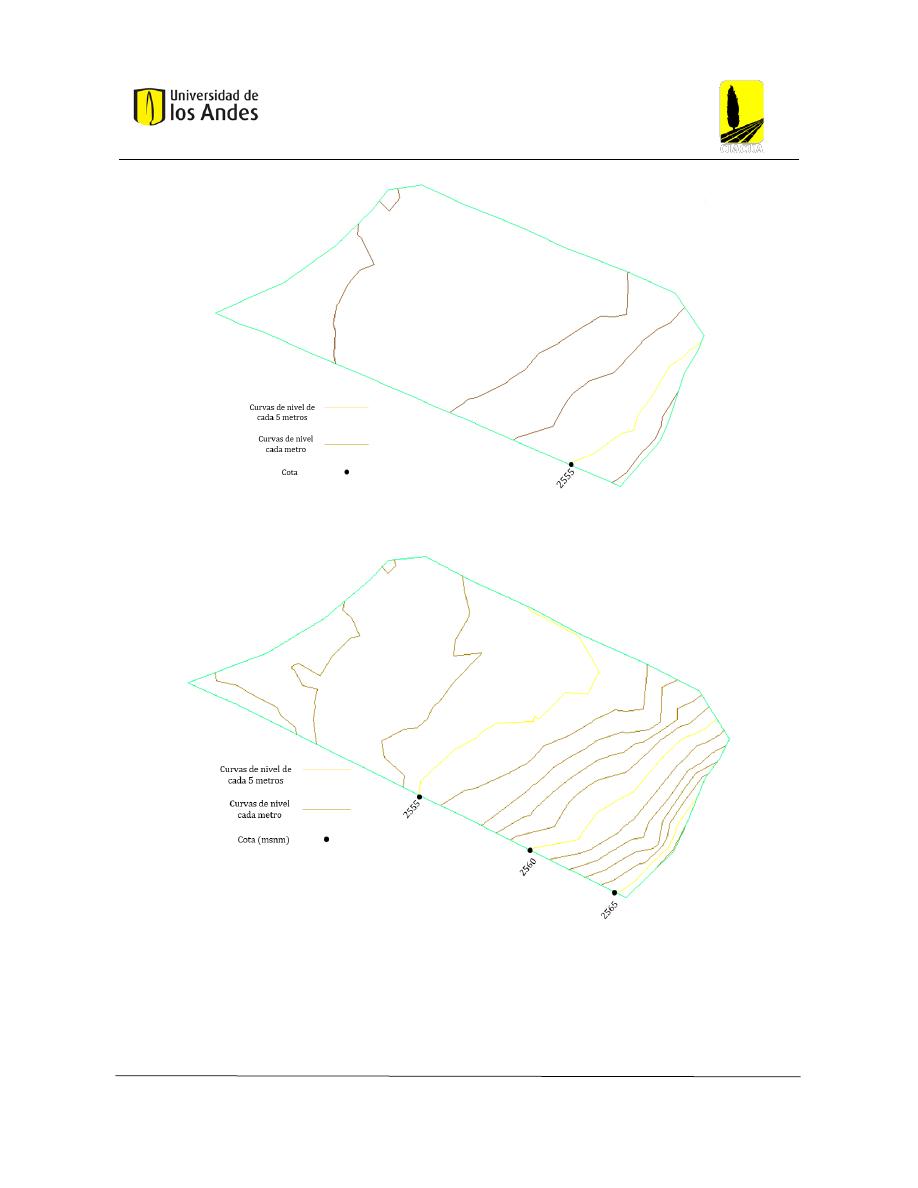
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 63
Figura 41: Topografía del terreno V
2
Figura 42: Topografía del terreno V
3
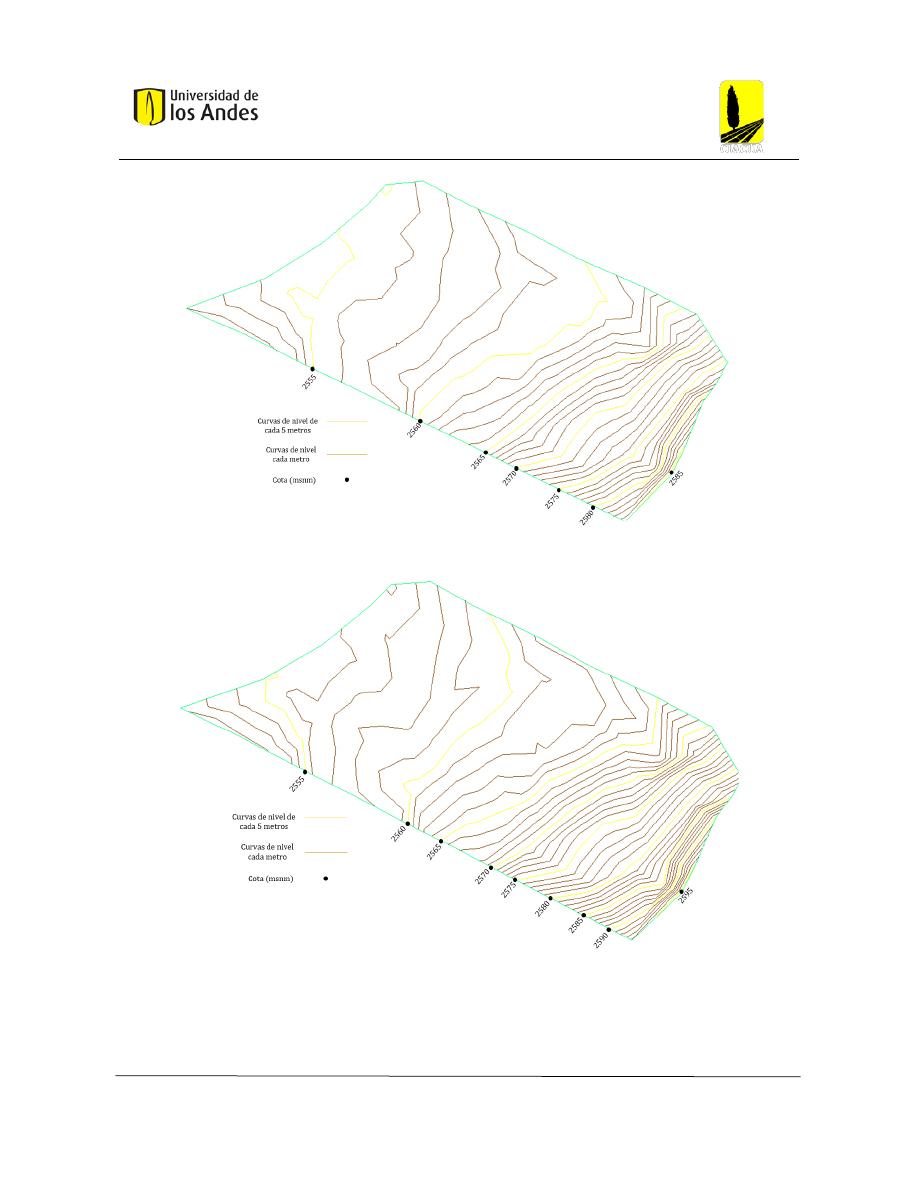
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 64
Figura 43: Topografía para el terreno V
5
Figura 44: Topografía del terreno V
6
Además, se presenta un perfil topográfico de una parte del terreno. Esto con el objetivo de
mostrar cómo es la variación del terreno visto de perfil.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 65
Figura 45: Serie de tuberías para exponer el perfil topográfico
Figura 46: Perfil topográfico: variación topográfica del terreno
2.545
2.550
2.555
2.560
2.565
2.570
2.575
2.580
2.585
2.590
2.595
2.600
0
200
400
600
800
1000
1200
1400
1600
Cota
(m
snm)
Distancia horizontal(m)
Variación topográfica - Chico Sur
V1
V2
V3
V4
V5
V6
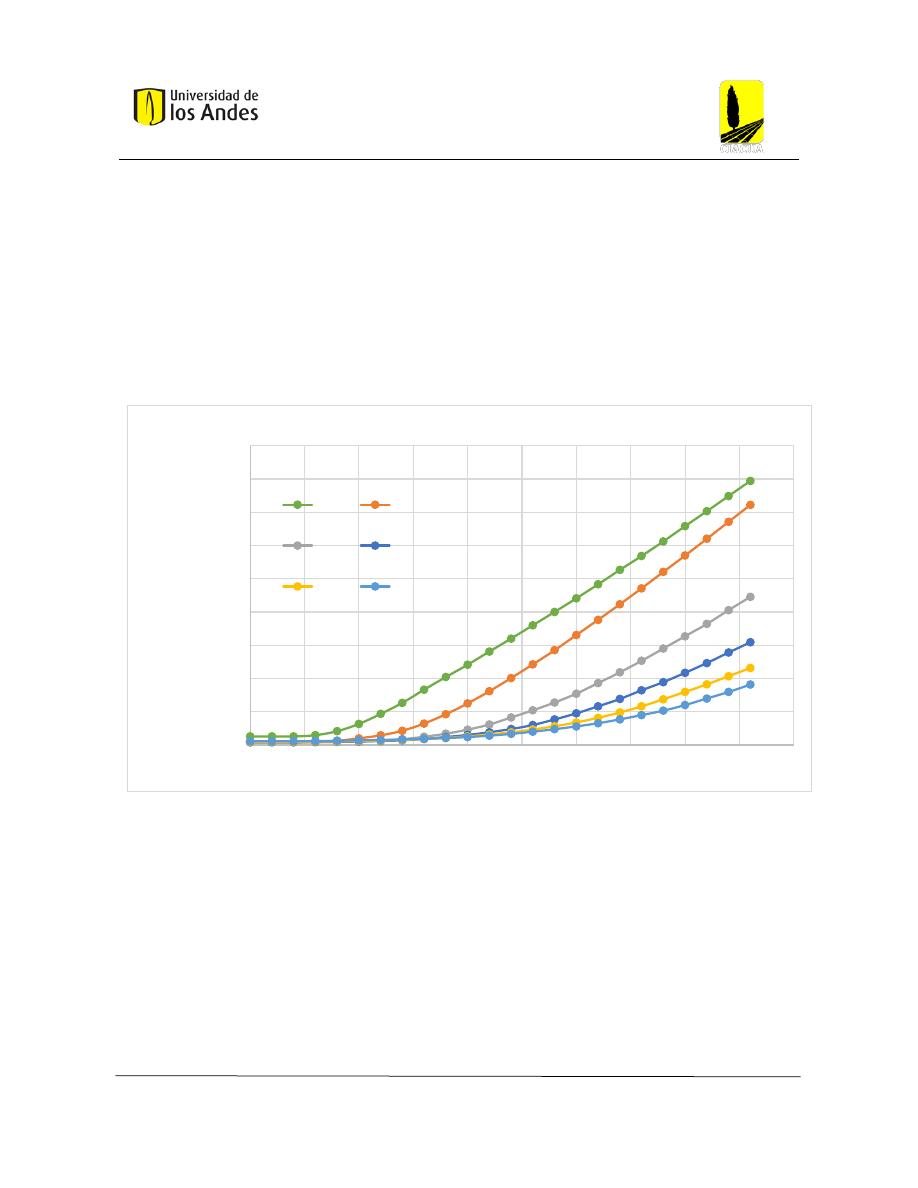
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 66
10.2.
VARIACIÓN DE LAS RESTRICCIONES DE DISEÑO
10.2.1. PROFUNDIDAD MÁXIMA DE EXCAVACIÓN
A partir de los análisis preliminares, se determinó que la profundidad máxima de excavación
no influye en los diseños y, en consecuencia, en los costos de la red.
10.2.2. ESFUERZO CORTANTE MÍNIMO
A continuación, se presenta los resultados de los costos del diseño de la red Chicó Sur, cuando
hay variación en el esfuerzo cortante mínimo. Los costos tabulados de esta restricción se
encuentran en el Anexo C.
Gráfica 1: Costo de la red ante la variación del esfuerzo cortante mínimo
Además, se muestra la variación de costos para esfuerzos cortantes mínimo entre 0 y 0.8
pascales.
2.900.000
3.900.000
4.900.000
5.900.000
6.900.000
7.900.000
8.900.000
9.900.000
10.900.000
11.900.000
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
C
ost
o (
US
D$)
Esfuerzo cortante mínimo (Pa)
Costo del diseño
V1
V2
V3
V4
V5
V6
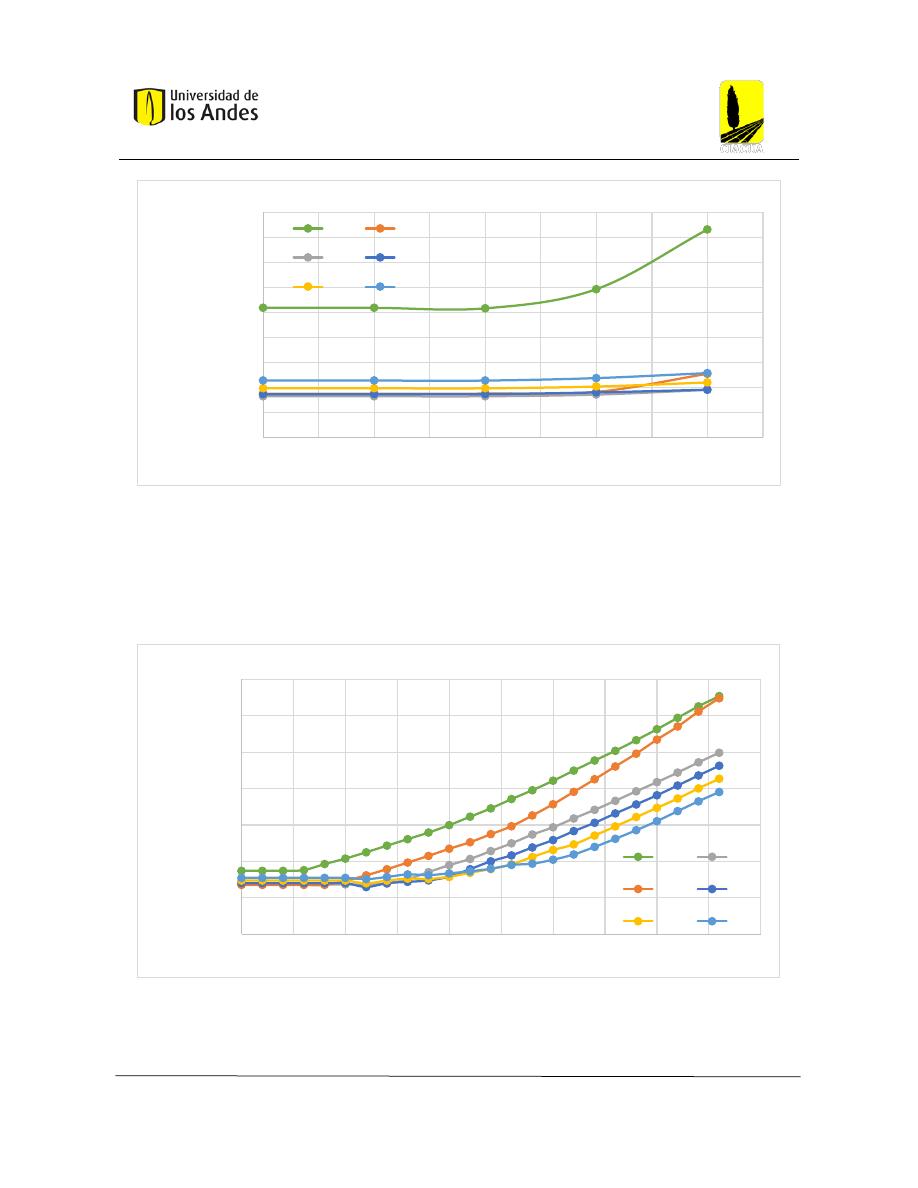
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 67
Gráfica 2: Costo de la red ante la variación de bajos esfuerzos cortantes mínimos
Por otro lado, en la ecuación de costos de Maurer, la profundidad de excavación es un
parámetro determinante para calcular los costos del diseño. Cada pozo de la red tiene una
profundidad de excavación. En este sentido, se determinó la máxima profundidad excavada
que se evidenció en cada diseño y se graficó en función del esfuerzo cortante mínimo.
Gráfica 3: Profundidad máxima en la red ante variación del esfuerzo cortante mínimo
2.900.000
2.950.000
3.000.000
3.050.000
3.100.000
3.150.000
3.200.000
3.250.000
3.300.000
3.350.000
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
C
ost
o (
US
D$)
Esfuerzo cortante mínimo (Pa)
Costo del diseño
V1
V2
V3
V4
V5
V6
0
2
4
6
8
10
12
14
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
Pr
of
und
idad
máx
ima (
m)
Esfuerzo cortante mínimo (Pa)
Profundidad máxima en el diseño
V1
V2
V3
V4
V5
V6
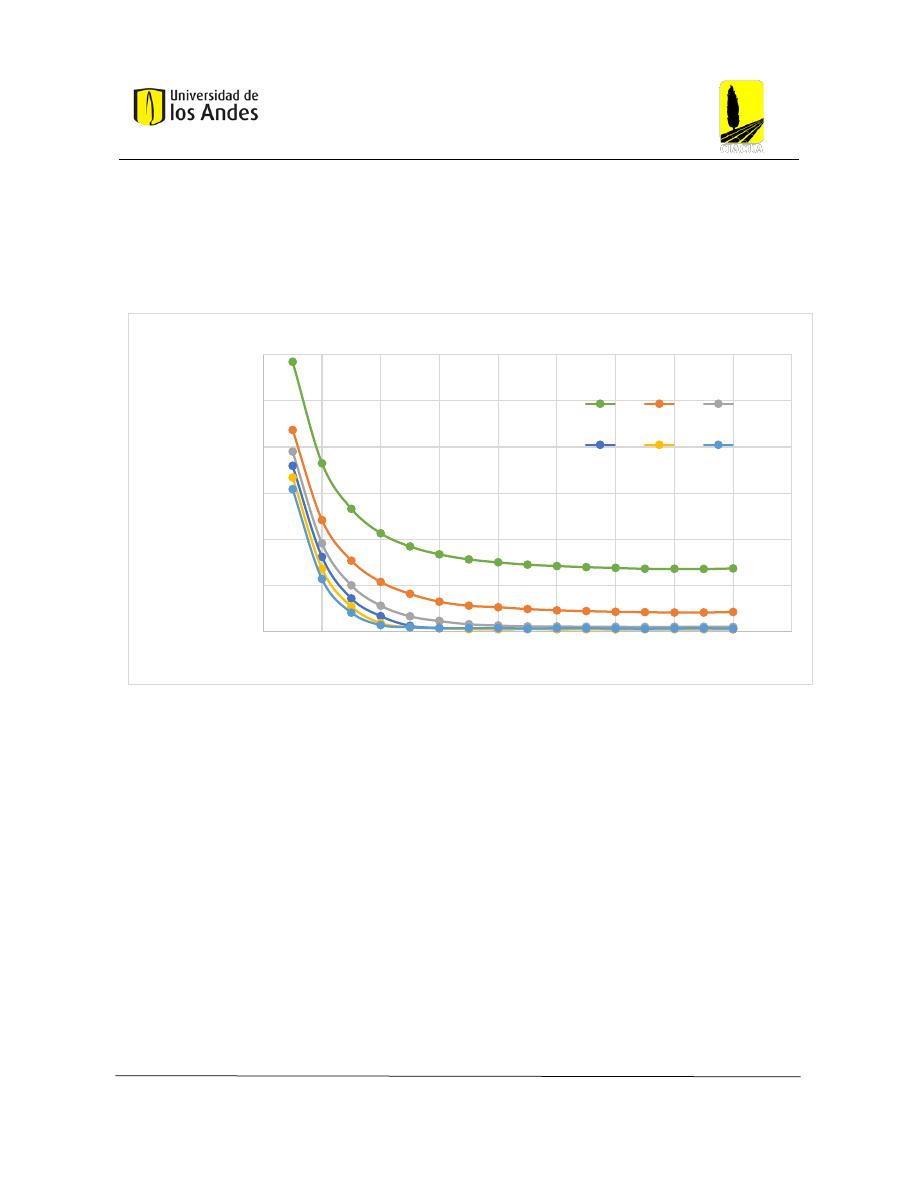
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 68
10.2.3. RELACIÓN DE LLENADO MÁXIMA
De igual forma, estos fueron los resultados para los costos del diseño cuando se varió la
restricción de máxima relación de llenado. Los costos tabulados de esta restricción se
encuentran en el Anexo D.
Gráfica 4: Costo de la red ante la variación de la máxima relación de llenado
Del mismo modo, se determinó la profundidad máxima evidenciada en cada diseño y se
graficó en función de la máxima relación de llenado.
3.000.000
4.000.000
5.000.000
6.000.000
7.000.000
8.000.000
9.000.000
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
Co
sto
(US
D$
)
Relación de llenado máxima (-)
Costo del diseño
V1
V2
V3
V4
V5
V6
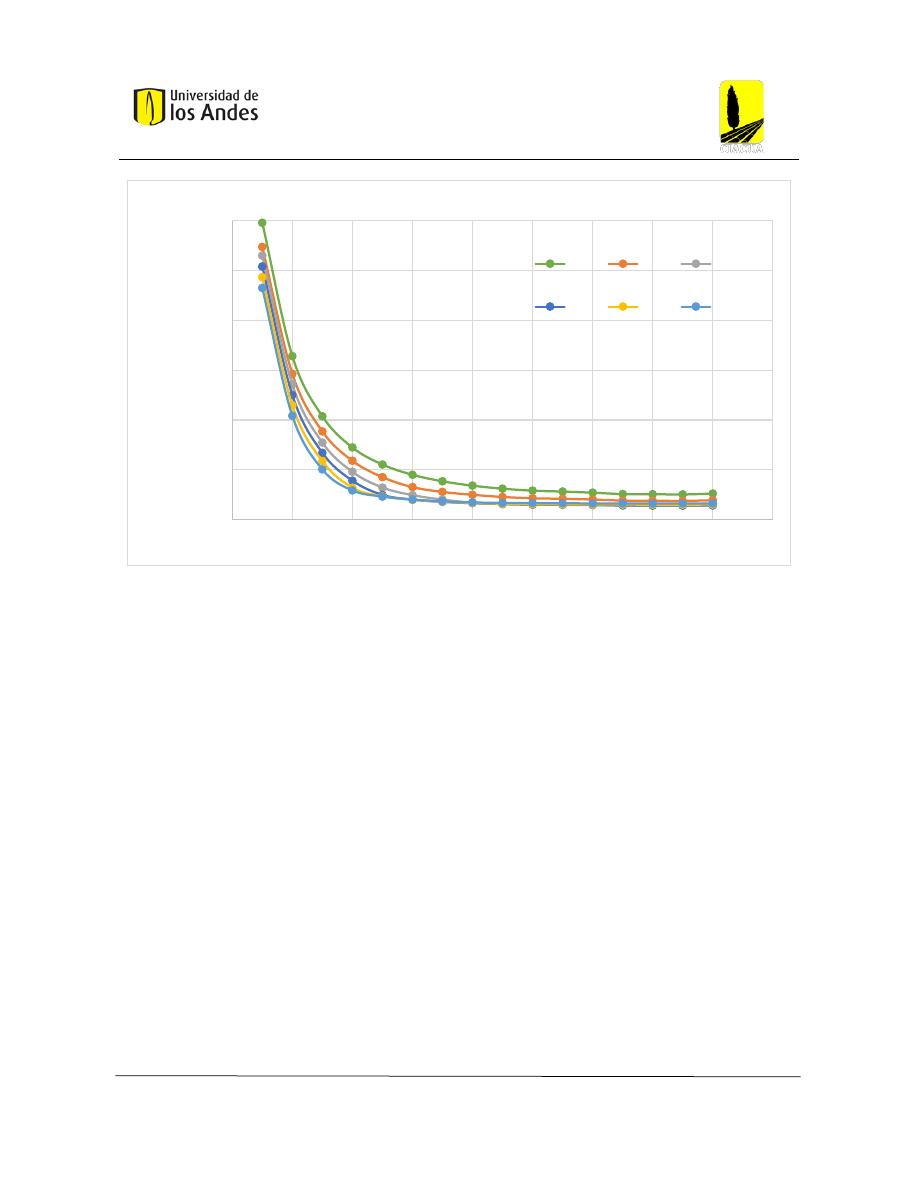
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 69
Gráfica 5: Profundidad máxima en la red ante variación de la máxima relación de llenado
Ahora, se muestran los costos para relaciones de llenado entre el 80% y 100% para todos los
terrenos. Estos costos tabulados se encuentran en el Anexo E.
0
10
20
30
40
50
60
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
Pr
of
und
idad
máx
ima (
m)
Relación de llenado máxima (-)
Profundidad máxima en el diseño
V1
V2
V3
V4
V5
V6
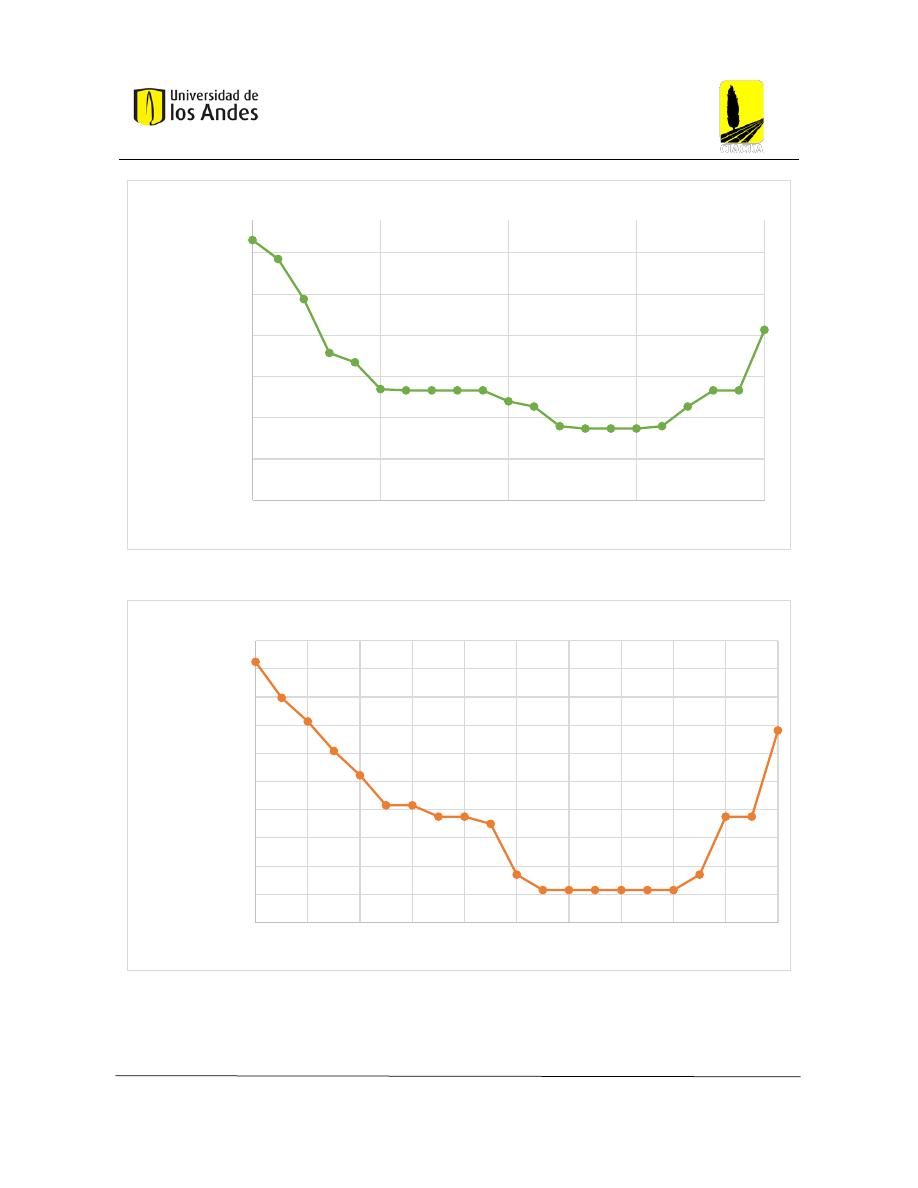
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 70
Gráfica 6: Costo de la red para altas relaciones de llenado máximas: terreno V
1
Gráfica 7: Costo de la red para altas relaciones de llenado máximas: terreno V
2
4.350.000
4.355.000
4.360.000
4.365.000
4.370.000
4.375.000
4.380.000
0,8
0,85
0,9
0,95
1
C
ost
o (
US
D$)
Relación de llenado máxima (-)
Costo del diseño (V
1
)
3.415.000
3.417.000
3.419.000
3.421.000
3.423.000
3.425.000
3.427.000
3.429.000
3.431.000
3.433.000
3.435.000
0,8
0,82
0,84
0,86
0,88
0,9
0,92
0,94
0,96
0,98
1
C
ost
o (
US
D$)
Relación de llenado máxima (-)
Costo del diseño (V
2
)
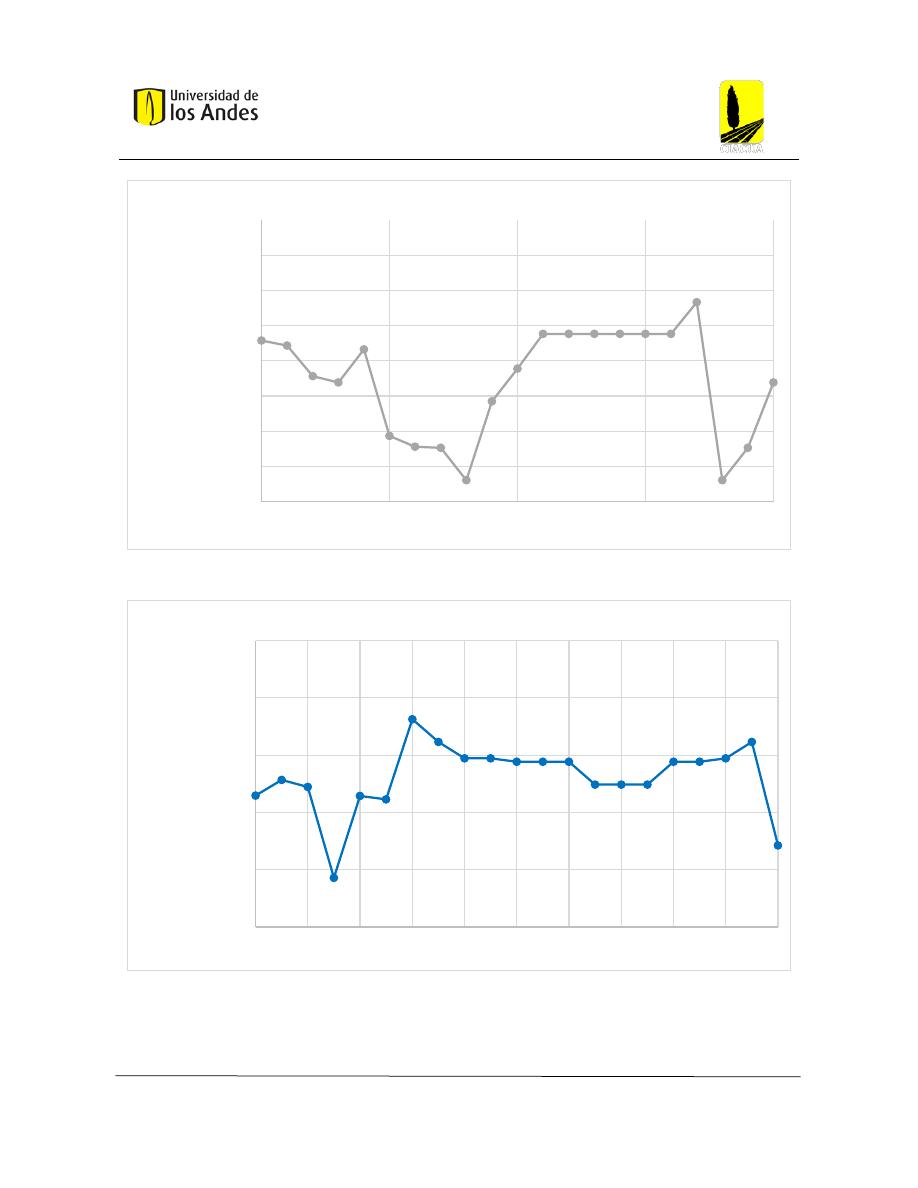
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 71
Gráfica 8: Costo de la red para altas relaciones de llenado máximas: terreno V
3
Gráfica 9: Costo de la red para altas relaciones de llenado máximas: terreno V
4
3.100.000
3.102.000
3.104.000
3.106.000
3.108.000
3.110.000
3.112.000
3.114.000
0,8
0,85
0,9
0,95
1
C
ost
o (
US
D$)
Relación de llenado máxima (-)
Costo del diseño (V
3
)
3.055.000
3.056.000
3.057.000
3.058.000
3.059.000
3.060.000
0,8
0,82
0,84
0,86
0,88
0,9
0,92
0,94
0,96
0,98
1
C
ost
o (
US
D$)
Relación de llenado máxima (-)
Costo del diseño (V
4
)
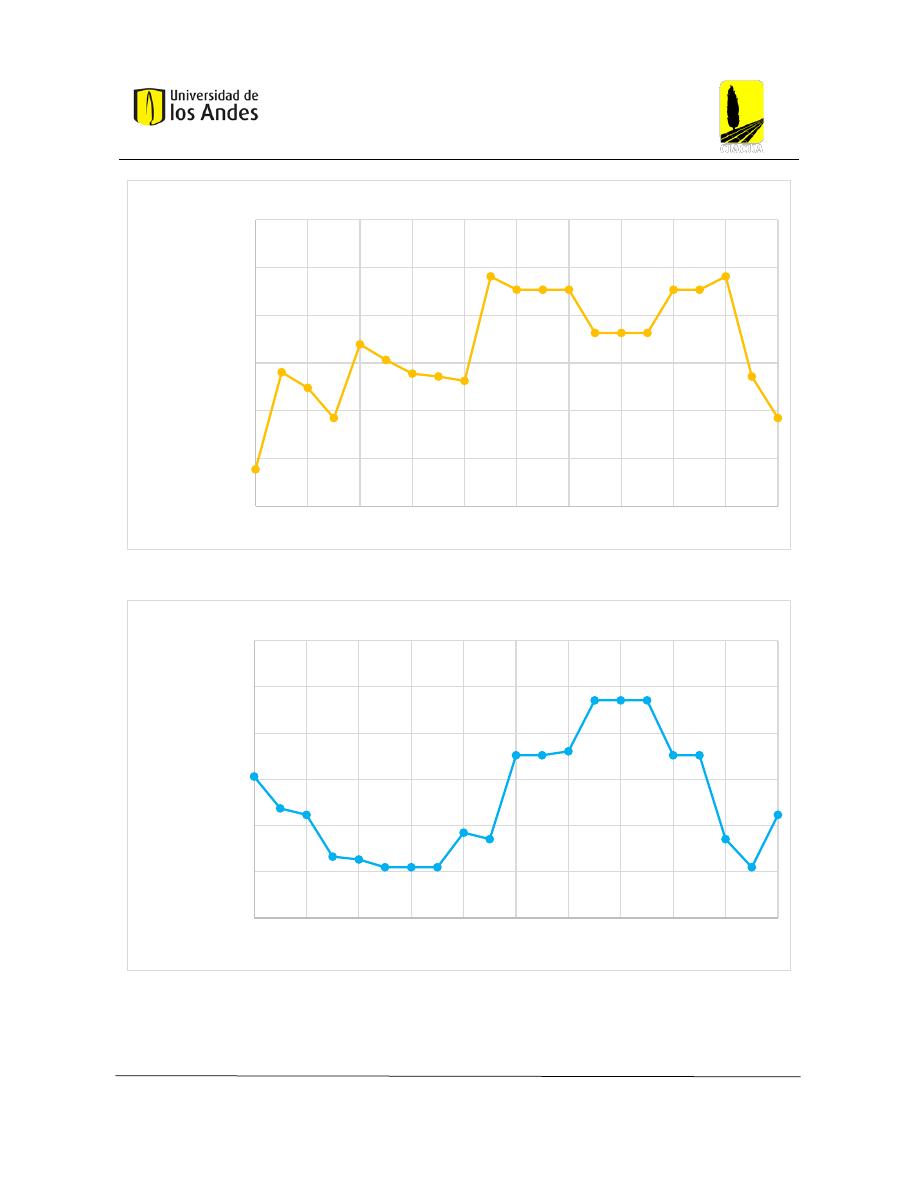
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 72
Gráfica 10: Costo de la red para altas relaciones de llenado máximas: terreno V
5
Gráfica 11: Costo de la red para altas relaciones de llenado máximas: terreno V
6
3.059.000
3.060.000
3.061.000
3.062.000
3.063.000
3.064.000
3.065.000
0,8
0,82
0,84
0,86
0,88
0,9
0,92
0,94
0,96
0,98
1
C
ost
o (
US
D$)
Relación de llenado máxima (-)
Costo del diseño (V
5
)
3.066.000
3.068.000
3.070.000
3.072.000
3.074.000
3.076.000
3.078.000
0,8
0,82
0,84
0,86
0,88
0,9
0,92
0,94
0,96
0,98
1
Cost
o
(USD$
)
Relación de llenado máxima (-)
Costo del diseño (V
6
)
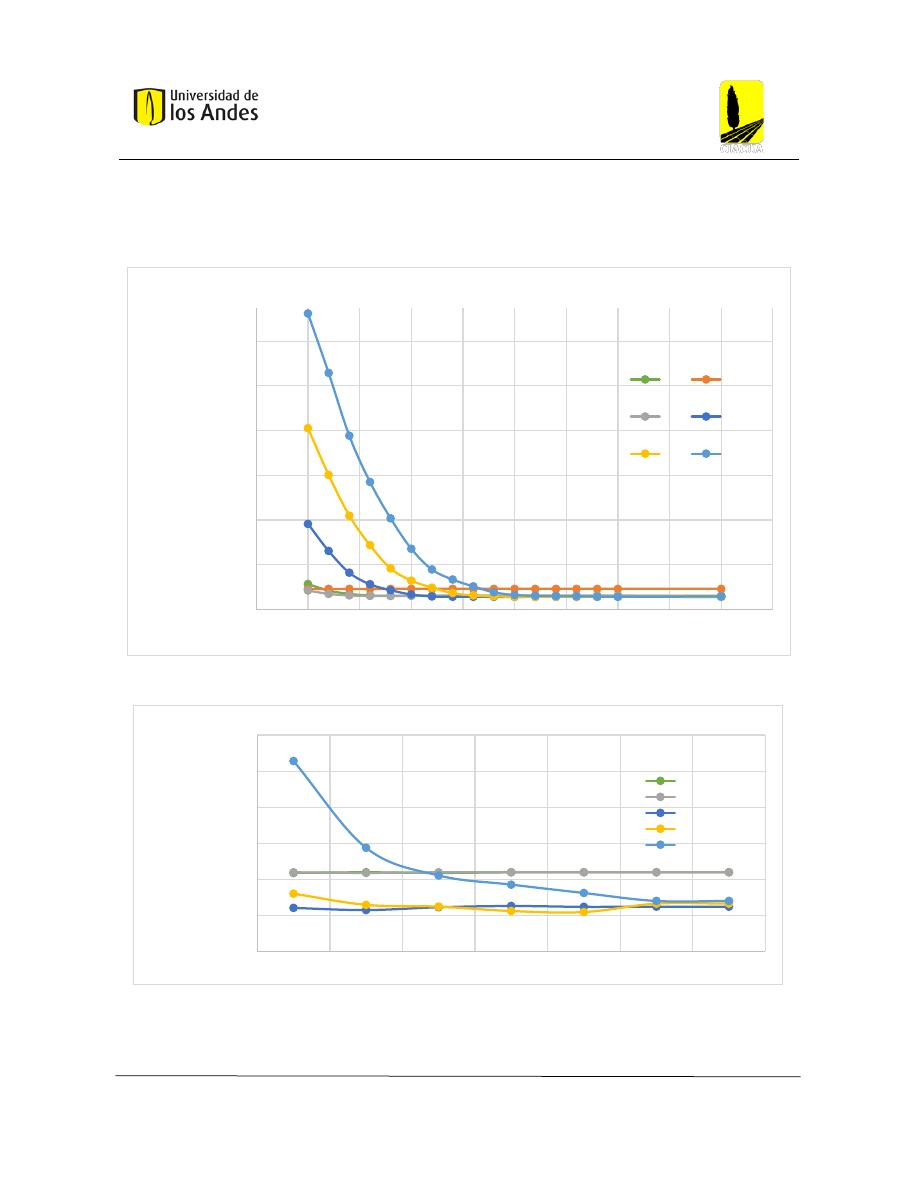
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 73
10.2.4. VELOCIDAD MÁXIMA
Seguidamente, para la restricción de velocidad máxima, los costos por terreno fueron los
siguientes. Los costos tabulados de esta restricción se encuentran en el Anexo F.
Gráfica 12: Costo de la red ante la variación de la velocidad máxima
Gráfica 13: Costo de la red ante la variación de altas velocidades máximas
2.500.000
4.500.000
6.500.000
8.500.000
10.500.000
12.500.000
14.500.000
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
6,5
Cost
o (
U
S
D$
)
Velocidad máxima (m/s)
Costo del diseño
V1
V2
V3
V4
V5
V6
3.000.000
3.050.000
3.100.000
3.150.000
3.200.000
3.250.000
3.300.000
3,7
3,9
4,1
4,3
4,5
4,7
4,9
5,1
C
ost
o (
US
D$)
Velocidad máxima (m/s)
Costo del diseño
V1
V3
V4
V5
V6
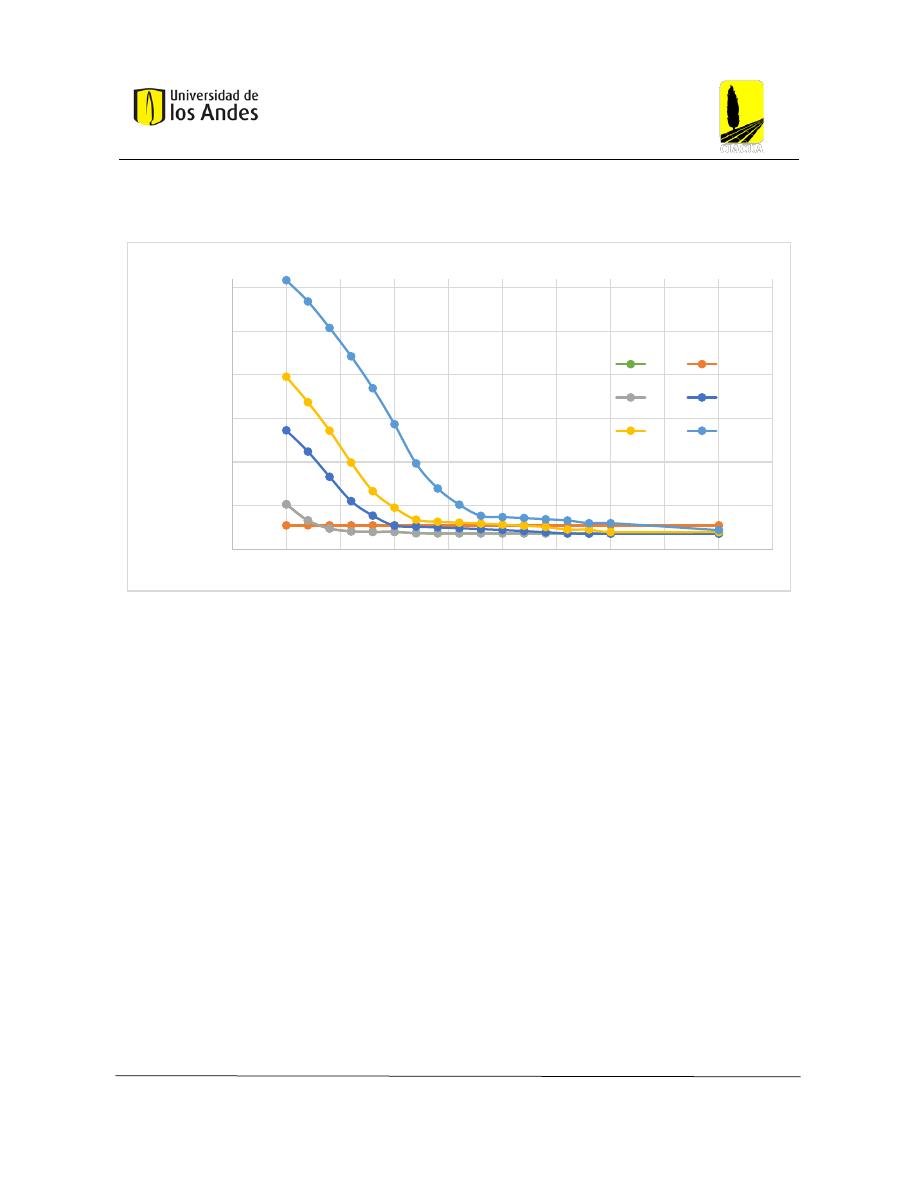
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 74
Del mismo modo, la máxima profundidad evidenciada en el diseño se determinó en función
de la restricción de velocidad máxima.
Gráfica 14: Profundidad máxima en la red ante la variación de la velocidad máxima
10.2.5. VELOCIDAD MÍNIMA
A continuación, se muestran los costos del diseño de la red variando la velocidad mínima de
diseño. Los costos tabulados de esta restricción se encuentran en el Anexo G.
1
6
11
16
21
26
31
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
6,5
Pr
of
und
idad
máx
ima (
m
)
Velocidad máxima (m/s)
Profundidad máxima en el diseño
V1
V2
V3
V4
V5
V6
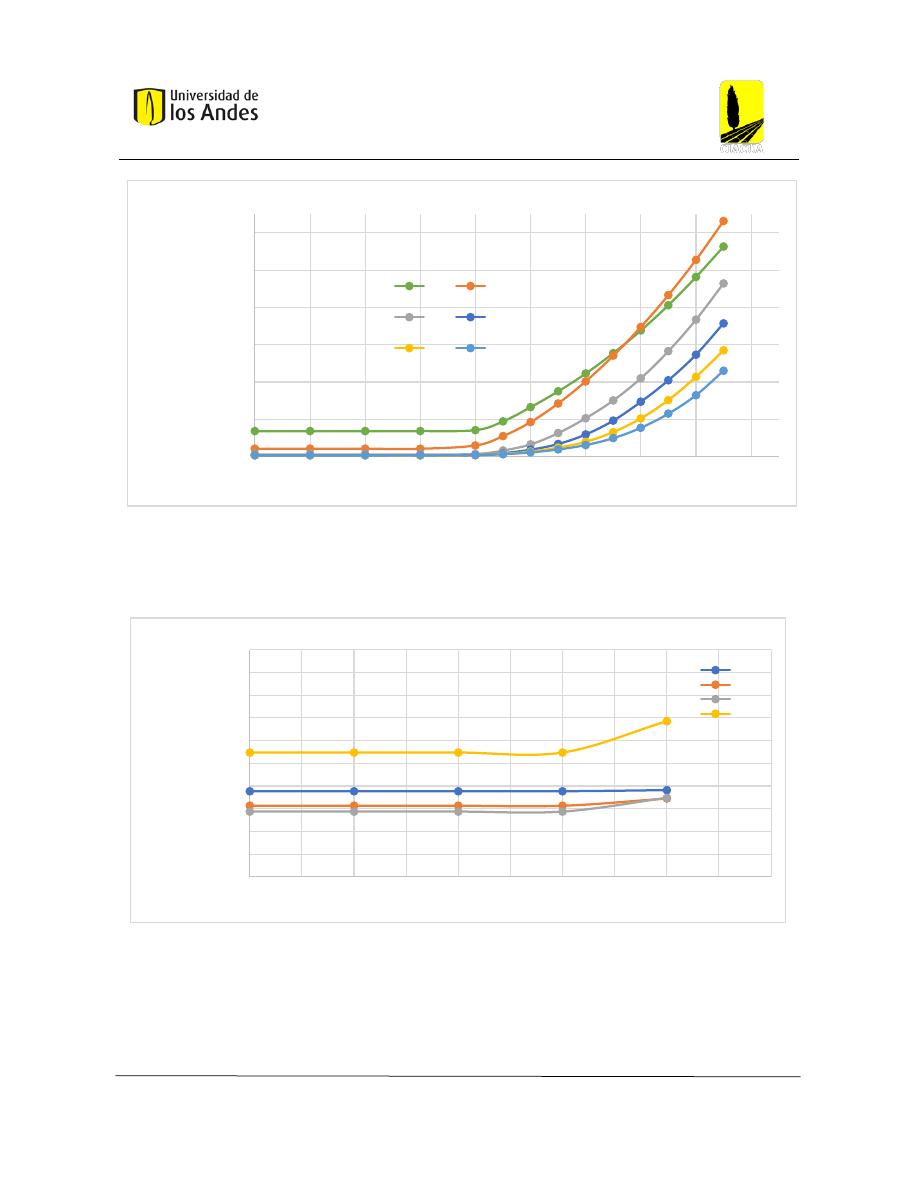
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 75
Gráfica 15: Costo de la red ante la variación de la velocidad mínima
Más detalladamente, se muestran los costos de 0 a 0.8 m/s para exponer el comportamiento
de los costos en este intervalo.
Gráfica 16: Costo de la red ante la variación de bajas velocidades mínimas
Para terminar, se presenta la profundidad máxima encontrada en la red para cada diseño, en
función de la velocidad mínima.
3.000.000
5.000.000
7.000.000
9.000.000
11.000.000
13.000.000
15.000.000
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
C
ost
o (
US
D$)
Velocidad mínima (m/s)
Costo del diseño
V1
V2
V3
V4
V5
V6
3.000.000
3.020.000
3.040.000
3.060.000
3.080.000
3.100.000
3.120.000
3.140.000
3.160.000
3.180.000
3.200.000
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
C
ost
o (
Do
lar
es)
Velocidad mínima (m/s)
Costo del diseño
V6
V5
V4
V3
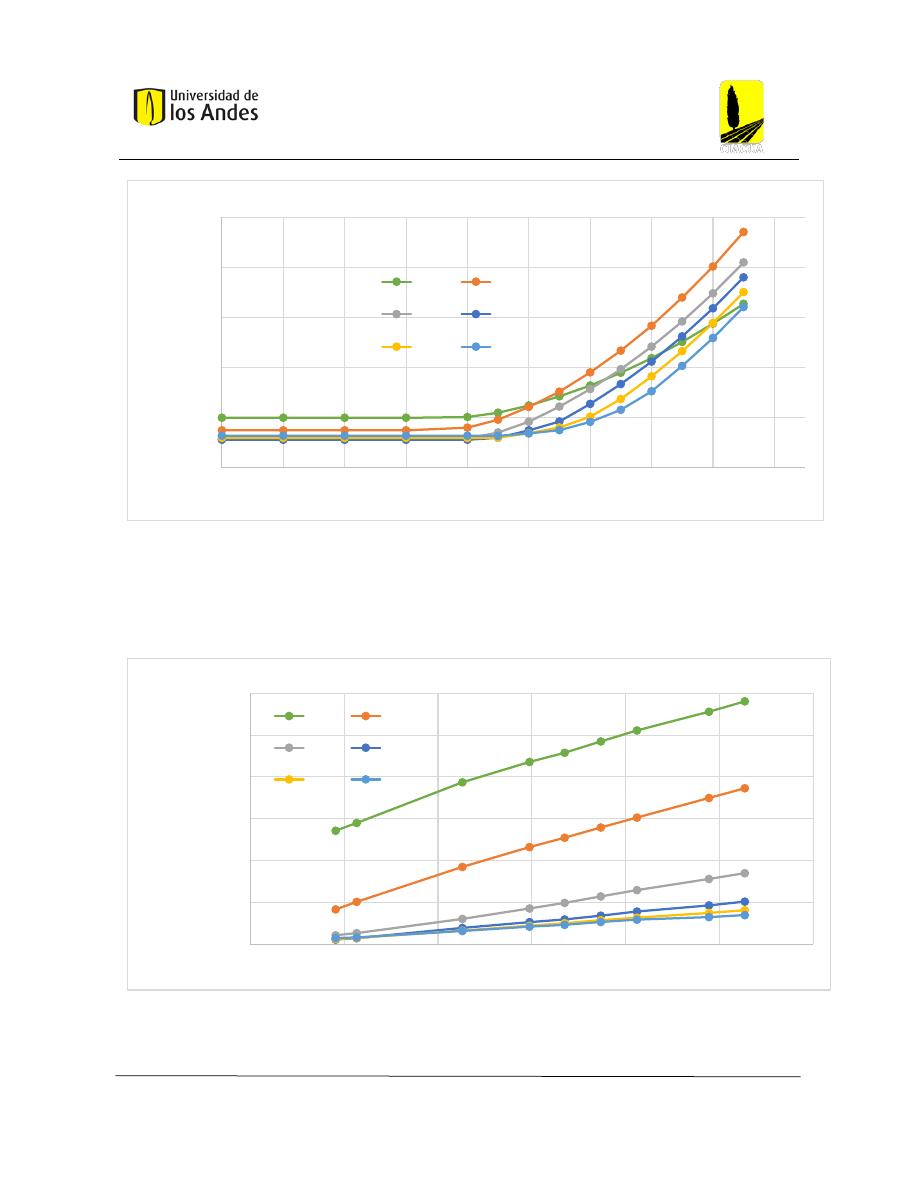
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 76
Gráfica 17: Profundidad máxima en la red ante la variación de la velocidad mínima
10.2.6. DIÁMETRO MÍNIMO
La última restricción hidráulica de diseño es el diámetro comercial mínimo. Los costos
tabulados de esta restricción se encuentran en el Anexo H.
Gráfica 18: Costo de la red ante la variación del diámetro mínimo
0
5
10
15
20
25
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
Pr
of
u
n
d
id
ad
má
xima
(m)
Velocidad mínima (m/s
)
Profundidad máxima en el diseño
V1
V2
V3
V4
V5
V6
3.000.000
3.500.000
4.000.000
4.500.000
5.000.000
5.500.000
6.000.000
0
0,2
0,4
0,6
0,8
1
1,2
C
osto
(U
S
D$)
Diámetro mínimo(m
)
Costo del diseño
V1
V2
V3
V4
V5
V6
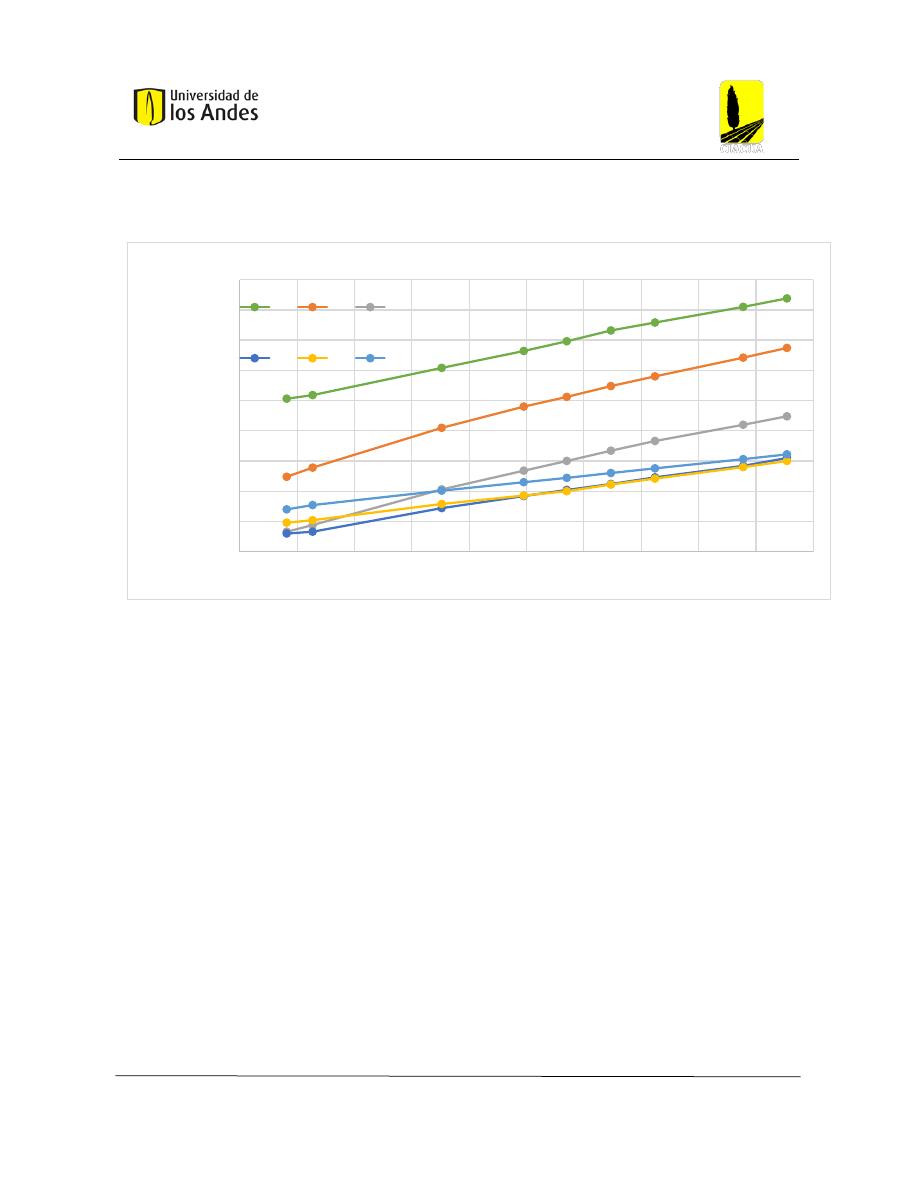
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 77
En cuanto a la profundidad máxima de diseño en función del diámetro mínimo, se determinó
lo siguiente.
Gráfica 19: Profundidad máxima en la red ante la variación del diámetro mínimo
2,50
3,00
3,50
4,00
4,50
5,00
5,50
6,00
6,50
7,00
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
Pr
of
und
idad
máx
ima (
m)
Diámetro mínimo(m
)
Profundidad máxima en el diseño
V1
V2
V3
V4
V5
V6
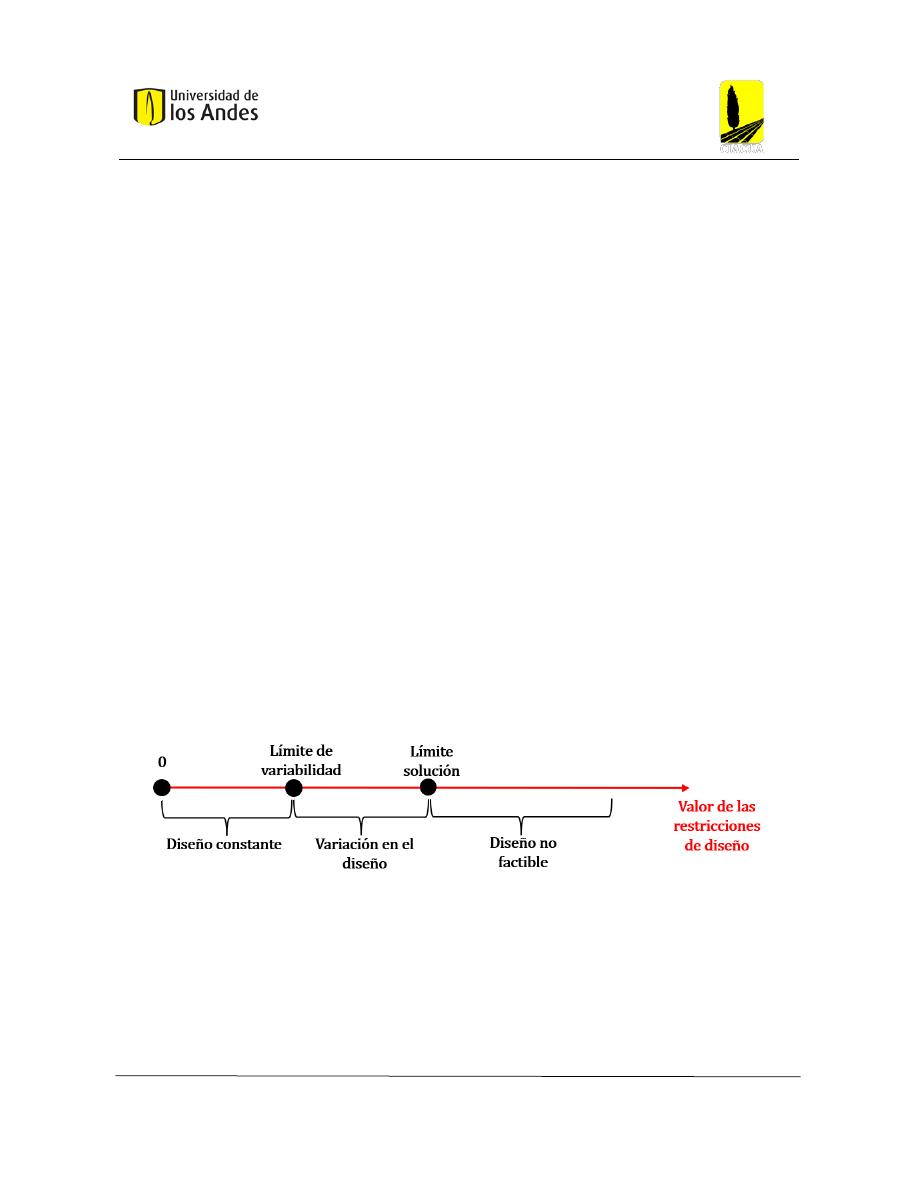
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 78
11. ANÁLISIS DE RESULTADOS
11.1.
LIMITE DE VARIABILIDAD Y LÍMITE SOLUCIÓN
En primer lugar, es posible notar que la mayoría de las restricciones tienen un patrón en
común. Esto es: límites de variabilidad. Es decir, existe un límite en los valores de la
restricción que condiciona el comportamiento del diseño y, por lo tanto, de los costos. Dicho
límite separa el dominio de valores en dos conjuntos finitos: en el primero, no existe variación
en el diseño. En el segundo, sí hay variación en el diseño de la red.
Complementariamente, el conjunto de valores para los cuales existe variación en el diseño
está dividido en dos límites. El límite de variabilidad ya mencionado, y el límite solución.
Este segundo límite se puede entender como un límite de valores para los cuales existe un
diseño factible. Por fuera de este límite, el programa UTOPIA no puede realizar el diseño de
la red.
El origen del límite solución está asociado a la profundidad máxima de excavación. Entre
mayor sea la profundidad de excavación, el rango de variaciones en el diseño será más
grande. Esto ocurre dado que, para determinadas restricciones de diseño, si la profundidad
máxima no es lo suficientemente alta, no será posible obtener un diseño. De modo que, para
garantizar condiciones hidráulicas y cumplir con estas restricciones, es necesario aumentar
la profundidad máxima de excavación.
Es posible ilustrar todo lo anterior con base en los siguientes esquemas. Para restricciones de
diseño mínimas como: esfuerzo cortante mínimo y velocidad de mínima, se tiene el siguiente
comportamiento:
Figura 47: Límite de variabilidad y límite solución para restricciones mínimas
Por otro lado, la restricción máxima que presenta este patrón es la velocidad máxima. Esta
sigue el siguiente comportamiento.
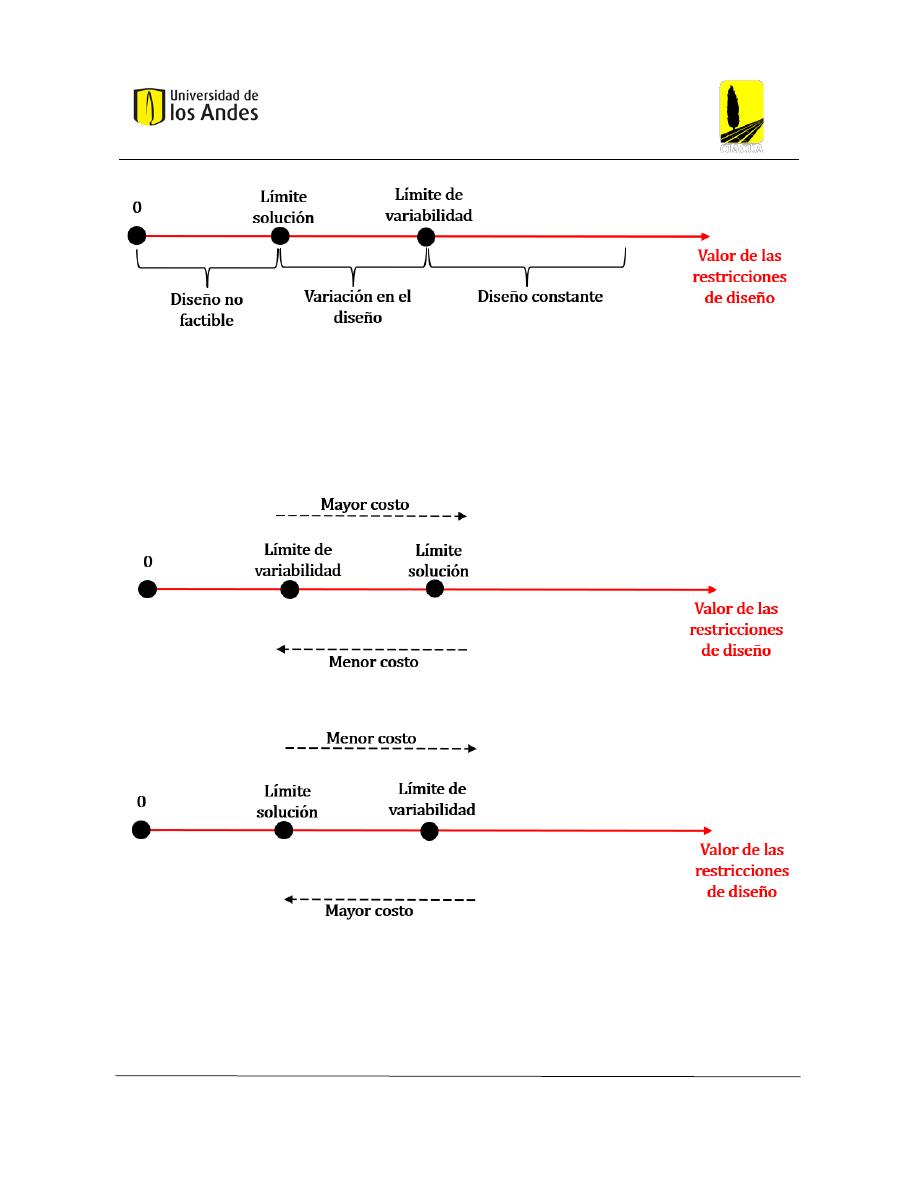
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 79
Figura 48: Límite de variabilidad y límite solución para restricciones máximas
Adicionalmente, este patrón tiene la siguiente característica: el diseño constante es el diseño
más económico. En este sentido, a medida que el valor de la restricción se acerca al límite
solución, se vuelve más costosa. A continuación, se presenta la dirección de mayor y menor
costo para las restricciones máximas y mínimas.
Figura 49: Costo en función de los límites para restricciones mínimas
Figura 50: Costo en función de los límites para restricciones máximas
Por otra parte, para la máxima relación de llenado, no se identificó un límite de variabilidad.
Sin embargo, sí se identificó un límite solución cercano a máximas relaciones de llenado
bajas. Por otro lado, para la profundidad máxima y el diámetro mínimo, no se encontró
ningún límite.
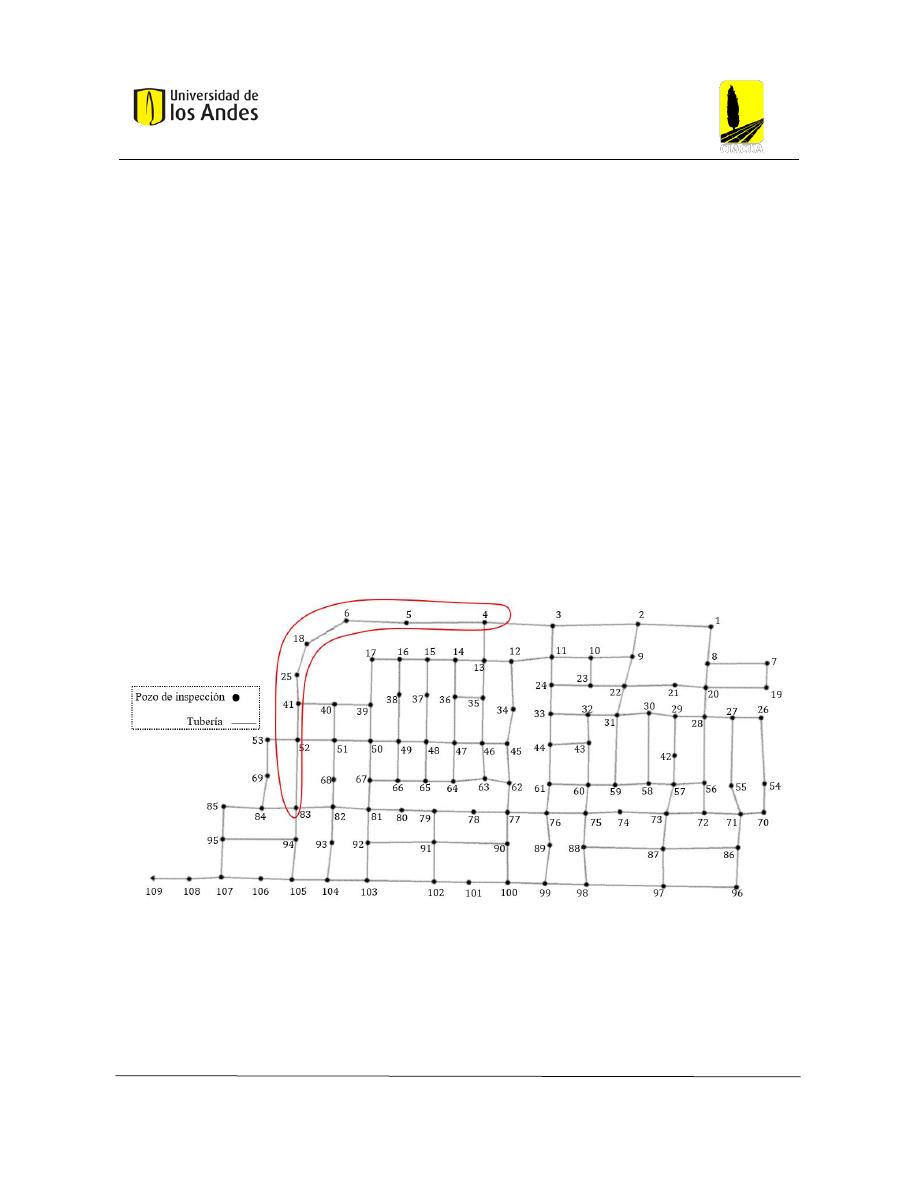
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 80
En conclusión, se puede afirmar que entre más altas sean las restricciones en el diseño, más
costoso será el diseño de la red de alcantarillado.
11.2.
ANÁLISIS DE SENSIBILIDAD: RESTRICCIONES DE DISEÑO
A partir de los resultados, se puede afirmar que sí existen cambios en los costos cuando hay
cambios en las restricciones de diseño. Sin embargo, para la variación en la profundidad
máxima no se evidenció un cambio en los costos para los terrenos analizados.
En primer lugar, en cuanto al esfuerzo cortante mínimo y la velocidad mínima: existe un
óptimo diseño constante para estas restricciones en todos los terrenos. Después de este límite,
el costo empieza a aumentar a medida que aumentan las restricciones. Esto ocurre debido a
que, para cumplir con velocidades y esfuerzos cortantes mínimos más altos, UTOPIA
aumenta la profundidad de excavación de los pozos. Así, se aumenta la pendiente en las
tuberías y, en ellas, se generan velocidades y esfuerzos cortantes más altos.
Esto se puede sustentar gráficamente a partir de los resultados del siguiente perfil. En este se
presentará el cambio en las profundidades de excavación y pendientes de las tuberías cuando
hay baja, intermedia y alta restricción para la velocidad mínima.
Figura 51: Serie de tuberías para el análisis de perfiles: velocidad mínima
Se escogió esta serie de tuberías puesto que es una zona relativamente plana, y permite
evidenciar de mejor forma los cambios en las profundidades. Se muestran los siguientes
perfiles para estas tuberías.
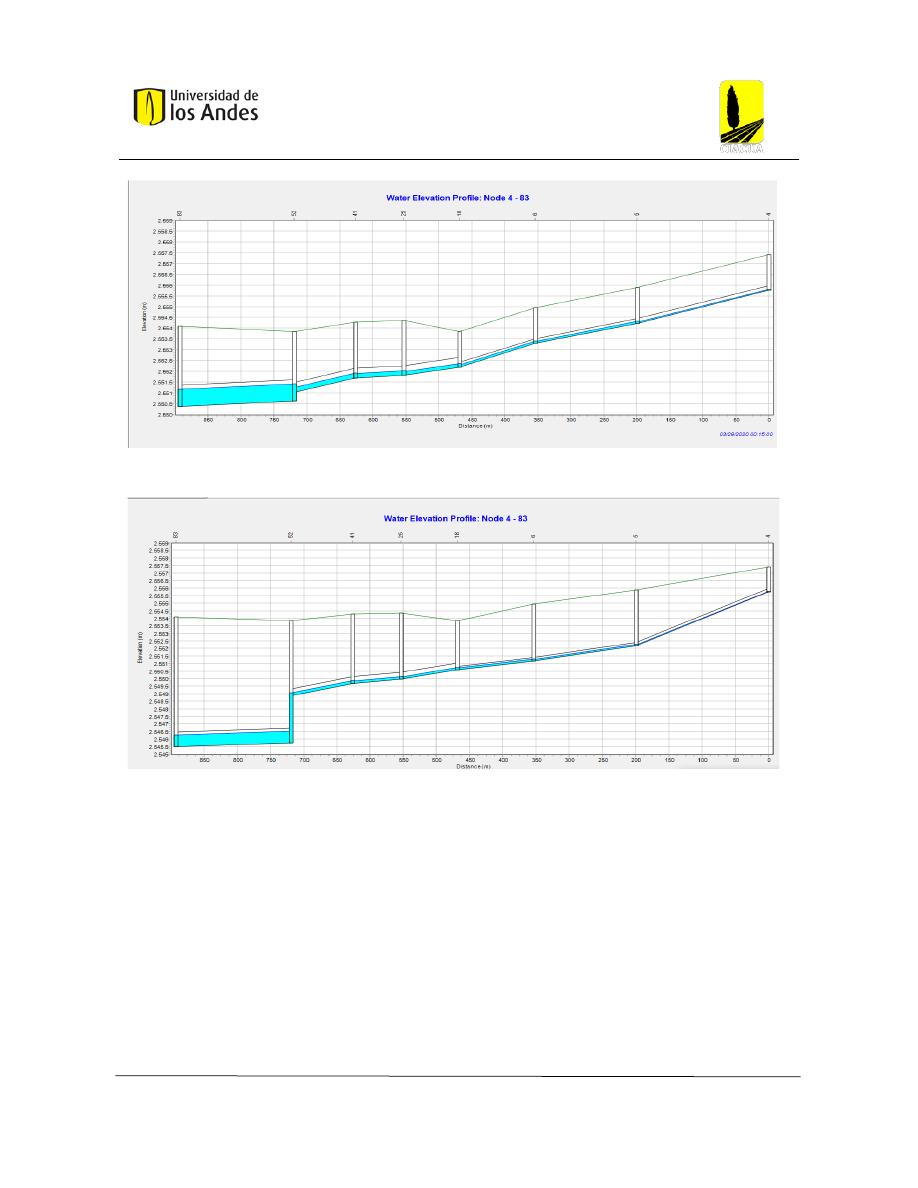
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 81
Figura 52: Diseño de la serie de tuberías para una velocidad mínima de 0.4 m/s (restricción baja)
Figura 53: Diseño de la serie de tuberías para una velocidad mínima de 1.3 m/s (restricción intermedia)
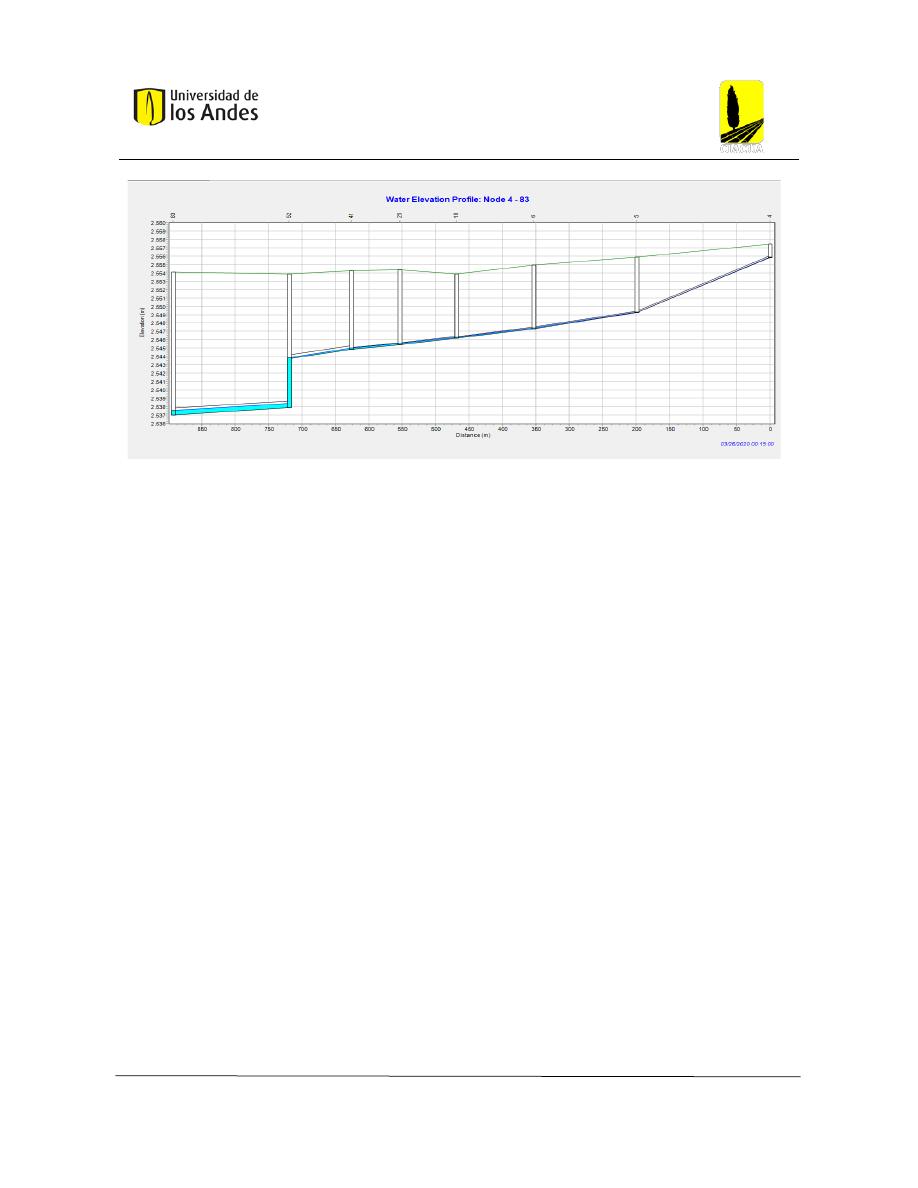
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 82
Figura 54: Diseño de la serie de tuberías para una velocidad mínima de 1.7 m/s (restricción alta)
En segundo lugar, para la máxima relación de llenado, no se determinó un límite de
variabilidad. De este modo, no se presentó un diseño que permaneciese constante a medida
que variaba el valor de esta restricción. Como puede verse en el capítulo 10.2.3, desde la
Gráfica 6 hasta la Gráfica 11, no necesariamente un aumento en la restricción implica
aumento en los costos.
Por otra parte, como se ve en la Gráfica 4 es evidente que el costo del diseño es más alto
para bajas relaciones de llenado máximas. Lo anterior tiene sentido ya que se
sobredimensiona la red de alcantarillado (diámetros y profundidades de excavación más
altos). De este modo, es evidente que el diseño más económico se encuentra en altas
relaciones de llenado máximas. Sin embargo, para un rango entre 80% y 100%, no se
encontró un comportamiento similar comparando los resultados de todos los terrenos. Por
tanto, se realizará en el capítulo 11.5, un análisis de la máxima relación de llenado óptima
para el terreno original de la red Chicó Sur.
En tercer lugar, a medida que se restringe la velocidad máxima, se obtienen diseños más
costosos. Lo anterior ocurre ya que UTOPIA aumenta la profundidad de excavación para
disminuir las pendientes en las tuberías. Así, se obtienen velocidades menores a la velocidad
máxima establecida. Esta variación de la pendiente se expone a partir del perfil de análisis.
Se escogió esta serie de tuberías puesto que es una zona empinada, y permite evidenciar de
mejor forma los cambios en las profundidades.
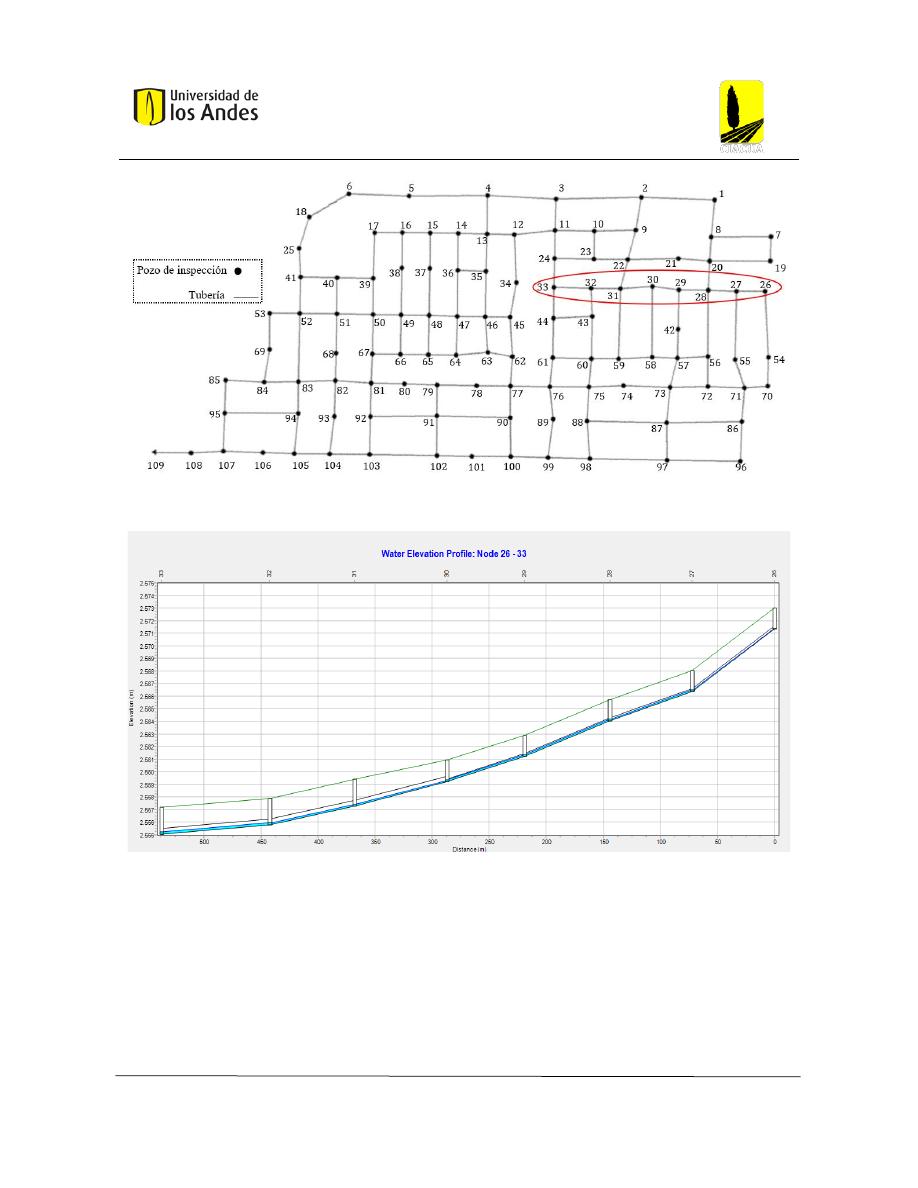
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 83
Figura 55: Serie de tuberías para el análisis de perfiles: velocidad máxima
Figura 56: Diseño de la serie de tuberías para una velocidad máxima de 5 m/s (restricción baja)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 84
Figura 57: Diseño de la serie de tuberías para una velocidad máxima de 2.8 m/s (restricción intermedia)
Figura 58: Diseño de la serie de tuberías para una velocidad máxima de 2m/s (restricción alta)
Finalmente, a medida que aumenta el diámetro mínimo, se obtienen diseños más costos. Esto
ocurre principalmente porque el diámetro afecta de forma directa la ecuación de Maurer. Es
decir, el diámetro y los costos de la tubería son directamente proporcionales. Por esta razón
también es evidente una tendencia lineal en los resultados de esta restricción.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 85
11.3.
EVALUACIÓN DE LA FUNCIÓN DE COSTOS
En este apartado, se analizará el rol de la ecuación de Maurer en la variación de las
restricciones hidráulicas de diseño. Esta ecuación cuenta con dos principales parámetros para
determinar los costos: el diámetro y la profundidad de excavación de cada tubería. En este
sentido, la ecuación acompañada de la metodología de Zambrano (2019), priorizó la
modificación de los diámetros y procuró obtener profundidades de excavación bajas. Cuando
la restricción era muy alta y el diámetro no se podía modificar más, UTOPIA procedió a
aumentar la profundidad de excavación para cumplir con dicha restricción.
Por ejemplo, cuando había alta restricción en la velocidad mínima, UTOPIA disminuía
primero el diámetro para aumentar la velocidad, y cumplir la restricción. No obstante, cuando
la restricción era muy alta y ya se estaba diseñando con el diámetro más pequeño, UTOPIA
procedió a aumentar la profundidad de excavación. Este tipo de problemas ocurrió con todas
las restricciones de diseño, menos con el diámetro mínimo y la profundidad máxima de
excavación.
En la variación de las restricciones de diseño, la profundidad de excavación tuvo mayor
impacto en los costos que el diámetro. Es decir, en el análisis, los diámetros comerciales
fueron una variable discreta y limitada. Por lo tanto, como se mencionó, el programa al no
poder aumentar más el diámetro recurre a aumentar las profundidades para cumplir las
restricciones. De igual forma, las profundidades máximas de excavación tienen una tendencia
similar a los costos de la red cuando se varían las restricciones. Así, la profundidad de
excavación es el principal parámetro en el aumento de los costos de la red Chicó Sur.
11.4.
RESTRICCIONES DE DISEÑO: EVALUACIÓN DE LA VARIACIÓN TOPOGRÁFICA
La variación topográfica del terreno aferente a la red Chicó Sur, tuvo impactos en los costos
del diseño. A partir de los resultados de la variación de las restricciones cuando hubo
variación en la topografía del terreno, se llegó a las siguientes conclusiones. Estas, se dividen
en dos partes: la primera, cuando hay altas restricciones en el diseño. Como por ejemplo baja
velocidad máxima, alto esfuerzo cortante y alta velocidad mínima. Y, la segunda parte,
cuando hay bajas restricciones en el diseño. Así como una relación de llenado alta, mínimo
esfuerzo cortante bajo, etc.
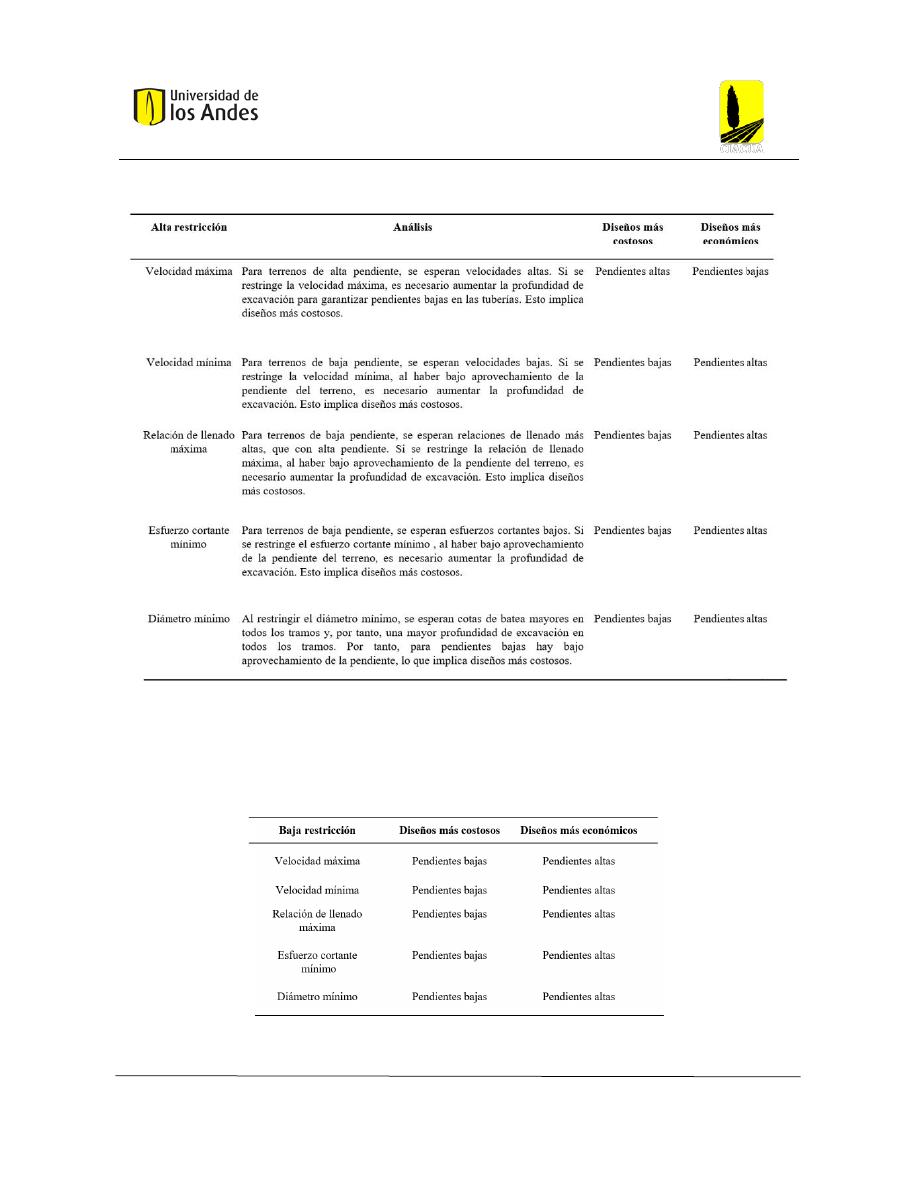
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 86
Tabla 15: Relación entre el costo de la red, la topografía y restricciones altas de diseño
Por su parte, cuando no hay restricciones o las restricciones son bajas, el criterio más importante es
el aprovechamiento de la pendiente. Por lo que los diseños más costosos se relacionan con
pendientes bajas.
Tabla 16: Relación entre el costo de la red, la topografía y restricciones bajas de diseño

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 87
11.5.
MÁXIMA RELACIÓN DE LLENADO ÓPTIMA
11.5.1. A PARTIR DE RESTRICCIONES CONSTANTES INICIALES
Como se puede ver en la Gráfica 9,existe una relación de llenado óptima del 83% para el
terreno original. No obstante, dado que los diseños se realizaron con las restricciones
establecidas en la Tabla 7, es posible que esta relación de llenado óptima sea mayor si se
omiten las restricciones que están afectando los diseños. Estas restricciones son el esfuerzo
cortante y velocidad mínimos.
Igualmente, otra causa puede ser la implementación de diámetros comerciales como variable
discreta. El hecho de considerar pocos diámetros puede afectar la máxima relación de llenado
óptima. De manera que, planteando un análisis que se aproxime a diámetros como variable
continua, es posible que se tenga un resultado claro sobre esta relación de llenado en cuestión.
11.5.2. ESFUERZO CORTANTE MÍNIMO
De este modo, se realizó un análisis variando simultáneamente dos restricciones: la máxima
relación de llenado y el esfuerzo cortante mínimo (Tau). Es importante aclarar que la
velocidad mínima toma un valor de 0 m/s para este análisis y se considerará exclusivamente
el terreno original. A continuación, se muestran los resultados de la máxima relación de
llenado óptima para cada esfuerzo cortante mínimo. Los gráficos se pueden evidenciar el
Anexo I.
Tabla 17: Máxima relación de llenado óptima para distintos esfuerzos cortantes mínimos
𝝉
𝒎𝒊𝒏
(Pa)
𝒚
𝒏
/d óptima (%)
0
94
0.2
94
0.4
94
0.6
94
0.8
94
1
94
1.2
94
1.4
84
1.5
100

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 88
Es evidente que, para bajas restricciones, se obtiene una máxima relación de llenado óptima
del 94%. Cuando restringe el esfuerzo cortante mínimo, esta máxima relación de llenado
empieza a variar.
11.5.3. VELOCIDAD MÍNIMA
De igual forma, se realizó un análisis variando simultáneamente dos restricciones: la máxima
relación de llenado y velocidad mínima. Se muestran los resultados de la máxima relación
de llenado óptima para cada velocidad mínima. Es importante aclarar que, para este análisis,
el esfuerzo cortante mínimo tomó un valor de 0 Pa. Los gráficos se pueden evidenciar el
Anexo J.
Tabla 18: Máxima relación de llenado óptima para distintas velocidades mínimas
𝒗
𝒎𝒊𝒏
(m/s)
𝒚
𝒏
/d óptima (%)
0
94
0.2
94
0.4
94
0.6
94
0.8
84
1
94
A partir de la anterior tabla, se puede ver un resultado similar al de esfuerzo cortante mínimo.
Para bajas restricciones, se da una máxima relación de llenado óptima del 94%.
11.5.4. DIÁMETROS COMERCIALES CONTINUOS
Para plantear un escenario en el cual se aproxime los diámetros comerciales a una variable
continua, para el terreno original, se estableció el siguiente intervalo: se inicia desde 0.02
metros hasta 1 metro, con un paso de 0.02 metros. Esto, para obtener un total de 50 diámetros
comerciales. Del mismo modo, las otras restricciones de diseño permanecerán con el valor
establecido en la Tabla 7. Los costos tabulados de este análisis se encuentran en el Anexo K.
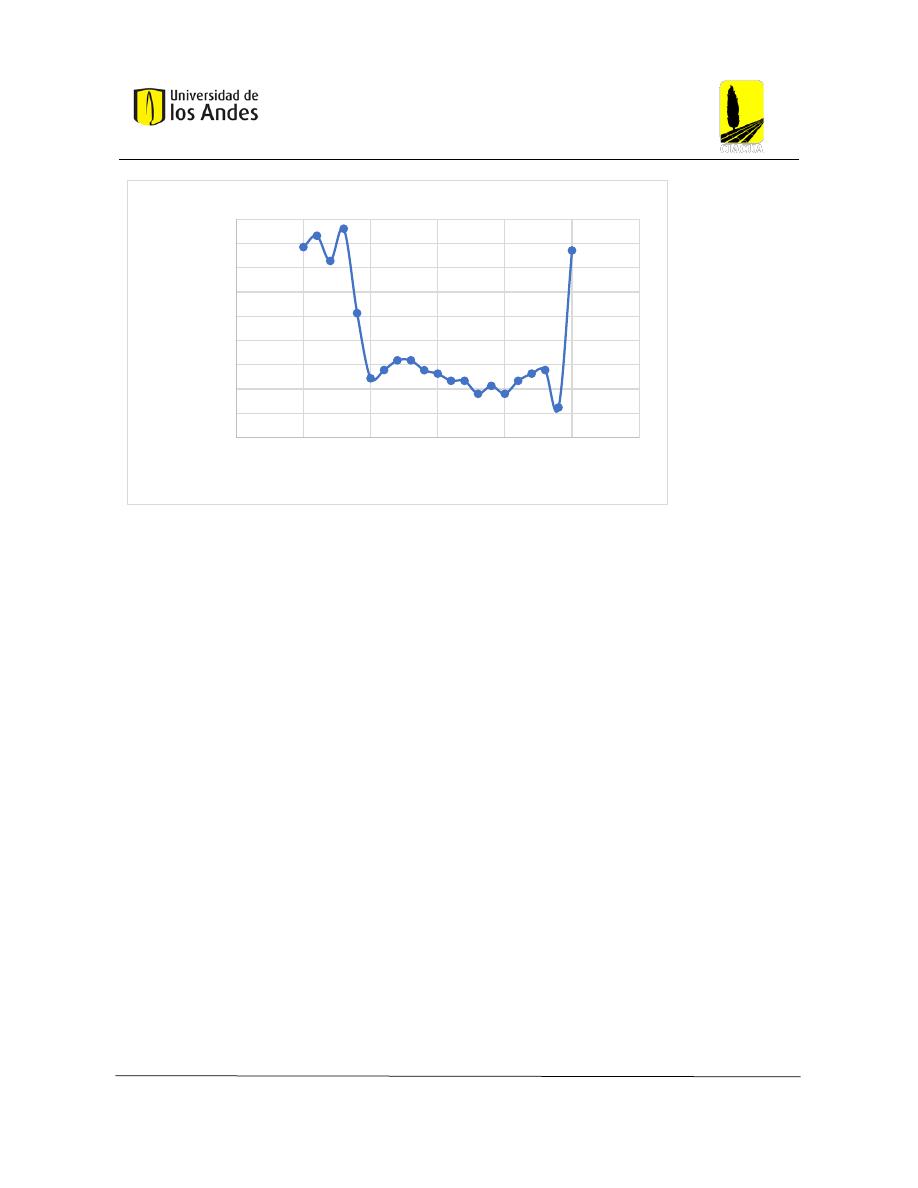
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 89
Gráfica 20: Máxima relación de llenado para diámetros continuos
Se evidencia entonces una máxima relación de llenado óptima del 99%. Este resultado es
distinto al análisis de esfuerzo cortante y velocidad mínimos. No obstante, es probable que
esta máxima relación de llenado óptima se encuentre entre el 90% y 100% para el terreno
original de la red Chicó Sur.
3.036.000
3.038.000
3.040.000
3.042.000
3.044.000
3.046.000
3.048.000
3.050.000
3.052.000
3.054.000
0,75
0,8
0,85
0,9
0,95
1
1,05
C
osto
(U
S
D$)
Relación de llenado máxima (-)
Costo del diseño

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 90
12. CONCLUSIONES Y RECOMENDACIONES
• Existe variación en los costos, cuando hay modificaciones en las restricciones de
diseño. Estas restricciones son: esfuerzo cortante mínimo, velocidad mínima y
máxima, relación de llenado máxima y diámetro mínimo.
• Se proponen dos límites que condicionan la variación en las restricciones de diseño:
el límite de variación y el límite de solución. Estos límites son útiles para definir el
comportamiento del diseño de la red a causa de estas variaciones. Hay un intervalo
para el cual el diseño es constante, y otro para el cual varía el diseño.
• El diseño que permanece constante antes de llegar al límite de variabilidad es el
diseño más económico. Cuando se pasa este límite, los diseños siempre resultan ser
más costos, debido a que las restricciones aumentan. Por tanto, entre más bajas sean
las restricciones en los diseños, más económicos serán.
• La ecuación de Maurer prioriza la modificación del diámetro para cumplir las
restricciones de diseño. Cuando el diámetro no se puede variar más, procede a
aumentar la profundidad de excavación.
• Las profundidades máximas de excavación tienen una tendencia similar a los costos
de la red cuando se varían las restricciones. En este sentido, la profundidad de
excavación es el principal motivo de aumento en los costos de la red Chicó Sur
cuando hay variación en las restricciones.
• La topografía del terreno influye en el costo de la red cuando hay variación en cada
restricción de diseño.
• A excepción de la restricción de velocidad máxima, los terrenos con pendientes bajas
siempre implican un mayor costo que terrenos con pendientes altas cuando hay
variación en las restricciones de diseño. Esto, debido a que no hay aprovechamiento
en la pendiente, por lo que hay mayores profundidades de excavación.
• La máxima relación de llenado óptima para la red Chicó Sur se encuentra entre 90%
y 100%. Se recomienda profundizar el análisis considerando más alternativas de
diseño, para determinar esta relación de llenado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 91
• Se puede considerar como alternativa la metodología propuesta para variar la
topología de una red de alcantarillado y su terreno aferente.
• Se recomienda realizar un análisis de restricciones de diseño para otras ecuaciones de
costos y para otras redes de alcantarillado, para tener un contraste más robusto sobre
los resultados obtenidos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 92
13. REFERENCIAS
Aguilar, A. (2017). Análisis de Sensibilidad de la Metodología Exhaustiva para el diseño optimizado
de redes de drenaje urbano . Bogotá: Universidad de los Andes.
Aguilar, A. (2019). Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje Urbano
. Bogotá: Universidad de los Andes .
Ahuja, R., Magnanti, T., & Orlin, J. (1993). Theory, Algorithms, and Applications. Nueva Jersey:
Prentice-Hall.
Benito, L. (3 de enero de 2015). BIOGUIA. Obtenido de Cómo construir un recolector de agua de
lluvia:
https://www.bioguia.com/ambiente/como-construir-un-recolector-de-agua-de-
lluvia_29269976.html
Butler , D., & Davies, J. (2004). Urban Drainage (Segunda ed.). Londres y Nueva York: Spon Press.
Butler, D., & Davies, J. (2011). Urban drainage. Londres: Spon Press.
Duque, N. (2013). Metodología para la optimización del diseño de tuberías en serie en sistemas de
alcantarillado. Bogotá: Universidad de los Andes.
Duque, N. (2015). Metodología para el Diseño Optimizado de Redes de Alcantarillado. Bogotá:
Universidad de los Andes.
Eurolimpiezas. (s.f.). Recuperado el 24 de junio de 2020, de LA SOLUCIÓN CONTRA LAS RAÍCES EN
LAS TUBERÍAS: http://www.eurolimpiezasmarmenor.es/desatascos/blog/18/la-solucion-
contra-las-raices-en-las-tuberias.html
Haghighi, A., & Bakhshipour, A. (2012). Optimization of Sewer Networks Using an Adaptive. Water
Resour Manage (2012) 26:3441–3456.
Haghighi, A., & Bakhshipour, A. (2015). Deterministic Integrated Optimization Model for Sewage
Collection Networks Using Tabu Search. ASCE. Obtenido de https://ascelibrary-
org.ezproxy.uniandes.edu.co:8443/doi/pdf/10.1061/%28ASCE%29WR.1943-5452.0000435
Hertz, A., & Werra, D. (1987). Using Tabu Search Techniques for Graph Coloring. Springer-Verlag.
Obtenido
de
https://www.researchgate.net/publication/37437164_Werra_D_Using_Tabu_Search_Tec
hniques_for_Graph_Coloring_Computing_39_345-351
Instituto Fraunhofer de Tecnología Medioambiental, de Seguridad y Energética UMSICHT. (2016).
Ensayo de la resistencia a la corrosión por ácido sulfúrico biogénico de MasterSeal 7000CR.
Osterfeld: Fraunhofer UMSICHT.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 93
Israelsen, O., & Hansen, V. (1985). Principios y aplicaciones de riego. Logan: EDITORIAL REVERTÉ , S.
A.
LA CALLE Digital. (4 de marzo de 2012). Alcantarilla desbordada Urbanización La Monserrate,
Hormigueros. Obtenido de https://www.youtube.com/watch?v=Sm11rIhO8XE
López, R. (2003). Elementos de diseño para acueductos y alcantarillados. Colombia: Escuela
Colombiana de Ingeniería.
MADERPLAST.
(febrero
de
2016).
Recuperado
el
2
de
julio
de
2020,
de
https://www.maderplast.com/images/2
Mata, A., & Quevedo, F. (2005). Diccionario didáctico de ecología. San José: Universidad de Costa
Rica.
Maurer, M., Scheidegger, A., & Herlyn, A. (2012). Quantifying costs and lengths of urban drainage
systems with a simple static sewer. Dübendorf: Taylor & Francis,.
Maurer, M., Wolfram, M., & Anja, H. (2010). Factors affecting economies of scale in combined sewer.
Londres: Water Science and Technology, 36-41.
NOTIFE. (5 de mayo de 2019). Obtenido de Informe sobre la lluvia caída en la ciudad:
https://notife.com/670130-informe-sobre-la-lluvia-caida-en-la-ciudad/
NYC Environmental Protection. (s.f.). Combined Sewer Overflows. Recuperado el 7 de julio de 2020,
de https://www1.nyc.gov/site/dep/water/combined-sewer-overflows.page
Park, K., Lee, H., Phelan, S., Liyanaarachchi, S., Marleni, N., Navaratna, D., . . . Shu, L. (2014).
Mitigation strategies of hydrogen sulphide emission in sewer networks – A review. ELSEVIER,
251-261.
Reglamento Técnico del Sector de Agua Potable y Saneamiento Básico - RAS. (2016). Título D:
Sistemas de Recolección y Evacuación de Aguas Residuales Domésticas y Aguas Lluvias.
Recuperado el 6 de junio de 2020
Resende , M., & Pardalos, P. (2006). Handbook of Optimization in Telecommunications. Nueva York:
Springer.
Rodríguez, H., & Matamoros, H. (2017). Rehabilitación de sistemas de alcantarillado. Colombia:
Escuela Colombiana de Ingeniería.
Safavi, H., & Geranmehr, M. (2016). Optimization of sewer networks using the mixed-integer linear
programming. Isfahan: Urban Water Journal, 2017.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 94
Saldarriaga , J. (2019). Curso Sistemas de Drenaje Urbano. Bogotá: Universidad de los Andes.
Saldarriaga , J. (2019). Hidráulica de tuberías (Cuarta ed.). Bogotá, Colombia: Alfaomega
Colombiana. Recuperado el 1 de julio de 2020
Torres, A. (2004). Apuntes de clase sobre hidrología urbana. Bogotá: Editorial Pontificia Universidad
Javeriana.
Zambrano, J. (2019). Diseño optimizado de Redes de Drenaje Urbano. Casos de estudio variando la
topografía del terreno, la densidad de las viviendas, los coeficientes de impermeabilidad y la
rugosidad de las tuberías . Bogotá: Universidad de los Andes .

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 95
14. ANEXOS
Anexo A: cotas y caudales de diseño para cada pozo del terreno original
Pozo
𝑸
𝑫𝑰𝑺𝑬Ñ𝑶
(𝒎
𝟑
/𝒔)
X
Y
Z
1
0.01240
2145.39
7352.39
2561.93
2
0.02219
1982.51
7441.01
2558.90
3
0.02170
1784.49
7532.93
2557.41
4
0.02085
1632.28
7617.99
2557.42
5
0.01566
1452.89
7704.76
2555.87
6
0.01194
1317.86
7779.49
2554.95
7
0.01101
2233.12
7204.60
2568.56
8
0.01520
2097.16
7271.09
2563.11
9
0.01334
1932.99
7372.47
2557.93
10
0.01345
1835.94
7416.57
2557.33
11
0.01762
1747.32
7462.52
2556.90
12
0.01430
1650.50
7499.21
2556.72
13
0.01709
1588.00
7531.50
2556.62
14
0.01273
1524.17
7564.57
2555.87
15
0.01259
1460.84
7597.47
2555.78
Pozo
𝑸
𝑫𝑰𝑺𝑬Ñ𝑶
(𝒎
𝟑
/𝒔)
X
Y
Z
16
0.01260
1397.46
7630.55
2555.37
17
0.00945
1333.26
7661.29
2554.93
18
0.00942
1202.87
7770.98
2553.85
19
0.01118
2204.20
7149.60
2570.03
20
0.01979
2065.54
7218.98
2564.85
21
0.01000
1996.74
7259.19
2559.70
22
0.01861
1880.41
7313.67
2558.70
23
0.01305
1803.79
7353.82
2557.34
24
0.01305
1715.03
7400.08
2557.00
25
0.00862
1144.17
7710.55
2554.38
26
0.01173
2157.49
7087.17
2573.00
27
0.01633
2093.60
7119.76
2568.05
28
0.02038
2029.41
7153.10
2565.71
29
0.01304
1963.14
7187.67
2562.88
30
0.01653
1905.84
7224.42
2560.93

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 96
Pozo
𝑸
𝑫𝑰𝑺𝑬Ñ𝑶
(𝒎
𝟑
/𝒔)
X
Y
Z
31
0.02083
1831.54
7256.25
2559.41
32
0.01281
1765.15
7289.85
2557.90
33
0.01281
1681.29
7333.85
2557.17
34
0.00934
1600.04
7388.10
2557.14
35
0.01359
1544.46
7448.03
2556.11
36
0.01362
1481.47
7481.98
2555.69
37
0.00929
1419.46
7517.89
2555.84
38
0.00930
1356.12
7550.70
2555.25
39
0.01329
1279.69
7558.36
2554.69
40
0.01227
1197.64
7600.63
2554.59
41
0.01256
1114.68
7643.68
2554.29
42
0.00873
1917.32
7098.98
2564.33
43
0.01342
1735.70
7224.20
2558.97
44
0.01314
1645.68
7265.07
2557.40
45
0.01271
1548.16
7315.99
2556.96
Pozo
𝑸
𝑫𝑰𝑺𝑬Ñ𝑶
(𝒎
𝟑
/𝒔)
X
Y
Z
46
0.01778
1491.40
7345.58
2556.45
47
0.01824
1427.55
7377.92
2555.93
48
0.01837
1364.27
7411.31
2555.47
49
0.01837
1300.92
7444.20
2554.96
50
0.00887
1237.38
7477.06
2554.76
51
0.01673
1155.71
7519.68
2554.23
52
0.02023
1072.14
7561.27
2553.85
53
0.00837
1004.44
7596.19
2553.74
54
0.01173
2090.90
6933.35
2575.89
55
0.01203
2013.31
6965.14
2569.71
56
0.01607
1954.28
7002.50
2566.98
57
0.01723
1882.86
7032.93
2565.49
58
0.00409
1826.73
7064.10
2564.64
59
0.01608
1746.82
7099.01
2562.24
60
0.01773
1686.22
7129.44
2560.50

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 97
Pozo
𝑸
𝑫𝑰𝑺𝑬Ñ𝑶
(𝒎
𝟑
/𝒔)
X
Y
Z
61
0.01314
1599.01
7175.99
2558.14
62
0.01308
1508.10
7223.40
2557.71
63
0.01267
1456.74
7260.95
2557.01
64
0.01304
1381.43
7289.20
2556.29
65
0.01305
1318.17
7322.35
2555.57
66
0.01306
1254.73
7355.18
2555.04
67
0.01305
1191.38
7388.10
2554.88
68
0.00878
1109.34
7429.94
2554.65
69
0.00837
962.53
7514.74
2553.57
70
0.00862
2056.96
6866.81
2576.09
71
0.01707
2002.76
6889.27
2570.15
72
0.01276
1920.35
6933.78
2567.70
73
0.01789
1832.90
6975.88
2565.94
74
0.00912
1728.08
7031.72
2563.69
75
0.01649
1649.08
7068.52
2561.04
Pozo
𝑸
𝑫𝑰𝑺𝑬Ñ𝑶
(𝒎
𝟑
/𝒔)
X
Y
Z
76
0.01743
1559.39
7112.63
2559.04
77
0.01687
1471.37
7158.01
2557.99
78
0.00829
1393.92
7198.28
2557.27
79
0.01304
1305.24
7244.35
2555.82
80
0.00862
1230.89
7282.92
2555.43
81
0.01695
1155.26
7322.23
2555.31
82
0.01644
1076.77
7368.03
2554.96
83
0.02002
992.30
7407.29
2554.09
84
0.01257
913.30
7446.36
2554.13
85
0.00867
826.81
7493.27
2553.36
86
0.01726
1958.45
6815.65
2573.03
87
0.02575
1785.75
6898.33
2566.15
88
0.01717
1604.82
6992.61
2561.96
89
0.00873
1530.58
7035.67
2559.86
90
0.01701
1434.47
7086.98
2558.71

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 98
Pozo
𝑸
𝑫𝑰𝑺𝑬Ñ𝑶
(𝒎
𝟑
/𝒔)
X
Y
Z
91
0.02456
1268.27
7173.47
2556.42
92
0.01605
1116.00
7247.09
2555.27
93
0.00827
1035.11
7288.28
2554.51
94
0.01714
955.69
7336.90
2553.91
95
0.01687
788.20
7419.13
2553.05
96
0.01274
1910.25
6726.98
2575.19
97
0.02123
1744.42
6812.62
2569.26
98
0.01769
1569.16
6903.75
2564.49
99
0.01333
1475.04
6952.68
2560.78
100
0.01301
1391.34
6997.48
2560.00
101
0.00829
1302.31
7041.85
2558.00
102
0.01599
1224.80
7082.59
2555.33
103
0.01637
1071.64
7162.13
2554.82
104
0.01276
981.54
7207.82
2554.22
105
0.01287
901.30
7249.35
2552.05
Pozo
𝑸
𝑫𝑰𝑺𝑬Ñ𝑶
(𝒎
𝟑
/𝒔)
X
Y
Z
106
0.00882
831.25
7286.18
2551.72
107
0.01312
741.36
7334.18
2551.63
108
0.00840
667.44
7367.24
2551.46
109
-1.51799
584.86
7408.61
2551.85

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 99
Anexo B: nuevas cotas de los pozos para cada terreno
Terreno
Pozo
∆𝒛
𝒊
V
1
V
2
V
3
V
4
V
5
V
6
1
2.094
2551.463 2553.557 2557.744 2561.931 2566.118 2570.305
2
1.487
2551.463 2552.950 2555.923 2558.897 2561.871 2564.844
3
1.190
2551.463 2552.653 2555.032 2557.411 2559.790 2562.169
4
1.191
2551.463 2552.654 2555.036 2557.418 2559.800 2562.182
5
0.882
2551.463 2552.345 2554.110 2555.874 2557.638 2559.403
6
0.698
2551.463 2552.161 2553.556 2554.951 2556.346 2557.741
7
3.419
2551.463 2554.882 2561.721 2568.560 2575.399 2582.238
8
2.330
2551.463 2553.793 2558.452 2563.112 2567.772 2572.431
9
1.294
2551.463 2552.757 2555.344 2557.932 2560.520 2563.107
10
1.173
2551.463 2552.636 2554.981 2557.326 2559.671 2562.016
11
1.088
2551.463 2552.551 2554.726 2556.901 2559.076 2561.251
12
1.051
2551.463 2552.514 2554.617 2556.719 2558.821 2560.924
13
1.031
2551.463 2552.494 2554.555 2556.617 2558.679 2560.740
14
0.881
2551.463 2552.344 2554.107 2555.869 2557.631 2559.394
15
0.864
2551.463 2552.327 2554.054 2555.782 2557.510 2559.237
Terreno
Pozo
∆𝒛
𝒊
V
1
V
2
V
3
V
4
V
5
V
6
16
0.781
2551.463 2552.244 2553.807 2555.370 2556.933 2558.496
17
0.693
2551.463 2552.156 2553.543 2554.930 2556.317 2557.704
18
0.477
2551.463 2551.940 2552.894 2553.848 2554.802 2555.756
19
3.714
2551.463 2555.177 2562.606 2570.034 2577.462 2584.891
20
2.677
2551.463 2554.140 2559.495 2564.849 2570.203 2575.558
21
1.646
2551.463 2553.109 2556.402 2559.695 2562.988 2566.281
22
1.447
2551.463 2552.910 2555.803 2558.696 2561.589 2564.482
23
1.175
2551.463 2552.638 2554.987 2557.337 2559.687 2562.036
24
1.107
2551.463 2552.570 2554.783 2556.997 2559.211 2561.424
25
0.582
2551.463 2552.045 2553.210 2554.375 2555.540 2556.705
26
4.307
2551.463 2555.770 2564.384 2572.998 2581.612 2590.226
27
3.317
2551.463 2554.780 2561.413 2568.046 2574.679 2581.312
28
2.849
2551.463 2554.312 2560.009 2565.707 2571.405 2577.102
29
2.283
2551.463 2553.746 2558.311 2562.876 2567.441 2572.006
30
1.893
2551.463 2553.356 2557.143 2560.929 2564.715 2568.502

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 100
Terreno
Pozo
∆𝒛
𝒊
V
1
V
2
V
3
V
4
V
5
V
6
31
1.589
2551.463 2553.052 2556.229 2559.406 2562.583 2565.760
32
1.288
2551.463 2552.751 2555.328 2557.904 2560.480 2563.057
33
1.140
2551.463 2552.603 2554.884 2557.165 2559.446 2561.727
34
1.136
2551.463 2552.599 2554.871 2557.143 2559.415 2561.687
35
0.930
2551.463 2552.393 2554.252 2556.112 2557.972 2559.831
36
0.845
2551.463 2552.308 2553.998 2555.688 2557.378 2559.068
37
0.876
2551.463 2552.339 2554.091 2555.843 2557.595 2559.347
38
0.758
2551.463 2552.221 2553.737 2555.253 2556.769 2558.285
39
0.645
2551.463 2552.108 2553.397 2554.687 2555.977 2557.266
40
0.625
2551.463 2552.088 2553.337 2554.587 2555.837 2557.086
41
0.565
2551.463 2552.028 2553.158 2554.288 2555.418 2556.548
42
2.574
2551.463 2554.037 2559.184 2564.332 2569.480 2574.627
43
1.502
2551.463 2552.965 2555.968 2558.971 2561.974 2564.977
44
1.188
2551.463 2552.651 2555.027 2557.403 2559.779 2562.155
45
1.099
2551.463 2552.562 2554.761 2556.960 2559.159 2561.358
Terreno
Pozo
∆𝒛
𝒊
V
1
V
2
V
3
V
4
V
5
V
6
46
0.998
2551.463 2552.461 2554.458 2556.454 2558.450 2560.447
47
0.893
2551.463 2552.356 2554.142 2555.928 2557.714 2559.500
48
0.802
2551.463 2552.265 2553.868 2555.472 2557.076 2558.679
49
0.700
2551.463 2552.163 2553.562 2554.961 2556.360 2557.759
50
0.659
2551.463 2552.122 2553.439 2554.756 2556.073 2557.390
51
0.554
2551.463 2552.017 2553.124 2554.232 2555.340 2556.447
52
0.477
2551.463 2551.940 2552.895 2553.849 2554.803 2555.758
53
0.455
2551.463 2551.918 2552.829 2553.740 2554.651 2555.562
54
4.886
2551.463 2556.349 2566.120 2575.891 2585.662 2595.433
55
3.649
2551.463 2555.112 2562.410 2569.708 2577.006 2584.304
56
3.102
2551.463 2554.565 2560.770 2566.975 2573.180 2579.385
57
2.805
2551.463 2554.268 2559.879 2565.490 2571.101 2576.712
58
2.634
2551.463 2554.097 2559.366 2564.635 2569.904 2575.173
59
2.155
2551.463 2553.618 2557.929 2562.239 2566.549 2570.860
60
1.808
2551.463 2553.271 2556.887 2560.503 2564.119 2567.735

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 101
Terreno
Pozo
∆𝒛
𝒊
V
1
V
2
V
3
V
4
V
5
V
6
61
1.336
2551.463 2552.799 2555.472 2558.144 2560.816 2563.489
62
1.248
2551.463 2552.711 2555.208 2557.705 2560.202 2562.699
63
1.110
2551.463 2552.573 2554.794 2557.014 2559.234 2561.455
64
0.966
2551.463 2552.429 2554.360 2556.292 2558.224 2560.155
65
0.822
2551.463 2552.285 2553.928 2555.571 2557.214 2558.857
66
0.714
2551.463 2552.177 2553.606 2555.035 2556.464 2557.893
67
0.684
2551.463 2552.147 2553.516 2554.884 2556.252 2557.621
68
0.638
2551.463 2552.101 2553.378 2554.654 2555.930 2557.207
69
0.420
2551.463 2551.883 2552.724 2553.565 2554.406 2555.247
70
4.925
2551.463 2556.388 2566.238 2576.088 2585.938 2595.788
71
3.738
2551.463 2555.201 2562.677 2570.153 2577.629 2585.105
72
3.247
2551.463 2554.710 2561.205 2567.700 2574.195 2580.690
73
2.895
2551.463 2554.358 2560.149 2565.940 2571.731 2577.522
74
2.445
2551.463 2553.908 2558.799 2563.690 2568.581 2573.472
75
1.916
2551.463 2553.379 2557.210 2561.041 2564.872 2568.703
Terreno
Pozo
∆𝒛
𝒊
V
1
V
2
V
3
V
4
V
5
V
6
76
1.515
2551.463 2552.978 2556.008 2559.038 2562.068 2565.098
77
1.305
2551.463 2552.768 2555.379 2557.989 2560.599 2563.210
78
1.161
2551.463 2552.624 2554.947 2557.270 2559.593 2561.916
79
0.872
2551.463 2552.335 2554.079 2555.823 2557.567 2559.311
80
0.793
2551.463 2552.256 2553.843 2555.429 2557.015 2558.602
81
0.769
2551.463 2552.232 2553.771 2555.309 2556.847 2558.386
82
0.700
2551.463 2552.163 2553.562 2554.962 2556.362 2557.761
83
0.526
2551.463 2551.989 2553.040 2554.092 2555.144 2556.195
84
0.534
2551.463 2551.997 2553.066 2554.134 2555.202 2556.271
85
0.379
2551.463 2551.842 2552.601 2553.360 2554.119 2554.878
86
4.313
2551.463 2555.776 2564.401 2573.027 2581.653 2590.278
87
2.938
2551.463 2554.401 2560.276 2566.152 2572.028 2577.903
88
2.100
2551.463 2553.563 2557.762 2561.961 2566.160 2570.359
89
1.680
2551.463 2553.143 2556.503 2559.863 2563.223 2566.583
90
1.449
2551.463 2552.912 2555.811 2558.709 2561.607 2564.506

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 102
Terreno
Pozo
∆𝒛
𝒊
V
1
V
2
V
3
V
4
V
5
V
6
91
0.991
2551.463 2552.454 2554.435 2556.416 2558.397 2560.378
92
0.761
2551.463 2552.224 2553.746 2555.268 2556.790 2558.312
93
0.610
2551.463 2552.073 2553.293 2554.513 2555.733 2556.953
94
0.489
2551.463 2551.952 2552.931 2553.910 2554.889 2555.868
95
0.317
2551.463 2551.780 2552.414 2553.048 2553.682 2554.316
96
4.744
2551.463 2556.207 2565.696 2575.185 2584.674 2594.163
97
3.560
2551.463 2555.023 2562.144 2569.264 2576.384 2583.505
98
2.605
2551.463 2554.068 2559.278 2564.488 2569.698 2574.908
99
1.864
2551.463 2553.327 2557.054 2560.781 2564.508 2568.235
100
1.706
2551.463 2553.169 2556.582 2559.995 2563.408 2566.821
101
1.307
2551.463 2552.770 2555.385 2558.000 2560.615 2563.230
102
0.773
2551.463 2552.236 2553.781 2555.326 2556.871 2558.416
103
0.670
2551.463 2552.133 2553.474 2554.815 2556.156 2557.497
104
0.551
2551.463 2552.014 2553.117 2554.220 2555.323 2556.426
105
0.117
2551.463 2551.580 2551.813 2552.046 2552.279 2552.512
Terreno
Pozo
∆𝒛
𝒊
V
1
V
2
V
3
V
4
V
5
V
6
106
0,050
2551.463 2551.513 2551.614 2551.715 2551.816 2551.917
107
0,033
2551.463 2551.496 2551.563 2551.630 2551.697 2551.764
108
0,000
2551.463 2551.463 2551.463 2551.463 2551.463 2551.463
109
0,078
2551.463 2551.541 2551.696 2551.851 2552.006 2552.161

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 103
Anexo C: costos en USD$ de la red para cada terreno, variando el esfuerzo cortante
mínimo
Terreno
𝝉
𝒎𝒊𝒏
(Pa)
V
1
V
2
V
3
V
4
V
5
V
6
0.0
3,158,795.2
2,987,515.4
2,982,190.3 2,986,513.4 2,998,121.9 3,013,581.6
0.2
3,158,795.2
2,987,515.4
2,982,190.3 2,986,513.4 2,998,121.9 3,013,581.6
0.4
3,157,846.3
2,987,617.7
2,982,190.3 2,986,513.4 2,998,121.9 3,013,581.6
0.6
3,196,108.3
2,991,046.1
2,985,552.9 2,989,893.9 3,001,648.6 3,018,498.6
0.8
3,315,407.2
3,027,097.2
2,994,973.4 2,995,333.4 3,009,715.8 3,028,480.2
1.0
3,534,734.3
3,102,266.5
3,007,125.9 3,005,230.5 3,019,739.4 3,041,190.7
Terreno
𝝉
𝒎𝒊𝒏
(Pa)
V
1
V
2
V
3
V
4
V
5
V
6
1.2
3,834,264.3
3,190,050.6
3,034,609.9 3,021,929.3 3,036,014.4 3,051,482.1
1.4
4,168,406.6
3,329,958.2
3,075,459.6 3,040,554.5 3,054,186.9 3,067,120.4
1.6
4,563,706.0
3,545,573.5
3,148,854.4 3,083,767.5 3,078,093.4 3,085,256.1
1.8
4,944,088.2
3,825,404.1
3,240,352.4 3,139,288.2 3,114,009.1 3,110,556.9
2.0
5,313,970.1
4,150,902.8
3,362,442.7 3,202,524.2 3,159,443.9 3,139,887.1
2.2
5,709,742.0
4,516,788.9
3,516,583.9 3,284,596.9 3,216,579.3 3,181,106.1

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 104
Terreno
𝝉
𝒎𝒊𝒏
(Pa)
V
1
V
2
V
3
V
4
V
5
V
6
2.4
6,100,146.4
4,912,787.4
3,727,447.7 3,380,568.7 3,281,850.6 3,234,593.3
2.6
6,501,044.0
5,325,908.0
3,943,476.1 3,501,699.5 3,365,380.1 3,301,192.2
2.8
6,900,886.9
5,749,352.3
4,178,859.4 3,668,265.1 3,464,236.8 3,374,743.9
3.0
7,309,601.6
6,208,050.8
4,444,339.3 3,853,074.1 3,578,147.3 3,460,095.3
3.2
7,731,530.7
6,663,204.0
4,762,310.6 4,063,110.0 3,718,795.5 3,555,091.4
3.4
8,163,290.2
7,131,027.4
5,085,284.8 4,284,417.2 3,877,658.4 3,670,638.4
Terreno
𝝉
𝒎𝒊𝒏
(Pa)
V
1
V
2
V
3
V
4
V
5
V
6
3.6
8,583,033.3
7,609,679.4
5,430,903.5 4,545,423.1 4,062,383.5 3,799,899.0
3.8
9,021,547.9
8,104,380.5
5,801,353.4 4,791,050.8 4,275,283.9 3,933,043.7
4.0
9,479,903.2
8,595,930.2
6,170,831.1 5,072,158.5 4,497,644.2 4,101,855.8
4.2
9,928,054.9
9,099,933.5
6,539,408.5 5,364,568.2 4,725,134.0 4,298,181.5
4.4
10,384,384.1
9,609,197.1
6,953,770.4 5,680,330.3 4,968,521.2 4,494,801.6
4.6
10,839,308.4 10,118,499.9 7,354,211.7 5,987,948.8 5,218,550.3 4,717,189.5

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 105
Anexo D: costos en USD$ de la red para cada terreno, variando la máxima relación de
llenado
Terreno
𝒚𝒏/𝒅 (-)
V
1
V
2
V
3
V
4
V
5
V
6
0.25
8,843,031.1
7,368,739.1
6,899,427.8
6,590,961.0
6,339,586.7
6,086,234.5
0.30
6,647,505.0
5,417,414.4
4,913,302.1
4,620,917.0
4,364,145.0
4,140,847.4
0.35
5,662,121.3
4,540,562.4
4,003,936.3
3,721,530.5
3,547,357.8
3,414,473.6
0.40
5,132,050.4
4,078,752.5
3,564,171.2
3,337,839.1
3,187,988.0
3,145,216.1
0.45
4,845,270.2
3,820,982.1
3,333,982.4
3,130,269.2
3,098,613.8
3,099,113.7
0.50
4,675,792.4
3,650,674.9
3,232,245.2
3,081,861.3
3,075,647.8
3,077,171.8
Terreno
𝒚𝒏/𝒅 (-)
V
1
V
2
V
3
V
4
V
5
V
6
0.55
4,567,400.4
3,563,449.9
3,163,244.5
3,067,768.6
3,056,409.8
3,077,934.5
0.60
4,502,677.7
3,531,960.1
3,135,962.6
3,056,906.7
3,059,772.4
3,080,708.6
0.65
4,453,130.7
3,491,993.7
3,115,826.9
3,060,291.9
3,064,700.4
3,070,093.4
0.70
4,422,886.5
3,465,031.8
3,115,638.2
3,057,667.8
3,058,716.5
3,076,321.9
0.75
4,399,388.8
3,446,728.8
3,109,570.4
3,059,299.3
3,057,598.2
3,076,074.2
0.80
4,381,551.0
3,433,487.7
3,109,156.0
3,057,293.1
3,056,496.7
3,072,122.0

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 106
Terreno
𝒚𝒏/𝒅 (-)
V
1
V
2
V
3
V
4
V
5
V
6
0.85
4,363,484.6
3,423,313.1
3,103,740.8
3,057,227.8
3,062,065.8
3,068,193.3
0.90
4,361,993.3
3,418,393.8
3,107,552.7
3,057,885.7
3,063,535.1
3,073,042.6
0.95
4,358,693.5
3,417,299.7
3,109,524.9
3,057,486.2
3,062,631.1
3,075,415.0
1.00
4,370,646.1
3,428,626.7
3,106,771.0
3,056,425.1
3,060,846.8
3,070,463.7

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 107
Anexo E: costos en USD$ de la red para cada terreno, variando las máximas relaciones
de llenado altas
Terreno
𝒚𝒏/𝒅 (-)
V
1
V
2
V
3
V
4
V
5
V
6
0.8
4,381,551.0
3,433,487.7
3,109,156.0
3,057,293.1
3,059,772.4
3,072,122.0
0.81
4,379,254.0
3,430,931.8
3,108,868.7
3,057,566.8
3,061,809.5
3,070,742.4
0.82
4,374,391.3
3,429,263.4
3,107,125.9
3,057,446.0
3,061,480.4
3,070,463.7
0.83
4,367,866.0
3,427,167.3
3,106,771.0
3,055,859.2
3,060,846.8
3,068,651.8
0.84
4,366,720.0
3,425,443.8
3,108,651.2
3,057,286.9
3,062,394.6
3,068,531.2
0.85
4,363,484.6
3,423,313.1
3,103,740.8
3,057,227.8
3,062,065.8
3,068,193.3
0.86
4,363,314.5
3,423,313.1
3,103,121.1
3,058,627.3
3,061,777.7
3,068,193.3
Terreno
𝒚𝒏/𝒅 (-)
V
1
V
2
V
3
V
4
V
5
V
6
0.87
4,363,314.5
3,422,514.5
3,103,061.9
3,058,231.8
3,061,718.6
3,068,193.3
0.88
4,363,314.5
3,422,514.5
3,101,220.1
3,057,944.8
3,061,627.7
3,069,693.3
0.89
4,363,314.5
3,421,994.6
3,105,694.8
3,057,944.8
3,063,813.8
3,069,414.6
0.9
4,361,993.3
3,418,393.8
3,107,552.7
3,057,885.7
3,063,535.1
3,073,042.6
0.91
4,361,359.0
3,417,299.7
3,109,524.9
3,057,885.7
3,063,535.1
3,073,042.6
0.92
4,358,980.8
3,417,299.7
3,109,524.9
3,057,885.7
3,063,535.1
3,073,210.3
0.93
4,358,693.5
3,417,299.7
3,109,524.9
3,057,486.2
3,062,631.1
3,075,415.0

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 108
Terreno
𝒚𝒏/𝒅 (-)
V
1
V
2
V
3
V
4
V
5
V
6
0.94
4,358,693.5
3,417,299.7
3,109,524.9
3,057,486.2
3,062,631.1
3,075,415.0
0.95
4,358,693.5
3,417,299.7
3,109,524.9
3,057,486.2
3,062,631.1
3,075,415.0
0.96
4,358,980.8
3,417,299.7
3,109,524.9
3,057,885.7
3,063,535.1
3,073,042.6
0.97
4,361,359.0
3,418,393.8
3,111,323.5
3,057,885.7
3,063,535.1
3,073,042.6
0.98
4,363,314.5
3,422,514.5
3,101,220.1
3,057,944.8
3,063,813.8
3,069,414.6
0.99
4,363,314.5
3,422,514.5
3,103,061.9
3,058,231.8
3,061,718.6
3,068,193.3
1
4,370,646.1
3,428,626.7
3,106,771.0
3,056,425.1
3,060,846.8
3,070,463.7

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 109
Anexo F : costos en USD$ de la red para cada terreno, variando la velocidad máxima
Terreno
𝒗
𝒎𝒂𝒙
(m/s)
V
1
V
2
V
3
V
4
V
5
V
6
6.0
3109524.9
3417299.7
3075415.0
3057486.2
3062203.5
3071171.6
5.0
3109524.9
3417299.7
3109524.9
3061866.6
3066076.1
3069761.1
4.8
3109524.9
3417299.7
3109524.9
3061866.6
3066076.1
3069761.1
4.6
3109524.9
3417299.7
3109524.9
3061608.3
3054364.3
3080807.5
4.4
3109524.9
3417299.7
3109524.9
3062776.4
3055809.4
3092444.3
4.2
3108675.3
3417299.7
3109524.9
3061056.9
3061882.3
3105129.6
Terreno
𝒗
𝒎𝒂𝒙
(m/s)
V
1
V
2
V
3
V
4
V
5
V
6
4.0
3109524.9
3417299.7
3108675.3
3057127.0
3064383.2
3143439.2
3.8
3108675.3
3417299.7
3109524.9
3060094.7
3079863.1
3263788.6
3.6
3108208.5
3417299.7
3108675.3
3059861.2
3120508.1
3527870.8
3.4
3108059.6
3417299.7
3108208.5
3062643.6
3227406.0
3833527.0
3.2
3106850.9
3417299.7
3108059.6
3077377.2
3473887.4
4282061.8
3.0
3104500.5
3417299.7
3106850.9
3164949.5
3787465.9
5212205.2
𝒗
𝒎𝒂𝒙
(m/s)
V
1
V
2
V
3
V
4
V
5
V
6
2.8
3102118.7
3417299.7
3104500.5
3358049.0
4329213.8
6570710.3
2.6
3123261.5
3415761.2
3102118.7
3620403.8
5369742.4
8201763.2
2.4
3191009.9
3415880.5
3123261.5
4139590.7
6696892.3
10267681.9
2.2
3341088.3
3415795.1
3191009.9
5113483.5
8517915.6
13080115.6

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 110
Anexo G: costos en USD$ de la red para cada terreno, variando la velocidad mínima
Terreno
𝒗
𝒎𝒊𝒏
(m/s)
V
1
V
2
V
3
V
4
V
5
V
6
0.0
4362692.8
3417299.7
3109524.9
3057486.2
3062631.1
3075415.0
0.2
4362692.8
3417299.7
3109524.9
3057486.2
3062631.1
3075415.0
0.4
4362692.8
3417299.7
3109524.9
3057486.2
3062631.1
3075415.0
0.6
4362692.8
3417299.7
3109524.9
3057486.2
3062631.1
3075415.0
0.8
4416179.4
3593012.3
3137091.3
3069557.4
3068966.1
3076374.6
0.9
4884250.4
4092947.7
3320121.7
3179572.7
3139998.2
3122080.9
1.0
5644807.0
4846499.1
3651204.1
3365357.9
3266446.5
3221329.2
Terreno
𝒗
𝒎𝒊𝒏
(m/s)
V
1
V
2
V
3
V
4
V
5
V
6
1.1
6496209.1
5845755.7
4255752.1
3671762.4
3476988.3
3376568.7
1.2
7452162.8
7034011.3
5055063.5
4182671.8
3789709.9
3615327.9
1.3
8545781.2
8407729.8
6007107.7
4926970.4
4311242.8
3985606.9
1.4
9763179.3
9949866.9
7197342.6
5935413.2
5045805.6
4539739.0
1.5
11121530.4
11661627.8
8652293.7
7092282.0
6029584.5
5298301.9
1.6
12630400.7
13552390.8
10343115.9
8464892.4
7275748.3
6289040.6
1.7
14265010.2
15632999.7
12287306.6
10144644.0
8695710.6
7600778.2

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 111
Anexo H: costos en USD$ de la red para cada terreno, variando el diámetro mínimo
Terreno
𝒅
𝒎𝒊𝒏
(m)
V
1
V
2
V
3
V
4
V
5
V
6
0.1820
4,358,693.5
3,417,299.7
3,109,524.9
3,057,486.2
3,062,631.1
3,075,415.0
0.2270
4,450,678.2
3,509,239.5
3,134,560.8
3,074,122.2
3,075,451.5
3,082,537.3
0.4520
4,935,491.3
3,925,005.7
3,304,721.8
3,197,008.4
3,165,569.1
3,160,230.1
0.5950
5,178,985.1
4,161,792.3
3,428,731.7
3,265,016.6
3,222,616.0
3,211,144.1
0.6700
5,290,038.7
4,274,935.9
3,495,180.0
3,297,913.3
3,253,369.3
3,233,300.5
0.7470
5,424,125.5
4,396,935.1
3,574,159.5
3,342,342.8
3,289,400.8
3,267,996.4
0.8240
5,556,770.5
4,515,462.2
3,647,741.3
3,392,465.2
3,320,430.1
3,296,026.9
0.9776
5,779,653.8
4,749,875.8
3,781,858.6
3,465,634.5
3,375,368.3
3,325,195.5
1.0540
5,903,287.6
4,865,081.4
3,851,096.6
3,511,013.6
3,408,322.5
3,350,308.7
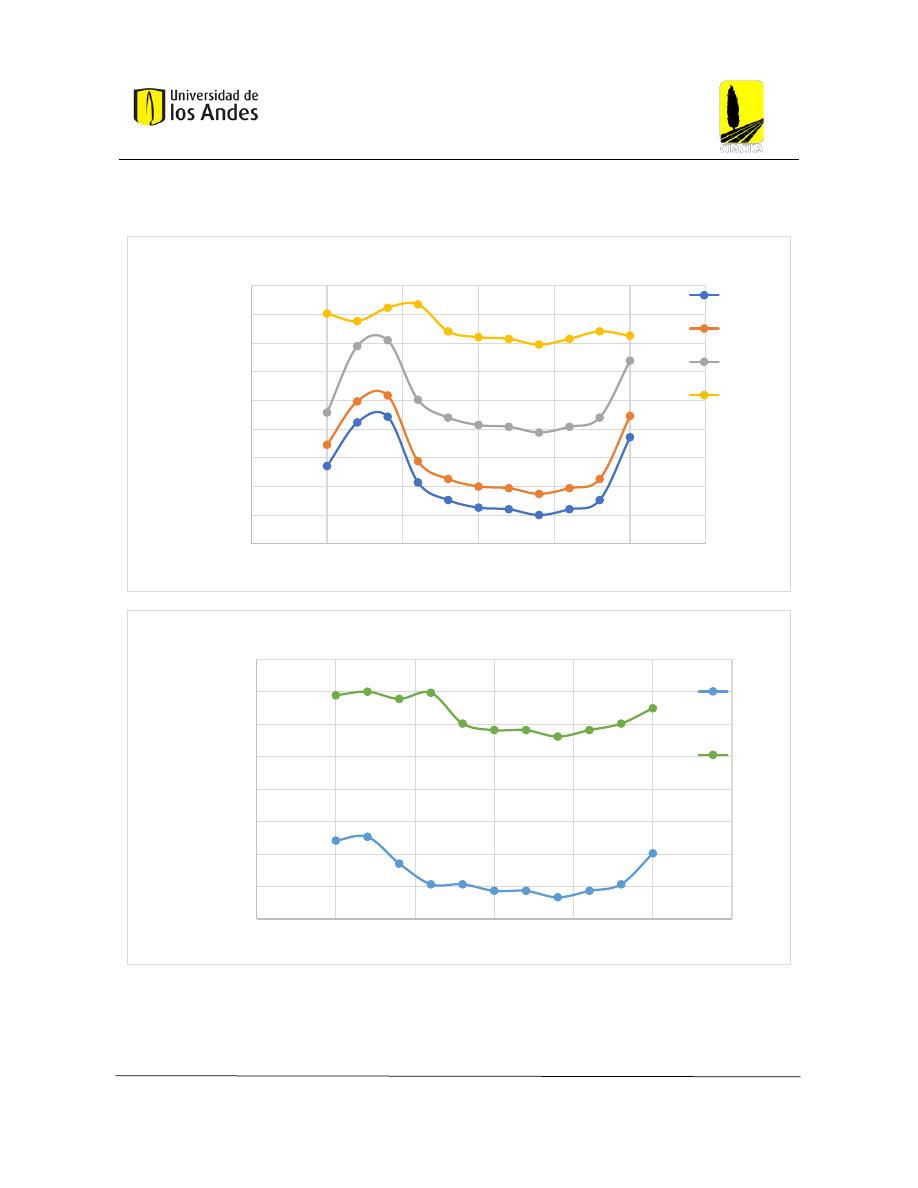
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 112
Anexo I: costos en (USD$) de la red variando la máxima relación de llenado y el esfuerzo
cortante mínimo en Pa
2.976.000
2.978.000
2.980.000
2.982.000
2.984.000
2.986.000
2.988.000
2.990.000
2.992.000
2.994.000
0,75
0,8
0,85
0,9
0,95
1
1,05
C
ost
o (
US
D$)
Relación de llenado máxima(-)
Costo del diseño
Tau 0
Tau 0.2
Tau 0.4
Tau 0.6
2.994.000
2.996.000
2.998.000
3.000.000
3.002.000
3.004.000
3.006.000
3.008.000
3.010.000
0,75
0,8
0,85
0,9
0,95
1
1,05
C
ost
o (
US
D$)
Relación de llenado máxima(-)
Costo del diseño
Tau 0.8
Tau 1
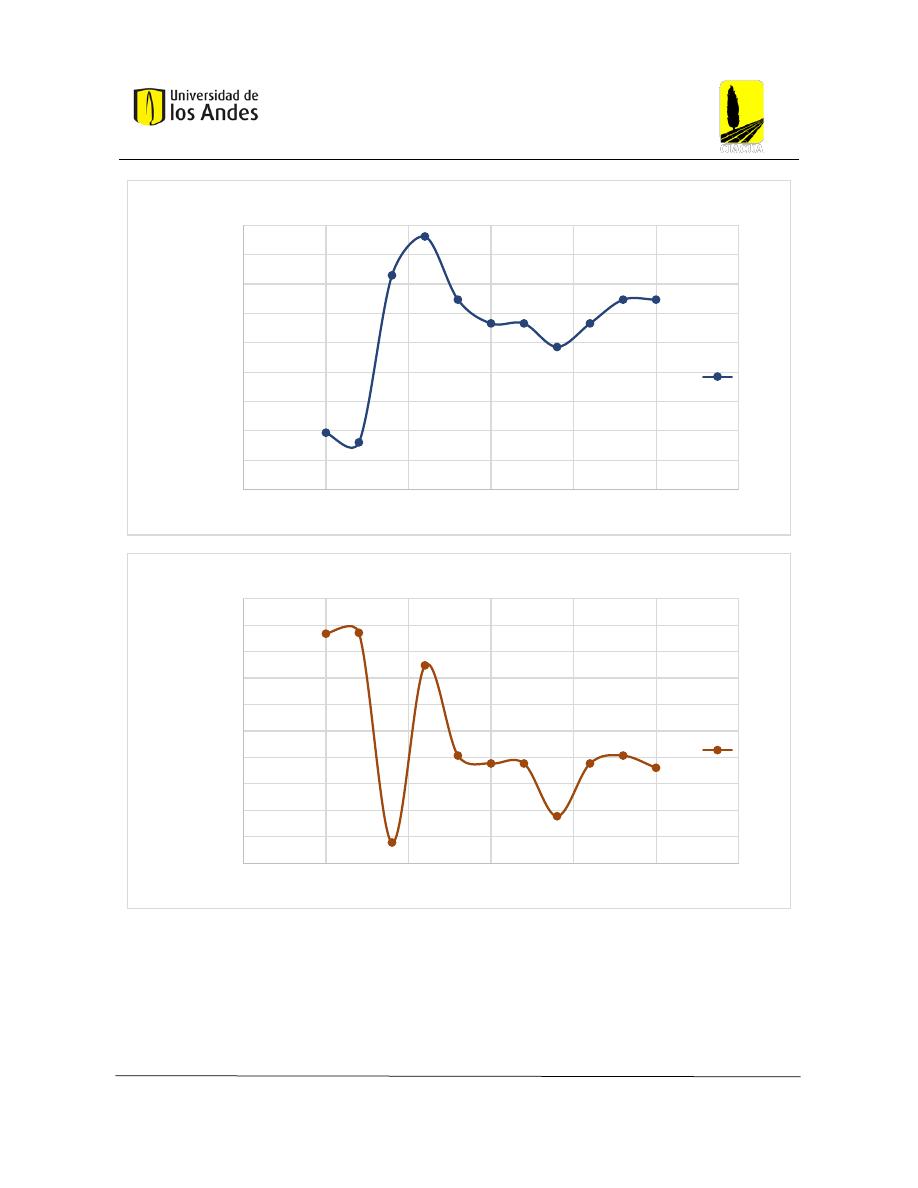
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 113
3.019.500
3.020.000
3.020.500
3.021.000
3.021.500
3.022.000
3.022.500
3.023.000
3.023.500
3.024.000
0,75
0,8
0,85
0,9
0,95
1
1,05
C
ost
o (
US
D$)
Relación de llenado máxima (-)
Costo del diseño
Tau 1.2
3.040.200
3.040.400
3.040.600
3.040.800
3.041.000
3.041.200
3.041.400
3.041.600
3.041.800
3.042.000
3.042.200
0,75
0,8
0,85
0,9
0,95
1
1,05
C
ost
o (
US
D$)
Relación de llenado máxima (-)
Costo del diseño
Tau 1.4
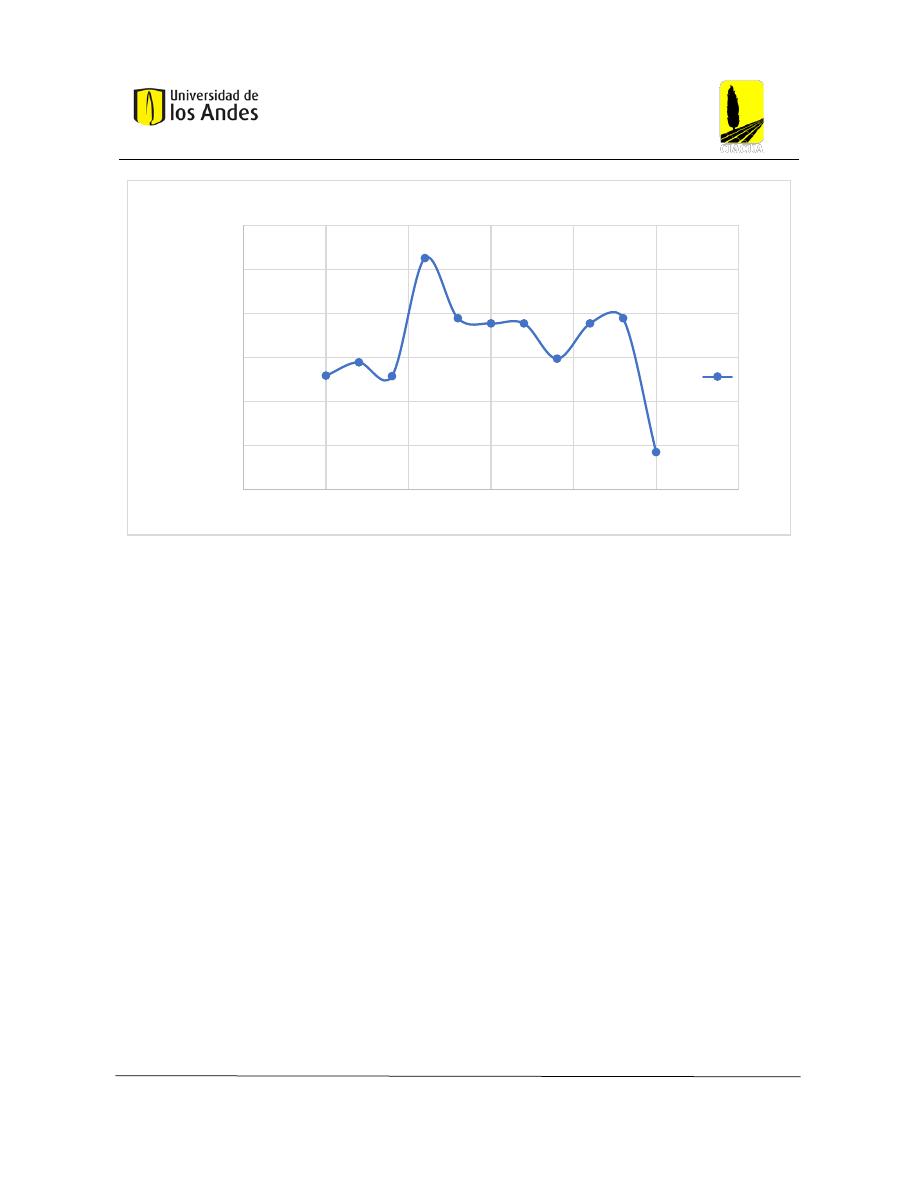
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 114
3.056.000
3.056.500
3.057.000
3.057.500
3.058.000
3.058.500
3.059.000
0,75
0,8
0,85
0,9
0,95
1
1,05
C
ost
o (
US
D$)
Relación de llenado máxima (-)
Costo del diseño
Tau 1.5
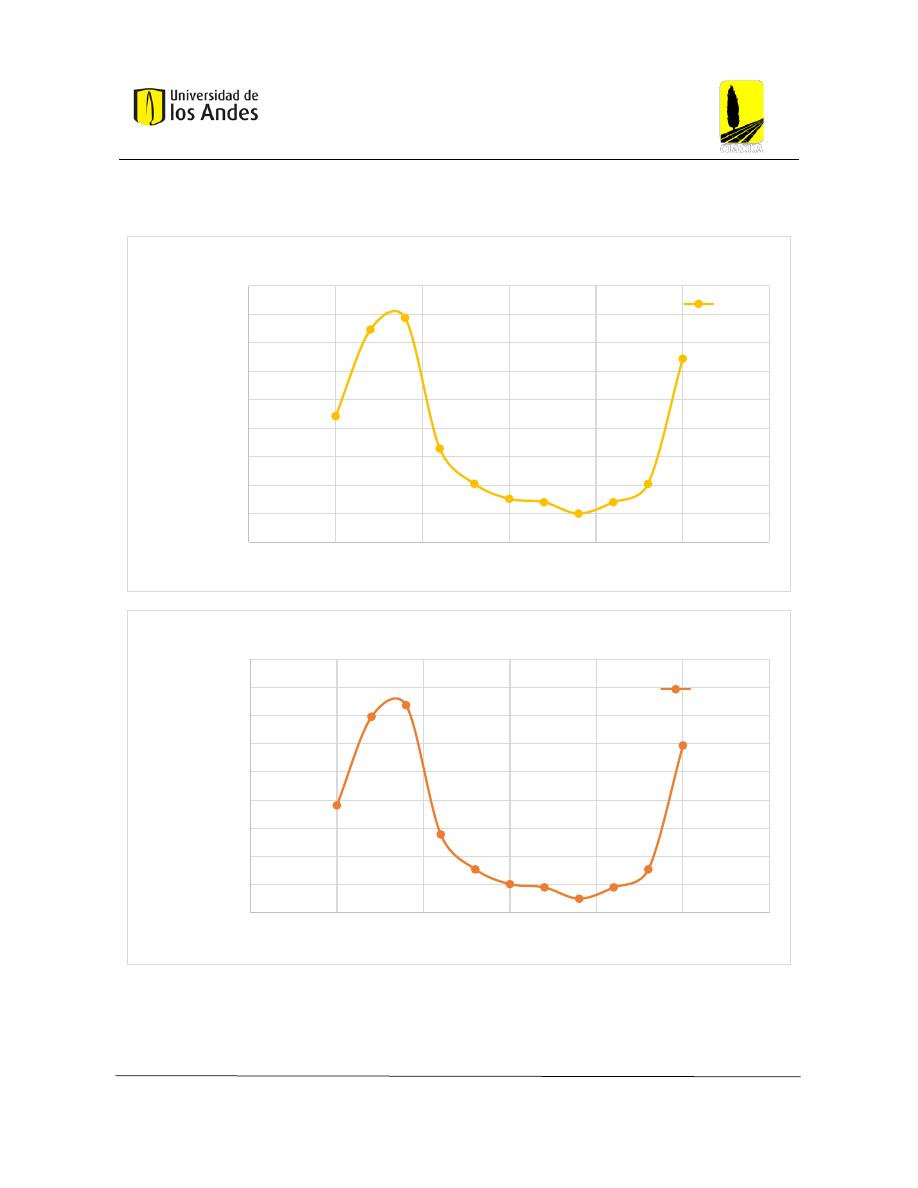
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 115
Anexo J: costos en (USD$) de la red variando la máxima relación de llenado y la
velocidad mínima en m/s
2.977.000
2.978.000
2.979.000
2.980.000
2.981.000
2.982.000
2.983.000
2.984.000
2.985.000
2.986.000
0,75
0,8
0,85
0,9
0,95
1
1,05
C
ost
o (
US
D$)
Relación de llenado máxima(%)
Costo del diseño
v min 0
2.978.000
2.979.000
2.980.000
2.981.000
2.982.000
2.983.000
2.984.000
2.985.000
2.986.000
2.987.000
0,75
0,8
0,85
0,9
0,95
1
1,05
C
ost
o (
US
D$)
Relación de llenado máxima(%)
Costo del diseño
v min 0.2
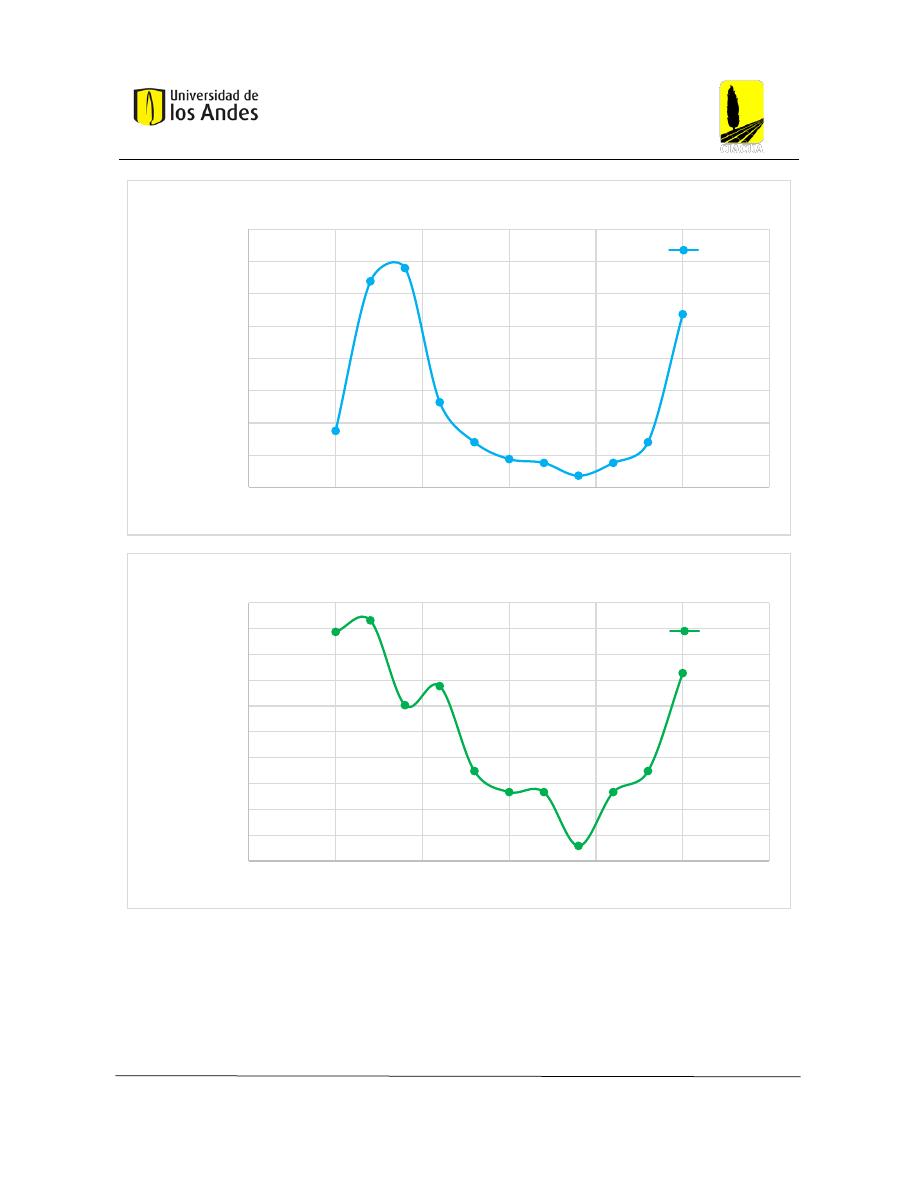
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 116
2.983.000
2.984.000
2.985.000
2.986.000
2.987.000
2.988.000
2.989.000
2.990.000
2.991.000
0,75
0,8
0,85
0,9
0,95
1
1,05
C
ost
o (
US
D$)
Relación de llenado máxima(%)
Costo del diseño
v min 0.4
2.997.500
2.998.000
2.998.500
2.999.000
2.999.500
3.000.000
3.000.500
3.001.000
3.001.500
3.002.000
3.002.500
0,75
0,8
0,85
0,9
0,95
1
1,05
C
ost
o (
US
D$)
Relación de llenado máxima(%)
Costo del diseño
v min 0.6
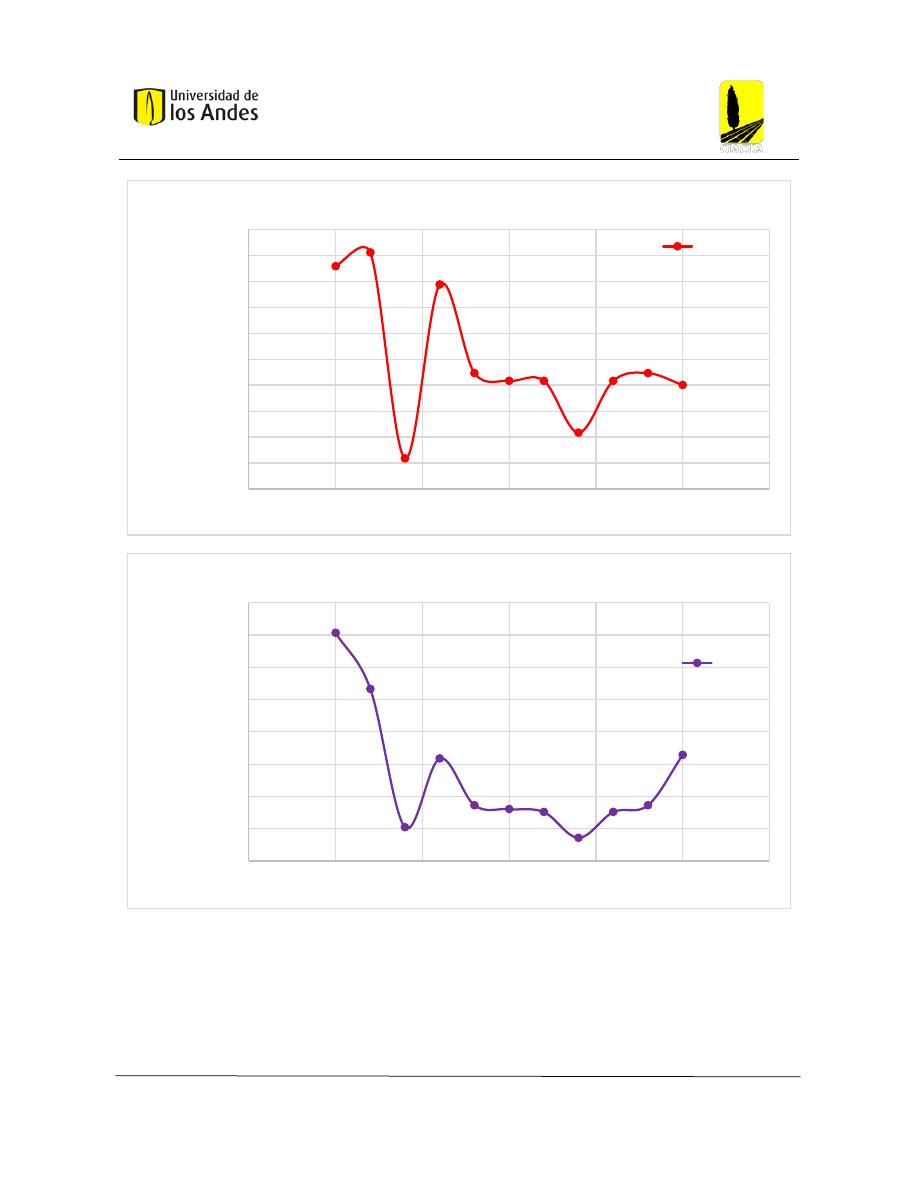
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 117
3.059.000
3.059.200
3.059.400
3.059.600
3.059.800
3.060.000
3.060.200
3.060.400
3.060.600
3.060.800
3.061.000
0,75
0,8
0,85
0,9
0,95
1
1,05
C
ost
o (
US
D$)
Relación de llenado máxima(%)
Costo del diseño
v min 0.8
3.365.000
3.365.500
3.366.000
3.366.500
3.367.000
3.367.500
3.368.000
3.368.500
3.369.000
0,75
0,8
0,85
0,9
0,95
1
1,05
C
ost
o (
US
D$)
Relación de llenado máxima(%)
Costo del diseño
v min 1

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 118
Anexo K: costos en USD$ de la red para el análisis de diámetros comerciales continuos
𝒚𝒏/𝒅 (-)
Costo (USD$)
0.80
3,051,692.83
0.81
3,052,634.49
0.82
3,050,563.58
0.83
3,053,207.69
0.84
3,046,248.56
0.85
3,040,874.91
0.86
3,041,555.16
0.87
3,042,357.76
0.88
3,042,357.76
0.89
3,041,546.14
0.90
3,041,259.31

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de redes de drenaje urbano: Análisis de sensibilidad de
restricciones de diseño y variación topográfica
Andrés Felipe Noriega Garzón Proyecto de Grado 119
𝒚𝒏/𝒅 (-)
Costo (USD$)
0.91
3,040,676.55
0.92
3,040,676.55
0.93
3,039,608.53
0.94
3,040,257.45
0.95
3,039,608.53
0.96
3,040,676.55
0.97
3,041,259.31
0.98
3,041,556.87
0.99
3,038,468.65
1.00
3,051,420.73
