
DISEÑO OPTIMIZADO DE REDES ABIERTAS CON DEMANDAS
DEPENDIENTES DE LA PRESIÓN USANDO PROGRAMACIÓN LINEAL
“XII Simposio Iberoamericano sobre planificación de sistemas de
abastecimiento y drenaje”
Camilo Salcedo (1), Diego Páez (2), David Hernández (3), Laura Manrique (4), Juan
Saldarriaga (5)
(1) Investigador, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de los
Andes (CIACUA), Carrera 1 No. 18ª-10, Bogotá, Colombia. Teléfono: 3394949 Ext: 2810. Email:
ca.salcedo959@uniandes.edu.co.
(2) Profesor Instructor, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad
de los Andes (CIACUA), Carrera 1 No. 18ª-10, Bogotá, Colombia. Teléfono: 3394949 Ext: 2810.
Email:da.paez27@uniandes.edu.co.
(3, 4) Investigador, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de los
Andes (CIACUA), Carrera 1 No. 18ª-10, Bogotá, Colombia. Teléfono: 3394949 Ext: 2810. Email:
da.hernandez39@uniandes.edu.co, l.manrique83@uniandes.edu.co,
(5) Profesor Titular, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de
los Andes (CIACUA), Carrera 1 No. 18ª-10, Bogotá, Colombia. Teléfono: 3394949 Ext: 2810. Email:
jsaldarr@uniandes.edu.co.
RESUMEN
El presente documento describe una aproximación al diseño optimizado de redes de distribución de agua
potable (RDAP) a través de metodologías que combinan Programación Lineal con conceptos relacionados
con el uso energético de la red. Con lo anterior, se busca obtener la combinación de diámetros de menor
costo para la red en el menor tiempo posible, asegurando su validez hidráulica. Esta aproximación fue
aplicada a diferentes redes abiertas con demandas dependientes de la presión (DDP), las cuales se modelaron
a través de emisores, alcanzando así un primer paso para el establecimiento de metodologías que permitan
diseñar redes con DDP de mayor complejidad.
Palabras claves: Emisores, Programación Lineal, Tuberías en Serie, RDAP, Demandas Dependientes de la
Presión.
ABSTRACT
This paper describes an approximation to the optimal design of water distribution networks (WDN) through
a methodology which combines linear programming with energy-based concepts. As result, it is expected to
obtain a set of diameters which have the minimum cost in the least computational time possible, and also
ensuring its hydraulic operation. This approximation was applied to different WDN’s with pressure driven
demands (PDD), which were modeled through the use of emitters, and establishing the first step of a
methodology that allows the design of more complex networks whose demands behave as PDD.
Key words: Emitters, Linear Programming, Pipes in Series, WDN, Pressure-Driven Demands.
SOBRE EL AUTOR PRINCIPAL
Camilo Andrés Salcedo Ballesteros: Estudiante de Maestría en Ingeniería Civil con énfasis en Recursos
Hídricos e Hidroinformática en la Universidad de los Andes, Colombia, en donde también obtuvo sus títulos
de pregrado como Ingeniero Civil e Ingeniero Industrial en Marzo del 2013. Actualmente se desempeña
como investigador del Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de los
Andes (CIACUA).

INTRODUCCIÓN Y ANTECEDENTES
Una red abierta está conformada por un conjunto de
tuberías formando un sistema en árbol con al menos
un embalse de alimentación, y distintos nudos de
demanda, comformando así a un tipo de sistema de
distribución de agua potable (RDAP). En la
clasificación de las redes de distribución según sus
demandas se pueden diferenciar dos tipos: Aquellas
en donde la demanda en cada nudo es conocida o
independiente, y aquellas en donde esta es
dependiente de la presión en al menos uno de los
nudos de la red. Estas últimas se conocen como
redes con demandas dependientes de la presión
(DDP).
Para el diseño optimizado de los sistemas con
demandas independientes se han desarrollado
metodologías
y
metaheurísiticas
de
diseño
optimizado enfocadas a la minimización de los
costos constructivos del sistema, las cuales se
encargan de escoger una combinación de diámetros
para la red tal que para cada nudo se cumpla con una
presión mayor o igual a la mínima establecida y se
entreguen los caudales demandados. Dentro de las
metaheurísticas probadas en este tipo de sistemas se
pueden mencionar los Algoritmos Genéticos (Savic
& Waters (1997); Wu & Simpson (2001); Reca et
al., 2006), Simulated Annealing (Cunha & Sousa
(1999); Reca, et al., 2007), Búsqueda de Armonía
(Geem (2002); Gemm (2009)), y la Colonia de
Hormigas (Zecchin et al., 2006, Ostfled et al.,
2008), entre otros. También investigadores como
Ipai Wu (1975) y Ochoa y Saldarriaga (2009) han
propuesto y desarrollado metodologías que utilizan
el conocimiento hidráulico de una red cerrada para
optimizar el uso de la energía disponible y llevar a
diseños de mínimos costo; entre estas últimas se
encuentran los métodos de superficie óptima de
gradiente hidráulico (SOGH) y superficie de uso
óptimo de potencia (OPUS).
Por su parte, en el caso de los modelos dependientes
de la presión se han probado un número menor de
metaheurísticas, dentro de las cuales la mayoría se
han aplicado para diseñar redes de riego haciendo
uso de emisores en cada uno de sus nudos. Dentro de
dichas metaheurísticas se pueden encontrar los
Algorítmos Genéticos (Farmani et al., 2007),
Programación Lineal Difusa (Spiliotis et al., 2007) y
Diseños Recursivos (González-Cebollada et al.,
2011).
Usualmente, el diseño de las redes de distribución se
ha realizado de forma tal que la demanda es
independiente de la presión en los nudos, hecho que
no refleja la realidad de todas las RDAP. Para esta
investigación, por el contrario, el tipo de RDAPs
utilizado incluye demandas dependientes de la
presión, haciendo uso de emisores, los cuales han
probado ser útiles al modelar fugas, redes contra
incendios y sistemas de riego. Este documento
muestra los resultados obtenidos al aplicar una
metodología donde se combinan los conceptos de
energía
anteriormente
expuestos
con
una
formulación de Programación Lineal en un software
especializado, buscando alcanzar diseños cuyos
costos constructivos sean mínimos, en el menor
tiempo posible. Para lo anterior, se diseñaron varias
RDAP con DDP utilizando las metodologías
convencionales de diseño óptimo y la metodología
propuesta. Las redes diseñadas están conformadas
por varias tuberías en serie, y se diferenciaban entre
sí por su topografía y los parámetros utilizados para
modelar los emisores.
Esta investigación puede ser considerada como el
primer paso para establecer metodologías enfocadas
a solucionar el problema de diseño optimizado de
redes de distribución de agua potable aplicado al
caso de sistemas cuyas demandas sean dependientes
de la presión, con un nivel de complejidad mayor, y
fundamentándose en conceptos hidráulicos en vez de
basarse en métodos heurísticos.
MARCO TEÓRICO
Línea Óptima de Gradiente Hidráulico Para
Tuberías en Serie
Basados en los resultados de Ipai-Wu (1975),
Ochoa
y
Saldarriaga
(2009)
definieron
la
metodología de diseño conocida como Superficie
Óptima
de
Gradiente
Hidráulico
(SOGH),
posteriormente modificada en Superficie de Uso
Óptimo de Potencia (OPUS), la cual se encuentra
basada en la hidráulica de la red. De acuerdo con los
resultados de Wu, el diseño de mínimo costo en un
tramo de tuberías en serie usualmente forma una
línea de gradiente hidráulico (LGH) parabólica.
Para establecer el comportamiento de la ecuación
cuadrática del gradiente hidráulico se deben conocer
tres puntos que describan la función parabólica.
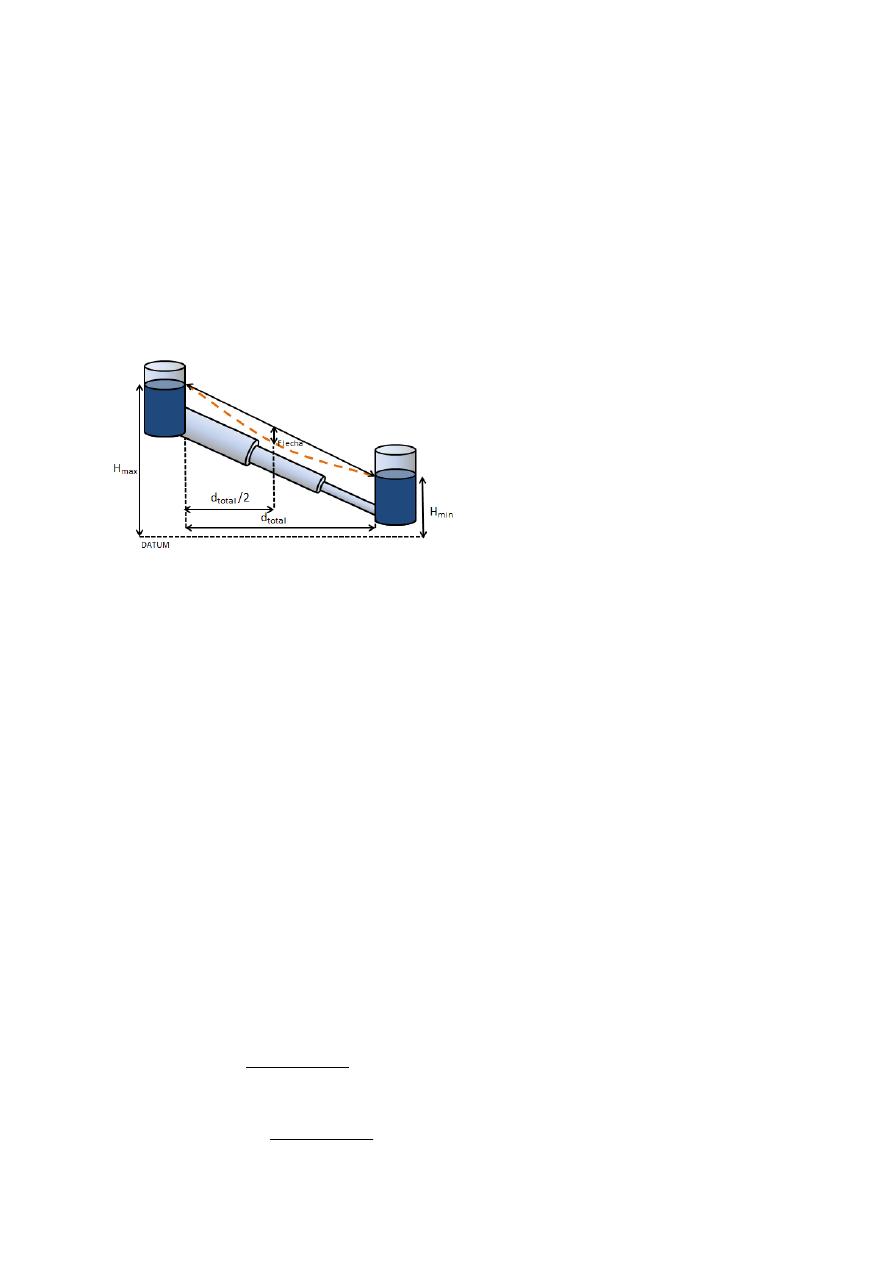
Estos puntos se muestran en la Figura 1, y son:
H
max
: La altura piezométrica disponible para
toda la red, y así como la altura del embalse,
se encuentra ubicado en la abscisa d = 0.
H
min
: La altura piezométrica mínima para el
nudo crítico, el cual bien puede ser la unión
final de la red, o bien aquel que tenga una
altura total cercana a la mínima como
consecuencia de su elevación. En caso que
esta sea definida en el nudo final, se
encontrará en la abscisa d = d
total
.
H
flecha
: Corresponde a la altura en el punto
de máxima curvatura de la línea de gradiente
hidráulico (LGH). Este punto se define por
la flecha, la cual es un porcentaje de la
altura disponible en la red, es decir, la
diferencia entre H
max
y H
min
. Este punto
siempre se localiza en la abscisa d = d
total
/2.
Figura 1. Línea de Gradiente Hidráulico
Objetivo, Basada en Tres Puntos Conocidos
Como se puede observar en la Figura 1, existe una
línea recta correspondiente al caso cuando la LGH
es lineal. Cuando la flecha es igual a 0%, el
gradiente será igual a esta línea recta, pero cuando
este porcentaje es distinto a 0% la altura en la mitad
de la serie de tuberías será igual a la altura en el
punto medio de la línea recta menos la flecha
multiplicada por la altura disponible en el sistema.
De acuerdo con lo anterior, la línea de gradiente
hidráulico objetivo se puede encontrar a partir de la
Ecuación 1.
d
d
LGH
j
2
(1)
En donde LGH
j
corresponde a la altura en el nudo j
ubicada a una distancia d desde la reserva, F es la
flecha seleccionada y H
max
y H
min
son las alturas en
los puntos mencionados. Asimismo, cada uno de los
coeficientes utilizados (α, β y
)
se describe en las
ecuaciones a continuación:
2
m in
m ax
)
(
4
total
d
H
H
F
(2)
total
d
H
H
F
)
(
)
4
1
(
m in
m ax
(3)
m ax
H
(4)
Formulación Para el Diseño Optimizado de
Redes Abiertas Utilizando Programación
Lineal
El diseño optimizado consiste en encontrar la
combinación de diámetros con el menor costo
constructivo posible a partir de parámetros dados de
una red tales como su topología, la longitud de las
tuberías, su topografía, el requerimiento de presión
mínima y la conexión entre nudos y conductos. La
solución obtenida debe obedecer los principios de
conservación de masa y energía, así como los
requerimientos mínimos de presión en cada nudo.
Asimismo, es importante mencionar que dentro del
alcance de la presente investigación no se
consideraron otro tipo de restricciones como las
velocidades máxima ni mínima.
La formulación matemática de este problema se
muestra a continuación.
Función Objetivo
La función objetivo consiste en minimizar los costos
constructivos de la red, los cuales se calculan a
través de la Ecuación 5.
∑
(5)
en donde NP corresponde a número de tuberías de la
red,
es la longitud de la tubería i,
es el
diámetro de la tubería i, y los parámetros K y x se
obtienen a partir de una regresión ajustada a la curva
de costos unitarios de las tuberías en función de su
diámetro.
Restricciones del Problema
Las restricciones del problema de optimización
asociado con el diseño se describen a continuación:
Conservación de la masa
∑
(
)
(6)

donde
es el caudal total en la tubería i,
es la
demanda base en el nudo j, y
es el caudal del
emisor en el nudo j, el cual depende de la presión en
dicho nudo.
Conservación de la Energía
∑ (
)
(7)
donde
es la altura total en el nudo j,
es la
altura total en el embalse,
son las pérdidas por
fricción en la tubería i,
las pérdidas menores en
la tubería i, y NN representa el número total de
nudos en la red. Para esta investigación, las pérdidas
por fricción se calcularon utilizando la ecuación de
Darcy-Weisbach.
Presión Mínima en Nudos de Demanda
(8)
donde
es la altura mínima requerida en el
nudo j, la cual corresponde a la mínima presión
admisible.
Diámetros de las Tuberías
(9)
Los diámetros de las tuberías únicamente pueden
tomar valores discretos, pertenecientes a la lista
comercial representada por
.
Finalmente, es importante recordar que al tratarse de
demandas dependientes de la presión, el caudal en
cada nudo no se conoce con antelación a la
realización del diseño. Por esta razón, no se puede
aplicar directamente Programación
Lineal al
problema para encontrar su óptimo global.
Diseño de Submódulos de Riego Utilizando
Programación Lineal
Para el diseño de redes abiertas con demandas
constantes
se
han
propuesto
formulaciones
utilizando Programación Lineal, las cuales han
obtenido buenos resultados. Sin embargo, cuando se
trata de redes con demandas dependientes de la
presión, estas formulaciones dejan de ser aplicables
directamente al problema de optimización asociado
ya que el caudal en cada nudo va a depender de la
presión que se tenga en un dado instante de tiempo,
razón por la cual no se puede conocer la demanda de
forma previa a la realización del diseño (Hernández,
2012). Como solución a este problema se propuso la
utilización de una superficie de gradiente hidráulico,
con el fin de poder asignar a cada emisor una
presión, y así conocer el caudal demandado por este.
Sin embargo, se detectó un segundo problema en el
uso de programación lineal atribuido al uso de
emisores; este fue la sensibilidad del diseño a la
flecha inicial utilizada. Por lo anterior, se buscó
establecer un rango de flechas que permitieran
obtener resultados factibles, y a su vez que arrojaran
el diseño de menor costo posible.
Para resolver los problemas descritos anteriormente
de forma simultánea, Hernández (2012) planteó un
algoritmo de 11 pasos en donde se combina la
Programación Lineal con la metodología conocida
como OPUS con el fin de realizar diseños de
submódulos de riego. Los pasos de dicho algoritmo
son:
1. Conocer la topología del submódulo de riego, el
caudal medio demandado por planta, el número de
emisores en cada nudo con su respectivas
ecuaciones, el coeficiente de uniformidad (CU) y el
de variabilidad (CV).
2. Determinar la Presión de Entrada al Submódulo
(PES) y la presión mínima aceptable en los
emisores.
3. Establecer la superficie de gradiente hidráulico
deseado utilizando la metodología OPUS. Esto se
debe realizar para la flecha de 0 y de 0.25.
4. Luego de obtener las presiones en la red, calcular
los caudales en cada nudo, y luego asignarlos como
demanda base a cada unión, suponiéndose
constantes en la modelación. Se debe recordar que
este procedimiento se debe realizar para ambas
flechas estudiadas (0 y 0.25).
5. Calcular las matrices de costo, de pérdidas totales,
de conectividad, y de LGH mínimas. Con lo anterior
y
la
formulación
de
programación
lineal
implementada, realizar el diseño del submódulo de
interés. Se obtendrán dos diseños, el más económico
asociado con la flecha de 0.25, y el más costoso
asociado con la flecha de 0.

6. Dado que en el paso anterior se realizó el diseño
considerando demandas constantes, es necesario
verificar el comportamiento del sistema una vez se
modelen los emisores. Por lo tanto, utilizando los
diseños obtenidos en el paso anterior con emisores
se obtendrá para cada nudo el caudal emitido.
Posteriormente, se deben sumar los caudales
emitidos por cada nudo, para cada una de las flechas
utilizadas (0 y 0.25).
7. En cada nudo, se deben promediar los caudales
emitidos para las flechas de 0 y 0.25, y
posteriormente se asignará esta demanda constante a
dichas uniones. Como resultado de esto, se obtuvo
un nuevo submódulo de riego con las mismas
características topológicas iniciales, pero con
caudales constantes obtenidos a partir de promediar
los resultantes del paso 6.
Los pasos 8 y 9 de la metodología propuesta por
Hernández (2012) consisten en repetir el paso 5 y 6,
pero esta vez utilizando únicamente los caudales
promediados, obtenidos en el paso 7.
10. Comprobar la factibilidad del diseño obtenido en
el paso anterior, verificando que el coeficiente de
uniformidad (CU) sea mayor al establecido, y que en
ningún nudo del sistema se presenten presiones
inferiores a la mínima. Si el diseño resulta ser
factible, el algoritmo termina y se concluye que se
obtuvo una solución. En caso contrario se debe
proceder al paso 11.
11. Para continuar con la búsqueda de la solución
óptima se debe establecer a cual diseño se le
asignará el encontrado en el paso 9. Para esto, se
establecerá que si existen nudos con déficit de
presión, el diseño de la flecha 0.25 asumirá los
valores de la iteración anterior; por el contrario, si
no hay nudos con déficit de presión, será el diseño
de la flecha 0 quien tomará el valor de la iteración
anterior. Una vez reasignado este valor, se debe
volver al paso 7 hasta que el diseño resulte factible.
Este procedimiento sigue un algoritmo de bisección,
el cual alcanza el diseño óptimo luego de la quinta o
sexta iteración.
Luego de probar el algoritmo descrito en diferentes
submódulos de riego utilizados como casos de
estudio se pudo llegar a algunas conclusiones, con
las cuales se logró extrapolar la metodología que se
describirá más adelante.
Dentro de las conclusiones más importantes se
encontró que el diseño de mínimo costo para este
tipo de sistemas tiene una flecha ubicada en el rango
entre 0 y 0.25. Asimismo, se obtuvo que al iniciar el
proceso de optimización con una flecha de 0 se
obtenía una solución factible, en donde todos los
nudos cumplían con la restricción de presión mínima
pero sus costos constructivos eran los más altos. Por
el contrario, al iniciar con una flecha de 0.25 se
obtenían alternativas no factibles ya que algunos
nudos incumplían la restricción de presión mínimas,
pero tenían el costo constructivo más bajo. Estas
últimas alternativas se podían volver válidas a través
del proceso iterativo, llegando así a la solución
óptima del diseño (Hernández, 2012). Por lo
anterior, se sugiere que la superficie de gradiente
hidráulico inicial se encuentre lo más cerca posible a
la flecha de 0.25.
Emisores en Redes con Demandas
Dependientes de la Presión (DDP)
Como ya se mencionó, las redes con demandas
dependientes de la presión (DDP) se caracterizan por
la inclusión de emisores, los cuales son accesorios
presentes en los sistemas de riego encargados de
suministrar a cada planta de un cultivo el caudal y
nutrientes
necesarios
para
su
desarrollo
(Saldarriaga, 2007).
Sin embargo, dado que su caudal es función de su
presión, han resultado bastante útiles también en la
modelación de fugas en redes de distribución, y
redes contra incendio.
En cuanto al comportamiento hidráulico de estos
accesorios, se puede observar que relacionan la
presión en el nudo con el caudal demandado a través
de la curva descrita en la Ecuación 10.
(10)
en donde Q es el caudal del emisor, h la altura de
presión, k el coeficiente del accesorio y x su
exponente. Es importante recordar que esta
ecuación no es dimensionalmente homogénea, razón
por la cual k y x dependen del sistema de unidades
utilizado (Saldarriaga, 2007).
METODOLOGÍA PARA EL DISEÑO
OPTIMIZADO DE REDES ABIERTAS CON
DEMANDAS DEPENDIENTES DE LA
PRESIÓN
La metodología utilizada para el diseño optimizado
de redes abiertas con demandas dependientes de la
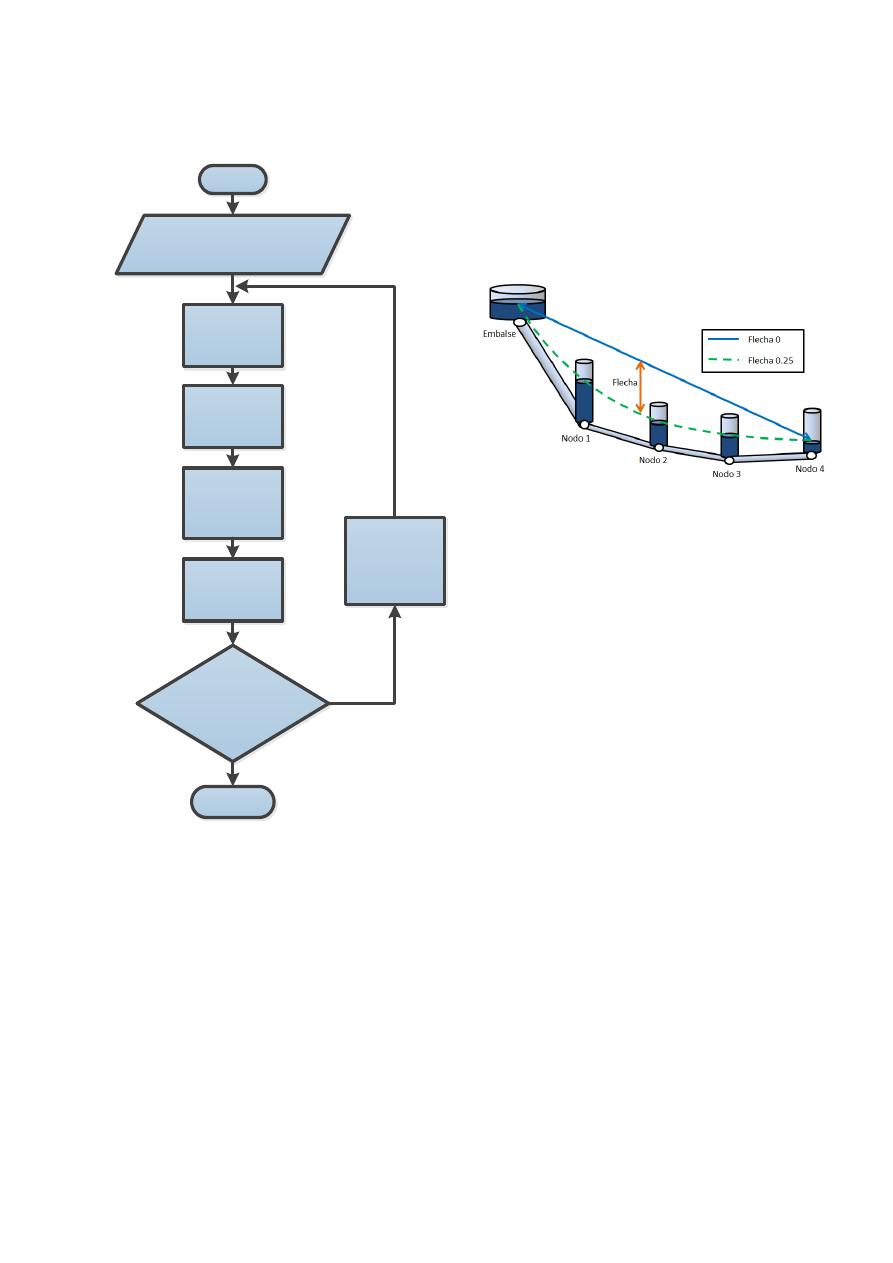
presión se muestra en la Figura 2, y su descripción
se realiza a continuación.
Figura 2. Diagrama de Flujo de la
Metodología Utilizada
Definición de la LGH Ideal
Como ya fue descrito por Hernández (2012), como
primer paso para resolver el problema de diseño de
redes abiertas con demandas dependientes de la
presión se debe establecer una superficie de
gradiente hidráulico para así poder asignar una
demanda constante a cada nudo de la red. Para este
fin, se buscó que la LGH estuviera lo más cercana
posible a la flecha de 0.25, como se muestra en la
Figura 3, lo cual se logró asignando la presión
mínima en cada nudo de la red. Para esta
investigación se estableció que la presión mínima en
cada nudo debía ser 15 mca.
Este procedimiento se realizó como consecuencia de
lo establecido por Hernández (2012) respecto a la
sensibilidad del diseño a la flecha inicial utilizada,
en donde se encontró al iniciar el algoritmo con una
flecha de 0.25 se obtienen los menores costos
constructivos, pero no se satisface la restricción de
presiones por la subestimación de los caudales de los
emisores.
Figura 3. LGH Ideal para comenzar el Diseño
Comparado con la Flecha 0
Cálculo de las Demandas de la Red
El caudal demandado en cada uno de los nudos de la
red se puede dividir en dos términos: La demanda
base y el caudal del emisor.
La demanda base de los nudos se establece por el
diseñador. Por su parte, el caudal de cada uno de los
emisores presentes en la red se obtiene haciendo uso
de la Ecuación 10, en donde k es un coeficiente y x
el exponente del accesorio.
Finalmente, el caudal demandado en cada nudo se
puede establecer a través de la Ecuación 11.
(11)
Diseño de la Red Utilizando Programación
Lineal
Una vez calculados los caudales en cada nudo se
debe realizar el diseño de la red haciendo uso de la
Programación Lineal. Para este fin se siguió la
metodología de Hernández (2012), en donde con los
caudales se formaba un archivo que sería ingresado
al software optimizador, y el cual se compone de 4
matrices:
1. Matriz de Costo: Dado la longitud de cada tramo
de la red, y la lista de diámetros comerciales, esta
matriz relaciona cada tramo de tubería de la red con
INICIO
Topología del sistema,
Hmin, Hmax, Presión
Mínima, Diámetros, ks
Definición de la
LGH Ideal
Cálculo de las
Demandas de la
Red
Diseño de la red
utilizando
Programación
Lineal
Ejecución
Hidráulica de la
Red con DDP
¿La presión en todos los
nodos es mayor a 15 mca?
FIN
Asignar
P = Pmin en los
nodos con
déficit de
presión
SI
NO

su costo, mostrando como alternativas los diferentes
diámetros disponibles.
2. Matriz de Pérdidas Totales: Para cada tramo de la
red, reúne el valor de las pérdidas de presión para
cada uno de los diámetros disponibles. Este cálculo
se realiza a través de la ecuación de Darcy-
Weisbach.
3. Matriz de Conectividad: Indica las conexiones en
la topología del sistema a través de tuberías
asignando el valor de 1.0 donde esta condición se
cumpla.
4. Matriz de LGH Mínimas: Para cada nudo de la
red, recopila la línea de gradiente hidráulico mínima.
Una vez definidas las matrices, se ingresa esta
información al software optimizador, en donde
previamente se implementó la formulación mostrada
a continuación.
Formulación
Para comenzar, se definió N como el conjunto de
nudos en la red,
como el conjunto de diámetros
comerciales disponibles, y
como una variable
de decisión la cual tomará el valor de 1 si a la
tubería que va desde el nudo i
N hasta el nudo j
N se le asignó el diámetro d
, o toma el valor de
0 en caso contrario. Asimismo, se definió la variable
auxiliar
, la cual representa la altura total en el
nudo i
N.
La función objetivo utilizada en la formulación del
problema de optimización asociado con el diseño de
la red se muestra a continuación en la Ecuación 12.
∑ ∑ ∑
(12)
en donde
es el costo de asignarle el diámetro d
D a la tubería que va del nudo i N hasta el nudo
j
N.
En cuanto a las restricciones utilizadas, estas se
describen a continuación:
Restricción de la presión mínima permitida, la
cual se estableció en la Ecuación 8, mostrada en
el marco teórico.
Restricción que asegura la conservación de
energía para cada tubería. La altura total en el
nudo j
N aguas abajo del nudo i N será igual
a la altura total en el nudo i menos las pérdidas
totales de presión producidas en el tubo que va
del nudo i
N al nudo j N cuando el diámetro
d
D fue asignado.
∑
(13)
en donde
es la altura aguas abajo del nudo,
la
altura aguas arriba del mismo,
las pérdidas
totales de presión que ocurren en el tubo que conecta
al nudo i
N con el nudo j N cuando el diámetro d
D es asignado, y w(i,j) es una función que toma el
valor de 1 cuando el tubo que va de i a j existe, y 0
en caso contrario.
Restricción que asegura que solamente un
diámetro sea asignado a cada tubería.
∑
(14)
Luego de realizar el diseño con la presentación
formulada, se obtiene como resultado un conjunto de
diámetros para toda la red.
Ejecución Hidráulica de la Red con
Demandas Dependientes de la Presión
Recordando que el diseño obtenido en el paso
anterior fue realizado con demandas constantes, es
importante verificar el comportamiento hidráulico de
la solución obtenida al ser modelada con demandas
dependientes de la presión.
Para este fin, se realiza una ejecución hidráulica de
la red calculando las presiones en cada uno de los
nudos. Con este paso se termina la primera iteración
del algoritmo propuesto.
Proceso Iterativo
Una vez obtenidas las presiones a partir de la
ejecución hidráulica del paso anterior, se debe
verificar que se cumpla la restricción de presión
mínima en cada uno de los nudos de la red. Para
todos aquellos nudos que presenten déficit de
presión, se les deberá asignar el valor mínimo (15
mca) y se iniciará una nueva iteración. El proceso
iterativo finaliza una vez no se tenga ningún nudo en
la red con déficit de presión.
CASOS DE ESTUDIO
La metodología propuesta se probó en un total de 12
redes, las cuales tenían una configuración igual en
cuanto a la cantidad de tubos (25 tuberías en serie) y
su topología, así como en la demanda base en cada
uno de los nudos, la cual se fue de 4.5 L/s. La lista
de diámetros comerciales utilizada en los diseños se
compuso por tubos de 50, 75, 100, 150, 200, 250,
300, 350, 400, 450, 500, 600 y 750 milímetros, con
una rugosidad absoluta (k
s
) igual a 0.0015 mm. Los
parámetros utilizados en la función de costos
asociados con la tubería se muestran en la
Ecuación15.
(15)
Asimismo, se utilizó una presión mínima de 15 mca,
las pérdidas por fricción se calcularon utilizando la
ecuación de Darcy-Weisbach y se consideró que no
se tenían pérdidas menores en el sistema.
Las redes utilizadas como casos de estudio fueron
diseñadas también con la metodología SOGH con
flechas entre 0 y 0.25 a fin de tener valores base para
comparar con los resultados obtenidos por la
aproximación propuesta.
En cuanto a las características que diferenciaban
cada uno de los 12 sistemas respecto los demás se
tenía en primer lugar la topografía de la red, y en
segundo lugar, los parámetros característicos de los
emisores
utilizados.
Como
se
mostrará
a
continuación, se analizaron 4 combinaciones
posibles de emisores en la red, así como 3
topografías distintas, resultando un total de 12 redes
distintas para ser analizadas.
En cuanto a los parámetros utilizados para la
modelación de los emisores, se consideraron dos
coeficientes diferentes, así como cuatro exponentes
de estos. Estos emisores fueron colocados en todos
los nudos de la red según diferentes combinaciones,
las cuales se muestran en la Tabla 1.
Tabla 1. Coeficientes y Exponentes
Utilizados en los Emisores
Combinación
Coeficiente
Exponente
1
0.3
0.25
2
0.3
0.5
3
0.3
1.0
4
0.03
2.0
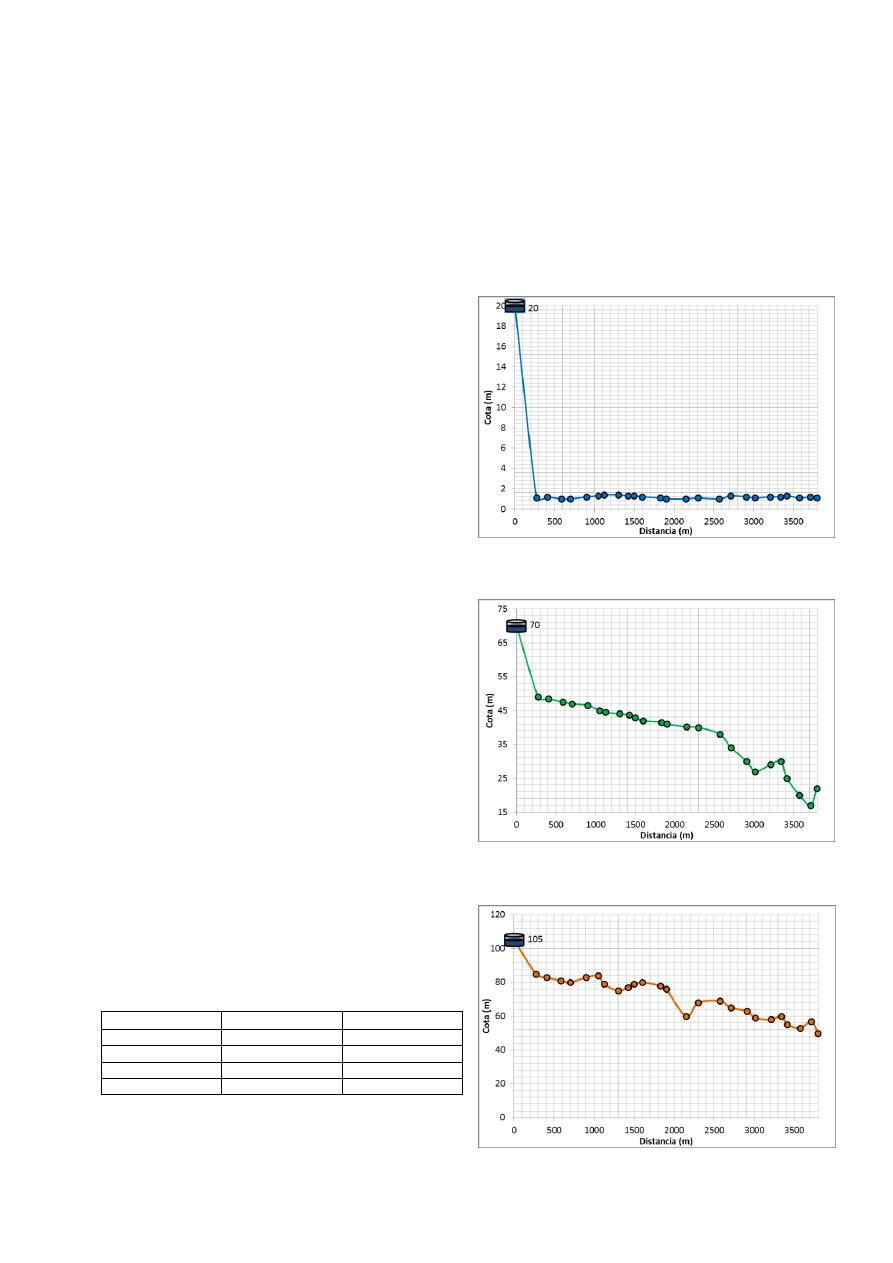
Para la topografía de la red, se plantearon tres casos,
los cuales se muestran en las figuras a continuación.
El primer caso, mostrado en la Figura 4 y
denominado MA, corresponde a una topografía
suave, con un embalse cuya altura total es de 20 m.
El segundo caso, mostrado en la Figura 5 y
denominado SA, se trata de una topografía empinada
con orientación descendiente, y cuyo embalse posee
una altura total de 70 m. Finalmente, el tercer caso
mostrado en la Figura 6 y denominado SB, se trata
de una topografía empinada, cuyo embalse se
encuentra a una altura total de 105 m.
Figura 4. Topografía Suave (M)
Figura 5. Topografía Empinada A (SA)
Figura 6. Topografía Empinada B (SB)
PRESENTACIÓN Y ANÁLISIS DE
RESULTADOS
Una vez aplicada la metodología a las 12 redes
utilizadas como caso de estudio se obtuvieron los
resultados que se describirán a continuación.
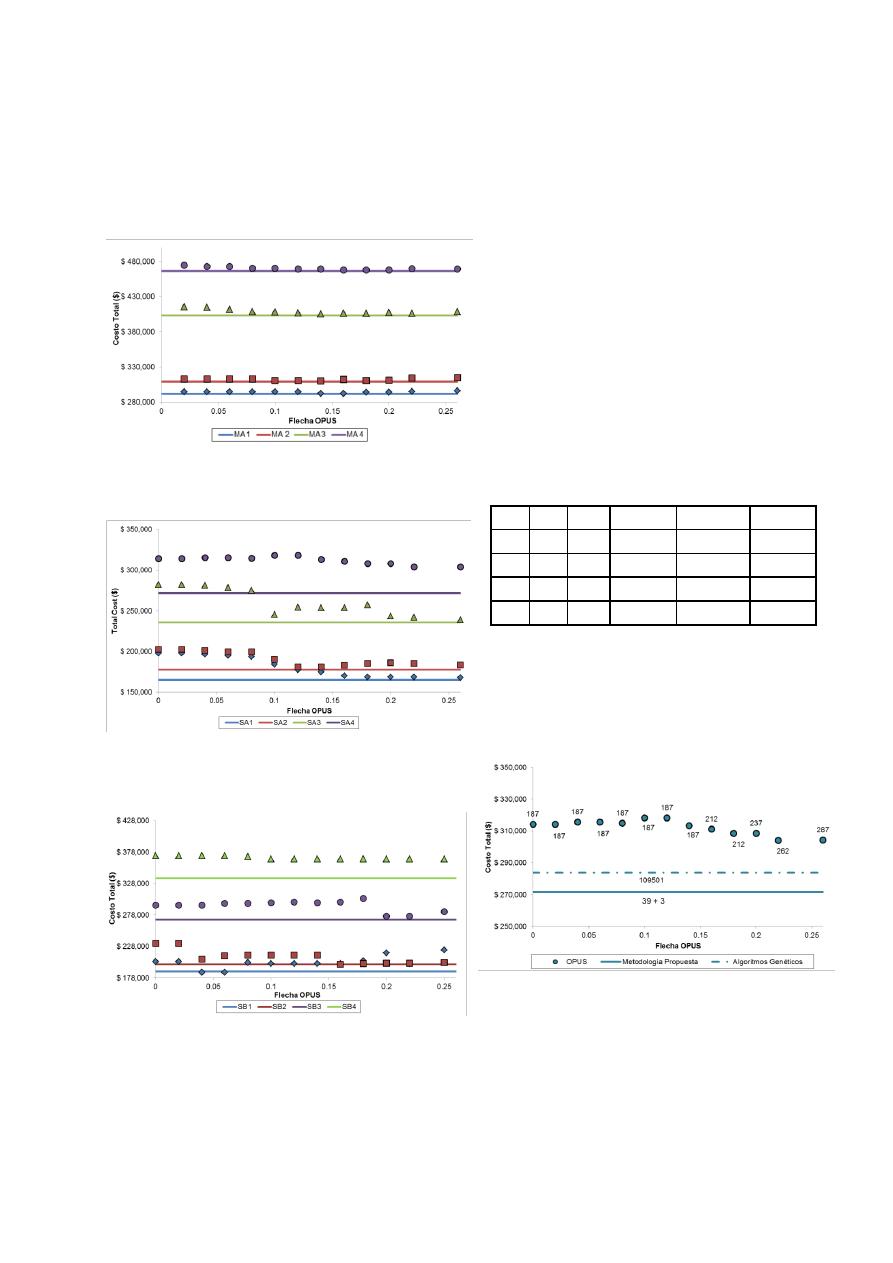
Figura 7. Costos Totales de las Redes en la
Topografía Suave A (MA)
Figura 8. Costos Totales de las Redes en la
Topografía Empinada A (SA)
Figura 9. Costos Totales de las Redes en la
Topografía Empinada B (SB)
El primer resultado destacable de la metodología
propuesta corresponde a la reducción en costos de
los diseños resultantes. A continuación, en las
Figuras 7, 8 y 9, se muestran los resultados
obtenidos para cada una de las redes tanto para
OPUS y las flechas entre 0 y 0.25 así como para la
metodología propuesta (línea recta en las gráficas).
Como ya se mencionó, para cada topografía se
tienen combinaciones de parámetros de emisores
como (0.3, 0.25), (0.3, 0.5), (0.3, 1.0) y (0.03, 2.0),
correspondientes a los números 1, 2, 3 y 4 en cada
figura.
Como se puede observar en la Figura 8, así como en
la Tabla 2, la mayor reducción en los costos se logró
en la Red SA-4. Por su parte, en la Red SB-1 se
presentó un sobrecosto de la metodología propuesta
respecto a OPUS. Dado que de los 12 casos de
estudio analizados, en 11 se obtuvieron costos
menores a los de OPUS, se puede concluir que el
algoritmo propuesto está encontrando soluciones
muy cercanas a la óptima en todas las redes.
Tabla 2. Reducción en Costos en Cada Una
de las Redes
Red
K
x
SA
SB
MA
1
0,3
0,25 $ 2,891.28 $ -1,082.81 $ 429.17
2
0,3
0,5 $ 2,273.03 $ 170.35 $ 951.07
3
0,3
1,0 $ 3,082.67 $ 5,019.52 $ 1,904.25
4
0,03
2,0 $ 32,440.1 $ 281,44.26 $ 1,857.13
El segundo resultado destacable de la metodología
propuesta es el número de iteraciones requerido para
llegar a la solución óptima respecto a otras
metodologías utilizadas como OPUS o Algoritmos
Genéticos.
Figura 10. Número de Iteraciones Según la
Metodología Utilizada para la Red SA-4
Como se puede observar en la Figura 10, al diseñar
la Red SA-4 se realizaron solamente 42 iteraciones
de la metodología propuesta, mientras que a OPUS
le tomó en promedio 209 iteraciones y a Algoritmos
Genéticos le tomó 109,501 iteraciones. Es
importante mencionar que dentro de las 42
iteraciones realizadas por la aproximación propuesta
se
encuentran
39
repeticiones
considerando
demandas constantes, mientras que 3 de ellas si
consideran las demandas dependientes de la presión
a través de los emisores. Por su parte, a pesar que
OPUS y AG consideran los caudales en función de
la presión, se demoran una cantidad significativa de
iteraciones adicionales a las de la metodología
propuesta, mostrando así una de las principales
ventajas de esta respecto a las demás.
Ahora bien, al analizar la Tabla 3 se puede observar
la reducción porcentual en el número de iteraciones
de la metodología propuesta respecto a las realizadas
por OPUS para alcanzar el óptimo (únicamente para
la flecha óptima). De acuerdo con lo anterior, las
mayores reducciones, superiores al 52%, se
obtuvieron para la topografía suave (MA), y para la
empinada (SA). En el caso de la topografía SB fue
necesario realizar más iteraciones, las cuales se
pueden atribuir a que esta topografía presenta más
oscilaciones en el terreno, e incluso un pico, lo cual
afecta el cumplimiento del requerimiento de las
presiones.
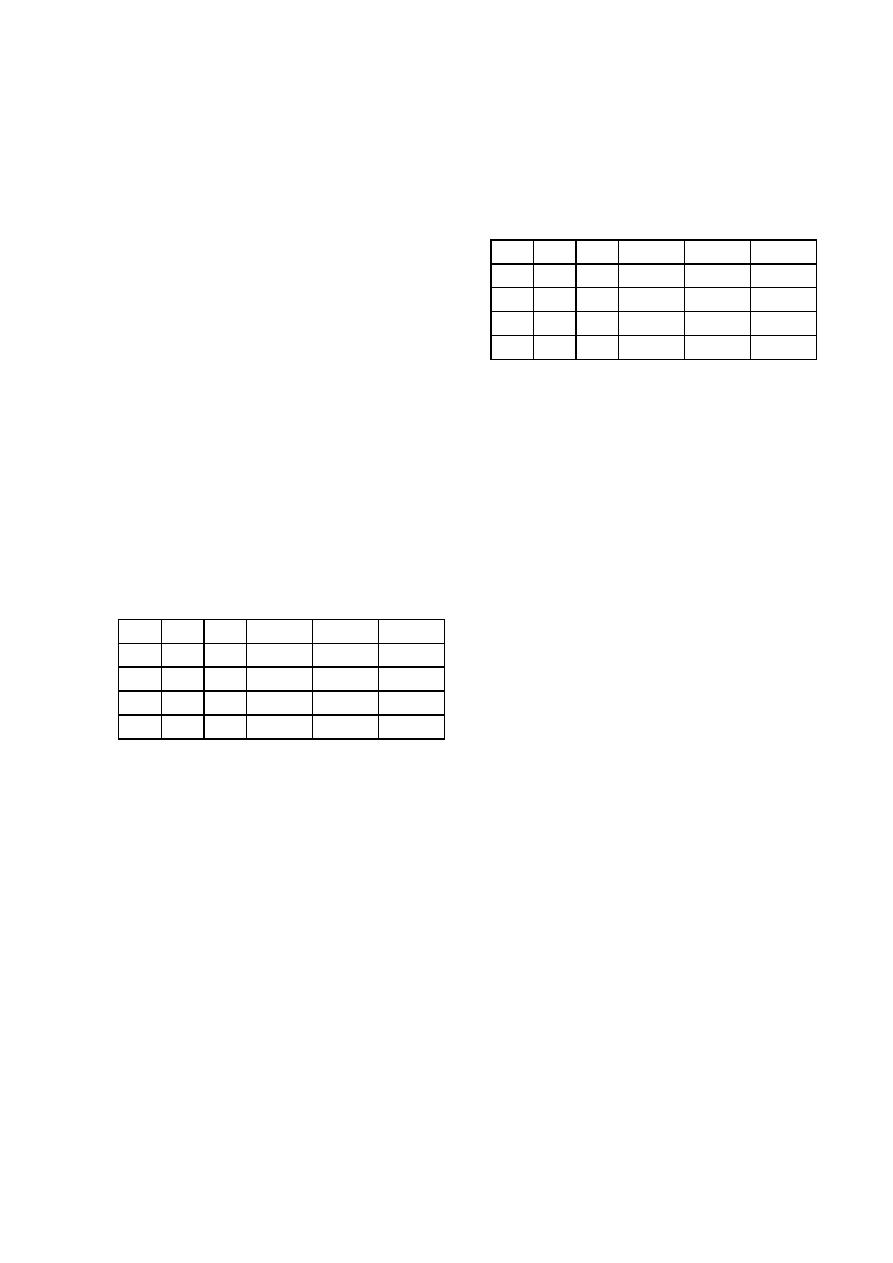
Tabla 3. Reducción Porcentual de
Iteraciones Respecto OPUS Para Alcanzar el
Óptimo
Red
K
x
SA
SB
MA
1
0,3
0,25
78.95%
17.65%
52.54%
2
0,3
0,5
79.90%
59.22%
79.41%
3
0,3
1,0
66.67%
18.25%
68.42%
4
0,03
2,0
82.28%
27.84%
65.22%
Es importante recordar que en la Tabla 3 se muestra
la reducción de iteraciones de la metodología
propuesta respecto a OPUS, pero únicamente
considerando la flecha que llegó a la solución
óptima. Dado que se trató con demandas
dependientes de la presión no fue posible identificar
a priori la flecha que llevaría a la solución óptima ya
que esta depende de la distribución de demandas en
el sistema, y estas no se conocen antes de realizar el
diseño. Por lo anterior, resulta interesante analizar la
reducción de iteraciones que tuvo la metodología
propuesta respecto al número total de ejecuciones
hidráulicas realizadas por OPUS para el total de
flechas probadas.
Como se puede observar en la Tabla 4, en la
topografía que se logró una mayor reducción en el
número de iteraciones fue en la SB, lo cual resulta
interesante ya que al analizar la reducción en la
cantidad de ejecuciones hidráulicas para alcanzar el
óptimo en este tipo de terreno fue el que obtuvo la
menor reducción. Finalmente, dado que en las tres
topografías se obtuvo una reducción superior al 95%
respecto OPUS se puede concluir que la
metodología propuesta es muy eficiente en cuanto el
tiempo computacional requerido.
Tabla 4. Reducción Porcentual del Total de
Iteraciones Respecto OPUS
Red
K
x
SA
SB
MA
1
0,3
0,25
98.62%
99.96%
97.56%
2
0,3
0,5
98.00%
99.98%
97.50%
3
0,3
1,0
97.41%
99.95%
96.55%
4
0,03
2,0
98.88%
99.95%
95.79%
CONCLUSIONES, RECOMENDACIONES, Y
TRABAJO FUTURO
Se presentó, y aplicó a 12 redes diferentes una
metodología de diseño que combina criterios
hidráulicos para predefinir una línea de gradiente
hidráulico objetivo con Programación Lineal
enfocada hacia sistemas con demandas dependientes
de la presión. Como resultado, esta mostró
beneficios en cuanto a la calidad de la solución, y la
cantidad de tiempo computacional requerido. El
primer beneficio se reflejó en la obtención de
menores costos constructivos que OPUS en todas las
redes analizadas, la cual se utilizó como valor base
al fin de comparar los resultados. Asimismo, la
segunda ventaja se hizo evidente al lograr una mayor
eficiencia en el tiempo computacional requerido,
reflejándose esto en un menor número de
ejecuciones hidráulicas realizadas para alcanzar el
óptimo respecto a la metodología utilizada
anteriormente (OPUS).
Se ratificó la importancia de la flecha inicial
utilizada en la generación de la superficie de
gradiente hidráulico, la cual como concluyó
Hernández (2012), obtendrá resultados con menores
costos constructivos entre esta más cercana sea a
0.25.
Esta investigación establece el primer paso de
futuros desarrollos en cuanto a metodologías que
resuelvan el problema de diseño optimizado de
RDAP
aplicado
a
sistemas
con
demandas
dependientes de la presión en redes de mayor
complejidad. Lo anterior resulta muy útil en el
diseño de redes contra incendios, la modelación de
RDAP considerando fugas, entre otros.

BIBLIOGRAFÍA
Farmani, R., Abadia, R. y Savic, D. (2007).
“Optimum Design and Management of
Pressurized Branched Irrigation Networks.”
Journal
of
Irrigation
and
Drainage
Engineering, 133(6), pp. 528-537.
González-Cebollada, C., Macarulla, B., y Sallán, D.
(2011). “Recursive Design of Pressurized
Branched Irrigation Networks.” Journal of
Irrigation and Drainage Engineering, 137(6),
pp. 375-382.
Hernández, D. (2012). “Diseño Optimizado de
Submódulos
de
Sistemas
de
Riego
Localizado de Alta Frecuencia”. Bogotá:
Universidad de los Andes.
Ochoa, S. (2009). “Diseño Optimizado de Redes de
Distribución de Agua Potable con Base en el
Concepto Energético de Superficie Óptima
de
Gradiente
Hidráulico”.
Bogotá:
Universidad de los Andes.
Ostfeld, A. y Tubaltzev, A. (2008). “Ant Colony
Optimization for Least-Cost Design and
Operation of Pumping Water Distribution
Systems.” Journal of Water Resources
Planning Management, 134(2), pp. 107-118.
Pizarro, F. (1996). “Riegos Localizados de Alta
Frecuencia (RLAF). Goteo, Microaspersión,
Exudación”. Madrid: Mundi-Prensa.
Reca, J., Martínez, J., Gil, C. y Baños, R. (2007).
“Application of Several Metaheuristic
Techniques to the Optimization of Real
Looped Water Distribution Networks.”
Water Resources Management, 22(10), pp.
1367-1379.
Saldarriaga, J. (2007). “Hidráulica de Tuberías.
Abastecimiento de Agua, Redes, Riego”.
Bogotá: Alfaomega. ISBN 978-958-682-
680-8.
Savic, D. y Walters, G. (1997). “Genetic Algorithms
for Least Cost Design of Water Distribution
Networks.” Journal of Water Resources
Planning Management, 123(2), pp. 67-77.
Spiliotis, M. y Tsakiris, G. (2007). “Minimum Cost
Irrigation Network Design Using Fuzzy
Integer Programming.” Journal of Irrigation
and Drainage Engineering, 133(3), pp. 242-
248.
Wu, I. (1975). “Design of Drip Irrigation Main
Lines.” Journal of Irrigation and Drainage
Division, 101(4), pp. 265-278.
Wu, Z. y Simpson, A. (2001). “Competent Genetic-
Evolutionary
Optimization
of
Water
Distribution
Systems.”
Journal
of
Computing in Civil Engineering, 15(2), pp.
89-101.
