
Universidad de los Andes
Facultad De Ingeniería
Departamento de Ingeniería Civil y Ambiental
Tesis 2
Estudio del comportamiento de resaltos hidráulicos en tuberías
parcialmente llenas de sección circular, con Números de Froude
supercríticos menores a 4
Preparado por:
Ing. Laura Elizabeth Montaño Luna
Asesor:
Ing. Juan Saldarriaga
Informe Final Proyecto de grado
Bogotá, Junio 2013

Agradecimientos
Para culminar cualquier trabajo se requiere de dedicación, esfuerzos y sacrificios, los cuales son
superados gracias a todas aquellas personas que de una u otra forma fueron un apoyo en la escalera
para culminar con éxito esta etapa. Por esta razón quiero agradecer primero que todo a Dios que me
ha permitido ir avanzado poco a poco en mi proyecto de vida, a mis padres que han sido siempre un
apoyo incondicional y mi fuerza en el camino, a mi asesor de tesis Juan Saldarriaga, quien me fue
orientando poco a poco hasta obtener el resultado de éste proyecto, a Jaysson Guerrero por
acompañarme desde un inicio en ésta etapa, a John Calvo por brindarme el tiempo y la dedicación
en el Laboratorio de Hidráulica, y finalmente a CIACUA y a todas aquellas personas que de una u
otra forma participaron en éste proyecto, dedicándome su tiempo, su amistad y colaboración.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
I
Tabla de contenido
Índice de Tablas ................................................................................................................................ IV
Índice de Ilustraciones ....................................................................................................................... VI
Índice de Ecuaciones ........................................................................................................................ VII
Notación ............................................................................................................................................. X
1.
Introducción ................................................................................................................................ 1
1.1 Objetivos .................................................................................................................... 3
1.1.1.
Objetivo General ............................................................................................. 3
1.1.2.
Objetivos Específicos ...................................................................................... 3
2.
Antecedentes ................................................................................................................ 4
3.
Marco Teórico ............................................................................................................ 29
3.1.
Resaltos Hidráulicos ............................................................................................. 29
3.1.1.
Definición .................................................................................................... 29
3.1.2.
Tipos de Resaltos Hidráulicos ......................................................................... 30
3.1.3.
Cálculo de profundidades subsecuentes en el Resalto Hidráulico......................... 31
3.1.4.
Análisis del comportamiento del resalto hidráulico ............................................ 35
4.
Diseño del modelo ....................................................................................................... 37
4.1.
Ubicación ............................................................................................................ 37
4.2.
Proceso de diseño ................................................................................................. 37
4.3.
Aparatos de medición ........................................................................................... 38
4.3.1.
Sensor Ultrasónico U – GAGE T30 ................................................................. 38
4.3.2.
ADV (Velocímetro Doppler acústico) .............................................................. 39
4.3.3.
Piezómetros .................................................................................................. 40
4.3.4.
Caudalímetro ................................................................................................ 41
4.4.
Metodología y proceso de medición ....................................................................... 41
4.4.1.
Profundidad del flujo ..................................................................................... 41
4.4.1.1.
Parámetros de medición ............................................................................. 41
4.4.1.2.
Metodología de medición............................................................................ 42
4.1.1.3.
Lista de caudales y pendientes .................................................................... 42

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
II
4.4.2.
Distribución de velocidades ............................................................................ 46
4.4.2.1.
Parámetros de medición ............................................................................. 46
4.4.2.2.
Metodología de medición............................................................................ 46
4.4.2.3.
Lista de caudales y pendientes .................................................................... 46
5.
Pruebas de verificación de los parámetros hidráulicos de la tubería.................................... 48
5.1.
Comprobación de Diseño ...................................................................................... 48
5.2.
Análisis caudales máximos para diferentes pendientes .............................................. 51
5.3.
Análisis del valor máximo del Número de Froude .................................................... 52
5.4 Análisis Comparativo con otros autores para el cálculo de la profundidad subsecuente al
resalto hidráulico ............................................................................................................ 56
5.4.1 Silvester ............................................................................................................. 56
5.4.2 Straub ................................................................................................................ 61
5.4.3 French ............................................................................................................... 62
5.4.4 Hager ................................................................................................................. 65
5.4.5 FHWA ............................................................................................................... 68
5.4.5 Conclusiones ...................................................................................................... 71
5.5 Análisis comparativo con otros autores para el cálculo de la longitud del resalto hidráulico 72
5.5.1 Silvester ............................................................................................................. 72
5.5.2 Hager ................................................................................................................. 74
5.5.3 FWHA ............................................................................................................... 74
6.
Resultados y Análisis de Resultados .............................................................................. 76
6.1.
Resultados ........................................................................................................... 76
6.1.1.
Registro Fotográfico ...................................................................................... 76
6.1.2.
Profundidad de flujo ...................................................................................... 78
6.1.3.
Longitud del resalto hidráulico........................................................................ 80
6.1.4.
Distribución de Velocidades ........................................................................... 84
6.2.
Análisis de Resultados .......................................................................................... 87
6.2.1.
Análisis profundidades subsecuentes ............................................................... 87
6.2.2.
Análisis del comportamiento de la Energía en el resalto hidráulico ...................... 92
6.2.3.
Análisis Conservación del Momentum ............................................................. 96

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
III
6.2.4.
Comparación entre los resultados empíricos y teóricos de las profundidades
subsecuentes ............................................................................................................... 99
6.2.5.
Ecuación profundidades subsecuentes en el Resalto Hidráulico ......................... 101
6.2.6.
Análisis del comportamiento de la longitud en el Resalto Hidráulico ................. 102
6.2.7.
Comparación entre los resultados empíricos y teóricos de la longitud del resalto
hidráulico ................................................................................................................. 105
6.2.8.
Ecuación longitud del resalto hidráulico para tuberías circulares ....................... 105
6.2.9.
Análisis de disipación de energía en el Resalto Hidráulico ............................... 105
6.2.10.
Análisis del comportamiento de la distribución de velocidades en el resalto
hidráulico ................................................................................................................. 107
7.
Conclusiones ............................................................................................................ 112
8.
Recomendaciones ...................................................................................................... 113
8.1.
Recomendaciones de diseño ................................................................................ 113
8.2.
Recomendaciones para futuras pruebas ................................................................. 113
9.
Glosario ................................................................................................................... 114
10.
Bibliografía ........................................................................................................... 115
11.
Anexos ................................................................................................................. 117
11.1.
Cálculo de la profundidad normal del flujo ........................................................ 118
11.2.
Cálculo de la profundidad subsecuente del resalto hidráulico mediante el método
desarrollado por Silvester .............................................................................................. 121
11.3.
Cálculo de la profundidad subsecuente del resalto hidráulico por el Método
desarrollado por French ................................................................................................. 124
11.4.
Cálculo de la profundidad subsecuente del resalto hidráulico por el Método
desarrollado por Hager ................................................................................................. 126
11.5.
Cálculo de la profundidad subsecuente del resalto hidráulico por el Método
desarrollado por FHWA. ............................................................................................... 128

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
IV
Índice de Tablas
Tabla 1. Valores de k' dependiendo de la relación de llenado (Silvester, 1964). .............................. 10
Tabla 2. Coeficientes para tuberías circulares horizontales (FHWA, 2006). .................................... 27
Tabla 3. Tipos de Resaltos Hidráulicos en fondos sin pendiente (Gonzales Rodríguez, 1992). ....... 30
Tabla 4. Lista de caudales y pendientes. .......................................................................................... 42
Tabla 5. Lista de caudales y pendientes para el análisis del comportamiento de la velocidad. ....... 46
Tabla 6. Diámetros seleccionados que superen el caudal de diseño y no superen los 48 cm de altura
con relaciones de llenado del 50 %. .................................................................................................. 50
Tabla 7. Diámetros seleccionados que superen el caudal de diseño y no superen los 48 cm de altura
con relaciones de llenado del 85 %. .................................................................................................. 50
Tabla 8. Diámetros seleccionados que superen el caudal de diseño y no superen los 48 cm de altura
con relaciones de llenado del 92.9 %. ............................................................................................... 51
Tabla 9. Valores de k' dependiendo de la relación de llenado (Silvester, 1964). .............................. 57
Tabla 10. Cálculo de la profundidad subsecuente para una pendiente del 1.9%. .............................. 57
Tabla 11. Cálculo de la profundidad subsecuente para una pendiente del 3.1%. .............................. 58
Tabla 12. Cálculo de la profundidad subsecuente para un caudal de 0.01 m
3
/s. ............................... 59
Tabla 13. Cálculo de la profundidad subsecuente para un caudal de 0.1 m
3
/s. ................................. 60
Tabla 14. Cálculo de la profundidad subsecuente para una pendiente de 0.019 mediante la
metodología planteada por Straub. .................................................................................................... 62
Tabla 15. Cálculo de la profundidad subsecuente para una pendiente de 0.031 mediante la
metodología planteada por Straub. .................................................................................................... 62
Tabla 16. Resultados obtenidos mediante la metodología de French para una S = 0.019. ............... 64
Tabla 17. Resultados obtenidos mediante la metodología de French para una S = 0.031. ............... 64
Tabla 18. Resultados obtenidos para una pendiente de 0.019 con la metodología planteada por
Hager. ................................................................................................................................................ 65
Tabla 19. Resultados obtenidos para una pendiente de 0.031 con la metodología planteada por
Hager. ................................................................................................................................................ 66
Tabla 20. Resultados de la profundidad subsecuente del resalto hidráulico para la aproximación
teórica con una pendiente de 0.019. .................................................................................................. 67
Tabla 21. Resultados de la profundidad subsecuente del resalto hidráulico para la aproximación
teórica con una pendiente de 0.031. .................................................................................................. 67
Tabla 22. Resultados para el cálculo de la profundidad subsecuente del resalto mediante la
metodología planteada por la FHWA, para una pendiente de 0.019. ................................................ 69
Tabla 23. Resultados para el cálculo de la profundidad subsecuente del resalto mediante la
metodología planteada por la FHWA, para una pendiente de 0.031. ................................................ 69
Tabla 24. Cálculo de la longitud mediante la metodología planteada por Silvester. ........................ 73
Tabla 25. Cálculo longitudes en el resalto hidráulico de acuerdo con la metodología planteada por
Hager. ................................................................................................................................................ 74

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
V
Tabla 26. Cálculo de la longitud del resalto con la metodología de FWHA. .................................... 75
Tabla 27. Registro fotográfico del resalto hidráulico para caudales cercanos a 30 L/s. ................... 76
Tabla 28. Comportamiento de la velocidad de las partículas en diferentes secciones transversales
para S = 1.2 % y Q = 24 L/s. ............................................................................................................. 84
Tabla 29. Comportamiento de la velocidad de las partículas en diferentes secciones verticales para S
= 1.2 % y Q = 24 L/s. ........................................................................................................................ 85
Tabla 30. Comportamiento de la velocidad de las partículas en diferentes secciones transversales
para S = 1.6 % y Q = 24 L/s. ............................................................................................................. 86
Tabla 31. Comportamiento de la velocidad de las partículas en diferentes secciones verticales para S
= 1.6 % y Q = 24 L/s. ........................................................................................................................ 87
Tabla 32. Ecuaciones sin corrección que describen el comportamiento del resalto hidráulico en
tuberías. ............................................................................................................................................. 93
Tabla 33. "m" y "k" para cada pendiente. ........................................................................................ 94
Tabla 34. Ecuaciones sin corrección que describen el comportamiento del resalto hidráulico en
tuberías. ............................................................................................................................................. 97
Tabla 35. “m” y “k” para cada pendiente. ......................................................................................... 98
Tabla 36. Error cuadrático medio para las diferentes ecuaciones evaluadas................................... 100
Tabla 37. Rango de validez de laEcuación 84 y la Ecuación 85. ................................................... 100
Tabla 38. Error cuadrático medio para las diferentes ecuaciones evaluadas................................... 105
Tabla 39. Comportamiento de la distribución de la velocidad en el resalto hidráulico. ................. 108

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
VI
Índice de Ilustraciones
Ilustración 1. Montaje realizado por Kindsvater y Lane (Kindsvater, 1938). ..................................... 4
Ilustración 2. Montaje de Kalinske y Robertson (Robertson & Kalinske, 1943). ............................... 5
Ilustración 3. Datos típicos de profundidades y presiones en un Resalto Hidráulico (Robertson &
Kalinske, 1943). .................................................................................................................................. 7
Ilustración 4. Diagrama de niveles en la tubería. .............................................................................. 15
Ilustración 5. Vista lateral de diferentes resaltos hidráulicos (Stahl & Hager, 1999). ...................... 19
Ilustración 6. Vista en perfil de los diferentes tipos de Resalto Hidráulico (Stahl & Hager, 1999). . 20
Ilustración 7. Longitudes del resalto hidráulico planteadas por Hager (Stahl & Hager, 1999). ........ 20
Ilustración 8. Resalto Hidráulico (Akan, 2006). ............................................................................... 29
Ilustración 9. Profundidad subsecuente menor al diámetro de la tubería (Ghamry, Shames, &
Branch, 2002). ................................................................................................................................... 29
Ilustración 10. Profundidad subsecuente mayor al diámetro de la tubería (Ghamry, Shames, &
Branch, 2002). ................................................................................................................................... 29
Ilustración 11. Tipos de Resaltos Hidráulicos (Gonzales Rodríguez, 1992). .................................... 31
Ilustración 12. Canal donde su ubicó el montaje. .............................................................................. 37
Ilustración 13. Vista dentro de la tubería. ......................................................................................... 38
Ilustración 14. Vista de la compuerta con el neumático. ................................................................... 38
Ilustración 15. Vista de la compuerta en el montaje. ........................................................................ 38
Ilustración 16. Vista perfil de la compuerta. ..................................................................................... 38
Ilustración 17. Características del U - GAGE T30 (Banner Engineering). ...................................... 39
Ilustración 18. U - GAGE T30. ......................................................................................................... 39
Ilustración 19. ADV (SonTek, 2012). ............................................................................................... 40
Ilustración 20. Adaptación del ADV en la tubería. ........................................................................... 40
Ilustración 21. Piezómetros en la tubería. ......................................................................................... 41
Ilustración 22. Caudalímetro ABB. ................................................................................................... 41
Ilustración 23.Matriz geométrica de medición de la Distribución de Velocidades. .......................... 46

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
VII
Índice de Ecuaciones
Ecuación 1. Ecuación para hallar la ecuación de fuerza del resalto (Silvester, 1964). ....................... 8
Ecuación 2. Ecuación para hallar la fuerza del resalto (Silvester, 1964). ........................................... 8
Ecuación 3. Número de Froude. .......................................................................................................... 8
Ecuación 4. Proceso para encontrar profundidades subsecuentes. ...................................................... 8
Ecuación 5. Proceso para hallar profundidades subsecuentes. ............................................................ 8
Ecuación 6. Ecuación 5 reorganizada.................................................................................................. 8
Ecuación 7. Relación Número de Froude (Silvester, 1964). ............................................................... 9
Ecuación 8. Número de Froude aguas abajo del resalto. ..................................................................... 9
Ecuación 9. Proceso para encontrar las profundidades subsecuentes en cualquier forma de canal. ... 9
Ecuación 10. Profundidades subsecuentes para cualquier tipo de canal (Silvester, 1964). ................ 9
Ecuación 11. Valor de la proporción entre la profundidad de llenado y el centro de masa para
tuberías parcialmente llenas (Silvester, 1964). .................................................................................. 10
Ecuación 12. Profundidades subsecuentes para tuberías parcialmente llenas (Silvester, 1964). ...... 10
Ecuación 13. Valor de la proporción entre la profundidad de llenado y el centro de gravedad para
tuberías llenas (Silvester, 1964). ....................................................................................................... 10
Ecuación 14. Profundidades subsecuentes para tuberías llenas (Silvester, 1964). ............................ 10
Ecuación 15. Longitud de un resalto hidráulico para cualquier tipo de sección (Silvester, 1964). ... 11
Ecuación 16. Cálculo del Momentum en Resaltos Hidráulicos (Rajaratnam, 1965). ....................... 12
Ecuación 17. Conservación del Momentum (Rajaratnam, 1965)...................................................... 13
Ecuación 18. Ecuación del Número de Froude según Rajaratnam (Rajaratnam, 1965). .................. 13
Ecuación 19. Conservación del Momentum (Rajaratnam, 1965)...................................................... 13
Ecuación 20. Cálculo de la profundidad crítica. ............................................................................... 14
Ecuación 21. Aproximación Número de Froude (French, 2007). ..................................................... 14
Ecuación 22. Cálculo profundidad subsecuente para Números de Froude menores a 1.7 (French,
2007). ................................................................................................................................................ 14
Ecuación 23. Cálculo profundidad subsecuente para Números de Froude mayores a 1.7 (French,
2007). ................................................................................................................................................ 14
Ecuación 24. Cálculo del Momentum. (French, 2007). .................................................................... 15
Ecuación 25. Distancia del centro de la tubería de agua. .................................................................. 15
Ecuación 26. Distancia del centro de la tubería al centroide de masa de agua. ................................ 16
Ecuación 27. Distancia desde la superficie de agua hasta el centroide de la masa de agua. ............. 16
Ecuación 28. Igualando Momentums. ............................................................................................... 16
Ecuación 29. Aproximación del área (Stahl & Hager, 1999). ........................................................... 16
Ecuación 30. Aproximación Presión (Stahl & Hager, 1999). ........................................................... 16
Ecuación 31. Ecuación del Momentum (Stahl & Hager, 1999). ....................................................... 17
Ecuación 32. Aproximación del Número de Froude (Hager, 1990). ................................................. 17
Ecuación 33. Proceso para encontrar la profundidad subsecuente del resalto hidráulico. ................ 17

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
VIII
Ecuación 34. Relación entre las relaciones de llenado aguas arriba y aguas abajo del resalto (Stahl
& Hager, 1999). ................................................................................................................................. 17
Ecuación 35. Proceso para encontrar la profundidad subsecuente en un resalto hidráulico. ............ 18
Ecuación 36. Profundidad subsecuente en el resalto hidráulico (Stahl & Hager, 1999). .................. 18
Ecuación 37. Profundidad subsecuente con Números de Froude mayores a 2 (Stahl & Hager, 1999).
........................................................................................................................................................... 18
Ecuación 38. Profundidad subsecuente para Números de Froude mayores a 2 (Stahl & Hager,
1999). ................................................................................................................................................ 19
Ecuación 39. Relación entre la longitud de recirculación y la profundidad aguas abajo del resalto
(Stahl & Hager, 1999). ...................................................................................................................... 21
Ecuación 40. Determinación de la longitud de recirculación a partir del Número de Froude. ......... 21
Ecuación 41. Relación entre la longitud de aireación y la profundidad aguas abajo del resalto (Stahl
& Hager, 1999). ................................................................................................................................. 21
Ecuación 42. Determinación de la longitud de aireación a partir del Número de Froude (Stahl &
Hager, 1999). ..................................................................................................................................... 21
Ecuación 43. Estimación para resaltos Ondulares Tipo C y D (Gargano & Hager, 2002). .............. 22
Ecuación 44. Sumergencia en la compuerta (Ghamry, Shames, & Branch, 2002). .......................... 23
Ecuación 45. Sumergencia (Ghamry, Shames, & Branch, 2002). .................................................... 23
Ecuación 46. Cálculo Momentum Específico en Canales Rectangulares (Akan, 2006). .................. 24
Ecuación 47. Procedimiento cálculo altura subsecuente de los resaltos hidráulicos en canales
rectangulares (Akan, 2006). .............................................................................................................. 24
Ecuación 48. Caudal por unidad de ancho. ....................................................................................... 24
Ecuación 49. Procedimiento cálculo profundidades subsecuentes. ................................................... 25
Ecuación 50. Conservación de la masa. ............................................................................................ 25
Ecuación 51. Cálculo velocidad aguas abajo a partir de los parámetros aguas arriba. ..................... 25
Ecuación 52. Cálculo profundidades subsecuentes en canales rectangulares. .................................. 26
Ecuación 53. Cálculo profundidad subsecuente para profundidades subsecuentes menores al
diámetro (FHWA, 2006). .................................................................................................................. 26
Ecuación 54. Cálculo profundidad subsecuente para profundidades subsecuentes mayores al
diámetro (FHWA, 2006). .................................................................................................................. 27
Ecuación 55. Determinación de la longitud del resalto cuando la profundidad aguas abajo es menor
al diámetro. (FHWA, 2006) .............................................................................................................. 28
Ecuación 56. Determinación longitud del resalto cuando la profundidad aguas abajo es mayor al
diámetro (FHWA, 2006). .................................................................................................................. 28
Ecuación 57. Conservación del Momentum Específico. ................................................................... 31
Ecuación 58. Dimensiones del Resalto Hidráulico en canales cuadrados reorganizada (SMITH &
CHEN, 1989). .................................................................................................................................... 32
Ecuación 59. Profundidad subsecuente en el resalto hidráulico (Stahl & Hager, 1999). .................. 34
Ecuación 60. Profundidad subsecuente con Números de Froude mayores a 2 (Stahl & Hager, 1999).
........................................................................................................................................................... 34

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
IX
Ecuación 61. Cálculo de la intensidad de la turbulencia (Lopardo, 2012). ....................................... 36
Ecuación 62. Cálculo del parámetro adimensional para determinar la turbulencia del resalto
hidráulico (Lopardo, 2012). .............................................................................................................. 36
Ecuación 63. Cálculo de la relación de llenado. ................................................................................ 48
Ecuación 64. Cálculo de
. ............................................................................................................... 48
Ecuación 65. Cálculo del área mojada. ............................................................................................. 48
Ecuación 66. Cálculo del perímetro mojado. .................................................................................... 48
Ecuación 67. Cálculo del radio hidráulico. ....................................................................................... 49
Ecuación 68. Cálculo de la velocidad. .............................................................................................. 49
Ecuación 69. Cálculo del caudal. ...................................................................................................... 49
Ecuación 70. Cálculo del Número de Reynodls. ............................................................................... 49
Ecuación 71. Cálculo del ancho de la superficie. .............................................................................. 49
Ecuación 72. Cálculo de la profundidad hidráulica. ......................................................................... 49
Ecuación 73. Cálculo del Número de Froude.................................................................................... 49
Ecuación 74. Cálculo de la altura total del soporte. .......................................................................... 49
Ecuación 75. Curva que describe el Número de Froude máximo. .................................................... 56
Ecuación 76. Cálculo de la profundidad crítica. ............................................................................... 61
Ecuación 77. Aproximación Número de Froude (French, 2007). ..................................................... 61
Ecuación 78. Cálculo de la profundidad subsecuente del resalto hidráulico por un método iterativo
de acuerdo con la metodología planteada por Hager. ....................................................................... 65
Ecuación 79. Aproximación teórica para cálculos de la profundidad subsecuente del resalto
hidráulico........................................................................................................................................... 66
Ecuación 80. Aproximación empírica para el cálculo de la profundidad subsecuente del resalto
hidráulico........................................................................................................................................... 67
Ecuación 81. Cálculo de la profundidad subsecuente del resalto hidráulico menor al diámetro. ..... 69
Ecuación 82. Cálculo de la profundidad subsecuente del resalto hidráulico mayor al diámetro. ..... 69
Ecuación 83. Relación entre el caudal y la gravedad y el diámetro de la tubería. (Sturm, 2010) ..... 89
Ecuación 84. Ecuación empírica de la profundidad subsecuente para
. ............................... 91
Ecuación 85. Ecuación empírica de la profundidad subsecuente para
. ............................... 91
Ecuación 86. Ecuación empírica de la profundidad subsecuente de acuerdo a la Energía Específica.
........................................................................................................................................................... 95
Ecuación 87. Ecuación empírica de la profundidad subsecuente de acuerdo al Momentum
Específico. ......................................................................................................................................... 99
Ecuación 88. Cálculo del Error Cuadrático Medio. .......................................................................... 99
Ecuación 89. Cálculo del Error Cuadrático Medio Promedio. .......................................................... 99
Ecuación 90. Ecuación lineal para determinar la longitud del resalto hidráulico en tuberías. ........ 104
Ecuación 91. Ecuación potencial para determinar la longitud del resalto hidráulico en tuberías. .. 104
Ecuación 92. Ecuación para determinar el valor de la disipación de energía. ................................ 107
Ecuación 93. Cálculo disipación de Energía ................................................................................... 114

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
X
Notación
SÍMBOLO UNIDADES S.I. DEFINICIÓN
m²
Área mojada de la sección.
m
Diámetro de la tubería.
%
Disipación de Energía relativa respecto a la energía aguas arriba.
m
Energía específica aguas arriba del resalto.
m
Energía específica aguas abajo del resalto.
-
Número de Froude aguas arriba del resalto.
m/s²
Aceleración de la gravedad.
m
Longitud del resalto hidráulico.
m³
Momentum específico aguas arriba del resalto hidráulico.
m
3
Momentum específico aguas abajo del resalto hidráulico.
m
Perímetro mojado de la sección.
m³/s
Caudal.
%
Coeficiente de determinación.
-
Número de Reynolds.
-
Pendiente de la tubería.
m/s
Velocidad del flujo.
m/s
Componente de la velocidad en la dirección longitudinal.
m/s
Componente de la velocidad en la dirección transversal.
m/s
Componente de la velocidad en la dirección vertical.
m
Profundidad crítica del flujo.
m
Profundidad normal del flujo.
m
Profundidad subsecuente aguas arriba del resalto
m
Profundidad subsecuente aguas abajo del resalto

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
1
1. Introducción
El estudio del fenómeno de resaltos hidráulicos en tuberías ha sido un tema de baja investigación a nivel
nacional e internacional dada la dificultad de su análisis. Sin embargo, dada la importancia de analizar
los alcantarillados y sus fenómenos de sobrecarga, es importante realizar un estudio para definir ciertas
características de los resaltos hidráulicos en tuberías fluyendo parcialmente llenas.
El resalto hidráulico es un fenómeno generado cuando la profundidad del flujo varía rápidamente; es
decir, cuando en un canal (abierto o cerrado) existe un cambio de flujo supercrítico a subcrítico. Éste
fenómeno ocurre por la presencia de altas pendientes u obstáculos (como las compuertas) que generan
un aumento importante del flujo aguas abajo, afectando las condiciones del flujo aguas arriba.
Adicionalmente, cuando los Números de Froude sean más grandes (flujo supercrítico), la altura
subsecuente aguas abajo del resalto será mayor.
Las principales características de un resalto hidráulico son: las pérdidas de energía, la longitud del
resalto y su localización. Las pérdidas de energía son causadas por la turbulencia generada en el resalto,
y se calculan como la diferencia de energía específica entre el flujo aguas abajo del resalto y el flujo
aguas arriba. La longitud del resalto se mide desde el lugar donde inicia la turbulencia hasta el lugar
donde finaliza: según la literatura encontrada, existen relaciones empíricas que permiten encontrar la
longitud del resalto hidráulico dependiendo del Número de Froude y de la altura del flujo aguas arriba
del resalto en canales rectangulares, trapeciales, triangulares y en el caso de tuberías circulares, se
encontró una ecuación empírica en el artículo de Silvester (Silvester, 1964) con un rango de validez
muy pequeño, dada la dificultad de medir resaltos cuando la tubería se presuriza. Por último, la
localización del resalto varía de acuerdo con el impacto que genere el obstáculo que se encuentre aguas
abajo, por lo tanto, es una variable que en estudios del resalto en el laboratorio puede ser modificada.
Por lo tanto, el presente trabajo presenta un estudio de resaltos hidráulicos en tuberías, el cual se realiza
en un modelo realizado en el Laboratorio de Hidráulica de la Universidad de Los Andes. El diseño y
construcción del modelo se realizaron previamente a este trabajo, por lo cual, en éste proyecto se
muestran los resultados de la construcción previa y sus modificaciones para ubicar aparatos que
permitan realizar la medición de las variables a estudiar. Adicionalmente, presenta una revisión
bibliográfica de estudios anteriores en el tema, una comparación de las diferentes metodologías
planteadas, y un estudio de los resultados esperados en el modelo construido.
El Capítulo 2 presenta todos los estudios y metodologías planteadas previamente para el análisis de
resaltos hidráulicos en tuberías, presentando gráficas y ecuaciones desarrolladas. El Capítulo 3 explica
el fenómeno de los resaltos hidráulicos en tuberías, los diferentes tipos de resaltos hidráulicos
planteados y las diferentes características que puede tener este fenómeno. En el Capítulo 4 se muestra el
resultado del diseño y construcción del montaje, los aparatos de medición requeridos para la toma de
datos de las variables a analizar, y la metodología que se llevará a cabo en el proceso de análisis. En el
siguiente capítulo se realiza un análisis para determinar los comportamientos esperados en el resalto
hidráulico, determinando profundidades que generarán un resalto hidráulico más fuerte, y un análisis
teórico de las metodologías encontradas en el Capítulo 2, tanto para el cálculo de la profundidad
subsecuente aguas abajo del resalto como para el cálculo de la longitud del mismo. En el Capítulo 6 se

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
2
encuentran los resultados obtenidos con los datos tomados para las variables medidas (y
1
, y
2
, L)
1
,
mediante gráficos e ilustrando los perfiles del flujo cuando la profundidad aguas abajo del resalto es
mayor al diámetro de la tubería; en este capítulo también se muestra el análisis de los resultados
obtenidos, mediante la comparación con las metodologías analizadas previamente y gráficos que
permitan inferir el comportamiento del resalto hidráulico en la tubería. En el Capítulo 7 y 8 se describen
algunas conclusiones mostradas en el proyecto y las recomendaciones que se plantearán para futuras
investigaciones en el tema. En el siguiente capítulo se presenta un glosario con los términos importantes
llevados a cabo en el proyecto, y posteriormente se presenta la bibliografía requerida e investigada, y
finalmente en el Capítulo 11 se presentan los anexos, los cuales se componen de diferentes códigos
desarrollados en Macros de Excel, y los planos diseñados y requeridos para la construcción del montaje.
1
Ir a la página X.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
3
1.1 Objetivos
1.1.1. Objetivo General
Estudiar el comportamiento de los resaltos hidráulicos en tuberías fluyendo parcialmente llenas de
sección circular mediante la toma de datos experimentales en el modelo físico construido anteriormente.
El estudio se realizará teniendo como restricción Números de Froude menores a 4.0 y pendientes
menores al 2.5%.
1.1.2. Objetivos Específicos
Para llevar a cabo el estudio de resaltos hidráulicos en tuberías se requiere realizar una recopilación
bibliográfica de modelos y estudios realizados anteriormente, analizando las metodologías encontradas
en esta recopilación, y aplicarlas a las condiciones físicas que tiene el montaje realizado.
Adicionalmente, se deben determinar las variables que se trabajarán en el modelo, las cuales deben
cumplir con las condiciones físicas e hidráulicas de este; y con las variables identificadas, se debe
proceder a realizar la toma de datos en el modelo, las cuales deben permitir realizar un análisis del
comportamiento de los resaltos hidráulicos en tuberías. Es importante tener en cuenta que el modelo se
debe adaptar para la ubicación de los sensores, por lo cual, se requiere un diseño de las modificaciones
necesarias para medir los diferentes parámetros.
Por otra parte, se determinarán ecuaciones empíricas que describan el comportamiento de los resaltos
hidráulicos en las tuberías, mostrando la diferencia de éstas ecuaciones empíricas respecto a las
ecuaciones encontradas en la literatura, con lo cual se obtendrán las herramientas suficientes para
determinar el comportamiento de los resaltos hidráulicos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
4
2. Antecedentes
Los antecedentes mostrados a continuación se encuentran en la tesis de pregrado denominada “Diseño y
construcción de un modelo para estudiar el comportamiento de resaltos hidráulicos en tuberías fluyendo
parcialmente llenas de sección circular, con Números de Froude supercríticos menores a 4” (Montaño
Luna, 2012).
El proceso para entender la formación y el comportamiento de resaltos hidráulicos en tuberías ha sido
estudiando experimental y teóricamente. En éste capítulo se mostrarán los diferentes estudios que han
trabajado algunos investigadores para entender el fenómeno.
Kindsvater y Lane (1938)
El primer análisis de resaltos hidráulicos en tuberías circulares fluyendo parcialmente llenas fue
realizado por Kindsvater y Lane en el año 1938, a raíz de los estudios que se venían realizando de
resaltos hidráulicos en canales rectangulares.
Kindsvater y Lane, en la Universidad de Iowa, establecieron que la mejor forma para analizar el
comportamiento de resaltos hidráulicos en tuberías circulares, era mediante análisis experimentales; por
lo tanto, para su montaje usaron una tubería transparente de 150 mm de diámetro y 6 m de longitud en
posición horizontal. Los resaltos hidráulicos los produjeron con 3 obstrucciones: la primera que ocupaba
el 40% del diámetro, la segunda el 60% y la tercera el 80% del diámetro. (Ver Ilustración 1).
Ilustración 1. Montaje realizado por Kindsvater y Lane (Kindsvater, 1938).
La variación del nivel del agua era medida mediante piezómetros aguas abajo de las constricciones; por
lo tanto, se podía analizar la variación de la altura del resalto a medida que aumentaba o disminuía el
caudal de entrada, y la longitud a la cual ocurría tal como se muestra en la Gráfica 1.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
5
Gráfica 1. Alturas medidas con caudal variable (Kindsvater, 1938).
Kindsvater y Lane concluyeron que con caudales muy bajos, la tubería no se alcanzaba a presurizar
aguas abajo del resalto; mientras que a caudales grandes, el resalto presurizaba completamente la
tubería. También, como el montaje tenía ventilación, el aire aumentaba la presión sobre la superficie del
agua, lo cual hacía que el resalto se moviera hacia la contracción y lo terminara ahogando.
Finalmente, como los análisis de resaltos hidráulicos se basan en la variación del Momentum aguas
arriba y aguas abajo de la contracción, Kindsvater y Lane observaron que el Momentum era
relativamente mayor aguas arriba de la constricción que aguas abajo; a lo que argumentaban la fricción
causada por la tubería, la falta de uniformidad de la velocidad aguas abajo del resalto y la omisión de las
burbujas de agua en los cálculos del Momentum.
Kalinske y Robertson (1943)
Posteriormente, en 1943, Kalinske y Robertson estudiaron la salida de paquetes de aire como
consecuencia de la formación de resaltos hidráulicos en tuberías con pendiente; su montaje consistió en
una tubería de diámetro de 150 mm, y aproximadamente 10 m de longitud; y las pendientes que
estudiaron fueron de 0.2%, 2%, 5%, 10%, 20% y 30%. En la Ilustración 2 se puede observar el montaje
para pendientes del 2% y el 30%.
Ilustración 2. Montaje de Kalinske y Robertson (Robertson & Kalinske, 1943).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
6
Previo a éste artículo, Kennison había indicado en el artículo “The Design of Pipes Lines” publicado en
la Revista Americana N.E.W.W.A. (New England Water Works Association) en 1933, que si la
pendiente de la tubería es menor a la línea de gradiente hidráulico, las burbujas se moverán a lo largo de
la tubería sin ninguna dificultad. Por lo tanto, Kalinske y Robertson aplicando este criterio, buscarían en
su montaje el aire entrante en las tuberías.
Los resultados de su estudio arrojaron que la intensidad del resalto es dependiente del Número de
Froude aguas arriba del resalto, de la pendiente, ya que ésta determina la entrada de aire en la tubería y
finalmente de la relación de llenado, la cual va relacionada directamente con la pendiente de la tubería.
Por lo tanto, para entender el comportamiento, realizaron una relación entre el caudal de aire que
entraba en la tubería (
) y el Caudal de agua (
) y lo graficaron respecto al Número de Froude; se
observa que con cualquier pendiente, mientras mayor es la relación entre los caudales, el Número de
Froude aumenta.
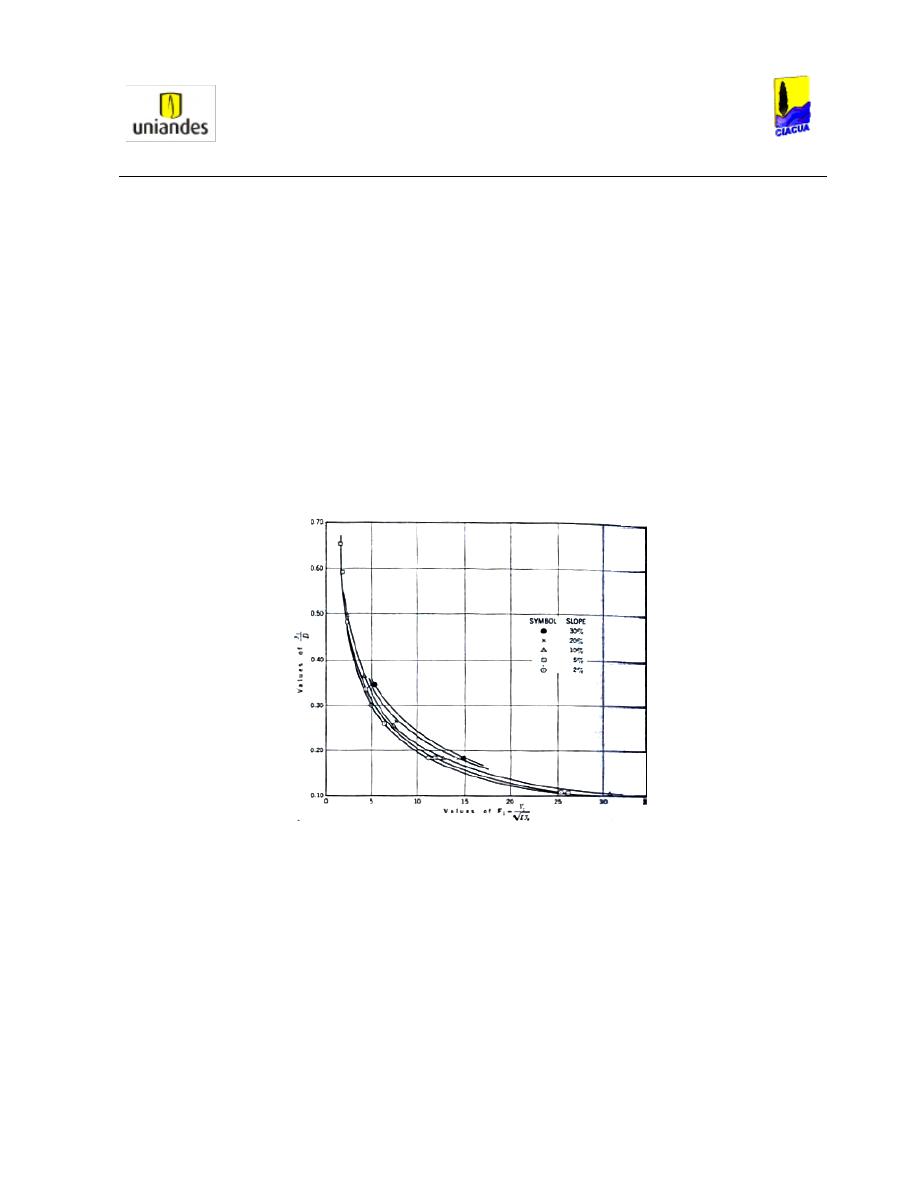
También analizaron que para diferentes relaciones de llenado, existe un Número de Froude crítico en
donde la tubería solo transporta parte del aire en el resalto (Ver Gráfica 2):
Gráfica 2. Valores críticos experimentales del Número Froude para diferentes relaciones de llenado (Robertson & Kalinske,
1943).
En la Gráfica 2
se observa que con un Número de Froude seleccionado, la relación de llenado es más
alta en la pendiente más alta, y más baja cuando la pendiente es más baja; por ejemplo, con un Número
de Froude de 10, la pendiente del 2% tiene una relación de llenado cercana a 0.19; con una pendiente
del 5%, la relación de llenado es cercana a 0.21; con una pendiente del 10%, la relación de llenado es de
0.22; con una pendiente de 20% la relación es de 0.24 y con una pendiente del 30%, la relación de
llenado es de 0.25. Además cuando la pendiente es de 2%, el Número de Froude se mantiene constante
en un valor cercano a 2 mientras la relación de llenado varía entre 0.58 y 0.68.
Adicionalmente, en la Ilustración 3 se observan diferentes comportamientos del flujo para diversos
caudales con sus respectivos datos típicos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
7
(a)
0.147
8.2
0.720
0.060
2 %
(b)
0.127
7.5
0.482
0.039
5 %
(c)
0.290
2.6
0.848
0.014
10 %
Ilustración 3. Datos típicos de profundidades y presiones en un Resalto Hidráulico (Robertson & Kalinske, 1943).
En la Ilustración 3 se puede analizar que cuando la pendiente es más alta hay más resaltos. Además,
según Robertson y Kalinske, con cada resalto hidráulico, la cantidad de presión de aire que hay en la
tubería aumenta mientras el Número de Froude y la profundidad subsecuente se mantienen constantes,
tal como se observa en la Imagen C de la Ilustración 3, donde la altura aguas abajo de cada uno de los
tres resaltos tiene a tener un valor constante. También Robertson y Kalinske observan que cuando la
profundidad aguas arriba del primer resalto es menor que la profundidad aguas arriba del segundo
resalto, el primer resalto entregará mayor cantidad de aire a la segunda profundidad y por lo tanto la
separación entre estos dos resaltos será mayor. Mientras que cuando la profundidad aguas arriba del
segundo resalto es mayor a la profundidad del primer resalto, el primer resalto entregará menor cantidad
de aire y se encontrarán a menor distancia.
Richard Silvester (1964)
En el año 1964, Richard Silvester realizó un análisis de resaltos hidráulicos que se formaban en
cualquier tipo de canal horizontal (rectangular, triangular, parabólico, circular y trapecial). El planteó
que las características principales para cualquier disipador de energía (incluido el resalto hidráulico);
son: la relación de las profundidades subsecuentes, las pérdidas de energía y la longitud del resalto.
En cuanto a las profundidades subsecuentes, se debe tener en cuenta el radio, la relación entre las
profundidades (d
1
/d
2
), el caudal, y para tuberías circulares, el centro de masa del agua. Silvester incluye
en su artículo la ecuación de fuerza del resalto para cualquier tipo de canal horizontal (Ver Ecuación 1):

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
8
(
) (
)
Ecuación 1. Ecuación para hallar la ecuación de fuerza del resalto (Silvester, 1964).
donde:
= Área de la sección de agua
= Proporción de la profundidad al centro de gravedad del canal circular
= Caudal
= Gravedad
La Ecuación 1 puede escribirse como:
(
)
Ecuación 2. Ecuación para hallar la fuerza del resalto (Silvester, 1964).
También se conoce que el Número de Froude es (Ver Ecuación 3):
Ecuación 3. Número de Froude.
donde:
= Número de Froude
= Profundidad de sección
Por lo tanto, se puede inferir que:
(
)
Ecuación 4. Proceso para encontrar profundidades subsecuentes.
Luego, reemplazando la Ecuación 4 en la Ecuación 2, se tiene que:
Ecuación 5. Proceso para hallar profundidades subsecuentes.
La Ecuación 5 se puede reescribir como:
Ecuación 6. Ecuación 5 reorganizada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
9
Por otra parte, la relación entre el Número de Froude aguas abajo del resalto sobre el Número de Froude
aguas arriba del resalto se muestra en la Ecuación 7:
Ecuación 7. Relación Número de Froude (Silvester, 1964).
Y si se despeja el Número de Froude aguas abajo del resalto:
Ecuación 8. Número de Froude aguas abajo del resalto.
Entonces, reemplazando la Ecuación 8 en la Ecuación 6:
(
)
Ecuación 9. Proceso para encontrar las profundidades subsecuentes en cualquier forma de canal.
Y para encontrar las profundidades subsecuentes, se divide la Ecuación 9 por el Área y la profundidad
de sección aguas arriba del resalto (
):
(
)
[
]
Ecuación 10. Profundidades subsecuentes para cualquier tipo de canal (Silvester, 1964).
Cómo en tuberías circulares la profundidad subsecuente puede tener dos condiciones (mayor o menor al
diámetro), el cálculo de ésta profundidad se divide en dos casos:
Tubería Parcialmente Llena:
Cuando la tubería está parcialmente llena, la proporción de la profundidad del agua al centro de masa
del agua (
) es variable, y se calcula con la Ecuación 11:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
10
( (
)
(
)
)
Ecuación 11. Valor de la proporción entre la profundidad de llenado y el centro de masa para tuberías parcialmente llenas
(Silvester, 1964).
donde:
= Proporción de la profundidad del flujo respecto al centro de gravedad
= Altura del flujo
= Diámetro de la tubería
= Área mojada de la tubería
Y los respectivos valores de k para diferentes profundidades de llenado son:
Tabla 1. Valores de k' dependiendo de la relación de llenado (Silvester, 1964).
d/D
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
k'
0.41
0.413
0.416
0.419
0.424
0.432 0.445 0.462 0.473
0.5
Finalmente, reemplazando la Ecuación 11 en la Ecuación 10 se tiene que:
[
]
Ecuación 12. Profundidades subsecuentes para tuberías parcialmente llenas (Silvester, 1964).
Tubería Llena
En aquellas tuberías que quedan presurizadas luego de un resalto hidráulico, la ecuación de la
proporción entre la profundidad de llenado y el centro de gravedad se calcula con la Ecuación 13
.
(
)
Ecuación 13. Valor de la proporción entre la profundidad de llenado y el centro de gravedad para tuberías llenas (Silvester,
1964).
Y reemplazando la Ecuación 13 en la Ecuación 10 se tiene que:
[
]
Ecuación 14. Profundidades subsecuentes para tuberías llenas (Silvester, 1964).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
11
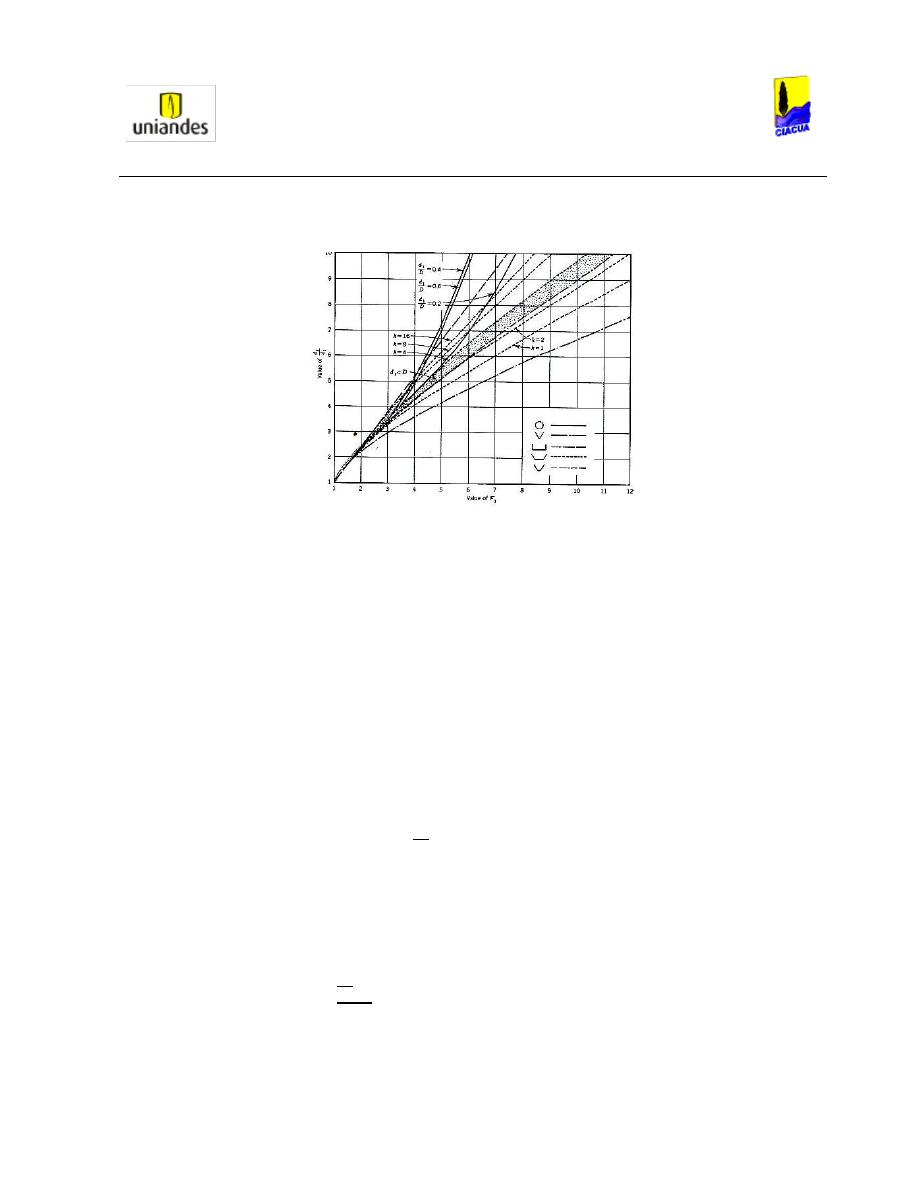
Luego, Silvester en su artículo, muestra un diagrama en el cual compara el valor del Número de Froude
respecto a la profundidad de llenado en diferentes tipos de secciones (Ver Gráfica 3):
Gráfica 3. Curvas Analíticas para d
2
/d
1
y F
1
(Silvester, 1964).
En la Gráfica 3 se puede observar que en tuberías circulares, para relaciones de llenado bajas aguas
arriba del resalto (d
1
/D = 0.2), el Número de Froude es más alto que para relaciones de llenado altas
(d
1
/D = 0.6). También se puede observar que cuando la tubería fluye parcialmente llena luego del resalto
hidráulico, existe una región válida de resultados, la cual se va incrementando a medida que aumenta la
relación d
2
/d
1
. Otro aspecto importante que se debe considerar, es que la relación de llenado del 20%
presenta el Número de Froude más alto, el cual se va aproximando a 8.
Adicionalmente, Silvester fue el primer investigador que aproximó una ecuación para hallar la longitud
del resalto hidráulico en tuberías circulares, teniendo como parámetros L/d
1
, L/d
2
, y L/(d
2
– d
1
). Por lo
tanto, para comparar las longitudes en la tubería, Silvester tomó el experimento realizado por
Kindsvater en 1934, y supuso las longitudes como la distancia entre el inicio del resalto, hasta el punto
donde la altura aguas abajo alcanzaba un máximo, teniendo en cuenta las pérdidas por fricción.
Su aproximación se basó en usar la Ecuación 15 y adaptarla para cada tipo de sección.
(
)
Ecuación 15. Longitud de un resalto hidráulico para cualquier tipo de sección (Silvester, 1964).
donde:
: Relación entre la longitud y la altura aguas arriba del resalto. Depende de la sección del canal
: Constante determinada experimentalmente según la sección del canal
: Se determina por la relación
En tuberías circulares, la longitud del resalto se determinó en el experimento realizado por Kindsvater
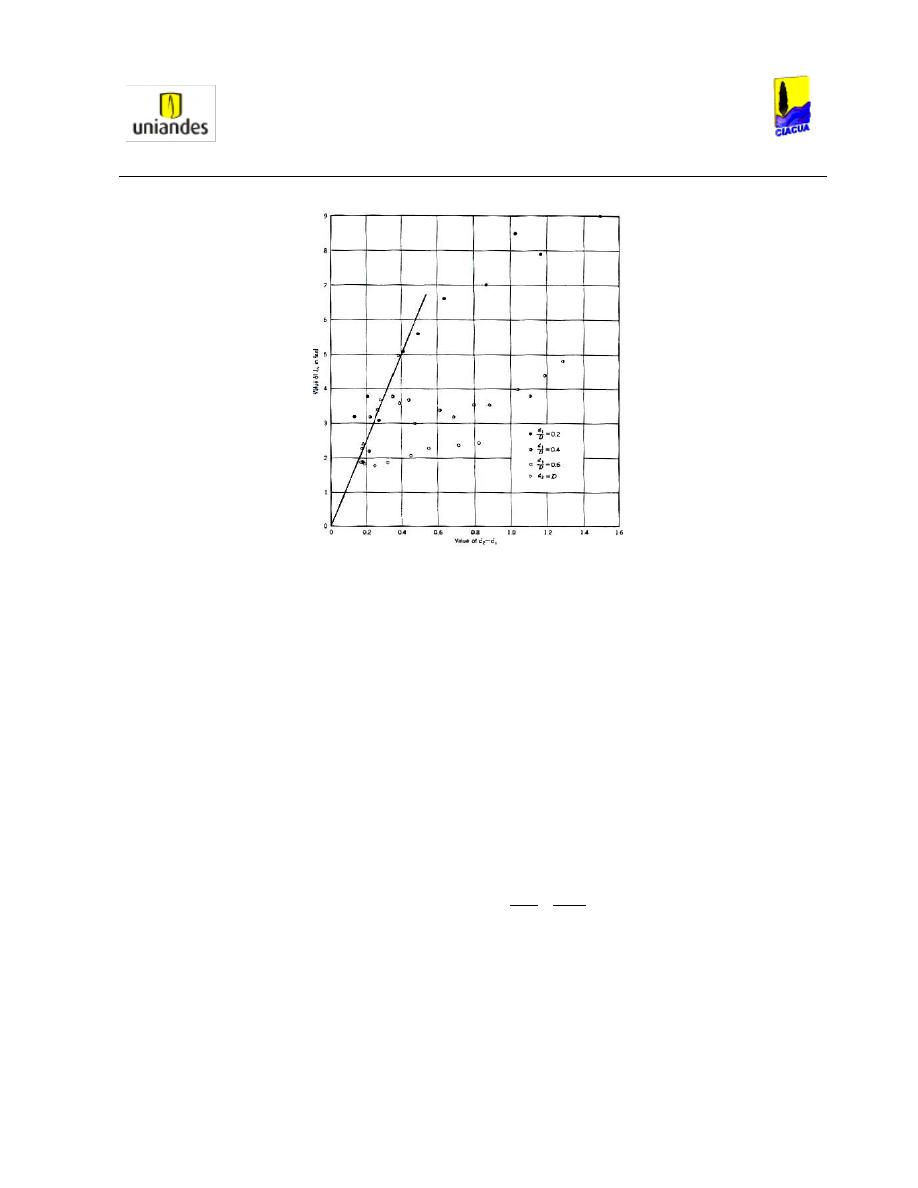
en 1934, con el cual, Silvester adaptó las mediciones y estableció la Gráfica 4:
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
12
Gráfica 4. Variación diferencia de alturas del resalto vs Longitud (Silvester, 1964).
En la Gráfica 4 se puede observar que a medida que aumenta la relación de llenado aguas arriba del
resalto, la longitud del resalto es menor; esto puede ir relacionado conjuntamente con la disminución del
Número de Froude a medida que disminuye la relación de llenado (Ver Gráfica 3). Esto ocurre porque
cuando hay menor relación de llenado, la velocidad aumenta por lo cual el Número de Froude aumenta,
haciendo que el resalto adquiera más fuerza y se aumente la longitud.
Rajaratnam (1965)
En 1965, Rajaratnam realizó un nuevo análisis de resaltos hidráulicos en tuberías de sección
exponencial y circular para canales horizontales. Su análisis de basó nuevamente en las conclusiones
dadas por Kindsvater (1938), y el análisis realizado por Kalinske (1943) para las masas de aire que salen
por la tubería luego de un resalto hidráulico.
Por lo tanto, teniendo en cuenta el análisis de Momentum mediante la Ecuación 16:
Ecuación 16. Cálculo del Momentum en Resaltos Hidráulicos (Rajaratnam, 1965).
donde:
: Peso específico del agua
: Presión
Momentum

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
13
: Son funciones de la relación de llenado aguas arriba (y
1
/D)
: Diámetro de la tubería
: Caudal
: Altura en el punto de medición
Y conociendo que el Momentum se conserva (Ver Ecuación 17):
Ecuación 17. Conservación del Momentum (Rajaratnam, 1965).
Y tomando el Número de Froude como:
Ecuación 18. Ecuación del Número de Froude según Rajaratnam (Rajaratnam, 1965).
donde
y
son funciones de
, se reemplaza la Ecuación 17 en la Ecuación 16 y se simplifica
obteniendo finalmente la ecuación de conservación del Momentum:
(
)
Ecuación 19. Conservación del Momentum (Rajaratnam, 1965).
A partir de la Ecuación 19, Rajaratnam estableció una gráfica con relaciones de llenado inferiores a 0.8
(Ver Gráfica 5), ya que en el análisis, Rajaratnam observó que para relaciones de llenado superiores a
0.8, el comportamiento del flujo no permite ningún análisis
Gráfica 5. Análisis de Froude vs y
2
/y
1
(Rajaratnam, 1965).
En la Gráfica 5, Rajaratnam analiza que cuando el Número de Froude llega aproximadamente a 3, las
curvas de las diferentes relaciones de llenado empiezan a diverger, y sus límites se encuentran entre las
relaciones de llenado de 0.2 y 0.5.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
14
Straub (1978)
En 1978, Straub planteó las siguientes ecuaciones para determinar las profundidades subsecuentes en
resaltos hidráulicos, partiendo de la siguiente ecuación semiempírica:
(
) (
)
Ecuación 20. Cálculo de la profundidad crítica.
La Ecuación 20 es válida únicamente si:
Posteriormente, se calcula el Número de Froude aguas arriba del resalto mediante la Ecuación 21:
(
)
Ecuación 21. Aproximación Número de Froude (French, 2007).
donde:
: Número de Froude aguas arriba del resalto [-]
: Profundidad crítica [m]
: Profundidad aguas arriba del resalto [m]
Luego realiza dos aproximaciones de la profundidad subsecuente con base en el Número de Froude,
dependiendo si el Número de Froude es menor a 1.7 o mayor.
Cuando el Número de Froude es menor a 1.7, la profundidad subsecuente es calculada como:
Ecuación 22. Cálculo profundidad subsecuente para Números de Froude menores a 1.7 (French, 2007).
Y cuando el Número de Froude es mayor a 1.7:
Ecuación 23. Cálculo profundidad subsecuente para Números de Froude mayores a 1.7 (French, 2007).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
15
Richard H. French (1988)
Richard French propuso igualar momentos tal cual lo hicieron otros autores, pero con la siguiente
ecuación:
(
) ̅
Ecuación 24. Cálculo del Momentum. (French, 2007).
donde:
: Momentum [m
3
]
: Caudal [m
3
/s]
: Gravedad [m/s
2
]
̅: Distancia desde la superficie de agua al centroide de masa [m]
: Área [m
2
]
Para hallar la distancia desde la superficie de agua al centroide se realiza el siguiente procedimiento:
Ilustración 4. Diagrama de niveles en la tubería.
1. Calcular el radio de la tubería (r).
2. Calcular la distancia del centro de la tubería a la superficie de agua (z)
Ecuación 25. Distancia del centro de la tubería de agua.
3. Calcular la distancia desde el centro de la tubería al centroide de masa del agua (
̂).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
16
̂
(
)
Ecuación 26. Distancia del centro de la tubería al centroide de masa de agua.
4. Calcular la distancia desde la superficie de agua hasta el centroide de la masa de agua (
̅).
̅ ( ̂)
Ecuación 27. Distancia desde la superficie de agua hasta el centroide de la masa de agua.
Entonces igualando los momentos se tiene que:
(
)
̅
(
)
̅
Ecuación 28. Igualando Momentums.
Luego, con la Ecuación 28 se despeja la altura subsecuente al resalto mediante un método iterativo.
Hager y Stahl (1999)
En 1999 Willi H. Hager y Helmut Stahl realizaron un nuevo análisis enfocado en tuberías circulares
fluyendo parcialmente llenas en una sola fase (sin tener en cuenta la relación aire – agua analizada
anteriormente por otros autores como Smith y Chen).
Para calcular la profundidad subsecuente, tuvieron en cuenta aproximaciones a las ecuaciones que
calcular el área y la fuerza de presión en una tubería circular:
Ecuación 29. Aproximación del área (Stahl & Hager, 1999).
2
Ecuación 30. Aproximación Presión (Stahl & Hager, 1999).
donde:
Área
: Diámetro de la tubería
2
Las Ecuación 29 y Ecuación 30 tienen un error máximo del 20% cuando y se encuentra entre 0.2 y 0.9, el cual es
aceptable para Stahl y Hager porque se ajustarán empíricamente.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
17
: Relación de llenado
Presión
: Densidad
: Gravedad
Por lo tanto la Ecuación del Momentum resulta en:
Ecuación 31. Ecuación del Momentum (Stahl & Hager, 1999).
Por otra parte, Hager realizó otro análisis en 1990 en el libro “Froudezahl im Kreisprofil (Froude
number in circular conduits)” para determinar que el Número de Froude en tuberías podía aproximarse
a:
√
Ecuación 32. Aproximación del Número de Froude (Hager, 1990).
donde:
: Número de Froude
: Caudal
: Diámetro de la tubería
: Profundidad del flujo
Ahora, dividiendo la Ecuación 31 entre
:
(
)
Ecuación 33. Proceso para encontrar la profundidad subsecuente del resalto hidráulico.
Y sabiendo que:
Ecuación 34. Relación entre las relaciones de llenado aguas arriba y aguas abajo del resalto (Stahl & Hager, 1999).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
18
Y aproximando 3.75
4 y remplazando las Ecuación 34 y Ecuación 32 en la Ecuación 33:
(
)
Ecuación 35. Proceso para encontrar la profundidad subsecuente en un resalto hidráulico.
Ecuación 36. Profundidad subsecuente en el resalto hidráulico (Stahl & Hager, 1999).
Además, la Ecuación 36 puede modificarse a la Ecuación 37 cuando
:
Ecuación 37. Profundidad subsecuente con Números de Froude mayores a 2 (Stahl & Hager, 1999).
Analizando la parte teórica, Stahl y Hager realizaron un experimento para verificar la Ecuación 37,
determinar un criterio de choque y determinar el comportamiento de los resaltos hidráulicos en tuberías
circulares. El diámetro de la tubería en acrílico que utilizaron fue de 240 mm, la pendiente fue de 0.5%
y la longitud fue de 6 m (equivalente a 25 veces el diámetro). El resalto se formó colocando placas al
final de la tubería y el caudal fue medido con un vertedero en V.
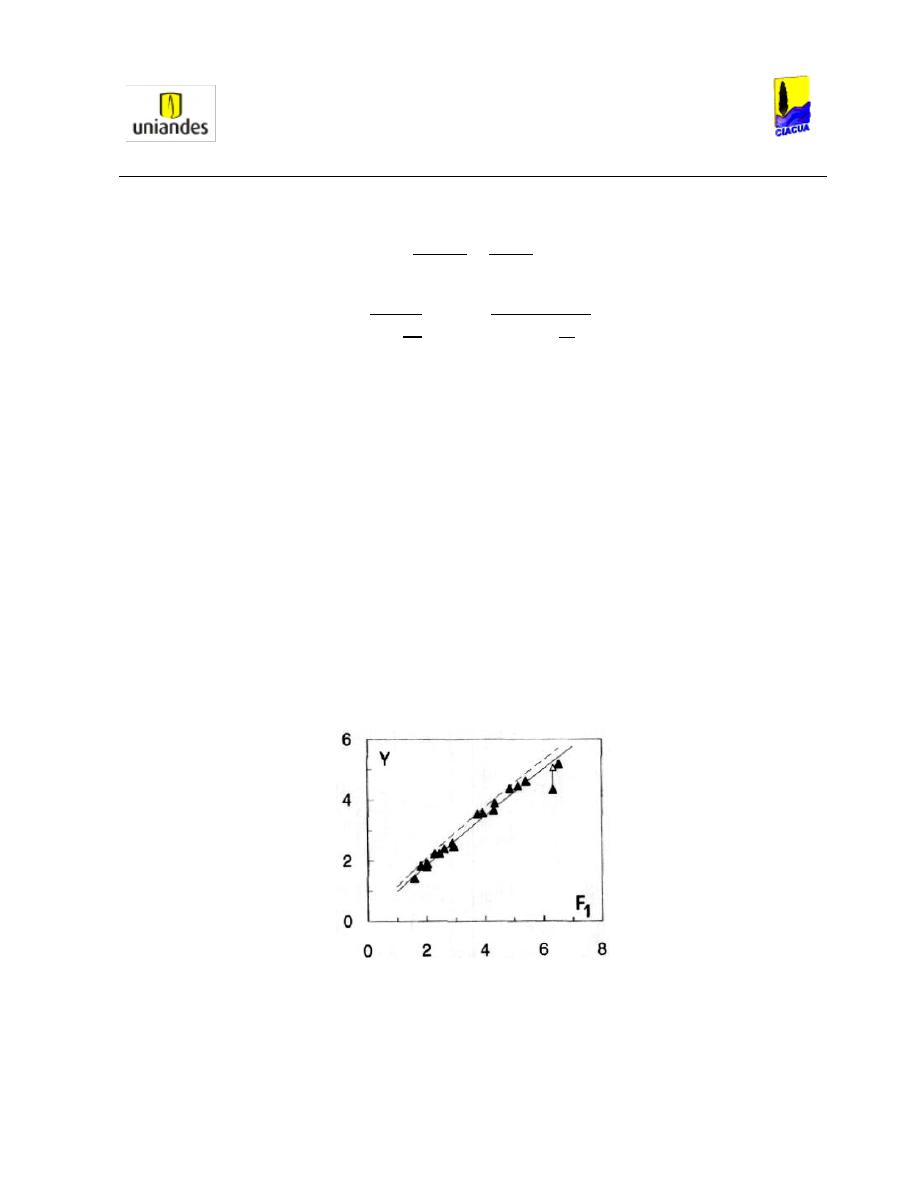
Gráfica 6. Profundidad subsecuente según el Número de Froude (Stahl & Hager, 1999).
En las 18 medidas realizadas, los Números de Froude oscilaron entre 1.5 y 6.5 (siempre en el rango
supercrítico), y se estableció que la Ecuación 37 había sido sobrestimada a causa de la viscosidad. Por lo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
19
tanto, la Ecuación 37 podía ser reemplazada por la Ecuación 38 (estimada con los resultados obtenidos
en los experimentos y mostrados en la Gráfica 6).
Ecuación 38. Profundidad subsecuente para Números de Froude mayores a 2 (Stahl & Hager, 1999).
Adicionalmente, Stahl y Hager realizaron un análisis para los tipos de resaltos
3
que se pueden formar:
Cuando el Número de Froude es 1.5, el tipo de resalto hidráulico que se forma es ondular y permanece a
lo largo de la tubería; cuando el Número de Froude oscila entre 1.5 y 2, las ondas del resalto hidráulico
se pierden aguas abajo porque la tubería se presuriza; cuando el Número de Froude es mayor a 2, se
producen dos tipos de resaltos hidráulicos, los cuales dependen de la relación de llenado de la tubería:
cuando la relación de llenado es inferior a 1/3, se forman remolinos laterales que recirculan, mientras el
flujo que continua se concentra en la superficie, cuando la relación de llenado es superior a 1/3, el
resalto se comporta normalmente, teniendo la zona de recirculación en la superficie.
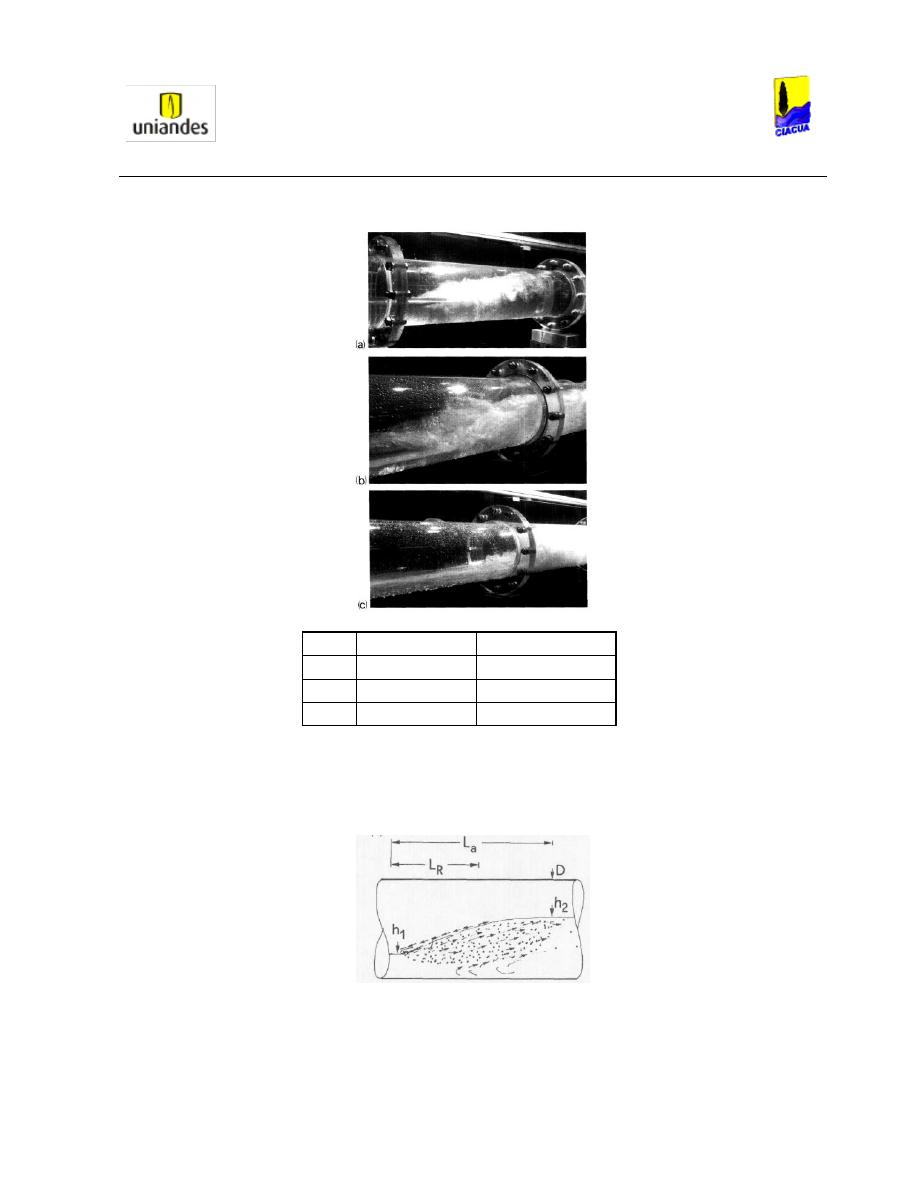
En la Ilustración 5 se muestran diferentes tipos de resaltos hidráulicos dependiendo del Número de
Froude:
Imagen Número de Froude
Tipo de Resalto
a
1.1
Ondular
b
2.3
Normal
c
4.1
Flujo recirculante
d
6.5
Con tubería presurizada
Ilustración 5. Vista lateral de diferentes resaltos hidráulicos (Stahl & Hager, 1999).
3
Los tipos de resaltos hidráulicos se explicarán en el Numeral 3 (Marco Teórico).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
20
En la Ilustración 6 se observan las fluctuaciones ocurridas en los flujos, y las zonas de recirculación.
Ilustración 6. Vista en perfil de los diferentes tipos de Resalto Hidráulico (Stahl & Hager, 1999).
Hager y Stahl analizan las longitudes desde dos perspectivas: longitudes de recirculación y longitudes
de aireación (Ver Ilustración 7).
Ilustración 7. Longitudes del resalto hidráulico planteadas por Hager (Stahl & Hager, 1999).
Imagen Número de Froude
Tipo de Resalto
a
2.3
Normal
b
4.1
Flujo recirculante
c
6.5
Con tubería presurizada

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
21
La longitud de recirculación (
) se mide desde el extremo aguas arriba de los remolinos hasta el punto
de estancamiento. Por lo tanto, para expresar una ecuación que determine la longitud de recirculación
del resalto hidráulico, Hager y Stahl determinan una relación entre longitud y altura del flujo aguas
abajo del resalto:
Ecuación 39. Relación entre la longitud de recirculación y la profundidad aguas abajo del resalto (Stahl & Hager, 1999).
Y
se calcula en función del Número de Froude:
Ecuación 40. Determinación de la longitud de recirculación a partir del Número de Froude.
La longitud de aireación se mide desde el extremo aguas arriba del resalto donde comienzan los
remolinos hasta el lugar donde no hay burbujas de aire (Esta longitud es base para encontrar la longitud
del resalto). Para determinarla, Hager y Stahl nuevamente calcularon una relación entre la longitud del
resalto y la profundidad aguas abajo del resalto y encontraron una ecuación en función del Número de
Froude:
Ecuación 41. Relación entre la longitud de aireación y la profundidad aguas abajo del resalto (Stahl & Hager, 1999).
Ecuación 42. Determinación de la longitud de aireación a partir del Número de Froude (Stahl & Hager, 1999).
Rudy Gargano y Willi H. Hager (2002)
En el año 2002, el investigador Willi H. Hager realizó otro análisis en resaltos hidráulicos pero
enfocados únicamente en los resaltos hidráulicos ondulares, analizando la longitud de las olas y los
perfiles. El experimento se realizó en un modelo similar al usado en 1999 (diámetro de 240 mm y de 6
m de longitud y el material de construcción fue acrílico).
Las relaciones de llenado oscilaron entre 0.3 y 0.8, variándolas cada 0.05. Se trabajaron 3 pendientes:
0.001, 0.0015 y 0.003, y los Números de Froude oscilaron entre 1.25 y 2.0 (Números de Froude
característicos de resaltos hidráulicos ondulares).
Como los resaltos hidráulicos ondulares son muy inestables, cualquier perturbación afecta el flujo en el
resalto; además, dependiendo del Número de Froude aguas arriba del resalto, se pueden determinar los
siguientes tipos de resaltos hidráulicos ondulares:
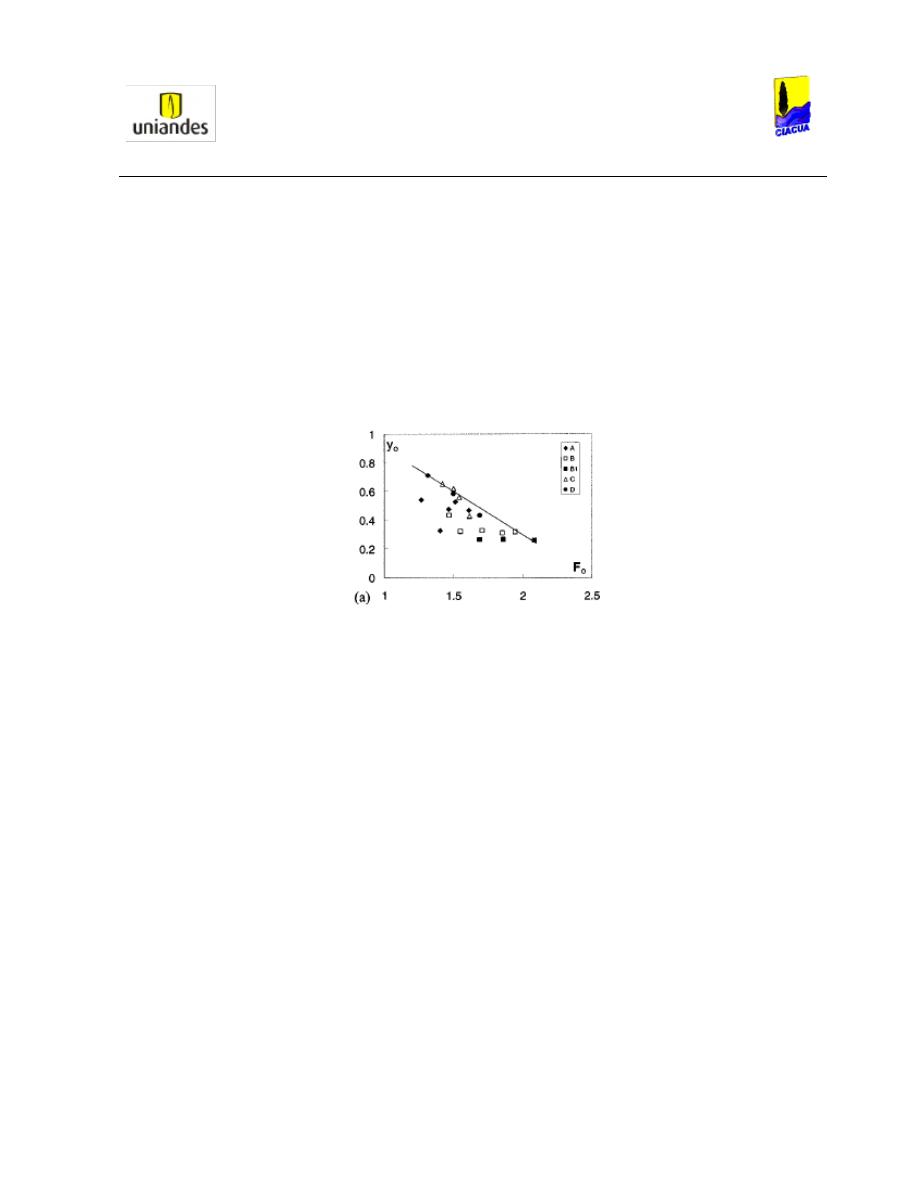
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
22
1. Resalto Ondular Tipo A: Ocurre cuando los Números de Froude aguas arriba del resalto son bajos
(F<1.20). Las ondas fluyen libremente en el flujo.
2.
Resalto Ondular Tipo B: Ocurre cuando la pendiente es pronunciada y el flujo va aumentado de
aguas arriba hacia aguas abajo sin la formación de ondas. (1.20<F<1.28)
3.
Resalto Ondular Tipo C: Ocurre cuando el Número de Froude oscila entre 1.28 y 1.36.
4.
Resaltos Ondular Tipo D: Ocurre cuando los Números de Froude aguas arriba del resalto son
grandes (1.28<F<1.60).
En la Gráfica 7 se muestran los diferentes tipos de resaltos hidráulicos generados en los experimentos
realizados:
Gráfica 7. Tipos de resaltos hidráulicos generados en los experimentos realizados por Hager y Gargano (Gargano & Hager,
2002).
Por lo tanto, según la Gráfica 7, se obtienen los siguientes resultados:
1. Resalto Ondular Tipo A: Ocurre para Números de Froude menores a 1.5
2. Resalto Ondular Tipo B: Ocurre para relaciones de llenado entre 0.3 y 0.45.
3. Resaltos Ondulares Tipo C y D: Se forman de acuerdo con la siguiente ecuación:
Ecuación 43. Estimación para resaltos Ondulares Tipo C y D (Gargano & Hager, 2002).
Como conclusión Gargano y Hager comentan que el pico de la onda ocurre en la primera onda, además
la longitud de la onda depende exclusivamente de
⁄ . Por último, para evitar problemas en las redes
de alcantarillado, los Números de Froude deben ser menores a 0.75 o mayores a 2 para evitar la
inestabilidad del flujo y no producir resaltos ondulares, los cuales tienen las mismas características que
un resalto normal.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
23
H.K. Ghamry, Ain Shames y Fayoum Branch (2002)
En el año 2002 se realizó otro experimento para analizar los resaltos hidráulicos en tuberías; el diámetro
era de 0.3 m, longitud de 1.37 m, el caudal variaba entre 7 y 35 L/s y la variación de los Números de
Froude oscilaban entre 1.29 y 6.43.
Para calcular el resalto, introducen el término de sumergencia (S):
Ecuación 44. Sumergencia en la compuerta (Ghamry, Shames, & Branch, 2002).
donde:
: Sumergencia en la compuerta
: Altura aguas arriba de la compuerta
: Altura en la compuerta
Ecuación 45. Sumergencia (Ghamry, Shames, & Branch, 2002).
donde:
: Sumergencia
: Altura aguas arriba del resalto
: Altura aguas abajo del resalto
Estos investigadores realizaron una comparación entre la sumergencia en la compuerta y la sumergencia
en el resalto y concluyeron que la relación es proporcional, aunque para una sumergencia del resalto
específica, la sumergencia en la compuerta empieza a aumentar cuando aumenta el Número de Froude
(Ver Gráfica 8).
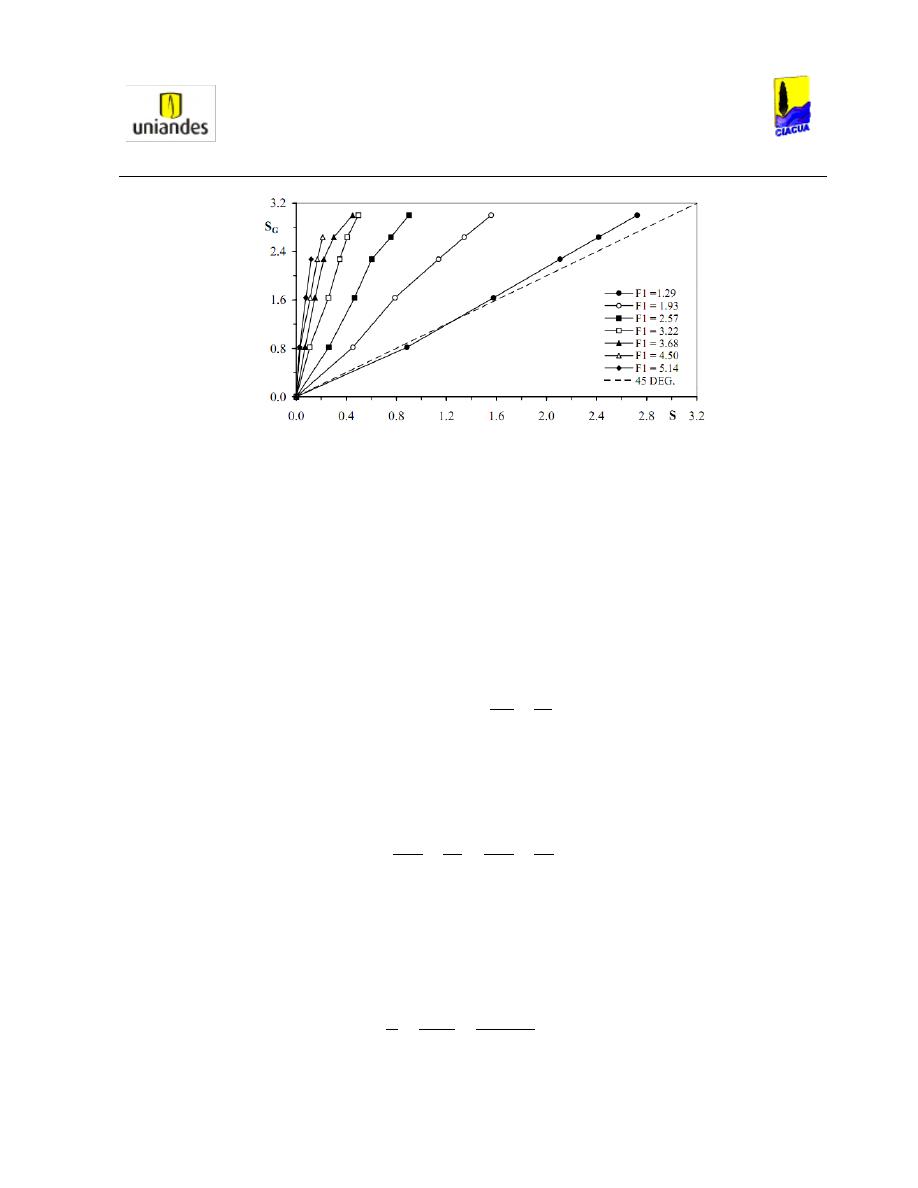
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
24
Gráfica 8. Comparación sumergencia del resalto vs sumersión de la compuerta (Ghamry, Shames, & Branch, 2002).
Por último, para Números de Froude bajos, con variaciones bajas en la sumergencia, varía de manera
importante la sumergencia en la compuerta; sin embargo, a medida que aumenta el Número de Froude,
la sumergencia en la compuerta y la sumergencia varían igual. Además, la relación entre la energía
específica en la compuerta respecto a las diferentes energías a lo largo del resalto tiene un leve aumento
cuando la sumergencia aumenta.
Osman Akan (2006)
La profundidad subsecuente de un resalto hidráulico en canales rectangulares fue planteada por Akan
como la igualdad de los momentos específicos aguas arriba y aguas abajo del resalto hidráulico:
Ecuación 46. Cálculo Momentum Específico en Canales Rectangulares (Akan, 2006).
Igualando los momentos específicos aguas arriba y aguas abajo usando la Ecuación 46 se tiene que:
Ecuación 47. Procedimiento cálculo altura subsecuente de los resaltos hidráulicos en canales rectangulares (Akan, 2006).
Y conociendo que el caudal por unidad de ancho es igual a:
Ecuación 48. Caudal por unidad de ancho.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
25
donde:
: Caudal [m³/s]
: Caudal por unidad de ancho [m³/s*m]
: Ancho del canal [m]
Reemplazando la Ecuación 48 en la Ecuación 47:
Ecuación 49. Procedimiento cálculo profundidades subsecuentes.
Teniendo en cuenta la ecuación de conservación de la masa:
Ecuación 50. Conservación de la masa.
Ecuación 51. Cálculo velocidad aguas abajo a partir de los parámetros aguas arriba.
Reemplazando la Ecuación 51 y la Ecuación 47 en la Ecuación 49:
(
)
y reorganizando:
(
)
(
)
(
)
(
)
(
)(
)
(
)
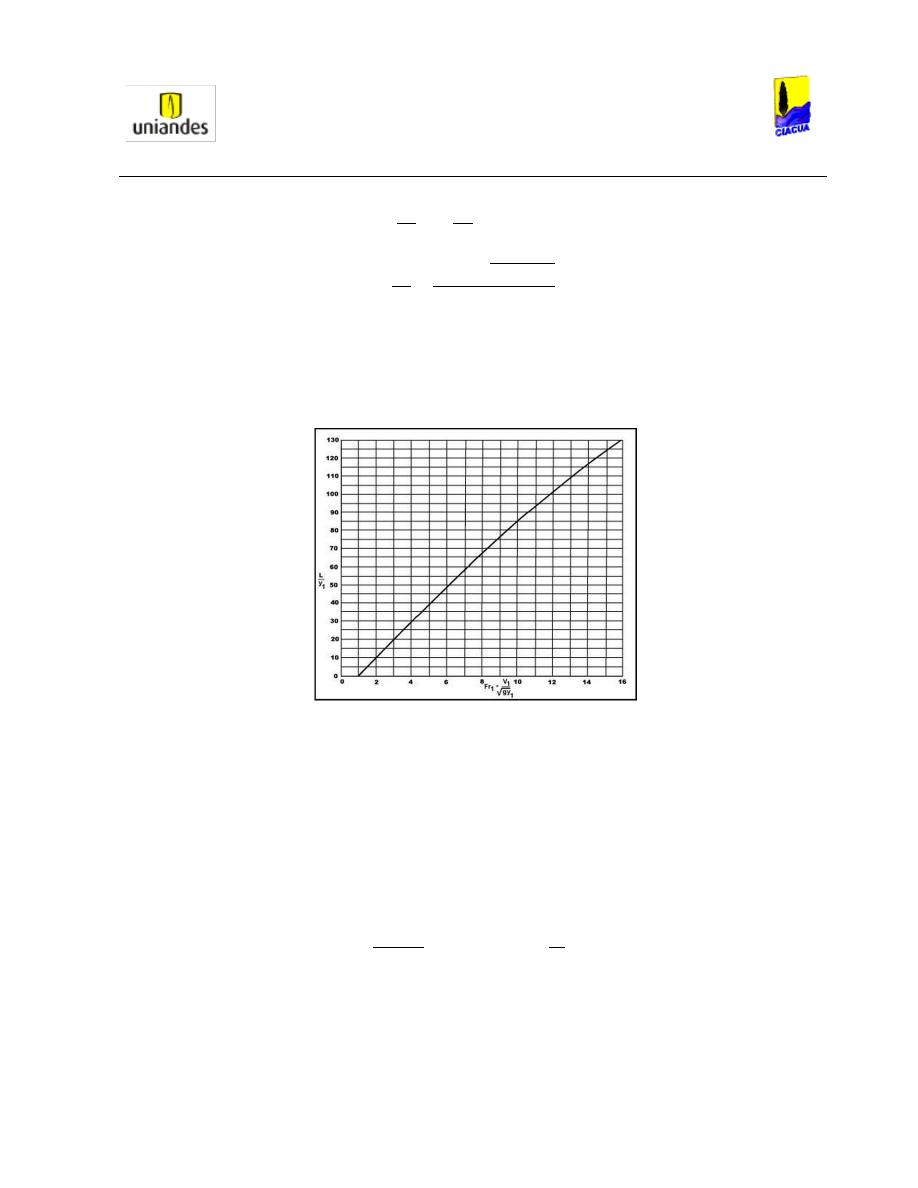
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
26
(
)
√
Ecuación 52. Cálculo profundidades subsecuentes en canales rectangulares.
La longitud del resalto hidráulico para canales rectangulares puede ser medida mediante la Gráfica 9, la
cual puede presentar errores cuando el resalto hidráulico presenta una superficie muy plana.
Gráfica 9. Cálculo de la longitud del Resalto Hidráulico. (FHWA, 2006).
National Highway Institute (2006)
En el 2006 aparecen publicadas en la Circular de Ingeniería Hidráulica N° 14 del Departamento de
Transporte de Estados Unidos (U.S. Department of Transportation), ecuaciones y gráficas para
determinar resaltos hidráulicos en tuberías. Estas ecuaciones se escogen dependiendo si la profundidad
aguas abajo es menor o mayor al diámetro:
Cuando la profundidad aguas abajo es menor al diámetro se tiene que:
(
)
Ecuación 53. Cálculo profundidad subsecuente para profundidades subsecuentes menores al diámetro (FHWA, 2006).
donde:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
27
: Profundidad aguas abajo del resalto
: Profundidad aguas arriba del resalto
: Número de Froude aguas arriba del resalto
: Funciones de y/D, y sus valores se encuentran en la Tabla 2.
Cuando la profundidad aguas abajo es mayor al diámetro, se realizan los cálculos con la Ecuación 54:
(
)
(
)
Ecuación 54. Cálculo profundidad subsecuente para profundidades subsecuentes mayores al diámetro (FHWA, 2006).
donde:
: Profundidad aguas abajo del resalto
: Profundidad aguas arriba del resalto
: Número de Froude aguas arriba del resalto
: Funciones de y/D, y sus valores se encuentran en la Tabla 2.
Tabla 2. Coeficientes para tuberías circulares horizontales (FHWA, 2006).
y/D
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1,000
K
0.41 0.413 0.416 0.419 0.424 0.432 0.445 0.462 0.473
0.5
C
0.041 0.112 0.198 0.293 0.393 0.494 0.587 0.674 0.745 0.748
Adicionalmente, la longitud del resalto (medida desde el punto donde inicia la turbulencia hasta el lugar
donde la profundidad aguas abajo alcanza el máximo) cuando la profundidad aguas abajo es menor al
diámetro se puede determinar mediante la Gráfica 10:
Gráfica 10. Determinación de la longitud del resalto para profundidades subsecuentes menores al diámetro (FHWA, 2006).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
28
En la Gráfica 10 se puede observar que existe una aproximación experimental para hallar la longitud del
resalto dependiendo si
es mayor o menor al diámetro:
Cuando la profundidad aguas abajo del resalto es menor al diámetro y para Números de Froude menores
a 6:
Ecuación 55. Determinación de la longitud del resalto cuando la profundidad aguas abajo es menor al diámetro. (FHWA,
2006)
Cuando la profundidad aguas abajo del resalto es mayor al diámetro:
(
)
Ecuación 56. Determinación longitud del resalto cuando la profundidad aguas abajo es mayor al diámetro (FHWA, 2006).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
29
3. Marco Teórico
El marco teórico presentado a continuación se encuentra en la tesis de pregrado denominada “Diseño y
construcción de un modelo para estudiar el comportamiento de resaltos hidráulicos en tuberías fluyendo
parcialmente llenas de sección circular, con Números de Froude supercríticos menores a 4” (Montaño
Luna, 2012).
3.1. Resaltos Hidráulicos
3.1.1. Definición
Los resaltos hidráulicos son fenómenos físicos presentados cuando hay un cambio de flujo supercrítico a
flujo subcrítico, lo cual genera pérdidas de energía, turbulencia, rompimiento en la superficie del flujo
(en algunos casos) y entrampamiento de aire. Su comportamiento se puede observar en la Ilustración 8:
Ilustración 8. Resalto Hidráulico (Akan, 2006).
En tuberías circulares, existen dos tipos de resaltos; el primero ocurre cuando la profundidad
subsecuente del resalto es menor al diámetro de la tubería (y
2
<D), (Ver Ilustración 9), y el segundo tipo,
cuando la profundidad subsecuente supera el diámetro (y
2
>D) (Ilustración 10).
Ilustración 9. Profundidad subsecuente menor al diámetro de la tubería (Ghamry, Shames, & Branch, 2002).
Ilustración 10. Profundidad subsecuente mayor al diámetro de la tubería (Ghamry, Shames, & Branch, 2002).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
30
Los resaltos hidráulicos cumplen la función de disipar energía debido a la turbulencia generada en éste
fenómeno y la incorporación de aire; por lo tanto son útiles en zonas donde la potencia del agua puede
causar daños en las estructuras y erosiones en los canales, o en las plantas de tratamiento de agua
residual o plantas de tratamiento de agua potable, donde se usan para mezclar sustancias mientras ocurre
el fenómeno.
A continuación se mencionan otras funciones del resalto hidráulico en canales abiertos (CIVIL
ENGINEERING PORTAL, 2011):
Disipación de energía en flujos sobre diques, vertederos y otras estructuras hidráulicas.
Establecimiento de alturas altas, apropiadas para canales usados en la distribución de agua o
irrigación de cultivos.
Reducción de las presiones altas que se encuentran debajo de las estructuras.
Mezcla de sustancias químicas usadas para tratamiento de agua.
Aireación de flujos y declorinado en los procesos de tratamiento de agua.
Eliminación de paquetes de aire presentados en canales circulares.
Identificación de las condiciones del flujo mediante mediciones, y así tomar medidas de
regulación.
Adicionalmente, la formación de resaltos hidráulicos se presenta cuando el canal tiene altas pendientes,
obstáculos en el canal o cambios de pendiente.
3.1.2. Tipos de Resaltos Hidráulicos
Según la US Bureau of Reclamation, los resaltos hidráulicos se identifican de acuerdo con el Número de
Froude:
Tabla 3. Tipos de Resaltos Hidráulicos en fondos sin pendiente (Gonzales Rodríguez, 1992).
Número de Froude
Características
Froude = 1.0
No existe formación de Resalto
Hidráulico porque se encuentra en la
profundidad crítica
1.0 < Froude < 1.7
Resalto Ondular
1.7 < Froude < 2.5
Resalto Débil
2.5 < Froude < 4.5
Resalto Oscilante
4.5 < Froude < 9.0
Resalto Permanente
Froude > 9.0
Resalto Fuerte
Resalto Ondular: Cómo se explicó en los Antecedentes, un resalto hidráulico ondular genera baja
disipación de energía, su disipación oscila entre el 0 y el 8%.
Resalto Débil: En la superficie del resalto se presenta una pequeña turbulencia, con disipaciones de
energía entre el 10 y el 20%.
Resalto Oscilante: Hay una turbulencia no periódica, la cual va generando a su paso problemas de
erosión tanto en las orillas del canal como en el fondo. La disipación de energía oscila entre 20 y
45%.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
31
Resalto Permanente: Éste resalto no tiene en cuenta el comportamiento del flujo aguas abajo, por lo
tanto, su comportamiento es más periódico. La disipación de energía oscila entre 45 – 70%.
Resalto fuerte: Es un resalto violento, que alcanza disipaciones de energía del 85%.
Ilustración 11. Tipos de Resaltos Hidráulicos (Gonzales Rodríguez, 1992).
3.1.3. Cálculo de profundidades subsecuentes en el Resalto Hidráulico
Cómo las pérdidas de energía son considerables, no se puede usar la ecuación de conservación de la
energía para encontrar la relación entre las profundidades aguas arriba del resalto y aguas abajo, sino
que se debe usar la conservación del Momentum planteada en la Ecuación 57.
Ecuación 57. Conservación del Momentum Específico.
En canales rectangulares el análisis de la profundidad subsecuente del resalto hidráulico se realiza
mediante la demostración planteada por Akan, obteniendo como resultado la Ecuación 52:
√
Ecuación 52. Cálculo profundidades subsecuentes en canales rectangulares.
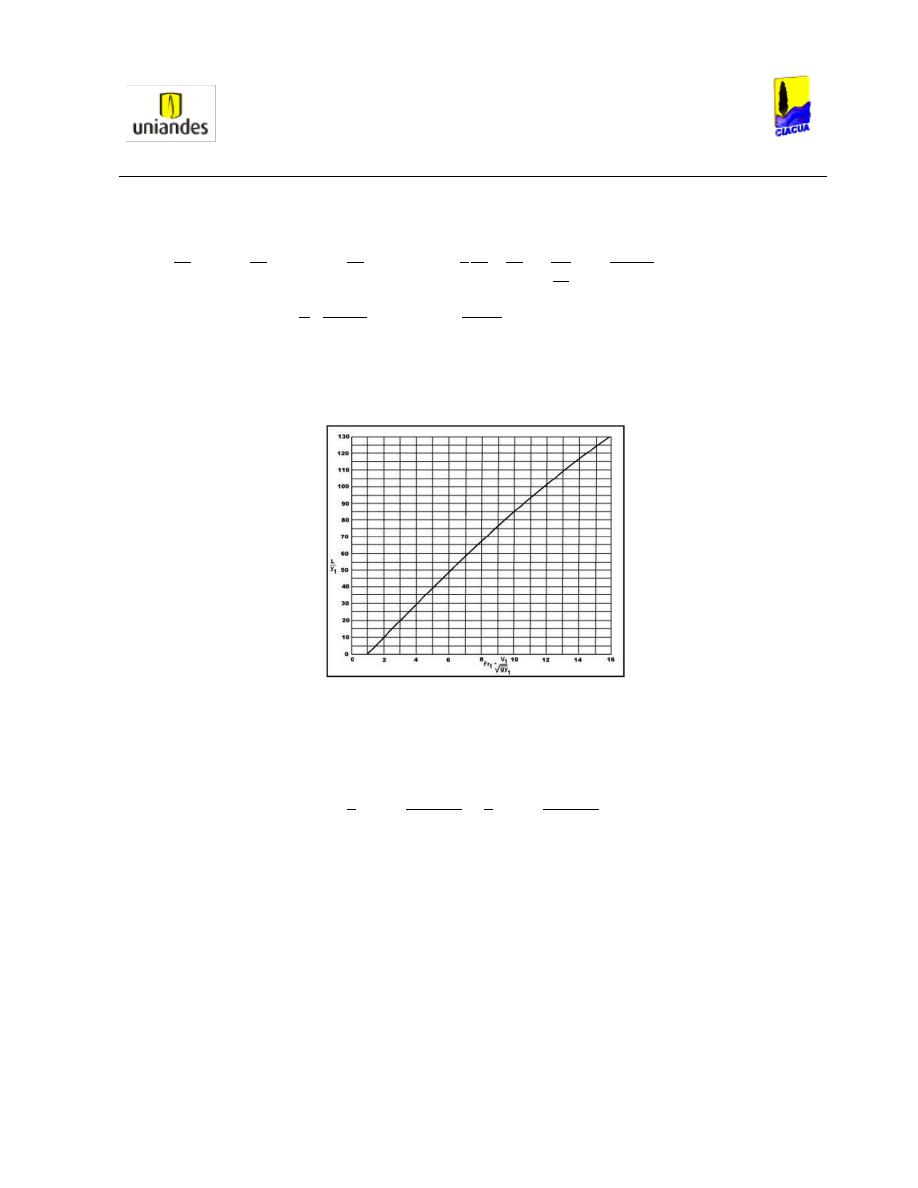
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
32
O mediante la
Ecuación 58
planteada por Smith y Chen:
(
)
[
(
) ]
[(
)
(
) ]
(
)
Ecuación 58.
Dimensiones del Resalto Hidráulico en canales cuadrados reorganizada (SMITH & CHEN, 1989).
Además, la longitud del resalto se puede medir mediante la Gráfica 11:
Gráfica 11. Cálculo de la longitud del Resalto Hidráulico (FHWA, 2006).
El análisis de Momentum para tuberías circulares se puede explicar en el análisis planteado por Stahl y
Hager (Ver Ecuación 31), en el cual se obtiene la siguiente ecuación de conservación del Momentum:
Ecuación 31. Ecuación del Momentum (Stahl & Hager, 1999).
Adicionalmente, en otro análisis, realizado por Osman Akan en el libro Open Channel Hydraulics, la
solución de la Ecuación 31 requiere de procedimientos de prueba y error, por lo tanto se han graficado
diagramas de Momentum para encontrar la solución en canales circulares:
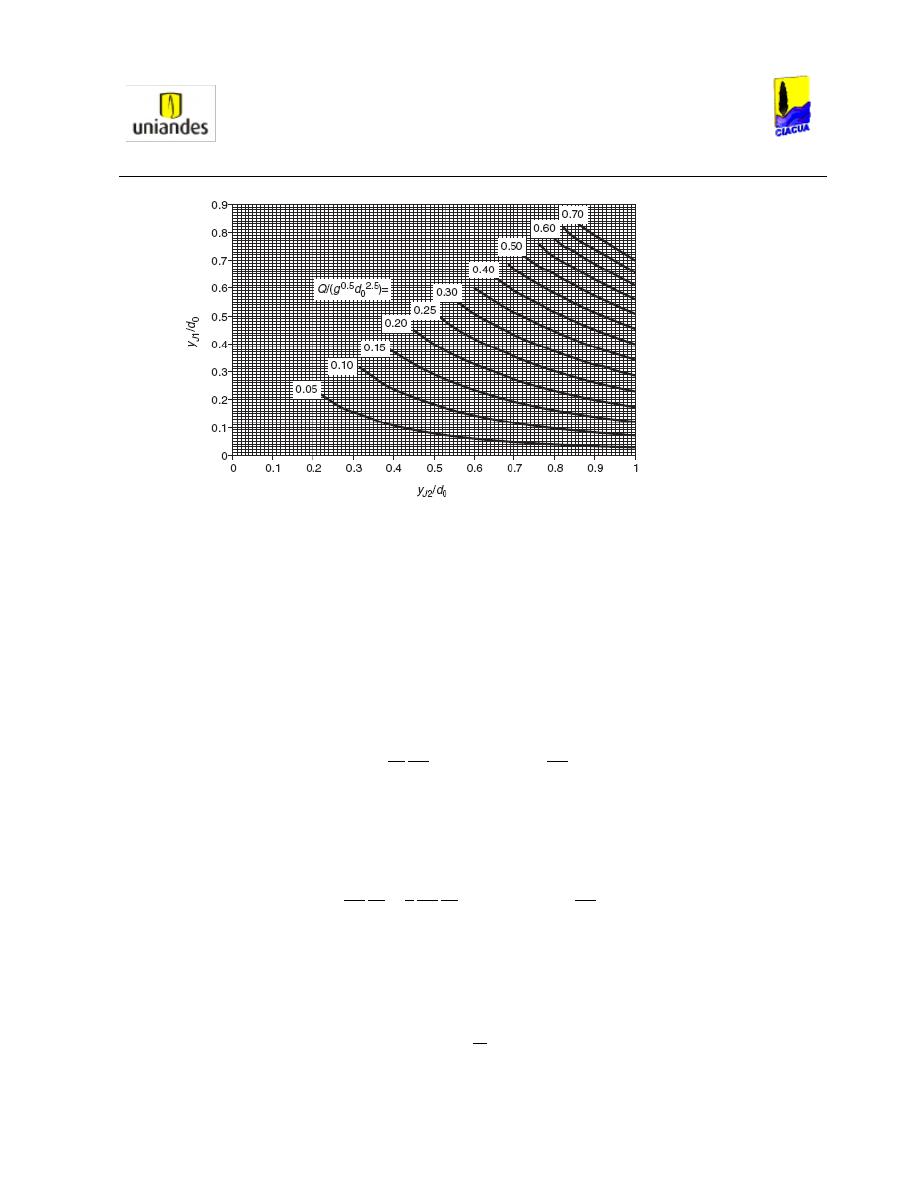
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
33
Gráfica 12. Diagrama de Momentum en canales circulares (Akan, 2006).
Como se observa en la Gráfica 12, todas las líneas tienen un límite en el inicio de la curva, lo que indica
que en tuberías circulares, siempre se tendrá una zona supercrítica antes de la formación del resalto, y
aguas abajo se tienen dos opciones, que el flujo siga a superficie libre o que la tubería se presurice.
Por lo tanto, partiendo de las Ecuaciones de Momentum y diversos experimentos, se encuentran las
siguientes ecuaciones para encontrar las profundidades subsecuentes:
La primera ecuación fue calculada por Silvester en 1964 a partir de los datos obtenidos en el
experimento de Kindsvater. La Ecuación 12 funciona para tuberías fluyendo parcialmente llenas:
[
]
Ecuación 12. Profundidades subsecuentes para tuberías parcialmente llenas (Silvester, 1964).
La Ecuación 14 se utiliza en tuberías presurizadas:
[
]
Ecuación 14. Profundidades subsecuentes para tuberías llenas.
En 1978, Straub plantea ecuaciones para determinar la profundidad subsecuente del resalto hidráulico a
partir de una aproximación en el cálculo del Número de Froude:
(
)
Ecuación 21. Aproximación Número de Froude (French, 2007).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
34
Cuando el Número de Froude es menor a 1.7:
Ecuación 22. Cálculo profundidad subsecuente para Números de Froude menores a 1.7 (French, 2007).
Y cuando el Número de Froude es mayor a 1.7:
Ecuación 23. Cálculo profundidad subsecuente para Números de Froude mayores a 1.7 (French, 2007).
En 1999 Stahl y Hager plantearon dos ecuaciones a partir de sus resultados experimentales, la primera
calculada para Números de Froude generales:
Ecuación 59. Profundidad subsecuente en el resalto hidráulico (Stahl & Hager, 1999).
donde
Y la siguiente para Números de Froude mayores a 2:
Ecuación 60. Profundidad subsecuente con Números de Froude mayores a 2 (Stahl & Hager, 1999).
Y por último, en la Circular 14 de Ingeniería Hidráulica del Departamento de Transporte de Estados
Unidos se establecen las siguientes ecuaciones para encontrar las profundidades subsecuentes:
Cuando la profundidad aguas abajo es menor al diámetro se tiene que:
(
)
Ecuación 53. Cálculo profundidad subsecuente para profundidades subsecuentes menores al diámetro (FHWA, 2006).
donde:
: Profundidad aguas abajo del resalto
: Profundidad aguas arriba del resalto
: Número de Froude aguas arriba del resalto

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
35
: Funciones de y/D, y sus valores se encuentran en la Tabla 2
Cuando la profundidad aguas abajo es mayor al diámetro, se realizan los cálculos con la Ecuación 54:
(
)
(
)
Ecuación 54. Cálculo profundidad subsecuente para profundidades subsecuentes mayores al diámetro (FHWA, 2006).
donde:
: Profundidad aguas abajo del resalto
: Profundidad aguas arriba del resalto
: Número de Froude aguas arriba del resalto
: Funciones de y/D, y sus valores se encuentran en la Tabla 2
Adicionalmente, la longitud del resalto (medida desde el punto donde inicia la turbulencia hasta el lugar
donde la profundidad aguas abajo alcanza el máximo) cuando la profundidad aguas abajo es menor al
diámetro se puede determinar mediante la Gráfica 13:
Gráfica 13. Determinación de la longitud del resalto para profundidades subsecuentes menores al diámetro (FHWA, 2006).
3.1.4. Análisis del comportamiento del resalto hidráulico
El comportamiento del resalto hidráulico es inestable y no se puede medir, salvo por análisis
probabilísticos; sin embargo, se puede evaluar la variación de la turbulencia en diferentes zonas del
resalto hidráulico, mediante la medición de velocidad y presión.
Para medir la intensidad de la turbulencia isotrópica, se usa la siguiente ecuación:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
36
√
̅̅̅̅
Ecuación 61. Cálculo de la intensidad de la turbulencia (Lopardo, 2012).
donde:
: Velocidad de fluctuación
: Velocidad media en el punto considerado
Ésta intensidad también puede ser calculada mediante un parámetro adimensional (
):
√
̅̅̅̅̅
Ecuación 62. Cálculo del parámetro adimensional para determinar la turbulencia del resalto hidráulico (Lopardo, 2012).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
37
4. Diseño del modelo
4.1.
Ubicación
El montaje se realizó en el laboratorio de Hidráulica de la Universidad de los Andes, sobre el canal
rectangular ubicado en el extremo derecho del laboratorio (Ver plano anexo).
Ilustración 12. Canal donde su ubicó el montaje.
4.2.
Proceso de diseño
El proceso ampliado de construcción del montaje se encuentra en la Tesis “Diseño y Construcción de un
modelo para estudiar el comportamiento de resaltos hidráulicos en tuberías parcialmente llenas de
sección circular, con Números de Froude supercríticos menores a 4 (Montaño Luna, 2012)”.
En general, el montaje consta de 6 tuberías de 2 m de longitud, y una tubería de 1 m de longitud, la cual
cuenta con una compuerta para controlar la ubicación del resalto hidráulico. Para sostener la tubería, se
realizó un soporte de acero dividido en 4 secciones de 3 m, el cual permite variar la pendiente de la
tubería sin poner en riesgo la estructura de la misma.
El montaje final realizado en la tesis de Montaño se muestra a continuación:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
38
Ilustración 13. Vista dentro de la tubería.
Ilustración 14. Vista de la compuerta con el neumático.
Ilustración 15. Vista de la compuerta en el montaje.
Ilustración 16. Vista perfil de la compuerta.
Posteriormente, para la lectura de los diferentes parámetros, se adaptaron en la tubería soportes y
adiciones para colocar los sensores de nivel y caudal, lo cual se puede observar en el Numeral 4.3.
4.3.
Aparatos de medición
4.3.1. Sensor Ultrasónico U – GAGE T30
El medidor ultrasónico de nivel U – GAGE T30, es un medidor de fácil manejo y programación. Su
funcionamiento consiste en lanzar un pulso de ultrasonido sobre una superficie, cuando el pulso
encuentra la superficie se refleja y emite la señal al receptor.
Las características del equipo son:
Su rango de acción se encuentra entre los 15 cm hasta 1 m.
El rango de temperatura varía entre – 20°C y 70°C.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
39
El tiempo de respuesta es de 48 milisegundos para la salida discreta y la análoga.
Ilustración 17. Características del U - GAGE T30 (Banner Engineering).
Sin embargo, como el sensor tiene una zona muerta de 15 cm, se requirió una adaptación de la tubería
para colocar los sensores, la cual consistió en adaptar un tubo en cada tubería donde se requiriera el
sensor; y en los casos en los cuales la tubería se presurice aguas abajo, el sensor será retirado y el nivel
del flujo se medirá con los piezómetros.
Ilustración 18. U - GAGE T30.
4.3.2. ADV (Velocímetro Doppler acústico)
El velocímetro Doppler acústico, es un instrumento que permite medir con alta precisión el
comportamiento de la velocidad en las 3 dimensiones.
Consta de 3 elementos para ejecutar la medición: una sonda, un módulo de acondicionamiento de la
señal y un procesador. El área muerta de medición del equipo es de 5 cm, por lo cual todas las
mediciones que se realizan en el resalto deben superar dicha altura. El rango de velocidad de medición
posible está entre
3 cm/s a 250 cm/s.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
40
Ilustración 19. ADV (SonTek, 2012).
Para adaptar el ADV en la tubería, se realizó un montaje que permite el movimiento tridimensional del
equipo, así poder medir el comportamiento de la velocidad en determinados puntos.
Ilustración 20. Adaptación del ADV en la tubería.
4.3.3. Piezómetros
Para medir el nivel de la tubería aguas abajo del resalto, cuando la tubería se encuentre presurizada, se
adaptaron unos piezómetros aguas abajo del sensor ADV. Estos piezómetros se encuentran a una
distancia de 20 cm entre ellos, dando lugar a 17 piezómetros de medición.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
41
Ilustración 21. Piezómetros en la tubería.
4.3.4. Caudalímetro
El caudal que pasa por la tubería es medido por un Caudalímetro Electromagnético ABB, el cual
funciona bajo la Ley de inducción de Faraday. El caudal máximo que puede pasar por el tanque de
abastecimiento es de 110 L/s, sin embargo, debido a las condiciones del canal, de la tubería y los
tanques aguas arriba y aguas abajo del montaje, el caudal máximo que pasará por la tubería fue de 80
L/s.
Ilustración 22. Caudalímetro ABB
.
4.4.
Metodología y proceso de medición
4.4.1. Profundidad del flujo
4.4.1.1.
Parámetros de medición
Los parámetros a medir en la tubería son:
Altura del nivel del flujo aguas arriba y aguas abajo del resalto hidráulico.
Longitud del resalto hidráulico (Longitud de la formación de las burbujas y del resalto
hidráulico como tal).
Temperatura del resalto hidráulico.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
42
Temperatura del flujo aguas arriba y aguas abajo del resalto hidráulico.
4.4.1.2.
Metodología de medición
1. Variación de las pendientes
4
.
2. Abertura de la válvula.
3. Purga de piezómetros.
4. Variación de los caudales.
5. Toma de datos de niveles, caudal y velocidad.
6. Medición de la temperatura aguas arriba y aguas abajo del resalto hidráulico.
7. Medición de la longitud de las burbujas y la longitud del resalto.
4.1.1.3. Lista de caudales y pendientes
Teniendo en cuenta el caudal y la pendiente máxima permitidos en el montaje, se realizó la siguiente
lista, en la cual también se muestra el valor del Número de Froude, ya que con este valor se puede
estimar la fuerza del resalto hidráulico:
Tabla 4. Lista de caudales y pendientes.
5
# Escenario
S
(-)
Q
(m
3
/s)
y
n
(m)
y
n
/d
(-)
Número de
Froude
(-)
1
0.005
0.005
0.048
0.198
0.241
2
0.005
0.015
0.084
0.346
0.699
3
0.005
0.025
0.111
0.458
1.137
4
0.005
0.035
0.135
0.559
1.555
5
0.005
0.045
0.160
0.661
1.956
6
0.005
0.055
0.188
0.776
2.331
7
0.007
0.005
0.044
0.181
0.242
8
0.007
0.015
0.076
0.314
0.705
9
0.007
0.025
0.100
0.412
1.148
10
0.007
0.035
0.121
0.500
1.576
11
0.007
0.045
0.141
0.583
1.989
12
0.007
0.055
0.162
0.668
2.386
13
0.007
0.065
0.185
0.763
2.762
14
0.007
0.075
0.222
0.919
3.082
15
0.009
0.005
0.041
0.169
0.243
16
0.009
0.015
0.071
0.292
0.708
17
0.009
0.025
0.093
0.382
1.156
18
0.009
0.035
0.112
0.461
1.590
4
Las pendientes y los caudales variarán de acuerdo con la lista presentada en el Numeral 4.1.1.3.
5
La convención (-) indica que la variable es adimensional.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
43
Continuación Tabla 4. Lista de caudales y pendientes.
# Escenario
S
(-)
Q
(m
3
/s)
y
n
(m)
y
n
/d
(-)
Número de
Froude
(-)
19
0.009
0.045
0.129
0.535
2.011
20
0.009
0.055
0.147
0.608
2.418
21
0.009
0.065
0.165
0.683
2.811
22
0.009
0.075
0.186
0.767
3.185
23
0.011
0.005
0.039
0.160
0.243
24
0.011
0.015
0.067
0.276
0.711
25
0.011
0.025
0.087
0.360
1.162
26
0.011
0.035
0.105
0.433
1.600
27
0.011
0.045
0.121
0.501
2.026
28
0.011
0.055
0.137
0.566
2.441
29
0.011
0.065
0.153
0.631
2.843
30
0.011
0.075
0.169
0.700
3.231
31
0.013
0.005
0.037
0.153
0.244
32
0.013
0.015
0.064
0.263
0.713
33
0.013
0.025
0.083
0.343
1.166
34
0.013
0.035
0.100
0.411
1.608
35
0.013
0.045
0.115
0.474
2.038
36
0.013
0.055
0.129
0.535
2.458
37
0.013
0.065
0.144
0.594
2.867
38
0.013
0.075
0.158
0.655
3.264
39
0.015
0.005
0.036
0.147
0.244
40
0.015
0.015
0.061
0.253
0.715
41
0.015
0.025
0.080
0.329
1.170
42
0.015
0.035
0.095
0.394
1.614
43
0.015
0.045
0.110
0.453
2.048
44
0.015
0.055
0.123
0.510
2.471
45
0.015
0.065
0.137
0.565
2.885
46
0.015
0.075
0.150
0.620
3.289
47
0.017
0.005
0.034
0.142
0.244
48
0.017
0.015
0.059
0.244
0.716
49
0.017
0.025
0.077
0.317
1.173
50
0.017
0.035
0.092
0.380
1.620
51
0.017
0.045
0.106
0.436
2.056
52
0.017
0.055
0.118
0.489
2.483
53
0.017
0.065
0.131
0.541
2.900
54
0.017
0.075
0.143
0.593
3.309
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
44
Continuación Tabla 4. Lista de caudales y pendientes.
# Escenario
S
(-)
Q
(m
3
/s)
y
n
(m)
y
n
/d
(-)
Número de
Froude
(-)
55
0.019
0.005
0.033
0.138
0.245
56
0.019
0.015
0.057
0.237
0.717
57
0.019
0.025
0.074
0.307
1.176
58
0.019
0.035
0.089
0.367
1.624
59
0.019
0.045
0.102
0.421
2.063
60
0.019
0.055
0.114
0.472
2.492
61
0.019
0.065
0.126
0.521
2.913
62
0.019
0.075
0.138
0.570
3.325
63
0.021
0.005
0.033
0.134
0.245
64
0.021
0.015
0.056
0.230
0.718
65
0.021
0.025
0.072
0.299
1.178
66
0.021
0.035
0.086
0.356
1.628
67
0.021
0.045
0.099
0.409
2.069
68
0.021
0.055
0.111
0.458
2.500
69
0.021
0.065
0.122
0.505
2.924
70
0.021
0.075
0.133
0.550
3.340
71
0.023
0.005
0.032
0.131
0.245
72
0.023
0.015
0.054
0.224
0.719
73
0.023
0.025
0.070
0.291
1.180
74
0.023
0.035
0.084
0.347
1.632
75
0.023
0.045
0.096
0.398
2.074
76
0.023
0.055
0.108
0.445
2.508
77
0.023
0.065
0.119
0.490
2.934
78
0.023
0.075
0.129
0.534
3.352
79
0.025
0.005
0.031
0.128
0.245
80
0.025
0.015
0.053
0.219
0.720
81
0.025
0.025
0.069
0.284
1.182
82
0.025
0.035
0.082
0.339
1.635
83
0.025
0.045
0.094
0.388
2.078
84
0.025
0.055
0.105
0.433
2.514
85
0.025
0.065
0.115
0.477
2.942
86
0.025
0.075
0.126
0.519
3.363
87
0.027
0.005
0.030
0.126
0.245
88
0.027
0.015
0.052
0.215
0.721
89
0.027
0.025
0.067
0.278
1.184
90
0.027
0.035
0.080
0.331
1.637
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
45
Continuación Tabla 4. Lista de caudales y pendientes.
# Escenario
S
(-)
Q
(m
3
/s)
y
n
(m)
y
n
/d
(-)
Número de
Froude
(-)
91
0.027
0.045
0.092
0.379
2.083
92
0.027
0.055
0.102
0.423
2.520
93
0.027
0.065
0.113
0.465
2.950
94
0.027
0.075
0.123
0.506
3.373
95
0.029
0.005
0.030
0.123
0.245
96
0.029
0.015
0.051
0.211
0.722
97
0.029
0.025
0.066
0.272
1.185
98
0.029
0.035
0.079
0.324
1.640
99
0.029
0.045
0.090
0.371
2.086
100
0.029
0.055
0.100
0.414
2.525
101
0.029
0.065
0.110
0.455
2.957
102
0.029
0.075
0.120
0.495
3.382
103
0.031
0.005
0.029
0.121
0.246
104
0.031
0.015
0.050
0.207
0.722
105
0.031
0.025
0.065
0.267
1.187
106
0.031
0.035
0.077
0.318
1.642
107
0.031
0.045
0.088
0.364
2.090
108
0.031
0.055
0.098
0.406
2.530
109
0.031
0.065
0.108
0.446
2.963
110
0.031
0.075
0.117
0.484
3.390

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
46
4.4.2. Distribución de velocidades
4.4.2.1.
Parámetros de medición
Los parámetros necesarios para entender el comportamiento de la distribución de la velocidad del flujo
son:
Velocidad en cada uno de los puntos de medición.
Profundidad del flujo aguas arriba del resalto.
Caudal de entrada en la tubería.
4.4.2.2.
Metodología de medición
La medición de los datos está organizada de acuerdo con la siguiente matriz geométrica:
Ilustración 23.Matriz geométrica de medición de la Distribución de Velocidades.
Con la matriz de medición establecida, se variaba la ubicación del ADV para cubrir cada uno de los
puntos deseados, mediante el montaje expuesto en el Numeral 4.3.2.
4.4.2.3.
Lista de caudales y pendientes
El listado de caudales y pendientes que se evaluarán, cumplirán con la condición de generar un resalto
hidráulico estable, es decir, solo se tomarán caudales y pendientes tales que el caudal sea mayor a 10 L/s
y menor a 50 L/s, y pendientes mayores al 1.1%.
Tabla 5. Lista de caudales y pendientes para el análisis del comportamiento de la velocidad.
# Escenario
Pendiente (-)
Caudal (m³/s)
1
0.012
0.024
2
0.012
0.030

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
47
# Escenario
Pendiente (-)
Caudal (m³/s)
3
0.016
0.019
4
0.016
0.024
5
0.017
0.019
6
0.017
0.026
7
0.020
0.020
8
0.020
0.025
9
0.021
0.019
10
0.021
0.025
11
0.022
0.021
12
0.022
0.026

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
48
5. Pruebas de verificación de los parámetros hidráulicos de la tubería
Los Numerales 5.1, 5.2 y 5.3 se encuentran en la tesis de pregrado denominada “Diseño y construcción
de un modelo para estudiar el comportamiento de resaltos hidráulicos en tuberías fluyendo parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4” (Montaño Luna, 2012).
5.1. Comprobación de Diseño
El proceso de comprobación de diseño se realizó para determinar cuál era el diámetro que se debía
elegir para transportar el caudal de 77.6 L/s, evitando tener una relación de llenado muy baja, y alturas
menores a 48 cm (altura máxima permitida por el canal en la compuerta aguas arriba).
Por lo tanto, se realizó un análisis para relaciones de llenado del 50%, 85 % y 92.9% con una pendiente
del 1.88%, y una variación del diámetro cada 0.05 m.
A continuación se presentan los cálculos realizados para la primera iteración, la cual se llevó a cabo para
un diámetro de 0.2 m:
1. Cálculo de la profundidad normal:
( )
Ecuación 63. Cálculo de la relación de llenado.
2. Cálculo de
:
(
)
(
)
Ecuación 64. Cálculo de
.
3. Cálculo del área
( ( ))
( ( ))
Ecuación 65. Cálculo del área mojada.
4. Cálculo del perímetro
Ecuación 66. Cálculo del perímetro mojado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
49
5. Cálculo del radio hidráulico
Ecuación 67. Cálculo del radio hidráulico.
6. Cálculo de la velocidad
√
((
)
( )
√
)
Ecuación 68. Cálculo de la velocidad.
7. Cálculo del caudal
Ecuación 69. Cálculo del caudal.
8. Cálculo del Número de Reynolds
Ecuación 70. Cálculo del Número de Reynodls.
9. Cálculo del ancho de la superficie
( (
))
Ecuación 71. Cálculo del ancho de la superficie.
10. Cálculo de la profundidad hidráulica
Ecuación 72. Cálculo de la profundidad hidráulica.
11. Cálculo del Número de Froude
√
√
Ecuación 73. Cálculo del Número de Froude.
12. Altura total del soporte y el diámetro de la tubería
Ecuación 74. Cálculo de la altura total del soporte.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
50
Siguiendo el procedimiento planteado, se obtienen las siguientes tablas:
Tabla 6. Diámetros seleccionados que superen el caudal de diseño y no superen los 48 cm de altura con relaciones de llenado
del 50 %.
d
(m)
yn
(m)
(-)
Á
(m²)
P
(m)
R
(m)
V
(m)
Q
(m³/s)
Re
(-)
T
(m)
D
(m)
Número
de
Froude
(-)
h
soporte
(m)
d +
soporte
(m)
0,2
0,1
3,142 0,016
0,314
0,050
2,315
0,036
406173,515
0,200 0,079
2,638
0,100
0,300
0,25
0,125
3,142 0,025
0,393
0,063
2,676
0,066
586753,110
0,250 0,098
2,726
0,100
0,350
0,3
0,15
3,142 0,035
0,471
0,075
3,009
0,106
791802,752
0,300 0,118
2,799
0,100
0,400
0,35
0,175
3,142 0,048
0,550
0,088
3,321
0,160
1019595,837
0,350 0,137
2,860
0,100
0,450
0,4
0,2
3,142 0,063
0,628
0,100
3,616
0,227
1268764,140
0,400 0,157
2,913
0,100
0,500
0,45
0,225
3,142 0,080
0,707
0,113
3,897
0,310
1538186,062
0,450 0,177
2,960
0,100
0,550
0,5
0,25
3,142 0,098
0,785
0,125
4,165
0,409
1826918,772
0,500 0,196
3,001
0,100
0,600
0,55
0,275
3,142 0,119
0,864
0,138
4,424
0,525
2134154,161
0,550 0,216
3,039
0,100
0,650
En la Tabla 6 se resaltan los diámetros que cumplen con caudales cercanos al caudal máximo permitido
en el montaje y no superan los 48 cm de la compuerta. Cabe destacar, que las tuberías con diámetros de
200 mm y 250 mm mueven un caudal menor que el caudal máximo con una relación de llenado del
50%, lo que indica que se puede realizar una variación mayor de las relaciones de llenado en éstos
diámetros respecto a los diámetros de 300 mm.
Tabla 7. Diámetros seleccionados que superen el caudal de diseño y no superen los 48 cm de altura con relaciones de llenado
del 85 %.
d
(m)
yn
(m)
(-)
Á
(m²)
P
(m)
R
(m)
V
(m)
Q
(m³/s)
Re
(-)
T
(m)
D
(m)
Número
de
Froude
(-)
h
soporte
(m)
d +
soporte
(m)
0.1
0.085
4.692
0.007
0.235
0.030
2.158
0.015
229631.7
0.071
0.100
2.183
0.1
0.200
0.15
0.128
4.692
0.016
0.352
0.045
2.814
0.045
449084.9
0.107
0.149
2.324
0.1
0.250
0.2
0.17
4.692
0.028
0.469
0.061
3.388
0.096
721077.9
0.143
0.199
2.423
0.1
0.300
0.25
0.213
4.692
0.044
0.587
0.076
3.909
0.174
1039829.5
0.179
0.249
2.501
0.1
0.350
0.3
0.255
4.692
0.064
0.704
0.091
4.390
0.281
1401297.5
0.214
0.299
2.563
0.1
0.400
0.35
0.298
4.692
0.087
0.821
0.106
4.840
0.422
1802433.9
0.250
0.349
2.617
0.1
0.450
0.4
0.34
4.692
0.114
0.938
0.121
5.265
0.599
2240825.9
0.286
0.399
2.663
0.1
0.500
0.45
0.383
4.692
0.144
1.056
0.136
5.669
0.817
2714497.0
0.321
0.448
2.703
0.1
0.550
0.5
0.425
4.692
0.178
1.173
0.152
6.055
1.077
3221787.4
0.357
0.498
2.739
0.1
0.600
0.55
0.468
4.692
0.215
1.290
0.167
6.427
1.383
3761274.8
0.393
0.548
2.772
0.1
0.650
En la Tabla 7 se puede observar que con relaciones de llenado del 85 % (relación de llenado máxima
permitida por el RAS), los diámetros cercanos al caudal máximo son los de 200 mm, 250 mm y 300

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
51
mm; pero al igual que con la relación de llenado del 50 %, los diámetros de 200 mm y 250 mm
permiten análisis con relaciones de llenado más altas dado que el caudal que transportan sigue siendo
menor que el caudal máximo que puede transportar el montaje.
Tabla 8. Diámetros seleccionados que superen el caudal de diseño y no superen los 48 cm de altura con relaciones de llenado
del 92.9 %.
d
(m)
yn
(m)
(-)
A
(m²)
P
(m)
R
(m)
V
(m/s)
Q
(m³/s)
Re
(-)
h
(m)
d + soporte
(m)
0,1
0,093 5,204
0,008
0,260
0,029
1,627
0,012
166855,528
0,100
0,200
0,15
0,139 5,204
0,017
0,390
0,044
2,125
0,036
326990,425
0,100
0,250
0,2
0,186 5,204
0,030
0,520
0,058
2,563
0,078
525738,360
0,100
0,300
0,25
0,232 5,204
0,048
0,651
0,073
2,959
0,141
758879,656
0,100
0,350
0,3
0,279 5,204
0,068
0,781
0,088
3,326
0,228
1023461,122
0,100
0,400
0,35
0,325 5,204
0,093
0,911
0,102
3,669
0,342
1317254,232
0,100
0,450
0,4
0,372 5,204
0,122
1,041
0,117
3,993
0,486
1638493,834
0,100
0,500
0,45
0,418 5,204
0,154
1,171
0,132
4,302
0,663
1985733,499
0,100
0,550
0,5
0,465 5,204
0,190
1,301
0,146
4,597
0,874
2357757,724
0,100
0,600
0,55
0,511 5,204
0,230
1,431
0,161
4,881
1,123
2753524,982
0,100
0,650
En la Tabla 8 se está realizando el mismo análisis pero con la relación de llenado que produce el
máximo caudal posible que puede transportar la tubería; por lo tanto, como supera la normatividad, se
esperaría que no se encuentren relaciones de llenado del 92.9 % en los alcantarillados del país. Sin
embargo, para analizar un ejemplo extremo, se realiza éste análisis, el cual muestra que el único
diámetro que cumple con el caudal cercano al caudal máximo que puede pasar por la tubería es el de
200 mm, mientras que el diámetro de 250 mm ya se ha alejado 70 L/s del caudal máximo, por lo cual el
único diámetro que permitiría realizar un análisis con todas las posibles relaciones de llenado sería el de
200 mm, pero con base en la norma y en la capacidad de visualizar el resalto, se elige el diámetro de
250 mm.
5.2. Análisis caudales máximos para diferentes pendientes
Luego de elegir el diámetro, se realizó un análisis con dos tipos de pendientes y diferentes relaciones de
llenado para observar la variación del Número de Froude obteniendo los siguientes resultados:
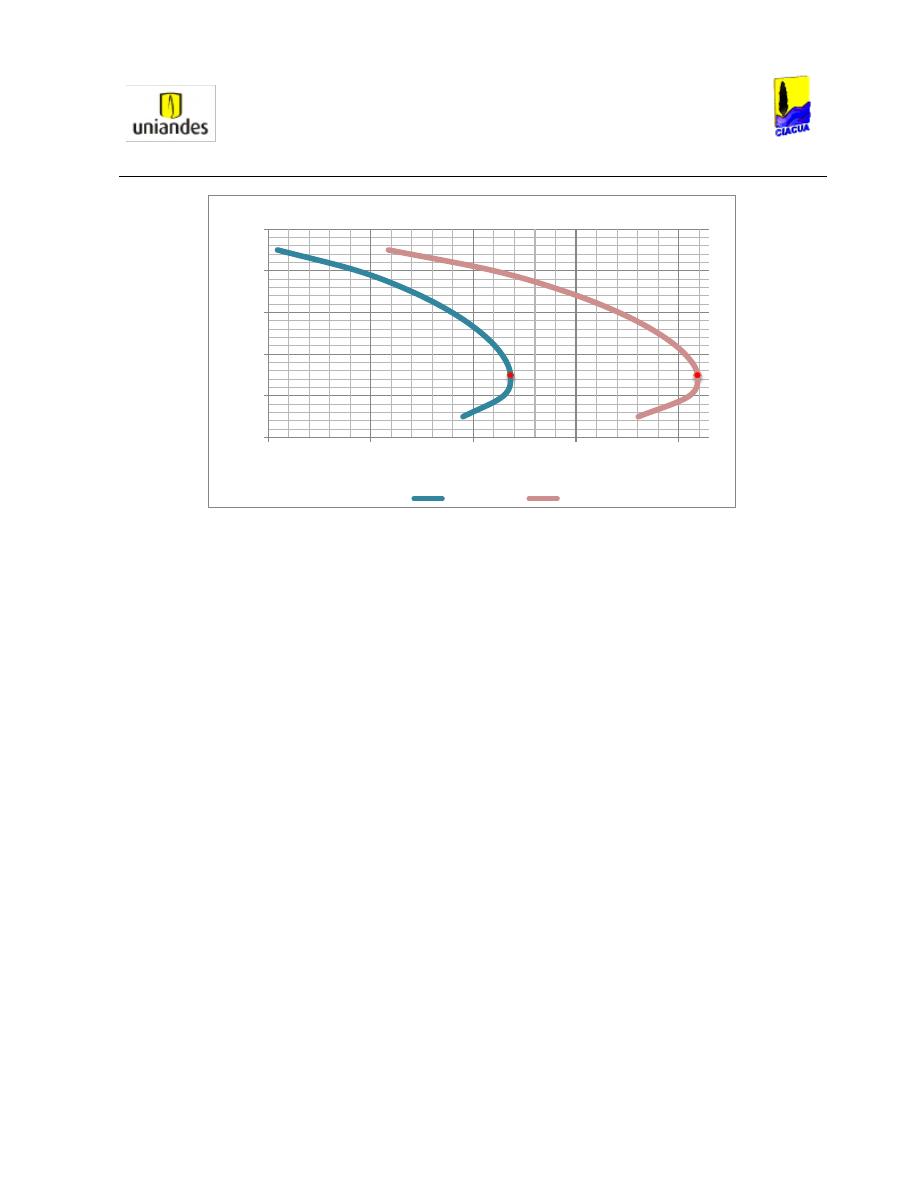
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
52
Gráfica 14. Variación del Número de Froude respecto a la relación de llenado para diferentes pendientes.
La línea azul se calculó con la pendiente original del canal (1.9%), el coeficiente de rugosidad del PVC,
la viscosidad del agua de
y con relaciones de llenado variantes entre el 10% y el
100% y la línea rosada se calculó con una pendiente de 3.1 % (pendiente máxima que podrá tomar el
montaje) y los demás valores idénticos a la línea azul.
Por lo tanto, observando la Gráfica 14, se puede observar que para relaciones de llenado menores al
30%, el Número de Froude aumenta a medida que aumenta la relación de llenado; para relaciones de
llenado mayores al 30%, el Número de Froude disminuye a medida que aumenta la relación de llenado
y cuando la relación de llenado es aproximadamente del 30%, se observa el valor máximo del Número
de Froude. También se observa que el rango de variación del Número de Froude es mayor en la línea
rosada que en la línea azul, debido a que el aumento de la pendiente aumenta la variación en la
velocidad del flujo.
Para corroborar el valor máximo del Número de Froude, se realizó un análisis más detallado de
diferentes pendientes y diferentes caudales para encontrar la curva que representa la variación del
Número de Froude respecto a las relaciones de llenado.
5.3. Análisis del valor máximo del Número de Froude
Para encontrar la curva que describiría en qué relaciones de llenado se encuentran los valores máximos
del Número de Froude, se realizó un análisis con diferentes pendientes (las cuales variaban entre el
0.5% al 2.5%) para encontrar las relaciones de llenado qué cumplían con un rango de caudales entre
0.01 L/s hasta 77.6 L/s. El proceso del análisis de describirá mediante las gráficas mostradas
posteriormente.
La primera gráfica refleja la forma como varía el caudal n respecto a la relación de llenado (Ver Gráfica
15):
0
0.2
0.4
0.6
0.8
1
1.650
2.150
2.650
3.150
3.650
y/
d
(
-)
Froude (-)
Variación Froude vs y/d
So = 0.019
So = 0.031
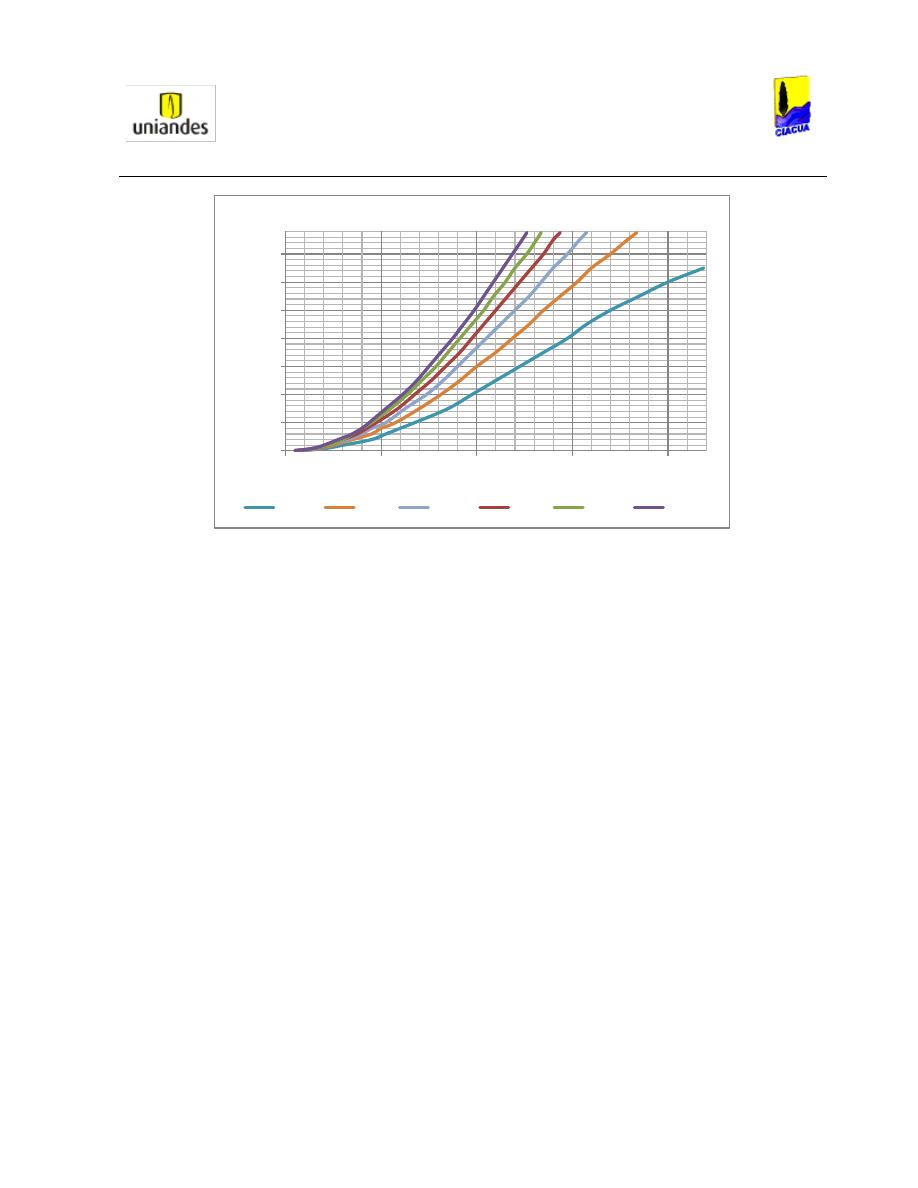
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
53
Gráfica 15. Variación del caudal respecto a la relación de llenado.
La Gráfica 15 permite observar que cuando la pendiente es más baja, la variación de la relación de
llenado mueve un rango de caudales más bajo que las pendientes más altas. Ésta afirmación se
explicaba también con la Gráfica 14, puesto que en la pendiente más alta (3.1%), el Número de Froude
tenía mayor rango de variación, y como el Número de Froude y el caudal son proporcionales a la
velocidad, se concluye que cuando aumenta la pendiente, el rango de variación de la velocidad aumenta.
También se observa que cuando las pendientes aumentan, las curvas se van acercando entre sí, lo que
indica que el comportamiento del flujo empieza a ser similar.
Posteriormente, se compara la variación del Número de Froude para diversos caudales (Ver Gráfica 16):
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0
0.2
0.4
0.6
0.8
Q
(m
³/
s)
y/d (-)
Comparación Pendientes
S = 0.005
S = 0.01
S = 0.015
S = 0.02
S = 0.025
S = 0.03
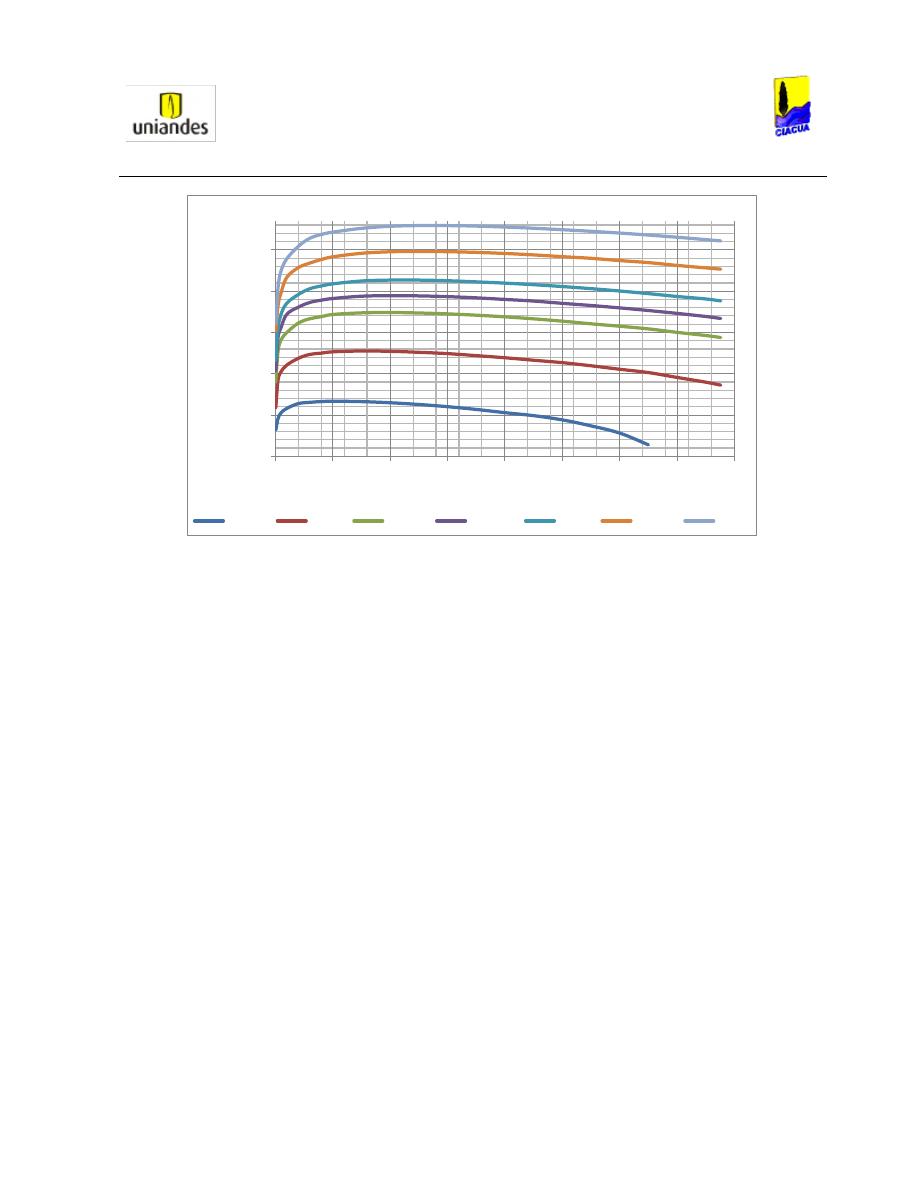
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
54
Gráfica 16. Variación del Número de Froude para diversos caudales.
En la Gráfica 16 se observa un valor del Número de Froude máximo para diferentes caudales, el cual se
va desplazando hacia la derecha a medida que aumenta la pendiente, lo que permite concluir que a
mayor pendiente, el máximo valor del Número de Froude se encuentra en caudales más altos. Además
los rangos del Número de Froude aumentan con el incremento de la pendiente, lo que sustenta las
afirmaciones expuestas en las anteriores gráficas, donde a mayor pendiente, mayor velocidad, es decir,
mayor Número de Froude.
Luego, se realiza una gráfica similar a la Gráfica 16 pero para los caudales expuestos en éste análisis, lo
cual se observa en la siguiente ilustración:
0.800
1.300
1.800
2.300
2.800
3.300
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
N
ú
m
e
ro
d
e
Fr
o
u
d
e
(
-)
Q (m
3
/s)
Comparación de Pendientes
S = 0.005
S = 0.01
S = 0.015
S = 0.0175
S = 0.02
S = 0.025
S = 0.03
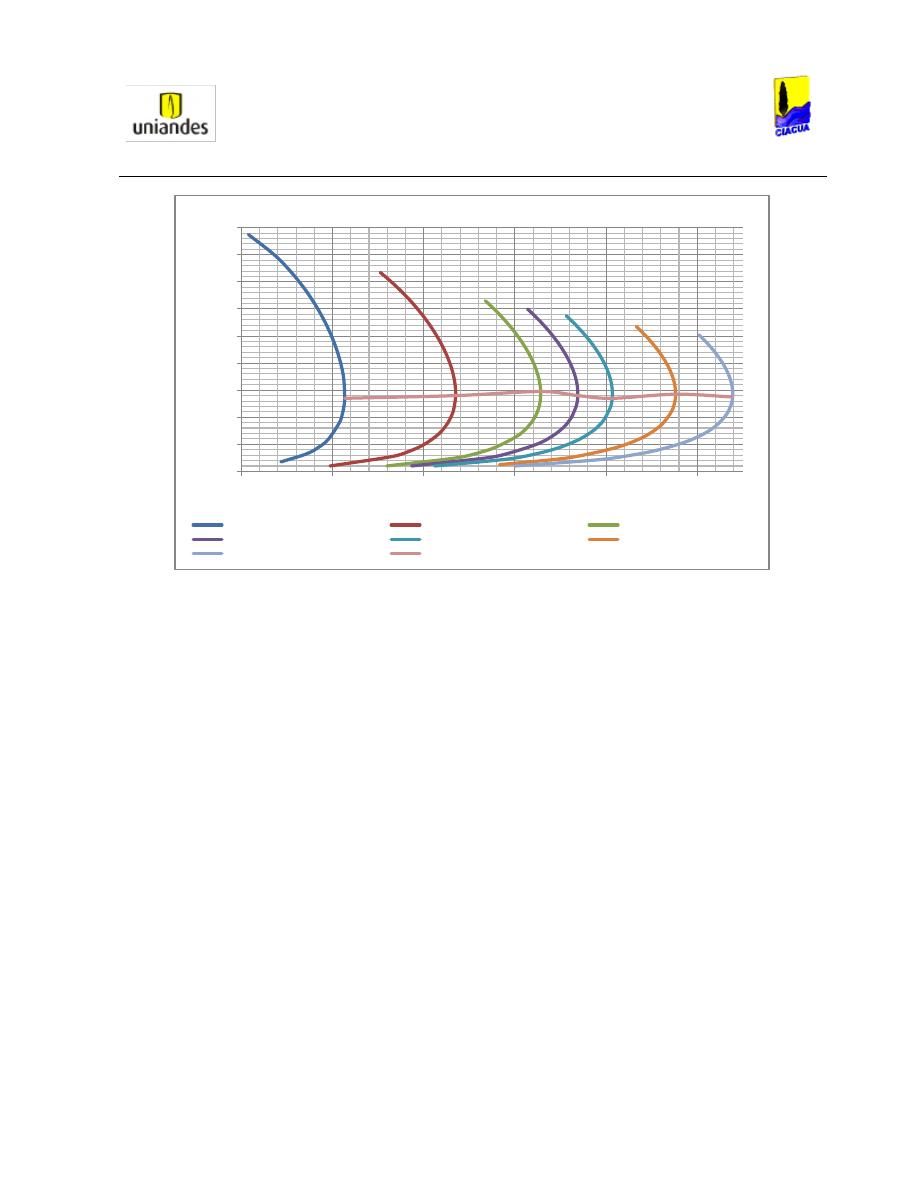
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
55
Gráfica 17. Variación del Número de Froude para diferentes relaciones de llenado.
La Gráfica 17 muestra nuevamente que el Número de Froude máximo se encuentra con relaciones de
llenado cercanas al 30%, pero la ilustración no permite obtener una ecuación coherente de la recta; por
lo tanto, se requiere otro tipo de análisis para encontrar una curva que pueda representar el máximo en el
Número de Froude para el montaje.
El análisis requiere aumentar el número de caudales elegidos para el análisis, puesto que con los
caudales analizados, se está parcializando el valor de las relaciones de llenado; por lo tanto, para
encontrar ésta curva se hizo uso de una macro en Excel con el lenguaje VBA (Anexo 1), la cual
converge mediante el método de la bisección (Ver Gráfica 18), en la cual el caudal aumenta cada 0.25
L/s:
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
0.900
1.400
1.900
2.400
2.900
3.400
y/d
(
-)
Froude (-)
Froude vs y/d (S total)
S = 0.005
S = 0.01
S = 0.015
S = 0.0175
S = 0.02
S = 0.025
S = 0.03
Número de Froude Máximo
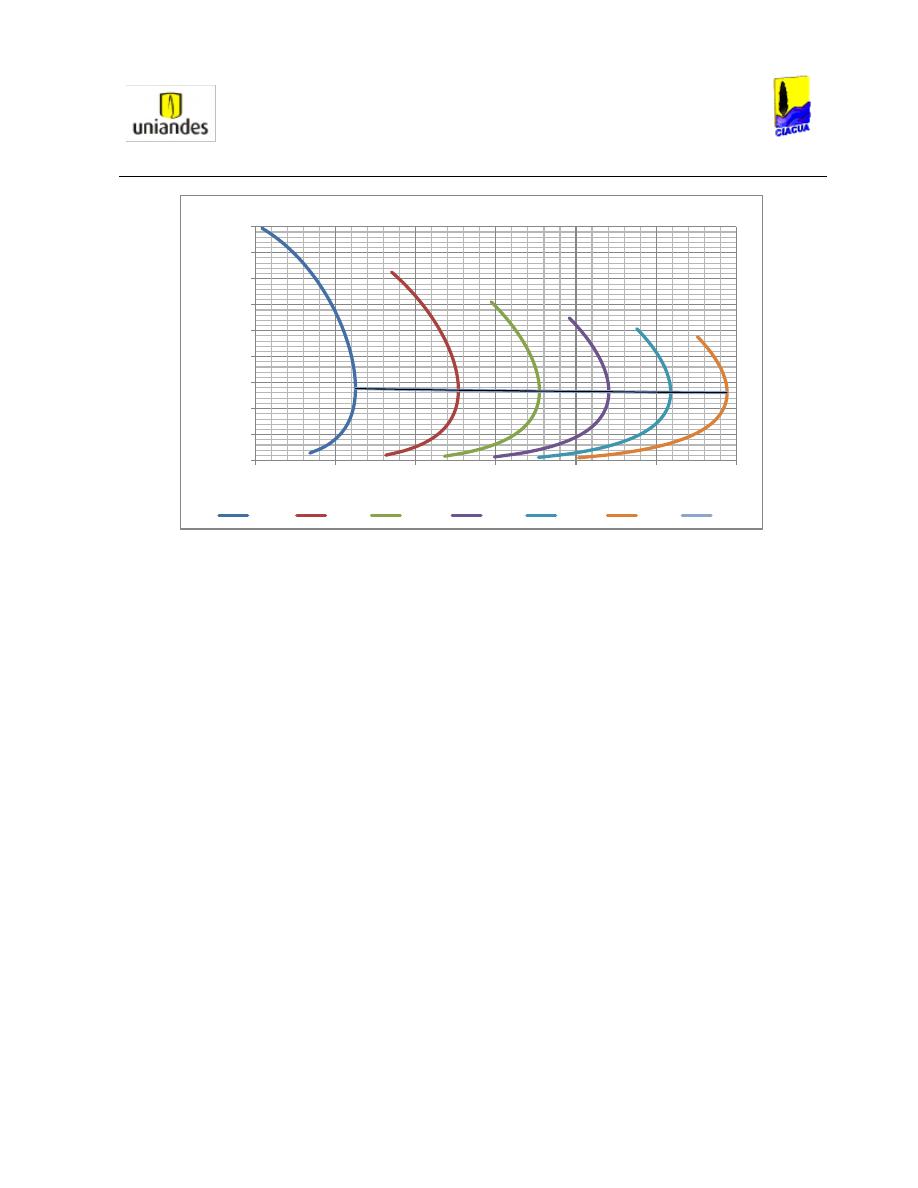
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
56
Gráfica 18. Comparación Número de Froude respecto a diferentes relaciones de llenado.
La Gráfica 18 permite demostrar que la curva que describe mejor en qué relación de llenado se
encuentran los Números de Froude máximos se ajusta a una curva potencial, la cual se calcula mediante
la Ecuación 75:
Ecuación 75. Curva que describe el Número de Froude máximo.
Por lo cual, en el montaje que se realizará, los Números de Froude máximos se encontrarán entre las
relaciones de llenado de 0.28 y 0.30, es decir, que el resalto hidráulico más fuerte se presentará cuando
la profundidad aguas arriba del resalto se encuentre entre 0.28 a 0.30 veces el diámetro.
5.4 Análisis Comparativo con otros autores para el cálculo de la profundidad
subsecuente al resalto hidráulico
El análisis comparativo que se mostrará a continuación para el cálculo de la profundidad subsecuente al
resalto hidráulico, se realizará con los datos del montaje realizado; es decir, el material de la tubería es
acrílico, con una rugosidad de
m, una longitud de 13 m, diámetro interno de 0.242 m,
viscosidad dinámica de
y con dos pendientes posibles del canal: 0.019 y 0.031.
A continuación se presentan los cálculos realizados con las ecuaciones mostradas en el Numeral 2.
5.4.1 Silvester
De acuerdo con lo establecido por Silvester, se graficó una curva para determinar el k’:
0.020
0.120
0.220
0.320
0.420
0.520
0.620
0.720
0.820
0.920
0.750
1.250
1.750
2.250
2.750
3.250
3.750
y/
d
(
-)
Froude (-)
Comparación Froude vs y/d
S =0.005
S = 0.01
S = 0.015
S = 0.02
S = 0.025
S = 0.03
MAX
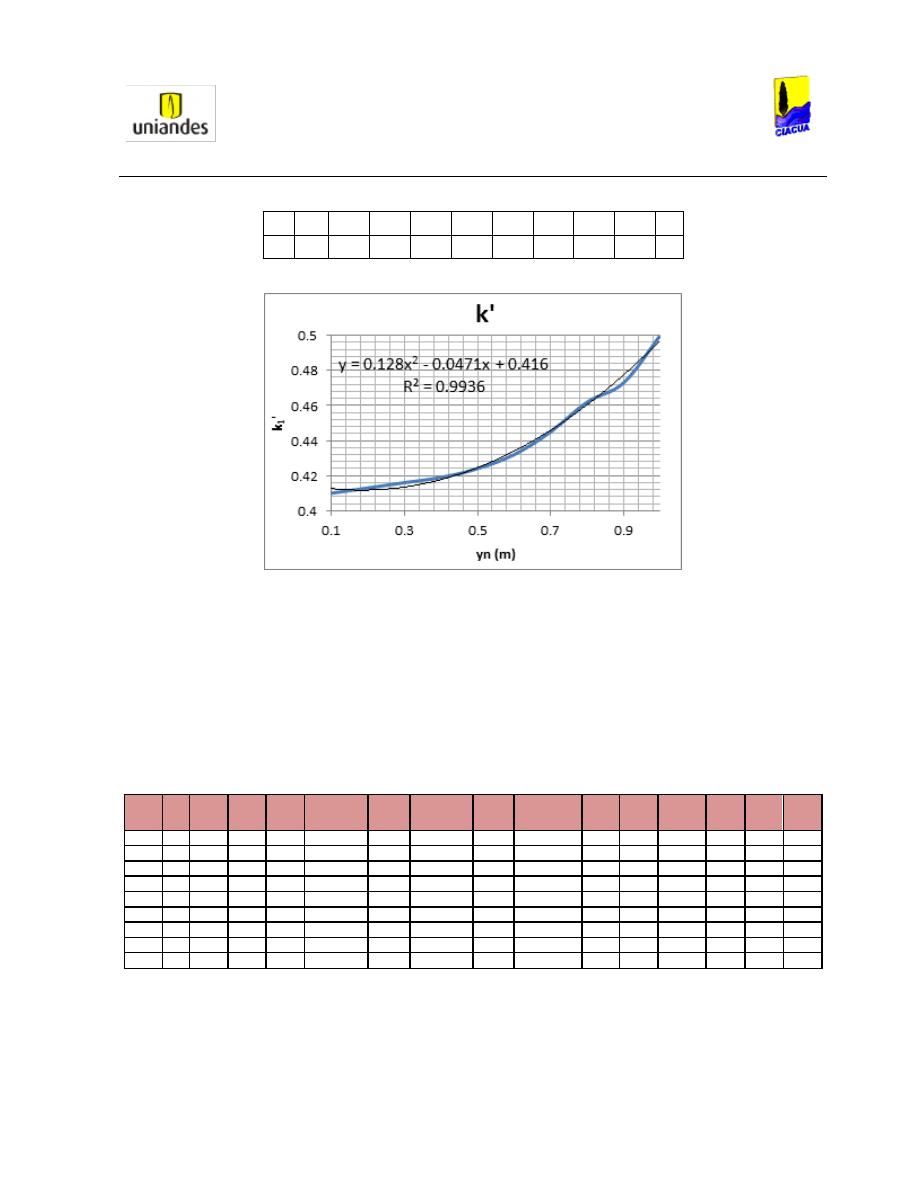
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
57
Tabla 9. Valores de k' dependiendo de la relación de llenado (Silvester, 1964).
d/D 0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
k'
0.41 0.413 0.416 0.419 0.424 0.432 0.445 0.462 0.473 0.5
Gráfica 19. Curva para determinar k'.
Teniendo el k’, entonces se calcula la profundidad subsecuente del resalto hidráulico teniendo en cuenta
la variación de las ecuaciones cuando la profundidad subsecuente es menor o mayor al diámetro. Para
tal fin, se desarrolló una macro (Anexo 2) que calculara la profundidad subsecuente para dos pendientes:
la primera corresponde a 0.019, la cual corresponde a la pendiente promedio que se presentará en el
montaje, y la segunda corresponde a 0.031 que correspondería a la pendiente máxima.
Así se obtuvieron los siguientes resultados:
Tabla 10. Cálculo de la profundidad subsecuente para una pendiente del 1.9%.
d
(m)
y/d
(-)
y
1
(m)
teta
(-)
Área
(m
2
)
Perímetro
(m)
Radio
(m)
Velocidad
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
k
1
'
(-)
y
2
(m)
y
2/
y
1
(-)
0.242 0.1 0.024 1.287 0.002
0.156
0.015
1.045
0.003
56377.905 0.145 0.016
2.599
0.413 0.071 2.942
0.242 0.2 0.048 1.855 0.007
0.224
0.029
1.611
0.011 164939.800 0.194 0.034
2.796
0.412 0.154 3.182
0.242 0.3 0.073 2.319 0.012
0.281
0.041
2.028
0.024 294376.898 0.222 0.052
2.831
0.413 0.238 3.280
0.242 0.4 0.097 2.739 0.017
0.331
0.052
2.350
0.040 427500.511 0.237 0.072
2.787
0.418 0.312 3.224
0.242 0.5 0.121 3.142 0.023
0.380
0.061
2.598
0.060 551433.772 0.242 0.095
2.690
0.424 0.366 3.022
0.242 0.6 0.145 3.544 0.029
0.429
0.067
2.780
0.080 655306.625 0.237 0.122
2.546
0.434 0.381 2.622
0.242 0.7 0.169 3.965 0.034
0.480
0.072
2.898
0.100 728969.002 0.222 0.155
2.350
0.446 0.354 2.089
0.242 0.8 0.194 4.429 0.039
0.536
0.074
2.948
0.116 761416.848 0.194 0.204
2.085
0.460 0.300 1.551
0.242 0.9 0.218 4.996 0.044
0.605
0.072
2.909
0.127 736268.556 0.145 0.300
1.695
0.477 0.250 1.150
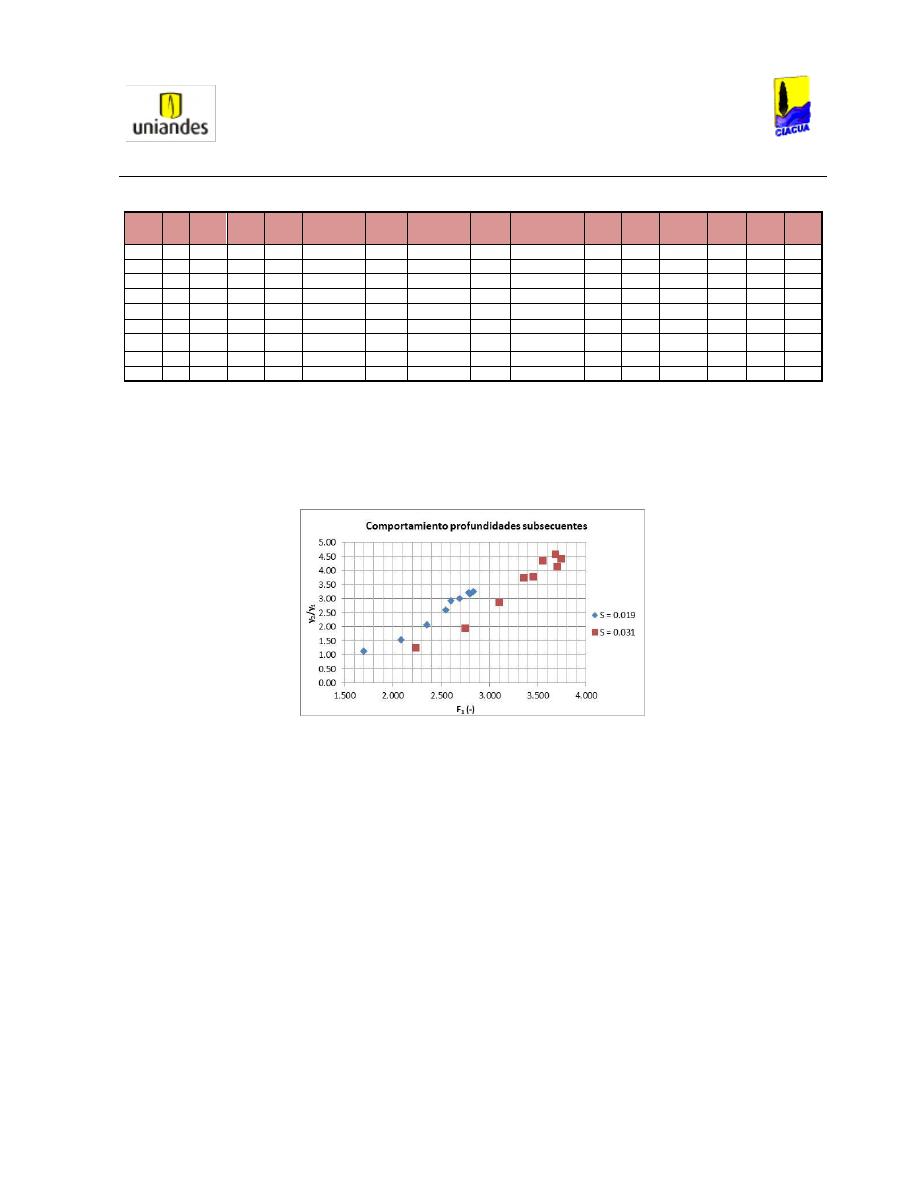
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
58
Tabla 11. Cálculo de la profundidad subsecuente para una pendiente del 3.1%.
d
(m)
y/d
(-)
y
1
(m)
teta
(-)
Área
(m
2
)
Perímetro
(m)
Radio
(m)
Velocidad
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
k
1
'
(-)
y
2
(m)
y
2
/y
1
(-)
0.242 0.1 0.024 1.287 0.002
0.156
0.015
1.389
0.003
74903.831
0.145 0.016
3.453
0.413 0.092 3.792
0.242 0.2 0.048 1.855 0.007
0.224
0.029
2.133
0.014
218395.095 0.194 0.034
3.702
0.412 0.200 4.131
0.242 0.3 0.073 2.319 0.012
0.281
0.041
2.681
0.031
389159.110 0.222 0.052
3.742
0.413 0.320 4.413
0.242 0.4 0.097 2.739 0.017
0.331
0.052
3.104
0.053
564604.302 0.237 0.072
3.681
0.418 0.443 4.578
0.242 0.5 0.121 3.142 0.023
0.380
0.061
3.429
0.079
727829.080 0.242 0.095
3.551
0.424 0.528 4.365
0.242 0.6 0.145 3.544 0.029
0.429
0.067
3.667
0.106
864573.169 0.237 0.122
3.359
0.434 0.544 3.745
0.242 0.7 0.169 3.965 0.034
0.480
0.072
3.823
0.131
961518.952 0.222 0.155
3.099
0.446 0.484 2.860
0.242 0.8 0.194 4.429 0.039
0.536
0.074
3.888
0.153 1004216.549 0.194 0.204
2.750
0.460 0.376 1.943
0.242 0.9 0.218 4.996 0.044
0.605
0.072
3.837
0.167
971124.647 0.145 0.300
2.236
0.477 0.273 1.255
En las Tabla 10 y Tabla
11 se observa que mientras el flujo sea más supercrítico, la relación entre las
profundidades aguas arriba y aguas abajo del resalto será más alta, por lo tanto, para los valores
obtenidos en la pendiente más alta, la relación entre las alturas del resalto son mayores, lo cual se
confirma con la siguiente gráfica:
Gráfica 20. Comportamiento de las profundidades subsecuentes.
En la Gráfica 20 también se observa para un mismo Número de Froude, la relación entre las
profundidades del resalto se ven afectadas por la pendiente de la tubería, en donde a mayor pendiente, se
tienen valores menores en la relación entre las profundidades.
Por otra parte, se realizó otro análisis en el cual se establecieron dos caudales fijos y se variaba la
pendiente para cada uno de ellos. El primer caudal es de 0.01 m
3
/s, y el segundo de 0.1 m
3
/s. Los
resultados se observan en las siguientes tablas:
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
59
Tabla 12. Cálculo de la profundidad subsecuente para un caudal de 0.01 m
3
/s.
s
(-)
y/d
(-)
y
n
(m)
teta
(-)
Área
(m
2
)
Perímetro
(m)
Radio
(m)
Velocidad
(m/s)
Caudal
(m
3
/s)
Re
(-)
T
(m)
D
(m)
F
(-)
k
1
'
(-)
y
2
(m)
y
2
/y
1
(-)
0.050 0.149 0.036 1.583 0.004
0.192
0.022
2.334
0.01
495567.5 0.172 0.025 4.733 0.412 0.183 5.097
0.051 0.148 0.036 1.579 0.004
0.191
0.022
2.354
0.01
499633.3 0.172 0.025 4.783 0.412 0.184 5.144
0.052 0.147 0.036 1.576 0.004
0.191
0.022
2.372
0.01
503618.2 0.172 0.025 4.832 0.412 0.185 5.192
0.053 0.147 0.035 1.571 0.004
0.190
0.022
2.389
0.01
507048.2 0.171 0.024 4.881 0.412 0.186 5.238
0.054 0.146 0.035 1.567 0.004
0.190
0.022
2.407
0.01
510870.2 0.171 0.024 4.929 0.412 0.186 5.284
0.055 0.145 0.035 1.563 0.004
0.189
0.022
2.424
0.01
514615.9 0.170 0.024 4.977 0.412 0.187 5.330
0.056 0.144 0.035 1.559 0.004
0.189
0.022
2.442
0.01
518286.8 0.170 0.024 5.025 0.412 0.188 5.375
0.057 0.144 0.035 1.555 0.004
0.188
0.022
2.458
0.01
521884.1 0.170 0.024 5.072 0.412 0.188 5.420
0.058 0.143 0.035 1.551 0.004
0.188
0.022
2.475
0.01
525409.2 0.169 0.024 5.119 0.412 0.189 5.463
0.059 0.142 0.034 1.548 0.004
0.187
0.021
2.491
0.01
528863.3 0.169 0.024 5.165 0.412 0.190 5.507
0.060 0.142 0.034 1.544 0.004
0.187
0.021
2.507
0.01
532247.5 0.169 0.024 5.211 0.412 0.190 5.550
0.061 0.141 0.034 1.540 0.004
0.186
0.021
2.523
0.01
535563.0 0.168 0.023 5.256 0.412 0.191 5.593
0.062 0.140 0.034 1.536 0.004
0.186
0.021
2.538
0.01
538810.8 0.168 0.023 5.301 0.412 0.191 5.636
0.063 0.140 0.034 1.533 0.004
0.186
0.021
2.556
0.01
542526.7 0.168 0.023 5.347 0.412 0.192 5.679
0.064 0.139 0.034 1.530 0.004
0.185
0.021
2.570
0.01
545648.1 0.168 0.023 5.391 0.412 0.193 5.720
0.065 0.139 0.034 1.527 0.004
0.185
0.021
2.587
0.01
549250.8 0.167 0.023 5.436 0.412 0.194 5.762
0.066 0.138 0.033 1.523 0.004
0.184
0.021
2.602
0.01
552249.6 0.167 0.023 5.479 0.412 0.194 5.803
0.067 0.138 0.033 1.520 0.004
0.184
0.021
2.618
0.01
555742.8 0.167 0.023 5.523 0.412 0.195 5.844
0.068 0.137 0.033 1.517 0.004
0.184
0.021
2.632
0.01
558622.5 0.166 0.023 5.566 0.412 0.195 5.884
0.069 0.137 0.033 1.514 0.004
0.183
0.021
2.647
0.01
562009.4 0.166 0.023 5.609 0.412 0.196 5.924
0.070 0.136 0.033 1.510 0.004
0.183
0.021
2.661
0.01
564773.1 0.166 0.023 5.651 0.412 0.196 5.963
0.071 0.136 0.033 1.507 0.004
0.182
0.020
2.676
0.01
568056.9 0.166 0.023 5.694 0.412 0.197 6.003
0.072 0.135 0.033 1.505 0.004
0.182
0.020
2.691
0.01
571292.8 0.165 0.022 5.736 0.412 0.197 6.043
0.073 0.135 0.033 1.502 0.004
0.182
0.020
2.706
0.01
574481.7 0.165 0.022 5.778 0.412 0.198 6.083
0.074 0.134 0.032 1.498 0.004
0.181
0.020
2.718
0.01
577028.3 0.165 0.022 5.818 0.412 0.198 6.119
0.075 0.134 0.032 1.496 0.004
0.181
0.020
2.733
0.01
580119.5 0.165 0.022 5.860 0.412 0.199 6.158
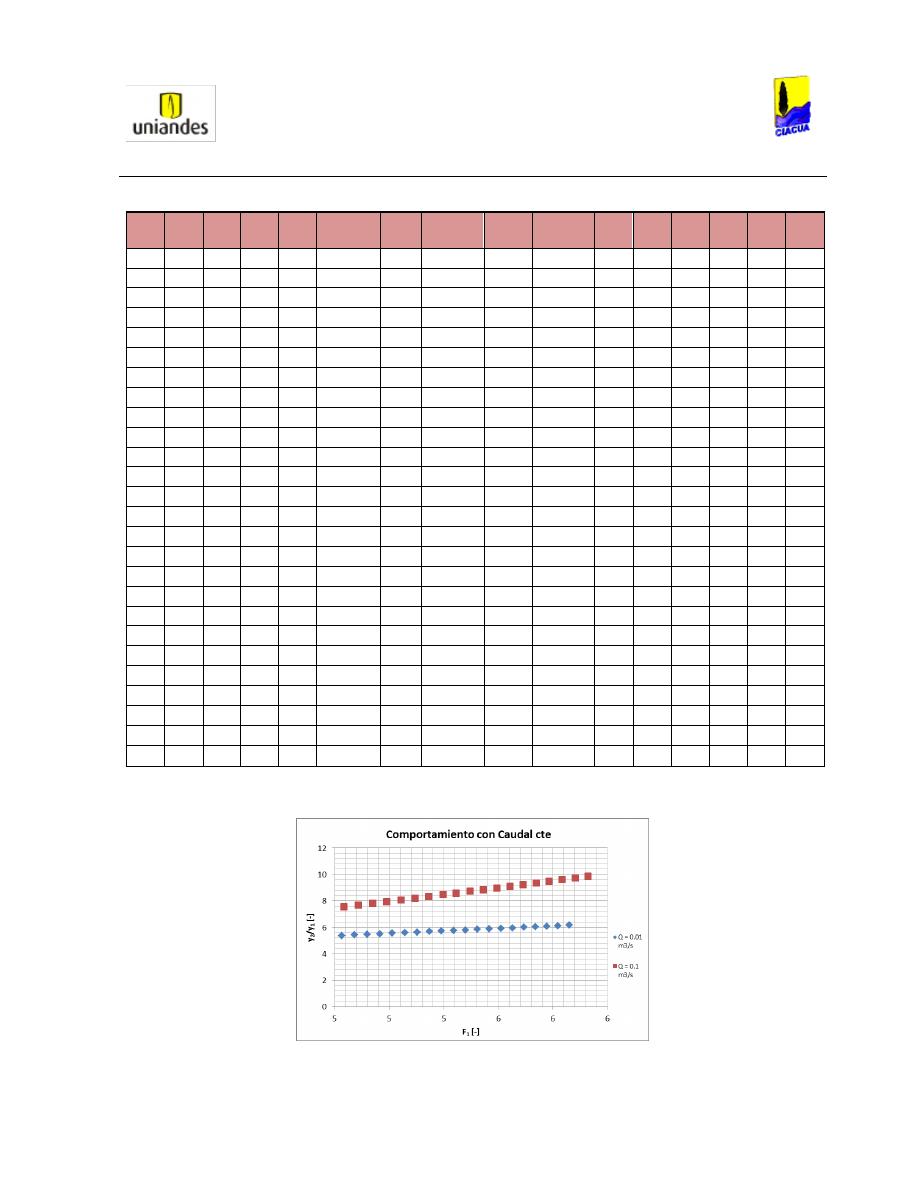
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
60
Tabla 13. Cálculo de la profundidad subsecuente para un caudal de 0.1 m
3
/s.
s
(-)
y/d
(-)
y
n
(m)
teta
(-)
Área
(m
2
)
Perímetro
(m)
Radio
(m)
Velocidad
(m/s)
Caudal
(m
3
/s)
Re
(-)
T
(m)
D
(m)
F
(-)
k
1
'
(-)
y
2
(m)
y
2
/y
1
(-)
0.050 0.492 0.119 3.109 0.023
0.376
0.060
4.439
0.100
942370.7
0.242 0.093 4.645 0.424 0.788 6.617
0.051 0.489 0.118 3.095 0.022
0.374
0.060
4.474
0.100
949699.2
0.242 0.092 4.703 0.424 0.798 6.754
0.052 0.486 0.118 3.084 0.022
0.373
0.059
4.511
0.100
957583.8
0.242 0.092 4.759 0.423 0.809 6.887
0.053 0.483 0.117 3.070 0.022
0.371
0.059
4.544
0.100
964563.4
0.242 0.091 4.816 0.423 0.819 7.025
0.054 0.480 0.116 3.059 0.022
0.370
0.059
4.579
0.100
972132.8
0.242 0.090 4.870 0.423 0.830 7.157
0.055 0.477 0.115 3.048 0.022
0.369
0.059
4.614
0.100
979554.8
0.242 0.089 4.925 0.423 0.841 7.290
0.056 0.474 0.115 3.037 0.021
0.368
0.058
4.649
0.100
986831.7
0.242 0.089 4.979 0.423 0.851 7.422
0.057 0.472 0.114 3.027 0.021
0.366
0.058
4.682
0.100
993965.6
0.242 0.088 5.033 0.422 0.862 7.555
0.058 0.469 0.113 3.016 0.021
0.365
0.058
4.715
0.100
1000958.5 0.242 0.088 5.086 0.422 0.872 7.687
0.059 0.466 0.113 3.005 0.021
0.364
0.058
4.748
0.100
1007812.3 0.241 0.087 5.139 0.422 0.882 7.819
0.060 0.464 0.112 2.998 0.021
0.363
0.058
4.783
0.100
1015377.9 0.241 0.087 5.190 0.422 0.893 7.947
0.061 0.461 0.112 2.987 0.021
0.361
0.057
4.814
0.100
1021972.8 0.241 0.086 5.243 0.422 0.902 8.079
0.062 0.459 0.111 2.976 0.021
0.360
0.057
4.845
0.100
1028433.7 0.241 0.085 5.295 0.421 0.911 8.210
0.063 0.457 0.111 2.969 0.020
0.359
0.057
4.879
0.100
1035651.8 0.241 0.085 5.345 0.421 0.922 8.338
0.064 0.455 0.110 2.958 0.020
0.358
0.057
4.908
0.100
1041863.8 0.241 0.084 5.396 0.421 0.931 8.467
0.065 0.452 0.109 2.951 0.020
0.357
0.057
4.941
0.100
1048862.2 0.241 0.084 5.445 0.421 0.941 8.595
0.066 0.450 0.109 2.940 0.020
0.356
0.056
4.969
0.100
1054831.2 0.241 0.083 5.496 0.421 0.950 8.725
0.067 0.448 0.109 2.935 0.020
0.355
0.056
5.003
0.100
1062086.0 0.241 0.083 5.544 0.421 0.960 8.850
0.068 0.446 0.108 2.926 0.020
0.354
0.056
5.032
0.100
1068301.6 0.241 0.083 5.594 0.421 0.969 8.978
0.069 0.444 0.108 2.919 0.020
0.353
0.056
5.064
0.100
1074890.1 0.240 0.082 5.642 0.420 0.979 9.105
0.070 0.442 0.107 2.910 0.020
0.352
0.056
5.092
0.100
1080893.3 0.240 0.082 5.691 0.420 0.988 9.231
0.071 0.440 0.107 2.902 0.020
0.351
0.056
5.122
0.100
1087284.6 0.240 0.081 5.738 0.420 0.997 9.357
0.072 0.439 0.106 2.895 0.019
0.350
0.055
5.152
0.100
1093582.3 0.240 0.081 5.786 0.420 1.006 9.482
0.073 0.437 0.106 2.886 0.019
0.349
0.055
5.178
0.100
1099279.1 0.240 0.080 5.834 0.420 1.014 9.608
0.074 0.435 0.105 2.879 0.019
0.348
0.055
5.207
0.100
1105386.5 0.240 0.080 5.881 0.420 1.023 9.733
0.075 0.433 0.105 2.872 0.019
0.347
0.055
5.236
0.100
1111403.4 0.240 0.080 5.928 0.420 1.032 9.857
El análisis de los datos obtenidos en la Tabla
12
y en la Tabla
13
se presenta en la Gráfica 21:
Gráfica 21. Comportamiento de las profundidades subsecuentes con caudal constante.
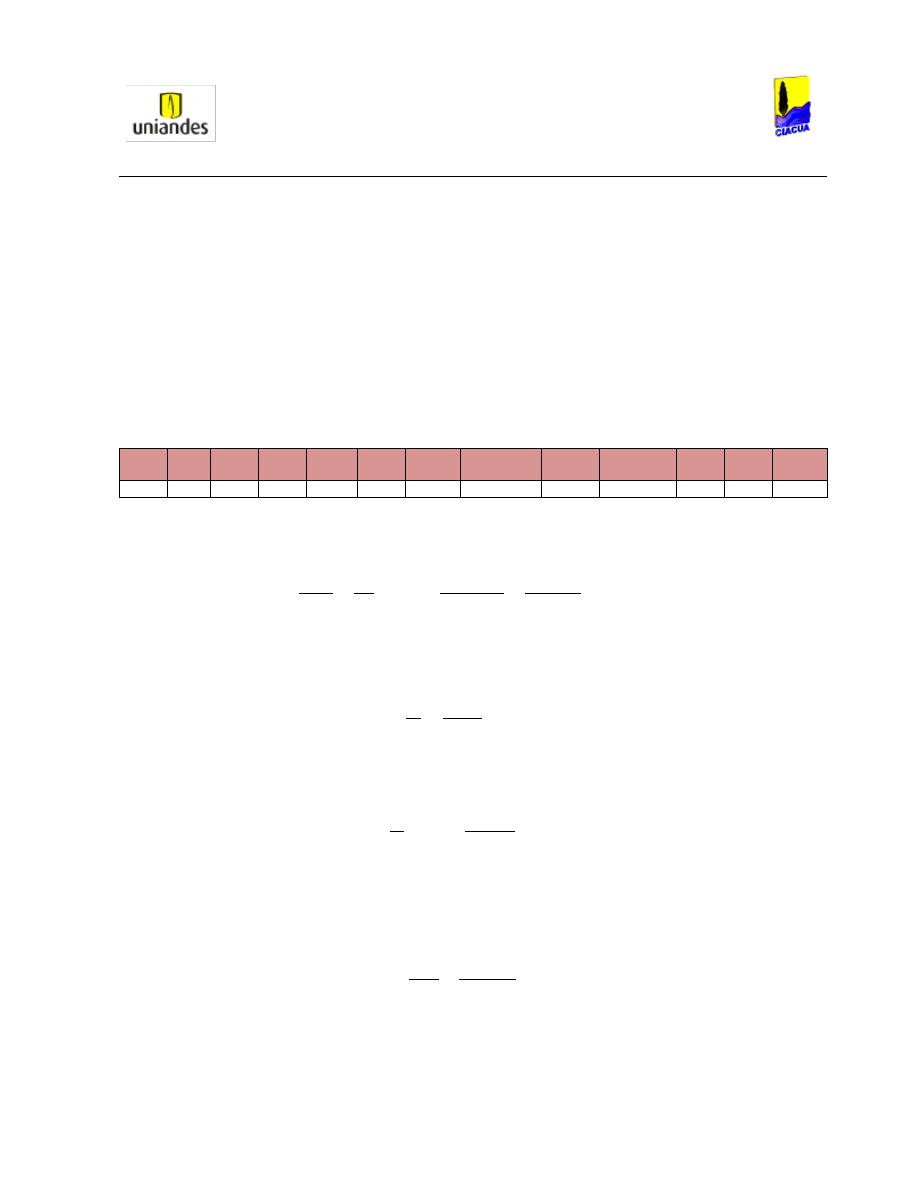
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
61
En la Gráfica 21 se observa que a mayor caudal, aumenta la relación entre las profundidades
subsecuentes del resalto, y ésta variación aumenta a medida que aumenta el Número de Froude.
También se observa que para el caudal más alto, la pendiente que representa la variación de la relación
de llenado es más alta que la pendiente obtenida con el caudal más bajo.
5.4.2 Straub
Siguiendo la metodología planteada por Straub, se calculan las ecuaciones para calcular la profundidad
crítica, el Número de Froude, y según el valor de este número se establece la ecuación para calcular la
profundidad subsecuente.
A continuación se presenta la iteración para la primera fila calculada:
d
(m)
y/d
(-)
y
n
(m)
teta
(-)
Área
(m
2
)
P
(m)
Radio
(m)
Velocidad
(m/s)
Q
(m
3
/s)
Reynolds
(-)
T (m)
D
(m)
Froude
(-)
0.242
0.1
0.024
1.287
0.002
0.156
0.015
1.045
0.0025
56377.905
0.145
0.016
2.599
Entonces el primer paso es calcular la profundidad crítica mediante la Ecuación 20:
(
) (
)
(
) (
)
Ecuación 76. Cálculo de la profundidad crítica.
Luego se comprueba que la Ecuación 20 es válida mediante la siguiente condición:
Posteriormente, se calcula el Número de Froude aguas arriba del resalto mediante la Ecuación 21:
(
)
(
)
Ecuación 77. Aproximación Número de Froude (French, 2007).
Teniendo el Número de Froude, se procede a calcular la profundidad subsecuente de acuerdo con el
valor de este número. Como el Número de Froude es mayor a 1.7 se tiene que:
Realizando el mismo proceso para todas las relaciones de llenado en la tubería se tiene que:
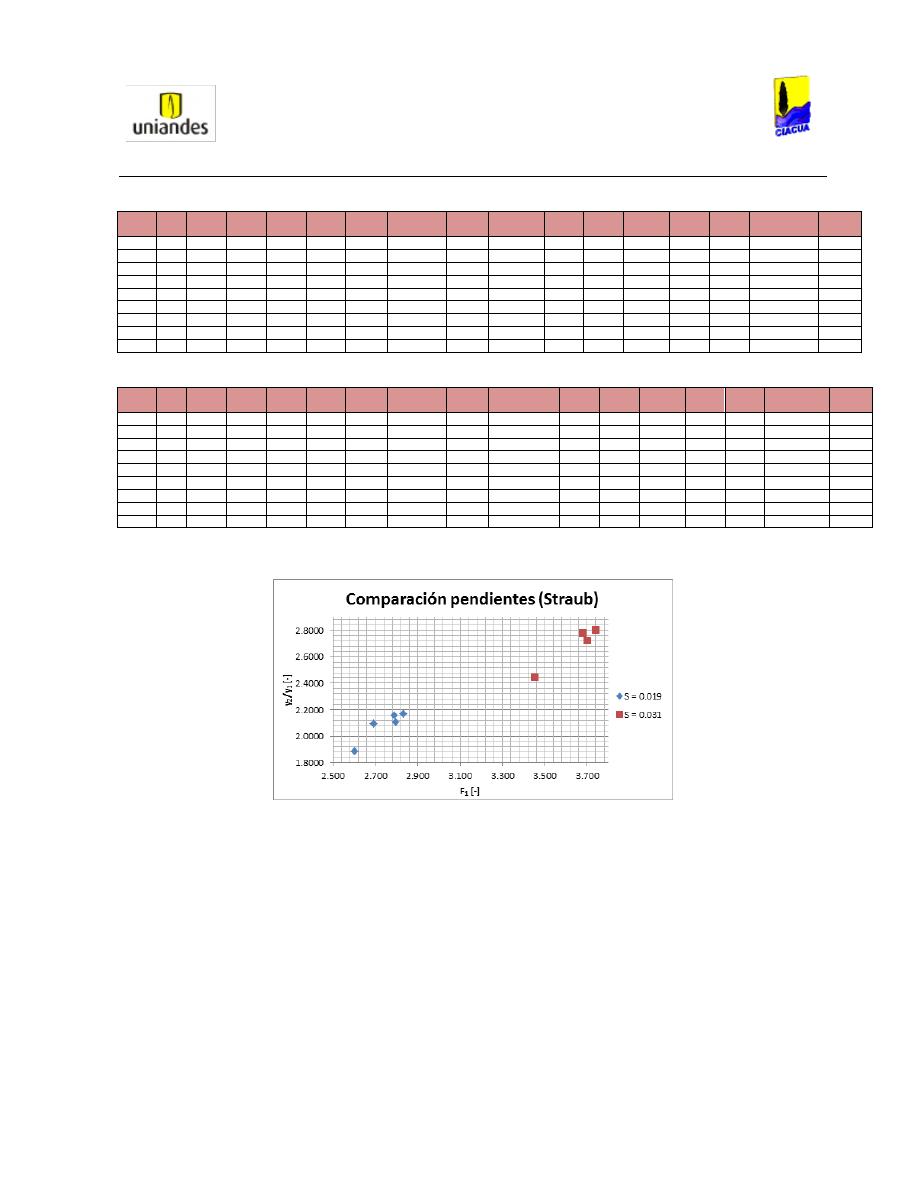
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
62
Tabla 14. Cálculo de la profundidad subsecuente para una pendiente de 0.019 mediante la metodología planteada por Straub.
d
(m)
y/d
(-)
y
n
(m)
teta
(-)
Área
(m
2
)
P
(m)
Radio
(m)
Velocidad
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
y
c
(m)
y
c
/d
(-)
y
2
(m)
y
2
/y
1
(-)
0.242
0.1
0.024
1.287
0.002
0.156
0.015
1.045
0.003
56377.9
0.145
0.016
2.599
0.040
0.164
0.046
1.885
0.242
0.2
0.048
1.855
0.007
0.224
0.029
1.611
0.011
164939.8
0.194
0.034
2.796
0.085
0.340
0.102
2.107
0.242
0.3
0.073
2.319
0.012
0.281
0.041
2.028
0.024
294376.9
0.222
0.052
2.831
0.124
0.511
0.158
2.170
0.242
0.4
0.097
2.739
0.017
0.331
0.052
2.350
0.040
427500.5
0.237
0.072
2.787
0.162
0.671
0.209
2.157
0.242
0.5
0.121
3.142
0.023
0.380
0.061
2.598
0.060
551433.8
0.242
0.095
2.690
0.198
0.819
0.254
2.095
0.242
0.6
0.145
3.544
0.029
0.429
0.067
2.780
0.080
655306.6
0.237
0.122
2.546
0.230
0.950
No cumple
0.242
0.7
0.169
3.965
0.034
0.480
0.072
2.898
0.100
728969.0
0.222
0.155
2.350
0.257
1.061
No cumple
0.242
0.8
0.194
4.429
0.039
0.536
0.074
2.948
0.113
761416.8
0.194
0.204
2.085
0.277
1.147
No cumple
0.242
0.9
0.218
4.996
0.044
0.605
0.072
2.909
0.127
736268.6
0.145
0.300
1.695
0.290
1.198
No cumple
Tabla 15. Cálculo de la profundidad subsecuente para una pendiente de 0.031 mediante la metodología planteada por Straub.
d
(m)
y/d
(-)
y
n
(m)
teta
(-)
Área
(m
2
)
P
(m)
Radio
(m)
Velocidad
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
y
c
(m)
y
c
/d
(-)
y
2
(m)
y
2
/y
1
(-)
0.242
0.1
0.024
1.287
0.002
0.156
0.015
1.389
0.003
74903.831
0.145
0.016
3.453
0.046
0.190
0.046
1.885
0.242
0.2
0.048
1.855
0.007
0.224
0.029
2.133
0.014
218395.095
0.194
0.034
3.702
0.095
0.392
0.102
2.107
0.242
0.3
0.073
2.319
0.012
0.281
0.041
2.681
0.031
389159.110
0.222
0.052
3.742
0.142
0.588
0.158
2.170
0.242
0.4
0.097
2.739
0.017
0.331
0.052
3.104
0.053
564604.302
0.237
0.072
3.681
0.187
0.773
0.209
2.157
0.242
0.5
0.121
3.142
0.023
0.380
0.061
3.429
0.079
727829.080
0.242
0.095
3.551
0.228
0.942
0.254
2.095
0.242
0.6
0.145
3.544
0.029
0.429
0.067
3.667
0.106
864573.169
0.237
0.122
3.359
0.264
1.092
No cumple
0.242
0.7
0.169
3.965
0.034
0.480
0.072
3.823
0.131
961518.952
0.222
0.155
3.099
0.295
1.220
No cumple
0.242
0.8
0.194
4.429
0.039
0.536
0.074
3.888
0.153
1004216.549
0.194
0.204
2.750
0.319
1.319
No cumple
0.242
0.9
0.218
4.996
0.044
0.605
0.072
3.837
0.167
971124.647
0.145
0.300
2.236
0.334
1.378
No cumple
El análisis de los resultados obtenidos en las Tabla 14 y Tabla 15 se presenta en la Gráfica 22:
Gráfica 22. Comparación de los valores obtenidos en las dos pendientes.
La Gráfica 22 muestra que la pendiente más alta presenta valores más altos del Número de Froude, y
para valores más altos de este número, la relación entre las profundidades del resalto es mayor. También
se observa que para cada pendiente, en los valores más altos del Número de Froude, existe un dato
atípico en el valor de la relación de las profundidades subsecuentes.
5.4.3 French
De acuerdo con lo establecido por French, se calcula la posición del centroide del flujo y se calcula el
Momentum respectivo aguas arriba, para posteriormente despejar por métodos iterativos, la profundidad
subsecuente del resalto hidráulico aguas abajo.
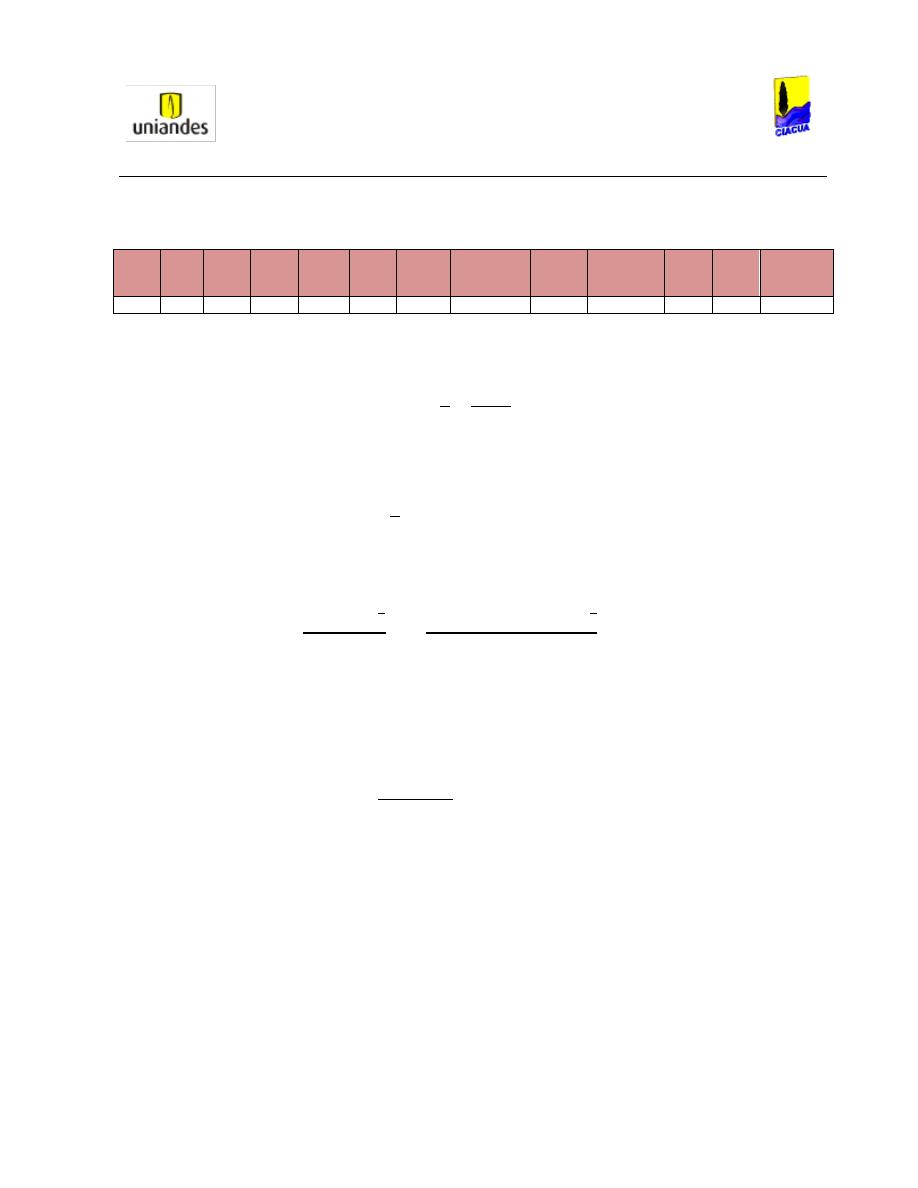
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
63
A continuación se presentarán los cálculos realizados para una pendiente de 0.019, y una relación de
llenado de 0.1, y con las siguientes características hidráulicas:
d
(m)
y/d
(-)
y
n
(m)
teta
(-)
Área
(m
2
)
P
(m)
Radio
(m)
v
(m/s)
Q
(m
3
/s)
Reynolds
(-)
T
(m)
D
(m)
Número
de Froude
(-)
0.242
0.1
0.024
1.287
0.002
0.156
0.015
1.045
0.0025
56377.905
0.145
0.016
2.599
1. Calcular el radio de la tubería (r).
2. Calcular la distancia del centro de la tubería a la superficie de agua (z)
3. Calcular la distancia desde el centro de la tubería al centroide de masa del agua (
̂).
̂
(
)
(
( )
)
4. Calcular la distancia desde la superficie de agua hasta el centroide de la masa de agua (
̅).
̅ ( ̂) ( ( ))
5. Calcular el Momento para el flujo aguas arriba del resalto:
(
)
6. Calcular la altura del flujo aguas abajo mediante un método iterativo, el cual se logra mediante
el método de la bisección (Ver Anexo 3), en este caso, la altura de flujo subsecuente que
satisface la condición en la cual el Momentum aguas arriba sea igual al Momentum aguas abajo
es y
2
= 0.06 m.
Finalmente, los resultados obtenidos se muestran en la Tabla 16 y la Tabla 17:
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
64
Tabla 16. Resultados obtenidos mediante la metodología de French para una S = 0.019.
d
(m)
y/d
(-)
y
n
(m)
teta
(-)
Á
(m
2
)
P
(m)
Radio
(m)
v
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
z
1
(m)
̂
(m)
̅
(m)
M
1
(m
3
)
y
2
(m)
̅
(m)
Á
2
(m
2
)
Prueba
M
(m
3
)
0.242
0.1
0.024
1.287 0.002 0.156 0.015
1.045
0.003
56362.599
0.145
0.016
2.598
-
0.097
-
0.107
0.010 0.0003 0.054 0.022 0.008 0.0003
0.242
0.2
0.048
1.855 0.007 0.224 0.029
1.610
0.011
164895.568
0.194
0.034
2.795
-
0.073
-
0.092
0.020 0.0019 0.117 0.050 0.022 0.0016
0.242
0.3
0.073
2.319 0.012 0.281 0.041
2.028
0.024
294298.411
0.222
0.052
2.830
-
0.048
-
0.078
0.030 0.0052 0.181 0.081 0.037 0.0045
0.242
0.4
0.097
2.739 0.017 0.331 0.052
2.350
0.040
427386.929
0.237
0.072
2.787
-
0.024
-
0.065
0.040 0.0104 0.241 0.120 0.046 0.0091
0.242
0.5
0.121
3.142 0.023 0.380 0.061
2.597
0.060
551287.595
0.242
0.095
2.690
0.000
-
0.051
0.051 0.0170 0.187 0.084 0.038 0.0128
0.242
0.6
0.145
3.544 0.029 0.429 0.067
2.779
0.080
655133.174
0.237
0.122
2.545
0.024
-
0.039
0.063 0.0245 0.199 0.091 0.040 0.0198
0.242
0.7
0.169
3.965 0.034 0.480 0.072
2.897
0.100
728776.229
0.222
0.155
2.349
0.048
-
0.026
0.075 0.0320 0.211 0.098 0.043 0.0280
0.242
0.8
0.194
4.429 0.039 0.536 0.074
2.947
0.116
761215.568
0.194
0.204
2.084
0.073
-
0.015
0.088 0.0384 0.223 0.106 0.044 0.0358
0.242
0.9
0.218
4.996 0.044 0.605 0.072
2.909
0.127
736073.869
0.145
0.300
1.695
0.097
-
0.006
0.103 0.0421 0.235 0.115 0.046 0.0412
En la Tabla 16 se observa que los valores resaltados indican los puntos donde la altura subsecuente del
resalto cumple con el Momentum aguas arriba, mientras que las filas que no se encuentran resaltadas,
encuentran alturas del flujo subsecuentes que no satisfacen el Momentum, es decir, que con las alturas
aguas arriba (y
1
) no se alcanza a formar un resalto hidráulico.
También se observan los resultados obtenidos para una pendiente S = 0.031.
Tabla 17. Resultados obtenidos mediante la metodología de French para una S = 0.031.
d
(m)
y/d
(-)
y
n
(m)
teta
(-)
Área
(m
2
)
P
(m)
Radio
(m)
v
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
z
1
(m)
̂
(m)
̅
(m)
M
1
(m
3
)
y
2
(m)
̅
(m)
Área
2
(m
2
)
Prueba
M
(m
3
)
0.242 0.1 0.024 1.287 0.002 0.156 0.015 1.389 0.003
74903.83
0.145 0.016
3.453
-
0.097
-
0.107
0.010 0.0005 0.077 0.032 0.013 0.0005
0.242 0.2 0.048 1.855 0.007 0.224 0.029 2.133 0.014
218395.10
0.194 0.034
3.702
-
0.073
-
0.092
0.020 0.0032 0.170 0.075 0.034 0.0032
0.242 0.3 0.073 2.319 0.012 0.281 0.041 2.681 0.031
389159.11
0.222 0.052
3.742
-
0.048
-
0.078
0.030 0.0089 0.162 0.071 0.033 0.0053
0.242 0.4 0.097 2.739 0.017 0.331 0.052 3.104 0.053
564604.30
0.237 0.072
3.681
-
0.024
-
0.065
0.040 0.0176 0.174 0.077 0.035 0.0109
0.242 0.5 0.121 3.142 0.023 0.380 0.061 3.429 0.079
727829.08
0.242 0.095
3.551
0.000
-
0.051
0.051 0.0287 0.187 0.084 0.038 0.0199
0.242 0.6 0.145 3.544 0.029 0.429 0.067 3.667 0.106
864573.17
0.237 0.122
3.359
0.024
-
0.039
0.063 0.0413 0.199 0.091
0.04
0.0318
0.242 0.7 0.169 3.965 0.034 0.480 0.072 3.823 0.131
961518.95
0.222 0.155
3.099
0.048
-
0.026
0.075 0.0538 0.211 0.098 0.043 0.0456
0.242 0.8 0.194 4.429 0.039 0.536 0.074 3.888 0.153 1004216.55 0.194 0.204
2.750
0.073
-
0.015
0.088 0.0642 0.223 0.106 0.044 0.0588
0.242 0.9 0.218 4.996 0.044 0.605 0.072 3.837 0.167
971124.65
0.145 0.300
2.236
0.097
-
0.006
0.103 0.0699 0.235 0.115 0.046 0.0678
En la Tabla 17 se observa que tan solo dos alturas aguas arriba satisfacen la condición de generar un
resalto hidráulico para una pendiente del 3.1%. Las otras alturas no satisfacen la condición en la cual el
Momentum aguas arriba del resalto sea igual al Momentum aguas abajo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
65
Gráfica 23. Comportamiento de las profundidades subsecuentes.
En la Gráfica 23 se tiene que para pendientes más altas, la relación entre las profundidades subsecuentes
del resalto es más alta y con Números de Froude mayores.
5.4.4 Hager
Hager plantea tres ecuaciones para el cálculo de la profundidad subsecuente al resalto hidráulico. La
primera ecuación planteada, se basa en igualar los Momentos aguas arriba y aguas abajo del resalto, y la
forma de resolverla es por un método iterativo:
(
)
(
)
Ecuación 78. Cálculo de la profundidad subsecuente del resalto hidráulico por un método iterativo de acuerdo con la
metodología planteada por Hager.
El método iterativo que se usó, fue el método de la bisección, el cuál se encuentra en el Anexo 4, y los
resultados obtenidos se presentan en las Tabla 18 y
Tabla
19
:
Tabla 18. Resultados obtenidos para una pendiente de 0.019 con la metodología planteada por Hager.
d
(m)
y/d
(-)
y
1
(m)
teta
(-)
Área
(m
2
)
Perímetro
(m)
Radio
(m)
Velocidad
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
A
y
2
(m)
0.242
0.1
0.0242
1.287
0.00239
0.156
0.015
1.045
0.003
56377.905
0.145
0.016
2.599
14.511
0.064
0.242
0.2
0.0484
1.855
0.00655
0.224
0.029
1.611
0.011
164939.800
0.194
0.034
2.796
16.638
0.136
0.242
0.3
0.0726
2.319
0.01161
0.281
0.041
2.028
0.024
294376.898
0.222
0.052
2.831
17.026
0.207
0.242
0.4
0.0968
2.739
0.01718
0.331
0.052
2.350
0.040
427500.511
0.237
0.072
2.787
16.540 Presurizado
0.242
0.5
0.1210
3.142
0.02300
0.380
0.061
2.598
0.060
551433.772
0.242
0.095
2.690
15.476 Presurizado
0.242
0.6
0.1452
3.544
0.02882
0.429
0.067
2.780
0.080
655306.625
0.237
0.122
2.546
13.962 Presurizado
0.242
0.7
0.1694
3.965
0.03439
0.480
0.072
2.898
0.100
728969.002
0.222
0.155
2.350
12.043 Presurizado
0.242
0.8
0.1936
4.429
0.03945
0.536
0.074
2.948
0.116
761416.848
0.194
0.204
2.085
9.695
Presurizado
0.242
0.9
0.2178
4.996
0.04360
0.605
0.072
2.909
0.127
736268.556
0.145
0.300
1.695
6.747
Presurizado

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
66
Tabla 19. Resultados obtenidos para una pendiente de 0.031 con la metodología planteada por Hager.
d
(m)
y/d
(-)
y
1
(m)
teta
(-)
Área
(m
2
)
Perímetro
(m)
Radio
(m)
Velocidad
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
A
y
2
(m)
0.242
0.1
0.02420
1.287
0.00239
0.156
0.015
1.389
0.003
74903.831
0.145
0.016
3.453
24.850
0.082
0.242
0.2
0.04840
1.855
0.00655
0.224
0.029
2.133
0.014
218395.095
0.194
0.034
3.702
28.417
0.174
0.242
0.3
0.07260
2.319
0.01161
0.281
0.041
2.681
0.031
389159.110
0.222
0.052
3.742
29.007 Presurizado
0.242
0.4
0.09680
2.739
0.01718
0.331
0.052
3.104
0.053
564604.302
0.237
0.072
3.681
28.106 Presurizado
0.242
0.5
0.12100
3.142
0.02300
0.380
0.061
3.429
0.079
727829.080
0.242
0.095
3.551
26.219 Presurizado
0.242
0.6
0.14520
3.544
0.02882
0.429
0.067
3.667
0.106
864573.169
0.237
0.122
3.359
23.562 Presurizado
0.242
0.7
0.16940
3.965
0.03439
0.480
0.072
3.823
0.131
961518.952
0.222
0.155
3.099
20.212 Presurizado
0.242
0.8
0.19360
4.429
0.03945
0.536
0.074
3.888
0.153
1004216.549
0.194
0.204
2.750
16.124 Presurizado
0.242
0.9
0.21780
4.996
0.04360
0.605
0.072
3.837
0.167
971124.647
0.145
0.300
2.236
10.997 Presurizado
De acuerdo con los resultados obtenidos, se observa que con la pendiente más alta, los valores de la
profundidad subsecuente al resalto son mayores. Por lo mismo, en la pendiente de 3.1%, la tubería se
presuriza más rápido. Adicionalmente, para ver el comportamiento de la variación del Número de
Froude con respecto a la relación de llenado, se realiza la Gráfica 24.
Gráfica 24. Comparación de la variación de las pendientes con el método iterativo de Hager
La Gráfica 24 muestra que para Números de Froude mayores, se presenta mayor relación entre las
profundidades de flujo, al igual que en todas las comparaciones anteriores.
La segunda ecuación planteada por Hager, resulta en una aproximación que corresponde a un error de
2 %, y solo aplica para valores del Número de Froude mayores a 2:
6
Ecuación 79. Aproximación teórica para cálculos de la profundidad subsecuente del resalto hidráulico.
6
se refiere a la altura subsecuente aguas abajo del resalto, y se le adiciona el subíndice “a” para diferenciar el
de las otras ecuaciones planteadas por Hager.
0,000
0,001
0,002
0,003
0,004
0,003
0,003
0,004
0,004
y
2
/y
1
[
-]
F
1
[-]
Comparación pendientes (Hager - iterativo)
S = 0.019
S = 0.031

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
67
Y luego de realizar los experimentos, Hager observó que podía corregir la Ecuación 79 a una mejor
aproximación:
7
Ecuación 80. Aproximación empírica para el cálculo de la profundidad subsecuente del resalto hidráulico.
Los valores obtenidos aplicando la Ecuación 79 y Ecuación
80
se encuentran en las siguientes tablas:
Tabla 20. Resultados de la profundidad subsecuente del resalto hidráulico para la aproximación teórica con una pendiente de
0.019.
d
(m)
y/d
(-)
y
1
(m)
teta
(-)
Área
(m
2
)
P
(m)
Radio
(m)
v
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
y
2
(m)
y
2
a
(m)
y
2
b
(m)
0.242 0.1
0.0242
1.287
0.00239
0.156
0.015
1.045
0.003
56377.905
0.145
0.016
2.599
0.064
0.063
0.057
0.242 0.2
0.0484
1.855
0.00655
0.224
0.029
1.611
0.011
164939.800
0.194
0.034
2.796
0.136
0.135
0.122
0.242 0.3
0.0726
2.319
0.01161
0.281
0.041
2.028
0.024
294376.898
0.222
0.052
2.831
0.207
0.204
0.185
0.242 0.4
0.0968
2.739
0.01718
0.331
0.052
2.350
0.040
427500.511
0.237
0.072
2.787
Presurizado
0.268
0.244
0.242 0.5
0.1210
3.142
0.02300
0.380
0.061
2.598
0.060
551433.772
0.242
0.095
2.690
Presurizado
0.326
0.295
0.242 0.6
0.1452
3.544
0.02882
0.429
0.067
2.780
0.080
655306.625
0.237
0.122
2.546
Presurizado
0.373
0.337
0.242 0.7
0.1694
3.965
0.03439
0.480
0.072
2.898
0.100
728969.002
0.222
0.155
2.350
Presurizado
0.406
0.365
0.242 0.8
0.1936
4.429
0.03945
0.536
0.074
2.948
0.116
761416.848
0.194
0.204
2.085
Presurizado
0.419
0.375
0.242 0.9
0.2178
4.996
0.04360
0.605
0.072
2.909
0.127
736268.556
0.145
0.300
1.695
Presurizado
0.396
0.350
Tabla 21. Resultados de la profundidad subsecuente del resalto hidráulico para la aproximación teórica con una pendiente de
0.031.
d
(m)
y/d
(-)
y
1
(m)
teta
(-)
Área
(m
2
)
P
(m)
Radio
(m)
v
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
y
2
(m)
y
2
a
(m)
y
2
b
(m)
0.242
0.1
0.024
1.287
0.002
0.156
0.015
1.389
0.003
74903.831
0.145
0.016
3.453
0.082
0.080
0.074
0.242
0.2
0.048
1.855
0.007
0.224
0.029
2.133
0.014
218395.095
0.194
0.034
3.702
0.174
0.171
0.157
0.242
0.3
0.073
2.319
0.012
0.281
0.041
2.681
0.031
389159.110
0.222
0.052
3.742
Presurizado
0.259
0.238
0.242
0.4
0.097
2.739
0.017
0.331
0.052
3.104
0.053
564604.302
0.237
0.072
3.681
Presurizado
0.340
0.313
0.242
0.5
0.121
3.142
0.023
0.380
0.061
3.429
0.079
727829.080
0.242
0.095
3.551
Presurizado
0.412
0.379
0.242
0.6
0.145
3.544
0.029
0.429
0.067
3.667
0.106
864573.169
0.237
0.122
3.359
Presurizado
0.472
0.432
0.242
0.7
0.169
3.965
0.034
0.480
0.072
3.823
0.131
961518.952
0.222
0.155
3.099
Presurizado
0.514
0.469
0.242
0.8
0.194
4.429
0.039
0.536
0.074
3.888
0.153
1004216.549
0.194
0.204
2.750
Presurizado
0.531
0.481
0.242
0.9
0.218
4.996
0.044
0.605
0.072
3.837
0.167
971124.647
0.145
0.300
2.236
Presurizado
0.501
0.449
7
se refiere a la altura subsecuente aguas abajo del resalto, y se le adiciona el subíndice “b” para diferenciar el
de las otras ecuaciones planteadas por Hager.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
68
Gráfica 25.Comparación de las pendientes para los tres métodos propuestos por Hager.
En la Gráfica 25 se observan los resultados para los tres métodos propuestos por Hager. Se puede
observar que los dos métodos teóricos tienen la misma tendencia, y solo difieren por un error de 1.43 %,
mientras que al comparar el método teórico iterativo con el método empírico, el error sube a 10.15 %, y
al comparar el método aproximado y el método empírico el error es de 8.85 %. Con estos resultados se
podría inferir que se deben revisar los datos obtenidos en el método empírico, para acercar más los
resultados a los métodos teóricos.
5.4.5 FHWA
El Departamento de Transporte de Estados Unidos establece una metodología muy parecida a la
planteada por Silvester, es decir, plantean una ecuación basada en el coeficiente k´, y también usan dos
ecuaciones diferentes para calcular la profundidad subsecuente del resalto hidráulico. Sin embargo, a
diferencia de Silvester, no usan el área como una variable a calcular en las ecuaciones, sino que se basan
en un nuevo coeficiente “C”, el cual es un número fijo para relaciones de llenado definidas:
Gráfica 26. Coeficiente para determinar la profundidad subsecuente en el resalto hidráulico en tuberías.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
69
Entonces, las ecuaciones establecidas son:
Para profundidades subsecuentes del resalto hidráulico menores al diámetro:
Ecuación 81. Cálculo de la profundidad subsecuente del resalto hidráulico menor al diámetro.
Para profundidades subsecuentes del resalto hidráulico mayores al diámetro:
(
)
Ecuación 82. Cálculo de la profundidad subsecuente del resalto hidráulico mayor al diámetro.
Por lo cual, mediante el método de la bisección (Anexo 5), se obtienen los siguientes resultados:
Tabla 22. Resultados para el cálculo de la profundidad subsecuente del resalto mediante la metodología planteada por la
FHWA, para una pendiente de 0.019.
d
(m)
y/d
(-)
y
1
(m)
teta
(-)
Área
(m
2
)
Perímetro
(m)
Radio
(m)
Velocidad
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
y2
(m)
y
2
/y
1
(-)
0.242
0.1
0.024
1.287
0.002
0.156
0.015
1.045
0.003
56377.905
0.145
0.016
2.599
0.074
3.065
0.242
0.2
0.048
1.855
0.007
0.224
0.029
1.611
0.011
164939.800
0.194
0.034
2.796
0.152
3.136
0.242
0.3
0.073
2.319
0.012
0.281
0.041
2.028
0.024
294376.898
0.222
0.052
2.831
0.240
3.300
0.242
0.4
0.097
2.739
0.017
0.331
0.052
2.350
0.040
427500.511
0.237
0.072
2.787
0.328
3.388
0.242
0.5
0.121
3.142
0.023
0.380
0.061
2.598
0.060
551433.772
0.242
0.095
2.690
0.324
2.681
0.242
0.6
0.145
3.544
0.029
0.429
0.067
2.780
0.080
655306.625
0.237
0.122
2.546
0.311
2.142
0.242
0.7
0.169
3.965
0.034
0.480
0.072
2.898
0.100
728969.002
0.222
0.155
2.350
0.293
1.732
0.242
0.8
0.194
4.429
0.039
0.536
0.074
2.948
0.116
761416.848
0.194
0.204
2.085
0.271
1.401
0.242
0.9
0.218
4.996
0.044
0.605
0.072
2.909
0.127
736268.556
0.145
0.300
1.695
0.243
1.116
Con el método planteado por la FHWA se observa que al igual que en la metodología de Silvester, para
una pendiente de 1.9%, la tubería se presuriza con relaciones de llenado mayores al 30%.
Tabla 23. Resultados para el cálculo de la profundidad subsecuente del resalto mediante la metodología planteada por la
FHWA, para una pendiente de 0.031.
d
(m)
y/d
(-)
y
1
(m)
teta
(-)
Área
(m
2
)
Perímetro
(m)
Radio
(m)
Velocidad
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
y
2
(m)
y
2
/y
1
(-)
0.242
0.1
0.024
1.287
0.002
0.156
0.015
1.395
0.003
75243.481
0.145
0.016
3.469
0.096
3.952
0.242
0.2
0.048
1.855
0.007
0.224
0.029
2.142
0.014
219373.764
0.194
0.034
3.719
0.199
4.114
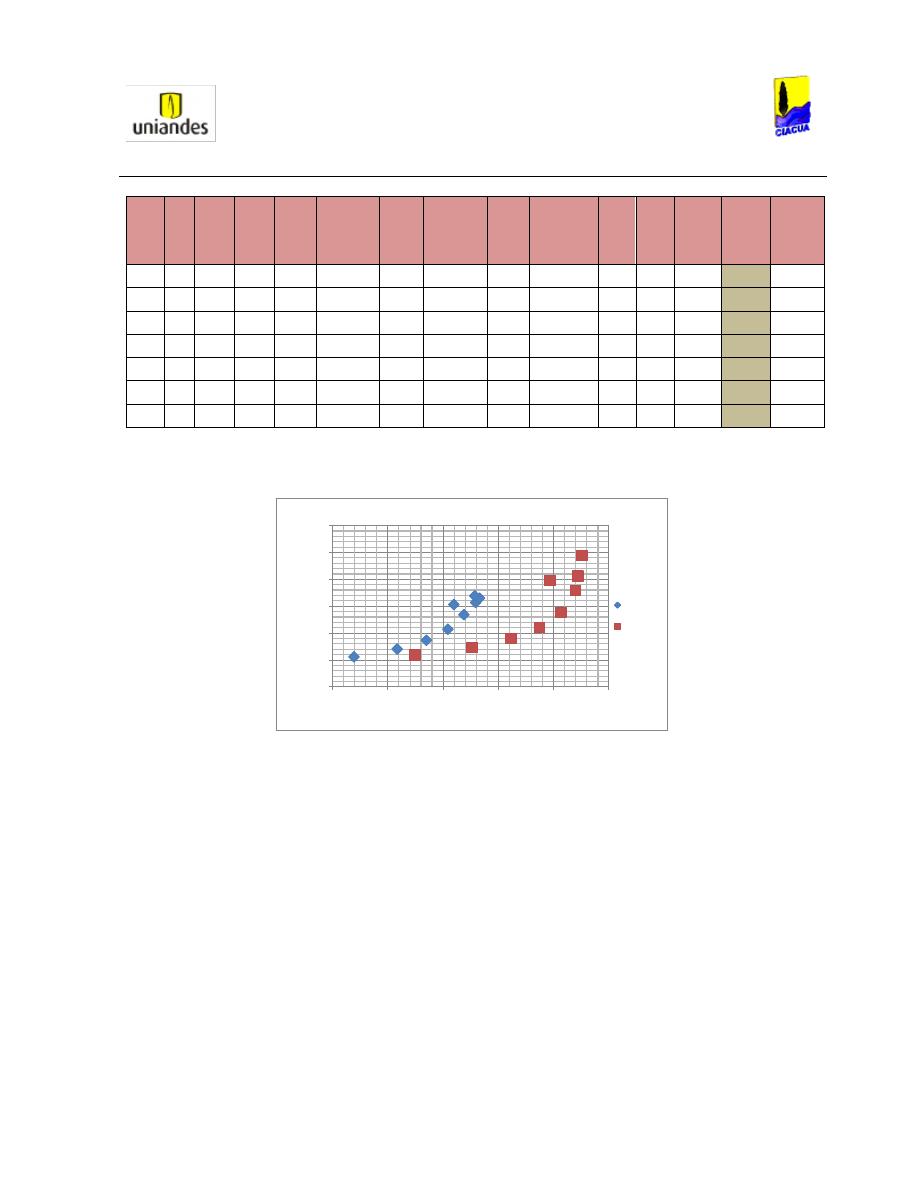
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
70
d
(m)
y/d
(-)
y
1
(m)
teta
(-)
Área
(m
2
)
Perímetro
(m)
Radio
(m)
Velocidad
(m/s)
Q
(m³/s)
Reynolds
(-)
T
(m)
D
(m)
Froude
(-)
y
2
(m)
y
2
/y
1
(-)
0.242
0.3
0.073
2.319
0.012
0.281
0.041
2.693
0.031
390893.219
0.222
0.052
3.759
0.355
4.895
0.242
0.4
0.097
2.739
0.017
0.331
0.052
3.118
0.054
567111.670
0.237
0.072
3.698
0.347
3.585
0.242
0.5
0.121
3.142
0.023
0.380
0.061
3.444
0.079
731054.123
0.242
0.095
3.567
0.335
2.770
0.242
0.6
0.145
3.544
0.029
0.429
0.067
3.683
0.106
868398.496
0.237
0.122
3.374
0.321
2.210
0.242
0.7
0.169
3.965
0.034
0.480
0.072
3.839
0.132
965769.414
0.222
0.155
3.113
0.304
1.794
0.242
0.8
0.194
4.429
0.039
0.536
0.074
3.905
0.154
1008654.150
0.194
0.204
2.762
0.284
1.465
0.242
0.9
0.218
4.996
0.044
0.605
0.072
3.854
0.168
975417.216
0.145
0.300
2.246
0.257
1.182
En cambio, para pendientes del 3.1%, la tubería se presuriza con relaciones de llenado mayores al 20%.
Gráfica 27. Comparación de las pendientes con el método de la FWHA.
El comportamiento de las profundidades subsecuentes con el método planteado por la FWHA presenta
un comportamiento similar al observado en la metodología de Silvester, ya que para pendientes más
altas se presentan Números de Froude más altos y valores más altos de las relaciones entre las
profundidades de llenado.
0.000
1.000
2.000
3.000
4.000
5.000
6.000
1.500
2.000
2.500
3.000
3.500
4.000
y
2
/y
1
[
-]
F
1
[-]
Comparación pendientes (FWHA)
S = 0.019
S = 0.031
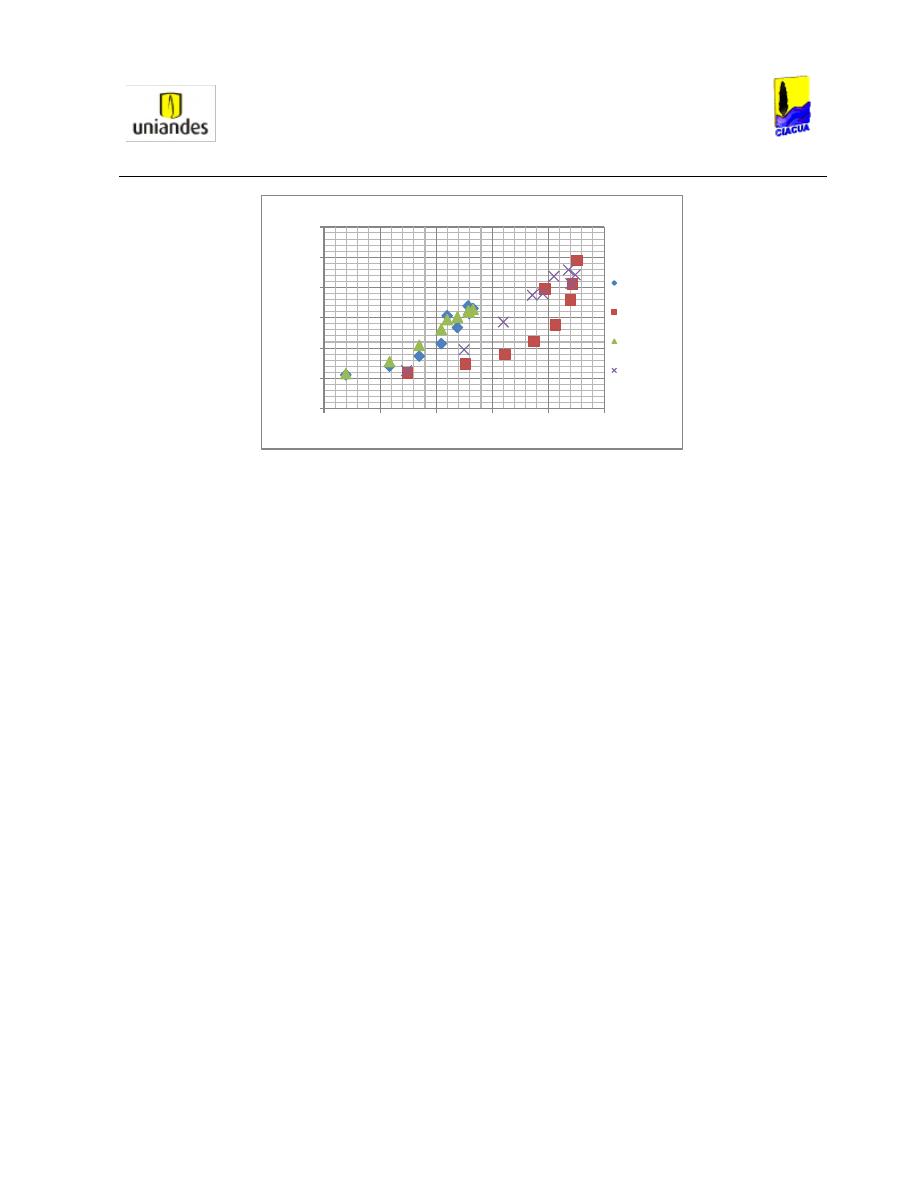
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
71
Gráfica 28. Comparación entre la metodología de Silvester y la metodología planteada por la FWHA.
En la Gráfica 28 se observa que en general la metodología planteada por la FWHA presenta un
comportamiento más uniforme que el observado en la metodología planteada por Silvester. Para la
pendiente de 1.9%, los valores obtenidos por las dos metodologías son muy similares y no se presenta
ninguna tendencia a tener valores mayores o menores en ninguna de las dos metodologías, mientras que
para la pendiente de 3.1%, los valores obtenidos por Silvester para la relación entre las relaciones de
llenado son mayores, mientras que la metodología planteada por la FWHA presenta una curva más
uniforme y con menores valores, ya que no se está evaluando el área mojada de la tubería para hallar la
profundidad subsecuente sino un coeficiente que varía con la profundidad de llenado. Por lo tanto, se
considera conveniente que en el montaje realizado se evalúe cuál de los dos parámetros representa
mayor influencia en el cálculo de la profundidad de llenado.
5.4.5 Conclusiones
Finalmente, se obtiene la siguiente gráfica en la cual se observa el comportamiento de las profundidades
subsecuentes según las ecuaciones de los diferentes autores:
0.000
1.000
2.000
3.000
4.000
5.000
6.000
1.500
2.000
2.500
3.000
3.500
4.000
y
2
/y
1
[
-]
F
1
[-]
Comparación pendientes (Silvester y FWHA)
S = 0.019 FWHA
S = 0.031 FWHA
S = 0.019
Silvester
S = 0.031
Silvester
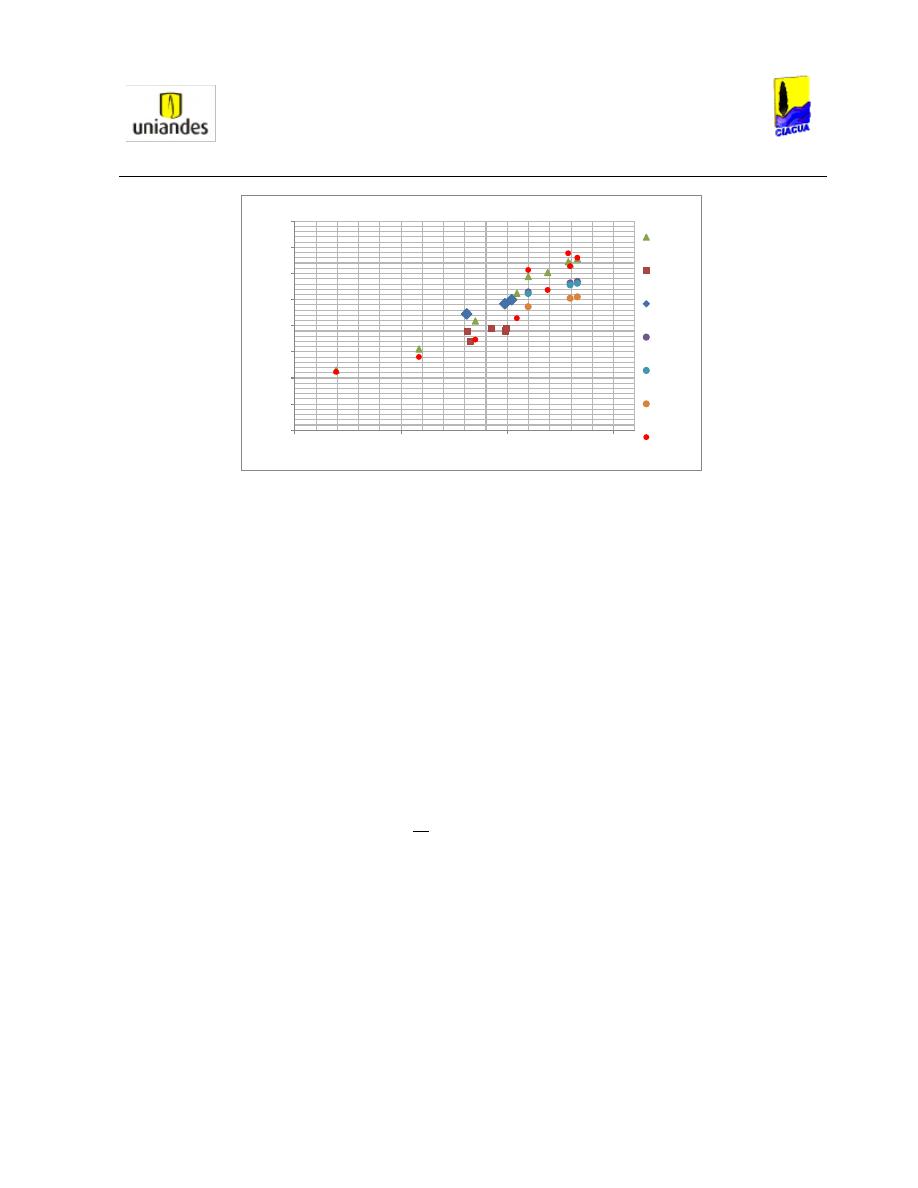
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
72
Gráfica 29. Comparación entre los diferentes autores para el cálculo de las profundidades subsecuentes.
En la Gráfica 29 se observa que a medida que aumenta el Número de Froude aumenta la relación entre
las profundidades subsecuentes para todos los autores. El comportamiento entre las ecuaciones de
Silvester y la FHWA es muy similar, mientras que las ecuaciones de Hager y de Straub sobrestiman el
aumento de la relación entre las profundidades subsecuentes.
5.5 Análisis comparativo con otros autores para el cálculo de la longitud del resalto
hidráulico
5.5.1 Silvester
Tal como se explicó en el Numeral 2, Silvester estableció la Ecuación 15 para el cálculo de la Longitud
del Resalto Hidráulico:
(
)
Ecuación 15. Longitud de un resalto hidráulico para cualquier tipo de sección (Silvester, 1964).
Ahora bien, Silvester a partir de la Gráfica 3 establece los valores de k y
, con los cuales se puede
estimar la longitud del resalto hidráulico, dependiendo de los valores del Número de Froude y la
relación entre las profundidades subsecuentes en el resalto.
Para entender la gráfica y aplicarla a los valores obtenidos en los análisis de las profundidades
subsecuentes realizados anteriormente, se realizó un programa que permitió ilustrar la gráfica planteada
por Silvester, y colocar los obtenidos en los anteriores análisis. La gráfica se muestra a continuación:
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
1.500
2.000
2.500
3.000
y
2
/y
1
[
-]
F
1
[-]
Comparación diferentes autores S = 0.019
Silvester
Straub
French
Hager
Hager 1.16
Hager 1.00
FHWA
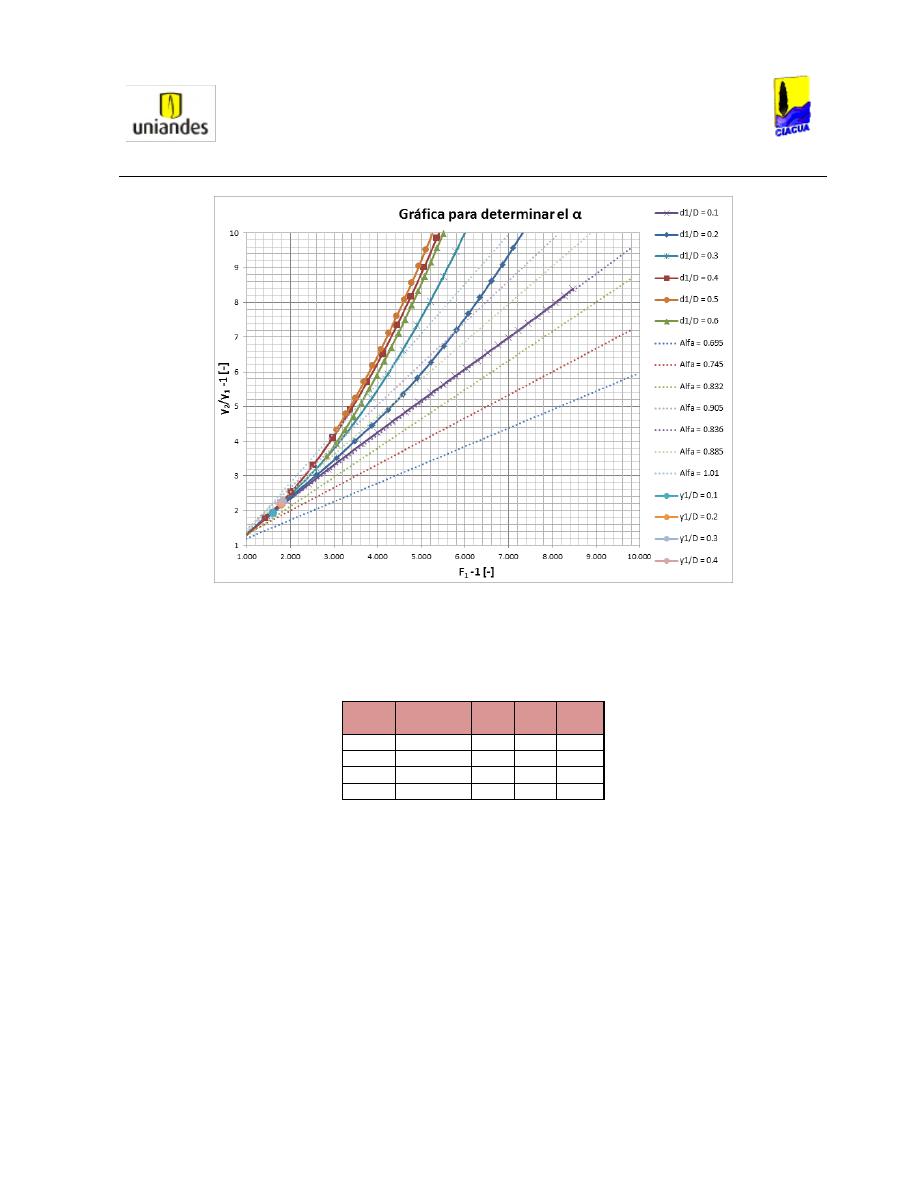
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
73
Gráfica 30. Datos obtenidos para calcular los coeficientes que permiten calcual la longitud del resalto hidráulico.
Con la Gráfica 30 se estableció el valor de
, obteniendo así los siguientes valores de longitud:
Tabla 24. Cálculo de la longitud mediante la metodología planteada por Silvester.
F
1
-1
(-)
(y
2
/y
1
) - 1
(-)
(-)
K
(-)
L
(m)
1.599
1.942
0.836 4.000 0.143
1.796
2.182
0.836 4.000 0.316
1.831
2.280
0.885 8.000 0.992
1.787
2.224
0.885 8.000 1.295
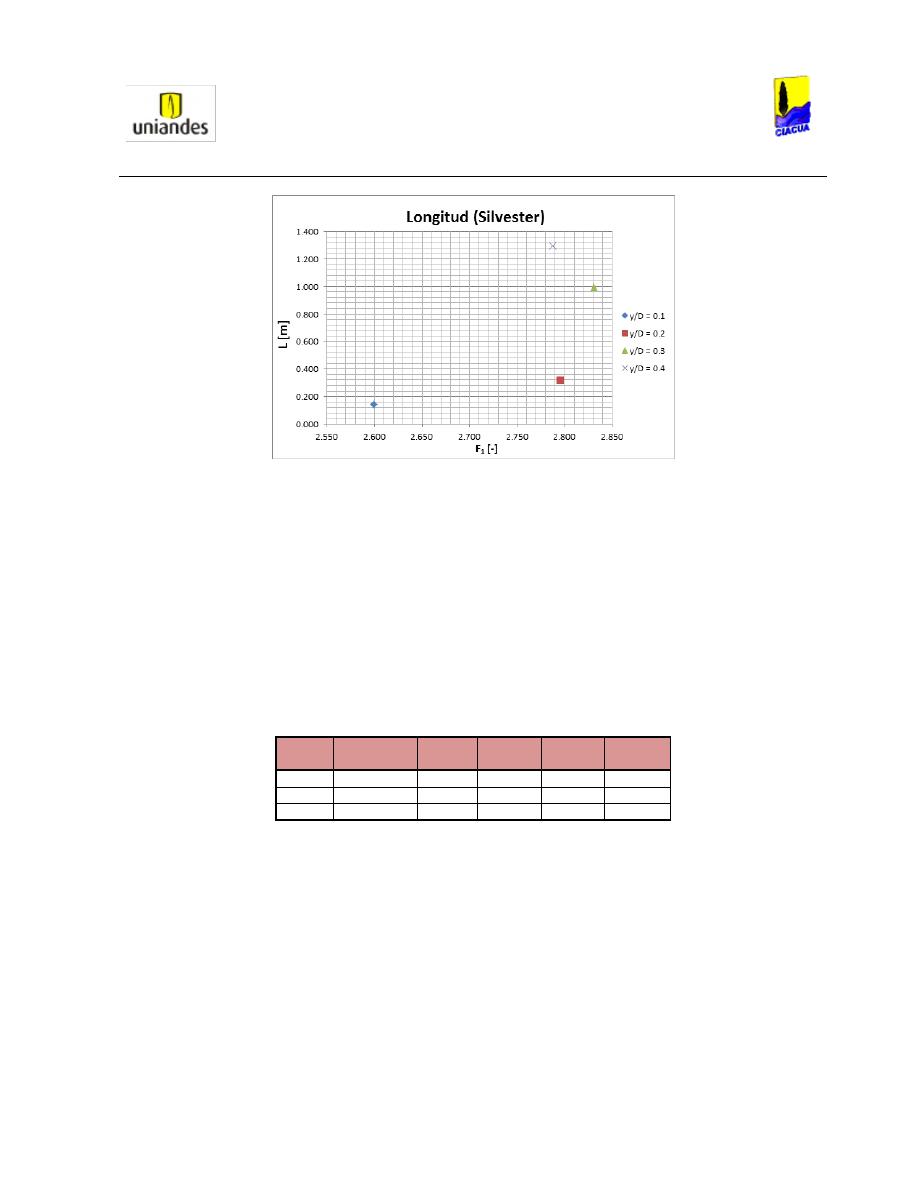
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
74
Gráfica 31. Longitud del resalto mediante la metodología planteada por Silvester.
En la Gráfica 31, se observa que para mayores Números de Froude, la longitud del resalto hidráulico es
mayor; hasta que se alcanza la profundidad de llenado que genera el resalto hidráulico más fuerte
(
). Para las demás profundidades de llenado, empieza a disminuir la longitud.
5.5.2 Hager
De acuerdo con la Ecuación
39
y la Ecuación
41
, se calcula la longitud de aireación y de recirculación en
el resalto hidráulico, a partir de las profundidades subsecuentes calculadas con la metodología iterativa
de Hager:
Tabla 25. Cálculo longitudes en el resalto hidráulico de acuerdo con la metodología planteada por Hager.
Froude
(-)
y
2
(m)
(-)
(m)
(-)
(m)
2.599
0.064
3.224
0.206
6.449
0.413
2.796
0.136
3.344
0.456
6.689
0.912
2.831
0.207
3.365
0.696
6.730
1.392
En la Tabla 25 se observa que a mayor Número de Froude, tanto la longitud de aireación, como la
longitud de recirculación aumentan. No se puede realizar el análisis para relaciones de llenado mayores
al 30%, ya que la tubería en estos casos se encuentra presurizada.
5.5.3 FWHA
La FWHA dice que para calcular la longitud del resalto hidráulico, se use la Gráfica 10 y la Ecuación
56, con lo cual se obtiene que:
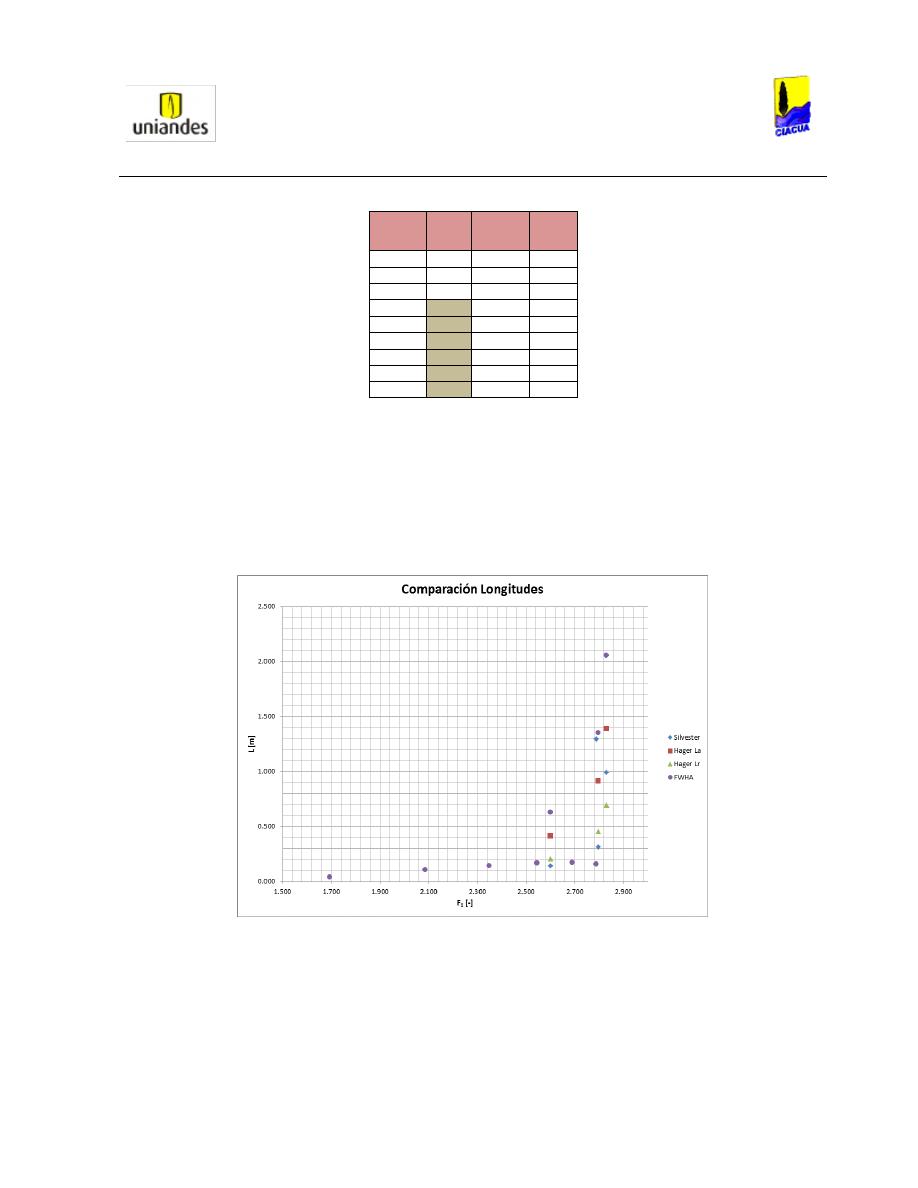
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
75
Tabla 26. Cálculo de la longitud del resalto con la metodología de FWHA.
Froude
(-)
y
2
(m)
y
2
/y
1
(-)
L
(m)
2.599
0.074
3.065
0.629
2.796
0.152
3.136
1.353
2.831
0.240
3.300
2.055
2.787
0.328
3.388
0.157
2.690
0.324
2.681
0.172
2.546
0.311
2.142
0.168
2.350
0.293
1.732
0.147
2.085
0.271
1.401
0.105
1.695
0.243
1.116
0.039
En la Tabla 26 se observa que cuando la tubería no está presurizada (sin sombreado), la longitud del
resalto aumenta a medida que aumenta el Número de Froude, mientras que cuando la tubería se
encuentra presurizada, el comportamiento del valor de la longitud del resalto hidráulico varía sin
ninguna tendencia.
A continuación se presenta la gráfica con todos los resultados obtenidos para el cálculo de la longitud en
las diferentes metodologías:
Gráfica 32. Comparación entre las diferentes metodologías para el cálculo de las longitudes.
En la Gráfica 32 se observa que todas las metodologías presentan un aumento de la longitud a medida
que aumenta el Número de Froude; sin embargo presentan puntos en los cuales los valores para un
mismo Número de Froude tienen como resultado valores diferentes en la longitud, como sucede en el
caso de un Número de Froude igual a 2.599.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
76
6. Resultados y Análisis de Resultados
6.1. Resultados
6.1.1. Registro Fotográfico
A continuación se presenta un registro fotográfico de algunos escenarios medidos con caudales cercanos
a 30 L/s.
Tabla 27. Registro fotográfico del resalto hidráulico para caudales cercanos a 30 L/s.
REGISTRO FOTOGRÁFICO PARA CAUDALES CERCANOS A 30 L/s
S = 0.7 % y Q = 34 L/s
S = 0.9 % y Q = 30 L/s
S = 1.1 % y Q = 30 L/s
S = 1.3 % y Q = 40 L/s

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
77
REGISTRO FOTOGRÁFICO PARA CAUDALES CERCANOS A 30 L/s
S = 1.5 % y Q = 30 L/s
S = 1.7 % y Q = 30 L/s
S = 1.9 % y Q = 30 L/s
S = 2.1 % y Q = 40 L/s
S = 2.5 % y Q = 30 L/s
Se puede observar que aunque se esté midiendo el mismo caudal, a medida que aumenta la pendiente, la
profundidad subsecuente aguas abajo del resalto hidráulico es más alta; y esto ocurre dado que el flujo
aguas arriba del resalto es más supercrítico en las pendientes altas que en las pendientes bajas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
78
6.1.2. Profundidad de flujo
Los resultados presentados en el presente informe se realizaron para diferentes pendientes, cada una,
con su respectiva variación de caudales, de acuerdo con el análisis mostrado en la Tabla 4.
El primer ensayo se realizó para una pendiente del 0.5%, la cual presentó en general resaltos muy
débiles, los cuales no permitían inferir fácilmente ni la longitud total de recirculación, ni la longitud de
aireación ya que no existía formación de burbujas en el resalto. Por otra parte, se hicieron mediciones de
temperatura aguas arriba y aguas abajo del resalto para comprobar si existía algún tipo de variación por
la formación del resalto hidráulico; sin embargo, no se obtuvo variación alguna en estas temperaturas.
Los datos obtenidos de medición de profundidades de flujo se muestran a continuación:
Gráfica 33. Profundidades aguas arriba y aguas abajo del resalto hidráulico para S = 0.005.
En la Gráfica 33 se observa que salvo la primera medición (Q = 0.0124 m
3
/s), a mayor caudal, aumenta
el nivel medido en los dos sensores. Es importante observar que el comportamiento en general para las
dos profundidades (aguas arriba y aguas abajo del resalto), es similar y presentan la misma tendencia. A
continuación se presenta el resultado para los otros escenarios medidos:
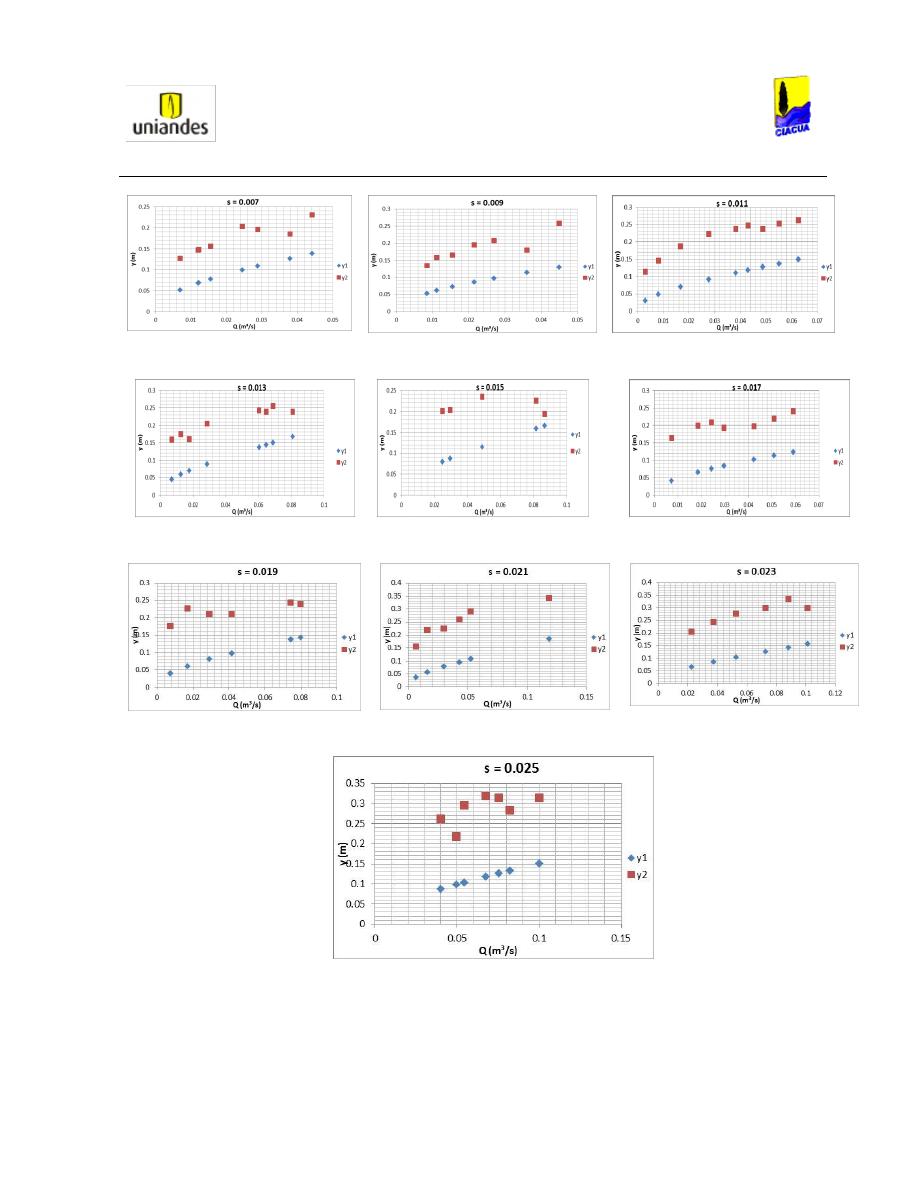
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
79
Gráfica 34. Profundidades aguas arriba
y aguas abajo del resalto hidráulico para
S = 0.007.
Gráfica 35. Profundidades aguas arriba y
aguas abajo del resalto hidráulico para S
= 0.009.
Gráfica 36. Profundidades aguas arriba
y aguas abajo del resalto hidráulico para
S = 0.011.
Gráfica 37. Profundidades aguas arriba y
aguas abajo del resalto hidráulico para S =
0.013.
Gráfica 38. Profundidades aguas arriba y
aguas abajo del resalto hidráulico para S =
0.015.
Gráfica 39. Profundidades aguas arriba y
aguas abajo del resalto hidráulico para S =
0.017.
Gráfica 40. Profundidades aguas arriba y
aguas abajo del resalto hidráulico para S =
0.019.
Gráfica 41. Profundidades aguas arriba y
aguas abajo del resalto hidráulico para S =
0.021.
Gráfica 42. Profundidades aguas arriba y
aguas abajo del resalto hidráulico para S =
0.023.
Gráfica 43. Profundidades aguas arriba y aguas abajo del resalto hidráulico para S = 0.025.
De acuerdo con las gráficas anteriores, se puede observar que para S
1.1%, se presenta un
comportamiento más estable, con lo cual se puede identificar de manera más clara, los niveles aguas
arriba y aguas abajo del resalto hidráulico. Vale la pena mencionar que existieron varios

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
80
comportamientos inusuales en el flujo, ya que como se estaba manejando una pendiente tan baja, el flujo
tiende a ser cuasicrítico, y no es estable. Por ejemplo, para S = 0.7% y Q = 0.012 m
3
/s, se presentaron
dos resaltos hidráulicos en una longitud menor a 7 m, y los dos presentaban características muy
similares, con resaltos hidráulicos muy débiles y poca formación de burbujas.
6.1.3. Longitud del resalto hidráulico
La longitud del resalto hidráulico se midió por medio de fotografías, y está definida como la distancia
que comprende el final de la profundidad aguas arriba del resalto y el inicio de la profundidad aguas
abajo. A continuación se muestra el comportamiento de la longitud del resalto hidráulico para una
pendiente de 0.005:
Gráfica 44. Longitud del Resalto Hidráulico para S = 0.005.
En la Gráfica 44 no se observa ninguna tendencia en el aumento de longitud cuando aumenta el caudal o
el Número de Froude. Es importante mencionar que la medida de la longitud tiene alta incertidumbre
dado que el resalto hidráulico es muy débil e inestable, y la magnitud de la medición anotada puede
tener un error aproximado de 10 cm.
A continuación se muestran todos los escenarios medidos:
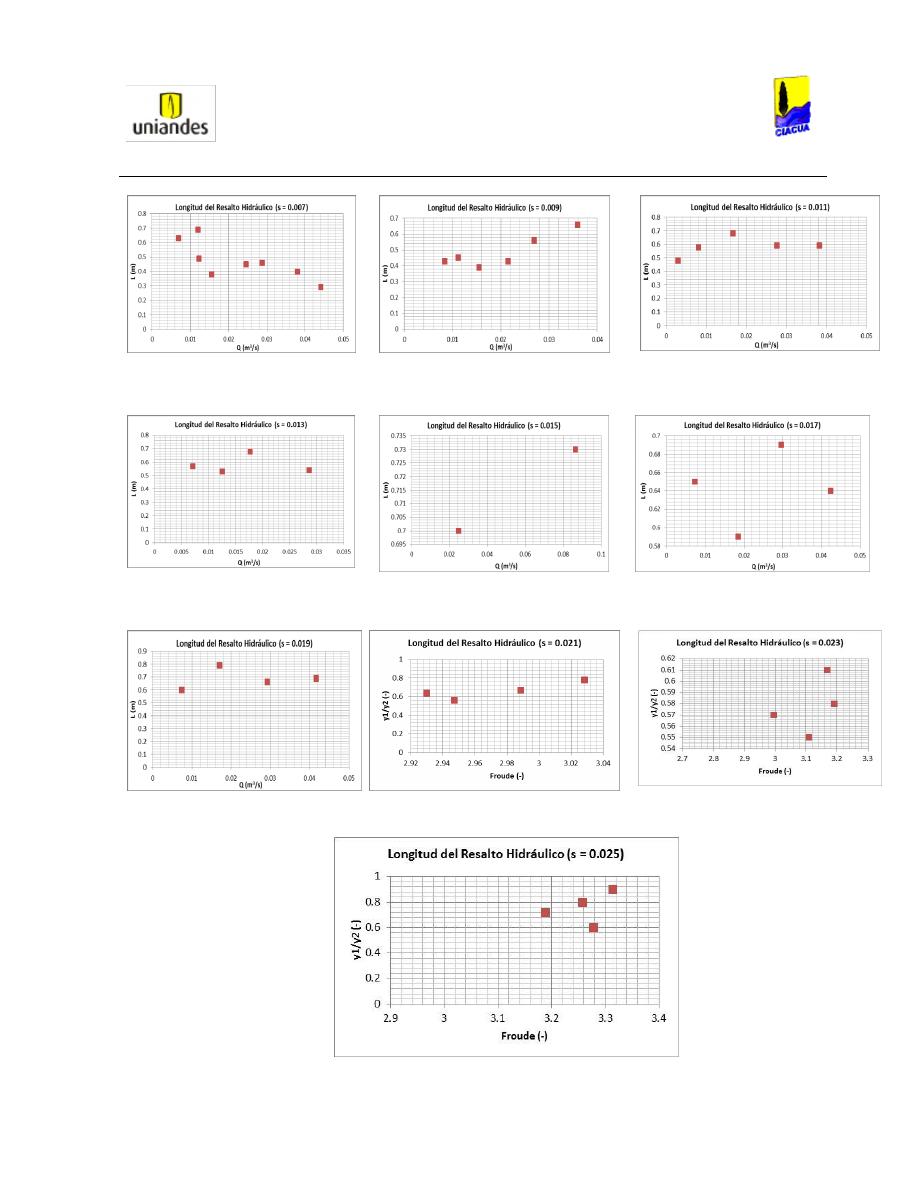
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
81
Gráfica 45. Longitud del Resalto
Hidráulico para S = 0.007.
Gráfica 46. Longitud del Resalto Hidráulico
para S = 0.009.
Gráfica 47. Longitud del Resalto Hidráulico
para S = 0.011.
Gráfica 48. Longitud del Resalto
Hidráulico para S = 0.013.
Gráfica 49. Longitud del Resalto Hidráulico
para S = 0.015.
Gráfica 50. Longitud del Resalto Hidráulico
para S = 0.017.
Gráfica 51. Longitud del Resalto
Hidráulico para S = 0.019.
Gráfica 52. Longitud del Resalto Hidráulico
para S = 0.021.
Gráfica 53. Longitud del Resalto Hidráulico
para S = 0.023.
Gráfica 54. Longitud del Resalto Hidráulico para S = 0.025.
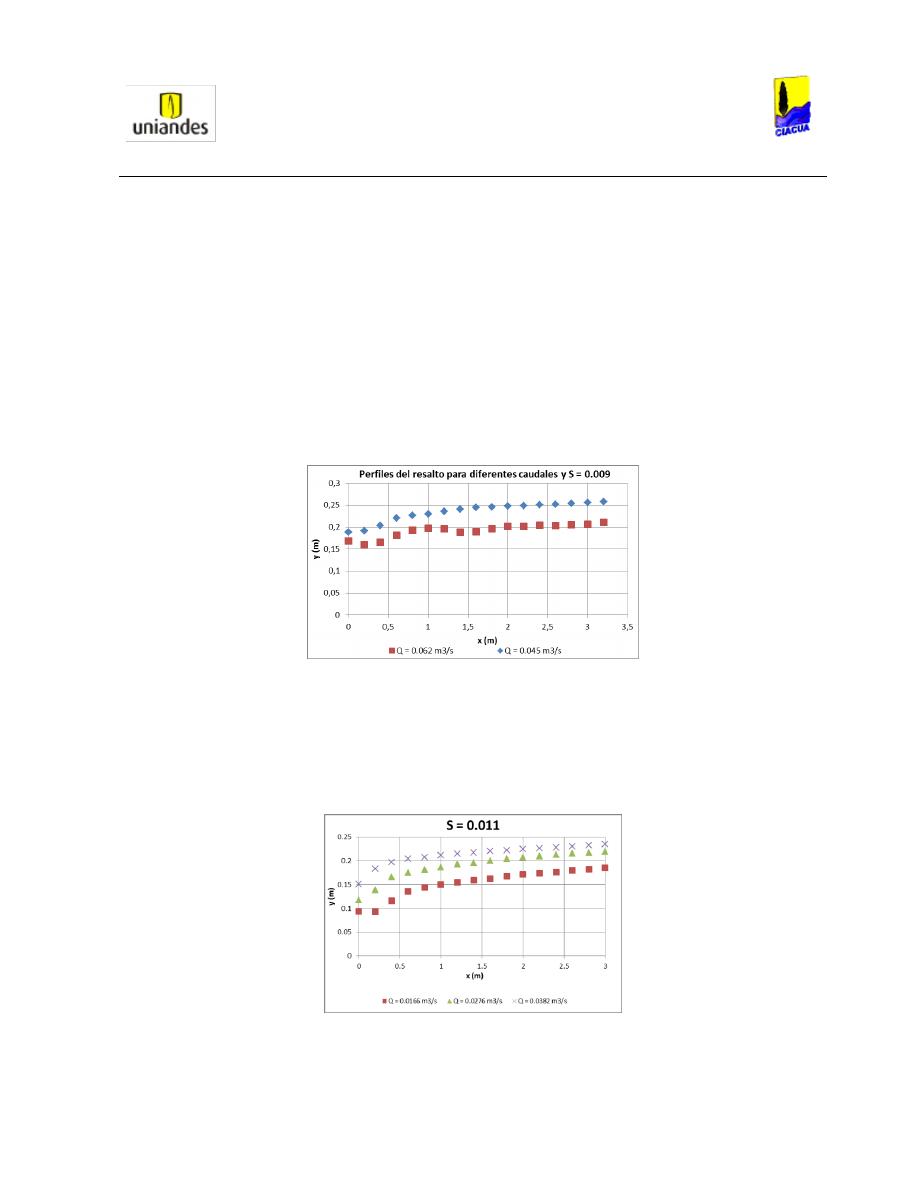
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
82
Para S = 0.7% y Q = 0.029 m
3
/s, el resalto hidráulico no logró ubicarse en un solo sitio, y su
movimiento variaba longitudinalmente 10 cm aproximadamente. En general, el comportamiento de la
longitud es variable y no aumenta proporcionalmente con el caudal, es decir, no aumenta con el
aumento de la profundidad subsecuente aguas arriba del resalto hidráulico.
Es importante aclarar que, de los datos tomados, únicamente para los resaltos hidráulicos generados con
pendientes mayores a 1.1% y con caudales mayores a 0.3 m
3
/s, se generó claramente la región de
burbujas mencionada por Hager; para las otras mediciones había formación de burbujas, pero la zona no
podía ser medida dada la inestabilidad del resalto.
Por otra parte, para S
0.9%, la profundidad subsecuente aguas abajo del resalto hidráulico superó el
diámetro de la tubería, por lo cual, se midió la profundidad del flujo con los piezómetros. De acuerdo
con lo anterior, se presentan los resultados en la siguiente gráfica:
Gráfica 55. Perfil del resalto hidráulico para S = 0.009.
En la Gráfica 55 se puede observar que el resalto hidráulico es inestable y presenta dos curvas en el
nivel del flujo. Sin embargo, para Q = 0.045 m
3
/s, el perfil del flujo es más estable, e incluso se puede
inferir rápidamente cuál es la profundidad subsecuente aguas abajo del resalto hidráulico; por otro lado
la profundidad subsecuente para Q = 0.062 m
3
/s, no se puede determinar claramente.
Gráfica 56. Perfil del resalto hidráulico para S = 0.011.
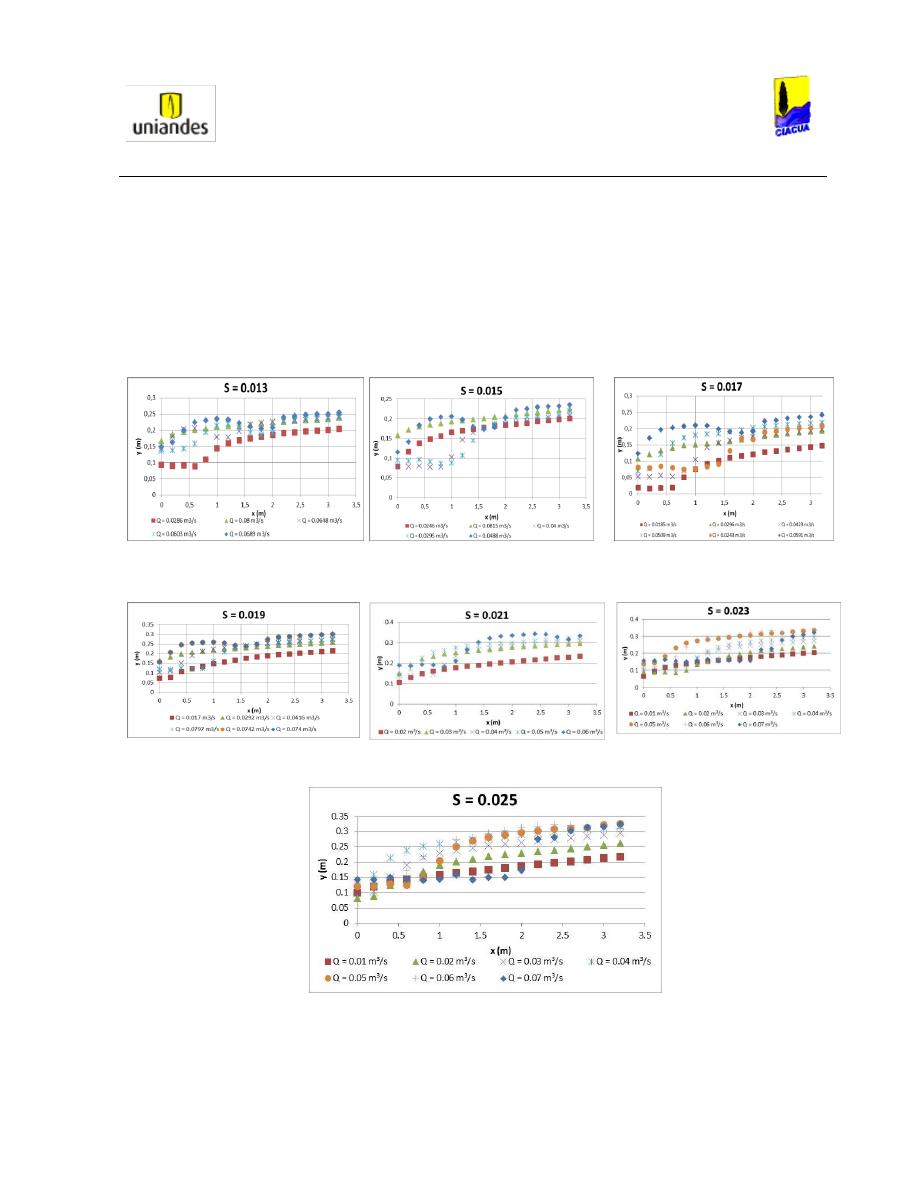
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
83
Para S = 0.011, los perfiles de flujo medidos son mucho más estables, y como es de esperarse, a mayor
caudal, mayor nivel en el flujo. Es importante resaltar, que a pesar de que la variación entre los 3
caudales mostrados es la misma, existe mayor distancia entre los datos tomados con el caudal más bajo
(0.0166 m
3
/s) con respecto al caudal medio, que la distancia existente entre el caudal medio y el caudal
más alto medido (0.0382 m
3
/s). Con éste resultado se podría inferir que a medida que aumenta el caudal,
las profundidades subsecuentes aguas abajo del resalto se van pareciendo entre sí. También se puede
observar que a mayor caudal, la longitud del resalto hidráulico es mayor.
A continuación se presentan los resultados para las pendientes entre 0.013 y 0.025:
Gráfica 57. Perfil del Resalto
Hidráulico para S = 0.013.
Gráfica 58. Perfil del Resalto Hidráulico
para S = 0.015.
Gráfica 59. Perfil del Resalto Hidráulico
para S = 0.017.
Gráfica 60. Perfil del Resalto Hidráulico
para S = 0.019.
Gráfica 61. Perfil del Resalto Hidráulico
para S = 0.021.
Gráfica 62. Perfil del Resalto Hidráulico
para S = 0.023
.
Gráfica 63. Perfil del Resalto Hidráulico para S = 0.025.
En general, en las anteriores gráficas se observa que para los caudales muy altos, el perfil del flujo es
muy inestable, y no se puede observar claramente cuál es la profundidad subsecuente aguas abajo del

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
84
resalto hidráulico. También se observa, que a mayor pendiente, la altura del nivel del perfil a lo largo
del resalto es mayor.
6.1.4. Distribución de Velocidades
Los datos obtenidos para el análisis de la distribución de velocidades se dividen de acuerdo con los 12
escenarios planteados en el Numeral 4.4.2.3. Sin embargo, solo se mostrarán 2 escenarios en éste
capítulo. Los demás escenarios se encuentran en ANEXOS.
Tabla 28. Comportamiento de la velocidad de las partículas en diferentes secciones transversales para S = 1.2 % y Q = 24 L/s.
PERFIL DE VELOCIDADES – VISTA LATERAL (S = 0.012 y Q = 0.024 m
3
/s)
Py
8
= 0 cm
Py = 0.04 m
Py = 0.08 m
8
Py corresponde a la posición medida en la coordenada y.
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
x (m) - Sección Longitudinal
z
(
m
)
-
S
e
c
c
ió
n
V
e
rt
ic
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.012 y Q = 0.024 m3/s) Py = 1
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
x (m) - Sección Longitudinal
z
(m
)
-
S
ec
ci
ón
V
er
tic
al
PERFIL DE VELOCIDADES EN EL RESALTO HIDRÁULICO (S = 0.012 y Q = 0.024 m3/s) Py = 2
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
x (m) - Sección Longitudinal
z
(
m
)
-
S
e
c
c
ió
n
V
e
rt
ic
a
l
PERFIL DE VELOCIDADES DEL RESALTO HIDRÁULICO (S = 0.012 y Q = 0.024 m3/s) Py = 4
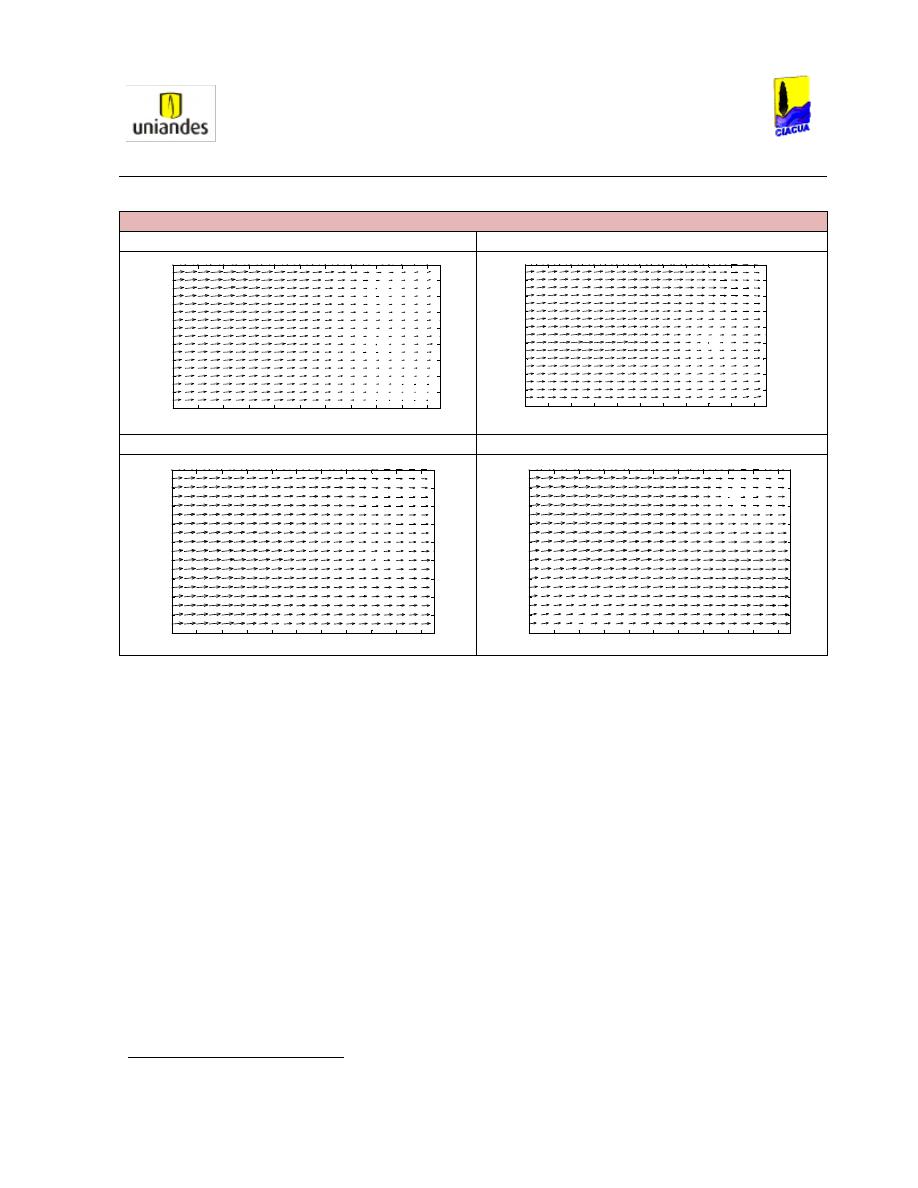
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
85
Tabla 29. Comportamiento de la velocidad de las partículas en diferentes secciones verticales para S = 1.2 % y Q = 24 L/s.
PERFIL DE VELOCIDADES – VISTA EN PLANTA (S = 0.012 y Q = 0.024 m
3
/s)
Pz
9
= 0.01 cm
Pz = 0.02 m
Pz = 0.03 cm
Pz = 0.04 m
Para el escenario 1, el cual corresponde a una pendiente de 1.2 % y un caudal de 24 L/s, se observa que
en el perfil lateral existen remolinos en la parte central de la medición, sin embargo, la mayoría de las
partículas siguen en promedio la velocidad en la dirección x del flujo. En el perfil lateral no se observa
ningún movimiento transversal de las partículas.
9
Pz corresponde a la posición medida en la coordenada z.
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
x (m) - Sección Longitudinal
y
(
m
)
-
S
e
c
c
ió
n
T
ra
n
s
v
e
rs
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.012 y Q = 0.024 m3/s) Pz = 1
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
x (m) - Sección Longitudinal
y
(
m
)
-
S
e
c
c
ió
n
T
ra
n
s
v
e
rs
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.012 y Q = 0.024 m3/s) Pz = 2
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
x (m) - Sección Longitudinal
y
(
m
)
-
S
e
c
c
ió
n
T
ra
n
s
v
e
rs
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.012 y Q = 0.024 m3/s) Pz = 3
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
x (m) - Sección Longitudinal
y
(
m
)
-
S
e
c
c
ió
n
T
ra
n
s
v
e
rs
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.012 y Q = 0.024 m3/s) Pz = 4
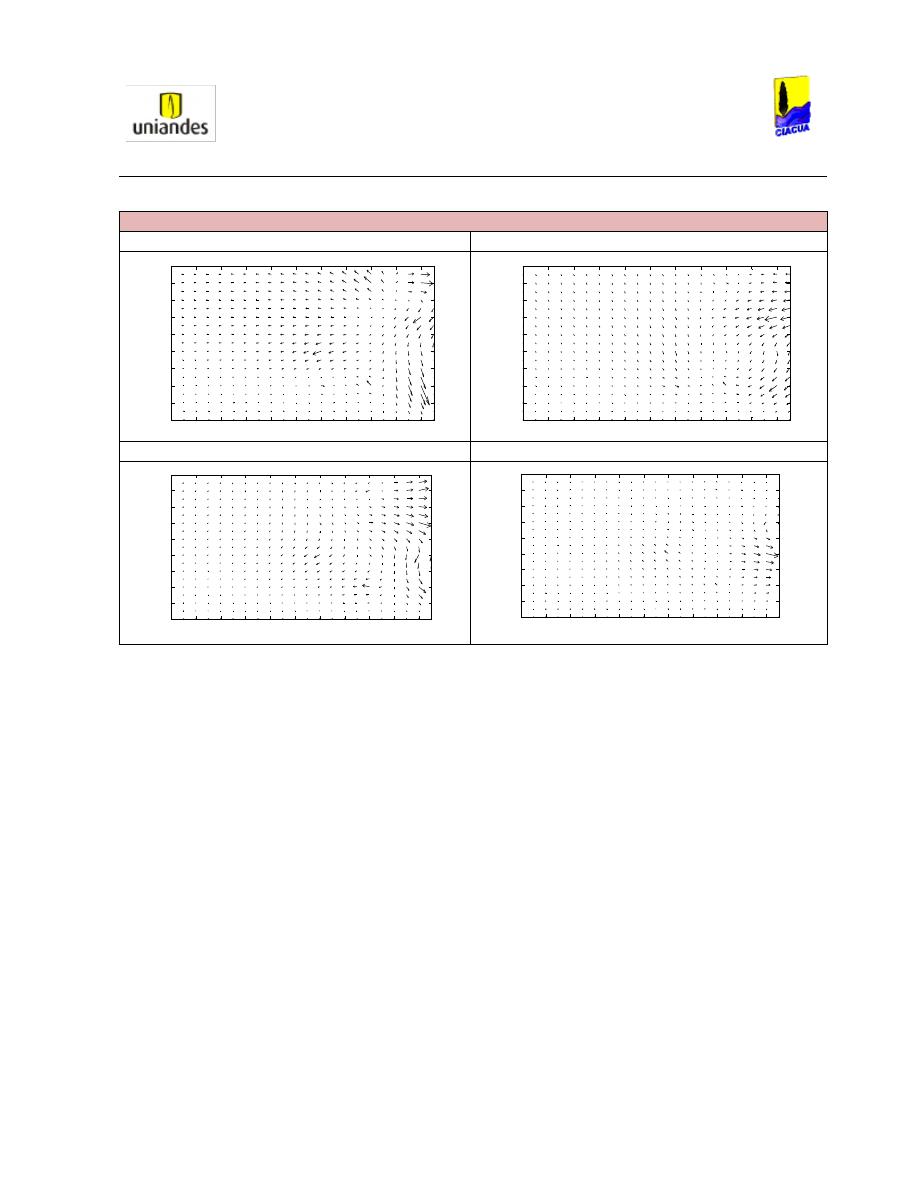
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
86
Tabla 30. Comportamiento de la velocidad de las partículas en diferentes secciones transversales para S = 1.6 % y Q = 24 L/s.
PERFIL DE VELOCIDADES – VISTA LATERAL (S = 0.016 y Q = 0.024 m
3
/s)
Py = 0 cm
Py = 0.04 m
Py = 0.08 cm
Py = 0.12 m
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
x (m) - Sección Longitudinal
z
(
m
)
-
S
e
c
c
ió
n
V
e
rt
ic
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.016 y Q = 0.024 m3/s) Py = 1
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
x (m) - Sección Longitudinal
z
(
m
)
-
S
e
c
c
ió
n
V
e
rt
ic
a
l
PERFIL VELOCIDAD RESALTO HIDRÁULICO (S = 0.016 y Q = 0.024 m3/s) Py = 3
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
x (m) - Sección Longitudinal
z
(
m
)
-
S
e
c
c
ió
n
V
e
rt
ic
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.016 y Q = 0.024 m3/s) Py = 5
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
x (m) - Sección Longitudinal
z
(
m
)
-
S
e
c
c
ió
n
V
e
rt
ic
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.016 y Q = 0.024 m3/s) Py = 7
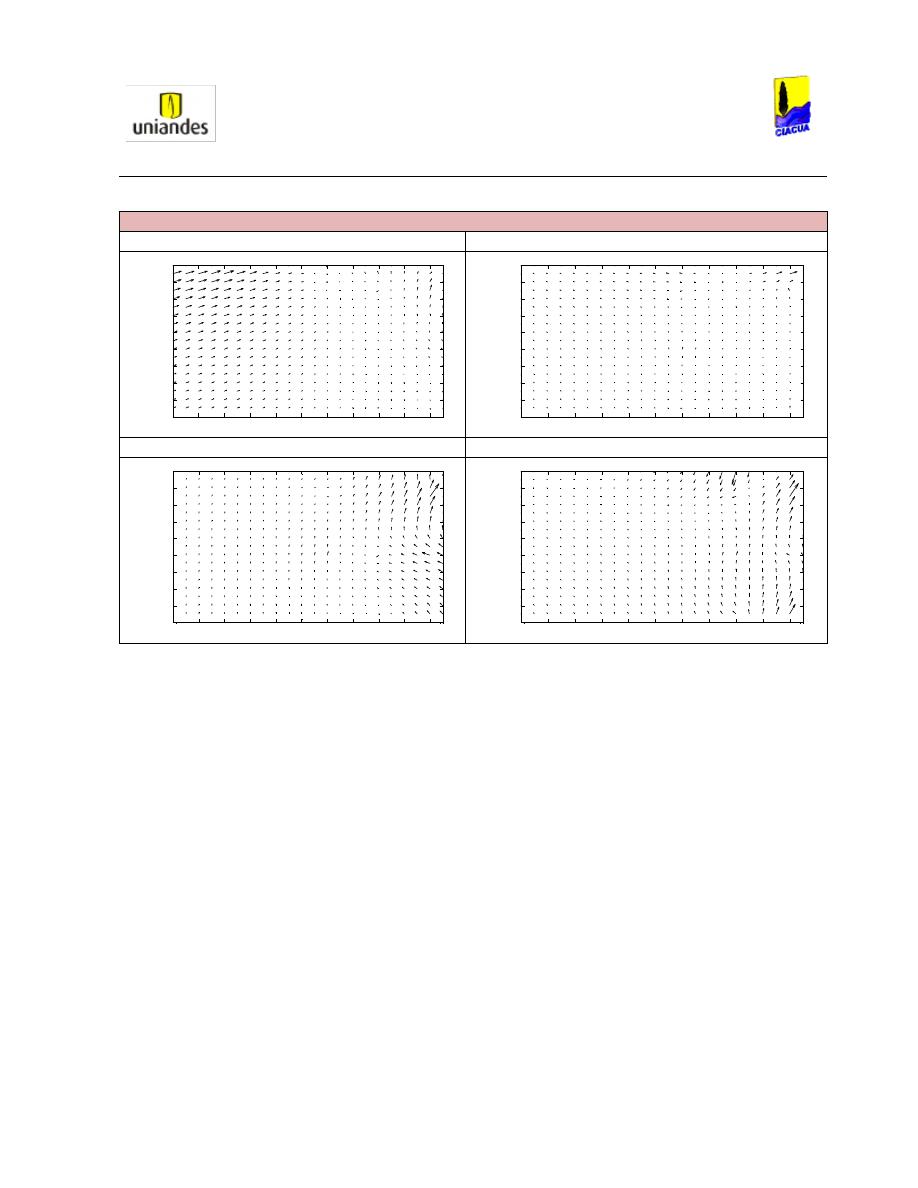
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
87
Tabla 31. Comportamiento de la velocidad de las partículas en diferentes secciones verticales para S = 1.6 % y Q = 24 L/s.
PERFIL DE VELOCIDADES – VISTA EN PLANTA (S = 0.016 y Q = 0.024 m
3
/s)
Pz = 0.01 cm
Pz = 0.02 m
Pz = 0.03 cm
Pz = 0.04 m
Para el escenario 3 se pueden observar remolinos a lo largo de los perfiles transversales de la tubería. En
la zona de los remolinos, la velocidad es mayor que en aquellas zonas donde no existen remolinos, lo
cual permite concluir que las partículas requieren mayor velocidad para cambiar la dirección del flujo.
En este escenario, las partículas si varían de dirección respecto a la sección vertical de la tubería. La
mayoría de las variaciones se observan en aquellas mediciones medidas en la zona cercana a la
superficie del resalto (Pz = 0.03 cm y Pz = 0.04 cm).
6.2. Análisis de Resultados
6.2.1. Análisis profundidades subsecuentes
A partir de los datos obtenidos, se realizarán las comparaciones con los resultados obtenidos por los
diferentes autores, los cuales fueron mencionados en el Numeral 5.4.
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
x (m) - Sección Longitudinal
y
(
m
)
-
S
e
c
c
ió
n
T
ra
n
s
v
e
rs
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.016 y Q = 0.024 m3/s) Pz = 1
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
x (m) - Sección Longitudinal
y
(
m
)
-
S
e
c
c
ió
n
T
ra
n
s
v
e
rs
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.016 y Q = 0.024 m3/s) Pz = 2
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
x (m) - Sección Longitudinal
y
(
m
)
-
S
e
c
c
ió
n
T
ra
n
s
v
e
rs
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.016 y Q = 0.024 m3/s) Pz = 3
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
x (m) - Sección Longitudinal
y
(
m
)
-
S
e
c
c
ió
n
T
ra
n
s
v
e
rs
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.016 y Q = 0.024 m3/s) Pz = 4
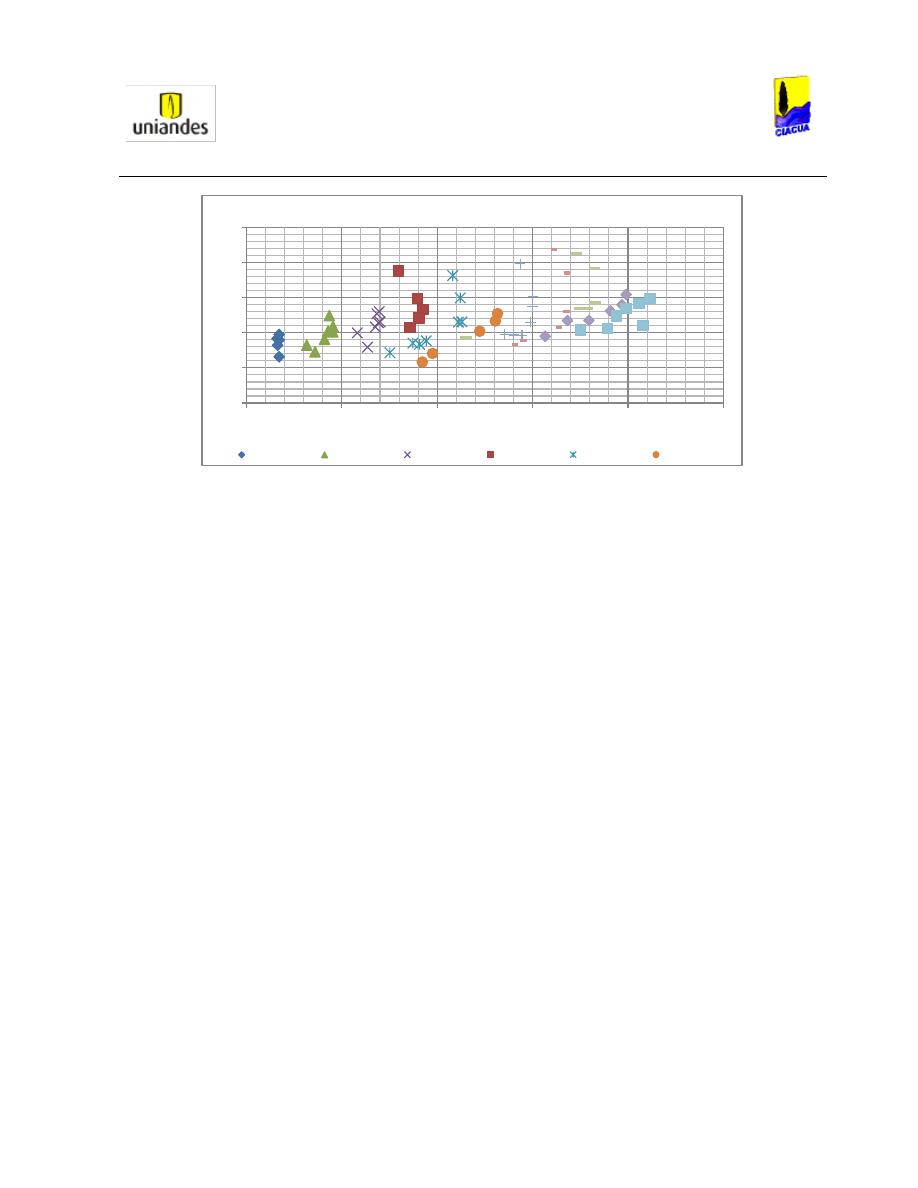
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
88
Gráfica 64. Resultados empíricos del comportamiento de las profundidades subsecuentes.
Los resultados obtenidos en la Gráfica 64 permiten observar un comportamiento similar para los 8 tipos
de pendiente evaluados. Se observa cierta tendencia a que cuando la relación entre las profundidades de
flujo alcanza el máximo Número de Froude, la gráfica presenta una variación en el sentido de la curva.
Por lo tanto, aquellas relaciones entre las profundidades de flujo que se encuentran por debajo del
máximo Número de Froude, se presenta que a mayor Número de Froude, existe mayor diferencia entre
la profundidad aguas abajo del resalto y la profundidad aguas arriba; mientras que cuando los valores
son superiores al máximo valor del Número de Froude, este disminuye a medida que la relación entre
las profundidades subsecuentes del flujo aumenta.
Por otro lado, al observar la Gráfica 18 se puede resaltar que el máximo Número de Froude encontrado
en el montaje se encuentra para relaciones de llenado del 30 %, lo cual concuerda con los Números de
Froude encontrados en la Gráfica 64, en donde el cambio de curvartura corresponde a un Número de
Froude formado con una relación de llenado del 30%.
Otra forma de analizar los datos, de acuerdo con lo planteado por Sturm, es comparar la relación entre
las profundidades subsecuentes del resalto hidráulico, clasificando el análisis por relaciones de llenado.
Éste análisis se realiza comparando un número parecido al Número de Froude, respecto a la relación
entre las profundidades subsecuentes:
0
1
2
3
4
5
1.2
1.7
2.2
2.7
3.2
3.7
y
2
/y
1
(
-)
Froude (-)
Comportamiento profundidades subsecuentes
S = 0.005
S = 0.007
S = 0.009
S = 0.011
S = 0.013
S = 0.015

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
89
Gráfica 65. Relación entre las profundidades subsecuentes del resalto hidráulico para tuberías circulares.
El
presentado en la Gráfica 65 se calcula mediante la siguiente ecuación:
Ecuación 83. Relación entre el caudal y la gravedad y el diámetro de la tubería. (Sturm, 2010)
En la Gráfica 65 se puede observar una clara tendencia a que cuando aumenta la relación de llenado
aguas arriba del resalto, disminuye la diferencia entre las profundidades aguas arriba del resalto y la
profundidad aguas abajo.
De acuerdo con el análisis realizado, se puede deducir que la profundidad del flujo aguas abajo del
resalto hidráulico depende de la pendiente, del caudal y de la profundidad aguas arriba; por lo cual se
desarrolla una regresión lineal por mínimos cuadrados para determinar una ecuación explícita para el
cálculo de
.
Después de varios análisis en los cuales se evaluaron diferentes parámetros, se obtuvieron dos
ecuaciones para el cálculo de la profundidad subsecuente; la primera ecuación calcula la profundidad
subsecuente del resalto hidráulico cuando
este es menor al diámetro, y la segunda cuando
es
mayor al diámetro.
A continuación se presentará el procedimiento para el cálculo de
cuando es menor al diámetro
10
.
10
Los resultados obtenidos por este método matricial se realizaron bajo la suposición de flujo gradualmente
variado, por lo cual la velocidad y el Número de Froude no son calculados con
sino con el caudal de entrada
medido con el Caudalímetro.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
90
1. Definir las variables independientes
(
)
2. Establecer la ecuación que determinará
(
)
(
)
Para realizar el análisis por mínimos cuadrados se debe linealizar, por lo tanto:
(
) (
) (
)
3. Establecer la ecuación que minimiza la suma del error:
∑ [ (
)
]
4. Determinar las ecuaciones que minimizan el error, las cuales consisten en derivadas parciales de
cada una de las constantes que son igualadas a cero:
( (
) (
) (
))
[ (
) (
) (
)]
Y aplicando la sumatoria se obtiene que
∑ (
) ∑ (
) ∑ (
)
Las otras ecuaciones son:
∑ (
) ∑ [ (
)]
∑ (
) (
) ∑ (
) (
)
∑ (
) ∑ (
) (
) ∑ [ (
)]
∑ (
) (
)
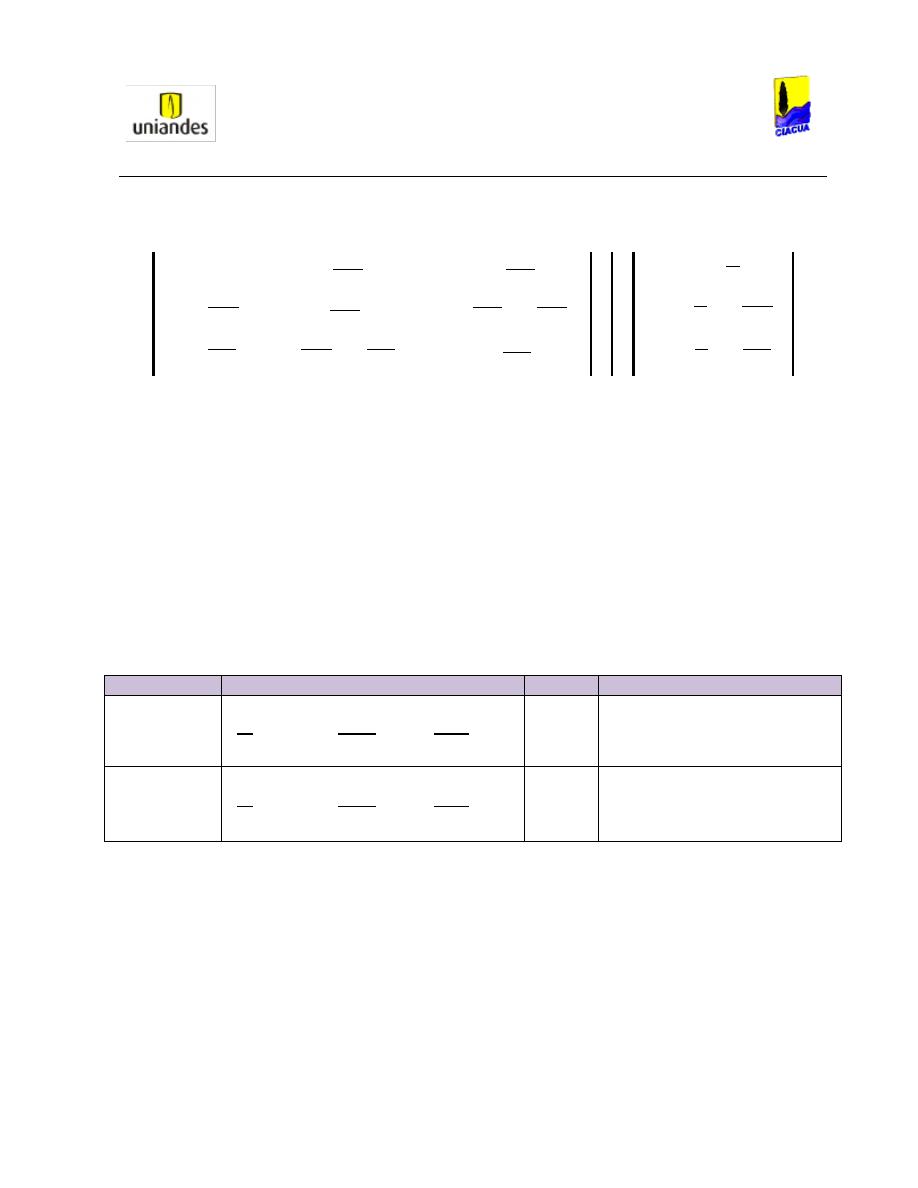
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
91
5. Plantear la matriz
n
∑ (
)
∑ (
)
a =
∑ (
)
∑ (
)
∑ [ (
)]
∑ (
) (
)
b =
∑ (
) (
)
∑ (
) ∑ (
) (
)
∑ [ (
)]
c =
∑ (
) (
)
6. Resolver la matriz
Al resolver la matriz planteada en el paso 5 se obtiene que:
Realizando el mismo proceso, se obtiene que las dos ecuaciones que calculan la profundidad
subsecuente aguas abajo del resalto hidráulico son:
Característica
Ecuación
R²
Numeración
(
)
(
)
85.3 %
Ecuación 84. Ecuación empírica de la
profundidad subsecuente para
.
(
)
(
)
90.7 %
Ecuación 85. Ecuación empírica de la
profundidad subsecuente para
.
Se observa que cuando la profundidad subsecuente aguas abajo del resalto es menor el diámetro, el
parámetro más relevante es la pendiente con un porcentaje de 63 %, mientras que el caudal tiene un
peso de 37%. Para
mayor al diámetro, el peso del caudal pasa a ser de 75.2% y la pendiente tiene un
peso 24.8%, lo que permite inferir la importancia que adquiere el caudal de entrada cuando la altura
subsecuente aguas abajo del resalto es mayor al diámetro.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
92
6.2.2. Análisis del comportamiento de la Energía en el resalto hidráulico
11
El concepto de energía específica de un fluido analiza el comportamiento de la energía potencial de
presión por unidad de peso y la energía cinética del flujo medidas desde el fondo de la tubería.
Para entender cómo se comporta la energía específica en la tubería, se realizó una gráfica teórica que
relaciona la variación del Número de Froude respecto a la energía específica para las diferentes
pendientes evaluadas en el laboratorio. Los datos de entrada para el cálculo corresponden a los
manejados en el canal:
,
y
. La gráfica obtenida se
muestra a continuación:
Gráfica 66. Comportamiento teórico de la Energía Específica respecto al Número de Froude para las diferentes pendientes
evaluadas en el laboratorio.
En la Gráfica 66 se observa que cada pendiente presenta un Número de Froude máximo, para el cual
cambia la curvatura de los datos, ya que el flujo empieza el cambio de flujo supercrítico a flujo
subcrítico. Los Números de Froude máximos se indican con la línea roja. También se puede observar
que a medida que aumenta la pendiente, los Números de Froude y la Energía Específica aumentan.
Ahora bien, retomando la Gráfica 64, se observa que presenta un Número de Froude máximo en el cual
inicia el cambio de curvatura en la gráfica para las distintas pendientes evaluadas; y ese Número de
11
Los resultados y gráficas obtenidos se hicieron bajo la suposición de Flujo Uniforme.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
0
0.5
1
1.5
2
2.5
3
3.5
En
e
rg
ia
Espec
íf
ic
a
[m]
Número de Froude [-]
Variación de la Energía dependiendo del Número de Froude
Máximos
S = 0.005
S = 0.007
S = 0.009
S = 0.011
S = 0.013
S = 0.015
S = 0.017
S = 0.019
S = 0.021
S = 0.023
S = 0.025

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
93
Froude máximo corresponde al máximo encontrado en la Gráfica 66; por lo cual existe una relación
entre las profundidades subsecuentes del resalto hidráulico y la energía específica:
Gráfica 67. Relación entre las profundidades subsecuentes del resalto hidráulico y la Energía Específica.
En la Gráfica 67 se observa cierta tendencia lineal al evaluar el comportamiento entre las profundidades
subsecuentes y la energía específica, y se observa que la pendiente y el punto de corte tienden a
aumentar a medida que aumenta la pendiente. Por lo tanto, para identificar las ecuaciones que evalúan
éstas variables, se realizó una regresión lineal para cada una de las pendientes evaluadas, las cuales se
muestran en la siguiente tabla
12
:
Tabla 32. Ecuaciones sin corrección que describen el comportamiento del resalto hidráulico en tuberías.
Pendiente (S)
Ecuación
R
2
0.007
(
) 0.8589
0.009
(
) 0.815
0.011
(
) 0.9626
12
La regresión lineal se llevó a cabo para los datos que representaran una desviación estándar menor al 3% por
cada medición.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0
1
2
3
4
5
6
7
E
1
[
-]
y
2
/y
1
[m]
Comportamiento de la relación entre las profundidades
subsecuentes en el resalto respecto a E
1
S = 0.005
S = 0.007
S = 0.009
S = 0.011
S = 0.013
S = 0.015
S = 0.017
S = 0.019
S = 0.021
S = 0.023
S = 0.025
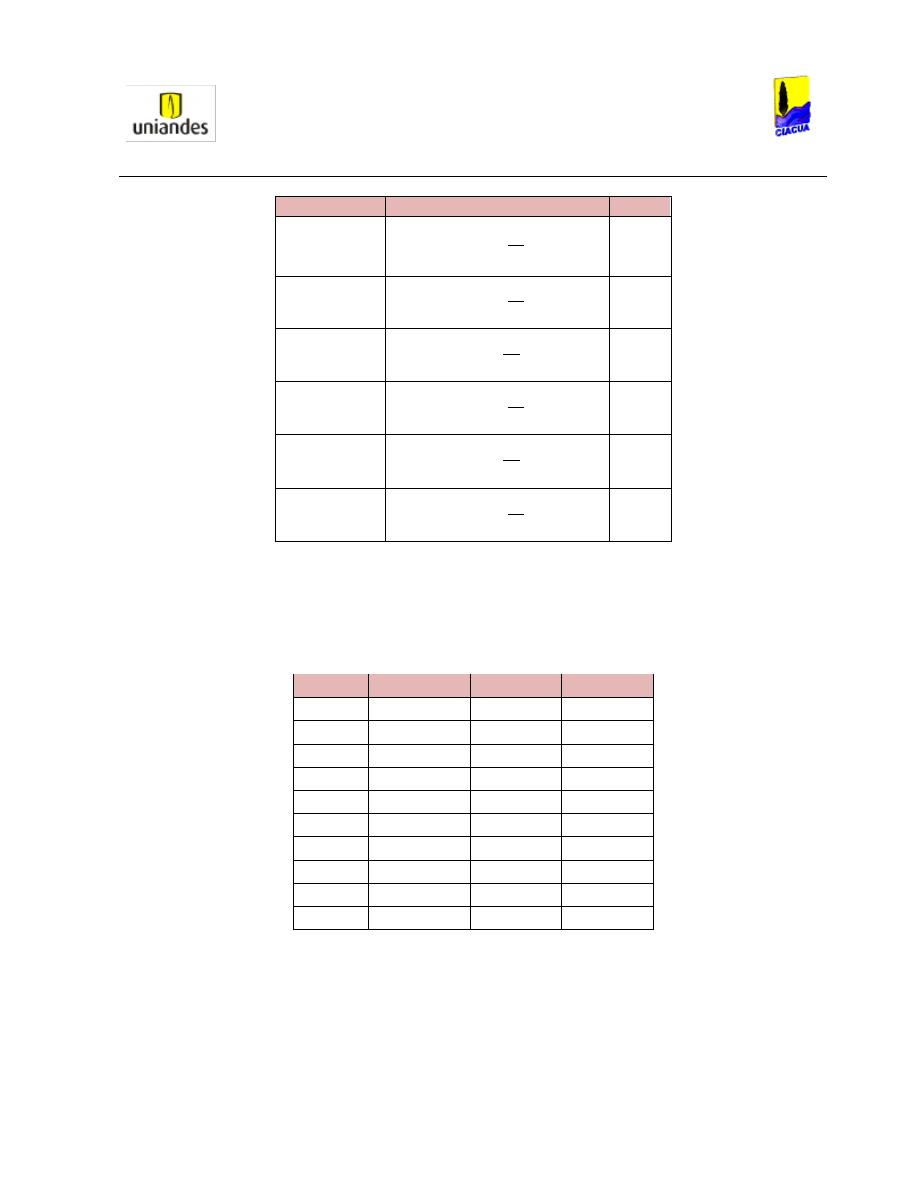
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
94
Pendiente (S)
Ecuación
R
2
0.013
(
) 0.9646
0.015
(
) 0.9773
0.017
(
)
0.911
0.019
(
) 0.9197
0.021
(
) 0.9926
0.023
(
) 0.9596
Para hallar alguna ecuación global que pueda representar el comportamiento de las profundidades
subsecuentes, se toma cada “m” y cada “k” de las ecuaciones presentadas en la Tabla 32, donde m
representa la pendiente de cada ecuación y k el punto de corte con el eje de las coordenadas:
Tabla 33. "m" y "k" para cada pendiente.
S [-]
m [-]
k [-]
R² [- ]
0.007
-0.161
0.4952
0.6942
0.009
-0.163
0.5604
0.851
0.011
-0.158
0.6311
0.9553
0.013
-0.1633
0.6687
0.8944
0.015
-0.1867
0.7384
0.9773
0.017
-0.1335
0.6521
0.9202
0.019
-0.138
0.7365
0.9308
0.021
-0.2117
1.025
0.9331
0.023
-0.3637
1.3591
0.8906
0.025
-0.1283
0.8808
0.326
Para ver el comportamiento de m y k a medida que aumenta la pendiente, se realizaron la Gráfica 68 y
la Gráfica 69:
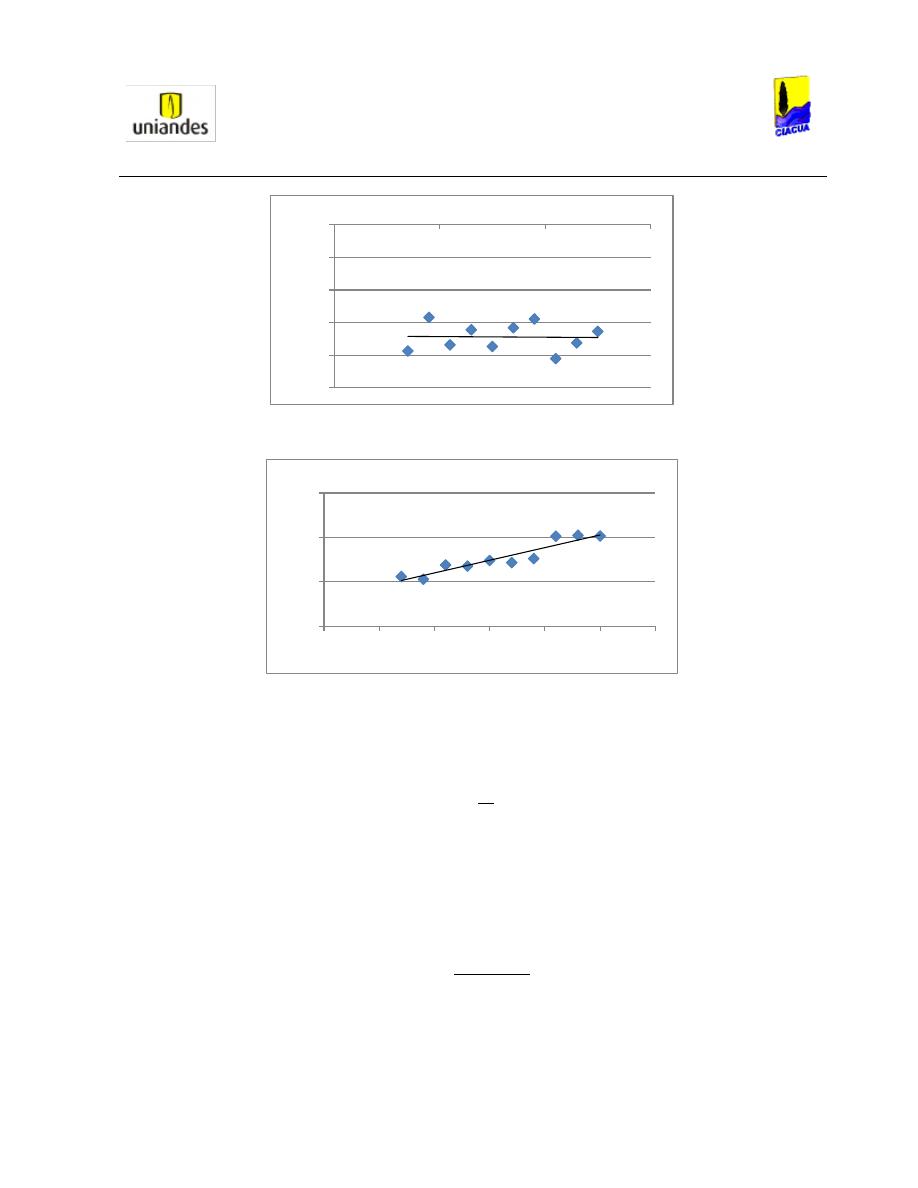
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
95
Gráfica 68. Comportamiento de "m" a medida que aumenta la pendiente.
Gráfica 69. Comportamiento de "k" a medida que aumenta la pendiente.
Por lo cual, la ecuación que relaciona la profundidad subsecuente del resalto hidráulico con la pendiente
es:
(
)
Por lo tanto,
es:
(
)
Ecuación 86. Ecuación empírica de la profundidad subsecuente de acuerdo a la Energía Específica.
Es decir,
(
).
y = -0.0906x - 0.1706
R² = 0.0007
-0.25
-0.2
-0.15
-0.1
-0.05
0
0
0.01
0.02
0.03
m
[
-]
S [-]
Comportamiento de m
y = 28.571x + 0.3143
R² = 0.8799
0
0.5
1
1.5
0
0.005
0.01
0.015
0.02
0.025
0.03
k[
-]
S [-]
Comportamiento de k
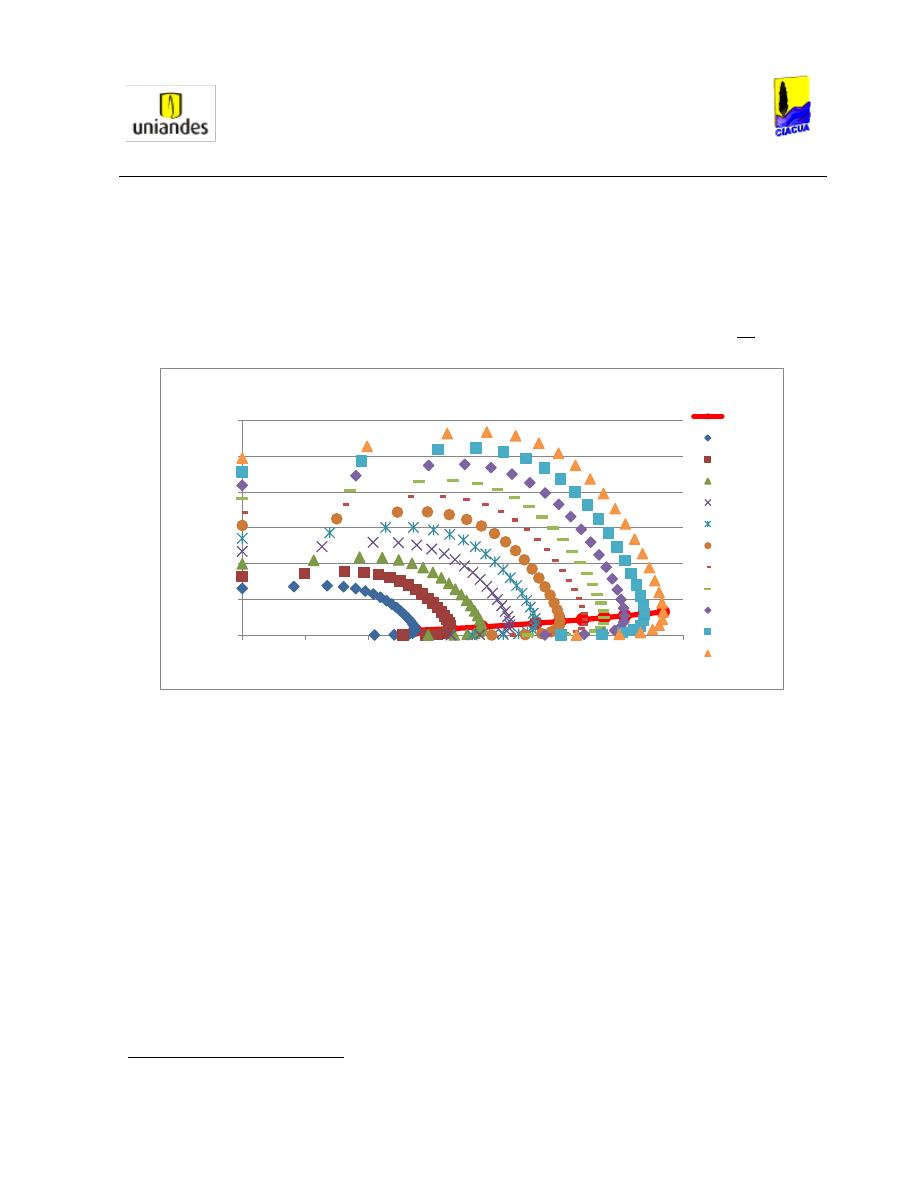
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
96
6.2.3. Análisis Conservación del Momentum
13
Para entender el comportamiento del Momentum en el resalto, se realiza una gráfica teórica que
compara el comportamiento del Momentum respecto a la variación en el Número de Froude para
diferentes pendientes. Los cálculos realizados se hicieron de acuerdo con las características iniciales que
se encuentran en el montaje realizado:
,
y
.
Gráfica 70. Comportamiento teórico del Momentum respecto al aumento en el Número de Froude para diferentes tipos de
pendientes.
Realizando el mismo proceso realizado en el Numeral 6.2.2, en el cual se observa que el Número de
Froude máximo corresponde al máximo encontrado en la Gráfica 64, se realiza la siguiente gráfica:
13
Los resultados y gráficas obtenidos se hicieron bajo la suposición de Flujo Uniforme.
0
0.01
0.02
0.03
0.04
0.05
0.06
0
0.5
1
1.5
2
2.5
3
3.5
M
o
m
e
n
tu
m
[m
3
]
Número de Froude [-]
Variación del Momentum dependiendo del Número de Froude
Máximos
S = 0.005
S = 0.007
S = 0.009
S = 0.011
S = 0.013
S = 0.015
S = 0.017
S = 0.019
S = 0.021
S = 0.023
S = 0.025
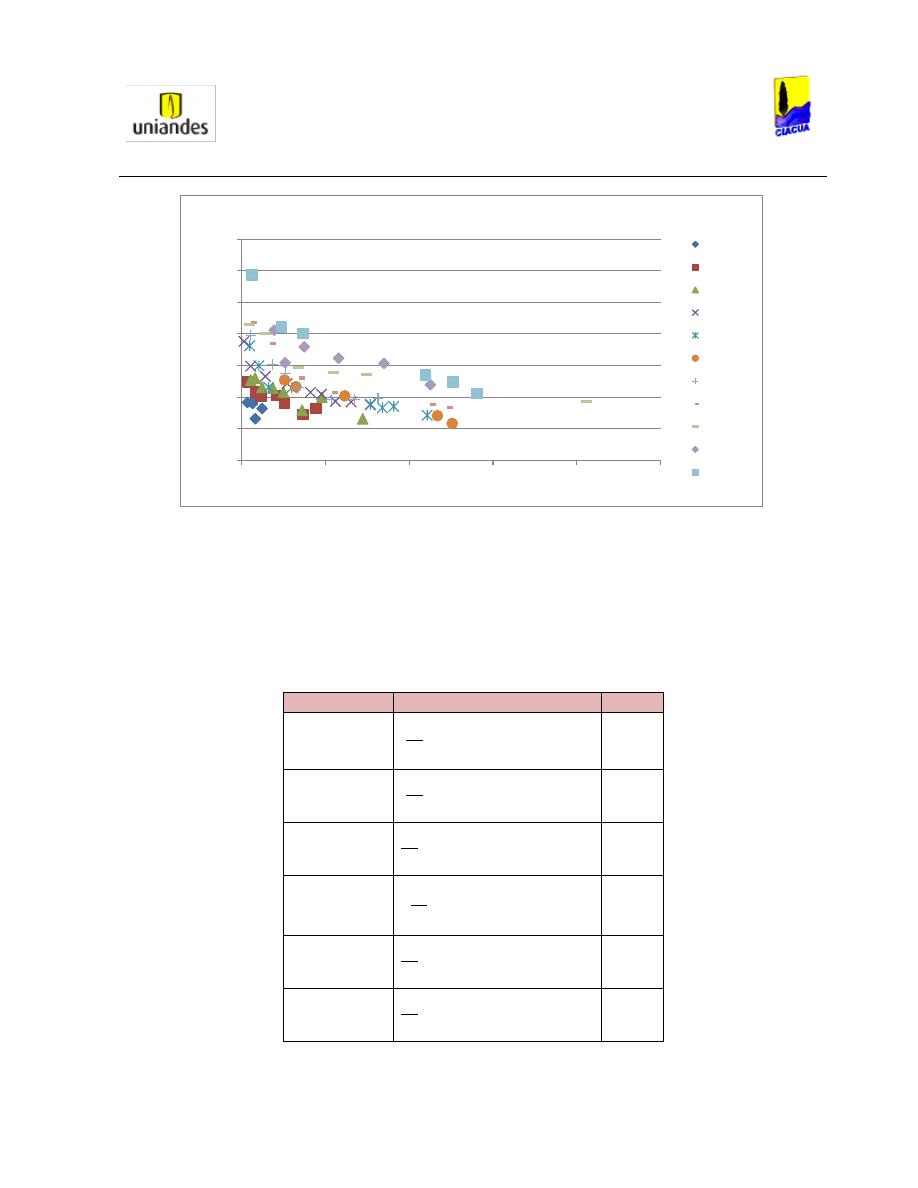
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
97
Gráfica 71. Comportamiento del Momentum respecto a la relación entre las profundidades subsecuentes en el resalto.
En la Gráfica 71 también se observa una tendencia lineal para cada tipo de pendiente. Por lo tanto, las
ecuaciones que describen el comportamiento de cada una de esas tendencias para cada tipo de pendiente
se observan en la siguiente tabla:
Tabla 34. Ecuaciones sin corrección que describen el comportamiento del resalto hidráulico en tuberías.
Pendiente (S)
Ecuación
R
2
0.007
0.8218
0.009
0.7683
0.011
0.9326
0.013
0.8889
0.015
0.9876
0.017
0.8495
0
1
2
3
4
5
6
7
0
0.01
0.02
0.03
0.04
0.05
y
2
/y
1
[
-]
M [m
3
]
Momentum vs relación profundidades de llenado
S = 0.005
S = 0.007
S = 0.009
S = 0.011
S = 0.013
S = 0.015
S = 0.017
S = 0.019
S = 0.021
S = 0.023
S = 0.025
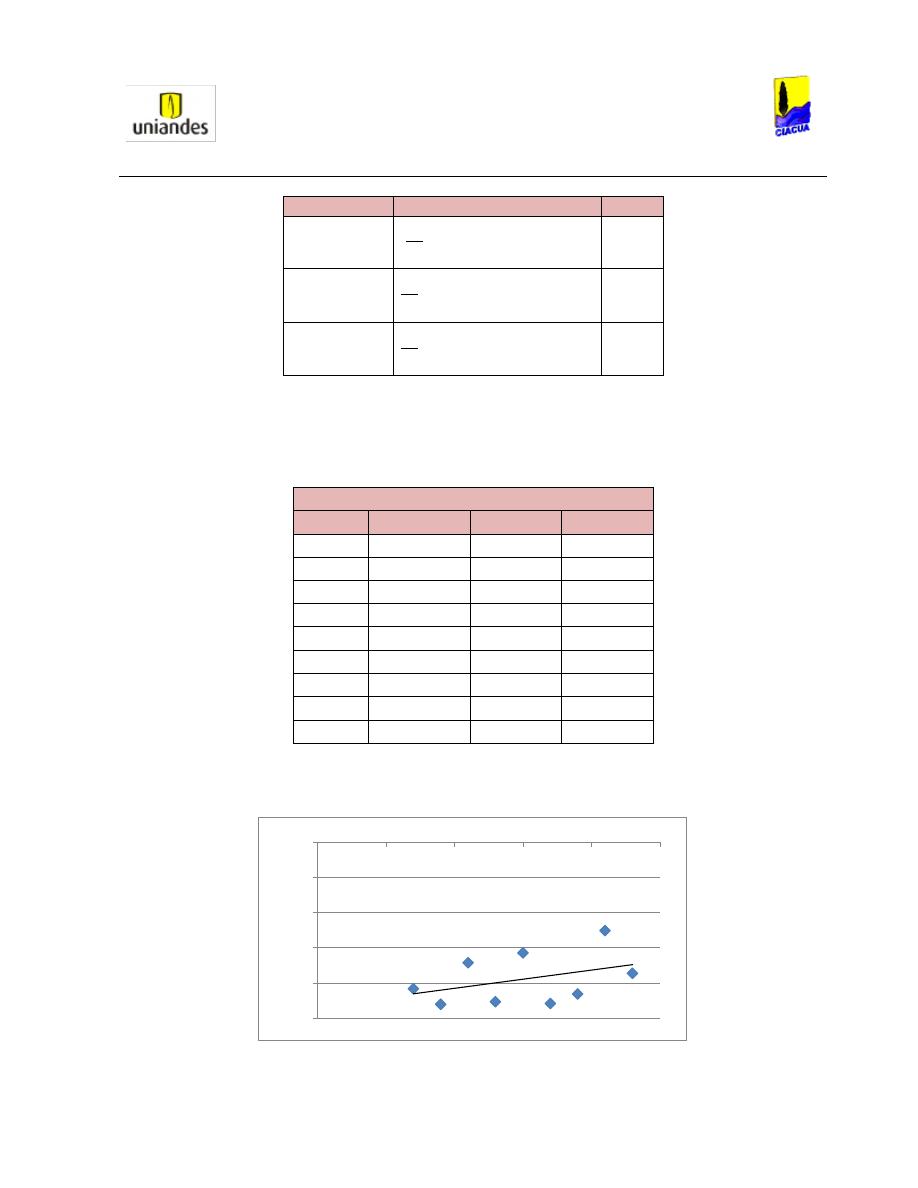
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
98
Pendiente (S)
Ecuación
R
2
0.019
0.8281
0.021
0.8951
0.023
0.9433
De la
Tabla 34
se analiza el comportamiento de la pendiente y el punto de corte de cada una de las
ecuaciones obtenidas en cada pendiente:
Tabla 35. “m” y “k” para cada pendiente.
Corregidos
S [-]
m [-]
k [-]
R² [- ]
0.007
-83.28
2.2459
0.8218
0.009
-91.972
2.632
0.7683
0.011
-68.451
2.7423
0.9326
0.013
-90.6
3.2693
0.8889
0.015
-62.919
2.8139
0.9876
0.017
-91.606
3.2273
0.8495
0.019
-86.15
3.6476
0.8281
0.021
-50.332
3.8838
0.8951
0.023
-74.473
4.1632
0.9433
Por lo tanto, realizando el mismo proceso desarrollado en el Numeral 6.2.2 se obtiene que:
Gráfica 72. Comportamiento de "m" a medida que aumenta la pendiente.
y = 1031.2x - 93.222
R² = 0.1476
-100
-80
-60
-40
-20
0
0
0.005
0.01
0.015
0.02
0.025
m
[
-]
S [-]
Comportamiento de m
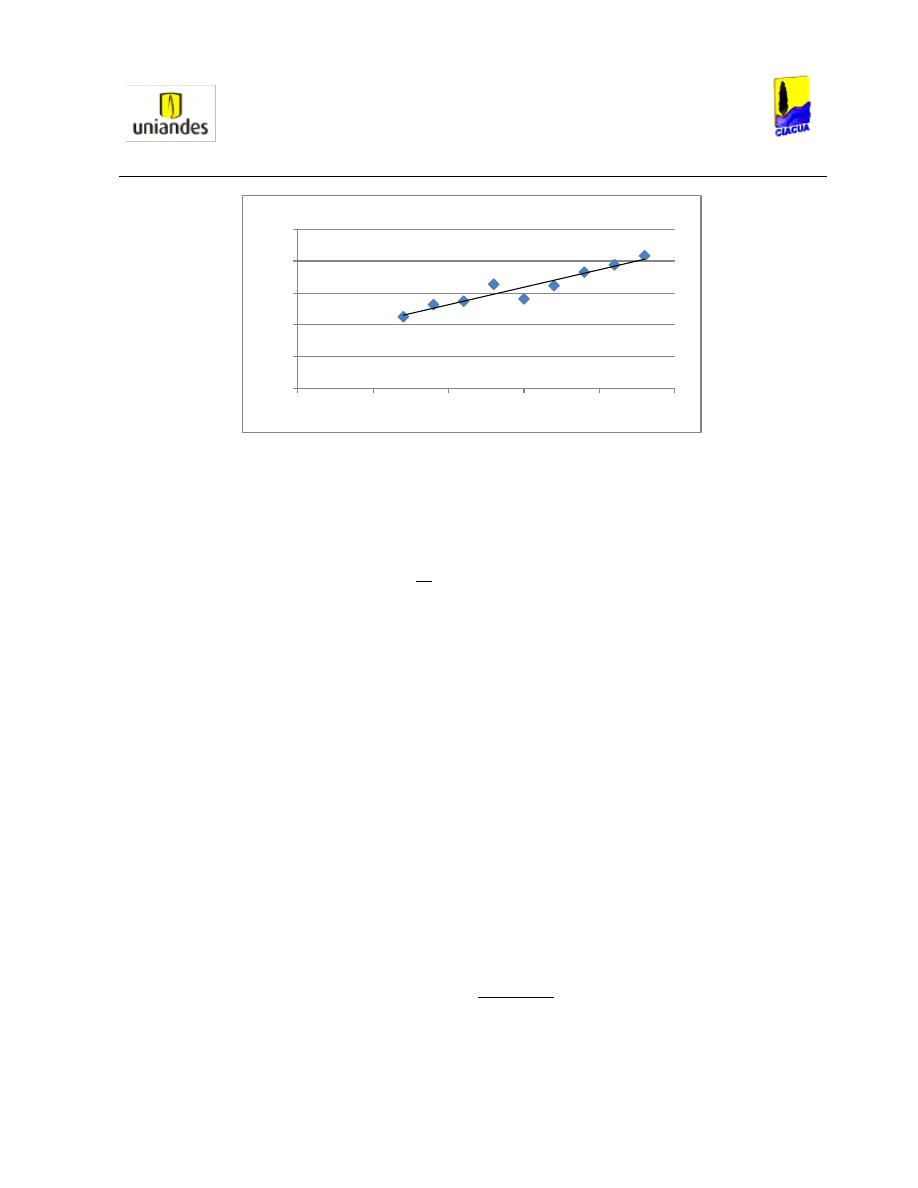
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
99
Gráfica 73. Comportamiento de "k" a medida que aumenta la pendiente.
Por lo tanto la ecuación que relaciona el comportamiento de las profundidades subsecuentes teniendo en
cuenta el Momentum es:
(
)
Ecuación 87. Ecuación empírica de la profundidad subsecuente de acuerdo al Momentum Específico.
6.2.4. Comparación entre los resultados empíricos y teóricos de las profundidades subsecuentes
Para comprobar la validez de las ecuaciones obtenidas se realizó una comparación con los resultados
obtenidos en laboratorio y los resultados obtenidos con las ecuaciones planteadas por autores y las
obtenidas empíricamente. La comparación se realizó mediante la comparación del error cuadrático
medio:
∑( ̅
)
Ecuación 88. Cálculo del Error Cuadrático Medio.
∑( ̅
)
Ecuación 89. Cálculo del Error Cuadrático Medio Promedio.
donde
y = 109.94x + 1.5314
R² = 0.9096
0
1
2
3
4
5
0
0.005
0.01
0.015
0.02
0.025
K
[
-]
S [-]
Comportamiento de k
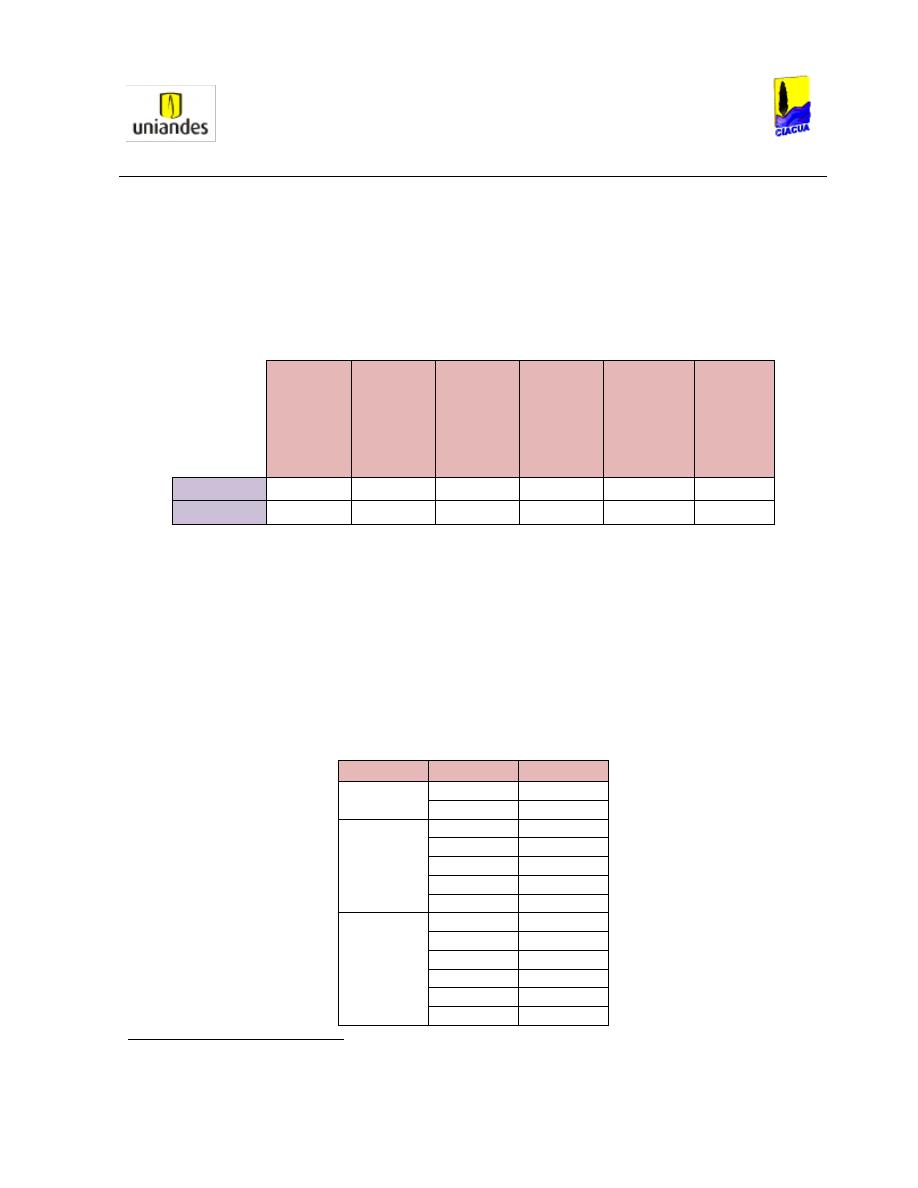
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
100
̅: Valor calculado con la ecuación.
: Valor real.
: Número total de datos medidos.
Por lo tanto, los ECM calculados con las ecuaciones de todos los autores se mostrarán en la Tabla 36.
Tabla 36. Error cuadrático medio para las diferentes ecuaciones evaluadas.
Ecuación
Silvester
[Ecuación 12
y Ecuación
14]
Ecuación
FHWA
[Ecuación 53
y Ecuación
54
]
Ecuación
Hager
[Ecuación
36
]
Ecuación
French
[Ecuación
28
]
Ecuación
empírica de
acuerdo
Potencial.
[Ecuación 84
y Ecuación
85
]
Ecuación
empírica
Lineal
[Ecuación
87]
[m]
0.0011
0.0012
0.0036
0.0022
0.0008
0.0003
[m]
0.3228
0.3601
1.0706
0.6543
0.253
0.0783
En la Tabla 36 se observa que la ecuación empírica que diferencia el cálculo de la profundidad
subsecuente cuando
es mayor o menor al diámetro es la que presenta menor error cuadrático medio
promedio. Y la ecuación que calcula
como función de la Energía es la que presenta menor error
cuadrático medio. Es importante tener en cuenta que la Ecuación 87 se calcula bajo la suposición de
flujo uniforme, mientras que las otras ecuaciones empíricas analizadas no trabajan bajo esta suposición.
Sin embargo, al realizar un análisis con diferentes diámetros y pendientes, el error medio cuadrático
aumenta, por lo cual, el rango de validez de la ecuación se limita a los siguientes casos:
Tabla 37. Rango de validez de laEcuación 84 y la Ecuación 85.
14
d (m)
Rango (y/d)
S (-)
0.150
0.47 - 0.70
0.200
0.35 - 0.38
0.300
0.200
0.29 - 0.38
0.01
0.33 - 0.35
0.015
0.26 - 0.28
0.02
0.33 - 0.36
0.2
0.27 - 0.28
0.3
0.250
0.21 - 0.26
0.01
0.20 - 0.25
0.015
0.20 - 0.24
0.02
0.19 - 0.23
0.025
0.19 - 0.23
0.03
0.19 - 0.2
0.04
14
Los rangos de validez se establecieron para aquellos datos que comparados con los valores obtenidos por la
ecuación de Silvester correspondieran a una diferencia menor al 10%.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
101
0.25 - 0.69
0.08
0.44 - 0.70
0.09
0.41 - 0.47
0.1
0.300
0.16 - 0.20
0.01
0.16 - 0.19
0.015
0.15 - 0.19
0.015
0.15 - 0.19
0.02
0.15 - 0.18
0.025
0.15 - 0.18
0.03
0.15 - 0.18
0.04
0.15 - 0.17
0.05
0.15 - 0.70
0.06
0.14 - 0.7
0.07
0.38 - 0.43
0.08
0.35 - 0.39
0.09
0.33 - 0.36
0.1
0.350
0.13 - 0.16
0.01
0.13 - 0.15
0.015
0.13 - 0.15
0.02
0.13 - 0.15
0.025
0.13 - 0.15
0.03
0.12 - 0.15
0.04
0.12 - 0.7
0.05
0.12 - 0.43
0.06
0.12 - 0.38
0.07
0.12 - 0.35
0.08
0.12 - 0.32
0.09
0.12 - 0.30
0.1
En la Tabla 37 se observa que el rango de validez de los resultados obtenidos con la Ecuación 84 y la
Ecuación 85 se encuentra para parámetros de entrada similares a los del montaje evaluado; es decir,
diámetros cercanos a 250 mm y pendientes bajas. Sin embargo, para un diámetro de 300 mm, la
ecuación se ajusta con una pendiente de 7%, y para un diámetro de 350 mm, la ecuación se ajusta para
una pendiente de 5 %.
6.2.5. Ecuación profundidades subsecuentes en el Resalto Hidráulico
De acuerdo con el análisis realizado en el Numeral 6.2.4 se puede concluir que las ecuaciones que
definen el comportamiento de la profundidad subsecuente aguas abajo del resalto hidráulico en tuberías
son la Ecuación 84 y la Ecuación 85.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
102
:
(
)
(
)
(
)
(
)
6.2.6. Análisis del comportamiento de la longitud en el Resalto Hidráulico
El análisis de la longitud en el resalto hidráulico se realizará respecto al Número de Froude, a las
diferentes pendientes evaluadas y a la relación entre las profundidades subsecuentes.
Respecto al Número de Froude se organizaron los datos de tal forma que para cada pendiente se
mostrara el comportamiento de la Longitud respecto al Número de Froude:
Gráfica 74. Longitud del resalto hidráulico para diferentes pendientes.
En la Gráfica 74 se puede observar que existe cierta tendencia entre la variación en la longitud del
resalto, el Número de Froude y la pendiente. Primero, se observa que a mayor Número de Froude, existe
una leve aumento de la longitud del resalto; también se presenta de manera evidente, que cuando
aumenta la pendiente en la tubería, aumenta el valor en el Número de Froude. Sin embargo, las
variaciones en la longitud del resalto no son relevantes ni representativas; en general, todos los puntos
se encuentran en el mismo rango de datos.
Respecto a los valores evaluados por otros autores (Ver Numeral 5.5), se observa la misma tendencia al
crecimiento rápido de la curva (para S = 0.019), sin embargo, los valores crecen más rápido que los
valores obtenidos experimentalmente.
Con respecto a los perfiles del resalto se tiene que:
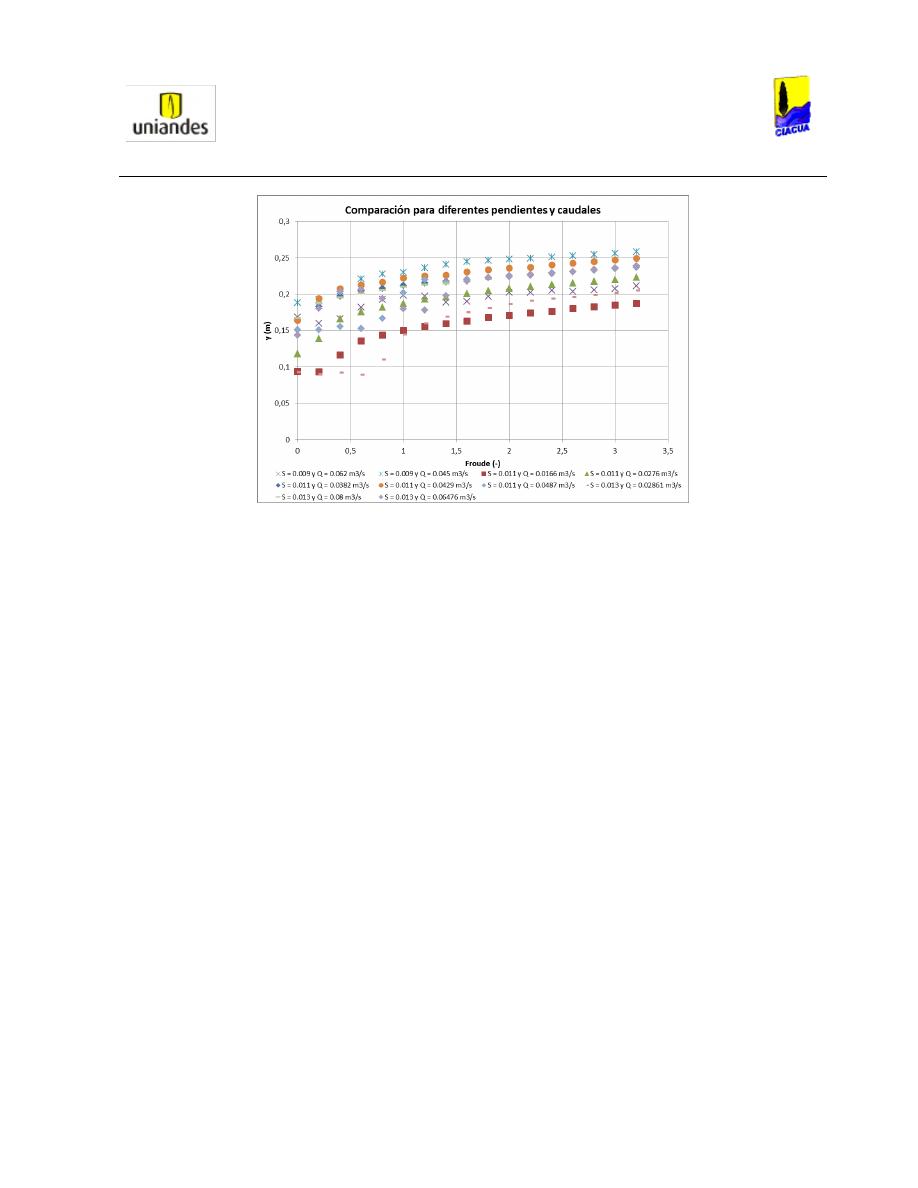
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
103
Gráfica 75. Comparación para diferentes pendientes y caudales.
En la Gráfica 75 se incluyen los perfiles de los resaltos evaluados con los piezómetros, los cuales
corresponden a pendientes mayores a 0.009; sin embargo, para observar más claramente los perfiles, no
se añaden en la gráfica todos los perfiles medidos. Se puede observar que el comportamiento para los
resaltos evaluados con S = 0.011 es mucho más estable, y no tiene tantas fluctuaciones, como las
presentadas en S = 0.009. Además, aunque no se alcanzó a medir, se puede inferir que la altura
subsecuente del resalto para S = 0.011 y Q = 0.05 m
3
/s, va a ser más baja, que la obtenida cuando S =
0.009, sin embargo, la diferencia entre la altura del resalto aguas abajo con respecto a la altura aguas
arriba es mayor a mayor pendiente, ya que el flujo adquiere mayor velocidad.
Por otra parte, se realizó un análisis de comparación entre la longitud del resalto hidráulico, la pendiente
y la relación entre las profundidades subsecuentes. Éste análisis se realizó también comparando el
Número de Froude; sin embargo el coeficiente de determinación calculado no era tan alto respecto a un
análisis sin el Número de Froude.
El primer paso para desarrollar el análisis fue comparar el comportamiento de la longitud divida entre la
profundidad aguas arriba del resalto, con respecto a la relación entre las profundidades subsecuentes:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
104
Gráfica 76. Comportamiento de la longitud en el Resalto Hidráulico.
En la Gráfica 76 se observa cierta tendencia a que con el aumento de la pendiente en el modelo
experimental, la pendiente de cada curva va aumentando. Por lo tanto, se puede establecer que la
longitud del resalto hidráulico está relacionada con la relación entre las profundidades subsecuentes y la
pendiente. Por lo tanto, se realizan dos análisis diferentes; el primero mediante una regresión lineal y el
segundo mediante un análisis de mínimos cuadrados por medio de la función cftool de Matlab.
La ecuación lineal analizada es la siguiente:
(
)
Ecuación 90. Ecuación lineal para determinar la longitud del resalto hidráulico en tuberías.
Por otro lado, la ecuación encontrada por el método cftool de Matlab es:
(
)
Ecuación 91. Ecuación potencial para determinar la longitud del resalto hidráulico en tuberías.
la cual tiene un coeficiente de determinación de 70.7% y un EMC de 1.974.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
105
6.2.7. Comparación entre los resultados empíricos y teóricos de la longitud del resalto hidráulico
Para comprobar la validez de las ecuaciones obtenidas se realizó una comparación con los resultados
obtenidos en laboratorio y los resultados obtenidos con las ecuaciones planteadas por autores y las
obtenidas empíricamente. La comparación se realizó mediante la comparación del error cuadrático
medio:
Tabla 38. Error cuadrático medio para las diferentes ecuaciones evaluadas.
Ecuación
Hager
[Ecuación 41]
Ecuación
FHWA
[Ecuación 55
y Ecuación
56]
Ecuación
Empírica
Lineal
[Ecuación 90]
Ecuación
Empírica
Potencial
[Ecuación 91]
ECM Prom [-]
0.426
1.828
0.025
0.023
ECM [-]
20.026
85.921
1.155
1.072
En la Tabla 38 se observa que la ecuación que presenta el menor error cuadrático medio promedio y
normal es la ecuación potencial, ajustándose mucho mejor que las ecuaciones empíricas encontradas
anteriormente. Es importante tener en cuenta que las ecuaciones obtenidas por Hager y por la FHWA no
tienen en cuenta la pendiente, sino exclusivamente el Número de Froude, y de acuerdo con los
resultados obtenidos en el modelo, la pendiente varía el comportamiento de la curva en la recta.
6.2.8. Ecuación longitud del resalto hidráulico para tuberías circulares
La ecuación que representa mejor el comportamiento de la longitud en el resalto hidráulico es:
(
(
)
)
Ecuación 91. Ecuación potencial para determinar la longitud del resalto hidráulico en tuberías.
6.2.9. Análisis de disipación de energía en el Resalto Hidráulico
Para analizar la eficiencia del resalto hidráulico, se desarrolla el análisis de disipación de energía, el
cual, con los datos obtenidos en laboratorio, se realiza comparando la variación del Número de Froude y
de la relación entre las profundidades subsecuentes respecto a la disipación de Energía para diferentes
caudales.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
106
Gráfica 77. Comportamiento de la disipación de energía respecto al Número de Froude.
En la Gráfica 77 se observa que la relación entre el Número de Froude y la disipación de Energía es
lineal y directamente proporcional. El aumento de la pendiente y del caudal afectan el valor del Número
de Froude pero no afectan el valor de la disipación de Energía.
Por otra parte, al analizar el comportamiento de la disipación de energía respecto a la relación entre las
profundidades subsecuentes se tiene que:
Gráfica 78. Comportamiento de la disipación de energía respecto a la relación entre las profundidades subsecuentes.
En la Gráfica 78 se observa que el comportamiento entre la relación de las profundidades subsecuentes
y la disipación de energía también es directamente proporcional; sin embargo el crecimiento no es

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
107
lineal, sino que tiende a aumentar lento al inicio (para valores de la disipación de energía bajos) y
aumentar más rápido para deltas de energía más altos.
Con las gráficas anteriores se puede establecer una clara relación entre la disipación de energía y el
Número de Froude y la relación entre las profundidades subsecuentes; por lo tanto usando el método
cftool de Matlab se obtiene la siguiente regresión potencial:
(
)
(
)
(
(
)
(
)
)
Ecuación 92. Ecuación para determinar el valor de la disipación de energía.
La ecuación obtenida tiene un coeficiente de determinación de 84.5%, con lo cual se establece que la
Ecuación 92 representa de manera apropiada el comportamiento de la disipación de energía.
6.2.10. Análisis del comportamiento de la distribución de velocidades en el resalto hidráulico
Para entender el comportamiento de la velocidad en la zona de un resalto hidráulico en la tubería, se
realizaron dos tipos de análisis; el primer análisis se basa en determinar la importancia de los diferentes
componentes de la velocidad (v
x
, v
y
, v
z
) respecto a la magnitud total de la velocidad, con lo cual se
puede definir si la dirección de cada partícula se ve afectada por los remolinos generados en el resalto.
El segundo análisis evalúa si existe mayor varianza en la toma de datos medidos cerca al fondo del canal
o a la superficie del resalto.
La importancia de cada uno de los componentes de la velocidad se observa en la Gráfica 79:
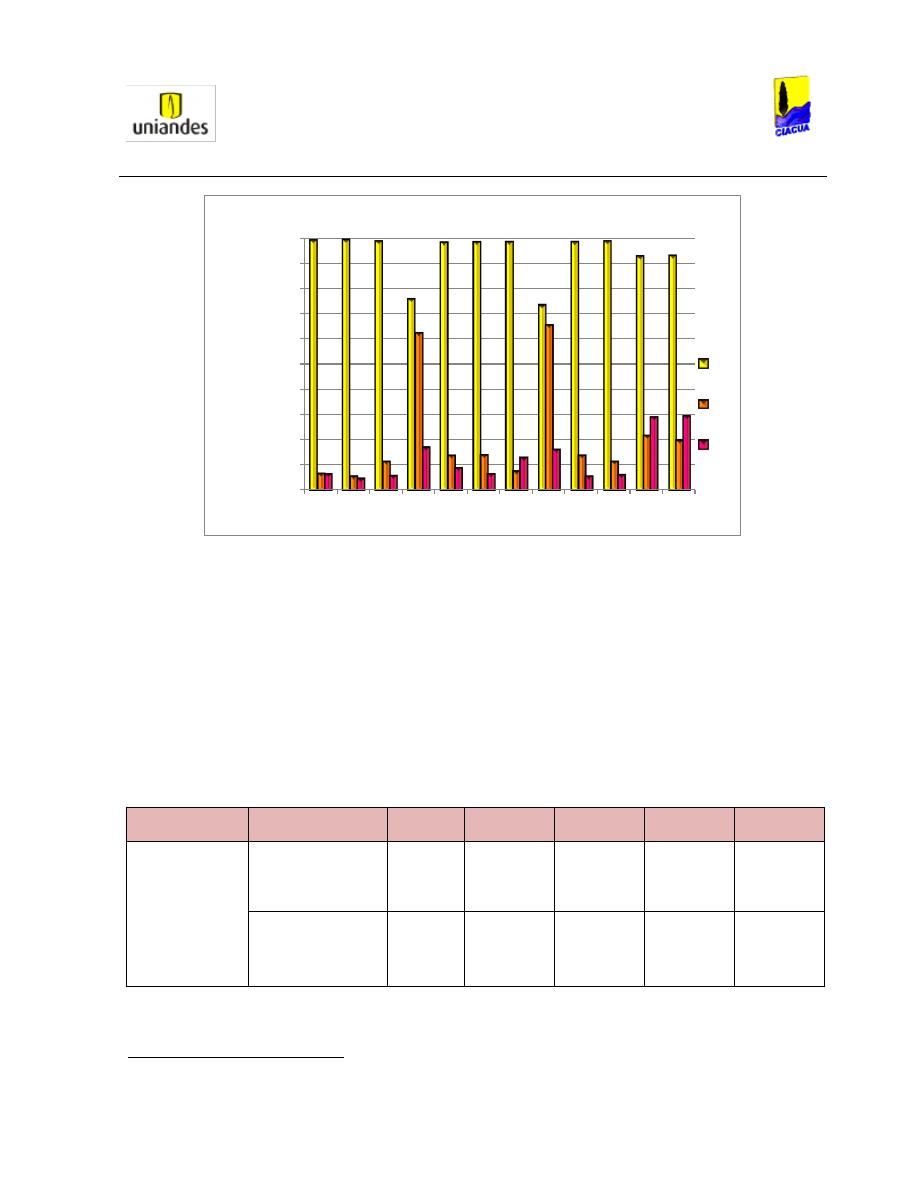
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
108
Gráfica 79. Importancia de los diferentes componentes de la velocidad.
15
En la Gráfica 79 se observa que en la mayoría de casos, el vector de la velocidad en el eje x corresponde
a más del 90% de la magnitud total de la velocidad, es decir, que a pesar de los remolinos generados en
el resalto hidráulico, la velocidad que rige el comportamiento de las partículas es la velocidad en x.
Por otro lado, se realizó un análisis de la varianza de los datos respecto a la posición de los puntos
medidos. El análisis se realizó comparando la desviación estándar de cada uno de los puntos de
medición en el perfil vertical y en el perfil transversal; sin embargo, la tendencia solo se presentó en el
análisis de los datos realizado en el perfil vertical.
Tabla 39. Comportamiento de la distribución de la velocidad en el resalto hidráulico.
Escenario
Ubicación puntos de
medición
Desviación
(cm/s)
Media
(cm/s)
Per 20
(cm/s)
Per 80
(cm/s)
Diferencia
(cm/s)
S = 0.012
Q = 0.024 m³/s
Lejos del fondo de
la tubería
70.239
68.447
-9.938
121.156
131.094
Cerca al fondo de
la tubería
23.746
76.977
59.839
95.323
35.484
15
Cada ID del escenario se explica en la Tabla 5.
0.00%
10.00%
20.00%
30.00%
40.00%
50.00%
60.00%
70.00%
80.00%
90.00%
100.00%
1
2
3
4
5
6
7
8
9
10
11
12
Im
p
o
rtan
ci
a
d
e
la var
iab
le
[%
]
Escenario [-]
Importancia de cada vector de velocidad
Vx
Vy
Vz
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
109
Escenario
Ubicación puntos de
medición
Desviación
(cm/s)
Media
(cm/s)
Per 20
(cm/s)
Per 80
(cm/s)
Diferencia
(cm/s)
S = 0.016
Q = 0.019 m³/s
Lejos del fondo de
la tubería
76.985
48.083
15.854
95.668
79.814
Cerca al fondo de
la tubería
54.307
62.608
37.619
100.883
63.264
S = 0.016
Q = 0.024 m³/s
Lejos del fondo de
la tubería
15.211
-0.651
-21.857
-11.176
10.681
Cerca al fondo de
la tubería
19.424
-3.050
-28.315
-4.230
24.085
S = 0.017
Q = 0.019 m³/s
Lejos del fondo de
la tubería
71.379
19.675
-37.135
72.133
109.268
Cerca al fondo de
la tubería
30.398
31.046
10.380
54.327
43.947
S = 0.017
Q = 0.026 m³/s
Lejos del fondo de
la tubería
78.630
44.017
-20.093
94.872
114.965
Cerca al fondo de
la tubería
29.338
32.145
11.914
53.399
41.485
S = 0.020
Q = 0.020 m³/s
Lejos del fondo de
la tubería
84.401
-4.648
-71.762
66.851
138.613
Cerca al fondo de
la tubería
63.650
56.851
22.004
101.663
79.660
S = 0.020
Q = 0.025 m³/s
Lejos del fondo de
la tubería
16.622
0.695
-12.204
-0.311
11.894
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
110
Escenario
Ubicación puntos de
medición
Desviación
(cm/s)
Media
(cm/s)
Per 20
(cm/s)
Per 80
(cm/s)
Diferencia
(cm/s)
Cerca al fondo de
la tubería
19.189
-1.489
-14.882
-0.771
14.111
S = 0.021
Q = 0.019 m³/s
Lejos del fondo de
la tubería
68.106
49.150
-1.426
100.926
102.352
Cerca al fondo de
la tubería
39.116
37.056
11.976
66.866
54.890
S = 0.021
Q = 0.025 m³/s
Lejos del fondo de
la tubería
76.832
21.242
-32.576
84.583
117.159
Cerca al fondo de
la tubería
44.714
49.802
23.761
82.661
58.900
S = 0.022
Q = 0.021 m³/s
Lejos del fondo de
la tubería
80.663
-11.696
-78.252
66.426
144.678
Cerca al fondo de
la tubería
95.946
30.901
-72.795
104.683
177.478
S = 0.022
Q = 0.026 m³/s
Lejos del fondo de
la tubería
68.747
-14.471
-69.753
45.699
115.452
Cerca al fondo de
la tubería
79.956
30.249
-62.398
102.312
164.709
En la Tabla 39 existen 7 columnas; la primera columna hace referencia a las características del escenario
evaluado; la segunda columna indica si los datos presentados en esa fila fueron medidos cerca del fondo
del canal o en la parte superior del resalto; la tercera columna muestra la desviación estándar de todos
los datos tomados en cada punto de medición; la cuarta columna hace referencia a la media de todos los
datos tomados en cada punto de medición; la quinta y sexta columna representan el percentil 20 y 80 de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
111
la muestra respectivamente, para lo cual se organizaron los datos de menor a mayor. Por último la
séptima columna hace referencia a la diferencia que hay entre el percentil 80 y el percentil 20.
Con los datos obtenidos se observa que en la mayoría de los escenarios existe mayor variación de los
datos en los puntos medidos lejos del fondo de la tubería, mientras que existe menor variación de los
datos en aquellos puntos medidos al fondo de la tubería, esto se comprueba al observar que existe mayor
diferencia entre el percentil 20 y 80 en aquellos puntos medidos cerca de la superficie del resalto que
aquellos puntos medidos en el fondo de la tubería. Éste comportamiento es similar al que ocurre en la
distribución de la velocidad en tuberías fluyendo a presión, donde la velocidad en el fondo de la tubería
es igual a cero.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
112
7. Conclusiones
En todas las metodologías estudiadas, se observa que siempre que aumente el valor en el
Número de Froude, la relación entre las profundidades subsecuentes será mayor.
El valor del Número de Froude para pendientes más altas es mayor, lo cual también aumenta la
relación entre las profundidades subsecuentes en el resalto.
Según las metodologías estudiadas, a mayor Número de Froude, la longitud del resalto será
mayor.
Para las pendientes del montaje menores a 0.010, la estabilidad del resalto es muy baja, y no se
puede ubicar exactamente en la zona requerida para la medición; además los resaltos hidráulicos
son muy inestables y no se puede inferir claramente cuál es la longitud del resalto, ya que no
existe una clara diferencia entre la profundidad aguas arriba y aguas abajo del resalto hidráulico.
Esto ocurre ya que el Número de Froude aguas arriba del resalto es muy bajo, y no permite
generar la fuerza suficiente para presentar un resalto hidráulico estable.
Cuando las pendientes en el resalto son mayores a 0.010, pero el caudal es menor o igual a 0.01
m³/s, el resalto también es débil y no se puede inferir la longitud ni las profundidades
subsecuentes en el resalto claramente.
Para caudales mayores a 0.05 m³/s, el perfil del resalto hidráulico empieza a generar muchas
ondas en la zona subcrítica; y el resalto deja de ser estable ya que la profundidad aguas abajo
del resalto se acerca a la zona de flujo cuasicrítico.
Entre los resultados obtenidos hasta los datos medidos (S <= 0.019), se observa una clara
tendencia a una variación en el comportamiento de la relación entre las profundidades
subsecuentes cuando se alcanza el máximo Número de Froude por cada pendiente. Es decir,
cuando las relaciones entre las profundidades del resalto, son menores al máximo Número de
Froude, la diferencia entre la profundidad aguas abajo del resalto y la profundidad aguas arriba
aumenta con el aumento en el Número de Froude; mientras que en el valor máximo del Número
de Froude, la diferencia aumenta a medida que el Número de Froude disminuye.
Los resultados de las longitudes permiten inferir que a mayor pendiente, aumenta el valor en los
Número de Froude, y la longitud del resalto aumenta con un aumento muy leve en este número.
El comportamiento de la profundidad subsecuente aguas abajo del resalto hidráulico depende
del caudal, de la pendiente y de la profundidad subsecuente aguas arriba.
La longitud del resalto hidráulico depende de las profundidades subsecuentes del resalto y de la
pendiente medida.
La disipación de energía depende del Número de Froude y de la relación entre las
profundidades subsecuentes, lo cual sucede en los resaltos hidráulicos que ocurren en canales
rectangulares.
La velocidad principal que rige la dirección de las partículas ubicadas en los remolinos del
resalto hidráulico es la velocidad en x.
La distribución de velocidades cercana al fondo del canal es más estable que la presentada en
puntos cercanos a la superficie del resalto, donde se presenta mayor turbulencia.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
113
8. Recomendaciones
8.1. Recomendaciones de diseño
A continuación se presentarán algunas recomendaciones para el diseño de tuberías de alcantarillado de
250 mm de diámetro y que presenten el riesgo de la formación de un resalto hidráulico, con el fin de
evitar el fenómeno de sobrecarga en la tubería:
Para un diámetro de 250 mm y cualquier pendiente, se deben evitar caudales mayores a 50 L/s.
Para pendientes menores a 1.5 %, se pueden permitir caudales menores a 50 L/s.
Para pendientes entre 1.5 % y 1.9 %, no se deben permitir caudales mayores a 20 L/s.
Para pendientes mayores a 2 %, la tubería se presuriza con caudales iguales o mayores a 20 L/s.
Con pendientes superiores a 2%, se debe evitar cualquier obstáculo en el flujo aguas abajo de la
tubería, ya que la velocidad del flujo hace que se generen resaltos hidráulicos con caudales
bajos.
8.2. Recomendaciones para futuras pruebas
Para estudiar el comportamiento de resaltos hidráulicos se recomienda:
Realizar un montaje que permita evaluar pendientes mayores a 3%.
Variar el diámetro de la tubería con el fin de observar cuánto varía la relación de llenado en la
formación del resalto hidráulico.
Realizar un montaje que permita forzar la profundidad aguas arriba del resalto con una
compuerta ubicada aguas arriba.
Medir las direcciones de los vectores de velocidad por medio de mediciones instantáneas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
114
9. Glosario
Disipación de Energía: Porcentaje de energía que fue disipado a causa del resalto hidráulico. Su cálculo
se realiza por medio de la Ecuación 93.:
Ecuación 93. Cálculo disipación de Energía
Flujo Aguas Abajo: Profundidad del flujo que se encuentra después del resalto hidráulico.
Flujo Aguas Arriba: Profundidad del flujo que se encuentra antes del resalto hidráulico.
Flujo Crítico: El flujo crítico se presenta cuando las fuerzas inerciales y las fuerzas de gravedad son
iguales, por lo tanto el Número de Froude es igual a 1.0. Se caracteriza por ser un flujo inestable.
Flujo Subcrítico: Flujo caracterizado por tener profundidades altas, velocidades bajas, pérdidas por
fricción bajas y Números de Froude inferiores a 1.0. Además las fuerzas gravitacionales son mayores a
las fuerzas inerciales.
Flujo Supercrítico: Flujo caracterizado por tener profundidades bajas, velocidades altas pérdidas por
fricción altas y Números de Froude mayores a 1.0. Además las fuerzas inerciales son mayores a las
fuerzas gravitacionales.
Línea de Gradiente Hidráulico: Línea que indica la altura del flujo desde el datum, es decir, teniendo
en cuenta la energía potencial y de presión.
Número de Froude: Valor adimensional que permite determinar a partir de las fuerzas gravitaciones y
las fuerzas inerciales el tipo de flujo: supercrítico, crítico o subcrítico.
Piezómetro: Instrumento para la medición de pérdidas de altura del flujo como consecuencia de
fricción, obstrucciones, pérdidas menores, etc.
Profundidad Subsecuente: Profundidad aguas abajo del resalto.
Relación de llenado: Porcentaje de llenado de la tubería, es decir, la altura del flujo dividida entre el
diámetro de la tubería.
Resalto Hidráulico: Fenómeno generado por el cambio de flujo supercrítico a flujo subcrítico.
Tubería presurizada: Cuando la profundidad del flujo es mayor al diámetro de la tubería.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
115
10. Bibliografía
Akan, A. O. (2006). OPEN CHANNEL HYDRAULICS. Canada: ELSEVIER.
Banner Engineering. (n.d.). U - GAGE T30 Series with Analog and Discrete Outputs.
Minneapolis.
CIVIL ENGINEERING PORTAL. (2011). What are the effects of Hydraulic Jump? Retrieved
Noviembre 28, 2011, from http://www.engineeringcivil.com/what-are-the-effects-of-
hydraulic-jump.html
FHWA. (2006). Hydraulic Design of Energy Dissipators for Culverts and Channels. Hydraulic
Engineering Circular, 6-1 a 6-14.
French, R. H. (2007). The Momentum Principle. In R. H. French, Open Channel Hydraulics
(pp. 93 - 111). Colorado, USA: Copyright.
Gargano, R., & Hager, W. H. (2002). Undular Hydraulic Jump in Circular Conduits. JOURNAL
OF HYDRAULIC ENGINEERING, 1008-1013.
Ghamry, H. K., Shames, A., & Branch, F. (2002). Hydraulic Jumps in Circular Conduits .
Québec: CSCE.
Gonzales Rodríguez, M. (1992). Estudio Experimental de Flujos Disipativos: I. Resalto
Hidráulico. Cantabria: Universidad de Cantabria.
Hager, W. H. (1990). CRITICAL FLOW. In W. Hager, Wastewater Hydraulics (pp. 137 - 172).
Berlin: Springer.
Kindsvater, E. W. (1938). Hydraulic Jump In Enclosed Conduits. Engineering News Record,
815 - 817.
Lopardo, R. (2012). INTERNAL FLOW OF FREE HYDRAULIC JUMP IN STILLING BASINS.
4th IAHR International Symposium on Hydraulic Structures, 8.
Montaño Luna, L. E. (2012). Diseño y construcción de un modelo para estudiar el
comportamiento de resalto hidráulicos en tuberías parcialmente llenas de sección
circular, con Números de Froude supercríticos menores a 4. Bogotá.
Rajaratnam, N. (1965). Hydraulic Jump in Horizontal Conduits. WATER POWER, 80 - 83.
Robertson, J. M., & Kalinske, A. A. (1943). Closed Conduit Flow. Transactions of the American
Society of Civil Engineers, 1435-1447.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
116
Silvester, R. (1964). HYDRAULIC JUMP IN ALL SHAPES OF HORIZONTAL CHANNELS.
Proceedings of the American Society of Civil Engineers, 23 - 55.
SMITH, C. D., & CHEN, W. (1989). The hydraulic jump in a steeply sloping square conduit.
JOURNAL OF HYDRAULIC RESEARCH, 385 - 399.
SonTek. (2012, Octubre). SonTek-IQ Series. San Diego, USA.
Stahl, H., & Hager, W. H. (1999). Hydraulic jump in circular pipes. Canadian Journal of Civil
Engineering, 368 -373.
Sturm, T. W. (2010). Open Channel Hydraulics. Singapore: McGraw-Hill.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
117
11. Anexos
1. Programación en VBA de Excel para calcular la profundidad normal del flujo.
2. Programación en VBA de Excel para calcular la profundidad subsecuente del resalto
hidráulico mediante el método planteado por Silvester.
3. Programación en VBA de Excel para calcular la profundidad subsecuente del resalto
hidráulico mediante el método planteado por French.
4. Programación en VBA de Excel para calcular la profundidad subsecuente del resalto
hidráulico mediante el método planteado por Hager.
5. Programación en VBA de Excel para calcular la profundidad subsecuente del resalto
hidráulico mediante el método planteado por FHWA.
6. Mapa de la ubicación del montaje
7. Plano de la tubería en Perfil
8. Plano de la tubería en Planta
9. Plano en Autocad 3D de la tubería

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
118
11.1.
Cálculo de la profundidad normal del flujo
Sub caudal ()
d = 0.242
“Diámetro de la tubería”
ks = 0.0000015
“ks del acrílico”
nu = 0.00000114
“Viscosidad”
Pi = 3.141592654
“Valor del Número de Pi”
suma = 0.01
s = 0.005
e = 0
For i = 1 To 6
For w = 1 To 308
yd = 0.929
“Porcentaje con el cual fluye el máximo caudal”
yd0 = 0.01
“Porcentaje con el cual fluye una altura mínima”
yp1 = 0
For j = 1 To 90
qe = Cells(e + w + 4, 6)
“Caudal para el cual se quiere encontrar la profundidad normal”
yn0 = d * yd0
“Cálculo de la profundidad normal con yd0”
“Cálculo de los parámetros hidráulicos para el porcentaje yd0”
teta0 = Pi + 2 * WorksheetFunction.Asin((yn0 - (0.5 * d)) / (0.5 * d))
a0 = ((d ^ 2) / (8)) * (teta0 - Sin(teta0))
“Cálculo del area mojada”
p0 = (d * teta0) / 2 “Cálculo del perímetro mojado”
sa
r0 = a0 / p0
“Cálculo del radio hidráulico”
“Cálculo de la velocidad”
vel0 = -2 * ((8 * 9.81 * r0 * s) ^ 0.5) * WorksheetFunction.Log10((ks / (14.8 * r0)) + ((2.51 *
nu) / (4 * r0 * ((8 * 9.81 * r0 * s) ^ (0.5)))))
q0 = (vel0 * a0) – qe
“Cálculo del error”
re = (d * vel0) / un
“Cálculo del Número de Reynolds”
“Ancho de la superficie”

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
119
ancho = d * Cos(WorksheetFunction.Asin((yn0 - (0.5 * d)) / (0.5 * d)))
prof = a0 / ancho
“Cálculo de la profundidad hidráulica”
froude = (vel0) / ((9.81 * prof) ^ (0.5))
“Cálculo del Número de Froude”
“Cálculo de los parámetros hidráulicos para el porcentaje yd”
yn = d * yd
teta = Pi + 2 * WorksheetFunction.Asin((yn - (0.5 * d)) / (0.5 * d))
a = ((d ^ 2) / (8)) * (teta - Sin(teta))
p = (d * teta) / 2
r = a / p
vel = -2 * ((8 * 9.81 * r * s) ^ 0.5) * WorksheetFunction.Log10((ks / (14.8 * r)) + ((2.51 * nu)
/ (4 * r * ((8 * 9.81 * r * s) ^ (0.5)))))
q = (vel * a) - qe
“Cálculo de los parámetros hidráulicos para el promedio de las profundidades”
ydp = (yd + yd0) / 2
ynp = d * ydp
tetap = Pi + 2 * WorksheetFunction.Asin((ynp - (0.5 * d)) / (0.5 * d))
ap = ((d ^ 2) / (8)) * (tetap - Sin(tetap))
pp = (d * tetap) / 2
rp = ap / pp
velp = -2 * ((8 * 9.81 * rp * s) ^ 0.5) * WorksheetFunction.Log10((ks / (14.8 * rp)) + ((2.51 *
nu) / (4 * rp * ((8 * 9.81 * rp * s) ^ (0.5)))))
qp = (velp * ap) - qe
“Aplicación del método de la bisección”
If (qp * q) < 0 Then
yd0 = ydp
Else
yd0 = yd0
End If
If (qp * q0) < 0 Then

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
120
yd = ydp
Else
yd = yd
End If
If (Abs((ydp - yp1) / (ydp))) < 0.0000001 Then
GoTo 100
End If
yp1 = ydp
Next
100
Next
s = 0.005 + s
e = 308 + e
Next
End Sub

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
121
11.2.
Cálculo de la profundidad subsecuente del resalto hidráulico
mediante el método desarrollado por Silvester
Sub subs()
For i = 1 To 10
“Se realizará un ciclo con 10 iteraciones”
F = Cells(i + 8, 18)
“Número de Froude”
M1 = Cells(i + 8, 10)
“Área mojada para la altura aguas arriba”
d = Cells(i + 8, 6)
“Diámetro”
d1 = Cells(i + 8, 8)
“Altura aguas arriba”
k1 = Cells(i + 8, 19)
“Proporción de la profundidad del flujo”
yi = d1 + 0.001
“Altura minima del flujo”
yf = d
“Altura maxima del flujo”
mtk = 10
“Error”
A = F ^ 2 + k1
“Parámetro que establece si la aproximación es correcta”
While mtk > 0.0001
“Contador que finaliza cuando el error es menor a 0.0001”
If yi > d Then
“Si yi es mayor al diámetro”
“Cálculo de teta”
tetai = WorksheetFunction.Pi + 2 * WorksheetFunction.Asin((d - (0.5 * d)) / (0.5 * d))
“Cálculo del área”
areai = ((d ^ 2) / 8) * (tetai - Sin(tetai))
“Cálculo del error”
Ai = ((areai / M1) * ((yi / d1) - (0.5 * (d / d1)))) + ((F ^ 2) * (M1 / (areai))) - A
Else
“Si yi es menor al diámetro”
tetai = WorksheetFunction.Pi + 2 * WorksheetFunction.Asin((yi - (0.5 * d)) / (0.5 * d))
area1 = ((d ^ 2) / 8) * (tetai - Sin(tetai))
Ai = (((0.128 * (yi / d) ^ 2) - (0.047 * (yi / d)) + 0.416) * (((yi) / (d1)) * ((area1) /
(M1)))) + ((F ^ 2) * ((M1) / (area1))) - A
End If

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
122
If yf > d Then
“Si yf es mayor al diámetro”
“Cálculo de teta”
tetaf = WorksheetFunction.Pi + 2 * WorksheetFunction.Asin((d - (0.5 * d)) / (0.5 * d))
“Cálculo del área”
areaf = ((d ^ 2) / 8) * (tetaf - Sin(tetaf))
“Cálculo del error”
Af = ((areaf / M1) * ((yf / d1) - (0.5 * (d / d1)))) + ((F ^ 2) * (M1 / (areaf))) - A
Else
tetaf = WorksheetFunction.Pi + 2 * WorksheetFunction.Asin((yf - (0.5 * d)) / (0.5 * d))
areaf = ((d ^ 2) / 8) * (tetaf - Sin(tetaf))
Af = (((0.128 * (yf / d) ^ 2) - (0.047 * (yf / d)) + 0.416) * (((yf) / (d1)) * ((areaf) /
(M1)))) + ((F ^ 2) * ((M1) / (areaf))) - A
End If
If Af < 0 Then
“En aquellos casos en que las dos condiciones sean menores a 0”
Delta = 0.001
“Se aumenta un delta a la profundidad subsecuente aguas abajo”
While Af < 0
“Se recalcula el parámetro que nos determina el error”
Af = ((areaf / M1) * (((yf + Delta) / d1) - (0.5 * (d / d1)))) + ((F ^ 2) * (M1 / (areaf))) -
A
yf = yf + Delta
“Se aumenta la profundidad subsecuente aguas abajo del resalto
hasta que Af sea mayor a 0”
Wend
End If
yp = 0.5 * (yi + yf)
“Se estima la altura promedio”
“Se calcula teta, area y el parámetro para determiner el error de la altura promedio”
If yp > d Then
tetap = WorksheetFunction.Pi + 2 * WorksheetFunction.Asin((d - (0.5 * d)) /
(0.5 * d))
areap = ((d ^ 2) / 8) * (tetap - Sin(tetap))
Ap = ((areap / M1) * ((yp / d1) - (0.5 * (d / d1)))) + ((F ^ 2) * (M1 / (areap))) - A

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
123
Else
tetap = WorksheetFunction.Pi + 2 * WorksheetFunction.Asin((yp - (0.5 * d)) / (0.5 * d))
areap = ((d ^ 2) / 8) * (tetap - Sin(tetap))
Ap = (((0.128 * (yp / d) ^ 2) - (0.047 * (yp / d)) + 0.416) * (((yp) / (d1)) * ((areap) /
(M1)))) + ((F ^ 2) * ((M1) / (areap))) - A
End If
“Se procede a implementar el método de la bisección”
If Ai * Ap < 0 Then
yi = yi
Else
yi = yp
End If
If Af * Ap < 0 Then
yf = yf
Else
yf = yp
End If
mtk = (Abs(yf - yi) / (yf))
Wend
Cells(i + 8, 20) = yp
“Mostrar cuál es el valor de y en la hoja de Excel”
Next
End Sub

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
124
11.3.
Cálculo de la profundidad subsecuente del resalto hidráulico por el
Método desarrollado por French
16
Sub French0019()
For i = 1 To 10
q = Caudal
g = 9.81
y1 = altura aguas arriba
yi = y1 + 0.01
d = Diámetro
r = d / 2
yf = d
mtk = 10
M1 = Momento 1
While mtk > 0.0001
tetai = WorksheetFunction.Pi() + (2 * WorksheetFunction.Asin((yi - (0.5 * d)) / (0.5 * d)))
areai = ((d ^ 2) / 8) * (tetai - Sin(tetai))
zi = yi - 0.5 * d
zgorroi = (-2 * (((r ^ 2) - (zi ^ 2)) ^ (3 / 2))) / (3 * areai)
zpromi = yi - (r + zgorroi)
m2i = ((q ^ 2) / (g * areai)) + (zpromi * areai)
mi = ((q ^ 2) / (g * areai)) + (zpromi * areai) - M1
tetaf = WorksheetFunction.Pi() + (2 * WorksheetFunction.Asin((yf - (0.5 * d)) / (0.5 * d)))
areaf = ((d ^ 2) / 8) * (tetaf - Sin(tetaf))
zf = yf - 0.5 * d
zgorrof = (-2 * (((r ^ 2) - (zf ^ 2)) ^ (3 / 2))) / (3 * areaf)
zpromf = yf - (r + zgorrof)
m2f = ((q ^ 2) / (g * areaf)) + (zpromf * areaf)
16
Los comentarios del código se presentan en el cálculo de la profundidad subsecuente del resalto
mediante el método desarrollado por Silvester (Numeral 11.2)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
125
mf = ((q ^ 2) / (g * areaf)) + (zpromf * areaf) - M1
yp = 0.5 * (yi + yf)
tetap = WorksheetFunction.Pi() + (2 * WorksheetFunction.Asin((yp - (0.5 * d)) / (0.5 *
d)))
areap = ((d ^ 2) / 8) * (tetap - Sin(tetap))
zp = yp - 0.5 * d
zgorrop = (-2 * (((r ^ 2) - (zp ^ 2)) ^ (3 / 2))) / (3 * areap)
zpromp = yp - (r + zgorrop)
m2p = ((q ^ 2) / (g * areap)) + (zpromp * areap)
mp = ((q ^ 2) / (g * areap)) + (zpromp * areap) - M1
If mi * mp < 0 Then
yi = yi
Else
yi = yp
End If
If mf * mp < 0 Then
yf = yf
Else
yf = yp
End If
mtk = Abs((yf - yi) / (yf))
Wend
Next
End Sub

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
126
11.4.
Cálculo de la profundidad subsecuente del resalto hidráulico por el
Método desarrollado por Hager
17
Sub Hager()
For i = 1 To 10
y1 = Cells(8 + i, 8)
F1 = Cells(8 + i, 18)
A = Cells(8 + i, 19)
d = Cells(8 + i, 6)
mtk = 10
y2i = y1 + 0.01
y2f = d
While mtk > 0.00001
yp = 0.5 * (y2i + y2f)
Ai = ((y2i / y1) ^ 2.5) + (2 * (F1 ^ 2) * ((y2i / y1) ^ -1.5)) - A
Af = ((y2f / y1) ^ 2.5) + (2 * (F1 ^ 2) * ((y2f / y1) ^ -1.5)) - A
Ap = ((yp / y1) ^ 2.5) + (2 * (F1 ^ 2) * ((yp / y1) ^ -1.5)) - A
If Ai * Af > 0 Then
Cells(i + 8, 20) = "Presurizado"
GoTo 100
End If
If Ap * Af < 0 Then
y2i = yp
Else
y2i = y2i
End If
17
Los comentarios del código se presentan en el cálculo de la profundidad subsecuente del resalto
mediante el método desarrollado por Silvester (Numeral 11.2)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
127
If Ap * Ai < 0 Then
y2f = yp
Else
y2f = y2f
End If
mtk = Abs((y2i - y2f) / y2f)
Wend
Cells(i + 8, 20) = y2i
100
Next
End Sub

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
128
11.5.
Cálculo de la profundidad subsecuente del resalto hidráulico por el
Método desarrollado por FHWA.
18
Sub FWHA()
For i = 1 To 9
F1 = Cells(i + 8, 19)
k1 = Cells(i + 8, 20)
y1 = Cells(i + 8, 9)
c1 = Cells(i + 8, 21)
d = Cells(i + 8, 7)
yi = y1 + 0.01
yf = d
mtk = 10
A = k1 + F1 ^ 2
While mtk > 0.00001
If yi > d Then
k2i = (0.128 * (yi / d) ^ 2) - (0.0471 * (yi / d)) + 0.416
c2i = (-1.1954 * ((yi / d) ^ 3)) + (1.7406 * (yi / d) ^ 2) + 0.2033 * (yi / d) + 0.0082
Ai = ((yi * c2i) / (y1 * c1)) - (0.5 * ((c2i * d) / (c1 * y1))) + ((F1 ^ 2) * (c1 / c2i)) - A
Else
k2i = (0.128 * (yi / d) ^ 2) - (0.0471 * (yi / d)) + 0.416
c2i = (-1.1954 * ((yi / d) ^ 3)) + (1.7406 * (yi / d) ^ 2) + 0.2033 * (yi / d) + 0.0082
Ai = ((k2i * yi * c2i) / (y1 * c1)) + ((F1 ^ 2) * (c1 / c2i)) - A
End If
If yf > d Then
k2f = (0.128 * (yf / d) ^ 2) - (0.0471 * (yf / d)) + 0.416
c2f = (-1.1954 * ((yf / d) ^ 3)) + (1.7406 * (yf / d) ^ 2) + 0.2033 * (yf / d) + 0.0082
Af = ((yf * c2f) / (y1 * c1)) - (0.5 * ((c2f * d) / (c1 * y1))) + ((F1 ^ 2) * (c1 / c2f)) - A
18
Los comentarios del código se presentan en el cálculo de la profundidad subsecuente del resalto
mediante el método desarrollado por Silvester (Numeral 11.2)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
129
Else
k2f = (0.128 * (yf / d) ^ 2) - (0.0471 * (yf / d)) + 0.416
c2f = (-1.1954 * ((yf / d) ^ 3)) + (1.7406 * (yf / d) ^ 2) + 0.2033 * (yf / d) + 0.0082
Af = ((k2f * yf * c2f) / (y1 * c1)) + ((F1 ^ 2) * (c1 / c2f)) - A
End If
If Af < 0 Then
Delta = 0.001
While Af < 0
Af = ((yf * c2f) / (y1 * c1)) - (0.5 * ((c2f * d) / (c1 * y1))) + ((F1 ^ 2) * (c1 / c2f)) - A
yf = yf + Delta
Wend
End If
yp = 0.5 * (yi + yf)
If yp > d Then
k2p = (0.128 * (yp / d) ^ 2) - (0.0471 * (yp / d)) + 0.416
c2p = (-1.1954 * ((yp / d) ^ 3)) + (1.7406 * (yp / d) ^ 2) + 0.2033 * (yp / d) + 0.0082
Ap = ((yp * c2p) / (y1 * c1)) - (0.5 * ((c2p * d) / (c1 * y1))) + ((F1 ^ 2) * (c1 / c2p)) - A
Else
k2p = (0.128 * (yp / d) ^ 2) - (0.0471 * (yp / d)) + 0.416
c2p = (-1.1954 * ((yp / d) ^ 3)) + (1.7406 * (yp / d) ^ 2) + 0.2033 * (yp / d) + 0.0082
Ap = ((k2p * yp * c2p) / (y1 * c1)) + ((F1 ^ 2) * (c1 / c2p)) - A
End If
If Ap * Af < 0 Then
yi = yp
Else

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio del comportamiento de resaltos hidráulicos en tuberías parcialmente
llenas de sección circular, con Números de Froude supercríticos menores a 4
130
yi = yi
End If
If Ap * Ai < 0 Then
yf = yp
Else
yf = yf
End If
mtk = Abs((yf - yi) / (yf))
Wend
Cells(i + 8, 23) = yp
Next
End Sub
