
TESIS DE MAESTRÍA
ANÁLISIS GEÓMETRICO AVANZADO DE REDES DE DISTRIBUCIÓN DE AGUA
POTABLE (RDAP) DISEÑADAS ÓPTIMAMENTE
Juan Diego Carvajal Cruz
Asesor: Juan G. Saldarriaga Valderrama
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
MAESTRÍA EN INGENIERÍA CIVIL
BOGOTÁ D.C.
Enero, 2020


AGRADECIMIENTOS
A Dios, por su fidelidad.
A mi familia; en especial a mis abuelos Fermín, Alcyra, Luis Jesús y Alba y a mis padres
Juan Carlos y Julieth. Gracias por su apoyo incondicional a lo largo de estos años.
A mi asesor, Juan Saldarriaga. Gracias por todos los consejos y las enseñanzas. Gracias
por ser más que un profesor, un tutor de vida.
A Daniela Rodríguez, por la paciencia y amor brindado en el desarrollo de esta
investigación. Gracias por siempre creer en mí y animarme a dar siempre lo mejor de mí.
A mis compañeros del CIACUA, por su amistad.


Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
1
TABLA DE CONTENIDO
1.
INTRODUCCIÓN Y OBJETIVOS ................................................................................ 8
1.1.
Introducción ......................................................................................................... 8
1.2.
Objetivos ............................................................................................................. 9
1.2.1.
Objetivo General ........................................................................................... 9
1.2.2.
Objetivos Específicos ................................................................................... 9
2.
OPTIMIZACIÓN EN REDES DE DISTRIBUCIÓN DE AGUA POTABLE .................. 10
2.1.
Optimización y problemas abordados en RDAP ................................................ 11
2.1.1.
Diseño de Redes de Distribución de Agua Potable ..................................... 11
2.1.2.
Operación de RDAP ................................................................................... 13
2.1.3.
Otros usos de optimización en sistemas de distribución de agua potable ... 14
2.2.
Métodos de optimización ................................................................................... 15
2.2.1.
Optimización Determinística ....................................................................... 15
2.2.2.
Metaheurísticas .......................................................................................... 16
2.3.
Resumen optimización en RDAP ....................................................................... 16
3.
GEOMETRÍA DE REDES DE DISTRIBUCIÓN DE AGUA POTABLE ....................... 18
3.1.
Complex Network Theory .................................................................................. 18
3.2.
CNT y su aplicación en RDAP ........................................................................... 20
3.3.
Teoría de grafos
– Topología de redes .............................................................. 22
3.3.1.
Métricas topológicas (teoría de grafos) implementadas en RDAP .............. 31
3.3.2.
Branch Index y sistema de clasificación ...................................................... 40
3.4.
Propiedades geométricas de componentes de la red ........................................ 41
4.
ANÁLISIS GEOMÉTRICO DE RDAP ........................................................................ 44
4.1.
Selección de índices para el análisis de RDAP .................................................. 45
4.1.1.
Herramientas computacionales .................................................................. 45
4.1.2.
Evaluación de índices en RDAP ................................................................. 45
4.1.3.
Caracterización geométrica de RDAP......................................................... 55

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
2
4.2.
Ajuste de índices de CNT seleccionados ........................................................... 62
4.2.1.
Índices de CNT con peso............................................................................ 62
5.
METODOLOGÍA DE OPTIMIZACIÓN ....................................................................... 67
5.1.
Metodología OPUS ............................................................................................ 68
5.2.
Algoritmos genéticos ......................................................................................... 70
5.3.
Ecuación de costo ............................................................................................. 72
5.4.
Resiliencia de RDAP ......................................................................................... 72
6.
CASOS DE ESTUDIO .............................................................................................. 74
7.
ANÁLISIS Y RESULTADOS ..................................................................................... 77
7.1.
Caracterización geométrica diseños originales .................................................. 77
7.2.
Optimización de RDAP ...................................................................................... 78
7.2.1.
Diámetros ................................................................................................... 80
7.2.2.
Índices de CNT ajustados con peso ........................................................... 82
7.2.3.
Centroides .................................................................................................. 89
8.
CONCLUSIONES Y RECOMENDACIONES ............................................................ 97
9.
Referencias ............................................................................................................ 100

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
3
ÍNDICE DE FIGURAS
Figura 2-1. Diagrama de investigación en optimización en RDAP ................................................... 17
Figura 3-1. Problema "The Bridges of Konisberg" (Barabási, Towlson, & Cornelius, 2018) ............ 23
Figura 3-2. Grafo (no dirigido - sin peso) .......................................................................................... 24
Figura 3-3. Grafo dirigido .................................................................................................................. 24
Figura 3-4. Grafo dirigido y con peso ................................................................................................ 24
Figura 3-5. Grado para grafos no dirigidos ....................................................................................... 25
Figura 3-6. Grado para grafos dirigidos ............................................................................................ 25
Figura 3-7. Grado promedio del grafo ............................................................................................... 25
Figura 3-8. Distribución del grado P(k) ............................................................................................. 26
Figura 3-9. Vecindario (nodo 4)......................................................................................................... 27
Figura 3-10. Matriz de adyacencia .................................................................................................... 27
Figura 3-11. Caminos y ciclos en grafos ........................................................................................... 28
Figura 3-12. Distancias, diámetro y longitud promedio de los caminos de un grafo ........................ 28
Figura 3-13. Conectividad de un grafo .............................................................................................. 29
Figura 3-14. Coeficiente de agrupación ............................................................................................ 30
Figura 3-15. Intermediación (Betweenness) ..................................................................................... 30
Figura 3-16. Cercanía (Closeness) ................................................................................................... 31
Figura 3-17. Diagrama de clasificación de RDAP (Hwang & Lansey, 2017) .................................... 41
Figura 4-1. Relación entre nodos y tuberías de las redes analizadas .............................................. 47
Figura 4-2. Relación entre el diámetro promedio y el BI ................................................................... 49
Figura 4-3. Topología de redes KY15, Bogotá, KY3 y KY14 ............................................................ 50
Figura 4-4. Relación entre k y Rm..................................................................................................... 54
Figura 4-5. Relación entre diámetro de la red y longitud promedio de los caminos ......................... 54
Figura 4-6. Relación entre la eficiencia de la red y longitud promedio de los caminos .................... 55
Figura 4-7. Resultados de cada una de las métricas para la caracterización .................................. 56
Figura 4-8. Clasificación de las RDAP (Conectividad) ...................................................................... 57
Figura 4-9. Clasificación de RDAP (Eficiencia) ................................................................................. 58
Figura 4-10. Clasificación de RDAP (Centralidad) ............................................................................ 59
Figura 4-11. Clasificación RDAP (Diversidad) .................................................................................. 60

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
4
Figura 4-12. Clasificación de RDAP (Robustez) ............................................................................... 61
Figura 4-13. Clasificación RDAP (Modularidad) ............................................................................... 62
Figura 4-14. Conectividad algebraica con pesos .............................................................................. 64
Figura 4-15. Dominancia del punto central con pesos ...................................................................... 64
Figura 4-16. Brecha espectral con pesos ......................................................................................... 65
Figura 4-17. Modularidad con pesos ................................................................................................. 65
Figura 4-18. Eficiencia con pesos ..................................................................................................... 65
Figura 5-1. Parámetros generales - optimización REDES ................................................................ 68
Figura 5-2. Diámetros comerciales disponibles para optimización (RDE 26 PVC - PAVCO) .......... 72
Figura 6-1. Casos de estudio. En rojo se señala la ubicación de los tanques ................................. 75
Figura 7-1. Distribución de diámetros para todos los diseños .......................................................... 82
Figura 7-2. Resultados conectividad algebraica ............................................................................... 83
Figura 7-3. Resultados centralidad ................................................................................................... 85
Figura 7-4. Resultados brecha espectral .......................................................................................... 87
Figura 7-5. Resultados modularidad ................................................................................................. 89
Figura 7-6. Centroides Blacksburg .................................................................................................... 91
Figura 7-7. Centroides Mamatoco ..................................................................................................... 92
Figura 7-8. Centroides Mesolandia ................................................................................................... 93
Figura 7-9. Centroides La Esperanza ............................................................................................... 94
Figura 7-10. Centroides Andalucia Alta ............................................................................................ 95
Figura 7-11. Centroides Candelaria .................................................................................................. 96

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
5
ÍNDICE DE TABLAS
Tabla 2-
1. Bibliografía en sistemas de distribución de agua potable (Savić et al., 2018) ................ 10
Tabla 3-1. Métricas implementadas en el análisis de RDAP (grafos sin peso y sin dirección) ........ 37
Tabla 4-1. Características generales de RDAP - caracterización topológica ................................... 46
Tabla 4-2. Rangos de características generales de las redes .......................................................... 47
Tabla 4-3. Cálculo de BI y sistema de clasificación .......................................................................... 48
Tabla 4-4. Cálculo de métricas de CNT para redes analizadas ....................................................... 52
Tabla 4-5. Coeficiente de correlación métricas CNT ........................................................................ 53
Tabla 4-6. Métricas para la caracterización geométrica de RDAP ................................................... 55
Tabla 6-1. Características generales casos de estudio .................................................................... 74
Tabla 6-2. Presión mínima, costo y resiliencia de casos de estudio ................................................ 76
Tabla 6-3. Diámetros originales casos de estudio ............................................................................ 76
Tabla 7-1. Resultados de clasificación topológica según Hwang y Lansey ..................................... 77
Tabla 7-2. Resultados métricos CNT ................................................................................................ 77
Tabla 7-3. Resultados generales optimización ................................................................................. 78
Tabla 7-4. Resultados resiliencia ...................................................................................................... 79
Tabla 7-5. Resultados de diámetros para todos los diseños ............................................................ 80
Tabla 7-6. Resultados conectividad algebraica ................................................................................ 82
Tabla 7-7. Resultados centralidad..................................................................................................... 84
Tabla 7-8. Resultados brecha espectral ........................................................................................... 86
Tabla 7-9. Resultados modularidad .................................................................................................. 88
Tabla 7-10. Resultados centroides.................................................................................................... 89

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
6
ÍNDICE DE ECUACIONES
Ecuación 1. Densidad de enlaces ..................................................................................................... 32
Ecuación 2. Grado promedio de los nodos ....................................................................................... 32
Ecuación 3. Grado del nodo vecino .................................................................................................. 32
Ecuación 4. Índice Beta ..................................................................................................................... 32
Ecuación 5. Heterogeneidad ............................................................................................................. 32
Ecuación 6. Coeficiente de agrupación del grafo.............................................................................. 33
Ecuación 7. Transitividad del nodo ................................................................................................... 33
Ecuación 8. Coeficiente Meshedness ............................................................................................... 33
Ecuación 9. Longitud promedio de los caminos ................................................................................ 33
Ecuación 10. Diámetro del grafo ....................................................................................................... 34
Ecuación 11. Eficiencia de la red ...................................................................................................... 34
Ecuación 12. Factor de ruta .............................................................................................................. 34
Ecuación 13. Densidad de puentes .................................................................................................. 34
Ecuación 14. Densidad de puntos de articulación ............................................................................ 35
Ecuación 15. Brecha espectral.......................................................................................................... 35
Ecuación 16. Centralidad Betweenness ........................................................................................... 35
Ecuación 17. Dominancia del punto central ...................................................................................... 36
Ecuación 18. Closeness .................................................................................................................... 36
Ecuación 19. Límite eliminación nodos aleatorios ............................................................................ 36
Ecuación 20. Indicador de Modularidad ............................................................................................ 37
Ecuación 21. Grado entrópico ajustado (demanda).......................................................................... 39
Ecuación 22. Intermediación ajustada (Tailored Edge Betweenness).............................................. 40
Ecuación 23. Branch Index ............................................................................................................... 40
Ecuación 24. Diámetro promedio de red (ponderado por la longitud) .............................................. 41
Ecuación 25. Centroide de Volumen RDAP ...................................................................................... 42
Ecuación 26. Centroide de Potencia Específica RDAP .................................................................... 42
Ecuación 27. Centroide de Diámetro RDAP ..................................................................................... 42
Ecuación 28. Centroide de Potencia RDAP ...................................................................................... 42
Ecuación 29. Cálculo de distancias centroides de red ..................................................................... 42

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
7
Ecuación 30. Peso (diámetro) ........................................................................................................... 63
Ecuación 31. Peso (Volumen) ........................................................................................................... 63
Ecuación 32. Peso (Caudal) .............................................................................................................. 63
Ecuación 33. Peso (Pérdidas) ........................................................................................................... 63
Ecuación 34. Índice de resiliencia ..................................................................................................... 73

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
8
1. INTRODUCCIÓN Y OBJETIVOS
1.1. Introducción
De los diferentes temas de investigación en el área de recursos hídricos e hidroinformática,
las investigaciones en la gerencia integral de redes de distribución de agua potable (RDAP)
son de gran importancia para la comunidad por el alto impacto y la aplicabilidad de los
resultados obtenidos. Las empresas prestadoras del servicio, por ejemplo, siempre buscan
determinar nuevas herramientas o formas de analizar redes con el fin de realizar una
adecuada planeación a futuro para la operación, mantenimiento y diseño de RDAP.
En la actualidad, el problema del diseño optimizado de RDAP ha sido abordado por
diferentes investigadores de forma exhaustiva. Sin embargo, en el análisis de RDAP
diseñadas óptimamente, se ha dejado a un lado la posible relación entre los parámetros
geométricos de una red y los parámetros hidráulicos obtenidos del diseño óptimo. La
presente investigación, mediante el desarrollo de un estado del arte, busca realizar un
análisis geométrico robusto de las RDAP diseñadas óptimamente, con el fin de brindar una
respuesta a las posibles relaciones existentes entre la geometría de la red y su diseño
optimizado.
En investigaciones previas, diferentes autores han estudiado las relaciones existentes entre
la teoría de redes complejas (Complex Network Theory - CNT) y los sistemas de distribución
de agua potable. Recientemente, Saldarriaga y Robles (2018), implementaron diferentes
métricas de teoría de grafos (geometría) para comparar redes reales y redes virtuales en
términos de estructura, eficiencia y robustez. En cuanto a la estructura, los índices
estudiados fueron: Link Density, Average Node Degree, Average Clustering y Meshedness
Coefficient; eficiencia y accesibilidad: Characteristic Path Length y Diamater; robustez y
vulnerabilidad: Density of Bridges, Spectral Gap y Algebraic Connectivity. Del mismo modo,
Moreno, Rojas y Saldarriaga (2018), crearon 4 índices geométricos para estudiar la relación
entre la densidad de población y la topología en RDAP. Los 4 índices creados fueron:
Volume Centroid, Specific Power Centroid, Diameter Centroid y Power Centroid. Como
estas, existen otras investigaciones que conectan la CNT con las RDAP y evalúan gran
cantidad de índices topológicos, no obstante, no existe una documentación detallada que
permita el entendimiento y la relación entre estos índices y los diseños optimizados de
RDAP.
Con esta investigación, se busca abrir un camino y entender cómo es la geometría de las
redes de distribución de agua potable diseñadas óptimamente. En primer lugar, se realiza
una recopilación bibliográfica de los dos temas fundamentales de este estudio, optimización
y geometría de RDAP enfocada en la teoría de grafos, ya que es fundamental para el
análisis geométrico. Finalizada esta etapa de recopilación bibliográfica, se plantea cómo
analizar la geometría de la RDAP diseñadas óptimamente. Esto se hace mediante la
escogencia de los mejores índices recopilados del estudio de CNT, complementado de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
9
otros índices que también analizan la geometría de las redes (por ejemplo, los centroides
de la red). Así mismo, en esta etapa de la investigación se plantea la proposición de nuevos
índices que junten la CNT con las características hidráulicas de la red. Finalmente, se
realizan los cálculos con sus respectivos análisis, conclusiones y recomendaciones.
Durante el desarrollo de la investigación, se espera encontrar cuáles son los índices
geométricos que verdaderamente permiten entender y relacionar la topología de la red con
su hidráulica.
1.2. Objetivos
1.2.1. Objetivo General
Realizar un análisis geométrico robusto de redes de distribución de agua potable diseñadas
óptimamente con el fin de abrir un camino y entender las posibles relaciones existentes
entre la geometría de la red y su diseño optimizado.
1.2.2. Objetivos Específicos
Recopilar y analizar la información disponible, mediante búsqueda bibliográfica,
sobre los trabajos desarrollados en el campo de optimización de RDAP.
Recopilar y analizar la información disponible, mediante búsqueda bibliográfica,
sobre las investigaciones desarrolladas en el campo de las redes complejas para el
análisis de RDAP.
Seleccionar de los diferentes índices encontrados en la literatura los más
significativos para el análisis geométrico de las RDAP.
Proponer una metodología para el análisis geométrico de RDAP que junten métricas
de CNT con otras métricas de la geometría de las redes, así como sus
características hidráulicas.
Proponer nuevos índices que combinen la geometría y la hidráulica de la red para
poder realizar comparaciones significativas entre los diseños optimizados y los no-
optimizados.
Comparar los resultados de los índices geométricos e hidráulicos obtenidos en el
análisis de RDAP diseñadas óptimamente y las RDAP diseñadas sin optimización
de costos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
10
2. OPTIMIZACIÓN EN REDES DE DISTRIBUCIÓN DE AGUA POTABLE
La optimización en sistemas de distribución de agua potable es un tema de investigación
que ha sido abordado de forma exhaustiva. Así mismo, las publicaciones relacionadas con
estos temas han crecido rápidamente debido a los desarrollos computacionales de los
últimos siglos. Esto puede verse reflejado en que en las últimas tres décadas hay más de
300 artículos de revista publicados sobre la optimización en el diseño y la operación de
RDAP
(Savić, Mala-Jetmarova, & Sultanova, 2018). En la Tabla 2-1 se pueden observar las
diferentes publicaciones que analizan en detalle toda la literatura publicada.
Tabla 2-1. Bibliografía en sistemas de distribución de agua potable
(Savić et al., 2018)
Autor (año)
Título
Periodo abarcado
Shamir (1974)
Optimal design and operation of water distribution
systems
1961-1972
Shamir (1979)
Optimization in water distribution systems engineering
1963-1977
Walski (1985)
State-of-the-art pipe network optimization
1931 – 1939
1968 - 1985
Lansey & Mays
(1989)
Optimization models for design of water distribution
systems
1939, 1961 - 1988
Walters (1992)
A review of pipe network optimisation techniques
1966-1991
Goulter (1992)
Systems analysis in water-distribution network design.
From theory to practice
1969-1991
Walters and
Cembrovicz (1993)
Optimal design of water distribution networks
1968-1994
Dandy et al. (1993)
A review of pipe network optimisation techniques
1936, 1963–1992
Ostfeld and Shamir
(1993)
Incorporating reliability in optimal design of wáter
distribution networks – review and new concepts
1972-1992
Ormsbee and
Lansey (1994)
Optimal control of water supply pumping system
1968-1994
Simpson et al.
(1994)
Genetic algorithms compared to other techniques for
pipe optimisation
1973-1992
Engelhardt et al.
(2000)
Rehabilitation strategies for water distribution
networks: a literature review with a UK perspective
1972-1999
Lansey (2006)
The evolution of optimizing water distribution system
applications
1939, 1961–2006
Savić et al. (2009)
Quo vadis water distribution model calibration?
1974-2008
Mala-Jetmarova et
al. (2017)
Lost in optimisation of water distribution systems? A
literature review of system operation
1969-2016
Mala-Jetmarova et
al. (2018)
Lost in Optimisation of Water Distribution Systems? A
literature review of system design
1895-2017
Como se puede observar, las últimas dos publicaciones abarcan los periodos de tiempo
más extensos. Mala-Jetmarova, Sultanova, & Savic, (2017) realizan una recopilación

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
11
bibliográfica de la literatura disponible sobre la optimización enfocada en el problema de la
operación del sistema, y luego, Mala-Jetmarova, Savic, & Sultanova, (2018) se enfocan en
el problema del diseño del sistema.
En la siguiente sección se realiza un resumen en donde se presenta una descripción de los
diferentes tipos de problemas abordados, las metodologías de optimización implementadas
y la aplicación de la optimización en sistemas de distribución de agua potable teniendo en
cuenta los desarrollos claves a lo largo de la historia.
2.1. Optimización y problemas abordados en RDAP
Diferentes problemas han sido abordados por los métodos de optimización en RDAP a lo
largo del tiempo, siendo el diseño del sistema como un todo el problema fundamental en
cuestión
(Savić et al., 2018). El diseño del sistema es una tarea de gran complejidad ya que
involucra la solución simultánea de un sistema de ecuaciones no-lineales junto con el
establecimiento del tamaño, ubicación y estado operacional de los componentes de la red
(tuberías, bombas, tanques y válvulas). Además, requiere que los sistemas diseñados sean
asequibles, desde el punto de vista económico, y duraderos, teniendo en cuenta que deben
satisfacer de forma continua diferentes criterios hidráulicos junto con los requisitos de los
usuarios
(Savić et al., 2018). Adicionalmente, los problemas relacionados con RDAP
pertenecen a la clase de problemas de optimización duros (Yates, Templeman, & Boffey,
1984), por lo cual se convierte en un problema intratable de manera formal.
En términos generales, estos problemas pueden ser clasificados en dos grupos: 1) diseño
de RDAP (determinación del tamaño de sus componentes) y 2) operación de RDAP. A
continuación, se presenta una descripción de cada tipo de problema.
2.1.1. Diseño de Redes de Distribución de Agua Potable
Este tipo de problemas se enfoca en determinar las dimensiones de los diferentes
componentes de una red de distribución de agua potable. En general, se habla de
determinar los diámetros de las tuberías de la red, no obstante, los diferentes avances en
el tema de investigación han incluido en el diseño de RDAP otros componentes como
válvulas, tanques y bombas.
Diámetro de las tuberías.
El diseño de una RDAP consiste en determinar los diámetros de cada una de las tuberías
que la conforman dados un caudal de consumo en cada uno de los nudos fijados por la
demanda de agua potable y una presión mínima en las horas de máximo consumo fijada
por una norma local (Saldarriaga, 2016). Es decir, dada una topología de una red, el
problema consiste en determinar un conjunto de diámetros en forma tal que se minimice
una función de costo sujeta a restricciones hidráulicas, comerciales y de construcción
(Saldarriaga, 2016). Las variables de decisión del problema son los diámetros de cada una

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
12
de las tuberías de la red. Estas variables son discretas, puesto que sus valores dependen
de los diámetros comerciales producidos por la industria. El problema de optimización, en
el caso más simple (únicamente un estado operacional), involucra un número posible de
diseños discretos equivalente a
𝑑
𝑝
, donde
𝑑 son los diámetros comerciales disponibles y 𝑝
es el número de tuberías de la red.
Otros componentes: tanques, válvulas, bombas.
Con los avances en la modelación de RDAP, estos componentes empezaron a
considerarse importantes en el proceso del diseño optimizado. Por ejemplo, las válvulas
suelen usarse para aislar porciones de la red durante emergencias, lo que hace que definir
la cantidad y su ubicación sea importante, especialmente cuando se quiere medir la
confiabilidad y la resiliencia de la red. No obstante, incluir tanques, válvulas y bombas como
variables de decisión, hacen que se incremente el tamaño y la complejidad (por cuestiones
operativas de cada componente) del problema. Un ejemplo claro que demuestra la
complejidad a tratar puede observarse de los resultados obtenidos en el evento “Battle of
the Network Model
s”, en donde se compararon las diferentes aproximaciones al diseño
optimizado la red patrón Anytown (Walski et al., 1987). Los participantes utilizaron
optimización para determinar los diámetros de las tuberías, pero escogieron la ubicación y
el tamaño de los tanques manualmente. El problema ha sido abordado en diferentes
investigaciones (A.R Simpson, Murphy, & Dandy, 1993), (Giustolisi, Berardi, & Laucelli,
2012).
Optimización en el diseño de sistemas existentes.
La optimización en el diseño de sistemas existentes se centra en el fortalecimiento, la
rehabilitación y la expansión de sistemas que ya están en operación (Mala-Jetmarova et
al., 2018). El fortalecimiento de un sistema representa la mejora del mismo mediante la
adición de tuberías paralelas a las existentes con el fin de satisfacer la demanda futura
(Savić et al., 2018). En cuanto a la rehabilitación, se hace referencia al remplazo de las
tuberías del sistema que, por deterioro a causa de diferentes factores, han reducido su
diámetro o necesitan revestimiento. Por último, la expansión del sistema es la extensión de
la red actual para cubrir una nueva zona por fuera de los límites.
Estos problemas suelen formularse de la misma forma que el diseño de una RDAP nueva,
no obstante más del 80% de las investigaciones publicadas han utilizado como caso de
estudio redes pequeñas, computacionalmente económicas (menos de 100 nodos) (Mala-
Jetmarova et al., 2018). Estudios en redes más grandes se han realizado en las
competiciones organizadas durante los congresos de
“Water Distribution System Analysis
– WDSA”.
Diseño escalonado y diseño flexible.
El problema del diseño escalonado es definido por (Mala-Jetmarova et al., 2018) como la
optimización de una RDAP a través del horizonte de planeación en el cual la construcción

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
13
del sistema es dividida en distintas fases o etapas. Este horizonte de planeación puede
expandirse por los años llegando incluso al ciclo de vida esperado del sistema. Los mismos
autores definen el diseño flexible de la igual que el diseño escalonado, pero considerando
la incertidumbre asociada a las demandas, el deterioro de las tuberías, la expansión urbana,
entre otras. Para ambos casos, el problema de optimización aumenta su complejidad por la
introducción de pasos (delta tiempo) y la necesidad de continuidad entre las soluciones
escalonadas
(Savić et al., 2018).
2.1.2. Operación de RDAP
La optimización en la operación de RDAP ha sido investigada de forma activa por casi 50
años (Mala-Jetmarova et al., 2017). Esta incluye: 1) La operación de las bombas
(planeación y operación en tiempo real), 2) el manejo de la calidad del agua del sistema y
3) la operación de válvulas.
Operación de bombas
La operación de bombas es el tema más investigado en la optimización de la operación de
RDAP. El objetivo es optimizar la forma en la que las bombas son operadas para minimizar
la cantidad de energía consumida por ellas. El control explicito considera los tiempos de
operación de las bombas, mientras que el control implícito se aproxima al problema
teniendo en cuenta caudales, presiones, niveles de los tanques e incluso la velocidad de
las bombas
(Savić et al., 2018). Todos estos controles son variables de decisión en el
problema de optimización y su formulación puede encontrarse en (Ormsbee, Lingireddy, &
Chase, 2009). Adicionalmente, es necesario tener en cuenta los costos derivados de la
demanda de energía y del mantenimiento de las bombas en el proceso de optimización.
Todas estas consideraciones hacen que el problema de la optimización del sistema de
bombeo de una RDAP sea un desafío complejo.
Calidad del agua
Ulanicki y Orr (1991) fueron de los primeros en considerar las restricciones de calidad de
agua en conjunto con la optimización en la operación de bombas en las RDAP. Otra
formulación del problema fue introducida por Boccelli et al., (2002), quienes, se aproximaron
al problema usando la minimización de la cantidad de masa de desinfectante suministrada
por las estaciones de bombeo como sustituto de los costos. Una variante de esta
aproximación involucra la minimización de la desviación en concentración del desinfectante
en los nodos de consumo
(Savić et al., 2018). Es interesante saber que existe una
compensación entre la calidad del agua y lo costos operacionales, en donde los costos de
bombeo son significativamente reducidos si la calidad de agua está ausente del modelo de
optimización, y, por el contrario, los mejores resultados de calidad de agua corresponden a
los costos más altos de operación en el bombeo (Ostfeld & Salomons, 2006).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
14
Operación de Válvulas
Las válvulas como variables de decisión se usan en conjunto con la optimización de la
operación de bombas y la calidad de agua del sistema. Las variables de decisión pueden
ser: estados continuos de la válvula, estado binario de la válvula, posición de la válvula o
ratio de apertura de la válvula, caudal a través de la válvula, coeficientes de pérdidas de la
válvula y, la configuración de las válvulas reductoras de presión (PRV de sus siglas en
inglés)
(Savić et al., 2018). Diferentes formulaciones pueden encontrarse en (Mala-
Jetmarova et al., 2017).
2.1.3. Otros usos de optimización en sistemas de distribución de agua potable
Es posible encontrar otras aplicaciones a las mencionadas anteriormente en problemas de
optimización en RDAP. Estas áreas están principalmente relacionadas con la calibración,
la sectorización y el manejo de la confiabilidad, robustez y resiliencia del sistema.
Calibración de modelos de RDAP
La calibración de modelos de RDAP consiste en determinar las características físicas y
operacionales del sistema mediante la determinación de diferentes parámetros que reducen
el error entre lo medido y lo simulado. Las variables que usualmente se utilizan para medir
este error son los caudales de las tuberías, las presiones en los nodos y la calidad de agua.
Es importante entender que un modelo bien calibrado de una RDAP es un requerimiento
para el análisis del comportamiento de la red, lo que hace que la calibración sea
fundamental.
Sectorización de la red
La sectorización del sistema o “partición de la red”, hace referencia a la división de la red
en zonas más pequeñas mediante el aislamiento de sectores con válvulas. Esas zonas,
también conocidas como sectores hidráulicos (District Metered Areas - DMA), fueron
utilizadas por primera vez en el Reino Unido para permitir la identificación más eficiente de
fugas y para implementar zonas de reducción de presión mediante la utilización de PRV.
Así mismo, la sectorización de la red puede ser útil en caso de emergencias por
contaminantes, ya que permite aislar las zonas contaminadas
(Savić et al., 2018).
Confiabilidad, robustez y resiliencia
Es claro que un modelo de optimización basado únicamente en el costo, sin una medida
explicita, va a eliminar la redundancia del sistema (Angus R. Simpson, Dandy, & Murphy,
1994). La confiabilidad, robustez y resiliencia de la red son consideradas medidas de
desempeño con respecto a las condiciones de incertidumbre inmediata y por venir. Mala-
Jetmarova et al. (2017) realiza una compilación de alguna de las diferentes definiciones
para cada una de las métricas: En primer lugar, (i) es posible definir la confiabilidad como
la habilidad que tiene el sistema para proveer el servicio esperado y puede ser expresada
como la probabilidad de que el sistema esté en servicio durante un periodo específico del

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
15
tiempo; (ii) la robustez representa la habilidad del sistema de mantener su funcionalidad
bajo diferentes circunstancias, o bajo las fluctuaciones diarias presentes en la red que
tienen el potencial de causar disminución del rendimiento; y (iii) la resiliencia es definida
como la habilidad de una RDAP para adaptarse o recuperarse de alteraciones significativas
de la red. Como no existe una función en común para cada una de estas métricas, existen
diferentes aproximaciones en la optimización de RDAP.
2.2. Métodos de optimización
Si bien es cierto que los métodos de optimización se han beneficiado del desarrollo digital
del computador, las primeras aproximaciones de optimización basada en cálculo datan
antes de la era digital a los años 90 del siglo 19. Mala-Jetmarova et al. (2015) reportan una
aproximación inicial por Tuttle, quien, en 1985, desarrolló un método para calcular la
“economic velocity”, la cual minimiza el diámetro de una tubería basado en los costos
anuales de una RDAP incluyendo el costo del capital inicial, el interés anual más la
depreciación y el costo anual de la operación del sistema de bombeo. A continuación, se
presentan los métodos de optimización que han sido aplicados para el diseño, la planeación
y el manejo de RDAP.
2.2.1. Optimización Determinística
Programación lineal (PL)
Las aproximaciones por optimización determinística (exacta) usan a su favor las
propiedades analíticas del problema para generar una secuencia de soluciones candidatas
que buscan converger en una solución óptima global
(Savić et al., 2018). La programación
lineal (PL) es una de las metodologías de optimización determinística más usadas, ya que
garantiza encontrar el óptimo en un problema continuo con una función objetivo lineal sujeta
a restricciones
(Savić et al., 2018). No obstante, como los problemas de optimización de
RDAP son no-lineales, ya que la relación entre el caudal y las pérdidas son casi cuadráticas,
el uso de PL en RDAP requiere de linealización. Así mismo, por su naturaleza continua, la
solución óptima tiene que ser redondeada al valor discreto del diámetro comercial
disponible. El primer éxito del uso de PL en el diseño de una RDAP con circuitos fue
concebido por Schaake & Lai (1969) y de ahí en adelante aparecieron otras aplicaciones
de PL en el diseño y la operación. Aunque los ejemplos del uso de PL para el diseño de
RDAP ha disminuido en el tiempo, el uso de esta metodología sigue prevaleciendo en la
planeación de la operación del sistema de bombeo y en el control en tiempo real por su alta
eficiencia
(Savić et al., 2018).
Programación dinámica (PD)
La PD es otra metodología determinística que se ajusta a los problemas con múltiples
etapas de optimización al descomponer estas etapas en una secuencia de procesos de
toma de decisión (single-stage decisión-making). Se ajusta muy bien para aplicaciones en

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
16
operación de bombas (Chase & Ormsbee, 1993), pero sufre de la maldición de la dimensión,
por lo cual limita su aplicación en RDAP grandes.
Programación no – lineal (PNL)
La PNL usada en RDAP se basa en el método del gradiente, la programación cuadrática
sucesiva, o programación lineal sucesiva (Angus R. Simpson et al., 1994). Debido al límite
de variables y restricciones que la PNL puede manejar, su implementación se limita a RDAP
pequeñas. Al igual que con la PL, la PNL trabaja con variables continuas, pero a diferencia
de la PL, la PNL no necesariamente converge a un óptimo global en RDAP
(Savić et al.,
2018).
2.2.2. Metaheurísticas
La aproximación a la optimización de RDAP vivió un cambio importante con la aparición de
computadores más potentes y las metaheurísticas en los años 90. Una metaheurística es
un algoritmo multipropósito diseñado para resolver de forma aproximada una gran variedad
de problemas de optimización duros (encuentra un buen resultado, pero no necesariamente
el óptimo global) sin la necesidad de ser adaptado para cada problema. Todas las
metaheurísticas tienen en común que: (i) se inspiran en la naturaleza (por ejemplo,
principios de la física, biología, entre otros); (ii) son de naturaleza estocástica; (iii) no
requieren de linealización, ni del cálculo de derivadas de la función objetivo; (iv)
dependiendo del problema, tienen parámetros de calentamiento para conseguir un mejor
rendimiento (Nicklow et al., 2010). La mayoría de metaheurísticas son poblacionales, lo que
las hace fácilmente adaptables a optimizaciones multiobjetivo para obtener soluciones
cercanas a la frontera de Pareto en una sola corrida. La ventaja principal de estos algoritmos
de optimización es que son capaces de encontrar soluciones a problemas de alta
complejidad que no se encuentran con algoritmos determinísticos
(Savić et al., 2018). Mela-
Jetmarova et al. (2018) lista una gran variedad de metaheurísticas implementadas en la
optimización de RDAP.
2.3. Resumen optimización en RDAP
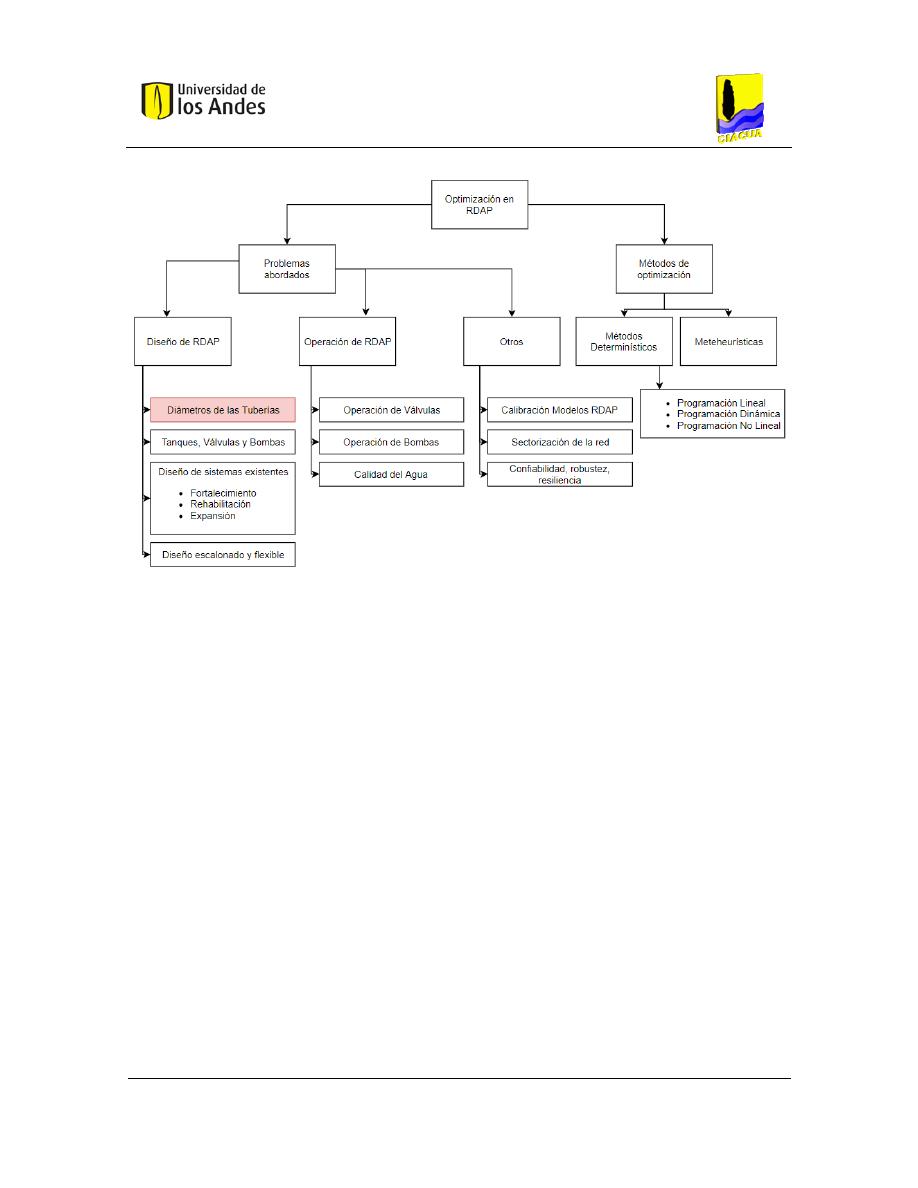
En general, es posible organizar la investigación del estado actual de la optimización en
RDAP con el diagrama que se presenta en Figura 2-1.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
17
Figura 2-1. Diagrama de investigación en optimización en RDAP
El diagrama expone las ramas de los estudios en optimización en RDAP. De los descritos,
el problema que más se ha trabajado es el de la determinación del tamaño de los
componentes de las RDAP, en especial del diámetro de las tuberías. Debido a esto, es
posible decir que este problema es en el que más se ha avanzado en optimización de
RDAP, y del cual, ya se puede considerar que varios de los algoritmos de optimización
propuestos permiten la correcta determinación de costos bajos (mínimos) en el diseño de
la red. No obstante, aún no se ha profundizado en las posibles relaciones existentes entre
geometría de la red y su diseño optimizado.
Estudiar la geometría de los diseños optimizados puede ser clave para abrir un camino y
entender cómo formular modelos detallados que describan los costos y el comportamiento
del sistema, lo cual, según Sávic et al. (2018), es uno de los temas a abordar en
investigaciones futuras. Además, la identificación del mejor esquema de optimización para
cada RDAP puede ser importante debido a que una sola aproximación no basta para todas
las redes. Según (Hwang & Lansey, 2017) la efectividad y eficiencia de los diferentes
algoritmos de optimización para diseñar una RDAP se ve afectada por la topología de la
red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
18
3. GEOMETRÍA DE REDES DE DISTRIBUCIÓN DE AGUA POTABLE
La geometría de las RDAP se ha estudiado desde dos enfoques complementarios que
permiten plantear una base para lo que debería ser un análisis robusto de la geometría de
la red. En primer lugar, se ha estudiado la geometría de la red analizando su topología
mediante la evaluación de diferentes métricas estructurales y estadísticas del mundo de las
redes complejas (Complex Network Theory). Acá, se estudian las redes mediante su
representación matemática a través de un grafo
𝐺 = 𝐺(𝑉, 𝐸), en donde 𝑉 es un conjunto de
nodos con
𝑛 elementos (tamaño del grafo) y 𝐸 es el conjunto de links con 𝑚 elementos
(orden del grafo) (Giustolisi & Savic, 2010; Yazdani & Jeffrey, 2012a). En segundo lugar, el
estudio de las propiedades geométricas de los componentes de la red mediante la
evaluación de diferentes índices como los propuestos por (Moreno, Rojas, & Saldarriaga,
2018) que tienen en cuenta características de las tuberías y el comportamiento hidráulico
de la red.
3.1. Complex Network Theory
La teoría de redes complejas (CNT) - Complex Networks Theory, nace hace más de dos
siglos con Euler (1741 teoría de grafos) y en las últimas dos décadas se ha convertido en
una herramienta útil y potente para estudiar, describir y entender el mundo (Barabási, 2012).
CNT permite el estudio y la interpretación de una gran cantidad de sistemas, por ejemplo:
físicos, sociales biológicos, de infraestructura, etc., ya que la mayoría de estos funcionan
como redes. Es cierto que cada red exhibe sus propias propiedades topológicas y
estructurales, no obstante, redes muy diferentes comparten características similares (Albert
& Barabási, 2002; Newman, 2010).
La investigación en el campo de redes complejas y sus propiedades estructurales ha
crecido rápidamente, llevando al desarrollo de nuevas aproximaciones, métricas y teorías
para explorar y entender las características de la red (ej. Boccaletti, Latora, Moreno,
Chavez, & Hwang, 2006; Newman, 2010). Los temas más investigados, dentro del análisis
de CNT y sus métricas, se relacionan con la robustez, vulnerabilidad, resiliencia y eficiencia
de sistemas reales (Giustolisi, Simone, & Ridolfi, 2017).
Las redes complejas son representadas como un conjunto de vértices
𝑉 (nodos,
intersecciones, actores, etc.) y la conexión entre estos como un conjunto de aristas
𝐸 (links,
tuberías, relaciones, etc.). Para cada red:
i)
Es posible evaluar características básicas para clasificar la estructura y
conectividad de la red (Boccaletti et al., 2006; Newman, 2010). Como: matriz de
adyacencia, grado (degree), diámetro, camino y camino más corto (path and
shortest path), coeficiente de agrupación (clustering coefficient), etc.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
19
Una métrica clave de entender es la distribución del grado de los nodos, ya que describe la
distribución de probabilidad del número de aristas conectadas con cada vértice de la red, y
diferentes características de la red están asociadas con la forma de esta distribución
(Giustolisi et al., 2017). Estudios relacionados con la clasificación y generación de redes
definieron tres tipos de redes basados en la distribución del grado: 1) aleatorias (Erdös &
Rényi, 1960; 1959), 2
) small world “mundo pequeño” (Watts & Strogatz, 1998) y 3) scale-
free “libres de escala” (Barabási & Albert, 1999). En las redes aleatorias, la distribución del
grado es aleatoria y similar alrededor de un valor promedio, siguiendo un modelo de
Poisson. Las redes de mundo pequeño se basan en el concepto de seis grados de
separación (Travers & Milgram, 1969) y muestran un comportamiento intermedio entre
redes regulares y redes aleatorias (modelo de Poission). Por último, en las redes libres de
escala, el grado de distribución sigue un modelo de Pareto con muchos nodos con baja
conectividad y otros (hubs) con muchas conexiones. Esta clasificación es útil para analizar
las redes con respecto a su comportamiento como consecuencia de fallas espontaneas o
amenazas intencionales.
ii)
Algunos componentes (enlaces y nodos) son más centrales que otros (Cadini,
Zio, & Petrescu, 2009; Everett & Borgatti, 1998; Freeman, 1977).
Por lo cual, existen diferentes métricas basadas en el concepto de grado del elemento para
medir centralidad y determinar cuál o cuáles son los componentes más importantes (los
más centrales). Algunas de estas métricas son: (1) grado (Nieminen, 1974) , (2) proximidad
closeness (Freeman, 1978) (3) betweenness (Freeman, 1977), Vector propio (Bonacich,
1972), etc.
iii)
Es un reto definir criterios para la detección de comunidades o la división en
módulos para entender mejor y analizar las diferentes porciones de una red.
(Newman, 2006) propuso una aproximación mediante la optimización de la modularidad de
la red sobre el número posible de divisiones de la red. (Girvan & Newman, 2002) también
propusieron un algoritmo para detectar comunidades usando una métrica de centralidad
(edge betweenness) la cual progresivamente removía aristas con los mayores valores de
betweenness.
Cada día se proponen nuevos métodos de redes complejas basados en características de
conectividad, métricas de centralidad y detección de comunidades.
Varios estudios de CNT se han centrado en entender el comportamiento de redes de
infraestructura como carreteras, redes de energía y las RDAP, por ejemplo: (Barthelemy,
2003; Barthélemy, 2011; Barthélemy & Flammini, 2008; Buhl et al., 2006; Cardillo, Scellato,
Latora, & Porta, 2006; Carvalho et al., 2009; Crucitti, Latora, & Marchiori, 2005; Deuerlein,
2008; Giustolisi et al., 2017; Masucci, Smith, Crooks, & Batty, 2009; Rosas-Casals,
Valverde, & Solé, 2007; Yazdani & Jeffrey, 2011). En cuanto a la susceptibilidad de la red
al daño: (Berardi, Ugarelli, Røstum, & Giustolisi, 2014; Berche, Von Ferber, Holovatch, &

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
20
Holovatch, 2009; Latora & Marchiori, 2005; Soldi, Candelieri, & Archetti, 2015; Yazdani &
Jeffrey, 2010, 2012b).
CNT, en efecto, estudia sistemas complejos compuestos por múltiples componentes
interconectados (nodos y enlaces) estructurados en configuraciones no triviales en donde
el comportamiento de la red está afectado por su estructura dependiendo de la complejidad
organizacional y del nivel de interacción entre los componentes (Yazdani & Jeffrey, 2011).
3.2. CNT y su aplicación en RDAP
Las RDAP son redes de infraestructura con características especiales porque son redes de
ciudad (Barthélemy, 2011), en las cuales la topología está restringida a factores
ambientales como las calles y los edificios, los cuales conducen la planeación y
construcción de la red (Giustolisi et al., 2017). Debido a lo anterior, existen serias
limitaciones en la conectividad de la red y en su diseño, haciendo que las RDAP se estudien
de forma distinta a otras redes complejas. En la última década, el estudio de RDAP usando
CNT ha crecido rápidamente y ha atraído a muchos investigadores, aun cuando sus
primeros estudios datan a 1972.
Kesevan y Chandrashekar (1972) utilizaron teoría de grafos para obtener modelos para el
análisis de redes de tuberías no-lineales. Jacobs y Goulter (1988, 1989) mostraron que las
redes que son menos vulnerables a fallas son las redes regulares con el mismo número de
links incidentes a cada nodo. Ostfeld y Shamir (1996) utilizaron teoría de redes para estudiar
la selec
ción de sistema de redundancia “backups” en una RDAP susceptible a fallas. Kumar
et al. (1999) propusieron una metodología para encontrar el trazado óptimo de un sistema
de detección en una RDAP municipal basados en el concepto de shortesth path (ruta más
corta). Gupta y Prasad (2002) propusieron un método numérico basado en teoría lineal de
grafos para el análisis de flujo uniforme y presiones en una red de tuberías incluyendo sus
componentes hidráulicos (bombas, válvulas, uniones). Deuerelin (2008) propuso un nuevo
concepto de descomposición del grafo de una red de acuerdo con las propiedades de
conectividad de esta y teniendo en cuenta mediciones de vulnerabilidad de la red, así como
varias fases de simplificación de la red las cuales pueden mejorar el entendimiento de los
componentes de las redes y su interacción.
Entre 2010 y 2012, Yazdani y Jeffrey representaron una RDAP como un grafo plano y
disperso con características de redes complejas y estudiaron la relación entre importantes
atributos topológicos de la red con la resiliencia del sistema, introduciendo dos métricas,
Meshed-ness y conectividad algebraica - algebraic connectivity, para cuantificar la
redundancia y robustez, respectivamente, en modelos de diseños optimizados. En el 2011
(Yazdani & Jeffrey, 2012a) exploraron una variedad de estrategias para entender la
formación, estructura, eficiencia y vulnerabilidad de RDAP. Las métricas estructurales
fueron usadas para cuantificar propiedades como la redundancia y la conectividad óptima,
usadas como restricciones en el diseño de RDAP. Así mismo, (2012a) propusieron la

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
21
representación link-nodo de una RDAP y una gran variedad de métricas para estudiar los
elementos fundamentales de los sistemas. Ellos cuantificaron propiedades como la
redundancia y la tolerancia a fallas con el propósito de establecer relaciones entre métricas
estructurales y el rendimiento de RDAP. En el (2012c), estudiaron la conectividad de los
sistemas de distribución de agua potable, sus relaciones con la robustez y susceptibilidad
al daño, modelando redes con dirección y peso.
Hawick (2012) aplicó análisis teórico de grafos a RDAP reales con el fin de estudiar su
robustez y propiedades de fragmentación a través de simulación de fallas en los
componentes de la red; uso la métrica de centralidad - betweenness para clasificar los
componentes y luego fue retirando los componentes más importantes. Gutiérrez-Pérez et
al. (2013) introdujeron una metodología basada en medidas espectrales de teoría de grafos
para establecer la importancia relativa de diferentes sectores en RDAP usando dos
algoritmos de clasificación (PageRank y HITS), con el propósito de lograr un análisis
eficiente de vulnerabilidad. Este método está basado en medidas de grafos como la
clasificación de la importancia relativa del grado de los vértices. Sheng et al. (2013)
exploraron la formación de comunidades en RDAP basados en CNT usando un modelo
grafo-algebraico para detectar las comunidades potenciales debido a fallas en las tuberías.
Shuang et al. (2014) propusieron evaluar la vulnerabilidad de los nodos de RDAP bajo fallas
en cascada. Nazempour et al. (2016) desarrollaron una nueva aproximación a la
modelación de la ubicación óptima de sensores para detectar la contaminación en RDAP
combinando la optimización clásica con CNT. Giustolisi et al. (2017) crearon una métrica
llamada neighborhood nodal degree
“grado vecino del nodo” mostrando que la distribución
de esta métrica si era apta para clasificar redes de infraestructura. Modelaron varias RDAP
usando el neighborhood nodal degree obteniendo una distribución de Poisson, y
demostrando que las redes presentan una buena resistencia estructural contra fallas
aleatorias y amenazas intencionales, así como una buena conectividad estructural.
En el 2017, Hwang y Lansey desarrollaron un esquema para clasificar RDAP basado en el
funcionamiento del sistema y en su topología. Examinaron varias métricas de CNT para
determinar los más adecuados para describir RDAP. Meng et al., (2018) estudiaron la
relación entre la resiliencia de un sistema y métricas topológicas de teoría de grafos y
encontraron que la resiliencia se veía afectada por algunos atributos topológicos. Por último,
Giustolisi et al. (2019) realizaron el ajuste de una métrica de centralidad de teoría de grafos
para poder determinar cuáles eran las tuberías más importantes de una red únicamente
con el análisis de su topología. La métrica ajustada la llamaron tailored Edge betweenness.
Los conceptos de teoría de grafos también se han implementado en sistemas de
distribución de agua potable con fines de monitoreo, operación y control. Se ha investigado
en calibración de modelos, medición de consumo de agua potable, detección de
contaminación temprana, control de presión y de fallas (Laucelli, Simone, Berardi, &
Giustolisi, 2017). Muchos algoritmos y métricas se han usado para definir la división óptima
de RDAP con respecto a su topología y las características de sus componentes, como por

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
22
ejemplo el diámetro y la longitud de las tuberías, las elevaciones de los nodos, fugas, etc.
Torres et al. (2017), por ejemplo, investigaron los patrones estructurales y las conexiones
basados en grafos utilizando redes en malladas (lattice-like). Perelman y Ostfeld (2011)
propusieron un esquema de fragmentación para análisis topológico/conectividad con el
objetico de desarrollar y demostrar un algoritmo basado en la conectividad para el análisis
de RDAP.
Por último, la segmentación óptima y división de RDAP para el análisis, la planeación y el
manejo de RDAP. El índice de modularidad es el índice más aceptado y usado para medir
que tan propensa es una red a dividirse en módulos (Newman & Girvan, 2004). Scibetta et
al. (2013) y Diao et al. (2013) aplicaron el índice de modularidad para la segmentación de
una RDAP usando la formulación original de Newman. Barthelemy (2011) explicó que la
formulación original estaba hecha para redes inmateriales (intangibles). Giustolisi y Ridolfi
(2014b) adaptaron el índice original de modularidad para obtener un índice orientado a
RDAP, teniendo en cuenta las características de estas. También propusieron un índice de
modularidad de infraestructuras (2014a) modificando el índice orientado a RDAP con el fin
de sobreponer el límite de resolución del índice de modularidad original (Fortunato &
Barthélemy, 2007) que causaba la no-identificación de módulos pequeños dependiendo del
tamaño de la red. Finalmente, Giustolisi et al. (2015) reportaron un marco comprehensivo
de índices de modularidad orientados a RDAP. Simone et al. (2016) extendieron los
conceptos de segmentación de redes a diseño por muestreo de presiones, introduciendo el
índice de modularidad orientado a muestras y el concepto de sectores por presión,
extendiendo el concepto de sectores por caudal relacionado con la forma clásica de
segmentación hidráulica.
3.3. Teoría de grafos – Topología de redes
La teoría de grafos es la base fundamental de la CNT, ya que una red, independiente de su
complejidad, es un grafo con un conjunto de nodos conectados por un conjunto de enlaces.
La teoría de grafos nace con Euler en 1735 intentando dar solución al problema de los
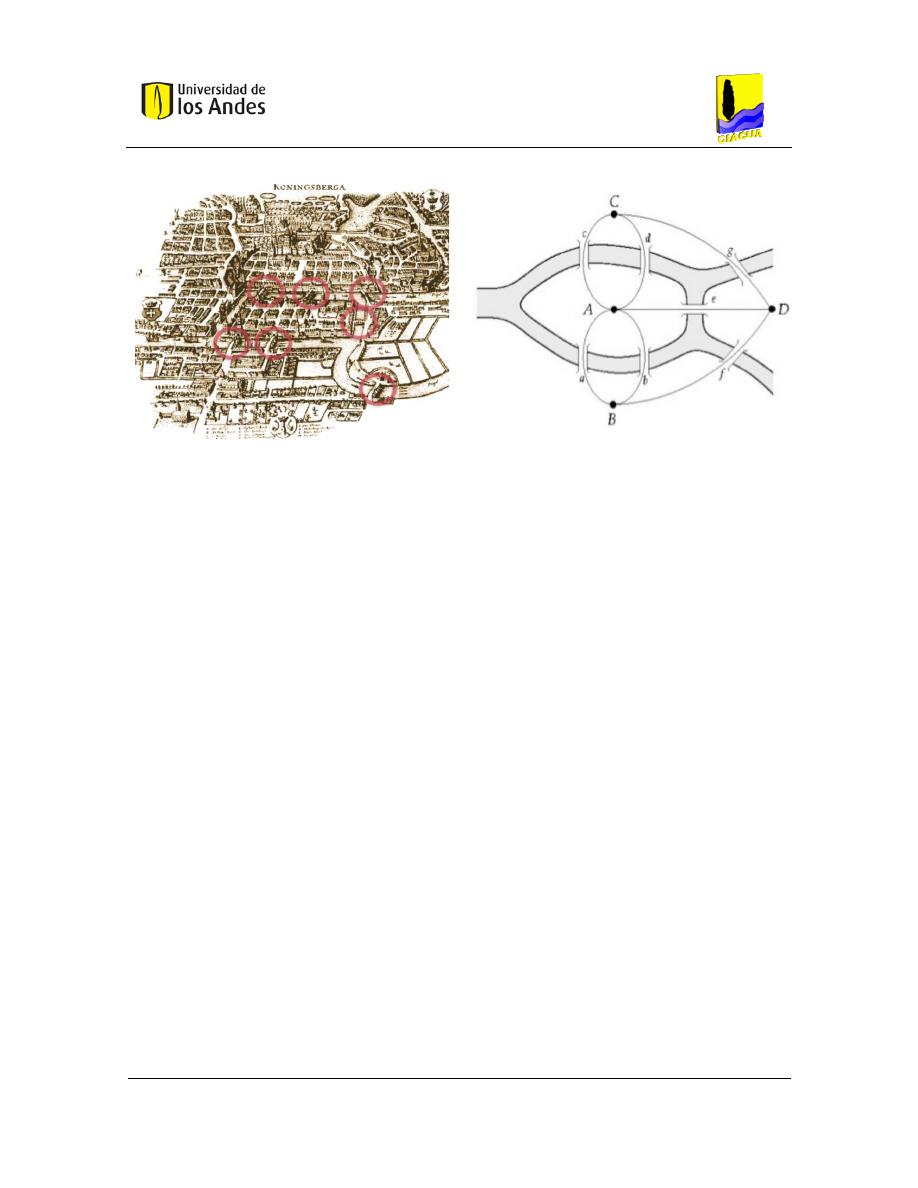
puentes de Konigsberg (The Bridges of Konigsberg). El problema intenta solucionar la
pregunta: ¿puede alguien cruzar los 7 puentes de Konigsberg sin cruzar por más de un
puente a la vez?
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
23
Figura 3-1. Problema "The Bridges of Konisberg" (Barabási, Towlson, & Cornelius, 2018)
Euler soluciona esta pregunta diciendo que no es posible y establece que (1735
– Teorema
de Euler):
a) Si un grafo tiene más de dos nodos con grado impar, no existe un camino.
b) Si un grafo está conectado y no tiene nodos con grado impar, tiene al menos un
camino.
Con este teorema nace el estudio de los grafos y se plantea la representación geométrica
de los sistemas mediante la caracterización de su topología.
Un grafo se puede representar como
𝐺 = 𝐺(𝑉, 𝐸), en donde 𝑉 es un conjunto de nodos con
𝑛 elementos (tamaño del grafo) y 𝐸 es el conjunto de links con 𝑚 elementos (orden del
grafo). En el caso más simple, los grafos son representaciones planas sin peso y sin
dirección, no obstante, es posible realizar la representación matemática de una red teniendo
en cuenta la dirección de los enlaces (aristas dirigidas) y la información en los nodos
(pesos).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
24
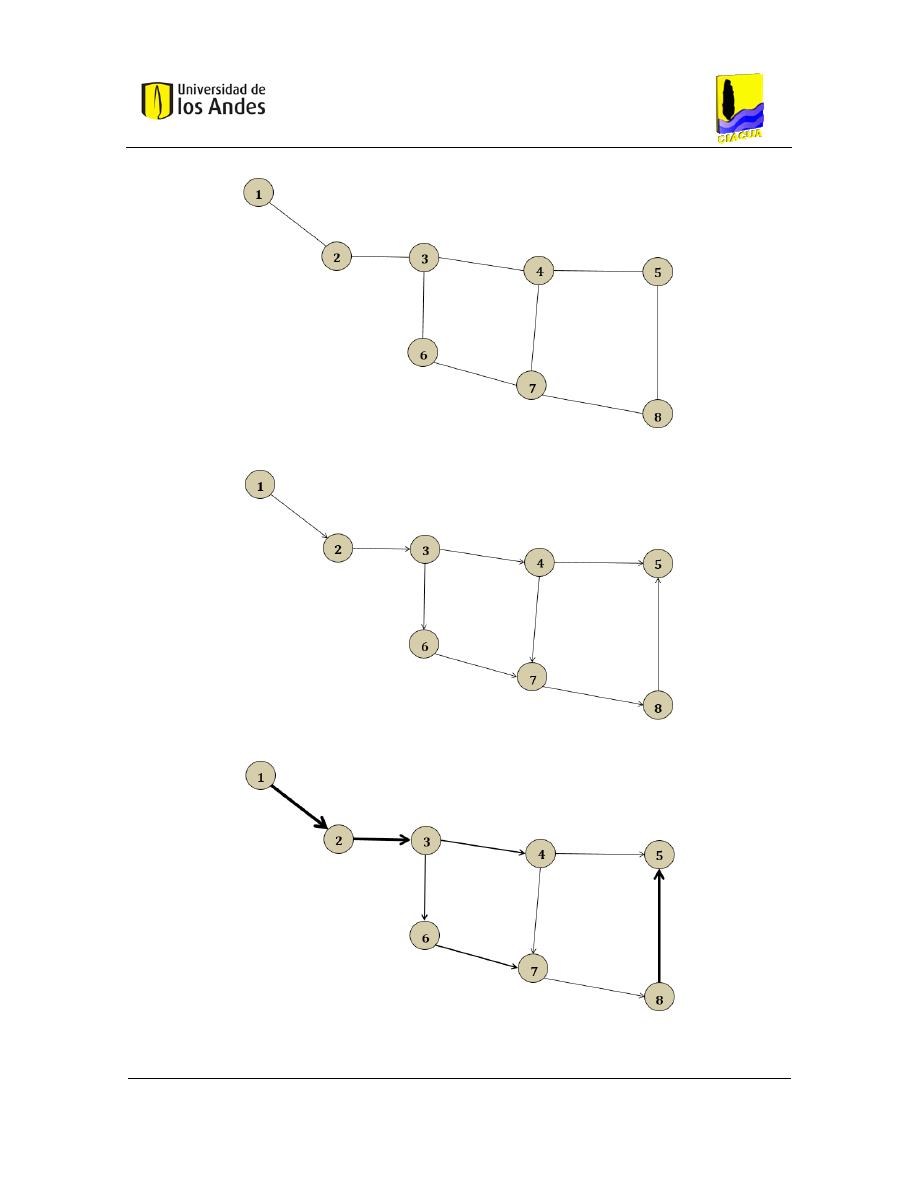
Figura 3-2. Grafo (no dirigido - sin peso)
Figura 3-3. Grafo dirigido
Figura 3-4. Grafo dirigido y con peso
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
25
A continuación, se presenta una serie de características generales de los grafos.
Grado, grado promedio y distribuciones de grados
El grado del nodo es el número de links conectados al nodo. Usualmente se denota con la
letra
𝑘. En redes con dirección (dirigidas) se puede definir el grado de entrada y el grado de
salida, el grado total sería la suma del grado entrante y el saliente (Barabási et al., 2018).
𝑘
6
= 2
𝑘
4
= 3
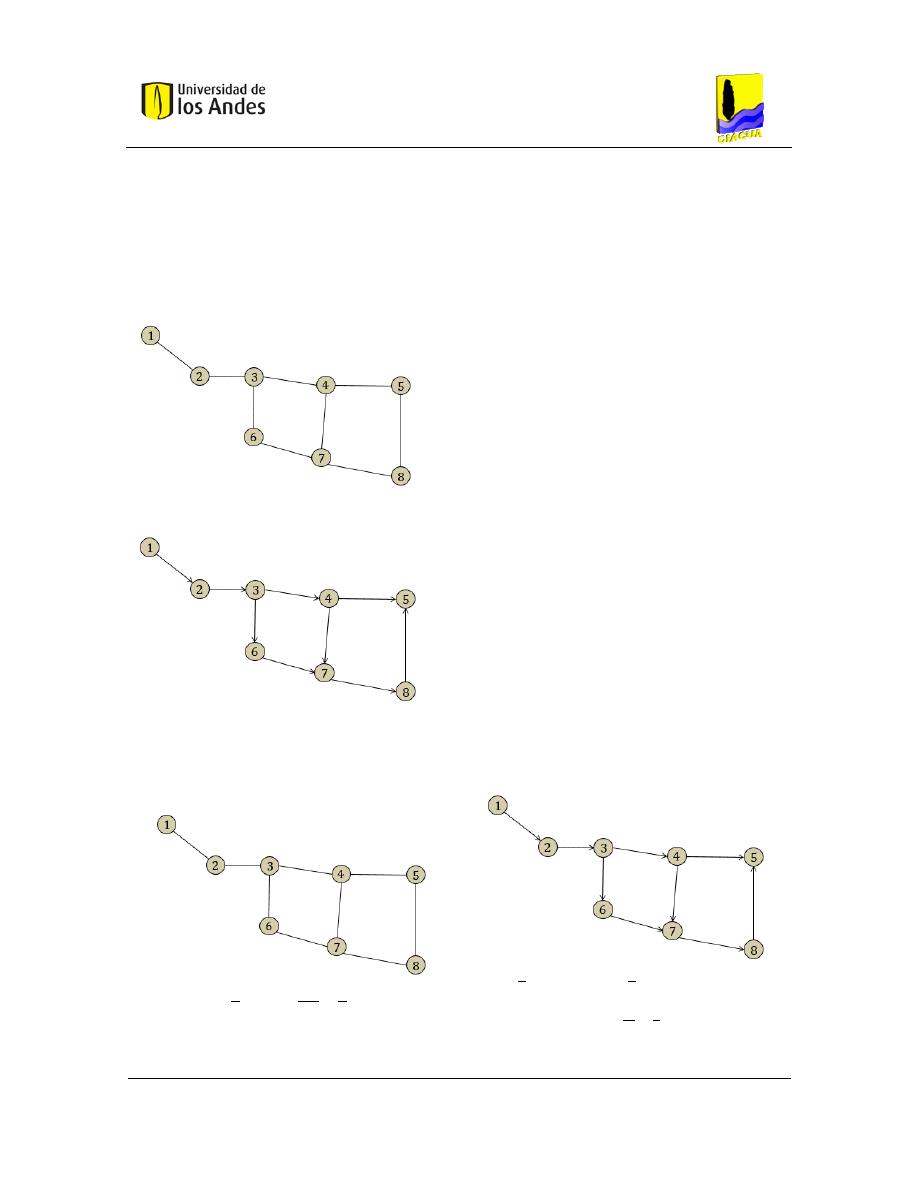
Figura 3-5. Grado para grafos no dirigidos
𝑘
7
𝑖𝑛
= 2
𝑘
7
𝑜𝑢𝑡
= 1
𝑘
7
= 3
Figura 3-6. Grado para grafos dirigidos
El grado promedio del grafo 〈
𝑘〉 es simplemente la suma de cada uno de los grados de los
nodos dividido en el número total de nodos.
〈𝑘〉 =
1
𝑛
∑ 𝑘
𝑖
𝑖=1
=
2𝑚
𝑛
=
9
4
= 2.25
〈𝑘
𝑖𝑛
〉 =
1
𝑛
∑ 𝑘
𝑖
𝑖𝑛
; 〈𝑘
𝑜𝑢𝑡
〉 =
1
𝑛
∑ 𝑘
𝑖
𝑜𝑢𝑡
; 〈𝑘
𝑖𝑛
〉 = 〈𝑘
𝑜𝑢𝑡
〉
𝑖=1
𝑖=1
〈𝑘〉 =
𝑚
𝑛
=
9
8
Figura 3-7. Grado promedio del grafo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
26
La distribución del grado
𝑃(𝑘) es la probabilidad de que un nodo tenga el grado 𝑘.
Figura 3-8. Distribución del grado P(k)
Vecindarios
De cada nodo dentro de un grafo es posible hablar de vecindarios, haciendo referencia al
conjunto de nodos que se conectan a él. Si el grafo es dirigido, existen vecindarios de
entrada y de salida.
0
0.2
0.4
0.6
0.8
1
1.2
0
1
2
3
P(
k)
k
0
0.2
0.4
0.6
0.8
1
1.2
0
1
2
3
P(
k)
k
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
27
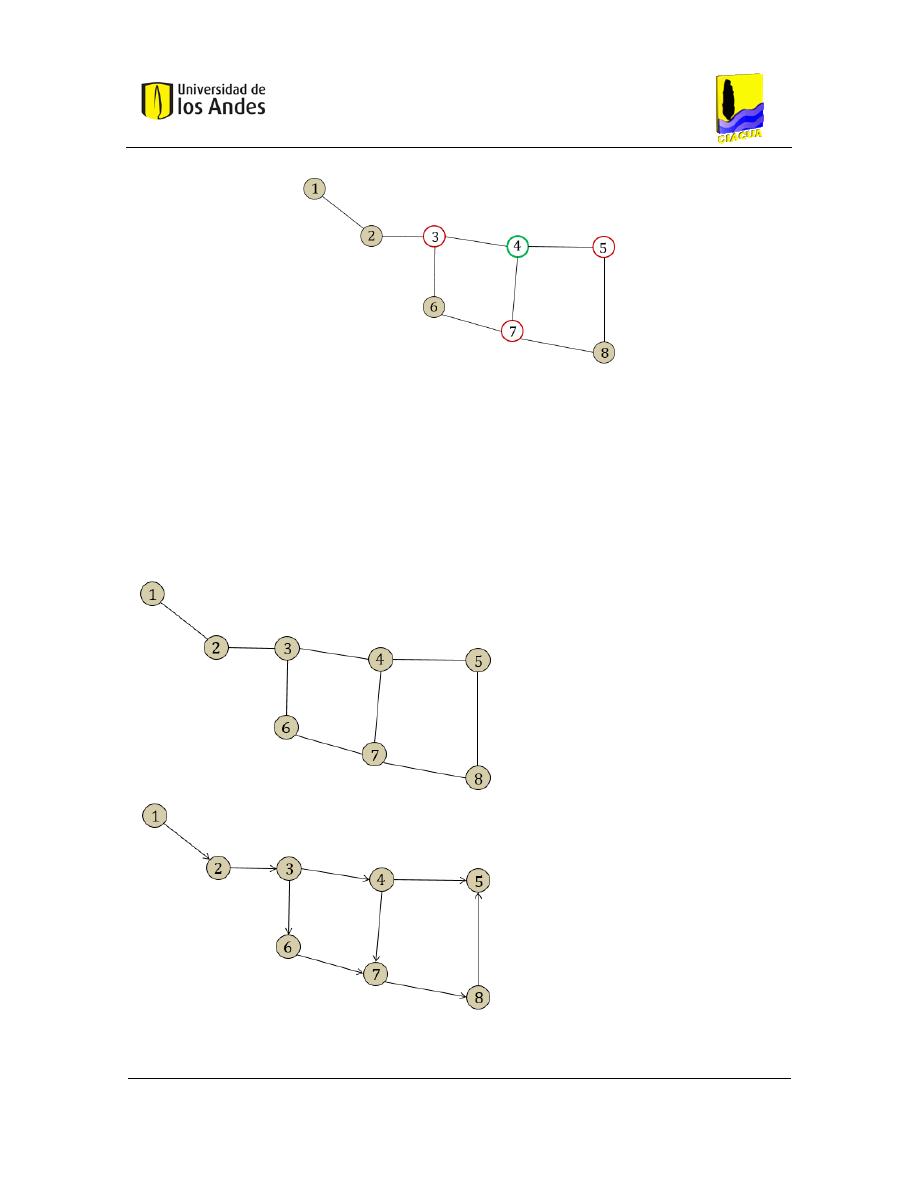
Figura 3-9. Vecindario (nodo 4)
Matriz de adyacencia – representación del grafo
La representación del grafo se realiza mediante la matriz de adyacencia [
𝐴]. Esta matriz,
de tamaño
𝑛 𝑥 𝑛 y está compuesta por unos (1 si hay conexión entre nodos) y 0 (si no existe
conexión entre los nodos) cuando es un grafo sin peso. En caso de que se tenga en cuenta
el peso, los valores 1 y 0 son remplazados por el peso respectivo
(𝐴
𝑖𝑗
= 𝑤
𝑖𝑗
) (Barabási et
al., 2018).
𝐴
𝑖𝑗
=
[
0
1 0 0 0 0 0 0
1
0 1 0 0 0 0 0
0
1 0 1 0 1 0 0
0
0 1 0 1 0 1 0
0
0 0 1 0 0 0 1
0
0 1 0 0 0 1 0
0
0 0 1 0 1 0 1
0
0 0 0 1 0 1 0]
𝐴
𝑖𝑗
=
[
0
1 0 0 0 0 0 0
0
0 1 0 0 0 0 0
0
0 0 1 0 1 0 0
0
0 0 0 1 0 1 0
0
0 0 0 0 0 0 0
0
0 0 0 0 0 1 0
0
0 0 0 0 0 0 1
0
0 0 0 1 0 0 0]
Figura 3-10. Matriz de adyacencia
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
28
Caminos y ciclos
Si un grafo está completamente conectado (grafo conexo), existen caminos entre todos los
nodos de la red. Un camino entre un nodo
𝑖 y un nodo 𝑗 es una sucesión de nodos que
comienza en
𝑖 y termina en 𝑗 en donde cada par de nodos consecutivos está conectado por
un enlace. Se dice que es un camino simple si todos los nodos son distintos entre sí y un
ciclo si el nodo inicial es el mismo que el final. Los caminos tienen una longitud y un peso
(grafos con peso), la primera hace referencia al número de aristas del camino y el peso, es
la suma de los pesos de las aristas del camino (en caso de que haya) (Barabási et al.,
2018).
𝐶𝑎𝑚𝑖𝑛𝑜
3,8
→ 𝐿𝑜𝑛𝑔𝑖𝑡𝑢𝑑 = 3
𝐶𝑖𝑐𝑙𝑜
4
→ 𝐿𝑜𝑛𝑔𝑖𝑡𝑢𝑑 = 4
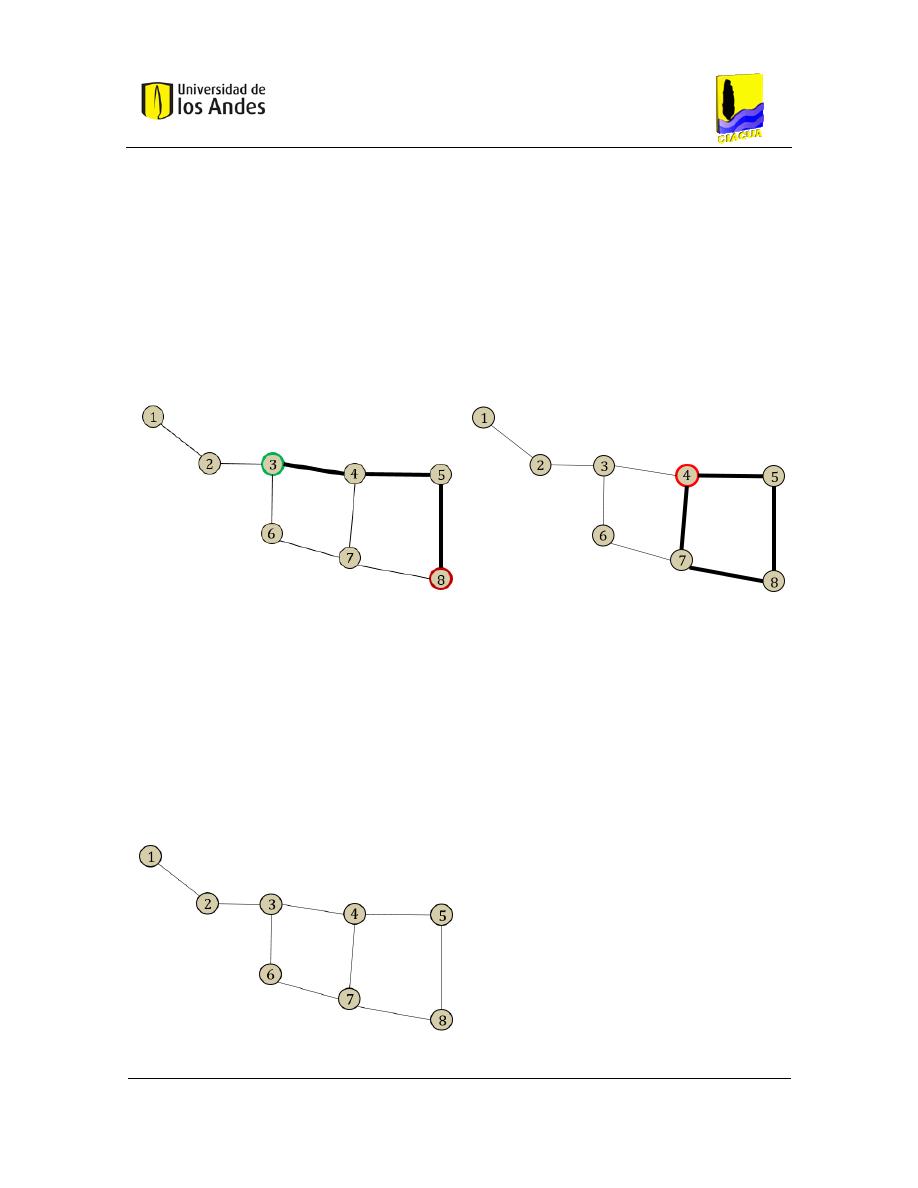
Figura 3-11. Caminos y ciclos en grafos
La distancia
𝑑 (camino más corto, camino geodésico) entre dos nodos se define como el
número de links totales en el camino más corto que los conecta. Si dos nodos están
desconectados, la distancia sería infinita. Para grafos dirigidos, cada camino sigue la
secuencia de los arcos, por lo cual, usualmente la diferencia entre dos nodos
𝑖 y 𝑗 es
diferente a la distancia entre
𝑗 e 𝑖. El diámetro 𝑑
𝑚á𝑥
es la distancia máxima entre cualquier
par de nodos en un grafo (Barabási et al., 2018).
𝑑
𝑖𝑗
=
[
0 1
2 3
4 3
4 5
1 0
1 2
3 2
3 4
2 1
0 1
2 1
2 3
3 2
1 0
1 2
1 2
4 3
2 1
0 3
2 1
3 2
1 2
3 0
1 2
4 3
2 1
2 1
0 1
5 4
3 2
1 2
1 0]
→ ∑
|
|
|
22
16
12
12
16
14
14
18
|
|
|
∑𝑑
𝑖𝑗
= 124
𝑑
𝑚á𝑥
= 5
〈𝑑〉 = 2.214
Figura 3-12. Distancias, diámetro y longitud promedio de los caminos de un grafo
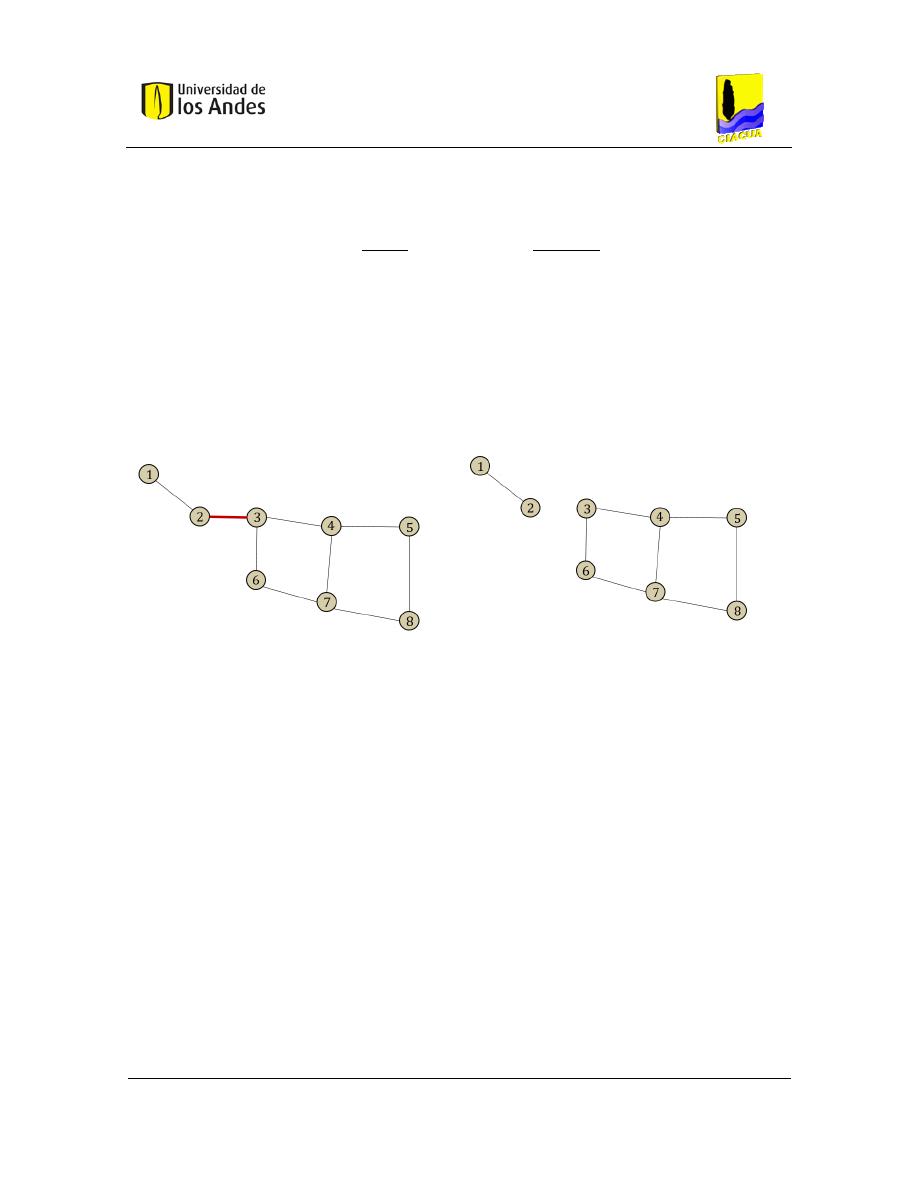
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
29
Para un grafo conexo, la longitud promedio de los caminos 〈
𝑑〉 (average path length)
equivale a:
〈𝑑〉 ≡
1
2 𝐿
𝑚á𝑥
∑ 𝑑
𝑖𝑗
𝑖,𝑗≠𝑖
; 𝐿
𝑚á𝑥
=
𝑁(𝑁 − 1)
2
donde
𝑑
𝑖𝑗
es la distancia del nodo
𝑖 al nodo 𝑗 (Barabási et al., 2018).
Conectividad
En un grafo no dirigido, se dice que es conexo si todo par de nodos están conectados por
un camino. Un grafo no-conexo está hecho por dos o más componentes conexos. Se
considera como un puente a un enlace que al quitarse desconecta el grafo (
𝑃𝑢𝑒𝑛𝑡𝑒 = 𝑁
2
→
𝑁
3
).
Figura 3-13. Conectividad de un grafo
Para grafos dirigidos, se dice que es un grafo fuertemente conexo si existe un camino entre
cada nodo de ida y de vuelta, es decir, si existe un camino AB y BA. Un grafo con conexión
débil es aquel que es conexo ignorando las direcciones de los enlaces.
Otras medidas comunes de los grafos
A continuación, se presentan algunas medidas comunes de los grafos. Un estudio completo
de las diferentes métricas de los grafos puede encontrarse en (Costa, Rodrigues, Travieso,
& Boas, 2007) y (Boccaletti et al., 2006).
Coeficiente de Clustering (agrupación) o Transitividad (Barabási et al., 2018). Es la
probabilidad de que dos nodos vecinos a uno dado sean vecinos entre sí. En otras palabras,
calcula la fracción de los nodos vecinos conectados.
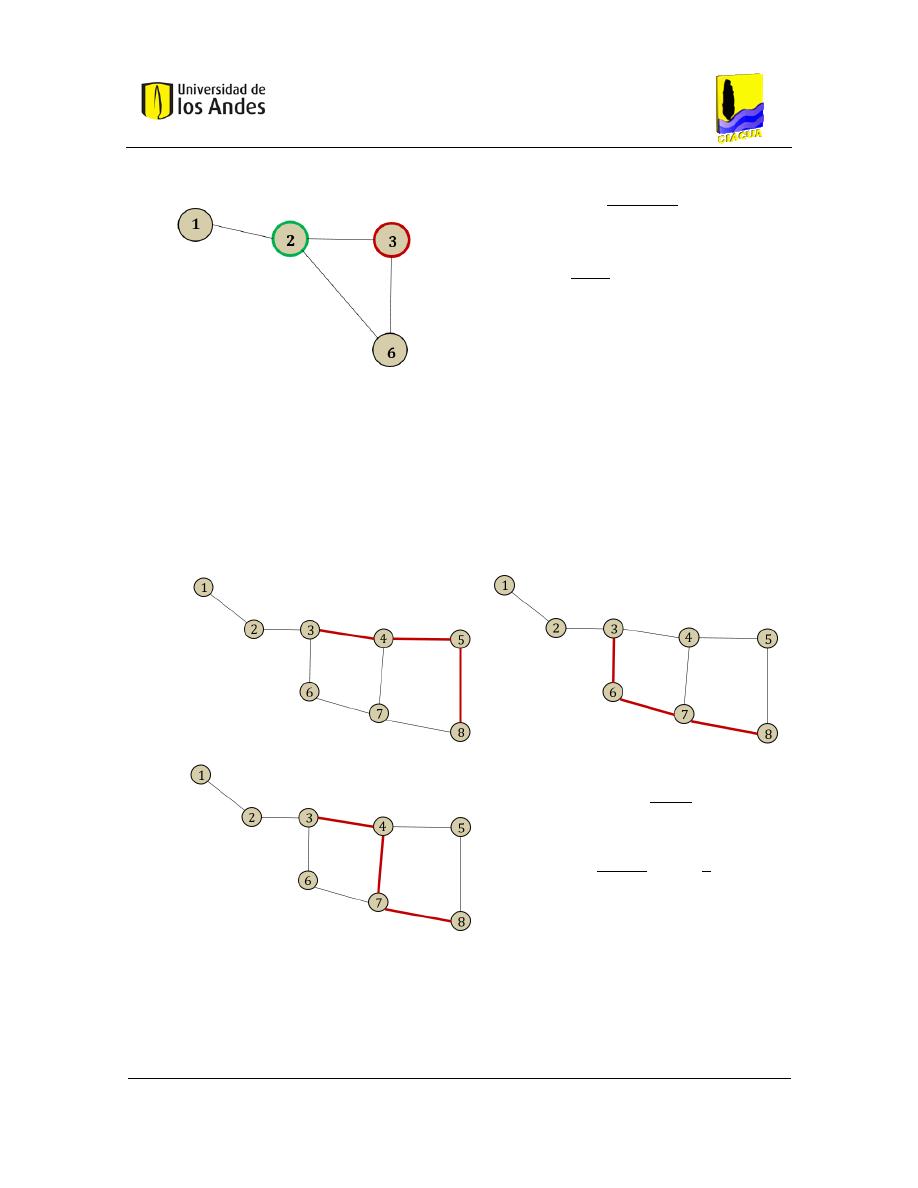
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
30
𝐶
𝑖
=
2𝑒
𝑖
𝑘
𝑖
(𝑘
𝑖
− 1)
𝐶
3
=
2(1)
2(2−1)
= 1 ; 𝐶
2
= 0
𝑒
𝑖
es el número de aristas que conectan entre sí los
nodos adyacentes al nodo i.
Figura 3-14. Coeficiente de agrupación
Medidas de centralidad.
Betweenness, Carga o Intermediación (Barabási et al., 2018). La carga del nodo
𝑘
es la porción de caminos más cortos que van de un nodo
𝑖 a un nodo 𝑗 pasando por
el nodo
𝑘. Es una métrica que da una idea de la conectividad relativa y de la porción
de veces que el nodo (o enlace) puede actuar como puente. Es clasificada como
una medida de centralidad.
𝐶
𝑖
𝐵
= ∑
𝑑
𝑗𝑘
(𝑖)
𝑑
𝑗𝑘
𝑗<𝑘
𝐶
7
𝐵
= ∑
𝑑
3,8
(3)
𝑑
3,8
+ ⋯ =
2
3
+ ⋯
𝑗<𝑘
Figura 3-15. Intermediación (Betweenness)
En la figura se puede observar el proceso del cálculo de la intermediación del nodo
7 teniendo en cuenta únicamente los caminos más cortos entre los nodos 3 y 8. Se
debe realizar el cálculo teniendo todos los pares de nodos. Es posible normalizar la
intermediación del nodo
𝑖 por el número total de pares de nodos excluyendo al nodo
𝑖.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
31
𝐶
𝑖
𝐵
𝑁𝑜𝑟𝑚
=
𝐶
𝑖
𝐵
(𝑁 − 1)(𝑁 − 2)/2
-
Closeness (cercanía) (Barabási et al., 2018). Es el promedio de las distancias más
cortas desde un nodo hacia todos los demás. Mide la centralidad como la
importancia que tiene un vértice en esparcir la información a los otros nodos a través
de las distancias más cortas.
𝐷𝑖𝑠𝑡 =
[
0 1
2
3
4 3
4 5
1 0
1
2
3 2
3 4
2 1
0
1
2 1
2 3
3 2
1
0
1 2
1 2
4 3
2
1
0 3
2 1
3 2
1
2
3 0
1 2
4 3
2
1
2 1
0 1
5 4
3
2
1 2
1 0]
→ ∑
|
|
|
22
16
12
12
16
14
14
18
|
|
|
𝐶
𝑖
𝐶
= [∑ 𝑑
𝑖𝑗
𝑛
𝑗=𝑖
]
−1
𝐶
3
𝐶
=
1
12
= 0.083
Figura 3-16. Cercanía (Closeness)
Esta centralidad también puede normalizarse dividiendo por
(𝑛 − 1).
3.3.1. Métricas topológicas (teoría de grafos) implementadas en RDAP
En esta sección se presentan las diferentes métricas de CNT o teoría de grafos
implementadas en el estudio de RDAP. Las métricas se obtuvieron de recopilar y analizar
toda la información disponible, mediante búsqueda bibliográfica, sobre índices de redes
utilizados en el análisis de RDAP. Para el caso de análisis, los vértices hacen referencia a
los nodos (
𝑛) y los enlaces a las tuberías (𝑚) de la RDAP.
3.3.1.1 Métricas para el estudio de RDAP (grafos no dirigidos y sin peso)
Densidad de enlaces (Link Density) → 𝑞 (Yazdani, Otoo, & Jeffrey, 2011)
La densidad de enlaces es el indicador más básico del (linkedness o sparseness) de la
estructura de una red. Se define como la razón entre el número de enlaces
𝑚 en la red y el
número máximo posible de enlaces de esta misma. Las densidades altas indican RDAP de
mayor conectividad. Es una medida global de la red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
32
𝑞 =
2𝑚
𝑛(𝑛 − 1)
Ecuación 1. Densidad de enlaces
Grado promedio del nodo (Average Node Degree) → 〈𝑘〉 (Newman, 2010; Yazdani
et al., 2011)
El grado promedio del nodo, junto con su histograma, es una medida básica de la
conectividad de la red. Refleja qué tan similar es la red a una red en forma de grilla (lattice-
like), importante hacia la distribución por igual del caudal y la presión bajo demanda
variable. Se define como el número promedio de enlaces conectados a los nodos.
〈𝑘〉 =
2𝑚
𝑛
Ecuación 2. Grado promedio de los nodos
Grado del nodo vecino (Neighborhood Nodal Degree) → 𝑘
𝑛
(Giustolisi et al., 2017)
Es una extensión al grado estándar del nodo. Corresponde a la suma de los grados de los
nodos adyacentes al nodo en cuestión y sirve para clasificar RDAP.
𝑘
𝑛
(𝑖) = ∑ 𝐴
𝑖𝑗
𝑘(𝑗)
𝑗∈𝑁(𝑖)
Ecuación 3. Grado del nodo vecino
donde
𝑘
𝑛
(𝑖) es el grado vecino (integra los nodos adyacentes) del nodo 𝑖, 𝐴
𝑖𝑗
son los
elementos de la matriz adyacente,
𝑘(𝑗) es el grado del nodo estándar y 𝑁(𝑖)es el vecindario
topológico del nodo
𝑖 (el set de nodos adyacentes).
Índice Beta (Beta index) → 𝛽 (Beckmann & Kansky, 2006)
El índice beta es una métrica simple de la estructura de la red. Es la razón entre el número
de enlaces y nodos.
𝛽 =
𝑚
𝑛
Ecuación 4. Índice Beta
Heterogeneidad (Heterogenity) (Gao, Barzel, & Barabási, 2016)
La heterogeneidad es una métrica que mide la diversidad de la red. Se mide como la
varianza de los grados de los nodos.
1
𝑘̅
× ∑(𝑘
𝑖
− 𝑘)
2
𝑛
𝑖=1
Ecuación 5. Heterogeneidad
donde
𝑘̅ es equivalente a 〈𝑘〉, el grado promedio de los nodos de la red y 𝑘
𝑖
es el grado del
nodo
𝑖.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
33
Coeficiente de agrupación (Clustering coefficient) → 𝐶
𝑐
(Wasserman & Faust, 1994;
Yazdani et al., 2011)
También conocida como transitividad, es la probabilidad de que dos nodos vecinos a un
nodo cualesquiera sean vecinos entre sí. Es una medida de redundancia que cuantifica la
densidad de ciclos triangulares y el grado en el que los nodos tienden a estar conectados.
Para redes con estructura de grilla (como muchas RDAP), en las cuales los ciclos tienen
formas geométricas diferentes a las triangulares, el valor del coeficiente de agrupación
tiende a ser bajo. Se mide como la razón entre el número de triángulos de la red y el número
máximo de triángulos posibles.
𝐶
𝑐
=
3𝑁
∆
𝑁
3
Ecuación 6. Coeficiente de agrupación del grafo
donde
𝑁
∆
es el número de triángulos y
𝑁
3
es el número de tripletes de nodos conectados.
Otra forma de medir la transitividad del nodo es mediante la ecuación:
𝐶
𝑖
=
𝑒
𝑖
1
2 𝑘
𝑖
(𝑘
𝑖
− 1)
Ecuación 7. Transitividad del nodo
donde
𝑒
𝑖
es el número de aristas que conectan entre sí los nodos adyacentes al nodo i. El
coeficiente de agrupación total de la red es la sumatoria de los coeficientes individuales de
cada nodo dividido en el número total de nodos.
Coeficiente de “enmallado” (Meshedness coefficient) → 𝑅
𝑚
(Buhl et al., 2006)
Cuantifica el estado general de los bucles (circuitos) en la red. Provee una estimación de la
redundancia topológica en un grafo plano de una RDAP al encontrar el número de circuitos
independientes presentes en la red
(𝑚 − 𝑛 + 1) como un porcentaje del número máximo de
circuitos posibles en la red (
2𝑛 − 5).
𝑅
𝑚
=
𝑚 − 𝑛 + 1
2𝑛 − 5
*
𝑚 − 𝑛 𝑒𝑛 𝑒𝑙 𝑛𝑢𝑚𝑒𝑟𝑎𝑑𝑜𝑟 𝑠𝑖 ℎ𝑎𝑦 𝑚á𝑠 𝑑𝑒 𝑢𝑛𝑎 𝑓𝑢𝑒𝑛𝑡𝑒
Ecuación 8. Coeficiente Meshedness
Longitud promedio de los caminos (Average Path Length) → 𝑙 (Yazdani et al., 2011)
Es la distancia (camino más corto, camino geodésico) promedio
𝑑 entre todos los nodos de
la red. Estima el número promedio mínimo de enlaces que tienen que recorrerse para ir de
un nodo a otro.
𝑙 =
1
𝑛(𝑛 − 1)
× ∑ 𝑑
𝑖,𝑗
𝑛
𝑖,𝑗=1
Ecuación 9. Longitud promedio de los caminos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
34
donde
𝑑
𝑖,𝑗
equivale a la longitud del camino más corto los nodos 𝑖 y 𝑗.
Diámetro (diameter) → 𝑑
𝑇
(Yazdani et al., 2011)
El diámetro de la red es la máxima distancia geodésica de los caminos más cortos entre
cualquier par de nodos de la red.
𝑑
𝑇
= 𝑚á𝑥(𝑑
𝑖,𝑗
)
Ecuación 10. Diámetro del grafo
Eficiencia de la red (Network Efficiency) → 𝐸 (Boccaletti et al., 2006; Torres et al.,
2017)
La eficiencia de la red se puede medir como la distancia física harmónica promedio entre
los nodos de la red. Varía entre 0 para redes con baja eficiencia y 100% para redes de
eficiencia alta. Puede tomarse como una medida indicativa (sustituta) para el tiempo
promedio del viaje del agua en la red.
𝐸 =
1
𝑛(𝑛 − 1)
∑
1
𝑑
𝑖𝑗
𝑖,𝑗∈𝑁,𝑖≠𝑗
Ecuación 11. Eficiencia de la red
Factor de ruta/camino (Route Factor) → 𝑔 (Yazdani & Jeffrey, 2011)
Es una medida de eficiencia basada en la conectividad entre el nodo raíz (un embalse) y el
resto de los nodos de la red.
𝑔
𝑅
=
1
(𝑛 − 1)
∑
∈
𝑠,𝑖
𝛿
𝑠,𝑖
𝑛−1
𝑖=1
Ecuación 12. Factor de ruta
donde
∈
𝑠,𝑖
es la distancia (Euclidiana) combinada de los nodos que conectan al nodo
𝑖 con
la fuente
𝑠, y 𝛿
𝑠,𝑖
es la distancia Euclidiana directa.
Densidad de puentes (Density of bridges) → 𝐷
𝑏𝑟
(Paez & Filion, 2017; Yazdani et
al., 2011)
Es una medida de robustez de la red. Mide el número de enlaces que al removerse de la
red desconectan la desconectan sobre el número total de enlaces. En términos de RDAP,
calcula el porcentaje de las tuberías cuya falla puede potencialmente interrumpir el
suministro de agua al aislar una parte de la red de la fuente de suministro.
𝐷
𝑏𝑟
=
𝑁
𝑏𝑟
𝑚
Ecuación 13. Densidad de puentes
donde
𝑁
𝑏𝑟
es el número de puentes en la red. Un puente es un enlace cuya eliminación
desconecta la red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
35
Densidad de puntos de articulación (Density of Articulation Points) → 𝐷
𝑎𝑝
(Yazdani
et al., 2011)
Al igual que la densidad de los puentes, es una medida de robustez de la red. Calcula el
porcentaje de los nodos cuya falla puede potencialmente interrumpir el suministro de agua
al aislar una parte de la red de la fuente de suministro. Un punto de articulación es un nodo
que, al removerlo, junto con sus enlaces incidentes, desconecta la red. Es la razón entre el
número de puntos de articulación
𝑁
𝑎𝑝
sobre el número total de nodos.
𝐷
𝑎𝑝
=
𝑁
𝑎𝑝
𝑛
Ecuación 14. Densidad de puntos de articulación
Brecha espectral (Spectral Gap) → λ∆ (Estrada, 2006; Yazdani et al., 2011)
Está métrica provee información de la robustez de la red. Es usada con el fin de detectar
redes con
“buenas” propiedades de expansión (es decir, redes que poseen un trazado
óptimo de conectividad). Si el valor de la brecha espectral es grande, se habla de una red
con buenas propiedades de expansión. Si, por el contrario, el valor de la brecha espectral
es pequeño, probablemente indicará la presencia de puentes o puntos de articulación que
al removerse causarán serias disrupciones en el sistema de suministro. La brecha espectral
se calcula como la resta entre los dos valores propios más grandes de la matriz de
adyacencia.
λ∆= λ
1
(𝐴) − λ
2
(𝐴)
Ecuación 15. Brecha espectral
Intermediación (Betweenness Centrality) → 𝐶
𝑏
(Freeman, 1977)
La intermediación, o también llamada carga del nodo, es una medida de centralidad del
nodo. Se calcula como una relación entre el número de caminos más cortos entre dos nodos
que atraviesan cierto nodo sobre el número total de caminos más cortos entre estos dos
puntos. En otras palabras, la carga del nodo
𝑘 es la porción de caminos más cortos que van
de un nodo
𝑖 a un nodo 𝑗 pasando por el nodo 𝑘. Esta métrica da una idea de la conectividad
relativa y de la porción de veces que el nodo (o enlace) puede actuar como puente.
𝐶
𝑏
(𝑘) = ∑
𝑔
𝑖𝑗
(𝑘)
𝑔
𝑖𝑗
𝑖≠𝑗≠𝑘
Ecuación 16. Centralidad Betweenness
donde
𝐶
𝑏
es la intermediación del nodo
𝑘 y 𝑔
𝑖𝑗
(𝑘) es el número de caminos más cortos
entre los nodos
𝑖 y 𝑗 que pasan por el nodo 𝑘, 𝑔
𝑖𝑗
equivale al número total de caminos más
cortos entre
𝑖 y 𝑗.
Dominancia del punto central (Central-point Dominance) → 𝐶
𝐵
(Freeman, 1977;
Yazdani et al., 2011)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
36
Mide la concentración de la topología de la red alrededor de punto más central. Puede
considerarse como un cuantificador de la vulnerabilidad de la red ante fallas cerca al punto
más central de la red. El cálculo de la dominancia del punto central depende del
betweenness o la intermediación de los demás nodos de la red. El valor de la dominancia
del punto central varía entre 0 (para redes regulares con el mismo número de conexiones
en cada nodo) y 1 (para redes con topología de estrella).
𝐶
𝐵
=
1
𝑛 − 1
∑(𝐶
𝑏𝑚á𝑥
− 𝐶
𝑏𝑖
)
𝑖
Ecuación 17. Dominancia del punto central
donde
𝐵
𝑚á𝑥
es la intermediación normalizada máxima de la red y
𝐵
𝑖
es la intermediación
normalizada del nodo
𝑖. La intermediación se normaliza por el factor
𝑛
2
−3𝑛+2
2
.
Cercanía (Closeness) → 𝐶
𝐶
(Freeman, 1977)
Es el promedio de las distancias más cortas desde un nodo hacia todos los demás. Mide la
centralidad como la importancia que tiene un vértice en esparcir la información a los otros
nodos a través de las distancias más cortas.
𝐶
𝑖
𝐶
=
1
∑ 𝑑
𝑖,𝑗
𝑗
Ecuación 18. Closeness
donde
𝐶
𝑖
𝐶
es la cercanía del nodo
𝑖 y 𝑑
𝑖,𝑗
son las distancias de los caminos más cortos entre
el resto de nodos de la red.
Conectividad Algebraica (Algebraic Connectivity) → 𝜆
2
(Yazdani et al., 2011)
Refleja la conectividad del grafo en general. Así mismo, puede implementarse como métrica
para cuantificar la robustez y la tolerancia a fallas de la red en términos de su conectividad.
Se calcula como el segundo valor propio más pequeño de la matriz laplaciana del grafo. La
matriz laplaciana se obtiene de restar la matriz del grado de los nodos con la matriz de
adyacencia.
Límite de eliminación de nodos aleatorios (Threshold for random removal of nodes)
→ 𝑓
𝑐
(Cohen, Erez, Ben-Avraham, & Havlin, 2000)
Esta métrica provee un valor teórico de la fracción critica de nodos que deben ser retirados
de la red para que esta pierda su propiedad de conectividad a gran escala (se da mediante
la destrucción completa del grupo más grande en la red).
𝑓
𝑐
= 1 −
1
〈𝑘
2
〉
〈𝑘〉
− 1
Ecuación 19. Límite eliminación nodos
aleatorios

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
37
Indicador de Modularidad (Modularity Indicator) → 𝚀 (Newman, 2004)
El indicador de modularidad cuantifica la mejor división de redes en comunidades. Se
calcula como la diferencia máxima entre la fracción de enlaces que caen dentro de
comunidades ∑
𝑒
𝑖𝑖
𝑖
y el valor esperado de esta misma cantidad si los enlaces caen al azar
sin tener en cuenta la estructura de comunidad ∑
𝑒
𝑖𝑗
𝑒
𝑘𝑖
𝑖𝑗𝑘
.
max (∑ 𝑒
𝑖𝑖
− ∑ 𝑒
𝑖𝑗
𝑒
𝑘𝑖
𝑖𝑗𝑘
𝑖
)
Ecuación 20. Indicador de Modularidad
En la Tabla 3-1 se presenta un resumen de las métricas presentadas anteriormente.
Tabla 3-1. Métricas implementadas en el análisis de RDAP (grafos sin peso y sin dirección)
Métrica
(Metric)
Ecuación
Cuantifica
Referencia
Densidad de enlaces
(Link Density)
𝑞 =
2𝑚
𝑛(𝑛 − 1)
Estructura
Conectividad
Redundancia
Yazdani et al., 2011
Grado promedio del nodo
(Average Node Degree)
𝑘 =
2𝑚
𝑛
Estructura
Robustez
Conectividad
Yazdani et al., 2011
–
Newman 2010
Grado del nodo vecino
(Neighborhood Nodal
Degree)
𝑘
𝑛
(𝑖) = ∑ 𝐴
𝑖𝑗
𝑘(𝑗)
𝑗∈𝑁(𝑖)
Estructura
Conectividad
Giustolisi et al., 2017
Índice Beta
(Beta Index)
𝛽 =
𝑚
𝑛
Estructura
Kansky, 1963
Heterogeneidad
(Heterogenity)
1
𝑘
× ∑(𝑘
𝑖
− 𝑘)
2
𝑛
𝑖=1
Diversidad
Gao et al., 2016
Coeficiente de
agrupación
(Clustering coefficient)
𝐶
𝑐
=
3𝑁
∆
𝑁
3
Redundancia
(loops)
Yazdani and Jeffrey, 2011
–
Wasserman and Faust, 1994
Coeficiente de enmallado
(Meshedness Coefficient)
𝑅
𝑚
=
𝑚 − 𝑛 + 1
2𝑛 − 5
*
𝑚 −
𝑛 si hay mas de una fuente
Redundancia
Robustez
(loops)
Buhl et al., 2006
Longitud promedio de los
caminos
(Average Path Length)
𝑙 =
1
𝑛(𝑛 − 1)
× ∑ 𝑑
𝑖,𝑗
𝑛
𝑖,𝑗=1
Robustez
Eficiencia
Yazdani and Jeffrey, 2011
Diametro
(Diameter)
𝑑
𝑇
= 𝑚á𝑥(𝑑
𝑖,𝑗
)
Eficiencia
Robustez
Yazdani et al., 2011
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
38
Métrica
(Metric)
Ecuación
Cuantifica
Referencia
Eficiencia de la red
(Network Efficiency)
𝐸 =
1
𝑛(𝑛 − 1)
∑
1
𝑑
𝑖𝑗
𝑖,𝑗∈𝑁,𝑖≠𝑗
Eficiencia
Boccaletti et al., 2006;
Torres et al., 2017)
Factor de ruta/camino
(Route Factor)
𝑔 =
1
(𝑛 − 1)
∑
∈
𝑠,𝑖
𝛿
𝑠,𝑖
𝑛−1
𝑖=1
Eficiencia
Yazdani et al., 2011; Black
W., 2003
Densidad de los puentes
(Density of Bridges)
𝐷
𝑏𝑟
=
𝑁
𝑏𝑟
𝑚
Robustez
Yazdani and Jeffrey, 2011;
Paez and Fillion, 2017
Densidad de puntos de
articulación
(Density of Articulation
Points)
𝐷
𝑎𝑝
=
𝑁
𝑎𝑝
𝑛
Robustez
Yazdani et al., 2011
Brecha espectral
(Spectral Gap)
λ∆= λ
1
(𝐴) − λ
2
(𝐴)
Robustez
Yazdani and Jeffrey, 2011 -
Estrada, 2006
Dominancia del punto
central
(Central Point
Dominance)
𝐶
𝐵
=
1
𝑛 − 1
∑(𝐵
𝑚𝑎𝑥
− 𝐵
𝑖
)
𝑖
B es la intermediación normalizada
𝐵
𝑖
=
2 𝐶
𝑏
(𝑖)
𝑛
2
− 3𝑛 + 2
Robustez
Yazdani et al., 2011;
Freeman, 1977
Intermediación
(Betweenness Centrality)
𝐶
𝑏
(𝑘) = ∑
𝑔
𝑖𝑗
(𝑘)
𝑔
𝑖𝑗
𝑖≠𝑗≠𝑘
Centralidad del
Nodo
Freeman, 1977
Cercanía
(Closeness)
𝐶
𝑖
𝐶
=
1
∑ 𝑑
𝑖,𝑗
𝑗
Centralidad del
Nodo
Freeman, 1977
Conectividad algebraica
Algebraic Connectivity
λ
2
Conectividad
Robustez
Yazdani and Jeffrey, 2011
Límite de eliminación de
nodos aleatorios
Threshold for random
removal of nodes
𝑓
𝑐
= 1 −
1
〈𝑘
2
〉
〈𝑘〉
− 1
Conectividad
Cohen et al., 2000
Indicador de modularidad
Modularity indicator
max (∑ 𝑒
𝑖𝑖
− ∑ 𝑒
𝑖𝑗
𝑒
𝑘𝑖
𝑖𝑗𝑘
𝑖
)
Modularidad
Newman, 2004

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
39
3.3.1.2 Métricas ajustadas para el estudio de RDAP
Como se mencionó anteriormente, es posible que la representación de una red a través de
un grafo considere la dirección y el peso de sus enlaces. Muchos investigadores han
concluido que esto puede mejorar el análisis de la red, no obstante, son pocos los que han
incorporado esto en sus análisis. A continuación, se mostrarán dos métricas encontradas
en la literatura que incorporan el peso o la dirección para el análisis de las RDAP.
Grado entrópico ajustado por demanda (Demand- Adjusted Entropic Degree) → 𝑓
𝑖
(Yazdani & Jeffrey, 2012c)
El grado entrópico ajustado por demanda es una adaptación del grado entrópico
𝑔
𝑖
, una
medida cuantitativa de la importancia del nodo (Bompard et al., 2009) presentada por
Yazdani y Jeffrey (2012). Con esta medida es posible clasificar los nodos de la red de
acuerdo con su centralidad y el impacto que generaría en el rendimiento de la red si llegase
a fallar.
𝑓
𝑖
=
g
i
2
(1 +
𝑑
𝑖
𝑀
𝑑
)
𝑀
𝑑
= 𝑑𝑒𝑚𝑎𝑛𝑑𝑎 𝑚á𝑥𝑖𝑚𝑎
𝑑
𝑖
= 𝑑𝑒𝑚𝑎𝑛𝑑𝑎 𝑛𝑜𝑚𝑖𝑛𝑎𝑙
𝑔
𝑖
= (1 − ∑ 𝑝
𝑖𝑗
log(𝑝
𝑖𝑗
)) ∑ 𝑤
𝑖𝑗
𝑗
𝑗
𝑝
𝑖𝑗
= 𝑤
𝑖𝑗
/ ∑ 𝑤
𝑖𝑗
𝑗
𝑤
𝑖𝑗
=
𝜋𝐿
𝑖𝑗
𝐷
𝑖𝑗
2
4
𝑑𝑜𝑛𝑑𝑒 𝐿
𝑖𝑗
𝑦 𝐷
𝑖𝑗
ℎ𝑎𝑐𝑒𝑛 𝑟𝑒𝑓𝑒𝑟𝑒𝑛𝑐𝑖𝑎 𝑎
𝑙𝑎 𝑙ó𝑛𝑔𝑖𝑡𝑢𝑑 𝑦 𝑒𝑙 𝑑𝑖á𝑚𝑒𝑡𝑟𝑜 𝑑𝑒 𝑙𝑎 𝑡𝑢𝑏𝑒𝑟𝑖𝑎, 𝑟𝑒𝑠𝑝𝑒𝑐𝑡𝑖𝑣𝑎𝑚𝑒𝑛𝑡𝑒.
Ecuación 21. Grado entrópico
ajustado (demanda)
Como se puede observar, el grado entrópico ajustado por demanda tienen cuenta
características de la red (demandas) y utiliza como peso el volumen de cada tubería. Esto
permite una mejor clasificación de la importancia de los nodos de la red.
Intermediación ajustada (Tailored edge betweenness) → 𝐵
𝑒
(Giustolisi, Ridolfi, &
Simone, 2019)
La intermediación ajustada propuesta por Giustolisi et al., es un ajuste de la métrica de
centralidad por intermediación (betweenness). Este ajuste tiene en cuenta la centralidad de
los enlaces (en vez de los nodos), el tipo de nodo (clasificación de nodos) y la
implementación de peso y dirección en el grafo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
40
𝐵
𝑒
(𝑘) = ∑
ℎ
𝑖𝑗
(𝑘)
ℎ
𝑖𝑗
𝑖≠𝑗≠𝑘
Ecuación 22. Intermediación ajustada (Tailored
Edge Betweenness)
donde
𝐵
𝑒
(𝑘) es la intermediación ajustada del enlace 𝑘, ℎ
𝑖𝑗
(𝑘) es el número de caminos
más cortos entre
𝑖 y 𝑗 que atraviesan el enlace 𝑘 y ℎ
𝑖𝑗
es el número de caminos más cortos
entre
𝑖 y 𝑗.
3.3.2. Branch Index y sistema de clasificación
Según su topología, una RDAP se puede clasificar como una red ramificada (branch) o
como una red enmallada (grid) y debido a que ninguno de los indicadores propuestos por
la teoría de grafos logra caracterizar la red en las dos características mencionadas
anteriormente, Hwang & Lansey (2017)
plantearon el “Branch Index (BI)”.
𝐵𝐼 =
𝑒
𝑏
𝑒
𝑟
+ 𝑒
𝑏
Ecuación 23. Branch Index
Donde
𝑒
𝑟
y
𝑒
𝑏
equivalen al número de enlaces de la red reducida y el número de enlaces
ramificados, respectivamente. La red reducida se obtiene mediante la implementación del
“node-reduction algorithm” creado por Hwang & Lansey. En términos generales, el algoritmo
elimina los nodos y tuberías no esenciales para la clasificación topológica de la red.
Si se relaciona el
𝐵𝐼 con la red reducida, en especial con el coeficiente de enmallado de la
red reducida y el diámetro promedio de la red (ponderado por la longitud de las tuberías),
es posible realizar una clasificación topológica de las RDAP. A continuación, se muestra el
diagrama de clasificación propuesto por Hwang & Lansey (2017) para la clasificación
topológica y funcional de RDAP.
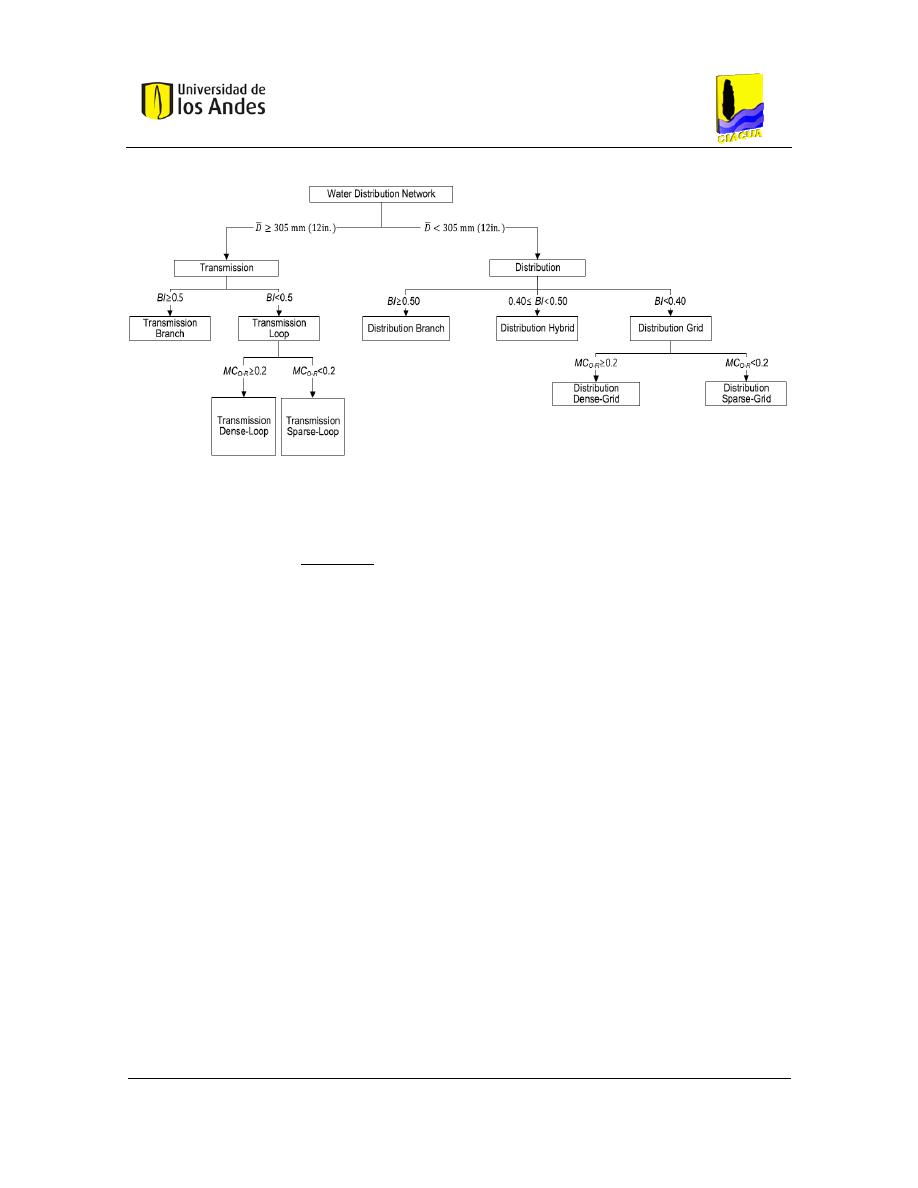
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
41
Figura 3-17. Diagrama de clasificación de RDAP (Hwang & Lansey, 2017)
El cálculo del diámetro promedio se realiza de la siguiente forma:
𝐷
̅
=
∑
𝐷
𝑘
𝐿
𝑘
𝑚
𝑘=1
∑
𝐿
𝑘
𝑚
𝑘=1
Ecuación 24. Diámetro promedio de red
(ponderado por la longitud)
donde
𝐷
𝑘
= diámetro del tubo
𝑘; 𝐿
𝑘
= longitud del tubo
𝑘; and 𝑚 = número de tubos en la
RDAP. Si
𝐷
̅
es igual o mayor a 305 mm (12 in), se puede decir que es un sistema de
trasmisión (red matriz) mientras que si
𝐷
̅
es menor a 305 mm (12 in), se habla de un sistema
de distribución. El
𝑀𝐶
𝑂−𝑅
hace referencia al coeficiente de enmallado de la red reducida.
3.4. Propiedades geométricas de componentes de la red
Como complemento al estudio de la topología de la red, se han estudiado las propiedades
geométricas mediante la evaluación de índices que tienen en cuenta características propias
de la RDAP (como diámetro, longitud de las tuberías, ubicación espacial de los nodos, entre
otros). Así mismo, es posible evaluar algunos atributos geométricos que miden centroides
en la red como los descritos por Moreno et al. (2018). Estas propiedades geométricas se
separan de la teoría de grafos ya que, son propiedades propias de las RDAP.
Características básicas
Las características básicas son aquellas que se pueden calcular sin realizar simulaciones
hidráulicas de la red. Estas características están asociadas a los componentes que son
variables de decisión y restricciones en el problema de optimización de RDAP. Sirven para
clasificar las redes en términos de masa transportada, tamaño e importancia. En general,
están asociadas con las características de las tuberías y los nodos. Como, por ejemplo: la

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
42
distribución de diámetros de las tuberías; longitud promedio de las tuberías; demandas en
los nodos, entre otras.
Centroides
Moreno et al. (2018) estudiaron la relación entre la densidad poblacional y la topología en
RDAP. Como parte de su estudio, presentaron diferentes indicadores para evaluar atributos
geométricos de la red. Estos indicadores fueron calculados utilizando las coordenadas X y
Y de los nodos y los valores obtenidos fueron llamados centorides. Estos centroides fueron
calculados para el volumen, la potencia, la potencia específica y el diámetro. Se debe
mencionar que para realizar el cálculo de estos índices se debe realizar una simulación
hidráulica.
𝐶
𝑉
=
∑
𝑉
𝑖
𝑛𝑡
𝑖=1
∗ 𝐷
𝑖𝑠𝑡 𝑖
𝑉
𝑇
Ecuación 25. Centroide de Volumen RDAP
𝐶𝑃
𝑠
=
∑
𝑃
𝑆𝑖
𝑛𝑡
𝑖=1
∗ 𝐷
𝑖𝑠𝑡 𝑖
𝑃
𝑆𝑇
𝑃
𝑠𝑖
= 𝑞
𝑖
(ℎ
𝑖,𝑖𝑛𝑖
− ℎ
𝑖,𝑓𝑖𝑛
)
Ecuación 26. Centroide de Potencia Específica
RDAP
𝐶
𝑑
=
∑
𝑑
𝑖
∗ 𝐷
𝑖𝑠𝑡 𝑖
𝑛
𝑡
𝑖=1
∑
𝑑
𝑖
𝑛
𝑡
𝑖=1
Ecuación 27. Centroide de Diámetro RDAP
𝐶
𝑃
=
∑
𝑄
𝐷
𝑛
𝑛
𝑖=1
∗ ℎ
𝑖
∗ 𝐷
𝑖𝑠𝑡 𝑖
∑
𝑄
𝐷
𝑛
𝑛
𝑖=1
∗ ℎ
𝑖
Ecuación 28. Centroide de Potencia RDAP
donde
𝑉
𝑖
es el volumen de la tubería
𝑖; 𝑉
𝑇
es el volumen total;
𝑃
𝑠𝑖
es la potencia específica
de la tubería
𝑖; 𝑞
𝑖
es el caudal en la tubería
𝑖; ℎ
𝑖,𝑖𝑛
, ℎ
𝑖,𝑓𝑖𝑛
son las alturas piezométricas en el
nodo inicial y el nodo final de la tubería
𝑖; 𝑃
𝑆𝑇
es la potencia específica total; 𝑑
𝑖
es el diámetro
de la tubería
𝑖; 𝑄
𝐷
es el caudal demandado en el nodo
𝑖; ℎ
𝑖
es la altura piezométrica del
nodo
𝑖, 𝑛
𝑡
es el número de tuberías y
𝑛
𝑛
es el número de nodos de demanda. En la ecuación
de centroide de potencia, la distancia
𝐷𝑖𝑠𝑡
𝑖
se calcula con las coordenadas X y Y de los
nodos, para el resto de las ecuaciones:
𝐷𝑖𝑠𝑡
(𝑥
𝑖
)
=
|𝐶
𝑥
𝑖𝑛𝑖
− 𝐶
𝑥
𝑓𝑖𝑛
|
2
+ min (𝐶
𝑥
𝑖𝑛𝑖
, 𝐶
𝑥
𝑓𝑖𝑛
)
Ecuación 29. Cálculo de distancias centroides
de red

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
43
𝐷𝑖𝑠𝑡
(𝑦
𝑖
)
=
|𝐶
𝑦
𝑖𝑛𝑖
− 𝐶
𝑦
𝑓𝑖𝑛
|
2
+ min (𝐶
𝑦
𝑖𝑛𝑖
, 𝐶
𝑦
𝑓𝑖𝑛
)
donde
𝐶
𝑥
𝑖𝑛𝑖
,
𝐶
𝑥
𝑓𝑖𝑛
,
𝐶
𝑦
𝑖𝑛𝑖
y
𝐶
𝑦
𝑓𝑖𝑛
son las coordenadas X y Y de los nodos iniciales y finales
de la tubería
𝑖.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
44
4. ANÁLISIS GEOMÉTRICO DE RDAP
Teniendo en cuenta la recopilación bibliográfica hecha sobre la optimización y el estudio de
la geometría de RDAP, es posible concluir:
-
La optimización de RDAP abarca una gran variedad de problemas, todos descritos
previamente. De estos, en el que más se ha avanzado es en la optimización de los
componentes de la red, en especial del diámetro de sus tuberías. Así mismo, podría
considerarse como el problema más simple de tratar para comenzar a abrir un
camino y entender la geometría de los diseños optimizados de RDAP. Por estas
razones, la realización del análisis geométrico de RDAP diseñadas óptimamente se
debe enfocar principalmente en la geometría de los diseños optimizados en costos
de sus tuberías.
-
La gran mayoría de estudios en RDAP que implementan teoría de redes complejas
ha supuesto grafos sin peso, por lo cual, no han incluido características geométricas
de los componentes de la red en el análisis realizado. (Yazdani & Jeffrey, 2012c),
(Hwang & Lansey, 2017) y (Giustolisi et al., 2019) han realizado esfuerzos para
considerar características de RDAP en el cálculo de métricas topológicas, más sin
embargo se han concentrado en métricas locales.
-
Las métricas del mundo de la teoría de grafos son de alta eficiencia computacional.
Por lo cual, la adaptación de estas para el análisis de RDAP puede traer consigo
grandes beneficios en el análisis de redes muy extensas.
-
Otros componentes que permiten analizar la topología de la red, como los centroides
de la red, pueden ser un complemento importante para el análisis geométrico de las
RDAP.
-
Con el fin de poder comparar los diseños de RDAP optimizados en costos vs. los
diseños no optimizados, es necesario proponer nuevos índices que midan
características hidráulicas del sistema, así como el diámetro de sus tuberías
optimizadas.
Con estas conclusiones, se plantea una metodología para realizar el análisis geométrico de
RDAP diseñadas óptimamente, la cual consiste en los siguientes pasos:
1. Selección de índices para el análisis de RDAP (identificación de índices más adecuados
para la caracterización geométrica de RDAP)
a. Evaluación de índices en RDAP
b. Caracterización de RDAP
2. Ajuste de índices seleccionados para análisis geométrico de RDAP
a. Índices de teoría de grafos ajustados a características hidráulicas y
geométricas de la red.
b. Evaluación de índices
3. Análisis geométrico de RDAP diseñadas óptimamente

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
45
a. Evaluación de índices en diseños no optimizados
b. Optimización de redes
c. Evaluación de índices en diseños optimizados
En este capítulo se muestra el paso a paso seguido para determinar lo expuesto en los
pasos anteriormente descritos debido a que no existe una metodología establecida para
realizar un análisis geométrico de las redes de distribución de agua potable. En el capítulo
siguiente (capítulo 5) se establece la metodología de optimización y posteriormente se
analizan una serie de redes (casos de estudio).
4.1. Selección de índices para el análisis de RDAP
Teniendo en cuenta que existe gran cantidad de índices de CNT, es necesario realizar una
selección de cuáles de estos son más adecuados para el análisis de RDAP. Para esto, se
escogen diferentes RDAP y se evalúan los índices de CNT para grafos simples (sin peso y
sin dirección) con el fin de observar el comportamiento general de los índices (establecer
relaciones). Es importante mencionar que únicamente se trabajó con índices globales, las
métricas de CNT para la cuantificación de cada elemento (métricas locales), no son tenidas
en cuenta para la caracterización general de la red. Así mismo, se tuvo en cuenta que,
basado en la revisión de la literatura mencionada en la sección 3.3., existen 6 características
fundamentales para el análisis topológico de RDAP, estas características son: conectividad,
eficiencia, centralidad, diversidad, robustez y modularidad.
4.1.1. Herramientas computacionales
Se desarrolló una herramienta en con el lenguaje de programación R para calcular los
indicadores de teoría de grafos. Este lenguaje de programación cuenta con un paquete
denominado Igraph (Csardi G., 2016) el cual permite calcular la mayoría de los indicadores
de teoría de grafos a partir de la información de la conectividad de la red. Así mismo,
también cuenta con una librería denominada epanet2toolkit que permite la conexión del
lenguaje R con el software hidráulico de EPANET2 (Rossman, 1994), lo que permite que la
información de la red se pueda obtener a través de la lectura del archivo .inp (input file -
archivo de texto) de cada red y que desde R se puedan realizar simulaciones hidráulicas.
4.1.2. Evaluación de índices en RDAP
Para el cálculo inicial de los índices se escogieron 42 RDAP (41 sistemas reales y 1 teórico
– Net3) de diferentes características. En Tabla 4-1 es posible se presentan las
características generales de las redes estudiadas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
46
Tabla 4-1. Características generales de RDAP - caracterización topológica
Red
Tuberías
Nodos
Bombas
Tanques
Embalses
Válvulas
Demanda
(LPS)
KY1
984
856
1
2
1
0
87.27
KY2
1124
811
1
3
1
0
91.55
KY3
366
269
5
3
3
0
87.93
KY4
1156
959
2
4
1
0
65.65
KY5
496
420
9
3
4
0
99.37
KY6
644
543
2
3
2
1
71.80
KY7
603
481
1
3
1
0
67.00
KY8
1614
1325
4
5
2
0
107.97
KY9
1270
1242
17
15
4
56
58.74
KY10
1043
920
13
15
2
5
94.72
KY11
846
802
21
28
1
15
76.54
KY12
2426
2347
15
7
1
22
60.04
KY13
940
778
4
5
2
0
103.33
KY14
548
377
5
3
4
0
45.66
KY15
662
659
13
8
2
28
64.72
Net3
117
92
2
3
2
0
192.56
Richmond
949
865
7
6
1
1
15.12
Sector 13 (BOG)
7616
6692
0
0
3
8
426.36
Sector 25 (BOG)
531
609
0
0
1
109
19.85
Sector 35 (BOG)
1291
1191
0
0
1
0
53.27
Zona 2 Sector 10 (BOG)
4193
4673
0
0
2
958
265.40
Zona 2 Sector 14-33 (BOG)
2003
2231
0
0
5
360
126.42
Zona 2 Sector 16 (BOG)
3748
4116
0
0
1
724
178.27
Zona 2 Sector 18 (BOG)
2022
2272
0
0
1
454
128.40
Sector 8-1 (BOG)
754
642
0
0
2
0
18.36
Sector 8-2 (BOG)
688
593
0
0
1
0
38.21
Sector 8-3 (BOG)
976
845
0
0
1
0
52.90
Sector 8-4 (BOG)
432
378
0
0
1
0
28.80
Sector Estadio (BGA)
6977
6196
0
0
1
12
266.52
Subsectores v3 (BGA)
3051
2671
0
2
2
19
64.90
Morro Alto (BGA)
5621
4819
0
0
2
0
383.00
Cabecera (BGA)
982
906
0
0
3
2
79.75
Cañaveral (BGA)
3854
3411
0
1
2
0
322.52
Trinidad Tejar (BGA)
2479
2176
0
0
2
0
117.54
Barrancabermeja
6814
6469
5
1
1
801
589.79
T9 - Belén (MAN)
322
290
0
0
1
1
11.74
Bolivar (VC)
333
285
0
0
1
0
20.14
Bugalagrande (VC)
654
582
0
0
1
1
29.29
Candelaria (VC)
567
463
0
0
2
0
50.38
Ginebra (VC)
545
474
0
0
3
0
20.96
Medellin
736
865
0
0
3
0
7759.50
Bogotá
4478
4369
0
15
4
30
14956.45
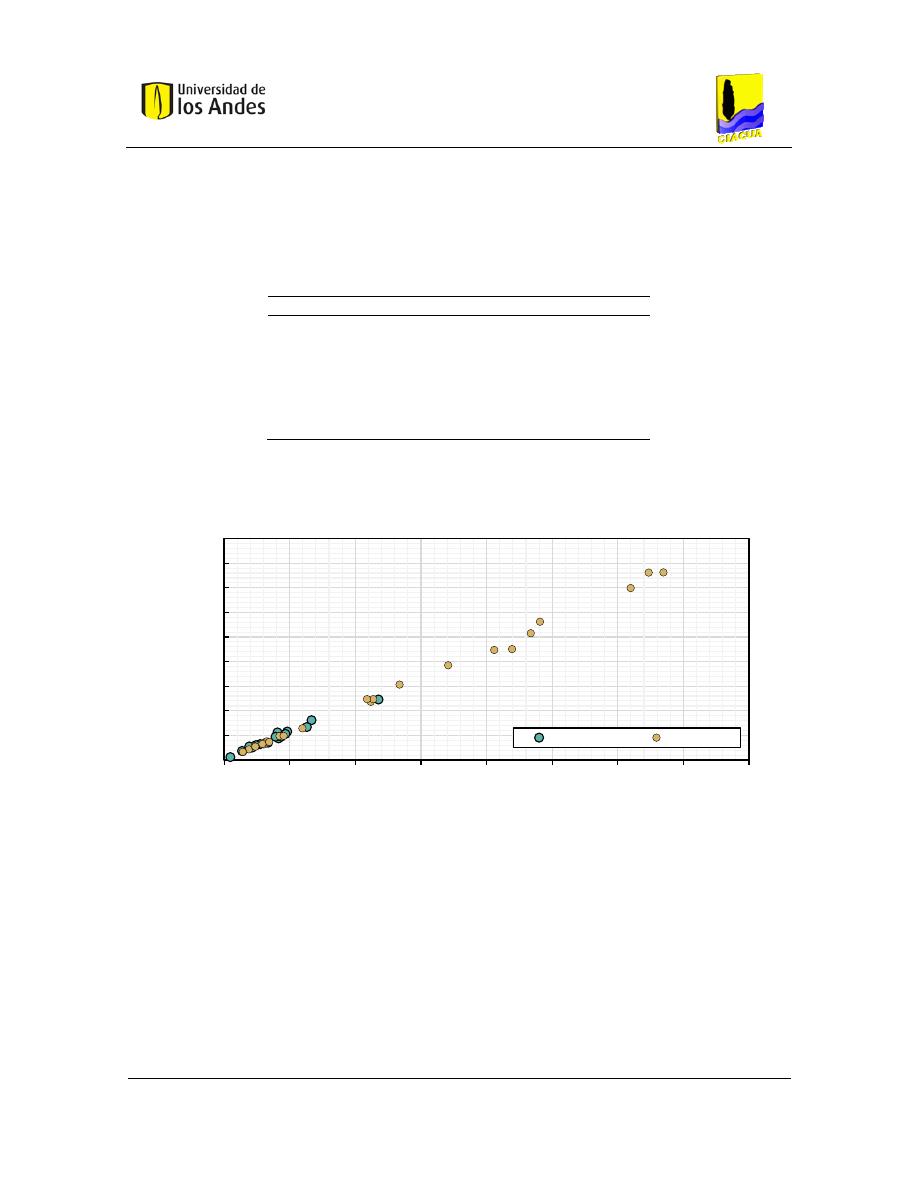
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
47
Como se observa, las redes analizadas varían en todas sus características. De las 41 RDAP
reales escogidas, 25 de ellas son redes colombianas y 16 redes son internacionales. En la
Tabla 4-2 se muestran los diferentes rangos para nodos, tuberías, tanques, embalses,
válvulas y demanda base.
Tabla 4-2. Rangos de características generales de las redes
Elemento
Min
Max
Nodos
92
6692
Tuberías
117
7616
Bombas
0
21
Tanques
0
28
Embalses
0
5
Válvulas
0.0
958.0
Demanda total (LPS)
12
14956
Así mismo, en la Figura 4-1. Relación entre nodos y tuberías de las redes analizadas se
presenta la variación del tamaño de las redes analizadas en términos de nodos y tuberías
(links). Además, esta imagen segrega las redes entre las colombianas y las internacionales.
Figura 4-1. Relación entre nodos y tuberías de las redes analizadas
4.1.2.1 Branch Index y sistema de clasificación
Una vez escogidas las redes, es posible realizar el cálculo de las métricas de teoría de
grafos. En primer lugar, se procede a clasificar estas redes con base en el esquema de
clasificación de Hwang y Lansey (2017), mencionado previamente. La Tabla 4-3. Cálculo
de BI y sistema de clasificación presenta el diámetro promedio ponderado por la
longitud
𝐷
̅ (tuberías), el Branch Index y la clasificación general de la red.
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
0
1000
2000
3000
4000
5000
6000
7000
8000
tu
be
rí
as
nodos
International
Colombia

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
48
Tabla 4-3. Cálculo de BI y sistema de clasificación
Red
D (mm)
BI
Clasificación
KY1
203.18
0.39
Distribution Sparse-Grid(DSG)
KY2
145.10
0.19
Distribution Dense-Grid(DDG)
KY3
242.01
0.15
Distribution Dense-Grid(DDG)
KY4
178.36
0.31
Distribution Sparse-Grid(DSG)
KY5
219.39
0.36
Distribution Sparse-Grid(DSG)
KY6
200.73
0.36
Distribution Dense-Grid(DDG)
KY7
195.81
0.32
Distribution Dense-Grid(DDG)
KY8
213.27
0.32
Distribution Sparse-Grid(DSG)
KY9
120.53
0.61
Distribution Branch (DB)
KY10
143.19
0.49
Distribution Hybrid (DH)
KY11
146.92
0.66
Distribution Branch (DB)
KY12
116.85
0.69
Distribution Branch (DB)
KY13
216.21
0.39
Distribution Sparse-Grid(DSG)
KY14
269.25
0.15
Distribution Dense-Grid(DDG)
KY15
136.50
0.71
Distribution Branch (DB)
Net3
454.05
0.25
Transmission Dense-Loop(TDL)
Richmond
113.20
0.44
Distribution Hybrid (DH)
Sector 13 (BOG)
144.34
0.28
Distribution Dense-Grid(DDG)
Sector 25 (BOG)
123.16
0.62
Distribution Branch (DB)
Sector 35 (BOG)
123.27
0.50
Distribution Hybrid (DH)
Zona 2 Sector 10 (BOG)
138.94
0.37
Distribution Sparse-Grid(DSG)
Zona 2 Sector 14-33 (BOG)
159.07
0.57
Distribution Branch (DB)
Zona 2 Sector 16 (BOG)
185.05
0.38
Distribution Sparse-Grid(DSG)
Zona 2 Sector 18 (BOG)
178.76
0.37
Distribution Sparse-Grid(DSG)
Sector 8-1 (BOG)
212.05
0.27
Distribution Dense-Grid(DDG)
Sector 8-2 (BOG)
121.97
0.20
Distribution Dense-Grid(DDG)
Sector 8-3 (BOG)
129.22
0.19
Distribution Dense-Grid(DDG)
Sector 8-4 (BOG)
119.65
0.29
Distribution Dense-Grid(DDG)
Barrancabermeja
87.60
0.37
Distribution Dense-Grid(DDG)
Sector Estadio (BGA)
82.17
0.25
Distribution Dense-Grid(DDG)
Subsectores v3 (BGA)
90.74
0.19
Distribution Dense-Grid(DDG)
Morro Alto (BGA)
104.52
0.24
Distribution Hybrid (DH)
Cabecera (BGA)
104.88
0.45
Distribution Dense-Grid(DDG)
Cañaveral (BGA)
93.35
0.35
Distribution Dense-Grid(DDG)
Trinidad Tejar (BGA)
111.90
0.31
Distribution Dense-Grid(DDG)
T9 - Belén (MAN)
85.28
0.43
Distribution Hybrid (DH)
Bolivar (VC)
65.57
0.30
Distribution Dense-Grid(DDG)
Bugalagrande (VC)
95.54
0.43
Distribution Hybrid (DH)
Candelaria (VC)
94.00
0.24
Distribution Dense-Grid(DDG)
Ginebra (VC)
80.99
0.45
Distribution Hybrid (DH)
Medellin
611.97
0.58
Transmission Branch (TB)
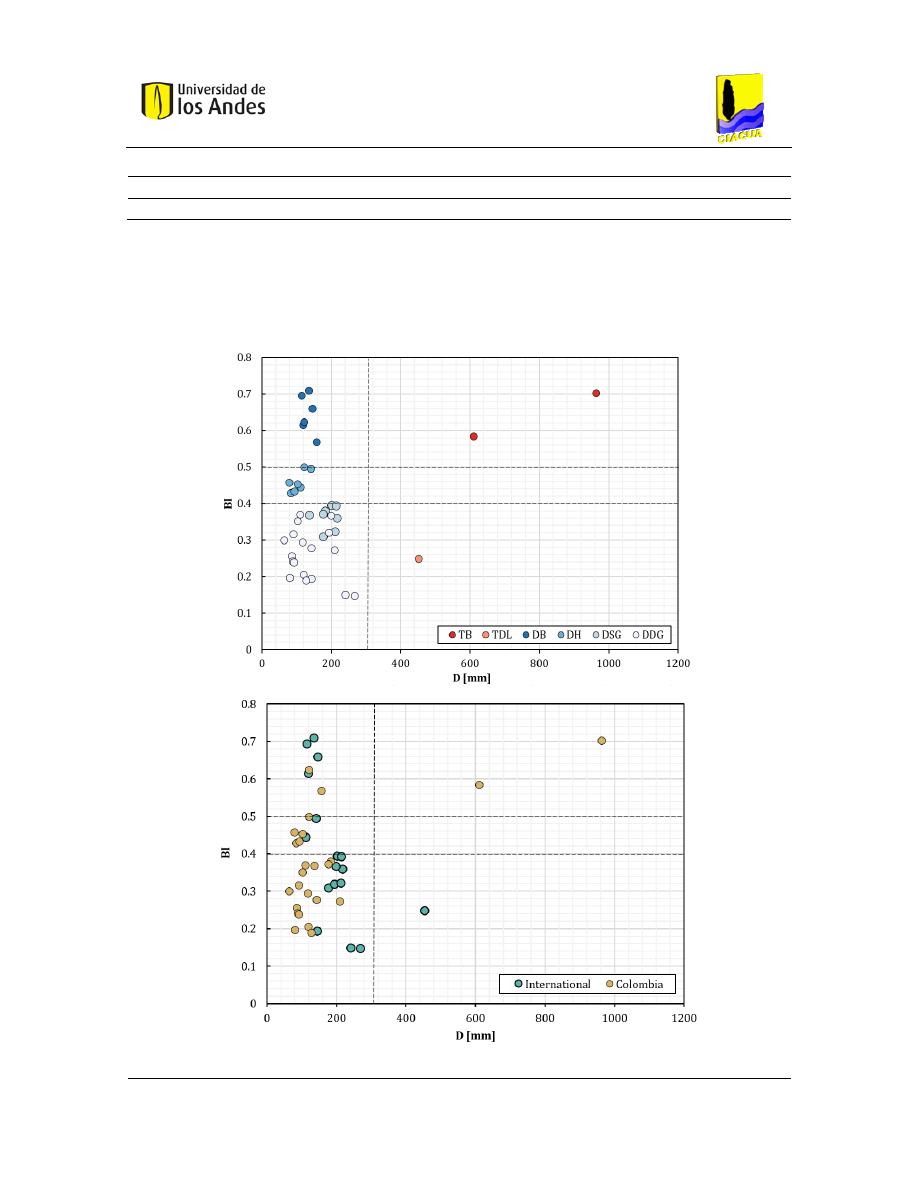
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
49
Red
D (mm)
BI
Clasificación
Bogotá
965.15
0.70
Transmission Branch (TB)
Como se puede observar, dentro de las redes analizadas hay variedad de topologías (redes
enmalladas, redes ramificadas y en circuitos) y en términos de función de la red, también
se pueden encontrar redes de transmisión (redes matrices) y redes de distribución. La
Figura 4-2 clasifica las redes de acuerdo con su topología y muestra la relación entre
𝐷
̅ y el
Branch Index.
Figura 4-2. Relación entre el diámetro promedio y el BI
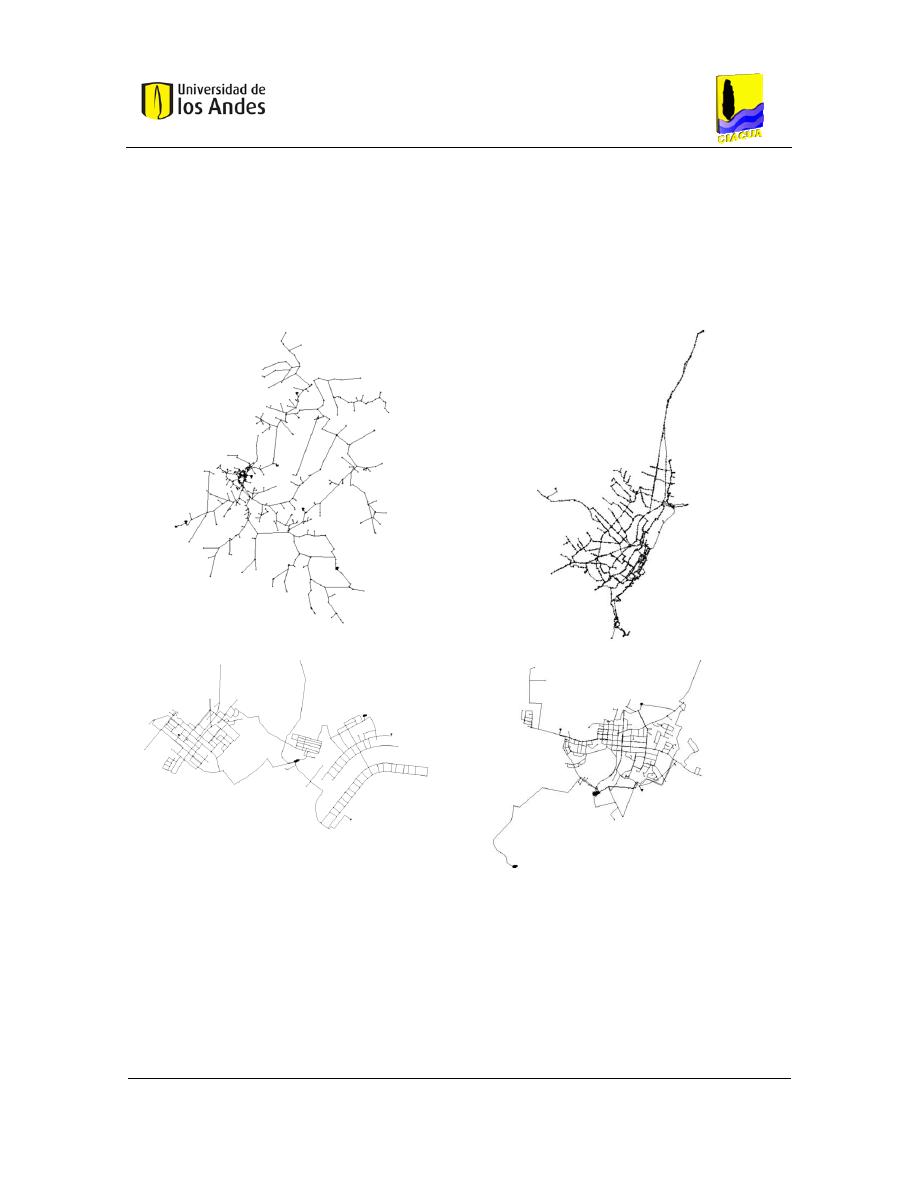
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
50
Las gráficas y los resultados del
𝐵𝐼 permiten identificar cuáles son los sistemas con mayor
ramificación y densidad (grillas). Según los valores obtenidos, las redes KY15 junto con la
red matriz de Bogotá son las redes más ramificadas, y las redes KY 3 y KY 14 las menos
ramificadas (haciendo referencia a que su topología es en forma de grilla). Para comprobar
esto, se analiza visualmente cada una de estas redes. La Figura 4-3 muestra la estructura
de las redes KY 15, Bogotá, KY 3 y KY 14.
Figura 4-3. Topología de redes KY15, Bogotá, KY3 y KY14
En general, la implementación del esquema de clasificación propuesto por Hwang y Lansey
muestran buenos resultados, acordes con la realidad de las RDAP, por lo cual, este (junto
con sus métricas
𝐷
̅ y 𝐵𝐼) deben ser tenidos en cuenta para en análisis geométrico de las
RDAP.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
51
4.1.2.2 Cálculo de métricas de CNT
El cálculo de las métricas de CNT se realiza teniendo en cuenta que existen seis
características fundamentales para el análisis topológico de las RDAP. Estas características
son: (i) conectividad, (ii) eficiencia, (iii) centralidad, (iv) diversidad, (v) robustez y (vi)
modularidad (Meng, Fu, Farmani, Sweetapple, & Butler, 2018). Con base en esto, se toman
las siguientes métricas de CNT para el cálculo de las características fundamentales:
Característica
Métrica
Definición
Conectividad
Grado promedio de nodos
(Average node degree)
𝑘 =
2𝑚
𝑛
Densidad de enlaces
(Link density)
𝑞 =
2𝑚
𝑛(𝑛 − 1)
Coeficiente de enmallado
(Meshedness coefficient)
𝑅
𝑚
=
𝑚 − 𝑛 + 1
2𝑛 − 5
Conectividad algebraica
(Algebraic connectivity)
λ
2
Coeficiente de agrupación
(Clustering coefficient)
𝐶
𝑐
=
3𝑁
∆
𝑁
3
Eficiencia
Longitud promedio de los caminos
(Average path length)
𝑙 =
1
𝑛(𝑛 − 1)
× ∑ 𝑑
𝑖,𝑗
𝑛
𝑖,𝑗=1
Diámetro (red)
(Diameter (Net))
𝑑
𝑇
= 𝑚á𝑥(𝑑
𝑖,𝑗
)
Eficiencia de red
(Net Efficiency)
𝐸 =
1
𝑛(𝑛 − 1)
∑
1
𝑑
𝑖𝑗
𝑖,𝑗∈𝑁,𝑖≠𝑗
Centralidad
Dominancia del punto central
(Central point dominance)
𝐶
𝐵
=
1
𝑛 − 1
∑(𝐵
𝑚𝑎𝑥
− 𝐵
𝑖
)
𝑖
B es la intermediación normalizada
𝐵
𝑖
=
2 𝐶
𝑏
(𝑖)
𝑛
2
− 3𝑛 + 2
Diversidad
Heterogeneidad
(Heterogeneity)
1
𝑘
× ∑
(𝑘
𝑖
− 𝑘)
2
𝑛
𝑖=1
Robustez
Brecha espectral
(Spectral gap)
λ∆= λ
1
(𝐴) − λ
2
(𝐴)
Modularidad
Indicador de modularidad
(Modularity indicator)
max (∑ 𝑒
𝑖𝑖
− ∑ 𝑒
𝑖𝑗
𝑒
𝑘𝑖
𝑖𝑗𝑘
𝑖
)
Cada una de estas métricas se calcula para las redes estudiadas. Los resultados se
presentan en la Tabla 2-1.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
52
Tabla 4-4. Cálculo de métricas de CNT para redes analizadas
Red
𝑘
𝑙
𝑑
𝑇
𝑞
𝐶
𝑐
𝑅
𝑚
𝐶𝑏
𝜆𝛥
𝜆
2
𝐻𝑒𝑡
𝐸
Mod
KY1
2.29
24.84
69
0.0027 0.0092 0.07 0.25 0.26 0.000436 0.40 0.06 0.86
KY2
2.74
17.36
42
0.0034 0.0420 0.19 0.16 0.07 0.001727 0.37 0.08 0.83
KY3
2.70
15.29
42
0.0098 0.0447 0.18 0.39 0.14 0.001065 0.33 0.11 0.82
KY4
2.36
23.53
61
0.0024 0.0488 0.10 0.34 0.02 0.000379 0.40 0.06 0.88
KY5
2.36
15.44
41
0.0055 0.0235 0.09 0.27 0.18 0.001646 0.42 0.09 0.83
KY6
2.34
17.16
41
0.0043 0.0213 0.09 0.23 0.04 0.001635 0.42 0.08 0.85
KY7
2.48
15.46
44
0.0051 0.0241 0.12 0.26 0.15 0.001824 0.40 0.09 0.82
KY8
2.42
25.88
69
0.0018 0.0328 0.11 0.24 0.10 0.000482 0.41 0.05 0.88
KY9
2.11
40.62
96
0.0017 0.0271 0.03 0.48 0.04 0.000086 0.43 0.04 0.91
KY10
2.27
29.44
89
0.0024 0.0154 0.07 0.28 0.04 0.000197 0.42 0.05 0.88
KY11
2.12
42.52
112 0.0026 0.0336 0.03 0.57 0.05 0.000139 0.44 0.04 0.91
KY12
2.08
84.96
216 0.0009 0.0176 0.02 0.54 0.13 0.000016 0.34 0.02 0.93
KY13
2.38
19.84
53
0.0030 0.0569 0.10 0.32 0.09 0.000753 0.45 0.07 0.84
KY14
2.83
12.88
37
0.0074 0.0401 0.22 0.23 0.14 0.002915 0.36 0.11 0.78
KY15
2.10
26.01
76
0.0031 0.0030 0.03 0.39 0.07 0.000484 0.39 0.06 0.86
Net3
2.45
10.26
30
0.0256 0.0429 0.12 0.27 0.14 0.003481 0.36 0.16 0.73
Richmond
2.19
51.44
135 0.0025 0.0402 0.05 0.56 0.07 0.000061 0.36 0.04 0.91
Sector 13 (BOG)
2.27
64.46
175 0.0003 0.0005 0.07 0.34 0.11 0.000016 0.29 0.02 0.94
Sector 25 (BOG)
2.10
32.90
86
0.0034 0.0037 0.03 0.52 0.02 0.000225 0.29 0.05 0.88
Sector 35 (BOG)
2.17
42.99
100 0.0018 0.0000 0.04 0.30 0.35 0.000123 0.33 0.04 0.91
Zona 2 Sector 10 (BOG)
2.20
54.08
146 0.0005 0.0004 0.05 0.32 0.14 0.000066 0.26 0.03 0.93
Zona 2 Sector 14-33 (BOG) 2.11
57.55
143 0.0009 0.0020 0.03 0.50 0.03 0.000037 0.29 0.03 0.92
Zona 2 Sector 16 (BOG)
2.17
55.17
154 0.0005 0.0020 0.04 0.36 0.03 0.000065 0.26 0.03 0.93
Zona 2 Sector 18 (BOG)
2.18
40.36
96
0.0010 0.0000 0.04 0.33 0.03 0.000137 0.25 0.03 0.90
Sector 8-1 (BOG)
2.34
27.54
70
0.0036 0.0026 0.09 0.37 0.01 0.000000 0.30 0.05 0.90
Sector 8-2 (BOG)
2.31
18.99
44
0.0039 0.0000 0.08 0.24 0.06 0.001154 0.29 0.07 0.85
Sector 8-3 (BOG)
2.31
23.32
58
0.0027 0.0021 0.08 0.23 0.13 0.000594 0.27 0.06 0.87
Sector 8-4 (BOG)
2.28
19.23
46
0.0060 0.0000 0.07 0.36 0.22 0.000618 0.32 0.08 0.80
Barrancabermeja
2.35
59.68
165 0.0004 0.0242 0.09 0.65 0.06 0.000014 0.39 0.02 0.94
Sector Estadio (BGA)
2.25
62.60
179 0.0004 0.0027 0.06 0.35 0.04 0.000045 0.28 0.02 0.93
Subsectores v3 (BGA)
2.29
53.55
130 0.0009 0.0067 0.07 0.39 0.16 0.000041 0.27 0.03 0.94
Morro Alto (BGA)
2.33
46.39
144 0.0005 0.0000 0.08 0.20 0.07 0.000090 0.31 0.03 0.92
Cabecera (BGA)
2.17
61.62
177 0.0024 0.0000 0.04 0.39 0.02 0.000045 0.30 0.04 0.89
Cañaveral (BGA)
2.26
55.33
150 0.0007 0.0005 0.06 0.48 0.04 0.000035 0.30 0.03 0.94
Trinidad Tejar (BGA)
2.28
56.12
155 0.0010 0.0008 0.07 0.34 0.06 0.000044 0.31 0.03 0.93
T9 - Belén (MAN)
2.19
21.03
61
0.0076 0.0195 0.06 0.38 0.05 0.000612 0.34 0.08 0.86
Bolivar (VC)
2.33
16.17
52
0.0082 0.0000 0.08 0.22 0.06 0.001563 0.37 0.10 0.79
Bugalagrande (VC)
2.25
24.69
69
0.0039 0.0000 0.06 0.37 0.10 0.000418 0.36 0.06 0.85
Candelaria (VC)
2.44
17.18
49
0.0053 0.0030 0.11 0.21 0.09 0.001452 0.37 0.09 0.82
Ginebra (VC)
2.29
20.28
57
0.0048 0.0066 0.07 0.27 0.18 0.000945 0.40 0.08 0.82
Medellin
2.14
33.04
113 0.0031 0.0032 0.04 0.24 0.06 0.000335 0.25 0.05 0.87
Bogotá
2.05 116.61 340 0.0005 0.0006 0.01 0.25 0.07 0.000028 0.20 0.01 0.95

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
53
Una vez calculadas las métricas en las RDAP, re realiza un análisis de correlación para
determinar la independencia de cada una de estas. Este análisis se lleva a cabo calculando
el coeficiente de correlación lineal de Pearson, el cual varía en -1 y +1. Entre más cercano
sea este valor a sus extremos, indica una alta correlación negativa o positiva,
respectivamente. Generalmente, valores de Pearson mayores a
± 0.8, indican
correlaciones fuertes y valores menores a
± 0.5, indican correlaciones débiles. La Tabla
4-5 presenta los valores de coeficiente de correlación para las métricas calculadas.
Tabla 4-5. Coeficiente de correlación métricas CNT
Métrica
𝑘
𝑙
𝑑
𝑇
𝑞
𝐶
𝑐
𝑅
𝑚
𝐶𝑏
𝜆𝛥
𝜆
2
𝐻𝑒𝑡
𝐸
𝑀𝑜𝑑
𝑘
1.00
-
-
-
-
-
-
-
-
-
-
-
𝑙
-0.57 1.00
-
-
-
-
-
-
-
-
-
-
𝑑
𝑇
-0.55 0.99
1.00
-
-
-
-
-
-
-
-
-
𝑞
0.41 -0.55 -0.53
1.00
-
-
-
-
-
-
-
-
𝐶
𝑐
0.53 -0.35 -0.36
0.38
1.00
-
-
-
-
-
-
-
𝑅
𝑚
1.00 -0.58 -0.56
0.43
0.56
1.00
-
-
-
-
-
-
𝐶
𝑏
-0.45 0.41
0.35
-0.24 0.08 -0.45 1.00
-
-
-
-
-
𝜆𝛥
0.19 -0.19 -0.22
0.19
0.00
0.18 -0.27 1.00
-
-
-
-
𝜆
2
0.70 -0.65 -0.62
0.73
0.44
0.71 -0.51 0.23
1.00
-
-
-
𝐻𝑒𝑡
0.30 -0.55 -0.55
0.23
0.62
0.32
0.02
0.13
0.35
1.00
-
-
𝐸
0.67 -0.86 -0.83 0.93
0.39
0.48 -0.47 0.23
0.87
0.48
1.00
-
𝑀𝑜𝑑
-0.59 0.82
0.78 -0.82 -0.36 -0.60 0.49 -0.27 -0.88 -0.42 -0.97 1.00
Es posible observar que existe alta correlación entre diferentes variables. Para el caso del
grado promedio de nodos, se muestra una correlación exacta con el coeficiente de
enmallado, por lo cual el cálculo de ambos para definir la conectividad de la red es
redundante. Así mismo, para el caso de la eficiencia, se muestra una alta relación con
respecto a la longitud promedio de los caminos y el diámetro de la red. De las figuras 4-4 a
la 4-6 se muestran las relaciones entre las métricas calculadas.
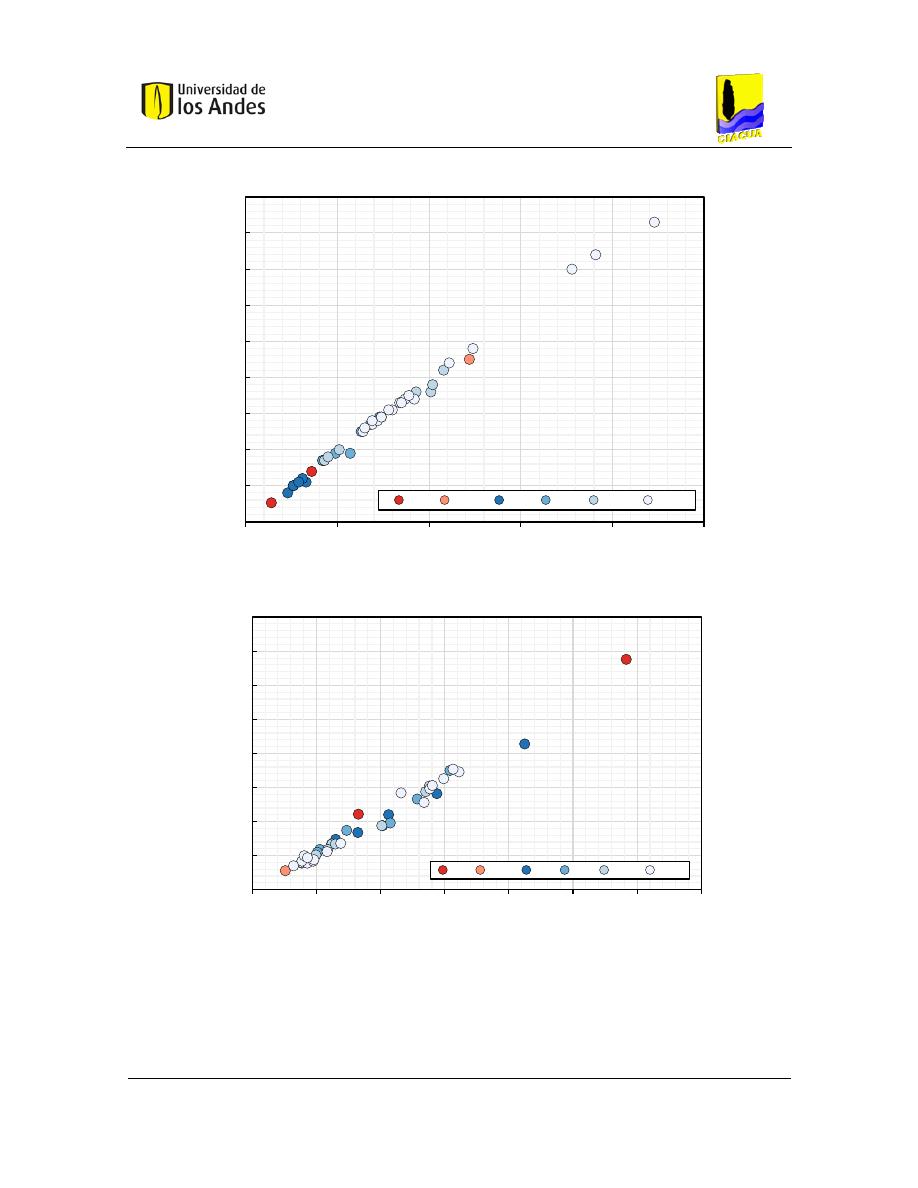
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
54
Figura 4-4. Relación entre k y Rm
Figura 4-5. Relación entre diámetro de la red y longitud promedio de los caminos
2
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
0
0.05
0.1
0.15
0.2
0.25
k
Rm
TB
TDL
DB
DH
DSG
DDG
2
52
102
152
202
252
302
352
402
0
20
40
60
80
100
120
140
d
T
l
TB
TDL
DB
DH
DSG
DDG
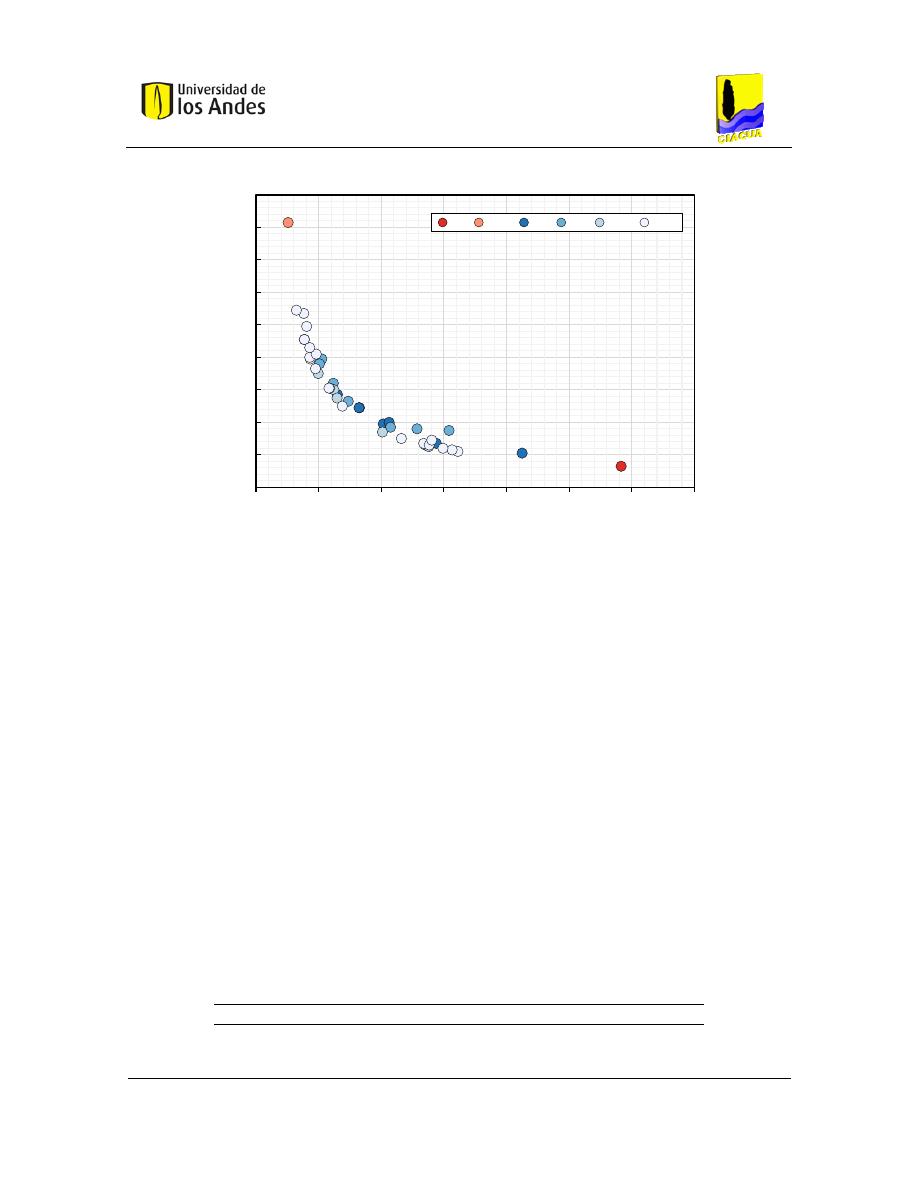
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
55
Figura 4-6. Relación entre la eficiencia de la red y longitud promedio de los caminos
Analizando las relaciones entre las métricas calculadas y los valores obtenidos, es posible
determinar cuáles son las más adecuadas para la caracterización geométrica de las RDAP.
En términos de la conectividad, se determina que el grado promedio de los nodos
𝑘 tiene
una alta correlación con el coeficiente de enmallado, por lo cual, su cálculo es redundante.
Además, los valores obtenidos de
𝑘 para RDAP no varían mucho ya que estas redes son
espacialmente restringidas (usualmente los valores varían entre 2 y 3). Con respecto al
coeficiente de agrupación, es extraño encontrar estructuras triangulares dentro de las
RDAP, es por esto por lo que la mayoría de RDAP tienen valores de
𝐶
𝑐
iguales o muy
cercanos a 0. La eficiencia de la red muestra una alta correlación con la longitud promedio
de los caminos y el diámetro de la red. Esto era de esperarse ya que la formulación
matemática de las tres métricas es muy similar. Se analizará la eficiencia de las redes con
la métrica de
𝑁𝑒𝑡 𝑒𝑓𝑓𝑖𝑐𝑖𝑒𝑛𝑐𝑦 ya que es la única que da valores entre 0 y 1, lo que la hace
de más fácil interpretación. Las características de centralidad, diversidad, robustez y
modularidad se pueden calcular con las métricas establecidas inicialmente.
4.1.3. Caracterización geométrica de RDAP
La caracterización geométrica de las RDAP con base en métricas de CNT quedaría de la
siguiente forma:
Tabla 4-6. Métricas para la caracterización geométrica de RDAP
Característica
Métrica
Conectividad
Densidad de enlaces
𝑞
Coeficiente de enmallado*
𝑅
𝑚
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0
20
40
60
80
100
120
140
E
l
TB
TDL
DB
DH
DSG
DDG

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
56
Característica
Métrica
Conectividad algebraica
𝜆
2
Eficiencia
Net Efficiency
𝐸
Centralidad
Central point dominance
𝐶
𝑏
Diversidad
Heterogeneity
𝐻𝐸𝑇
Robustez
Spectral gap
𝜆∆
Modularidad
Modularity indicator
𝑀𝑂𝐷
*El coeficiente de enmallado caracteriza mejor las RDAP si se hace con la red reducida mediante el node-
reduction algorithm (Hwang y Lansey, 2017).
Adicionalmente, el esquema de clasificación de RDAP propuesto por Hwang y Lansey, junto
con el cálculo de sus variables (
𝐵𝐼, 𝑅
𝑚
y
𝐷
̅) también será utilizado para determinar el tipo
de red según su función y su topología.
Con base en esto, es posible caracterizar las RDAP analizadas previamente. En las figuras
4-8 a 4-13 se presenta la clasificación de las RDAP, la cual se realiza mediante la
ponderación del resultado mayor para cada métrica.
Figura 4-7. Resultados de cada una de las métricas para la caracterización
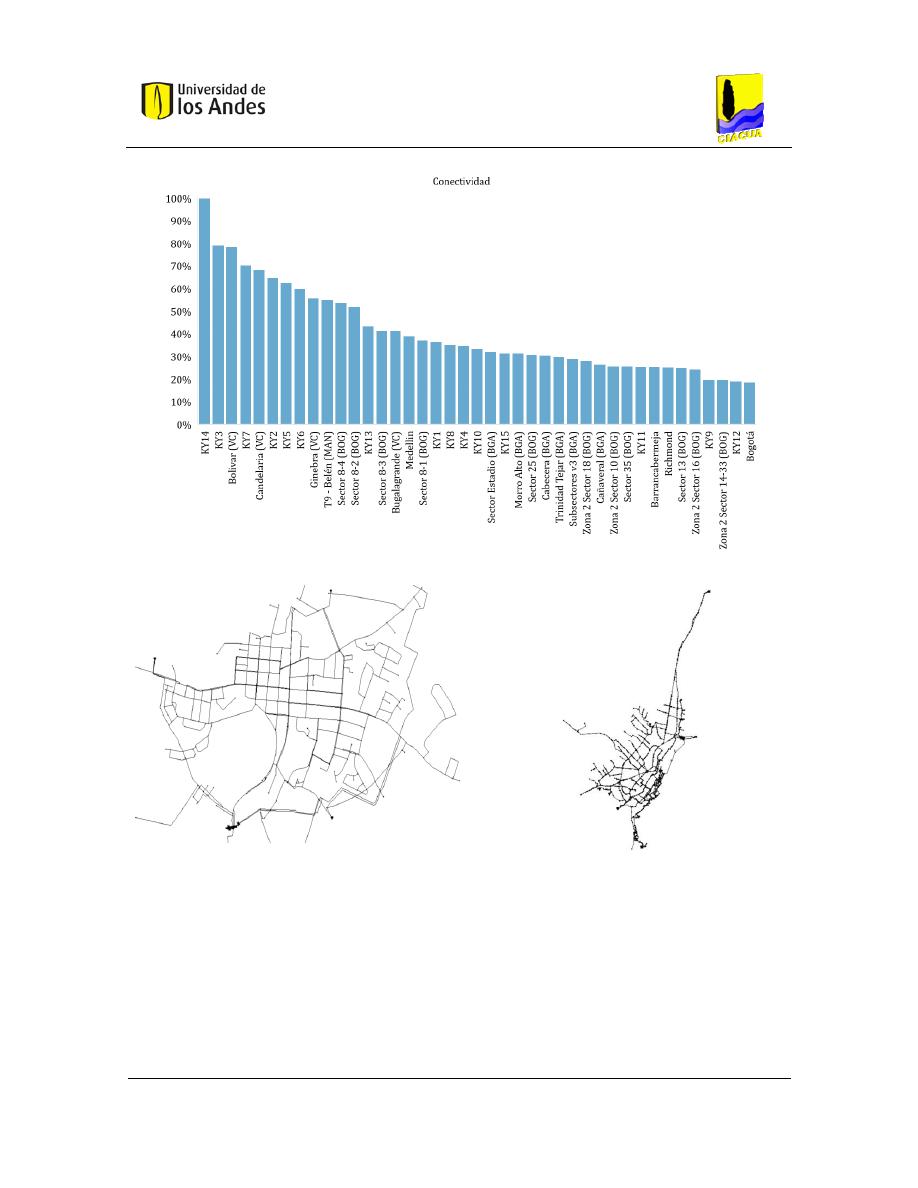
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
57
KY 14
Bogotá
Figura 4-8. Clasificación de las RDAP (Conectividad)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
58
KY 14
Bogotá
Figura 4-9. Clasificación de RDAP (Eficiencia)
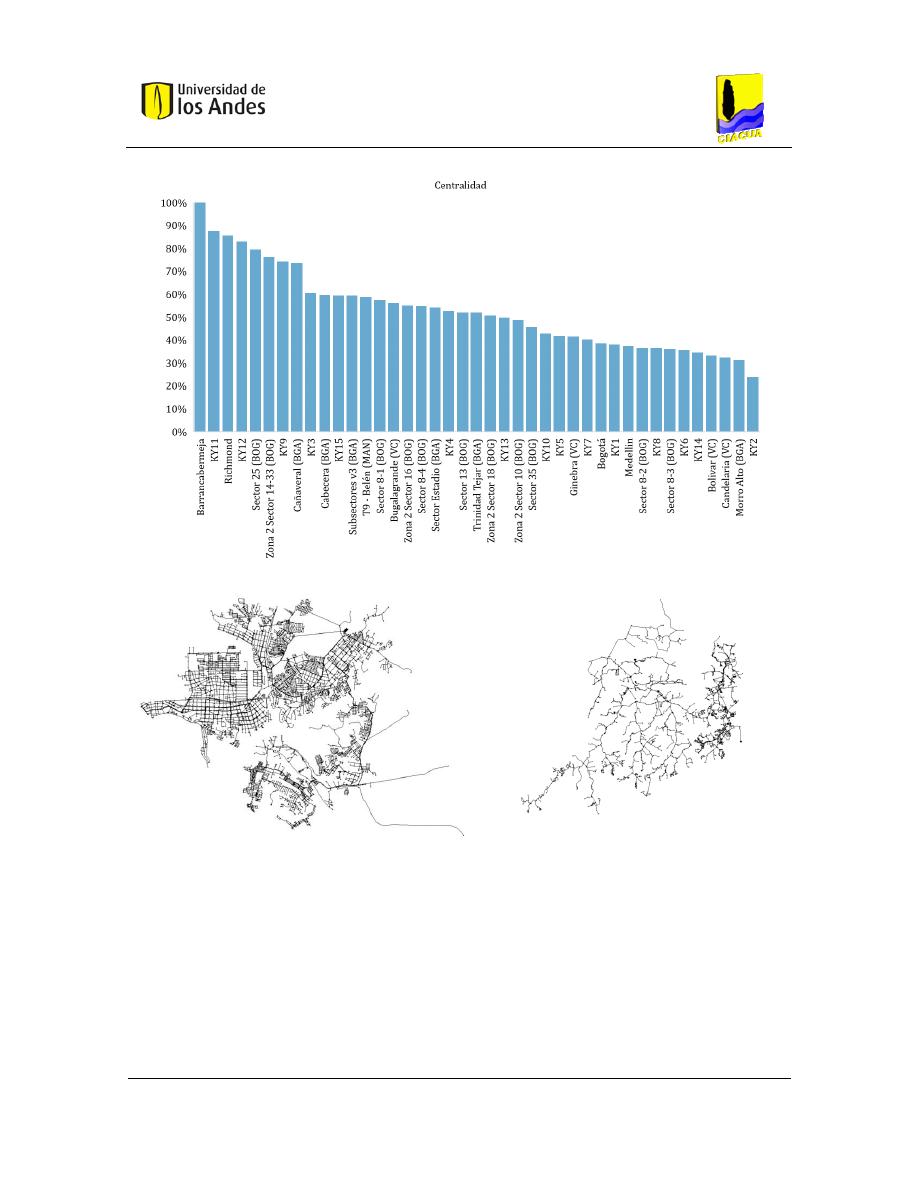
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
59
Barrancabermeja
KY12
Figura 4-10. Clasificación de RDAP (Centralidad)
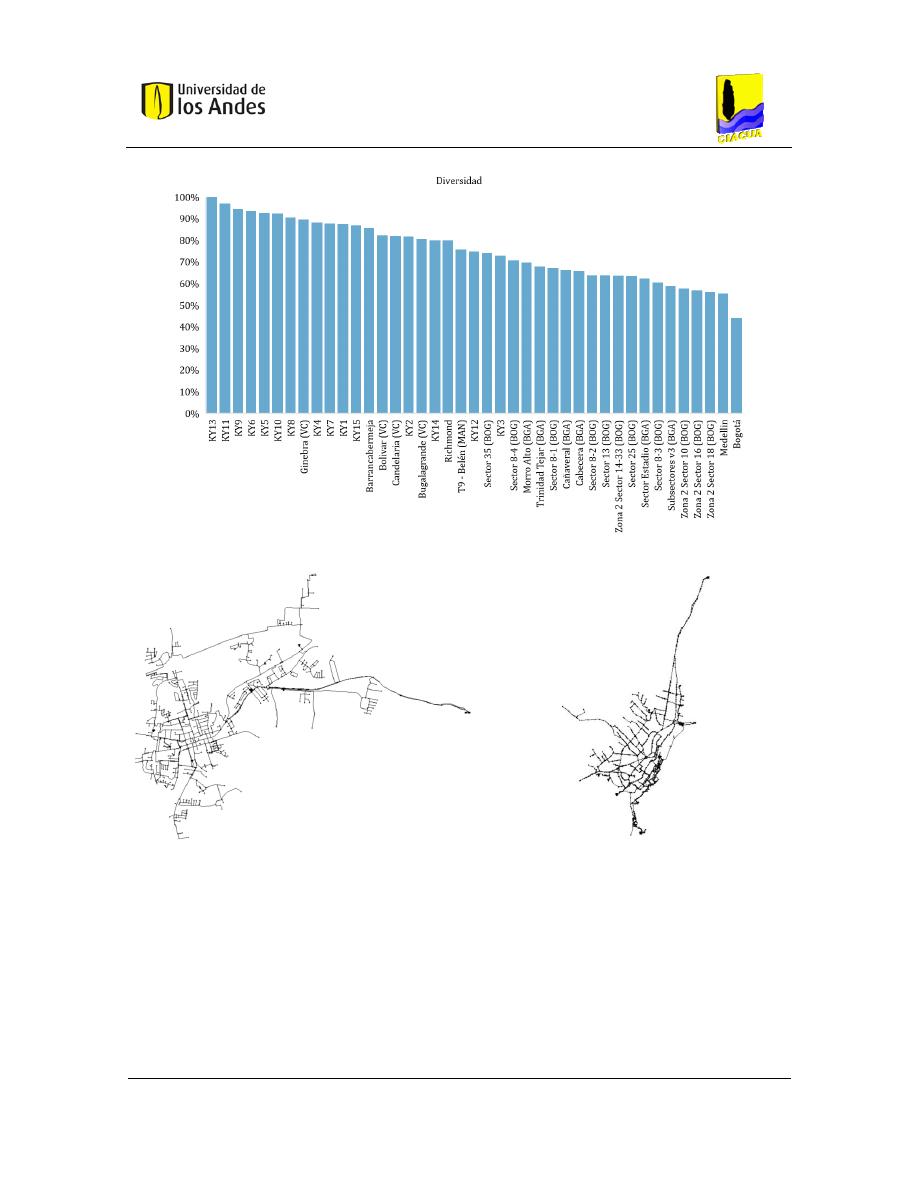
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
60
KY 13
Bogotá
Figura 4-11. Clasificación RDAP (Diversidad)
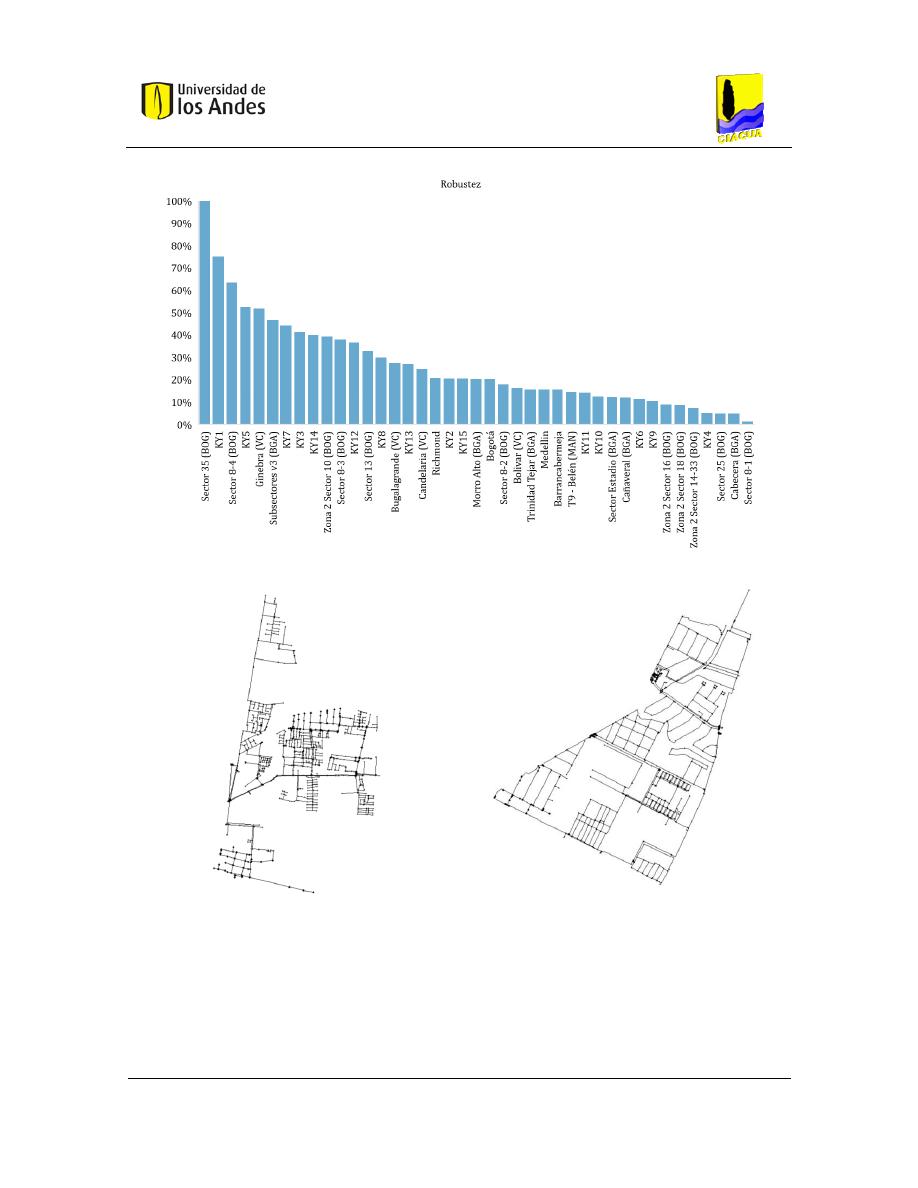
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
61
Sector 35 (BOG)
Sector 8-1 (BOG)
Figura 4-12. Clasificación de RDAP (Robustez)
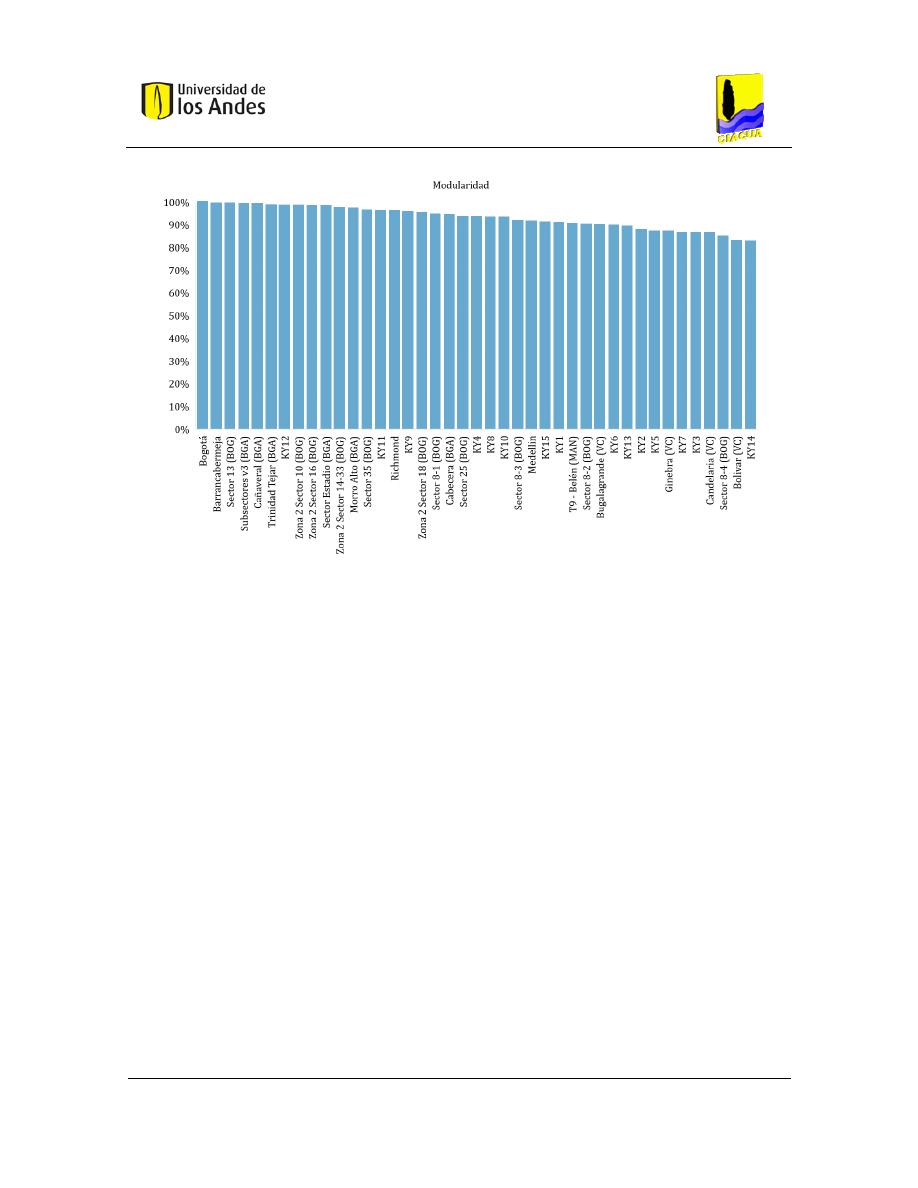
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
62
Figura 4-13. Clasificación RDAP (Modularidad)
4.2. Ajuste de índices de CNT seleccionados
Una vez seleccionados los índices de CNT para la caracterización de las RDAP, es
necesario ajustarlos con elementos de las RDAP. Es importante recalcar que los índices
previamente seleccionados se calculan con base a grafos planos y sin dirección, por lo cual
únicamente están analizando el árbol (trazado) de las RDAP. La caracterización previa
permite distinguir entre diferentes características de los trazados de las RDAP y sus
resultados no deben confundirse con la caracterización hidráulica de la red. El único índice
que se ha ajustado hasta el momento es el
𝑅
𝑚
ya que se está calculando después de que
se realiza el node-reduction algoritm (eliminación de nodos no esenciales de la red).
Dicho lo anterior, se realiza un ajuste (adaptación) de las métricas mencionadas mediante
la implementación de grafos con peso, en donde entra en consideración las características
hidráulicas y geométricas (como, por ejemplo, el diámetro de las tuberías) específicas de
las RDAP.
4.2.1. Índices de CNT con peso
Un grafo se puede representar como
𝐺 = 𝐺(𝑉, 𝐸), en donde 𝑉 es un conjunto de nodos con
𝑛 elementos (tamaño del grafo) y 𝐸 es el conjunto de links con 𝑚 elementos (orden del
grafo). En el caso más simple, los grafos son representaciones planas sin peso y sin
dirección (como la caracterización hecha previamente) no obstante, es posible realizar la

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
63
representación matemática de una red teniendo en cuenta la dirección de los enlaces
(aristas dirigidas) y la información en los nodos y tuberías (pesos).
Para la presente investigación, se propone el ajuste de las métricas mediante la
implementación de pesos que tengan en cuenta características hidráulicas y geométricas
de la red. Los pesos implementados son:
𝑤
𝑑𝑖𝑎𝑚𝑒𝑡𝑟𝑜
→ 𝑤
𝑑
= 𝑑
𝑖,𝑗
=
𝑑
𝑖,𝑗
max 𝑑
𝑖,𝑗
Ecuación 30. Peso (diámetro)
𝑤
𝑣𝑜𝑙
→ 𝑤
𝑣𝑜𝑙
= 𝑉
𝑖,𝑗
=
𝑉
𝑖,𝑗
max 𝑉
𝑖,𝑗
𝑉
𝑖,𝑗
=
𝜋𝐿
𝑖,𝑗
𝑑
𝑖,𝑗
2
4
Ecuación 31. Peso (Volumen)
𝑤
𝑐𝑎𝑢𝑑𝑎𝑙
→ 𝑤
𝑄
= 𝑄
𝑖,𝑗
=
𝑄
𝑖,𝑗
𝑚𝑎𝑥 𝑄
𝑖,𝑗
Ecuación 32. Peso (Caudal)
𝑤
𝑝é𝑟𝑑𝑖𝑑𝑎𝑠
→ 𝑤
ℎ
= ℎ
𝑖,𝑗
=
ℎ
𝑖,𝑗
𝑃é𝑟𝑑𝑖𝑑𝑎 𝑡𝑜𝑡𝑎𝑙 𝑑𝑒 𝑙𝑎 𝑟𝑒𝑑
ℎ
𝑖,𝑗
= 𝑟
𝑖,𝑗
𝑄
𝑖,𝑗
2
𝑟
𝑖,𝑗
=
8𝑓𝐿
𝑖,𝑗
𝜋
2
𝑔𝑑
𝑖,𝑗
5
Ecuación 33. Peso (Pérdidas)
Donde
𝑑
𝑖,𝑗
; equivale al diámetro de la tubería entre los nodos 𝑖 y 𝑗; 𝐿
𝑖,𝑗
es la longitud de la
tubería entre los nodos
𝑖 y 𝑗; 𝑄
𝑖,𝑗
es el caudal de la tubería entre los nodos
𝑖 y 𝑗; 𝑉
𝑖,𝑗
es el
volumen de la tubería entre los nodos
𝑖 y 𝑗 y 𝑓 es el factor de fricción (Darcy-Weisbach).
Los pesos de diámetro y volumen hacen referencia a características geométricas de las
tuberías de la red y los pesos de caudal y pérdidas tienen en cuenta las características
hidráulicas de la misma. Una vez establecido estos, se vuelve a realizar el cálculo de las
métricas de CNT escogidas para la caracterización de las RDAP. En las figuras 4-14 a 4-
18 se muestra el resultado de las métricas que varían por la inclusión de pesos para el
análisis de RDAP.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
64
Figura 4-14. Conectividad algebraica con pesos
Figura 4-15. Dominancia del punto central con pesos
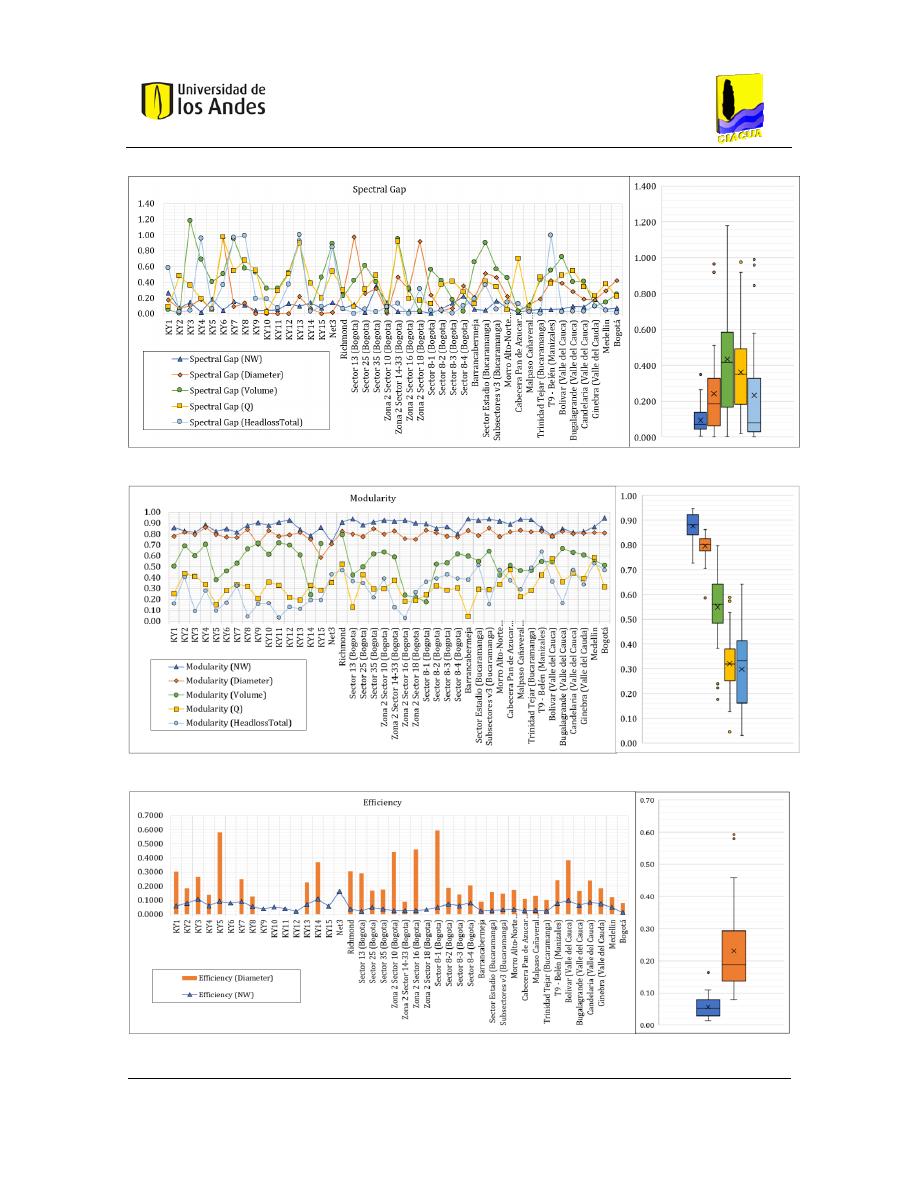
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
65
Figura 4-16. Brecha espectral con pesos
Figura 4-17. Modularidad con pesos
Figura 4-18. Eficiencia con pesos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
66
Únicamente 5 métricas de las 8 previamente escogidas varían al momento de implementar
pesos (conectividad algebraica, dominancia del punto central, brecha espectral,
modularidad de la red y eficiencia). Las otras métricas (densidad de enlaces,
heterogeneidad y coeficiente de enmallado) no cambian debido a que su cálculo se basa
únicamente en la cantidad de enlaces y nodos. Las figuras muestran las variaciones para
cada una de las redes analizadas y permiten observar como las métricas espectarles son
muy sensibles a los pesos implementados, en especial a los pesos de volumen
(característica geométrica) y pérdidas (característica hidráulica). La gráfica de eficiencia
únicamente se muestra con el peso del diámetro debido a que los valores obtenidos para
los demás pesos varían mucho con respecto a los originales (para algunas redes se
obtienen valores de eficiencia de 5 órdenes de magnitud mayor a la original).
Al analizar las variaciones encontradas, se determina que para simplificar el análisis y poder
obtener conclusiones sobre las RDAP, únicamente se trabajará con los pesos de cada tipo
que menos variación generan con respecto a las métricas originales. Estos pesos son:
diámetro
𝑤
𝑑
(geométrico) y caudal
𝑤
𝑄
(hidráulico). Adicionalmente, se determina que la
eficiencia de la red se calculará sin peso debido a que se obtienen valores de diferente
orden de magnitud.
Con la implementación de los pesos se espera poder comparar las geometrías obtenidas
al momento de optimizar las redes de distribución de agua potable.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
67
5. METODOLOGÍA DE OPTIMIZACIÓN
La optimización de las RDAP fue descrita previamente en la sección 2. Como conclusiones
de la recopilación bibliográfica se estableció que para abrir un camino y entender la
geometría de los diseños optimizados de RDAP se debe comenzar por la aproximación
tradicional al diseño optimizado, la cual puede describirse de la siguiente manera:
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑎𝑟 𝐶 = ∑ 𝑓
𝑖
(𝑥
𝑖
)
𝑛
𝑖=1
𝑃
𝑗
≥ 𝑃
𝑚í𝑛
𝑄
𝑗
≥ 𝑄𝑑
𝑗
𝐷
𝑘
∈ (𝐷𝑐
𝑚í𝑛
, 𝐷𝑐
𝑚á𝑥
)
donde
𝐶= costo total de la red; 𝑥𝑖= variable asociada al costo; 𝑓𝑖= función de costo asociada
a cada variable
𝑥𝑖; 𝑃𝑗= presión de servicio en cada nodo de la red; 𝑃𝑚𝑖𝑛= presión mínima
de diseño;
𝑄𝑗= caudal entregado en cada nodo de la red; 𝑄𝑑𝑗= caudal demandado en cada
nodo de la red.
En otras palabras, el diseño optimizado de una RDAP consiste en determinar los diámetros
de cada una de las tuberías que la conforman dados un caudal de consumo en cada uno
de los nudos fijados por la demanda de agua potable y una presión mínima en las horas de
máximo consumo fijada por una norma local (Saldarriaga, 2016). Es decir, dada una
topología de una red, el problema consiste en determinar un conjunto de diámetros en forma
tal que se minimice una función de costo sujeta a restricciones hidráulicas, comerciales y
de construcción (Saldarriaga, 2016). Las variables de decisión del problema son los
diámetros de cada una de las tuberías de la red. Estas variables son discretas, puesto que
sus valores dependen de los diámetros comerciales producidos por la industria. El problema
de optimización, en el caso más simple (únicamente un estado operacional), involucra un
número posible de diseños discretos equivalente a
𝑑
𝑝
, donde
𝑑 son los diámetros
comerciales disponibles y
𝑝 es el número de tuberías de la red.
A continuación, se describe los dos algoritmos de optimización implementados en la
presente investigación. Ambos de estos algoritmos se encuentran en el programa REDES
El diseño optimizado de las RDAP implementadas como casos de estudio se realizó con el
programa REDES, el cual fue desarrollado por el Centro de Investigaciones en Acueductos
y Alcantarillados (CIACUA) de la Universidad de los Andes. Se utilizó la metodología OPUS
y Algoritmos Genéticos para el diseño optimizado de dichas redes. Ambas metodologías se
encuentran programadas en el código fuente del programa REDES. Para estas
metodologías el programa permite ajustar el valor de la presión mínima de diseño, la función
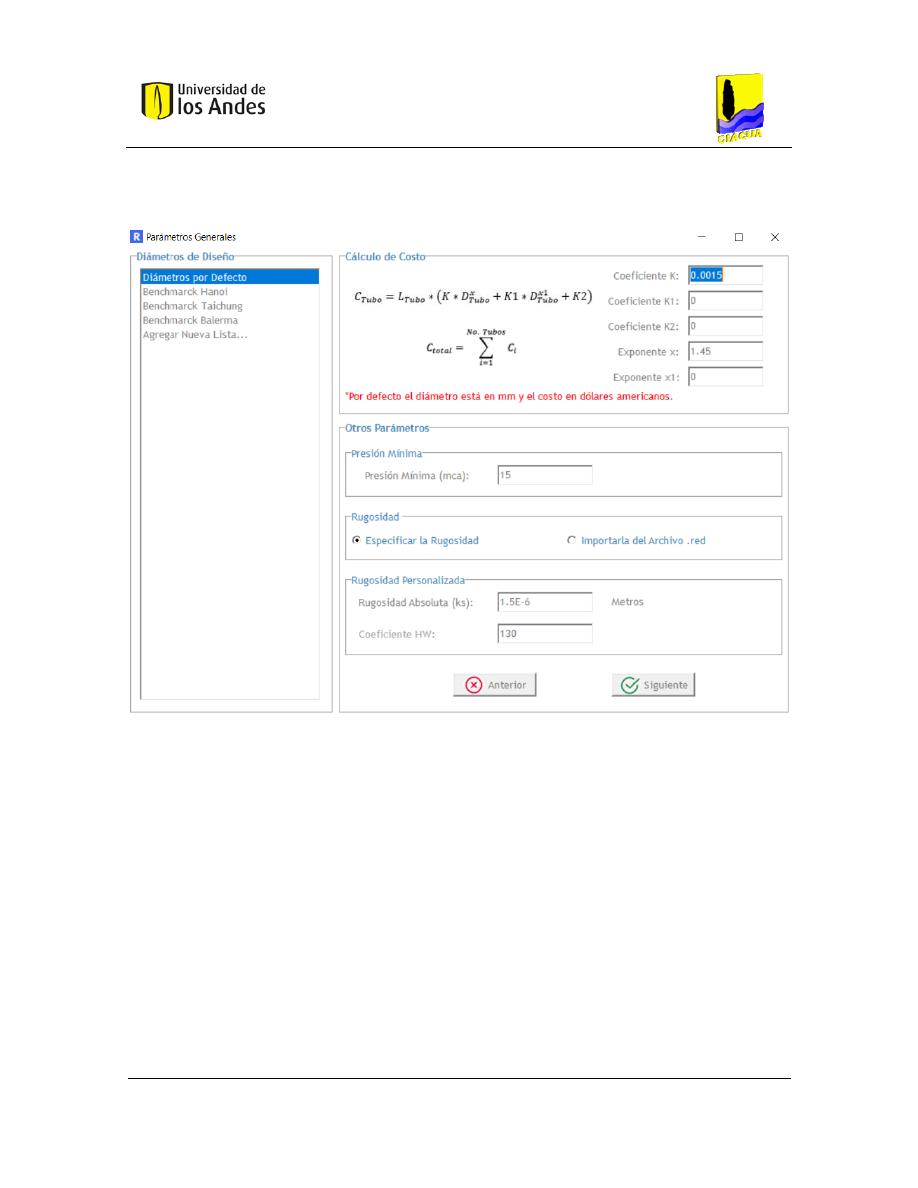
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
68
de costos a minimizar, la lista de diámetros comerciales y la rugosidad del material de las
tuberías, tal como se muestra en la ventana encontrada a continuación:
Figura 5-1. Parámetros generales - optimización REDES
5.1. Metodología OPUS
La metodología Superficie de Uso Óptimo de Potencia (OPUS) fue desarrollada por el
Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA) de la Universidad de
los Andes con base en el trabajo de Wu (1975). OPUS es una metodología determinística,
basada en principios hidráulicos. Su objetivo es minimizar los costos de la red mediante el
establecimiento de formas eficientes de disipación de energía y distribución del flujo a lo
largo del sistema. Esta metodología fue introducida por primera vez por Saldarriaga et al.
(2010) y ha demostrado un gran desempeño de optimización en cuanto a la evaluación de
la función objetivo y el bajo costo computacional que requiere su implementación. De
manera general, OPUS consiste en seis pasos:
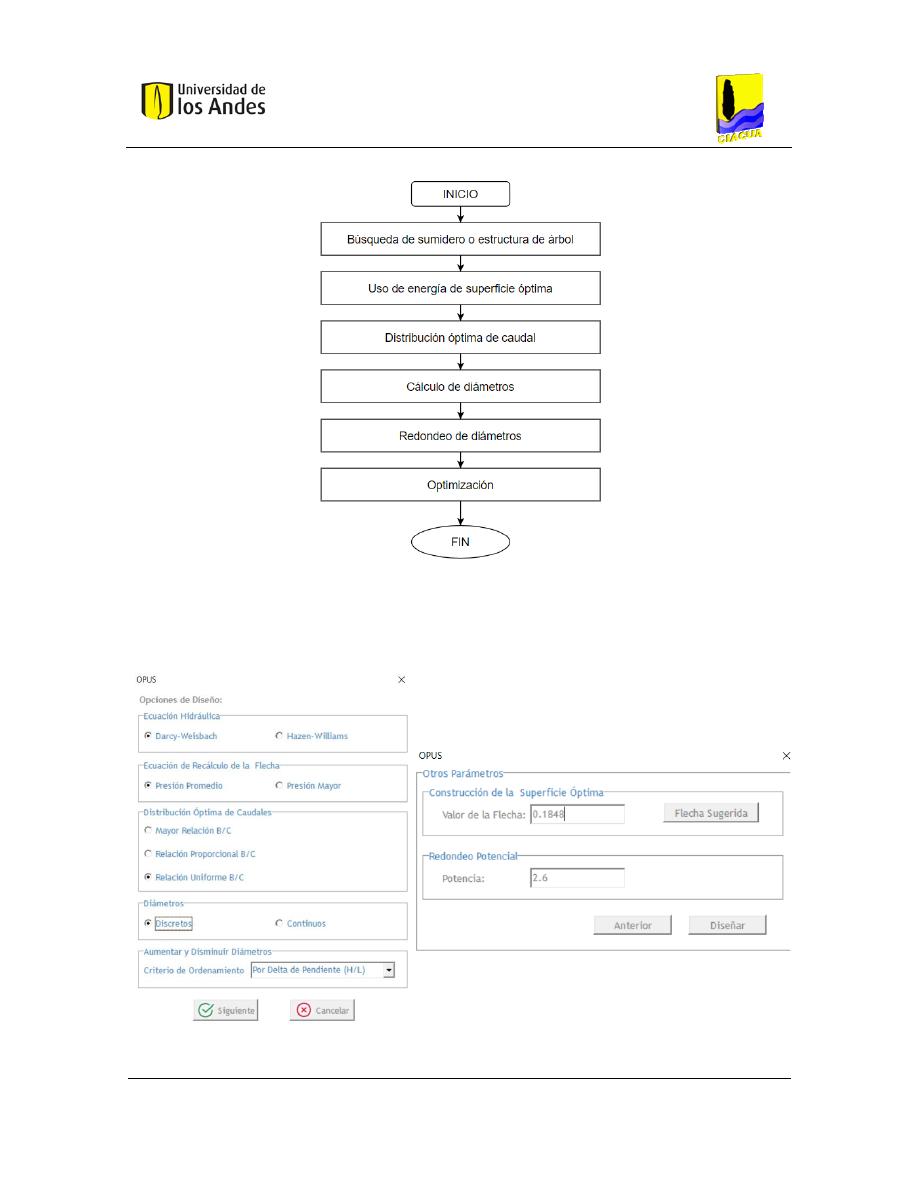
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
69
5.1.1.1 Configuración metodología OPUS
A continuación, se muestran las ventanas en las cuales se configuran las opciones y
parámetros particulares del diseño mediante la metodología OPUS:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
70
En la sección Ecuación Hidráulica se selecciona la ecuación con la cual son evaluadas las
pérdidas por fricción durante cada iteración del diseño. La ecuación hidráulica escogida
corresponde a la ecuación de Darcy-Weisbach. En el apartado Diámetros se indica si se va
a implementar una lista de diámetros discretos (lista comercial) o si se diseña con diámetros
continuos. Para todos los diseños optimizados realizados en esta investigación se
implementaron diámetros discretos (en la sección de ecuación de costo se muestran los
diámetros implementados). Se seleccionó solo un método de aproximación de diámetros
para todos los diseños con el con fin de tener parámetros uniformes que permitieran el
análisis de los resultados de la optimización de los diseños. En la ventana mostrada en la
siguiente figura se establece el valor de la flecha de energía y el exponente de la función
de redondeo potencial. Los valores que se presentan la segunda fueron los mismos para
cada uno de los diseños. El resto de los parámetros de la metodología OPUS del programa
REDES se deja con los valores que vienen por defecto.
5.2. Algoritmos genéticos
Los Algoritmos Genéticos (GA) son un método de búsqueda aleatoria que simula el proceso
de la selección natural de la teoría de la evolución de las especies. De acuerdo con
Saldarriaga (2016), los GA son métodos de optimización combinatoria usados ampliamente
en los últimos años para el diseño óptimo de RDAP. Debido a su carácter estocástico esta
metodología no garantiza el encuentro la solución óptima global ni tampoco un resultado
óptimo local. Aun así, se consideran eficientes en la búsqueda dentro de espacios de
solución tan complejos como el del diseño optimizado de RDAPs (Simpson et al., 1994). A
continuación, se muestra un diagrama que explica una metodología que contempla GA en
un proceso de diseño optimizado multiobjetivo:
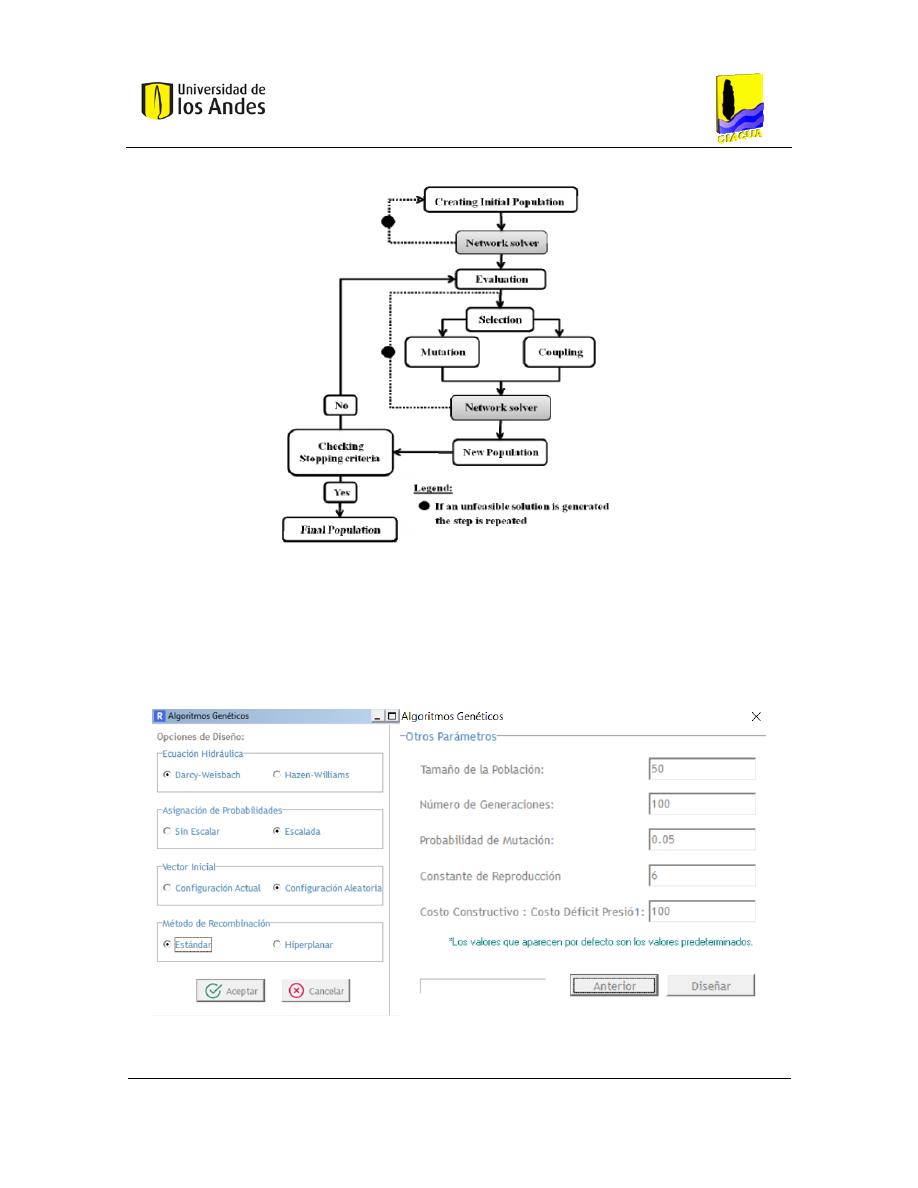
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
71
5.2.1.1 Configuración Algoritmos Genéticos
El Algoritmo Genético implementado en REDES utiliza la reproducción generacional con
recombinación estándar y la selección rueda de ruleta como método de reproducción. Para
el diseño de las redes se dejaron los valores que venían definidos por defecto en el
programa REDES. Únicamente se realizaron cambios en los tamaños poblacionales y el
número de generaciones, esto con el fin de encontrar mejores diseños.
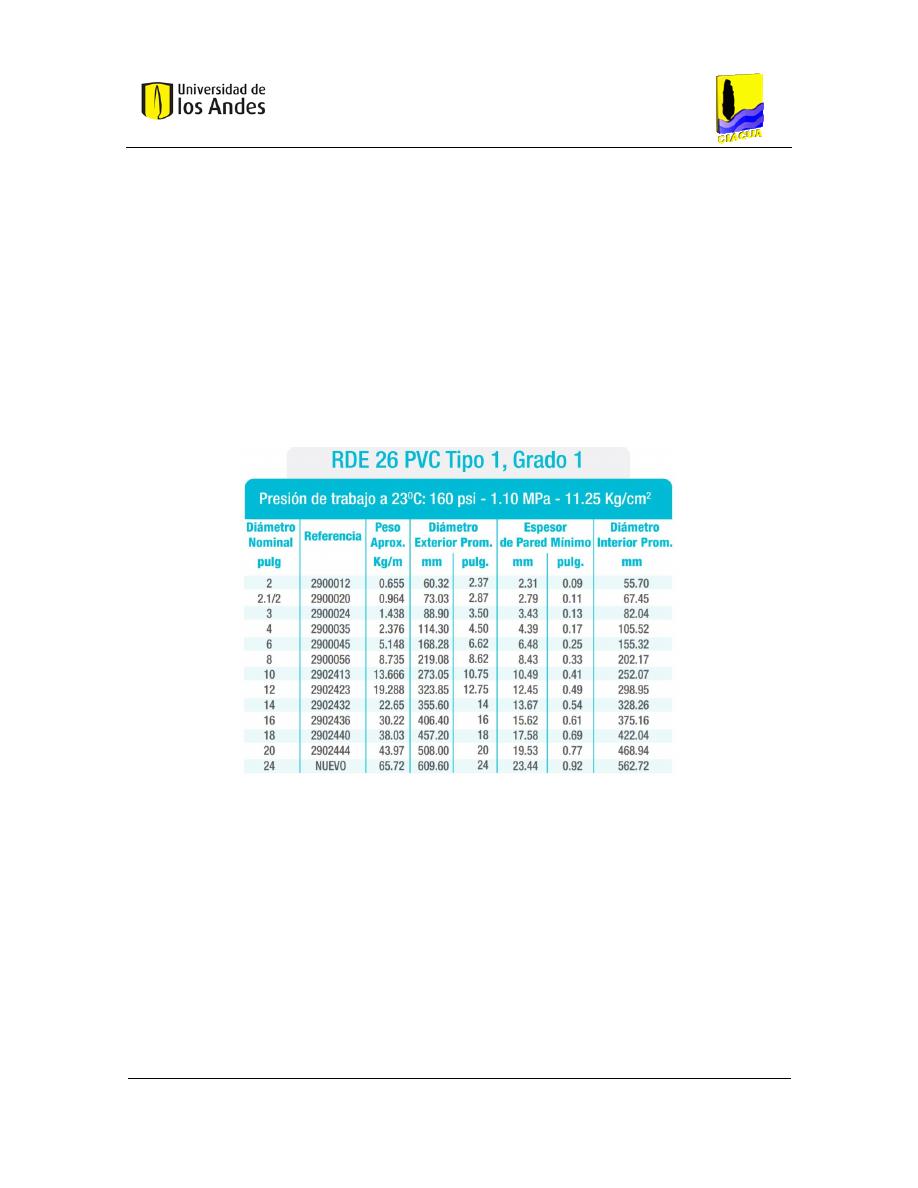
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
72
5.3. Ecuación de costo
La ecuación de costo seleccionada para el diseño optimizado es la ecuación de Peinado
(2016) ya que es la que mejor se ajusta a los costos reales para las tuberías de PVC,
implementadas en los diseños optimizados. Esta ecuación se ajustó a dólares americanos
(USD) y a valor presente, teniendo en cuenta la tasa promedio de inflación entre los años
2016 y 2019. La ecuación es la siguiente:
𝐶 = ∑ 0.005973 ∗ 𝐿
𝑖
∗ 𝐷
𝑖
1.5927
𝑁𝑇
𝑖=1
Así mismo, se trabajó con la lista de diámetros comerciales correspondientes a esa
ecuación, estos se presentan la Figura 5-2.
Figura 5-2. Diámetros comerciales disponibles para optimización (RDE 26 PVC - PAVCO)
5.4. Resiliencia de RDAP
La resiliencia de una RDAP hace referencia a la capacidad que tiene la red de mantener su
servicio por encima del estándar de satisfacción estipulado (las presiones y caudales
demandados en cada uno de los nodos de la red) durante la ocurrencia de un evento
adverso, como una falla. En otras palabras, la resiliencia de una RDAP es una medida de
la tolerancia a fallas de una red. Uno de las formas más conocidas y utilizadas a nivel
mundial para medir la resiliencia de una RDAP es mediante el cálculo del índice de
resiliencia de Todini (2000), el cual se calcula de la siguiente manera:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
73
Ecuación 34. Índice de resiliencia
𝐼
𝑟
=
∑
𝑞
𝑗
∗
(ℎ
𝑗
− ℎ
𝑗
∗
)
𝑛
𝑛
𝑗=1
(∑
𝑄
𝑒
𝐻
𝑒
𝑛
𝑒
𝑒=1
+ ∑
𝑃
𝑖
)
𝑛
𝑏
𝑖=1
− ∑
𝑞
𝑗
∗
ℎ
𝑗
∗
𝑛
𝑛
𝑖=1
donde
𝐼
𝑟
=
índice de resiliencia de una red [-]; 𝑞
𝑗
∗
=
caudal demandado en el nodo 𝑗 de la red
[𝑙/𝑠]; ℎ
𝑗
∗
= mínima cabeza requerida en el nodo
𝑗 de la red [m] ; ℎ
𝑗
= cabeza real en el nodo
𝑗 de la red [m]; 𝑄
𝑒
= caudal ingresado desde el embalse 𝑒 de la red (𝑙/𝑠); 𝐻
𝑒
= cabeza real
en el embalse
𝑒 de la red [𝑚]; 𝑃
𝑖
= potencia adicionada por la bomba 𝑖 de la red [𝑚∗𝑙/𝑠];
𝑛
𝑛
= número de nodos en la red; 𝑛
𝑒
= número de embalses en la red; 𝑛
𝑏
= número de bombas
en la red. Este índice puede tomar valores entre [0,1], donde 0 represente una red sin
resiliencia y 1 representa una red con resiliencia ideal.
El cálculo de este índice es importante para la comparación entre diseños optimizados y no
optimizados. Se espera que, con la optimización de las RDAP, el índice de resiliencia
disminuya de forma significativa.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
74
6. CASOS DE ESTUDIO
Seis redes de distribución de agua potable (5 redes reales colombianas y una red patrón)
fueron seleccionadas para realizar el análisis geométrico de los diseños optimizados. En la
Tabla 6-1 se presentan las características generales de cada una de las redes y en la Figura
6-1 la topología de estas.
Tabla 6-1. Características generales casos de estudio
Red
Tuberías Nodos
Bombas
Válvulas Tanques/Embalses
Demanda
base
(LPS)
Blacksburg*
35
30
0
0
1
97.68
Mamatoco
101
77
0
0
1
17.64
Mesolandia
104
89
0
0
1
20.39
La Esperanza
141
96
0
0
1
18.28
Andalucia Alta
360
329
0
0
1
35.48
Candelaria
567
463
0
0
2
95.56
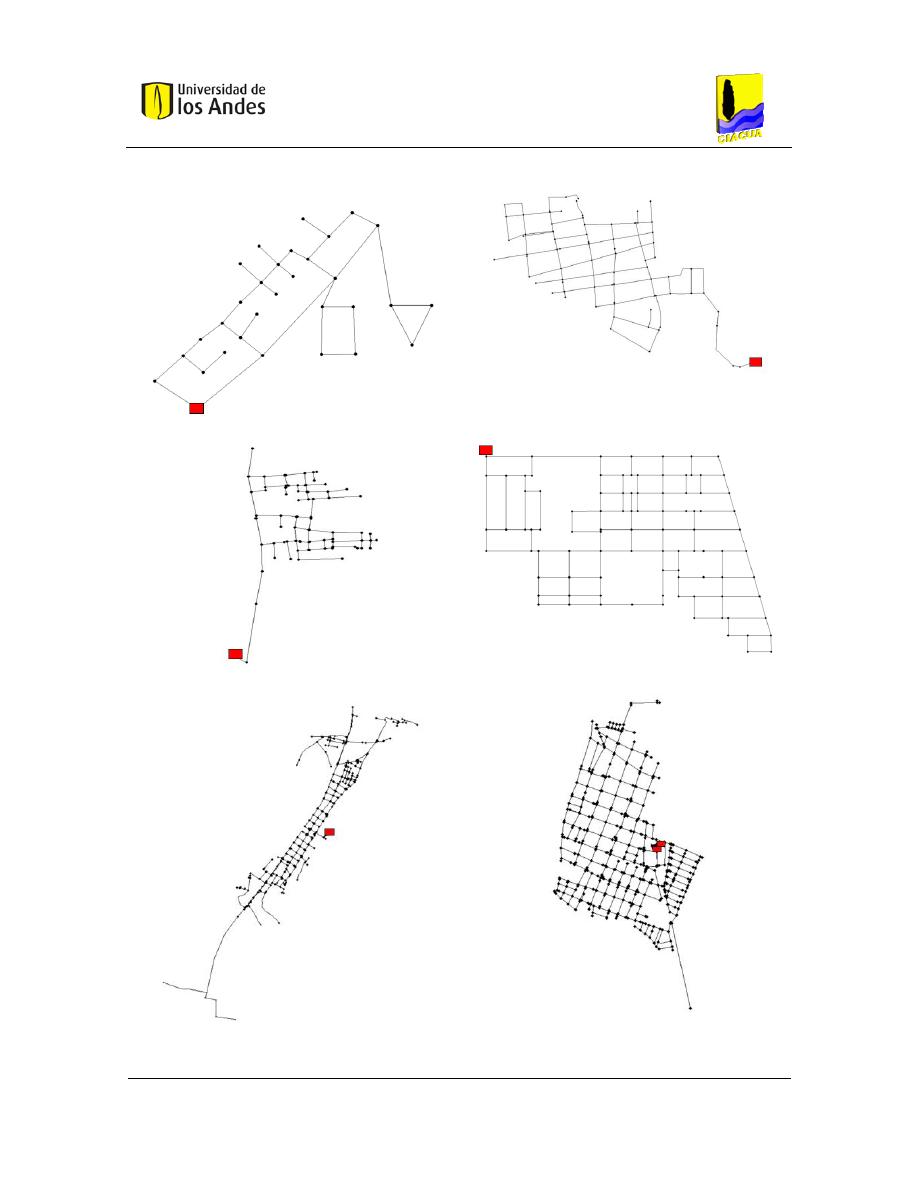
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
75
Blacksburg
Mamatoco
Mesolandia
La Esperanza
Andalucia Alta
Candelaria
Figura 6-1. Casos de estudio. En rojo se señala la ubicación de los tanques
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
76
Cada una de estas redes cuenta con un diseño original, el cual es adapatado para poder
realizar las comparaciones respectivas con el diseño optimizado. La adaptación consta
principalmente de dos factores: en primer lugar se cambian todas las tuberías al material
de PVC, y en segundo lugar, se ajusta la altura del embalse (cabeza de energía) para que
la presión mínima de cada diseño sea mayor a 15 m.c.a. Si para el diseño original se tienen
presiones mayores a los 15 m.c.a, no se realiza el ajuste a la altura del tanque. Así mismo,
se calcula el costo y el índice de resiliencia original de la red con base a la ecuación de
costo presentada en la sección anterior.
Tabla 6-2. Presión mínima, costo y resiliencia de casos de estudio
Red
Presión mínima
(m.c.a)
Costo (USD)
IR
Blacksburg
38.68
$ 105,808.88
0.78
Mamatoco
17.23
$ 69,634.72
0.98
Mesolandia
18.11
$ 52,656.83
0.60
La Esperanza
23.12
$ 40,847.51
0.92
Andalucia Alta
18.38
$ 178,437.43
0.71
Candelaria
23.93
$ 206,049.85
0.68
En la Tabla 6-3 se presenta un resumen de las tuberías de cada uno de los diseños
originales.
Tabla 6-3. Diámetros originales casos de estudio
Diámetros
Blacksburg Mamatoco Mesolandia La Esperanza Andalucia Alta Candelaria
< 60mm
23%
0%
0%
75%
16%
1%
60mm - 100mm
6%
74%
91%
14%
58%
66%
100mm - 200mm
57%
14%
9%
11%
17%
15%
200mm - 350mm
14%
10%
0%
0%
1%
5%
> 350 mm
0%
2%
0%
0%
9%
13%
Volumen (m3)
114
69
46
32
147
185
Área (m2)
2663
2105
1810
1638
6650
6885
Longitud (m)
6185
6642
6170
7558
26400
23312
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
Blacksburg
Mamatoco
Mesolandia
La Esperanza
Andalucia Alta
Candelaria
> 350 mm
200mm - 350mm
100mm - 200mm
60mm - 100mm
< 60mm

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
77
7. ANÁLISIS Y RESULTADOS
7.1. Caracterización geométrica diseños originales
La caracterización geométrica inicial permite identificar el tipo de redes estudiadas. En la
Tabla 7-1 se presentan los resultados de la caracterización geométrica inicial con base en
el esquema de clasificación propuesto por Hwang y Lansey (2017).
Tabla 7-1. Resultados de clasificación topológica según Hwang y Lansey
Network
BI
D (mm)
Class
Blacksburg
0.29
137.1
Distribution Sparse-Grid(DSG)
Mamatoco
0.23
100.9
Distribution Dense-Grid(DDG)
Mesolandia
0.33
93.4
Distribution Dense-Grid(DDG)
La Esperanza
0.02
69.0
Distribution Dense-Grid(DDG)
Andalucia Alta
0.53
80.2
Distribution Branch (DB)
Candelaria
0.24
94.0
Distribution Dense-Grid(DDG)
El número del BI varía entre [0.23, 0.53] mostrando así que la mayoría de las redes
estudiadas son redes en forma de grilla, únicamente Andalucia Alta presenta una
configuración con alto grado de ramificación. En términos del diámetro ponderado por la
longitud
𝐷
̅, las redes estudiadas varían entre [69.0, 137.1] milímetros, por lo cual, todas las
redes clasifican como función en redes de distribución. La clasificación general permite
identificar que, de las seis redes estudiadas, cuatro de ellas (Mamatoco, Mesolandia, La
Esperanza, y Candelaria) son redes de distribución con alta densidad de malla, una
(Blacksburg) es de malla dispersa y una (Andalucia) es una ramificada. Estos cálculos
permiten son importantes porque permiten clasificar de forma inicial la topología de la red,
eliminando el sesgo al momento de clasificar la red únicamente con su topología de forma
visual (como comúnmente se realiza). Se espera que con la optimización, el
𝐷
̅ disminuya
de forma significativa.
En términos de las métricas de CNT, los cálculos para conectividad, eficiencia, centralidad,
robustez, diversidad y modularidad, se presentan en la Tabla 7-2. Esta clasificación permite
una caracterización del grafo, no tiene en cuenta las características propias (pesos) de las
RDAP determinados previamente.
Tabla 7-2. Resultados métricos CNT
Red
𝑞
𝑅
𝑚
𝜆
2
Eficiencia
𝐶
𝑏
𝜆∆
𝐻𝐸𝑇
MOD
Blacksburg
0.08 0.19
0.0419
0.31
0.44
0.31
0.41
0.62
Mamatoco
0.03 0.16
0.0153
0.22
0.23
0.21
0.38
0.67
Mesolandia
0.03 0.09
0.0076
0.17
0.31
0.19
0.37
0.70
La Esperanza
0.03 0.24
0.0125
0.20
0.24
0.32
0.23
0.70
Andalucia Alta 0.01 0.05
0.0005
0.08
0.45
0.06
0.42
0.82
Candelaria
0.01 0.11
0.0015
0.09
0.21
0.09
0.37
0.82

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
78
En cuanto a la conectividad de las redes, es posible determinar que la red con mejor
conectividad es la red patrón Blacksburg, ya que es la que cuenta con mayor densidad de
enlaces y conectividad algebraica. Esto se esperaba ya que esta red no es una red real,
por lo cual su configuración no se rige por las normas de las redes espacialmente
restringidas (por calles y carreteras) como en las demás redes analizadas. En segundo
lugar, se encuentra la red La Esperanza (alto coeficiente de enmallado), la cual comparte
resultados muy similares con la red Mamatoco (tercer lugar en términos de conectividad).
La red con peores propiedades de conectividad es la red Andalucía Alta, comprobando lo
confirmado en la clasificación inicial al terminar que se trataba de una red ramificada.
En términos de eficiencia, la red más eficiente es Blacksburg (0.31) y las redes menos
eficientes son Andalucía Alta (0.08) y Candelaria (0.09). Esto va de la mano con la densidad
de los enlaces y la cantidad de nodos de la red, a medida que aumentan los nodos deberían
aumentar los enlaces para mantener la eficiencia de la red. La red con mayor dominancia
del punto central es la red Andalucía y la que menos tiene dominancia del punto central es
Candelaria. Indicando qué, en términos topológicos, la red Andalucía es más dependiente
de sus nodos y tuberías centrales.
La robustez medida a través de la brecha espectral permite identificar que La Esperanza es
la red más robusta y con mejores propiedades de expansión. Por el contrario, la red
Andalucía es la menos robusta indicando que su topología no es la más adecuada para la
expansión de la red. La red más diversa es Andalucia, ya que si diversidad, medida a través
de la heterogeneidad (coeficiente de variación del grado de los nodos) es la más alta, no
obstante, los valores en comparación con las otras redes no varían mucho, como es de
esperarse en RDAP espacialmente restringidas. Por último, la modularidad indica que las
redes de Andalucía y Candelaria son las más modulares, mientras qué, Blacksburg y
Mamatoco son menos propensas a la segregación en comunidades.
El cálculo de las métricas con peso se analizará una vez optimizadas las redes.
7.2. Optimización de RDAP
La optimización de los casos de estudio se llevó a cabo bajo la metodología establecida en
la sección de metodología de optimización. En la Tabla 7-3 se presenta un resumen de los
resultados obtenidos para cada una de las redes. Las siglas N.O. significan No-
Optimización.
Tabla 7-3. Resultados generales optimización
Red
Costo [USD]
Reducción
costo [USD]
#
Simulaciones
Blacksburg
N.O.
$ 105,809
[-]
[-]
G.A
$ 55,972
47.1%
332501
OPUS
$ 62,244
41.2%
37
Mamatoco
N.O.
$ 69,635
[-]
[-]

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
79
Red
Costo [USD]
Reducción
costo [USD]
#
Simulaciones
G.A
$ 38,490
44.7%
332501
OPUS
$ 27,564
60.4%
62
Mesolandia
N.O.
$ 52,657
[-]
[-]
G.A
$ 37,689
28.4%
332501
OPUS
$ 36,131
31.4%
54
La Esperanza
N.O.
$ 40,848
[-]
[-]
G.A
$ 33,753
17.4%
332501
OPUS
$ 30,374
25.6%
41
Andalucia Alta
N.O.
$ 178,437
[-]
[-]
G.A
$ 138,249
22.5%
1165001
OPUS
$ 120,498
32.5%
208
Candelaria
N.O.
$ 206,050
[-]
[-]
G.A
$ 130,862
36.5%
332501
OPUS
$ 108,961
47.1%
338
Como se puede observar, los cambios obtenidos en los costos de las redes son
significativos, incluso, alcanzando valores de hasta el 60% (OPUS
– Mamatoco) para
algunas redes. También es importante analizar la alta eficiencia computacional de la
metodología OPUS sobre G.A, mostrando que para alcanzar costos similares en G.A se
deben realizar muchas más iteraciones. Esto se debe a la naturaleza de cada metodología
de optimización, no obstante, es importante de mencionar porque permite entender que
algunas metodologías son más eficientes que otras para la optimización de algunas RDAP.
El único caso en donde se obtiene una mejor reducción del costo por parte de G.A. es para
la red de Blacksburg, la cual, como se mencionó previamente, es una red patrón.
Los resultados obtenidos para el análisis de resiliencia de las redes se presentan en la
Tabla 7-4. Los resultados indican lo esperado, con la reducción de los diámetros en cada
una de las redes, la tolerancia a fallas debe disminuir. No obstante, esta relación no es lineal
en ya que para algunos diseños optimizados se obtiene mejor resiliencia aun cuando el
𝐷
̅
es menor (Mesolandia, comparativa entre G.A. y OPUS). Así mismo, el caso de la red
Mesolandia es llamativo ya que los diseños optimizados no reducen de forma significativa
la resiliencia original, mostrando que el diseño original de la red no es el más adecuado (en
términos económicos y de tolerancia a fallas).
Tabla 7-4. Resultados resiliencia
Network
Presión minima
(mca)
IR
𝐷
̅ [𝑚𝑚]
Blacksburg
N.O.
38.68
0.78
137.1
G.A
17.10
0.32
90.5
OPUS
15.09
0.46
96.7
Mamatoco
N.O.
17.23
0.98
100.9
G.A
16.35
0.14
69.3

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
80
OPUS
15.42
0.10
59.9
Mesolandia
N.O.
18.11
0.60
93.4
G.A
15.00
0.49
73.8
OPUS
15.01
0.58
71.2
La Esperanza
N.O.
23.12
0.92
69.0
G.A
15.37
0.25
62.9
OPUS
15.00
0.23
58.9
Andalucia Alta
N.O.
18.38
0.71
80.2
G.A
15.46
0.42
68.5
OPUS
15.00
0.42
62.5
Candelaria
N.O.
23.93
0.68
94.0
G.A
15.06
0.24
71.3
OPUS
15.00
0.31
62.3
7.2.1. Diámetros
La distribución de los diámetros obtenidos en los diseños optimizados se puede observar
en la Tabla 7-5 y en la Figura 7-1. Los resultados muestran lo esperado, entre mayor sea
la reducción de costos de la red, mayor es el cambio en la distribución de los diámetros de
la misma. En general, los diseños optimizados aumentaron de forma significativa la
implementación de tuberías con diámetros menores a los 60 mm (diámetro de 55.87 mm,
valor mínimo comercial estudiado).
Tabla 7-5. Resultados de diámetros para todos los diseños
Blacksburg
Mamatoco
Diametros
N.O.
AG
OPUS
Diámetros
N.O.
AG
OPUS
< 60mm
22.86% 65.71% 51.43%
< 60mm
0%
71%
89%
60mm - 100mm
5.71%
20.00% 14.29%
60mm - 100mm
74%
26%
4%
100mm - 200mm
57.14%
8.57% 14.29% 100mm - 200mm
14%
0%
7%
200mm - 350mm
14.29%
5.71% 20.00% 200mm - 350mm
10%
3%
0%
> 350 mm
0.00%
0.00%
0.00%
> 350 mm
2%
0%
0%
Volumen (m3)
114.1
53.8
61.1
Volumen (m3)
68.7
33.5
19.6
Area (m2)
2663.4
1757.8
1878.1
Area (m2)
2105.0 1445.9 1249.9
Longitud total (m)
6184.7
Longitud total (m)
6642.17
Mesolandia
La Esperanza
Diámetros
N.O.
AG
OPUS
Diámetros
N.O.
AG
OPUS
< 60mm
0%
68%
87%
< 60mm
75%
72%
87%
60mm - 100mm
91%
27%
8%
60mm - 100mm
14%
28%
10%
100mm - 200mm
9%
5%
6%
100mm - 200mm
11%
1%
3%
200mm - 350mm
0%
0%
0%
200mm - 350mm
0%
0%
0%
> 350 mm
0%
0%
0%
> 350 mm
0%
0%
0%
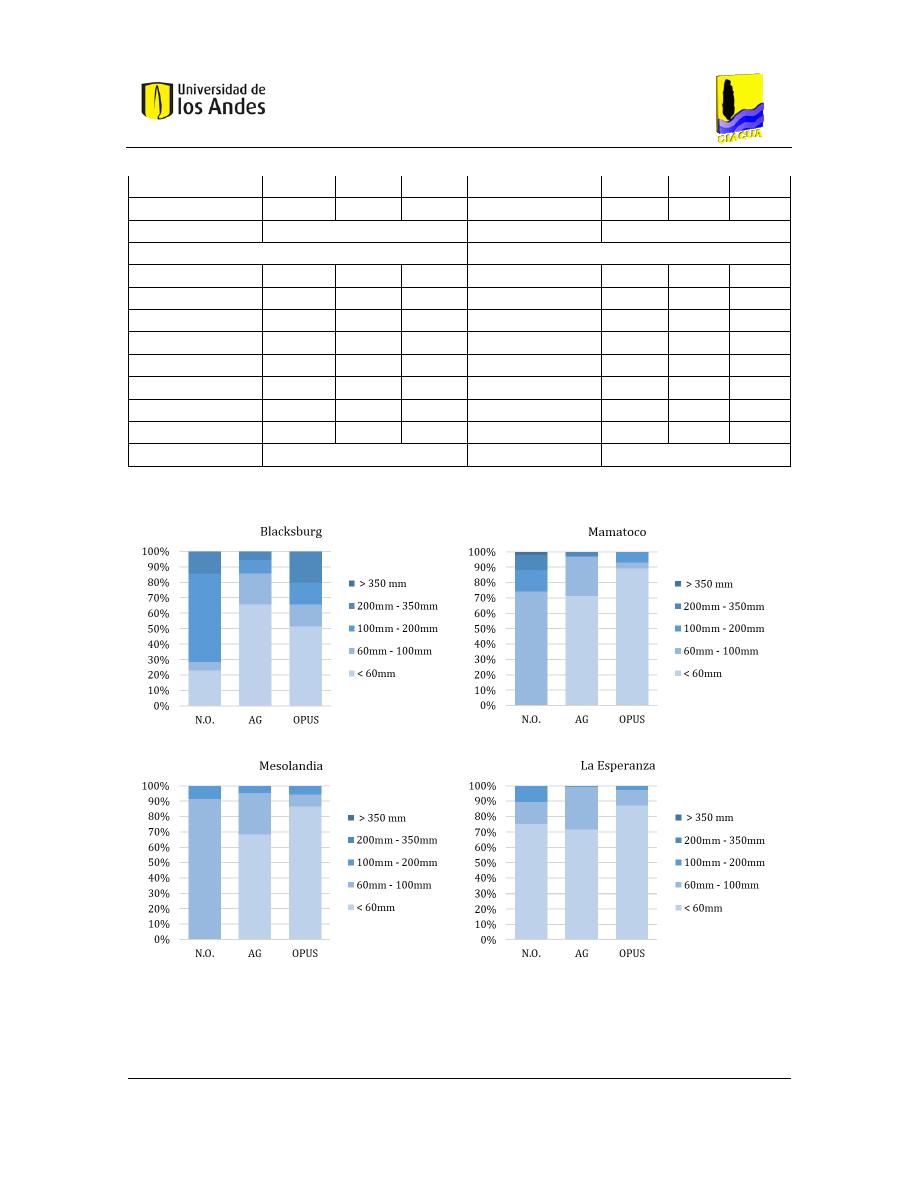
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
81
Volumen (m3)
45.5
31.0
29.9
Volumen (m3)
32.3
24.3
21.3
Area (m2)
1810.0
1431.4
1379.9
Area (m2)
1638.1 1493.0 1399.6
Longitud total (m)
6170
Longitud total (m)
7558.2
Andalucia Alta
Candelaria
Diámetros
N.O.
AG
OPUS
Diámetros
N.O.
AG
OPUS
< 60mm
16%
49%
83%
< 60mm
1%
48%
90%
60mm - 100mm
58%
49%
9%
60mm - 100mm
66%
48%
4%
100mm - 200mm
17%
1%
8%
100mm -200mm
15%
1%
3%
200mm - 350mm
1%
0%
1%
200mm - 350mm
5%
1%
2%
> 350 mm
9%
1%
0%
> 350 mm
13%
2%
0%
Volumen (m3)
146.9
106.5
90.7
Pipe Volume (m3)
184.8
103.2
85.8
Area (m2)
6650.2
5680.0
5183.8
Pipe Area (m2)
6884.5 5220.8 4564.2
Longitud total (m)
26400.3
Pipe length (m)
23312.27
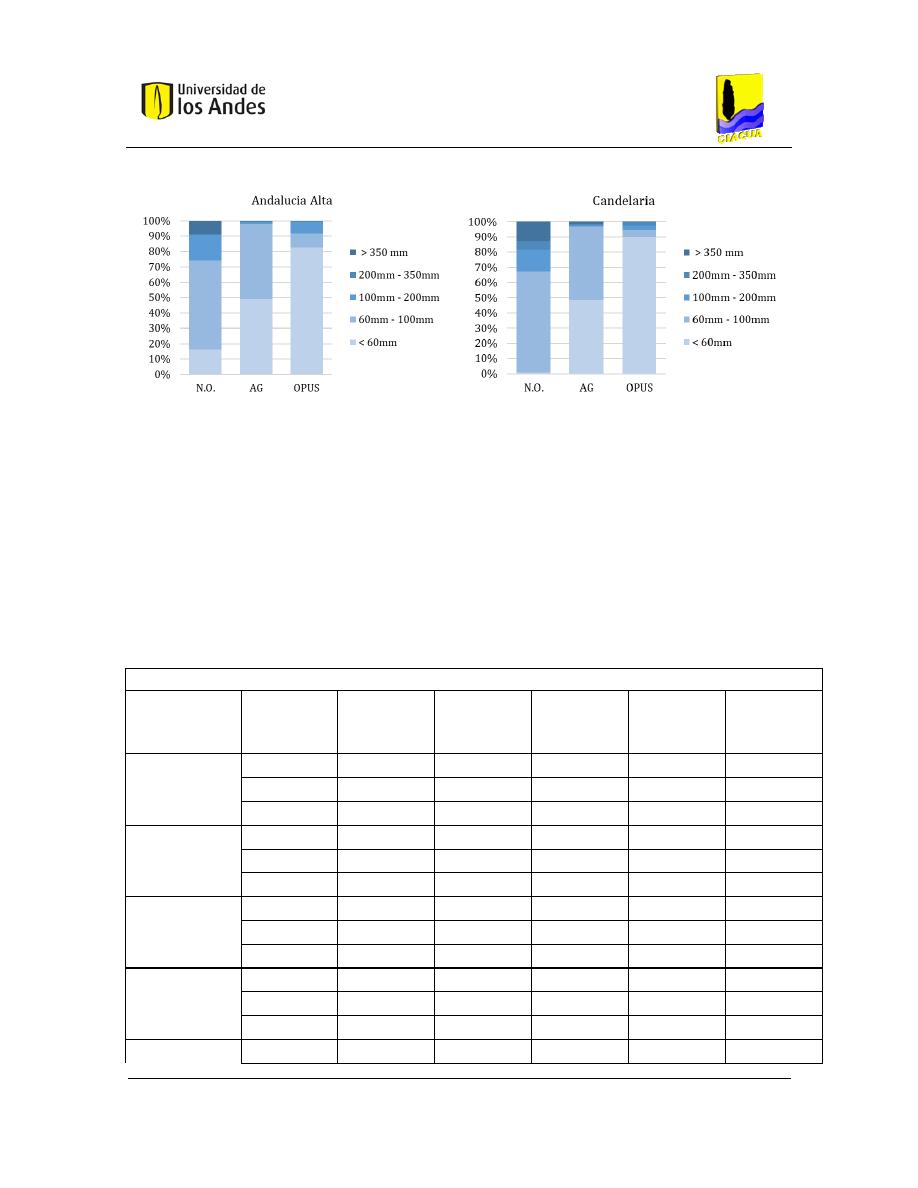
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
82
Figura 7-1. Distribución de diámetros para todos los diseños
7.2.2. Índices de CNT ajustados con peso
7.2.2.1 Conectividad algebraica
En la tabla 7-6 se presentan los resultados obtenidos del cambio de la conectividad
algebraica para los diseños optimizados. La tabla muestra los resultados separados en
peso (
𝑤
𝑑
y
𝑤
𝑄
), diseño (N.O-No Optimización, G.A y OPUS), y en el cambio relativo de la
métrica con respecto a su valor del diseño original. La figura 7-2 permite visualizar lo
descrito en la tabla 7-6.
Tabla 7-6. Resultados conectividad algebraica
Conectividad algebraica - 𝝀
𝟐
Red
Peso
N.O.
G.A.
OPUS
Cambio
relativo
G.A.
Cambio
relativo
OPUS
Blacksburg
[-]
0.042
0.042
0.042
0.000000
0.000000
𝑤
𝑑
0.033
0.063
0.040
0.945701
0.233940
𝑤
𝑄
0.061
0.122
0.039
1.003634
-0.364745
Mamatoco
[-]
0.015
0.015
0.015
0.000000
0.000000
𝑤
𝑑
0.012
0.011
0.013
-0.130471
0.088686
𝑤
𝑄
0.016
0.019
0.019
0.187669
0.204071
Mesolandia
[-]
0.008
0.008
0.008
0.000000
0.000000
𝑤
𝑑
0.008
0.008
0.008
0.002561
0.027000
𝑤
𝑄
0.014
0.014
0.015
0.010614
0.113522
La Esperanza
[-]
0.013
0.013
0.013
0.000000
0.000000
𝑤
𝑑
0.013
0.012
0.013
-0.076233
-0.016848
𝑤
𝑄
0.019
0.016
0.016
-0.137025
-0.134490
[-]
0.000
0.000
0.000
0.000000
0.000000
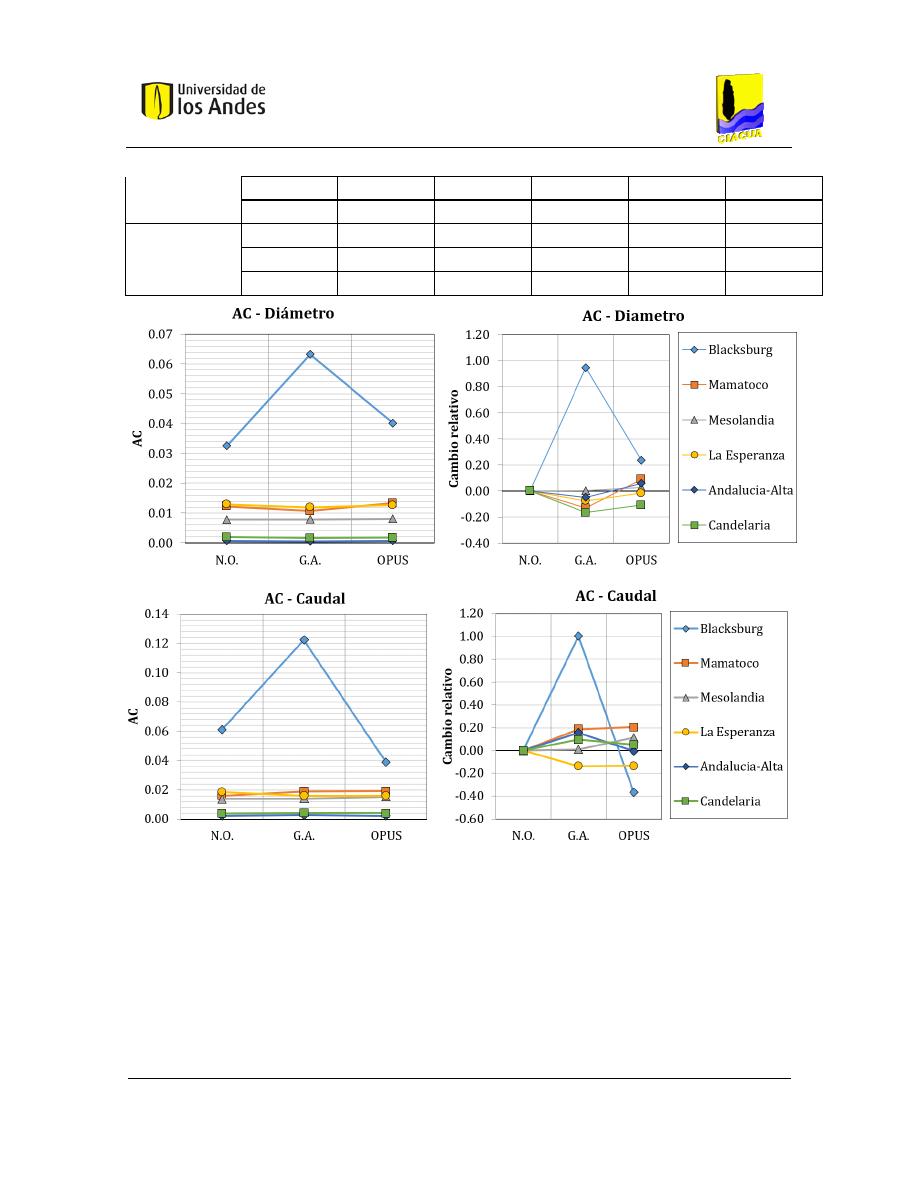
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
83
Andalucia-
Alta
𝑤
𝑑
0.001
0.001
0.001
-0.049675
0.058040
𝑤
𝑄
0.002
0.003
0.002
0.157190
-0.004974
Candelaria
[-]
0.001
0.001
0.001
0.000000
0.000000
𝑤
𝑑
0.002
0.002
0.002
-0.165224
-0.108235
𝑤
𝑄
0.004
0.004
0.004
0.095947
0.051264
Figura 7-2. Resultados conectividad algebraica
Diámetro 𝑤
𝑑
Las figuras 7-2 muestran que las redes se comportan de forma diferente para cada caso,
por lo cual, no es posible realizar una generalización de los cambios en conectividad
obtenidos al optimizar los diseños. Para la conectividad en términos del diámetro, los
resultados muestran que la red Blacksburg es la de mayor conectividad, y con su
optimización, esta conectividad aumenta significativamente (100% para AG y 25% OPUS).
Para el resto de las redes, se puede observar que la optimización no altera de forma
significativa su conectividad inicial, los cambios relativos para cada una de ellas son

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
84
inferiores al 20%. Las redes con menor conectividad son las redes de Andalucia Alta y
Candelaria, tal como se mostraba en el análisis inicial sin pesos.
Caudal 𝑤
𝑄
En cuanto a la conectividad en términos del caudal, los resultados obtenidos muestran un
comportamiento similar al descrito anteriormente, siendo Blacksburg la red con mayor
conectividad y a su vez, la red más sensible a la optimización. En este caso, al optimizar
Blacksburg con OPUS, la conectividad algebraica de la red disminuye.
7.2.2.2 Centralidad
En la 7-7 se presentan los resultados obtenidos del cambio de la dominancia del punto
central para los diseños optimizados. La tabla muestra los resultados separados en peso
(
𝑤
𝑑
y
𝑤
𝑄
), diseño (N.O-No Optimización, G.A y OPUS), y en el cambio relativo de la métrica
con respecto a su valor del diseño original. La figura 7-3 permite visualizar lo descrito en la
tabla 7-7.
Tabla 7-7. Resultados centralidad
Centralidad - 𝑪
𝒃
Red
Peso
N.O.
G.A.
OPUS
Cambio
relativo
G.A.
Cambio
relativo
OPUS
Blacksburg
[-]
0.437
0.437
0.437
0.000000
0.000000
𝑤
𝑑
0.452
0.263
0.410
-0.417741
-0.091418
𝑤
𝑄
0.345
0.400
0.429
0.158829
0.242014
Mamatoco
[-]
0.227
0.227
0.227
0.000000
0.000000
𝑤
𝑑
0.230
0.224
0.224
-0.025220
-0.026436
𝑤
𝑄
0.347
0.304
0.347
-0.124923
-0.000690
Mesolandia
[-]
0.313
0.313
0.313
0.000000
0.000000
𝑤
𝑑
0.329
0.347
0.323
0.053978
-0.018930
𝑤
𝑄
0.412
0.530
0.388
0.285888
-0.059049
La Esperanza
[-]
0.244
0.244
0.244
0.000000
0.000000
𝑤
𝑑
0.255
0.205
0.242
-0.198174
-0.051664
𝑤
𝑄
0.372
0.438
0.306
0.176165
-0.176570
Andalucia-
Alta
[-]
0.452
0.452
0.452
0.000000
0.000000
𝑤
𝑑
0.451
0.450
0.450
-0.002249
-0.003549
𝑤
𝑄
0.445
0.441
0.445
-0.010629
-0.001949
Candelaria
[-]
0.210
0.210
0.210
0.000000
0.000000
𝑤
𝑑
0.306
0.265
0.237
-0.133117
-0.226051
𝑤
𝑄
0.436
0.384
0.319
-0.119828
-0.267312
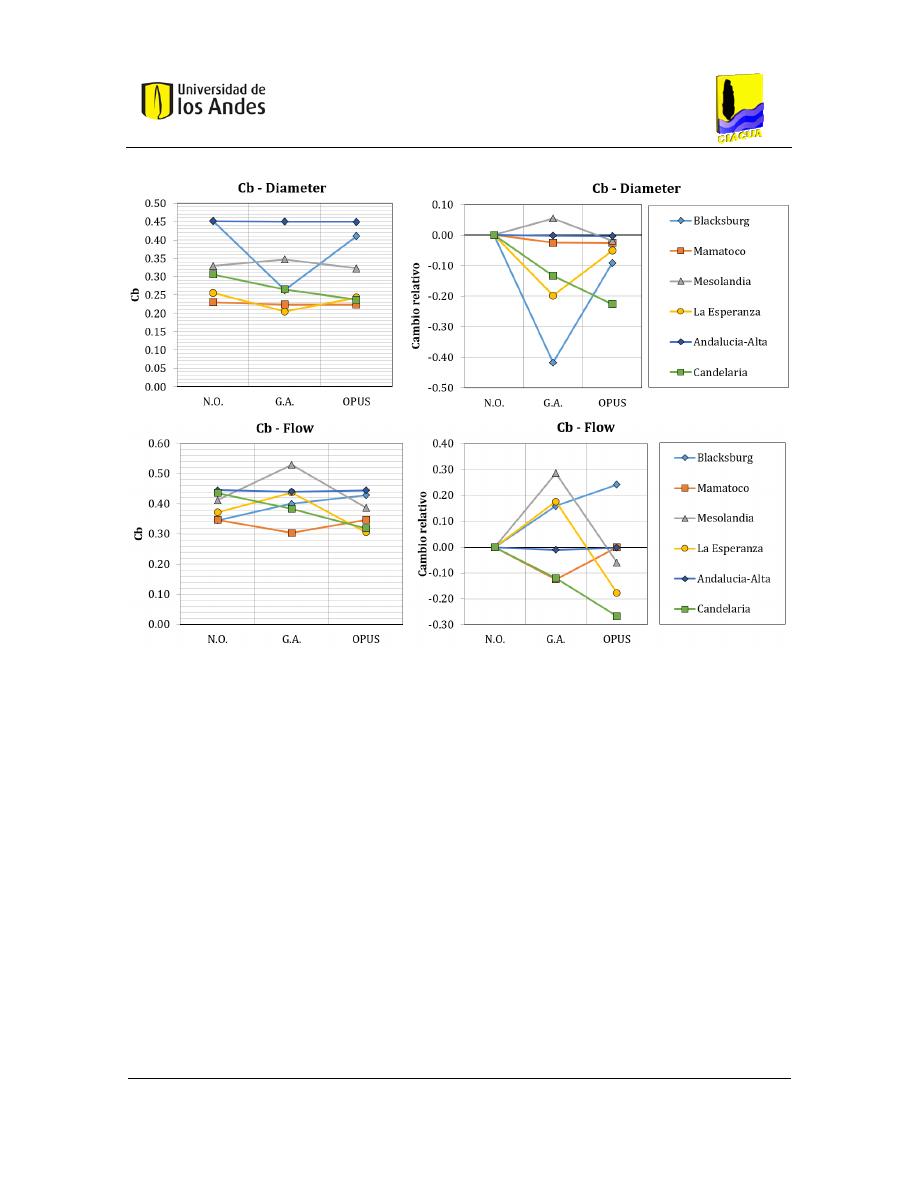
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
85
Figura 7-3. Resultados centralidad
Diámetro 𝑤
𝑑
El cálculo de la dominancia del punto central con respecto a los diámetros de la red muestra
una posible relación negativa con respecto a la optimización. Esto se puede observar en la
figura 7-3 (diámetro), en donde se muestra que, para todas las redes, los resultados
obtenidos en el diseño optimizado por la metodología OPUS, disminuyen la dominancia del
punto central. Si bien no es un cambio relativo significativo, si puede reflejar que los diseños
optimizados disminuyen la centralidad de la red. Así mismo, se puede observar que para la
red Andalucia, los cambios en la centralidad son muy bajos (casi nulos) y esto se debe a
que esta red es de estructura ramificada, por lo cual, su centralidad no se afecta por los
cambios generados en la optimización.
Caudal 𝑤
𝑄
En términos de la centralidad a través del caudal, se evidencia que el comportamiento es
diferente para cada red. El único comportamiento que se mantiene constante, con respecto
al diámetro, es el de la red Andalucía, comprobando así que su centralidad no se ve
afectada por la optimización. La metodología de OPUS muestra una disminución de la
centralidad para las redes de Candelaria, La Esperanza y Mesolandia, mientras que A.G

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
86
únicamente muestran disminución en Candelaria y Mamatoco. La red de Blacksburg
presenta un aumento significativo con su optimización.
7.2.2.3 Robustez
En la Tabla 7-8 presentan los resultados obtenidos de la brecha espectral para los diseños
optimizados. La tabla muestra los resultados separados en peso (
𝑤
𝑑
y
𝑤
𝑄
), diseño (N.O-No
Optimización, G.A y OPUS), y en el cambio relativo de la métrica con respecto a su valor
del diseño original.
Tabla 7-8. Resultados brecha espectral
Brecha Espectral - 𝝀∆
Red
Peso
N.O.
G.A.
OPUS
Cambio
relativo
G.A.
Cambio
relativo
OPUS
Blacksburg
[-]
0.308
0.308
0.308
0.000000
0.000000
𝑤
𝑑
0.206
0.766
0.275
2.718272
0.336267
𝑤
𝑄
0.588
0.898
0.485
0.528550
-0.174625
Mamatoco
[-]
0.206
0.206
0.206
0.000000
0.000000
𝑤
𝑑
0.204
0.184
0.339
-0.094999
0.662867
𝑤
𝑄
0.286
0.420
0.392
0.469005
0.371109
Mesolandia
[-]
0.193
0.193
0.193
0.000000
0.000000
𝑤
𝑑
0.263
0.450
0.556
0.707232
1.111048
𝑤
𝑄
0.614
0.643
0.640
0.047200
0.042878
La Esperanza
[-]
0.319
0.319
0.319
0.000000
0.000000
𝑤
𝑑
0.452
0.022
0.111
-0.951868
-0.754014
𝑤
𝑄
0.752
0.667
0.605
-0.113155
-0.194916
Andalucia-
Alta
[-]
0.058
0.058
0.058
0.000000
0.000000
𝑤
𝑑
0.537
0.494
0.436
-0.079417
-0.188442
𝑤
𝑄
0.645
0.639
0.629
-0.008834
-0.024279
Candelaria
[-]
0.086
0.086
0.086
0.000000
0.000000
𝑤
𝑑
0.182
0.125
0.289
-0.312379
0.587870
𝑤
𝑄
0.365
0.393
0.282
0.077154
-0.226412
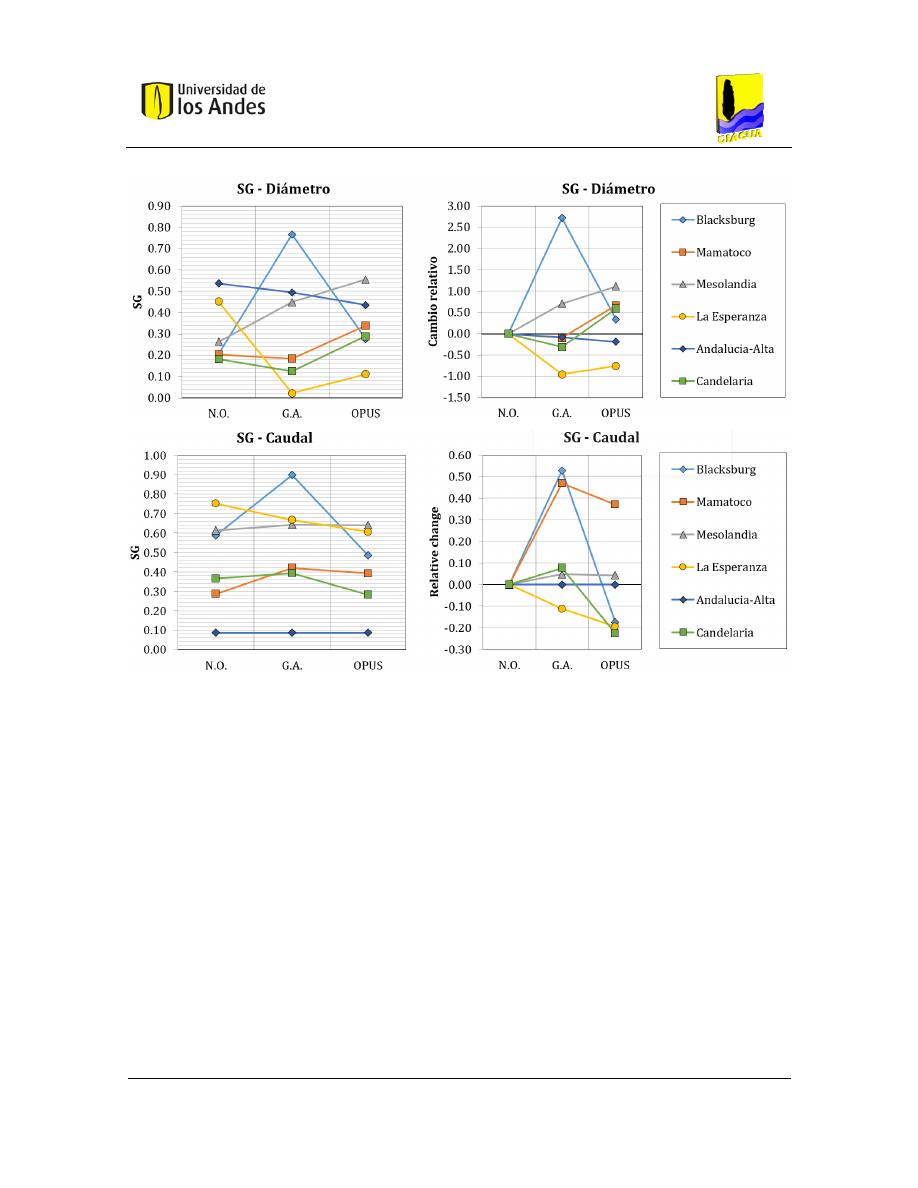
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
87
Figura 7-4. Resultados brecha espectral
Diámetro 𝑤
𝑑
Los resultados de la brecha espectral, por tratarse de una métrica espectral, son muy
sensibles a los pesos utilizados, por lo cual, es de esperarse que los resultados obtenidos
sean muy distintos para cada red. Inicialmente, se puede apreciar que la red de Andalucía
Alta tenía el valor más alto de robustez, no obstante, esta disminuyó con el diseño
optimizado. La metodología de OPUS mejora la robustez de los diseños de Mesolandia,
Candelaria y Mamatoco. Nuevamente, Blacksburg muestra un comportamiento atípico entre
el diseño de G.A y OPUS.
Caudal 𝑤
𝑄
Para el caso de Andalucía Alta, la robustez medida con la brecha espectral y utilizando
como peso el caudal no cambia con su optimización. Inicialmente se tiene la Esperanza
como la red más robusta, pero al optimizar, Mesolandia mejora su resultado. En general,
los resultados no siguen ningún comportamiento específico.
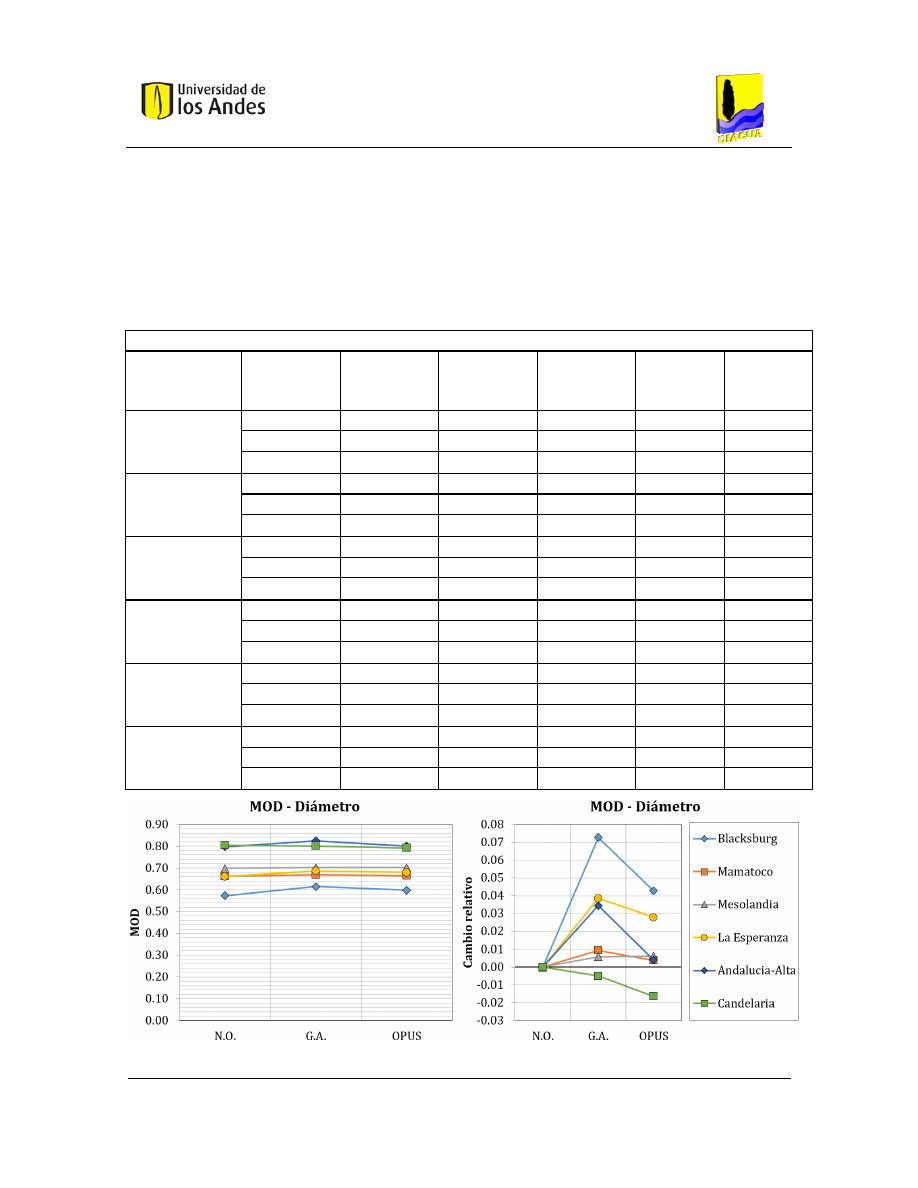
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
88
7.2.2.4 Modularidad
En la Tabla 7-9 se presentan los resultados obtenidos de la modularidad para los diseños
optimizados. La tabla muestra los resultados separados en peso (
𝑤
𝑑
y
𝑤
𝑄
), diseño (N.O-No
Optimización, G.A y OPUS), y en el cambio relativo de la métrica con respecto a su valor
del diseño original.
Tabla 7-9. Resultados modularidad
Modularidad – 𝑴𝑶𝑫
Red
Peso
N.O.
G.A.
OPUS
Cambio
relativo
G.A.
Cambio
relativo
OPUS
Blacksburg
[-]
0.621
0.621
0.621
0.000000 0.000000
𝑤
𝑑
0.573
0.615
0.598
0.072650 0.042735
𝑤
𝑄
0.464
0.511
0.513
0.101143 0.104662
Mamatoco
[-]
0.665
0.665
0.665
0.000000 0.000000
𝑤
𝑑
0.663
0.669
0.666
0.009348 0.003694
𝑤
𝑄
0.421
0.435
0.425
0.033959 0.009499
Mesolandia
[-]
0.703
0.703
0.703
0.000000 0.000000
𝑤
𝑑
0.698
0.702
0.702
0.005764 0.006161
𝑤
𝑄
0.599
0.546
0.445
-0.08954
-0.25698
La Esperanza
[-]
0.697
0.697
0.697
0.000000 0.000000
𝑤
𝑑
0.661
0.686
0.679
0.038598 0.027939
𝑤
𝑄
0.539
0.481
0.505
-0.10919
-0.06457
Andalucia-
Alta
[-]
0.823
0.823
0.823
0.000000 0.000000
𝑤
𝑑
0.798
0.825
0.801
0.034450 0.003908
𝑤
𝑄
0.428
0.459
0.406
0.074589 -0.05116
Candelaria
[-]
0.818
0.818
0.818
0.000000 0.000000
𝑤
𝑑
0.805
0.801
0.791
-0.00498
-0.01646
𝑤
𝑄
0.454
0.308
0.265
-0.32157
-0.41722

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
89
Figura 7-5. Resultados modularidad
Diámetro 𝑤
𝑑
En general, la modularidad de las redes calculada con el peso del diámetro muestra una
mejora a medida que se optimiza. Únicamente una red (Candelaria) empeora su
modularidad. No obstante, los cambios relativos obtenidos para la modularidad son muy
bajos, todos menores al 8% con respecto a su valor inicial.
Caudal 𝑤
𝑄
La modularidad calculada con el caudal si permite ver un cambio significativo con la
optimización, en especial para la red de Candelaria, la cual disminuye hasta casi 40%. Las
redes de Mesolandia y La Esperanza también presentan una disminución en si modularidad
para ambos algoritmos de optimización.
7.2.3. Centroides
Los centroides de las redes se calculan para analizar los desplazamientos obtenidos con la
optimización de los diseños. En la tabla XX se presentan todos los centroides para las redes
analizadas.
Tabla 7-10. Resultados centroides
Red
Volumen
Potencia Específica
Diámetro
Potencia
Cx
Cy
Cx
Cy
Cx
Cy
Cx
Cy
Blacksburg NO
5377
6412
3369
4844
5139
6537
5404
6541
AG
5373
5894
4257
5574
5253
6392
5420
6539
OPUS
4557
6394
2932
5515
4718
6474
5381
6538
Mamatoco NO
990439 1733400 990562 1733334 990356 1733455 990313 1733436
AG
990477 1733388 990607 1733343 990346 1733471 990319 1733434
OPUS 990371 1733453 990625 1733311 990331 1733481 990319 1733434
Mesolandia NO
924487 1695590 924348 1695176 924568 1695693 924525 1695609
AG
924466 1695497 924366 1695284 924563 1695675 924519 1695600
OPUS 924456 1695441 924389 1695358 924563 1695666 924522 1695596
NO
934053 1097565 933904 1097649 934109 1097533 934086 1097575

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
90
Red
Volumen
Potencia Específica
Diámetro
Potencia
Cx
Cy
Cx
Cy
Cx
Cy
Cx
Cy
La
Esperanza
AG
934107 1097527 933859 1097642 934125 1097525 934086 1097575
OPUS 934099 1097539 933842 1097651 934125 1097527 934085 1097575
Andalucia
Alta
NO
1101161 952932 1101273 952927 1101216 952994 1101227 953014
AG
1101131 952866 1101279 953002 1101208 952985 1101226 953012
OPUS 1101138 952856 1101283 952981 1101220 952988 1101226 953012
Candelaria NO
1081190 868594 1081214 868681 1081183 868564 1081105 868762
AG
1081151 868631 1081236 868710 1081163 868588 1081105 868762
OPUS 1081149 868655 1081150 868736 1081165 868594 1081105 868762
En las figuras 7-6 a 7-10 se presentan la ubicación de los distintos centroides calculados
para cada red. En términos generales ser observa que únicamente los centroides de
potencia especifica y volumen muestran un desplazamiento significativo. Así mismo, el
centroide de potencia muestra desplazamientos muy bajos (casi nulos) en cuanto a los
diseños optimizados, mostrando que la distribución de potencia de la red no se afecta con
la optimización del diseño. Para los centroides de diámetro, su desplazamiento no es tan
importante y se concentra en el centroide de coordenadas de los nodos y las tuberías de la
red. Si bien si existe un desplazamiento debido a los cambios en los diseños optimizados,
este no resulta ser tan significativo.
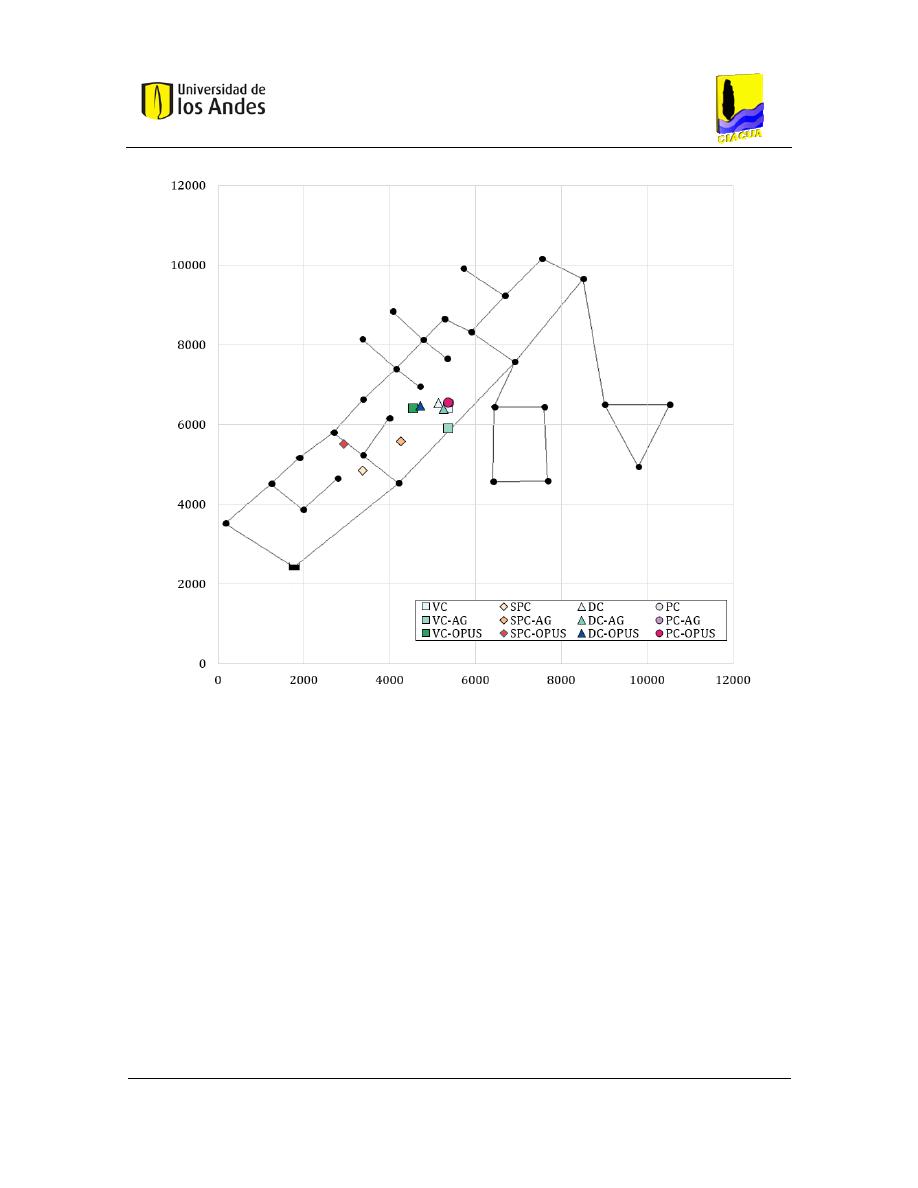
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
91
Figura 7-6. Centroides Blacksburg
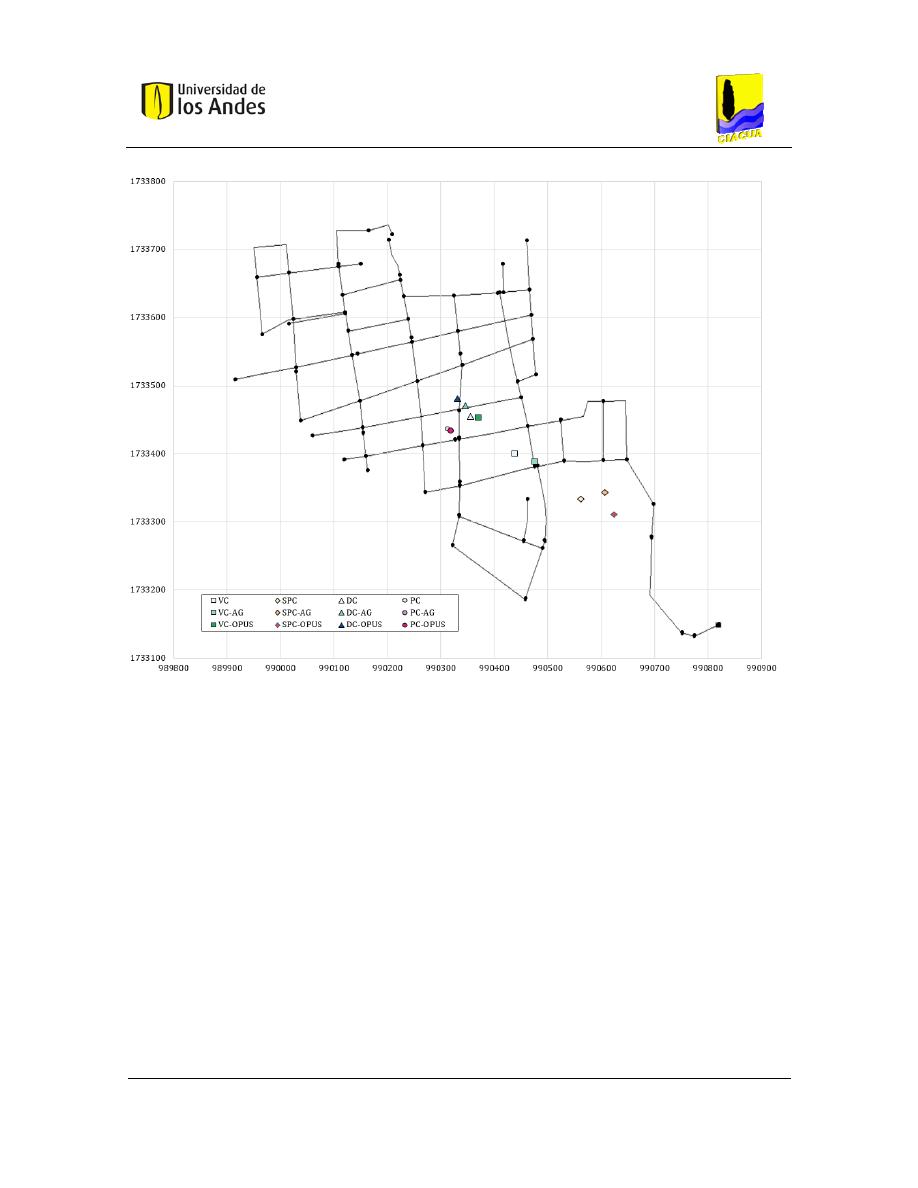
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
92
Figura 7-7. Centroides Mamatoco
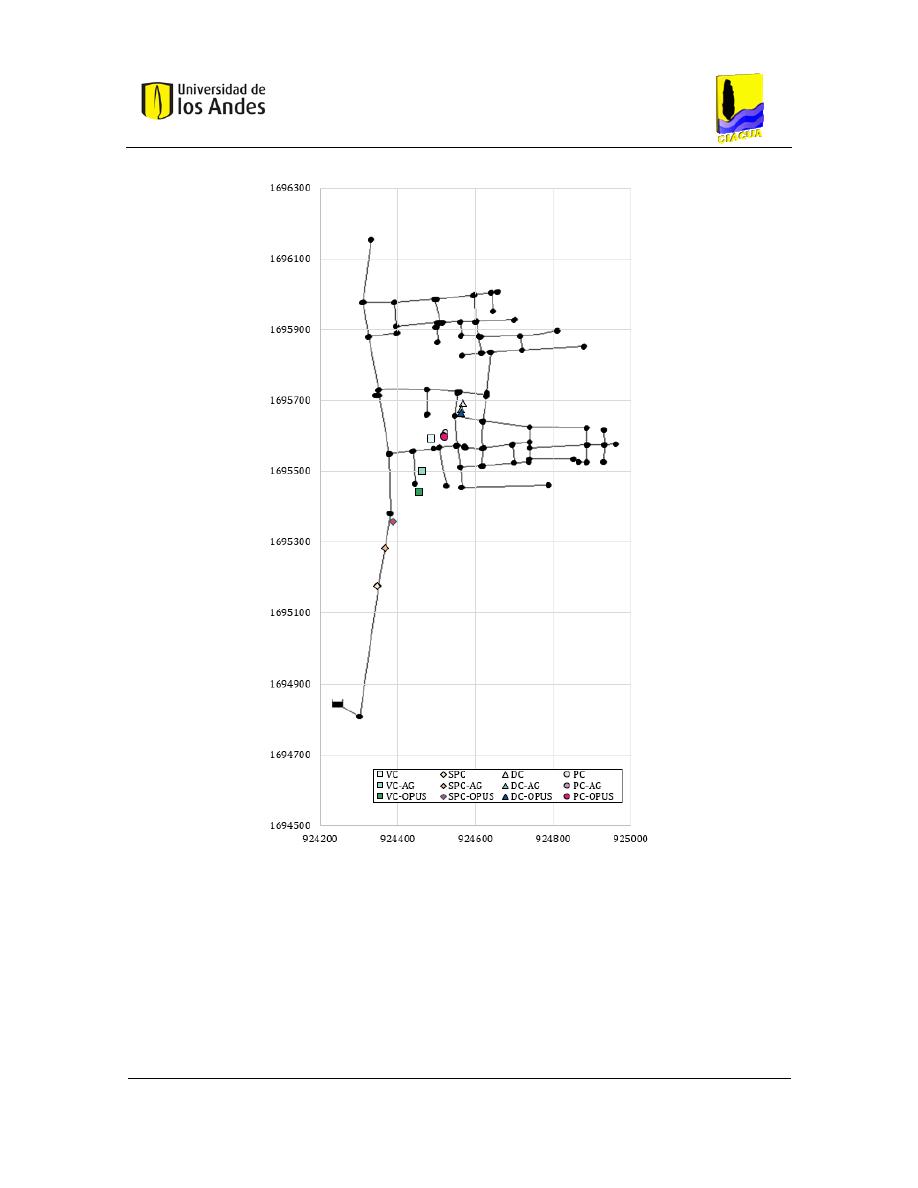
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
93
Figura 7-8. Centroides Mesolandia

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
94
Figura 7-9. Centroides La Esperanza
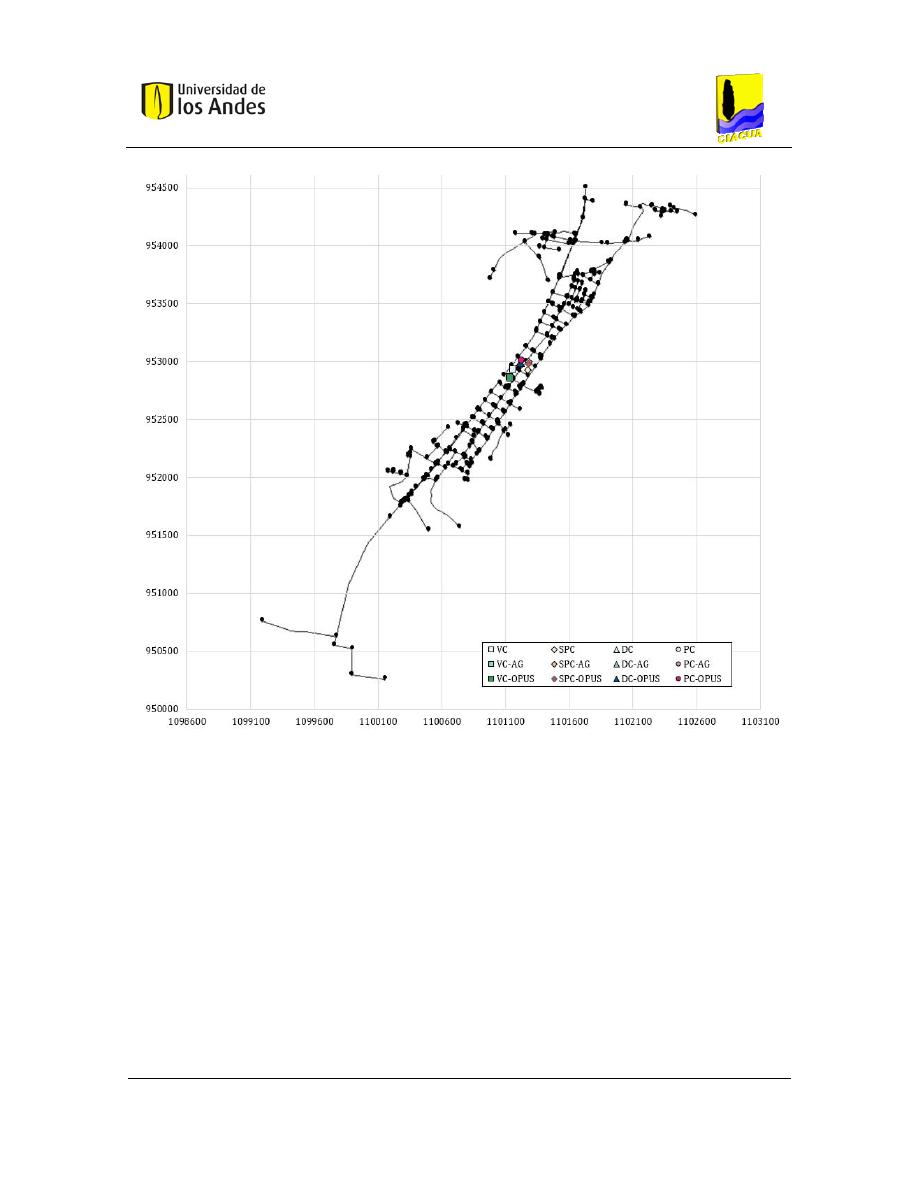
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
95
Figura 7-10. Centroides Andalucia Alta

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
96
Figura 7-11. Centroides Candelaria

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
97
8. CONCLUSIONES Y RECOMENDACIONES
En la presente investigación, mediante la realización de un estado del arte, se buscó abrir
un camino para entender las posibles relaciones existentes entre la geometría de las redes
de distribución de agua potable y su diseño optimizado. Para tal fin, se realizó inicialmente
una recopilación bibliográfica exhaustiva en la cual se determinó el estado actual de las
investigaciones en términos de geometrías de RDAP y sus diseños optimizados. De esta
recopilación fue posible concluir:
-
La optimización de RDAP abarca una gran variedad de problemas, todos descritos
previamente. De estos, en el que más se ha avanzado es en la optimización de los
componentes de la red, en especial del diámetro de sus tuberías. Así mismo, podría
considerarse como el problema más simple de tratar para entender la geometría de
los diseños optimizados de RDAP. Por estas razones, la realización del análisis
geométrico de RDAP diseñadas óptimamente se debe enfocar principalmente en la
geometría de los diseños optimizados en costos de sus tuberías.
-
La mayoría de estudios en RDAP que implementan teoría de redes complejas ha
supuesto grafos sin peso, no han incluido características geométricas de los
componentes de la red en el análisis realizado. (Yazdani & Jeffrey, 2012c), (Hwang
& Lansey, 2017) y (Giustolisi et al., 2019) han realizado esfuerzos para considerar
características de RDAP en el cálculo de métricas topológicas, no obstante, se han
enfocado en la adaptación de métricas locales.
-
Las métricas del mundo de la teoría de grafos son de alta eficiencia computacional.
Por lo cual, la adaptación de estas para el análisis de RDAP puede traer consigo
grandes beneficios en el análisis de redes muy extensas.
-
Otros componentes que permiten analizar la topología de la red, como los
centroides, pueden ser un complemento importante para el análisis geométrico de
las RDAP.
-
Con el fin de poder comparar los diseños de RDAP optimizados en costos vs. los
diseños no optimizados, es necesario proponer nuevos índices (o ajustar índices)
que midan características hidráulicas del sistema, así como el diámetro de sus
tuberías optimizadas.
Teniendo en cuenta las conclusiones de la recopilación bibliográfica, se planteó una
metodología para realizar un análisis geométrico de RDAP diseñadas óptimamente. Esta
metodología permitió: i) identificar las métricas más adecuadas de CNT para la
caracterización topológica de RDAP, en donde se analizan 6 características principales de
las RDAP (conectividad, eficiencia, centralidad, robustez, modularidad y diversidad); ii)
realizar un ajuste a las métricas encontradas para tener en cuenta propiedades de las
tuberías, así como propiedades hidráulicas de la red (mediante la definición de pesos como
el diámetro y el caudal) y iii) definir una metodología de optimización para evaluar los
resultados obtenidos al momento de realizar diseños optimizados de RDAP.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
98
Los resultados permiten concluir que los cambios geométricos obtenidos con los diseños
optimizados, en términos de conectividad, centralidad, robustez y modularidad, no se
ajustan a una metodología de optimización especifica. Cada red tiene variaciones
independientes al algoritmo de optimización utilizado, dando a entender que los cambios
en las geometrías de los diseños optimizados obedecen más a la estructura topológica
original de la red que a lo que sucede en realidad en términos hidráulicos dentro de los
algoritmos de optimización.
Para el caso de clasificación de la red según su topología y función, se confirma que el
esquema de clasificación propuesto por Hwang y Lansey (2017) es adecuado para la
caracterización de redes de distribución y redes de transmisión (matrices) de agua potable.
Dependiendo de la normativa de cada país, se puede ajustar los límites del diámetro
promedio ponderado por la longitud para separar las redes de distribución con las redes de
transmisión (matrices). Del mismo modo, el cálculo del coeficiente en mallado de la red
𝑅
𝑚
para las redes reducidas, se adapta de mejor manera a la realidad de las RDAP.
Las métricas de CNT, comúnmente utilizadas para la caracterización de redes complejas,
sirven para realizar una clasificación inicial de la topología de las RDAP, no obstante, se
debe tener presente que estas métricas no permiten sacar conclusiones hidráulicas ya que
no tienen en cuenta los componentes de la red y lo que sucede en su interior desde el punto
de vista hidráulico.
El esfuerzo por ajustar estas métricas mediante la implementación de pesos permite evaluar
algunas características topológicas como la conectividad algebraica, la centralidad, la
modularidad y la robustez en términos de características reales de las RDAP. Sin embargo,
la formulación matemática de estas métricas es ajena a las ecuaciones de continuidad y
masa, y las condiciones de frontera (demandas, tanques, niveles de los tanques, entre
otras) que determinan el comportamiento de las redes de distribución de agua potable. No
existe una relación simple de ver entre la geometría de la red y el resultado de su diseño
optimizado; se recomienda realizar más comparaciones entre RDAP con mismos niveles
de complejidad. Así mismo, las métricas espectrales de las redes (
𝜆
2
y
𝜆∆), por su
formulación matemática, son muy sensibles a los pesos escogidos, se recomienda analizar
otras formulaciones que se adapten mejor a las RDAP.
La evaluación geométrica de los diseños de la red mediante características básicas como
las distribuciones de los diámetros, longitudes de tuberías, entre otras, sirven como
indicadores simples para definir la complejidad y diversidad de las redes.
El cálculo de los centroides de la red permite comparar las distribuciones del volumen, los
diámetros, la potencia y la potencia específica para diferentes tipos de diseños. No
obstante, los resultados obtenidos muestran que no hay desplazamientos significativos
entre los diseños originales y los diseños optimizados de las redes. Para la mayoría de las
redes, los centroides de diámetro, volumen y potencia se concentran en el medio de la

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
99
topología, en cambio, el centroide de potencia específica tiende a ubicarse más cerca al
tanque de alimentación.
Debido a que las redes de distribución de agua potable son redes espacialmente
restringidas, se recomienda realizar una comparativa entre la topología de esta misma y la
expansión urbana.
Como continuación a esta investigación, se recomienda realizar un análisis de sensibilidad
en los parámetros de los diferentes algoritmos de optimización implementados en el análisis
geométrico de las redes. Del mismo modo, comparar los resultados de optimización con
algoritmos multiobjetivos que permitan diseñar RDAP de bajo costo, pero alta resiliencia
(por ejemplo). En esta optimización multiobjetivo, comparar las geometrías de las RDAP.
Se recomienda analizar la trazabilidad de la red dada una topología. Estudiar diferentes
trazados para los mismos nodos de demanda y comparar qué tanto influye el trazado y la
topología inicial en los resultados de la optimización.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
100
9. Referencias
Albert, R., & Barabási, A. L. (2002). Statistical mechanics of complex networks. Reviews of
Modern Physics, 74(1264), 553
–554.
Barabási, A. L. (2012). The network takeover. Nature Physics, 8(1), 14
–16.
Barabási, A. L., & Albert, R. (1999). Emergence of scaling in random networks. Science.
https://doi.org/10.1126/science.286.5439.509
Barabási, A. L., Towlson, E. K., & Cornelius, S. P. (2018). Course PHYS 5116: Complex
Networks. Retrieved from Notheastern University, Network Science Institute website:
https://www.barabasilab.com/course
Barthelemy, M. (2003). Crossover from Scale-Free to Spatial Networks. Europhysisc
Letters, 63, 915
–921.
Barthélemy, M. (2011). Spatial networks. Physics Reports, 499(1
–3), 1–101.
https://doi.org/10.1016/j.physrep.2010.11.002
Barthélemy, M., & Flammini, A. (2008). Modeling Urban street patterns. Physical Review
Letters, 100(13), 3
–6. https://doi.org/10.1103/PhysRevLett.100.138702
Beckmann, M. J., & Kansky, K. J. (2006). Structure of Transportation Networks.
Relationships
between
Network
Geometry
and
Regional
Characteristics.
Econometrica. https://doi.org/10.2307/1905669
Berardi, L., Ugarelli, R., Røstum, J., & Giustolisi, O. (2014). Assessing mechanical
vulnerability in water distribution networks under multiple failures. Water Resources
Research. https://doi.org/10.1002/2013WR014770
Berche, B., Von Ferber, C., Holovatch, T., & Holovatch, Y. (2009). Resilience of public
transport networks against attacks. European Physical Journal B, 71(1), 125
–137.
https://doi.org/10.1140/epjb/e2009-00291-3
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., & Hwang, D. U. (2006). Complex
networks: Structure and dynamics. Physics Reports, 424(4
–5), 175–308.
https://doi.org/10.1016/j.physrep.2005.10.009
Boccelli, D. L., Tryby, M. E., Uber, J. G., Rossman, L. A., Zierolf, M. L., & Polycarpou, M. M.
(2002). Optimal Scheduling of Booster Disinfection in Water Distribution Systems.
Journal
of
Water
Resources
Planning
and
Management.
https://doi.org/10.1061/(asce)0733-9496(1998)124:2(99)
Bonacich, P. (1972). Factoring and weighting approaches to status scores and clique
identification. The Journal of Mathematical Sociology, 2(1), 113
–120.
Buhl, J., Gautrais, J., Reeves, N., Solé, R. V., Valverde, S., Kuntz, P., & Theraulaz, G.
(2006). Topological patterns in street networks of self-organized urban settlements.
European Physical Journal B, 49(4), 513
–522. https://doi.org/10.1140/epjb/e2006-
00085-1
Cadini, F., Zio, E., & Petrescu, C. A. (2009). Using centrality measures to rank the
importance of the components of a complex network infrastructure. Lecture Notes in

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
101
Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and
Lecture Notes in Bioinformatics), 5508 LNCS, 155
–167. https://doi.org/10.1007/978-3-
642-03552-4_14
Cardillo, A., Scellato, S., Latora, V., & Porta, S. (2006). Structural properties of planar graphs
of urban street patterns. Physical Review E - Statistical, Nonlinear, and Soft Matter
Physics, 73(6), 1
–8. https://doi.org/10.1103/PhysRevE.73.066107
Carvalho, R., Buzna, L., Bono, F., Gutiérrez, E., Just, W., & Arrowsmith, D. (2009).
Robustness of trans-European gas networks. Physical Review E - Statistical,
Nonlinear,
and
Soft
Matter
Physics,
80(1),
1
–11.
https://doi.org/10.1103/PhysRevE.80.016106
Chase, D. V., & Ormsbee, L. E. (1993). Computer-generated pumping schedules for
satisfying operational objectives. Journal / American Water Works Association.
Cohen, R., Erez, K., Ben-Avraham, D., & Havlin, S. (2000). Resilience of the Internet to
random
breakdowns.
Physical
Review
Letters.
https://doi.org/10.1103/PhysRevLett.85.4626
Costa, L. D. F., Rodrigues, F. A., Travieso, G., & Boas, P. R. V. (2007). Characterization of
complex
networks:
A
survey
of
measurements.
Advances
in
Physics.
https://doi.org/10.1080/00018730601170527
Crucitti, P., Latora, V., & Marchiori, M. (2005). Locating Critical Lines in High-Voltage
Electrical Power Grids. Fluctuation and Noise Letters, 05(02), L201
–L208.
https://doi.org/10.1142/s0219477505002562
Csardi G, Nepusz T (2006). “The igraph software package for complex network
research.” InterJournal, Complex Systems, 1695.
http://igraph.org
.
Deuerlein, J. W. (2008). Decomposition Model of a General Water Supply Network. Journal
of Hydraulic Engineering, 134(6), 822
–832.
Diao, K., Butler, D., & Ulanicki, B. (2017). Fractality in water distribution networks.
Computing and Control for the Water Industry, Sheffield, September, 1(September).
https://doi.org/10.15131/shef.data.5364151.v1
Diao, K., Zhou, Y., & Rauch, W. (2013). Automated Creation of District Metered Area
Boundaries in Water Distribution Systems. Journal of Water Resources Planning and
Management, 139, 184
–190. https://doi.org/10.1061/(asce)wr.1943-5452.0000247
Erdös, P., & Rényi, A. (1959). On random graphs 1. Publ. Math. Debrecen.
Erdös, P., & Rényi, A. (1960). On the evolution of random graphs. Publication of the
Mathematical Institute of the Hungarian Academy of Sciences.
Estrada, E. (2006). Network robustness to targeted attacks. the interplay of expansibility and
degree distribution. European Physical Journal B. https://doi.org/10.1140/epjb/e2006-
00330-7
Everett, M. G., & Borgatti, S. P. (1998). Analyzing Clique Overlap. Connections, 21(1), 49
–

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
102
61.
Fortunato, S., & Barthélemy, M. (2007). Resolution limit in community detection. PNAS,
104(1), 36
–41. https://doi.org/https://doi.org/10.1073/pnas.0605965104
Freeman, L. C. (1977). A Set of Measures of Centrality Based on Betweenness. Sociometry,
40(1), 35
–41. https://doi.org/10.2307/3033543
Freeman, L. C. (1978). Centrality in Social Networks Conceptual Clarification. Social
Networks, 179(1968), 215
–239.
Gao, J., Barzel, B., & Barabási, A. L. (2016). Universal resilience patterns in complex
networks. Nature. https://doi.org/10.1038/nature16948
Girvan, M., & Newman, M. (2002). Community structure in social and biological networks.
Proceedings of the National Academy of Sciences of the United States of America,
99(12), 7821
–7826. https://doi.org/10.1073/pnas.122653799
Giustolisi, O., Berardi, L., & Laucelli, D. (2012). Optimal Water Distribution Network Design
Accounting for Valve Shutdowns. Journal of Water Resources Planning and
Management. https://doi.org/10.1061/(asce)wr.1943-5452.0000327
Giustolisi, O., & Ridolfi, L. (2014a). A novel infrastructure modularity index for the
segmentation of water distribution networks. Water Resources Management, 50,
7648
–7661. https://doi.org/10.1002/ 2014WR016067
Giustolisi, O., & Ridolfi, L. (2014b). New Modularity-Based Approach to Segmentation of
Water
Distribution
Networks.
Journal
of
Hydraulic
Engineering,
140.
https://doi.org/10.1061/(asce)hy.1943-7900.0000916
Giustolisi, O., Ridolfi, L., & Berardi, L. (2015). General metrics for segmenting infrastructure
networks.
Journal
of
Hydroinformatics,
17(4),
505
–517.
https://doi.org/10.2166/hydro.2015.102
Giustolisi, O., Ridolfi, L., & Simone, A. (2019). Tailoring Centrality Metrics for Water
Distribution
Networks.
Water
Resources
Research,
55(3),
2348
–2369.
https://doi.org/10.1029/2018WR023966
Giustolisi, O., & Savic, D. (2010). Identification of segments and optimal isolation valve
system design in water distribution networks. Urban Water Journal, 7(1), 1
–15.
https://doi.org/10.1080/15730620903287530
Giustolisi, O., Simone, A., & Ridolfi, L. (2017). Network structure classification and features
of water distribution systems. Water Resources Research, 53, 3407
–3423.
https://doi.org/10.1002/2016WR020071
Gupta, R., & Prasad, T. D. (2002). Extended Use of Linear Graph Theory for Analysis of
Pipe Networks. Journal of Hydraulic Engineering. https://doi.org/10.1061/(asce)0733-
9429(2000)126:1(56)
Gutiérrez-Pérez, J. A., Herrera, M., Pérez-García, R., & Ramos-Martínez, E. (2013).
Application of graph-spectral methods in the vulnerability assessment of water supply
networks.
Mathematical
and
Computer
Modelling,
57(7
–8), 1853–1859.
https://doi.org/10.1016/j.mcm.2011.12.008

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
103
Hawick, K. A. (2012). Water Distribution Network Robustness and Fragmentation using
Graph Metrics. Proc. Int. Conf. on Water Resource Management (AfricaWRM 2012),
304
–310. https://doi.org/10.2316/p.2012.762-037
Hwang, H., & Lansey, K. (2017). Water Distribution System Classification Using System
Characteristics and Graph-Theory Metrics. Journal of Water Resources Planning and
Management,
143(12),
04017071.
https://doi.org/10.1061/(asce)wr.1943-
5452.0000850
Jacobs, P., & Goulter, I. (1988). Evaluation of methods for decomposition of water
distribution networks for reliability analysis. Civil Engineering Systems, 5(2), 58
–64.
https://doi.org/10.1080/02630258808970505
Jacobs, P., & Goulter, I. (1989). Optimization of redundancy in water distribution networks
using graph theoretic principles. Engineering Optimization, 15(1), 71
–82.
https://doi.org/10.1080/03052158908941143
Kesavan, H. K., & Chandrashekar, M. (1972). Graph-theoretic models for pipe network
analysis. J. Hydraul. Div.,ASCE.
Kumar, A., & Kansal, M. L. (1999). DETECTING ACCIDENTAL CONTAMINATIONS IN
MUNICIPAL WATER NETWORKS. 125(October), 308
–310.
Latora, V., & Marchiori, M. (2005). Vulnerability and protection of infrastructure networks.
Physical Review E - Statistical, Nonlinear, and Soft Matter Physics, 71(1), 1
–4.
https://doi.org/10.1103/PhysRevE.71.015103
Laucelli, D. B., Simone, A., Berardi, L., & Giustolisi, O. (2017). Optimal Design of District
Metering Areas for the Reduction of Leakages. Journal of Water Resources Planning
and
Management,
143(6),
04017017.
https://doi.org/10.1061/(asce)wr.1943-
5452.0000768
Mala-Jetmarova, H., Barton, A., & Bagirov, A. (2015). A history of Water distribution systems
and their optimisation. Water Science and Technology: Water Supply.
https://doi.org/10.2166/ws.2014.115
Mala-Jetmarova, H., Savic, D., & Sultanova, N. (2018). Lost in Optimisation of water
distribution systems? A literature review of system design. Water (Switzerland).
Mala-Jetmarova, H., Sultanova, N., & Savic, D. (2017). Lost in optimisation of water
distribution systems? A literature review of system operation. Environmental Modelling
and Software. https://doi.org/10.1016/j.envsoft.2017.02.009
Masucci, A. P., Smith, D., Crooks, A., & Batty, M. (2009). Random planar graphs and the
London street network. European Physical Journal B, 71(2), 259
–271.
https://doi.org/10.1140/epjb/e2009-00290-4
Meng, F., Fu, G., Farmani, R., Sweetapple, C., & Butler, D. (2018). Topological attributes of
network resilience: A study in water distribution systems. Water Research, 143, 376
–
386. https://doi.org/10.1016/j.watres.2018.06.048
Moreno, C., Rojas, D., & Saldarriaga, J. (2018). RELATION BETWEEN POPULATION
DENSITY AND TOPOLOGY IN POTABLE WATER DISTRIBUTION NETWORKS
Methodology Optimal Design of RDAP. WDSA / CCWI 2018 Joint Conference

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
104
Proceedings, 1. Retrieved from https://ojs.library.queensu.ca/index.php/wdsa-
ccw/article/view/12351
Nazempour, R., Monfared, M. A. S., & Zio, E. (2016). A complex network theory approach
for optimizing contamination warning sensor location in water distribution networks.
International
Journal
of
Disaster
Risk
Reduction.
https://doi.org/10.1016/j.ijdrr.2018.04.029
Newman, M. (2004). Fast algorithm for detecting community structure in networks. Physical
Review E - Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics,
69(6), 5. https://doi.org/10.1103/PhysRevE.69.066133
Newman, M. (2006). Modularity and community structure in networks. 103(23), 8577
–8582.
https://doi.org/10.1073/pnas.0601602103
Newman, M. (2010). Networks: An Introduction. In Networks: An Introduction.
https://doi.org/10.1093/acprof:oso/9780199206650.001.0001
Newman, M., & Girvan, M. (2004). Finding and evaluating community structure in networks.
Physical Review E - Statistical, Nonlinear, and Soft Matter Physics, 69(2 2), 1
–15.
https://doi.org/10.1103/PhysRevE.69.026113
Nicklow, J., Reed, P., Savic, D., Dessalegne, T., Harrell, L., Chan-
Hilton, A., … Zechman,
E. (2010). State of the Art for Genetic Algorithms and Beyond in Water Resources
Planning and Management. Journal of Water Resources Planning and Management.
https://doi.org/10.1061/(ASCE)WR.1943-5452.0000053
Nieminen, U. J. (1974). On centrality in a graph. Scandinavian Journal of Psychology.
Ormsbee, L., Lingireddy, S., & Chase, D. (2009). Optimal Pump Scheduling For Water
Distribution Systems. Mistaconference.Org.
Ostfeld, A., & Salomons, E. (2006). Conjunctive optimal scheduling of pumping and booster
chlorine injections in water distribution systems. Engineering Optimization.
https://doi.org/10.1080/03052150500478007
Ostfeld, A., & Shamir, U. (1996). Design of Optimal Reliable Multiquality Water-Supply
Systems. Journal of Water Resources Planning and Management, 122(5), 322
–333.
Paez, D., & Filion, Y. (2017). Generation and Validation of Synthetic WDS Case Studies
Using Graph Theory and Reliability Indexes. Procedia Engineering, 186, 143
–151.
https://doi.org/10.1016/j.proeng.2017.03.220
Peinado, C. (2016). Ecuaciones de Costo para el Diseño Optimizado de Redes de Agua
Potable y Alcantarillado. Universidad de los Andes, Bogotá D.C.
Perelman, L., & Ostfeld, A. (2011). Topological clustering for water distribution systems
analysis.
Environmental
Modelling
and
Software,
26(7),
969
–972.
https://doi.org/10.1016/j.envsoft.2011.01.006
R Core Team (2013).R:A Language and enviroment for statistical computing. R Foundation
for Statistical computing.R Foundation for Statistical Computing, Vienna, Austria. URL

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
105
http://www.R-project.org/.
Rosas-Casals, M., Valverde, S., & Solé, R. V. (2007). Topological Vulnerability of the
European Power Grid Under Errors and Attacks. International Journal of Bifurcation
and Chaos, 17(07), 2465
–2475. https://doi.org/10.1142/s0218127407018531
Rossman, Lewis A. (1994). EPANET users manual : project summary. Cincinnati, OH :U.S.
Environmental Protection Agency, Risk Reduction Engineering Laboratory
Saldarriaga, Juan. (2016). Hidráulica de Tuberías, Abastecimiento de Agua, Redes y Riegos
(Third). Bogotá D.C.: ALFAOMEGA.
Saldarriaga, J., Takahashi, S., Hernéndez, F., Díaz, D. M., & Ochoa, S. (2010). An Energy
Methodology for the Design of Water Distribution Systems. En World Environmental
and Water Resources Congress 2010 (pp. 4303
–4313). Providence, Rhode Island,
United
States:
American
Society
of
Civil
Engineers.
https://doi.org/10.1061/41114(371)437
Savić, D. A., Mala-Jetmarova, H., & Sultanova, N. (2018). History of Optimization in Water
Distribution System Analysis. WDSA / CCWI Joint Conference Proceedings. Retrieved
from https://ojs.library.queensu.ca/index.php/wdsa-ccw/article/view/11973
Schaake, J., & Lai, F. H. (1969). Linear programming and dynamic programming application
to water distribution network design. M.I.T. -Dept Civ Eng-Hydrodynamics Laboratory-
Report 116.
Scibetta, M., Boano, F., Revelli, R., & Ridolfi, L. (2013). Community detection as a tool for
complex pipe network clustering. EPL. https://doi.org/10.1209/0295-5075/103/48001
Shamir, U. (1974). Optimal Design and Operation of Water Distribution Systems. Water
Resources Research. https://doi.org/10.1029/WR010i001p00027
Sheng, N., Jia, Y., Xu, Z., Ho, S. L., & Wai Kan, C. (2013). A complex network based model
for detecting isolated communities in water distribution networks. Chaos, 23(4).
https://doi.org/10.1063/1.4823803
Shuang, Q., Zhang, M., & Yuan, Y. (2014). Node vulnerability of water distribution networks
under cascading failures. Reliability Engineering and System Safety, 124, 132
–141.
https://doi.org/10.1016/j.ress.2013.12.002
Simone, A., Giustolisi, O., & Laucelli, D. B. (2016). A proposal of optimal sampling design
using a modularity strategy. Water Resources Research, 52, 6171
–6185.
https://doi.org/10.1002/2016WR018944
Simpson, A.R, Murphy, L. ., & Dandy, G. . (1993). Pipe network optimisation using genetic
algorithms. American Society of Civil Engineers.
Simpson, Angus R., Dandy, G. C., & Murphy, L. J. (1994). Genetic Algorithms Compared to
Other Techniques for Pipe Optimization. Journal of Water Resources Planning and
Management. https://doi.org/10.1061/(asce)0733-9496(1994)120:4(423)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
106
Soldi, D., Candelieri, A., & Archetti, F. (2015). Resilience and vulnerability in urban water
distribution networks through network theory and hydraulic simulation. Procedia
Engineering, 119(1), 1259
–1268. https://doi.org/10.1016/j.proeng.2015.08.990
Song, C., Gallos, L. K., Havlin, S., & Makse, H. A. (2007). How to calculate the fractal
dimension of a complex network: The box covering algorithm. Journal of Statistical
Mechanics:
Theory
and
Experiment.
https://doi.org/10.1088/1742-
5468/2007/03/P03006
Todini, E. (2000). Looped water distribution networks design using a resilience index based
heuristic approach. Urban Water, 2(2), 115
–122. https://doi.org/10.1016/S1462-
0758(00)00049-2
Torres, J. M., Duenas-Osorio, L., Li, Q., & Yazdani, A. (2017). Exploring Topological Effects
on Water Distribution System Performance Using Graph Theory and Statistical Models.
Journal of Water Resources Planning and Management, 143(1), 04016068.
https://doi.org/10.1061/(asce)wr.1943-5452.0000709
Travers, J., & Milgram, S. (1969). An Experimental Study of the Small World Problem.
Sociometry. https://doi.org/10.2307/2786545
Vargas, K., & Saldarriaga, J. (2019). Analysis of Fractality in Water Distribution Networks
Using Hydraulic Criteria. World Environmental and Water Resources Congress 2019,
564
–572. https://doi.org/10.1061/9780784482353.054
Walski, T. M., Brill, E. D., Gessler, J., Goulter, I. C., Jeppson, R. M., Lansey, K., … Ormsbee,
L. (2008). Battle of the Network Models: Epilogue. Journal of Water Resources
Planning and Management. https://doi.org/10.1061/(asce)0733-9496(1987)113:2(191)
Wasserman, S., & Faust, K. (1994). Social network analysis: methods and applications II.
In American Ethnologist. https://doi.org/10.1525/ae.1997.24.1.219
Watts, D., & Strogatz, S. (1998). Collective dynamics of networks. Nature, 393, 440
–442.
Yates, D. F., Templeman, A. B., & Boffey, T. B. (1984). The computational complexity of the
problem of determining least capital cost designs for water supply networks.
Engineering Optimization. https://doi.org/10.1080/03052158408960635
Yazdani, A., & Jeffrey, P. (2010). A complex network approach to robustness and
vulnerability of spatially organized water distribution networks. 1
–18. Retrieved from
http://arxiv.org/abs/1008.1770
Yazdani, A., & Jeffrey, P. (2011). Complex network analysis of water distribution systems.
Chaos, 21(1). https://doi.org/10.1063/1.3540339
Yazdani, A., & Jeffrey, P. (2012a). Applying Network Theory to Quantify the Redundancy
and Structural Robustness of Water Distribution Systems. Journal of Water Resources
Planning and Management, 138(2), 153
–161. https://doi.org/10.1061/(asce)wr.1943-
5452.0000159
Yazdani, A., & Jeffrey, P. (2012b). Robustness and Vulnerability Analysis of Water
Distribution Networks Using Graph Theoretic and Complex Network Principles.
https://doi.org/10.1061/41203(425)85

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados
– CIACUA
Análisis geométrico avanzado de redes de distribución de agua potable
(RDAP) diseñadas óptimamente.
ICYA 4213-201920
Juan D. Carvajal Cruz
Tesis II
107
Yazdani, A., & Jeffrey, P. (2012c). Water distribution system vulnerability analysis using
weighted and directed network models. Water Resources Research, 48(6), 1
–10.
https://doi.org/10.1029/2012WR011897
Yazdani, A., Otoo, R. A., & Jeffrey, P. (2011). Resilience enhancing expansion strategies
for water distribution systems: A network theory approach. Environmental Modelling
and Software, 26(12), 1574
–1582. https://doi.org/10.1016/j.envsoft.2011.07.016
Wu, I. P. (1975). Design on Drip Irrigation Main Lines. Journal of the Irrigation and Drainage
Division, ASCE.
