
TESIS DE MAESTRÍA
ANÁLISIS DE REDES INTERNAS DE DISTRIBUCIÓN DE AGUA
POTABLE UTILIZANDO SIMULACIÓN DE EVENTOS DISCRETOS
Diego Alejandro Páez Ángel
Asesor: Juan G. Saldarriaga Valderrama
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
MAESTRÍA EN INGENIERÍA CIVIL
BOGOTÁ D.C.
2011

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
i
Tabla de contenido
1
Introducción .......................................................................................................................... 1
1.1
Objetivos ....................................................................................................................... 4
1.1.1
Objetivo general .................................................................................................... 4
1.1.2
Objetivos específicos ............................................................................................. 4
2
Análisis preliminar del sistema .............................................................................................. 5
2.1
Descripción del sistema ................................................................................................. 5
2.1.1
Prototipo ............................................................................................................... 5
2.1.2
Modelo .................................................................................................................. 5
2.2
Diseño del sistema ........................................................................................................ 9
2.2.1
Determinación de los escenarios o condiciones de diseño .................................. 9
2.2.2
Determinación del valor de los parámetros. ....................................................... 15
2.3
Estimación de la demanda en el sistema con métodos modernos ............................. 23
2.3.1
Modelo de PRP (Poisson Rectangular Pulses) ..................................................... 24
2.3.2
Modelo de NSRP (Neyman-Scott Rectangular Pulses) ........................................ 27
2.3.3
Modelo estocástico de uso último (stochastic end-use model) ......................... 27
2.3.4
Modelo estocástico de demanda aplicado a RIDAPs .......................................... 30
3
Metodología de modelación propuesta .............................................................................. 35
3.1
Modelación de los aparatos sanitarios ....................................................................... 35
3.2
Modelación de la simultaneidad de uso de los aparatos ............................................ 38
3.2.1
Modelo basado en Blokker .................................................................................. 38
3.2.2
Modelo basado en Blokker con simulación de eventos discretos ...................... 46
4
Casos de estudio.................................................................................................................. 54
4.1
Análisis de la simultaneidad de uso según el modelo basado en Blokker .................. 59
4.2
Análisis de la simultaneidad de uso según el modelo basado en Blokker con
simulación de eventos discretos. ............................................................................................ 64
4.3
Análisis de caudales a partir de ambas metodologías ................................................ 73
5
Procedimiento de diseño propuesto ................................................................................... 79
5.1
Asignación de una Línea de Gradiente Hidráulico (LGH) ............................................ 80
5.2
Cálculo de los caudales emitidos................................................................................. 81

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
ii
5.3
Cálculo del caudal de diseño de un tubo .................................................................... 81
5.3.1
Análisis estocástico para nudos independientes ................................................ 82
5.3.2
Análisis estocástico para nudos dependientes ................................................... 96
5.4
Cálculo y redondeo del diámetro del tubo ................................................................. 98
5.5
Asignación de una LGH para la red aguas abajo del tubo ........................................... 99
5.6
Proceso iterativo ......................................................................................................... 99
6
Comprobación de diseño propuesta ................................................................................. 101
6.1
Discretización de las Curvas Únicas y ajuste de la función ....................................... 101
6.2
Interpolación e iteración ........................................................................................... 104
6.3
Cálculo de los demás resultados hidráulicos............................................................. 105
6.4
Software desarrollado ............................................................................................... 105
7
Casos de estudio................................................................................................................ 107
7.1
Caso de estudio 1: Red Interna Conjunto OASIS IV ................................................... 110
7.1.1
Asignación de una Línea de Gradiente Hidráulico (LGH) .................................. 111
7.1.2
Cálculo de los caudales emitidos ....................................................................... 111
7.1.3
Cálculo de los caudales de diseño ..................................................................... 114
7.1.4
Cálculo y redondeo del diámetro del tubo ....................................................... 115
7.1.5
Asignación de una LGH para la red aguas abajo del tubo ................................. 115
7.1.6
Resultados para toda la red .............................................................................. 116
7.2
Caso de estudio 2: Red Interna APTOS ACERO ......................................................... 120
7.2.1
Asignación de una Línea de Gradiente Hidráulico (LGH) .................................. 121
7.2.2
Cálculo de los caudales emitidos ....................................................................... 122
7.2.3
Cálculo de los caudales de diseño ..................................................................... 124
7.2.4
Cálculo y redondeo del diámetro del tubo ....................................................... 125
7.2.5
Resultados para toda la red .............................................................................. 126
8
Conclusiones...................................................................................................................... 130
8.1
Conclusiones de la modelación de RIDAPs................................................................ 130
8.2
Conclusiones del diseño y comprobación de diseño de RIDAPs ............................... 131
9
Recomendaciones ............................................................................................................. 133
10
Referencias .................................................................................................................... 135
11
Anexos ........................................................................................................................... 138
11.1 Demostraciones del dominio de la variable .......................................................... 138

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
iii
11.2 Parametrizaciones de la distribución Lognormal ...................................................... 141

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
iv
Índice de Figuras
Figura 1. Esquema de asignación de Altura Piezométrica según una ecuación cuadrática. ....... 17
Figura 2. Sistema de tuberías en serie con longitudes diferenciales. ......................................... 19
Figura 3. Sistema de tuberías en serie con longitud conocida. ................................................... 20
Figura 4. Sistema de tuberías en serie con longitud conocida y con diámetro máximo. ........... 22
Figura 5. Modelo de Pulsos Rectangulares de Poisson (PRP). (GARCÍA et Al, 2004). ................. 30
Figura 6. Ejemplo de configuración ordenada de los posibles escenarios de demanda de una
RIDAP con . .................................................................................................................... 32
Figura 7. Diagrama de transición estados para una cadena de Markov asociada a una RIDAP
con . ............................................................................................................................... 32
Figura 8. Relación entre Caudal Emitido y Altura piezométrica aguas arriba del aparato, para
diferentes porcentajes de apertura de válvula de un mismo aparato. ...................................... 35
Figura 9. Partes de la curva única de relación entre Caudal Emitido y Altura piezométrica aguas
arriba del aparato, para aparatos con apertura de válvula variable........................................... 37
Figura 10. Curva única de relación entre Caudal Emitido y Altura piezométrica aguas arriba del
aparato, para aparatos con apertura de válvula variable, para el problema de estimación de
demanda para diseño. ................................................................................................................. 38
Figura 11. Distribución temporal supuesta de la frecuencia de uso de un lavamanos. ............. 41
Figura 12. Serie de tiempo de la frecuencia horaria de uso por persona de un lavamanos. ...... 42
Figura 13. Serie de tiempo de la frecuencia horaria de uso de un lavamanos. .......................... 43
Figura 14. Serie de tiempo de la utilización de un lavamanos. ................................................... 44
Figura 15. Esquema del caso de estudio correspondiente a un baño. ....................................... 54
Figura 16. Vista en planta del baño, con diagrama de las tuberías de la red. ............................ 55
Figura 17. Implementación del modelo de un baño residencial en el programa ARENA. .......... 66
Figura 18. Esquema del modelo de un baño residencia implementado en ARENA. .................. 67
Figura 19. Función de densidad de probabilidad del caudal transportado por el tubo, utilizando
la metodología basada en Blokker para un baño con 4 personas aferentes. ............................. 74
Figura 20. Función acumulada de probabilidad del caudal transportado por el tubo, utilizando
la metodología basada en Blokker para un baño con 4 personas aferentes. ............................. 74
Figura 21. Función de densidad de probabilidad del caudal transportado por el tubo, utilizando
la metodología basada en Blokker con simulación de eventos discretos para un baño con 4
personas aferentes. ..................................................................................................................... 75
Figura 22. Función acumulada de probabilidad del caudal transportado por el tubo, utilizando
la metodología basada en Blokker con simulación de eventos discretos para un baño con 4
personas aferentes. ..................................................................................................................... 75
Figura 23. Función de densidad de probabilidad del caudal transportado por el tubo dado que
el sistema está en uso, utilizando la metodología basada en Blokker para un baño con 4
personas aferentes. ..................................................................................................................... 76

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
v
Figura 24. Función acumulada de probabilidad del caudal transportado por el tubo dado que el
sistema está en uso, utilizando la metodología basada en Blokker para un baño con 4 personas
aferentes. .................................................................................................................................... 76
Figura 25. Función de densidad de probabilidad del caudal transportado por el tubo dado que
el sistema está en uso, utilizando la metodología basada en Blokker con simulación de eventos
discretos para un baño con 4 personas aferentes. ..................................................................... 77
Figura 26. Función acumulada de probabilidad del caudal transportado por el tubo dado que el
sistema está en uso, utilizando la metodología basada en Blokker con simulación de eventos
discretos para un baño con 4 personas aferentes. ..................................................................... 77
Figura 27. Diagrama de flujo del procedimiento de diseño propuesto. ..................................... 79
Figura 28. Ejemplo de configuración ordenada de los posibles escenarios de demanda de una
RIDAP con . .................................................................................................................... 82
Figura 29. Justificación de la ecuación de probabilidad de falla. ................................................ 84
Figura 30. Comportamiento de la función de la Ecuación 48. .................................................... 87
Figura 31. Relación entre el error en la estimación de la probabilidad de un estado y la
desviación estándar de las probabilidades de uso de los aparatos. ........................................... 89
Figura 32. Error en la estimación de la probabilidad de un estado para desviaciones estándar
entre 0.15 y 0.45. ........................................................................................................................ 90
Figura 33. Error en la estimación de la probabilidad de un estado para desviaciones estándar
entre 0.02 y 0.20. ........................................................................................................................ 91
Figura 34. Error en la estimación de la probabilidad de un estado para desviaciones estándar
entre 0.28 y 0.50. ........................................................................................................................ 92
Figura 35. Diagrama de flujo del algoritmo de ejecución hidráulica para RIDAPs. ................... 102
Figura 36. Interfaz principal del software. ................................................................................ 106
Figura 37. Modelo casa OASIS IV tipo C - Vista en perfil. Aparatos conectados a la red. ......... 110
Figura 38. Modelo casa OASIS IV tipo C – LGH ideal en mca (izquierda) y Presión ideal
correspondiente en mca (derecha). .......................................................................................... 112
Figura 39. Modelo casa OASIS IV tipo C – Caudal emitido en L/s para el caso basado en Acero
(izquierda) y para el caso basado en ICONTEC. (derecha). ....................................................... 113
Figura 40. Modelo casa OASIS IV tipo C - Resultados del cálculo del estado de diseño para cada
tubería de la red. ....................................................................................................................... 116
Figura 41. Modelo casa OASIS IV tipo C - Resultados del diseño para el caso basado en Acero
(izquierda) y para el caso basado en ICONTEC (derecha). Diámetros en pulgadas. ................. 117
Figura 42. Prototipo casa OASIS IV tipo C – Diámetros reales del sistema en pulgadas. .......... 119
Figura 43. Modelo APTO ACERO tipo 1 - Vista en planta. Aparatos conectados a la red. ........ 121
Figura 44. Modelo APTO ACERO tipo 1 – LGH ideal en psi. ...................................................... 122
Figura 45. Modelo APTO ACERO tipo 1 – Caudal emitido en L/s para el caso basado en Acero
(izquierda) y para el caso basado en ICONTEC (derecha). ........................................................ 123
Figura 46. Modelo APTO ACERO tipo 1 – Resultados del cálculo del estado de diseño para cada
tubería de la red. ....................................................................................................................... 127
Figura 47. Modelo APTO ACERO tipo 1 – Resultados del diseño para el caso basado en Acero
(izquierda) y para el caso basado en ICONTEC (derecha). Diámetros en pulgadas. ................. 128

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
vi
Índice de Tablas
Tabla 1. Asignación de unidades a cada aparato (Gonzalez, 2010). ........................................... 10
Tabla 2. Asignación del caudal de diseño para cada valor de las unidades (Granados Robayo,
2002). .......................................................................................................................................... 11
Tabla 3. Asignación de caudales de diseño a partir de los caudales máximos posibles (García
Sosa, 2001). ................................................................................................................................. 12
Tabla 4. Frecuencia, duración e intensidad para los ocho usos últimos definidos en el modelo –
Datos medidos en Holanda. (Blokker, 2006, 2010a y 2010b). .................................................... 28
Tabla 5. Frecuencia, duración e intensidad para siete de los ocho usos últimos definidos en el
modelo – Datos medidos en Milford, Ohio. (Blokker, 2010a). ................................................... 29
Tabla 6. Frecuencia, duración e intensidad para los ocho usos últimos definidos en el modelo –
Datos medidos en Holanda. (Blokker, 2006, 2010a y 2010b). .................................................... 39
Tabla 7. Principales procedimientos del programa ARENA para simulación de eventos discretos.
..................................................................................................................................................... 47
Tabla 8. Funciones de la curva única de los aparatos de un baño residencial. ........................... 55
Tabla 9. Frecuencia y Duración de uso para los aparatos de un baño residencial (basada en la
Tabla 6 y en Blokker, 2010a). ...................................................................................................... 56
Tabla 10. Distribuciones temporales de la frecuencia de uso para los aparatos de un baño
residencial. .................................................................................................................................. 56
Tabla 11. Series de tiempo de la frecuencia horaria de uso por persona para los aparatos de un
baño residencial. ......................................................................................................................... 58
Tabla 12. Cálculo de la duración promedio total para el lavamanos de un baño residencial. ... 59
Tabla 13. Series de tiempo de la utilización de cada aparato de un baño residencial con 4
personas aferentes. ..................................................................................................................... 60
Tabla 14. Descripción y notación de los 8 posibles escenarios para un baño residencial. ......... 61
Tabla 15. Series de tiempo de la probabilidad de ocurrencia de cada escenario de un baño
residencial con 4 personas aferentes. ......................................................................................... 61
Tabla 16. Series de tiempo de la probabilidad de ocurrencia de cada escenario de un baño
residencial con 4 personas aferentes. ......................................................................................... 70
Tabla 17. Caudal transportado por el tubo más aguas arriba del sistema para cada escenario. 73
Tabla 18. Funciones de la curva única de los aparatos sanitarios en las redes ejemplo con base
en Acero (2009). ........................................................................................................................ 107
Tabla 19. Funciones de la curva única de los aparatos sanitarios en las redes ejemplo con base
en ICONTEC (2004). ................................................................................................................... 107
Tabla 20. Frecuencia y Duración de uso para los aparatos sanitarios en las redes ejemplo con
base en Blokker (2010a). ........................................................................................................... 108
Tabla 21. Cálculo de la duración promedio total para los lavamanos de las redes ejemplo. ... 108
Tabla 22. Cálculo de la duración promedio total para los lavaplatos de las redes ejemplo. .... 109
Tabla 23. Presiones mínimas aceptables y frecuencias de diseño. ........................................... 109
Tabla 24. Probabilidades de uso de los aparatos para el diseño de la RIDAP. .......................... 114

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
vii
Tabla 25. Probabilidades de ocurrencia de los estados. ........................................................... 114
Tabla 26. Diámetros disponibles para las tuberías de la red. ................................................... 115
Tabla 27. Probabilidades de ocurrencia de los estados – Metodología Exacta. ....................... 124
Tabla 28. Probabilidades de ocurrencia de los estados – Metodología Aproximada. .............. 125

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
1
1 Introducción
Las redes internas de distribución de agua potable (RIDAP), son el componente final del
sistema de distribución de agua potable de cualquier asentamiento urbano. Estas redes son las
encargadas llevar el recurso líquido a los usuarios finales desde la conexión al sistema de
acueducto de la ciudad. Los usuarios entonces, son los habitantes o visitantes de la edificación
en donde está construida la red, de manera que pueden ser residentes de una vivienda o
trabajadores y visitantes de una edificación comercial, industrial, escolar u hospitalaria, entre
otras. Lo que tienen en común todos estos potenciales usuarios, es que esperan que al utilizar
un aparato sanitario conectado a la RIDAP (e.g., lavamanos, duchas, inodoros, tinas, lavaplatos,
lavadoras, etc.) éste les proporcione agua con unas características de flujo aceptable para
satisfacer sus necesidades.
Para lograr tener un sistema que cumpla con los requerimientos hechos por los usuarios del
mismo, es necesario conocer el comportamiento del sistema y de su demanda, de manera que
desde hace más de medio siglo se han hecho análisis de las redes internas, procurando
caracterizar su comportamiento hidráulico y las demandas a las que está sometido a lo largo
de su vida útil. Si bien la simulación hidráulica de estas redes tiene muchos elementos en
común con la simulación hidráulica de las redes de acueducto, existen otros elementos que no
pueden ser bien representados de igual manera que en las redes de acueducto, y por lo tanto
se hace necesario caracterizar ese comportamiento hidráulico haciendo uso de otros
elementos matemáticos como los emisores (Acero, 2009).
Por otro lado el análisis de la demanda en una RIDAP, ha tenido aproximaciones hechas para la
solución del problema de diseño del sistema, las cuales se basan en datos, conocimientos y
modelos bastante antiguos que pueden ser considerados obsoletos, si se tiene en cuenta que
con el paso del tiempo han surgido nuevas herramientas para la simulación de diferentes
sistemas, además de conocimientos y datos basados en el comportamiento actual de los
usuarios de los sistemas, el cual no debe suponerse igual al de los usuarios de hace cincuenta
años.
De esta manera se tiene un sistema vigente y ampliamente usado como lo son las RIDAPs, y
metodologías de análisis y simulación del sistema un tanto obsoletas y basadas en supuestos
que ya no son necesarios para lograr representar de mejor manera lo observado en los
prototipos. Así, en esta investigación se busca realizar un análisis de las RIDAPs basado en
conocimientos contemporáneos que se ajustan más a las necesidades y comportamientos de
estos sistemas, y en especial se centra en la caracterización y simulación de la demanda
haciendo uso de mediciones recientes y de herramientas como la simulación de eventos
discretos, que es una herramienta informática basada en las capacidades actuales de los
computadores y que permite tener en cuenta correlaciones entre variables, difícilmente
representables de otra forma.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
2
Con el avance logrado en la modelación de estos sistemas, se consiguió una base para el
posterior desarrollo de una metodología de diseño de RIDAPs basada específicamente en los
resultados de las mencionadas metodologías de modelación de la demanda acá desarrolladas.
Ese desarrollo de una metodología de diseño, al igual su implementación en casos de estudio
también es presentado en este documento, junto con el proceso deductivo realizado y los
estudios específicos de la función de probabilidad Binomial de Poisson necesarios para su
implementación en sistemas con un alto número de aparatos.
Así mismo se desarrolló un software capaz de ejecutar la hidráulica de estos sistemas
incluyendo los comportamientos de los aparatos que se encontraron y utilizaron para este
documento, haciendo uso de éste en los casos de estudio de diseño mencionados
anteriormente.
El contendido de este documento está dividido en once capítulos. El primero de ellos incluye la
introducción y los objetivos del proyecto. El segundo capítulo hace referencia a conocimiento
previo o útil que se requiere para el desarrollo de las metodologías de modelación de la
demanda y futuro diseño, incluyendo entre otras cosas, leyes físicas que rigen la hidráulica de
tuberías con flujo presurizado, conocimientos de los procedimientos de diseño de sistemas de
varias tuberías y conocimientos previos de modelación de la demanda para el problema de
diseño, incluyendo enfoques tradiciones y algunos enfoques y conocimientos más recientes. El
Capítulo 3 presenta las dos metodologías desarrolladas para la modelación estocástica de la
demanda en RIDAPs con base en deducciones y en información disponible, así como algunas
recomendaciones de implementación de la metodología basada en simulación de eventos
discretos. El cuarto capítulo incluye un caso de estudio simple en el que se muestra
explícitamente la implementación de las metodologías desarrolladas en el Capítulo 3,
presentando resultados para ese caso, y sacando algunas conclusiones de las observaciones
hechas a los resultados encontrados. El Capítulo 5 muestra el desarrollo de la metodología de
diseño que resulta consistente con las metodologías de modelación explicadas en el Capítulo
3, haciendo un análisis de la función de probabilidad Binomial de Poisson que resulta necesario
para aproximar los resultados exactos pero altamente demandantes computacionalmente. El
capítulo sexto explica el algoritmo desarrollado en esta investigación para la ejecución
hidráulica de RIDAPs que hacen uso del concepto de Curva Única, explicado en el Capítulo 3,
así como el software creado para su fácil implementación. El Capítulo 7 presenta 4 casos de
estudio de la metodología de diseño que hace uso de los conceptos del Capítulo 5 y del
software expuesto en el Capítulo 6, presentando además un análisis de los resultados
encontrados que evidencian la consistencia del método de diseño y algunos aspectos de
mejora del mismo. El octavo capítulo resume las conclusiones encontradas a lo largo del
documento, en especial las relacionadas con las observaciones a los resultados del cuarto y
sétimo capítulo. El Capítulo 9 hace recomendaciones para futuras investigaciones en el tema y
para una potencial aplicación de las metodologías desarrolladas en esta investigación en casos
de sistemas reales con diferentes condiciones de ocupación. El décimo capítulo presenta las
referencias bibliográficas citadas en este documento, las cuales fueron utilizadas para describir

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
3
o analizar algún procedimiento relativo a las RIDAPs o en general a los sistemas de tuberías
con flujo presurizado. Finalmente el Capítulo 11 presenta unos anexos al documento que
facilitan el entendimiento más profundo de algunas partes de éste.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
4
1.1 Objetivos
1.1.1 Objetivo general
Desarrollar una metodología de modelación de la demanda en redes internas de distribución
de agua potable, así como una metodología de diseño acorde con la metodología de
modelación de la demanda.
1.1.2 Objetivos específicos
A fin de cumplir con el objetivo general del proyecto se plantearon y desarrollaron los
siguientes objetivos específicos:
Hacer una revisión bibliográfica de los métodos de modelación de la demanda tanto
tradicionales como modernos a fin de tener una base teórica para el desarrollo de la
metodología propuesta.
Desarrollar un caso de estudio de la metodología de modelación con uso de simulación de
eventos discretos para definir procedimientos y recomendaciones de creación de modelos
haciendo uso del programa ARENA.
Buscar formas de aproximación de la función de probabilidad Binomial de Poisson para
permitir su cálculo o estimación de manera eficiente y aceptable en el procedimiento de
diseño planteado.
Hacer una revisión y análisis del procedimiento de diseño optimizado de sistemas de series de
tuberías basado en el criterio de Wu (1975), a fin de entenderlo y definir su aplicación en la
metodología de diseño.
Desarrollar dos casos de estudio de la metodología de diseño para verificar su correcto
funcionamiento y potenciales aspectos de mejora.
Desarrollar un algoritmo y un software que permitan ejecutar la hidráulica de redes con flujo
presurizado con nudos cuyo caudal emitido es función no potencial de la presión en el nudo, a
fin de disponer de una herramienta que permita hacer comprobaciones de diseño consistentes
con la metodología de modelación hidráulica.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
5
2 Análisis preliminar del sistema
2.1 Descripción del sistema
2.1.1 Prototipo
El proceso típico de abastecimiento de agua potable incluye: 1) la captación del recurso en
cuerpos de agua como lagos, ríos, acuíferos, etcétera; 2) la potabilización del recurso
usualmente realizada en plantas de tratamiento de agua potable (PTAP); 3) el almacenamiento
del recurso en tanques elevados o subterráneos, o en embalses; 4) la distribución del recurso a
través de la red de distribución de agua potable (RDAP); y 5) el uso último del recurso
mediante los aparatos sanitarios conectados a la red. La RDAP usualmente es dividida de
acuerdo con la magnitud de los caudales que transporta y al ente encargado de su
construcción, operación y/o mantenimiento, generando así redes matrices, redes de
distribución propiamente dichas y redes internas de distribución. A éstas últimas son a las que
resultan conectados los aparatos sanitarios tales como duchas, lavamanos, inodoros, llaves y
demás, y usualmente incluyen dentro del sistema a todos los tubos y accesorios que se
encuentran aguas abajo de una conexión particular de una edificación al sistema de acueducto
municipal (red de distribución).
Las redes internas de distribución de agua potable (RIDAP) son, entonces, las redes ubicadas al
interior de cada edificación y, para este documento, se considerará que incluyen todos los
aparatos sanitarios conectados a ésta. Respecto a estos aparatos, se puede encontrar una gran
variedad incluyendo diferentes funciones y comportamientos hidráulicos, que además
continuamente se renuevan para ajustarse a los nuevos requerimientos de los usuarios
directos del aparato. Sin embargo la mayoría de aparatos típicos, tienen en común que se
observa una relación biunívoca entre el caudal emitido por el aparato y la presión de flujo
inmediatamente aguas arriba del mismo, simplificando así su modelado.
2.1.2 Modelo
El modelo matemático de una RIDAP se compone de arcos o links y de vértices o nudos. Cada
link representa una tubería de la red, y cada nudo representa un accesorio, una unión de varias
tuberías, una conexión de un aparato sanitario a la red o una conexión de la RIDAP a la red de
acueducto municipal. Los atributos de las tuberías incluyen los nudos que conectan, la
longitud, el diámetro real interno, la rugosidad absoluta del material y el coeficiente de
pérdidas menores a lo largo de toda la tubería. Por otro lado los atributos de los nudos
incluyen sus coordenadas , y y los parámetros de caracterización del comportamiento
hidráulico del aparato sanitario conectado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
6
Para caracterizar el comportamiento hidráulico de cada aparato, es posible utilizar el concepto
de “Emisores” (Acero, 2009), en el cuál se supone que el caudal emitido por el aparato cumple
la siguiente relación potencial:
Ecuación 1
Donde:
: Caudal emitido por el aparato.
: Presión en el nudo al que está conectado el aparato, usualmente escrita en
unidades de altura piezométrica (m.c.a. o mca: metros-columna de agua).
: Parámetros de la función potencial.
Datos de entrada al modelo
Dado un modelo de una RIDAP, existen datos de entrada que en conjunto con los parámetros
del modelo (atributos de los nudos y links), determinan la respuesta hidráulica simulada del
sistema. Estos datos de entrada incluyen las siguientes variables: 1) La altura piezométrica
disponible en el nudo de entrada de la red (conexión de la RIDAP con la red de acueducto
municipal), y 2) El escenario de demanda (configuración de aparatos encendidos y apagados
que están demandando agua a la RIDAP de acuerdo con la Ecuación 1).
Para determinar la altura piezométrica disponible a la entrada de la red, se debe disponer de
los resultados hidráulicos de la simulación de la red de acueducto a la cual está conectada la
RIDAP. Dentro de los resultados de esa simulación, se encuentran alturas piezométricas en
cada nudo de la red de acueducto, y para establecer la altura piezométrica a utilizar basta
tomar dicho resultado evaluado en el nudo de entrada de la RIDAP.
El problema de la determinación de los escenarios de demanda es considerablemente más
complejo, y su complejidad radica en la naturaleza estocástica de estos procesos,
fundamentada en la naturaleza estocástica de la frecuencia y la duración de uso de cada
aparato sanitario. Éstas variables (duración y frecuencia) dependen de la función para la que
fue diseñado cada aparato sanitario y de las personas que esperan utilizarlo para sus
diferentes necesidades. Así, por ejemplo, la frecuencia de uso de un lavamanos ubicado en un
baño residencial, es diferente de la frecuencia de uso de una ducha también ubicada en el
mismo baño residencial, e inclusive es diferente del mismo lavamanos ubicado en otro baño
residencial que tiene mayor (o menor) número de personas aferentes a este. Similarmente la
duración de un uso de una ducha es considerablemente diferente a la duración de un uso de
un lavamanos, e inclusive es diferente la duración de uso de esa misma ducha para diferentes
personas (e.g., según Blokker et Al. (2010), los niños y adolecentes toman duchas más largas
que los adultos).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
7
La complejidad del problema de simulación de la demanda en RIDAPs, hace que diferentes
problemas alrededor de éstas sean de difícil solución o que, análogamente, sean solucionados
con metodologías basadas en suposiciones difícilmente aplicables (e.g., los procedimientos
tradicionales de diseño de RIDAPs).
Simulación del sistema
1
(Basado en Saldarriaga, 2007)
Una vez determinado en su totalidad el modelo (i.e., todos los atributos de los nudos y los links
del modelo son conocidos), y conocidos los datos de entrada para los que se simulará el
sistema (i.e., altura piezométrica a la entrada de la red y el escenario de demanda que se
simulará), se deben aplicar dos principios físicos que gobiernan el movimiento de un fluido en
una red cualquiera: Conservación de la Masa y Conservación de la Energía
2
.
El principio de Conservación de Masa establece que el caudal en cualquier punto a lo largo de
una tubería es constante e igual al producto de la velocidad media del flujo y el área de la
sección transversal (suponiendo que el agua es un fluido incompresible). Así mismo para todo
nudo de la red, la diferencia de la suma de caudales que entran y la suma de caudales que
salen debe ser exactamente igual a cero (incluyendo el caudal emitido por el aparato
conectado a ese nudo).
El principio de Conservación de la Energía establece que la energía del flujo en el nudo inicial
de la tubería debe ser igual a la energía del flujo en el nudo final de la misma más la suma de la
energía perdida por fricción del fluido con la tubería y con el mismo fluido y, la energía perdida
por accesorios y discontinuidades que alteren el flujo (pérdidas menores). Para caracterizar las
pérdidas menores, se asocia un coeficiente global para cada tubería, el cual, al multiplicarse
por la altura piezométrica (cabeza) de velocidad, resulta en la energía perdida por dicho efecto
(Ecuación 2).
Ecuación 2
Donde:
: Energía por unidad de peso específico del fluido (Altura piezométrica) que es
disipada por las pérdidas menores.
: Velocidad media del flujo a lo largo de la tubería.
: Aceleración producida por la gravedad.
: Coeficiente global de pérdidas menores de la tubería seleccionada.
1
También denominado “Ejecución del modelo”.
2
Si bien la Conservación de Momentum también se cumple, éste principio no resulta de utilidad para la
solución de los problemas típicamente estudiados en el sistema.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
8
Para caracterizar las pérdidas por fricción, existen varias ecuaciones, dentro de las que se
encuentra la ecuación de Darcy-Weisbach (Ecuación 3) en conjunto con la ecuación de
Colebrooke-White (Ecuación 4), que tiene como ventajas, su deducción físicamente basada y
consecuentemente su aplicabilidad a todos los casos que se llegan a presentar en una RIDAP.
(e.g., flujo de agua a temperaturas cercanas a los 40°C).
Ecuación 3
√
(
√
)
Ecuación 4
Donde:
: Altura piezométrica que es disipada por la fricción del flujo con las paredes de la
tubería y por la turbulencia del mismo.
: Factor de fricción adimensional que relaciona las pérdidas por fricción con la altura
piezométrica de velocidad, con el diámetro de la tubería y con la longitud de la misma.
: Longitud de la tubería.
: Diámetro real interno de la tubería.
: Rugosidad absoluta del material de la tubería.
: Número de Reynolds del flujo que pasa por la tubería.
Teniendo en cuenta que el anterior principio aplica para todas las tuberías de la red, y dado
que la energía en un nudo debe ser única, se puede plantear la Conservación de la Energía en
redes de flujo presurizado de manera que para cada circuito cerrado de la red, la suma de la
pérdidas por fricción y las pérdidas menores de todos sus tubos es igual a cero si se tiene en
cuenta el signo de cada sumando dependiendo de la manera de recorrer el circuito.
Así, para simular el comportamiento hidráulico de una red de flujo presurizado se pueden
plantear ecuaciones, donde es el número de circuitos cerrados de la red, y
es el número de nudos de la red (en donde se debe cumplir la Conservación de la Masa).
Por otro lado, las incógnitas del procedimiento son el caudal en cada tubo de la red, y la altura
piezométrica disponible en cada nudo de la misma. Sin embargo al conocer una de las
respuestas hidráulicas (caudales en los tubos o alturas piezométricas en los nudos), es posible
conocer la otra, utilizando las ecuaciones de fricción mostradas (Ecuación 3 y Ecuación 4).
De esta manera se pueden simplificar las incógnitas a (Número de tubos en la red), y es
posible demostrar que, para cualquier red dada, el término es exactamente
igual a , y por lo tanto la simulación del modelo, consiste en la solución de un sistema de
ecuaciones. Existen diferentes métodos de solución de estos sistemas, dentro de los que se

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
9
encuentra el Método del Gradiente (Todini & Pilati, 1987), el cuál ha sido implementado en
diferentes programas de computador, tales como Epanet (Rossman, 2000) y Redes (CIACUA,
2006). Estos programas entregan la respuesta hidráulica del sistema (datos de salida),
incluyendo las presiones en los nudos y, por lo tanto, los caudales emitidos por el aparato
conectado.
2.2 Diseño del sistema
El problema de diseño de cualquier sistema, siempre puede ser dividido en dos problemas. El
primero es la determinación de los escenarios para los que será diseñado el sistema (i.e., las
configuraciones de datos de entrada para los que el sistema, al ser simulado, generará
respuestas o datos de salida dentro de un rango aceptable para los usuarios del mismo). El
segundo es un problema de optimización que consiste en determinar el valor de cada uno de
los parámetros a diseñar del sistema, teniendo como restricciones el hecho de que para cada
escenario establecido en el anterior problema, la simulación del sistema, debe generar datos
de salida dentro de un rango aceptable, y con una función a minimizar que usualmente
representa los costos constructivos y/o de operación, aunque también se llegan a incluir
variables que representan la confiabilidad del sistema, el impacto ambiental del mismo y
demás consideraciones propias de cada problema particular.
2.2.1 Determinación de los escenarios o condiciones de diseño
3
Para el caso de diseño de RIDAPs, el primer problema ha sido ampliamente estudiado desde
1932 (Hunter, 1940) hasta la presente fecha, y ha generado diferentes metodologías de
estimación de caudales de diseño, a partir de diferentes aproximaciones al problema.
Método de Hunter
Es un método que considera la percepción de que sólo pocos de los aparatos conectados a la
RIDAP, operan de manera simultánea durante un cierto intervalo de tiempo. Así, define
como la probabilidad de que haya más de aparatos encendidos en un sistema con
aparatos totales. Esta probabilidad la calcula utilizando la Ecuación 5.
∑ (
)
Ecuación 5
3
Basado en: CIACUA (2011).
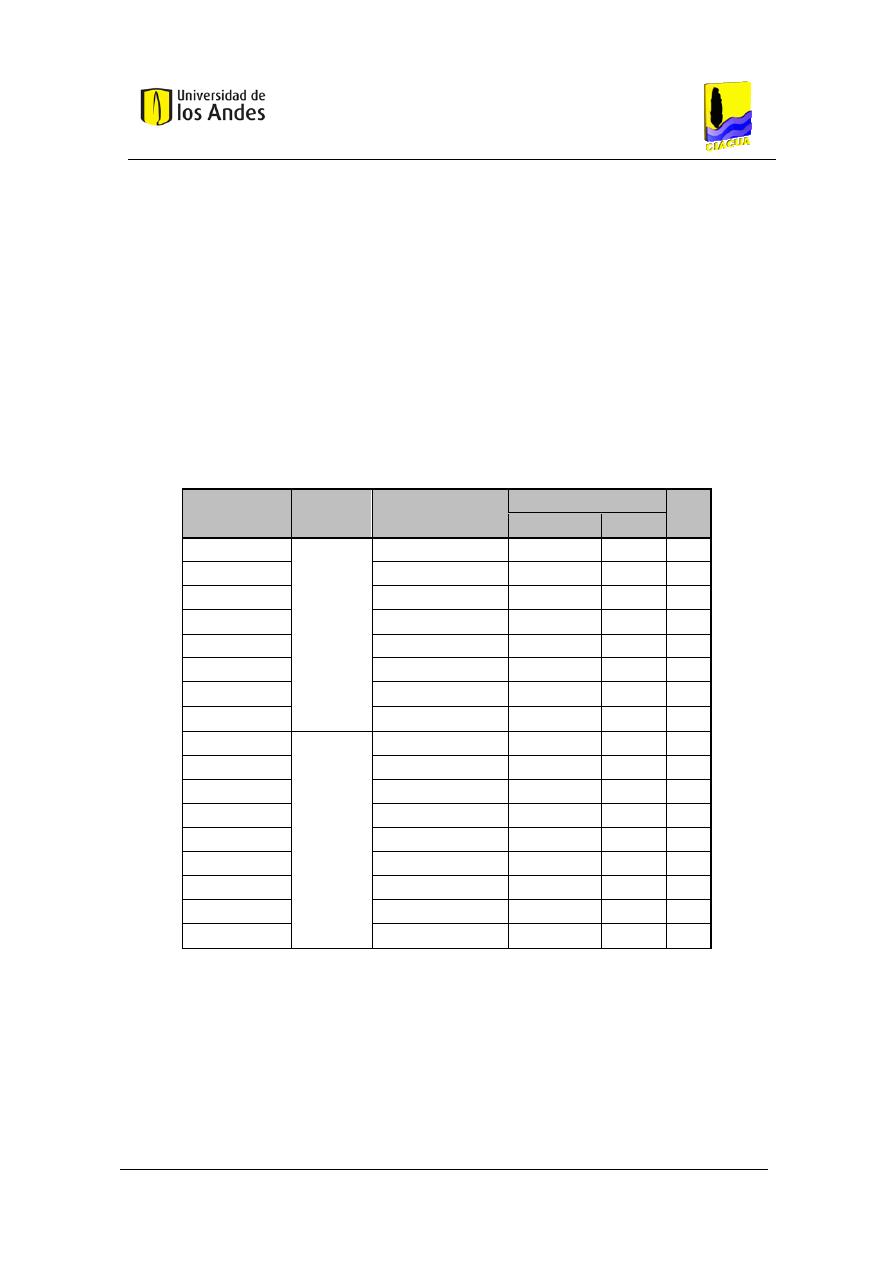
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
10
donde:
: Probabilidad de un aparato de estar encendido.
Dado que la Ecuación 5 se basa en una acumulación de una Distribución Binomial, que
representa una adición de ensayos Bernoulli con probabilidad de éxito (probabilidad de
estar encendido), es necesario estimar esta probabilidad de manera que sea constante para
todos los aparatos de la red. Teniendo en cuenta ésta suposición, y el hecho de que cada
aparato tiene un caudal promedio emitido diferente, el método estandariza los aparatos
sanitarios más comunes respecto a un fluxómetro de uso público, asignando “Unidades” a
cada aparato (Tabla 1), y definiendo un caudal de diseño para posible acumulación de dichas
unidades en una RIDAP (Tabla 2).
Tabla 1. Asignación de unidades a cada aparato (Gonzalez, 2010).
Aparato
Tipo de uso Tipo de suministro
Unidades de aparto
Total
Agua caliente Agua fría
Sanitario
Pú
b
lic
o
Fluxómetro
-
10,00
10,00
Sanitario
Tanque
-
5,00
5,00
Orinal pedestal
Fluxómetro 1"
-
10,00
10,00
Orinal pared
Fluxómetro 3/4"
-
5,00
5,00
Lavamanos
-
1,50
1,50
2,00
Tina
-
3,00
3,00
4,00
Regadera ducha
Mezclador
3,00
3,00
4,00
Lavaplatos
Mezclador
3,00
3,00
4,00
Sanitario
Priv
ad
o
Fluxómetro
-
6,00
6,00
Sanitario
Tanque
-
3,00
3,00
Lavamanos
Mezclador
0,75
0,75
1,00
Tina
Mezclador
1,50
1,50
2,00
Regadera ducha
Mezclador
1,50
1,50
2,00
Grupo de baño
Sanitario fluxómetro
2,25
6,75
8,00
Grupo de baño
Sanitario tanque
2,25
4,50
6,00
Lavaplatos
Mezclador
1,50
1,50
2,00
Lavadora
-
2,25
2,25
3,00
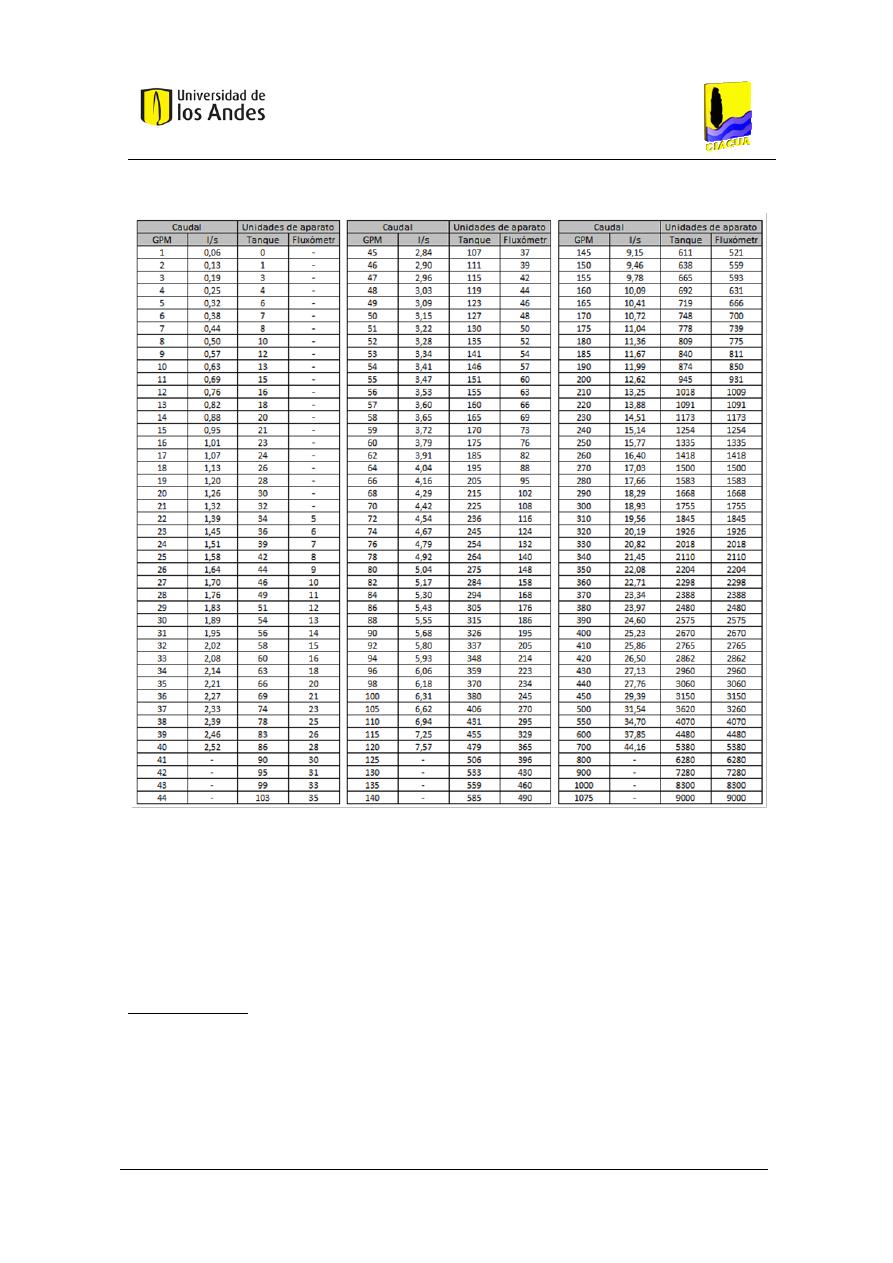
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
11
Tabla 2. Asignación del caudal de diseño para cada valor de las unidades (Granados Robayo, 2002).
La determinación de ese caudal de diseño se basa en la suposición de que el escenario de
diseño no debe ser superado en más del 1.0% del tiempo, y por lo tanto se plantea una
igualdad entre la Ecuación 5 y dicha probabilidad aceptable de “falla”, de manera que se
encuentra el número de aparatos encendidos que debe ser tenido en cuenta ( ) para cumplir
esa ecuación y por lo tanto para diseñar el sistema.
Método Británico
El Método Británico consiste en calcular el caudal máximo posible, entendido como la suma de
los caudales emitidos promedio de cada aparato sanitario conectado a la RIDAP. Una vez
conocido dicho caudal, se utiliza la Tabla 3 para encontrar el caudal de diseño y así se
encuentra el escenario de diseño de cada tubería de la red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
12
Tabla 3. Asignación de caudales de diseño a partir de los caudales máximos posibles (García Sosa, 2001).
Caudal emitido
promedio (L/min)
Caudal de
diseño
(L/min)
Caudal emitido
promedio (L/min)
Caudal de
diseño
(L/min)
Hasta 12
100% del
máximo
posible
318,0
147,0
405,0
159,0
53,0
49,2
465,6
170,3
60,6
54,9
537,5
181,7
68,1
60,6
617,0
196,8
75,7
66,2
711,7
212,0
87,1
71,9
817,6
230,9
98,4
77,6
938,8
246,1
113,6
85,2
1082,8
268,8
132,5
90,8
1245,4
291,5
151,4
98,4
1430,9
321,8
174,1
106,0
1646,6
359,6
200,6
113,6
1892,7
393,7
230,9
121,1
Más de 1892,7
20% del
máximo
posible
268,8
128,7
306,3
140,1
Existe una variante del Método Británico, denominada Método de Dawson y Bowman, que fue
desarrollado en la Universidad de Wisconsin, y que tiene como única diferencia la asignación
de caudales de diseño para pequeñas instalaciones hidráulicas ubicadas en edificaciones de
tipo residencial.
Método alemán o de Raíz Cuadrada
Este método asignó un “factor de carga” a cada aparato sanitario existente en el momento de
su desarrollo, representando así el comportamiento de la demanda típica de cada aparato, y
su caudal emitido promedio. Dicho factor es unitario para el caso de una llave de 3/8”, cuyo
caudal emitido promedio es de 0.25L/s, siendo éste caudal, el utilizado como caudal unitario
base (Ecuación 6):
√∑
Ecuación 6
donde:
: Caudal de diseño de la tubería analizada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
13
: Caudal unitario base. Corresponde al caudal emitido promedio de una llave de
3/8” (
).
: Factor de carga de los aparatos de tipo . Para una llave de 3/8” el factor de carga
es unitario.
: Número de aparatos de tipo aguas abajo de la tubería analizada.
: Número total de tipos de aparatos.
Método del Factor de Simultaneidad
El Método del Factor de Simultaneidad, calcula el caudal de diseño como el producto del
caudal máximo posible, de nuevo entendido como la suma de los caudales emitidos promedio
de cada aparato sanitario conectado a la RIDAP, y un factor de simultaneidad que es función
del número de aparatos aguas abajo del tubo analizado (Ecuación 8).
∑
Ecuación 7
donde:
: Factor de simultaneidad de la tubería analizada.
: Caudal emitido promedio de los aparatos de tipo .
√
Ecuación 8
donde:
: Número total de aparatos sanitarios aguas abajo de la tubería analizada.
Este método tiene algunas recomendaciones de uso, dentro de las que se encuentra el valor
mínimo de
como . Además, existe una variante del método que incluye un segundo
factor (
) función del número de viviendas aguas abajo del tubo analizado (Ecuación 9). Así,
este factor es considerable, solo para tuberías por fuera de las RIDAPs de cada unidad
residencial (Roca & Carratalá).
Ecuación 9
donde:
: Factor de simultaneidad por varias residencias.
: Número de unidades residenciales aguas abajo del tubo analizado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
14
El principal problema de los anteriores métodos radica en su naturaleza sobre-simplificada y,
en algunos casos, empírica, que se basa en mediciones hechas en sus periodos de desarrollo y
que, por lo tanto, no se ajustan de manera aceptable a las condiciones actuales de las RIDAPs.
Por otro lado, hacen algunas suposiciones un tanto fuertes de cumplir en el prototipo, dentro
de las cuales se encuentra la aplicabilidad de sus observaciones a sistemas con diferentes
condiciones socio-ambientales así como la representación de los aparatos sanitarios con un
caudal promedio determinado con aparatos de la época. Así, los métodos anteriormente
mencionados fueron pensados para una labor ingenieril considerablemente más limitada en
términos de recursos computacionales que la actual, y por lo tanto se considera conveniente
una revaluación de este aspecto del diseño a la luz de los recursos disponibles en la actualidad.
Métodos basados en modelos modernos
Buchberger & Wu (1995) y Buchberger & Wells (1996) presentaron un modelo para simular la
demanda de agua en edificaciones residenciales, con base en Pulsos Rectangulares de Poisson
(PRP). Si bien el objetivo original de estas investigaciones, y de muchas otras que le siguieron
(ver Sección 2.3), era desarrollar un modelo que estimara los caudales que se están
demandando en cada nudo de la RDAP en cada instante de tiempo para así predecir de
manera más precisa el comportamiento de la calidad del agua, es posible hacer uso de estos
métodos para encontrar uno o varios escenarios de demanda a tener en cuenta en el
procedimiento de diseño de las RIDAPs (e.g., CIACUA, 2011).
Método propuesto por Acero (2009)
Acero en su investigación propone un método de diseño de RIDAPs que incluye un paso de
determinación de las condiciones de diseño del sistema. Dicho paso, según la investigación, se
basa en , que no son más que posibles escenarios de demanda que deben ser
determinados por el ingeniero diseñador con base en su experiencia y juicio. Así, para cada
escenario, realiza el procedimiento de diseño (determinación del valor de los parámetros)
utilizando una metodología similar a la descrita en la Sección 2.2.2, para después tomar como
valores definitivos de los parámetros de diseño los valores máximos de todos los escenarios
(valores envolventes).
Sin embargo la escogencia de los escenarios de diseño depende del criterio del diseñador, y
por lo tanto un mismo sistema puede resultar con dos diseños diferentes, dependiendo de la
experiencia y el juicio del ingeniero diseñador. Además el número de escenarios necesarios
para diseñar una red de una edificación de tamaño medio o grande puede resultar
considerablemente alto, haciendo difícil la aplicación correcta por parte del diseñador. Por lo
tanto dicho método sólo es recomendado para una posterior comprobación de diseño en
donde se verifiquen escenarios de demanda determinados por el diseñador según su criterio.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
15
2.2.2 Determinación del valor de los parámetros.
La determinación del valor de los parámetros de un sistema, es el procedimiento mediante el
cual se asigna un valor a cada parámetro “diseñable” del sistema, de manera que al simular su
respuesta a los datos de entrada determinados en el paso anterior, se llega a
comportamientos aceptables para cada dato de salida. Sin embargo en la mayoría de los casos
existen muchas configuraciones de valores de los parámetros que cumplen con esas
restricciones, por lo que este procedimiento incluye la búsqueda de aquella solución que
optimiza una función objetivo.
En el caso de redes de distribución de agua con flujo presurizado (tanto RDAPs como RIDAPs)
los parámetros a determinar en el diseño son los diámetros reales internos de las tuberías de
la red y el material que se utilizará para éstas (usualmente se predefine de acuerdo con la
disponibilidad de materiales en el mercado). Las restricciones, por otro lado, incluyen
presiones en los nudos, velocidades en las tuberías, y para el caso específico de las RIDAPs,
también se incluyen caudales mínimos y máximos en cada nudo de la red. Como función
objetivo en RDAPs se han utilizado funciones relacionadas con el costo constructivo de la red
así como con la confiabilidad del sistema, de manera que se han desarrollado diferentes
metodologías, incluyendo algunas que acoplan heurísticas al diseño, para optimizar esa
función logrando que el sistema diseñado cumpla con las restricciones y que a la vez minimice
los costos constructivos y/o maximice la confiabilidad del sistema (minimizar la probabilidad
de falla). En el caso de las RIDAPs, este procedimiento de optimización no presenta
antecedentes en la literatura, y muy seguramente en el ejercicio profesional se toma como
solución al problema, la primera configuración de valores de los parámetros que cumple con
todas las restricciones, de manera que no se minimizan costos constructivos, ni se maximiza la
confiabilidad.
Sin embargo CIACUA (2011), hace una aproximación novedosa al problema de diseño de
RIDAPs, al definir los mismos parámetros a diseñar y las mismas restricciones, pero
adicionando una función objetivo que representa los costos constructivos de la red. Esta
función es tomada de estudios realizados para RDAPs donde sí existe dicha función y su forma
típica es:
∑
Ecuación 10
donde:
: Costo constructivo total de la red.
: Longitud de la -ésima tubería de la red.
: Diámetro de la -ésima tubería de la red.
: Parámetros de la función de costos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
16
Para minimizar la función descrita por la Ecuación 10, CIACUA utiliza los resultados de I-Pai Wu
(1975) en donde se encuentra que una manera rápida y efectiva para realizar esta tarea
consiste en predefinir la superficie de presiones
4
de la red, generando una superficie objetivo,
de manera que al diseñar cada tubería por separado se llegue a un sistema que, cuando es
simulado con los datos de entrada de diseño, genera dicha superficie de presiones. Según I-Pai
Wu el diseño óptimo no difiere considerablemente del diseño al que se llega si se utiliza una
superficie de presiones plana, definida para cada trayectoria de una RIDAP a partir de la
siguiente ecuación:
(
)
Ecuación 11
donde:
: Línea de gradiente hidráulico
5
(LGH) evaluada en .
: Máximo valor de la LGH para esa trayectoria. Dada la forma abierta de las
RIDAPs, y la ausencia de bombas dentro de ésta,
es igual a la altura
piezométrica en la conexión de la RIDAP con el sistema de acueducto o a la altura
piezométrica aguas abajo de la bomba que conecta la RIDAP con la RDAP.
: Mínimo valor de la LGH para esa trayectoria. Este valor corresponde a la
mínima altura piezométrica aceptable en el nudo final de la trayectoria (el más aguas
abajo), y se determina a partir de los requisitos de los aparatos conectados en ese
nudo.
: Longitud de la trayectoria a la cual pertenece el punto analizado. Se calcula
como la distancia topológica entre la conexión de la RIDAP a la RDAP y el nudo final de
la trayectoria.
: Distancia topológica entre la conexión de la RIDAP a la RDAP y el punto en donde se
quiere calcular la LGH objetivo.
De esta manera CIACUA calcula la superficie objetivo para cada nudo de la red utilizando la
Ecuación 11, y conociendo los caudales de diseño a partir de una metodología moderna de
Determinación de los escenarios de diseño (ver Sección 2.3.4), puede calcular los diámetros
internos reales de cada tubería de la red, de manera que se minimiza en buena medida el
costo constructivo de la misma.
Sin embargo la deducción de I Pai Wu (1975), se basa en un sistema de tuberías en serie con
flujo presurizado, que tiene como principal característica una longitud uniforme de todos sus
4
Es la superficie que representa la cabeza hidráulica total en cada punto de la red. Se calcula como la
suma de la altura piezométrica de velocidad, de presión y la elevación de dicho punto.
5
Es la línea perteneciente a la superficie de presiones, correspondiente a los valores de cada punto
sobre una trayectoria dada, en este caso una rama de la red.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
17
tubos, y un caudal de demanda uniforme en todos sus nudos Esas condiciones son típicamente
encontradas en redes de riego de alta frecuencia, pero no en una RIDAP o en una RDAP, por lo
que es posible que el diseño óptimo difiera de manera considerable del diseño encontrado
utilizando la aproximación de CIACUA (2011), para el caso de RIDAPs.
De esta manera, se debe considerar la fórmula completa de I Pai Wu (1975), para esa línea de
gradiente hidráulico objetivo correspondiente a la superficie de presiones objetivo evaluada en
una trayectoria única con forma topológicamente similar a la de una tubería en serie,
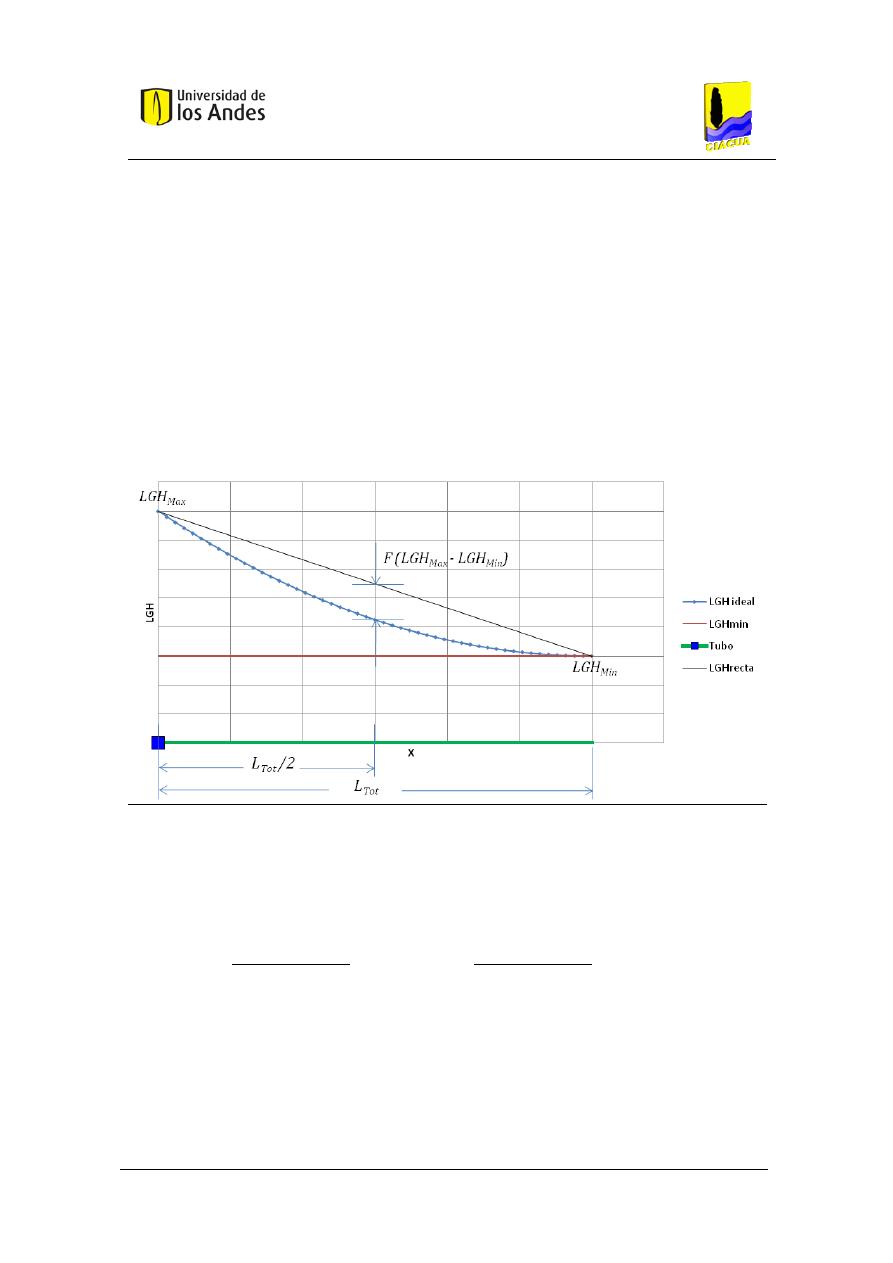
caracterizada como una ecuación cuadrática con una función descrita por la Ecuación 12 que
puede verse representada en la Figura 1, y así utilizar resultados de estudios posteriores a I Pai
Wu acerca de esa línea de gradiente hidráulico objetivo que minimiza los costos constructivos
(e.g., Villalba, 2004; Ochoa, 2009).
Figura 1. Esquema de asignación de Altura Piezométrica según una ecuación cuadrática.
Es importante notar que la Ecuación 12, y la posterior descripción de sus variables es aplicable
para cualquier sistema de tuberías en serie, incluyendo las trayectorias que se generan en una
RIDAP.
Ecuación 12
donde:
: Línea de gradiente hidráulico (LGH) evaluada en el punto medido desde la
entrada del sistema.
: Máximo valor de la LGH para esa trayectoria analizada. Corresponde con la
altura piezométrica disponible en la entrada del sistema.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
18
: Mínimo valor de la LGH para esa trayectoria. Este valor corresponde a la
mínima altura piezométrica aceptable en el nudo final de la trayectoria (el de más
aguas abajo).
: Longitud total de la trayectoria a la cual pertenece el punto analizado. Se calcula
como la distancia topológica entre la entrada del sistema y el nudo final de la rama.
: Flecha de la ecuación cuadrática de LGH. Representa la diferencia de alturas
piezométricas entre una LGH recta calculada con la Ecuación 11, y la que se desea
calcular con la Ecuación 12, escrita de manera porcentual respecto a la diferencia entre
la
y la
. Se considera positiva si el valor calculado con la ecuación
cuadrática es menor que el calculado con la ecuación lineal, y negativa en caso
contrario.
: Distancia topológica entre la conexión de la RIDAP a la RDAP y el punto en donde se
quiere calcular la LGH objetivo.
A diferencia de la Ecuación 11, la Ecuación 12 tiene un grado de libertad representado por la
variable , que implica que existe una variable que debe ser ajustada por el diseñador para
buscar un diseño que minimice la función objetivo. I Pai Wu (1975) encuentra que, para
sistemas de tuberías en serie con longitudes de tubos uniformes y con caudales demandados
en los nudos también uniformes, ese valor óptimo es . Por otro lado, Ochoa
(2009) sugiere un procedimiento de cálculo del valor de óptimo a partir de las características
de la demanda de agua a lo largo del sistema. Sin embargo en ninguna de las dos
investigaciones se encuentra un estudio del dominio de la variable para el que la función
genera valores físicamente posibles, por lo que dicho análisis se presenta a
continuación, a fin de hacer uso de los resultados en un futuro método de diseño de RIDAPs:
Análisis del dominio de y de
El dominio de una función es el conjunto de valores que pueden tomar las variables
independientes de manera que la función pueda ser evaluada. Dado que la función descrita
por la Ecuación 12 tiene como variable independiente a , pero tiene como parámetro para su
cálculo la variable , que es independiente de , ésta puede ser entendida como otra variable
independiente, haciendo que la función de asignación de línea de gradiente hidráulico objetivo
sea una función con dos variables independientes .
Por un lado el dominio de , entendido como el conjunto de valores de la variable para los que
es posible calcular la función, es fácilmente identificable como:
[ ] [
]
Ecuación 13
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
19
Teniendo en cuenta que, si bien la función cuadrática puede ser evaluada para cualquier valor
real de , sólo para aquellos valores que pertenezcan al sistema de tuberías en serie de
longitud
, dicha función tendría sentido físico.
Por otro lado el dominio de requiere un análisis un poco más complejo, que tiene como
principal consideración la conservación de la energía a lo largo del sistema. Así, el valor de
nunca debe implicar una ganancia de energía del flujo, dado que ello es físicamente imposible
en los sistemas analizados (series de tuberías sin bombas o elementos de aumento de la altura
piezométrica), y de hecho no puede siquiera implicar una energía constante del flujo, dado que
el trasporte a lo largo de la tubería siempre generará pérdidas de energía por fricción.
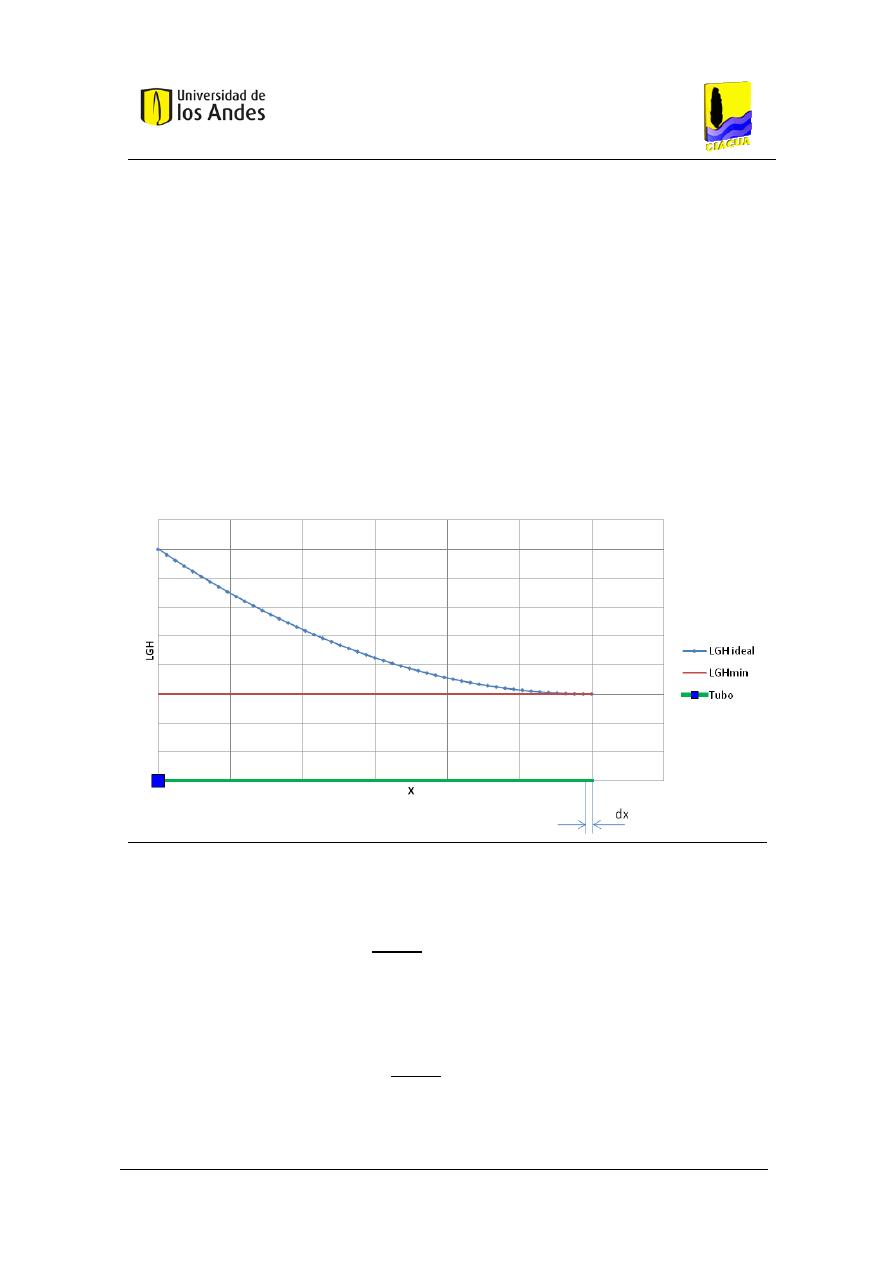
De esta manera si se considera un sistema compuesto por tuberías de longitud diferencial
como la mostrada en la Figura 2, el dominio de serán todos los valores de la variable que no
implican una pendiente de la LGH positiva o cero para ningún valor de [
].
Figura 2. Sistema de tuberías en serie con longitudes diferenciales.
La anterior consideración puede ser expresada con la siguiente expresión:
|
[
]
que tiene como casos críticos y
. Así, el valor máximo de para este sistema
puede ser calculado como (la demostración completa se encuentra en el Anexo 11.1):
(
|
)
Ecuación 14
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
20
Similarmente se puede plantear la desigualdad para , llegando a:
Ecuación 15
Lo que implica que el dominio de para el sistema de tuberías en serie con longitudes
diferenciales es el descrito por la Ecuación 29:
[ ]
Ecuación 16
Sin embargo cuando se considera que el sistema no está compuesto por tuberías de longitud
diferencial, sino de hecho por tuberías de longitud real y conocida, se puede presentar el caso
mostrado en la Figura 3, en donde existe un rango para el que se viola la LGH mínima y más
grave aún, un rango para el que se viola la conservación de energía (rango en donde la LGH
tiene pendiente positiva), pero sin embargo el procedimiento tendría sentido físico y podría
ser implementado teniendo en cuenta que el algoritmo sólo asigna LGH a los nudos del
sistema y no a toda la longitud del mismo, por lo que el sistema mostrado en la Figura 3,
podría ser perfectamente diseñado cuando se asignara la LGH mínima al último y al penúltimo
nudo del sistema. Así, si se considera que la última tubería tiene longitud
, el valor máximo
de se calcularía a partir de la Ecuación 18.
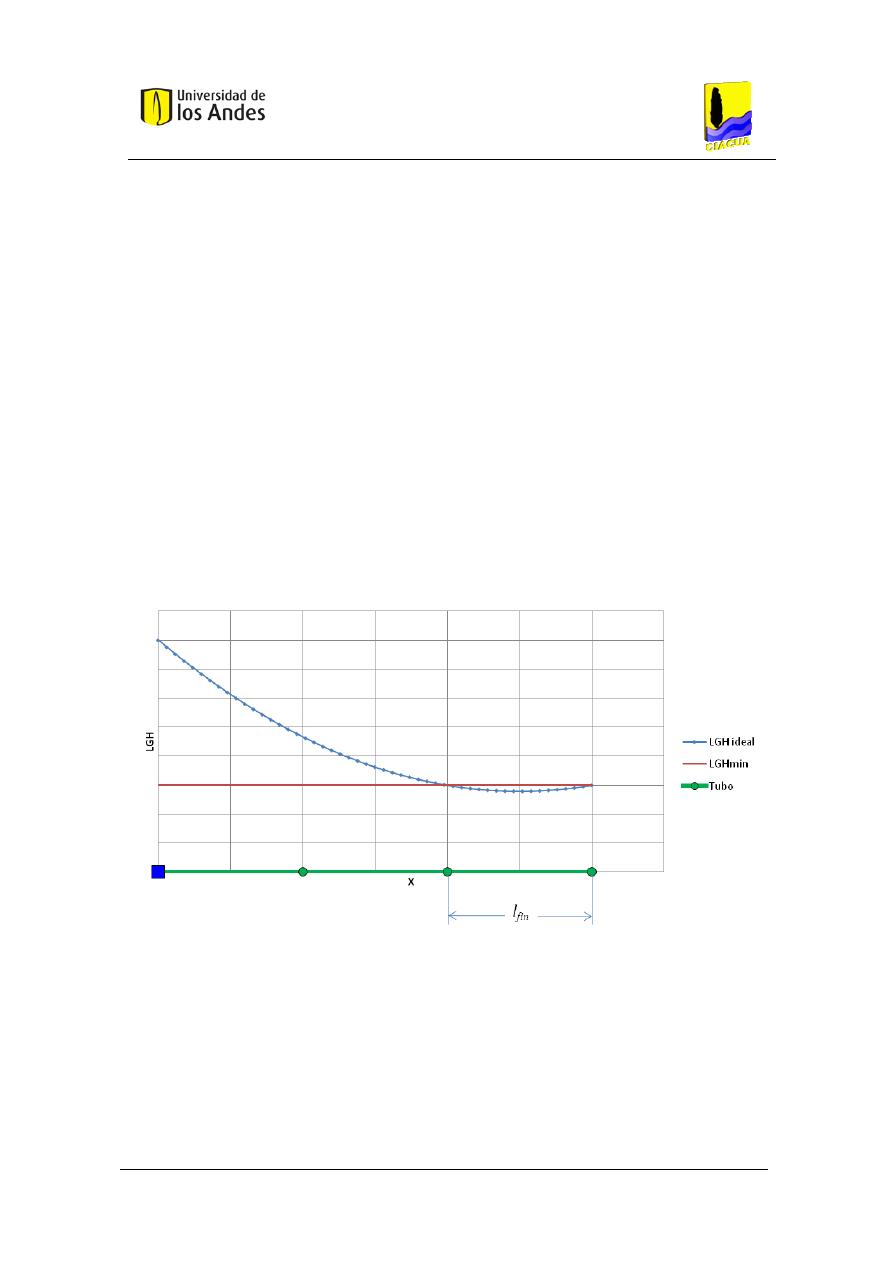
Figura 3. Sistema de tuberías en serie con longitud conocida.
La evaluación de la LGH para el último y el penúltimo nudo, en el caso crítico, daría como
resultado
y por lo tanto la diferencia entre las dos expresiones sería cero tal y como se
muestra a continuación (la demostración completa se encuentra en el Anexo 11.1):
(
)
Ecuación 17

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
21
(
)
Ecuación 18
Similarmente al caso de las tuberías diferenciales, el cálculo de
consiste en plantear la
misma expresión anterior, pero considerando que la LGH se debe evaluar en el primer y en el
segundo tubo, de manera que, si la longitud de la primera tubería del sistema es
,
entonces se tiene que:
Ecuación 19
Lo que implica que el dominio de para el sistema de tuberías en serie con longitudes no
diferenciales y conocidas es el descrito por la Ecuación 20:
[ ] (
(
)
)
Ecuación 20
Tanto para la deducción de la Ecuación 16 como para la deducción de la Ecuación 20, las
diferencias de LGH se han igualado a cero, indicando que el caso crítico es aquel en el que se
asigna cero altura piezométrica disponible al tubo más aguas abajo o más aguas arriba. Dicha
deducción igualando a cero, es la que genera que los intervalos de dominio de sean
abiertos, indicando que los valores allí escritos son valores y , pero
no ni . Es decir que nunca puede ser exactamente igual a ninguno
de estos valores, porque implicaría cero altura piezométrica disponible para mover el flujo, y
por lo tanto se requeriría un diámetro real interno infinito (ver Ecuación 3).
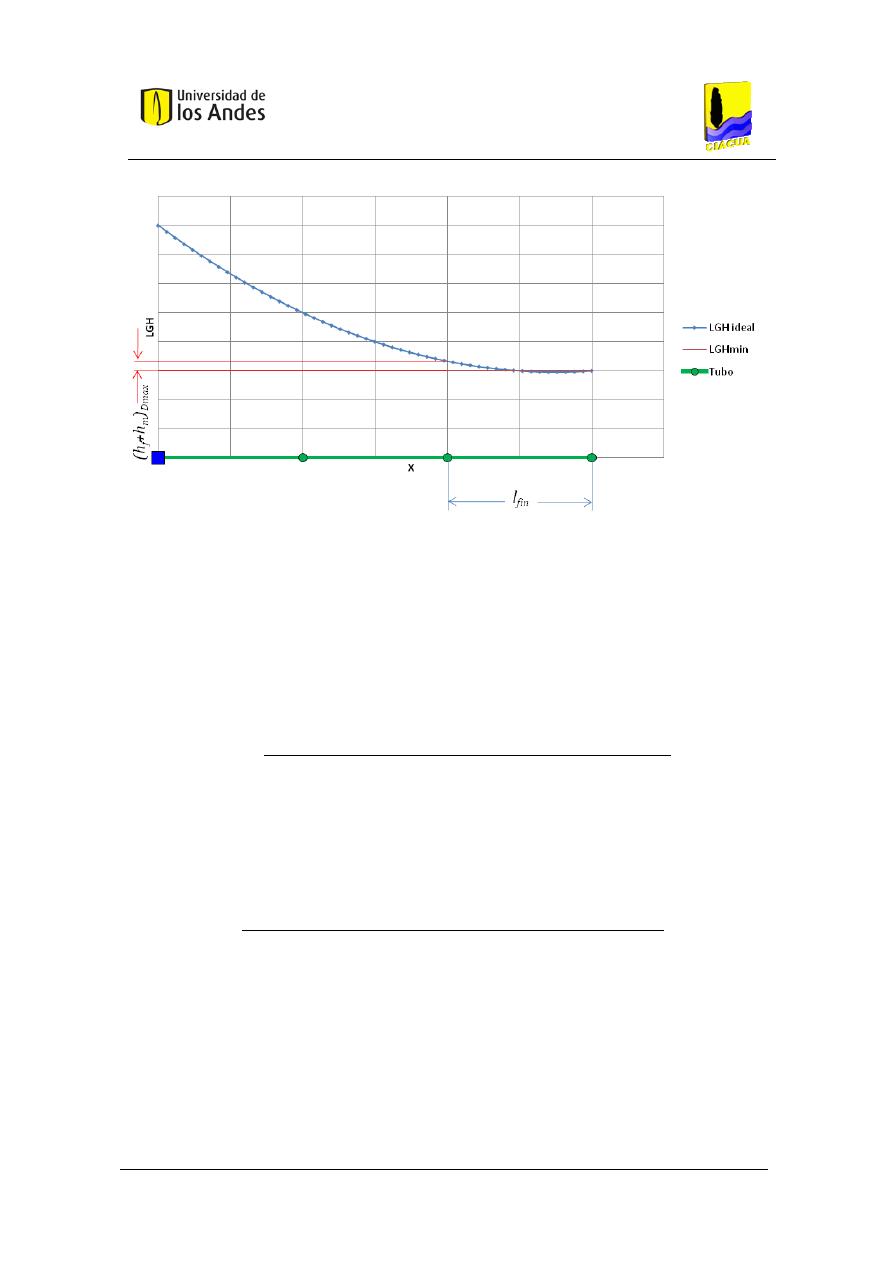
De esta manera, si se desea considerar que el rango de valores del diámetro, en un caso real,
tiene un máximo, la expresión de la Ecuación 17 no se debe igualar a cero, sino a una altura
piezométrica disponible mínima necesaria para mover el flujo. Teniendo en cuenta la Ecuación
3, el flujo requerirá menos altura piezométrica para su movimiento mientras más grande sea el
diámetro real interno, de manera que si
es el máximo diámetro disponible en el
mercado, y
en el caudal demandado en el último nudo del sistema, entonces la mínima
altura piezométrica requerida para mover el flujo por la última tubería será:
(
)
(
∑
)
(
)
Ecuación 21
De manera que se tendrá una condición crítica como la mostrada en la Figura 4:
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
22
Figura 4. Sistema de tuberías en serie con longitud conocida y con diámetro máximo.
Planteando las ecuaciones para el cálculo de
en el caso de un sistema de tuberías en
serie con longitud conocida y con diámetro máximo, se tendría que (la demostración completa
se encuentra en el Anexo 11.1):
(
(
)
)
(
(
)
)
(
)
Ecuación 22
Y haciendo un análisis análogo para la primera tubería se llegaría a la Ecuación 23, suponiendo
que (
)
ahora es calculado con
en vez de
, donde
es el caudal
total demandado en el sistema y que por lo tanto tendrá que pasar por la primera tubería:
(
(
)
)
Ecuación 23
Lo que implica que el dominio de para el sistema de tuberías en serie con longitudes no
diferenciales y conocidas y con diámetro máximo disponible es el descrito por la Ecuación 24:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
23
[ ]
[
(
(
)
)
(
(
)
)
(
)
]
Ecuación 24
En la Ecuación 24 se puede notar que el intervalo dominio de la variable se encuentra
descrito como un intervalo cerrado, indicando que para este caso los valores que definen el
intervalo son valores y , y a la vez y de
manera que la variable puede ser inclusive exactamente igual a dichos valores, y aun así la
función estará definida y tendrá sentido físico para su uso en el diseño de las
tuberías.
De esta manera se tienen tres conjuntos de dominio de (Ecuación 16, Ecuación 20 y Ecuación
24) que describen, dependiendo del sistema a considerar, el espacio de búsqueda de ese valor
óptimo de para el que el diseño de la tubería en serie minimizará los costos constructivos
asociados. Es decir que en el caso de la determinación de los valores de los parámetros de una
RIDAP, una buena política sería realizar el procedimiento de diseño sugerido por I Pai Wu
(1975) para tuberías en serie y extendido a redes abiertas y cerradas por VILLALBA (2004) y
OCHOA (2009), pero recorriendo todo el dominio de F, hasta encontrar la solución de menor
costo.
2.3 Estimación de la demanda en el sistema con métodos modernos
Una de las ramas de investigación relativa a RDAPs se encarga de estimar el comportamiento
de la demanda de dichos sistemas, para tener valores de demanda en cada nudo de la red más
ajustados a lo que ocurre en el prototipo, a fin de simular el comportamiento hidráulico típico
de la red y así poder simular el comportamiento de la calidad del agua en términos de
concentraciones de diferentes sustancias, formación y desprendimiento de películas en las
tuberías y demás aspectos importantes para asegurar una potabilidad del agua entregada.
Teniendo en cuenta dicho objetivo, se han desarrollado metodologías para describir y predecir
la demanda en cada nudo de la red, y como resultado se ha llegado, en algunos casos, a
metodologías que sirven para estimar la demanda en RIDAPs.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
24
2.3.1 Modelo de PRP (Poisson Rectangular Pulses)
El modelo de Pulsos Rectangulares de Poisson fue propuesto por Buchberger & Wu (1995) y
toma como base la teoría de colas cuyo uso más conocido es en la descripción de la dinámica
de un sistema de atención de llamadas (callcenter).
Teoría de colas
La teoría de colas busca analizar la dinámica de sistemas donde ciertas entidades llegan con
una distribución de probabilidad dada, y buscan ser atendidas por un cierto número de
servidores que tardan un tiempo aleatorio en atender a cada entidad, de manera que se
generan filas o colas de entidades esperando para ser atendidas por los servidores. Un sistema
de formación de colas queda completamente definido si se conocen cuatro características
principales del sistema y dos características de la población a la que atiende:
: Función de probabilidad del tiempo entre llegadas de las entidades que esperan ser
atendidas al sistema.
: Función de probabilidad del tiempo de atención o servicio por parte de los
servidores del sistema.
: Número de servidores en el sistema.
: Disciplina de la fila. Se refiere a la manera como se selecciona la entidad que será
servida dentro del conjunto de entidades en espera, una vez se desocupe un servidor.
: Capacidad del sistema. Se refiere al número máximo de entidades que puede haber
dentro del sistema, incluyendo las entidades que están siendo servidas y las entidades
que están en cola.
: Tamaño de la población de la cual provienen las entidades que esperan ser
atendidas.
De esta manera surgió la notación de Kendall-Lee-Taha usualmente conocida como la notación
de Kendall, en la cual cada sistema tiene asignada una cadena de caracteres como se muestra
a continuación:
Ecuación 25
donde cada letra corresponde con la descripción hecha anteriormente, y existen una serie de
códigos asignados a valores específicos de cada característica:
Los valores relacionados con distribuciones de probabilidad ( , ) pueden tomar alguno
de los siguientes valores (CIACUA, 2011):

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
25
: Distribución exponencial. (Se asigna una M para entender el proceso como
Markoviano).
: Distribución Erlang con fases.
: Distribución hiperexponencial con fases.
: Distribución Cox con fases.
: Distribución determinística.
: Distribución general. Se refiere a una distribución de probabilidad cualquiera.
: Distribución general con tiempos entre llegadas independientes.
Los valores numéricos ( , , ) toman valores enteros positivos, o infinito ( ) entendido
como un valor suficientemente grande en comparación con las demás variables del
análisis.
La disciplina de la fila ( ) puede tomar alguno de los siguientes valores:
: Las entidades son atendidas de acuerdo con el orden de llegada. (First In First
Out).
: Las entidades son atendidas de manera inversa al orden de llegada. (Last In
First Out).
: Las entidades son atendidas en un orden aleatorio. (Service In Random Order).
: La disciplina de la fila es general. Se refiere a una disciplina de fila cualquiera.
(General Discipline).
Así, existen soluciones analíticas a una serie de posibles sistemas, y soluciones numéricas para
otros cuantos. La solución de un sistema de colas, consiste en calcular el valor de una serie de
medidas de desempeño dentro de las que se encuentran la utilización promedio del sistema, el
número de entidades en el sistema en estado estable
6
, el tiempo promedio de estadía de una
entidad en el sistema en estado estable, y la probabilidad de tener entidades en el sistema en
estado estable (
). La solución de un gran número de estos sistemas se basa en la utilización
de Cadenas de Markov, que es una herramienta que permite calcular cada
suponiendo que
el sistema es un proceso de nacimiento y muerte, y las distribuciones del tiempo entre llegadas
y del tiempo de servicio son exponenciales.
6
Se entiende que un sistema está en estado estable si el valor de cada medida de desempeño no varía
con el paso del tiempo. Para su cálculo se calcula el límite de la medida de desempeño instantánea
cuando el tiempo tiende a infinito.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
26
Modelo
Buchberger & Wu (1995), propusieron este modelo, también denominado sistema de pérdidas
Erlang (Erlang’s loss system), para caracterizar la demanda de agua en una RIDAP
correspondiente a una única vivienda. Para ello define los aparatos sanitarios como servidores,
de manera que el tiempo de servicio corresponde con el tiempo de uso del aparato, y los
residentes de la vivienda como entidades que entran al sistema para ser “atendidos” por los
servidores.
De la notación, se puede deducir que tanto el tiempo entre llegadas de las personas (o de sus
necesidades) como el tiempo de servicio (o de uso) de cada aparato se distribuyen
exponencialmente, indicando que éstas siguen un proceso de Poisson con tasa igual al inverso
del valor esperado del tiempo:
[ ]
Ecuación 26
[ ]
Ecuación 27
Donde:
: Tasa de llegada de las personas al sistema. Corresponde al parámetro de la
distribución de Poisson que describe las llegadas.
: Tasa de servicio de los servidores. Corresponde al parámetro de la distribución de
Poisson que describe el servicio.
Además se deduce que el sistema está compuesto por aparatos sanitarios, que la disciplina
de la cola no es de incumbencia, que el sistema tiene una capacidad máxima de personas, y
que la población se considera infinita. De lo anterior es significativo el hecho de que la
capacidad del sistema coincide con el número de servidores en el mismo, indicando que si una
persona llega al sistema y nota que todos los aparatos sanitarios están siendo utilizados, no
hace ningún tipo de fila (dado que ya hay personas en el sistema y no hay capacidad para
nadie más), y por lo tanto se “pierde” esa llegada, (de donde sale el nombre de Sistema de
Pérdidas de Erlang).
En su investigación, Buchberger & Wu (1995), aplican la solución encontrada por Erlang para la
solución del sistema, implicando que suponen, además de lo ya expuesto, que la tasa de
llegada de personas es independiente del número de personas en el sistema, que el tiempo de
servicio de todos los servidores es independiente e idénticamente distribuido para todos y que
la necesidad de un usuario puede ser satisfecha por cualquiera de los servidores (aparatos).
Como resultado del proceso encuentran la probabilidad de que haya aparatos encendidos al
tiempo en la vivienda, y a continuación presentan una aproximación a la distribución de
probabilidad de la intensidad de cada uso de un aparato, entendido como el caudal emitido en
el momento en que hay una persona en él. Para dicho resultado, de nuevo se supone que la

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
27
intensidad de los usos de los aparatos es independiente e idénticamente distribuida para todos
los usos.
Como se puede notar, la metodología planteada por Buchberger & Wu (1995) se basa en una
serie de suposiciones que hacen que el modelo no se ajuste de manera suficiente al
comportamiento que se desea simular, dado su difícil cumplimiento en las condiciones reales
del prototipo. Si bien en el resto del documento Buchberger & Wu, presentan otros modelos
para un nivel de agregación mayor, para el caso de la estimación de demanda en RIDAPs, sólo
el modelo acá expuesto busca cumplir con este fin.
2.3.2 Modelo de NSRP (Neyman-Scott Rectangular Pulses)
Alcocer-Yamanaka et Al. (2008), presentan un modelo un tanto diferente del propuesto por
Buchberger & Wu (1995), al suponer la frecuencia de llegadas como un proceso de Neyman-
Scott. Este modelo presenta una ventaja significativa al permitir diferentes intervalos de
tiempo para su obtención, por lo que la estimación de sus parámetros resulta más fácil y
robusta. Sin embargo, y al igual que las demás investigaciones presentadas en esta sección, su
objetivo es estimar la demanda en un nudo de una RDAP que representa la demanda en una
cuadra o sector de edificaciones residenciales, y no en una única vivienda.
2.3.3 Modelo estocástico de uso último (stochastic end-use model)
Blokker & Vreeburg (2005) presentan un modelo completamente diferente a las
aproximaciones hasta el momento desarrolladas por los investigadores, al proponer una
estimación de los caudales de demanda en los nudos de una RDAP basada en conocimiento del
uso último del agua. Para ello utiliza mediciones hechas por diferentes encuestas y mediciones
realizadas en Holanda (e.g., Foekema & Engelsman, 2001) que le permiten definir ocho
posibles usos últimos, los cuales coinciden con los aparatos utilizados para ello, así como las
funciones de densidad de probabilidad de su frecuencia, duración e intensidad (caudal
emitido) (Ver Tabla 4).
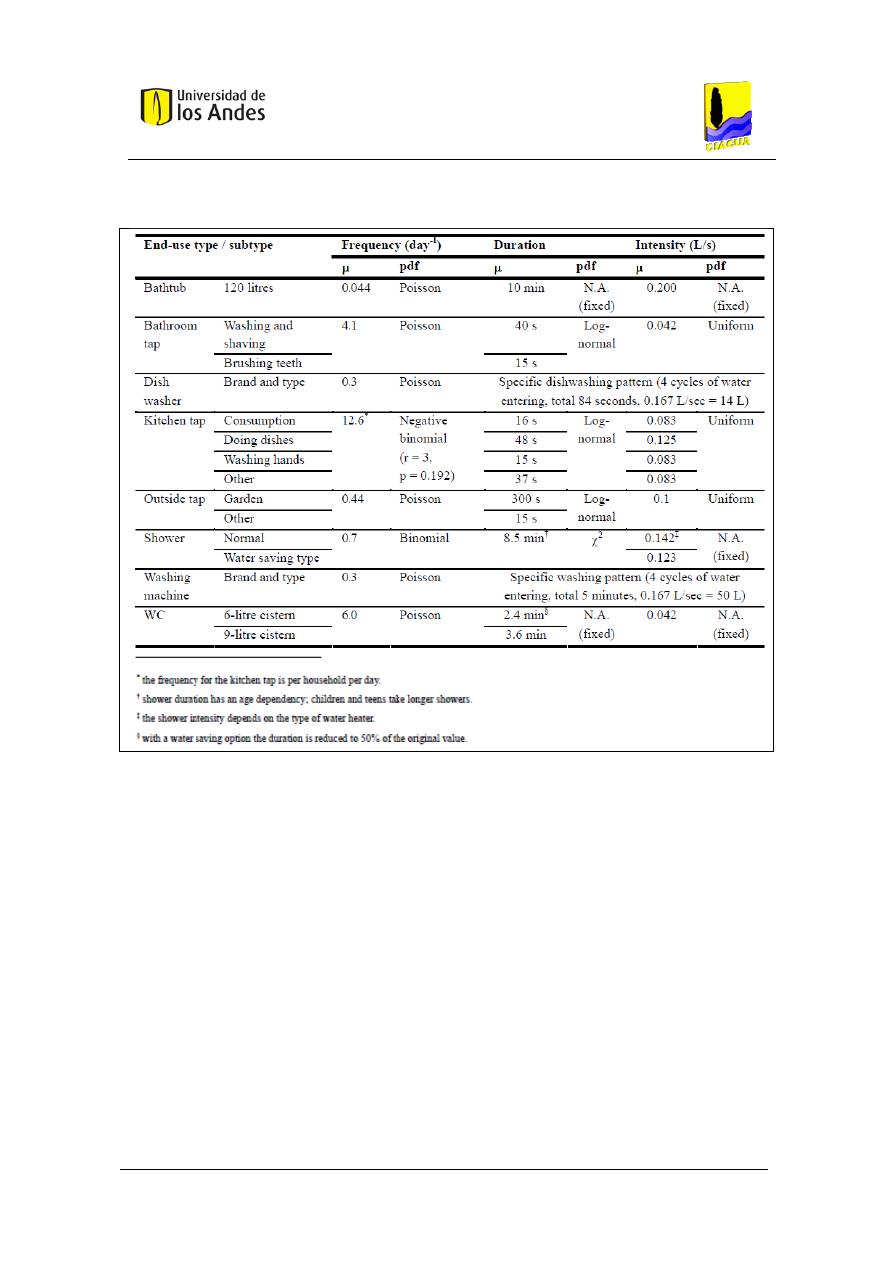
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
28
Tabla 4. Frecuencia, duración e intensidad para los ocho usos últimos definidos en el modelo – Datos medidos en
Holanda. (Blokker, 2006, 2010a y 2010b).
En sus posteriores investigaciones (Blokker, 2006; Blokker, 2010a; Blokker, 2010b; Blokker et
Al., 2010; Blokker et Al., 2011) desarrollan y muestran un software denominado SIMDEUM
(Simulation of water demand, an end-use model) desarrollado en MATLAB, cuyo principal
objetivo es generar simulaciones de los caudales a lo largo del día que serán demandados en
un sector de una zona urbana con unas características específicas. Sin embargo, para ello hace
uso de una serie de mediciones que resultan de gran utilidad a la hora de analizar la demanda
en RIDAPs, tales como patrones diarios de consumo de agua y comportamiento humano.
En la Tabla 4, Blokker logra asignar a cada uso último una distribución de probabilidad para la
frecuencia de uso, para la duración de uso y para la intensidad de uso (caudal emitido). Esta
tabla resulta de mediciones realizadas en zonas residenciales de Holanda, y tiene como ventaja
respecto a las demás metodologías de estimación de demandas, el hecho de que estas
mediciones no dependen significativamente de la ubicación geográfica del sistema, como se
puede ver en la Tabla 5, medida en Milford, Ohio, en donde los parámetros de las
distribuciones y las mismas distribuciones no presentan diferencias significativas respecto a las
medidas en Holanda. Ello resulta muy conveniente a la hora de predecir la demanda de agua
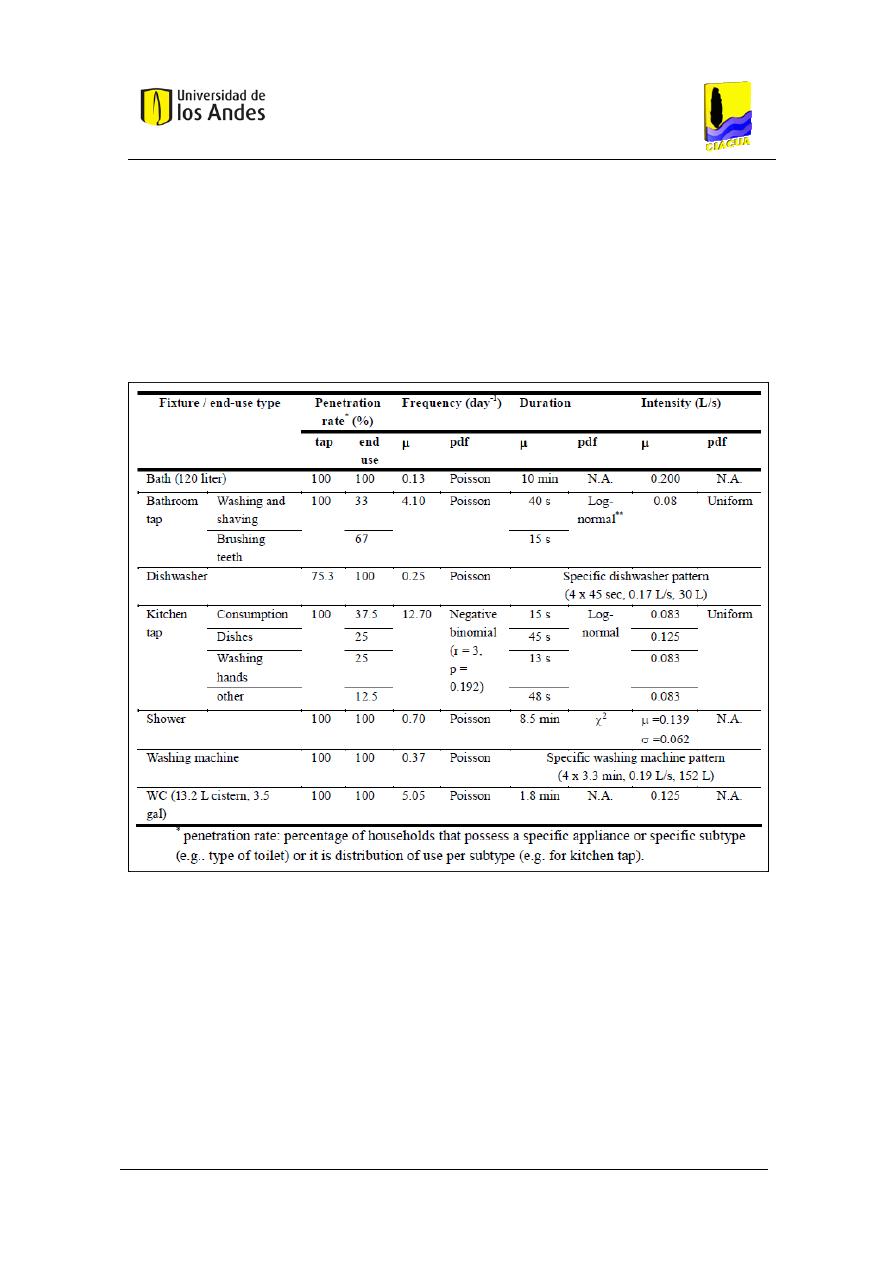
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
29
en un escenario hipotético, dado que no requiere de mediciones en el prototipo para
caracterizar la demanda (cosa que si ocurre con los otros modelos, que presentan variaciones
significativas entre sistemas, de acuerdo con su ubicación geográfica). Además Blokker et Al.
(2011), muestran cómo utilizar el mismo modelo para la caracterización y posible predicción
de demandas en zonas no residenciales a partir de una recolección de datos muy similar a la
hecha para zonas residenciales.
Tabla 5. Frecuencia, duración e intensidad para siete de los ocho usos últimos definidos en el modelo – Datos
medidos en Milford, Ohio. (Blokker, 2010a).
Si bien Blokker presenta otros resultados potencialmente útiles para caracterizar la demanda
en RIDAPS (tanto residenciales como no residenciales), tales como patrones diarios
(distribuciones de frecuencia de cada actividad en horas) de variables como la duración del
sueño de una persona, la hora en la que se levanta, la hora en la que sale del hogar y la
duración fuera de éste además de los porcentajes de hogares que disponen de los aparatos
asociados con cada uso último y las estadísticas de tamaño de hogar y su discriminación por
edad de los ocupantes; estos datos no son presentados en este documento dado que no son
utilizados directamente.
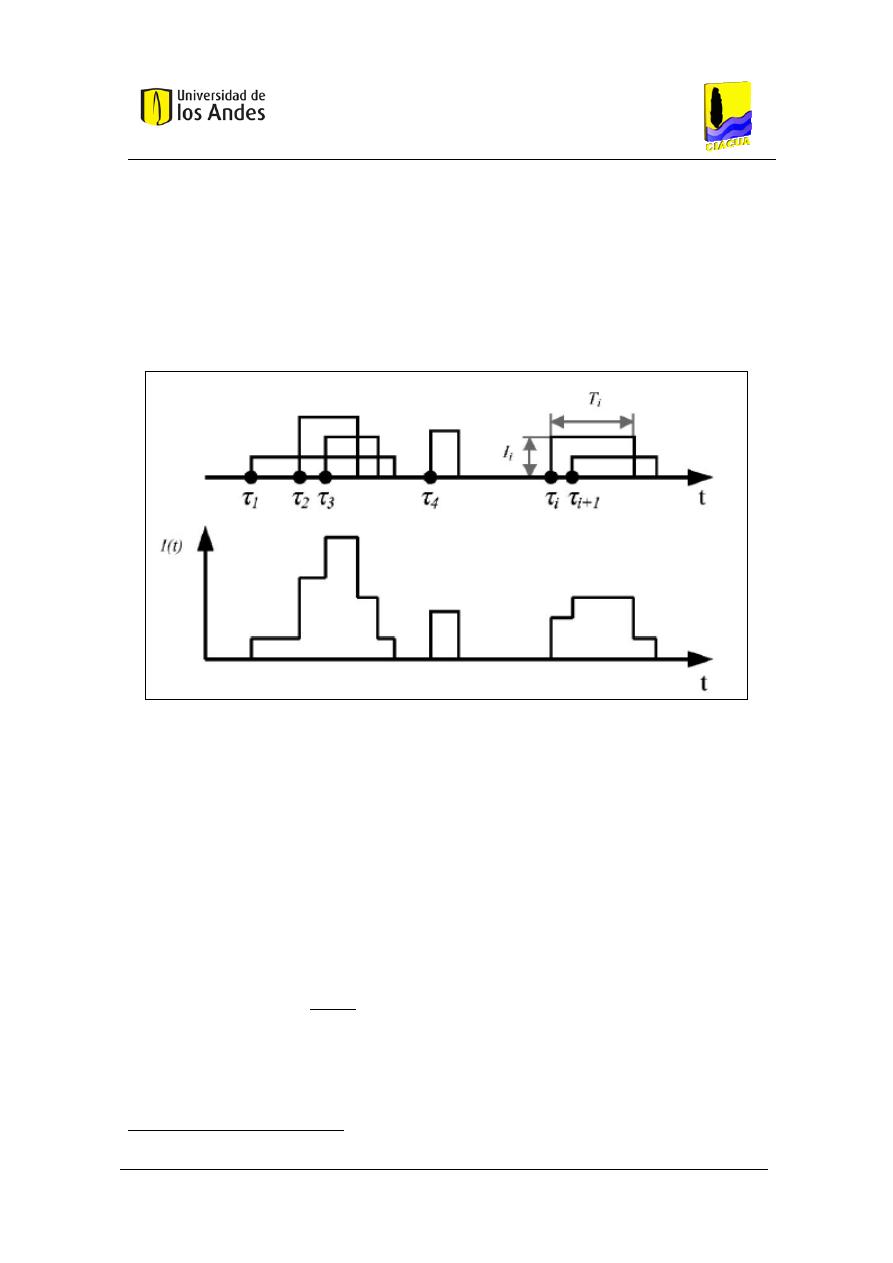
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
30
2.3.4 Modelo estocástico de demanda aplicado a RIDAPs
7
García et Al., (2004), presentan un modelo de estimación de demanda en RDAPs basado en el
modelo de PRP propuesto por Buchberger & Wu (1995). Para este modelo, se supone que la
demanda de agua está representada por pulsos rectangulares de demanda constante que
pueden ocurrir de manera tal que en un instante dado de tiempo están ocurriendo a la vez
varios de estos pulsos (ver Figura 5), y por lo tanto la demanda total en dicho instante resulta
ser la suma de las intensidades de cada uno de los pulsos que están ocurriendo.
Figura 5. Modelo de Pulsos Rectangulares de Poisson (PRP). (GARCÍA et Al, 2004).
García et Al., (2004), suponen que la duración de cada pulso de demanda se distribuye de
manera exponencial mientras la intensidad de cada pulso (caudal emitido) se distribuye
Weibull. Estas dos suposiciones se basan en mediciones realizadas por otras investigaciones,
aunque los parámetros de cada una de las funciones de densidad de probabilidad son
calculados para los casos de estudio presentados por García et Al. Respecto a la frecuencia de
aparición de los pulsos, el modelo PRP supone que la distribución de la frecuencia sigue un
proceso de Poisson no homogéneo, de manera que el número de pulsos por unidad de tiempo
se puede calcular a partir de la Ecuación 28.
Ecuación 28
[
] [ ]
Ecuación 29
donde
: Número de pulsos por unidad de tiempo.
7
Basado en: CIACUA (2011) y García et Al.(2004).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
31
: Valor esperado del número de pulsos en un día.
: Componente aleatorio de la frecuencia. Tiene valor esperado igual a cero.
: Función que distribuye el total de pulsos diarios a lo largo del día. Cumple que:
∫
: Parámetros de la función de distribución de pulsos a lo largo del día.
: Instante de tiempo en que se desea conocer la frecuencia de aparición de pulsos.
Se mide desde el inicio de día en horas.
De esta manera García et Al. plantean una metodología de estimación de los parámetros de su
modelo, aplicándola a dos casos de estudio en Milford, Ohio y Valencia, España. Los resultados
de dicha investigación son adoptados por CIACUA (2011) para desarrollar una metodología de
diseño de RIDAPS. CIACUA plantea el problema de la estimación de demandas de diseño
considerando lo siguiente:
Si se supone que un aparato sólo tiene dos posibles configuraciones
(encendido/apagado), y se tiene una RIDAP con nudos de demanda con solo
aparato conectado a cada uno, entonces el número de posibles escenarios de
demanda
8
es
.
Se entiende que un escenario es de otro escenario cuando el conjunto de
nudos encendidos en el estado es subconjunto del conjunto de nudos encendidos
en el estado . Dicha relación de representa que el escenario es
indiscutiblemente más demandante hidráulicamente que el escenario , y por lo
tanto un diseño que cumpla con los requerimientos hidráulicos de , necesariamente
cumplirá con los requerimientos hidráulicos de . Además es claro que la relación
es transitiva, es decir que si es de y es de , entonces es
de . Haciendo posible que se puedan ordenar los
posibles escenarios de
demanda de acuerdo con la relación , de la siguiente manera:
8
Escenario de demanda: Configuración de aparatos encendidos y apagados que están demandando
agua a la RIDAP. Ver Sección 2.1.2.
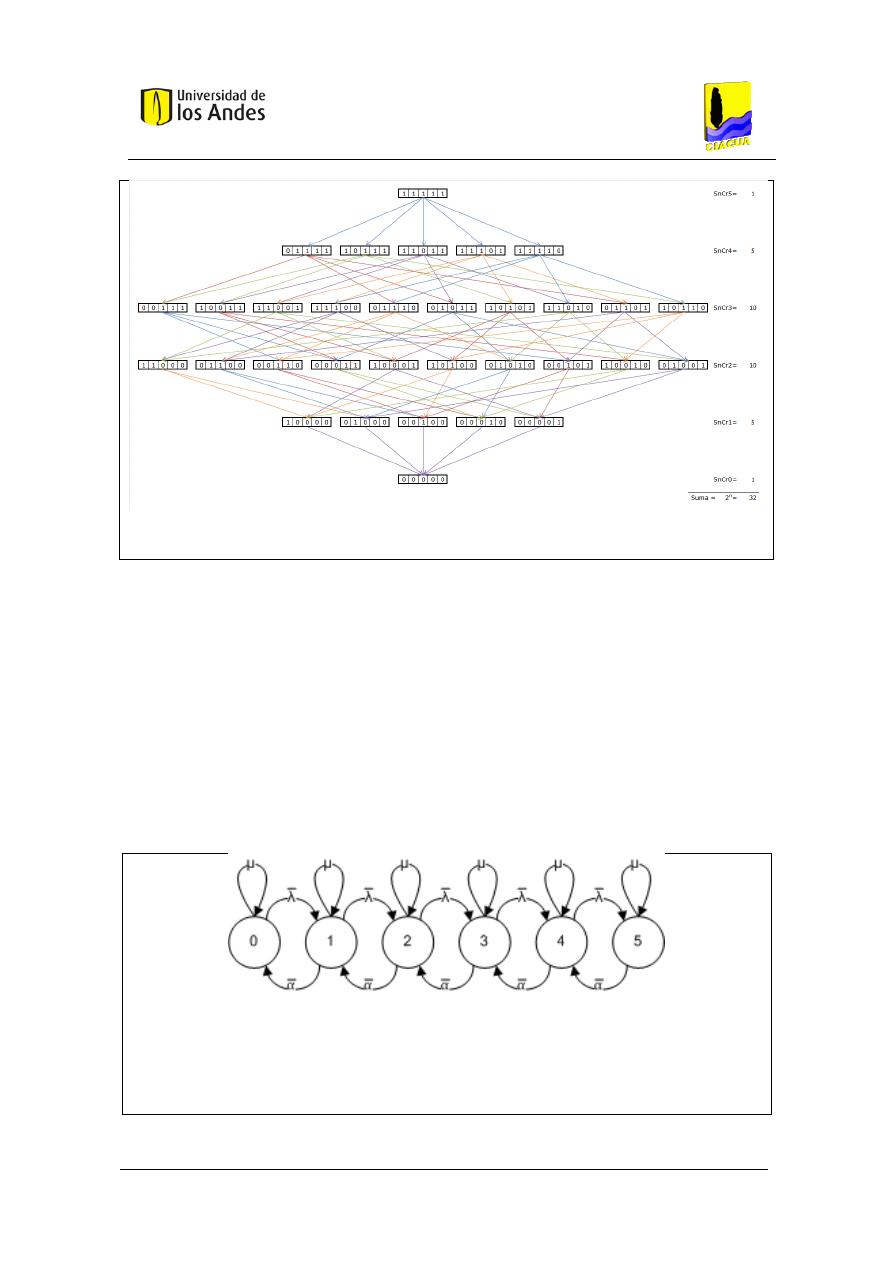
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
32
En el diagrama se entiende que, cada rectángulo con 5 casillas representa un escenario de demanda, en donde las
casillas con valor representan que el nudo está apagado y las casillas con valor representan que el nudo está
encendido; además una flecha que parte del escenario hacia el escenario significa que es de .
Figura 6. Ejemplo de configuración ordenada de los posibles escenarios de demanda de una RIDAP con .
En la Figura 6 se puede notar cómo se genera una clasificación natural de los
escenarios de acuerdo con el número de nudos encendidos que tiene cada uno. Para
ello se definirá cada uno de estos conjuntos de escenarios con igual número de nudos
encendidos como , donde es precisamente el número de nudos
encendidos { } .
Utilizando el modelo y los datos encontrados por García et Al., (2004), además de una
analogía a la Teoría de Colas, y más específicamente a las Cadenas de Markov, se
puede calcular la probabilidad en estado estable de que el sistema (la RIDAP), se
encuentre bajo un escenario de demanda perteneciente a un . Para ello la
cadena de Markov utilizada tiene el siguiente diagrama de transición de estados:
̅ : Probabilidad de que en el siguiente intervalo de tiempo se encienda un nudo que antes estaba apagado, en la
RIDAP. (Asociada con la frecuencia de aparición de pulsos).
̅ : Probabilidad de que en el siguiente intervalo de tiempo se apague un nudo que antes estaba encendido, en la
RIDAP. (Asociada con la duración de los pulsos).
: Probabilidad de que en el siguiente intervalo de tiempo, la RIDAP siga con la misma cantidad de nudos
encendidos.
Los círculos representan un estado con aparatos encendidos.
{ }
Figura 7. Diagrama de transición estados para una cadena de Markov asociada a una RIDAP con .

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
33
Conociendo el diagrama de transición de estados es posible calcular las probabilidades
en estado estable de cada uno de los estados, teniendo en cuenta que para cada
estado se debe cumplir que todas las probabilidades salientes sumen , haciéndose
posible el planteamiento de tantas ecuaciones como estados haya (ecuaciones de
balance), pero dado que estas ecuaciones son linealmente dependientes se debe
prescindir de una, tomando en su lugar la ecuación de normalización, que asegura que
las probabilidades de estado estable de todos los estados sumen . De esta manera
se tienen tantas ecuaciones como estados, y tantas incógnitas como estados
(probabilidad en estado estable de cada uno), haciendo posible la solución del sistema
de ecuaciones.
Al aplicar el cálculo de las probabilidades de cada estado al caso de las RIDAPs, es
posible asignar a cada fila de la Figura 6 una probabilidad en estado estable, y teniendo
en cuenta que un diseño de la RIDAP que cumpla con los requerimientos hidráulicos
para el estado , necesariamente cumplirá los requisitos de los estados {
}, se hace posible calcular la probabilidad de falla del sistema con dicho diseño
como:
∑
Ecuación 30
donde:
: Probabilidad de falla del sistema diseñado para cumplir con los
requerimientos hidráulicos de todos los escenarios de estado .
: Probabilidad de que el sistema este en el estado (bajo alguno de sus
escenarios) en estado estable.
: Máximo estado posible en la RIDAP. Coincide con el número de nudos de la
red .
: Estado para el cual el diseño cumple con los requisitos hidráulicos.
Teniendo en cuenta la posibilidad de calcular la probabilidad de falla de un diseño
generado a partir de un (conjunto de escenarios de diseño
pertenecientes a un mismo estado), es posible determinar el valor de para que la
probabilidad de falla del sistema diseñado sea igual o menor a la aceptable. Para ello
basta calcular la distribución acumulada de cada posible estado, tomando como estado
de diseño el estado de mínimo que cumpla con que su probabilidad acumulada
supera el valor (
).
El análisis anteriormente descrito fue hecho por CIACUA en su investigación, y en ella incluyen
el desarrollo de un software capaz de implementar la metodología propuesta (denominado
RIDAPS), en conjunto con una metodología de optimización de costos constructivos (ver

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
34
Sección 2.2.2). Es importante aclarar que la metodología propuesta por CIACUA tiene un
inconveniente a la hora de su implementación, que consiste en la aproximación de los
caudales correspondientes al estado de diseño, dado el tamaño que pueden alcanzar algunos
estados de diseño (el número de escenarios de un estado se calcula como , que
en el caso de una RIDAP con y un estado de diseño , resulta en un tamaño de
estado de , implicando escenarios de diseño y por lo tanto un número de
ejecuciones hidráulicas y de cálculos numéricos considerablemente grande). Dicha
aproximación y su consecuente consideración por parte de CIACUA, puede derivar en diseños
no ajustados al comportamiento esperado de la demanda, si se escogen mal algunos
parámetros del método de aproximación.
Por otro lado tiene como desventaja conceptual, el hecho de basarse en la metodología de
García et Al., (2004), la cual es originalmente desarrollada para RDAPs, y así supone que tanto
la duración como el tiempo entre arribos de usos se distribuyen de manera exponencial
9
. Así
mismo la modelación con cadenas de Markov, supone que una necesidad que llega al sistema,
puede ser atendida por cualquier servidor (aparato) libre. Además, el método de aproximación
anteriormente mencionado fue desarrollado con base en demandas en los nudos
independientes e idénticamente distribuidas, y aunque el software RIDAPS permite diferentes
valores esperados para las duraciones de los pulsos, es posible que el algoritmo de
aproximación no funcione bien bajo dicha condición con los valores de los parámetros
sugeridos en la investigación.
9
Para un proceso de Poisson, como el de apariciones de pulsos, el tiempo entre arribos se distribuye
exponencial con media igual al inverso multiplicativo del valor esperado de la frecuencia de llegada.
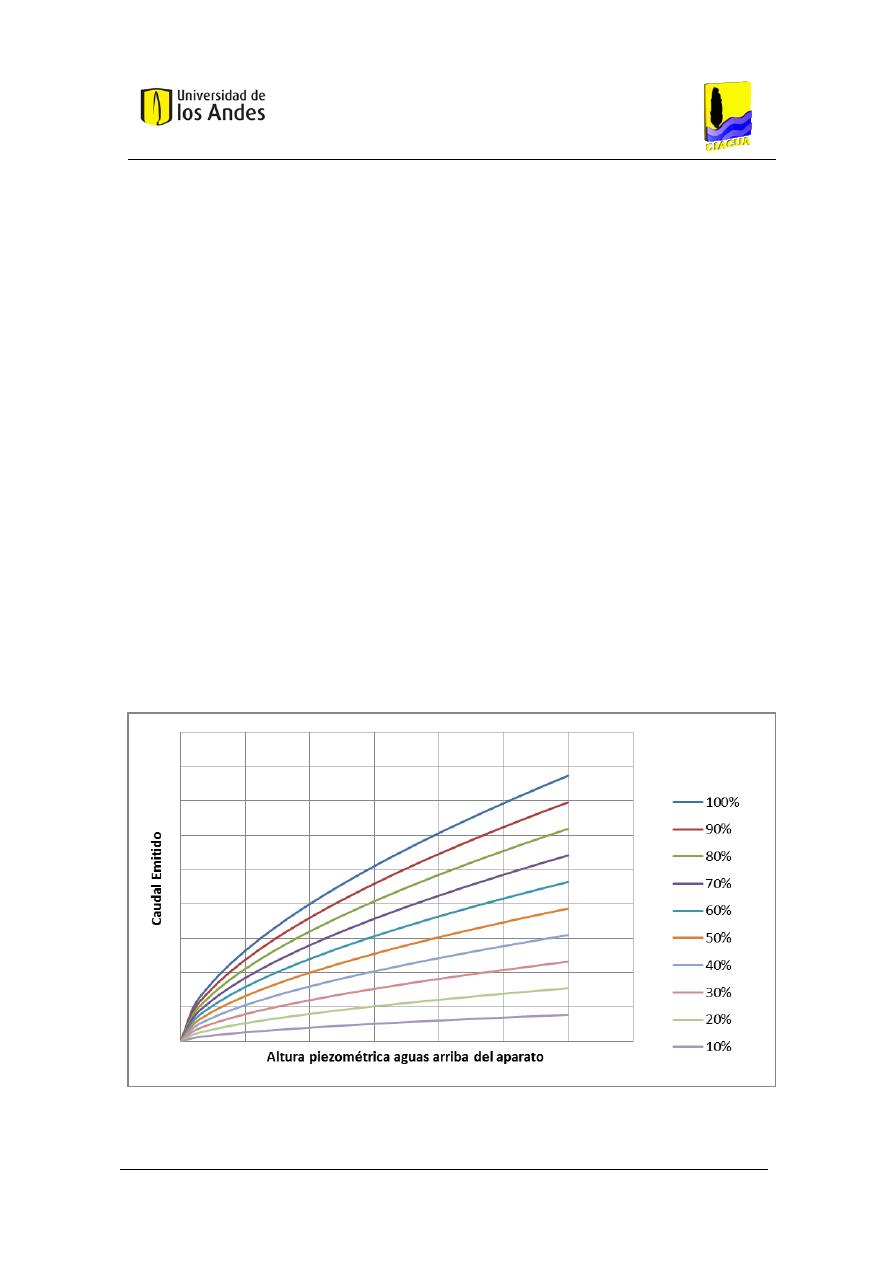
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
35
3 Metodología de modelación propuesta
3.1 Modelación de los aparatos sanitarios
Una RIDAP típica tiene conectados a sus nudos aparatos sanitarios tales como lavamanos,
inodoros, duchas, tinas, lavaplatos, llaves en general y aparatos como lavaplatos eléctricos y
lavadoras. Dada la naturaleza de estos aparatos, se puede observar que el caudal de salida o
caudal emitido por cada uno de estos aparatos no es un valor constante independiente de las
condiciones del flujo en la RIDAP, o de la manera como el usuario lo configura (porcentaje de
apertura de válvula en el caso de llaves). De hecho para una configuración dada del aparato,
Acero (2009), encontró que el caudal emitido se ajusta al comportamiento hidráulico de un
emisor, regido por la Ecuación 1.
Sin embargo, en la operación normal de una RIDAP, cada uso de un mismo aparato puede
tener una configuración diferente de éste. En el caso de un lavamos, por ejemplo, la apertura
de la válvula que controla el caudal emitido no es igual en cada ocasión en que se utiliza el
aparato. Ello implica que el estudio de Acero (2009) sólo describe el comportamiento
hidráulico de los aparatos sanitarios bajo una configuración dada, y dado que existen aparatos
con un sinnúmero de posibles configuraciones, en principio deben existir un sinnúmero de
curvas similares a las encontradas en dicha investigación para aquellos aparatos donde la
apertura de válvula es variable. En la Figura 8 se puede ver esquemáticamente como varía la
relación entre caudal emitido y altura piezométrica aguas arriba del aparato para diferentes
porcentajes de apertura de válvula.
Figura 8. Relación entre Caudal Emitido y Altura piezométrica aguas arriba del aparato, para diferentes
porcentajes de apertura de válvula de un mismo aparato.
Porcentaje de
apertura de
válvula:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
36
El uso práctico de un potencial estudio de las propiedades hidráulicas de un aparato sanitario
que busque ajustarse a un comportamiento similar al mostrado en la Figura 8, tendría que
incluir
una
función
de
densidad
de
probabilidad
para
la
variable
, de manera que se pudiese calcular la probabilidad
asociada a cada curva, y así se calculara la función de densidad de probabilidad del
para una altura piezométrica aguas arriba del aparato conocida.
Sin embargo para problemas como el de estimación de la demanda para diseño, es posible y
necesario simplificar el anterior modelo de manera que se tenga en cuenta el comportamiento
de emisor del aparato sin tener en cuenta todos los porcentajes de apertura de válvula
posibles. Para ello se propone asignar una única relación de vs
que represente un comportamiento “típico” de uso del aparato. La
definición de “típico” puede resultar ambigua y por lo tanto, para esta propuesta se plantea
considerar como ciertas las siguientes observaciones:
La reacción esperada de un usuario que nota una baja presión (Altura piezométrica) en
el aparato, es abrir la válvula a su máximo para lograr aumentar el caudal emitido y
esperar que dicho caudal, después de la apertura total, resulte mayor al
, entendido como el mínimo caudal que el usuario espera
recibir de su aparato sanitario sin que se éste considere que el sistema de distribución
de agua potable está presentando una falla o un mal funcionamiento.
La reacción esperada de un usuario que nota una presión demasiado grande en el
aparato, es cerrar la válvula hasta un porcentaje tal, que el caudal emitido, después del
cierre parcial, resulte menor al , entendido como el
máximo caudal que el usuario está dispuesto a recibir de su aparato sanitario sin que
se éste considere incómoda la presión y velocidad del flujo emitido por dicho aparato.
A partir de estas dos suposiciones, se pueden inferir dos partes de la curva que representa la
relación única de vs típica del uso de aparatos
sanitarios con apertura de válvula variable (curva única)
10
. Así, para presiones inferiores a la
presión que asegura que el caudal emitido por el aparato sea igual al
cuando el es igual a ,
se tiene que la curva única coincide con la curva del
. Además para presiones mayores a una presión , la curva única será una línea
horizontal de caudal emitido constante igual al (ver Figura 9).
10
Se debe notar que se está suponiendo, de manera implícita, que los valores de caudal mínimo
admisible y caudal máximo admisible, así como otras constantes utilizadas más adelante, son iguales
para todos los usuarios del sistema.
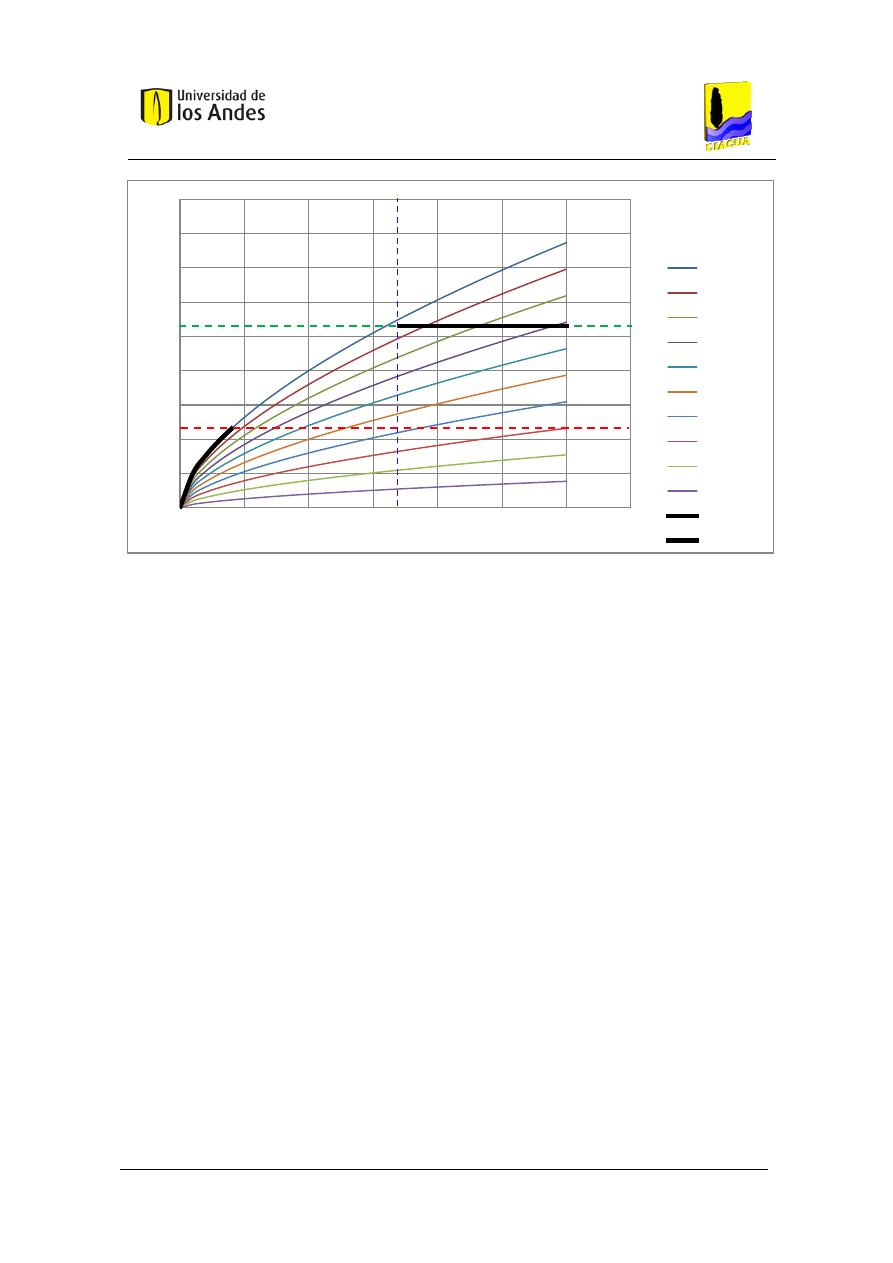
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
37
Figura 9. Partes de la curva única de relación entre Caudal Emitido y Altura piezométrica aguas arriba del aparato,
para aparatos con apertura de válvula variable.
Dado que es necesario conocer la parte intermedia de la curva, así como la presión a partir
de la cual el caudal emitido es constante, se hace necesario hacer alguna suposición adicional
respecto al comportamiento típico de los usuarios o bien realizar observaciones de uso de
aparatos con apertura de válvula variable, notando los porcentajes de apertura más comunes
y/o necesarios para un comportamiento aceptable del aparato. Sin embargo, para el problema
de estimación de la demanda para diseño, el comportamiento crítico sería aquel en el que se
considerara un porcentaje de apertura de válvula igual al para las presiones intermedias
de la curva única. Ello implicaría que la presión es la presión necesaria para que el caudal
emitido
por
el
aparato
sea
igual
al cuando
el
es igual a .
De esta manera la curva única a considerar para el problema de estimación de la demanda
para diseño, en caso de que no se disponga de observaciones de uso del aparato para
aperturas de válvula comunes, sería la curva con apertura de válvula del hasta llegar al
a partir del cual la curva se torna horizontal asegurando que el
caudal emitido no supera al máximo admisible (ver Figura 10). Se debe tener presente que
dicha curva única es útil solamente para los aparatos sanitarios con apertura de válvula
variable, y que para aparatos con apertura de válvula constante y/o binaria (o totalmente
cerrada o totalmente abierta) no hace falta realizar ninguna suposición respecto al
comportamiento típico de la demanda, dado que ya se dispone de una única curva que
caracteriza la relación vs .
Caud
al
E
m
iti
d
o
Altura piezométrica aguas arriba del aparato
100%
90%
80%
70%
60%
50%
40%
30%
20%
10%
Curva única
Curva única
Caudal máximo admisible
Caudal mínimo admisible
Presión X
Porcentaje de
apertura de
válvula:
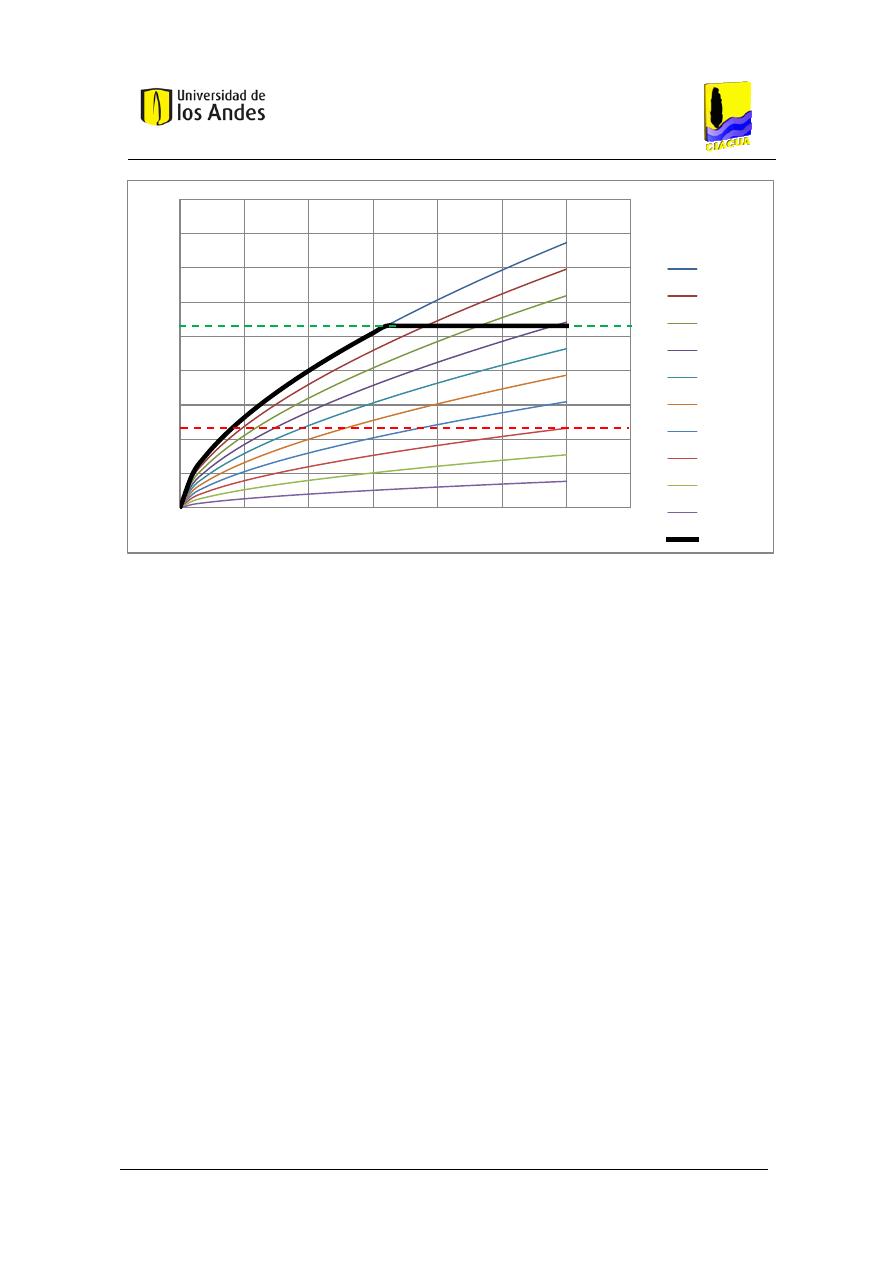
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
38
Figura 10. Curva única de relación entre Caudal Emitido y Altura piezométrica aguas arriba del aparato, para
aparatos con apertura de válvula variable, para el problema de estimación de demanda para diseño.
Independientemente de la manera como se haga, lo que se debe tener presente es que la
representación moderna de aparatos sanitarios debe asignar, no un caudal emitido constante,
sino una relación vs que según los resultados de Acero
(2009) se ajusta mucho mejor al comportamiento hidráulico observado de éstos.
3.2 Modelación de la simultaneidad de uso de los aparatos
El diseño de una RIDAP tiene, como principal problema, la naturaleza estocástica de la
demanda que dificulta la estimación de escenarios de diseño para una probabilidad de falla
dada. Dicho problema se ve representado en la simultaneidad de uso de los aparatos, dado
que la probabilidad de ocurrencia de cada posible escenario de demanda es función de cuáles
aparatos están encendidos, entendiéndose como la probabilidad de que dichos aparatos
encendidos estén siendo utilizados de manera simultánea por los usuarios de la edificación.
3.2.1 Modelo basado en Blokker
Utilizando mediciones hechas en Holanda (Tabla 6) y Estados Unidos, Blokker asigna a cada
aparato sanitario una función de densidad de probabilidad para la de uso y para la
de uso diaria por persona de dicho aparato. Si bien Blokker también asigna una
función de densidad de probabilidad para la de uso (caudal emitido) de cada
aparato, los resultados de Acero (2009) respecto al comportamiento hidráulico de los aparatos
Caud
al
E
m
iti
d
o
Altura piezométrica aguas arriba del aparato
100%
90%
80%
70%
60%
50%
40%
30%
20%
10%
Curva única
Caudal máximo admisible
Caudal mínimo admisible
Porcentaje de
apertura de
válvula:
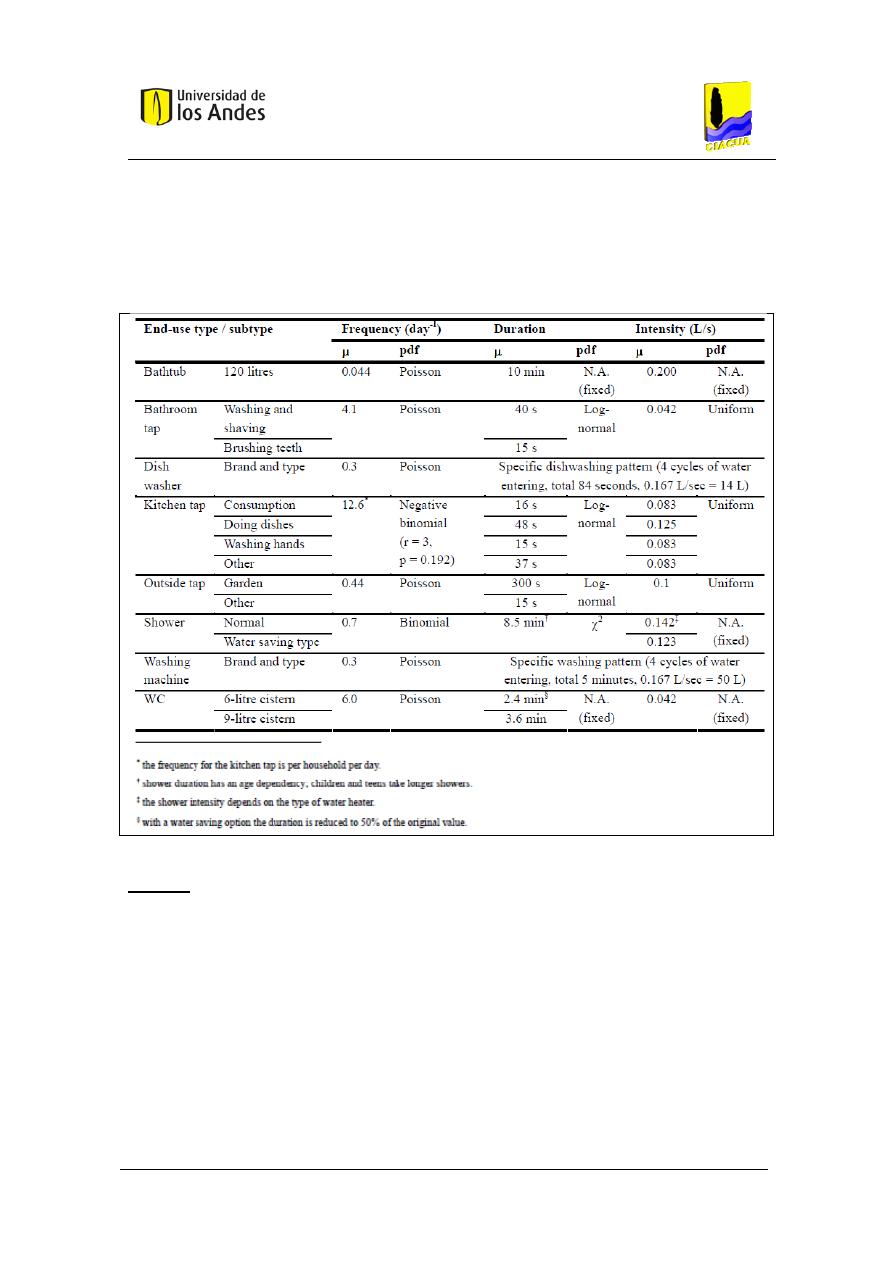
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
39
muestran que una modelación utilizando emisores representa mejor el comportamiento
observado, y por lo tanto para la representación de la variable se recomienda el
uso del análisis de la Sección 3.1.
Tabla 6. Frecuencia, duración e intensidad para los ocho usos últimos definidos en el modelo – Datos medidos en
Holanda. (Blokker, 2006, 2010a y 2010b).
Duración
Si se supone que la de uso de un aparato depende de los posibles usos últimos que
se hagan de éste, y teniendo en cuenta las estadísticas mostradas por Blokker para cada uno
de esos usos últimos, se hace necesario estimar una división del total de usos del aparato en
esos usos últimos de manera que se pueda estimar una única función de densidad de
probabilidad para la duración de uso del aparato. Por ejemplo, utilizando los datos de la Tabla
6 para un lavamanos (Bathroom tap), se tienen dos duraciones medias de uso para dos
posibles usos de un lavamanos: Lavarse y afeitarse o Cepillarse los dientes. Es decir que en este
caso se debe estimar qué porcentaje del total de usos de un lavamanos es para Lavarse y
afeitarse y qué porcentaje del total de usos de un lavamanos es para Cepillarse los dientes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
40
Una vez estimados los porcentajes de cada uso último del aparato, se pueden calcular los
valores de los parámetros de la función de densidad de probabilidad que representará todos
los usos del aparato. Así, por ejemplo, si para un lavamanos se estima que el 60% de los usos
corresponde a Lavarse y afeitarse, y el 40% restante es para Cepillarse los dientes, entonces el
valor esperado de la duración de un uso puede calcularse como:
Y teniendo en cuenta que Blokker propone como Coeficiente de Variación de la duración de
uso del lavamanos un valor de , se puede calcular la desviación estándar de la
duración de uso como:
De manera que la distribución Lognormal asignada para la duración de uso de un lavamanos
queda totalmente definida y cumpliendo el requerimiento de que sea única para el aparato.
Frecuencia
Para la de uso del aparato, los datos de Blokker ya vienen asignados con una
única distribución para cada aparato. Sin embargo dicha distribución está en unidades de
o en el caso del lavaplatos en , y ello representa
un inconveniente a la hora de estimar escenarios de diseño, dado que esas frecuencias pueden
y, de hecho usualmente, están concentradas en algunas horas del día. Esa concentración de
frecuencia es precisamente la razón por la que García et Al. (2004), plantea la curva de la
Ecuación 29.
El inconveniente de la curva de García et Al. (2004) de distribución temporal de la frecuencia,
radica en que los datos medidos en dicha investigación corresponden a hogares y RIDAPs
completas, y no a aparatos sanitarios por separado. Es por ello que se requieren curvas de
distribución temporal de la frecuencia para cada tipo de aparato, entendidas como:
Del total de usos que se espera tenga el aparato sanitario , qué porcentaje se espera
que ocurra en el instante de tiempo .
Dichas curvas pueden ser diferentes entre días laborales y días no laborales, pero en principio
no existen razones para esperar una diferencia causada por otra razón. Esa posible diferencia
entre días laborales y no laborales, puede implicar la evaluación de la simultaneidad de uso
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
41
para ambos casos, dado que es posible que los escenarios de diseño resultado de utilizar una
curva sean más o menos exigentes que si se utilizara otra, y ello podría conducir a posibles
subestimaciones del diseño.
Por otro lado, la naturaleza de dichas curvas es la de representar patrones diarios de
comportamiento humano tales como horas de sueño, horas de bañado, horas de ausencia y
presencia en la edificación, horas de disponibilidad o necesidad de uso de un aparato sanitario
etcétera, y por lo tanto una buena aproximación a dichas curvas es una discretización de las
mismas en intervalos de horas que son los que rigen en buena medida, muchos de los
comportamientos anteriormente descritos.
Una ventaja intrínseca de la discretización de la curva, es que el valor asignado a cada hora
corresponde al porcentaje del total de usos que se espera que ocurran a esa hora de manera
que son menores o a lo sumo iguales a , y aseguran que la suma total sea , a diferencia
de una curva continua donde la integral total es igual a , pero puede tener valores
superiores a para algunas horas. Esos porcentajes de la curva discretizada resultan
especialmente útiles para asignar una frecuencia de uso a cada hora, dado que simplifican el
proceso a una multiplicación del parámetro de la función de frecuencia con el porcentaje de la
hora seleccionada. Por ejemplo, si se supone que la curva de distribución temporal de la
frecuencia para un lavamanos es la presentada en la Figura 11, y se tiene en cuenta que según
la Tabla 6, la frecuencia diaria de uso por persona es de , entonces
la frecuencia horaria de uso por persona se podrá calcular como la multiplicación del
porcentaje de usos de cada hora, por la frecuencia diaria de usos, generando como resultado
para cada hora, la serie mostrada en la Figura 12.
Figura 11. Distribución temporal supuesta de la frecuencia de uso de un lavamanos.
0.0%
1.0%
2.0%
3.0%
4.0%
5.0%
6.0%
7.0%
8.0%
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:00
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Por
ce
n
taje
d
e
u
sos
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
42
Figura 12. Serie de tiempo de la frecuencia horaria de uso por persona de un lavamanos.
De esta manera es posible evaluar la concentración de usos a lo largo del día, en vez de
suponer una distribución uniforme de la frecuencia que resultaría en una frecuencia horaria de
⁄
⁄
⁄
, la cual
resulta considerablemente menor que la máxima frecuencia presentada en la Figura 12
⁄
.
Sin embargo hasta ahora todas las frecuencias encontradas se encuentran en unidades de
frecuencia por persona, y por lo tanto para el cálculo de la frecuencia efectiva de uso de un
aparato sanitario, es necesario conocer el número de personas aferentes a dicho aparato. Así,
por ejemplo, si un lavamanos puede ser utilizado por un total de tres personas, las frecuencias
efectivas de llegadas de usos al aparato serán el producto de las frecuencias de la Figura 12
con el número de personas que lo puede utilizar (tres en este caso), llegando a una serie de
frecuencias totales mostrada en la Figura 13:
0.00
0.05
0.10
0.15
0.20
0.25
0.30
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:00
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:00
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Fr
e
cu
e
n
ci
a
d
e
u
so
(u
sos/
(h
*p
e
rson
a))
Hora
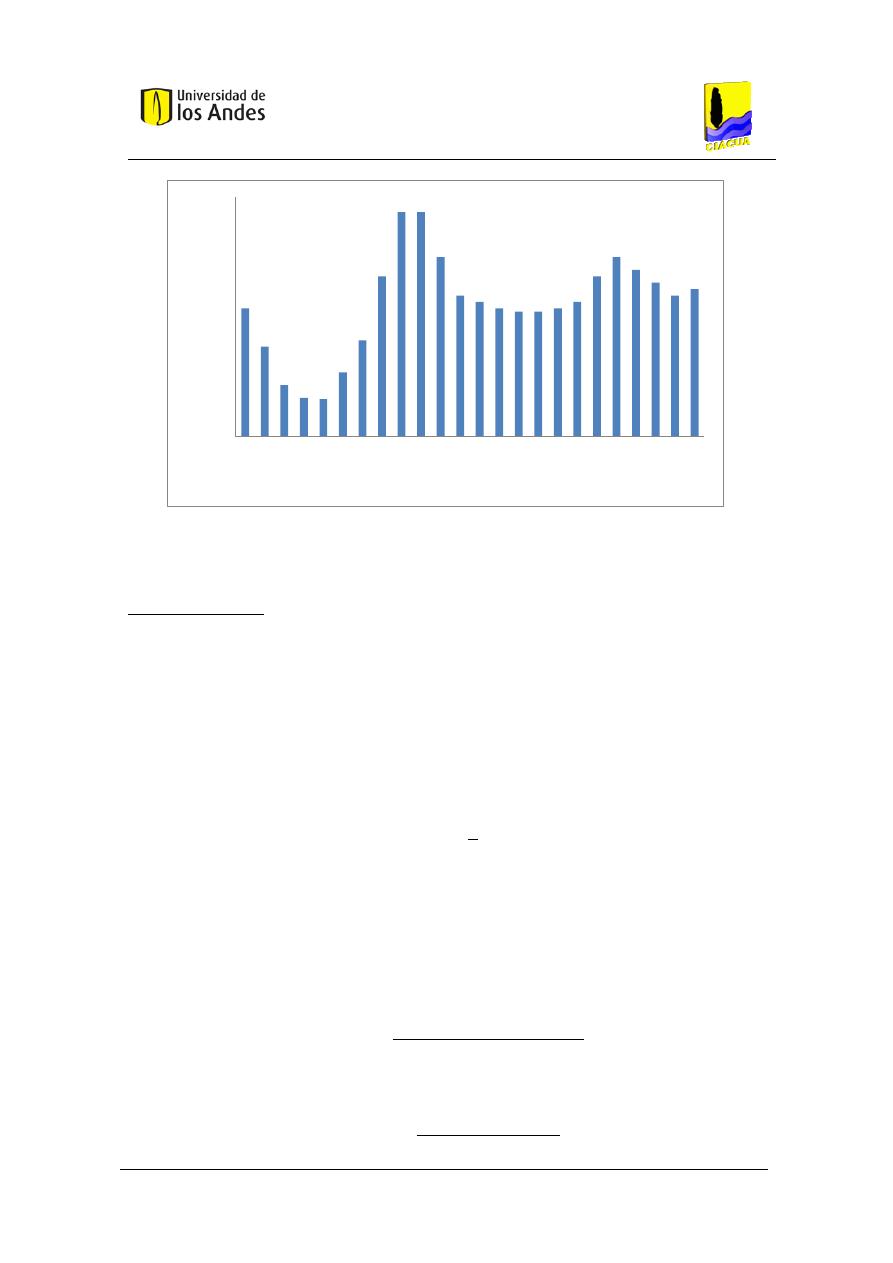
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
43
Figura 13. Serie de tiempo de la frecuencia horaria de uso de un lavamanos.
Probabilidad de uso
Una vez se conocen las funciones de densidad de probabilidad para la y la
de uso, es posible calcular la probabilidad de que en un instante dado el aparato
esté siendo utilizado por un usuario. Para ello se utiliza una variable de desempeño de una cola
según la Teoría de Colas, denominada o , entendida como
la fracción promedio del tiempo en que el sistema de atención a la cola está siendo ocupado.
Dicha variable está relacionada con esa probabilidad mencionada anteriormente de que en un
instante dado el sistema esté en uso, según la Ecuación 31:
Ecuación 31
donde:
: Probabilidad de que en un instante dado de tiempo el aparato se encuentre en uso.
: Utilización o Factor de Utilización del aparato.
: Tasa promedio de llegadas de usos al aparato. Se calcula como:
[ ]
: Tasa promedio de servicio del aparato. Se calcula como:
[ ]
0.00
0.10
0.20
0.30
0.40
0.50
0.60
0.70
0.80
0.90
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:00
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:00
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Fr
e
cu
e
n
ci
a
d
e
u
so
(u
sos/
h
)
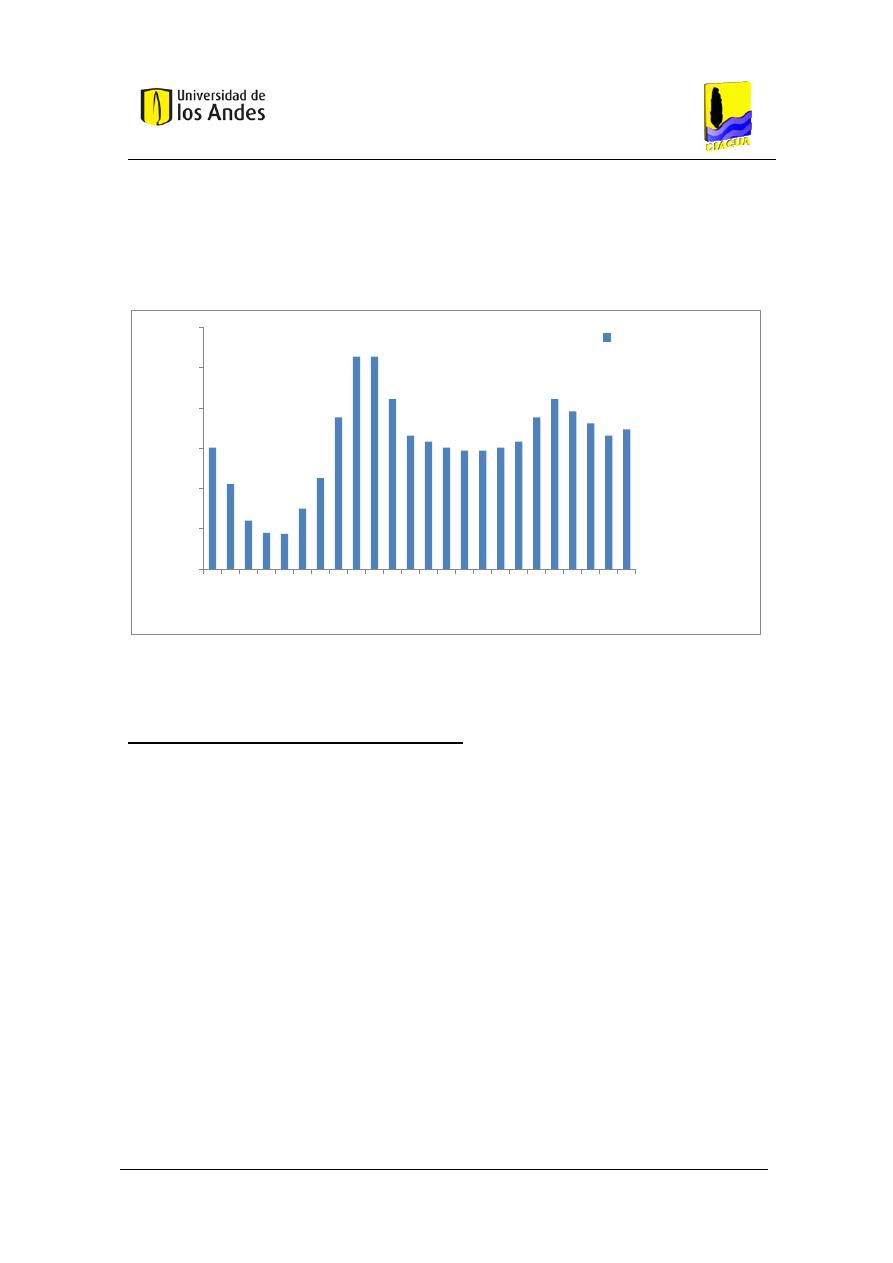
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
44
Así, se puede calcular esa probabilidad de uso de cada aparato para cada hora del día como el
producto de la duración promedio de uso del aparato y la frecuencia horaria total (incluyendo
el número de personas), de manera que en el caso de un lavamanos con duración promedio de
uso
y con frecuencias horarias totales descritas por la serie de la Figura 13, se
tiene una serie de tiempo de la utilización como la mostrada en la Figura 14:
Figura 14. Serie de tiempo de la utilización de un lavamanos.
Probabilidades conjuntas de uso (Simultaneidad)
Utilizando los resultados de cálculo de las probabilidades de uso de cada aparato, descritas
para cada hora del día, es posible calcular las probabilidades conjuntas de un sistema,
haciendo una serie de suposiciones que simplifican el comportamiento real del prototipo a un
modelo fácilmente calculable. Así, si se suponen conocidas las series de tiempo de la
utilización de cada aparato presente en un sistema, se pueden calcular las probabilidades de
cada posible escenario del sistema, suponiendo total independencia entre los usos de los
todos los aparatos sanitarios.
De esta manera, si se tiene un sistema con los siguientes aparatos sanitarios:
{
}
conectados a los nudos de la RIDAP, entonces la probabilidad de un escenario cualquiera,
en una hora dada, puede ser calculada como:
(
⁄
⁄
⁄
⁄
)|
0
0.0005
0.001
0.0015
0.002
0.0025
0.003
00
:0
0
01
:0
0
02
:00
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:00
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Uti
lizac
ió
n
()
Hora
Utilización Lavamanos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
45
∏
|
∏
|
Ecuación 32
donde:
: Probabilidad del escenario dado en la hora .
⁄
: Posibles configuraciones de un aparato. El aparato puede estar encendido
o apagado .
|
: Utilización del aparato en la hora . Es igual a la probabilidad de uso del
aparato en la hora .
|
: Probabilidad de NO uso del aparato en la hora . Es el complemento de
la probabilidad de uso.
De la Ecuación 32, se puede concluir que se está aplicando la suposición de independencia
entre eventos al considerar la probabilidad conjunta como el producto de las probabilidades
individuales de cada aparato. Si bien esta suposición puede ser bastante discutible en el caso
de las RIDAPS, con ella se hace posible calcular la probabilidad de cada uno de los
posibles
escenarios de la RIDAP, asegurándose de que la suma de todas esas probabilidades da como
resultado . Esto quiere decir que este modelo permite una caracterización estocástica de
los escenarios de la red, permitiendo una asignación de funciones de densidad de probabilidad
diferentes a la Exponencial para la duración y la frecuencia de uso, de manera que se puede
presentar un mejor ajuste entre datos medidos y datos simulados, a partir de funciones de
densidad de probabilidad más ajustadas al comportamiento medido de los usos (e.g., Tabla 6).
Otra ventaja respecto a otros métodos de caracterización de la demanda como el planteado
por CIACUA (2011), es el hecho de no asignar una misma probabilidad de ocurrencia para
cualquier escenario con el mismo número de aparatos encendidos, lo que es una mejor
aproximación al comportamiento esperado de una RIDAP real.
Por otro lado, para pasar de escenarios de demanda a caudales en los tubos de la red, basta
simular la respuesta hidráulica de la red para cada posible escenario, haciendo uso de la
caracterización del comportamiento hidráulico de los aparatos hecha en la Sección 3.1, y de
esta manera, para un tubo dado, la función de densidad de probabilidad del caudal que debe
transportar, puede ser calculada relacionando el caudal que pasa por dicho tubo según la
simulación hidráulica de la red para cada escenario con la probabilidad asociada con la
ocurrencia del escenario simulado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
46
3.2.2 Modelo basado en Blokker con simulación de eventos discretos
Si bien el modelo descrito en la Sección 3.2.1 representa un avance en la simulación de la
simultaneidad de uso de los aparatos sanitarios en una RIDAP, éste se basa en una suposición
bastante discutible para algunos casos de análisis de una RIDAP real. Así, suponer total
independencia entre los usos de los aparatos, puede alejarse de la realidad en el caso de
sistemas pequeños ubicados en unidades residenciales, por ejemplo.
Para entender mejor el problema de dicha suposición, se puede considerar el caso de un baño
residencial con un lavamanos, un inodoro y una ducha. Según el anterior modelo, la
probabilidad de que los tres aparatos se encuentren descargando al tiempo, se calcula como el
producto de la probabilidad de que la ducha esté descargando, con la probabilidad de que el
inodoro esté descargando y con la probabilidad de que el lavamanos esté descargando. Sin
embargo, el comportamiento esperado de un usuario que está utilizando la ducha, por
ejemplo, es el de cerrar la puerta del baño, denegando la entrada a otro usuario que desee
utilizar el lavamanos o el inodoro. Así, la probabilidad de que el lavamanos y/o el inodoro
también estén descargando sería nula, dada la manera activa en que se restringe su uso
cuando se usa una ducha.
Para mejorar en este aspecto el modelo basado en Blokker, se hace necesario utilizar
simulación de eventos discretos, que es básicamente una herramienta para el análisis de
sistemas difícilmente representables con modelos analíticos. En estos casos se prefiere una
simulación basada en las capacidades actuales de los computadores para procesar datos que
permiten acelerar el tiempo de simulación de un sistema y así concluir con base en resultados
numéricos que representan comportamientos del sistema ante diferentes condiciones de
entrada.
Este tipo de modelos se basa en una representación del sistema mediante entidades, eventos
y actividades, que se asemejan a la programación mediante el paradigma de POO
(programación orientada a objetos), y se basa en interacciones entre diferentes entidades u
objetos haciendo que el resultado global sea gobernado por esas interacciones, y no por una
fórmula o planteamiento matemático explícitamente escrito. Para su implementación existen
diferentes programas que permiten realizar simulaciones de eventos discretos, pero quizás el
más utilizado en el ámbito de la investigación de operaciones (rama de la ingeniería con mayor
uso de estas herramientas), es el desarrollado por Rockwell Automation, Inc. denominado
ARENA.
Programa ARENA
El programa ARENA es un programa de simulación de eventos discretos ampliamente utilizado
en diferentes problemas de la investigación de operaciones. Este programa define una serie de
procesos, que son objetos que actúan activamente con las entidades de manera que rigen la
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
47
dinámica del sistema con sus acciones. Dentro de los principales procesos que tiene el
programa, y que resultan de alguna utilidad para la modelación de RIDAPS se encuentran:
Tabla 7. Principales procedimientos del programa ARENA para simulación de eventos discretos.
Create:
Es el procedimiento encargado de crear entidades siguiendo
algún patrón de frecuencia o alguna distribución del tiempo
entre arribos (creación de entidades).
Assign:
Es el procedimiento encargado de asignar un cierto valor a los
atributos de las entidades o a variables globales del sistema,
cada vez que alguna condición se cumple o que alguna entidad
pasa por dicho procedimiento.
Process:
Es el procedimiento encargado de simular un proceso o tarea
que requiere un cierto tiempo y unos ciertos recursos. Se
encarga de registrar el tiempo de utilización de un recurso
registrándolo como “No disponible” hasta después de que la
entidad que ha entrado al procedimiento lo desocupa.
También retrasa el avance de las entidades que entran, un
tiempo igual al tiempo de ocupación del recurso. También
registra las estadísticas de una cola de entidades que se forma
para pasar por esa tarea.
Decide:
Es el procedimiento encargado de evaluar una condición de
una variable global o de un atributo de la entidad que pasa por
este procedimiento, de manera que asigna un camino a seguir
para la entidad en cuestión dependiendo del resultado del
condicional. Puede modelar condiciones de más de dos
opciones, evitando la anidación de procedimientos similares.
Hold:
Es el procedimiento encargado de retener una o varias
entidades que pasan por este procedimiento hasta que se
cumpla una condición dada. Permite registrar estadísticas de
una cola de entidades que se forma en espera de que la
condición para ser liberadas se cumpla.
Dispose:
Es el procedimiento encargado de eliminar entidades que
llegan a este procedimiento, tomando estadísticas de tiempos
entre llegadas de entidades. Se utiliza para facilitar la liberación
de memoria del computador después de cada ejecución.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
48
Por otro lado, el programa permite seleccionar las condiciones de finalización de una
simulación, ya sea por el cumplimiento de una condición, o por la finalización de un periodo de
tiempo de análisis. Además permite seleccionar el número de simulaciones que se desea
realizar en una misma ejecución del programa, permitiendo así calcular estadísticas de
diferentes variables de estudio del sistema.
Metodología utilizando simulación de eventos discretos
La metodología de análisis de la simultaneidad de uso de los aparatos de una RIDAP utilizando
simulación de eventos discretos consiste en una creación de un modelo para cada conjunto de
nudos que tenga una dependencia entre sus usos. Dicho modelo debe representar esa
dependencia de manera efectiva, para que las simulaciones que haga el programa sean lo más
ajustadas a la realidad.
Una vez se tenga un modelo que represente aceptablemente las condiciones de dependencia
deseadas, se deben ingresar los parámetros de caracterización de la demanda de cada
aparato, asegurándose de que cada uso de un aparato tenga asignada las funciones de
densidad de probabilidad medidas en un estudio como el presentado en la Tabla 6. Para ello se
recomienda poner en el modelo, tantos como aparatos haya en el sistema,
asignándole a cada uno la función de probabilidad que mejor describe la frecuencia de llegada
de usos. Una ventaja del programa ARENA, es que permite que el tenga series de
tiempo de frecuencia de llegada, de manera que es fácilmente acoplable un resultado como el
mostrado en la Figura 14.
Existen algunas excepciones a la anterior regla, y estas tienen que ver con algunas
consideraciones analíticas que permiten reducir el número de sin afectar la respuesta
del modelo. La primera excepción aplica cuando diferentes aparatos tienen una misma función
de densidad de probabilidad para la frecuencia (no necesariamente con los mismos
parámetros, pero sí con la misma función). En estos casos se puede utilizar un único
que en el caso de que represente llegadas de procesos de Poisson, debe tener como
parámetro de frecuencia el siguiente valor:
∑
Ecuación 33
donde:
: Frecuencia de creación de usuarios para la simulación de uso de los aparatos del
sistema con la misma función de densidad de probabilidad .
: Frecuencia de llegada de usuarios al aparato .

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
49
El anterior debe estar acompañado de un que asigna a las entidades creadas
un atributo relacionado con el aparato que el usuario desea utilizar. Para ello se debe tener en
cuenta que el más el deben hacer lo mismo que una serie de con una
misma función de densidad de probabilidad, pero diferente parámetro de frecuencia, y por lo
tanto se debe encontrar la fracción del total de entidades creadas que corresponde a cada
aparato resumido. Para ello existe una expresión (Ecuación 34) que permite calcular la fracción
del total de entidades creadas que corresponde con el aparato :
Ecuación 34
donde:
: Fracción del total de entidades creadas que corresponde con el aparato .
Es importante notar que el parámetro de la Ecuación 34, debe estar en unidades de
⁄
y dicha unidad de tiempo debe ser igual para todos los parámetros
de la Ecuación 33 y la Ecuación 34. De esta manera el asignará el aparato a utilizar a la
entidad de acuerdo con esas
, siendo así consistentes con el modelo no simplificado de
asignación de varios .
La segunda excepción de la regla, es un caso especial de la primera en el que el tipo de aparato
que van a utilizar las entidades creadas es el mismo, y se supone indiferencia por parte del
usuario a cuál aparato utilizar (siempre y cuando sea del tipo que requiere). En este caso sólo
se requiere el uso de la Ecuación 33, dejando que la selección del aparato a utilizar se realice
en un posterior relacionado con la disponibilidad de cada uno de los aparatos.
Independientemente del método de creación de entidades seleccionado, es recomendable
poner que asignen a cada entidad el tipo de aparato que desean utilizar, a fin de
reducir los procedimientos necesarios en el modelo, y simular esas interacciones entre las
entidades, sin perder la información acerca de cuál aparato desea utilizar cada entidad.
Igualmente se recomiendan poner tantos como aparatos sanitarios haya, para que
a cada uno se le asigne la función de densidad de probabilidad de la duración de descarga del
aparato, y así el aparato permanezca ocupado (encendido) durante ese intervalo de tiempo.
Esa anterior regla tiene una excepción relacionada con la operación de los inodoros, dado que
en su uso normal un inodoro es ocupado por el usuario en un intervalo de tiempo diferente al
intervalo en que ocurre la descarga efectiva del aparato. Así, un usuario que desea utilizar el
inodoro ocupa el recurso durante un cierto tiempo, y después de terminar su uso es que
comienza la descarga de agua del aparato. Teniendo en cuenta que el intervalo de tiempo en
que se está interesado es el de descarga de agua, es ese el que necesariamente debe estar
incluido en el modelo, pero dado que el intervalo de ocupación del recurso puede interactuar
con las llegadas y usos de los demás usuarios y demás aparatos (durante el intervalo de tiempo
de ocupación del recurso inodoro, es posible que no se permita el uso de la ducha o el
lavamanos en un baño residencial), se hace recomendable representar los inodoros con dos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
50
objetos que representen: 1) La ocupación del recurso inodoro y de todos los recursos
que su ocupación implique según el modelo, y 2) La descarga efectiva del aparato, en la cual se
puede suponer que no hay ocupación de ningún aparato, inclusive del inodoro (el inodoro
puede ser ocupado por un usuario mientras está descargando).
Finalmente el modelo debe tener al menos un en donde evacuar a los usuarios del
sistema, representando así, una finalización de uso e interacción con el sistema real (RIDAP), y
además haciendo un mejor uso de los recursos computacionales disponibles para la
modelación.
Respecto al periodo de simulación, éste debe analizarse de acuerdo con el comportamiento
esperado del sistema a lo largo del tiempo. En caso de utilizarse datos como los deducidos en
la Sección 3.2.1, no se esperan variaciones significativas con una procedencia diferente que la
mera aleatoriedad de los datos simulados, después de un día de simulación. Es decir que el
comportamiento esperado de cualquier variable de estudio, no debería cambiar
sustancialmente entre el primer día de la simulación y el último día de la simulación, dado que
todos los días tendrían los mismos datos de entrada, y el sistema ya se encuentra en un estado
estable que se evidencia en la frecuencia de ocurrencia del escenario en donde todos los
aparatos están apagados (ver Sección 4.3). Así un periodo de simulación de un día se considera
suficiente y necesario (dado que un intervalo menor implicaría una pérdida de información
acerca de la concentración de frecuencia a lo largo del día) para el caso de modelos de RIDAPs.
Por otro lado está la decisión del número de simulaciones por ejecución del programa. Estas
simulaciones son denominadas repeticiones, y se deben hacer suficientes para que las
estadísticas extraídas de los datos sean confiables. Así si se desea analizar, por ejemplo, el
porcentaje de tiempo que un sistema permanece en el escenario en donde todos los aparatos
están apagados, esa variable toma un valor por cada día de simulación, y para poder concluir
acerca del comportamiento de esa variable, es necesario observar el sistema días, teniendo
así valores del porcentaje de tiempo con todos los aparatos apagados, y permitiendo de esta
manera el cálculo de una estimación de la media de la variable, de la varianza y, si son de
interés, de los demás momentos estadísticos de la ésta. Es decir que en general se pueden
calcular estimaciones de los parámetros de la función de densidad de probabilidad de la
variable estudiada, y de esta manera se puede conocer y caracterizar su comportamiento
estocástico.
El cálculo del número de repeticiones entonces, es una selección del tamaño de la muestra
que se desea tener para extraer un comportamiento estadístico de una variable, y teniendo
esto en cuenta existen diversos criterios que permiten esa selección:
Criterio de la estadística acumulada: Este criterio consiste en calcular la estimación del
parámetro inmediatamente después de finalizar cada repetición y detener la ejecución
de repeticiones cuando la estadística calculada se estabilice en un valor. Así, después
de repeticiones se tienen valores de la variable estudiada, que permiten calcular la

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
51
estimación ̂
(que tiene en cuenta los datos de las repeticiones). Si después se
realiza una repetición más, se tendrán valores de la variable estudiada, que
permitirán calcular la nueva estimación ̂
. Si se compara ̂
con ̂
, se podrá
estimar el error en el que se incurre si se toma como valor definitivo del estimador el
valor ̂
, suponiendo que el valor teórico con el cual se compara es ̂
(que es la
mejor estimación hecha hasta el momento). De esta manera se debe detener la
ejecución de repeticiones cuando ese error se mantenga lo suficientemente pequeño
para las últimas repeticiones hechas, indicando así, que se ha llegado a un valor
aceptablemente estable del estimador ̂.
Criterio del intervalo de confianza: Si se dispone de suficiente información estadística y
de conocimiento de distribuciones probabilísticas y muéstrales, es posible encontrar
una expresión analítica para un intervalo de confianza del parámetro que se desea
estimar. Este intervalo de confianza, es función del que se desea
para el intervalo según la Ecuación 35:
[
]
Ecuación 35
donde:
[
] : Probabilidad de que el verdadero valor del parámetro se
encuentre en el intervalo [
].
: Nivel de confianza que se desea para el intervalo del parámetro. Los
valores típicos son , , y , entre otros.
De esta manera se tiene el intervalo [
], que puede ser reescrito como la Ecuación
36 quedando en términos del número del tamaño de la muestra que fue utilizada:
[
] [ ̂
( ) ̂
( )]
Ecuación 36
donde:
̂ : Mejor estimación hasta el momento del parámetro .
: Tamaño de la muestra de donde se calcula ̂.
: Funciones que representan la relación entre las
y el tamaño de la muestra, para un nivel de confianza dado.
Es decir que se puede calcular el ancho del intervalo de confianza como:
( )
( ) ( )
Ecuación 37
La Ecuación 37, relaciona el ancho del intervalo de confianza, con el tamaño de la
muestra y con el nivel de confianza del intervalo, permitiendo así, calcular el tamaño
de la muestra necesario para tener un intervalo con un nivel de confianza dado y con

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
52
un ancho máximo dado. Ese ancho máximo es una medida del error en que se puede
incurrir si se toma el valor ̂ como valor definitivo del parámetro, y por lo tanto se
puede seleccionar con base en qué tan precisa se desea la medición (se debe tener en
cuenta que está en las misma unidades que el parámetro ).
Dada la posibilidad de que las cantidades pivotales
sean también función de la
estimación ̂, es posible que para implementar esta metodología de cálculo del
tamaño de la muestra sea necesario tener resultados de repeticiones previas, de
manera que ̂
se estima con base en repeticiones, después se estima con base en
̂
, y después se calculan las repeticiones necesarias restantes como ,
teniendo en cuenta que ya se dispone de datos, y por lo tanto no es necesario
ejecutar todas las repeticiones. Se recomienda que después de realizadas todas las
repeticiones, se vuelva a calcular ̂
y se vuelva a calcular , para asegurarse que la
estimación ̂
, no subestimó dicho valor.
Si bien existen otras metodologías para el cálculo del tamaño de la muestra, o en este caso el
número de repeticiones a realizar, las dos anteriores se consideran suficientes para el cálculo
necesario en modelos de RIDAPs.
Acople de la metodología utilizando simulación de eventos discretos
La metodología de uso de simulación de eventos discretos para la simulación de la
simultaneidad de uso de los aparatos, es únicamente requerida en el caso en el que se tengan
nudos con demandas dependientes, y su uso en casos de independencia representa un uso
injustificado de recursos computacionales y de esfuerzo del modelador. De esta manera, se
requiere un acople entre los resultados de la metodología con simulación de eventos discretos
para conjuntos de nudos con demanda dependiente, y los demás nudos de la RIDAP con
demandas independientes.
Para ello se debe tener en cuenta que como resultado de la modelación en ARENA, se deben
tener resultados del porcentaje de tiempo que permanece el sistema en cada uno de los
posibles escenarios de demanda (donde
es el número de nudos del sistema que tiene
demanda dependiente entre ellos y que fueron simulados con eventos discretos). Es decir que
el resultado tiene la misma forma que el resultado de la metodología basada en Blokker, la
cual asigna a cada posible escenario una probabilidad de ocurrencia según la Ecuación 32. Esto
permite una forma natural de acoplar los resultados de la siguiente manera:
Una vez se dispone de las
probabilidades de ocurrencia de cada escenario para el
conjunto de nudos simulados con ARENA, se debe verificar que éstas sumen ,
indicando que reparten la totalidad del tiempo del sistema.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
53
Teniendo en cuenta que la metodología basada en Blokker asigna a cada nudo una
probabilidad de encendido y su complemento como probabilidad de apagado, esto
puede ser entendido como un sistema “simulado” de un nudo
que dio
como resultado que el escenario de encendido tiene una probabilidad de ocurrencia
y el escenario de apagado una probabilidad de ocurrencia de
, y por lo tanto la
manera como se acopla ese nudo al resto del sistema es una multiplicación de la
probabilidad correspondiente a su configuración (encendido/apagado) con las
probabilidades de las configuraciones del resto de nudos (ver Ecuación 32).
Algo similar a lo anteriormente descrito puede hacerse con los sistemas simulados con
eventos discretos, en donde los posibles escenarios no son dos, como en el sistema de
un nudo, sino
, pero dado que se tiene una probabilidad asociada con cada uno,
el acople consiste en multiplicar la probabilidad correspondiente al escenario del
sistema simulado con las probabilidades de las configuraciones del resto de los nudos
(los nudos no incluidos en ese sistema simulado). Así la probabilidad de un escenario
global de toda la RIDAP, será la multiplicación de las probabilidades asociadas a los
escenarios individuales de cada nudo (configuraciones) y los escenarios de cada
sistema de nudos simulado con eventos discretos.
Es decir que la metodología basada en simulación de eventos discretos, sólo se usa para
subconjuntos de nudos de la red, que después dejarán de ser caracterizados como nudos
individuales con dos únicas configuraciones, para ser caracterizados como partes de un
sistema al que se debe evaluar la probabilidad conjunta que es precisamente el resultado de la
simulación de eventos discretos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
54
4 Casos de estudio
A fin de mostrar de manera explícita la implementación de la metodología se desarrolló un
caso de estudio simple que busca mostrar cómo se utiliza cada uno de los conceptos,
algoritmos y programas mostrados en al anterior capítulo. El sistema a modelar consiste en un
baño residencial con un lavamanos, un inodoro y una ducha (ver Figura 15). Se supone que
todos los aparatos del baño son alimentados por una única tubería que transporta el agua fría
hasta cada uno de los nudos de demanda, y en el caso de la ducha, esta cuenta con un sistema
eléctrico propio que calienta el agua, de manera que la vivienda no dispone de calentador (ver
Figura 16). El número de personas aferentes a este baño, y por lo tanto a cada uno de sus
aparatos, se maneja como una variable, de manera que se buscarán los resultados para , , ,
, , y .
Figura 15. Esquema del caso de estudio correspondiente a un baño.
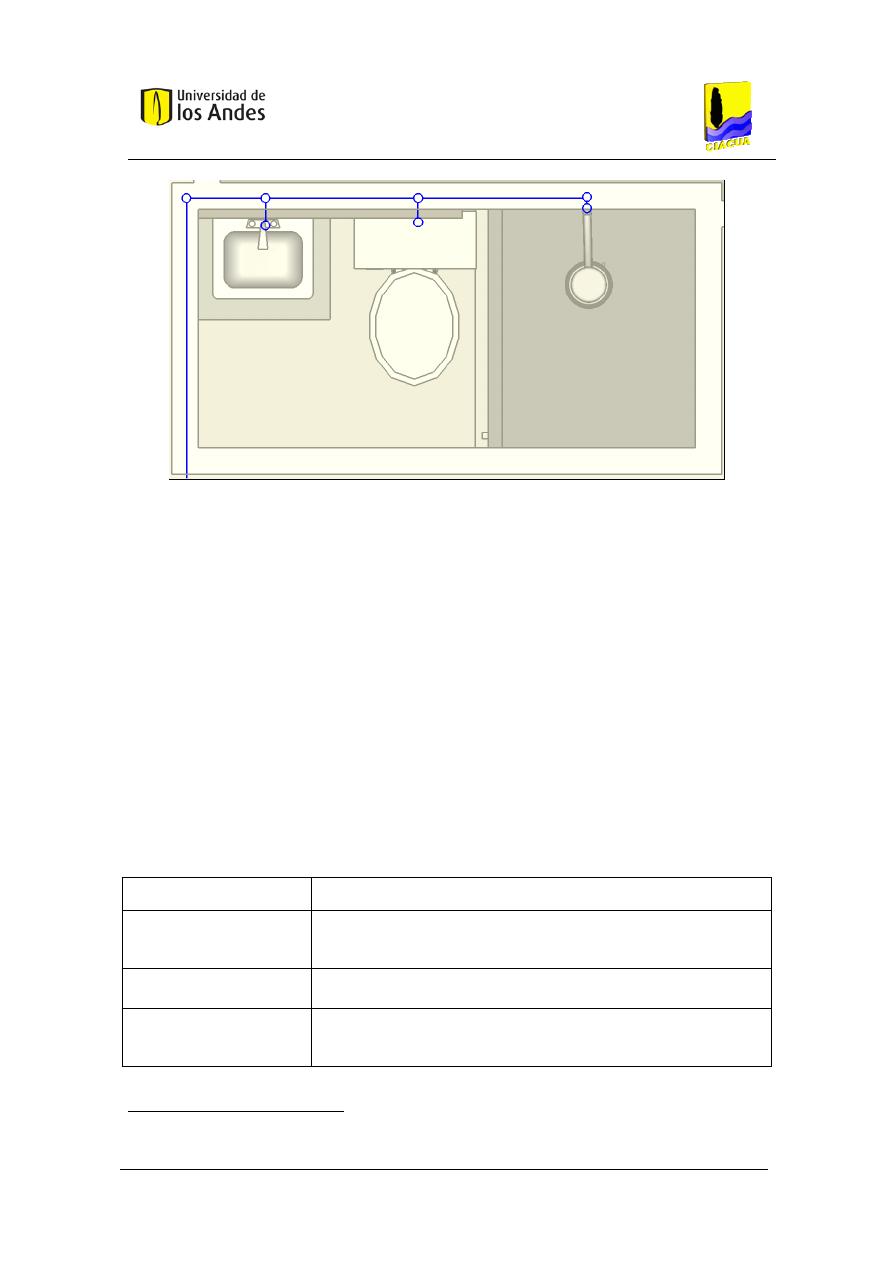
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
55
Figura 16. Vista en planta del baño, con diagrama de las tuberías de la red.
Para caracterizar la demanda de agua en el baño se utilizan las ecuaciones del
comportamiento hidráulico mostradas en la Tabla 8 que plasman lo analizado en la Sección 3.1
acerca de la curva única del aparato. También se hace uso de Tabla 9 acerca de la frecuencia y
duración de uso de cada uno de los aparatos. En esa Tabla 9 se utilizan los datos de la Tabla 6
para todas las frecuencias y para las duraciones del lavamanos y del inodoro, pero para la
ducha se prefiere la distribución encontrada por Blokker (2010a) de forma Lognormal, dado
que la distribución Ji (Chi) Cuadrado
(asignada por la Tabla 6) , es una distribución de mayor
complejidad y menor ajuste a los datos observados, y además no es linealmente escalable de
manera que sólo es válida si se expresa en minutos. Finalmente se utiliza una distribución
temporal de la frecuencia como la mostrada en Tabla 10 para cada uno de los aparatos
sanitarios. Estas distribuciones temporales de la frecuencia se basan en suposiciones de
patrones de comportamiento de los habitantes de la edificación en donde se encuentra el
baño analizado.
Tabla 8. Funciones de la curva única de los aparatos de un baño residencial.
Aparato sanitario
Curva única del aparato
Lavamanos
⁄ { ( )
Inodoro
11
⁄ ( )
Ducha
⁄ { ( )
11
Dado que el inodoro no dispone de una válvula de apertura variable, se rige por la ecuación del
emisor para todo el rango de presiones.
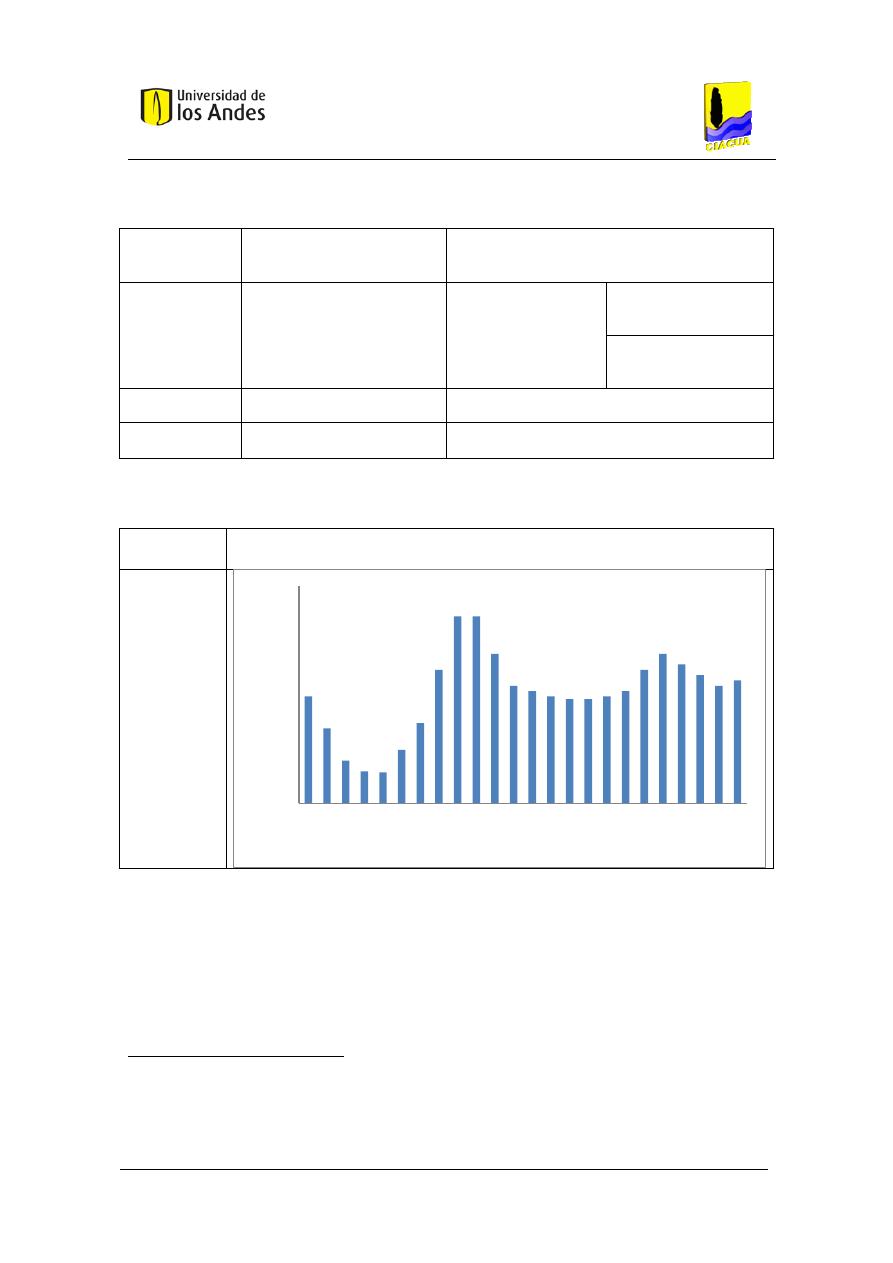
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
56
Tabla 9. Frecuencia y Duración de uso para los aparatos de un baño residencial (basada en la Tabla 6 y en Blokker,
2010a).
Aparato
sanitario
Frecuencia
(usos/(día*persona))
Duración
12
Lavamanos
Lavado y afeitado:
[ ]
Cepillado de dientes:
[ ]
Inodoro
Ducha
(
)
Tabla 10. Distribuciones temporales de la frecuencia de uso para los aparatos de un baño residencial.
Aparato
sanitario
Distribución temporal de la frecuencia de uso
Lavamanos
12
Las duraciones son representadas por distribuciones lognormales, que tienen como inconveniente la
diversidad de sus parámetros. Así en algunos casos esta distribución es parametrizada por la media y la
desviación estándar de la variable distribuida lognormal, y en otros casos está parametrizada por la
media y la desviación estándar del logaritmo natural de la variable distribuida lognormal, cuya
distribución es normal. (Ver Anexo 11.2).
0.0%
1.0%
2.0%
3.0%
4.0%
5.0%
6.0%
7.0%
8.0%
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:00
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:00
21
:0
0
22
:0
0
23
:0
0
Por
ce
n
taje
d
e
u
sos
(%
)
Hora
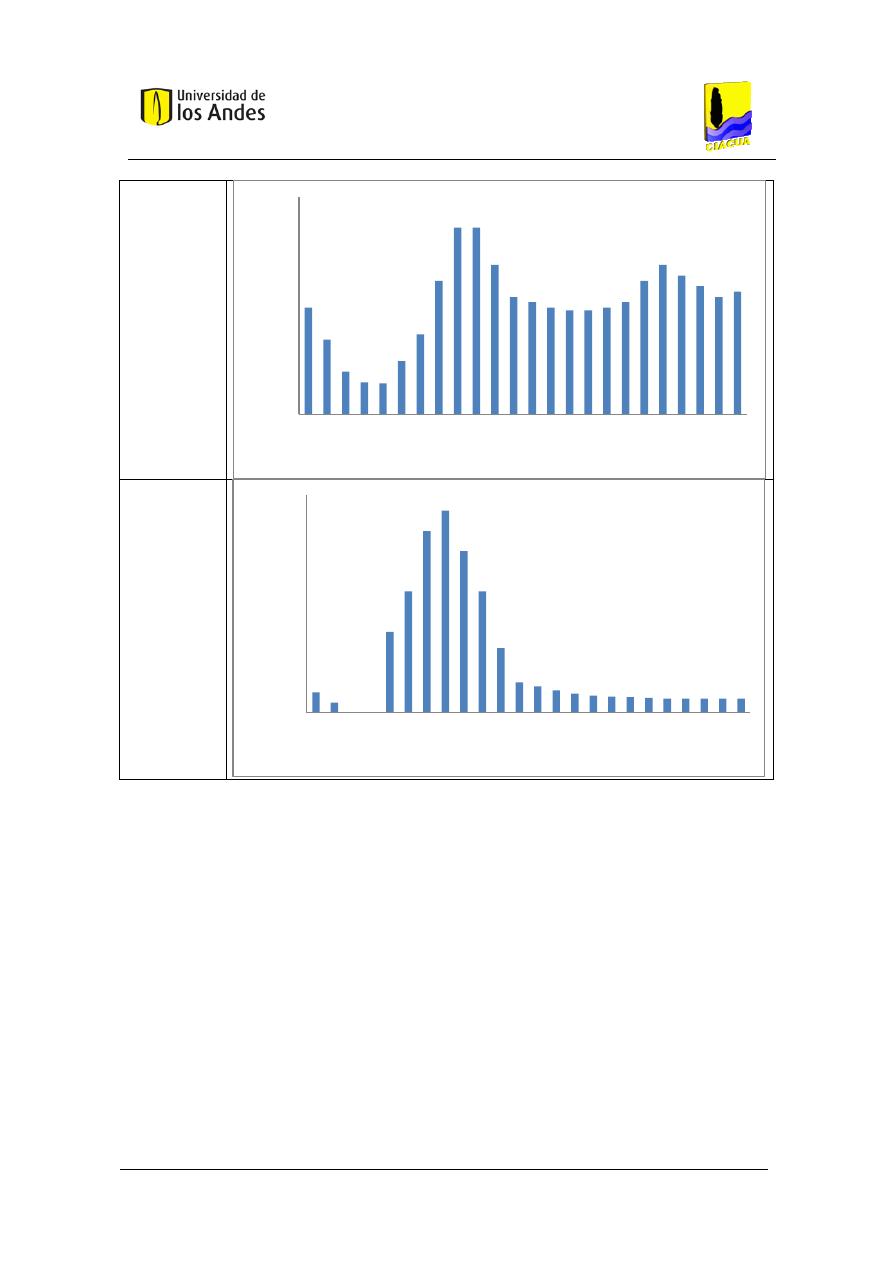
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
57
Inodoro
Ducha
Una vez se conocen las distribuciones temporales de la frecuencia, se pueden conocer las
series de tiempo de la frecuencia horaria de uso por persona de cada aparato sanitario en el
sistema como el producto de la frecuencia promedio (valor esperado de las distribuciones de
frecuencia de la Tabla 9) y el valor horario del porcentaje de usos del aparato analizado, tal y
como se ve en la Tabla 11.
0.0%
1.0%
2.0%
3.0%
4.0%
5.0%
6.0%
7.0%
8.0%
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:00
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:00
21
:0
0
22
:0
0
23
:0
0
Por
ce
n
taje
d
e
u
sos
(%
)
Hora
0.0%
2.0%
4.0%
6.0%
8.0%
10.0%
12.0%
14.0%
16.0%
18.0%
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Pr
o
ce
n
taje
d
e
u
sos
(%
)
Hora
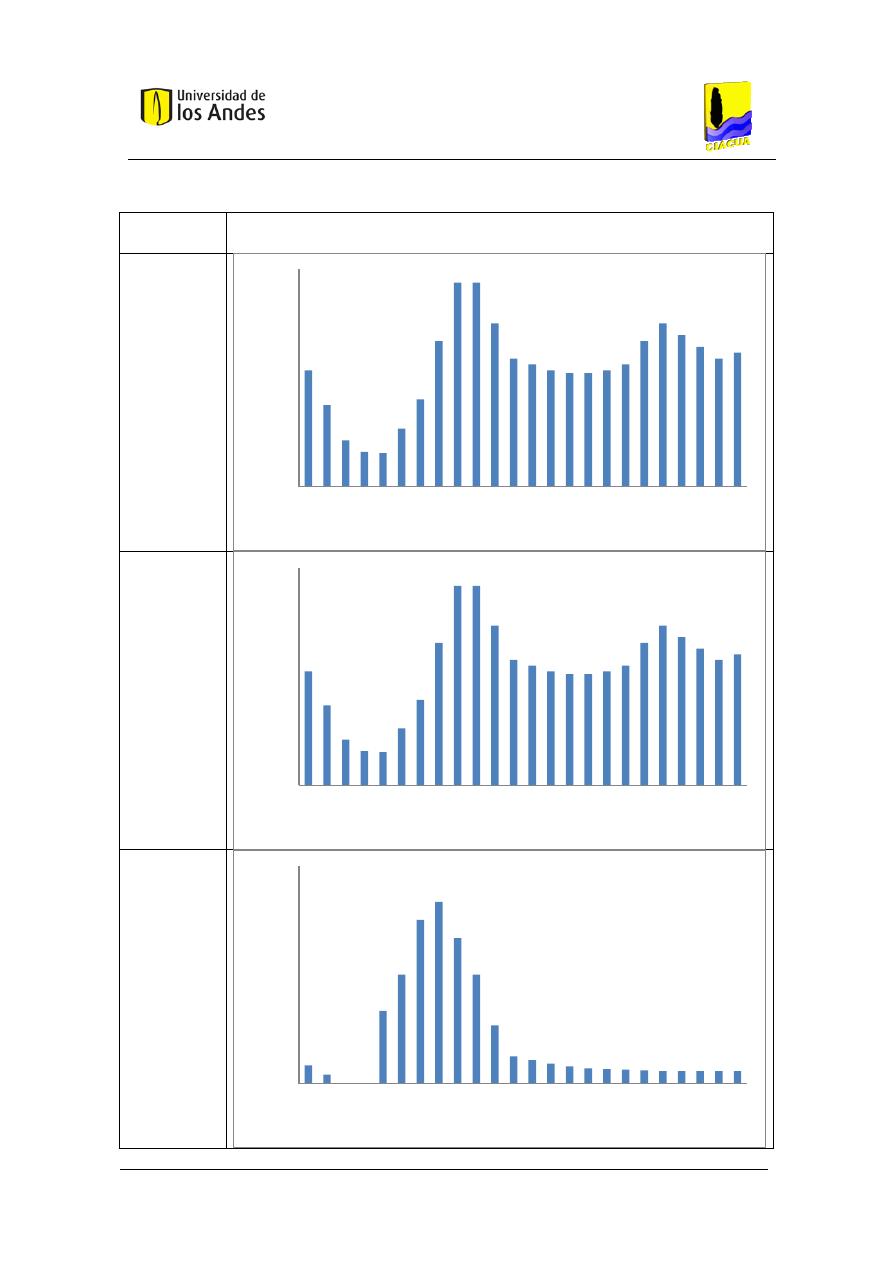
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
58
Tabla 11. Series de tiempo de la frecuencia horaria de uso por persona para los aparatos de un baño residencial.
Aparato
sanitario
Serie de tiempo de la frecuencia horaria de uso por persona
Lavamanos
Inodoro
Ducha
0.00
0.05
0.10
0.15
0.20
0.25
0.30
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:00
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:00
21
:0
0
22
:0
0
23
:0
0
Fr
e
cu
e
n
ci
a
d
e
u
so
(u
sos/
h
/p
e
rson
a)
Hora
0.00
0.05
0.10
0.15
0.20
0.25
0.30
0.35
0.40
0.45
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:00
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:00
21
:0
0
22
:0
0
23
:0
0
Fr
e
cu
e
n
ci
a
d
e
u
so
(u
sos/
h
/p
e
rson
a)
Hora
0.00
0.02
0.04
0.06
0.08
0.10
0.12
0.14
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:00
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:00
21
:0
0
22
:0
0
23
:0
0
Fr
e
cu
e
n
ci
a
d
e
u
so
(u
sos/
h
/p
e
rson
a)
Hora

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
59
Por otro lado es necesario realizar el análisis mostrado en la Sección 3.2.1 para la duración de
los usos de los aparatos. Dado que el lavamanos es el único aparato con duraciones diferentes
según el uso último que se haga de éste, sólo para este aparato es necesario hallar una única
función de densidad de probabilidad de la duración, siguiendo el procedimiento mostrado a
continuación:
Tabla 12. Cálculo de la duración promedio total para el lavamanos de un baño residencial.
Uso
Duración: [ ]
Porcentaje del total
de usos
[ ]
Lavado y afeitado
Cepillado de dientes
Promedio total
4.1 Análisis de la simultaneidad de uso según el modelo basado en
Blokker
Para implementar la metodología basada en Blokker para la simulación de la simultaneidad de
uso de los aparatos, se deben tener todos los datos anteriormente calculados, para calcular la
utilización horaria de cada aparato, haciendo uso de la Ecuación 31. Sin embargo este cálculo
depende de un resultado previo que es la serie de tiempo de la frecuencia horaria de uso de
cada aparato, teniendo en cuenta el número de personas aferente a éste. Para ese cálculo es
necesario multiplicar cada serie de tiempo de la Tabla 11 con ese número de personas que
puede tomar diferentes valores ( , , , , , y ), de manera que existen tantas series de
utilización para cada aparato, como casos de número de personas aferentes al sistema. En la
Tabla 13
13
, se muestra un conjunto de esas series de tiempo para todos los aparatos del
sistema analizado, con personas aferentes al baño y por lo tanto a cada uno de los éstos.
13
Algunas de las gráficas mostradas en esta tabla y en adelante en el documento, tienen en el eje de las
ordenadas un valor sin dimensiones, lo cual es representado como ().
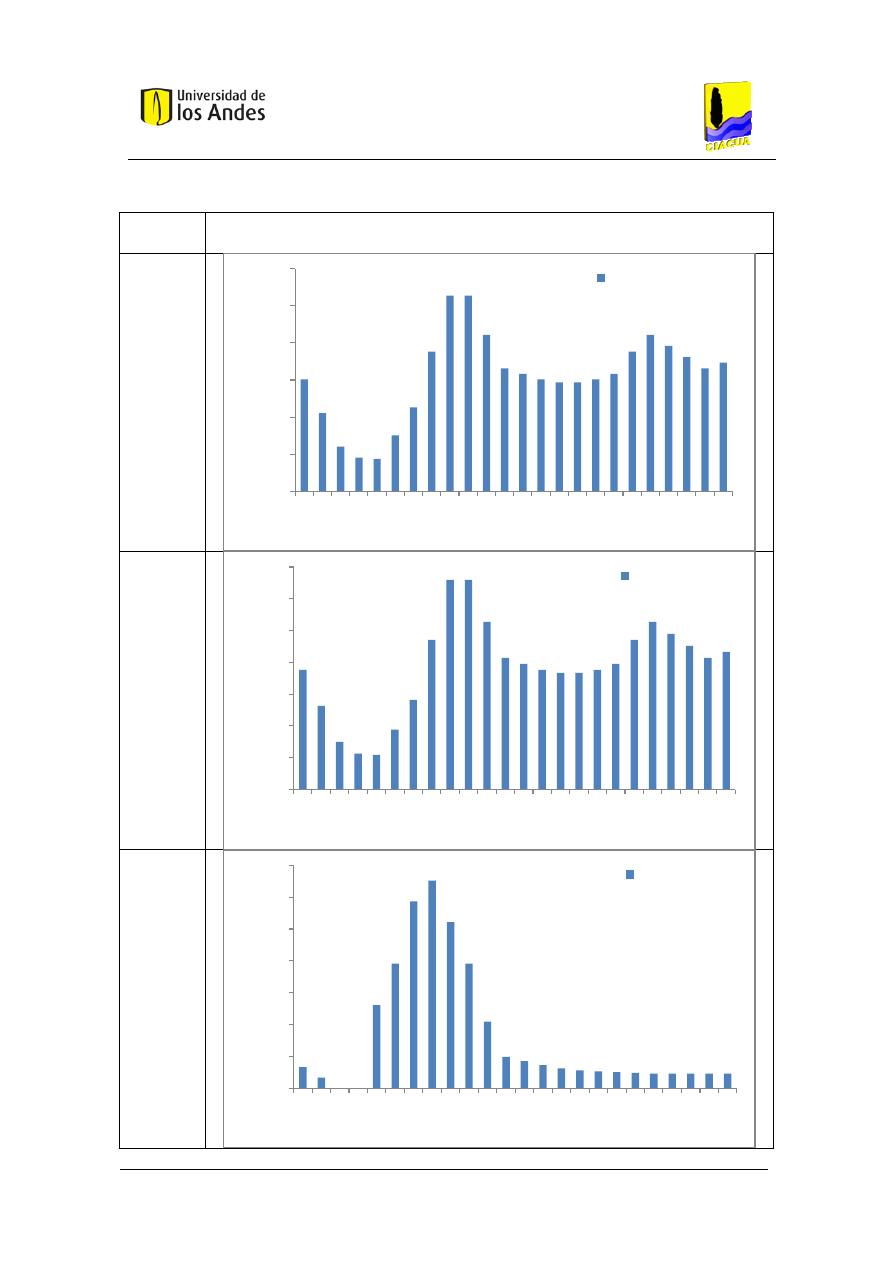
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
60
Tabla 13. Series de tiempo de la utilización de cada aparato de un baño residencial con 4 personas aferentes.
Aparato
sanitario
Serie de tiempo de la utilización del aparato
Lavamanos
Inodoro
Ducha
0
0.001
0.002
0.003
0.004
0.005
0.006
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:00
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:00
Uti
lizac
ió
n
()
Hora
Utilización Lavamanos
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Uti
lizac
ió
n
()
Hora
Utilización Inodoro
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
00
:0
0
01
:0
0
02
:00
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Uti
lizac
ió
n
()
Hora
Utilización Ducha
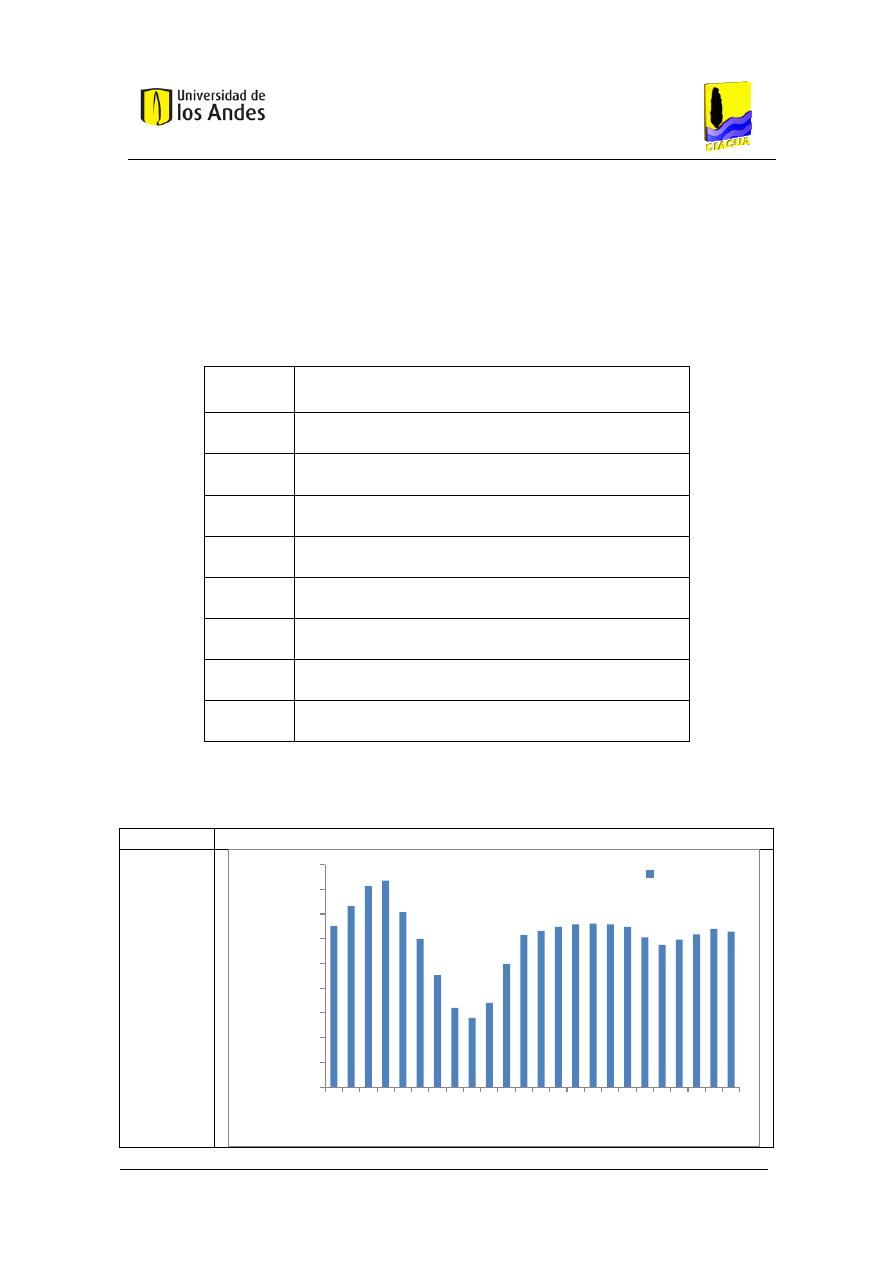
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
61
Teniendo en cuenta que el sistema tiene aparatos, el total de posibles escenarios es
(Ver Tabla 14), y por lo tanto el análisis completo de la simultaneidad incluye el
cálculo de cada una de las probabilidades de ocurrencia. Para ello es necesario hacer uso de
la Ecuación 32, para cada posible escenario y para cada hora del día. Como resultado se
obtienen series de tiempo de la probabilidad de ocurrencia de cada escenario a lo largo del
día, tal y como se muestra en la Tabla 15, para el caso de personas aferentes al baño.
Tabla 14. Descripción y notación de los 8 posibles escenarios para un baño residencial.
Notación
Escenario
Todos los tres aparatos del baño se encuentran
apagados
La ducha se encuentra encendida, pero el lavamanos y el
inodoro no.
El lavamanos se encuentra encendido, pero la ducha y el
inodoro no.
El inodoro se encuentra encendido (descargando), pero
el lavamanos y la ducha no.
Tanto la ducha como el lavamanos se encuentran
encendidos, pero el inodoro no.
Tanto la ducha como el inodoro se encuentran
encendidos, pero el lavamanos no
Tanto el lavamanos como el inodoro se encuentran
encendidos, pero la ducha no
Los tres aparatos del baño se encuentran encendidos
(descargando).
Tabla 15. Series de tiempo de la probabilidad de ocurrencia de cada escenario de un baño residencial con 4
personas aferentes.
Escenario
Serie de tiempo de la probabilidad de ocurrencia del escenario
8.20E-01
8.40E-01
8.60E-01
8.80E-01
9.00E-01
9.20E-01
9.40E-01
9.60E-01
9.80E-01
1.00E+00
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:00
19
:00
20
:00
21
:00
22
:00
23
:00
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Escenario (-)
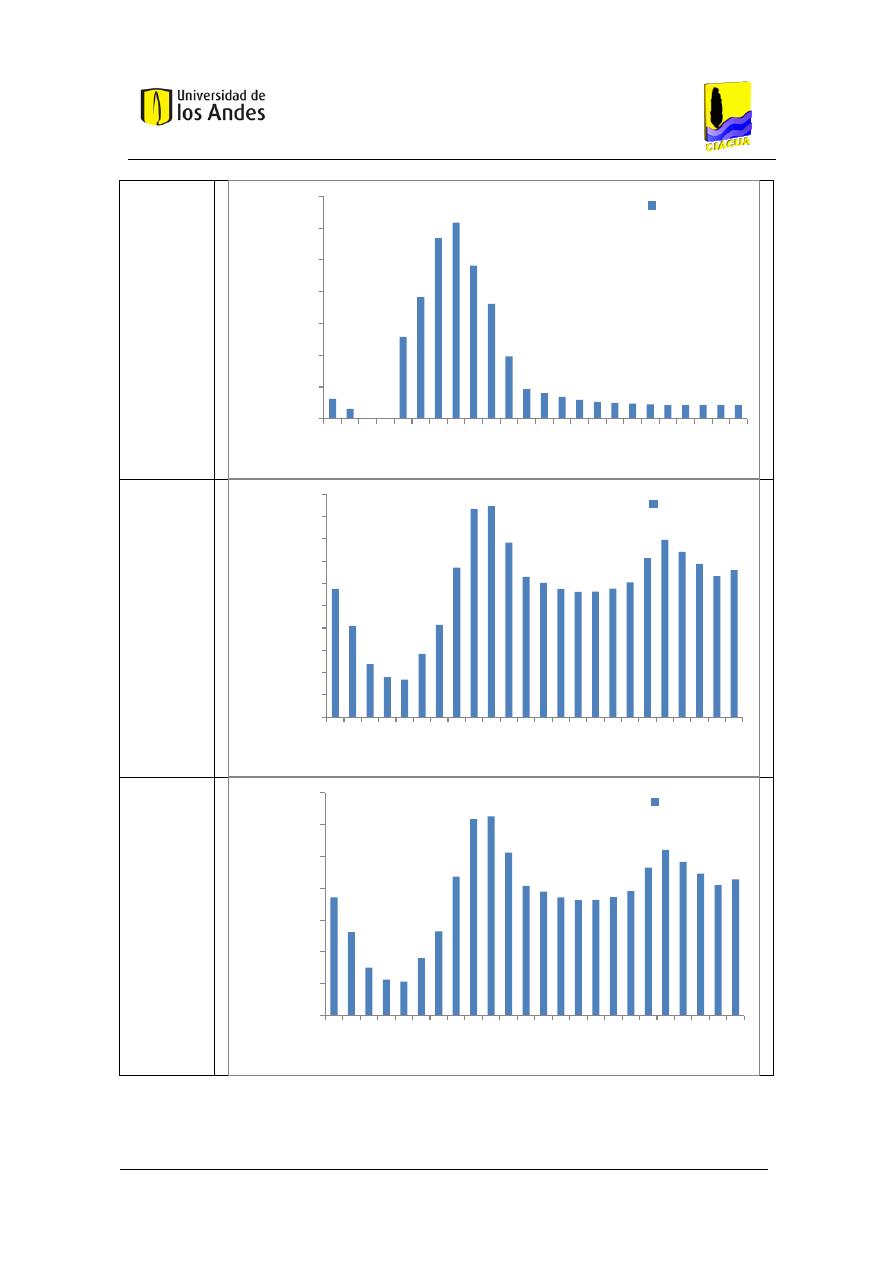
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
62
0.00E+00
1.00E-02
2.00E-02
3.00E-02
4.00E-02
5.00E-02
6.00E-02
7.00E-02
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:00
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
P
rob
abil
id
ad
d
e
op
cu
rr
en
cia
()
Escenario D
0.00E+00
1.00E-03
2.00E-03
3.00E-03
4.00E-03
5.00E-03
6.00E-03
7.00E-03
8.00E-03
9.00E-03
1.00E-02
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:00
18
:0
0
19
:0
0
20
:0
0
21
:00
22
:0
0
23
:0
0
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Escenario L
0.00E+00
1.00E-02
2.00E-02
3.00E-02
4.00E-02
5.00E-02
6.00E-02
7.00E-02
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:00
22
:0
0
23
:0
0
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Escenario I
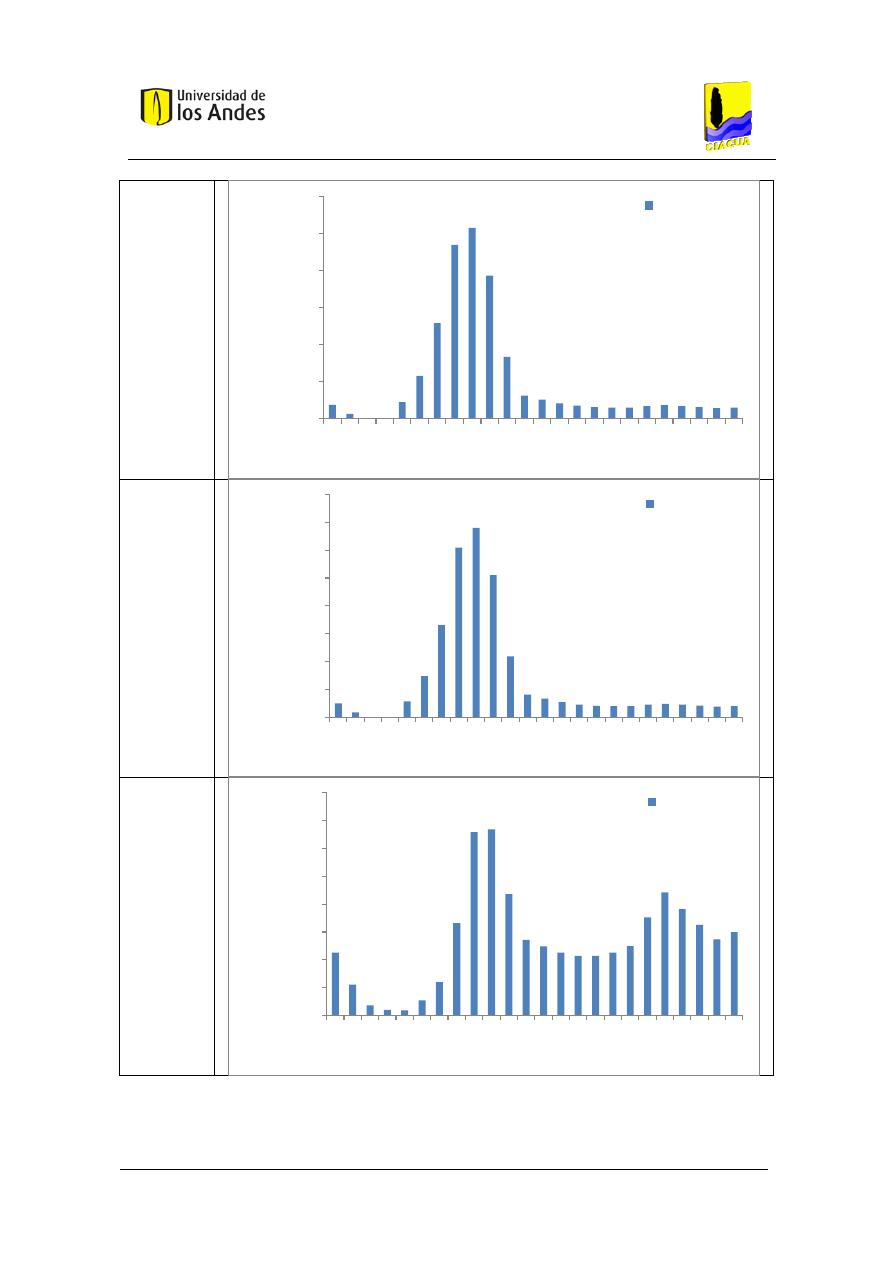
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
63
0.00E+00
1.00E-04
2.00E-04
3.00E-04
4.00E-04
5.00E-04
6.00E-04
00
:0
0
01
:00
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:00
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
P
rob
abil
id
ad
d
e
oc
u
rr
en
cia
()
Escenario DL
0.00E+00
5.00E-04
1.00E-03
1.50E-03
2.00E-03
2.50E-03
3.00E-03
3.50E-03
4.00E-03
00
:00
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:00
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Escenario DI
0.00E+00
1.00E-04
2.00E-04
3.00E-04
4.00E-04
5.00E-04
6.00E-04
7.00E-04
8.00E-04
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:00
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Escenario IL
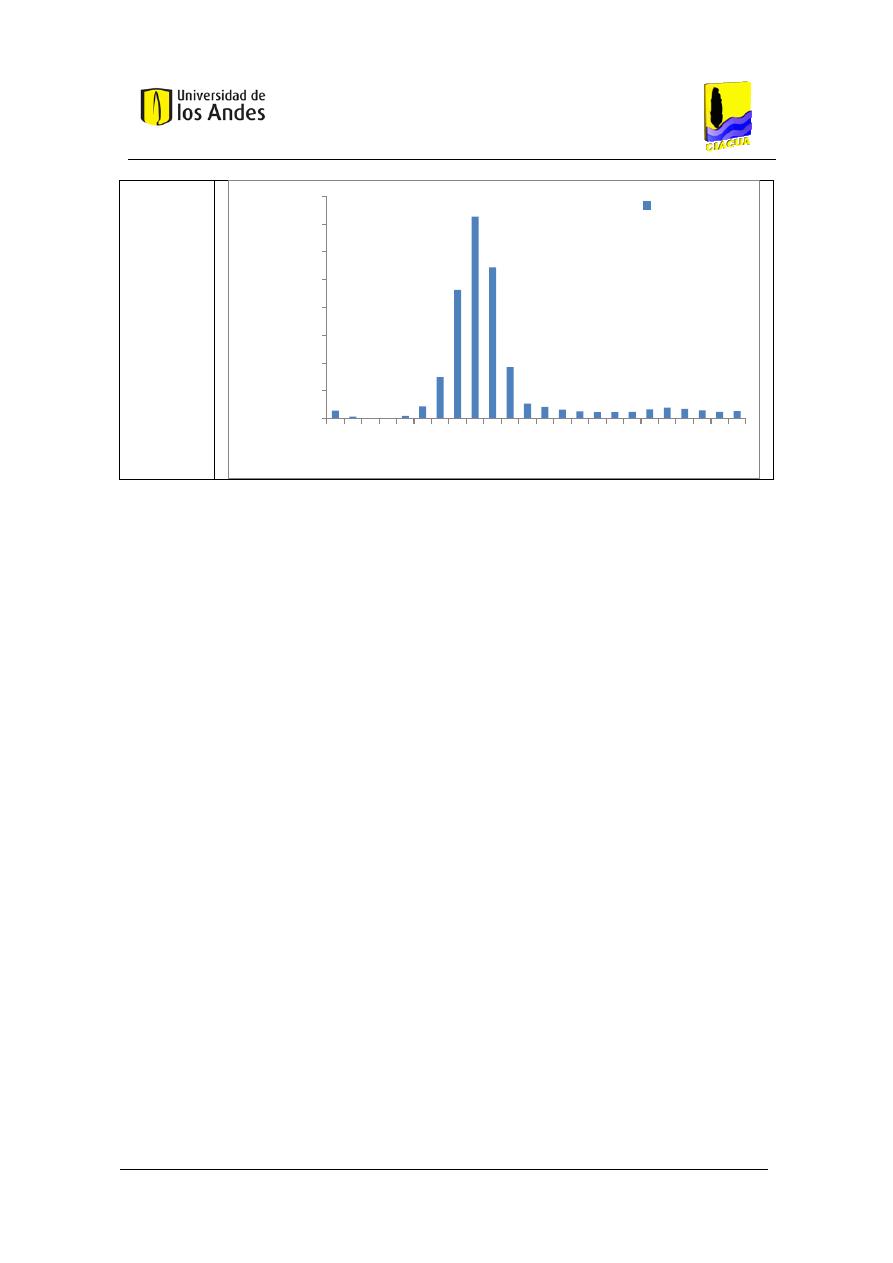
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
64
Como se puede ver en la Tabla 15, la probabilidad más alta en cualquier hora del día, es la del
escenario en donde todos los aparatos se encuentran apagados. Esto es una constante para
todos los casos intentados con diferente número de personas aferentes, incluyendo el más
extremo con personas. De igual manera, el caso en donde los tres aparatos se encuentran
encendidos al tiempo, tiene una probabilidad de ocurrencia extremadamente baja, donde sus
mayores probabilidades apenas llegan a
representando así lo extremo de este
escenario.
Sin embargo, para este sistema es posible hacer uso de la metodología basada en Blokker con
uso de simulación de eventos discretos, teniendo en cuenta que un comportamiento esperado
de un usuario de un baño residencial, es cerrar la puerta de ingreso al baño, restringiendo el
uso de los demás aparatos, y por lo tanto bloqueando de manera activa algunos escenarios, de
manera que tienen probabilidad cero de ocurrencia.
4.2 Análisis de la simultaneidad de uso según el modelo basado en
Blokker con simulación de eventos discretos.
Haciendo uso del programa ARENA de simulación de eventos discretos, se planteó un modelo
que representa la dinámica de un baño que tiene en cuenta el comportamiento esperado de
un usuario respecto a la ocupación total del recurso baño, cuando se hace uso de un aparato.
El modelo supuso que si un potencial usuario llega al sistema y lo encuentra reservado por otro
usuario, éste hará fila hasta que el recurso sea desocupado (se abra la puerta del baño).
Así, en la Figura 17 se muestra la implementación del modelo en el programa ARENA, en el
cuál se incluyeron las series de tiempo de la frecuencia de uso del aparato para cada caso de
número de personas aferentes, así como las funciones de densidad de probabilidad de las
duraciones de uso de cada aparato. Esas duraciones requirieron un cálculo previo antes de ser
0.00E+00
5.00E-06
1.00E-05
1.50E-05
2.00E-05
2.50E-05
3.00E-05
3.50E-05
4.00E-05
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:00
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:00
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Escenario DIL

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
65
ingresados en el programa, teniendo en cuenta que la parametrización de la función
Lognormal programada en ARENA es la mostrada en la Ecuación 38 (ver Anexo 11.2).
( [ ] [ ]
⁄
)
Ecuación 38
Así, las funciones asignadas para los tiempos de duración de uso del lavamanos y de la ducha
fueron:
Ecuación 39. Duración
de uso del lavamanos.
Ecuación 40. Duración
de uso de la ducha.
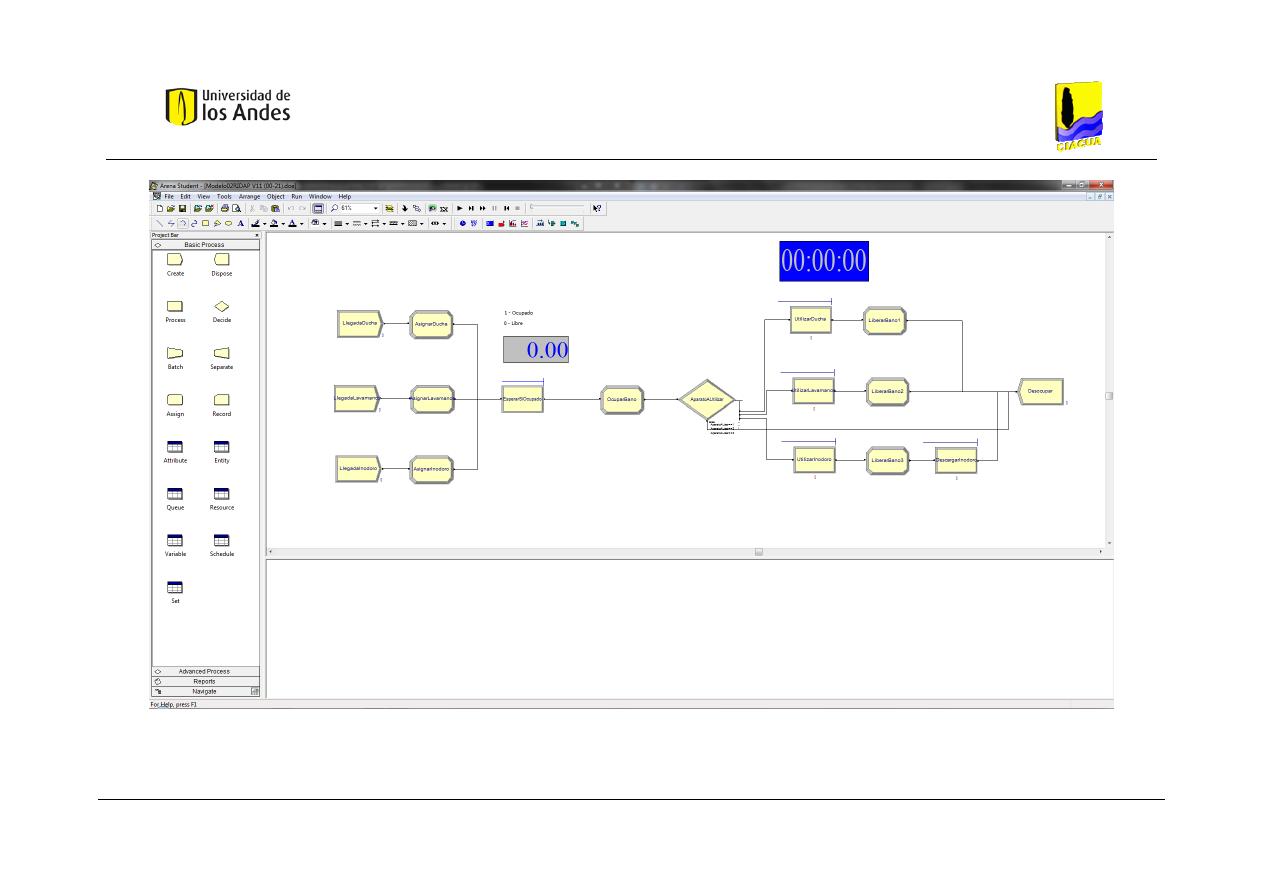
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
66
Figura 17. Implementación del modelo de un baño residencial en el programa ARENA.
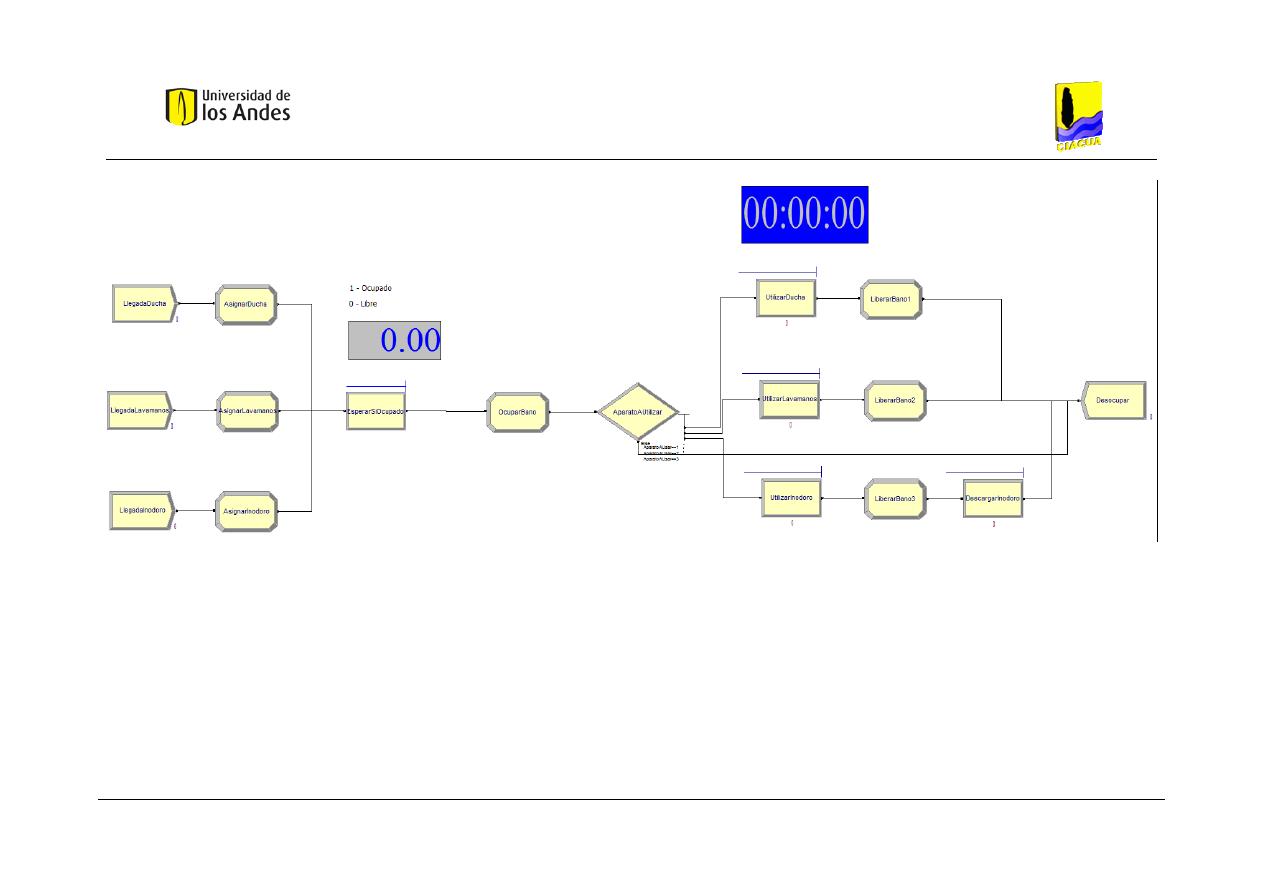
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
67
Figura 18. Esquema del modelo de un baño residencia implementado en ARENA.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
68
Respecto a la duración de uso y descarga del inodoro (teniendo en cuenta que se representan
los inodoros con dos objetos , para la ocupación del recurso y para la descarga
efectiva del aparato), se supuso una función de densidad de probabilidad como se
muestra en la Ecuación 41. Para la duración de la descarga del inodoro se utilizaron los datos
de la Tabla 9, de manera que la duración es fija tal y como se muestra en la Ecuación 42.
Ecuación 41. Duración de
uso del inodoro.
Ecuación 42. Duración de
descarga del inodoro.
Teniendo las anteriores funciones de densidad de probabilidad de las duraciones de uso y
descarga de los aparatos, se tuvieron todos los datos necesarios para la creación del modelo
esquematizado en la Figura 18. En este modelo, los primeros componentes son elementos
asignados a cada uno de los aparatos sanitarios que contienen las series de tiempo de
frecuencia de uso de los aparatos, y son precisamente estos componentes los que varían de
acuerdo con el caso del número de personas aferentes al baño. Estos elementos fueron
denominados , y , para representar su
naturaleza de representación de llegada de usuarios al sistema.
Después de cada elemento , sigue un elemento cuya función es asignar a las
entidades un atributo relacionado con el aparato sanitario que planea utilizar. Estos elementos
fuero denominados , y , para
representar su labor de asignar como atributo a las entidades (usuarios) el nombre del aparato
que desean utilizar.
El modelo tiene una variable global denominada que toma valor cuando el
baño está siendo ocupado por alguna entidad y por lo tanto tiene restringida la entrada para
las demás entidades, y cuando el baño está libre, listo para ser utilizado por la primera
entidad que entre al sistema. Dado que se supone que si una entidad llega al sistema y éste
está siendo ocupado, la entidad hará fila hasta que el sistema se desocupe, se utilizó un
elemento (ver Tabla 7), que permite generar y almacenar esa potencial fila de usuarios
que desea utilizar el baño, permitiendo que el primer usuario que llegó a la fila sea el primero
en utilizarlo una vez se ha desocupado. Este procedimiento se denominó
para que se entendiera que las entidades tendrían que hacer la fila del elemento en caso
de que la variable tuviera un valor igual a .
El siguiente componente del modelo es un elemento de tipo cuya función era cambiar
a la variable cada vez que una entidad pasara por el procedimiento,
indicando así, que el baño ha sido cerrado, y que toda entidad que llegue después de ésta,
tendrá que esperar en hasta que el baño sea liberado. Este se
denominó para representar su función de cambiar la variable haciendo que el
sistema esté ocupado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
69
Una vez el usuario ha cerrado la puerta (pasar por ), llega a un en donde
éste decide cuál aparato usará y descargará a partir del atributo signado por los
ubicados inmediatamente después de los . Dado que el sistema sólo tiene tres
aparatos, el sólo tiene tres caminos posibles a cada uno de los que
representan los aparatos. Si bien existe una cuarta salida del , esta sólo se ubica para
evitar errores de compilación del programa ARENA. El objeto fue denominado
para representar ese proceso de elección del aparato a usar.
Después del objeto , existen tres caminos, cada uno de los cuales lleva a un aparato
sanitario, representado por un . Dada la versatilidad del programa ARENA, los objetos
tienen diferentes posibles configuraciones dentro de la que se encuentra
, cuya función es ocupar el recurso, durar un tiempo de servicio
ocupando el recurso y la entidad, y después liberar el recurso para otro posterior uso por parte
de otra entidad. Esta opción se considera la mejor para representar la dinámica de uso de un
aparato sanitario, y ello permite ingresar la función de densidad de probabilidad de la duración
del “servicio” permitiendo así, ingresar las duraciones expresadas en la Ecuación 39, la
Ecuación 40 y la Ecuación 41.
Es importante notar que inmediatamente después de los objetos procesos de representación
de uso de los aparatos (denominados , y
), vienen objetos que modifican la variable para que
tome el valor de indicando así que el baño ya fue liberado y que un próximo usuario puede
hacer uso de éste. Estos objetos son denominados dada su función
análoga a la de .
En el caso del inodoro, existe un después de que representa la
descarga del aparato, y cuya ubicación en el modelo se pensó para representar la posibilidad
de que el baño sea utilizado, no mientras el inodoro está siendo utilizado, pero sí mientras está
descargando después de un uso, y es en este objeto donde se incorpora la Ecuación 42 de
duración de descarga del inodoro. Este se denomina dada su
función de representar la descarga efectiva del aparato.
Finalmente, cuando un usuario ha hecho uso del aparato y ha liberado el baño, se dirige a un
denominado , en donde se eliminan las entidades para así representar
una salida completa del sistema.
Respecto a las variables del programa ARENA sobre las características de las simulaciones y de
la ejecución del programa, se seleccionó un periodo de simulación de un día, tal y como se
recomendó en la Sección 3.2.2. El número de repeticiones se calculó con el Criterio de la
estadística acumulada pero para permitir una mejor comparación se aumentó ese número
hasta el punto de poder registrar esos eventos de muy baja probabilidad como aquellos para
los que la metodología basada en Blokker asigna probabilidades de cerca de
. Esto llevó a
un total de repeticiones que fue el número que equilibró la calidad de los datos de
salida, con el tiempo de ejecución del programa.
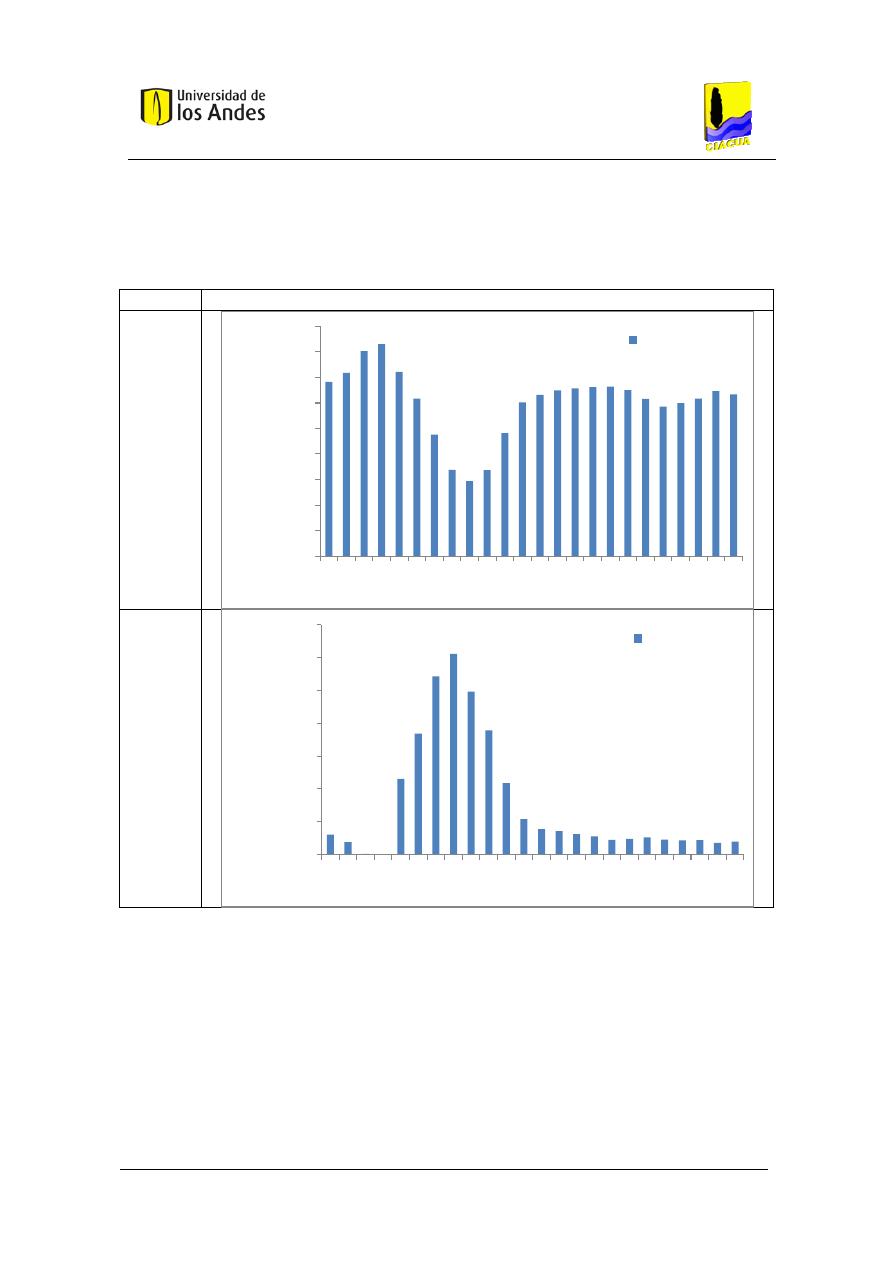
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
70
A continuación se muestran los resultados encontrados con esta metodología para el caso en
que el número de personas aferentes al baño es de :
Tabla 16. Series de tiempo de la probabilidad de ocurrencia de cada escenario de un baño residencial con 4
personas aferentes.
Escenario
Serie de tiempo de la probabilidad de ocurrencia del escenario
8.20E-01
8.40E-01
8.60E-01
8.80E-01
9.00E-01
9.20E-01
9.40E-01
9.60E-01
9.80E-01
1.00E+00
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:00
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Escenario (-)
0.00E+00
1.00E-02
2.00E-02
3.00E-02
4.00E-02
5.00E-02
6.00E-02
7.00E-02
00
:0
0
01
:0
0
02
:00
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Escenario D
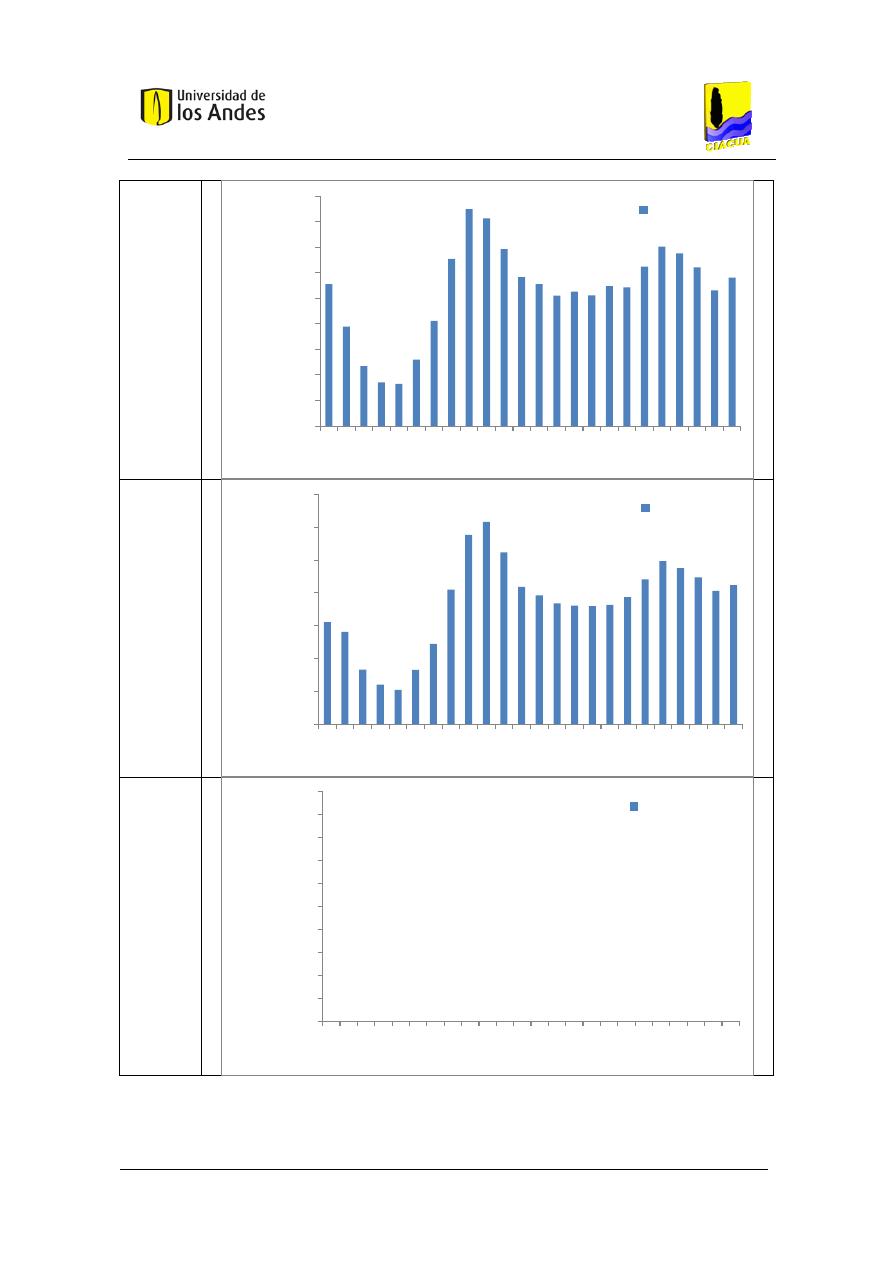
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
71
0.00E+00
1.00E-03
2.00E-03
3.00E-03
4.00E-03
5.00E-03
6.00E-03
7.00E-03
8.00E-03
9.00E-03
00
:0
0
01
:0
0
02
:00
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:00
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Escenario L
0.00E+00
1.00E-02
2.00E-02
3.00E-02
4.00E-02
5.00E-02
6.00E-02
7.00E-02
00
:0
0
01
:0
0
02
:00
03
:0
0
04
:0
0
05
:00
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Escenario I
0.00E+00
1.00E-01
2.00E-01
3.00E-01
4.00E-01
5.00E-01
6.00E-01
7.00E-01
8.00E-01
9.00E-01
1.00E+00
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:0
0
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Escenario DL
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
72
0.00E+00
5.00E-04
1.00E-03
1.50E-03
2.00E-03
2.50E-03
3.00E-03
3.50E-03
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:00
15
:00
16
:00
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Escenario DI
0.00E+00
5.00E-04
1.00E-03
1.50E-03
2.00E-03
2.50E-03
00
:0
0
01
:0
0
02
:0
0
03
:0
0
04
:0
0
05
:0
0
06
:0
0
07
:0
0
08
:0
0
09
:0
0
10
:0
0
11
:0
0
12
:0
0
13
:0
0
14
:0
0
15
:0
0
16
:00
17
:0
0
18
:0
0
19
:0
0
20
:0
0
21
:0
0
22
:0
0
23
:0
0
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Escenario IL
0.00E+00
1.00E-01
2.00E-01
3.00E-01
4.00E-01
5.00E-01
6.00E-01
7.00E-01
8.00E-01
9.00E-01
1.00E+00
00
:00
01
:0
0
02
:00
03
:0
0
04
:00
05
:0
0
06
:00
07
:0
0
08
:00
09
:0
0
10
:00
11
:0
0
12
:00
13
:0
0
14
:00
15
:0
0
16
:00
17
:0
0
18
:00
19
:0
0
20
:00
21
:0
0
22
:00
23
:0
0
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Escenario DIL

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
73
En la Tabla 16 se pueden ver las probabilidades de ocurrencia horarias de cada escenario del
sistema. Se debe notar que tanto el escenario como el escenario tienen
probabilidad nula en cualquier hora del día, siendo este un efecto de la suposición de
ocupación total del baño cuando se usa un aparato sanitario. Los escenarios con dos aparatos
encendidos, uno de los cuales es el inodoro, representan escenarios donde el lavamanos o la
ducha fueron utilizados mientras el inodoro descargaba inmediatamente después de haber
sido usado y por lo tanto no violan la restricción de un usuario por vez en el baño.
4.3 Análisis de caudales a partir de ambas metodologías
Una vez se ha asignado una probabilidad de ocurrencia a cada escenario de demanda del
sistema, es posible encontrar una función de densidad de probabilidad para el caudal que pasa
por cada tubería de la red. Para ello se utiliza la modelación de los aparatos sanitarios descrita
en la Sección 3.1, que para el caso del baño residencial previamente analizado, se rige por las
ecuaciones de la Tabla 8.
Así, si se desea conocer la función de densidad de probabilidad del caudal que transporta el
tubo que alimenta a todo el baño (ver Figura 16), es necesario modelar el comportamiento
hidráulico del sistema para cada escenario, suponiendo que en los nudos que representan a los
aparatos, se encuentran emisores con una curva igual a la de la Tabla 8 en caso de que el
escenario los tenga encendidos, y en caso contrario, serán nudos con demanda cero. Así, se
puede encontrar un caudal transportado por esa tubería para cada escenario, que en el caso
del ejemplo dio:
Tabla 17. Caudal transportado por el tubo más aguas arriba del sistema para cada escenario.
Escenario
Caudal (L/s)
0
0.142
0.042
0.042
0.184
0.184
0.084
0.226
Haciendo uso de la Tabla 17 que relaciona caudal en el tubo con el escenario de demanda, y la
Tabla 15 o la Tabla 16 que relacionan probabilidad de ocurrencia con cada escenario de
demanda, se pueden encontrar relaciones de caudal en el tubo con probabilidad de
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
74
ocurrencia, que es precisamente la función de densidad de probabilidad de la variable
aleatoria
14
.
Si se utiliza la Tabla 15, y por lo tanto la metodología basada en Blokker, se llega a la función de
densidad de probabilidad mostrada en la Figura 19 para el caso de personas aferentes al
sistema lo cual permite encontrar la función de probabilidad acumulada de la variable, la cual
se muestra en la Figura 20.
Figura 19. Función de densidad de probabilidad del caudal transportado por el tubo, utilizando la metodología
basada en Blokker para un baño con 4 personas aferentes.
Figura 20. Función acumulada de probabilidad del caudal transportado por el tubo, utilizando la metodología
basada en Blokker para un baño con 4 personas aferentes.
14
Si bien esa variable es discreta según lo mostrado en la Tabla 17, estos valores son sólo estimaciones
del caudal que pasará por el tubo, y por lo tanto la variable tiene una función de densidad de
probabilidad tal como cualquier variable continua.
0.00
0.10
0.20
0.30
0.40
0.50
0.60
0.70
0.80
0.90
1.00
0
0.05
0.1
0.15
0.2
0.25
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Caudal (L/s)
00:00
01:00
02:00
03:00
04:00
05:00
06:00
07:00
08:00
09:00
10:00
11:00
12:00
13:00
14:00
15:00
16:00
17:00
18:00
19:00
20:00
21:00
22:00
23:00
0.00
0.10
0.20
0.30
0.40
0.50
0.60
0.70
0.80
0.90
1.00
0
0.05
0.1
0.15
0.2
0.25
Pr
o
b
ab
ili
d
ad
n
o
ser
e
xce
d
id
o
()
Caudal (L/s)
00:00
01:00
02:00
03:00
04:00
05:00
06:00
07:00
08:00
09:00
10:00
11:00
12:00
13:00
14:00
15:00
16:00
17:00
18:00
19:00
20:00
21:00
22:00
23:00
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
75
Si, por otro lado, se utiliza la Tabla 16 para dicho cálculo, las funciones de densidad de
probabilidad y de probabilidad acumulada son las mostradas en la Figura 21 y la Figura 22:
Figura 21. Función de densidad de probabilidad del caudal transportado por el tubo, utilizando la metodología
basada en Blokker con simulación de eventos discretos para un baño con 4 personas aferentes.
Figura 22. Función acumulada de probabilidad del caudal transportado por el tubo, utilizando la metodología
basada en Blokker con simulación de eventos discretos para un baño con 4 personas aferentes.
En las anteriores figuras se puede notar que dada la alta probabilidad del escenario ,
todas las funciones acumuladas de probabilidad para cualquier hora inician con una
probabilidad considerablemente alta, que hace que, para un caudal cualquiera mayor a cero, la
probabilidad de no ser excedido sea cercana o superior al .
Para permitir una mejor visualización de las probabilidades encontradas, se decidió calcular y
graficar las funciones de densidad de probabilidad y las funciones de probabilidad acumulada
del caudal transportado por el tubo tomando como dado que el sistema sí está en uso y que
0.00
0.10
0.20
0.30
0.40
0.50
0.60
0.70
0.80
0.90
1.00
0
0.05
0.1
0.15
0.2
0.25
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Caudal (L/s)
00:00
01:00
02:00
03:00
04:00
05:00
06:00
07:00
08:00
09:00
10:00
11:00
12:00
13:00
14:00
15:00
16:00
17:00
18:00
19:00
20:00
21:00
22:00
23:00
0.00
0.10
0.20
0.30
0.40
0.50
0.60
0.70
0.80
0.90
1.00
0
0.05
0.1
0.15
0.2
0.25
Pr
o
b
ab
ili
d
ad
d
e
n
o
ser
e
xce
d
id
o
()
Caudal (L/s)
00:00
01:00
02:00
03:00
04:00
05:00
06:00
07:00
08:00
09:00
10:00
11:00
12:00
13:00
14:00
15:00
16:00
17:00
18:00
19:00
20:00
21:00
22:00
23:00
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
76
por lo tanto no se está en el escenario . Estas figuras permiten ver la forma de las
curvas para los caudales mayores a cero, y pueden ser utilizadas en un eventual análisis de
probabilidad de falla.
Figura 23. Función de densidad de probabilidad del caudal transportado por el tubo dado que el sistema está en
uso, utilizando la metodología basada en Blokker para un baño con 4 personas aferentes.
Figura 24. Función acumulada de probabilidad del caudal transportado por el tubo dado que el sistema está en
uso, utilizando la metodología basada en Blokker para un baño con 4 personas aferentes.
0.00
0.10
0.20
0.30
0.40
0.50
0.60
0.70
0.80
0.90
1.00
0
0.05
0.1
0.15
0.2
0.25
Pr
o
b
ab
ili
d
ad
d
e
o
u
rr
e
n
ci
a
()
Caudal (L/s)
00:00
01:00
02:00
03:00
04:00
05:00
06:00
07:00
08:00
09:00
10:00
11:00
12:00
13:00
14:00
15:00
16:00
17:00
18:00
19:00
20:00
21:00
22:00
23:00
0.00
0.10
0.20
0.30
0.40
0.50
0.60
0.70
0.80
0.90
1.00
0
0.05
0.1
0.15
0.2
0.25
Pr
o
b
ab
ili
d
ad
d
e
n
o
ser
e
xce
d
id
o
()
Caudal (L/s)
00:00
01:00
02:00
03:00
04:00
05:00
06:00
07:00
08:00
09:00
10:00
11:00
12:00
13:00
14:00
15:00
16:00
17:00
18:00
19:00
20:00
21:00
22:00
23:00
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
77
Figura 25. Función de densidad de probabilidad del caudal transportado por el tubo dado que el sistema está en
uso, utilizando la metodología basada en Blokker con simulación de eventos discretos para un baño con 4
personas aferentes.
Figura 26. Función acumulada de probabilidad del caudal transportado por el tubo dado que el sistema está en
uso, utilizando la metodología basada en Blokker con simulación de eventos discretos para un baño con 4
personas aferentes.
Comparativamente, las funciones de densidad de probabilidad asignadas por ambas
metodologías son similares en forma, pero tienen algunas diferencias en los valores de las
probabilidades, los cuales pueden resultar poco significativos para algunos procedimientos,
pero significativos para otros. Así, por ejemplo, para una eventual evaluación de las
condiciones de flujo en la red en búsqueda de posibles condiciones de crecimiento de
biopelículas o mineralopelículas, tendría en cuenta la recurrencia del escenario con caudal en
el tubo nulo, y en ese caso podría utilizar los resultados de las figuras entre la Figura 19 y la
0.00
0.10
0.20
0.30
0.40
0.50
0.60
0.70
0.80
0.90
1.00
0
0.05
0.1
0.15
0.2
0.25
Pr
o
b
ab
ili
d
ad
d
e
o
cu
rr
e
n
ci
a
()
Caudal (L/s)
00:00
01:00
02:00
03:00
04:00
05:00
06:00
07:00
08:00
09:00
10:00
11:00
12:00
13:00
14:00
15:00
16:00
17:00
18:00
19:00
20:00
21:00
22:00
23:00
0.00
0.10
0.20
0.30
0.40
0.50
0.60
0.70
0.80
0.90
1.00
0
0.05
0.1
0.15
0.2
0.25
P
rob
abil
id
ad
d
e
n
o
ser
e
xced
id
o(
)
Caudal (L/s)
00:00
01:00
02:00
03:00
04:00
05:00
06:00
07:00
08:00
09:00
10:00
11:00
12:00
13:00
14:00
15:00
16:00
17:00
18:00
19:00
20:00
21:00
22:00
23:00

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
78
Figura 22. Estas figuras, presentan diferencias despreciables en las probabilidades, y por lo
tanto los resultados de dicho análisis no variarían significativamente si se usa la metodología
basada en Blokker o la metodología basada en Blokker con simulación de eventos discretos.
Sin embargo, una evaluación del nivel de satisfacción promedio de los usuarios que utilizan el
sistema, sólo tendría en cuenta los escenarios donde hay una demanda efectiva, es decir que
utilizaría los resultados de las figuras entre la Figura 23 y la Figura 26, y en ese caso las
diferencias entre las metodologías puede ser significativa, con diferencias en las
probabilidades de hasta en valor absoluto de probabilidad, y de diferencias promedio de
entre las probabilidades para cada hora y para cada escenario relativas al valor estimado
con la metodología con simulación de eventos discretos, para el caso de 4 personas aferentes
al baño.
Es importante notar que los resultados mostrados en las anteriores figuras y los anteriores
cálculos, son similares a los encontrados para el resto de casos del número de personas
aferentes al sistema, con diferencias en valores pero no en forma. Por ejemplo en el caso de
las funciones de densidad de probabilidad y de probabilidad acumulada, a medida que
aumenta el número de personas aferentes, las probabilidades del escenario se reducen
mientras que para los demás escenarios se aumentan, haciendo más pronunciados los picos de
las funciones de densidad de probabilidad (e.g. Figura 19 y Figura 23). Análogamente cuando
se reduce el número de personas aferentes, las probabilidades del escenario aumentan
significativamente haciendo todas las curvas de probabilidad total más planas.
El
anterior
procedimiento
de
análisis
estocástico
hecho
para
la
variable
puede ser hecho también para otras variables del flujo
en la red, tales como los caudales en el resto de las tuberías, las presiones y alturas
piezométricas en cualquier nudo o punto de la red, los números de Reynolds, las velocidades, y
demás, teniendo en cuenta que la mayoría de los programas de simulación hidráulica de redes
con flujo presurizado entregan como resultados tablas en donde para cada nudo y para cada
tubo presentan características del flujo en dicho elemento, y por lo tanto al realizar
simulaciones hidráulicas para cada escenario, es posible tener una realización de la variable
estudiada, la cual puede relacionarse con la probabilidad de ocurrencia del escenario
simulado.
De esta manera concluye el caso de estudio correspondiente a un baño residencial, habiendo
mostrado la manera de la implementación de ambas metodologías propuestas, y mostrando
un resultado comparativo entre los resultados de ambas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
79
5 Procedimiento de diseño propuesto
Con base en los resultados de la metodología propuesta para la modelación de la demanda en
RIDAPs, es posible realizar un análisis estocástico e hidráulico que permita realizar diseños que
se ajusten satisfactoriamente a las demandas modeladas, y por lo tanto a la utilización típica
del sistema prototipo. A continuación se muestra un diagrama de flujo que resume las etapas
en las que se divide el procedimiento de diseño de RIDAPs planteado en esta investigación:
Figura 27. Diagrama de flujo del procedimiento de diseño propuesto.
Inicio
Asignación de una
Línea de
Gradiente
Hidráulico (
LGH)
para toda la red.
Cálculo de
caudales emitidos
en los aparatos
sanitarios.
t = 1
t = |T|
Cálculo del caudal
de diseño del tubo
t.
Cálculo y
redondeo del
diámetro del tubo
t.
Asignación de una
LGH para la red
aguas abajo del
tubo
t.
t = t + 1
Fin
No
Si

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
80
Las etapas del procedimiento de diseño mostrado en la Figura 27 son detalladas en las
siguientes secciones.
5.1 Asignación de una Línea de Gradiente Hidráulico (LGH)
La asignación de una LGH para toda la red, o para la red aguas abajo de una tubería cualquiera,
es un paso adoptado de algunas metodologías de diseño optimizado de RDAPs (Wu, 1975 y
Ochoa, 2009). Este paso consiste en predefinir la altura piezométrica de cada nudo de la red,
de manera que, con los caudales de diseño de cada tubo se pueden encontrar valores de los
diámetros de todas las tuberías que globalmente generan una red diseñada de costo cercano
al mínimo.
En la Sección 2.2.2 de este documento se presenta un análisis de la función típicamente
asignada como LGH para una tubería en serie (polinomio de segundo grado). Como resultado
se encuentran los dominios de cada una de las variables independientes de esta función,
permitiendo así definir completamente la familia de curvas cuadráticas que pueden ser
asignadas como LGH de una tubería en serie. Así, para realizar este subproceso del
procedimiento de diseño se hace uso de la Ecuación 12 presentada a continuación, con la cual
es posible asignar la altura piezométrica objetivo de cada nudo de la red o tramo de red
analizado:
Ecuación 43
donde:
: LGH evaluada en el punto medido desde la entrada del sistema. En la altura
piezométrica que se asignará al nudo ubicado a una distancia de la entrada del
sistema.
: Máximo valor de la LGH para esa trayectoria analizada. Corresponde con la
altura piezométrica disponible en la entrada del sistema.
: Mínimo valor de la LGH para esa trayectoria. Este valor corresponde a la
mínima altura piezométrica aceptable en el nudo final de la trayectoria (el de más
aguas abajo).
: Longitud total de la trayectoria a la cual pertenece el punto analizado. Se calcula
como la distancia topológica entre la entrada del sistema y el nudo final de la rama.
: Flecha de la ecuación cuadrática de LGH. Representa la diferencia de alturas
piezométricas entre una LGH recta calculada con la Ecuación 11, y la que se desea
calcular con la Ecuación 12, escrita de manera porcentual respecto a la diferencia entre
la
y la
. Se considera positiva si el valor calculado con la ecuación

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
81
cuadrática es menor que el calculado con la ecuación lineal, y negativa en caso
contrario.
: Distancia topológica entre la conexión de la RIDAP a la RDAP (entrada del sistema)
y el punto en donde se quiere calcular la LGH objetivo.
Según Wu (1975) el valor del parámetro independiente que minimiza los diseños de una
tubería en serie con caudales demandados homogéneamente distribuidos a lo largo de la
tubería es . Sin embargo, Wu también analiza el sobrecosto en el que se incurre al
seleccionar una curva con que genera una función lineal, llegando a un valor del
, lo cual se considera poco significativo para el problema de diseño de RIDAPs.
Adicionalmente, una LGH con asigna presiones objetivo más altas para todos los
nudos de la red, aumentando así la confiabilidad del sistema cuando ésta es medida con
índices como el Índice de Resiliencia (Todini, 2000) o la Potencia Unitaria (Saldarriaga, 2010).
Considerando lo anterior, se recomienda como LGH para el procedimiento de diseño, aquella
con . Sin embargo, la metodología puede ser utilizada con cualquier valor de y
eventualmente se podrían evaluar otros posibles valores para mejorar el diseño final de la red
ajustándolo a las necesidades específicas del problema respecto a costos constructivos y
confiabilidad.
5.2 Cálculo de los caudales emitidos
Teniendo en cuenta que las alturas piezométricas asignadas en el paso anterior son las alturas
piezométricas que deben registrarse cuando las condiciones de diseño son alcanzadas por la
demanda de la red, los caudales emitidos correspondientes a dichas presiones son los caudales
que deben ser tenidos en cuenta para el diseño de la misma. Para su cálculo basta evaluar la
presión correspondiente a la altura piezométrica asignada, en la curva del aparato que
relaciona el caudal emitido con la presión inmediatamente aguas arriba (ver Sección 3.1).
5.3 Cálculo del caudal de diseño de un tubo
Para poder diseñar un tubo es necesario conocer la diferencia de alturas piezométricas entre
sus dos nudos y el caudal que se espera pase por él. El paso de Asignación de LGH asigna una
altura piezométrica a cada nudo de la red, y por lo tanto la diferencia de alturas piezométricas
es conocida para cada tubo. Para determinar el caudal de diseño, es necesario realizar un
análisis estocástico de la demanda, que permita asignar como caudal de diseño, un caudal que
asegure una probabilidad de falla menor a la máxima aceptable sin incurrir en sobrecostos por
asignar caudales mayores al realmente necesario.
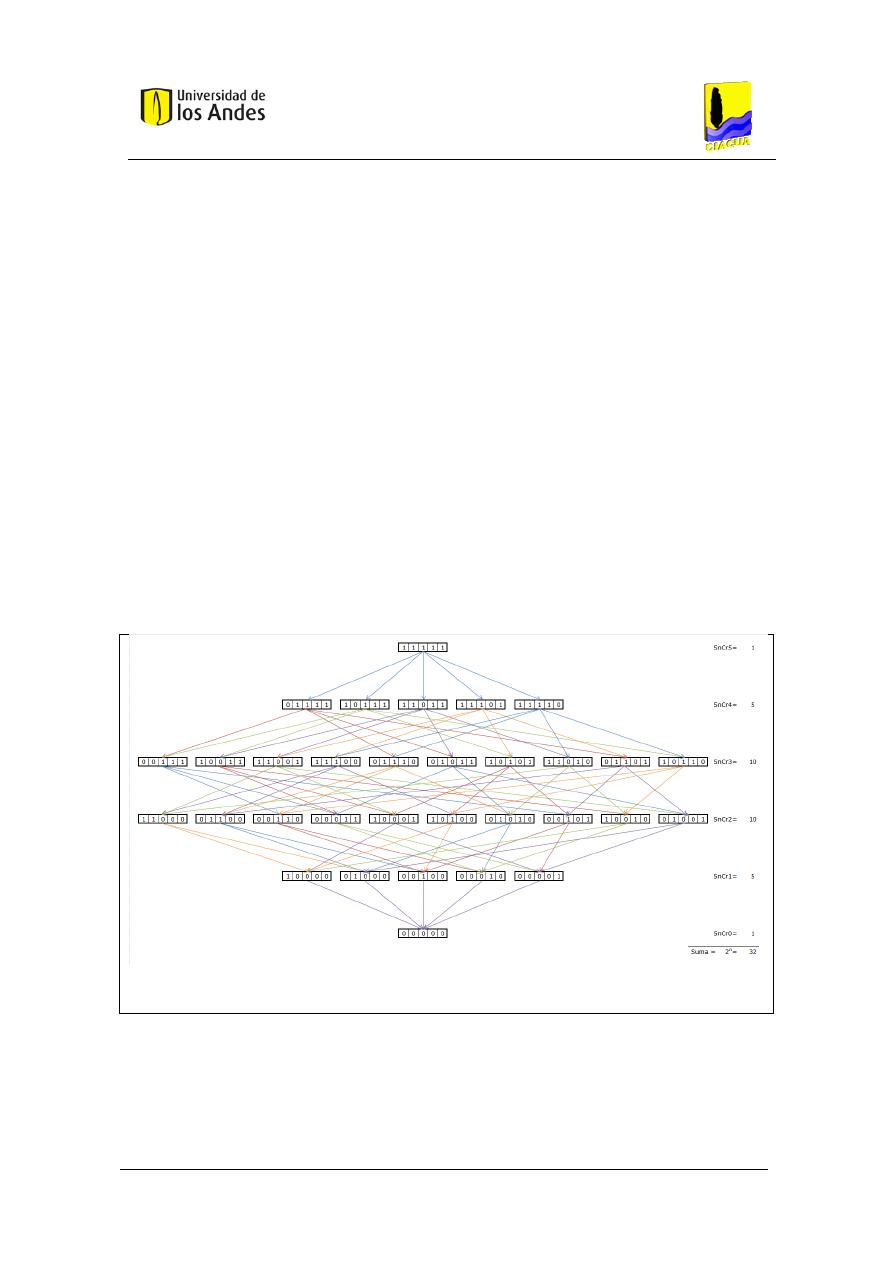
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
82
5.3.1 Análisis estocástico para nudos independientes
Haciendo un análisis similar al hecho por CIACUA (2011), es posible ordenar todos los posibles
escenarios de demanda de una RIDAP de mayor a menor exigencia hidráulica como se muestra
a continuación:
Si se supone que un aparato sólo tiene dos posibles configuraciones
(encendido/apagado), y se tiene una RIDAP con nudos de demanda con solo
aparato conectado a cada uno, entonces el número de posibles escenarios de
demanda es
.
Se entiende que un escenario es de otro escenario cuando el conjunto de
nudos encendidos en el estado es subconjunto del conjunto de nudos encendidos
en el estado . Dicha relación de representa que el escenario es
indiscutiblemente más demandante hidráulicamente que el escenario , y por lo
tanto un diseño que cumpla con los requerimientos hidráulicos de , necesariamente
cumplirá con los requerimientos hidráulicos de . Además es claro que la relación
es transitiva, es decir que si es de y es de , entonces es
de . Haciendo posible que se puedan ordenar los
posibles escenarios de
demanda de acuerdo con la relación , de la siguiente manera:
En el diagrama se entiende que, cada rectángulo con 5 casillas representa un escenario de demanda, en donde las
casillas con valor representan que el nudo está apagado y las casillas con valor representan que el nudo está
encendido; además una flecha que parte del escenario hacia el escenario significa que es de .
Figura 28. Ejemplo de configuración ordenada de los posibles escenarios de demanda de una RIDAP con .
En la Figura 28 se puede notar cómo se genera una clasificación natural de los
escenarios de acuerdo con el número de nudos encendidos que tiene cada uno. Para
ello se definirá cada uno de estos conjuntos de escenarios con igual número de nudos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
83
encendidos como , donde es precisamente el número de nudos
encendidos { } .
Dado que escenarios pertenecientes al mismo estado no pueden ser comparados respecto a su
exigencia hidráulica, teniendo en cuenta que un escenario puede ser más exigente que un
escenario para el tubo
, pero menos exigente para un tubo
; el algoritmo de selección
del caudal de diseño debe ser ejecutado para cada tubo de la red a fin de encontrar el caudal
con el que el diseño de dicho tubo asegura una probabilidad de falla menor a la máxima
aceptable.
Probabilidad de falla
Para que el procedimiento tenga validez, es necesario definir la , y así
asignarle un valor máximo admisible dependiendo de la aversión al riesgo que tenga el futuro
usuario del sistema y de los costos que pueda implicar una falla del mismo. La probabilidad de
falla de una RIDAP puede ser calculada y entendida como:
(
)
Ecuación 44
Ecuación 45
donde:
: Probabilidad de falla de la RIDAP.
: Probabilidad de falla del aparato conectado al nudo .
: Tiempo durante el cual el aparato del nudo está encendido pero el caudal
emitido es menor al de dicho aparato (ver Sección 3.1).
: Tiempo durante el cual el aparato del nudo está encendido.
Es decir que la probabilidad de falla de un aparato es la frecuencia con la que se desea hacer
uso de éste y, por las condiciones hidráulicas de la RIDAP en ese instante, el caudal emitido es
inferior al mínimo aceptable. Por otro lado, la probabilidad de falla de toda la red, podría ser
entendida como la probabilidad de que al menos un aparato esté fallando, y en ese caso la
probabilidad de falla sería la suma de las probabilidades de falla de cada aparato, suponiendo
independencia en la ocurrencia de la falla en un nudo.
Sin embargo, la ocurrencia de la falla en un nudo, no es independiente de la ocurrencia de la
falla en los demás nudos, dado que si un nudo está fallando es porque hay más aparatos
encendidos que los que el sistema puede soportar, y por lo tanto un aparato que se encienda
mientras el sistema está en dicho estado, también reportará una falla. Así, la fórmula
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
84
planteada en la Ecuación 44, se considera una mejor representación de la ocurrencia de las
fallas en una RIDAP considerando lo siguiente:
Ecuación 46
Cuando ocurre el evento (falla de un aparato que está encendido) es porque el sistema está
siendo sometido a una situación de demanda más exigente que la de diseño para al menos un
tubo aguas arriba del nudo con falla, y por lo tanto es muy probable que también esté
ocurriendo el evento (falla de otro aparato que está encendido y que también está aguas
abajo de dicho(s) tubos(s)). Es decir que la probabilidad de que ocurran los dos eventos al
tiempo ( ) debe ser muy similar a la menor de las probabilidades de los dos eventos
(ver Figura 29). Así, de la expresión de la derecha de la Ecuación 46 queda reducida a
, donde se entiende que la función entrega el evento de mayor
probabilidad asociada.
Figura 29. Justificación de la ecuación de probabilidad de falla.
En el caso de que ocurra el evento , pero el evento esté relacionado con la falla de un nudo
aguas arriba del tubo o tubos con un caudal mayor al de diseño, entonces la probabilidad del
evento será despreciable, y el resultado de la probabilidad de seguirá siendo
. Algo similar ocurre cuando el aparato relacionado con el evento esta
apagado. En este caso la probabilidad de que dicho nudo falle es nula, dado que la falla solo es
posible si se le exige algo al sistema, de manera que la probabilidad de falla sigue siendo la
mayor de la dos.
El anterior concepto puede ser fácilmente extendido a varios eventos (i.e. varios aparatos) de
manera que se llega a la expresión de la Ecuación 44 para cuantificar la probabilidad de falla de
una RIDAP.
Por otro lado, para determinar la máxima probabilidad de falla aceptable, se deben tener en
cuenta detalles como el costo de una falla del sistema, que en el caso de una RIDAP no es
usualmente alto, pero pueden existir excepciones como hospitales o laboratorios en donde
una falta de disponibilidad de agua con flujo adecuado (i.e. caudal mayor al mínimo
aceptable), puede implicar afectación en la integridad de los ocupantes de la edificación y/o
pérdidas económicas considerables. Usualmente existen entidades gubernamentales que dan
valores máximos para esa probabilidad de falla aceptable, o lo que es similar, valor mínimo de
confiabilidad del sistema y/o periodo de retorno de una falla.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
85
Cálculo del estado de diseño de un tubo
Una primera aproximación al procedimiento de cálculo del caudal de diseño de un tubo
considera que una vez se conoce la probabilidad de falla aceptable, es necesario encontrar el
caudal cuya probabilidad de ser igualado o excedido es menor que ésta, siendo dicho caudal el
caudal de diseño. Es decir que el caudal de diseño de un tubo podría ser encontrado haciendo
uso de las funciones de probabilidad acumuladas de caudal obtenidas mediante las
metodologías de modelación de la demanda (e.g. Figura 24 y Figura 26), conociendo la
probabilidad de no ser excedido (el complemento de la probabilidad de ser igualado o
excedido) y hallando el caudal correspondiente a dicho valor de probabilidad.
Sin embargo la anterior aproximación no es consistente con la definición de probabilidad de
falla hecha anteriormente y la razón se hace evidente con el siguiente ejemplo:
Suponga que se tiene una RIDAP con dos aparatos sanitarios y . Las probabilidades de
uso de estos dos aparatos son tales que , y las curvas de emisor son tales
que siempre se cumple que
. Dado que las probabilidades de uso deben ser
condicionadas con que el sistema esté en uso, entonces se cumple que
| | , y dado que la probabilidad de que esté
siendo utilizado es mucho mayor que la de entonces, si el sistema está en uso, es
mucho más probable que sea el (o uno de los) aparato(s) en uso, y por lo tanto
| implicando que el caudal
tiene una probabilidad acumulada
cercana a , y por lo tanto puede ser utilizado como caudal de diseño del tubo que
alimenta a los dos aparatos para probabilidades de falla aceptables mayores a (
| ) , es decir cualquier probabilidad de falla.
Sin embargo si el diseño es efectivamente hecho con
, cualquier escenario de demanda
en donde el aparato esté encendido generará una falla del sistema al ocurrir una falla
en dicho aparato, teniendo en cuenta que
. Es decir que la probabilidad de falla
de será
y por lo tanto, utilizando la Ecuación 44, la probabilidad de falla
del sistema será
, implicando así, que el diseño no cumple con las
condiciones de diseño.
El anterior ejemplo muestra cómo la selección del caudal de diseño debe ser realizada de una
manera diferente a la explicada que permita incorporar la definición de probabilidad de falla
hecha en la Ecuación 44. Para ello, se plantea una aproximación similar a la hecha por CIACUA
(2011) en donde se evalúan diferentes escenarios de un mismo estado seleccionado como
estado de diseño (ver Figura 28). La diferencia radica en que, como se ha explicado
anteriormente, la evaluación del caudal de diseño puede y debe realizarse para cada tubo de
manera independiente (pág. 83) y el cálculo de las probabilidades de los estados no hace uso
de un modelo con cadenas de Markov.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
86
Para calcular entonces las probabilidades de cada uno de los estados de un tubo, entendidos
como los estados de la red aguas abajo del tubo analizado, se puede hacer uso de la Ecuación
47 comúnmente denominada Distribución Binomial de Poisson:
∑
(∏
∏ (
)
)
Ecuación 47.
Distribución
Binomial de
Poisson
donde:
: Es la probabilidad de que se esté en el estado en una red con nudos
de demanda.
y
: Probabilidad de que el aparato (o ) esté encendido.
Dada la difícil indexación de las sumatorias y productorias de la Ecuación 47, se presenta
un ejemplo del cálculo:
(
)
(
)
(
)
(
)
(
)
Así, la Ecuación 47 simplemente suma las probabilidades de ocurrencia de todos los posibles
escenarios con aparatos encendidos, calculando cada una de esas probabilidades con el
método descrito en la Sección 3.2.1. Es importante notar que el número de sumandos de la
Ecuación 47 se calcula como (combinatoria de en ). Es fácil demostrar que el
máximo de una combinatoria ocurre cuando [
⁄ ]
⁄ (función
parte entera, que se define como el máximo entero que es menor que la variable
independiente para valores positivos). A continuación se muestra cómo crece la función de la
Ecuación 48 que representa la máxima combinatoria posible con aparatos en la red
analizada:
( [
])
Ecuación 48
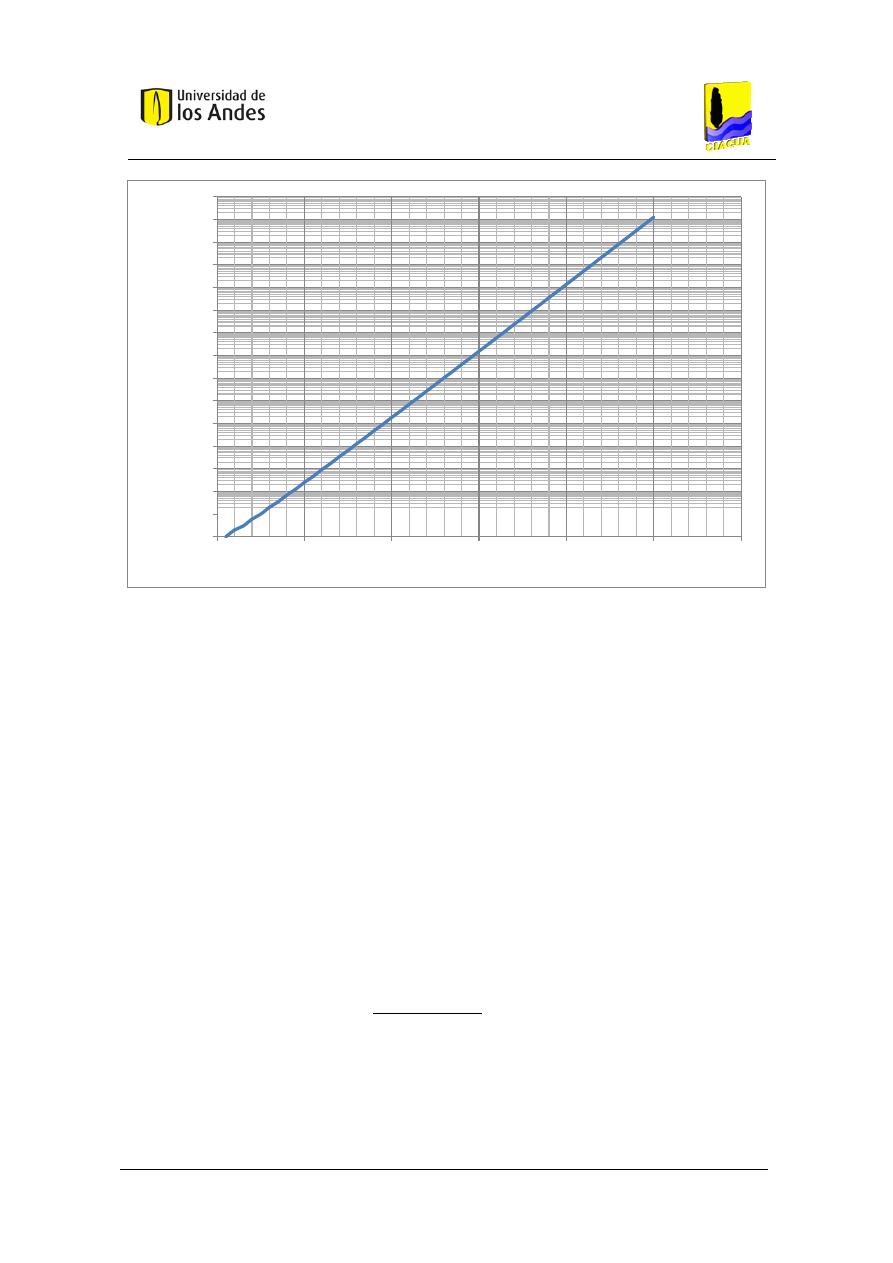
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
87
Figura 30. Comportamiento de la función de la Ecuación 48.
Como se puede ver en la Figura 30 el número de sumandos a tener en cuenta en la Ecuación
47, cuando supera los aparatos, supera los mil millones, implicando un esfuerzo
computacional considerable para realizar cálculo de la probabilidad del estado [
⁄ ]. Así, se
hace necesario buscar una manera más eficiente de calcular dicha probabilidad o de hacer una
estimación aceptable de su valor.
Para ello se puede hacer un análisis de las expresiones resultantes de expandir y simplificar la
Ecuación 47 para diferentes valores de y . Como resultado se llegó a la siguiente
igualdad:
∑
̅̅̅̅̅̅̅̅
Ecuación 49
(
) ∑
(
)
̅̅̅̅̅̅̅̅
̅̅̅
∑
(∏
)
Ecuación 50
donde:
: Es la probabilidad de que se esté en el estado en una red con nudos
de demanda.
1.0E+00
1.0E+01
1.0E+02
1.0E+03
1.0E+04
1.0E+05
1.0E+06
1.0E+07
1.0E+08
1.0E+09
1.0E+10
1.0E+11
1.0E+12
1.0E+13
1.0E+14
1.0E+15
0
10
20
30
40
50
60
n
Cr
(NN,
[NN/2])
NN

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
88
̅̅̅̅̅̅̅̅ : Sumatoria de las productorias de las probabilidades de encendido de
aparatos.
El
número
de
sumandos
de
la
sumatoria,
denominado
puede ser calculado como .
Para entender su indexación se presenta el siguiente ejemplo:
(
)
∑
(
)
̅̅̅̅̅
̅̅̅̅̅̅
̅̅̅
̅̅̅̅̅̅
̅̅̅
̅̅̅̅̅̅
̅̅̅
Se debe notar que en caso de que todas las probabilidades
fuesen iguales a un mismo , el
término
̅̅̅ seria igual a
. Adicionalmente, si todas las probabilidades son iguales, se puede
llegar a la conocida ecuación de la distribución Binomial:
Ecuación 51
(
)
La Ecuación 51 tiene una ventaja significativa respecto a la Ecuación 47, y es que está
compuesta por un único sumando sin importar o , pero por otro lado tiene la desventaja
de requerir que todas las probabilidades de uso de los aparatos sean iguales. Para poder
reducir el efecto negativo de dicha desventaja, que imposibilitaría el uso de la Ecuación 51 en
el cálculo del estado de diseño, se propone el uso de un valor representativo de las
probabilidades de uso de todos los aparatos. Es decir que se busca un único valor que
minimice la diferencia entre
calculado con la Ecuación 51 y
calculado con la
Ecuación 47.
Un análisis a la Ecuación 49 y la Ecuación 50 sugiere que la mejor manera de encontrar ese
valor es utilizando un promedio geométrico, teniendo en cuenta que el término
̅̅̅ puede
ser aceptablemente estimado como
. Para validar dicho postulado se realizaron cerca de
cálculos de
para diferentes valores de los
. Para cada cálculo se
computaron las probabilidades con la Ecuación 47 (valor real), y con la Ecuación 51 utilizando,
entre otros, promedios aritméticos y geométricos para el cálculo de .
Como resultado se encontró que el error en el que se incurre al utilizar la Ecuación 51,
independientemente de la forma de estimar , aumenta considerablemente cuando aumenta
la desviación estándar de las probabilidades de uso de los aparatos
(ver Figura 31).
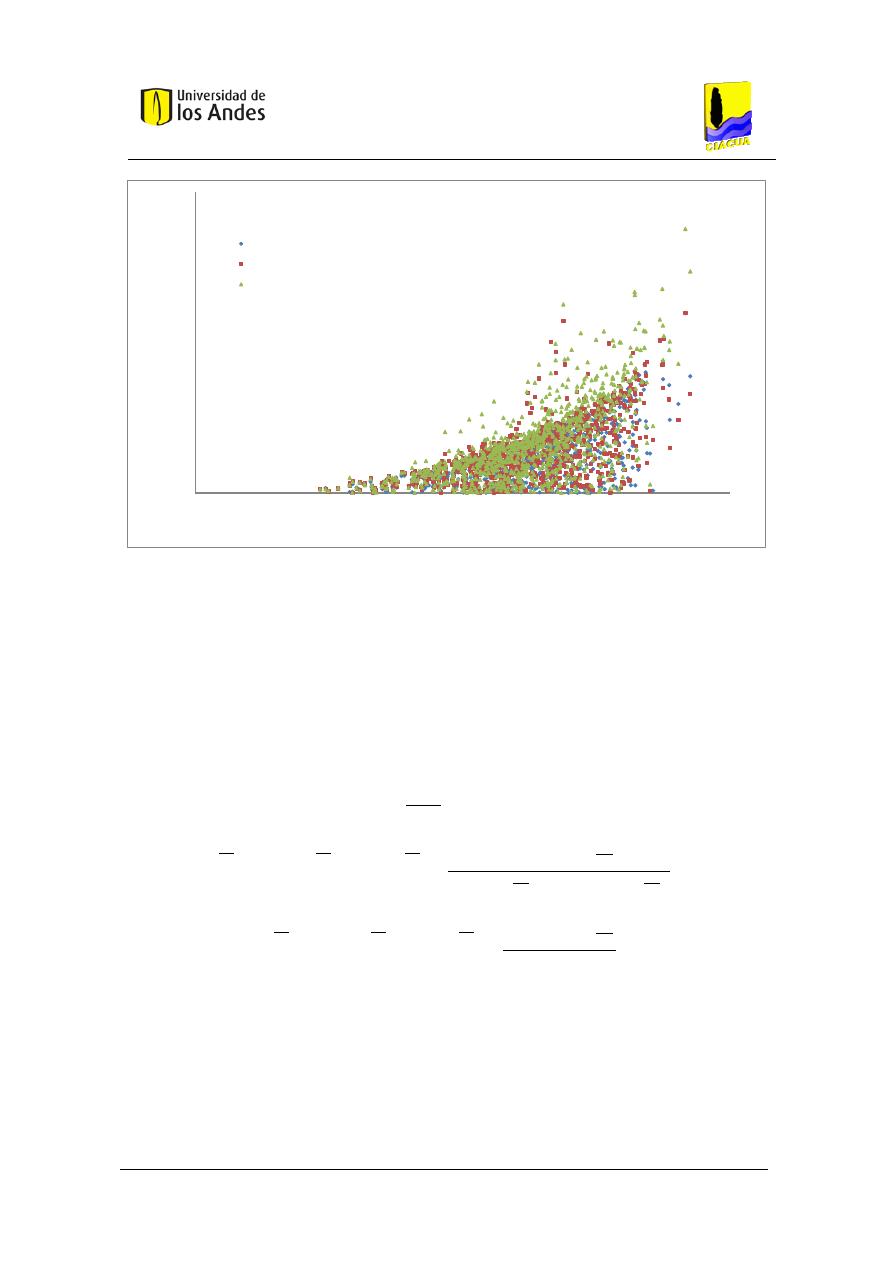
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
89
Figura 31. Relación entre el error en la estimación de la probabilidad de un estado y la desviación estándar de las
probabilidades de uso de los aparatos.
Si bien para el conjunto de pruebas presentado en la Figura 31 fueron probadas otras posibles
formas de estimar , las tres que presentaron mejores resultados fueron: estimación con un
promedio aritmético de las probabilidades de uso de cada aparato (Ecuación 52), estimación
con un promedio geométrico corregido (Ecuación 53) denominado
-
y estimación con un promedio geométrico simplificado (Ecuación 54) denominado
-
.
∑
Ecuación 52.
Promedio
Aritmético.
(∏
)
(
(
(∏
)
(∏
)
)
)
∏
( ∏
∏
)
Ecuación 53.
Promedio
Geometrico
(-1c).
(∏
)
(
(
(∏
)
(∏
)
)
)
∏
Ecuación 54.
Promedio
Geométrico
(-1).
Para realizar una comparación objetiva entre las tres posibilidades de estimación de se
realizaron diferentes cálculos de
para diferentes conjuntos de probabilidades
con diferentes rangos para la desviación estándar. Los resultados de los cálculos más
significativos se presentan de la Figura 32 a la Figura 34, en donde fueron graficadas las
funciones acumuladas del error absoluto de cada estimación respecto al valor real (Ecuación
47).
0.00
0.05
0.10
0.15
0.20
0.25
0.30
0.00
0.05
0.10
0.15
0.20
0.25
0.30
0.35
0.40
0.45
Er
ro
r
ab
solut
o
e
n
e
l val
o
r
d
e
p
ro
b
ab
ili
d
ad
(
)
Desviación estándar de p
i
()
Con promedio algebraico
Con promedio geométrico (-1c)
Con promedio geométrico (-1)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
90
Figura 32. Error en la estimación de la probabilidad de un estado para desviaciones estándar entre 0.15 y 0.45.
En la Figura 32 se puede notar como en el 50% de los casos las diferentes estimaciones
generaron errores menores a 0.04, pero para la otra mitad de los datos la estimación con
Promedio geométrico (-1) generó errores considerablemente mayores que los otros dos
métodos. Sin embargo, un procesamiento de los datos de dicha figura indicó que la estimación
con Promedio geométrico (-1) fue mejor en el 31.4% de los casos, con Promedio geométrico (-
1c) fue mejor en el 35.6%, con Promedio aritmético fue mejor en el 33.0%. Es decir, que a
pesar de que el Promedio geométrico (-1) incurre en errores considerables para la mitad de los
datos, para otro tercio de éstos es la mejor estimación evaluada.
La razón de dicho fenómeno, es precisamente la dispersión de los
que al ser cuantificada
con la desviación estándar, permite notar que ese 31.4% de los casos en donde el Promedio
geométrico (-1) fue mejor que las demás estimaciones, tiene como característica común una
baja desviación estándar. Así, se decidió realizar un nuevo conjunto de cálculos de
en donde el conjunto de
’s tuviera una desviación estándar acotada con un máximo, que
en el caso de la ejecución mostrada en la Figura 33, fue de 0.20.
0.00
0.02
0.04
0.06
0.08
0.10
0.12
0.14
0.16
0.18
0.0
0.2
0.4
0.6
0.8
1.0
1.2
Er
ro
r
ab
solut
o
e
n
e
l val
o
r
d
e
p
ro
b
ab
ili
d
ad
(
)
Percentil ()
Con promedio aritmético
Con promedio geométrico (-1c)
Con promedio geométrico (-1)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
91
Figura 33. Error en la estimación de la probabilidad de un estado para desviaciones estándar entre 0.02 y 0.20.
En la Figura 33 se puede notar como la estimación con Promedio geométrico (-1) tiene un
comportamiento considerablemente mejor que las demás estimaciones, que puede verse
evidenciado no solo en la menor magnitud de sus errores, sino en la frecuencia con la que
estos son inferiores a los generados por las otras estimaciones. Esta frecuencia para el caso
graficado en la mencionada figura fue del 78.3% de los casos, en comparación con el 7.9% del
Promedio geométrico (-1c) y con el 13.8% del Promedio aritmético.
Esto quiere decir que para desviaciones estándar bajas, la Ecuación 54 representa la mejor
manera de calcular el parámetro de la distribución Binomial. Para llegar a una conclusión
parecida para desviaciones estándar altas, se realizó otro conjunto de cálculos, pero esta vez
definiendo un valor mínimo para de desviación estándar, que en el caso de la Figura 34 fue de
0.50.
0
0.002
0.004
0.006
0.008
0.01
0.012
0.014
0
0.2
0.4
0.6
0.8
1
1.2
Er
ro
r
ab
solut
o
e
n
e
l val
o
r
d
e
p
ro
b
ab
ili
d
ad
(
)
Percentil ()
Con promedio aritmético
Con promedio geométrico (-1c)
Con promedio geométrico (-1)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
92
Figura 34. Error en la estimación de la probabilidad de un estado para desviaciones estándar entre 0.28 y 0.50.
En la Figura 34 se nota que la estimación con Promedio geométrico (-1) presenta problemas
importantes a la hora de estimar dichas probabilidades siendo la mejor estimación solo en el
12.9% de los casos, mientras que el Promedio geométrico (-1c) fue mejor en el 65.4%, y el
Promedio aritmético fue mejor en el 21.7%. Esta observación, y unas similares para otros
conjuntos de cálculos, permiten concluir que para desviaciones estándar altas es
recomendable utilizar la Ecuación 53.
Sin embargo, al tener en cuenta la magnitud de los errores para las desviaciones estándar
altas, se hace la recomendación adicional de dividir el conjunto de
en al menos 2
subconjuntos que minimicen las desviaciones estándar de cada uno (la forma natural de
hacerlo es definir un subconjunto con los aparatos de alta
y otro subconjunto con los
aparatos de baja
), para después calcular la representativa de cada subconjunto con el
Promedio geométrico (-1) y estimar
como la suma de las posibles combinaciones de
y
tal y como se muestra en el siguiente ejemplo:
Sea el conjunto de
’s: { } y se desea
calcular
. Entonces, dado que la desviación estándar de es 0.38, se hace
necesario
definir
los
subconjuntos
{ }
y
{ } para realizar una mejor estimación de la probabilidad del
estado 3. Teniendo en cuenta que la desviación estándar de
es 0.08 y de
es 0.07, la
estimación de los parámetros
y
se puede hacer utilizando la Ecuación 54:
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0
0.2
0.4
0.6
0.8
1
1.2
Er
ro
r
ab
solut
o
e
n
e
l val
o
r
d
e
p
ro
b
ab
ili
d
ad
(
)
Percentil ()
Con promedio aritmético
Con promedio geométrico (-1c)
Con promedio geométrico (-1)
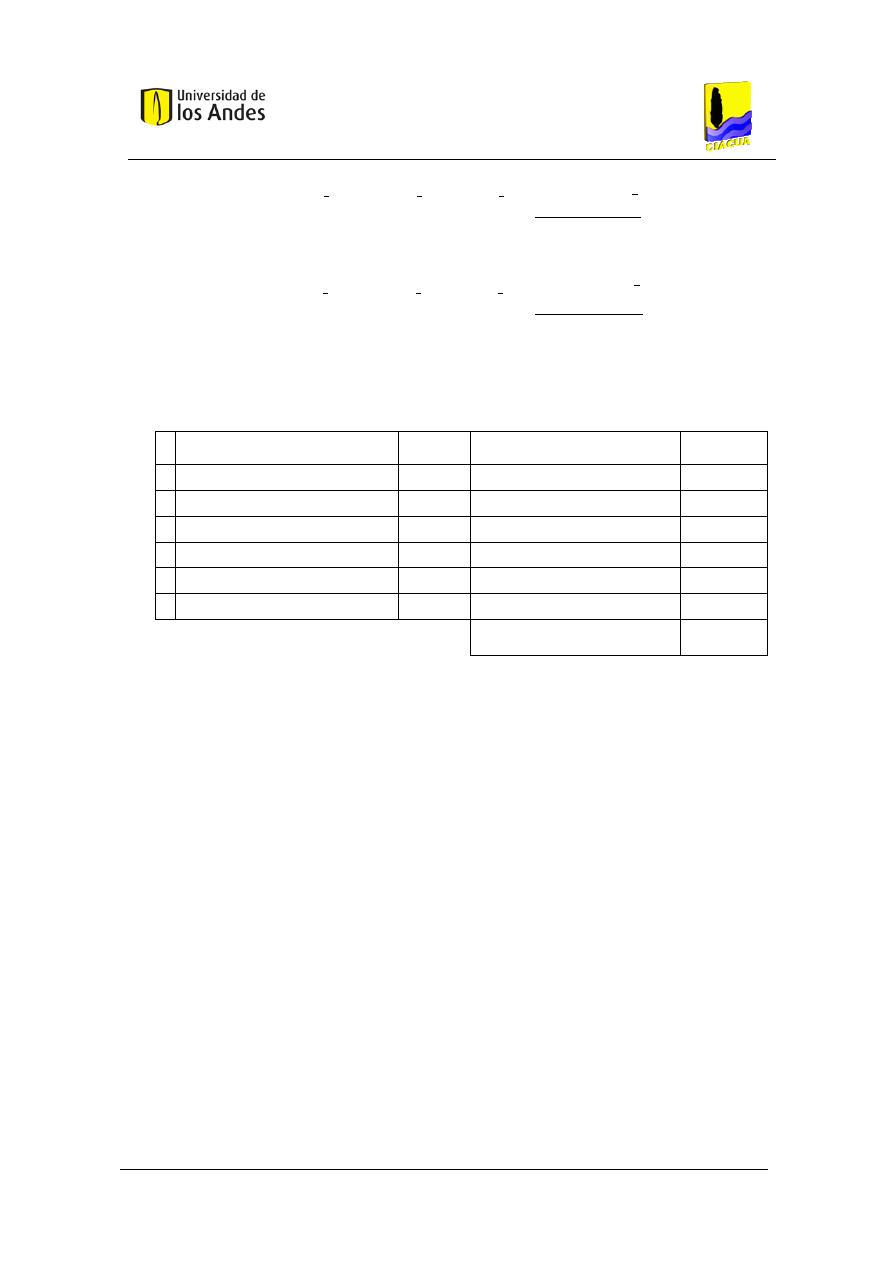
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
93
(∏
)
(
(
(∏
)
(∏
)
)
)
(∏
)
(∏
)
(
(
(∏
)
(∏
)
)
)
(∏
)
Una vez se conocen los parámetros se puede aplicar la Ecuación 51 para calcular
y
y calcular
como la suma del producto de dichos términos:
(
)
(
)
-
-
4
0.56
-
0
0.48
3
0.35
0.17
1
0.39
2
0.08
0.03
2
0.11
1
8.19E-03
9.41E-04
3
0.02
0
3.14E-04
4.80E-06
4
7.59E-04
-
-
-
∑
0.1996
Si se compara el valor estimado con la metodología sugerida con el valor real calculado
con la Ecuación 47
, se llega una diferencia de 0.0015 la cual
representa un error admisible para el cálculo de dicha probabilidad. Así, se tiene una
estimación que no requiere el cálculo de las probabilidades de
ocurrencia de cada escenario con 3 aparatos encendidos y que estima de manera
aceptable la probabilidad de este estado.
El anterior ejemplo muestra la aplicación de la metodología sugerida para el cálculo de la
probabilidad de ocurrencia de cada estado. Sin embargo no se debe olvidar que la metodología
de estimación debe ser utilizada sólo cuando el número de cálculos requerido para la
utilización de la Ecuación 47 implique un tiempo de cálculo muy alto.
Una vez se tiene una manera de calcular la probabilidad de cada estado, es posible determinar
el estado de diseño como el estado cuya probabilidad acumulada es mayor que el
complemento de la probabilidad de falla aceptable. Esa probabilidad acumulada de un estado
puede ser calculada entonces como:
∑
Ecuación 55

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
94
donde:
: Probabilidad de que el sistema esté en un escenario con o menos
aparatos encendidos. Denominada como probabilidad acumulada del estado .
: Probabilidad de que el sistema esté en un escenario con exactamente
aparatos encendidos.
Así, el estado de diseño es el menor estado
que cumple que:
Ecuación 56
donde:
: Probabilidad de falla máxima que se desea para el sistema diseñado.
El anterior análisis permite identificar el estado de diseño de cada tubo de la red a partir de
una probabilidad de falla aceptable dada. Se debe notar que como datos adicionales para la
ejecución del procedimiento es necesario conocer el número de aparatos aguas abajo del tubo
analizado así como la probabilidad de uso
de cada uno de dichos aparatos. Por un
lado, las probabilidades de uso, son halladas con el procedimiento descrito en la Sección 3.2.1,
y por otro lado, el número de aparatos aguas abajo del tubo puede ser determinado mediante
simple observación a la red, en caso de ser una red con geometría abierta, es decir que sólo
existe un camino entre dos puntos cualquiera de la red. Sin embargo en el caso de que la red
tenga topología cerrada, se hace necesario hacer uso de los resultados del procedimiento de
Asignación de una Línea de Gradiente Hidráulico (LGH) (Sección 5.1), que permiten conocer la
altura piezométrica total en cada nudo de la red y por lo tanto el sentido de flujo de cada
tubería. Estos sentidos de flujo permiten a su vez determinar los nudos alimentados por un
tubo y así contar el número de aparatos aguas abajo de éste.
Cálculo del caudal de diseño de un tubo
Una vez se conoce el estado de diseño
se debe seleccionar un escenario de dicho estado
con el cual se pueda evaluar el caudal en el tubo a diseñar, para así proceder a calcular el
diámetro de éste. Para ello, se debe considerar que, en caso de que la probabilidad acumulada
del estado
sea exactamente igual a (
), el caudal de diseño debe ser
exactamente igual al máximo caudal requerido por un escenario con
aparatos encendidos.
Es decir que una aproximación conservadora consistiría en tomar el máximo caudal que puede
ser requerido por un escenario con
aparatos encendidos para dicho tubo. Para ello bastaría
ordenar la lista de los aparatos aguas abajo del tubo a diseñar de mayor a menor caudal
emitido, para después tomar los primeros
aparatos y sumar dichos caudales, y así tomar
ese valor como el caudal de diseño.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
95
Por otro lado, si se tiene en cuenta que el procedimiento de cálculo del estado de diseño
puede seleccionar un estado
cuya probabilidad acumulada es considerablemente mayor
que (
) en vez de seleccionar el estado anterior
cuya probabilidad
acumulada es inferior, por muy poco, a dicho valor; entonces es claro que el caudal de diseño
del tubo debería ser un valor intermedio entre el caudal máximo del estado
y el
caudal máximo del estado
. Para determinar dicho valor se podría suponer una relación
lineal entre la probabilidad acumulada y el caudal de diseño, al menos dentro de dicho
intervalo de probabilidades acumuladas. Así el valor del caudal de diseño sería el
correspondiente a una interpolación lineal entre los caudales de diseño correspondientes al
estado
y al estado
, tal y como se muestra en el siguiente ejemplo:
Suponga que se tiene un tubo con 8 aparatos aguas abajo cuyo conjunto de
’s es:
{ } y se desea calcular su caudal de
diseño para una probabilidad de diseño de 5%. Entonces se debe calcular
hasta
que el valor acumulado de las probabilidades sea mayor a 95%.
Utilizando la Ecuación 47 para el cálculo de las probabilidades de cada estado, se llega a
las siguientes probabilidades:
0
1.08E-04
1.08E-04
1
3.38E-03
3.49E-03
2
3.91E-02
4.26E-02
3
1.99E-01
2.42E-01
4
4.16E-01
6.58E-01
5
2.65E-01
9.23E-01
6
6.91E-02
9.92E-01
7
7.84E-03
1.00E+00
8
3.23E-04
1.00E+00
Es decir que el estado es el que cumple la condición de que su probabilidad
acumulada es mayor al complemento de la probabilidad aceptable de falla
. Si el conjunto de los caudales emitidos por los aparatos es
{ } , entonces el caudal de diseño
según la aproximación conservadora sería correspondientes a la suma de los
mayores 6 caudales de
Si en cambio se utiliza la aproximación no conservadora, entonces se sabe que el caudal
de diseño estará entre correspondiente a y correspondiente a
. Suponiendo una relación lineal entre la probabilidad acumulada y el caudal para el
intervalo analizado, se tendría que el caudal de diseño para una probabilidad de falla de
exactamente 5% es:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
96
donde:
: Caudal de diseño del tubo analizado según la aproximación no conservadora.
y
: Caudales máximos con 5 y 6 aparatos encendidos, respectivamente.
y
: Probabilidad acumulada del estado 5 y el estado 6, respectivamente.
Como se puede ver en el anterior ejemplo, las dos formas de calcular el caudal de diseño no
difieren significativamente en el resultado, aunque esa diferencia puede llegar a verse
magnificada para tuberías con bajo número de aparatos aguas abajo, en cuyo caso se
recomienda tomar el caudal de diseño conservador.
5.3.2 Análisis estocástico para nudos dependientes
Teniendo en cuenta que se hizo la suposición de independencia entre las probabilidades de
uso de los nudos para el desarrollo de la formulación anteriormente mencionada, y dado que
existen posibles análisis en donde se considera conveniente incluir el efecto de la dependencia
entre los usos de un conjunto de aparatos, es necesario reajustar la metodología de cálculo del
caudal de diseño para nudos dependientes. Para ello es necesario notar que el análisis de los
escenarios que permite encontrar su orden según la exigencia hidráulica que implican (Figura
28) y el análisis de la probabilidad de falla, no se ven afectados por la dependencia o
independencia de los aparatos de la red. Así para realizar el cálculo del caudal de diseño de un
tubo con un conjunto de nudos dependientes aguas abajo de éste, debe realizarse la selección
de un estado de diseño y la posterior aplicación la misma metodología de cálculo de caudal de
diseño a partir de un estado de diseño que en el caso de nudos independientes.
Es decir que el único paso que se debe ver afectado por la dependencia del uso de los nudos es
aquel en el que se calculan las probabilidades de ocurrencia de cada estado, de manera que la
Ecuación 47 deja de ser válida para calcular
entendido como la probabilidad de
que se esté en el estado en una red con nudos de demanda.
Sin embargo si se analiza el caso cuando un tubo tiene un número de nudos aguas abajo con
demanda
todos independientes entre sí, y el tubo inmediatamente aguas arriba tiene los
mismos
nudos más un conjunto de
aparatos dependientes entre sí, resulta claro que
la probabilidad de que ocurra el estado para el tubo aguas arriba será:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
97
∑
Ecuación 57
donde:
: Probabilidad de que un tubo con
nudos independientes aguas
abajo y
nudos dependientes aguas abajo se encuentre en un escenario del estado
.
: Probabilidad de que un tubo con los mismos
nudos del tubo
mencionado arriba se encuentre en un escenario del estado . Dado que son
aparatos independientes, este valor puede ser calculado con la Ecuación 47 o con alguna
de sus aproximaciones mencionadas en la Sección 5.3.1.
: Probabilidad de que un tubo con los mismos
nudos del tubo
mencionado arriba se encuentre en un escenario del estado . Dado que son
aparatos dependientes entre sí, este valor debe ser calculado con base en los resultados
de la simulación con eventos discretos utilizada para la modelación de la dependencia.
y
: Número de nudos con demanda independiente y dependiente,
respectivamente, ubicados aguas abajo del tubo analizado.
Y si se generaliza la expresión de la Ecuación 57 para tubos con más de un conjunto de
aparatos dependientes entre sí, se llega a la Ecuación 58 y la Ecuación 59:
∑[
]
Ecuación 58
∑
(
)
Ecuación 59
donde:
∑
: Número total de nudos con alguna dependencia, aguas abajo del tubo
analizado. Corresponde a la suma de los nudos de cada uno de los conjuntos de nudos
dependientes entre sí.
: Número total de nudos con dependencia entre sí del conjunto de nudos
dependientes.
: Probabilidad de que un tubo (posiblemente hipotético) con los mismos
∑
nudos dependientes del tubo analizado se encuentre en un escenario del estado
.
: Probabilidad de que un tubo con los mismos
nudos
dependientes del tubo analizado se encuentre en un escenario del estado
.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
98
: Estados evaluados para cada conjunto de nudos dependientes. Las posibles
combinaciones son todas aquellas combinaciones de valores de estos valores cuya suma
es igual a .
De esta manera se pueden incorporar a la metodología de cálculo del caudal de diseño, los
casos donde se presenten dependencias de uso entre los aparatos de una red. Se debe notar
que, si bien la notación de las ecuaciones anteriormente encontradas puede resultar
complicada, su implementación consiste en aplicar la metodología mostrada en el ejemplo de
la página 92 dividiendo la totalidad de los aparatos en dos subconjuntos correspondientes a los
aparatos independientes y al conjunto de aparatos dependientes. De manera que se calculan
las probabilidades de cada estado para el subconjunto de nudos independientes con la
Ecuación 47, y se utilizan los resultados de la simulación hecha para calcular las probabilidades
de cada estado del subconjunto de nudos dependientes, como la adición de las probabilidades
de cada escenario de un mismo estado.
5.4 Cálculo y redondeo del diámetro del tubo
Una vez se conoce el caudal de diseño del tubo y la altura piezométrica ideal en los nudos
aguas arriba y aguas abajo de éste, se debe calcular el diámetro que asegura que se presenten
dichas condiciones hidráulicas. Ese cálculo se basa en la ecuación de conservación de energía y
en la ecuación de fricción de flujo en una tubería presurizada. Así, cuando la ecuación de
fricción es Hazen-Williams, el cálculo del diámetro es explícito, mientras que cuando la
ecuación es Darcy-Weisbach en conjunto con Colebrooke-White, el cálculo se hace implícito
requiriendo de métodos numéricos para su solución.
Después de realizar el cálculo del diámetro continuo, se debe tener en cuenta una restricción
del problema de diseño que consiste en la disponibilidad de diámetros discretos en el mercado
local del sistema. Así, el diámetro hallado mediante la ecuación de fricción difícilmente estará
disponible en el mercado, y por lo tanto es necesario seleccionar uno de los disponibles. Este
paso se denomina redondeo, y puede ser realizado de diferentes maneras.
Sin embargo, Takahashi et al. (2011) presentan una manera de hacerlo en la que se selecciona
el diámetro discreto cuyo valor de caudal es más cercado al caudal de diseño. Para ello
proponen elevar el valor del diámetro continuo a un exponente de 2.6 (correspondiente a la
relación potencial entre diámetro y caudal) para después seleccionar el diámetro discreto que,
al ser elevado a la 2.6, tenga menor diferencia respecto éste valor.
Un análisis similar puede ser realizado, buscando seleccionar el diámetro cuyas pérdidas por
fricción sean las más cercanas a las ideales. En dicho caso se realizaría el mismo procedimiento
anterior, pero utilizando un exponente de -4.8655 (correspondiente a la relación potencial
entre diámetro y pérdidas por fricción).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
99
5.5 Asignación de una LGH para la red aguas abajo del tubo
Independientemente de la manera seleccionada para realizar el redondeo, si se dispone de
una altura piezométrica fija aguas arriba del tubo a diseñar, y se le asigna un diámetro
diferente al diámetro continuo calculado con la ecuación de fricción, entonces la altura
piezométrica aguas abajo diferirá de la asignada en la Sección 5.1 (Asignación de una Línea de
Gradiente Hidráulico (LGH)) en el momento en que fluya el caudal de diseño de dicho tubo. Es
decir que al redondear el diámetro del tubo se esta deformando la LGH y por lo tanto se
recomienda reajustar la superficie para tener en cuenta el déficit o superávit de energía que
dejó el redondeo del diámetro.
Si bien dicho reajuste puede ser realizado de diferentes maneras, se recomienda modificar
únicamente la LGH del nudo inmediatamente aguas abajo del tubo recién diseñado. Ello
implica que el déficit o superávit de energía debe ser asignado en su totalidad al tubo
inmediatamente aguas abajo, procurando así que en su diseño se llegue a una LGH aguas abajo
cercana a la asignada inicialmente, conservando de esta manera los caudales emitidos
calculados en el paso de la Sección 5.2.
Como inconveniente del anterior procedimiento se tiene que un posible déficit de energía
puede ser suficientemente alto como para generar una LGH del nudo aguas abajo inferior a la
LGH del siguiente nudo aguas abajo, llegando a una condición de diseño no factible en la que
se crearía energía. En dicho caso sería necesaria una modificación del diámetro del tubo recién
diseñado de manera que se tome como valor final el diámetro discreto inmediatamente mayor
al que había sido asignado.
Si por otro lado se supone que el mercado dispone de cualquier diámetro continuo encontrado
en el paso anterior, de manera que no ha sido necesario el redondeo, entonces la diferencia de
LGH con la que se diseñará el (o los) tubo(s) aguas abajo debe considerar que el caudal de
diseño del tubo a diseñar puede implicar, por conservación de la masa, que por el tubo ya
diseñado fluirá un caudal menor al de diseño de dicho tubo, haciendo que las pérdidas totales
sean menores a las de diseño y por lo tanto se dispondrá de mayor altura piezométrica para
trasportar el caudal de diseño del tubo a diseñar. Así, si se desean evitar los sobrediseños se
debe tener en cuenta esta diferencia adicional de energía, que aplica de igual manera para el
caso en donde el diámetro tuvo que ser redondeado.
5.6 Proceso iterativo
Los anteriores pasos realizan el diseño de un tubo seleccionado. Es decir que es necesario
realizar tantas veces esos pasos como tubos tenga la red. El orden en que se debe recorrer la
red diseñando sus tubos es de aguas arriba a aguas abajo, teniendo en cuenta que el redondeo
de un tubo aguas arriba afecta la superficie ideal de la red aguas abajo. Así, el diseño concluye

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
100
cuando se han diseñado todos los tubos, es decir cuando se han diseñado los tubos
conectados a los aparatos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
101
6 Comprobación de diseño propuesta
Independientemente de la manera en que se diseña, es conveniente poder evaluar el
comportamiento hidráulico de una RIDAP bajo diferentes condiciones de demanda para
determinar las velocidades del flujo y las presiones en cada nudo y así conocer la calidad de la
respuesta del sistema ante escenarios de demanda no necesariamente de diseño. Para ello es
necesario poder ejecutar la hidráulica de una red ya diseñada (todos sus parámetros están
determinados) incluyendo el comportamiento de los aparatos sanitarios, que no precisamente
emiten un caudal constante independientemente de la presión en el nudo al que están
conectados.
Así, motores de ejecución hidráulica como EPANET (Rossman, 2000) o REDES (CIACUA, 2006)
son capaces de modelar nudos con una demanda independiente de la presión y nudos con una
demanda relacionada con la presión mediante la expresión de la Ecuación 1, pero no incluyen
una modelación de curvas como la Curva Única definida en la Sección 3.1. Adicionalmente
EPANET sólo permite un único exponente para todos los nudos que se modelen con la
Ecuación 1, lo que restringe su utilidad para la modelación de RIDAPs.
A fin de disponer de un programa que permita la ejecución hidráulica de las RIDAPs incluyendo
la Curva Única, se desarrolló e implementó un algoritmo que permite definir la curva
(Caudal emitido vs. Presión en el nudo) para cada nudo de la red, de manera no
necesariamente potencial (ver Figura 35). Para ello se hizo uso del Toolkit de EPANET para su
acople a código desarrollado en MSExcel con VBA para Aplicaciones.
6.1 Discretización de las Curvas Únicas y ajuste de la función
Teniendo en cuenta la forma de las Curvas Únicas expuesta en la Sección 3.1, la función que
describe su comportamiento es una función a trozos o por partes. Esto representa un
inconveniente a la hora de buscar un algoritmo que utilice una función continua en la cual se
represente el emisor con curva única de manera similar a los emisores típicos descritos con la
Ecuación 1.
Así, se considera conveniente discretizar la curva única (o cualquier otra curva que se desee
asignar como caudal emitido dependiente de la presión) de manera que se realice una
interpolación entre los datos de manera continua. Adicionalmente, dicha discretización aporta
versatilidad al programa, teniendo en cuenta que se desarrolló en MSExcel y en éste es
necesario ingresar un conjunto de puntos para que sea graficado y reconocido como una
función.
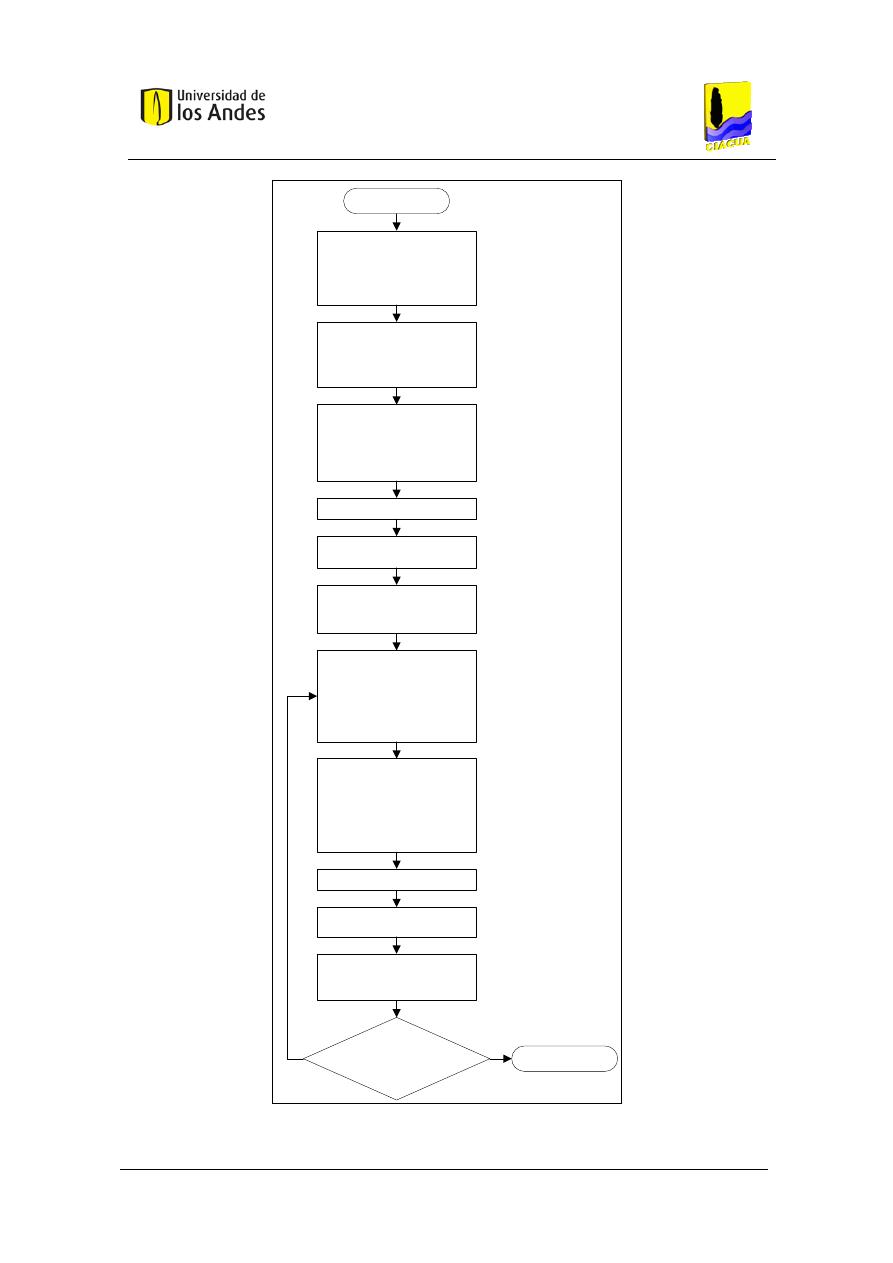
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
102
Figura 35. Diagrama de flujo del algoritmo de ejecución hidráulica para RIDAPs.
Inicio
Leer:
1. Curvas Únicas
discretizadas de cada nudo.
2. Exponente por defecto
para emisores:
x.
Ajustar una función de la
forma:
Q=Q
o
+ k*h
x
para cada curva única.
Asignar el coeficiente
k
como el coeficiente del
emisor y el caudal
Q
o
como
demanda base de cada
nudo.
Ejecutar la hidráulica
Leer la presión
h
i
y hallar el
intervalo
[h
inf
, h
sup
)
i
de la
curva única discretizada al
cual pertenece la presión
encontrada, para cada nudo
de la red.
Recalcular
k
y
Q
o
para el
intervalo de
h
haciendo que
la función:
Q=Q
o
+k*h
x
Pase por los puntos
(h
inf ,
Q
inf
)
i
y
(h
sup ,
Q
sup
)
i
.
i = 1
Leer el caudal total
Q
i
emitido por cada nudo de la
red.
i = i + 1
Ejecutar la hidráulica
Leer el caudal total
Q
i
emitido por cada nudo de la
red.
Max(|
Q
i
-Q
i-1
|) <
Error
Admisible
Fin

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
103
De esta manera, el programa requiere una tabla de puntos que describa de manera
aceptable la curva única del emisor que se desea simular. Teniendo en cuenta que para las
RIDAPs las curvas de emisores se repiten dentro de la red por cuenta de aparatos iguales
asignados a diferentes nudos de la red (e.g. todos los lavamanos tienen la misma curva
independientemente del nudo al que se conectan), el programa permite asignar a diferentes
nudos una misma curva, evitando la reiteración en el ingreso de información.
Así, una vez se tienen definidas de manera discretizada todas las curvas únicas y éstas se han
asignado a cada nudo de demanda de la red, se puede comenzar a resolver la ejecución
hidráulica de la misma. Para ello se hace una primera ejecución hidráulica asignándole a cada
nudo una función como la presentada en la Ecuación 60:
Ecuación 60
Dicha ecuación corresponde a la función que el programa EPANET puede ejecutar, en
donde
corresponde con la denominada demanda base, corresponde con el coeficiente de
emisor y corresponde con el exponente global del emisor que debe ser igual para todos los
nudos.
A fin de que la función inicial asignada a cada nudo sea representativa de la curva única
asignada, se pueden calcular los parámetros
y que minimizan el Error Cuadrático Medio
(ECM) respecto a todos los puntos que representan la curva única discretizada. El resultado del
cálculo analítico de la expresión para estos dos parámetros es entonces:
̅
∑
∑
Ecuación 61
̅̅̅̅
Ecuación 62
donde:
̅ : Estimación del parámetro que minimiza el ECM para los puntos de la curva única
discretizada.
̅̅̅̅ : Estimación del parámetro
que minimiza el ECM para los puntos de la curva única
discretizada.
,
: Valores de caudal y presión, respectivamente, que definen el punto de la curva
única discretizada.
: Valor del exponente del emisor que tenga por defecto el archivo de EPANET
(usualmente 0.5).
: Número de puntos que tiene la curva única discretizada.
: Caudal que se le ha asignado al nudo como demanda independiente
de la presión.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
104
Como resultado se tiene entonces una par de parámetros que ajustan una función a cada
curva única y que, por lo tanto, deben ser asignados a todos los nudos con esa curva única. Así,
al ejecutar la hidráulica se tendrá una primera aproximación de la presión y el caudal emitido
en cada nudo.
6.2 Interpolación e iteración
Teniendo en cuenta que como resultado de los pasos anteriores se tiene una primera
aproximación de la presión y del caudal emitido por cada nudo, se puede calcular el par de
puntos de la curva única discretizada cuyas presiones
y
son menor o igual y mayor,
respectivamente, que la presión encontrada en la primera ejecución hidráulica, para cada
nudo. Esto permite conocer el intervalo (
) (
) tentativo en donde puede
estar el punto que cumple con todas las ecuaciones de la ejecución hidráulica de la red.
Una vez se conoce este intervalo, es posible mejorar la estimación de los parámetros y
para que generen una función que cruce exactamente por los puntos (
) y
(
). Así, el cálculo de estas nuevas estimaciones se hace mediante la Ecuación 63 y la
Ecuación 64.
̅
(
)
(
)
Ecuación 63
̅̅̅̅
(
)
(
)
Ecuación 64
Esta estimación genera una manera natural de interpolación en la curva única, regida por la
Ecuación 60. Así, si después de dos iteraciones seguidas todos los nudos siguen en el mismo
intervalo de sus respectivas curvas, entonces se ha encontrado la solución a las ecuaciones de
ejecución hidráulica y el error en el caudal y la presión será cero respecto a la curva única
discretizada, dado que, para esos intervalos caracterizados con esas curvas de emisor, la
solución dada por EPANET resuelve las ecuaciones mediante el método del gradiente (ver
Saldarriaga, 2007) con una precisión mucho mayor a la requerida.
Sin embargo, el procedimiento resulta más eficiente si sólo se almacena como resultado de
cada iteración el caudal emitido en cada nudo, de manera que iteración a iteración se
comprara únicamente el caudal emitido en cada nudo y no el intervalo de la curva única
discretizada en el que se encuentra el nudo. Así la solución completa de la ejecución hidráulica
debe cumplir con que todos sus nudos tengan una diferencia entre iteraciones menor a la
mínima admisible, y por lo tanto se pueden calcular las diferencias y se compara únicamente la
mayor de todas éstas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
105
6.3 Cálculo de los demás resultados hidráulicos
Una vez se ha llegado a una caracterización de la curva de cada nudo que representa
aceptablemente su comportamiento para el rango de caudales y presiones que éste emite y
tiene, respectivamente, se tiene una solución de toda la hidráulica de la red, de manera que se
pueden conocer otras variables resultado de la ejecución como velocidades y esfuerzos
cortantes en las tuberías, alturas piezométricas totales en los nudos y demás.
Para ello basta tomar los resultados hidráulicos de la última ejecución hidráulica, calculados
por EPANET, y presentarlos como los resultados finales de la red. El programa desarrollado
para implementar este algoritmo y permitir la simulación hidráulica de RIDAPs mediante la
curva única, incluye entonces tablas de resultados de todas las variables disponibles para cada
nudo y tubo.
6.4 Software desarrollado
A fin de implementar el algoritmo desarrollado y disponer de un software que facilite la
comprobación de diseño para una RIDAP modelada mediante la curva única se desarrolló un
libro en MSEXCEL con VBA para Aplicaciones que en conjunto con el Toolkit de EPANET 2.0
(Rossman, 2000) permite conocer los resultados hidráulicos de una red con emisores variables
y no necesariamente potenciales.
El procedimiento para hacer uso del programa se divide en 5 subprocesos cada uno de los
cuales está listado en la interfaz principal del programa (ver Figura 36). El primer paso consiste
en limpiar todo el libro de EXCEL reiniciando cada una de las secciones. A continuación se debe
seleccionar un modelo de la red ya creado mediante EPANET, permitiendo al programa
conocer la lista de nudos y de tubos, así como la ubicación del archivo.
Una vez se tiene ingresado el modelo de la red se procede a ingresar las curvas únicas que
existen en el modelo. Así, se deben ingresar tantas curvas como aparatos sanitarios diferentes
se tengan, describiendo para cada una la lista de puntos
que describen, de manera
discretizada, la función . Es en este paso donde se nota la conveniencia de la
discretización, la cual permite definir curvas de funciones a trozos como la curva única de las
RIDAPs.
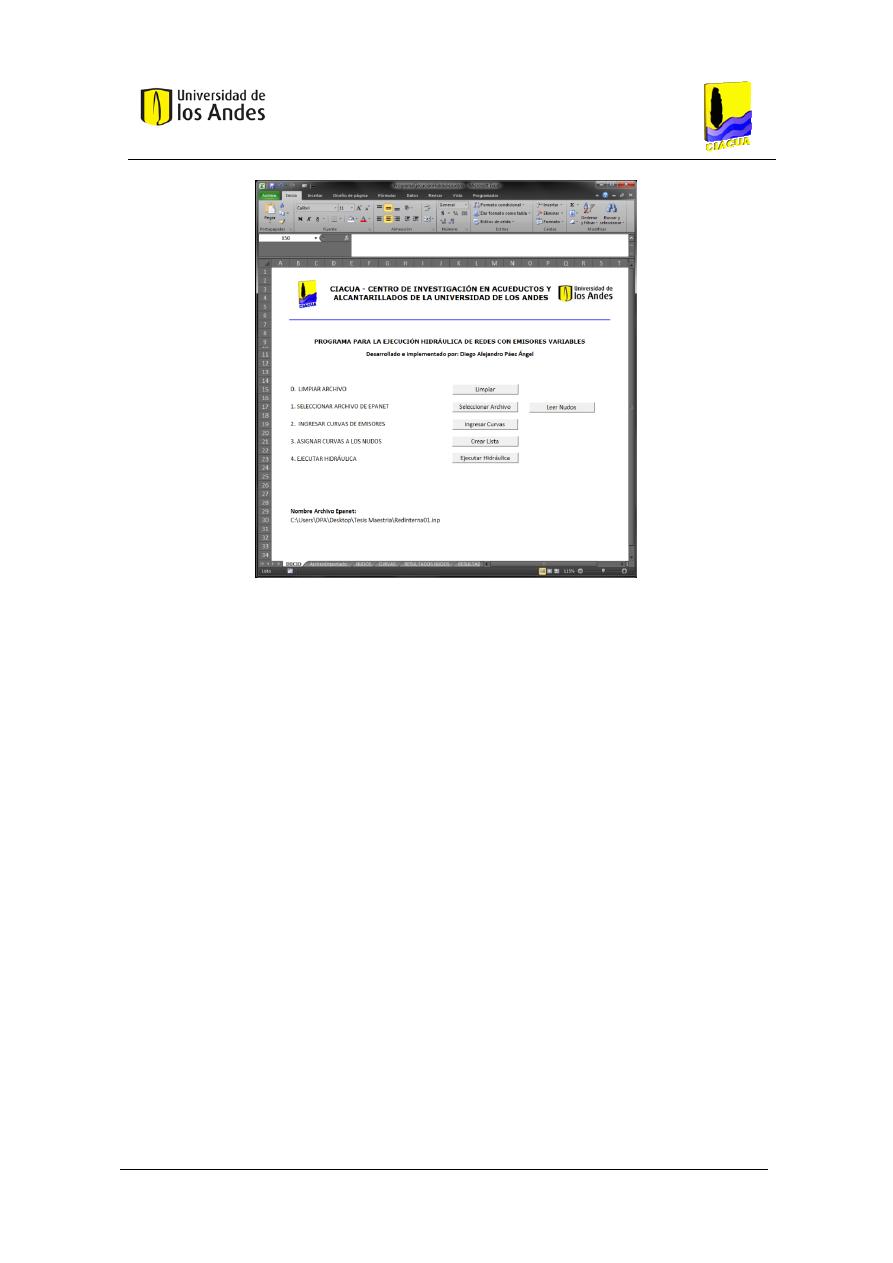
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
106
Figura 36. Interfaz principal del software.
Teniendo disponible una lista de curvas únicas definidas en el paso 2 del programa (sin incluir
la limpieza), se debe asignar a cada nudo una de estas curvas de manera que se caracterice el
comportamiento de la demanda en función de la presión en el nudo. Para ello el programa
genera una lista de las curvas exitosamente leídas para que el usuario seleccione de la lista el
nombre que corresponde a cada nudo. Adicionalmente se definen hipervínculos en las celdas
para que el usuario pueda revisar los datos ingresados en cada curva y así asegurar la correcta
asignación de curvas.
Finalmente el programa permite ejecutar la hidráulica, haciendo uso del algoritmo
anteriormente descrito y llamando a EPANET para cada ejecución hidráulica requerida. Así, es
posible presentar los resultados de la ejecución hidráulica final que para los nudos incluye los
datos de entrada y la altura piezométrica total, la presión, el caudal total de salida y de emisor
y el error en los caudales respecto a la iteración anterior. Asimismo para los tubos se
presentan los datos de entrada, y datos de salida como pérdidas totales en la tubería,
velocidad y caudal transportado.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
107
7 Casos de estudio
A fin de mostrar de manera explícita la implementación de la metodología de diseño
propuesta, se presentan 2 ejemplos de su uso en diferentes redes internas correspondientes a
sistemas reales ubicados en la ciudad de Bogotá, Colombia. Para ambos casos se supondrán los
mismos valores de los parámetros y funciones que caracterizan la demanda en los aparatos de
la red. Los parámetros de funcionamiento hidráulico de los aparatos presentes en los ejemplos
se basan en los resultados de Acero (2009) y en las recomendaciones de la Norma Técnica
Colombiana NTC 1500 (ICONTEC, 2004), mientras que los parámetros de caracterización
estocástica de la demanda se basan en los datos y mediciones de Blokker (2010a):
Tabla 18. Funciones de la curva única de los aparatos sanitarios en las redes ejemplo con base en Acero (2009).
Aparato sanitario
Curva única del aparato
Lavamanos
⁄ { ( )
Inodoro
⁄ ( )
Ducha
⁄ { ( )
Lavaplatos
⁄ { ( )
Fregadero/Llave
manguera/Lavadora
⁄ ( )
Tabla 19. Funciones de la curva única de los aparatos sanitarios en las redes ejemplo con base en ICONTEC (2004).
Aparato sanitario
Curva única del aparato
Lavamanos
⁄ { ( )
Inodoro
⁄ ( )
Ducha
⁄ { ( )
Lavaplatos
⁄ { ( )
Fregadero/Llave
manguera/Lavadora
⁄ ( )

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
108
Tabla 20. Frecuencia y Duración de uso para los aparatos sanitarios en las redes ejemplo con base en Blokker
(2010a).
Aparato sanitario
Frecuencia
(usos/(día*persona))
Duración
15
Lavamanos
Lavado y afeitado:
[ ]
Cepillado de dientes:
[ ]
Inodoro
Ducha
(
)
Lavaplatos
Consumo:
[ ]
Lavado de platos:
[ ]
Lavado de manos:
[ ]
Otros: [ ]
Fregadero/Llave
manguera/Lavadora
Tabla 21. Cálculo de la duración promedio total para los lavamanos de las redes ejemplo.
Uso
Duración: [ ]
Porcentaje del total
de usos
[ ]
Lavado y afeitado
Cepillado de dientes
Promedio total
15
Las duraciones son representadas por distribuciones lognormales, que tienen como inconveniente la
diversidad de sus parámetros. Así en algunos casos esta distribución es parametrizada por la media y la
desviación estándar de la variable distribuida lognormal, y en otros casos está parametrizada por la
media y la desviación estándar del logaritmo natural de la variable distribuida lognormal, cuya
distribución es normal. (Ver Anexo 11.2).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
109
Tabla 22. Cálculo de la duración promedio total para los lavaplatos de las redes ejemplo.
Uso
Duración: [ ]
Porcentaje del total
de usos
[ ]
Consumo
Lavado de platos
Lavado de manos
Otros
Promedio total
Por otro lado las condiciones de diseño seleccionadas con base en el comportamiento
hidráulico de los aparatos, las recomendaciones de ICONTEC (2004) y la confiabilidad deseada
del sistema
16
, se definieron los siguientes valores de los parámetros:
Tabla 23. Presiones mínimas aceptables y frecuencias de diseño.
Aparato sanitario
Presión correspondiente al
caudal mínimo admisible
(mca)
Frecuencia de diseño
(usos/(hora*persona))
Lavamanos
Inodoro
Ducha
Lavaplatos
17
Fregadero/Llave
manguera/Lavadora
Ecuación 65
Se debe notar que, si bien la frecuencia de uso tiene una distribución temporal en ciclos diarios
(e.g. Tabla 10 y Tabla 11), es necesario tomar un único valor de esta distribución para el cálculo
de las probabilidades de uso (utilización) que se asignaran a los aparatos para el cálculo de las
probabilidades de los estados. En este caso se han seleccionado las frecuencias
correspondientes a la hora en donde el caudal demandado esperado de toda la red es mayor a
lo largo del día, teniendo en cuenta la cercanía de los picos de cada distribución temporal. Para
distribuciones temporales muy diferentes entre lo aparatos, se recomienda la aproximación
hecha por CIACUA (2011) en donde se toma el percentil de la curva de distribución horaria
de la demanda, como valor de la frecuencia de uso de cada aparato.
16
Se entenderá confiabilidad como el complemento de la probabilidad de falla. Su definición para un
diseño se debe evaluar con base en un análisis de las pérdidas que implica una falla del sistema, tal y
como se explica en la Sección 5.3.1.
17
La frecuencia de uso del lavaplatos se encuentra en (usos/(hora*hogar)).
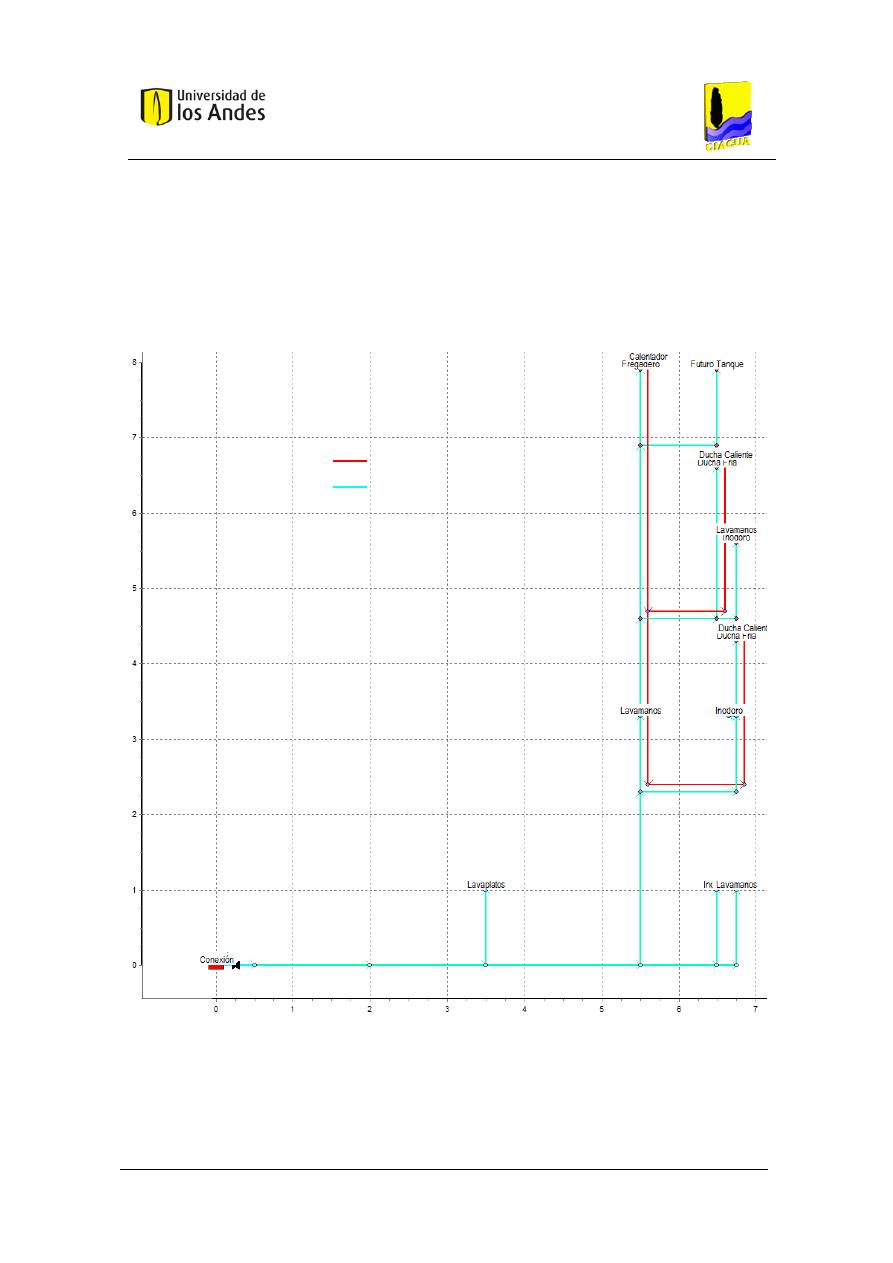
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
110
7.1 Caso de estudio 1: Red Interna Conjunto OASIS IV
Ubicado en la ciudad de Bogotá, Colombia, se encuentra un conjunto residencial con 183 casas
divididas en cuatro tipos de unidad: A, AA, C y CC. Teniendo en cuenta la complejidad de las
redes internas de cada una de las casas, se seleccionó la casa tipo C como la casa a modelar y
diseñar, ya que corresponde a una extensión de las casas tipo CC y a una red de mayor
exigencia hidráulica que las casas tipo A y AA.
Figura 37. Modelo casa OASIS IV tipo C - Vista en perfil. Aparatos conectados a la red.
Agua Caliente
Agua Fría

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
111
7.1.1 Asignación de una Línea de Gradiente Hidráulico (LGH)
Para la asignación de una LGH ideal para toda la red se hizo uso de la Ecuación 43 con un
, quedando escrita como:
(
)
Ecuación 66
Teniendo en cuenta que la Empresa de Acueducto de Bogotá (EAAB), asegura una presión
mínima de en cualquiera de las conexiones que se hagan a la red, y suponiendo un
diseño de la red de distribución interna del conjunto residencial que asegura una presión
similar a la entrada de las casas (ya sea mediante bombeo, mediante almacenamiento en
tanques elevados, o mediante diferencias topográficas dentro del conjunto), entonces la altura
piezométrica total disponible en la conexión se supone de es decir
Si por otro lado se nota que existen tantas trayectorias como sumideros
18
tenga la red,
entonces se notará que la Ecuación 66 deberá ser evaluada al menos 10 veces para la red
OASIS IV tipo C, y se requerirá una ejecución adicional por cada trayectoria en donde a un
nudo intermedio (no sumidero) se le asigne una LGH inferior a su LGH mínima
(correspondiente a la suma de su elevación y la presión mínima admisible de su aparato). Dado
que la red dispone de una válvula que representa el medidor de consumo y de un tubo con un
alto coeficiente de pérdidas menores que representa el calentador de agua, es necesario tener
en cuenta las pérdidas objetivo de estos dos accesorios a la hora de hacer la asignación de LGH
objetivo. Así el medidor de consumo siempre generará unas pérdidas de 3.0 mca, mientras que
el calentador generará pérdidas de 2.8 mca. En la Figura 38 se muestran los resultados de este
paso, presentando tanto la LGH asignada, como las presiones que corresponden con estas
alturas piezométricas.
7.1.2 Cálculo de los caudales emitidos
Haciendo uso de las curvas únicas de los aparatos descritas en la Tabla 18 para aparatos
ahorradores y en la Tabla 19 para aparatos de alto consumo, se calculó el caudal emitido por
cada aparato de la red de ejemplo cuando las presiones son iguales a las asignadas por el
procedimiento de la Sección 7.1.1 y presentadas en la Figura 38. Los resultados de este
procedimiento se muestran en la Figura 39.
18
Se entenderá como sumidero cualquier nudo que cumpla con que sus nudos adyacentes tienen mayor
LGH que él. Dada la geometría abierta de las RIDAPs, los sumideros deben ser aquellos nudos sin
tuberías o nudos aguas abajo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
112
Figura 38. Modelo casa OASIS IV tipo C – LGH ideal en mca (izquierda) y Presión ideal correspondiente en mca (derecha).
Agua Caliente
Agua Fría
Agua Caliente
Agua Fría
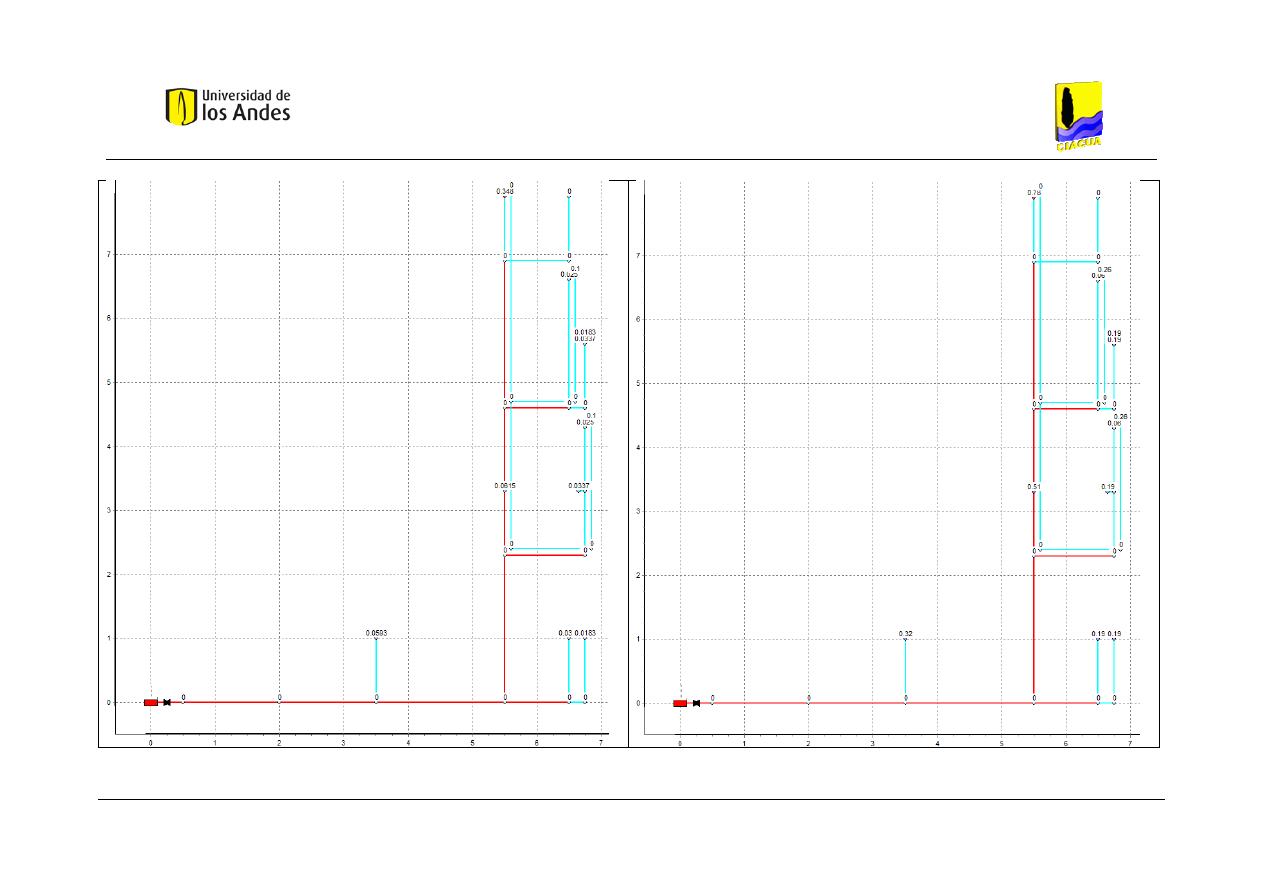
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
113
Figura 39. Modelo casa OASIS IV tipo C – Caudal emitido en L/s para el caso basado en Acero (izquierda) y para el caso basado en ICONTEC. (derecha).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
114
7.1.3 Cálculo de los caudales de diseño
Haciendo uso de los parámetros de caracterización estocástica de la demanda de los aparatos
mostrados en la Tabla 20 y suponiendo un total de 6 habitantes en la casa, se puede hacer uso
de la Ecuación 31 para encontrar el conjunto de probabilidades de uso de los aparatos:
Tabla 24. Probabilidades de uso de los aparatos para el diseño de la RIDAP.
Aparato sanitario
Probabilidad de uso
para diseño ()
Lavamanos
Inodoros
Duchas
Lavaplatos
Fregadero/Llave
manguera/Lavadora
Una vez se dispone del conjunto de probabilidades de uso y del conjunto de caudales
emitidos, es posible comenzar el procedimiento de cálculo del caudal de diseño para el primer
tubo aguas arriba. Teniendo en cuenta que la válvula que representa el medidor de consumo
de la red tiene fijado el valor de las pérdidas que genera, el primer tubo a diseñar
efectivamente es el ubicado aguas abajo de esta válvula, extendiendo después su diámetro al
tramo que incluye el medidor.
Dicho tubo tiene entonces 10 aparatos sanitarios aguas abajo, consistentes en 1 lavaplatos, 3
lavamanos, 3 inodoros, 2 duchas y 1 fregadero/lavadora. Así, se debe calcular la probabilidad
de ocurrencia de cada posible estado de la red aguas abajo del tubo a diseñar. Para ello se
hace uso de la Ecuación 47 llegando a los siguientes resultados:
Tabla 25. Probabilidades de ocurrencia de los estados.
Estado
Probabilidad
de ocurrencia
Probabilidad de ocurrencia dado
que el sistema está en uso
10
5.11E-14
1.01E-13
9
1.64E-11
3.26E-11
8
2.16E-09
4.29E-09
7
1.51E-07
2.99E-07
6
6.07E-06
1.20E-05
5
1.46E-04
2.91E-04
4
2.19E-03
4.34E-03
3
2.04E-02
4.04E-02
2
1.16E-01
2.29E-01
1
3.66E-01
7.26E-01
0
4.96E-01
-
Suma
1.00E+00
1.00E+00

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
115
A partir de los resultados de la Tabla 25, se puede concluir que el primer tubo de la red tiene
como estado de diseño , dado que la probabilidad acumulada para dicho estado supera
al complemento de la probabilidad de falla aceptable
. Si se tiene en
cuenta que la red se considera pequeña y que se recomienda tomar el caudal correspondiente
al caudal máximo del estado de diseño como caudal final de diseño, entonces éste será igual a
la suma de los dos mayores caudales emitidos aguas abajo del tubo.
Así, utilizando los valores de la Figura 39, se llega a que en el caso del diseño basado en Acero
(2009), el caudal de diseño es de
correspondiente a encender la llave del
fregadero/lavadora y una de las duchas de la casa. Similarmente el caudal de diseño según
ICONTEC (2006) corresponde a encender la llave del fregadero/lavadora y el lavamanos del
segundo piso:
.
7.1.4 Cálculo y redondeo del diámetro del tubo
Haciendo uso de la ecuación de Darcy-Weisbach (Ecuación 3) en conjunto con la ecuación de
Colebrooke-White (Ecuación 4), es posible hallar el diámetro continuo necesario para que el
caudal de diseño fluya por la tubería haciendo uso de la energía asignada en la Sección 7.1.1. El
procedimiento numérico necesario para su cálculo, puede ser revisado en Saldarriaga (2007).
Para el cálculo se tomó una aceleración de gravedad de
, una viscosidad cinemática
de
correspondiente a la del agua a , una rugosidad absoluta de
correspondiente a una tubería de PVC y un coeficiente de pérdidas menores de
que representa un codo estándar.
Como resultado se encuentra que para el caso basado en Acero el diámetro necesario es de
equivalente a , mientras que para el caso basado en ICONTEC se obtiene
un diámetro de equivalente a . Dado que en el mercado local no existen
tuberías de dicho diámetro, se hace necesario redondear el valor a uno de los comerciales
(Tabla 26). Si se utiliza el criterio de redondeo potencial con un exponente de 2.6, se tiene que
para el caso basado en Acero, el diámetro asignado a dicho tubo es de mientras que
para el caso basado en ICONTEC es de .
Tabla 26. Diámetros disponibles para las tuberías de la red.
Diámetro (in)
0.50
0.75
1.00
1.25
1.50
2.00
4.00
6.00
8.00
Diámetro (mm)
12.70
19.05
25.40
31.75
38.10
50.80
101.60
152.40
203.20
7.1.5 Asignación de una LGH para la red aguas abajo del tubo
Para el tubo inmediatamente aguas abajo del recién diseñado se debe considerar, por un lado
que el diámetro que efectivamente fue asignado al tubo difiere del que asegura la LGH ideal en
su nudo aguas abajo de manera que, para el caso de estudio, se tendrá una LGH menor a la
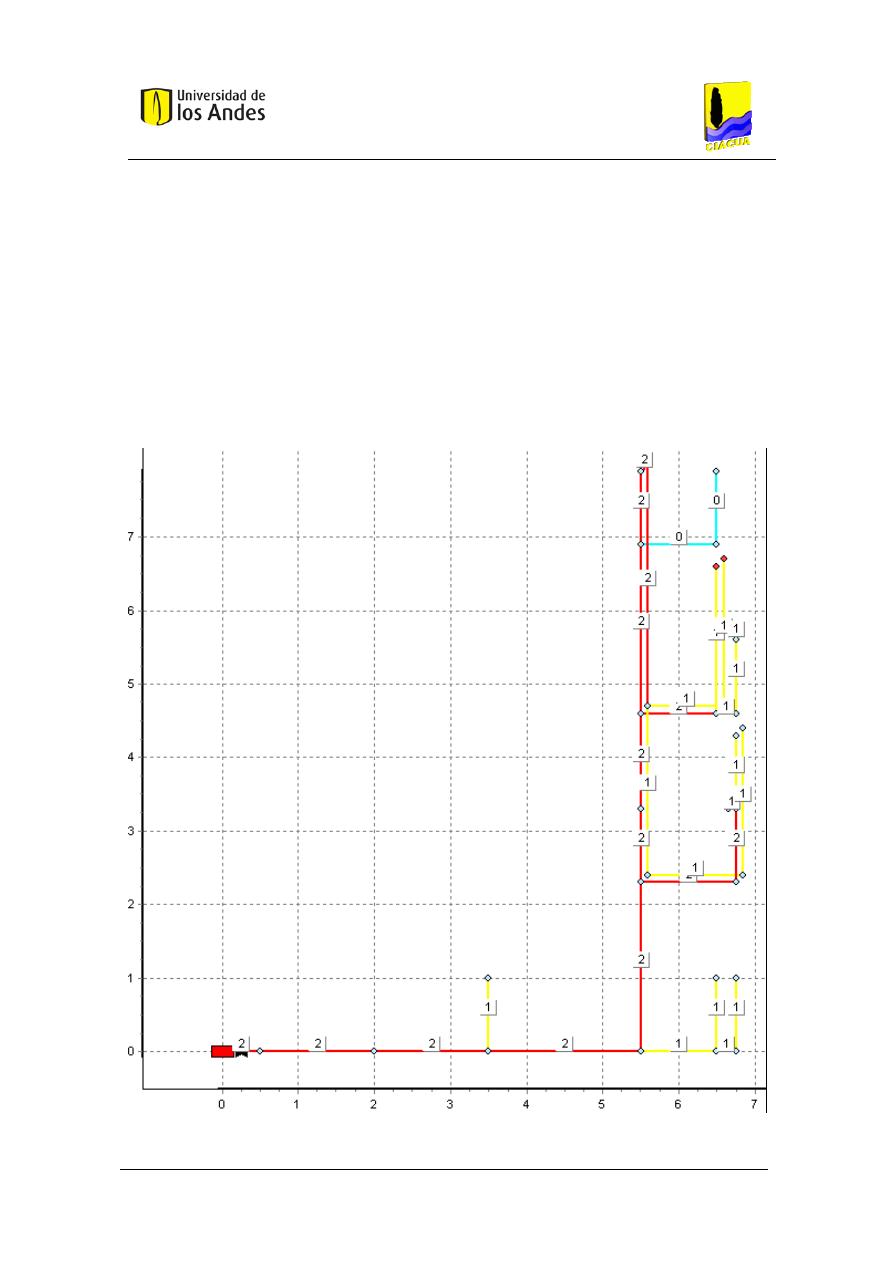
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
116
ideal cuando el caudal de diseño pase por el tubo, y por otro lado que por el tubo recién
diseñado no siempre está fluyendo su caudal de diseño. Así, la manera de calcular la LGH en el
nudo aguas arriba del nuevo tubo a diseñar consiste en hacer fluir su caudal de diseño por
toda la red aguas arriba (ya diseñada) encontrando la altura piezométrica con la que llega a
dicho nudo.
7.1.6 Resultados para toda la red
El anterior procedimiento fue aplicado para toda la res OASIS IV llegando a los siguientes
resultados:
Figura 40. Modelo casa OASIS IV tipo C - Resultados del cálculo del estado de diseño para cada tubería de la red.
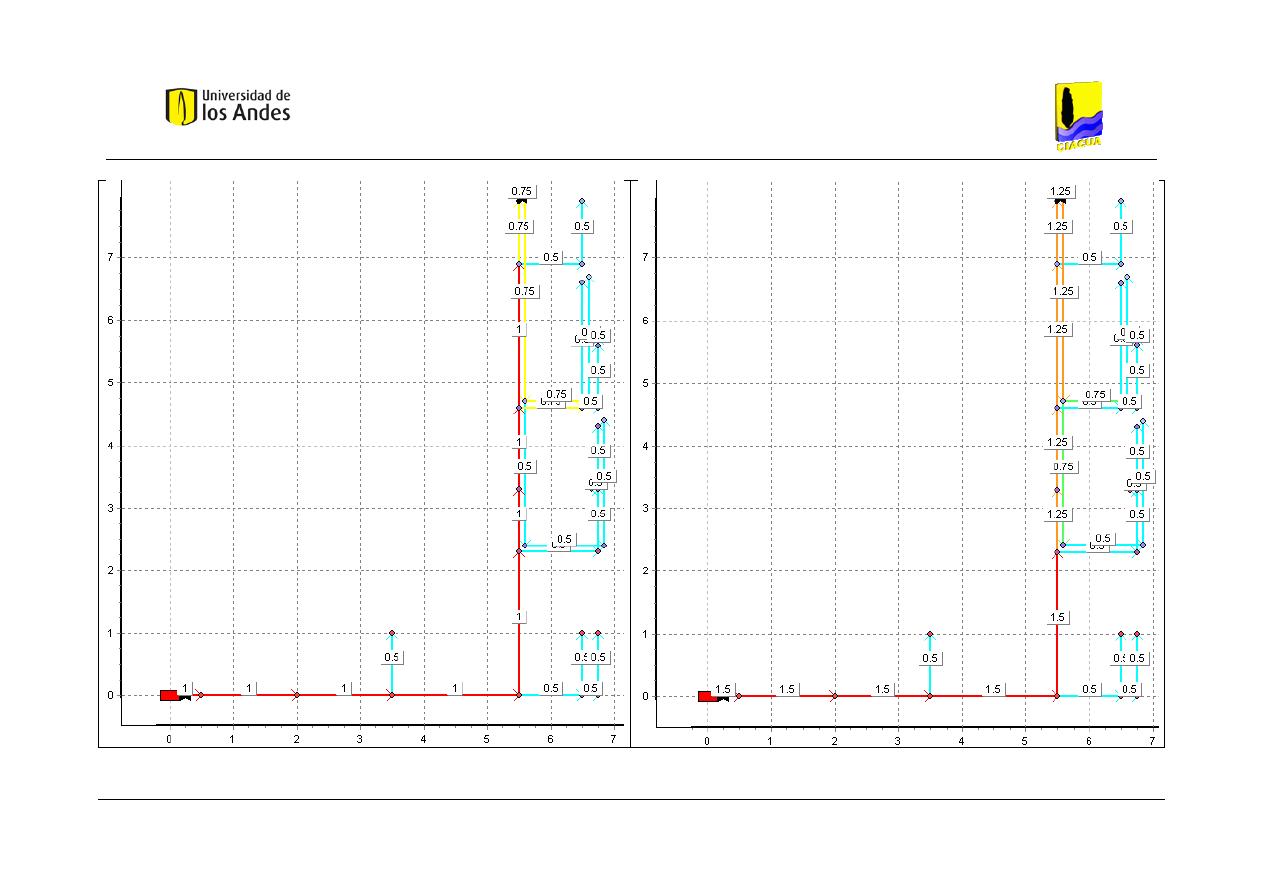
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
117
Figura 41. Modelo casa OASIS IV tipo C - Resultados del diseño para el caso basado en Acero (izquierda) y para el caso basado en ICONTEC (derecha). Diámetros en pulgadas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
118
Se debe notar que los resultados para el estado de diseño a utilizar no dependen del
comportamiento hidráulico del sistema, sino únicamente del comportamiento estocástico de
la demanda, que para los dos casos de análisis de la red OASIS IV tipo C, se considera igual. Así
el procedimiento de diseño sólo difiere en el cálculo del caudal de diseño de cada tubo y los
posteriores pasos basados en este resultado.
En el caso especial de este caso de estudio, existen dos tuberías con un estado de diseño igual
a cero, que presentan un requisito adicional para el diseño de la red, en el cual se desea dejar
tuberías disponibles para un potencial tanque de reserva de agua, pero que no es considerado
activamente en la metodología de diseño implementada. Así, dichas tuberías deben ser
diseñadas con otro criterio, y si bien por defecto se les asignó el diámetro mínimo, su
determinación juiciosa requiere información adicional a la disponible.
Un resultado esperado del cálculo del estado de diseño consiste en notar que un tubo aguas
arriba siempre tendrá un estado de diseño mayor o igual al estado de diseño de cualquiera de
sus tubos aguas abajo, teniendo en cuenta que se consideran únicamente redes abiertas, y que
al avanzar hacia aguas abajo por cualquier ruta, sólo se pueden estar reduciendo los aparatos a
alimentar. Este resultado permite agregar eficiencia al procedimiento dado que una vez se
llega a un tubo cuyo estado de diseño es , se puede asegurar que el estado de diseño de
todos sus tubos aguas abajo será también , considerando que, a excepción de casos
especiales como el del futuro tanque de almacenamiento, ninguna tubería puede tener estado
de diseño igual a cero.
Respecto al procedimiento de cálculo de los caudales de diseño, se puede hacer una
conclusión similar, al notar que su cálculo consiste en tomar los
caudales mayores de los
nudos aguas abajo, y dado que un tubo nunca tiene un estado de diseño mayor que cualquiera
de sus tubos aguas abajo, los caudales con los que se diseña este tubo serán a lo sumo iguales
a los de diseño de cualquiera de sus tubos aguas arriba sino mayores.
Por otro lado, la conclusión similar respecto al diámetro no siempre puede aplicarse, dado que
el cálculo de los diámetros depende no sólo del caudal de diseño, sino también de la
disponibilidad de energía asignada por la LGH ideal. Adicionalmente, dada la manera de
recorrer la red para calcular el diámetro y redondearlo, es posible que se afecte la superficie
de alturas piezométricas aguas abajo de un tubo recién diseñado, de manera que se disponga
de menos energía y por lo tanto se requieran mayores diámetros.
La anterior observación resulta inconveniente para la mayoría de las redes, dada la restricción
adicional que incluyen algunos diseñadores y constructores sobre la posibilidad de permitir
tuberías más grandes aguas abajo de tuberías más pequeñas. Si bien este problema no ocurre
en ninguno de los dos casos de estudio, se hizo evidente en un paso del redondeo en donde la
aproximación de un diámetro continuo presento valores iguales para el ponderador que
decide a cuál de los diámetros discretos se debe aproximar.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
119
Adicionalmente se deben notar las diferencias en los resultados finales de los dos
procedimientos de diseño, en los cuales difieren las curvas únicas de los emisores asignadas a
cada aparato. Esto permite ver la sensibilidad del procedimiento a variaciones en los caudales
de diseño de los aparatos de la red, que para estos resultados indica que conocer bien el
comportamiento hidráulico de los aparatos puede generar diferencias de costos de USD$26.40
en las redes hidráulicas de cada casa. Esta diferencia representa un 33% del costo de la red, y
teniendo en cuenta que se tiene un conjunto con 183 casas, esto representaría un total de
cerca USD$4800 que puede llegar a justificar el estudio hidráulico de los aparatos que se
utilizarán en la red.
Figura 42. Prototipo casa OASIS IV tipo C – Diámetros reales del sistema en pulgadas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
120
Finalmente, vale la pena notar que para ambos casos de estudio, la red resultado del
procedimiento de diseño presenta diámetros más grandes para la mayoría de tubos que
aquellos presentes en el sistema real de las casas de OASIS IV (ver Figura 42), lo cual resulta
consistente con el estado actual de las casas, en donde se conocen quejas por parte de los
usuarios por la calidad del servicio en términos específicos de presión y caudal emitido en los
aparatos. Es decir que, dado que el prototipo tiene diámetros menores que los encontrados en
este documento como necesarios para una confiabilidad de 95%, entonces el prototipo debe
tener una probabilidad de falla considerablemente mayor al 5%, lo cual es verificado al notar la
frecuencia de las quejas presentadas por los usuarios del sistema.
7.2 Caso de estudio 2: Red Interna APTOS ACERO
En Acero (2009) se muestran 4 redes internas diferentes correspondientes a los 4 tipos de
apartamentos que existen en un mismo edificio ubicado en Bogotá, Colombia. De estos, el más
complejo resulta ser el Tipo 1 cuya longitud total de tubería es de más de 85.5m, y tiene un
total de 17 aparatos sanitarios, de los cuales 10 tienen llaves de agua caliente y fría (ver Figura
43).
A fin de modelar los accesorios que existen en esta red (27 Tees y 67 Codos de 90°), Acero
propone distribuir los coeficientes de pérdidas menores uniformemente entre la longitud de
las tuberías, lo cual implica un coeficiente de pérdidas menores por unidad de longitud de
. Adicionalmente propone modelar el calentador de paso como una tubería con un
coeficiente de pérdidas menores de .

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
121
Figura 43. Modelo APTO ACERO tipo 1 - Vista en planta. Aparatos conectados a la red.
7.2.1 Asignación de una Línea de Gradiente Hidráulico (LGH)
Para la asignación de la LGH ideal se utilizó la misma relación lineal utilizada en los anteriores
casos de estudio y cuya función es la descrita en la Ecuación 66. Para ello se definió como
una altura piezométrica total iguala correspondiente a la altura piezométrica
asignada por Acero a la red. Este valor puede ser resultado de un análisis de los sistemas de
bombeo del edificio, o de una alta disponibilidad de energía en la conexión de edificio a la red
de acueducto.
Por otro lado, las presiones mínimas de operación de cada aparato son las mismas utilizadas
en el anterior caso de estudio, las cuales son expuestas en la Tabla 23. Los resultados de este
procedimiento se muestran en la Figura 44.
Agua Caliente
Agua Fría
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
122
Figura 44. Modelo APTO ACERO tipo 1 – LGH ideal en psi.
7.2.2 Cálculo de los caudales emitidos
Similarmente al caso de estudio anterior, el cálculo de los caudales emitidos se realiza
remplazando las presiones correspondientes a las alturas piezométricas totales mostradas en
la Figura 44. De nuevo son utilizados dos conjuntos de curvas únicas de los aparatos
correspondientes a los resultados de Acero (2009) y de ICONTEC (2006). Los resultados son
presentados en la Figura 45.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
123
Figura 45. Modelo APTO ACERO tipo 1 – Caudal emitido en L/s para el caso basado en Acero (izquierda) y para el caso basado en ICONTEC (derecha).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
124
7.2.3 Cálculo de los caudales de diseño
Haciendo uso de los parámetros de caracterización estocástica de la demanda de los aparatos
mostrados en la Tabla 20 y suponiendo un total de 6 habitantes en la casa, se tienen las
mismas probabilidades de diseño de la Tabla 24 calculadas para los casos de estudio ya
presentados. Esto permite comenzar el cálculo del caudal de diseño del tubo más aguas arriba
de la red APTO ACERO tipo 1 que tiene 17 aparatos sanitarios aguas abajo de éste.
Los 17 aparatos consisten en 5 lavamanos, 5 inodoros, 4 duchas, 1 lavaplatos y 2 fregaderos, y
sus probabilidades de uso para el diseño (ver Tabla 24) generan un conjunto de probabilidades
cuya desviación estándar es de . Dado que esta desviación estándar se considera
relativamente pequeña, es posible aproximar los resultados de la Ecuación 47 calculando una
única probabilidad conjunta de ocurrencia mediante la Ecuación 54 para así utilizar la Ecuación
51 que resulta considerablemente más fácil de utilizar.
Sin embargo, a fin de ilustrar la precisión de esta aproximación, fueron calculados los
resultados de las probabilidades de ocurrencia de cada estado mediante ambas metodologías.
Así, la metodología exacta, requirió el cálculo de probabilidades conjuntas, lo que
implica el procesamiento de probabilidades individuales que dan como resultado
las probabilidades mostradas en la Tabla 27:
Tabla 27. Probabilidades de ocurrencia de los estados – Metodología Exacta.
Estado
Probabilidad
de ocurrencia
Probabilidad de ocurrencia dado
que el sistema está en uso
17
1.39E-22
1.93E-22
16
6.82E-20
9.48E-20
15
1.49E-17
2.06E-17
14
1.90E-15
2.64E-15
13
1.59E-13
2.21E-13
12
9.18E-12
1.28E-11
11
3.80E-10
5.28E-10
10
1.15E-08
1.60E-08
9
2.59E-07
3.60E-07
8
4.39E-06
6.10E-06
7
5.64E-05
7.84E-05
6
5.51E-04
7.65E-04
5
4.05E-03
5.63E-03
4
2.21E-02
3.07E-02
3
8.66E-02
1.20E-01
2
2.31E-01
3.21E-01
1
3.75E-01
5.22E-01
0
2.80E-01
-
Suma
1.00E+00
1.00E+00

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
125
Por otro lado, el cálculo de las probabilidades de ocurrencia de los estados mediante la
aproximación detallada en la Sección 5.3.1, en la cuál es necesario el cálculo de una única
probabilidad representativa mediante la Ecuación 54, y el posterior uso de la Ecuación 51 un
total de veces, genera como resultados las probabilidades mostradas en la Tabla 28:
Tabla 28. Probabilidades de ocurrencia de los estados – Metodología Aproximada.
Estado
Probabilidad de
ocurrencia
Probabilidad de ocurrencia dado
que el sistema está en uso
17
2.69E-20
3.77E-20
16
6.01E-18
8.45E-18
15
6.33E-16
8.90E-16
14
4.17E-14
5.86E-14
13
1.92E-12
2.70E-12
12
6.58E-11
9.24E-11
11
1.73E-09
2.43E-09
10
3.58E-08
5.03E-08
9
5.89E-07
8.28E-07
8
7.76E-06
1.09E-05
7
8.17E-05
1.15E-04
6
6.85E-04
9.62E-04
5
4.51E-03
6.33E-03
4
2.28E-02
3.21E-02
3
8.58E-02
1.21E-01
2
2.26E-01
3.17E-01
1
3.72E-01
5.22E-01
0
2.88E-01
Suma
1.00E+00
1.00E+00
Así, ambos resultados indican que para una probabilidad de falla aceptable de , el estado
de diseño es (dado que
para el caso exacto y para el
caso aproximado), y por lo tanto el caudal de diseño del tubo más aguas arriba se calcula como
la suma de los aparatos sanitarios con mayor caudal de consumo, lo cual da como resultado
un caudal de para el caso basado en Acero (2009) y para el caso basado
en ICONTEC (2006).
7.2.4 Cálculo y redondeo del diámetro del tubo
De nuevo haciendo uso de la ecuación de Darcy-Weisbach (Ecuación 3) en conjunto con la
ecuación de Colebrooke-White (Ecuación 4), es posible hallar el diámetro continuo necesario
para que el caudal de diseño fluya por la tubería haciendo uso de la energía asignada en la
Sección 7.2.1.
Para el cálculo se tomó una aceleración de gravedad de
, una viscosidad cinemática
de
correspondiente a la del agua a , una rugosidad absoluta de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
126
correspondiente a una tubería de PVC y un coeficiente de pérdidas menores
consistente con la suposición de Acero (2009) de
pérdidas por unidad de longitud
.
Como resultado se obtuvo que, para el caso basado en Acero, el diámetro continuo necesario
es de o , mientras que para el caso basado en ICONTEC, es de o
. Así, al redondearlos se tiene que la diferencia entre
y
es
menor que la diferencia entre
y
y por lo tanto se toma como
diámetro de diseño el para el caso basado en Acero.
Algo análogo ocurre para el caso basado en ICONTEC, en donde se calcula la diferencia del
diámetro continuo y los diámetros de y , encontrando que el diámetro que se
debe asignar, según el criterio anteriormente mostrado, es de .
7.2.5 Resultados para toda la red
Una vez diseñado el primer tubo de la red, se procedió a diseñar los demás tubos aguas abajo,
siguiendo el mismo procedimiento para cada uno. Los resultados del cálculo del estado de
diseño de cada tubo son mostrados en la Figura 46, en donde se pueden apreciar un par de
tubos en los cuales el estado de diseño da cero, por cuenta de la condición del modelo
desarrollado por Acero (2009) en el cual no se asigna ningún aparato sanitario al nudo que
éstos alimentan, de manera que su número de aparatos aguas abajo es nulo y así mismo su
estado de diseño. Dado que no se conoce la naturaleza de la conexión que se hace a los dos
tubos mencionados, en el procedimiento de diseño se decidió asignar como diámetro
definitivo el diámetro mínimo disponible en el mercado .
A partir de la Figura 46 se puede verificar la conclusión hecha en el anterior caso de estudio
acerca de la manera como siempre decrece el estado de diseño mientras se avanza hacia
aguas abajo. Esta conclusión puede verse afectada por el uso de un procedimiento de cálculo
aproximado como el expuesto en la Sección 5.3.1 dado que para cada tubería se calcula la
probabilidad equivalente, y ello hace que no sea posible afirmar sin ningún grado de
incertidumbre que los estados de diseño efectivamente son menores o iguales para tubos
aguas abajo. Sin embargo en este ejemplo fue utilizada la metodología aproximada, dado el
tamaño del problema para aparatos sanitarios aguas abajo de un tubo, y la cantidad de
tuberías presentes en la red, y se evidenció que esto efectivamente se cumple.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
127
Figura 46. Modelo APTO ACERO tipo 1 – Resultados del cálculo del estado de diseño para cada tubería de la red.
Respecto a los resultados finales para los diámetros, se puede notar que en ambos casos se
evidencian diámetros mayores para tuberías más aguas abajo. Esto se genera por la
variabilidad de los coeficientes de pérdidas menores asignados a cada tubería y por el
procedimiento de redondeo que genera déficits y superávits de energía, que pueden afectar la
disponibilidad de la misma al punto de requerir diámetros cuyo posterior redondeo difiere del
valor asignado aguas arriba, en algunos casos de manera que aumenta el diámetro que se
tiene (ver Figura 47).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
128
Figura 47. Modelo APTO ACERO tipo 1 – Resultados del diseño para el caso basado en Acero (izquierda) y para el caso basado en ICONTEC (derecha). Diámetros en pulgadas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
129
Para el caso de estudio presentado no fue tenida en cuenta la restricción de no considerar
factibles diseños que impliquen tubos con diámetros mayores que algunas de sus tuberías
aguas arriba. Esto, debido a que la metodología de redondeo planteada en esta investigación
no considera esta restricción, y por lo tanto incluirla implicaría un replanteamiento del
procedimiento sugerido. Así en el caso de querer considerarla, los resultados del diseño
siguiendo la metodología desarrollada deberían ser tenidos en cuenta sin realizar el redondeo
en el paso descrito en la Sección 5.4.
Se debe notar que, dada la manera de modelación del calentador de paso sugerida por Acero
(2009), la tubería que lo representa resulta con un diámetro de diseño mayor que los demás
diámetros de la red. Así mismo las dos tuberías sin aparatos sanitarios aguas abajo, resultaron
con un diámetro asignado de correspondiente al diámetro mínimo disponible. Esto
evidencia que la metodología está diseñada para diseños cuyas consideraciones incluyan la
incertidumbre de la demanda de manera estocástica y el comportamiento hidráulico de
emisores de los aparatos conocidos que se conectarán a la RIDAP, pero no consideraciones
adicionales como posibles ampliaciones de la red, nudos con comportamiento diferente al
descrito en la Sección 3.1 y demás.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
130
8 Conclusiones
8.1 Conclusiones de la modelación de RIDAPs
A partir de lo observado en el caso de estudio, se encuentra que la selección de la metodología
de simulación de la simultaneidad debe realizarse con base en el uso que se vaya a hacer de
los resultados entregados por estos procedimientos, y así, en el caso de considerarse poco
ajustada y muy relevante la suposición de independencia entre usos de diferentes aparatos
sanitarios, se puede considerar el uso de una herramienta de simulación de eventos discretos
que tenga en cuenta, de manera simplificada, las posibles correlaciones existentes entre los
usos de los diferentes aparatos.
También se puede concluir que, al menos en el caso de sistemas pequeños como el del caso de
estudio de modelación (baño de tres aparatos), el escenario donde todos los aparatos están
apagados es significativamente probable y frecuente, indicando así, que el sistema
constantemente está en dicho escenario, y que por lo tanto, condiciones de demanda
periódicas pueden ser representadas y analizadas con base en la observación de un único
periodo, dado que el sistema se encuentra en un estado estable, que puede ser entendido
como un equilibrio estable del cual es sacado cuando se hace uso del sistema (de al menos uno
de sus aparatos), pero siempre éste tenderá a volver a su condición estable (escenario con
todos los aparatos apagados).
Según lo observado en las funciones de densidad de probabilidad del caudal transportado por
el tubo, inclusive para el caso en el que se da como dado que el sistema está en uso, éstas no
tienen un único pico de probabilidad como las funciones típicas de densidad de probabilidad
tanto de variables continuas como discretas, indicando así, que un ajuste de una distribución
de probabilidad teórica puede ser poco representativo de la realidad, al menos para sistemas
pequeños como el del caso de estudio, y más teniendo aparatos sanitarios sin porcentaje de
apertura de válvula variable o con porcentaje de apertura de válvula variable pero con muy
poca influencia en la curva final del aparato.
Para una efectiva implementación de las metodologías desarrolladas, se hace necesario un
conocimiento detallado de parámetros como los mostrados en la Tabla 4 y la Tabla 5 que
caractericen la demanda de agua para cada aparato tanto en su frecuencia de uso como en su
duración. Si bien esto puede resultar poco viable desde el punto de vista económico, los
resultados de la Tabla 4 y la Tabla 5 no difieren significativamente en sus valores a pesar de
provenir de mediciones en lugares geográficamente distintos y distantes (Holanda y Ohio,
Estados Unidos), indicando que tomar valores de sitios aceptablemente parecidos al lugar de
estudio es una buena aproximación para la implementación de las metodologías.
También se hace necesario el conocimiento de las curvas de distribución temporal de la
frecuencia de uso de cada aparato sanitario, las cuales pueden ser determinadas con base en
observaciones a sistemas ya construidos y utilizados, o mediante suposiciones razonables

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
131
acerca del comportamiento de los usuarios del sistema. Finalmente es necesario conocer y
caracterizar el comportamiento hidráulico de los aparatos sanitarios presentes o esperados en
la edificación a analizar, y para ello se requieren estudios como los desarrollados por Acero
(2009) para diferentes aparatos, de manera que sería ideal que los mismos fabricantes de los
aparatos se encargaran de entregar a los ingenieros encargados del análisis (y posible diseño)
las curvas de emisor de sus aparatos, así como las presiones mínimas y máximas aceptables de
operación de éstos.
8.2 Conclusiones del diseño y comprobación de diseño de RIDAPs
Respecto al análisis hecho acerca de la definición y cálculo de la probabilidad de falla de una
RIDAP, se puede concluir que las distribuciones de probabilidad encontradas mediante la
aplicación de la metodología de modelación de RIDAPs desarrollada en esta investigación no
pueden ser utilizadas directamente como un criterio para diseñar un tubo con una
probabilidad de falla aceptable dada. Es por ello que se considera conveniente en esta
investigación el desarrollo de una metodología que pueda ser consistente con la metodología
de modelación mencionada.
Para caracterizar la demanda de una RIDAP se puede utilizar la distribución Binomial de
Poisson en donde los parámetros
son las probabilidades de uso de los aparatos
(utilización). Adicionalmente se encontró que el cálculo de los valores de probabilidad
asignados por esta distribución puede requerir un alto esfuerzo computacional que lo hace de
difícil uso e implementación en casos reales. Sin embargo en esta investigación se dedujo una
aproximación aceptable para su cálculo que requiere que el conjunto de parámetros sea de
poca dispersión para la aceptable estimación de las probabilidades finales. Esta aproximación
se explica en la Sección 5.3.1 y hace uso de promedios geométricos ponderados.
Adicionalmente, para calcular las probabilidades de ocurrencia de conjuntos de escenarios de
demanda con igual número de aparatos encendidos en casos donde el conjunto de parámetros
de la distribución Binomial de Poisson tiene alta dispersión, se dedujo una manera de
aproximación que implica un mayor esfuerzo computacional que la solución para el caso de
poca dispersión de los
pero menor que el cálculo exhaustivo y exacto de dicha
probabilidad mediante la Ecuación 47. Además se encontró que la misma metodología que
soluciona el anterior problema, resulta útil para acoplar al problema, resultados de
probabilidades conjuntas de ocurrencia encontradas mediante simulación de eventos
discretos, permitiendo así el uso de esta herramienta para condiciones de demanda
claramente dependientes entre aparatos.
Respecto al algoritmo desarrollado para la ejecución hidráulica de las RIDAPs con curvas únicas
asignadas a sus nudos, se encontró que la interpolación potencial entre los datos de la curva
discretizada resulta mucho más conveniente que otros tipos de interpolación, dada la manera
en que motores de cálculo como EPANET (Rossman, 2000) o Redes (CIACUA, 2006) resuelven

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
132
las ecuaciones que gobiernan la hidráulica en redes presurizadas con emisores o nudos de
demanda constantes. Asimismo se encontró que la convergencia del algoritmo es
considerablemente buena al realizar la comprobación de diseño de redes reales en menos de
10 iteraciones.
Sobre el procedimiento de diseño desarrollado se puede concluir que el paso de asignación de
LGH ideal a los nudos puede hacer uso de cualquier función descrita por la Ecuación 12
siempre y cuando los parámetros que la describen se encuentren dentro de los dominios
hallados en la Sección 2.2.2. Esto resulta especialmente útil para un futuro análisis de
sensibilidad de la metodología a los valores de estos parámetros, especialmente en lo relativo
a los costos constructivos de la red.
Por otro lado, y con base en los resultados de los casos de estudio para la metodología de
diseño propuesta, y de un análisis metódico del procedimiento, se concluyó que la
metodología resulta consistente con lo esperado en términos de que un tubo aguas arriba
siempre tendrá un estado de diseño mayor o igual al estado de diseño de cualquiera de sus
tubos aguas abajo, teniendo en cuenta que se consideran únicamente redes abiertas, y que al
avanzar hacia aguas abajo por cualquier ruta, sólo se pueden estar reduciendo los aparatos a
alimentar.
Similarmente se evidenció que los caudales de diseño también resultan menores o iguales para
cualquier tubería aguas abajo, mostrando así un decremento del caudal de diseño. Sin
embargo respecto a los diámetros no se puede concluir lo mismo, dado que su valor depende
de la asignación de LGH, que dependiendo de la función utilizada puede asignar más o menos
energía a una tubería, y del redondeo previo que se haya hecho a las tuberías aguas arriba. Si
bien esto puede representar un inconveniente para algunas edificaciones, se espera que la
solución consista en omitir el paso de redondeo tubo a tubo, y realizar este procedimiento una
vez se tenga toda la red diseñada con diámetros continuos.
Finalmente se puede concluir que la metodología de diseño sí es consecuente con la
metodología de modelación de las RIDAPs, tanto en su parte hidráulica (comportamiento de
emisores con curva única) como en su parte estocástica (cálculo de las probabilidades de uso
de cada aparato y probabilidades conjuntas de escenarios). Además es una metodología que
permite definir las probabilidades de falla aceptables de cada RIDAP, de manera que se puede
incluir en consideración la aversión o propensión al riego de los dueños de un proyecto de
construcción dependiendo del carácter del mismo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
133
9 Recomendaciones
Con base en los resultados encontrados para el caso de estudio de modelación de
simultaneidad y los casos de estudio del procedimiento de diseño, se recomienda realizar
futuras investigaciones y mediciones que permitan conocer los parámetros de caracterización
estocástica de la demanda, similares a los mostrados en la Tabla 4 para Holanda y la Tabla 5
para Ohio, pero para la población específica de la región donde se planee implementar la
metodología desarrollada. El valor de una investigación como la sugerida no sólo aplicaría para
la población encuestada sino también para otras poblaciones, dada la aparente tendencia de
los datos medidos en Holanda y Ohio que presenta similitudes, y que a la luz de más datos
permitiría verificar la variabilidad de estos parámetros y el error en el que se puede llegar a
incurrir al tomar datos de una población para realizar modelaciones y diseños en otras
poblaciones sin mediciones disponibles.
Similarmente, para el caso de la modelación y eventualmente del diseño se recomiendan
investigaciones que permitan conocer las curvas de distribución de frecuencia de los usos de
cada aparato, a fin de conocer picos de uso y su simultaneidad de ocurrencia con los picos de
otros aparatos. Dada la naturaleza de una investigación como la sugerida en la recomendación
anterior, se podrían incluir dentro de los datos a medir las series de tiempo de uso de los
aparatos y así deducir las series de distribución temporal de la frecuencia.
Así mismo, conocer mejor las curvas únicas de los aparatos puede representar una mayor
exactitud en los diseños de las RIDAPs con lo cual se puede llegar a un ahorro en los costos
constructivos, o a un mejor ajuste del sistema a la probabilidad de falla deseada. Para ello se
recomienda realizar estudios similares a los conducidos por Acero (2009) para otros aparatos
sanitarios típicamente utilizados en las construcciones actuales, con la necesidad adicional de
incluir una evaluación de la posibilidad de controlar el porcentaje de apertura de válvula y de
los parámetros adicionales del aparato como caudal máximo admisible y caudal mínimo
admisible.
Respecto al procedimiento de diseño, se recomienda un análisis de sensibilidad del diseño
generado mediante la metodología ante cambios en el parámetro (flecha) de la función de
LGH ideal dado el potencial de la asignación de LGH de generar diseños más o menos costosos.
Además se pueden llegar a considerar externalidades al procedimiento de asignación de la LGH
como pendientes de fricción máximas y mínimas para un caudal dado de manera que se
tengan mejores estimativos de las presiones en los nudos para las condiciones de diseño.
Adicionalmente se recomiendan futuras investigaciones relacionadas con el redondeo de
diámetros para un diámetro continuo encontrado por la metodología, a fin de posibilitar la
consideración de una restricción posiblemente impuesta por algunos diseñadores y
constructores acerca de considerar no factibles diseños donde algún tubo aguas abajo de otro
pueda tener un diámetro más grande que éste.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
134
Finalmente se recomienda evaluar la aplicabilidad del algoritmo de comprobación de diseño
con nudos cuyo caudal en función de la presión no necesariamente se rige por una relación
potencial. Asimismo se considera conveniente implementar el algoritmo de diseño de RIDAPs
en este, u otro programa de cálculo hidráulico, a fin de facilitar su uso en el ambiente
profesional y la investigación en estos temas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
135
10 Referencias
Acero, M. F. (2009). “Revisión Crítica de los Métodos de Diseño de Abastecimiento de Agua
Potable al Interior de edificaciones”. Tesis de Maestría, Universidad de los Andes,
Bogotá.
Alcocer-Yamanaka, V. H. ;Tzatchkov, V. ;Garcia-Bartual, R. ;Buchberger, S. ;Arreguin-Cortes, F. I.
;Leon-Rodriguez, T. (2008). “Stochastic modeling of residential drinking water demand
using the Neyman-Scott scheme”. Ingeniería Hidráulica en México, 23(3), 105-121.
Blokker, E. & Vreeburg, J. (2005). “Monte Carlo simulation of residential water demand: A
stochastic end-use model”. EWRI 2005.
Blokker, E. (2006). “Modeling water demand patterns; description and evaluation of simulation
model SIMDEUM”. Kiwa N.V., Nieuwegein, Netherlands (en holandés).
Blokker, E., Vreeburg, J., & van Dijk, J. (2010). “Simulating residential water demand with a
stochastic end-use model”. Journal of Water Resources Planning and Management,
ASCE, 19-26.
Blokker, E. (2010a). “Stochastic water demand modeling for a better understanding of
hydraulics in water distribution networks”. PhD Thesis, Delft University, Netherlands.
ISBN: 978-90-8957-015-4.
Blokker, E. (2010b). “Simulating residential water demand with a stochastic end-use model”.
Journal of Water Resources Planning and Management, ASCE, 19-26.
Blokker, E., Pieterse-Quirijns, E., Vreeburg, J. & Van Dijk, J. (2011). “Simulating non-residential
water demand with a stochastic end-use model”. Journal of Water Resources Planning
and Management, ASCE, 1(1), 101.
Buchberger, S. G., & Wu, L. (1995). “Model for instantaneous residential water demands”.
Journal of Hydraulic Engineering, ASCE, 232-246.
Buchberger, S. G., & Wells, G. J. (1996). “Intensity, Duration, and Frequency of Residential
Water Demands”. Journal of Water Resources Planning and Management, ASCE, 122,
11-19.
CIACUA. (2006). Programa Redes. Bogotá: Universidad de los Andes.
CIACUA. (2011). “Desarrollo e implementación de una metodología moderna para el diseño de
redes internas de distribución de agua potable”. Colciencias, Bogotá: Universidad de
los Andes

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
136
Foekema, H. & Engelsman, O. (2001). “A different consumption pattern (domestic water use
2001)”. TNS NIPO, Amsterdam, commissioned by VEWIN. (en Holandés).
García, V., García-Bartual, R., Cabrera, E: Arregui, F. & García-Serra, J. (2004). “Stochastic
model to evaluate residential water demands”. Journal of Water Resources Planning
and Management, ASCE, 130(5), 386-394.
García Sosa, J. (2001). “Instalaciones Hidráulicas y Sanitarias”. México D.F.: Fernando Cuna
Rojas.
Granados Robayo, J. A. (2002). “Redes hidráulicas y sanitarias en edificios”. Bogotá, Colombia:
Unibiblos.
Hunter, R. (1940). “Methods of Estimating Loads in Plumbing Systems”. Building Materials and
Structures, National Bureau of Standards.
ICONTEC - Instituto Colombiano de Normas Técnicas y Certificación (2004). “Código
Colombiano de Fontanería – Norma Técnica Colombiana NTC 1500” Bogotá, Colombia:
Ed. ICONTEC, ISBN: 958-9383-49-1.
Ochoa, S. (2009). “Diseño optimizado de distribución de agua potable con base en el concepto
energético de superficie óptima de gradiente hidráulico”. Tesis de Maestría,
Universidad de los Andes, Bogotá.
Roca Suárez, M., & Carratalá Fuentes, J. “Manual de fontanería”. España: CA.
Rossman, L.A. (2000). “EPANET 2 User’s Manual”. Cincinnati OH: Risk Reduction Engineering
Laboratory, US Environmental Protection Agency.
Saldarriaga, J. G. (2007). “Hidráulica de tuberías Abastecimiento de Agua, Redes, Riegos”.
Bogotá: Alfaomega.
Saldarriaga, J. G. (2010) “Prioritized rehabilitation of water distribution networks using
dissipated power concept to reduce non-revenue water” Urban Water Journal, 1-20.
Takahashi, S., Saldarriaga, J., Hernández, F., Díaz, D. & Ochoa, S. (2011) “An energy
methodology for the design of water distribution systems”
Todini, E., & Pilati, S. (1987). “A gradient method for the analysis of pipe networks”.
International conference on Computer Applications for Water Supply and Distribution,
Leicester Polytechnic, UK.
Todini, E. (2000). “Looped water distribution networks design using a resilience index based
heuristic approach” Urban Water Journal, 115-122.
Villalba, G. (2004). “Algoritmos de optimización combinatoria aplicados al diseño de redes de
distribución de agua potable”. Tesis de Maestría, Universidad de los Andes, Bogotá.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
137
Wu, I-Pai, (1975). “Design of drip irrigation main lines”. Journal of the Irrigation and Drainage
Division, ASCE, Vol 101 No. IR4 Dic. 1975

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
138
11 Anexos
11.1 Demostraciones del dominio de la variable
Sea el grado de libertad de una ecuación cuadrática asignada a un sistema de tuberías en
serie como representación de la altura piezométrica total en cada punto de la trayectoria del
flujo:
Según la siguiente figura, la variable toma valores positivos cuando la curva se
encuentra por debajo de la curva , y negativos en caso de que la curva
se encuentre por encima de la curva :
Entonces existen tres posibles casos para los que se puede evaluar el dominio de la variable
a saber:
Dominio de suponiendo tubería diferencial y diámetros continuos infinitos:
Cálculo de
:
(
|
)
(
|
)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
139
|
Cálculo de
:
(
|
)
|
Rango de suponiendo tubería con longitudes dadas y diámetros continuos infinitos:
Sea
la longitud del último tramo del sistema de tuberías en serie.
Sea
la longitud del primer tramo del sistema de tuberías en serie.
Cálculo de
:
(
)
(
(
(
)
(
)
)
)
(
)
Notar que si
, entonces .
Cálculo de
:
(
)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
140
Notar que si
, entonces .
Rango de suponiendo tubería con longitudes dadas y diámetro máximo conocido:
Sea
el diámetro máximo disponible.
Sea
la longitud del último tramo del sistema de tuberías en serie.
Sea
el caudal demandado en
.
Sea
la longitud del primer tramo del sistema de tuberías en serie.
Sea
el caudal demandado en todo el sistema (caudal que pasa por el primer tramo del
sistema de tuberías en serie).
Cálculo de
:
Sea:
(
)
(
∑
)
(
)
Entonces la ecuación para hallar
es:
(
(
)
)
(
(
(
)
(
)
) (
)
)
(
(
)
)
(
)
Notar que si
, entonces (
)
, y entonces
(
)
.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
141
Cálculo de
:
Sea:
(
)
(
∑
)
Entonces la ecuación para hallar
es:
(
(
)
)
(
(
)
)
(
(
)
)
Notar que si
, entonces (
)
, y entonces
(
)
.
11.2 Parametrizaciones de la distribución Lognormal
19
Sea una variable aleatoria distribuida Lognormal. Entonces su función de densidad de
probabilidad será:
√
(
)
(
)
donde:
: Media o valor esperado de la variable aleatoria .
: Desviación estándar de la variable aleatoria .
Y tendrá como valor esperado y varianza las siguientes expresiones:
[ ]
(
)
[ ] (
(
)
)
(
)
19
Basado en: http://en.wikipedia.org/wiki/Log-normal_distribution

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos
MIC 201210-15
Diego Alejandro Páez Ángel
Tesis II
142
De manera que podrá ser parametrizado como:
(
)
O como:
( [ ] [ ]
⁄
)
Y en caso de ser utilizada la segunda expresión, los otros parámetros se podrán calcular como:
[ ]
(
[ ]
[ ]
)
( (
[ ]
[ ]
))
