
TESIS DE PREGRADO
ANÁLISIS DE LA GEOMETRÍA FRACTAL DE LA SUPERFICIE ÓPTIMA
DE PRESIONES EN EL DISEÑO OPTIMIZADO DE REDES DE
DISTRIBUCIÓN DE AGUA POTABLE
Andrés Felipe Jaramillo Pabón
Asesor: Juan G. Saldarriaga Valderrama
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
PREGRADO EN INGENIERÍA AMBIENTAL
BOGOTÁ D.C.
2020

AGRADECIMIENTOS
Agradezco a Dios por guiarme y brindarme fortaleza a lo largo de toda la carrera. A mis padres, por
motivarme, apoyarme y ser una fuente incondicional de confianza y amor. Al Centro de
Investigaciones en Acueductos y Alcantarillados (CIACUA) y a mi asesor, Juan G. Saldarriaga, por
brindarme las herramientas, conocimientos y consejos con los cuáles fue posible construir el
presente trabajo. Finalmente, a la Universidad de los Andes y a los demás profesores encargados
de mi formación, cuyos esfuerzos garantizaron mi aprendizaje en el área de la ingeniería civil y
ambiental.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
2
TABLA DE CONTENIDO
1
Introducción ............................................................................................................................... 36
2
Objetivos .................................................................................................................................... 37
2.1.1
Objetivo General ........................................................................................................ 37
2.1.2
Objetivos Específicos.................................................................................................. 37
3
Marco teórico ............................................................................................................................. 38
3.1
Conceptos de mecánica de fluidos .................................................................................... 38
3.1.1
Propiedades del agua ................................................................................................. 38
3.1.2
Principio de conservación de la masa ........................................................................ 39
3.1.3
Principio de conservación de la energía .................................................................... 40
3.2
Conceptos de hidráulica de tuberías ................................................................................. 41
3.2.1
Regímenes de flujo ..................................................................................................... 41
3.2.2
Pérdidas de energía en una tubería ........................................................................... 42
3.2.3
Método del gradiente en redes cerradas .................................................................. 45
3.3
Diseño optimizado de redes de distribución de agua potable .......................................... 51
3.3.1
Definiciones y restricciones ....................................................................................... 51
3.3.2
Criterio de Wu y metodología LOGH para tuberías en serie ..................................... 52
3.3.3
Métodos de optimización para redes cerradas ......................................................... 55
3.3.4
Redondeo de diámetros............................................................................................. 63
3.4
Herramientas computacionales ......................................................................................... 66
3.4.1
Programa REDES ........................................................................................................ 66
3.4.2
Programa MATLAB ..................................................................................................... 68
3.4.3
Programa ArcGIS ........................................................................................................ 70
3.5
Geometría fractal ............................................................................................................... 72
3.5.1
Autosimilitud .............................................................................................................. 72
3.5.2
Dimensión fractal – Hausdorff-Besicovitch................................................................ 72
3.5.3
Dimensión fractal – Box Counting.............................................................................. 73
3.6
Análisis fractal .................................................................................................................... 74

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
3
3.6.1
Algoritmo Box-Covering ............................................................................................. 74
3.6.2
Análisis de Rango Reescalado (R/S) ........................................................................... 76
3.6.3
Análisis de la lagunaridad........................................................................................... 78
4
Metodología ............................................................................................................................... 81
4.1
Definición de las redes ....................................................................................................... 81
4.2
Cálculo de diseños óptimos ............................................................................................... 83
4.3
Cálculo de diseños no óptimos .......................................................................................... 85
4.4
Análisis fractal de las redes ................................................................................................ 86
4.5
Trazado de la red................................................................................................................ 87
4.6
Generación de las Superficies de Gradiente Hidráulico .................................................... 89
4.7
Análisis fractal unidimensional de la superficie ................................................................. 92
4.8
Análisis fractal bidimensional de la superficie ................................................................... 94
5
Resultados .................................................................................................................................. 97
5.1
Diseños óptimos y no óptimos ........................................................................................... 97
5.1.1
Costos ......................................................................................................................... 97
5.1.2
Distribuciones de diámetros .................................................................................... 105
5.1.3
Superficies de Gradiente Hidráulico ........................................................................ 117
5.2
Análisis fractal unidimensional de las superficies ............................................................ 163
5.2.1
Perfil de dimensiones fractales – Eje X .................................................................... 163
5.2.2
Perfil de dimensiones fractales – Eje Y .................................................................... 174
5.3
Análisis fractal bidimensional de las superficies .............................................................. 186
5.3.1
Modelos Digitales de Elevaciones (DEM)................................................................. 186
5.3.2
Dimensiones fractales .............................................................................................. 198
5.3.3
Gráficas .................................................................................................................... 204
5.4
Correlación de dimensiones fractales – Red vs SOP ........................................................ 225
6
Análisis de resultados............................................................................................................... 228
6.1
Diseños óptimos y no óptimos ......................................................................................... 228
6.2
Superficies de Gradiente Hidráulico ................................................................................ 229
6.3
Análisis fractal .................................................................................................................. 230

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
4
7
Conclusiones ............................................................................................................................ 233
8
Recomendaciones .................................................................................................................... 234
9
Referencias ............................................................................................................................... 235
10
Anexos .................................................................................................................................. 246
10.1 Topología de las redes ..................................................................................................... 246
10.2 Curvas de costos .............................................................................................................. 251
10.3 Trazado de red – Algoritmo MATLAB............................................................................... 260
10.4 Generación de SGH – Algoritmo MATLAB ....................................................................... 263
10.5 Análisis fractal unidimensional – Algoritmo MATLAB...................................................... 266
10.6 Análisis fractal bidimensional – Algoritmo MATLAB ........................................................ 268
10.7 Costos - Diseños ............................................................................................................... 269
10.8 Conteo de diámetros – Algoritmo MATLAB ..................................................................... 270
10.9 Diámetros - Diseños ......................................................................................................... 271

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
5
ÍNDICE DE FIGURAS
Figura 1. Flujos similares. ................................................................................................................................... 41
Figura 2. Diagrama de flujo 1 - Método del gradiente. ..................................................................................... 50
Figura 3. Diagrama de Flujo 2 - Metodología SOGH Parte 1. ............................................................................ 60
Figura 4. Diagrama de Flujo 2 - Metodología SOGH Parte 2. ............................................................................ 61
Figura 5. Diagrama de Flujo 3 - Redondeo de diámetros Parte A. Adaptado de Saldarriaga (2016). ............... 64
Figura 6. Diagrama de flujo 3 - Redondeo de diámetros Parte B. Adaptado de Saldarriaga (2016). ................ 65
Figura 7. Interfaz REDES 2019 para la red de ejemplo. ..................................................................................... 66
Figura 8. Interfaz REDES 2019 visualización 3D de la SOP. ................................................................................ 67
Figura 9. Botones para la construcción de la red. ............................................................................................. 67
Figura 10. Ventana de edición de red. ............................................................................................................... 67
Figura 11. Pestaña Diseñar. ............................................................................................................................... 68
Figura 12. Ventana de resultados del diseño optimizado. ................................................................................ 68
Figura 13. Interfaz MATLAB R2018a. ................................................................................................................. 69
Figura 14. Interfaz ArcMap. ............................................................................................................................... 71
Figura 15. Herramientas de ArcToolbox. ........................................................................................................... 71
Figura 16. Diagrama de flujo - Análisis fractal de las redes. Recuperado de Vargas et. al. (2019). .................. 76
Figura 17. OPUS en REDES 2019. ....................................................................................................................... 83
Figura 18. Asignación de diámetros comerciales, restricciones y coeficientes de función de costos. ............. 84
Figura 19. Parámetros OPUS 1 - REDES 2019. ................................................................................................... 84
Figura 20. Parámetros OPUS 2 - REDES 2019. ................................................................................................... 84
Figura 21. Algoritmos Genéticos en REDES 2019. ............................................................................................. 85
Figura 22. Parámetros Algoritmos Genéticos 1 – REDES 2019. ......................................................................... 86
Figura 23. Parámetros Algoritmos Genéticos 2 - REDES 2019........................................................................... 86
Figura 24. Opción para el cálculo de la dimensión fractal en REDES 2019. ...................................................... 86
Figura 25. Ingreso de parámetros para la aplicación del algoritmo Box-Covering. .......................................... 87
Figura 26. Diagrama de flujo - Trazado de la red. .............................................................................................. 88
Figura 27. Diagrama de flujo - Generación de SGH - Parte 1. ............................................................................ 90
Figura 28. Diagrama de flujo - Generación SGH - Parte 2. ................................................................................. 91

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
6
Figura 29. Diagrama de flujo - Análisis fractal unidimensional. ........................................................................ 93
Figura 30. Herramienta IDW. ............................................................................................................................. 95
Figura 31. Generación de imágenes ".tif". ......................................................................................................... 95
Figura 32. Diagrama de flujo - Análisis fractal bidimensional............................................................................ 96
Figura 33. Costos - Red Two Loops .................................................................................................................... 97
Figura 34. Costos - Red Two Reservoirs. ............................................................................................................ 97
Figura 35. Costos - Red Taichung. ...................................................................................................................... 98
Figura 36. Costos - Red Hanoi. ........................................................................................................................... 98
Figura 37. Costos - Red Blacksburg. ................................................................................................................... 98
Figura 38. Costos - Red New York Tunnels. ....................................................................................................... 99
Figura 39. Costos - Red BakRyan. ....................................................................................................................... 99
Figura 40. Costos - Red Fossolo. ........................................................................................................................ 99
Figura 41. Costos - Red R28. ............................................................................................................................ 100
Figura 42. Costos - Red Pescara. ...................................................................................................................... 100
Figura 43. Costos - Red Modena. ..................................................................................................................... 100
Figura 44. Costos - Red Balerma. ..................................................................................................................... 101
Figura 45. Costos - Red San Vicente................................................................................................................. 101
Figura 46. Costos - Red Cazucá. ....................................................................................................................... 101
Figura 47. Costos - Red Elevada. ...................................................................................................................... 102
Figura 48. Costos - Red Bolívar. ....................................................................................................................... 102
Figura 49. Costos - Red La Cumbre. ................................................................................................................. 102
Figura 50. Costos - Red Candelaria. ................................................................................................................. 103
Figura 51. Costos - Red Bugalagrande. ............................................................................................................ 103
Figura 52. Costos - Red Carmen. ...................................................................................................................... 103
Figura 53. Costos - Red Chinú. ......................................................................................................................... 104
Figura 54. Costos - Red Sector 35. ................................................................................................................... 104
Figura 55. Costos - Red La Enea. ...................................................................................................................... 105
Figura 56. Distribución de diámetros - Red Two Loops. .................................................................................. 105
Figura 57. Distribución de diámetros - Red Taichung. ..................................................................................... 106
Figura 58. Distribución de diámetros - Red Two Reservoirs. ........................................................................... 106

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
7
Figura 59. Distribución de diámetros - Red Blacksburg. .................................................................................. 107
Figura 60. Distribución de diámetros - Red Hanoi. .......................................................................................... 107
Figura 61. Distribución de diámetros - Red BakRyan. ..................................................................................... 108
Figura 62. Distribución de diámetros - Red New York Tunnels. ...................................................................... 108
Figura 63. Distribución de diámetros - Red R28. ............................................................................................. 109
Figura 64. Distribución de diámetros - Red Fossolo. ....................................................................................... 109
Figura 65. Distribución de diámetros - Red Modena. ...................................................................................... 110
Figura 66. Distribución de diámetros - Red Pescara. ....................................................................................... 110
Figura 67. Distribución de diámetros - Red San Vicente. ................................................................................ 111
Figura 68. Distribución de diámetros - Red Balerma. ...................................................................................... 111
Figura 69. Distribución de diámetros - Red Cazucá. ........................................................................................ 112
Figura 70. Distribución de diámetros - Red Elevada. ....................................................................................... 112
Figura 71. Distribución de diámetros - Red La Cumbre. .................................................................................. 113
Figura 72. Distribución de diámetros - Red Bolívar. ........................................................................................ 113
Figura 73. Distribución de diámetros - Red Candelaria. .................................................................................. 114
Figura 74. Distribución de diámetros - Red Bugalagrande. ............................................................................. 114
Figura 75. Distribución de diámetros - Red Carmen. ....................................................................................... 115
Figura 76. Distribución de diámetros - Red Chinú. .......................................................................................... 115
Figura 77. Distribución de diámetros - Red Sector 35. .................................................................................... 116
Figura 78. Distribución de diámetros - Red La Enea. ....................................................................................... 116
Figura 79. SOP Red Two Loops - REDES 2019. ................................................................................................. 117
Figura 80. SOP Red Two Loops - MATLAB. ....................................................................................................... 117
Figura 81. Diseño No Óptimo 1 - Red Two Loops - REDES 2019. ..................................................................... 117
Figura 82. Diseño No Óptimo 1 - Red Two Loops - MATLAB. .......................................................................... 117
Figura 83. Diseño No Óptimo 2 - Red Two Loops - REDES 2019. ..................................................................... 117
Figura 84. Diseño No Óptimo 2 - Red Two Loops - MATLAB. .......................................................................... 117
Figura 85. Diseño No Óptimo 3 - Red Two Loops - REDES 2019. ..................................................................... 117
Figura 86. Diseño No Óptimo 3 - Red Two Loops - MATLAB. .......................................................................... 117
Figura 87. Diseño No Óptimo 4 - Red Two Loops - REDES 2019. ..................................................................... 118
Figura 88. Diseño No Óptimo 4 - Red Two Loops - MATLAB. .......................................................................... 118

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
8
Figura 89. Diseño No Óptimo 5 - Red Two Loops - REDES 2019. ..................................................................... 118
Figura 90. Diseño No Óptimo 5 - Red Two Loops - MATLAB. .......................................................................... 118
Figura 91. Diseño No Óptimo 6 - Red Two Loops - REDES 2019. ..................................................................... 118
Figura 92. Diseño No Óptimo 6 - Red Two Loops - MATLAB. .......................................................................... 118
Figura 93. SOP Red Two Reservoirs – REDES 2019. ......................................................................................... 119
Figura 94. SOP Red Two Reservoirs - MATLAB. ............................................................................................... 119
Figura 95. Diseño No Óptimo 1 - Red Two Reservoirs - REDES 2019. ............................................................. 119
Figura 96. Diseño No Óptimo 1 - Red Two Reservoirs - MATLAB. ................................................................... 119
Figura 97. Diseño No Óptimo 2 - Red Two Reservoirs - REDES 2019. ............................................................. 119
Figura 98. Diseño No Óptimo 2 - Red Two Reservoirs - MATLAB. ................................................................... 119
Figura 99. Diseño No Óptimo 3 - Red Two Reservoirs - REDES 2019. ............................................................. 119
Figura 100. Diseño No Óptimo 3 - Red Two Reservoirs - MATLAB. ................................................................. 119
Figura 101. Diseño No Óptimo 4 - Red Two Reservoirs - REDES 2019. ........................................................... 120
Figura 102. Diseño No Óptimo 4 - Red Two Reservoirs - MATLAB. ................................................................. 120
Figura 103. Diseño No Óptimo 5 - Red Two Reservoirs - REDES 2019. ........................................................... 120
Figura 104. Diseño No Óptimo 5 - Red Two Reservoirs - MATLAB. ................................................................. 120
Figura 105. Diseño No Óptimo 6 - Red Two Reservoirs - REDES 2019. ........................................................... 120
Figura 106. Diseño No Óptimo 6 - Red Two Reservoirs - MATLAB. ................................................................. 120
Figura 107- SOP Red Taichung - REDES 2019. .................................................................................................. 121
Figura 108. SOP Red Taichung - MATLAB. ....................................................................................................... 121
Figura 109. Diseño No Óptimo 1 - Red Taichung - REDES 2019. ..................................................................... 121
Figura 110. Diseño No Óptimo 1 - Red Taichung - MATLAB. ........................................................................... 121
Figura 111. Diseño No Óptimo 2 - Red Taichung - REDES 2019. ..................................................................... 121
Figura 112. Diseño No Óptimo 2 - Red Taichung - REDES 2019. ..................................................................... 121
Figura 113. Diseño No Óptimo 3 - Red Taichung - REDES 2019. ..................................................................... 121
Figura 114. Diseño No Óptimo 3 - Red Taichung - MATLAB. ........................................................................... 121
Figura 115. Diseño No Óptimo 4 - Red Taichung - REDES 2019. ..................................................................... 122
Figura 116. Diseño No Óptimo 4 - Red Taichung - REDES 2019. ..................................................................... 122
Figura 117. Diseño No Óptimo 5 - Red Taichung - REDES 2019. ..................................................................... 122
Figura 118. Diseño No Óptimo 5 - Red Taichung - MATLAB. ........................................................................... 122

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
9
Figura 119. Diseño No Óptimo 6 - Red Taichung - REDES 2019. ..................................................................... 122
Figura 120. Diseño No Óptimo 6 - Red Taichung - REDES 2019. ..................................................................... 122
Figura 121. SOP Red Hanoi - REDES 2019. ....................................................................................................... 123
Figura 122. SOP Red Hanoi - MATLAB.............................................................................................................. 123
Figura 123. Diseño No Óptimo 1 - Red Hanoi - REDES 2019............................................................................ 123
Figura 124. Diseño No Óptimo 1 - Red Hanoi - MATLAB. ................................................................................ 123
Figura 125. Diseño No Óptimo 2 - Red Hanoi - REDES 2019............................................................................ 123
Figura 126. Diseño No Óptimo 2 - Red Hanoi - MATLAB. ................................................................................ 123
Figura 127. Diseño No Óptimo 3 - Red Hanoi - REDES 2019............................................................................ 123
Figura 128. Diseño No Óptimo 3 - Red Hanoi - MATLAB. ................................................................................ 123
Figura 129. Diseño No Óptimo 4 - Red Hanoi - REDES 2019............................................................................ 123
Figura 130. Diseño No Óptimo 4 - Red Hanoi - MATLAB. ................................................................................ 123
Figura 131. Diseño No Óptimo 5 - Red Hanoi - REDES 2019............................................................................ 124
Figura 132. Diseño No Óptimo 5 - Red Hanoi - REDES 2019............................................................................ 124
Figura 133. Diseño No Óptimo 6 - Red Hanoi - REDES 2019............................................................................ 124
Figura 134. Diseño No Óptimo 6 - Red Hanoi – MATLAB. ............................................................................... 124
Figura 135. SOP Red Blacksburg - REDES 2019. ............................................................................................... 125
Figura 136. SOP Red Blacksburg - MATLAB...................................................................................................... 125
Figura 137. Diseño No Óptimo 1 - Red Blacksburg - REDES 2019.................................................................... 125
Figura 138. Diseño No Óptimo 1 - Red Blacksburg - MATLAB. ........................................................................ 125
Figura 139. Diseño No Óptimo 2 - Red Blacksburg - REDES 2019.................................................................... 125
Figura 140. Diseño No Óptimo 2 - Red Blacksburg - MATLAB. ........................................................................ 125
Figura 141. Diseño No Óptimo 3 - Red Blacksburg - REDES 2019.................................................................... 125
Figura 142. Diseño No Óptimo 3 - Red Blacksburg - MATLAB. ........................................................................ 125
Figura 143. Diseño No Óptimo 4 - Red Blacksburg - REDES 2019.................................................................... 125
Figura 144. Diseño No Óptimo 4 - Red Blacksburg - MATLAB. ........................................................................ 125
Figura 145. Diseño No Óptimo 5 - Red Blacksburg - REDES 2019.................................................................... 126
Figura 146. Diseño No Óptimo 5 - Red Blacksburg - MATLAB. ........................................................................ 126
Figura 147. Diseño No Óptimo 6 - Red Blacksburg - REDES 2019.................................................................... 126
Figura 148. Diseño No Óptimo 6 - Red Blacksburg - MATLAB. ........................................................................ 126

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
10
Figura 149. SOP Red New York Tunnels - REDES 2019. ................................................................................... 127
Figura 150. SOP Red New York Tunnels - MATLAB. ......................................................................................... 127
Figura 151. Diseño No Óptimo 1 - Red New York Tunnels - REDES 2019. ....................................................... 127
Figura 152. Diseño No Óptimo 1 - Red New York Tunnels - MATLAB. ............................................................ 127
Figura 153. Diseño No Óptimo 2 - Red New York Tunnels - REDES 2019. ....................................................... 127
Figura 154. Diseño No Óptimo 2 - Red New York Tunnels - MATLAB. ............................................................ 127
Figura 155. Diseño No Óptimo 3 - Red New York Tunnels - REDES 2019. ....................................................... 127
Figura 156. Diseño No Óptimo 3 - Red New York Tunnels - MATLAB. ............................................................ 127
Figura 157. Diseño No Óptimo 4 - Red New York Tunnels - REDES 2019. ....................................................... 127
Figura 158. Diseño No Óptimo 4 - Red New York Tunnels - MATLAB. ............................................................ 127
Figura 159. Diseño No Óptimo 5 - Red New York Tunnels - REDES 2019. ....................................................... 128
Figura 160. Diseño No Óptimo 5 - Red New York Tunnels - MATLAB. ............................................................ 128
Figura 161. Diseño No Óptimo 6 - Red New York Tunnels - REDES 2019. ....................................................... 128
Figura 162. Diseño No Óptimo 6 - Red New York Tunnels - MATLAB. ............................................................ 128
Figura 163. SOP Red BakRyan - REDES 2019. ................................................................................................... 129
Figura 164. SOP Red BakRyan - MATLAB. ........................................................................................................ 129
Figura 165. Diseño No Óptimo 1 - Red BakRyan - REDES 2019. ...................................................................... 129
Figura 166. Diseño No Óptimo 1 - Red BakRyan - MATLAB. ............................................................................ 129
Figura 167. Diseño No Óptimo 2 - Red BakRyan - REDES 2019. ...................................................................... 129
Figura 168. Diseño No Óptimo 2 - Red BakRyan - MATLAB. ............................................................................ 129
Figura 169. Diseño No Óptimo 3 - Red BakRyan - REDES 2019. ...................................................................... 129
Figura 170. Diseño No Óptimo 3 - Red BakRyan - MATLAB. ............................................................................ 129
Figura 171. Diseño No Óptimo 4 - Red BakRyan - REDES 2019. ...................................................................... 129
Figura 172. Diseño No Óptimo 4 - Red BakRyan - MATLAB. ............................................................................ 129
Figura 173. Diseño No Óptimo 5 - Red BakRyan - REDES 2019. ...................................................................... 130
Figura 174. Diseño No Óptimo 5 - Red BakRyan - MATLAB. ............................................................................ 130
Figura 175. Diseño No Óptimo 6 - Red BakRyan - REDES 2019. ...................................................................... 130
Figura 176. Diseño No Óptimo 6 - Red BakRyan - MATLAB. ............................................................................ 130
Figura 177. SOP Red Fossolo - REDES 2019. .................................................................................................... 131
Figura 178. SOP Red Fossolo - MATLAB. .......................................................................................................... 131

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
11
Figura 179. Diseño No Óptimo 1 - Red Fossolo - REDES 2019. ........................................................................ 131
Figura 180. Diseño No Óptimo 1 - Red Fossolo - MATLAB. ............................................................................. 131
Figura 181. Diseño No Óptimo 2 - Red Fossolo - REDES 2019. ........................................................................ 131
Figura 182. Diseño No Óptimo 2 - Red Fossolo - MATLAB. ............................................................................. 131
Figura 183. Diseño No Óptimo 3 - Red Fossolo - REDES 2019. ........................................................................ 131
Figura 184. Diseño No Óptimo 3 - Red Fossolo - MATLAB. ............................................................................. 131
Figura 185. Diseño No Óptimo 4 - Red Fossolo - REDES 2019. ........................................................................ 132
Figura 186. Diseño No Óptimo 4 - Red Fossolo - MATLAB. ............................................................................. 132
Figura 187. Diseño No Óptimo 5 - Red Fossolo - REDES 2019. ........................................................................ 132
Figura 188. Diseño No Óptimo 5 - Red Fossolo - MATLAB. ............................................................................. 132
Figura 189. Diseño No Óptimo 6 - Red Fossolo - REDES 2019. ........................................................................ 132
Figura 190. Diseño No Óptimo 6 - Red Fossolo - MATLAB. ............................................................................. 132
Figura 191. SOP Red R28 - REDES 2019. .......................................................................................................... 133
Figura 192. SOP Red R28 - MATLAB. ................................................................................................................ 133
Figura 193. Diseño No Óptimo 1 - Red R28 - REDES 2019. .............................................................................. 133
Figura 194. Diseño No Óptimo 1 - Red R28 - MATLAB. ................................................................................... 133
Figura 195. Diseño No Óptimo 2 - Red R28 - REDES 2019. .............................................................................. 133
Figura 196. Diseño No Óptimo 2 - Red R28 - MATLAB. ................................................................................... 133
Figura 197. Diseño No Óptimo 3 - Red R28 - REDES 2019. .............................................................................. 133
Figura 198. Diseño No Óptimo 3 - Red R28 - MATLAB. ................................................................................... 133
Figura 199. Diseño No Óptimo 4 - Red R28 - REDES 2019. .............................................................................. 134
Figura 200. Diseño No Óptimo 4 - Red R28 - MATLAB. ................................................................................... 134
Figura 201. Diseño No Óptimo 5 - Red R28 - REDES 2019. .............................................................................. 134
Figura 202. Diseño No Óptimo 5 - Red R28 - MATLAB. ................................................................................... 134
Figura 203. Diseño No Óptimo 6 – Red R28 – REDES 2019. ............................................................................ 134
Figura 204. Diseño No Óptimo 6 - Red R28 - MATLAB. ................................................................................... 134
Figura 205. SOP Red Pescara - REDES 2019. .................................................................................................... 135
Figura 206. SOP Red Pescara - MATLAB........................................................................................................... 135
Figura 207. Diseño No Óptimo 1 - Red Pescara - REDES 2019......................................................................... 135
Figura 208. Diseño No Óptimo 1 - Red Pescara - MATLAB. ............................................................................. 135

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
12
Figura 209. Diseño No Óptimo 2 - Red Pescara - REDES 2019......................................................................... 135
Figura 210. Diseño No Óptimo 2 - Red Pescara - MATLAB. ............................................................................. 135
Figura 211. Diseño No Óptimo 3 - Red Pescara - REDES 2019......................................................................... 135
Figura 212. Diseño No Óptimo 3 - Red Pescara - MATLAB. ............................................................................. 135
Figura 213. Diseño No Óptimo 4 - Red Pescara - REDES 2019......................................................................... 136
Figura 214. Diseño No Óptimo 4 - Red Pescara - MATLAB. ............................................................................. 136
Figura 215. Diseño No Óptimo 5 - Red Pescara - REDES 2019......................................................................... 136
Figura 216. Diseño No Óptimo 5 - Red Pescara - MATLAB. ............................................................................. 136
Figura 217. Diseño No Óptimo 6 - Red Pescara – REDES 2019. ....................................................................... 136
Figura 218. Diseño No Óptimo 6 - Red Pescara - MATLAB. ............................................................................. 136
Figura 219. SOP Red Modena - REDES 2019. ................................................................................................... 137
Figura 220. SOP Red Modena - MATLAB. ........................................................................................................ 137
Figura 221. Diseño No Óptimo 1 - Red Modena - REDES 2019. ...................................................................... 137
Figura 222. Diseño No Óptimo 1 - Red Modena - MATLAB. ............................................................................ 137
Figura 223. Diseño No Óptimo 2 - Red Modena - REDES 2019. ...................................................................... 137
Figura 224. Diseño No Óptimo 2 - Red Modena - MATLAB. ............................................................................ 137
Figura 225. Diseño No Óptimo 3 - Red Modena - REDES 2019. ...................................................................... 137
Figura 226. Diseño No Óptimo 3 - Red Modena - MATLAB. ............................................................................ 137
Figura 227. Diseño No Óptimo 4 - Red Modena - REDES 2019. ...................................................................... 138
Figura 228. Diseño No Óptimo 4 - Red Modena - MATLAB. ............................................................................ 138
Figura 229. Diseño No Óptimo 5 - Red Modena - REDES 2019. ...................................................................... 138
Figura 230. Diseño No Óptimo 5 - Red Modena - MATLAB. ............................................................................ 138
Figura 231. Diseño No Óptimo 6 - Red Modena - REDES 2019. ...................................................................... 138
Figura 232. Diseño No Óptimo 6 - Red Modena - MATLAB. ............................................................................ 138
Figura 233. SOP Red Balerma - REDES 2019. ................................................................................................... 139
Figura 234. SOP Red Balerma - MATLAB.......................................................................................................... 139
Figura 235. Diseño No Óptimo 1 - Red Balerma - REDES 2019........................................................................ 139
Figura 236. Diseño No Óptimo 1 - Red Balerma - MATLAB. ............................................................................ 139
Figura 237. Diseño No Óptimo 2 - Red Balerma - REDES 2019........................................................................ 139
Figura 238. Diseño No Óptimo 2 - Red Balerma - MATLAB. ............................................................................ 139

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
13
Figura 239. Diseño No Óptimo 3 - Red Balerma - REDES 2019........................................................................ 139
Figura 240. Diseño No Óptimo 3 - Red Balerma - MATLAB. ............................................................................ 139
Figura 241. Diseño No Óptimo 4 - Red Balerma - REDES 2019........................................................................ 139
Figura 242. Diseño No Óptimo 4 - Red Balerma - MATLAB. ............................................................................ 139
Figura 243. Diseño No Óptimo 5 – Red Balerma - REDES 2019. ...................................................................... 140
Figura 244. Diseño No Óptimo 5 - Red Balerma - MATLAB. ............................................................................ 140
Figura 245. Diseño No Óptimo 6 - Red Balerma - REDES 2019........................................................................ 140
Figura 246. Diseño No Óptimo 6 - Red Balerma - MATLAB. ............................................................................ 140
Figura 247. SOP San Vicente - REDES 2019. ..................................................................................................... 141
Figura 248. SOP San Vicente - MATLAB. .......................................................................................................... 141
Figura 249. Diseño No Óptimo 1 – Red San Vicente - REDES 2019. ................................................................ 141
Figura 250. Diseño No Óptimo 1 - Red San Vicente - MATLAB........................................................................ 141
Figura 251. Diseño No Óptimo 2 - Red San Vicente - REDES 2019. ................................................................. 141
Figura 252. Diseño No Óptimo 2 - Red San Vicente - MATLAB........................................................................ 141
Figura 253. Diseño No Óptimo 3 - Red San Vicente - REDES 2019. ................................................................. 141
Figura 254. Diseño No Óptimo 3 - Red San Vicente - MATLAB........................................................................ 141
Figura 255. Diseño No Óptimo 4 - Red San Vicente - REDES 2019. ................................................................. 142
Figura 256. Diseño No Óptimo 4 - Red San Vicente - MATLAB........................................................................ 142
Figura 257. Diseño No Óptimo 5 - Red San Vicente - REDES 2019. ................................................................. 142
Figura 258. Diseño No Óptimo 5 - Red San Vicente - MATLAB........................................................................ 142
Figura 259. Diseño No Óptimo 6 - Red San Vicente - REDES 2019. ................................................................. 142
Figura 260. Diseño No Óptimo 6 - Red San Vicente - MATLAB........................................................................ 142
Figura 261. SOP Red Cazucá - REDES 2019. ..................................................................................................... 143
Figura 262. SOP Red Cazucá - MATLAB. ........................................................................................................... 143
Figura 263. Diseño No Óptimo 1 - Red Cazucá - REDES 2019. ......................................................................... 143
Figura 264. Diseño No Óptimo 1 - Red Cazucá - MATLAB. .............................................................................. 143
Figura 265. Diseño No Óptimo 2 - Red Cazucá - REDES 2019. ......................................................................... 143
Figura 266. Diseño No Óptimo 2 - Red Cazucá - MATLAB. .............................................................................. 143
Figura 267. Diseño No Óptimo 3 - Red Cazucá - REDES 2019. ......................................................................... 143
Figura 268. Diseño No Óptimo 3 - Red Cazucá - MATLAB. .............................................................................. 143

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
14
Figura 269. Diseño No Óptimo 4 - Red Cazucá - REDES 2019. ......................................................................... 144
Figura 270. Diseño No Óptimo 4 - Red Cazucá - MATLAB. .............................................................................. 144
Figura 271. Diseño No Óptimo 5 - Red Cazucá - REDES 2019. ......................................................................... 144
Figura 272. Diseño No Óptimo 5 - Red Cazucá - MATLAB. .............................................................................. 144
Figura 273. Diseño No Óptimo 6 - Red Cazucá - REDES 2019. ......................................................................... 144
Figura 274. Diseño No Óptimo 6 - Red Cazucá - MATLAB. .............................................................................. 144
Figura 275. SOP Red Elevada - REDES 2019. .................................................................................................... 145
Figura 276. SOP Red Elevada - MATLAB. ......................................................................................................... 145
Figura 277. Diseño No Óptimo 1 - Red Elevada - REDES 2019. ....................................................................... 145
Figura 278. Diseño No Óptimo 1 - Red Elevada - MATLAB. ............................................................................. 145
Figura 279. Diseño No Óptimo 2 - Red Elevada - REDES 2019. ....................................................................... 145
Figura 280. Diseño No Óptimo 2 - Red Elevada - MATLAB. ............................................................................. 145
Figura 281. Diseño No Óptimo 3 - Red Elevada - REDES 2019. ....................................................................... 145
Figura 282. Diseño No Óptimo 3 - Red Elevada - MATLAB. ............................................................................. 145
Figura 283. Diseño No Óptimo 4 - Red Elevada - REDES 2019. ....................................................................... 145
Figura 284. Diseño No Óptimo 4 - Red Elevada - MATLAB. ............................................................................. 145
Figura 285. Diseño No Óptimo 5 - Red Elevada - REDES 2019. ....................................................................... 146
Figura 286. Diseño No Óptimo 5 - Red Elevada - MATLAB. ............................................................................. 146
Figura 287. Diseño No Óptimo 6 - Red Elevada - REDES 2019. ....................................................................... 146
Figura 288. Diseño No Óptimo 6 - Red Elevada - MATLAB. ............................................................................. 146
Figura 289. SOP Red Bolívar - REDES 2019. ..................................................................................................... 147
Figura 290. SOP Red Bolívar - MATLAB. ........................................................................................................... 147
Figura 291. Diseño No Óptimo 1 - Red Bolívar - REDES 2019. ......................................................................... 147
Figura 292. Diseño No Óptimo 1 - Red Bolívar - MATLAB. .............................................................................. 147
Figura 293. Diseño No Óptimo 2 - Red Bolívar - REDES 2019. ......................................................................... 147
Figura 294. Diseño No Óptimo 2 - Red Bolívar - MATLAB. .............................................................................. 147
Figura 295. Diseño No Óptimo 3 - Red Bolívar - REDES 2019. ......................................................................... 147
Figura 296. Diseño No Óptimo 3 - Red Bolívar - MATLAB. .............................................................................. 147
Figura 297. Diseño No Óptimo 4 - Red Bolívar - REDES 2019. ......................................................................... 148
Figura 298. Diseño No Óptima 4 - Red Bolívar - MATLAB................................................................................ 148

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
15
Figura 299. Diseño No Óptimo 5- Red Bolívar - REDES 2019. .......................................................................... 148
Figura 300. Diseño No Óptima 5 - Red Bolívar - MATLAB................................................................................ 148
Figura 301. Diseño No Óptimo 6 - Red Bolívar - REDES 2019. ......................................................................... 148
Figura 302. Diseño No Óptimo 6 - Red Bolívar - MATLAB. .............................................................................. 148
Figura 303. SOP Red La Cumbre - REDES 2019. ............................................................................................... 149
Figura 304. SOP Red La Cumbre - MATLAB. ..................................................................................................... 149
Figura 305. Diseño No Óptimo 1 - Red La Cumbre - REDES 2019. ................................................................... 149
Figura 306. Diseño No Óptimo 1 - Red La Cumbre - MATLAB. ........................................................................ 149
Figura 307. Diseño No Óptimo 2 - Red La Cumbre - REDES 2019. ................................................................... 149
Figura 308. Diseño No Óptimo 2 - Red La Cumbre - MATLAB. ........................................................................ 149
Figura 309. Diseño No Óptimo 3 - Red La Cumbre - REDES 2019. ................................................................... 149
Figura 310. Diseño No Óptimo 3 - Red La Cumbre - MATLAB. ........................................................................ 149
Figura 311. Diseño No Óptimo 4 - Red La Cumbre - REDES 2019. ................................................................... 150
Figura 312. Diseño No Óptimo 4 - Red La Cumbre - MATLAB. ........................................................................ 150
Figura 313. Diseño No Óptimo 5 - Red La Cumbre - REDES 2019. ................................................................... 150
Figura 314. Diseño No Óptimo 5 – Red La Cumbre - MATLAB. ....................................................................... 150
Figura 315. Diseño No Óptimo 6 - Red La Cumbre - REDES 2019. ................................................................... 150
Figura 316. Diseño No Óptimo 6 - Red La Cumbre - MATLAB. ........................................................................ 150
Figura 317. SOP Red Candelaria - REDES 2019. ............................................................................................... 151
Figura 318. SOP Red Candelaria - MATLAB. ..................................................................................................... 151
Figura 319. Diseño No Óptimo 1 - Red Candelaria – REDES 2019. .................................................................. 151
Figura 320. Diseño No Óptimo 1 - Red Candelaria - MATLAB. ........................................................................ 151
Figura 321. Diseño No Óptimo 2 - Red Candelaria - REDES 2019. ................................................................... 151
Figura 322. Diseño No Óptimo 2 - Red Candelaria - MATLAB. ........................................................................ 151
Figura 323. Diseño No Óptimo 3 - Red Candelaria - REDES 2019. ................................................................... 151
Figura 324. Diseño No Óptimo 3 - Red Candelaria - MATLAB. ........................................................................ 151
Figura 325. Diseño No Óptimo 4 - Red Candelaria - REDES 2019. ................................................................... 152
Figura 326. Diseño No Óptimo 4 - Red Candelaria - MATLAB. ........................................................................ 152
Figura 327. Diseño No Óptimo 5 - Red Candelaria - REDES 2019. ................................................................... 152
Figura 328. Diseño No Óptimo 5 - Red Candelaria - MATLAB. ........................................................................ 152

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
16
Figura 329. Diseño No Óptimo 6 - Red Candelaria - REDES 2019. ................................................................... 152
Figura 330. Diseño No Óptimo 6 - Red Candelaria - MATLAB. ........................................................................ 152
Figura 331. SOP Red Bugalagrande - REDES 2019. .......................................................................................... 153
Figura 332. SOP Bugalagrande - MATLAB. ....................................................................................................... 153
Figura 333. Diseño No Óptimo 1 - Red Bugalagrande - REDES 2019. .............................................................. 153
Figura 334. Diseño No Óptimo 1 - Red Bugalagrande - MATLAB. ................................................................... 153
Figura 335. Diseño No Óptimo 2 - Red Bugalagrande - REDES 2019. .............................................................. 153
Figura 336. Diseño No Óptimo 2 - Red Bugalagrande - MATLAB. ................................................................... 153
Figura 337. Diseño No Óptimo 3 - Red Bugalagrande - REDES 2019. .............................................................. 153
Figura 338. Diseño No Óptimo 3 - Red Bugalagrande - MATLAB. ................................................................... 153
Figura 339. Diseño No Óptimo 4 - Red Bugalagrande - REDES 2019. .............................................................. 153
Figura 340. Diseño No Óptimo 4 - Red Bugalagrande - MATLAB. ................................................................... 153
Figura 341. Diseño No Óptimo 5 - Red Bugalagrande - REDES 2019. .............................................................. 154
Figura 342. Diseño No Óptimo 5 - Red Bugalagrande - MATLAB. ................................................................... 154
Figura 343. Diseño No Óptimo 6 - Red Bugalagrande - REDES 2019. .............................................................. 154
Figura 344. Diseño No Óptimo 6 - Red Bugalagrande - MATLAB. ................................................................... 154
Figura 345. SOP Red Carmen - REDES 2019. .................................................................................................... 155
Figura 346. SOP Red Carmen - MATLAB. ......................................................................................................... 155
Figura 347. Diseño No Óptimo 1 - Red Carmen - REDES 2019. ....................................................................... 155
Figura 348. Diseño No Óptimo 1 - Red Carmen - MATLAB. ............................................................................. 155
Figura 349. Diseño No Óptimo 2 - Red Carmen - REDES 2019. ....................................................................... 155
Figura 350. Diseño No Óptimo 2 - Red Carmen - MATLAB. ............................................................................. 155
Figura 351. Diseño No Óptimo 3 - Red Carmen - REDES 2019. ....................................................................... 155
Figura 352. Diseño No Óptimo 3 - Red Carmen - MATLAB. ............................................................................. 155
Figura 353. Diseño No Óptimo 4 - Red Carmen - REDES 2019. ....................................................................... 155
Figura 354. Diseño No Óptimo 4 - Red Carmen - MATLAB. ............................................................................. 155
Figura 355. Diseño No Óptimo 5 - Red Carmen - REDES 2019. ....................................................................... 156
Figura 356. Diseño No Óptimo 5 - Red Carmen - MATLAB. ............................................................................. 156
Figura 357. Diseño No Óptimo 6 - Red Carmen - REDES 2019. ....................................................................... 156
Figura 358. Diseño No Óptimo 6 - Red Carmen - MATLAB. ............................................................................. 156

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
17
Figura 359. SOP Red Chinú - REDES 2019. ....................................................................................................... 157
Figura 360. SOP Red Chinú - MATLAB. ............................................................................................................. 157
Figura 361. Diseño No Óptimo 1 - Red Chinú - REDES 2019. ........................................................................... 157
Figura 362. Diseño No Óptimo 1 - Red Chinú - MATLAB. ................................................................................ 157
Figura 363. Diseño No Óptimo 2 - Red Chinú - REDES 2019. ........................................................................... 157
Figura 364. Diseño No Óptimo 2 - Red Chinú - MATLAB. ................................................................................ 157
Figura 365. Diseño No Óptimo 3 - Red Chinú - REDES 2019. ........................................................................... 157
Figura 366. Diseño No Óptimo 3 - Red Chinú - MATLAB. ................................................................................ 157
Figura 367. Diseño No Óptimo 4 - Red Chinú - REDES 2019. ........................................................................... 157
Figura 368. Diseño No Óptimo 4 - Red Chinú - MATLAB. ................................................................................ 157
Figura 369. Diseño No Óptimo 5 - Red Chinú - REDES 2019. ........................................................................... 158
Figura 370. Diseño No Óptimo 5 - Red Chinú - MATLAB. ................................................................................ 158
Figura 371. Diseño No Óptimo 6 - Red Chinú - REDES 2019. ........................................................................... 158
Figura 372. Diseño No Óptimo 6 - Red Chinú - MATLAB. ................................................................................ 158
Figura 373. SOP Sector 35 - REDES 2019. ........................................................................................................ 159
Figura 374. SOP Red Sector 35 - MATLAB. ....................................................................................................... 159
Figura 375. Diseño No Óptimo 1 - Red Sector 35 - REDES 2019. ..................................................................... 159
Figura 376. Diseño No Óptimo 1 - Red Sector 35 - MATLAB. .......................................................................... 159
Figura 377. Diseño No Óptimo 2 - Red Sector 35 - REDES 2019. ..................................................................... 159
Figura 378. Diseño No Óptimo 2 - Red Sector 35 - MATLAB. .......................................................................... 159
Figura 379. Diseño No Óptimo 3 - Red Sector 35 - REDES 2019. ..................................................................... 159
Figura 380. Diseño No Óptimo 3 - Red Sector 35 - MATLAB. .......................................................................... 159
Figura 381. Diseño No Óptimo 4 - Red Sector 35 - REDES 2019. ..................................................................... 160
Figura 382. Diseño No Óptimo 4 - Red Sector 35 - MATLAB. .......................................................................... 160
Figura 383. Diseño No Óptimo 5 - Red Sector 35 - REDES 2019. ..................................................................... 160
Figura 384. Diseño No Óptimo 5 - Red Sector 35 - MATLAB. .......................................................................... 160
Figura 385. Diseño No Óptimo 6 - Red Sector 35 - REDES 2019. ..................................................................... 160
Figura 386. Diseño No Óptimo 6 - Red Sector 35 - MATLAB. .......................................................................... 160
Figura 387. SOP Red La Enea - REDES 2019. .................................................................................................... 161
Figura 388. SOP Red La Enea - MATLAB. .......................................................................................................... 161

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
18
Figura 389. Diseño No Óptimo 1 - Red La Enea - REDES 2019. ........................................................................ 161
Figura 390. Diseño No Óptimo 1 - Red La Enea - MATLAB. ............................................................................. 161
Figura 391. Diseño No Óptimo 2 - Red La Enea - REDES 2019. ........................................................................ 161
Figura 392. Diseño No Óptimo 2 - Red La Enea - MATLAB. ............................................................................. 161
Figura 393. Diseño No Óptimo 3 - Red La Enea - REDES 2019. ........................................................................ 161
Figura 394. Diseño No Óptimo 3 - Red La Enea - MATLAB. ............................................................................. 161
Figura 395. Diseño No Óptimo 4 - Red La Enea - REDES 2019. ........................................................................ 162
Figura 396. Diseño No Óptimo 4 - Red La Enea - MATLAB. ............................................................................. 162
Figura 397. Diseño No Óptimo 5 - Red La Enea - REDES 2019. ........................................................................ 162
Figura 398. Diseño No Óptimo 5 - Red La Enea - MATLAB. ............................................................................. 162
Figura 399. Diseño No Óptimo 6 - Red La Enea - REDES 2019. ........................................................................ 162
Figura 400. Diseño No Óptimo 6 - Red La Enea - MATLAB. ............................................................................. 162
Figura 401. Perfil de dimensiones fractales en X - Red Two Loops. ................................................................ 163
Figura 402. Perfil de dimensiones fractales en X - Red Two Reservoirs. ......................................................... 163
Figura 403. Perfil de dimensiones fractales en X - Red Taichung. ................................................................... 164
Figura 404. Perfil de dimensiones fractales en X - Red Hanoi. ........................................................................ 164
Figura 405. Perfil de dimensiones fractales en X - Red Blacksburg. ................................................................ 165
Figura 406. Perfil de dimensiones fractales en X - Red New York Tunnels. .................................................... 165
Figura 407. Perfil de dimensiones fractales en X - Red BakRyan. .................................................................... 166
Figura 408. Perfil de dimensiones fractales en X - Red Fossolo. ..................................................................... 166
Figura 409. Perfil de dimensiones fractales en X - Red R28. ........................................................................... 167
Figura 410. Perfil de dimensiones fractales en X - Red Pescara. ..................................................................... 167
Figura 411. Perfil de dimensiones fractales en X - Red Modena. .................................................................... 168
Figura 412. Perfil de dimensiones fractales en X - Red Balerma. .................................................................... 168
Figura 413. Perfil de dimensiones fractales en X - Red San Vicente................................................................ 169
Figura 414. Perfil de dimensiones fractales en X - Red Cazucá. ...................................................................... 169
Figura 415. Perfil de dimensiones fractales en X - Red Elevada. ..................................................................... 170
Figura 416. Perfil de dimensiones fractales en X - Red Bolívar. ...................................................................... 170
Figura 417. Perfil de dimensiones fractales en X - Red La Cumbre. ................................................................ 171
Figura 418. Perfil de dimensiones fractales en X - Red Candelaria. ................................................................ 171

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
19
Figura 419. Perfil de dimensiones fractales en X - Red Bugalagrande. ........................................................... 172
Figura 420. Perfil de dimensiones fractales en X - Red Carmen. ..................................................................... 172
Figura 421. Perfil de dimensiones fractales en X - Red Chinú. ........................................................................ 173
Figura 422. Perfil de dimensiones fractales en X - Red Sector 35. .................................................................. 173
Figura 423. Perfil de dimensiones fractales en X - Red La Enea. ..................................................................... 174
Figura 424. Perfil de dimensiones fractales en Y - Red Two Loops. ................................................................ 174
Figura 425. Perfil de dimensiones fractales en Y - Red Two Reservoirs. ......................................................... 175
Figura 426. Perfil de dimensiones fractales en Y - Red Taichung. ................................................................... 175
Figura 427. Perfil de dimensiones fractales en Y - Red Hanoi. ........................................................................ 176
Figura 428. Perfil de dimensiones fractales en Y - Red Blacksburg. ................................................................ 176
Figura 429. Perfil de dimensiones fractales en Y - Red New York Tunnels. .................................................... 177
Figura 430. Perfil de dimensiones fractales en Y - Red BakRyan. .................................................................... 177
Figura 431. Perfil de dimensiones fractales en Y - Red Fossolo....................................................................... 178
Figura 432. Perfil de dimensiones fractales en Y - Red R28. ........................................................................... 178
Figura 433. Perfil de dimensiones fractales en Y - Red Pescara. ..................................................................... 179
Figura 434. Perfil de dimensiones fractales en Y - Red Modena. .................................................................... 179
Figura 435. Perfil de dimensiones fractales en Y - Red Balerma. .................................................................... 180
Figura 436. Perfil de dimensiones fractales en Y - Red San Vicente. ............................................................... 180
Figura 437. Perfil de dimensiones fractales en Y - Red Cazucá. ...................................................................... 181
Figura 438. Perfil de dimensiones fractales en Y - Red Elevada. ..................................................................... 181
Figura 439. Perfil de dimensiones fractales en Y - Red Bolívar. ...................................................................... 182
Figura 440. Perfil de dimensiones fractales en Y - Red La Cumbre. ................................................................ 182
Figura 441. Perfil de dimensiones fractales en Y - Red Candelaria. ................................................................ 183
Figura 442. Perfil de dimensiones fractales en Y - Red Bugalagrande. ........................................................... 183
Figura 443. Perfil de dimensiones fractales en Y - Red Carmen. ..................................................................... 184
Figura 444. Perfil de dimensiones fractales en Y - Red Carmen. ..................................................................... 184
Figura 445. Perfil de dimensiones fractales en Y - Red Sector 35. .................................................................. 185
Figura 446. Perfil de dimensiones fractales en Y - Red La Enea. ..................................................................... 185
Figura 447. DEM Two Loops - Óptimo. ............................................................................................................ 186
Figura 448. DEM Two Loops - No Óptimo 1..................................................................................................... 186

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
20
Figura 449. DEM Two Loops - No Óptimo 2..................................................................................................... 186
Figura 450. DEM Two Loops - No Óptimo 3..................................................................................................... 186
Figura 451. DEM Two Loops - No Óptimo 4..................................................................................................... 186
Figura 452. DEM Two Loops - No Óptimo 5..................................................................................................... 186
Figura 453. DEM Two Loops - No Óptimo 6..................................................................................................... 186
Figura 454. DEM Two Reservoirs - Óptimo. ..................................................................................................... 186
Figura 455. DEM Two Reservoirs - No Óptimo 1. ............................................................................................ 186
Figura 456. DEM Two Reservoirs - No Óptimo 2. ............................................................................................ 186
Figura 457. DEM Two Reservoirs - No Óptimo 3. ............................................................................................ 186
Figura 458. DEM Two Reservoirs - No Óptimo 4. ............................................................................................ 186
Figura 459. DEM Two Reservoirs - No Óptimo 5. ............................................................................................ 186
Figura 460. DEM Two Reservoirs - No Óptimo 6. ............................................................................................ 186
Figura 461. DEM Taichung - Óptimo. ............................................................................................................... 187
Figura 462. DEM Taichung - No Óptimo 1 ....................................................................................................... 187
Figura 463. DEM Taichung - No Óptimo 2. ...................................................................................................... 187
Figura 464. DEM Taichung - No Óptimo 3. ...................................................................................................... 187
Figura 465. DEM Taichung - No Óptimo 4. ...................................................................................................... 187
Figura 466. DEM Taichung - No Óptimo 5. ...................................................................................................... 187
Figura 467. DEM Taichung - No Óptimo 6. ...................................................................................................... 187
Figura 468. DEM Hanoi – Óptimo. ................................................................................................................... 187
Figura 469. DEM Hanoi - No Óptimo 1. ........................................................................................................... 187
Figura 470. DEM Hanoi - No Óptimo 2. ........................................................................................................... 187
Figura 471. DEM Hanoi - No Óptimo 3. ........................................................................................................... 187
Figura 472. DEM Hanoi - No Óptimo 4. ........................................................................................................... 187
Figura 473. DEM Hanoi - No Óptimo 5. ........................................................................................................... 187
Figura 474. DEM Hanoi - No Óptimo 6. ........................................................................................................... 187
Figura 475. DEM Blacksburg - Óptimo. ............................................................................................................ 188
Figura 476. DEM Blacksburg - No Óptimo 1. ................................................................................................... 188
Figura 477. DEM Blacksburg - No Óptimo 2. ................................................................................................... 188
Figura 478. DEM Blacksburg - No Óptimo 3. ................................................................................................... 188

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
21
Figura 479. DEM Blacksburg - No Óptimo 4. ................................................................................................... 188
Figura 480. DEM Blacksburg - No Óptimo 5. ................................................................................................... 188
Figura 481. DEM Blacksburg - No Óptimo 6. ................................................................................................... 188
Figura 482. DEM New York Tunnels - Óptimo. ................................................................................................ 188
Figura 483. DEM New York Tunnels - No Óptimo 1. ........................................................................................ 188
Figura 484. DEM New York Tunnels - No Óptimo 2. ........................................................................................ 188
Figura 485. DEM New York Tunnels - No Óptimo 3. ........................................................................................ 188
Figura 486. DEM New York Tunnels - No Óptimo 4. ........................................................................................ 188
Figura 487. DEM New York Tunnels - No Óptimo 5. ........................................................................................ 188
Figura 488. DEM New York Tunnels - No Óptimo 6. ........................................................................................ 188
Figura 489. DEM BakRyan - Óptimo................................................................................................................. 189
Figura 490. DEM BakRyan - No Óptimo 1. ....................................................................................................... 189
Figura 491. DEM BakRyan - No Óptimo 2. ....................................................................................................... 189
Figura 492. DEM BakRyan - No Óptimo 3. ....................................................................................................... 189
Figura 493. DEM BakRyan - No Óptimo 4. ....................................................................................................... 189
Figura 494. DEM BakRyan - No Óptimo 5. ....................................................................................................... 189
Figura 495. DEM BakRyan - No Óptimo 6. ....................................................................................................... 189
Figura 496. DEM Fossolo - Óptimo. ................................................................................................................. 189
Figura 497. DEM Fossolo - No Óptimo 1. ......................................................................................................... 189
Figura 498. DEM Fossolo - No Óptimo 2. ......................................................................................................... 189
Figura 499. DEM Fossolo - No Óptimo 3. ......................................................................................................... 189
Figura 500. DEM Fossolo - No Óptimo 4. ......................................................................................................... 189
Figura 501. DEM Fossolo - No Óptimo 5. ......................................................................................................... 189
Figura 502. DEM Fossolo - No Óptimo 6. ......................................................................................................... 189
Figura 503. DEM R28 - Óptimo. ....................................................................................................................... 190
Figura 504. DEM R28 - No Óptimo 1. ............................................................................................................... 190
Figura 505. DEM R28 - No Óptimo 2. ............................................................................................................... 190
Figura 506. DEM R28 - No Óptimo 3. ............................................................................................................... 190
Figura 507. DEM R28 - No Óptimo 4. ............................................................................................................... 190
Figura 508. DEM R28 - No Óptimo 5. ............................................................................................................... 190

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
22
Figura 509. DEM R28 - No Óptimo 6. ............................................................................................................... 190
Figura 510. DEM Pescara – Óptimo. ................................................................................................................ 190
Figura 511. DEM Pescara - No Óptimo 1. ........................................................................................................ 190
Figura 512. DEM Pescara - No Óptimo 2. ........................................................................................................ 190
Figura 513. DEM Pescara - No Óptimo 3. ........................................................................................................ 190
Figura 514. DEM Pescara - No Óptima 4. ......................................................................................................... 190
Figura 515. DEM Pescara - No Óptima 5. ......................................................................................................... 190
Figura 516. DEM Pescara - No Óptima 6. ......................................................................................................... 190
Figura 517. DEM Modena - Óptimo. ................................................................................................................ 191
Figura 518. DEM Modena - No Óptimo 1. ....................................................................................................... 191
Figura 519. DEM Modena - No Óptimo 2. ....................................................................................................... 191
Figura 520. DEM Modena - No Óptimo 3. ....................................................................................................... 191
Figura 521. DEM Modena - No Óptimo 4. ....................................................................................................... 191
Figura 522. DEM Modena - No Óptimo 5. ....................................................................................................... 191
Figura 523. DEM Modena - No Óptimo 6. ....................................................................................................... 191
Figura 524. DEM Balerma - Óptimo. ................................................................................................................ 191
Figura 525. DEM Balerma - No Óptimo 1. ....................................................................................................... 191
Figura 526. DEM Balerma - No Óptimo 2. ....................................................................................................... 191
Figura 527. DEM Balerma - No Óptimo 3. ....................................................................................................... 191
Figura 528. DEM Balerma - No Óptimo 4. ....................................................................................................... 191
Figura 529. DEM Balerma - No Óptimo 5. ....................................................................................................... 191
Figura 530. DEM Balerma - No Óptimo 6. ....................................................................................................... 191
Figura 531. DEM San Vicente - Óptimo. .......................................................................................................... 192
Figura 532. DEM San Vicente - No Óptimo 1. .................................................................................................. 192
Figura 533. DEM San Vicente - No Óptimo 2. .................................................................................................. 192
Figura 534. DEM San Vicente - No Óptimo 3. .................................................................................................. 192
Figura 535. DEM San Vicente - No Óptimo 4. .................................................................................................. 192
Figura 536. DEM San Vicente - No Óptimo 5. .................................................................................................. 192
Figura 537. DEM San Vicente - No Óptimo 6. .................................................................................................. 192
Figura 538. DEM Cazucá - Óptimo. .................................................................................................................. 192

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
23
Figura 539. DEM Cazucá - No Óptimo 1. .......................................................................................................... 192
Figura 540. DEM Cazucá - No Óptimo 2. .......................................................................................................... 192
Figura 541. DEM Cazucá - No Óptimo 3. .......................................................................................................... 192
Figura 542. DEM Cazucá - No Óptimo 4. .......................................................................................................... 192
Figura 543. DEM Cazucá - No Óptimo 5. .......................................................................................................... 192
Figura 544. DEM Cazucá - No Óptimo 6. .......................................................................................................... 192
Figura 545. DEM Elevada - Óptimo. ................................................................................................................. 193
Figura 546. DEM Elevada - No Óptimo 1. ........................................................................................................ 193
Figura 547. DEM Elevada - No Óptimo 2. ........................................................................................................ 193
Figura 548. DEM Elevada - No Óptimo 3. ........................................................................................................ 193
Figura 549. DEM Elevada - No Óptimo 4. ........................................................................................................ 193
Figura 550. DEM Elevada - No Óptimo 5. ........................................................................................................ 193
Figura 551. DEM Elevada - No Óptimo 6. ........................................................................................................ 193
Figura 552. DEM Bolívar - Óptimo. .................................................................................................................. 193
Figura 553. DEM Bolívar - No Óptimo 1. .......................................................................................................... 193
Figura 554. DEM Bolívar - No Óptimo 2. .......................................................................................................... 193
Figura 555. DEM Bolívar - No Óptimo 3. .......................................................................................................... 193
Figura 556. DEM Bolívar - No Óptimo 4. .......................................................................................................... 193
Figura 557. DEM Bolívar - No Óptimo 5. .......................................................................................................... 193
Figura 558. DEM Bolívar - No Óptimo 6. .......................................................................................................... 193
Figura 559. DEM La Cumbre - Óptimo. ............................................................................................................ 194
Figura 560. DEM La Cumbre - No Óptimo 1..................................................................................................... 194
Figura 561. DEM La Cumbre - No Óptimo 2..................................................................................................... 194
Figura 562. DEM La Cumbre - No Óptimo 3..................................................................................................... 194
Figura 563. DEM La Cumbre - No Óptimo 4..................................................................................................... 194
Figura 564. DEM La Cumbre - No Óptimo 5..................................................................................................... 194
Figura 565. DEM La Cumbre - No Óptimo 6..................................................................................................... 194
Figura 566. DEM Candelaria - Óptimo. ............................................................................................................ 194
Figura 567. DEM Candelaria - No Óptimo 1. .................................................................................................... 194
Figura 568. DEM Candelaria - No Óptimo 2. .................................................................................................... 194

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
24
Figura 569. DEM Candelaria - No Óptimo 3. .................................................................................................... 194
Figura 570. DEM Candelaria - No Óptimo 4. .................................................................................................... 194
Figura 571. DEM Candelaria - No Óptimo 5. .................................................................................................... 194
Figura 572. DEM Candelaria - No Óptimo 6. .................................................................................................... 194
Figura 573. DEM Bugalagrande - Óptimo. ....................................................................................................... 195
Figura 574. DEM Bugalagrande - No Óptimo 1. ............................................................................................... 195
Figura 575. DEM Bugalagrande - No Óptimo 2. ............................................................................................... 195
Figura 576. DEM Bugalagrande - No Óptimo 3. ............................................................................................... 195
Figura 577. DEM Bugalagrande - No Óptimo 4. ............................................................................................... 195
Figura 578. DEM Bugalagrande - No Óptimo 5. ............................................................................................... 195
Figura 579. DEM Bugalagrande - No Óptimo 6. ............................................................................................... 195
Figura 580. DEM Carmen - Óptimo. ................................................................................................................. 195
Figura 581. DEM Carmen - No Óptimo 1. ........................................................................................................ 195
Figura 582. DEM Carmen - No Óptimo 2. ........................................................................................................ 195
Figura 583. DEM Carmen - No Óptimo 3. ........................................................................................................ 195
Figura 584. DEM Carmen - No Óptimo 4. ........................................................................................................ 195
Figura 585. DEM Carmen - No Óptimo 5. ........................................................................................................ 195
Figura 586. DEM Carmen - No Óptimo 6. ........................................................................................................ 195
Figura 587. DEM Chinú - Óptimo. .................................................................................................................... 196
Figura 588. DEM Chinú - No Óptimo 1. ............................................................................................................ 196
Figura 589. DEM Chinú - No Óptimo 2. ............................................................................................................ 196
Figura 590. DEM Chinú - No Óptimo 3. ............................................................................................................ 196
Figura 591. DEM Chinú - No Óptimo 4. ............................................................................................................ 196
Figura 592. DEM Chinú - No Óptimo 5. ............................................................................................................ 196
Figura 593. DEM Chinú - No Óptimo 6. ............................................................................................................ 196
Figura 594. DEM Sector 35 - Óptimo. .............................................................................................................. 196
Figura 595. DEM Sector 35 - No Óptimo 1. ...................................................................................................... 196
Figura 596. DEM Sector 35 - No Óptimo 2. ...................................................................................................... 196
Figura 597. DEM Sector 35 - No Óptimo 3. ...................................................................................................... 196
Figura 598. DEM Sector 35 - No Óptimo 4. ...................................................................................................... 196

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
25
Figura 599. DEM Sector 35 - No Óptimo 5. ...................................................................................................... 196
Figura 600. DEM Sector 35 - No Óptimo 6. ...................................................................................................... 196
Figura 601. DEM La Enea - Óptimo. ................................................................................................................. 197
Figura 602. DEM La Enea - No Óptimo 1.......................................................................................................... 197
Figura 603. DEM La Enea - No Óptimo 2.......................................................................................................... 197
Figura 604. DEM La Enea - No Óptimo 3.......................................................................................................... 197
Figura 605. DEM La Enea - No Óptimo 4.......................................................................................................... 197
Figura 606. DEM La Enea - No Óptimo 5.......................................................................................................... 197
Figura 607. DEM La Enea - No Óptimo 6.......................................................................................................... 197
Figura 608. Análisis fractal bidimensional – Altura unitaria - Red Two Loops. ............................................... 204
Figura 609. Análisis fractal bidimensional – Altura unitaria - Red Two Reservoirs. ........................................ 205
Figura 610. Análisis fractal bidimensional – Altura unitaria - Red Taichung. .................................................. 205
Figura 611. Análisis fractal bidimensional – Altura unitaria - Red Hanoi. ....................................................... 206
Figura 612. Análisis fractal bidimensional – Altura unitaria - Red Blacksburg. ............................................... 206
Figura 613. Análisis fractal bidimensional – Altura unitaria - Red New York Tunnels..................................... 207
Figura 614. Análisis fractal bidimensional – Altura unitaria - Red BakRyan. ................................................... 207
Figura 615. Análisis fractal bidimensional – Altura unitaria - Red Fossolo. ..................................................... 208
Figura 616. Análisis fractal bidimensional – Altura unitaria - Red R28. ........................................................... 208
Figura 617. Análisis fractal bidimensional – Altura unitaria - Red Pescara. .................................................... 209
Figura 618. Análisis fractal bidimensional – Altura unitaria - Red Modena. ................................................... 209
Figura 619. Análisis fractal bidimensional – Altura unitaria - Red Balerma. ................................................... 210
Figura 620. Análisis fractal bidimensional – Altura unitaria - Red Cazucá. ..................................................... 210
Figura 621. Análisis fractal bidimensional – Altura unitaria - Red Bolívar....................................................... 211
Figura 622. Análisis fractal bidimensional – Altura unitaria - Red La Cumbre. ............................................... 211
Figura 623. Análisis fractal bidimensional - Altura unitaria - Red Candelaria. ................................................ 212
Figura 624. Análisis fractal bidimensional – Altura unitaria - Red Bugalagrande............................................ 212
Figura 625. Análisis fractal bidimensional – Altura unitaria - Red Carmen. .................................................... 213
Figura 626. Análisis fractal bidimensional – Altura unitaria - Red Chinú. ....................................................... 213
Figura 627. Análisis fractal bidimensional – Altura unitaria - Red Sector 35................................................... 214
Figura 628. Análisis fractal bidimensional – Altura unitaria - Red La Enea. .................................................... 214

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
26
Figura 629. Análisis fractal bidimensional - Altura por tanteo - Red Two Loops. ........................................... 215
Figura 630. Análisis fractal bidimensional - Altura por tanteo - Red Two Reservoirs. .................................... 215
Figura 631. Análisis fractal bidimensional - Altura por tanteo - Red Taichung. .............................................. 216
Figura 632. Análisis fractal bidimensional - Altura por tanteo - Red Hanoi. ................................................... 216
Figura 633. Análisis fractal bidimensional - Altura por tanteo - Red Blacksburg. ........................................... 217
Figura 634. Análisis fractal bidimensional - Altura por tanteo - Red Fossolo. ................................................. 217
Figura 635. Análisis fractal bidimensional – Altura por tanteo - Red R28. ...................................................... 218
Figura 636. Análisis fractal bidimensional - Altura por tanteo - Red Pescara. ................................................ 218
Figura 637. Análisis fractal bidimensional - Altura por tanteo - Red Modena. ............................................... 219
Figura 638. Análisis fractal bidimensional - Altura por tanteo - Red Balerma. ............................................... 219
Figura 639. Análisis fractal bidimensional - Altura por tanteo - Red San Vicente. .......................................... 220
Figura 640. Análisis fractal bidimensional - Altura por tanteo - Red Cazucá................................................... 220
Figura 641. Análisis fractal bidimensional - Altura por tanteo - Red Elevada. ................................................ 221
Figura 642. Análisis fractal bidimensional - Altura por tanteo - Red Bolívar. .................................................. 221
Figura 643. Análisis fractal bidimensional - Altura por tanteo - Red La Cumbre. ........................................... 222
Figura 644. Análisis fractal bidimensional - Altura por tanteo - Red Candelaria............................................. 222
Figura 645. Análisis fractal bidimensional - Altura por tanteo - Red Bugalagrande........................................ 223
Figura 646. Análisis fractal bidimensional - Altura por tanteo - Red Carmen. ................................................ 223
Figura 647. Análisis fractal bidimensional - Altura por tanteo - Red Chinú..................................................... 224
Figura 648. Análisis fractal bidimensional - Altura por tanteo - Red La Enea. ................................................ 224
Figura 649. Comparación de dimensiones fractales - Altura unitaria. ............................................................ 225
Figura 650. Comparación de dimensiones fractales - Altura por tanteo. ....................................................... 226
Figura 651. Dimensión fractal de la SOP vs Número de tuberías - Altura por tanteo. .................................... 226
Figura 652. Dimensión fractal de la SOP vs Número de nodos - Altura por tanteo. ....................................... 227
Figura 653. Dimensión fractal de la SOP. ......................................................................................................... 231
Figura 654. Red Two Loops 2D - REDES 2019. ................................................................................................. 246
Figura 655. Red Two Reservoirs 2D - REDES 2019. .......................................................................................... 246
Figura 656. Red Taichung 2D - REDES 2019. .................................................................................................... 246
Figura 657. Red Hanoi 2D - REDES 2019. ......................................................................................................... 246
Figura 658. Red New York Tunnels 2D - REDES 2019. ..................................................................................... 246

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
27
Figura 659. Red BakRyan 2D - REDES 2019. ..................................................................................................... 246
Figura 660. Red Fossolo 2D - REDES 2019. ...................................................................................................... 247
Figura 661. Red R28 2D - REDES 2019. ............................................................................................................ 247
Figura 662. Red Pescara 2D - REDES 2019. ...................................................................................................... 247
Figura 663. Red Modena 2D - REDES 2019. ..................................................................................................... 247
Figura 664. Red Balerma 2D - REDES 2019. ..................................................................................................... 247
Figura 665. Red San Vicente 2D - REDES 2019................................................................................................. 248
Figura 666. Red Cazucá 2D - REDES 2019. ....................................................................................................... 248
Figura 667. Red Elevada 2D - REDES 2019. ...................................................................................................... 248
Figura 668. Red Bolívar 2D - REDES 2019. ....................................................................................................... 248
Figura 669. Red La Cumbre 2D - REDES 2019. ................................................................................................. 248
Figura 670. Red Candelaria 2D - REDES 2019. ................................................................................................. 248
Figura 671. Red Bugalagrande 2D - REDES 2019. ............................................................................................ 249
Figura 672. Red Carmen 2D - REDES 2019. ...................................................................................................... 249
Figura 673. Red Chinú 2D - REDES 2019. ......................................................................................................... 249
Figura 674. Red Sector 35 2D - REDES 2019. ................................................................................................... 249
Figura 675. Red La Enea 2D - REDES 2019. ...................................................................................................... 250
Figura 676. Curva de costos - Red Two Loops. ................................................................................................ 254
Figura 677. Curva de costos - Red Two Reservoirs. ......................................................................................... 254
Figura 678. Curva de costos - Red Taichung. ................................................................................................... 255
Figura 679. Curva de costos - Red Hanoi. ........................................................................................................ 255
Figura 680. Curva de costos - Red Blacksburg. ................................................................................................ 255
Figura 681. Curva de costos - Red New York Tunnels...................................................................................... 256
Figura 682. Curva de costos - Red BakRyan. .................................................................................................... 256
Figura 683. Curva de costos - Red Fossolo....................................................................................................... 257
Figura 684. Curva de costos - Red R28............................................................................................................. 257
Figura 685. Curva de costos - Red Pescara. ..................................................................................................... 258
Figura 686. Curva de costos - Red Modena. .................................................................................................... 258
Figura 687. Curva de costos - Red Balerma. .................................................................................................... 259
Figura 688. Curva de costos - Tuberías biaxiales en PVC. ................................................................................ 259

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
28
Figura 689. Lectura de datos............................................................................................................................ 260
Figura 690. Definición de variables - Parte 1. .................................................................................................. 261
Figura 691. Definición de variables - Parte 2. .................................................................................................. 261
Figura 692. Definición de variables - Parte 3. .................................................................................................. 261
Figura 693. Trazado de la red - Parte 1. ........................................................................................................... 261
Figura 694. Trazado de la red - Parte 2. ........................................................................................................... 262
Figura 695. Trazado de la red - Parte 3. ........................................................................................................... 262
Figura 696. Generación de SGH - Parte 1. ....................................................................................................... 263
Figura 697. Generación de SGH - Parte 2. ....................................................................................................... 263
Figura 698. Generación SGH - Parte 3. ............................................................................................................ 263
Figura 699. Generación SGH - Parte 4. ............................................................................................................ 263
Figura 700. Generación SGH - Parte 5. ............................................................................................................ 264
Figura 701. Generación SGH - Parte 6. ............................................................................................................ 264
Figura 702. Generación SGH - Parte 7. ............................................................................................................ 264
Figura 703. Generación SGH - Parte 8. ............................................................................................................ 264
Figura 704. Generación SGH - Parte 9. ............................................................................................................ 265
Figura 705. Generación SGH - Parte 10. .......................................................................................................... 265
Figura 706. Generación SGH - Parte 11. .......................................................................................................... 266
Figura 707. Análisis R/S - Parte 1. .................................................................................................................... 266
Figura 708. Análisis R/S - Parte 2. .................................................................................................................... 267
Figura 709. Análisis R/S - Parte 3. .................................................................................................................... 267
Figura 710. Función R/S - Parte 1..................................................................................................................... 267
Figura 711. Función R/S - Parte 2..................................................................................................................... 267
Figura 712. Función R/S - Parte 3..................................................................................................................... 267
Figura 713. Función R/S - Parte 4..................................................................................................................... 267
Figura 714. Función R/S – Parte 5. ................................................................................................................... 268
Figura 715. Análisis fractal bidimensional - Parte 1. ........................................................................................ 268
Figura 716. Análisis fractal bidimensional - Parte 2. ........................................................................................ 268
Figura 717. Función de cálculo de masa de una caja....................................................................................... 268
Figura 718. Conteo de diámetros. ................................................................................................................... 270

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
29
ÍNDICE DE TABLAS
Tabla 1. Redes patrón. ....................................................................................................................................... 81
Tabla 2. Redes reales. ........................................................................................................................................ 82
Tabla 3. Dimensiones fractales - Altura unitaria - Red Two Loops. ................................................................. 198
Tabla 4. Dimensiones fractales - Altura unitaria - Red Two Loops. ................................................................. 198
Tabla 5. Dimensiones fractales - Altura unitaria - Red Taichung. .................................................................... 198
Tabla 6. Dimensiones fractales - Altura unitaria - Red Hanoi. ......................................................................... 198
Tabla 7. Dimensiones fractales - Altura unitaria - Red Blacksburg. ................................................................. 198
Tabla 8. Dimensiones fractales - Altura unitaria - Red New York Tunnels. ..................................................... 198
Tabla 9. Dimensiones fractales - Altura unitaria - Red BakRyan. .................................................................... 198
Tabla 10. Dimensiones fractales - Altura unitaria - Red Fossolo. .................................................................... 198
Tabla 11. Dimensiones fractales - Altura unitaria - Red R28. .......................................................................... 199
Tabla 12. Dimensiones fractales - Altura unitaria - Red Pescara. .................................................................... 199
Tabla 13. Dimensiones fractales - Altura unitaria - Red Modena. ................................................................... 199
Tabla 14. Dimensiones fractales - Altura unitaria - Red Balerma. ................................................................... 199
Tabla 15. Dimensiones fractales - Altura unitaria - Red Cazucá. ..................................................................... 199
Tabla 16. Dimensiones fractales - Altura unitaria - Red Bolívar. ..................................................................... 199
Tabla 17. Dimensiones fractales - Altura unitaria - Red La Cumbre. ............................................................... 199
Tabla 18. Dimensiones fractales - Altura unitaria - Red Candelaria. ............................................................... 199
Tabla 19. Dimensiones fractales - Altura unitaria - Red Bugalagrande. .......................................................... 199
Tabla 20. Dimensiones fractales - Altura unitaria - Red Carmen. .................................................................... 199
Tabla 21. Dimensiones fractales - Altura unitaria - Red Chinú. ....................................................................... 200
Tabla 22. Dimensiones fractales - Altura unitaria - Red Sector 35. ................................................................. 200
Tabla 23. Análisis fractal bidimensional - Altura unitaria - Red La Enea. ........................................................ 200
Tabla 24. Alturas de caja por tanteo. ............................................................................................................... 201
Tabla 25. Dimensiones fractales - Altura por tanteo - Red Two Loops. .......................................................... 202

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
30
Tabla 26. Dimensiones fractales - Altura por tanteo - Red Reservoirs. ........................................................... 202
Tabla 27. Dimensiones fractales - Altura por tanteo - Red Taichung. ............................................................. 202
Tabla 28. Dimensiones fractales - Altura por tanteo - Red Hanoi. .................................................................. 202
Tabla 29. Dimensiones fractales - Altura por tanteo - Red Blacksburg. .......................................................... 202
Tabla 30. Dimensiones fractales - Altura por tanteo - Red Fossolo. ............................................................... 202
Tabla 31. Dimensiones fractales - Altura por tanteo - Red R28. ..................................................................... 202
Tabla 32. Dimensiones fractales - Altura por tanteo - Red Pescara. ............................................................... 202
Tabla 33. Dimensiones fractales - Altura por tanteo - Red Modena. .............................................................. 203
Tabla 34. Dimensiones fractales - Altura por tanteo - Red Balerma. .............................................................. 203
Tabla 35. Dimensiones fractales - Altura por tanteo - Red San Vicente. ......................................................... 203
Tabla 36. Dimensiones fractales - Altura por tanteo - Red Cazucá. ................................................................ 203
Tabla 37. Dimensiones fractales - Altura por tanteo - Red Elevada. ............................................................... 203
Tabla 38. Dimensiones fractales - Altura por tanteo - Red Bolívar. ................................................................ 203
Tabla 39. Dimensiones fractales - Altura por tanteo - Red La Cumbre. .......................................................... 203
Tabla 40. Dimensiones fractales - Altura por tanteo - Red Candelaria. .......................................................... 203
Tabla 41. Dimensiones fractales - Altura por tanteo - Red Bugalagrande. ..................................................... 204
Tabla 42. Dimensiones fractales - Altura por tanteo - Red Carmen. ............................................................... 204
Tabla 43. Dimensiones fractales - Altura por tanteo - Red Chinú. .................................................................. 204
Tabla 44. Dimensiones fractales - Altura por tanteo - Red La Enea. ............................................................... 204
Tabla 45. Comparación de dimensiones fractales. .......................................................................................... 225
Tabla 46. Comportamiento fractal de la SOP - Altura unitaria. ....................................................................... 231
Tabla 47. Comportamiento fractal de la SOP - Altura por tanteo. .................................................................. 231
Tabla 48. Diámetros y costos unitarios - Red Two Loops. Adaptado de Keedwell y Khu (2006). ................... 251
Tabla 49. Diámetros y costos unitarios - Red Two Reservoirs. ........................................................................ 251
Tabla 50. Diámetros y costos unitarios - Red Taichung. Adaptado de Sung et. al. (2007). ............................. 251
Tabla 51. Diámetros y costos unitarios - Red Hanoi. Adaptado de Beygi et. al. (2014). ................................. 251
Tabla 52. Diámetros y costos unitarios - Red Blacksburg. Adaptado de University of Exeter (s.f). ................ 251
Tabla 53. Diámetros y costos unitarios - Red New York Tunnels. Adaptado de University of Exeter (s.f.). ... 251
Tabla 54. Diámetros y costos unitarios - Red BakRyan. Adaptado de Lee y Lee (2001).................................. 252
Tabla 55. Diámetros y costos unitarios - Red Fossolo. Adaptado de University of Exeter (s.f.). .................... 252

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
31
Tabla 56. Diámetros y costos unitarios - Red R28. Adaptado de Saldarriaga (2016). ..................................... 252
Tabla 57. Diámetros y costos unitarios - Red Pescara. Adaptado de University of Exeter (s.f.). .................... 252
Tabla 58. Diámetros y costos unitarios - Red Modena. Adaptado de University of Exeter (s.f.) .................... 252
Tabla 59. Diámetros y costos unitarios - Red Balerma. Adaptado de University of Exeter (s.f.). ................... 252
Tabla 60. Diámetros y costos unitarios - Red Exnet. ....................................................................................... 253
Tabla 61. Diámetros comerciales - Tuberías biaxiales en PVC. Adaptado de PAVCO Wavin, S.A (2019). ....... 253
Tabla 62. Costos - Diseños - Parte 1. ................................................................................................................ 269
Tabla 63. Costos - Diseños - Parte 2. ................................................................................................................ 269
Tabla 64. Costos - Diseños - Parte 3. ................................................................................................................ 270
Tabla 65. Diámetros de diseño - Red Two Loops. ............................................................................................ 271
Tabla 66. Diámetros de diseño - Red Two Reservoirs. .................................................................................... 271
Tabla 67. Diámetros de diseño - Red Taichung. .............................................................................................. 272
Tabla 68. Diámetros de diseño - Red Hanoi..................................................................................................... 272
Tabla 69. Diámetros de diseño - Red Blacksburg............................................................................................. 273
Tabla 70. Diámetros de diseño - Red New York Tunnels. ................................................................................ 273
Tabla 71. Diámetros de diseño - Red BakRyan. ............................................................................................... 273
Tabla 72. Diámetros de diseño - Red Fossolo. ................................................................................................. 274
Tabla 73. Diámetros de diseño - Red R28. ....................................................................................................... 274
Tabla 74. Diámetros de diseño - Red Pescara.................................................................................................. 274
Tabla 75. Diámetros de diseño - Red Modena. ............................................................................................... 275
Tabla 76. Diámetros de diseño - Red Balerma................................................................................................. 275
Tabla 77. Diámetros de diseño - Red San Vicente. .......................................................................................... 275
Tabla 78. Diámetros de diseño - Red Cazucá. .................................................................................................. 276
Tabla 79. Diámetros de diseño - Red Elevada. ................................................................................................ 276
Tabla 80. Diámetros de diseño - Red Bolívar. .................................................................................................. 276
Tabla 81. Diámetros de diseño - Red La Cumbre. ............................................................................................ 277
Tabla 82. Diámetros de diseño - Red Candelaria. ............................................................................................ 277
Tabla 83. Diámetros de diseño - Red Bugalagrande. ....................................................................................... 277
Tabla 84. Diámetros de diseño - Red Carmen. ................................................................................................ 278
Tabla 85. Diámetros de diseño - Red Chinú. .................................................................................................... 278

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
32
Tabla 86. Diámetros de diseño - Red Sector 35. .............................................................................................. 278
Tabla 87. Diámetros de diseño - Red La Enea. ................................................................................................. 279

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
33
ÍNDICE DE ECUACIONES
Ecuación 1. Ley de viscosidad de Newton. ........................................................................................................ 39
Ecuación 2. Viscosidad cinemática de un fluido. ............................................................................................... 39
Ecuación 3. Ecuación general de conservación para un volumen de control fijo y no deformable. ................ 39
Ecuación 4. Ecuación de conservación de la masa para flujo a presión en tuberías circulares. ....................... 40
Ecuación 5. Ecuación de Bernoulli. .................................................................................................................... 40
Ecuación 6. Número de Reynolds para flujo en tuberías a presión. .................................................................. 41
Ecuación 7. Pérdidas menores en una tubería. ................................................................................................. 43
Ecuación 8. Ecuación de Darcy-Weisbach. ........................................................................................................ 43
Ecuación 9. Factor de fricción para régimen de flujo laminar. .......................................................................... 43
Ecuación 10. Ecuación de Colebrook-White para el factor de fricción. ............................................................ 43
Ecuación 11. Ecuación para la velocidad media en flujo turbulento. ................................................................ 44
Ecuación 12. Ecuación de Hazen-Williams......................................................................................................... 44
Ecuación 13. Pérdidas por fricción según la Ecuación de Hazen-Williams. ....................................................... 44
Ecuación 14. Coeficiente de Hazen-Williams a la luz de la ecuación de Darcy-Weisbach. ............................... 44
Ecuación 15. Restricción de continuidad en el nudo i. ...................................................................................... 45
Ecuación 16. Pérdidas de energía en un tubo. .................................................................................................. 45
Ecuación 17. Restricción de energía en el circuito i........................................................................................... 46
Ecuación 18. Relación no lineal entre el caudal de flujo y las pérdidas por fricción. ........................................ 46
Ecuación 19. Caudal por la tubería ij. ................................................................................................................ 46
Ecuación 20. Ecuación de altura piezométrica en el nudo i. ............................................................................. 47
Ecuación 21. Ecuación de flujo en el circuito i. .................................................................................................. 47
Ecuación 22. Relación polinomial entre la cabeza disponible y el caudal de flujo. ........................................... 47
Ecuación 23. Vector solución para las alturas piezométricas en los nodos en una iteración k+1. ................... 49
Ecuación 24. Vector solución para los caudales en las tuberías en una iteración k+1...................................... 49
Ecuación 25. Sistema de ecuaciones lineales para las alturas piezométricas desconocidas. ........................... 49

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
34
Ecuación 26. Restricción de presión mínima. .................................................................................................... 51
Ecuación 27. Restricción de diámetros comerciales.......................................................................................... 51
Ecuación 28. Función de costos. ........................................................................................................................ 52
Ecuación 29. Centroide de demandas en metodología LOGH........................................................................... 53
Ecuación 30. Coeficiente de uniformidad en metodología LOGH. .................................................................... 53
Ecuación 31. Ecuación cuadrática de la flecha óptima. ..................................................................................... 53
Ecuación 32. Flecha óptima corregida según el exponente de la función de costos. ....................................... 54
Ecuación 33. Flecha óptima corregida según la relación Q
2
/L
3
. ........................................................................ 54
Ecuación 34. Línea óptima del gradiente hidráulico.......................................................................................... 54
Ecuación 35. Pérdidas objetivo en el tramo ij. .................................................................................................. 54
Ecuación 36. Distancia topológica mínima entre la fuente y un nodo. ............................................................. 57
Ecuación 37. LGH ideal mínima para la ruta al sumidero i. ............................................................................... 58
Ecuación 38. LGH ideal máxima para la ruta al sumidero i. .............................................................................. 58
Ecuación 39. Ecuación LOGH para una red cerrada. ......................................................................................... 58
Ecuación 40. Dimensión de Hausdorff-Besicovitch. .......................................................................................... 73
Ecuación 41. Medición de fractales mediante una ley de potencias. ............................................................... 73
Ecuación 42. Estimación de la dimensión fractal mediante ley de potencias. .................................................. 74
Ecuación 43. Peso según la topología del sistema............................................................................................. 75
Ecuación 44. Peso según el caudal..................................................................................................................... 75
Ecuación 45. Peso según el producto del caudal y la altura piezométrica. ....................................................... 75
Ecuación 46. Dimensión fractal a partir del exponente de Hurst. ..................................................................... 77
Ecuación 47. Media de la serie de tiempo. ........................................................................................................ 77
Ecuación 48. Serie de tiempo ajustada por la media......................................................................................... 77
Ecuación 49. Serie acumulativa. ........................................................................................................................ 77
Ecuación 50. Serie de rangos. ............................................................................................................................ 77
Ecuación 51. Desviación estándar de la serie de tiempo. ................................................................................. 78
Ecuación 52. Serie de rangos escalados............................................................................................................. 78
Ecuación 53. Función de probabilidad para cajas de lado R y masa M. ............................................................ 79
Ecuación 54. q-ésimo momento estadístico de la función Q. ........................................................................... 79
Ecuación 55. Análisis de la lagunaridad a una escala R. .................................................................................... 79

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
35
Ecuación 56. Masa de una caja de tamaño R. ................................................................................................... 80
Ecuación 57. Ecuación vectorial de la recta en el decaimiento de la LGH. ....................................................... 89

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
36
1 INTRODUCCIÓN
El diseño optimizado de las redes de distribución de agua potable (RDAPs) consiste en la búsqueda
de la configuración de diámetros comerciales que permite reducir al mínimo los costos del sistema
de tuberías, verificando que en cada uno de los nodos se obtenga la presión mínima que garantiza
un correcto funcionamiento de la red (Saldarriaga, 2016). Actualmente, el diseño optimizado ha
adquirido relevancia a nivel de la toma de decisiones, dado que el factor económico se constituye
como un aspecto importante a la hora de construir sistemas hidráulicos. De esta manera, reducir
los costos implica grandes ventajas en el mercado y en la viabilidad de obras civiles que mejoran la
cobertura en saneamiento básico y acueducto. Algunos métodos modernos de optimización
empleados para resolver el problema son: los Algoritmos Genéticos (AG), la Programación por
Restricciones (PR), la Superficie Óptima de Gradiente Hidráulico (SOGH) y la metodología de la
Superficie de Uso Óptimo de Potencia (OPUS). Tanto SOGH como OPUS suponen la existencia de
una superficie tridimensional discontinua conformada por las alturas piezométricas de cada nodo
que garantizan el mínimo costo, denominada la Superficie Óptima de Presiones (SOP). Se ha
demostrado que dichos métodos permiten obtener resultados satisfactorios con menor gasto
computacional.
Por otra parte, la geometría fractal se ha establecido como una opción viable para el análisis de
superficies comúnmente encontradas en la naturaleza, donde la irregularidad, fragmentación y
escabrosidad impiden aplicar los postulados de la geometría euclídea (Quintero y Ruíz, 2011). En
efecto, asumir las formas naturales como campos fractales permite estudiar aquellos aspectos
geométricos que son invariantes con el cambio de escala (Quintero y Ruíz, 2011). Específicamente,
se considera el estudio de la dimensión fractal, el exponente de Hurst y la lagunaridad, entidades
matemáticas que describen la rugosidad, persistencia y heterogeneidad de los fractales. Diversos
trabajos de investigación han sido enfocados al estudio de la fractalidad de superficies naturales o
fenómenos en el ámbito de la ingeniería. No obstante, para la Superficie Óptima de Presiones no
se ha realizado algún estudio similar. En los apartados subsecuentes se planteará el diseño
optimizado de diferentes RDAPs mediante la metodología OPUS y, al obtener las SOPs, se
empleará la modelación numérica para desarrollar un análisis de la geometría fractal a nivel de la
red y la superficie de alturas piezométricas. De esta manera, se espera identificar patrones en el
comportamiento de la fractalidad de las SOPs, a modo que se permita utilizar las propiedades
matemáticas de la superficie como herramienta para orientar los procesos existentes de diseño
optimizado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
37
2 OBJETIVOS
2.1.1 Objetivo General
• Analizar las propiedades fractales de la Superficie Óptima de Presiones (SOP).
2.1.2 Objetivos Específicos
• Implementar en el software REDES diferentes redes patrón y reales, incluyendo sus
características topológicas, hidráulicas, de costos y restricciones de presión mínima y
diámetros comerciales disponibles.
• Generar el diseño optimizado de las RDAPs implementadas en REDES mediante el método
OPUS.
• Aplicar algoritmos de Programación por Restricciones (PR) para efectuar el redondeo
optimizado de diámetros comerciales sobre los diseños resultantes de la metodología
OPUS.
• Construir la Superficie Óptima de Presiones (SOP) de las redes evaluadas mediante
modelación computacional en el software REDES y MATLAB.
• Aplicar una rutina de análisis de rango reescalado (R/S) para estimar la dimensión fractal
sobre diversos cortes en las Superficies Óptimas de Presiones empleando el software
MATLAB.
• Desarrollar un algoritmo de análisis de la fractalidad de las SOPs integrando el concepto de
lagunaridad mediante el uso de MATLAB y ArcGIS.
• Caracterizar la escabrosidad, persistencia y heterogeneidad de las SOPs calculadas.
• Establecer una comparación entre la fractalidad de las redes y de las SOPs estimadas.
• Investigar la relevancia del análisis fractal en el diseño optimizado de redes de distribución
de agua potable.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
38
3 MARCO TEÓRICO
3.1 Conceptos de mecánica de fluidos
3.1.1 Propiedades del agua
De manera preliminar, se conoce que un fluido es toda aquella sustancia que bajo la influencia de
cualquier esfuerzo cortante se deformará de manera continua en el espacio (White, 2008). Dichas
deformaciones se caracterizan como movimientos relativos de las capas del fluido con respecto a
un contorno sólido, fenómeno denominado como flujo (Saldarriaga, 2016). Todo compuesto en
fase líquida o gaseosa se enmarca en la anterior descripción (Fox y McDonald, 1995). Ahora bien,
en el contexto de la ingeniería civil, el fluido agua es tal vez el de mayor relevancia considerando
sus implicaciones a nivel de saneamiento básico y abastecimiento.
La densidad se define como la masa contenida por unidad de volumen
(Cengel y Cimbala, 2006).
Actualmente, se conoce que su valor puede verse afectado por las fluctuaciones de temperatura y
presión. En el primer caso, la afectación se manifiesta en la forma como se modifica el arreglo de
moléculas según los fenómenos físicos de dilatación (Cengel y Cimbala, 2006). Por su parte, los
cambios en la presión suponen modificaciones en el volumen acorde a la compresibilidad del
fluido (Fox y McDonald, 1995). Dada la suposición de incompresibilidad y temperatura constante,
en la modelación de las redes de distribución se asumirá que ninguno de los efectos es
significativo. Como consecuencia se trabajará con un único valor de densidad en el análisis físico
de los sistemas.
Por otra parte, se encuentra la viscosidad. Esta propiedad refleja la velocidad de deformación de
un fluido cuando se le aplica un esfuerzo cortante dado, obteniéndose una medida cuantitativa de
la resistencia del fluido al movimiento (White, 2008). La viscosidad en los líquidos se define según
las fuerzas de cohesión presentes dentro de la estructura molecular (Streeter et. al., 2000). Para el
caso del agua se conoce que la relación entre el esfuerzo cortante y la tasa (velocidad) de
deformación es directamente proporcional para el caso de flujo laminar, razón por la cual se
enmarca como un fluido newtoniano (Fox y McDonald, 1995). En este caso, dicha relación se
caracteriza según la presencia de una constante de proporcionalidad definida como la viscosidad
dinámica (Cengel y Cimbala, 2006). La descripción anterior puede expresarse correctamente según
la ley de viscosidad de Newton, donde las variaciones de velocidad perpendiculares a un campo de
flujo paralelo imprimen esfuerzos cortantes al inducir aceleraciones entre los paquetes de fluido
que viajan a velocidades diferentes (Shames, 1995).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
39
𝜏 = 𝜇
𝑑𝑣
𝑑𝑦
Ecuación 1. Ley de viscosidad de Newton.
Dónde:
𝜏[𝑃𝑎]
: Esfuerzo cortante.
𝜇[𝑃𝑎 ∗ 𝑠]
: Viscosidad dinámica.
𝑑𝑣/𝑑𝑦[1/𝑠]
:
Gradiente de velocidad vertical.
Una manera alternativa de caracterizar la viscosidad de un fluido es a partir de la viscosidad
cinemática. Por definición, esta se determina como el cociente entre la viscosidad dinámica y la
densidad del fluido como se expresa a continuación (Cengel y Cimbala, 2006):
𝜈 =
𝜇
𝜌
Ecuación 2. Viscosidad cinemática de un fluido.
Dónde:
𝜈[𝑚
2
/𝑠]
: Viscosidad cinemática.
𝜇[𝑃𝑎 ∗ 𝑠]
: Viscosidad dinámica.
𝜌[𝑘𝑔/𝑚
3
]
:
Densidad.
3.1.2 Principio de conservación de la masa
El primer principio aplicable a los sistemas de tuberías es el principio de conservación de la masa.
De manera general, se establece que, para cualquier volumen de control, la masa permanecerá
constante siempre y cuando la tasa de entrada y salida sean iguales, es decir, que no exista
acumulación (Fox y McDonald, 1995). Adicionalmente, considerando que la masa es una
propiedad extensiva, es posible aplicar la ecuación integral de conservación para un volumen de
control no deformable acorde al Teorema de Transporte de Reynolds (Streeter et. al. 2000).
𝑑𝑁
𝑑𝑡
=
𝜕
𝜕𝑡
∫ 𝜂𝜌𝑑𝑉
.
𝑉𝐶
+ ∫ 𝜂𝜌𝑣⃗ ∙ 𝑑𝐴⃗
.
𝑆𝐶
Ecuación 3. Ecuación general de conservación para un volumen de control fijo y no deformable.
Dónde:
𝑁[−]
: Propiedad extensiva.
𝑡[𝑠]
: Tiempo.
𝜂[𝑚
3
/𝑠]
:
Cantidad de 𝑁 por unidad de masa. 𝜌[𝑘𝑔/𝑚
3
]
:
Densidad.
𝑉[𝑚
3
]
: Volumen.
𝑣⃗
[𝑚/𝑠]
: Vector velocidad. 𝐴⃗[𝑚
2
]:
Vector de área transversal.
La Ecuación 3 se puede simplificar a la luz de las siguientes afirmaciones:
• Para las redes de distribución no se contemplará acumulación.
• Se asumirá al agua como fluido incompresible (Fox y McDonald, 1995).
• Los volúmenes de control no se deformarán. El cambio del volumen con respecto al
tiempo es nulo.
• El cálculo de los caudales implica suponer el desarrollo de flujo uniforme a lo largo de la
sección transversal de la tubería. La velocidad adquiere un valor constante representado
por el valor medio (Fox y McDonald, 1995).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
40
∑
𝑣̅𝐴
𝐸𝑛𝑡𝑟𝑎𝑑𝑎𝑠
= ∑ 𝑣̅𝐴
𝑆𝑎𝑙𝑖𝑑𝑎𝑠
∑
𝑄
𝐸𝑛𝑡𝑟𝑎𝑑𝑎𝑠
= ∑ 𝑄
𝑆𝑎𝑙𝑖𝑑𝑎𝑠
Ecuación 4. Ecuación de conservación de la masa para flujo a presión en tuberías circulares.
Dónde:
𝑣̅[𝑚/𝑠]
: Velocidad media.
𝐴[𝑚
2
]
: Área transversal.
𝑄[𝑚
3
/𝑠]
:
Caudal.
3.1.3 Principio de conservación de la energía
El segundo principio de conservación relevante corresponde a la conservación de la energía. Este
fenómeno se describe a partir de la Ecuación de Bernoulli, donde se sugiere la existencia de tres
formas de energía por unidad de peso intercambiables entre sí: la energía potencial por presión, la
energía potencial por posición y la energía cinética del flujo (White, 2008).
𝑝
𝜌𝑔
+
𝑣
2
2𝑔
+ 𝑧 = 𝑐𝑡𝑒
Ecuación 5. Ecuación de Bernoulli.
Dónde:
𝑝[𝑃𝑎]
: Presión.
𝜌[𝑘𝑔/𝑚
3
]
:
Densidad.
𝑔[𝑚/𝑠
2
]
:
Gravedad.
𝑣[𝑚/𝑠]
:
Velocidad.
𝑧[𝑚]
:
Altura
con respecto al datum.
No obstante, es importante recalcar que la aplicación de la Ecuación 5 debe garantizar el
cumplimiento de las siguientes afirmaciones:
• Los efectos viscosos deben ser suficientemente pequeños a comparación de los efectos
inerciales, gravitacionales y de presión (Cengel y Cimbala, 2006). Si se requiere incluir las
pérdidas por fricción, se debe contemplar un término adicional (Saldarriaga, 2016).
• El flujo debe ser permanente (White, 2008). La componente local de la aceleración se
puede despreciar.
• El fluido debe asumirse como incompresible (White, 2008). Particularmente cierto para el
agua líquida (Fox y McDonald, 1995).
• Los puntos de análisis deben encontrarse conectados por una línea de corriente (White,
2008).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
41
3.2 Conceptos de hidráulica de tuberías
3.2.1 Regímenes de flujo
A partir de los resultados del primer experimento de Reynolds fue posible describir la existencia de
tres regímenes de flujo según la relación entre las fuerzas viscosas e inerciales sobre algún punto
en una línea de corriente (Saldarriaga, 2016). Dicha descripción fue realizada según el número de
Reynolds. A partir de la similitud dinámica en mecánica de fluidos, se conoce que para condiciones
análogas de velocidad y geometría en dos campos de flujo similares se puede plantear triángulos
semejantes para las fuerzas relevantes (Saldarriaga, 2016). Para el caso de flujo en tuberías,
priman las fuerzas viscosas (FV), de presión (FP) y las inerciales (FI). Así pues, se puede establecer
la siguiente relación geométrica para dos flujos similares:
Figura 1. Flujos similares.
𝐹𝐼
𝐴
𝐹𝑉
𝐴
=
𝐹𝐼
𝐴′
𝐹𝑉
𝐴′
𝑅𝑒
𝐴
= 𝑅𝑒
𝐴′
Las fuerzas inerciales hacen referencia a la resistencia que presenta el fluido al cambiar su
velocidad (NASA, s.f.). Se sabe que dichas fuerzas deben relacionarse con el producto de la masa
por la aceleración según la segunda ley de Newton (Tesar, 2001). Por su parte, para las fuerzas
viscosas se conoce que son proporcionales al esfuerzo cortante multiplicado por el área en el que
actúa, siendo posible describir el esfuerzo como se estipula en la Ecuación 1 (Tesar, 2001). Al
desarrollar el cociente de la relación de triángulos semejantes se encuentra la expresión
adimensional conocida como el número de Reynolds. Para el flujo en tuberías dicha entidad se
describe como se estipula en la Ecuación 2.
𝑅𝑒 =
𝑣𝑑
𝜈
Ecuación 6. Número de Reynolds para flujo en tuberías a presión.
Dónde:
𝑅𝑒[−]
: Número de Reynolds.
𝑣[𝑚/𝑠]
:
Velocidad.
𝑑[𝑚]
:
Diámetro. 𝜈[𝑚
2
/𝑠]
: Viscosidad cinemática.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
42
La semejanza de triángulos estipulada en la Figura 1 demuestra que, para condiciones de flujo
similares, el número de Reynolds debería ser igual. Lo anterior sugiere que el flujo en cualquier red
de tuberías debe estar gobernado por fuerzas similares (Saldarriaga, 2016). Adicionalmente, según
Reynolds (1883), la expresión adimensional permite caracterizar la aparición de los remolinos
(“eddies”) para ciertos valores límite de caudal, lo cual conlleva a la descripción teórica de los tres
regímenes de flujo: laminar, transicional y turbulento.
El flujo laminar se caracteriza por patrones macroscópicos ordenados en el que las capas de fluido
se deslizan unas sobre otras sin intercambio másico significativo entre ellas (Shames, 1995). Dado
que el flujo laminar implica un comportamiento de flujo en líneas aproximadamente rectas y
paralelas, es posible aplicar la ley de viscosidad de Newton como se estipula en la Ecuación 1
(Shames, 1995). Según Bird et. al. (2002), este comportamiento es característico en números de
Reynolds cercanos o inferiores a 2100 para el caso de tuberías circulares. Los valores pequeños en
el número de Reynolds se explican considerando que las fuerzas viscosas, al sobreponerse sobre
las inerciales, atenúan las inestabilidades surgidas por el movimiento relativo entre capas de fluido
(Streeter et. al., 2000). En contraparte, el flujo turbulento se caracteriza por un movimiento
errático con intercambio másico importante (Streeter et. al., 2000). En efecto, jamás se tiene un
vector velocidad definido para el campo de flujo, resultando así en el uso de una velocidad
promedio (Saldarriaga, 2016). De manera opuesta al flujo laminar, se tendrán números de
Reynolds altos que reflejan una dominancia de las fuerzas inerciales que tienden a desestabilizar y
desordenar el flujo. Según Saldarriaga (2016), la turbulencia se materializa a partir de números de
Reynolds cercanos a 4500. Cabe resaltar que la Ecuación 1 se invalida bajo estas condiciones.
Finalmente, entre ambos límites se tiene un comportamiento transicional con algunas
ondulaciones manifiestas (Saldarriaga, 2016). Este último régimen ha sido caracterizado
experimentalmente, más que a nivel teórico debido a su complejidad.
3.2.2 Pérdidas de energía en una tubería
El flujo al interior de una tubería conlleva procesos de transformación de energía mecánica en
calor (Rennels y Hudson, 2012). Dicha disipación se explica bien sea a partir del rozamiento
generado por la interacción del flujo y la pared sólida, denominadas las pérdidas por fricción, o
según los fenómenos de turbulencia inducida por los accesorios y otros elementos, denominadas
las pérdidas menores (Rennels y Hudson, 2012). Los cambios en la energía se reflejan en
disminuciones sobre las cabezas de energía potencial por presión y posición (White, 2008). En
efecto, dado que la línea del gradiente hidráulico (LGH) refleja la sumatoria de las cabezas de
energía potencial por presión y posición, es de esperar que las pérdidas hidráulicas se traduzcan
en un comportamiento decreciente y gradual para los efectos de la fricción y repentinas para el
caso de las pérdidas menores (U.S. Army Corps of Engineers, 1957). Las pérdidas menores
usualmente se expresan como el producto entre un coeficiente característico del accesorio y la
cabeza de velocidad (Stephenson, 1989):

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
43
∑ ℎ
𝑚
= ∑ 𝑘
𝑚
∗
𝑣
2
2𝑔
Ecuación 7. Pérdidas menores en una tubería.
Dónde:
𝑣[𝑚/𝑠]
: Velocidad media.
𝑔[𝑚/𝑠
2
]
:
Gravedad.
𝑘
𝑚
[−]
:
Coeficiente de pérdidas menores.
Por su parte, las pérdidas por fricción se caracterizan a partir de la ecuación de Darcy-Weisbach,
que surge como resultado de un análisis dimensional combinado con la aplicación de las leyes de
Newton (Brown, 2002). Dado su origen, la ecuación se establece como una relación
dimensionalmente consistente y físicamente basada. A partir de la aplicación del teorema de Pi-
Buckingham se determina la relación estipulada a continuación (Shames, 1995):
ℎ
𝑓
= 𝑓
𝑙
𝑑
𝑣
2
2𝑔
Ecuación 8. Ecuación de Darcy-Weisbach.
Dónde:
ℎ
𝑓
[𝑚]
: Pérdidas por fricción.
𝑓[−]
: Factor de fricción de Darcy.
𝑙[𝑚]
:
Longitud.
𝑑[𝑚]
:
Diámetro.
𝑣[𝑚/𝑠]
: Velocidad de flujo. 𝑔[𝑚/𝑠
2
]
:
Gravedad.
La cantidad 𝑓 se conoce como el factor de fricción. Esta variable adimensional depende del
número de Reynolds y la rugosidad relativa de la tubería (Saldarriaga, 2016). Para el caso de flujo
laminar, el factor de fricción se deduce a partir de la ecuación de Hagen-Poiseuille, donde se
materializa un predominio del número de Reynolds sobre la caracterización de 𝑓 (Saldarriaga,
2016). Por su parte, para el cálculo del factor de fricción en régimen turbulento se requieren
aproximaciones experimentales acordes a la teoría de la capa límite desarrollada por Prandtl, los
aportes de Von Kárman, el desarrollo de los diagramas de Nikuradse-Moody y los trabajos de
Colebrook y White (Saldarriaga, 2016). La Ecuación 10 combina los casos para flujo
hidráulicamente liso y rugoso, por lo que se afirma que es válida para la totalidad del rango
turbulento.
𝑓 =
64
𝑅𝑒
Ecuación 9. Factor de fricción para régimen de flujo laminar.
1
√𝑓
= −2 log
10
(
𝑘
𝑠
3.7𝑑
+
2.51
𝑅𝑒√𝑓
)
Ecuación 10. Ecuación de Colebrook-White para el factor de fricción.
Dónde:
𝑓[−]
: Factor de fricción de Darcy.
𝑅𝑒[−]
:
Número de Reynolds. 𝑘
𝑠
[𝑚]: Rugosidad absoluta. 𝑑[𝑚]:
Diámetro.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
44
Finalmente, combinando la Ecuación 6, la Ecuación 8 y la Ecuación 10 se obtiene una ecuación
explícita de la velocidad aplicable para todo el rango turbulento (Saldarriaga, 2016).
𝑣 = −
2√2𝑔𝑑ℎ
𝑓
√𝑙
log
10
(
𝑘
𝑠
3.7𝑑
+
2.51𝜈√𝑙
𝑑√2𝑔𝑑ℎ
𝑓
)
Ecuación 11. Ecuación para la velocidad media en flujo turbulento.
Dónde:
𝑣[𝑚/𝑠]
: Velocidad de flujo. 𝑔[𝑚/𝑠
2
]
:
Gravedad. 𝑑[𝑚]:
Diámetro. ℎ
𝑓
[𝑚]
: Pérdidas por fricción.
𝑙[𝑚]
: Longitud.
𝑘
𝑠
[𝑚]: Rugosidad absoluta. 𝜈[𝑚
2
/𝑠]
: Viscosidad cinemática.
Dado que la ecuación de Colebrook-White requiere de la aplicación de métodos numéricos para
obtener el factor de fricción, su uso resultaba tedioso en la época previa a la popularización de los
computadores (Saldarriaga, 2016). Como consecuencia, surgieron diversas expresiones empíricas
que simplificaban el cálculo de las pérdidas hidráulicas. Una de las más relevantes es la ecuación
de Hazen-Williams, cuya ventaja radica en ser explícita con respecto a la velocidad. Según Liou
(1998), para unidades del sistema internacional, la fórmula de Hazen-Williams se expresa como
sigue:
𝑣 = 0.849𝐶𝑅
0.63
𝑆
0.54
Ecuación 12. Ecuación de Hazen-Williams.
Dónde:
𝑣[𝑚/𝑠]
: Velocidad de flujo.
𝐶[−]
:
Coeficiente de Hazen-Williams. 𝑅[𝑚]: Radio hidráulico. 𝑆[−]:
Pendiente de fricción.
Según las manipulaciones algebraicas propuestas por Diskin (1960) y Liou (1998) es posible
determinar expresiones para las pérdidas por fricción (Ecuación 13) y el coeficiente 𝐶
(Ecuación
14).
ℎ
𝑓
=
6.82𝐿
𝐶
1.85
𝑑
1.17
𝑣
1.851
Ecuación 13. Pérdidas por fricción según la Ecuación de Hazen-Williams.
𝐶 =
14.09
𝑓
0.54
𝑑
0.009
𝜈
0.081
𝑅𝑒
0.081
Ecuación 14. Coeficiente de Hazen-Williams a la luz de la ecuación de Darcy-Weisbach.
Dónde:
𝑣[𝑚/𝑠]
: Velocidad de flujo.
𝐶[−]
:
Coeficiente de Hazen-Williams. 𝑅[𝑚]: Radio hidráulico. 𝑆[−]:
Pendiente de fricción.
𝑓[−]
: Factor de fricción de Darcy. 𝑑[𝑚]:
Diámetro. 𝜈[𝑚
2
/𝑠]
: Viscosidad cinemática. 𝑅𝑒[−]: Número de Reynolds.
La Ecuación 14 sugiere que el coeficiente de Hazen-Williams depende no solo del ducto, sino
también de las características del fluido y el flujo (Liou, 1998). Dadas las condiciones
experimentales de donde se obtuvo la ecuación, existen ciertas limitaciones que deben

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
45
considerarse antes de aplicarla en el contexto de la hidráulica de tuberías (Liou, 1998). Según
Saldarriaga (2016), la ecuación de Hazen-Williams es aplicable siempre y cuando se cumplan las
siguientes restricciones: el fluido debe ser agua a temperaturas normales (~15°C), el diámetro de
la tubería debe ser superior o igual a tres pulgadas y la velocidad de flujo no puede sobrepasar 3
m/s.
3.2.3 Método del gradiente en redes cerradas
En general, el trazado de las redes de distribución de agua potable contempla la conformación de
circuitos o “loops” en la medida que intentan ajustarse a la disposición cuadricular de las calles y
avenidas de una ciudad. Este tipo de sistemas de tuberías se denominan redes cerradas
(Saldarriaga, 2016). A lo largo de los últimos dos siglos se han estipulado diversos métodos que
permiten calcular las condiciones hidráulicas de dichos sistemas (caudales, alturas piezométricas y
pérdidas de energía); no obstante, por sus ventajas a nivel computacional, el método del gradiente
se constituye como el más exitoso (Salgado et. al., 1987).
De acuerdo con el supuesto de que las redes de distribución se comportan bajo condiciones de
flujo permanente, es posible aplicar los principios de conservación de la masa y la energía
(Salgado, 1988). El primer principio se aplica a los nodos contabilizando el caudal de alimentación,
el demandado y los que recorren en cada una de las tuberías que divergen o convergen hacia el
nodo (Cross, 1936). Por su parte, el principio de conservación de la energía se puede modelar de
dos maneras. En primer lugar, se conoce que en cada tubería la energía total disponible debe
disiparse en pérdidas por fricción y menores (Saldarriaga, 2016). En segundo lugar, al realizar la
sumatoria de las pérdidas en un circuito, es de esperar que, al considerar el signo de las
magnitudes, el resultado sea igual a la altura provista por la bomba, si la hay, o cero, en caso de
que no exista (Ochoa y Saldarriaga, 2009). Los tres fenómenos físicos se estipulan en la Ecuación
15, Ecuación 16 y Ecuación 17.
∑ 𝑄
𝑖𝑗
− 𝑄
𝐷𝑖
+ 𝑄
𝑒𝑖
= 0
𝑁𝑇
𝑖
𝑗=1
Ecuación 15. Restricción de continuidad en el nudo i.
𝐻
𝑇
= ℎ
𝑓
+ ∑ ℎ
𝑚
Ecuación 16. Pérdidas de energía en un tubo.
Dónde:
𝑄
𝐷𝑖
[𝑚
3
/𝑠]
: Caudal consumido en el nodo i.
𝑄
𝑒𝑖
[𝑚
3
/𝑠]
: Caudal alimentado en el nodo i a la red.
𝑄
𝑖𝑗
[𝑚
3
/𝑠]
:
Caudal en la tubería ij del nodo j hacia el nodo i. 𝑁𝑇
𝑖
[−]: Número de tubos que convergen en el nodo i.
ℎ
𝑓
[𝑚]
: Pérdidas por fricción.
ℎ
𝑚
[𝑚]
: Pérdidas menores.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
46
∑ ℎ
𝑓
𝑖𝑗
𝑁𝑇
𝑖
′
𝑗=1
+ ∑ ℎ
𝑚
𝑖𝑗
𝑁𝑇
𝑖
′
𝑗=1
= 𝐻
𝐵𝑜𝑚𝑏𝑎
Ecuación 17. Restricción de energía en el circuito i.
Dónde:
𝑁𝑇
𝑖
′
[−]
: Número de tuberías del circuito i.
ℎ
𝑓
𝑖𝑗
[𝑚]
: Pérdidas por fricción en tubería j.
ℎ
𝑚
𝑖𝑗
[𝑚]
:
Pérdidas menores en tubería j. 𝐻
𝐵𝑜𝑚𝑏𝑎
[𝑚]: Altura provista por la bomba.
Las anteriores restricciones se pueden estipular para cada nodo, tubería y circuito de la red, lo cual
desemboca en la constitución de un sistema de ecuaciones de naturaleza no lineal que debe
resolverse de manera iterativa para conocer la hidráulica del sistema (Ormsbee y Wood, 1986). La
no linealidad surge como resultado de la aplicación de la ecuación de Darcy-Weisbach y,
consecuentemente, de Colebrook-White, en la medida que incluyen una relación no lineal entre
las pérdidas por fricción y la velocidad de flujo (Ecuación 11) para describir el caudal en una
tubería (Salgado, 1988).
𝑄 = −
2𝐴√2𝑔𝑑ℎ
𝑓
√𝑙
log
10
(
𝑘
𝑠
3.7𝑑
+
2.51𝜈√𝑙
𝑑√2𝑔𝑑ℎ
𝑓
)
Ecuación 18. Relación no lineal entre el caudal de flujo y las pérdidas por fricción.
Dónde:
𝐴[𝑚
2
]
: Área transversal. 𝑔[𝑚/𝑠
2
]
:
Gravedad. 𝑑[𝑚]:
Diámetro. ℎ
𝑓
[𝑚]
: Pérdidas por fricción.
𝑙[𝑚]
: Longitud.
𝑘
𝑠
[𝑚]: Rugosidad absoluta. 𝜈[𝑚
2
/𝑠]
: Viscosidad cinemática.
Para dos nodos conectados por un ducto, se puede establecer la caída en la presión piezométrica
según la Ecuación 16; a partir de las manipulaciones algebraicas planteadas por Saldarriaga (2016)
se obtienen ecuaciones para definir el caudal en cada tubería de la red y modelar la conservación
de la masa. A estas igualdades se les denomina ecuaciones de altura piezométrica por la necesidad
de conocer la cabeza de energía disponible en algún punto de la red para resolver el sistema
(Ormsbee y Wood, 1986). El valor absoluto contempla de manera automática la dirección del flujo,
descrita según el signo del caudal (Saldarriaga, 2016).
𝑄
𝑖𝑗
=
√
2𝑔𝐴
𝑖𝑗
(𝐻
𝑖
− 𝐻
𝑗
)
𝑓
𝑖𝑗
𝑙
𝑖𝑗
𝑑
𝑖𝑗
+ ∑ 𝑘
𝑚𝑖𝑗
Ecuación 19. Caudal por la tubería ij.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
47
∑
𝐻
𝑖
− 𝐻
𝑗
(|𝐻
𝑖
− 𝐻
𝑗
|)
−1/2
√
2𝑔𝐴
𝑖𝑗
𝑓
𝑖𝑗
𝑙
𝑖𝑗
𝑑
𝑖𝑗
+ ∑ 𝑘
𝑚𝑖𝑗
− 𝑄
𝐷𝑖
+ 𝑄
𝑒𝑖
= 0
𝑁𝑇
𝑖
𝑗=1
Ecuación 20. Ecuación de altura piezométrica en el nudo i.
Dónde:
𝐴
𝑖𝑗
[𝑚
2
]
: Área transversal tubería ij. 𝑔[𝑚/𝑠
2
]
:
Gravedad.
𝑑
𝑖𝑗
[𝑚]
:
Diámetro tubería ij.
𝑓
𝑖𝑗
[−]
: Factor de fricción tubería ij.
𝑙
𝑖𝑗
[𝑚]
: Longitud tubería ij. 𝑘
𝑠
[𝑚]: Rugosidad absoluta.
𝜈[𝑚
2
/𝑠]
: Viscosidad cinemática. 𝐻
𝑖
[𝑚]
: Altura piezométrica nodo i. 𝐻
𝑗
[𝑚]
: Altura piezométrica nodo j.
𝑄
𝐷𝑖
[𝑚
3
/𝑠]
: Caudal consumido en el nodo i.
𝑄
𝑒𝑖
[𝑚
3
/𝑠]
: Caudal alimentado en el nodo i a la red.
Un proceso algebraico similar se puede ejecutar sobre la restricción de energía sobre los circuitos
(Ecuación 17). En este caso, como el sistema de ecuaciones se expresa en términos del caudal, las
igualdades resultantes se denominan las ecuaciones de flujo (Ormsbee y Wood, 1986). El valor
absoluto contempla de manera automática el signo del caudal, siguiendo la convención hidráulica
de valores positivos para un recorrido del agua en el circuito en sentido horario (Saldarriaga,
2016).
∑(
𝑄
𝑖𝑗
|𝑄
𝑖𝑗
|
2𝑔𝐴
𝑖𝑗
2
(𝑓
𝑖𝑗
𝑙
𝑖𝑗
𝑑
𝑖𝑗
+ ∑ 𝑘
𝑚𝑖𝑗
))
𝑁𝑇
𝑖
′
𝑗=1
= 𝐻
𝐵𝑜𝑚𝑏𝑎
Ecuación 21. Ecuación de flujo en el circuito i.
La aplicación del método del gradiente permite resolver de manera eficiente los sistemas
estipulados por la Ecuación 20 y la Ecuación 21. Un paso preliminar corresponde a modelar la
energía total disponible entre dos nodos de la red con respecto al caudal de flujo al interior de la
tubería. Si se incluyen accesorios o bombas, se puede asumir una relación general de tipo
polinomial entre el caudal y la cabeza disponible como se estipula en la Ecuación 22 (Saldarriaga.
2016).
𝐻
𝑇
= 𝛼𝑄
𝑛
+ 𝛽𝑄 + 𝛾
Ecuación 22. Relación polinomial entre la cabeza disponible y el caudal de flujo.
Dónde:
𝐻
𝑇
[𝑚]
: Cabeza total. 𝑄[𝑚
3
/𝑠]
:
Caudal de flujo.
𝛼, 𝛽, 𝛾[−]
:
Coeficientes.
El método del gradiente supone una descripción matricial de la topología del sistema de tuberías.
Para esto, se debe recurrir a algunas definiciones adicionales según como lo estipulado por
Saldarriaga (2016).
• NT: Número de tuberías en la red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
48
• NN: Número de nodos con altura piezométrica desconocida.
• NS: Número de nodos con altura piezométrica fija y conocida.
• [A12]: Matriz de conectividad de dimensión NT x NN con elementos diferentes de cero en
la i-ésima fila: -1 en la columna correspondiente al nodo inicial del tramo i y 1 en la
columna correspondiente al nodo final.
• [A21]: Matriz transpuesta de [A12].
• [A10]: Matriz topológica de dimensión NT x NS tramo a nodo para los NS nodos con altura
piezométrica conocida. Tiene como elementos -1 en las filas asociadas a tramos
conectados con nodos de altura piezométrica fija y 0 en las demás.
• [A11]: Matriz diagonal de dimensión NT x NT definida a continuación (Todini y Pilati,
1987):
[𝐴11] =
[
𝛼
1
𝑄
1
(𝑛
1
−1)
+ 𝛽
1
+
𝛾
1
𝑄
1
0 ⋯ 0
0
0
⋮
⋱
0
⋮
0
0 ⋯ 0 𝛼
𝑁𝑇
𝑄
𝑁𝑇
(𝑛
𝑁𝑇
−1)
+ 𝛽
𝑁𝑇
+
𝛾
𝑁𝑇
𝑄
𝑁𝑇
]
• [A11]’: Matriz diagonal de dimensión NT x NT definida como (Saldarriaga, 2016):
[𝐴11]′ =
[
𝛼
1
𝑄
1
(𝑛
1
−1)
0 ⋯ 0
0
0
⋮
⋱
0
⋮
0
0 ⋯ 0 𝛼
𝑁𝑇
𝑄
𝑁𝑇
(𝑛
𝑁𝑇
−1)
]
• [N]: Matriz diagonal de dimensión NT x NT definida como sigue (Todini y Pilati, 1987):
[𝑁] = [
𝑛
1
0 ⋯ 0
0
0
⋮
⋱
0
⋮
0
0 ⋯ 0 𝑛
𝑁𝑇
]
• [Q]: Vector de caudales de cada tubería con dimensión NT x 1.
• [q]: Vector de consumo o de entrada de caudal en cada nudo de la red de dimensión NN
x1.
• [H]: Vector de alturas piezométricas desconocidas en los nodos con dimensión NN x 1.
• [Ho]: Vector de alturas piezométricas conocidas o fijas con dimensión NS x 1.
Según los establecido por Todini y Pilati (1987), creadores del método, la conservación de la masa
y la energía se puede modelar según un sistema matricial que contenga la descripción topológica y
la caracterización de las pérdidas como se ha explicado en párrafos anteriores. Todini y Pilati
(1987) describen el problema de manera compacta como sigue:
(
[𝐴11] [𝐴12]
[𝐴21]
[0]
) (
[𝑄]
[𝐻]
) = (
−[𝐴10][𝐻𝑜]
[𝑞]
)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
49
Posteriormente, los autores (1987) proponen derivar ambos lados de la igualdad con respecto a Q
y H mediante el operador gradiente, representando el resultado como un esquema Newton-
Raphson a partir de una serie de Taylor truncada.
(
[𝑁][𝐴11]′ [𝐴12]
[𝐴21]
[0]
) (
[𝑑𝑄]
[𝑑𝐻]
) = (
[𝑑𝐸]
[𝑑𝑞]
)
Los términos 𝑑𝐸 y 𝑑𝑞 representan las cantidades residuales o desbalances de energía y materia
que deben ser minimizados de manera iterativa por el método (Todini y Pilati, 1987). Retomando
la expresión matricial compacta original, se obtiene una expresión para los desbalances en alguna
iteración k (Todini y Pilati, 1987). Adicionalmente, aplicando los principios del álgebra lineal, se
pueden despejar los valores 𝑑𝑄 y 𝑑𝐻, permitiendo obtener expresiones para los caudales y alturas
piezométricas de una iteración k+1 (Saldarriaga, 2016).
[𝐻
𝑘+1
] = −([𝐴21]([𝑁][𝐴11]
′
)
−1
[𝐴12])
−1
× ([𝐴21]([𝑁][𝐴11]
′
)
−1
([𝐴11][𝑄
𝑘
] + [𝐴10][𝐻𝑜])
− ([𝐴21][𝑄
𝑘
] − [𝑞]))
Ecuación 23. Vector solución para las alturas piezométricas en los nodos en una iteración k+1.
[𝑄
𝑘+1
] = ([𝐼] − ([𝑁][𝐴11]′)
−1
− [𝐴11])[𝑄
𝑘
] − (([𝑁][𝐴11]
′
)
−1
([𝐴12][𝐻
𝑘+1
] + [𝐴10][𝐻𝑜]))
Ecuación 24. Vector solución para los caudales en las tuberías en una iteración k+1.
El sistema estipulado por la Ecuación 23 se puede reescribir como un sistema de ecuaciones
lineales (Saldarriaga, 2016).
([𝐴21]([𝑁][𝐴11]
′
)
−1
[𝐴12])
−1
[𝐻
𝑘+1
]
= −([𝐴21]([𝑁][𝐴11]
′
)
−1
([𝐴11][𝑄
𝑘
] + [𝐴10][𝐻𝑜]) − ([𝐴21][𝑄
𝑘
] − [𝑞]))
Ecuación 25. Sistema de ecuaciones lineales para las alturas piezométricas desconocidas.
El proceso de cálculo implica suponer caudales iniciales para cada tubería, insertarlos en el sistema
de la Ecuación 25, determinar las alturas piezométricas y los nuevos caudales. Dichos valores de
gasto volumétrico se reinsertan en el sistema de ecuaciones lineales de manera iterativa hasta
alcanzar la convergencia. El algoritmo se presenta en el siguiente diagrama de flujo.
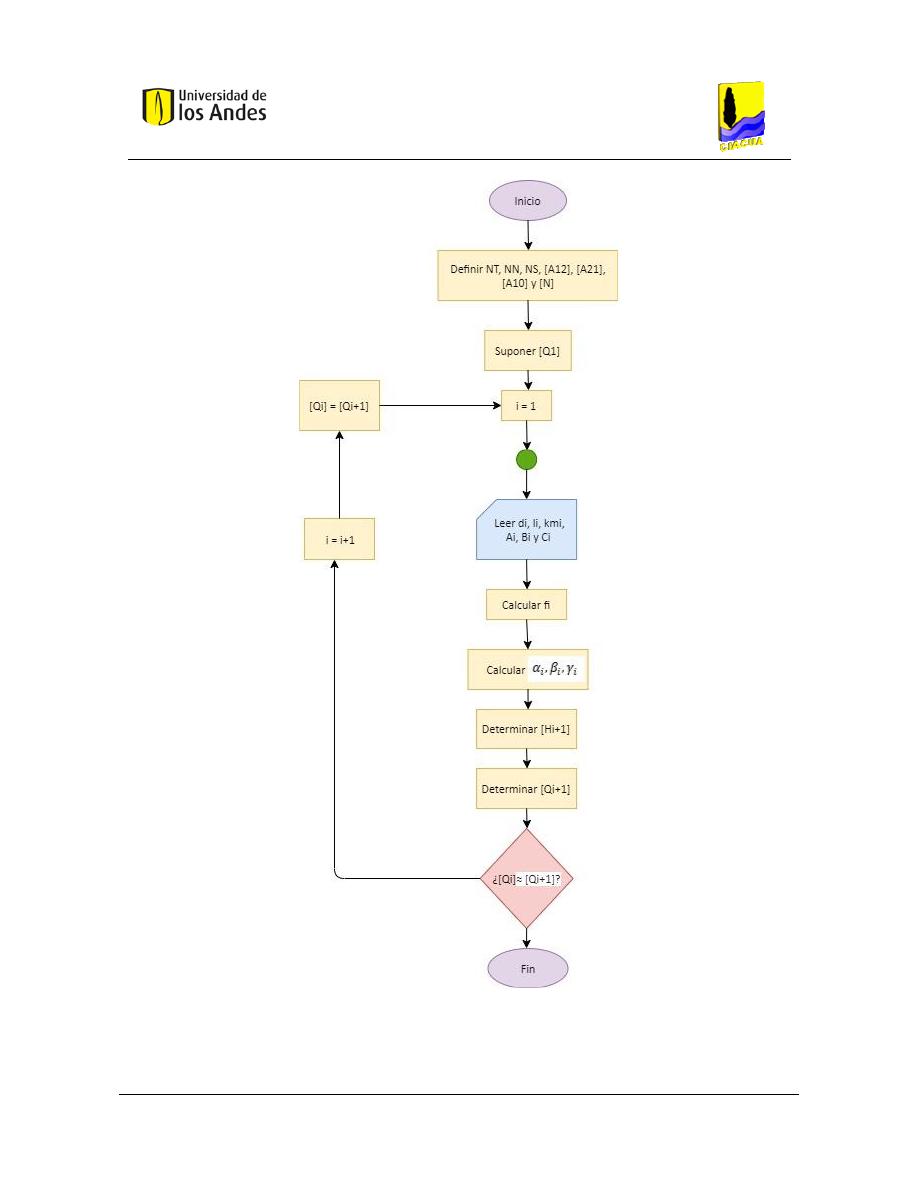
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
50
Figura 2. Diagrama de flujo 1 - Método del gradiente.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
51
3.3 Diseño optimizado de redes de distribución de agua potable
3.3.1 Definiciones y restricciones
Una red de distribución se refiere al conjunto de tuberías, accesorios y otras estructuras cuya
finalidad es facilitar el abastecimiento de agua potable a los usuarios (Conagua, s.f.). Dicho
abastecimiento consiste en el transporte del agua desde algún tanque de almacenamiento,
embalse o planta de tratamiento hasta el punto de demanda, bien sea aprovechando el
movimiento por gravedad o mediante el uso de un sistema de bombeo (Steel y McGhee, 1979).
Actualmente, el diseño de las redes de distribución de agua potable implica deducir aquella
configuración de diámetros comerciales que minimiza el costo de la red para condiciones
topológicas y de demanda específicas (Saldarriaga, 2016). Asimismo, implica garantizar aquellos
valores de presión mínima en los nodos acorde a la normatividad vigente y los requerimientos de
uso (Steel y McGhee, 1979). La restricción de la presión mínima y de los diámetros comerciales se
expresa matemáticamente como sigue:
min(𝑃
𝑖
) ≥ 𝑃
𝑚𝑖𝑛
Ecuación 26. Restricción de presión mínima.
𝑑
𝑖
∈ 𝐶𝐷
𝑐𝑜𝑚
Ecuación 27. Restricción de diámetros comerciales.
Dónde:
𝑃
𝑖
[𝑚. 𝑐. 𝑎]
: Presión nodo i.
𝑃
𝑚𝑖𝑛
[𝑚. 𝑐. 𝑎]
: Presión mínima admisible.
𝑑
𝑖
[𝑚]
:
Diámetro tubería i.
El problema de optimización se modela a partir de la teoría de grafos, incluyendo un conjunto de
arcos y nodos que representan las tuberías y las intersecciones entre ellas (Pereyra et. al., 2016).
Dicha modelación debe cumplir restricciones de continuidad en la totalidad de los nodos y
garantizar que las pérdidas sean a lo sumo iguales a la energía disponible (Narváez y Galeano,
2002). Según Saldarriaga (2016), las restricciones de continuidad en cada nudo y de energía en
cada circuito se pueden expresar según la Ecuación 15 y la Ecuación 17 estipuladas en la página 45.
En términos de los costos, Narváez y Galeano (2002) establecen que es importante contemplar
rubros concernientes a la infraestructura y la instalación. El primero se relaciona con los costos de
las tuberías y accesorios, mientras que en el segundo se incluye la mano de obra, la excavación, la
maquinaria y otras obras geotécnicas. Estos rubros se resumen en una función de costos que
contempla una regresión potencial con respecto al diámetro incluyendo la longitud del tubo (Pino
et. al., 2017). Si bien es evidente que los costos deberían contemplar otros rubros concernientes al
mantenimiento y la operación, en el presente trabajo solo se trabajará con los costos iniciales de
infraestructura. Según Saldarriaga et. al. (2018), la ecuación potencial que modela los costos se
establece como sigue:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
52
𝐶 = ∑ 𝐾 ∙ 𝐿
𝑖
∙ 𝑑
𝑖
𝑥
𝑁
𝑡
𝑖=1
Ecuación 28. Función de costos.
Dónde:
𝐶[$]
: Costo de la red. 𝑁
𝑡
[−]
: Número de tuberías. 𝐾[−]: Coeficiente.
𝐿
𝑖
[𝑚]
:
Longitud tubería i.
𝑑
𝑖
[𝑚]
:
Diámetro
tubería i.
Encontrar la solución que minimiza la ecuación de costos resulta ser particularmente difícil.
Considerando que para cualquier conjunto de valores discretos de diámetros comerciales existe
una gran cantidad de combinaciones factibles que cumplen con los requerimientos hidráulicos,
métodos como la búsqueda exhaustiva deben descartarse en el camino para encontrar el óptimo
global (Saldarriaga, 2016). Yates et. al. (1984) demostraron que el problema se encuentra dentro
del conjunto NP-Complejo, lo cual implica que el diseño optimizado de RDAPs se asemeja a otros
problemas que, en algunas instancias, reflejan intratabilidad computacional. Dadas sus
características como NP-Complejo, cualquier aproximación o algoritmo determinista que procure
encontrar una solución exacta no lo logrará en un tiempo polinomial (Yates et. al., 1984). Por
consiguiente, el problema se debe resolver mediante heurísticas no deterministas (Villalba et. al.,
2005).
3.3.2 Criterio de Wu y metodología LOGH para tuberías en serie
La complejidad del problema de diseño de redes de distribución se puede empezar a materializar
desde las tuberías en serie. Wu (1975) demostró que, para cualquier número de tuberías en serie,
el mínimo costo se obtiene cuando la línea del gradiente hidráulico (LGH) se comporta como una
curva parabólica cóncava hacia arriba con una depresión del 15% de la cabeza disponible en su
centro con respecto a la línea recta que une las alturas de energía totales al inicio y final de la
serie. Inclusive, tomando la recta que une los nodos inicial y final, el costo varía en apenas un 2%
(Saldarriaga, 2016). Cabe resaltar que dicha demostración se planteó para una distribución
uniforme de las demandas (Wu et. al., 1979).
Los hallazgos de Wu permitieron demostrar la posibilidad de predeterminar los valores de altura
piezométrica en los nodos para obtener de manera directa los diámetros sin recurrir a técnicas de
búsqueda estocástica (Saldarriaga et. al., 2010). Lo anterior funcionó como un primer paso para
establecer una mejor metodología de optimización: la Línea Óptima del Gradiente Hidráulico
(LOGH). A diferencia del criterio de Wu, la metodología LOGH se basa en obtener aquella flecha o
depresión óptima para cualquier topología, demanda hidráulica y función de costos (Saldarriaga,
2016). De esta manera, se pueden incluir sistemas con caudales de demanda de magnitud y
distanciamiento variables.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
53
La determinación de la flecha óptima se realiza en base al centroide de demandas y el coeficiente
de uniformidad (Saldarriaga, 2016). El centroide de demandas se obtiene ponderando las
distancias en las que se presenta demanda de caudal con respecto a la fuente de abastecimiento.
Dicha ponderación se realiza según la longitud de la serie de tuberías y el caudal total fluyendo en
el sistema. Según Saldarriaga (2016), el centroide de demandas se calcula según la Ecuación 29.
𝑥̅ =
∑
𝑄
𝑖
𝐷
𝑖
𝑁𝑁
𝑖=0
𝑄
𝑇
𝑙
𝑇
Ecuación 29. Centroide de demandas en metodología LOGH.
Dónde:
𝑁𝑁[−]
: Número de nodos.
𝑄
𝑖
[𝑚
3
/𝑠]
: Caudal demandado en el nodo i. 𝐷
𝑖
[𝑚]
: Distancia topológica al nodo i.
𝑙
𝑇
[𝑚]
: Longitud total.
𝑄
𝑇
[𝑚
3
/𝑠]:
Caudal total.
Por su parte, el coeficiente de uniformidad es un indicador de la localización de las demandas de
caudal. Puede interpretarse como una constante que relativiza la posición de cada uno de los
nodos con extracción de flujo volumétrico con respecto al centroide de demandas. El coeficiente
se obtiene dividiendo la serie de tuberías en dos tramos según 𝑥̅ y ponderando los dos centroides
obtenidos para cada tramo según la posición y magnitud de los requerimientos de caudal. Según
Saldarriaga (2016), el coeficiente de uniformidad se determina según la Ecuación 30.
𝐶𝑈 = (
∑
𝑄
𝑖
𝑁𝑁
𝑇𝑟𝑎𝑚𝑜1
𝑖=0
𝐷̅
𝑇𝑟𝑎𝑚𝑜1
𝑖
𝑙
𝑇
∑
𝑄
𝑖
𝑁𝑁
𝑇𝑟𝑎𝑚𝑜1
𝑖=0
)
𝑙
𝑇𝑟𝑎𝑚𝑜1
𝑙
𝑇
+ (
∑
𝑄
𝑖
𝑁𝑁
𝑇𝑟𝑎𝑚𝑜2
𝑖=0
𝐷̅
𝑇𝑟𝑎𝑚𝑜2
𝑖
𝑙
𝑇
∑
𝑄
𝑖
𝑁𝑁
𝑇𝑟𝑎𝑚𝑜2
𝑖=0
)
𝑙
𝑇𝑟𝑎𝑚𝑜2
𝑙
𝑇
Ecuación 30. Coeficiente de uniformidad en metodología LOGH.
Dónde:
𝑁𝑁[−]
: Número de nodos.
𝑄
𝑖
[𝑚
3
/𝑠]
: Caudal demandado en el nodo i. 𝐷̅
𝑇𝑟𝑎𝑚𝑜1
𝑖
[𝑚]
: Distancia del nodo i a la fuente
de abastecimiento en el centroide de demandas. 𝑙
𝑇
[𝑚]
: Longitud total.
𝑙
𝑇𝑟𝑎𝑚𝑜
[𝑚
3
/𝑠]:
Longitud de tramo.
Los números que se obtienen en la Ecuación 29 y Ecuación 30 se pueden insertar en la función
cuadrática de la flecha óptima (Ecuación 31). Esta se deduce mediante un ajuste estadístico que
describe en más de un 85% la variación de la flecha óptima (Saldarriaga, 2016). Dado que el ajuste
se realiza empleando un exponente en la función de costos de 1.46 y una relación Q
2
/L
3
de 1*10
-9
m
3
/s
2
, se deben incluir dos correcciones para adaptar la parábola de la flecha óptima a las
condiciones particulares del sistema a analizar (aplicación de la Ecuación 32 y Ecuación 33)
(Saldarriaga, 2016).
𝐹 = 0.436 − 0.177𝑥̅ − 0.977𝐶𝑈 + 0.906𝐶𝑈
2
Ecuación 31. Ecuación cuadrática de la flecha óptima.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
54
𝐹
𝑛
= (−0.1134𝐹 + 0.0032)𝑛
2
+ (0.6443𝐹 + 0.0043)𝑛 + 0.2835𝐹 − 0.0111
Ecuación 32. Flecha óptima corregida según el exponente de la función de costos.
𝐹
𝑄
2
/𝑙
3
= (0.00868𝐹
𝑛
+ 0.00066) ln (
𝑄
𝑇
2
𝑙
𝑇
3
) + 1.18069𝐹
𝑛
+ 0.01345
Ecuación 33. Flecha óptima corregida según la relación Q
2
/L
3
.
Dónde:
𝑥̅[−]
: Centroide de demandas.
𝐶𝑈
[−]
: Coeficiente de uniformidad. 𝑛[−]: Exponente de la función de costos.
𝑙
𝑇
[𝑚]
: Longitud total.
𝑄
𝑇
[𝑚
3
/𝑠]:
Caudal total.
Con la flecha óptima corregida se puede obtener la LOGH. En este caso, se conoce la cabeza
disponible al inicio, al final y en el punto medio según la flecha, por lo que es posible calcular una
ecuación cuadrática cóncava hacia arriba que intercepte los tres puntos (Saldarriaga, 2016).
Omitiendo el procedimiento matemático, se encuentra la función que describe la línea óptima del
gradiente hidráulico.
𝐿𝑂𝐺𝐻(𝑥) = 4𝐹
𝑄
2
𝑙
3
𝐿𝑂𝐺𝐻
𝑚𝑎𝑥
− 𝐿𝑂𝐺𝐻
𝑚𝑖𝑛
𝑙
𝑇
2
𝑥
2
− (1 + 4𝐹
𝑄
2
𝑙
3
)
𝐿𝑂𝐺𝐻
𝑚𝑎𝑥
− 𝐿𝑂𝐺𝐻
𝑚𝑖𝑛
𝑙
𝑇
𝑥 + 𝐿𝑂𝐺𝐻
𝑚𝑎𝑥
Ecuación 34. Línea óptima del gradiente hidráulico.
Dónde:
𝐿𝑂𝐺𝐻
𝑚𝑎𝑥
[𝑚]
: Altura piezométrica máxima.
𝐿𝑂𝐺𝐻
𝑚𝑖𝑛
[𝑚]
: Altura piezométrica mínima. 𝑙
𝑇
[𝑚]
: Longitud total.
𝐹
𝑄2
𝑙3
[−]: Flecha óptima corregida.
𝑥[𝑚]:
Distancia topológica.
Por último, empleando la Ecuación 34, se determinan las pérdidas objetivo en cada tubería de la
red. Con las pérdidas se puede despejar el diámetro continuo correspondiente según la ecuación
de Darcy-Weisbach o Hazen-Williams (Saldarriaga, 2016). Es importante mencionar que, dadas la
restricción de los diámetros comerciales (Ecuación 27), es necesario redondear los diámetros de
tal modo que se minimicen los costos y se cumplan los requerimientos hidráulicos. La heurística
para redondear los diámetros se tratará más adelante.
Δ𝐻
𝑖𝑗
= 𝐿𝑂𝐺𝐻
𝑖
− 𝐿𝑂𝐺𝐻
𝑗
Ecuación 35. Pérdidas objetivo en el tramo ij.
Dónde:
𝐿𝑂𝐺𝐻
𝑖
[𝑚]
: Altura piezométrica en el nodo i.
𝐿𝑂𝐺𝐻
𝑗
[𝑚]
: Altura piezométrica en el nodo j.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
55
3.3.3 Métodos de optimización para redes cerradas
Como se mencionaba en apartados anteriores, la búsqueda de la configuración óptima en redes de
distribución implica la aplicación de heurísticas no deterministas. En los siguientes apartados se
desarrollarán algunas de estas metodologías según su relevancia en el desarrollo de la presente
investigación.
3.3.3.1 Algoritmos genéticos (AG)
Los algoritmos genéticos corresponden a un proceso de búsqueda de soluciones análogo a los
mecanismos de evolución característicos en el fenómeno biológico de selección natural (Goldberg,
1953). Cada una de las soluciones pertenecientes al espacio de búsqueda se puede tratar como un
“cromosoma”, cuyas características o “genes” le atribuyen su aptitud para cumplir con los
requerimientos establecidos por el problema a optimizar (Mitchell, 1999). El algoritmo ejecuta de
manera iterativa un proceso de procreación entre los individuos de la población, propiciando una
mejoría automática de las opciones disponibles al momento de producir nuevas generaciones
(Sivanandam y Deepa, 2008). La implementación computacional del apareamiento desarrolla los
procesos de adaptación y supervivencia de los mejores especímenes, avanzando hacia soluciones
con mejor genotipo en cada repetición de las rutinas programadas.
Una de las grandes ventajas de la metodología corresponde a la flexibilidad. El autor se encuentra
en la potestad de definir aspectos como los operadores de reproducción, el número de
descendientes, la función de aptitud que evalúa a cada individuo, la población inicial, entre otros
parámetros relevantes (Sivanandam y Deepa, 2008). Inclusive, es usual encontrar modelos que
incorporan fenómenos de mutación, donde algún fragmento del cromosoma de un individuo
aleatorio puede cambiar de manera esporádica según el modelo probabilístico que se considere
adecuado (Mitchell, 1999). Por otra parte, se encuentran las desventajas. En lo que concierne al
diseño de RDAPs, la aplicación de algoritmos genéticos no corresponde a un proceso de
optimización en sentido estricto; la aleatoriedad intrínseca al proceso implica que no existan
garantías de encontrar algún óptimo local, mucho menos el global (Saldarriaga, 2016). Asimismo, a
no ser que se simule explícitamente mediante criterios de penalización, las rutinas de algoritmos
genéticos no incluyen de antemano los requerimientos hidráulicos de los sistemas (Saldarriaga,
2016). No obstante, si el número de iteraciones es suficientemente alto, es posible que los
resultados sean satisfactorios.
3.3.3.2 Programación por Restricciones (PR)
El principio de la Programación por Restricciones (PR) consiste en asimilar el diseño optimizado de
redes de distribución de agua potable como varias instancias de un problema de satisfacción por
restricciones (CSP). Dicho CSP (𝑃 = (𝑉, 𝐶)) se describe mediante un conjunto finito de variables
𝑉
que pueden asumir valores de una tupla de dominios finitos 𝐷, buscando aquellas
combinaciones que garantizan el cumplimiento de ciertas restricciones o “constraints”

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
56
pertenecientes a otro conjunto finito 𝐶 (Xia y Yap, 2013). Se dice que una tupla de asignaciones 𝐴
es solución al CSP siempre y cuando sus valores para cada variable de 𝑉 pertenezca al dominio 𝐷 y
cumpla con los requerimientos de 𝐶 (Xia y Yap, 2013). En otras palabras, la solución corresponde a
una tupla consistente de asignaciones (Barták et. al., 2004).
En este caso, las variables a trabajar corresponden a los diámetros de cada una de las tuberías de
la red, que pueden asumir valores correspondientes a un dominio de diámetros comerciales. Para
el caso de las RDAPs, las restricciones deben contemplar la presión mínima admisible en los nodos
y las demandas de caudal, ambas describibles en función de los diámetros. Según Barber y Salido
(2003), en los problemas CSP las restricciones se describen según su aridad, es decir, según el
número de variables involucradas en la restricción; de esta manera, para el diseño optimizado se
pueden emplear restricciones unarias (una sola variable), binarias (dos variables) o n-arias (tres o
más variables) según como se desee modelar las restricciones de alturas piezométricas y de
caudal.
La ventaja de la PR radica en la posibilidad de usar activamente las restricciones para reducir el
esfuerzo computacional necesario (Villalba et. al., 2005). En efecto, a medida que transcurre el
algoritmo, ocurren reducciones en el dominio de análisis debido a la generación de nuevas
restricciones o a la detección de inconsistencias (Saldarriaga, 2016). Al decidir el diámetro de un
ducto se establece una nueva restricción que acota el espacio de búsqueda. Las variaciones en la
eficiencia y el gasto computacional del método dependen directamente de las heurísticas de
búsqueda que se implementen en el algoritmo. En general, el mecanismo de funcionamiento
cambia según la metodología de avance o toma de decisiones al momento de contemplar
diferentes posibilidades de asignación y al retroceso una vez se encuentre una inconsistencia o un
escenario desfavorable (Barták et. al., 2004). Cabe resaltar que este último esquema usualmente
se representa mediante árboles de búsqueda (Saldarriaga, 2016).
3.3.3.3
Superficie Óptima del Gradiente Hidráulico (SOGH)
El concepto de las pérdidas hidráulicas objetivo, establecidas en un principio por el criterio
geométrico de Wu, puede extenderse para el caso de las RDAPs. La analogía corresponde a
plantear un gradiente hidráulico que asegura el diseño de menor costo (Featherstone y El-Juamily,
1983). Estas condiciones de presión pueden describirse mediante el ajuste a una superficie
tridimensional (Superficie Óptima de Presiones – SOP). En este contexto surge el criterio de
Featherstone (1983), cuya aproximación consiste en definir un decaimiento de la energía
disponible como una superficie plana. Sin embargo, la aproximación presenta problemas para
modelar casos con topografías abruptas (Villalba et. al., 2005).
La metodología de la Superficie Óptima del Gradiente Hidráulico (SOGH) corresponde a una
alternativa mejorada tanto del criterio de Wu como el de Featherstone. A diferencia de los
criterios presentados y de manera similar a la metodología LOGH, es posible variar la flecha para

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
57
encontrar aquel número que mejor se ajuste a las características hidráulicas y topológicas del
sistema (Saldarriaga, 2016). De esta manera, se obtiene una solución que respeta las restricciones
de conservación de la masa y la energía, demandas de caudal, presión mínima y ventajas
computacionales asociadas a una convergencia en un tiempo polinomial no mayor a O(n) (Villalba
et. al., 2005). No obstante, es importante aclarar que el método resulta en diseños con diámetros
continuos, requiriéndose entonces la aplicación de otras heurísticas para el redondeo a las
medidas comerciales disponibles (Villalba et. al., 2005).
A continuación, se resume la lista de pasos a implementar según los trabajos de Saldarriaga
(2016), Villalba et. al. (2005), Ochoa y Saldarriaga (2009) y Ochoa et. al. (2010):
1. Calcular la distancia topológica de los nodos a las fuentes de abastecimiento. Cabe resaltar
que esta corresponde a la distancia mínima asociada a la trayectoria real que puede
recorrer el agua en el sistema (Villalba et. al., 2005). Por consiguiente, se debe
implementar un algoritmo que determine la longitud mínima entre dos vértices de un
grafo como se establece en la Ecuación 36 (Villalba et. al., 2005). Una aproximación inicial
para conocer la hidráulica de la red corresponde a asignar, como suposición preliminar,
algún diámetro comercial pequeño para asegurar que el agua fluya de las fuentes a los
nodos (Saldarriaga, 2016). Si un nodo es alimentado por más de una fuente, se le asigna
aquella que le aporta mayor LGH (Ochoa et. al., 2010). De esta manera, se obtendrán las
rutas desde cada embalse hasta sus correspondientes sumideros, es decir, hasta aquellos
nodos que no alimentan ningún otro nodo.
𝐷
𝑡
= 𝐷𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎 𝑚í𝑛𝑖𝑚𝑎 𝑔𝑟𝑎𝑓𝑜(𝑓𝑢𝑒𝑛𝑡𝑒, 𝑛𝑢𝑑𝑜)
Ecuación 36. Distancia topológica mínima entre la fuente y un nodo.
2. Asignar a cada tubería uno de los diámetros comerciales de manera proporcional a la
distancia calculada en la Ecuación 36 (Ochoa et. al., 2010).
3. Estimar la flecha óptima. De manera análoga a la metodología LOGH, se estima el
centroide de demandas, el coeficiente de uniformidad, la flecha según la ecuación
cuadrática y las debidas correcciones dadas por el ajuste estadístico (Saldarriaga, 2016).
Retomando la Ecuación 29, Ecuación 30, Ecuación 31, Ecuación 32 y la Ecuación 33, para el
caso de las redes cerradas se emplea la distancia topológica en vez de la longitud y la
distancia topológica máxima recorrida por el agua en vez de la longitud total (Saldarriaga,
2016).
4. Aplicar una simulación hidráulica para conocer los sentidos de flujo y caudales iniciales en
cada ducto. De esta manera, se puede identificar que fuentes abastecen cada uno de los
nodos, así como los sumideros de la red. Si un nodo es abastecido por más de una fuente,
se le asigna aquella que le aporta mayor LGH (Ochoa et. al., 2010). Adicionalmente, se

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
58
logran estipular nuevas distancias topológicas según la Ecuación 36. Cabe resaltar que la
hidráulica puede variar en la medida que se tiene una nueva configuración de diámetros
comerciales.
5. Ordenar los nuevos sumideros de mayor a menor distancia topológica.
6. Identificar las rutas de alimentación o trayectorias de flujo desde las fuentes hasta los
sumideros.
7. Para cada ruta o trayectoria de flujo, determinar la LGH ideal mínima según la Ecuación 37.
𝐿𝑂𝐺𝐻
𝑚𝑖𝑛
= 𝑍
𝑆𝑢𝑚𝑖𝑑𝑒𝑟𝑜𝑖
+ 𝑃
min
i
Ecuación 37. LGH ideal mínima para la ruta al sumidero i.
Dónde:
𝑍
𝑆𝑢𝑚𝑖𝑑𝑒𝑟𝑜𝑖
[𝑚]
: Altura topográfica del sumidero i.
𝑃
min 𝑖
[𝑚]
: Presión mínima admisible en el nodo i.
8. Para cada ruta se determina la LGH ideal en cada nodo siguiendo algunos lineamientos. En
primer lugar, la LGH ideal máxima corresponde a la de la fuente que alimenta la ruta
(Saldarriaga, 2016).
𝐿𝑂𝐺𝐻
𝑚𝑎𝑥
= 𝐿𝑂𝐺𝐻
𝑜
Ecuación 38. LGH ideal máxima para la ruta al sumidero i.
Dónde:
𝐿𝑂𝐺𝐻
𝑜
[𝑚]
: Altura piezométrica en la fuente.
En segundo lugar, la LGH ideal para cada nodo debe encontrarse entre la LGH mínima y
máxima. La forma de describir el valor según la distancia topológica se realiza mediante
alguna ecuación de ajuste. Se han encontrado excelentes resultados implementando la
relación cuadrática de la LOGH al acercarse al criterio de Wu. Se retoma la Ecuación 34
generalizando para una red cerrada.
𝐿𝑂𝐺𝐻(𝑑) = 4𝐹
𝑄
2
𝑙
3
𝐿𝑂𝐺𝐻
𝑚𝑎𝑥
− 𝐿𝑂𝐺𝐻
𝑚𝑖𝑛
𝑑
𝑚𝑎𝑥
2
𝑑
2
− (1 + 4𝐹
𝑄
2
𝑙
3
)
𝐿𝑂𝐺𝐻
𝑚𝑎𝑥
− 𝐿𝑂𝐺𝐻
𝑚𝑖𝑛
𝑑
𝑚𝑎𝑥
2
𝑑 + 𝐿𝑂𝐺𝐻
𝑚𝑎𝑥
Ecuación 39. Ecuación LOGH para una red cerrada.
Dónde:
𝑑[𝑚]
: Distancia topológica.
𝐿𝑂𝐺𝐻
𝑚𝑎𝑥
[𝑚]
: Altura piezométrica máxima.
𝐿𝑂𝐺𝐻
𝑚𝑖𝑛
[𝑚]
: Altura piezométrica mínima.
𝐹
𝑄2
𝑙3
[−]: Flecha óptima corregida.
𝑑
𝑚𝑎𝑥
[𝑚]:
Distancia topológica máxima.
9. Definir para cada tubo una pérdida de energía objetivo igual a la diferencia entre las
alturas piezométricas entre el nodo final e inicial (Ochoa y Saldarriaga, 2009). Lo anterior
se describe en la Ecuación 35.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
59
10. Conociendo las pérdidas hidráulicas objetivo y el caudal determinado por la simulación
hidráulica del paso 4 se aplica un algoritmo de diseño de tuberías simples para cada ducto
del sistema.
11. Mediante el modelo de simulación se realiza una comprobación de caudal y estimación de
las pérdidas reales en cada tubería.
12. Si la diferencia entre las pérdidas reales y objetivo es menor al error admisible
contemplado por el diseñador se continua al paso 13. De lo contrario, se regresa al paso 4.
13. Verificar que en la totalidad de los nodos se cumpla con la presión mínima admisible. En
aquellos donde no se cumpla el requisito de altura piezométrica se deben realizar
correcciones. El proceso consiste en asignar una nueva LGH mínima igual a la altura
topográfica mayor de los nodos que incumplen (Ochoa et. al., 2010). Luego, se determina
una nueva distancia topológica máxima asociada al nodo con presión inadmisible más
alejado. Finalmente, se recalculan los parámetros de la Ecuación 39. Los nuevos valores
LGH según la distancia topológica serán los valores corregidos.
14. Aplicar alguna heurística para redondear los diámetros a las restricciones comerciales.
La lista de pasos se puede ilustrar, de manera sintética, en un diagrama de flujo. A modo de
ejemplo, se presenta el caso en el que se escogen líneas de ajuste cuadráticas.
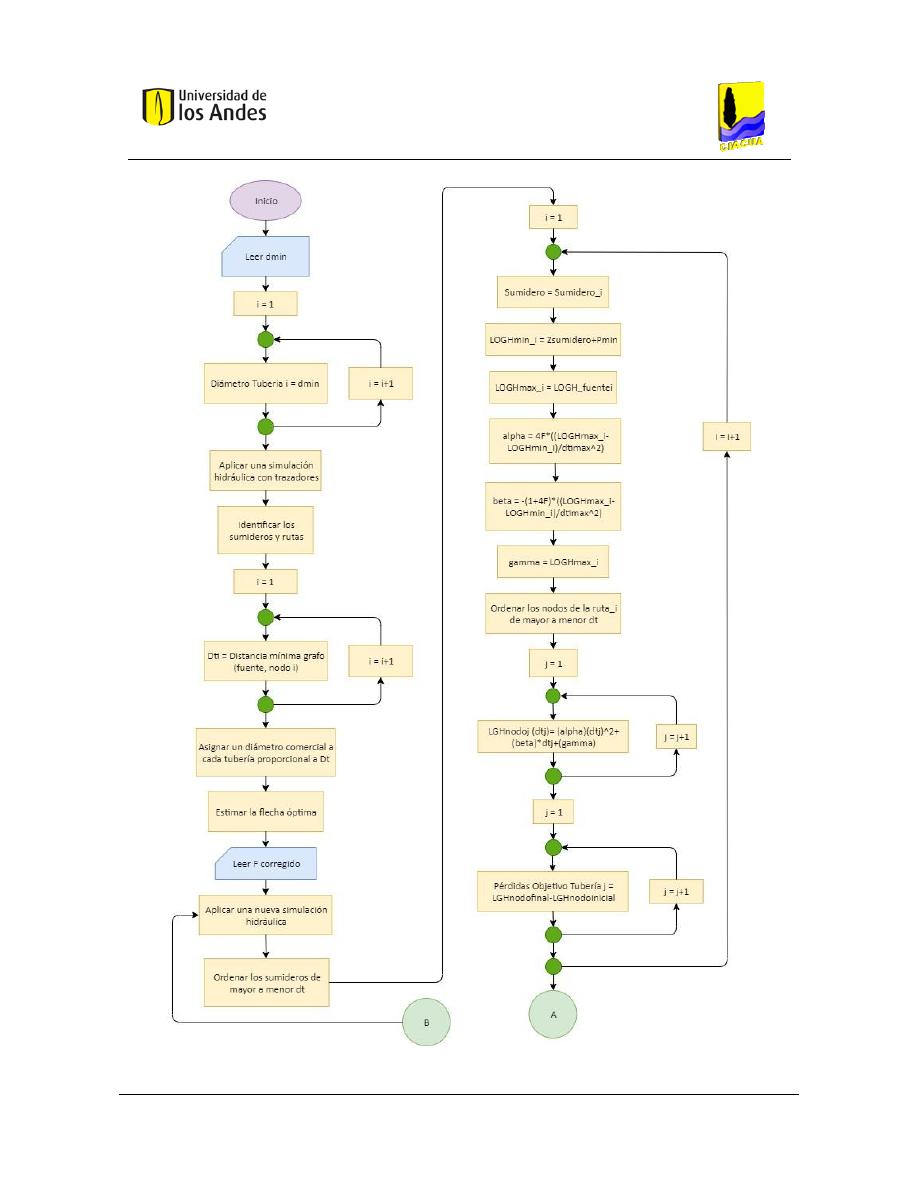
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
60
Figura 3. Diagrama de Flujo 2 - Metodología SOGH Parte 1.
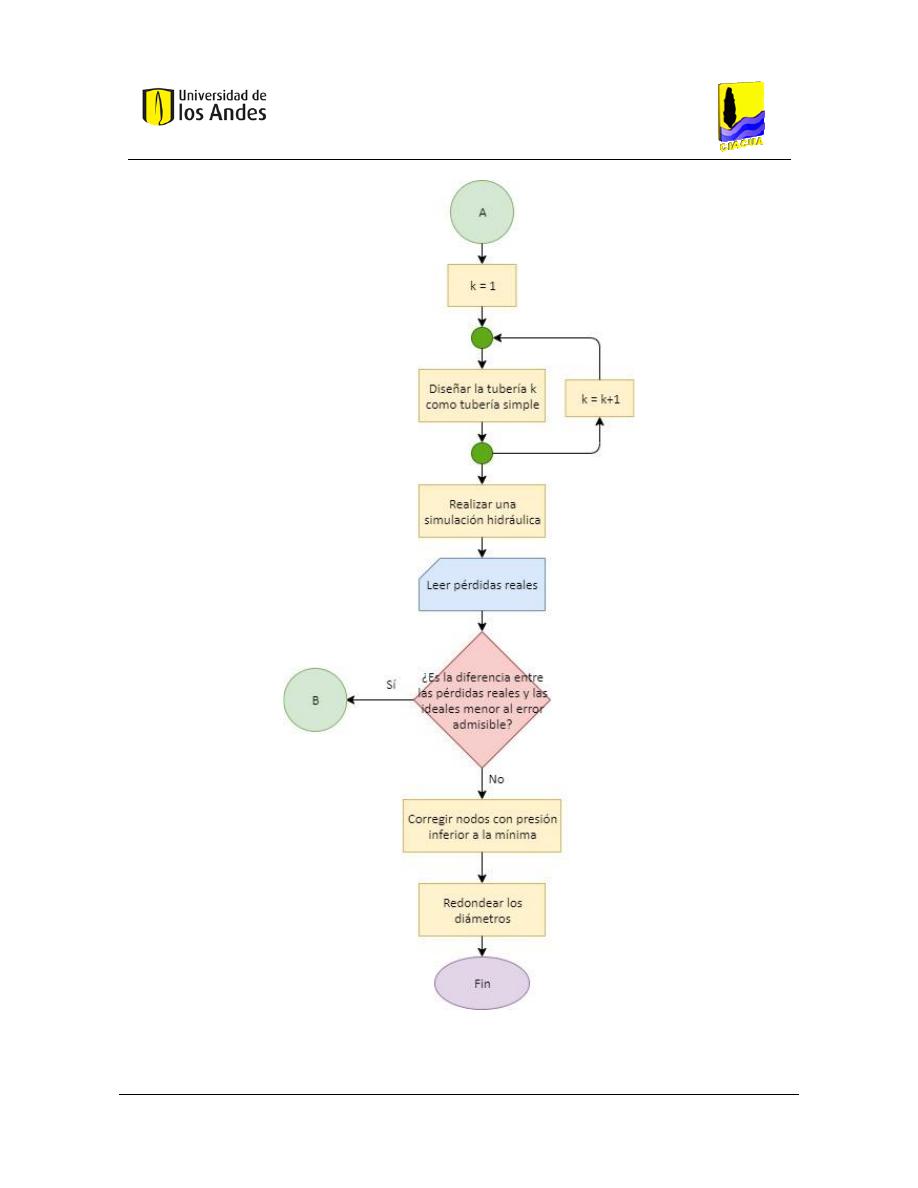
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
61
Figura 4. Diagrama de Flujo 2 - Metodología SOGH Parte 2.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
62
3.3.3.4 OPUS (Optimal Power Use Surface)
La metodología OPUS corresponde a una alternativa al algoritmo de la Superficie Óptima del
Gradiente Hidráulico. Su ventaja radica en reducir el número de iteraciones necesarias con
pequeñas variaciones con respecto al costo óptimo de la red. La diferencia del método se asocia al
tratamiento de las redes como mallas abiertas, en la medida que un sistema redundante, típico de
analizar desde la perspectiva de una red cerrada, resulta desventajoso a nivel de costos (López et.
al., 2013). De esta manera, OPUS supone el tratamiento de las redes bajo un esquema de árbol, de
tal manera que las ramificaciones conformadas por las trayectorias de flujo se comporten de
manera análoga a una red abierta (Saldarriaga et. al., 2013). Los subprocesos de la metodología se
resumen a continuación según lo planteado en los trabajos de Saldarriaga et. al. (2013) y López et.
al. (2013):
1. Estructura de árbol: Corresponde a un proceso iterativo de adición de pares nodo-tubería
hasta alcanzar un sumidero de la red. La asignación se realiza mediante una función
costo/beneficio, donde se determina el cociente entre la demanda del nodo nuevo y el
costo marginal de conectarlo a la fuente de abastecimiento (Saldarriaga et. al., 2013). A
partir de la estructura de árbol se espera favorecer la creación de pocas rutas principales
donde se transporte la mayor proporción del caudal disponible.
2. Uso de superficie óptima de energía: Se retoman los principios de optimización
establecidos por Wu (1975) y perfeccionados por Ochoa (2009) para asignar una altura
piezométrica objetivo a todos los nodos de la red, considerando las rutas estipuladas en la
estructura de árbol. En este paso se establecen las LGH con flecha variable según la
distribución de las demandas en la red.
3. Distribución óptima de caudal: Una vez definida la SOP, procede determinar la
distribución de caudales en cada ducto a modo que se minimicen los costos, se respete el
principio de conservación de la masa y el criterio de pérdidas de energía establecido en el
paso anterior. El proceso consiste en partir de cada sumidero y, mediante una función de
ajuste (usualmente H/L
2
), determinar la tubería principal que alimenta el nudo. Esta
tubería llevará dentro de sí el valor máximo de caudal, mientras que las demás contendrán
el caudal asociado al diámetro mínimo disponible. Cabe resaltar que el análisis se realiza
sobre el grafo original en vez del esquema modificado por la estructura de árbol.
4. Cálculo del diámetro: Mediante las pérdidas objetivo y el caudal de diseño, se ejecuta un
proceso iterativo para determinar el diámetro que cumple las restricciones. Al finalizar el
proceso se obtiene un diámetro óptimo en un espacio continuo de soluciones.
5. Redondeo de diámetros: Se trata del procedimiento de redondeo de los diámetros
continuos a los valores discretos disponibles según el catálogo de diámetros comerciales.
Es común utilizar el redondeo potencial a la 2.6 (Saldarriaga, 2016).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
63
6. Optimización: De manera similar al algoritmo de optimización por programación por
restricciones, se realiza una reducción iterativa de todos los diámetros posibles sin violar
el requerimiento de presión mínima en los nodos.
3.3.4 Redondeo de diámetros
Retomando la restricción estipulada en la Ecuación 27, se conoce que el diseño de una red de
distribución de agua potable debe contemplar la condición de contar con un número limitado de
diámetros comerciales según la disponibilidad que ofrezca el fabricante. Por consiguiente, el
conjunto de diámetros comerciales debe establecerse como una serie de valores discretos. Dado
que las metodologías de optimización LOGH y SOGH determinan los diámetros en un espacio de
solución continuo (conjunto de los números reales), es indispensable plantear alguna heurística
que permita aproximar los diámetros calculados a valores discretos sin apartarse, en lo posible, del
óptimo económico (Saldarriaga, 2016).
El redondeo de los diámetros puede llevarse a cabo de diferentes maneras. Una primera opción
consiste en aproximar al diámetro comercial inmediatamente superior (Saldarriaga, 2016). A pesar
del incremento en la capacidad de caudal de las tuberías, el costo del sistema incrementa en la
medida que un diámetro mayor implica un encarecimiento potencial del precio. De esta manera, si
se desea reducir el costo del sistema, es prioritario reducir la mayor cantidad de diámetros. Otras
metodologías corresponden a aproximar al diámetro comercial más cercano o realizar
correcciones que permitan ajustar el diámetro a un valor proporcional según el caudal de flujo
(Saldarriaga et. al., 2010). Independiente de la metodología, es importante reconocer que el
comportamiento hidráulico del diseño cambiará, por lo que es imprescindible establecer si en
algún punto de la red se incumple con el límite de presión mínima (Saldarriaga et. al., 2010).
La heurística para obtener los diámetros comerciales óptimos consiste en un algoritmo de
programación combinatoria en la medida que incluye tanto la técnica SOGH como la Programación
por Restricciones según lo propuesto por Villalba et. al. (2005). El primer paso consiste en aplicar
la metodología SOGH para obtener los diámetros continuos (Ochoa y Saldarriaga, 2009). Después,
se aplica un algoritmo de Programación por Restricciones, el cual consiste en incrementar todos
los diámetros a los inmediatamente superiores (Villalba et. al., 2005). En caso tal que el diámetro
sea superior al máximo, deberá reducirse a este valor. Si en algún nodo no se cumple con la
presión mínima, inicia un proceso iterativo en el que se aumenta el diámetro al inmediatamente
superior a la tubería con la máxima pendiente de fricción hasta cumplir con el requisito (Ochoa y
Saldarriaga, 2009). Posteriormente, se aplica otro algoritmo de programación por Restricciones
para reducir los diámetros del sistema (Villalba et. al., 2005). La red se recorre dos veces según la
posición del ducto: una en orden ascendente a la distancia topológica y otra en orden
descendente (Ochoa y Saldarriaga, 2009). Para cada caso se reduce el diámetro de cada tubo al
mínimo sin incumplir con la restricción de la presión mínima. Villalba et. al. (2005) demostraron
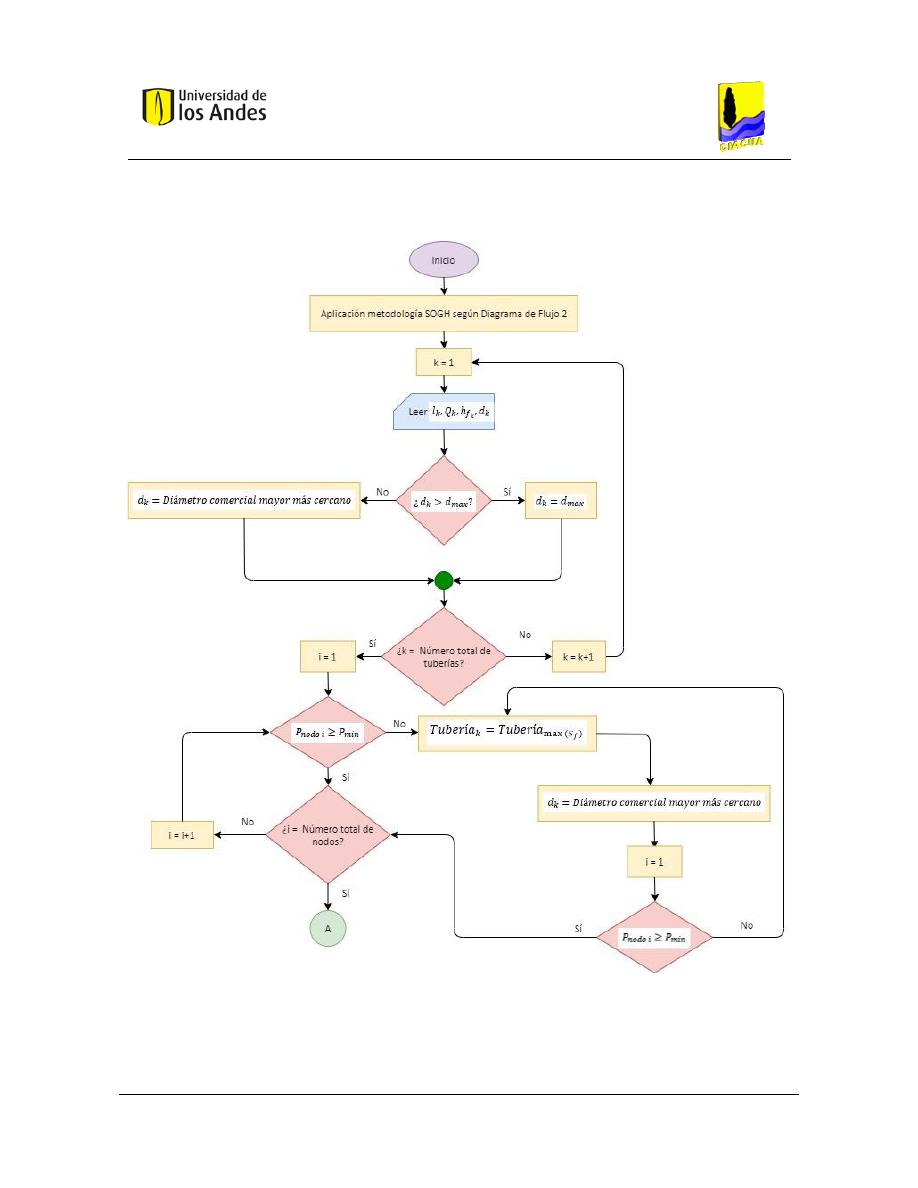
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
64
que la metodología arroja resultados relativamente buenos. En el siguiente diagrama de flujo se
ilustran los pasos estipulados para redondear los diámetros.
Figura 5. Diagrama de Flujo 3 - Redondeo de diámetros Parte A. Adaptado de Saldarriaga (2016).
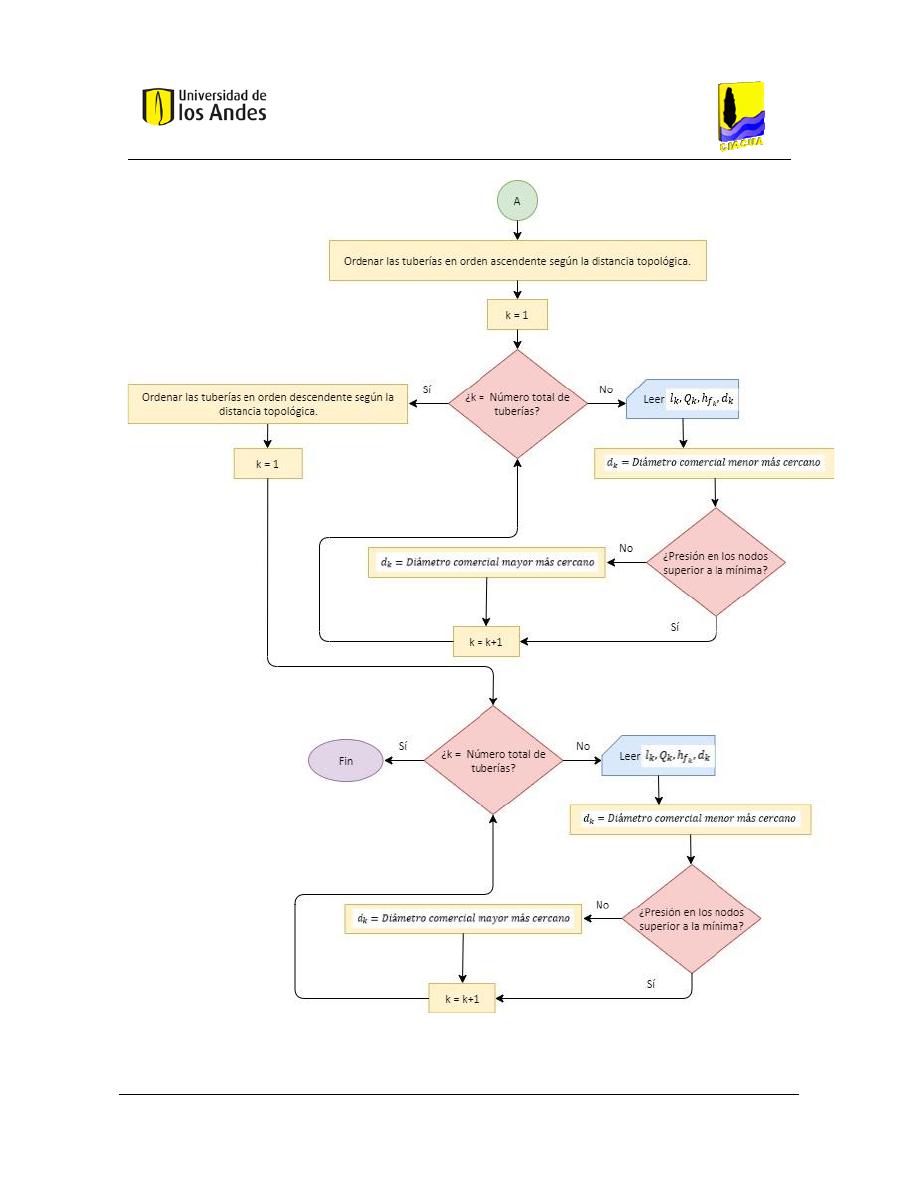
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
65
Figura 6. Diagrama de flujo 3 - Redondeo de diámetros Parte B. Adaptado de Saldarriaga (2016).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
66
3.4 Herramientas computacionales
3.4.1 Programa REDES
REDES es un software desarrollado por el Centro de Investigaciones en Acueductos y
Alcantarillados (CIACUA) del Departamento de Ingeniería Civil y Ambiental de la Universidad de los
Andes. Se trata de una herramienta para el análisis, diseño, simulación hidráulica y de calidad del
agua de sistemas de tuberías con flujo a presión, tanto para escenarios estáticos como para
períodos extendidos (Saldarriaga et. al., 2018). Entre sus características computacionales más
importantes se encuentra el lenguaje de programación PASCAL, una implementación en el entorno
de desarrollo Delphi, funcionamiento en el sistema operacional Windows y el seguimiento del
paradigma de programación orientada a objetos (Saldarriaga, 2016). Cabe resaltar que para el
presente trabajo se empleará la versión del año 2019.
REDES cuenta con una interfaz gráfica que permite visualizar la red a modelar por el usuario. En
ella se pueden ubicar geográficamente los nodos, embalses, tuberías, distinguir superficies y
curvas de nivel y obtener un mapeo de la topografía tridimensional del sistema. En la Figura 7 y
Figura 8 se visualiza la interfaz gráfica de REDES para el caso de un sistema en dos y tres
dimensiones, respectivamente, para la red de ejemplo incluida en la licencia. Con respecto a la
teoría hidráulica, REDES incorpora la ecuación de Darcy-Weisbach, Colebrook-White y Hazen-
Williams para caracterizar las pérdidas por fricción, así como el Método del Gradiente para el
cálculo de los circuitos, empleando rutinas que desarrollan la factorización incompleta de Cholesky
en la operación de las matrices (Saldarriaga, 2016). A comparación de otros softwares de uso
similar, REDES tiene la capacidad de ejecutar cálculos hidráulicos de alta complejidad con un
ahorro importante de tiempo y gasto computacional (Bernal y Saldarriaga, 2008).
Figura 7. Interfaz REDES 2019 para la red de ejemplo.
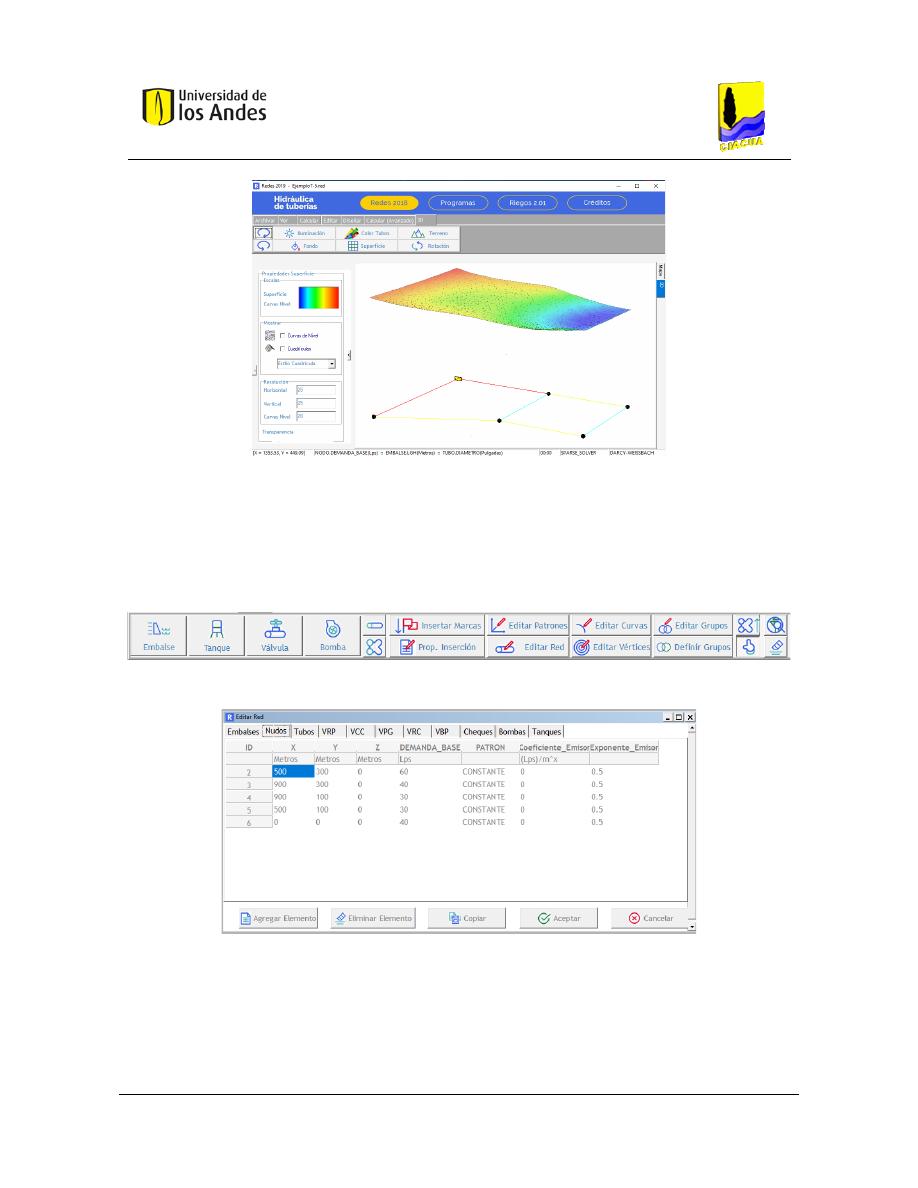
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
67
Figura 8. Interfaz REDES 2019 visualización 3D de la SOP.
En la pestaña Editar se encuentran los botones para materializar la red sobre el lienzo. Cada uno
de los elementos se puede agregar bien sea presionando el ícono que lo representa y ubicándolo
sobre la interfaz o ingresando en Editar Red para especificar las coordenadas, caudal demandado,
longitud, línea del gradiente hidráulico o cualquier otra característica pertinente para el programa.
Figura 9. Botones para la construcción de la red.
Figura 10. Ventana de edición de red.
En cuanto al diseño optimizado, REDES incorpora cinco metodologías para minimizar la Ecuación
28 en la pestaña Diseñar: OPUS, Algoritmos Genéticos (AG), Superficie Óptima de Gradiente
Hidráulico (SOGH), Algoritmos de Programación Combinatoria y Búsqueda de Armonía. Las rutinas
se basan en el principio de mantener la presión mínima en todos los nudos, la reducción del costo
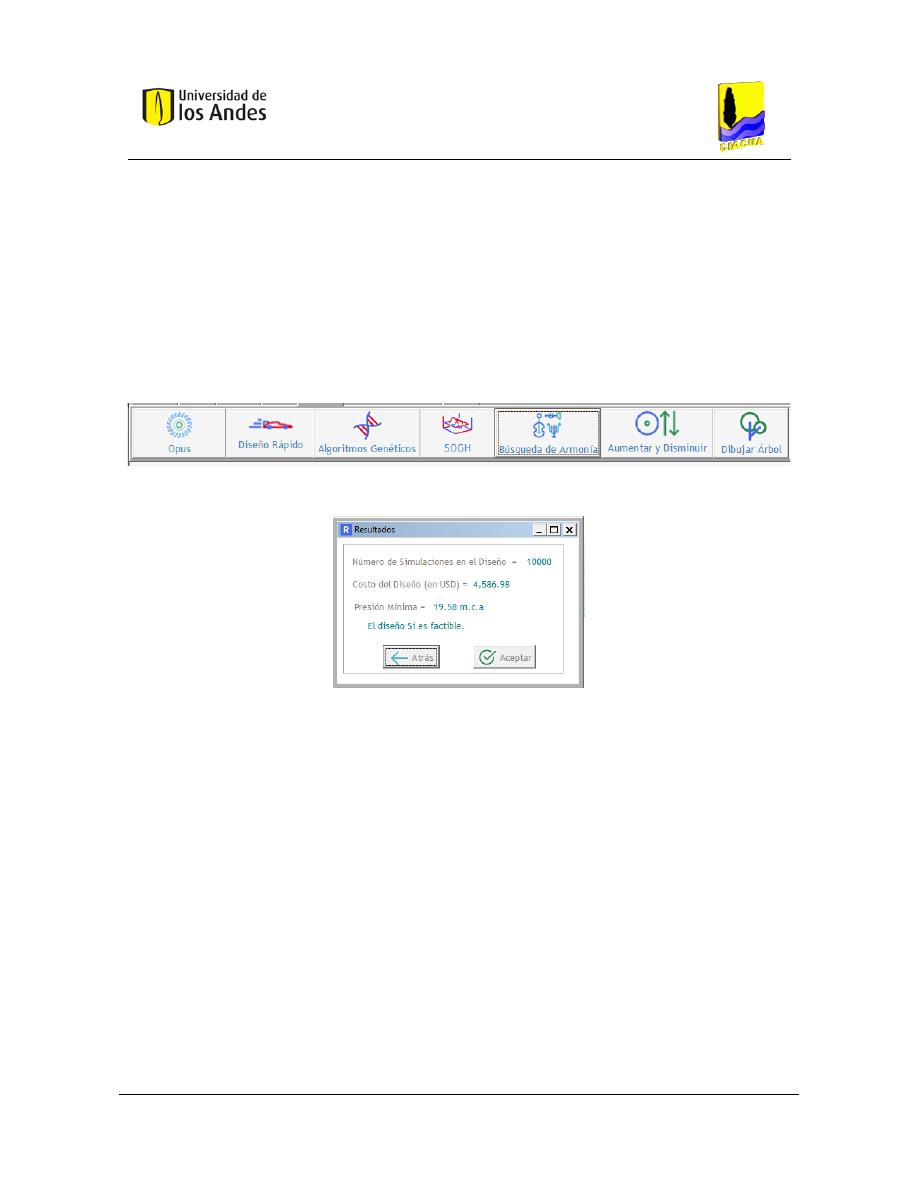
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
68
de la red y el diseño contemplando un conjunto discreto de diámetros según lo que el usuario
defina (Saldarriaga, 2016). Asimismo, el software integra las restricciones estipuladas en la
Ecuación 15, Ecuación 17, Ecuación 26 y en la Ecuación 27. En la pestaña “Diseñar” se le permite
escoger al usuario su metodología de preferencia. Cabe resaltar que se debe contar con
parámetros como la rugosidad absoluta, el coeficiente de la Ecuación de Hazen-Williams, la
presión mínima admisible, el conjunto discreto de diámetros comerciales, las constantes de la
curva de costos, entre otros valores para ejecutar el diseño de manera adecuada. Finalizado el
proceso, el programa muestra en pantalla una ventana emergente que comunica el costo final, el
tiempo transcurrido y el número de iteraciones necesarias para alcanzar el resultado.
Figura 11. Pestaña Diseñar.
Figura 12. Ventana de resultados del diseño optimizado.
3.4.2 Programa MATLAB
La plataforma de programación MATLAB es un software matemático y privativo desarrollado por
la empresa MathWorks. El programa se especializa en la resolución de problemas concernientes
con el análisis numérico, la computación y visualización de los resultados, siendo ampliamente
utilizado en el campo de la ingeniería y las ciencias exactas (Sigmon, 1993). A nivel general,
pueden atribuírsele aplicaciones en las áreas de análisis de datos, modelación numérica,
optimización, ecuaciones diferenciales, estadística, procesamiento de señales, programación
lineal, entre otras (Gjendemsjo, 2006). Estas funciones pueden utilizarse bien sea mediante la
declaración de código en un entorno interactivo de desarrollo integrado o mediante el uso de una
amplia variedad de rutinas ya instaladas en complementos o Toolboxes (Houcque, 2005). Estos
últimos abarcan una serie de procesos y cálculos matemáticos en alguno de los campos de
especialidad ya mencionados.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
69
El nombre de la plataforma surge como una abreviación de “Matrix Laboratory”, lo cual refleja la
naturaleza de su lenguaje de programación de alto nivel (M). A diferencia de otros lenguajes que
trabajan con un número al tiempo, MATLAB opta por arreglos multidimensionales o matrices
completas independiente de la naturaleza de la información (MathWorks, 2019). Asimismo, este
cuenta con sus debidas estructuras de control, de datos y otras características del paradigma de
programación orientada a objetos. Según Gjendemsjo (2006), el lenguaje es del tipo intérprete,
por lo que no depende de la máquina (máquina virtual). Algunas de las ventajas que se atribuyen a
MATLAB son: la depuración eficiente, la posibilidad de llamar librerías externas, la facilidad de
implementar los algoritmos, la sencillez para desarrollar código y la capacidad de procesar
imágenes (University of Cincinnati, 2019).
En la Figura 13 se muestra la disposición predeterminada de la interfaz de MATLAB versión R2018a
de la licencia adquirida por la Universidad de los Andes. Se pueden señalar tres paneles
principales: Carpeta actual o “Current Folder”, Ventana de comandos o “Command Window” y
Área de trabajo o “Workspace” (MathWorks, 2019). El primero de ellos se emplea para acceder a
los archivos, bien sea rutinas, funciones, entre otros, el segundo para ingresar los comandos y el
tercero para explorar los datos creados (arreglos, matrices o variables, por ejemplo) e importados
(MathWorks, 2019). El panel superior contiene una serie de botones que permiten ejecutar
comandos específicos, como por ejemplo la limpieza de la ventana, la creación de variables o la
ejecución de algún complemento (Griffiths, 2018).
Figura 13. Interfaz MATLAB R2018a.
El desarrollo de los algoritmos implica el uso de algunas funciones preestablecidas en MATLAB
para los procesos de lectura de datos, trazado de gráficas e interpolación:
• Función xlsread: Lee un archivo de hoja de cálculo de Microsoft Excel y permite su
almacenamiento en una matriz (Mathworks, 2020).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
70
• Función scatter3: Dibuja un diagrama de dispersión tridimensional a partir de las
coordenadas X, Y y Z que se ingresan como parámetros (Mathworlks, 2020).
• Función line: Traza una línea entre dos puntos en el espacio a partir de las coordenadas X,
Y y Z que se ingresan como parámetros (Mathworks, 2020).
• Función griddata: Interpola información a partir de nubes de puntos en dos o tres
dimensiones (Mathworks, 2020). El método recibe como parámetro el dominio sobre el
cuál interpolar, es decir, un teselado o enmallado donde se sitúan los puntos de análisis.
De manera preliminar, la función obtiene la envolvente convexa de la nube, es decir, aquel
polígono convexo de mínima área que encierra la totalidad de los puntos (Buitrago et. al.,
2015). Posteriormente, la función interpola la información según el método de preferencia
estipulado por el usuario. Mathworks (2020) ofrece cinco opciones: interpolación lineal,
del vecino más cercano, natural, cúbica y biharmónica.
• Función delaunay: Desarrolla una triangulación de Delaunay sobre la envolvente convexa
de una serie de puntos en el espacio (Mathworks, 2020). La subdivisión en triángulos se
realiza asegurando que la circunferencia circunscrita a cada uno de ellos no encierre
puntos diferentes a los vértices del triángulo en cuestión (Lee y Schachter, 1980). Las
ventajas del método radican en la posibilidad de desarrollar la triangulación de manera
independiente al orden de los puntos, reducir problemas de precisión al optar, en lo
posible, por triángulos equiángulos y por garantizar que todos los puntos se encuentran lo
más cerca posible a alguno de los vértices (Tchoukanski, s.f.).
• Función trisurf: Dibuja la superficie definida por una triangulación tridimensional,
conectando planos entre los vértices de los triángulos según la conectividad definida por el
método de Delaunay (Mathworks, 2020).
3.4.3 Programa ArcGIS
ArcGIS es un sistema de información geográfica (SIG) que integra herramientas computacionales
para crear y trabajar con datos geográficos (ESRI, 2002). El software ofrece modelos de alto nivel
que representan información espacial mediante capas shapefile, ráster, grid, imágenes, redes de
triángulos irregulares (TIN), entre otras estructuras (ESRI, 2002). Asimismo, integra un sistema
DBMS para el manejo de bases de datos geográficas o geodatabases (ESRI, 2002). Como resultado,
el software permite el desarrollo de tareas avanzadas en mapeo, geoprocesamiento, edición y
administración de datos y análisis geográfico (ESRI, 2002).
Para el presente proyecto se emplearon dos de las aplicaciones del programa: ArcMap y
ArcToolbox. La primera aplicación se enfoca en la cartografía. Mediante la interfaz y las vistas,
ArcMap permite implementar análisis basados en mapas o en la representación visual de la
información (ESRI, 2002). Por su parte, la aplicación ArcToolbox permite procesar los datos a partir
de las herramientas SIG especializadas según los requerimientos científicos o ingenieriles (ESRI,
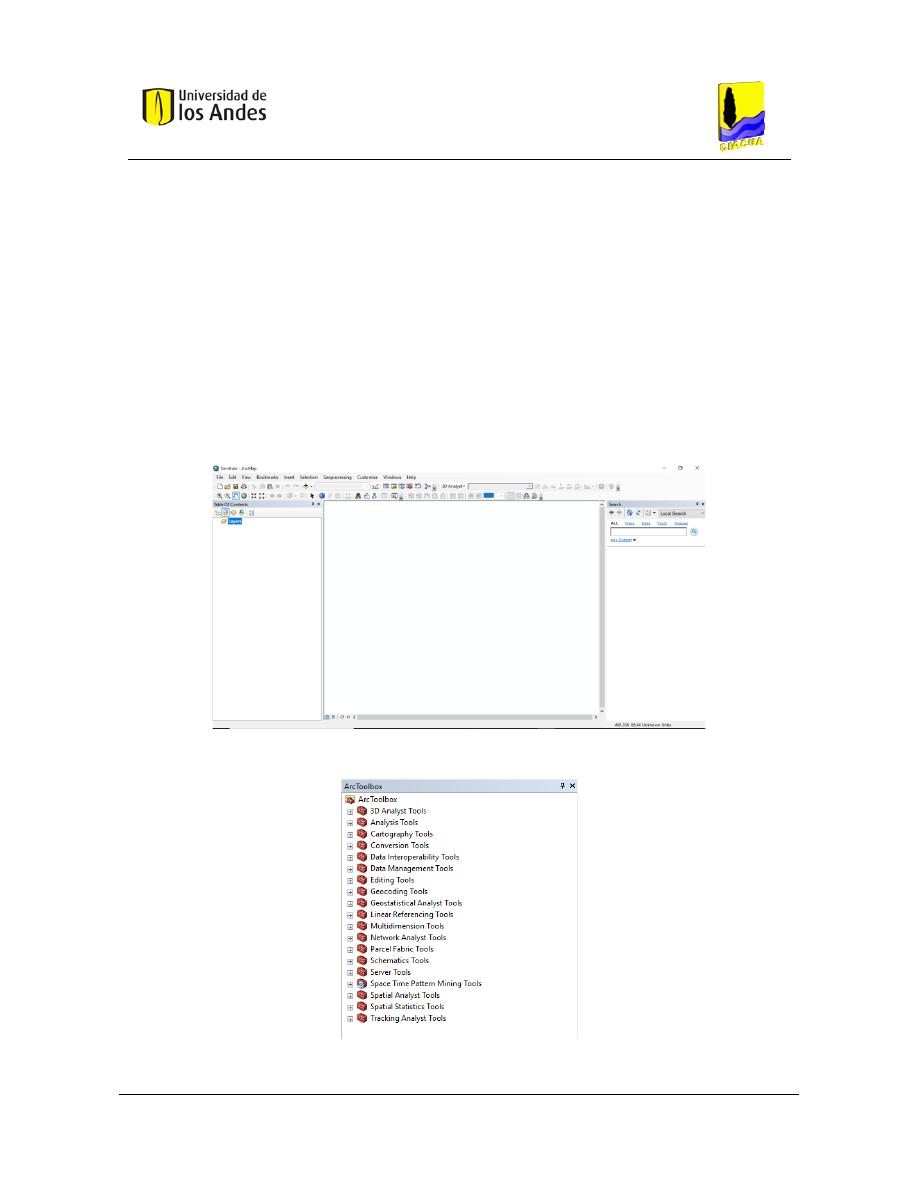
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
71
2002). Una de las posibles aplicaciones corresponde a los procesos de interpolación, para lo cual
se cuenta con rutinas de IDW, Kriging, vecino natural, splines, entre otras (ESRI, 2016).
El método de la distancia inversa ponderada (IDW) se basa en el cálculo de los puntos interpolados
a través de una combinación lineal ponderada de un conjunto de puntos de muestra (ESRI, 2016).
La aplicación de IDW supone que la variable a interpolar, dependiente de la ubicación, disminuye
su influencia a mayor distancia desde la ubicación de los puntos de muestra (ESRI, 2016). Como se
estipula en su nombre, el método IDW asume que la influencia de un punto conocido se encuentra
inversamente correlacionada con la distancia del punto donde se desea interpolar la información
(Azpurua y Dos Ramos, 2010). La ventaja del método se asocia a su simplicidad y eficiencia, en la
medida que se permite definir la potencia de la ecuación de cálculo, los radios de influencia de los
puntos de muestra y el uso de barreras (ESRI, 2016).
Figura 14. Interfaz ArcMap.
Figura 15. Herramientas de ArcToolbox.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
72
3.5 Geometría fractal
Los fractales pueden definirse, a grandes rasgos, como objetos geométricos de alta irregularidad,
escabrosidad y fragmentación (Mandelbrot, 1993). La utilidad de estas entidades radica en su
capacidad para recrear una amplia variedad de figuras amorfas encontradas de manera común en
la naturaleza, donde es imposible aplicar los principios de la geometría euclídea (Mandelbrot,
1983). En los siguientes apartados se examinarán algunos aspectos relevantes de la geometría
fractal, incluyendo las propiedades principales que permiten la caracterización de estos.
3.5.1 Autosimilitud
Cuando se establece que un objeto fractal es autosimilar, se afirma que cualquier parte del objeto
presenta similitud geométrica tanto con otras partes como con el objeto completo (Falconer,
1990). Por lo tanto, la característica de autosimilitud les confiere a los fractales las mismas (o
similares) propiedades geométricas independiente del cambio de escala (Falconer, 1990). De
manera formal, se puede establecer que un conjunto compacto 𝑋 es autosimilar si existe un
conjunto finito de semejanzas contractivas 𝐹
𝑁
= {𝐹
1
, 𝐹
2
, … , 𝐹
𝑛
}
tal que 𝑋 = ⋃
𝐹
𝑖
(𝑋)
𝑛
𝑖=1
y los
subconjuntos de 𝑋 de la forma 𝐹
𝑖
(𝑋)
se sobreponen únicamente en las fronteras (Cardona y
Múnera, 2016). El conjunto 𝐹
𝑁
usualmente se caracteriza como un sistema iterado de funciones
(Prusinkiewicz, 2004).
Esta autosimilitud puede ser exacta, aproximada o estadística, dependiendo de la naturaleza del
objeto fractal. Para el primer caso, se tienen semejanzas exactas independiente de si se analiza el
objeto a nivel infinitesimal (Mandelbrot, 1977). Esta afirmación solo puede cumplirse en la teoría,
en la medida que los objetos naturales no mantienen el comportamiento fractal si se desea seguir
reduciendo la escala de manera indefinida. No obstante, los fenómenos naturales pueden
aproximarse a un fractal considerando que, a nivel estadístico, su comportamiento es autosimilar
(Mandelbrot, 1977). En este caso, se afirma que la autosimilitud se manifiesta de manera
estadística.
3.5.2 Dimensión fractal – Hausdorff-Besicovitch
Las propiedades de autosimilitud de un fractal le confieren características que los hacen
intratables si se analizan desde la perspectiva tradicional de la longitud. Es así como surge el
concepto de dimensión fractal, cuyo objetivo es establecer una estrategia alterna a los
planteamientos tradicionales de la geometría euclídea. En particular, la dimensión fractal intenta
describir la forma como los objetos fractales llenan el espacio (Falconer, 1990). Una primera
definición corresponde al concepto de dimensión de Hausdorff-Besicovitch. Considérese cualquier
subconjunto no vacío 𝑈 de 𝑅
𝑛
. El diámetro de 𝑈 se define como la máxima distancia entre
cualquier par de puntos en 𝑈 (|𝑈| = sup{|𝑥 − 𝑦|: 𝑥, 𝑦 ∈ 𝑈}) (Falconer, 1990). Una familia
contable {𝑈
𝑖
}
es una 𝛿-cobertura de un subespacio 𝐹 de 𝑅
𝑛
si 𝐹 ⊂ ⋃
𝑈
𝑖
∞
𝑖=1
con diámetro 0 <

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
73
|𝑈
𝑖
| ≤ 𝛿 para todo 𝑖 ∈ 𝐼 (Fernández y Sánchez, 2015). Defínase para cualquier número 𝑠 no
negativo la medida s-dimensional de Hausdorff de F como:
𝐻
𝛿
𝑠
(𝐹) = inf{∑|𝑈
𝑖
|
𝑠
: {𝑈
𝑖
} 𝑒𝑠 𝑢𝑛𝑎 𝛿 − 𝑐𝑜𝑏𝑒𝑟𝑡𝑢𝑟𝑎 𝑑𝑒 𝐹}
∞
𝑖=1
𝐻
𝛿
𝑠
(𝐹) = lim
𝛿→0
𝐻
𝛿
𝑠
(𝐹)
De la anterior expresión, se conoce que a medida que 𝛿 decrece, la cantidad de coberturas
permisibles de 𝐹 se reduce, implicando que el valor de 𝐻
𝛿
𝑠
(𝐹) incremente (Edgar, 1990). En el
límite cuando 𝛿 → 0
+
, el valor de 𝐻
𝛿
𝑠
(𝐹) usualmente toma el valor de 0 o ∞, con la existencia de
un cambio brusco para un valor 𝑠
𝑜
(Fernández y Sánchez, 2015). Este valor se denomina la
dimensión de Hausdorff, cuya expresión formal se muestra a continuación:
𝑠
𝑜
= dim
𝐻
𝐹 = inf{𝑠: 𝐻
𝑠
(𝐹) = 0} = sup {𝑠: 𝐻
𝑠
(𝐹) = ∞}
Ecuación 40. Dimensión de Hausdorff-Besicovitch.
Dónde:
𝑠
𝑜
: Dimensión fractal de Hausdorff-Besicovitch.
𝐻
𝑠
(𝐹): Medida s-dimensional de F.
Para valores pequeños de s, las potencias de los diámetros tienden a 1 y, por ende, la sumatoria
diverge, mientras que, para valores grandes de s, los valores de la sumatoria convergen a cero. La
dimensión de Hausdorff es precisamente el punto donde la medida s-dimensional de Hausdorff
salta espontáneamente entre cero e infinito (Falconer, 1990). Los conceptos anteriores deben
entenderse como una manera para medir los objetos fractales. En otras palabras, las coberturas
pueden entenderse como conjuntos que “encierran” a los objetos fractales, permitiendo describir
su medida a partir de las características geométricas de la cobertura.
3.5.3 Dimensión fractal – Box Counting
Aunque la dimensión de Hausdorff se constituye como uno de los planteamientos teóricos más
importantes para caracterizar los fractales, su implementación a nivel computacional es
ineficiente. Es así como surgen otras definiciones alternativas de dimensión fractal que, en muchas
ocasiones, pueden utilizarse para resolver problemas en el computador. Una medida a escala 𝛿
puede representarse de manera aproximada a partir de una ley de potencia, donde el exponente
que acompaña a 𝛿 corresponde al negativo de la dimensión del fractal a analizar (Falconer, 1990).
𝑀
𝛿
(𝐹) ≈ 𝑐 ∗ 𝛿
−𝑠
Ecuación 41. Medición de fractales mediante una ley de potencias.
Dónde:
𝑠
: Dimensión fractal.
𝛿
: Escala.
𝑐:
Coeficiente.
𝑀
𝛿
(𝐹): Medición de F a escala
𝛿
.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
74
Si se toma el logaritmo a ambos lados de la ecuación y se despeja s, se haya un cociente que
determina la dimensión fractal del objeto. Ahora bien, para cualquier 𝛿, el análisis ignora las
irregularidades de tamaño inferior, por lo que una caracterización exacta del fractal se obtiene
cuando 𝛿 → 0 (Falconer, 1990).
𝑠 = lim
𝛿→0
log 𝑀
𝛿
(𝐹)
− log(𝛿)
Ecuación 42. Estimación de la dimensión fractal mediante ley de potencias.
Dónde:
𝑠
: Dimensión fractal.
𝛿
: Escala.
𝑀
𝛿
(𝐹): Medición de F a escala
𝛿
.
A partir de la Ecuación 42, y recobrando los conceptos de cobertura de la dimensión de Hausdorff,
se puede establecer el concepto de dimensión caja o “box dimension”. Si se considera cualquier
subespacio F no vacío y acotado de 𝑅
𝑛
, la dimensión fractal se puede describir según el número
mínimo de conjuntos de diámetro de a lo sumo 𝛿 que pueden recubrir F, en particular cuando 𝛿 →
0
y el límite existe (Falconer, 1990). Los conjuntos pueden representarse bien sea como cubos de
lado 𝛿, bolas cerradas de radio 𝛿, cuadrículas de cubos de lado 𝛿, entre otras formas (Falconer,
1990). El método recibe su nombre debido a la preferencia de plantear la cobertura mediante
grillas de cubos. En efecto, 𝑀
𝛿
(𝐹) será igual al número de cajas necesarias (proceso de conteo o
“counting” para recubrir el fractal.
3.6 Análisis fractal
A partir de los preceptos matemáticos es posible establecer algunas metodologías que suponen
una caracterización de los fractales. Para el caso particular de las redes de distribución, se pueden
establecer tres algoritmos para determinar las características fractales de los fenómenos
hidráulicos asociados al diseño optimizado: el algoritmo box-covering, el análisis de rango
reescalado (R/S) y el análisis de la lagunaridad.
3.6.1 Algoritmo Box-Covering
El algoritmo Box-Covering aplica los principios de dimensión fractal según el conteo de cajas. El
método intenta determinar el número mínimo de cajas necesarias (𝑁
𝑏
), de un tamaño dado, para
cubrir una red compleja en su totalidad (Schneider et. al., 2018). Bajo este contexto, una caja se
define como un conjunto de nodos donde todas las distancias 𝑙
𝑖𝑗
entre dos nodos 𝑖 y 𝑗 no superan
un tamaño 𝑙
𝑏
predefinido (Song et. al., 2007). Un par de nodos no pueden pertenecer a una misma
caja si 𝑙
𝑖𝑗
> 𝑙
𝑏
; de manera contraria, dos nodos pueden pertenecer a una misma caja si 𝑙
𝑖𝑗
< 𝑙
𝑏
(Song et. al., 2007). La situación puede describirse mediante un problema de optimización
pertenece a la familia NP-complejo, lo cual sugiere la implementación de alguna heurística que
aporte soluciones aproximadas (Song et. al., 2007).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
75
Para el caso de las RDAPs, el cálculo del número de cajas puede realizarse según las características
hidráulicas y topológicas del sistema, condiciones que se representan mediante la asignación de
un peso para cada una de las uniones. El análisis de la topología del sistema se efectúa mediante la
implementación de un peso unitario para cada nodo (ver Ecuación 43) (Wei et. al., 2013). Por su
parte, si se desea considerar la hidráulica, los pesos pueden representarse según la sumatoria de
caudales que ingresan al nodo en cuestión o al producto de dicha sumatoria por la altura
piezométrica (ver Ecuación 44 y Ecuación 45) (Vargas et. al., 2019).
𝑤
𝑖
= 1
Ecuación 43. Peso según la topología del sistema.
𝑤
𝑖
= ∑ 𝑄
𝑖
Ecuación 44. Peso según el caudal.
𝑤
𝑖
= 𝐿𝐺𝐻
𝑖
∗ ∑ 𝑄
𝑖
Ecuación 45. Peso según el producto del caudal y la altura piezométrica.
Dónde:
𝑤[−]
: Peso.
𝑄
𝑖
[𝑚
3
/𝑠]
: Caudal nodo i.
𝐿𝐺𝐻
𝑖
[𝑚]
:
Altura piezométrica nodo i.
A partir de los planteamientos de Vargas et. al. (2019) y Song et. al. (2007), se puede establecer el
siguiente procedimiento para determinar la dimensión fractal:
1. Determinar 𝑙
𝑏𝑚𝑖𝑛
y 𝑙
𝑏𝑚𝑎𝑥
. Según Vargas et. al. (2019), se recomienda el uso de valores
impares.
2. Definir el tamaño 𝑙
𝑏
. Según Vargas et. al. (2019), se recomienda el uso de valores impares.
3. Definir el tamaño del paso, en términos del número de uniones, como (𝑙
𝑏
− 1)/2
. De esta
manera, la máxima distancia entre dos uniones cualquiera de una misma caja, siguiendo la
ruta más corta, resulta ser menor o igual a 𝑙
𝑏
− 1
(Vargas et. al., 2019).
4. Calcular el peso de cada unión según algún criterio hidráulico o topológico.
5. A partir del tamaño del paso, se suman los pesos de todos los nodos encerrados por una
hipotética caja generada para cada unión. Cabe resaltar que solo se consideran los nodos
que no han sido acaparados por alguna otra caja.
6. La unión con el mayor peso se escoge como el centro de la nueva caja, cubriendo además
los nodos al interior de sus fronteras.
7. El proceso se repite hasta que todos los nodos sean cubiertos.
8. Contar el número de cajas 𝑁
𝐵
necesarias para cubrir todos los nodos.
9. Repetir el proceso para todos los 𝑙
𝑏
entre 𝑙
𝑏𝑚𝑖𝑛
y 𝑙
𝑏𝑚𝑎𝑥
.
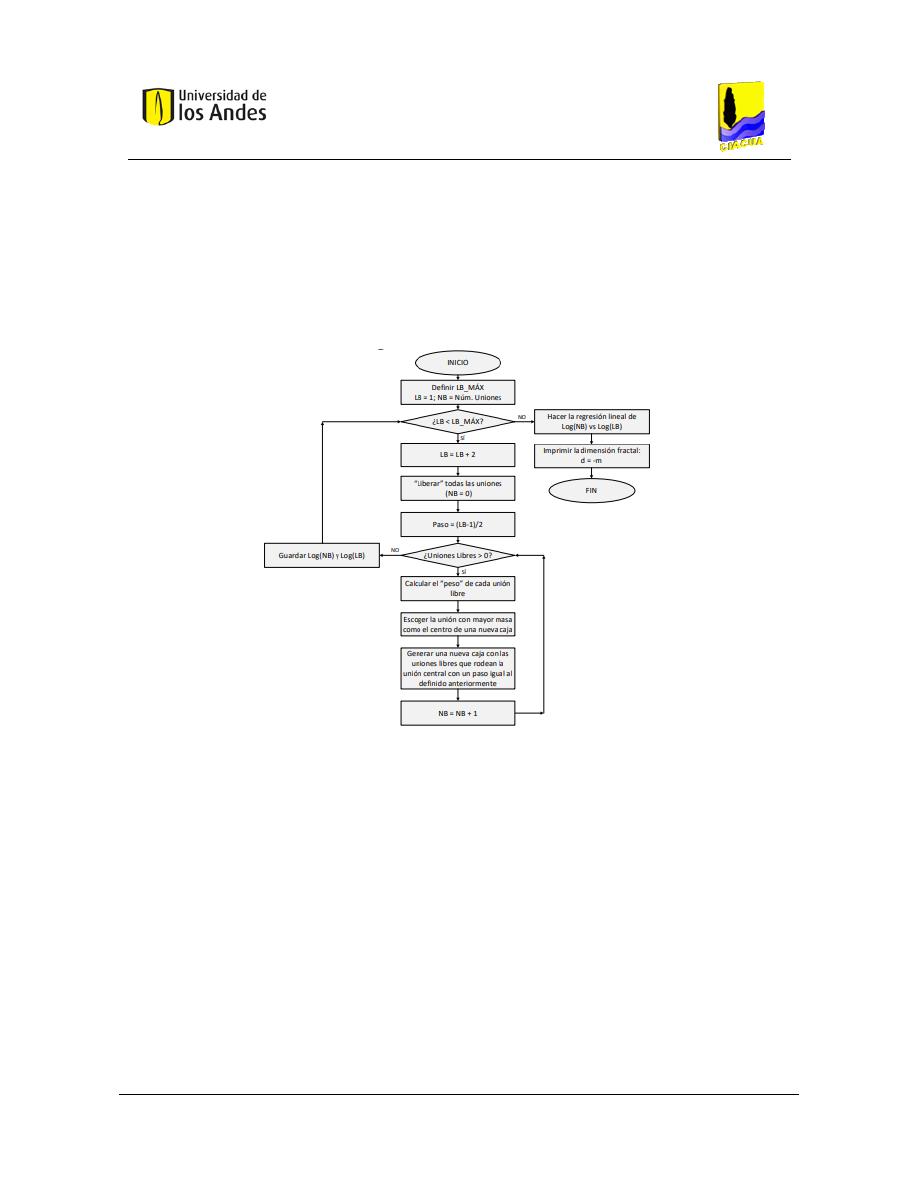
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
76
10. Obtener la regresión log(𝑁
𝐵
) 𝑣𝑠 log(𝑙
𝑏
)
. La pendiente de la recta de ajuste corresponderá
al negativo de la dimensión fractal. Si se encuentra un coeficiente de determinación
cercano a la unidad, puede afirmarse que la red presenta propiedades que se ajustan al
modelo potencial de medida de fractales.
La lista de pasos se puede resumir en el siguiente diagrama de flujo acorde al algoritmo
implementado en REDES 2019:
Figura 16. Diagrama de flujo - Análisis fractal de las redes. Recuperado de Vargas et. al. (2019).
3.6.2 Análisis de Rango Reescalado (R/S)
Otra manera de afrontar el problema de la fractalidad es a través de la perspectiva estadística. En
este contexto, es usual recurrir a una cantidad denominada el coeficiente o exponente de Hurst
(𝐻), cuyo objetivo es realizar una caracterización de cualquier serie de tiempo en términos de sus
propiedades fractales y memoria a largo plazo (Qian y Rasheed, 2004). En teoría, el exponente de
Hurst puede tomar cualquier valor entre 0 y 1; si 𝐻 > 0.5 se dice que la serie de tiempo presenta
un comportamiento persistente o de autocorrelación positiva, mientras que para valores
inferiores a 0.5 se presenta una naturaleza antipersistente (Gilmore et. al., 2002). Cuando 𝐻 es
igual a 0.5, se dice que la serie tiene un comportamiento errático (Qian y Rasheed, 2004).
La importancia del exponente de Hurst corresponde a su relación con la dimensión fractal. Según
Kleinow (2002), para procesos autosimiliares es común relacionar la dimensión fractal a partir de
𝐻
como se establece en la Ecuación 46. De esta manera, determinar 𝐻 supone una medida

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
77
indirecta del comportamiento fractal de algún fenómeno que se pueda representar mediante una
serie de tiempo.
𝐷 = 2 − 𝐻
Ecuación 46. Dimensión fractal a partir del exponente de Hurst.
Dónde:
𝐷[−]
: Dimensión fractal.
𝐻[−]
: Exponente de Hurst.
Una manera recurrente de calcular 𝐻 corresponde al Análisis de Rango Reescalado (R/S), que
funciona como una medida estadística de la variabilidad de una serie de tiempo dada (Quintero y
Ruíz, 2011). A partir de lo establecido por Qian y Rasheed (2004) se define una serie de pasos para
aplicar un análisis R/S sobre cualquier serie de tiempo 𝑋
1
, 𝑋
2
, … , 𝑋
𝑛
:
1. Determinar la media 𝑋̅.
𝑋̅ =
1
𝑛
∑ 𝑋
𝑖
𝑛
𝑖=1
Ecuación 47. Media de la serie de tiempo.
Dónde:
𝑛[−]
: Número total de datos.
𝑋
𝑖
[−]
: Valor de la serie en el tiempo i.
2. Calcular una serie ajustada por la media.
𝑌
𝑖
= 𝑋
𝑖
− 𝑋̅ 𝑖 ∈ [1,2, … , 𝑛]
Ecuación 48. Serie de tiempo ajustada por la media.
3. Obtener una serie acumulativa a partir de la serie ajustada por la media.
𝑍
𝑖
= ∑ 𝑌
𝑘
𝑖
𝑘=1
𝑖 ∈ [1,2, … , 𝑛]
Ecuación 49. Serie acumulativa.
4. Calcular la serie de rangos según la serie acumulativa.
𝑅
𝑖
= max(𝑍
1
, 𝑍
2
, … , 𝑍
𝑖
) − min(𝑍
1
, 𝑍
2
, … , 𝑍
𝑖
) 𝑖 ∈ [1,2, … , 𝑛]
Ecuación 50. Serie de rangos.
5. Determinar una serie de desviaciones estándar a partir de los valores originales de la serie.
En este caso, “u” corresponde a la media entre X
1
y X
i
.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
78
𝑆
𝑖
= √
1
𝑖
∗ ∑(𝑋
𝑘
− 𝑢)
2
𝑖
𝑘=1
𝑖 ∈ [1,2, … , 𝑛]
Ecuación 51. Desviación estándar de la serie de tiempo.
Dónde:
𝑖[−]
: Índice del número del dato.
𝑋
𝑘
[−]
: Valor de la serie en el tiempo k. 𝑢[−]: Media de los datos entre X1 y Xi.
6. Obtener la serie de rangos reescalados o normalizados por la desviación estándar.
(
𝑅
𝑆
)
𝑖
=
𝑅
𝑖
𝑆
𝑖
𝑖 ∈ [1,2, … , 𝑛]
Ecuación 52. Serie de rangos escalados.
A partir de la serie de rangos reescalados es posible determinar el exponente de Hurst si se retoma
el comportamiento potencial característico de los fractales. De manera similar a la perspectiva
Box-Counting de la dimensión fractal, existe una relación potencial entre cada valor R/S y el
tiempo 𝑖 en el que ocurre, presentando el valor 𝐻 como el exponente (Qian y Rasheed, 2004). Por
lo tanto, a partir de regresiones lineales sobre curvas log(𝑅/𝑆) 𝑣𝑠 log(𝑖) se puede determinar el
exponente de Hurst como la pendiente de la recta de ajuste y, por consiguiente, la dimensión
fractal a partir de la Ecuación 46 (Qian y Rasheed, 2004).
3.6.3 Análisis de la lagunaridad
Una tercera alternativa para efectuar el análisis fractal de la SOP corresponde a un estudio de la
lagunaridad asociada. El término de lagunaridad se vincula a una entidad matemática que permite
determinar las propiedades de aquellos fractales que cuentan con la misma dimensión a pesar de
presentar diferentes texturas (Yang et. al., 2012). La lagunaridad mide la desviación de un objeto
fractal de la invarianza traslacional; en otras palabras, corresponde a una medida de la
homogeneidad espacial de un cuerpo geométrico a partir de una caracterización de las “lagunas”,
“gaps” o “vacíos” en el dominio de estudio (Dong, 2000). Un objeto se puede catalogar como
homogéneo si presenta una baja lagunaridad, en la medida que la distribución de los tamaños de
los vacíos es uniforme (Dong, 2000). Por su parte, los objetos heterogéneos presentan diversos
tamaños de lagunas, reflejando valores elevados de lagunaridad (Dong, 2000). La lagunaridad
representa que tan similares son las regiones que conforman un objeto geométrico con respecto a
las demás. No obstante, es importante recalcar que, a diferencia de la dimensión fractal, la
medición de la lagunaridad depende de la escala a la que se analiza el objeto geométrico de
interés (Dong, 2000).
Actualmente existen diversas alternativas para estudiar la lagunaridad de objetos fractales. Una de
las opciones consiste en representar los objetos como imágenes, donde a cada píxel se le asocia

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
79
un peso o valor específico que lo represente. De esta manera, la imagen se puede discretizar como
una malla de puntos que pueden ser cubiertos por una caja cuadrada hipotética de lado R (Allain y
Cloitre, 1991). Dicha caja puede deslizarse a lo largo del dominio de análisis, cumpliendo la
restricción de no situarse fuera de las fronteras o los bordes de la imagen (algoritmo “Box-
Gliding”) (Allain y Coitre, 1991). El movimiento de la caja implica encerrar un conjunto diferente de
pixeles para cada iteración.
Sea 𝑁 el número total de cajas de tamaño R que pueden situarse al interior de la imagen;
asimismo, denótese 𝑛(𝑀, 𝑅) como el número de cajas de masa M y lado R pertenecientes a las N
cajas totales (Allan y Coitre, 1991). La función de probabilidad Q que describe la posibilidad de
encontrar una caja de tamaño R y masa M se describe como sigue (Allain y Coitre, 1991):
𝑄(𝑀, 𝑅) =
𝑛(𝑀, 𝑅)
𝑁
Ecuación 53. Función de probabilidad para cajas de lado R y masa M.
Dichas definiciones conllevan la necesidad de implementar un conteo de cajas (“box-counting”) al
interior del dominio de análisis. La función de probabilidad Q puede estudiarse a la luz de los
momentos estadísticos 𝑍
𝑄
𝑞
(𝑅)
como se expresa en la Ecuación 54 (Allain y Coitre, 1991). Por
definición, la lagunaridad se expresa como la desviación media cuadrática (“mean-square
deviation”) de las fluctuaciones de la función de distribución de probabilidad Q dividida por la
media al cuadrado (Yang et. al., 2012). Como resultado, se deberá involucrar el primer y segundo
momento estadístico como propone Allain y Coitre (1991). Cabe resaltar que el tamaño de caja
define la escala a la que se estudia la lagunaridad del cuerpo geométrico.
𝑍
𝑄
𝑞
(𝑅) = ∑ 𝑀
𝑞
𝑄(𝑀, 𝑅)
𝑀
Ecuación 54. q-ésimo momento estadístico de la función Q.
Λ(𝑅) =
𝑍
𝑄
2
(𝑅)
(𝑍
𝑄
1
(𝑅))
2
=
∑ 𝑀
2
𝑄(𝑀, 𝑅)
𝑀
(∑ 𝑀
1
𝑄(𝑀, 𝑅)
𝑀
)
2
Ecuación 55. Análisis de la lagunaridad a una escala R.
El cálculo de la masa varía según el autor. Según Sarkar y Chaudhuri (1992), una manera eficiente
de establecer el cálculo es a partir de un método de conteo diferencial de cajas (DBC). Si la imagen
de análisis se interpreta como un modelo digital de elevaciones (DEM), el valor intrínseco a cada
píxel se puede entender como la altura de una columna justo sobre el píxel (Dong, 2000). De esta
manera, dependiendo de la altura de la caja definida por el usuario, se requerirá una o más para
cubrir todas las columnas (Dong, 2000). La masa al interior de una caja cuadrada se estima

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
80
entonces como la altura relativa de columna, definida como la resta entre el número máximo de
cajas para cubrir la columna más alta y el número mínimo requerido para cubrir la columna de
menor altura más uno (Yang et. al., 2012).
𝑀 = 𝑣 − 𝑢 + 1
Ecuación 56. Masa de una caja de tamaño R.
Dónde:
𝑣[−]
: Número máximo de cajas para cubrir la columna más alta.
𝑢[−]
: Número mínimo de cajas requerido para cubrir la columna de menor altura.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
81
4 METODOLOGÍA
4.1 Definición de las redes
Inicialmente, se definirán los ejemplares a estudiar. Se opta por la selección de un conjunto de
redes patrón y reales con diversas condiciones topográficas, de disponibilidad energética,
distanciamiento entre nodos, conectividad, presencia de elementos especiales, pérdidas menores
y distribución de las demandas de caudal, a modo que el análisis fractal considere diferentes
aspectos topológicos e hidráulicos que influyen en el diseño. Las redes patrón corresponden a
planteamientos teóricos que han sido estudiados en múltiples ocasiones y de los que se cuenta
con amplia información bibliográfica de referencia. Por su parte, las redes reales corresponden a
sistemas de distribución existentes en municipios colombianos.
En la Tabla 1 se presentan las redes patrón escogidas, precisando el número de tuberías, nodos,
embalses, presión mínima de diseño, rugosidad absoluta y fuente bibliográfica de consulta. Por su
parte, las redes reales se resumen en la Tabla 2. La implementación computacional de estos
sistemas se obtiene de trabajos previos desarrollados por el CIACUA, incluyendo los trabajos de
Araque y Saldarriaga (2005) y Posada y Saldarriaga (2018). La topología de los sistemas se describe
mediante el trazado bidimensional en REDES 2019; las figuras se muestran en Anexos.
Tabla 1. Redes patrón.
Nombre
Número de tuberías Número de nodos Número de embalses Pmin (m.c.a) ks (mm)
Referencias
Two Loops
8
7
1
30.00
0.0015
Alperovits y Shamir (1977)
Beygi et. al. (2014)
Ezzeldin et. al. (2014)
Two Reservoirs
17
10
2
36.00
0.0015
Gessler (1985)
Taichung
31
20
1
15.00
0.0015
Sung et. al. (2007)
Saldarriaga et. al. (2015)
Hanoi
34
32
1
30.00
0.0015
Fujiwara y Khang (1990)
Kadu et. al. (2008)
Beygi et. al. (2014)
Blacksburg
35
30
1
30.00
0.0015
Sherali et. al. (2001)
New York Tunnels
42
19
1
77.72
0.0015
Schaake y Lai (1969)
BakRyan
58
35
1
15.00
0.0015
Lee y Lee (2001)
Fossolo
58
36
1
40.00
0.0015
Bragalli et. al. (2012)
R28
67
39
1
20.00
0.0015
Saldarriaga et. al. (2010)
Saldarriaga et. al. (2015)
Saldarriaga (2016)
Pescara
99
68
3
20.00
0.0015
Bragalli et. al. (2012)
Modena
317
268
4
20.00
0.0015
Bragalli et. al. (2012)
Balerma
454
443
4
20.00
0.0025
Reca y Martínez (2006)
Geem (2009)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
82
Tabla 2. Redes reales.
Algunos aspectos adicionales contemplados en la caracterización de las redes y el posterior cálculo
de los diseños se plantean a continuación:
• La totalidad de los diseños se desarrollan empleando la ecuación de fricción de Darcy-
Weisbach, independiente de si la red fue concebida bajo la ecuación de Hazen-Williams. La
disponibilidad de herramientas computacionales facilita la aplicación de ecuaciones
físicamente basadas en lugar de relaciones empíricas.
• En la mayoría de los casos se asumió una rugosidad absoluta de 0.0015 mm asociada al
PVC. Las excepciones corresponden a aquellas redes que fueron concebidas bajo un valor
de rugosidad absoluta diferente.
• Para el caso de las redes reales, los diseños se plantean a partir del catálogo de diámetros
comerciales de tuberías en PVC a septiembre de 2019 de PAVCO Wavin S.A. En particular,
se utilizaron las referencias de tuberías biaxiales con resistencia de 200 psi a 23°C.
• En Anexos se presentan las curvas de costos según la lista de diámetros disponibles y los
costos unitarios asociados. Los valores de los coeficientes de la curva se obtienen
mediante una regresión potencial (Saldarriaga, 2016). Para el caso de las redes reales, se
extrapolan tres diámetros mayores adicionales asumiendo que el comportamiento de los
costos se ajusta a la regresión potencial. Cabe resaltar que los esquemas planteados son
exclusivamente de carácter teórico.
• La presión mínima de diseño para las redes reales se toma según el estándar
recomendado por el RAS Título A (2000) para un nivel de complejidad alto, es decir, las
condiciones hidráulicas más exigentes. Por ende, se toma un valor de 15 m.c.a. como
presión mínima admisible. En aquellos casos donde las condiciones de diseño impidan
alcanzar soluciones factibles con la presión mínima establecida, se permitirá el cálculo
bajo una restricción de cabeza menos demandante.
• Por simplicidad, no se contemplan restricciones de presión máxima en los nodos como se
establece en algunas de las redes patrón.
Nombre
Número de tuberías Número de nodos Número de embalses Pmin (m.c.a) ks (mm)
San Vicente
71
62
1
10.00
0.0015
Cazucá
150
145
1
15.00
0.0015
Elevada
263
255
1
1.00
0.0015
Bolívar
333
285
1
15.00
0.0015
La Cumbre
378
338
1
15.00
0.0015
Candelaria
567
463
2
15.00
0.0015
Bugalagrande
655
582
1
15.00
0.0015
Carmen
754
716
1
15.00
0.0015
Chinú
1089
828
2
15.00
0.0015
Sector 35
1289
1190
2
15.00
0.0015
La Enea
1592
1413
1
15.00
0.0015

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
83
4.2 Cálculo de diseños óptimos
El cálculo de los diseños óptimos se realiza acorde a la metodología OPUS. Como se mencionó
anteriormente, se ha demostrado que los resultados que ofrece OPUS son excepcionales no solo
en términos de la minimización del costo sino también en la reducción del esfuerzo computacional
requerido para alcanzar la solución (López et. al., 2013). Si bien los resultados presentan un
distanciamiento con respecto a los récords mundiales para el caso de las redes patrón, la agilidad
del método lo convierte en la opción de mayor eficiencia para el desarrollo de la presente
investigación (López et. al., 2013). Se aclara que los diseños que se presentan como óptimos no se
suponen como la solución óptima global al problema, sino como la alternativa de menor costo a
comparación de los demás diseños estudiados.
Para el cálculo de los diseños óptimos se implementan los siguientes pasos:
1. Cargar el sistema en REDES.
2. Ingresar a la pestaña “Diseñar” y presionar el botón de “OPUS”.
3. Definir la ecuación hidráulica de Darcy-Weisbach. Asignar la ecuación de recálculo de la
flecha, la distribución óptima de caudales, diámetros discretos y el criterio de
ordenamiento según corresponda (ver Figura 19).
4. Asignar el conjunto de diámetros comerciales, los coeficientes de la ecuación de costos, la
rugosidad de las tuberías y la restricción de presión mínima (ver Figura 18).
5. Definir la flecha óptima y la potencia para el redondeo de los diámetros. Se sugiere una
potencia de 2.6 para obtener valores proporcionales al flujo (ver Figura 20) (Saldarriaga,
2016).
6. Correr la rutina.
7. Almacenar los resultados de costo, configuración de diámetros comerciales, caudales de
flujo en tuberías y altura piezométrica en los nodos en un archivo de Microsoft Excel.
Figura 17. OPUS en REDES 2019.
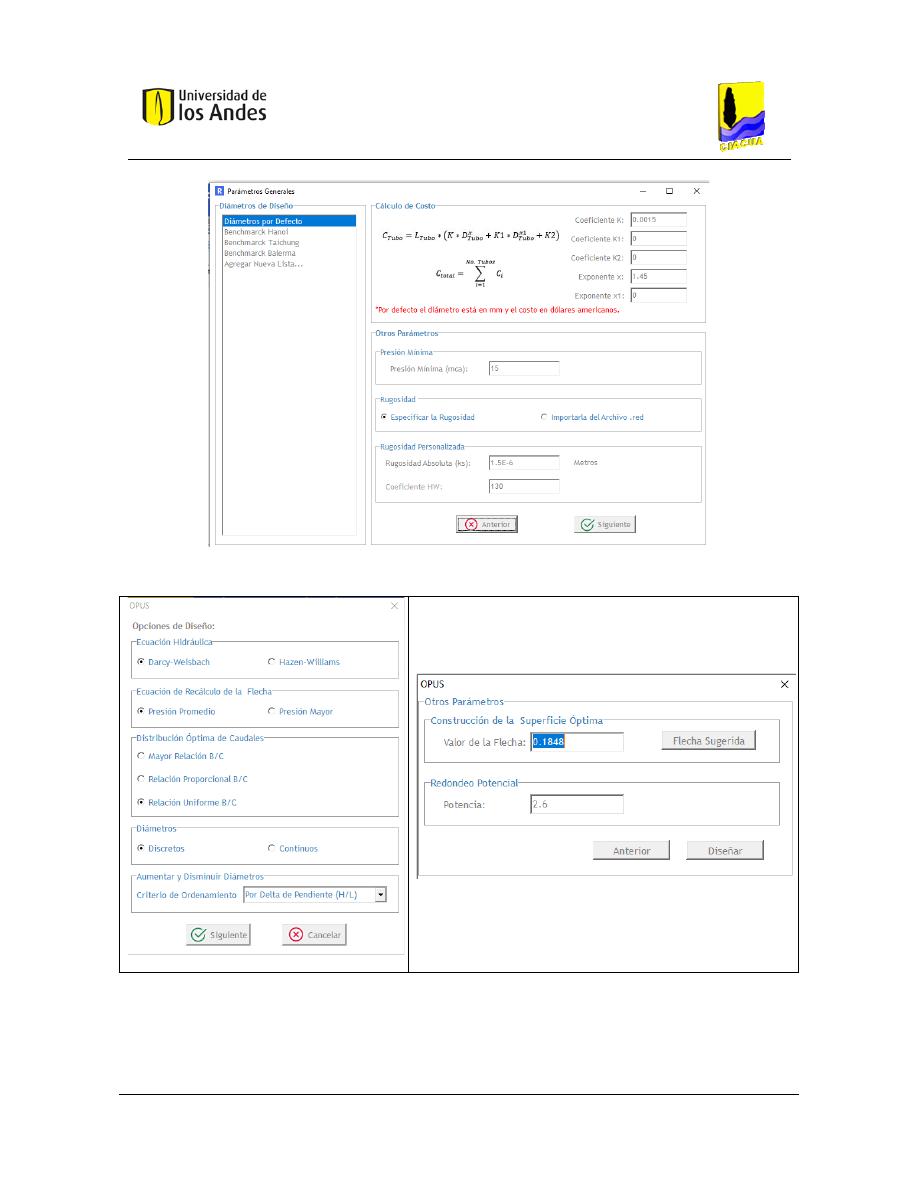
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
84
Figura 18. Asignación de diámetros comerciales, restricciones y coeficientes de función de costos.
Figura 19. Parámetros OPUS 1 - REDES 2019.
Figura 20. Parámetros OPUS 2 - REDES 2019.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
85
4.3 Cálculo de diseños no óptimos
El concepto de la superficie de alturas piezométricas puede extenderse a redes no óptimas. Para el
planteamiento de diseños no optimizados se pueden construir superficies similares con la presión
en cada nodo, bajo la salvedad de que no corresponderán a los valores de mínimo costo. Con el
objetivo de comparar las diferencias en el comportamiento fractal, se decide plantear alternativas
no óptimas mediante la ejecución de algoritmos genéticos, en la medida que corresponden a una
técnica usual para la generación de poblaciones aleatorias. En algunas ocasiones se aplicaron las
rutinas de SOGH y redondeo de diámetros mediante Programación por Restricciones con el fin de
buscar ejemplares con configuraciones variadas.
Para cada red se determinan seis diseños no óptimos a comparación de la alternativa calculada
con OPUS. Se contemplan las mismas restricciones de presión, rugosidad, catálogo de diámetros
comerciales y constantes de curvas de costos que se emplearon para el cálculo de las redes
óptimas. La generación de los diseños no óptimos se realizó acorde a la siguiente metodología:
1. Cargar el sistema en REDES.
2. Ingresar a la pestaña “Diseñar” y presionar el botón de “Algoritmos Genéticos”.
3. Definir la ecuación hidráulica de Darcy-Weisbach. La asignación de probabilidades, el
vector inicial y el método de recombinación se realiza según como se considere
conveniente (ver Figura 22).
4. Implementar la lista de diámetros comerciales y definir parámetros como la rugosidad, la
presión mínima y los coeficientes de la curva de costos (ver Figura 18).
5. Definir el tamaño de la población, el número de generaciones, la probabilidad de mutación
y la constante de reproducción como se considere conveniente (ver Figura 23).
6. Correr la rutina.
7. Almacenar los resultados de costo, configuración de diámetros comerciales, caudales de
flujo en tuberías y altura piezométrica en los nodos en un archivo de Microsoft Excel.
Figura 21. Algoritmos Genéticos en REDES 2019.
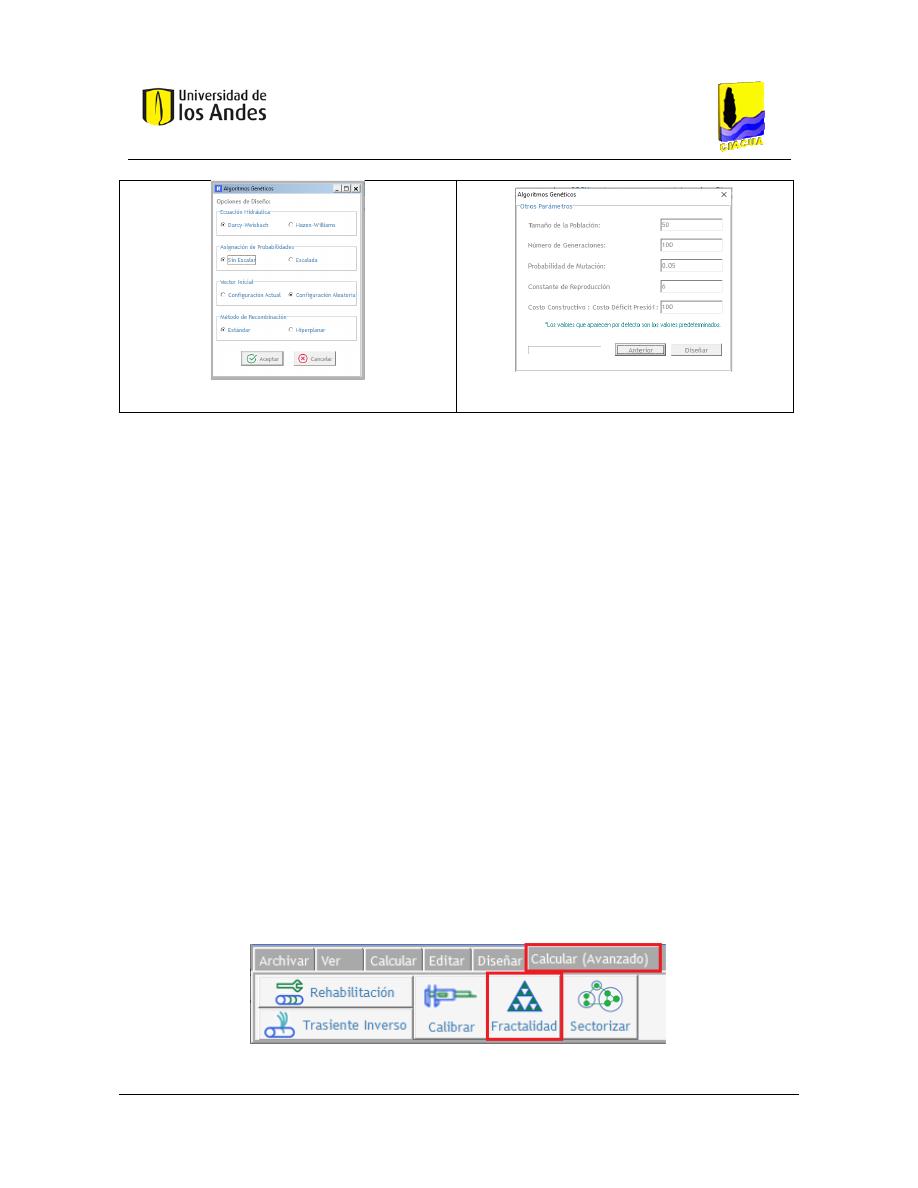
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
86
Figura 22. Parámetros Algoritmos Genéticos 1 – REDES
2019.
Figura 23. Parámetros Algoritmos Genéticos 2 - REDES
2019.
4.4 Análisis fractal de las redes
El análisis fractal de las redes se llevará a cabo acorde a lo estipulado en el algoritmo Box-Covering
propuesto por Vargas et. al. (2019). El proceso considerará únicamente el criterio de asignación de
pesos según la topología del sistema. No se contempla el criterio de caudales en la medida que las
demandas en los nodos no cambian entre los diseños; por su parte, el criterio de alturas
piezométricas no se incluye dado que su análisis se realizará a detalle a partir de los algoritmos de
análisis R/S y cálculo de la lagunaridad. De esta manera, el proceso de análisis fractal de la red se
enfocará en identificar la influencia de la distribución espacial de los nodos y la conectividad entre
ellos en las características fractales de la SOP en cuestión. El proceso de obtención de las
dimensiones fractales se resume como sigue:
1. Cargar el sistema en REDES.
2. Ingresar a la pestaña “Calcular (Avanzado)” y presionar el botón “Fractalidad” (ver Figura
24).
3. Definir el criterio de asignación de pesos según la topología (ver Figura 25).
4. Asignar un tamaño mínimo y máximo de caja. En todos los casos, el tamaño mínimo será
de un nodo, mientras que el máximo corresponde al número impar de nodos más cercano
al total (ver Figura 25).
5. Correr el algoritmo y leer la dimensión fractal en conjunto con el coeficiente de
determinación.
Figura 24. Opción para el cálculo de la dimensión fractal en REDES 2019.
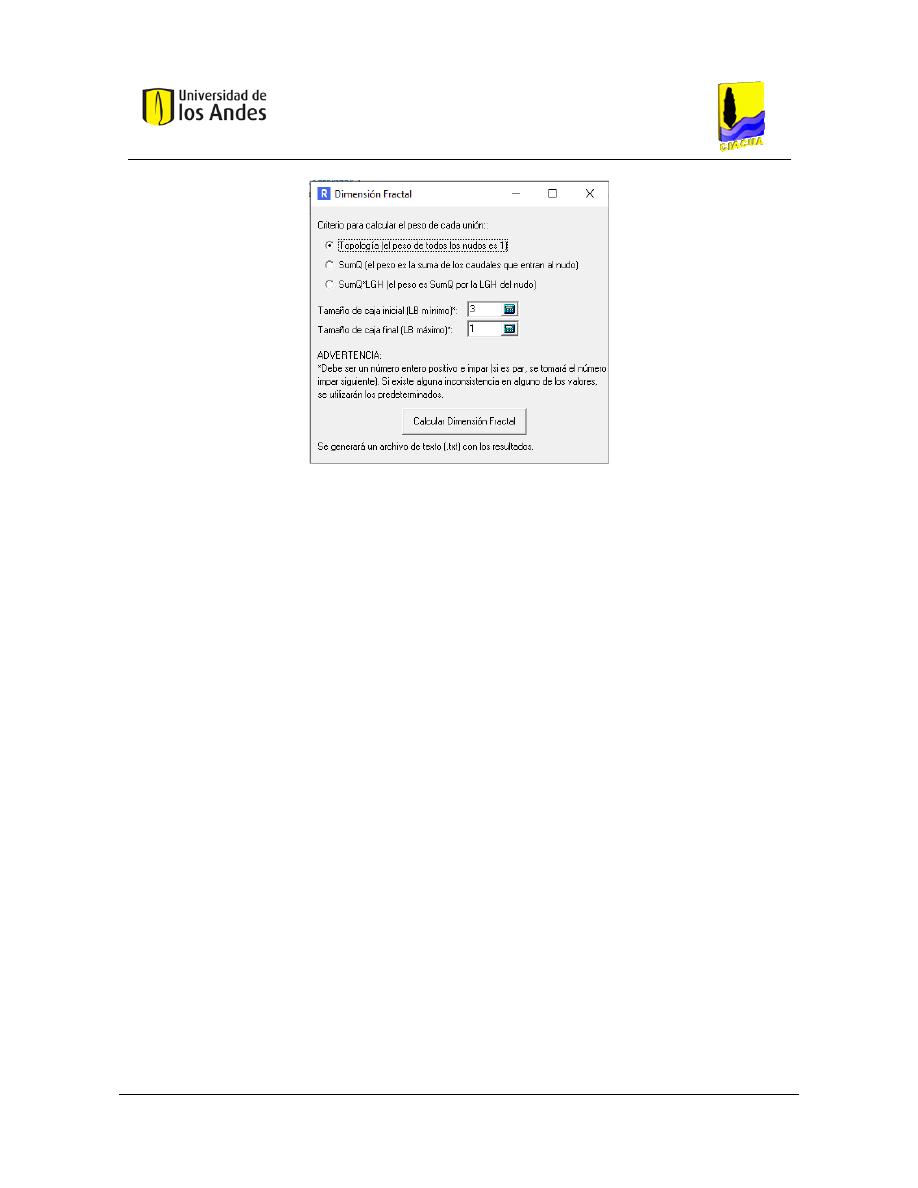
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
87
Figura 25. Ingreso de parámetros para la aplicación del algoritmo Box-Covering.
4.5 Trazado de la red
Las rutinas de análisis fractal en MATLAB contemplan el trazado de los componentes de la red con
el fin de visualizar y corroborar la correcta lectura de los datos contenidos en los archivos en
Microsoft Excel donde se almacenan los diseños. En Anexos se muestran recortes del código en
MATLAB propuesto. La lista de pasos se estipula a continuación:
1. Se realiza una lectura del número de nodos, embalses y tuberías. Los valores se almacenan
en variables. Se emplea la función integrada “xlsread” (Mathworks, 2020).
2. Se ejecuta una lectura de las propiedades de cada elemento de la red. Los valores se
almacenan en matrices. Se emplean las funciones integradas “xlsread”, “strcat” y
“num2str” (Mathworks, 2020).
3. Mediante el uso de ciclos definidos se declaran arreglos asociativos que almacenan las
propiedades de cada objeto. Cada nodo cuenta con una identificación, sus coordenadas,
demanda base y altura piezométrica. Los embalses con una identificación, coordenadas y
cabeza de energía disponible. Finalmente, a cada tubería se le asigna una identificación, su
nodo inicial, final, el diámetro de diseño, su longitud, el coeficiente de pérdidas menores y
el caudal de flujo.
4. Las coordenadas de nodos y embalses se almacenan en vectores.
5. Mediante la función integrada “scatter3” se dibujan los nodos y embalses en el lienzo
(Mathworks, 2020).
6. En un proceso iterativo se dibujan las tuberías empleando la función integrada “line”
(Mathworks, 2020). Mediante ciclos definidos y condicionales anidados se buscan las
coordenadas iniciales y finales de las tuberías acorde a los nodos.
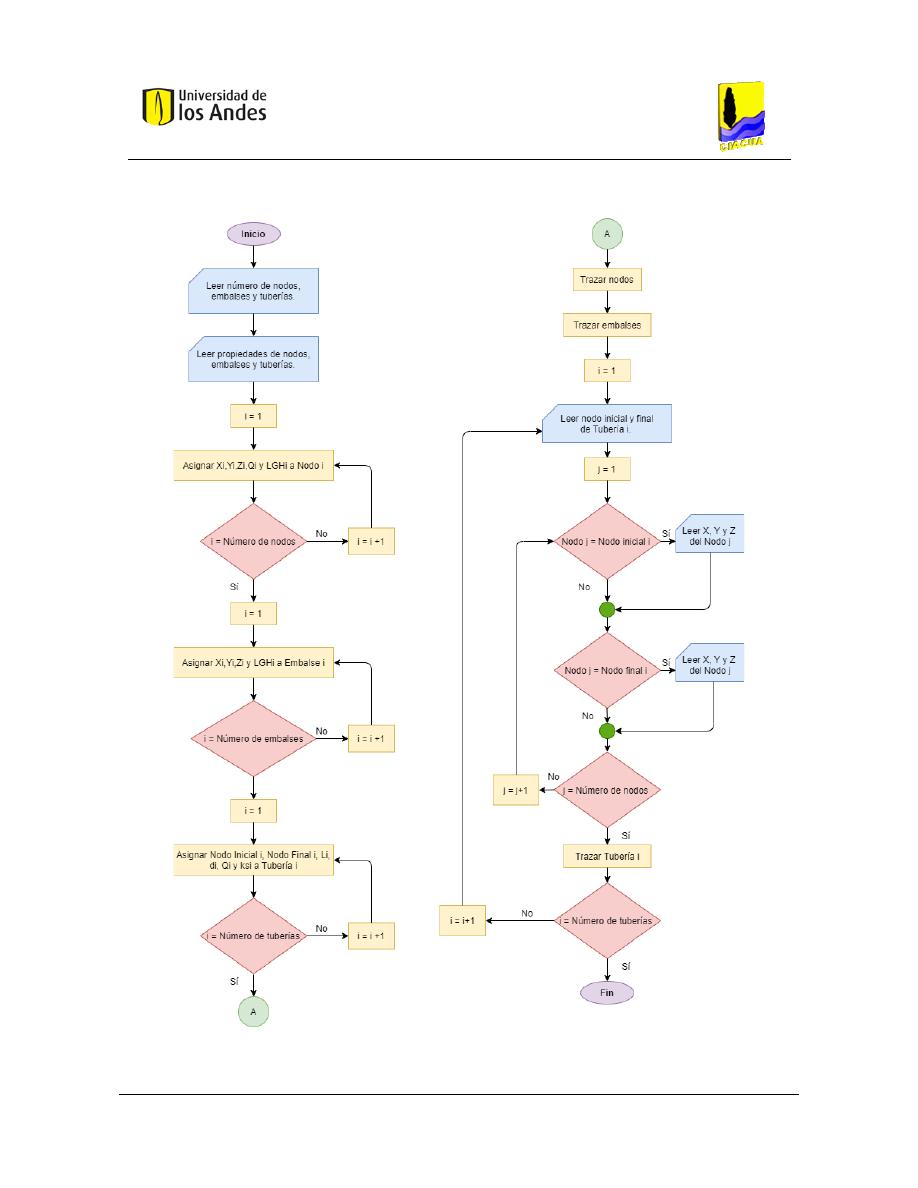
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
88
La lista de pasos se resume en el siguiente diagrama de flujo:
Figura 26. Diagrama de flujo - Trazado de la red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
89
4.6 Generación de las Superficies de Gradiente Hidráulico
El proceso de creación de las superficies conlleva la aplicación de los métodos de interpolación y
representación gráfica explicados en el marco teórico. El algoritmo planteado en MATLAB se
alimenta de la información declarada en el trazado de la red. En Anexos se presentan recortes del
algoritmo. La lista de pasos se enuncia a continuación:
1. Almacenar la información de alturas piezométricas en nodos y embalses en un vector
junto con sus coordenadas en X y Y.
2. Trazar los puntos de presión conocida sobre la red trazada. Se emplea la función integrada
“scatter3” (Mathworks, 2020).
3. Dibujar las LGHs entre nodos empleando el mismo algoritmo para el trazado de las
tuberías.
4. Aprovechando el decaimiento lineal de la altura piezométrica a lo largo de cada tubería,
generar nuevos puntos conocidos sobre las LGHs empleando la ecuación vectorial de la
recta (interpolación lineal) (Grossman y Flores, 2012). En particular, se determinan tres
nuevos puntos sobre cada tubería.
[𝑋, 𝑌, 𝐿𝐺𝐻] = [𝑋
𝑜
, 𝑌
𝑜
, 𝐿𝐺𝐻
𝑜
] + 𝛼 ∗ [𝑋
𝑓
− 𝑋
𝑜
, 𝑌
𝑓
− 𝑌
𝑜
, 𝐿𝐺𝐻
𝑓
− 𝐿𝐺𝐻
𝑜
]
Ecuación 57. Ecuación vectorial de la recta en el decaimiento de la LGH.
5. Determinar las coordenadas máximas X y Y del sistema. Si los valores presentan una
fracción decimal, redondear hacia arriba empleando la función integrada “ceil”
(Mathworks, 2020).
6. A partir de las coordenadas máximas y el espaciamiento que defina el usuario, definir el
enmallado rectangular sobre el cuál interpolar los valores de altura piezométrica.
7. Recorrer el enmallado en las dos direcciones para determinar el valor de altura
piezométrica. La rutina emplea la función “griddata” como mecanismo de interpolación,
optando bien sea por interpolación lineal o natural (Mathworks, 2020). Estas últimas
opciones se escogen esperando evitar alguna atenuación en las diferencias de las
propiedades fractales de los sistemas.
8. A partir de los resultados, utilizar la función integrada “scatter3” para graficar los puntos
sobre la red (Mathworks, 2020).
9. Mediante la aplicación de la triangulación de Delaunay, implementar las funciones
integradas “delaunay” y “trisurf” para dibujar la SGH a partir de planos triangulares entre
los valores de LGH interpolados (Mathworks, 2020).
En el siguiente diagrama de flujo se resumen los pasos:
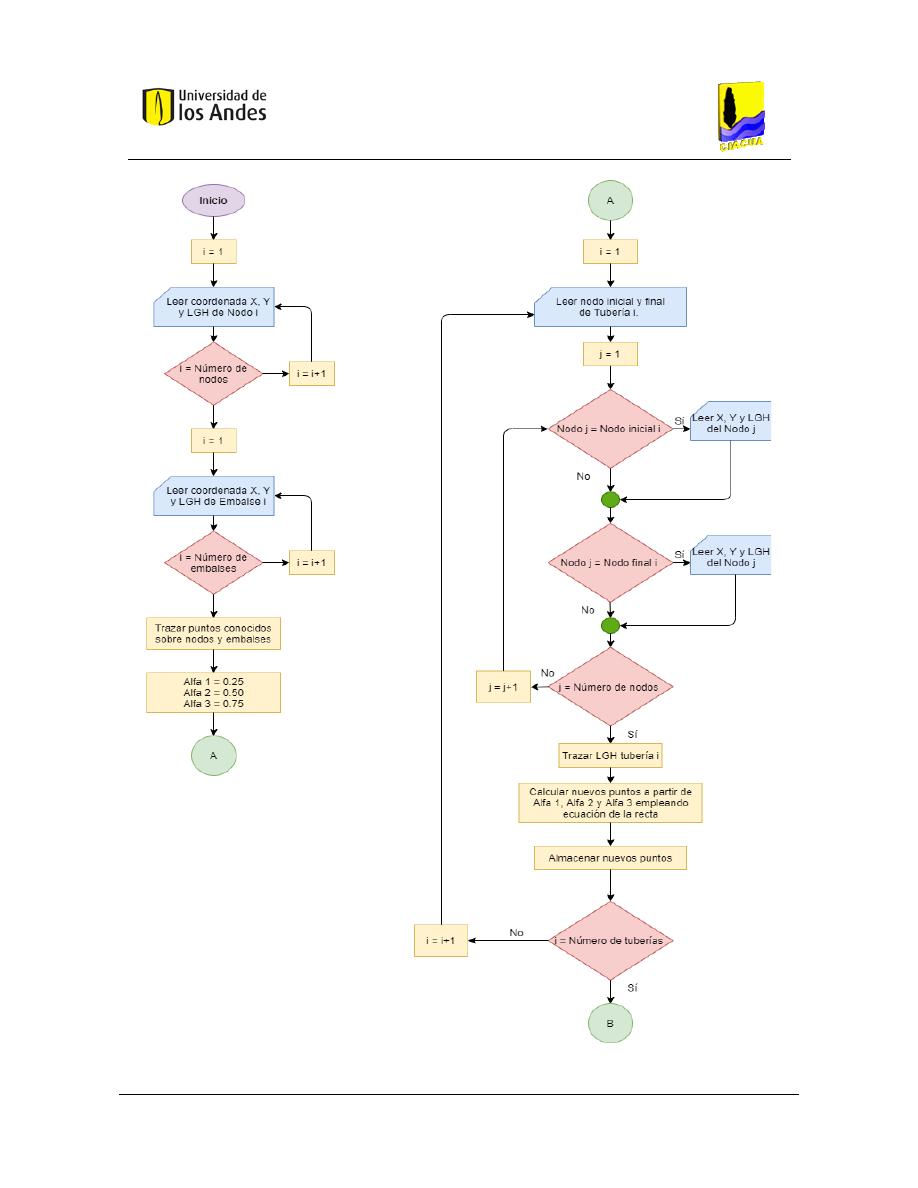
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
90
Figura 27. Diagrama de flujo - Generación de SGH - Parte 1.
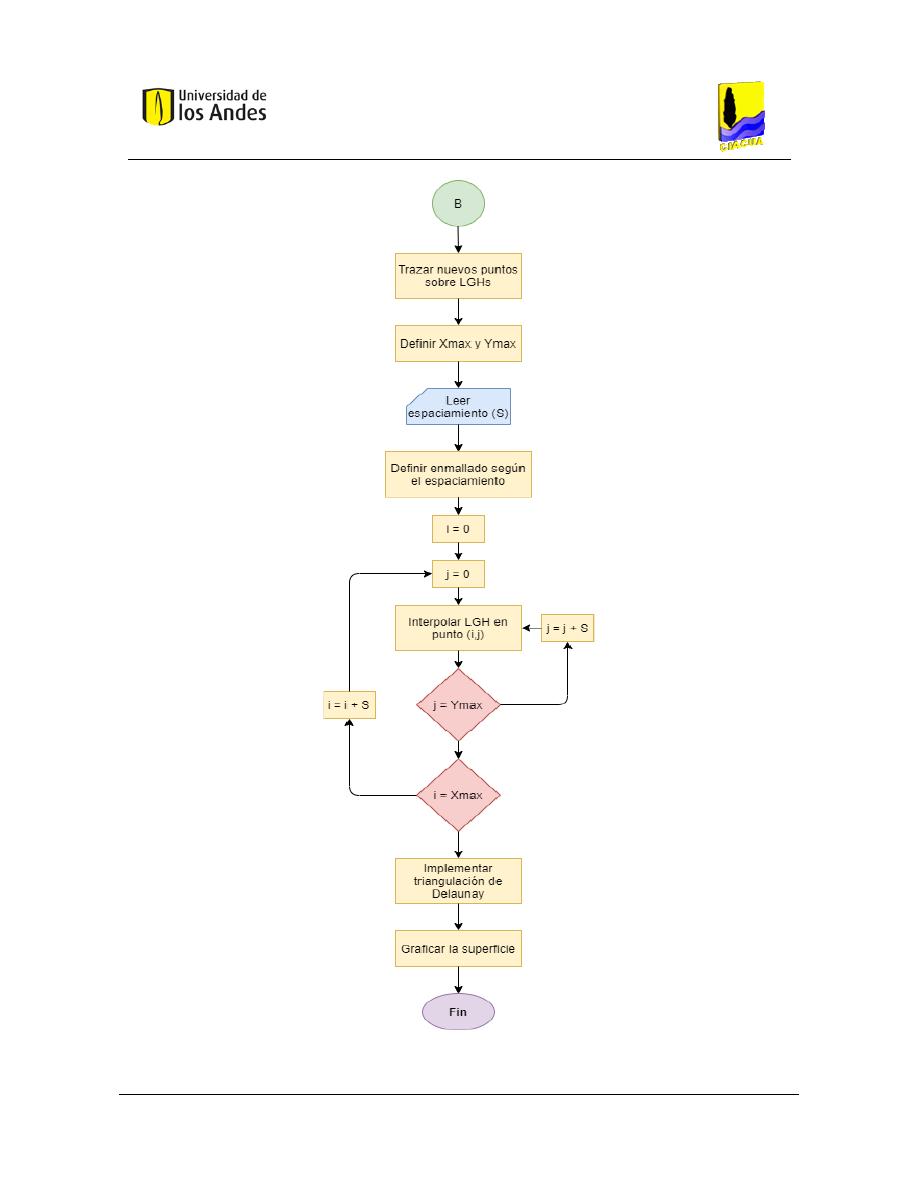
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
91
Figura 28. Diagrama de flujo - Generación SGH - Parte 2.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
92
4.7 Análisis fractal unidimensional de la superficie
Una de las posibles formas de efectuar un analizar fractal de la superficie es mediante la definición
de cortes a lo largo de alguna dirección predefinida. Los valores de altura piezométrica contenidos
en el corte se pueden interpretar como una serie de tiempo, donde en vez de incluir una variable
temporal se toma el valor de la distancia a lo largo del eje de corte. El proceso de cálculo de la
dimensión fractal a lo largo del corte corresponde al algoritmo de análisis de rango reescalado
(R/S) planteado en el marco teórico.
Mediante la creación de una función en MATLAB y su aplicación sobre la rutina principal descrita
en párrafos anteriores, se plantea un proceso iterativo para calcular la dimensión fractal sobre
diferentes cortes sobre la SGH. En Anexos se presenta el código. En los siguientes pasos se
describe el procedimiento:
1. Definir el espaciamiento de corte en cada dirección de análisis según los intervalos de
interpolación. Por simplicidad, se decide realizar cortes paralelos a los ejes X y Y.
2. Determinar las coordenadas iniciales y finales del corte de interés acorde a la distribución
espacial de los puntos interpolados.
3. Invocar la función de análisis de rango reescalado ingresando como parámetro la
información de los pasos 1 y 2.
4. Calcular la media de los valores de altura piezométrica contenidos en el corte como se
estipula en la Ecuación 46.
5. Ajustar los valores de altura piezométrica por la media como se establece en la Ecuación
48.
6. Acumular las alturas piezométricas ajustadas según la Ecuación 49.
7. Obtener la serie de rangos según los valores acumulados como se describe en la Ecuación
50.
8. Estimar la desviación estándar de la serie de alturas piezométricas originales como se
enuncia en la Ecuación 51.
9. Escalar cada elemento de la serie de rangos por la desviación estándar correspondiente
(ver Ecuación 52).
10. Determinar el logaritmo base 10 tanto de la serie de rangos reescalados como de los
valores de distancia a lo largo del corte.
11. Implementar una regresión lineal sobre la nube de puntos. La serie R/S debe encontrarse
en las ordenadas y la distancia sobre la abscisa.
12. Calcular la dimensión fractal y el exponente de Hurst a partir de la pendiente de la
regresión lineal.
13. Repetir el proceso para cada corte.
El diagrama de flujo asociado se presenta a continuación:
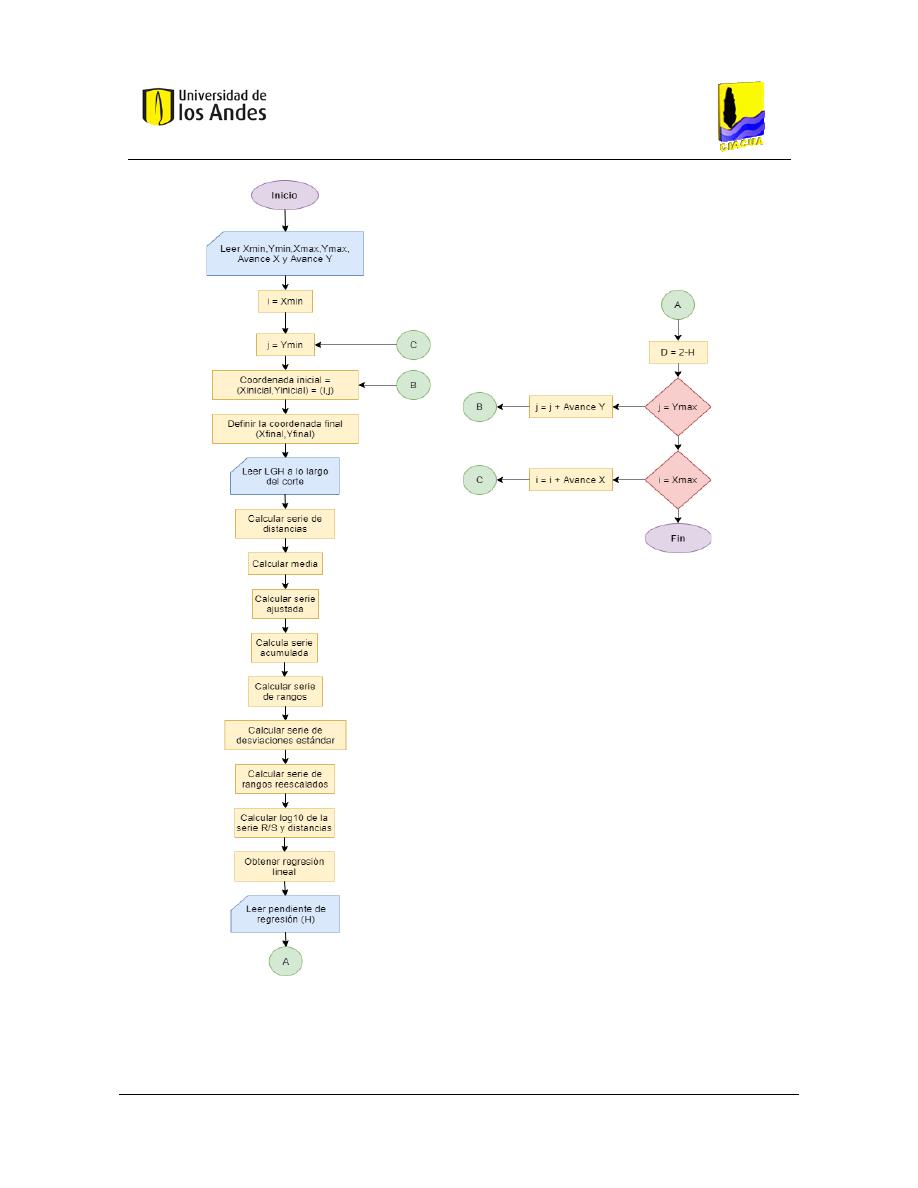
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
93
Figura 29. Diagrama de flujo - Análisis fractal unidimensional.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
94
4.8 Análisis fractal bidimensional de la superficie
La superficie de gradiente hidráulico puede interpretarse como un modelo digital de elevaciones
(DEM) donde el valor asociado a cada píxel corresponde a la altura piezométrica del punto de
interpolación y la resolución se establece según la malla de puntos. Adicionalmente, según el
método DBC, la LGH se interpretará como la altura de columna del píxel.
Los resultados generados pueden analizarse a la luz de la lagunaridad empleando la acción
conjunta de ArcGIS y MATLAB. Para el presente proyecto se implementa una rutina que permite
establecer la fractalidad estadística de las superficies, optando por obtener coberturas de los DEM
mediante conjuntos rectangulares de altura fija. En particular, se proponen dos alternativas de
análisis: cajas con alturas unitarias y cajas con alturas que mejoran la correlación del modelo
fractal mediante una búsqueda por tanteo. A diferencia de lo estipulado por Dong (2000), no se
establecen cajas cúbicas, por lo que el algoritmo no itera sobre las alturas de caja. En Anexos se
muestra el código en MATLAB. Los pasos se estipulan en la siguiente lista:
1. Generar la SGH a partir de la rutina explicada en apartados anteriores.
2. Exportar las coordenadas de los puntos conocidos e interpolados a una hoja de cálculo en
Microsoft Excel.
3. Importar la serie de puntos en ArcMap como una capa shapefile.
4. Utilizar la función de interpolación IDW de la caja de herramientas “Spatial Analyst” para
generar un archivo ráster con las alturas piezométricas de la capa shapefile. La resolución
del ráster, potencia y radio de búsqueda se definió acorde a los valores predeterminados.
La capa resultante se interpreta como el modelo digital de elevaciones de la SGH.
5. Exportar el archivo ráster a formato de imagen “.tif”.
6. Leer y almacenar la información de la imagen en una matriz en MATLAB.
7. Determinar el tamaño mínimo y máximo de caja según el tamaño de la imagen.
8. Obtener los valores de masa para el deslizamiento de una caja de cada uno de los posibles
tamaños R acorde al método DBC. Se emplea una variable estructural y un ciclo definido
para almacenar los resultados y desarrollar las iteraciones, respectivamente.
9. Calcular el número de posibles cajas N de tamaño R.
10. Determinar la probabilidad de cada dupla (M,R) usando la función Q.
11. Obtener el valor de lagunaridad para cada tamaño de caja R.
12. Estimar el logaritmo natural de la serie de lagunaridad versus radio de caja.
13. Aplicar una regresión lineal sobre la nube de puntos ln(Λ) 𝑣𝑠 ln(𝑅) y leer el valor de la
pendiente. Asumiendo a la lagunaridad como una manera para medir los fractales, se
aplica el modelo potencial para obtener una cantidad análoga a la dimensión fractal
(pendiente de la recta de ajuste a escala logarítmica). Este valor debe interpretarse como
una medida de la fractalidad propia del presente proyecto y no debe considerarse como
comparable a las nociones de dimensión fractal de otros trabajos de investigación.
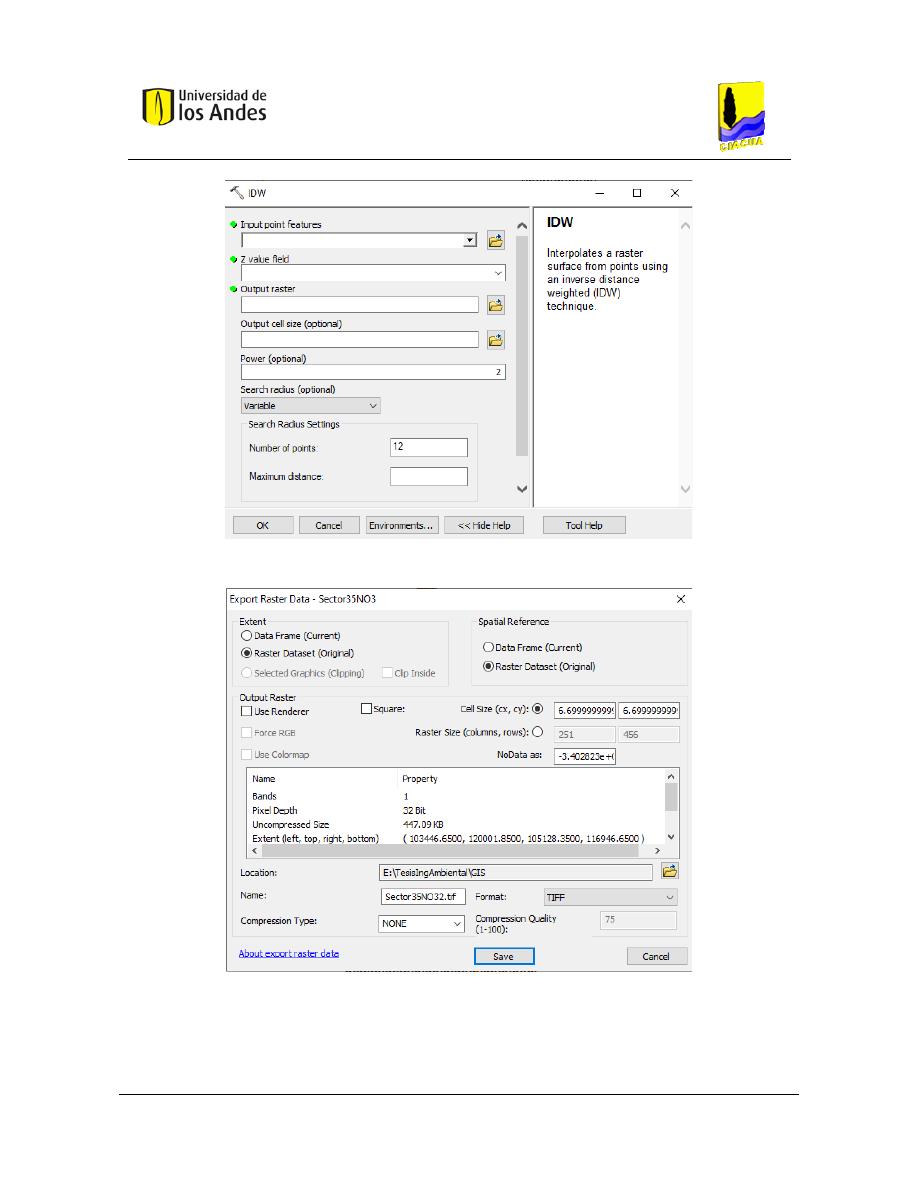
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
95
Figura 30. Herramienta IDW.
Figura 31. Generación de imágenes ".tif".
La lista de pasos se puede resumir en el siguiente diagrama de flujo:
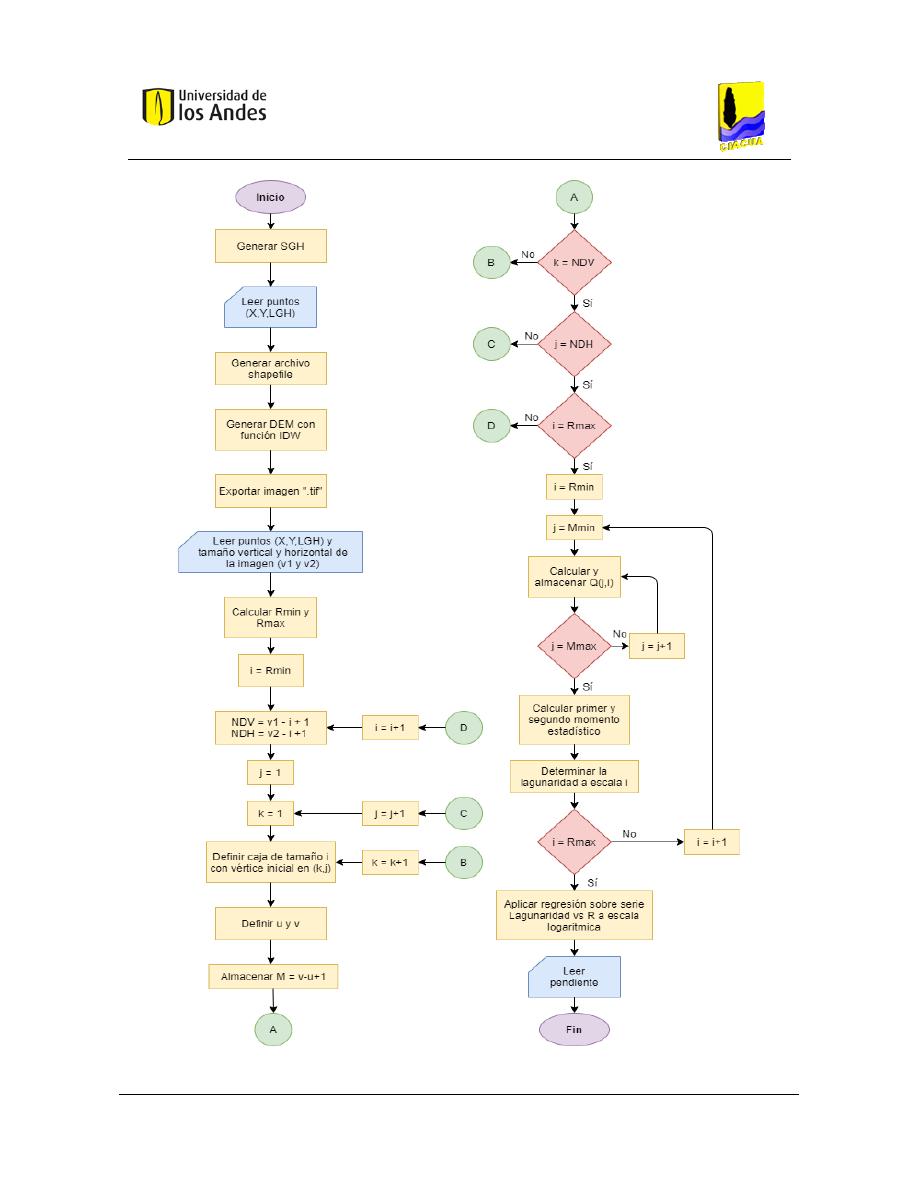
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
96
Figura 32. Diagrama de flujo - Análisis fractal bidimensional.
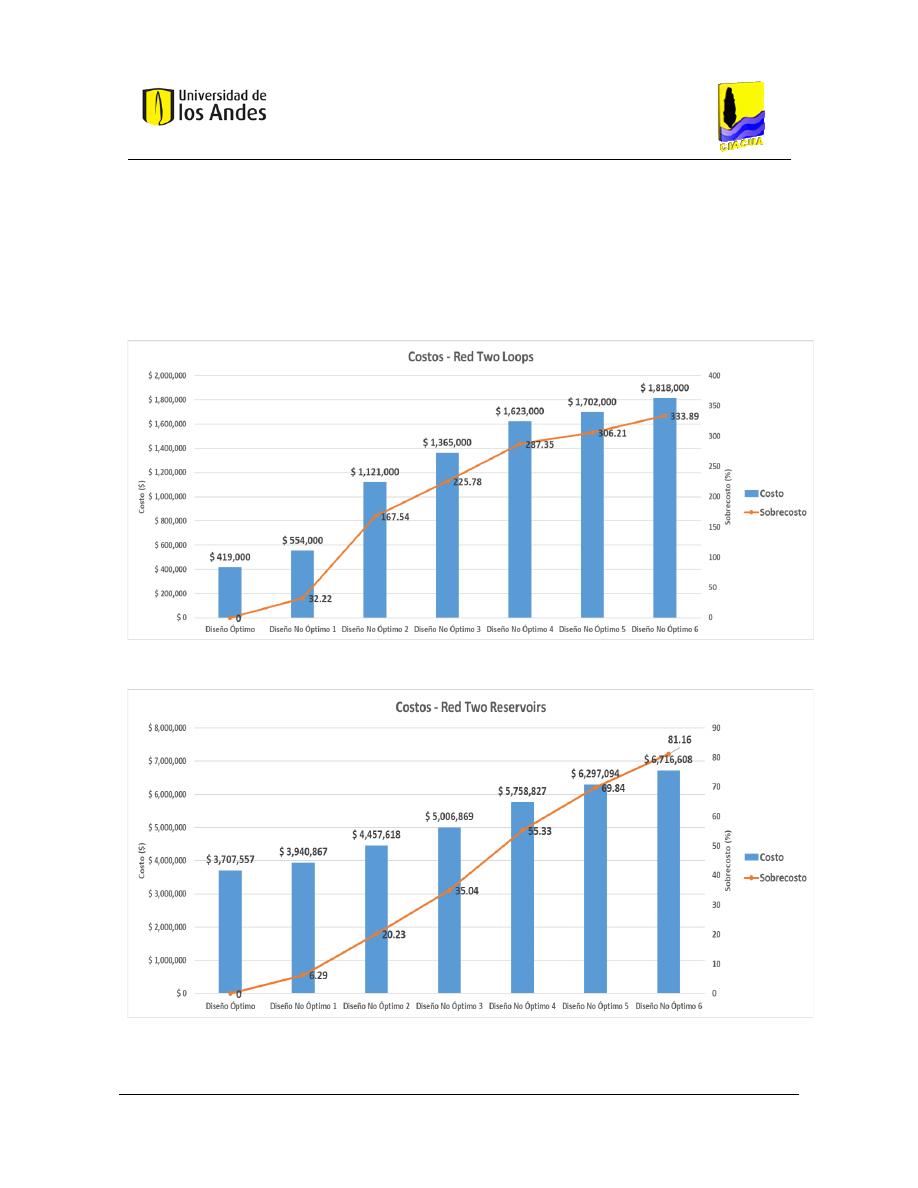
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
97
5 RESULTADOS
5.1 Diseños óptimos y no óptimos
5.1.1 Costos
Figura 33. Costos - Red Two Loops
Figura 34. Costos - Red Two Reservoirs.
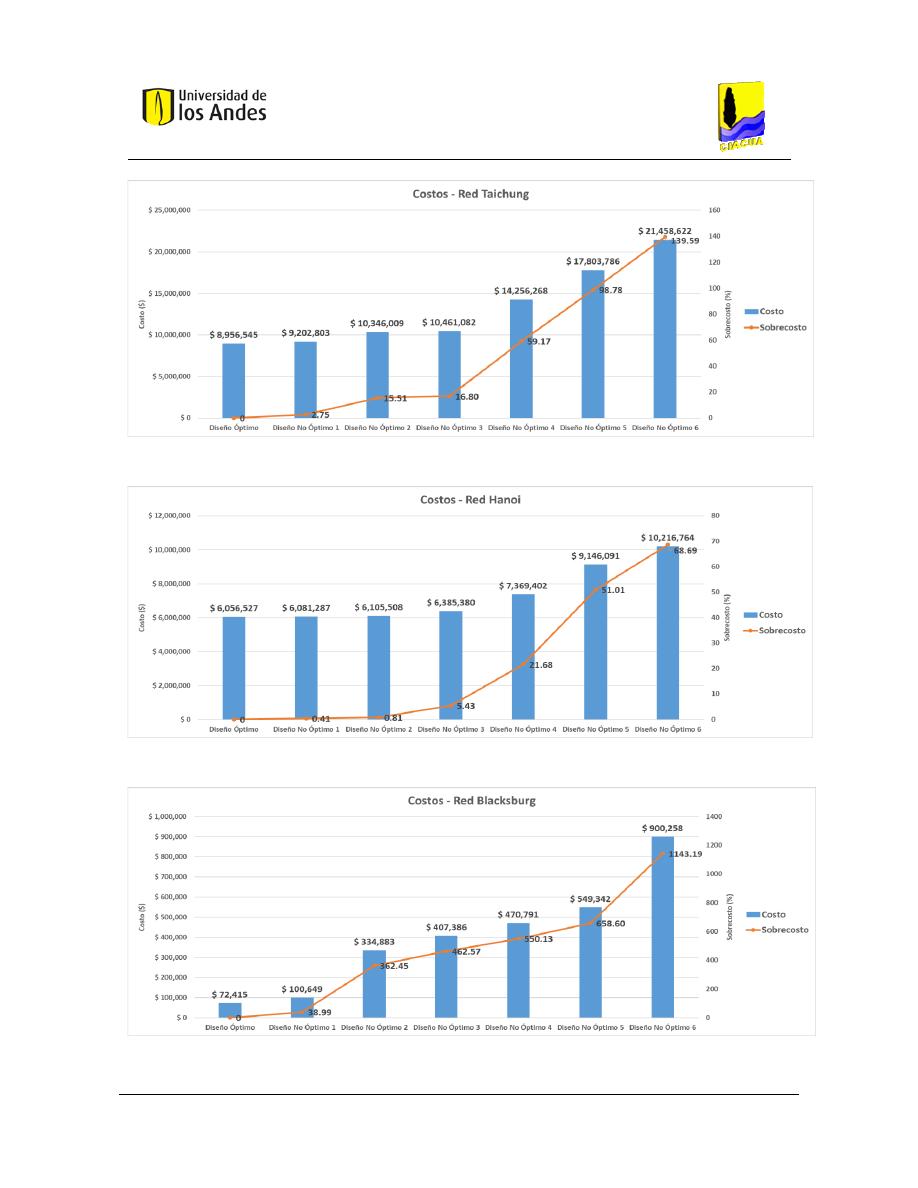
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
98
Figura 35. Costos - Red Taichung.
Figura 36. Costos - Red Hanoi.
Figura 37. Costos - Red Blacksburg.
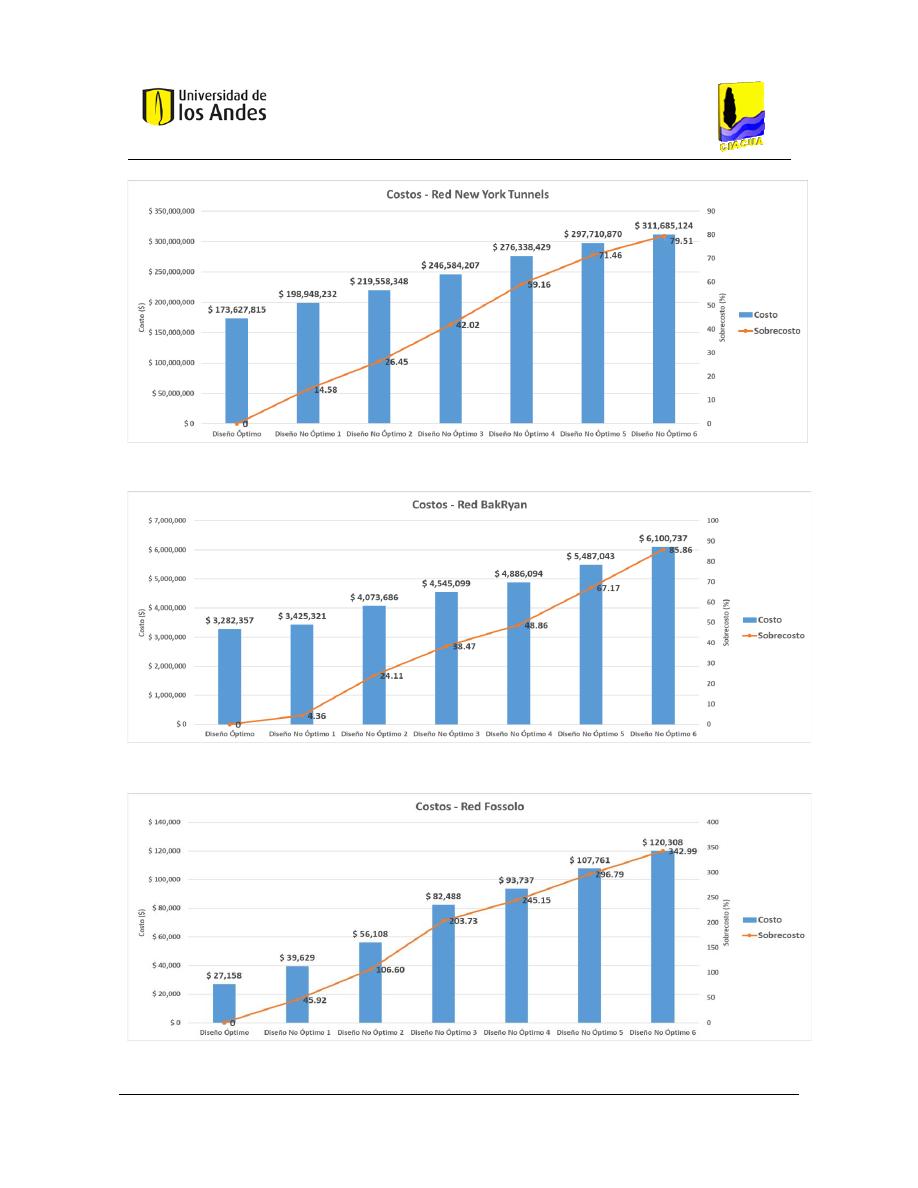
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
99
Figura 38. Costos - Red New York Tunnels.
Figura 39. Costos - Red BakRyan.
Figura 40. Costos - Red Fossolo.
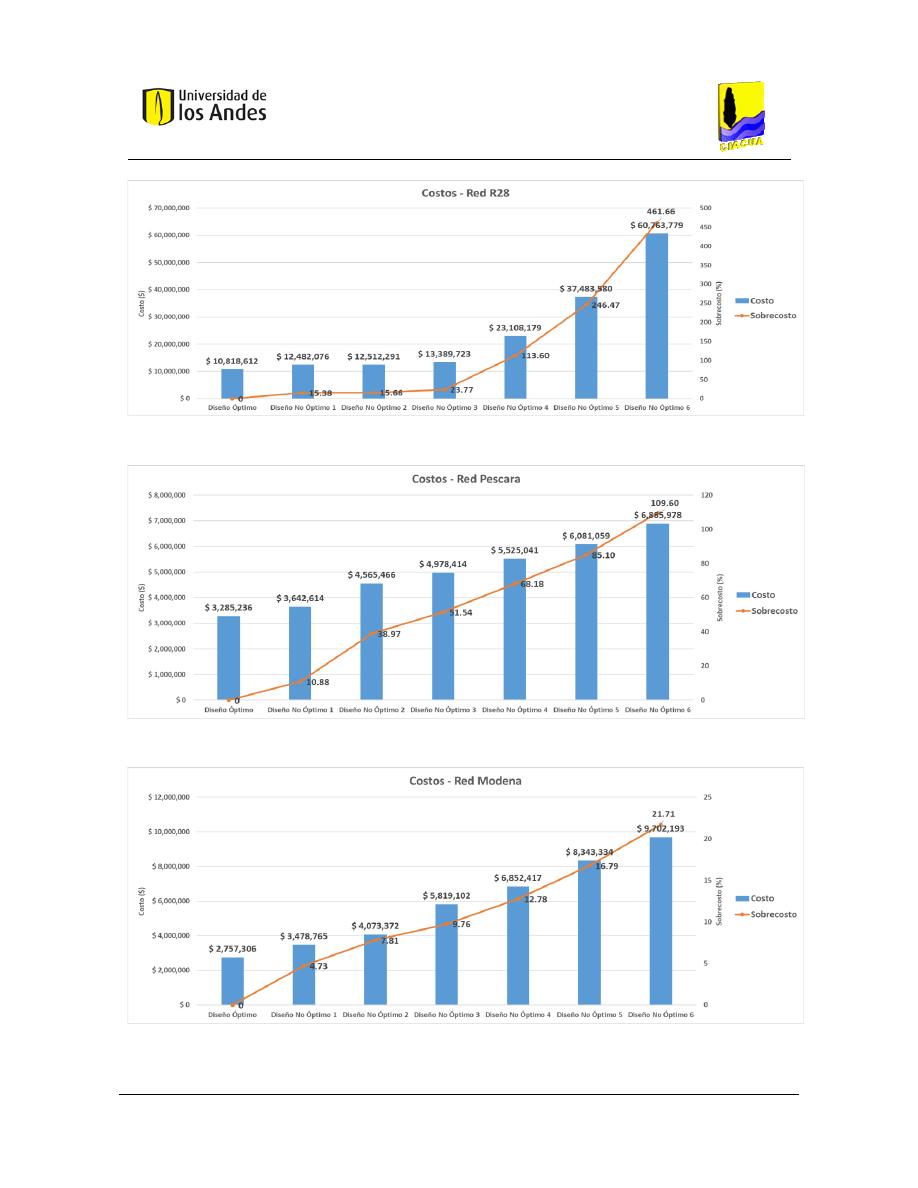
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
100
Figura 41. Costos - Red R28.
Figura 42. Costos - Red Pescara.
Figura 43. Costos - Red Modena.
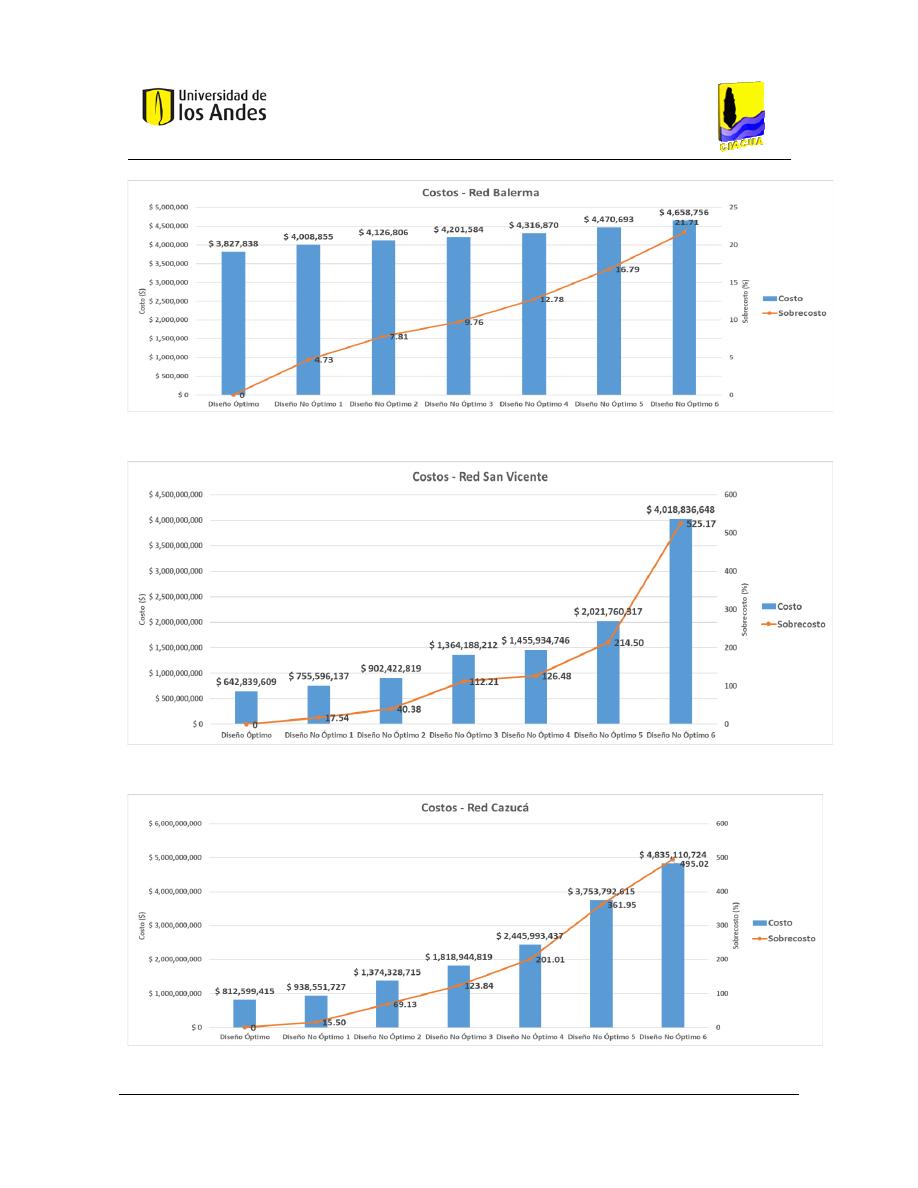
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
101
Figura 44. Costos - Red Balerma.
Figura 45. Costos - Red San Vicente.
Figura 46. Costos - Red Cazucá.
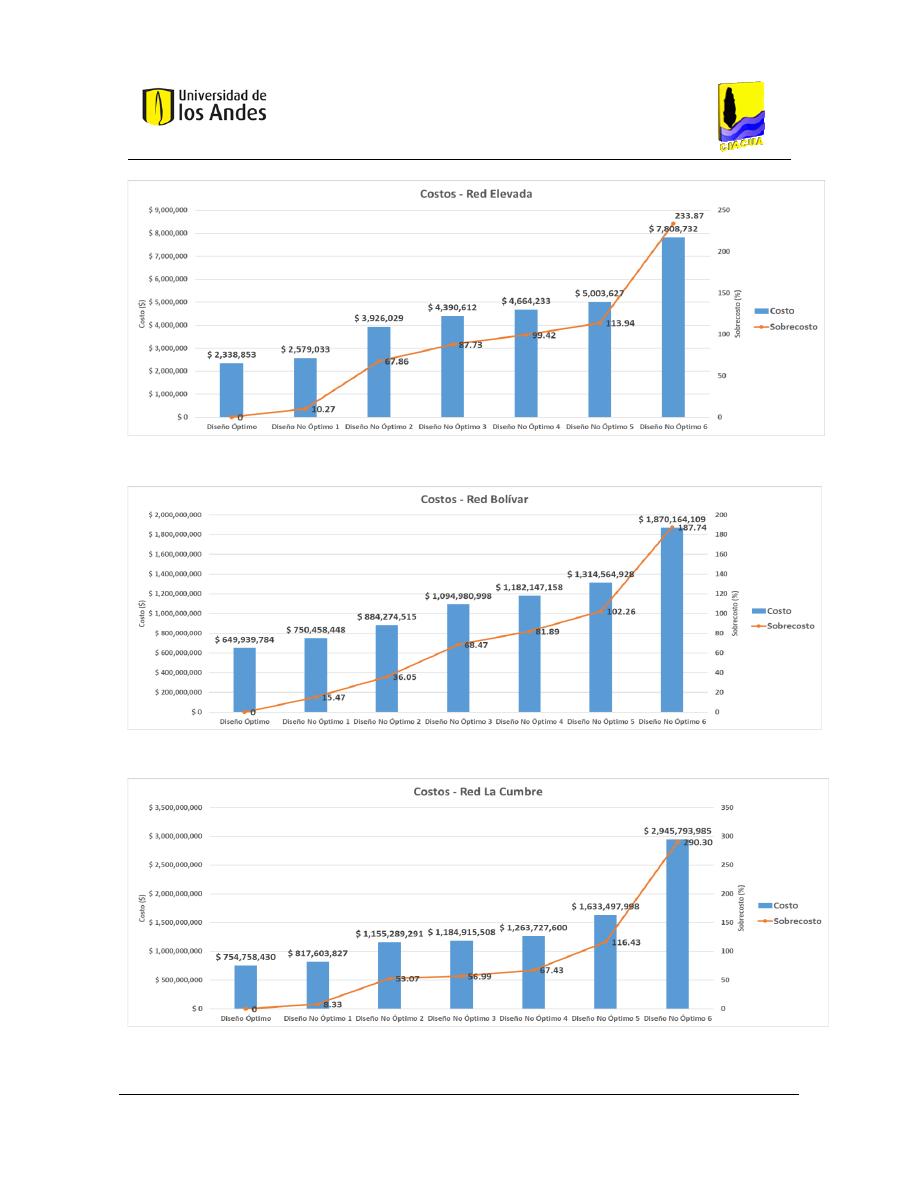
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
102
Figura 47. Costos - Red Elevada.
Figura 48. Costos - Red Bolívar.
Figura 49. Costos - Red La Cumbre.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
103
Figura 50. Costos - Red Candelaria.
Figura 51. Costos - Red Bugalagrande.
Figura 52. Costos - Red Carmen.
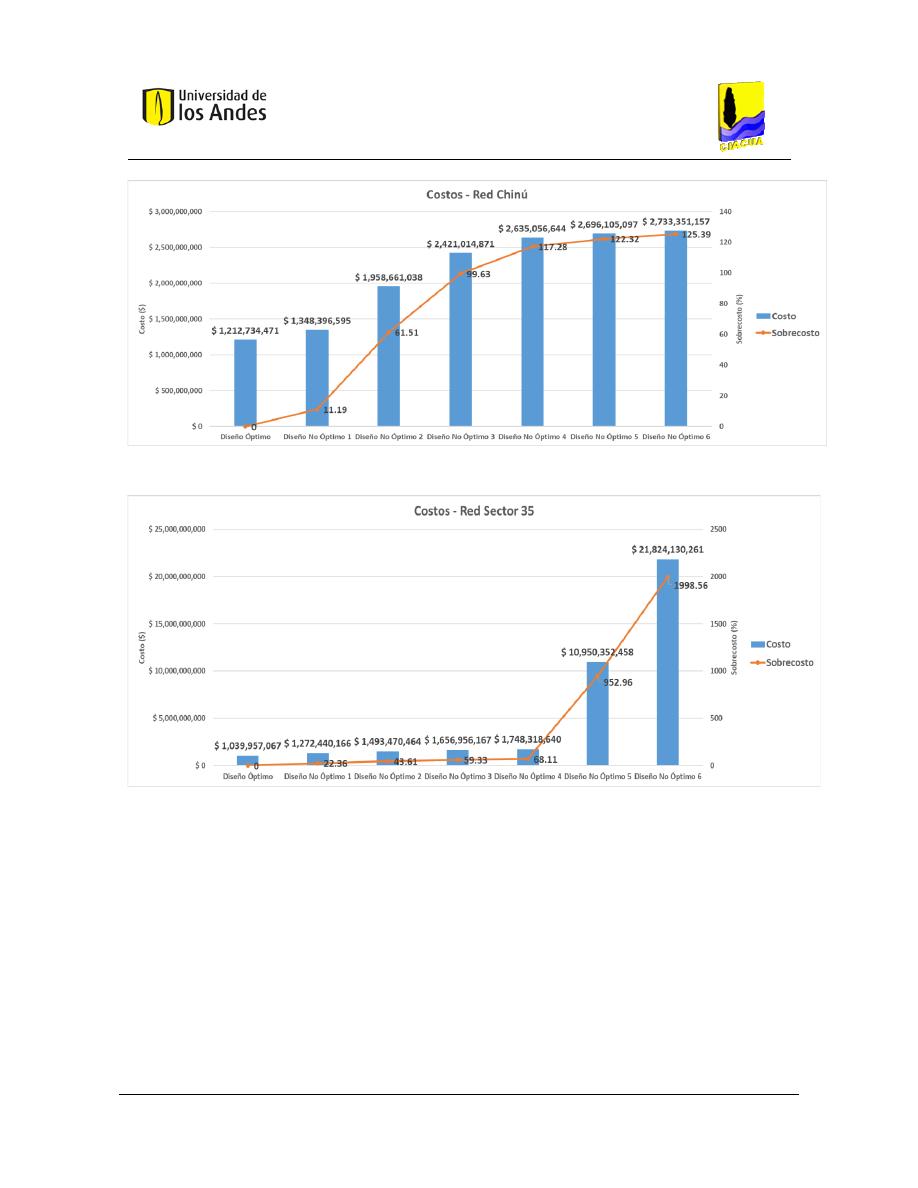
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
104
Figura 53. Costos - Red Chinú.
Figura 54. Costos - Red Sector 35.
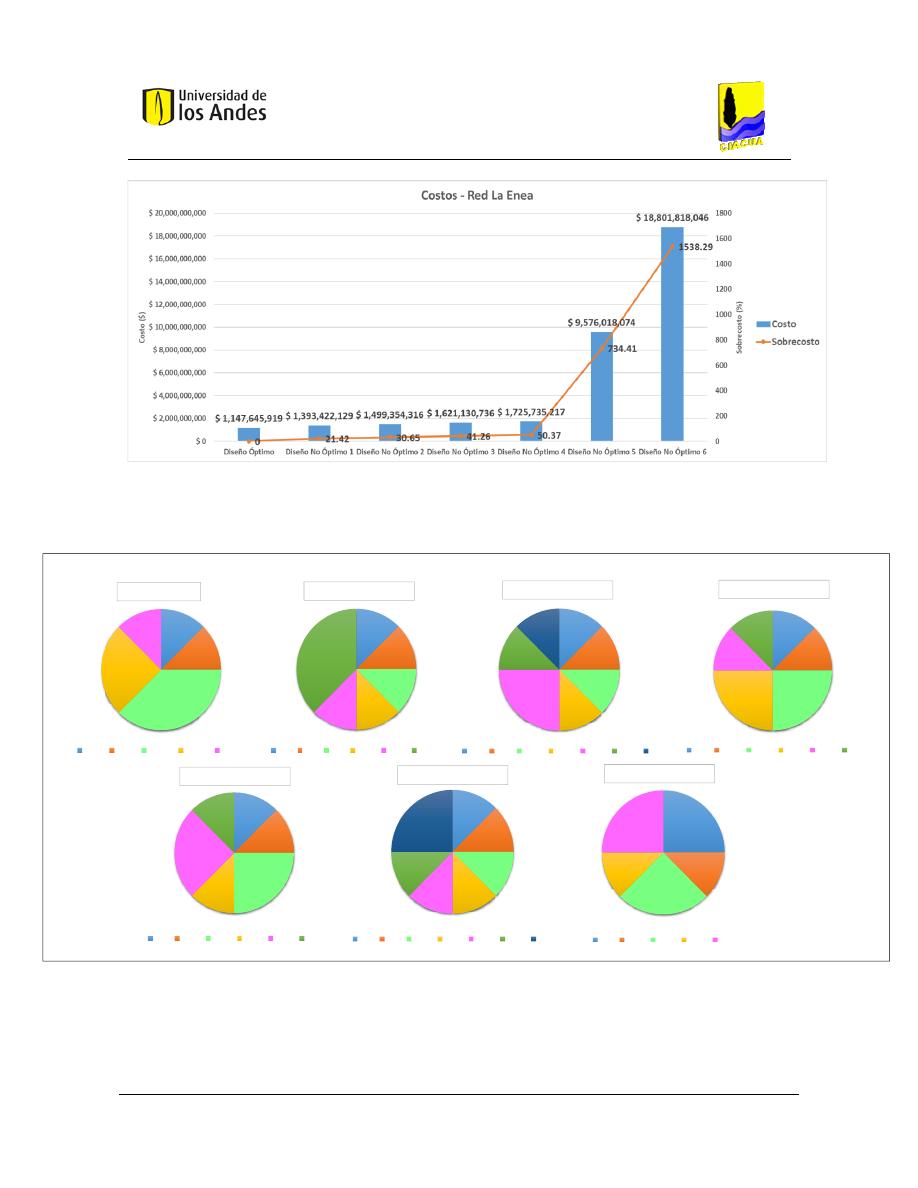
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
105
12.5%
12.5%
37.5%
25.0%
12.5%
Diámetros - Red Two Loops
1 in
4 in
10 in
16 in
18 in
12.5%
12.5%
12.5%
12.5%
12.5%
37.5%
3 in
4 in
8 in
10 in
16 in
18 in
12.5%
12.5%
12.5%
12.5%
25.0%
12.5%
12.5%
3 in
8 in
12 in
14 in
18 in
20 in
24 in
12.5%
12.5%
25.0%
25.0%
12.5%
12.5%
8 in
10 in
14 in
20 in
22 in
24 in
12.5%
12.5%
25.0%
12.5%
25.0%
12.5%
4 in
10 in
18 in
20 in
22 in
24 in
12.5%
12.5%
12.5%
12.5%
12.5%
12.5%
25.0%
1 in
3 in
10 in
16 in
20 in
22 in
24 in
25.0%
12.5%
25.0%
12.5%
25.0%
8 in
10 in
20 in
22 in
24 in
Diseño Óptimo
Diseño No Óptimo 1
Diseño No Óptimo 2
Diseño No Óptimo 3
Diseño No Óptimo 4
Diseño No Óptimo 5
Diseño No Óptimo 6
Figura 56. Distribución de diámetros - Red Two Loops.
Figura 55. Costos - Red La Enea.
5.1.2 Distribuciones de diámetros
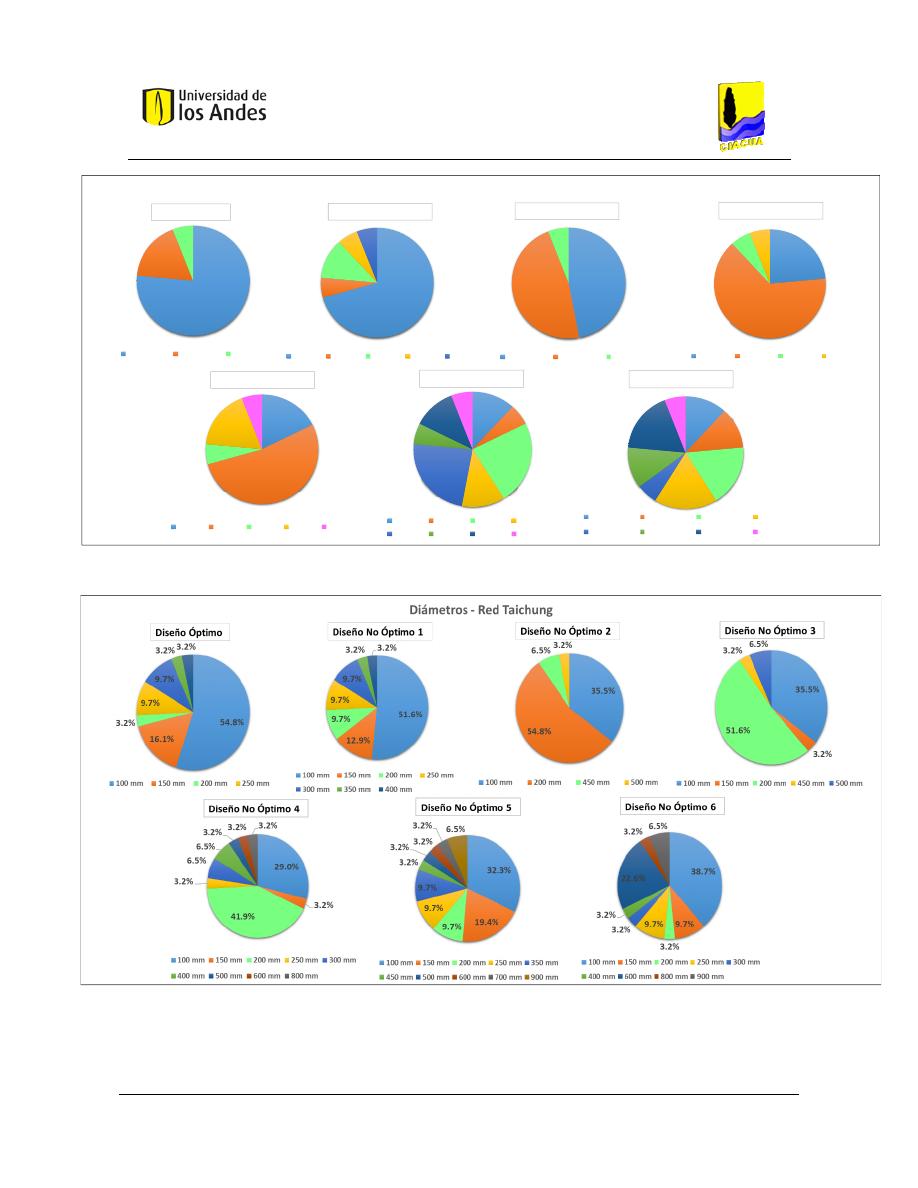
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
106
76.5%
17.6%
5.9%
Diámetros - Red Two Reservoirs
152 mm
254 mm
509 mm
70.6%
5.9%
11.8%
5.9%
5.9%
152 mm
203 mm
254 mm
305 mm
458 mm
47.1%
47.1%
5.9%
152 mm
254 mm
509 mm
23.5%
64.7%
5.9%
5.9%
152 mm
254 mm
458 mm
509 mm
17.6%
52.9%
5.9%
17.6%
5.9%
152 mm
254 mm
356 mm
407 mm
458 mm
11.8%
5.9%
23.5%
11.8%
23.5%
5.9%
11.8%
5.9%
152 mm
203 mm
254 mm
305 mm
356 mm
407 mm
458 mm
509 mm
11.8%
11.8%
17.6%
17.6%
5.9%
11.8%
17.6%
5.9%
152 mm
203 mm
254 mm
305 mm
356 mm
407 mm
458 mm
509 mm
Diseño Óptimo
Diseño No Óptimo 1
Diseño No Óptimo 2
Diseño No Óptimo 3
Diseño No Óptimo 4
Diseño No Óptimo 5
Diseño No Óptimo 6
Figura 58. Distribución de diámetros - Red Two Reservoirs.
Figura 57. Distribución de diámetros - Red Taichung.
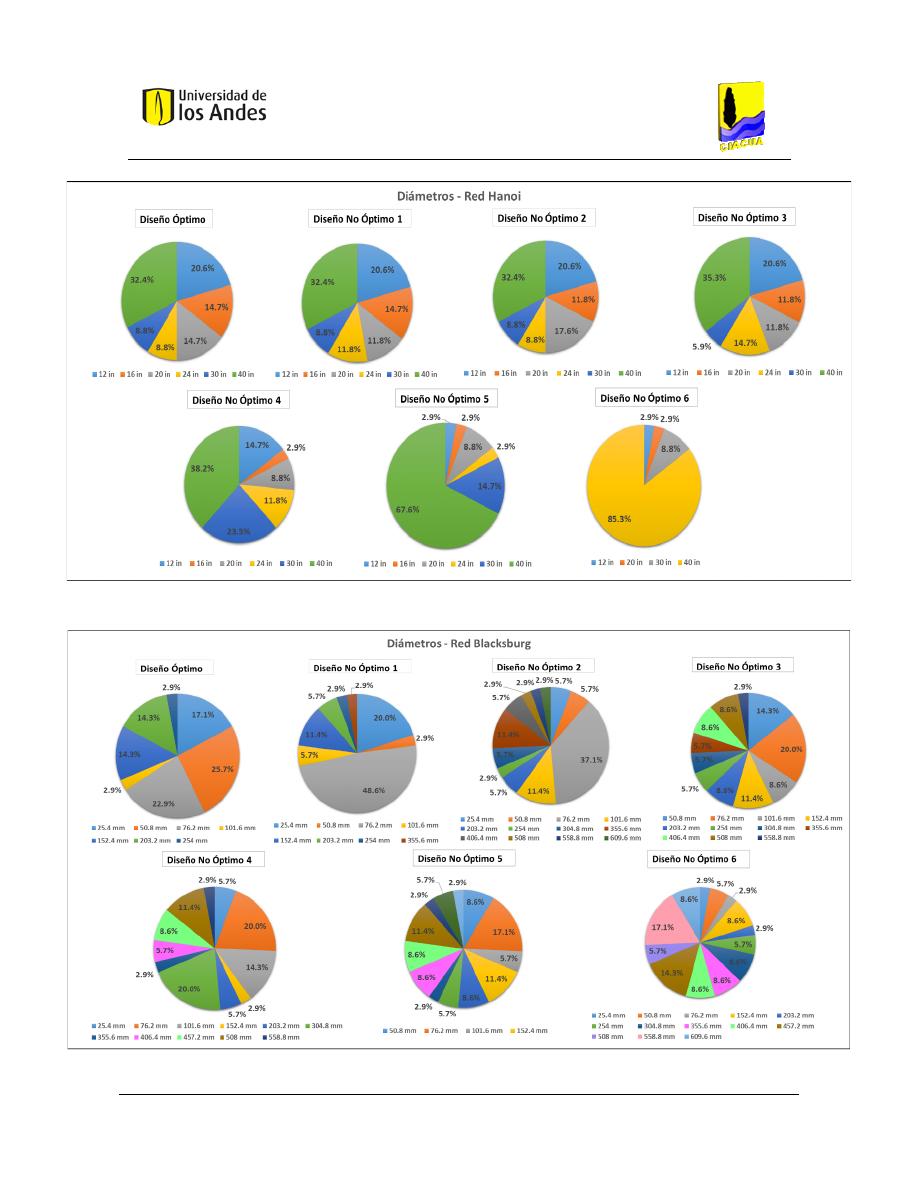
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
107
Figura 60. Distribución de diámetros - Red Hanoi.
Figura 59. Distribución de diámetros - Red Blacksburg.
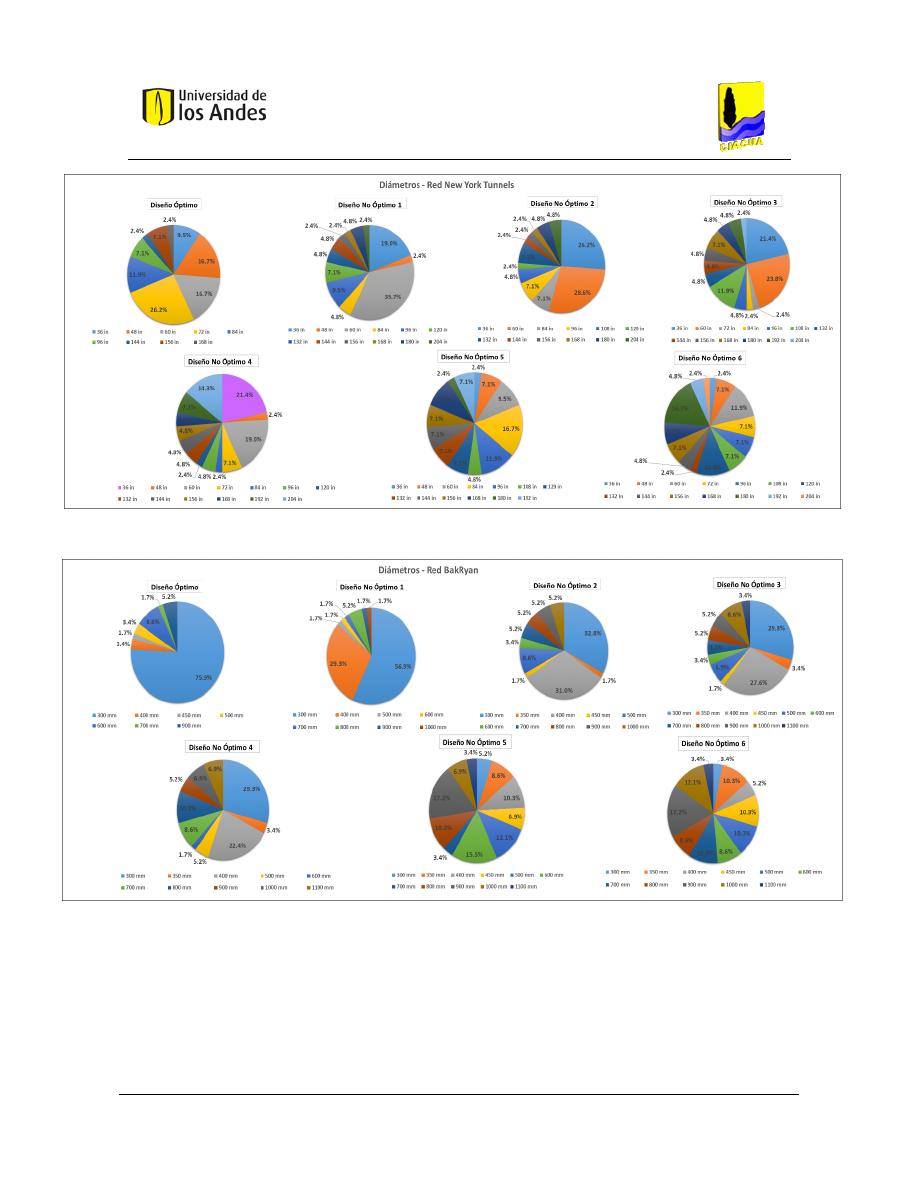
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
108
Figura 62. Distribución de diámetros - Red New York Tunnels.
Figura 61. Distribución de diámetros - Red BakRyan.
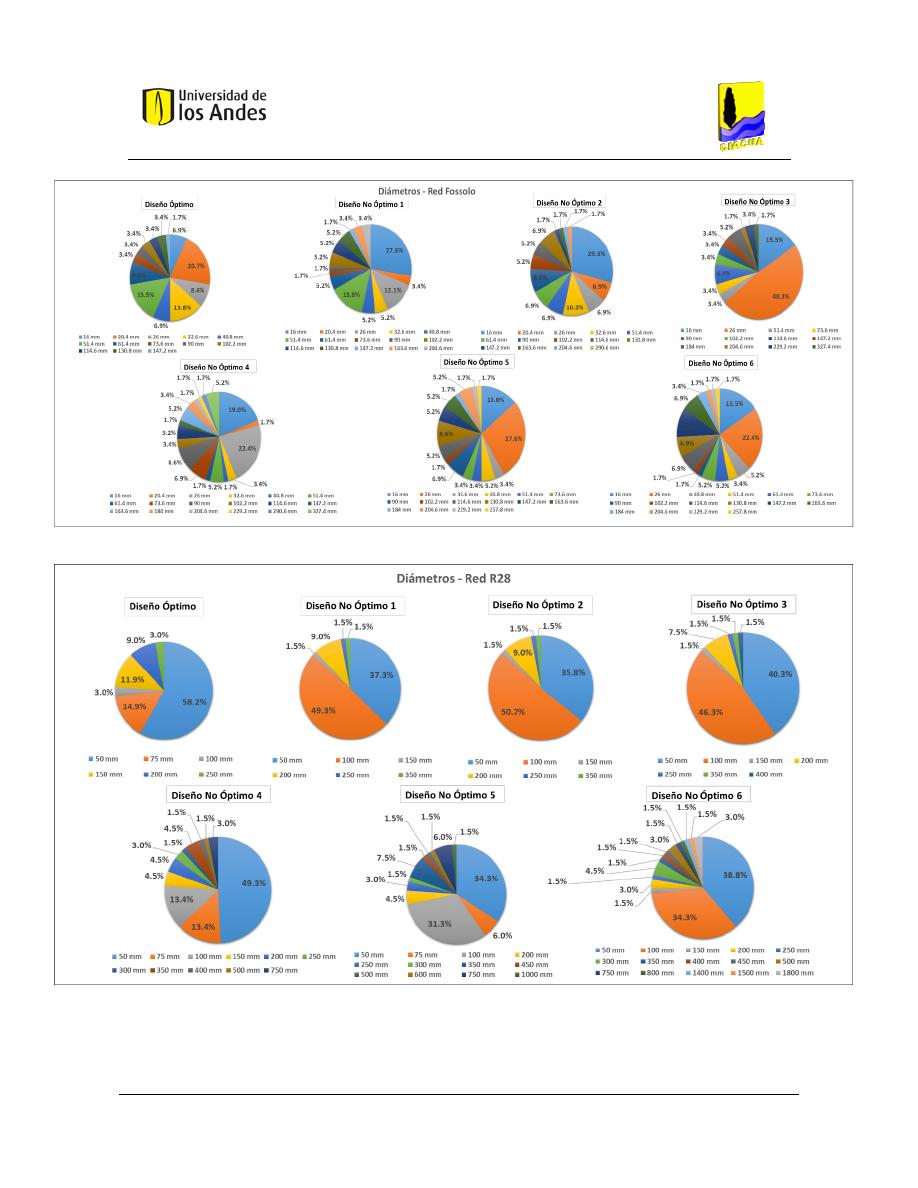
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
109
Figura 64. Distribución de diámetros - Red Fossolo.
Figura 63. Distribución de diámetros - Red R28.
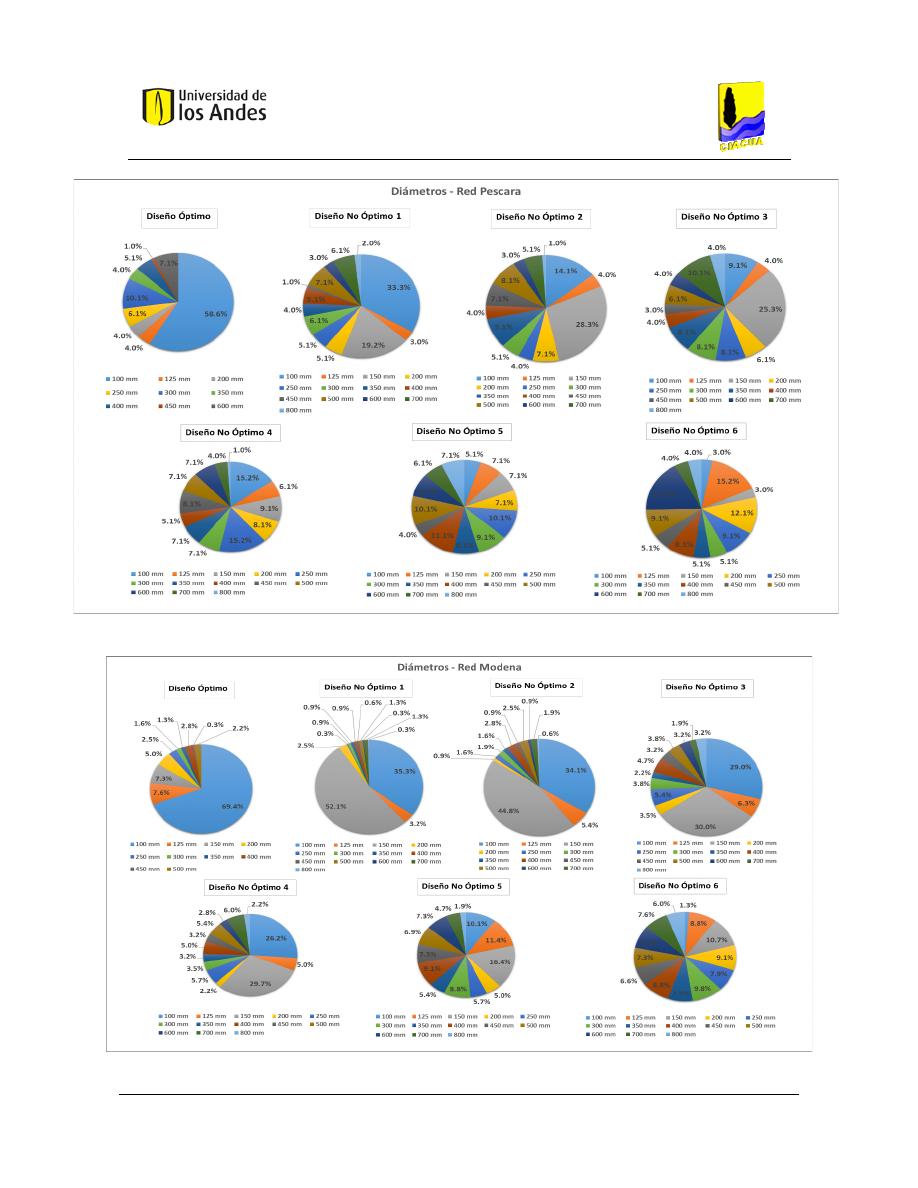
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
110
Figura 66. Distribución de diámetros - Red Pescara.
Figura 65. Distribución de diámetros - Red Modena.
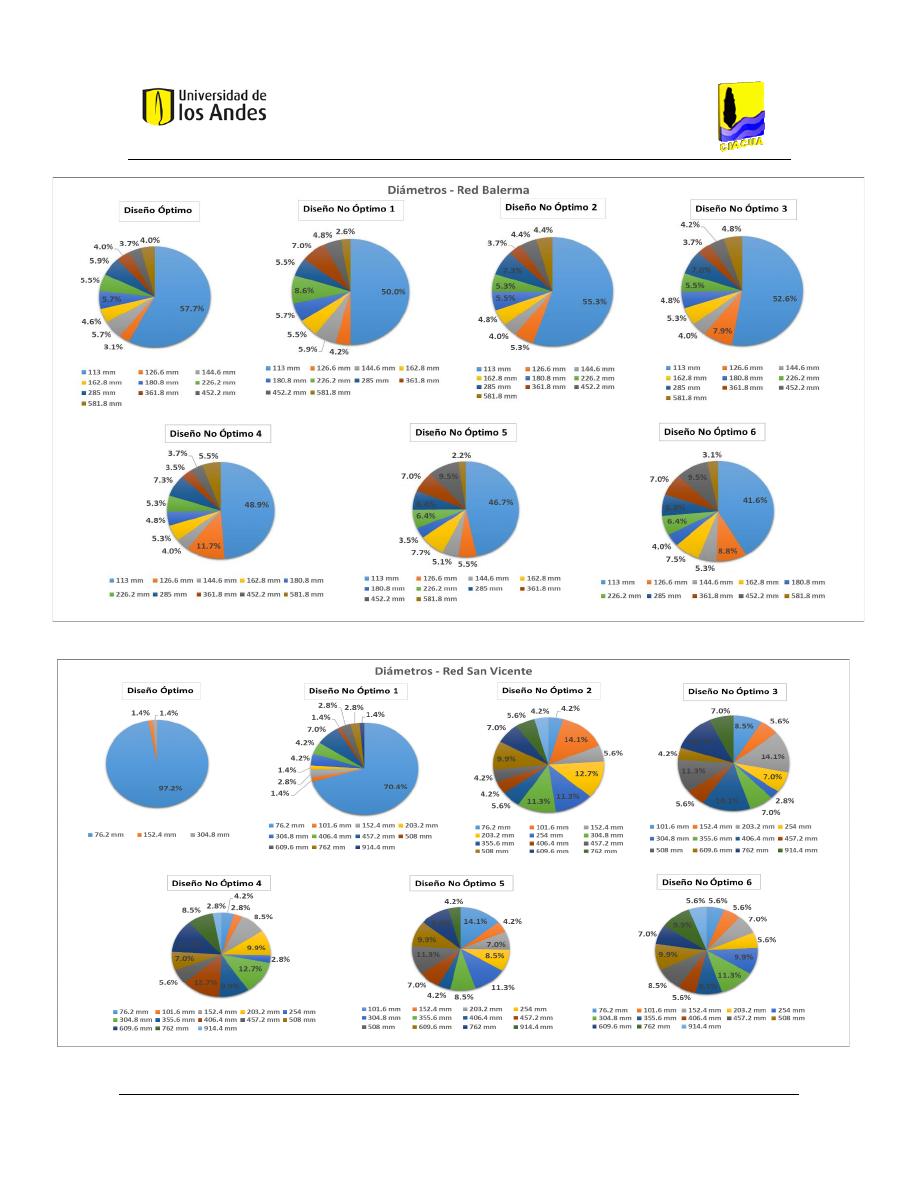
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
111
Figura 67. Distribución de diámetros - Red San Vicente.
Figura 68. Distribución de diámetros - Red Balerma.
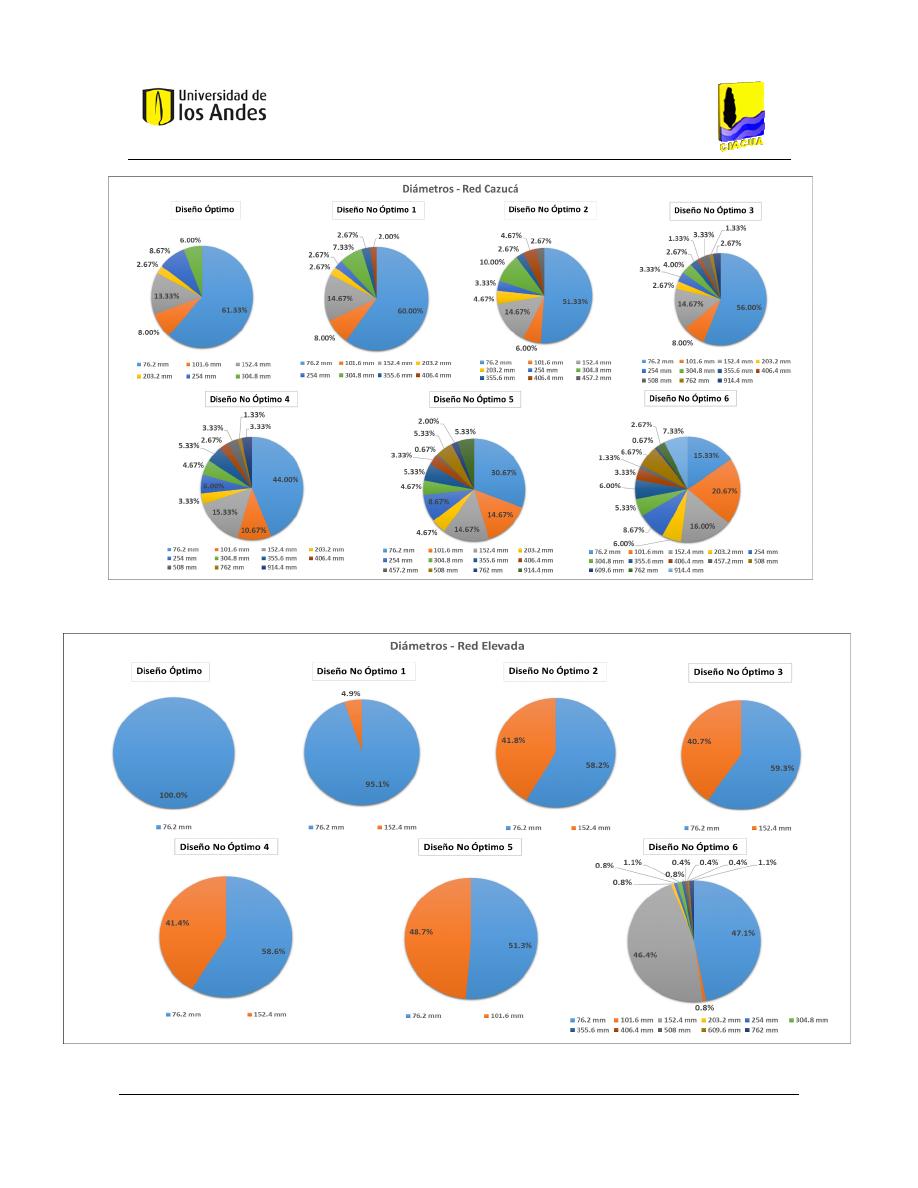
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
112
Figura 70. Distribución de diámetros - Red Elevada.
Figura 69. Distribución de diámetros - Red Cazucá.
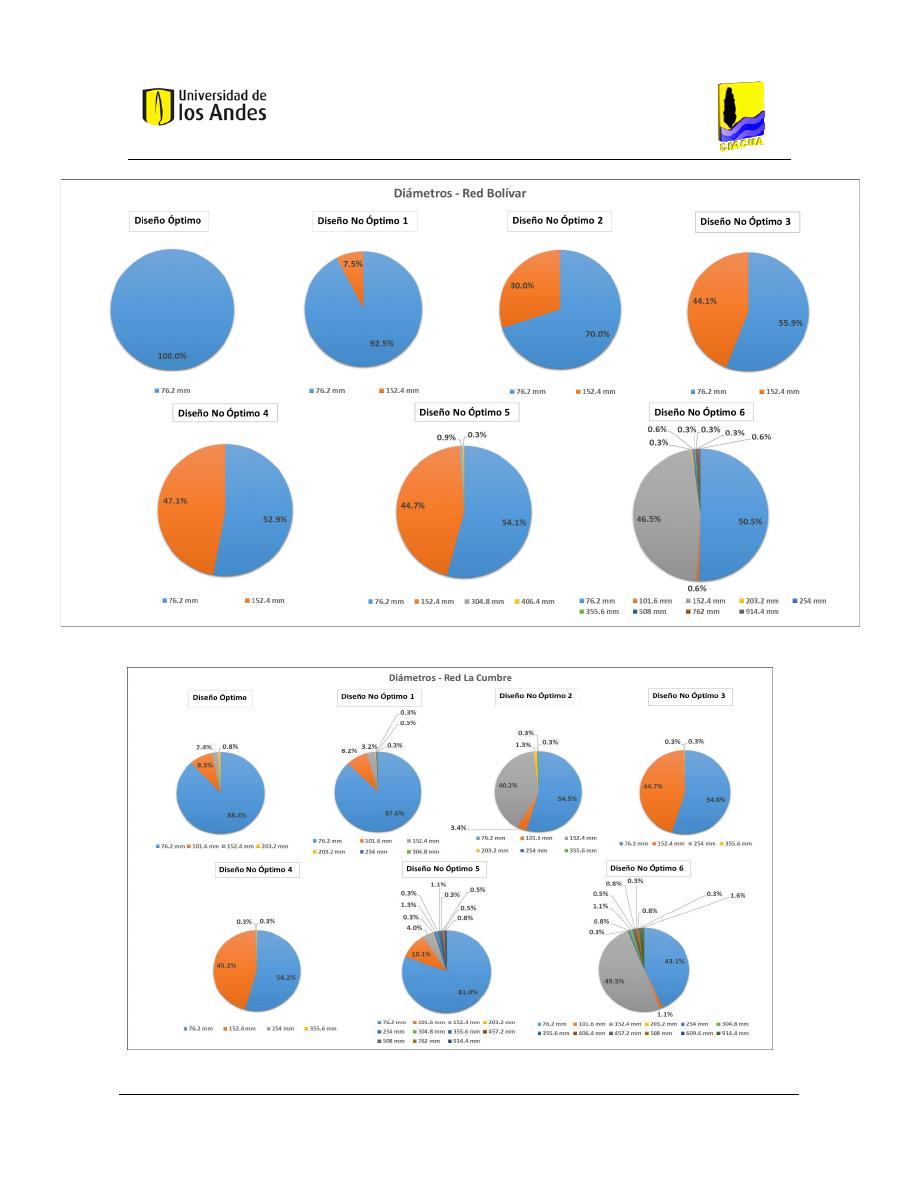
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
113
Figura 71. Distribución de diámetros - Red La Cumbre.
Figura 72. Distribución de diámetros - Red Bolívar.
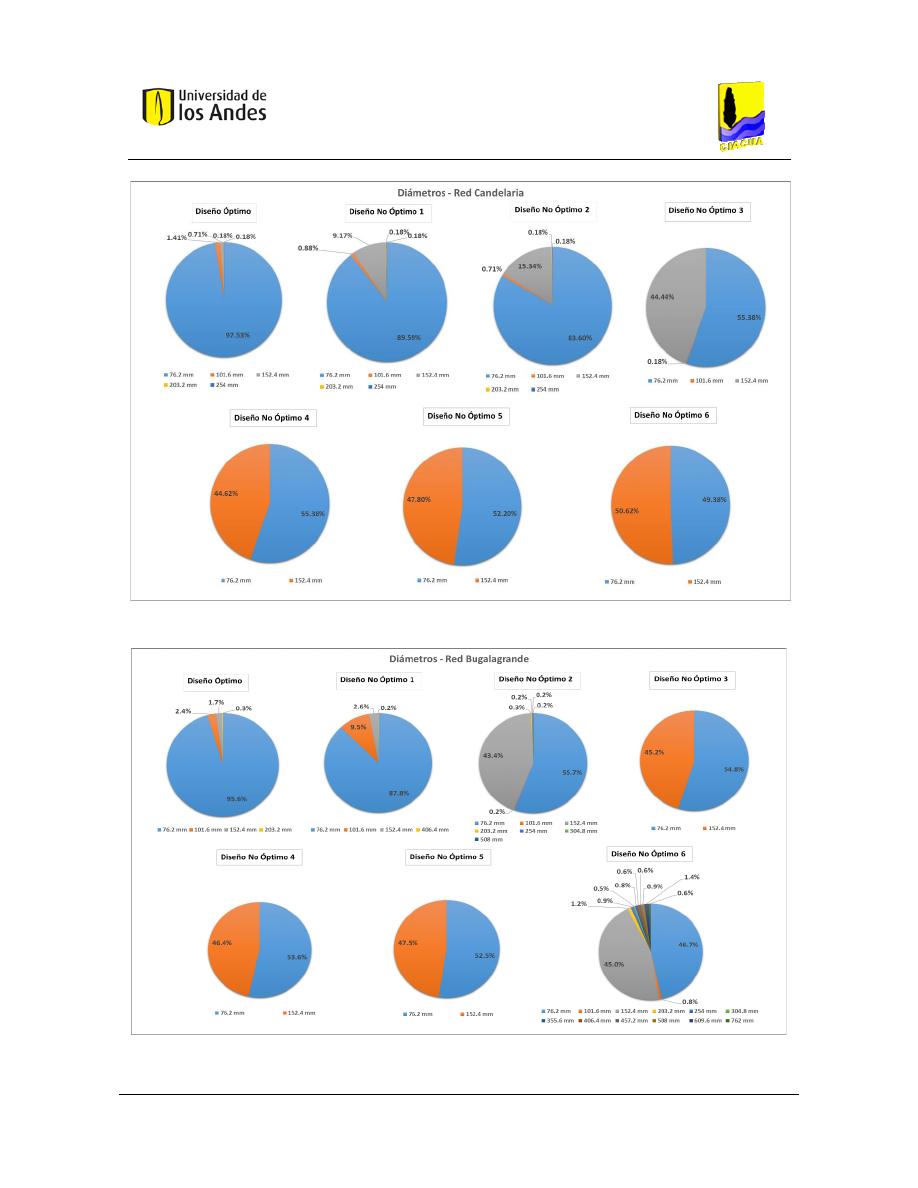
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
114
Figura 74. Distribución de diámetros - Red Bugalagrande.
Figura 73. Distribución de diámetros - Red Candelaria.
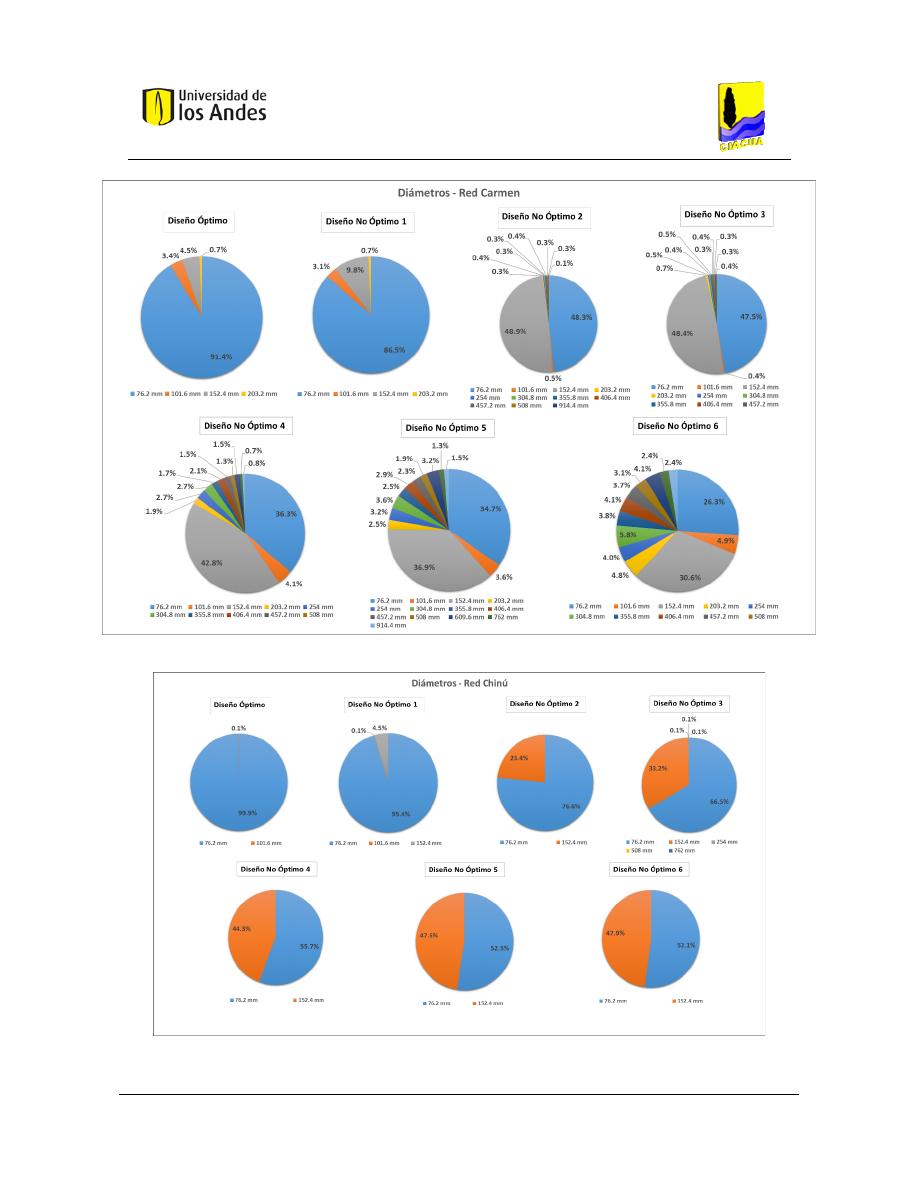
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
115
Figura 76. Distribución de diámetros - Red Chinú.
Figura 75. Distribución de diámetros - Red Carmen.
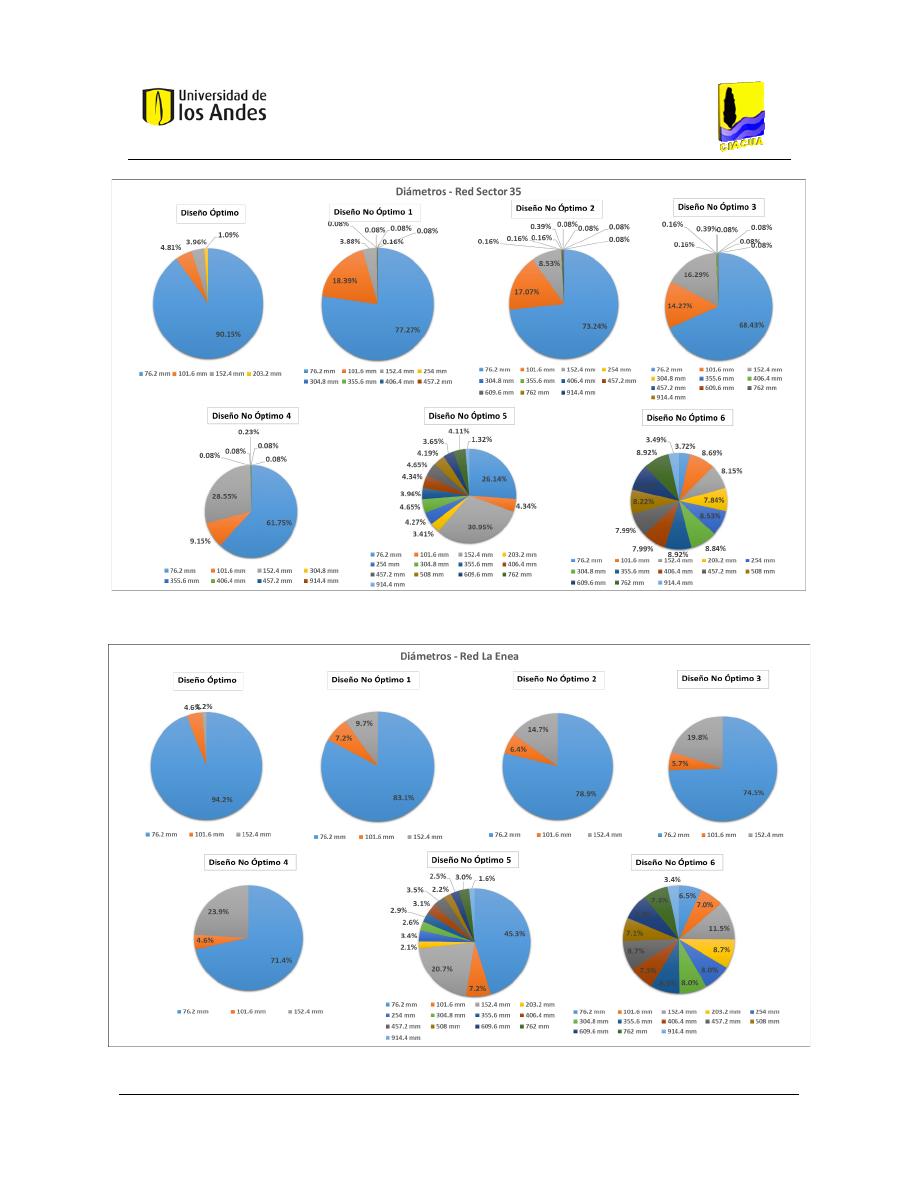
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
116
Figura 78. Distribución de diámetros - Red La Enea.
Figura 77. Distribución de diámetros - Red Sector 35.
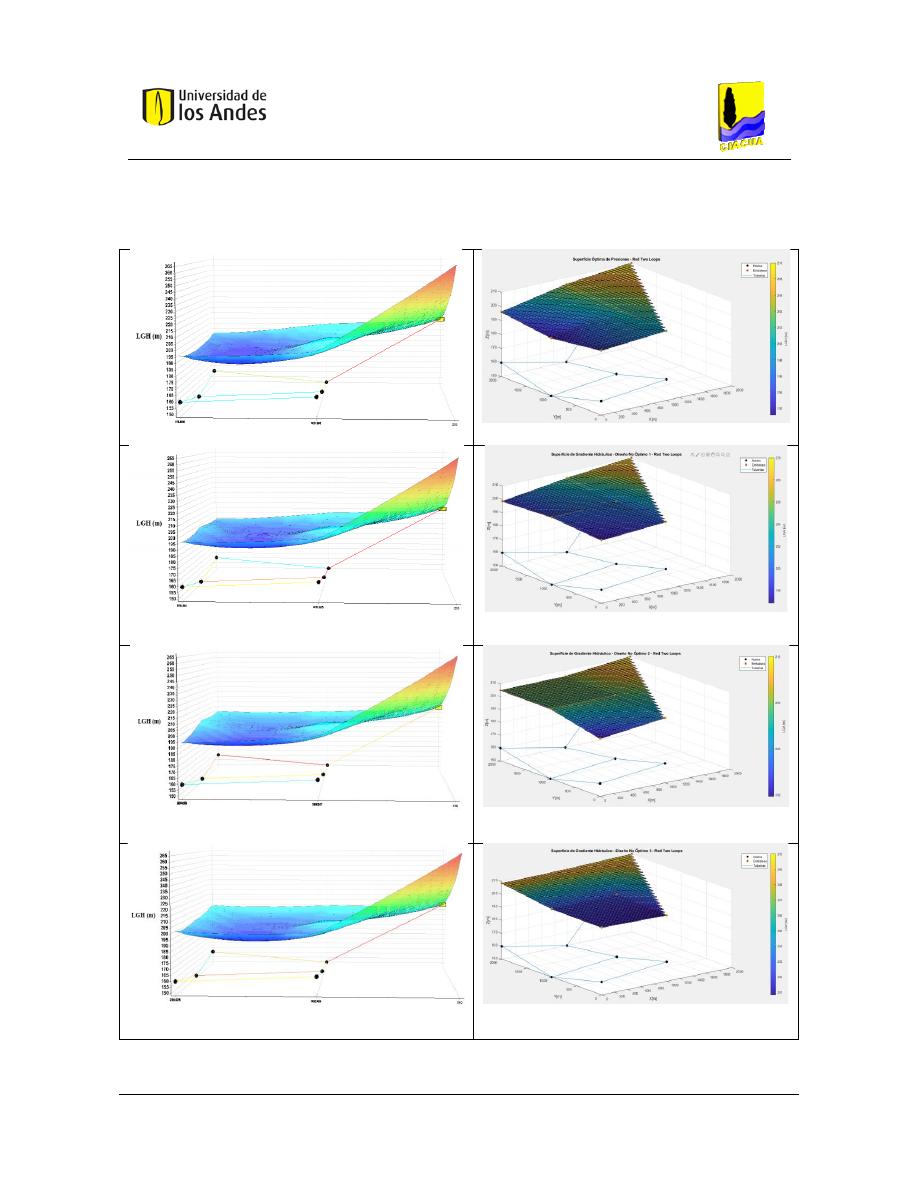
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
117
5.1.3 Superficies de Gradiente Hidráulico
5.1.3.1 Red Two Loops
Figura 79. SOP Red Two Loops - REDES 2019.
Figura 80. SOP Red Two Loops - MATLAB.
Figura 81. Diseño No Óptimo 1 - Red Two Loops - REDES
2019.
Figura 82. Diseño No Óptimo 1 - Red Two Loops -
MATLAB.
Figura 83. Diseño No Óptimo 2 - Red Two Loops - REDES
2019.
Figura 84. Diseño No Óptimo 2 - Red Two Loops -
MATLAB.
Figura 85. Diseño No Óptimo 3 - Red Two Loops - REDES
2019.
Figura 86. Diseño No Óptimo 3 - Red Two Loops -
MATLAB.
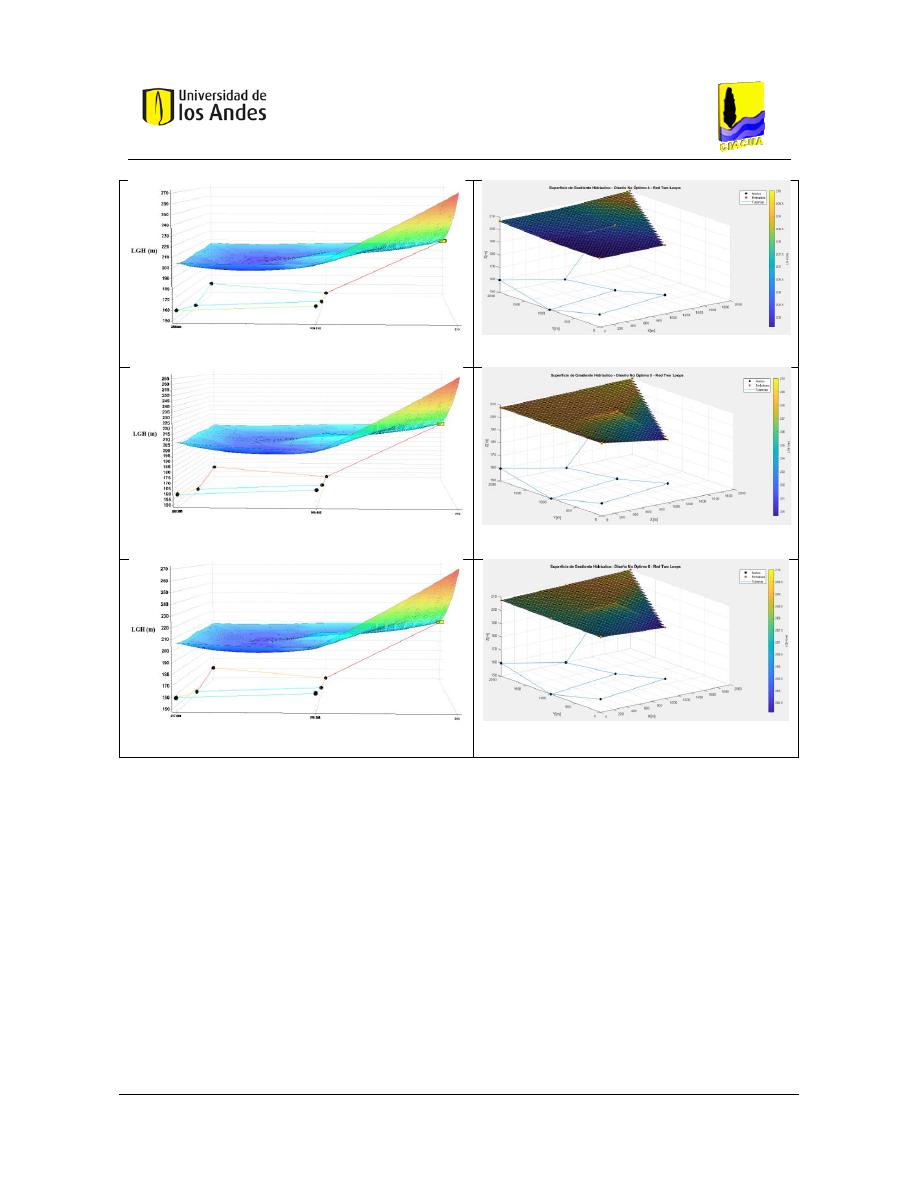
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
118
Figura 87. Diseño No Óptimo 4 - Red Two Loops - REDES
2019.
Figura 88. Diseño No Óptimo 4 - Red Two Loops -
MATLAB.
Figura 89. Diseño No Óptimo 5 - Red Two Loops - REDES
2019.
Figura 90. Diseño No Óptimo 5 - Red Two Loops -
MATLAB.
Figura 91. Diseño No Óptimo 6 - Red Two Loops - REDES
2019.
Figura 92. Diseño No Óptimo 6 - Red Two Loops -
MATLAB.
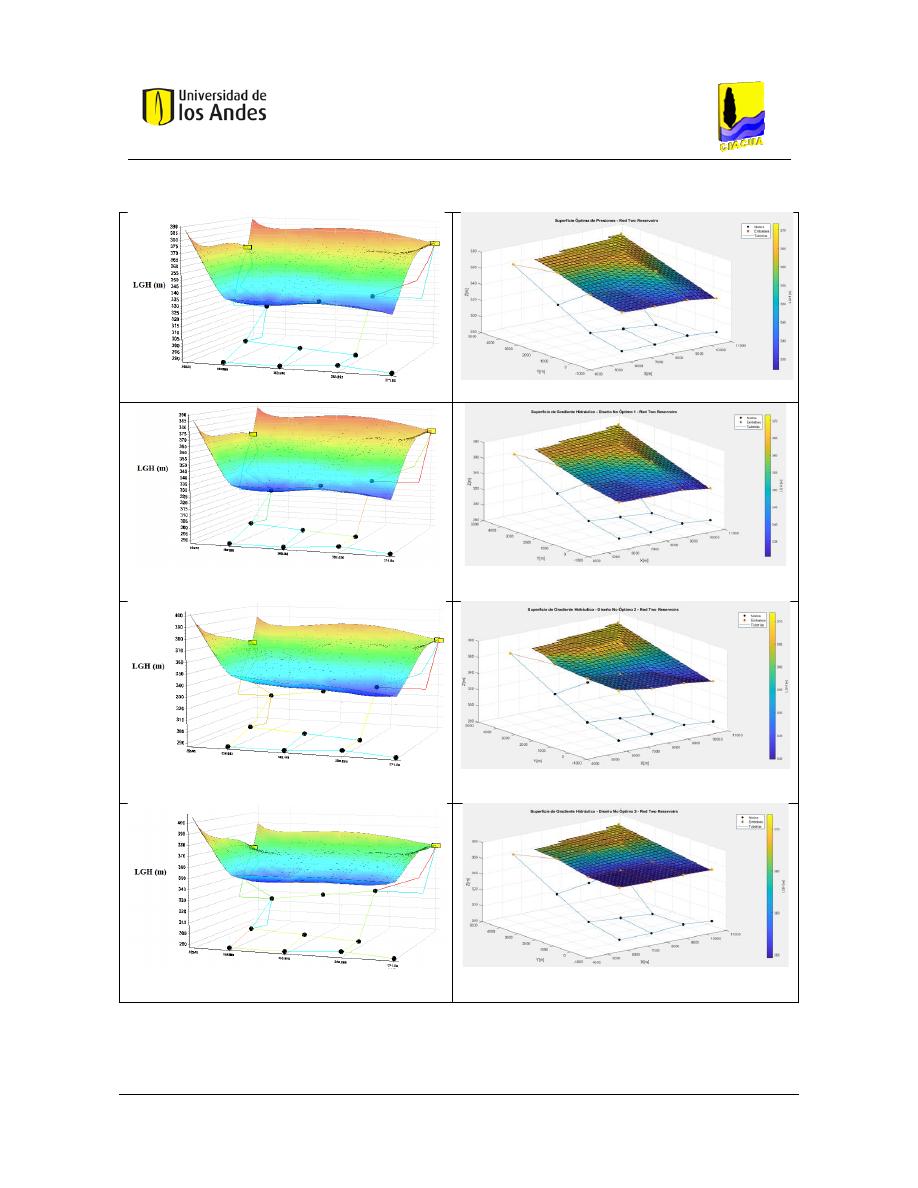
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
119
5.1.3.2 Red Two Reservoirs
Figura 93. SOP Red Two Reservoirs – REDES 2019.
Figura 94. SOP Red Two Reservoirs - MATLAB.
Figura 95. Diseño No Óptimo 1 - Red Two Reservoirs -
REDES 2019.
Figura 96. Diseño No Óptimo 1 - Red Two Reservoirs -
MATLAB.
Figura 97. Diseño No Óptimo 2 - Red Two Reservoirs -
REDES 2019.
Figura 98. Diseño No Óptimo 2 - Red Two Reservoirs -
MATLAB.
Figura 99. Diseño No Óptimo 3 - Red Two Reservoirs -
REDES 2019.
Figura 100. Diseño No Óptimo 3 - Red Two Reservoirs -
MATLAB.
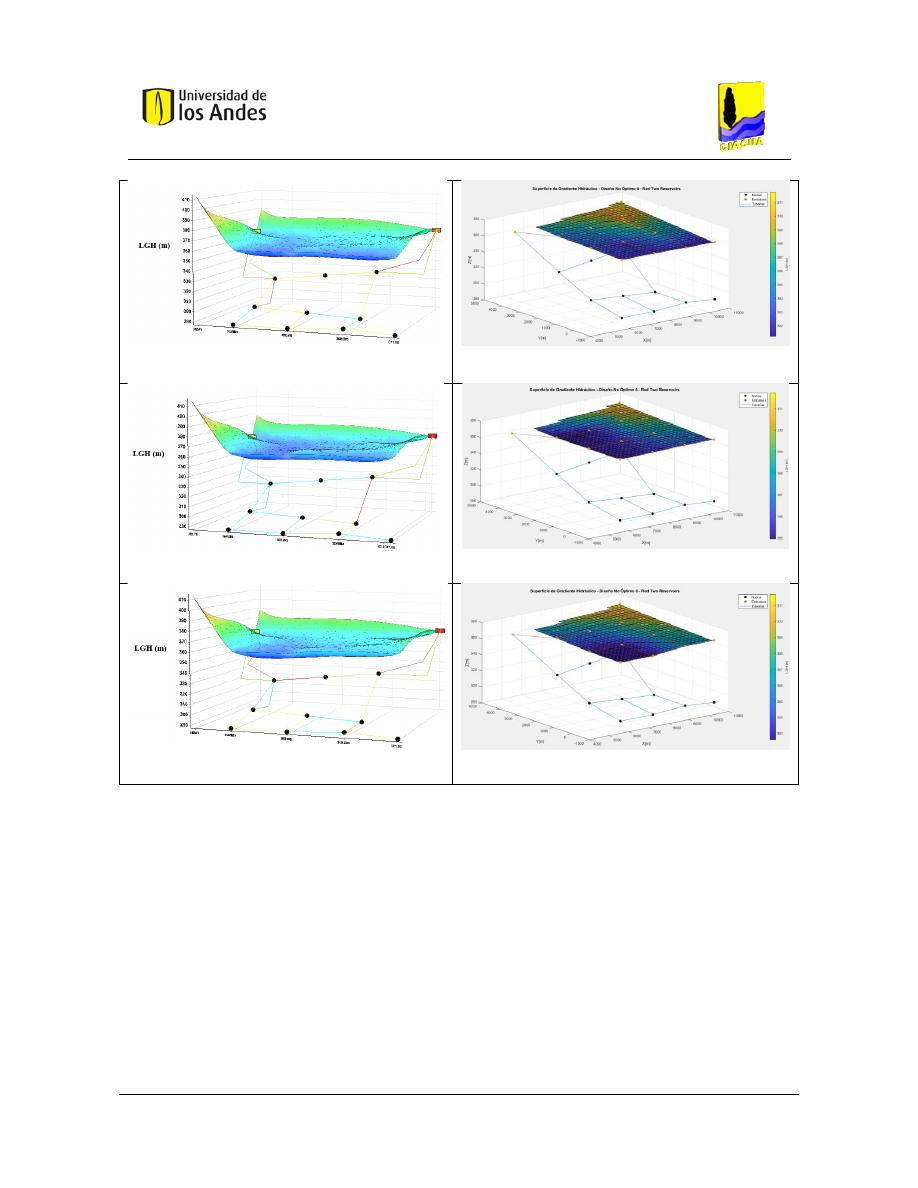
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
120
Figura 101. Diseño No Óptimo 4 - Red Two Reservoirs -
REDES 2019.
Figura 102. Diseño No Óptimo 4 - Red Two Reservoirs -
MATLAB.
Figura 103. Diseño No Óptimo 5 - Red Two Reservoirs -
REDES 2019.
Figura 104. Diseño No Óptimo 5 - Red Two Reservoirs -
MATLAB.
Figura 105. Diseño No Óptimo 6 - Red Two Reservoirs -
REDES 2019.
Figura 106. Diseño No Óptimo 6 - Red Two Reservoirs -
MATLAB.
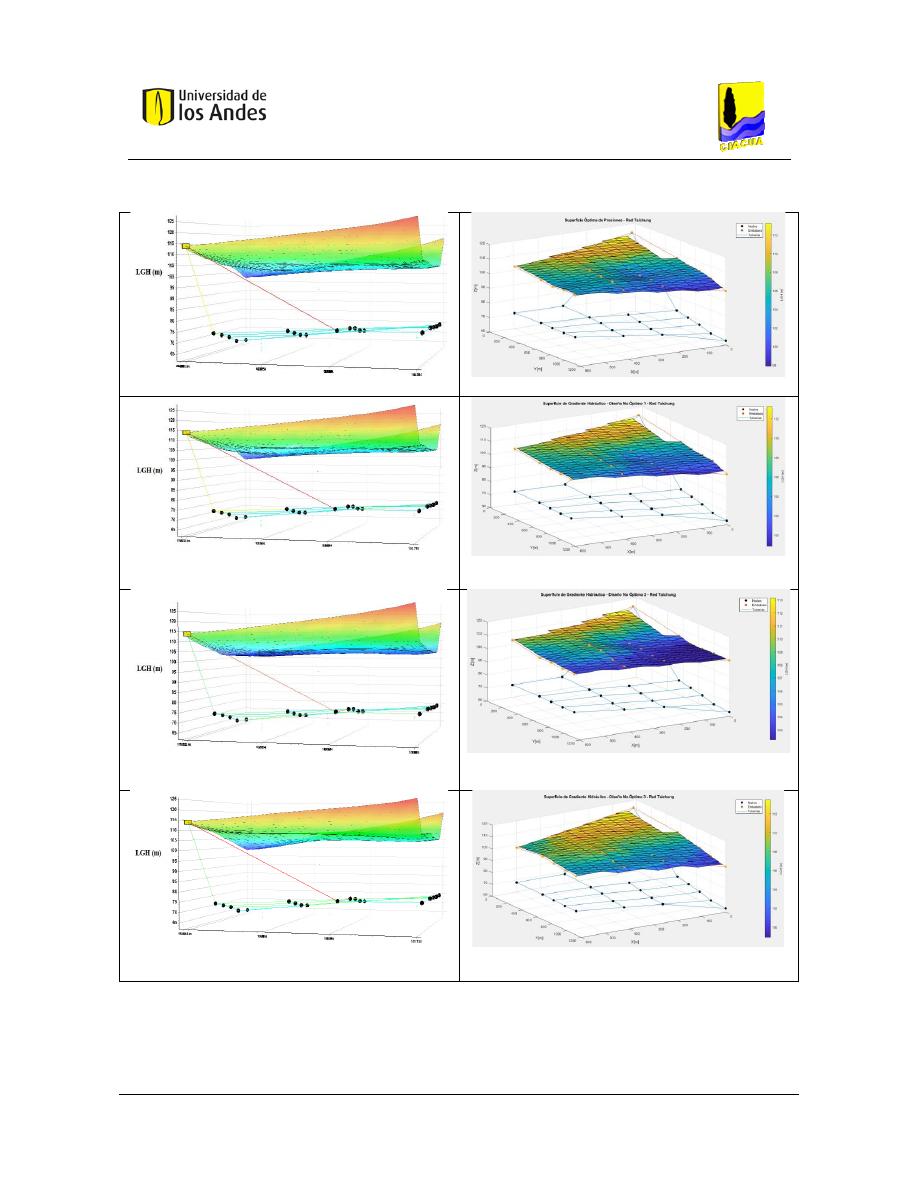
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
121
5.1.3.3 Red Taichung
Figura 107- SOP Red Taichung - REDES 2019.
Figura 108. SOP Red Taichung - MATLAB.
Figura 109. Diseño No Óptimo 1 - Red Taichung - REDES
2019.
Figura 110. Diseño No Óptimo 1 - Red Taichung -
MATLAB.
Figura 111. Diseño No Óptimo 2 - Red Taichung - REDES
2019.
Figura 112. Diseño No Óptimo 2 - Red Taichung - REDES
2019.
Figura 113. Diseño No Óptimo 3 - Red Taichung - REDES
2019.
Figura 114. Diseño No Óptimo 3 - Red Taichung -
MATLAB.
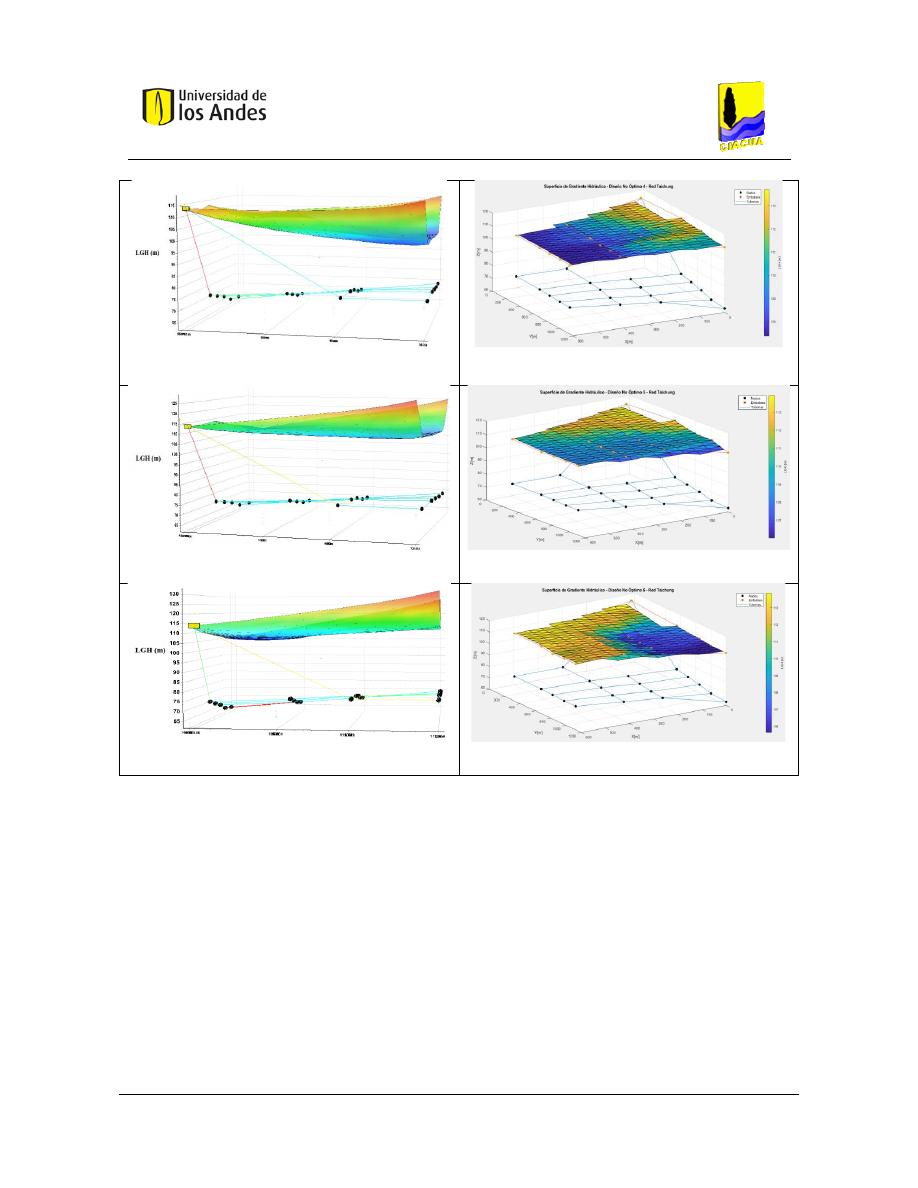
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
122
Figura 115. Diseño No Óptimo 4 - Red Taichung - REDES
2019.
Figura 116. Diseño No Óptimo 4 - Red Taichung - REDES
2019.
Figura 117. Diseño No Óptimo 5 - Red Taichung - REDES
2019.
Figura 118. Diseño No Óptimo 5 - Red Taichung -
MATLAB.
Figura 119. Diseño No Óptimo 6 - Red Taichung - REDES
2019.
Figura 120. Diseño No Óptimo 6 - Red Taichung - REDES
2019.
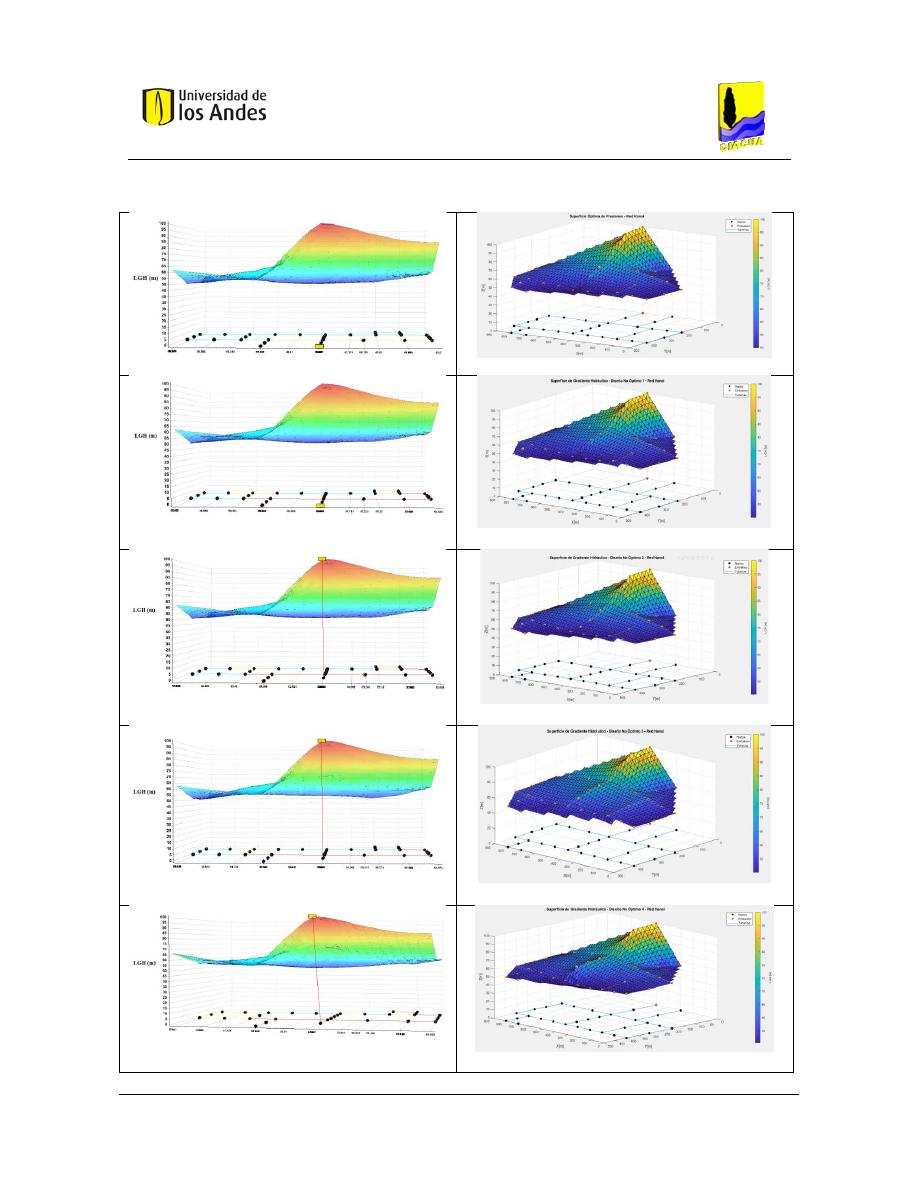
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
123
5.1.3.4 Red Hanoi
Figura 121. SOP Red Hanoi - REDES 2019.
Figura 122. SOP Red Hanoi - MATLAB.
Figura 123. Diseño No Óptimo 1 - Red Hanoi - REDES
2019.
Figura 124. Diseño No Óptimo 1 - Red Hanoi - MATLAB.
Figura 125. Diseño No Óptimo 2 - Red Hanoi - REDES
2019.
Figura 126. Diseño No Óptimo 2 - Red Hanoi - MATLAB.
Figura 127. Diseño No Óptimo 3 - Red Hanoi - REDES
2019.
Figura 128. Diseño No Óptimo 3 - Red Hanoi - MATLAB.
Figura 129. Diseño No Óptimo 4 - Red Hanoi - REDES
2019.
Figura 130. Diseño No Óptimo 4 - Red Hanoi - MATLAB.
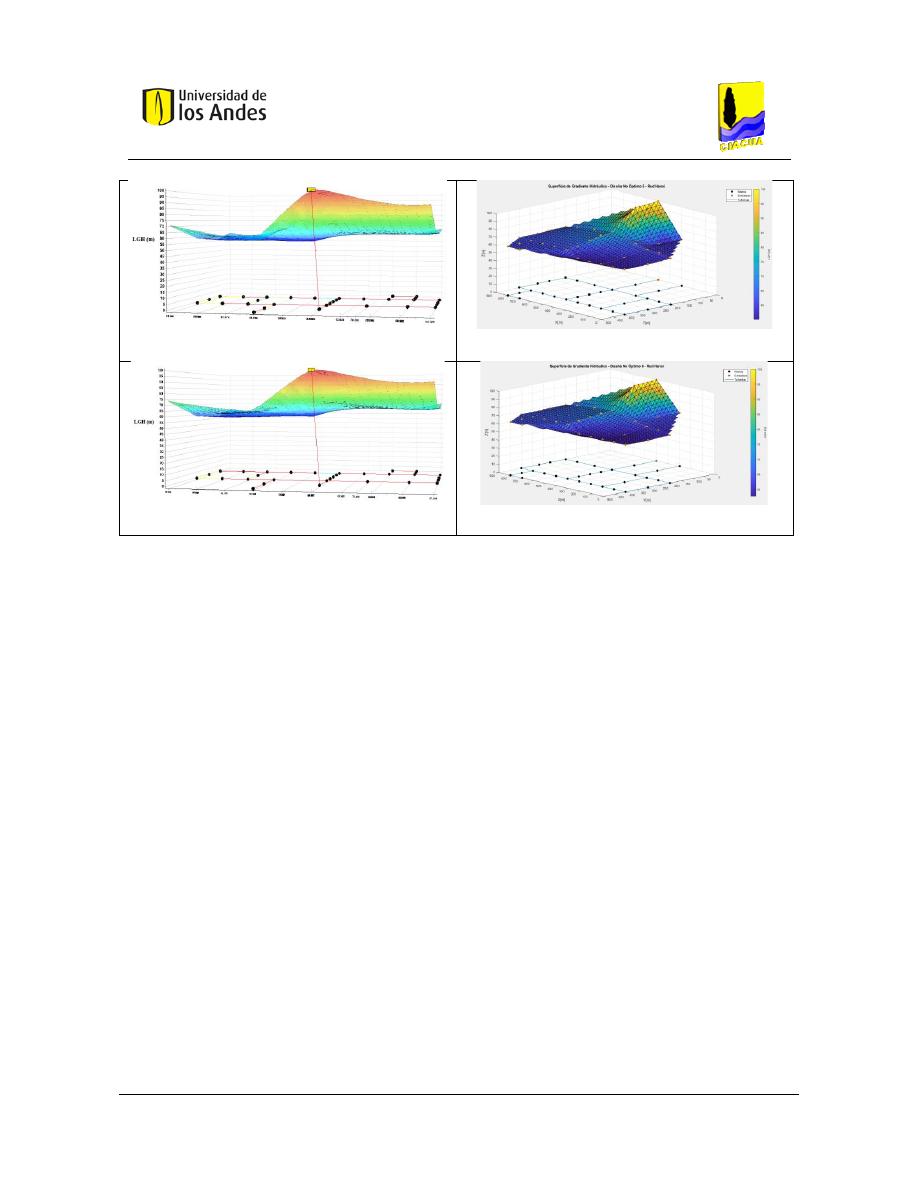
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
124
Figura 131. Diseño No Óptimo 5 - Red Hanoi - REDES
2019.
Figura 132. Diseño No Óptimo 5 - Red Hanoi - REDES
2019.
Figura 133. Diseño No Óptimo 6 - Red Hanoi - REDES
2019.
Figura 134. Diseño No Óptimo 6 - Red Hanoi – MATLAB.
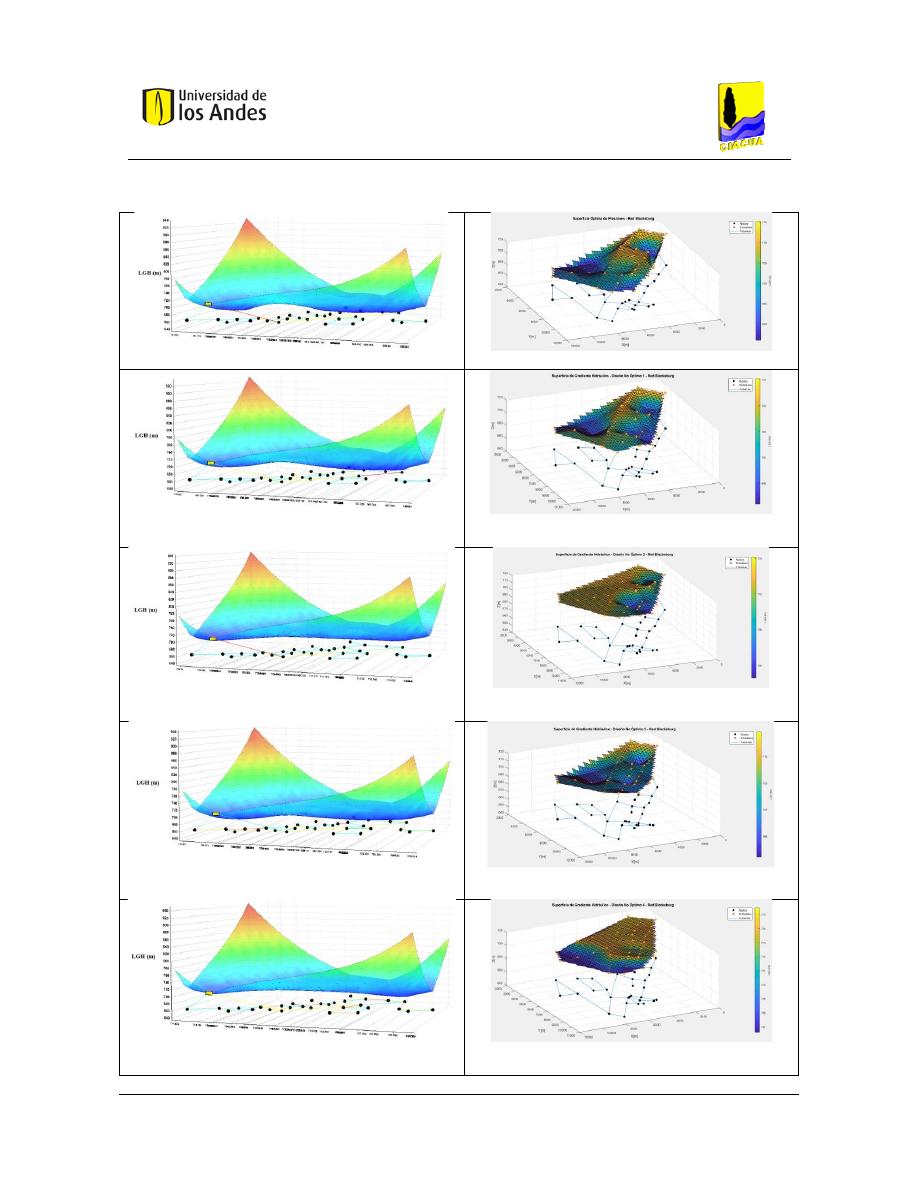
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
125
5.1.3.5 Red Blacksburg
Figura 135. SOP Red Blacksburg - REDES 2019.
Figura 136. SOP Red Blacksburg - MATLAB.
Figura 137. Diseño No Óptimo 1 - Red Blacksburg - REDES
2019.
Figura 138. Diseño No Óptimo 1 - Red Blacksburg -
MATLAB.
Figura 139. Diseño No Óptimo 2 - Red Blacksburg - REDES
2019.
Figura 140. Diseño No Óptimo 2 - Red Blacksburg -
MATLAB.
Figura 141. Diseño No Óptimo 3 - Red Blacksburg - REDES
2019.
Figura 142. Diseño No Óptimo 3 - Red Blacksburg -
MATLAB.
Figura 143. Diseño No Óptimo 4 - Red Blacksburg - REDES
2019.
Figura 144. Diseño No Óptimo 4 - Red Blacksburg -
MATLAB.
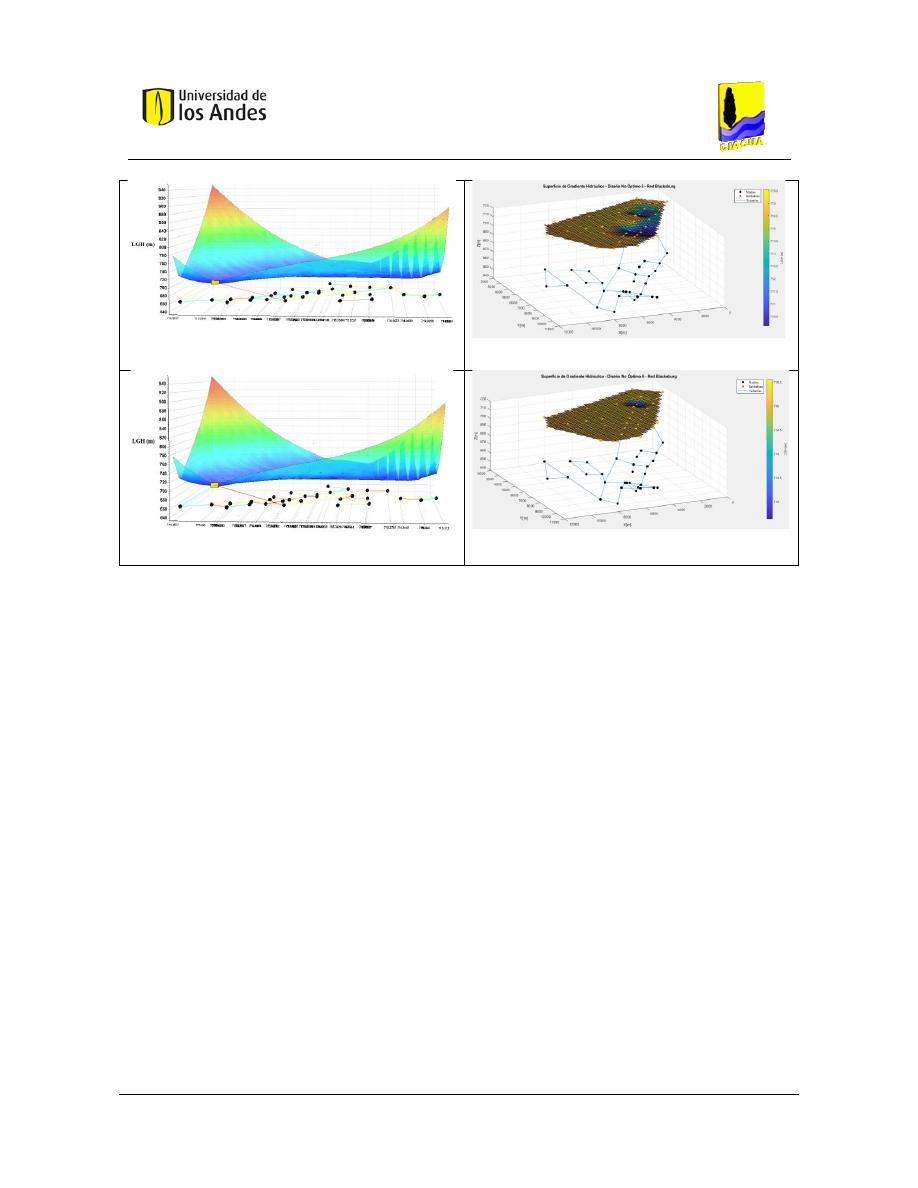
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
126
Figura 145. Diseño No Óptimo 5 - Red Blacksburg - REDES
2019.
Figura 146. Diseño No Óptimo 5 - Red Blacksburg -
MATLAB.
Figura 147. Diseño No Óptimo 6 - Red Blacksburg - REDES
2019.
Figura 148. Diseño No Óptimo 6 - Red Blacksburg -
MATLAB.
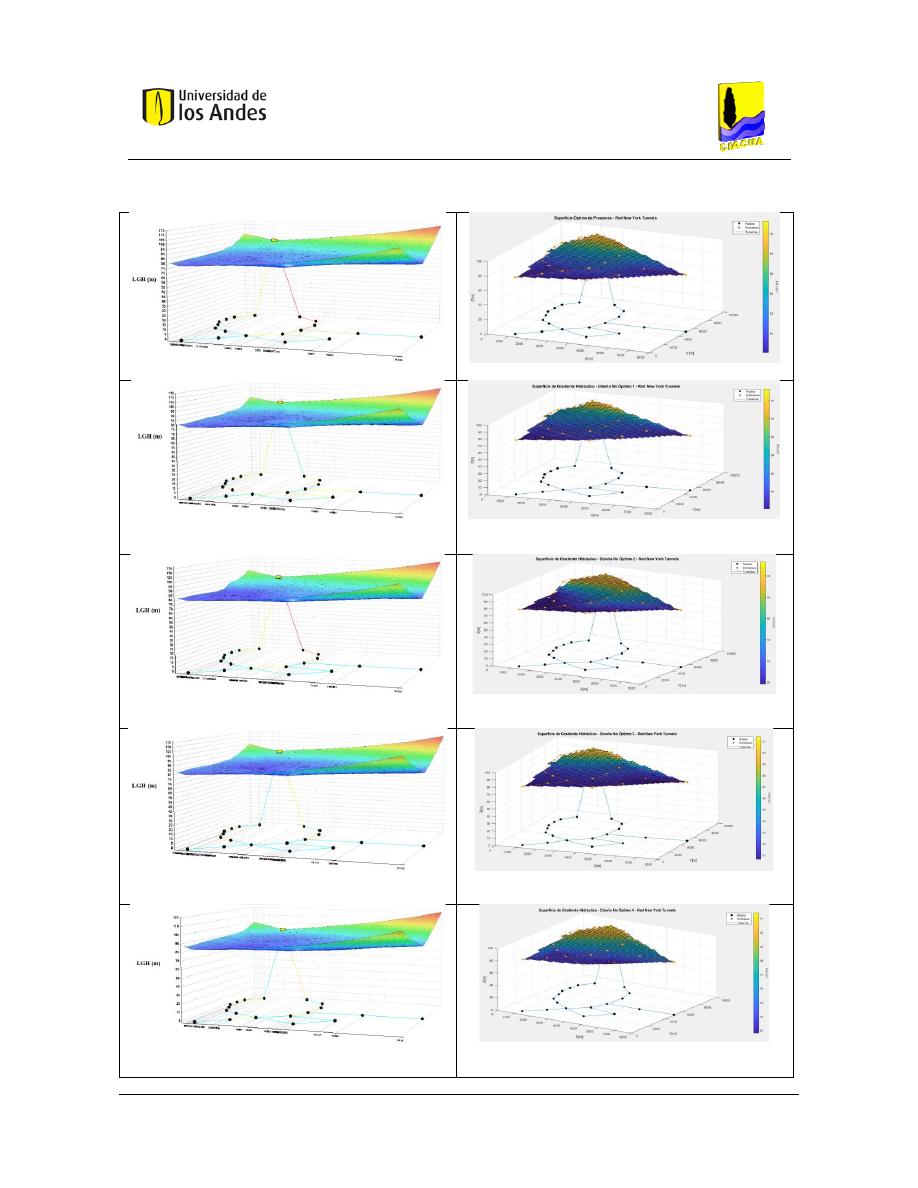
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
127
5.1.3.6 Red New York Tunnels
Figura 149. SOP Red New York Tunnels - REDES 2019.
Figura 150. SOP Red New York Tunnels - MATLAB.
Figura 151. Diseño No Óptimo 1 - Red New York Tunnels
- REDES 2019.
Figura 152. Diseño No Óptimo 1 - Red New York Tunnels
- MATLAB.
Figura 153. Diseño No Óptimo 2 - Red New York Tunnels
- REDES 2019.
Figura 154. Diseño No Óptimo 2 - Red New York Tunnels
- MATLAB.
Figura 155. Diseño No Óptimo 3 - Red New York Tunnels
- REDES 2019.
Figura 156. Diseño No Óptimo 3 - Red New York Tunnels
- MATLAB.
Figura 157. Diseño No Óptimo 4 - Red New York Tunnels
- REDES 2019.
Figura 158. Diseño No Óptimo 4 - Red New York Tunnels
- MATLAB.
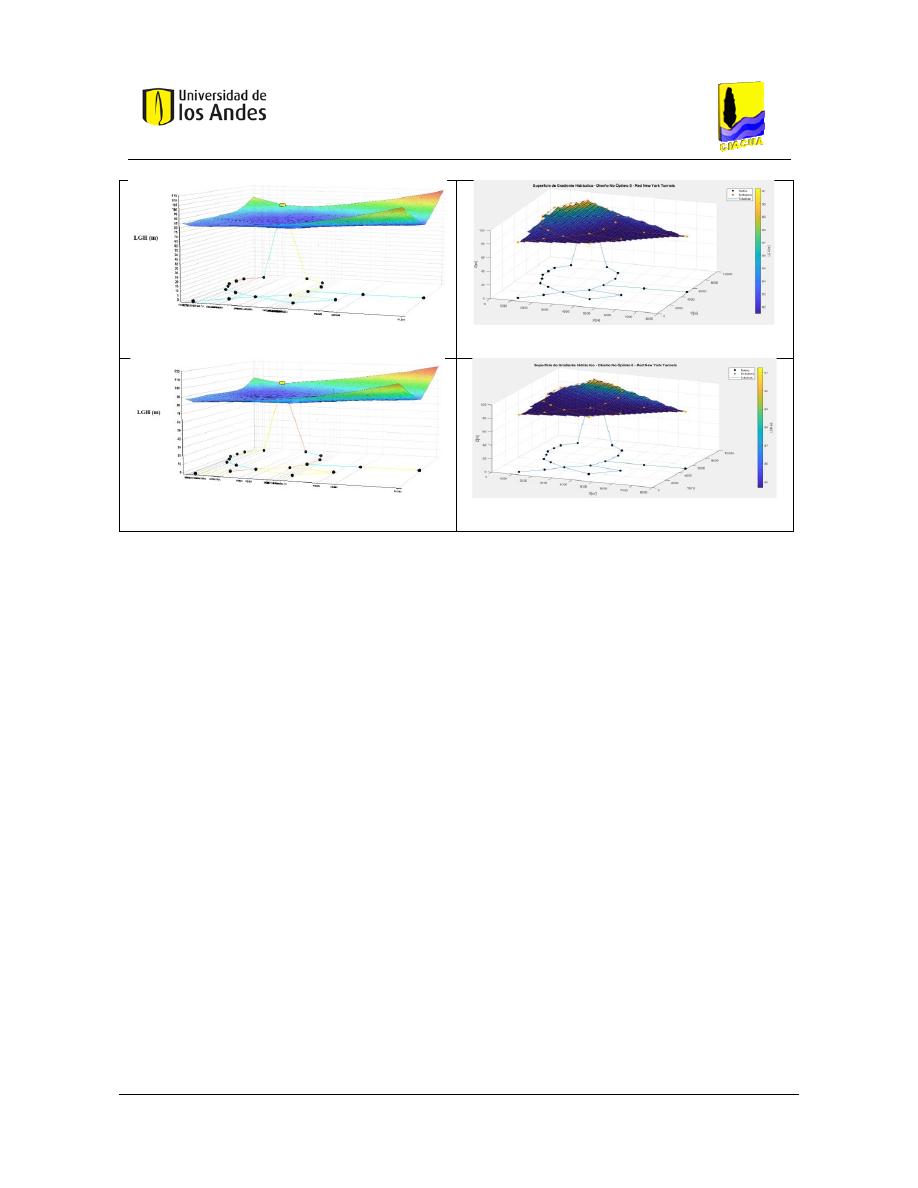
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
128
Figura 159. Diseño No Óptimo 5 - Red New York Tunnels
- REDES 2019.
Figura 160. Diseño No Óptimo 5 - Red New York Tunnels
- MATLAB.
Figura 161. Diseño No Óptimo 6 - Red New York Tunnels
- REDES 2019.
Figura 162. Diseño No Óptimo 6 - Red New York Tunnels
- MATLAB.
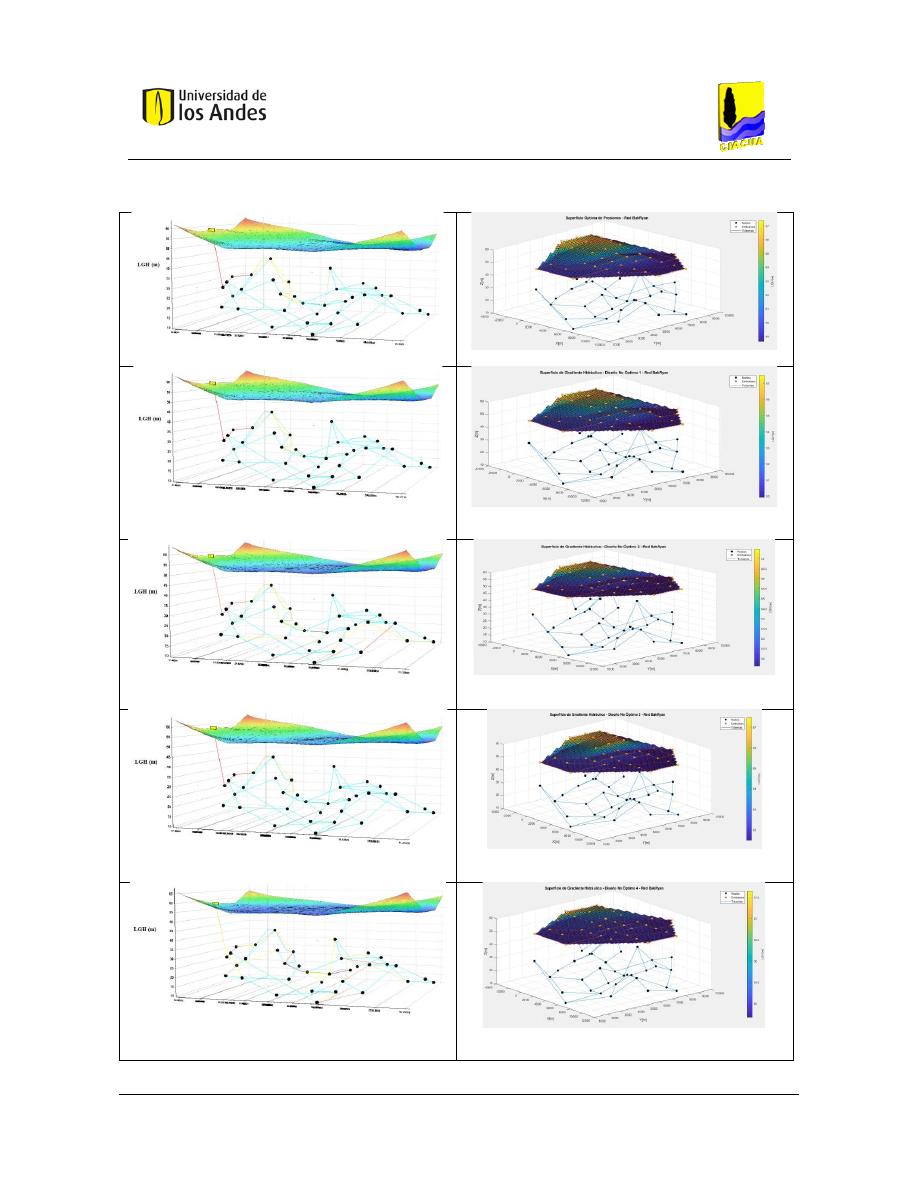
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
129
5.1.3.7 Red BakRyan
Figura 163. SOP Red BakRyan - REDES 2019.
Figura 164. SOP Red BakRyan - MATLAB.
Figura 165. Diseño No Óptimo 1 - Red BakRyan - REDES
2019.
Figura 166. Diseño No Óptimo 1 - Red BakRyan -
MATLAB.
Figura 167. Diseño No Óptimo 2 - Red BakRyan - REDES
2019.
Figura 168. Diseño No Óptimo 2 - Red BakRyan -
MATLAB.
Figura 169. Diseño No Óptimo 3 - Red BakRyan - REDES
2019.
Figura 170. Diseño No Óptimo 3 - Red BakRyan -
MATLAB.
Figura 171. Diseño No Óptimo 4 - Red BakRyan - REDES
2019.
Figura 172. Diseño No Óptimo 4 - Red BakRyan -
MATLAB.
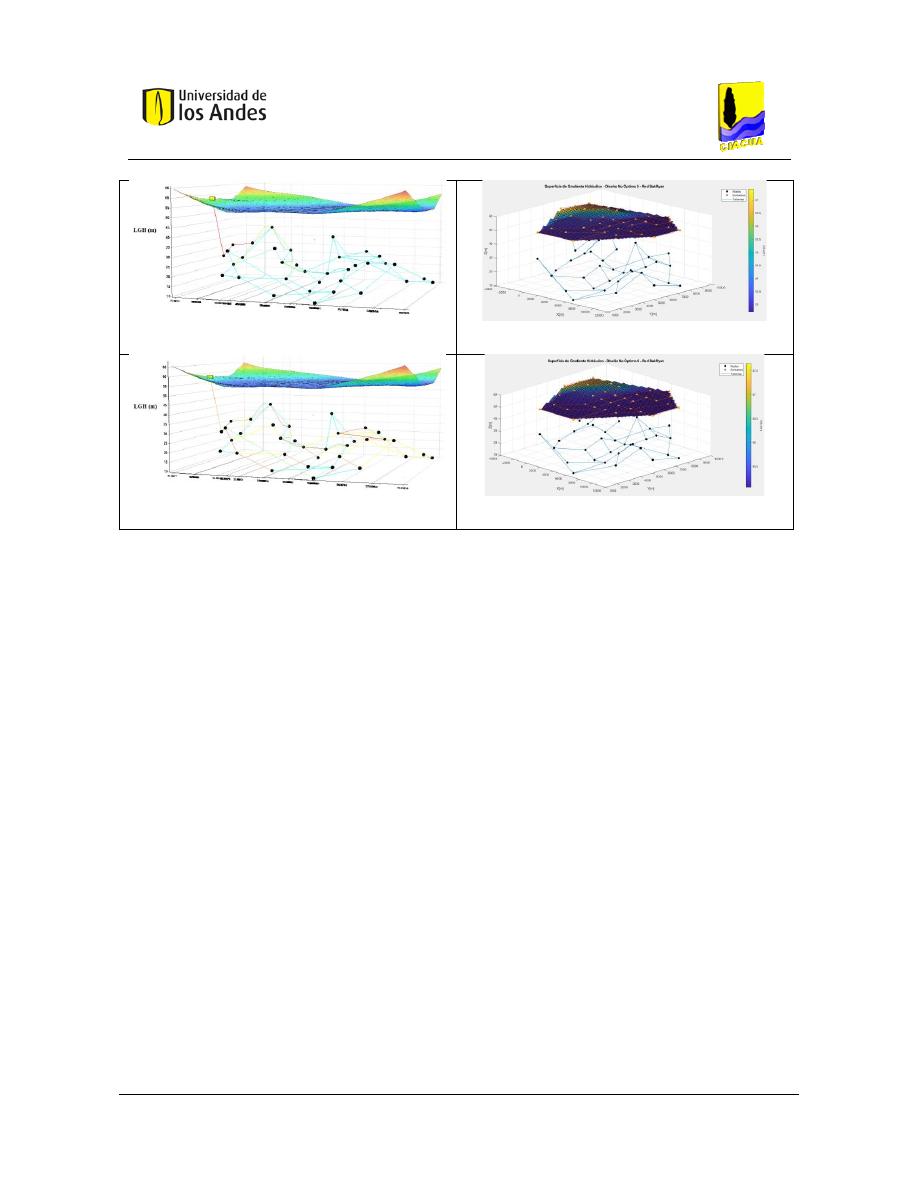
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
130
Figura 173. Diseño No Óptimo 5 - Red BakRyan - REDES
2019.
Figura 174. Diseño No Óptimo 5 - Red BakRyan -
MATLAB.
Figura 175. Diseño No Óptimo 6 - Red BakRyan - REDES
2019.
Figura 176. Diseño No Óptimo 6 - Red BakRyan -
MATLAB.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
131
5.1.3.8 Red Fossolo
Figura 177. SOP Red Fossolo - REDES 2019.
Figura 178. SOP Red Fossolo - MATLAB.
Figura 179. Diseño No Óptimo 1 - Red Fossolo - REDES
2019.
Figura 180. Diseño No Óptimo 1 - Red Fossolo - MATLAB.
Figura 181. Diseño No Óptimo 2 - Red Fossolo - REDES
2019.
Figura 182. Diseño No Óptimo 2 - Red Fossolo - MATLAB.
Figura 183. Diseño No Óptimo 3 - Red Fossolo - REDES
2019.
Figura 184. Diseño No Óptimo 3 - Red Fossolo - MATLAB.
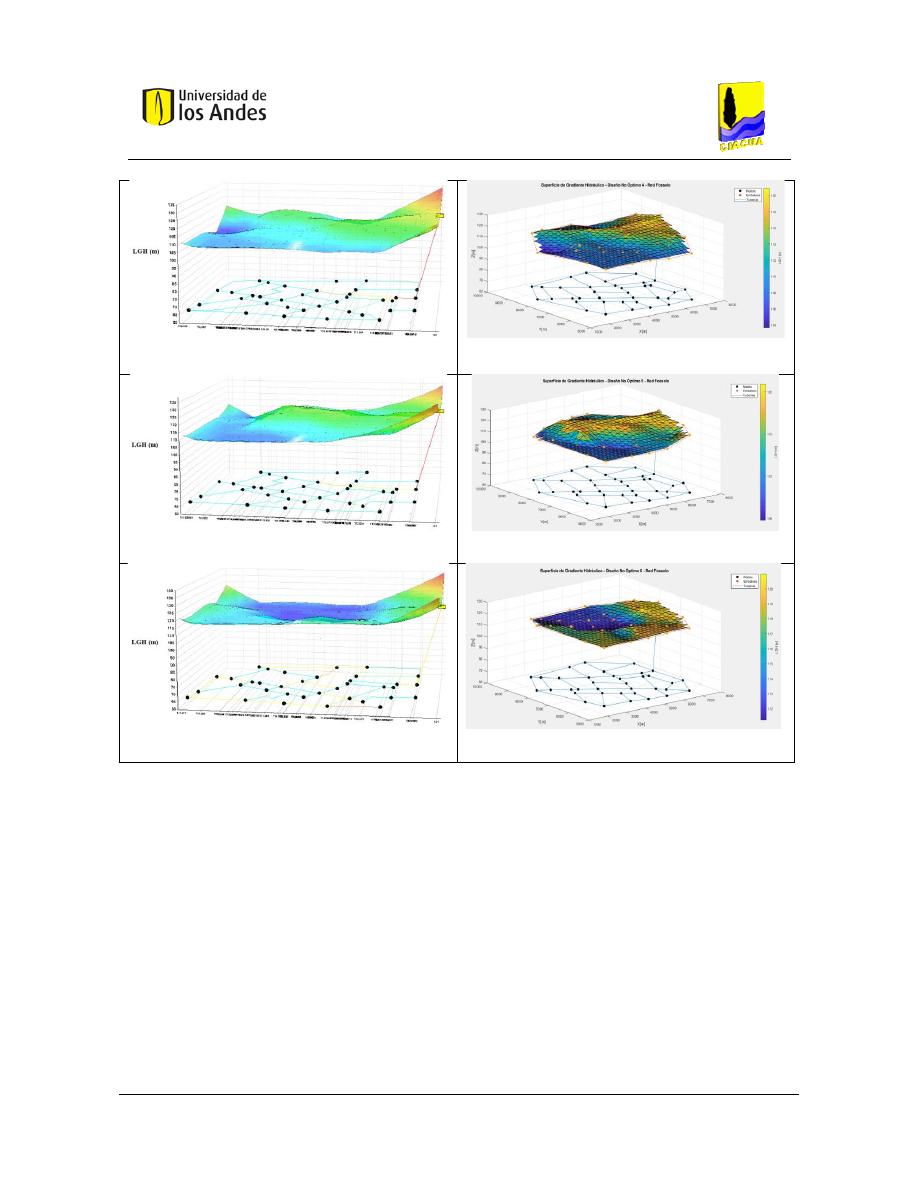
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
132
Figura 185. Diseño No Óptimo 4 - Red Fossolo - REDES
2019.
Figura 186. Diseño No Óptimo 4 - Red Fossolo - MATLAB.
Figura 187. Diseño No Óptimo 5 - Red Fossolo - REDES
2019.
Figura 188. Diseño No Óptimo 5 - Red Fossolo - MATLAB.
Figura 189. Diseño No Óptimo 6 - Red Fossolo - REDES
2019.
Figura 190. Diseño No Óptimo 6 - Red Fossolo - MATLAB.
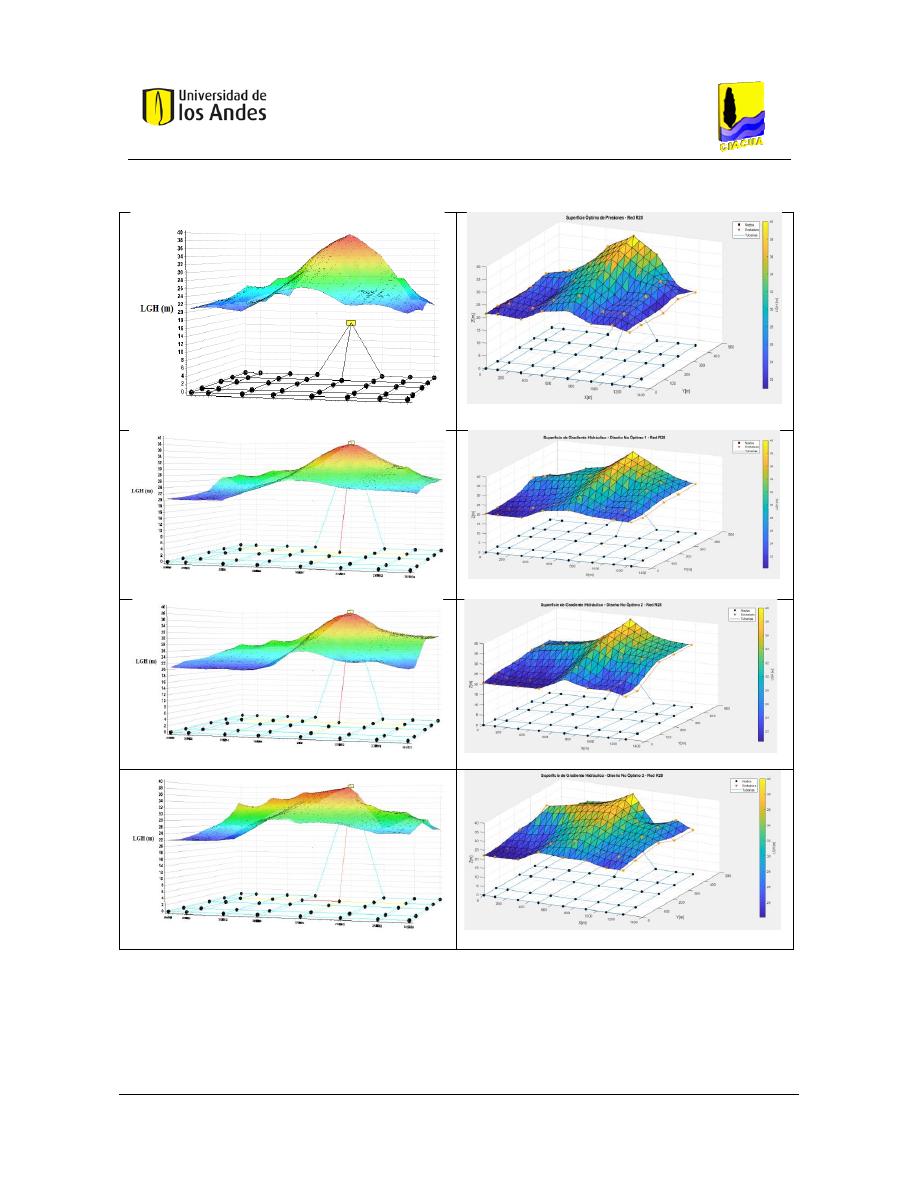
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
133
5.1.3.9 Red R28
Figura 191. SOP Red R28 - REDES 2019.
Figura 192. SOP Red R28 - MATLAB.
Figura 193. Diseño No Óptimo 1 - Red R28 - REDES 2019.
Figura 194. Diseño No Óptimo 1 - Red R28 - MATLAB.
Figura 195. Diseño No Óptimo 2 - Red R28 - REDES 2019.
Figura 196. Diseño No Óptimo 2 - Red R28 - MATLAB.
Figura 197. Diseño No Óptimo 3 - Red R28 - REDES 2019.
Figura 198. Diseño No Óptimo 3 - Red R28 - MATLAB.
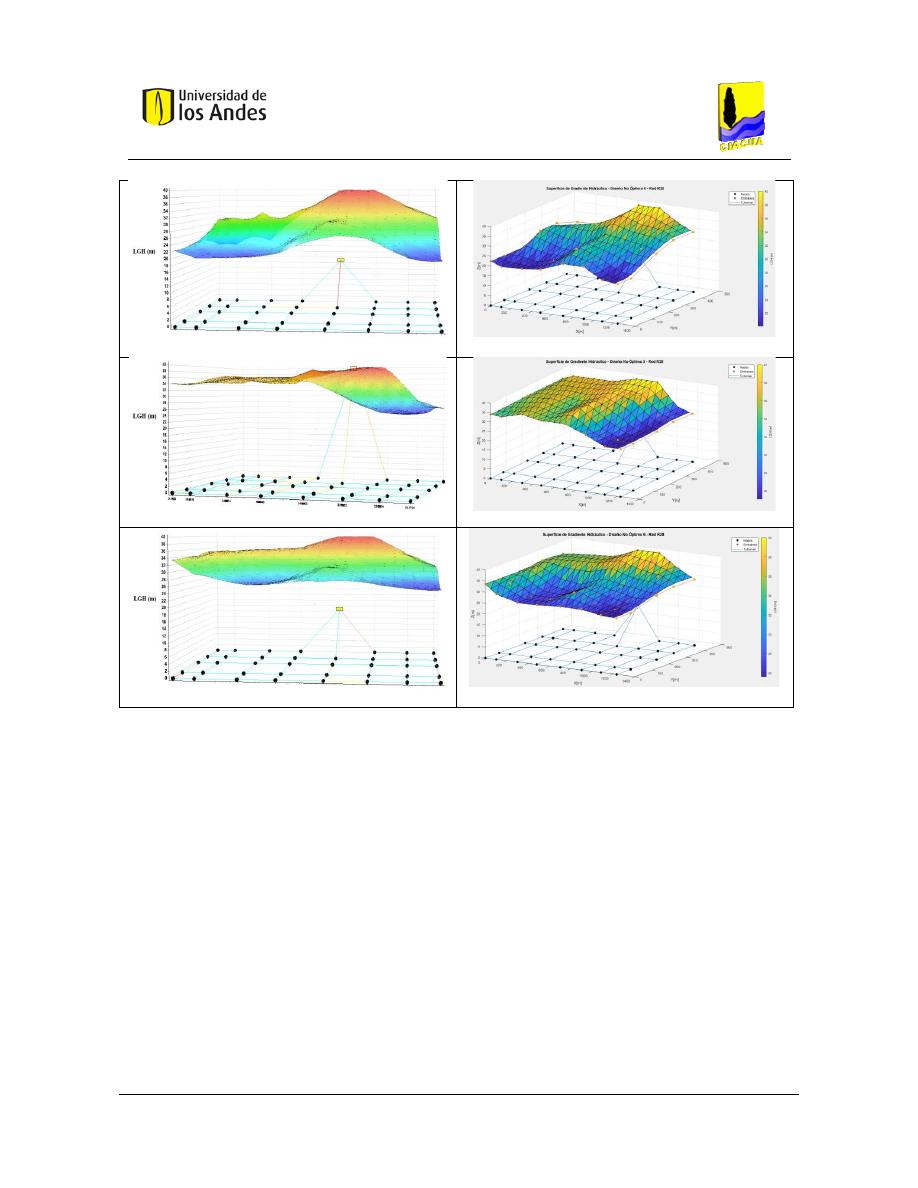
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
134
Figura 199. Diseño No Óptimo 4 - Red R28 - REDES 2019.
Figura 200. Diseño No Óptimo 4 - Red R28 - MATLAB.
Figura 201. Diseño No Óptimo 5 - Red R28 - REDES 2019.
Figura 202. Diseño No Óptimo 5 - Red R28 - MATLAB.
Figura 203. Diseño No Óptimo 6 – Red R28 – REDES 2019.
Figura 204. Diseño No Óptimo 6 - Red R28 - MATLAB.
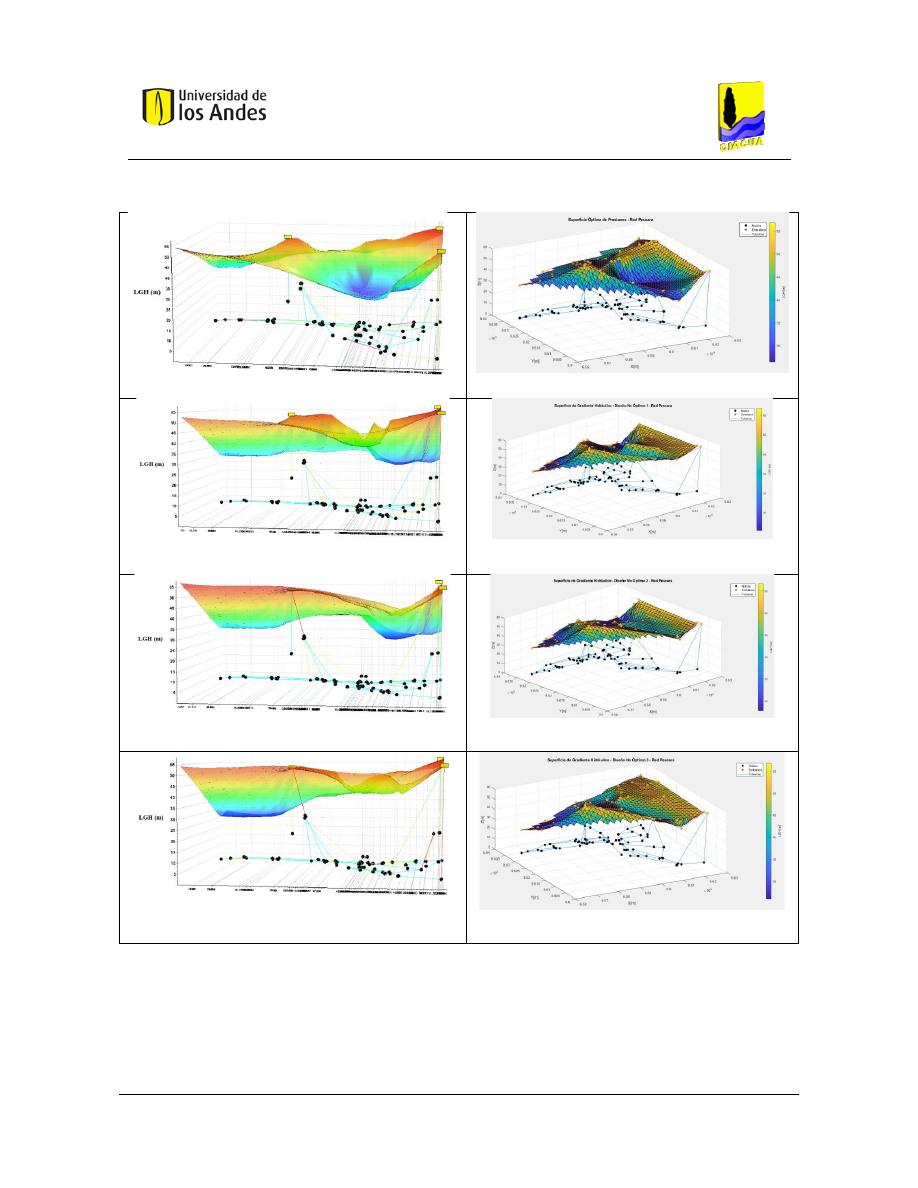
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
135
5.1.3.10 Red Pescara
Figura 205. SOP Red Pescara - REDES 2019.
Figura 206. SOP Red Pescara - MATLAB.
Figura 207. Diseño No Óptimo 1 - Red Pescara - REDES
2019.
Figura 208. Diseño No Óptimo 1 - Red Pescara -
MATLAB.
Figura 209. Diseño No Óptimo 2 - Red Pescara - REDES
2019.
Figura 210. Diseño No Óptimo 2 - Red Pescara -
MATLAB.
Figura 211. Diseño No Óptimo 3 - Red Pescara - REDES
2019.
Figura 212. Diseño No Óptimo 3 - Red Pescara -
MATLAB.
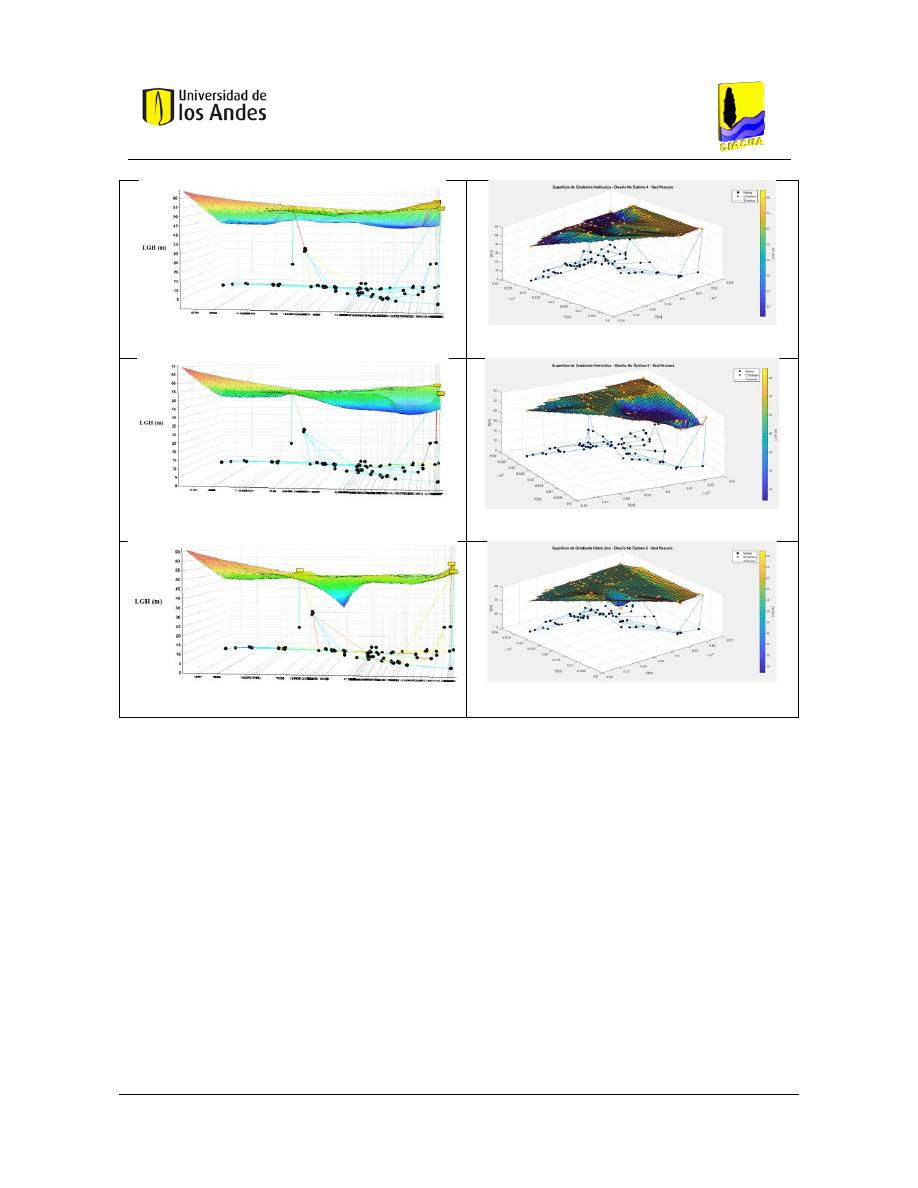
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
136
Figura 213. Diseño No Óptimo 4 - Red Pescara - REDES
2019.
Figura 214. Diseño No Óptimo 4 - Red Pescara -
MATLAB.
Figura 215. Diseño No Óptimo 5 - Red Pescara - REDES
2019.
Figura 216. Diseño No Óptimo 5 - Red Pescara -
MATLAB.
Figura 217. Diseño No Óptimo 6 - Red Pescara – REDES
2019.
Figura 218. Diseño No Óptimo 6 - Red Pescara -
MATLAB.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
137
5.1.3.11 Red Modena
Figura 219. SOP Red Modena - REDES 2019.
Figura 220. SOP Red Modena - MATLAB.
Figura 221. Diseño No Óptimo 1 - Red Modena - REDES
2019.
Figura 222. Diseño No Óptimo 1 - Red Modena -
MATLAB.
Figura 223. Diseño No Óptimo 2 - Red Modena - REDES
2019.
Figura 224. Diseño No Óptimo 2 - Red Modena -
MATLAB.
Figura 225. Diseño No Óptimo 3 - Red Modena - REDES
2019.
Figura 226. Diseño No Óptimo 3 - Red Modena -
MATLAB.
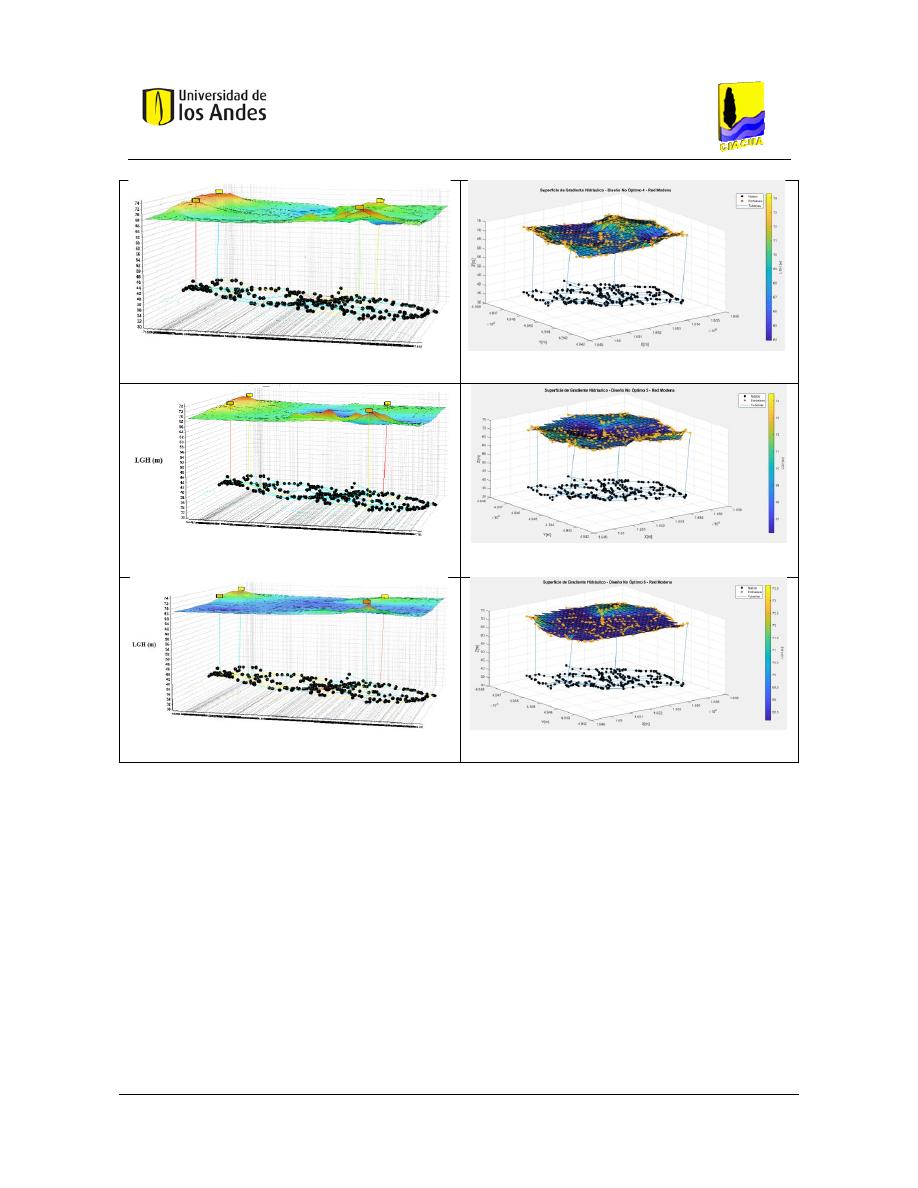
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
138
Figura 227. Diseño No Óptimo 4 - Red Modena - REDES
2019.
Figura 228. Diseño No Óptimo 4 - Red Modena -
MATLAB.
Figura 229. Diseño No Óptimo 5 - Red Modena - REDES
2019.
Figura 230. Diseño No Óptimo 5 - Red Modena -
MATLAB.
Figura 231. Diseño No Óptimo 6 - Red Modena - REDES
2019.
Figura 232. Diseño No Óptimo 6 - Red Modena -
MATLAB.
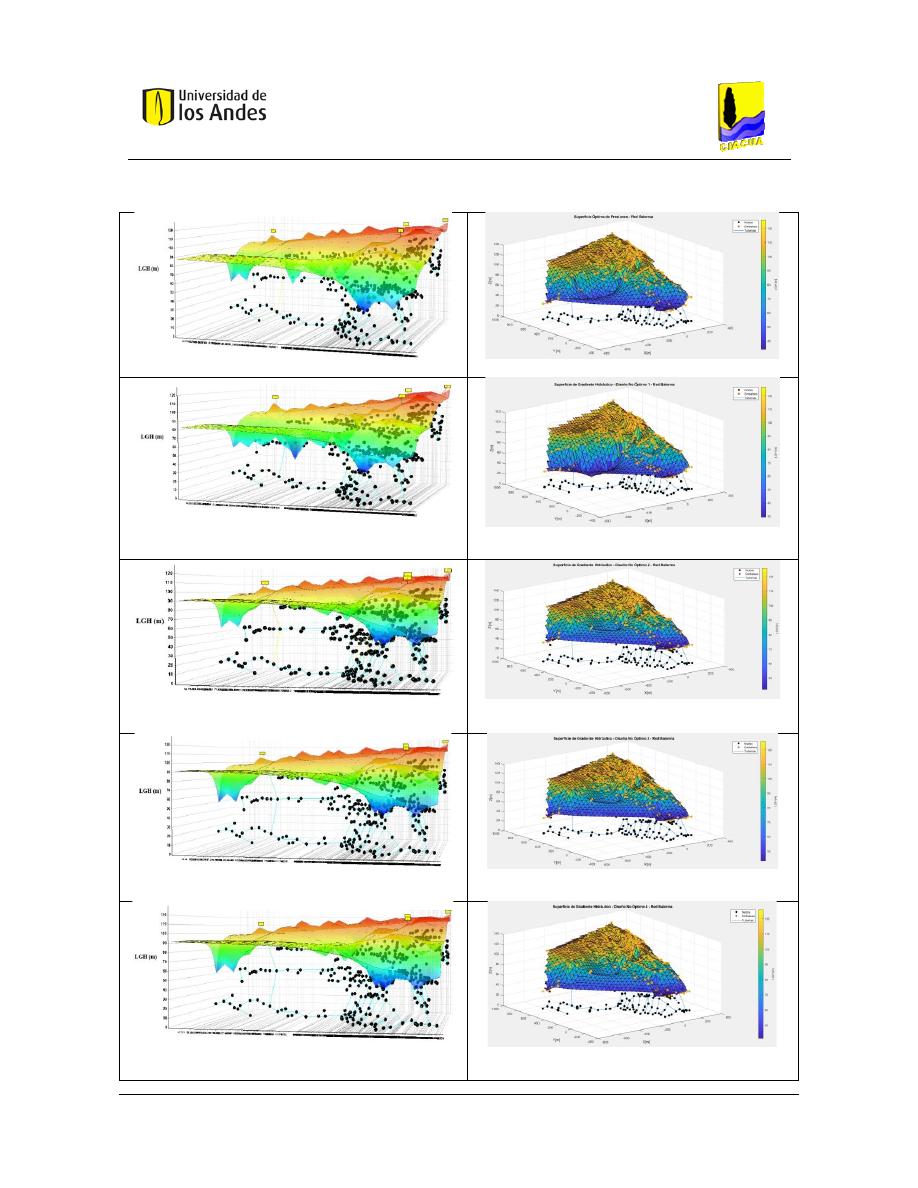
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
139
5.1.3.12 Red Balerma
Figura 233. SOP Red Balerma - REDES 2019.
Figura 234. SOP Red Balerma - MATLAB.
Figura 235. Diseño No Óptimo 1 - Red Balerma - REDES
2019.
Figura 236. Diseño No Óptimo 1 - Red Balerma -
MATLAB.
Figura 237. Diseño No Óptimo 2 - Red Balerma - REDES
2019.
Figura 238. Diseño No Óptimo 2 - Red Balerma -
MATLAB.
Figura 239. Diseño No Óptimo 3 - Red Balerma - REDES
2019.
Figura 240. Diseño No Óptimo 3 - Red Balerma -
MATLAB.
Figura 241. Diseño No Óptimo 4 - Red Balerma - REDES
2019.
Figura 242. Diseño No Óptimo 4 - Red Balerma -
MATLAB.
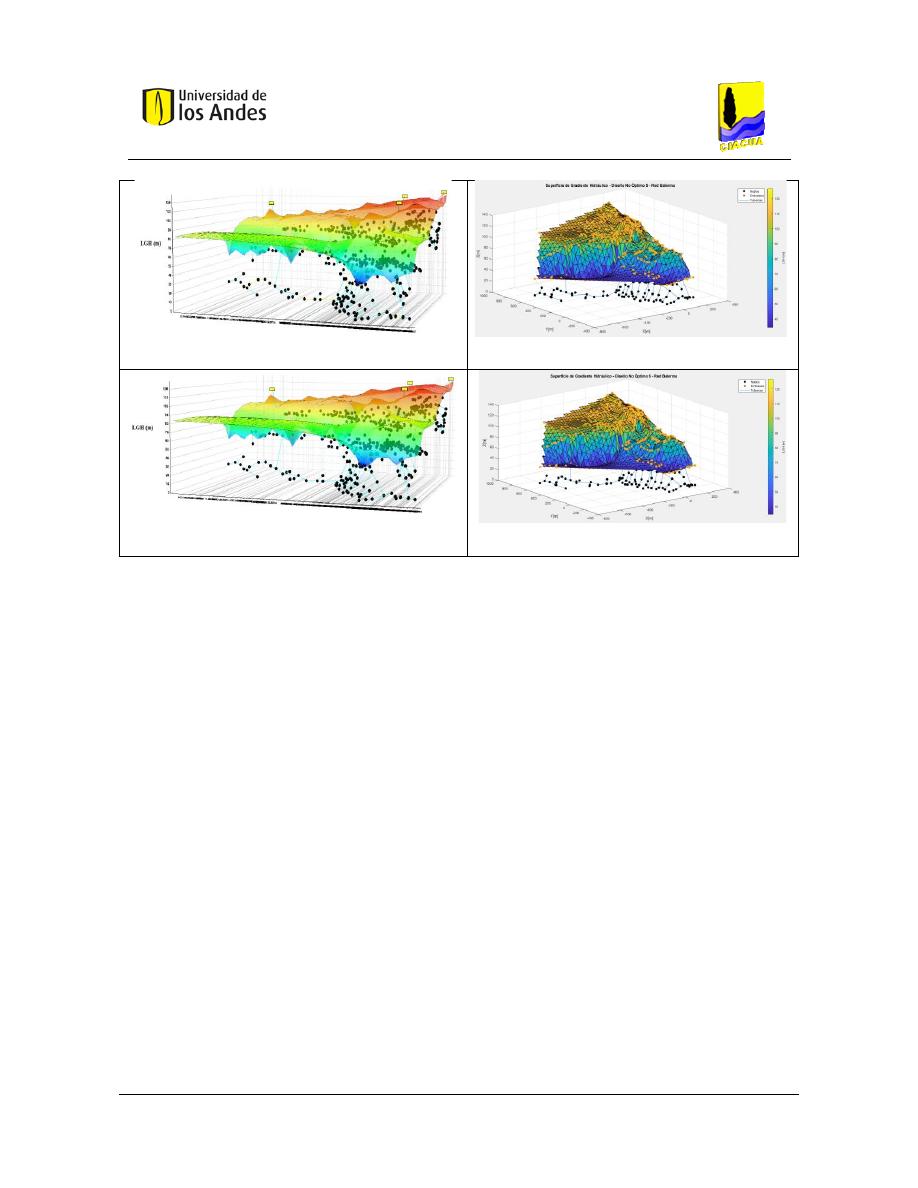
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
140
Figura 243. Diseño No Óptimo 5 – Red Balerma - REDES
2019.
Figura 244. Diseño No Óptimo 5 - Red Balerma -
MATLAB.
Figura 245. Diseño No Óptimo 6 - Red Balerma - REDES
2019.
Figura 246. Diseño No Óptimo 6 - Red Balerma -
MATLAB.
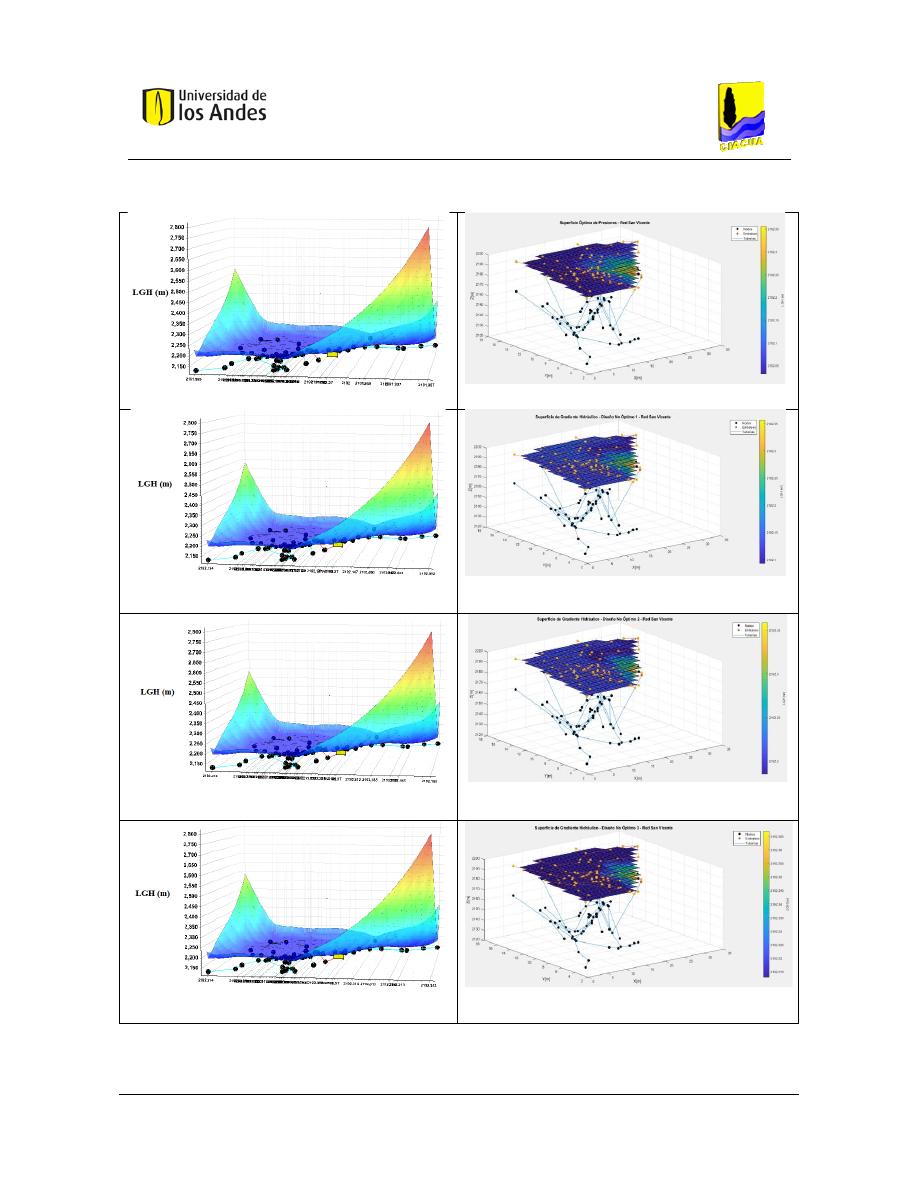
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
141
5.1.3.13 Red San Vicente
Figura 247. SOP San Vicente - REDES 2019.
Figura 248. SOP San Vicente - MATLAB.
Figura 249. Diseño No Óptimo 1 – Red San Vicente -
REDES 2019.
Figura 250. Diseño No Óptimo 1 - Red San Vicente -
MATLAB.
Figura 251. Diseño No Óptimo 2 - Red San Vicente -
REDES 2019.
Figura 252. Diseño No Óptimo 2 - Red San Vicente -
MATLAB.
Figura 253. Diseño No Óptimo 3 - Red San Vicente -
REDES 2019.
Figura 254. Diseño No Óptimo 3 - Red San Vicente -
MATLAB.
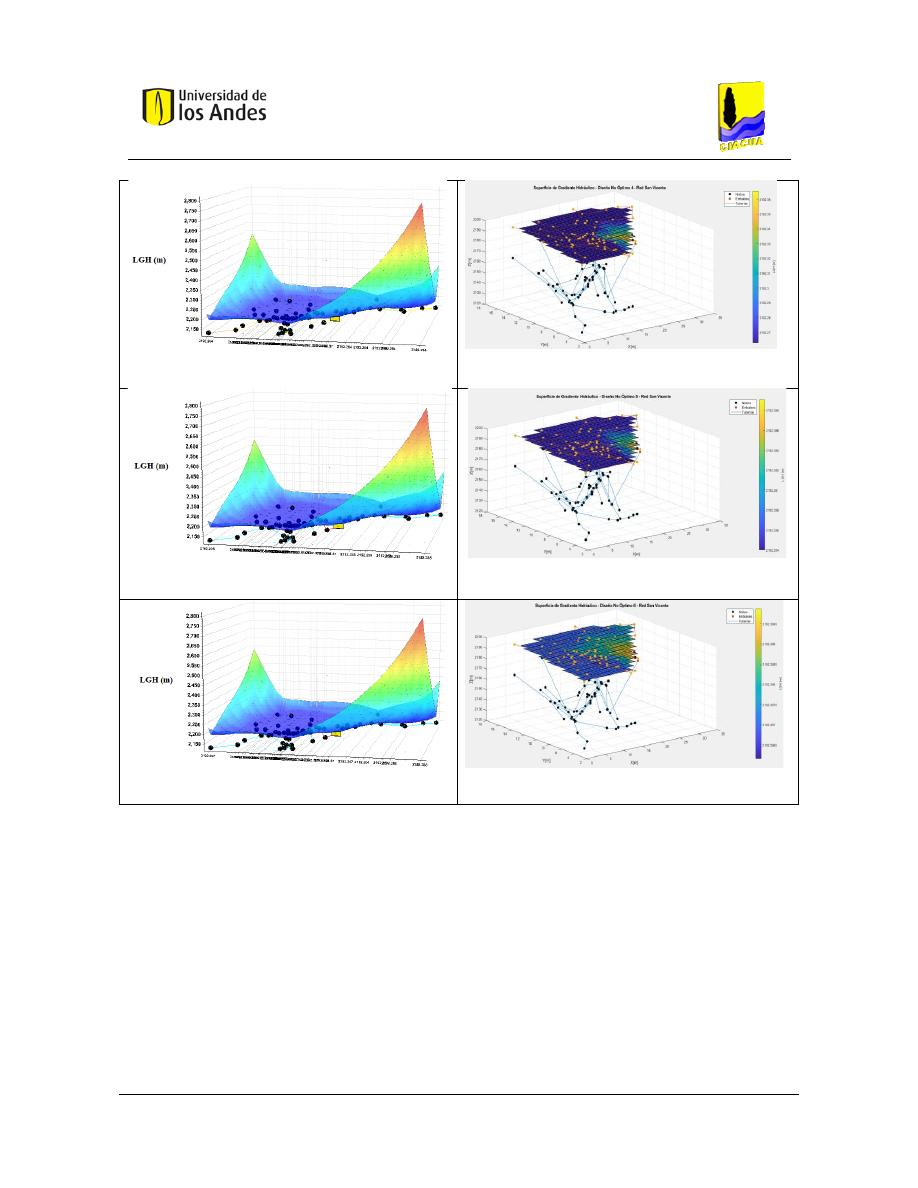
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
142
Figura 255. Diseño No Óptimo 4 - Red San Vicente -
REDES 2019.
Figura 256. Diseño No Óptimo 4 - Red San Vicente -
MATLAB.
Figura 257. Diseño No Óptimo 5 - Red San Vicente -
REDES 2019.
Figura 258. Diseño No Óptimo 5 - Red San Vicente -
MATLAB.
Figura 259. Diseño No Óptimo 6 - Red San Vicente -
REDES 2019.
Figura 260. Diseño No Óptimo 6 - Red San Vicente -
MATLAB.
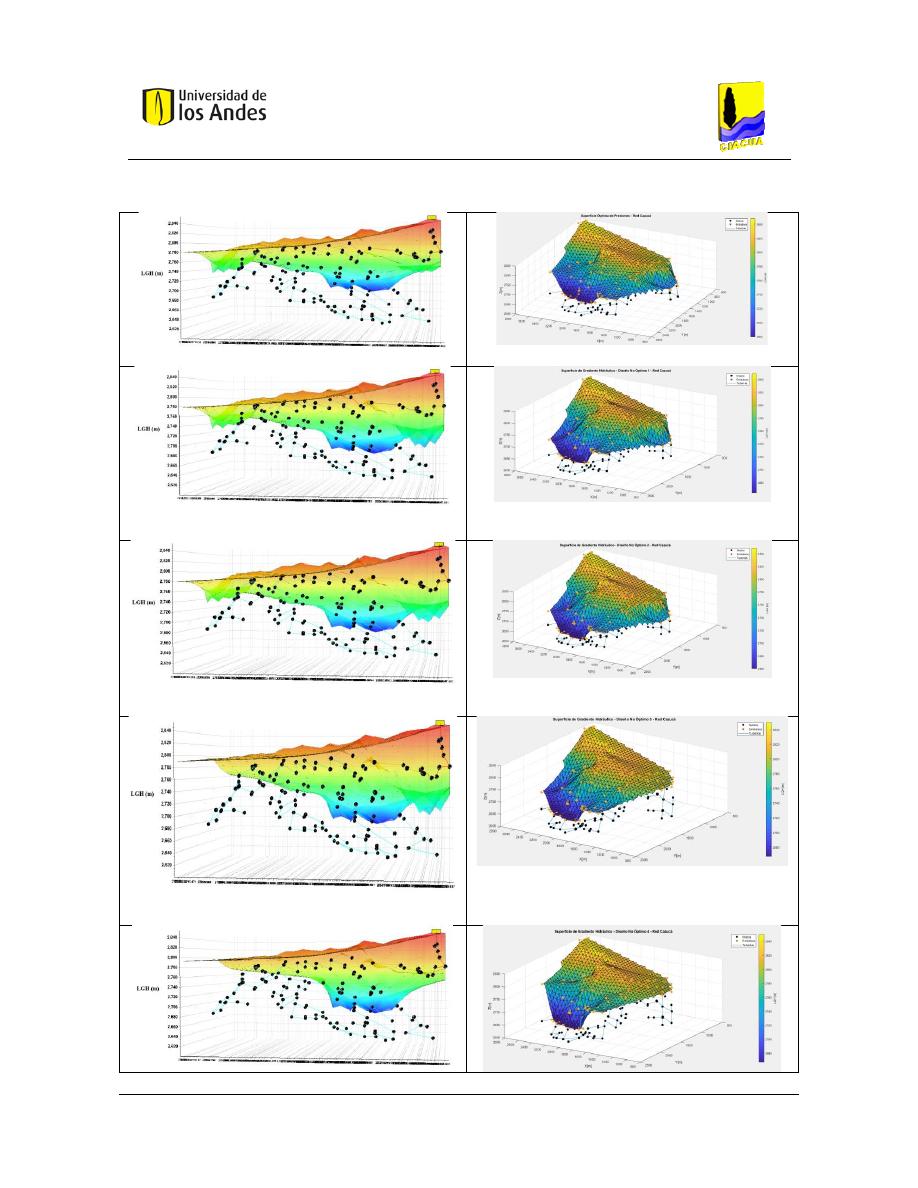
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
143
5.1.3.14 Red Cazucá
Figura 261. SOP Red Cazucá - REDES 2019.
Figura 262. SOP Red Cazucá - MATLAB.
Figura 263. Diseño No Óptimo 1 - Red Cazucá - REDES
2019.
Figura 264. Diseño No Óptimo 1 - Red Cazucá - MATLAB.
Figura 265. Diseño No Óptimo 2 - Red Cazucá - REDES
2019.
Figura 266. Diseño No Óptimo 2 - Red Cazucá - MATLAB.
Figura 267. Diseño No Óptimo 3 - Red Cazucá - REDES
2019.
Figura 268. Diseño No Óptimo 3 - Red Cazucá - MATLAB.
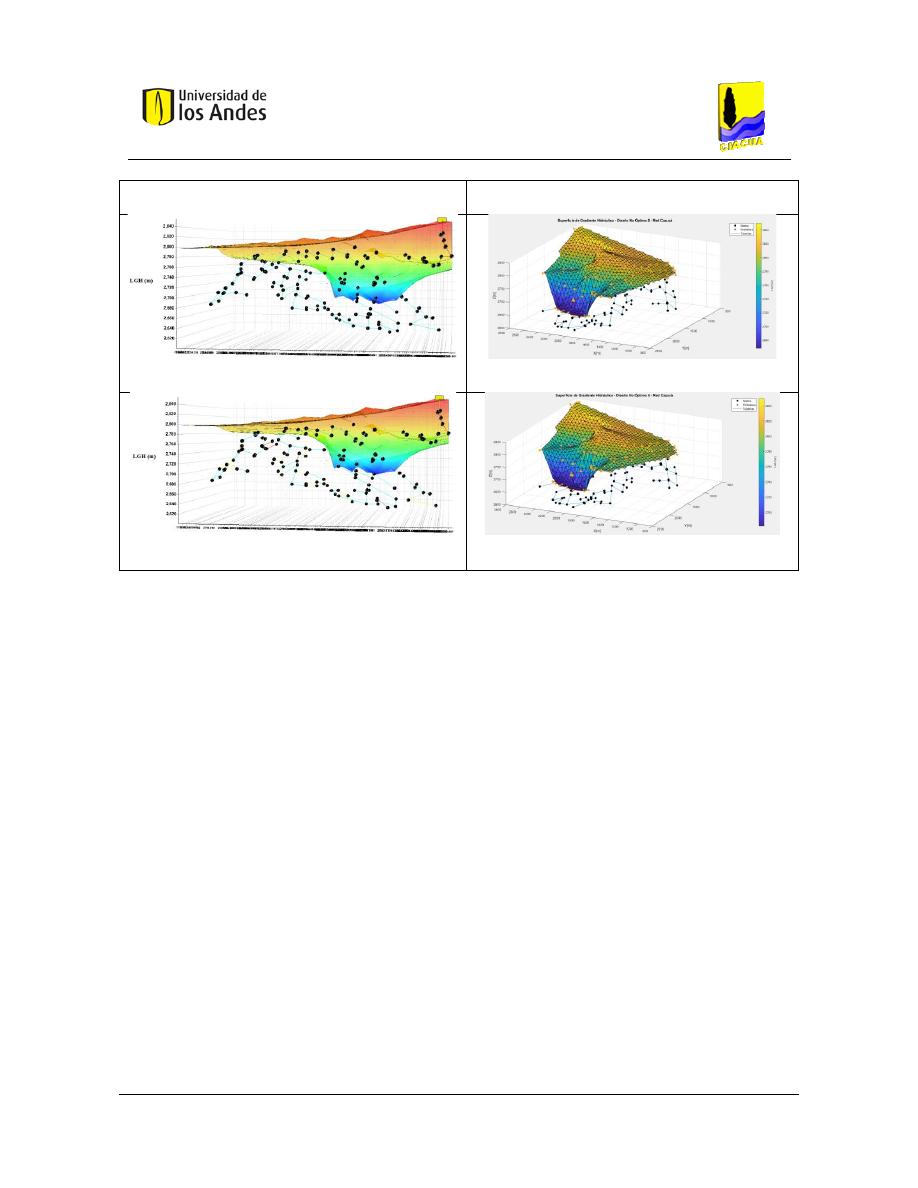
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
144
Figura 269. Diseño No Óptimo 4 - Red Cazucá - REDES
2019.
Figura 270. Diseño No Óptimo 4 - Red Cazucá - MATLAB.
Figura 271. Diseño No Óptimo 5 - Red Cazucá - REDES
2019.
Figura 272. Diseño No Óptimo 5 - Red Cazucá - MATLAB.
Figura 273. Diseño No Óptimo 6 - Red Cazucá - REDES
2019.
Figura 274. Diseño No Óptimo 6 - Red Cazucá - MATLAB.
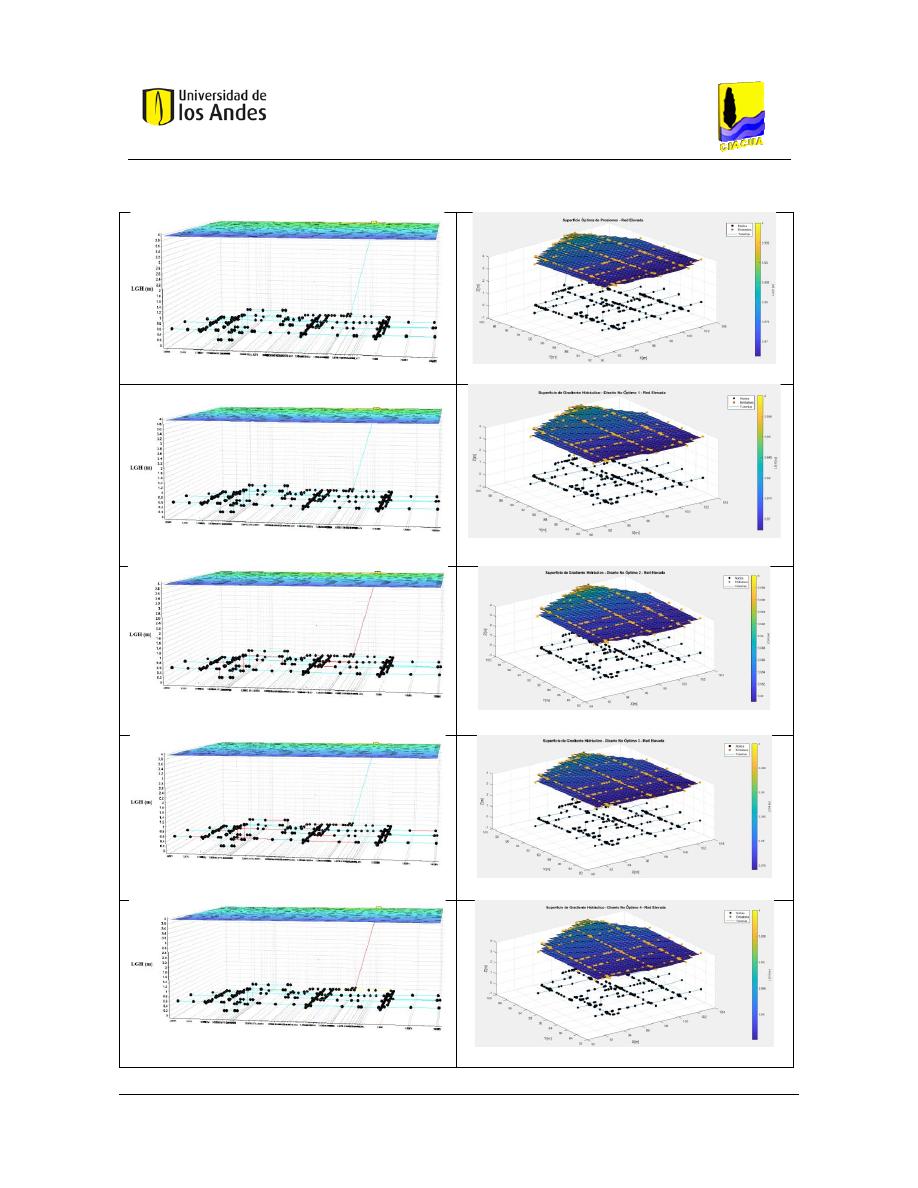
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
145
5.1.3.15 Red Elevada
Figura 275. SOP Red Elevada - REDES 2019.
Figura 276. SOP Red Elevada - MATLAB.
Figura 277. Diseño No Óptimo 1 - Red Elevada - REDES
2019.
Figura 278. Diseño No Óptimo 1 - Red Elevada - MATLAB.
Figura 279. Diseño No Óptimo 2 - Red Elevada - REDES
2019.
Figura 280. Diseño No Óptimo 2 - Red Elevada - MATLAB.
Figura 281. Diseño No Óptimo 3 - Red Elevada - REDES
2019.
Figura 282. Diseño No Óptimo 3 - Red Elevada - MATLAB.
Figura 283. Diseño No Óptimo 4 - Red Elevada - REDES
2019.
Figura 284. Diseño No Óptimo 4 - Red Elevada - MATLAB.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
146
Figura 285. Diseño No Óptimo 5 - Red Elevada - REDES
2019.
Figura 286. Diseño No Óptimo 5 - Red Elevada - MATLAB.
Figura 287. Diseño No Óptimo 6 - Red Elevada - REDES
2019.
Figura 288. Diseño No Óptimo 6 - Red Elevada - MATLAB.
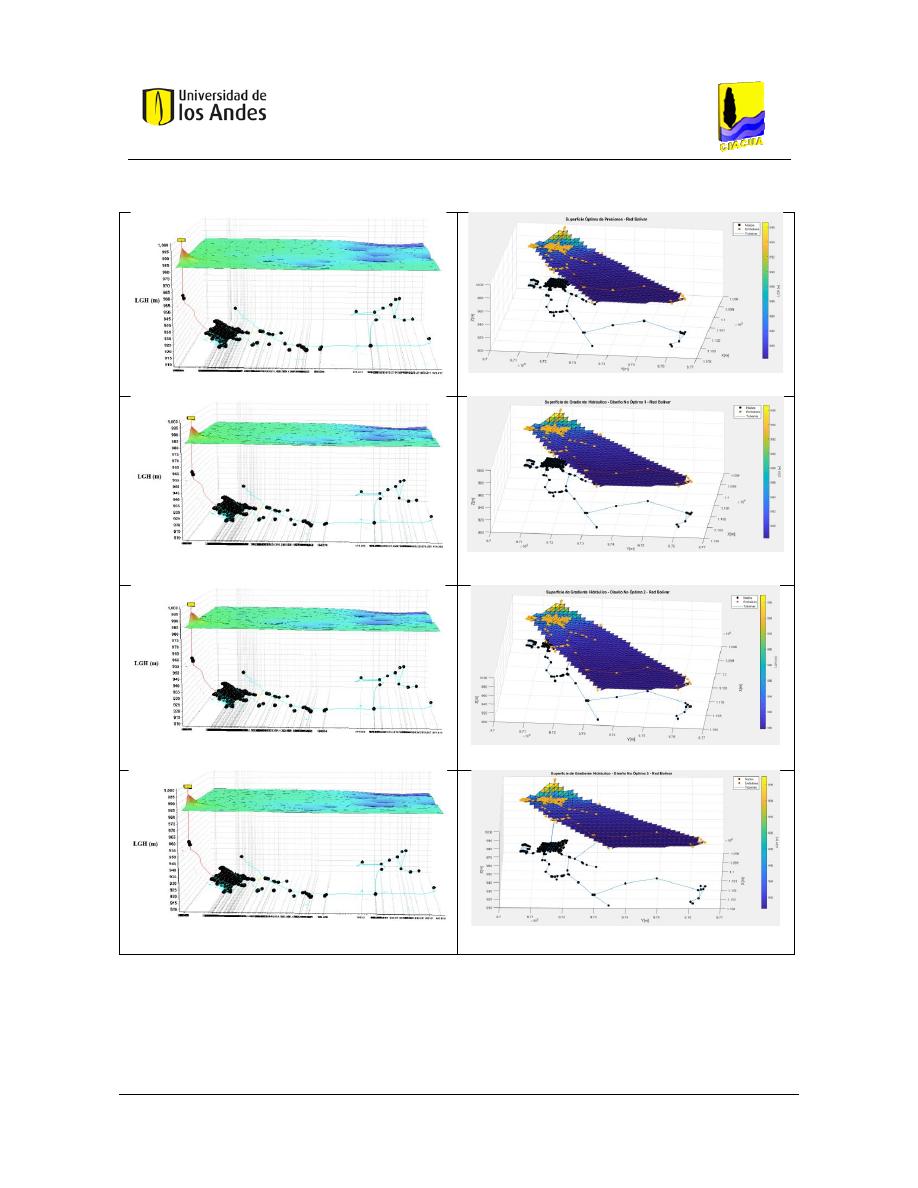
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
147
5.1.3.16 Red Bolívar
Figura 289. SOP Red Bolívar - REDES 2019.
Figura 290. SOP Red Bolívar - MATLAB.
Figura 291. Diseño No Óptimo 1 - Red Bolívar - REDES
2019.
Figura 292. Diseño No Óptimo 1 - Red Bolívar - MATLAB.
Figura 293. Diseño No Óptimo 2 - Red Bolívar - REDES
2019.
Figura 294. Diseño No Óptimo 2 - Red Bolívar - MATLAB.
Figura 295. Diseño No Óptimo 3 - Red Bolívar - REDES
2019.
Figura 296. Diseño No Óptimo 3 - Red Bolívar - MATLAB.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
148
Figura 297. Diseño No Óptimo 4 - Red Bolívar - REDES
2019.
Figura 298. Diseño No Óptima 4 - Red Bolívar - MATLAB.
Figura 299. Diseño No Óptimo 5- Red Bolívar - REDES
2019.
Figura 300. Diseño No Óptima 5 - Red Bolívar - MATLAB.
Figura 301. Diseño No Óptimo 6 - Red Bolívar - REDES
2019.
Figura 302. Diseño No Óptimo 6 - Red Bolívar - MATLAB.
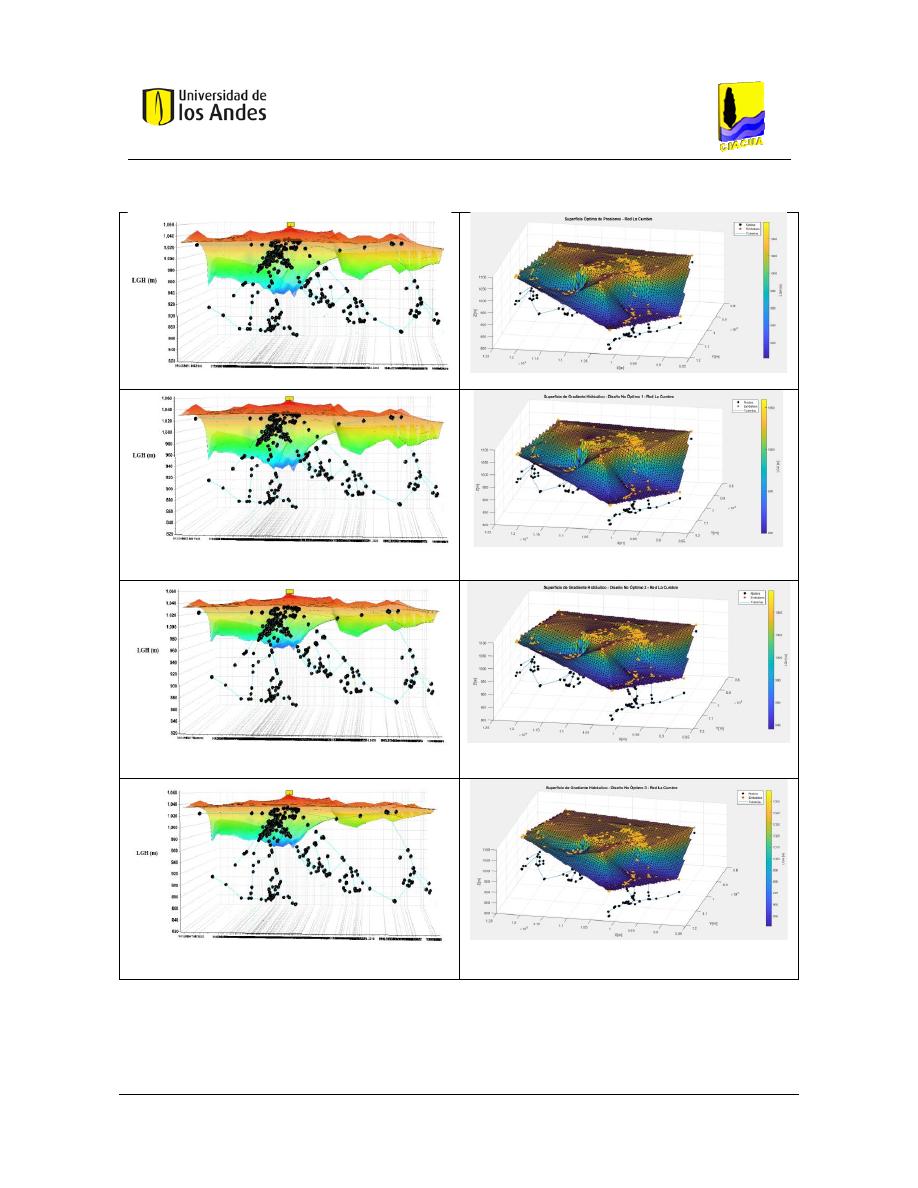
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
149
5.1.3.17 Red La Cumbre
Figura 303. SOP Red La Cumbre - REDES 2019.
Figura 304. SOP Red La Cumbre - MATLAB.
Figura 305. Diseño No Óptimo 1 - Red La Cumbre - REDES
2019.
Figura 306. Diseño No Óptimo 1 - Red La Cumbre -
MATLAB.
Figura 307. Diseño No Óptimo 2 - Red La Cumbre - REDES
2019.
Figura 308. Diseño No Óptimo 2 - Red La Cumbre -
MATLAB.
Figura 309. Diseño No Óptimo 3 - Red La Cumbre - REDES
2019.
Figura 310. Diseño No Óptimo 3 - Red La Cumbre -
MATLAB.
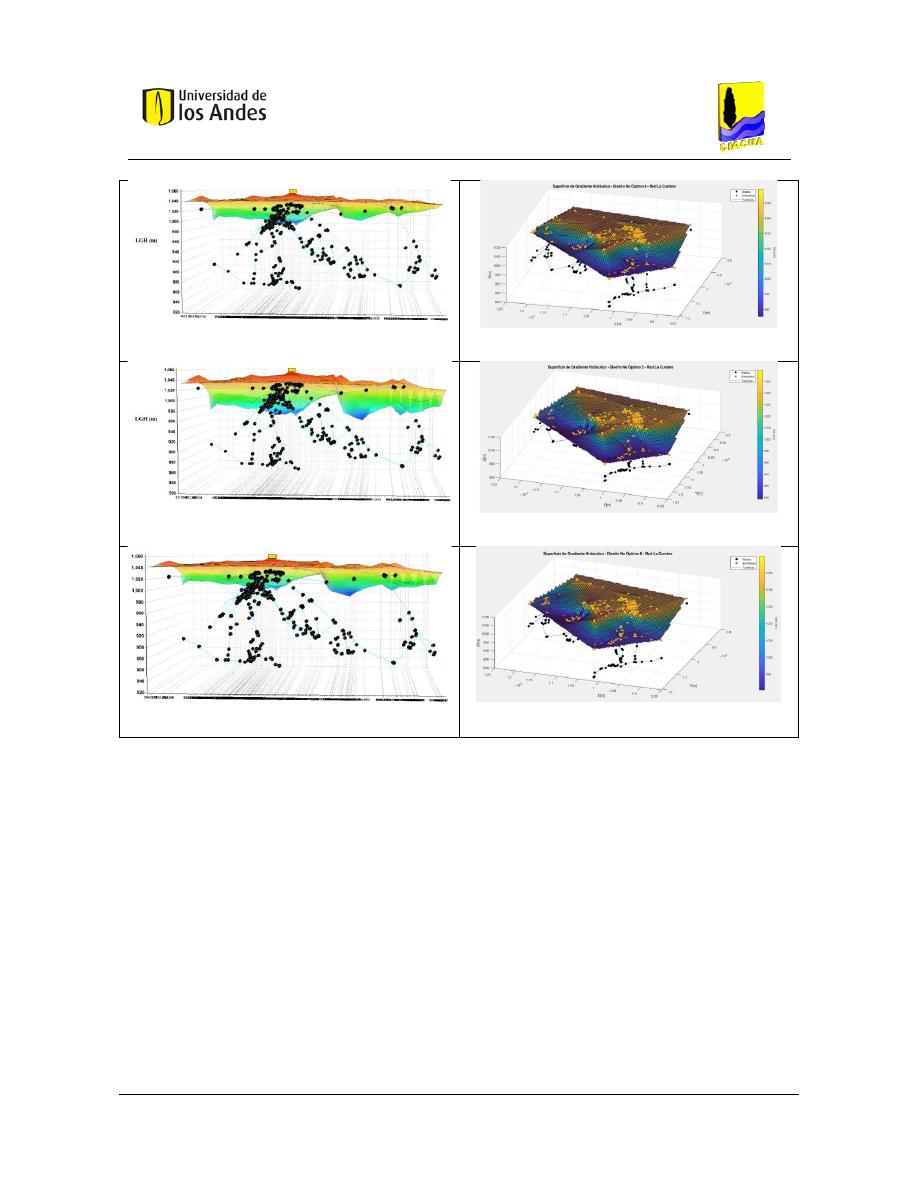
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
150
Figura 311. Diseño No Óptimo 4 - Red La Cumbre - REDES
2019.
Figura 312. Diseño No Óptimo 4 - Red La Cumbre -
MATLAB.
Figura 313. Diseño No Óptimo 5 - Red La Cumbre - REDES
2019.
Figura 314. Diseño No Óptimo 5 – Red La Cumbre -
MATLAB.
Figura 315. Diseño No Óptimo 6 - Red La Cumbre - REDES
2019.
Figura 316. Diseño No Óptimo 6 - Red La Cumbre -
MATLAB.
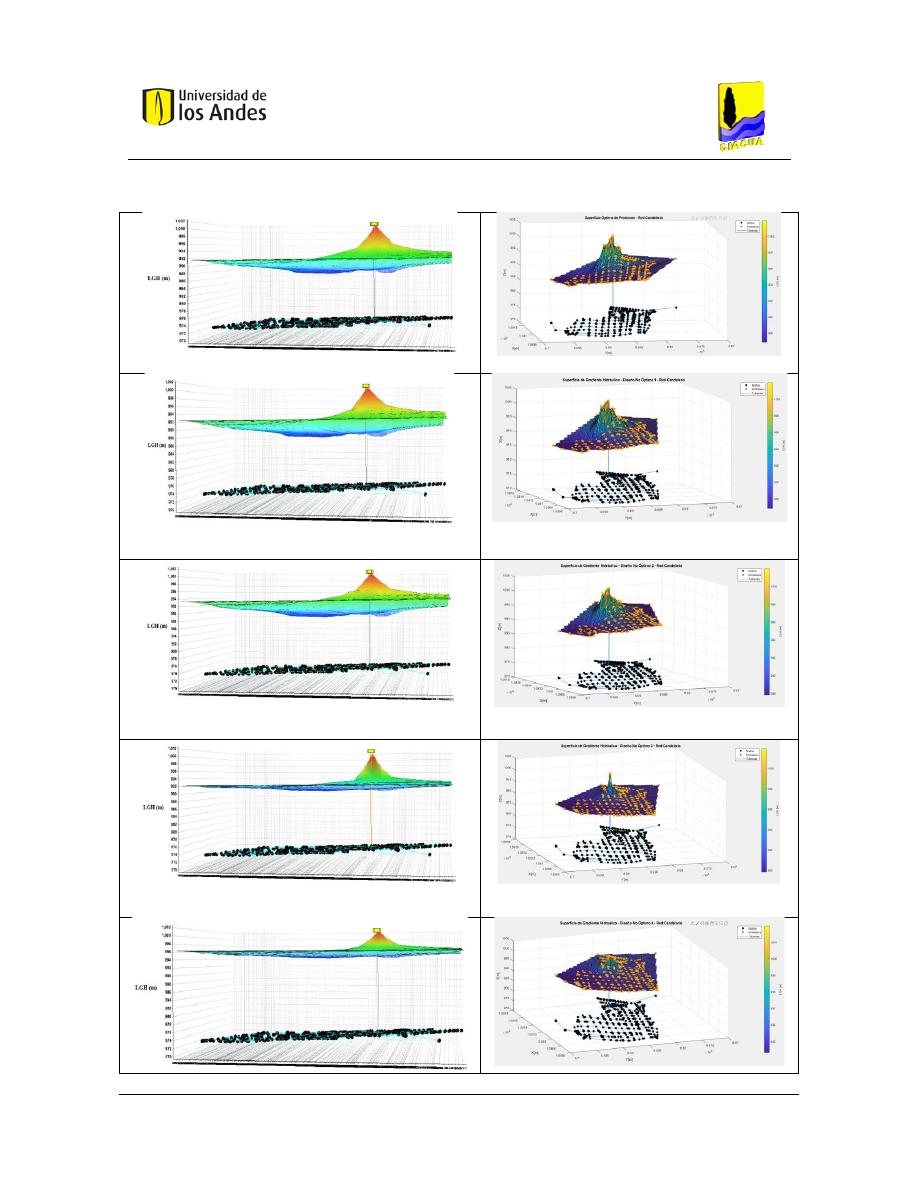
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
151
5.1.3.18 Red Candelaria
Figura 317. SOP Red Candelaria - REDES 2019.
Figura 318. SOP Red Candelaria - MATLAB.
Figura 319. Diseño No Óptimo 1 - Red Candelaria – REDES
2019.
Figura 320. Diseño No Óptimo 1 - Red Candelaria -
MATLAB.
Figura 321. Diseño No Óptimo 2 - Red Candelaria - REDES
2019.
Figura 322. Diseño No Óptimo 2 - Red Candelaria -
MATLAB.
Figura 323. Diseño No Óptimo 3 - Red Candelaria - REDES
2019.
Figura 324. Diseño No Óptimo 3 - Red Candelaria -
MATLAB.
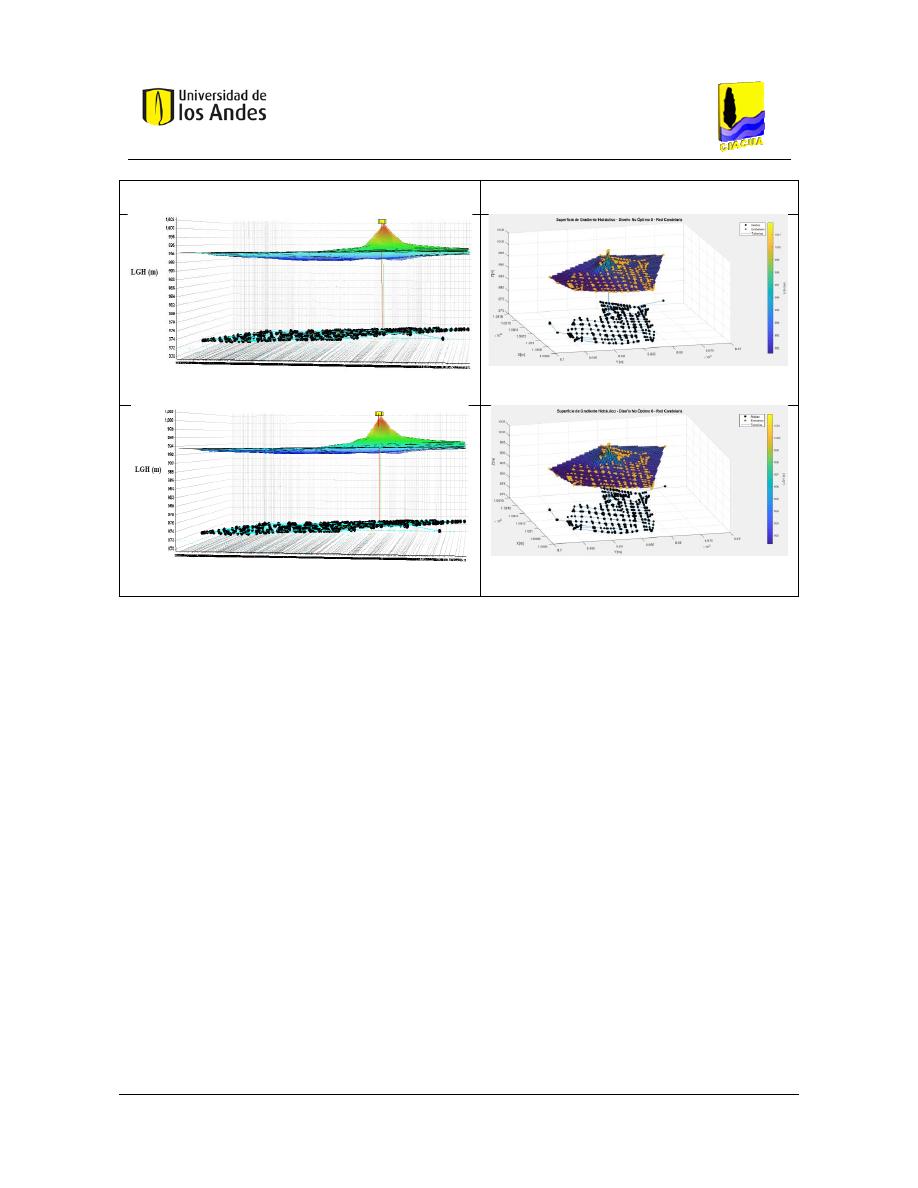
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
152
Figura 325. Diseño No Óptimo 4 - Red Candelaria - REDES
2019.
Figura 326. Diseño No Óptimo 4 - Red Candelaria -
MATLAB.
Figura 327. Diseño No Óptimo 5 - Red Candelaria - REDES
2019.
Figura 328. Diseño No Óptimo 5 - Red Candelaria -
MATLAB.
Figura 329. Diseño No Óptimo 6 - Red Candelaria - REDES
2019.
Figura 330. Diseño No Óptimo 6 - Red Candelaria -
MATLAB.
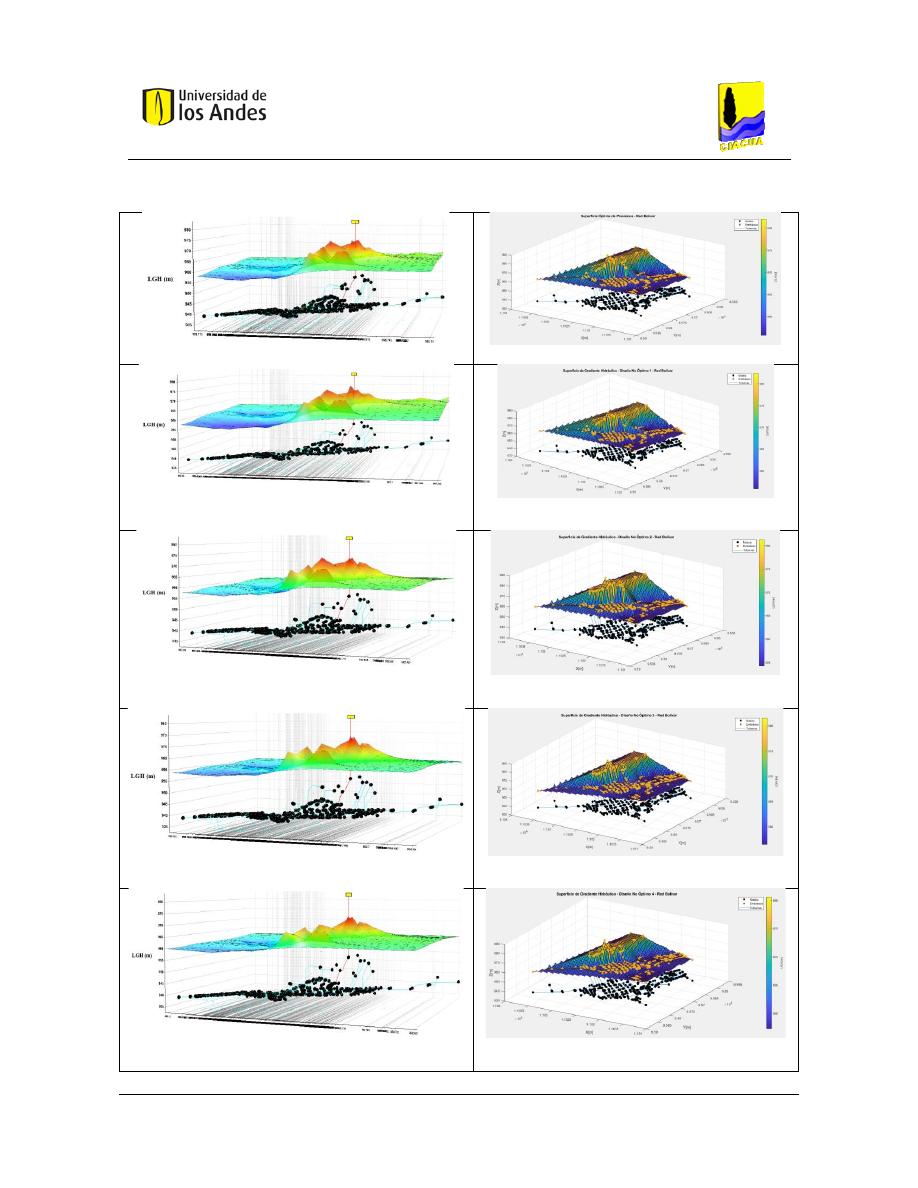
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
153
5.1.3.19 Red Bugalagrande
Figura 331. SOP Red Bugalagrande - REDES 2019.
Figura 332. SOP Bugalagrande - MATLAB.
Figura 333. Diseño No Óptimo 1 - Red Bugalagrande - REDES
2019.
Figura 334. Diseño No Óptimo 1 - Red Bugalagrande -
MATLAB.
Figura 335. Diseño No Óptimo 2 - Red Bugalagrande - REDES
2019.
Figura 336. Diseño No Óptimo 2 - Red Bugalagrande -
MATLAB.
Figura 337. Diseño No Óptimo 3 - Red Bugalagrande - REDES
2019.
Figura 338. Diseño No Óptimo 3 - Red Bugalagrande -
MATLAB.
Figura 339. Diseño No Óptimo 4 - Red Bugalagrande - REDES
2019.
Figura 340. Diseño No Óptimo 4 - Red Bugalagrande -
MATLAB.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
154
Figura 341. Diseño No Óptimo 5 - Red Bugalagrande - REDES
2019.
Figura 342. Diseño No Óptimo 5 - Red Bugalagrande -
MATLAB.
Figura 343. Diseño No Óptimo 6 - Red Bugalagrande - REDES
2019.
Figura 344. Diseño No Óptimo 6 - Red Bugalagrande -
MATLAB.
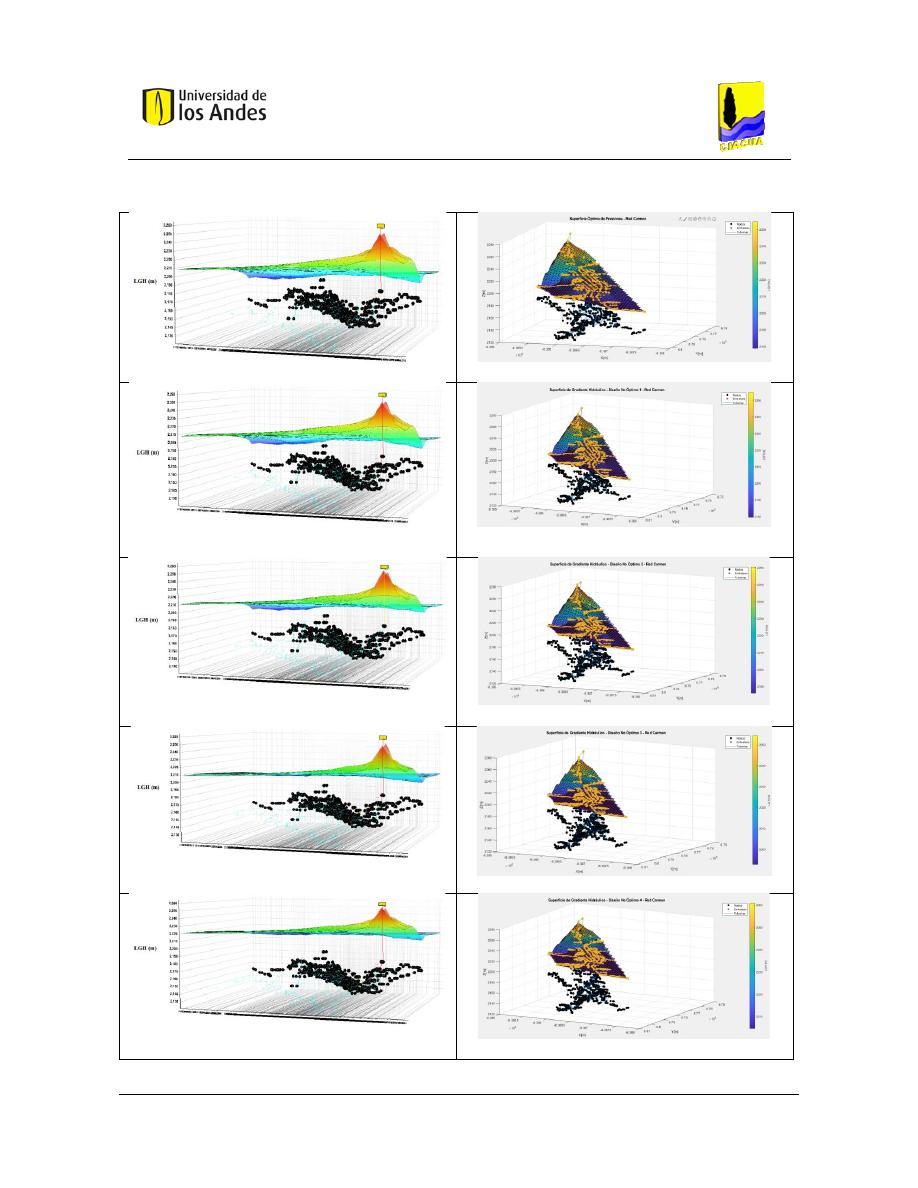
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
155
5.1.3.20 Red Carmen
Figura 345. SOP Red Carmen - REDES 2019.
Figura 346. SOP Red Carmen - MATLAB.
Figura 347. Diseño No Óptimo 1 - Red Carmen - REDES
2019.
Figura 348. Diseño No Óptimo 1 - Red Carmen - MATLAB.
Figura 349. Diseño No Óptimo 2 - Red Carmen - REDES
2019.
Figura 350. Diseño No Óptimo 2 - Red Carmen - MATLAB.
Figura 351. Diseño No Óptimo 3 - Red Carmen - REDES
2019.
Figura 352. Diseño No Óptimo 3 - Red Carmen - MATLAB.
Figura 353. Diseño No Óptimo 4 - Red Carmen - REDES
2019.
Figura 354. Diseño No Óptimo 4 - Red Carmen - MATLAB.
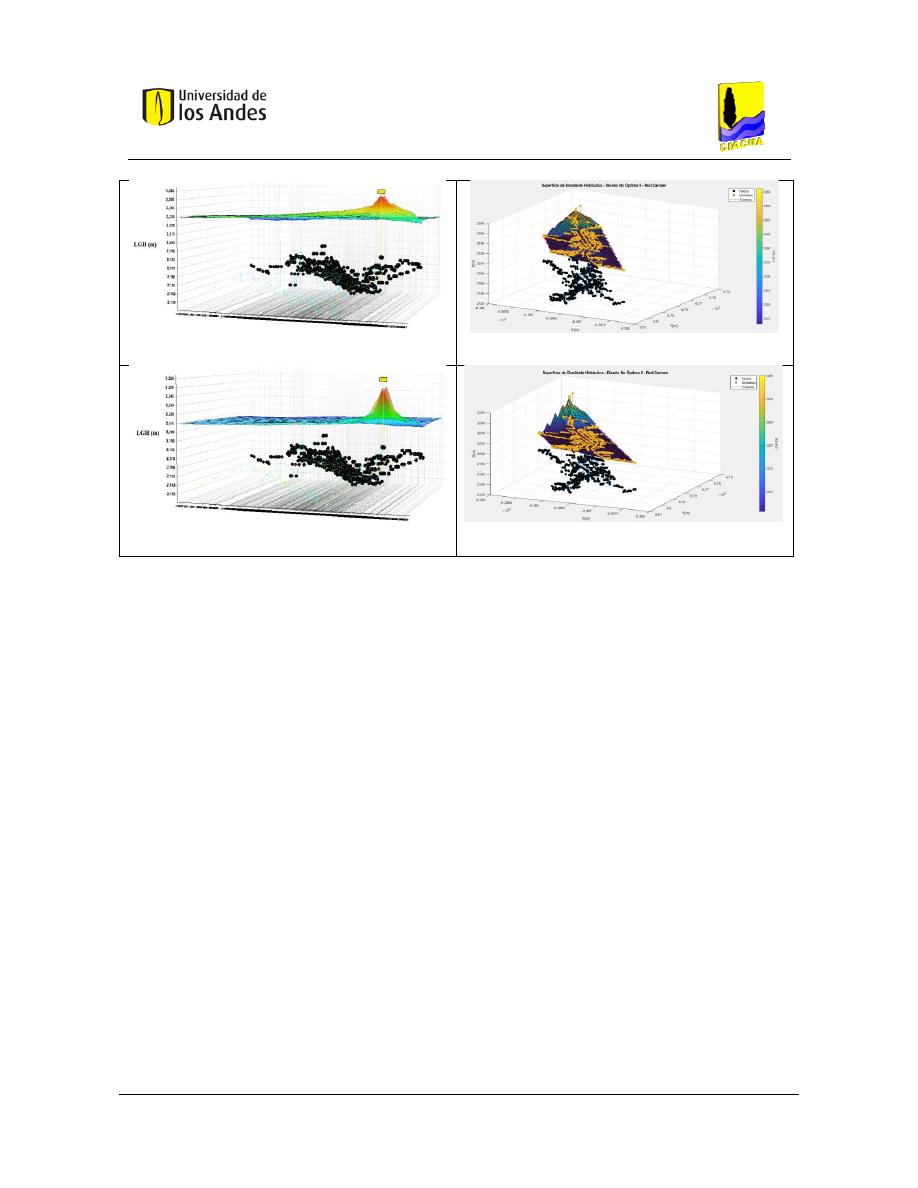
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
156
Figura 355. Diseño No Óptimo 5 - Red Carmen - REDES
2019.
Figura 356. Diseño No Óptimo 5 - Red Carmen - MATLAB.
Figura 357. Diseño No Óptimo 6 - Red Carmen - REDES
2019.
Figura 358. Diseño No Óptimo 6 - Red Carmen - MATLAB.
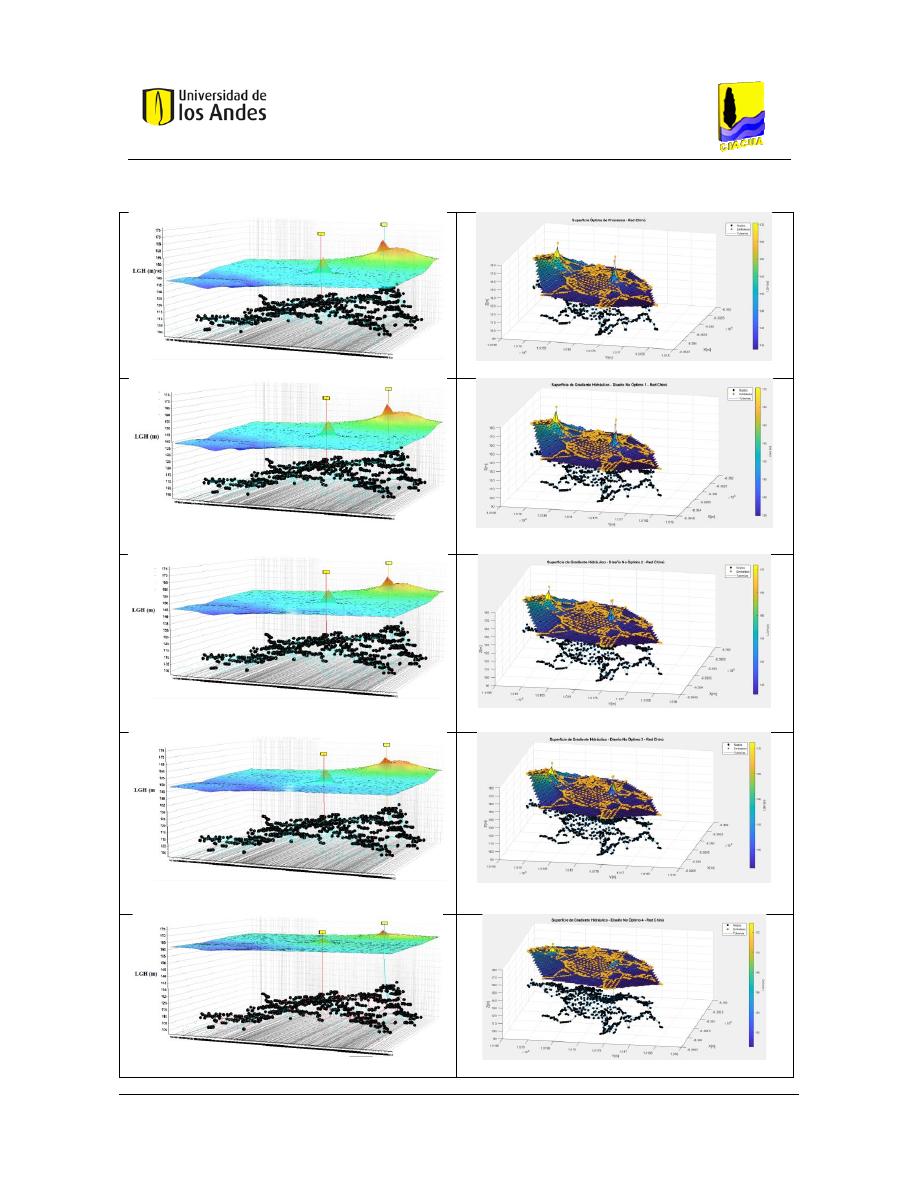
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
157
5.1.3.21 Red Chinú
Figura 359. SOP Red Chinú - REDES 2019.
Figura 360. SOP Red Chinú - MATLAB.
Figura 361. Diseño No Óptimo 1 - Red Chinú - REDES
2019.
Figura 362. Diseño No Óptimo 1 - Red Chinú - MATLAB.
Figura 363. Diseño No Óptimo 2 - Red Chinú - REDES
2019.
Figura 364. Diseño No Óptimo 2 - Red Chinú - MATLAB.
Figura 365. Diseño No Óptimo 3 - Red Chinú - REDES
2019.
Figura 366. Diseño No Óptimo 3 - Red Chinú - MATLAB.
Figura 367. Diseño No Óptimo 4 - Red Chinú - REDES
Figura 368. Diseño No Óptimo 4 - Red Chinú - MATLAB.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
158
2019.
Figura 369. Diseño No Óptimo 5 - Red Chinú - REDES
2019.
Figura 370. Diseño No Óptimo 5 - Red Chinú - MATLAB.
Figura 371. Diseño No Óptimo 6 - Red Chinú - REDES
2019.
Figura 372. Diseño No Óptimo 6 - Red Chinú - MATLAB.
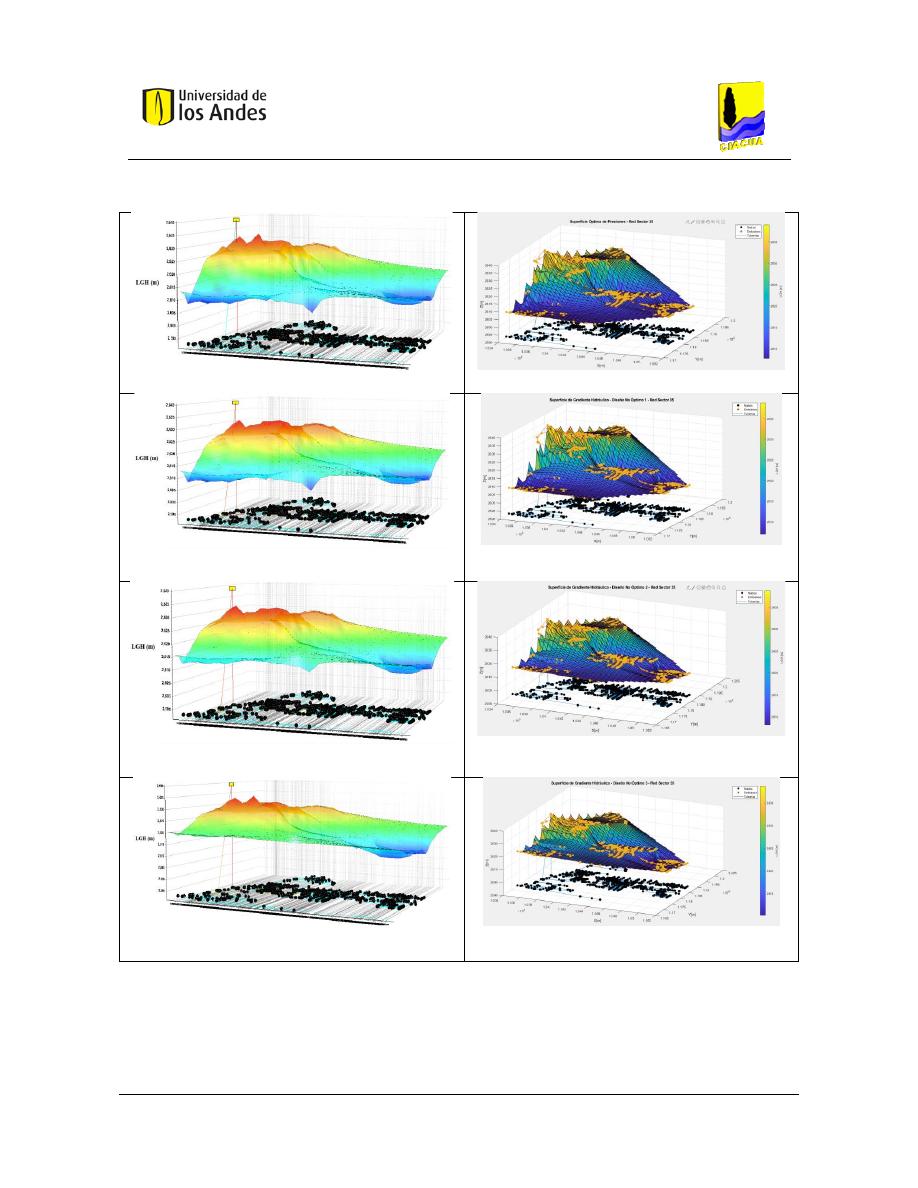
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
159
5.1.3.22 Red Sector 35
Figura 373. SOP Sector 35 - REDES 2019.
Figura 374. SOP Red Sector 35 - MATLAB.
Figura 375. Diseño No Óptimo 1 - Red Sector 35 - REDES
2019.
Figura 376. Diseño No Óptimo 1 - Red Sector 35 -
MATLAB.
Figura 377. Diseño No Óptimo 2 - Red Sector 35 - REDES
2019.
Figura 378. Diseño No Óptimo 2 - Red Sector 35 -
MATLAB.
Figura 379. Diseño No Óptimo 3 - Red Sector 35 - REDES
2019.
Figura 380. Diseño No Óptimo 3 - Red Sector 35 -
MATLAB.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
160
Figura 381. Diseño No Óptimo 4 - Red Sector 35 - REDES
2019.
Figura 382. Diseño No Óptimo 4 - Red Sector 35 -
MATLAB.
Figura 383. Diseño No Óptimo 5 - Red Sector 35 - REDES
2019.
Figura 384. Diseño No Óptimo 5 - Red Sector 35 -
MATLAB.
Figura 385. Diseño No Óptimo 6 - Red Sector 35 - REDES
2019.
Figura 386. Diseño No Óptimo 6 - Red Sector 35 -
MATLAB.
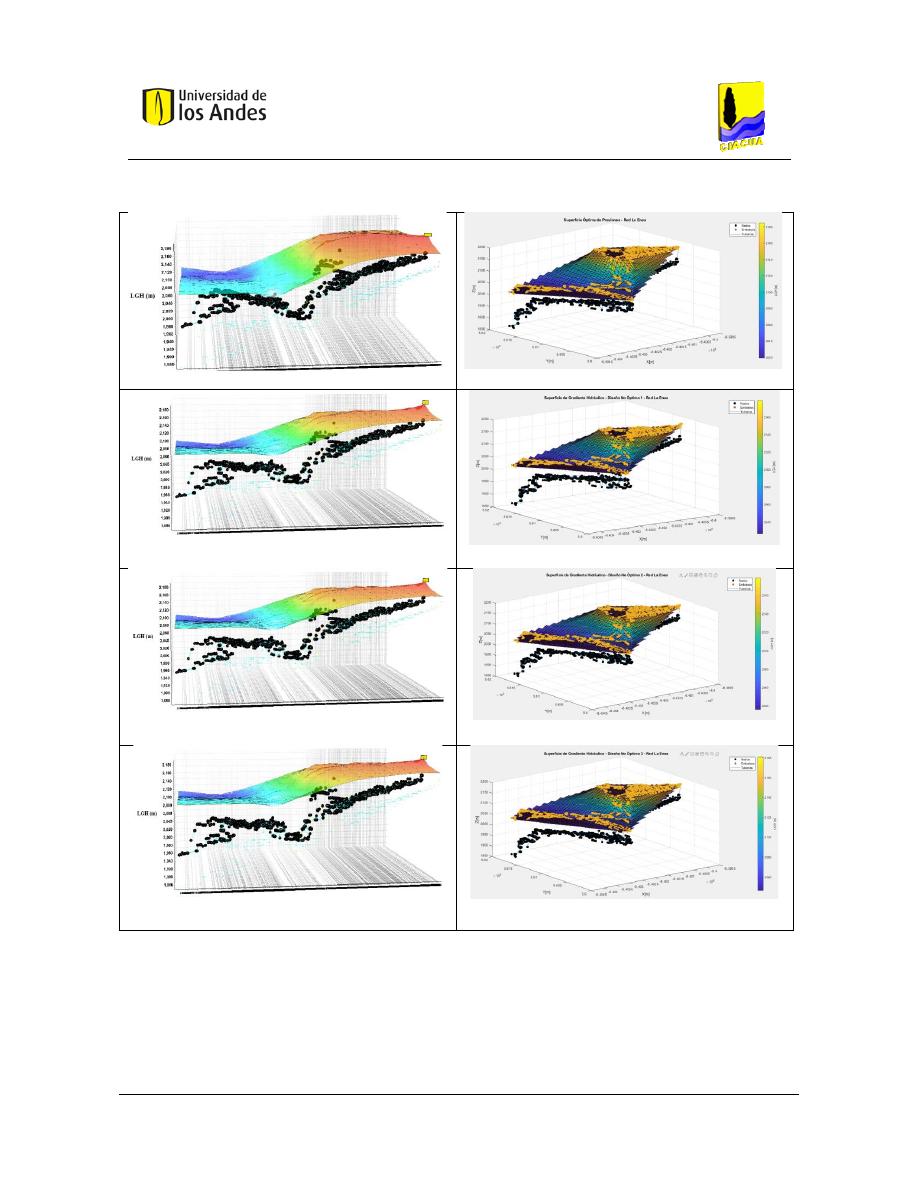
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
161
5.1.3.23 Red La Enea
Figura 387. SOP Red La Enea - REDES 2019.
Figura 388. SOP Red La Enea - MATLAB.
Figura 389. Diseño No Óptimo 1 - Red La Enea - REDES
2019.
Figura 390. Diseño No Óptimo 1 - Red La Enea - MATLAB.
Figura 391. Diseño No Óptimo 2 - Red La Enea - REDES
2019.
Figura 392. Diseño No Óptimo 2 - Red La Enea - MATLAB.
Figura 393. Diseño No Óptimo 3 - Red La Enea - REDES
2019.
Figura 394. Diseño No Óptimo 3 - Red La Enea - MATLAB.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
162
Figura 395. Diseño No Óptimo 4 - Red La Enea - REDES
2019.
Figura 396. Diseño No Óptimo 4 - Red La Enea - MATLAB.
Figura 397. Diseño No Óptimo 5 - Red La Enea - REDES
2019.
Figura 398. Diseño No Óptimo 5 - Red La Enea - MATLAB.
Figura 399. Diseño No Óptimo 6 - Red La Enea - REDES
2019.
Figura 400. Diseño No Óptimo 6 - Red La Enea - MATLAB.
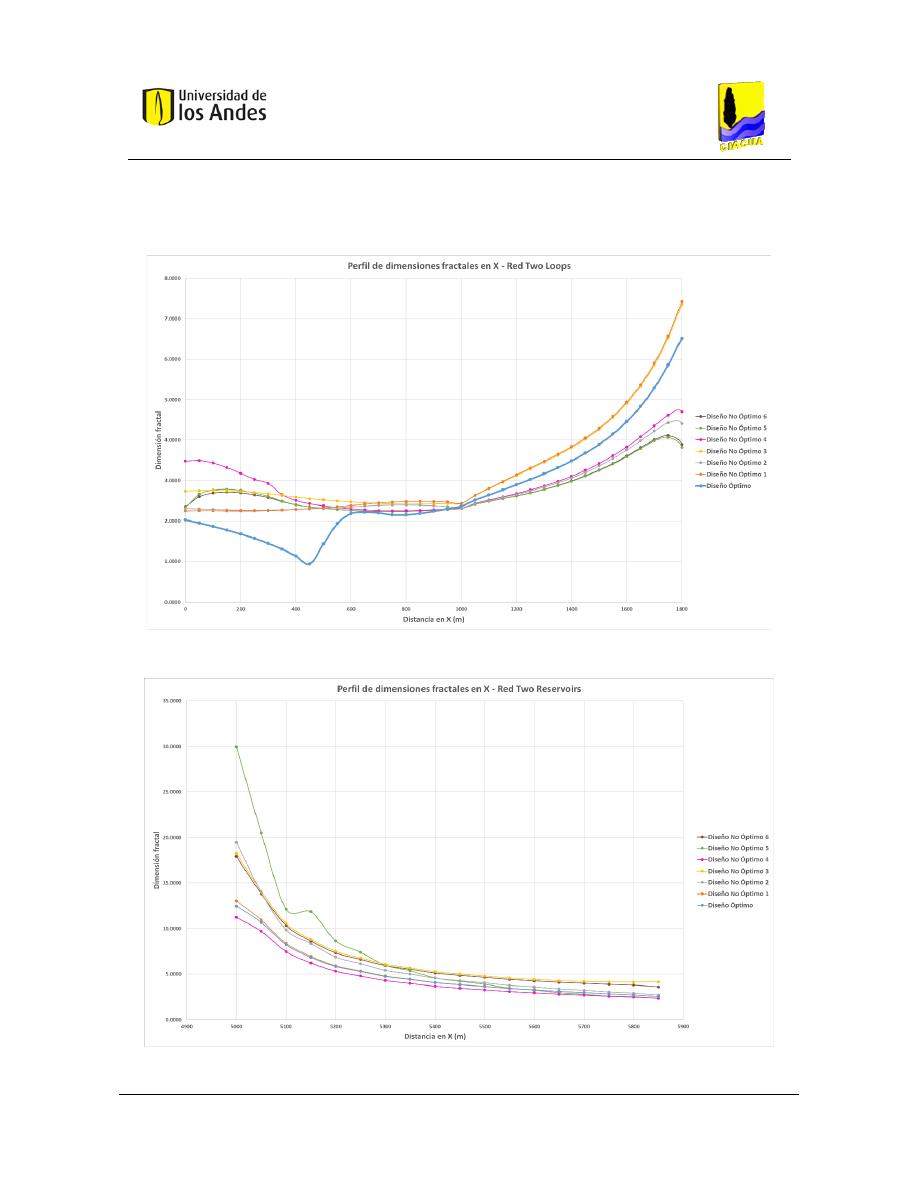
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
163
5.2 Análisis fractal unidimensional de las superficies
5.2.1 Perfil de dimensiones fractales – Eje X
Figura 401. Perfil de dimensiones fractales en X - Red Two Loops.
Figura 402. Perfil de dimensiones fractales en X - Red Two Reservoirs.
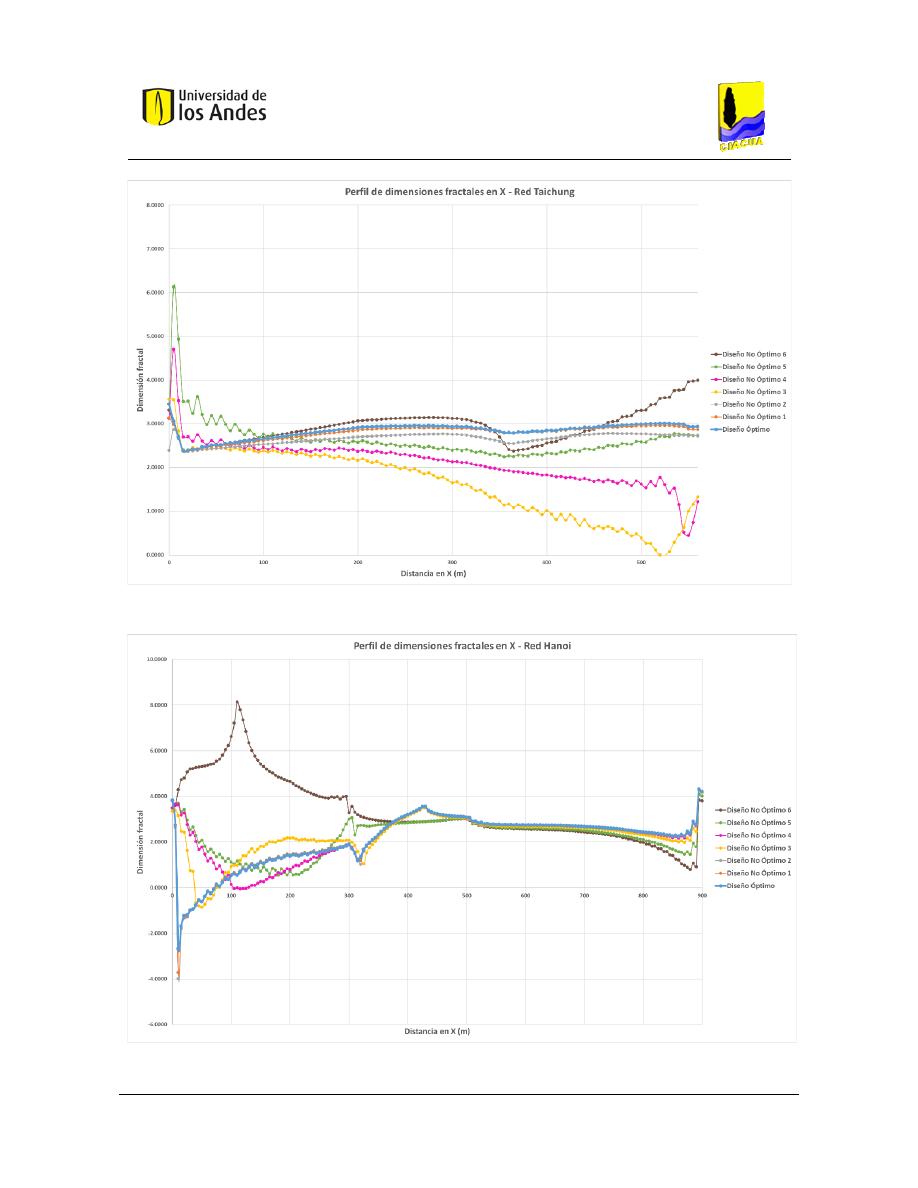
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
164
Figura 403. Perfil de dimensiones fractales en X - Red Taichung.
Figura 404. Perfil de dimensiones fractales en X - Red Hanoi.
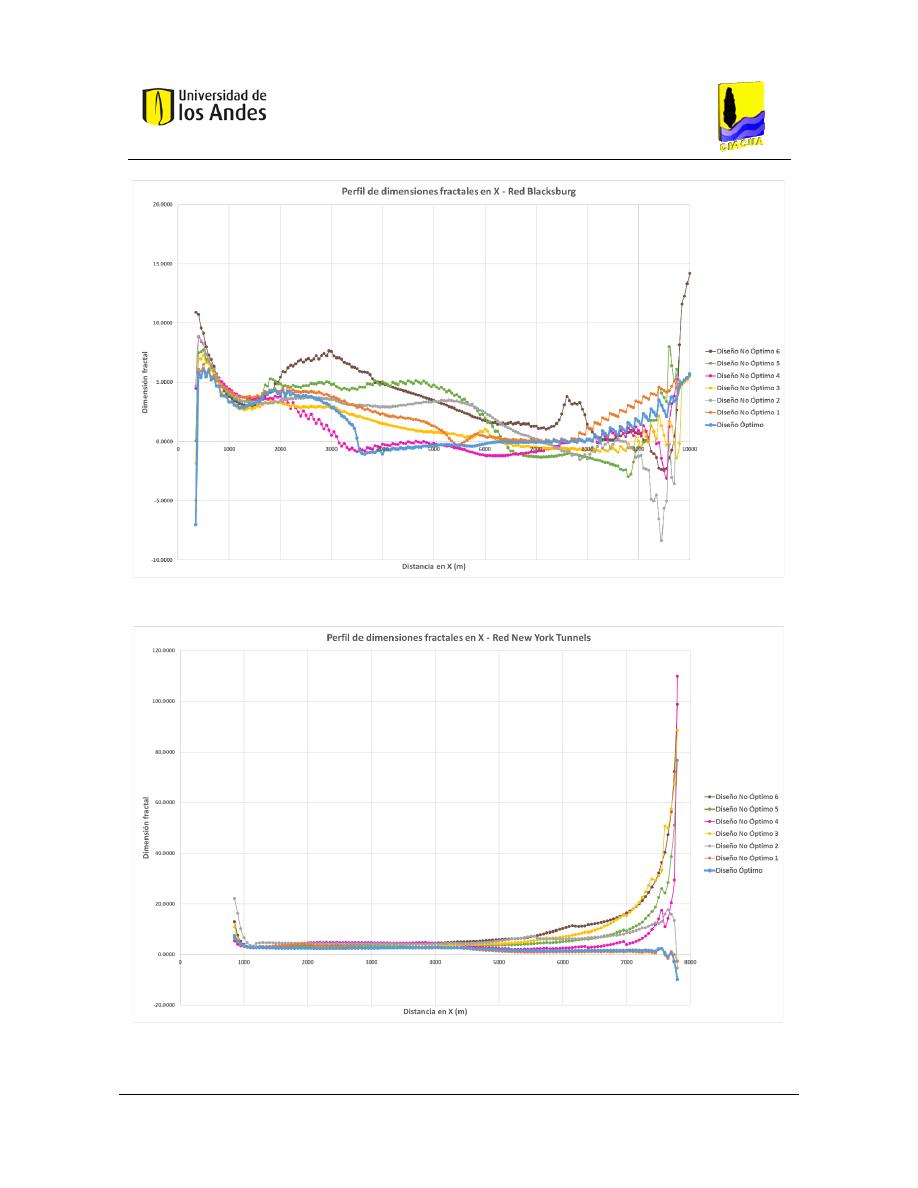
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
165
Figura 405. Perfil de dimensiones fractales en X - Red Blacksburg.
Figura 406. Perfil de dimensiones fractales en X - Red New York Tunnels.
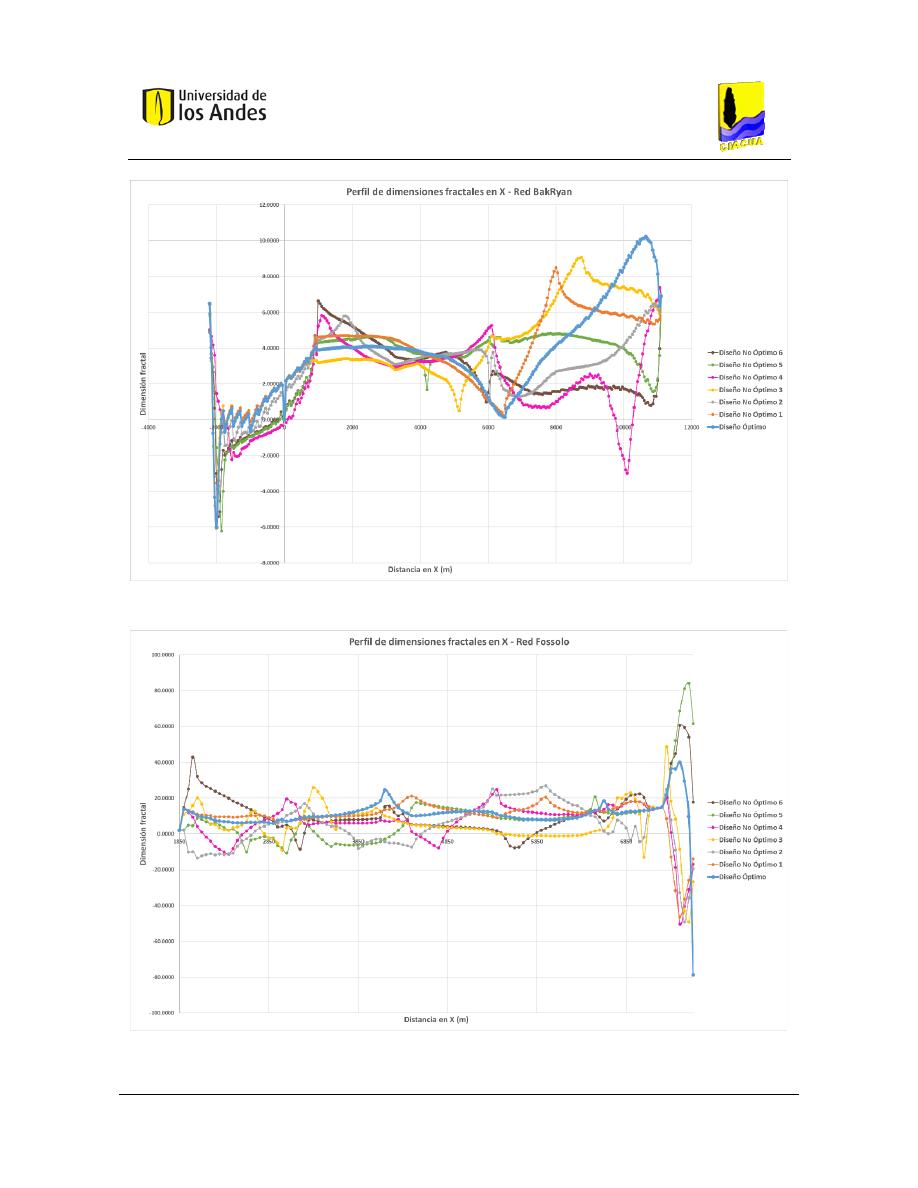
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
166
Figura 407. Perfil de dimensiones fractales en X - Red BakRyan.
Figura 408. Perfil de dimensiones fractales en X - Red Fossolo.
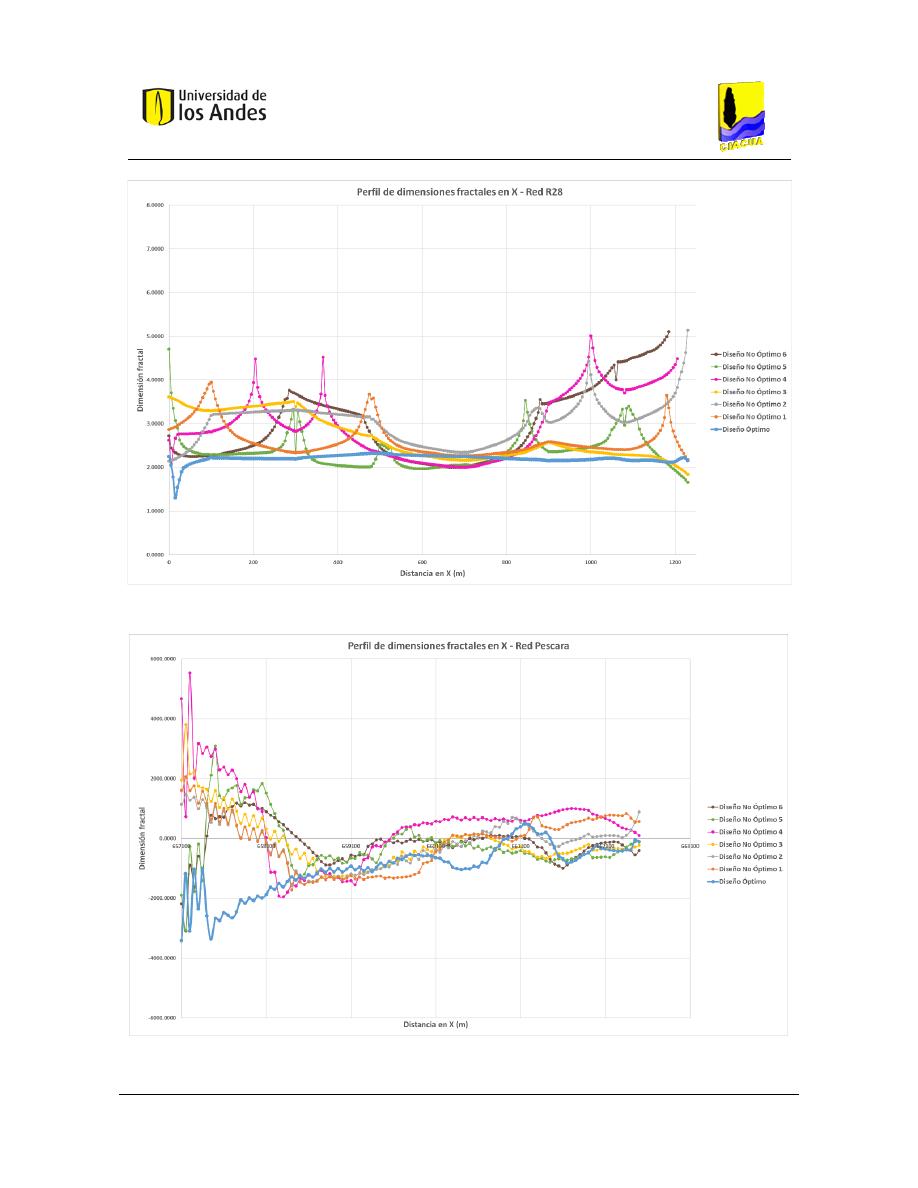
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
167
Figura 409. Perfil de dimensiones fractales en X - Red R28.
Figura 410. Perfil de dimensiones fractales en X - Red Pescara.
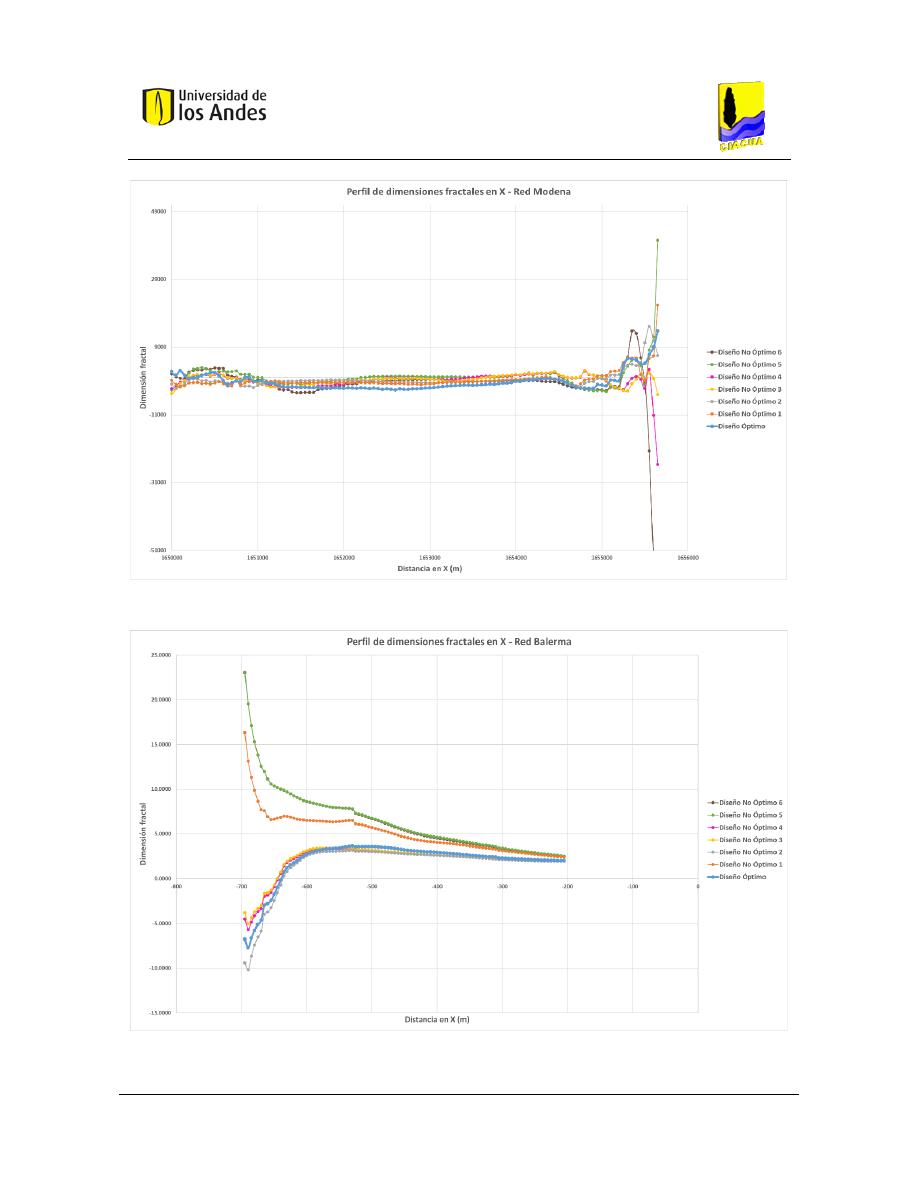
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
168
Figura 411. Perfil de dimensiones fractales en X - Red Modena.
Figura 412. Perfil de dimensiones fractales en X - Red Balerma.
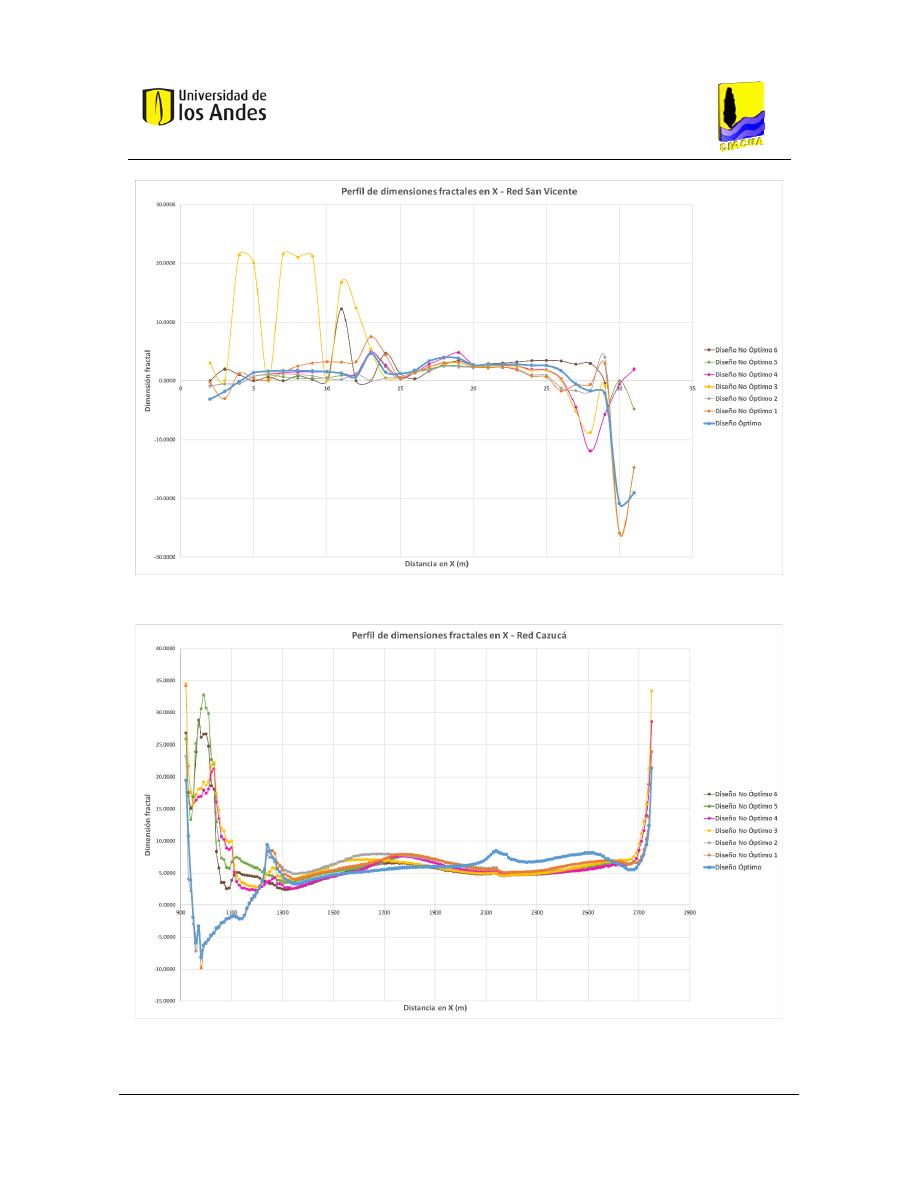
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
169
Figura 413. Perfil de dimensiones fractales en X - Red San Vicente.
Figura 414. Perfil de dimensiones fractales en X - Red Cazucá.
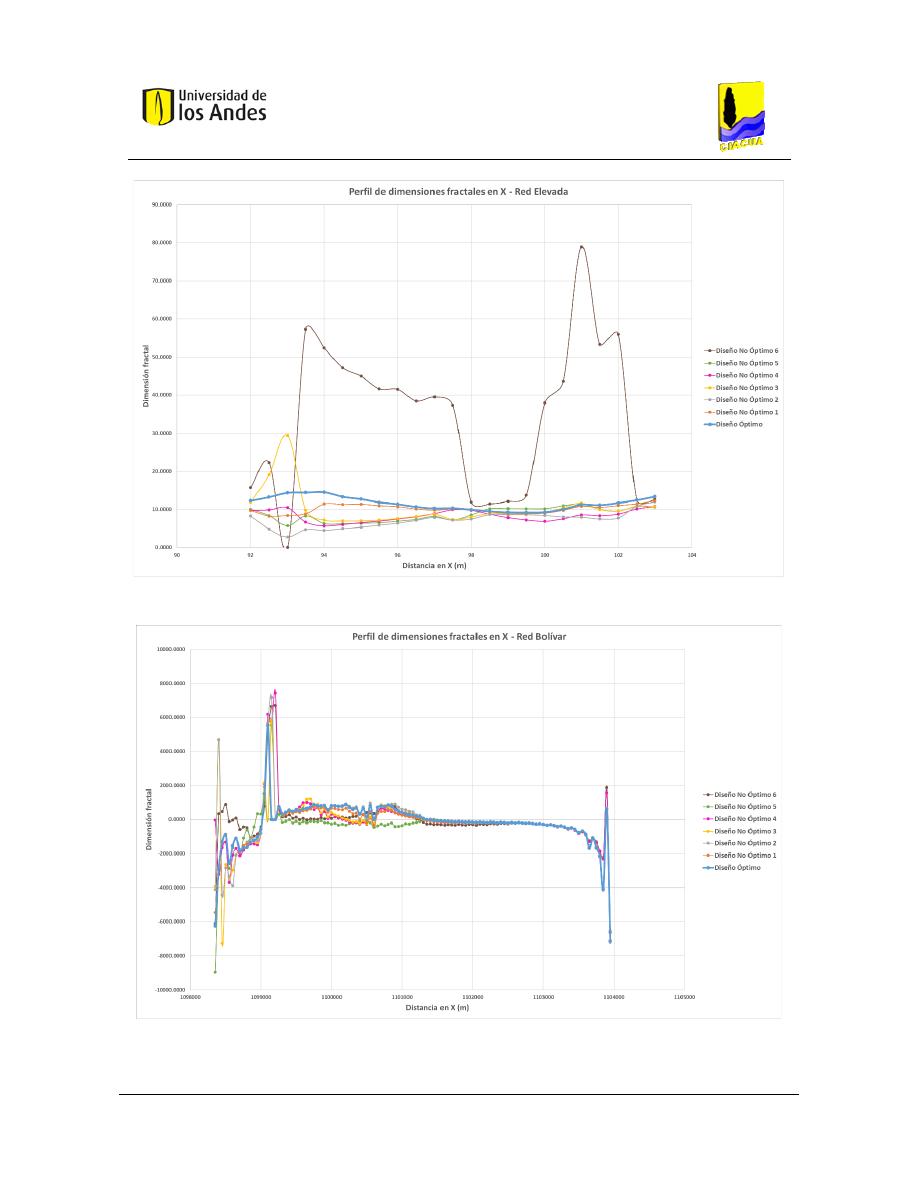
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
170
Figura 415. Perfil de dimensiones fractales en X - Red Elevada.
Figura 416. Perfil de dimensiones fractales en X - Red Bolívar.
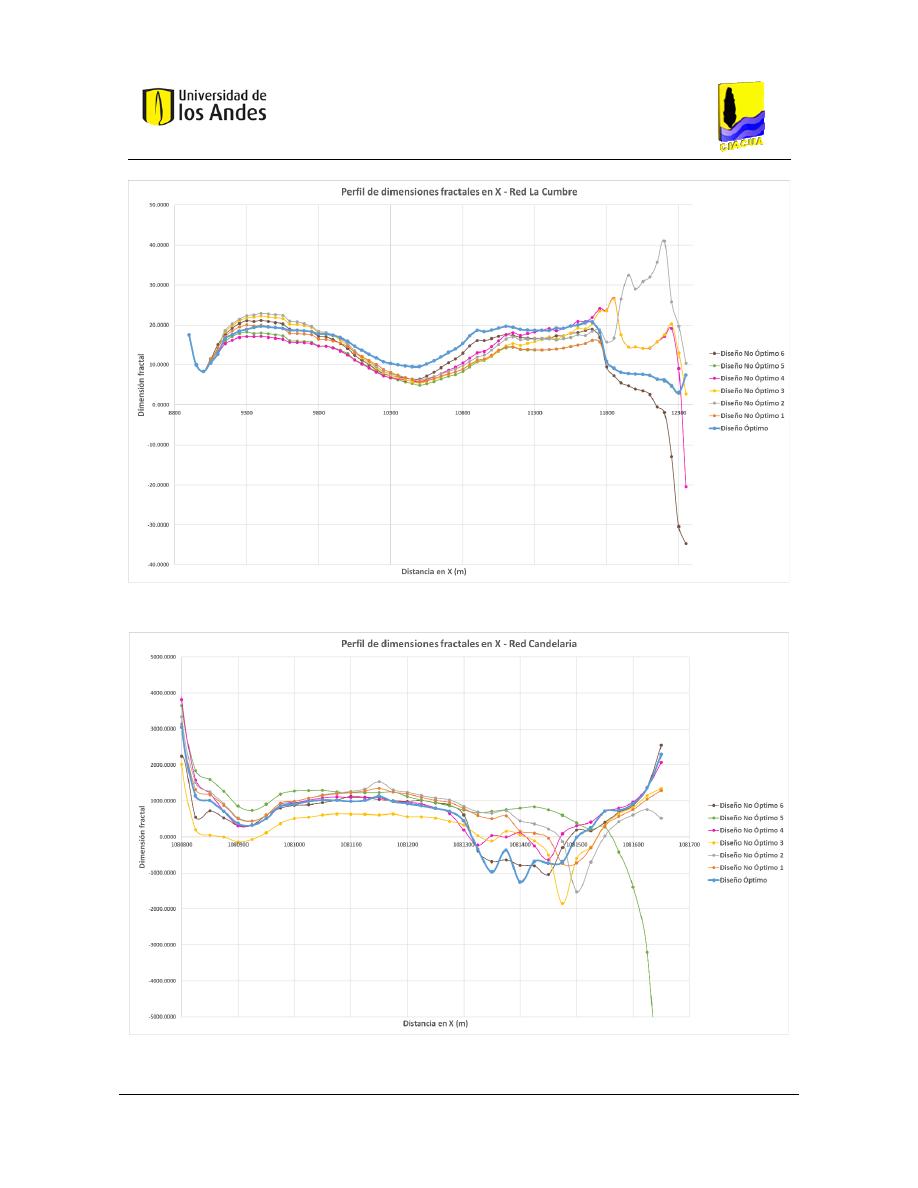
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
171
Figura 417. Perfil de dimensiones fractales en X - Red La Cumbre.
Figura 418. Perfil de dimensiones fractales en X - Red Candelaria.
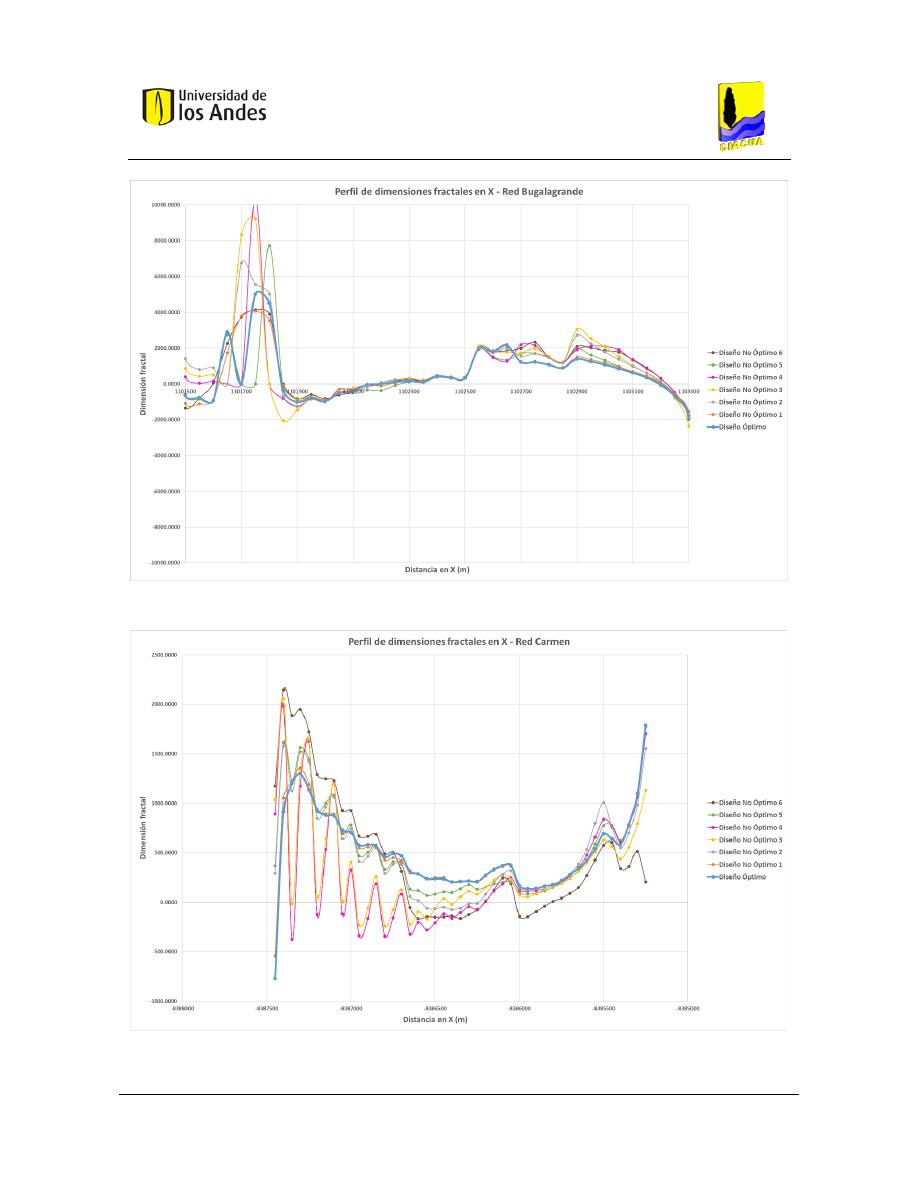
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
172
Figura 419. Perfil de dimensiones fractales en X - Red Bugalagrande.
Figura 420. Perfil de dimensiones fractales en X - Red Carmen.
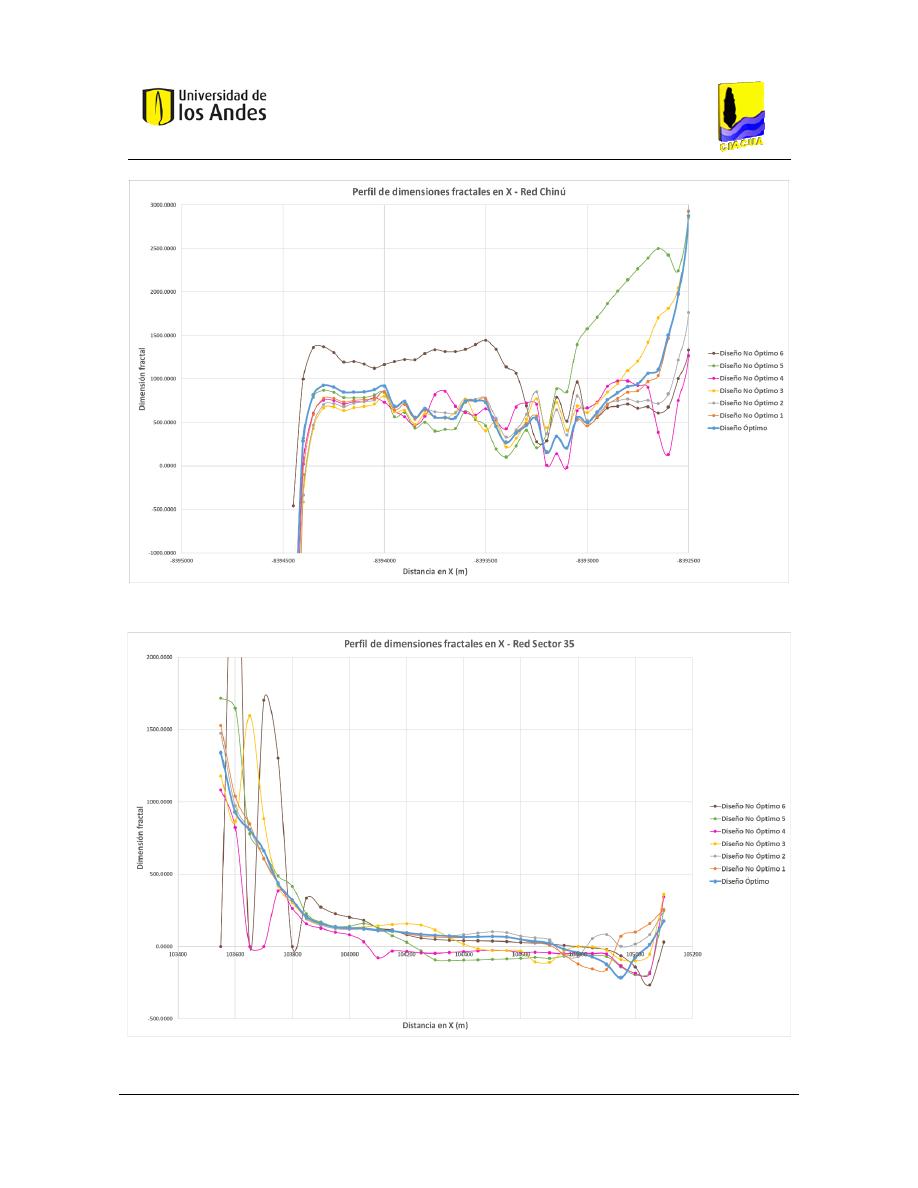
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
173
Figura 421. Perfil de dimensiones fractales en X - Red Chinú.
Figura 422. Perfil de dimensiones fractales en X - Red Sector 35.
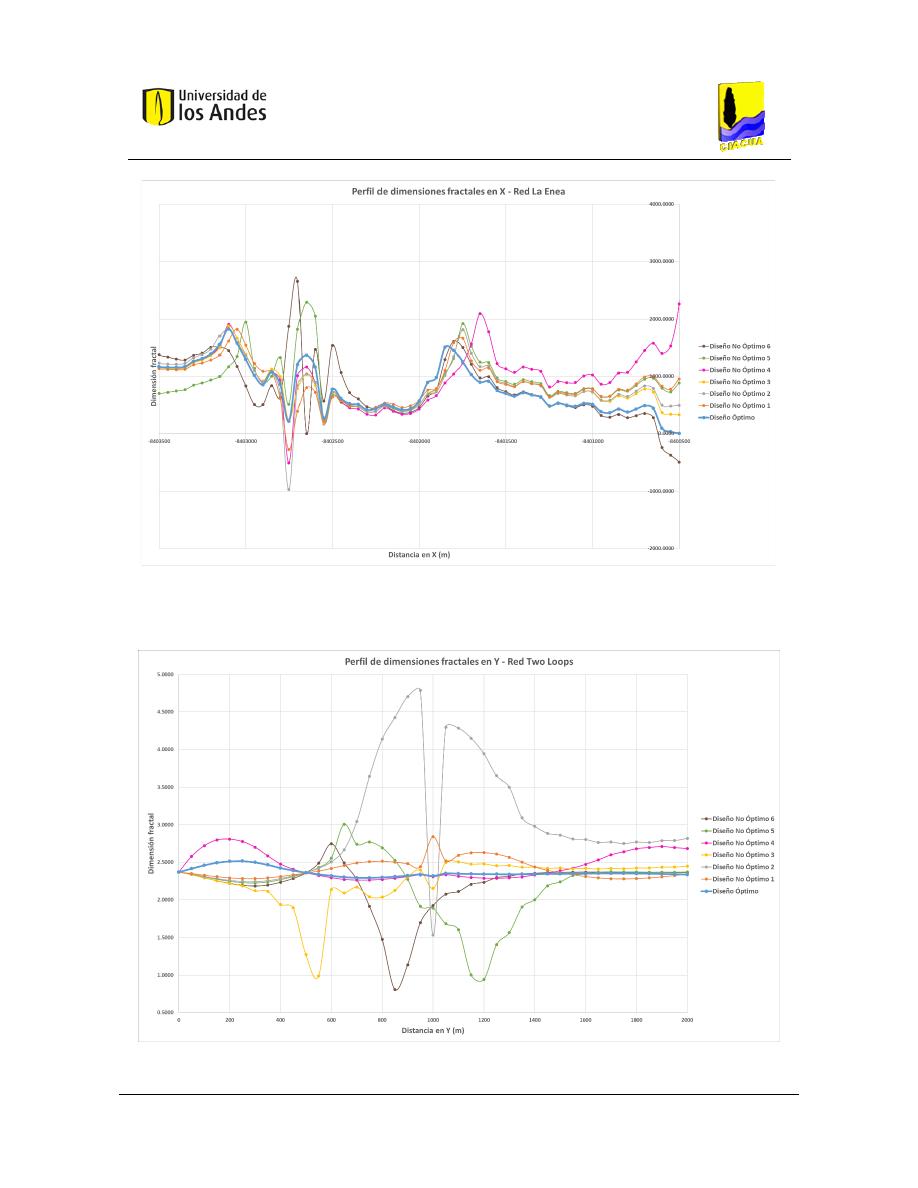
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
174
Figura 423. Perfil de dimensiones fractales en X - Red La Enea.
5.2.2 Perfil de dimensiones fractales – Eje Y
Figura 424. Perfil de dimensiones fractales en Y - Red Two Loops.
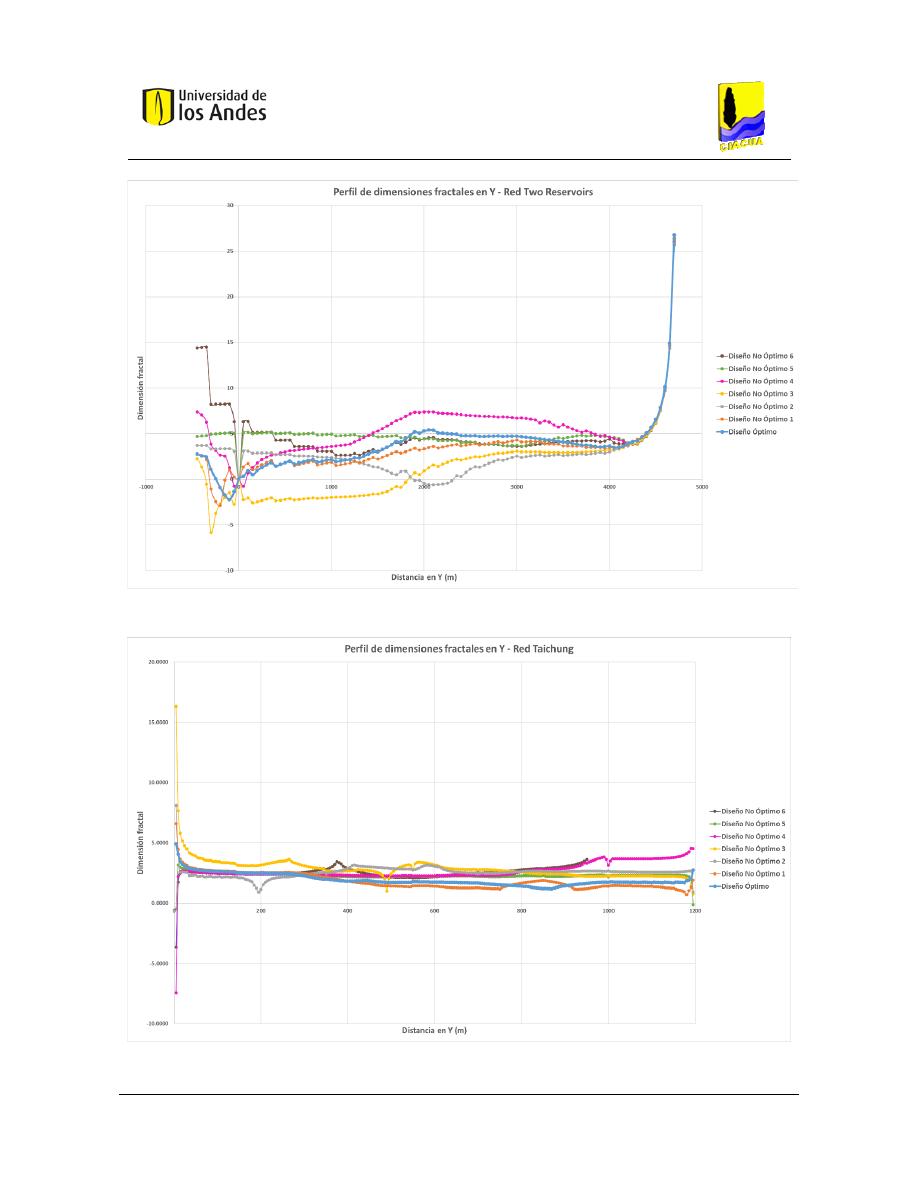
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
175
Figura 425. Perfil de dimensiones fractales en Y - Red Two Reservoirs.
Figura 426. Perfil de dimensiones fractales en Y - Red Taichung.
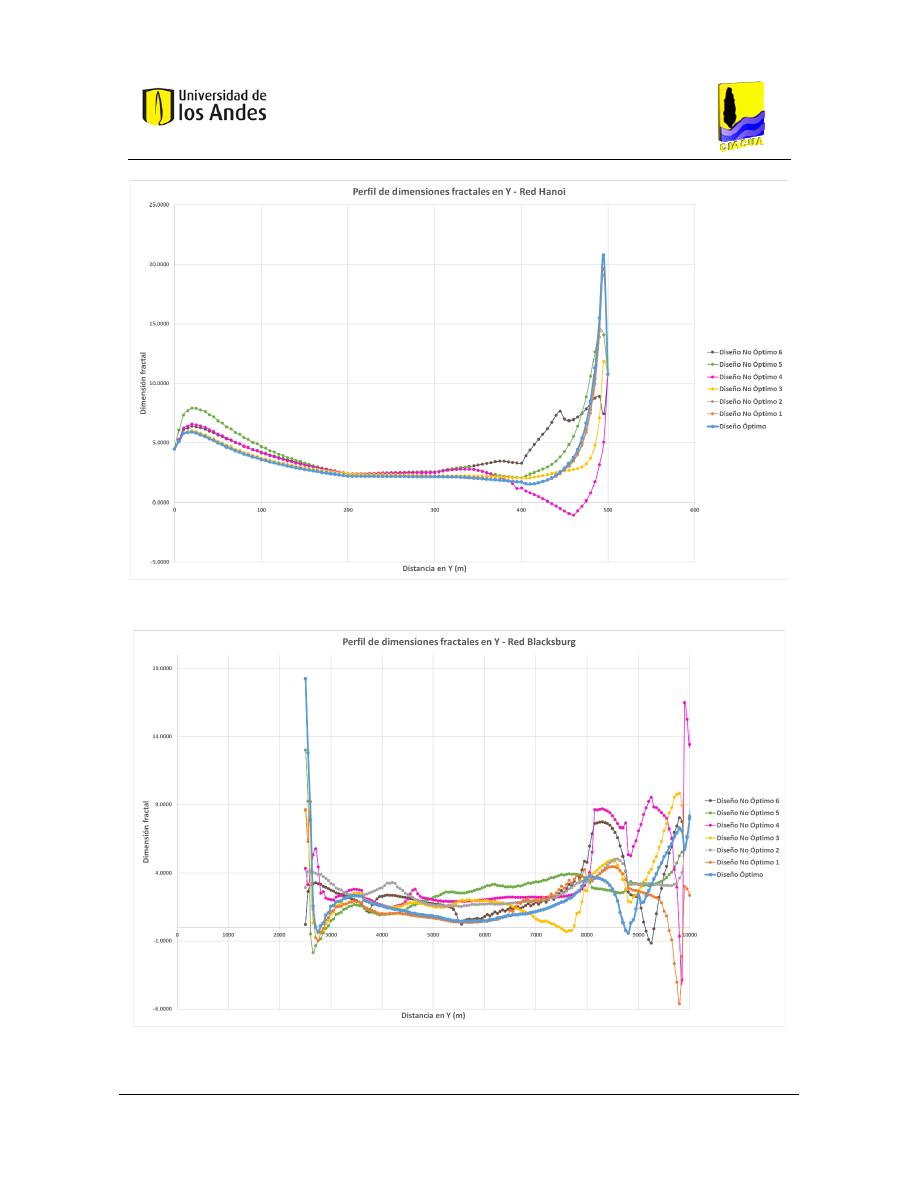
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
176
Figura 427. Perfil de dimensiones fractales en Y - Red Hanoi.
Figura 428. Perfil de dimensiones fractales en Y - Red Blacksburg.
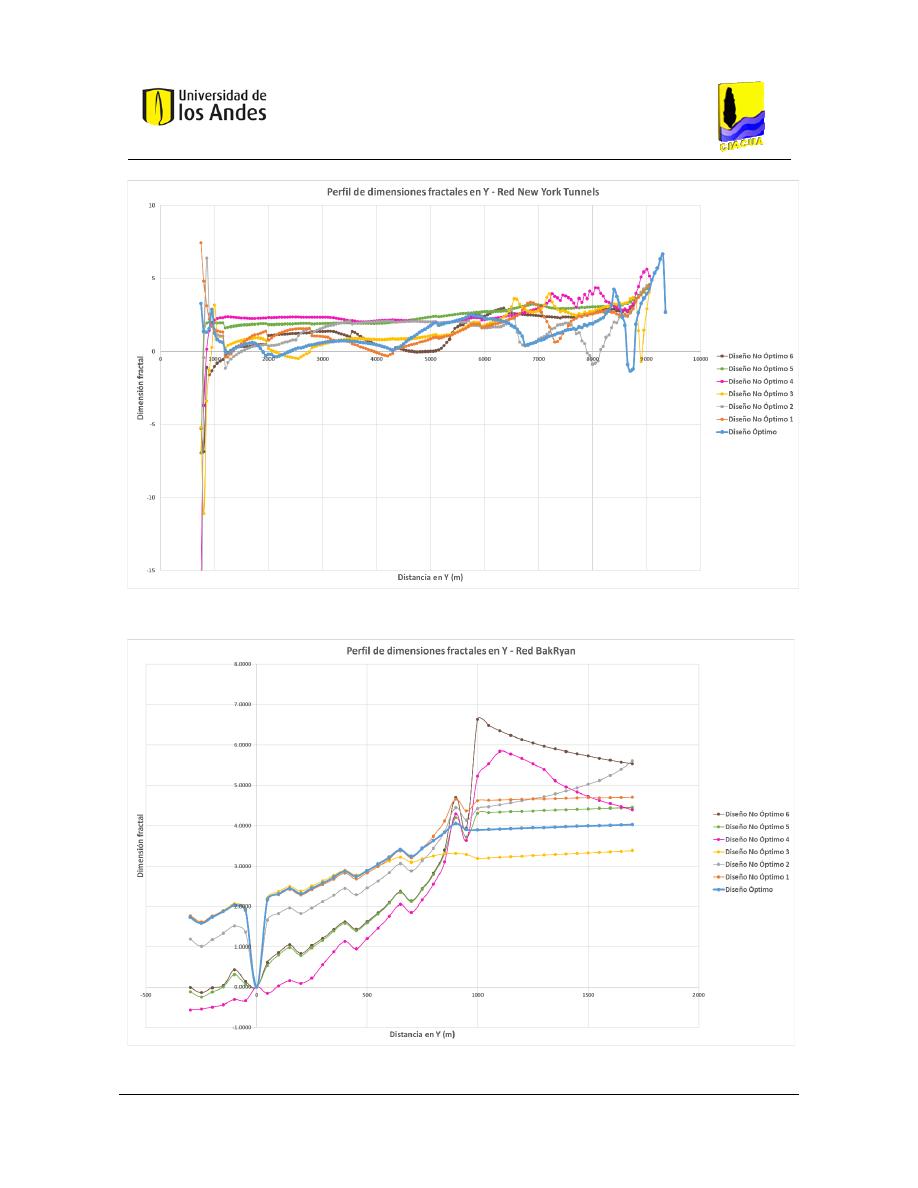
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
177
Figura 429. Perfil de dimensiones fractales en Y - Red New York Tunnels.
Figura 430. Perfil de dimensiones fractales en Y - Red BakRyan.
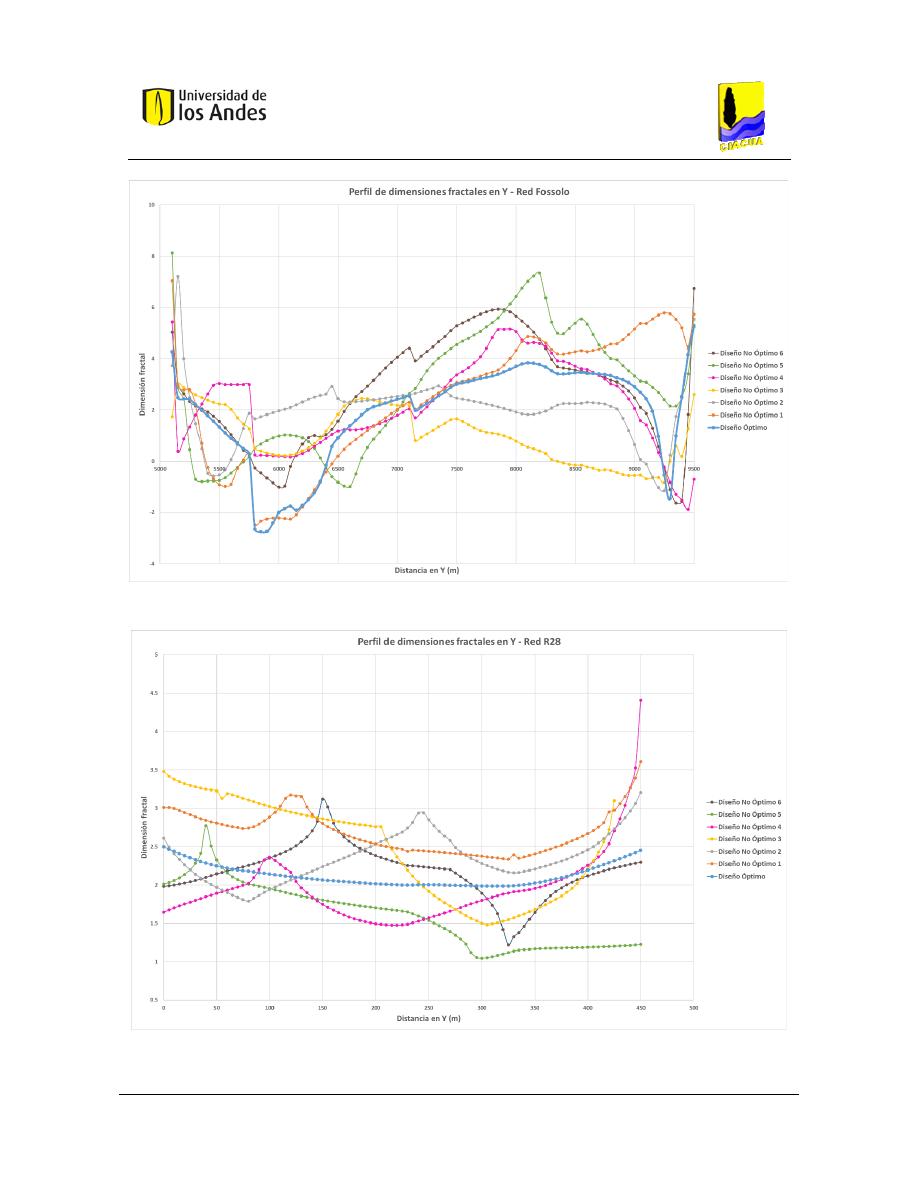
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
178
Figura 431. Perfil de dimensiones fractales en Y - Red Fossolo.
Figura 432. Perfil de dimensiones fractales en Y - Red R28.
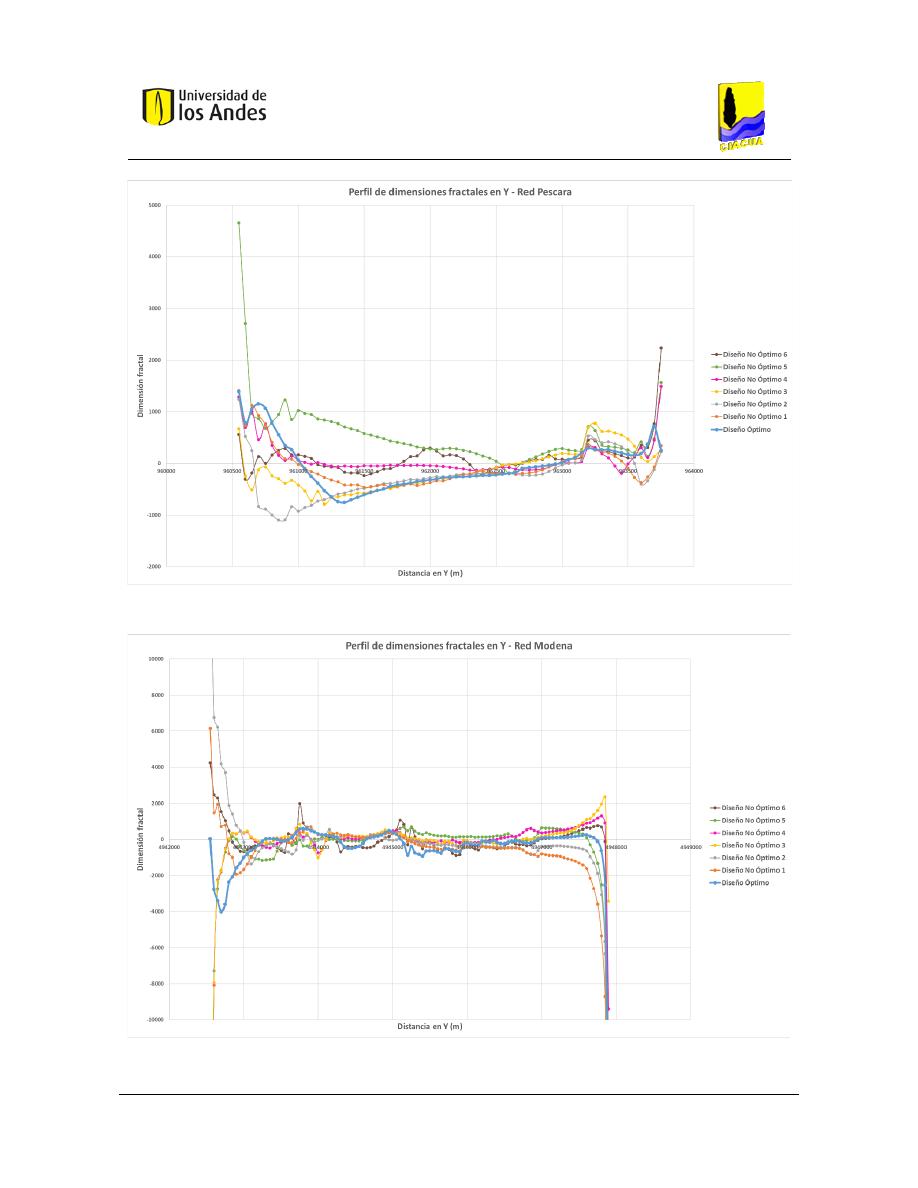
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
179
Figura 433. Perfil de dimensiones fractales en Y - Red Pescara.
Figura 434. Perfil de dimensiones fractales en Y - Red Modena.
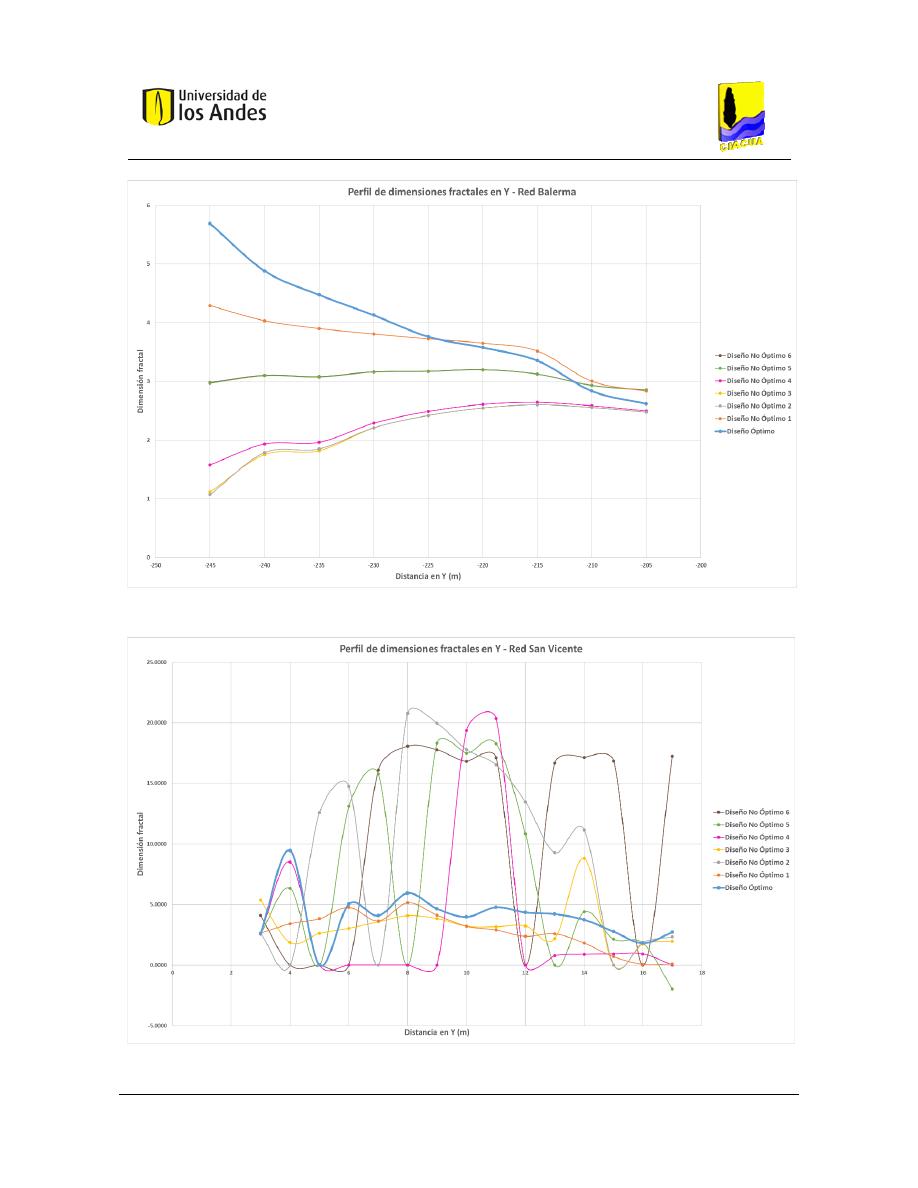
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
180
Figura 435. Perfil de dimensiones fractales en Y - Red Balerma.
Figura 436. Perfil de dimensiones fractales en Y - Red San Vicente.
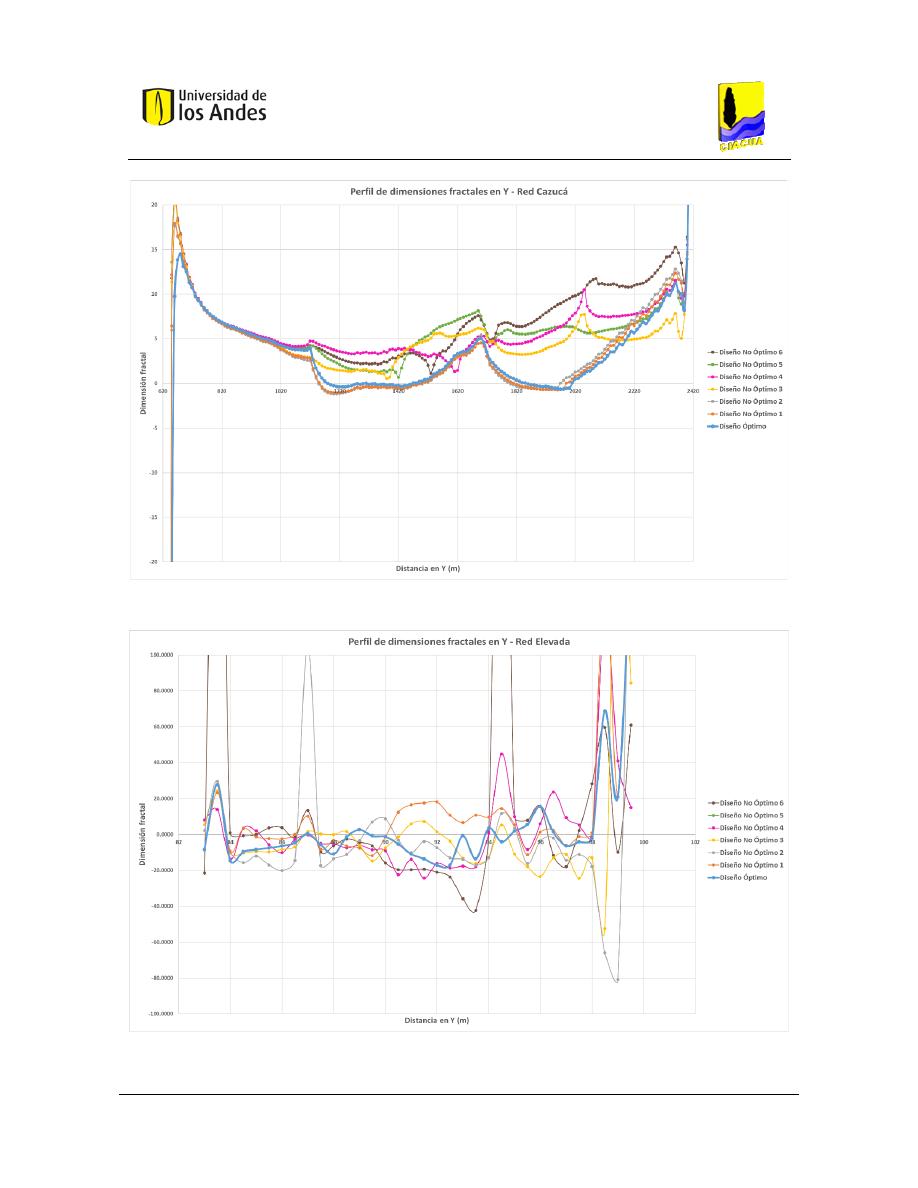
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
181
Figura 437. Perfil de dimensiones fractales en Y - Red Cazucá.
Figura 438. Perfil de dimensiones fractales en Y - Red Elevada.
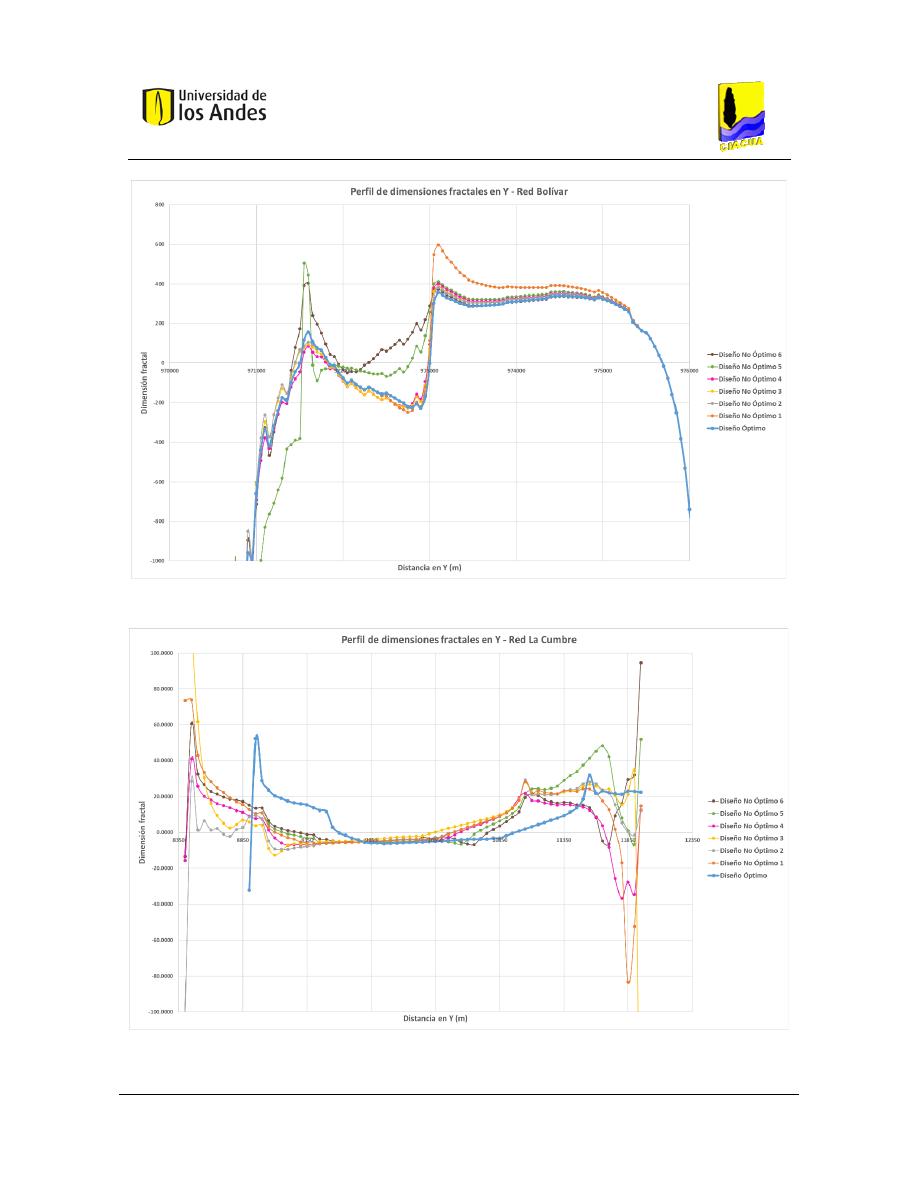
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
182
Figura 439. Perfil de dimensiones fractales en Y - Red Bolívar.
Figura 440. Perfil de dimensiones fractales en Y - Red La Cumbre.
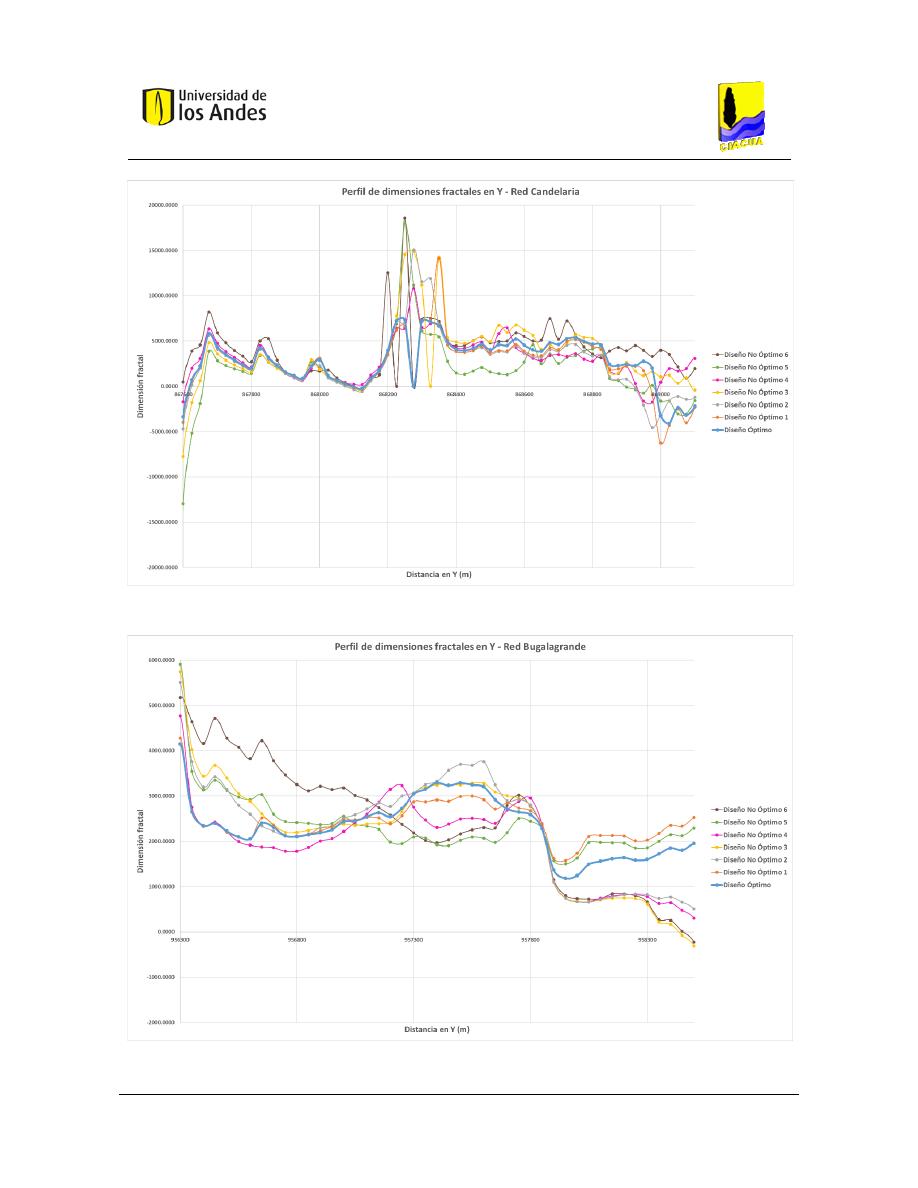
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
183
Figura 441. Perfil de dimensiones fractales en Y - Red Candelaria.
Figura 442. Perfil de dimensiones fractales en Y - Red Bugalagrande.
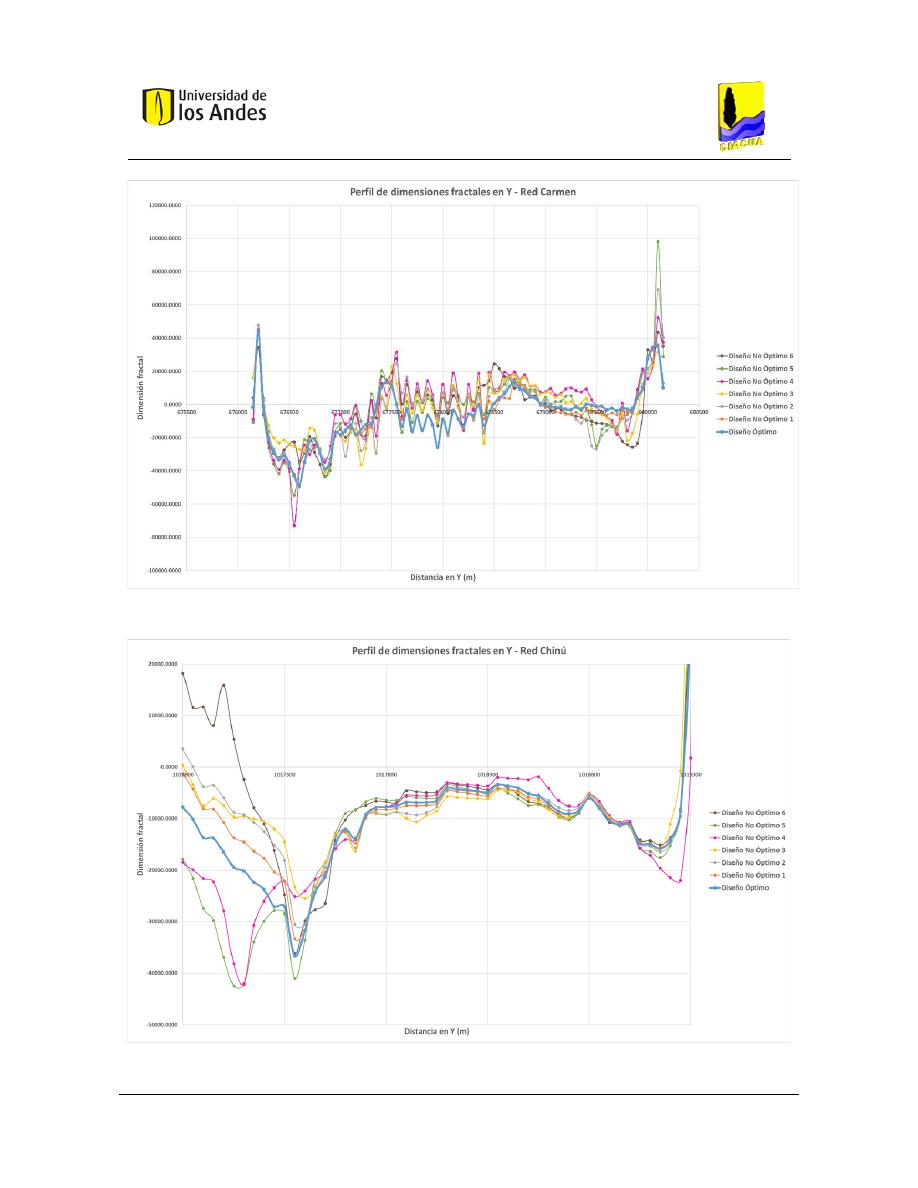
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
184
Figura 443. Perfil de dimensiones fractales en Y - Red Carmen.
Figura 444. Perfil de dimensiones fractales en Y - Red Carmen.
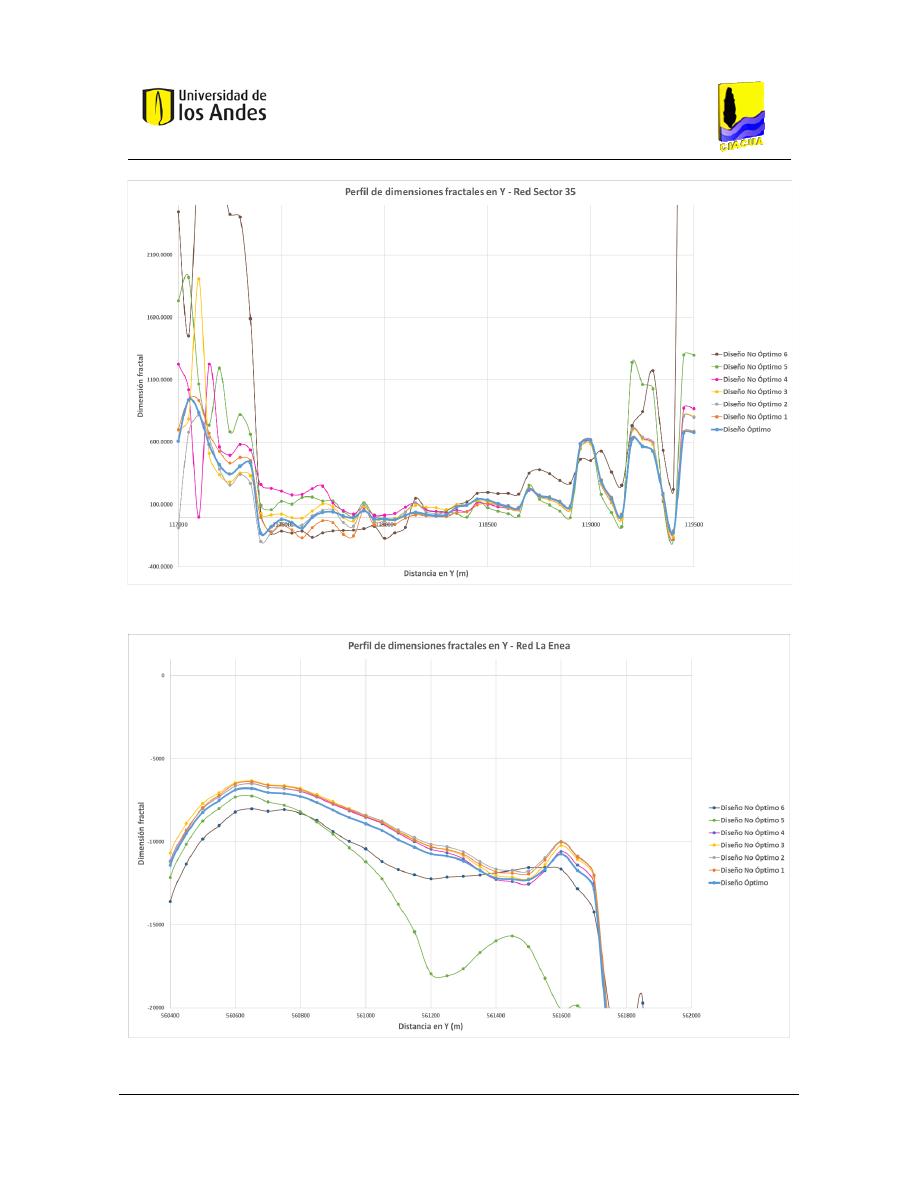
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
185
Figura 445. Perfil de dimensiones fractales en Y - Red Sector 35.
Figura 446. Perfil de dimensiones fractales en Y - Red La Enea.
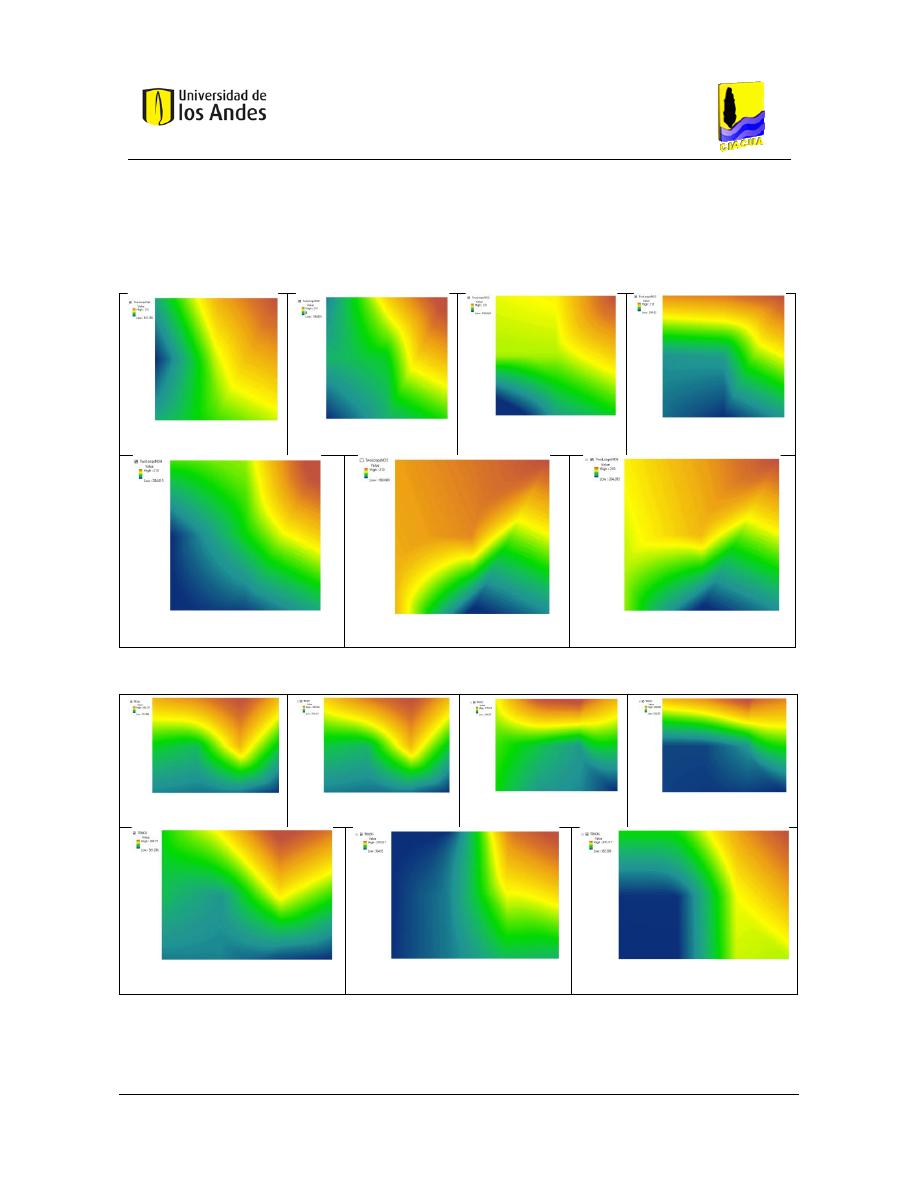
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
186
5.3 Análisis fractal bidimensional de las superficies
5.3.1 Modelos Digitales de Elevaciones (DEM)
5.3.1.1 Red Two Loops
Figura 447. DEM Two
Loops - Óptimo.
Figura 448. DEM Two
Loops - No Óptimo 1.
Figura 449. DEM Two
Loops - No Óptimo 2.
Figura 450. DEM Two
Loops - No Óptimo 3.
Figura 451. DEM Two Loops - No
Óptimo 4.
Figura 452. DEM Two Loops - No
Óptimo 5.
Figura 453. DEM Two Loops - No
Óptimo 6.
5.3.1.2 Red Two Reservoirs
Figura 454. DEM Two
Reservoirs - Óptimo.
Figura 455. DEM Two
Reservoirs - No Óptimo 1.
Figura 456. DEM Two
Reservoirs - No Óptimo 2.
Figura 457. DEM Two
Reservoirs - No Óptimo 3.
Figura 458. DEM Two Reservoirs - No
Óptimo 4.
Figura 459. DEM Two Reservoirs - No
Óptimo 5.
Figura 460. DEM Two Reservoirs - No
Óptimo 6.
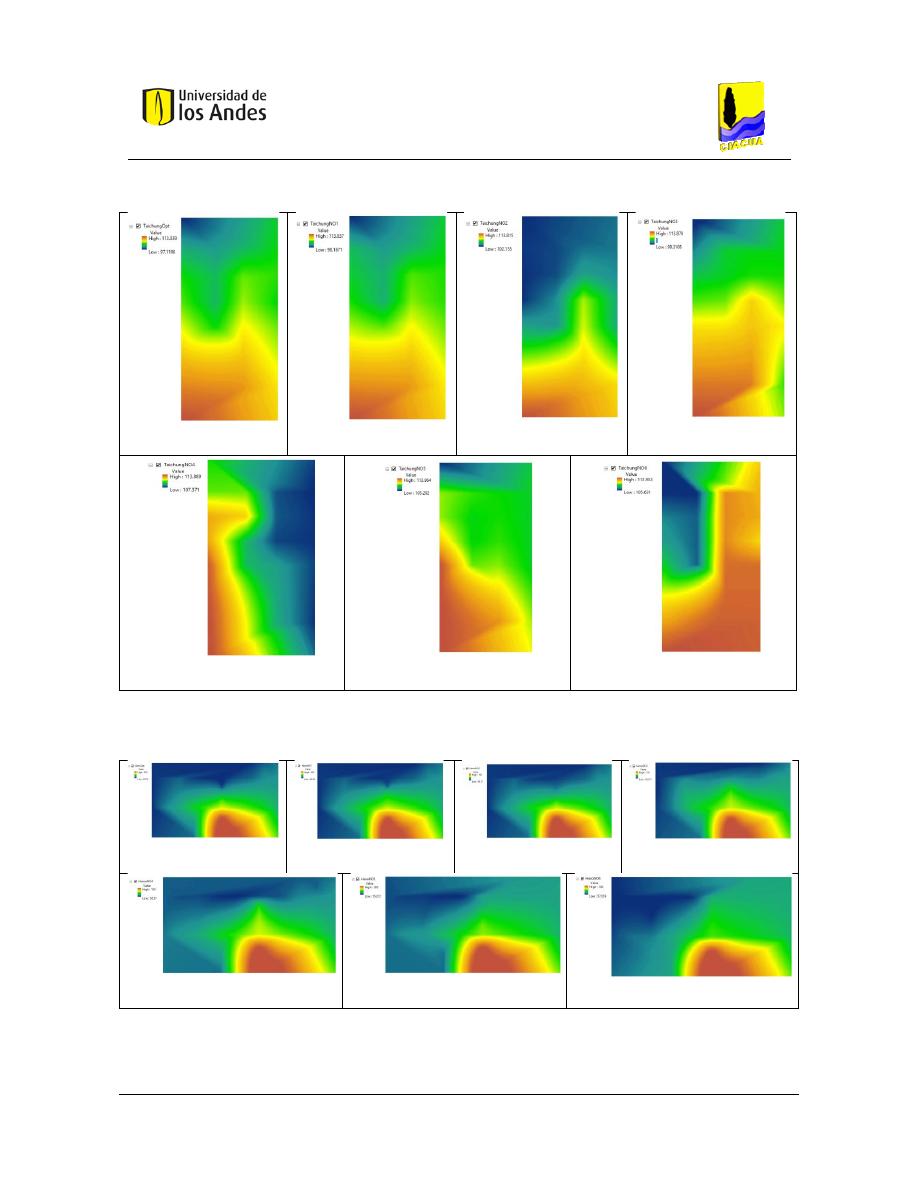
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
187
5.3.1.3 Red Taichung
Figura 461. DEM Taichung
- Óptimo.
Figura 462. DEM Taichung
- No Óptimo 1
Figura 463. DEM Taichung -
No Óptimo 2.
Figura 464. DEM Taichung
- No Óptimo 3.
Figura 465. DEM Taichung - No
Óptimo 4.
Figura 466. DEM Taichung - No
Óptimo 5.
Figura 467. DEM Taichung - No
Óptimo 6.
5.3.1.4 Red Hanoi
Figura 468. DEM Hanoi –
Óptimo.
Figura 469. DEM Hanoi -
No Óptimo 1.
Figura 470. DEM Hanoi -
No Óptimo 2.
Figura 471. DEM Hanoi - No
Óptimo 3.
Figura 472. DEM Hanoi - No Óptimo
4.
Figura 473. DEM Hanoi - No Óptimo
5.
Figura 474. DEM Hanoi - No Óptimo 6.
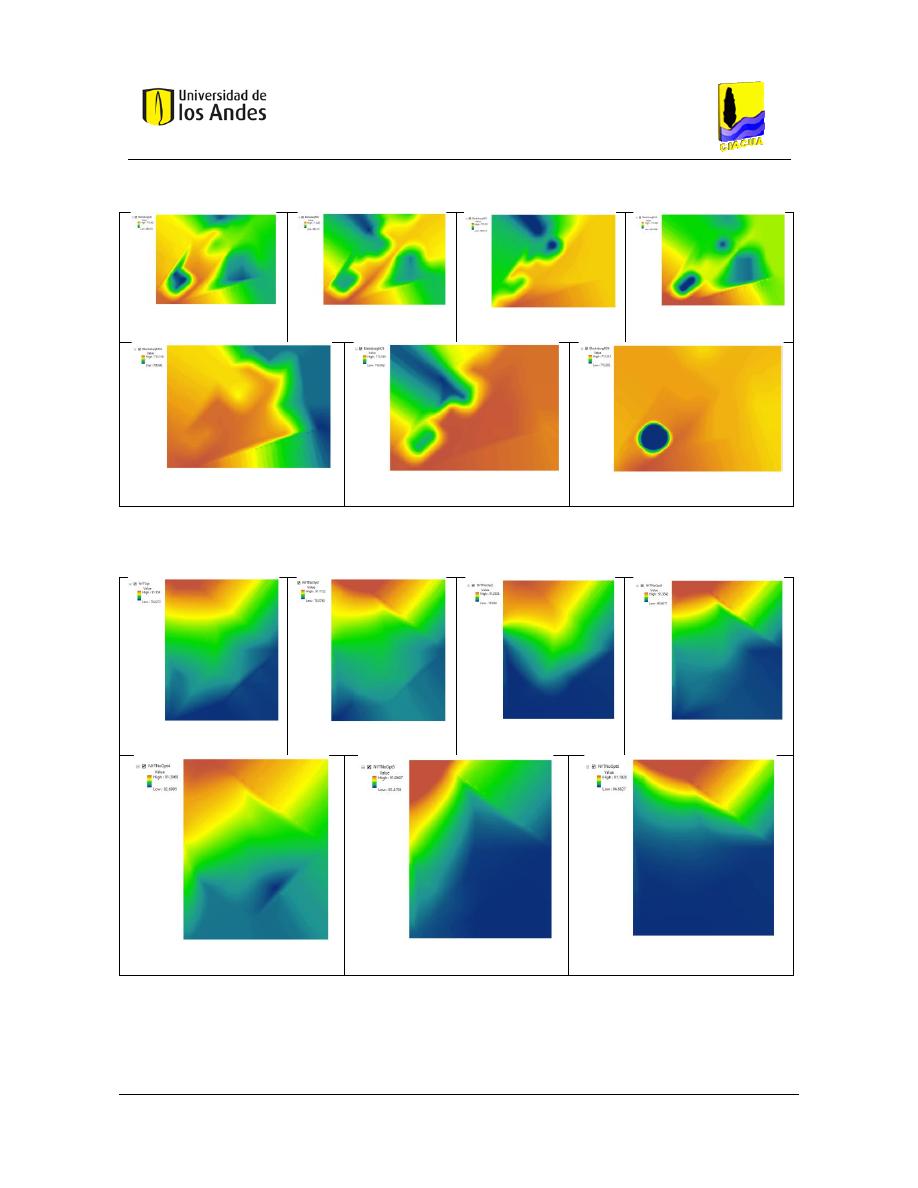
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
188
5.3.1.5 Red Blacksburg
Figura 475. DEM
Blacksburg - Óptimo.
Figura 476. DEM
Blacksburg - No Óptimo 1.
Figura 477. DEM
Blacksburg - No Óptimo 2.
Figura
478.
DEM
Blacksburg - No Óptimo 3.
Figura 479. DEM Blacksburg - No
Óptimo 4.
Figura 480. DEM Blacksburg - No
Óptimo 5.
Figura 481. DEM Blacksburg - No
Óptimo 6.
5.3.1.6 Red New York Tunnels
Figura 482. DEM New York
Tunnels - Óptimo.
Figura 483. DEM New York
Tunnels - No Óptimo 1.
Figura 484. DEM New York
Tunnels - No Óptimo 2.
Figura 485. DEM New York
Tunnels - No Óptimo 3.
Figura 486. DEM New York Tunnels -
No Óptimo 4.
Figura 487. DEM New York Tunnels -
No Óptimo 5.
Figura 488. DEM New York Tunnels -
No Óptimo 6.
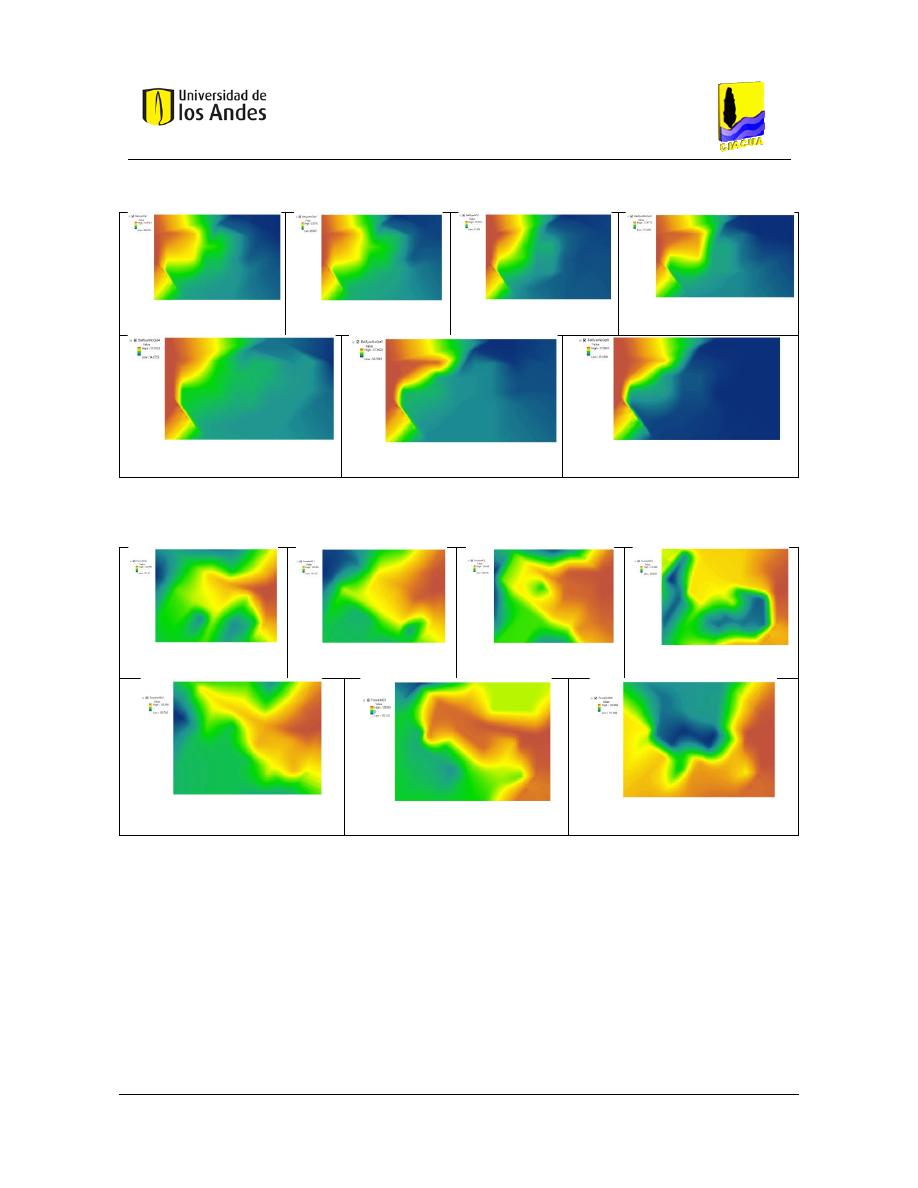
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
189
5.3.1.7 Red BakRyan
Figura 489. DEM BakRyan
- Óptimo.
Figura 490. DEM BakRyan
- No Óptimo 1.
Figura 491. DEM BakRyan -
No Óptimo 2.
Figura 492. DEM BakRyan -
No Óptimo 3.
Figura 493. DEM BakRyan - No
Óptimo 4.
Figura 494. DEM BakRyan - No
Óptimo 5.
Figura 495. DEM BakRyan - No Óptimo
6.
5.3.1.8 Red Fossolo
Figura 496. DEM Fossolo -
Óptimo.
Figura 497. DEM Fossolo -
No Óptimo 1.
Figura 498. DEM Fossolo -
No Óptimo 2.
Figura 499. DEM Fossolo -
No Óptimo 3.
Figura 500. DEM Fossolo - No
Óptimo 4.
Figura 501. DEM Fossolo - No
Óptimo 5.
Figura 502. DEM Fossolo - No Óptimo
6.
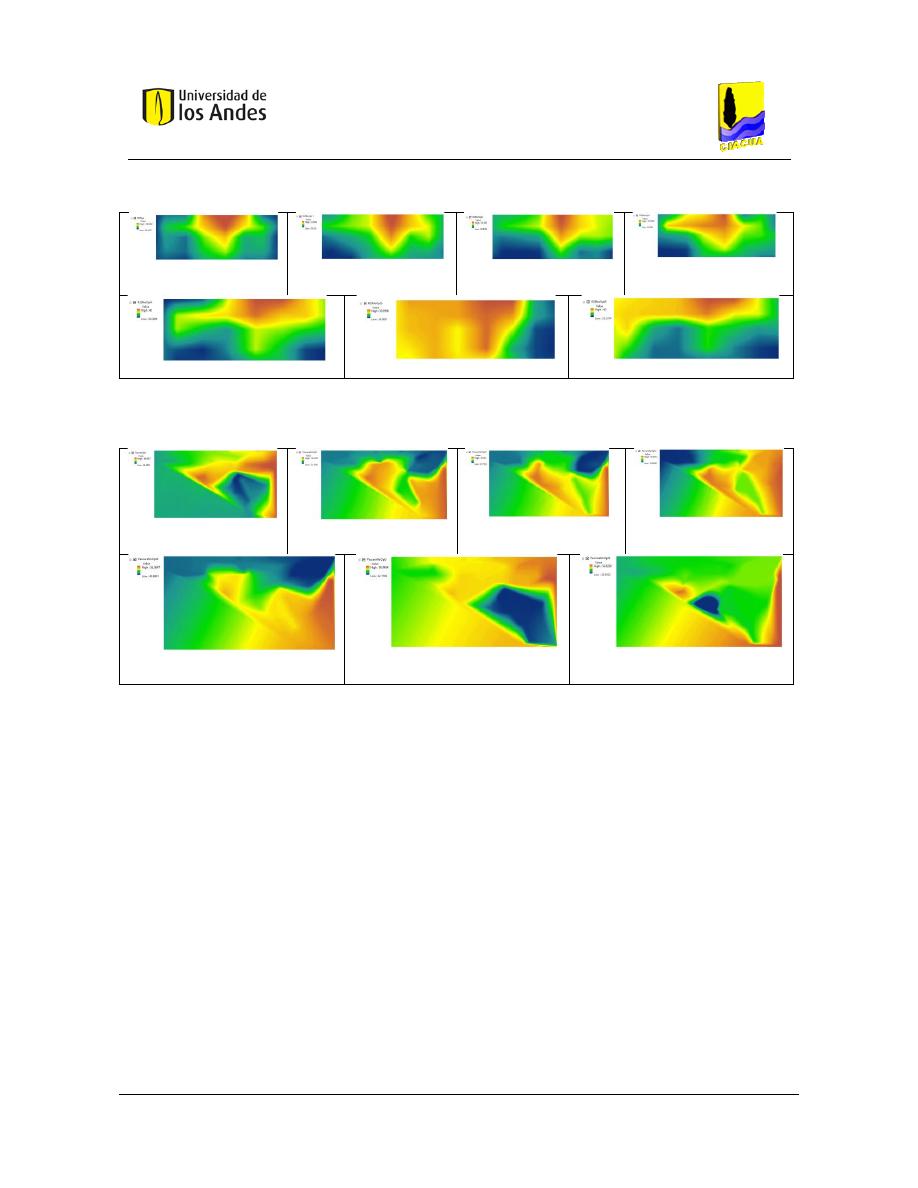
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
190
5.3.1.9 Red R28
Figura 503. DEM R28 -
Óptimo.
Figura 504. DEM R28 - No
Óptimo 1.
Figura 505. DEM R28 - No
Óptimo 2.
Figura 506. DEM R28 - No
Óptimo 3.
Figura 507. DEM R28 - No Óptimo 4.
Figura 508. DEM R28 - No Óptimo 5.
Figura 509. DEM R28 - No Óptimo 6.
5.3.1.10 Red Pescara
Figura 510. DEM Pescara –
Óptimo.
Figura 511. DEM Pescara -
No Óptimo 1.
Figura 512. DEM Pescara -
No Óptimo 2.
Figura 513. DEM Pescara -
No Óptimo 3.
Figura 514. DEM Pescara - No
Óptima 4.
Figura 515. DEM Pescara - No
Óptima 5.
Figura 516. DEM Pescara - No
Óptima 6.
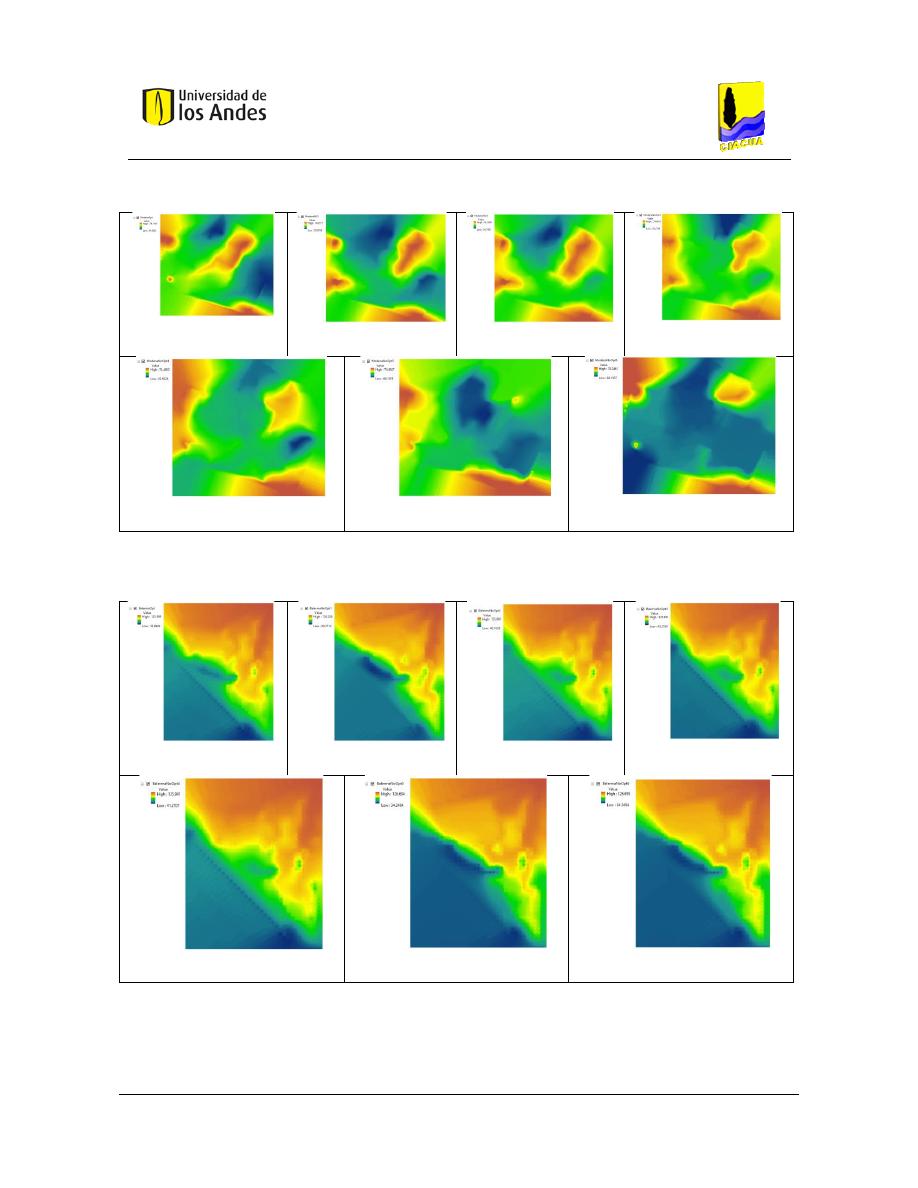
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
191
5.3.1.11 Red Modena
Figura 517. DEM Modena -
Óptimo.
Figura 518. DEM Modena -
No Óptimo 1.
Figura 519. DEM Modena -
No Óptimo 2.
Figura 520. DEM Modena -
No Óptimo 3.
Figura 521. DEM Modena - No
Óptimo 4.
Figura 522. DEM Modena - No
Óptimo 5.
Figura 523. DEM Modena - No
Óptimo 6.
5.3.1.12 Red Balerma
Figura 524. DEM Balerma -
Óptimo.
Figura 525. DEM Balerma -
No Óptimo 1.
Figura 526. DEM Balerma -
No Óptimo 2.
Figura 527. DEM Balerma -
No Óptimo 3.
Figura 528. DEM Balerma - No
Óptimo 4.
Figura 529. DEM Balerma - No
Óptimo 5.
Figura 530. DEM Balerma - No
Óptimo 6.
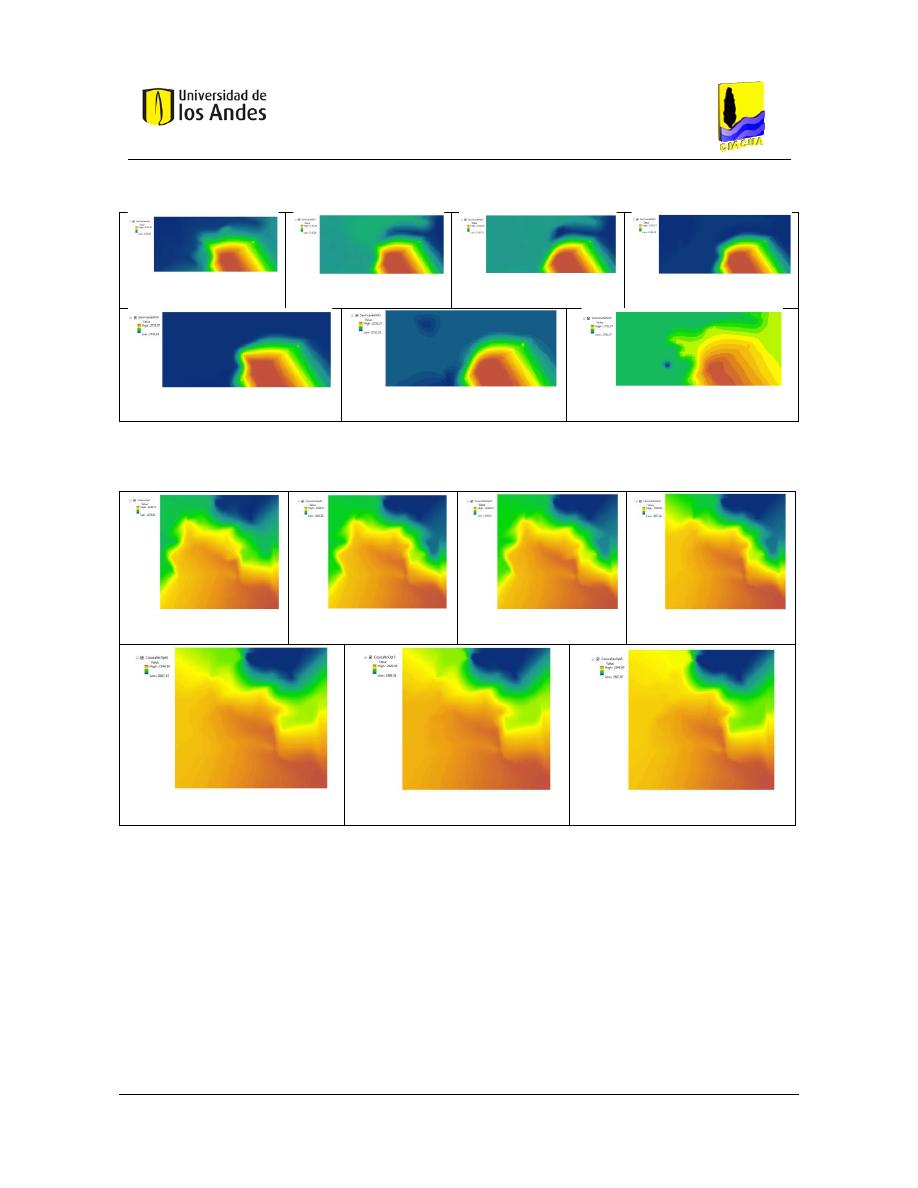
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
192
5.3.1.13 Red San Vicente
Figura 531. DEM San
Vicente - Óptimo.
Figura 532. DEM San
Vicente - No Óptimo 1.
Figura 533. DEM San
Vicente - No Óptimo 2.
Figura 534. DEM San
Vicente - No Óptimo 3.
Figura 535. DEM San Vicente - No
Óptimo 4.
Figura 536. DEM San Vicente - No
Óptimo 5.
Figura 537. DEM San Vicente - No
Óptimo 6.
5.3.1.14 Red Cazucá
Figura 538. DEM Cazucá -
Óptimo.
Figura 539. DEM Cazucá -
No Óptimo 1.
Figura 540. DEM Cazucá -
No Óptimo 2.
Figura 541. DEM Cazucá -
No Óptimo 3.
Figura 542. DEM Cazucá - No Óptimo
4.
Figura 543. DEM Cazucá - No Óptimo
5.
Figura 544. DEM Cazucá - No Óptimo
6.
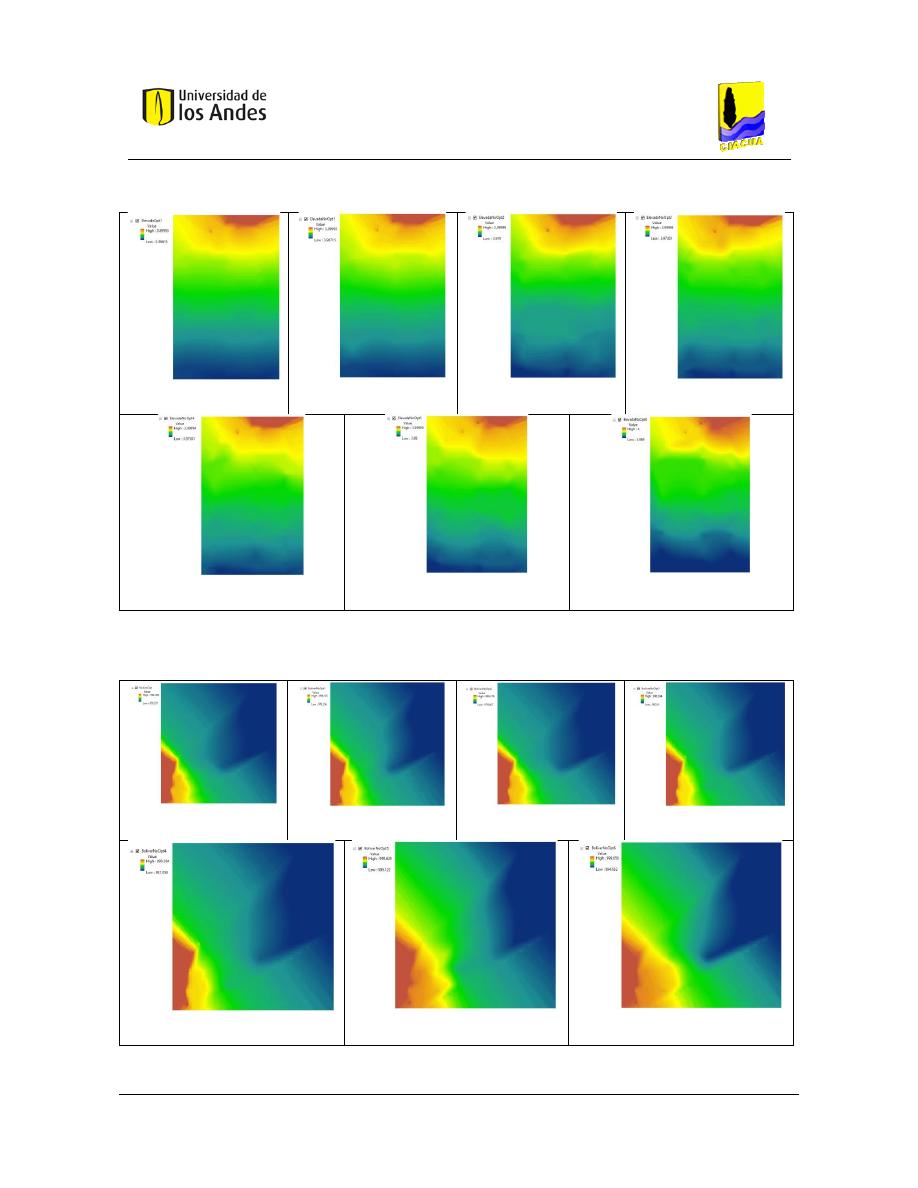
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
193
5.3.1.15 Red Elevada
Figura 545. DEM Elevada -
Óptimo.
Figura 546. DEM Elevada -
No Óptimo 1.
Figura 547. DEM Elevada -
No Óptimo 2.
Figura 548. DEM Elevada -
No Óptimo 3.
Figura 549. DEM Elevada - No
Óptimo 4.
Figura 550. DEM Elevada - No
Óptimo 5.
Figura 551. DEM Elevada - No
Óptimo 6.
5.3.1.16 Red Bolívar
Figura 552. DEM Bolívar -
Óptimo.
Figura 553. DEM Bolívar -
No Óptimo 1.
Figura 554. DEM Bolívar -
No Óptimo 2.
Figura 555. DEM Bolívar -
No Óptimo 3.
Figura 556. DEM Bolívar - No Óptimo
4.
Figura 557. DEM Bolívar - No Óptimo
5.
Figura 558. DEM Bolívar - No Óptimo
6.
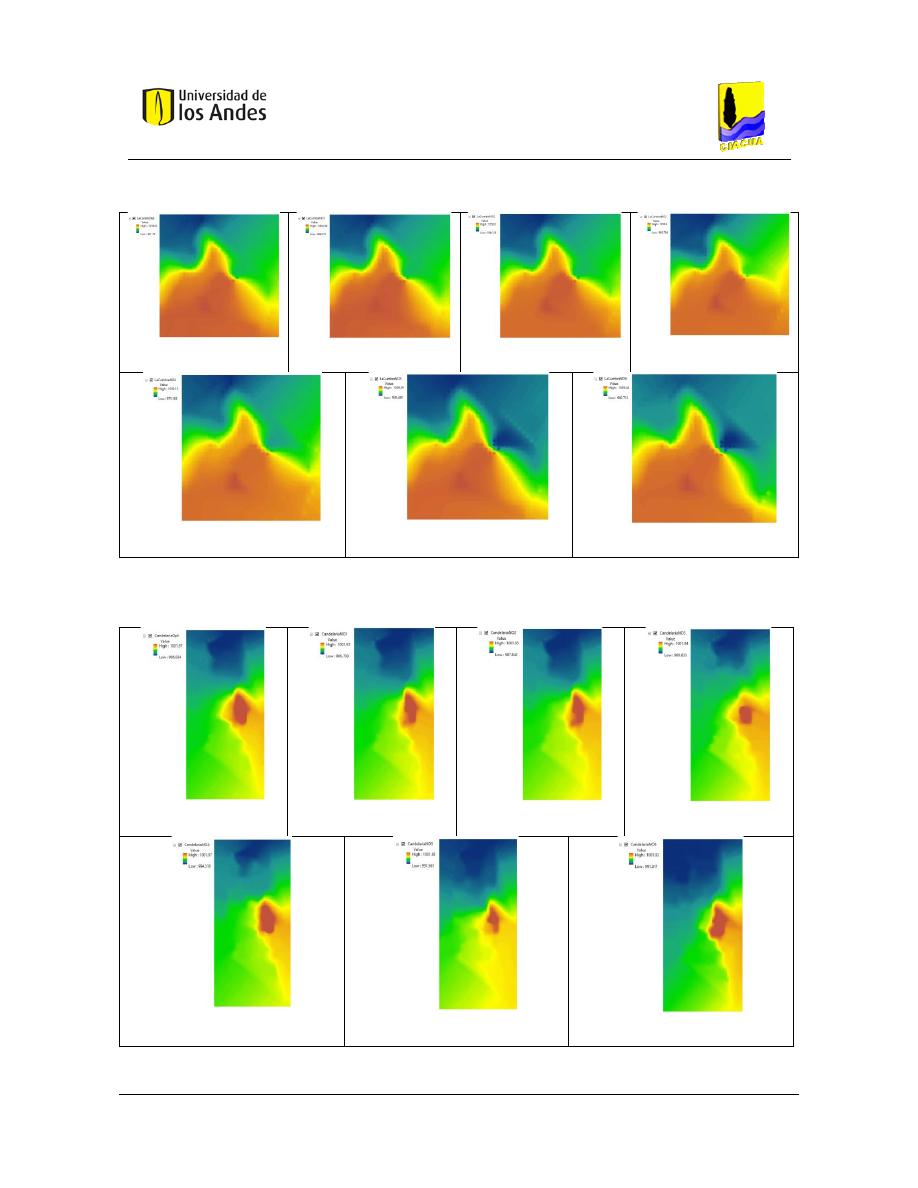
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
194
5.3.1.17 Red La Cumbre
Figura 559. DEM La
Cumbre - Óptimo.
Figura 560. DEM La Cumbre
- No Óptimo 1.
Figura 561. DEM La
Cumbre - No Óptimo 2.
Figura 562. DEM La
Cumbre - No Óptimo 3.
Figura 563. DEM La Cumbre - No
Óptimo 4.
Figura 564. DEM La Cumbre - No
Óptimo 5.
Figura 565. DEM La Cumbre - No
Óptimo 6.
5.3.1.18 Red Candelaria
Figura 566. DEM
Candelaria - Óptimo.
Figura 567. DEM
Candelaria - No Óptimo 1.
Figura 568. DEM
Candelaria - No Óptimo 2.
Figura 569. DEM
Candelaria - No Óptimo 3.
Figura 570. DEM Candelaria - No
Óptimo 4.
Figura 571. DEM Candelaria - No
Óptimo 5.
Figura 572. DEM Candelaria - No
Óptimo 6.
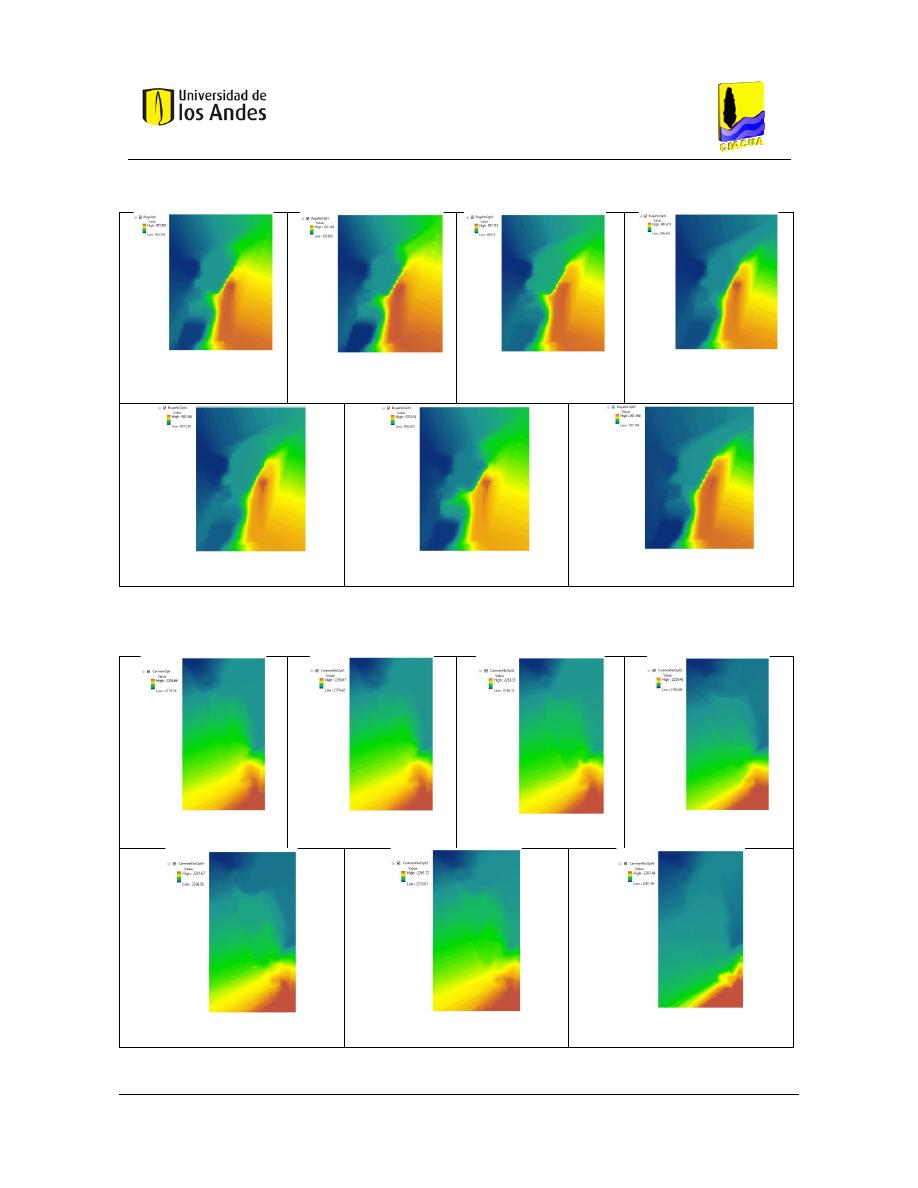
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
195
5.3.1.19 Red Bugalagrande
Figura 573. DEM
Bugalagrande - Óptimo.
Figura 574. DEM
Bugalagrande - No Óptimo
1.
Figura 575. DEM
Bugalagrande - No Óptimo
2.
Figura 576. DEM
Bugalagrande - No Óptimo
3.
Figura 577. DEM Bugalagrande - No
Óptimo 4.
Figura 578. DEM Bugalagrande - No
Óptimo 5.
Figura 579. DEM Bugalagrande - No
Óptimo 6.
5.3.1.20 Red Carmen
Figura 580. DEM Carmen -
Óptimo.
Figura 581. DEM Carmen -
No Óptimo 1.
Figura 582. DEM Carmen -
No Óptimo 2.
Figura 583. DEM Carmen -
No Óptimo 3.
Figura 584. DEM Carmen - No
Óptimo 4.
Figura 585. DEM Carmen - No
Óptimo 5.
Figura 586. DEM Carmen - No
Óptimo 6.
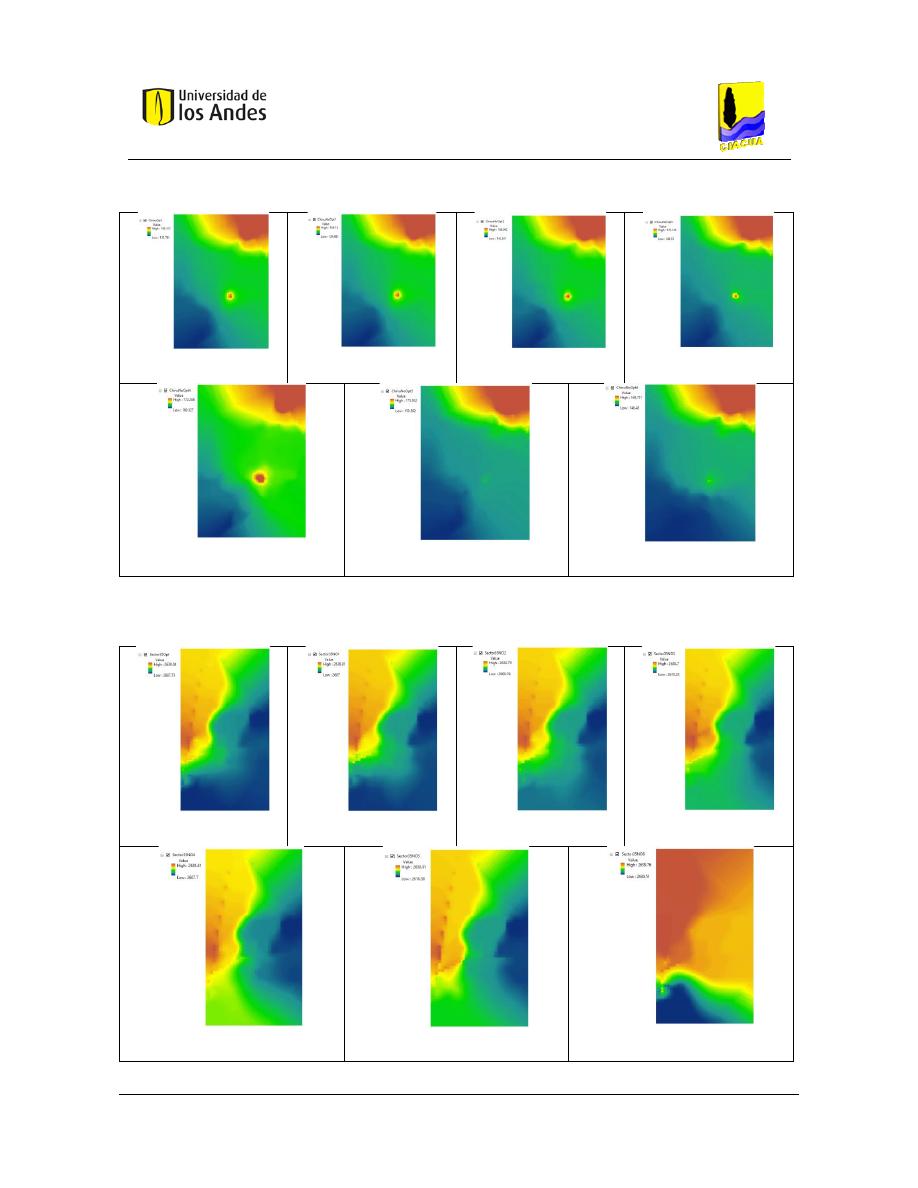
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
196
5.3.1.21 Red Chinú
Figura 587. DEM Chinú -
Óptimo.
Figura 588. DEM Chinú -
No Óptimo 1.
Figura 589. DEM Chinú -
No Óptimo 2.
Figura 590. DEM Chinú -
No Óptimo 3.
Figura 591. DEM Chinú - No Óptimo
4.
Figura 592. DEM Chinú - No Óptimo
5.
Figura 593. DEM Chinú - No Óptimo
6.
5.3.1.22 Red Sector 35
Figura 594. DEM Sector 35
- Óptimo.
Figura 595. DEM Sector 35
- No Óptimo 1.
Figura 596. DEM Sector 35
- No Óptimo 2.
Figura 597. DEM Sector 35
- No Óptimo 3.
Figura 598. DEM Sector 35 - No
Óptimo 4.
Figura 599. DEM Sector 35 - No
Óptimo 5.
Figura 600. DEM Sector 35 - No
Óptimo 6.
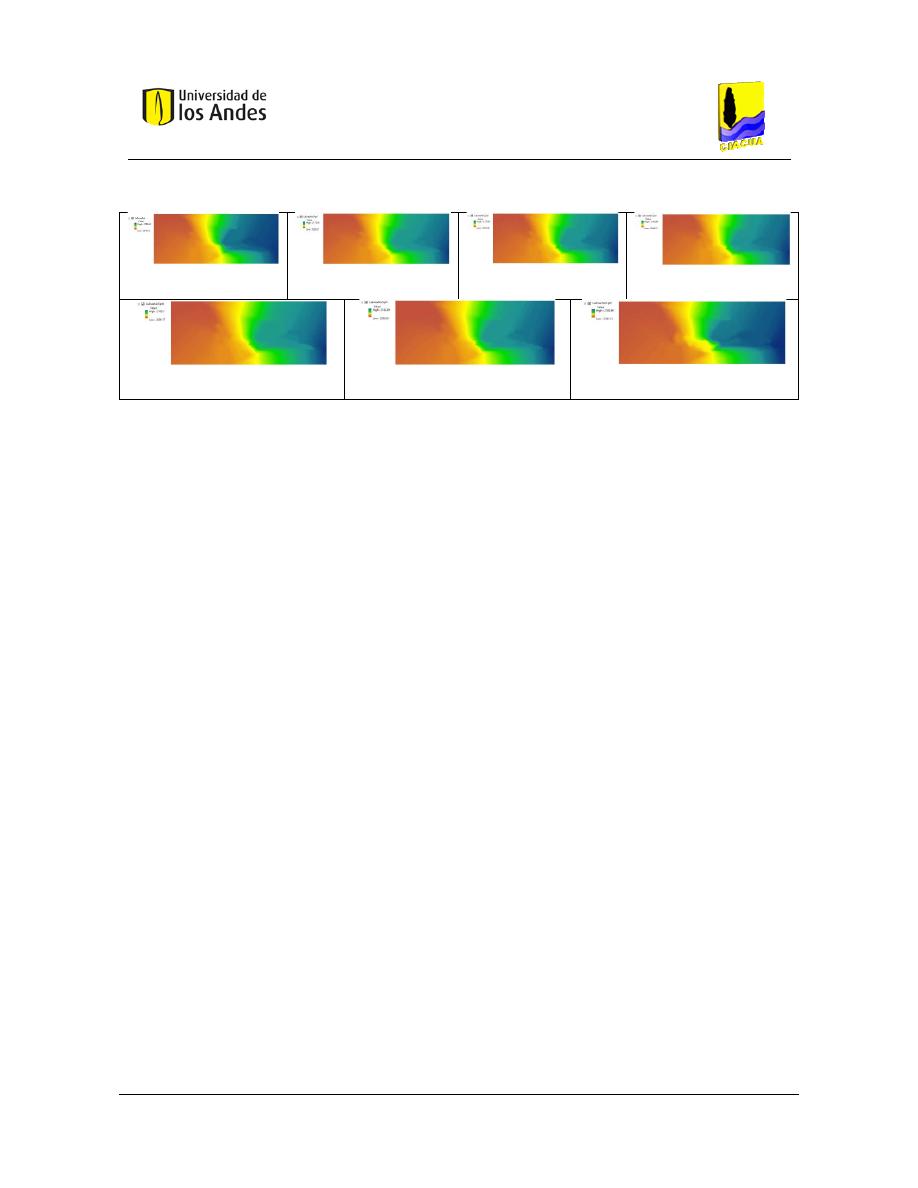
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
197
5.3.1.23 Red La Enea
Figura 601. DEM La Enea -
Óptimo.
Figura 602. DEM La Enea -
No Óptimo 1.
Figura 603. DEM La Enea -
No Óptimo 2.
Figura 604. DEM La Enea -
No Óptimo 3.
Figura 605. DEM La Enea - No
Óptimo 4.
Figura 606. DEM La Enea - No Óptimo
5.
Figura 607. DEM La Enea - No Óptimo
6.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
198
5.3.2 Dimensiones fractales
5.3.2.1 Altura de caja unitaria
Tabla 3. Dimensiones fractales - Altura unitaria - Red
Two Loops.
Tabla 4. Dimensiones fractales - Altura unitaria - Red
Two Loops.
Tabla 5. Dimensiones fractales - Altura unitaria - Red
Taichung.
Tabla 6. Dimensiones fractales - Altura unitaria - Red
Hanoi.
Tabla 7. Dimensiones fractales - Altura unitaria - Red
Blacksburg.
Tabla 8. Dimensiones fractales - Altura unitaria - Red
New York Tunnels.
Tabla 9. Dimensiones fractales - Altura unitaria - Red
BakRyan.
Tabla 10. Dimensiones fractales - Altura unitaria - Red
Fossolo.
Diseño
Dimensión Fractal
R^2
Óptimo
0.05774
0.79
No Óptimo 1
0.04926
0.63
No Óptimo 2
0.10320
0.74
No Óptimo 3
0.03887
0.63
No Óptimo 4
0.03500
0.59
No Óptimo 5
0.07014
0.88
No Óptimo 6
0.03750
0.73
Red Two Loops
Diseño
Dimensión Fractal
R^2
Óptimo
0.04947
0.78
No Óptimo 1
0.04747
0.78
No Óptimo 2
0.05990
0.84
No Óptimo 3
0.04779
0.78
No Óptimo 4
0.04622
0.75
No Óptimo 5
0.05201
0.74
No Óptimo 6
0.05942
0.70
Red Two Reservoirs
Diseño
Dimensión Fractal
R^2
Óptimo
0.02420
0.46
No Óptimo 1
0.01915
0.39
No Óptimo 2
0.05187
0.89
No Óptimo 3
0.00682
0.21
No Óptimo 4
0.01233
0.32
No Óptimo 5
0.00787
0.09
No Óptimo 6
0.05448
0.52
Red Taichung
Diseño
Dimensión Fractal
R^2
Óptimo
0.01580
0.05
No Óptimo 1
0.00774
0.01
No Óptimo 2
0.01650
0.07
No Óptimo 3
0.03478
0.26
No Óptimo 4
0.01637
0.07
No Óptimo 5
0.02138
0.12
No Óptimo 6
0.03228
0.33
Red Hanoi
Diseño
Dimensión Fractal
R^2
Óptimo
0.00122
0.00
No Óptimo 1
0.01207
0.07
No Óptimo 2
0.02965
0.09
No Óptimo 3
0.03864
0.48
No Óptimo 4
0.01573
0.07
No Óptimo 5
0.05030
0.68
No Óptimo 6
0.11497
0.37
Red Blacksburg
Diseño
Dimensión Fractal
R^2
Óptimo
0.06398
0.95
No Óptimo 1
0.05821
0.97
No Óptimo 2
0.07005
0.79
No Óptimo 3
0.07955
0.91
No Óptimo 4
0.05256
0.67
No Óptimo 5
0.07063
0.50
No Óptimo 6
0.05013
0.86
Red New York Tunnels
Diseño
Dimensión Fractal
R^2
Óptimo
0.06608
0.90
No Óptimo 1
0.04618
0.70
No Óptimo 2
0.06480
0.87
No Óptimo 3
0.05112
0.78
No Óptimo 4
0.01912
0.47
No Óptimo 5
0.05046
0.97
No Óptimo 6
0.05514
0.90
Red BakRyan
Diseño
Dimensión Fractal
R^2
Óptimo
0.02652
0.78
No Óptimo 1
0.02285
0.86
No Óptimo 2
-0.02503
0.12
No Óptimo 3
-0.09170
0.41
No Óptimo 4
0.00028
0.00
No Óptimo 5
-0.07504
0.34
No Óptimo 6
-0.00096
0.00
Red Fossolo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
199
Tabla 11. Dimensiones fractales - Altura unitaria - Red
R28.
Tabla 12. Dimensiones fractales - Altura unitaria - Red
Pescara.
Tabla 13. Dimensiones fractales - Altura unitaria - Red
Modena.
Tabla 14. Dimensiones fractales - Altura unitaria - Red
Balerma.
Tabla 15. Dimensiones fractales - Altura unitaria - Red
Cazucá.
Tabla 16. Dimensiones fractales - Altura unitaria - Red
Bolívar.
Tabla 17. Dimensiones fractales - Altura unitaria - Red La
Cumbre.
Tabla 18. Dimensiones fractales - Altura unitaria - Red
Candelaria.
Tabla 19. Dimensiones fractales - Altura unitaria - Red
Bugalagrande.
Tabla 20. Dimensiones fractales - Altura unitaria - Red
Carmen.
Diseño
Dimensión Fractal
R^2
Óptimo
0.03631
0.67
No Óptimo 1
0.03337
0.67
No Óptimo 2
0.03108
0.89
No Óptimo 3
0.00926
0.21
No Óptimo 4
0.00038
0.00
No Óptimo 5
0.06454
0.77
No Óptimo 6
0.04142
0.86
Red R28
Diseño
Dimensión Fractal
R^2
Óptimo
-0.05113
0.27
No Óptimo 1
-0.12111
0.67
No Óptimo 2
-0.10704
0.65
No Óptimo 3
0.01616
0.51
No Óptimo 4
-0.09817
0.54
No Óptimo 5
-0.09898
0.51
No Óptimo 6
-0.02575
0.07
Red Pescara
Diseño
Dimensión Fractal
R^2
Óptimo
-0.02120
0.27
No Óptimo 1
-0.02550
0.31
No Óptimo 2
-0.01241
0.18
No Óptimo 3
0.01152
0.56
No Óptimo 4
0.01294
0.64
No Óptimo 5
-0.02687
0.18
No Óptimo 6
0.00310
0.03
Red Modena
Diseño
Dimensión Fractal
R^2
Óptimo
-0.05649
0.40
No Óptimo 1
-0.04797
0.45
No Óptimo 2
-0.06618
0.43
No Óptimo 3
-0.06386
0.43
No Óptimo 4
-0.06917
0.45
No Óptimo 5
-0.07275
0.49
No Óptimo 6
-0.07916
0.51
Red Balerma
Diseño
Dimensión Fractal
R^2
Óptimo
-0.02464
0.12
No Óptimo 1
-0.09929
0.42
No Óptimo 2
-0.08102
0.38
No Óptimo 3
-0.06156
0.34
No Óptimo 4
-0.02891
0.13
No Óptimo 5
-0.03447
0.16
No Óptimo 6
-0.05286
0.24
Red Cazucá
Diseño
Dimensión Fractal
R^2
Óptimo
0.15250
0.48
No Óptimo 1
0.14340
0.45
No Óptimo 2
0.13716
0.41
No Óptimo 3
0.13443
0.44
No Óptimo 4
0.14570
0.51
No Óptimo 5
0.05966
0.71
No Óptimo 6
0.03720
0.39
Red Bolívar
Diseño
Dimensión Fractal
R^2
Óptimo
0.04899
0.64
No Óptimo 1
0.04692
0.57
No Óptimo 2
0.05348
0.70
No Óptimo 3
0.07815
0.83
No Óptimo 4
0.04967
0.77
No Óptimo 5
-0.03712
0.22
No Óptimo 6
-0.04363
0.26
Red La Cumbre
Diseño
Dimensión Fractal
R^2
Óptimo
0.13102
0.77
No Óptimo 1
0.12437
0.79
No Óptimo 2
0.12292
0.79
No Óptimo 3
0.18384
0.64
No Óptimo 4
0.14446
0.71
No Óptimo 5
0.17943
0.71
No Óptimo 6
0.16991
0.70
Red Candelaria

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
200
Tabla 21. Dimensiones fractales - Altura unitaria - Red
Chinú.
Tabla 22. Dimensiones fractales - Altura unitaria - Red
Sector 35.
Tabla 23. Análisis fractal bidimensional - Altura unitaria - Red La Enea.
5.3.2.2 Altura de caja por tanteo
Mediante ensayo y error se obtienen las siguientes alturas de caja como posibles opciones que
mejoran la correlación del modelo fractal a comparación de la altura unitaria. Si el coeficiente de
determinación de la red para una altura unitaria es superior a 0.90, no se realiza la búsqueda de
una nueva altura.
Diseño
Dimensión Fractal
R^2
Óptimo
0.12632
0.70
No Óptimo 1
0.12714
0.73
No Óptimo 2
0.11630
0.78
No Óptimo 3
0.09962
0.89
No Óptimo 4
0.11470
0.83
No Óptimo 5
0.12841
0.70
No Óptimo 6
0.09472
0.92
Red Bugalagrande
Diseño
Dimensión Fractal
R^2
Óptimo
-0.06574
0.22
No Óptimo 1
-0.06395
0.21
No Óptimo 2
-0.04994
0.12
No Óptimo 3
-0.00229
0.00
No Óptimo 4
-0.02677
0.04
No Óptimo 5
-0.01631
0.02
No Óptimo 6
0.00266
0.00
Red Carmen
Diseño
Dimensión Fractal
R^2
Óptimo
0.03018
0.09
No Óptimo 1
0.03083
0.08
No Óptimo 2
0.04874
0.17
No Óptimo 3
0.03188
0.09
No Óptimo 4
0.07879
0.40
No Óptimo 5
0.07330
0.61
No Óptimo 6
0.11612
0.62
Red Chinú
Diseño
Dimensión Fractal
R^2
Óptimo
0.07538
0.93
No Óptimo 1
0.06820
0.89
No Óptimo 2
0.07717
0.90
No Óptimo 3
0.07273
0.80
No Óptimo 4
0.04265
0.70
No Óptimo 5
0.06078
0.71
No Óptimo 6
0.09070
0.94
Red Sector 35
Diseño
Dimensión Fractal
R^2
Óptimo
0.01665
0.08
No Óptimo 1
0.03985
0.73
No Óptimo 2
0.04021
0.67
No Óptimo 3
0.04221
0.66
No Óptimo 4
0.04959
0.89
No Óptimo 5
0.04395
0.66
No Óptimo 6
0.08423
0.87
Red La Enea
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
201
Tabla 24. Alturas de caja por tanteo.
Nombre
Altura de caja (m)
Two Loops
5.00
Two Reservoirs
0.10
Taichung
14.00
Hanoi
20.00
Blacksburg
7.00
New York Tunnels
1.00
Bakryan
1.00
Fossolo
0.50
R28
5.00
Pescara
1.00.E-03
Modena
5.00.E-03
Balerma
5.00.E-03
San Vicente
1.00.E-05
Cazucá
15.00
Elevada
1.00.E-06
Bolívar
2.80
La Cumbre
25.00
Candelaria
4.00
Bugalagrande
4.00
Carmen
5.00.E-04
Chinú
17.00
Sector 35
1.00
La Enea
15.00
Redes
patrón
Redes
reales

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
202
Tabla 25. Dimensiones fractales - Altura por tanteo - Red
Two Loops.
Tabla 26. Dimensiones fractales - Altura por tanteo - Red
Reservoirs.
Tabla 27. Dimensiones fractales - Altura por tanteo - Red
Taichung.
Tabla 28. Dimensiones fractales - Altura por tanteo - Red
Hanoi.
Tabla 29. Dimensiones fractales - Altura por tanteo - Red
Blacksburg.
Tabla 30. Dimensiones fractales - Altura por tanteo - Red
Fossolo.
Tabla 31. Dimensiones fractales - Altura por tanteo - Red
R28.
Tabla 32. Dimensiones fractales - Altura por tanteo - Red
Pescara.
Diseño
Dimensión Fractal
R^2
Óptimo
0.03008
0.93
No Óptimo 1
0.01549
0.31
No Óptimo 2
0.01630
0.30
No Óptimo 3
0.00846
0.20
No Óptimo 4
0.03838
0.54
No Óptimo 5
0.05099
0.89
No Óptimo 6
0.03820
0.80
Red Two Loops
Diseño
Dimensión Fractal
R^2
Óptimo
0.05596
0.90
No Óptimo 1
0.05317
0.89
No Óptimo 2
0.05638
0.83
No Óptimo 3
0.05637
0.88
No Óptimo 4
0.06922
0.87
No Óptimo 5
0.09161
0.95
No Óptimo 6
0.10018
0.86
Red Two Reservoirs
Diseño
Dimensión Fractal
R^2
Óptimo
0.02831
0.92
No Óptimo 1
0.02913
0.42
No Óptimo 2
0.03621
0.55
No Óptimo 3
0.04208
0.61
No Óptimo 4
0.03030
0.44
No Óptimo 5
0.04179
0.65
No Óptimo 6
0.00427
0.05
Red Taichung
Diseño
Dimensión Fractal
R^2
Óptimo
0.03369
0.92
No Óptimo 1
0.03383
0.93
No Óptimo 2
0.03420
0.91
No Óptimo 3
0.03011
0.69
No Óptimo 4
0.03444
0.87
No Óptimo 5
0.02513
0.62
No Óptimo 6
0.02457
0.63
Red Hanoi
Diseño
Dimensión Fractal
R^2
Óptimo
0.04121
0.67
No Óptimo 1
0.01797
0.63
No Óptimo 2
0.04878
0.71
No Óptimo 3
0.04111
0.55
No Óptimo 4
0.02216
0.77
No Óptimo 5
0.02238
0.71
No Óptimo 6
0.03215
0.35
Red Blacksburg
Diseño
Dimensión Fractal
R^2
Óptimo
0.03034
0.82
No Óptimo 1
0.02278
0.78
No Óptimo 2
-0.03997
0.24
No Óptimo 3
-0.14650
0.54
No Óptimo 4
-0.00059
0.00
No Óptimo 5
-0.11162
0.47
No Óptimo 6
-0.01775
0.08
Red Fossolo
Diseño
Dimensión Fractal
R^2
Óptimo
0.02300
0.69
No Óptimo 1
0.00453
0.05
No Óptimo 2
0.01779
0.69
No Óptimo 3
-0.00580
0.09
No Óptimo 4
0.00689
0.11
No Óptimo 5
0.00344
0.01
No Óptimo 6
0.00948
0.20
Red R28
Diseño
Dimensión Fractal
R^2
Óptimo
-0.13371
0.68
No Óptimo 1
-0.21642
0.74
No Óptimo 2
-0.19020
0.75
No Óptimo 3
-0.04555
0.40
No Óptimo 4
-0.26270
0.74
No Óptimo 5
-0.26169
0.80
No Óptimo 6
-0.23261
0.70
Red Pescara

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
203
Tabla 33. Dimensiones fractales - Altura por tanteo - Red
Modena.
Tabla 34. Dimensiones fractales - Altura por tanteo - Red
Balerma.
Tabla 35. Dimensiones fractales - Altura por tanteo - Red
San Vicente.
Tabla 36. Dimensiones fractales - Altura por tanteo - Red
Cazucá.
Tabla 37. Dimensiones fractales - Altura por tanteo - Red
Elevada.
Tabla 38. Dimensiones fractales - Altura por tanteo - Red
Bolívar.
Tabla 39. Dimensiones fractales - Altura por tanteo - Red
La Cumbre.
Tabla 40. Dimensiones fractales - Altura por tanteo - Red
Candelaria.
Diseño
Dimensión Fractal
R^2
Óptimo
-0.08694
0.72
No Óptimo 1
-0.12696
0.77
No Óptimo 2
-0.09830
0.69
No Óptimo 3
-0.04581
0.49
No Óptimo 4
-0.05365
0.53
No Óptimo 5
-0.23764
0.78
No Óptimo 6
-0.05795
0.70
Red Modena
Diseño
Dimensión Fractal
R^2
Óptimo
-0.10807
0.72
No Óptimo 1
-0.09217
0.74
No Óptimo 2
-0.11819
0.72
No Óptimo 3
-0.11684
0.72
No Óptimo 4
-0.12246
0.73
No Óptimo 5
-0.12226
0.74
No Óptimo 6
-0.13029
0.75
Red Balerma
Diseño
Dimensión Fractal
R^2
Óptimo
-0.21341
0.63
No Óptimo 1
-0.14559
0.63
No Óptimo 2
-0.22756
0.73
No Óptimo 3
-0.44976
0.74
No Óptimo 4
-0.60339
0.76
No Óptimo 5
-0.46482
0.75
No Óptimo 6
-0.31417
0.66
Red San Vicente
Diseño
Dimensión Fractal
R^2
Óptimo
0.04331
0.89
No Óptimo 1
0.01046
0.06
No Óptimo 2
0.01532
0.15
No Óptimo 3
0.02167
0.42
No Óptimo 4
0.05251
0.83
No Óptimo 5
0.05020
0.82
No Óptimo 6
0.04419
0.64
Red Cazucá
Diseño
Dimensión Fractal
R^2
Óptimo
-0.15043
0.69
No Óptimo 1
-0.15463
0.69
No Óptimo 2
-0.11915
0.66
No Óptimo 3
-0.18478
0.70
No Óptimo 4
-0.16858
0.69
No Óptimo 5
-0.17682
0.72
No Óptimo 6
-0.05063
0.48
Red Elevada
Diseño
Dimensión Fractal
R^2
Óptimo
0.11855
0.54
No Óptimo 1
0.09665
0.54
No Óptimo 2
0.09721
0.45
No Óptimo 3
0.12352
0.49
No Óptimo 4
0.09141
0.59
No Óptimo 5
0.04248
0.46
No Óptimo 6
0.04216
0.44
Red Bolívar
Diseño
Dimensión Fractal
R^2
Óptimo
0.05175
0.86
No Óptimo 1
0.05032
0.82
No Óptimo 2
0.05237
0.89
No Óptimo 3
0.06752
0.89
No Óptimo 4
0.05435
0.91
No Óptimo 5
0.02739
0.40
No Óptimo 6
0.02533
0.72
Red La Cumbre
Diseño
Dimensión Fractal
R^2
Óptimo
0.05033
0.93
No Óptimo 1
0.07236
0.83
No Óptimo 2
0.07695
0.92
No Óptimo 3
0.09775
0.68
No Óptimo 4
0.05874
0.78
No Óptimo 5
0.07350
0.90
No Óptimo 6
0.09963
0.85
Red Candelaria
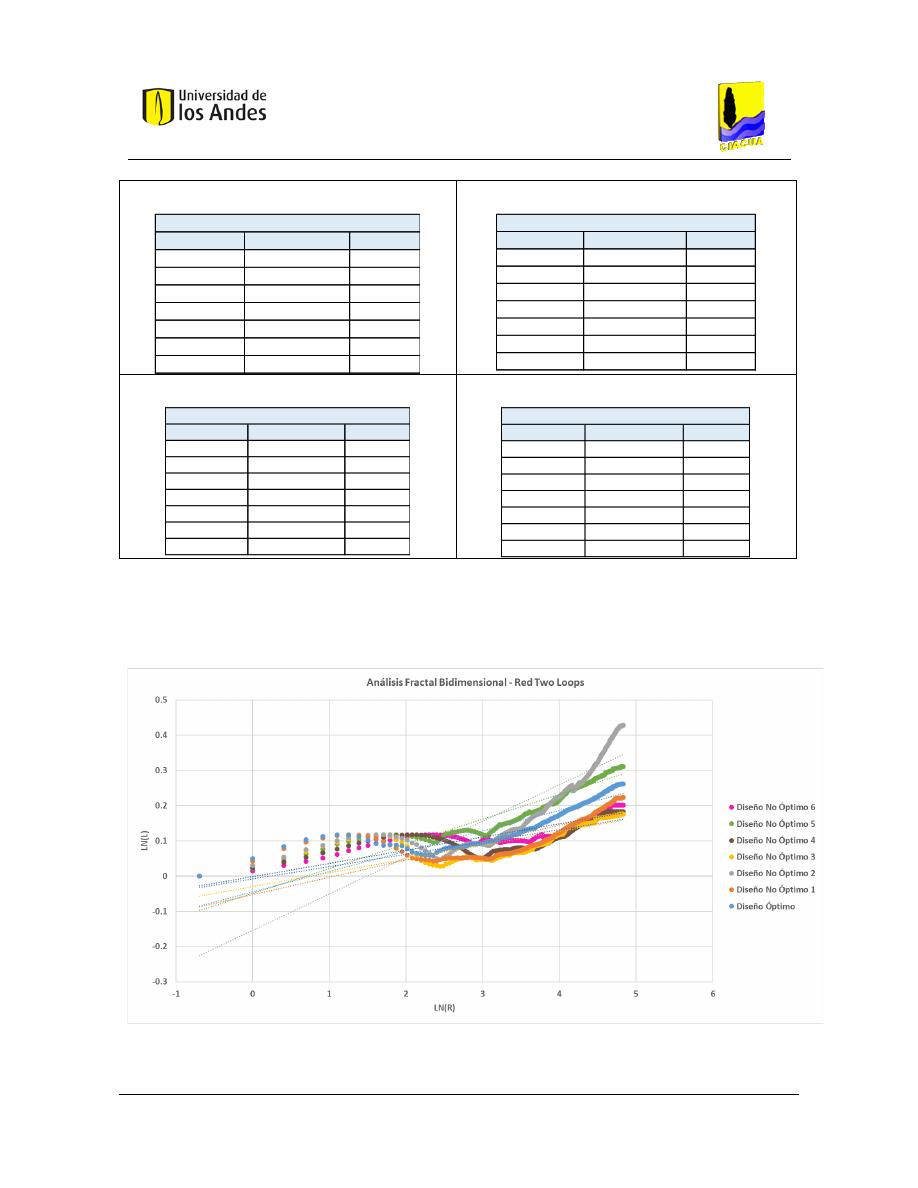
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
204
Tabla 41. Dimensiones fractales - Altura por tanteo - Red
Bugalagrande.
Tabla 42. Dimensiones fractales - Altura por tanteo - Red
Carmen.
Tabla 43. Dimensiones fractales - Altura por tanteo - Red
Chinú.
Tabla 44. Dimensiones fractales - Altura por tanteo - Red
La Enea.
5.3.3 Gráficas
5.3.3.1 Altura de caja unitaria
Figura 608. Análisis fractal bidimensional – Altura unitaria - Red Two Loops.
Diseño
Dimensión Fractal
R^2
Óptimo
0.09402
0.79
No Óptimo 1
0.08367
0.72
No Óptimo 2
0.08062
0.75
No Óptimo 3
0.08751
0.84
No Óptimo 4
0.09636
0.84
No Óptimo 5
0.06878
0.77
No Óptimo 6
0.08666
0.88
Red Bugalagrande
Diseño
Dimensión Fractal
R^2
Óptimo
-0.20511
0.76
No Óptimo 1
-0.20111
0.76
No Óptimo 2
-0.19752
0.75
No Óptimo 3
-0.17352
0.70
No Óptimo 4
-0.20410
0.75
No Óptimo 5
-0.18820
0.76
No Óptimo 6
-0.18246
0.56
Red Carmen
Diseño
Dimensión Fractal
R^2
Óptimo
0.04778
0.82
No Óptimo 1
0.04055
0.77
No Óptimo 2
0.00817
0.15
No Óptimo 3
0.02256
0.48
No Óptimo 4
0.03643
0.67
No Óptimo 5
0.02107
0.77
No Óptimo 6
0.02127
0.78
Red Chinú
Diseño
Dimensión Fractal
R^2
Óptimo
0.06912
0.93
No Óptimo 1
0.06956
0.91
No Óptimo 2
0.04939
0.94
No Óptimo 3
0.05570
0.96
No Óptimo 4
0.04235
0.77
No Óptimo 5
0.05520
0.95
No Óptimo 6
0.00000
0.00
Red La Enea
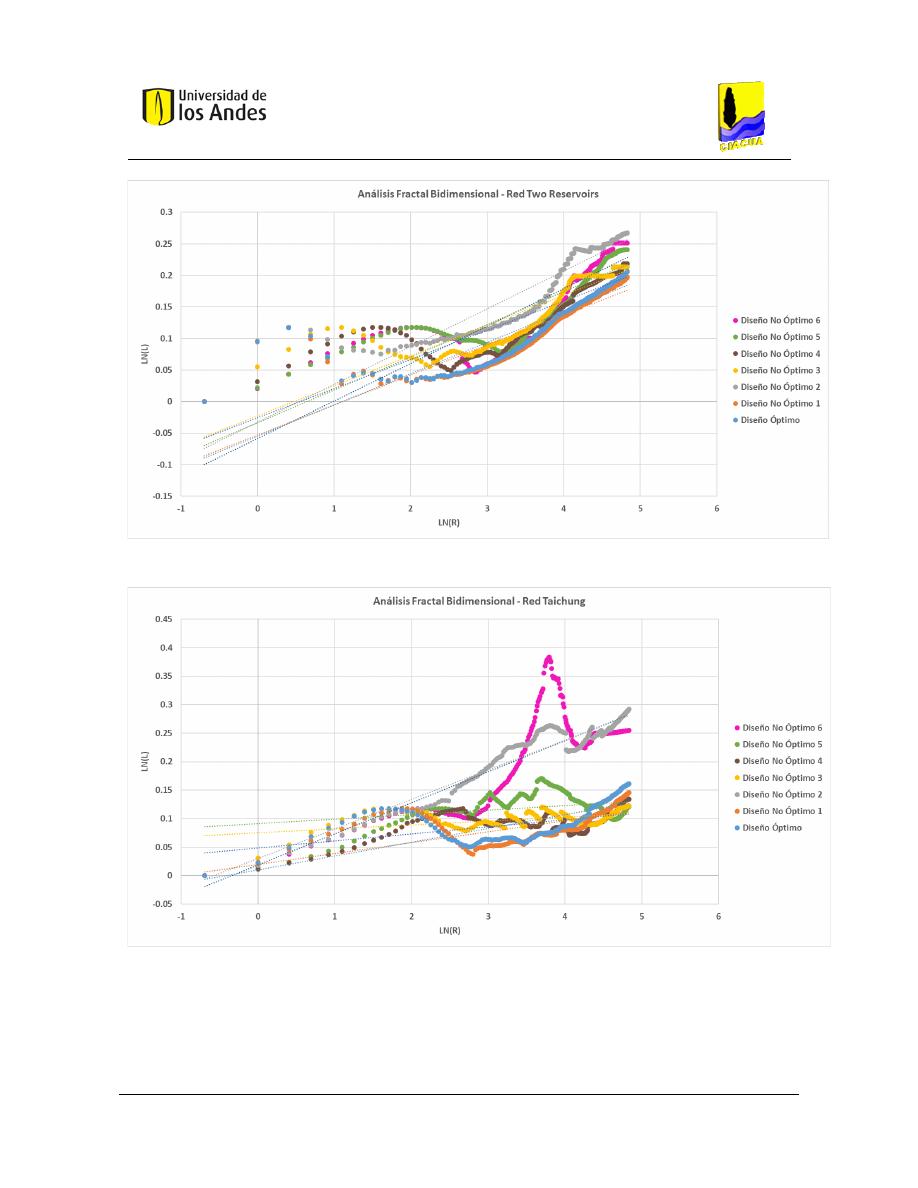
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
205
Figura 609. Análisis fractal bidimensional – Altura unitaria - Red Two Reservoirs.
Figura 610. Análisis fractal bidimensional – Altura unitaria - Red Taichung.
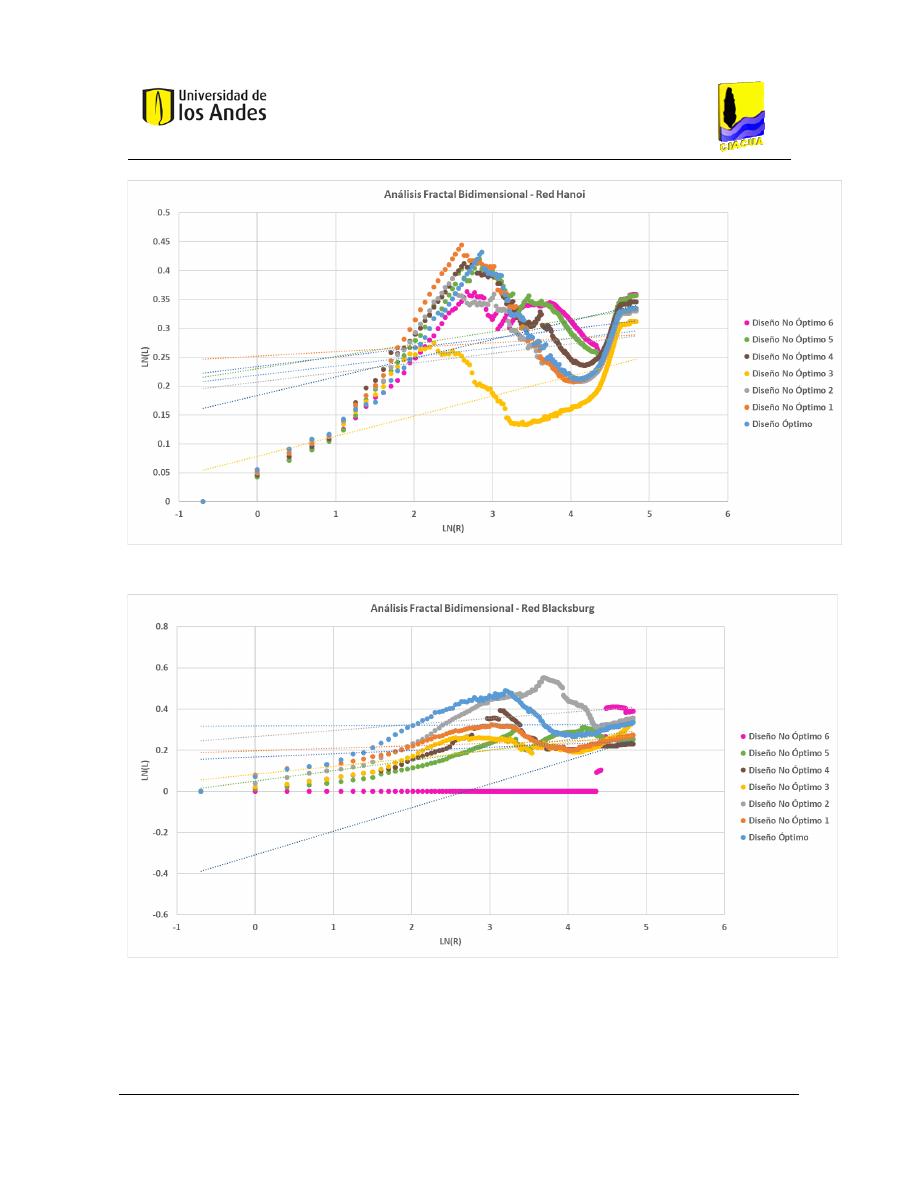
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
206
Figura 611. Análisis fractal bidimensional – Altura unitaria - Red Hanoi.
Figura 612. Análisis fractal bidimensional – Altura unitaria - Red Blacksburg.
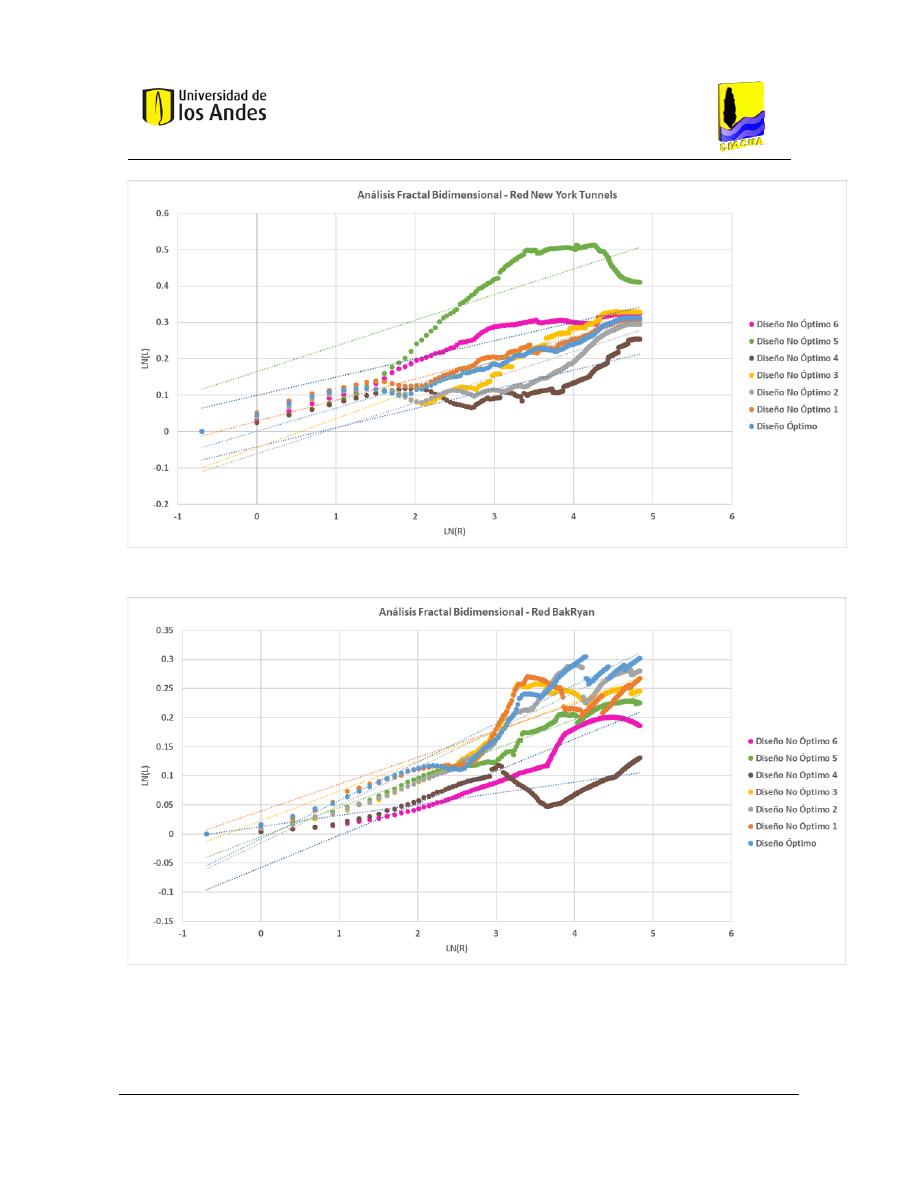
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
207
Figura 613. Análisis fractal bidimensional – Altura unitaria - Red New York Tunnels.
Figura 614. Análisis fractal bidimensional – Altura unitaria - Red BakRyan.
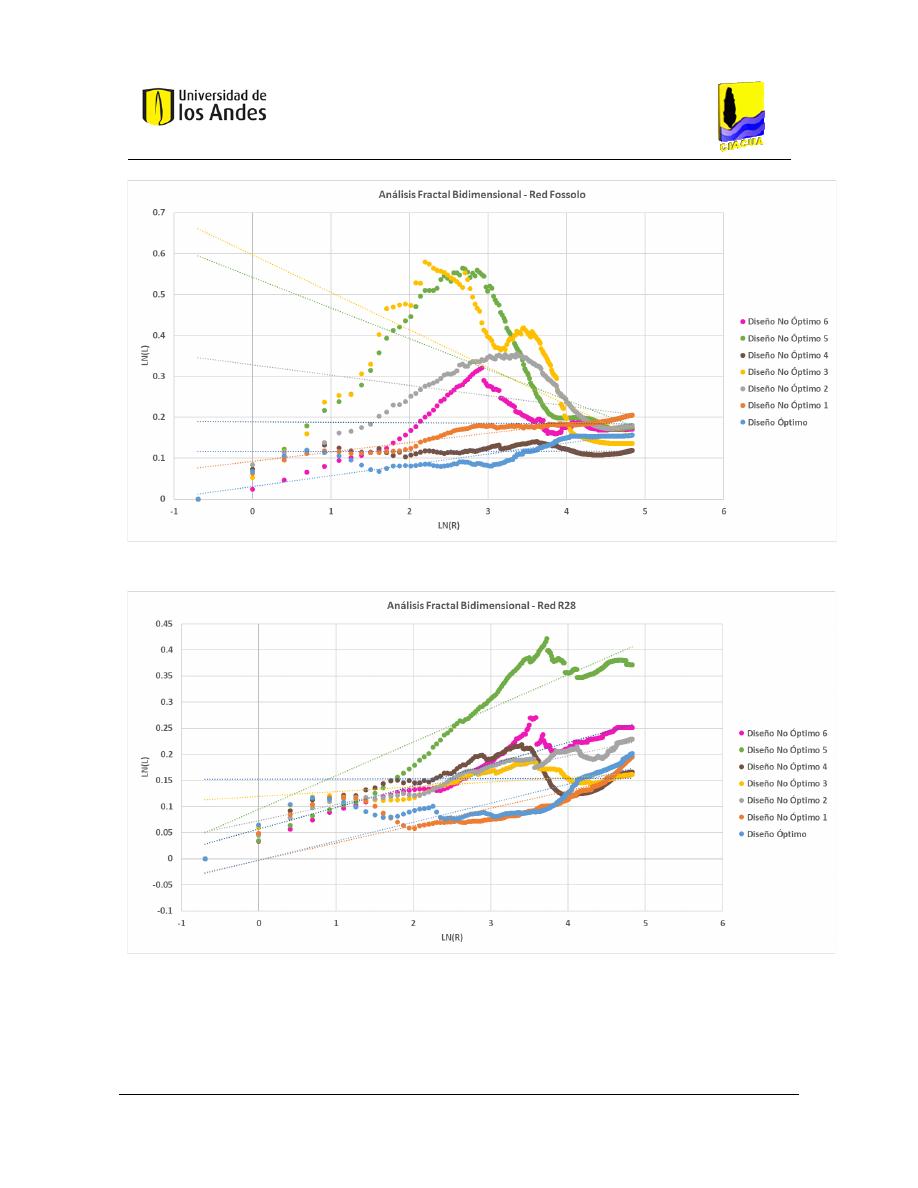
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
208
Figura 615. Análisis fractal bidimensional – Altura unitaria - Red Fossolo.
Figura 616. Análisis fractal bidimensional – Altura unitaria - Red R28.
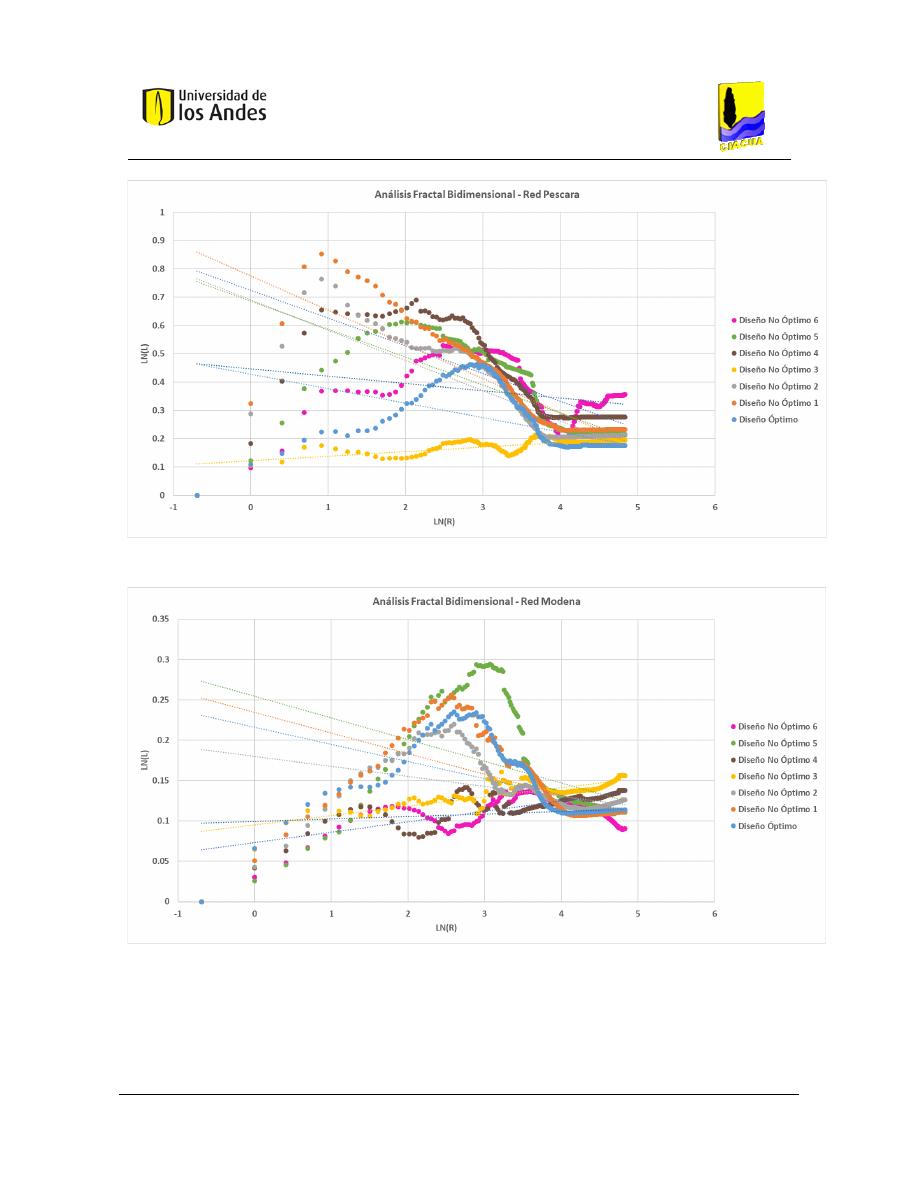
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
209
Figura 617. Análisis fractal bidimensional – Altura unitaria - Red Pescara.
Figura 618. Análisis fractal bidimensional – Altura unitaria - Red Modena.
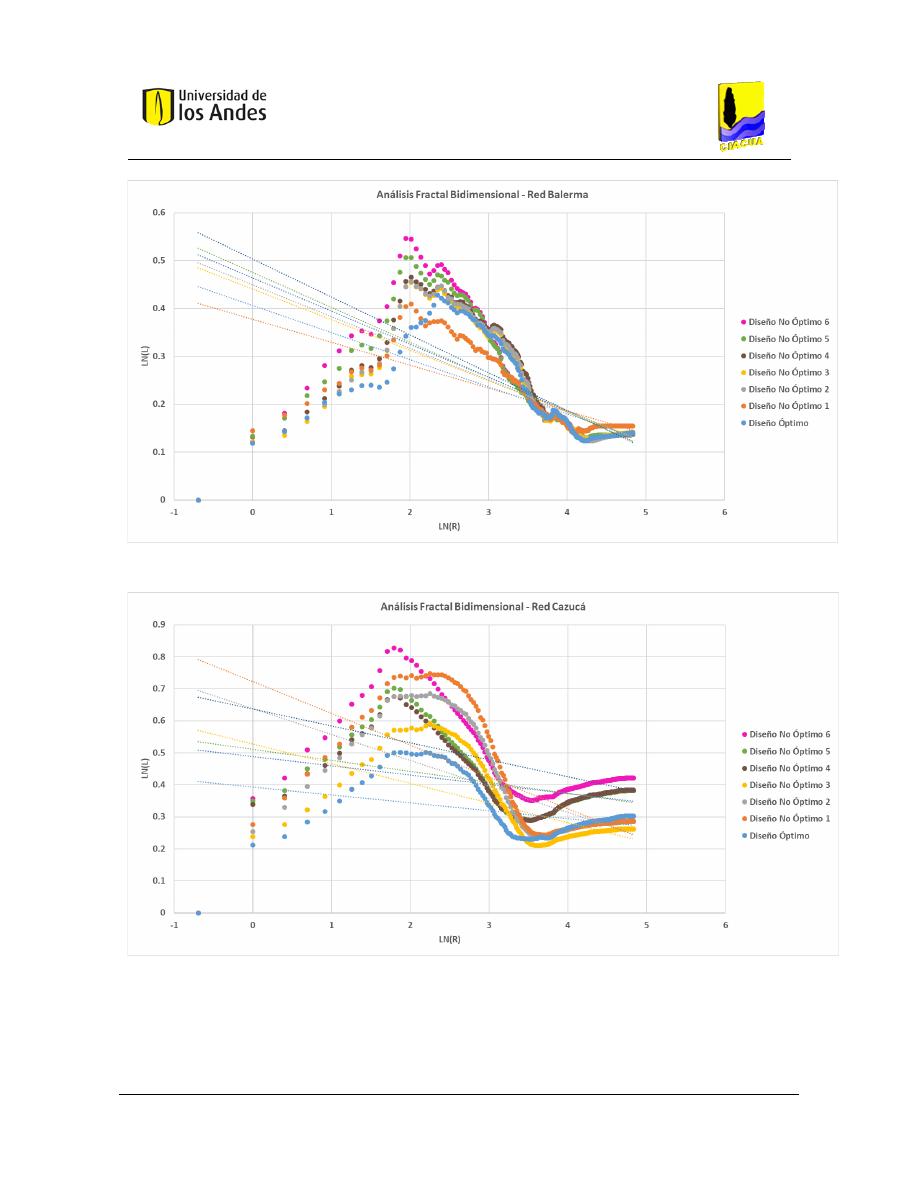
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
210
Figura 619. Análisis fractal bidimensional – Altura unitaria - Red Balerma.
Figura 620. Análisis fractal bidimensional – Altura unitaria - Red Cazucá.
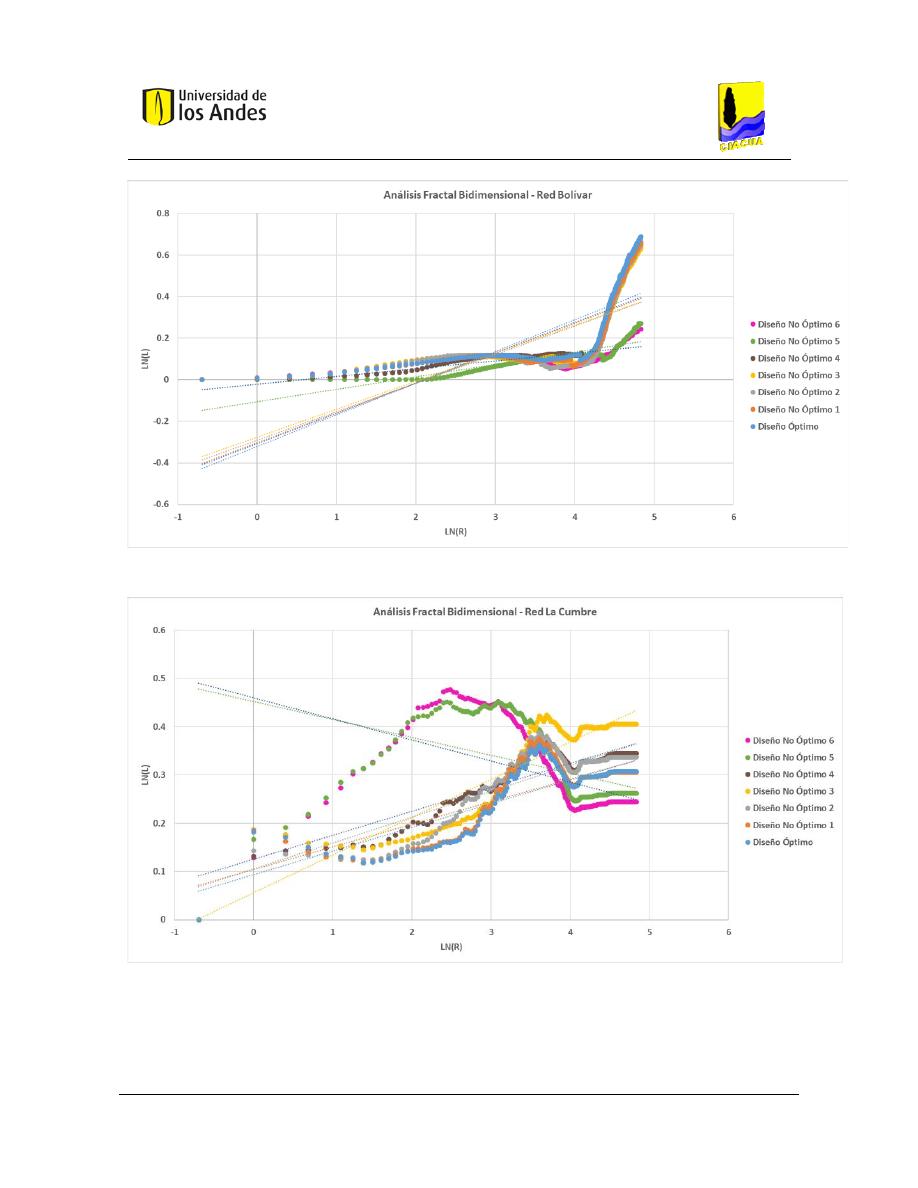
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
211
Figura 621. Análisis fractal bidimensional – Altura unitaria - Red Bolívar.
Figura 622. Análisis fractal bidimensional – Altura unitaria - Red La Cumbre.
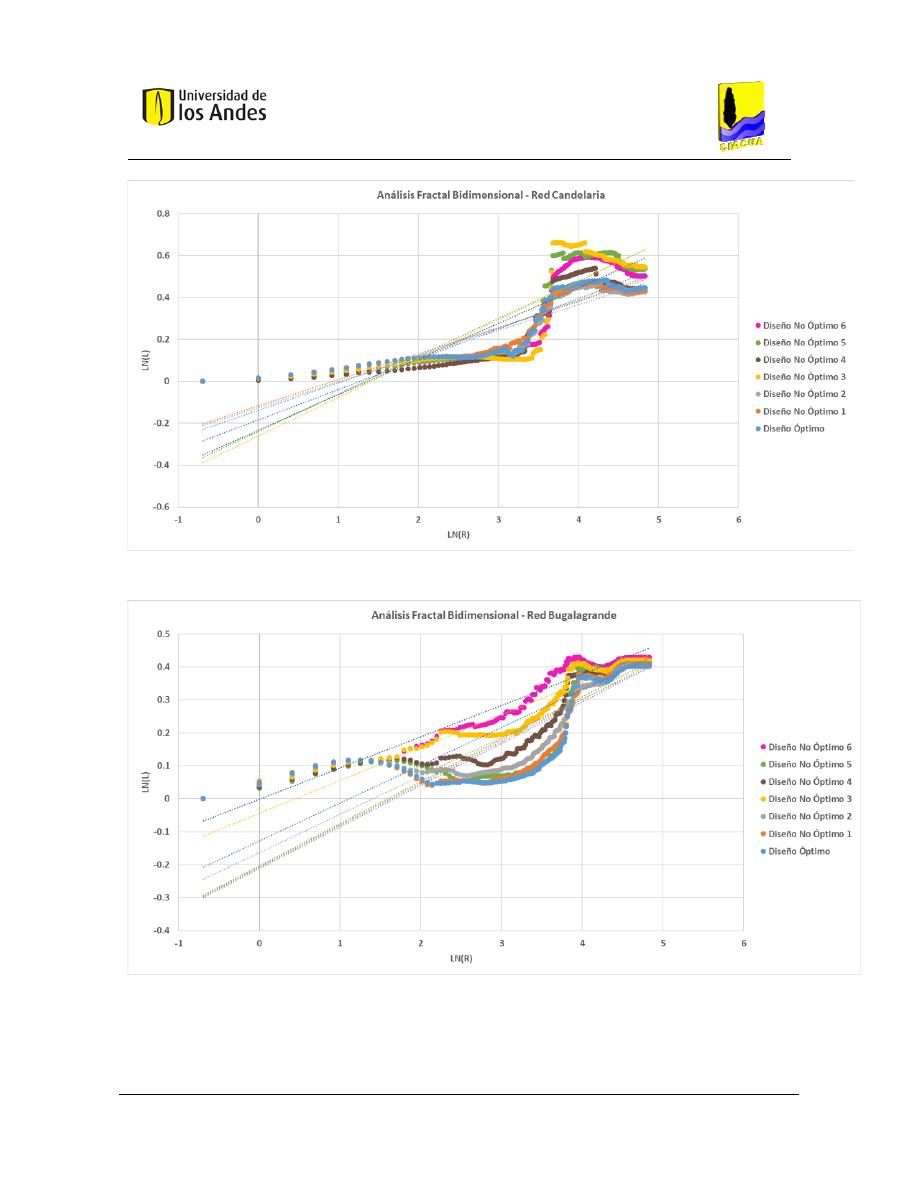
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
212
Figura 623. Análisis fractal bidimensional - Altura unitaria - Red Candelaria.
Figura 624. Análisis fractal bidimensional – Altura unitaria - Red Bugalagrande.
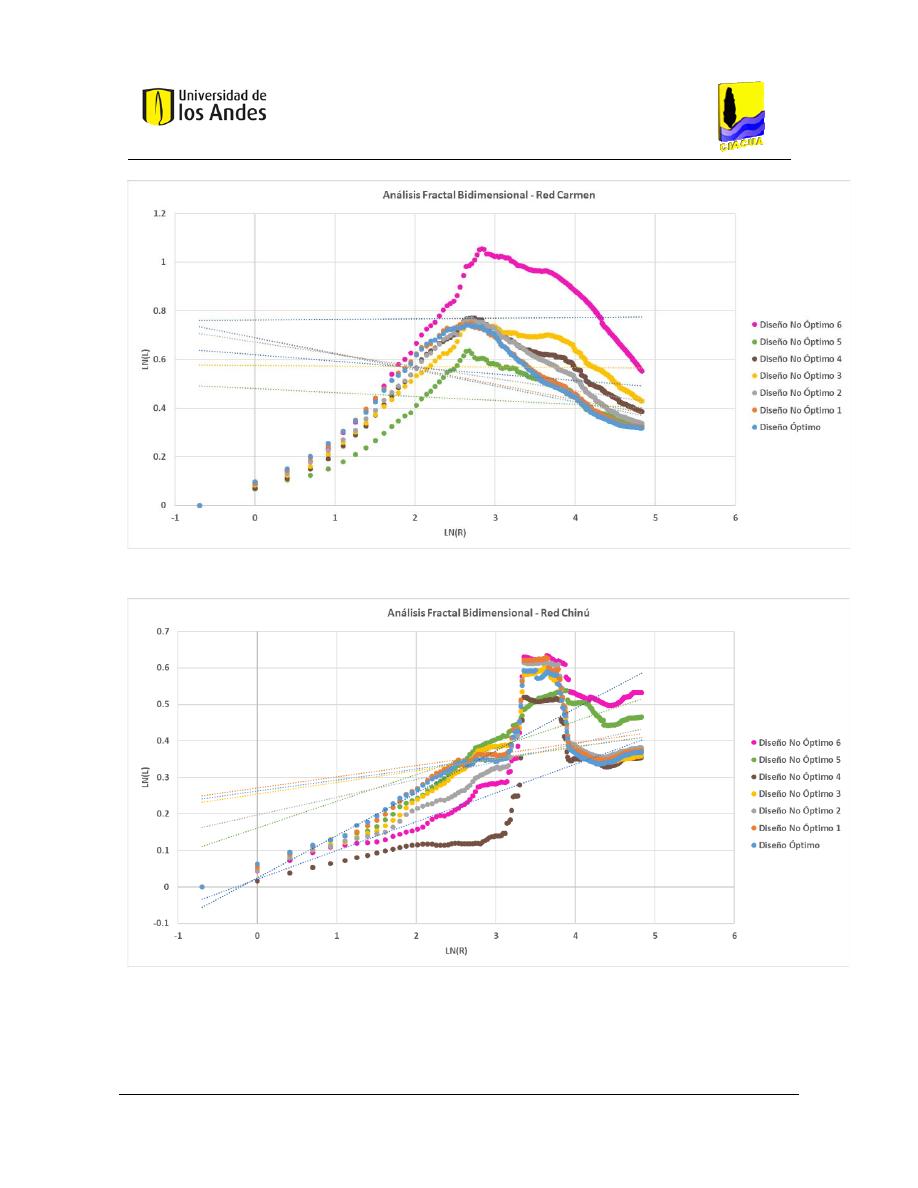
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
213
Figura 625. Análisis fractal bidimensional – Altura unitaria - Red Carmen.
Figura 626. Análisis fractal bidimensional – Altura unitaria - Red Chinú.
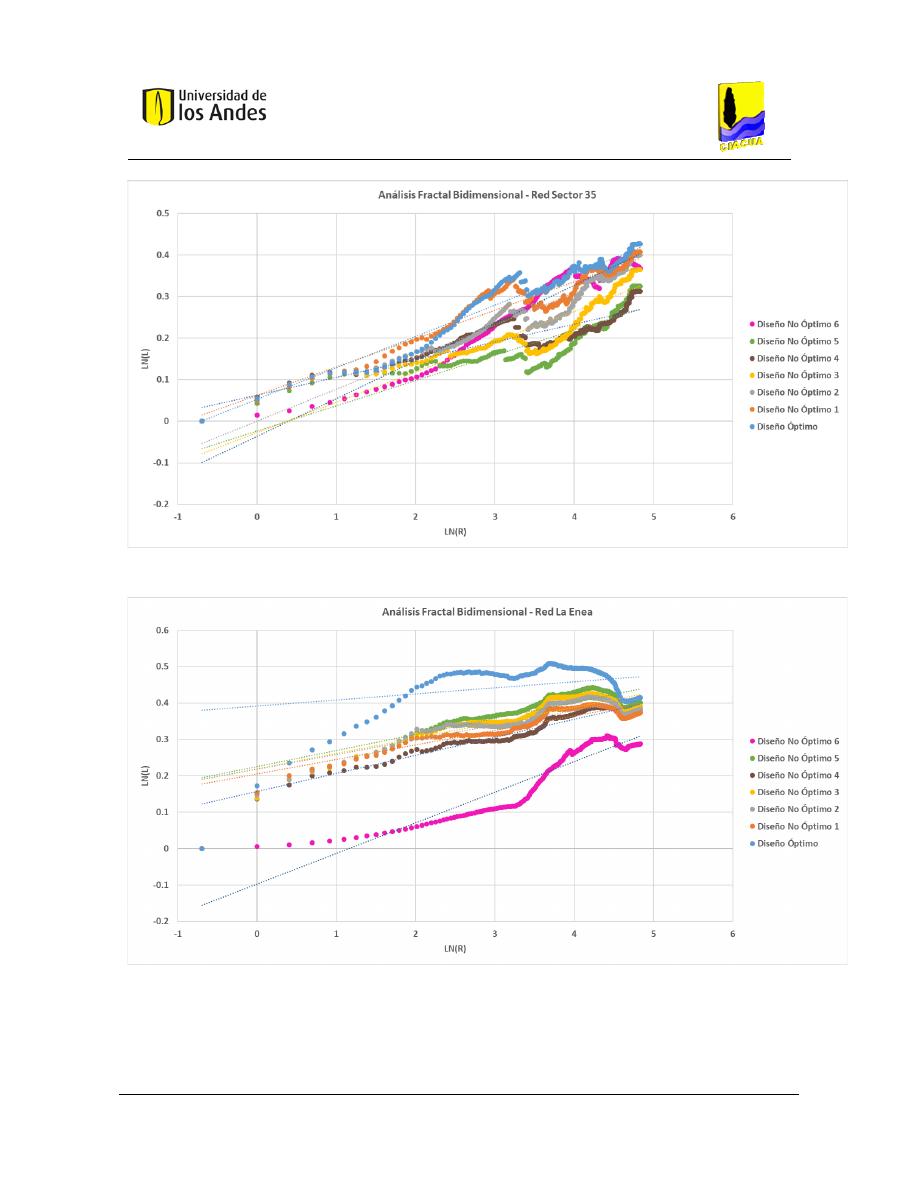
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
214
Figura 627. Análisis fractal bidimensional – Altura unitaria - Red Sector 35.
Figura 628. Análisis fractal bidimensional – Altura unitaria - Red La Enea.
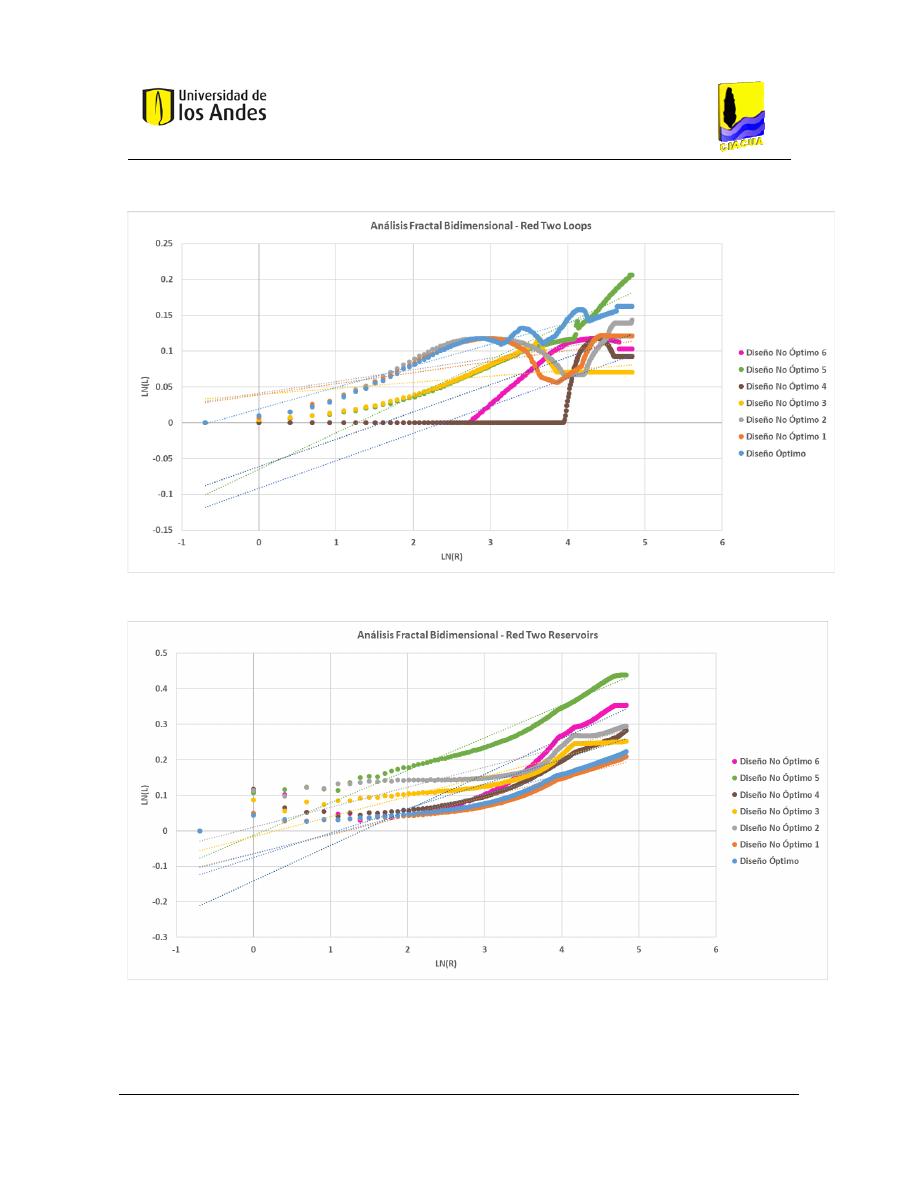
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
215
5.3.3.2 Altura de caja por tanteo
Figura 629. Análisis fractal bidimensional - Altura por tanteo - Red Two Loops.
Figura 630. Análisis fractal bidimensional - Altura por tanteo - Red Two Reservoirs.
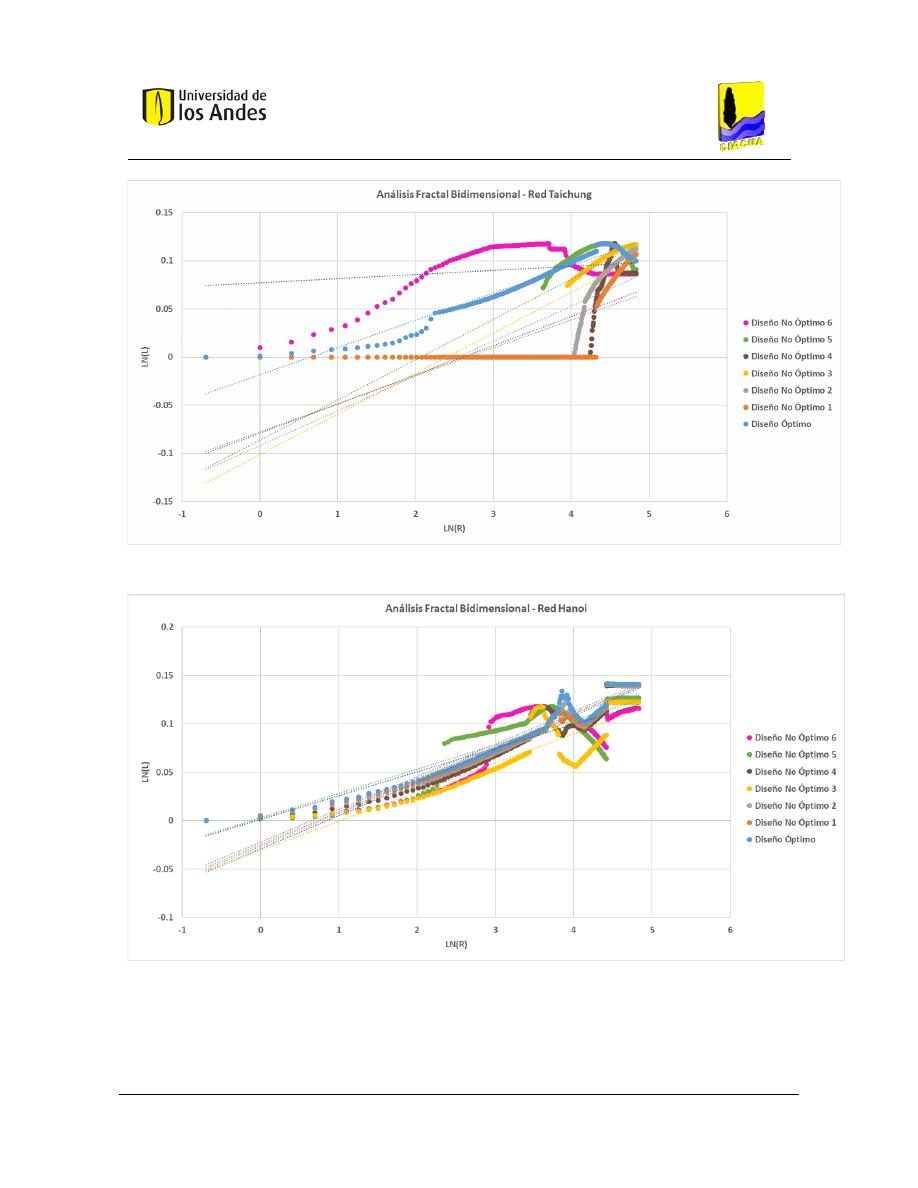
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
216
Figura 631. Análisis fractal bidimensional - Altura por tanteo - Red Taichung.
Figura 632. Análisis fractal bidimensional - Altura por tanteo - Red Hanoi.
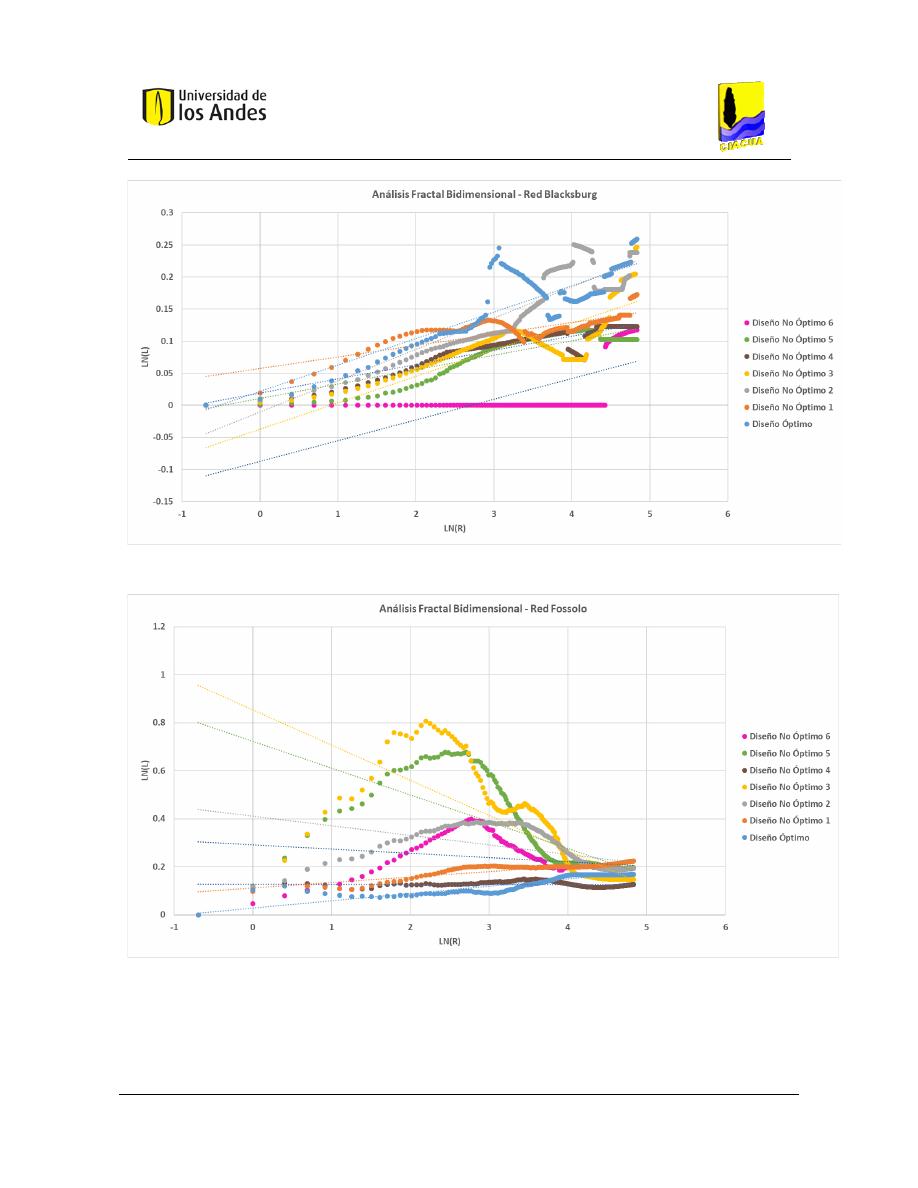
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
217
Figura 633. Análisis fractal bidimensional - Altura por tanteo - Red Blacksburg.
Figura 634. Análisis fractal bidimensional - Altura por tanteo - Red Fossolo.
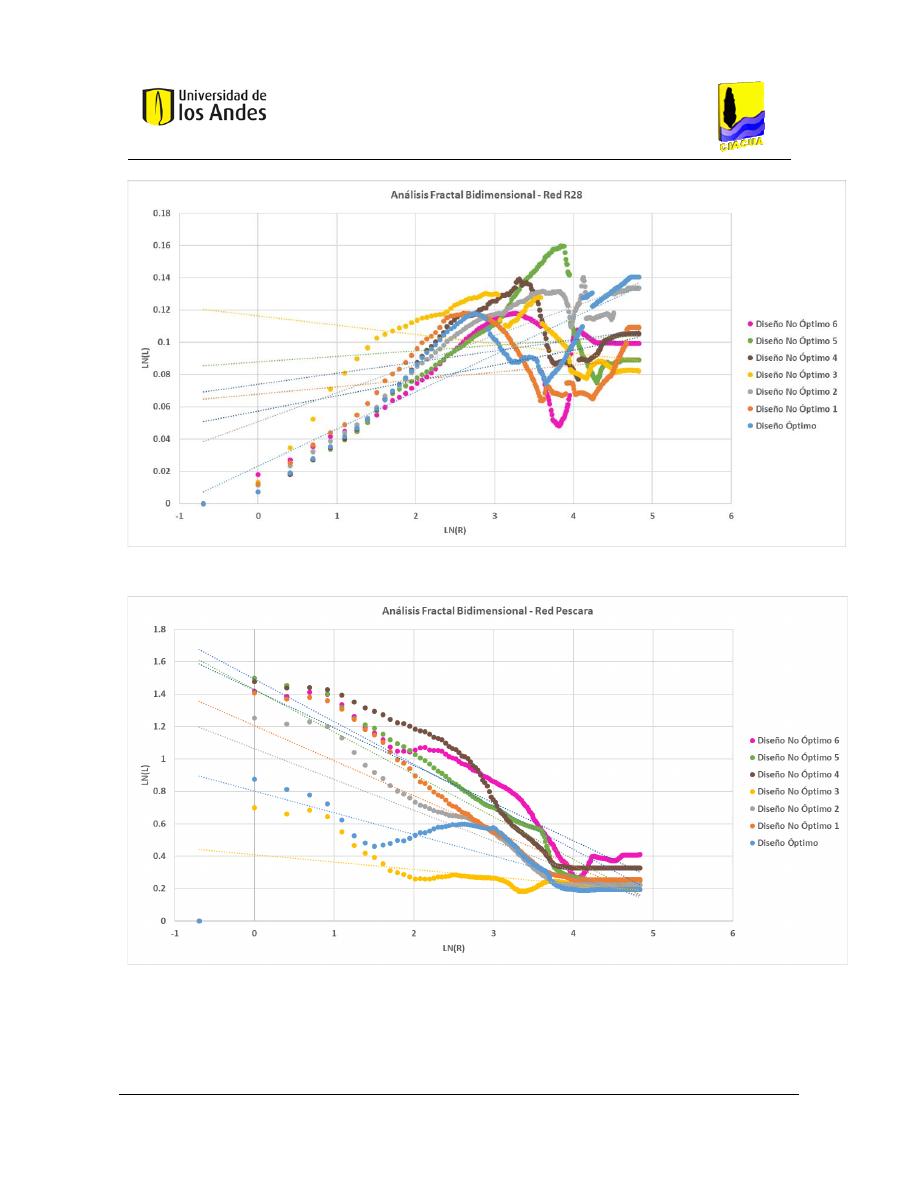
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
218
Figura 635. Análisis fractal bidimensional – Altura por tanteo - Red R28.
Figura 636. Análisis fractal bidimensional - Altura por tanteo - Red Pescara.
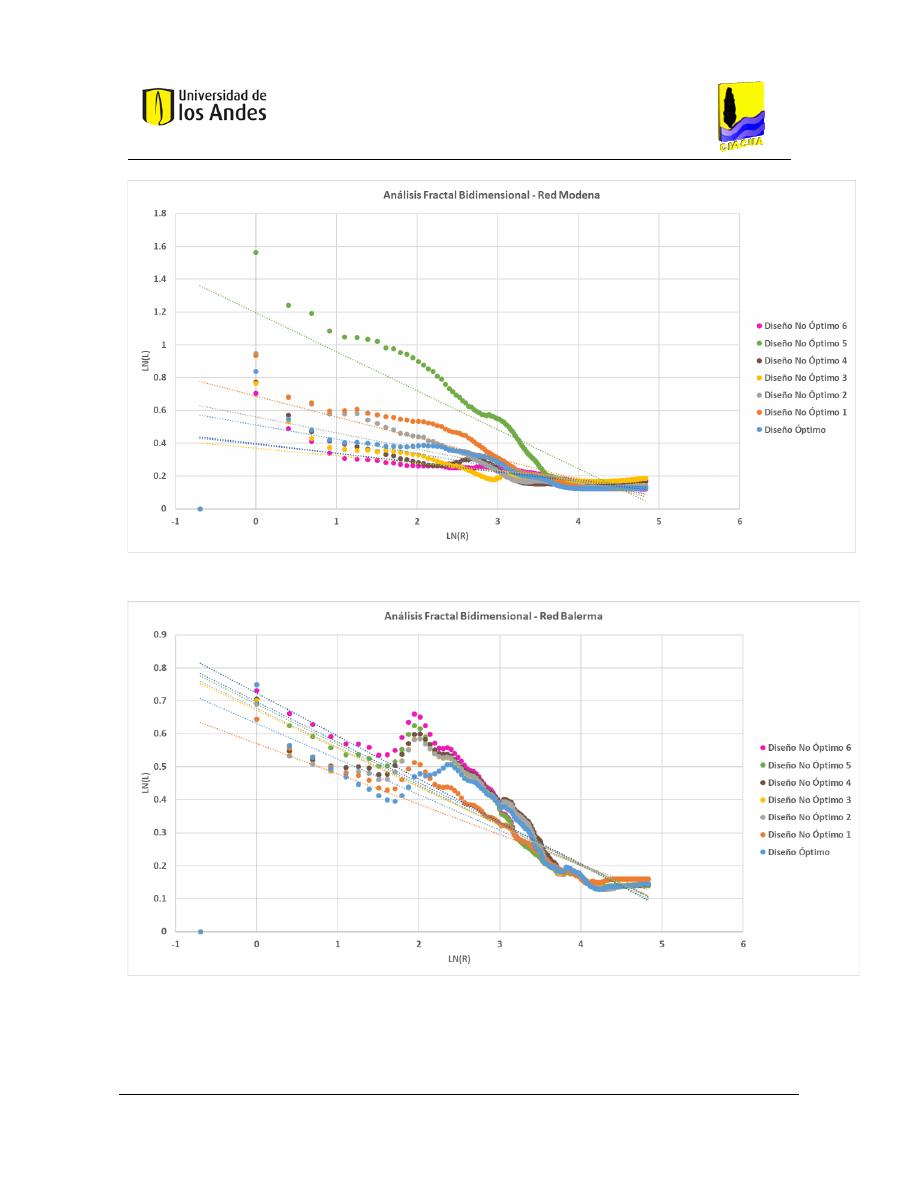
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
219
Figura 637. Análisis fractal bidimensional - Altura por tanteo - Red Modena.
Figura 638. Análisis fractal bidimensional - Altura por tanteo - Red Balerma.
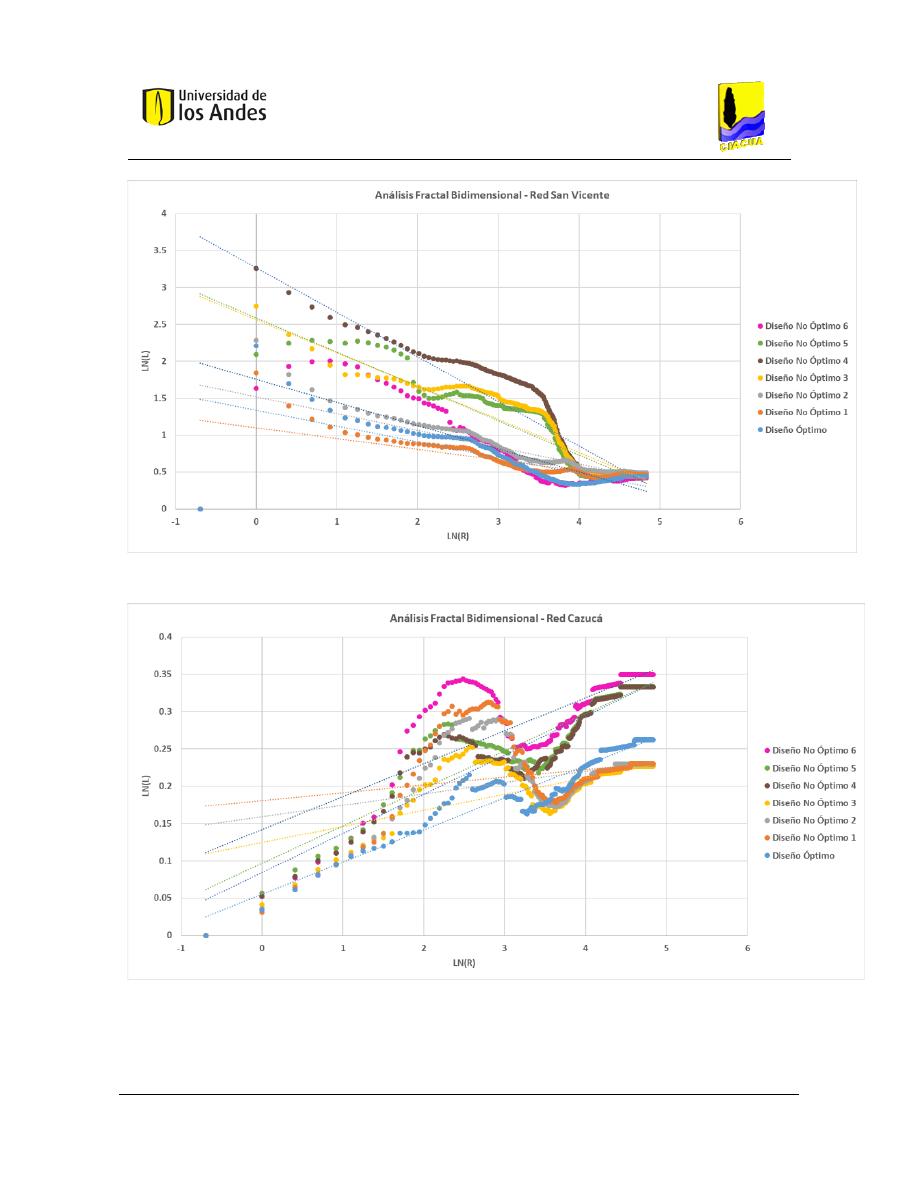
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
220
Figura 639. Análisis fractal bidimensional - Altura por tanteo - Red San Vicente.
Figura 640. Análisis fractal bidimensional - Altura por tanteo - Red Cazucá.
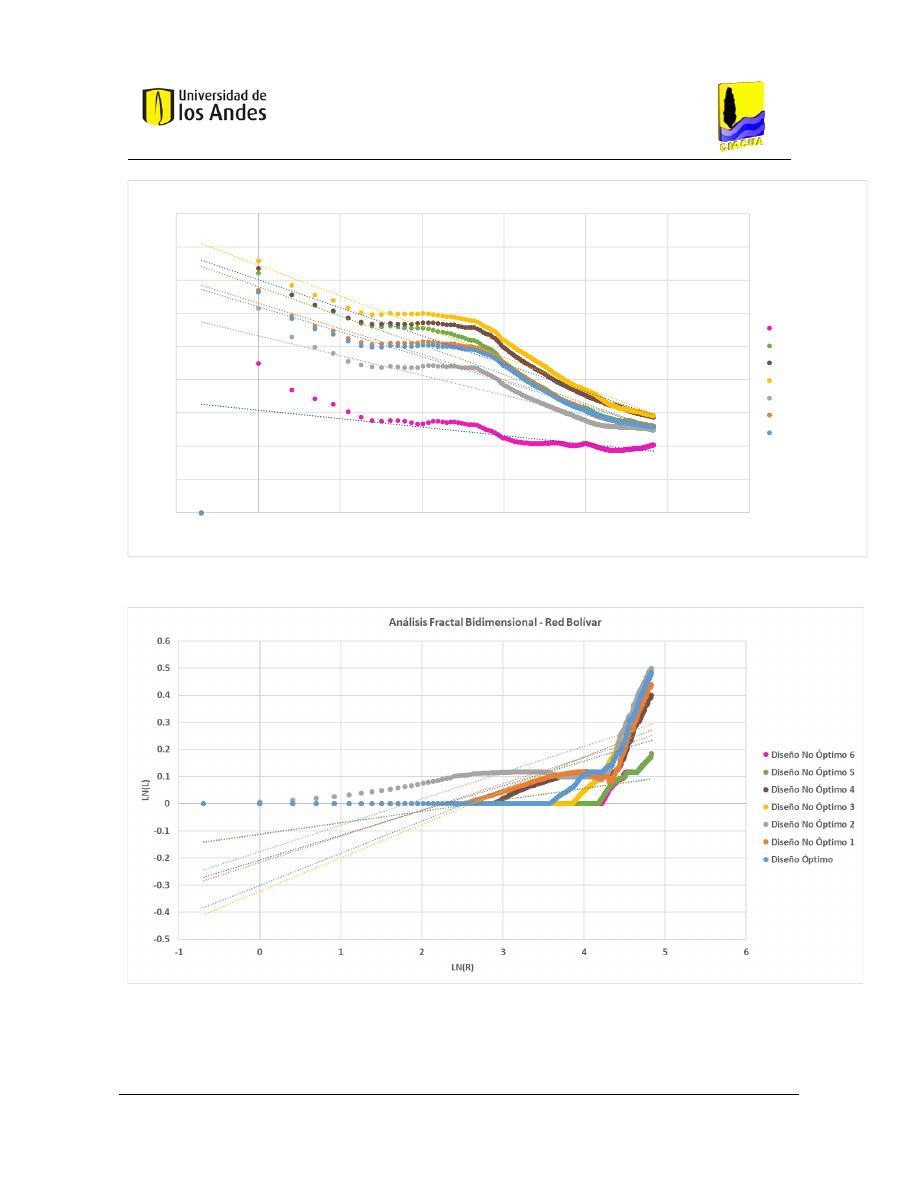
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
221
Figura 641. Análisis fractal bidimensional - Altura por tanteo - Red Elevada.
Figura 642. Análisis fractal bidimensional - Altura por tanteo - Red Bolívar.
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
-1
0
1
2
3
4
5
6
LN
(L
)
LN(R)
Análisis Fractal Bidimensional - Red Elevada
Diseño No Óptimo 6
Diseño No Óptimo 5
Diseño No Óptimo 4
Diseño No Óptimo 3
Diseño No Óptimo 2
Diseño No Óptimo 1
Diseño Óptimo
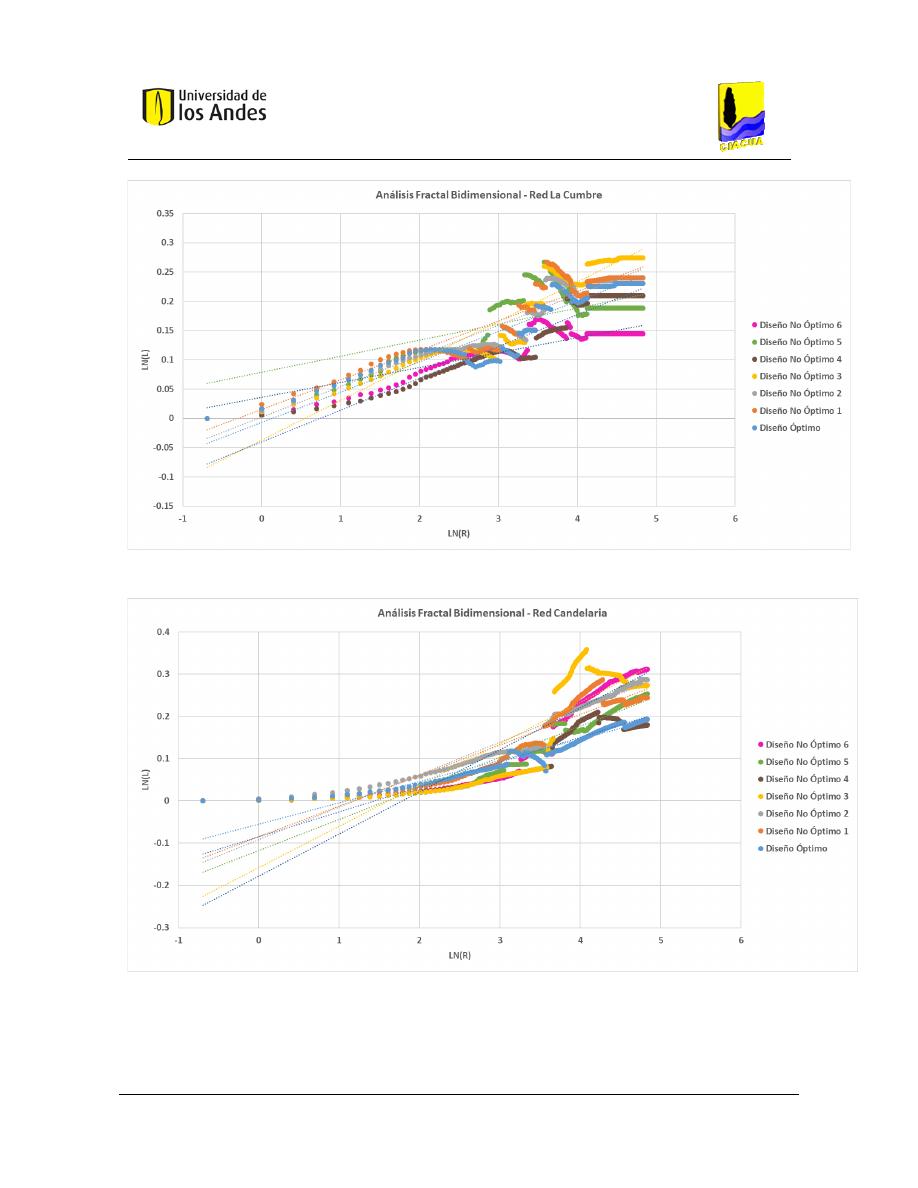
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
222
Figura 643. Análisis fractal bidimensional - Altura por tanteo - Red La Cumbre.
Figura 644. Análisis fractal bidimensional - Altura por tanteo - Red Candelaria.
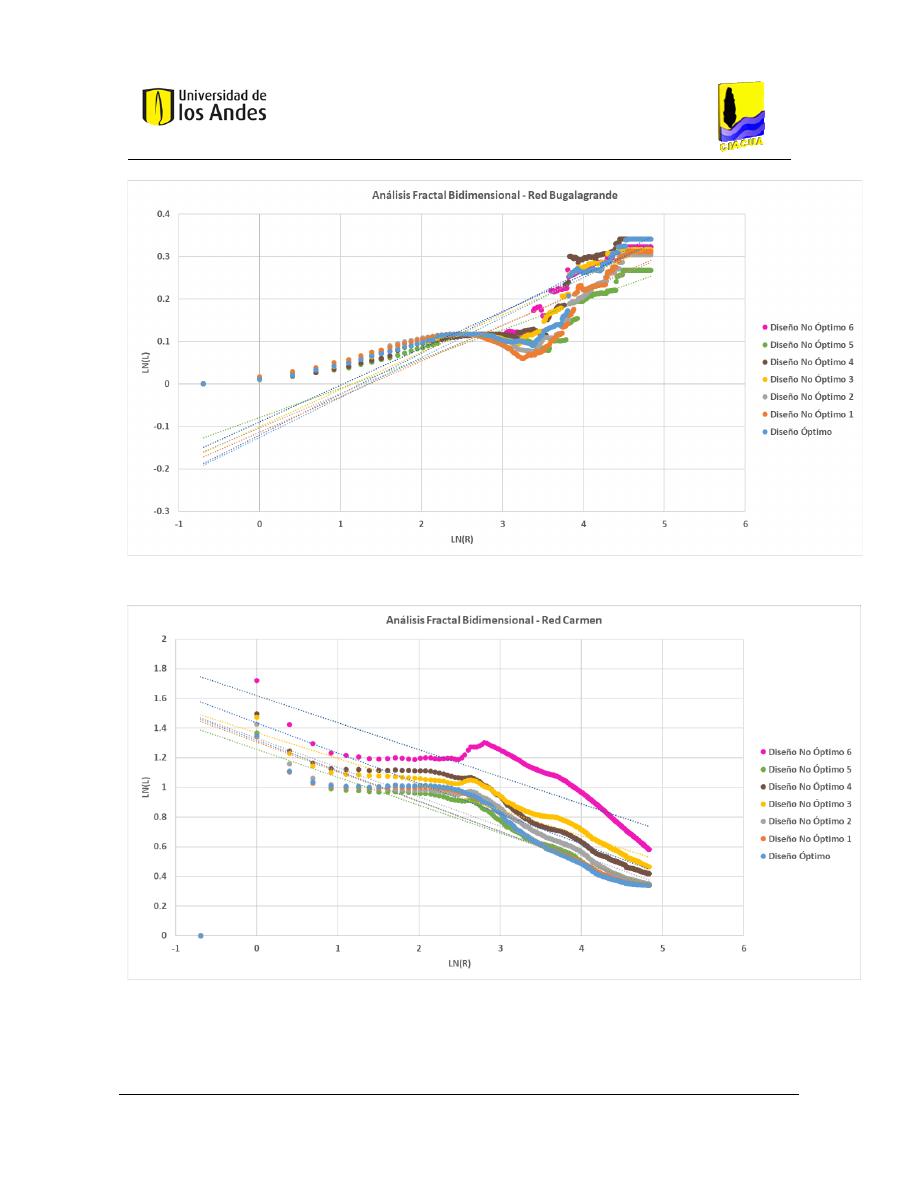
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
223
Figura 645. Análisis fractal bidimensional - Altura por tanteo - Red Bugalagrande.
Figura 646. Análisis fractal bidimensional - Altura por tanteo - Red Carmen.
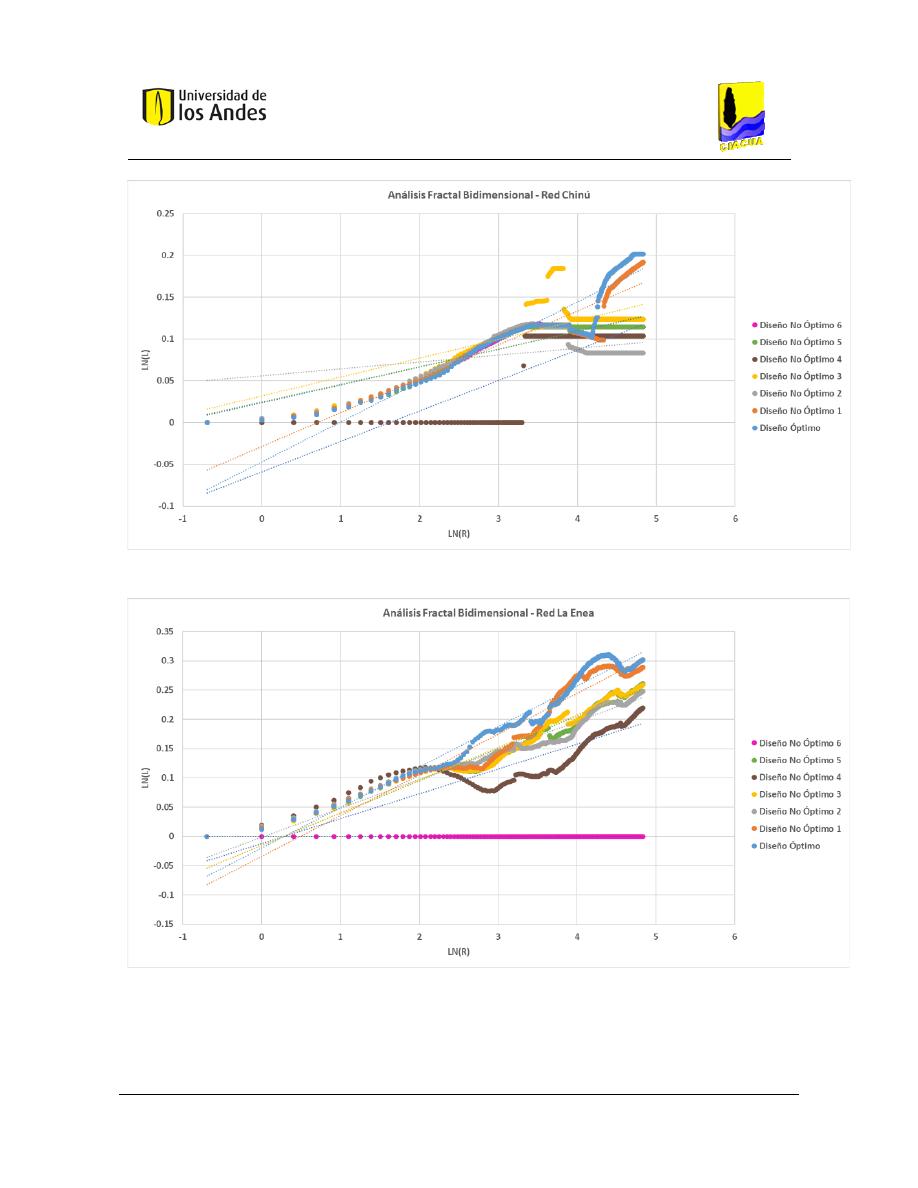
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
224
Figura 647. Análisis fractal bidimensional - Altura por tanteo - Red Chinú.
Figura 648. Análisis fractal bidimensional - Altura por tanteo - Red La Enea.
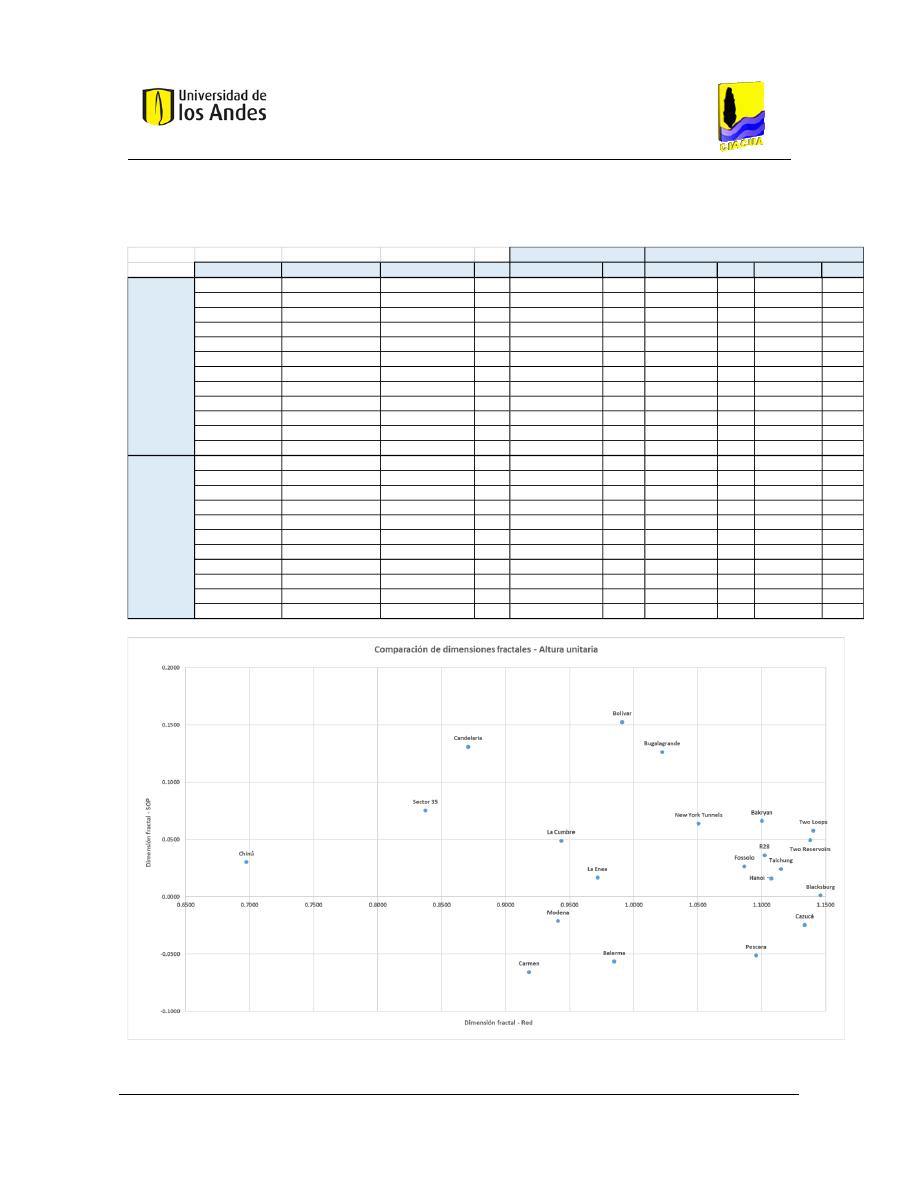
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
225
5.4 Correlación de dimensiones fractales – Red vs SOP
Tabla 45. Comparación de dimensiones fractales.
Figura 649. Comparación de dimensiones fractales - Altura unitaria.
Nombre
Número de tuberías Número de nodos lb max Criterio Topológico
R^2
Altura unitaria R^2
Altura tanteo
R^2
Two Loops
8
7
7
1.1403
1.00
0.0577
0.79
0.0301
0.93
Two Reservoirs
17
10
9
1.1379
0.96
0.0495
0.78
0.0560
0.90
Taichung
31
20
19
1.1152
0.96
0.0242
0.46
0.0283
0.92
Hanoi
34
32
31
1.1075
0.94
0.0158
0.05
0.0337
0.92
Blacksburg
35
30
29
1.1459
0.93
0.0012
0.00
0.0412
0.67
New York Tunnels
42
19
19
1.0507
0.97
0.0640
0.95
0.0640
0.95
Bakryan
58
35
35
1.1001
0.94
0.0661
0.90
0.0661
0.90
Fossolo
58
36
35
1.0865
0.92
0.0265
0.78
0.0303
0.82
R28
67
39
39
1.1022
0.93
0.0363
0.67
0.0230
0.69
Pescara
99
68
67
1.0956
0.92
-0.0511
0.27
-0.1337
0.68
Modena
317
268
267
0.9408
0.79
-0.0212
0.27
-0.0869
0.72
Balerma
454
443
443
0.9848
0.76
-0.0565
0.40
-0.1081
0.72
San Vicente
71
62
61
1.1399
0.92
-
-
-0.2134
0.63
Cazucá
150
145
145
1.1336
0.91
-0.0246
0.12
0.0433
0.89
Elevada
263
256
255
1.1172
0.91
-
-
-0.1504
0.69
Bolívar
333
286
285
0.9910
0.84
0.1525
0.48
0.1185
0.54
La Cumbre
378
339
339
0.9435
0.99
0.0490
0.64
0.0518
0.86
Candelaria
567
464
463
0.8706
0.72
0.1310
0.77
0.0503
0.93
Bugalagrande
656
583
583
1.0223
0.98
0.1263
0.70
0.0940
0.79
Carmen
754
716
715
0.9184
0.79
-0.0657
0.22
-0.2051
0.76
Chinú
1089
828
827
0.6974
0.60
0.0302
0.09
0.0478
0.82
Sector 35
1289
1190
1189
0.8374
0.66
0.0754
0.93
0.0754
0.93
La Enea
1592
1413
1413
0.9718
0.80
0.0167
0.08
0.0691
0.93
Dimensión Fractal (D) - Red
Redes patrón
Redes reales
Dimensión Fractal (D) - SOP

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
226
Figura 650. Comparación de dimensiones fractales - Altura por tanteo.
Figura 651. Dimensión fractal de la SOP vs Número de tuberías - Altura por tanteo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
227
Figura 652. Dimensión fractal de la SOP vs Número de nodos - Altura por tanteo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
228
6 ANÁLISIS DE RESULTADOS
6.1 Diseños óptimos y no óptimos
La generación de los diseños permite establecer un incremento en el costo a medida que se
establecen las configuraciones no óptimas. Las figuras (ver página 97) evidencian un
comportamiento creciente en el precio de los sistemas, que se demuestra a partir del ascenso de
las columnas entre la alternativa óptima y el sexto diseño no optimizado. Por otra parte, la
aplicación de las rutinas de algoritmos genéticos permitió obtener patrones variados en el
incremento del costo. Las series de porcentaje de sobrecosto (ver página 97) sugieren la
inexistencia de uniformidad en la transición entre cada configuración de una misma red o,
inclusive, en los patrones de evolución del costo de las diferentes redes. Cabe resaltar que las
brechas donde existen aumentos súbitos en el valor de la red se explican a partir de los cambios
sobre la probabilidad de mutación y la selección de individuos tras pocas generaciones. Por el
contrario, la ocurrencia de diseños con variaciones pequeñas en el precio muestra el
estancamiento de los algoritmos genéticos sobre ciertas soluciones particulares. El desarrollo de la
metodología permitió definir diseños con precios cercanos al óptimo y otros donde la
configuración de diámetros comerciales implicara porcentajes elevados de sobrecosto. Como
resultado, podría afirmarse el establecimiento de una muestra representativa de diseños en
términos de los costos.
Por otra parte, es importante recalcar la suposición del modelo potencial en el cálculo de los
costos. Los valores estipulados implican asumir que los catálogos de diámetros comerciales se
ajustan de manera perfecta a una función potencial, lo cual no es necesariamente cierto para
algunos de los ejemplares patrón trabajados (ver página 251). Las líneas de tendencia y los
coeficientes de determinación sugieren un distanciamiento con el modelo de ajuste, por lo que los
valores calculados pueden presentar diferencias con respecto al valor real si se calculara
directamente con los costos unitarios propuestos por la literatura. No obstante, el uso de las
curvas de costos sí garantiza un orden en el precio de los sistemas, en la medida que este
incrementa entre el primer y el sexto diseño no optimizado. Asimismo, el uso de las regresiones
para determinar el costo no influye en el análisis fractal posterior y debe asumirse únicamente
como un valor de referencia teórico para comparar los sistemas trabajados.
Adicionalmente, los costos de las redes patrón optimizadas no se asimilan a los valores usuales
registrados en la literatura. Lo anterior se puede explicar a partir de dos factores. El primero
corresponde al uso de la ecuación de fricción de Darcy-Weisbach en lugar de la relación empírica
de Hazen-Williams, en particular para aquellos casos donde la red fue originalmente concebida
bajo la última ecuación. Las diferencias en el cálculo de las pérdidas por fricción desembocan en la

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
229
definición de configuraciones óptimas distintas a los récords mundiales según la literatura. Por su
parte, el uso de la metodología OPUS implica resultados con costos ligeramente superiores a los
óptimos registrados, tal como se explicó en el marco teórico. No obstante, a pesar de las
discrepancias, los resultados expuestos en términos de alturas piezométricas y caudales al interior
de las tuberías corresponden a mejores aproximaciones al comportamiento real de los sistemas al
emplear ecuaciones físicamente basadas, en lugar de la relación empírica de Hazen-Williams. A
partir de lo expuesto, los resultados deben analizarse únicamente como referentes teóricos y no
deben asumirse como comparables con las configuraciones óptimas propuestas en la literatura.
A nivel de la distribución de diámetros, los resultados reflejan variedad en los sistemas analizados.
Los diagramas circulares (ver página 105) presentan configuraciones en las que se contemplan
alternativas con un único diámetro, pocos referentes o un rango amplio de las opciones
disponibles. En efecto, nuevamente se puede asumir la definición de una muestra representativa
de diseños, esta vez en términos de las configuraciones de diámetros comerciales. Sumado a lo
anterior, se observa que en la medida que incrementa el costo de los diseños, el número de
tuberías con los menores diámetros decrece, para ser reemplazados por los referentes de mayor
tamaño.
6.2 Superficies de Gradiente Hidráulico
La construcción de las superficies de gradiente hidráulico vía REDES 2019 y MATLAB permite
establecer una comparación entre ambas alternativas. Para empezar, se identifica que el algoritmo
en REDES 2019 presenta la superficie como un ente geométrico suave y continuo, a diferencia de
la rutina en MATLAB, donde el uso de la triangulación de Delaunay y la interpolación lineal-natural
le atribuye mayor escabrosidad y rugosidad a la superficie. Si bien la sensación de continuidad que
ofrece REDES permite mayor claridad en la interpretación del gradiente hidráulico, la metodología
de dibujo y colores en MATLAB ofrece mayor detalle independiente de si los cambios en las alturas
piezométricas son pequeños entre un diseño y otro. A nivel de la metodología de interpolación, el
algoritmo en MATLAB se establece como superior. El uso de la envolvente convexa garantiza que
el cálculo de las alturas piezométricas se lleve a cabo desde las fronteras hacia adentro,
reduciendo la obtención de valores equivocados en puntos localizados por fuera de la red de
distribución. Como se puede observar en algunos de los ejemplares (véase Two Loops, Two
Reservoirs, Taichung y Blacksburg, por ejemplo), la rutina en REDES genera picos incorrectos sobre
las fronteras de algunas SGH, con valores de altura piezométrica superiores a los puntos teóricos
de máxima energía (embalses).
A nivel de los diseños óptimos y no óptimos, se encuentran diferencias apreciables. Una
inspección visual de las superficies y revisión de los valores interpolados de alturas piezométricas
permiten detectar un incremento global en la cabeza hidráulica de los nodos a medida que el
sistema se encarece. Como se mencionaba previamente, la evolución del costo implica un

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
230
reemplazo de las tuberías con menores diámetros por otras con referentes de mayor tamaño. En
efecto, a la luz de la ecuación de Darcy-Weisbach, la disipación de energía y la pendiente de
fricción serían inferiores para los diseños no óptimos. Dado lo anterior, una revisión de la SOP
permite establecer concavidades, picos pronunciados y cambios súbitos de pendiente, a diferencia
de los diseños no optimizados, donde las tuberías atenúan las rugosidades descritas a
comparación del gradiente hidráulico óptimo. No obstante, es importante recalcar que dichos
cambios en la fractalidad se suponen a nivel local hasta este punto. La heterogeneidad global de la
superficie se evaluará con mayor precisión a la luz de la modelación numérica de la lagunaridad.
6.3 Análisis fractal
El análisis de la lagunaridad de las superficies de gradiente hidráulico permite establecer algunas
aseveraciones. En primer lugar, se encuentra la sensibilidad del método DBC a la altura de caja
para establecer los resultados. Como se observa en el cálculo de las dimensiones fractales y en las
figuras ln(𝛬) 𝑣𝑠 ln(𝑅) , el comportamiento fractal de los diseños cambia si se analiza con una
altura unitaria y otra definida por tanteo. Inclusive, se encuentra que para alturas específicas de
caja se obtiene una mejor caracterización del cuerpo fractal en la medida que los coeficientes de
determinación reflejan un ajuste más cercano al modelo potencial de medición. La gran ventaja
del método radica en su capacidad de detectar las diferencias en las propiedades fractales de los
diseños, independiente de si el cambio en las alturas piezométricas es considerable o de pequeña
magnitud. Lo anterior suponiendo la elección de una altura de caja apropiada.
En segundo lugar, se identifica que en la mayoría de los casos la dimensión fractal es superior en la
Superficie Óptima de Presiones. Lo anterior se afirma en aquellas redes dónde en al menos cuatro
diseños no óptimos se obtiene una dimensión fractal inferior a la de la SOP. Acorde a lo estipulado
en las referencias bibliográficas, un valor de dimensión fractal mayor supone un comportamiento
con mayor rugosidad, fragmentación y escabrosidad (Zhang, 2016). De esta manera, la mayoría de
los resultados reflejan la predominancia de gradientes hidráulicos tortuosos en los diseños
optimizados, a comparación de los ejemplares de mayor costo cuyas superficies reflejarían mayor
suavidad y atenuación de picos y concavidades. No obstante, en algunos casos no se puede
distinguir un comportamiento específico o, más bien, se visualizan propiedades fractales
contrarias. Lo primero se asocia a los casos dónde se encuentran tres de los seis diseños con una
dimensión fractal inferior, redes para las cuáles se requeriría el análisis de un número mayor de
diseños para establecer conclusiones definitivas. Por su parte, el segundo caso se materializa
cuando se obtienen dos o menos diseños con dimensiones fractales inferiores a la de la SOP,
discrepancias que sugieren comportamientos menos escabrosos en el diseño óptimo a
comparación de los ejemplares de mayor precio.
A continuación, se muestra el comportamiento individual de cada red según la altura de caja.
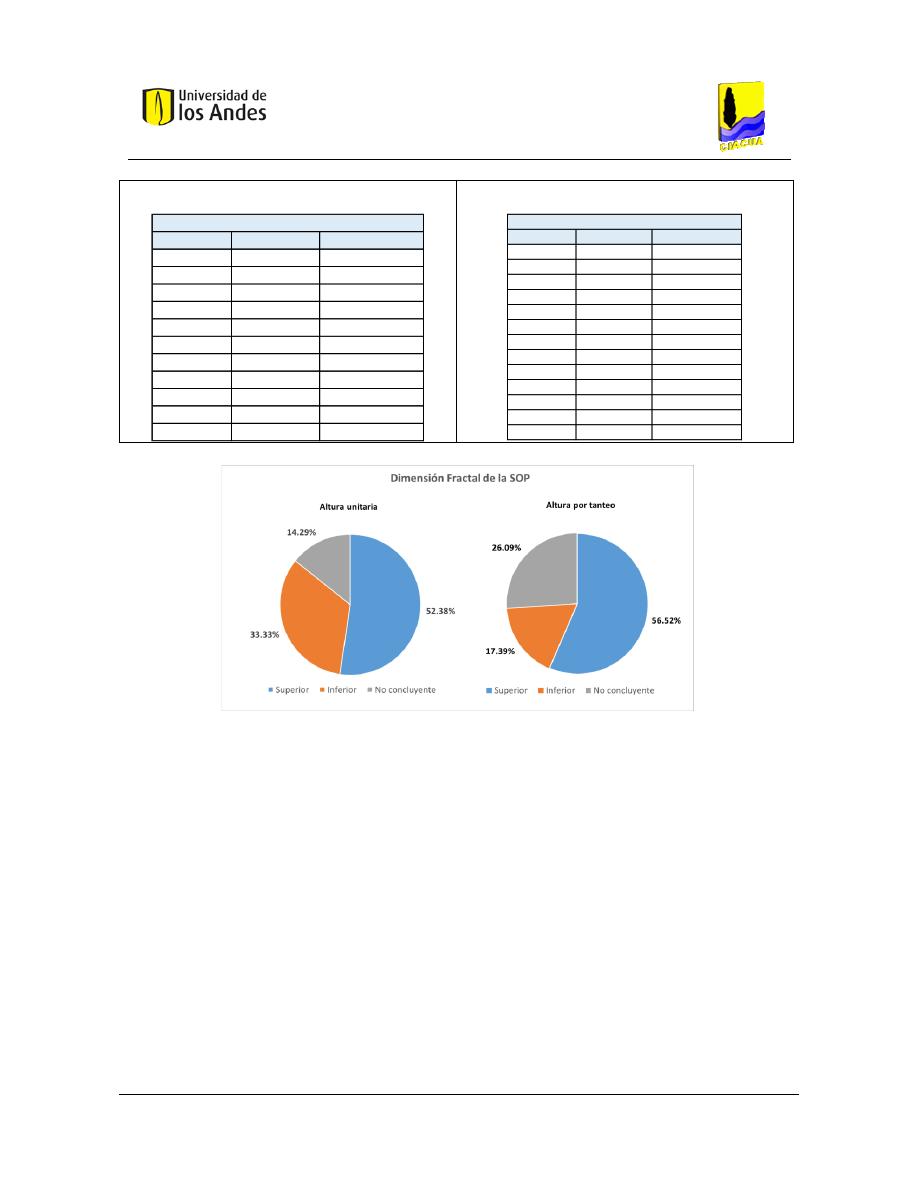
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
231
Tabla 46. Comportamiento fractal de la SOP - Altura
unitaria.
Tabla 47. Comportamiento fractal de la SOP - Altura por
tanteo.
Figura 653. Dimensión fractal de la SOP.
Revisando las figuras ln(𝛬) 𝑣𝑠 ln(𝑅) (ver página 204), se encuentran comportamientos variados
de la lagunaridad entre las redes. Inclusive, las propiedades lagunares entre diseños pueden variar
para una misma red dependiendo del tamaño de caja. De esta manera, se confirma la sujeción de
la lagunaridad a la escala de análisis como se estipula en el marco teórico. Adicionalmente, se
especula que la heterogeneidad espacial de las superficies presenta comportamientos
dependientes de las condiciones específicas de cada red, en la medida que no se tiene un patrón
de comportamiento único entre los diseños para la mayoría de los ejemplares trabajados. Si bien
no se establece una conclusión general definitiva en torno a la heterogeneidad espacial de las SOP,
sí se reitera la presencia de una distinción del diseño optimizado con respecto a los demás. Bien
sea que los valores de lagunaridad tiendan a ser superiores, inferiores o a localizarse en valores
intermedios, es posible encontrar un comportamiento distintivo de la heterogeneidad en la
alternativa de menor costo para la mayoría de los ejemplares trabajados. Cabe resaltar que las
redes pueden clasificarse en dos grupos según el signo de la dimensión fractal resultante. Para
aquellas donde el signo es negativo, se encuentra un decrecimiento de la heterogeneidad espacial
Superior
Inferior
No concluyente
BakRyan
Blacksburg
La Cumbre
Balerma
Candelaria
New York Tunnels
Bolívar
Carmen
Two Reservoirs
Bugalagrande
Chinú
Cazucá
Hanoi
Fossolo
La Enea
Pescara
Modena
R28
Sector 35
Taichung
Two Loops
Dimensión fractal SOP - Altura unitaria
Superior
Inferior
No concluyente
BakRyan
Candelaria
Cazucá
Balerma
Carmen
Hanoi
Blacksburg
Taichung
La Cumbre
Bolívar
Two Reservoirs
Modena
Bugalagrande
New York Tunnels
Chinú
Two Loops
Elevada
Fossolo
La Enea
Pescara
R28
San Vicente
Sector 35
Dimensión fractal SOP - Altura por tanteo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
232
en la transición del análisis fractal desde una escala local a una global dónde se comprende la
totalidad de la superficie. Caso contrario a lo que ocurre con un valor positivo, para el cuál la
heterogeneidad espacial crece junto al tamaño de caja de análisis.
Las figuras (ver página 225) no sugieren alguna función o curva de ajuste clara que permita
relacionar ambas cantidades. De esta manera, aún no se logra establecer una conclusión definitiva
frente a las propiedades fractales de la SOP y la topología de la red, es decir, la forma como se
distribuyen en el espacio e interconectan los nodos entre sí. Asimismo, el tamaño de los sistemas,
representado por el número de nodos y tuberías, tampoco presenta correlación con la dimensión
fractal de la superficie óptima.
Finalmente, a nivel del análisis de rango reescalado, se encuentran resultados parcialmente
satisfactorios. En algunos de los ejemplares, de manera similar a lo concluido para las curvas de
lagunaridad, se encuentra un comportamiento distintivo para el diseño optimizado a comparación
de los sistemas de mayor costo. En adición a lo anterior, las fluctuaciones en los valores de
dimensión fractal en las diferentes regiones de las SGH evidencian que las propiedades fractales
solo se pueden establecer a nivel estadístico, en la medida que los valores calculados sugieren un
distanciamiento de la autosimilitud matemática. No obstante, también se encuentra una cantidad
significativa de ejemplares cuyos perfiles de dimensiones fractales manifiestan comportamientos
erráticos que dificultan establecer un patrón distintivo en las dimensiones fractales para los
sentidos de corte propuestos. En consecuencia, en estos casos la modelación vía R/S no
desemboca en resultados concluyentes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
233
7 CONCLUSIONES
• La determinación de los diseños óptimos y no óptimos permite afirmar el establecimiento
de una muestra representativa de sistemas a nivel de configuraciones variadas de
diámetros comerciales y evolución del costo.
• La rutina de generación de las superficies de gradiente hidráulico en MATLAB se establece
como una mejor alternativa desde la perspectiva numérica. El algoritmo propuesto
permite un mayor nivel de detalle y la prevención de errores de interpolación sobre las
fronteras del dominio de análisis.
• Una inspección visual de las SGH permite concluir una atenuación local de la irregularidad,
escabrosidad y fragmentación para el caso de los ejemplares de mayor costo. Las
pendientes de fricción de las SOP se traducen en concavidades y picos marcados debido a
los fenómenos de disipación de energía en los diámetros comerciales de menor tamaño.
• En la mayoría de los ejemplares, para la metodología propuesta de cálculo de dimensiones
fractales, se encuentra que los diseños optimizados presentan un valor mayor a
comparación de las alternativas no óptimas. Lo anterior es coherente con las pendientes
suaves y pérdida de rugosidad local que evidencia la inspección visual de las SGH de los
diseños no óptimos.
• El método DBC es sensible a la altura de caja escogida. Se encuentran variaciones con
respecto a la bondad de ajuste del modelo fractal supuesto, los resultados de dimensiones
fractales y la aptitud del método para detectar las variaciones en las alturas piezométricas.
• Si bien la lagunaridad de la SGH no presenta un comportamiento único para el diseño
optimizado, es posible distinguir una tendencia distintiva según la red e intervalo de
tamaños de caja específico. Este patrón puede corresponder a curvas de lagunaridad de la
SOP superiores, con valores intermedios o inferiores comparadas con las de los diseños no
óptimos.
• El análisis R/S y de la lagunaridad reflejan las diferencias en las propiedades fractales de la
SOP dependiendo de la escala de análisis. Los valores de dimensión fractal y
heterogeneidad espacial pueden variar dependiendo de si el análisis se efectúa a nivel
local (cortes o regiones específicas de la SOP) o a nivel global (totalidad de la superficie de
gradiente hidráulico).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
234
8 RECOMENDACIONES
Para el desarrollo de próximos proyectos de investigación, se sugieren los siguientes puntos:
• El número de ejemplares se puede ampliar implementando redes patrón o reales con un
número superior de nodos y tuberías, a modo que se logre verificar la veracidad de las
conclusiones planteadas. En la literatura se pueden encontrar redes alternativas que no se
incluyeron en el presente trabajo.
• El cálculo de la dimensión fractal de la red se puede complementar incluyendo el valor de
la altura piezométrica o el caudal demandado en el criterio de asignación de pesos a los
nodos. De esta manera, se exploraría la dependencia del esquema de demandas en la
fractalidad de la red.
• Se recomienda la búsqueda de diseños no óptimos dónde se recurra a configuraciones de
diámetros comerciales no trabajadas en la presente investigación. Se pueden implementar
rutinas de algoritmos genéticos u otros métodos de optimización típicos de la literatura.
• Para el caso de las redes patrón, los diseños optimizados se estipularon según la
metodología OPUS, que ofrece resultados con discrepancias pequeñas con respecto a los
récords mundiales. Se recomienda establecer los diseños de estas redes a partir de las
configuraciones récord para obtener una mejor aproximación a la SOP.
• Se sugiere modificar la distribución y magnitud de las demandas de caudal en los nodos de
las redes trabajadas. Lo anterior implica investigar los cambios sobre las propiedades
fractales de la SOP de una red específica bajo diferentes esquemas de demandas de
caudal.
• Para mejorar el cálculo de los costos de los diseños se recomienda el uso de los precios
unitarios en lugar de las curvas obtenidas mediante las regresiones potenciales.
• Como se explicó en apartados anteriores, el proceso de interpolación durante la
construcción de las superficies de gradiente hidráulico se realizó optando por evitar la
atenuación de la fractalidad. Se sugiere explorar los cambios en la dimensión fractal
implementando métodos de interpolación alternativos.
• La implementación del método de conteo diferencial de cajas (DBC) se desarrolló para una
altura de caja unitaria y otra obtenida por tanteo. Se sugiere determinar las dimensiones
fractales permitiendo iterar sobre la altura de caja.
• Si bien el proceso de investigación concluye con planteamientos a nivel teórico, se
recomienda explorar la aplicabilidad del análisis fractal en el desarrollo de mejores
metodologías de optimización, sectorización u operación de las redes de distribución. Se
espera que los resultados de la presente investigación permitan orientar el desarrollo de
conocimiento que contribuya al estado del arte en redes de abastecimiento.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
235
9 REFERENCIAS
Allain, C. y Cloitre, M. (1991). Characterizing the lacunarity of random and deterministic fractal
sets. Physical Review A, 44(6), pp. 3552-3558. doi: 10.1103/physreva.44.3552.
Alperovits, E. y Shamir, U. (1977). Design of optimal water distribution systems. Water Resources
Research, 13(6). doi: 10.1029/WR013i006p00885
Araque, D.A. y Saldarriaga, J.G. (2005). Optimización operacional de redes de distribución de agua
potable con el fin de maximizar la uniformidad de presiones en los nodos de consumo.
Revista
de
Ingeniería,
48(22),
pp.
126-132.
Recuperado
de
https://ojsrevistaing.uniandes.edu.co/ojs/index.php/revista/article/view/394
Azpurua, M. y Dos Ramos, K. (2010). A comparison of spatial interpolation methods for estimation
of average electromagnetic field magnitude. Progress In Electromagnetics Research M, 14,
pp. 135-145. Recuperado de http://www.jpier.org/PIERM/pierm14/11.10083103.pdf
Barber, F. y Salido, M.A. (2003). Introducción a la Programación de Restricciones. Inteligencia
Artificial: Revista Iberoamericana de Inteligencia Artificial, 7(20), pp. 13-30. Recuperado de
https://www.redalyc.org/pdf/925/92572002.pdf
Barták, R., Salido, M.A. y Rossi, F. (2004). New Trends in Constraint Satisfaction, Planning, and
Scheduling: A Survey. The Knowledge Engineering Review, 0(0), pp.1-24. doi:
10.1017/S000000000000000
Benavides, H.M. (2010). EPAEX. Universidad Técnica Particular de Loja, Ecuador.
Bernal, A.E. y Saldarriaga, J.G. (2008). Diseño optimizado de ampliaciones de redes de distribución
utilizando los conceptos de Potencia y Resiliencia en la red (Tesis de maestría).
Recuperado
de
https://biblioteca.uniandes.edu.co/visor_de_tesis/web/?SessionID=L1Rlc2lzXzIwMDhfcHJ
pbWVyX3NlbWVzdHJlLzAwMDA2NTQucGRm
Beygi, S., Haddad, O.B., Mehdipour, E.F., Mariño, M.A. (2014). Bargaining Models for optimal
Design of Water Distribution Networks. Journal of Water Resources Planning and
Management, 140(1), pp. 92-99. doi: : 10.1061/(ASCE)WR.1943-5452.0000324
Bird, R.B., Stewart, W.E., Lightfoot, E.N. (2002). Transport Phenomena (2ª ed.). New York, United
States of America: John Wiley & Sons, Inc.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
236
Bragalli, C., D’Ambrosio, Lee, J., Lodi, A. y Toth, P. (2012). On the optimal design of water
distribution networks: a practical MINLP approach. Optimization and Engineering, 13,
pp.219-246. doi: 10.1007/s11081-011-9141-7.
Brown, G.O. (2002). The History of the Darcy-Weisbach Equation for Pipe Flow. Environmental and
Water Resources History. ASCE Civil Engineering Conference and Exposition. doi:
10.1061/40650(2003)4
Buitrago, O.Y., Ramírez, A.L. y Britto, R.A. (2015). Nuevo Algoritmo para la Construcción de la
Envolvente Convexa en el Plano. Información Tecnológica, 26(4), pp.137-144. doi:
10.4067/S0718-07642015000400017.
Cardona, L.F. y Múnera, L.E. (2016). Auto-similaridad de las Space Filling Curves. Ingeniería y
Competitividad,
18(2),
pp.113-124.
Recuperado
de
http://www.scielo.org.co/pdf/inco/v18n2/v18n2a10.pdf
Cengel, Y.A. y Cimbala, J.M. (2006). Mecánica de Fluidos: Fundamentos y Aplicaciones (1ª ed.) (V.
Campos, Trad.). Nueva York, Estados Unidos: McGraw-Hill (Trabajo original publicado en
2005).
Conagua. (s.f.). Manual de agua potable, alcantarillado y saneamiento: Diseño de redes de
distribución de agua potable. Tlalpan, México D.F.: Comisión Nacional del Agua.
Recuperado
de
https://sswm.info/sites/default/files/reference_attachments/CONAGUA%20s.f.a.%20Dise
%C3%B1o%20de%20redes%20de%20distribuci%C3%B3n%20de%20agua%20potable.pdf
Cross, H. (1936). Analysis of flow in networks of conduits or conductors (Bulletin No. 286).
University
of
Illinois
Bulletin,
34(22).
Recuperado
de
https://www.ideals.illinois.edu/bitstream/handle/2142/4433/engineeringexperv00000i00
286.pdf?seque.
Diskin, M.H. (1960). The limits of applicability of the Hazen-Williams formula. La Houille Blanche,
(6), pp. 720-726. doi: 10.1051/lhb/1960059.
Dong, P. (2000). Lacunarity for Spatial Heterogeneity Measurement in GIS. Geographic Information
Sciences, 6(1), pp. 20-26. doi: 10.1080/10824000009480530.
Dong, P. (2000). Test of a new lacunarity estimation method for image texture analysis.
International Journal of Remote Sensing, 21(17), pp. 3369-3373. doi:
10.1080/014311600750019985.
Edgar, G.A. (1990). Measure, Topology, and Fractal Geometry. New York, USA: Springer-Verlag.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
237
ESRI.
(2016).
Comparing
interpolation
methods.
Recuperado
de
https://desktop.arcgis.com/en/arcmap/10.3/tools/3d-analyst-toolbox/comparing-
interpolation-methods.htm
ESRI.
(2016).
How
IDW
works.
Recuperado
de
https://desktop.arcgis.com/en/arcmap/10.3/tools/3d-analyst-toolbox/how-idw-
works.htm
Ezzeldin, R., Djebedjian, B. y Saafan, T. (2014). Integer Discrete Particle Swarm Optimization of
Water Distribution Networks. Journal of Pipeline Systems Engineering and Practice, 5(1).
Recuperado
de
https://ascelibrary.org/doi/abs/10.1061/%28ASCE%29PS.1949-
1204.0000154
Falconer, K. (1990). Fractal Geometry: Mathematical Foundations and Applications. West Sussex,
England: John Wiley & Sons Ltd.
Featherstone, R.E. y El-Jumaily, K.K. (1983). Optimal Diameter Selection for Pipe Networks. Journal
of Hydraulic Engineering, 109(2), pp. 221-234. doi: 10.1061/(ASCE)0733-
9429(1983)109:2(221)
Fernández, M. y Sánchez, M.A. (2015). How to calculate the Hausdorff dimension using fractal
structures. Applied Mathematics and Computation, 264 (1), pp. 116-131. doi:
10.1016/j.amc.2015.04.059
Fox. R.W. y McDonald, A.T. (1995). Introducción a la mecánica de fluidos (4ª ed.) (G. Nagore,
Trad.). Nueva York, Estados Unidos: John Wiley & Sons, Inc (Trabajo original publicado en
1993).
Fujiwara, O. y Khang, D. (1990). A two phase decomposition methods for optimal design of looped
wáter distribution networks. Water Resources Research, 26(4), pp.539-549. doi:
10.1029/WR026i004p00539
Geem, Z.W. (2008). Particle-swarm harmony search for water network design. Engineering
Optimization, (41)4, pp. 297-311. doi: 10.1080/03052150802449227
Gessler, J. (1985). Pipe network optimization by enumeration. Procs. Speciality Conference on
Computer Applications/Water Resources, ASCE, New York, pp. 572-581.
Gilmore, M., Yu, C.X., Rhodes, T.L. y Peebles, W.A. (2002). Investigation of rescaled range analysis,
the Hurst exponent, and a long time correlations in plasma turbulence. Physics of Plasmas,
9(4), pp. 1312-1316. doi: 10.1063/1.1459707.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
238
Gjendemsjo, A. (2006). An Introduction to MATLAB. Trondheim, Noruega: Openstax CNX
Recuperado
de
https://cnx.org/exports/2100a51e-a5c9-4e41-9cb6-
087b755125ac@3.1.pdf/an-introduction-to-matlab-3.1.pdf
Goldberg, D.E. (1989). Genetic algorithms in search, optimization, and machine learning. Boston,
USA: Addison-Wesley Publishing Company, Inc.
Griffiths, D.F. (2018). An Introduction to Matlab (Reporte 4.1.). Scotland, United Kingdom: The
University
of
Dundee.
Recuperado
de
https://www.researchgate.net/publication/328077935_An_Introduction_to_Matlab_Revis
ed_Version_41
Grossman, S.I. y Flores, J.J. (2012). Álgebra Lineal (7ª ed.). Delegación Álvaro Obregón, México
D.F.: McGraw-Hill Interamericana Editores, S.A.
Houcque, D. (2005). Introduction to MATLAB for Engineering Students. Evanston, Estados Unidos:
Northwestern
University.
Recuperado
de
https://www.mccormick.northwestern.edu/documents/students/undergraduate/introduc
tion-to-matlab.pdf
Kadu, M.S., Gupta, R. y Bhave, P.R. (2008). Optimal Design of Water Networks Using a Modified
Algorithm with Reduction in Search Space. Journal of Water Resources Planning and
Management, 134(2), pp. 147-160. doi: 10.1061/(ASCE)0733-9496(2008)134:2(147)
Keedwell, E.C. y Khu, S.T. (2006). Novel Cellular Automata Approach to Optimal Water Distribution
Network Design. Journal of Computing in Civil Engineering, 20(1), pp. 49-56. doi:
10.1061/(ASCE)0887-3801(2006)20:1(49)
Kleinow, T. (2002). Testing Continuous Time Models in Financial Markets (Tesis Doctoral).
Universidad Humboldt de Berlín, Alemania. Recuperado de https://edoc.hu-
berlin.de/bitstream/handle/18452/15422/Kleinow.pdf?sequence=1&isAllowed=y
Lee, D.T. y Schachter, B.J. (1980). Two Algorithms for Constructing a Delaunay Triangulation.
International Journal of Computer and Information Sciences, 9(3), pp. 219-242.
Recuperado
de
http://www.personal.psu.edu/cxc11/AERSP560/DELAUNEY/13_Two_algorithms_Delauney
.pdf
Lee, S.C. y Lee, S.I. (2001). Genetic algorithms for optimal augmentation of water distribution
networks. Journal of Korea Water Resources Association, 34(5), pp. 567-575. Recuperado
de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
239
https://www.researchgate.net/publication/264077224_Genetic_Algorithms_for_Optimal_
Augmentation_of_Water_Distribution_Networks
Liou, C.P. (1998). Limitations and proper use of the Hazen-Williams equation. Journal of Hydraulic
Engineering, 124(9), pp. 951-954. doi: 10.1061/(ASCE)0733-9429(1998)124:9(951).
López, L., Cuero, P., Díaz, O., Páez, D. y Saldarriaga, J.G. (2013). Diseño de redes de distribución de
agua potable por medio de la metodología OPUS e inicio en caliente. XII Simposio
Iberoamericano sobre planificación de sistemas de abastecimiento y drenaje. Recuperado
de
https://es.scribd.com/document/230058089/DISENO-DE-RDAP-POR-MEDIO-DE-LA-
METODOLOG-A-OPUS-E-INICIO-EN-CALIENTE-pdf
Mandelbrot, B. (1977). Fractals: Form, chance and dimension. San Francisco, USA: W.H. Freeman
and Company.
Mandelbrot, B. (1983). The Fractal Geometry of Nature. New York, USA: W.H. Freeman and
Company.
Mandelbrot, B. (1993). Los objetos fractales (3a ed.) (J. Llosa, trad.). Barcelona, España:
Metatemas 13.
MathWorks.
(2019).
MATLAB
Primer
R2019b.
Recuperado
de
https://www.mathworks.com/help/pdf_doc/matlab/getstart.pdf
Mathworks.
(2020).
Delaunay.
Recuperado
de
https://la.mathworks.com/help/matlab/ref/delaunay.html
Mathworks.
(2020).
Griddata.
Recuperado
de
https://la.mathworks.com/help/matlab/ref/griddata.html
Mathworks. (2020). Line. Recuperado de https://la.mathworks.com/help/matlab/ref/line.html
Mathworks.
(2020).
Scatter3.
Recuperado
de
https://la.mathworks.com/help/matlab/ref/scatter3.html
Mathworks.
(2020).
Trisurf.
Recuperado
de
https://la.mathworks.com/help/matlab/ref/trisurf.html
Mathworks.
(2020).
Xlsread.
Recuperado
de
https://la.mathworks.com/help/matlab/ref/xlsread.html
Ministerio de Desarrollo Económico. (2000). Reglamento Técnico del Sector de Agua Potable y
Saneamiento Básico – Título A: Aspectos Generales de los Sistemas de Agua potable y

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
240
Saneamiento Básico. Bogotá D.C., República de Colombia. Recuperado de
http://www.minvivienda.gov.co/Documents/ViceministerioAgua/010710_ras_titulo_a_.pd
f
Mitchell, M. (1999). An Introduction to Genetic Algorithm. Cambridge, USA: Massachussetts
Institute of Technology.
Narváez, P.C y Galeano, H. (2002). Ecuación de costos y función objetivo para la optimización del
diseño de redes de flujo de líquidos a presión. Ingeniería e Investigación, 49, pp.23-29. doi:
10.15446/ing.investig
NASA.
(s.f.).
Reynolds
Number.
U.S.
Government.
Recuperado
de
https://www.grc.nasa.gov/www/k-12/airplane/reynolds.html
Ochoa, S. y Saldarriaga, J.G. (2009). Diseño optimizado de redes de distribución de agua potable
con base en el concepto energético de Superficie Óptima de Gradiente Hidráulico (Tesis de
Maestría).
Recuperado
de
https://es.scribd.com/document/48972610/06-Diseno-
optimizado-de-redes-con-base-en-el-concepto-energetico#download
Ochoa, S., Saldarriaga, J.G., Ñañez, P. y Galvis, C. (2010). Diseño optimizado de redes de
distribución de agua potable mediante la superficie óptima de gradiente hidráulico. XXIV
Congreso Latinoamericano de Hidráulica, Punta del Este, Uruguay. Recuperado de
https://www.academia.edu/6036607/Dise%C3%B1o_Optimizado_de_Acueductos_Median
te_la_Superficie_%C3%93ptima_de_Gradiente_Hidr%C3%A1ulico.
Ormsbee, L.E. y Wood, D.J. (1986). Hydraulic design algorithms for pipe networks. Journal of
Hydraulic Engineering, 112(12), pp. 1195-1206.
PAVCO Wavin S.A. (2019). Lista de precios: Septiembre 2019. Recuperado de
https://pavcowavin.com.co/tuberia-acueducto-pvco-biorientado-biaxial-pavco
Pereyra, G., Pandolfi, D.R, Villagra, N.A. (2017). Diseño y optimización de redes de distribución de
agua utilizando algoritmos genéticos. Informe Científico Técnica UNPA, 9(1), pp. 37-63.
Recuperado de https://dialnet.unirioja.es/servlet/articulo?codigo=5919083
Pino, V.E., Valle, C.A., Condori, P.F., Mejía, M.J., Chavarri, V.E. y Alfaro, R.L. (2017). Diseño Óptimo
de Redes de Distribución de Agua Usando Un Software Basado en Microalgoritmos
Genéticos Multiobjetivos. Ribagua, 4(1), pp. 6-23. doi: 10.1080/23863781.2017.1317087
Posada, A. y Saldarriaga, J.G. (2018). Comparación entre diseños optimizados y diseños reales en
RDAP: Efecto del aumento de la población a lo largo de la vida útil del proyecto. XXVIII

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
241
Congreso Latinoamericano de Hidráulica, Buenos Aires, Argentina. Recuperado de
https://www.ina.gob.ar/congreso_hidraulica/resumenes/LADHI_2018_RE_162.pdf
Prusinkiewicz, P. (2004). Self-Similarity in Plants: Integrating Mathematical and Biological
Perspectives. doi: 10.1142/9789812702746_0008
Qian, B. y Rasheed, K. (2004). Hurst exponent and financial market predictability. University of
Georgia,
USA.
Recuperado
de
https://pdfs.semanticscholar.org/0816/a5a989c8d2431a6d20076d27c4295c00fb77.pdf
Quintero, O.Y. y Ruiz, J. (2011). Estimación del exponente de Hurst y la dimensión fractal de una
superficie topográfica a través de la extracción de perfiles. UD y la Geomática, (5), 84-91.
Recuperado
de
https://revistas.udistrital.edu.co/index.php/UDGeo/article/view/3648/5248
Reca, J. y Martínez, J. (2006). Genetic algorithms for the design of looped irrigation water
distribution networks. Water Resources Research, 42(5). doi: 10.1029/2005WR004383
Rennels, D.C. y Hudson, H.M. (2012). Pipe Flow: A Practical and Comprehensive Guide. New Jersey,
United States of America: John Wiley & Sons, Inc. Recuperado de
http://ezproxy.uniandes.edu.co:8080/login?url=http://onlinelibrary.wiley.com/book/10.1
002/9781118275276
Reynolds, O. (1883). An experimental investigation of the circumstances which determine whether
the motion of water shall be direct or sinuous, and of the law of resistance in parallel
channels. The Royal Society, 174, 935-982. doi: 10.1098/rstl.1883.0029.
Saldarriaga, J.G. (2016). Hidráulica de tuberías: Abastecimiento de agua, Redes y Riegos (3ª ed.).
Bogotá D.C., República de Colombia: Alfaomega Colombiana.
Saldarriaga, J.G., López, L., Páez, D., Luna, D., González, S. (2018). Diseño Optimizado de Redes de
Distribución de Agua Potable (Programa REDES). XV Seminario Iberoamericano de Redes
de
Agua
y
Drenaje,
SEREA2017.
Recuperado
de
https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3112868
Saldarriaga, J.G., Ochoa, S., Moreno, M., Romero, N. y Cortés, O. (2010). Renovación priorizada de
redes de distribución utilizando el concepto de potencia unitaria. Revista de Ingeniería,
(31), pp. 7-15. Recuperado de http://www.scielo.org.co/pdf/ring/n31/n31a2.pdf
Saldarriaga, J.G., Páez, D., Cuero, P. y León, N. (2013). Optimal Design of Water Distribution
Networks Using Mock Open Tree Topology. World Environmental and Water Resources
Congress 2013: Showcasing the Future, pp. 869-880. doi: 10.1061/9780784412947.083.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
242
Saldarriaga, J.G., Páez, D., León, N., López, L. y Cuero, P. (2015). Power use methods for optimal
design of WDS: History and their use as post-optimization warm starts. Journal of
Hydroinformatics, 17(3), pp. 404-421. doi: 10.2166/hydro.2014.013
Saldarriaga, J.G., Pulgarín, L., Cuero, P. y Duque, N. (2018). Software para la Enseñanza de
Hidráulica de Tuberías. XV Seminario Iberoamericano de Redes de Agua y Denaje , SEREA
2017.
Recuperado
de
https://poseidon01.ssrn.com/delivery.php?ID=43910510311912112509408111608702412
300000503602101100406406902309110400906410009207510606301603205800100002
209207308612007600001603507500302100007308602800907012211601807709511308
109611810211811801612408311509402802906710006508309110208512600609801309
6&EXT=pdf
Saldarriaga, J.G., Takahashi, S., Hernández, F. y Escovar, M.A. (2010). Diseño optimizado de
sistemas de distribución de agua: una nueva perspectiva. Recuperado de
https://www.researchgate.net/publication/320331618_Diseno_optimizado_de_sistemas_
de_distribucion_de_agua_Una_nueva_perspectiva
Salgado, R., Todini, E. y O’Connell, P.E. (1987). Comparison of the Gradient Method with some
traditional methods for the analysis of water supply distribution networks. En Computer
Applications in Water Supply: Volume 1- Systems Analysis and Simulation (pp. 38-62).
Letchworth, England: John Wiley & Sons, Inc.
Salgado, R.O. (1988). Computer modelling of water supply distribution networks using the gradient
method
(Tesis
de
doctorado).
Recuperado
de
http://scholar.google.com.co/scholar_url?url=https://theses.ncl.ac.uk/jspui/bitstream/10
443/287/1/Salgado-
Castro88v.1.pdf&hl=es&sa=X&scisig=AAGBfm1LKxR9RNIjXvhhdqlYdnc4tkek7Q&nossl=1&o
i=scholarr
Sarkar, N. y Chaudhuri, B.B. (1992). An efficient approach to estimate fractal dimension of textural
images. Pattern Recognition, 25(9), pp. 1035-1041. doi: 10.1016/0031-3203(92)90066-R.
Schaake, J. y Lai, D. (1969). Linear programming and dynamic programming application to water
distribution network design. Department of Civil Engineering, Massachusetts Institute of
Technology, Cambridge, Massachusetts.
Schneider, C.M., Kesselring, T.A., Andrade Jr., J.S. y Hermann, H.J. (2018). Optimal box-covering
algorithm for fractal dimension of complex networks. Physical review. E, Statistical physics,
plasmas,
fluids,
and
related
interdisciplinary
topics,
86(1).
doi:
10.1103/PhysRevE.86.016707

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
243
Shames, I.H. (1995). Mecánica de fluidos (3ª ed.) (J.G. Saldarriaga, Trad.). Nueva York, Estados
Unidos: McGraw-Hill (Trabajo original publicado en 1992).
Sherali, H.D., Subramanian, S. y Loganathan, G.V. (2001). Effective Relaxations and Partitioning
Schemes for Solving Water Distribution Network Design Problems to Global Optimality.
Journal
of
Global
Optimization,
19,
pp.
1-26.
Recuperado
de
https://link.springer.com/content/pdf/10.1023/A:1008368330827.pdf
Sigmon, K. (1993). MATLAB Primer (3ª ed.). Cambridge, Estados Unidos: Massachusetts Institute of
Technology. Recuperado de http://web.mit.edu/6.777/www/downloads/primer.pdf
Sivanandam, S.N y Deepa, S.N. (2008). Introduction to Genetic Algorithms. New York, USA:
Springer-Verlag Berling Heidelberg.
Song, C., Gallos, L.K., Havlin, S. y Makse, H.A. (2007). How to calculate the fractal dimension of a
complex network: The box covering algorithm. Journal of Statistical Mechanics Theory and
Experiment, (3). doi: 10.1088/1742-5468/2007/03/P03006.
Steel, E.W. y McGhee, T.J. (1979). Water Supply and Sewerage (5th ed.). Tokyo: McGraw-Hill
Kogakusha.
Stephenson, D. (1989). Pipeline Design for Water Engineers (3ª ed.). Amsterdam, Netherlands:
Elsevier Science Publishers.
Streeter V.L., Wylie, E.B. y Bedford, K.W. (2000). Mecánica de Fluidos (9ª ed.) (J.G. Saldarriaga,
Trad.). Nueva York, Estados Unidos: McGraw-Hill Companies, Inc (Trabajo original
publicado en 1998).
Sung, Y.H., Lin, M.D., Lin, Y.H. y Liu, Y.L. (2007). Tabu search solution of water distribution network
optimization. Journal of Environmental Engineering and Management, 17(3), pp. 177-187.
Tchoukanski, I. (s.f). Triangulated Irregular Network. ET Spatial Techniques. Recuperado de
https://www.ian-ko.com/resources/triangulated_irregular_network.htm
Tesar, V. (2001). Microfluidic Valves for Flow Control at Low Reynolds Numbers. Journal of
Visualization, 4(1), 51-60. doi: 10.1007/BF03182455.
Todini, E. y Pilati, S. (1987). A Gradient Algorithm for the Analysis of Pipe Networks. En Computer
Applications in Water Supply: Volume 1- Systems Analysis and Simulation (pp. 1-20).
Letchworth, England: John Wiley & Sons, Inc.
Todini, E. y Pilati, S. (1987). A gradient method for the analysis of pipe networks. International
Conference on Computer Applications for Water Supply and Distribution, Leicester

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
244
Polytechnic,
United
Kingdom.
Recuperado
de
http://theodores-
pro.ttu.edu/ncimm/research-documents/Todini%20and%20Pilati%201987.pdf
U.S. Army Corps of Engineers. (1957). Military Hydrology Bulletin 12. Washington D.C., United
States of America: Military Hydrology R&D Branch, U.S. Army Engineer District.
Recuperado
de
https://www.cia.gov/library/readingroom/docs/CIA-RDP81-
01043R002300060004-2.pdf
University of Cincinnati. (2019). MATLAB Resources. Cincinnati, Estados Unidos: University of
Cincinnati
Libraries.
Recuperado
de
https://guides.libraries.uc.edu/c.php?g=461109&p=3152738
University of Exeter. (s.f.). Benchmarks – Design/Resiliance – Medium Problems. Centre for Water
Systems.
Recuperado
de
http://emps.exeter.ac.uk/engineering/research/cws/resources/benchmarks/design-
resiliance-pareto-fronts/medium-problems/
University of Exeter. (s.f.). Benchmarks – Design/Resilience – Intermediate Problems. Centre for
Water
Systems.
Recuperado
de
http://emps.exeter.ac.uk/engineering/research/cws/resources/benchmarks/design-
resiliance-pareto-fronts/intermediate-problems/
University of Exeter. (s.f.). Benchmarks – Design/Resilience – Large Problems. Centre for Water
Systems.
Recuperado
de
http://emps.exeter.ac.uk/engineering/research/cws/resources/benchmarks/design-
resiliance-pareto-fronts/large-problems/
University of Exeter. (s.f.). Two Objective Design/Resilience: Towards the Best-Known
Approximation
to
the
True
Pareto
Front.
Recuperado
de
http://emps.exeter.ac.uk/engineering/research/cws/resources/benchmarks/design-
resiliance-pareto-fronts/
Vargas, K., Salcedo, C. y Saldarriaga, J.G. (2019). Dimensión fractal e identificación de potenciales
sectores de servicio en redes de distribución de agua potable utilizando criterios
hidráulicos. Revista Recursos Hídricos, 40(2), pp. 27-38. doi: 10.5894/rh40n2-cti3
Villalba, G., Saldarriaga, J.G., Takahashi, S. (2005). Algoritmos de optimización combinatoria
aplicados al diseño de redes de distribución de agua potable (Tesis de maestría).
Recuperado
de
https://es.scribd.com/document/48973715/08-Algoritmos-de-
optimizacion-Combinatoria-aplicados-al-diseno-de-redes

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
245
Wang, Q., Guidolin, M., Savic, D. y Kapelan, Z. (2014). Two-Objective Design of Benchmark
Problems of a Water Distribution System via MOEAs: Towards the Best-Known
Approximation of the True Pareto Front. Journal of Water Resources Planning and
Management,
141(3).
Recuperado
de
https://ascelibrary-
org.ezproxy.uniandes.edu.co:8443/doi/full/10.1061/%28ASCE%29WR.1943-5452.0000460
Wei, D.J., Liu, Q., Zhang, H.X., Hu, Y., Deng, Y. y Mahadevan, S. (2013). Box-covering algorithm for
fractal dimension of weighted networks. Scientific Reports, 3(3049), pp. 1-8. doi:
10.1038/srep03049.
White, F.M. (2008). Mecánica de Fluidos (6ª ed.). Madrid, España: McGraw-Hill.
Wu, I.P. (1975). Design of Drip Irrigation Main Lines. Journal of the Irrigation and Drainage
Division, 101(4), pp. 265-278.
Wu, I.P., Howell, T.A. y Hiler, E.A. (1979). Hydraulic Design of Drip Irrigation Systems (Technical
Bulletin No. 105). Hawaii Agricultural Experiment Station, University of Hawaii: Western
Regional
Research
Project
W-128.
Recuperado
de
https://core.ac.uk/download/pdf/19333341.pdf.
Xia, W. y Yap, R.H.C. (2013). Optimizing STR Algorithms with Tuple Compression. En Principles and
Practice of Constraint Programming – 19th International Conference (pp.724-732).
Uppsala, Sweden: Springer-Verlag Berlin Heidelberg.
Yang, T., Guo’an, T. y Strobl, J. (2012). Spatial Structure Characteristics Detecting of Landform
based on Improved 3D Lacunarity Model. Chinese Geographical Science, 22(1), pp. 88-96.
doi: 10.1007/s11769-012-0516-2.
Yates, D.F., Templeman, A.B. y Boffey, T.B. (1984). The computational complexity of the problem
of determining least capital cost designs for water supply networks. Engineering
Optimization, 7, pp. 143-155. doi: 10.1080/03052158408960635.
Zhang, Z.X. (2016). Rock Fracture and Blasting: Theory and Applications. Doi: 10.1016/C2014-0-
01408-6
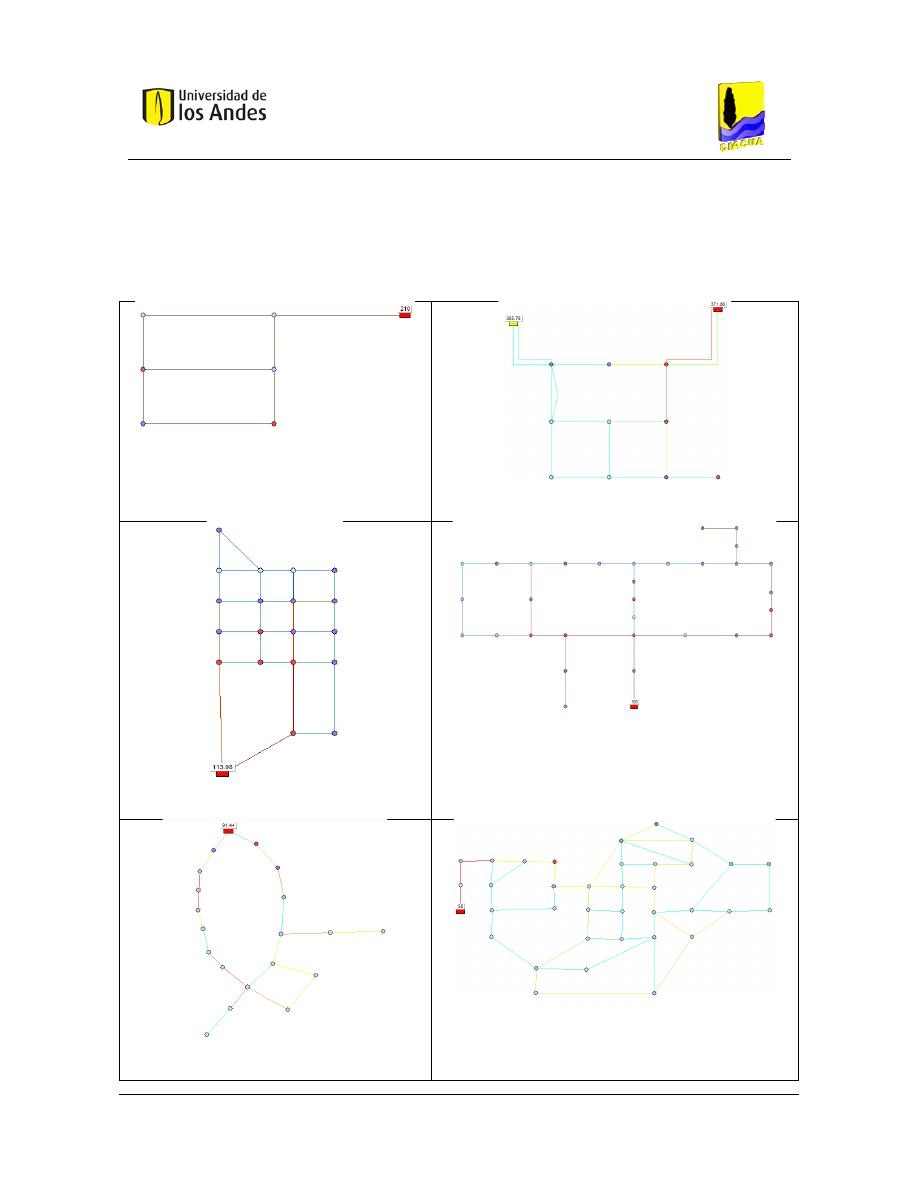
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
246
10 ANEXOS
10.1 Topología de las redes
Figura 654. Red Two Loops 2D - REDES 2019.
Figura 655. Red Two Reservoirs 2D - REDES 2019.
Figura 656. Red Taichung 2D - REDES 2019.
Figura 657. Red Hanoi 2D - REDES 2019.
Figura 658. Red New York Tunnels 2D - REDES 2019.
Figura 659. Red BakRyan 2D - REDES 2019.
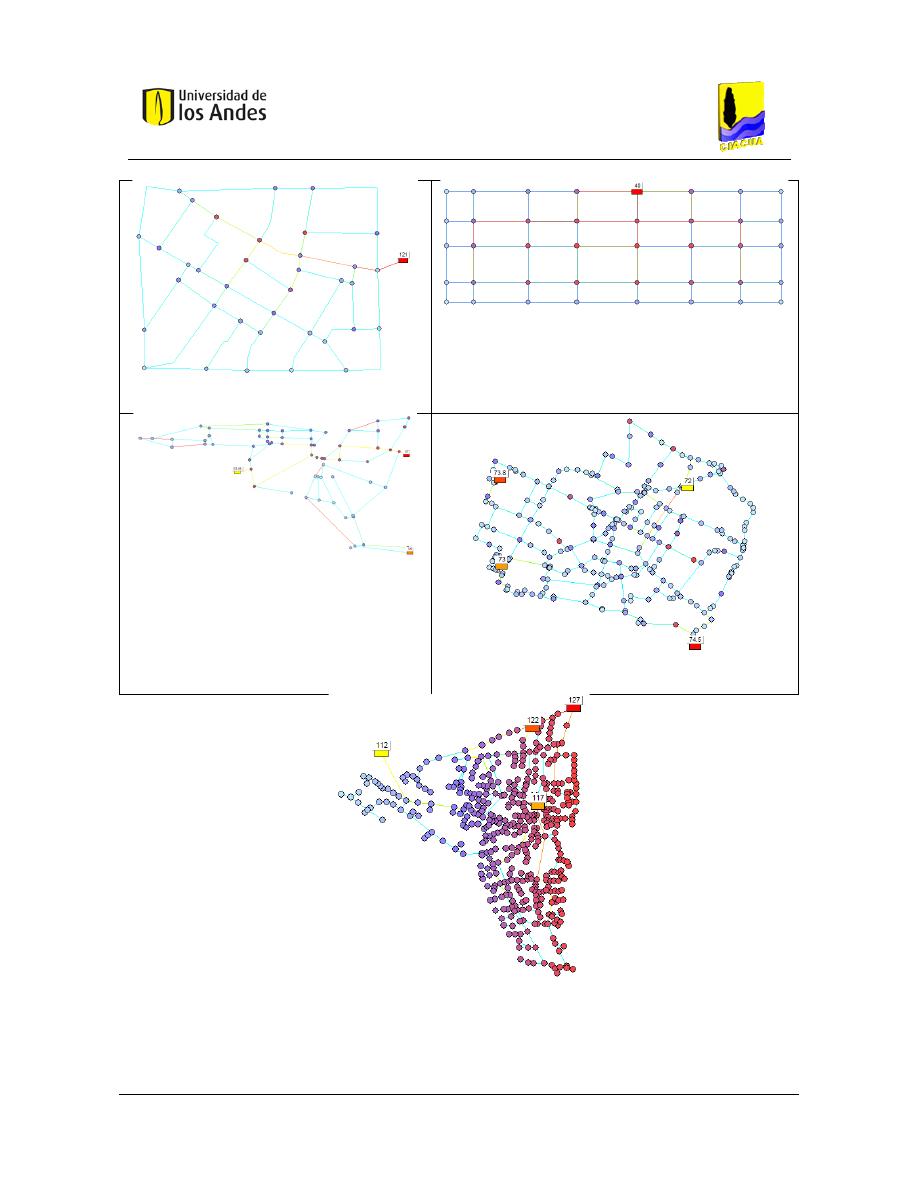
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
247
Figura 660. Red Fossolo 2D - REDES 2019.
Figura 661. Red R28 2D - REDES 2019.
Figura 662. Red Pescara 2D - REDES 2019.
Figura 663. Red Modena 2D - REDES 2019.
Figura 664. Red Balerma 2D - REDES 2019.
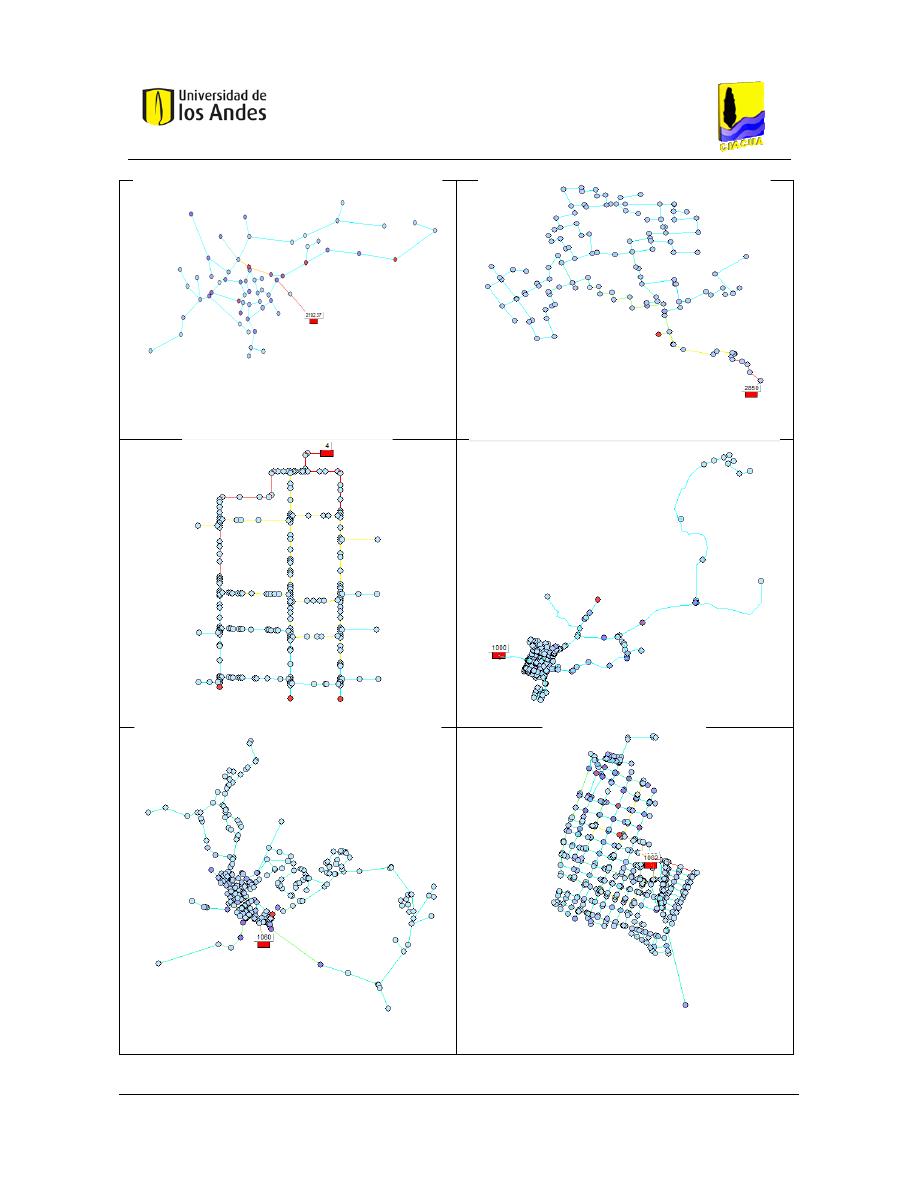
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
248
Figura 665. Red San Vicente 2D - REDES 2019.
Figura 666. Red Cazucá 2D - REDES 2019.
Figura 667. Red Elevada 2D - REDES 2019.
Figura 668. Red Bolívar 2D - REDES 2019.
Figura 669. Red La Cumbre 2D - REDES 2019.
Figura 670. Red Candelaria 2D - REDES 2019.
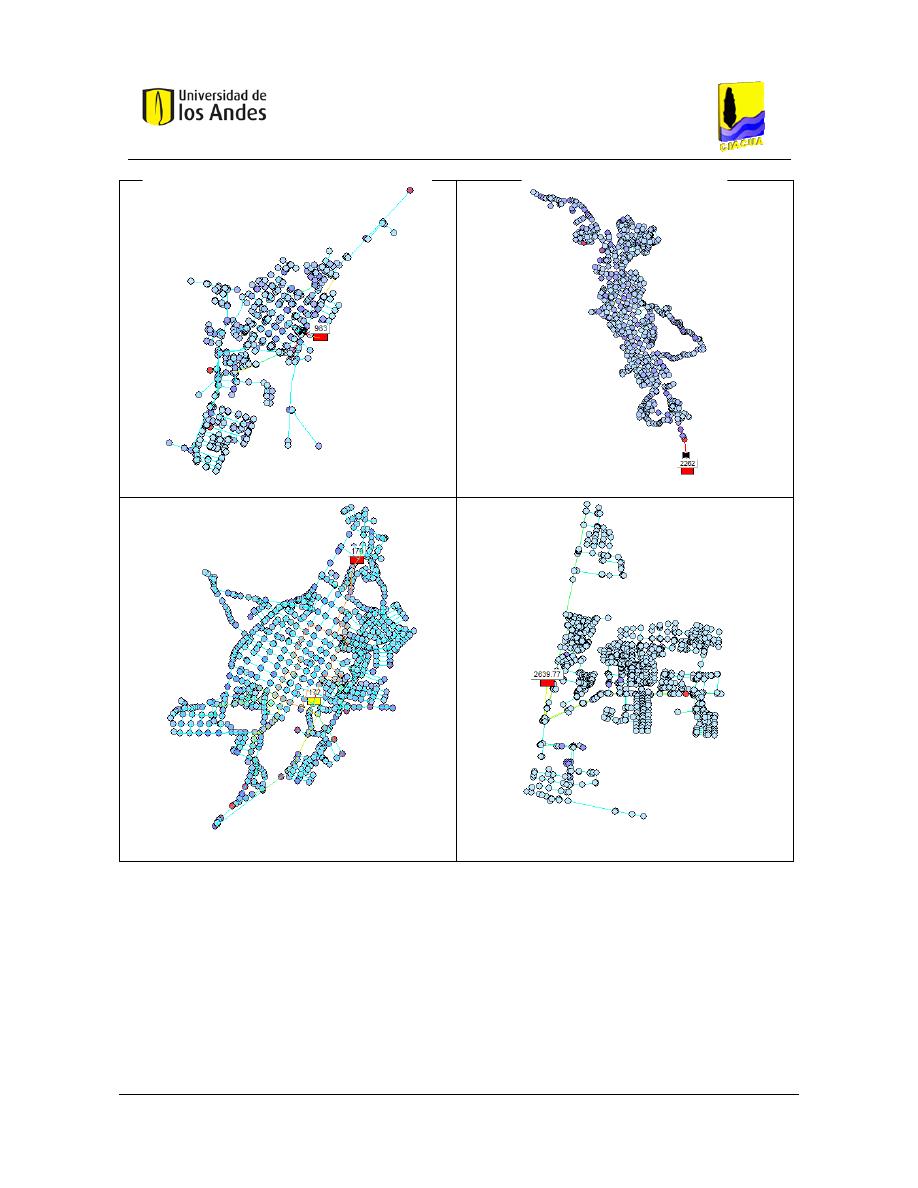
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
249
Figura 671. Red Bugalagrande 2D - REDES 2019.
Figura 672. Red Carmen 2D - REDES 2019.
Figura 673. Red Chinú 2D - REDES 2019.
Figura 674. Red Sector 35 2D - REDES 2019.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
250
Figura 675. Red La Enea 2D - REDES 2019.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
251
10.2 Curvas de costos
Tabla 48. Diámetros y costos unitarios - Red Two Loops.
Adaptado de Keedwell y Khu (2006).
Tabla 49. Diámetros y costos unitarios - Red Two
Reservoirs.
Tabla 50. Diámetros y costos unitarios - Red Taichung.
Adaptado de Sung et. al. (2007).
Tabla 51. Diámetros y costos unitarios - Red Hanoi.
Adaptado de Beygi et. al. (2014).
Tabla 52. Diámetros y costos unitarios - Red Blacksburg.
Adaptado de University of Exeter (s.f).
Tabla 53. Diámetros y costos unitarios - Red New York
Tunnels. Adaptado de University of Exeter (s.f.).
Diámetro (in)
Costo unitario ($USD/m)
1
2
2
5
3
8
4
11
6
16
8
23
10
32
12
50
14
60
16
90
18
130
20
170
22
300
24
550
Diámetro (mm)
Costo unitario ($/m)
152
49.54
203
63.32
254
94.82
305
132.87
356
170.93
407
194.88
458
232.94
509
264.1
Diámetro (mm) Costo unitario ($TWD/m)
100
860
150
1160
200
1470
250
1700
300
2080
350
2640
400
3240
450
3810
500
4400
600
5580
700
8360
800
10400
900
12800
Diámetro (in)
Costo unitario ($USD/m)
12
45.7
16
70.4
20
98.4
24
129.3
30
180.7
40
278.3
Diámetro (mm) Costo unitario ($/m)
25.4
0.52
50.8
2.1
76.2
4.72
101.6
8.4
152.4
18.9
203.2
33.6
254
52.5
304.8
75.59
355.6
102.89
406.4
134.39
457.2
170.09
508
209.98
558.8
254.08
609.6
302.37
Diámetro (in) Costo unitario ($/ft)
36
93.59
48
133.70
60
176.32
72
221.05
84
267.61
96
315.80
108
365.46
120
416.46
132
468.71
144
522.11
156
576.59
168
632.09
180
688.54
192
745.91
204
804.14

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
252
Tabla 54. Diámetros y costos unitarios - Red BakRyan.
Adaptado de Lee y Lee (2001).
Tabla 55. Diámetros y costos unitarios - Red Fossolo.
Adaptado de University of Exeter (s.f.).
Tabla 56. Diámetros y costos unitarios - Red R28.
Adaptado de Saldarriaga (2016).
Tabla 57. Diámetros y costos unitarios - Red Pescara.
Adaptado de University of Exeter (s.f.).
Tabla 58. Diámetros y costos unitarios - Red Modena.
Adaptado de University of Exeter (s.f.)
Tabla 59. Diámetros y costos unitarios - Red Balerma.
Adaptado de University of Exeter (s.f.).
Diámetro (mm) Costo unitario ($/m)
300
118
350
129
400
145
450
160
500
181
600
214
700
242
800
285
900
325
1000
370
1100
434
Diámetro (mm) Costo unitario (€/m)
16.0
0.38
20.4
0.56
26.0
0.88
32.6
1.35
40.8
2.02
51.4
3.21
61.4
4.44
73.6
6.45
90.0
9.59
102.2
11.98
114.6
14.93
130.8
19.61
147.2
24.78
163.6
30.55
184.0
38.71
204.6
47.63
229.2
59.70
257.8
75.61
290.6
99.58
327.4
126.48
368.2
160.29
409.2
197.71
Diámetro (mm)
Costo unitario ($/m)
50
0.019
75
0.035
100
0.053
150
0.096
200
0.145
250
0.201
300
0.262
350
0.327
400
0.397
450
0.471
500
0.549
600
0.715
750
0.988
800
1.085
1000
1.500
1200
1.954
1400
2.443
1500
2.700
1800
3.518
Diámetro (mm) Costo unitario (€/m)
100
27.7
125
38.0
150
40.5
200
55.4
250
75.0
300
92.4
350
123.1
400
141.9
450
169.3
500
191.5
600
246.0
700
319.6
800
391.1
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
253
Tabla 60. Diámetros y costos unitarios - Red Exnet.
Tabla 61. Diámetros comerciales - Tuberías biaxiales en PVC. Adaptado de PAVCO Wavin, S.A (2019).
Diámetro (mm)
Costo unitario (€/m)
100
27.7
125
38.0
150
40.5
200
55.4
250
75.0
300
92.4
350
123.1
400
141.9
450
169.3
500
191.5
600
246.0
700
319.6
800
391.1
Diámetro (mm)
Costo unitario (€/m)
113.0
7.22
126.6
9.10
144.6
11.92
162.8
14.84
180.8
18.38
226.2
28.60
285.0
45.39
361.8
76.32
452.2
124.64
581.8
215.85
Diámetro (mm) Costo unitario (£/m)
110
100
159
120
200
140
250
190
300
240
400
290
500
340
600
410
750
500
900
625
Referencia
d (mm)
Costo ($/Ud.) Costo unitario ($/m)
2905079
76.2
134,391
$
22,399
$
2900109
101.6
221,737
$
36,956
$
2900111
152.4
484,167
$
80,695
$
2900113
203.2
820,122
$
136,687
$
2900105
254.0
1,291,037
$
215,173
$
2900107
304.8
1,806,408
$
301,068
$
2900524
355.6
2,240,167
$
373,361
$
2905388
406.4
2,940,252
$
490,042
$
2905393
457.2
3,773,764
$
628,961
$
2905395
508.0
4,700,652
$
783,442
$
-
609.6
6,429,662
$
1,071,610
$
-
762.0
9,753,225
$
1,625,537
$
-
914.4
13,708,924
$
2,284,821
$
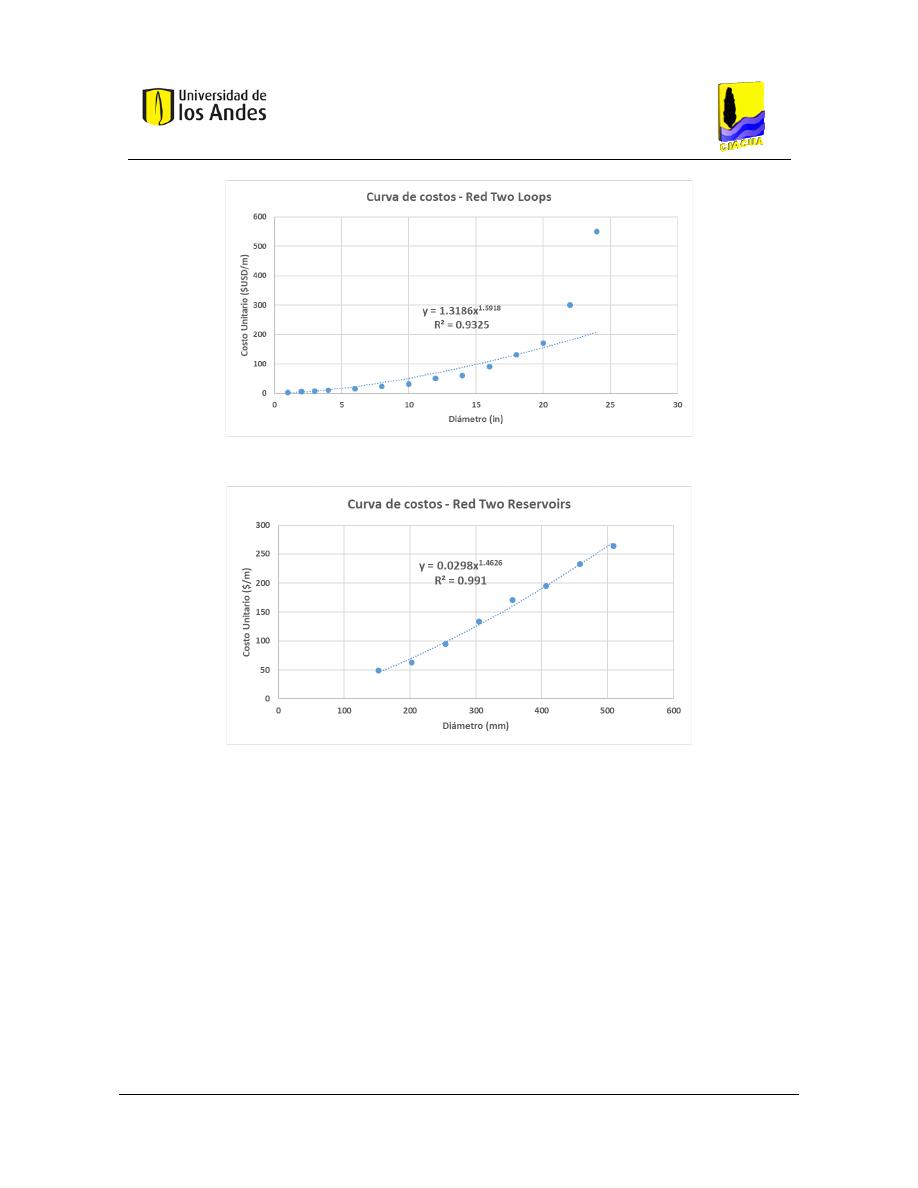
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
254
Figura 676. Curva de costos - Red Two Loops.
Figura 677. Curva de costos - Red Two Reservoirs.
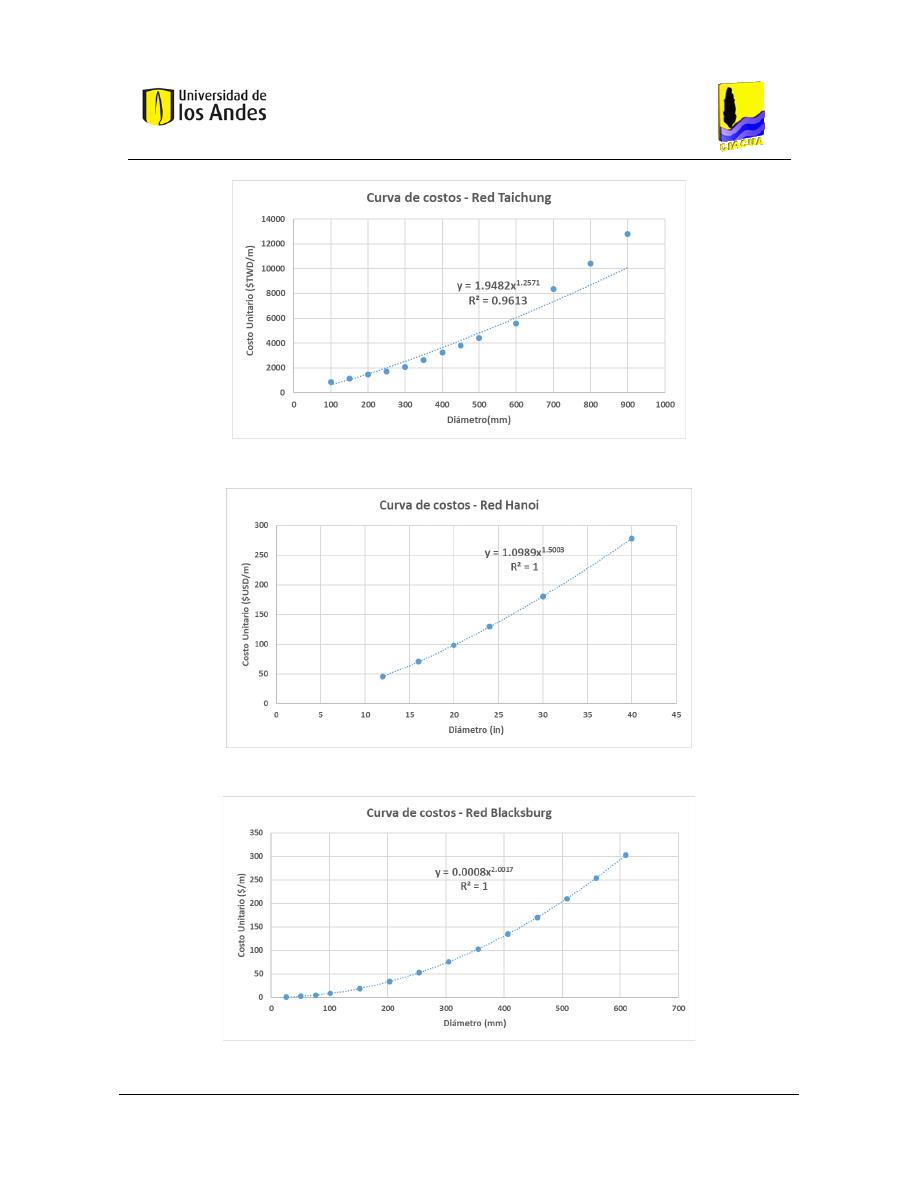
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
255
Figura 678. Curva de costos - Red Taichung.
Figura 679. Curva de costos - Red Hanoi.
Figura 680. Curva de costos - Red Blacksburg.
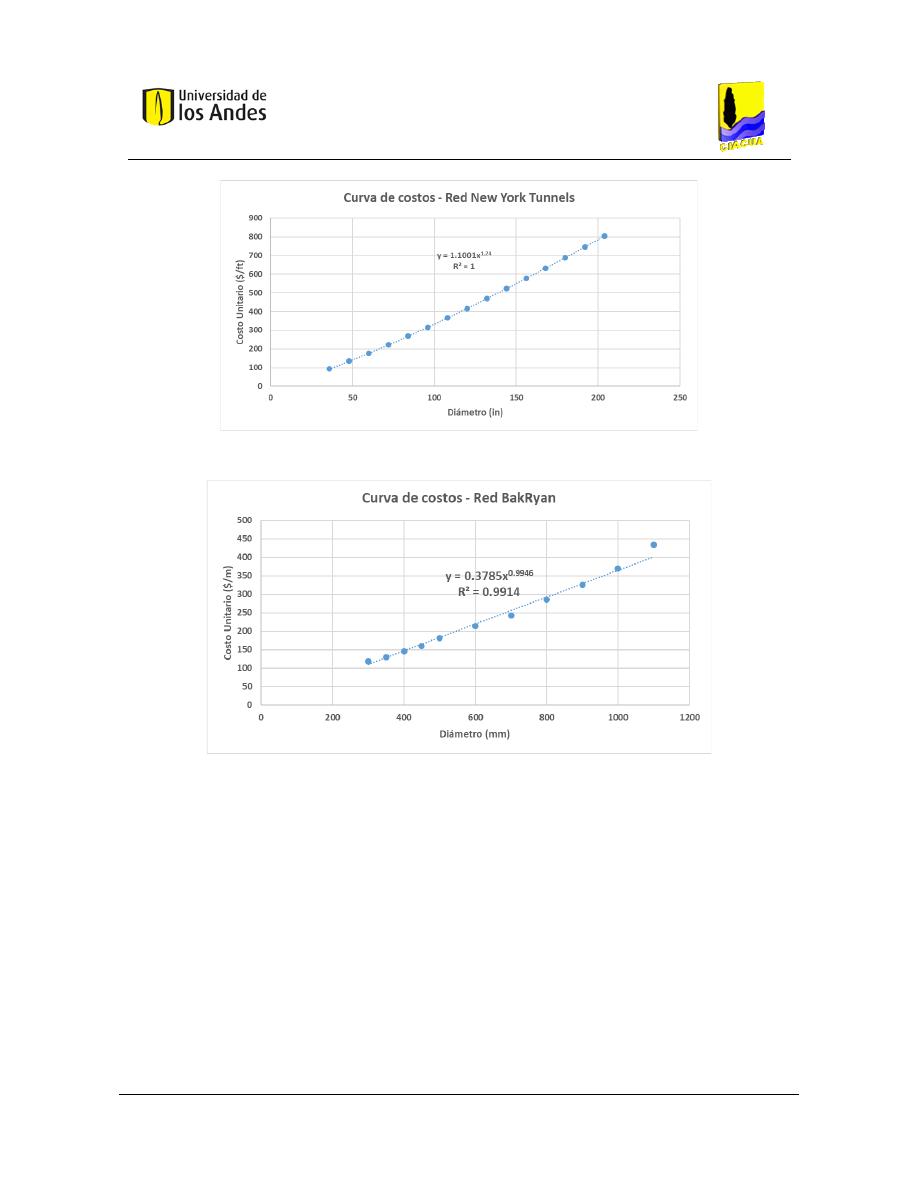
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
256
Figura 681. Curva de costos - Red New York Tunnels.
Figura 682. Curva de costos - Red BakRyan.
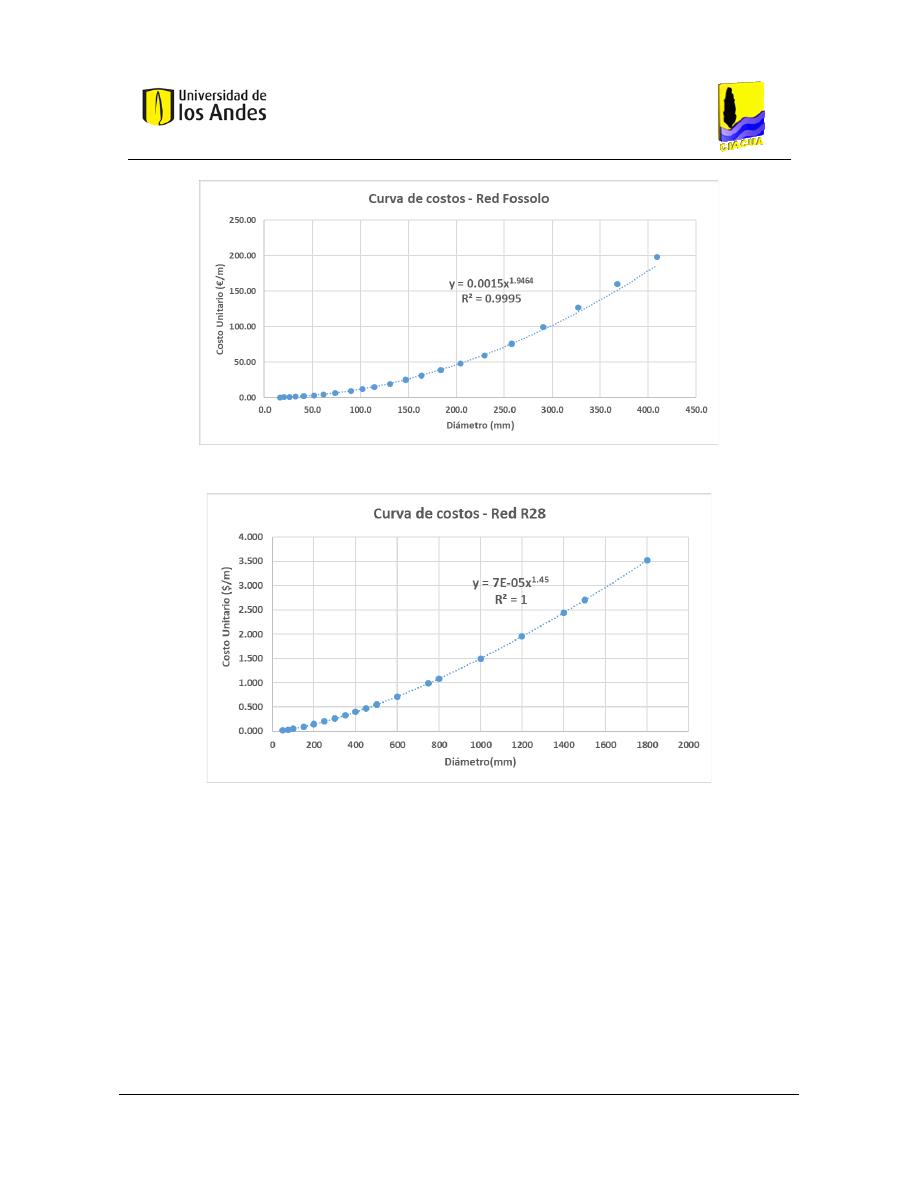
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
257
Figura 683. Curva de costos - Red Fossolo.
Figura 684. Curva de costos - Red R28.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
258
Figura 685. Curva de costos - Red Pescara.
Figura 686. Curva de costos - Red Modena.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
259
Figura 687. Curva de costos - Red Balerma.
Figura 688. Curva de costos - Tuberías biaxiales en PVC.
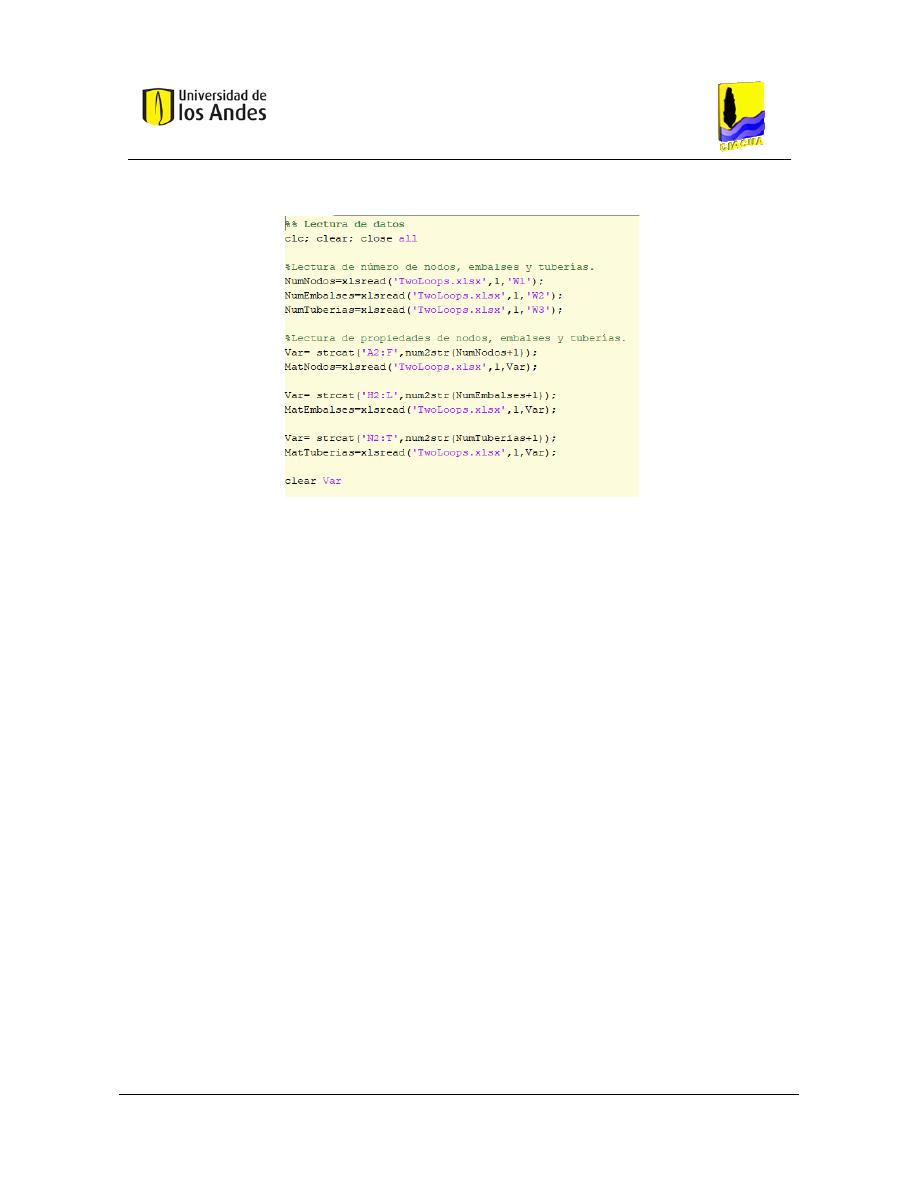
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
260
10.3 Trazado de red – Algoritmo MATLAB
Figura 689. Lectura de datos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
261
Figura 690. Definición de variables - Parte 1.
Figura 691. Definición de variables - Parte 2.
Figura 692. Definición de variables - Parte 3.
Figura 693. Trazado de la red - Parte 1.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
262
Figura 694. Trazado de la red - Parte 2.
Figura 695. Trazado de la red - Parte 3.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
263
10.4 Generación de SGH – Algoritmo MATLAB
Figura 696. Generación de SGH - Parte 1.
Figura 697. Generación de SGH - Parte 2.
Figura 698. Generación SGH - Parte 3.
Figura 699. Generación SGH - Parte 4.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
264
Figura 700. Generación SGH - Parte 5.
Figura 701. Generación SGH - Parte 6.
Figura 702. Generación SGH - Parte 7.
Figura 703. Generación SGH - Parte 8.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
265
Figura 704. Generación SGH - Parte 9.
Figura 705. Generación SGH - Parte 10.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
266
Figura 706. Generación SGH - Parte 11.
10.5 Análisis fractal unidimensional – Algoritmo MATLAB
Figura 707. Análisis R/S - Parte 1.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
267
Figura 708. Análisis R/S - Parte 2.
Figura 709. Análisis R/S - Parte 3.
Figura 710. Función R/S - Parte 1.
Figura 711. Función R/S - Parte 2.
Figura 712. Función R/S - Parte 3.
Figura 713. Función R/S - Parte 4.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
268
Figura 714. Función R/S – Parte 5.
10.6 Análisis fractal bidimensional – Algoritmo MATLAB
Figura 715. Análisis fractal bidimensional - Parte 1.
Figura 716. Análisis fractal bidimensional - Parte 2.
Figura 717. Función de cálculo de masa de una caja.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
269
10.7 Costos - Diseños
Tabla 62. Costos - Diseños - Parte 1.
Tabla 63. Costos - Diseños - Parte 2.
Diseño Óptimo
Nombre
Costo ($)
Costo ($)
Sobrecosto (%)
Costo ($)
Sobrecosto (%)
Two Loops
$ 419,000
$ 554,000
32.22
$ 1,121,000
167.54
Two Reservoirs
$ 3,707,557
$ 3,940,867
6.29
$ 4,457,618
20.23
Taichung
$ 8,956,545
$ 9,202,803
2.75
$ 10,346,009
15.51
Hanoi
$ 6,056,527
$ 6,081,287
0.41
$ 6,105,508
0.81
Blacksburg
$ 72,415
$ 100,649
38.99
$ 334,883
362.45
New York Tunnels
$ 173,627,815
$ 198,948,232
14.58
$ 219,558,348
26.45
BakRyan
$ 3,282,357
$ 3,425,321
4.36
$ 4,073,686
24.11
Fossolo
$ 27,158
$ 39,629
45.92
$ 56,108
106.60
R28
$ 10,818,612
$ 12,482,076
15.38
$ 12,512,291
15.66
Pescara
$ 3,285,236
$ 3,642,614
10.88
$ 4,565,466
38.97
Modena
$ 2,757,306
$ 3,478,765
26.17
$ 4,073,372
47.73
Balerma
$ 3,827,838
$ 4,008,855
4.73
$ 4,126,806
7.81
San Vicente
$ 642,839,609
$ 755,596,137
17.54
$ 902,422,819
40.38
Cazucá
$ 812,599,415
$ 938,551,727
15.50
$ 1,374,328,715
69.13
Elevada
$ 2,338,853
$ 2,579,033
10.27
$ 3,926,029
67.86
Bolívar
$ 649,939,784
$ 750,458,448
15.47
$ 884,274,515
36.05
La Cumbre
$ 754,758,430
$ 817,603,827
8.33
$ 1,155,289,291
53.07
Candelaria
$ 524,020,452
$ 626,286,779
19.52
$ 692,470,851
32.15
Bugalagrande
$ 769,061,246
$ 833,780,046
8.42
$ 1,365,034,219
77.49
Carmen
$ 1,207,394,858 $ 1,322,030,749
9.49
$ 2,677,577,405
121.76
Chinú
$ 1,212,734,471 $ 1,348,396,595
11.19
$ 1,958,661,038
61.51
Sector 35
$ 1,039,957,067 $ 1,272,440,166
22.36
$ 1,493,470,464
43.61
La Enea
$ 1,147,645,919 $ 1,393,422,129
21.42
$ 1,499,354,316
30.65
Diseño No Óptimo 1
Diseño No Óptimo 2
Diseño Óptimo
Nombre
Costo ($)
Costo ($)
Sobrecosto (%)
Costo ($)
Sobrecosto (%)
Two Loops
$ 419,000
$ 1,365,000
225.78
$ 1,623,000
287.35
Two Reservoirs
$ 3,707,557
$ 5,006,869
35.04
$ 5,758,827
55.33
Taichung
$ 8,956,545
$ 10,461,082
16.80
$ 14,256,268
59.17
Hanoi
$ 6,056,527
$ 6,385,380
5.43
$ 7,369,402
21.68
Blacksburg
$ 72,415
$ 407,386
462.57
$ 470,791
550.13
New York Tunnels
$ 173,627,815
$ 246,584,207
42.02
$ 276,338,429
59.16
BakRyan
$ 3,282,357
$ 4,545,099
38.47
$ 4,886,094
48.86
Fossolo
$ 27,158
$ 82,488
203.73
$ 93,737
245.15
R28
$ 10,818,612
$ 13,389,723
23.77
$ 23,108,179
113.60
Pescara
$ 3,285,236
$ 4,978,414
51.54
$ 5,525,041
68.18
Modena
$ 2,757,306
$ 5,819,102
111.04
$ 6,852,417
148.52
Balerma
$ 3,827,838
$ 4,201,584
9.76
$ 4,316,870
12.78
San Vicente
$ 642,839,609 $ 1,364,188,212
112.21
$ 1,455,934,746
126.48
Cazucá
$ 812,599,415 $ 1,818,944,819
123.84
$ 2,445,993,437
201.01
Elevada
$ 2,338,853
$ 4,390,612
87.73
$ 4,664,233
99.42
Bolívar
$ 649,939,784 $ 1,094,980,998
68.47
$ 1,182,147,158
81.89
La Cumbre
$ 754,758,430 $ 1,184,915,508
56.99
$ 1,263,727,600
67.43
Candelaria
$ 524,020,452 $ 1,061,984,619
102.66
$ 1,091,035,672
108.20
Bugalagrande
$ 769,061,246 $ 1,467,243,385
90.78
$ 1,514,573,452
96.94
Carmen
$ 1,207,394,858 $ 3,123,241,966
158.68
$ 6,255,891,596
418.13
Chinú
$ 1,212,734,471 $ 2,421,014,871
99.63
$ 2,635,056,644
117.28
Sector 35
$ 1,039,957,067 $ 1,656,956,167
59.33
$ 1,748,318,640
68.11
La Enea
$ 1,147,645,919 $ 1,621,130,736
41.26
$ 1,725,735,217
50.37
Diseño No Óptimo 3
Diseño No Óptimo 4
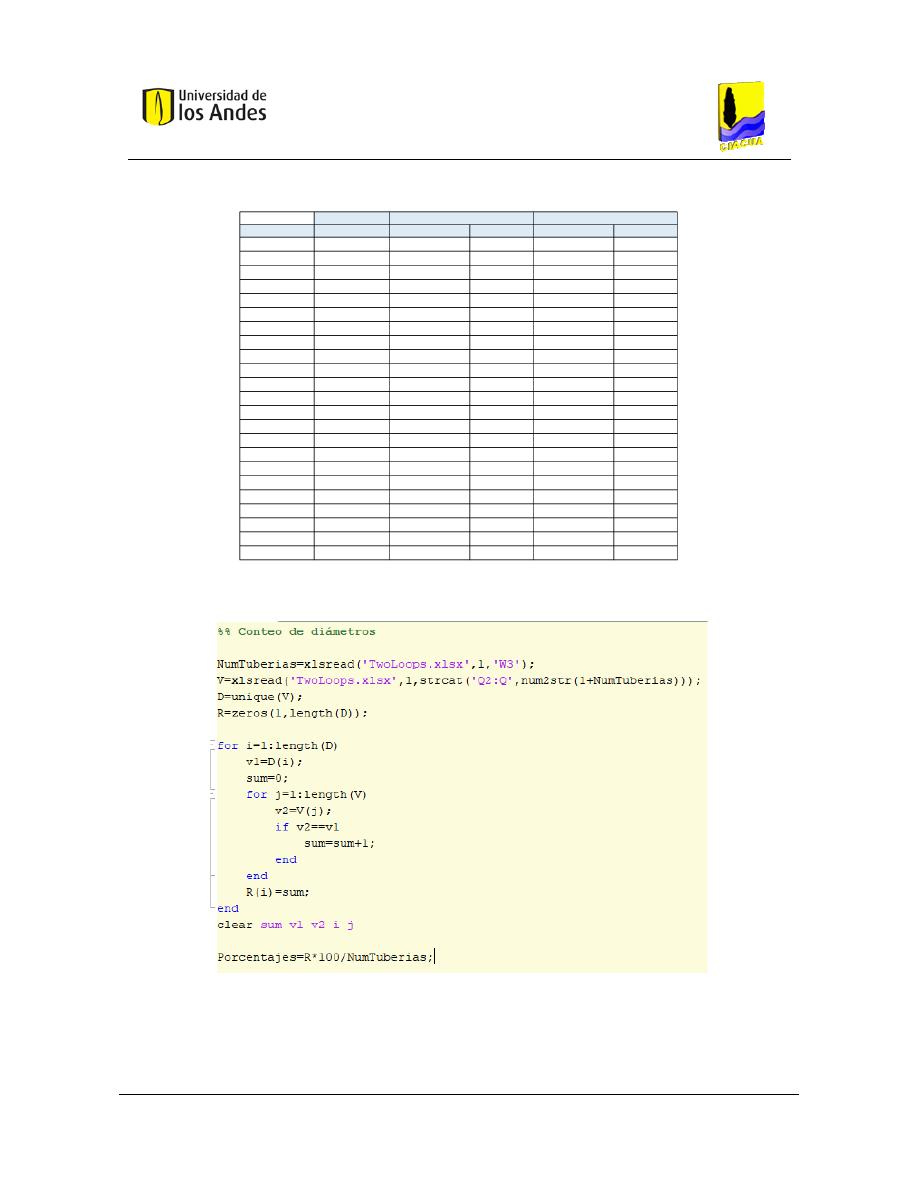
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
270
Tabla 64. Costos - Diseños - Parte 3.
10.8 Conteo de diámetros – Algoritmo MATLAB
Figura 718. Conteo de diámetros.
Diseño Óptimo
Nombre
Costo ($)
Costo ($)
Sobrecosto (%)
Costo ($)
Sobrecosto (%)
Two Loops
$ 419,000
$ 1,702,000
306.21
$ 1,818,000
333.89
Two Reservoirs
$ 3,707,557
$ 6,297,094
69.84
$ 6,716,608
81.16
Taichung
$ 8,956,545
$ 17,803,786
98.78
$ 21,458,622
139.59
Hanoi
$ 6,056,527
$ 9,146,091
51.01
$ 10,216,764
68.69
Blacksburg
$ 72,415
$ 549,342
658.60
$ 900,258
1143.19
New York Tunnels
$ 173,627,815
$ 297,710,870
71.46
$ 311,685,124
79.51
BakRyan
$ 3,282,357
$ 5,487,043
67.17
$ 6,100,737
85.86
Fossolo
$ 27,158
$ 107,761
296.79
$ 120,308
342.99
R28
$ 10,818,612
$ 37,483,580
246.47
$ 60,763,779
461.66
Pescara
$ 3,285,236
$ 6,081,059
85.10
$ 6,885,978
109.60
Modena
$ 2,757,306
$ 8,343,334
202.59
$ 9,702,193
251.87
Balerma
$ 3,827,838
$ 4,470,693
16.79
$ 4,658,756
21.71
San Vicente
$ 642,839,609 $ 2,021,760,317
214.50
$ 4,018,836,648
525.17
Cazucá
$ 812,599,415 $ 3,753,792,615
361.95
$ 4,835,110,724
495.02
Elevada
$ 2,338,853
$ 5,003,627
113.94
$ 7,808,732
233.87
Bolívar
$ 649,939,784 $ 1,314,564,928
102.26
$ 1,870,164,109
187.74
La Cumbre
$ 754,758,430 $ 1,633,497,998
116.43
$ 2,945,793,985
290.30
Candelaria
$ 524,020,452 $ 1,105,234,523
110.91
$ 1,182,221,059
125.61
Bugalagrande
$ 769,061,246 $ 1,602,950,448
108.43
$ 3,347,277,066
335.24
Carmen
$ 1,207,394,858 $ 8,809,063,274
629.59
$ 12,862,736,066
965.33
Chinú
$ 1,212,734,471 $ 2,696,105,097
122.32
$ 2,733,351,157
125.39
Sector 35
$ 1,039,957,067 $ 10,950,352,458
952.96
$ 21,824,130,261
1998.56
La Enea
$ 1,147,645,919 $ 9,576,018,074
734.41
$ 18,801,818,046
1538.29
Diseño No Óptimo 5
Diseño No Óptimo 6

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
271
10.9 Diámetros - Diseños
Tabla 65. Diámetros de diseño - Red Two Loops.
Tabla 66. Diámetros de diseño - Red Two Reservoirs.
Diámetro (in)
1
4
10
16
18
Cantidad
1
1
3
2
1
Porcentaje (%)
12.50
12.50
37.50
25.00
12.50
Diámetro (in)
3
4
8
10
16
18
Cantidad
1
1
1
1
1
3
Porcentaje (%)
12.50
12.50
12.50
12.50
12.50
37.50
Diámetro (in)
3
8
12
14
18
20
24
Cantidad
1
1
1
1
2
1
1
Porcentaje (%)
12.50
12.50
12.50
12.50
25.00
12.50
12.50
Diámetro (in)
8
10
14
20
22
24
Cantidad
1
1
2
2
1
1
Porcentaje (%)
12.50
12.50
25.00
25.00
12.50
12.50
Diámetro (in)
4
10
18
20
22
24
Cantidad
1
1
2
1
2
1
Porcentaje (%)
12.50
12.50
25.00
12.50
25.00
12.50
Diámetro (in)
1
3
10
16
20
22
24
Cantidad
1
1
1
1
1
1
2
Porcentaje (%)
12.50
12.50
12.50
12.50
12.50
12.50
25.00
Diámetro (in)
8
10
20
22
24
Cantidad
2
1
2
1
2
Porcentaje (%)
25.00
12.50
25.00
12.50
25.00
No Óptimo 5
No Óptimo 6
Two Loops
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
Diámetro (mm)
152
254
509
Cantidad
13
3
1
Porcentaje (%)
76.47
17.65
5.88
Diámetro (mm)
152
203
254
305
458
Cantidad
12
1
2
1
1
Porcentaje (%)
70.59
5.88
11.76
5.88
5.88
Diámetro (mm)
152
254
509
Cantidad
8
8
1
Porcentaje (%)
47.06
47.06
5.88
Diámetro (mm)
152
254
458
509
Cantidad
4
11
1
1
Porcentaje (%)
23.53
64.71
5.88
5.88
Diámetro (mm)
152
254
356
407
458
Cantidad
3
9
1
3
1
Porcentaje (%)
17.65
52.94
5.88
17.65
5.88
Diámetro (mm)
152
203
254
305
356
407
458
509
Cantidad
2
1
4
2
4
1
2
1
Porcentaje (%)
11.76
5.88
23.53
11.76
23.53
5.88
11.76
5.88
Diámetro (mm)
152
203
254
305
356
407
458
509
Cantidad
2
2
3
3
1
2
3
1
Porcentaje (%)
11.76
11.76
17.65
17.65
5.88
11.76
17.65
5.88
Two
Reservoirs
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
272
Tabla 67. Diámetros de diseño - Red Taichung.
Tabla 68. Diámetros de diseño - Red Hanoi.
Diámetro (mm)
100
150
200
250
300
350
400
Cantidad
17
5
1
3
3
1
1
Porcentaje (%)
54.84
16.13
3.23
9.68
9.68
3.23
3.23
Diámetro (mm)
100
150
200
250
300
350
400
Cantidad
16
4
3
3
3
1
1
Porcentaje (%)
51.61
12.90
9.68
9.68
9.68
3.23
3.23
Diámetro (mm)
100
200
450
500
Cantidad
11
17
2
1
Porcentaje (%)
35.48
54.84
6.45
3.23
Diámetro (mm)
100
150
200
450
500
Cantidad
11
1
16
1
2
Porcentaje (%)
35.48
3.23
51.61
3.23
6.45
Diámetro (mm)
100
150
200
250
300
400
500
600
800
Cantidad
9
1
13
1
2
2
1
1
1
Porcentaje (%)
29.03
3.23
41.94
3.23
6.45
6.45
3.23
3.23
3.23
Diámetro (mm)
100
150
200
250
350
450
500
600
700
900
Cantidad
10
6
3
3
3
1
1
1
1
2
Porcentaje (%)
32.26
19.35
9.68
9.68
9.68
3.23
3.23
3.23
3.23
6.45
Diámetro (mm)
100
150
200
250
300
400
600
800
900
Cantidad
12
3
1
3
1
1
7
1
2
Porcentaje (%)
38.71
9.68
3.23
9.68
3.23
3.23
22.58
3.23
6.45
Taichung
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Diámetro (in)
12
16
20
24
30
40
Cantidad
7
5
5
3
3
11
Porcentaje (%)
20.59
14.71
14.71
8.82
8.82
32.35
Diámetro (in)
12
16
20
24
30
40
Cantidad
7
5
4
4
3
11
Porcentaje (%)
20.59
14.71
11.76
11.76
8.82
32.35
Diámetro (in)
12
16
20
24
30
40
Cantidad
7
4
6
3
3
11
Porcentaje (%)
20.59
11.76
17.65
8.82
8.82
32.35
Diámetro (in)
12
16
20
24
30
40
Cantidad
7
4
4
5
2
12
Porcentaje (%)
20.59
11.76
11.76
14.71
5.88
35.29
Diámetro (in)
12
16
20
24
30
40
Cantidad
5
1
3
4
8
13
Porcentaje (%)
14.71
2.94
8.82
11.76
23.53
38.24
Diámetro (in)
12
16
20
24
30
40
Cantidad
1
1
3
1
5
23
Porcentaje (%)
2.94
2.94
8.82
2.94
14.71
67.65
Diámetro (in)
12
20
30
40
Cantidad
1
1
3
29
Porcentaje (%)
2.94
2.94
8.82
85.29
Hanoi
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
273
Tabla 69. Diámetros de diseño - Red Blacksburg.
Tabla 70. Diámetros de diseño - Red New York Tunnels.
Tabla 71. Diámetros de diseño - Red BakRyan.
Diámetro (mm)
25.4
50.8
76.2
101.6
152.4
203.2
254.0
Cantidad
6
9
8
1
5
5
1
Porcentaje (%)
17.14
25.71
22.86
2.86
14.29
14.29
2.86
Diámetro (mm)
25.4
50.8
76.2
101.6
152.4
203.2
254.0
355.6
Cantidad
7
1
17
2
4
2
1
1
Porcentaje (%)
20.00
2.86
48.57
5.71
11.43
5.71
2.86
2.86
Diámetro (mm)
25.4
50.8
76.2
101.6
203.2
254.0
304.8
355.6
406.4
508.0
558.8
609.6
Cantidad
2
2
13
4
2
1
2
4
2
1
1
1
Porcentaje (%)
5.71
5.71
37.14
11.43
5.71
2.86
5.71
11.43
5.71
2.86
2.86
2.86
Diámetro (mm)
50.8
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
508.0
558.8
Cantidad
5
7
3
4
3
2
2
2
3
3
1
Porcentaje (%)
14.29
20.00
8.57
11.43
8.57
5.71
5.71
5.71
8.57
8.57
2.86
Diámetro (mm)
25.4
76.2
101.6
152.4
203.2
304.8
355.6
406.4
457.2
508.0
558.8
Cantidad
2
7
5
1
2
7
1
2
3
4
1
Porcentaje (%)
5.71
20.00
14.29
2.86
5.71
20.00
2.86
5.71
8.57
11.43
2.86
Diámetro (mm)
50.8
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508.0
558.8
609.6
Cantidad
3
6
2
4
3
2
1
3
3
4
1
2
1
Porcentaje (%)
8.57
17.14
5.71
11.43
8.57
5.71
2.86
8.57
8.57
11.43
2.86
5.71
2.86
Diámetro (mm)
25.4
50.8
76.2
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508.0
558.8
609.6
Cantidad
1
2
1
3
1
2
3
3
3
5
2
6
3
Porcentaje (%)
2.86
5.71
2.86
8.57
2.86
5.71
8.57
8.57
8.57
14.29
5.71
17.14
8.57
Blacksburg
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Diámetro (in)
36
48
60
72
84
96
144
156
168
Cantidad
4
7
7
11
5
3
1
3
1
Porcentaje (%)
9.52
16.67
16.67
26.19
11.90
7.14
2.38
7.14
2.38
Diámetro (in)
36
48
60
84
96
120
132
144
156
168
180
204
Cantidad
8
1
15
2
4
3
2
2
1
1
2
1
Porcentaje (%)
19.05
2.38
35.71
4.76
9.52
7.14
4.76
4.76
2.38
2.38
4.76
2.38
Diámetro (in)
36
60
84
96
108
120
132
144
156
168
180
204
Cantidad
11
12
3
3
2
1
3
1
1
1
2
2
Porcentaje (%)
26.19
28.57
7.14
7.14
4.76
2.38
7.14
2.38
2.38
2.38
4.76
4.76
Diámetro (in)
36
60
72
84
96
108
132
144
156
168
180
192
204
Cantidad
9
10
1
1
2
5
2
2
2
3
2
2
1
Porcentaje (%)
21.43
23.81
2.38
2.38
4.76
11.90
4.76
4.76
4.76
7.14
4.76
4.76
2.38
Diámetro (in)
36
48
60
72
84
96
120
132
144
156
168
192
204
Cantidad
9
1
8
3
1
2
1
2
2
2
2
3
6
Porcentaje (%)
21.43
2.38
19.05
7.14
2.38
4.76
2.38
4.76
4.76
4.76
4.76
7.14
14.29
Diámetro (in)
36
48
60
84
96
108
120
132
144
156
168
180
192
Cantidad
1
3
4
7
5
2
3
3
3
3
4
1
3
Porcentaje (%)
2.38
7.14
9.52
16.67
11.90
4.76
7.14
7.14
7.14
7.14
9.52
2.38
7.14
Diámetro (in)
36
48
60
72
96
108
120
132
144
156
168
180
192
204
Cantidad
1
3
5
3
3
3
5
1
2
3
3
7
2
1
Porcentaje (%)
2.38
7.14
11.90
7.14
7.14
7.14
11.90
2.38
4.76
7.14
7.14
16.67
4.76
2.38
New York
Tunnels
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Diámetro (mm)
300
400
450
500
600
700
900
Cantidad
44
2
1
2
5
1
3
Porcentaje (%)
75.86
3.45
1.72
3.45
8.62
1.72
5.17
Diámetro (mm)
300
400
500
600
700
800
900
1000
Cantidad
33
17
1
1
1
3
1
1
Porcentaje (%)
56.90
29.31
1.72
1.72
1.72
5.17
1.72
1.72
Diámetro (mm)
300
350
400
450
500
600
700
800
900
1000
Cantidad
19
1
18
1
5
2
3
3
3
3
Porcentaje (%)
32.76
1.72
31.03
1.72
8.62
3.45
5.17
5.17
5.17
5.17
Diámetro (mm)
300
350
400
450
500
600
700
800
900
1000
1100
Cantidad
17
2
16
1
4
2
3
3
3
5
2
Porcentaje (%)
29.31
3.45
27.59
1.72
6.90
3.45
5.17
5.17
5.17
8.62
3.45
Diámetro (mm)
300
350
400
500
600
700
800
900
1000
1100
Cantidad
17
2
13
3
1
5
6
3
4
4
Porcentaje (%)
29.31
3.45
22.41
5.17
1.72
8.62
10.34
5.17
6.90
6.90
Diámetro (mm)
300
350
400
450
500
600
700
800
900
1000
1100
Cantidad
3
5
6
4
7
9
2
6
10
4
2
Porcentaje (%)
5.17
8.62
10.34
6.90
12.07
15.52
3.45
10.34
17.24
6.90
3.45
Diámetro (mm)
300
350
400
450
500
600
700
800
900
1000
1100
Cantidad
2
6
3
6
6
5
6
5
10
7
2
Porcentaje (%)
3.45
10.34
5.17
10.34
10.34
8.62
10.34
8.62
17.24
12.07
3.45
BakRyan
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
274
Tabla 72. Diámetros de diseño - Red Fossolo.
Tabla 73. Diámetros de diseño - Red R28.
Tabla 74. Diámetros de diseño - Red Pescara.
Diámetro (mm)
16.0
20.4
26.0
32.6
40.8
51.4
61.4
73.6
90.0
102.2
114.6
130.8
147.2
Cantidad
4
12
5
8
4
9
5
2
2
2
2
2
1
Porcentaje (%)
6.90
20.69
8.62
13.79
6.90
15.52
8.62
3.45
3.45
3.45
3.45
3.45
1.72
Diámetro (mm)
16.0
20.4
26.0
32.6
40.8
51.4
61.4
73.6
90.0
102.2
114.6
130.8
147.2
163.6
204.6
Cantidad
16
2
7
3
3
8
3
1
1
3
3
3
1
2
2
Porcentaje (%)
27.59
3.45
12.07
5.17
5.17
13.79
5.17
1.72
1.72
5.17
5.17
5.17
1.72
3.45
3.45
Diámetro (mm)
16.0
20.4
26.0
32.6
51.4
61.4
90.0
102.2
114.6
130.8
147.2
163.6
204.6
290.6
Cantidad
17
4
4
6
4
4
5
3
3
4
1
1
1
1
Porcentaje (%)
29.31
6.90
6.90
10.34
6.90
6.90
8.62
5.17
5.17
6.90
1.72
1.72
1.72
1.72
Diámetro (mm)
16.0
26.0
51.4
73.6
90.0
102.2
114.6
147.2
184.0
204.6
229.2
327.4
Cantidad
9
28
2
2
4
2
2
2
3
1
2
1
Porcentaje (%)
15.52
48.28
3.45
3.45
6.90
3.45
3.45
3.45
5.17
1.72
3.45
1.72
Diámetro (mm)
16.0
20.4
26.0
32.6
40.8
51.4
61.4
73.6
90.0
102.2
114.6
147.2
163.6
184.0
204.6
229.2
290.6
327.4
Cantidad
11
1
13
2
1
3
1
4
5
2
3
1
3
2
1
1
1
3
Porcentaje (%)
18.97
1.72
22.41
3.45
1.72
5.17
1.72
6.90
8.62
3.45
5.17
1.72
5.17
3.45
1.72
1.72
1.72
5.17
Diámetro (mm)
16.0
26.0
32.6
40.8
51.4
73.6
90.0
102.2
114.6
130.8
147.2
163.6
184.0
204.6
229.2
257.8
Cantidad
8
16
2
3
2
2
4
1
3
5
3
3
1
3
1
1
Porcentaje (%)
13.79
27.59
3.45
5.17
3.45
3.45
6.90
1.72
5.17
8.62
5.17
5.17
1.72
5.17
1.72
1.72
Diámetro (mm)
16.0
26.0
40.8
51.4
61.4
73.6
90.0
102.2
114.6
130.8
147.2
163.6
184.0
204.6
229.2
257.8
Cantidad
9
13
3
2
3
3
1
1
4
4
6
4
2
1
1
1
Porcentaje (%)
15.52
22.41
5.17
3.45
5.17
5.17
1.72
1.72
6.90
6.90
10.34
6.90
3.45
1.72
1.72
1.72
Fossolo
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Diámetro (mm)
50
75
100
150
200
250
Cantidad
39
10
2
8
6
2
Porcentaje (%)
58.21
14.93
2.99
11.94
8.96
2.99
Diámetro (mm)
50
100
150
200
250
350
Cantidad
25
33
1
6
1
1
Porcentaje (%)
37.31
49.25
1.49
8.96
1.49
1.49
Diámetro (mm)
50
100
150
200
250
350
Cantidad
24
34
1
6
1
1
Porcentaje (%)
35.82
50.75
1.49
8.96
1.49
1.49
Diámetro (mm)
50
100
150
200
250
350
400
Cantidad
27
31
1
5
1
1
1
Porcentaje (%)
40.30
46.27
1.49
7.46
1.49
1.49
1.49
Diámetro (mm)
50
75
100
150
200
250
300
350
400
500
750
Cantidad
33
9
9
3
3
2
1
3
1
1
2
Porcentaje (%)
49.25
13.43
13.43
4.48
4.48
2.99
1.49
4.48
1.49
1.49
2.99
Diámetro (mm)
50
75
100
200
250
300
350
450
500
600
750
1000
Cantidad
23
4
21
3
2
1
5
1
1
1
4
1
Porcentaje (%)
34.33
5.97
31.34
4.48
2.99
1.49
7.46
1.49
1.49
1.49
5.97
1.49
Diámetro (mm)
50
100
150
200
250
300
350
400
450
500
750
800
1400
1500
1800
Cantidad
26
23
1
2
1
3
1
1
1
2
1
1
1
1
2
Porcentaje (%)
38.81
34.33
1.49
2.99
1.49
4.48
1.49
1.49
1.49
2.99
1.49
1.49
1.49
1.49
2.99
R28
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Diámetro (mm)
100
125
200
250
300
350
400
450
600
Cantidad
58
4
4
6
10
4
5
1
7
Porcentaje (%)
58.59
4.04
4.04
6.06
10.10
4.04
5.05
1.01
7.07
Diámetro (mm)
100
125
150
200
250
300
350
400
450
500
600
700
800
Cantidad
33
3
19
5
5
6
4
5
1
7
3
6
2
Porcentaje (%)
33.33
3.03
19.19
5.05
5.05
6.06
4.04
5.05
1.01
7.07
3.03
6.06
2.02
Diámetro (mm)
100
125
150
200
250
300
350
400
450
500
600
700
800
Cantidad
14
4
28
7
4
5
9
4
7
8
3
5
1
Porcentaje (%)
14.14
4.04
28.28
7.07
4.04
5.05
9.09
4.04
7.07
8.08
3.03
5.05
1.01
Diámetro (mm)
100
125
150
200
250
300
350
400
450
500
600
700
800
Cantidad
9
4
25
6
8
8
8
4
3
6
4
10
4
Porcentaje (%)
9.09
4.04
25.25
6.06
8.08
8.08
8.08
4.04
3.03
6.06
4.04
10.10
4.04
Diámetro (mm)
100
125
150
200
250
300
350
400
450
500
600
700
800
Cantidad
15
6
9
8
15
7
7
5
8
7
7
4
1
Porcentaje (%)
15.15
6.06
9.09
8.08
15.15
7.07
7.07
5.05
8.08
7.07
7.07
4.04
1.01
Diámetro (mm)
100
125
150
200
250
300
350
400
450
500
600
700
800
Cantidad
5
7
7
7
10
9
8
11
4
10
8
6
7
Porcentaje (%)
5.05
7.07
7.07
7.07
10.10
9.09
8.08
11.11
4.04
10.10
8.08
6.06
7.07
Diámetro (mm)
100
125
150
200
250
300
350
400
450
500
600
700
800
Cantidad
3
15
3
12
9
5
5
8
5
9
17
4
4
Porcentaje (%)
3.03
15.15
3.03
12.12
9.09
5.05
5.05
8.08
5.05
9.09
17.17
4.04
4.04
Pescara
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
275
Tabla 75. Diámetros de diseño - Red Modena.
Tabla 76. Diámetros de diseño - Red Balerma.
Tabla 77. Diámetros de diseño - Red San Vicente.
Diámetro (mm)
100
125
150
200
250
300
350
400
450
500
Cantidad
220
24
23
16
8
5
4
9
1
7
Porcentaje (%)
69.40
7.57
7.26
5.05
2.52
1.58
1.26
2.84
0.32
2.21
Diámetro (mm)
100
125
150
200
250
300
350
400
450
500
600
700
800
Cantidad
112
10
165
8
1
3
3
3
2
4
1
4
1
Porcentaje (%)
35.33
3.15
52.05
2.52
0.32
0.95
0.95
0.95
0.63
1.26
0.32
1.26
0.32
Diámetro (mm)
100
125
150
200
250
300
350
400
450
500
600
700
800
Cantidad
108
17
142
3
5
6
5
9
3
8
3
6
2
Porcentaje (%)
34.07
5.36
44.79
0.95
1.58
1.89
1.58
2.84
0.95
2.52
0.95
1.89
0.63
Diámetro (mm)
100
125
150
200
250
300
350
400
450
500
600
700
800
Cantidad
92
20
95
11
17
12
7
15
10
12
10
6
10
Porcentaje (%)
29.02
6.31
29.97
3.47
5.36
3.79
2.21
4.73
3.15
3.79
3.15
1.89
3.15
Diámetro (mm)
100
125
150
200
250
300
350
400
450
500
600
700
800
Cantidad
83
16
94
7
18
11
10
16
10
17
9
19
7
Porcentaje (%)
26.18
5.05
29.65
2.21
5.68
3.47
3.15
5.05
3.15
5.36
2.84
5.99
2.21
Diámetro (mm)
100
125
150
200
250
300
350
400
450
500
600
700
800
Cantidad
32
36
52
16
18
28
17
29
23
22
23
15
6
Porcentaje (%)
10.09
11.36
16.40
5.05
5.68
8.83
5.36
9.15
7.26
6.94
7.26
4.73
1.89
Diámetro (mm)
100
125
150
200
250
300
350
400
450
500
600
700
800
Cantidad
4
28
34
29
25
31
25
28
21
23
26
24
19
Porcentaje (%)
1.26
8.83
10.73
9.15
7.89
9.78
7.89
8.83
6.62
7.26
8.20
7.57
5.99
Modena
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Diámetro (mm)
113.0
126.6
144.6
162.8
180.8
226.2
285.0
361.8
452.2
581.8
Cantidad
262
14
26
21
26
25
27
18
17
18
Porcentaje (%)
57.71
3.08
5.73
4.63
5.73
5.51
5.95
3.96
3.74
3.96
Diámetro (mm)
113.0
126.6
144.6
162.8
180.8
226.2
285.0
361.8
452.2
581.8
Cantidad
227
19
27
25
26
39
25
32
22
12
Porcentaje (%)
50.00
4.19
5.95
5.51
5.73
8.59
5.51
7.05
4.85
2.64
Diámetro (mm)
113.0
126.6
144.6
162.8
180.8
226.2
285.0
361.8
452.2
581.8
Cantidad
251
24
18
22
25
24
33
17
20
20
Porcentaje (%)
55.29
5.29
3.96
4.85
5.51
5.29
7.27
3.74
4.41
4.41
Diámetro (mm)
113.0
126.6
144.6
162.8
180.8
226.2
285.0
361.8
452.2
581.8
Cantidad
239
36
18
24
22
25
32
17
19
22
Porcentaje (%)
52.64
7.93
3.96
5.29
4.85
5.51
7.05
3.74
4.19
4.85
Diámetro (mm)
113.0
126.6
144.6
162.8
180.8
226.2
285.0
361.8
452.2
581.8
Cantidad
222
53
18
24
22
24
33
16
17
25
Porcentaje (%)
48.90
11.67
3.96
5.29
4.85
5.29
7.27
3.52
3.74
5.51
Diámetro (mm)
113.0
126.6
144.6
162.8
180.8
226.2
285.0
361.8
452.2
581.8
Cantidad
212
25
23
35
16
29
29
32
43
10
Porcentaje (%)
46.70
5.51
5.07
7.71
3.52
6.39
6.39
7.05
9.47
2.20
Diámetro (mm)
113.0
126.6
144.6
162.8
180.8
226.2
285.0
361.8
452.2
581.8
Cantidad
189
40
24
34
18
29
31
32
43
14
Porcentaje (%)
41.63
8.81
5.29
7.49
3.96
6.39
6.83
7.05
9.47
3.08
Balerma
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Diámetro (mm)
76.2
152.4
304.8
Cantidad
69
1
1
Porcentaje (%)
97.18
1.41
1.41
Diámetro (mm)
76.2
101.6
152.4
203.2
304.8
406.4
457.2
508.0
609.6
762.0
914.4
Cantidad
50
1
2
1
3
3
5
1
2
2
1
Porcentaje (%)
70.42
1.41
2.82
1.41
4.23
4.23
7.04
1.41
2.82
2.82
1.41
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508.0
609.6
762.0
914.4
Cantidad
3
10
4
9
8
8
4
3
3
7
5
4
3
Porcentaje (%)
4.23
14.08
5.63
12.68
11.27
11.27
5.63
4.23
4.23
9.86
7.04
5.63
4.23
Diámetro (mm)
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508.0
609.6
762.0
914.4
Cantidad
6
4
10
5
2
5
10
4
8
3
9
5
Porcentaje (%)
8.45
5.63
14.08
7.04
2.82
7.04
14.08
5.63
11.27
4.23
12.68
7.04
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508.0
609.6
762.0
914.4
Cantidad
3
2
6
7
2
9
7
9
4
5
9
6
2
Porcentaje (%)
4.23
2.82
8.45
9.86
2.82
12.68
9.86
12.68
5.63
7.04
12.68
8.45
2.82
Diámetro (mm)
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508.0
609.6
762.0
914.4
Cantidad
10
3
5
6
8
6
3
5
8
7
7
3
Porcentaje (%)
14.08
4.23
7.04
8.45
11.27
8.45
4.23
7.04
11.27
9.86
9.86
4.23
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508.0
609.6
762.0
914.4
Cantidad
4
4
5
4
7
8
6
4
6
7
5
7
4
Porcentaje (%)
5.63
5.63
7.04
5.63
9.86
11.27
8.45
5.63
8.45
9.86
7.04
9.86
5.63
San Vicente
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
276
Tabla 78. Diámetros de diseño - Red Cazucá.
Tabla 79. Diámetros de diseño - Red Elevada.
Tabla 80. Diámetros de diseño - Red Bolívar.
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
Cantidad
92
12
20
4
13
9
Porcentaje (%)
61.33
8.00
13.33
2.67
8.67
6.00
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
Cantidad
90
12
22
4
4
11
4
3
Porcentaje (%)
60.00
8.00
14.67
2.67
2.67
7.33
2.67
2.00
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
Cantidad
77
9
22
7
5
15
4
7
4
Porcentaje (%)
51.33
6.00
14.67
4.67
3.33
10.00
2.67
4.67
2.67
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
508
762
914.4
Cantidad
84
12
22
4
5
6
4
2
5
2
4
Porcentaje (%)
56.00
8.00
14.67
2.67
3.33
4.00
2.67
1.33
3.33
1.33
2.67
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
508
762
914.4
Cantidad
66
16
23
5
9
7
8
4
5
2
5
Porcentaje (%)
44.00
10.67
15.33
3.33
6.00
4.67
5.33
2.67
3.33
1.33
3.33
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508
762
914.4
Cantidad
46
22
22
7
13
7
8
5
1
8
3
8
Porcentaje (%)
30.67
14.67
14.67
4.67
8.67
4.67
5.33
3.33
0.67
5.33
2.00
5.33
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508
609.6
762
914.4
Cantidad
23
31
24
9
13
8
9
5
2
10
1
4
11
Porcentaje (%)
15.33
20.67
16.00
6.00
8.67
5.33
6.00
3.33
1.33
6.67
0.67
2.67
7.33
Cazucá
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Diámetro (mm)
76.2
Cantidad
263
Porcentaje (%)
100.00
Diámetro (mm)
76.2
152.4
Cantidad
250
13
Porcentaje (%)
95.06
4.94
Diámetro (mm)
76.2
152.4
Cantidad
153
110
Porcentaje (%)
58.17
41.83
Diámetro (mm)
76.2
152.4
Cantidad
156
107
Porcentaje (%)
59.32
40.68
Diámetro (mm)
76.2
152.4
Cantidad
154
109
Porcentaje (%)
58.56
41.44
Diámetro (mm)
76.2
152.4
Cantidad
135
128
Porcentaje (%)
51.33
48.67
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
508.0
609.6
762.0
Cantidad
124
2
122
2
2
3
2
1
1
1
3
Porcentaje (%)
47.15
0.76
46.39
0.76
0.76
1.14
0.76
0.38
0.38
0.38
1.14
Elevada
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Diámetro (mm)
76.2
Cantidad
333
Porcentaje (%)
100.00
Diámetro (mm)
76.2
152.4
Cantidad
308
25
Porcentaje (%)
92.49
7.51
Diámetro (mm)
76.2
152.4
Cantidad
233
100
Porcentaje (%)
69.97
30.03
Diámetro (mm)
76.2
152.4
Cantidad
186
147
Porcentaje (%)
55.86
44.14
Diámetro (mm)
76.2
152.4
Cantidad
176
157
Porcentaje (%)
52.85
47.15
Diámetro (mm)
76.2
152.4
304.8
406.4
Cantidad
180
149
3
1
Porcentaje (%)
54.05
44.74
0.90
0.30
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
355.6
508.0
762.0
914.4
Cantidad
168
2
155
1
2
1
1
1
2
Porcentaje (%)
50.45
0.60
46.55
0.30
0.60
0.30
0.30
0.30
0.60
Bolívar
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
277
Tabla 81. Diámetros de diseño - Red La Cumbre.
Tabla 82. Diámetros de diseño - Red Candelaria.
Tabla 83. Diámetros de diseño - Red Bugalagrande.
Diámetro (mm)
76.2
101.6
152.4
203.2
Cantidad
334
32
9
3
Porcentaje (%)
88.36
8.47
2.38
0.79
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
Cantidad
331
31
12
1
2
1
Porcentaje (%)
87.57
8.20
3.17
0.26
0.53
0.26
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
355.6
Cantidad
206
13
152
5
1
1
Porcentaje (%)
54.50
3.44
40.21
1.32
0.26
0.26
Diámetro (mm)
76.2
152.4
254.0
355.6
Cantidad
207
169
1
1
Porcentaje (%)
54.76
44.71
0.26
0.26
Diámetro (mm)
76.2
152.4
254.0
355.6
Cantidad
205
171
1
1
Porcentaje (%)
54.23
45.24
0.26
0.26
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
457.2
508.0
762.0
914.4
Cantidad
306
38
15
1
5
1
4
1
2
2
3
Porcentaje (%)
80.95
10.05
3.97
0.26
1.32
0.26
1.06
0.26
0.53
0.53
0.79
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508.0
609.6
914.4
Cantidad
163
4
187
1
3
4
2
3
1
3
1
6
Porcentaje (%)
43.12
1.06
49.47
0.26
0.79
1.06
0.53
0.79
0.26
0.79
0.26
1.59
La Cumbre
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
Cantidad
553
8
4
1
1
Porcentaje (%)
97.53
1.41
0.71
0.18
0.18
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
Cantidad
508
5
52
1
1
Porcentaje (%)
89.59
0.88
9.17
0.18
0.18
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
Cantidad
474
4
87
1
1
Porcentaje (%)
83.60
0.71
15.34
0.18
0.18
Diámetro (mm)
76.2
101.6
152.4
Cantidad
314
1
252
Porcentaje (%)
55.38
0.18
44.44
Diámetro (mm)
76.2
152.4
Cantidad
314
253
Porcentaje (%)
55.38
44.62
Diámetro (mm)
76.2
152.4
Cantidad
296
271
Porcentaje (%)
52.20
47.80
Diámetro (mm)
76.2
152.4
Cantidad
280
287
Porcentaje (%)
49.38
50.62
Candelaria
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Diámetro (mm)
76.2
101.6
152.4
203.2
Cantidad
626
16
11
2
Porcentaje (%)
95.57
2.44
1.68
0.31
Diámetro (mm)
76.2
101.6
152.4
406.4
Cantidad
575
62
17
1
Porcentaje (%)
87.79
9.47
2.60
0.15
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
508.0
Cantidad
365
1
284
2
1
1
1
Porcentaje (%)
55.73
0.15
43.36
0.31
0.15
0.15
0.15
Diámetro (mm)
76.2
152.4
Cantidad
359
296
Porcentaje (%)
54.81
45.19
Diámetro (mm)
76.2
152.4
Cantidad
351
304
Porcentaje (%)
53.59
46.41
Diámetro (mm)
76.2
152.4
Cantidad
344
311
Porcentaje (%)
52.52
47.48
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508.0
609.6
762.0
Cantidad
306
5
295
8
6
3
5
4
4
6
9
4
Porcentaje (%)
46.72
0.76
45.04
1.22
0.92
0.46
0.76
0.61
0.61
0.92
1.37
0.61
Bugalagrande
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
278
Tabla 84. Diámetros de diseño - Red Carmen.
Tabla 85. Diámetros de diseño - Red Chinú.
Tabla 86. Diámetros de diseño - Red Sector 35.
Diámetro (mm)
76.2
101.6
152.4
203.2
Cantidad
689
26
34
5
Porcentaje (%)
91.38
3.45
4.51
0.66
Diámetro (mm)
76.2
101.6
152.4
203.2
Cantidad
652
23
74
5
Porcentaje (%)
86.47
3.05
9.81
0.66
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.8
406.4
457.2
508.0
914.4
Cantidad
364
4
369
2
3
2
2
3
2
2
1
Porcentaje (%)
48.28
0.53
48.94
0.27
0.40
0.27
0.27
0.40
0.27
0.27
0.13
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.8
406.4
457.2
508.0
609.6
762.0
Cantidad
358
3
365
5
4
3
4
2
3
2
2
3
Porcentaje (%)
47.48
0.40
48.41
0.66
0.53
0.40
0.53
0.27
0.40
0.27
0.27
0.40
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.8
406.4
457.2
508.0
609.6
762.0
914.4
Cantidad
274
31
323
14
20
20
13
16
11
10
11
5
6
Porcentaje (%)
36.34
4.11
42.84
1.86
2.65
2.65
1.72
2.12
1.46
1.33
1.46
0.66
0.80
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.8
406.4
457.2
508.0
609.6
762.0
914.4
Cantidad
262
27
278
19
24
27
19
22
17
14
24
10
11
Porcentaje (%)
34.75
3.58
36.87
2.52
3.18
3.58
2.52
2.92
2.25
1.86
3.18
1.33
1.46
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.8
406.4
457.2
508.0
609.6
762.0
914.4
Cantidad
198
37
231
36
30
44
29
31
28
23
31
18
18
Porcentaje (%)
26.26
4.91
30.64
4.77
3.98
5.84
3.85
4.11
3.71
3.05
4.11
2.39
2.39
Carmen
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Diámetro (mm)
76.2
101.6
Cantidad
1088
1
Porcentaje (%)
99.91
0.09
Diámetro (mm)
76.2
101.6
152.4
Cantidad
1039
1
49
Porcentaje (%)
95.41
0.09
4.50
Diámetro (mm)
76.2
152.4
Cantidad
834
255
Porcentaje (%)
76.58
23.42
Diámetro (mm)
76.2
152.4
254.0
508.0
762.0
Cantidad
724
362
1
1
1
Porcentaje (%)
66.48
33.24
0.09
0.09
0.09
Diámetro (mm)
76.2
152.4
Cantidad
607
482
Porcentaje (%)
55.74
44.26
Diámetro (mm)
76.2
152.4
Cantidad
572
517
Porcentaje (%)
52.53
47.47
Diámetro (mm)
76.2
152.4
Cantidad
567
522
Porcentaje (%)
52.07
47.93
Chinú
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
Diámetro (mm)
76.2
101.6
152.4
203.2
Cantidad
1162
62
51
14
Porcentaje (%)
90.15
4.81
3.96
1.09
Diámetro (mm)
76.2
101.6
152.4
254.0
304.8
355.6
406.4
457.2
Cantidad
996
237
50
1
1
1
2
1
Porcentaje (%)
77.27
18.39
3.88
0.08
0.08
0.08
0.16
0.08
Diámetro (mm)
76.2
101.6
152.4
254.0
304.8
355.6
406.4
457.2
609.6
762.0
914.4
Cantidad
944
220
110
2
2
2
5
1
1
1
1
Porcentaje (%)
73.24
17.07
8.53
0.16
0.16
0.16
0.39
0.08
0.08
0.08
0.08
Diámetro (mm)
76.2
101.6
152.4
304.8
355.6
406.4
457.2
609.6
762.0
914.4
Cantidad
882
184
210
2
2
5
1
1
1
1
Porcentaje (%)
68.43
14.27
16.29
0.16
0.16
0.39
0.08
0.08
0.08
0.08
Diámetro (mm)
76.2
101.6
152.4
304.8
355.6
406.4
457.2
914.4
Cantidad
796
118
368
1
1
3
1
1
Porcentaje (%)
61.75
9.15
28.55
0.08
0.08
0.23
0.08
0.08
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508.0
609.6
762.0
914.4
Cantidad
337
56
399
44
55
60
51
56
60
54
47
53
17
Porcentaje (%)
26.14
4.34
30.95
3.41
4.27
4.65
3.96
4.34
4.65
4.19
3.65
4.11
1.32
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508.0
609.6
762.0
914.4
Cantidad
48
112
105
101
110
114
115
103
103
106
112
115
45
Porcentaje (%)
3.72
8.69
8.15
7.84
8.53
8.84
8.92
7.99
7.99
8.22
8.69
8.92
3.49
Sector 35
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Análisis de la geometría fractal de la Superficie Óptima de Presiones
en el diseño optimizado de redes de distribución de agua potable.
IAMB 202010
Andrés Felipe Jaramillo Pabón
Tesis de Pregrado
279
Tabla 87. Diámetros de diseño - Red La Enea.
Diámetro (mm)
76.2
101.6
152.4
Cantidad
1499
74
19
Porcentaje (%)
94.16
4.65
1.19
Diámetro (mm)
76.2
101.6
152.4
Cantidad
1323
115
154
Porcentaje (%)
83.10
7.22
9.67
Diámetro (mm)
76.2
101.6
152.4
Cantidad
1256
102
234
Porcentaje (%)
78.89
6.41
14.70
Diámetro (mm)
76.2
101.6
152.4
Cantidad
1186
90
316
Porcentaje (%)
74.50
5.65
19.85
Diámetro (mm)
76.2
101.6
152.4
Cantidad
1137
74
381
Porcentaje (%)
71.42
4.65
23.93
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508.0
609.6
762.0
914.4
Cantidad
721
114
329
34
54
42
46
49
56
35
40
47
25
Porcentaje (%)
45.29
7.16
20.67
2.14
3.39
2.64
2.89
3.08
3.52
2.20
2.51
2.95
1.57
Diámetro (mm)
76.2
101.6
152.4
203.2
254.0
304.8
355.6
406.4
457.2
508.0
609.6
762.0
914.4
Cantidad
104
112
183
139
128
127
135
117
139
113
125
116
54
Porcentaje (%)
6.53
7.04
11.49
8.73
8.04
7.98
8.48
7.35
8.73
7.10
7.85
7.29
3.39
La Enea
Óptimo
No Óptimo 1
No Óptimo 2
No Óptimo 3
No Óptimo 4
No Óptimo 5
No Óptimo 6
