
FACULTAD DE INGENIERIA.
“ESPECIALIZACIÓN EN INGENIERIA DE SISTEMAS HIDRICOS URBANOS”
PROYECTO DE GRADO
“Análisis de la dilución de concentraciones de NaCl en una unión
tipo cruz”
JUAN GUILLERMO SALDARRIAGA VALDERRAMA
TESIS DE ESPECIALIZACIÓN
Buitrago León, Iván Alexander.
02/11/2014

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
i
A Dios por todas sus bendiciones pasadas, presentes y venideras.
A mi madre y a mi padre, que con su esfuerzo en medio de las dificultades orientaron mi vida con
amor y responsabilidad.
A Clara por su amor, apoyo y comprensión; con su ternura y cariño hace de mí un mejor hombre
cada día.
A Hugo Forero y Williams Torres quienes han creído en mí en estos últimos años y a quienes debo
mi éxito, formación profesional y personal.
A la Universidad de los Andes, a sus docentes y mis compañeros en la especialización, con quienes
tuve la oportunidad de compartir y aprender de sus experiencias y conocimientos. Me enorgullece
haber estudiado en esta Universidad y haber compartido una parte de mi vida con ellos. Me
divertí mucho.
A Sebastián y Alfredo, por su apoyo en mis labores diarias durante este último año.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
ii
Contenido
Lista de figuras ............................................................................................................................... 5
Lista de fotografías......................................................................................................................... 6
Lista de gráficas ............................................................................................................................. 6
Lista de tablas ................................................................................................................................ 7
Lista de ecuaciones ........................................................................................................................ 8
1
Introducción ........................................................................................................................... 1
2
Objetivos ................................................................................................................................ 3
2.1
Objetivo general ............................................................................................................. 3
2.2
Objetivo particular .......................................................................................................... 3
2.3
Objetivo específico ......................................................................................................... 3
3
Justificación............................................................................................................................ 4
3.1
Estado del arte: comentarios .......................................................................................... 5
4
Marco teórico ........................................................................................................................ 6
4.1
Análisis de redes de tuberías: redes cerradas .................................................................. 6
4.1.1
Método del gradiente ............................................................................................. 6
4.1.1.1 Descripción matemática ...................................................................................... 7
4.1.1.2 Ejemplo del método ............................................................................................ 8
4.2
Análisis de calidad de agua: concentración de un soluto (NaCl), en un nudo ................. 20
4.2.1
Desinfección ......................................................................................................... 20
4.2.2
Difusión ................................................................................................................ 22
4.3
Modelo de mezcla completa: método tradicional ......................................................... 22
4.4
Modelo de mezcla parcial: concepción moderna........................................................... 23
5
Observaciones sobre el experimento .................................................................................... 29
5.1
¿Por qué lo lógico es suponer predominio de mezclas parciales y no totales en una
unión? 29
5.1.1
Caudales confluyentes en una cruz........................................................................ 29
5.1.1.1 Primer caso ....................................................................................................... 29
5.1.1.2 Segundo caso .................................................................................................... 30
5.1.1.3 Tercer caso........................................................................................................ 31
5.1.1.4 Cuarto caso ....................................................................................................... 32
5.1.1.4.1 Tipo a. ......................................................................................................... 32
5.1.1.4.2 Tipo b. ......................................................................................................... 33

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
iii
5.1.2
Mezcla de soluciones acuosas ............................................................................... 34
5.1.2.1 Mezcla de soluciones sin reacción química ........................................................ 34
5.1.2.2 Fuerza (impulso), de fluidos que discurren en la cruz ........................................ 36
5.2
Estrategia metodológica para acertar en la solución del objetivo del experimento ........ 37
5.2.1
Conservación de la masa en el nudo (cruz) ............................................................ 37
5.2.2
Variables, factores y niveles .................................................................................. 38
5.2.3
Metodología propuesta “Estrategia y consideraciones”......................................... 39
5.2.3.1 Determinar la función general objetivo ............................................................. 39
5.2.3.2 Determinar las restricciones iniciales para el experimentoplaneado .................. 39
5.2.3.3 Proponer relaciones entre las variables ............................................................. 39
5.2.3.4 Determinar la ecuación de relación ................................................................... 40
5.2.4
Diagrama de flujo de la estrategia planteada ........................................................ 41
6
Modelo físico y digital .......................................................................................................... 42
6.1
Partes del modelo físico ................................................................................................ 42
6.2
Modelo digital en EPANET ............................................................................................ 43
6.3
Instrumentos utilizados en el modelo físico .................................................................. 45
6.3.1
Medidor de agua volumétrico. .............................................................................. 45
6.3.1.1 Ajuste de las medidas de caudal. ....................................................................... 47
6.3.2
Termómetro digital ............................................................................................... 48
6.3.2.1 Ajuste de las medidas de temperatura .............................................................. 49
6.3.3
Medidor de conductividad .................................................................................... 50
6.3.3.1 Ajuste de la medida de conductividad ............................................................... 51
6.3.4
Cámaras de tipo WEB y toma de imágenes ............................................................ 51
6.4
Soluto utilizado en el experimento................................................................................ 53
6.5
Tuberías y accesorios en PVC ........................................................................................ 53
7
Desarrollo del experimento y metodología ........................................................................... 54
7.1
Paso a paso de ejecución de cada prueba del experimento. .......................................... 54
7.2
Escenarios del experimento .......................................................................................... 55
7.2.1
Escenario #1 ......................................................................................................... 56
7.2.2
Escenario #2 ......................................................................................................... 56
7.2.3
Escenario #3 ......................................................................................................... 56
7.2.4
Escenario #4 ......................................................................................................... 56

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
iv
7.2.5
Escenario #5 ......................................................................................................... 56
7.2.6
Escenario #6 ......................................................................................................... 57
7.2.7
Escenario #7 ......................................................................................................... 57
7.2.8
Escenario #8 ......................................................................................................... 57
7.2.9
Escenario #9 ......................................................................................................... 57
7.2.10
Escenario #10........................................................................................................ 57
7.2.11
Escenario #11........................................................................................................ 57
7.2.12
Escenario #12........................................................................................................ 57
7.3
Toma de los datos......................................................................................................... 58
7.4
Relación entre la conductividad y la concentración de sal en la solución ....................... 59
7.5
Estimación de la viscosidad cinemática y densidad del agua ......................................... 60
7.6
Cálculos hidráulicos ...................................................................................................... 61
7.7
Cálculos de la conductividad y concentración del soluto ............................................... 62
7.7.1
Formulación para el cálculo de la concentración a partir de la ecuación de Clifford K.
Ho
63
7.7.2
Formulación para el cálculo de la concentración a partir de la ecuación de Pedro
Romero-Gómez .................................................................................................................... 63
7.8
Calculo de las concentraciones con la estrategia propuesta .......................................... 65
8
Análisis de los resultados obtenidos ..................................................................................... 72
8.1
Resultados obtenidos para la concentración C
4
............................................................. 72
8.2
Resultados obtenidos para la concentración C
3
............................................................. 74
8.3
Resultado general C
3
y C
4
.............................................................................................. 76
9
Conclusiones, recomendaciones y comentarios sobre las conclusiones ................................ 79
9.1
Conclusiones ................................................................................................................ 79
9.2
Recomendaciones ........................................................................................................ 80
9.3
Comentarios ................................................................................................................. 80
9.3.1
Mezclas reales dentro de las uniones en cruz ........................................................ 80
9.3.1.1 Características de las uniones en cruz ................................................................ 81
9.3.1.1.1 Consideraciones geométricas por procesos de fabricación. ......................... 81
9.3.1.1.2 Consideraciones del método de unión ......................................................... 82
9.3.1.1.3 Consideraciones al respecto del material de fabricación .............................. 83
9.3.2
Aplicación computacional del modelo planteado .................................................. 83
10
Bibliografía ....................................................................................................................... 86

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
v
10.1 Artículos y otros documentos ....................................................................................... 86
10.2 Tesis ............................................................................................................................. 87
ANEXO No. 1 Datos obtenidos en el experimento........................................................................ 88
ANEXO No. 2 Ajuste del error para los medidores de agua usados ............................................. 107
ANEXO No. 3 Cálculo de caudales............................................................................................... 109
ANEXO No. 4 Cálculo de parámetros hidráulicos ........................................................................ 121
ANEXO No. 5 Relación entre conductividad y concentración de soluto para el agua utilizada en el
experimento .............................................................................................................................. 133
ANEXO No. 6 Cálculo de la concentración mediante las diferentes ecuaciones estudiadas ......... 134
ANEXO No.7 Lecturas de los medidores de agua ........................................................................ 152
ANEXO No.8 Certificados de calibración de los medidores de agua ............................................ 170
Lista de figuras
Figura 1. Geometría de la red para el método del gradiente. .......................................................... 9
Figura 2. Datos para el desarrollo de los análisis de la red. ........................................................... 10
Figura 3. Curva de demanda de Cloro. .......................................................................................... 22
Figura 4. Características internas de la tee de PVC de 1” usada como unión en el experimento. ... 24
Figura 5. Mayor impulso en la dirección vertical ........................................................................... 25
Figura 6. Mayor impulso en la dirección horizontal ...................................................................... 25
Figura 7. Mayor impulso en la dirección vertical ........................................................................... 27
Figura 8. Única entrada de flujo con su concentración a la cruz. ................................................... 30
Figura 9. Flujo por entradas encontradas hacia el centro de la cruz. ............................................. 31
Figura 10. Tres caudales que confluyen en el centro de la cruz. .................................................... 32
Figura 11. Dos caudales de entrada con diferentes concentraciones confluyen en el centro de la
cruz sin que exista mezcla ............................................................................................................ 33
Figura 12. Mezcla parcial dentro de la cruz, cuarto caso. .............................................................. 34
Figura 13. Diagrama de flujo de la estrategia planteada ............................................................... 41
Figura 14. Modelo físico ensamblado. .......................................................................................... 42
Figura 15. Traductores de la versión utilizada de EpaNet a español .............................................. 44
Figura 16. Modelo digital de EpaNet para la prueba No. 4 ............................................................ 44
Figura 17. Identificación de las tuberías de entrada y salida de acuerdo con una base
georreferenciada ......................................................................................................................... 84
Figura 18. Diagrama de flujo propuesto para la aplicación computacional del modelo planteado
con base en un posicionamiento georreferenciado ...................................................................... 85

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
vi
Lista de fotografías
Fotografía 1. Modelo físico del experimento. ............................................................................... 43
Fotografía 2. Medidor volumétrico utilizado para el experimento ................................................ 45
Fotografía 3. Lecturas iniciales de los medidores para una de las pruebas realizadas .................... 46
Fotografía 4. Lecturas finales de los medidores para una de las pruebas realizadas ...................... 46
Fotografía 5. Montaje de la cámara web y ajuste de la imagen en el software de video ............... 47
Fotografía 6. Dispositivo termo-resistivo digital utilizado para el experimento ............................. 49
Fotografía 7. Lectura de temperatura en el patrón ....................................................................... 50
Fotografía 8. Comparación temperatura en el patrón con los equipos termo-resistivos utilizados 50
Fotografía 9. Medidor de conductividad utilizado en el experimento ........................................... 51
Fotografía 10. Verificación de la lectura de la conductividad respecto a la temperatura del agua
según certificación del fabricante ................................................................................................. 51
Fotografía 11. Posicionamiento de la cámara web sobre el medidor de volumen ......................... 52
Fotografía 12. Ejecución del experimento y control de los datos .................................................. 53
Fotografía 13. Soluto utilizado...................................................................................................... 53
Fotografía 14. Medición de conductividad y temperatura del agua durante el experimento ......... 58
Fotografía 15. Imperfecciones derivadas del proceso de fabricación (cruz PVC soldada) ............... 81
Fotografía 16. Imperfecciones derivadas del proceso de fabricación (cruz PVC roscada)............... 82
Fotografía 17. Imperfecciones derivadas del proceso de fabricación (cruz hierro galvanizado
roscada) ....................................................................................................................................... 82
Lista de gráficas
Gráfica 1. Convergencia del método del gradiente ....................................................................... 19
Gráfica 2. Conservación de la masa ............................................................................................. 38
Gráfica 3. Corrección del error en porcentaje en el medidor No. 1 - 13 006070 ............................ 48
Gráfica 4. Relación existente entre la conductividad y la concentración del soluto en el agua ...... 60
Gráfica 5. Relación existente entre la temperatura del agua y su densidad ................................... 61
Gráfica 6. Relación existente entre la temperatura del agua y su viscosidad cinemática ............... 61
Gráfica 7. Relación encontrada entre la distribución de masas de entrada y de salida de la cruz, en
el tiempo ..................................................................................................................................... 69
Gráfica 8. Exactitud de las ecuaciones estudiadas en relación a la concentración medida para C4.
Pruebas que cumplen con las restricciones del modelo. Promedio de las tomas para cada prueba.
.................................................................................................................................................... 73
Gráfica 9. Error calculado para el valor de C4 hallado mediante las diferentes ecuaciones
estudiadas respecto a los valores medidos en el experimento. Pruebas que cumplen con las
restricciones del modelo. ............................................................................................................. 74
Gráfica 10. Exactitud de las ecuaciones estudiadas en relación a la concentración medida para C3.
Pruebas que cumplen con las restricciones del modelo. Promedio de las tomas para cada muestra
.................................................................................................................................................... 75

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
vii
Gráfica 11. Error calculado para el valor de C3 hallado mediante las diferentes ecuaciones
estudiadas respecto a los valores medidos en el experimento. Pruebas que cumplen con las
restricciones del modelo. ............................................................................................................. 76
Gráfica 12. Exactitud de las ecuaciones estudiadas en relación a la concentración medida para C4.
Todas las pruebas. ....................................................................................................................... 77
Gráfica 13. Exactitud de las ecuaciones estudiadas en relación a la concentración medida para C3.
Todas las pruebas. ....................................................................................................................... 78
Lista de tablas
Tabla 1. Datos de inicio para la primera iteración ......................................................................... 13
Tabla 2. Datos para la segunda iteración ...................................................................................... 19
Tabla 3. Datos de la última iteración ............................................................................................ 20
Tabla 4. Cálculo del caudal ajustado para la prueba No. 4, toma 2 ................................................ 48
Tabla 5. Estado de operación de las válvulas para los diferentes escenarios ................................. 54
Tabla 6. Mediciones realizadas durante la ejecución de la prueba No. 4, toma 2 .......................... 58
Tabla 7. Cálculo de la concentración de soluto como función de la conductividad medida ........... 59
Tabla 8. Relación de la densidad y la viscosidad cinemática del agua con la temperatura ............. 60
Tabla 9. Parámetros hidráulicos calculados para la prueba No. 4, toma 2 ..................................... 62
Tabla 10. Concentración calculada del soluto durante la prueba No. 4, toma 2 y concentraciones
calculadas mediante las ecuaciones estudiadas. ........................................................................... 62
Tabla 11. Ecuaciones para el cálculo de C3 y C4 de acuerdo con la relación existente entre Q1 y Q2,
según las restricciones planteadas a partir de la ecuación de Ho .................................................. 63
Tabla 12. Ecuaciones para el cálculo de C3 y C4 de acuerdo con la relación existente entre Q1 y Q2,
según las restricciones planteadas a partir de la ecuación de Romero-Gómez .............................. 64
Tabla 13. Cálculo de C4 mediante las ecuaciones anteriores ........................................................ 65
Tabla 14. Cálculo de C3 mediante las ecuaciones anteriores ........................................................ 66
Tabla 15. Cumplimiento de las restricciones planteadas ............................................................... 68
Tabla 16. Cálculo de la razón entre las masas entrantes y entre las masas salientes con relación al
tiempo ......................................................................................................................................... 68
Tabla 17. Cálculo de C4 mediante las ecuaciones estudiadas y la ecuación propuesta, para las
pruebas que cumplen las restricciones incluyendo la totalidad de las tomas ................................ 71
Tabla 18. Cálculo de C3 mediante las ecuaciones estudiadas y la ecuación propuesta, para las
pruebas que cumplen las restricciones incluyendo la totalidad de las tomas ................................ 71
Tabla 19. Cálculo de C4 mediante las ecuaciones estudiadas y la ecuación propuesta, para las
pruebas que cumplen las restricciones. Promedio de las tomas para cada prueba ....................... 72
Tabla 20. Cálculo de C3 mediante las ecuaciones estudiadas y la ecuación propuesta, para las
pruebas que cumplen las restricciones. Promedio de las tomas para cada prueba ....................... 75

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
viii
Lista de ecuaciones
Ecuación 1. Ecuación de continuidad para cada nudo ..................................................................... 7
Ecuación 2. Ecuación de balance de enrgía para cada tubo............................................................. 7
Ecuación 3. Cálculo del factor de fricción f para flujo en trancisión o trubulento ............................ 7
Ecuación 4. Ecuación explícita para el caudal con base en Colebrook-White ................................... 7
Ecuación 5. Ecuación general que relaciona la altura de energía con el caudal que fluye por la
tubería ........................................................................................................................................... 7
Ecuación 6. Ecuación general que relaciona la altura de energía con el caudal que fluye por la
tubería, para sistemas sin bombeo ni válvulas de control ............................................................... 8
Ecuación 7. Cálculo del término
.................................................................................................. 8
Ecuación 8. Cálculo del caudal por el método del gradiente ........................................................... 8
Ecuación 9. Ecuación vectorial del método del gradiente ............................................................... 8
Ecuación 10. Tasa de destrucción de microorganismos en función del agente letal ...................... 20
Ecuación 11. Ecuación de cálculo del cloro consumiso para la desinfección .................................. 21
Ecuación 12. Reacción química del cloro con el agua .................................................................... 21
Ecuación 13. Reacción química del cloro con el agua .................................................................... 21
Ecuación 14. Componentes del ácido hipocloroso ........................................................................ 21
Ecuación 15. Componentes del ácido hipocloroso ........................................................................ 21
Ecuación 16. Balance de masa para mezcla completa en un nudo ................................................ 23
Ecuación 17. Balance de masa para mezcla completa en un nudo en WaterCad ........................... 23
Ecuación 18. Ecuación para la tasa de cambio del impulso ........................................................... 26
Ecuación 19. Criterio del impulso con base en los caudales entrantes y salientes en un nudo....... 26
Ecuación 20. Hipótesis de igualdad de las concentraciones en 1 y 4 ............................................. 27
Ecuación 21. Balance de masa del soluto en una unión ................................................................ 27
Ecuación 22. Balance de masa del soluto en una unión con C
1
= C
4
............................................... 27
Ecuación 23. Cálculo de C
3
en función de caudales y concentraciones conocidas .......................... 28
Ecuación 24. Variables x y y de acuerdo a la ecuación de Romero-Gómez ................................... 28
Ecuación 25. Conservación de masa en un nudo de acuerdo con Romero-Gómez ........................ 28
Ecuación 26. Combinación de las ecuaciones 24 y 25 para Q
2
y Q
3
................................................ 28
Ecuación 27. Combinación de las ecuaciones 24 y 25 para Q
1
y Q
3
................................................ 28
Ecuación 28. Cálculo de C
3
de acuerdo con las ecuaciones planteadas por Romero-Gómez .......... 28
Ecuación 29. Cálculo de Q
1
según la ecuación de balance de masa ............................................... 30
Ecuación 30. Ecuación para la mezcla de soluciones sin reacción química de los solutos .............. 35
Ecuación 31. Ecuación para la mezcla de soluciones sin reacción química de los solutos dividida en
la unidad de tiempo para el tercer caso ....................................................................................... 35
Ecuación 32. Cálculo de C
4
con base en la ecuación 31 ................................................................. 35
Ecuación 33. Ecuación para la mezcla de soluciones sin reacción química de los solutos dividida en
la unidad de tiempo para el cuarto caso ....................................................................................... 35
Ecuación 34. Desarrollo de la metodología de Ho cuando C
1
es igual a C
4
. Paso 1 ......................... 35
Ecuación 35. Desarrollo de la metodología de Ho cuando C1 es igual a C4. Paso 2 ........................ 35
Ecuación 36. Desarrollo de la metodología de Ho cuando C1 es igual a C4. Paso 3 ........................ 35
Ecuación 37. Cálculo de C
3
según la metodología de Ho cuando C1 es igual a C4. Paso 3 .............. 35
Ecuación 38. Desigualdad de las concentraciones 1, 2 y 3 en un nudo si C
2
es mayor que C
1
......... 36
Ecuación 39. Desigualdad de las concentraciones 1, 2 y 3 en un nudo si C2 es menor que C1 ....... 36

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
ix
Ecuación 40. Segunda ley de Newton ........................................................................................... 36
Ecuación 41. Integración de la segunda ley de Newton en función del tiempo ............................. 36
Ecuación 42. Segunda ley de Newton con base en deltas de tiempo y de velocidad ..................... 37
Ecuación 43. Cálculo de la fuerza en función a la densidad del líquido y un volumen de control ... 37
Ecuación 44. Cálculo de la fuerza en función a la densidad del líquido y el caudal ........................ 37
Ecuación 45. Cálculo de la fuerza en función al caudal y el área.................................................... 37
Ecuación 46. Conservación de la masa entrante y saliente en un nudo ......................................... 37
Ecuación 47. Conservación del caudal entrante y saliente en un nudo.......................................... 37
Ecuación 48. Ecuación de balance de la masa en un nudo ............................................................ 38
Ecuación 49. Concentraciones 3 y 4 en función de caudales y concentraciones conocidas ............ 39
Ecuación 50. Relación propuesta en consideración a las restricciones establecidas ...................... 39
Ecuación 51. Definición de y y f(x) en función de las relaciones propuestas .................................. 40
Ecuación 52. Definición de y como función de x ........................................................................... 40
Ecuación 53. Despeje de Q
3
C
3
desde las ecuaciones 51 y 52 ........................................................ 40
Ecuación 54. Despeje de Q
3
C
3
desde la ecuación de balance de la masa en un nudo ................... 40
Ecuación 55. Reemplazo de f(x) en la ecuación 54. Paso 1 ............................................................ 40
Ecuación 56. Reemplazo de f(x) en la ecuación 54. Paso 2 ............................................................ 40
Ecuación 57. Reemplazo de f(x) en la ecuación 54. Paso 3 ............................................................ 40
Ecuación 58. Despeje de C
4
con base en la relación propuesta ..................................................... 40
Ecuación 59. Despeje de C
3
con base en la relación propuesta ..................................................... 41
Ecuación 60. Cálculo del caudal medido en cada una de las pruebas ........................................... 46
Ecuación 61. Ecuación de balance de masas en un nudo .............................................................. 63
Ecuación 62. Cálculo de C
3
desde la ecuación de balance de masas en un nudo, según Ho ........... 63
Ecuación 63. Cálculo de C
4
desde la ecuación de balance de masas en un nudo, según Ho ........... 63
Ecuación 64. Cálculo de C
3
según Romero-Gómez ........................................................................ 64
Ecuación 65. Cálculo de C
4
según Romero-Gómez ........................................................................ 64
Ecuación 66. Cálculo del error respecto a las concentraciones medidas en el experimento .......... 64
Ecuación 67. Relación propuesta para el experimento ................................................................. 67
Ecuación 68. Ecuación que relaciona Q
1
C
1
/Q
2
C
2
con Q
3
C
3
/Q
4
C
4
.................................................... 69
Ecuación 69. Desarrollo de la ecuación 68. Paso 1 ........................................................................ 69
Ecuación 70. Despeje de Q
3
C
3
con base en las relaciones propuestas ........................................... 69
Ecuación 71. Despeje de Q
3
C
3
desde la ecuación estándar para las soluciones acuosas ................ 69
Ecuación 72. Igualación de las ecuaciones 70 y 71 ........................................................................ 69
Ecuación 73. Cálculo de C
4
con base en las relaciones propuestas ................................................ 70
Ecuación 74. Despeje de Q
4
C
4
con base en las relaciones propuestas ........................................... 70
Ecuación 75. Despeje de Q
4
C
4
desde la ecuación estándar para las soluciones acuosas ................ 70
Ecuación 76. Igualación de las ecuaciones 74 y 75. Paso 1 ............................................................ 70
Ecuación 77. Igualación de las ecuaciones 74 y 75. Paso 2 ............................................................ 70
Ecuación 78. Cálculo de C3 con base en las relaciones propuestas ............................................... 70

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones en una unión de tuberías tipo
cruz de soluciones de NaCl”

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
1
1 Introducción
El agua es un elemento especial para el desarrollo de la vida y de vital importancia para el hombre,
está presente en muchos aspectos de su vida diaria, en la salud, no solo regula en gran medida el
sistema endocrino del cuerpo, agua contaminada y consumida es la responsable enfermedades
como el cólera, la fiebre tifoidea, diarreas y gastroenteritis ente otras, y vector de otras como
dengue y la malaria
1
. En el desarrollo con equidad, el suministro de agua potable es la base de la
igualdad social en la prestación de los servicios públicos. En el ámbito industrial el agua hace parte
de la mayoría de procesos productivos industriales modernos, ya sea como materia prima, insumo
directo del producto o bien necesario para regular o controlar los diferentes procesos. El agua en
si es el motor del desarrollo y crecimiento poblacional.
Dada la importancia del agua, una gran cantidad de recursos (económicos y humanos), se invierte
en todo el mundo para abastecer de agua potable a toda la población, no solo en sistemas nuevos
de captación, purificación, almacenamiento, transporte y distribución del agua potable, también
en el mantenimiento, rehabilitación y actualización técnica de la estructuras existentes, siendo la
operación y mantenimiento de la red de distribución uno de los rubros que más pesa en la
estructura tarifaria.
Las empresas de agua potable en la actualidad se apoyan en programas informáticos que ayudan a
desarrollar modelos virtuales de la red de distribución, que les permita su fácil operación
hidráulica y apreciación de la calidad del agua distribuida. La confiabilidad y grado de exactitud de
estos programas tiene un alto grado de responsabilidad social en la medida que con base en los
resultados emitidos por los mismos se toman decisiones que afectan la salud de la población
atendida.
Según explica Clifford K. Ho
2
, En la actualidad el transporte de solutos en los sistemas de
distribución de agua es una preocupación creciente debido a la posibilidad de eventos de
contaminación accidental o intencional. Tal como lo menciona Ho, la comprensión de cómo los
solutos se mueven y se mezclan a través de una red de tuberías y uniones es crítica para el
desarrollo planes de mitigación que deberían producirse un evento de contaminación.
Este documento contiene una recopilación básica del estado del arte en la evaluación de la mezcla
de aguas con diferentes o iguales concentraciones de un soluto, que permitan establecer una
1
Según la Unesco, las enfermedades relacionadas con el agua matan a un niño cada 8 segundos y, son
responsables del 80% de todas las enfermedades y muertes de los países en vías de desarrollo; cobran la
vida de más de 5 millones de personas cada año, más de 10 veces el número de personas que mueren a
causa de los conflictos armados. La diarrea está causada por una serie de microorganismos que incluyen
virus, bacterias y protozoos. Esta enfermedad provoca que una persona pierda agua y electrólitos, lo que
conduce a la deshidratación y, en algunos casos, a la muerte. Unos 4.000 millones de casos de diarrea al año
causan 1,8 millones de víctimas mortales, más del 90% de los cuales (1,6 millones) son niños menores de
cinco años. Recuperado el 2 de diciembre de 2013 de UNESCO:
http://www.unesco.org/water/news/newsletter/161_es.shtml#know
2
Ho. Clifford. (2008). Solute Mixing Models for Water-Distribution Pipe Networks. Recuperado el de octubre
de 2013, de ASCE: http://gsgc.gzhu.edu.cn/gpsgd/UploadFile/200942623229730.pdf

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
2
aproximación al proceso de mezcla en cruces de tuberías, así como una propuesta metodológica
con base en un modelo físico desarrollado para este proyecto, que relaciona la teoría actual de
mezcla completa y parcial, para determinar la concentración del soluto en las tuberías de salida de
los cruces en redes de distribución de agua potable.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
3
2 Objetivos
2.1 Objetivo general
Desarrollar un experimento que permita a través de un modelo físico estudiar la mezcla de agua
con diferentes concentraciones de NaCl al discurrir a través de un accesorio (cruz comercial), e
interpretar los resultados de las concentraciones resultantes a la luz de las teorías actuales.
2.2 Objetivo particular
Conocer e interpretar el comportamiento del agua que fluye a través de una unión tipo cruz, con
diferentes grados de concentración de NaCl y caudal que discurre
2.3 Objetivo específico
Plantear con base en los resultados obtenidos una metodología nueva que permita estimar las
concentraciones de NaCl de salida de la cruz, tomando como base las teorías actuales y buscando
una relación con las medidas realizadas. Metodología que permita determinar ecuaciones que
estimen concentraciones de salida de NaCl y su aplicación a sistemas informáticos de modelación
de redes de distribución de agua potable a presión.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
4
3 Justificación
En cada país, el gobierno de la nación tiene como obligación velar por la integridad y salud de sus
ciudadanos, siendo el abastecimiento y distribución de agua potable uno de los pilares de la salud
pública. En Colombia, a través del decreto 1575 del 9 de mayo de 2007, se establece el sistema de
protección y control de la calidad del agua para consumo humano, esto con el fin de monitorear,
prevenir y controlar los riesgos para la salud humana causados por el consumo de agua. El agua
potable o para consumo humano, tiene que cumplir con las características físicas, químicas y
microbiológicas, en las condiciones señaladas en el decreto y demás legislación complementaria.
Para el control de la calidad de agua en la red de distribución, el gobierno Colombiano a través del
Ministerio de la Protección Social y el Ministerio de Ambiente, Vivienda y Desarrollo Territorial,
expidieron la Resolución número 0811 DE 2008, “por medio de la cual se definen los lineamientos
a partir de los cuales la autoridad sanitaria y las personas prestadoras, concertadamente definirán
en su área de influencia los lugares y puntos de muestreo para el control y la vigilancia de la
calidad del agua para consumo humano en la red de distribución”. El cumplimiento de esta
resolución, implica por parte de los prestadores del servicio de agua potable una labor técnica
idónea para la ubicación de los puntos de muestreo; esto involucra el uso de un modelo hidráulico
de la red que ayude a identificar los puntos más críticos y con deficiencias en la calidad del agua
distribuida.
La ubicación técnica e idónea de los puntos de muestreo se debe hacer con la ayuda de programas
informáticos que permita hacer un modelo virtual de la red de distribución, entender su hidráulica
y relación de esta última con la variación de la calidad del agua en cualquier punto de la red. Una
ubicación errada conlleva elevados costos de ensayos en laboratorios acreditados, un control
ineficiente de la calidad del agua en la red, conflictos entre el prestador del servicio y los entes de
control, desconfianza y conflictos internos entre las dependencias de la empresa prestadora del
servicio; producción de agua con la de operación de la red (encargados de la distribución de agua)
e inconformidad de los usuarios por la calidad del servicio prestado.
Como se mencionó anteriormente, la confiabilidad y grado de exactitud de estos programas tiene
un alto grado de responsabilidad social en la medida que con base en los resultados emitidos por
los mismos se toman decisiones que afectan la salud de la población atendida.
Si bien se considera, que el tema del modelo matemático que soporta la hidráulica de una red de
distribución la cual permite hacer un modelo computacional de la misma, es un tema abordado
con profundidad, tiene el inconveniente que para crear la malla de distribución del agua en el
modelo y hallar su solución numérica no profundiza en el comportamiento del agua a través de los
nudos que dan forma a la malla evaluada. Esto trae como consecuencia que aunque
hidráulicamente el problema de la modelación esté resuelto, la valoración de la calidad del agua
en la red y de manera más precisa el transporte de solutos por la misma aun no tenga una solución
satisfactoria que represente de manera sustancial la realidad.
Tal como lo menciona Clifford K. Ho, la comprensión de cómo los solutos se mueven y se mezclan
a través de una red de tuberías y uniones es crítica. Conocer el comportamiento de los solutos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
5
que discurren por las uniones de las tuberías en el modelo y como relacionar los resultados de
estos análisis con las redes de distribución de agua potable existentes, permitirán a los usuarios de
estos programas informáticos ajustar sus modelos con las redes existentes y con base en los
resultados obtenidos tomar acciones en tiempo real para; eventos de contaminación de la red,
ubicación de los puntos de control sobre la misma u operación de la red, tomando en cuenta las
variaciones de la calidad del agua derivadas a la manipulación de válvulas o variación de los
circuitos de distribución.
Lo esencial en todo modelo es la representación más cercana de la realidad a través de una
representación conceptual y gráfica de lo estudiado; el éxito de todo modelo depende del grado
de exactitud con el que se relacionen las variables que intervienen en el modelo con la realidad y
el grado de precisión con el cual estas variables soporten el modelo en el tiempo. Conocer con
claridad, e interpretar de manera correcta el comportamiento físico y químico del agua que
discurre a través de tuberías y accesorios de una red, fortalecerán los modelos brindando una
mayor confiablidad a los usuarios de los mismos.
3.1 Estado del arte: comentarios
En la actualidad el campo de la modelación hidráulica de redes de distribución de agua potable ha
llegado a un punto en el cual el avance científico y tecnológico de la concepción hidráulica del
problema del modelo de distribución ya ha sido resuelto. En la medida que este problema de la
modelación de la redes de distribución de agua potable ha sido resuelto para su hidráulica, hasta
hace unos años la investigación referente al comportamiento de las partículas que están
contenidas en el agua transportada y su comportamiento (mezcla, degradación, reacciones), al
pasar a través de diferentes estructuras de control y accesorios (válvulas y conexiones), de la red
misma ha evolucionado.
Diferentes investigadores, en trabajos de tesis para Maestría o Doctorado han abordado el tema
de la mezcla o el transporte de sustancias en redes de distribución, y sus mezclas y reacciones,
estas han arrojado resultados que a través de los modelos hidráulicos convencionales no se
hubieran podido evidenciar.
El comportamiento de la mezcla de sustancias y/o partículas en accesorios y en especial en cruces
de tuberías ha sido estudiado de manera dedicada solo en los últimos años; esto en cierta medida
es coherente ya que sólo en la última década el costo de los instrumentos e instalaciones de
ensayo con sistemas de medición el línea de parámetros de calidad de agua y medición de presión,
caudal y volumen han bajado, facilitando su adquisición. Por otra parte, en la misma medida en
que los costos de adquisición tecnológica han bajado, la capacidad metrológica de los mismos
(sensibilidad, resolución, exactitud, baja incertidumbre entre otros), ha aumentado, permitiendo
analizar los procesos de mezcla de manera más exacta y evidenciando la relación entre las
diferentes variables envueltas en el tema de estudio.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
6
4 Marco teórico
Para el análisis de calidad de agua en redes de distribución, se deben considerar en el modelo los
dos componentes que interactúan; el primero que hace referencia al modelo hidráulico y el
segundo que corresponde al modelo de calidad de agua, ambos con las ecuaciones que los
componen.
El modelo hidráulico tiene como base el método del gradiente y las ecuaciones que los soportan y
el modelo de calidad de agua incluye los modelos de mezcla completa y de mezcla parcial. De
manera alterna con lo anterior se debe conocer la relación que existe entre el modelo hidráulico
y el modelo de calidad de agua.
4.1 Análisis de redes de tuberías: redes cerradas
Una red de tuberías es analizada para determinar dos variables características del sistema: los
caudales que fluyen por sus tuberías y las alturas de presión en cada uno de sus nudos. Dado que
la demanda de agua cambia con el tiempo, los caudales en las tuberías y las presiones en los
nudos también cambian con esta. El análisis de la red se realiza entonces con el ánimo de
conocer en cada instante los valores de caudal y presión en los diferentes puntos y tramos de la
red, ya sea para el diseño de un sistema nuevo, la mejora de un sistema existente, rehabilitación
de zonas específicas de la red o simplemente para las maniobras de operación que se presentan
en el día a día. Tal como lo comenta Prabhata K. Swamee
3
, el análisis de redes es fundamental
para la operación y mantenimiento adecuado de un sistema de suministro de agua potable.
El modelo hidráulico permite analizar la red como un todo. Aunque existen diferentes
metodologías reportadas por la literatura técnica para el análisis de redes de tuberías, en este
documento solamente se menciona el método más usado, confiable y físicamente basado, que
corresponde al método del gradiente hidráulico.
El método del gradiente realiza un análisis a régimen permanente del fluido dentro de la red de
distribución de agua, tomando como base la conservación de masa en nudos y la conservación de
la energía en los circuitos del sistema. Todo lo anterior bajo la presunción que; el fluido es
incompresible, está fluyendo a régimen permanente, esta en una sola fase, esta presurizado y que
los cambios en la temperatura, densidad y viscosidad son mínimos y no afectan el cálculo de
manera significativa.
4.1.1 Método del gradiente
Es sin duda el método más extendido para la resolución de las ecuaciones que conforman una red
de tuberías cerradas, se basa en una formulación híbrida entre la formulación por nudos y
formulación por tuberías. Originalmente el método fue desarrollado por los profesores E. Todini y
3
Swamee, P.K. & Sharma A.K. (2.007). Design of Water Supply Pipe Networks. New Jersey: John Wiley &
Sons, INC.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
7
Pilati en 1987 y posteriormente fue ampliado en su uso y aplicación por Salgado en 1.993. Este
método es bastante similar al planteado por Hamman y Drameller en 1971; tal como lo describe
García-Serra ambos métodos obtienen para cada iteración los valores de las aturas de las
piezométricas en los nudos, y antes de proceder con la siguiente iteración en la resolución del
sistema debe obtenerse también los caudales de las tuberías.
4.1.1.1 Descripción matemática
Como se comentó anteriormente, el método toma como base el hecho que las redes de los
sistemas de distribución de agua trabajan de manera continua y su flujo es permanente,
cumpliendo con la conservación de masa en los nudos y la conservación de energía en los
circuitos, contemplando las siguientes condiciones
4
:
1. Ecuación de continuidad para cada nudo
∑
Ecuación 1
2. Ecuación de balance de energía para cada tubo
(
∑
)
Ecuación 2
El factor de fricción f se calcula con la siguiente ecuación (para flujo en transición o turbulento)
√
(
√
)
Ecuación 3
3. Relación no lineal entre el caudal y las pérdidas por fricción para cada tubo
√
(
√
)
Ecuación 4
En el caso que la red contenga dispositivos que modifiquen las condiciones de caudal o presión,
tales como bombas o válvulas de control, la Ecuación 2, toma la siguiente forma, válida para todo
tipo de tubería.
Ecuación 5
4
Saldarriaga V. Juan G. (2009). Hidráulica de tuberías: Abastecimiento de Agua, Redes y Riegos. Bogotá:
Alfaomega.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
8
Si no existen bombas o válvulas de control en la red analizada la ecuación 5, se simplifica así;
Ecuación 6
donde el término
se calcula de la siguiente manera:
( ∑
)
Ecuación 7
4.1.1.2 Ejemplo del método
5
Este método busca una representación matemática con una aproximación lineal de las ecuaciones
de energía. De acuerdo con Saldarriaga, las ecuaciones se resuelven utilizando un esquema
imaginativo que se basa en la inversión de la matriz de coeficientes originales.
El método del gradiente resuelve un sistema de dimensión NN x NN, mientras que el método de la
teoría lineal resuelve un sistema de NT x NT. Debido a que NN <NT, el método del gradiente llega a
una solución más rápida, calculando y ajustando simultáneamente los caudales y las alturas
piezométricas, dado que no requiere la definición de caminos de energía o circuitos, implica
menor número de datos que el diseñador debe ingresar y a la vez menor probabilidad de error.
Para el cálculo del caudal se utiliza la siguiente ecuación:
0
1
1
1
1
10
12
'
11
11
'
11
H
A
H
A
A
N
Q
A
A
N
I
Q
i
i
j
Ecuación 8
El vector final de cálculo es:
q
Q
A
H
A
Q
A
A
N
A
H
A
A
N
A
i
i
i
21
10
11
11
21
12
11
21
0
1
1
1
Ecuación 9
Para mayor compresión del método se desarrollara un ejercicio paso a paso
1. Convención de signos
Las convenciones usadas son las siguientes:
5
Fuente: ejercicio de Hidráulica de tuberías 2013, desarrollado por el autor.
+
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
9
Con relación al sentido de circulación del agua dentro de cada circuito de la red, su valor su
signo será positivo si este es tomado en el mismo sentido en que rotan las manecillas de un
reloj.
Para el caso de los nudos, todo caudal que entre al nudo se considera con signo positivo y todo
caudal que salga del nudo se considera con signo negativo.
2. Las propiedades del fluido para el desarrollo del ejemplo son evaluadas con agua a 15°C, con
las siguientes características:
⁄
⁄
3. Para las tuberías se tomó el valor del diámetro interno efectivo del tubo como el valor dado en
el esquema de la red y con un valor de;
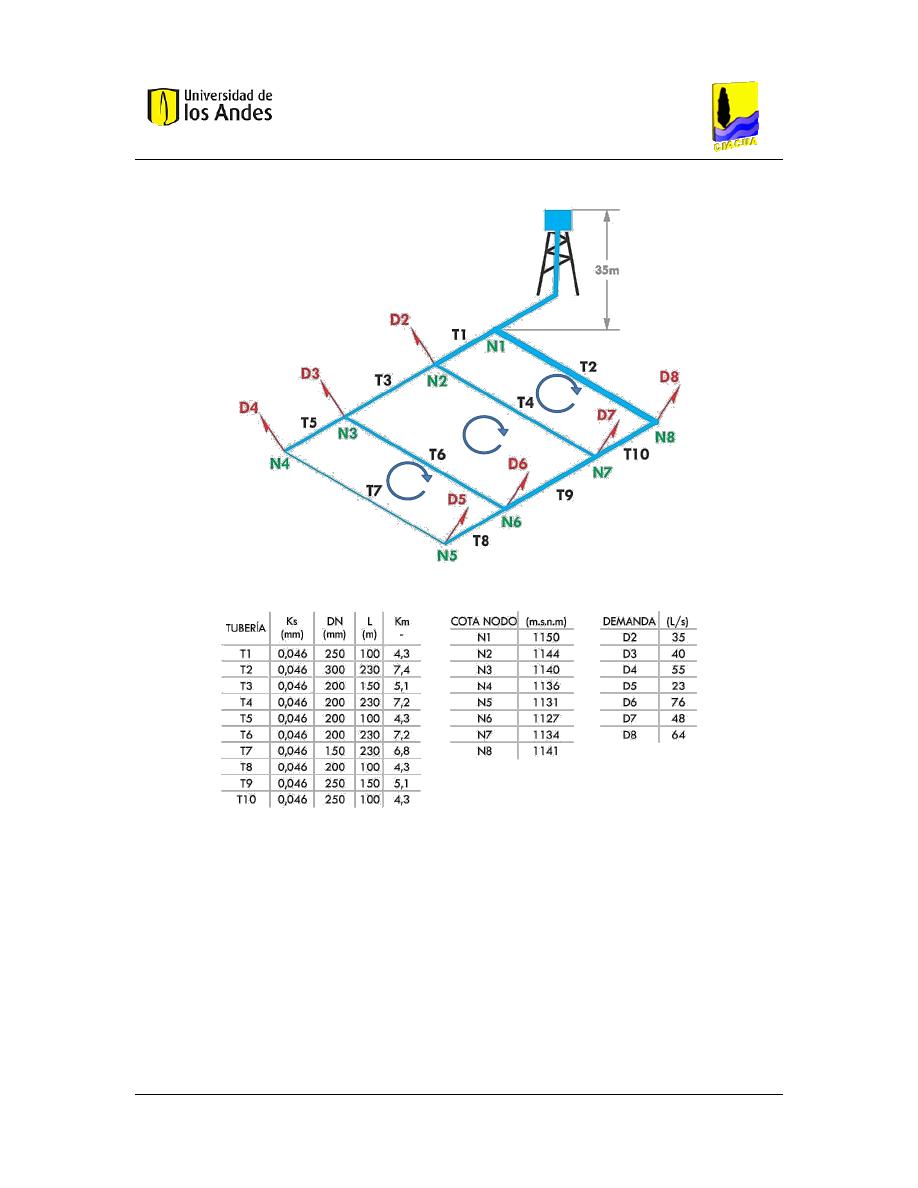
La geometría de la red se muestra en la siguiente grafica;
Figura 1. Geometría de la red para el método del gradiente.
-
+
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
10
Figura 2. Datos para el desarrollo de los análisis de la red.
4. Inicio del procedimiento de análisis
En el proceso de cálculo de la red por el método del gradiente se siguen los siguientes pasos;
Se suponen el caudal para cada tubo, en este caso 1,1 L/s, para todos los tubos.
Número de tubos
NT = 10 tuberías
Número de nudos de presión desconocida
NN = 7 nudos
Número de nudos de presión conocida
NS = 1 nudo
+
+
+

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
11
Se define la matriz de conectividad (NT x NN); el valor de 1 corresponde al nudo de llegada
y el -1 al nudo de salida de la tubería en análisis (ver ¡Error! No se encuentra el origen de
la referencia.), luego se escribe la matriz transpuesta de matriz de conectividad.
[A12]
Matriz de conectividad ( 10 X 7 )
N 2
N 3
N 4
N 5
N 6
N 7
N 8
T 1
1
0
0
0
0
0
0
T 2
0
0
0
0
0
0
1
T 3
-1
1
0
0
0
0
0
T 4
-1
0
0
0
0
1
0
T 5
0
-1
1
0
0
0
0
T 6
0
-1
0
0
1
0
0
T 7
0
0
1
-1
0
0
0
T 8
0
0
0
1
-1
0
0
T 9
0
0
0
0
1
-1
0
T 10
0
0
0
0
0
1
-1
[A21]
Matriz transpuesta ( 7 X 10 )
1
0
-1
-1
0
0
0
0
0
0
0
0
1
0
-1
-1
0
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
0
0
0
-1
1
0
0
0
0
0
0
0
1
0
-1
1
0
0
0
0
1
0
0
0
0
-1
1
0
1
0
0
0
0
0
0
0
-1
Se define la matriz topológica, tramo a nudo para los NS nudos de altura piezométrica fija; su
dimensión es NT x NS. El valor -1 en la fila corresponde a tuberías conectadas a un nudo con
altura piezométrica fija.
Se define el vector de caudales para cada tubería, su dimensión es NT x 1. El valor allí escrito
es la semilla de caudal con el cual el método inicia su proceso de iteración.
Se define el vector de alturas piezométricas desconocidas, su dimensión es NN x 1.
Se define el vector de alturas piezométricas fijas, su dimensión es NS x 1.
Se define el vector de consumos, en cada nudo de la red, su dimensión es, NN x 1
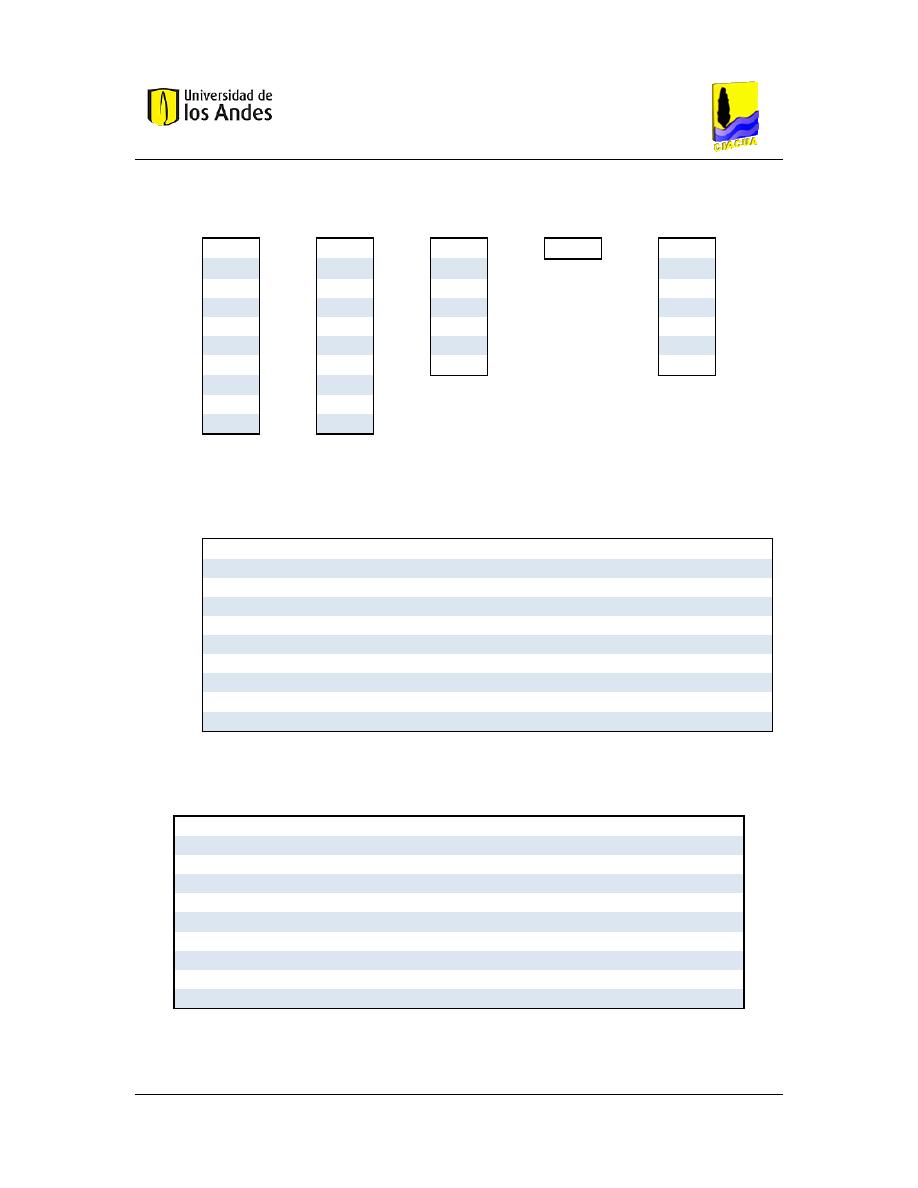
[A10]
Matriz topológica ( 10 X 1 )
[Q]
Vector de caudales (-) sentido de flujo (10 X 1)
[H]
Vector de alturas piezométricas desconocidas ( 7 X 1 )
[Ho]
Vector de alturas piezométricas fijas ( 1 X 1 )
[q]
Vector de consumos ( 7 X 1 )
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
12
[A10]
[Q]
[H]
[Ho]
[q]
( 10 X 1 )
( 10 X 1 )
( 7 X 1 )
( 1 X 1 )
( 7 X 1 )
-1
0,0011
H2
35
-0,035
-1
0,0011
H3
-0,040
0
0,0011
H4
-0,055
0
0,0011
H5
-0,023
0
0,0011
H6
-0,076
0
0,0011
H7
-0,048
0
0,0011
H8
-0,064
0
0,0011
0
0,0011
0
0,0011
Se define una matriz diagonal con dimensión NT x NT, en cuya línea diagonal se escriben el
coeficiente de la ecuación de Darcy – Weisbach. Para este caso de 2.
[N]
Matriz de coeficientes Darcy - Weisbach ( 10 X 10 )
T 1
2
0
0
0
0
0
0
0
0
0
T 2
0
2
0
0
0
0
0
0
0
0
T 3
0
0
2
0
0
0
0
0
0
0
T 4
0
0
0
2
0
0
0
0
0
0
T 5
0
0
0
0
2
0
0
0
0
0
T 6
0
0
0
0
0
2
0
0
0
0
T 7
0
0
0
0
0
0
2
0
0
0
T 8
0
0
0
0
0
0
0
2
0
0
T 9
0
0
0
0
0
0
0
0
2
0
T 10
0
0
0
0
0
0
0
0
0
2
Se define la matriz identidad, con dimensión NT x NT.
[I]
Matriz identidad ( 10 X 10 )
1
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
1

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
13
Con el caudal supuesto en cada tubería y los datos suministrados en el enunciado del
ejercicio, se procede a valuar los parámetros hidráulicos que darán inicio a la primera
iteración, tal como se observa en la Tabla 1.
Tabla 1. Datos de inicio para la primera iteración
TUBERÍA
CAUDAL DIÁMETRO REYNOLDS
f
LONGITUD
COEFIC.
VEL.
ÁREA
h
f
+
h
m
j - i
(m^3/s)
(m)
(m)
km
m/s
m^2
(m)
1 - 2
0,0011
0,25
4910
0,0378
100
4,3
0,02
0,049
4,97E-04
410,7
1 - 8
0,0011
0,30
4092
0,0398
230
7,4
0,02
0,071
4,68E-04
386,7
2 - 3
0,0011
0,20
6137
0,0356
150
5,1
0,04
0,031
1,99E-03
1640,6
2 - 7
0,0011
0,20
6137
0,0356
230
7,2
0,04
0,031
3,01E-03
2483,6
3 - 4
0,0011
0,20
6137
0,0356
100
4,3
0,04
0,031
1,38E-03
1140,2
3 - 6
0,0011
0,20
6137
0,0356
230
7,2
0,04
0,031
3,01E-03
2483,6
5 - 4
0,0011
0,15
8183
0,0330
230
6,8
0,06
0,018
1,13E-02
9372,2
6 - 5
0,0011
0,20
6137
0,0356
100
4,3
0,04
0,031
1,38E-03
1140,2
7 - 6
0,0011
0,25
4910
0,0378
150
5,1
0,02
0,049
7,11E-04
587,5
8 - 7
0,0011
0,25
4910
0,0378
100
4,3
0,02
0,049
4,97E-04
410,7
El valor de cada coeficiente corresponde a la multiplicación del caudal por
[A11]
Matriz de coeficientes ( 10 X 10 )
0,452
0
0
0
0
0
0
0
0
0
0
0,425
0
0
0
0
0
0
0
0
0
0
1,805
0
0
0
0
0
0
0
0
0
0
2,732
0
0
0
0
0
0
0
0
0
0
1,254
0
0
0
0
0
0
0
0
0
0
2,732
0
0
0
0
0
0
0
0
0
0
10,309
0
0
0
0
0
0
0
0
0
0
1,254
0
0
0
0
0
0
0
0
0
0
0,646
0
0
0
0
0
0
0
0
0
0
0,452
Se transpone la matriz calculada anteriormente
[A11]'
Matriz de coeficientes ( 10 X 10 )
0,452
0
0
0
0
0
0
0
0
0
0
0,425
0
0
0
0
0
0
0
0
0
0
1,805
0
0
0
0
0
0
0
0
0
0
2,732
0
0
0
0
0
0
0
0
0
0
1,254
0
0
0
0
0
0
0
0
0
0
2,732
0
0
0
0
0
0
0
0
0
0
10,309
0
0
0
0
0
0
0
0
0
0
1,254
0
0
0
0
0
0
0
0
0
0
0,646
0
0
0
0
0
0
0
0
0
0
0,452

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
14
Se multiplica la matriz de coeficiente de Darcy con la matriz transpuesta anterior.
( [N] [A11]' )
( 10 X 10 ) ( 10 X 10 )
( 10 x 10 )
0,904
0
0
0
0
0
0
0
0
0
0
0,851
0
0
0
0
0
0
0
0
0
0
3,609
0
0
0
0
0
0
0
0
0
0
5,464
0
0
0
0
0
0
0
0
0
0
2,509
0
0
0
0
0
0
0
0
0
0
5,464
0
0
0
0
0
0
0
0
0
0
20,619
0
0
0
0
0
0
0
0
0
0
2,509
0
0
0
0
0
0
0
0
0
0
1,293
0
0
0
0
0
0
0
0
0
0
0,904
Se halla la matriz inversa de la anterior.
( [N] [A11]' ) ^-1
( 10 X 10 ) ( 10 X 10 )
( 10 x 10 )
1,107
0
0
0
0
0
0
0
0
0
0
1,175
0
0
0
0
0
0
0
0
0
0
0,277
0
0
0
0
0
0
0
0
0
0
0,183
0
0
0
0
0
0
0
0
0
0
0,399
0
0
0
0
0
0
0
0
0
0
0,183
0
0
0
0
0
0
0
0
0
0
0,048
0
0
0
0
0
0
0
0
0
0
0,399
0
0
0
0
0
0
0
0
0
0
0,774
0
0
0
0
0
0
0
0
0
0
1,107
Se multiplica la matriz transpuesta de la conectividad con la matriz anterior (matriz base 1)
[A21] ( [N] [A11]' ) ^-1
( 7 X 10 ) ( 10 X 10 )
( 7 x 10 )
1,10671
0
-0,27706
-0,18302
0
0
0
0
0
0
0
0
0,27706
0
-0,39864
-0,18302
0
0
0
0
0
0
0
0
0,39864
0
0,0485
0
0
0
0
0
0
0
0
0
-0,0485
0,39864
0
0
0
0
0
0
0
0,18302
0
-0,39864
0,77366
0
0
0
0
0,18302
0
0
0
0
-0,77366
1,10671
0
1,17535
0
0
0
0
0
0
0
-1,10671

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
15
La matriz anterior se multiplica por la matriz de conectividad
[A21] ( [N] [A11]' ) ^-1 [A12]
( 7 X 10 ) ( 10 X 7 )
( 7 x 7 )
1,56678
-0,277056
0
0
0
-0,18301
0
-0,27706
0,858718
-0,39864
0
-0,18302
0
0
0
-0,398644
0,44714
-0,0485
0
0
0
0
0
-0,0485
0,44714
-0,39864
0
0
0
-0,183018
0
-0,39864
1,35533
-0,77366
0
-0,18302
0
0
0
-0,77366
2,06338
-1,10671
0
0
0
0
0
-1,10670
2,28206
Se halla inversa de la matriz calculada anteriormente y se multiplica por -1 (Matriz base 2)
- ( [A21] ( [N] [A11]' ) ^-1 [A12] )^-1
( 7 X 10 ) ( 10 X 7 )
( 7 X 7 )
-0,770
-0,574
-0,550
-0,353
-0,329
-0,259
-0,126
-0,574
-2,824
-2,658
-1,293
-1,127
-0,640
-0,310
-0,550
-2,658
-4,780
-1,610
-1,224
-0,686
-0,333
-0,353
-1,293
-1,610
-4,216
-2,024
-1,068
-0,518
-0,329
-1,127
-1,224
-2,024
-2,122
-1,115
-0,541
-0,259
-0,640
-0,686
-1,068
-1,115
-1,251
-0,607
-0,126
-0,310
-0,333
-0,518
-0,541
-0,607
-0,732
Se multiplica la matriz del número de tuberías con el vector de caudal, a su vez se
multiplica la matriz topológica por el vector de alturas piezométricas fijas, luego se suman
estas dos matrices. (Matriz base 3)
[A11] [Q]
[A10] [Ho]
[A11] [Q] + [A10] [Ho]
( 10 X 1 )
( 10 X 1 )
( 10 X 1 )
0,0005
-35,0
-35,000
0,0005
-35,0
-35,000
0,0020
0,0
0,002
0,0030
0,0
0,003
0,0014
0,0
0,001
0,0030
0,0
0,003
0,0113
0,0
0,011
0,0014
0,0
0,001
0,0007
0,0
0,001
0,0005
0,0
0,000

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
16
Se multiplica la matriz base 1 por la matriz base 2, y a este resultado se le suma el
resultado de la multiplicación de la matriz transpuesta de la conectividad por el vector de
caudales y se le resta el vector de consumos. (Matriz base 4)
( [A21] ( [N] [A11]' ) ^-1 ( [A11] [Q] + [A10] [Ho] ) -
[A21] [Q]
-
[q]
=
[R]
( 7 x 1 )
( 7 X 1 )
( 7 X 1 )
( 7 X 1 )
-38,735
-0,0011
-0,035
-38,699
-0,001
-0,0011
-0,040
0,041
0,001
0,0022
-0,055
0,054
0,000
0,0000
-0,023
0,023
0,001
0,0011
-0,076
0,075
0,001
0,0011
-0,048
0,047
-41,137
0,0000
-0,064
-41,073
Se multiplica la matriz base 2 con la matriz base 4, y se determinan así las alturas
piezométricas.
ALTURAS PIEZOMÉTRICAS
[H i+1] = - ( [A21] ( [N] [A11]' ) ^-1 [A12] )^-1 ) ( [R] )
( 7 X 1 )
34,87
34,56
34,43
34,51
34,58
34,72
34,84
Se multiplica la matriz de conectividad con la matriz de las alturas piezométricas,
encontrada anteriormente, a este resultado se le suma el resultado de la multiplicación de
la matriz topológica por el vector de alturas piezométricas fijas dando como resultado la
matriz R2.
Se halla la inversa de la multiplicación de la matriz diagonal de coeficientes de Darcy con la
matriz diagonal, este resultado se multiplica por la matriz R2. (Matriz base 5)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
17
CAUDALES
[A12] [H i+1]
+
[A10]
[Ho]
=
[R2]
( [N] [A11]' )^-1 ( [R2] )
( 10 X 1 )
( 10 X 1 )
( 10 X 1 )
( 10 X 1 )
34,866
-35,00
-0,134
-0,1479
34,837
-35,00
-0,163
-0,192
-0,309
0,00
-0,309
-0,08574
-0,145
0,00
-0,145
-0,02661
-0,125
0,00
-0,125
-0,04988
0,026
0,00
0,026
0,00468
-0,083
0,00
-0,083
-0,00402
-0,068
0,00
-0,068
-0,02702
-0,139
0,00
-0,139
-0,10716
-0,116
0,00
-0,116
-0,128
Se halla la inversa de la multiplicación de la matriz diagonal de coeficientes de Darcy con la
matriz diagonal y se multiplica nuevamente por la matriz diagonal.
( [N] [A11]' )^-1 [A11]
( 10 X 10 )
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
18
A la matriz identidad se le resta la matriz hallada anteriormente
[I] - ( [N] [A11]' )^-1 [A11]
( 10 X 10 )
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
0
0
0
0
0
0
0
0
0
0
0,500
Se multiplica la matriz anterior por el resultado de la multiplicación de la matriz diagonal
de coeficiente por el vector de caudales.
Finalmente el caudal calculado en cada tubería corresponde a la resta de la matriz
calculada anteriormente menos la matriz base 5.
( [I] - ( [N] [A11]' )^-1 [A11] ) ([A11] [Q])
( 10 X 1 )
TUBERÍA
j - i
(m^3/s)
L/s
0,00055
1 - 2
0,1484
148,45
0,00055
1 - 8
0,1926
192,55
0,00055
2 - 3
0,0863
86,29
0,00055
2 - 7
0,0272
27,16
0,00055
3 - 4
0,0504
50,43
0,00055
3 - 6
-0,0041
-4,13
0,00055
5 - 4
0,0046
4,57
0,00055
6 - 5
0,0276
27,57
0,00055
7 - 6
0,1077
107,71
0,00055
8 - 7
0,1286
128,55
Con los caudales estimados se inicia la segunda iteración.
Los caudales estimados en la primera iteración son la semilla para determinar el valor del
coeficiente
el cual se usara como base de la matriz [A11] en el nuevo cálculo.
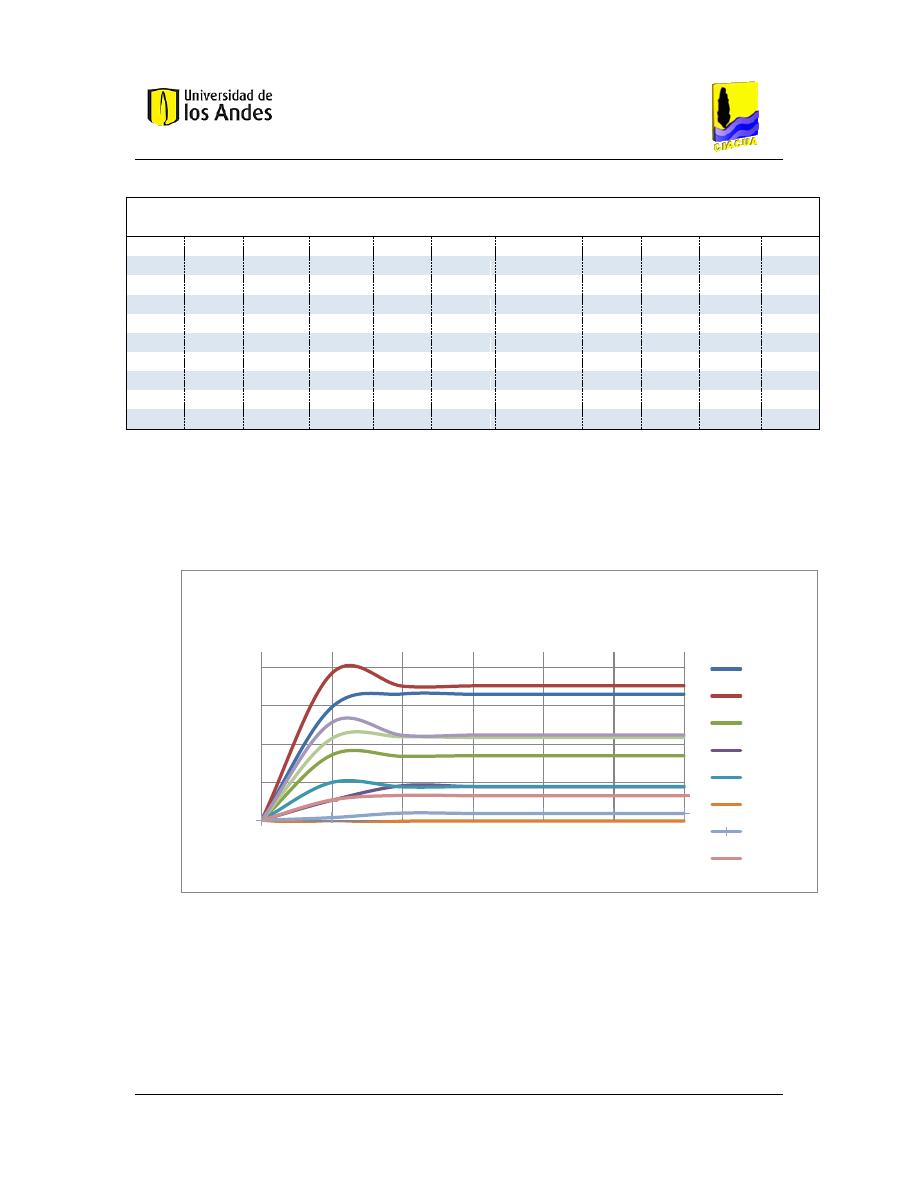
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
19
Tabla 2. Datos para la segunda iteración
TUBERÍA
CAUDAL DIÁMETRO REYNOLDS
f
LONGITUD
COEFIC.
VEL.
ÁREA
h
f
+
h
m
j - i
(m^3/s)
(m)
(m)
km
m/s
m^2
(m)
1 - 2
0,1484
0,25
662618
0,0149
100
4,3
3,02
0,049
4,79E+00
217,3
1 - 8
0,1926
0,30
716223
0,0145
230
7,4
2,72
0,071
7,00E+00
188,9
2 - 3
0,0863
0,20
481471
0,0158
150
5,1
2,75
0,031
6,50E+00
873,4
2 - 7
0,0272
0,20
151519
0,0180
230
7,2
0,86
0,031
1,06E+00
1441,8
3 - 4
0,0504
0,20
281362
0,0166
100
4,3
1,61
0,031
1,65E+00
649,7
3 - 6
-0,0041
0,20
23070
0,0243
230
7,2
-0,13
0,031
3,11E-02
1817,8
5 - 4
0,0046
0,15
34014
0,0248
230
6,8
0,26
0,018
1,53E-01
7314,7
6 - 5
0,0276
0,20
153838
0,0180
100
4,3
0,88
0,031
5,22E-01
687,0
7 - 6
0,1077
0,25
480760
0,0153
150
5,1
2,19
0,049
3,51E+00
302,6
8 - 7
0,1286
0,25
573797
0,0151
100
4,3
2,62
0,049
3,61E+00
218,7
Se repite este procedimiento hasta verificar que el sistema ha convergido con base en un valor de
un error de exactitud entre el penúltimo y último caudal; para este ejemplo el método llegó a un
valor aceptable en la sexta iteración. La velocidad de con la que converge el método para este
ejemplo por tubería se observa en la ¡Error! No se encuentra el origen de la referencia..
Gráfica 1. Convergencia del método del gradiente
0
50
100
150
200
0
1
2
3
4
5
6
Q
(
L/
s)
NUMERO DE ITERACIÓN
VELOCIDAD DE CONVERGENCIA - METODO DEL
GRADIENTE
TUBO 1-2
TUBO 1-8
TUBO 2-3
TUBO 2-7
TUBO 3-4
TUBO 3-6
TUBO 5-4
TUBO 6-5

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
20
Tabla 3. Datos de la última iteración
TUBERÍA
CAUDAL DIÁMETRO REYNOLDS
f
LONGITUD
COEFIC.
VEL.
ÁREA
h
f
+
h
m
j - i
(m^3/s)
(m)
(m)
km
m/s
m^2
(m)
1 - 2
0,1650
0,25
736488
0,0148
100
4,3
3,36
0,049
5,89E+00
216,2
1 - 8
0,1760
0,30
654664
0,0146
230
7,4
2,49
0,071
5,88E+00
189,8
2 - 3
0,0852
0,20
475137
0,0158
150
5,1
2,71
0,031
6,34E+00
874,0
2 - 7
0,0448
0,20
250190
0,0168
230
7,2
1,43
0,031
2,76E+00
1370,7
3 - 4
0,0451
0,20
251787
0,0168
100
4,3
1,44
0,031
1,34E+00
656,0
3 - 6
0,0000
0,20
171
0,3745
230
7,2
0,00
0,031
2,12E-05
22609,7
5 - 4
0,0099
0,15
73447
0,0205
230
6,8
0,56
0,018
6,08E-01
6238,6
6 - 5
0,0329
0,20
183413
0,0175
100
4,3
1,05
0,031
7,28E-01
673,6
7 - 6
0,1088
0,25
485827
0,0153
150
5,1
2,22
0,049
3,58E+00
302,4
8 - 7
0,1120
0,25
499927
0,0153
100
4,3
2,28
0,049
2,76E+00
220,3
4.2 Análisis de calidad de agua: concentración de un soluto (NaCl), en un nudo
Antes de analizar el comportamiento de la calidad del agua es necesario determinar el tipo de
sustancia que como soluto es objeto de este proyecto y su relación con la calidad del agua en la
red. Conocida la sustancia y su incidencia en la calidad del agua potable, se establecerán las
teorías actuales de mezcla en las uniones (nudos correspondientes al modelo hidráulico), de una
red de distribución de agua potable y se establecerán la bases para el desarrollo del experimento
que busca una nueva aproximación para estimar las concentraciones de Cloro libre (con base en
lo observado con NaCl), del agua de salida de una cruz (nudo).
4.2.1 Desinfección
La desinfección, es el proceso unitario final que se encarga de eliminar a los microorganismos
patógenos que se encuentran en el agua, tales como; Bacterias, protozoarios, virus y tremátodos.
Como lo define Jairo A. Romero R.
6
, El propósito primerio de la desinfección del agua es el impedir
la diseminación de enfermedades hídricas.
Como lo explica María P. Villegas
7
, la destrucción de los microorganismos mediante la desinfección
es función tanto del tiempo de exposición al agente letal (tiempo de contacto), como del
desinfectante usado, como se muestra a continuación, para el Cloro:
(
)
Ecuación 10
Para un pH de 7, k toma los siguientes valores
k = 1,6 x 10
-2
, residual de Cloro libre
k = 1,6 x 10
-5
, residual de Cloro combinado
6
Romero R., Jairo A. (2002). Calidad del Agua. Bogotá. Escuela Colombiana de Ingeniería.
7
Villegas de B., María P. (2008). Purificación de Aguas, Ejercicios. Bogotá. Escuela Colombiana de Ingeniería.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
21
La anterior ecuación, muestra finalmente que el proceso de desinfección con Cloro, es función
básicamente de: el tiempo de contacto, la temperatura del agua, el pH del agua, el número de
microorganismos, la dosis de Cloro y tipo de Cloro residual.
Aunque existen diferentes tipos de desinfectante, el Cloro es el desinfectante más usado, ya que
es un agente oxidante fuerte, económico y fácil de conseguir. La característica más importante del
Cloro es que a bajas concentraciones, y después de reaccionar con elementos presentes en el agua
filtrada, deja un residual en solución dentro de la red de distribución de agua que actúa como un
desinfectante en el tiempo, sin dejar sabor y siendo inocuo para el consumo humano. La porción
de Cloro que queda en solución en el agua después de un determinado tiempo de contacto ya sea
como ácido hipocloroso o ión hipoclorito se conoce como Cloro residual libre. El valor del Cloro
residual libre exigido en Colombia debe estar en el rango de 0,3 y 2,0 mg/L. Por otra parte el Cloro
consumido, corresponde a la cantidad Cloro utilizado en la reacción para eliminar los
microorganismos en el agua; así se establece la siguiente igualdad;
Ecuación 11
La reacción química que se presenta es:
Ecuación 12
Ecuación 13
A su vez:
Ecuación 14
Ecuación 15
Siendo el ácido hipoclorito el de mayor efectividad relativa en el proceso de desinfección.
El Cloro tiene la desventaja de ser muy inestable con la temperatura del agua que lo contiene, con
la exposición a la luz y a la variación del pH entre otros
8
.
8
Por ello para el desarrollo del experimento se utilizara NaCl como soluto e inferir con los resultados la
metodología que permita aplicar el cálculo de concentraciones obtenidas para NaCl al Cloro residual libre.
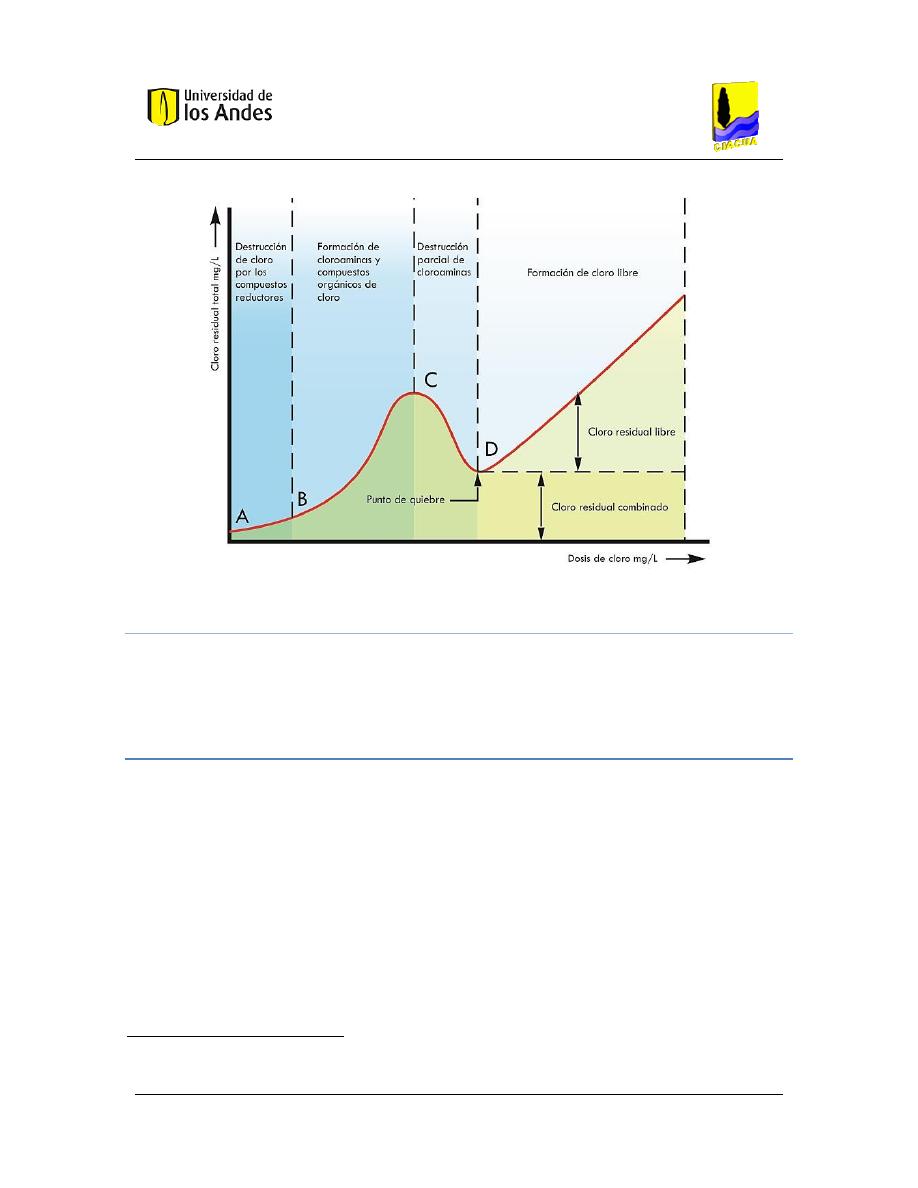
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
22
Figura 3. Curva de demanda de Cloro.
9
4.2.2 Difusión
En la difusión, pequeñas partículas como moléculas, iones u otras, y gracias a la entropía del
sistema, se mezclan de manera lenta y espontánea, a través de desplazamientos de zonas de alta
concentración de esas partículas a zonas de baja concentración de las mismas.
4.3 Modelo de mezcla completa: método tradicional
El modelo de mezcla completa, es el más usado por los programas informáticos que permiten la
realización de modelos de calidad de agua en redes de distribución. EPANET y otros programas
comerciales usan este método para estimar el tipo de mezcla de un soluto en las uniones del
modelo. El modelo supone una mezcla completa e instantánea en las uniones (nudos de la red), la
facilidad de la formula permite un cálculo rápido y aproximado de fenómeno de mezcla, siendo de
fácil incorporación a un programa informático.
Dado que el modelo se basa en la mezcla completa e instantánea del soluto a través de los flujos
de agua que discurren por la unión, este modelo prevé la mayor mezcla posible que puede ocurrir
dentro de la misma. Sin embargo la anterior premisa deja de lado las interacciones físicas de los
flujos que discurren: diferencia de caudales, presiones y derivadas de las dos anteriores las fuerzas
de impulso, generando datos antagónicos entre el modelo informático y los datos obtenidos en
9
Adaptado por el autor de: Romero R., Jairo A. (2002). Calidad del Agua. Bogotá. Escuela Colombiana de
Ingeniería.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
23
campo en modelos físicos o en la red misma. Un balance de masa del soluto en la unión se puede
evaluar con la siguiente ecuación, para un solo caudal de salida.
∑
Ecuación 16
De manera más general y tal como lo describe el modelo que usa WaterCad
10
, la concentración
resultante de una mezcla total en un nudo se puede calcular de la siguiente manera:
∑
∑
Ecuación 17
dónde:
C
out, j
: Concentración saliente del accesorio en el nudo j (M/L
3
)
Out
j
: Grupo de tuberías que salen del nudo j
In
j
: Grupo de tuberías que entran al nudo j
Q
i
: Caudal que entra al nudo por la tubería i (L
3
/T)
C
i,ni
: Concentración que entra al nudo por la tubería i (M/L
3
)
U
j
: Suministro externo de concentración al nudo j (M/T)
4.4 Modelo de mezcla parcial: concepción moderna.
Resultado de diferentes investigaciones, modelos físicos y modelos realizados a través de la
Computational Fluid Dynamics (CFD), se corroboró que el modelo de mezcla completa no era el
más acertado para predecir la concentración de un soluto a la salida de una unión. Con las
observaciones efectuadas y los datos obtenidos experimentalmente, se desarrolló el modelo de
mezcla parcial.
10
Bentley Institute Press. (2007), primera edición. Advanced Water Distribution Modeling and
Management. Exton Pennsylvania. Bentley Systems Inc.
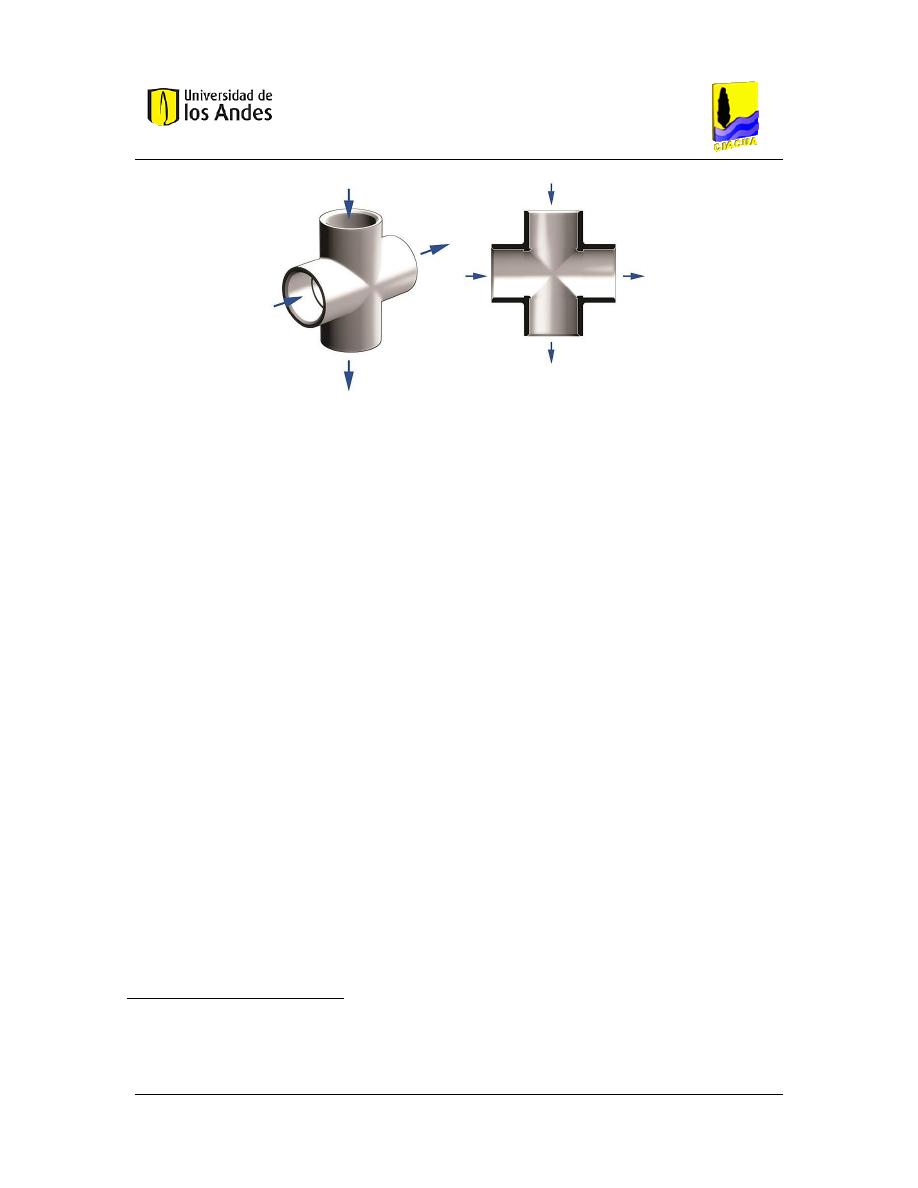
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
24
Figura 4. Características internas de la tee de PVC de 1” usada como unión en el experimento
11
.
Este modelo complementa el modelo tradicional de mezcla completa, proporcionando un
acercamiento real al fenómeno de mezcla, tomando en cuenta las reacciones físicas (velocidad del
agua, impulso) y químicas (variación de la concentración), del flujo que discurre por cada tubería
de ingreso a la unión y su interacción con las paredes y geometría del accesorio que los contiene y
une.
En el modelo de mezcla parcial, el impulso desigual de los flujos que discurren a través de la unión
que en conjunto con otras variables hidráulicas en los modelos hacen que a la salida de la misma
exista una diferencia en los caudales, sin mantener una relación de proporción o igualdad con los
caudales de entrada (salvo en algunos casos), tal como es de esperarse debido a resultado del
modelo hidráulico.
Dada esta independencia de los caudales de salida, el impulso de flujo por alguna de las entradas
(fuerza resultante del tubo de ingreso 1), podrá ser tal que supere al impulso de la otra (fuerza
resultante del tubo de ingreso 2), la sumatoria final de fuerzas en la unión hará que parte del
flujo del líquido que ingresa a la unión por el extremo 1, desplace espacialmente (dentro de punto
de convergencia de los flujos en la unión) , al flujo del líquido que ingresa a la unión por el extremo
2, modificando la concentración del soluto que ingresa con el líquido a través del extremo 2 y que
sale a través del extremo 3 de la unión
11
Adaptado por el autor de: Ho. Clifford. (2008). Solute Mixing Models for Water-Distribution Pipe
Networks. Recuperado el de octubre de 2013, de ASCE:
http://gsgc.gzhu.edu.cn/gpsgd/UploadFile/200942623229730.pdf
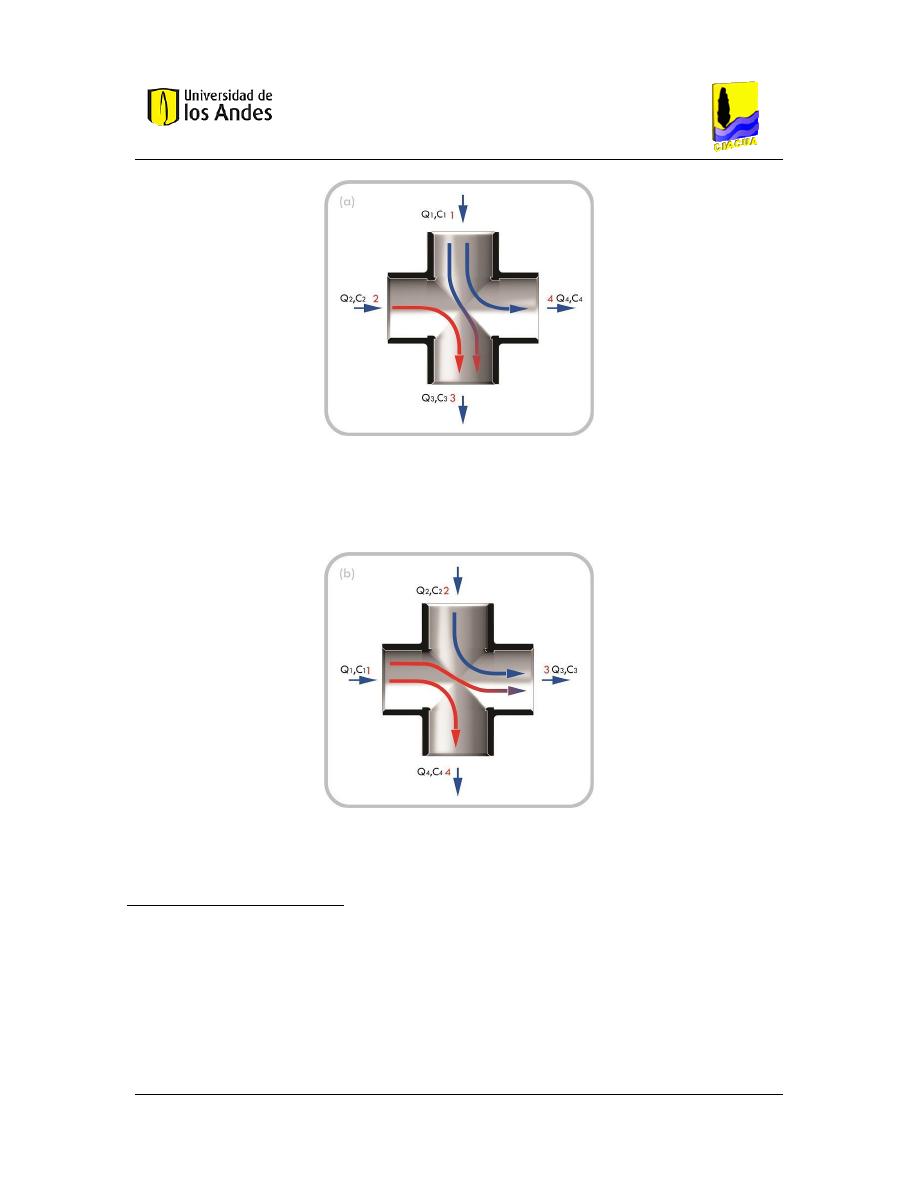
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
25
Figura 5. Mayor impulso en la dirección vertical
12
De igual manera puede ocurrir si el impulso es mayor en el líquido que fluye e ingresa por el
extremo 2 de la unión, que el impulso el líquido que fluye e ingresa por el extremo 1 de la unión
como se observa a continuación.
Figura 6. Mayor impulso en la dirección horizontal
13
Se puede presentar también el caso en el cual no exista mezcla alguna; esto se da si:
12
Adaptado por el autor de: Ho. Clifford. (2008). Solute Mixing Models for Water-Distribution Pipe
Networks. Recuperado el de octubre de 2013, de ASCE:
http://gsgc.gzhu.edu.cn/gpsgd/UploadFile/200942623229730.pdf
13
Adaptado por el autor de: Ho. Clifford. (2008). Solute Mixing Models for Water-Distribution Pipe
Networks. Recuperado el de octubre de 2013, de ASCE:
http://gsgc.gzhu.edu.cn/gpsgd/UploadFile/200942623229730.pdf

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
26
1. Si los caudales que ingresan a la unión son iguales, y poseen el mismo impulso
2. Si el caudal que fluye por la tubería de entrada y salida colindantes son iguales.
Bajo estas circunstancias los flujos chocan, la sumatoria de las fuerzas derivadas del impulso se
anulan y por tanto el flujo se bifurca completamente y no existirá mezcla.
Para la aplicación del modelo de mezcla parcial se realizan los siguientes pasos:
1. Calcular la tasa de cambio del impulso del fluido tuberías que ingresan a la unión, y en las que
salen de la unión, es decir, entradas y salidas situados a 180° entre ellas.
⃗
Ecuación 18
2. Asignar el número 1, al flujo del líquido que discurre la entrada en la unión y que tiene mayor
impulso, asignar el número 3, a la salida de la unión enfrentada al ingreso en 1*.
3. Asignar el número 2, al flujo del líquido que discurre la entrada en la unión y que tiene menor
impulso, asignar el número 4, a la salida de la unión enfrentada al ingreso en 2*.
* Ver ilustraciones siguientes.
Dado que el cambio de temperatura en el agua que fluye por las redes de distribución de agua
durante un día potable varía muy poco (no más de 10°C), su densidad puede tomarse como
constante y bajo estas condiciones el criterio de impulso es el siguiente:
Ecuación 19
La anterior ecuación está fundamentada bajo la consideración que las conexiones en la
unión contengan tuberías con el mismo diámetro interno, siendo sólo aplicable para estos
casos. Para uniones con diferentes diámetros se debe hallar otra ecuación.
Con las conexiones identificadas, es posible establecer las diferentes concentraciones de salida,
con base en las siguientes suposiciones:
1. El modelo hidráulico suministra el valor de los caudales que entran o salen de la unión (no se
toman en cuenta las demandas), Q
1
, Q
2
, Q
3
y Q
4
.
2. Se conocen las concentraciones del soluto en cada una de las entradas del fluido a la unión. C
1
y C
2.
3. El soluto transportado por el fluido y que ingresa a la unión proveniente de las tuberías, está
totalmente disuelto y perfectamente mezclado en él.
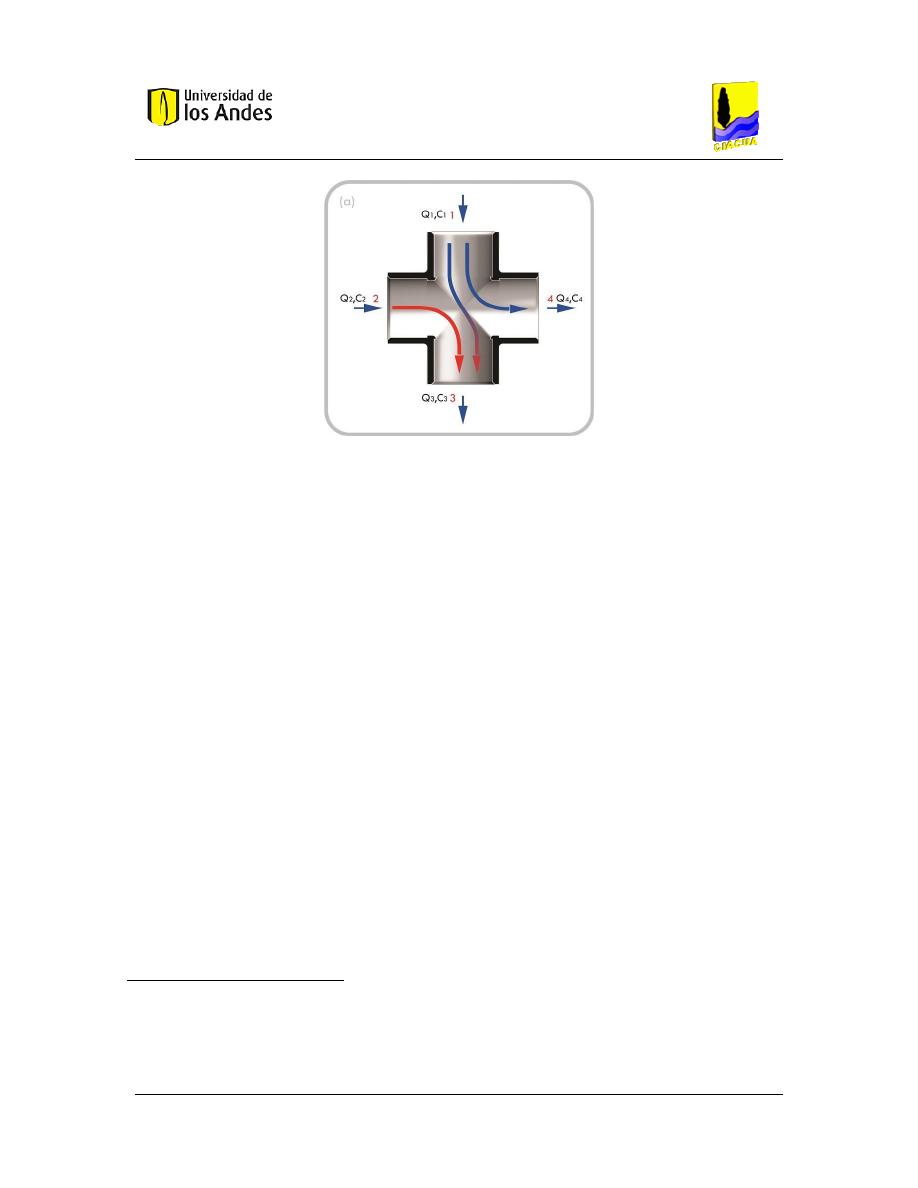
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
27
Figura 7. Mayor impulso en la dirección vertical
14
Analizando la figura anterior es evidente que el caudal de agua que sale por el extremo 4 de la
unión (
), proviene de 1, y como se aprecia, este caudal no tiene contacto con el que
ingresa por 2, de tal manera que las características químicas de 1 se conservan y son las que están
contenidas en 4 (
), matemáticamente esto se puede representar como sigue:
Ecuación 20
Siendo la anterior expresión el balance de masa del soluto de que sale de la tubería 4.
La concentración del soluto que sale por el extremo 3 hacia la tubería, se halla realizando un
balance de masa del soluto a través de la unión.
Ecuación 21
Como (
),
Ecuación 22
Despejando C
3
14
Adaptado por el autor de: Ho. Clifford. (2008). Solute Mixing Models for Water-Distribution Pipe
Networks. Recuperado el de octubre de 2013, de ASCE:
http://gsgc.gzhu.edu.cn/gpsgd/UploadFile/200942623229730.pdf

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
28
(
)
Ecuación 23
La ecuación anterior determina que conociendo los caudales de entrada y salida, y la
concentración del soluto en una entrada y una salida en la unión en cruz, se puede determinar la
concentración en la salida faltante. El valor de los caudales se evalúa previamente a través de
métodos como el del gradiente. La forma de la ecuación permite ser implantada fácilmente en el
algoritmo de un programa computacional para la modelación de redes de tuberías.
Existe otra manera para determinar la concentración de un soluto que sale por el extremo 3 hacia
la tubería; Romero-Gómez
15
, propusieron una metodología basada en la razón que existe entre los
caudales de entrada Q
1
y Q
2
, como resultado de sus experimentos. La metodología es como se
presenta a continuación:
Primero se definen dos variables x y y, así:
Ecuación 24
Aplicando la conservación de masa de agua que fluye a través de la unión, se tienen;
Ecuación 25
Combinando las anteriores ecuaciones se tienen las siguientes razones entre caudales y las
variables x y y
Ecuación 26
De igual manera se tiene
Ecuación 27
Combinando las dos anteriores ecuaciones y combinándolas con la relación de concentraciones se
tiene;
(
)
(
)
Ecuación 28
15
Ho. Clifford. (2008). Solute Mixing Models for Water-Distribution Pipe Networks. Recuperado el de
octubre de 2013, de ASCE: http://gsgc.gzhu.edu.cn/gpsgd/UploadFile/200942623229730.pdf

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
29
5 Observaciones sobre el experimento
Para realizar el experimento y poder cotejar los resultados obtenidos en el mismo vs el marco
teórico descrito en el numeral anterior, es necesario conocer la procedencia de las ecuaciones y
parámetros descritos. Conocer qué bases físicas y químicas tiene lo anterior es fundamental para
el desarrollo del experimento y la comparación de los resultados de mismo.
Se propone primero determinar las ecuaciones anteriormente halladas; posteriormente se plantea
hacer un modelo de la instalación del experimento con EPANET e interpretar sus resultados
hidráulicos con la teoría aquí expuesta.
5.1 ¿Por qué lo lógico es suponer predominio de mezclas parciales y no totales en
una unión?
Tomando en consideración que el elemento de estudio corresponde a una cruz cuyos diámetros
de entrada y salida son iguales, y que además su configuración geométrica interna es simétrica (en
teoría), se pueden identificar cuatro (4) posibles configuraciones de flujo de la solución dentro de
la unión.
De estas configuraciones, el caso número 4 es el más común en los nudos de sistemas de
distribución de agua potable, siendo además este caso el que afecta de manera significativa la
distribución de las concentraciones de un soluto en un red de tuberías.
Para el caso del Cloro Residual, aunque este se degrada a medida que fluye mezclado con el agua a
través de la red de tuberías de distribución, por las reacciones con la pared de las mismas y de los
accesorios que la conforman, la distribución de la concentración del mismo en los nudos genera un
mayor impacto en el modelo de simulación de calidad de agua distribuida en la red.
5.1.1 Caudales confluyentes en una cruz.
5.1.1.1 Primer caso
Una primera configuración corresponde a una única entrada de flujo en la cruz y con tres salidas,
tal como aparece en la figura que sigue.
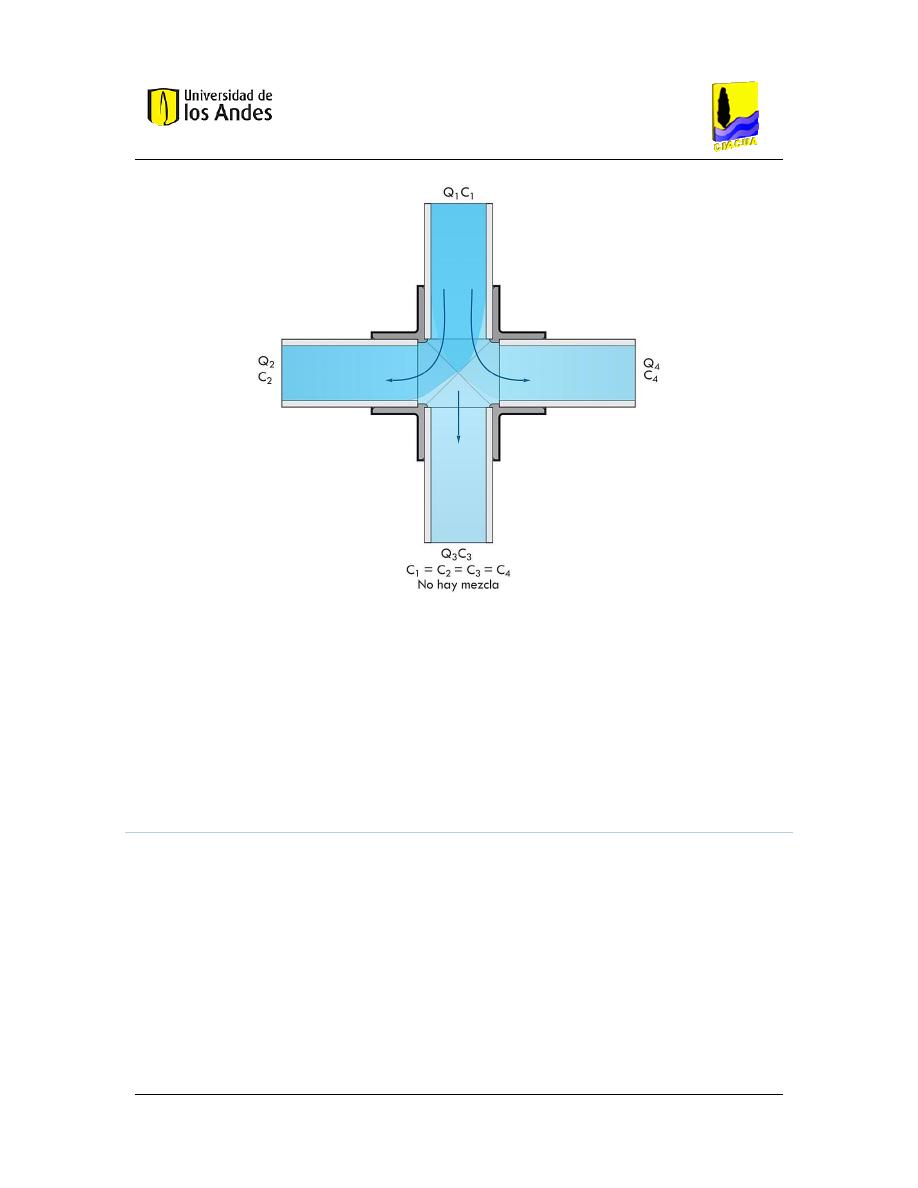
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
30
Figura 8. Única entrada de flujo con su concentración a la cruz.
En esta configuración se observa que el caudal de entrada, con su respectiva concentración, se
distribuye en las tres salidas, manteniéndose en cada una de ellas la misma concentración.
Ecuación 29
5.1.1.2 Segundo caso
Una segunda configuración corresponde al ingreso de dos caudales por los extremos opuestos de
la cruz, los cuales se encuentran en el centro de esta y se distribuyen por las salidas que quedan
perpendiculares a la dirección del flujo de ingreso del soluto. En este caso si los caudales son
iguales, la mitad del caudal entrante por cada uno de los ingresos se desplazará hacia cada una de
las salidas, e igualmente ocurrirá con las respectivas concentraciones, dando como resultado una
mezcla total.
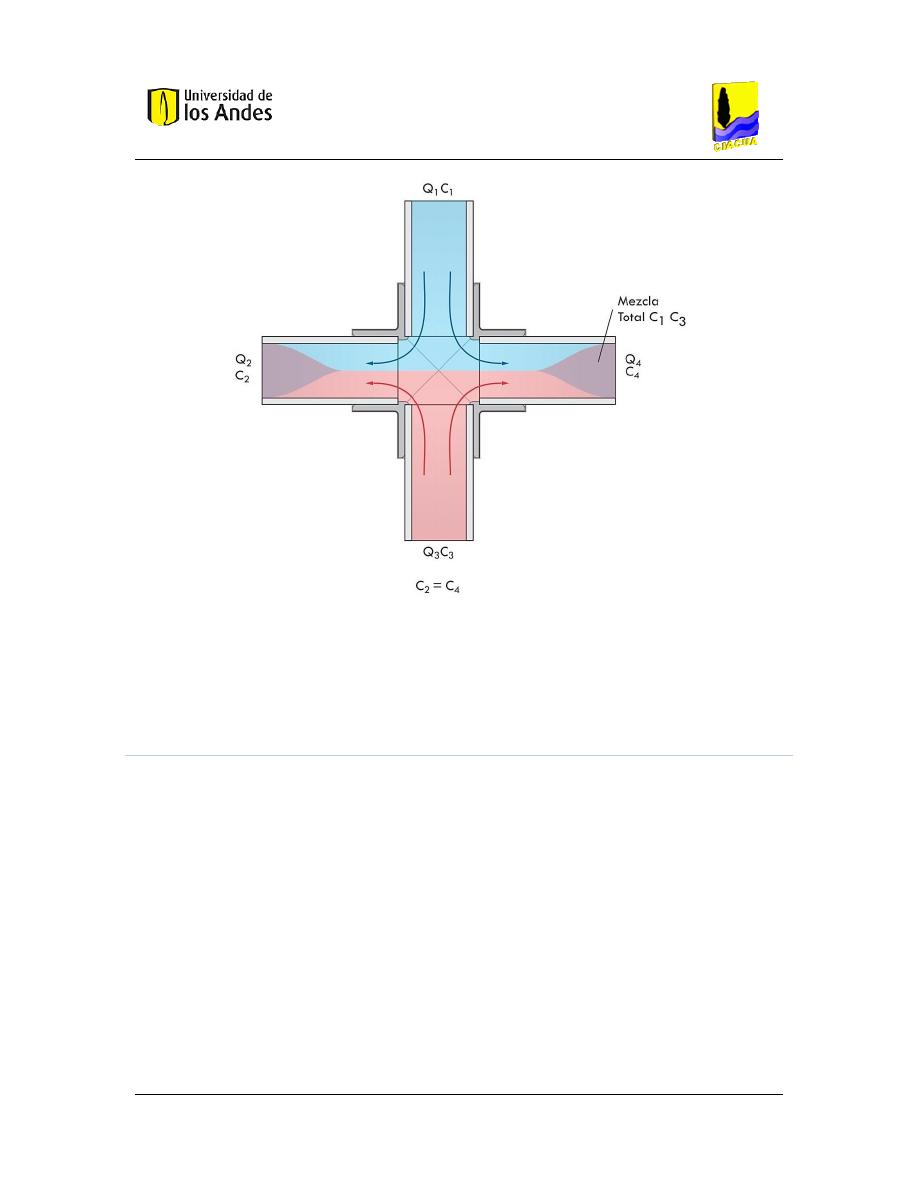
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
31
Figura 9. Flujo por entradas encontradas hacia el centro de la cruz.
En una variación de esta configuración, donde un caudal de entrada es mayor que el otro, los
caudales de salida estarán compuestos por una proporción de los caudales de entrada, que
corresponde a la suma de las mitades de los caudales de entrada.
5.1.1.3 Tercer caso
Es el caso en el cual tres caudales con sus correspondientes concentraciones confluyen al centro
de la cruz, saliendo de esta un caudal total que corresponde a la suma de los mencionados y con
una concentración correspondiente a la combinación de las iniciales. En este caso la mezcla a la
salida es total, tal como se observa en la siguiente ilustración.
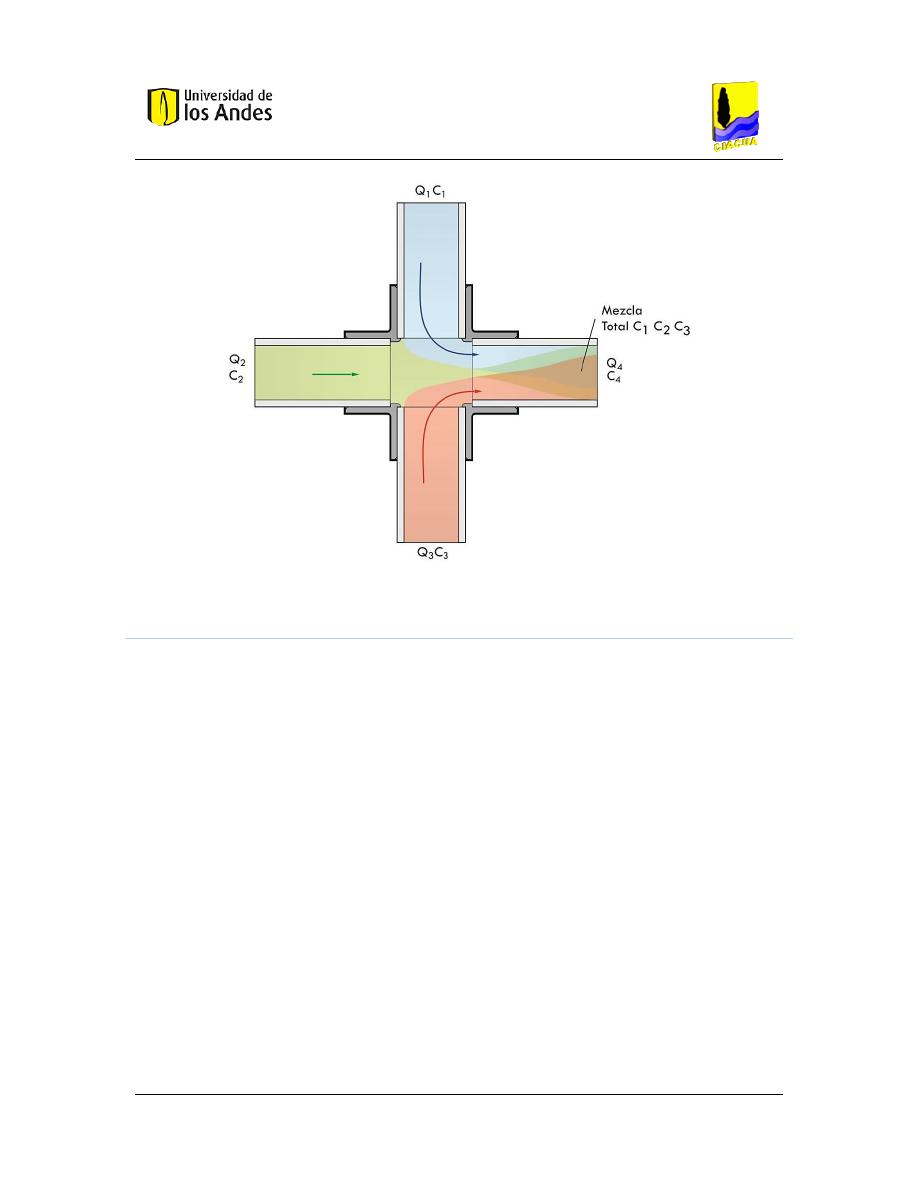
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
32
Figura 10. Tres caudales que confluyen en el centro de la cruz.
5.1.1.4 Cuarto caso
Una cuarta configuración consiste en dos caudales de entrada, pero esta vez ingresando por
ramales adyacentes.
5.1.1.4.1 Tipo a.
Si los caudales de entrada son iguales, la colisión que se produce en el centro de la cruz provocará
que se separen hacia la salida más próxima, sin existir mezcla, manteniendo (en teoría), en cada
salida la concentración original de la entrada adyacente.
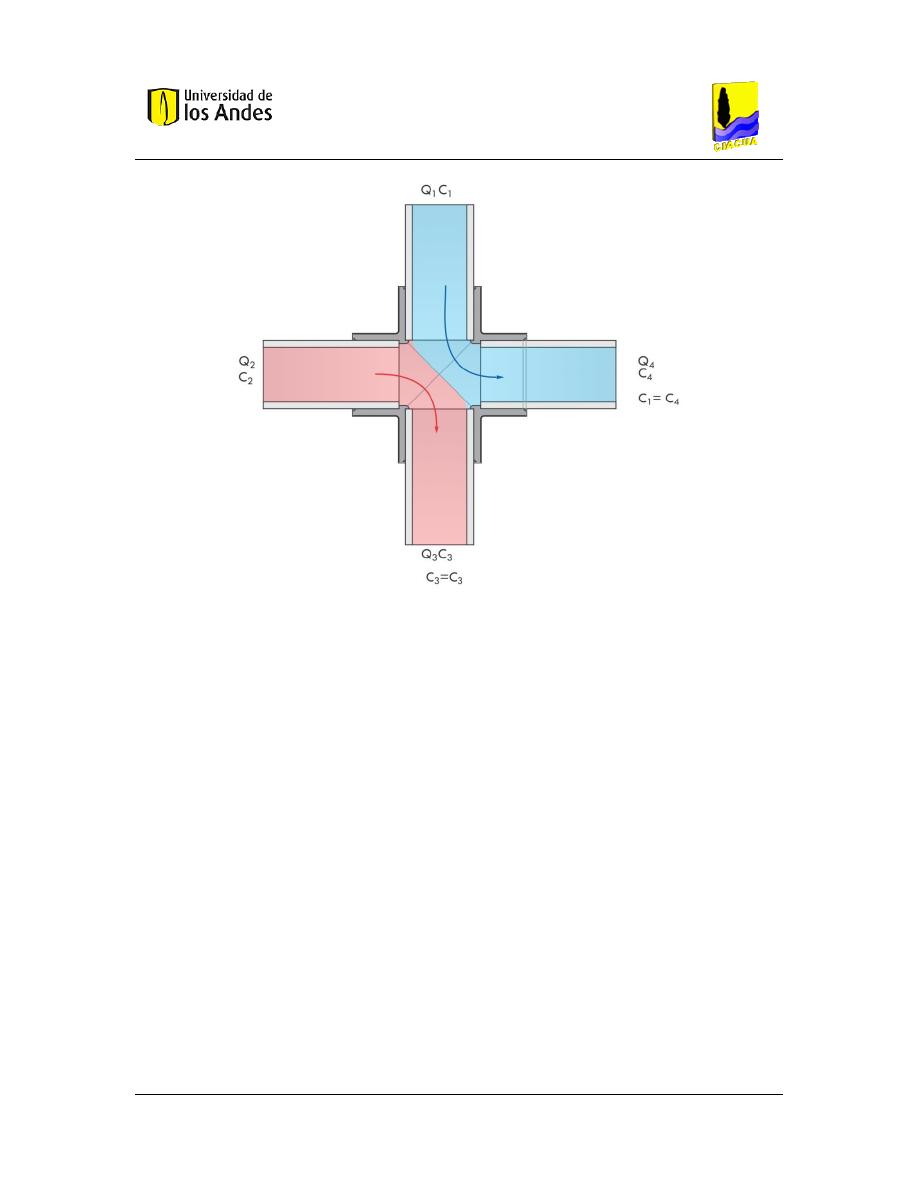
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
33
Figura 11. Dos caudales de entrada con diferentes concentraciones confluyen en el centro de la cruz sin que exista
mezcla
5.1.1.4.2 Tipo b.
Una variación de esta configuración muestra igualmente dos entradas adyacentes pero esta vez
transportando caudales diferentes. En teoría en este caso el caudal mayor tiende a empujar al
caudal menor hacia la salida opuesta, manteniendo la concentración original del caudal mayor en
la salida adyacente y permitiendo una mezcla parcial entre los dos caudales, y por consiguiente
entre las dos configuraciones, en la salida opuesta a la entrada con el mayor caudal.
Este es el caso explicado por Ho, en el modelo de mezcla parcial.
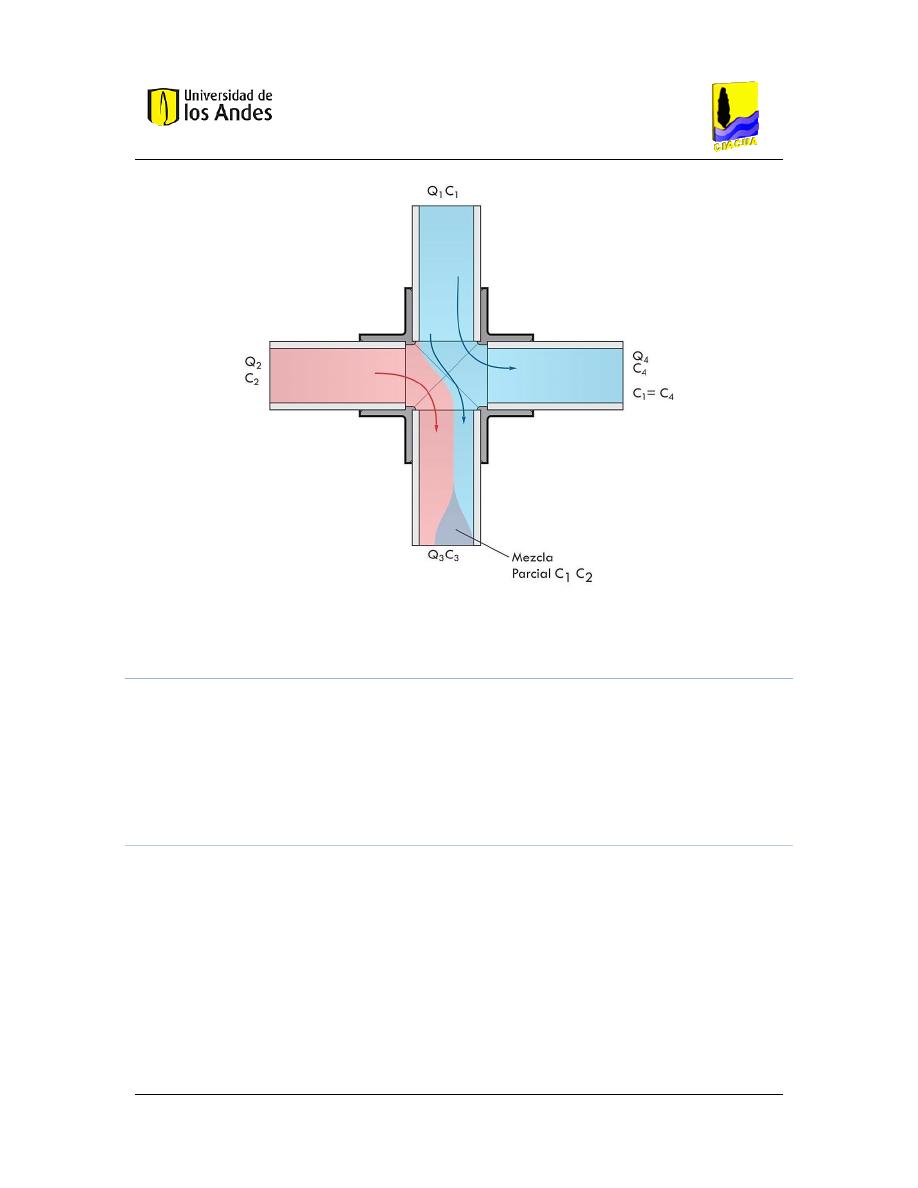
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
34
Figura 12. Mezcla parcial dentro de la cruz, cuarto caso.
5.1.2 Mezcla de soluciones acuosas
La mezcla de soluciones acuosas es un proceso que ocurre cotidianamente dentro de las tuberías
de una red de distribución de agua potable. La mezcla de estas soluciones se puede ocurrir con o
sin reacción química de los solutos. Para el caso del experimento que se desarrolla en este
trabajo, se considera que al ser las soluciones del mismo soluto no existirá una reacción química
dentro de la mezcla.
5.1.2.1 Mezcla de soluciones sin reacción química
La mezcla de dos o más soluciones acuosas sin que ocurra una reacción química dentro de ella, se
presenta cuando el soluto principal (objeto de estudio), es el mismo o cuando solutos que
acompañan a los principales son diferentes pero inertes entre sí y el soluto principal.
Para hallar la concentración final resultado de la mezcla de dos o más soluciones con el mismo
soluto, se toma como base el principio de conservación de la materia. Las cantidades del soluto
común que se mezcla se deben conservar y la cantidad total de soluto en la mezcla final debe ser
igual a la suma de los solutos que se mezclan.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
35
Dado que la solución tiene como base además del mismo soluto, el mismo solvente (agua), se
considera que los volúmenes de las soluciones que se mezclan se pueden sumar. De allí se tiene
para el tercer caso:
Ecuación 30
Dividiendo el volumen en la base de tiempo unitaria, estos pasan a ser caudales, reescribiendo se
tiene que para el tercer caso:
Ecuación 31
Despejando la concentración en C
4
se tiene:
[
]
Ecuación 32
Para el caso cuatro se tiene:
Ecuación 33
Si C
1
es igual a C
4
, entonces:
Ecuación 34
Ecuación 35
Ecuación 36
[
]
Ecuación 37
Esta última ecuación, corresponde en términos generales a la misma utilizada por Ho y descrita en
el marco teórico.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
36
Es evidente además, que para este caso la concentración resultante C
3
, debe corresponder a un
valor localizado entre las concentraciones C
1
y C
2
(recordar que en teoría C
1
= C
4
), así:
Ecuación 38
Si C
2
es mayor a C
1
, o
Ecuación 39
Si C
1
es mayor a C
2
5.1.2.2 Fuerza (impulso), de fluidos que discurren en la cruz
El impulso o de la cantidad de movimiento es una de las ecuaciones fundamentales en la
resolución de problemas de mecánica de fluidos.
Tomando como base la segunda Ley de Newton, la fuerza es el producto de la masa por la
aceleración. Dado que la aceleración es la variación de la velocidad con respecto al tiempo se
tiene que:
̅
̅
Ecuación 40
Ahora, si una partícula de fluido de masa conocida y constante m es sometida a una fuerza F
durante un intervalo de tiempo (t
2
– t
1
), se puede multiplicar los dos miembros de la ecuación por
dt e integrando, se tiene:
∫ ̅
Ecuación 41
donde:
∫ ̅
:
Impulso de la fuerza ̅ que en general variará con el tiempo en el intervalo t
2
– t
1
̅ :
Cantidad de movimiento de la partícula de fluido
La ecuación anterior es el teorema del impulso aplicado a una partícula de fluido.
La anterior ecuación puede escribirse de la siguiente manera, dado que la masa m de la partícula
del fluido, es igual a la densidad del fluido (a la temperatura que discurre), por un volumen
(volumen de control), la ecuación anterior se puede escribir así:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
37
Ecuación 42
Despejando la fuerza se tiene:
Ecuación 43
Tomando en cuenta que caudal es volumen sobre tiempo la anterior ecuación cambia a:
Ecuación 44
Por otra parte la velocidad es igual al caudal dividido el área, finalmente la ecuación se convierte
en:
Ecuación 45
Esta última ecuación, corresponde a sugerida por Ho, para la aplicación del modelo de mezcla
parcial.
5.2 Estrategia metodológica para acertar en la solución del objetivo del
experimento
16
5.2.1 Conservación de la masa en el nudo (cruz)
Del principio de la conservación de la masa en la cruz en cada instante de tiempo, se define la
premisa de que la sumatoria de la masa de NaCl en las tuberías de entrada es igual a la sumatoria
de la masa de NaCl en las tuberías de salida, así:
Ecuación 46
A lo anterior se suma que, bajo el mismo principio, la sumatoria de los caudales de entrada es
igual a la sumatoria de los caudales de salida:
Ecuación 47
16
Cambio de condiciones de operación de un sistema o proceso, que se hace con el objetivo de medir el
efecto del cambio sobre una o varias propiedades del producto o resultado. Así mismo, el experimento
permite aumentar el conocimiento acerca del sistema. Gutiérrez, P. H. & De la Vara. S.R. (2008). Análisis y
diseño de experimentos. Bogotá. Mc Graw Hill.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
38
Si se tiene que el producto del volumen por la concentración de un soluto en él, es igual a la masa
este último, al evaluar dicha situación en una unidad de tiempo, se tiene que el producto del
caudal por la concentración es igual a la masa sobre dicha unidad de tiempo, y esto se incluye en
la ecuación de balance de la masa en el nudo, se tiene:
Ecuación 48
Lo anterior se cumple siempre y cuando dentro de las pruebas realizadas se dé cumplimiento al
principio inicialmente enunciado, el de la conservación de la masa, condición que se pudo
comprobar al graficar la sumatoria de los caudales de entrada por sus respectivas
concentraciones, contra la sumatoria de los caudales de salida por sus respectivas
concentraciones, es decir, masa de entrada contra masa de salida, obteniendo los resultados
mostrados en la gráfica siguiente
Gráfica 2. Conservación de la masa
5.2.2 Variables, factores y niveles
Las variables de respuesta que permiten conocer el efecto resultante de la aplicación de cada
análisis que de la prueba que se hace sobre el experimento, de manera directa es la medida en la
conductividad del agua a la salida en los tanques de recolección T3 y T4, de manera indirecta la
relación que existe entre la concentración del soluto en el agua recolectada C
3
y C
4
, y la
conductividad medida.
Los factores controlables en experimento corresponden al conocimiento y ajuste preciso de los
caudales de entrada y salida al nudo, así como las concentraciones del soluto en la solución que
discurrirán a través del nudo con el caudal que ingresa al mismo.
y = 1,01x - 0,03
R² = 1,00
0,00
0,50
1,00
1,50
2,00
2,50
3,00
3,50
0,00
0,50
1,00
1,50
2,00
2,50
3,00
3,50
Q
3
C
3
+
Q
4
C
4
(
g/
s)
Q1C1 + Q2C2 (g/s)
Conservación de la masa
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
39
Los factores no controlables o de ruido son las características internas de la cruz utilizada, como la
rugosidad del material, geometría interna y calidad y tipo de la conexión con las tuberías entrantes
o salientes. Otros factores no controlables son las incertidumbres del proceso derivados de
variaciones aleatorias en la medida de las variables confluyentes en el experimento o en la
ejecución del mismo.
Los factores de estudio corresponden a la relación que existe entre los caudales de entrada Q
1
y
Q
2
, y sus concentraciones con los caudales de salida Q
3
y Q
4
, sus las concentraciones.
5.2.3 Metodología propuesta “Estrategia y consideraciones”
5.2.3.1 Determinar la función general objetivo
Dado que lo anterior se cumple se plantea una relación entre los caudales de entrada y de salida,
se plante a la siguiente función:
Ecuación 49
Dónde: Q
1
, Q
2
, Q
3
, Q
4.
, C
1
y C
2
, son conocidas
5.2.3.2 Determinar las restricciones iniciales para el experimentoplaneado
Se determinan las siguientes restricciones para el experimento planteado. Se identifican para la
solución cuantitativa de este experimento:
Siempre Q
1
≥ Q
2
, Q
3
y Q
4.
Siempre Q
3
≥ Q
4.
Siempre C
1
> C
2
, C
3
y C
4.
Siempre C
3
≤ C
4.
Siempre C
3
> C
2.
Para cada relación entre las variables, identifique todas las restricciones posibles.
5.2.3.3 Proponer relaciones entre las variables
17
Para este experimento se propone la siguiente relación en consideración a las restricciones
iniciales:
Ecuación 50
17
Se deben proponer tantas relaciones como posibilidades de cambio existan en las variables de salida.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
40
5.2.3.4 Determinar la ecuación de relación
Hallando la relación para C
3
Si
(
)
Ecuación 51
Entonces
Ecuación 52
Ecuación 53
Partiendo de la ecuación de mezcla y conservación de masa se despeja Q
3
C
3
:
Ecuación 54
Igualando las dos anteriores ecuaciones:
Ecuación 55
Ecuación 56
[ ]
Ecuación 57
Despejando C
4
se tiene:
[ ]
Ecuación 58
Con lo que se obtiene la ecuación explícita para el cálculo de C
4
a partir de las variables conocidas
de entrada, esto es caudales y concentraciones, y caudal de salida sobre la tubería requerida.
De manera análoga se desarrolla para la concentración C
3
obteniendo:
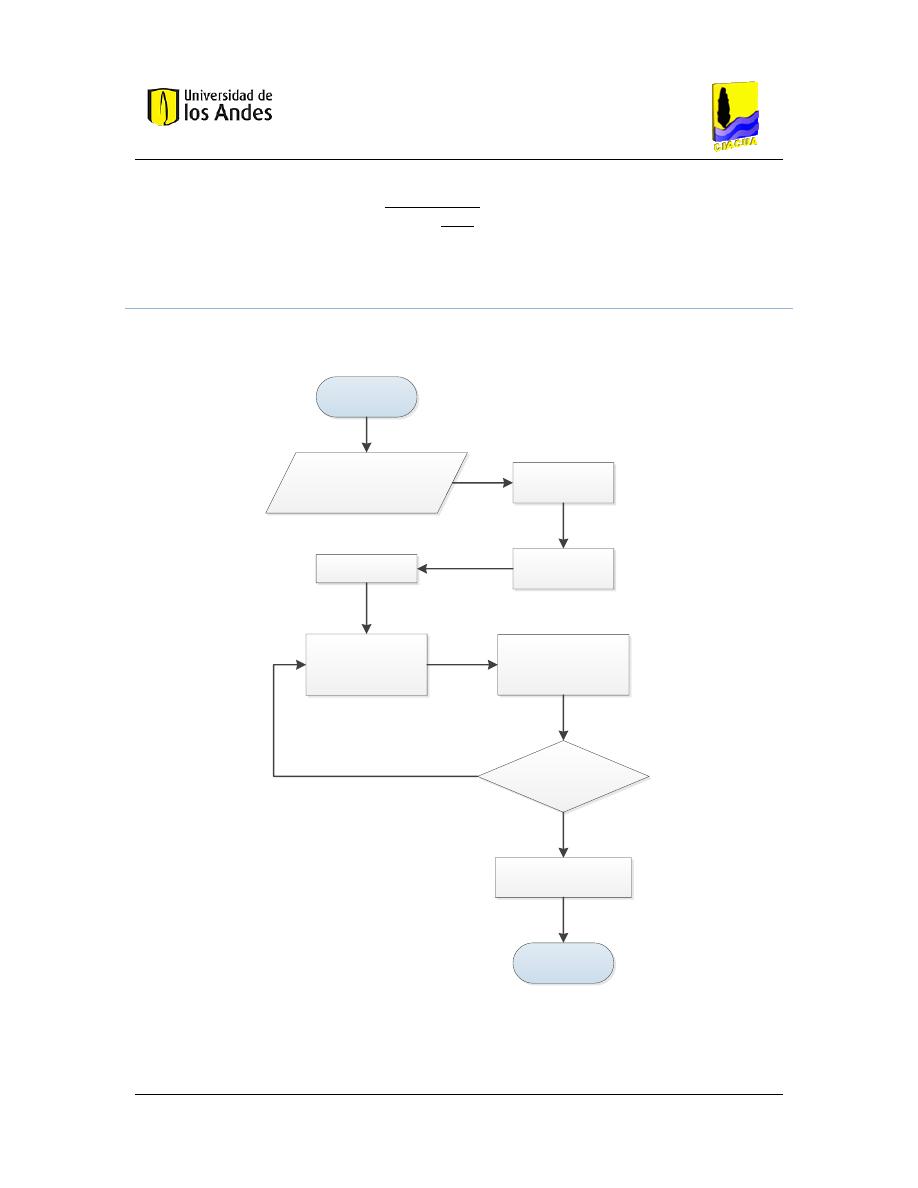
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
41
[
]
Ecuación 59
5.2.4 Diagrama de flujo de la estrategia planteada
La estrategia para hallar el valor de las concentraciones de manera general se muestra a
continuación:
Figura 13. Diagrama de flujo de la estrategia planteada
Inicio
Datos de entrada: Q1 a
Q4, Concentraciones
de entrada, error
máximo aceptable
Definir la función
objetivo
Proponer relaciones
entre las variables
Definir restricciones
Proponer ecuación que
relacione las variables
dentro de las
restricciones propuestas
Igualar la ecuación
obtenida con la ec.
General de mezcla para las
incógnitas a calcular
Calcular concentraciones de
salida e imprimir resultados
Fin
El error obtenido es igual o
menor al máximo aceptable
SI
NO

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
42
6 Modelo físico y digital
El modelo físico del experimento se diseñó con el objetivo de generar diferentes tipos de caudales
en las entradas y salidas de la cruz, y conocer en cada caso el caudal transportado. Se permitió una
variación máxima del nivel del agua en los tanques de suministro, del 5%, lo que garantiza un
caudal estable y uniforme. La imagen del modelo físico se muestra a continuación.
Figura 14. Modelo físico ensamblado.
6.1 Partes del modelo físico
El modelo físico está constituido por:
a. Sistema de alimentación; constituido por una manguera conectada a una llave de agua
potable que proviene de la red de Acueducto de Bogotá.
b. Tanques de suministro; uno con agua con una solución acuosa de agua y sal de comedor,
y otro con agua potable, ambos tipo botella marca PAVCO con una capacidad individual de
300 L (T1 y T2).
c. Sistema de tuberías y válvulas; compuesto por tuberías de PVC (RDE 21)
marca PAVCO de
1 pulgada de diámetro nominal cortadas a 0,5m de longitud y refrentadas y refiladas en
sus extremos, válvulas en PVC tipo bola de ¼ de vuelta con unión universal marca
ControlAgua, dos de control (C1 y C2), y cuatro de regulación de caudal (V1, V2, V3 y V4),
y una cruz comercial en PVC de 1 pulgada.
d. Sistema de recolección; compuesto por dos tanques de 60L cada uno. (T3 y T4)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
43
e. Sistema de control de caudal; constituido por un sistema de cuatro medidores
volumétricos de 1 pulgada (M1, M2, M3 y M4).
f. Sistema de instrumentación: compuesto por un medidor de temperatura (PT 100), con un
rango de 0 a 50°C y un medidor de Conductividad de 0 a 20 mS.
g. Sistema de cámaras de video: compuesto por cuatro cámaras de video WEB para gravar el
volumen de agua acumulado en tiempo real durante la prueba.
Fotografía 1. Modelo físico del experimento.
6.2 Modelo digital en EPANET
Diseñado el modelo físico del experimento, este se digitalizo en el software de modelación
hidráulica de tuberías a presión EPANET, versión 2.0.12 vE, traducido por la Universidad
Politécnica de Valencia.
El propósito del desarrollo del modelo físico en EPANET, tiene como objeto predecir el
comportamiento hidráulico del modelo al variar los caudales en cada una de las entradas y salidas
de la cruz y tener un punto de referencia con relación a los posibles resultados que se esperarían
del modelo físico.
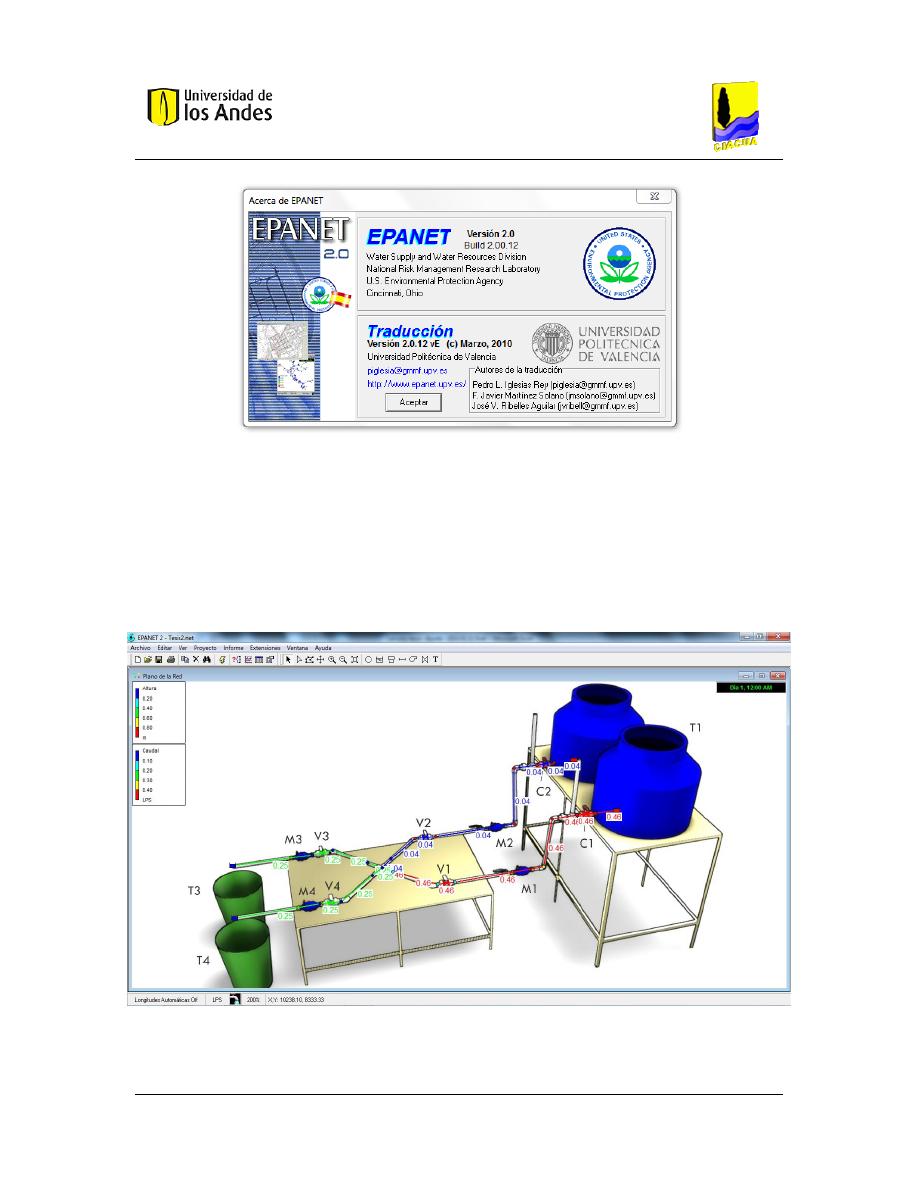
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
44
Figura 15. Traductores de la versión utilizada de EpaNet a español
Se ajustó el modelo de manera que fuera posible simular los doce (12) escenarios planteados.
Dado que algunos de los escenarios planteaban perdidas de energía derivadas del cierre de una o
dos válvulas y su consecuente cambio de caudal en la línea controlada, se planteó hacer esto con
el modelo en EPANET, encontrando que al utilizar una válvula reguladora por estrangulación
debida al cambio del coeficiente de la válvula, esta no generaba ningún cambio en la pérdida por
fricción en la misma. Debido a lo anterior fue necesario hacer la correspondiente perdida sobre la
tubería a controlar, incrementando en ella el coeficiente de pérdidas menores que la componen.
Figura 16. Modelo digital de EpaNet para la prueba No. 4
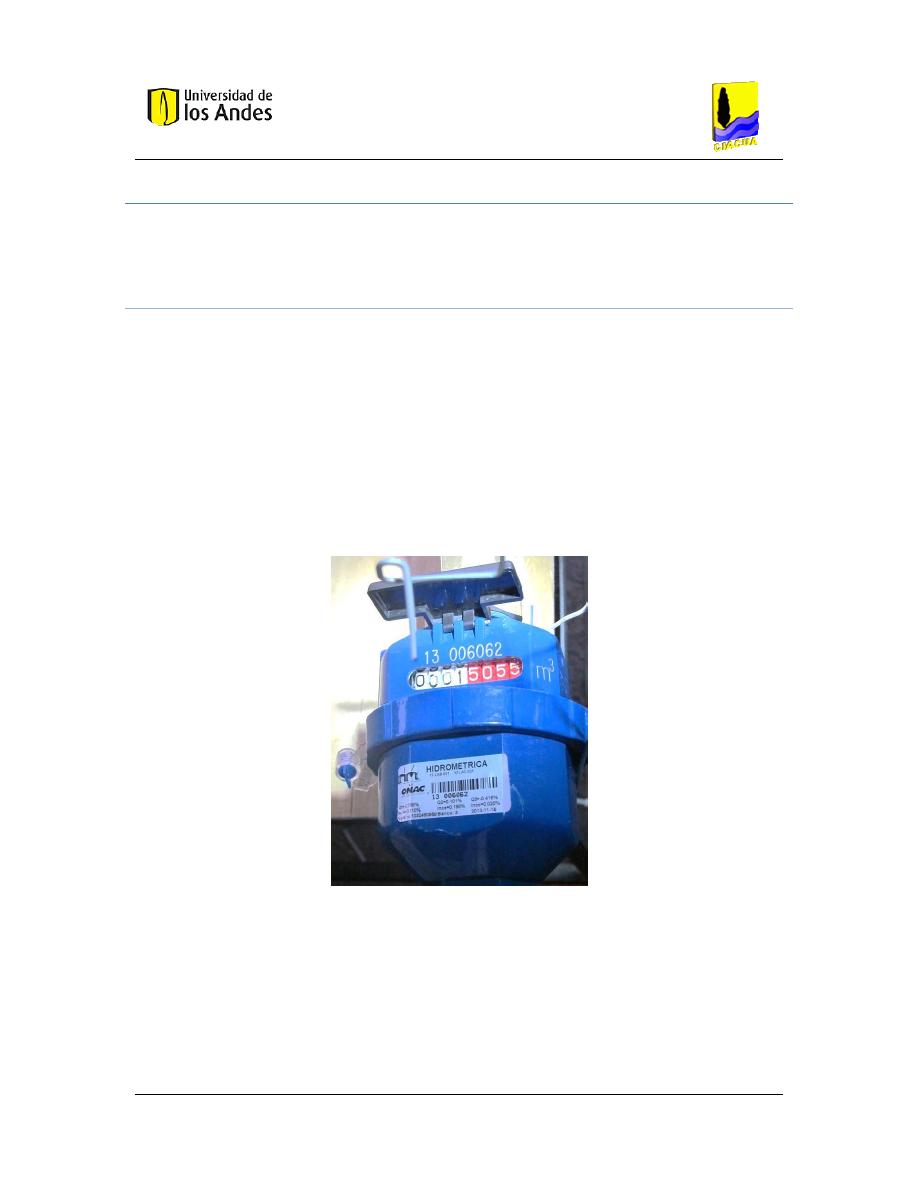
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
45
6.3 Instrumentos utilizados en el modelo físico
Los instrumentos utilizados en el modelo físico son; medidores de agua potable, termómetro
digital, equipo para medir la conductividad del agua y cámaras de video tipo WEB. Las
características de los instrumentos utilizados se describen a continuación.
6.3.1 Medidor de agua volumétrico.
Para realizar la medida del caudal que fluye por cada una de las tuberías que se unen con la cruz,
se utilizan medidores para agua potable tipo volumétrico con un diámetro nominal de 1pulgada
marca ControlAgua. Estos medidores cumplen con la Norma Técnica Colombiana NTC 1063 de
2007 y corresponden a la clase metrológica R160, con una resolución de 0,02 L y fabricados en el
año 2013. Los medidores han sido calibrados por un laboratorio acreditado para tal fin
(Hidrométrica SA), y corresponden a los siguientes números de serie:
M1:
13 006070
M2:
13 006062
M3:
13 006046
M4:
13 006064
Fotografía 2. Medidor volumétrico utilizado para el experimento
El valor del caudal que discurre por cada medidor (y a su vez por cada tubería), se calcula hallando
las diferencias de los volúmenes
Con el agua fluyendo a través del medidor de manera estable, se toma una fotografía instantánea
del video del inicio del cronometraje de la prueba y la final del tiempo de la misma, de tal manera
que se conoce el volumen inicial, el volumen final, dando el volumen de agua que discurre a través

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
46
del medidor. Este volumen dividido el tiempo cronometrado nos indica el caudal que fluyó a
través del medidor, así:
Ecuación 60
Fotografía 3. Lecturas iniciales de los medidores para una de las pruebas realizadas
Fotografía 4. Lecturas finales de los medidores para una de las pruebas realizadas

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
47
Fotografía 5. Montaje de la cámara web y ajuste de la imagen en el software de video
6.3.1.1 Ajuste de las medidas de caudal.
Los medidores utilizados están calibrados por Hidrométrica S.A.
18
, laboratorio acreditado para tal
fin por la ONAC
19
, los correspondientes certificados de calibración se encuentra adjuntos en los
anexos.
El ajuste del volumen medido se realiza a través de la información contenida en los certificados de
calibración individuales de cada medidor.
Los datos metrológicos de todos los medidores según la NTC 1063 de 2007, son:
Q
3
, Caudal nominal de 4 000 L/h (error relativo máximo de ±2%)
Q
4
, Caudal máximo de 5 000 L/h (error relativo máximo de ±2%)
Q
1
, Caudal mínimo de 25 L/h (R160) (error relativo máximo de ±5%)
Q
2
, Caudal de transición de 40 L/h (error relativo máximo de ±2%)
Dado que todos los caudales de la pruebas fueron superiores a Q
2
e inferiores a Q
3
, se toman los
errores relativos de los certificados de calibración de cada medidor y se realiza una línea que una
los dos puntos coordenados (Caudal, Error relativo %); para Q
2
y Q
3
, se halla la ecuación de esa
línea recta y se utiliza para corregir todos los caudales de la prueba para cada medidor. Un
ejemplo se muestra a continuación con la línea realizada para el medidor de agua M1: 13
006070
20
.
18
Laboratorio Nacional de Calibración de Medidores e Hidráulica, Hidrométrica S.A.
19
ONAC, Organismo Nacional de Acreditación de Colombia
20
Ver certificado anexo de Hidrométrica S.A. CC1303201907.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
48
Gráfica 3. Corrección del error en porcentaje en el medidor No. 1 - 13 006070
Con la ecuación obtenida, se calcula el error y con este se ajusta el caudal medido, obteniendo el
caudal ajustado. Realizadas las anteriores operaciones se hace una tabla de ajuste da caudales
para cada prueba y toma de datos como se muestra a continuación.
Tabla 4. Cálculo del caudal ajustado para la prueba No. 4, toma 2
Prueba No. 4 - Toma No. 2
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
971,63
950,16
21,47
0,477
1.717,6
-0,12%
0,478
2
791,82
789,95
1,87
0,042
149,6
0,09%
0,042
3
968,72
956,55
12,17
0,270
973,6
-0,14%
0,271
4
810,32
799,10
11,22
0,249
897,6
0,09%
0,249
6.3.2 Termómetro digital
Durante el desarrollo del experimento y para cada prueba, se midió la temperatura del agua, en
los cuatro tanques. El sensor usado para la verificación de la temperatura durante las pruebas,
corresponde a una RTD (Resistance Temperature Detector), detector de temperatura resistivo.
y = -2,51E-06x + 3,12E-03
R² = 1,00E+00
-0,80%
-0,60%
-0,40%
-0,20%
0,00%
0,20%
0,40%
30
300
3000
Er
ro
r
(
%
)
Caudal (L/h)
Medidor No.1 13 006070

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
49
Fotografía 6. Dispositivo termo-resistivo digital utilizado para el experimento
Este dispositivo termo-resistivo corresponde a una PT100
21
, es de marca EBCHQ, referencia 58103
y tiene las siguientes características metrológicas:
Rango de medición de -50°C a 300°C
Resolución de 0,1°C
Profundidad de inmersión del bulbo de hasta 70mm
Exactitud de ±1°C de 0°C a 100°C y ±2°C de 100°C en adelante
Modelo S-HO3 Ref. 58103
6.3.2.1 Ajuste de las medidas de temperatura
Para el ajuste de la medida de temperatura del agua se utiliza un termómetro de precisión patrón
marca H-B instrument Enviro-Safe, con las siguientes características metrológicas:
Rango de medición de -1°C a 51°C
División de escala de 0,1°C
Profundidad de inmersión del bulbo de 76mm
Exactitud de ±0,5°C en toda la escala
Longitud de 460mm
Modelo 20504
Este medidor patrón fue calibrado por MetroCal Ltda
22
, según el certificado de calibración número
TE-0022-10 (ver anexo). Según este certificado de calibración la corrección de la temperatura para
15°C es de 0,2°C y para 20°C es de 0,1°C y en ambos casos la incertidumbre de medida es de
±0,18°C. Dado estos datos las temperaturas medidas están dentro del rango de 16°C a 19°C, por
tanto la corrección del valor medido está dentro del rango de la incertidumbre, de manera tal,
que para efectos prácticos el valor leído del termómetro patrón se tomara como el de referencia
para ajustar la lectura de la PT100.
Al comparar el patrón con la PT100, se observa que la temperatura indicada por la PT100 es la
misma indicada por el medidor patrón, tal como se muestra en las fotografías subsiguientes.
21
PT100. Sensor de temperatura basado en la resistencia eléctrica que impide el flujo de corriente a través
de un alambre de platino y cuyo valor cambia con la temperatura. Para una temperatura de 0°C el valor de
la resistencia corresponde a 100Ω.
22
MetroCal Ltda, Metrologia y Calibración Ltda, acreditado por la SIC para calibración de instrumentos de
medida de temperatura.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
50
Fotografía 7. Lectura de temperatura en el patrón
Fotografía 8. Comparación temperatura en el patrón con los equipos termo-resistivos utilizados
Ya que la temperatura medida es igual a la del patrón se decide no hacer ninguna corrección por
temperatura a los datos medios de esta unidad.
6.3.3 Medidor de conductividad
La medición de la conductividad se realizó con un equipo producido por la firma Hanna
Instruments, modelo DiST 4, con las siguientes características metrológicas:
Rango de medición de 0 a 19,99 mS/cm
Resolución de 0,01 nS/cm
Profundidad de inmersión del instrumento 90mm
Exactitud de ±2% de toda la escala (±0,4 mS/cm)
Compensación por temperatura de manera automática entre 0°C y 50°C
Modelo DiST 4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
51
Fotografía 9. Medidor de conductividad utilizado en el experimento
6.3.3.1 Ajuste de la medida de conductividad
El ajuste de la medida de conductividad se realiza con una solución patrón suministrada por el
fabricante. El equipo se calibra en un solo punto. La solución patrón está en medio acuosa y tiene
un valor de 12,88 mS/cm a una temperatura de 25°C.
Fotografía 10. Verificación de la lectura de la conductividad respecto a la temperatura del agua según certificación del
fabricante
Con la temperatura medida por la PT100, se confirma si se ajusta el valor de la conductividad
según la tabla de variación de la conductividad con respecto a la temperatura suministrada por el
fabricante de la solución patrón.
6.3.4 Cámaras de tipo WEB y toma de imágenes
La captura de los vídeos se realizó por medio de 4 cámaras web, una por cada medidor de agua,
marca Genius FaceCam 321 de 8 Mega pixeles con conexión USB 2.0, micrófono incorporado,

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
52
velocidad de fotogramas de 30 fps (fotogramas por segundo) y enfoque manual. Las señales
fueron concentradas en un par de ordenadores, que utilizan el software nativo de la cámara web
para registra en formato digital los vídeos de cada una de las pruebas de las cuatro cámaras al
mismo tiempo.
Fotografía 11. Posicionamiento de la cámara web sobre el medidor de volumen
En el procedimiento de realización de la prueba una persona accionaba una claqueta y su sonido
era registrado por cada una de las cámaras, este sonido permite que en el momento de la edición
se sincronicen todas las muestras de vídeo alineando en el mismo punto el pico de la onda de
sonido generado por la claqueta. En la edición se realizó, por cada prueba, una impresión de
pantalla en los momentos: de inicio (marcado por el sonido de la claqueta) y final (45 segundos
exactos determinados por el cronometro del software de vídeo con exactitud de 0.03 segundos) a
partir de dichas imágenes (inicio y final) era posible determinar cuánto volumen había sido
registrado por cada uno de los medidores en el tiempo mencionado y así calcular el caudal en cada
uno de los puntos de medición.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
53
Fotografía 12. Ejecución del experimento y control de los datos
6.4 Soluto utilizado en el experimento
Como soluto para realizar el experimento se usó sal de cocina refinada de alta pureza marca
Refisal con las siguientes características:
Fotografía 13. Soluto utilizado
Granulometría fina, para que la sal se disuelva rápidamente en el agua (solvente)
Concentración de Fluor de 180 a 220 ppm
Concentración de Yodo de 50 a 100 ppm
6.5 Tuberías y accesorios en PVC
Las tuberías utilizadas para la prueba fueron suministradas por la firma PAVCO, fabricadas en PVC.
La norma de fabricación de la tubería corresponde a la ASTM D2241-09, tubos de policloruro de
vinilo (PVC), clasificados según la presión (serie RDE), RDE 21, con un diámetro nominal de 1
pulgada y diámetro interno de 30,20 mm.
La unión tipo cruz usada para el experimento está fabricada en PVC, por la firma LASCO y
corresponde a la norma ASTM D2466 – 13, "accesorios de policloruro de vinilo (PVC) Schedule
40”.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
54
7 Desarrollo del experimento y metodología
Para el desarrollo del experimento se cuenta con un sistema de distribución de tuberías y
suministro de agua concebido para tal fin. El procedimiento metodológico se describe a
continuación, así como los escenarios que se dispusieron para el experimento.
7.1 Paso a paso de ejecución de cada prueba del experimento.
Los pasos seguidos para el desarrollo de cada prueba del experimento se detallan a continuación.
1. Verificar que todos los elementos necesarios para el desarrollo del experimento se encuentren
en perfectas condiciones de uso, en la cantidad y calidad suficiente para el desarrollo del
mismo (Tales como el sistema de suministro de agua potable, medidores de caudal, sistema
de aforo, medidor de temperatura, medidor de conductividad, sistema de cámaras de video y
otros).
2. Confirmar el estado inicial de las válvulas que componen el sistema según muestra en la tabla
a continuación, y el estado de las válvulas para cada escenario.
Tabla 5. Estado de operación de las válvulas para los diferentes escenarios
Escenario
Válvulas
C1
C2
V1
V2
V3
V4
Inicio
Cerrada Cerrada
Abierta
Abierta
Abierta
Abierta
1
Abierta Abierta
Abierta
Abierta
Abierta
Abierta
2
Abierta Abierta
Abierta
Cerrada 25°
Abierta
Abierta
3
Abierta Abierta
Abierta
Cerrada 45°
Abierta
Abierta
4
Abierta Abierta
Abierta
Cerrada 65°
Abierta
Abierta
5
Abierta Abierta Cerrada 25°
Abierta
Abierta
Abierta
6
Abierta Abierta Cerrada 45°
Abierta
Abierta
Abierta
7
Abierta Abierta Cerrada 65°
Abierta
Abierta
Abierta
8
Abierta Abierta
Abierta
Abierta
Cerrada 25°
Abierta
9
Abierta Abierta
Abierta
Abierta
Cerrada 45°
Abierta
10
Abierta Abierta
Abierta
Abierta
Cerrada 65°
Abierta
11
Abierta Abierta Cerrada 45°
Abierta
Abierta
Cerrada 45°
12
Abierta Abierta Cerrada 45°
Abierta
Cerrada 45°
Abierta
3. Llenar los tanques T
1
y T
2
con agua potable hasta la mitad de su capacidad. Abrir las válvulas C
1
y C
2
, totalmente, manteniendo V
1
y V
2
cerradas, confirmar que no existen fugas en el sistema.
Abrir las válvulas V
1
y V
2
, si no hay fugas en el sistema abrir las válvulas V
3
y V
4
, y dejar fluir el
agua totalmente.
4. Una vez desocupados los tanques, cerrar las válvulas C
1
y C
2
.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
55
5. Llenar los tanques T
1
y T
2
con agua potable con el volumen necesario para el experimento (250
L). Agregar al tanque T
1
suficiente sal de cocina, de tal manera que su conductividad llegue al
menos a 11 mS; agitar el tanque T
1
de manera tal que asegure una dilución de la sal de cocina
dentro del agua potable.
6. Regular el caudal de salida de los tanques con las válvulas V
1
o V
2
(Depende del experimento a
realizar los caudales pueden ser iguales o diferentes; confirmar la relación de caudales para
cada experimento de la tabla del numeral 2)
7. Medir la temperatura del agua en cada uno de los tanques T
1
y T
2
, y registrarla en el formato
de toma de datos.
8. Medir la conductividad del agua en cada uno de los tanques T
1
y T
2
, y registrarla en el formato
de toma de datos.
9. Preparar el sistema de video cámaras para los medidores de agua.
10. Preparar y desocupar los tanques de recolección T
3
y T
4
11. Regular las válvulas V
1
, V
2
, V
3
o V
4
según sea el caso de la prueba experimental.
12. Iniciar el sistema de grabación de video.
13. Abrir las válvulas de control C
1
y C
2
al tiempo y totalmente
14. Dejar fluir agua a través del sistema durante al menos 15 segundos para que el flujo se
estabilice.
15. Marcar el inicio del conteo en el sistema de grabación y al mismo tiempo dirigir los flujos de
salida a los tanques T
3
y T
4
16. Dejar fluir el agua durante 45 s, inmediatamente cumplido este tiempo, cerrar las válvulas C
1
y
C
2
y retirar el flujo de agua de salida que va hacia los tanques de recolección T
3
y T
4
.
17. Medir la conductividad del agua y su temperatura del tanque de recolección T
3
y registrarlo.
18. Medir la conductividad del agua y su temperatura del tanque de recolección T
4
y registrarlo.
19. Purgar todo el sistema de tuberías y agregar agua limpia a través de las almenaras de los
tanques T
1
y T
2
para la limpieza del modelo.
20. Desocupar los tanques de recolección T
3
y T
4
, y lavarlos con agua suficiente.
21. Confirmar el estado de las válvulas para la siguiente prueba.
22. Repetir los pasos anteriores para realizar una nueva prueba.
7.2 Escenarios del experimento
Para determinara la validez de las ecuaciones propuestas por Ho y Romero, así como para
entender el discurrir del agua a través de una cruz y la distribución de las concentraciones se ha
propuesto desarrollar 12 escenarios que cubran diferentes formas de distribución del flujo del
agua a través de la cruz, con diferentes concentraciones y caudales.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
56
7.2.1 Escenario #1
Para el escenario #1, se prepara una solución acuosa para el tanque 1, que contiene agua del
sistema de acueducto de Bogotá y sal de comedor, en determinada concentración que permita
alcanzar una conductividad superior a 10 mS. Se llena el tanque #1 (T
1
), con la solución se agua y
sal preparada y el tanque #2 con agua del sistema de acueducto de Bogotá. Ambos tanques de
agua se llenan hasta el mismo nivel. Todas las válvulas del modelo se dejan totalmente abiertas
(V
1
, V
2
, V
3
y V
4
). Se permite que fluya el agua abriendo rápidamente las válvulas de control C
1
y C
2
.
Luego de un determinado tiempo, se evalúa el valor de la conductividad en los tanques de
recolección T
3
y T
4
. Con los medidores de agua instalados se confirma el valor del caudal que fluye
a través de cada tubería conectada a la cruz.
Se espera en este escenario que los caudales de ingreso sean idénticos, de manera tal que no
exista mezcla alguna de los flujos que ingresan a la cruz por la V
1
y la V
2
, obteniendo en T
3
y T
4
, las
mismas concentraciones que en T
2
y T
1
respectivamente.
7.2.2 Escenario #2
Idéntico al Escenario #1, pero con la válvula V2 cerrada 25° aproximadamente. Se espera en este
escenario, que ingrese a la cruz un mayor caudal de agua a través de la válvula V
1
y que los
caudales de salida sean muy similares a través de las válvulas V
3
y V
4
. El valor final de las
concentraciones se estimará la final para cada tanque de recolección T
3
y T
4
.
7.2.3 Escenario #3
Idéntico al Escenario #2, pero con la válvula V
2
cerrada 45° aproximadamente. Se espera en este
escenario, que ingrese a la cruz un mayor caudal de agua a través de la válvula V
1
y que los
caudales de salida sean un poco diferentes a través de las válvulas V
3
y V
4
. Teniendo V
3
un mayor
caudal que V
4
. El valor final de las concentraciones se estimará la final para cada tanque de
recolección T
3
y T
4
.
7.2.4 Escenario #4
Idéntico al Escenario #3, pero con la válvula V
2
cerrada 65° aproximadamente. Se espera en este
escenario, que ingrese a la cruz un mayor caudal de agua a través de la válvula V
1
y que los
caudales de salida sean significativamente diferentes a través de las válvulas V
3
y V
4
. Teniendo V
3
un mayor caudal que V
4
. El valor final de las concentraciones se estimará la final para cada tanque
de recolección T
3
y T
4
.
7.2.5 Escenario #5
Idéntico al Escenario #1, pero con la válvula V
1
cerrada 25° aproximadamente. Se espera en este
escenario, que ingrese a la cruz un mayor caudal de agua a través de la válvula V
2
y que los
caudales de salida sean muy similares a través de las válvulas V
3
y V
4
. El valor final de las
concentraciones se estimará la final para cada tanque de recolección T
3
y T
4
.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
57
7.2.6 Escenario #6
Idéntico al Escenario #5, pero con la válvula V
1
cerrada 45° aproximadamente. Se espera en este
escenario, que ingrese a la cruz un mayor caudal de agua a través de la válvula V
2
y que los
caudales de salida sean un poco diferentes a través de las válvulas V
3
y V
4
. Teniendo V
4
un mayor
caudal que V
3
. El valor final de las concentraciones se estimara la final para cada tanque de
recolección T
3
y T
4
.
7.2.7 Escenario #7
Idéntico al Escenario #6, pero con la válvula V
2
cerrada 65° aproximadamente. Se espera en este
escenario, que ingrese a la cruz un mayor caudal de agua a través de la válvula V
2
y que los
caudales de salida sean un poco diferentes a través de las válvulas V
3
y V
4
. Teniendo V
4
un mayor
caudal que V
3
. El valor final de las concentraciones se estimara la final para cada tanque de
recolección T
3
y T
4
.
7.2.8 Escenario #8
Idéntico al Escenario #1, pero con la válvula V
3
cerrada 25° aproximadamente. Se espera en este
escenario, que salga de la cruz un mayor caudal de agua a través de la válvula V
4
y que los caudales
de entrada sean muy similares a través de las válvulas V
1
y V
2
. El valor final de las concentraciones
se estimara la final para cada tanque de recolección T
3
y T
4
.
7.2.9 Escenario #9
Idéntico al Escenario #8, pero con la válvula V
3
cerrada 45° aproximadamente. Se espera en este
escenario, que salga de la cruz un mayor caudal de agua a través de la válvula V
4
y que los caudales
de entrada sean un poco diferentes a través de las válvulas V
1
y V
2
. El valor final de las
concentraciones se estimara la final para cada tanque de recolección T
3
y T
4
.
7.2.10 Escenario #10
Idéntico al Escenario #9, pero con la válvula V
3
cerrada 65° aproximadamente. Se espera en este
escenario, que salga de la cruz un mayor caudal de agua a través de la válvula V
4
y que los caudales
de entrada sean diferentes a través de las válvulas V
1
y V
2
. El valor final de las concentraciones se
estimara la final para cada tanque de recolección T
3
y T
4
.
7.2.11 Escenario #11
Idéntico al Escenario #1, pero con las válvulas V
1
y V
4
cerradas 45° aproximadamente. Se espera
en este escenario, que salga de la cruz un mayor caudal de agua a través de la válvula V
4
y que los
caudales de entrada sean muy diferentes a través de las válvulas V
1
y V
2
. El valor final de las
concentraciones se estimara la final para cada tanque de recolección T
3
y T
4
.
7.2.12 Escenario #12
Idéntico al Escenario #11, pero con las válvulas V
1
y V
3
cerradas 45° aproximadamente. Se espera
en este escenario, que salga de la cruz un mayor caudal de agua a través de la válvula V
4
y que los
caudales de entrada sean muy diferentes a través de las válvulas V
1
y V
2
. El valor final de las
concentraciones se estimara la final para cada tanque de recolección T
3
y T
4
.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
58
7.3 Toma de los datos
La toma de los datos durante el desarrollo del experimento se realizó con la instrumentación
descrita anteriormente. Todos los datos de temperatura y conductividad fueron consignados en el
formato realizado para tal fin en computador. Para tener la medida confiable se esperó en cada
toma de la medida el tiempo necesario para que los instrumentos indicaran una medida estable,
aproximadamente 2 minutos por toma. Para garantizar la calidad de la medida se limpia cada
instrumento con agua potable antes de ser utilizado para evitar trazas de las anteriores
mediciones.
Fotografía 14. Medición de conductividad y temperatura del agua durante el experimento
Tabla 6. Mediciones realizadas durante la ejecución de la prueba No. 4, toma 2
Prueba No. 4 - Toma No. 2
Condición:
Válvula 2 cerrada 67,5°
Tanque No 1
Muestra 1
Muestra 2
Muestra 3
Promedio
Conductividad (mS/cm)
11,65
11,65
11,64
11,647
Temperatura (°C)
15,90
15,90
15,80
15,867
Tanque No 3
Muestra 1
Muestra 2
Muestra 3
Promedio
Conductividad (mS/cm)
10,44
10,43
10,43
10,433
Temperatura (°C)
16,30
16,40
16,50
16,400
Tanque No 4
Muestra 1
Muestra 2
Muestra 3
Promedio
Conductividad (mS/cm)
11,24
11,25
11,26
11,250
Temperatura (°C)
16,40
16,30
16,40
16,367
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
59
7.4 Relación entre la conductividad y la concentración de sal en la solución
Para poder determinar la cantidad de gramos sal necesaria para realizar una concentración
determinada y poderla evaluar a través de la conductividad se realiza un ensayo que relacione el
cambio de la conductividad del agua con base en una cantidad de masa de sal medida y adicionada
a un volumen de agua conocido (agua del acueducto de Bogotá en el lugar del experimento).
En un vaso de Griffin de 1L se llena con agua potable igual a la que se usará durante la prueba. Se
mide la temperatura del agua y la conductividad de la misma. Luego en una pesa de precisión con
resolución de 0,01g, se pesa pequeñas cantidades de sal de cocina; esta cantidad se adiciona al
volumen de agua se mezcla vigorosamente y se mide de nuevo la temperatura y la conductividad,
desarrollando la tabla que se observa a continuación:
Tabla 7. Cálculo de la concentración de soluto como función de la conductividad medida
#
DOSIS
SAL
AGREGADA
(g)
SAL
TOTAL (g)
CONDUCTIVIDAD
(mS/cm)
TEMPERATURA
°C
VOLUMEN
AGUA (L)
CONCENTRACIÓN
(g/L)
0
0,00
0,00
0,042
17,70
1,00
0,000
1
0,77
0,77
1,505
17,70
1,00
0,770
2
0,65
1,42
2,675
17,80
1,00
1,415
3
0,78
2,20
4,05
17,90
0,99
2,217
4
0,74
2,93
5,29
18,00
0,99
2,960
5
1,08
4,01
7,08
18,30
0,98
4,092
6
0,74
4,75
8,28
18,50
0,98
4,847
7
0,63
5,38
9,27
18,60
0,97
5,546
8
0,81
6,19
10,53
18,70
0,97
6,381
9
0,91
7,10
11,89
18,70
0,97
7,320
Con los datos obtenidos se grafica la concentración como función de la conductividad, y se halla la
ecuación correspondiente, tal como se muestra a continuación:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
60
Gráfica 4. Relación existente entre la conductividad y la concentración del soluto en el agua
La ecuación hallada se utiliza para determinar la concentración del soluto en la solución y poder
desarrollar la metodología que permita hallar una fórmula para inferir las concentraciones del
soluto a la salida de una cruz.
7.5 Estimación de la viscosidad cinemática y densidad del agua
Para determinar la densidad y la viscosidad cinemática
23
del agua se graficó los datos que se
encuentran en la Tabla A.1.1, del libro de Hidráulica de Tuberías, así:
Tabla 8. Relación de la densidad y la viscosidad cinemática del agua con la temperatura
Temperatura
°C
Densidad
(kg/m
3
)
Viscosidad
cinemática
(m
2
/s)
0
999,90
1,79E-06
5
1000,00
1,52E-06
10
999,70
1,31E-06
15
999,10
1,14E-06
20
998,20
1,01E-06
25
997,10
8,97E-07
30
995,70
8,04E-07
Aunque la densidad del agua cambia al agregar la sal, la cantidad es tan mínima que se supone que
la densidad no cambia por agregar está.
23
Saldarriaga V. Juan G. (2009). Hidráulica de tuberías: Abastecimiento de Agua, Redes y Riegos. Bogotá:
Alfaomega.
y = -0,00026x
3
+ 0,01274x
2
+ 0,50129x - 0,00981
R² = 0,99997
0,0
2,0
4,0
6,0
8,0
0,00
2,00
4,00
6,00
8,00
10,00
12,00
C
o
n
ce
n
tr
ac
ió
n
(
g/
L)
Conductividad (mS/cm)
Relación Conductividad - Concentración

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
61
Gráfica 5. Relación existente entre la temperatura del agua y su densidad
Gráfica 6. Relación existente entre la temperatura del agua y su viscosidad cinemática
7.6 Cálculos hidráulicos
Con base en la información obtenida correspondiente al caudal que fluye a través de cada tubería
para cada prueba y toma de datos, se procedió a determinar la velocidad, el Número de Reynolds
y la fuerza derivada de la cantidad de movimiento dentro de cada tubería, esta información es
valiosa para realizar comparaciones de otros métodos propuestos por Romero-Gómez y Ho, para
estimar las concentraciones de salida y su relación con el Número de Reynolds.
y = -5,76E-03x
2
+ 3,07E-02x + 1,00E+03
R² = 9,99E-01
9,95E+02
9,96E+02
9,96E+02
9,97E+02
9,97E+02
9,98E+02
9,98E+02
9,99E+02
9,99E+02
1,00E+03
1,00E+03
1,00E+03
0,00
5,00
10,00
15,00
20,00
25,00
30,00
Den
si
d
ad
d
el
a
gu
a
(kg/
m
3
)
Temperatura (°C)
Temperatura vs. Densidad del agua
y = 7,00E-10x
2
- 5,32E-08x + 1,78E-06
R² = 9,99E-01
0,00E+00
2,00E-07
4,00E-07
6,00E-07
8,00E-07
1,00E-06
1,20E-06
1,40E-06
1,60E-06
1,80E-06
2,00E-06
0,00
5,00
10,00
15,00
20,00
25,00
30,00
V
is
co
si
d
ad
C
in
e
m
áti
ca
(
m
2
/s
)
Temperatura (°C)
Temperatura vs. Viscosidad cinemática
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
62
Tabla 9. Parámetros hidráulicos calculados para la prueba No. 4, toma 2
Prueba No. 4 - Toma No. 2
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m
2
/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,48
15,87
1,112E-06
0,67
18.106
0,318
2
0,04
15,87
1,112E-06
0,06
1.574
0,002
3
0,27
16,40
1,096E-06
0,38
10.418
0,102
4
0,25
16,37
1,097E-06
0,35
9.575
0,087
7.7 Cálculos de la conductividad y concentración del soluto
Para determinar la conductividad final en cada prueba, está se midió con el equipo descrito
anteriormente, dado que el mismo hace corrección por temperatura, se deja el mismo valor
medido. La temperatura indicada se mide con la PT100.
Para determinar el valor de la concentración presente en el agua que se tienen en T1 y T2,
recolectada en T3 y T4, se utiliza la ecuación hallada en el numeral que relaciona la conductividad
con la concentración del agua los resultados se muestran continuación:
Tabla 10. Concentración calculada del soluto durante la prueba No. 4, toma 2 y concentraciones calculadas mediante
las ecuaciones estudiadas.
Prueba No. 4 - Toma No. 2
Tubería
Caudal
(L/s)
Conductividad
(mS/cm)
Temperatura
°C
Conductividad
corregida por
(mS/cm)
Concentración
(g/L)
1
0,48
11,65
15,87
11,65
7,15
2
0,04
0,05
15,87
0,05
0,01
3
0,27
10,43
16,40
10,43
6,32
4
0,25
11,25
16,37
11,25
6,88
Concentración
Unidad
Valor medido
Ho. C. K.
Romero-
Gómez
Concentración
estándar
T3
Valor (mg/L)
6,32
6,04
6,06
6,29
Error (%)
0%
-4%
-4%
0%
T4
Valor (mg/L)
6,88
7,15
7,15
6,85
Error (%)
0%
4%
4%
0%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
63
Con el fin de evaluar el comportamiento de las ecuaciones propuestas para las concentraciones de
salida y compararlo con otros sistemas de cálculo, se incluye además en la anterior tabla, el valor
de las concentraciones C
3
y C
4
, calculadas con las ecuaciones de Ho y Romero-Gómez, y se
comparan con el valor medido de los tanques T3 y T4. Para calcular C
3
y C
4
para cada uno de los
escenarios involucrados en el experimento mediante las teorías de Clifford K. Ho y Pedro Romero-
Gómez, se identifica la formulación correspondiente a cada una de las condiciones simuladas,
Q
1
>Q
2
y Q
2
>Q
1
:
7.7.1 Formulación para el cálculo de la concentración a partir de la ecuación de
Clifford K. Ho
Partiendo de la teoría de Clifford K. Ho, en donde Q
1
>Q
2
y por lo tanto C
1
=C
4
, se tiene que:
Ecuación 61
Ecuación 62
Ahora, suponiendo que Q
2
>Q
1
, y que por lo tanto C
2
=C
3
, se tiene que:
Ecuación 63
Las condiciones de cálculo se pueden resumir de la siguiente forma:
Tabla 11. Ecuaciones para el cálculo de C3 y C4 de acuerdo con la relación existente entre Q1 y Q2, según las
restricciones planteadas a partir de la ecuación de Ho
7.7.2 Formulación para el cálculo de la concentración a partir de la ecuación de
Pedro Romero-Gómez
Romero-Gómez reescribe la ecuación de Ho, con base en los siguientes términos:
donde:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
64
Con lo que se tiene que si Q
1
>Q
2
y por lo tanto C
1
=C
4
:
(
(
)
(
)
)
(
(
) (
)
(
)
)
Ecuación 64
Pero si Q
2
>Q
1
y por lo tanto C
2
=C
3
:
(
(
)
(
)
)
(
(
) (
)
(
)
)
Ecuación 65
Resumiendo:
Tabla 12. Ecuaciones para el cálculo de C3 y C4 de acuerdo con la relación existente entre Q1 y Q2, según las
restricciones planteadas a partir de la ecuación de Romero-Gómez
(
(
)
(
)
)
(
(
) (
)
(
)
)
(
(
)
(
)
)
(
(
) (
)
(
)
)
La ecuación que se usa para la comparación de los resultados de las concentraciones es la del
error relativo:
(
)
Ecuación 66
donde:
C
c
Es el valor de concentración calculado con las ecuaciones correspondientes a Ho, Romero-
Gómez y de concentración estándar (mezcla universal de soluciones acuosas).
V
m
Valor de la concentración medido en el experimento.
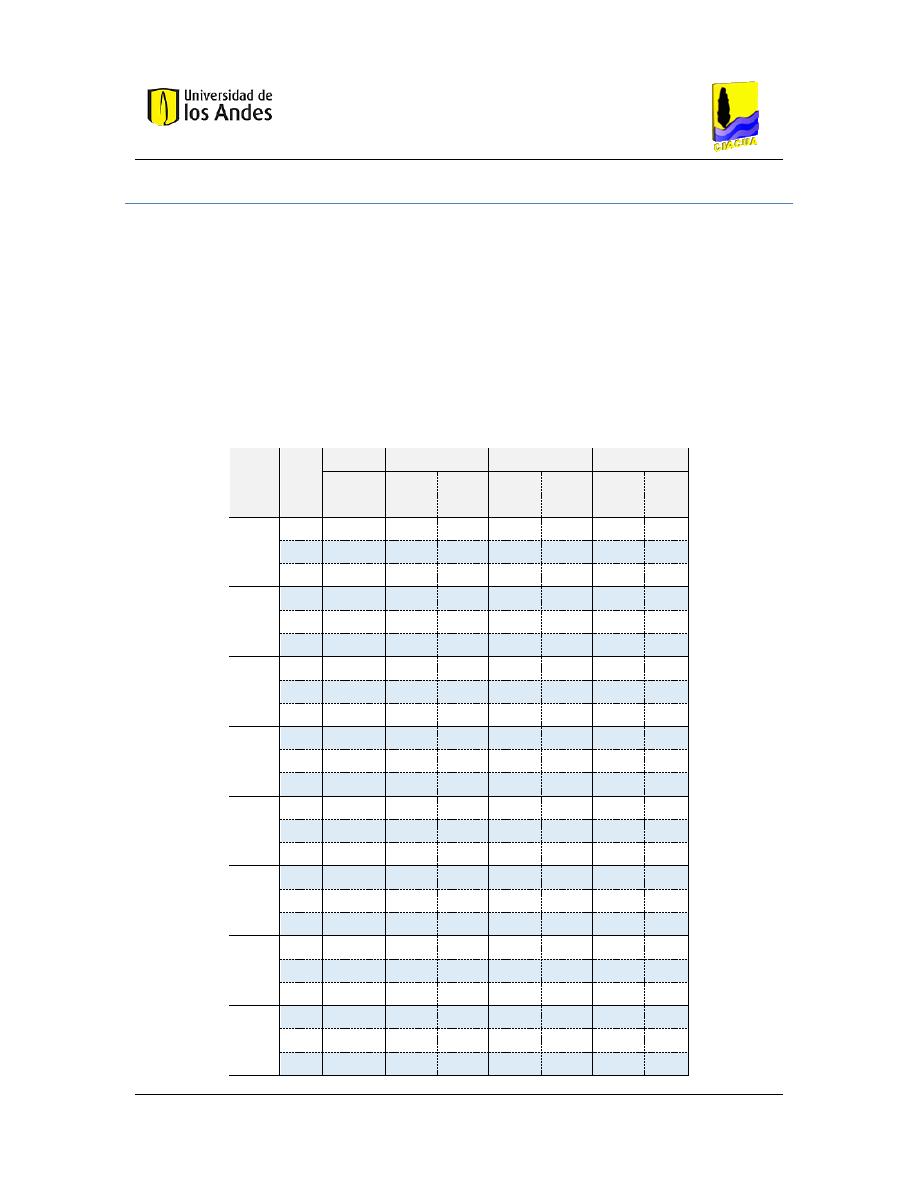
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
65
7.8 Calculo de las concentraciones con la estrategia propuesta
Según la estrategia definida para determinar la ecuación de cada concentración, se procede de la
siguiente manera:
Tomando todos los valores de las concentraciones (la medida y las calculadas, según lo indicado
anteriormente), de las pruebas del experimento, se realiza una tabla para estos datos, para la
concentración C
3
como para la concentración C
4
.
La tabla de datos para la concentración C
4
, se muestra a continuación:
Tabla 13. Cálculo de C4 mediante las ecuaciones anteriores
Prueba Toma
Medición
Ho
Gómez
Ec. Estándar
Conc.
(g/L)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
1
1,00
6,40
7,31
14,4%
7,31
14,4%
6,49
1,5%
2,00
6,29
7,30
16,0%
7,31
16,1%
6,34
0,8%
3,00
6,25
7,28
16,5%
7,29
16,5%
6,30
0,7%
2
1,00
6,62
7,27
9,7%
7,27
9,7%
6,64
0,2%
2,00
6,56
7,24
10,3%
7,24
10,3%
6,56
0,0%
3,00
6,54
7,21
10,2%
7,21
10,2%
6,57
0,5%
3
1,00
6,63
7,04
6,2%
7,04
6,2%
6,58
-0,6%
2,00
6,63
7,02
5,9%
7,02
5,9%
6,65
0,3%
3,00
6,61
6,98
5,7%
6,98
5,7%
6,65
0,6%
4
1,00
6,90
7,16
3,7%
7,16
3,7%
6,86
-0,5%
2,00
6,88
7,15
4,0%
7,15
4,0%
6,85
-0,4%
3,00
6,82
7,08
3,8%
7,08
3,8%
6,66
-2,3%
5
1,00
5,91
6,57
11,1%
6,58
11,3%
5,93
0,4%
2,00
5,91
6,56
11,1%
6,58
11,3%
5,92
0,3%
3,00
5,84
6,49
11,1%
6,50
11,3%
5,84
0,1%
6
1,00
2,97
3,35
12,8%
3,35
12,9%
3,01
1,6%
2,00
2,94
3,35
14,0%
3,36
14,2%
3,00
2,1%
3,00
2,93
3,31
12,9%
3,32
13,2%
2,97
1,3%
7
1,00
0,50
0,81
60,4%
0,81
60,8%
0,55
10,3%
2,00
0,53
0,81
54,3%
0,81
55,1%
0,56
7,3%
3,00
0,55
0,81
47,9%
0,81
48,2%
0,56
3,4%
8
1,00
6,09
7,23
18,8%
7,23
18,8%
6,11
0,4%
2,00
6,02
7,24
20,3%
7,24
20,3%
6,05
0,5%
3,00
6,16
7,21
17,1%
7,21
17,1%
6,08
-1,3%
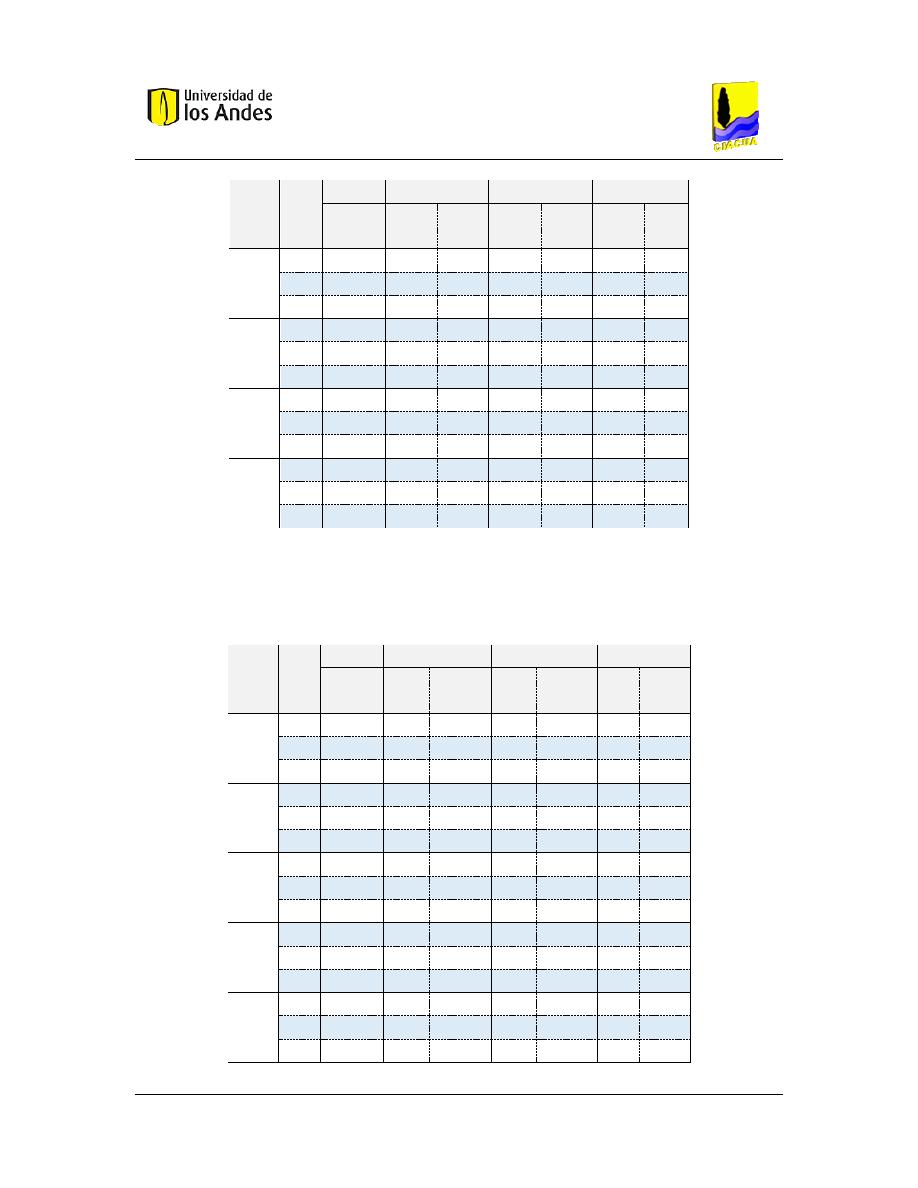
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
66
Prueba Toma
Medición
Ho
Gómez
Ec. Estándar
Conc.
(g/L)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
9
1,00
5,05
7,22
42,9%
7,22
42,9%
5,00
-1,0%
2,00
4,68
4,82
2,9%
4,83
3,0%
4,71
0,5%
3,00
5,13
7,21
40,4%
7,21
40,4%
5,09
-0,9%
10
1,00
3,97
4,09
3,2%
4,09
3,2%
4,06
2,4%
2,00
4,55
7,28
60,0%
7,28
60,0%
4,53
-0,5%
3,00
4,30
7,27
69,0%
7,27
69,0%
4,28
-0,3%
11
1,00
5,23
10,46 100,0% 10,47 100,1%
5,91
12,9%
2,00
5,38
10,34
92,1%
10,34
92,2%
5,77
7,2%
3,00
5,35
10,35
93,4%
10,35
93,4%
5,80
8,5%
12
1,00
2,67
2,85
7,0%
2,85
7,0%
2,77
3,9%
2,00
2,66
2,81
5,8%
2,81
5,6%
2,73
2,6%
3,00
2,69
2,89
7,5%
2,89
7,4%
2,80
4,1%
La tabla de datos para la concentración C
3
, se muestra a continuación:
Tabla 14. Cálculo de C3 mediante las ecuaciones anteriores
Prueba Toma
Medición
Ho
Gómez
Ec. Estándar
Conc.
(g/L)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
1
1,00
0,94
0,15
-83,5%
0,36
-61,5%
1,03
10,0%
2,00
0,93
0,01
-98,5%
0,01
-98,5%
0,98
5,2%
3,00
0,97
0,01
-98,6%
0,01
-98,6%
1,01
4,5%
2
1,00
1,26
0,65
-48,5%
0,66
-48,1%
1,28
1,2%
2,00
1,32
0,65
-50,3%
0,66
-49,8%
1,32
0,0%
3,00
1,22
0,60
-51,2%
0,60
-51,2%
1,25
2,4%
3
1,00
4,29
3,87
-9,8%
3,90
-9,1%
4,25
-0,9%
2,00
4,24
3,90
-8,1%
3,90
-8,1%
4,26
0,4%
3,00
4,20
3,88
-7,4%
3,87
-7,7%
4,24
0,9%
4
1,00
6,33
6,05
-4,3%
6,10
-3,6%
6,29
-0,5%
2,00
6,32
6,04
-4,4%
6,06
-4,1%
6,29
-0,4%
3,00
6,34
5,96
-6,0%
6,00
-5,5%
6,20
-2,3%
5
1,00
0,64
0,01
-97,9%
0,01
-97,9%
0,66
3,5%
2,00
0,65
0,01
-97,9%
0,01
-97,9%
0,66
2,4%
3,00
0,65
0,01
-97,9%
0,01
-97,9%
0,65
0,7%
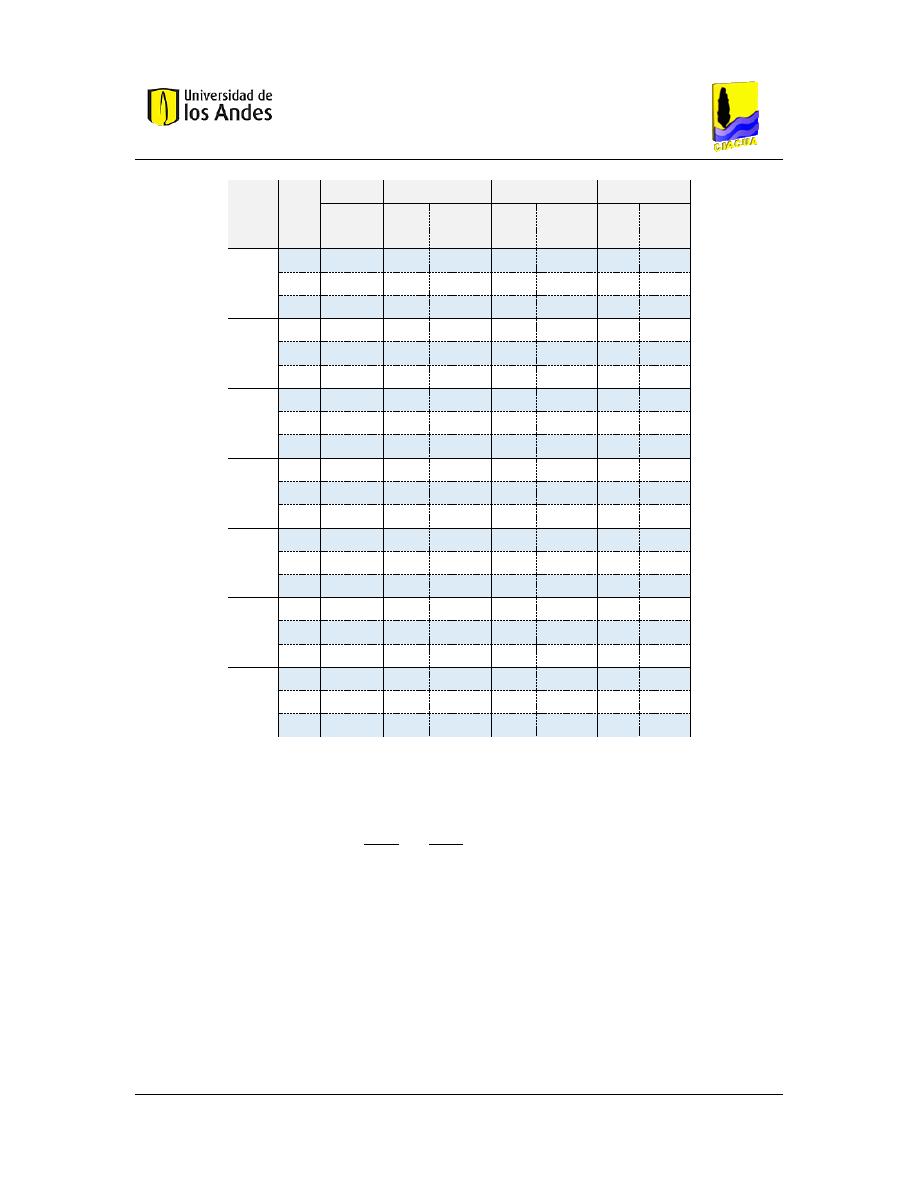
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
67
Prueba Toma
Medición
Ho
Gómez
Ec. Estándar
Conc.
(g/L)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
6
1,00
0,35
0,01
-96,1%
0,01
-96,1%
0,40
13,5%
2,00
0,37
0,01
-96,3%
0,01
-96,3%
0,43
17,1%
3,00
0,36
0,01
-96,2%
0,01
-96,2%
0,40
10,5%
7
1,00
0,27
0,01
-95,0%
0,01
-95,0%
0,33
19,4%
2,00
0,27
0,01
-94,9%
0,01
-94,9%
0,31
14,8%
3,00
0,26
0,01
-94,9%
0,01
-94,9%
0,28
7,3%
8
1,00
0,66
-0,69
-203,2%
-0,68
-202,5%
0,70
4,9%
2,00
0,75
-0,68
-190,7%
-0,68
-189,8%
0,79
4,8%
3,00
0,81
-0,56
-168,4%
-0,54
-166,7%
0,72 -11,9%
9
1,00
0,41
-5,83 -1522,0% -5,82 -1520,1% 0,26 -35,6%
2,00
0,34
0,01
-95,9%
0,01
-95,9%
0,40
19,9%
3,00
0,40
-5,61 -1504,0% -5,63 -1509,2% 0,27 -31,4%
10
1,00
0,20
0,01
-93,3%
0,01
-93,3%
0,75 270,5%
2,00
0,26
-15,68 -6145,1% -15,71 -6157,6% 0,13 -50,5%
3,00
0,31
-17,01 -5661,8% -17,00 -5658,9% 0,23 -24,4%
11
1,00
0,99
0,01
-98,6%
0,01
-98,6%
1,14
14,6%
2,00
0,99
0,01
-98,6%
0,01
-98,6%
1,08
8,4%
3,00
0,99
0,01
-98,6%
0,01
-98,6%
1,09
9,8%
12
1,00
0,24
0,01
-94,3%
0,01
-94,3%
0,53 122,8%
2,00
0,25
0,01
-95,9%
0,01
-95,9%
0,45
77,4%
3,00
0,27
0,01
-96,1%
0,01
-96,1%
0,58 118,1%
Se propone la relación entre las variables, para este caso se propone:
Ecuación 67
Se determinan las restricciones para el desarrollo de la ecuación, así:
R1 = Siempre Q
1
≥ Q
2
, Q
3
y Q
4.
R2 = Siempre Q
3
≥ Q
4.
R3 = Siempre C
1
> C
2
, C
3
y C
4.
R4 = Siempre C
3
≤ C
4.
R5 = Siempre C
3
> C
2.
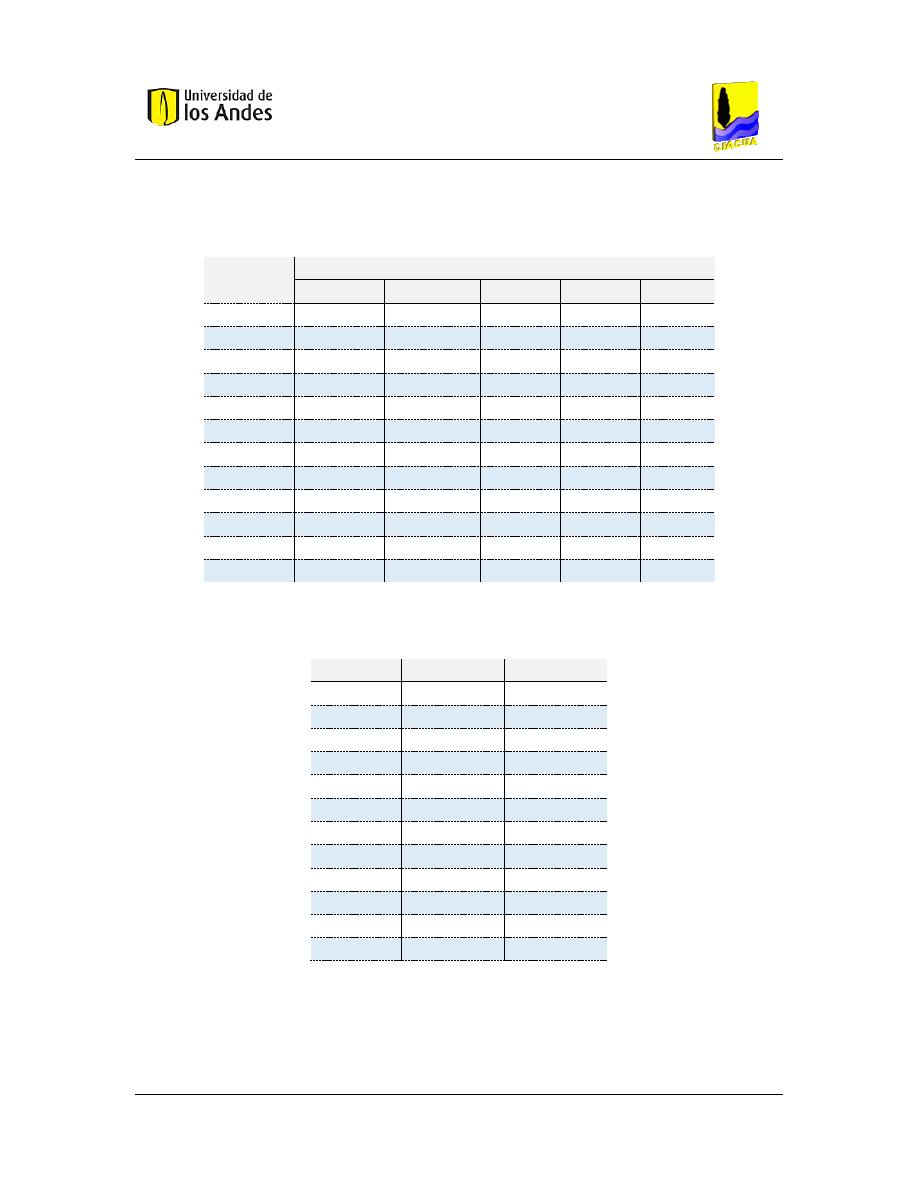
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
68
Se determina cuales pruebas cumplen con todas las restricciones, tal como aparece a
continuación:
Tabla 15. Cumplimiento de las restricciones planteadas
Prueba No.
Restricciones
R1
R2
R3
R4
R5
1
Ok
Ok
Ok
Ok
Ok
2
Ok
Ok
Ok
Ok
Ok
3
Ok
Ok
Ok
Ok
Ok
4
Ok
Ok
Ok
Ok
Ok
5
Q
2
mayor
Ok
Ok
Ok
Ok
6
Q
2
mayor
Ok
Ok
Ok
Ok
7
Q
2
mayor
Q
4
> Q
3
Ok
Ok
Ok
8
Q
4
mayor
Q
4
> Q
3
Ok
Ok
Ok
9
Q
4
mayor
Q
4
> Q
3
Ok
Ok
Ok
10
Q
4
mayor
Q
4
> Q
3
Ok
Ok
Ok
11
Q
3
mayor
Ok
Ok
Ok
Ok
12
Q
4
mayor
Q
4
> Q
3
Ok
Ok
Ok
Con las pruebas que cumplen las restricciones se procede a hallar la ecuación de relación, así
Tabla 16. Cálculo de la razón entre las masas entrantes y entre las masas salientes con relación al tiempo
Pru. / toma
Q
1
C
1
/Q
2
C
2
Q
3
C
3
/Q
4
C
4
P1/t1
566,82
0,15
P1/t2
517,95
0,15
P1/t3
524,75
0,16
P2/t1
623,63
0,20
P2/t2
623,17
0,21
P2/t3
610,43
0,19
P3/t1
1.715,33
0,70
P3/t2
1.717,64
0,69
P3/t3
1.705,32
0,68
P4/t1
6.282,40
1,00
P4/t2
6.045,39
1,00
P4/t3
5.989,72
1,02
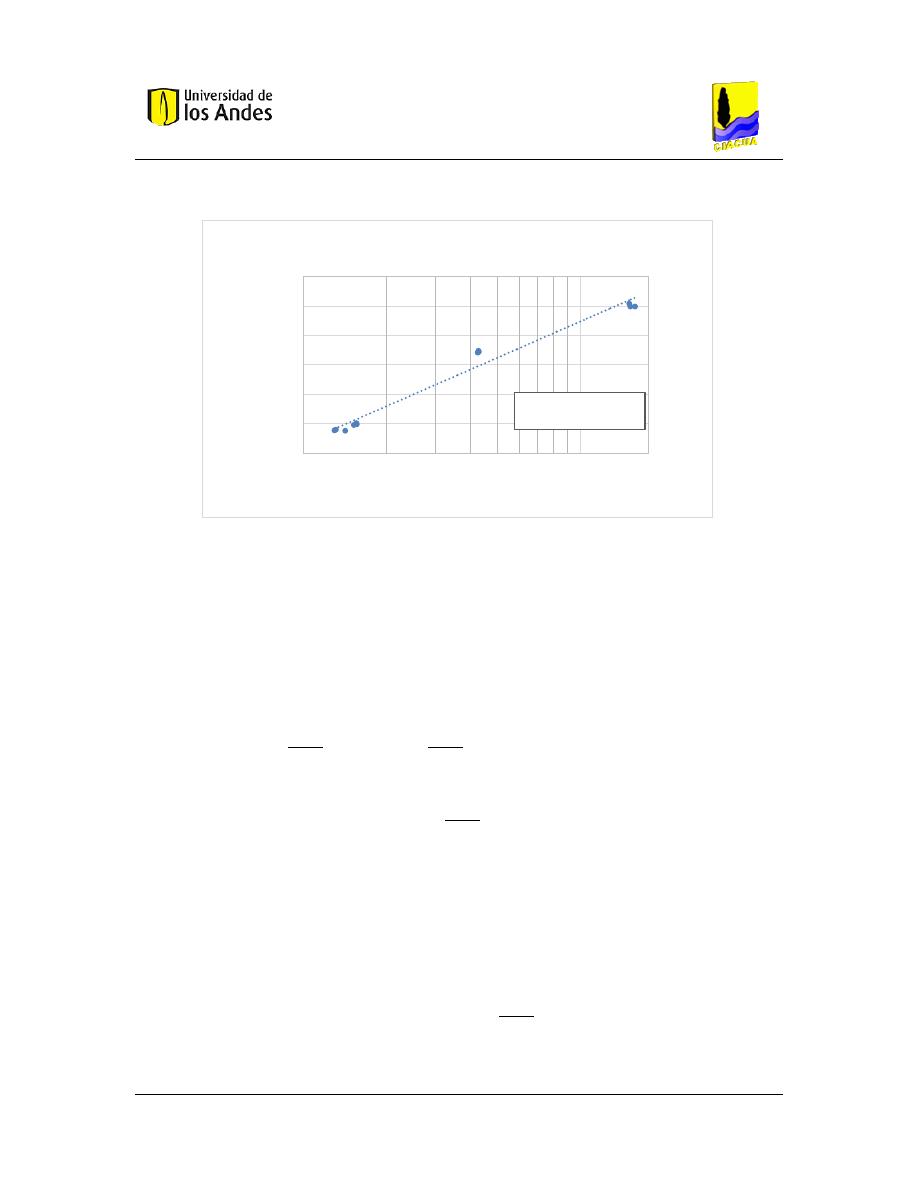
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
69
La ecuación resultante de la regresión se muestra en la siguiente gráfica:
Gráfica 7. Relación encontrada entre la distribución de masas de entrada y de salida de la cruz, en el tiempo
Con base en la gráfica anterior se obtuvo la ecuación que relaciona las dos relaciones expuestas
anteriormente y que permitirá, en conjunción con la ecuación estándar para las soluciones
acuosas, definir un par de ecuaciones explícitas para el cálculo de C
4
, así:
Ecuación 68
Remplazando
(
)
Ecuación 69
[ (
) ]
Ecuación 70
Partiendo de la ecuación estándar para las soluciones acuosas de donde se despeja Q
3
C
3
:
Ecuación 71
Igualando
[ (
) ]
Ecuación 72
y = 0,358ln(x) - 2,0724
R² = 0,974
-
0,20
0,40
0,60
0,80
1,00
1,20
400,00
4.000,00
Q
3
C
3
/Q
4
C
4
Q
1
C
1
/Q
2
C
2
Relación Concentraciones y Caudales

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
70
[ (
) ]
Ecuación 73
Con lo que se obtiene la ecuación explícita para el cálculo de C
4
a partir de las variables conocidas
de entrada, esto es caudales y concentraciones, y caudal de salida sobre la tubería requerida.
De manera similar se realiza para la concentración en C
3
, así:
(
)
Ecuación 74
Y partiendo de la ecuación estándar para las soluciones acuosas, de donde se despeja Q
4
C
4
:
Ecuación 75
Igualando se obtiene
(
)
Ecuación 76
(
)
Ecuación 77
[
(
)
]
Ecuación 78
Finalmente se realiza una tabla que muestre todas las concentraciones calculadas y la medida,
tanto para C
3
, como para C
4
, tal como sigue:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
71
Tabla 17. Cálculo de C4 mediante las ecuaciones estudiadas y la ecuación propuesta, para las pruebas que cumplen las
restricciones incluyendo la totalidad de las tomas
Prueba
Toma
Medición
Ho
Gómez
Ec. Estándar
Ec. Propuesta
Conc.
(g/L)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
1
1,00
6,40
7,31
14,4%
7,31
14,4%
6,49
1,5%
6,24
-2,4%
2,00
6,29
7,30
16,0%
7,31
16,1%
6,34
0,8%
6,28
-0,2%
3,00
6,25
7,28
16,5%
7,29
16,5%
6,30
0,7%
6,24
-0,2%
2
1,00
6,62
7,27
9,7%
7,27
9,7%
6,64
0,2%
6,44
-2,8%
2,00
6,56
7,24
10,3%
7,24
10,3%
6,56
0,0%
6,43
-2,1%
3,00
6,54
7,21
10,2%
7,21
10,2%
6,57
0,5%
6,39
-2,3%
3
1,00
6,63
7,04
6,2%
7,04
6,2%
6,58
-0,6%
7,03
6,0%
2,00
6,63
7,02
5,9%
7,02
5,9%
6,65
0,3%
7,04
6,1%
3,00
6,61
6,98
5,7%
6,98
5,7%
6,65
0,6%
7,01
6,1%
4
1,00
6,90
7,16
3,7%
7,16
3,7%
6,86
-0,5%
6,67
-3,3%
2,00
6,88
7,15
4,0%
7,15
4,0%
6,85
-0,4%
6,71
-2,5%
3,00
6,82
7,08
3,8%
7,08
3,8%
6,66
-2,3%
6,66
-2,3%
Tabla 18. Cálculo de C3 mediante las ecuaciones estudiadas y la ecuación propuesta, para las pruebas que cumplen las
restricciones incluyendo la totalidad de las tomas
Prueba
Toma
Medición
Ho
Gómez
Ec. Estándar
Ec. Propuesta
Conc.
(g/L)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
1
1,00
0,94
0,15
-83,5%
0,36
-61,5%
1,03
10,0%
1,18
25,5%
2,00
0,93
0,01
-98,5%
0,01
-98,5%
0,98
5,2%
0,99
6,7%
3,00
0,97
0,01
-98,6%
0,01
-98,6%
1,01
4,5%
1,02
5,8%
2
1,00
1,26
0,65
-48,5%
0,66
-48,1%
1,28
1,2%
1,46
15,2%
2,00
1,32
0,65
-50,3%
0,66
-49,8%
1,32
0,0%
1,45
10,4%
3,00
1,22
0,60
-51,2%
0,60
-51,2%
1,25
2,4%
1,40
14,3%
3
1,00
4,29
3,87
-9,8%
3,90
-9,1%
4,25
-0,9%
3,88
-9,6%
2,00
4,24
3,90
-8,1%
3,90
-8,1%
4,26
0,4%
3,89
-8,4%
3,00
4,20
3,88
-7,4%
3,87
-7,7%
4,24
0,9%
3,86
-8,0%
4
1,00
6,33
6,05
-4,3%
6,10
-3,6%
6,29
-0,5%
6,50
2,7%
2,00
6,32
6,04
-4,4%
6,06
-4,1%
6,29
-0,4%
6,45
2,1%
3,00
6,34
5,96
-6,0%
6,00
-5,5%
6,20
-2,3%
6,34
0,0%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
72
8 Análisis de los resultados obtenidos
Una vez calculado el valor de las concentraciones de salida, C
3
y C
4
, mediante las ecuaciones de
Ho, Romero-Gómez, ecuación de mezcla estándar y la propuesta en el desarrollo del experimento,
se parte a comparar los resultados obtenidos con el promedio de los valores medidos con el fin de
confirmar que la propuesta metodológica para determinar un ecuación que relacione las
concentraciones de salida en función de las variables conocidas se aproxime a los valores
obtenidos en las mediciones realizadas sobre el modelo físico del experimento. Dichos resultados
se ilustran en las tablas y gráficas siguientes.
Es importante mencionar que en todos los casos las concentraciones en las tuberías 3 y 4 se
encontraron dentro del rango definido por las concentraciones en 1 y 2, sin ser en ningún caso las
primeras iguales a las segundas, lo que confirma que sea cual sea a configuración del sistema y de
los caudales entrantes y salientes del accesorio, en todos los casos ocurre algún grado de dilución
y por lo tanto mezcla en alguna proporción.
8.1 Resultados obtenidos para la concentración C
4
Para el caso de la concentración C
4
se obtiene los resultados transcritos en la siguiente tabla:
Tabla 19. Cálculo de C4 mediante las ecuaciones estudiadas y la ecuación propuesta, para las pruebas que cumplen las
restricciones. Promedio de las tomas para cada prueba
Prueba
Medición
Ho
Romero-Gómez
Ec. Estándar
Ec. Propuesta No. 1
Conc.
(g/L)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
Conc.
(g/L)
Error
(%)
1
6,31
7,30
15,6%
7,30
15,7%
6,38
1,0%
6,25
-1,0%
2
6,57
7,24
10,1%
7,24
10,1%
6,59
0,2%
6,42
-2,4%
3
6,62
7,01
5,9%
7,01
5,9%
6,63
0,1%
7,02
6,1%
4
6,87
7,13
3,8%
7,13
3,8%
6,79
-1,1%
6,68
-2,7%
Con los valores anteriores se elaboró una gráfica de dispersión de datos que permite observar la
aproximación de los resultados de cada una de las ecuaciones respecto a los valores medidos,
representados por la línea punteada en color azul, tal como se muestra a continuación:
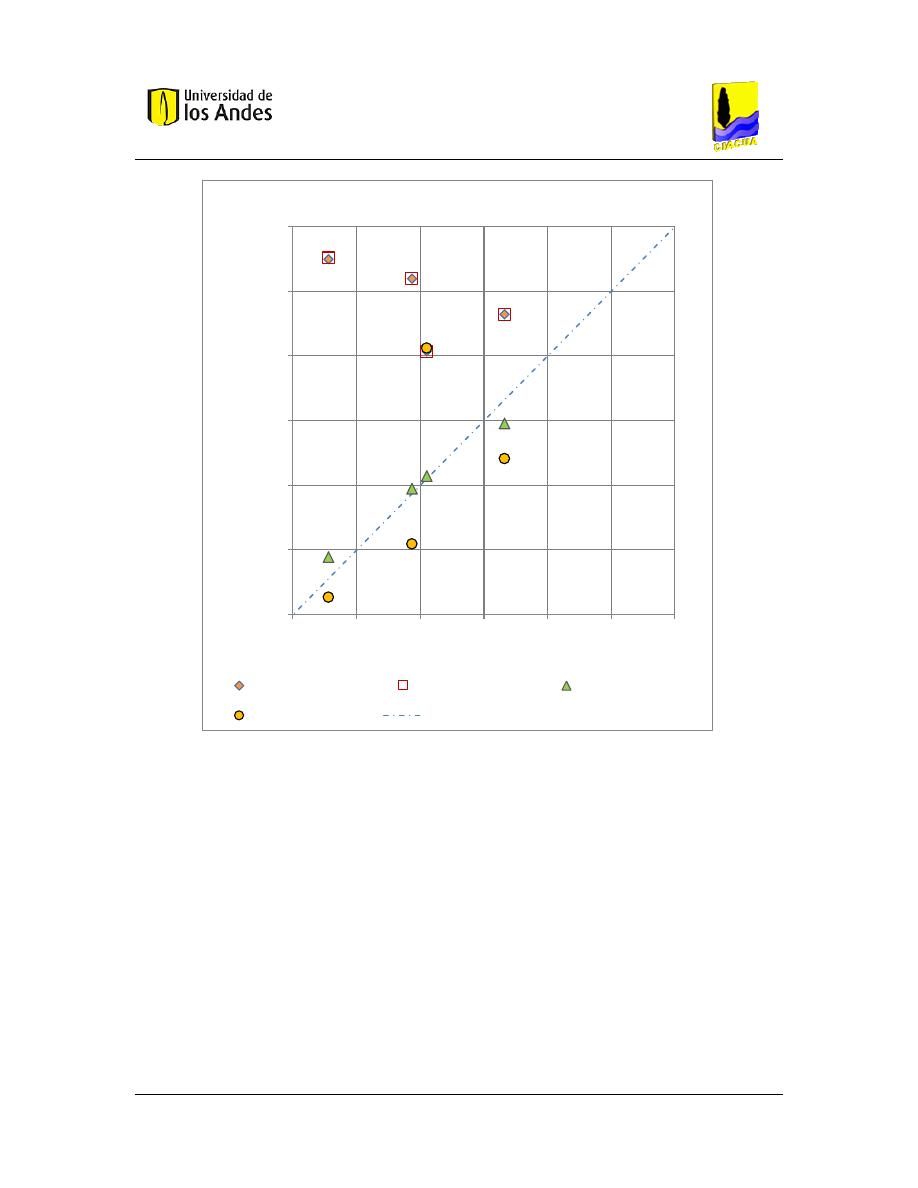
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
73
Gráfica 8. Exactitud de las ecuaciones estudiadas en relación a la concentración medida para C4. Pruebas que cumplen
con las restricciones del modelo. Promedio de las tomas para cada prueba.
Como se puede observar, la ecuación estándar es de las cuatro evaluadas la que más se ajusta a
las mediciones realizadas; sin embargo es importante tener en cuenta que su uso se restringe al
conocimiento de las concentraciones de tres de las tuberías que componen la cruz, situación que
no es real debido a que en los modelos hidráulicos de redes de distribución de agua a presión las
concentraciones de salida son de por sí las incógnitas. Entre las ecuaciones explícitas para el
cálculo de C
4
, se puede observar que la propuesta en el presente estudio es la que más se ajusta a
los valores medidos, incluso más que las ecuaciones de Ho y Romero-Gómez debido a las
diferencias notables en el modelo físico de los experimentos realizados por los diferentes autores,
como se comentará más a detalle en las conclusiones.
6,2
6,4
6,6
6,8
7,0
7,2
7,4
6,2
6,4
6,6
6,8
7,0
7,2
7,4
C
o
n
ce
n
tra
ci
ó
n
c
al
cu
la
d
a
(g/L
)
Concentración medida (g/L)
Concentración medida vs. calculada
Ho
Romero-Gómez
Ec. Estándar
Ec. Propuesta
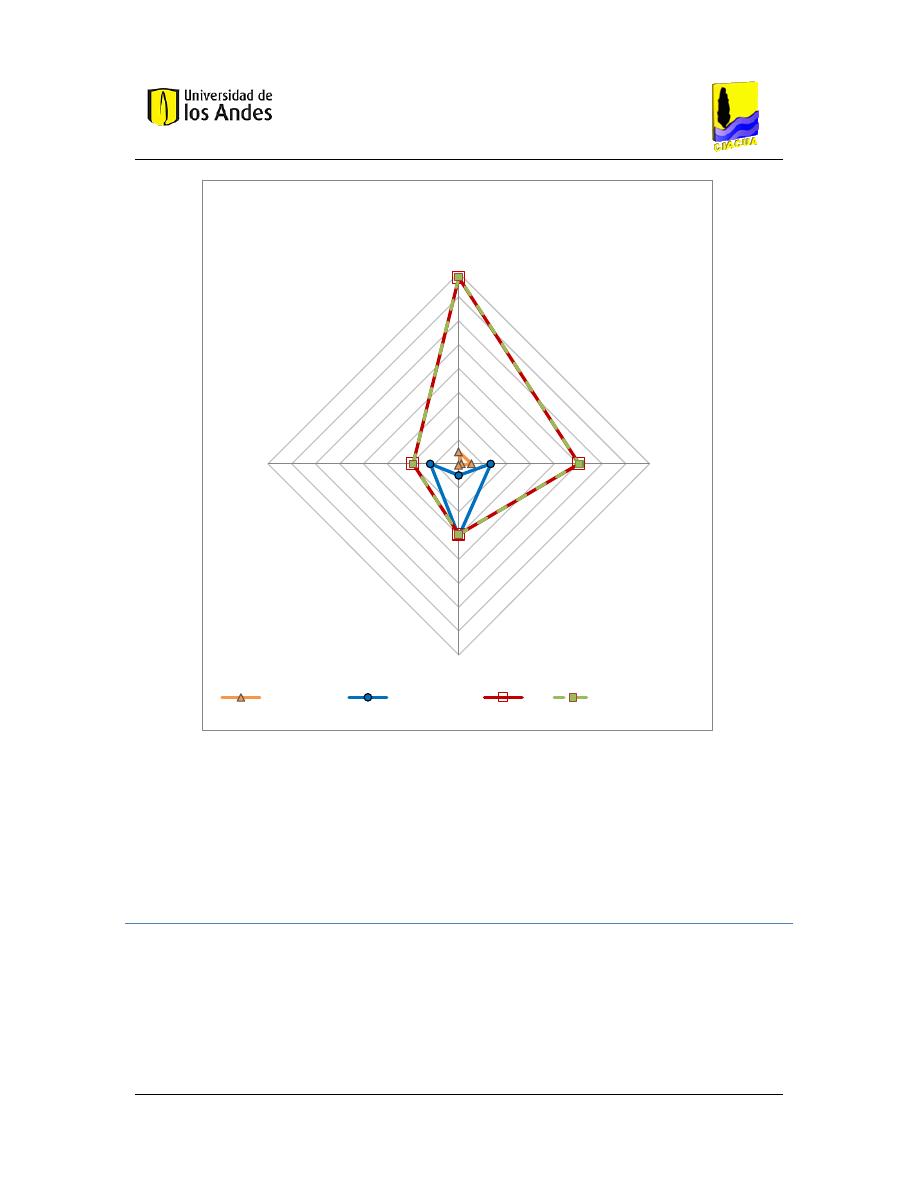
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
74
Gráfica 9. Error calculado para el valor de C4 hallado mediante las diferentes ecuaciones estudiadas respecto a los
valores medidos en el experimento. Pruebas que cumplen con las restricciones del modelo.
En la gráfica radial anterior se observa que los valores correspondientes a los errores relativos de
cada ecuación respecto a los valores promedio de cada prueba del experimento, que mejor ajuste
presentan corresponden a la ecuación de mezcla estándar, y dentro de las ecuaciones explícitas la
que más exacta es la ecuación propuesta.
8.2 Resultados obtenidos para la concentración C
3
Para el caso de la concentración C
3
se realizó el mismo procedimiento, obteniendo los siguientes
resultados:
0,0%
2,0%
4,0%
6,0%
8,0%
10,0%
12,0%
14,0%
16,0%
1
2
3
4
Error calculado respecto a los valores medidos
para C4
Ec. Estándar
Ec. Propuesta
Ho
Romero-Gómez
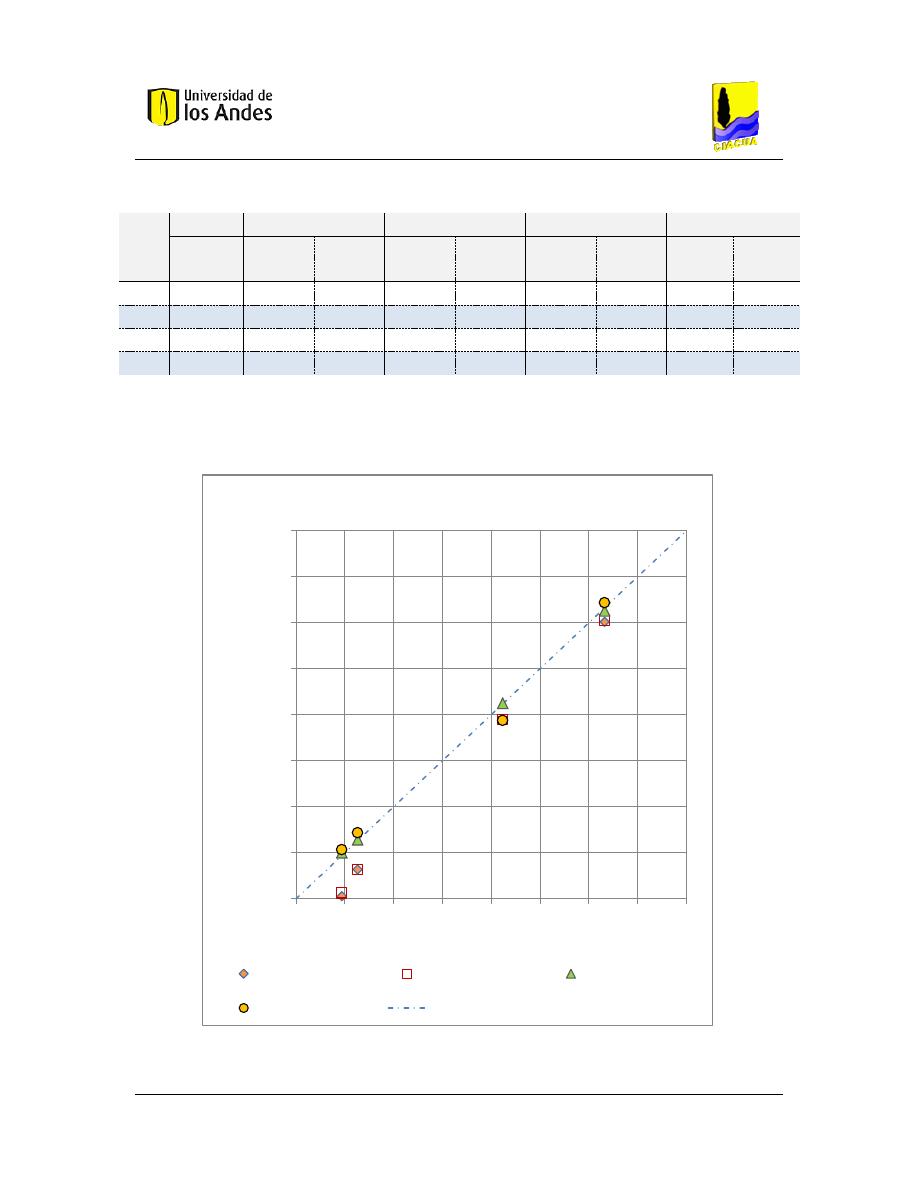
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
75
Tabla 20. Cálculo de C3 mediante las ecuaciones estudiadas y la ecuación propuesta, para las pruebas que cumplen las
restricciones. Promedio de las tomas para cada prueba
Prueba
Medición
Ho
Gómez
Ec. Estándar
Ec. Propuesta 1
Concen.
(g/L)
Concen.
(g/L)
Error
(%)
Concen.
(g/L)
Error
(%)
Concen.
(g/L)
Error
(%)
Concen.
(g/L)
Error
(%)
1
0,95
0,06
-93,6%
0,13
-86,3%
1,01
6,5%
1,06
12,6%
2
1,27
0,63
-50,0%
0,64
-49,7%
1,28
1,1%
1,44
13,3%
3
4,24
3,88
-8,4%
3,89
-8,3%
4,25
0,1%
3,87
-8,7%
4
6,33
6,02
-4,9%
6,05
-4,4%
6,26
-1,1%
6,43
1,6%
Con los valores anteriores se elaboró una gráfica de dispersión de datos que permite observar la
aproximación de los resultados de cada una de las ecuaciones respecto a los valores medidos,
representados por la línea punteada en color azul, tal como se muestra a continuación:
Gráfica 10. Exactitud de las ecuaciones estudiadas en relación a la concentración medida para C3. Pruebas que
cumplen con las restricciones del modelo. Promedio de las tomas para cada muestra
0,0
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
0,0
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
C
o
n
ce
n
tra
ci
ó
n
c
al
cu
la
d
a
(g/L
)
Concentración medida (g/L)
Concentración medida vs. calculada
Ho
Romero-Gómez
Ec. Estándar
Ec. Propuesta
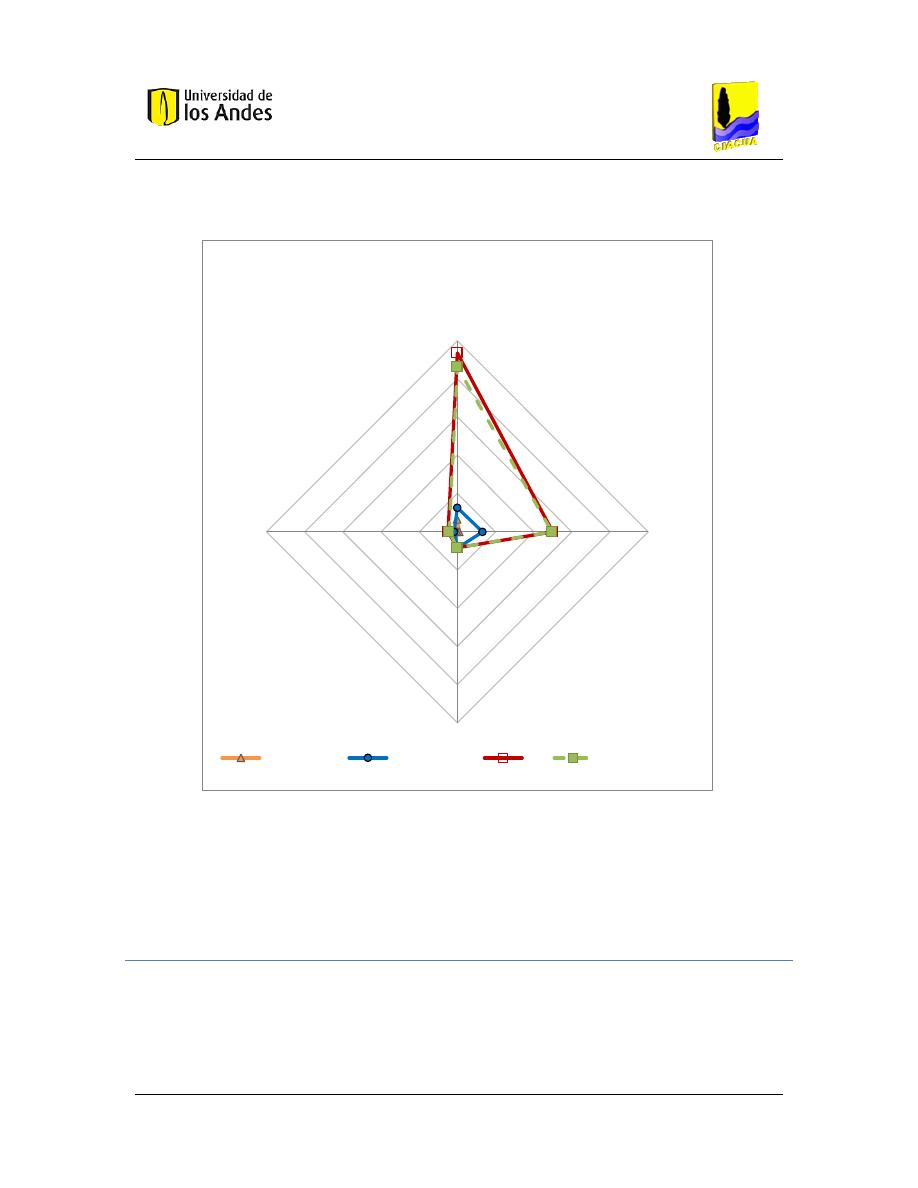
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
76
En este caso se puede observar que tal como ocurrió en el caso anterior, la ecuación propuesta
muestra un alto nivel de ajuste a las mediciones realizadas en las pruebas del experimento.
Gráfica 11. Error calculado para el valor de C3 hallado mediante las diferentes ecuaciones estudiadas respecto a los
valores medidos en el experimento. Pruebas que cumplen con las restricciones del modelo.
Nuevamente, la gráfica radial en el caso de C3 muestra que después de la ecuación de mezcla
estándar, la ecuación más exacta es la propuesta.
8.3 Resultado general C
3
y C
4
Tanto las tablas como los gráficos anteriores corresponden a las pruebas que cumplen a cabalidad
las restricciones arriba mencionadas; sin embargo se decidió graficar los resultados de los datos
promedio de cada una de las pruebas realizadas y evaluar el ajuste de la ecuación propuesta en los
casos en que no se cumplió con alguna de las restricciones propuestas.
0,0%
20,0%
40,0%
60,0%
80,0%
100,0%
1
2
3
4
Error calculado respecto a los valores medidos
para C3
Ec. Estándar
Ec. Propuesta
Ho
Romero-Gómez
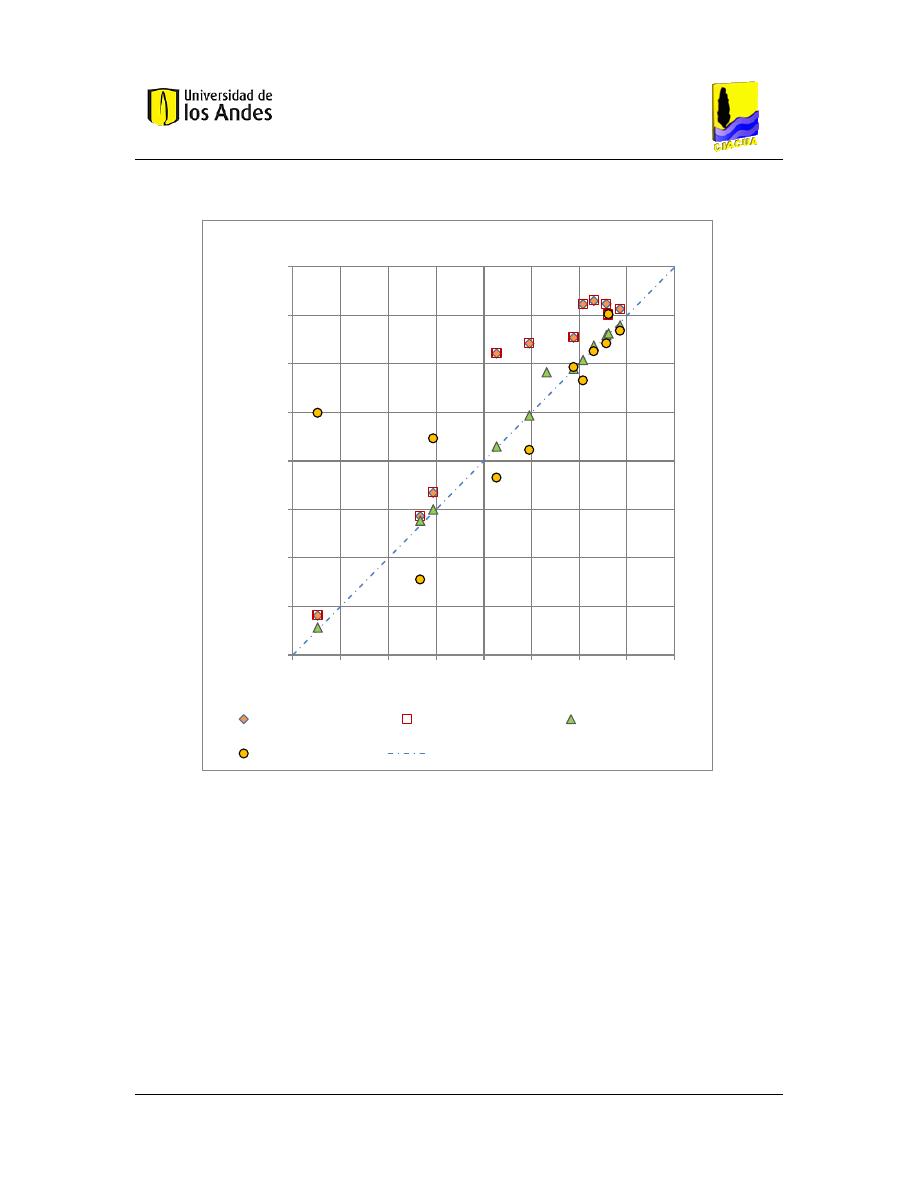
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
77
Los resultados obtenidos para C
4
se muestran en la siguiente gráfica:
Gráfica 12. Exactitud de las ecuaciones estudiadas en relación a la concentración medida para C4. Todas las pruebas.
Como se puede observar, algunos de los valores obtenidos se alejan significativamente de los
valores obtenidos durante el experimento. Al hacer un análisis del comportamiento de los
resultados se evidenció un error de procedimiento en la toma de los datos respecto al instrumento
utilizado para medir la conductividad, situación que se explicará con mayor detalle en las
conclusiones del informe.
Para el caso de la concentración C
3
se desarrolló el mismo procedimiento, alcanzando los
siguientes resultados:
0,00
1,00
2,00
3,00
4,00
5,00
6,00
7,00
8,00
0,00
1,00
2,00
3,00
4,00
5,00
6,00
7,00
8,00
C
o
n
ce
n
tra
ci
ó
n
c
al
cu
la
d
a
(g/L
)
Concentración medida (g/L)
Concentración medida vs. calculada
Ho
Romero-Gómez
Ec. Estándar
Ec. Propuesta
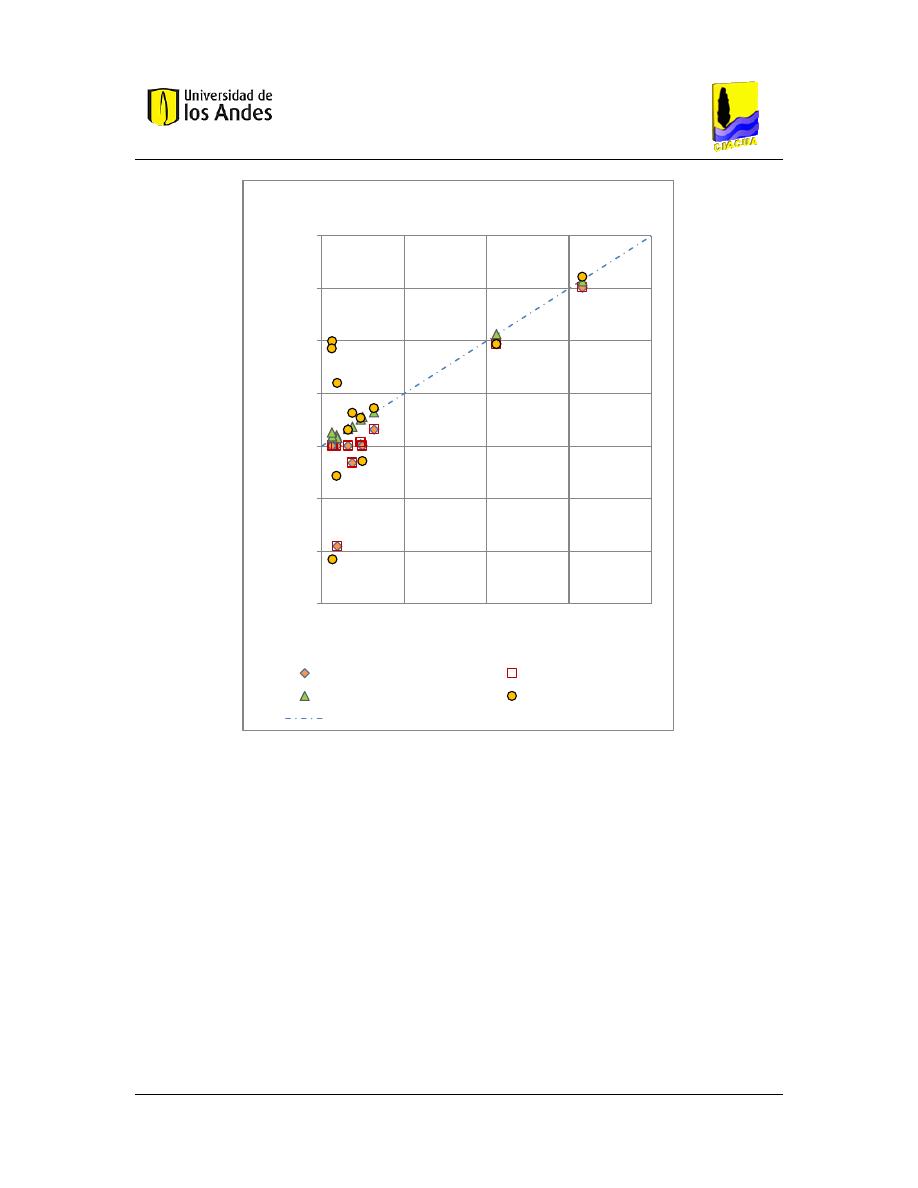
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
78
Gráfica 13. Exactitud de las ecuaciones estudiadas en relación a la concentración medida para C3. Todas las pruebas.
Se observa igualmente mayor dispersión en algunas de las pruebas donde no se cumplen las
restricciones, incluso mayores errores porcentuales que en el caso anterior dado que por regla
general los valores de la concentración en la tubería 3 son significativamente menores que en la
tubería 4, acercándose en algunos de los casos a la conductividad en la tubería 2, la cual era
mínima.
-6,00
-4,00
-2,00
0,00
2,00
4,00
6,00
8,00
0,00
2,00
4,00
6,00
8,00
C
o
n
ce
n
tra
ci
ó
n
c
al
cu
la
d
a
(g/L
)
Concentración medida (g/L)
Concentración medida vs. calculada
Ho
Romero-Gómez
Ec. Estándar
Ec. Propuesta

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
79
9 Conclusiones, recomendaciones y comentarios sobre las conclusiones
Las conclusiones y recomendaciones resultado del experimento se muestran continuación.
9.1 Conclusiones
Realizado el experimento y analizados los elementos que intervinieron en él, así como sus
resultados se puede concluir lo siguiente:
Se confirma que la metodología usada para este experimento con las restricciones planteadas
para el mismo, es coherente y brinda resultados óptimos para estimar las concentraciones C
3
y
C
4
.
Para estimar las concentraciones C
3
y C
4
con otras restricciones se hace necesario determinar
e incluir en la metodología propuesta nuevas relaciones entre caudales de entrada y salida y
sus concentraciones, de manera tal que se pueda hallar otra ecuación que ajuste los
resultados reales al modelo.
Se confirma que efectivamente, para las circunstancias comunes de los sistemas de
distribución de agua potable a presión correspondientes a las uniones de tuberías en cruz se
cumplen la mayoría de las situaciones el caso 4 tipo b. con la salvedad que las concentraciones
son diferentes en todas las tuberías (C
1
≠ C
2
).
Se observa que las consideraciones y evaluaciones realizadas por diferentes investigadores
donde se supone para el caso 4 tipo a y b, que la concentración C
1
es igual a la C
4
, solo es
correcta en condiciones controladas de laboratorio y con cruces sin mayores cambios
geométricos en su sección interior y con unas paredes interinas lisas, aunque es posible que
para grandes diámetros esta suposición sea una buena aproximación a la realidad.
Para todo sistema de distribución de agua potable a presión, que tenga en su red uniones de
tuberías por medio de cruces, si el valor de las concentraciones de entrada a la cruz, son
diferentes, todas las concentraciones de salida también serán diferentes, debido a las
características mismas de la unión en cruz que afectan el perfil de velocidad y la cantidad de
movimiento de los fluidos que discurren a través de ella, ver comentarios.
Dado que en una red de distribución de agua potable existen cambios de velocidad y sentido
de flujo se puede inferir con base en el experimento, que al existir gran cantidad de estas
uniones, las concentraciones en sectores de la red tenderán a igualarse, y en general en toda
la red se presentara una mezcla total de las soluciones. Los valores de estas concentraciones
variaran en el tiempo debido a la afectación derivada de la reacción de las soluciones con las
paredes internas de las tuberías, válvulas y accesorios, de ahí que aunque exista una mezcla
total en toda la red el valor de las concentraciones de la solución sea diferente por sectores.
Dado que para modelar una red de agua potable a presión, se hace necesario determinar
unos consumos por nudo que representa en el modelo el consumo de agua por parte de los
suscritores alrededor del mismo, para determinar la concentración del soluto para estos no es
acertado estimar la calidad del agua en el nudo, en la medida que las concentraciones de
salida por cada tubería (caso tipo 4 b), son diferentes, de manera tal que la concentración por
tubería es diferente a la que se estimaría como si se extrajera un cantidad de agua de la cruz
(nudo), la concentración de esta salida sería diferente a la correspondiente al usuario
dependiendo de la tubería donde tenga su acometida. Todos los usuarios de conectados a

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
80
una tubería deben tener asignada la concentración del soluto correspondiente a la misma.
Esto se puede realizar haciendo una adaptación al software de modelación hidráulica con base
en un SIG, que identifique a usuario con su correspondiente tubería de alimentación.
Al comparar el modelo digital (EPANET), con el modelo real, se observa en el modelo real que
cuando una de las tuberías que discurre el agua hacia la cruz tiene un caudal muy bajo, por
ejemplo Q
2
, en comparación con Q
1
, el flujo a través de la unión tipo cruz se asemeja al flujo a
través de una tee, lo cual no lo entiende físicamente el programa de EPANET, reportando así
caudales iguales a la salida de la cruz, siendo un error ya que en la realidad fluye más agua a
través de la salida Q
3
que por la salida Q
4
.
Se observa que el experimento es muy sensible en la medida de la conductividad, por el uso
de instrumentos no adecuados y con rangos de medida de la conductividad extremos a los
preparados para el experimento.
9.2 Recomendaciones
Para desarrollar un método de cálculo robusto de las concentraciones de salida, se debe
desarrollar más experimentos con diferentes diámetros de tuberías, caudales de entrada y
salida en cada tubería, diferentes tipos de uniones en cruz.
Para mejorar la toma de datos es imprescindible la compra de instrumentos que evalúen los
valores de las variables en tiempo real, calibrados y con los rangos ajustados a las medidas que
se planteen en el experimento. No se debe realizar el experimento con valores extremos de
conductividad, lo ideal es que los valores de la conductividad de las soluciones preparadas
estén muy cerca del valor óptimo de medida del instrumento utilizado, por ejemplo si el valor
de medida optimo del instrumento de conductividad es de 12 mS, lo recomendable es que una
de las concentraciones este alrededor de 14 mS y la otra alrededor de los 10 mS, de tal maner
que sus mezclas estén cercanas al valor óptimo de medida del equipo.
Para mejores resultados se debe desarrollar un experimento con modelos más complejos que
simulen una red de distribución de agua y evaluar en varios nudos al tiempo el
comportamiento de los caudales y las concentraciones
Verificar los modelos de Redes, Epanet y WaterCad.
9.3 Comentarios
Adjunto con las conclusiones y recomendaciones, resultado del experimento aparecen algunos
temas que deben ser comentados pero que no hacen parte de las dos anteriores, para este caso
ellos son:
9.3.1 Mezclas reales dentro de las uniones en cruz
Aunque pruebas en laboratorio y modelos desarrollados en software de modelación de fluidos
hacen suponer que para el caso 4 (tipo a y b), la concentración C
1
es igual a la concentración C
4
,
en la realidad las redes de distribución de agua potable cuentan con uniones de tipo cruz que se
alejan significativamente de las usadas comúnmente en los prototipos físicos de laboratorio
(acrílico o vidrio), lo que hace que la suposición que C
1
es igual a la concentración C
4
, es
meramente académica, aunque eficiente para entender de manera general el fenómeno y brindar
explicaciones al respecto y aproximaciones matemáticas útiles.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
81
Algunas de las razones por las cuales afirmar que la concentración C
1
es igual a la concentración
C
4
, no es cierta en redes de distribución de agua potable a presión se comentan a continuación.
9.3.1.1 Características de las uniones en cruz
Las uniones en cruz tienen una serie de características que afectan la cantidad de movimiento de
los fluidos que discurren a través de ella, generando pequeñas turbulencias que hacen que exista
mezcla de las aguas convergentes en el interior de la misma.
9.3.1.1.1 Consideraciones geométricas por procesos de fabricación.
Dentro de las consideraciones a tener en cuenta están las características de configuración
geométrica derivadas de los procesos de fabricación de la unión, tal como se muestra en la foto
siguiente; se observa la sección transversal de la unión cruz usada en el experimento (PVC), tiene
las huellas de los machos contenidos en el molde de inyección, que sirven para configurar la parte
interna de la unión. La altura de las huellas de estos machos se midió con un pie de rey y es de 0,5
mm.
Fotografía 15. Imperfecciones derivadas del proceso de fabricación (cruz PVC soldada)
De igual manera para uniones en cruz fabricadas en PVC, pero con conexión roscada NPT, tal como
se observa en la siguiente fotografía, se distinguen zonas con rugosidades (rebabas), debidas a los
machos de fabricación y al sistema de conexión.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
82
Fotografía 16. Imperfecciones derivadas del proceso de fabricación (cruz PVC roscada)
Para el caso de otros tipos de procesos de fabricación como el de las cruces de Acero Galvanizado
se puede observar una cavidad propia del macho que conforma la parte interna de la unión en el
proceso de fundición del metal, esta cavidad fue medida obteniendo una altura de la parte más
baja al filete de la rosca de 2 mm
Fotografía 17. Imperfecciones derivadas del proceso de fabricación (cruz hierro galvanizado roscada)
De igual manera ocurre con otro tipo de uniones en cruz usada en los sistemas de distribución de
agua, como las fabricadas en hierro dúctil donde también necesita de machos de arena para
conformar la parte interna de la cruz, generando saltos o diferencias concéntricas en la cruz
derivados de la fuerza de desplazamiento del hierro fundido a través del molde de arena. Esta
diferencia disminuye de manera relativa al diámetro interno de la tubería a usar; así a mayor
diámetro interno menor es esta diferencia de altura relativa al mismo.
9.3.1.1.2 Consideraciones del método de unión
Otra consideración a tener en cuenta es la correspondiente al método de unión en la cruz. Para el
caso de esta unión en PVC, la unión se realiza a través de pegamento para PVC (Soldadura
solvente); esto implica que el material en contacto entre el tubo y la cruz, se derrite y se mezcla
para luego secarse y hacerse una sola pieza. Esto implica que el diámetro exterior de la tubería
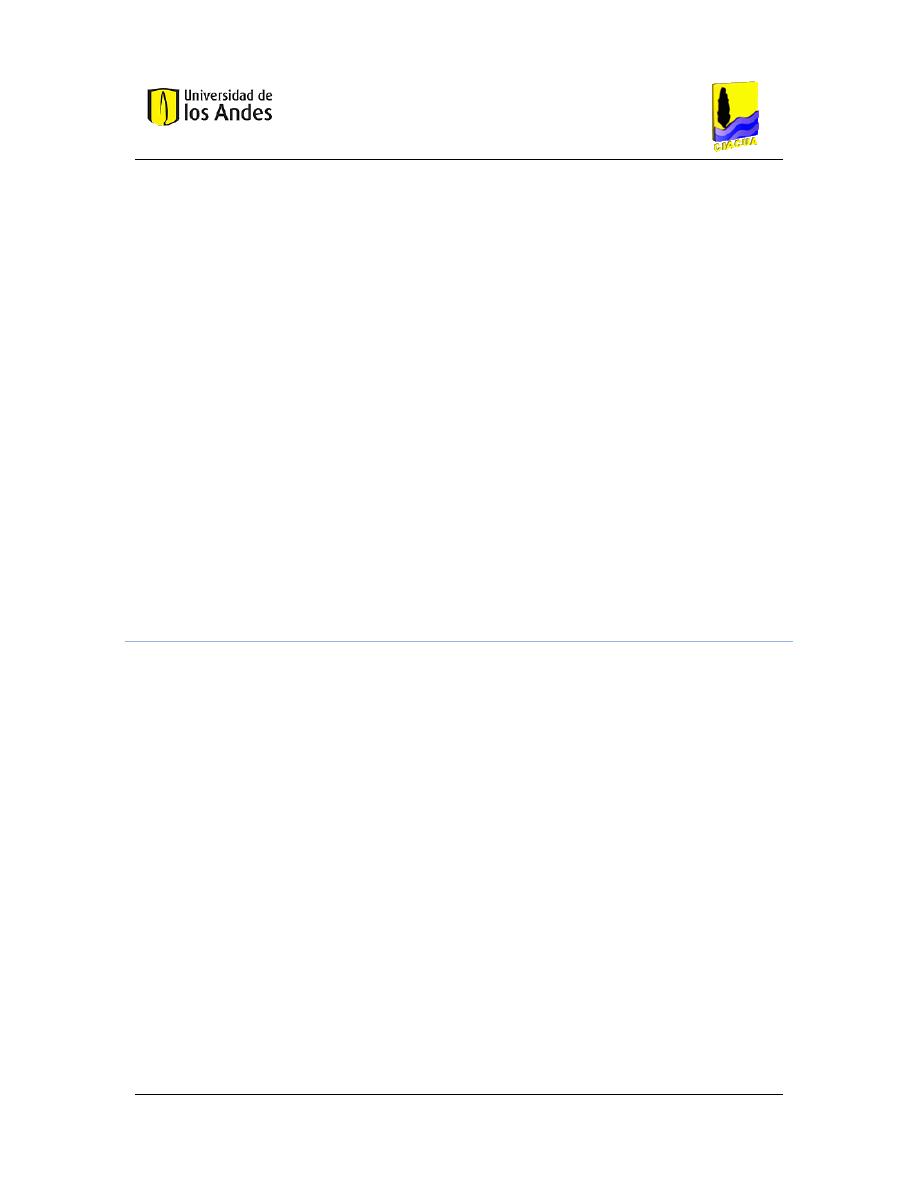
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
83
debe ingresar dentro de la unión, generando dentro de la cruz un escalón que corresponde en
altura casi al espesor mismo del tubo que se une, tal como se observa en la foto anterior.
Para el caso de la tubería de Acero Galvanizado, la conexión es roscada de tipo cónico que hace
sello a través de los filetes de la rosca, por tanto y como aparece en la foto la rosca del tubo no
entra plenamente dentro de la cruz, por tanto al fluir el agua hacia adentro de la cruz esta choca
con los filetes de la rosca generando turbulencias que interrumpen el discurrir uniforme del agua.
Otros tipos de conexiones en uniones de cruz, son las bridadas o las conexiones hidráulicas; en
ambos casos la unión genera saltos internos dentro de la cruz que perturba el discurrir del flujo
hacia el centro de la cruz.
9.3.1.1.3 Consideraciones al respecto del material de fabricación
Otro aspecto importante es el material con el cual se fabrica la unión. Así por ejemplo, para el caso
del PVC es un material con una rugosidad muy baja y sin afectación por corrosión metálica y solo
afectado en parte por la biocorrosión. Para el caso del Acero Galvanizado, este es un material con
una rugosidad alta, que se afecta por corrosión metálica y biocorrosión. Para el caso del hierro
dúctil, aunque este tipo de unión está recubierto por una pintura epóxica que disminuye la
rugosidad del material en contacto con el agua, esta sigue siendo mayor a la del PVC y susceptible
de desgastarse y permitir la formación de corrosión metálica y en todo caso biocorrosión.
9.3.2 Aplicación computacional del modelo planteado
Todo experimento tiene como objetivo conocer más de aquello sobre lo que se experimenta y
como fin último aplicar lo conocido a situaciones prácticas de la vida, la sociedad o la industria de
todo tipo, y este experimento la metodología aquí propuesta y sus resultados no se alejan de este
fin.
La aplicación práctica de lo aquí desarrollado es llevarlo a un modelo computacional que con
bastante exactitud permita modelar el flujo de agua con su concentración a través de la red de
distribución de agua modelada y predecir el valor de la concentración del agua de manera espacial
y temporal en la red.
A continuación se muestra el diagrama de flujo propuesto para determinar el valor de salida de las
concentraciones de agua que discurre a través de un nudo en un modelo hidráulico, donde se
conocen los caudales de entrada y salida (cuatro en total), y al menos dos de las cuatro
concentraciones que discurren hacia el nudo.
El diagrama propone que conocido los caudales de entrada y salida de cada nudo y conocidas dos
de las concentraciones que ingresan a él, determinar el valor de las concentraciones de salida de
manera eficiente y exacta, evaluando las características de los caudales que confluyen a la unión.
El método propone evaluar qué caso de caudales que confluyen en la cruz, de los aquí descritos en
este documento ocurre en el nudo del modelo y con base en esto continuar con el diagrama de
flujo y determinar el valor de las concentraciones a través de las diferentes ecuaciones propuestas.
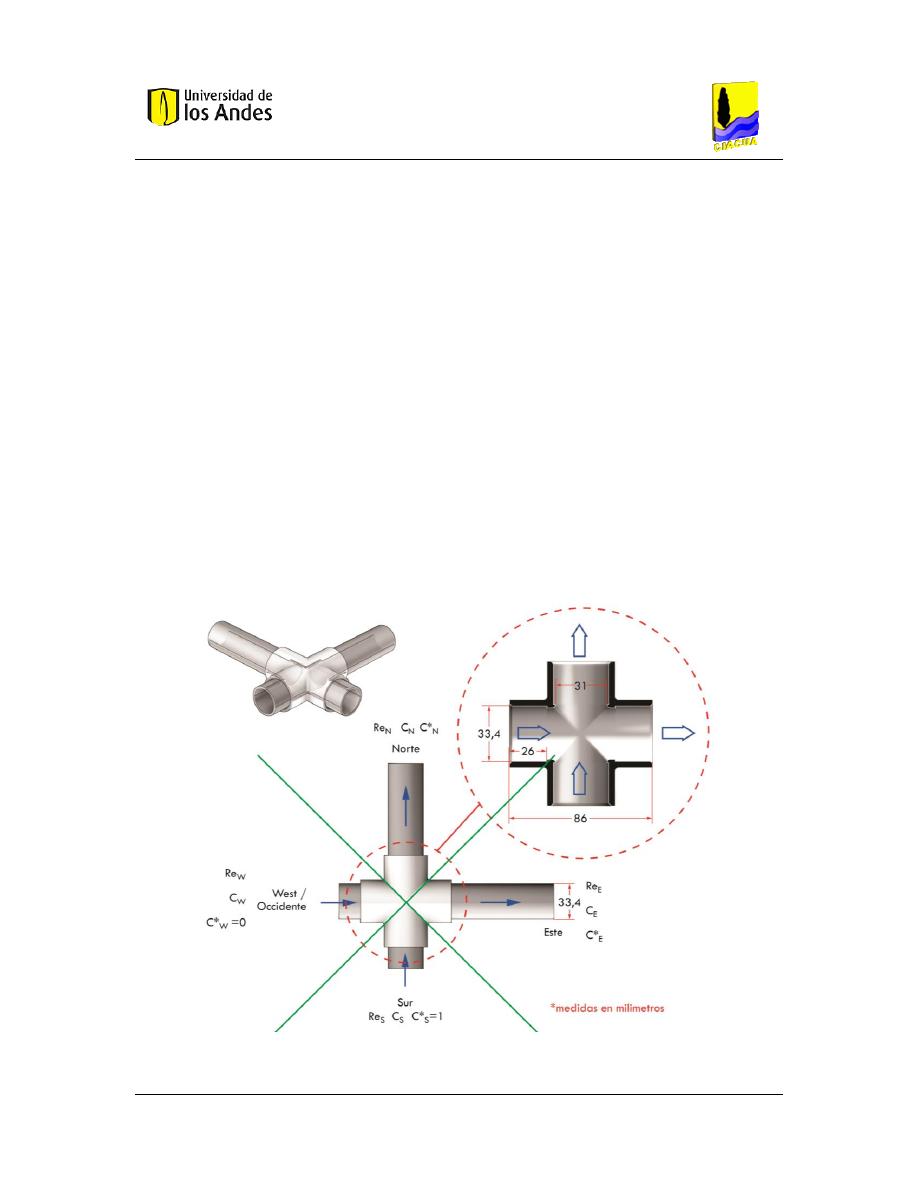
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
84
Para determinar si los caudales que confluyen al nudo son de entrada o salida se toma como base
la información suministrada por el software de modelación hidráulica que se toma como base el
cual debe tener la posibilidad de a través de una aplicación de GIS (o de manera propia del sistema
a través de un sistema cartesiano propio que ubique espacialmente los nudos dentro de una foto
satelital o de otro tipo), ubicar los nudos en coordenadas (x,y) o latitud (Norte y Sur) y longitud
(Este y Oeste), de tal manera que pueda determinar a través de un algoritmo si la entrada de una
tubería a la cruz en comparación a otra, es adyacente o está enfrentada, tal como se muestra en la
figura siguiente.
El algoritmo deberá evaluar si el punto de origen del tubo está en las zona correspondiente al
norte (N), al sur (S), al este (E) u oeste (W); estas zonas están delimitadas por líneas imaginarias
trazadas desde el nudo en dirección (NE), (NW), (SW) y (SE), así una tubería cuyo punto de origen
en dirección al nudo en estudio (las coordenadas del nudo son el punto de llegada de la tubería),
está ubicada en coordenadas que la ubique en la zona comprendida entre las líneas (NE) y (NW),
será adyacente a una tubería cuyas coordenadas de origen este ubicadas en la zona delimitada por
la líneas imaginarias (NE) y (SE) o (NW) y (SW). Un algoritmo similar es posible realizarlo para
sistemas coordenados, tal como lo utiliza EPANET, haciendo por ejemplo f(x) = x, y f(x) = -x,
desarrollando desigualdades para la ubicación de los puntos de origen y llegada de las tuberías y
determinando las áreas de influencia.
Figura 17. Identificación de las tuberías de entrada y salida de acuerdo con una base georreferenciada
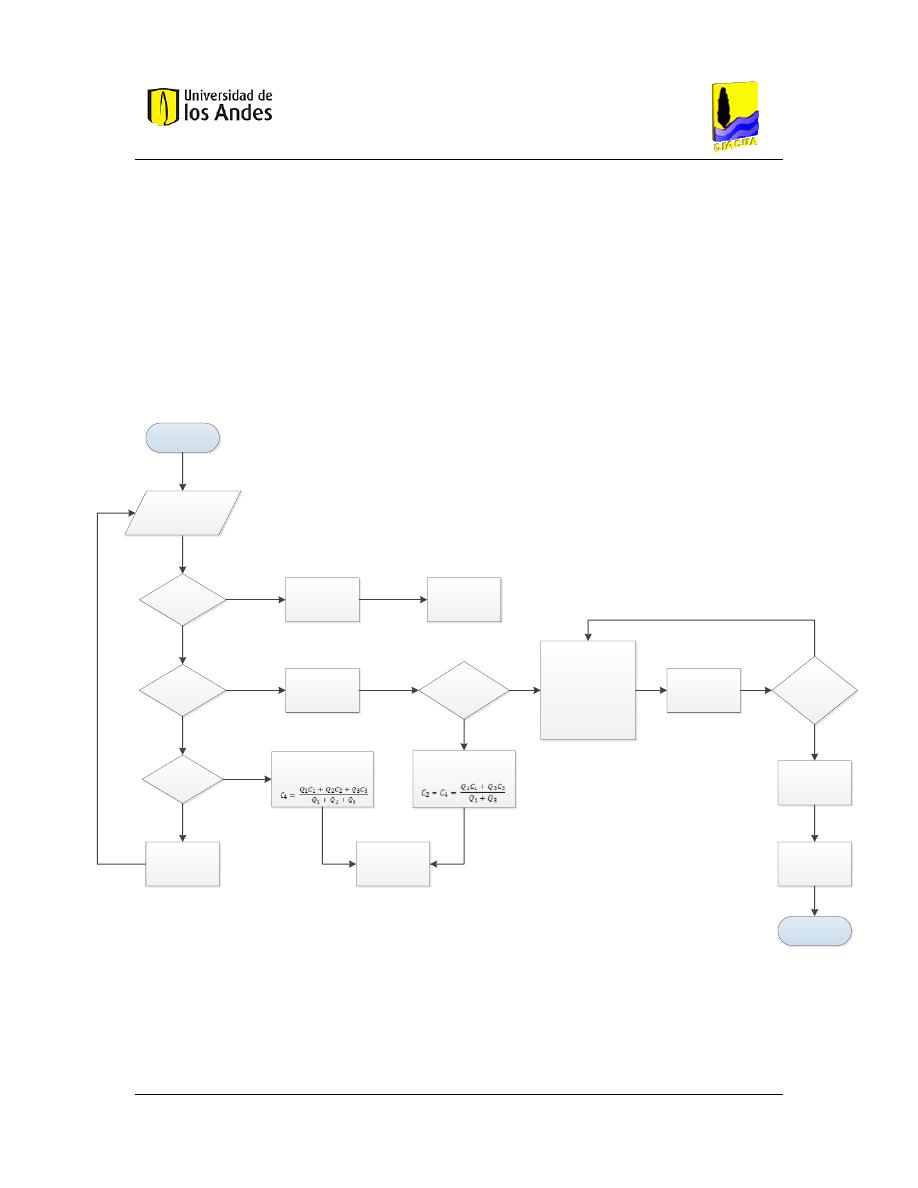
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
85
Para el caso 4 tipo b. es necesario complementar el método de cálculo con una o varias ecuaciones
que cubran todas las posibilidades de relaciones y restricciones de los caudales de entrada y salida
con sus correspondientes concentraciones y agregarlas a esta parte del diagrama de flujo
propuesto. Para el caso aquí evaluado, se agregaron las relaciones y restricciones que hacen parte
de este documento y su correspondiente ecuación para la valoración de las concentraciones de
salida. Este diagrama de flujo debe conllevar al desarrollo de un algoritmo lo suficientemente
robusto para ser incorporado en un software de modelación hidráulica convencional y determinar
con mayor exactitud el valor de las concentraciones salientes de los nudos de estudio.
El diagrama de flujo desarrollado para este caso particular se muestra a continuación.
Figura 18. Diagrama de flujo propuesto para la aplicación computacional del modelo planteado con base en un
posicionamiento georreferenciado
Inicio
No. Caudales
positivos = 1 ?
Mezcla completa
C1 = C2 = C3 = C4
No. Caudales
positivos = 2 ?
SI
NO
SI
Georreferencie los
caudales positivos
Son los
caudales positivos
adyacentes ?
No. Caudales
positivos = 3 ?
NO
SI
Mezcla completa
Aplique la ecuación
Mezcla completa
Aplique la ecuación
NO
NO
Imprima resultados
y vaya a FIN
Imprima resultados
y vaya a FIN
Revise la
información de
entrada
Evaluar restricciones y
relaciones entre las
variables. Para este caso,
las siguientes :
a. Q
1
>= Q
2
, Q
3
, Q
4
b. Q
3
>= Q
4
c. C
1
> C
2
, C
3
, C
4
d. C
3
<= C
4
e. C
3
> C
2
Se cumplen dichas
consideraciones?
Calcule C3 y C4
mediante las
ecuaciones
propuestas
SI
SI
NO
Imprima resultados
FIN
Lea Q1, Q2, Q3,
Q4 y
concentraciones
de entrada
Defina las
ecuaciones con base
en lo anterior

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
86
10 Bibliografía
10.1 Artículos y otros documentos
Cabrera, M. E. & Espert, A. V. (2005). Análisis de la evolución de la calidad del agua en
redes. Modelación matemática de redes. Formación ITA. Memorias de curso, Tomo 1.
UPV.
Chiu, C. L., & Hsu, S. M. (2006). Probabilistic approach to modeling of velocity distributions
in fluid flows. Journal of Hydrology , Vol 316, 119-149.
Chiu, C. -L., Lin, G. F., & Lu, G. F. (1993). Application of probability and entropy concepts in
pipe flow study. Journal of Hydraulic Engineering , Vol 119, 742 - 756.
Fuentes, M. O & Mompremier, R. (2012). Resultados de pruebas de laboratorio para
analizar la difusión del Cloro en cruces de tuberías. Recuperado el 10 de Septiembre de
2013, de XXII Congreso Nacional de Ingeniería Hidráulica, Acapulco, México, memorias:
http://www.revistatlaloc.org.mx/amh_congreso/articulos/InfraestructuraParaAbastecimie
ntoySaneamientoDelAgua/182Art_fmoa_6.pdf
García, C. V.& García-Serra, J. (2005). Modelación matemática de redes. Formación ITA.
Memorias de curso, Tomo 1. UPV.
Grayman, W., Clarck, R., & Males, R. (1988). Modeling Distribution System Quality
Dynamic Approach. Journal of Water Resources Planning and Management , Vol 114, 295 -
312.
Hernández, O. (2005). Metodología del gradiente para la solución de redes de tuberías a
presión. Revista Escuela Colombiana de Ingeniería, Vol. 59, Pag 16 a 23.
Ho, C. K. (2008). Solute Mixing Model for Water-Distribution Pipe Networks. Recuperado
el
10
de
Marzo
de
2013,
de
ASCE:
http://gsgc.gzhu.edu.cn/gpsgd/UploadFile/200942623229730.pdf
Ho, C. K., Choi, C. Y., & McKenna, S. A. (2007). Evaluation of complete and incomplete
mixing models in water distribution pipe network simulations. Recuperado el 3 de Junio de
2013,
de
World
Environmental
and
Water
Resources
congress
(ASCE):
http://ascelibrary.org.biblioteca.uniandes.edu.co:8080/doi/abs/10.1061/40927%28243%2
9486?prevSearch=%28evaluation+of+complete+and+incomplete+mixing+models%29+and
+%5BFulltext%3A+evaluation+of+complete+and+incomplete+mixing+models%5D&search
HistoryKey=
Liou, C., & Kroon, J. R. (1987). Modelling the Propagation of Waterborne Substances in
Distribution Networks. Journal of American Water Works Association , Vol 119, 54 - 58.
Rossman, L., & Boulos, P. (1993). Discrete Volume Element Method for Network Water
Quality Models. Jurnal of Water Resources Planning and Managament , Vol. 119, 505-515.
Rossman, L., & Boulos, P. (1996). Numerical methods for modellingwater quality in
distribution systems. Journal of Water Resources Planning and Management , Vol 122, 137
- 146.
Taylor, G. (1954). The dispersion of matter in turbulent flow through a pipe. Proceedings
of the London Mathematical Society , Series A, 446-463.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
87
Todini, E., & Pilati, S. (1987). A gradient method for the analysis of pipe networks.
International Conference on Computer Applications for Water Supply and Distribution,
Leicester Polytechnic .
Vidal, R., Martinez, F., & Ayza, M. (1994). Aplicaciones de los modelos de calidad en la
simulación de las redes de distribución de agua potable. Ingeniería del Agua, 55 - 68.
10.2 Tesis
Felix, Z. (2005). Verificación experimental de la aplicabilidad de un modelo simplificado de
transporte de solutos en tuberías. Tesis para optar título de maestría, Universidad de los
Andes, Departamento de Ingeniería Civil, Bogotá, Colombia.
Fonnegra, J. C. (2002). Modelo de Calidad del Agua en Sistemas de Distribución de Agua
Potable. Tesis de Maestría en Ingeniería Civil, Universidad de los Andes, Departamento de
Ingeniería Civil, Bogotá, Colombia.
Hernández F. M. A. (2010). Verificación Experimental de la Capacidad Predictiva de
Modelos de Transporte de Solutos en Redes de Tuberías a Presión.
Tesis presentada
como requisito parcial para optar al título de Magister en Ingeniería de Recursos
Hidráulicos. Universidad Nacional de Colombia, Bogotá, Colombia.
González, M. (2004). Modelo de contaminantes en la red de distribución de agua potable
en la ciudad de Bogotá y sus efectos en la población. Tesis de Maestría en Ingeniería Civil,
Universidad de Los Andes, Bogotá, Colombia.
Guevara, G. (2002). Desarrollo de un modelo simplificado de transporte de solutos en
redes de distribución de agua potable. Tesis de Maestría en Ingeniería Civil, Universidad de
los Andes, Departamento de Ingeniería Civil, Bogotá, Colombia.
Mompremier, R. (2009). Difusión de sustancias en redes de tuberías a presión. Tesis de
Maestría en Ciencias en Hidráulica. Instituto Politécnico Nacional. México, México.
Palacios, W., & Rincón, F. (2008). Red experimental de flujo a presión para el estudio de la
hidráulica y transporte de solutos. Tesis de grado en Ingeniería Civil, Universidad Nacional
de Colombia, Departamento de Ingeniería Civil y Agrícola, Bogotá, Colombia.
Pantoja, C. A. (2005). Verificación Experimental de un modelo transporte de solutos en
sistemas de distribución de agua potable. Tesis de Maestría en Ingeniería Civil, Universidad
de Los Andes, Departamento de Ingeniería Civil, Bogotá, Colombia.
Trujillo López, J. A. (2007). Diseño e implementación de una red experimental de flujo a
presión para el estudio de la hidráulica y el transporte de solutos. Universidad Nacional de
Colombia, Departamento de Ingeniería Civil y Agrícola, Bogotá, Colombia.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
88
ANEXO No. 1 Datos obtenidos en el experimento
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
0,050 0,045 0,045 0,047
Temperatura (°T)
16,90 17,00 16,80 16,900
Tanque No 2
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
0,050 0,045 0,045 0,047
Temperatura (°T)
17,00 16,90 16,90 16,933
Prueba No. 1 - Toma No. 1
Contenido sal
2 Kg
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
11,88 11,88 11,88 11,880
Temperatura (°T)
16,70 16,70 16,70 16,700
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
1,80 1,82 1,82 1,813
Temperatura (°T)
16,70 16,80 16,80 16,767
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
10,55 10,54 10,56 10,550
Temperatura (°T)
16,70 16,70 16,80 16,733

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
89
Prueba No. 1 - Toma No. 2
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
11,80 11,78 11,80 11,793
Temperatura (°T)
17,10 16,80 16,80 16,900
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
1,79 1,80 1,80 1,797
Temperatura (°T)
17,00 17,00 17,00 17,000
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
10,40 10,40 10,39 10,397
Temperatura (°T)
17,00 16,90 16,80 16,900
Prueba No. 1 - Toma No. 3
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
11,66 11,67 11,67 11,667
Temperatura (°T)
16,70 16,70 16,70 16,700
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
1,86 1,86 1,86 1,860
Temperatura (°T)
16,60 16,70 16,70 16,667
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
10,32 10,34 10,36 10,340
Temperatura (°T)
16,90 16,80 16,80 16,833

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
90
Prueba No. 2 - Toma No. 1
Condición:
Válvula 2 cerrada 22,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,82 11,82 11,79 11,810
Temperatura (°T) 15,40 15,20 15,10 15,233
Tanque No 2
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,04 0,04 0,04 0,040
Temperatura (°T) 15,30 15,20 15,20 15,233
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 2,40 2,40 2,40 2,400
Temperatura (°T) 15,60 15,60 15,60 15,600
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 10,88 10,88 10,88 10,880
Temperatura (°T) 15,70 15,70 15,70 15,700
Prueba No. 2 - Toma No. 2
Condición:
Válvula 2 cerrada 22,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,79 11,77 11,77 11,777
Temperatura (°T) 15,50 15,30 15,30 15,367
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 2,50 2,49 2,49 2,493
Temperatura (°T) 16,00 15,80 15,80 15,867
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 10,80 10,80 10,79 10,797
Temperatura (°T) 15,70 15,60 15,70 15,667

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
91
Prueba No. 2 - Toma No. 3
Condición:
Válvula 2 cerrada 22,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,73 11,72 11,73 11,727
Temperatura (°T) 15,70 15,50 15,40 15,533
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 2,34 2,33 2,32 2,330
Temperatura (°T) 16,20 15,90 16,00 16,033
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 10,76 10,76 10,75 10,757
Temperatura (°T) 15,70 15,70 15,70 15,700
Prueba No. 3 - Toma No. 1
Condición:
Válvula 2 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,48 11,48 11,48 11,480
Temperatura (°T) 16,40 16,50 16,50 16,467
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 7,38 7,39 7,40 7,390
Temperatura (°T) 16,80 16,80 16,80 16,800
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 10,88 10,89 10,89 10,887
Temperatura (°T) 16,70 16,70 16,70 16,700

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
92
Prueba No. 3 - Toma No. 2
Condición:
Válvula 2 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,46 11,46 11,46 11,460
Temperatura (°T) 16,70 16,60 16,70 16,667
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 7,32 7,32 7,32 7,320
Temperatura (°T) 16,70 16,60 16,70 16,667
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 10,89 10,90 10,90 10,897
Temperatura (°T) 16,70 16,70 16,70 16,700
Prueba No. 3 - Toma No. 3
Condición:
Válvula 2 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,39 11,41 11,41 11,403
Temperatura (°T) 16,50 16,70 16,70 16,633
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 7,25 7,25 7,25 7,250
Temperatura (°T) 16,30 16,40 16,40 16,367
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 10,86 10,86 10,85 10,857
Temperatura (°T) 16,40 16,40 16,40 16,400

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
93
Prueba No. 4 - Toma No. 1
Condición:
Válvula 2 cerrada 67,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,65 11,65 11,66 11,653
Temperatura (°T) 15,70 15,70 15,60 15,667
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 10,45 10,44 10,45 10,447
Temperatura (°T) 16,30 16,10 16,30 16,233
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,28 11,28 11,28 11,280
Temperatura (°T) 16,30 16,20 16,10 16,200
Prueba No. 4 - Toma No. 2
Condición:
Válvula 2 cerrada 67,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,65 11,65 11,64 11,647
Temperatura (°T) 15,90 15,90 15,80 15,867
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 10,44 10,43 10,43 10,433
Temperatura (°T) 16,30 16,40 16,50 16,400
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,24 11,25 11,26 11,250
Temperatura (°T) 16,40 16,30 16,40 16,367

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
94
Prueba No. 4 - Toma No. 3
Condición:
Válvula 2 cerrada 67,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,54 11,54 11,54 11,540
Temperatura (°T) 16,00 16,00 16,00 16,000
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 10,48 10,47 10,47 10,473
Temperatura (°T) 16,60 16,50 16,60 16,567
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,17 11,17 11,17 11,170
Temperatura (°T) 16,40 16,40 16,40 16,400
Prueba No. 5 - Toma No. 1
Condición:
Válvula 2 cerrada 67,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,78 11,77 11,77 11,773
Temperatura (°T) 16,50 16,40 16,40 16,433
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 1,26 1,25 1,25 1,253
Temperatura (°T) 17,20 17,20 17,20 17,200
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 9,84 9,84 9,84 9,840
Temperatura (°T) 16,90 17,00 17,00 16,967

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
95
Prueba No. 5 - Toma No. 2
Condición:
Válvula 2 cerrada 67,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,66 11,66 11,65 11,657
Temperatura (°T) 16,90 16,80 16,80 16,833
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 1,27 1,26 1,27 1,267
Temperatura (°T) 17,80 17,70 17,70 17,733
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 9,83 9,83 9,83 9,830
Temperatura (°T) 17,50 17,40 17,50 17,467
Prueba No. 5 - Toma No. 3
Condición:
Válvula 2 cerrada 67,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,53 11,52 11,52 11,523
Temperatura (°T) 16,80 16,80 16,80 16,800
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 1,27 1,27 1,27 1,270
Temperatura (°T) 17,60 17,50 17,50 17,533
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 9,74 9,73 9,73 9,733
Temperatura (°T) 17,50 17,30 17,40 17,400

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
96
Prueba No. 6 - Toma No. 1
Condición:
Válvula 1 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,40 11,40 11,39 11,397
Temperatura (°T) 17,40 17,30 16,80 17,167
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,71 0,71 0,71 0,710
Temperatura (°T) 17,90 18,00 18,00 17,967
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 5,30 5,30 5,30 5,300
Temperatura (°T) 18,10 18,20 18,20 18,167
Prueba No. 6 - Toma No. 2
Condición:
Válvula 1 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,42 11,41 11,40 11,410
Temperatura (°T) 17,50 17,30 17,50 17,433
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,74 0,74 0,74 0,740
Temperatura (°T) 18,40 18,40 18,40 18,400
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 5,26 5,26 5,26 5,260
Temperatura (°T) 18,30 18,30 18,30 18,300

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
97
Prueba No. 6 - Toma No. 3
Condición:
Válvula 1 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
11,42
11,41 11,41 11,413
Temperatura (°T)
17,50
17,40 17,40 17,433
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
0,73
0,73 0,73 0,730
Temperatura (°T)
18,40
18,30 18,30 18,333
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
5,25
5,25 5,24 5,247
Temperatura (°T)
18,10
18,00 18,10 18,067
Prueba No. 7 - Toma No. 1
Condición:
Válvula 1 cerrada 67,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
11,42
11,42 11,41 11,417
Temperatura (°T)
17,50
17,40 17,50 17,467
Tanque No 2
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Temperatura (°T)
17,90
17,90 18,00 17,933
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
0,56
0,56 0,56 0,560
Temperatura (°T)
18,40
18,40 18,40 18,400
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS)
1,00
1,00 0,99 0,997
Temperatura (°T)
18,50
18,50 18,50 18,500

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
98
Prueba No. 7 - Toma No. 2
Condición:
Válvula 1 cerrada 67,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,43 11,43 11,41 11,423
Temperatura (°T) 17,50 17,50 17,40 17,467
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,55 0,55 0,545 0,548
Temperatura (°T) 18,40 18,30 18,30 18,333
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 1,04 1,04 1,04 1,040
Temperatura (°T) 18,40 18,40 18,40 18,400
Prueba No. 7 - Toma No. 3
Condición:
Válvula 1 cerrada 67,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,44 11,44 11,43 11,437
Temperatura (°T) 17,60 17,60 17,60 17,600
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,54 0,54 0,54 0,540
Temperatura (°T) 18,30 18,20 18,20 18,233
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 1,08 1,08 1,08 1,080
Temperatura (°T) 18,30 18,40 18,30 18,333

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
99
Prueba No. 8 - Toma No. 1
Condición:
Válvula 1 cerrada 22,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,75 11,76 11,76 11,757
Temperatura (°T) 17,70 17,80 17,80 17,767
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 1,31 1,30 1,30 1,303
Temperatura (°T) 18,20 18,10 18,10 18,133
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 10,09 10,10 10,10 10,097
Temperatura (°T) 17,90 17,90 17,80 17,867
Prueba No. 8 - Toma No. 2
Condición:
Válvula 1 cerrada 22,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,77 11,77 11,76 11,767
Temperatura (°T) 17,40 17,50 17,50 17,467
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 1,47 1,47 1,47 1,470
Temperatura (°T) 17,80 17,80 17,80 17,800
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 9,99 10,00 9,99 9,993
Temperatura (°T) 17,60 17,70 17,80 17,700

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
100
Prueba No. 8 - Toma No. 3
Condición:
Válvula 1 cerrada 22,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,73 11,74 11,74 11,737
Temperatura (°T) 17,70 17,70 17,50 17,633
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 1,59 1,58 1,58 1,583
Temperatura (°T) 18,40 18,20 18,10 18,233
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 10,20 10,21 10,21 10,207
Temperatura (°T) 17,80 17,90 17,70 17,800
Prueba No. 9 - Toma No. 1
Condición:
Válvula 1 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,75 11,75 11,75 11,750
Temperatura (°T) 17,10 17,20 17,10 17,133
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,82 0,82 0,82 0,820
Temperatura (°T) 17,30 17,30 17,30 17,300
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 8,56 8,56 8,56 8,560
Temperatura (°T) 17,20 17,20 17,20 17,200

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
101
Prueba No. 9 - Toma No. 2
Condición:
Válvula 1 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,70 11,70 11,70 11,700
Temperatura (°T) 17,30 17,30 17,40 17,333
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,67 0,68 0,68 0,677
Temperatura (°T) 17,80 17,80 17,80 17,800
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 8,00 8,00 8,00 8,000
Temperatura (°T) 17,70 17,70 17,60 17,667
Prueba No. 9 - Toma No. 3
Condición:
Válvula 1 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,72 11,73 11,73 11,727
Temperatura (°T) 17,30 17,20 17,30 17,267
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,80 0,80 0,80 0,800
Temperatura (°T) 17,80 17,70 17,70 17,733
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 8,68 8,68 8,68 8,680
Temperatura (°T) 17,40 17,40 17,40 17,400

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
102
Prueba No. 10 - Toma No. 1
Condición:
Válvula 1 cerrada 67,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,84 11,84 11,85 11,843
Temperatura (°T) 17,20 17,10 17,20 17,167
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,42 0,42 0,42 0,420
Temperatura (°T) 17,20 17,20 17,20 17,200
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 6,89 6,89 6,90 6,893
Temperatura (°T) 17,20 17,20 17,20 17,200
Prueba No. 10 - Toma No. 2
Condición:
Válvula 1 cerrada 67,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,83 11,84 11,84 11,837
Temperatura (°T) 17,10 17,10 17,10 17,100
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,53 0,53 0,53 0,530
Temperatura (°T) 17,20 17,20 17,20 17,200
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 7,80 7,80 7,80 7,800
Temperatura (°T) 17,20 17,20 17,20 17,200

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
103
Prueba No. 10 - Toma No. 3
Condición:
Válvula 1 cerrada 67,5°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,81 11,81 11,81 11,810
Temperatura (°T) 17,10 17,10 17,10 17,100
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,62 0,62 0,62 0,620
Temperatura (°T) 17,10 17,10 17,10 17,100
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 7,40 7,41 7,41 7,407
Temperatura (°T) 17,10 17,10 17,10 17,100
Prueba No. 11 - Toma No. 1
Condición:
Válvula 1 cerrada 45° - Válvula 4 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,24 11,24 11,24 11,240
Temperatura (°T) 16,90 17,00 17,00 16,967
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 1,91 1,91 1,91 1,910
Temperatura (°T) 16,90 17,00 17,00 16,967
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 8,83 8,84 8,82 8,830
Temperatura (°T) 16,80 16,80 16,70 16,767

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
104
Prueba No. 11 - Toma No. 2
Condición:
Válvula 1 cerrada 45° - Válvula 4 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,14 11,14 11,14 11,140
Temperatura (°T) 16,80 16,80 16,80 16,800
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 1,91 1,91 1,92 1,913
Temperatura (°T) 16,90 17,00 17,00 16,967
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 9,05 9,05 9,05 9,050
Temperatura (°T) 16,70 16,70 16,70 16,700
Prueba No. 11 - Toma No. 3
Condición:
Válvula 1 cerrada 45° - Válvula 4 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,20 11,20 11,20 11,200
Temperatura (°T) 16,80 16,80 16,90 16,833
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 1,91 1,91 1,91 1,910
Temperatura (°T) 16,80 16,80 16,80 16,800
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 9,00 9,01 9,01 9,007
Temperatura (°T) 16,60 16,60 16,60 16,600

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
105
Prueba No. 12 - Toma No. 1
Condición:
Válvula 1 cerrada 45° - Válvula 3 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,18 11,18 11,18 11,180
Temperatura (°T) 16,60 16,60 16,70 16,633
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,49 0,49 0,49 0,490
Temperatura (°T) 16,60 16,60 16,60 16,600
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 4,80 4,81 4,81 4,807
Temperatura (°T) 16,60 16,60 16,60 16,600
Prueba No. 12 - Toma No. 2
Condición:
Válvula 1 cerrada 45° - Válvula 3 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,17 11,16 11,16 11,163
Temperatura (°T) 16,70 16,70 16,70 16,700
Tanque No 2
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,04 0,04 0,04 0,040
Temperatura (°T) 16,60 16,60 16,60 16,600
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,51 0,52 0,52 0,517
Temperatura (°T) 16,60 16,60 16,60 16,600
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 4,79 4,80 4,80 4,797
Temperatura (°T) 16,60 16,60 16,60 16,600

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
106
Prueba No. 12 - Toma No. 3
Condición:
Válvula 1 cerrada 45° - Válvula 3 cerrada 45°
Tanque No 1
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 11,19 11,19 11,19 11,190
Temperatura (°T) 16,70 16,70 16,70 16,700
Recipiente No 3
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 0,54 0,55 0,54 0,543
Temperatura (°T) 16,50 16,60 16,60 16,567
Recipiente No 4
Muestra No. 1
Muestra No. 2
Muestra No. 3
Promedio
Conductividad (mS) 4,84 4,85 4,85 4,847
Temperatura (°T) 16,50 16,60 16,60 16,567
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
107
ANEXO No. 2 Ajuste del error para los medidores de agua usados
Medidor No.1
13 006070
Caudal
L/h
Error
48,00
0,30%
0,30%
0,00000%
3.666,32
-0,61%
-0,61%
0,00102%
1.452,80
-0,05%
Medidor No.2
13 006062
Caudal
L/h
Error
48,00
0,10%
0,10%
0,00000%
3.666,32
-0,42%
-0,42%
-0,00001%
1.376,80
-0,09%
y = -2,51E-06x + 3,12E-03
R² = 1,00E+00
-0,80%
-0,60%
-0,40%
-0,20%
0,00%
0,20%
0,40%
30,00
300,00
3.000,00
Er
ro
r
(
%
)
Caudal (L/h)
Medidor No.1 13 006070
y = -1,44E-06x + 1,07E-03
R² = 1,00E+00
-0,50%
-0,40%
-0,30%
-0,20%
-0,10%
0,00%
0,10%
0,20%
30,00
300,00
3.000,00
Er
ro
r
(
%
)
Caudal (L/h)
Medidor No.2 13 006062
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
108
Medidor No.3
13 006046
Caudal
L/h
Error
41,31
0,00%
0,00%
0,00000%
3.824,74
-0,56%
-0,56%
-0,00001%
1.485,60
-0,21%
Medidor No.4 13 006064
Caudal
L/h
Error
48,00
0,30%
0,30%
0,00000%
3.666,32
-0,61%
-0,61%
0,00001%
1.424,00
-0,05%
y = -1,48E-06x + 6,11E-05
R² = 1,00E+00
-0,60%
-0,50%
-0,40%
-0,30%
-0,20%
-0,10%
0,00%
30,00
300,00
3.000,00
Er
ro
r
(
%
)
Caudal (L/h)
Medidor No.3 13 006046
y = -2,51E-06x + 3,12E-03
R² = 1,00E+00
-0,80%
-0,60%
-0,40%
-0,20%
0,00%
0,20%
0,40%
40,00
400,00
4.000,00
Er
ro
r
(
%
)
Caudal (L/h)
Medidor No.4 13 006064

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
109
ANEXO No. 3 Cálculo de caudales
Prueba No. 1 - Toma No. 1
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
535,44
517,28
18,16
0,404
1.452,8
-0,05%
0,404
2
512,19
494,98
17,21
0,382
1.376,8
-0,09%
0,383
3
573,55
554,98
18,57
0,413
1.485,6
-0,21%
0,414
4
471,84
454,04
17,8
0,396
1.424,0
-0,05%
0,396
Prueba No. 1 - Toma No. 2
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
570,20
552,22
17,98
0,400
1.438,4
-0,05%
0,400
2
541,88
523,39
18,49
0,411
1.479,2
-0,11%
0,411
3
610,86
592,24
18,62
0,414
1.489,6
-0,21%
0,415
4
501,79
483,92
17,87
0,397
1.429,6
-0,05%
0,397
Prueba No. 1 - Toma No. 3
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
604,89
586,96
17,93
0,398
1.434,4
-0,05%
0,399
2
579,34
561,36
17,98
0,400
1.438,4
-0,10%
0,400
3
651,16
632,90
18,26
0,406
1.460,8
-0,21%
0,407
4
536,65
519,01
17,64
0,392
1.411,2
-0,04%
0,392

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
110
Prueba No. 2 - Toma No. 1
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
809,64
790,42
19,22
0,427
1.537,6
-0,08%
0,427
2
711,60
695,15
16,45
0,366
1.316,0
-0,08%
0,366
3
836,34
818,30
18,04
0,401
1.443,2
-0,21%
0,402
4
697,00
679,36
17,64
0,392
1.411,2
-0,04%
0,392
Prueba No. 2 - Toma No. 2
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
838,04
818,96
19,08
0,424
1.526,4
-0,07%
0,424
2
736,79
720,50
16,29
0,362
1.303,2
-0,08%
0,362
3
864,42
846,54
17,88
0,397
1.430,4
-0,21%
0,398
4
723,46
705,96
17,5
0,389
1.400,0
-0,04%
0,389
Prueba No. 2 - Toma No. 3
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
871,56
852,71
18,85
0,419
1.508,0
-0,07%
0,419
2
765,14
748,79
16,35
0,363
1.308,0
-0,08%
0,364
3
895,53
877,76
17,77
0,395
1.421,6
-0,20%
0,396
4
754,34
736,93
17,41
0,387
1.392,8
-0,04%
0,387

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
111
Prueba No. 3 - Toma No. 1
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
708,52
688,67
19,85
0,441
1.588,0
-0,09%
0,441
2
649,79
643,80
5,99
0,133
479,2
0,04%
0,133
3
745,32
731,90
13,42
0,298
1.073,6
-0,15%
0,299
4
620,67
608,17
12,5
0,278
1.000,0
0,06%
0,278
Prueba No. 3 - Toma No. 2
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
740,04
720,29
19,75
0,439
1.580,0
-0,09%
0,439
2
664,34
658,40
5,94
0,132
475,2
0,04%
0,132
3
771,60
758,30
13,3
0,296
1.064,0
-0,15%
0,296
4
641,62
629,23
12,39
0,275
991,2
0,06%
0,275
Prueba No. 3 - Toma No. 3
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
772,88
753,36
19,52
0,434
1.561,6
-0,08%
0,434
2
677,14
671,26
5,88
0,131
470,4
0,04%
0,131
3
796,37
783,24
13,13
0,292
1.050,4
-0,15%
0,292
4
662,80
650,56
12,24
0,272
979,2
0,07%
0,272

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
112
Prueba No. 4 - Toma No. 1
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
938,67
916,97
21,7
0,482
1.736,0
-0,13%
0,483
2
787,70
785,88
1,82
0,040
145,6
0,09%
0,040
3
948,71
936,42
12,29
0,273
983,2
-0,14%
0,273
4
792,40
781,07
11,33
0,252
906,4
0,08%
0,252
Prueba No. 4 - Toma No. 2
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
971,63
950,16
21,47
0,477
1.717,6
-0,12%
0,478
2
791,82
789,95
1,87
0,042
149,6
0,09%
0,042
3
968,72
956,55
12,17
0,270
973,6
-0,14%
0,271
4
810,32
799,10
11,22
0,249
897,6
0,09%
0,249
Prueba No. 4 - Toma No. 3
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
999,30
977,92
21,38
0,475
1.710,4
-0,12%
0,476
2
795,35
793,49
1,86
0,041
148,8
0,09%
0,041
3
986,52
974,35
12,17
0,270
973,6
-0,14%
0,271
4
824,94
813,79
11,15
0,248
892,0
0,09%
0,248

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
113
Prueba No. 5 - Toma No. 1
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1024,50
1008,88
15,62
0,347
1.249,6
0,00%
0,347
2
824,48
805,45
19,03
0,423
1.522,4
-0,11%
0,423
3
1015,20
997,72
17,48
0,388
1.398,4
-0,20%
0,389
4
851,53
834,32
17,21
0,382
1.376,8
-0,03%
0,383
Prueba No. 5 - Toma No. 2
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1049,22
1033,57
15,65
0,348
1.252,0
0,00%
0,348
2
853,58
834,90
18,68
0,415
1.494,4
-0,11%
0,416
3
1042,34
1025,03
17,31
0,385
1.384,8
-0,20%
0,385
4
878,54
861,47
17,07
0,379
1.365,6
-0,03%
0,379
Prueba No. 5 - Toma No. 3
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1075,58
1060,02
15,56
0,346
1.244,8
0,00%
0,346
2
884,98
866,50
18,48
0,411
1.478,4
-0,11%
0,411
3
1072,11
1054,97
17,14
0,381
1.371,2
-0,20%
0,382
4
907,07
890,12
16,95
0,377
1.356,0
-0,03%
0,377

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
114
Prueba No. 6 - Toma No. 1
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1990,46
1983,86
6,6
0,147
528,0
0,18%
0,146
2
915,70
895,02
20,68
0,460
1.654,4
-0,13%
0,460
3
1094,90
1081,37
13,53
0,301
1.082,4
-0,15%
0,301
4
930,04
916,27
13,77
0,306
1.101,6
0,04%
0,306
Prueba No. 6 - Toma No. 2
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1104,12
1097,58
6,54
0,145
523,2
0,18%
0,145
2
945,29
924,85
20,44
0,454
1.635,2
-0,13%
0,455
3
1117,27
1103,88
13,39
0,298
1.071,2
-0,15%
0,298
4
951,68
938,04
13,64
0,303
1.091,2
0,04%
0,303
Prueba No. 6 - Toma No. 3
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1119,31
1112,85
6,46
0,144
516,8
0,18%
0,143
2
977,04
956,60
20,44
0,454
1.635,2
-0,13%
0,455
3
1141,54
1128,22
13,32
0,296
1.065,6
-0,15%
0,296
4
975,24
961,60
13,64
0,303
1.091,2
0,04%
0,303

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
115
Prueba No. 7 - Toma No. 1
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1128,71
1127,40
1,31
0,029
104,8
0,29%
0,029
2
1011,69
990,48
21,21
0,471
1.696,8
-0,14%
0,472
3
1164,33
1153,25
11,08
0,246
886,4
-0,13%
0,247
4
997,27
985,75
11,52
0,256
921,6
0,08%
0,256
Prueba No. 7 - Toma No. 2
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1131,77
1130,46
1,31
0,029
104,8
0,29%
0,029
2
1039,17
1018,10
21,07
0,468
1.685,6
-0,14%
0,469
3
1180,74
1169,69
11,05
0,246
884,0
-0,12%
0,246
4
1012,20
1000,74
11,46
0,255
916,8
0,08%
0,254
Prueba No. 7 - Toma No. 3
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1135,06
1133,76
1,3
0,029
104,0
0,29%
0,029
2
1070,37
1049,27
21,1
0,469
1.688,0
-0,14%
0,470
3
1198,99
1187,95
11,04
0,245
883,2
-0,12%
0,246
4
1029,11
1017,69
11,42
0,254
913,6
0,08%
0,254

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
116
Prueba No. 8 - Toma No. 1
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1168,62
1151,08
17,54
0,390
1.403,2
-0,04%
0,390
2
1103,56
1086,32
17,24
0,383
1.379,2
-0,09%
0,383
3
1231,86
1216,14
15,72
0,349
1.257,6
-0,18%
0,350
4
1064,03
1044,97
19,06
0,424
1.524,8
-0,07%
0,424
Prueba No. 8 - Toma No. 2
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1194,47
1177,36
17,11
0,380
1.368,8
-0,03%
0,380
2
1130,98
1114,15
16,83
0,374
1.346,4
-0,09%
0,374
3
1254,92
1239,56
15,36
0,341
1.228,8
-0,18%
0,342
4
1094,54
1075,95
18,59
0,413
1.487,2
-0,06%
0,413
Prueba No. 8 - Toma No. 3
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1215,20
1198,30
16,9
0,376
1.352,0
-0,03%
0,376
2
1150,01
1133,96
16,05
0,357
1.284,0
-0,08%
0,357
3
1273,60
1258,69
14,91
0,331
1.192,8
-0,17%
0,332
4
1116,20
1098,12
18,08
0,402
1.446,4
-0,05%
0,402

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
117
Prueba No. 9 - Toma No. 1
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1234,90
1219,87
15,03
0,334
1.202,4
0,01%
0,334
2
1167,32
1153,72
13,6
0,302
1.088,0
-0,05%
0,302
3
1284,59
1277,07
7,52
0,167
601,6
-0,08%
0,167
4
1142,80
1121,70
21,1
0,469
1.688,0
-0,11%
0,469
Prueba No. 9 - Toma No. 2
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1251,18
1238,70
12,48
0,312
1.123,2
0,03%
0,312
2
1183,84
1171,18
12,66
0,316
1.139,4
-0,06%
0,317
3
1293,33
1286,78
6,55
0,164
589,5
-0,08%
0,164
4
1166,92
1148,32
18,6
0,465
1.674,0
-0,11%
0,466
Prueba No. 9 - Toma No. 3
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1271,52
1256,84
14,68
0,326
1.174,4
0,02%
0,326
2
1201,52
1188,76
12,76
0,284
1.020,8
-0,04%
0,284
3
1303,93
1296,79
7,14
0,159
571,2
-0,08%
0,159
4
1194,74
1174,50
20,24
0,450
1.619,2
-0,10%
0,450

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
118
Prueba No. 10 - Toma No. 1
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1320,88
1308,41
12,47
0,277
997,6
0,06%
0,277
2
1250,33
1236,77
13,56
0,301
1.084,8
-0,05%
0,301
3
1329,09
1325,28
3,81
0,085
304,8
-0,04%
0,085
4
1268,19
1246,00
22,19
0,493
1.775,2
-0,13%
0,494
Prueba No. 10 - Toma No. 2
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1339,52
1326,07
13,45
0,299
1.076,0
0,04%
0,299
2
1266,40
1254,68
11,72
0,260
937,6
-0,03%
0,261
3
1336,94
1333,24
3,7
0,082
296,0
-0,04%
0,082
4
1296,98
1275,57
21,41
0,476
1.712,8
-0,12%
0,476
Prueba No. 10 - Toma No. 3
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1356,79
1344,14
12,65
0,281
1.012,0
0,06%
0,281
2
1282,96
1270,75
12,21
0,271
976,8
-0,03%
0,271
3
1345,16
1341,51
3,65
0,081
292,0
-0,04%
0,081
4
1324,79
1303,60
21,19
0,471
1.695,2
-0,11%
0,471

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
119
Prueba No. 11 - Toma No. 1
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1384,66
1378,20
6,46
0,144
516,8
0,18%
0,143
2
1318,99
1301,55
17,44
0,388
1.395,2
-0,09%
0,388
3
1387,93
1368,28
19,65
0,437
1.572,0
-0,23%
0,438
4
1346,74
1342,50
4,24
0,094
339,2
0,23%
0,094
Prueba No. 11 - Toma No. 2
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1394,24
1387,84
6,4
0,142
512,0
0,18%
0,142
2
1342,66
1325,31
17,35
0,386
1.388,0
-0,09%
0,386
3
1416,96
1397,44
19,52
0,434
1.561,6
-0,23%
0,435
4
1352,99
1348,78
4,21
0,094
336,8
0,23%
0,093
Prueba No. 11 - Toma No. 3
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1403,68
1397,34
6,34
0,141
507,2
0,18%
0,141
2
1366,65
1349,38
17,27
0,384
1.381,6
-0,09%
0,384
3
1446,18
1426,80
19,38
0,431
1.550,4
-0,22%
0,432
4
1359,34
1355,15
4,19
0,093
335,2
0,23%
0,093

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
120
Prueba No. 12 - Toma No. 1
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1419,04
1411,38
7,66
0,170
612,8
0,16%
0,170
2
1393,65
1376,38
17,27
0,384
1.381,6
-0,09%
0,384
3
1464,34
1457,78
6,56
0,146
524,8
-0,07%
0,146
4
1385,96
1367,60
18,36
0,408
1.468,8
-0,06%
0,408
Prueba No. 12 - Toma No. 2
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1429,76
1422,24
7,52
0,167
601,6
0,16%
0,167
2
1417,10
1399,92
17,18
0,382
1.374,4
-0,09%
0,382
3
1476,26
1469,84
6,42
0,143
513,6
-0,07%
0,143
4
1410,16
1391,94
18,22
0,405
1.457,6
-0,05%
0,405
Prueba No. 12 - Toma No. 3
Medidor
Lectura
final
Lectura
inicial
Volumen
(L)
Caudal
(L/s)
Caudal
(L/h)
Error
Caudal
ajustado
(L/s)
1
1440,74
1433,26
7,48
0,166
598,4
0,16%
0,166
2
1440,66
1424,20
16,46
0,366
1.316,8
-0,08%
0,366
3
1488,08
1481,86
6,22
0,138
497,6
-0,07%
0,138
4
1434,88
1417,19
17,69
0,393
1.415,2
-0,04%
0,393

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
121
ANEXO No. 4 Cálculo de parámetros hidráulicos
Prueba No. 1 - Toma No. 1
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,40
16,70
1,087E-06
0,56
15.662
0,227
2
0,38
16,70
1,087E-06
0,53
14.848
0,204
3
0,41
16,77
1,085E-06
0,58
16.070
0,238
4
0,40
16,73
1,086E-06
0,55
15.364
0,218
Prueba No. 1 - Toma No. 2
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,40
16,90
1,081E-06
0,56
15.591
0,223
2
0,41
16,90
1,081E-06
0,57
16.042
0,236
3
0,41
17,00
1,078E-06
0,58
16.217
0,240
4
0,40
16,90
1,081E-06
0,55
15.495
0,220
Prueba No. 1 - Toma No. 3
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,40
16,70
1,087E-06
0,56
15.462
0,222
2
0,40
16,70
1,087E-06
0,56
15.513
0,223
3
0,41
16,67
1,088E-06
0,57
15.758
0,231
4
0,39
16,83
1,083E-06
0,55
15.267
0,214

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
122
Prueba No. 2 - Toma No. 1
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,43
15,23
1,132E-06
0,60
15.917
0,255
2
0,37
15,23
1,132E-06
0,51
13.624
0,187
3
0,40
15,60
1,121E-06
0,56
15.114
0,225
4
0,39
15,70
1,117E-06
0,55
14.796
0,214
Prueba No. 2 - Toma No. 2
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,42
15,37
1,128E-06
0,59
15.860
0,251
2
0,36
15,37
1,128E-06
0,51
13.542
0,183
3
0,40
15,87
1,112E-06
0,56
15.092
0,221
4
0,39
15,67
1,119E-06
0,54
14.664
0,211
Prueba No. 2 - Toma No. 3
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,42
15,53
1,123E-06
0,59
15.741
0,245
2
0,36
15,53
1,123E-06
0,51
13.655
0,184
3
0,40
16,03
1,107E-06
0,55
15.068
0,218
4
0,39
15,70
1,117E-06
0,54
14.602
0,209

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
123
Prueba No. 3 - Toma No. 1
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,44
16,47
1,094E-06
0,62
17.015
0,272
2
0,13
16,47
1,094E-06
0,19
5.128
0,025
3
0,30
16,80
1,084E-06
0,42
11.617
0,124
4
0,28
16,70
1,087E-06
0,39
10.768
0,107
Prueba No. 3 - Toma No. 2
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,44
16,67
1,088E-06
0,61
17.023
0,269
2
0,13
16,67
1,088E-06
0,18
5.113
0,024
3
0,30
16,67
1,088E-06
0,41
11.471
0,122
4
0,28
16,70
1,087E-06
0,38
10.673
0,106
Prueba No. 3 - Toma No. 3
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,43
16,63
1,089E-06
0,61
16.808
0,263
2
0,13
16,63
1,089E-06
0,18
5.057
0,024
3
0,29
16,37
1,097E-06
0,41
11.231
0,119
4
0,27
16,40
1,096E-06
0,38
10.457
0,103

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
124
Prueba No. 4 - Toma No. 1
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,48
15,67
1,119E-06
0,67
18.199
0,325
2
0,04
15,67
1,119E-06
0,06
1.523
0,002
3
0,27
16,23
1,101E-06
0,38
10.473
0,104
4
0,25
16,20
1,102E-06
0,35
9.624
0,088
Prueba No. 4 - Toma No. 2
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,48
15,87
1,112E-06
0,67
18.106
0,318
2
0,04
15,87
1,112E-06
0,06
1.574
0,002
3
0,27
16,40
1,096E-06
0,38
10.418
0,102
4
0,25
16,37
1,097E-06
0,35
9.575
0,087
Prueba No. 4 - Toma No. 3
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,48
16,00
1,108E-06
0,66
18.097
0,316
2
0,04
16,00
1,108E-06
0,06
1.571
0,002
3
0,27
16,57
1,091E-06
0,38
10.466
0,102
4
0,25
16,40
1,096E-06
0,35
9.523
0,085
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
125
Prueba No. 5 - Toma No. 1
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,35
16,43
1,095E-06
0,48
13.366
0,168
2
0,42
16,43
1,095E-06
0,59
16.301
0,250
3
0,39
17,20
1,072E-06
0,54
15.305
0,211
4
0,38
16,97
1,079E-06
0,53
14.948
0,204
Prueba No. 5 - Toma No. 2
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,35
16,83
1,083E-06
0,49
13.539
0,169
2
0,42
16,83
1,083E-06
0,58
16.178
0,241
3
0,39
17,73
1,057E-06
0,54
15.376
0,207
4
0,38
17,47
1,064E-06
0,53
15.029
0,201
Prueba No. 5 - Toma No. 3
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,35
16,80
1,084E-06
0,48
13.449
0,167
2
0,41
16,80
1,084E-06
0,57
15.990
0,236
3
0,38
17,53
1,063E-06
0,53
15.143
0,203
4
0,38
17,40
1,066E-06
0,53
14.896
0,198

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
126
Prueba No. 6 - Toma No. 1
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,15
17,17
1,073E-06
0,20
5.752
0,030
2
0,46
17,17
1,073E-06
0,64
18.078
0,295
3
0,30
17,97
1,050E-06
0,42
12.088
0,126
4
0,31
18,17
1,045E-06
0,43
12.345
0,130
Prueba No. 6 - Toma No. 2
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,15
17,43
1,065E-06
0,20
5.741
0,029
2
0,45
17,43
1,065E-06
0,63
17.997
0,288
3
0,30
18,40
1,038E-06
0,42
12.101
0,124
4
0,30
18,30
1,041E-06
0,42
12.271
0,128
Prueba No. 6 - Toma No. 3
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,14
17,43
1,065E-06
0,20
5.670
0,029
2
0,45
17,43
1,065E-06
0,63
17.997
0,288
3
0,30
18,33
1,040E-06
0,41
12.017
0,123
4
0,30
18,07
1,047E-06
0,42
12.195
0,128

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
127
Prueba No. 7 - Toma No. 1
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,03
17,47
1,064E-06
0,04
1.150
0,001
2
0,47
17,93
1,051E-06
0,66
18.929
0,311
3
0,25
18,40
1,038E-06
0,34
10.011
0,085
4
0,26
18,50
1,036E-06
0,36
10.414
0,091
Prueba No. 7 - Toma No. 2
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,03
17,47
1,064E-06
0,04
1.150
0,001
2
0,47
17,47
1,064E-06
0,65
18.570
0,306
3
0,25
18,33
1,040E-06
0,34
9.966
0,084
4
0,25
18,40
1,038E-06
0,36
10.333
0,090
Prueba No. 7 - Toma No. 3
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,03
17,60
1,061E-06
0,04
1.145
0,001
2
0,47
17,60
1,061E-06
0,66
18.663
0,307
3
0,25
18,23
1,043E-06
0,34
9.931
0,084
4
0,25
18,33
1,040E-06
0,35
10.278
0,090

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
128
Prueba No. 8 - Toma No. 1
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,39
17,77
1,056E-06
0,54
15.569
0,212
2
0,38
17,77
1,056E-06
0,54
15.311
0,205
3
0,35
18,13
1,046E-06
0,49
14.111
0,171
4
0,42
17,87
1,053E-06
0,59
16.969
0,250
Prueba No. 8 - Toma No. 2
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,38
17,47
1,064E-06
0,53
15.064
0,202
2
0,37
17,47
1,064E-06
0,52
14.826
0,195
3
0,34
17,80
1,055E-06
0,48
13.665
0,163
4
0,41
17,70
1,058E-06
0,58
16.475
0,238
Prueba No. 8 - Toma No. 3
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,38
17,63
1,060E-06
0,52
14.946
0,197
2
0,36
17,63
1,060E-06
0,50
14.201
0,178
3
0,33
18,23
1,043E-06
0,46
13.418
0,154
4
0,40
17,80
1,055E-06
0,56
16.065
0,225

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
129
Prueba No. 9 - Toma No. 1
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,33
17,13
1,074E-06
0,47
13.108
0,156
2
0,30
17,13
1,074E-06
0,42
11.868
0,127
3
0,17
17,30
1,069E-06
0,23
6.594
0,039
4
0,47
17,20
1,072E-06
0,66
18.458
0,307
Prueba No. 9 - Toma No. 2
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,31
17,33
1,068E-06
0,44
12.309
0,136
2
0,32
17,33
1,068E-06
0,44
12.497
0,140
3
0,16
17,80
1,055E-06
0,23
6.549
0,037
4
0,47
17,67
1,059E-06
0,65
18.537
0,302
Prueba No. 9 - Toma No. 3
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,33
17,27
1,070E-06
0,46
12.849
0,148
2
0,28
17,27
1,070E-06
0,40
11.174
0,112
3
0,16
17,73
1,057E-06
0,22
6.334
0,035
4
0,45
17,40
1,066E-06
0,63
17.799
0,283

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
130
Prueba No. 10 - Toma No. 1
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,28
17,17
1,073E-06
0,39
10.880
0,107
2
0,30
17,17
1,073E-06
0,42
11.844
0,127
3
0,08
17,20
1,072E-06
0,12
3.330
0,010
4
0,49
17,20
1,072E-06
0,69
19.416
0,340
Prueba No. 10 - Toma No. 2
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,30
17,10
1,075E-06
0,42
11.716
0,124
2
0,26
17,10
1,075E-06
0,36
10.216
0,095
3
0,08
17,20
1,072E-06
0,11
3.234
0,009
4
0,48
17,20
1,072E-06
0,66
18.730
0,316
Prueba No. 10 - Toma No. 3
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,28
17,10
1,075E-06
0,39
11.017
0,110
2
0,27
17,10
1,075E-06
0,38
10.644
0,103
3
0,08
17,10
1,075E-06
0,11
3.182
0,009
4
0,47
17,10
1,075E-06
0,66
18.487
0,310

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
131
Prueba No. 11 - Toma No. 1
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,14
16,97
1,079E-06
0,20
5.599
0,029
2
0,39
16,97
1,079E-06
0,54
15.157
0,210
3
0,44
16,97
1,079E-06
0,61
17.100
0,267
4
0,09
16,77
1,085E-06
0,13
3.653
0,012
Prueba No. 11 - Toma No. 2
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,14
16,80
1,084E-06
0,20
5.522
0,028
2
0,39
16,80
1,084E-06
0,54
15.010
0,208
3
0,43
16,97
1,079E-06
0,61
16.987
0,264
4
0,09
16,70
1,087E-06
0,13
3.621
0,012
Prueba No. 11 - Toma No. 3
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,14
16,83
1,083E-06
0,20
5.475
0,028
2
0,38
16,83
1,083E-06
0,54
14.954
0,206
3
0,43
16,80
1,084E-06
0,60
16.788
0,260
4
0,09
16,60
1,090E-06
0,13
3.594
0,012

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
132
Prueba No. 12 - Toma No. 1
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,17
16,63
1,089E-06
0,24
6.580
0,040
2
0,38
16,63
1,089E-06
0,54
14.872
0,206
3
0,15
16,60
1,090E-06
0,20
5.643
0,030
4
0,41
16,60
1,090E-06
0,57
15.791
0,232
Prueba No. 12 - Toma No. 2
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,17
16,70
1,087E-06
0,23
6.472
0,039
2
0,38
16,70
1,087E-06
0,53
14.822
0,204
3
0,14
16,60
1,090E-06
0,20
5.522
0,028
4
0,41
16,60
1,090E-06
0,57
15.670
0,229
Prueba No. 12 - Toma No. 3
Tubería
Caudal
(L/s)
Temperatura
°C
Viscosidad
cinemática
(m2/s)
Velocidad
(m/s)
Re
Cantidad
movimiento
(N)
1
0,17
16,70
1,087E-06
0,23
6.437
0,038
2
0,37
16,70
1,087E-06
0,51
14.200
0,187
3
0,14
16,57
1,091E-06
0,19
5.345
0,027
4
0,39
16,57
1,091E-06
0,55
15.199
0,216
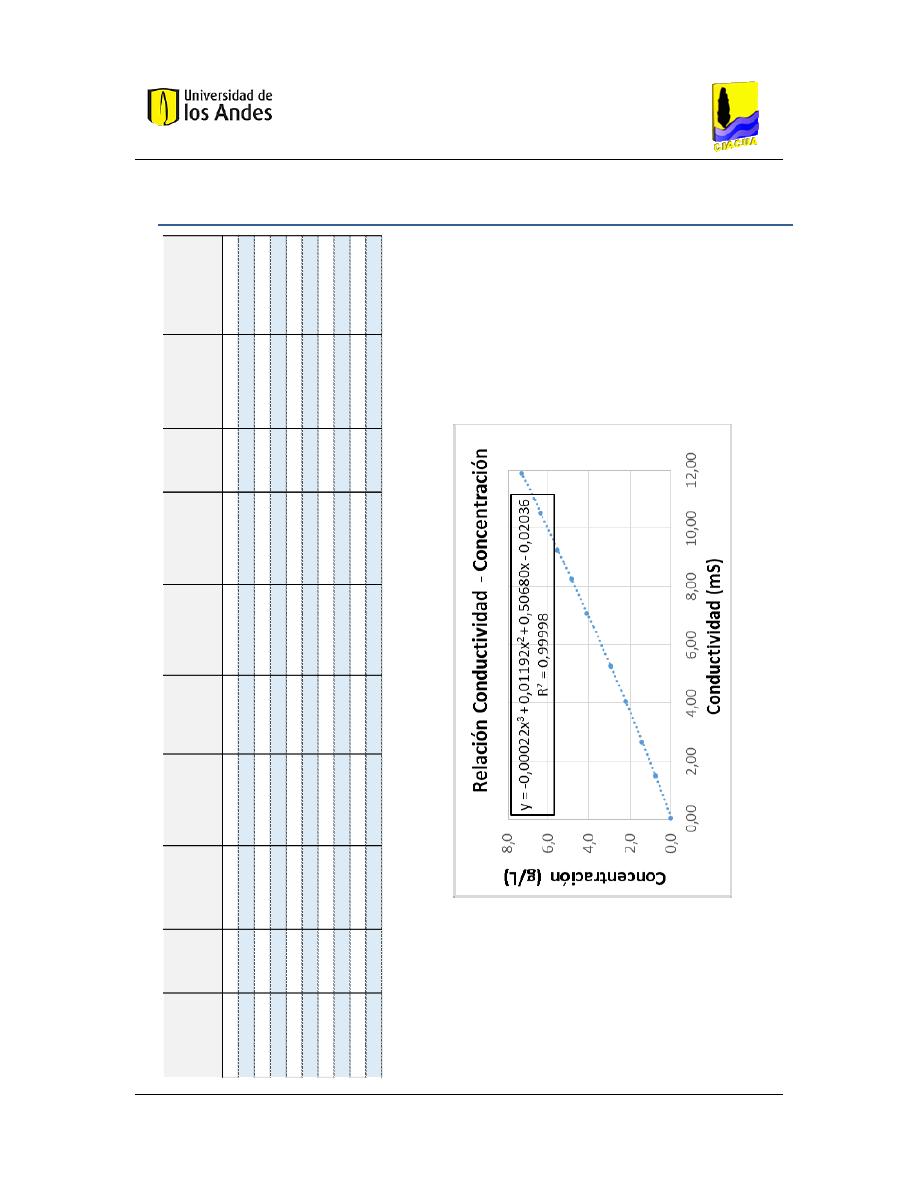
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
133
ANEXO No. 5 Relación entre conductividad y concentración de soluto para el
agua utilizada en el experimento
N
o
. PR
U
EB
A
SA
L
A
G
R
EG
A
D
A
CO
N
TE
N
ID
O
S
A
L
(g
)
CO
N
D
U
CT
IV
ID
A
D
(M
s)
TE
M
PE
R
A
TU
R
A
°T
CO
R
R
ECC
IÓ
N
CO
N
D
U
CT
IV
ID
A
D
PO
R
°
T
CO
N
D
U
CT
IV
ID
A
D
CO
R
R
EG
ID
A
(
M
s)
V
O
LU
M
EN
A
G
U
A
(
L)
CO
N
CE
N
TR
A
CIÓ
N
(g
/L
)
EN
TR
A
CO
N
D
U
CT
IV
=
CO
N
CE
N
TR
A
CIO
N
0
0,
00
0,
00
0,
04
2
17
,7
0
-1
4,
53
%
0,
04
2
1,
00
0,
00
0
0,
01
1
1
0,
77
0,
77
1,
50
5
17
,7
0
-1
4,
53
%
1,
50
5
1,
00
0,
77
0
0,
77
3
2
0,
65
1,
42
2,
67
5
17
,8
0
-1
4,
36
%
2,
67
5
1,
00
1,
41
5
1,
41
7
3
0,
78
2,
20
4,
05
17
,9
0
-1
4,
19
%
4,
05
0
0,
99
2,
21
7
2,
21
2
4
0,
74
2,
93
5,
29
18
,0
0
-1
4,
01
%
5,
29
0
0,
99
2,
96
0
2,
96
1
5
1,
08
4,
01
7,
08
18
,3
0
-1
3,
41
%
7,
08
0
0,
98
4,
09
2
4,
08
7
6
0,
74
4,
75
8,
28
18
,5
0
-1
2,
95
%
8,
28
0
0,
98
4,
84
7
4,
86
9
7
0,
63
5,
38
9,
27
18
,6
0
-1
2,
71
%
9,
27
0
0,
97
5,
54
6
5,
52
8
8
0,
81
6,
19
10
,5
3
18
,7
0
-1
2,
45
%
10
,5
30
0,
97
6,
38
1
6,
38
2
9
0,
91
7,
10
11
,8
9
18
,7
0
-1
2,
45
%
11
,8
90
0,
97
7,
32
0
7,
32
1

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
134
ANEXO No. 6 Cálculo de la concentración mediante las diferentes ecuaciones
estudiadas
Prueba No. 1 - Toma No. 1
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,404 11,880 16,700 11,880 7,314
2
0,383 0,047 16,700 0,047 0,014
3
0,414 1,813 16,767 1,813 0,940
4
0,396 10,550 16,733 10,550 6,396
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,94 0,15 0,36 1,03
Error (%)
0%
-84%
-62%
10%
T4
Valor (mg/L) 6,40 7,31 7,31 6,49
Error (%)
0%
14%
14%
2%
Prueba No. 1 - Toma No. 2
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,400 11,793 16,900 11,793 7,254
2
0,411 0,047 16,900 0,047 0,014
3
0,415 1,797 17,000 1,797 0,930
4
0,397 10,397 16,900 10,397 6,291
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,93 0,01 0,01 0,98
Error (%)
0%
-99%
-99%
5%
T4
Valor (mg/L) 6,29 7,30 7,31 6,34
Error (%)
0%
16%
16%
1%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
135
Prueba No. 1 - Toma No. 3
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,399 11,667 16,700 11,667 7,166
2
0,400 0,047 16,700 0,047 0,014
3
0,407 1,860 16,667 1,860 0,965
4
0,392 10,340 16,833 10,340 6,252
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,97 0,01 0,01 1,01
Error (%)
0%
-99%
-99%
4%
T4
Valor (mg/L) 6,25 7,28 7,29 6,30
Error (%)
0%
16%
17%
1%
Prueba No. 2 - Toma No. 1
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,427 11,810 15,233 11,810 7,265
2
0,366 0,047 15,233 0,047 0,014
3
0,402 2,400 15,600 2,400 1,263
4
0,392 10,880 15,700 10,880 6,622
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 1,26 0,65 0,66 1,28
Error (%)
0%
-49%
-48%
1%
T4
Valor (mg/L) 6,62 7,27 7,27 6,64
Error (%)
0%
10%
10%
0%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
136
Prueba No. 2 - Toma No. 2
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,424 11,777 15,367 11,777 7,242
2
0,362 0,047 15,367 0,047 0,014
3
0,398 2,493 15,867 2,493 1,315
4
0,389 10,797 15,667 10,797 6,565
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 1,32 0,65 0,66 1,32
Error (%)
0%
-50%
-50%
0%
T4
Valor (mg/L) 6,56 7,24 7,24 6,56
Error (%)
0%
10%
10%
0%
Prueba No. 2 - Toma No. 3
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,419 11,727 15,533 11,727 7,207
2
0,364 0,047 15,533 0,047 0,014
3
0,396 2,330 16,033 2,330 1,224
4
0,387 10,757 15,700 10,757 6,537
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 1,22 0,60 0,60 1,25
Error (%)
0%
-51%
-51%
2%
T4
Valor (mg/L) 6,54 7,21 7,21 6,57
Error (%)
0%
10%
10%
0%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
137
Prueba No. 3 - Toma No. 1
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,441 11,480 16,467 11,480 7,036
2
0,133 0,047 16,467 0,047 0,014
3
0,299 7,390 16,800 7,390 4,287
4
0,278 10,887 16,700 10,887 6,627
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 4,29 3,87 3,90 4,25
Error (%)
0%
-10%
-9%
-1%
T4
Valor (mg/L) 6,63 7,04 7,04 6,58
Error (%)
0%
6%
6%
-1%
Prueba No. 3 - Toma No. 2
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,439 11,460 16,667 11,460 7,022
2
0,132 0,047 16,667 0,047 0,014
3
0,296 7,320 16,667 7,320 4,242
4
0,275 10,897 16,700 10,897 6,634
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 4,24 3,90 3,90 4,26
Error (%)
0%
-8%
-8%
0%
T4
Valor (mg/L) 6,63 7,02 7,02 6,65
Error (%)
0%
6%
6%
0%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
138
Prueba No. 3 - Toma No. 3
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,434 11,403 16,633 11,403 6,983
2
0,131 0,047 16,633 0,047 0,014
3
0,292 7,250 16,367 7,250 4,196
4
0,272 10,857 16,400 10,857 6,606
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 4,20 3,88 3,87 4,24
Error (%)
0%
-7%
-8%
1%
T4
Valor (mg/L) 6,61 6,98 6,98 6,65
Error (%)
0%
6%
6%
1%
Prueba No. 4 - Toma No. 1
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,483 11,653 15,667 11,653 7,156
2
0,040 0,047 15,667 0,047 0,014
3
0,273 10,447 16,233 10,447 6,325
4
0,252 11,280 16,200 11,280 6,898
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 6,33 6,05 6,10 6,29
Error (%)
0%
-4%
-4%
-1%
T4
Valor (mg/L) 6,90 7,16 7,16 6,86
Error (%)
0%
4%
4%
-1%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
139
Prueba No. 4 - Toma No. 2
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,478 11,647 15,867 11,647 7,152
2
0,042 0,047 15,867 0,047 0,014
3
0,271 10,433 16,400 10,433 6,316
4
0,249 11,250 16,367 11,250 6,877
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 6,32 6,04 6,06 6,29
Error (%)
0%
-4%
-4%
0%
T4
Valor (mg/L) 6,88 7,15 7,15 6,85
Error (%)
0%
4%
4%
0%
Prueba No. 4 - Toma No. 3
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,476 11,540 16,000 11,540 7,078
2
0,041 0,047 16,000 0,047 0,014
3
0,271 10,473 16,567 10,473 6,343
4
0,248 11,170 16,400 11,170 6,822
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 6,34 5,96 6,00 6,20
Error (%)
0%
-6%
-5%
-2%
T4
Valor (mg/L) 6,82 7,08 7,08 6,66
Error (%)
0%
4%
4%
-2%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
140
Prueba No. 5 - Toma No. 1
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,347 11,773 16,433 11,773 7,240
2
0,423 0,047 16,433 0,047 0,014
3
0,389 1,253 17,200 1,253 0,638
4
0,383 9,840 16,967 9,840 5,912
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,64 0,01 0,01 0,66
Error (%)
0%
-98%
-98%
3%
T4
Valor (mg/L) 5,91 6,57 6,58 5,93
Error (%)
0%
11%
11%
0%
Prueba No. 5 - Toma No. 2
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,348 11,657 16,833 11,657 7,159
2
0,416 0,047 16,833 0,047 0,014
3
0,385 1,267 17,733 1,267 0,645
4
0,379 9,830 17,467 9,830 5,905
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,65 0,01 0,01 0,66
Error (%)
0%
-98%
-98%
2%
T4
Valor (mg/L) 5,91 6,56 6,58 5,92
Error (%)
0%
11%
11%
0%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
141
Prueba No. 5 - Toma No. 3
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,346 11,523 16,800 11,523 7,066
2
0,411 0,047 16,800 0,047 0,014
3
0,382 1,270 17,533 1,270 0,647
4
0,377 9,733 17,400 9,733 5,840
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,65 0,01 0,01 0,65
Error (%)
0%
-98%
-98%
1%
T4
Valor (mg/L) 5,84 6,49 6,50 5,84
Error (%)
0%
11%
11%
0%
Prueba No. 6 - Toma No. 1
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,146 11,397 17,167 11,397 6,979
2
0,460 0,047 17,167 0,047 0,014
3
0,301 0,710 17,967 0,710 0,352
4
0,306 5,300 18,167 5,300 2,967
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,35 0,01 0,01 0,40
Error (%)
0%
-96%
-96%
14%
T4
Valor (mg/L) 2,97 3,35 3,35 3,01
Error (%)
0%
13%
13%
2%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
142
Prueba No. 6 - Toma No. 2
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,145 11,410 17,433 11,410 6,988
2
0,455 0,047 17,433 0,047 0,014
3
0,298 0,740 18,400 0,740 0,368
4
0,303 5,260 18,300 5,260 2,942
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,37 0,01 0,01 0,43
Error (%)
0%
-96%
-96%
17%
T4
Valor (mg/L) 2,94 3,35 3,36 3,00
Error (%)
0%
14%
14%
2%
Prueba No. 6 - Toma No. 3
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,143 11,413 17,433 11,413 6,990
2
0,455 0,047 17,433 0,047 0,014
3
0,296 0,730 18,333 0,730 0,363
4
0,303 5,247 18,067 5,247 2,934
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,36 0,01 0,01 0,40
Error (%)
0%
-96%
-96%
11%
T4
Valor (mg/L) 2,93 3,31 3,32 2,97
Error (%)
0%
13%
13%
1%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
143
Prueba No. 7 - Toma No. 1
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,029 11,417 17,467 11,417 6,992
2
0,472 0,047 17,933 0,047 0,014
3
0,247 0,560 18,400 0,560 0,275
4
0,256 0,997 18,500 0,997 0,502
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,27 0,01 0,01 0,33
Error (%)
0%
-95%
-95%
19%
T4
Valor (mg/L) 0,50 0,81 0,81 0,55
Error (%)
0%
60%
61%
10%
Prueba No. 7 - Toma No. 2
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,029 11,423 17,467 11,423 6,997
2
0,469 0,047 17,467 0,047 0,014
3
0,246 0,548 18,333 0,548 0,269
4
0,254 1,040 18,400 1,040 0,525
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,27 0,01 0,01 0,31
Error (%)
0%
-95%
-95%
15%
T4
Valor (mg/L) 0,53 0,81 0,81 0,56
Error (%)
0%
54%
55%
7%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
144
Prueba No. 7 - Toma No. 3
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,029 11,437 17,600 11,437 7,006
2
0,470 0,047 17,600 0,047 0,014
3
0,246 0,540 18,233 0,540 0,265
4
0,254 1,080 18,333 1,080 0,546
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,26 0,01 0,01 0,28
Error (%)
0%
-95%
-95%
7%
T4
Valor (mg/L) 0,55 0,81 0,81 0,56
Error (%)
0%
48%
48%
3%
Prueba No. 8 - Toma No. 1
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,390 11,757 17,767 11,757 7,228
2
0,383 0,047 17,767 0,047 0,014
3
0,350 1,303 18,133 1,303 0,665
4
0,424 10,097 17,867 10,097 6,086
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,66 - 0,69 - 0,68 0,70
Error (%)
0%
-203%
-203%
5%
T4
Valor (mg/L) 6,09 7,23 7,23 6,11
Error (%)
0%
19%
19%
0%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
145
Prueba No. 8 - Toma No. 2
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,380 11,767 17,467 11,767 7,235
2
0,374 0,047 17,467 0,047 0,014
3
0,342 1,470 17,800 1,470 0,754
4
0,413 9,993 17,700 9,993 6,016
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,75 - 0,68 - 0,68 0,79
Error (%)
0%
-191%
-190%
5%
T4
Valor (mg/L) 6,02 7,24 7,24 6,05
Error (%)
0%
20%
20%
0%
Prueba No. 8 - Toma No. 3
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,376 11,737 17,633 11,737 7,214
2
0,357 0,047 17,633 0,047 0,014
3
0,332 1,583 18,233 1,583 0,815
4
0,402 10,207 17,800 10,207 6,161
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,81 - 0,56 - 0,54 0,72
Error (%)
0%
-168%
-167%
-12%
T4
Valor (mg/L) 6,16 7,21 7,21 6,08
Error (%)
0%
17%
17%
-1%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
146
Prueba No. 9 - Toma No. 1
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,334 11,750 17,133 11,750 7,223
2
0,302 0,047 17,133 0,047 0,014
3
0,167 0,820 17,300 0,820 0,410
4
0,469 8,560 17,200 8,560 5,054
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,41 - 5,83 - 5,82 0,26
Error (%)
0%
-1522%
-1520%
-36%
T4
Valor (mg/L) 5,05 7,22 7,22 5,00
Error (%)
0%
43%
43%
-1%
Prueba No. 9 - Toma No. 2
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,312 11,700 17,333 11,700 7,189
2
0,317 0,047 17,333 0,047 0,014
3
0,164 0,677 17,800 0,677 0,335
4
0,466 8,000 17,667 8,000 4,685
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,34 0,01 0,01 0,40
Error (%)
0%
-96%
-96%
20%
T4
Valor (mg/L) 4,68 4,82 4,83 4,71
Error (%)
0%
3%
3%
1%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
147
Prueba No. 9 - Toma No. 3
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,326 11,727 17,267 11,727 7,207
2
0,284 0,047 17,267 0,047 0,014
3
0,159 0,800 17,733 0,800 0,399
4
0,450 8,680 17,400 8,680 5,134
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,40 - 5,61 - 5,63 0,27
Error (%)
0%
-1504%
-1509%
-31%
T4
Valor (mg/L) 5,13 7,21 7,21 5,09
Error (%)
0%
40%
40%
-1%
Prueba No. 10 - Toma No. 1
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,277 11,843 17,167 11,843 7,288
2
0,301 0,047 17,167 0,047 0,014
3
0,085 0,420 17,200 0,420 0,203
4
0,494 6,893 17,200 6,893 3,967
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,20 0,01 0,01 0,75
Error (%)
0%
-93%
-93%
270%
T4
Valor (mg/L) 3,97 4,09 4,09 4,06
Error (%)
0%
3%
3%
2%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
148
Prueba No. 10 - Toma No. 2
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,299 11,837 17,100 11,837 7,284
2
0,261 0,047 17,100 0,047 0,014
3
0,082 0,530 17,200 0,530 0,259
4
0,476 7,800 17,200 7,800 4,554
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,26 - 15,68 - 15,71 0,13
Error (%)
0%
-6145%
-6158%
-51%
T4
Valor (mg/L) 4,55 7,28 7,28 4,53
Error (%)
0%
60%
60%
0%
Prueba No. 10 - Toma No. 3
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,281 11,810 17,100 11,810 7,265
2
0,271 0,047 17,100 0,047 0,014
3
0,081 0,620 17,100 0,620 0,306
4
0,471 7,407 17,100 7,407 4,298
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,31 - 17,01 - 17,00 0,23
Error (%)
0%
-5662%
-5659%
-24%
T4
Valor (mg/L) 4,30 7,27 7,27 4,28
Error (%)
0%
69%
69%
0%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
149
Prueba No. 11 - Toma No. 1
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,143 11,240 16,967 11,240 6,870
2
0,388 0,047 16,967 0,047 0,014
3
0,438 1,910 16,967 1,910 0,992
4
0,094 8,830 16,767 8,830 5,233
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,99 0,01 0,01 1,14
Error (%)
0%
-99%
-99%
15%
T4
Valor (mg/L) 5,23 10,46 10,47 5,91
Error (%)
0%
100%
100%
13%
Prueba No. 11 - Toma No. 2
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,142 11,140 16,800 11,140 6,801
2
0,386 0,047 16,800 0,047 0,014
3
0,435 1,913 16,967 1,913 0,994
4
0,093 9,050 16,700 9,050 5,380
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,99 0,01 0,01 1,08
Error (%)
0%
-99%
-99%
8%
T4
Valor (mg/L) 5,38 10,34 10,34 5,77
Error (%)
0%
92%
92%
7%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
150
Prueba No. 11 - Toma No. 3
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,141 11,200 16,833 11,200 6,843
2
0,384 0,047 16,833 0,047 0,014
3
0,432 1,910 16,800 1,910 0,992
4
0,093 9,007 16,600 9,007 5,351
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,99 0,01 0,01 1,09
Error (%)
0%
-99%
-99%
10%
T4
Valor (mg/L) 5,35 10,35 10,35 5,80
Error (%)
0%
93%
93%
8%
Prueba No. 12 - Toma No. 1
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,170 11,180 16,633 11,180 6,829
2
0,384 0,047 16,633 0,047 0,014
3
0,146 0,490 16,600 0,490 0,239
4
0,408 4,807 16,600 4,807 2,666
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,24 0,01 0,01 0,53
Error (%)
0%
-94%
-94%
123%
T4
Valor (mg/L) 2,67 2,85 2,85 2,77
Error (%)
0%
7%
7%
4%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
151
Prueba No. 12 - Toma No. 2
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,167 11,163 16,700 11,163 6,817
2
0,382 0,040 16,700 0,040 0,010
3
0,143 0,517 16,600 0,517 0,253
4
0,405 4,797 16,600 4,797 2,660
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,25 0,01 0,01 0,45
Error (%)
0%
-96%
-96%
77%
T4
Valor (mg/L) 2,66 2,81 2,81 2,73
Error (%)
0%
6%
6%
3%
Prueba No. 12 - Toma No. 3
Tubería
Caudal
(L/s)
Conductividad
(mS)
Temperatura
°C
Conductividad
corregida por °T
(mS)
Concentración
(g/L)
1
0,166 11,190 16,700 11,190 6,836
2
0,366 0,040 16,700 0,040 0,010
3
0,138 0,543 16,567 0,543 0,266
4
0,393 4,847 16,567 4,847 2,690
Concentración
Unidad
Valor medido
Ho
Gómez
Concentración
estándar
T3
Valor (mg/L) 0,27 0,01 0,01 0,58
Error (%)
0%
-96%
-96%
118%
T4
Valor (mg/L) 2,69 2,89 2,89 2,80
Error (%)
0%
7%
7%
4%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
152
ANEXO No.7 Lecturas de los medidores de agua

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
153

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
154

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
155

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
156

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
157

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
158

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
159

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
160

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
161

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
162

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
163

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
164

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
165

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
166

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
167

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
168

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
169

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
170
ANEXO No.8 Certificados de calibración de los medidores de agua

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
171

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
172

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
173

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
174
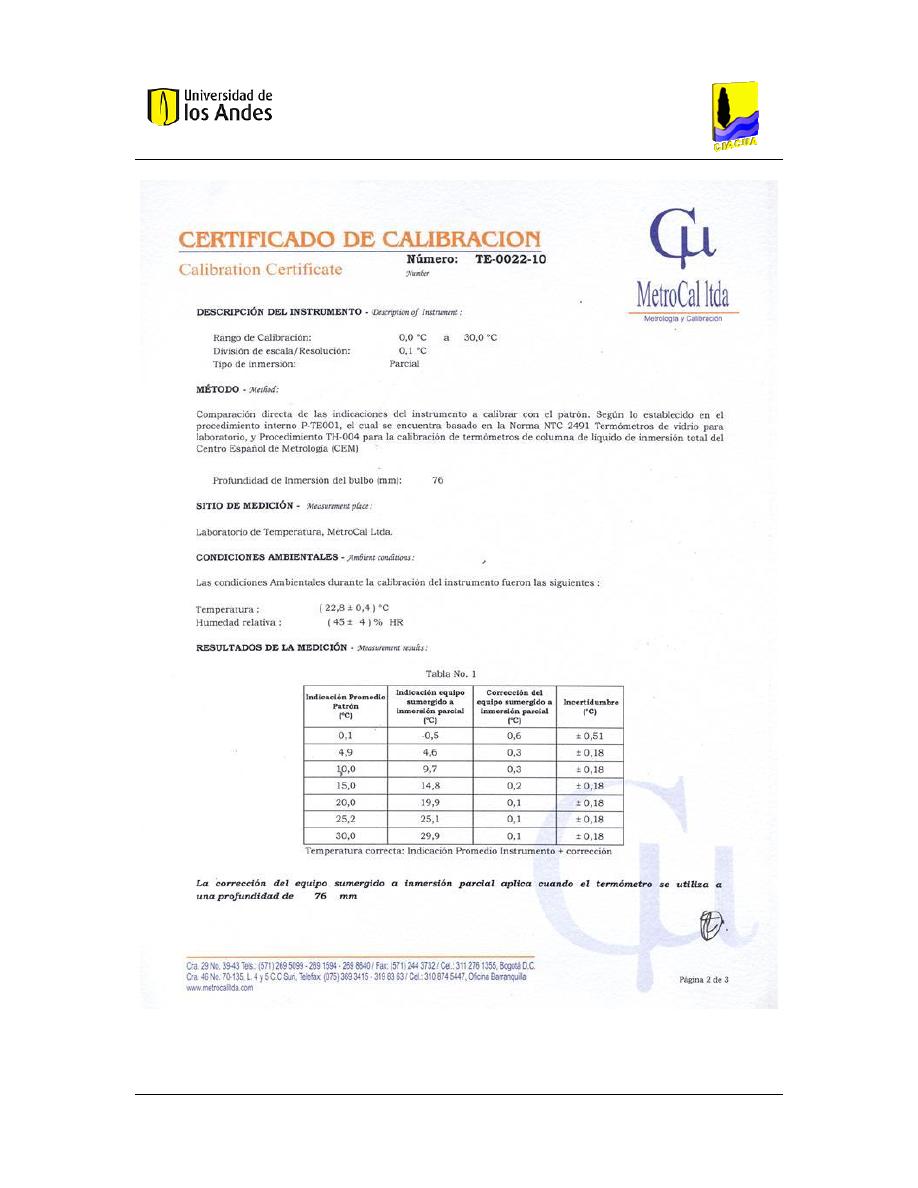
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
175

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Análisis de la mezcla de concentraciones de soluciones de NaCl en una
unión de tuberías tipo cruz”
Iván Alexander Buitrago León
Proyecto de Grado
176
