
IAHR
CIC
XXV CONGRESO LATINOAMERICANO DE HIDRÁULICA
SAN JOSÉ, COSTA RICA, 9 AL 12 DE SEPTIEMBRE DE 2012
ANÁLISIS CRÍTICO DE LA TRANSICIÓN ENTRE EL FLUJO
TURBULENTO HIDRAULICAMENTE LISO Y FLUJO TURBULENTO
TRANSICIONAL
Rafael A. Flechas
Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA), Departamento de Ingeniería Civil y Ambiental,
Universidad de los Andes, Bogotá, Colombia
<ra.flechas30@uniandes.edu.co>
RESUMEN:
De todos los parámetros de la ecuación de Darcy-Weisbach, el factor de fricción fue el más difícil
de cuantificar. Este problema ocasionó la aparición de ecuaciones empíricas como la de Hazen-
Williams, pero también dio origen a métodos gráficos como el Diagrama de Moody. En este, Lewis
Moody delimitó la zona de transición utilizando las ecuaciones de Prandtl-Von Kármán y el
Diagrama de Nikuradse, sin tener en cuenta la ecuación de Colebrook-White y los límites definidos
por estos dos investigadores para esta zona. Por lo anterior, en el presente artículo se pretende
mostrar un proceso deductivo de las ecuaciones que describen el límite inferior y superior de la
zona de transición a partir de la ecuación de Colebrook-White, y los efectos que pueden tener estos
nuevos límites en el Diagrama de Moody. Con base en este análisis, se obtuvo que el límite
inferior de la zona de transición definido a partir de la ecuación de Colebrook-White difiere del
demarcado por la ecuación de Prandtl-Von Kármán en dicho Diagrama. Por ello, se sugiere revisar
dicho límite y establecer, realmente, si la rugosidad en el flujo turbulento hidráulicamente liso se
puede despreciar para el cálculo del factor de fricción
ABSTRACT:
Of all the parameters in the Darcy-Weisbach equation, the friction factor was by far the hardest to
quantify. This issue led to the development of the empiric Hazen-Williams equation and graphying
methods, like the Moody Diagram. Lewis Moody delimits the transition zone that is based on
Prandtl-Von Kármán equation and Nikuradse diagram, but he does not take into account the
Colebrook-White equations or the limits that according to these researchers, define this zone. This
paper shows the deductive process of equations that describe the upper and lower limits of the
transition zone according to Colebrook and White. It also demonstrates the effects of these limits on
the Moody Diagram. The article shows how the lower limit proposed by Colebrook’s and White’s
transition zone differs to that shown by the Prandtl-Von Kármán equation. This way, the article
suggests a revision of this lower limit. It also seeks to establish whether the roughness can be
depreciated when calculating the friction factor in smooth pipes.
PALABRAS CLAVES: Ecuación de Darcy-Weisbach, Tuberías lisas y Diagrama de Moody

INTRODUCCIÓN
En las redes de distribución de agua potable (RDAP), tanto para el diseño como para el análisis
hidráulico de estos sistemas, la ecuación de Darcy-Weisbach [1] ha sido ampliamente utilizada para
determinar las pérdidas por fricción que se generan en las tuberías. Sin embargo, en la primera
mitad del Siglo XX, el cálculo de estas pérdidas haciendo uso de dicha ecuación era complicado
debido a que el factor de fricción era un parámetro difícil de calcular, por ser una función no
explícita de la rugosidad relativa (ks/d) y del número de Reynolds (Re).
ℎ𝑓 = 𝑓
𝐿
𝐷
𝑉
2
2𝑔 [𝟏]
donde hf son las pérdidas por fricción, L es la longitud de la tubería, V la velocidad de flujo, g es la
aceleración de la gravedad y f es el factor de fricción.
Esta complejidad se reflejó en los intentos realizados por investigadores como Paul Richard
Heinrich Blasius (1883-1970), Johann Nikuradse (1894-1979), Ludwig Prandtl (1875-1953),
Theodor Von Kármán (1881-1963) y C.F. Colebrook y H. White para predecir analíticamente la
magnitud del factor de fricción en el flujo turbulento (Re>4000), ya que para el flujo laminar
(Re< 2000) Weisbach dedujo como cuantificar dicho factor con base en la ecuación de Hagen
(1794-1884)-Poiseuille (1799-1869), como se ilustra en la siguiente ecuación:
𝑓 =
64
𝑅𝑒 [𝟐]
En 1911, Blasius, alumno de Prandtl, encontró empíricamente una Ecuación [3] para calcular el
factor de fricción para el Flujo Turbulento Hidráulicamente Liso (FTHL), donde el espesor de la
subcapa laminar viscosa es mayor a la rugosidad absoluta de tuberías, para un rango de número de
Reynolds entre 5000 y 100.000:
𝑓 =
0.316
𝑅𝑒
0.25
[𝟑]
Luego en 1933, Nikuradse efectuó una serie de experimentos en tuberías con rugosidades
artificiales para estudiar la naturaleza del factor de fricción. Con base en estos experimentos,
Prandtl y su estudiante Von Kármán plantearon ecuaciones para calcular el factor de fricción para
FTHL
[𝟒] y Flujo Turbulento Hidráulicamente Rugoso (FTHR) [𝟓], donde la rugosidad absoluta de
la tubería es mayor al espesor de la subcapa laminar viscosa:
1
�𝑓
= −2𝑙𝑜𝑔
10
�
2.51
𝑅𝑒�𝑓
� [𝟒]
1
�𝑓
= −2𝑙𝑜𝑔
10
�
𝑘𝑠
3.7𝐷� [𝟓]
Sin embargo, estas dos últimas ecuaciones no resultaron ser de gran aplicabilidad para el diseño y
análisis de RDAP, ya que la gran mayoría de los flujos en tuberías se ubicaban en el Flujo
Turbulento Transicional (FTT) o zona de transición, zona delimitada entre el FTHL y FTHR.
Para solucionar este inconveniente, C.F. Colebrook y H. White (1939) lograron definir claramente
los límites de esta zona [6] (Vennard, 1961) y la ecuación implícita [7] definitiva para calcular el
factor de fricción en el FTT.
0.305𝛿´ < 𝑘𝑠 < 6.1𝛿´ [𝟔]
donde δ' es el espesor de la subcapa laminar viscosa. La ecuación es:
1
�𝑓
= −2𝑙𝑜𝑔
10
�
𝑘𝑠
3.7𝐷 +
2.51
𝑅𝑒�𝑓
� [𝟕]
A pesar de todos los esfuerzos realizados por estos investigadores, en la primera mitad del siglo
XX, no fue posible aplicar las ecuaciones implícitas propuestas por Prandtl, Von Kármán,
Colebrook y White en el diseño de tuberías, ya que en esta época no existían herramientas
computacionales para resolver ecuaciones implícitas por medio de algún método numérico. Por
ello, este problema ocasionó la aparición de ecuaciones empíricas tales como la ecuación de Hazen-
Williams:
𝑉 = 0.849𝐶
𝐻𝑊
𝑅
0.63
𝑆
0.54
[𝟖]
donde C
HW
es el coeficiente de la ecuación de Hazen-Williams, el cual depende del material y edad
de la tubería, R es el radio hidráulico y S la Pendiente de la línea de fricción. Sin embargo, este
problema también dio origen al desarrollo de métodos gráficos como el Diagrama de Moody,
propuesto por Lewis Moody (Moody, 1944), para facilitar el cálculo del factor de fricción con base
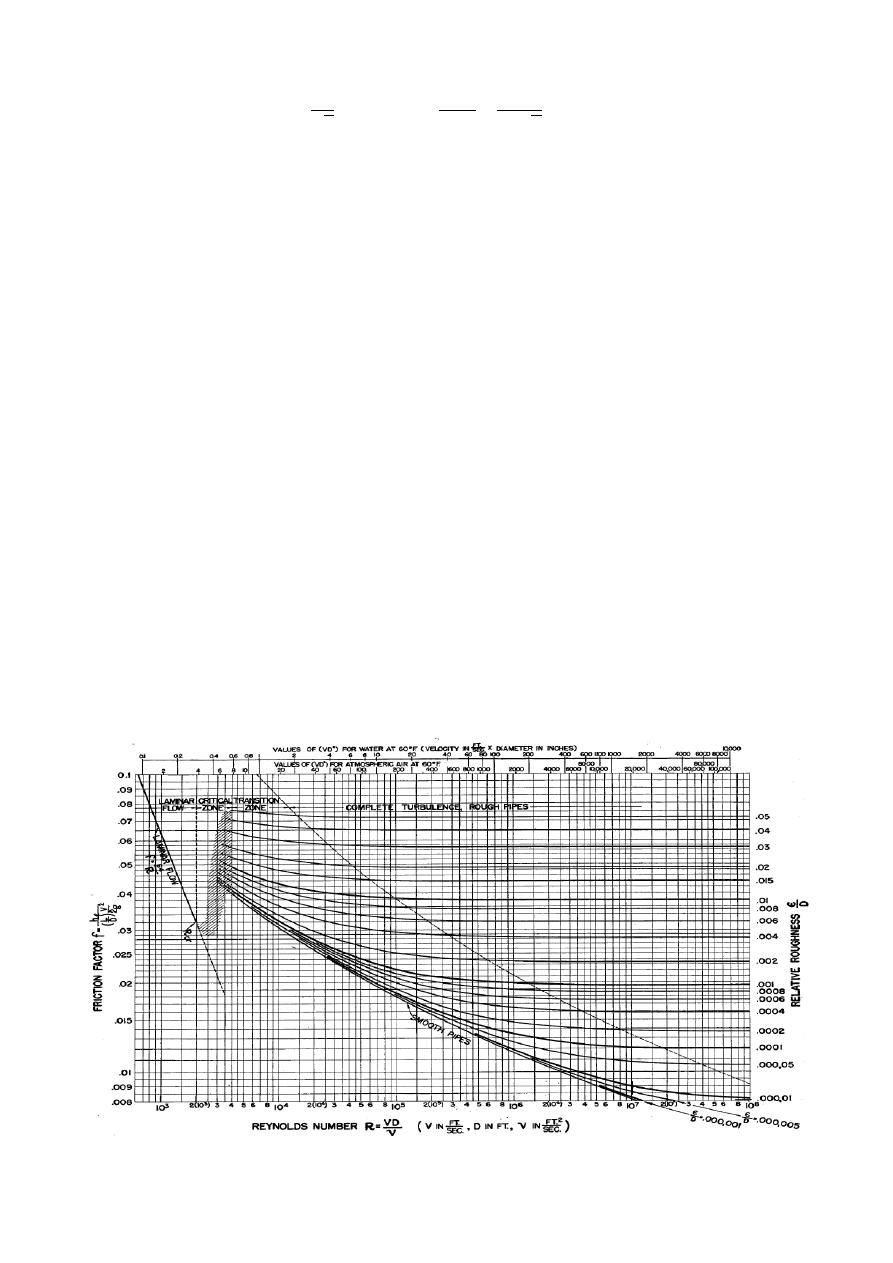
en el número de Reynolds y la rugosidad relativa, como se puede ver en la Figura 1.
En este Diagrama, Moody delimitó cinco áreas, las cuales son: flujo laminar, zona crítica, zona lisa,
zona de transición y turbulencia completa. La primera región está delimitada por números de
Reynolds menores a 2000 y esta descrita por la Ecuación [2]. La segunda área, por su parte, está
delimitada por números de Reynolds entre 2000 y 4000, donde el factor de fricción es difícil de
cuantificar ya que no fue posible encontrar una expresión matemática para calcular dicho parámetro
por la inestabilidad que se presenta en dicha zona. Para números de Reynolds superiores a 4000, en
el Diagrama de Moody se pueden ver tres regiones adicionales, la zona lisa, la zona de transición y
la zona de turbulencia completa. En relación a la zona de transición, Moody utilizó las Ecuaciones
[4] y [5] para demarcar el límite inferior (zona lisa) y superior (turbulencia completa) de esta zona
respectivamente. Adicionalmente, este investigador utilizó la ecuación de Colebrook-White [7]
para dibujar las líneas dentro de la zona de transición, como se puede ver en la Figura 1.
Figura 1. Diagrama de Moody

A partir de lo anterior, los límites de la zona de transición demarcados en el Diagrama Moody se
basaron en las ecuaciones propuestas por Prandtl y Von Kármán para FTHL y FTHR. Sin embargo,
para delimitar el FTT, Moody (1944) nunca se basó en la ecuación Colebrook-White (ver Ecuación
[7]) y los límites definidos claramente por estos dos investigadores para la zona de transición en
función de la rugosidad y el espesor de la subcapa laminar viscosa (Vennard, 1961).
Por esta razón y teniendo en cuenta la importancia de la zona de transición en el diseño de tuberías,
en el presente artículo se presentará la delimitación de la zona de transición o FTT en el Diagrama
de Moody con base en la ecuación de Colebrook-White y los efectos que puede tener esta nueva
zona en dicho Diagrama. Para ello, primero se ilustrará el proceso deductivo que se efectuó para
encontrar las ecuaciones que describen los límites del FTT basado en las Ecuaciones [6] y [7].
Posteriormente, se diseñarán distintas redes hipotéticas basadas en redes reales de Colombia tales
como Red San Vicente, Red Bogotá-Cazucá y Red La Cumbre, para analizar el efecto que puede
tener la demarcación de estos nuevos límites en el Diagrama de Moody en el análisis y diseño de
RDAP. Finalmente, se mostrarán algunas conclusiones con base en dicho análisis.
PROCESO DEDUCTIVO
El paso de flujo laminar a flujo turbulento no se hace de forma súbita sino gradual; por ello el flujo
que describe dicho cambio es el flujo turbulento transicional (FTT), el cual está definido desde el
límite máximo donde se puede presentar Flujo Turbulento Hidráulicamente liso (FTHL) hasta el
límite mínimo donde se puede presentar Flujo Turbulento Hidráulicamente Rugoso (FTHR). Estos
límites fueron definidos claramente por Colebrook y White mediante la Ecuación [6]. Con base en
ello, a continuación se ilustra el proceso deductivo para el límite inferior y el límite superior del
FTT a partir de dicha ecuación.
Límite inferior zona de transición
El límite inferior de la zona de transición está definido por los flujos que se pueden clasificar
máximo como FTHL. Según Colebrook y White (1939), este se presenta cuando la rugosidad de la
tubería es igual al 30% del espesor de la subcapa laminar viscosa como se puede ver en la Ecuación
[6]. Por ello, si el tamaño de la rugosidad de la tubería es inferior a dicho valor, el flujo es
hidráulicamente liso. Teniendo en cuenta lo anterior, a continuación se ilustra el proceso deductivo
de la ecuación que describe el límite inferior de la zona de transición basado en la ecuación de
Colebrook-White [7] y la Ecuación [6].
Primero, se reemplaza en la ecuación de Colebrook-White [7] la rugosidad (ks) por el 30% del
espesor de la subcapa laminar viscosa (
𝛿´):
1
�𝑓
= −2𝑙𝑜𝑔
10
�
0.305𝛿´
3.7𝑑 +
2.51
𝑅𝑒�𝑓
� [𝟗]
El espesor de la subcapa laminar viscosa se define mediante la siguiente ecuación:
𝛿´ =
11.6 𝜈
v
∗
[𝟏𝟎]
donde
𝜈 es la viscosidad cinemática del fluido y v
*
es la velocidad de corte, la cual se calcula de la
siguiente manera:
v
∗
= �
𝜏
𝑜
𝜌
[𝟏𝟏]
donde
𝜏
𝑜
es el esfuerzo cortante y
ρ es la densidad del fluido.

Teniendo en cuenta lo anterior, se procede a reemplazar en la Ecuación [9] el espesor de la subcapa
laminar viscosa por las ecuaciones [10] y [11], como se muestra a continuación:
1
�𝑓
= −2𝑙𝑜𝑔
10
(
0.305
3.7𝑑 (
11.6 𝜈
�
𝜏
𝑜
𝜌
) +
2.51
𝑅𝑒�𝑓
) [𝟏𝟐]
Luego, para expresar la Ecuación [12] en términos del factor de fricción (f), es necesario conocer la
relación que existe entre el factor de fricción (f) y el esfuerzo cortante
(𝜏
𝑜
), la cual se ilustra en la
siguiente ecuación:
𝑓 =
8𝜏
𝑜
𝜌v
2
[𝟏𝟑]
donde v es la velocidad media del flujo.
Con base en la Ecuación [13], se reemplaza en la Ecuación [12] el esfuerzo cortante por el factor de
fricción, la densidad del fluido y la velocidad media de flujo, como se muestra a continuación:
1
�𝑓
= −2𝑙𝑜𝑔
10
(
0.305
3.7𝑑 (
11.6 𝜈
�
𝑓𝜌v2
8
𝜌
) +
2.51
𝑅𝑒�𝑓
)
1
�𝑓
= −2𝑙𝑜𝑔
10
�
2.7 𝜈
�𝑓v𝑑
+
2.51
𝑅𝑒�𝑓
� [𝟏𝟒]
Posteriormente en la Ecuación [14], se expresa la velocidad media de flujo en términos del número
de Reynolds (Re), la viscosidad cinemática del fluido
(𝜈) y el diámetro de la tubería, con base en la
definición de este número adimensional, tal como se ilustra a continuación:
1
�𝑓
= −2𝑙𝑜𝑔
10
(
2.7 𝜈
�𝑓(
𝑅𝑒𝜈
𝑑
) 𝑑
+
2.51
𝑅𝑒�𝑓
)
1
�𝑓
= −2𝑙𝑜𝑔
10
�
2.7
𝑅𝑒�𝑓
+
2.51
𝑅𝑒�𝑓
� [𝟏𝟓]
Finalmente, si se suman los factores en común de la Ecuación [15], se obtiene la siguiente ecuación
que define el límite inferior de la zona de transición basado en la ecuación de Colebrook-White y
los límites definidos claramente por estos investigadores para la zona de transición.
1
�𝑓
= −2𝑙𝑜𝑔
10
�
5.21
𝑅𝑒�𝑓
� [𝟏𝟔]
Límite superior zona de transición
El límite superior del FTT está definido por los flujos que pueden mínimo clasificarse como FTHR.
Según Colebrook-White (1939), estos se presentan cuando la rugosidad de la tubería (ks) es igual a
6.1 veces el espesor de la subcapa laminar viscosa
(𝛿´) como se puede ver en la Ecuación [6]. Por
ello, si la rugosidad de la tubería es superior a dicho valor, el flujo es hidráulicamente rugoso.
Teniendo en cuenta lo anterior y llevando a cabo el mismo proceso deductivo para el límite inferior
de la zona de transición, se obtuvo la siguiente ecuación que describe el límite superior de esta zona
con base en la ecuación de Colebrook-White y la Ecuación [6]:
1
�𝑓
= −2𝑙𝑜𝑔
10
�
56.6
𝑅𝑒�𝑓
� [𝟏𝟕]
ANÁLISIS
Para entender el efecto que puede tener estos nuevos límites de la zona de transición en el Diagrama
de Moody, se dibujó el límite inferior y superior de la zona de transición en el Diagrama de Moody
con base en las Ecuaciones [16] y [17] respectivamente. Luego, se demarcaron los límites de esta
zona en dicho Diagrama a partir de las ecuaciones de Blasius [2] y Prandtl-Von Kármán (ver
Ecuaciones [4] y [5]), para luego compararlos con los límites obtenidos a partir de la ecuación de
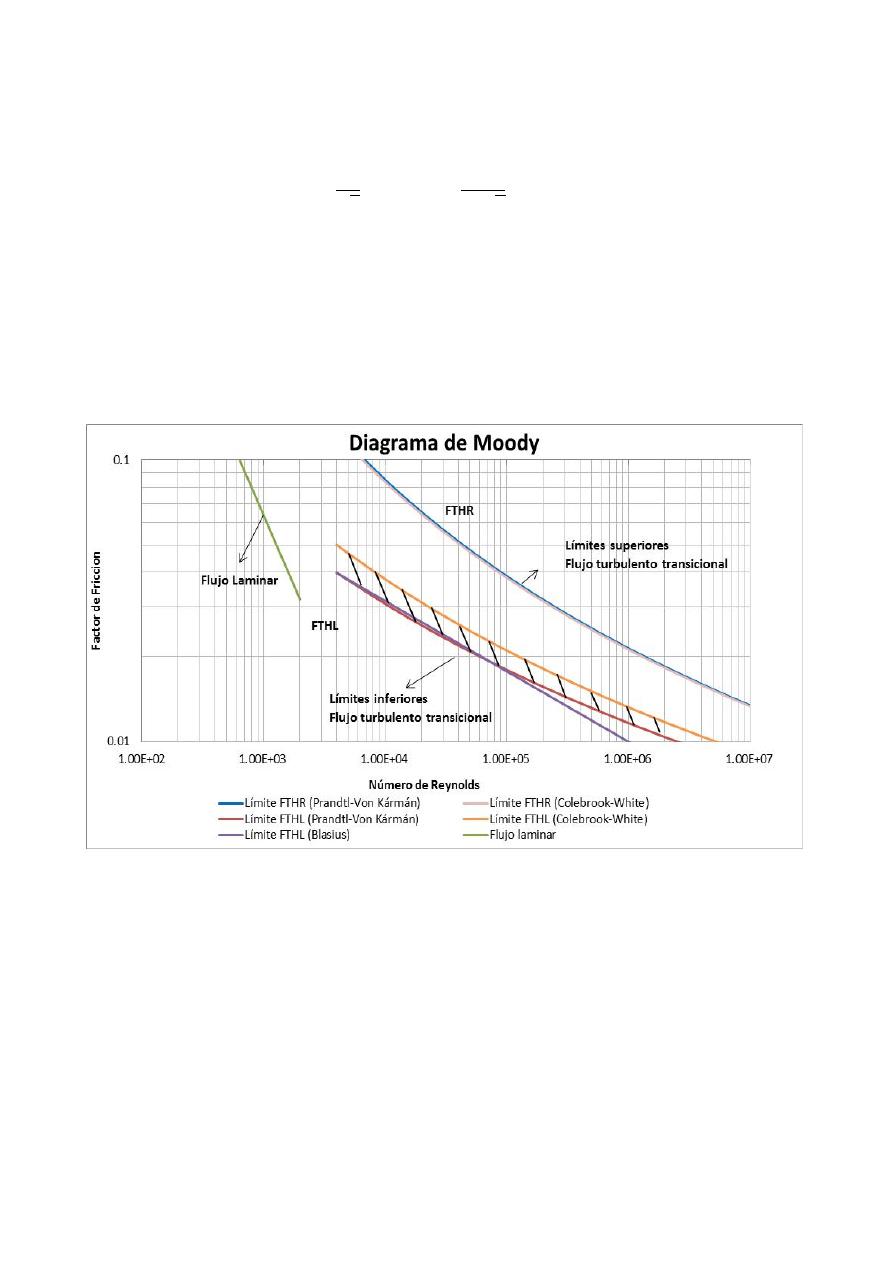
Colebrook-White. Lo anterior se puede ver en la Figura 2.
Figura 2. Delimitación del flujo turbulento transicional en el Diagrama de Moody.
Si se compara el límite superior de la zona de transición obtenido a partir de la ecuación de
Colebrook-White (ver Ecuación [17]) vs. la ecuación de Prandtl-Von Kármán (ver Ecuación [5]), se
puede ver en la Figura 2 que estos coinciden en toda la extensión del Diagrama de Moody. Sin
embargo, el límite inferior del FTT demarcado a partir de la Ecuación [4] difiere del dibujado en el
Diagrama de Moody, ya que el obtenido a partir de la ecuación de Colebrook-White [2] hace más
estrecha la zona que describe este tipo de flujo en dicho Diagrama, lo que implica que la ocurrencia
del FTHL sería más común en el diseño de tuberías en comparación con la ecuación de Prandtl-
Von Kármán para este tipo de flujo. Esto se refleja claramente en la región sombreada de la Figura
1 y se presenta debido a que el orden de magnitud del primer sumando del paréntesis de la
ecuación de Colebrook-White (ver Ecuación [2]) es igual al orden de magnitud del segundo
sumando con base en el proceso deductivo de la Ecuación [16]. Este resultado, modifica la
concepción que se tiene que la rugosidad relativa no se debe considerar en el análisis de tuberías
que presentan FTHL.
Teniendo en cuenta lo anterior, es necesario analizar el efecto que pueden tener estos nuevos límites
de la zona de transición del Diagrama de Moody. Para ello, se diseñaron diversas redes hipotéticas
basadas en redes de distribución de agua potable (RDAP) de Colombia tales como Red La Cumbre,
Red Bogotá-Cazucá y Red San Vicente utilizando las ecuaciones de Darcy-Weisbach y Hazen-
Williams (ver Ecuación [8]). Para diseñar estas redes se utilizó el programa REDES, programa
creado en la Universidad de los Andes Bogotá, Colombia (1988) para realizar el análisis y diseño
optimizado de RDAP, por medio de la metodología de diseño Superficie Óptima del Gradiente
Hidráulico (Ochoa, 2009), teniendo en cuenta los siguientes parámetros de diseño en común para
estas tres redes:
• Presión mínima de diseño: 20 metros de columna de agua.
• Los materiales utilizados para el diseño de estas redes fueron el PVC, Hierro dúctil, polietileno y
acero. Por ello, se adoptó la rugosidad absolutas (ks) y los coeficientes de Hazen-Williams
(CHw) de dichos materiales de las normas de las Empresas Públicas de Medellín (EPM,2009):
Tabla 1.
Rugosidades de las tuberías.
Material\Rugosidad
tubería
ks (mm)
C
HW
Acero
0.45
120
Hierro dúctil
0.25
140
Polietileno
0.007
150
PVC
0.0015
150
• Se adoptó el valor de viscosidad cinemática del agua para una temperatura de 20°C.
• La estimación de la demanda en cada uno de los nudos se hizo de forma uniforme en toda en la
red, dividiendo la demanda total de esta por el número de nudos totales de la red de diseño, de tal
forma que en ninguno de los nudos se presentara un caudal de consumo inferior a 1.48 L/s o
mayor a 2.6 L/s.
A partir de lo anterior, se definió la demanda total de la red, consumo por nudo y línea de gradiente
hidráulico (LGH) de la fuente de abastecimiento de cada una de las redes mencionadas
anteriormente con respecto al nivel del mar (m.s.n.m), tal como se ilustra en la siguiente tabla.
Tabla 2.
Parámetros de diseño de las Redes La Cumbre, Bogotá-Cazucá y Red Elevada.
Parámetro\RDAP
Red San Vicente
Bogotá-Cazucá
La Cumbre
No Nudos
62
145
338
No Tubos
71
150
378
Demanda total (L/s)
135
315
500
Consumo por nudo (L/s)
2.18
2.17
1.48
Altura promedio (m.s.n.m)
2150
2720
950
Línea del gradiente hidráulico de la
fuente de Abastecimiento (m.s.n.m)
2300
2930
1200
Posteriormente, se localizaron los factores hidráulicos obtenidos a partir de cada uno de los diseños
de la Red San Vicente, Red Bogotá
–
Cazucá y Red La Cumbre en el Diagrama de Moody de la
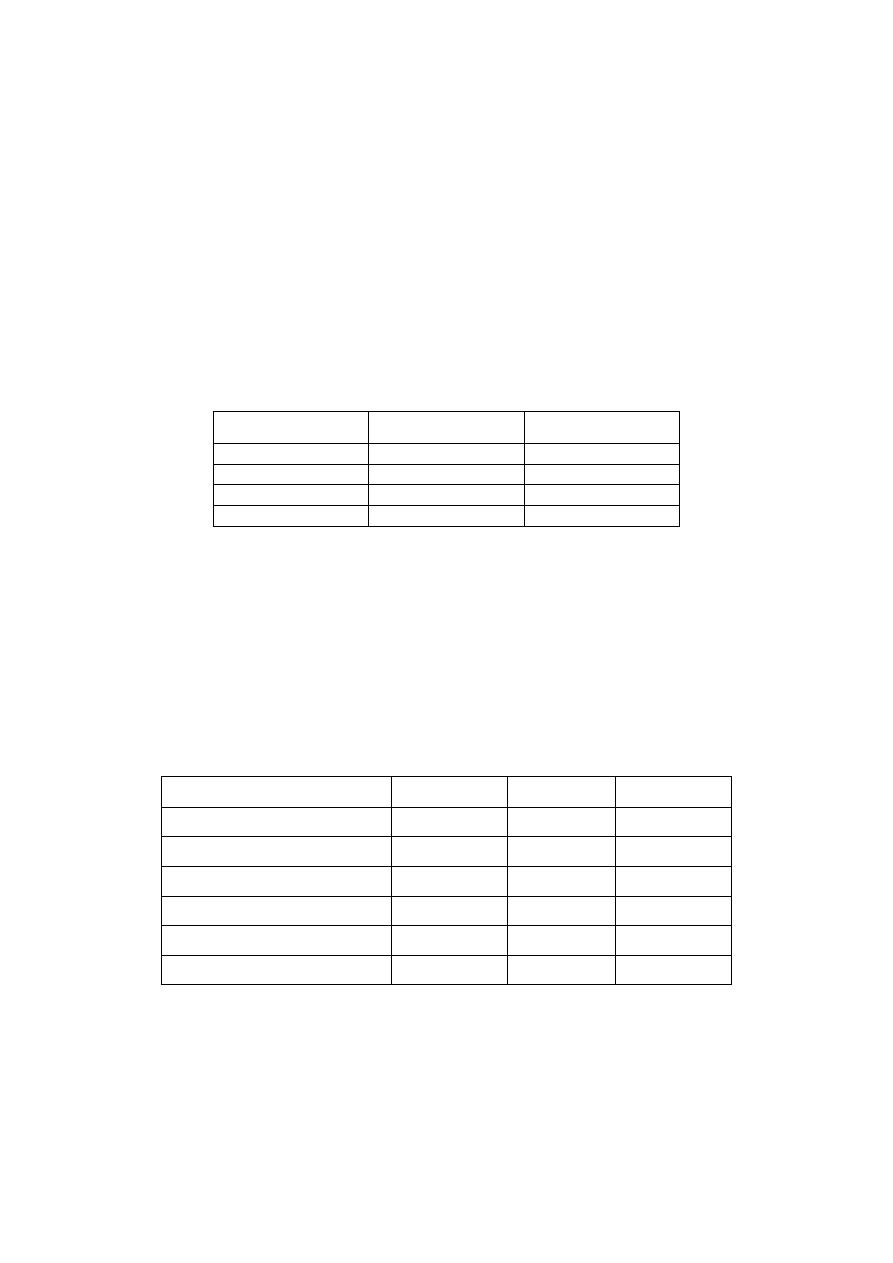
Figura 2, como se puede ver en las Figuras 3, 4 y 5 respectivamente.
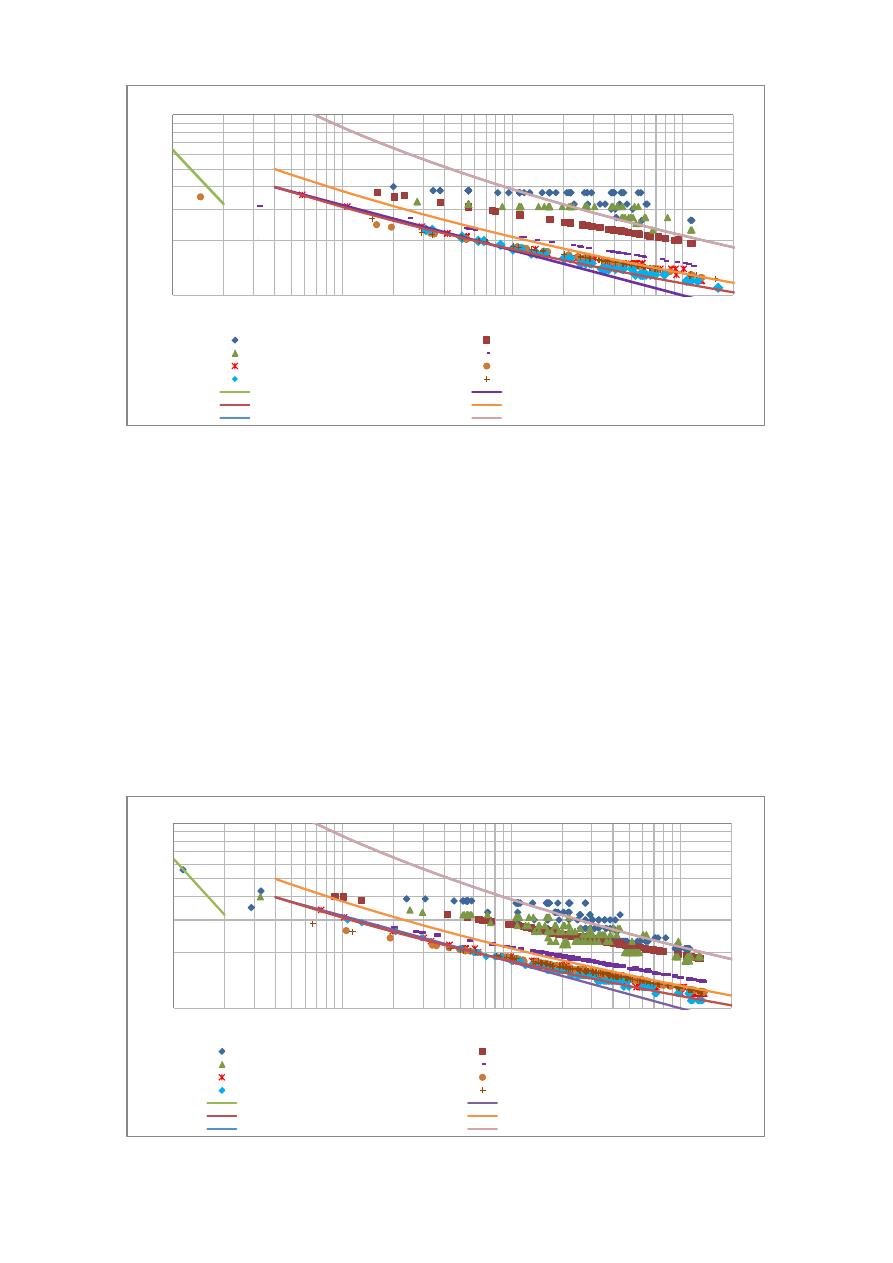
Figura 3. Factores hidráulicos obtenidos para la Red San Vicente.
En relación con el diseño de la Red San Vicente, en la Figura 3 se puede ver que los factores
hidráulicos obtenidos para el diseño de esta red con el Acero y Hierro Dúctil, se localizan en su
mayoría en la zona de FTHR cuando se utiliza en el diseño la ecuación de fricción de Darcy-
Weisbach. Sin embargo, se puede observar que los factores hidráulicos obtenidos por medio de la
ecuación de Hazen-Williams se ubican en su mayoría en la zona de transición definida a partir de
las ecuaciones de Prandtl-Von Kármán y Colebrook-White, pero se distingue claramente que para
números de Reynolds inferiores a 100000 los factores hidráulicos calculados para el Hierro dúctil
con esta última ecuación se localizan dentro de la zona de FTHL definida a partir de la ecuación de
Colebrook-White. Igualmente, en esta figura se puede observar que la tendencia que se presenta
para el Acero y Hierro Dúctil no sucede de igual forma para el PVC y el Polietileno, debido a que
los factores de fricción obtenidos por medio de la ecuación de Darcy-Weisbach tienden a igualarse
con los calculados en la ecuación de Hazen-Williams, los cuales se ubican en su mayoría en la
región sombreada de la Figura 2, y específicamente en la zona de FTHL con base en el nuevo límite
inferior de la zona de transición definido a partir de la ecuación de Colebrook-White y la zona de
transición demarcada con base en la ecuación de Prandtl-Von Kármán.
Figura 4. Factores hidráulicos obtenidos para la Red Bogotá-Cazucá.
0.01
0.1
1.00E+03
1.00E+04
1.00E+05
1.00E+06
Fac
to
r d
e
Fr
ic
ció
n
Número de Reynolds
Red San Vicente (LGH:2300 m, 20
o
C)
Darcy-Weisbach (Acero, ks=0.45mm)
Hazen-Williams( Acero ,CHW=120)
Darcy-Weisbach (Hierro Dúctil, ks=0.25mm)
Hazen Williams (Hierro Dúctil, CHW:140)
Darcy-Weisbach (Polietileno, ks=0.007mm)
Hazen-Williams (Polietileno, CH=150)
Darcy-Weisbach(PVC, ks=0.0015mm)
Hazen-Williams(PVC, CHW:150)
Flujo laminar
Límite FTHL (Blasius)
Límite FTHL (Prandtl- Von Kármán)
Límite FTHL (Colebrook-White)
Límite FTHR (Prandtl- Von Kármán)
Límite FTHR (Colebrook-White)
0.01
0.1
1.00E+03
1.00E+04
1.00E+05
1.00E+06
Fa
ct
or
d
e
fr
ic
ci
ón
Número de Reynolds
Red Bogotá-Cazucá (LGH:2930 m, 20
o
C)
Darcy-Weisbach(Acero,ks:0.45mm)
Hazen-Williams(Acero, CHW:120)
Darcy-Weisbach(Hierro Dúctil, ks:0.25mm)
Hazen-Williams(Hierro Dúctil, CHW:140)
Darcy-Weisbach(Polietileno, ks:0.007mm)
Hazen-Williams(Polietileno, CHW:150)
Darcy-Weisbach(PVC, ks:0.0015mm)
Hazen-Williams(PVC, CHW:150)
Flujo laminar
Límite FTHL (Blasius)
Límite FTHL (Prandtl- Von Kármán)
Límite FTHL (Colebrook-White)
Límite FTHR (Prandtl- Von Kármán)
Límite FTHR (Colebrook-White)

Por su parte, en la Figura 4 se puede observar que los factores de fricción obtenidos para el diseño
de la Red Bogotá-Cazucá con el Acero y Hierro Dúctil, se localizan en su mayoría en la zona de
transición cuando se utiliza en el diseño la ecuación de fricción de Darcy-Weisbach. Por otro lado,
se puede ver que los factores hidráulicos obtenidos por medio de la ecuación de Hazen-Williams se
ubican por debajo de los calculados por esta ecuación o se alejan del límite superior de la zona de
transición dibujado a partir de la ecuación de Prandtl-Von Kármán o la ecuación de Colebrook-
White. Así mismo; se puede observar que la tendencia que se presenta para el Acero y Hierro
Dúctil no ocurre de igual forma para el Polietileno y PVC, ya que los factores de fricción obtenidos
por la ecuación de Darcy-Weisbach tienden a igualarse con los calculados en la ecuación de Hazen-
Williams y se ubican en su mayoría en la región sombreada de la Figura 2 o en el FTHL con base
en el nuevo límite inferior del FTT. Es importante aclarar que, para números de Reynolds inferiores
a 10000, los factores hidráulicos calculados para el Polietileno y PVC se ubican en la zona de FTHL
definida a partir de la ecuación de Colebrook-White y la ecuación de Prandtl-Von Kármán, pero
después de dicho número este comportamiento no se presenta.
Figura 5. Factores hidráulicos obtenidos para la Red La Cumbre.
Finalmente, con base en la Figura 5 se puede observar que, para una temperatura de 20
o
C y
LGH=1200 m.s.n.m, los factores hidráulicos obtenidos en el diseño de la Red La Cumbre con el
Acero y Hierro Dúctil, se localizan cerca al límite superior de la zona de transición cuando se
utiliza en el diseño la ecuación de fricción de Darcy-Weisbach. Por otro lado, se puede ver que los
factores hidráulicos obtenidos por medio de la ecuación de Hazen-Williams para estos materiales se
alejan de este límite descrito por la ecuación de Prandtl-Von Kármán y la ecuación de Colebrook-
White. Adicionalmente, de esta misma figura se puede apreciar que la tendencia que se presenta
para el Acero y Hierro Dúctil es similar para el Polietileno y el PVC para números de Reynolds
inferiores a 100000 ya que los factores de fricción obtenidos por la ecuación de Darcy-Weisbach
tienden a ser mayores comparados con los calculados con la ecuación de Hazen-Williams. Sin
embargo, es importante mencionar que los factores de fricción obtenidos por estas ecuaciones
tienden a igualarse para estos dos materiales, los cuales se ubican en su mayoría en la región
sombreada de la Figura 2, y específicamente en el FTHL con base en el nuevo límite inferior de la
zona de transición definido a partir de la ecuación de Colebrook-White. Por último, en esta figura
se puede ver que en comparación al diseño de la Red San Vicente y la Red Bogotá-Cazucá, para
números de Reynolds inferiores a 100000, se obtienen factores hidráulicos dentro del FTHL para
materiales rugosos como el Hierro Dúctil a partir del nuevo límite inferior del FTT, cuando se
diseña con la ecuación de Hazen-Williams.
0.01
0.1
1.00E+03
1.00E+04
1.00E+05
1.00E+06
Fac
to
r d
e
Fr
ic
ció
n
Número de Reynolds
Red La Cumbre (LGH: 1200 m, 20
o
C)
Darcy-Weisbach(Acero, ks:0.45mm)
Hazen-Williams (Acero, CHW:120)
Darcy-Weisbach (Hierro Dúctil, ks:0.25mm)
Hazen-Williams (Hierro Dúctil, CHW:140)
Darcy-Weisbach (Polietileno, ks:0.007mm)
Hazen-Williams( Polietileno, CHW:150)
Darcy-Weisbach (PVC, Ks:0.0015mm)
Hazen-Williams (PVC, CHW:150)
Flujo laminar
Límite FTHL (Blasius)
Límite FTHL (Prandtl- Von Kármán)
Límite FTHL (Colebrook-White)
Límite FTHR (Prandtl- Von Kármán)
Límite FTHR (Colebrook-White)

CONCLUSIONES
• Para materiales que presentan rugosidades absolutas inferiores a 0.007 mm o coeficientes de
Hazen-Williams superiores a 140, los factores hidráulicos obtenidos a partir del diseño de las
redes analizadas en este artículo, utilizando las ecuaciones de Darcy-Weisbach y Hazen-
Williams, se localizaron en la región sombreada de la Figura [2]. Por lo anterior, se puede
concluir que el límite inferior de la zona de transición del Diagrama de Moody debe ser revisado,
para establecer si el nuevo límite definido a partir de la ecuación de Colebrook-White puede
contribuir a entender mejor el comportamiento de las tuberías en el FTHL.
•
Con base en el proceso deductivo de la Ecuación [16], se puede concluir que el factor de fricción
en FTHL no depende únicamente del número de Reynolds sino también de la rugosidad de la
tubería, ya que el orden de magnitud del primer sumando del paréntesis de la ecuación de
Colebrook-White (ver Ecuación [6]) es igual al orden de magnitud del segundo sumando. Por lo
anterior, se debería establecer, realmente, si la rugosidad en este tipo de flujo puede afectar el
cálculo del factor de fricción.
REFERENCIAS
Bombardelli F. & Garcia M. (Noviembre de 2003). "Hydraulic Design of Large-Diameter Pipes".
Recuperado el Marzo de 13 de 2010, de ascelibrary: http//: www.ascelibrary.com.
Brown, G. O. (2004). "The History of the Darcy-Weisbach Equation for Pipe flow resistance". Recuperado
el 4 de Marzo de 2010, de ascelibrary: http://www.ascelibrary.org.
Colebrook, C.F (1939). "Turbulent flow in pipes, whit particular reference to the transition region between
the smooth and rough pipe laws". Journal of Institution of Civil Engineers, Vol 11, 133-156.
Diskin, M. (1960). "The limits of applicability of the Hazen-Williams formula". Houille Blanche , 720-723.
EPM. (2009). Normas de diseño de sistemas de acueducto. Medellin.
Liou, C. P. (1998). "Limitations and proper use of the Hazen-Williams equation". Recuperado el 5 de Marzo
de 2010, de ascelibrary: http://www.ascelibrary.com
Moody, L. (1944). "Friction factors for pipe flow". Trans. ASME. 671-684.
Ochoa, S. (2009). Diseño optimizado de redes de distribucion de agua potable con base en el concepto
enérgetico de superficie óptima de gradiente hidráulico. Bogotá D.C.: Trabajo de grado, Universidad de los
Andes.
Saldarriaga Valderrama, J. G. (2007). Hidráulica de tuberías: abastecimiento de agua, redes, riegos .
Bogotá, D.C.: Alfaomega: Uniandes.
Vennard, D. (1961). Elementary Fluid Mechanics. Fourth edition, New York: Jhon Wiley & Sons.
