
TESIS DE MAESTRÍA
TRÁNSITO DE CRECIENTES A TRAVÉS DE CANALES DE AGUAS LLUVIA
UTILIZANDO REDES NEURONALES
PRESENTADO POR:
LAINER J. BOHÓRQUEZ MEZA
ASESOR:
JUAN GUILLERMO SALDARRIAGA VALDERRAMA
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
MAESTRÍA EN INGENIERÍA CIVIL
BOGOTÁ D.C.
AGOSTO DE 2015

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza Tesis de maestría

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza Tesis de maestría
AGRADECIMIENTOS
Agradezco a Dios primeramente por brindarme la
oportunidad de iniciar y culminar esta importante etapa en
mi vida profesional y personal, superando con éxito todos
los obstáculos presentados.
A mi familia, en especial a mis padres Carmen Meza y
Wilson Bohórquez y a mis hermanas que desde la distancia
siempre me brindaron palabras de apoyo, ánimo y
bendiciones.
A mi novia Lina Solano, doy gracias por animarme,
apoyarme y comprenderme durante el tiempo que dediqué
a la culminación de mis estudios.
También agradezco a todos mis compañeros de maestría,
en especial a Adriana, Néstor e Iván con los cuales
compartí momentos arduos de estudio y muchas alegrías.
Nunca consideres el estudio como una obligación, sino como una oportunidad
para penetrar en el bello y maravilloso mundo del saber.
Albert Einstein

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
i
TABLA DE CONTENIDO
1.
INTRODUCCIÓN ......................................................................................... 1
1.1 OBJETIVOS GENERALES ...................................................................... 4
1.2 OBJETIVOS ESPECIFICOS .................................................................... 4
2.
CONTEXTUALIZACIÓN Y MARCO TEÓRICO ........................................... 6
2.1
REDES NEURONALES – MODELO BIOLOGICO ................................ 6
2.1.1
Naturaleza bioeléctrica de la neurona ............................................. 7
2.1.2
Sinapsis ........................................................................................... 7
2.2
REDES NEURONALES ARTIFICIALES ................................................ 8
2.3
DESARROLLO HISTÓRICO DE LAS REDES NEURONALES ........... 10
2.4
VENTAJAS DE LAS REDES NEURONALES ...................................... 13
2.4.1
Aprendizaje adaptativo .................................................................. 13
2.4.2
Autoorganización........................................................................... 14
2.4.3
Tolerancia a fallos ......................................................................... 14
2.4.4
Operación en tiempo real .............................................................. 15
2.4.5
Fácil inserción dentro de la tecnología existente ........................... 15
2.5
ELEMENTOS DE UNA RED NEURONAL ARTIFICIAL ....................... 15
2.5.1
Unidades de Proceso - Neurona Artificial ...................................... 16
2.5.2
Estado de Activación ..................................................................... 17
2.5.3
Conexiones entre neuronas .......................................................... 17
2.5.4
Función de Salida o Transferencia ................................................ 18
2.5.5
Función o Regla de Activación ...................................................... 21
2.5.6
Regla de Aprendizaje .................................................................... 23
2.6
CARACTERÍSTICAS DE LAS REDES NEURONALES....................... 23
2.6.1
Topología de la Red Neuronal ...................................................... 24
2.6.2
Mecanismo de Aprendizaje ........................................................... 24
2.6.3
Tipo de asociación entre la información de entrada y salida ......... 28
3.
MANEJO DE LA HERRAMIENTA DE SIMULACIÓN – MATLAB
®
............ 29

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
ii
3.1
USO DEL TOOLBOX EN MATLAB
®
.................................................... 29
3.2
SERIES DE TIEMPO DINÁMICAS ...................................................... 31
3.2.1
Definición del problema ................................................................. 31
3.2.2
Estructuras de datos ..................................................................... 31
3.3
USO DE LA INTERFAZ GRÁFICA PARA SERIES DE TIEMPO ......... 32
3.4
USO DE LAS FUNCIONES DE LA LÍNEA DE COMANDO ................. 43
4.
METODOLOGÍA DESARROLLADA .......................................................... 52
5.
ANÁLISIS DE RESULTADOS ................................................................... 64
5.1
CASO DE ESTUDIO 1 ......................................................................... 64
5.1.1
Desempeño de las Redes Neuronales – Caso de Estudio 1 ......... 71
5.1.2
Correlación de Resultados – Caso de Estudio 1 ........................... 76
5.1.3
Análisis de sensibilidad – Caso de Estudio 1 ................................ 79
5.1.4
Otras distribuciones de hidrogramas - Caso de Estudio 1 ............ 81
5.2
CASO DE ESTUDIO 2 ......................................................................... 87
5.3
CASO DE ESTUDIO 3 ......................................................................... 95
6.
ANÁLISIS DE COSTOS........................................................................... 102
6.1
CASO DE ESTUDIO 1 ....................................................................... 102
6.2
CASO DE ESTUDIO 2 ....................................................................... 103
7.
CONCLUSIONES Y RECOMENDACIONES ........................................... 105
8.
BIBLIOGRAFÍA ........................................................................................ 108
9.
ANEXOS .................................................................................................. 110

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
iii
ÍNDICE DE FIGURAS
Figura 2.1. Esquema de una neurona biológica. Fuente:
(www.histologiaub.blogspot.com). ...................................................................... 6
Figura 2.2. Salto sináptico. Fuente: (IZAURIETA & SAAVEDRA)....................... 8
Figura 2.3. Red neuronal artificial simple. Fuente: (MOLINA AGUILAR &
APARICIO, 2006). ............................................................................................... 9
Figura 2.4. Función de Transferencia tipo escalón. Fuente: (IZAURIETA &
SAAVEDRA). .................................................................................................... 19
Figura 2.5. Función de transferencia lineal (Fuente: Toolbox MATLAB
®
). ........ 19
Figura 2.6. Función de transferencia sigmoidal (Fuente: Toolbox MATLAB
®
). . 20
Figura 2.7. Función de transferencia Gaussiana (Fuente: Toolbox MATLAB
®
). 20
Figura 3.1. Acceso principal a la herramienta de redes neuronales (Fuente:
Toolbox MATLAB
®
). .......................................................................................... 30
Figura 3.2. Acceso a la herramienta de series de tiempo dinámicas (Fuente:
Toolbox MATLAB
®
). .......................................................................................... 32
Figura 3.3. Panel para cargar datos y objetivos – Red tipo NARX (Fuente:
Toolbox MATLAB
®
). .......................................................................................... 34
Figura 3.4. Panel para validación y prueba de datos (Fuente: Toolbox
MATLAB
®
). ........................................................................................................ 35
Figura 3.5. Panel para ajustar arquitectura de la red (Fuente: Toolbox
MATLAB
®
). ........................................................................................................ 36
Figura 3.6. Panel para entrenamiento de la red (Fuente: Toolbox MATLAB
®
).. 37
Figura 3.7. Variables de decisión e información del entrenamiento (Fuente:
Toolbox MATLAB
®
). .......................................................................................... 38
Figura 3.8. Panel para pruebas de la red (Fuente: Toolbox MATLAB
®
). .......... 42
Figura 3.9. Panel para validación y prueba de datos (Fuente: Toolbox
MATLAB
®
). ........................................................................................................ 43
Figura 3.10. Ventana de proceso del entrenamiento (Fuente: Toolbox
MATLAB
®
). ........................................................................................................ 48
Figura 3.11. Red NARX de circuito cerrado (Fuente: Toolbox MATLAB
®
). ....... 50
Figura 4.1 Trazado en planta – Caso de Estudio 1. .......................................... 53
Figura 4.2 Perfil del fondo del cauce – Caso de Estudio 1. .............................. 53
Figura 4.3 Modelo digital del Caso de Estudio 1. .............................................. 54
Figura 4.4 Trazado en planta – Caso de Estudio 2. .......................................... 61
Figura 4.5 Perfil del fondo del cauce – Caso de Estudio 2. .............................. 61
Figura 4.6 Trazado en planta – Caso de Estudio 3. .......................................... 62

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
iv
Figura 4.7 Perfil del fondo del cauce – Caso de Estudio 3. .............................. 63

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
v
ÍNDICE DE TABLAS
Tabla 2.1 Funciones de transferencia y rango de aplicación. Fuente: (MOLINA
AGUILAR & APARICIO, 2006). ......................................................................... 21
Tabla 3.1 Funciones para división de datos (Fuente: Toolbox MATLAB
®
). ...... 45
Tabla 3.2 Algoritmos de entrenamiento ofrecidos por MATLAB
®
(Fuente:
Toolbox MATLAB
®
). .......................................................................................... 47
Tabla 4.1. Distribución de neuronas según el número de capas ocultas. ......... 55
Tabla 4.2 Arquitecturas de redes neuronales utilizadas para el análisis del Caso
de Estudio 1 – Distribución 1. ........................................................................... 59
Tabla 5.1 Resultados del proceso de entrenamiento para cada arquitectura –
Caso de Estudio 1 – Distribución 1. .................................................................. 70
Tabla 5.2 Análisis de sensibilidad mediante la ANN_5 para cambios en la
pendiente de fondo – Caso de Estudio 1 – Distribución 1. ............................... 80
Tabla 5.3 Análisis de sensibilidad mediante la ANN_5 para cambios en el
coeficiente de rugosidad – Caso de Estudio 1 – Distribución 1. ....................... 80
Tabla 5.4 Porcentaje de datos para cada etapa según la distribución de
hidrogramas – Caso de Estudio 1. .................................................................... 81
Tabla 5.5 Desempeño para cada una de las redes neuronales según la
distribución de la serie de hidrogramas – Caso de Estudio 1. .......................... 85
Tabla 5.6 Coeficiente de correlación para cada una de las redes neuronales
según la distribución de la serie de hidrogramas – Caso de Estudio 1. ............ 86
Tabla 5.7 Porcentaje de datos para cada etapa según la distribución de
hidrogramas – Caso de Estudio 2. .................................................................... 88
Tabla 5.8 Desempeño para cada una de las redes neuronales según la
distribución de la serie de hidrogramas – Caso de Estudio 2. .......................... 93
Tabla 5.9 Coeficiente de correlación para cada una de las redes neuronales
según la distribución de la serie de hidrogramas – Caso de Estudio 2. ............ 94
Tabla 5.10 Porcentaje de datos para cada etapa según la distribución de
hidrogramas – Caso de Estudio 3. .................................................................... 95
Tabla 5.11 Desempeño para cada una de las redes neuronales según la
distribución de la serie de hidrogramas – Caso de Estudio 3. ........................ 100
Tabla 5.12 Coeficiente de correlación para cada una de las redes neuronales
según la distribución de la serie de hidrogramas – Caso de Estudio 3. .......... 101

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
vi
ÍNDICE DE GRÁFICAS
Gráfica 3.1. Panel para validación y prueba de datos (Fuente: Toolbox
MATLAB
®
). ........................................................................................................ 39
Gráfica 3.2. Error de autocorrelación (Fuente: Toolbox MATLAB
®
). ................. 40
Gráfica 3.3. Correlación entre entradas y errores (Fuente: Toolbox MATLAB
®
).
.......................................................................................................................... 41
Gráfica 3.4 Desempeño de la red neuronal (Fuente: Toolbox MATLAB
®
). ....... 49
Gráfica 4.1 Hidrogramas de entrada al modelo en HEC-RAS – Caso de Estudio
1 – Distribución 1. ............................................................................................. 58
Gráfica 5.1Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso de
Estudio 1 - Distribución 1. ................................................................................. 68
Gráfica 5.2. Desempeño (MSE) para cada una de la Redes neuronales
analizadas – Caso de Estudio 1 – Distribución 1. ............................................. 72
Gráfica 5.3. Coeficiente de correlación (R
2
) para cada una de las Redes
neuronales analizadas – Caso de Estudio 1 – Distribución 1. .......................... 73
Gráfica 5.4. Redes neuronales con mejor desempeño según el algoritmo de
entrenamiento – Caso de Estudio 1 – Distribución 1. ....................................... 74
Gráfica 5.5. Redes neuronales con mejor desempeño en la etapa de prueba –
Caso de Estudio 1 – Distribución 1. .................................................................. 75
Gráfica 5.6 Correlación de datos para arquitectura 1 (ANN_1). ....................... 77
Gráfica 5.7 Correlación de datos para arquitectura 5 (ANN_5). ....................... 77
Gráfica 5.8 Correlación de datos para arquitectura 18 (ANN_18)..................... 78
Gráfica 5.9 Correlación de datos para arquitectura 19 (ANN_19)..................... 78
Gráfica 5.10 Correlación de datos para arquitectura 21 (ANN_21)................... 79
Gráfica 5.11 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso
de Estudio 1 - Distribución 2. ............................................................................ 82
Gráfica 5.12 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso
de Estudio 1 - Distribución 3. ............................................................................ 83
Gráfica 5.13 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso
de Estudio 2 – Distribución 1. ........................................................................... 89
Gráfica 5.14 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso
de Estudio 2 – Distribución 2. ........................................................................... 90
Gráfica 5.15 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso
de Estudio 2 – Distribución 3. ........................................................................... 91

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
vii
Gráfica 5.16 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso
de Estudio 3 – Distribución 1. ........................................................................... 96
Gráfica 5.17 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso
de Estudio 3 – Distribución 2. ........................................................................... 97
Gráfica 5.18 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso
de Estudio 3 – Distribución 3. ........................................................................... 98

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
1
1. INTRODUCCIÓN
La consecución de información de campo y el grado de certeza de está en el
área de los Hidrosistemas o cualquier otra área de trabajo es uno de los
problemas más comunes en el desarrollo de proyectos actualmente. Ante esta
situación generalmente se recurre a métodos matemáticos y/o estadísticos que
permitan estimar o simular las condiciones que un hidrosistema dado presenta
en un momento determinado. Para el tránsito de crecientes en un canal de
aguas lluvias, tema objeto de este estudio, entre las variables más difíciles de
estimar con total certeza se encuentran los hidrogramas de entrada
(Información base para el tránsito de crecientes), hidrogramas de salida y el
coeficiente de rugosidad; ante esta situación muchas veces se recurre a la
experiencia del diseñador para obtener la información requerida.
Existen en la actualidad diversos métodos matemáticos para estimar los
parámetros desconocidos necesarios para el tránsito de una creciente. La
Inteligencia Artificial o Algoritmos Genéticos hacen parte de una serie de
instrumentos matemáticos y computacionales que debido al desarrollo logrado
en el campo de la informática en los últimos años están ganando espacio en
cuanto a su uso en la resolución de problemas en muchas áreas de estudio,
puesto que permite simular situaciones ocurridas con antelación y definir una
nueva condición dada en el presente. En el campo de la ingeniería,
específicamente la Ingeniería Civil, esta herramienta de análisis tiene una gran
aplicabilidad ya sea en el área de estructuras, geotecnia, hidrología e hidráulica,
etc.
En lo que tiene que ver con el área de interés de esta investigación (hidrología e
hidráulica), el uso de redes neuronales artificiales son de gran ayuda en los
procesos de estimación o tránsito de caudales en una cuenca dada, pues como
es sabido, a pesar de la existencia de diversos métodos para la estimación de
caudales, la determinación de los parámetros requeridos por dichos métodos
algunas veces se basa en la subjetividad del diseñador y en la experiencia que
este ha adquirido a lo largo de su vida profesional. La metodología empleada
para transformar la precipitación en escorrentía o caudal, se basa en etapas o
niveles; el primero lo constituye la obtención de los datos de precipitación
mediante registros históricos en la zona de interés, definidos como datos de
entrada, el segundo nivel lo define la función de transferencia utilizada o etapa

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
2
donde se desarrollan los procesos matemáticos que toman los datos de entrada
y mediante una secuencia de cálculos proporciona los datos de salida (nivel 3).
La selección de una adecuada función de transferencia brinda resultados de
mayor confianza mientras que con un método de menor soporte técnico y/o
científico ocurre lo opuesto.
Debido a los inconvenientes mencionados la utilización de redes neuronales en
la resolución de problemas en el campo de los hidrosistemas se abre paso
como una opción o método alterno a los tradicionalmente empleados, pues su
concepción o estructura puede ser sujeta a entrenamiento y así ser capaz de
relacionar información histórica que servirá de base para adaptarla y obtener un
resultado de mayor certeza en el problema que se esté considerando,
posicionándolas como una alternativa de alto valor. Las redes neuronales
artificiales utilizan una gran cantidad de información del hidrosistema en
estudio, al igual que una variedad de parámetros para un eficiente proceso de
cálculo, lo que es de gran ayuda cuando no es posible el uso de modelos físicos
o cuando la información de trabajo es poca; en algunos casos estas pueden
servir de complemento a la información existente. El mecanismo de solución o
algoritmo de trabajo, es una secuencia que se va modificando y adaptando
paso a paso hasta que la solución obtenida con la red neuronal sea lo más
cercana a la solución esperada.
“Las redes neuronales artificiales –RNA– intentan ser una emulación inteligente
del comportamiento de los sistemas biológicos, en donde los sistemas
nerviosos se basan en la neurona como elemento fundamental. Actualmente,
una RNA puede ser considerada como un modelo de “caja negra”, es decir, un
modelo en donde se tiene certeza de que es lo que se hace pero sin dar
importancia a como lo hace. Entre las principales características de una RNA,
cabe destacar que es un modelo con múltiples parámetros, capaz de reproducir
complejas relaciones no lineales, cuyo proceso de calibración (entrenamiento)
requiere de gran cantidad de información.” (OBREGÓN, FRAGALA, & PRADA).
Algunas características para considerar una red neuronal como óptima son:
-
Menos problemas de convergencia en el proceso de entrenamiento.
-
Menor número de parámetros a ajustar.
-
Menor número de ciclos de entrenamiento.
-
Mejor respuesta en situaciones extremas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
3
“El aprendizaje en una red neuronal consiste en la determinación de los valores
precisos de los pesos para todas sus conexiones; con los pesos ajustados la
red podría modelar de forma acertada y eficiente un problema específico. El
proceso general de aprendizaje consiste en ir agregando paulatinamente todos
los ejemplos del conjunto de aprendizaje y modificar los pesos de las
conexiones siguiendo un determinado esquema o algoritmo de aprendizaje. Los
algoritmos que permiten refinar los pesos de la red, se basan por lo general en
rutinas de gradientes que intentan recorrer un espacio de solución de la forma
más eficiente para alcanzar el mínimo global en la superficie de la función de
error. Dentro de estos métodos son conocidos los algoritmos de
retropropagación, retropropagación con Momentum y los de búsqueda aleatoria.
El algoritmo de aprendizaje de una red neuronal artificial es lo que determina el
tipo de problemas que es capaz de resolver. La gran utilidad de las redes
neuronales se debe a que son sistemas de aprendizaje basados en ejemplos.”
(MORALES V., 2004).
El tránsito de crecientes es un procedimiento para determinar valores de caudal
y niveles en un tiempo determinado en una sección de un canal a partir de
hidrogramas de entrada conocidos. Como herramientas de cálculo se utilizan la
ecuación de continuidad y la ecuación de Momentum. El tránsito de crecientes
en canales se basa en que se utiliza una serie de secciones y con estas se
simula un canal de longitud “L”, esto se hace por la dificultad de obtener la
topología y/o topografía exacta del canal lo que indica que se tiene un
conocimiento muy limitado de este, pues es posible que entre secciones
simultáneas se presenten cambios abruptos de las condiciones topográficas e
hidráulicas. Adicional a la estimación del trazado del canal se debe tratar de
ajustar un coeficiente de rugosidad, que en este caso es el definido por la
ecuación de Manning (n de Manning), dicho coeficiente debe involucrar los
cambios de sección, de pendiente, de superficies y cualquier otra variable
desconocida entre dos secciones. Todo este procedimiento se considera
problemático debido a que la obtención en campo y la calibración de este valor
es muy complicada y costosa a la vez. El objetivo del tránsito de crecientes es
obtener un hidrograma aguas abajo del canal, dado un hidrograma de diseño
aguas arriba. El hidrograma de diseño representa la variación del caudal en una
sección determinada de un canal reflejando los efectos de la cuenca aportante
aguas arriba de la sección considerada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
4
Teniendo en cuenta lo anteriormente expuesto, el objetivo de la investigación se
basa en definir y entrenar una o varias redes neuronales mediante el uso de un
software apropiado –MATLAB
®
– con la cual sea posible realizar el tránsito de
crecientes a través de canales de aguas lluvias sin contar con las
características geométricas e hidráulicas de este o de contar con la totalidad de
parámetros hidráulicos, además de esto, analizar si la respuesta de las redes
neuronales artificiales –ANN– es sensible a cambios en la pendiente de fondo y
coeficiente de rugosidad de un canal determinado y estimar con buena
precisión la creciente de salida como método alterno de cálculo a los
tradicionalmente utilizados.
1.1 OBJETIVOS GENERALES
• Establecer el tipo de red neuronal y las características apropiadas de
esta –arquitectura de la red– para realizar el tránsito de crecientes a
través de canales de aguas lluvias con la ayuda del software MATLAB®.
• Realizar el Tránsito de crecientes a través de canales de aguas lluvia
utilizando Redes Neuronales artificiales y determinar las ventajas y
desventajas de este con relación a los métodos tradicionales.
1.2 OBJETIVOS ESPECIFICOS
• Recopilación de información sobre el uso de las redes neuronales
artificiales para el tránsito de crecientes tanto a nivel local como a nivel
global.
• Recopilación de información topográfica de canales para la simulación
del tránsito de una creciente con redes neuronales artificiales.
• Definir las formas de los hidrogramas de entrada para la simulación de
los casos de estudio con redes neuronales artificiales.
• Determinar el tipo de algoritmo de entrenamiento que se debe aplicar a
las redes neuronales a partir del Caso de Estudio 1.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
5
• Obtener una estimación del número de neuronas y/o capas ocultas
adecuadas para las redes neuronales a partir del Caso de Estudio 1.
• Definir la función de desempeño que mejor evalué el comportamiento de
los resultados obtenidos.
• Realizar el tránsito de una creciente con redes neuronales artificiales
para todos los casos de estudio analizados.
• Realizar para los casos de estudio un análisis de costos y tiempo entre el
tránsito de una creciente con redes neuronales artificiales y el tránsito
con un método tradicional.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
6
2. CONTEXTUALIZACIÓN Y MARCO TEÓRICO
2.1 REDES NEURONALES – MODELO BIOLOGICO
El cerebro está conformado por millones de elementos o unidades de
procesamiento básicas interconectadas entre sí; estas unidades se denominan
neuronas. En una neurona se pueden considerar tres partes básicas, el cuerpo
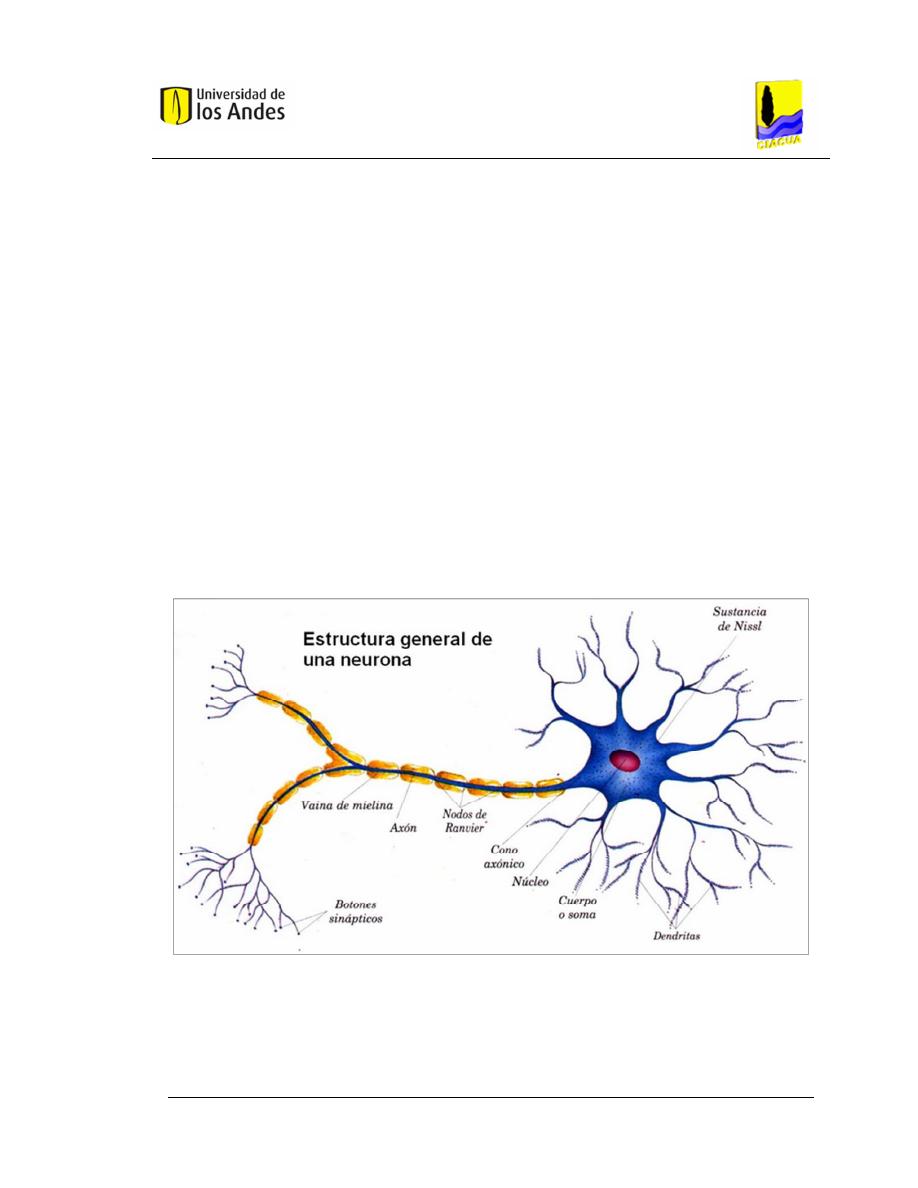
celular, del que se desprende una rama principal denominada axón y las
dendritas. La Figura 2.1 (www.histologiaub.blogspot.com) muestra las partes de
una neurona biológica, además de las principales ya mencionadas.
De forma general, el funcionamiento de una neurona inicia a través de las
dendritas, las cuales reciben señales de entrada y las conducen al cuerpo
celular que se encarga de combinarlas e integrarlas para posteriormente emitir
señales de salida. El axón transporta esas señales a los terminales axónicos, a
partir de los cuales la información pasa a otras neuronas. Por lo general, una
neurona recibe información de miles de otras neuronas, y a su vez envía
información a miles de neuronas más.
Figura 2.1. Esquema de una neurona biológica. Fuente: (www.histologiaub.blogspot.com).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
7
2.1.1 Naturaleza bioeléctrica de la neurona
Las señales que permiten la comunicación entre neuronas, son de dos tipos
distintos: eléctricas y químicas. La señal generada por la neurona y
transportada a lo largo del axón es un impulso eléctrico, mientras que la señal
que se transmite entre los terminales axónicos de una neurona y las dendritas
de las neuronas siguientes es de origen químico y se realiza mediante
moléculas de sustancias transmisoras (neurotransmisores) que fluyen a través
de unos contactos especiales, llamados sinapsis, que tienen la función de
receptor y están localizados entre los terminales axónicos y las dendritas de la
neurona siguiente. La generación de las señales eléctricas está íntimamente
relacionada con la composición de la membrana celular.
La llegada de señales procedentes de otras neuronas a través de las dendritas
actúa acumulativamente, bajando ligeramente el valor del potencial de reposo.
Dicho potencial modifica la permeabilidad de la membrana, de manera que
cuando llega a cierto valor crítico comienza una entrada masiva de iones sodio
que invierte la polaridad de la membrana. La inversión del voltaje de la cara
interior de la membrana cierra el paso a los iones sodio y abre el paso a los
iones potasio hasta que se restablece el equilibrio en reposo. Después de un
periodo refractario, puede seguir un segundo impulso. El resultado de esto es la
emisión por parte de la neurona de trenes de impulsos cuya frecuencia varía en
función de la cantidad de neurotransmisores recibidos (HILERA & MARTÍNEZ,
2000).
2.1.2 Sinapsis
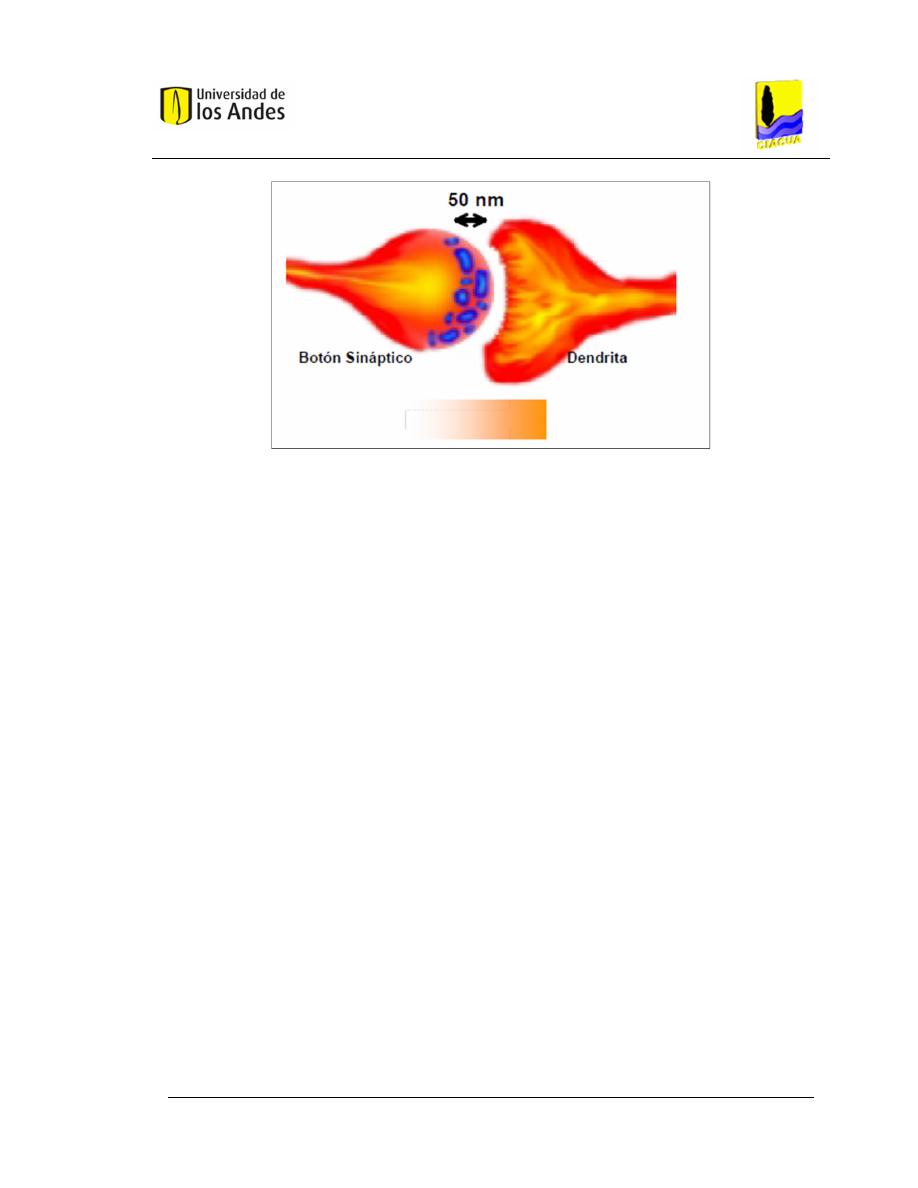
La interconexión entre dos neuronas se denomina Sinapsis (véase Figura 2.2).
La sinapsis química es el tipo más común de interacción; en ésta una señal
eléctrica llega al botón sináptico o parte terminal de la neurona izquierda (véase
Figura 2.2) lo que origina que se liberen neurotransmisores, que son captados
por la dendrita de la neurona de la derecha lo que causa un pulso eléctrico
desde la neurona izquierda a la de la derecha. Según la cantidad de
neurotransmisor liberada el pulso se reforzará o debilitará entre una y otra
neurona, además de esto se debe tener en cuenta el hecho de que si la
sumatoria de las entradas captadas por todas las dendritas de la neurona
supera un determinado umbral, el pulso se transmite a lo largo del axón pero de
no ser así este no se transmitirá a la siguiente neurona.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
8
Figura 2.2. Salto sináptico. Fuente: (IZAURIETA & SAAVEDRA).
2.2 REDES NEURONALES ARTIFICIALES
Una red neuronal es un procesador paralelo de información que tiene una
inclinación natural a almacenar conocimiento experimental y tenerlo a
disposición en cualquier momento para su uso. Por otro lado, también se puede
decir que, las redes neuronales artificiales son dispositivos de procesamiento de
información no lineal (señales), construidos a partir de dispositivos elementales
de procesamiento interconectados, llamados neuronas; el tipo más común de
neurona artificial es la de McCulloch-Pitts. Una red neuronal artificial (RNA) o
ANN por las siglas en inglés de “artificial neural network”, es un instrumento de
procesamiento de información inspirado en la forma como el cerebro procesa la
información. Tal como ocurre en el cerebro de las personas o animales, las
redes neuronales logran el aprendizaje a partir de ejemplos o mediante la
repetición de un proceso; estas son configuradas para una aplicación
específica, por ejemplo, reconocimiento de patrones, clasificación de
información, funciones de ajuste o predicciones de series de tiempo dinámicas.
El aprendizaje en sistemas biológicos involucra ajustes en las conexiones
sinápticas que existen entre las neuronas. Este también es el caso de las redes
neuronales artificiales pero aquí el ajuste se da en los pesos sinápticos de las
conexiones entre una y otra neurona, dichas conexiones son utilizadas para
almacenar el conocimiento adquirido por la red. Algunas características para
determinar una RNA son:
• Arquitectura (conexión entre neuronas).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
9
• Tipo de entrenamiento o aprendizaje (determinación del peso de las
conexiones).
• Función de activación.
Las redes neuronales pueden ser definidas a nivel general como un algoritmo
computacional parametrizado no lineal para procesamiento (numérico) de
datos, señales o imágenes. En consecuencia las RNA son un sistema de
procesamiento de información en donde las señales son transmitidas por medio
de enlaces; estos poseen un peso asociado el cual es multiplicado por la señal
de entrada para cualquier red neuronal típica. La señal de salida se obtiene
aplicando una función de activación a la entrada de la red.
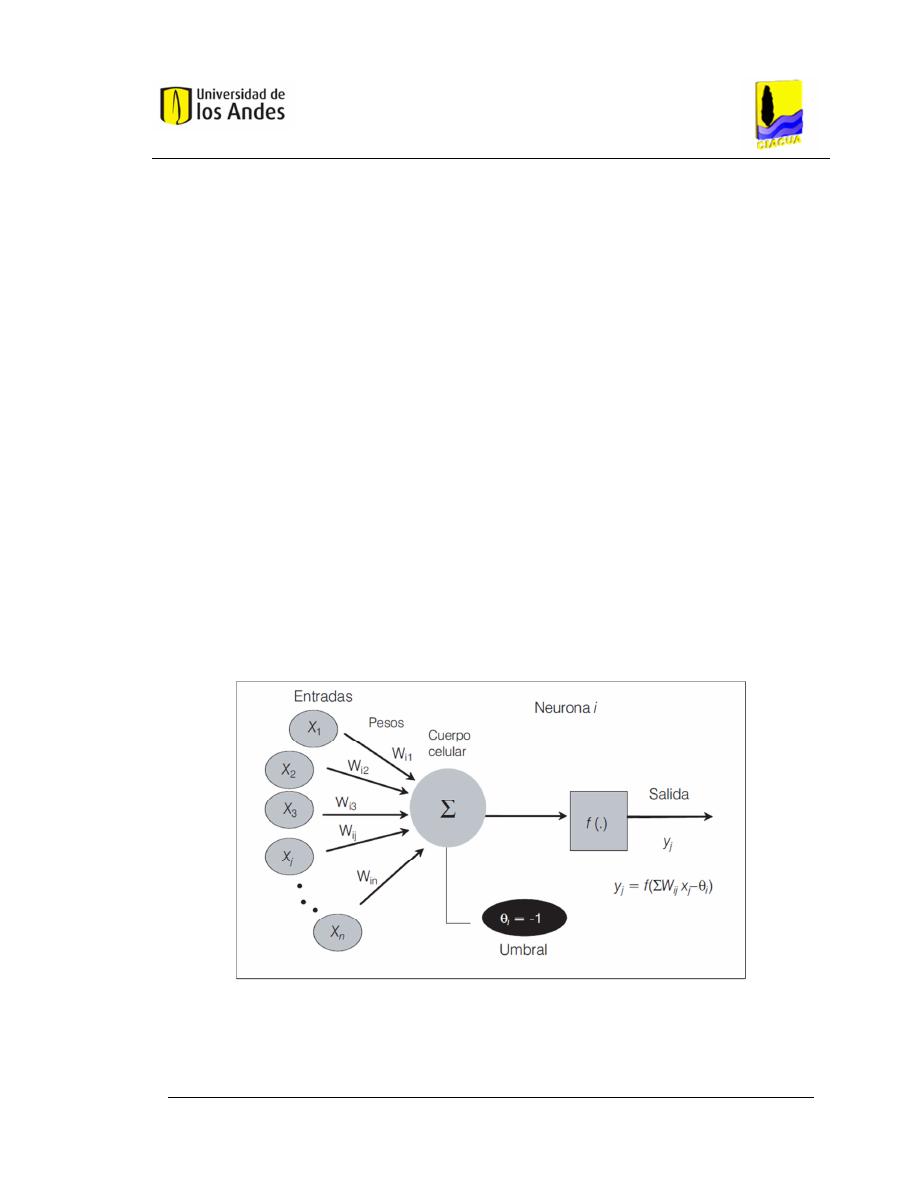
La Figura 2.3 muestra una ANN donde se indican cada uno de los parámetros
enunciados anteriormente. En esta se tienen un número n de neuronas de
entrada (x
1
, x
2
,…, x
n
) y una neurona de salida (y
j
), los pesos interconectados
están dados por w
i1
a w
in
. En la Figura 2.3 varias entradas a la red son
representadas por el símbolo matemático x
n
y cada una de estas entradas es
multiplicada por el peso respectivo de su conexión, w
in
. En el caso más simple,
este producto simplemente se suma a través de una función de transferencia
(véase Numeral 2.5) y se genera así la salida y
j
tal como se muestra en la
figura.
Figura 2.3. Red neuronal artificial simple. Fuente: (MOLINA AGUILAR & APARICIO, 2006).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
10
2.3 DESARROLLO HISTÓRICO DE LAS REDES NEURONALES
De acuerdo con la fecha de aparición o publicación de la contribución realizada
en este campo, el desarrollo histórico de las redes neuronales puede ser
trazado cronológicamente de la siguiente forma según (SIVANANDAM,
SUMATHI, & DEEPA, 2006).
• 1943 – McCulloch and Pitts: Inicio de la era moderna de las redes
neuronales.
Estos establecen un cálculo lógico para las redes neuronales. Una red
consta de un número suficiente de neuronas (usando un modelo simple),
y estas, conectadas adecuadamente pueden calcular cualquier función
computable. Una simple función lógica es desarrollada por una neurona,
en el caso de la neurona de McCulloch-Pitts basada en el ajuste de los
pesos de esta. El arreglo o disposición de neuronas en este caso puede
ser representado como una combinación de funciones lógicas. La
característica más importante de este tipo de neurona es el concepto de
umbral; cuando la entrada a una neurona particular es más grande que el
umbral especificado por el usuario entonces la neurona se activa.
Circuitos lógicos son creados para usar de forma extensa este tipo de
neurona.
• 1949 – El Libro de Hebb - “The organization of behavior”.
En este libro fue presentada por primera vez una declaración explícita de
una regla para el aprendizaje psicológico para modificación sináptica.
Hebb propuso que la conectividad del cerebro está cambiando
continuamente como un organismo que aprende diferentes tareas
funcionales, y que los montajes neuronales son creados por tales
cambios. El concepto detrás de la teoría de Hebb es que si dos neuronas
son creadas para ser activadas simultáneamente, la fuerza de conexión
entre las dos neuronas debería ser incrementada. Este concepto es
similar al del aprendizaje de la matriz de correlación.
• 1958 – Rosenblatt introduce el concepto de Perceptrón.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
11
En una red perceptrón los pesos de las rutas de conexión pueden ser
ajustados; un método iterativo para el ajuste de los pesos puede ser
utilizado. La red Perceptrón está creada para converger si los pesos
obtenidos le permiten reproducir exactamente todas las parejas de
vectores de entradas y objetivos de salida en el entrenamiento.
• 1960 – Widrow and Hoff introducen el término ADALINE.
ADALINE, es la abreviatura para adaptive linear neuron (Neurona Lineal
Adaptativa). Esta utiliza una regla de aprendizaje conocida como regla de
los mínimos cuadrados o regla delta, creada para ajustar los pesos así
como para reducir la diferencia entre la entrada a la red para la unidad de
salida y la salida deseada. El criterio de convergencia en este caso es la
reducción del valor del error cuadrado a un valor mínimo. Esta regla delta
para una red de una sola capa puede ser denominada como la
precursora de la red backpropagation utilizada para redes multicapas. La
extensión multicapa de Adaline formó la Madaline.
• 1982 – La red de John Hopfield.
Hopfield mostró cómo usar “Ising spin glass”, un tipo de modelo para
almacenar información en redes dinámicamente estables. Su trabajo
forjó el camino a los físicos para introducirse a la modelación neuronal y
de este modo transformar el campo de las redes neuronales. Hay redes
extensamente utilizadas como redes de memoria asociativa. Las redes
Hopfield son creadas para ser valoradas como continua y discreta a la
vez.
• 1972 – Mapas de autoorganización de Kohonen (Self-Organizing
Maps
- SOM).
Los mapas de auto-organización de Kohonen son capaces de reproducir
aspectos importantes de la estructura de una red neuronal biológica.
Ellos hacen uso de representación de datos utilizando mapas
topográficos, los cuales son comunes en los sistemas nerviosos. Los
SOM muestran como la capa de salida puede recuperar la estructura

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
12
correlacional (de la entrada) en forma del arreglo espacial de unidades.
Estas redes son aplicadas en muchos problemas de reconocimiento.
• 1985 – Parker, 1986 – Lecum.
Durante este periodo la red de retropropagación (backpropagation) forjó
su camino dentro de las redes neuronales. Este método reparte la
información de error en la unidad de salida de nuevo a las unidades
ocultas utilizando la regla delta generalizada. Esta red es básicamente
una red multicapa, feedforward (alimentación hacia adelante) entrenada
por medio del algoritmo backpropagation (retropropagación).
Originalmente, aunque el trabajo fue desarrollado por Parker (1985) el
crédito de publicar esta red es para Rumelhart, Hinton y Williams (1986).
La red de retropropagación (backpropagation) surgió como el más
popular algoritmo de aprendizaje para el entrenamiento de perceptrones
multicapa y ha sido el caballo de batalla para muchas aplicaciones de
redes neuronales.
• 1988 – Grossberg.
Grossberg desarrolló una regla de aprendizaje similar a la de Kohonen,
la cual es ampliamente utilizada en la red Counter propagation. Este tipo
de aprendizaje Grossberg, es también utilizado como aprendizaje outstar
y se produce para todas las unidades en una capa particular.
• 1987, 1990 – Carpenter y Grossberg.
Carpenter y Grossberg inventaron la teoría de resonancia adaptativa
(Adaptive Resonance Theory – ART). ART fue diseñada para entradas
binarias y para entradas continuas. El diseño para las entradas binarias
ART1 y ART2 entró en vigor cuando el diseño llegó a ser aplicable a las
entradas continuas. La característica más importante de estas redes es
que los patrones de entrada pueden ser presentados en cualquier orden.
• 1988 – Broomhead y Lowe desarrollaron las funciones de base
radial (Radial Basis Functions – RBF).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
13
Esta es una red multicapa similar a la red de retropropagación
(backpropagation).
• 1990 – Vapnik desarrollo la máquina de vector de soporte.
Las máquinas de vectores de soporte o SVM por las siglas en inglés de
“Support Vector Machine” se basan en minimizar el riesgo estructural, a
diferencia de las redes neuronales convencionales que utilizan el
principio de minimizar el riesgo empírico. El fundamento de esta teoría se
utiliza para aplicaciones como reconocimiento de imágenes y
categorización de textos.
2.4 VENTAJAS DE LAS REDES NEURONALES
Según (HILERA & MARTÍNEZ, 2000) algunas ventajas de utilizar redes
neuronales artificiales pueden ser:
“Debido a su constitución y fundamentos, las redes neuronales artifíciales
(RNA) ofrecen numerosas ventajas entre las que se incluyen:
• Aprendizaje adaptativo. Capacidad de aprender a realizar tareas
basadas en un entrenamiento o experiencia inicial.
• Autoorganización. Una red neuronal puede crear su propia organización
o representación de la información que recibe mediante una etapa de
aprendizaje.
• Tolerancia a fallos. El daño parcial de una red conduce a una
degradación de su estructura; sin embargo, algunas capacidades de la
red se pueden retener, incluso sufriendo un daño serio.
• Operación en tiempo real.
• Fácil inserción dentro de la tecnología existente.
2.4.1 Aprendizaje adaptativo
Esto consiste en aprender a llevar a cabo ciertas tareas mediante un
entrenamiento con ejemplos ilustrativos, por ello no es necesario elaborar
modelos a priori ni es necesario especificar funciones de distribución de
probabilidad.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
14
Una red neuronal puede generar su propia distribución de pesos en los enlaces,
esto mediante el aprendizaje; en éste, los enlaces ponderados de las neuronas
(pesos sinápticos) se ajustan de manera que se obtengan unos resultados
específicos. La función del diseñador es únicamente la obtención de la
arquitectura apropiada para la red sin considerar la forma como esta aprenderá
a discriminar, por lo que se deberá desarrollar un buen algoritmo de
aprendizaje.
2.4.2 Autoorganización
Las redes neuronales usan su capacidad de aprendizaje adaptativo para
autoorganizar la información que reciben durante el aprendizaje y/o la
operación. Mientras que el aprendizaje es la modificación de cada elemento
procesal, la autoorganización consiste en la modificación de la red neuronal
completa para llevar a cabo un objetivo específico. Esta autoorganización
provoca la generalización, la cual es una facultad de las redes neuronales de
responder apropiadamente cuando se les presentan datos o situaciones a las
que no habían sido expuestas anteriormente. Esta característica es muy
importante cuando se tienen que solucionar problemas en los cuales la
información de entrada es poco clara, ya que permite que el sistema de una
solución incluso cuando la información de entrada está incompleta.
2.4.3 Tolerancia a fallos
Las redes neuronales son los primeros métodos computacionales con la
capacidad inherente de tolerancia a fallos. En las redes neuronales, si se
produce un fallo en un pequeño número de neuronas, aunque el
comportamiento del sistema se ve influenciado este no sufre una falla repentina.
Hay dos aspectos distintos respecto a la tolerancia a fallos:
• Tolerancia a fallo según los datos; las redes pueden aprender a
reconocer patrones con ruido, distorsionados o incompletos.
• Pueden seguir realizando su función aunque se destruya parte de la red.
La razón por la que las redes neuronales son tolerantes a los fallos es que
tienen su información distribuida en las conexiones entre neuronas, existiendo
cierto grado de redundancia en este tipo de almacenamiento. La mayoría de los
ordenadores algorítmicos y sistemas de recuperación de datos almacenan cada
pieza de información en un espacio único, localizado y direccionable. Las redes
neuronales almacenan información no localizada, por lo tanto, la mayoría de las

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
15
interconexiones entre los nodos de la red tendrán unos valores en función de
los estímulos recibidos, y se generará un patrón de salida que represente la
información almacenada.
2.4.4 Operación en tiempo real
Una de las mayores prioridades de la mayoría de las áreas de aplicación es la
necesidad de realizar grandes procesos con datos de forma muy rápida. Las
redes neuronales se adaptan bien a esto debido a su implementación paralela.
Para que la mayoría de las redes puedan operar en un entorno de tiempo real,
la necesidad de cambio en los pesos de las conexiones o entrenamiento es
mínima. Por tanto, de todos los métodos posibles, las redes neuronales son la
mejor alternativa para reconocimiento y clasificación de patrones en tiempo real.
2.4.5 Fácil inserción dentro de la tecnología existente
Una red individual puede ser entrenada para desarrollar una única y bien
definida tarea. Debido a que una red puede ser rápidamente entrenada,
comprobada, verificada y trasladada a un hardware de bajo costo, es fácil
insertar redes neuronales para aplicaciones específicas dentro de sistemas
existentes. De esta manera, las redes neuronales se pueden utilizar para
mejorar sistemas de forma incremental, y cada paso puede ser evaluado antes
de acometer un desarrollo más amplio”.
2.5 ELEMENTOS DE UNA RED NEURONAL ARTIFICIAL
Una correcta elección de las características y una adecuada estructura son los
pilares fundamentales para construir una red neuronal que le dé solución al
problema que se quiere resolver. Cualquier modelo de red neuronal está
conformado por neuronas, a partir de las cuales se pueden generar
representaciones específicas como letras, números o cualquier otro objeto.
Cada neurona de una red está caracterizada en cualquier instante de tiempo
por un valor numérico denominado valor o estado de activación,
, al cual
está asociado una función de salida,
, que transforma el estado de activación
en ese instante en una señal de salida,
, la cual esta afecta por la sinapsis o
peso sináptico,
, de la conexión entre la neurona de entrada y la neurona de
salida. La sumatoria de las señales que llegan a una neurona j,
, se puede
expresar matemáticamente como lo indica la Ecuación 1.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
16
Ecuación 1.
Una función de activación, F, determina el nuevo estado de activación
1
de la neurona, teniendo en cuenta la entrada total calculada y el anterior estado
de activación
. Las variables anteriormente mencionadas se muestran
esquemáticamente en la Figura 2.3.
(HILERA & MARTÍNEZ, 2000), estructuran y definen los componentes más
importantes de una red neuronal artificial como sigue:
• Unidad de procesamiento (Neurona artificial)
• Estado de activación de cada neurona
• Conexiones entre neuronas
• Función de salida o transferencia
• Función o Regla de activación
• Regla de aprendizaje.
2.5.1 Unidades de Proceso - Neurona Artificial
El conjunto de neuronas cuyas entradas provienen de la misma fuente y cuyas
salidas se dirigen al mismo destino se conoce como capa o nivel. Si se tienen N
neuronas o unidades, estas se pueden ordenar arbitrariamente y designar la i-
ésima neurona como
. Su trabajo es simple y único, y consiste en recibir las
entradas de las células vecinas y calcular un valor de salida, el cual es enviado
a todas las células restantes.
En cualquier sistema modelado, se pueden caracterizar tres tipos de unidades o
capas: entradas, salidas y ocultas. Las unidades de entrada reciben señales
desde el entorno; dichas entradas pueden ser señales provenientes de
sensores o de otros sectores del sistema. Las unidades de salida son las
encargadas de enviar la señal fuera del sistema y las unidades ocultas son
aquellas cuyas entradas y salidas se encuentran dentro del sistema, es decir,
no tienen contacto con el exterior.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
17
2.5.2 Estado de Activación
Adicionalmente al conjunto de neuronas, la representación de la red neuronal
necesita los estados del sistema en un tiempo t. Esto se especifica por un
vector de N números reales
, que representan el estado de activación del
conjunto de unidades de procesamiento (Véase Ecuación 2). Cada elemento
del vector representa la activación de una neurona en el tiempo t. La activación
de una neurona
en el tiempo t se designa por
, es decir:
,
, … ,
, … ,
Ecuación 2.
Todas las neuronas que componen la red se hallan en cierto estado de
activación, este puede ser reposo o excitado y a cada uno de ellos se le asigna
un valor. Dichos valores de activación pueden ser continuos o discretos o
también limitados o ilimitados. Si son discretos suelen tomar valores pequeños
o binarios. El estado activo se caracteriza por la emisión de un impulso por
parte de la neurona, mientas que el estado pasivo indica que la neurona está en
reposo. Para determinar el estado de activación de una neurona se deben
considerar dos factores: el mecanismo de interacción entre neuronas y la señal
que envía cada una a las neuronas vecinas.
2.5.3 Conexiones entre neuronas
Las conexiones que unen a las neuronas que forman una RNA tienen asociado
un peso (w), que es el que hace que la red adquiera conocimiento.
Considerando
y
como el valor de salida de la neurona i en un instante dado y
que cada conexión (sinapsis) entre la neurona i y la neurona j está definida por
un peso
w
, se tiene que la entrada neta que recibe una neurona
Net
es la
suma del producto de cada señal individual por el valor de la sinapsis que
conecta ambas neuronas, esto se conoce como regla de propagación (Véase
Ecuación 3).
.
Ecuación 3.
Si
w
es positivo indica que la interacción entre las neuronas i y j es excitadora,
es decir, siempre que la neurona i este activada, la neurona j recibirá una señal

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
18
de i que tenderá a activarla. Si
w
es negativo, la sinapsis será inhibidora. En
este caso, si i esta activada, enviará una señal a j que tenderá a desactivarla.
Por último, si
w
es igual a 0, se considera que no hay conexión entre ambas.
2.5.4 Función de Salida o Transferencia
Entre las unidades o neuronas que forman una ANN existe un conjunto de
conexiones que unen unas a otras. Cada neurona transmite señales a aquellas
que están conectadas con su salida. Asociada con cada neurona
hay una
función de salida
, que transforma el estado actual de activación
en una señal de salida
(véase Ecuación 4).
"
Ecuación 4.
El vector que contiene las salidas de todas las neuronas en un instante t se
puede definir como lo muestra la Ecuación 5.
" #
$
%,
$
%, … ,
$
%, … ,
$
%&
Ecuación 5.
En algunos modelos, esta salida es igual al nivel de activación de la neurona,
en cuyo caso la función
es la función identidad,
. Existen
cuatro tipos de funciones de transferencia, aunque generalmente la función de
salida o de transferencia es de tipo sigmoidal.
-
Función escalón
-
Función lineal y mixta
-
Función sigmoidal
-
Función gaussiana
Función Escalón. Esta se utiliza cuando las salidas de la red son binarias. La
salida de una neurona se activa solo cuando el estado de activación es mayor o
igual a cierto valor umbral. La función escalón no puede definir la derivada en
un punto de transición, razón por la que esta no es muy útil a los métodos de
aprendizaje donde se utilizan derivadas. Las redes formadas por este tipo de
neuronas son fáciles de implementar en hardware (véase Figura 2.4).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
19
Figura 2.4. Función de Transferencia tipo escalón. Fuente: (IZAURIETA & SAAVEDRA).
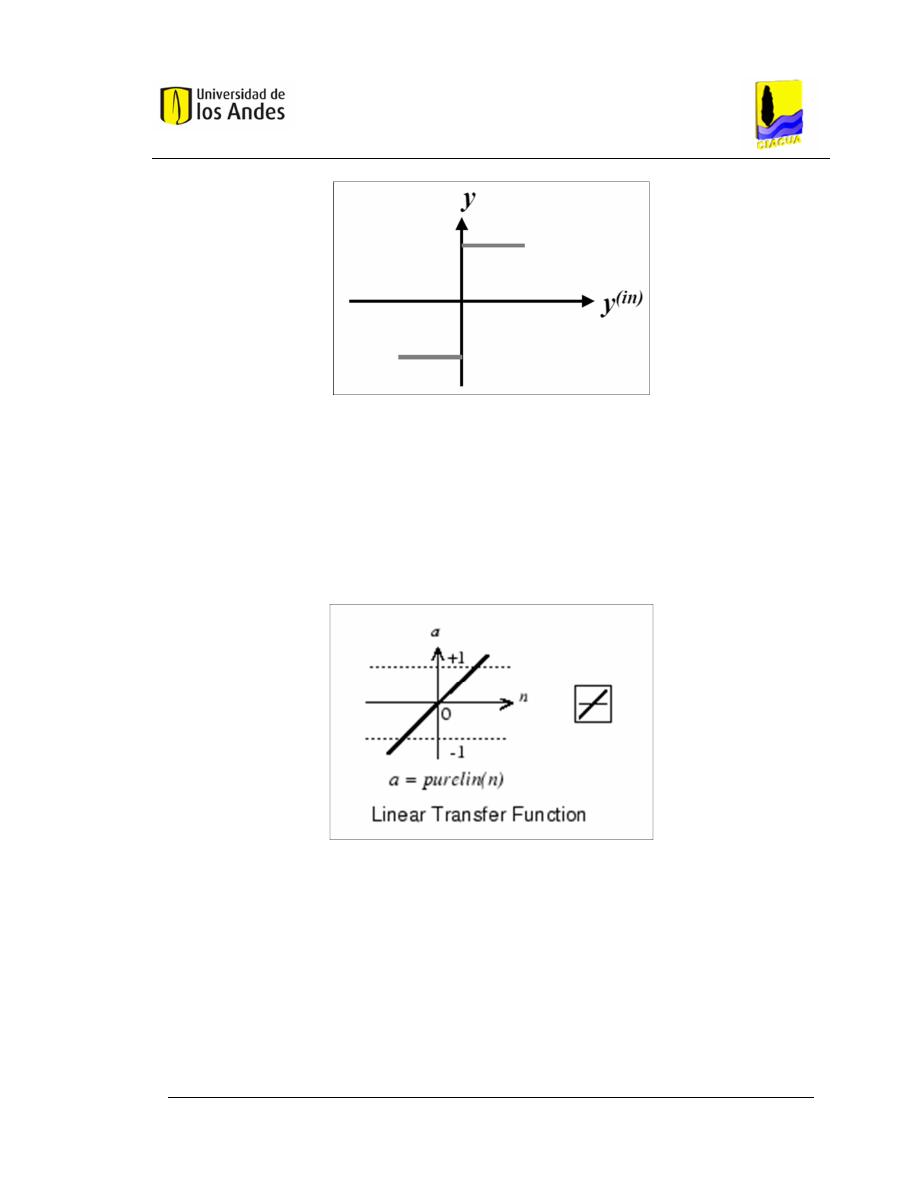
Función lineal y mixta. Esta responde a la expresión f(x)=x. En las neuronas
con función mixta, si la suma de las señales de entrada es menor a un límite
inferior, la activación se define como 0 o -1. Si dicha suma es mayor o igual que
el límite superior, entonces la activación es 1. Si la suma de las entradas está
comprendida entre ambos límites entonces la activación se define como una
función lineal de la suma de las señales de entrada (véase Figura 2.5).
Figura 2.5. Función de transferencia lineal (Fuente: Toolbox MATLAB
®
).
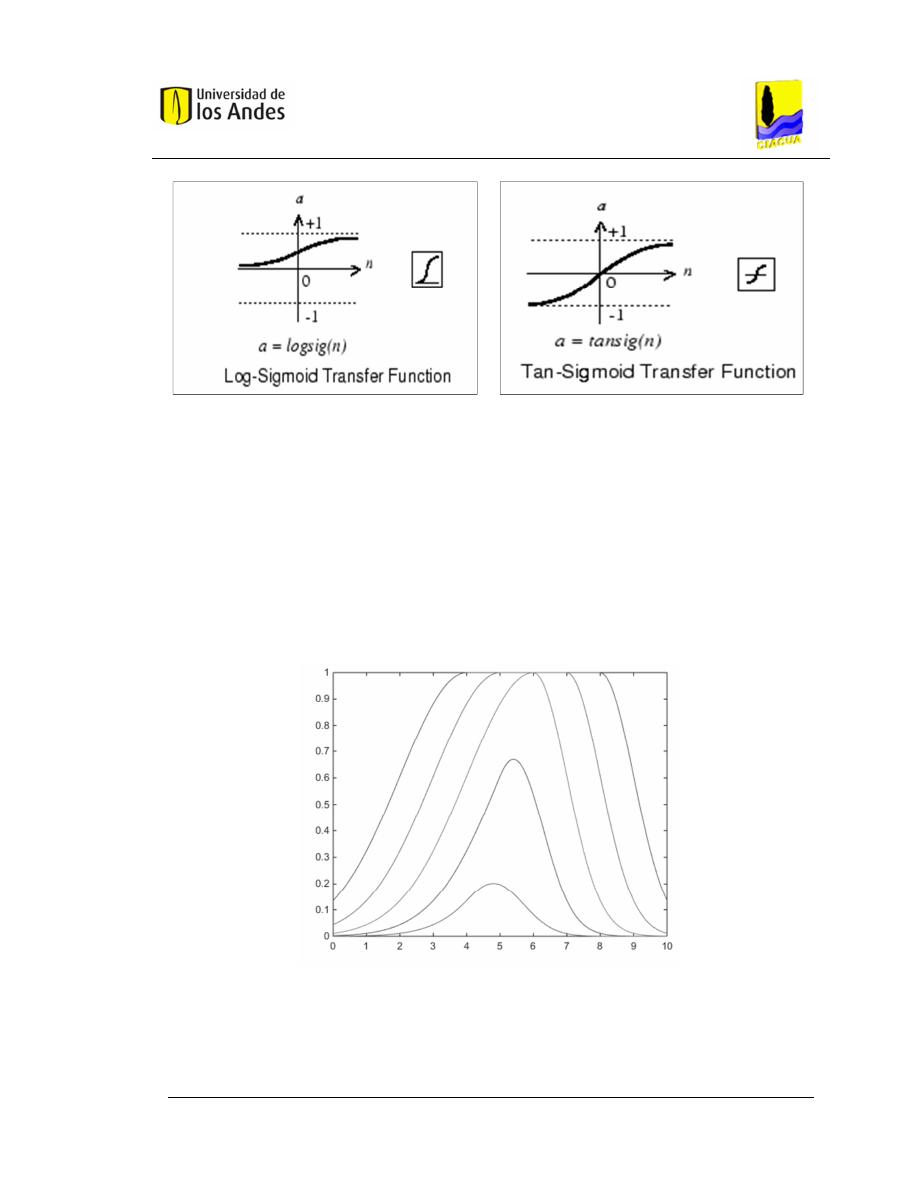
Función Continua o Sigmoidal. Con la función sigmoidal, para la mayoría de
los valores de entrada, el valor dado por la función es cercano a uno de los
valores asintóticos. Esto hace que en la mayoría de los casos, el valor de salida
esté comprendido en la zona alta o baja del sigmoide. Cuando la pendiente es
elevada esta función tiende a la función escalón. La importancia de la función
sigmoidal radica en el hecho de que su derivada es siempre positiva y cercana
a cero para valores grandes positivos o negativos y toma su valor máximo
cuando x es igual a 0 (véase Figura 2.6).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
20
Figura 2.6. Función de transferencia sigmoidal (Fuente: Toolbox MATLAB
®
).
Las funciones logsig y tansig calcula la salida de una capa a partir de su
entrada a la red y retorna elementos entre 0 y 1 y entre 1 y -1 respectivamente.
Función Gaussiana. Los centros y alto de estas funciones pueden ser
adaptados, lo cual las hace más adaptativas que las funciones sigmoidales.
Mapeos que suelen requerir dos capas ocultas utilizando la función sigmoidal,
algunas veces se pueden realizar con una sola capa en redes con neuronas de
función gaussiana (véase Figura 2.7).
Figura 2.7. Función de transferencia Gaussiana (Fuente: Toolbox MATLAB
®
).
En la Tabla 2.1 se muestran las funciones de transferencia mencionadas, la
ecuación que la representa y el rango de valores de aplicación.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
21
Tabla 2.1 Funciones de transferencia y rango de aplicación. Fuente: (MOLINA AGUILAR &
APARICIO, 2006).
2.5.5 Función o Regla de Activación
Así como es necesaria una regla que combine las entradas a una neurona con
los pesos de las conexiones, también se requiere una regla que combine las
entradas con el estado actual de la neurona para producir un nuevo estado de
activación. Esta función que se podría denominar, F, produce un nuevo estado
de activación en una neurona a partir del estado
que existía y la combinación
de las entradas con los pesos de las conexiones (
). Dado el estado de
activación
de la unidad
y la entrada total que llega a ella,
, el estado
de activación siguiente,
1, se obtiene aplicando la llamada función de
activación, como se muestra en la Ecuación 6.
1 '
,
Ecuación 6.
En la mayoría de los casos, F es la función identidad, por lo que el estado de
activación de una neurona en t+1 coincidirá con el Net de la misma en t. En
este caso, el parámetro que se le pasa a la función de salida, f, de la neurona
será directamente el Net. La salida de una neurona i (
) se puede expresar
como lo indica la Ecuación 7.
1
(
.
)
Ecuación 7.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
22
Normalmente la función de activación no está centrada en el origen del eje que
representa el valor de la entrada neta, sino que existe cierto desplazamiento
debido a las características internas de la propia neurona lo cual no es igual en
todas. Este valor se denota como
*
, y representa el umbral de activación de la
neurona i. De acuerdo con lo anterior la salida de la neurona para esta situación
se puede reescribir como lo indica la Ecuación 8.
1
+ *
(
.
+ *
)
Ecuación 8.
La salida que se obtiene en una neurona considerando el tipo de función de
activación utilizada puede tomar múltiples valores como se muestra a
continuación para cada una de las funciones de activación.
• Función de activación tipo escalón. Si el conjunto de los estados de
activación es E = [0, 1], se tiene que la salida para un tiempo t+1 puede
ser:
1 ,
1 -. /
0 *
1
-. /
*
1
0 -. /
3 *
1
,
Si el conjunto de los estados de activación es E = [-1, 1], se tiene que:
1 ,
1 -. /
0 *
1
-. /
*
1
+1 -. /
3 *
1
,
• Función de activación lineal o identidad. En esta el conjunto de
estados E puede contener cualquier número real (véase Ecuación 9).
1
+ *
Ecuación 9.
• Función de activación lineal-mixta. Con esta función, el estado de
activación de la neurona está obligado a permanecer dentro de un
intervalo de valores reales prefijados como se muestra a continuación:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
23
1 4
5
6 5 *
+ *
5 *
3
3 7 *
7
8 7
4
• Función de activación sigmoidal. Esta es una función continua, por lo
que el espacio de los estados de activación es un intervalo del eje central
(véase Ecuación 10).
1
1
1
9:;
<
9 =
<
Ecuación 10.
Para simplificar la expresión de la salida de una neurona se puede considerar
una neurona ficticia con valor de salida 1 y peso
+ *
para la conexión con la
neurona de entrada. De acuerdo con esta premisa la salida se puede expresar
como lo indica la Ecuación 11.
1 (
.
+ *
∗ 1) ?
.
@
A
Ecuación 11.
2.5.6 Regla de Aprendizaje
El aprendizaje se puede definir como la modificación del comportamiento
inducido por la interacción con el entorno y como resultado de la experiencia
conducente al establecimiento de nuevos modelos de respuesta a estímulos
externos. Cada modelo de red neuronal dispone de una o varias técnicas de
aprendizaje y este depende del número de neuronas y de cómo estén
conectadas entre sí.
2.6 CARACTERÍSTICAS DE LAS REDES NEURONALES
Según (HILERA & MARTÍNEZ, 2000), existen tres aspectos que caracterizan
una red neuronal, estos son:
• La topología
• El mecanismo de aprendizaje
• Tipo de asociación realizada entre la información de entrada y salida

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
24
2.6.1 Topología de la Red Neuronal
Esta se refiere a la organización y disposición de las neuronas en la red
formando capas. Los parámetros fundamentales de la red son: el número de
capas, el número de neuronas por capa, el grado de conectividad y el tipo de
conexión entre neuronas. Según la topología se pueden tener redes de una
capa o monocapa y redes con múltiples capas o multicapas.
Las redes monocapa se utilizan generalmente para obtener o completar
información cuando esta se tiene incompleta o distorsionada. Las redes
multicapa son aquellas que disponen de conjuntos de neuronas agrupados en
varios niveles o capas. Estas redes pueden ser de los siguientes tipos:
• Feedforward o con conexiones hacia adelante. Las redes más conocidas
de este tipo son: Perceptrón, Adaline. Madaline, Linear Adaptative
Memory (LAM), Drive_Reinforcement, Backpropagation. Todas estas son
muy útiles en aplicaciones de reconocimiento o clasificación de parones.
• Feedback o con conexión hacia atrás.
• Además de estas dos también se tienen redes que disponen de
conexiones tanto hacia adelante como hacia atrás o redes
feedforward/feedback. Los modelos más conocidos de este tipo son: La
red ART (Adaptative Resonance Theory) y la red BAM (Bidirectional
Associative Memory). Dentro de este grupo se pueden incluir la red
Neocognitron en la que las neuronas se disponen en planos
superpuestos y la red CABAM (Competitive Adaptative Bidirectional
Associative Memory) que es un tipo de red con conexiones laterales
entre neuronas de la misma capa.
2.6.2 Mecanismo de Aprendizaje
Este es el proceso por el cual una red neuronal modifica sus pesos en
respuesta a la información de entrada. En un modelo de red neuronal artificial,
la creación de una nueva conexión implica que el peso de esta pasa a tener un
valor distinto de cero, en caso contrario la conexión se destruye. Durante el
proceso de aprendizaje, los pesos de las conexiones de la red sufren
modificaciones; bajo esta premisa cuando los pesos permanecen estables entre
iteraciones sucesivas se puede afirmar que el proceso ha terminado o que la
red ha aprendido.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
25
Considerando la presencia o no de un agente externo que controle el proceso
de aprendizaje, las redes neuronales se pueden clasificar como:
• Redes con aprendizaje supervisado
• Rede con aprendizaje no supervisado
• Redes con aprendizaje híbrido
• Redes con aprendizaje reforzado
Redes con aprendizaje supervisado. Se caracterizan por que el proceso de
aprendizaje se realiza mediante un entrenamiento controlado por un agente
externo que determina la respuesta que debería generar la red a partir de una
entrada determinada. Para este tipo de aprendizaje se consideran tres formas
de llevarlo a cabo:
-
Aprendizaje por corrección de error. Consiste en ajustar los pesos de las
conexiones de la red en función de la diferencia entre los valores
deseados y los valores obtenidos en la salida de la red. La Ecuación 12
ilustra este proceso:
∆
∝
$D
+
%
Ecuación 12.
siendo,
∆
= Variación en el peso de la conexión entre las neuronas i y j
$∆
EF;GEH
+
E;:IJI
%
= Valor de salida de la neurona i
D
= Valor de salida deseado para la neurona j
= Valor de salida obtenido en la neurona j
∝ = Factor de aprendizaje (0 < ∝ ≤ 1) que regula la velocidad con que
este se realiza.
Una limitación de este tipo de algoritmo es que no considera la magnitud
del error global cometido durante el proceso de aprendizaje, pues solo
tiene en cuenta el error individual. La regla de aprendizaje del perceptrón
es un ejemplo de este tipo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
26
Un algoritmo con mayor rango de aplicabilidad y mucho más rápido, es el
desarrollado por Widrof y Hoff, conocido como Regla Delta, en este se
considera el error global para así determinar la variación del peso. La
Ecuación 13 define la forma de cálculo del error global, mientras que la
Ecuación 14 muestra como calcular la variación en el peso de las
conexiones.
KLLML
NHJOEH
1
2Q
R
S
#
S
+ D
S
&
Ecuación 13.
siendo,
N = Numero de neuronas de salida
P = Numero de datos de la Información que debe aprender la red
∑ #
S
+ D
S
&
= Error cometido en el aprendizaje de la información
k-ésima.
∆
U
V KLLML
NHJOEH
V
Ecuación 14.
Aplicando la Ecuación 13 y la Ecuación 14 se obtiene un conjunto de
pesos con los que se consigue minimizar el error. El algoritmo de la
Regla Delta Generalizada, es una modificación de este para poderlo
aplicar a redes con capas de entrada, oculta y de salida.
-
Aprendizaje por refuerzo. Este es más lento que el aprendizaje por
corrección de errores, y se basa en la idea de no disponer de un ejemplo
completo del comportamiento deseado, es decir, de no indicar durante el
entrenamiento exactamente la salida que se desea que proporcione la
red ante una determinada entrada. Ejemplos de este tipo de algoritmos
son el denominado Linear Reward Penalty o Lr-p (Algoritmo lineal con
recompensa y penalización) y el conocido como Adaptive Heuristic Critic,
que se utiliza en redes feedforward de tres capas especialmente
diseñadas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
27
-
Aprendizaje estocástico. Este consiste en realizar cambios aleatorios en
los valores de los pesos de las conexiones de la red y evaluar su efecto a
partir del objetivo deseado y de distribuciones de probabilidad. La red
conocida como Boltzmann Machine utiliza este tipo de aprendizaje y lo
combina con el aprendizaje Hebbiano o con el aprendizaje por corrección
de error. El procedimiento de utilizar ruido y combinarlo con asignación
probabilística mediante capas ocultas, es lo que se conoce como
aprendizaje estocástico.
Redes con aprendizaje no supervisado. Estas no reciben ninguna
información por parte del entorno que le indique si la salida generada en
respuesta a una determinada entrada es o no correcta, por lo que se dice que
este tipo de redes se pueden autoorganizar. En cuanto a los algoritmos de
aprendizaje no supervisado, en general se suelen considerar dos tipos, los
cuales dan lugar a los siguientes aprendizajes: el aprendizaje Hebbiano y el
aprendizaje competitivo o cooperativo.
-
Aprendizaje Hebbiano. El aprendizaje Hebbiano consiste básicamente en
el ajuste de los pesos de las conexiones de acuerdo con la correlación
de los valores de activación (Salidas) de las dos neuronas conectadas,
como se muestra en la Ecuación 15.
∆
.
Ecuación 15.
De la Ecuación 15, se tiene que si las dos unidades son activas
(Positivas), se produce un reforzamiento de la conexión, pero cuando
una es activa y la otra pasiva (Negativa), se produce un debilitamiento de
la conexión.
-
Aprendizaje competitivo y cooperativo; este suele orientarse hacia la
clasificación de los datos de entrada. Con este tipo de aprendizaje se
pretende que cuando se presente a la red cierta información de entrada,
solo una de las neuronas de salida de la red, o una por cierto grupo de
neuronas, se active. En este tipo de redes, cada neurona tiene asignado
un peso total, que equivale a la suma de todos los pesos de las
conexiones que tiene a su entrada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
28
Redes con aprendizaje híbrido. Para este tipo de aprendizaje unas capas de
la red tienen un aprendizaje supervisado y otras capas de la red tienen un
aprendizaje no supervisado.
Redes con aprendizaje forzado. Es un aprendizaje con características del
supervisado y con características del autoorganizado, diferenciándose del
híbrido en que en este solo se proporciona un porcentaje de error que debe
cumplirse al no indicarle la salida deseada.
2.6.3 Tipo de asociación entre la información de entrada y salida
Existen dos formas primarias de realizar la asociación entre la información de
entrada y salida según la naturaleza de la información almacenada en la red.
La primera se denomina heteroasociación, que se refiere al caso en el que la
red aprende parejas de datos (A
1
, B
1
), (A
2
, B
2
)… (A
n
, B
n
), de tal forma que
cuando se presenta cierta información de entrada A
i
, deberá responder
generando la correspondiente salida asociada B
i
. En cuanto a su conectividad,
existen redes heteroasociativas con conexiones hacia adelante o feedforward,
redes con conexión hacia atrás feedforward/feedback, redes con conexiones
laterales y redes con capas multidimensionales como la Neocognitron. El
aprendizaje de este tipo de red puede ser con supervisión o sin supervisión.
La segunda forma se conoce como autoasociación, donde la red aprende cierta
información A
1
, A
2
,…, A
n
, de tal forma que cuando se le presenta una
información de entrada realizara una autocorrelación, respondiendo con uno de
los datos almacenados más parecido al de entrada. Estas redes suelen
utilizarse en tareas de filtrado de información para la reconstrucción de datos,
eliminando distorsiones o ruido; también se utilizan para facilitar la búsqueda
por contenido en bases de datos y para resolver problemas de optimización.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
29
3. MANEJO DE LA HERRAMIENTA DE SIMULACIÓN – MATLAB
®
En este capítulo se describe paso a paso la forma como se realiza el montaje y
simulación de una red neuronal artificial. La totalidad de la información aquí
resumida se extrajo de las ayudas y tutoriales proporcionados por el software
de diseño (MATLAB
®
) con la finalidad de que cualquiera pueda reproducir lo
aquí desarrollado.
En la actualidad existen diversos mecanismos y lenguajes de programación
para realzar el montaje y simulación de un determinado caso de estudio
utilizando redes neuronales artificiales (RNA). En esta investigación, se utilizará
la herramienta de redes neuronales artificiales que proporciona el software
MATLAB
®
en su versión R2012b, pues este presenta una interfaz de manejo de
fácil comprensión para el usuario y de interacción amigable.
El toolbox de redes neuronales artificiales en MATLAB
®
ofrece funciones y
aplicaciones para modelar complejos sistemas no lineales que no son fáciles de
representar con una ecuación; también permite realizar aprendizaje supervisado
con redes de alimentación hacia adelante (feedforward), redes de base radial
(radial basis), y redes dinámicas. Con las herramientas del toolbox se puede
diseñar, entrenar, visualizar y simular redes neuronales; además se puede
utilizar para aplicaciones tales como ajuste de datos, reconocimiento de
patrones, predicción de series de tiempo y modelado y control de sistemas
dinámicos.
3.1 USO DEL TOOLBOX EN MATLAB
®
Hay cuatro formas de utilizar el toolbox de redes neuronales artificiales ofrecido
por MATLAB
®
.
• La primera forma es a través de una de las cuatro interfaces gráficas de
usuario o GUI, por las siglas en inglés de Graphical User Interfaces.
También se pueden abrir estas GUIs desde una interfaz gráfica de
usuario principal, con el comando nnstart. Estas proporcionan una
manera rápida y fácil para acceder a los beneficios del toolbox para las
siguientes tareas:
-
Fitting function (Función de ajuste)
-
Pattern recognition (Reconocimiento de patrones)
-
Data clustering (Agrupación de datos)
-
Time series analysis (Análisis de series de tiempo)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
30
En la Figura 3.1 se muestra la forma como se presenta la interfaz gráfica para
esta versión del software, utilizando el comando nnstart.
Figura 3.1. Acceso principal a la herramienta de redes neuronales (Fuente: Toolbox MATLAB
®
).
En esta investigación para la simulación de las redes neuronales artificiales se
utilizará el análisis de series de tiempo dinámicas (Opción resaltada en color
azul); por esta razón se enfatizará solo en el montaje de las redes neuronales a
través de esta opción.
• La segunda manera de utilizar el toolbox es a través de las operaciones
básicas de la línea de comandos, estas ofrecen más flexibilidad que la
interfaz gráfica de usuario, pero con algo de complejidad añadida. La
GUI puede generar scripts de código MATLAB
®
para crear funciones
personalizadas.
• La tercera forma de utilizar el toolbox es a través de la personalización.
Esta capacidad permite crear redes neuronales propias, sin dejar de
tener acceso a todas las funciones del toolbox. Se puede crear además
redes con conexiones arbitrarias, y todavía será capaz de entrenarlas
utilizando las funciones de entrenamiento existentes en la herramienta.
• La cuarta forma de utilizar el toolbox es a través de la capacidad de
modificar cualquiera de las funciones contenidas en este. Cada
componente computacional es escrito en código MATLAB
®
y es
totalmente accesible.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
31
3.2 SERIES DE TIEMPO DINÁMICAS
Las redes neuronales dinámicas son buenas para la predicción de series de
tiempo. Como se mencionó anteriormente, este tipo de problemas se pueden
resolver de dos formas:
1. Utilizando la interfaz gráfica del usuario (GUI), con el comando ntstool,
la cual despliega la ventana mostrada en la Figura 3.1.
2. Utilizando las funciones de la línea de comando.
La guía de análisis ofrecida por MATLAB
®
sugiere que generalmente es mejor
empezar con la interfaz gráfica, y luego utilizar la GUI para generar
automáticamente scripts para la línea de comandos; este consejo se consideró
para el desarrollo y personalización de las RNA analizadas en la investigación.
3.2.1 Definición del problema
Para definir un problema de series de tiempo del toolbox, se debe organizar un
conjunto de vectores de entrada TS como columnas en una matriz de celdas. A
continuación, organizar otro conjunto de vectores objetivo TS (los vectores de
salida correctos para cada uno de los vectores de entrada) en una segunda
matriz de celdas. Sin embargo, hay casos en los que sólo se necesita un
conjunto de datos objetivo. La forma de organizar los datos es como sigue:
targets = {1 2 3 4 5};
3.2.2 Estructuras de datos
En esta se hace referencia a cómo el formato de la estructura de los datos de
entrada afecta la simulación de redes. Se inicia con redes estáticas, y luego se
continúa con redes dinámicas. Hay dos tipos básicos de vectores de entrada:
los que se producen simultáneamente (al mismo tiempo, o en ninguna
secuencia de tiempo particular), y los que se producen secuencialmente en el
tiempo. Para los vectores concurrentes, el orden no es importante, y si hay un
número de redes que funcionan en paralelo, se podría presentar un vector de
entrada para cada una de las redes. Para los vectores secuenciales, el orden
en que aparecen los vectores es importante.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
32
3.3 USO DE LA INTERFAZ GRÁFICA PARA SERIES DE TIEMPO
Este capítulo describe la secuencia de pasos seguida para el montaje de las
redes neuronales artificiales analizadas en esta etapa de la investigación,
comenzando por el uso de la interfaz gráfica (GUI) y luego realizando
modificaciones a cada script según el requerimiento del investigador.
1. Inicialmente se necesita desplegar la interfaz gráfica de redes neuronales
con el comando, nnstart, con lo cual se despliega la ventana mostrada
en la Figura 3.1.
2. Dando clic en la opción Time Series Tool se abre la ventana que muestra
la herramienta de redes neuronales para series de tiempo dinámicas
(Véase Figura 3.2).
Figura 3.2. Acceso a la herramienta de series de tiempo dinámicas (Fuente: Toolbox MATLAB
®
).
El panel abierto muestra que esta opción (ntstool) se puede utilizar para
resolver tres tipos de problemas de series de tiempo.
-
En el primer tipo de problema se quiere predecir los valores futuros de
una serie de tiempo
a partir de los valores pasados de la serie y
valores pasados de una segunda serie de tiempo
W. Esta forma de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
33
predicción se denomina autorregresiva no lineal con entrada exógena
(externa), o NARX, y se puede escribir como lo muestra la Ecuación 16.
+ 1, … , + D, W + 1, … , + D Ecuación 16.
Este modelo podría ser utilizado para predecir los valores futuros de una
acción de una compañía, basado en variables económicas como las
tasas de desempleo, PIB, etc.
-
En el segundo tipo de problema, hay solo una serie involucrada. Los
valores futuros de una serie de tiempo
son predichos solo desde
valores pasados de esa serie. Esta forma de predicción es llamada no
lineal autorregresiva, o NAR y puede ser escrita como lo muestra la
Ecuación 17.
+ 1, … , + D
Ecuación 17.
Este modelo también se podría utilizar para predecir instrumentos
financieros, pero sin el uso de una serie compañera.
-
El tercer problema de series de tiempo es similar al primero, en el que
dos series están involucradas, una serie de entrada
W y una serie de
salida/objetivo
. En esta se quiere predecir valores de a partir de
valores previos de
W, pero sin el conocimiento de valores previos de
. Este modelo entradas/salidas puede ser escrito como lo indica la
Ecuación 18.
W + 1, … , W + D
Ecuación 18.
En esta investigación se utilizará el modelo NARX ya que proporciona mejores
predicciones que los otros modelos modelo de entrada-salida, pues como se
mencionó, puede utilizar información adicional contenida en los valores
anteriores de
para obtener una mejor respuesta. Sin embargo, puede
haber algunas aplicaciones en las que los valores anteriores de
no estarían
disponibles. Esos son los únicos casos en los que se querría utilizar otro de
estos modelos en lugar del tipo NARX.
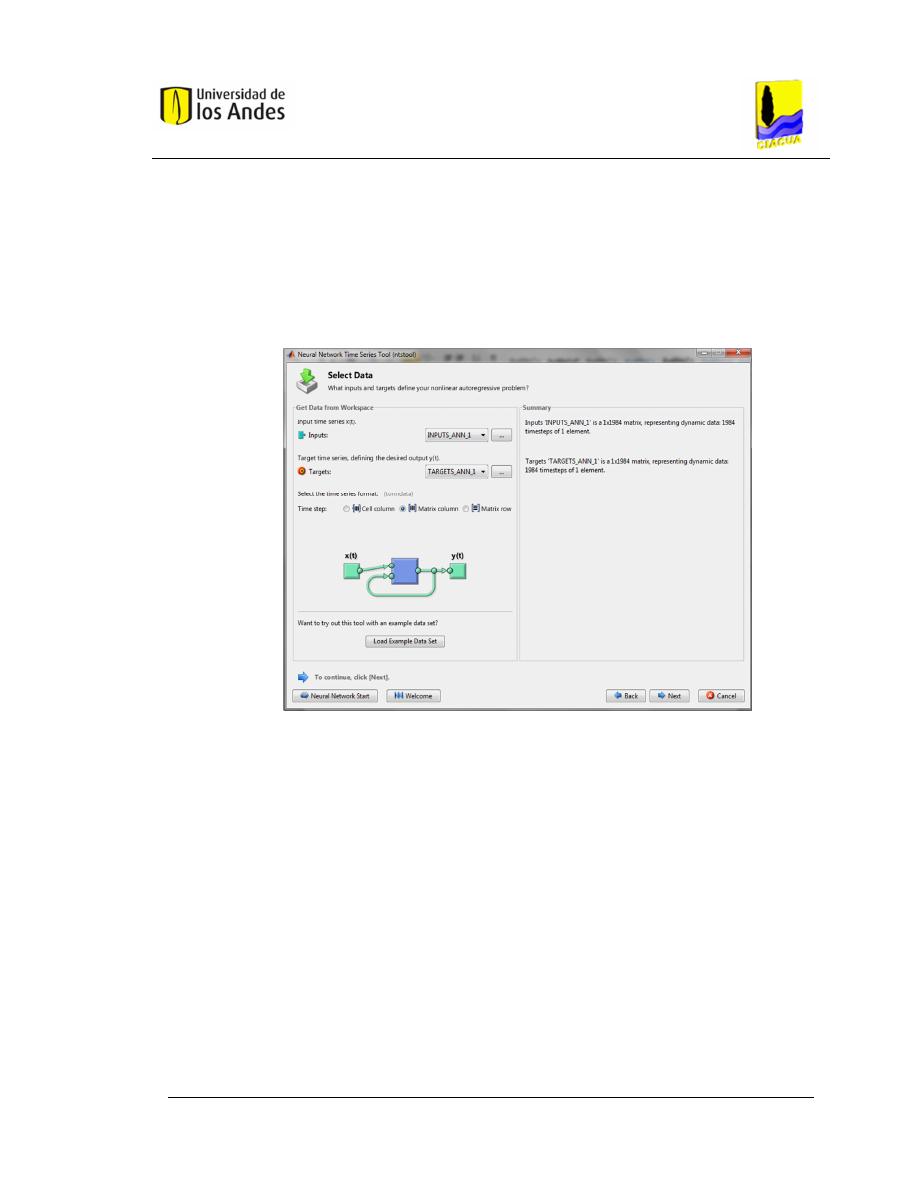
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
34
3. Para escoger el modelo tipo NARX se selecciona dicha opción, como lo
muestra la Figura 3.2, y se da clic en next para proceder. Luego de esto
se despliega la ventana donde se deberán cargar los datos de entrada
(Inputs) y los objetivos (Targets) de la red, además se debe escoger el
tipo de formato de la serie de tiempo, para este caso se selecciona
Matrix column (Véase Figura 3.3).
Figura 3.3. Panel para cargar datos y objetivos – Red tipo NARX (Fuente: Toolbox MATLAB
®
).
4. Después de cargar los datos de entradas y objetivos, se da clic en el
botón Next para abrir la ventana de validación y prueba de datos (Véase
Figura 3.4). En esta primera aproximación a través de la interfaz gráfica,
se observa que de manera predeterminada el porcentaje de datos para
entrenamiento (Training) es del 70%, mientas que un 15% será utilizado
para validar (Validation) que la red está generalizando y para detener el
entrenamiento cuando se detecte sobreentrenamiento y el restante 15%
será utilizado para una prueba completamente independiente de
generalización de la red (Testing).
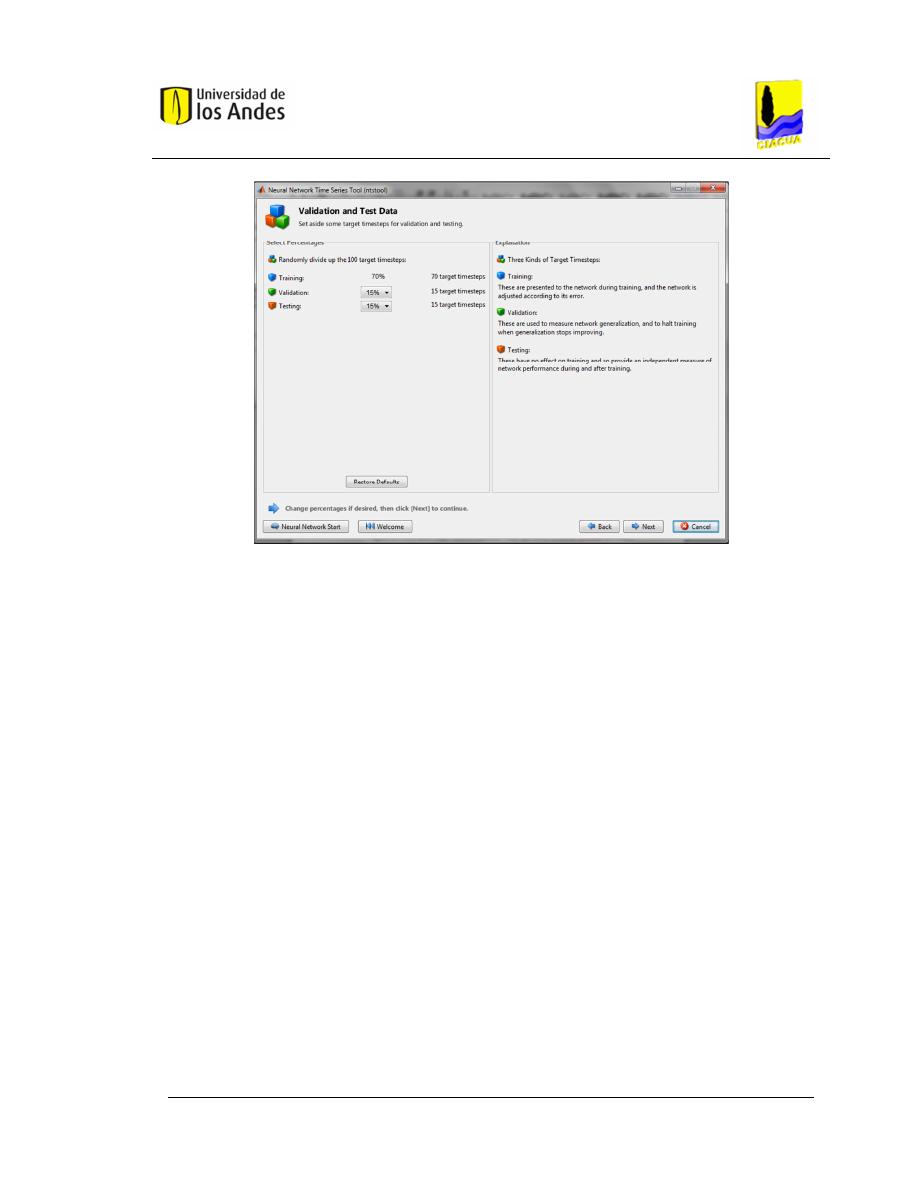
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
35
Figura 3.4. Panel para validación y prueba de datos (Fuente: Toolbox MATLAB
®
).
De acuerdo con la cantidad de datos cargados para la ejecución de la red
neuronal este porcentaje deberá o no ser ajustado. Para este caso se debió
ajustar cada uno de estos porcentajes con el objetivo de tener una adecuada
división de datos, dicho ajuste se realizará directamente en el script de la red
como se indica en el Numeral 3.4.
5. Dando clic en el botón Next, se despliega la ventana donde se muestra la
arquitectura predeterminada para la red tipo NARX; esta es una red
feedforward de dos capas, con una función de transferencia sigmoidal en
la capa oculta y una función de transferencia lineal en la capa de salida.
El número predeterminado de neuronas ocultas es 10 y el número
predeterminado de retrasos en 2 (Véase Figura 3.5). Si el desempeño
del entrenamiento de la red es deficiente, estos datos se podrán ajustar
en busca de una mejor respuesta.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
36
Figura 3.5. Panel para ajustar arquitectura de la red (Fuente: Toolbox MATLAB
®
).
Este tipo de red utiliza líneas de retardo para almacenar los valores
anteriores de las secuencias
W y . Nótese que la salida de la red
NARX,
, retroalimenta la entrada de la red (a través de los retrasos),
ya que
es una función de + 1, + 2, … , + D. Sin
embargo, para un entrenamiento eficiente se puede abrir este ciclo de
retroalimentación.
Debido a que la salida verdadera está disponible durante el entrenamiento de la
red, se puede utilizar la arquitectura de bucle abierto mostrada en la Figura 3.5,
en la que la salida real se utiliza en lugar de retroalimentar la salida estimada,
esto tiene dos ventajas. La primera es que la entrada a la red feedforward es
más precisa. La segunda es que la red resultante tiene una arquitectura
puramente feedforward, y por lo tanto un algoritmo más eficiente puede ser
utilizado para el entrenamiento.
6. Haciendo clic en el botón Next se despliega la ventana para
entrenamiento (Véase Figura 3.6). De forma predeterminada la red viene
ajustada con el algoritmo de entrenamiento de Levenberg-Marquardt
(trainlm) el cual puede ser modificado dependiendo de los
requerimientos del investigador. Para este caso de estudio se utilizó el
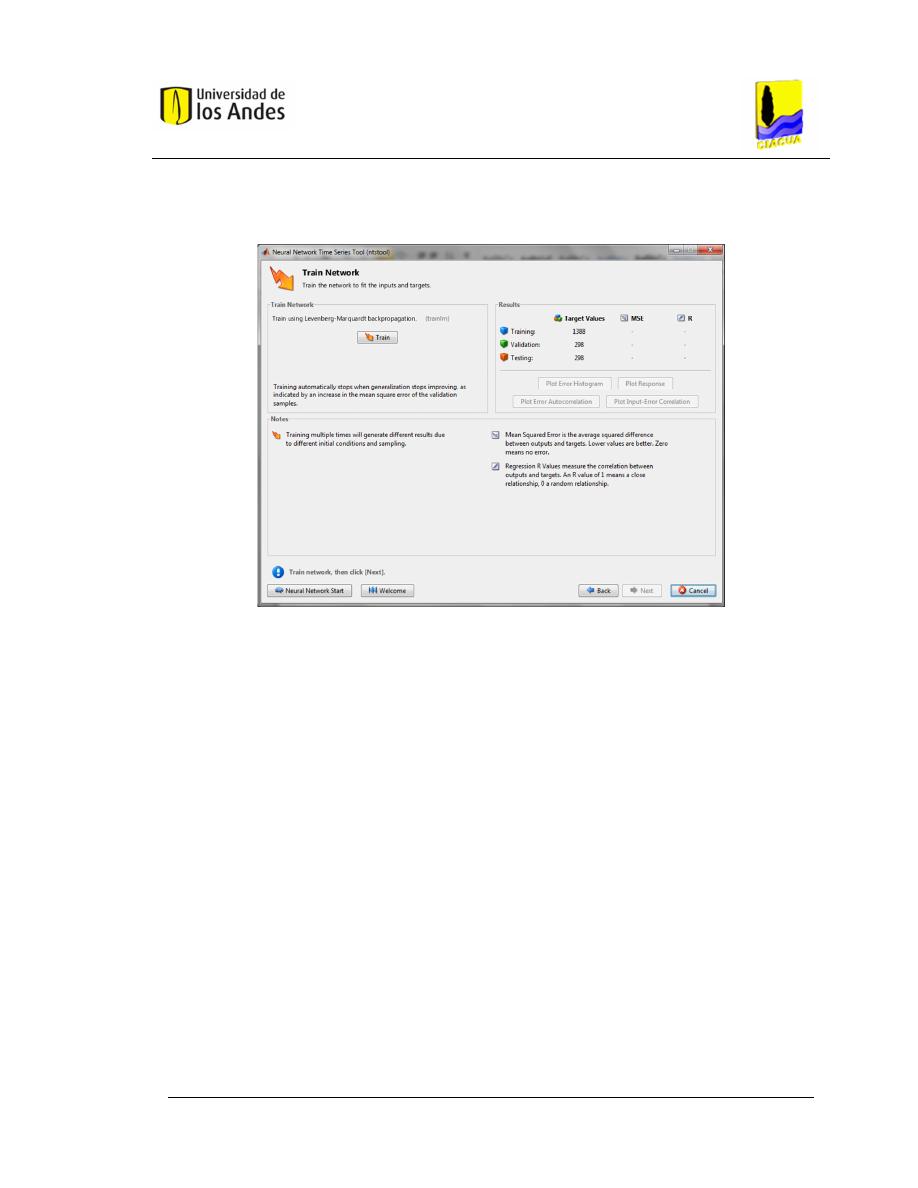
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
37
algoritmo de entrenamiento como una variable de diseño, por lo que se
debió variar el tipo de algoritmo utilizado.
Figura 3.6. Panel para entrenamiento de la red (Fuente: Toolbox MATLAB
®
).
7. Al hacer clic en la opción Train se inicia el entrenamiento de la red, el
cual continúa hasta que el error de validación no logra disminuir durante
seis iteraciones. Una vez finaliza el entrenamiento se despliega una
nueva ventana (Véase Figura 3.7), a través de la cual se puede observar
el comportamiento de variables como Performance, Training state, Error
histogram, Regression, Time-Series Respose, Error Autocorrelation e
Input-Error Cross-Correlation. Además se puede observar la arquitectura
utilizada para la red y otras variables de decisión.
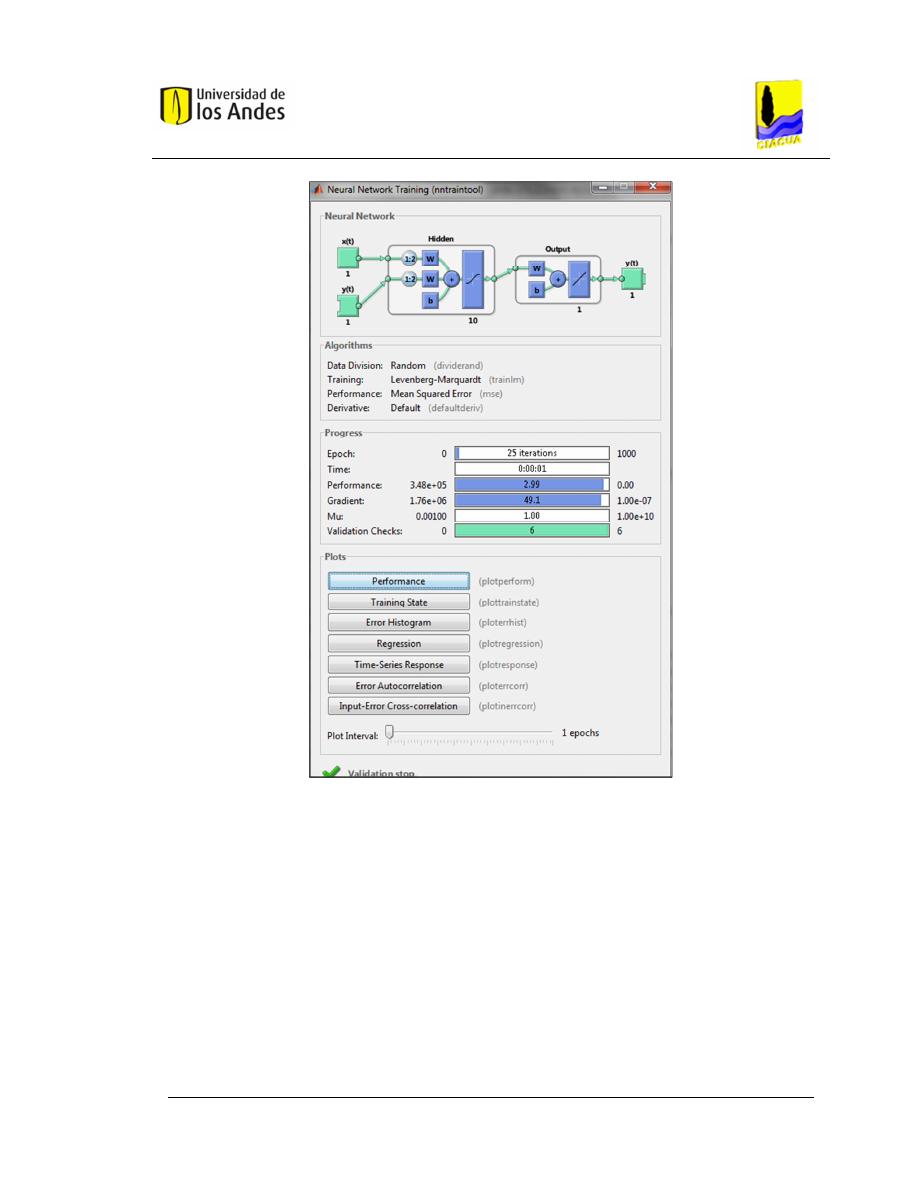
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
38
Figura 3.7. Variables de decisión e información del entrenamiento (Fuente: Toolbox MATLAB
®
).
8. En la parte baja del panel dando clic en la opción Time Series Respose,
se muestran los objetivos y errores versus tiempo. También indica que
puntos fueron seleccionados para entrenamiento, prueba y validación
(Véase Gráfica 3.1).
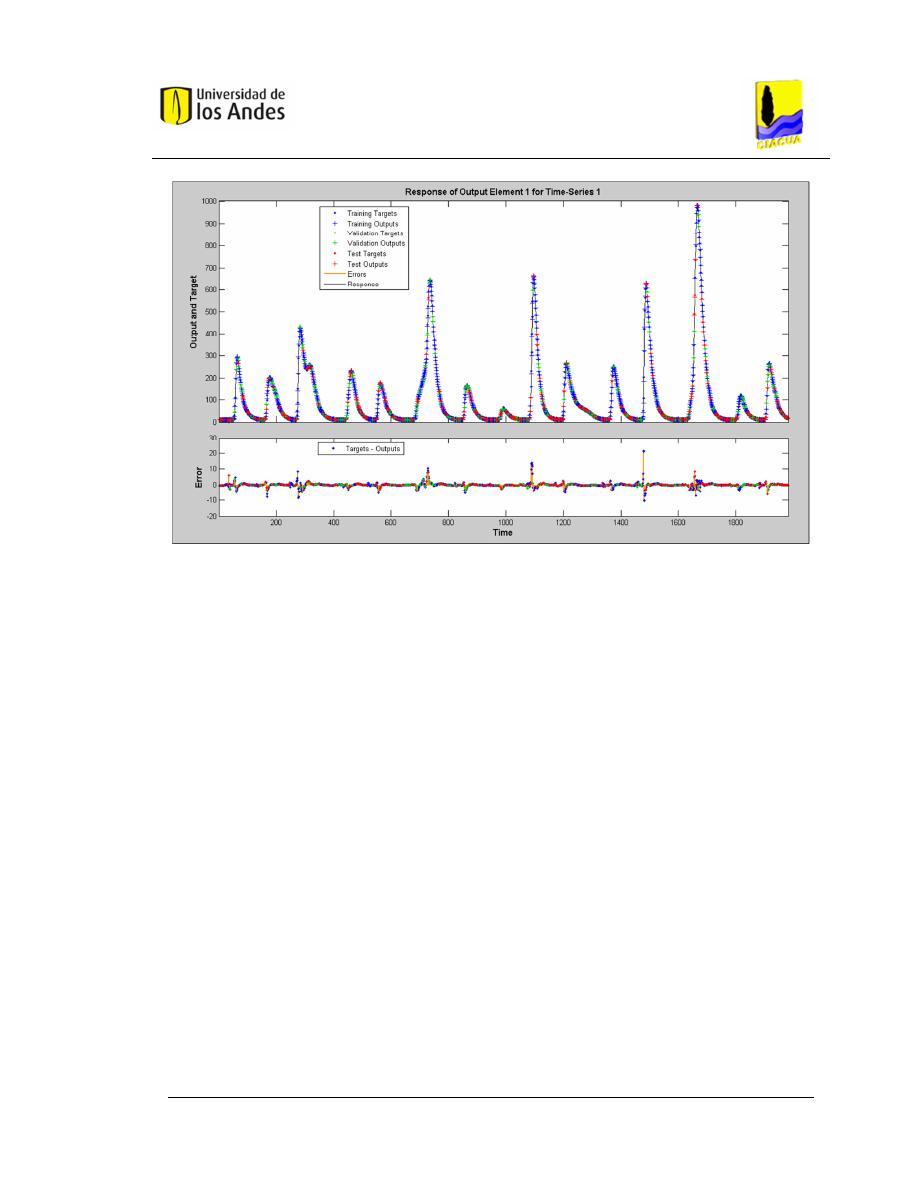
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
39
Gráfica 3.1. Panel para validación y prueba de datos (Fuente: Toolbox MATLAB
®
).
Como se observa en la Gráfica 3.1, los datos escogidos para entrenamiento,
validación y prueba están seleccionados en forma aleatoria; esto se puede
ajustar cambiando en el script de la red neuronal la forma de división de datos
mediante la escogencia de la opción divideblock (véase Tabla 3.1). Esto se
definirá en detalle en el Numeral 3.4.
9. Otra de las variables de decisión que se puede obtener una vez realizado el
entrenamiento de la red es la opción Error Autocorrelation, la cual se utiliza
para validar el desempeño de la ANN. En la Gráfica 3.2 se muestra la
función de autocorrelación de errores para el ejemplo utilizado.
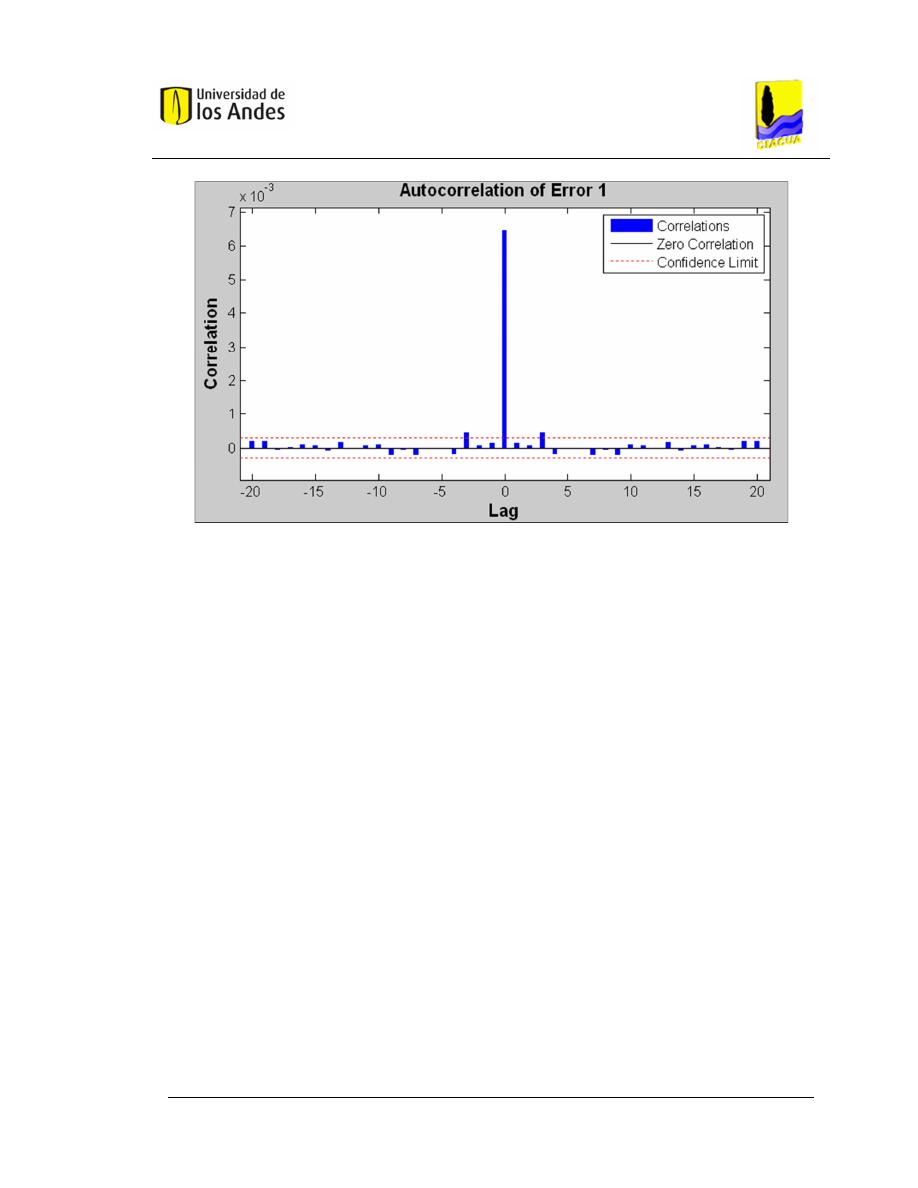
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
40
Gráfica 3.2. Error de autocorrelación (Fuente: Toolbox MATLAB
®
).
La Gráfica 3.2 describe cómo los errores de predicción se relacionan en el
tiempo. Para un modelo de predicción perfecto, sólo debe haber un valor
distinto de cero en la función de autocorrelación, y debería ocurrir en retraso
cero (cero lag), este es el error cuadrático medio. Lo anterior significa que los
errores de predicción están completamente no correlacionados entre sí (ruido
blanco). Si se tiene una correlación significativa en los errores de predicción,
entonces debería ser posible mejorar la predicción, tal vez aumentando el
número de retrasos en las líneas de retardo. En este caso (Gráfica 3.2), las
correlaciones, a excepción de la que está en retraso cero, caen
aproximadamente dentro de los límites de confianza del 95% alrededor de cero,
por lo que podría decirse que el modelo es adecuado. Si se requieren
resultados aún más precisos, se puede reentrenar la red haciendo clic en
Retrain en ntstool. Este procedimiento cambia los pesos iniciales y los
umbrales de la red, y puede producir una red mejorada después del
reentrenamiento.
10. Para realizar una verificación adicional del desempeño de la red se
puede desplegar también la función Input-Error Cross-Correlation, dando
clic en el botón del mismo nombre, véase Figura 3.7. Realizado el
anterior procedimiento se podrá ver una representación como la
mostrada en la Gráfica 3.3.
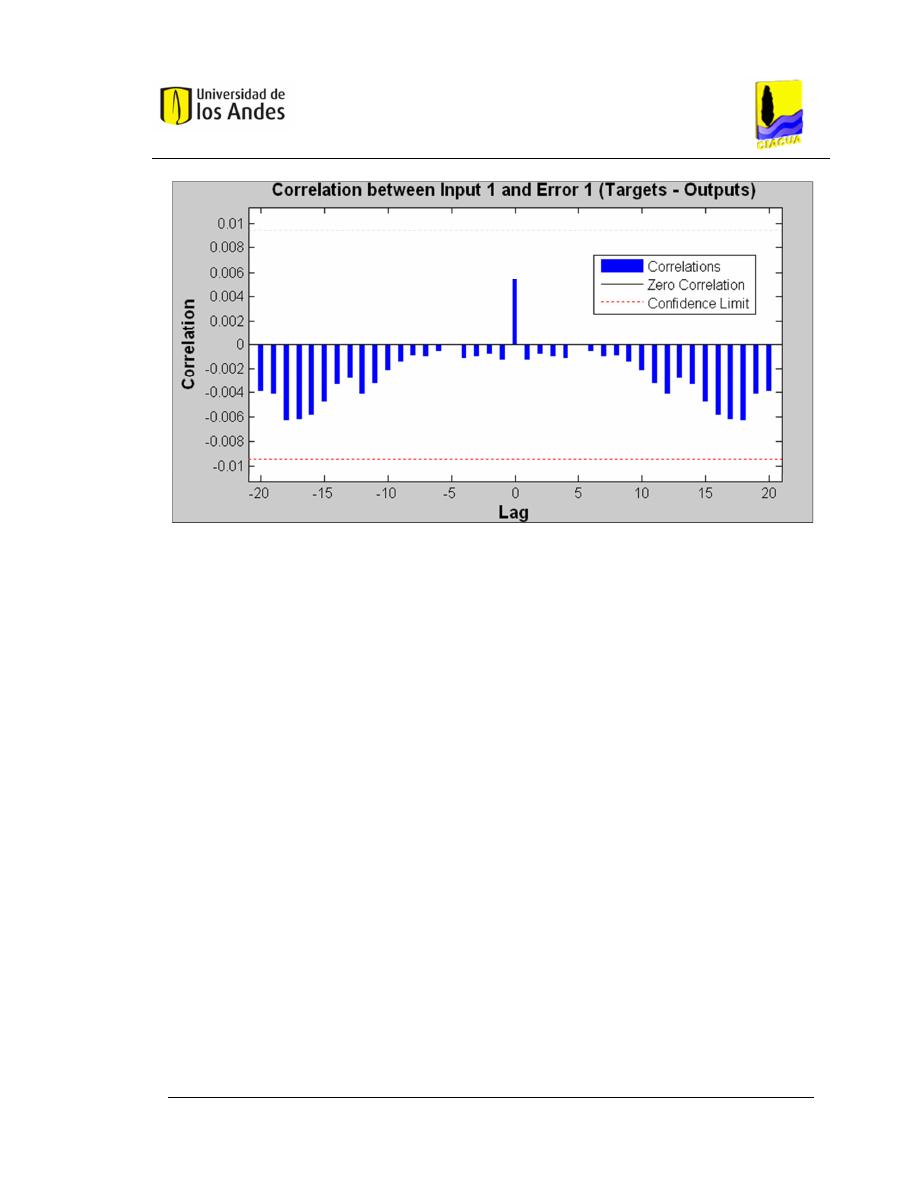
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
41
Gráfica 3.3. Correlación entre entradas y errores (Fuente: Toolbox MATLAB
®
).
La gráfica de la función input-error cross-correlation muestra como los errores
están correlacionados con la secuencia de entrada x(t). Para un modelo
perfecto de predicción, todas las correlaciones deberían ser cero. Si la entrada
se correlaciona con el error, entonces debería ser posible mejorar la predicción,
tal vez incrementando el número de retrasos en las líneas de retardo. En este
caso, todas las correlaciones caen dentro de los límites de confianza alrededor
de cero.
11. Dando clic en el botón Next en la herramienta de series de tiempo para
evaluar la red (véase Figura 3.6), es posible probar la red con nuevos
datos en el nuevo panel que se despliega (véase Figura 3.8). Si no se
está satisfecho con el desempeño de la red con los datos de origen o con
los nuevos se puede probar con los ajustes siguientes:
-
Entrenar de nuevo la red.
-
Incrementar el número de neuronas y/o el número de retrasos.
-
Obtener un conjunto de datos de entrenamiento más amplio.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
42
Figura 3.8. Panel para pruebas de la red (Fuente: Toolbox MATLAB
®
).
Si el desempeño en el conjunto de entrenamiento es bueno, pero el desempeño
en el conjunto de prueba no es el adecuado, esto podría indicar
sobreentrenamiento, entonces reduciendo el número de neuronas se pueden
mejorar los resultados.
Si no se está satisfecho con los resultados obtenidos a través de la interfaz
gráfica, es posible personalizar la estructura de la red dando clic en la opción
advanced script (véase Figura 3.9) con lo cual el investigador puede cambiar
parámetros como el tipo de algoritmo de entrenamiento, el número de neuronas
y/o capas ocultas, el tipo de división de datos, etc. En el numeral 3.4 se da una
descripción de la forma como se edita un determinado script.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
43
Figura 3.9. Panel para validación y prueba de datos (Fuente: Toolbox MATLAB
®
).
3.4 USO DE LAS FUNCIONES DE LA LÍNEA DE COMANDO
La forma fácil para aprender cómo utilizar la funcionalidad de la línea de
comando del toolbox de redes neuronales artificiales (RNA) disponible en
MATLAB
®
es generando scripts desde la interfaz gráfica (GUI), y luego
modificarlos para personalizar el entrenamiento de la red. Para editar un script
se puede seguir el procedimiento sugerido a continuación:
1. Cargar entradas y objetivos. El script asume que los vectores de entrada
y vectores objetivo ya están cargados en el espacio de trabajo. Si no lo
están, pueden cargarse como sigue para un caso determinado, para este
estudio las entradas se denominan INPUTS_n y los objetivos
TARGETS_n siendo n un consecutivo desde 1 hasta la cantidad total de
redes requeridas.
load ANN_1_dataset
inputSeries = INPUTS_1;
targetSeries = TARGETS_1;
2. Crear una red. En esta investigación como ya se mencionó anteriormente
se utilizará una red tipo NARX para la simulación de las redes

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
44
neuronales. La red NARX, narxnet, es una red feedforward con una
función de transferencia sigmoidal en la capa oculta y una función de
transferencia lineal en la capa de salida, ambas predeterminadas. Esta
red tiene dos entradas, una es una entrada externa y la otra es una
conexión de realimentación desde la salida de la red, como se observa
en la Figura 3.5. Para asignar la arquitectura a una red tipo NARX, se
deben seleccionar los retrasos asociados con cada línea de retardo, y
también el número de neuronas de la capa oculta. En las líneas de
ejemplo siguientes se indica cómo se asignan los retrasos de entrada y
los retrasos de retroalimentación, para este caso en un rango de 1 a 4 y
el número de neuronas ocultas como 10.
inputDelays = 1:4;
feedbackDelays = 1:4;
hiddenLayerSize = 10;
net = narxnet(inputDelays,feedbackDelays,hiddenLayerSize);
NOTA: Aumentar el número de neuronas y el número de retrasos requiere más
cálculo, y esto tiene una tendencia a sobreentrenar la red cuando los números
son demasiado altos, pero permite a la red resolver problemas más
complicados. Más capas requieren más cálculo, pero su uso podría resultar en
una red resolviendo problemas complejos de manera más eficiente. Para utilizar
más de una capa oculta, se ingresa el tamaño de la capa oculta como
elementos de un matriz en el comando fitnet, es decir, si se requiere una red
con dos capas ocultas, teniéndose 10 neuronas en la primera capa y 5
neuronas en la segunda capa, el ajuste se debe realizar como se indica:
hiddenLayerSize = [10,5];
3. Ajustar la división de datos. Al entrenar redes multicapas, la práctica
general es dividir primero los datos en tres subconjuntos. El primer
subconjunto es el conjunto de entrenamiento (training), el cual se utiliza
para calcular el gradiente y actualizar los pesos y los umbrales de la red.
El segundo subconjunto es el grupo de validación (validation), el error en
este conjunto es monitoreado constantemente durante el proceso de
entrenamiento. El error de validación normalmente disminuye durante la
fase inicial de entrenamiento, al igual que el error del conjunto de
entrenamiento; sin embargo, cuando la red comienza a sobreentrenar los

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
45
datos, el error en el conjunto de validación típicamente comienza a
elevarse. Los pesos de la red y los umbrales se guardan para el mínimo
valor de error del conjunto de validación. El tercer subconjunto es el de
prueba (testing); el error del conjunto de prueba no es utilizado durante el
entrenamiento, pero si es utilizado para comparar diferentes modelos. Si
el error en el conjunto de prueba alcanza un mínimo en un número de
iteración significativamente diferente que el error del conjunto de
validación, esto podría indicar una pobre división del conjunto de datos.
De forma predeterminada MATLAB
®
proporciona el siguiente ajuste:
net.divideParam.trainRatio = 70/100;
net.divideParam.valRatio = 15/100;
net.divideParam.testRatio = 15/100;
Con este ajuste los vectores de entrada y objetivo serán aleatoriamente
divididos, con 70% para entrenamiento, 15% para prueba y 15% para
validación.
Hay cuatro funciones provistas por MATLAB
®
para dividir los datos en
grupos de entrenamiento, validación y prueba. Estas son dividerand
(función por defecto), divideblock, divideint y divideind. La Tabla 3.1
indica la forma de división de datos según la función seleccionada.
FUNCIÓN
ALGORITMO
dividerand
Divide los datos aleatoriamente (Función por defecto)
divideblock
Divide los datos en bloques contiguos
divideint
Divide los datos mediante una selección intercalada
divideind
Divide los datos por un índice o clasificación
Tabla 3.1 Funciones para división de datos (Fuente: Toolbox MATLAB
®
).
La función de división
net.divideFcn
se incluye de forma automática
cada vez que la red es entrenada, y se utiliza para dividir los datos en
subgrupos de entrenamiento, validación y de prueba. Si
net.divideFcn
se establece en 'dividerand' (función por defecto), entonces los datos se
dividen al azar en tres subconjuntos utilizando los parámetros de división
net.divideParam.trainRatio,
net.divideParam.valRatio
y
net.divideParam.testRatio
. La fracción de los datos que se coloca
en el conjunto de entrenamiento es
trainRatio / (trainRatio +
valRatio + testRatio)
, una fórmula similar aplica para los otros dos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
46
grupos. Los valores por defecto para entrenamiento, prueba y validación
son 0.7, 0.15 y 0.15, respectivamente.
Si
net.divideFcn
se establece en 'divideblock', entonces los datos se
dividen en tres subgrupos utilizando tres bloques contiguos del conjunto
de datos original (para entrenamiento toma el primer bloque, para
validación el segundo y para prueba el tercero). La fracción de los datos
originales que entra en cada subconjunto se determina por los mismos
tres parámetros de división utilizados para dividerand o el investigador
puede asignar diferentes porcentajes según sus requerimientos.
Si
net.divideFcn
se establece en 'divideint', entonces los datos se
dividen mediante un método intercalado, como en el tratamiento de una
baraja de cartas. Está hecho para que diferentes porcentajes de datos
entren en los tres subgrupos. La fracción de los datos originales que
entra en cada subconjunto se determina por los mismos tres parámetros
de división utilizados para dividerand.
Cuando
net.divideFcn
se establece en 'divideind', los datos se dividen
por el índice. Los índices para los tres subgrupos están definidos por los
parámetros
de
división
net.divideParam.trainInd
,
net.divideParam.valInd
y
net.divideParam.testInd
. La asignación
predeterminada de estos índices es la matriz nula, por lo que se deben
establecer los índices al utilizar esta opción.
4. Entrenar la red. Una vez se inician los pesos y biases (umbrales), la red
está lista para el entrenamiento. La red multicapas feedforward puede
ser entrenada para aproximación de funciones (regresión no lineal) o
para reconocimiento de patrones. El proceso de entrenamiento requiere
un adecuado conjunto de entradas a la red “p” y salidas objetivo “t”.
El proceso de entrenar una red neuronal implica afinar los valores de los
pesos y biases para optimizar el rendimiento de la red, de acuerdo con la
definición de la función de desempeño de la red
net.performFcn
. La
función de desempeño predeterminada para redes feedforward es el
error cuadrado medio (MSE) entre la salida de la red “a” y la salida
objetivo “t”. La Ecuación 19 define esta expresión:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
47
' X-
1
1
+
Ecuación 19.
Hay dos maneras diferentes como el entrenamiento se puede
implementar: el modo incremental y el modo por grupos. En el modo
incremental, el gradiente se calcula y los pesos se actualizan después
que cada entrada se aplica a la red. En el modo por grupos, todas las
entradas en el conjunto de entrenamiento se aplican a la red antes de
que se actualicen los pesos. Para la mayoría de los problemas, cuando
se utiliza en el toolbox de red neuronal, el entrenamiento por grupos es
significativamente más rápido y produce errores de menor tamaño que el
entrenamiento incremental.
Las redes neuronales artificiales en MATLAB
®
utilizan por defecto para
entrenamiento el algoritmo de Levenberg-Marquardt. La Tabla 3.2
muestra los algoritmos disponibles en el toolbox de redes neuronales del
software. Estos algoritmos están basados en los métodos del gradiente y
en el jacobiano.
FUNCIÓN
ALGORITMO
trainlm
Levenberg-Marquardt
trainbr
Bayesian Regularization
trainbfg
BFGS Quasi-Newton
trainrp
Resilient Backpropagation
trainscg
Scaled Conjugate Gradient
traincgb
Conjugate Gradient with Powell/Beale Restarts
traincgf
Fletcher-Powell Conjugate Gradient
traincgp
Polak-Ribiére Conjugate Gradient
trainoss
One Step Secant
traingdx
Variable Learning Rate Gradient Descent
traingdm
Gradient Descent with Momentum
traingd
Gradient Descent
Tabla 3.2 Algoritmos de entrenamiento ofrecidos por MATLAB
®
(Fuente: Toolbox MATLAB
®
).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
48
La función de entrenamiento más rápida es generalmente trainlm, y es la
función por defecto para redes feedforward. El método cuasi-Newton,
trainbfg, también es bastante rápido. Ambos métodos tienden a ser
menos eficiente para redes grandes (con miles de pesos), ya que
requieren más memoria y más tiempo de cálculo. La función trainlm
realiza mejor problemas de función de ajuste (regresión no lineal) que
problemas de reconocimiento de patrones.
Cuando se tienen redes de gran tamaño y redes para reconocimiento de
patrones, trainscg y trainrp son buenas opciones. Sus requisitos de
memoria son relativamente pequeños y sin embargo son mucho más
rápidos que los algoritmos de descenso de gradiente estándar. Durante
el entrenamiento de una red se abre la ventana mostrada en la Figura
3.10; el entrenamiento se detiene en forma automática cuando el error de
validación aumenta luego de 6 iteraciones.
Figura 3.10. Ventana de proceso del entrenamiento (Fuente: Toolbox MATLAB
®
).
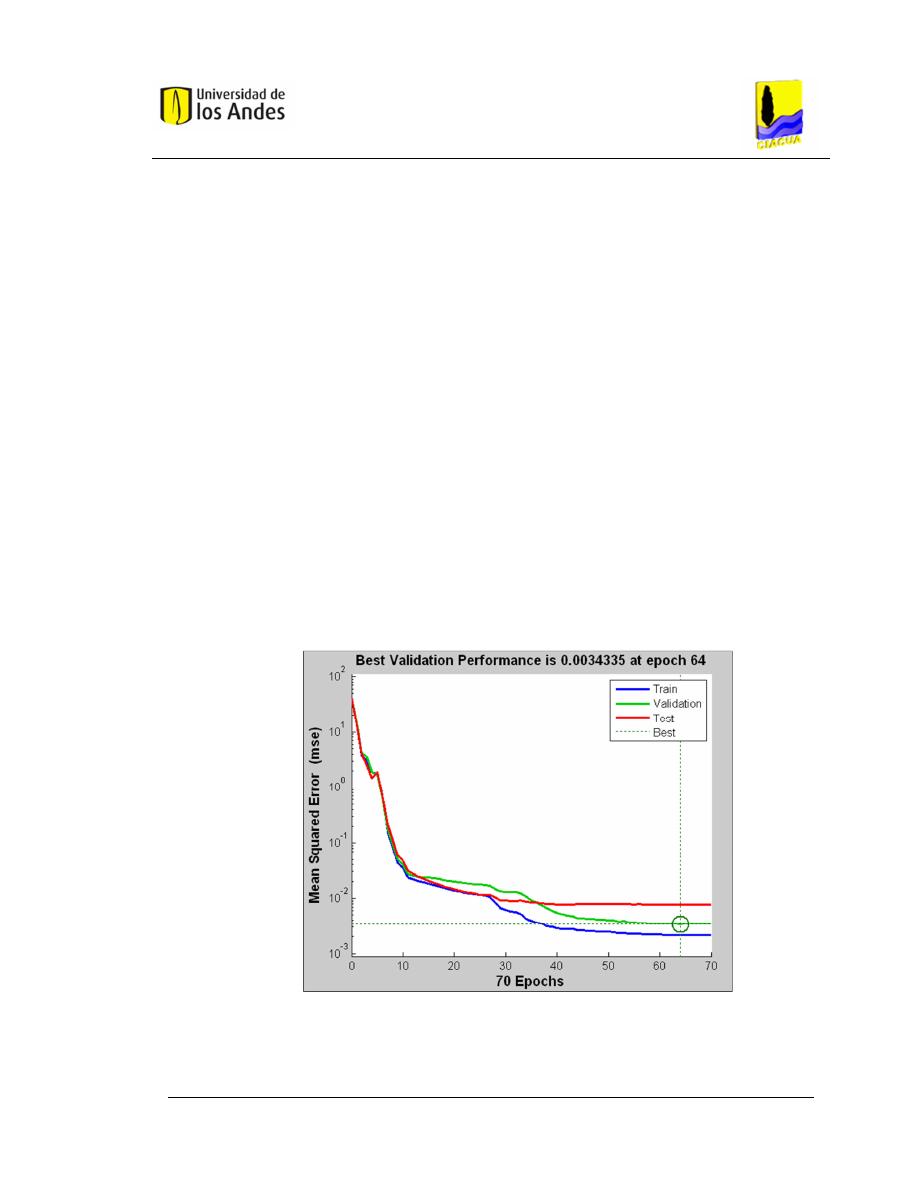
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
49
5. Probar la red. Después que la red ha sido entrenada, se puede utilizar
para calcular las salidas de la misma. El siguiente código calcula las
salidas de la red, errores y desempeño total.
outputs = net(inputs,inputStates,layerStates);
errors = gsubtract(targets,outputs);
performance = perform(net,targets,outputs)
6. Desempeño del entrenamiento. Este se determina para comprobar si hay
un potencial sobreentrenamiento en la red. La función
figure,
plotperform(tr)
muestra la Gráfica 3.4 donde se ve el comportamiento
de la red. De esta grafica se puede afirmar que en cuanto a los errores
de entrenamiento, validación y prueba, todos disminuyeron hasta
aproximadamente la iteración 64. No parece que se haya producido
algún sobreentrenamiento, ya que ningún error de prueba o de validación
aumento antes de la iteración 64, de observarse en la curva de prueba
un aumentado de manera significativa antes que la curva de validación
aumentara, entonces es posible que algún sobreentrenamiento pudiera
haber ocurrido.
Gráfica 3.4 Desempeño de la red neuronal (Fuente: Toolbox MATLAB
®
).
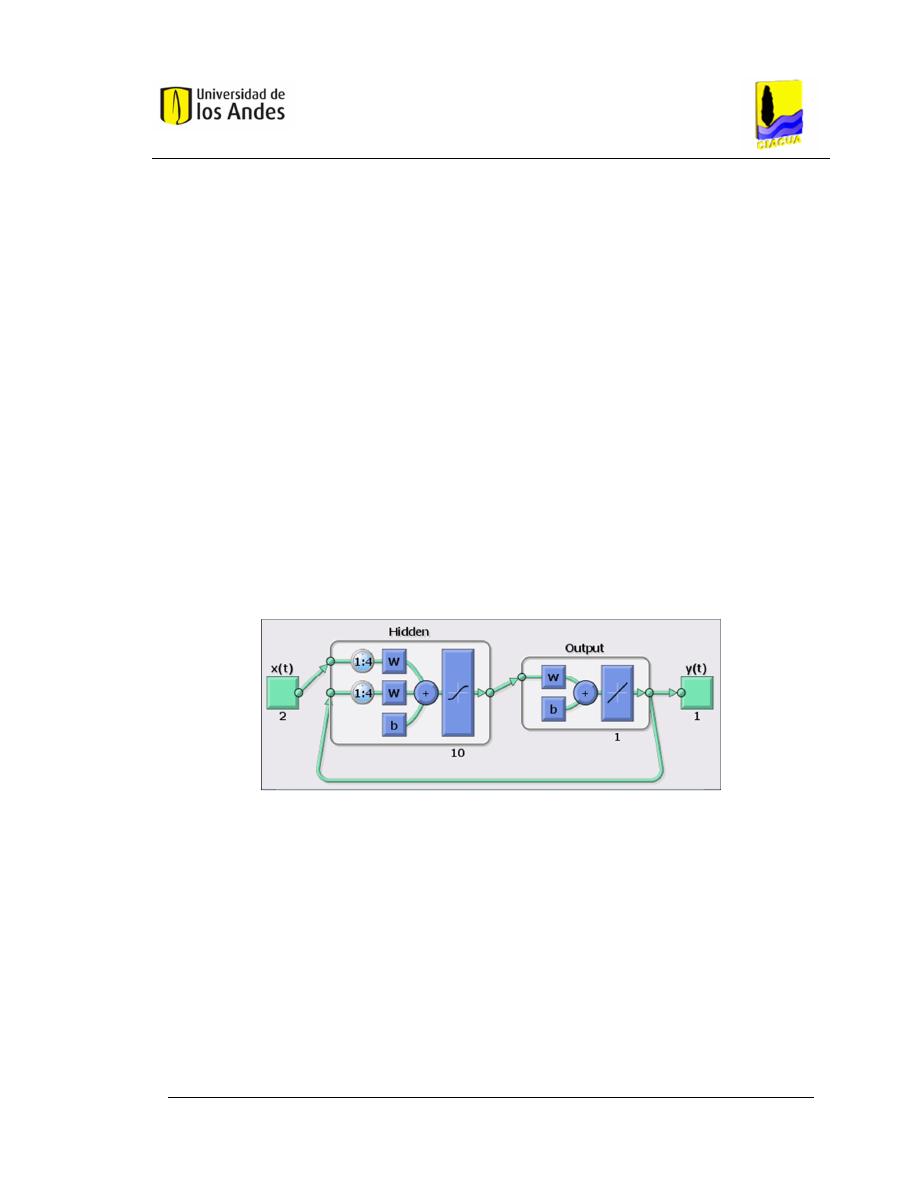
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
50
7. Cerrar el ciclo en la red NARX. Cuando el bucle de retroalimentación
está abierto en la red NARX, se está realizando una predicción de un
solo paso hacia adelante, se predice el siguiente valor de y (t) a partir de
los valores anteriores de y(t) y x(t). Con el bucle de realimentación
cerrado, este se puede utilizar para realizar predicciones multi-paso
hacia adelante. Esto es porque las predicciones de y(t) se utilizan en
lugar de los valores reales futuros de y(t). Los siguientes comandos se
pueden utilizar para cerrar el bucle y calcular el rendimiento del circuito
cerrado.
netc = closeloop(net);
netc.name = [net.name ' - Closed Loop'];
view(netc)
[xc,xic,aic,tc] =
preparets(netc,inputSeries,{},targetSeries);
yc = netc(xc,xic,aic);
perfc = perform(netc,tc,yc)
La Figura 3.11 muestra una red NARX con el circuito cerrado.
Figura 3.11. Red NARX de circuito cerrado (Fuente: Toolbox MATLAB
®
).
8. Eliminar un retraso de la red. Para obtener la predicción un paso en el
tiempo más temprano, el siguiente código permite realizar esta
operación.
nets = removedelay(net);
nets.name = [net.name ' - Predict One Step Ahead'];
view(nets)
[xs,xis,ais,ts]=
preparets(nets,inputSeries,{},targetSeries);
ys = nets(xs,xis,ais);
earlyPredictPerformance = perform(nets,ts,ys)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
51
Cuando los resultados y el desempeño de la red no son satisfactorios se puede
intentar alguna de las siguientes aproximaciones:
• Restablecer los pesos y umbrales iniciales de la red a nuevos valores
con
init
y entrenar de nuevo.
• Incrementar el número de neuronas ocultas o retrasos.
• Incrementar el número de vectores de entrenamiento.
• Incrementar el número de valores de entrada, si está disponible más
información relevante.
• Probar un algoritmo de entrenamiento diferente.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
52
4. METODOLOGÍA DESARROLLADA
En esta investigación, posterior a la etapa de búsqueda y recopilación del
material bibliográfico existente y reconocimiento del estado del arte de este tipo
de metodologías tanto a nivel local como a nivel general, se seguirán las etapas
indicadas más adelante con el fin de lograr el objetivo de la investigación, el
cual se fundamenta en determinar la viabilidad de utilizar un método basado en
inteligencia artificial (ANN) para realizar en forma adecuada el tránsito de
crecientes a través de un tramo de canal o cauce determinado. Para los casos
de análisis o como se denominaran de aquí en adelante “Caso de Estudio 1,
Caso de Estudio 2 y Caso de Estudio 3”, el alcance de la investigación se indica
en las etapas 1 a 5, las cuales se describen a continuación.
Etapa 1. En la parte inicial de la investigación se define en principio un tramo de
canal o cauce con características hidráulicas sencillas, es decir, con una sola
entrada de caudal y una sola salida. Se resalta que en las siguientes etapas de
la investigación se considerarán modelos más complejos con varias entradas y
una o varias salidas, para validar y reforzar los resultados obtenidos. El cauce
utilizado como Caso de Estudio 1, corresponde a un tramo de río del territorio
colombiano de aproximadamente 30 Km de longitud, con algunas curvas en su
recorrido, la pendiente de fondo es del orden de 0,0012 m/m y el ancho de la
sección del orden de 150 m. La Figura 4.1 muestra un trazado en planta del
caso de estudio mencionado; indicados con puntos de color rojo se muestran
los sitios donde se localizan las secciones batimétricas. La Figura 4.2 muestra
además de forma esquemática el perfil de fondo del cauce analizado; en esta
se exagera la escala vertical para observar las irregularidades que este pueda
tener.
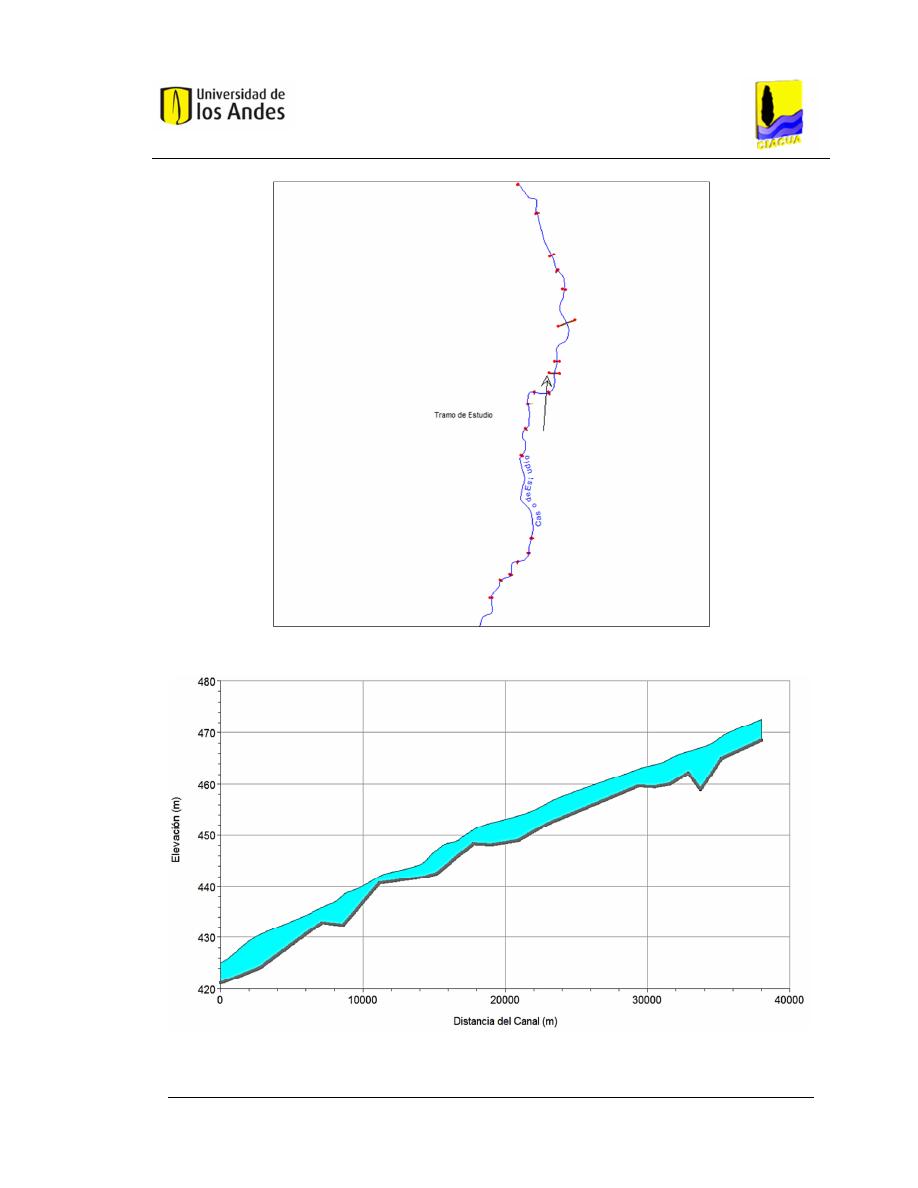
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
53
Figura 4.1 Trazado en planta – Caso de Estudio 1.
Figura 4.2 Perfil del fondo del cauce – Caso de Estudio 1.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
54
Teniendo la información básica del Caso de Estudio 1, a partir de un
hidrograma de diseño inicial se elaboran una serie de hidrogramas de diferentes
tamaños y formas, buscando con esto tener un rango de información amplio
que permita abarcar un mayor y más significativo grupo de datos para el
aprendizaje de las redes neuronales. Esta misma metodología se utilizará para
determinar los hidrogramas de entrada (Datos de entrada) en el Caso de
Estudio 2 y en el Caso de Estudio 3.
Seguido a esto, con la serie de hidrogramas definidos se procede al ejecutar el
tránsito en el tramo de canal del Caso de Estudio 1, este se hace en primera
instancia con ayuda de un software confiable, para este ejercicio se utiliza HEC-
RAS. La información de entrada para comenzar el proceso de simulación está
conformada por un grupo de 20 secciones batimétricas, con las cuales se
genera un modelo digital del cauce a analizar. La Figura 4.3 muestra una
imagen tridimensional del tramo en mención y la Gráfica 4.1 muestra los
hidrogramas utilizados para el tránsito en el modelo digital. Se resalta que el
espaciamiento entre uno y otro hidrograma se determinó con el objetivo de
evitar que la respuesta de un determinado hidrograma afectara la respuesta del
hidrograma siguiente.
Figura 4.3 Modelo digital del Caso de Estudio 1.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
55
Con la información batimétrica, la serie de hidrogramas y demás variables de
entrada al modelo, se procede a determinar la serie de hidrogramas de salida
en la última sección aguas abajo del modelo digital en HEC-RAS; el resultado
de esto se muestra en la Gráfica 5.1.
Etapa 2. En esta etapa de la investigación se realiza la escogencia de las
arquitecturas de las redes neuronales cuyo entrenamiento, calibración y/o grupo
de prueba muestre el mejor comportamiento o desempeño; dicha selección se
basa en someter una red neuronal definida a múltiples procesos de cálculo
variando algunos parámetros que definen su arquitectura, como son:
• Número de neuronas en la capa oculta. Se consideró evaluar este
parámetro para 5, 10, 15 y 20 neuronas. Según el número de capas
ocultas, el total de neuronas se distribuyó en el total de capas como se
muestra en la Tabla 4.1.
• Número de capas ocultas. De acuerdo con el número de estas (máximo
3), la cantidad total de neuronas se distribuyó según se muestra en la
Tabla 4.1.
Número
total de
neuronas
Distribución de neuronas por capa
1 capa oculta
2 capas ocultas
3 capas ocultas
5
5
3 y 2
2, 2 y 1
10
10
5 y 5
4, 3 y 3
15
15
10 y 5
5, 5 y 5
20
20
10 y 10
10, 5 y 5
Tabla 4.1. Distribución de neuronas según el número de capas ocultas.
• Tipo de algoritmo de entrenamiento utilizado por la red. En cuanto a
algoritmos de entrenamiento, MATLAB
®
proporciona las opciones
indicadas en la Tabla 3.2. Para este análisis sólo se utilizaron los
algoritmos siguientes, los cuales mostraron resultados con mejor ajuste a
los objetivos o targets deseados.
-
Levenberg-Marquardt
-
Bayesian Regularization
-
BFGS Quasi-Newton
-
Resilient Backpropagation

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
56
-
Variable Learning Rate Gradient Descent
-
Scaled Conjugate Gradient
-
One Step Secant
• Tipo de división de datos. La escogencia del conjunto de datos a analizar
se puede realizar de cuatro formas diferentes; estas son: aleatoriamente,
por bloques contiguos, mediante una selección intercalada o con la
ayuda de un índice. En el Numeral 3.4 se explica en detalle cómo opera
cada una de estas opciones. Para este caso se seleccionará la forma de
división por bloques contiguos, escogiendo un 60% de los datos para
entrenamiento, 22% para validación y 18% para evaluar la red. El por
qué de esta división se explica por el hecho de evitar que un mismo
hidrograma haga parte de dos bloques, es decir, entrenamiento y
validación o validación y prueba. Para el Caso de Estudio 2, el Caso de
Estudio 3 y las demás distribuciones de hidrogramas del Caso de Estudio
1, los porcentajes mencionados varían debido a que el número de datos
analizados es diferente.
Bajo las anteriores consideraciones se construyó un total de 84 arquitecturas de
redes neuronales diferentes, las cuales se evalúan considerando el error medio
cuadrado (MSE) para calificar o valorar el comportamiento de una determinada
arquitectura; dicho valor indica el nivel de desempeño logrado por cada red
neuronal (véase Ecuación 20). Para este parámetro se tiene que entre más
cercano a cero se encuentre el valor, el desempeño de una determinada
arquitectura de red neuronal será mejor. La Tabla 4.2 muestra las diferentes
arquitecturas utilizadas para cada red neurona. Aunque MATLAB
®
proporciona
otros algoritmos de entrenamiento sólo se analizan los ya mencionados, pues
los demás, en pruebas previas no muestran un desempeño confiable. De aquí
se seleccionarán las redes neuronales que muestren el mejor desempeño y a
partir de estas se continuará el análisis en las etapas 3, 4 y 5 de la
investigación, pero como ya se había mencionado, con los modelos de los
Casos de Estudio 2 y 3.
YZK
∑ [
JO\:I]E^J
+ [
:\;_E^J
Ecuación 20.
siendo,

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
57
[
JO\:I]E^J
= Caudal Observado (HEC-RAS)
[
:\;_E^J
= Caudal Estimado (MATLAB
®)
N = Número de datos
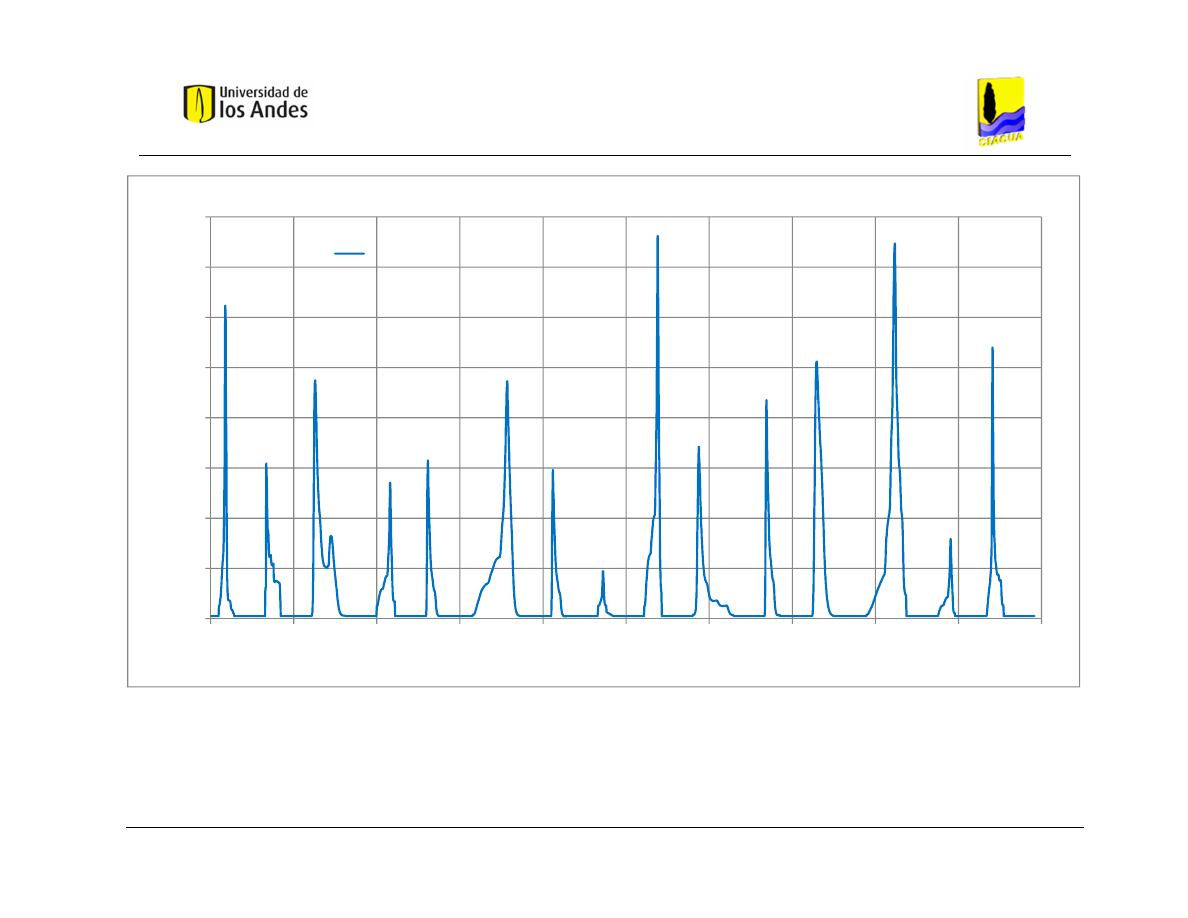
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
58
Gráfica 4.1 Hidrogramas de entrada al modelo en HEC-RAS – Caso de Estudio 1 – Distribución 1.
0
200
400
600
800
1000
1200
1400
1600
0
50
100
150
200
250
300
350
400
450
500
C
a
u
d
a
l
(m
3
/s
)
Tiempo (Horas)
HIDROGRAMAS DE ENTRADA - CASO DE ESTUDIO 1 - DISTRIBUCIÓN 1
Hidrogramas de Entrada
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
59
Tabla 4.2 Arquitecturas de redes neuronales utilizadas para el análisis del Caso de Estudio 1 –
Distribución 1.
NOMBRE
ALGORITMO DE
ENTRENAMIENTO
NEURONAS
EN LA CAPA
OCULTA
NEURONAS
POR CAPA
CAPAS
OCULTAS
TIME STEP
NOMBRE
ALGORITMO DE
ENTRENAMIENTO
NEURONAS
EN LA CAPA
OCULTA
NEURONAS
POR CAPA
CAPAS
OCULTAS
TIME STEP
ANN_1
5
5
1
2
ANN_49
5
5
1
2
ANN_2
10
10
1
2
ANN_50
10
10
1
2
ANN_3
15
15
1
2
ANN_51
15
15
1
2
ANN_4
20
20
1
2
ANN_52
20
20
1
2
ANN_5
5
3,2
2
2
ANN_53
5
3,2
2
2
ANN_6
10
5,5
2
2
ANN_54
10
5,5
2
2
ANN_7
15
10,5
2
2
ANN_55
15
10,5
2
2
ANN_8
20
10,10
2
2
ANN_56
20
10,10
2
2
ANN_9
5
2,2,1
3
2
ANN_57
5
2,2,1
3
2
ANN_10
10
4,3,3
3
2
ANN_58
10
4,3,3
3
2
ANN_11
15
5,5,5
3
2
ANN_59
15
5,5,5
3
2
ANN_12
20
10,5,5
3
2
ANN_60
20
10,5,5
3
2
ANN_13
5
5
1
2
ANN_61
5
5
1
2
ANN_14
10
10
1
2
ANN_62
10
10
1
2
ANN_15
15
15
1
2
ANN_63
15
15
1
2
ANN_16
20
20
1
2
ANN_64
20
20
1
2
ANN_17
5
3,2
2
2
ANN_65
5
3,2
2
2
ANN_18
10
5,5
2
2
ANN_66
10
5,5
2
2
ANN_19
15
10,5
2
2
ANN_67
15
10,5
2
2
ANN_20
20
10,10
2
2
ANN_68
20
10,10
2
2
ANN_21
5
2,2,1
3
2
ANN_69
5
2,2,1
3
2
ANN_22
10
4,3,3
3
2
ANN_70
10
4,3,3
3
2
ANN_23
15
5,5,5
3
2
ANN_71
15
5,5,5
3
2
ANN_24
20
10,5,5
3
2
ANN_72
20
10,5,5
3
2
ANN_25
5
5
1
2
ANN_73
5
5
1
2
ANN_26
10
10
1
2
ANN_74
10
10
1
2
ANN_27
15
15
1
2
ANN_75
15
15
1
2
ANN_28
20
20
1
2
ANN_76
20
20
1
2
ANN_29
5
3,2
2
2
ANN_77
5
3,2
2
2
ANN_30
10
5,5
2
2
ANN_78
10
5,5
2
2
ANN_31
15
10,5
2
2
ANN_79
15
10,5
2
2
ANN_32
20
10,10
2
2
ANN_80
20
10,10
2
2
ANN_33
5
2,2,1
3
2
ANN_81
5
2,2,1
3
2
ANN_34
10
4,3,3
3
2
ANN_82
10
4,3,3
3
2
ANN_35
15
5,5,5
3
2
ANN_83
15
5,5,5
3
2
ANN_36
20
10,5,5
3
2
ANN_84
20
10,5,5
3
2
ANN_37
5
5
1
2
ANN_38
10
10
1
2
ANN_39
15
15
1
2
ANN_40
20
20
1
2
ANN_41
5
3,2
2
2
ANN_42
10
5,5
2
2
ANN_43
15
10,5
2
2
ANN_44
20
10,10
2
2
ANN_45
5
2,2,1
3
2
ANN_46
10
4,3,3
3
2
ANN_47
15
5,5,5
3
2
ANN_48
20
10,5,5
3
2
One Step Secant -
trainoss
Levenberg-
Marquardt -
trainlm
Bayesian
Regularization -
trainbr
BFGS Quasi-
Newton - trainbfg
Resilient
Backpropagation -
trainrp
Variable Learning
Rate Gradient
Descent -
traingdx
Scaled Conjugate
Gradient -
trainscg

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
60
Etapa 3. Con las mejores arquitecturas de redes neuronales se realizará un
análisis de sensibilidad al modelo del Caso de Estudio 1 para observar el
comportamiento de la respuesta proporcionada por las redes neuronales ante
cambios en parámetros importantes como la pendiente de fondo del cauce y el
coeficiente de rugosidad.
Luego de analizar los resultados obtenidos, se analizarán otros canales o
sistemas de canales con características geométricas e hidráulicas más
complejas (Caso de Estudio 2 y Caso de Estudio 3), pero esta vez solo se
tendrá los datos de los hidrogramas de entrada y de los hidrogramas de salida.
La idea principal de esto es que con las mejores arquitecturas de las redes
neuronales definidas en la anterior etapa y con los datos de entrada y los datos
objetivos conocidos evaluar la nueva respuesta de las redes neuronales para
una condición diferente de varias entradas y una salida. A continuación se
describen los modelos utilizados para los Casos de Estudio 2 y 3.
• Caso de Estudio 2. El sistema utilizado como Caso de Estudio 2, está
conformado por el tramo principal de un río del territorio colombiano
(Cauce 3) de aproximadamente 1,60 Km de longitud, con varias curvas
cerradas en la zona de análisis, la pendiente de fondo es del orden de
0,0015 m/m y el ancho de la sección varía entre 20 y 30 m. A este cauce
principal descargan 2 cauces de menor capacidad denominados Cauce 1
y Cauce 2. El Cauce 1 tiene aproximadamente 1,3 Km de longitud, pocos
cambios de dirección en su recorrido, la pendiente promedio del fondo es
del orden de 0,004 m/m y el ancho de la sección varía entre 5 y 10 m. En
cuanto al Cauce 2, este tiene aproximadamente 1,5 Km de longitud,
pocos cambios de dirección en su recorrido, la pendiente promedio del
fondo es del orden de 0,009 m/m y el ancho de la sección varía entre 5 y
12 m. La Figura 4.4 muestra la configuración en planta del caso de
estudio mencionado, indicados con puntos de color rojo se muestran los
sitios donde se localizan las secciones batimétricas. La Figura 4.5
muestra además de forma esquemática el perfil de fondo de los tres
cauces analizados, exagerando la escala vertical para observar las
irregularidades que estos puedan tener.
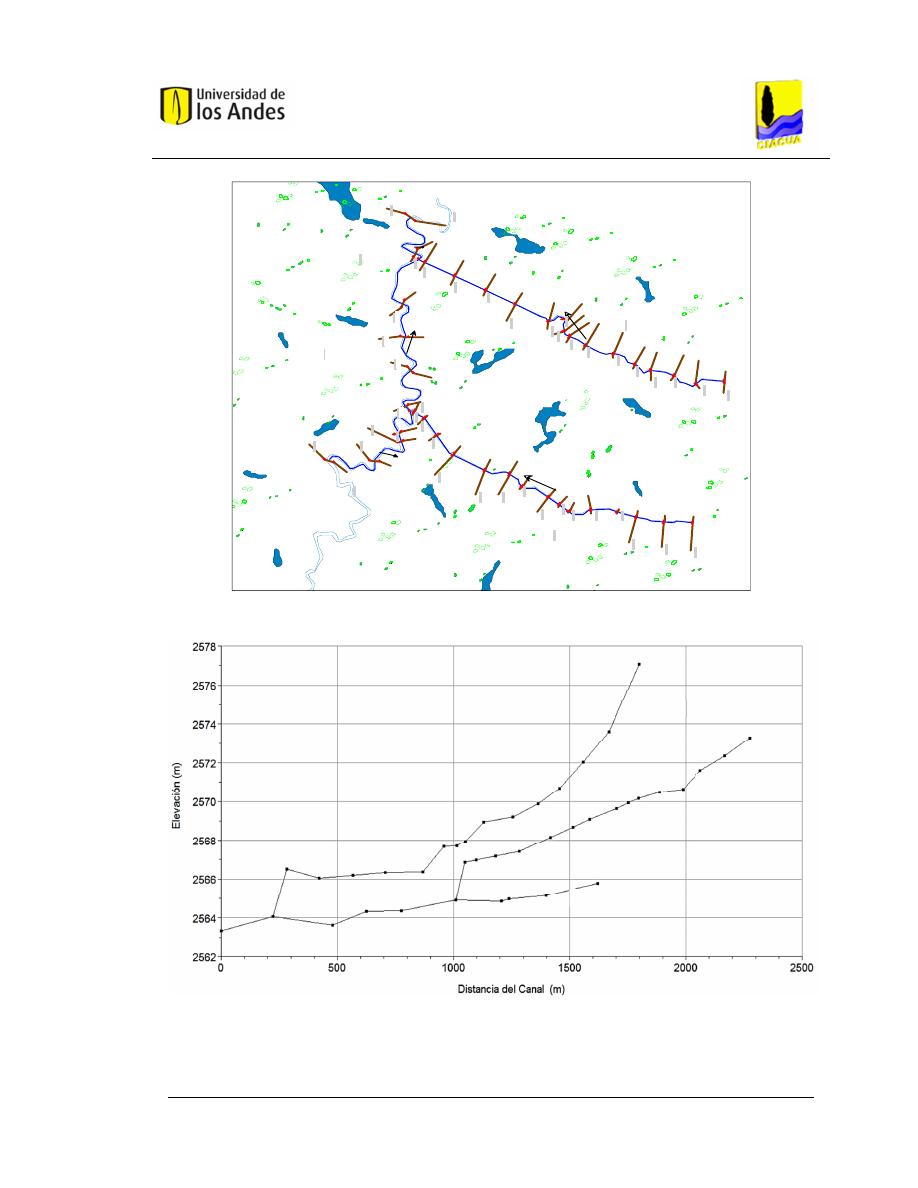
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
61
Figura 4.4 Trazado en planta – Caso de Estudio 2.
Figura 4.5 Perfil del fondo del cauce – Caso de Estudio 2.
CAUCE_3.2
6
5
4
3
C
AUC
E
_ 3
CAUCE_3.1
2
1
CAUCE_1
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
1
CAUCE_2
19
18
17
16
15
14
13
12
11
10
9
4
3
2
1
2
CAUCE_3.3
10
9
8
7
3
NODO_1
NODO_2
CAUCE 2
CAUCE 1
CAUCE 3
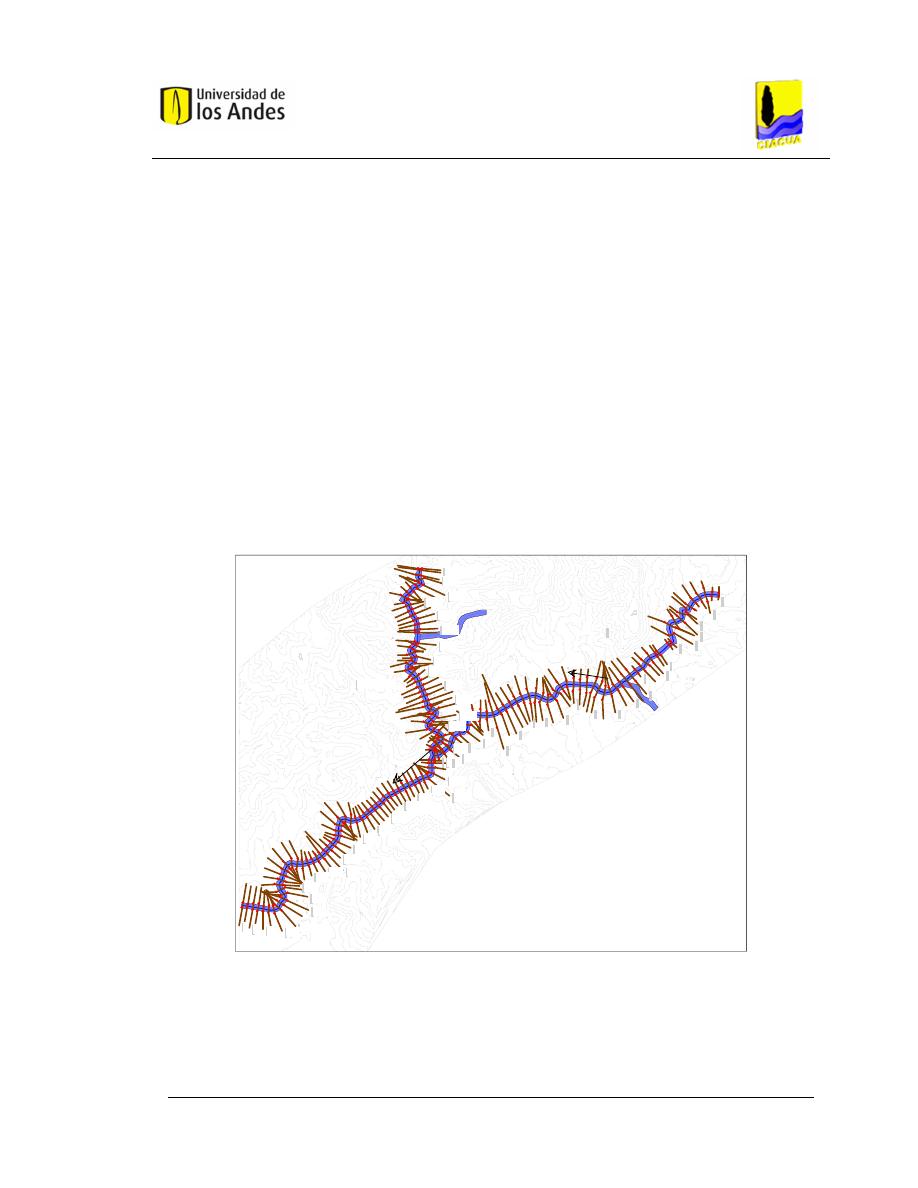
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
62
• Caso de Estudio 3. El Caso de Estudio 3, está conformado por un tramo
principal de un río del territorio colombiano (Cauce 1) de
aproximadamente 2,0 Km de longitud, con varias curvas cerradas en la
zona de análisis, la pendiente de fondo es del orden de 0,003 m/m y el
ancho de la sección principal del cauce varía entre 12 y 30 m. A este
cauce principal descarga un tributario denominado Cauce 2, el cual tiene
aproximadamente 1,2 Km de longitud, con varios cambios de dirección
en el recorrido analizado, la pendiente promedio del fondo es del orden
de 0,009 m/m y el ancho de la sección varía entre 8 y 30 m en el cauce
principal. La Figura 4.6 muestra la configuración en planta del caso de
estudio mencionado; indicados con puntos de color rojo y líneas de color
café se muestran los sitios donde se localizan las secciones batimétricas.
La Figura 4.7 muestra además de forma esquemática el perfil del fondo
de los dos cauces analizados; se exagera la escala vertical para
observar las irregularidades que este pueda tener.
Figura 4.6 Trazado en planta – Caso de Estudio 3.
CAUCE_1
1985.25
1960
1920
1880
1740
1700
1650
1580
1480
1420
1360
1300
1260
1160
1070
1020
1000
980
920
860
780
720
680
540
500
480
440
400
240
200
180
140
120
80
40
0
CA
U
C
E
_1
CAUCE_2
1160
1120
1020
1000
930
900
850
820
760
740
700
660
620
540
460
420
360
300
260
240
140
100
60
40
20
C A
UC
E_
2
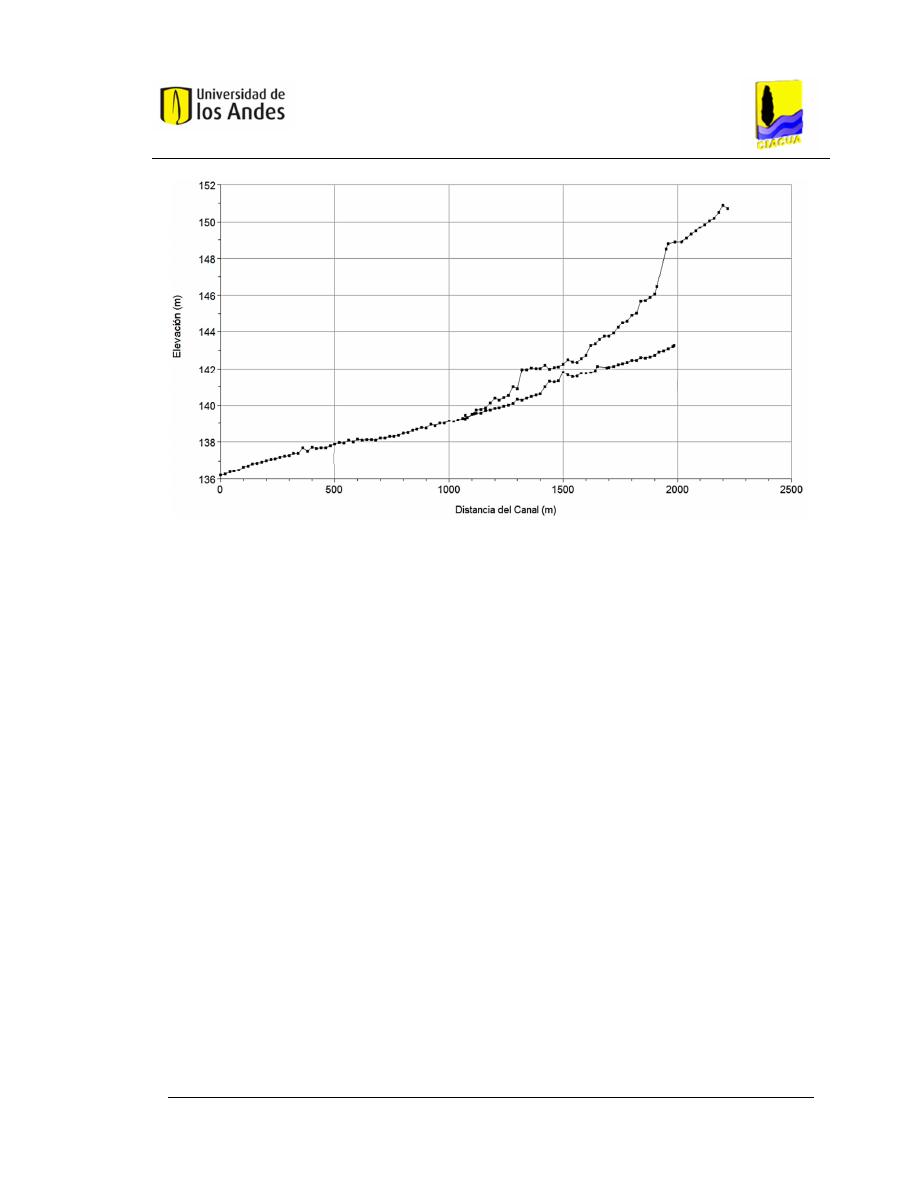
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
63
Figura 4.7 Perfil del fondo del cauce – Caso de Estudio 3.
Etapa 4. En este nivel de la investigación se busca validar u observar el
comportamiento de la respuesta de las redes neuronales para condiciones de
análisis diferentes. En esta etapa se somete nuevamente a evaluación por parte
de las ANN los tres casos de estudio mencionados, pero esta vez las series de
hidrogramas de entrada tendrán variaciones en la magnitud de los picos, en la
localización de los mismos, en la forma y duración de los hidrogramas, lo que
proporcionara salidas diferentes para alimentar las redes neuronales escogidas,
es decir, aquellas con mejor desempeño en las Etapas 1 y 2.
Etapa 5. Finalmente se compararan todos los resultados logrados con las ANN
y con el software de comprobación (HEC-RAS). De acuerdo con los resultados
obtenidos en las Etapas 3 y 4 se podrá dar un juicio, sustentado en los
resultados obtenidos mostrando las ventajas y desventajas de las redes
neuronales artificiales en el tránsito de crecientes en canales con respecto a los
métodos tradicionales. Además del análisis hidráulico se considerará como
parámetro adicional de decisión un análisis de costos entre ambos métodos
para determinar la viabilidad o no de utilizar ANN.
CAUCE 2
CAUCE 1
CAUCE 1

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
64
5. ANÁLISIS DE RESULTADOS
Como se describió en el capítulo anterior, el Caso de Estudio 1 es el más
sencillo de los tres Casos de Estudio evaluados, este se utilizó como base para
la evaluación de los Casos de Estudio 2 y 3, es decir, los resultados del análisis
inicial para determinar qué tipos de arquitectura de redes neuronales son las
que mejor desempeño presentan servirán de base para el desarrollo de los
Casos de Estudio 2 y 3. Esto indica que para el análisis de los tres casos de
estudio se utilizarán las mismas arquitecturas de ANN. A continuación se
describe el procedimiento para determinar que arquitecturas de redes
neuronales tienen el mejor desempeño, es decir, cuales se ajustan mejor al
objetivo deseado.
5.1 CASO DE ESTUDIO 1
Una vez definido el modelo digital para el Caso de Estudio 1 y la información
que sirve de entrada para dicho modelo, se realizó un análisis de flujo no
uniforme con ayuda del software HEC-RAS, obteniéndose como resultado para
la serie de hidrogramas de entrada de la Gráfica 4.1 la serie de hidrogramas de
salida mostrada en la Gráfica 5.1.
Esta serie de hidrogramas de salida obtenidos pasan a ser ahora el objetivo
buscado de cada una de las 84 arquitecturas de redes neuronales configuradas.
El procedimiento utilizado para el montaje de cada red neuronal es el descrito
en el Capítulo 3, mientras que la topología utilizada para cada red se muestra
en la Tabla 4.2. Como ya se ha mencionado, uno de los objetivos es definir cuál
configuración de red neuronal simulada tiene la mejor sensibilidad en cuanto a
la predicción de la información, es decir, cual proporciona resultados más
aproximados a los definidos como objetivos o targets, como se denominan en la
interfaz del software de análisis, MATLAB
®
. A continuación se presenta el script
general (en este caso el de la red neuronal 1, ANN_1) a partir del cual se
realizan las modificaciones a los parámetros de diseño de la red neuronal, las
líneas de código donde se muestran dichos parámetros se indican resaltadas
en color rojo.
% Solve an Autoregression Problem with External Input with a NARX
Neural Network
% Script generated by NTSTOOL
% Created Fri Nov 07 20:58:53 COT 2014
%
% This script assumes these variables are defined:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
65
%
% IN_ANN_1 - input time series.
% TAR_ANN_1 - feedback time series.
inputSeries = tonndata(IN_ANN_1,true,false);
targetSeries = tonndata(TAR_ANN_1,true,false);
% Create a Nonlinear Autoregressive Network with External Input
inputDelays = 1:2;
feedbackDelays = 1:2;
hiddenLayerSize = 5;
net = narxnet(inputDelays,feedbackDelays,hiddenLayerSize);
% Choose Input and Feedback Pre/Post-Processing Functions
% Settings for feedback input are automatically applied to feedback
output
% For a list of all processing functions type: help nnprocess
% Customize input parameters at: net.inputs{i}.processParam
% Customize output parameters at: net.outputs{i}.processParam
net.inputs{1}.processFcns = {'removeconstantrows','mapminmax'};
net.inputs{2}.processFcns = {'removeconstantrows','mapminmax'};
% Prepare the Data for Training and Simulation
% The function PREPARETS prepares timeseries data for a particular
network,
% shifting time by the minimum amount to fill input states and layer
states.
% Using PREPARETS allows you to keep your original time series data
unchanged, while
% easily customizing it for networks with differing numbers of delays,
with
% open loop or closed loop feedback modes.
[inputs,inputStates,layerStates,targets] =
preparets(net,inputSeries,{},targetSeries);
% Setup Division of Data for Training, Validation, Testing
% The function DIVIDERAND randomly assigns target values to training,
% validation and test sets during training.
% For a list of all data division functions type: help nndivide
net.divideFcn = 'divideblock'
;
% Divide data randomly
% The property DIVIDEMODE set to TIMESTEP means that targets are
divided
% into training, validation and test sets according to timesteps.
% For a list of data division modes type: help
nntype_data_division_mode
net.divideMode = 'value'; % Divide up every value
net.divideParam.trainRatio = 60/100;
net.divideParam.valRatio = 22/100;
net.divideParam.testRatio = 18/100;
% Choose a Training Function

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
66
% For a list of all training functions type: help nntrain
% Customize training parameters at: net.trainParam
net.trainFcn = 'trainlm'; % Levenberg-Marquardt
% Choose a Performance Function
% For a list of all performance functions type: help nnperformance
% Customize performance parameters at: net.performParam
net.performFcn = 'mse'; % Mean squared error
% Choose Plot Functions
% For a list of all plot functions type: help nnplot
% Customize plot parameters at: net.plotParam
net.plotFcns = {'plotperform','plottrainstate','plotresponse', ...
'ploterrcorr', 'plotinerrcorr'};
% Train the Network
[net,tr] = train(net,inputs,targets,inputStates,layerStates);
% Test the Network
outputs = net(inputs,inputStates,layerStates);
errors = gsubtract(targets,outputs);
performance = perform(net,targets,outputs)
% Recalculate Training, Validation and Test Performance
trainTargets = gmultiply(targets,tr.trainMask);
valTargets = gmultiply(targets,tr.valMask);
testTargets = gmultiply(targets,tr.testMask);
trainPerformance = perform(net,trainTargets,outputs)
valPerformance = perform(net,valTargets,outputs)
testPerformance = perform(net,testTargets,outputs)
% View the Network
view(net)
% Plots
% Uncomment these lines to enable various plots.
%figure, plotperform(tr)
%figure, plottrainstate(tr)
%figure, plotregression(targets,outputs)
%figure, plotresponse(targets,outputs)
%figure, ploterrcorr(errors)
%figure, plotinerrcorr(inputs,errors)
% Closed Loop Network
% Use this network to do multi-step prediction.
% The function CLOSELOOP replaces the feedback input with a direct
% connection from the outout layer.
netc = closeloop(net);
netc.name = [net.name ' - Closed Loop'];
view(netc)
[xc,xic,aic,tc] = preparets(netc,inputSeries,{},targetSeries);

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
67
yc = netc(xc,xic,aic);
closedLoopPerformance = perform(netc,tc,yc)
% Early Prediction Network
% For some applications it helps to get the prediction a timestep
early.
% The original network returns predicted y(t+1) at the same time it is
given y(t+1).
% For some applications such as decision making, it would help to have
predicted
% y(t+1) once y(t) is available, but before the actual y(t+1) occurs.
% The network can be made to return its output a timestep early by
removing one delay
% so that its minimal tap delay is now 0 instead of 1. The new network
returns the
% same outputs as the original network, but outputs are shifted left
one timestep.
nets = removedelay(net);
nets.name = [net.name ' - Predict One Step Ahead'];
view(nets)
[xs,xis,ais,ts] = preparets(nets,inputSeries,{},targetSeries);
ys = nets(xs,xis,ais);
earlyPredictPerformance = perform(nets,ts,ys)
Con este script se realiza el montaje y ejecución de las 84 arquitecturas de
redes neuronales. En la Tabla 5.1 se muestra el desempeño para cada red
neuronal en el Caso de Estudio 1, utilizando para la valoración y/o evaluación
los indicadores, error medio cuadrático (MSE) y coeficiente de correlación (R
2
),
en color verde se resalta la red neuronal con mejor desempeño para cada
algoritmo de entrenamiento utilizado. Por otro lado, la Gráfica 5.2 y la Gráfica
5.3 muestran mediante un diagrama de barras los valores obtenidos para el
error medio cuadrático y el coeficiente de correlación de cada una de las
arquitecturas analizadas.
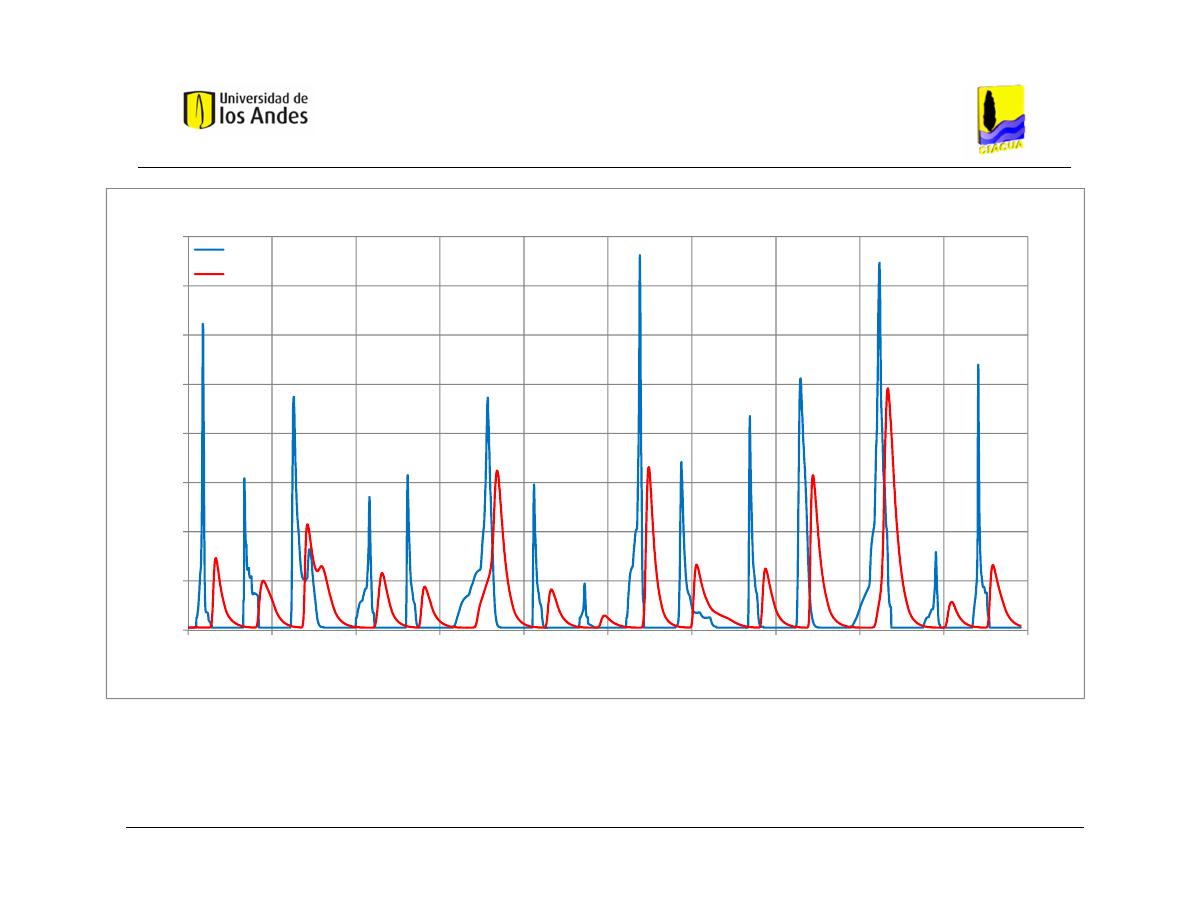
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
68
Gráfica 5.1Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso de Estudio 1 - Distribución 1.
0
200
400
600
800
1000
1200
1400
1600
0
50
100
150
200
250
300
350
400
450
500
C
a
u
d
a
l
(m
3
/s
)
Tiempo (Horas)
HIDROGRAMAS CASO DE ESTUDIO 1 - DISTRIBUCIÓN 1
Hidrogramas de Entrada
Hidrogramas de Salida

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
69
NOMBRE
TRAINING VALIDATON
TEST
TRINING
VALIDATON
TEST
TRAINING
VALIDATION
TEST
TOTAL
(%)
ANN_1
18.68
37.81
34.16
0.00
0.00
0.00
3.21
8.62
31.69
9.53
99.96
ANN_2
12.49
23.31
91.49
0.00
0.00
0.00
1.61
4.71
217.18
41.10
99.85
ANN_3
11.54
24.23
83.72
0.00
0.00
0.00
1.74
4.69
232.88
43.99
99.84
ANN_4
13.77
22.36
240.49
0.00
0.00
0.00
1.66
4.08
1269.56
230.42
99.10
ANN_5
13.20
24.59
29.82
0.00
0.00
0.00
2.00
4.76
29.57
7.57
99.97
ANN_6
10.86
24.47
133.31
0.00
0.00
0.00
1.81
4.74
462.07
85.30
99.68
ANN_7
7.80
17.53
73.94
0.00
0.00
0.00
0.81
2.00
117.23
22.03
99.90
ANN_8
8.34
16.26
124.18
0.00
0.00
0.00
0.79
3.01
430.90
78.70
99.66
ANN_9
18.02
36.86
51.29
0.00
0.00
0.01
3.69
8.30
64.54
15.66
99.94
ANN_10
16.25
32.15
85.25
0.00
0.00
0.00
2.56
7.84
150.71
30.39
99.88
ANN_11
17.72
20.92
52.12
0.00
0.00
0.00
2.02
4.97
72.77
15.40
99.94
ANN_12
16.68
37.36
158.98
0.00
0.00
0.01
6.02
10.73
1021.31
189.81
99.23
ANN_13
14.22
0
60.79
0.00
0
0.00
1.21
0
108.11
20.45
99.92
ANN_14
7.42
0
209.20
0.00
0
0.00
0.39
0
814.45
146.92
99.93
ANN_15
6.81
0
148.15
0.00
0
0.00
0.31
0
590.19
106.49
99.56
ANN_16
6.94
0
264.06
0.00
0
0.00
0.31
0
1182.90
213.18
99.10
ANN_17
15.68
0
106.65
0.00
0
0.00
1.66
0
197.56
36.92
99.85
ANN_18
7.17
0
71.14
0.00
0
0.00
0.41
0
70.28
12.99
99.95
ANN_19
6.30
0
58.38
0.00
0
0.00
0.33
0
55.46
10.25
99.96
ANN_20
7.59
0
176.89
0.00
0
0.00
0.40
0
579.14
104.57
99.62
ANN_21
32.68
0
49.94
0.00
0
0.00
3.84
0
59.87
13.92
99.95
ANN_22
9.01
0
132.30
0.00
0
0.00
0.74
0
551.81
99.93
99.63
ANN_23
9.21
0
104.14
0.00
0
0.00
0.83
0
189.23
34.74
99.84
ANN_24
7.02
0
181.20
0.00
0
0.00
0.38
0
672.83
121.42
99.47
ANN_25
140.74
172.32
210.45
0.02
0.03
0.11
278.45
417.92
1421.25
514.84
97.67
ANN_26
60.96
87.63
182.65
0.01
0.02
0.11
57.24
74.94
1044.00
238.75
98.95
ANN_27
124.71
83.53
248.71
0.02
0.01
0.03
128.72
138.81
1584.23
392.93
98.33
ANN_28
172.07
167.52
248.61
0.00
0.11
0.04
344.46
412.93
1951.39
648.77
97.65
ANN_29
159.19
182.06
401.32
0.01
0.01
0.37
349.75
470.51
6572.45
1496.40
95.56
ANN_30
131.61
163.76
292.23
0.00
0.04
0.03
417.71
466.05
4076.67
1086.96
95.28
ANN_31
132.86
159.98
542.38
0.03
0.04
0.00
197.76
289.07
7055.15
1452.18
93.55
ANN_32
159.65
176.70
214.75
0.03
0.02
0.09
357.13
488.86
1165.71
531.65
97.45
ANN_33
127.99
149.58
395.47
0.00
0.03
0.07
615.64
486.19
5701.84
1502.68
93.36
ANN_34
176.43
138.53
255.77
0.01
0.06
0.02
410.93
276.20
2661.45
786.38
96.32
ANN_35
124.40
139.55
218.92
0.00
0.02
0.00
209.26
300.05
1464.15
455.11
97.98
ANN_36
153.34
188.68
222.89
0.01
0.01
0.05
291.30
460.55
1627.50
569.05
97.45
ANN_37
169.51
163.32
374.91
0.04
0.00
0.03
488.99
482.69
4451.34
1200.83
94.44
ANN_38
113.26
72.86
356.63
0.00
0.03
0.01
75.53
63.59
3069.95
611.90
97.48
ANN_39
159.04
185.04
165.78
0.00
0.05
0.04
392.44
511.37
1060.50
538.86
97.61
ANN_40
61.70
52.69
528.06
0.00
0.00
0.03
35.90
41.75
3603.58
679.37
97.47
ANN_41
152.38
189.93
274.14
0.01
0.01
0.02
830.91
677.09
2909.51
1171.22
94.57
ANN_42
62.08
81.84
241.24
0.00
0.02
0.05
52.38
76.94
1904.18
391.10
98.46
ANN_43
86.94
100.91
132.21
0.01
0.01
0.10
89.19
88.37
561.56
174.04
99.18
ANN_44
170.11
95.99
302.10
0.00
0.12
0.15
356.39
217.36
3628.97
914.87
96.12
ANN_45
91.50
92.64
358.44
0.02
0.03
0.03
295.08
274.50
4621.78
1069.36
95.52
ANN_46
57.50
89.70
329.55
0.00
0.00
0.02
56.26
60.03
3761.17
723.97
97.00
ANN_47
53.93
74.66
283.01
0.00
0.00
0.01
34.71
50.80
2056.44
402.16
98.40
ANN_48
41.56
55.98
462.17
0.00
0.01
0.03
23.37
31.41
5548.11
1019.59
95.69
ERROR MAXIMO
ERROR MINIMO
DESEMPEÑO - MSE
X
`
-
⁄
X
`
-
⁄
X
3
-
⁄
c

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
70
Tabla 5.1 Resultados del proceso de entrenamiento para cada arquitectura – Caso de Estudio 1 –
Distribución 1.
NOMBRE
TRAINING VALIDATON
TEST
TRINING
VALIDATON
TEST
TRAINING
VALIDATION
TEST
TOTAL
(%)
ANN_49
203.46
233.31
403.52
0.01
0.00
0.02
755.62
850.93
5575.43
1644.16
92.39
ANN_50
150.95
163.12
405.79
0.01
0.00
0.00
506.11
480.50
3642.82
1065.09
95.89
ANN_51
345.48
222.41
565.26
0.03
0.06
0.01
1445.87
1543.26
5097.62
2124.61
91.73
ANN_52
372.72
184.67
384.66
0.01
0.01
0.02
1119.84
791.86
4736.37
1698.66
91.87
ANN_53
247.64
242.80
435.74
0.02
0.08
0.23
1581.69
912.12
6212.10
2267.85
89.21
ANN_54
148.30
201.61
442.86
0.01
0.03
0.03
796.69
807.47
7113.90
1936.16
91.45
ANN_55
132.59
187.05
238.08
0.01
0.05
0.07
404.43
515.17
1546.57
634.38
97.09
ANN_56
157.89
120.81
314.66
0.02
0.01
0.07
471.09
406.93
4274.45
1141.58
94.87
ANN_57
165.15
135.71
654.60
0.03
0.13
0.00
755.97
792.61
12778.84
2928.15
86.71
ANN_58
279.14
254.61
507.54
0.20
0.13
0.31
1881.40
1050.60
8864.37
2955.56
86.43
ANN_59
371.62
265.02
419.06
0.00
0.00
0.03
1022.41
913.60
7170.32
2105.09
90.38
ANN_60
229.89
177.36
494.23
0.04
0.07
0.03
1799.70
1288.53
10273.82
3212.59
86.04
ANN_61
158.57
194.16
364.74
0.01
0.01
0.06
408.99
557.70
4749.15
1222.94
94.71
ANN_62
64.54
53.94
543.51
0.01
0.01
0.02
102.95
80.02
8038.45
1526.30
93.30
ANN_63
100.65
53.27
347.81
0.01
0.04
0.02
155.74
83.87
2941.45
641.35
97.63
ANN_64
147.30
166.62
183.65
0.01
0.07
0.08
521.89
511.23
1077.30
619.52
97.42
ANN_65
246.72
240.36
435.50
0.00
0.08
0.11
1566.76
863.78
6464.23
2293.65
89.22
ANN_66
63.30
80.38
247.34
0.00
0.05
0.00
72.63
89.87
1633.97
357.46
98.40
ANN_67
163.77
184.64
317.67
0.00
0.03
0.00
403.37
510.81
2882.02
873.16
96.14
ANN_68
126.56
176.01
397.15
0.01
0.03
0.00
327.20
449.27
4076.28
1028.89
95.37
ANN_69
31.54
54.87
113.94
0.01
0.00
0.01
18.41
23.48
400.51
88.30
99.68
ANN_70
183.46
185.26
265.63
0.02
0.01
0.02
682.53
443.95
1503.44
777.80
96.28
ANN_71
140.73
163.93
272.14
0.08
0.02
0.02
438.49
498.77
2523.27
827.01
96.29
ANN_72
130.10
146.98
443.66
0.02
0.01
0.06
395.64
430.95
6139.48
1437.30
93.62
ANN_73
117.04
148.15
256.73
0.01
0.01
0.13
286.43
382.31
2127.96
639.00
97.12
ANN_74
125.70
139.93
386.89
0.01
0.04
0.00
309.95
392.11
3481.83
898.96
95.81
ANN_75
136.58
183.58
417.16
0.00
0.02
0.05
372.21
502.52
3983.01
1050.82
95.22
ANN_76
142.31
156.49
208.86
0.01
0.07
0.04
269.13
370.07
1311.49
478.96
98.07
ANN_77
41.04
46.91
151.85
0.00
0.00
0.01
26.29
26.45
753.35
157.19
99.37
ANN_78
149.51
204.57
401.50
0.03
0.10
0.27
397.11
580.46
4251.01
1131.15
95.36
ANN_79
136.01
188.23
245.16
0.03
0.01
0.04
433.20
506.56
1750.49
686.45
97.22
ANN_80
101.88
120.43
142.00
0.01
0.02
0.00
210.53
238.29
877.56
336.70
98.54
ANN_81
42.94
50.48
376.41
0.02
0.02
0.03
41.84
40.02
3362.99
639.25
97.61
ANN_82
164.06
162.81
202.29
0.01
0.00
0.02
460.50
405.25
1748.85
680.25
96.80
ANN_83
152.55
191.90
124.50
0.01
0.07
0.01
291.94
402.74
438.82
342.76
98.36
ANN_84
119.71
137.72
323.07
0.02
0.01
0.05
283.76
363.51
3922.09
956.21
95.79
ERROR MAXIMO
ERROR MINIMO
DESEMPEÑO - MSE
X
`
-
⁄
X
`
-
⁄
X
3
-
⁄
c

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
71
5.1.1 Desempeño de las Redes Neuronales – Caso de Estudio 1
Las arquitecturas con el mejor desempeño según el tipo de algoritmo de
entrenamiento, es decir, la mejor para cada uno de estos son las siguientes
redes: ANN_5, ANN_19, ANN_26, ANN_43, ANN_55, ANN_69 y ANN_77
(véase valores resaltados en la Tabla 5.1). La Gráfica 5.4 muestra el
comportamiento de los datos arrojados por estas redes en la etapa de prueba,
ya que dicha etapa define que tan bien es la generalización de una red
neuronal, con esto no se quiere decir que estas sean las arquitecturas con
mejor desempeño a nivel general.
En la Gráfica 5.2 y Gráfica 5.3 se observa que las redes neuronales que
presentan un mejor desempeño son las 24 primeras arquitecturas, es decir,
aquellas que utilizan el algoritmo de entrenamiento de Levenberg-Marquardt y
el algoritmo de Bayesian Regularization, pues son las que muestran un R
2
más
próximo al 100% y el error medio cuadrático más cercano a cero. En la Tabla
5.1 se nota además que, para la mayoría de redes con un mayor número de
neuronas ocultas, 20 en este caso, el desempeño mostrado en relación a las
demás es bajo, y que las configuraciones con dos capas ocultas muestran los
mejores valores de desempeño. En cuanto a los valores de desempeño más
bajos, estos se presentan en redes con el mayor número de neuronas y mayor
número de capas ocultas (3 capas ocultas).
Teniendo en cuenta lo anterior, se escogió para el análisis del Caso de Estudio
1 las cinco redes con el mejor desempeño, es decir, aquellas cuyo error medio
cuadrado (MSE) sea lo más cercano a cero y R
2
lo más cercano al 100%. Entre
las que utilizan el algoritmo de Levenberg-Marquardt se seleccionan la red
ANN_1 y la ANN_5, mientras que las mejores utilizando el algoritmo de
Bayesian Regularization son la ANN_18, ANN_19 y ANN_21. En la Gráfica 5.5
se muestra los resultados obtenidos con estas redes en la etapa de prueba; en
esta se aprecia que tan buenos son los resultados en comparación con los
targets. Al igual que para la gran mayoría de arquitecturas utilizadas, el mayor
grado de imprecisión se observa en la estimación de los caudales pico, tal como
se puede notar en la Gráfica 5.4 y Gráfica 5.5.
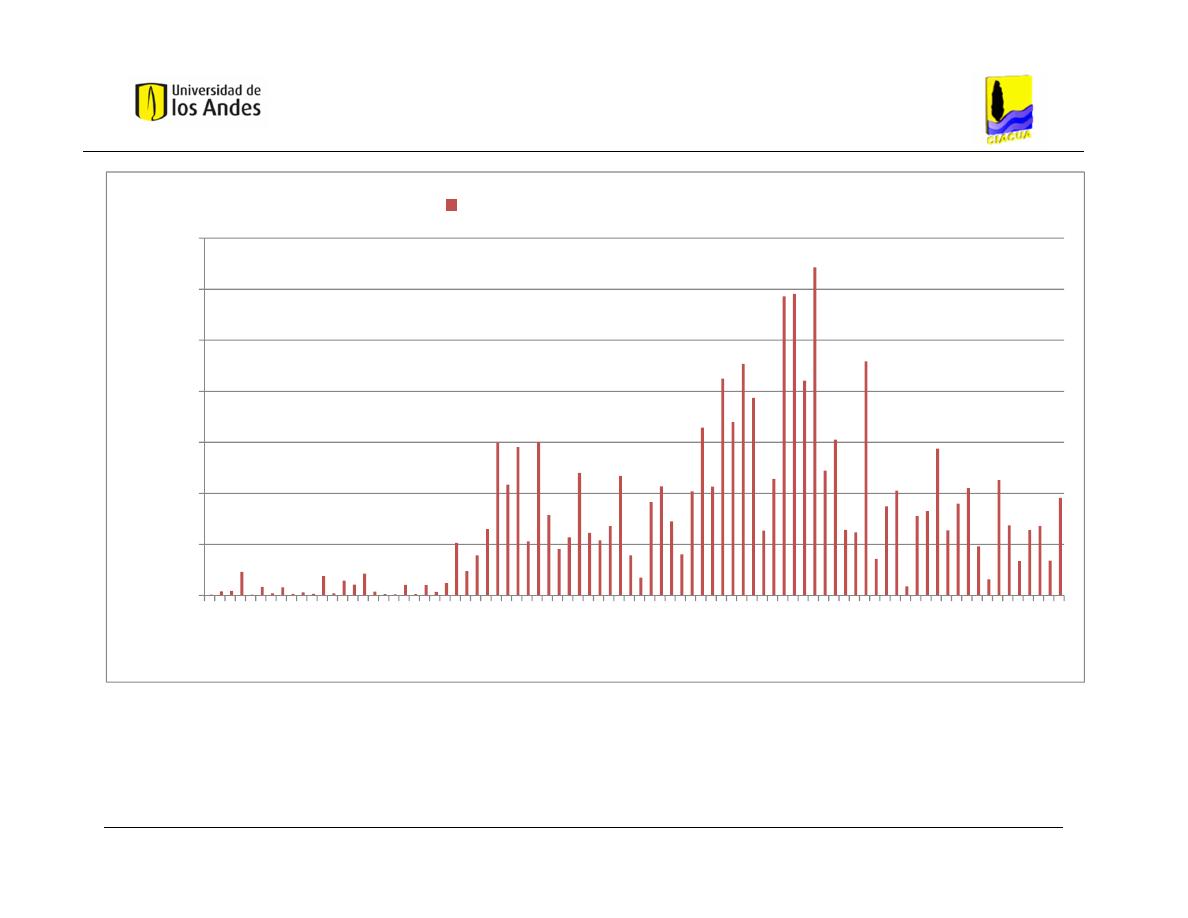
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
72
Gráfica 5.2. Desempeño (MSE) para cada una de la Redes neuronales analizadas – Caso de Estudio 1 – Distribución 1.
0
500
1000
1500
2000
2500
3000
3500
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 83
E
rr
o
m
e
d
io
C
u
a
d
ra
ti
co
(
(m
3
∕-
)
2
)
Arquitectura de la Red Neuronal
ERROR MEDIO CUADRATICO (MSE)
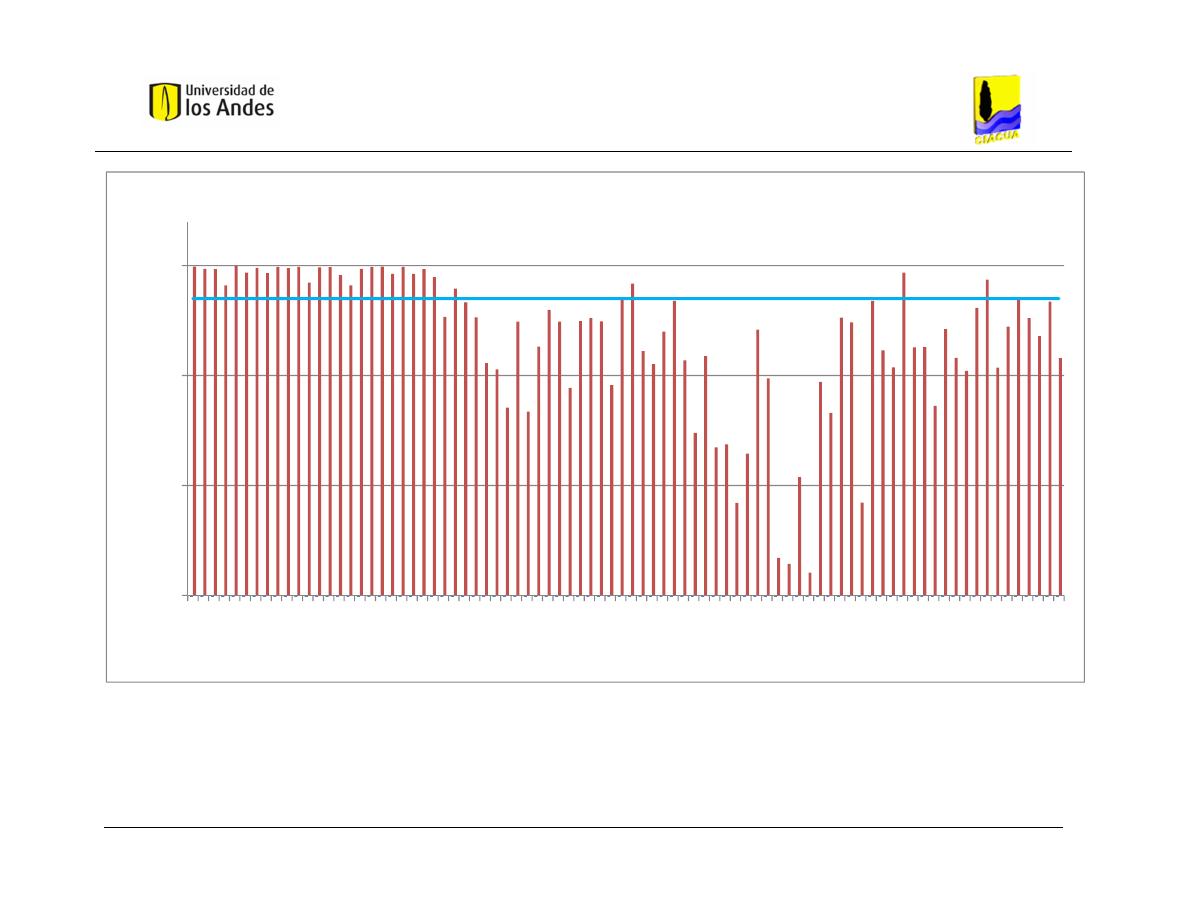
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
73
Gráfica 5.3. Coeficiente de correlación (R
2
) para cada una de las Redes neuronales analizadas – Caso de Estudio 1 – Distribución 1.
98.5%
85
90
95
100
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 83
C
o
e
fi
ci
e
n
te
d
e
C
o
rr
e
la
ci
ó
n
(
%
)
Arquitectura de la Red Neuronal
COEFICIENTE DE CORRELACIÓN (R
2
)
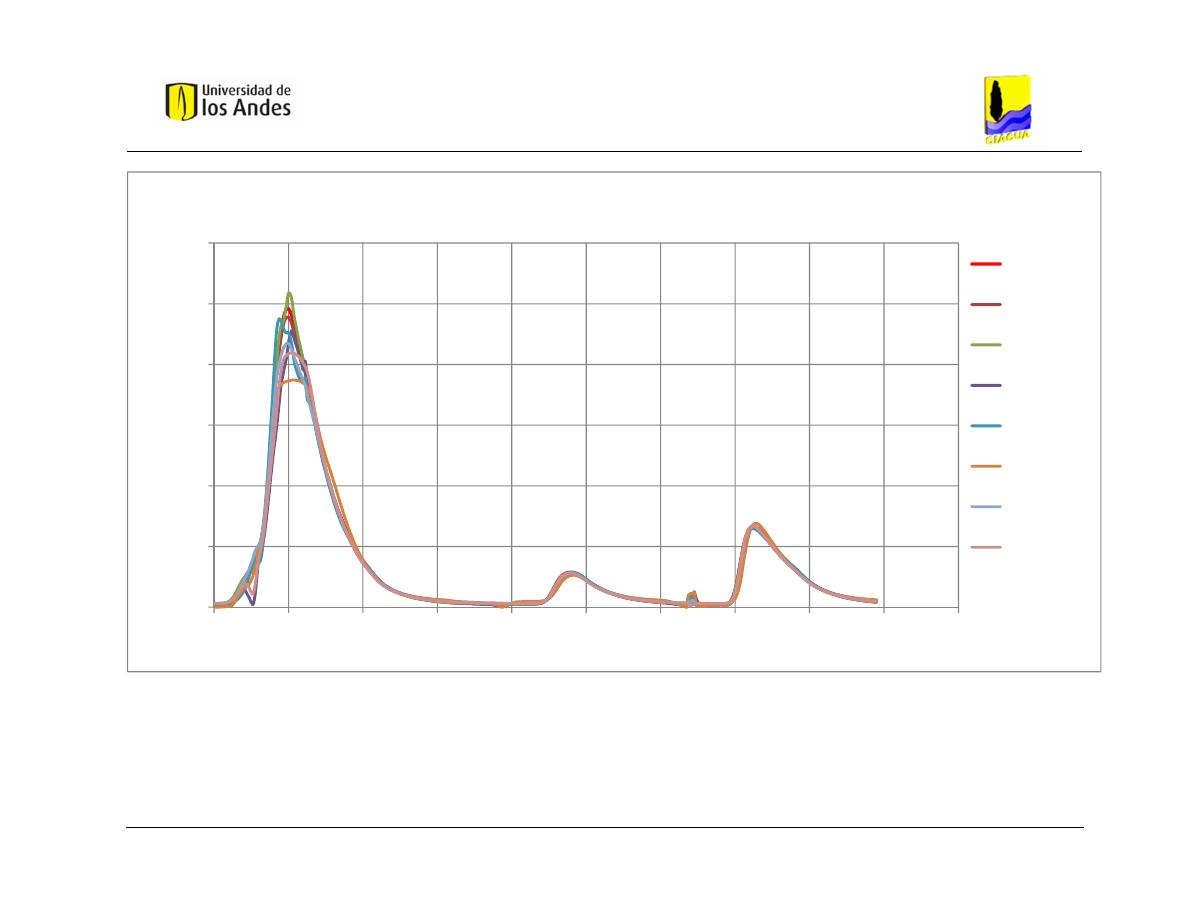
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
74
Gráfica 5.4. Redes neuronales con mejor desempeño según el algoritmo de entrenamiento – Caso de Estudio 1 – Distribución 1.
0
200
400
600
800
1000
1200
0
10
20
30
40
50
60
70
80
90
100
C
a
u
d
a
l
(m
3
/s
)
Tiempo (Horas)
REDES NEURONALES CON MEJOR DESEMPEÑO SEGÚN ALGORITMO DE
ENTRENAMIENTO - ETAPA DE PRUEBAS
Q Esperado
ANN_5
ANN_19
ANN_26
ANN_43
ANN_55
ANN_69
ANN_77
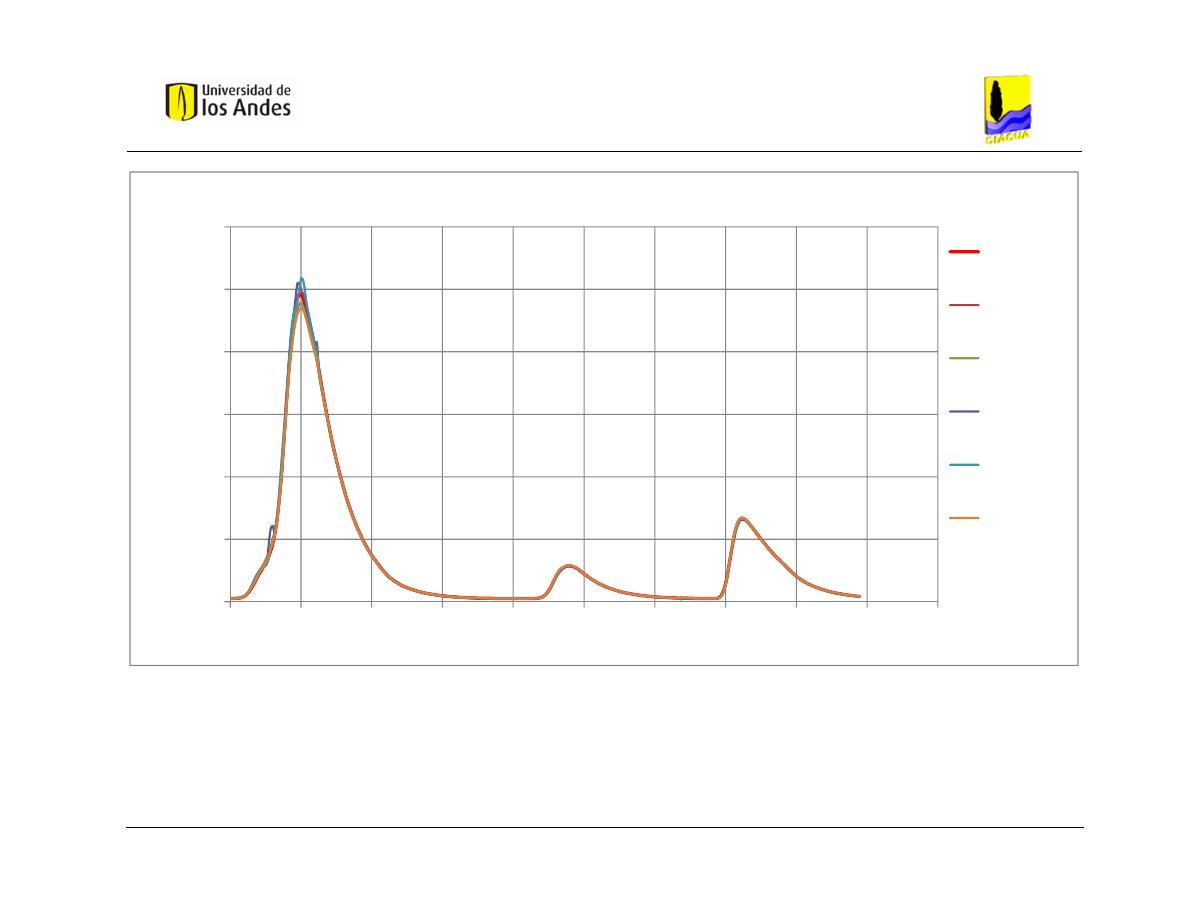
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
75
Gráfica 5.5. Redes neuronales con mejor desempeño en la etapa de prueba – Caso de Estudio 1 – Distribución 1.
0
200
400
600
800
1000
1200
0
10
20
30
40
50
60
70
80
90
100
C
a
u
d
a
l
(m
3
/s
)
Tiempo (Horas)
REDES NEURONALES CON MEJOR DESEMPEÑO - ETAPA DE PRUEBAS
Q Esperado
ANN_1
ANN_5
ANN_18
ANN_19
ANN_21

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
76
5.1.2 Correlación de Resultados – Caso de Estudio 1
Además de la evaluación de las redes mediante la función de desempeño MSE,
se tiene en cuenta también el valor del coeficiente de correlación (R
2
) para
estimar que arquitecturas muestran el mejor comportamiento. El criterio R
2
es,
en esencia, una medida global del rendimiento del modelo analizado con
respecto al del modelo de base, y está estrechamente relacionado con el de
mínimos cuadrados. Matemáticamente se pude expresar como lo muestra la
Ecuación 21.
c
'
@
+ '
'
@
Ecuación 21.
donde,
' [
d\;_E^J
+ [
eO\:I]E^J
[
d\;_E^J
= Caudal estimado por la red neuronal (m
3
/s)
[
eO\:I]E^J
= Caudal observado o medido en HEC-RAS (m
3
/s)
'
@
[
eO\:I]E^J
+ [
RIJ_:^J
[
RIJ_:^J
= Promedio de los caudales observados para el periodo de
Calibración escogido
La Tabla 5.1 y la Gráfica 5.3 muestran el valor del coeficiente de correlación
para cada una de las redes neuronales estudiadas; de estos resultados se
puede resaltar que el rango de variación de la respuesta para el total de redes
neuronales se encuentra entre el 86,04% y el 99,97%, y que para valores de R
2
superiores al 98.5% los resultados obtenidos tienen una buena aproximación y
son muy cercanos a los objetivos. Por otro lado, para las cinco arquitecturas
con mejor desempeño (ANN_1, ANN_5, ANN_18, ANN_19 y ANN_21) el
mínimo valor de R
2
se sitúa en 99,95% mostrando así el buen desempeño de
las redes. Las Gráfica 5.6 a Gráfica 5.10 muestran la forma como se
correlacionan los datos para cada una de estas.
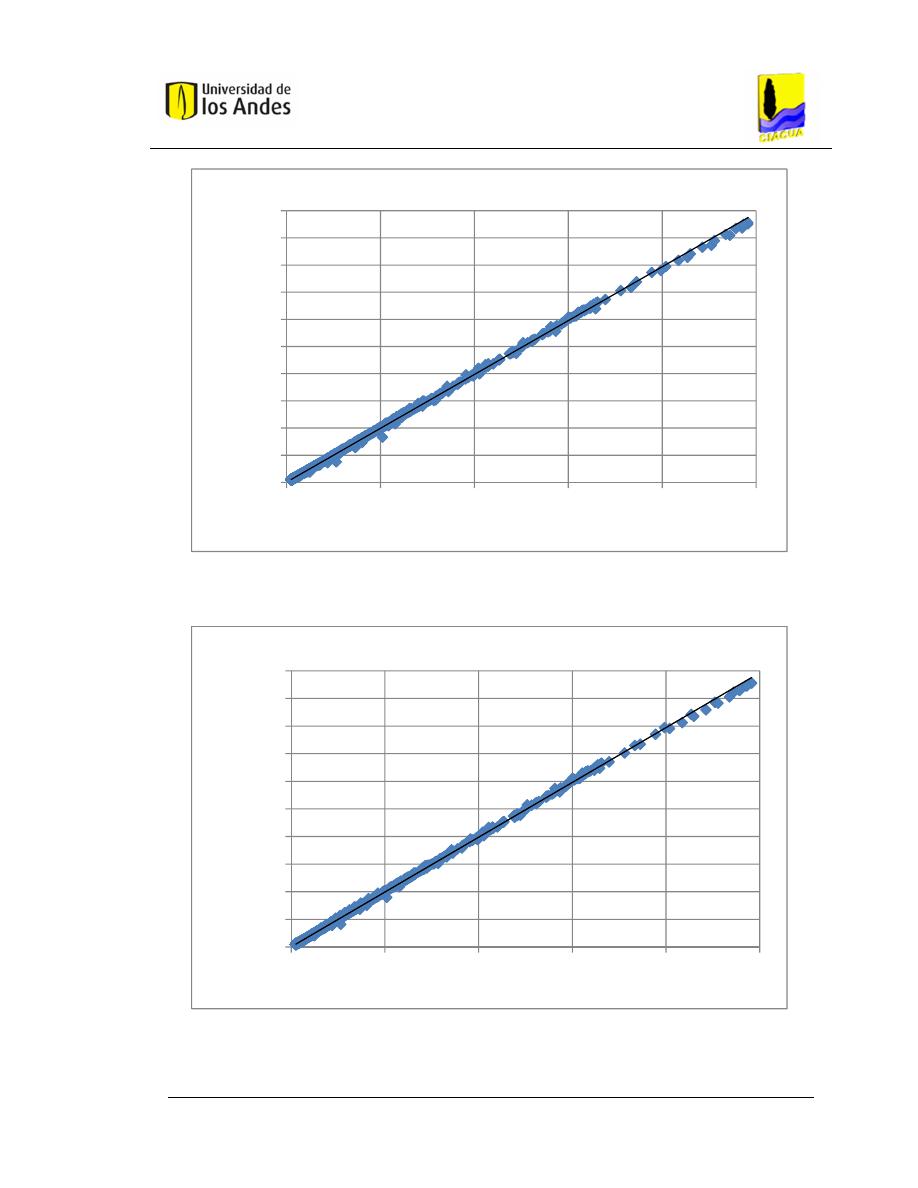
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
77
Gráfica 5.6 Correlación de datos para arquitectura 1 (ANN_1).
Gráfica 5.7 Correlación de datos para arquitectura 5 (ANN_5).
0
100
200
300
400
500
600
700
800
900
1000
0
200
400
600
800
1000
C
a
u
d
a
l
E
st
im
a
d
o
(
m
3
/s
)
Caudal Observado (m
3
/s)
ANN_1
0
100
200
300
400
500
600
700
800
900
1000
0
200
400
600
800
1000
C
a
u
d
a
l
E
st
im
a
d
o
(
m
3
/s
)
Caudal Observado (m
3
/s)
ANN_5
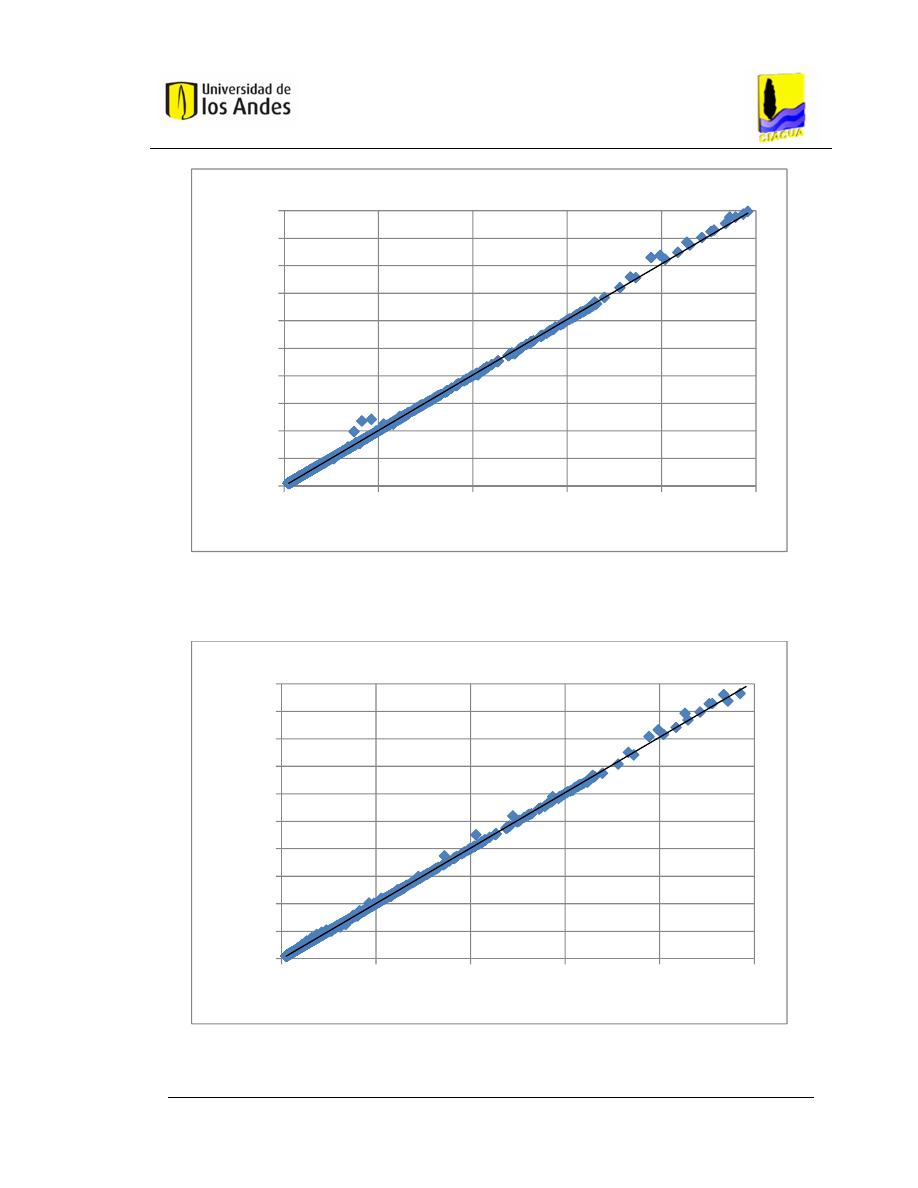
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
78
Gráfica 5.8 Correlación de datos para arquitectura 18 (ANN_18).
Gráfica 5.9 Correlación de datos para arquitectura 19 (ANN_19).
0
100
200
300
400
500
600
700
800
900
1000
0
200
400
600
800
1000
C
a
u
d
a
l
E
st
im
a
d
o
(
m
3
/s
)
Caudal Observado (m
3
/s)
ANN_18
0
100
200
300
400
500
600
700
800
900
1000
0
200
400
600
800
1000
C
a
u
d
a
l
E
st
im
a
d
o
(
m
3
/s
)
Caudal Observado (m
3
/s)
ANN_19
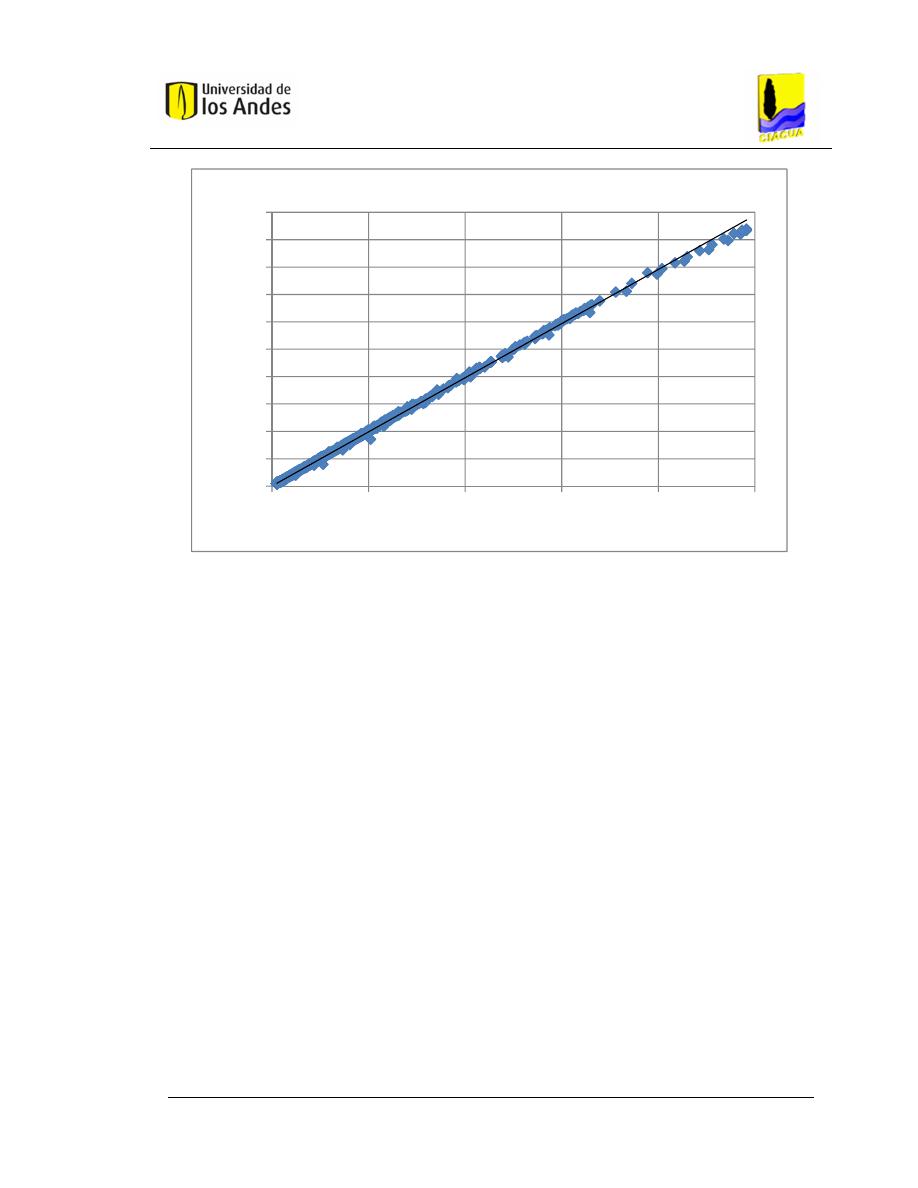
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
79
Gráfica 5.10 Correlación de datos para arquitectura 21 (ANN_21).
De las anteriores graficas se puede resaltar que el ajuste de los datos es muy
bueno en comparación con los datos buscados, lo que permite concluir que
estas redes neuronales serán las utilizadas para evaluar y analizar los modelos
de los Casos de Estudio 2 y 3.
5.1.3 Análisis de sensibilidad – Caso de Estudio 1
Con el fin de determinar si el desempeño de las redes neuronales artificiales se
ve influenciado por la variación de los parámetros hidráulicos de un canal, por
ejemplo, pendiente de fondo y coeficiente de rugosidad, se analizó la respuesta
proporcionada por la arquitectura con mejor desempeño, es decir, la ANN_5
para diferentes valores de pendiente y coeficiente de rugosidad del canal
utilizado como Caso de Estudio 1. Los resultados de esta evaluación se
muestran en la Tabla 5.2 y en la Tabla 5.3. Resaltado en color verde se observa
en ambas tablas el valor de los parámetros de diseño del modelo, mientras que
los demás valores corresponden a la variación hecha.
0
100
200
300
400
500
600
700
800
900
1000
0
200
400
600
800
1000
C
a
u
d
a
l
E
st
im
a
d
o
(
m
3
/s
)
Caudal Observado (m
3
/s)
ANN_21

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
80
PENDIENTE
(m/m)
DESEMPEÑO - MSE (m
3
/s)
2
DESEMPEÑO
TOTAL - MSE
(m
3
/s)
2
R
2
ENTRENAMIENTO VALIDACIÓN PRUEBA
0,00001
0,00366
0,00377
0,19880
0,03881 100,00%
0,00005
0,01705
0,02400
1,59252
0,30216
99,99%
0,0001
0,03813
0,05565
3,22481
0,61559
99,99%
0,0005
0,15948
0,27049
0,73701
0,28786 100,00%
0,001
2,76193
5,56715 780,47515
143,36746
99,48%
0,00125
4,12771
8,83056 457,08656
86,69493
99,69%
0,005
26,57324
46,96720 788,53342
168,21274
99,49%
Tabla 5.2 Análisis de sensibilidad mediante la ANN_5 para cambios en la pendiente de fondo –
Caso de Estudio 1 – Distribución 1.
Tabla 5.3 Análisis de sensibilidad mediante la ANN_5 para cambios en el coeficiente de rugosidad –
Caso de Estudio 1 – Distribución 1.
Analizando los resultados se observa que el desempeño de la red neuronal
evaluada (ANN_5) no presenta una gran variación con respecto a los valores
objetivos deseados para diferentes valores de pendiente y coeficiente de
rugosidad. Basados en los resultados obtenidos para el Caso de Estudio 1, se
puede afirmar que las ANN no son sensibles a variaciones de pendiente o
rugosidad, es decir, la respuesta de la red neuronal no se ve afectada.
ENTRENAMIENTO VALIDACIÓN
PRUEBA
0,010
0,001881
0,00373
0,37562
0,06956
100,00%
0,020
11,17993
19,22280
57,45330
21,27857
99,92%
0,035
5,92042
15,01370
38,39107
13,76566
99,95%
0,040
3,63528
9,41462
22,78181
8,35311
99,97%
0,045
3,03588
7,38430
181,94375
36,19595
99,87%
0,050
3,89135
8,51126
402,33391
76,62739
99,72%
0,070
1,91737
3,53659
9,97218
3,72346
99,98%
0,090
1,67460
2,63508
26,98906
6,44251
99,96%
0,100
1,36033
1,93455
18,63533
4,59616
99,97%
0,150
0,26091
0,35282
2,29447
0,64717
99,99%
0,200
0,10342
0,09854
10,83091
2,03330
99,98%
0,300
0,05757
0,02715
1,97001
0,39511
99,99%
0,500
0,001883
0,00375
0,37554
0,06955
100,00%
COEFICIENTE
DE RUGOSIDAD
(n)
DESEMPEÑO - MSE (m
3
/s)
2
DESEMPEÑO
TOTAL - MSE
(m
3
/s)
2
R
2
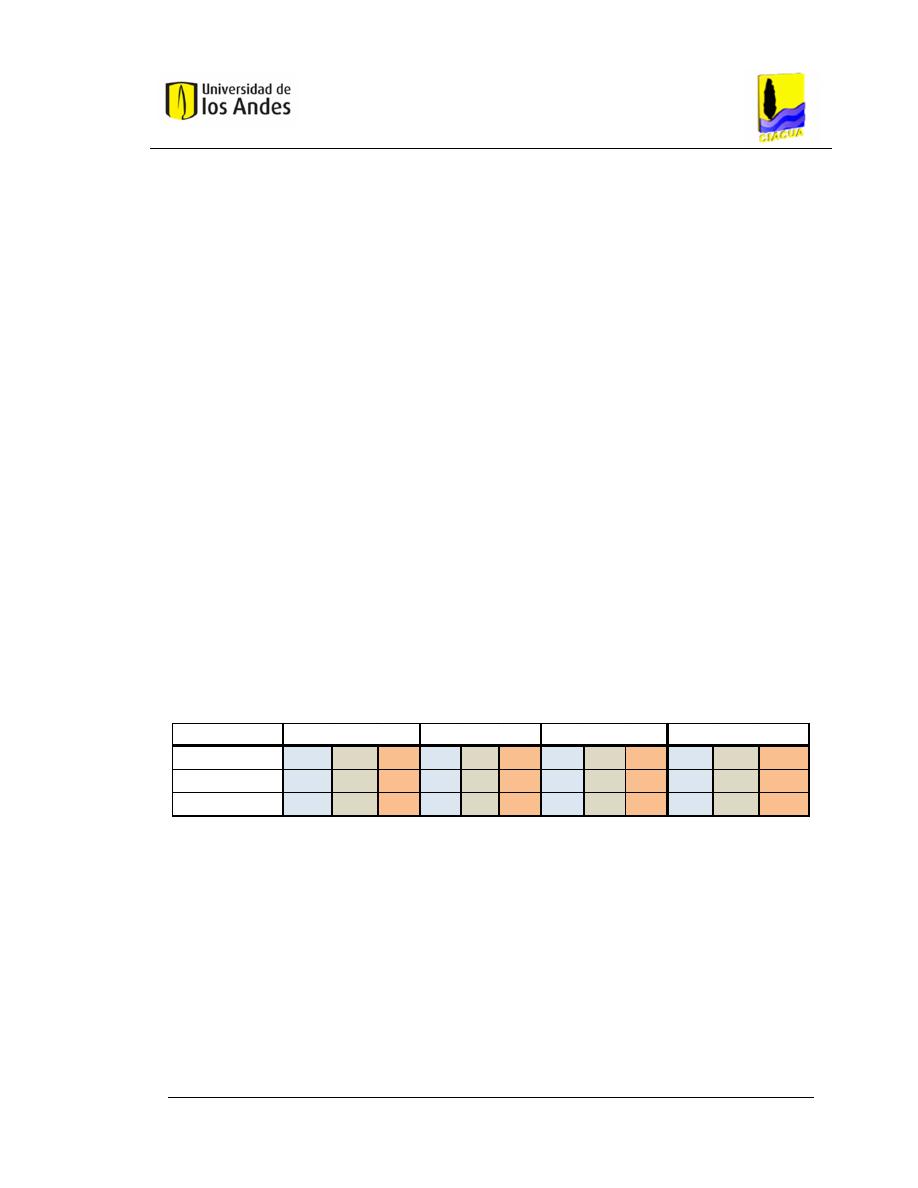
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
81
5.1.4 Otras distribuciones de hidrogramas - Caso de Estudio 1
Para continuar evaluando el desempeño de las redes neuronales artificiales
seleccionadas y el grado de acierto de la respuesta proporcionada por estas, en
esta etapa se busca determinar cómo afecta la configuración y la distribución de
la serie de hidrogramas de entrada la respuesta dada por las redes neuronales
o si por el contrario le es indiferente. Para esto, adicional a la serie de
hidrogramas evaluada inicialmente para el Caso de Estudio 1, se construyeron
dos series de hidrogramas de entrada diferentes entre sí; para lograr esto se
cambió la duración, la forma, la magnitud y localización de los picos de los
hidrogramas, lo que proporcionó series de hidrogramas diferentes que fueron
evaluados para cada una de las cinco arquitecturas de redes neuronales
escogidas. Para evitar que las redes neuronales analizadas quedaran
sobreentrenadas a causa de una inadecuada escogencia y disposición de los
datos de entrada, se evitó que hidrogramas con alturas o picos similares
quedaran juntos en un mismo grupo de datos, es decir, entrenamiento, prueba
y/o validación. La serie de hidrogramas analizada en principio se denominará
Distribución 1, mientas que las otras dos se denominaran Distribución 2 y
Distribución 3. En la Gráfica 5.11 se muestran los hidrogramas de entrada y
objetivo para la Distribución 2 mientras la Gráfica 5.12 muestra los hidrogramas
de entrada y objetivo para la Distribución 3. La forma como se realizó la división
de los datos de entrada para cada distribución de hidrogramas se muestra en la
Tabla 5.4.
Tabla 5.4 Porcentaje de datos para cada etapa según la distribución de hidrogramas – Caso de
Estudio 1.
DISTRIBUCIÓN
1
60%
49% 33% 22% 19% 20% 18% 32% 47% 100% 100% 100%
2
52%
43% 33% 23% 20% 20% 25% 37% 47% 100% 100% 100%
3
55%
44% 35% 20% 19% 20% 25% 37% 45% 100% 100% 100%
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
TOTAL
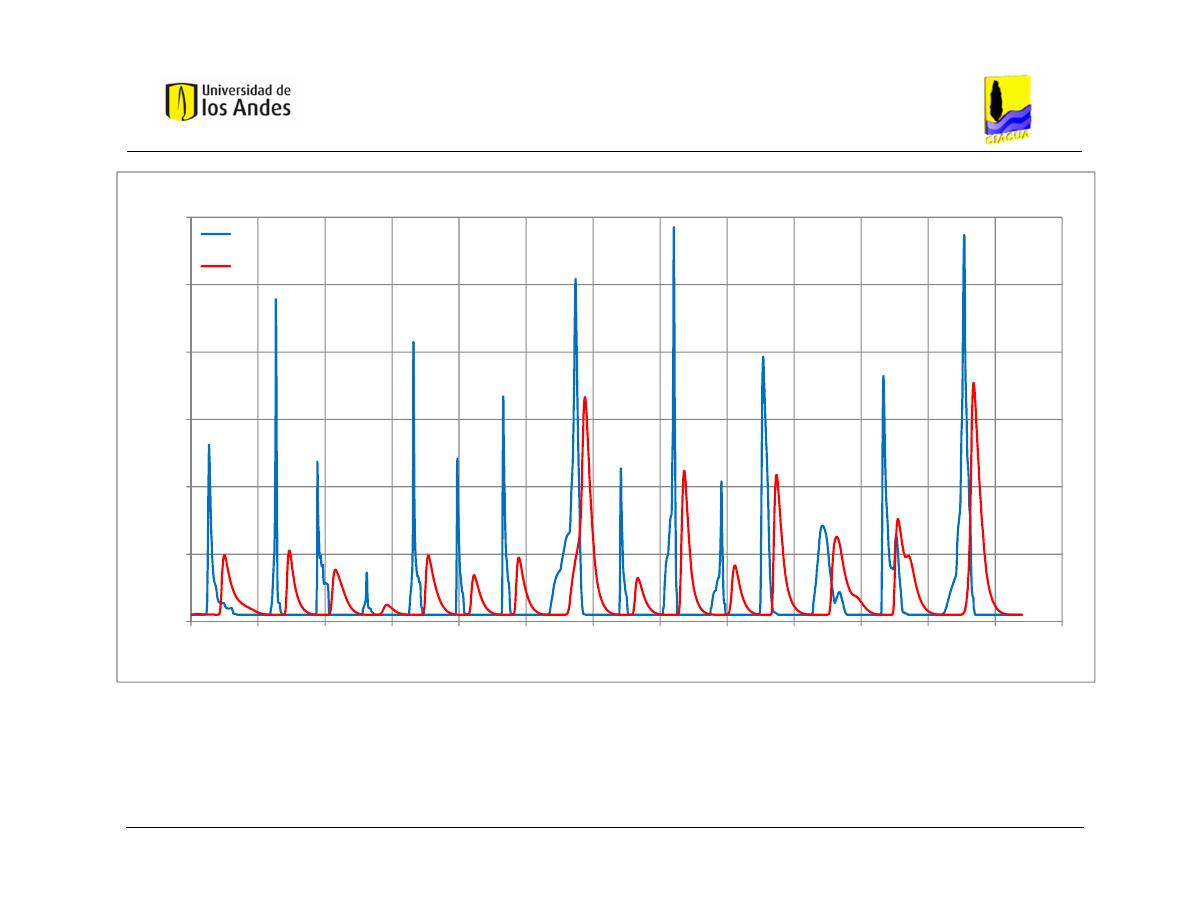
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
82
Gráfica 5.11 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso de Estudio 1 - Distribución 2.
0
100
200
300
400
500
600
0
50
100
150
200
250
300
350
400
450
500
550
600
650
C
a
u
d
a
l
(m
3
/s
)
Tiempo (Horas)
HIDROGRAMAS CASO DE ESTUDIO 1 - DISTRIBUCIÓN 2
Hidrogramas de Entrada
Hidrogramas de Salida
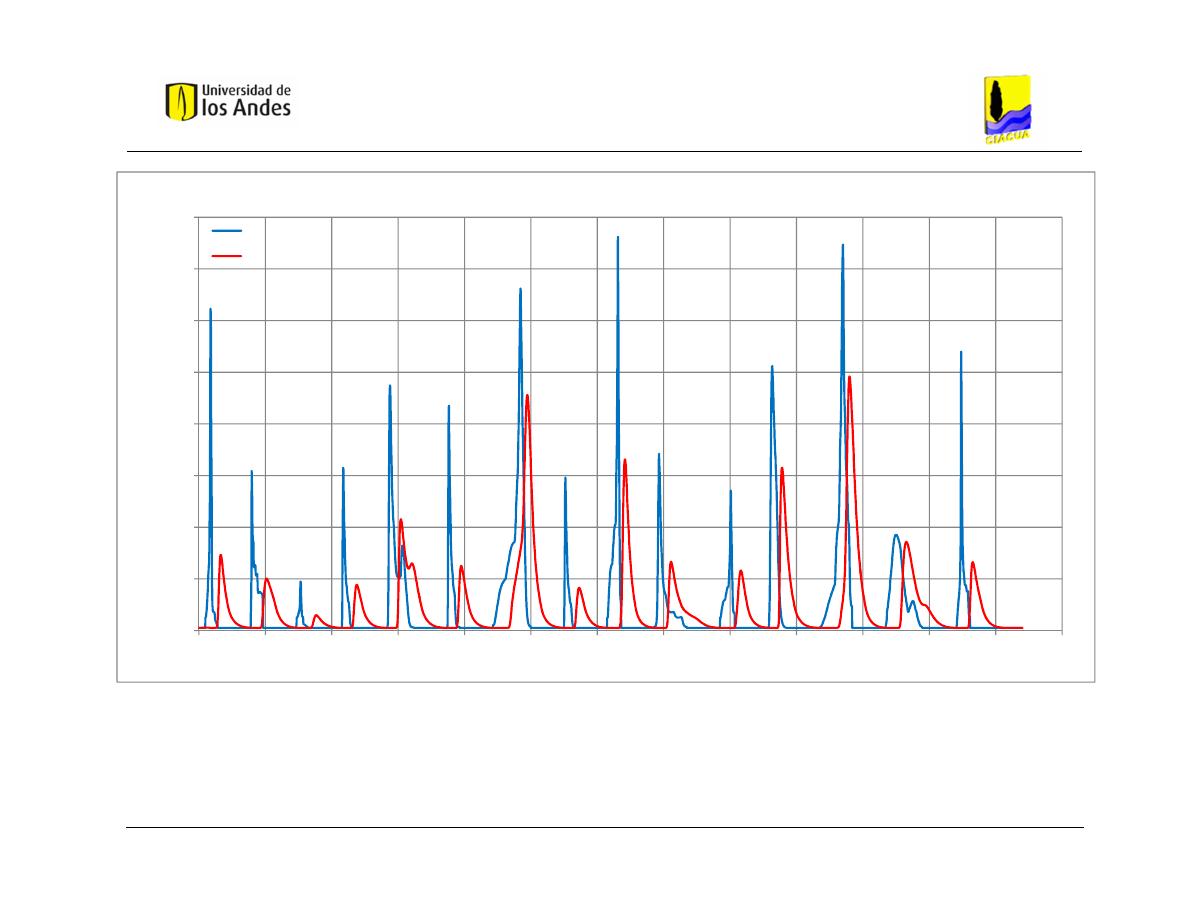
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
83
Gráfica 5.12 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso de Estudio 1 - Distribución 3.
0
200
400
600
800
1000
1200
1400
1600
0
50
100
150
200
250
300
350
400
450
500
550
600
650
C
a
u
d
a
l
(m
3
/s
)
Tiempo (Horas)
HIDROGRAMAS CASO DE ESTUDIO 1 - DISTRIBUCIÓN 3
Hidrogramas de Entrada
Hidrogramas de Salida

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
84
Para cada una de las tres series de hidrogramas se varió el porcentaje de datos
utilizados para entrenamiento, validación y prueba de las cinco redes
neuronales ya seleccionadas como de mejor desempeño (Véase Tabla 5.4). La
finalidad de este ejercicio fue la de conocer la forma como varía el desempeño
de las redes neuronales a medida que disminuye el porcentaje de datos
utilizados para entrenamiento y validación. En la Tabla 5.5 y en la Tabla 5.6 se
muestra el desempeño (MSE) y el coeficiente de correlación (R
2
) entre los datos
esperados y los arrojados por las redes neuronales según la distribución de los
datos en las series de hidrogramas.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
85
Tabla 5.5 Desempeño para cada una de las redes neuronales según la distribución de la serie de hidrogramas – Caso de Estudio 1.
60%
49%
33%
22%
19%
20%
18%
32%
47%
100%
100%
100%
ANN_1
3,215
1,891
1,487
8,615
4,383
22,676
31,691
85,755
232,471
9,529
29,201
114,287
ANN_5
1,995
3,077
2,251
4,762
4,011
71,661
29,568
111,260
392,258
7,567
37,873
199,436
ANN_18
0,412
0,317
0,189
-
-
-
70,276
101,340
134,023
12,988
32,644
63,091
ANN_19
0,327
0,356
0,153
-
-
-
55,455
66,682
191,048
10,250
21,580
89,873
ANN_21
3,837
2,569
1,947
-
-
-
59,870
88,070
79,010
13,923
29,929
38,166
52%
43%
33%
23%
20%
20%
25%
37%
47%
100%
100%
100%
ANN_1
0,141
1,985
3,714
0,492
23,290
53,977
0,337
16,891
49,033
0,271
11,761
35,066
ANN_5
0,394
10,544
0,077
0,385
119,275
26,696
0,981
105,967
22,250
0,539
67,597
15,822
ANN_18
0,014
0,011
0,017
-
-
-
2,766
2,603
1,903
0,702
0,970
0,904
ANN_19
0,029
0,013
0,010
-
-
-
4,121
3,577
1,808
1,052
1,332
0,855
ANN_21
0,155
0,155
0,129
-
-
-
0,319
0,440
0,796
0,196
0,261
0,443
55%
44%
35%
20%
19%
20%
25%
37%
45%
100%
100%
100%
ANN_1
2,760
2,869
3,354
6,652
4,810
23,460
2,898
8,021
11,396
3,573
5,144
10,994
ANN_5
2,529
2,217
1,575
6,771
4,399
60,991
6,235
5,770
55,149
4,304
3,946
37,566
ANN_18
0,526
0,643
0,427
-
-
-
41,311
39,697
20,286
10,722
15,093
9,364
ANN_19
0,307
0,286
0,251
-
-
-
42,147
95,584
121,180
10,767
35,546
54,669
ANN_21
3,831
2,781
3,549
-
-
-
3,721
5,611
5,343
3,803
3,828
4,356
CASO DE ESTUDIO 1 - MSE (m
3
/s)
2
DISTRIBUCIÓN
DE
HIDROGRÁMAS
N°1
RED
NEURONAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
TOTAL
TOTAL
DISTRIBUCIÓN
DE
HIDROGRÁMAS
N°2
RED
NEURONAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
DISTRIBUCIÓN
DE
HIDROGRÁMAS
N°3
RED
NEURONAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
TOTAL
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
86
Tabla 5.6 Coeficiente de correlación para cada una de las redes neuronales según la distribución de la serie de hidrogramas – Caso de Estudio 1.
60%
49%
33%
22%
19%
20%
18%
32%
47%
100%
100%
100%
ANN_1
99,98%
99,99%
99,98%
99,94%
99,97%
99,97%
99,98%
99,85%
99,72%
99,96%
99,89%
99,73%
ANN_5
99,99%
99,98%
99,97%
99,97%
99,98%
99,75%
99,98%
99,82%
99,44%
99,97%
99,86%
99,46%
ANN_18
100,00%
100,00%
100,00%
-
-
-
99,90%
99,82%
99,62%
99,95%
99,88%
99,73%
ANN_19
100,00%
100,00%
100,00%
-
-
-
99,92%
99,83%
99,51%
99,96%
99,90%
99,64%
ANN_21
99,98%
99,98%
99,98%
-
-
-
99,95%
99,85%
99,82%
99,95%
99,89%
99,85%
52%
43%
33%
23%
20%
20%
25%
37%
47%
100%
100%
100%
ANN_1
99,99%
99,64%
99,83%
99,98%
99,63%
98,80%
99,99%
99,55%
98,62%
99,99%
99,59%
98,75%
ANN_5
99,98%
98,16%
99,99%
99,99%
97,70%
99,44%
99,98%
97,24%
99,47%
99,98%
97,61%
99,50%
ANN_18
100,00%
100,00%
100,00%
-
-
-
99,94%
99,94%
99,95%
99,97%
99,97%
99,97%
ANN_19
100,00%
100,00%
100,00%
-
-
-
99,91%
99,93%
99,96%
99,96%
99,96%
99,97%
ANN_21
99,99%
99,99%
99,99%
-
-
-
99,99%
99,99%
99,98%
99,99%
99,99%
99,99%
55%
44%
35%
20%
19%
20%
25%
37%
45%
100%
100%
100%
ANN_1
99,99%
99,99%
99,95%
99,95%
99,97%
99,96%
99,99%
99,97%
99,97%
99,98%
99,98%
99,96%
ANN_5
99,99%
99,99%
99,98%
99,95%
99,97%
99,86%
99,98%
99,98%
99,78%
99,98%
99,98%
99,83%
ANN_18
100,00%
100,00%
100,00%
-
-
-
99,87%
99,86%
99,92%
99,95%
99,93%
99,96%
ANN_19
100,00%
100,00%
100,00%
-
-
-
99,89%
99,66%
99,51%
99,95%
99,84%
99,75%
ANN_21
99,98%
99,98%
99,98%
-
-
-
99,99%
99,98%
99,98%
99,98%
99,98%
99,98%
DISTRIBUCIÓN
DE
HIDROGRÁMAS
N°3
RED
NEURONAL
TOTAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
DISTRIBUCIÓN
DE
HIDROGRÁMAS
N°2
RED
NEURONAL
TOTAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
CASO DE ESTUDIO 1 - R
2
(%)
DISTRIBUCIÓN
DE
HIDROGRÁMAS
N°1
RED
NEURONAL
TOTAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
87
De los resultados del análisis mostrado en la Tabla 5.5 y en la Tabla 5.6 se
puede afirmar que, a medida que se disminuye el porcentaje de datos utilizados
para entrenamiento y validación de una red neuronal, en la mayoría de los
casos disminuye la precisión en la estimación de la respuesta en la etapa de
prueba por parte de las redes neuronales analizadas; dicho comportamiento se
puede apreciar en la forma como decrece el rendimiento (MSE) y el coeficiente
de correlación (R
2
) de los datos o series de hidrogramas utilizados en la etapa
de prueba.
Esta afirmación se aprecia con mayor claridad en la columna que muestra el
coeficiente de correlación y el desempeño total de las redes neuronales.
Además de lo anterior se puede concluir que la distribución de hidrogramas N°2
es la que muestra la respuesta de las redes neuronales con el error medio
cuadrado (MSE) más bajo de las tres, siendo las arquitecturas ANN_5, ANN_18
y ANN_19 las que producen un hidrograma de salida con mayor distorsión para
las tres distribuciones si se compara con la salida deseada (Targets), con un
coeficiente de correlación (R
2
) mínimo de 97,24% en la etapa de prueba. Una
causa probable del menor desempeño podría ser el hecho de que la serie de
hidrogramas en el grupo para entrenamiento y validación no es lo
suficientemente variada como para que las redes simulen de forma satisfactoria
los hidrogramas de la etapa de prueba.
En el ANEXO A se muestran los resultados de las simulaciones realizadas en la
etapa de prueba y los errores de las redes neuronales evaluadas para las
Distribuciones 1, 2 y 3. En las gráficas del anexo se puede apreciar que la
mayor dificultad para las redes neuronales del Caso de Estudio 1 se presenta
cuando estas requieren simular hidrogramas con picos altos.
5.2 CASO DE ESTUDIO 2
Como se mencionó en el Capítulo 4, el Caso de Estudio 2 es un hidrosistema
conformado por un cauce principal y dos afluentes (Véase Figura 4.4). Para el
montaje del modelo en MATLAB
®
, esta condición indica una ANN de 3
entradas, siendo estas, los hidrogramas de los dos afluentes y de la entrada al
tramo de estudio y 1 salida, que en este caso es el hidrograma en la descarga
del tramo principal.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
88
Para este caso de estudio los análisis realizados son similares a los del Caso
de Estudio 1, salvo que en este no se evaluó el comportamiento de las 84 ANN
mencionadas en la Tabla 4.2, sino que se consideró para análisis únicamente
las redes neuronales ya definidas como de mejor desempeño (ANN_1, ANN_5,
ANN_18, ANN_19 y ANN_21). El análisis de sensibilidad a cambios de
pendiente y rugosidad también se omitió, pues en el Caso de Estudio 1 se
concluyó que la respuesta de las redes neuronales artificiales no se ve afectada
por el cambio de dichas variables.
Igual que para el Caso de Estudio 1, en este también se generaron 3 series de
hidrogramas diferentes, la Distribución 1 se refiere a la condición inicial de
análisis, mientras que las Distribuciones 2 y 3, son variaciones de esta en
cuanto a la localización, altura de los picos, duración y forma de los
hidrogramas de entrada. La Gráfica 5.13, Gráfica 5.14 y la Gráfica 5.15
muestran las series de hidrogramas para cada una de las 3 distribuciones. La
forma como se realizó la división de los datos de entrada para cada serie de
hidrogramas se muestra en la Tabla 5.7.
Tabla 5.7 Porcentaje de datos para cada etapa según la distribución de hidrogramas – Caso de
Estudio 2.
DISTRIBUCIÓN
1
63%
50% 37% 15% 19% 19% 22% 31% 44% 100% 100% 100%
2
58%
48% 37% 18% 22% 18% 24% 30% 45% 100% 100% 100%
3
58%
51% 36% 18% 18% 15% 24% 31% 49% 100% 100% 100%
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
TOTAL
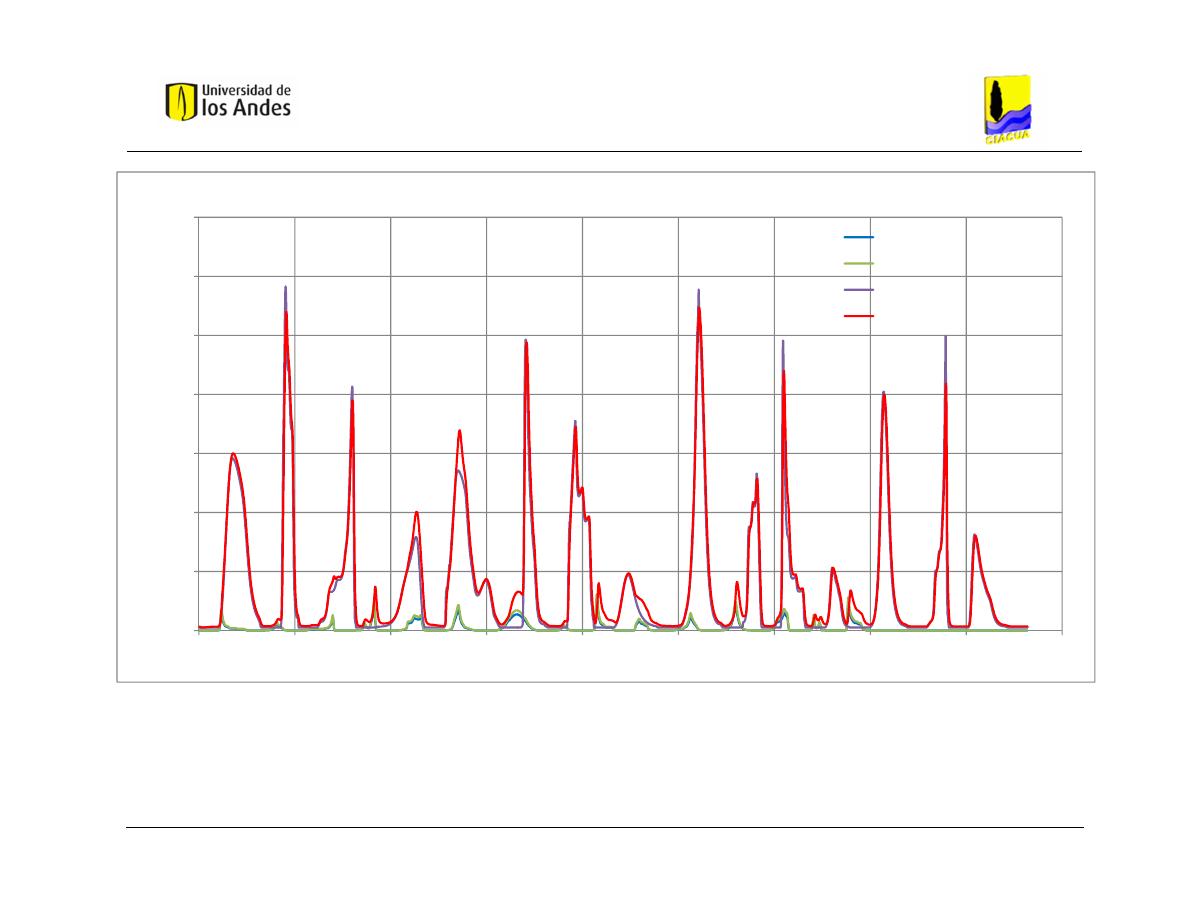
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
89
Gráfica 5.13 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso de Estudio 2 – Distribución 1.
0
20
40
60
80
100
120
140
0
50
100
150
200
250
300
350
400
450
C
a
u
d
a
l
(m
3
/s
)
Tiempo (Horas)
HIDROGRAMAS CASO DE ESTUDIO 2 - DISTRIBUCIÓN 1
Hidrogramas de Entrada 1
Hidrogramas de Entrada 2
Hidrogramas de Entrada 3
Hidrogramas de Salida
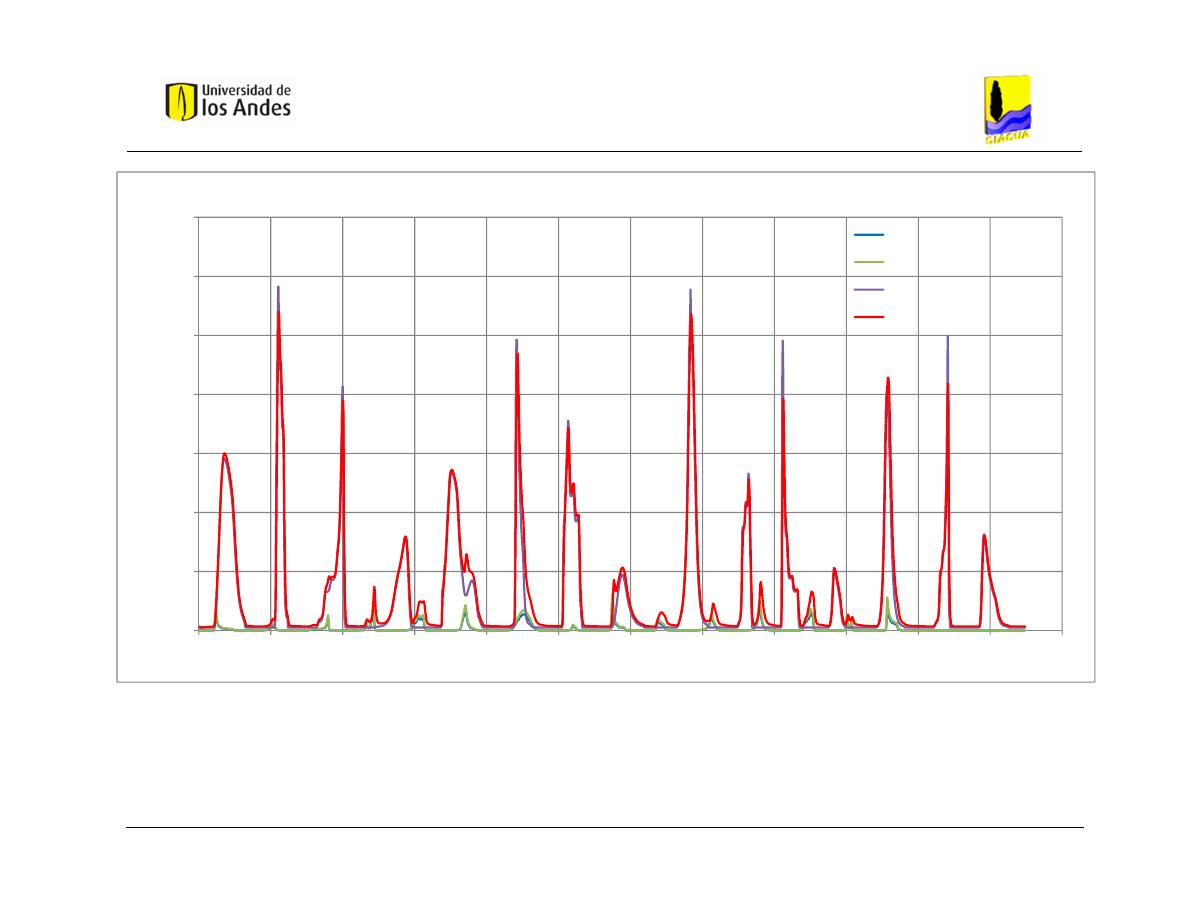
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
90
Gráfica 5.14 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso de Estudio 2 – Distribución 2.
0
20
40
60
80
100
120
140
0
50
100
150
200
250
300
350
400
450
500
550
600
C
a
u
d
a
l
(m
3
/s
)
Tiempo (Horas)
HIDROGRAMAS CASO DE ESTUDIO 2 - DISTRIBUCIÓN 2
Hidrogramas de Entrada 1
Hidrogramas de Entrada 2
Hidrogramas de Entrada 3
Hidrogramas de Salida
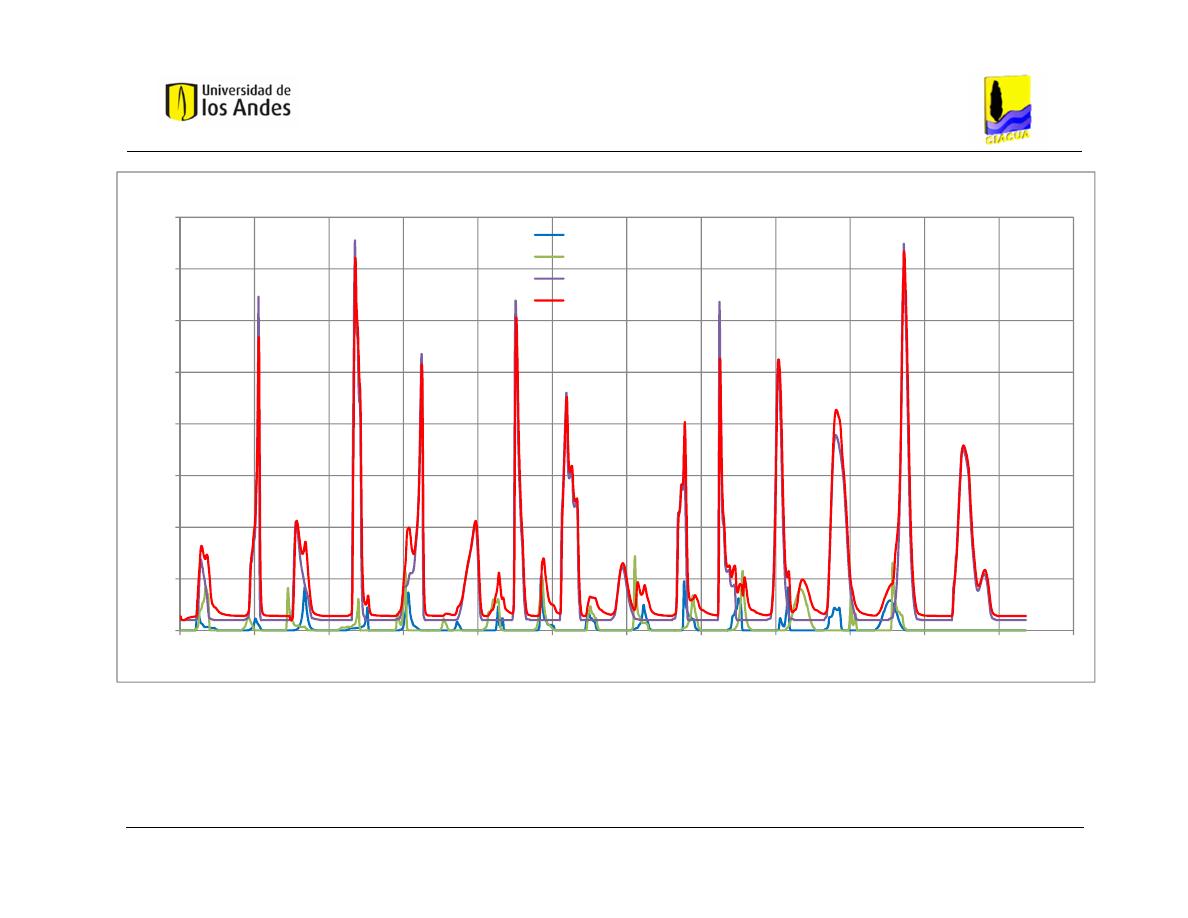
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
91
Gráfica 5.15 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso de Estudio 2 – Distribución 3.
0
5
10
15
20
25
30
35
40
0
50
100
150
200
250
300
350
400
450
500
550
600
C
a
u
d
a
l
(m
3
/s
)
Tiempo (Horas)
HIDROGRAMAS CASO DE ESTUDIO 2 - DISTRIBUCIÓN 3
Hidrogramas de Entrada 1
Hidrogramas de Entrada 2
Hidrogramas de Entrada 3
Hidrogramas de Salida

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
92
Para cada una de las tres distribuciones de hidrogramas, como se mencionó
anteriormente, se varió el porcentaje de datos utilizados para entrenamiento,
validación y prueba. En la Tabla 5.8 y en la Tabla 5.9 se muestra el desempeño
(MSE) y el coeficiente de correlación (R
2
) entre los datos esperados y los
arrojados por las redes neuronales. Igual que para el Caso de Estudio 1, se
puede afirmar que, a medida que se disminuye el porcentaje de datos utilizados
para entrenamiento y validación de una red neuronal, en la mayoría de los
casos disminuye la precisión en la estimación de la respuesta en la etapa de
prueba por parte de las redes neuronales analizadas; esta afirmación se aprecia
con mayor claridad en la columna que muestra el coeficiente de correlación y el
desempeño total de las redes neuronales, donde el MSE aumenta y el
coeficiente de correlación disminuye.
Además de lo anterior se puede concluir que la distribución de hidrogramas N°3
es la que muestra la respuesta de las redes neuronales con el error medio
cuadrado (MSE) más bajo de las tres, siendo las arquitecturas ANN_18 y
ANN_19 las que producen un hidrograma de salida con mayor distorsión para
las tres distribuciones si se compara con la salida deseada (Targets), con un
coeficiente de correlación (R
2
) mínimo de 94,65% en la etapa de prueba.
En el ANEXO B se muestran los resultados de las simulaciones realizadas en la
etapa de prueba y los errores de las redes neuronales evaluadas para las
Distribuciones 1, 2 y 3. Igual que para el Caso de Estudio 1, la respuesta de las
redes neuronales en este caso presentan las mayores distorsiones al momento
de simular los picos de los hidrogramas, pues estos se desarrollan en poco
tiempo y para valores de caudal altos.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
93
Tabla 5.8 Desempeño para cada una de las redes neuronales según la distribución de la serie de hidrogramas – Caso de Estudio 2.
63%
50%
37%
15%
19%
19%
22%
31%
44%
100%
100%
100%
ANN_1
0,272
0,306
0,214
0,435
0,204
0,271
0,837
0,717
0,416
0,420
0,414
0,314
ANN_5
0,285
0,325
0,326
0,416
0,144
0,239
0,843
0,652
0,606
0,427
0,391
0,433
ANN_18
0,070
0,123
0,045
-
-
-
1,044
1,010
4,684
0,284
0,397
2,086
ANN_19
0,035
0,046
0,022
-
-
-
2,662
6,136
2,985
0,612
1,932
1,326
ANN_21
0,267
0,204
0,199
-
-
-
0,686
0,783
2,432
0,358
0,383
1,181
58%
48%
37%
18%
22%
18%
24%
30%
45%
100%
100%
100%
ANN_1
0,189
0,146
0,256
0,322
0,136
0,347
0,586
0,437
0,539
0,308
0,232
0,400
ANN_5
0,185
0,235
0,243
0,328
0,160
0,272
0,588
2,185
2,529
0,308
0,804
1,277
ANN_18
0,100
0,067
0,039
-
-
-
0,774
9,771
3,309
0,244
2,964
1,510
ANN_19
0,066
0,034
0,021
-
-
-
1,779
14,755
7,557
0,465
4,443
3,412
ANN_21
0,240
0,177
0,127
-
-
-
0,452
0,559
0,706
0,248
0,292
0,387
58%
51%
36%
18%
18%
15%
24%
31%
49%
100%
100%
100%
ANN_1
0,016
0,026
0,041
0,035
0,024
0,071
0,021
0,033
0,089
0,020
0,028
0,069
ANN_5
0,039
0,032
0,043
0,025
0,032
0,036
0,030
0,024
0,030
0,034
0,029
0,036
ANN_18
0,006
0,006
0,003
-
-
-
0,040
0,153
0,364
0,014
0,052
0,180
ANN_19
0,002
0,002
0,002
-
-
-
0,226
1,048
0,526
0,056
0,326
0,258
ANN_21
0,018
0,028
0,019
-
-
-
0,010
0,020
0,017
0,016
0,025
0,018
CASO DE ESTUDIO 2 - MSE (m
3
/s)
2
DISTRIBUCIÓN DE
HIDROGRÁMAS
N°1
RED
NEURONAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
TOTAL
DISTRIBUCIÓN DE
HIDROGRÁMAS
N°2
RED
NEURONAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
TOTAL
DISTRIBUCIÓN DE
HIDROGRÁMAS
N°3
RED
NEURONAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
TOTAL
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
94
Tabla 5.9 Coeficiente de correlación para cada una de las redes neuronales según la distribución de la serie de hidrogramas – Caso de Estudio 2.
63%
50%
37%
15%
19%
19%
22%
31%
44%
100%
100%
100%
ANN_1
99,95%
99,94%
99,96%
99,88%
99,96%
99,94%
99,74%
99,77%
99,90%
99,91%
99,91%
99,93%
ANN_5
99,95%
99,93%
99,93%
99,86%
99,97%
99,94%
99,72%
99,79%
99,86%
99,90%
99,91%
99,90%
ANN_18
99,99%
99,98%
99,99%
-
-
-
99,66%
99,67%
98,93%
99,94%
99,91%
99,53%
ANN_19
99,99%
99,99% 100,00%
-
-
-
99,12%
98,18%
99,32%
99,86%
99,58%
99,70%
ANN_21
99,94%
99,96%
99,96%
-
-
-
99,77%
99,75%
99,45%
99,92%
99,91%
99,74%
58%
48%
37%
18%
22%
18%
24%
30%
45%
100%
100%
100%
ANN_1
99,95%
99,97%
99,94%
99,93%
99,96%
99,91%
99,77%
99,83%
99,84%
99,91%
99,94%
99,89%
ANN_5
99,95%
99,94%
99,94%
99,93%
99,96%
99,93%
99,78%
99,33%
99,35%
99,92%
99,79%
99,67%
ANN_18
99,98%
99,99%
99,99%
-
-
-
99,75%
96,21%
99,03%
99,93%
99,18%
99,58%
ANN_19
99,99%
99,99%
99,99%
-
-
-
99,33%
94,65%
97,79%
99,87%
98,79%
99,06%
ANN_21
99,95%
99,96%
99,97%
-
-
-
99,83%
99,79%
99,79%
99,93%
99,92%
99,89%
58%
51%
36%
18%
18%
15%
24%
31%
49%
100%
100%
100%
ANN_1
99,95%
99,92%
99,87%
99,90%
99,86%
99,83%
99,96%
99,96%
99,79%
99,95%
99,93%
99,81%
ANN_5
99,87%
99,90%
99,86%
99,92%
99,83%
99,91%
99,95%
99,95%
99,92%
99,91%
99,92%
99,90%
ANN_18
99,98%
99,98%
99,99%
-
-
-
99,93%
99,80%
99,08%
99,96%
99,88%
99,51%
ANN_19
99,99%
99,99% 100,00%
-
-
-
99,58%
97,95%
98,73%
99,85%
99,10%
99,31%
ANN_21
99,94%
99,90%
99,94%
-
-
-
99,98%
99,96%
99,96%
99,96%
99,93%
99,95%
TOTAL
DISTRIBUCIÓN DE
HIDROGRÁMAS
N°1
CASO DE ESTUDIO 2 - R
2
(%)
DISTRIBUCIÓN DE
HIDROGRÁMAS
N°2
RED
NEURONAL
TOTAL
TOTAL
RED
NEURONAL
ENTRENAMIENTO
DISTRIBUCIÓN DE
HIDROGRÁMAS
N°3
RED
NEURONAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
VALIDACIÓN
PRUEBA
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
95
5.3 CASO DE ESTUDIO 3
El Caso de Estudio 3 es un hidrosistema conformado por un cauce principal y
un tributario (Véase Figura 4.6). Para el montaje del modelo en MATLAB
®
, esta
condición indica que se debe configurar una ANN de 2 entradas, siendo estas,
las series de hidrogramas del cauce tributario y del cauce principal y 1 salida
que corresponde a la serie de hidrogramas en la descarga del tramo principal.
Para este caso de estudio los análisis realizados son similares a los descritos
paras los demás casos, es decir, se consideró para análisis únicamente las
redes neuronales ANN_1, ANN_5, ANN_18, ANN_19 y ANN_21. Al igual que
en los dos casos anteriores se generaron 3 series de hidrogramas, donde, la
Distribución 1 hace referencia a la condición inicial de estudio, mientras que las
Distribuciones 2 y 3, son variaciones de esta en cuanto a la localización, altura
de los picos, duración y forma de los hidrogramas de entrada. La Gráfica 5.16,
Gráfica 5.17 y Gráfica 5.18, muestran las series de hidrogramas de entrada y
salida para cada una de las 3 distribuciones. La forma como se realizó la
división de los datos de entrada para cada distribución de hidrogramas se
muestra en la Tabla 5.10.
Tabla 5.10 Porcentaje de datos para cada etapa según la distribución de hidrogramas – Caso de
Estudio 3.
DISTRIBUCIÓN
1
64%
50% 36% 16% 19% 21% 20% 31% 43% 100% 100% 100%
2
62%
50% 38% 17% 18% 18% 21% 32% 44% 100% 100% 100%
3
60%
48% 35% 17% 17% 19% 23% 35% 46% 100% 100% 100%
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
TOTAL
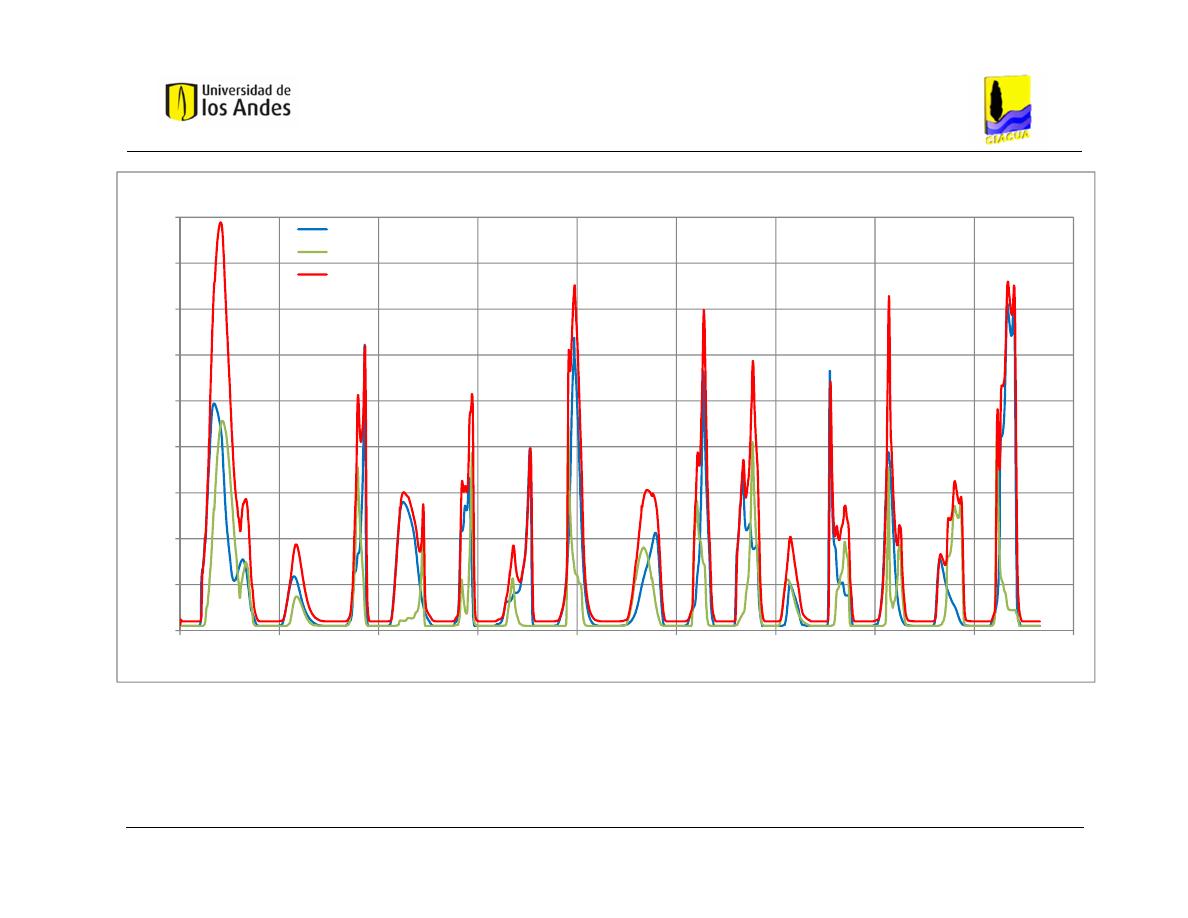
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
96
Gráfica 5.16 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso de Estudio 3 – Distribución 1.
0
10
20
30
40
50
60
70
80
90
0
50
100
150
200
250
300
350
400
450
C
a
u
d
a
l
(m
3
/s
)
Tiempo (Horas)
HIDROGRAMAS CASO DE ESTUDIO 3 - DISTRIBUCIÓN 1
Hidrogramas de Entrada 1
Hidrogramas de Entrada 2
Hidrogramas de Salida
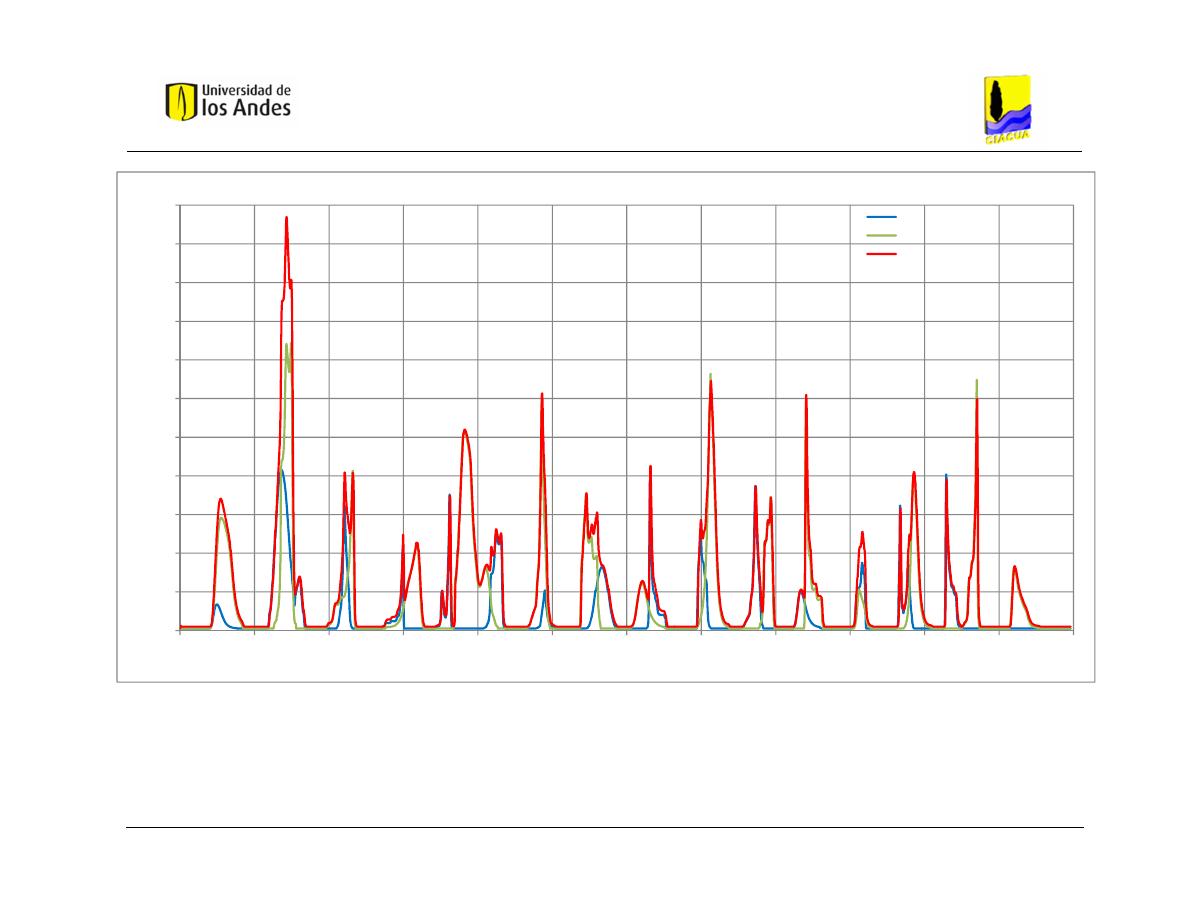
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
97
Gráfica 5.17 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso de Estudio 3 – Distribución 2.
0
20
40
60
80
100
120
140
160
180
200
220
0
50
100
150
200
250
300
350
400
450
500
550
600
C
a
u
d
a
l
(m
3
/s
)
Tiempo (Horas)
HIDROGRAMAS CASO DE ESTUDIO 3 - DISTRIBUCIÓN 2
Hidrogramas de Entrada 1
Hidrogramas de Entrada 2
Hidrogramas de Salida
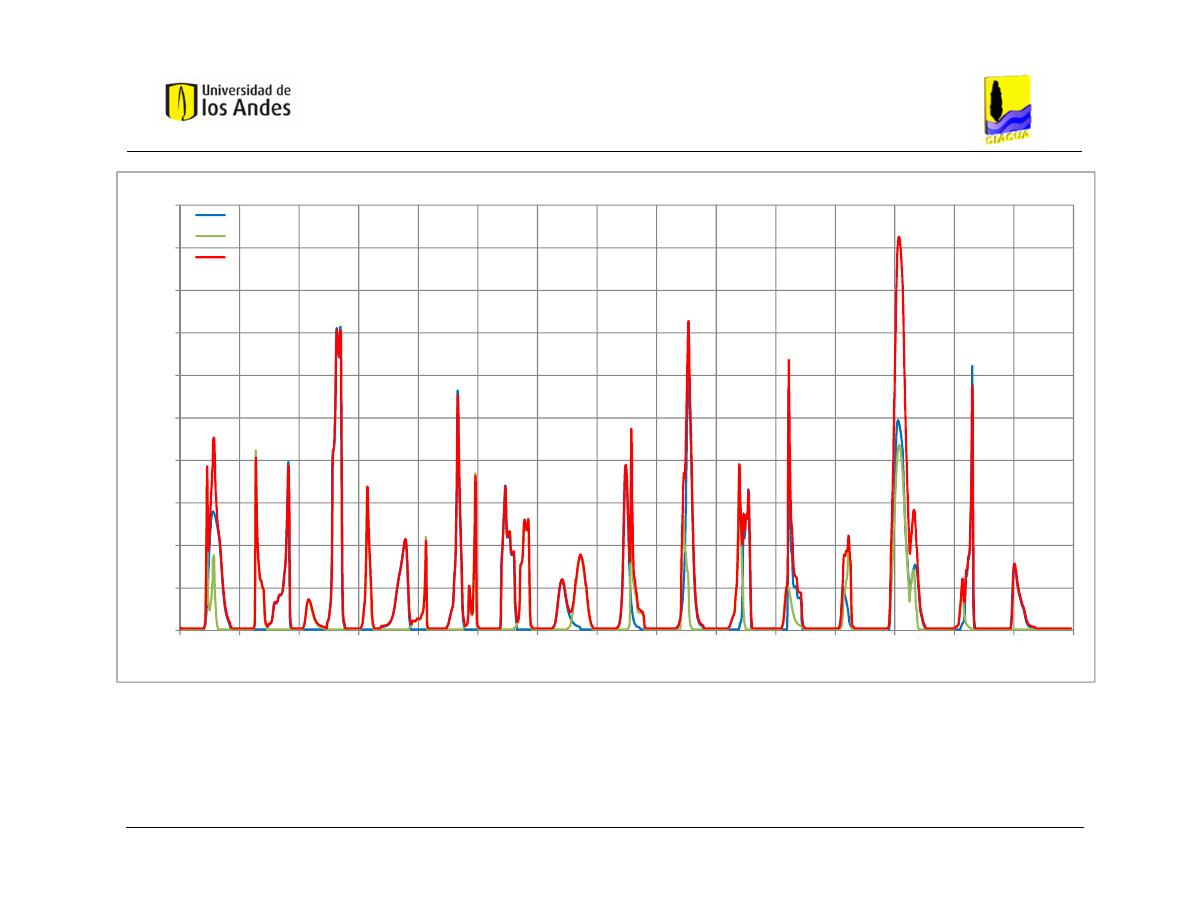
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
98
Gráfica 5.18 Hidrogramas de entrada y salida obtenidos con HEC-RAS – Caso de Estudio 3 – Distribución 3.
0
40
80
120
160
200
240
280
320
360
400
0
50
100
150
200
250
300
350
400
450
500
550
600
650
700
750
C
a
u
d
a
l
(m
3
/s
)
Tiempo (Horas)
HIDROGRAMAS CASO DE ESTUDIO 3 - DISTRIBUCIÓN 3
Hidrogramas de Entrada 1
Hidrogramas de Entrada 2
Hidrogramas de Salida

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
99
En la Tabla 5.11 y en la Tabla 5.12 se muestra el desempeño (MSE) y el
coeficiente de correlación (R
2
) entre los datos esperados y los arrojados por las
redes neuronales; se observa que a medida que se disminuye el porcentaje de
datos utilizados para entrenamiento y validación de una red neuronal decrece la
precisión en la estimación de la respuesta en la etapa de prueba por parte de
las redes neuronales analizadas. Dicho comportamiento se puede apreciar en la
forma como aumenta el error medio cuadrado (MSE) y en la disminución del
coeficiente de correlación (R
2
) de los datos o series de hidrogramas utilizados
en la etapa de prueba.
Además de lo anterior se puede concluir que la distribución de hidrogramas N°2
es la que muestra la respuesta de las redes neuronales con el error medio
cuadrado (MSE) más bajo de las tres, siendo las arquitecturas ANN_18 y
ANN_19 junto con la ANN_5 en la Distribución 3 las que producen un
hidrograma de salida con mayor distorsión para las tres distribuciones si se
compara con la salida deseada (Targets), con un coeficiente de correlación (R
2
)
de 98,11% en la etapa de prueba. Una causa probable del menor desempeño
podría ser la irregularidad en la forma de los hidrogramas de salida, pues para
este caso de estudio, todos tienen una configuración diferente y con picos altos
y de corta duración.
El ANEXO C muestra los resultados de las simulaciones realizadas en la etapa
de prueba y los errores de las redes neuronales evaluadas para las
Distribuciones de Hidrogramas 1, 2 y 3. En las gráficas del anexo se puede
apreciar que la mayor dificultad para las redes neuronales del Caso de Estudio
3 se presenta cuando estas requieren simular hidrogramas con picos altos y
con formas irregulares.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
100
Tabla 5.11 Desempeño para cada una de las redes neuronales según la distribución de la serie de hidrogramas – Caso de Estudio 3.
64%
50%
36%
16%
19%
21%
20%
31%
43%
100%
100%
100%
ANN_1
0,055
0,051
0,072
0,084
0,049
0,104
0,139
0,154
0,680
0,076
0,083
0,340
ANN_5
0,073
0,063
0,092
0,080
0,046
0,082
0,288
0,153
0,223
0,117
0,088
0,146
ANN_18
0,026
0,019
0,013
-
-
-
1,928
3,344
3,885
0,406
1,050
1,678
ANN_19
0,011
0,015
0,008
-
-
-
6,853
6,366
4,055
1,380
1,984
1,748
ANN_21
0,057
0,059
0,059
-
-
-
0,098
0,117
0,103
0,065
0,077
0,078
62%
50%
38%
17%
18%
18%
21%
32%
44%
100%
100%
100%
ANN_1
0,245
0,239
0,254
0,498
0,298
0,394
0,489
0,454
0,790
0,339
0,318
0,515
ANN_5
0,348
0,399
0,421
0,302
0,291
0,229
0,728
0,512
0,448
0,420
0,416
0,398
ANN_18
0,083
0,086
0,082
-
-
-
0,252
0,826
0,694
0,119
0,323
0,352
ANN_19
0,067
0,071
0,045
-
-
-
0,351
1,126
3,023
0,126
0,409
1,355
ANN_21
0,282
0,202
0,187
-
-
-
2,455
2,733
0,719
0,739
1,012
0,421
60%
48%
35%
17%
17%
19%
23%
35%
46%
100%
100%
100%
ANN_1
1,598
1,714
1,704
1,299
1,798
0,537
5,630
6,320
11,135
2,476
3,341
5,821
ANN_5
1,986
1,557
1,874
1,013
2,547
0,407
65,271
32,650
41,859
16,387
12,608
19,988
ANN_18
0,525
0,508
0,417
-
-
-
42,870
152,971
24,075
10,271
53,870
11,300
ANN_19
0,304
0,208
0,198
-
-
-
48,863
96,653
58,207
11,480
33,963
26,882
ANN_21
1,336
1,005
0,943
-
-
-
14,963
11,128
4,007
4,473
4,548
2,352
CASO DE ESTUDIO 3 - MSE (m
3
/s)
2
TOTAL
RED
NEURONAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
DISTRIBUCIÓN
DE
HIDROGRÁMAS
N°1
TOTAL
DISTRIBUCIÓN
DE
HIDROGRÁMAS
N°2
RED
NEURONAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
DISTRIBUCIÓN
DE
HIDROGRÁMAS
N°3
RED
NEURONAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
TOTAL
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
101
Tabla 5.12 Coeficiente de correlación para cada una de las redes neuronales según la distribución de la serie de hidrogramas – Caso de Estudio 3.
64%
50%
36%
16%
19%
21%
20%
31%
43%
100%
100%
100%
ANN_1
99,99%
99,99%
99,98%
99,96%
99,98%
99,96%
99,97%
99,95%
99,82%
99,98%
99,98%
99,91%
ANN_5
99,98%
99,98%
99,98%
99,96%
99,98%
99,97%
99,94%
99,95%
99,94%
99,97%
99,98%
99,96%
ANN_18
99,99%
99,99%
100,00%
-
-
-
99,63%
99,21%
99,00%
99,89%
99,72%
99,55%
ANN_19
100,00%
100,00%
100,00%
-
-
-
98,39%
98,48%
98,80%
99,61%
99,47%
99,51%
ANN_21
99,98%
99,98%
99,98%
-
-
-
99,98%
99,96%
99,97%
99,98%
99,98%
99,98%
62%
50%
38%
17%
18%
18%
21%
32%
44%
100%
100%
100%
ANN_1
99,98%
99,98%
99,98%
99,89%
99,96%
99,93%
99,88%
99,90%
99,86%
99,96%
99,97%
99,95%
ANN_5
99,97%
99,97%
99,97%
99,93%
99,96%
99,96%
99,82%
99,88%
99,92%
99,96%
99,96%
99,96%
ANN_18
99,99%
99,99%
99,99%
-
-
-
99,94%
99,80%
99,88%
99,99%
99,97%
99,96%
ANN_19
99,99%
99,99%
100,00%
-
-
-
99,91%
99,72%
99,47%
99,99%
99,96%
99,86%
ANN_21
99,97%
99,98%
99,98%
-
-
-
99,44%
99,32%
99,87%
99,92%
99,89%
99,96%
60%
48%
35%
17%
17%
19%
23%
35%
46%
100%
100%
100%
ANN_1
99,94%
99,93%
99,94%
99,92%
99,95%
99,97%
99,93%
99,91%
99,77%
99,93%
99,91%
99,84%
ANN_5
99,93%
99,93%
99,93%
99,94%
99,94%
99,97%
99,54%
99,67%
99,54%
99,61%
99,71%
99,57%
ANN_18
99,98%
99,98%
99,98%
-
-
-
99,29%
98,11%
99,71%
99,69%
98,66%
99,76%
ANN_19
99,99%
99,99%
99,99%
-
-
-
99,31%
98,57%
98,75%
99,67%
99,12%
99,21%
ANN_21
99,95%
99,96%
99,96%
-
-
-
99,87%
99,84%
99,93%
99,88%
99,88%
99,94%
CASO DE ESTUDIO 3 - R
2
(%)
DISTRIBUCIÓN
DE
HIDROGRÁMAS
N°1
RED
NEURONAL
TOTAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
TOTAL
RED
NEURONAL
TOTAL
ENTRENAMIENTO
VALIDACIÓN
PRUEBA
DISTRIBUCIÓN
DE
HIDROGRÁMAS
N°3
RED
NEURONAL
DISTRIBUCIÓN
DE
HIDROGRÁMAS
N°2
ENTRENAMIENTO
VALIDACIÓN
PRUEBA

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
102
6. ANÁLISIS DE COSTOS
Una de las premisas planteadas al inicio de la investigación para definir la
viabilidad de utilizar las ANN como método alterno para realizar el tránsito de
crecientes en un canal o cauce determinado además de la precisión en la
estimación de las series de hidrogramas objetivo, fue la posibilidad de reducir
los costos operacionales entre utilizar ANN u otro método alterno. Entre los
insumos que se requieren para desarrollar estas metodologías se pueden listar:
obtención de secciones batimétricas (Trabajo de campo), las cuales requieren
una gran inversión de dinero y tiempo, análisis hidrológicos, análisis hidráulico y
el montaje del modelo digital, ya sea con algún software de diseño (HEC-RAS
en este caso) o utilizando ANN.
Para el análisis de costos de esta investigación no fue posible obtener la
información monetaria de las actividades, materiales y procesos requeridos
para el Caso de Estudio 3, por lo que el análisis solo se realizó para los Casos
de Estudio 1 y 2. Debido a que los costos de las actividades no están referidos
a la fecha actual sino a la fecha de realización de las mismas, los costos se
manejarán en dólares utilizando como tasa de cambio el promedio de la
cotización de esta moneda durante el desarrollo de las actividades. A
continuación se muestra el gasto de dinero y tiempo que requieren las
actividades necesarias para realizar el tránsito de crecientes en un canal a
través de la metodología tradicional y utilizando ANN.
6.1 CASO DE ESTUDIO 1
•
Trabajos de Campo
– Batimetrías: 18 Secciones – 40 días
– Costos Batimetría (Unidad): $ 2´320.000 o US 1.268
– Costo Total Batimetrías: $ 41´760.000 o US 22.820
•
Trabajos de Oficina
– Montaje de modelo digital: 15 días
– Costo personal / día: $ 100.000 o US 54,65
– Costo total montaje de modelo digital: $ 1´500.000 o US 819,68
•
Montaje de redes neuronales artificiales (ANN)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
103
– Montaje de ANN: 5 días
– Costo personal / día: $ 100.000 o US 54,65
– Costo total montaje de ANN: $ 500.000 o US 273,23
•
Registros hidrológicos o de caudales
– Análisis hidrológico: 5 a 10 días
– Costo personal /día: $ 100.000 o US 54,65
– Información disponible por el IDEAM u otras entidades de forma
libre.
– Entrega de información IDEAM: 3 a 10 días
Promedio dólar mes, Marzo - Mayo 2013: $ 1.829,99
6.2 CASO DE ESTUDIO 2
•
Trabajos De Campo
– Batimetrías: 40 Secciones – 15 días
– Costos promedio batimetría (Unidad): $ 750.000 o US 425,71
– Costo total batimetrías: $ 30´000.000 o US 17.028,52
•
Trabajos de Oficina
– Montaje de modelo digital: 7 días
– Costo personal /día: $ 100.000 o US 56,76
– Costo total montaje de modelo digital: $ 700.000 o US 397,33
•
Montaje de redes neuronales artificiales (ANN)
– Montaje de ANN: 5 días
– Costo personal /día: $ 100.000 o US 56,76
– Costo total montaje de ANN: $ 500.000 o US 283,81
•
Registros hidrológicos o de caudales
– Análisis hidrológico: 5 días

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
104
– Costo personal /día: $ 100.000 o US 56,76
– Información disponible por el IDEAM u otras entidades de forma
libre.
– Entrega de información 3 a 10 días
Promedio dólar mes, Julio 2011: $ 1.761,75
Analizando la información anterior se aprecia que la actividad que demanda
mayor gasto de tiempo y dinero es la consecución de la información topológica
del cauce (Secciones batimétricas) la cual no es requerida para el montaje de
una red neuronal, lo que le da una ventaja a estas sobre los métodos
tradicionales. El ahorro en tiempo por cuenta de esta actividad, para el Caso de
Estudio 1 es del orden de 40 días y para el Caso de Estudio 2 del orden de 15
días, mientras que el ahorro en dinero es de aproximadamente 22.800 dólares
para el Caso de Estudio 1 y de aproximadamente 17.000 dólares para el Caso
de Estudio 2.
A demás de esto, se destaca que el tiempo de montaje y calibración del modelo
digital de un cauce es un poco mayor que el que se requiere para seleccionar y
entrenar una determinada red neuronal. Una característica que diferencia las
redes neuronales de los métodos tradicionales es el hecho de que el adecuado
funcionamiento de estas se ve influenciado por la cantidad de información de
entrada con la que se cuente, es decir, entre mayor sea el rango de información
o registros con el que se cuente la respuesta proporcionadas por la redes
neuronales tendrá una probabilidad mucho mayor de ajustarse adecuadamente
a la realidad o a la respuesta deseada.
De acuerdo con los costos de las actividades definidos anteriormente, para el
Caso de Estudio 1, el ahorro en dinero sería del orden de 23.360,00 dólares y
en tiempo del orden de unos 50 días, mientras que para el Caso de Estudio 2 el
ahorro en dinero sería del orden de 17.140,00 dólares y en tiempo del orden de
unos 17días.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
105
7. CONCLUSIONES Y RECOMENDACIONES
• Al realizar la búsqueda bibliográfica se nota que a nivel local en el campo
de los Hidrosistemas las investigaciones son pocas y solo se encuentran
algunas aplicaciones a nivel general y en redes húmedas.
• Como lo indica el material bibliográfico proporcionado por MATLAB
®
, se
pudo corroborar que las redes neuronales que utilizan el algoritmo de
entrenamiento de Levenberg-Marquardt y además de estas, las que
utilizan el algoritmo de Bayesian Regularization son la que muestran un
mejor desempeño considerando como parámetros de evaluación el error
medio cuadrado (MSE) y el coeficiente de correlación (R
2
). Para un
análisis rápido se podría partir de estos algoritmos de entrenamiento,
pero se deberá verificar para cada caso de estudio particular si
proporcionan el mejor desempeño.
• En cuanto a la investigación se observó que para un mayor número de
neuronas combinado con un mayor número de capas ocultas, la
generalización de las redes neuronales es menos acertada.
• Para un coeficiente de correlación (R
2
) superior al 98.5% las redes
neuronales muestran una muy buena generalización en los datos de
salida en la etapa de prueba.
• Las arquitecturas de las cinco redes neuronales con mejor desempeño,
ANN_1, ANN_5, ANN_18, ANN_19 y ANN_21, fueron las utilizadas como
base para el tránsito de crecientes en cada uno de los tres casos de
estudio. La ANN_1 y ANN_5 utilizan el algoritmo de Levenberg-
Marquardt mientras que las demás arquitecturas utilizan el algoritmo de
Bayesian Regularization.
• Realizado un análisis de sensibilidad al Caso de Estudio 1, se observó
que el desempeño de las redes neuronales no se ve afectado en gran
medida por variaciones en el coeficiente de rugosidad (n de Manning) o
en la pendiente de fondo del cauce, razón por la cual se puede afirmar
en primera instancia que las redes neuronales no son sensibles a la
variación de dichos parámetros.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
106
• Las redes neuronales analizadas en los Casos de Estudio 1, 2 y 3
muestran algún grado de dificultad para lograr una buena generalización
o ajuste en hidrogramas de la serie con picos altos y de corta duración.
Para lograr un mejor ajuste en la respuesta de la red neuronal se podría
aumentar el tamaño de la serie de datos de entrada incluyendo aún más
hidrogramas con formas y tamaños diversos.
• En la mayoría de casos analizados, a medida que se disminuye el
porcentaje de datos de entrenamiento de la serie de hidrogramas, se
observa una reducción en el coeficiente de correlación en la etapa de
prueba entre los datos esperados y los simulados con las redes
neuronales artificiales. Para esta investigación el porcentaje de datos
para entrenamiento, validación y prueba de los tres casos de estudio en
la distribución 1 se ubicaron en los siguientes rangos de datos.
-
Entrenamiento: 60% - 64% de los datos.
-
Validación: 15% - 22% de los datos.
-
Prueba: 18% - 22% de los datos.
• En cuanto al Error Medio Cuadrado de los datos simulados con las redes
neuronales (MSE), en la mayoría de los casos este aumenta a medida
que se disminuye el porcentaje de datos de entrenamiento de la serie de
hidrogramas. Se podría recomendar mantenerse en el orden de
porcentaje de datos dado, aunque lo ideal sería estimar la distribución
adecuada para cada caso de estudio particular.
• Para las distintas distribuciones de hidrogramas de los tres casos de
estudio analizados se obtuvo un Coeficiente de Correlación total variable
entre los datos esperados y los obtenidos con las redes neuronales
artificiales en el rango mostrado a continuación:
Caso de Estudio 1: 99,46% – 99,99%
Caso de Estudio 2: 98,79% – 99,96%
Caso de Estudio 3: 98,66% – 99,99%
• Las redes neuronales por la naturaleza de los datos que requieren para
ejecutar un análisis determinado permiten reducir el tiempo de ejecución
del tránsito de una creciente, ya que no requiere toma de información en
campo como secciones batimétricas ni el montaje y calibración de un

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
107
modelo digital. Estos procesos son los que mayor tiempo y recursos
requieren en el desarrollo de un adecuado tránsito de crecientes.
• En cuanto a los costos de análisis, las redes neuronales requieren una
menor cantidad de recursos; estas solo necesitan registros históricos de
precipitación o caudales en los sitios de análisis sin considerar la
geometría o morfología del cauce estudiado. De acuerdo con los costos
de las actividades definidos en el Capítulo 6, para el Caso de Estudio 1,
el ahorro en dinero sería del orden de 23.360,00 dólares y en tiempo del
orden de unos 50 días, mientras que para el Caso de Estudio 2 el ahorro
en dinero sería del orden de 17.140,00 dólares y en tiempo del orden de
unos 17días.
• A diferencia de un tránsito normal, para obtener un mejor desempeño en
el tránsito de una creciente utilizando ANN, se requieren de un registro
de datos históricos amplio para evitar que al presentarse datos por fuera
de un rango determinado la red neuronal presente inconvenientes en
cuanto a la estimación o predicción de la información y además para
evitar que estas se sobreentrenen por la presencia de datos muy
parecidos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
108
8. BIBLIOGRAFÍA
CAMPOLO, M., SOLDATI, A., & ANDREUSSI, P. (2003). Artificial neural
network approach to flood forecasting in the River Arno. Hydrological
Sciences–Journal–des Sciences Hydrologiques, 19.
DIBIKE, Y., & SOLOMATINE, D. (2001). River Flow Forecasting Using Artificial
Neural Networks. 7 Páginas. Netherlands.
HILERA, J., & MARTÍNEZ, V. (2000). REDES NEURONALES ARTIFICIALES.
Fundamentos, modelos y aplicaciones. México D.F.: EDITORIAL
ALFAOMEGA S.A.
IZAURIETA, F., & SAAVEDRA, C. (n.d.). Redes Neuronales Artificiales.
Concepción, Chile: Departamento de Física, Universidad de Concepción.
MOLINA AGUILAR, J. P., & APARICIO, J. (2006). Tránsito de avenidas en
cauces mediante redes neuronales artificiales . México.
MORALES V., J. (2004). Tránsito de crecientes en sistemas de alcantarillado
utilizando redes neuronales artificiales (RNA). Bogotá, Colombia:
Universidad de Los Andes.
OBREGÓN, N., FRAGALA, F., & PRADA, L. (n.d.). Redes neuronales
artificiales en hidroinformátiSeminario Internacional La Hidroinformática
en la Gestión Integrada de los Recursos Hídricos. Cali, Colombia:
Universidad del Valle/Instituto CINARA.
PARTAL, T. (2009). River flow forecasting using different artificial neural
network algorithms and wavelet transform. NRC Research Press, 15.
SHAMSELDIN, A. (2010). Artificial neural network model for river flow
forecasting in a developing country. Journal of Hydroinformatics, 14.
SIVANANDAM, S., SUMATHI, S., & DEEPA, S. (2006). Introduction to neural
networks using MATLAB 6.0. New Delhi: McGraw-Hill.
www.histologiaub.blogspot.com. (n.d.). Retrieved 11 17, 2014, from
https://www.google.com.co/search?q=neurona&client=firefox-
a&hs=wO&rls=org.mozilla:es-
ES:official&channel=sb&source=lnms&tbm=isch&sa=X&ei=o0d1VISuEIG

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
109
qggSA14O4Cg&ved=0CAgQ_AUoAQ&biw=1366&bih=639#facrc=_&img
dii=_&imgrc=qa7tgqlMHlTyNM%253A%3BTgKwYYz52x2ohM%3B

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
“Tránsito de crecientes a través de canales de aguas lluvia utilizando
Redes Neuronales”
Lainer J. Bohórquez Meza
Tesis de maestría
110
9. ANEXOS
