
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Tesis de Maestría en Ingeniería Civil
Tiempo de Respuesta Típico de Operaciones en
Redes de Distribución de Agua Potable
Presentado por:
Juan Pablo Paris Valencia
Asesor:
Profesor Juan Saldarriaga
Informe Final – Tesis 2
Bogotá, Junio 2015

“A man should keep his little brain attic stocked with all the furniture that he is
likely to use, and the rest he can put away in the lumber room of his library, where
he can get if he wants it”- Sir Arthur Conan Doyle
A mis padres y mi hermano gracias por su incondicional apoyo y conocimiento
aportado.
A ustedes dedico y dedicaré siempre mis logros.
A Juan Saldarriaga, gracias por sus enseñanzas que me desarrollaron como
profesional y persona.
A Diego Páez, gracias por introducirme en este tema y los conocimientos
adquiridos.
A Jessica Bohórquez gracias por la ideas sugeridas y por la ayuda constante en el
proceso de esta investigación.

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
i
TABLA DE CONTENIDO
TABLA DE CONTENIDO ............................................................................................................ I
ÍNDICE DE FIGURAS ................................................................................................................. 3
ÍNDICE DE TABLAS ................................................................................................................... 8
1.
INTRODUCCIÓN Y OBJETIVOS .................................................................................... 1
1.1.
I
NTRODUCCIÓN
.............................................................................................................. 1
1.2.
O
BJETIVOS
...................................................................................................................... 3
1.2.1.
Objetivo General ....................................................................................................... 3
1.2.2.
Objetivos Específicos ................................................................................................. 3
2.
ANTECEDENTES ................................................................................................................ 4
3.
MARCO TEÓRICO ........................................................................................................... 14
3.1.
T
IPOS DE FLUJO
............................................................................................................ 14
3.2.
H
IDRÁULICA DE FLUJO TRANSIENTE
............................................................................ 14
3.3.
M
ÉTODO DE LAS CARACTERÍSTICAS
............................................................................ 18
4.
METODOLOGÍA ............................................................................................................... 23
4.1.
U
BICACIÓN DE VÁLVULAS
........................................................................................... 23
4.2.
M
EDIDAS DE TENDENCIA
............................................................................................. 24
5.
HAMMER ........................................................................................................................... 26
5.1.
D
EMANDAS
................................................................................................................... 26
5.2.
F
ACTORES DE FRICCIÓN
............................................................................................... 27
5.2.1.
Métodos de Cálculo ................................................................................................. 27
5.2.2.
Análisis de Sensibilidad ........................................................................................... 28
6.
REDES DE PRUEBA ......................................................................................................... 34
6.1.
R
ED DE
B
UCARAMANGA
(S
ECTOR
E
STADIO
) ............................................................... 34
6.1.1.
Patrónes ................................................................................................................... 35
6.1.2.
Sectorización ........................................................................................................... 36
6.2.
R
ED
M
ATRIZ DE
M
EDELLÍN
......................................................................................... 41
6.2.1.
Sectorización ........................................................................................................... 42
7.
RESULTADOS Y ANÁLISIS............................................................................................ 49
7.1.
ANÁLISIS
DE
SENSIBILIDAD
CASO
SIMPLE....................................................... 49
7.1.1.
AUMENTO DE LA LONGITUD ............................................................................. 51
7.1.2.
DISMINUCIÓN DE LA LONGITUD ...................................................................... 53
7.1.3.
AUMENTO DE LA RUGOSIDAD ........................................................................... 54
7.1.4.
DISMINUCIÓN DE LA RUGOSIDAD .................................................................... 55
7.1.5.
AUMENTO DE LA CELERIDAD DE LA ONDA .................................................... 56
7.1.6.
DISMINUCIÓN DE LA CELERIDAD DE LA ONDA ............................................. 58
7.1.7.
AUMENTO DEL DIÁMETRO DE LA TUBERÍA .................................................... 59
7.1.8.
DISMINUCIÓN DEL DIÁMETRO DE LA TUBERÍA ............................................. 60
7.1.9.
AUMENTO DE LA ALTURA DEL EMBALSE ........................................................ 61
7.2.
REDES
PROBADAS ................................................................................................... 63
7.2.1.
RED MATRIZ DE MEDELLÍN ................................................................................ 63

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
ii
7.2.1.1.
Válvula 1 ............................................................................................................. 64
7.2.1.2.
Válvula 2 ............................................................................................................. 72
7.2.1.3.
Válvula 3 ............................................................................................................. 74
7.2.1.4.
Válvula 4 ............................................................................................................. 76
7.2.1.5.
Válvula 5 ............................................................................................................. 80
7.2.1.6.
Válvula 6 ............................................................................................................. 84
7.2.1.7.
Válvula 7 ............................................................................................................. 86
7.2.2.
RED DE BUCARAMANGA (SECTOR ESTADIO) .................................................. 91
7.2.2.1.
Red Original ........................................................................................................ 91
7.2.2.1.1.
Válvula 1 ......................................................................................................... 92
7.2.2.1.2.
Válvula 2 ......................................................................................................... 93
7.2.2.1.3.
Válvula 3 ......................................................................................................... 94
7.2.2.1.4.
Válvula 4 ......................................................................................................... 96
7.2.2.1.5.
Válvula 5 ......................................................................................................... 97
7.2.2.1.6.
Válvula 6 ......................................................................................................... 99
7.2.2.1.7.
Válvula 7 ....................................................................................................... 100
7.2.2.2.
Análisis de Sensibilidad..................................................................................... 101
7.2.2.2.1.
Válvula 1 ....................................................................................................... 101
7.2.2.2.2.
Válvula 2 ....................................................................................................... 106
7.2.2.2.3.
Válvula 3 ....................................................................................................... 110
7.2.2.2.4.
Válvula 4 ....................................................................................................... 113
8.
CONCLUSIONES Y TRABAJO FUTURO ................................................................... 116
8.1.
Conclusiones .......................................................................................................... 116
8.2.
Trabajo Futuro ...................................................................................................... 118
9.
REFERENCIAS ................................................................................................................ 119

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
iii
ÍNDICE DE FIGURAS
F
IGURA
1.
R
ED UTILIZADA EN EL TRABAJO DE
D
UAN ET AL
.
(2010). ............................................................... 4
F
IGURA
2.
R
ED UTILIZADA PARA EL MODELO PRESENTADO EN EL TRABAJO DE
F
ILION ET AL
.
(2002). ............ 5
F
IGURA
3.
R
ESULTADOS DEL TRABAJO DE
F
ILION ET AL
.
(2002). .................................................................... 6
F
IGURA
4.
M
ODELO UTILIZADO EN EL TRABAJO DE
K
ARNEY ET AL
.
(2006) .................................................... 7
F
IGURA
5.
R
ESULTADOS DEL TRABAJO DE
K
ARNEY ET AL
.
(2006)
CON UNA BASE DE
1
M
2
DEL TANQUE
......... 8
F
IGURA
6.
R
ESULTADOS DEL TRABAJO DE
K
ARNEY ET AL
.
(2006)
CON UNA BASE DE
0.2
M
2
DEL TANQUE
. ..... 8
F
IGURA
7.
R
ESULTADOS DEL TRABAJO DE
K
ARNEY ET AL
.
(2006)
RESPECTO AL TIEMPO DE CIERRE DE LA
VÁLVULA
. .............................................................................................................................................. 9
F
IGURA
8.
R
ED
"A
NYTOWN
"
UTILIZADA EN EL TRABAJO DE
S
IEW ET AL
.
(2012). ..........................................10
F
IGURA
9.
R
ESULTADOS DEL FACTOR DE SATISFACCIÓN DE LA DEMANDA EN LA INVESTIGACIÓN DE
S
IEW ET
AL
.
(2012). ............................................................................................................................................11
F
IGURA
10.
P
RESIONES EN LOS NUDOS DE LA RED
"A
NYTOWN
"
A LAS
10
HORAS
(S
IEW ET AL
.,
2012). ..........11
F
IGURA
11.
A
NÁLISIS DE LA ONDA DE PRESIÓN POR MEDIO DEL MÉTODO DE LA CARACTERÍSTICA DE LA ONDA
(W
OOD
,
2005). .....................................................................................................................................12
F
IGURA
12.
R
ED DE ESTUDIO EN EL TRABAJO DE
W
OOD
(2005). ....................................................................13
F
IGURA
13.
D
IAGRAMA DE CUERPO LIBRE PARA LA APLICACIÓN DE LA ECUACIÓN DE CONSERVACIÓN DE LA
CANTIDAD DE MOVIMIENTO
(W
YLIE
&
S
TREETER
,
1978). ....................................................................15
F
IGURA
14.
D
IAGRAMA DE CUERPO LIBRE PARA LA APLICACIÓN DE LA ECUACIÓN DE CONSERVACIÓN DE LA
MASA
(W
YLIE
&
S
TREETER
,
1978). ......................................................................................................16
F
IGURA
15.
G
RILLA DE XT PARA LA SOLUCIÓN DEL SISTEMA DE ECUACIONES DIFERENCIALES
(W
YLIE
&
S
TREETER
,
1978). .................................................................................................................................20
F
IGURA
16.
D
IAGRAMA DE FLUJO PARA LA UBICACIÓN DE LAS VÁLVULAS
. ...................................................23
F
IGURA
17.
R
ED UTILIZADA PARA ESTUDIAR LAS DEMANDAS EN
HAMMER. ...............................................26
F
IGURA
18.
E
RRORES PORCENTUALES DE LOS MÉTODOS DE CÁLCULO DEL FACTOR DE FRICCIÓN
(C
IERRE DEL
20%). ....................................................................................................................................................29
F
IGURA
19.
E
RRORES PORCENTUALES DE LOS MÉTODOS DE CÁLCULO DEL FACTOR DE FRICCIÓN
(C
IERRE DEL
40%). ....................................................................................................................................................30
F
IGURA
20.
E
RRORES PORCENTUALES DE LOS MÉTODOS DE CÁLCULO DEL FACTOR DE FRICCIÓN
(C
IERRE DEL
60%). ....................................................................................................................................................30
F
IGURA
21.
E
RRORES PORCENTUALES DE LOS MÉTODOS DE CÁLCULO DEL FACTOR DE FRICCIÓN
(C
IERRE DEL
80%). ....................................................................................................................................................31
F
IGURA
22.
E
RRORES PORCENTUALES DE LOS MÉTODOS DE CÁLCULO DEL FACTOR DE FRICCIÓN
(C
IERRE DEL
90%). ....................................................................................................................................................32
F
IGURA
23.
E
RRORES PORCENTUALES DE LOS MÉTODOS DE CÁLCULO DEL FACTOR DE FRICCIÓN
(C
IERRE DEL
100%). ..................................................................................................................................................32
F
IGURA
24.
E
RRORES PORCENTUALES PROMEDIOS DE LOS DIFERENTES MÉTODOS DE CÁLCULO DE FACTOR DE
FRICCIÓN
,
EN LOS DIFERENTES PORCENTAJES DE CIERRE
. .....................................................................33
F
IGURA
25.
C
ASO DE ESTUDIO
R
ED DE
B
UCARAMANGA
(S
ECTOR
E
STADIO
). ................................................34
F
IGURA
26.
P
ATRÓN
B
IENESTAR DE LA RED DE
B
UCARAMANGA
(S
ECTOR
E
STADIO
). ...................................35
F
IGURA
27.
P
ATRÓN
E
STADIO DE LA RED DE
B
UCARAMANGA
(S
ECTOR
E
STADIO
). .......................................36
F
IGURA
28.
P
ATRÓN
R
EGADERO DE LA RED DE
B
UCARGAMANGA
(S
ECTOR
E
STADIO
). .................................36
F
IGURA
29.
U
BICACIÓN Y AFECTACIÓN QUE GENERA LA VÁLVULA
TCV-1. ...................................................37
F
IGURA
30.
U
BICACIÓN Y AFECTACIÓN QUE GENERA LA VÁLVULA
TCV-2. ...................................................37
F
IGURA
31.
U
BICACIÓN Y AFECTACIÓN QUE GENERA LA VÁLVULA
TCV-3. ...................................................38
F
IGURA
32.
U
BICACIÓN Y AFECTACIÓN QUE GENERA LA VÁLVULA
TCV-4. ...................................................38
F
IGURA
33.
U
BICACIÓN Y AFECTACIÓN QUE GENERA LA VÁLVULA
TCV-5. ...................................................39
F
IGURA
34.
U
BICACIÓN Y AFECTACIÓN QUE GENERA LA VÁLVULA
TCV-6. ...................................................39
F
IGURA
35.
U
BICACIÓN Y AFECTACIÓN QUE GENERA LA VÁLVULA
TCV-7. ...................................................40
F
IGURA
36.
U
BICACIÓN Y AFECTACIÓN QUE GENERA LA VÁLVULA
TCV-8. ...................................................40

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
iv
F
IGURA
37.
C
ASO DE ESTUDIO
R
ED
M
ATRIZ DE
M
EDELLÍN
............................................................................41
F
IGURA
38.
D
IAGRAMA DE FLUJO IMPLEMENTADO PARA UBICAR LAS VÁLVULAS EN LA
R
ED
M
ATRIZ DE
M
EDELLÍN
. ...........................................................................................................................................42
F
IGURA
39.
C
OMPORTAMIENTO DE LA VARIACIÓN DEL CAUDAL RESPECTO AL ESTADO INICIAL
. ...................43
F
IGURA
40.
E
STADO
I
NICIAL DE LA RED
M
ATRIZ DE
M
EDELLÍN
.....................................................................44
F
IGURA
41.
U
BICACIÓN Y AFECTACIÓN QUE GENERA LA
V
ÁLVULA
-1
EN LA RED
M
ATRIZ DE
M
EDELLÍN
. .....45
F
IGURA
42.
U
BICACIÓN Y AFECTACIÓN QUE GENERA LA
V
ÁLVULA
-2
EN LA RED
M
ATRIZ DE
M
EDELLÍN
. .....45
F
IGURA
43.U
BICACIÓN Y AFECTACIÓN QUE GENERA LA
V
ÁLVULA
-3
EN LA RED
M
ATRIZ DE
M
EDELLÍN
. ......46
F
IGURA
44.U
BICACIÓN Y AFECTACIÓN QUE GENERA LA
V
ÁLVULA
-4
EN LA RED
M
ATRIZ DE
M
EDELLÍN
. ......46
F
IGURA
45.U
BICACIÓN Y AFECTACIÓN QUE GENERA LA
V
ÁLVULA
-5
EN LA RED
M
ATRIZ DE
M
EDELLÍN
. ......47
F
IGURA
46.U
BICACIÓN Y AFECTACIÓN QUE GENERA LA
V
ÁLVULA
-6
EN LA RED
M
ATRIZ DE
M
EDELLÍN
. ......47
F
IGURA
47.
U
BICACIÓN Y AFECTACIÓN QUE GENERA LA
V
ÁLVULA
-7
EN LA RED
M
ATRIZ DE
M
EDELLÍN
. .....48
F
IGURA
48.
E
JEMPLO SIMPLE PARA REALIZAR EL ANÁLISIS DE SENSIBILIDAD A LAS VARIABLES RELEVANTES
DEL FENÓMENO DE TRANSIENTE
. ..........................................................................................................49
F
IGURA
49.
C
OMPORTAMIENTO DE LA PRESIÓN EN LA VÁLVULA DEL EJEMPLO SIMPLE CON SUS VALORES
INICIALES
. .............................................................................................................................................50
F
IGURA
50.
C
OMPORTAMIENTO DEL CAUDAL DEL EJEMPLO SIMPLE CON SUS VALORES INICIALES
. ................50
F
IGURA
51.
C
OMPORTAMIENTO DE LA PRESIÓN EN LA VÁLVULA DEL EJEMPLO SIMPLE INCREMENTADO LA
LONGITUD
. ............................................................................................................................................51
F
IGURA
52.
C
OMPORTAMIENTO DEL CAUDAL DEL EJEMPLO SIMPLE INCREMENTANDO LA LONGITUD
. ...........52
F
IGURA
53.
C
OMPORTAMIENTO DE LA PRESIÓN EN LA VÁLVULA DEL EJEMPLO SIMPLE DISMINUYENDO LA
LONGITUD
. ............................................................................................................................................53
F
IGURA
54.
C
OMPORTAMIENTO DEL CAUDAL DEL EJEMPLO SIMPLE DISMINUYENDO LA LONGITUD
. ..............53
F
IGURA
55.
C
OMPORTAMIENTO DE LA PRESIÓN EN LA VÁLVULA DEL EJEMPLO SIMPLE AUMENTANDO LA
RUGOSIDAD
. ..........................................................................................................................................54
F
IGURA
56.
C
OMPORTAMIENTO DEL CAUDAL DEL EJEMPLO SIMPLE AUMENTANDO LA RUGOSIDAD
. ..............55
F
IGURA
57.
C
OMPORTAMIENTO DE LA PRESIÓN EN LA VÁLVULA DEL EJEMPLO SIMPLE DISMINUYENDO LA
RUGOSIDAD
. ..........................................................................................................................................55
F
IGURA
58.
C
OMPORTAMIENTO DEL CAUDAL DEL EJEMPLO SIMPLE DISMINUYENDO LA RUGOSIDAD
. ............56
F
IGURA
59.
C
OMPORTAMIENTO DE LA PRESIÓN EN LA VÁLVULA DEL EJEMPLO SIMPLE AUMENTANDO LA
CELERIDAD DE ONDA
. ...........................................................................................................................57
F
IGURA
60.
C
OMPORTAMIENTO DEL CAUDAL DEL EJEMPLO SIMPLE AUMENTANDO LA CELERIDAD DE ONDA
.57
F
IGURA
61.
C
OMPORTAMIENTO DE LA PRESIÓN EN LA VÁLVULA DEL EJEMPLO SIMPLE DISMINUYENDO LA
CELERIDAD DE ONDA
. ...........................................................................................................................58
F
IGURA
62.
C
OMPORTAMIENTO DEL CAUDAL DEL EJEMPLO SIMPLE DISMINUYENDO LA CELERIDAD DE ONDA
.
.............................................................................................................................................................58
F
IGURA
63.
C
OMPORTAMIENTO DE LA PRESIÓN EN LA VÁLVULA DEL EJEMPLO SIMPLE AUMENTANDO EL
DIÁMETRO DE LA TUBERÍA
. ...................................................................................................................59
F
IGURA
64.
C
OMPORTAMIENTO DEL CAUDAL DEL EJEMPLO SIMPLE AUMENTANDO EL DIÁMETRO
. ................60
F
IGURA
65.
C
OMPORTAMIENTO DE LA PRESIÓN EN LA VÁLVULA DEL EJEMPLO SIMPLE DISMINUYENDO EL
DIÁMETRO DE LA TUBERÍA
. ...................................................................................................................60
F
IGURA
66.
C
OMPORTAMIENTO DEL CAUDAL DEL EJEMPLO SIMPLE DISMINUYENDO EL DIÁMETRO
. ..............61
F
IGURA
67.
C
OMPORTAMIENTO DE LA PRESIÓN EN LA VÁLVULA DEL EJEMPLO SIMPLE AUMENTANDO LA
ALTURA DEL EMBALSE
. .........................................................................................................................62
F
IGURA
68.
C
OMPORTAMIENTO DEL CAUDAL DEL EJEMPLO SIMPLE AUMENTANDO LA ALTURA DE EMBALSE
.
.............................................................................................................................................................62
F
IGURA
69.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
95%
DE LA
V
ÁLVULA
1
EN LA RED MATRIZ
DE
M
EDELLÍN
. ......................................................................................................................................64
F
IGURA
70.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
90%
DE LA
V
ÁLVULA
1
EN LA RED MATRIZ
DE
M
EDELLÍN
. ......................................................................................................................................65
F
IGURA
71.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
80%
DE LA
V
ÁLVULA
1
EN LA RED MATRIZ
DE
M
EDELLÍN
. ......................................................................................................................................66

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
v
F
IGURA
72.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
60%
DE LA
V
ÁLVULA
1
EN LA RED MATRIZ
DE
M
EDELLÍN
. ......................................................................................................................................68
F
IGURA
73.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
40%
DE LA
V
ÁLVULA
1
EN LA RED MATRIZ
DE
M
EDELLÍN
. ......................................................................................................................................68
F
IGURA
74.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
95%
DE LA
V
ÁLVULA
1
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................69
F
IGURA
75.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
90%
DE LA
V
ÁLVULA
1
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................70
F
IGURA
76.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
80%
DE LA
V
ÁLVULA
1
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................70
F
IGURA
77.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
60%
DE LA
V
ÁLVULA
1
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................71
F
IGURA
78.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
40%
DE LA
V
ÁLVULA
1
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................72
F
IGURA
79.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
95%
DE LA
V
ÁLVULA
2
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................73
F
IGURA
80.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
90%
DE LA
V
ÁLVULA
2
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................73
F
IGURA
81.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
95%
DE LA
V
ÁLVULA
2
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................74
F
IGURA
82.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
95%
DE LA
V
ÁLVULA
3
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................75
F
IGURA
83.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
90%
DE LA
V
ÁLVULA
3
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................75
F
IGURA
84.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
95%
DE LA
V
ÁLVULA
3
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................76
F
IGURA
85.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
95%
DE LA
V
ÁLVULA
4
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................77
F
IGURA
86.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
90%
DE LA
V
ÁLVULA
4
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................78
F
IGURA
87.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
80%
DE LA
V
ÁLVULA
4
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................78
F
IGURA
88.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
95%
DE LA
V
ÁLVULA
4
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................79
F
IGURA
89.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
90%
DE LA
V
ÁLVULA
4
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................79
F
IGURA
90.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
95%
DE LA
V
ÁLVULA
5
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................80
F
IGURA
91.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
90%
DE LA
V
ÁLVULA
5
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................81
F
IGURA
92.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
80%
DE LA
V
ÁLVULA
5
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................81
F
IGURA
93.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
95%
DE LA
V
ÁLVULA
5
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................82
F
IGURA
94.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
90%
DE LA
V
ÁLVULA
5
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................83
F
IGURA
95.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
80%
DE LA
V
ÁLVULA
5
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................83
F
IGURA
96.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
95%
DE LA
V
ÁLVULA
6
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................84
F
IGURA
97.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
90%
DE LA
V
ÁLVULA
6
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................85

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
vi
F
IGURA
98.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
80%
DE LA
V
ÁLVULA
6
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................85
F
IGURA
99.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
95%
DE LA
V
ÁLVULA
6
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................86
F
IGURA
100.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
95%
DE LA
V
ÁLVULA
7
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................87
F
IGURA
101.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
90%
DE LA
V
ÁLVULA
7
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................87
F
IGURA
102.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
80%
DE LA
V
ÁLVULA
7
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................88
F
IGURA
103.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
60%
DE LA
V
ÁLVULA
7
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................89
F
IGURA
104.
C
OMPORTAMIENTO DEL CAUDAL PARA EL CIERRE DEL
40%
DE LA
V
ÁLVULA
7
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................89
F
IGURA
105.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
95%
DE LA
V
ÁLVULA
7
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................90
F
IGURA
106.
C
OMPORTAMIENTO DE LA PRESIÓN PARA EL CIERRE DEL
90%
DE LA
V
ÁLVULA
7
EN LA RED
MATRIZ DE
M
EDELLÍN
. .........................................................................................................................90
F
IGURA
107.
C
OMPORTAMIENTO DE LOS CAUDALES FRENTE AL CIERRE DE LA VÁLVULA
1
AL
95%. .............92
F
IGURA
108.
C
OMPORTAMIENTO DE LAS PRESIONES FRENTE AL CIERRE DE LA VÁLVULA
1
AL
95%. .............93
F
IGURA
109.
C
OMPORTAMIENTO DE LOS CAUDALES FRENTE AL CIERRE DE LA VÁLVULA
2
AL
95%. .............93
F
IGURA
110.
C
OMPORTAMIENTO DE LAS PRESIONES FRENTE AL CIERRE DE LA VÁLVULA
2
AL
95%. .............94
F
IGURA
111.
C
OMPORTAMIENTO DE LOS CAUDALES FRENTE AL CIERRE DE LA VÁLVULA
3
AL
95%. .............95
F
IGURA
112.
C
OMPORTAMIENTO DE LAS PRESIONES FRENTE AL CIERRE DE LA VÁLVULA
3
AL
95%. .............96
F
IGURA
113.C
OMPORTAMIENTO DE LOS CAUDALES FRENTE AL CIERRE DE LA VÁLVULA
4
AL
95%. ..............96
F
IGURA
114.C
OMPORTAMIENTO DE LAS PRESIONES FRENTE AL CIERRE DE LA VÁLVULA
4
AL
95%. ..............97
F
IGURA
115.
C
OMPORTAMIENTO DE LOS CAUDALES FRENTE AL CIERRE DE LA VÁLVULA
5
AL
95%. .............98
F
IGURA
116.
C
OMPORTAMIENTO DE LAS PRESIONES FRENTE AL CIERRE DE LA VÁLVULA
5
AL
95%. .............98
F
IGURA
117.
C
OMPORTAMIENTO DE LOS CAUDALES FRENTE AL CIERRE DE LA VÁLVULA
6
AL
95%. .............99
F
IGURA
118.
C
OMPORTAMIENTO DE LAS PRESIONES FRENTE AL CIERRE DE LA VÁLVULA
6
AL
95%. ...........100
F
IGURA
119.
C
OMPORTAMIENTO DE LOS CAUDALES FRENTE AL CIERRE DE LA VÁLVULA
7
AL
95%. ...........100
F
IGURA
120.
C
OMPORTAMIENTO DE LAS PRESIONES FRENTE AL CIERRE DE LA VÁLVULA
7
AL
95%. ...........101
F
IGURA
121.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
95%
DE LA VÁLVULA
1
EN LA RED DE
B
UCARAMANGA
(C
AUDAL
). ...............................................................................................................102
F
IGURA
122.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
90%
DE LA VÁLVULA
1
EN LA RED DE
B
UCARAMANGA
(C
AUDAL
). ...............................................................................................................103
F
IGURA
123.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
80%
DE LA VÁLVULA
1
EN LA RED DE
B
UCARAMANGA
(C
AUDAL
). ...............................................................................................................103
F
IGURA
124.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
60%
DE LA VÁLVULA
1
EN LA RED DE
B
UCARAMANGA
(C
AUDAL
). ...............................................................................................................104
F
IGURA
125.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
95%
DE LA VÁLVULA
1
EN LA RED DE
B
UCARAMANGA
(P
RESIÓN
). ...............................................................................................................105
F
IGURA
126.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
90%
DE LA VÁLVULA
1
EN LA RED DE
B
UCARAMANGA
(P
RESIÓN
). ...............................................................................................................105
F
IGURA
127.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
80%
DE LA VÁLVULA
1
EN LA RED DE
B
UCARAMANGA
(P
RESIÓN
). ...............................................................................................................106
F
IGURA
128.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
95%
DE LA VÁLVULA
2
EN LA RED DE
B
UCARAMANGA
(C
AUDAL
). ...............................................................................................................107
F
IGURA
129.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
90%
DE LA VÁLVULA
2
EN LA RED DE
B
UCARAMANGA
(C
AUDAL
). ...............................................................................................................107
F
IGURA
130.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
80%
DE LA VÁLVULA
2
EN LA RED DE
B
UCARAMANGA
(C
AUDAL
). ...............................................................................................................108

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
vii
F
IGURA
131.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
60%
DE LA VÁLVULA
2
EN LA RED DE
B
UCARAMANGA
(C
AUDAL
). ...............................................................................................................108
F
IGURA
132.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
95%
DE LA VÁLVULA
2
EN LA RED DE
B
UCARAMANGA
(P
RESIÓN
). ...............................................................................................................109
F
IGURA
133.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
90%
DE LA VÁLVULA
2
EN LA RED DE
B
UCARAMANGA
(P
RESIÓN
). ...............................................................................................................109
F
IGURA
134.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
95%
DE LA VÁLVULA
3
EN LA RED DE
B
UCARAMANGA
(C
AUDAL
). ...............................................................................................................110
F
IGURA
135.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
90%
DE LA VÁLVULA
3
EN LA RED DE
B
UCARAMANGA
(C
AUDAL
). ...............................................................................................................111
F
IGURA
136.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
80%
DE LA VÁLVULA
3
EN LA RED DE
B
UCARAMANGA
(C
AUDAL
). ...............................................................................................................111
F
IGURA
137.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
95%
DE LA VÁLVULA
3
EN LA RED DE
B
UCARAMANGA
(P
RESIÓN
). ...............................................................................................................112
F
IGURA
138.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
90%
DE LA VÁLVULA
3
EN LA RED DE
B
UCARAMANGA
(P
RESIÓN
). ...............................................................................................................112
F
IGURA
139.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
95%
DE LA VÁLVULA
4
EN LA RED DE
B
UCARAMANGA
(C
AUDAL
). ...............................................................................................................113
F
IGURA
140.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
90%
DE LA VÁLVULA
4
EN LA RED DE
B
UCARAMANGA
(C
AUDAL
). ...............................................................................................................114
F
IGURA
141.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
80%
DE LA VÁLVULA
4
EN LA RED DE
B
UCARAMANGA
(C
AUDAL
). ...............................................................................................................114
F
IGURA
142.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
95%
DE LA VÁLVULA
4
EN LA RED DE
B
UCARAMANGA
(P
RESIÓN
). ...............................................................................................................115
F
IGURA
143.
A
NÁLISIS DE SENSIBILIDAD DEL CIERRE DEL
90%
DE LA VÁLVULA
4
EN LA RED DE
B
UCARAMANGA
(P
RESIÓN
). ...............................................................................................................115

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
viii
ÍNDICE DE TABLAS
T
ABLA
1.
T
UBERÍAS EN LAS CUALES SE SITUARON LAS VÁLVULAS DE
M
EDELLÍN
. ........................................43
T
ABLA
2.
T
IEMPO MÍNIMO DE CIERRE DE LAS VÁLVULAS DEPENDIENDO DEL DIÁMETRO
(S
ILVA
G.
&
L.F.,
1975). ...................................................................................................................................................63
T
ABLA
3.
C
ASOS SIMULADOS PARA LA RED MATRIZ DE
M
EDELLÍN
. ...............................................................63
T
ABLA
4.
C
ASOS SIMULADOS PARA LA RED DE
B
UCARAMANGA
. ...................................................................91

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
1
1. Introducción y Objetivos
1.1. Introducción
El agua potable es un recurso que es heterogéneo en el espacio y tiempo, sin embargo, la
demanda del mismo está en constante crecimiento. La supervivencia de las grandes
civilizaciones ha dependido en gran medida del agua; por esta razón, no es gratuito que
las grandes urbes se hayan situado junto a ríos o fuentes considerables de este bien. Por
otra parte, a lo largo de la historia las sociedades han encontrado la necesidad de hallar y
desarrollar soluciones que permitan tener una oferta continua o al menos de fácil acceso a
este bien de consumo.
Frente a esta necesidad continua, las sociedades prehistóricas encontraron que una
posible solución era la construcción de pozos. Sin embargo, esta opción requiere que las
personas sean quienes transporten el bien de consumo desde la fuente hasta el punto de
uso, haciendo que las cantidades transportadas sean de pequeña magnitud. Por otra parte,
la continua evolución y avance del conocimiento permitió que las sociedades
desarrollaran soluciones que permitieran la oferta continua del agua en la ciudad. Entre
éstas se puede ver los acueductos construidos por los romanos, griegos, persas, entre
otros, los cuales tenían como función llevar el agua desde una fuente lejana hasta la
ciudad.
En el siglo XVII se implementó uno de los proyectos que promovió el desarrollo de los
grandes acueductos; éste fue desarrollado en Londres y consistía en abastecer la pequeña
población de aquel momento con agua del Río Lea. Posteriormente, en el siglo XVIII,
Londres experimentó un crecimiento poblacional considerable, esto impulsó la necesidad
de tener una red de distribución de agua potable. Por aquel entonces la Chelsea
Waterworks Company, establecida en el año 1723, creó una gran cantidad de estanques
en la ciudad que eran abastecidos con el agua del Río Támesis. La importancia de este
proyecto yace en la implementación del uso de bombas en una red de distribución de
agua potable.
De esta manera, se inició el desarrollo de este tipo de redes, las cuales tienen como
objetivo abastecer a la población de la ciudad a partir de una fuente (Planta de
Tratamiento de Agua Potable). Así, una red de distribución de agua potable es una
interconexión de tuberías, válvulas, bombas, tanques de almacenamiento que permite
abastecer de agua a los pobladores de la ciudad. Sin embargo, algunos de estos
componentes (Válvulas y Bombas) se pueden operar para disminuir o aumentar el flujo
en la red.
Adicionalmente, los individuos de la sociedad tienen un comportamiento rutinario en
donde se tiene un alto consumo en algunos momentos del día y otros en donde la

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
2
situación es totalmente opuesta. Por lo tanto, la red se enfrenta a cambios continuos en la
demanda a lo largo del día y la semana.
En consecuencia, la red experimenta cambios en la operación (p. ej. Apertura y cierre de
válvulas) y la demanda; esto hace que el análisis operativo de las redes de agua potable
sea dinámico y no estático. Sin embargo, en la actualidad la simulación dinámica de las
redes se ha realizado bajo el análisis de periodo extendido y no de transiente, el cual no
tiene en cuenta que la hidráulica deja de ser de flujo permanente y pasa a ser no
permanente o de transiente.
Es importante establecer que el realizar un análisis de periodo extendido no permite
analizar la presencia de fenómenos de cavitación, estallidos de tuberías, desprendimiento
de biopelículas, entre otros. Además, en caso de que se tengan tanques de
almacenamiento y se esté operando continuamente las válvulas y bombas, los niveles del
tanque pueden variar considerablemente dependiendo del análisis que se emplee. De
forma similar, es relevante tener en cuenta que los modelos de calidad del agua dependen
directamente de los resultados que se tengan del modelo hidráulico. De esta manera, en
caso de que se tengan valores erróneos en el flujo de cada tubería y los niveles de los
tanques, se estaría incurriendo en desviaciones importantes de la calidad real que se tenga
en el sistema.
Por otra parte, la operación de válvulas es de gran utilidad para la empresa prestadora del
servicio, dado que la manipulación de éstas permite la reparación o rehabilitación de
tuberías. Adicionalmente, se debe saber que en la red existen fugas en las tuberías y la
pérdida de agua está en función de la presión que tenga la misma. Por esta razón, la
operación de válvulas juega un papel relevante en la disminución del desperdicio de agua.
Además, en algunos casos donde se tengan nudos con presiones bajas, la operación
eficiente de válvulas permitirá aumentar en cierta medida la presión en estos puntos. Sin
embargo, para poder realizar estas operaciones es necesario llevar a cabo un análisis de
transiente para ver los tiempos de respuesta de la red frente a estos cambios.
A pesar de tener todos estos posibles objetivos, el presente trabajo se centra en validar la
veracidad que tiene el análisis de periodo extendido. Es decir, se desea estudiar el tiempo
que requiere la red para llegar nuevamente a un estado estable. De esta forma, el
encontrar esta cantidad de tiempo permitirá establecer la resolución máxima que pueden
tener los patrones de demanda en la red, para aquellos casos en donde se realiza un
análisis de periodo extendido.
Por lo tanto, para lograr el objetivo se realizará una extensa revisión bibliográfica acerca
del tema de transiente en redes de distribución de agua potable. Adicionalmente, se
emplearán distintos modelos de redes de agua potable en donde se pueda realizar varios
análisis de sensibilidad. En consecuencia, será necesario emplear algún software que
permita llevar a cabo este análisis; de esta manera, se utilizará HAMMER como la
principal herramienta.

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
3
El documento constará de siete secciones principales. En la primera de ellas se expondrá
con detenimiento las investigaciones pasadas que se han realizado en el tema.
Posteriormente, se realizará una explicación acerca de las ecuaciones gobernantes en este
fenómeno. En la tercera parte se hará una explicación detallada de la metodología que
fue implementada para la ubicación de las válvulas y el procesamiento de las señales
obtenidas. Luego, se hará una explicación detallada de la herramienta computacional que
se utilizó para realizar las simulaciones del fenómeno de transiente. En la sexta sección
se describirán con detalle las redes que se utilizarán para el análisis. Más adelante, se
tendrá una sección en donde se presentarán los resultados y su interpretación.
Finalmente, la última parte constará de las conclusiones que se encontraron en la
investigación, en conjunto con recomendaciones para trabajos futuros.
1.2. Objetivos
1.2.1. Objetivo General
El objetivo principal de este trabajo es comprender y cuantificar el tiempo de respuesta de
las redes de distribución de agua potable, frente a cambios operativos asociados al cierre
o apertura de válvulas. De esta manera, se podrá comparar la veracidad del uso del
análisis de periodo extendido frente al análisis de transiente.
1.2.2. Objetivos Específicos
Para llevar a cabo el objetivo general del presente trabajo, se establecen los siguientes
objetivos específicos:
Realizar una revisión bibliográfica sobre el fenómeno de transiente; revisar los
conceptos fundamentales del fenómeno y estudiar investigaciones donde se
realice una crítica o comparación del análisis de periodo extendido.
Entender cómo funciona el motor de cálculo del software que se utilizará y las
variables que requiere para desarrollar el análisis de flujo transiente.
Desarrollar una metodología que permita dar las ubicaciones de las válvulas que
se emplearán para el análisis.
Estudiar qué redes son las que se van a estudiar a lo largo de toda la investigación.
Desarrollar una medida de tendencia que permita cuantificar las variaciones que
tiene la red. Asimismo, emplearla para definir en que instante la red llega a un
nuevo estado estable.
Entender la dinámica que tienen las redes frente a la operación de válvulas. Es
decir, entender hasta que distancia y en que tiempo la manipulación de las
válvulas perturba el flujo en la red.
Realizar un análisis de sensibilidad de las variables que se consideren relevantes
en el análisis (longitud, contenido de aire, etc.).
Establecer los tiempos de estabilización de las redes en términos de caudal y
presión de las mismas.
Establecer tiempos de simulación para cada caso que se vaya a estudiar.
Establecer los tiempos, curvas y porcentajes de cierre para las válvulas.
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
4
2. Antecedentes
Después de realizar una extensa revisión bibliográfica acerca de las investigaciones más
relevantes sobre el presente tema, se encontró una constante crítica hacia el uso de los
análisis de periodo extendido. Sin embargo, en muchos de ellos también se establece que
si los patrones de consumo y operación son de tiempos considerables, los resultados
obtenidos son aceptables.
Adicionalmente, se plantea constantemente que los análisis se deben realizar teniendo en
cuenta una demanda dependiente de la presión y no fija. Por otra parte, en algunos de los
artículos revisados se establece la importancia y la influencia de ciertos parámetros
cuando se realiza un análisis de flujo de transiente. A continuación se presenta un
resumen de los artículos y los aspectos más relevantes de estos para la investigación
presente.
En el trabajo de Duan, Tung, Ghidaoui (2010), realizado en la Universidad de Ciencia y
Tecnología de Hong Kong, se llevó a cabo un análisis probabilístico de los parámetros
más influyentes en el estudio de flujo transiente. De esta manera, se tomaron como
parámetros con incertidumbre el diámetro y longitud de la tubería, en conjunto con el
factor de fricción y celeridad de la onda. Se encuentra relevante mencionar que éste
último parámetro tiene en cuenta otras incertidumbres tales como los módulos de
elasticidad, densidades, contenido de aire en el agua, espesores y coeficiente de Poisson
de la tubería.
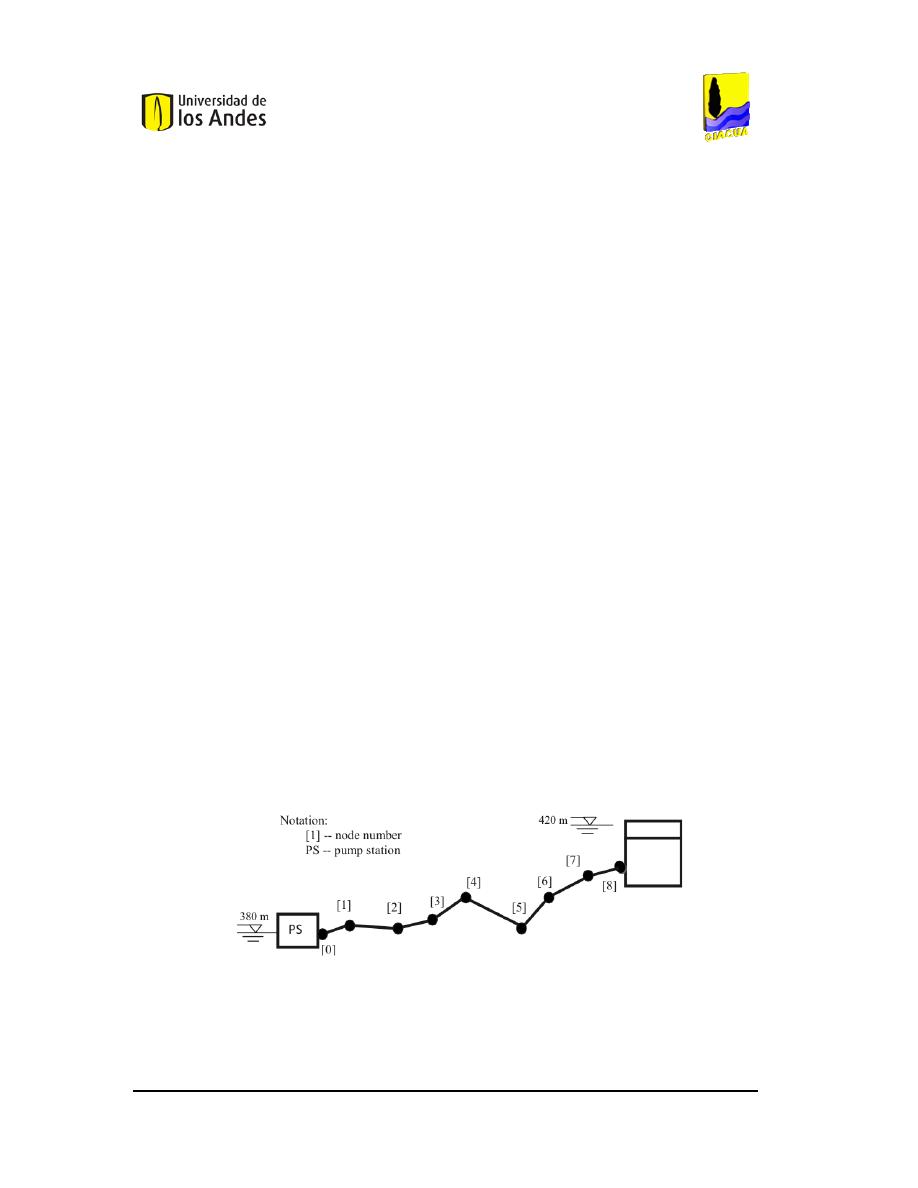
El sistema analizado se presenta en la
Figura 1
, el cual consta de una serie de tuberías de
acero de 1,000 mm de diámetro y una longitud total de 1.8 Km. De esta manera, al tener
el material y el diámetro empleado se puede calcular la velocidad de onda, la cual tiene
un valor de 1,100 m/s. El sistema cuenta con un bomba al inicio del sistema (PS), la cual
se encuentra al lado izquierdo del nudo [0]. La manera en que generaron el flujo
transiente en el sistema es por medio de la falla de la bomba y el cerrado automático de
una válvula que se encuentra en el nudo [1].
Figura 1. Red utilizada en el trabajo de Duan et al. (2010).
Uno de los aspectos más relevante de la investigación es que la velocidad de onda tiene
una alta variación con respecto al valor encontrado cuando se supone que la
concentración de aire en el agua es de 0. Es decir, el valor promedio encontrado para la
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
5
velocidad de onda, a partir del análisis de incertidumbre, es de 480 m/s con un coeficiente
de variación del 32%. Se debe tener en cuenta que para encontrar éste valor utilizaron
una concentración promedio de aire de 0.05% con un coeficiente de variación del 80%.
Posteriormente, al realizar el análisis de transiente se encontró que cuando se realiza un
estudio determinístico del sistema, la probabilidad de falla se distribuye uniformemente
entre los diferentes tubos. Sin embargo, cuando se lleva a cabo el mismo análisis
teniendo en cuenta la variabilidad de los diferentes parámetros de entrada, la probabilidad
de falla se concentra en los puntos más cercanos a la válvula y no en su totalidad.
El mayor aporte que da este trabajo a la presente investigación es la noción de la
relevancia que puede llegar a tener la concentración de aire en el cálculo de la velocidad
de onda y, por lo tanto, en los resultados finales obtenidos.
La siguiente investigación que se presenta es el trabajo realizado por Filion y Karney
(2002), el cual muestra un modelo denominado “Extended Dynamic”. Adicionalmente,
los investigadores describen el inconveniente principal que tiene el análisis de periodo
extendido, el cual supone que las variaciones de los flujos y las presiones son graduales.
De esta manera, si se tiene un tiempo de análisis de periodo extendido corto, se podrá
incurrir en errores significativos en los niveles de los tanques de almacenamiento, flujo y
presiones de la red.
Los autores plantean un modelo que conecta un tipo de análisis de periodo extendido y de
transiente. Es decir, en un instante de tiempo
𝑡 se realiza un análisis de transiente que
permite saber la tasa de llenado que tendrán los tanques hasta el instante
𝑡 + ∆𝑡
𝑡𝑟𝑎𝑛𝑠𝑖𝑒𝑛𝑡𝑒
.
Posteriormente, se utiliza este valor y un predictor para suponer la tasa de llenado que
tendrán los tanques desde el instante
𝑡 + ∆𝑡
𝑡𝑟𝑎𝑛𝑠𝑖𝑒𝑛𝑡𝑒
hasta
𝑡 + ∆𝑡
𝑡𝑟𝑎𝑛𝑠𝑖𝑒𝑛𝑡𝑒
+
∆𝑡
𝑝𝑒𝑟𝑖𝑜𝑑𝑜 𝑒𝑥𝑡𝑒𝑛𝑑𝑖𝑑𝑜
. De esta manera, se calcula el nivel de los tanques al final de este
último instante de tiempo, y luego se vuelve a realizar un análisis de transiente para
repetir el procedimiento nuevamente.
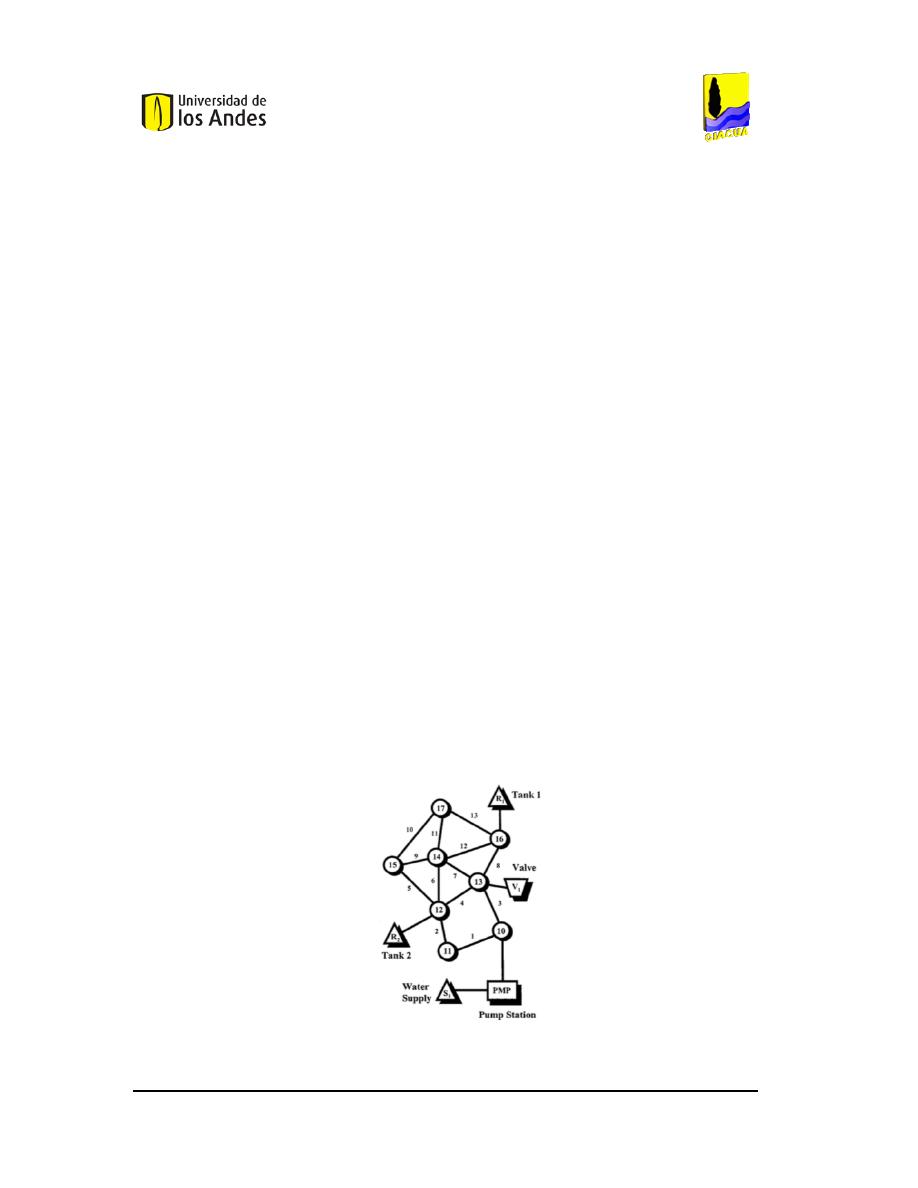
Figura 2. Red utilizada para el modelo presentado en el trabajo de Filion et al. (2002).
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
6
El modelo fue probado en la red que se presenta en la
Figura 2
y los resultados fueron
comparados con TransAM y EPANET, siendo el primero un simulador de flujo transiente
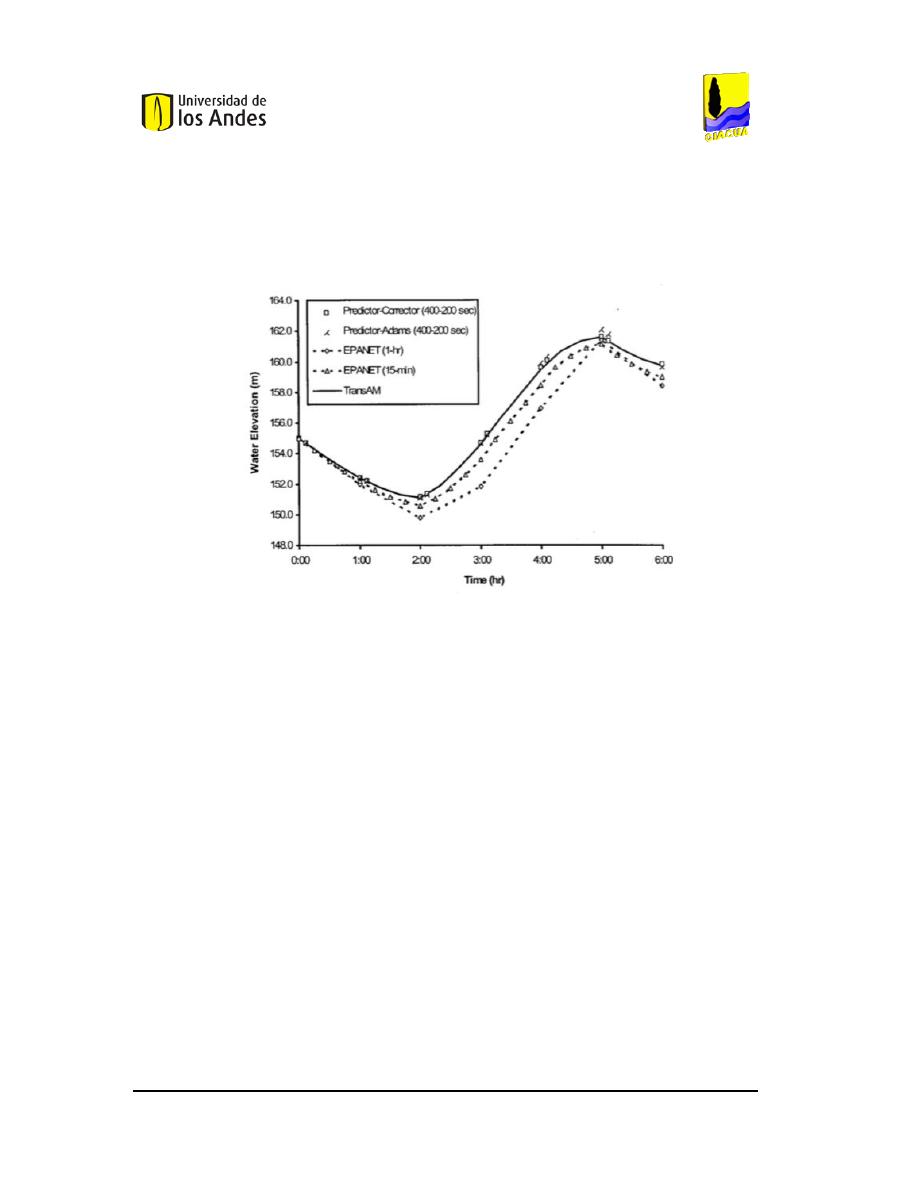
y el segundo uno de periodo extendido. En la
Figura 3
se muestran los resultados
obtenidos; cabe resaltar que el modelo planteado por los investigadores tiene dos tipos de
predictores. Es por esto que en la figura se presentan dos resultados del mismo modelo.
Figura 3. Resultados del trabajo de Filion et al. (2002).
A partir de la figura anterior se puede ver que el modelo planteado tiene una alta
precisión para definir el nivel de los tanques en el tiempo. Esto se puede ver ya que los
puntos de los predictores se encuentran justo encima de la línea continua obtenida del
programa TransAM. Por otra parte, se puede ver que EPANET se aleja de ésta última
línea; sin embargo, el disminuir el paso del tiempo hace que el error disminuya
considerablemente. Es relevante mencionar que la dinámica de la red se debe al
encendido y apagado de bombas, en conjunto con la operación de la única válvula del
sistema.
Lo relevante del anterior estudio es que cuantifica y muestra los errores que se pueden
tener si realiza un análisis de periodo extendido durante la operación de válvulas y
bombas.
El siguiente artículo que se presenta tiene como objetivo mostrar que en la industria se ha
llevado a cabo el análisis de transiente para redes pequeñas y no para redes de gran
magnitud. El trabajo fue realizado por Allen Davis (2004), en él se presentan tres casos
de estudio donde se analizaron los riesgos que tenían las redes de distribución de agua
frente a fenómenos de transiente.
Las redes estudiadas fueron las de Salt Lake County, Utah; Rockdale County, Georgia y
City of Atlanta, Georgia. Se encuentra relevante mencionar que el mecanismo para
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
7
generar el flujo transiente fue a partir de una falla en el sistema de bombeo. La primera de
éstas tiene una longitud total de tubería de 220,000 metros, con 313 tuberías y 292 nudos.
A partir del análisis realizado se encontró que existían dos áreas alejadas en la red, las
cuales eran susceptibles a tener presiones inferiores a la de vapor. Por otra parte, luego
de ocurrido el primer evento, éstas zonas se veían nuevamente afectadas por las altas
presiones que superaban las máximas permitidas. Para remediar la situación se crearon
19 almenaras con un volumen total de 225 m
3
.
El siguiente caso de estudio tenía una longitud de tubería de 197,000 metros, 150 tuberías
y 124 nudos. Ésta red presentaba nuevamente bajas presiones y sobrepresiones en varios
puntos de la red, por lo tanto, para remediar el problema fue necesario construir una torre
piezométrica de 85 m
3
de volumen. De esta manera, se logró disminuir las altas
presiones hasta conseguir que las máximas presiones coincidieran con aquellas
encontradas en el estado estable de la red.
Finalmente, el último caso tenía una longitud total de tubería de 366,000 metros, 232
tuberías y 198 nudos. Esta red solo presentó problemas de baja presión; la solución
presentada fue la instalación de varias torres piezométricas de 113 m
3
. El aspecto de
mayor relevancia de éste artículo es ver el tamaño de las redes que se han estudiado, las
cuales no superan las 500 tuberías.
El siguiente artículo es de los trabajos que se considera de mayor relevancia para la
presente investigación, dado que presenta una comparación entre los métodos de cálculo
para el flujo de transiente. La investigación fue realizada por Karney, Jung y Alkozai
(2006).
La comparación se centra en los métodos de: golpe de ariete (Convencional), la teoría de
columna rígida de agua y el periodo extendido. El primero de estos supone que la
velocidad de la onda es superior a la del flujo, el fluido es compresible y la tubería tiene
un comportamiento elástico. El segundo supone que el fluido es incompresible y que la
tubería es indeformable. Cabe resaltar que los tres métodos mencionados tienen en
cuenta las pérdidas por fricción. Para realizar la comparación de los tres métodos se
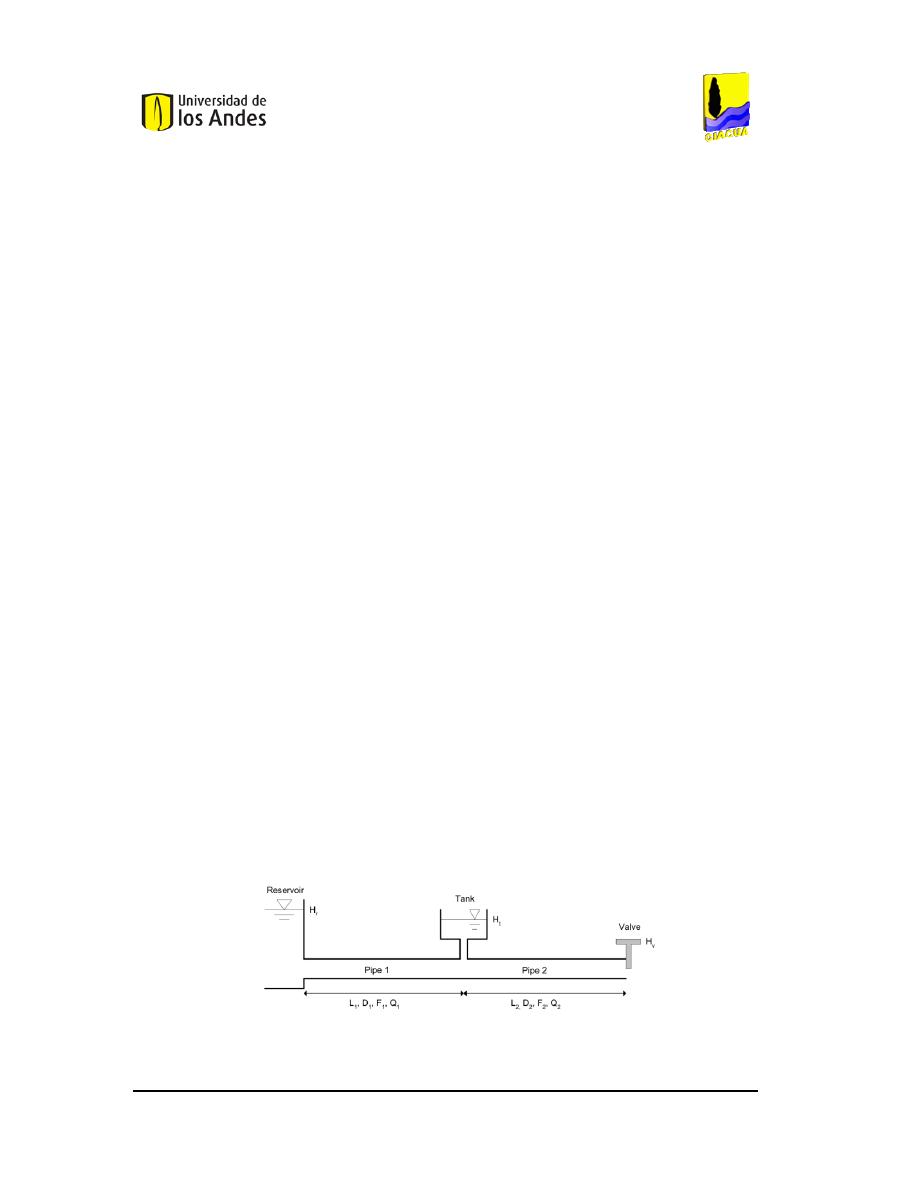
utilizó el modelo que se presenta en
Figura 4
, el cual consta de un reservorio, un tanque de
almacenamiento, dos tuberías y una válvula con la cual se generan los flujos transientes.
Figura 4. Modelo utilizado en el trabajo de Karney et al. (2006)
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
8
Con el uso del modelo se realizaron dos análisis de sensibilidad, en el primero se varió la
base del tanque de almacenamiento, el cual funciona como amortiguamiento al transiente.
El segundo análisis que se realizó fue variar los tiempos de cierre de la válvula para ver
de qué forma se comportaban los tres métodos de cálculo.
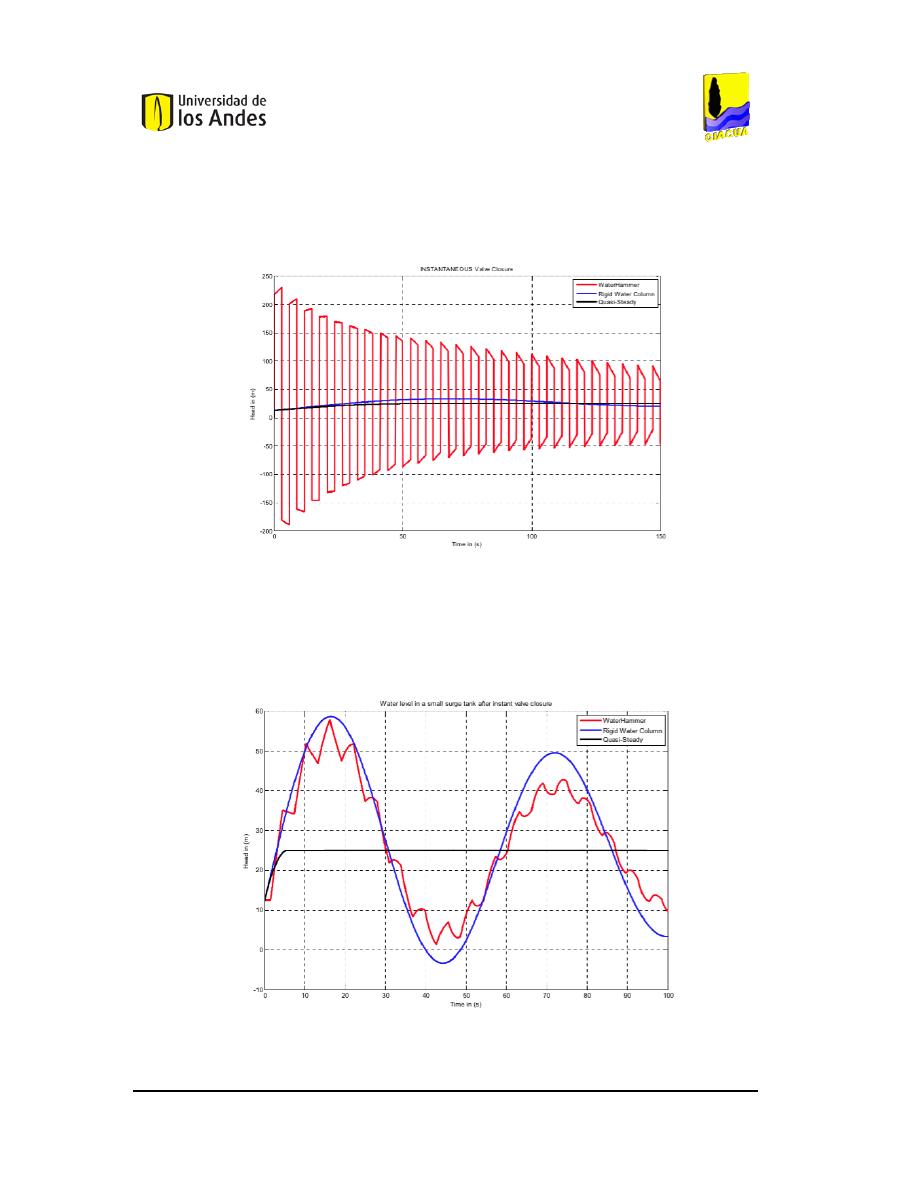
Figura 5. Resultados del trabajo de Karney et al. (2006) con una base de 1 m
2
del tanque.
A partir de la
Figura 5
se puede ver como el modelo convencional de transiente
(WaterHammer), tiene un comportamiento que se aleja de la realidad. Sin embargo, es
relevante que es el único capaz de captar las variaciones de presión que se pueden
generar en este fenómeno.
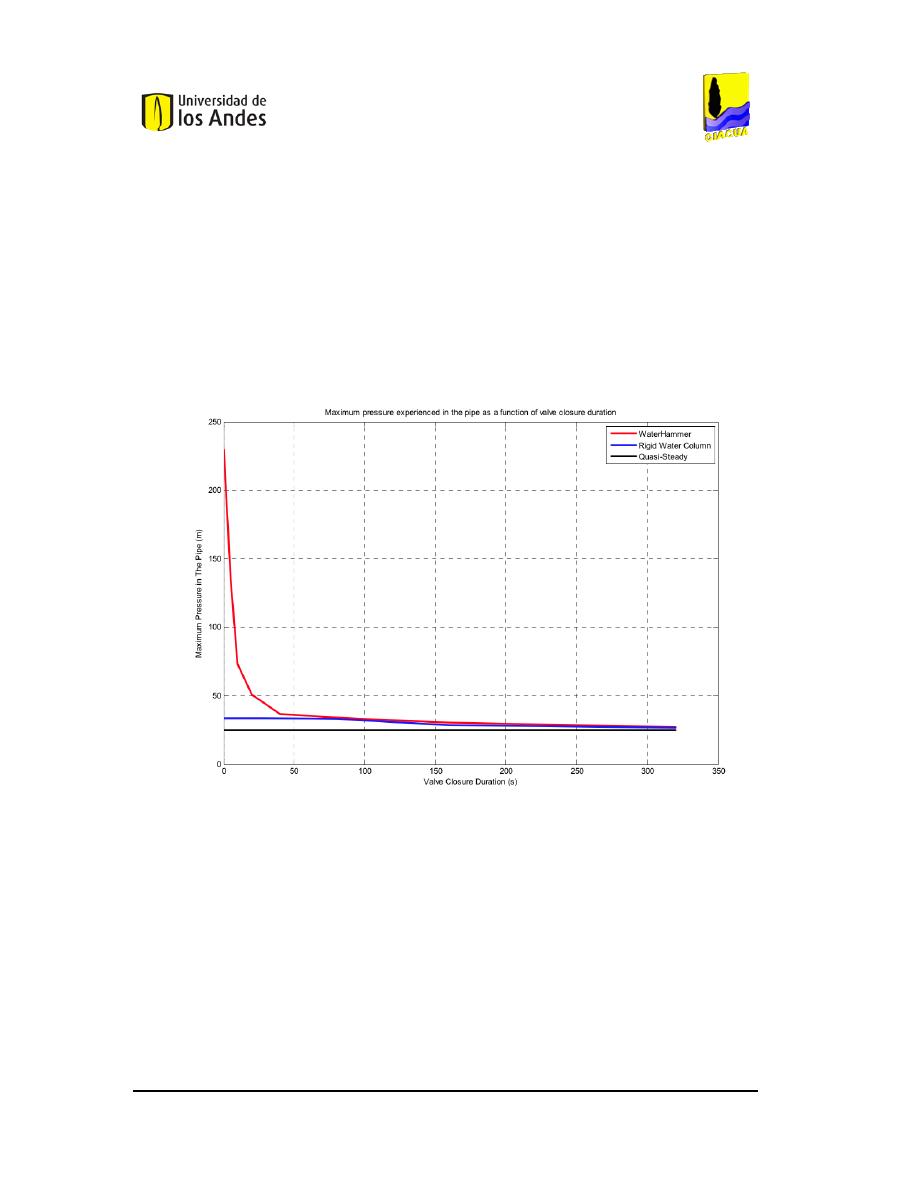
Figura 6. Resultados del trabajo de Karney et al. (2006) con una base de 0.2 m
2
del tanque.
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
9
Por otra parte, cuando se disminuye la base del tanque del modelo se puede ver que los
efectos de inercia y compresibilidad se vuelven más evidentes (Ver Figura 6). Por esta
razón, el modelo de columna rígida de agua se separa del comportamiento que tiene el
modelo de periodo extendido. Se encuentra relevante mencionar la ineficiencia que tiene
éste último para representar las variaciones considerables de presión que existen.
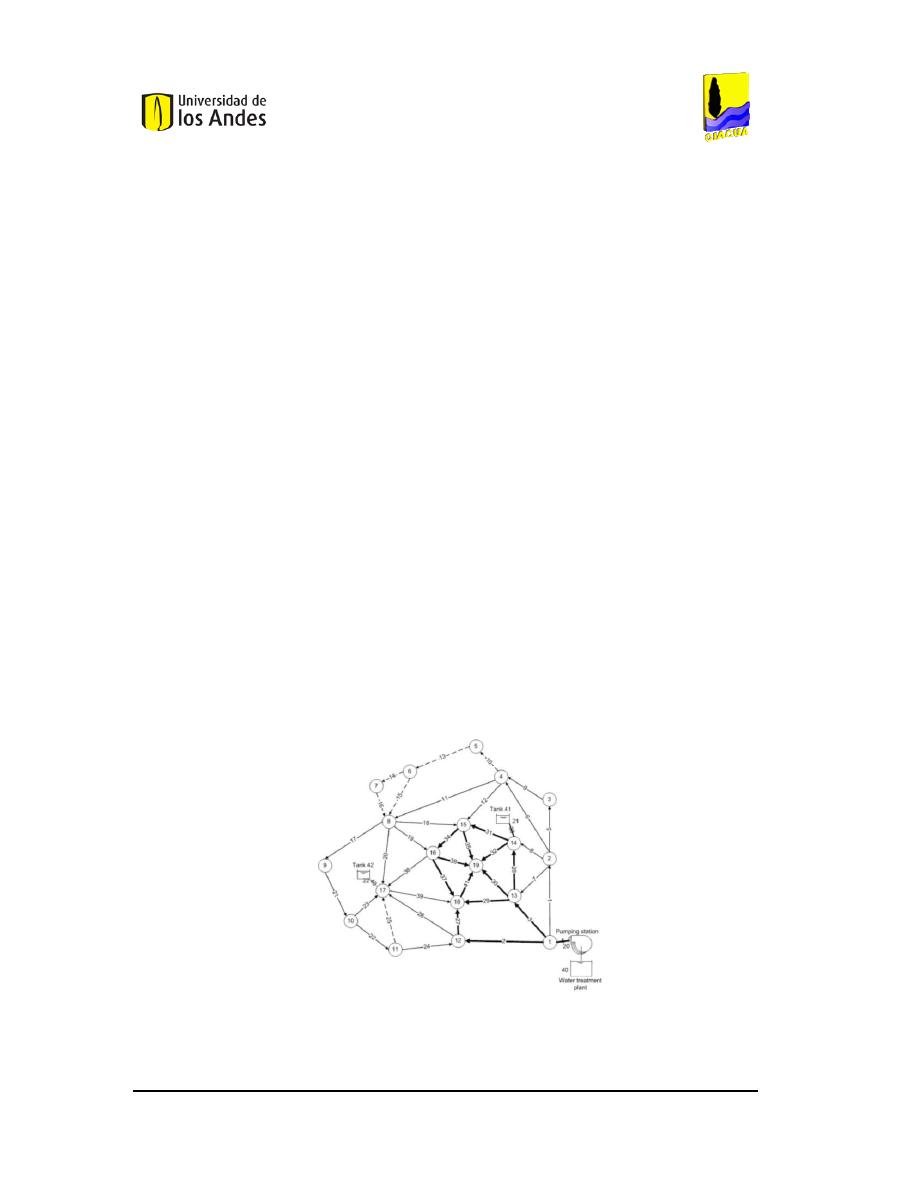
Finalmente, al realizar el análisis de sensibilidad respecto al tiempo de cierre de la
válvula se encontró que a medida que éste aumentaba, los efectos de inercia y
compresibilidad pierden importancia y, los tres modelos llegan a tener resultados muy
similares. Sin embargo, cuando el tiempo de cierre es menor a 50 segundos (Ver
Figura
7
), el modelo de golpe de ariete es el único capaz de captar las sobrepresiones.
Figura 7. Resultados del trabajo de Karney et al. (2006) respecto al tiempo de cierre de la válvula.
A partir de esta investigación se pudo ver en qué casos vale la pena realizar un análisis de
flujo de transiente. Por otra parte, es relevante mencionar que la teoría de columna rígida
de agua es válida solo para los casos en los que los efectos inerciales y de
compresibilidad comienzan a ser relevantes. Sin embargo, a partir de la
Figura 7
se puede
ver que, para tiempos de cierre de la válvula inferiores a 50 segundos, la teoría de
columna rígida pierde la capacidad de describir las sobrepresiones que se pueden generar
en el sistema.
De esta manera, los investigadores establecen que si se tiene un flujo transiente suave, el
modelo de periodo extendido es válido. Por otra parte, si las variaciones del flujo son un
poco más rápidas, el modelo de la teoría de columna rígida de agua es el que se debería
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
10
realizar. Finalmente, cuando las variaciones de cambio de flujo son drásticas, se
considera necesario llevar a cabo un análisis exhaustivo de flujo transiente.
Otro aspecto que se consideró de gran relevancia para la presente investigación fue ver la
influencia que tenía el análisis si se consideran demandas fijas o dependientes de la
presión. Por esta razón, a continuación se presenta una investigación que muestra la
relevancia que tiene este aspecto sobre el análisis de la red.
La primera de ellas fue realizada por Siew y Tanyinboh (2012), en ella se comparan los
resultados de periodo extendido para los casos en que se consideran las demandas fijas y
dependientes de la presión. Sin embargo, un aspecto relevante de esta investigación es
que las demandas dependientes de la presión no se simularon por medio de emisores sino
con el uso de una función logística. Es decir, no porque exista presión en el nudo habrá
un caudal demandado; se debe superar un valor mínimo de presión (40 psi) para dar un
caudal en aquel nudo. De forma similar, existe un valor máximo de presión para el cual
el caudal demandado no tiene aumento alguno y permanece estable.
Por otra parte, los investigadores plantearon un factor de satisfacción de la demanda
(DSR), el cual tiene como objetivo medir el porcentaje de la demanda fija que se está
abasteciendo. De esta manera, se cuantificó qué tan deficiente es la red en su operación
usual. Se encuentra relevante mencionar que la forma de cálculo del llenado y vaciado de
los tanques es a partir del modelo que trae por defecto EPANET. Sin embargo, los
investigadores establecen que se tendrán errores en el cálculo de los niveles, para mitigar
esto se disminuyó el tiempo de cálculo.
La red que se utilizó para evaluar el modelo fue la de “Anytown” (Ver
Figura 8
), la cual es
un benchmark mundial para el análisis de redes de distribución de agua potable.
Figura 8. Red "Anytown" utilizada en el trabajo de Siew et al. (2012).
A partir de la modelación se encontró que para el intervalo de tiempo entre 7 y 15 horas
(Ver
Figura 9
), la red tiene un DSR menor a 1. Es decir, existen nudos en donde no se está

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
11
abasteciendo la totalidad del caudal establecido como demanda fija. Sin embargo, es
relevante ver que el índice no es inferior a 0.6 y, de cierta forma, se está abasteciendo
gran parte de la demanda en la totalidad del tiempo de simulación.
Figura 9. Resultados del factor de satisfacción de la demanda en la investigación de Siew et al. (2012).
Por otra parte, se puede ver a partir de la
Figura 9
que a las 10 horas es el momento en el
que se tiene el menor DSR. Por esta razón, los investigadores consideraron de alta
relevancia ver las presiones que se estaban teniendo en el sistema en este momento. A
partir de la
Figura 10
se puede ver que en la mayoría de los nudos se tienen presiones
negativas cuando se analizan las demandas como fijas. Por lo contrario, cuando se
supone que las demandas dependen de la presión, en ningún nudo se tiene valores
negativos de esta variable. Adicionalmente, se puede ver que los puntos azules están por
debajo de los 40 psi. Sin embargo, en algunos casos la diferencia es mínima y, por lo
tanto, se puede estar abasteciendo una porción del caudal demandado.
Figura 10. Presiones en los nudos de la red "Anytown" a las 10 horas (Siew et al., 2012).
Se encuentra necesario establecer que los puntos azules y morados tienen la misma
tendencia. De esta manera, se encuentra que la suposición de que las demandas sean
dependientes de la presión no afecta la tendencia ni el comportamiento de la red. A partir
de los resultados obtenidos, los investigadores establecen que el análisis de demandas
fijas no permite cuantificar la deficiencia que tiene el sistema para abastecer todos los
nudos con sus demandas. De esta forma, plantean que el estudio de la red se debería
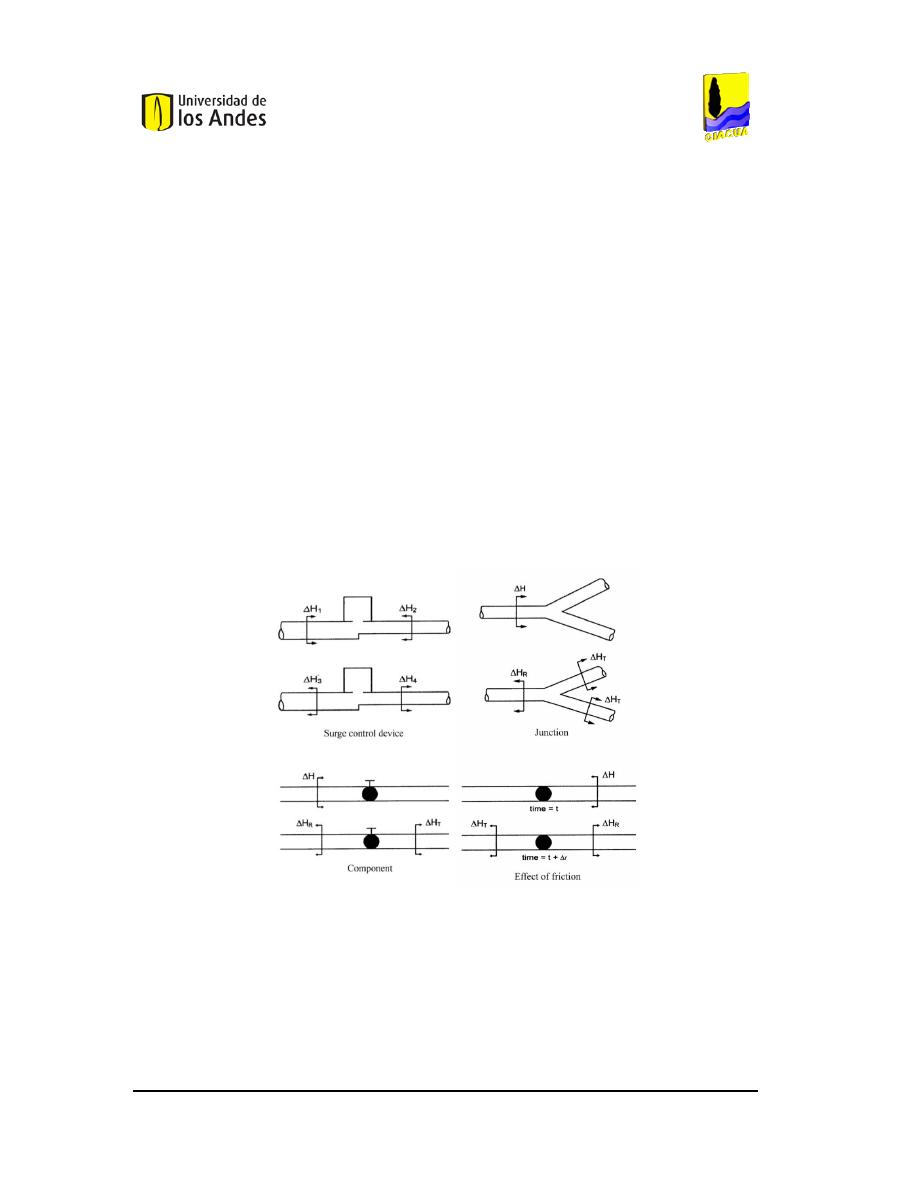
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
12
llevar a cabo suponiendo que los caudales de los nudos sean en función de la presión que
se tenga.
Finalmente, el último artículo que se considera relevante mencionar en la presente
investigación es el trabajo realizado por Don J. Wood (2005). En él se presenta una
comparación del cálculo de transiente por medio del método de las características y el
método de la característica de la onda. El primero de estos emplea las dos ecuaciones
diferenciales que rigen el fenómeno, en conjunto con dos ecuaciones de compatibilidad.
Estas últimas son solo válidas en aquellos casos en donde las ecuaciones características
son satisfechas. Adicionalmente, para la solución de este método, es necesario tener
distintas condiciones de fronteras tales como reservorios, válvulas, bombas, etc.
Por otra parte, el segundo método de cálculo se basa solo en dos análisis. El primero de
ellos consiste en analizar los componentes de la red, es decir, cuando la onda llega a una
válvula, tanque, entre otros. Este análisis se encarga de definir la propagación en
términos de transmisión y reflexión de la onda en ese componente. El segundo análisis se
concentra en estudiar estos mismos aspectos, pero en las uniones únicamente.
Adicionalmente, los efectos de fricción son simulados por medio de orificios en las
tuberías. En la
Figura 11
se muestra gráficamente el análisis que realiza este método.
Figura 11. Análisis de la onda de presión por medio del método de la característica de la onda
(Wood, 2005).
Los métodos de cálculo fueron evaluados en la red que se presenta en la Figura 12. La
forma de generar el flujo transiente fue cerrando la válvula en 0.6 segundos, por otra
parte, los nudos de análisis fueron el 4 y el 5. Los resultados obtenidos muestran la alta
exactitud que tiene el método de la característica de onda. Adicionalmente, los
investigadores encontraron que la precisión del método de las características tiene una
alta dependencia al paso de tiempo que se elija, caso contrario con el otro método.
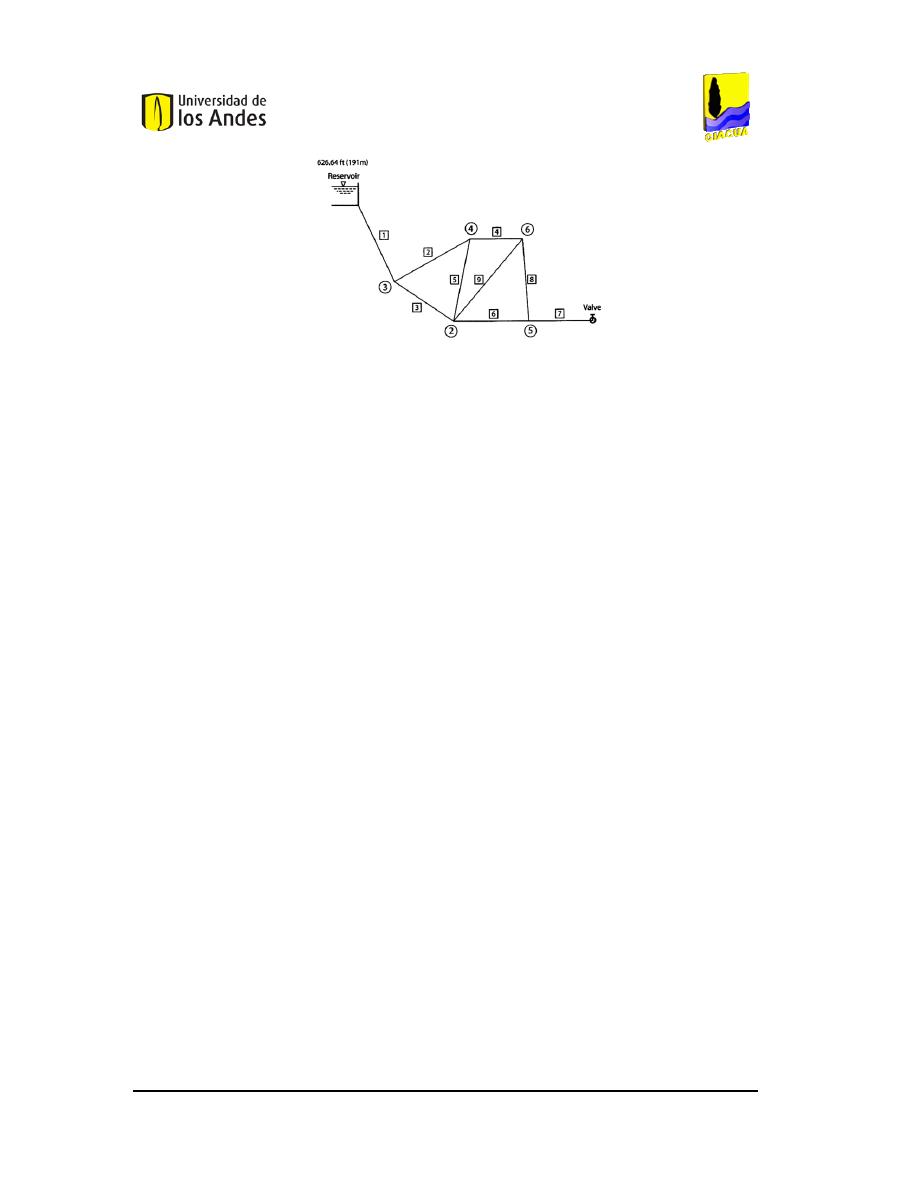
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
13
Figura 12. Red de estudio en el trabajo de Wood (2005).
Dado que en la presente investigación se va a usar el método de las características se
encuentra relevante la conclusión que tuvo Wood (2005) en su trabajo. Es decir, la alta
dependencia que tiene la precisión de éste método frente al paso de tiempo que se elija.
De esta manera, éste será un parámetro de alta relevancia para el análisis que se realice en
la investigación.

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
14
3. Marco Teórico
El flujo transiente involucra una gran cantidad de conocimiento hidráulico, incluyendo
ecuaciones diferenciales que definen la conservación de masa y de la energía.
Adicionalmente, al tener ecuaciones complejas de solucionar en sistemas de redes de
distribución de agua potable, es necesario tener un método de cálculo que permita la
solución de éstas. Por otra parte, para poder cumplir con el objetivo general, se considera
necesario conocer el comportamiento hidráulico que tienen las válvulas en su estado
estable y transiente. En este capítulo se mencionan los principales aspectos teóricos y del
método de cálculo utilizado. De esta manera, se podrá realizar una interpretación
correcta de los resultados obtenidos en las diferentes simulaciones que se lleven a cabo.
3.1. Tipos de flujo
Flujo Permanente: Las condiciones en los diferentes puntos permanecen estables
en el tiempo.
Flujo No Permanente: Las condiciones en los diferentes puntos varían en el
tiempo.
Flujo Uniforme: La velocidad promedio en los diferentes puntos del ducto es
igual.
Flujo No Uniforme: La velocidad varía a lo largo del ducto.
El caso de estudio de la presente investigación es el flujo transiente el cual es un flujo no
permanente. Por lo tanto, las características de velocidad, caudal y presión dependerán
de t. Se encuentra relevante mencionar que el flujo permanente es un caso especial del
flujo no permanente; por esta razón, las ecuaciones de flujo transiente deben satisfacer el
primer tipo de flujo (Wylie & Streeter, 1978).
3.2. Hidráulica de flujo transiente
Para definir correctamente la hidráulica de flujo de transiente, es necesario establecer las
ecuaciones que conservan la cantidad de movimiento y la masa. De esta manera, a
continuación se presenta la forma cómo se obtienen las ecuaciones que rigen este tipo de
flujo.
Ecuación de Conservación de la Cantidad de Movimiento
Para desarrollar la ecuación de movimiento se emplea el diagrama de cuerpo libre que se
encuentra en
Figura 13
. En él, se tienen en cuenta las fuerzas normales de contacto,
cortante y las presiones que son ejercidas en la periferia del cuerpo de control.

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
15
Figura 13. Diagrama de cuerpo libre para la aplicación de la ecuación de conservación de la cantidad
de movimiento (Wylie & Streeter, 1978).
Es necesario aclarar que el subíndice x o t tienen como significado la derivada parcial de
la variable dependiente respecto a x o t (
𝑒. 𝑔. 𝑝
𝑥
= 𝜕𝑝/𝜕𝑥). Adicionalmente, el punto que
tienen las variables independientes se refiere a la derivada total de esa variable respecto al
tiempo (
𝑒. 𝑔. 𝑉̇ = 𝑑𝑉/𝑑𝑡). A partir del diagrama de cuerpo libre se obtiene la siguiente
ecuación:
𝑝𝐴 − [𝑝𝐴 + (𝑝𝐴)
𝑥
𝛿𝑥] + (𝑝 + 𝑝
𝑥
𝛿𝑥
2
) 𝐴
𝑥
𝛿𝑥 − 𝜏
0
𝜋𝐷𝛿𝑥 − 𝛾𝐴𝛿𝑥 sin 𝛼 = 𝜌𝐴𝛿𝑥𝑣̇ (1)
Luego de quitar los dobles diferencial (
𝛿𝑥)
2
de la ecuación se obtiene:
𝑝
𝑥
𝐴 + 𝜏
0
𝜋𝐷 + 𝜌𝑔𝐴 sin 𝛼 + 𝜌𝐴𝑣̇ = 0 (2)
Por otra parte, se tienen las siguientes ecuaciones:
𝜏
0
= 𝛾𝑅𝑆
𝑓
(3)
ℎ
𝑓
= 𝑓
𝑙
𝑑
𝑣
2
2𝑔
= 𝑓
𝑙
4𝑅
𝑣
2
2𝑔
→
ℎ
𝑓
𝑙
= 𝑆
𝑓
=
𝑓
4𝑅
𝑣
2
2𝑔
(4)
Haciendo uso de las dos ecuaciones anteriores se encuentra que:
𝜏
0
=
𝜌𝑓𝑣|𝑣|
8
(5)
De esta manera, usando la ecuación (1) y (5) se obtiene:
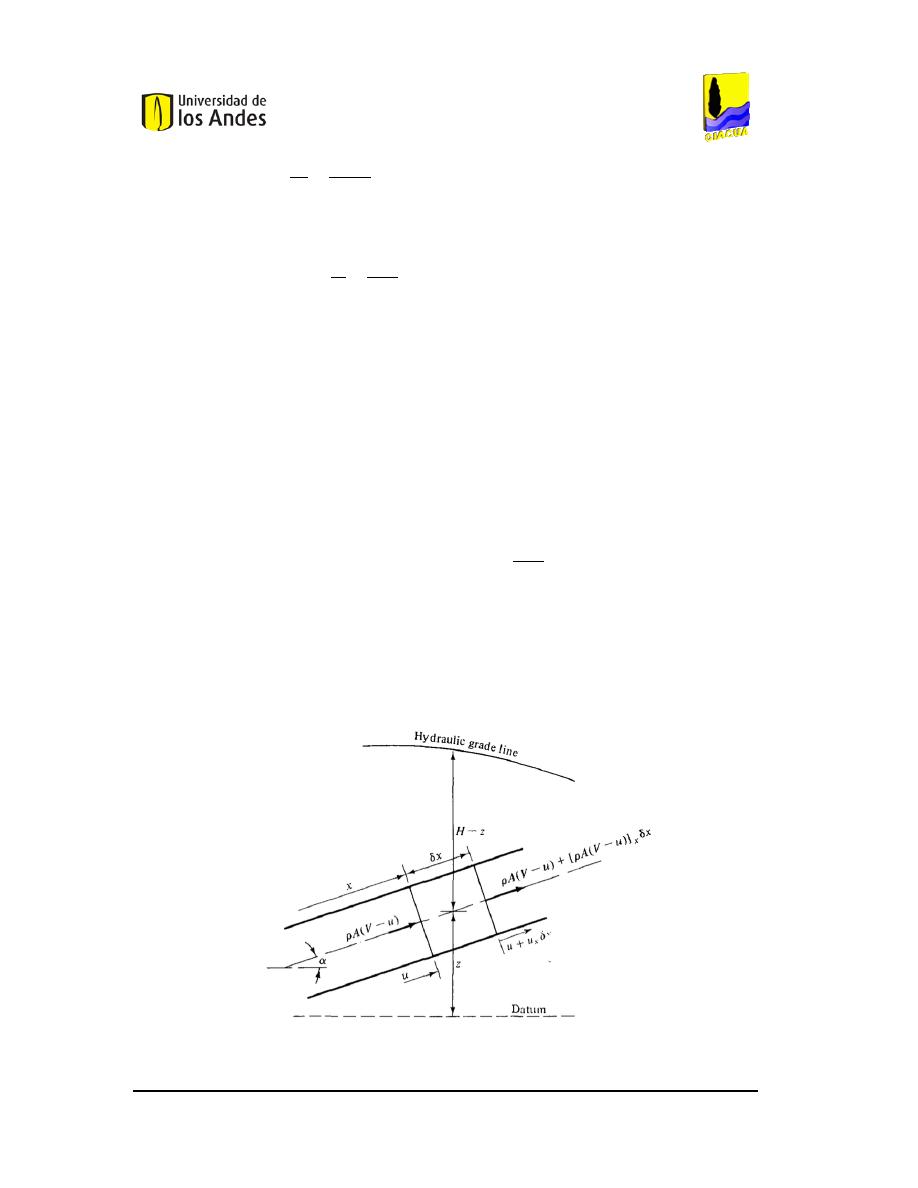
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
16
𝑝
𝑥
𝜌
+
𝑓𝑣|𝑣|
2𝐷
+ 𝑔 sin 𝛼 + 𝑣̇ = 0; 𝑣̇ = 𝑣𝑣
𝑥
+ 𝑣
𝑡
Por lo tanto:
𝑝
𝑥
𝜌
+
𝑓𝑣|𝑣|
2𝐷
+ 𝑔 sin 𝛼 + 𝑣𝑣
𝑥
+ 𝑣
𝑡
= 0 (6)
A partir de la
Figura 13
, se encuentra:
𝑝 = 𝜌𝑔(𝐻 − 𝑧)
Luego:
𝑝
𝑥
= [𝜌𝑔(𝐻 − 𝑧)]
𝑥
= 𝜌𝑔(𝐻
𝑥
− 𝑧
𝑥
) = 𝜌𝑔(𝐻
𝑥
− sin 𝛼)
De esta manera, la Ecuación (6) queda de la siguiente forma y es la ecuación de
conservación de la cantidad de movimiento.
𝑔𝐻
𝑥
+ 𝑣𝑣
𝑥
+ 𝑣
𝑡
+
𝑓𝑣|𝑣|
2𝐷
= 0 (7)
Ecuación de Conservación de la Cantidad de la Masa
Para el desarrollo de la ecuación de conservación de la cantidad de la masa, se emplea el
diagrama de cuerpo libre que se ve en la
Figura 14
. La conservación de la masa se
establece como el flujo de entrada al volumen de control es igual a la tasa de incremento
de la masa en el mismo.
Figura 14. Diagrama de cuerpo libre para la aplicación de la ecuación de conservación de la masa
(Wylie & Streeter, 1978).

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
17
Por lo tanto, se plantea la siguiente ecuación:
−[𝜌𝐴(𝑉 − 𝑢)]
𝑥
𝛿𝑥 =
𝐷´
𝐷𝑡
(𝜌𝐴𝛿𝑥) (8)
Se encuentra relevante mencionar que
𝒖 es la velocidad de las paredes del volumen de
control en la dirección x. Por otra parte, se tiene que:
𝐷´
𝐷𝑡
= 𝑢
𝜕
𝜕𝑥
+
𝜕
𝜕𝑡
(9)
De esta manera, se tiene que:
𝐷´
𝐷𝑡
𝛿𝑥 = 𝑢
𝑥
𝛿𝑥 (10)
A partir de la Ecuación (8) y la expansión de la derivada encontrada en las Ecuaciones (9)
y (10) se encuentra que:
(𝜌𝐴𝑉)
𝑥
− (𝜌𝐴)
𝑥
𝑢 − 𝜌𝐴𝑢
𝑥
+ 𝑢(𝜌𝐴)
𝑥
+ (𝜌𝐴)
𝑡
+ 𝜌𝐴𝑢
𝑥
= 0 (11)
Simplificando la ecuación anterior:
(𝜌𝐴𝑉)
𝑥
+ (𝜌𝐴)
𝑡
= 0 (12)
Desarrollando las derivadas parciales de la ecuación anterior se halla la siguiente
expresión:
𝜌𝐴𝑉
𝑥
+ 𝑉(𝜌𝐴)
𝑥
+ (𝜌𝐴)
𝑡
= 0 (13)
Si se mira con detalle los dos últimos términos de la ecuación anterior, se puede ver que
corresponden a la derivada total de
𝝆𝑨 respecto al tiempo. Por lo tanto, se tiene que:
1
𝜌𝐴
𝐷
𝐷𝑡
(𝜌𝐴) + 𝑉
𝑥
= 0 (14)
Desarrollando la ecuación anterior se puede llegar a:
1
𝜌𝐴
(𝜌𝐴̇ + 𝜌̇𝐴) + 𝑉
𝑥
= 0 (15)
Reordenando:
𝐴̇
𝐴
+
𝜌
𝜌
̇ + 𝑉
𝑥
= 0 (16)

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
18
Al no haber realizado ninguna suposición, la ecuación anterior es válida aún para tuberías
muy flexibles o para el flujo de gas. Adicionalmente, a partir de diferentes suposiciones
de cómo se va a comportar la tubería y el coeficiente de Poisson, se puede llegar a la
siguiente ecuación.
𝑉𝐻
𝑥
+ 𝐻
𝑡
− 𝑉 sin 𝛼 +
𝑎
2
𝑔
𝑉
𝑥
= 0 (17)
La anterior ecuación es la conservación de la masa definida de una manera pertinente,
dado que tiene como variables dependientes
𝑽 y 𝑯. Se encuentra necesario aclarar que el
término
𝒂, es la velocidad de la onda, la cual se define en la siguiente ecuación.
𝑎
2
=
𝐾/𝜌
1+[(
𝐾
𝐸
)(
𝐷
𝑒
)]𝑐
1
; 𝑐
1
= {
1 −
𝜇
2
1 − 𝜇
2
1
𝑑𝑒𝑝𝑒𝑛𝑑𝑒 𝑑𝑒 𝑙𝑎 𝑠𝑢𝑝𝑜𝑠𝑖𝑐𝑖ó𝑛 𝑞𝑢𝑒 𝑠𝑒 𝑟𝑒𝑎𝑙𝑖𝑐𝑒 (18)
Donde:
𝐾: Módulo de elasticidad del fluido.
𝜌: Densidad del fluido.
𝐸: Módulo de elasticidad de la tubería.
𝐷: Diámetro de la tubería.
𝑒: Espesor de la pared de la tubería.
𝜇: Coeficiente de Poisson de la tubería.
3.3. Método de las características
Para resolver las ecuaciones diferenciales parciales (Conservación de la masa y cantidad
de movimiento) se requiere un método numérico, dado que estas ecuaciones no tienen
una solución general. De esta manera, en la presente sección se muestra la metodología
de cálculo que emplea el software (HAMMER) que se utilizará en la investigación.
El método de las características utiliza las dos ecuaciones diferenciales parciales que
rigen el fenómeno y las transforma en cuatro ecuaciones diferenciales ordinarias que
podrán ser integradas posteriormente. A continuación se presenta el desarrollo de las
ecuaciones que utilizará el método. Se considera relevante mencionar que los términos
de menor importancia son omitidos; de esta manera, las ecuaciones de conservación de la
cantidad de movimiento y masa quedan de la siguiente forma.
𝐿
1
= 𝑔𝐻
𝑥
+ 𝑉
𝑡
+
𝑓
2𝐷
𝑉|𝑉| = 0 (19)
𝐿
2
= 𝐻
𝑡
+
𝑎
2
𝑔
𝑉
𝑥
= 0 (20)

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
19
Estas dos ecuaciones pueden ser combinadas linealmente por medio del uso de un
multiplicador
𝝀. De esta forma, se plantea la siguiente ecuación.
𝐿 = 𝐿
1
+ 𝜆𝐿
2
= 𝜆 [𝐻
𝑥
𝑔
𝜆
+ 𝐻
𝑡
] + [𝑉
𝑥
𝜆
𝑎
2
𝑔
+ 𝑉
𝑡
] +
𝑓𝑉|𝑉|
2𝐷
= 0 (21)
De esta manera, se tiene una ecuación en donde nuevamente hay dos variables
dependientes (
𝑽 y 𝑯) de x y t. Si se supone que la variable x está en función de t, se
puede establecer que:
𝑑𝐻
𝑑𝑡
= 𝐻
𝑥
𝑑𝑥
𝑑𝑡
+ 𝐻
𝑡
(22)
𝑑𝑉
𝑑𝑡
= 𝑉
𝑥
𝑑𝑥
𝑑𝑡
+ 𝑉
𝑡
(23)
Ahora bien, si se mira con detenimiento la Ecuación (21) y las Ecuaciones (22) y (23), se
puede ver que:
𝑑𝑥
𝑑𝑡
=
𝑔
𝜆
=
𝜆𝑎
2
𝑔
(24)
Por lo tanto, la Ecuación (21) se transforma en la siguiente ecuación diferencial ordinaria.
𝜆
𝑑𝐻
𝑑𝑡
+
𝑑𝑉
𝑑𝑡
+
𝑓𝑉|𝑉|
2𝐷
= 0 (25)
Adicionalmente, de la Ecuación (24) se encuentra que los valores que puede obtener el
multiplicador son:
𝜆 = √
𝑔
2
𝑎
2
= ±
𝑔
𝑎
(26)
Nuevamente, utilizando la Ecuación (24), en conjunto con la Ecuación (26) se encuentra
que:
𝑑𝑥
𝑑𝑡
= ±𝑎 (27)
A partir de las Ecuaciones (25), (26) y (27) se tienen las ecuaciones diferenciales
ordinarias que utiliza el método.
𝑔
𝑎
𝑑𝐻
𝑑𝑡
+
𝑑𝑉
𝑑𝑡
+
𝑓𝑉|𝑉|
2𝐷
= 0 (28)
𝑑𝑥
𝑑𝑡
= +𝑎 (29)
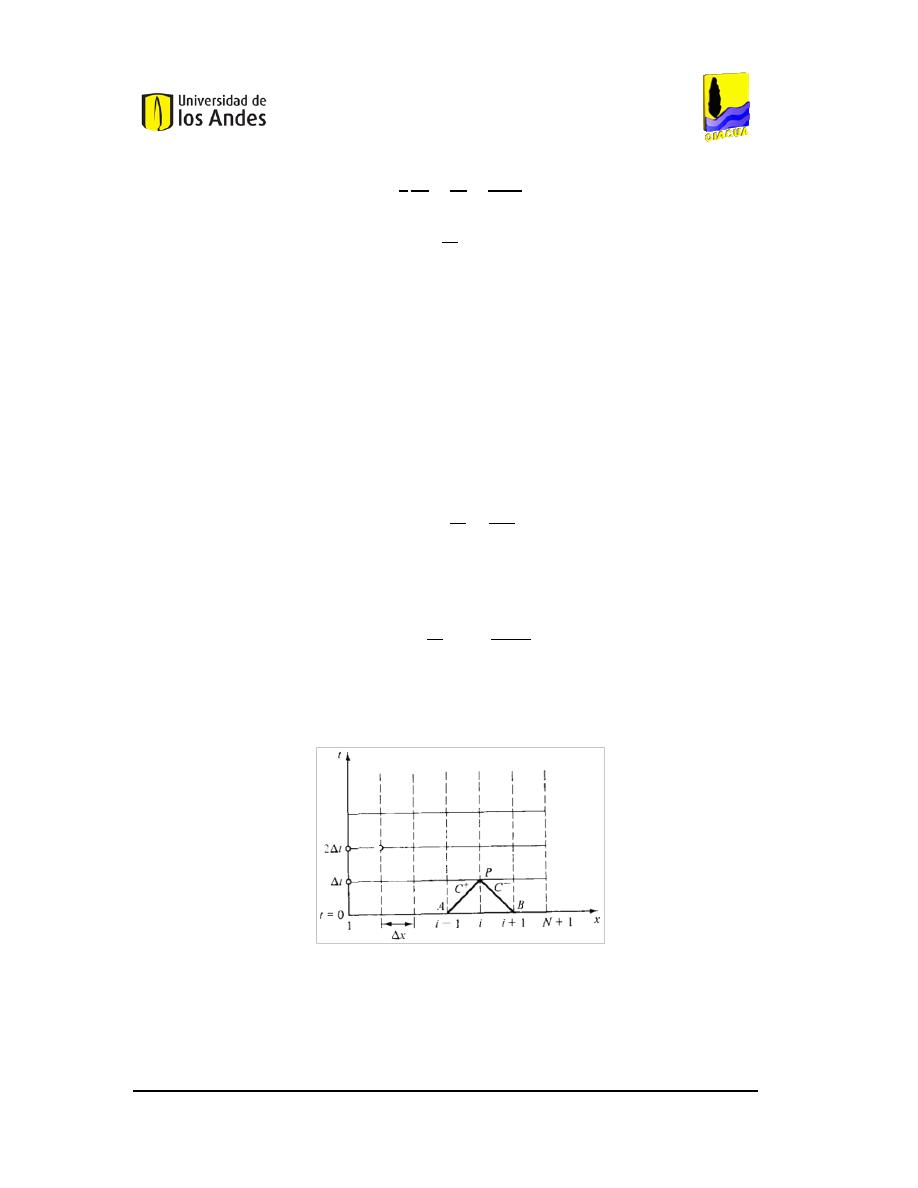
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
20
−
𝑔
𝑎
𝑑𝐻
𝑑𝑡
+
𝑑𝑉
𝑑𝑡
+
𝑓𝑉|𝑉|
2𝐷
= 0 (30)
𝑑𝑥
𝑑𝑡
= −𝑎 (31)
Dado que se utilizó los dos posibles valores de
𝝀 para desarrollar las ecuaciones
diferenciales ordinarias, las Ecuaciones (28) y (30) son solo válidas cuando las
Ecuaciones (29) y (31) son válidas.
Ecuaciones de diferencias finitas
Una vez que se tienen las ecuaciones diferenciales ordinarias, se realiza la integración de
las mismas para poder tener las ecuaciones de diferencias finitas que se utilizarán para el
análisis. Sin embargo, es necesario realizar una última modificación a las Ecuaciones
(28) y (30). Por lo tanto, a partir de las Ecuaciones (26) y (27) se puede encontrar la
siguiente relación.
𝑑𝑥
𝑔
=
𝑎 𝑑𝑡
𝑔
(32)
La Ecuación (28) será multiplicada por la Ecuación (32) y por el área de la sección de la
tubería. De esta manera, se tendrá la siguiente ecuación.
𝑑𝐻 +
𝑎
𝑔𝐴
𝑑𝑄 +
𝑓
2𝑔𝐷𝐴
2
𝑄|𝑄| = 0 (33)
Se encuentra necesario realizar un esquema de la forma de cálculo para poder establecer
los límites que tendrán las integrales que se desarrollen. A partir de la
Figura 15
, se puede
ver cuáles serán los límites de las integrales que se realicen.
Figura 15. Grilla de xt para la solución del sistema de ecuaciones diferenciales (Wylie & Streeter,
1978).

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
21
De esta manera la Ecuación (33) queda de la siguiente forma.
∫ 𝑑𝐻
𝐻
𝑃
𝐻
𝐴
+
𝑎
𝑔𝐴
∫ 𝑑𝑄
𝑄
𝑃
𝑄
𝐴
+
𝑓
2𝑔𝐷𝐴
2
∫ 𝑄|𝑄|𝑑𝑥
𝑥
𝑃
𝑥
𝐴
= 0 (34)
Aplicando el mismo procedimiento a la Ecuación (30), se obtienen las ecuaciones finales
que se utilizarán para desarrollo del flujo transiente. Estas se presentan a continuación.
𝐻
𝑃
− 𝐻
𝐴
+
𝑎
𝑔𝐴
(𝑄
𝑃
− 𝑄
𝐴
) +
𝑓Δ𝑥
2𝑔𝐷𝐴
2
𝑄
𝐴
|𝑄
𝐴
| = 0 (35)
𝐻
𝑃
− 𝐻
𝐵
−
𝑎
𝑔𝐴
(𝑄
𝑃
− 𝑄
𝐵
) −
𝑓Δ𝑥
2𝑔𝐷𝐴
2
𝑄
𝐵
|𝑄
𝐵
| = 0 (36)
Las ecuaciones anteriores quedan en la siguiente forma cuando se introducen al software.
𝐻
𝑃
𝑖
= 𝐻
𝑖−1
+
𝑎
𝑔𝐴
(𝑄
𝑖−1
) −
𝑓Δ𝑥
2𝑔𝐷𝐴
2
(𝑄
𝑖−1
)|𝑄
𝑖−1
| −
𝑎
𝑔𝐴
(𝑄
𝑃𝑖
) (37)
𝐻
𝑃
𝑖
= 𝐻
𝑖+1
−
𝑎
𝑔𝐴
(𝑄
𝑖+1
) +
𝑓Δ𝑥
2𝑔𝐷𝐴
2
(𝑄
𝑖+1
)|𝑄
𝑖+1
| +
𝑎
𝑔𝐴
(𝑄
𝑃
𝑖
) (38)
De las ecuaciones anteriores se encuentra que:
𝐻
𝑃
𝑖
= (
𝐻
𝑖−1
+
𝑎
𝑔𝐴
(𝑄
𝑖−1
)−
𝑓Δ𝑥
2𝑔𝐷𝐴2
(𝑄
𝑖−1
)|𝑄
𝑖−1
|
𝐻
𝑖+1
−
𝑎
𝑔𝐴
(𝑄
𝑖+1
)+
𝑓Δ𝑥
2𝑔𝐷𝐴2
(𝑄
𝑖+1
)|𝑄
𝑖+1
|
) /2 (39)
Es relevante mencionar que los términos que no tiene el subíndice P son términos
conocidos. Adicionalmente, los términos i+1 o i-1 corresponden a la posición y no al
Δ𝑡.
Condiciones básicas de frontera
En la presente investigación se utilizaron solo válvulas para generar el fenómeno de
transiente. Por lo tanto, a continuación se presenta cómo el método de cálculo utiliza este
elemento como una condición de frontera. La ecuación que se emplea para definir el
flujo a través de una válvula en un estado estable es la siguiente.
𝑄
0
= (𝐶
𝑑
𝐴
𝑔
)
0
√2𝑔𝐻
0
; 𝐶
𝑑
=
𝜋𝑑
2
√𝑔
√8
1
√𝑘𝑚
(40)
Donde:
𝐶
𝑑
: Coeficiente de descarga inicial de la válvula.
𝐴
𝑔
: Área de apertura de la válvula
Generalizando la anterior ecuación, para cualquier instante de tiempo u operación, el
flujo en la válvula será el siguiente.

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
22
𝑄
𝑝
=
𝑄
0
√𝐻
0
𝐶
𝑑
𝐴
𝑔
(𝐶
𝑑
𝐴
𝑔
)
0
√∆𝐻 =
𝑄
0
√𝐻
0
𝜏√∆𝐻 (41)
Donde:
τ: Es 1 para el estado estable y 0 en caso de que se cierre totalmente. De esta manera, si
la válvula se cierra en comparación a su estado estable, el valor será menor a 1. En caso
de que la válvula se abra en comparación al estado estable, el valor será mayor a 1.
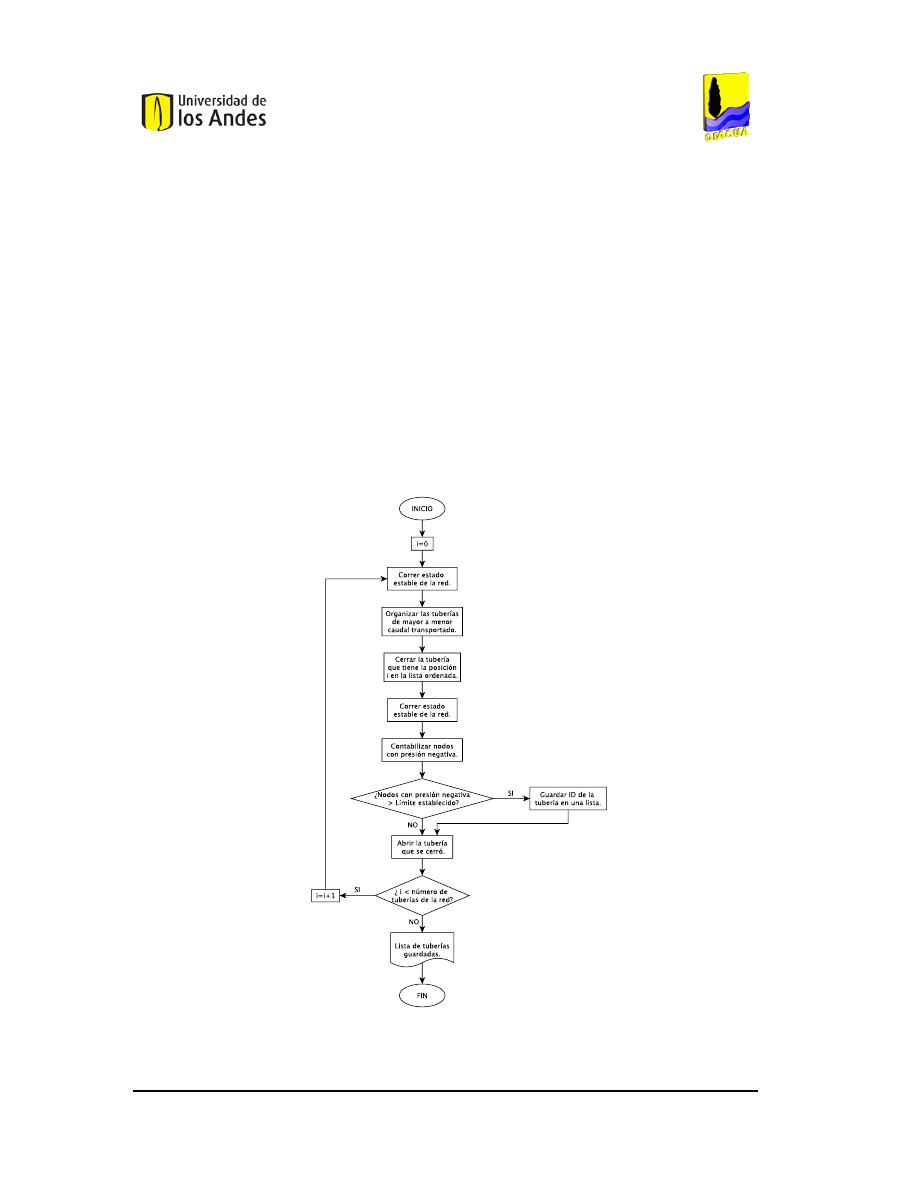
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
23
4. Metodología
Uno de los aspectos de mayor relevancia en la presente investigación fue establecer los
puntos dónde se iban a ubicar las válvulas. Adicionalmente, se desarrolló una
metodología para establecer la estabilización de la red. De esta manera, en la presente
sección se muestran los conocimientos que establecieron la metodología enunciada.
4.1. Ubicación de válvulas
Para obtener resultados fáciles de interpretar en esta primera etapa, se estableció que las
válvulas deberían afectar un área específica. Es decir, los puntos donde se ubicarán estos
componentes deben ser capaces de sectorizar la red. En otras palabras, las válvulas deben
ir en aquellas tuberías que, en caso de cierre, sean capaces de restringir en su totalidad el
suministro de agua a ciertos puntos de la red. Por lo tanto, las tuberías en las que se
deben ubicar las válvulas, deben ser aquellas que transporten caudales de gran magnitud.
A continuación, se presenta un diagrama de flujo que muestra la metodología adoptada.
Figura 16. Diagrama de flujo para la ubicación de las válvulas.

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
24
4.2. Medidas de tendencia
Uno de los mayores retos que se tuvo en la primera etapa del proyecto fue definir de qué
forma se iba a establecer si la red se encontraba nuevamente en un estado estable. Por lo
tanto, surgieron distintas formas de cuantificar las variaciones que se estaban teniendo en
el sistema. Sin embargo, se definió que para cuantificar esto, lo más racional era utilizar
valores porcentuales.
Adicionalmente, se estudió qué medida de tendencia podría ser la mejor para mostrar la
variación que estaba teniendo el sistema. De esta manera, se llegó a que la mejor opción
era utilizar una desviación estándar móvil. A continuación se presentan los análisis
realizados para llegar a las conclusiones que se enunciaron anteriormente.
En una primera instancia de la investigación se consideró que la diferencia porcentual del
caudal con respecto a su anterior dato podría ser la mejor medida de tendencia. Sin
embargo, algunas tuberías de la red al estabilizarse tenían ligeras oscilaciones numéricas.
De esta manera, para tuberías que tuvieran caudales pequeños la medida de tendencia
mostraría variaciones porcentuales de gran magnitud, las cuales no reflejaban lo que
estaba sucediendo.
Posteriormente, al ver el problema anterior se pensó que lo mejor sería ver las variaciones
netas de caudal. Sin embargo, cuando se obtuvieron los datos se encontró que era
necesario establecer un valor de caudal que concluyera si la tubería había llegado a
estabilizarse o no. De esta forma, se consideró que este valor debería tener en cuenta la
mayor precisión que pudiese tener un medidor de flujo en campo. Sin embargo, el
realizar esta suposición podría despreciar aquellas tuberías que transportaran caudales
pequeños.
Adicional a esto, el paso que se utilizó para las simulaciones fue menor a 0.5 segundos.
Por lo tanto, al ver esta cifra y los inconvenientes que se estaban teniendo con la medida
de tendencia, se consideró que el cuantificar la variación del caudal con el paso anterior
no iba a reflejar la situación real. Por lo tanto, se decidió que para ver las variaciones se
debía tener un grupo de datos que representaran un tiempo considerable.
En una primera instancia se pensó en comparar el valor que se tenía en el tiempo t con
aquel que se había tenido en 5 o 10 pasos atrás. Sin embargo, al realizar esto se encontró
que las variaciones permanecían constante a lo largo de la simulación, haciendo
inconcluyente el análisis. La solución que se encontró a esto fue tomar una medida que
fuera móvil y tomará varios datos. De esta manera, se optó por utilizar una desviación
estándar móvil de los datos como la medida de tendencia. Sin embargo, los valores a los
que se les tomaría la desviación estándar no serían valores netos sino porcentuales. De
esta manera, se estableció que los valores porcentuales debían estar respecto al caudal
inicial de cada tubería.

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
25
Adicionalmente, se realizó un análisis de sensibilidad de la desviación estándar móvil
para ver el tamaño que debía tener cada paquete. De esta forma, se utilizaron paquetes de
10, 20, 30, 60, 120 y 180 segundos. El resultado que se encontró fue que para los
paquetes pequeños, la medida de tendencia móvil no permitía ver las variaciones
considerables que se tenía en aquellos casos en donde el flujo tenía una oscilación
numérica. Por otra parte, cuando los paquetes eran muy grandes, la desviación estándar
móvil mostraba en mayor medida solo las variaciones grandes y no las oscilaciones
pequeñas que se consideraban inestabilidades de la red. De esta manera, se optó que el
paquete debía tener los datos de 60 segundos. A continuación se presenta la medida de
tendencia empleada; para facilitar la interpretación se supondrá que se tienen datos cada
segundo.
𝑀𝑇
𝑖
= 𝑠 =
∑
(𝑥
𝑖
−
∑
𝑥
𝑗
𝑖
𝑗=𝑖−60
60
)
2
𝑖
𝑗=𝑖−60
60 − 1
𝑥
𝑗
=
𝑄
𝑗
𝑄
0
Al tener una mayor cantidad de resultados en la segunda etapa de la investigación, se
modificó la metodología para evaluar la estabilización de la red. Para cada simulación
que se realizó se tenían diferentes puntos de medición. De esta manera, se optó por
sumar los caudales y las presiones de estos para cada instante de tiempo. Por lo tanto, al
final se tendría una sola línea que representaría el comportamiento de la red frente al
cierre de válvula que se estudiara.
Se encuentra relevante mencionar que al realizar una única serie de datos, las oscilaciones
que se tenían en algunas tuberías se veían disminuidas. De esta manera, al tener una línea
que fuera más consistente, se pudo emplear la derivada del caudal y la presión respecto al
tiempo. Al utilizar esta metodología se obtuvieron resultados concluyentes y, además,
ésta permitió realizar comparaciones más claras entre los diferentes cierres de válvulas
estudiados. Al tener datos discretos se debe emplear derivadas discretas; éstas se
presenta a continuación.
𝑑𝑄
𝑑𝑡
=
𝑄
𝑖+1
− 𝑄
𝑖
𝑡
𝑖+1
− 𝑡
𝑖
𝑑𝑃
𝑑𝑡
=
𝑃
𝑖+1
− 𝑃
𝑖
𝑡
𝑖+1
− 𝑡
𝑖
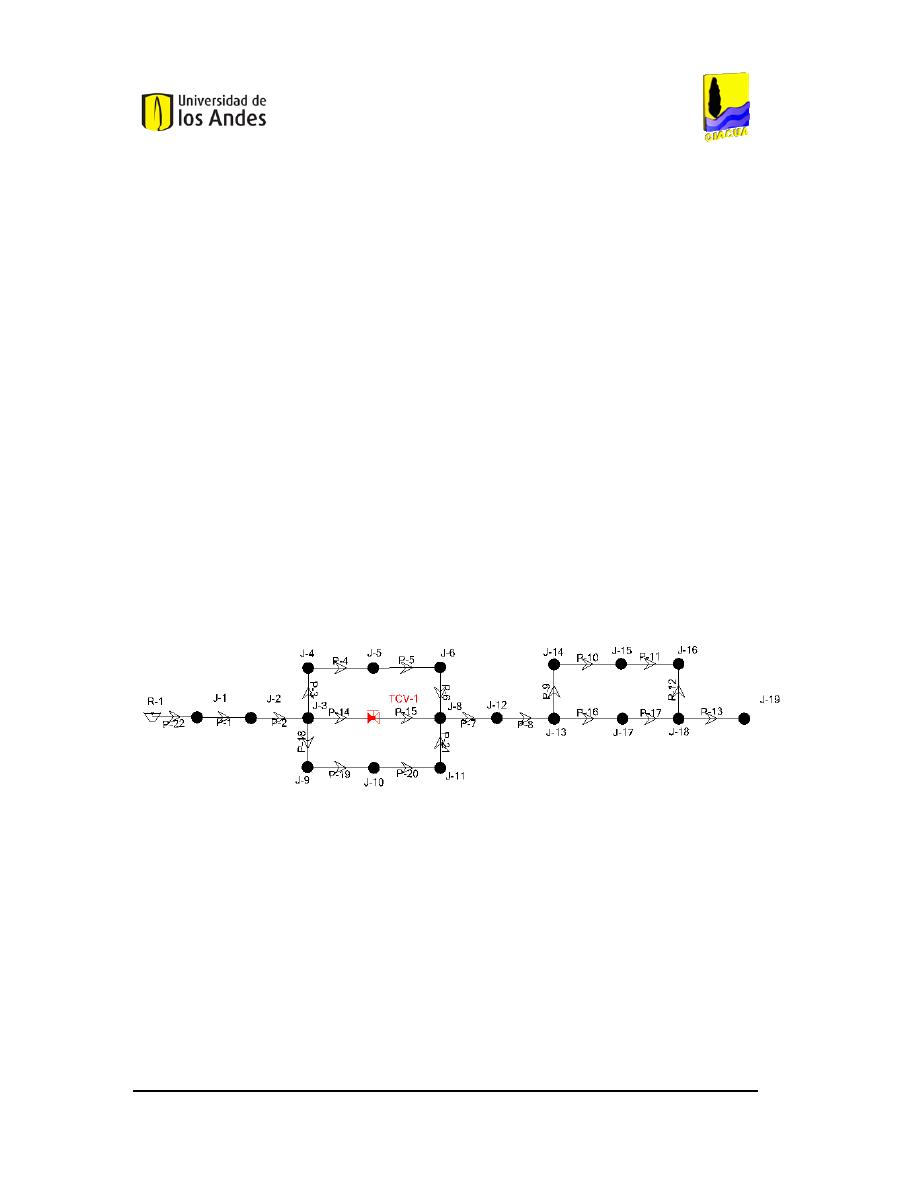
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
26
5. HAMMER
La presente sección tiene como objetivo presentar las características de mayor relevancia
que tiene el software utilizado. De esta manera, se presentará una red pequeña que se
utilizó para estudiar la forma en que HAMMER maneja las demandas cuando realiza el
análisis de transiente. Adicionalmente, esta herramienta computacional tiene varias
metodologías para el cálculo del factor de fricción; por lo tanto, se presenta el análisis de
sensibilidad realizado sobre esta variable.
5.1. Demandas
Como se estableció en secciones anteriores, HAMMER hace uso del método de las
características para realizar el cálculo del flujo transiente. Sin embargo, cuando se
realizaron las simulaciones se encontró que de cierta forma el software no estaba
conservando la masa en algunos casos. Por lo tanto, se creó una red pequeña de estudio
en la cual se analizó la forma en que HAMMER simula las demandas y conservaba la
masa.
La red utilizada para este análisis se muestra en la Figura 17; ésta tenía una demanda de
200 L/s en todos los nudos de la misma. Es importante resaltar que cuando se situó la
válvula en el nudo J-1, y se realizó un cierre del 100% de la misma, se tuvieron
problemas numéricos y en ningún momento la red se estabilizó. Por lo tanto, se optó por
situar la válvula en un sitio en donde no se ahogara la red.
Figura 17. Red utilizada para estudiar las demandas en HAMMER.
Para el análisis se realizaron cierres del 20%, 40%, 60%, 80% y 100%; para todos los
casos se revisó la conservación de la masa en los diferentes nudos. Sin embargo, siempre
se dejó la demanda del nudo como una variable a encontrar y no un dato predeterminado
del problema. Por lo tanto, la ecuación utilizada se presenta a continuación.
𝑄
𝑑𝑒𝑚𝑎𝑛𝑑𝑎
= 𝑄
𝑖𝑛
− 𝑄
𝑜𝑢𝑡
(42)
De esta manera, lo que se hizo fue encontrar el caudal demandado en todos los nudos,
para todos los cierres, en el instante donde la red ya se había estabilizado. Se encontró
que en algunos nudos la demanda era superior a 200 L/s y en otros era menor a ésta. Por
lo tanto, se pensó que HAMMER podía estar modelando la demanda como emisores. De

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
27
esta manera, se calculó el coeficiente del emisor de cada nudo con el estado estable
inicial.
Posteriormente, se modeló la red con los coeficientes encontrados y con las aperturas de
válvulas propuestas. Luego se realizó nuevamente la conservación de la masa para cada
nudo con el uso de la Ecuación (41), y se encontró que efectivamente HAMMER realiza
la modelación del transiente como si los nudos tuvieran emisores y no una demanda fija.
La Ecuación (43) muestra la forma de modelar un emisor y la Ecuación (44) presenta la
forma que utiliza el método de las características para simular una válvula u orificio. Al
comparar ambas ecuaciones se ve la gran similitud. Por otra parte, el modelar la
demanda de esta forma ofrece una gran ayuda al método de cálculo, ya que cada nudo
tendrá una condición básica de frontera para el proceso.
𝑄 = 𝑎 𝑃
0.5
(43)
𝑄 = 𝐶
𝑑
𝐴
𝑔
√2𝑔 𝐻 = 𝐶
𝑑
𝐴
𝑔
√2𝑔 𝐻
0.5
(44)
5.2. Factores de fricción
Adicionalmente, el software utilizado permite elegir la forma de cálculo del factor de
fricción durante el análisis del flujo transiente. A continuación se presentan las opciones
que ofrece el programa.
5.2.1. Métodos de Cálculo
Steady
Con el uso de esta herramienta el programa calcula el factor de fricción con la ecuación
de Colebrook-White en el estado estable; el cual será la condición inicial del sistema.
Luego, durante el análisis de transiente el programa dejará el factor de fricción como una
constante. A continuación se presenta la ecuación de Colebrook-White.
1
√𝑓
= −2 log
10
(
𝑘𝑠
3.7𝑑
+
2.51
𝑅𝑒 √𝑓
) (45)
Quasi-Steady
Con esta opción el programa realiza el cálculo del factor de fricción con la ecuación de
Colebrook-White en cada paso de tiempo que se realice. Es decir, el factor de fricción va
a ser cambiante y dependiente del caudal que se encuentre luego de aplicar las ecuaciones
de diferencias finitas del método de las características.
Unsteady
Cuando se elige esta opción el programa realiza los mismos cálculos de Quasi-Steady, es
decir, calcula el factor de fricción en cada paso de tiempo. Sin embargo, realiza una
corrección basada en la siguiente ecuación.

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
28
𝑓
𝑢𝑛𝑠𝑡𝑒𝑎𝑑𝑦
= 𝑓
𝑞𝑢𝑎𝑠𝑖−𝑠𝑡𝑒𝑎𝑑𝑦
(1 + min (
10,000|
𝜕𝑉
𝜕𝑡
|
𝑔
, 4)) (46)
Donde:
𝜕𝑉
𝜕𝑡
: Aceleración temporal.
Las razones que establecen los desarrolladores para el incremento del factor de fricción
son las variaciones rápidas de presión y flujo, las cuales aumentan el esfuerzo cortante.
Como se puede ver, el método tiene un costo de computación superior al método Quasi-
Steady.
Unsteady-Vitkovsky
Similar a la forma de cálculo del método anterior, este método de hallar el factor de
fricción utiliza el cálculo del factor Quasi-Steady. Sin embargo, nuevamente se realiza
una variación del mismo mediante la ecuación que se presenta a continuación.
𝑓
𝑢𝑛𝑠.−𝑉𝑖𝑡𝑘.
= 𝑓
𝑞𝑢𝑎𝑠𝑖−𝑠𝑡𝑒𝑎𝑑𝑦
+
𝑘𝑑
𝑣|𝑣|
(
𝜕𝑣
𝜕𝑡
+ 𝑎 𝑆𝑖𝑔𝑛(𝑣) |
𝜕𝑉
𝜕𝑥
|) (47)
𝑘 =
√𝐶
∗
2
;
𝐶
∗
= 0.00476 𝐹𝑙𝑢𝑗𝑜 𝐿𝑎𝑚𝑖𝑛𝑎𝑟
𝐶
∗
=
12.86
𝑅𝑒
log10(
15.29
𝑅𝑒0.0567
)
𝐹𝑙𝑢𝑗𝑜 𝑇𝑢𝑟𝑏𝑢𝑙𝑒𝑛𝑡𝑜 (48)
Donde:
𝑘: Coeficiente de Fricción de Brunone.
d: Diámetro de la tubería.
v: Velocidad media del flujo.
a: Velocidad de la onda.
C
*
: Coeficiente de decaimiento de Vardy & Brown.
Sign(v): Función que define que signo tiene la velocidad.
Este método es el de mayor costo computacional, dado que tienen que solucionar las
Ecuaciones (45), (47) y (48) en cada paso de tiempo que realice. Cabe aclarar que los
desarrolladores del programa establecen que esta debería ser la forma de calcular el factor
de fricción.
5.2.2. Análisis de Sensibilidad
Luego de ver la definición de la forma de cálculo de cada opción del programa, se
procedió a utilizar la red de la Figura 17 para realizar un análisis de sensibilidad. Cabe
aclarar que el haber hallado que HAMMER modela las demandas como emisores cuando
realiza el flujo transiente, ayudó a encontrar el valor al que deberían llegar los caudales
de las tuberías una vez que se haya llegado nuevamente a un estado estable. De esta
manera, se calcularon estos valores y se midió el error porcentual que tenían los métodos
de cálculo.
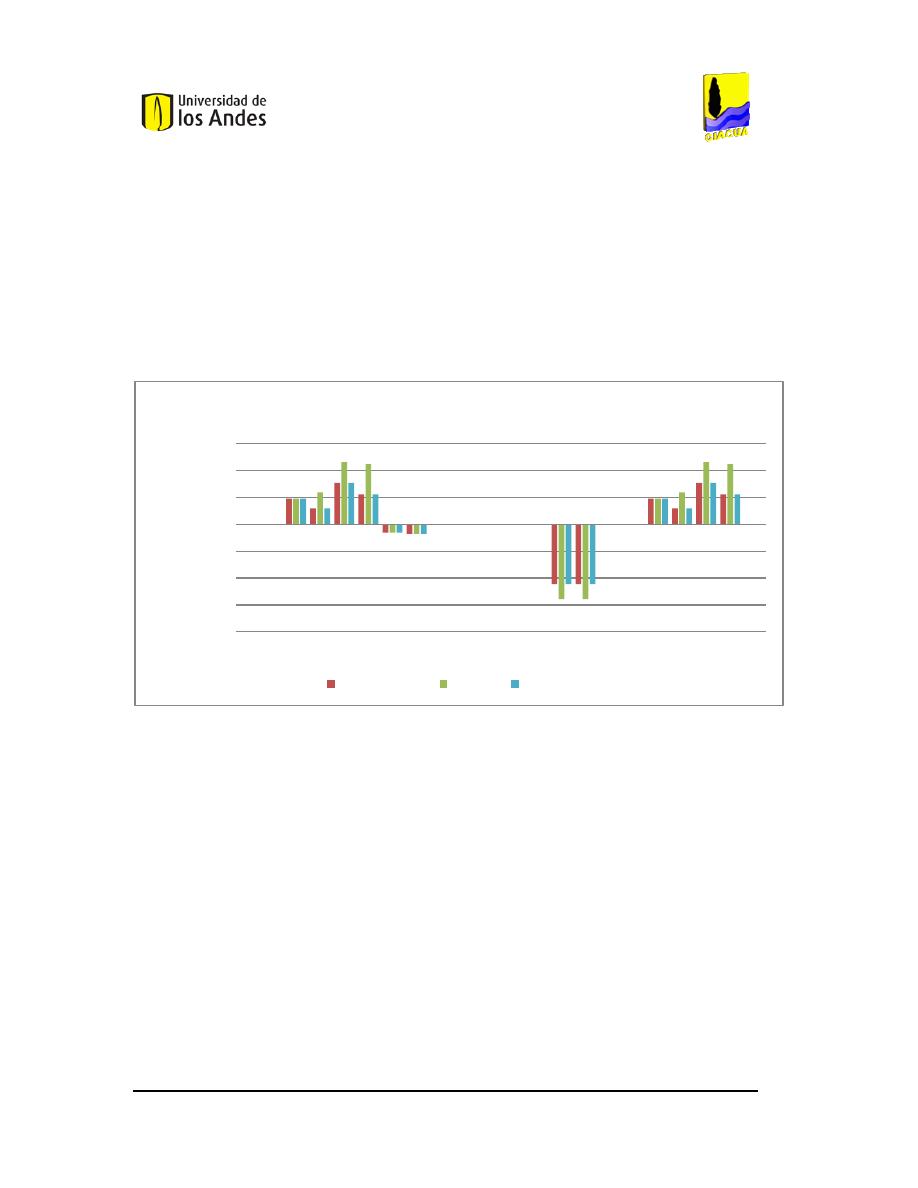
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
29
A continuación se presentan los resultados obtenidos; cabe aclarar que se emplearon
cierres de 20%, 40%, 60%, 80%, 90% y 100%. Adicionalmente, en todos los casos el
método Unsteady tuvo errores superiores al 30%. Por esta razón, éste no se presenta en
las gráficas dado que no dejaría ver el comportamiento de las otras metodologías.
Cierre del 20%
A partir de la
Figura 18
, se puede ver que los errores porcentuales de los métodos no
superan el 0.3%. Adicionalmente, se puede ver que el método Quasi-Steady y Unsteady-
Vitkovsky, tiene un comportamiento muy similar en las diferentes tuberías. Finalmente,
se puede apreciar que en 10 tuberías se tiene que no hay error alguno.
Figura 18. Errores porcentuales de los métodos de cálculo del factor de fricción (Cierre del 20%).
Se encuentra relevante mencionar nuevamente que si se hubiera puesto el método
Unsteady en la Figura 18, no se hubiera podido apreciar la variación de los errores de los
demás métodos de cálculo. Adicionalmente, en todos los casos y en todas las tuberías el
método Unsteady tuvo errores superiores al 30%.
Cierre del 40%
A partir de la
Figura 19
, se puede ver que los errores porcentuales aumentaron en los tres
métodos. Sin embargo, estos siguen siendo bajos dado que son inferiores al 0.7%.
Adicionalmente, se puede ver en las tuberías 7 y 8 que el error disminuyó. Por otra parte,
para las tuberías 1, 2 y 22 se puede apreciar un error, el cual no era apreciable en el caso
anterior.
-0,40%
-0,30%
-0,20%
-0,10%
0,00%
0,10%
0,20%
0,30%
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Err
or
Por
cent
u
al
ID de la Tubería
20% de Cierre de Válvula
Quasi-Steady
Steady
Unsteady-V
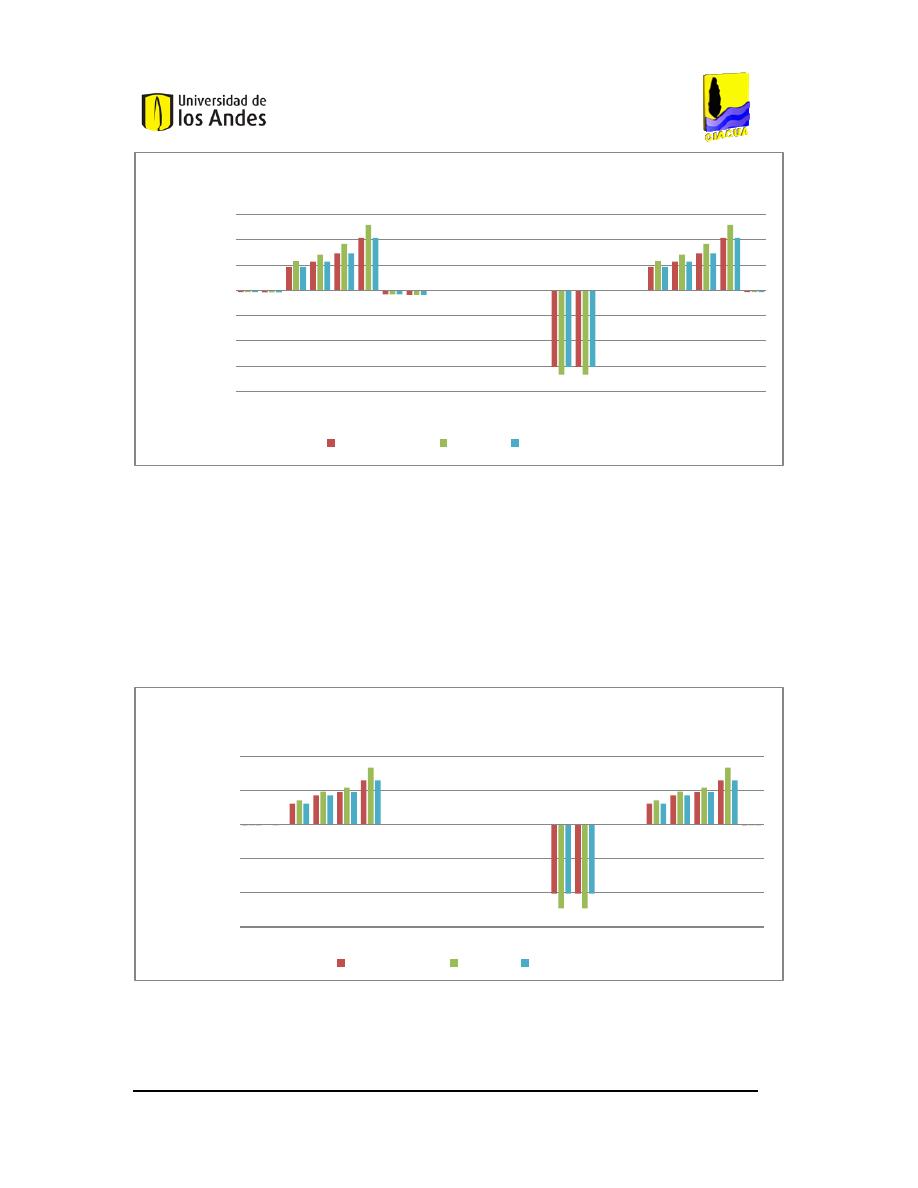
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
30
Figura 19. Errores porcentuales de los métodos de cálculo del factor de fricción (Cierre del 40%).
Un aspecto relevante es que los errores de los métodos de cálculo Quasi-Steady y
Unsteady-Vitkovsky siguen siendo similares. Además, el incremento en los errores en
ambos métodos fue de la misma magnitud.
Cierre del 60%
A partir de la
Figura 20
, se puede ver nuevamente que los errores siguen siendo de una
baja magnitud. Adicionalmente, se ve nuevamente la alta semejanza que tienen los
errores de los métodos Quasi-Steady y Unsteady-Vitkovsky.
Figura 20. Errores porcentuales de los métodos de cálculo del factor de fricción (Cierre del 60%).
Se encuentra relevante mencionar que las tuberías 14 y 15 son aquellas adyacentes a la
válvula. Adicionalmente, como se vio en secciones anteriores, las válvulas funcionan
-0,80%
-0,60%
-0,40%
-0,20%
0,00%
0,20%
0,40%
0,60%
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Err
or
Por
cent
u
al
ID de la Tubería
40% de Cierre de Válvula
Quasi-Steady
Steady
Unsteady-V
-1,50%
-1,00%
-0,50%
0,00%
0,50%
1,00%
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Err
or
Por
cent
u
al
ID de la Tubería
60% de Cierre de Válvula
Quasi-Steady
Steady
Unsteady-V
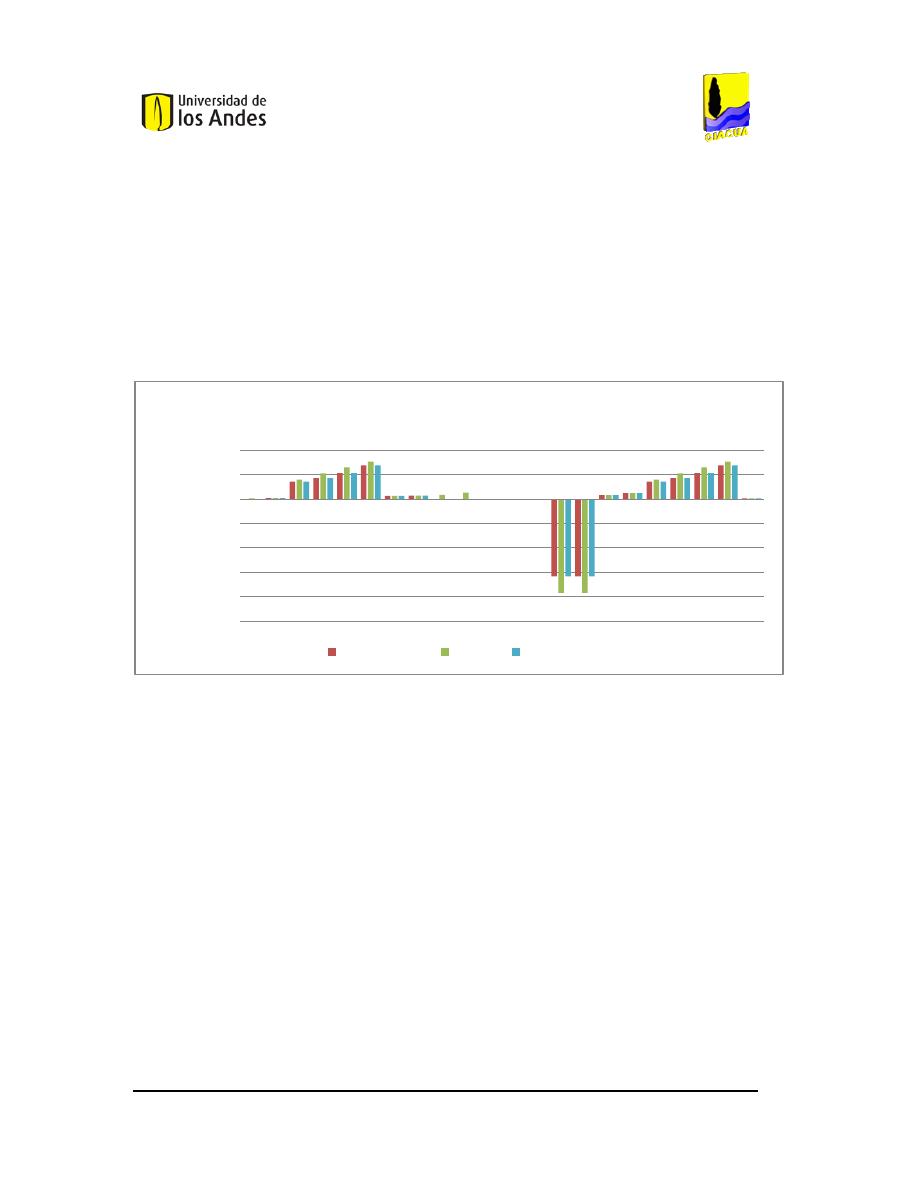
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
31
como condiciones de frontera en el método de cálculo. De esta manera, resulta llamativo
que las tuberías que tengan mayor error porcentual sean éstas y no las que se encuentran
más alejadas de la condición de frontera.
Cierre del 80%
A partir de la
Figura 21
se puede ver que los errores de las tuberías 14 y 15 tuvieron un
aumento del 0.5% aproximadamente. Adicionalmente, se encuentra llamativo que las
demás tuberías que tenían errores en el caso anterior, en éste no tuvieran aumento alguno
en su valor. Nuevamente se encuentra relevante mencionar la alta semejanza que tienen
los métodos Quasi-Steady y Unsteady-Vitkovsky.
Figura 21. Errores porcentuales de los métodos de cálculo del factor de fricción (Cierre del 80%).
Cierre del 90%
A partir de la
Figura 22
se puede ver que nuevamente hubo un aumento del error
porcentual de las tuberías 14 y 15. En este caso el valor llegó a superar el 2% en los 3
métodos. Por otra parte, resulta curioso que las tuberías que tenían errores entre 0.4% y
0.7% no hayan tenido un incremento significativo de este valor. Sin embargo, aquellas
tuberías en donde los errores eran menores a 0.1%, tuvieron un incremento del 0.2%. A
pesar de todo esto, se puede ver que los errores que se obtienen son de baja magnitud. Es
importante tener en cuenta que ésta es una red pequeña, y las ecuaciones del método de
las características pueden ser resueltas fácilmente. Esto factiblemente ayudará a que el
método sea muy preciso.
-2,50%
-2,00%
-1,50%
-1,00%
-0,50%
0,00%
0,50%
1,00%
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Err
or
Por
cent
u
al
ID de la Tubería
80% de Cierre de Válvula
Quasi-Steady
Steady
Unsteady-V
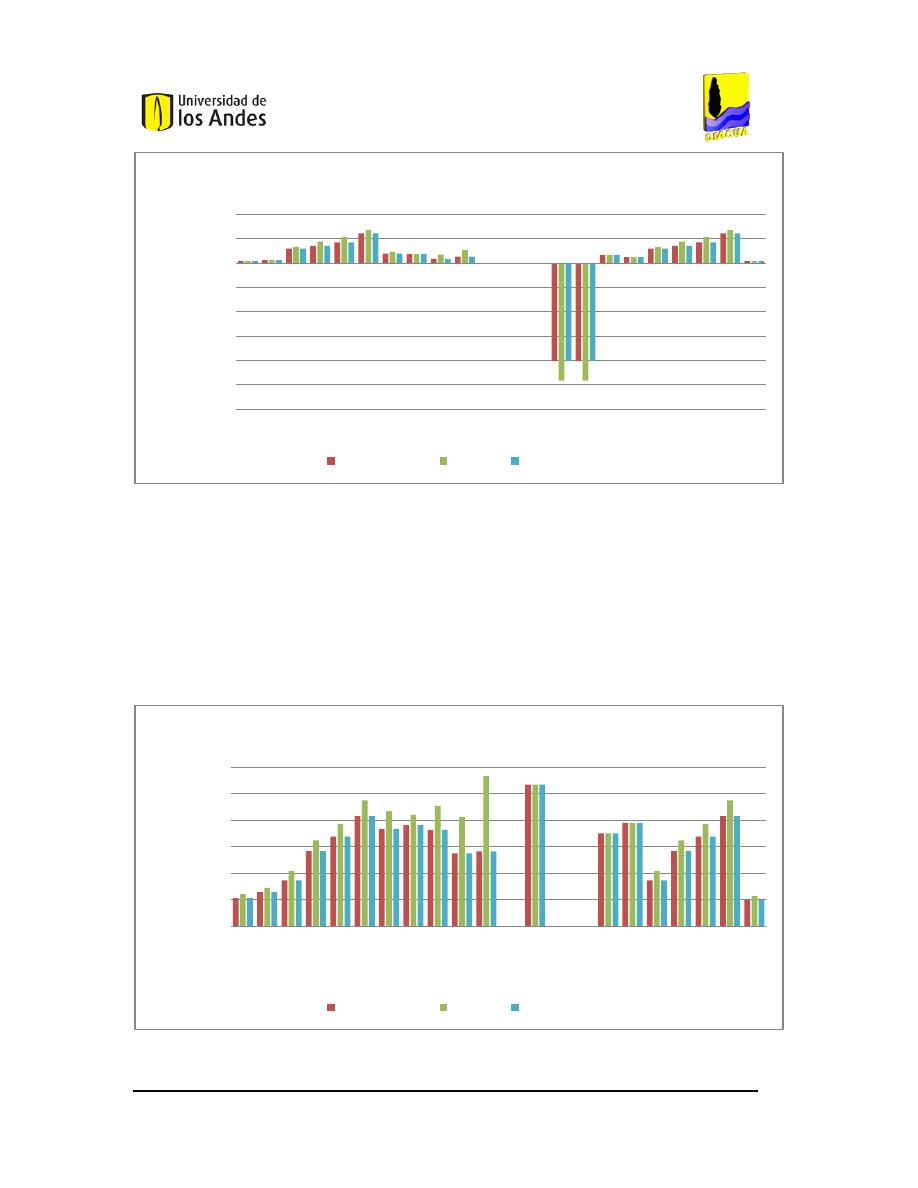
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
32
Figura 22. Errores porcentuales de los métodos de cálculo del factor de fricción (Cierre del 90%).
Cierre del 100%
A partir de la
Figura 23
se puede ver que todas las tuberías a excepción de la 12, 14 y 15
tienen error en su valor. Sin embargo, si se ve con detenimiento se puede ver que
ninguno de ellos supera el 0.6%. Se encuentra relevante mencionar que las tuberías 14 y
15, las cuales presentaban los mayores errores en los casos anteriores, en éste no tienen
error alguno. De esta manera, parece ser que la condición de frontera funciona mejor
cuando se tiene un cierre total de la válvula.
Figura 23. Errores porcentuales de los métodos de cálculo del factor de fricción (Cierre del 100%).
-3,00%
-2,50%
-2,00%
-1,50%
-1,00%
-0,50%
0,00%
0,50%
1,00%
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Err
or
Por
cent
u
al
ID de la Tubería
90% de Cierre de Válvula
Quasi-Steady
Steady
Unsteady-V
0,00%
0,10%
0,20%
0,30%
0,40%
0,50%
0,60%
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Err
or
Por
cent
u
al
ID de la Tubería
100% de Cierre de Válvula
Quasi-Steady
Steady
Unsteady-V
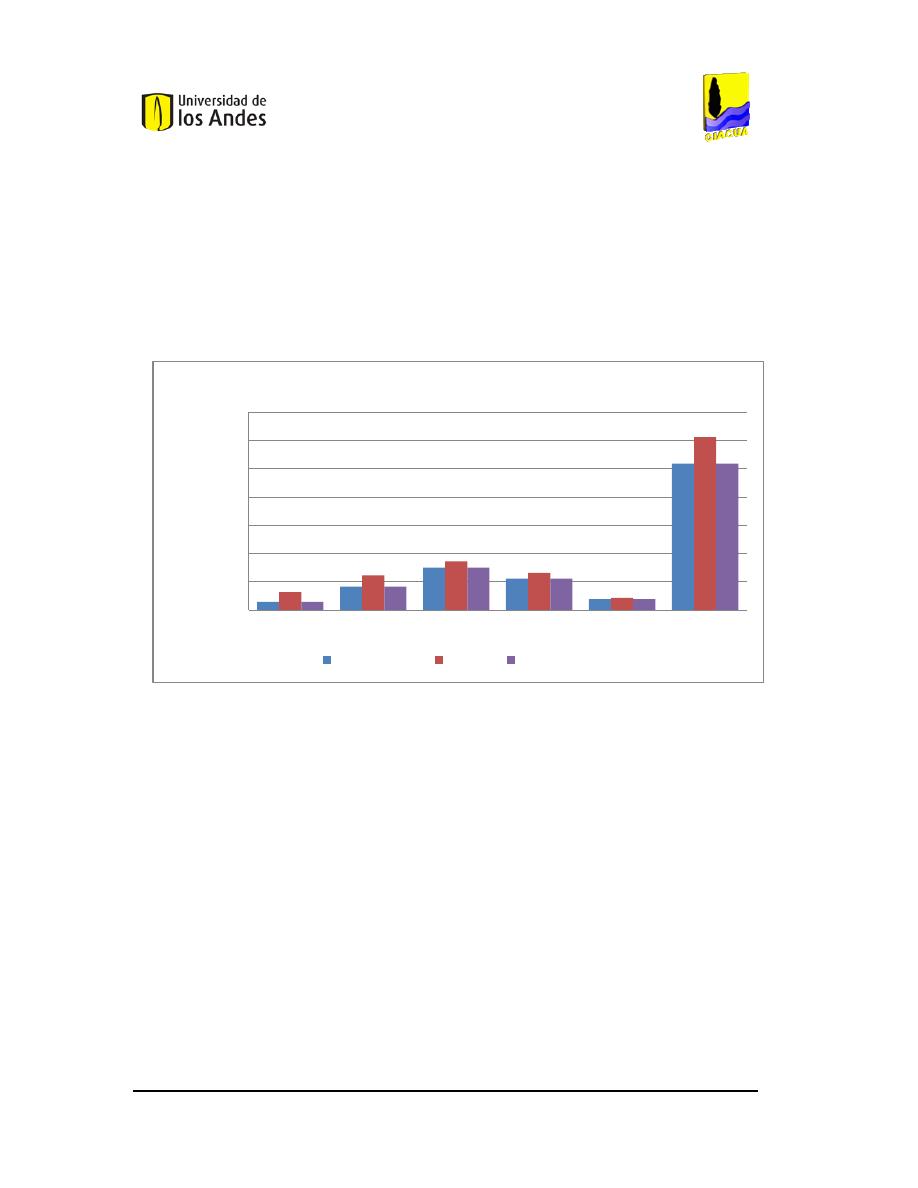
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
33
Comparación general
A partir de la
Figura 24
se pueden ver los errores porcentuales promedio de cada método
para cada porcentaje de cierre analizado. En ella se puede observar que el valor máximo,
para los tres casos, se tiene cuando la válvula se cierra totalmente. Resulta llamativo que
la tendencia no sea monótona creciente, sino que tenga un máximo local en 60% y luego
el máximo global en el 100%. Finalmente, se puede apreciar la constante semejanza que
tienen los métodos Quasi-Steady y Unsteady-Vitkovsky. De esta manera, se optará por
realizar las simulaciones con el método de Quasi-Steady, dado que tiene un menor costo
computacional comparado con Unsteady-Vitkovsky y el error porcentual más bajo.
Figura 24. Errores porcentuales promedios de los diferentes métodos de cálculo de factor de fricción,
en los diferentes porcentajes de cierre.
Se encuentra relevante mencionar que el método de cálculo Steady, a pesar de tener
errores porcentuales bajos y el menor costo computacional, no se tomará en cuenta. Esto,
dado que si existe una variación significativa en el caudal y, por tanto, en el número de
Reynolds, el método estará sub o sobreestimando en gran medida el valor real del factor
de fricción de Darcy.
0,00%
0,05%
0,10%
0,15%
0,20%
0,25%
0,30%
0,35%
20%
40%
60%
80%
90%
100%
Err
or
es
Por
cent
u
al
es
Pro
med
io
Errores Porcentuales Promedio vs Método de Cálculo
Quasi-Steady
Steady
Unsteady - V
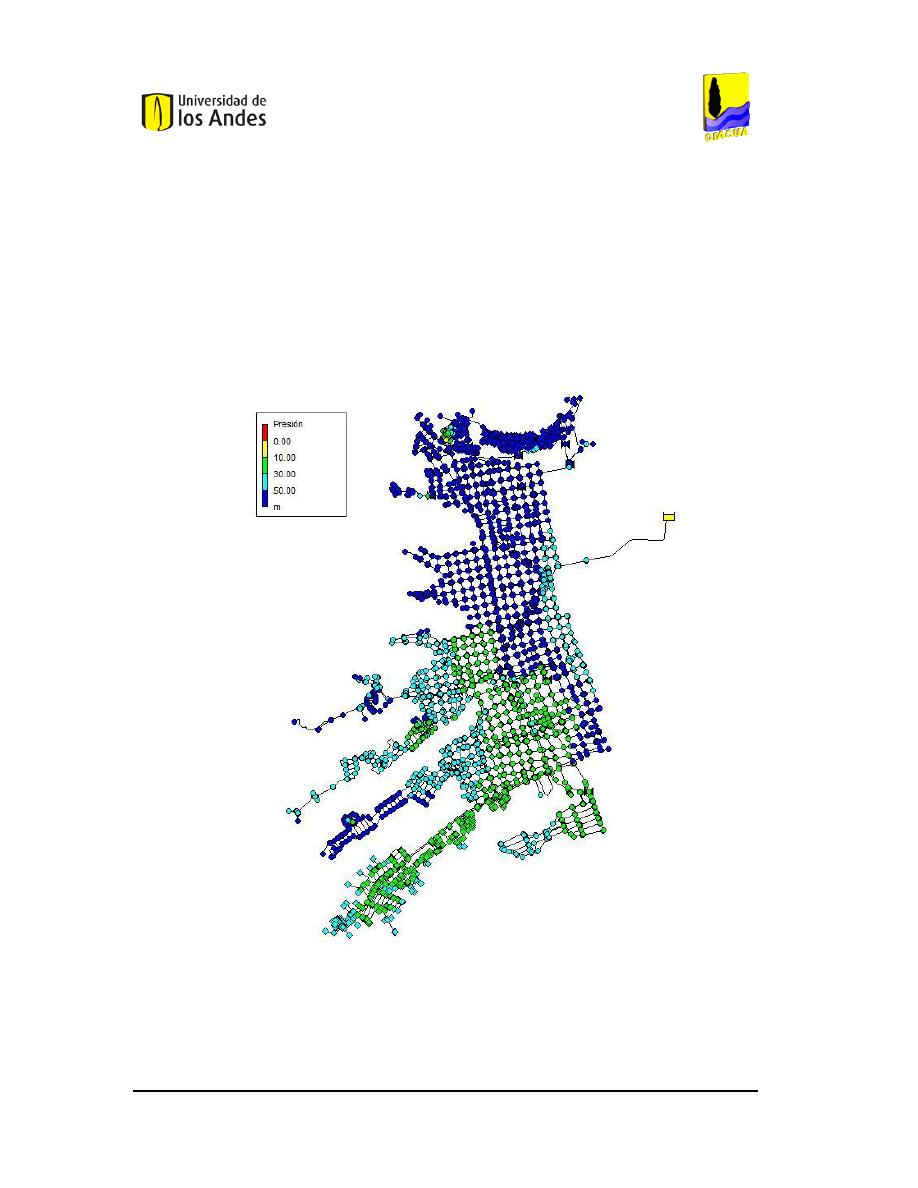
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
34
6. Redes de Prueba
En la presente sección se describirán detalladamente las redes de distribución de agua
potable que se emplearon para encontrar los resultados presentados más adelante.
6.1. Red de Bucaramanga (Sector Estadio)
La red de Bucaramanga, más específicamente el sector Estadio, es una red de un tamaño
considerable. Ésta tiene un número de 5,356 tuberías con 1,882,736 m de éstas.
Adicionalmente, tiene 4,545 nudos con una elevación promedio de 924.49 m y un
coeficiente de variación de 3.59%. La red tiene una única fuente de abastecimiento, y el
mismo es realizado por gravedad sin uso alguno de bombas.
Figura 25. Caso de estudio Red de Bucaramanga (Sector Estadio).
En la Figura 25 se puede ver lo compleja que es la red. Adicionalmente, en la parte
derecha de la figura, en amarillo, se ve el reservorio que abastece toda la red. Por otra
parte, con el uso de la escala de presiones se puede ver que la red en su mayor parte
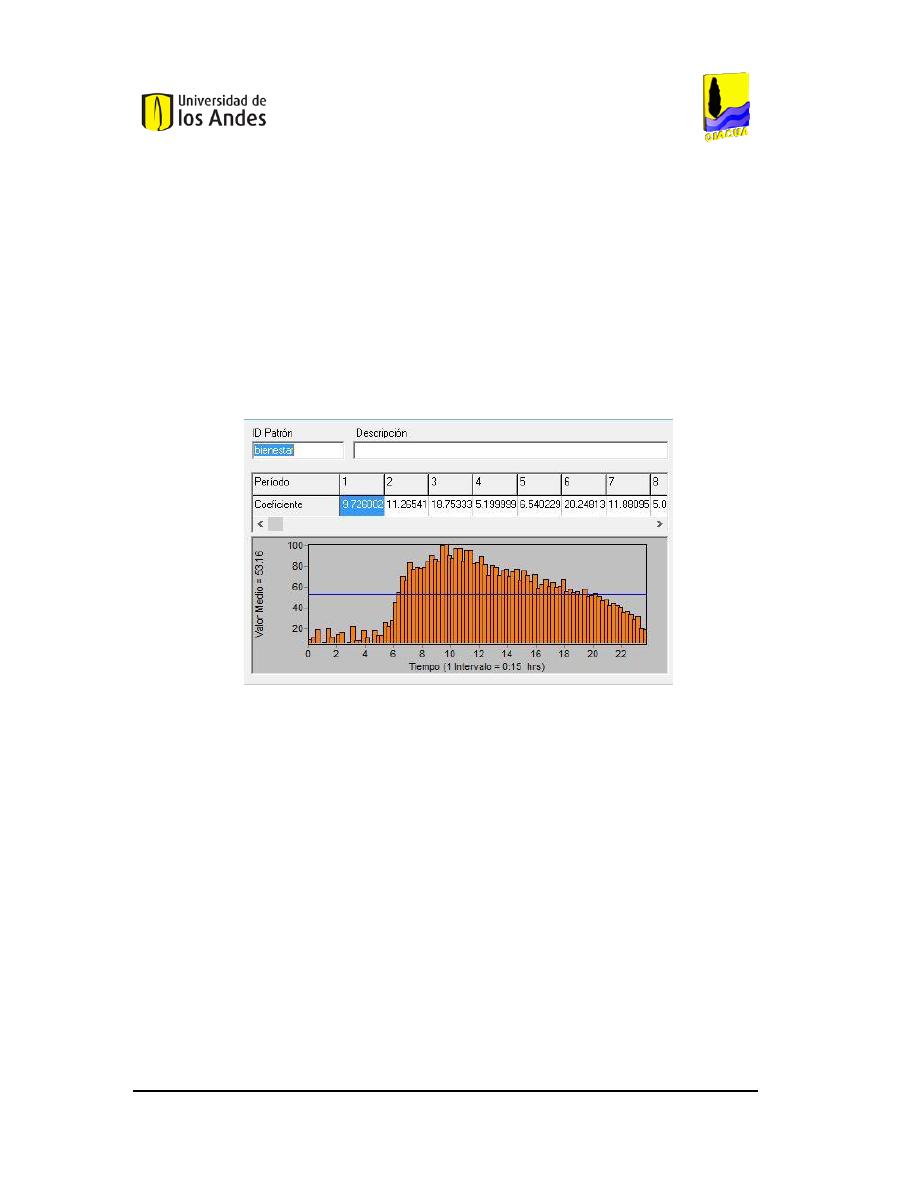
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
35
maneja una presión superior a 50 m de columna de agua. Se considera relevante
mencionar que en el estado estable la red en total tiene un consumo de 324 L/s.
6.1.1. Patrónes
La red tiene 3 patrones de consumo diferentes, los cuales se presentan a continuación.
Sin embargo, en casi el 98% de los nudos se presenta el mismo patrón, el cual es
denominado Estadio.
Bienestar
En la Figura 26 se puede ver la forma que tiene el patrón Bienestar en el tiempo. Se
considera relevante mencionar que los coeficientes son de gran magnitud, pues oscilan
entre 5 y 100.
Figura 26. Patrón Bienestar de la red de Bucaramanga (Sector Estadio).
Estadio
En la Figura 27 se puede apreciar el comportamiento que tiene el patrón que rige el 98%
de la red. Se puede apreciar que la demanda máxima estará cerca de las 11 horas y la
mínima a las 4 horas. Adicionalmente, se encuentra que las variaciones no son drástica y,
por lo tanto, tiene un comportamiento suave a lo largo del tiempo.
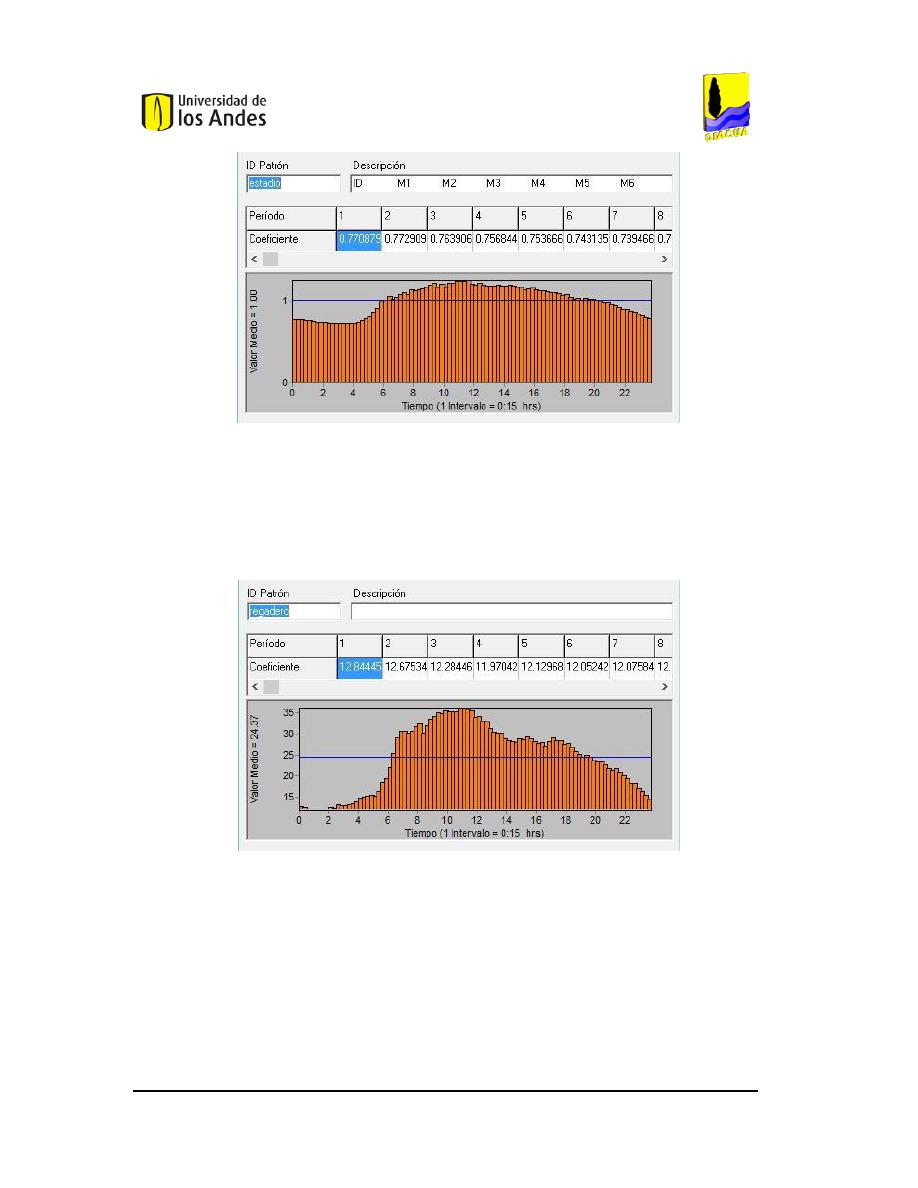
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
36
Figura 27. Patrón Estadio de la red de Bucaramanga (Sector Estadio).
Regadero
En la Figura 28 se puede ver el comportamiento del patrón Regadero. En ella se puede
apreciar que el patrón tiene una alta variación entre las 2 y 6 horas. Adicionalmente, si se
ve la escala se puede ver que los coeficientes son de gran magnitud. Sin embargo, estos
son menores que los que se pueden ver en el patrón Bienestar.
Figura 28. Patrón Regadero de la red de Bucargamanga (Sector Estadio).
6.1.2. Sectorización
Luego de haber establecido la metodología de ubicar las válvulas, ésta se aplicó a la
presente red. A continuación se muestran los resultados encontrados, y los sectores que
se crearon en el proceso. En total se crearon 8 válvulas en distintas partes de la red. Se
considera relevante mencionar que los nudos que están en rojo en las figuras que se
presentarán, son los afectados por la operación de la válvula que se esté describiendo.

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
37
TCV-1 (Sector Principal 1)
En la Figura 29, en la imagen del lado izquierdo se puede ver la ubicación de la válvula
donde está el punto rojo. En la imagen del lado derecho se puede apreciar la afectación
que genera el cerrar la válvula.
Figura 29. Ubicación y afectación que genera la válvula TCV-1.
TCV-2 (Sector Principal 2)
En la Figura 30 se puede ver la ubicación y los nudos que afecta la operación de la
válvula TCV-2. Se considera relevante decir que se utilizó esta ubicación para poder
estudiar el efecto que tiene el cierre de la válvula aguas arriba de ésta.
Figura 30. Ubicación y afectación que genera la válvula TCV-2.
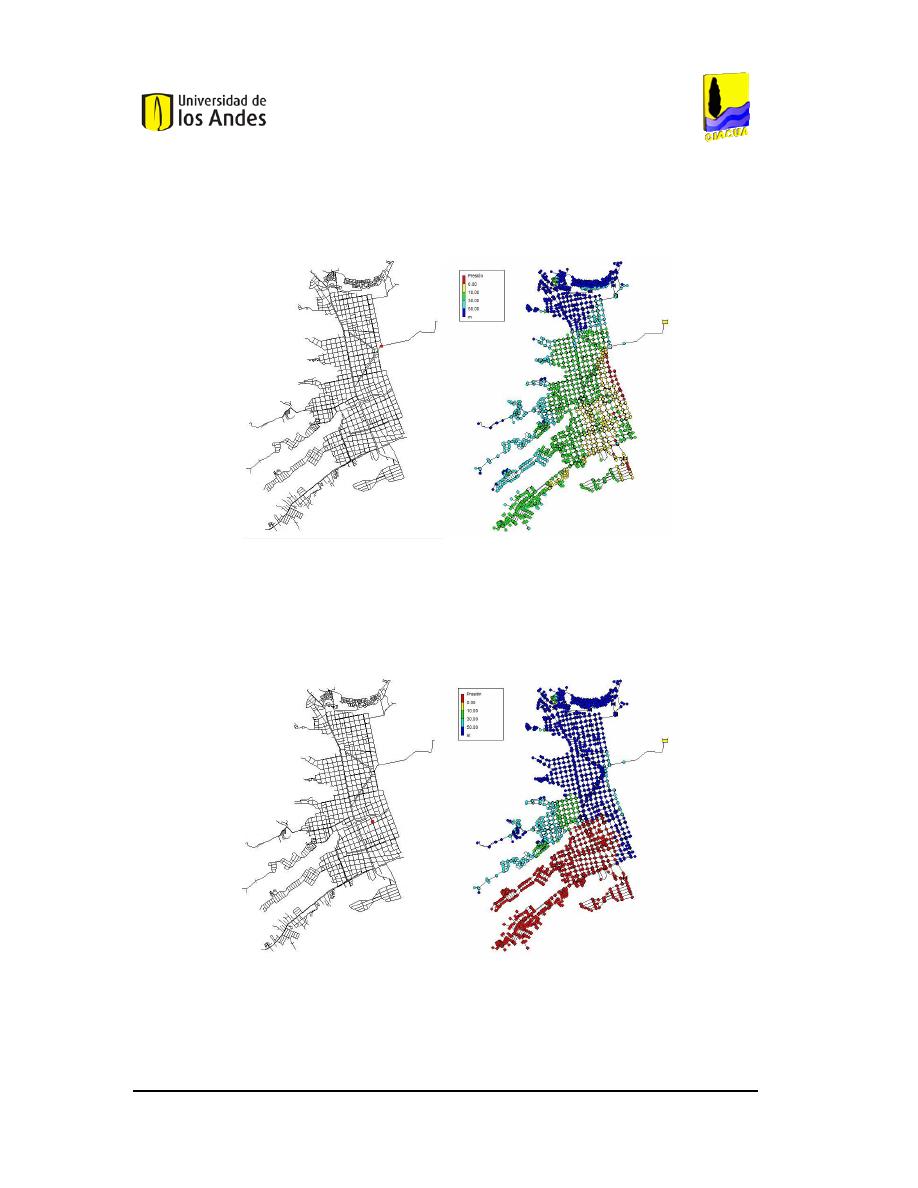
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
38
TCV-3 (Semi-Principal)
En la Figura 31 se puede ver la ubicación de la válvula TCV-3. Adicionalmente, al lado
derecho se puede ver que la operación de ésta válvula afecta una gran cantidad de nudos
en la red. Sin embargo, ésta no tiene la capacidad de ahogar la red.
Figura 31. Ubicación y afectación que genera la válvula TCV-3.
TCV-4 (Sector Abajo)
En la Figura 32 se puede ver la ubicación de la válvula TCV-4 y los nudos que afecta la
operación de la misma. De forma similar, se puede ver que esta válvula afecta solo un
sector de la red y deja otras partes de la misma intactas.
Figura 32. Ubicación y afectación que genera la válvula TCV-4.

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
39
TCV-5 (Sector Izquierdo)
En la Figura 33 se puede ver la ubicación y los nudos que afecta la operación de la
válvula TCV-5. Similar a la válvula anterior, se puede ver que la operación de ésta afecta
solo un sector de la red.
Figura 33. Ubicación y afectación que genera la válvula TCV-5.
TCV-6 (Arriba Derecha)
En la Figura 34 se puede ver la ubicación de la válvula TCV-5. De forma similar se
puede ver que el número de nudos que afecta esta válvula es reducido.
Figura 34. Ubicación y afectación que genera la válvula TCV-6.
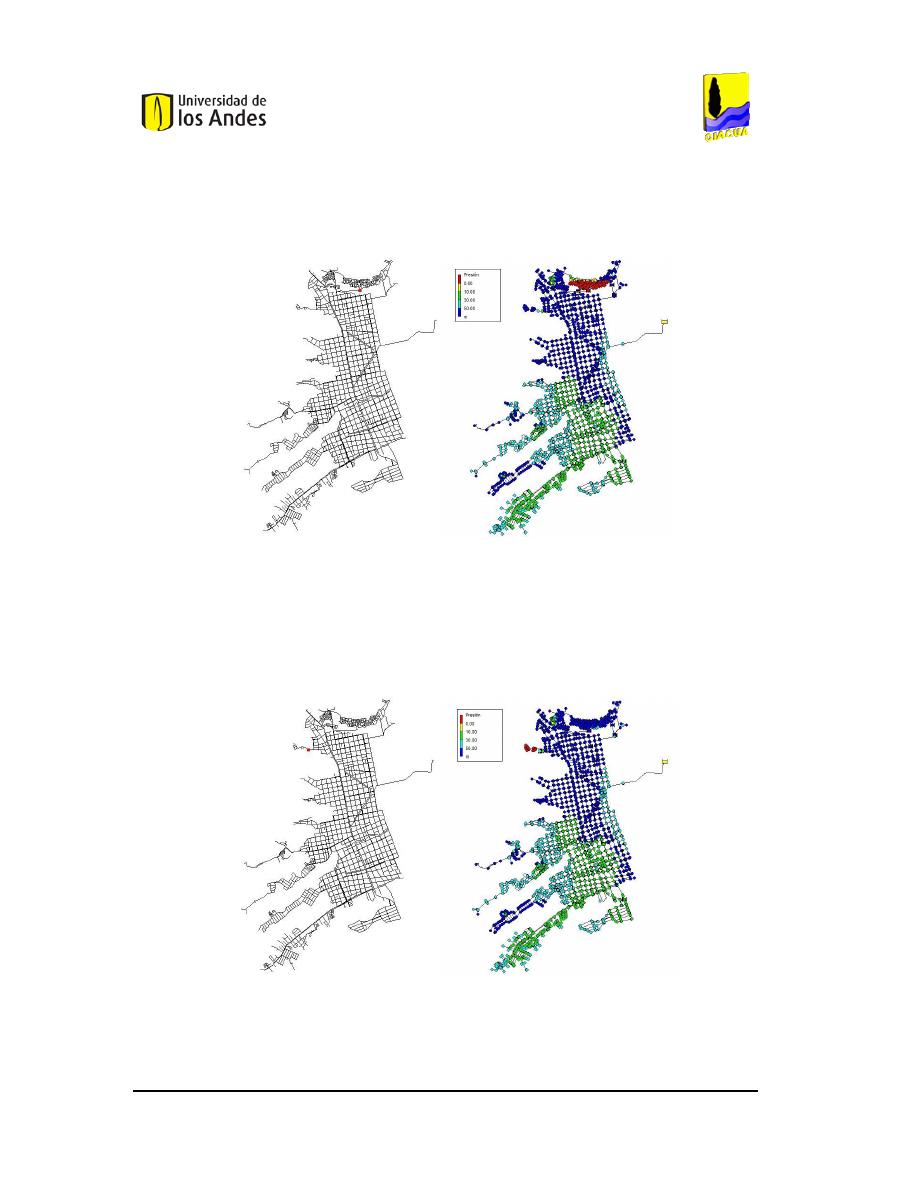
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
40
TCV-7 (Arriba Centro)
En la Figura 35 se puede ver la ubicación que tiene la válvula TCV-7, en conjunto con el
número de nudos que afecta la operación de la misma. Adicionalmente, se puede ver que
el cerrar esta válvula no afecta de forma significativa el resto de la red.
Figura 35. Ubicación y afectación que genera la válvula TCV-7.
TCV-8 (Pequeño)
En la Figura 36 se puede ver la ubicación de la válvula TCV-8. Adicionalmente, se
puede ver que la operación de esta válvula afecta una cantidad reducida de nudos. Sin
embargo, se optó por dejar esta válvula, pues se quiere ver el comportamiento que tiene
la red en caso de que se afecte una pequeña parte de la misma.
Figura 36. Ubicación y afectación que genera la válvula TCV-8.
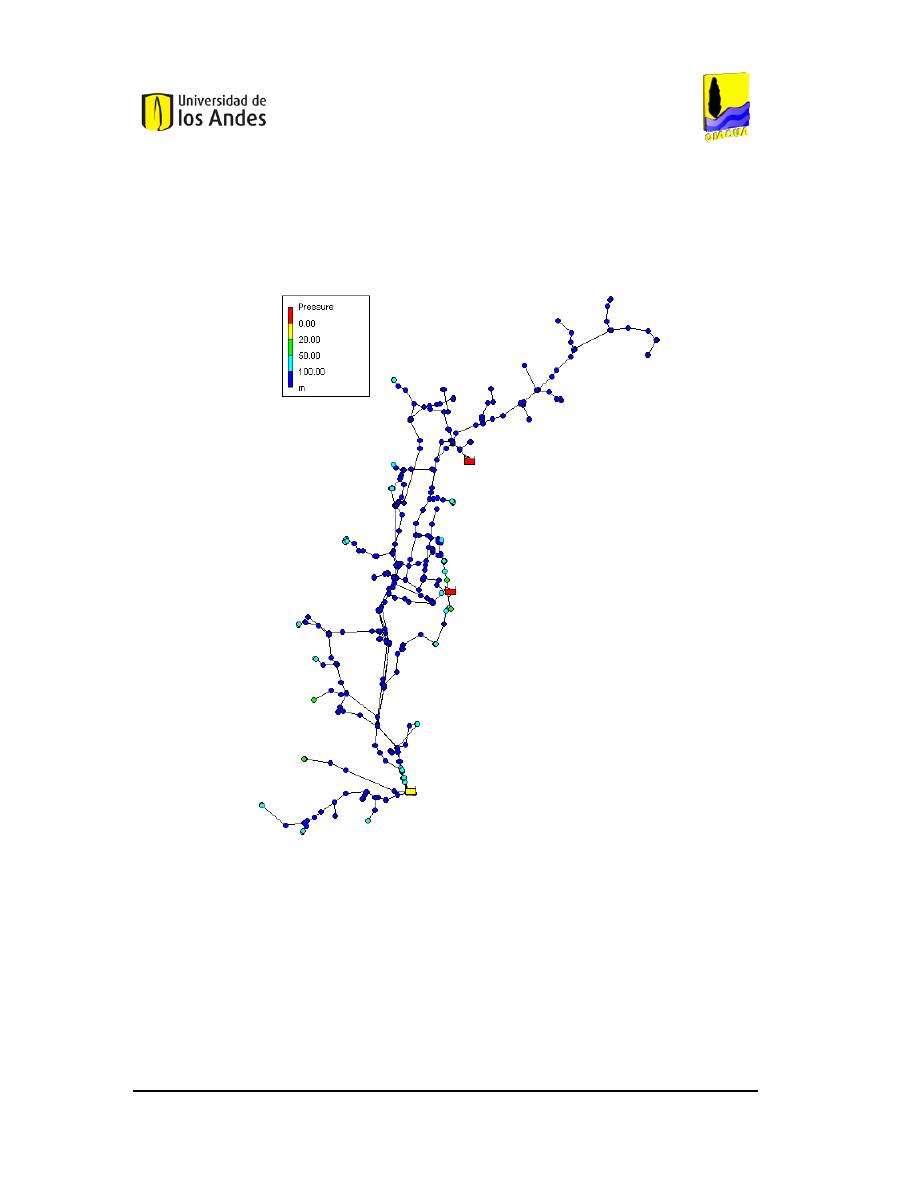
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
41
6.2. Red Matriz de Medellín
La red matriz de Medellín es una red de un tamaño considerable; sin embargo menos
compleja que la de Bucaramanga. Ésta tiene un número de 736 tuberías con 202.15 Km
de éstas. Adicionalmente, tiene 685 nudos con una elevación promedio de 1549 m y un
coeficiente de variación de 6.08%. La red tiene tres fuentes de abastecimiento, y el
mismo es realizado por gravedad sin uso alguno de bombas.
Figura 37. Caso de estudio Red Matriz de Medellín.
En la Figura 37 se puede ver que es una red menos compleja que la de Bucaramanga, esto
se ve reflejado en el número de elementos y en la disminución del tiempo computacional
de cálculo requerido. Adicionalmente, se puede ver que hay una alta conexión entre las
fuentes de agua.
Por otra parte, a partir de simulaciones realizadas se encontró que el cierre del reservorio
superior y el de la parte central no afecta una cantidad de nudos considerable. Sin
embargo, el cierre del reservorio de la parte inferior afecta en gran medida la red y el
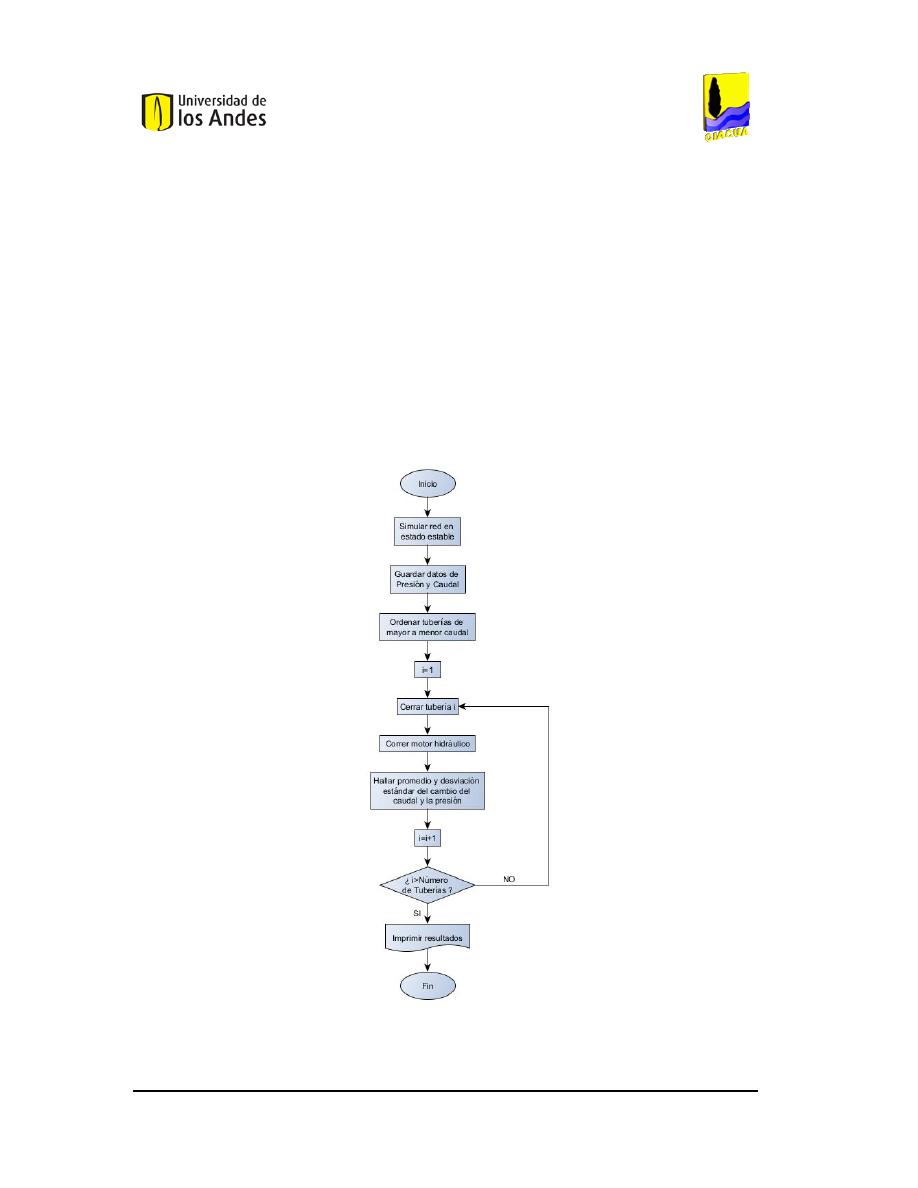
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
42
número de nudos que afecta es relevante. En la Figura 37 se puede ver que en la mayoría
de la red la presión que se tiene es superior a los 100 mca, y en su totalidad es mayor a 20
mca.
Finalmente, la red tiene 46 nudos de consumo los cuales en total consumen 7.759 m
3
/s;
cabe decir que estos no tienen patrones asociados. Es relevante establecer que, al realizar
el análisis de estado estable de la red, el reservorio que se encuentra en la parte central de
la red tiene un caudal de entrada y los otros dos son lo que suplen el caudal requerido.
6.2.1. Sectorización
Al emplear la metodología para la selección de válvulas se encontraron 6 tuberías las
cuales parecían ser prominentes para el análisis. Sin embargo, al realizar algunas
simulaciones se encontró que no todas perturbaban en gran medida la red. Al estudiar
con mayor precisión la red se encontró que al ser tan cerrada, con tres posibles fuentes y
con un bajo número de nudos de consumo la red ésta es muy resiliente.
Figura 38. Diagrama de flujo implementado para ubicar las válvulas en la Red Matriz de Medellín.
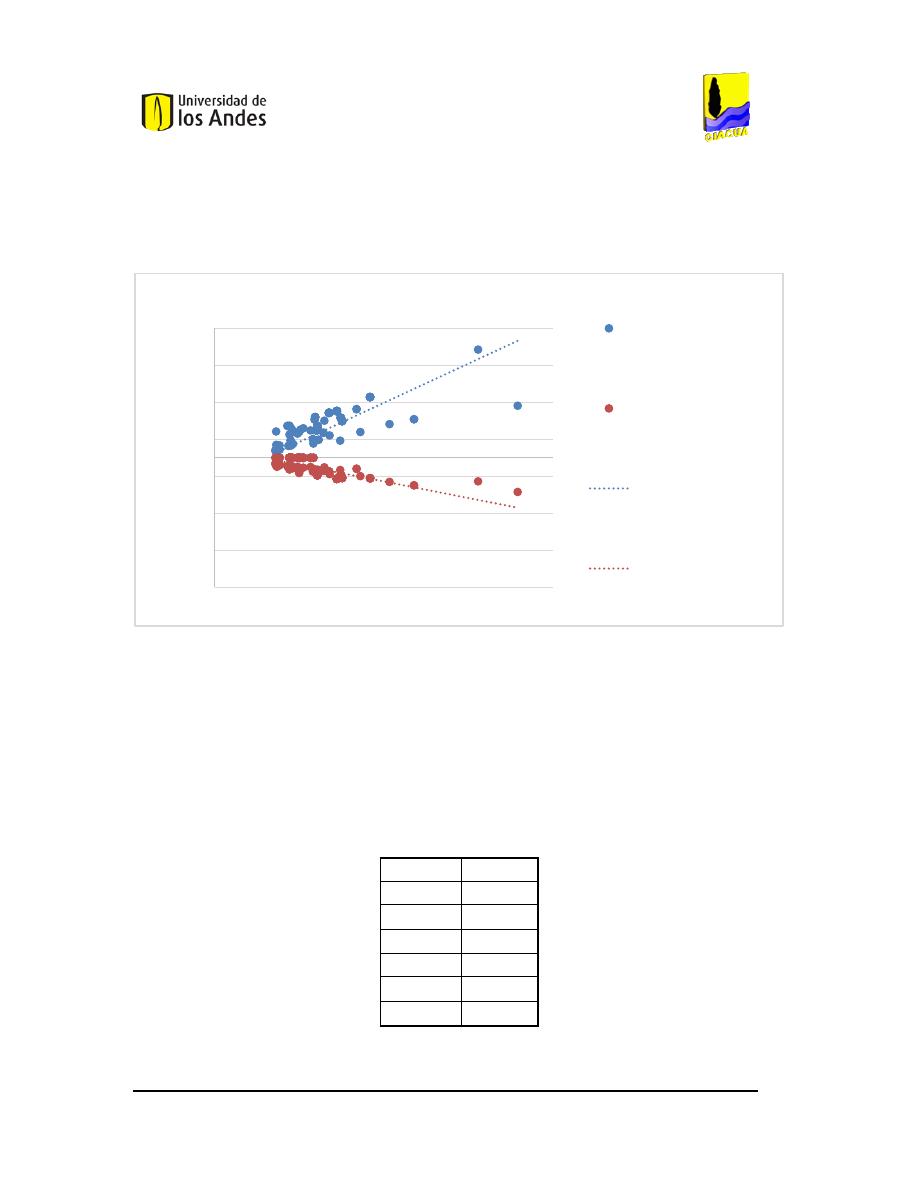
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
43
De esta manera, la metodología presentada en una sección anterior no llevó a situar las
válvulas en aquellas tuberías que perturbaban la red en mayor medida. Asimismo, se
optó por un cambio para la selección de la ubicación de las válvulas. En la Figura 38 se
puede ver el diagrama de flujo que se implementó para ubicar las válvulas en la red
Matriz de Medellín.
Figura 39. Comportamiento de la variación del caudal respecto al estado inicial.
En la Figura 39 se puede ver que a mayor caudal transportado por la tubería de cierre hay
una mayor perturbación de los caudales en la red. Adicionalmente, si se ven los R
2
obtenidos para las regresiones lineales se encuentra que la regresión elegida tiene la
capacidad de mostrar la tendencia general de los datos.
Al emplear la metodología descrita se encontró que las tuberías candidatas para situar las
válvulas fueron las siguientes.
Tabla 1. Tuberías en las cuales se situaron las válvulas de Medellín.
Válvula-1 Pipe 119
Válvula-2 Pipe 474
Válvula-3 Pipe 320
Válvula-4 Pipe 107
Válvula-5 Pipe 468
Válvula-6 Pipe 385
Válvula-7 Pipe 435
R² = 0,5852
R² = 0,6137
-350
-250
-150
-50
50
150
250
350
0
500
1000
1500
Va
ria
ción
de
l C
auda
l (
L/
s)
Caudal transportado por la tubería de cierre (L/s)
Variación del Caudal
Promedio + Desviación
Estándar
Promedio - Desviación
Estándar
Lineal (Promedio +
Desviación Estándar)
Lineal (Promedio -
Desviación Estándar)
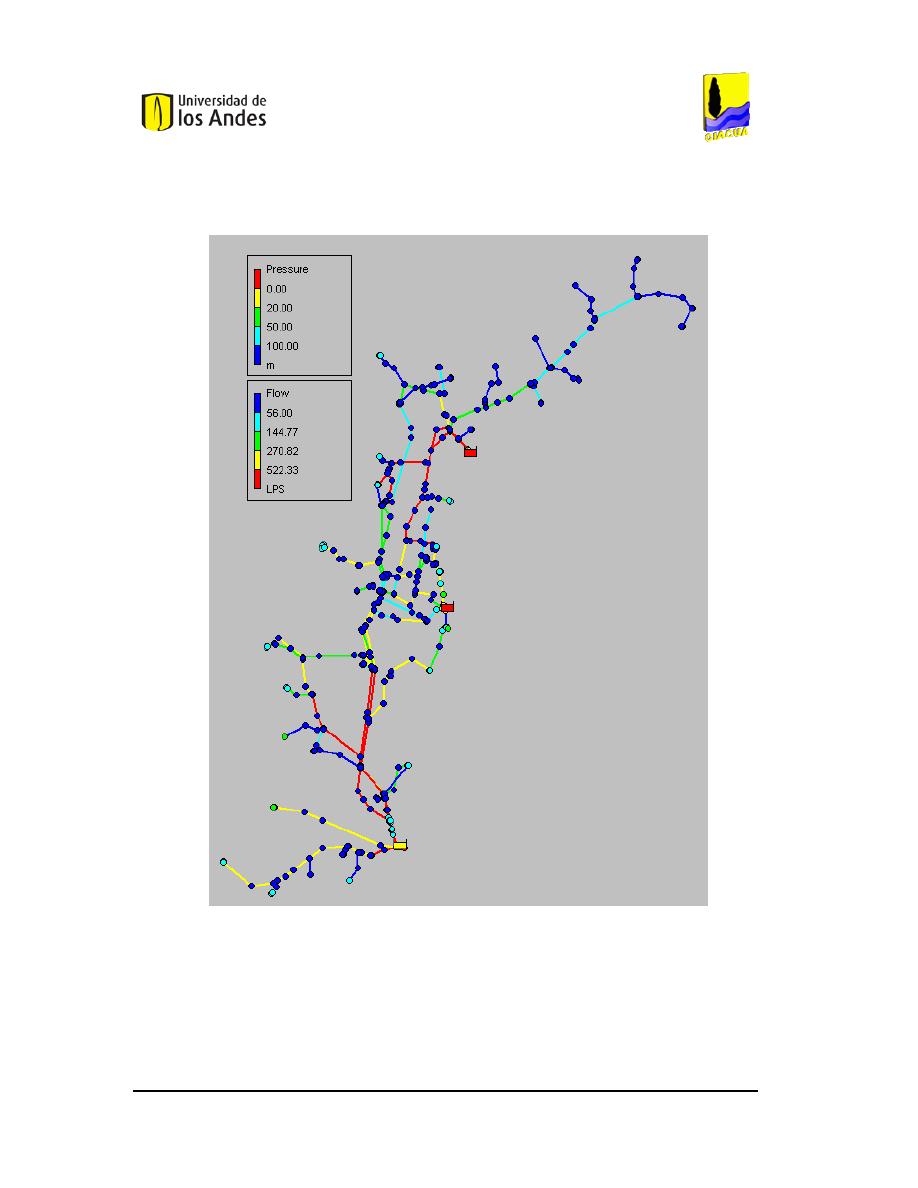
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
44
A continuación se presenta una ilustración que muestra los flujos y las presiones que
tienen la red Matriz de Medellín. De esta manera, se puede comparar y ver la influencia
que tiene el cierre de las diferentes válvulas situadas.
Figura 40. Estado Inicial de la red Matriz de Medellín.
Válvula-1
En la Figura 41 se puede ver la ubicación de la Válvula 1. Adicionalmente, si se observa
con detenimiento la figura, en la parte derecha ve la afectación generada por la válvula en
términos de presión y caudal. La gran variación de la primera variable se da en los nudos
más cercanos al reservorio de la parte inferior. Por otra parte, para los caudales ocurre en
la parte central de la red.
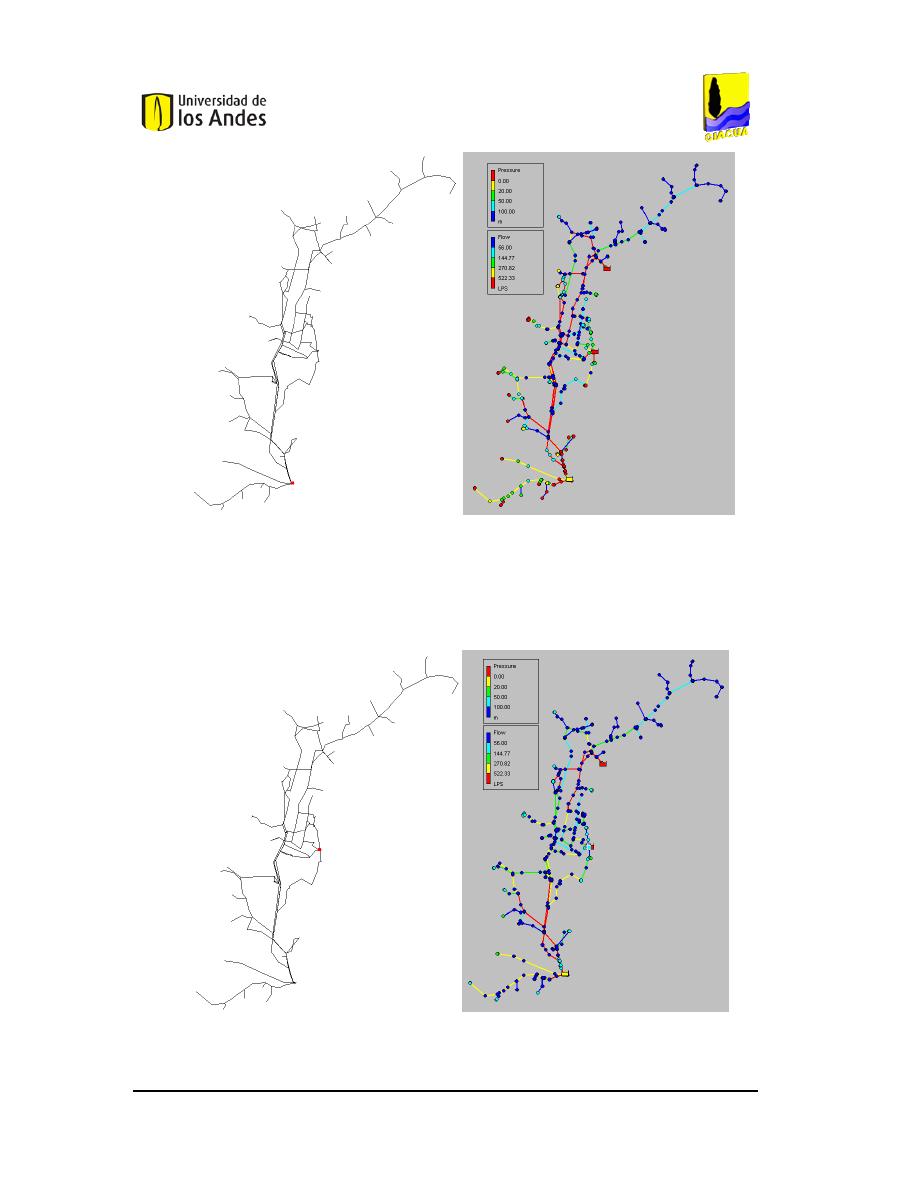
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
45
Figura 41. Ubicación y afectación que genera la Válvula-1 en la red Matriz de Medellín.
Válvula-2
En la Figura 42 se puede ver la ubicación de la Válvula-2. En adición, se encuentra la
afectación de los caudales en la parte central de la red generada por el cierre de la
Válvula-2. Se considera relevante mencionar que esta válvula no tiene la capacidad de
producir cambios relevantes en la presión.
Figura 42. Ubicación y afectación que genera la Válvula-2 en la red Matriz de Medellín.
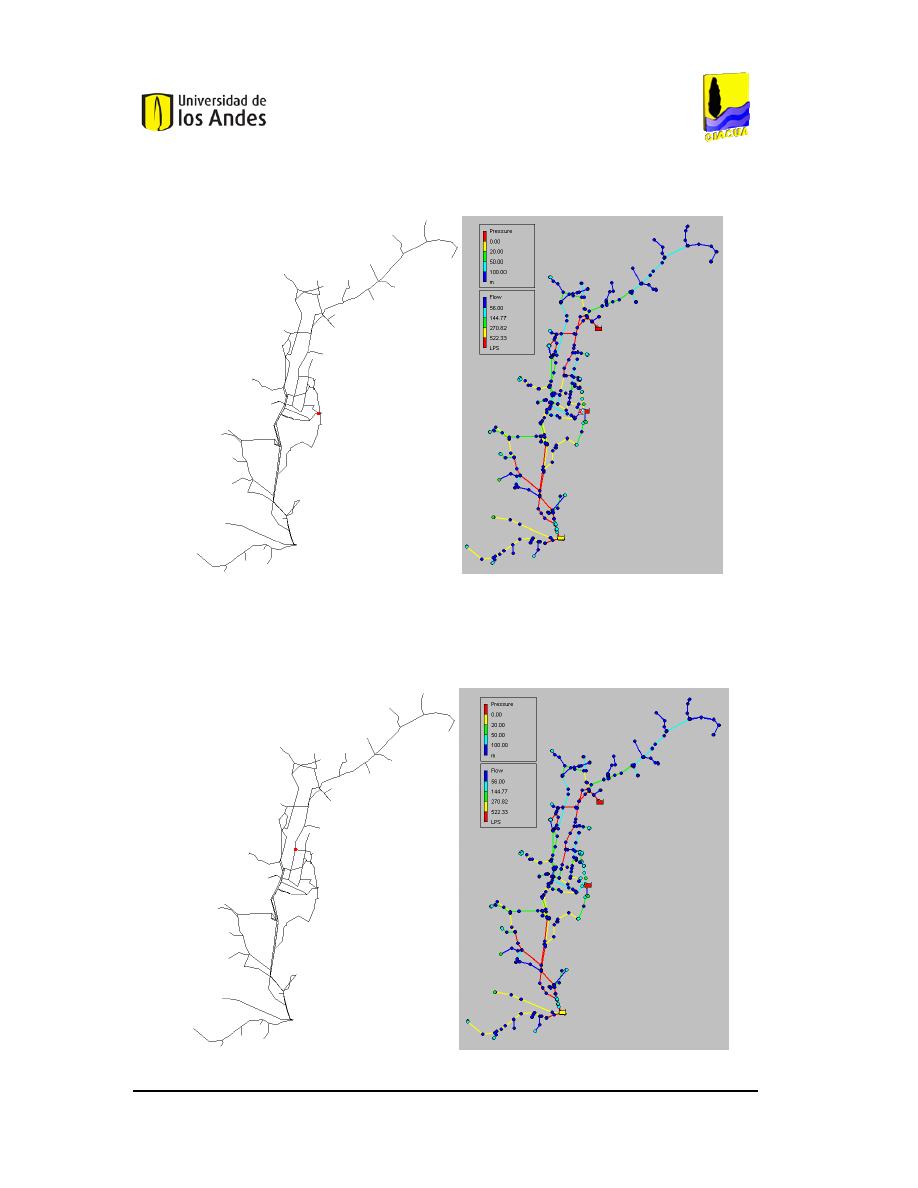
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
46
Válvula-3
En la Figura 43 se encuentra la ubicación de la Válvula 3 y la afectación en los caudales
que genera el cierre de ésta.
Figura 43.Ubicación y afectación que genera la Válvula-3 en la red Matriz de Medellín.
Válvula-4
En la Figura 44 se puede encontrar la ubicación de la Válvula 4. Nuevamente, con la
figura se puede ver la afectación de la válvula a la red, la cual se da en solo términos de
caudal.
Figura 44.Ubicación y afectación que genera la Válvula-4 en la red Matriz de Medellín.
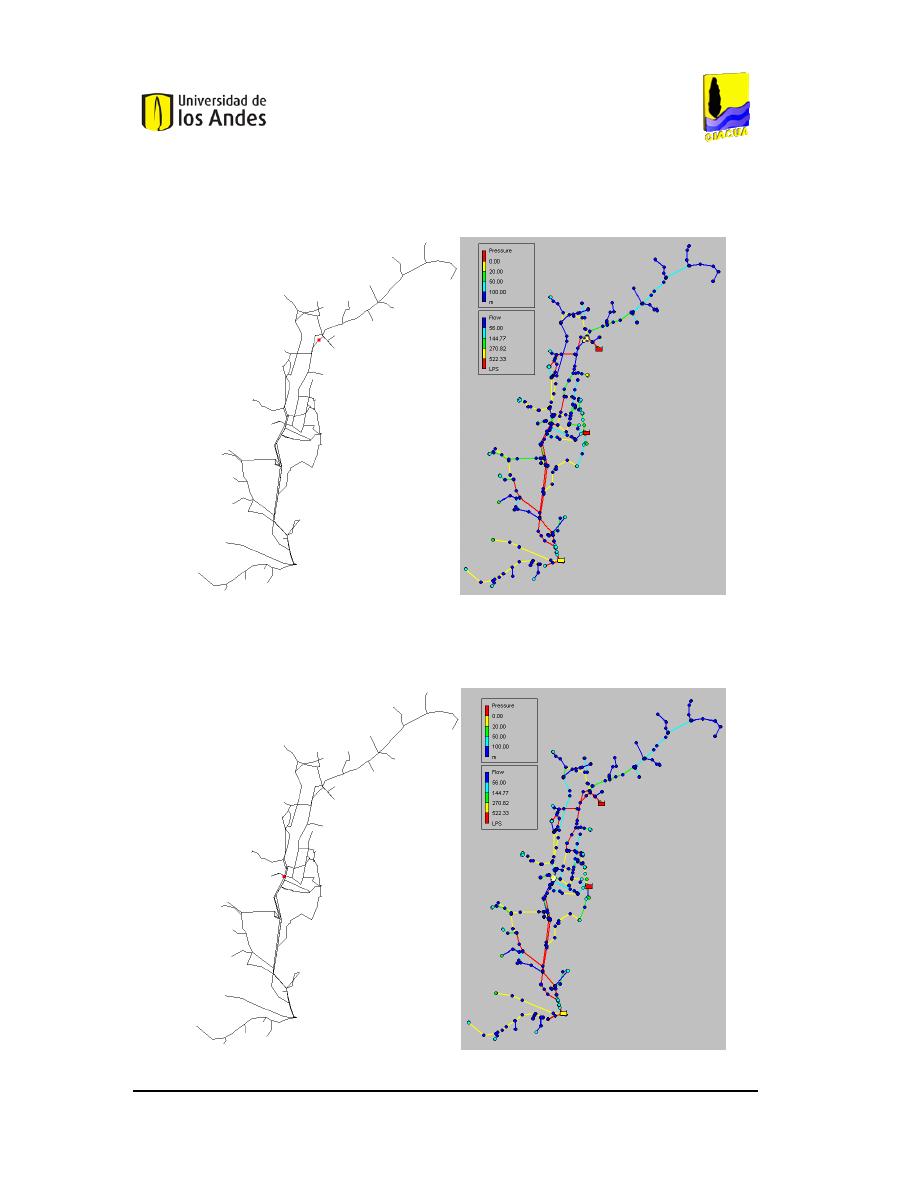
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
47
Válvula-5
En la Figura 45 se puede ver la posición de la Válvula 5 en la red. En adición se puede
ver que la afectación en términos de caudal de esta válvula es superior en comparación a
las dos anteriores. Sin embargo, ésta no es capaz de afectar las presiones en gran medida.
Figura 45.Ubicación y afectación que genera la Válvula-5 en la red Matriz de Medellín.
Válvula-6
En la Figura 46 se puede ver en donde se encuentra la Válvula 6. Por otra parte, se puede
ver que la afectación a los caudales es similar a la que se da con la Válvula 5.
Figura 46.Ubicación y afectación que genera la Válvula-6 en la red Matriz de Medellín.
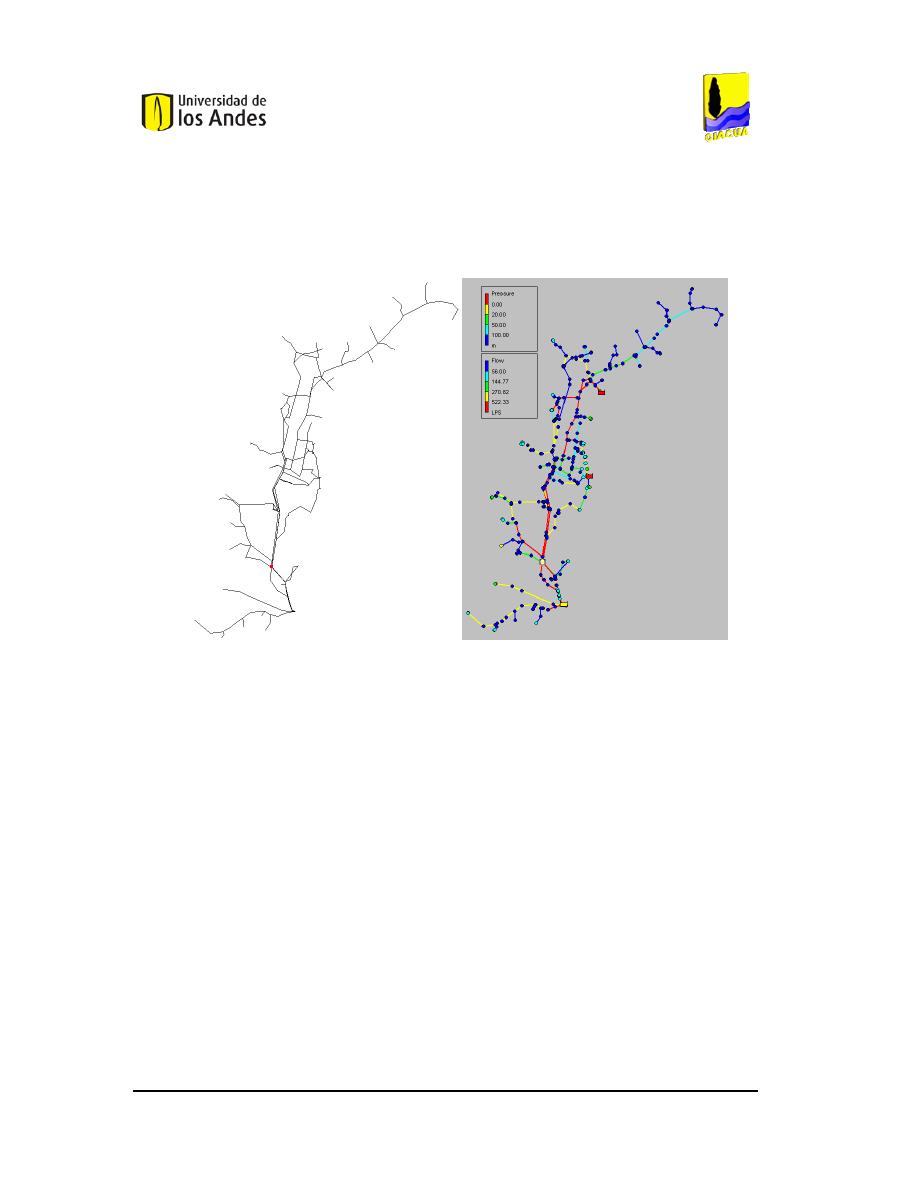
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
48
Válvula-7
En la Figura 47 se puede ver la ubicación de la Válvula 7. Adicionalmente, al ver la
afectación que esta genera se encuentra gran similitud con la generada en la Válvula 1 en
términos de caudal. Sin embargo, si se analiza en términos de presión se encuentra que el
cierre de ésta no produce cambios significativos en la red.
Figura 47. Ubicación y afectación que genera la Válvula-7 en la red Matriz de Medellín.
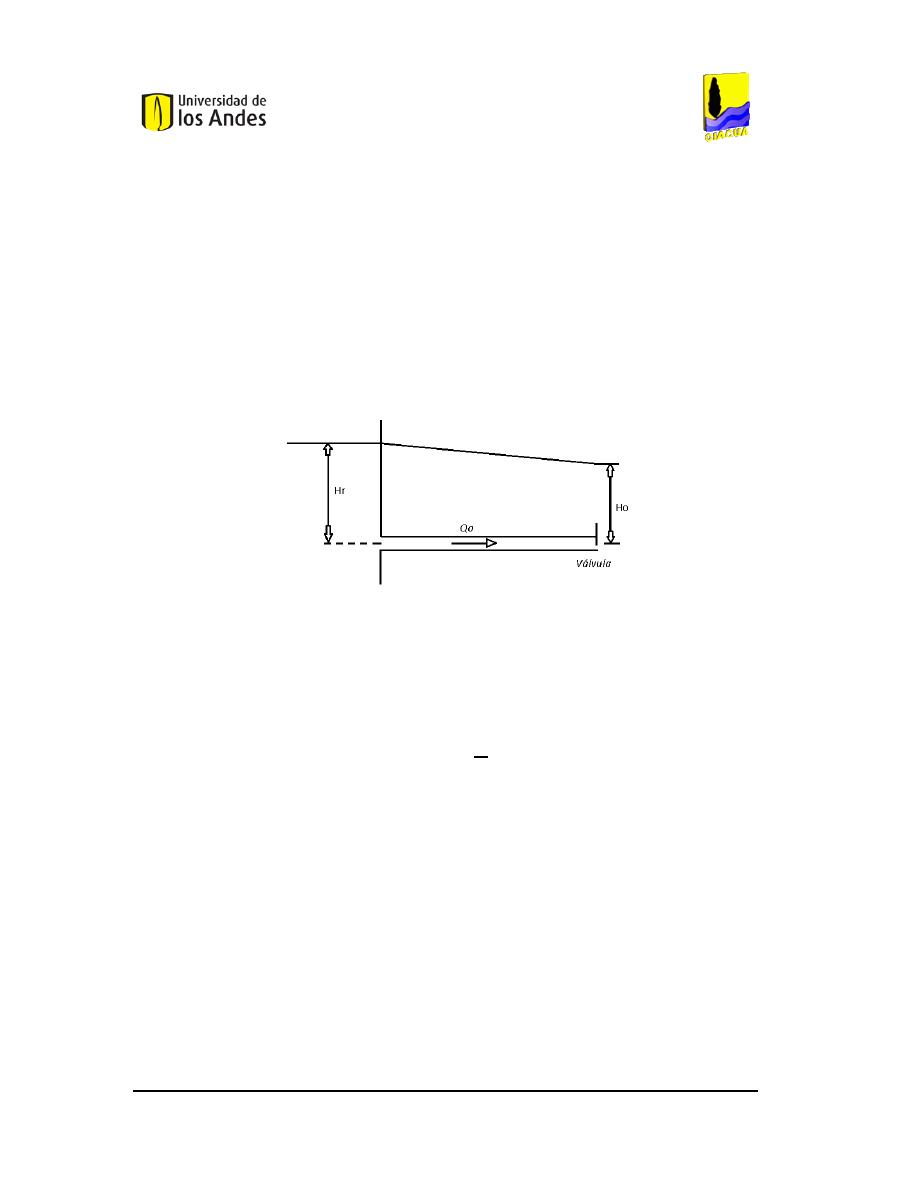
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
49
7. Resultados y Análisis
En la siguiente sección se presentarán los resultados y análisis correspondiente de los
datos obtenidos de las redes probadas. Adicionalmente, se presenta un breve análisis de
sensibilidad realizado para un caso simple. En éste se involucran las diferentes variables
que influyen en el fenómeno.
7.1. ANÁLISIS DE SENSIBILIDAD CASO SIMPLE
Se consideró relevante y necesario realizar un análisis de sensibilidad para un caso
simple, dado que si se realiza éste sobre las redes complejas que se enunciaron
anteriormente sin un análisis previo podría conllevar a generar conclusiones erróneas.
Para el estudio se utilizó un ejemplo simple que aparece en el libro de Wylie y Streeter
(1978), el cual se ilustra a continuación.
Figura 48. Ejemplo simple para realizar el análisis de sensibilidad a las variables relevantes del
fenómeno de transiente.
El modelo está compuesto por un reservorio de altura
𝐻
𝑟
, conectado a una tubería que
transporta un caudal
𝑄
𝑜
y éste es regulado por una válvula al final de la tubería. La curva
de cierre de la válvula está dada por la ecuación que se presenta a continuación.
𝜏 = (1 −
𝑡
𝑡
𝑐
)
𝐸
𝑚
Para el desarrollo del problema se plantean los siguientes valores iniciales para las
variables independientes del problema.
𝐿 = 600 m
𝑎 = 1,242 m/s
𝑑 = 0.5 m
𝐻
𝑟
= 150 m
𝑡
𝑐
= 2.1 s
𝐸
𝑚
= 1.5
(𝐶
𝑑
𝐴
𝐺
)
𝑜
= 0.009
𝐻
𝑟
=0.0003 m
A partir de la simulación realizada con los datos anteriores se encontraron los resultados
presentados en la siguiente figura.
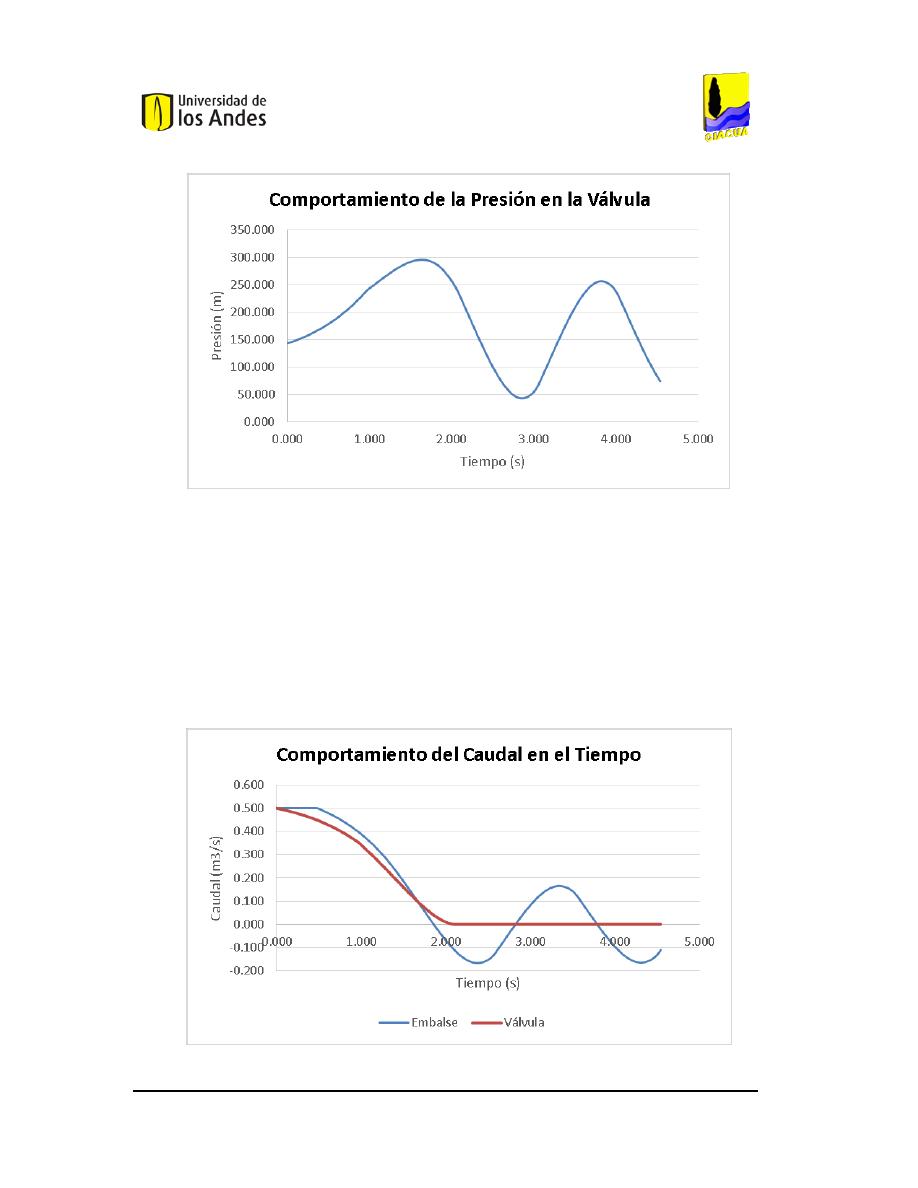
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
50
Figura 49. Comportamiento de la presión en la válvula del ejemplo simple con sus valores iniciales.
En la Figura 49 se puede ver el drástico cambio que produce el cierre de la válvula. Se
considera relevante mencionar que a partir de la revisión bibliográfica la definición de un
cierre rápido de válvula corresponde a aquel que el tiempo de cierre (
𝑡
𝑐
) sea menor a
2L/a. De esta manera, para el presente ejemplo si se realizan los cálculos se encuentra
que el cierre de la válvula no es considerado rápido, dado que 2.1 s > 0.966 s. A pesar de
tener un cierre lento se encuentra que hay una perturbación considerable en el sistema ya
que se puede llegar a tener el doble de la presión en un instante. De forma similar, se
puede ver que la amplitud de la onda es considerable, dado que en una primera instancia
puede llegar a tener un valor de 250 m.
Figura 50. Comportamiento del caudal del ejemplo simple con sus valores iniciales.
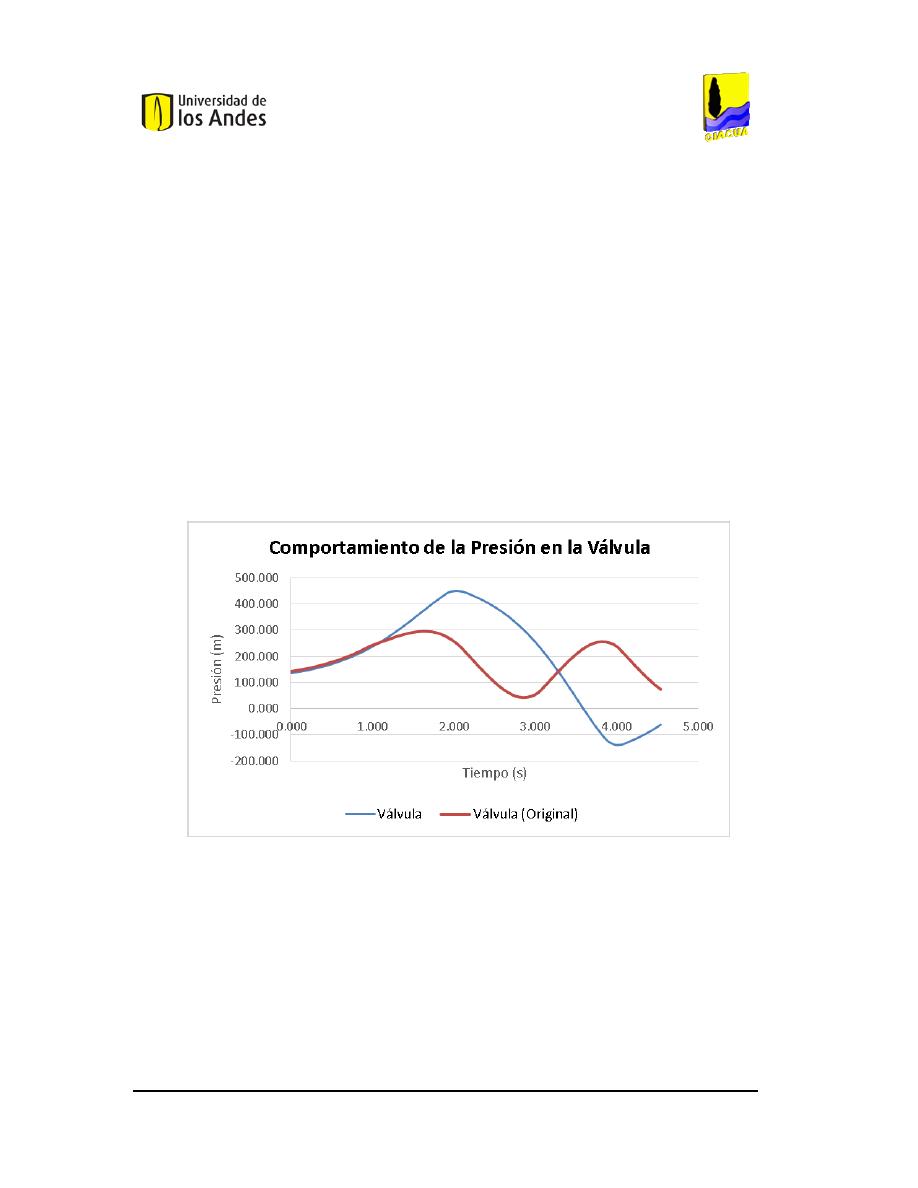
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
51
Por otra parte, al ver la
Figura 50
se puede ver el comportamiento que tiene el caudal en la
salida del embalse y la válvula. De esta manera, se puede ver que el caudal del último
elemento tiene un comportamiento suave y al final del tiempo de cierre de la válvula se
mantiene en 0. Sin embargo, el caudal de salida del embalse, al no tener una condición
de frontera del caudal, muestra oscilaciones considerables.
Se encuentra relevante mencionar que el caudal en este punto se demora 0.483 s en sentir
el cierre de la válvula. Dato que concuerda con el tiempo que requiere la onda en
recorrer la longitud total de la tubería. Adicionalmente, es necesario comentar que la
oscilación que presenta el caudal en la salida del embalse conlleva a que existan caudales
negativos, es decir, que haya agua entrando hacia el reservorio. Finalmente, es relevante
establecer que la amplitud de la onda del caudal en el embalse es de 0.3 m
3
/s, el cual
corresponde a un 60% del caudal inicial.
7.1.1. AUMENTO DE LA LONGITUD
Para los resultados que se presentan a continuación se realizó un incremento a la longitud
de la tubería, siendo ésta de 1200 m; dos veces el valor original.
Figura 51. Comportamiento de la presión en la válvula del ejemplo simple incrementado la longitud.
En la Figura 51 se puede ver que el incremento en la longitud conlleva a un aumento de
la amplitud y el periodo de la onda que es generada. Adicionalmente, se puede ver que el
incremento de la onda es tal que se llegan a tener presiones negativas en el sistema. De
esta manera, se encuentra que el aumentar la longitud afecta de forma negativa al sistema.
Además, por las ecuaciones de diferencias finitas que rigen el fenómeno se encuentra que
el sistema con doble longitud requerirá un mayor tiempo para que el sistema se
estabilice.
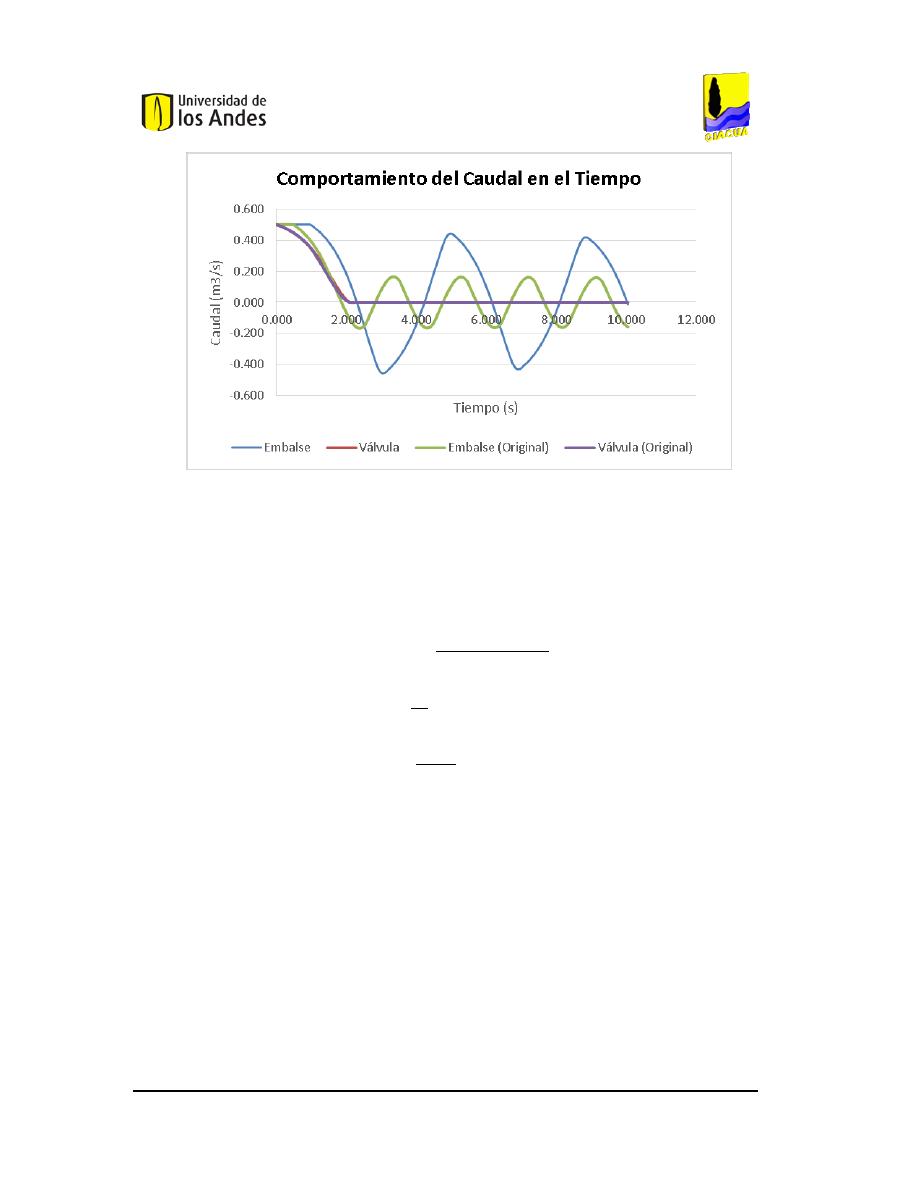
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
52
Figura 52. Comportamiento del caudal del ejemplo simple incrementando la longitud.
En la Figura 52 se puede ver que el comportamiento del caudal también es afectado de
forma negativa, dado que aumenta drásticamente el periodo de la onda. Adicionalmente,
se podría decir que la afectación es aún mayor dado que la amplitud de onda es mayor al
caudal inicial. Por otra parte, se puede ver que el caudal de salida de la válvula no es
afectado de manera drástica. Para explicar la razón de esto se encuentra necesario
presentar las siguientes ecuaciones que muestran la manera de definir el caudal de salida
de la válvula.
𝑄 = −𝐵𝐶
𝑣
+ √(𝐵𝐶
𝑣
) + 2𝐶
𝑣
𝐶
𝑝
(49)
𝐵 =
𝑎
𝑔𝐴
(50)
𝐶
𝑣
=
(𝑄
𝑜
𝜏)
2
2𝐻
𝑜
(51)
𝐶𝑝 = 𝐻
𝑖−1
− 𝐵𝑄
𝑖−1
− 𝑅𝑄
𝑖−1
|𝑄
𝑖−1
|
(52)
En la Ecuación 49 se pueden ver los factores que influyen en el caudal de salida de la
válvula. Adicionalmente, al ver la Ecuación 50 se puede ver que el término
𝐵 es una
variable constante a través del análisis. El componente
𝐶
𝑣
de la Ecuación 51 tiene una
variable cambiante, la cual es el
𝜏. Ésta última está definida por parámetros fijos y a su
vez es dependiente del tiempo. Finalmente, el componente
𝐶
𝑝
es el único que es
dependiente de los caudales y presiones que ocurren aguas arriba de la válvula. De esta
manera, se puede ver que 2 de los 3 términos que componen a la Ecuación 49,
corresponden a característica propias de la válvula y no de los demás componentes del
sistema. De esta manera, se encuentra la baja influencia que tiene el incremento de la
longitud en el caudal de salida de la válvula.
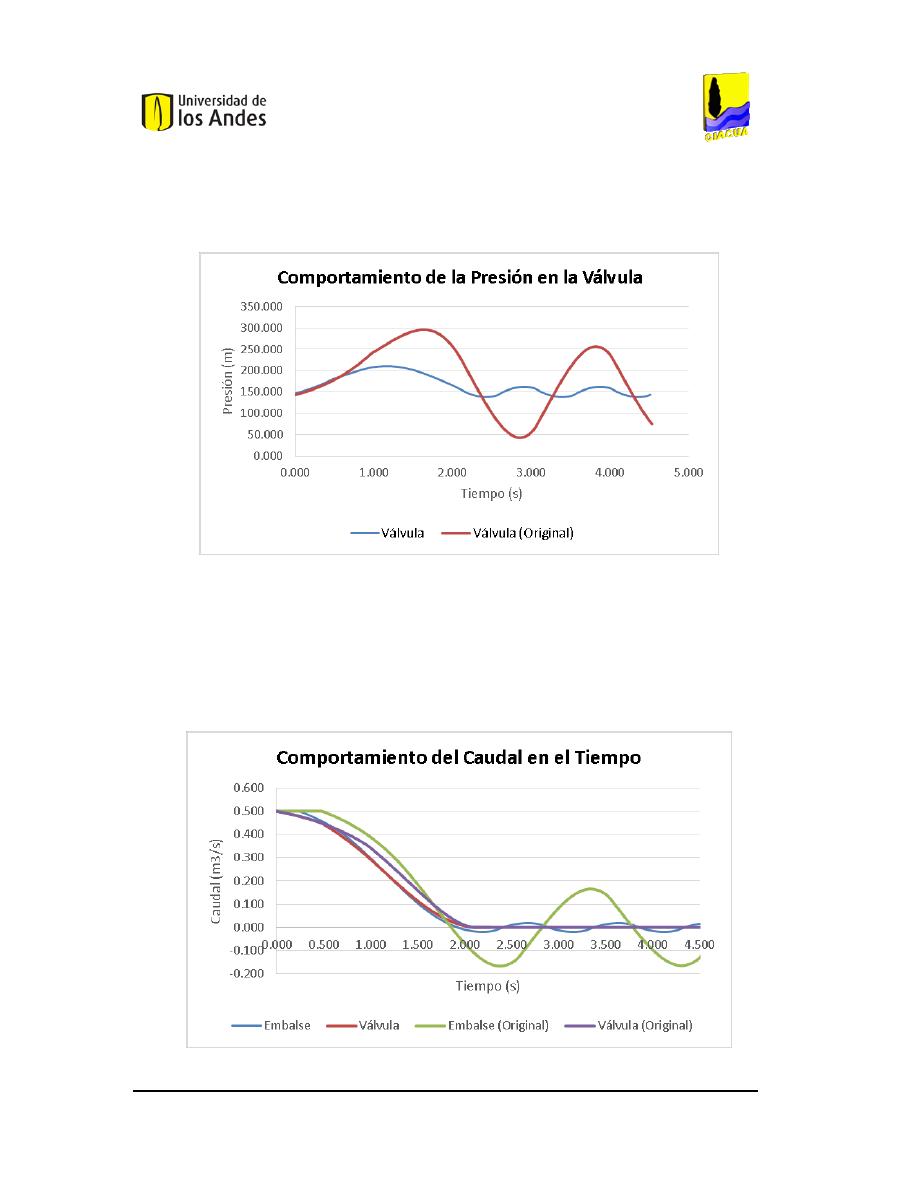
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
53
7.1.2. DISMINUCIÓN DE LA LONGITUD
Para los resultados que se presentan a continuación se disminuyó la longitud de la tubería
a la mitad del valor original, es decir, 300 m.
Figura 53. Comportamiento de la presión en la válvula del ejemplo simple disminuyendo la longitud.
En la Figura 53 se puede ver que la disminución de la longitud afecta positivamente al
sistema. La amplitud y el periodo de la onda disminuyen de forma sustancial, hasta tal
punto que no se sobrepasan las presiones que se habían tenido en los casos anteriores. La
razón de esto es atribuible a que al disminuir la longitud, la expresión que define el límite
de un cierre rápido (2L/a) toma un valor más pequeño, alejándose cada vez más del
tiempo de cierre de la válvula.
Figura 54. Comportamiento del caudal del ejemplo simple disminuyendo la longitud.
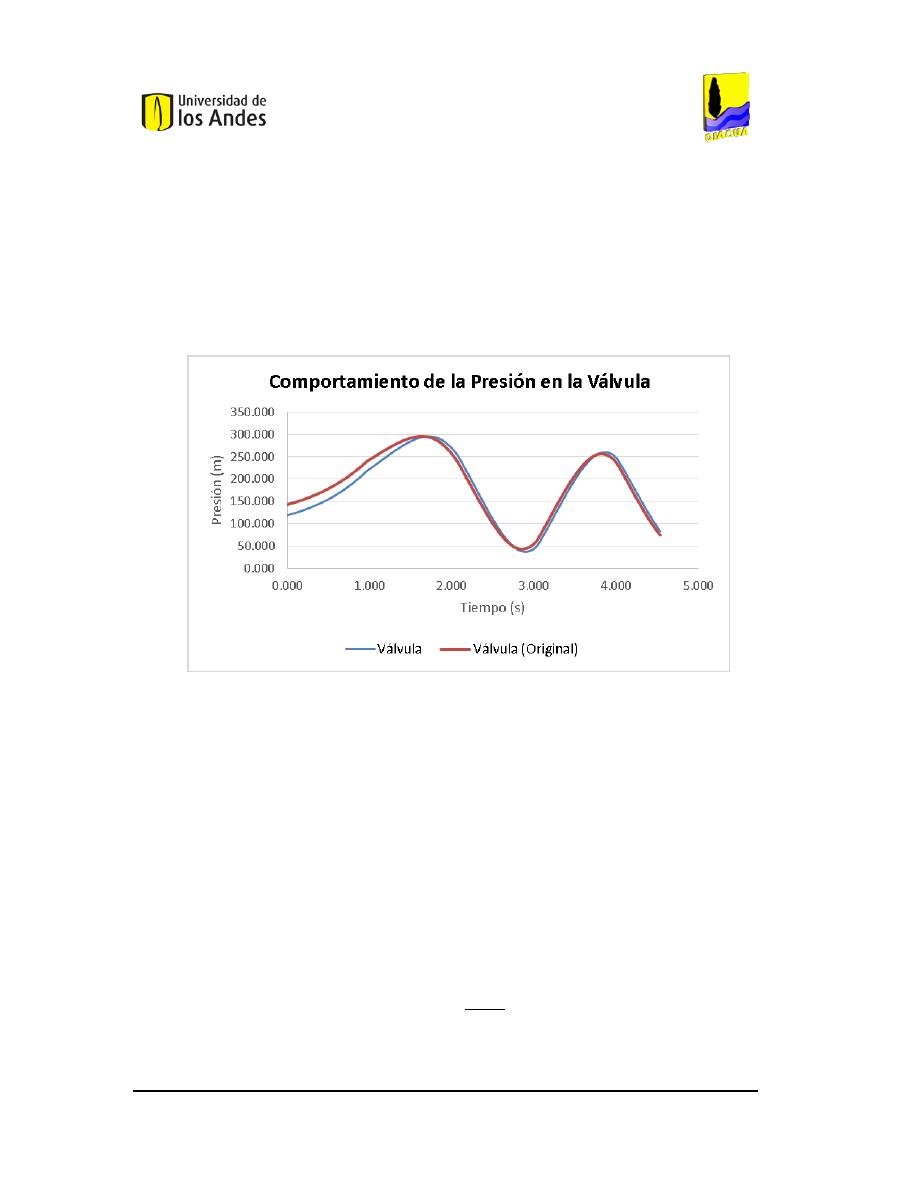
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
54
A partir de la
Figura 54
se puede concluir que el efecto positivo de la disminución de la
longitud es mayor en el caudal. La perturbación del sistema disminuye hasta tal punto en
donde las curvas del caudal de la válvula y el embalse tienen una alta similitud. Esto
hace que el cierre de la válvula se sienta rápidamente en el embalse y el sistema se
estabilice rápidamente.
7.1.3. AUMENTO DE LA RUGOSIDAD
Para los resultados que se presentan a continuación se incrementó la rugosidad de la
tubería a 0.03 m, lo cual corresponde a 100 veces el valor inicial.
Figura 55. Comportamiento de la presión en la válvula del ejemplo simple aumentando la rugosidad.
En la Figura 55 se puede ver que el incremento de la rugosidad no juega un papel
importante en el fenómeno de transiente. Desde luego se da una variación relevante en el
valor inicial dado que aumentan las pérdidas por fricción. Sin embargo, una vez que se
haya generado el cierre de la válvula, las ondas generadas en ambos casos son de gran
similitud en términos de periodo y amplitud.
Por otra parte, al mirar la
Figura 56
se puede ver que el efecto del aumento de la rugosidad
es aún menor en términos del caudal. Incluso es tan despreciable el efecto que es difícil
diferenciar la línea verde con la azul. Esta baja afectación se puede deber a que el
incremento de la rugosidad, manteniendo un mismo caudal, genera un incremento del
factor de fricción de 0.096. Desde luego para las pérdidas por fricción son relevantes, sin
embargo, para las ecuaciones de diferencias finitas que rigen el fenómeno no tiene gran
influencia por las demás variables que afectan la ecuación.
𝑅 =
𝑓∆𝑥
2𝑔𝐷𝐴
2
(53)
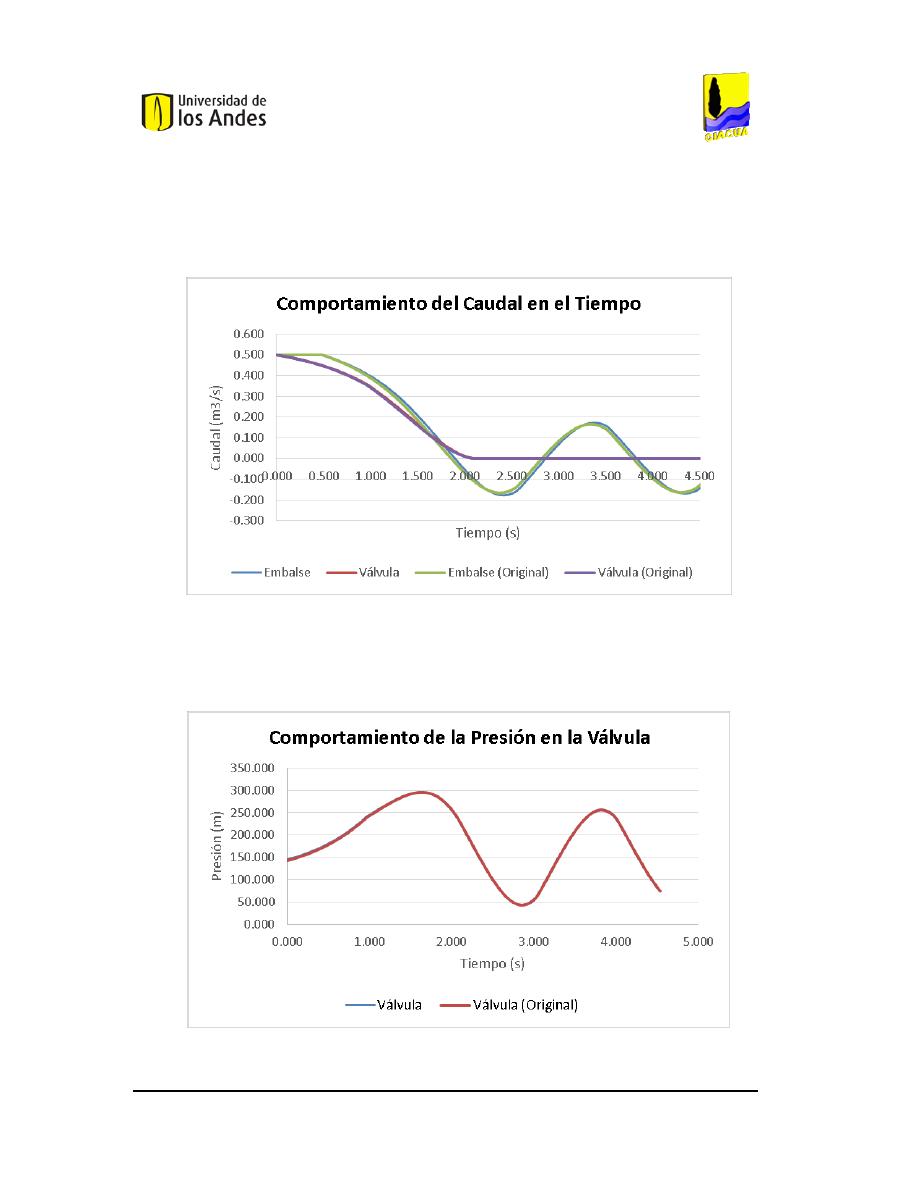
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
55
Si se estudia con detenimiento el término descrito en la Ecuación 53, el cual aparece en
las Ecuaciones 37, 38 y 39, se encuentra que la importancia de la rugosidad depende de
otras variables tales como el diámetro y el
∆𝑥 que depende de la celeridad de la onda. De
esta manera, para el presente caso el incrementar 100 veces la rugosidad hizo que el
término
𝑅 incrementara 4.38 veces.
Figura 56. Comportamiento del caudal del ejemplo simple aumentando la rugosidad.
7.1.4. DISMINUCIÓN DE LA RUGOSIDAD
Para los resultados que se presentan a continuación se disminuyó el valor de la rugosidad
a 0.000003 m, el cual es 100 veces menor que el valor original.
Figura 57. Comportamiento de la presión en la válvula del ejemplo simple disminuyendo la
rugosidad.
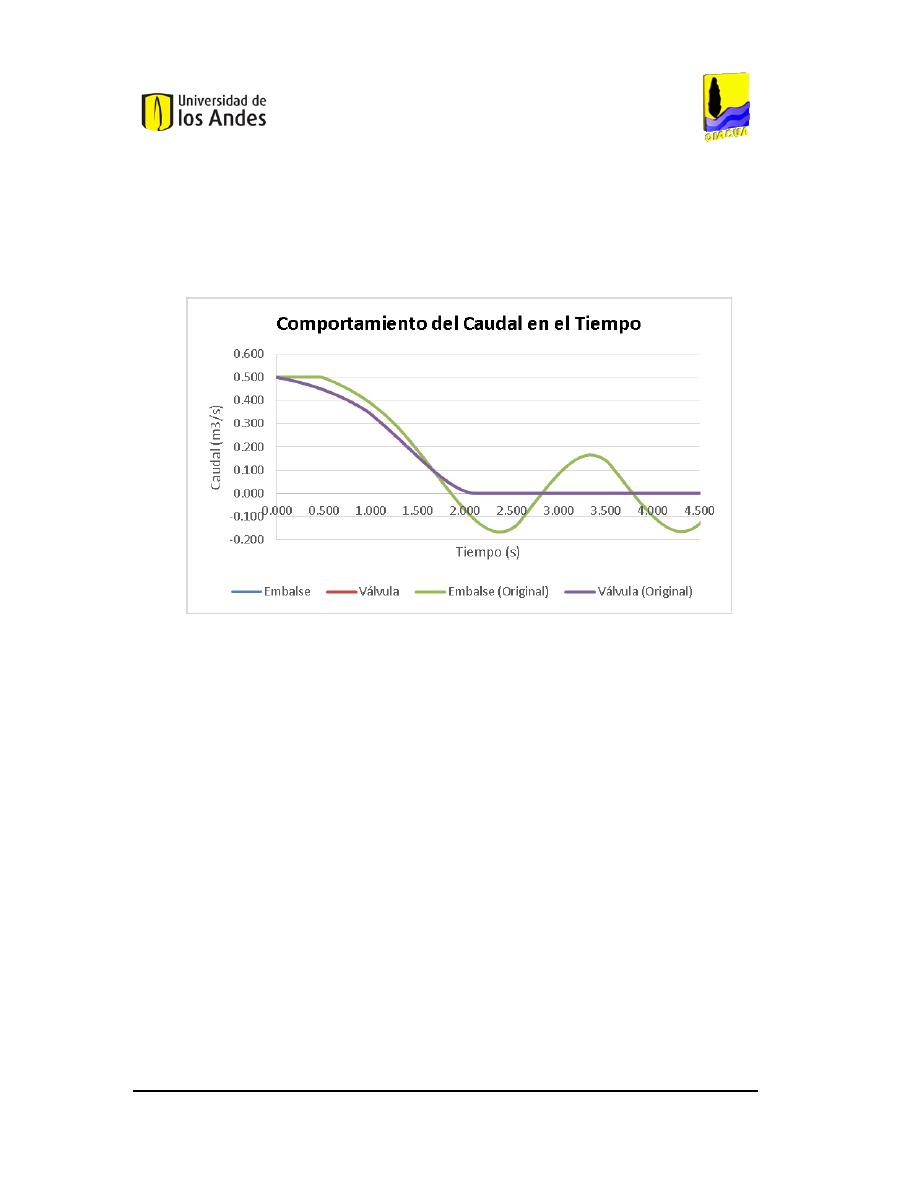
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
56
En la Figura 57 se puede ver que la influencia del disminuir la rugosidad de la tubería es
despreciable, haciendo que ambas curvas se sobrepongan. Nuevamente si se estudia el
factor de fricción se encuentra que el disminuir la rugosidad hace que éste disminuya en
0.0294. De forma similar, al evaluar el término descrito en la Ecuación 53, se encuentra
que el término es 0.65 veces el valor inicial. De esta manera, se encuentra la justificación
del por qué la rugosidad no influye de manera drástica el fenómeno.
Figura 58. Comportamiento del caudal del ejemplo simple disminuyendo la rugosidad.
Una vez más al ver la
Figura 58
se encuentra que las líneas de sobreponen, mostrando que
el efecto de la rugosidad no es significativo para el fenómeno de transiente. Es relevante
mencionar que si la tubería disminuye su diámetro es factible que la rugosidad afecte en
mayor medida.
7.1.5. AUMENTO DE LA CELERIDAD DE LA ONDA
Para los resultados que se presentan a continuación se incrementó la celeridad de onda a
1490 m/s, lo cual corresponde a 1.2 veces el valor inicial.
En la Figura 59 se encuentra que la variación de la celeridad de onda tiene un efecto
significativo en el sistema. Sin embargo, se considera que es favorable, dado que el
periodo y la amplitud de la onda disminuyen en cierta medida. De esta manera, se puede
decir que el incremento de la celeridad hace que los cambios se den en un menor tiempo
y sean menos drásticos. Esto hace que el tiempo de estabilización sea menor.
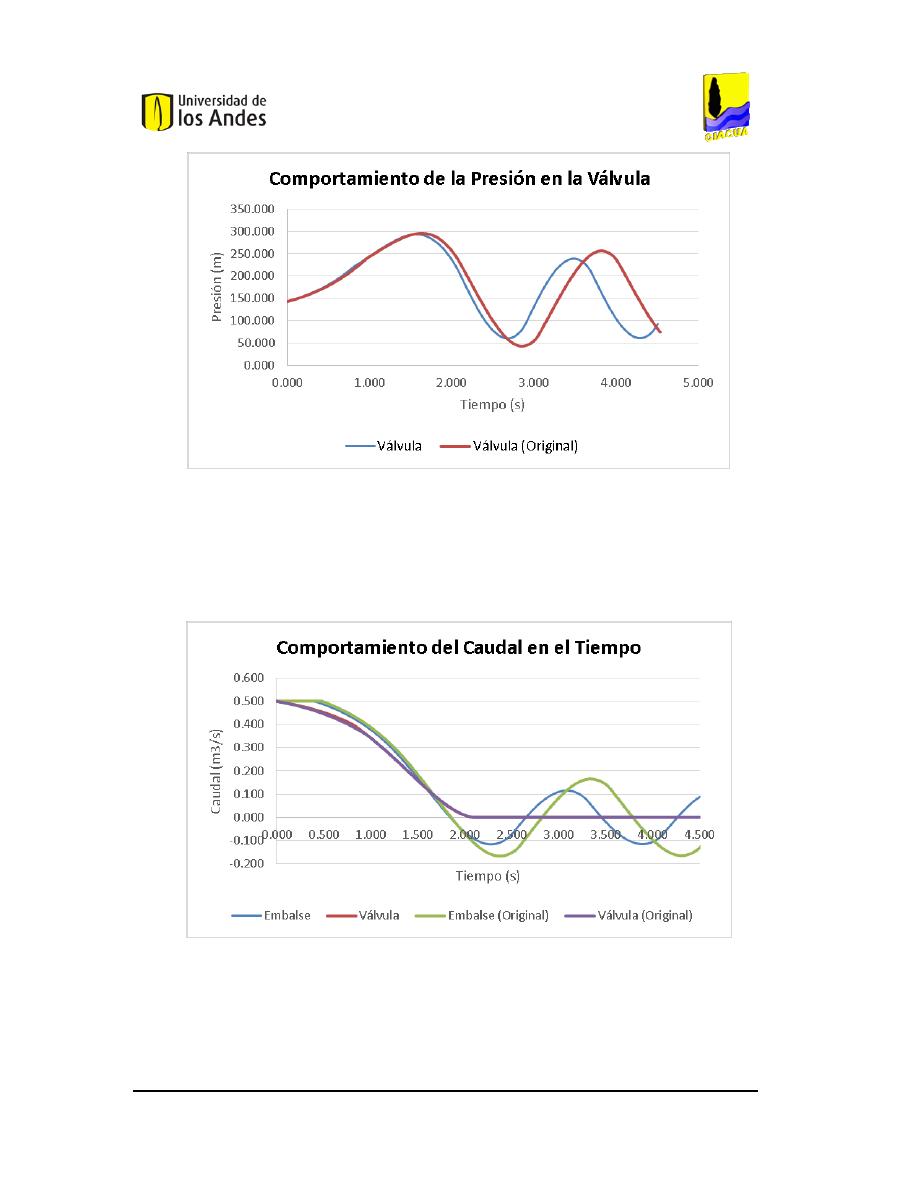
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
57
Figura 59. Comportamiento de la presión en la válvula del ejemplo simple aumentando la celeridad
de onda.
En la Figura 60 ver nuevamente que el aumentar la celeridad de la onda hace que la onda
disminuya su periodo y amplitud. Por lo tanto, nuevamente se puede establecer que esto
hará que el tiempo de estabilización sea menor dado que la onda recorre con mayor
velocidad el sistema y los cambios son menos drásticos.
Figura 60. Comportamiento del caudal del ejemplo simple aumentando la celeridad de onda.
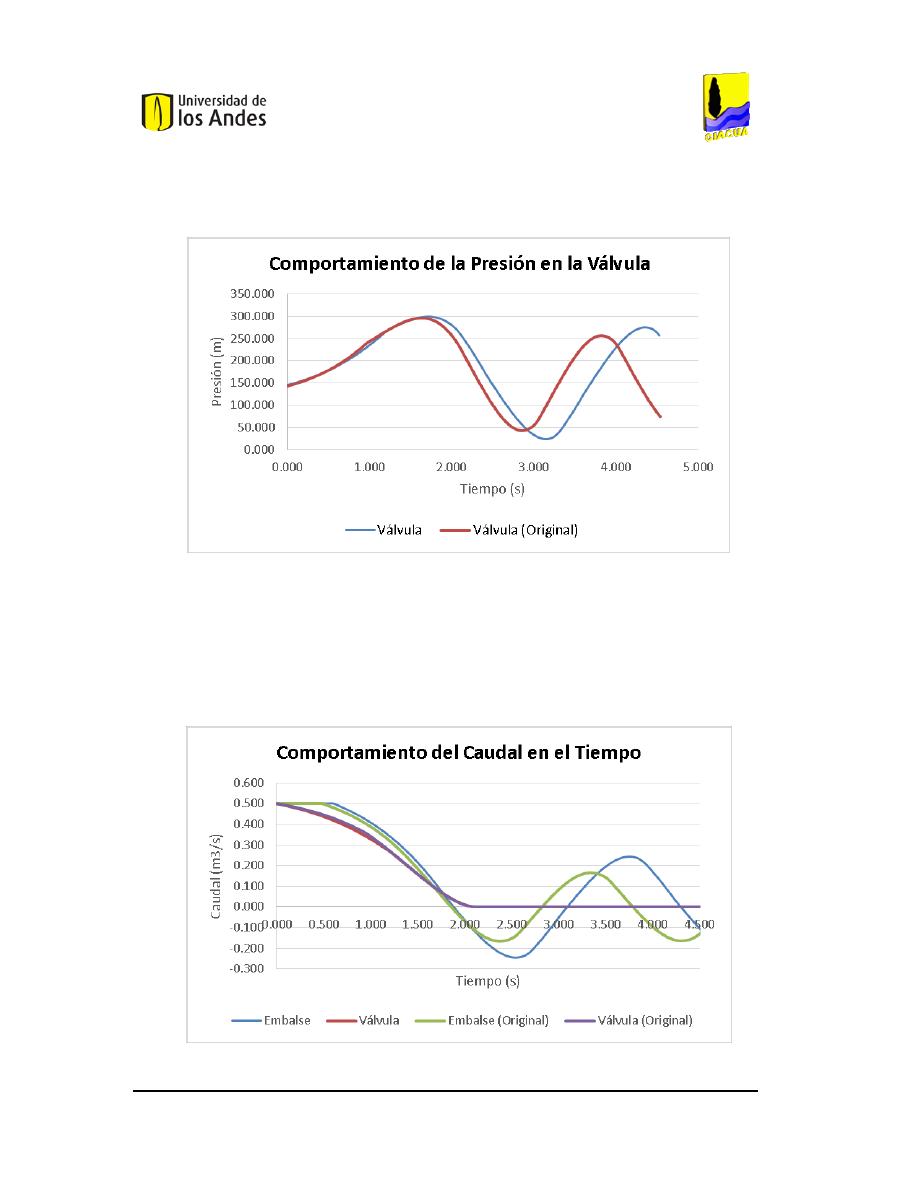
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
58
7.1.6. DISMINUCIÓN DE LA CELERIDAD DE LA ONDA
Para los resultados que se presentan a continuación ser disminuyó la celeridad de onda a
993 m/s, lo cual corresponde a 0.8 veces el valor inicial.
Figura 61. Comportamiento de la presión en la válvula del ejemplo simple disminuyendo la celeridad
de onda.
En la Figura 61 se puede ver que ocurre la situación contraria al disminuir la velocidad de
onda. Es decir, la amplitud y el periodo aumentan, sin embargo, el incremento de la
amplitud no es lo suficientemente considerable para establecer que es un problema para
el sistema. Sin embargo, el aumento de periodo es significativo y, de esta manera, se
puede establecer que el tiempo de estabilización del sistema se incrementa.
Figura 62. Comportamiento del caudal del ejemplo simple disminuyendo la celeridad de onda.
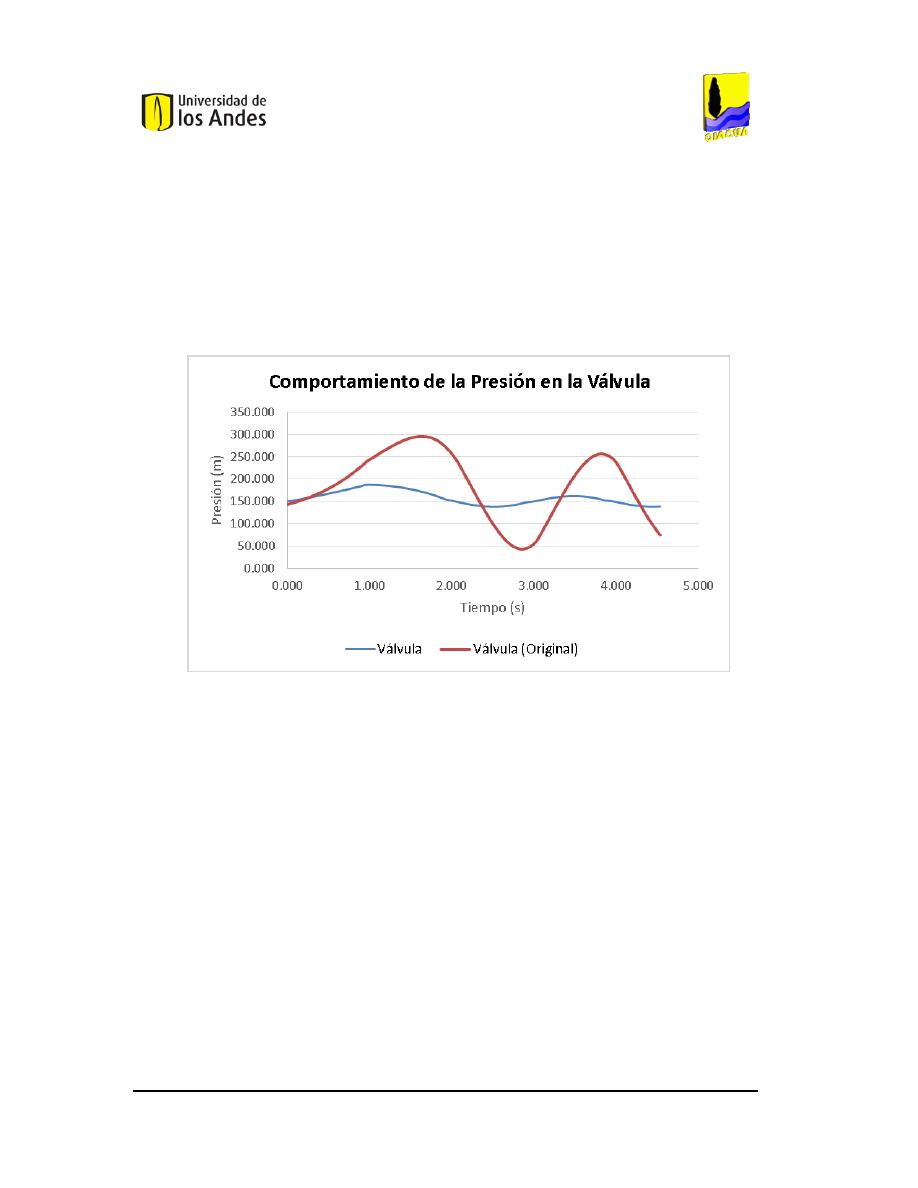
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
59
Al ver la Figura 62 se puede observar que para términos de caudal, la amplitud y periodo
de la onda aumentan. Sin embargo, a diferencia de la presión, la onda generada en el
caudal tiene un aumento considerable en la amplitud. De tal forma que llega a ser de la
misma magnitud del caudal inicial. Incluso, es tan alta que se llegan a tener cambios en
la dirección del flujo para los caudales de salida del embalse.
7.1.7. AUMENTO DEL DIÁMETRO DE LA TUBERÍA
Para los resultados que se presentan a continuación se incrementó el diámetro de la
tubería dos veces el valor inicial, es decir, el diámetro tiene un valor de 1 m.
Figura 63. Comportamiento de la presión en la válvula del ejemplo simple aumentando el diámetro
de la tubería.
En la Figura 63 se puede ver que el incrementar el diámetro de la tubería del sistema
ayuda a que los cambios de presión sean disminuidos. Adicionalmente, se puede apreciar
que a pesar de que no hay una variación considerable en el periodo de la onda, el
fenómeno de transiente ocurre en un menor tiempo. De esta manera, se encuentra que el
aumentar el diámetro ayuda a que se disminuyan las sobrepresiones y que el tiempo de
estabilización sea menor.
En la Figura 64 se puede ver que hay un cambio que no se había dado en ninguno de los
casos anteriores. Éste corresponde a que hay una variación considerable en la línea del
caudal que fluye por la válvula. La razón de esto corresponde a que afectar el diámetro
altera los términos de las Ecuaciones 50 y 53. De esta manera, si se ve la Ecuación 49
hay dos coeficientes que se afectan de manera directa. Adicionalmente, si se mira la
Ecuación 52 se encuentra que dos de los tres términos son afectados. Por lo tanto, al
final, la Ecuación 49 tendrá dos términos afectados directamente y un tercero afectado
indirectamente pero de manera significativa.
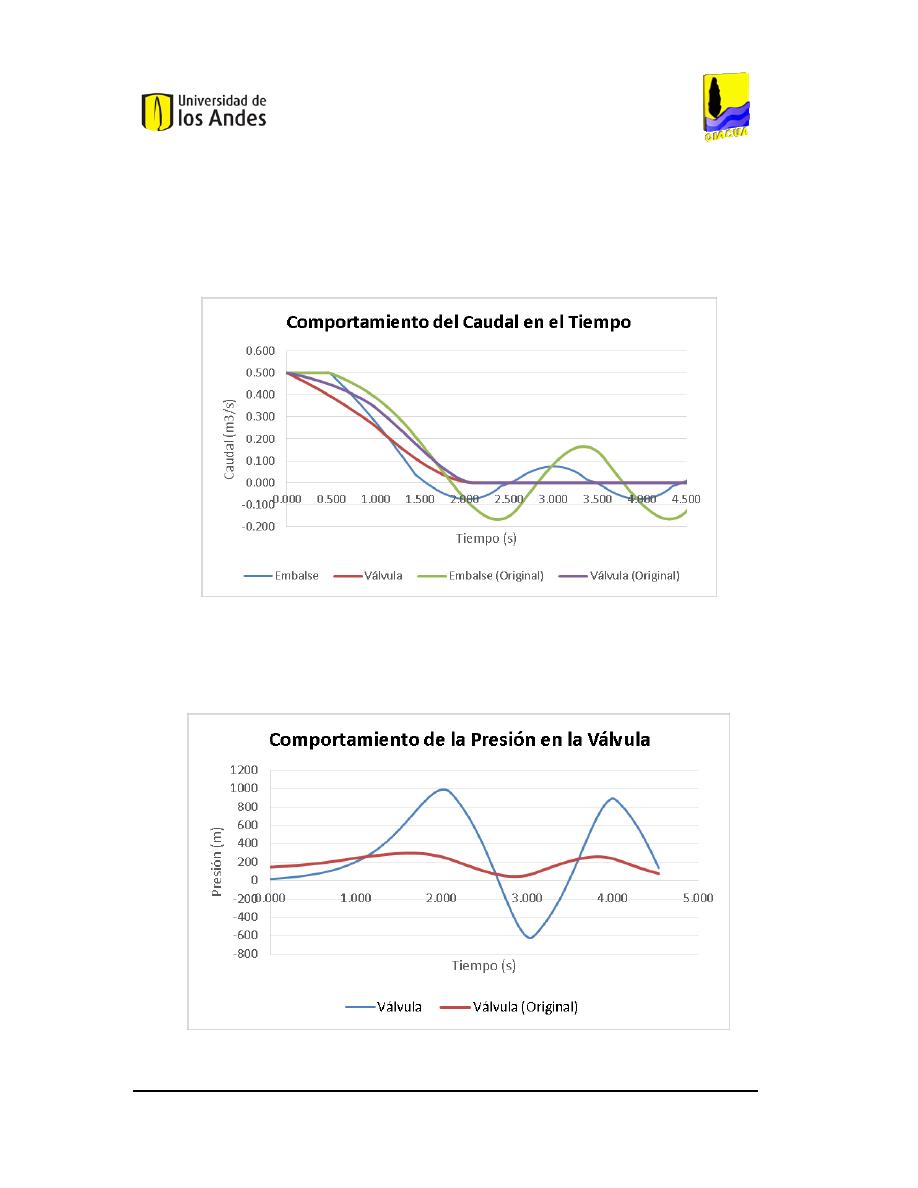
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
60
Para ambos caudales que son medidos en la
Figura 64
, se encuentra que el incrementar el
diámetro hace que las señales se suavicen y no tengan curvas tan pronunciadas como la
situación original. De esta forma, se recalca que el aumento de diámetro hace que el
sistema se estabilice en una menor cantidad de tiempo. La razón de esto es que al
incrementar el diámetro de la tubería se está aumentando el volumen de almacenamiento
del agua. Por lo tanto, los efectos de compresibilidad en el flujo se ven disminuidos.
Figura 64. Comportamiento del caudal del ejemplo simple aumentando el diámetro.
7.1.8. DISMINUCIÓN DEL DIÁMETRO DE LA TUBERÍA
Para los resultados que se presentan a continuación se disminuyó el diámetro a la mitad
del valor original. De esta manera, el valor de esta variable es de 0.25 m.
Figura 65. Comportamiento de la presión en la válvula del ejemplo simple disminuyendo el diámetro
de la tubería.
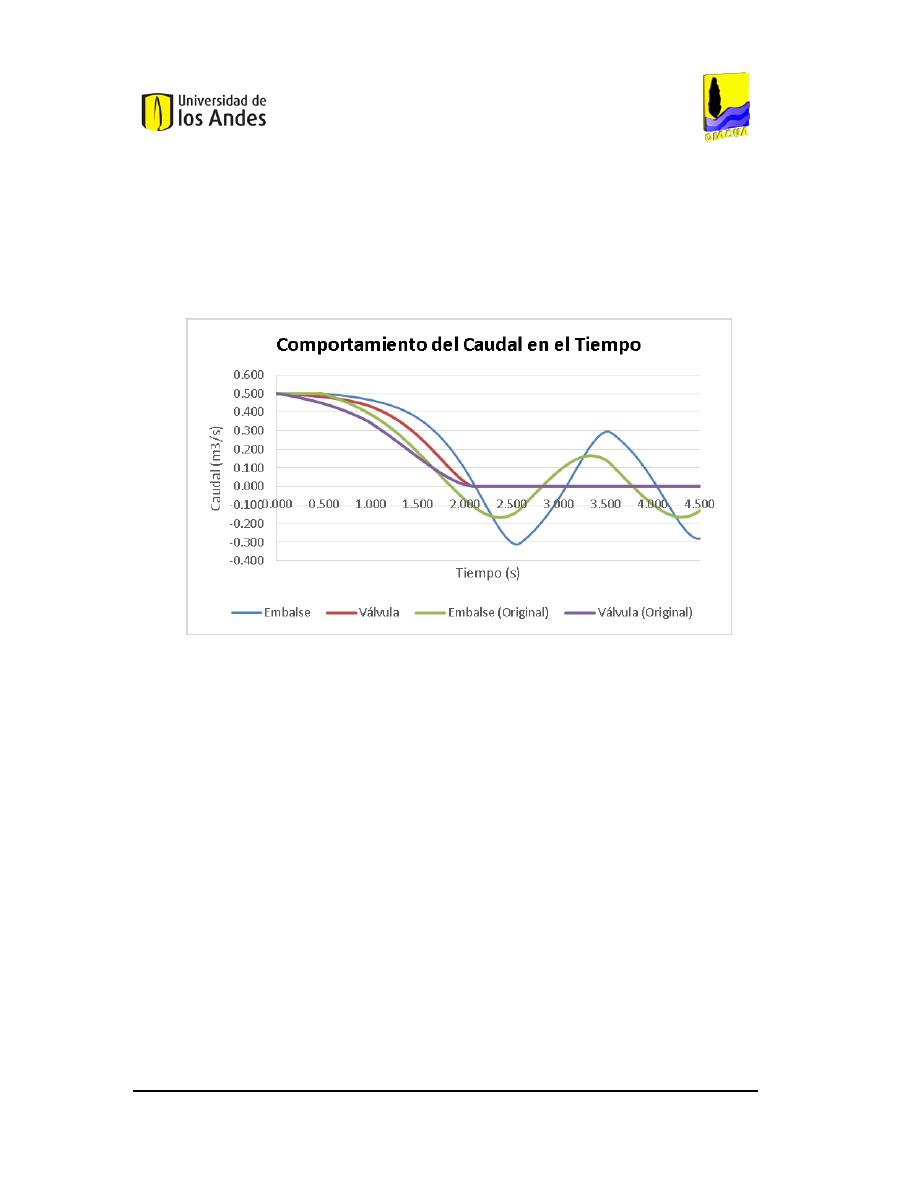
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
61
En la Figura 65 se puede ver que el disminuir el diámetro a la mitad conlleva a tener
aumentos de sobrepresiones considerable, en conjunto con valores sustanciales de
presiones negativas. Es de tal magnitud las presiones que se llegan a tener que sistema
fallaría instantáneamente. Por otra parte, si se analiza el periodo de la onda se encuentra
que no hay un cambio significativo. Sin embargo se puede establecer que el sistema
requiere de más tiempo para sentir las perturbaciones ocasionados por los cambios
operativos.
Figura 66. Comportamiento del caudal del ejemplo simple disminuyendo el diámetro.
Al observar la
Figura 66
se encuentra nuevamente que hay un cambio considerable y
atípico en el caudal de salida de la válvula. Adicionalmente, las líneas obtenidas tienen
curvas más pronunciadas y drásticas, haciendo así que el sistema experimente cambios
más bruscos. Sin embargo, es curioso que a pesar de tener cambios de la magnitud que
se tienen en la presión, para el caudal se tengan incrementos de baja magnitud. La razón
del incremento de la perturbación al sistema tanto en caudal como en presión se debe a
que el disminuir el diámetro hace que los efectos de compresibilidad sean más relevantes.
7.1.9. AUMENTO DE LA ALTURA DEL EMBALSE
Para los resultados que se presentan a continuación se incrementó la altura del embalse a
200 m.
En la Figura 67 se puede ver que el incrementar la altura del embalse solo hace que la
línea de presión se desplace hacia arriba, proporcionalmente al valor que sea aumentado
para el fondo del embalse. No se presenta ningún cambio en la curvatura; por lo tanto, el
aumento de presión no afecta el tiempo de estabilización del sistema. La razón de que no
haya cambio en el comportamiento de la presión se debe a que en la Ecuación 37 y 38, el
término correspondiente a la presión no tiene ningún coeficiente asociado. Por lo tanto,
las variaciones que se realicen de este término serán lineales al vector de respuesta.
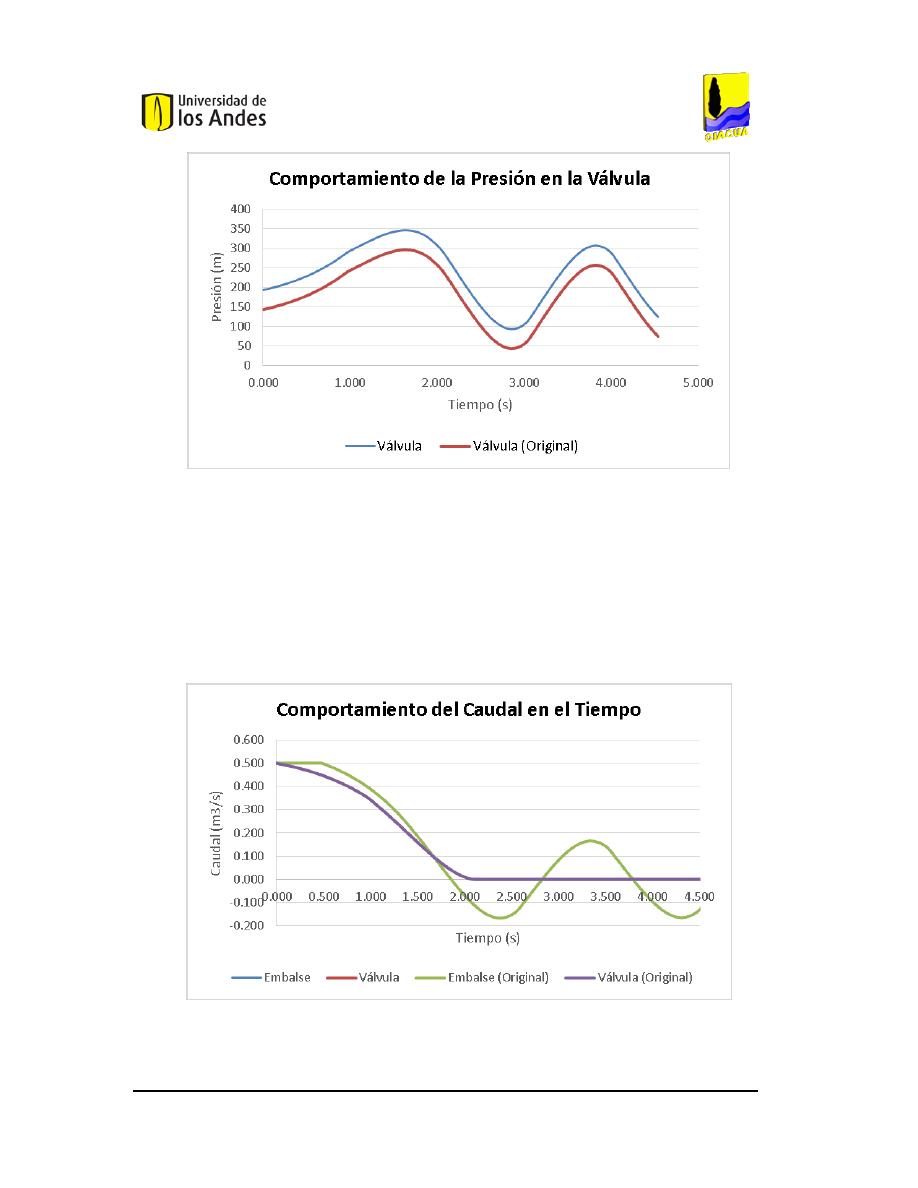
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
62
Figura 67. Comportamiento de la presión en la válvula del ejemplo simple aumentando la altura del
embalse.
En la Figura 68 se puede ver que de forma similar el caudal no siente el efecto del
incremento de la presión. Se considera relevante mencionar que se realizó la simulación
para el caso donde la altura del embalse era menor a la inicial. Sin embargo, al tener el
mismo desplazamiento de la
Figura 67
pero para la otra dirección. Adicionalmente, la
Figura 68
es la misma que se tendría si se grafican los resultados al haber disminuido la
altura del embalse. Por las razones enunciadas anteriormente no se presentan los
resultados de esta simulación.
Figura 68. Comportamiento del caudal del ejemplo simple aumentando la altura de embalse.
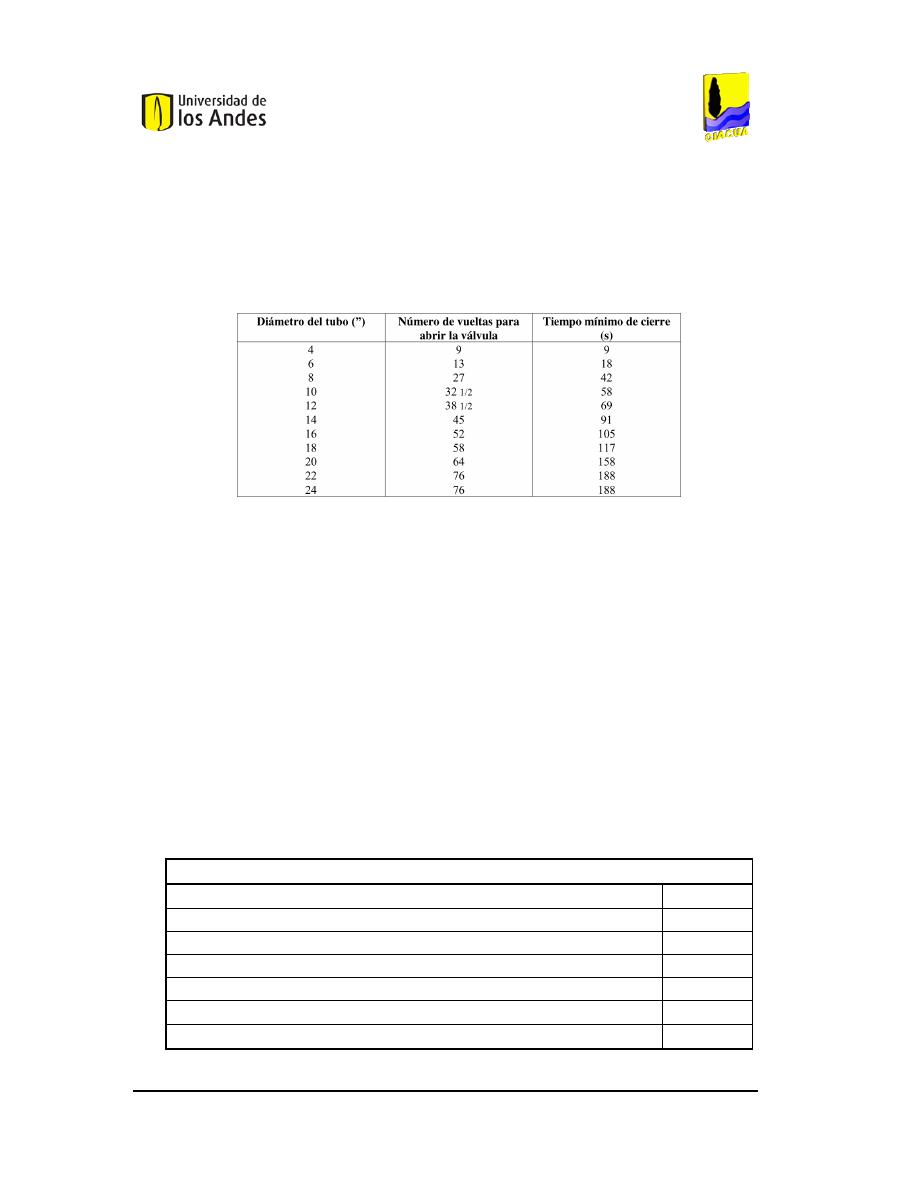
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
63
7.2. REDES PROBADAS
Un punto de gran importancia cuando se está estudiando el fenómeno de transiente, es el
tiempo de cerrado de las válvulas. Por lo tanto, se realizó una revisión bibliográfica para
saber cuáles eran los tiempos mínimos de cierre de las válvulas dependiendo de su
diámetro. El resultado de esta búsqueda se resume en la siguiente tabla.
Tabla 2. Tiempo mínimo de cierre de las válvulas dependiendo del diámetro (Silva G. & L.F., 1975).
Por otra parte, a partir de la revisión bibliográfica también se encontró que las curvas de
cierre de la válvula tenía una gran influencia en el fenómeno de transiente que se
generaría. De esta manera, se encuentra una gran cantidad de posibles curvas; sin
embargo, se consideró que la presente investigación no se iba a centrar en el análisis de
éstas. Por lo tanto, se optó por utilizar la curva de cierre más simple, la cual corresponde
a un cierre lineal.
7.2.1. RED MATRIZ DE MEDELLÍN
En la presente sección se muestran los resultados obtenidos en las simulaciones
realizadas. Es relevante establecer que se realizaron 6 casos en donde se variaron
condiciones de rugosidad, longitud de las tuberías y celeridad de la onda. De esta
manera, se presentarán los resultados encontrados y serán organizados por las válvulas
probadas. Es relevante establecer la nomenclatura de las gráficas, de esta manera, en la
siguiente tabla se presentan los diferentes casos modelados y sus siglas.
Tabla 3. Casos simulados para la red matriz de Medellín.
Caso simulado
Siglas
Red sin cambios
normal
Red con las tuberías con dos veces la longitud
ldnks
Red con las tuberías con dos veces la longitud y la rugosidad más alta
ldaks
Red con las tuberías con dos veces la longitud y la rugosidad más baja
lddks
Red con las tuberías con la mitad de la longitud
lm
Red con 1.5 veces la celeridad de la onda
lna1,5
Red con 0.5 veces la celeridad de la onda
lna0,5
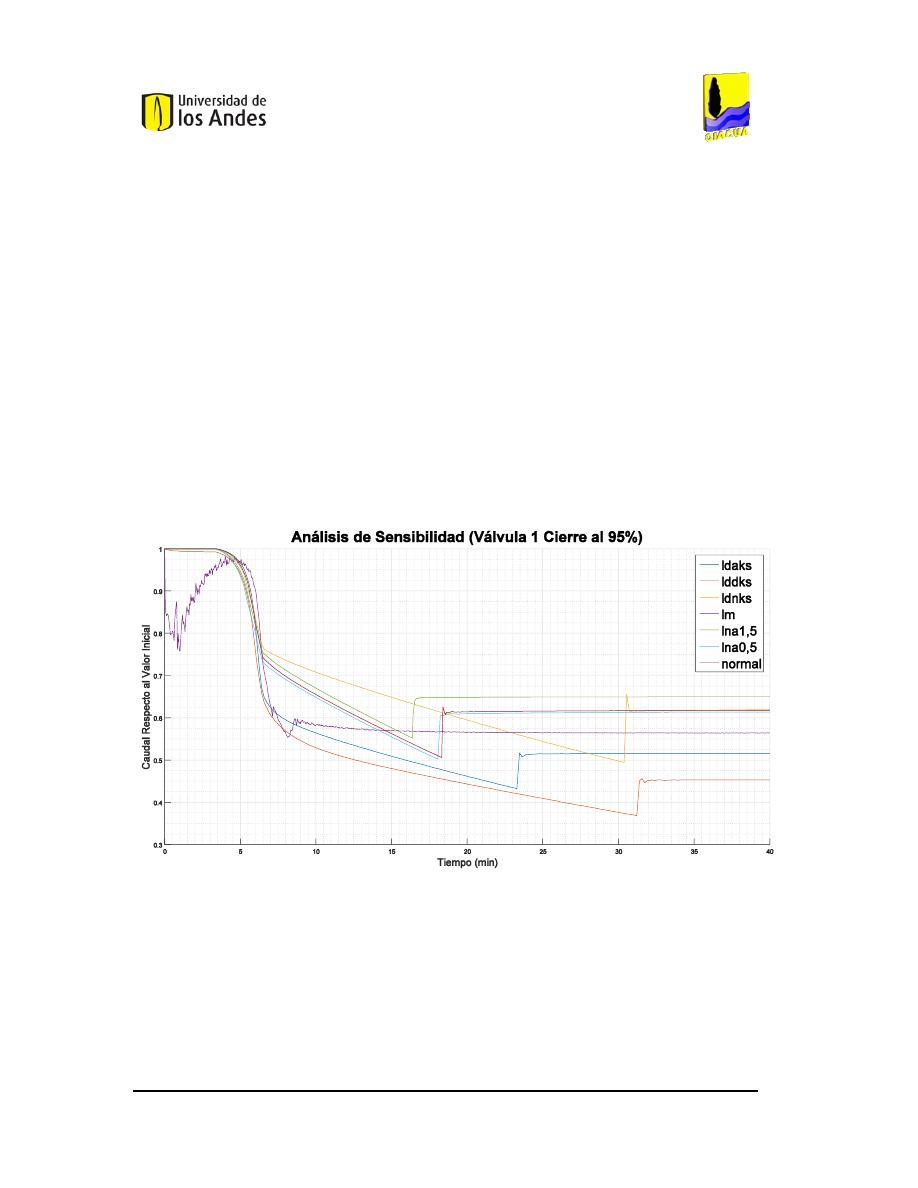
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
64
Por otra parte, es necesario establecer que los porcentajes de cierre que se realizaron
fueron de 95%, 90%, 80%, 60%, 40% y 20%. Sin embargo, para el último porcentaje de
cierre se encontró una baja incluso irrelevante perturbación de la red. De esta manera, se
presentan sólo los 5 primeros porcentajes de cierre.
7.2.1.1. Válvula 1
En la presente sección se presentan los porcentajes de cierre de la válvula 1, mostrando
primero el comportamiento de los caudales y luego de la presión.
CAUDAL
En la Figura 69 se puede ver la alta influencia que tiene el cierre de la válvula 1 en el
sistema. Por otra parte, se puede ver que el máximo tiempo de estabilización de los casos
estudiados es de 28 minutos.(lddks). En contraste con lo anterior, la simulación cuando
las longitudes son a la mitad (lm) es de 10 minutos. Adicionalmente, al ver las diferentes
líneas que se presentan se encuentra que el modelo que presenta mayor ruido es el de las
longitudes a la mitad.
Figura 69. Comportamiento del caudal para el cierre del 95% de la Válvula 1 en la red matriz de Medellín.
Agregando a lo anterior, al observar las tres simulaciones en donde se afectó la
rugosidad, se encuentra que la disminución de ésta no tiene un efecto considerable en el
tiempo de estabilización. Es necesario tener en cuenta que entre el caso que tiene la
rugosidad original y éste, existe un desplazamiento lineal en el eje vertical. Sin embargo,
esto se debe a que las pérdidas en el sistema disminuyen y, por lo tanto, las presiones en
los nudos de consumo aumentan. Una vez ocurre esto, los coeficientes de los emisores
empleados para realizar el análisis de transiente son menores en comparación con la
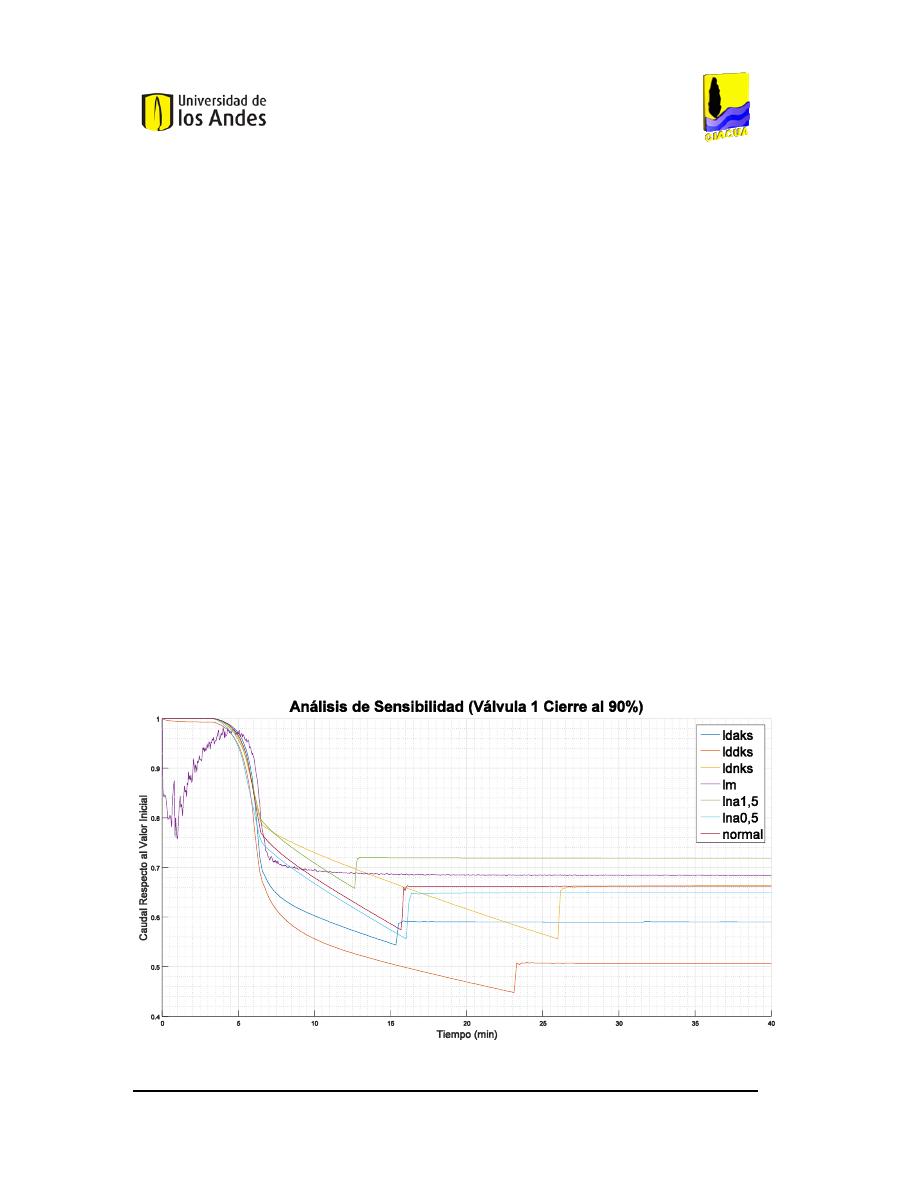
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
65
situación de las rugosidades originales. Sin embargo, para este caso existirá una
variación sustancial en la presión. Por esta razón, el caudal de estabilización es menor al
encontrado para el caso de la rugosidad original.
A su vez cuando se aumenta la rugosidad ocurre la situación contraria a lo expuesto
anteriormente. Sin embargo, al disminuir la presión, para obtener el mismo caudal del
emisor, el coeficiente de éste debe ser incrementado. Esto hace que las variaciones en
términos del caudal, dado la presión, sean amplificadas. Adicionalmente, se nota que hay
una disminución de 8 minutos en el tiempo de estabilización de la red. De esta manera,
se puede decir que el incremento de la rugosidad ayuda a que la red se estabilice en una
menor cantidad de tiempo.
Por otra parte, al observar los casos en los que se modificó la celeridad de la onda se
encuentra que existe una disminución de 2 minutos en el tiempo de estabilización para el
caso en el que se incrementó la celeridad de la onda. Para el caso en el que se disminuyó
el valor de esta variable se encontró una ligera (segundos) disminución del tiempo de
estabilización. Por lo tanto, se encuentra que, para este caso, la variación en el valor de la
celeridad de la onda no afecta de manera drástica el tiempo de estabilización de la red.
Finalmente, si se realiza una comparación de las variaciones de la longitud se encuentra
que el tiempo de estabilización sufre cambios importantes si se realiza alguna
modificación en esta variable. A partir de los resultados se encontró que si se disminuye
la longitud a la mitad, el tiempo de estabilización disminuye en 6 minutos. En
contraparte, cuando se incrementa la longitud a dos veces el valor inicial, la red requiere
de 13 minutos más para su estabilización. Es relevante mencionar que para el caso
original, la red requiere de 16 minutos de estabilización.
Figura 70. Comportamiento del caudal para el cierre del 90% de la Válvula 1 en la red matriz de Medellín.
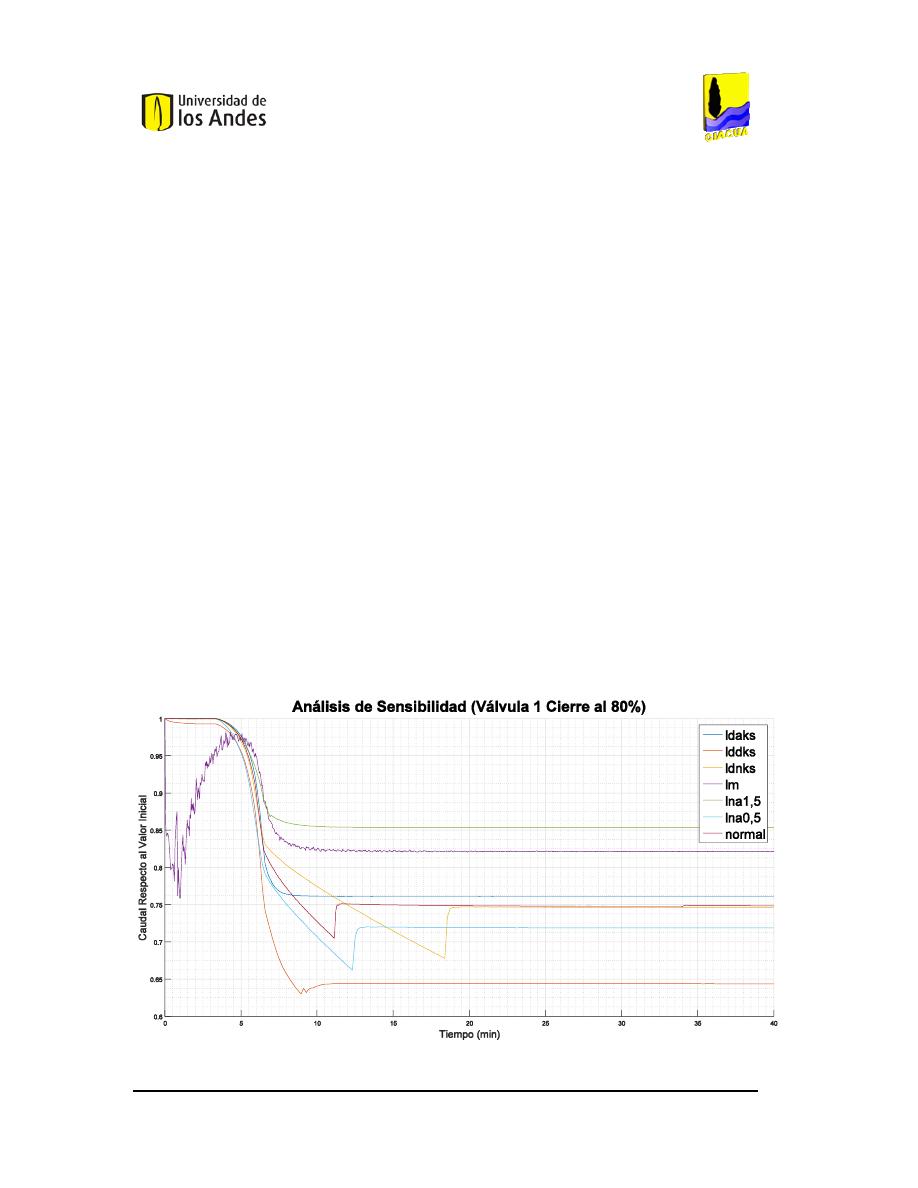
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
66
En la Figura 70 se puede ver las variaciones que se tienen en términos del caudal cuando
se realiza un cierre del 90% de la válvula 1. En ella se encuentra que en general los
tiempos de estabilización disminuyeron en comparación con la situación anterior. El
mayor tiempo de estabilización en este caso fue de 23 minutos (ldnks) y el menor de 7
minutos (lm).
Para la rugosidad en este caso se encontró que el aumento y la disminución de ésta hacen
que la red se estabilice en un tiempo menor. Sin embargo, el incremento de la rugosidad
hace que la red se estabilice en un tiempo considerablemente menor (11 minutos menos).
De forma contraria, el disminuir esta variable no afecta con tanta relevancia el tiempo de
estabilización dado que éste es disminuido en 4 minutos.
Al estudiar la celeridad de la onda se encontró que hubo un cambio y que la disminución
de este parámetro hace que la red requiera de unos segundos más para estabilizarse. De
forma similar al caso anterior, el incremento de la celeridad de la onda hace que la red
requiera 3 minutos menos para su estabilización. De esta manera, se encuentra
nuevamente que la celeridad de la onda parece no ser un parámetro de alta influencia en
el tiempo de estabilización de la red.
Respecto a la longitud se encontró que los resultados son consistentes con el caso
anterior, haciendo que el incremento de la longitud haga que la red requiera de un mayor
tiempo para la estabilización (10 minutos). En contraste, la disminución de la longitud
hace que la red se estabilice 6 minutos antes. Si se realiza una comparación con las
variaciones temporales que se tuvieron en el caso anterior, se encuentra que son
altamente similares. Por lo tanto, la sensibilidad de éste parámetro no se vio afectada con
el cambio en el porcentaje de cierre de la válvula.
Figura 71. Comportamiento del caudal para el cierre del 80% de la Válvula 1 en la red matriz de Medellín.

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
67
Al revisar la Figura 71 se encuentra nuevamente que el disminuir una vez más el
porcentaje de cierre de la válvula hace que el tiempo de estabilización de los casos
estudiados disminuya. Adicionalmente, se encuentra que el menor tiempo de
estabilización fue de 4 minutos (ldaks) y el más alto de 16 minutos (ldnks).
Al revisar con detenimiento la Figura 71 se encuentra que la rugosidad fue el parámetro
de mayor influencia para este caso. De esta manera, el aumento de ésta hace que la red
requiera de 12 minutos menos para su estabilización, y la disminución de ella que el
tiempo se reduzca en 5 minutos. Por lo tanto, parece que a medida que se disminuye el
porcentaje de cierre y, por tanto, la perturbación a la red, la rugosidad comienza a tener
mayor relevancia en el tiempo de estabilización.
De manera similar, a medida que se disminuye el porcentaje de cierre, la celeridad de la
onda comienza a tener una mayor relevancia en el tiempo de estabilización de la red.
Como se ve, al aumentar la celeridad de la onda, la red se estabiliza 4 minutos antes.
Para el caso contrario el tiempo incrementa en 1 minutos. De esta manera, se encuentra
que el porcentaje de cierre juega un rol importante en la sensibilidad de la celeridad de la
onda en el tiempo de estabilización. Sin embargo, una vez más se encuentra la baja
relevancia que tiene el disminuir la celeridad de la onda, pues el reducir el valor a la
mitad del inicial solo hizo que el tiempo de estabilización cambiara en un minuto.
En la Figura 71 se encuentra que la longitud sigue siendo un parámetro importante en la
estabilización de la red, dado que el aumentar esta variable hace que el tiempo de
estabilización incremente en 8 minutos. Contrariamente, el reducir esta variable hace que
la red requiera 2 minutos menos para estabilizarse. En comparación con los resultados
anteriores se encuentra que a medida que el porcentaje de cierre disminuye, las
diferencias entre la simulación de las longitudes originales y a la mitad se ve reducida.
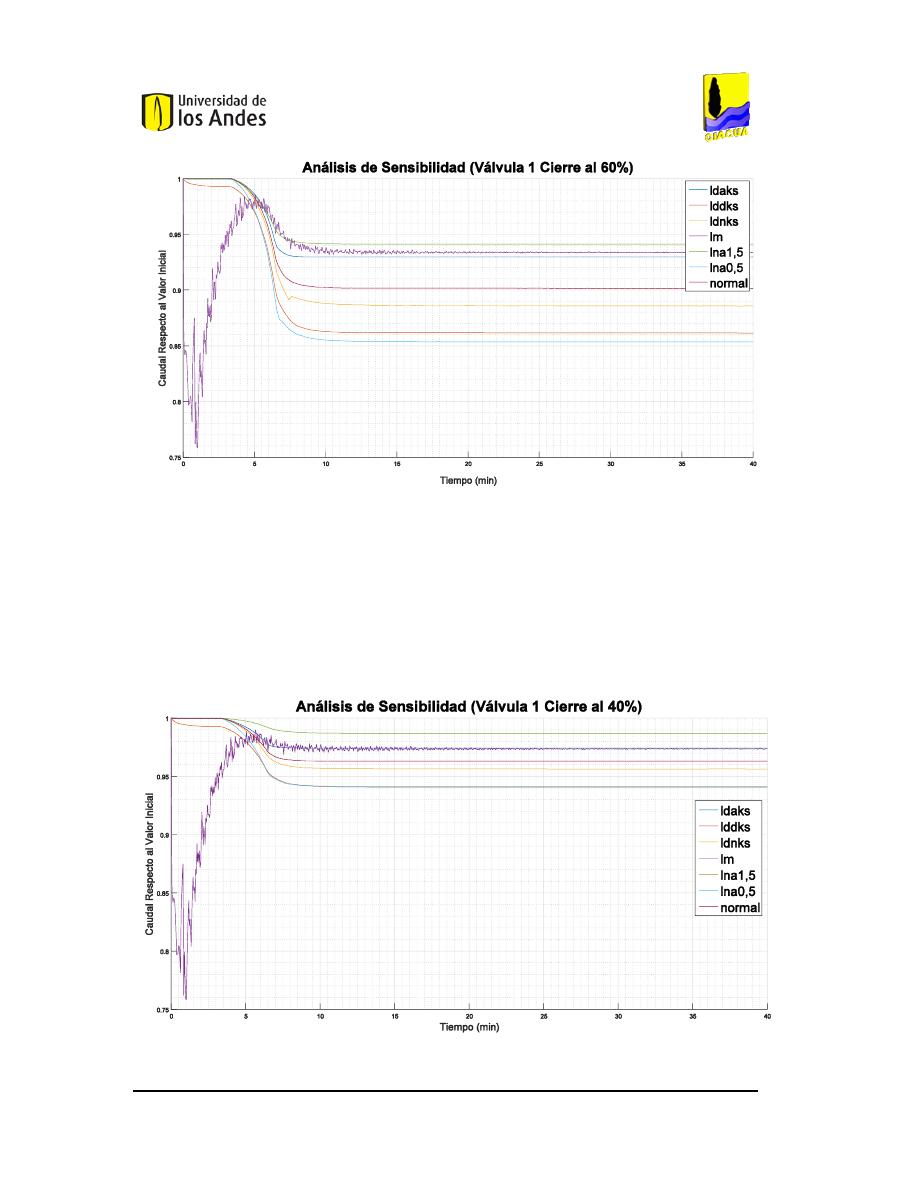
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
68
Figura 72. Comportamiento del caudal para el cierre del 60% de la Válvula 1 en la red matriz de Medellín.
De la Figura 72 se encuentra que el disminuir el cierre de la válvula al 60% hace que los
tiempos de estabilización disminuyan y tengan gran similitud entre ellos. Sin embargo,
es relevante mencionar que a pesar de tener variaciones en el caudal de 14% respecto al
valor inicial, la red requiere de alrededor de 6 minutos. Siendo esto relevante si se tiene
en cuenta que cuando se simulan redes de distribución de agua potable bajo el análisis de
periodo extendido, los patrones de consumo pueden llegar a tener una resolución de 5
minutos. Esto puede conllevar a errores significativos en los niveles de los tanques si se
realizan simulaciones por un periodo de tiempo considerable.
Figura 73. Comportamiento del caudal para el cierre del 40% de la Válvula 1 en la red matriz de Medellín.
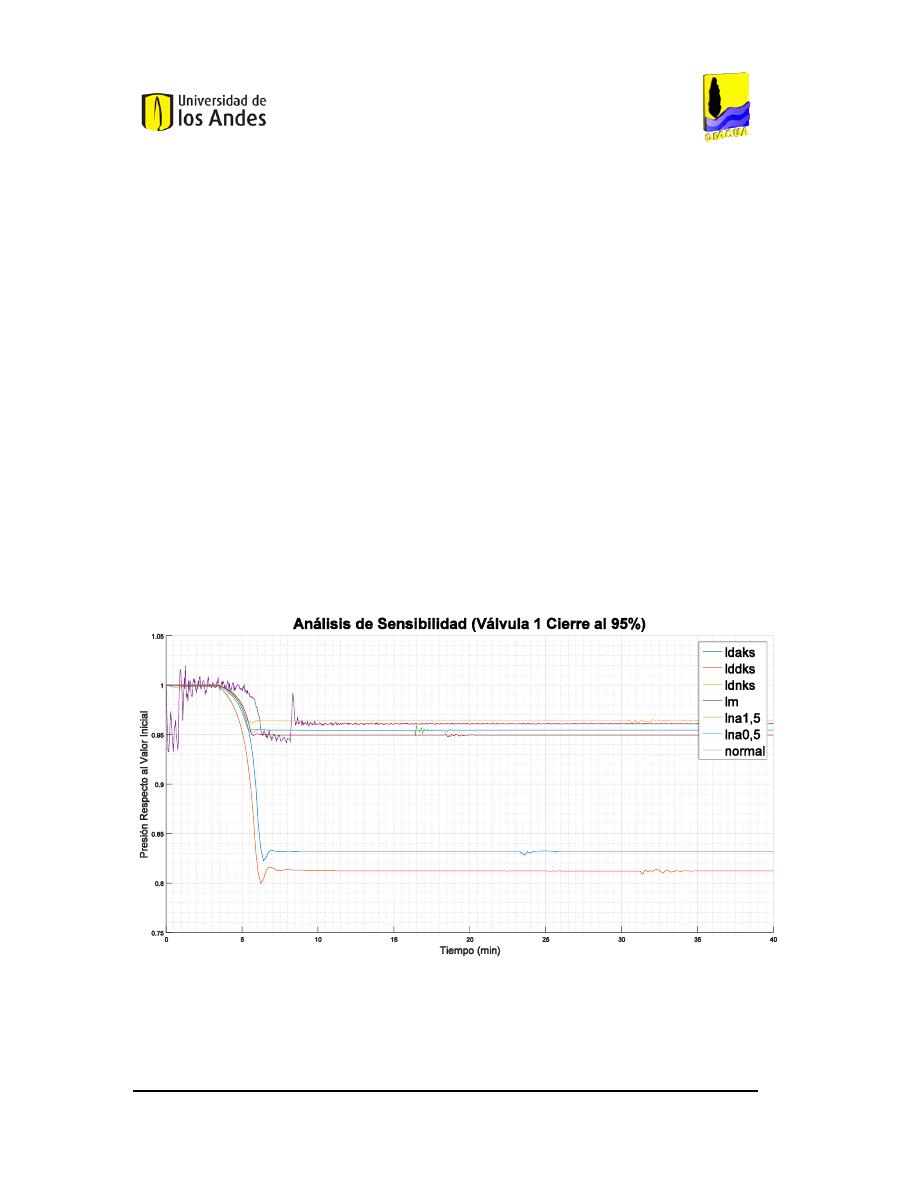
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
69
A partir de la Figura 73 se encuentra que para el cierre del 40% de la válvula, la red tiene
una alta capacidad para estabilizarse, pues los tiempos son cercanos a los 3 minutos. A
su vez es relevante ver que las señales tienen un comportamiento suave. Esto en conjunto
con el bajo tiempo de estabilización conlleva a que para estos casos el emplear el análisis
de periodo extendido puede llegar a resultados cercanos a la realidad.
PRESIÓN
En la Figura 74 se encuentra que las perturbaciones a la presión son sustancialmente
menores a las obtenidas en los caudales. Asimismo, se encuentra que el análisis de
sensibilidad pierde relevancia pues los tiempos de estabilización son muy similares entre
los casos estudiados. Para esto también se debe tener en cuenta que este es el caso más
drástico y, por lo tanto, debería ser aquel que muestre mayores diferencias. Es relevante
mencionar el comportamiento que tiene la señal cuando las longitudes de las tuberías se
ven reducidas a la mitad, pues se encuentra mucho ruido en la señal obtenida.
Por otra parte, es relevante mencionar que, a excepción de la simulación con alto
contenido de ruido, ninguno de los casos simulados presenta una sobrepresión
considerable. De esta forma, se encuentra que para la operación de la válvula 1 no se
tendrán problemas de estallidos de tuberías. Finalmente, en la Figura 74 se encuentra que
el tiempo de estabilización de las redes está entre los 2 y 3 minutos, si se tiene en cuenta
el comportamiento de la presión.
Figura 74. Comportamiento de la presión para el cierre del 95% de la Válvula 1 en la red matriz de Medellín.
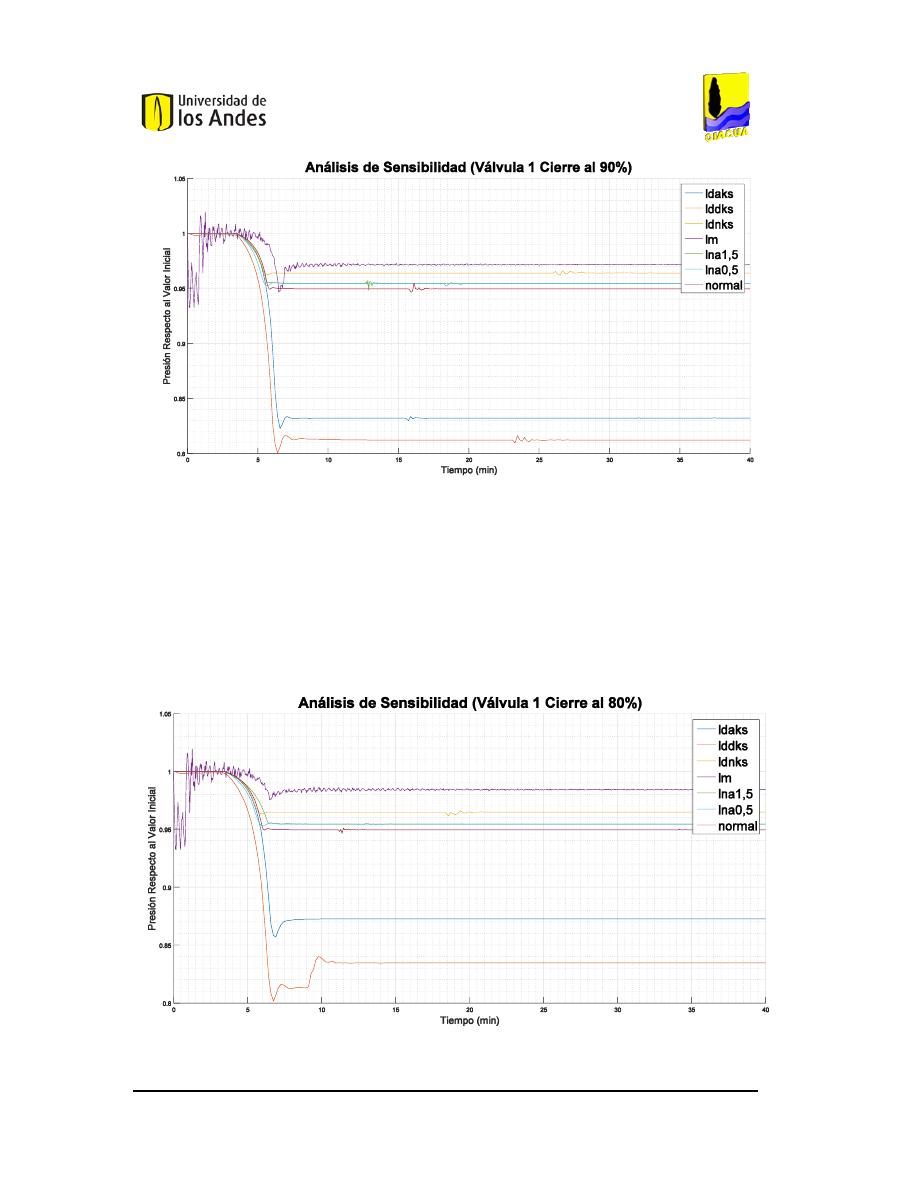
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
70
Figura 75. Comportamiento de la presión para el cierre del 90% de la Válvula 1 en la red matriz de Medellín.
Al observar la Figura 74 y la Figura 75 se puede ver que el disminuir 5% el porcentaje de
cierre no genera una diferencia perceptible en los valores de la presión cuando la red ya
se ha estabilizado. Asimismo, se encuentra que no hay una variación considerable en los
tiempos de estabilización. Por otra parte, una vez más, el realizar el análisis de
sensibilidad de las señales de presión obtenidas no tiene gran relevancia al estudiar el
tiempo de estabilización. Sin embargo, es relevante mencionar que los valores de la
presión cuando la red llega nuevamente a un estado estable son significativamente
menores para los casos en donde se modifica la rugosidad.
Figura 76. Comportamiento de la presión para el cierre del 80% de la Válvula 1 en la red matriz de Medellín.
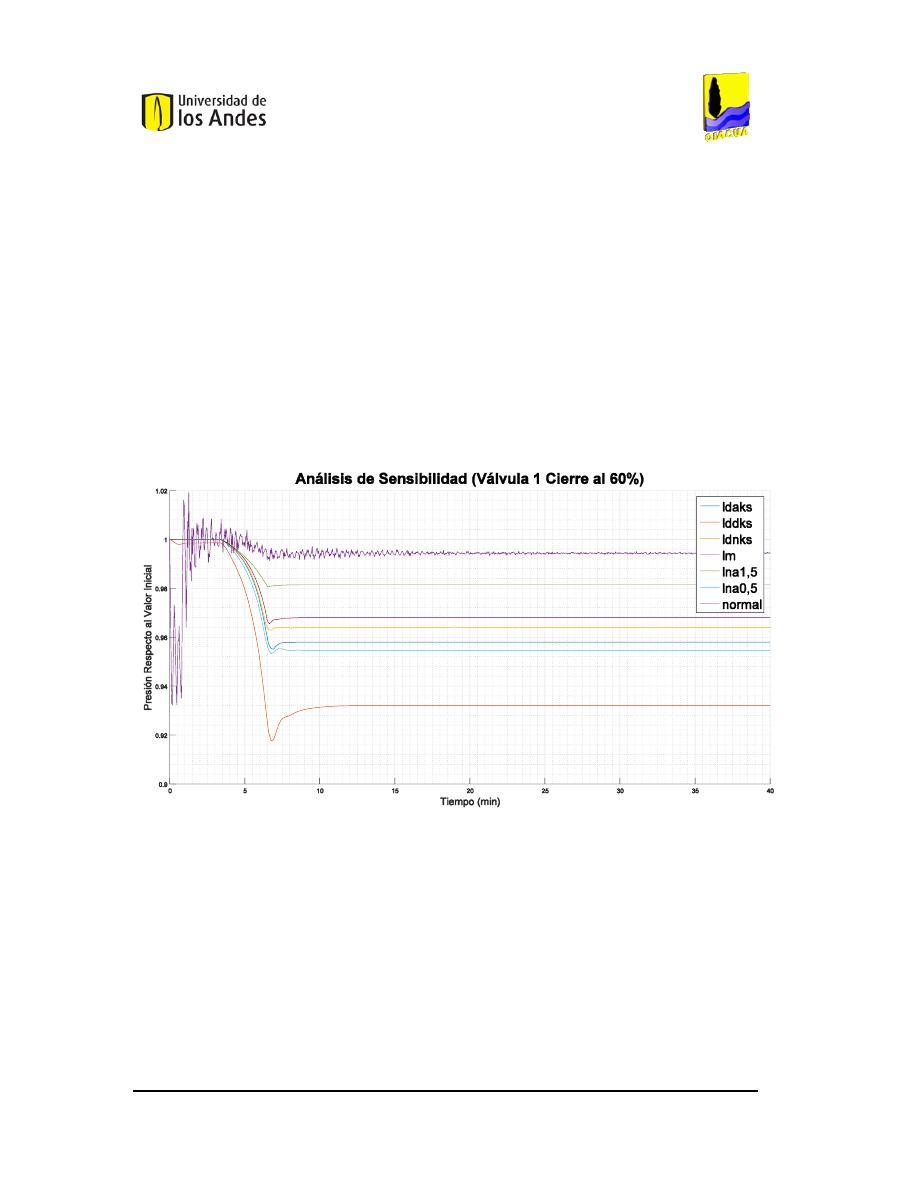
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
71
En la Figura 76 se encuentra que la disminución del porcentaje de cierre no afecta el
tiempo de estabilización en términos de presión. Sin embargo, llama la atención que esta
variación en el porcentaje de cierre parece no afectar de manera significativa el valor de
la presión, en el nuevo estado estable de la red, cuando se disminuye la rugosidad. Por
otra parte, para este mismo caso parece que el disminuir el porcentaje de cierre hace que
el tiempo de estabilización aumente 3 minutos. Situación que parece no tener coherencia
pues se está perturbando en menor medida la red.
En la Figura 77 se encuentra el comportamiento de la presión frente al cierre del 60% de
la válvula 1. Nuevamente, se encuentra que la red se estabiliza rápidamente si se emplea
esta variable para establecer cuando se llega a un nuevo estado estable. Sin embargo, una
vez más, el caso en el que se disminuye la rugosidad incrementa el tiempo de
estabilización en 1 minuto respecto al caso a anterior y en 4 minutos cuando se realiza un
cierre del 95%. A partir de esto se encuentra que la rugosidad comienza a tener un
aspecto relevante cuando los porcentajes de cierre disminuyen.
Figura 77. Comportamiento de la presión para el cierre del 60% de la Válvula 1 en la red matriz de Medellín.
Al observar la Figura 78 se encuentra que las variaciones de la presión se reducen
drásticamente, pues la máxima variación respecto al valor inicial es de 3%. Asimismo, se
puede ver en comparación con la Figura 77 que la variación en la rugosidad pierde su
efecto cuando el cierre de la válvula es del 40%. Finalmente, se establece que, para el
cierre de 40%, los diferentes casos simulados requieren de 3 a 4 minutos para llegar a un
estado estable.
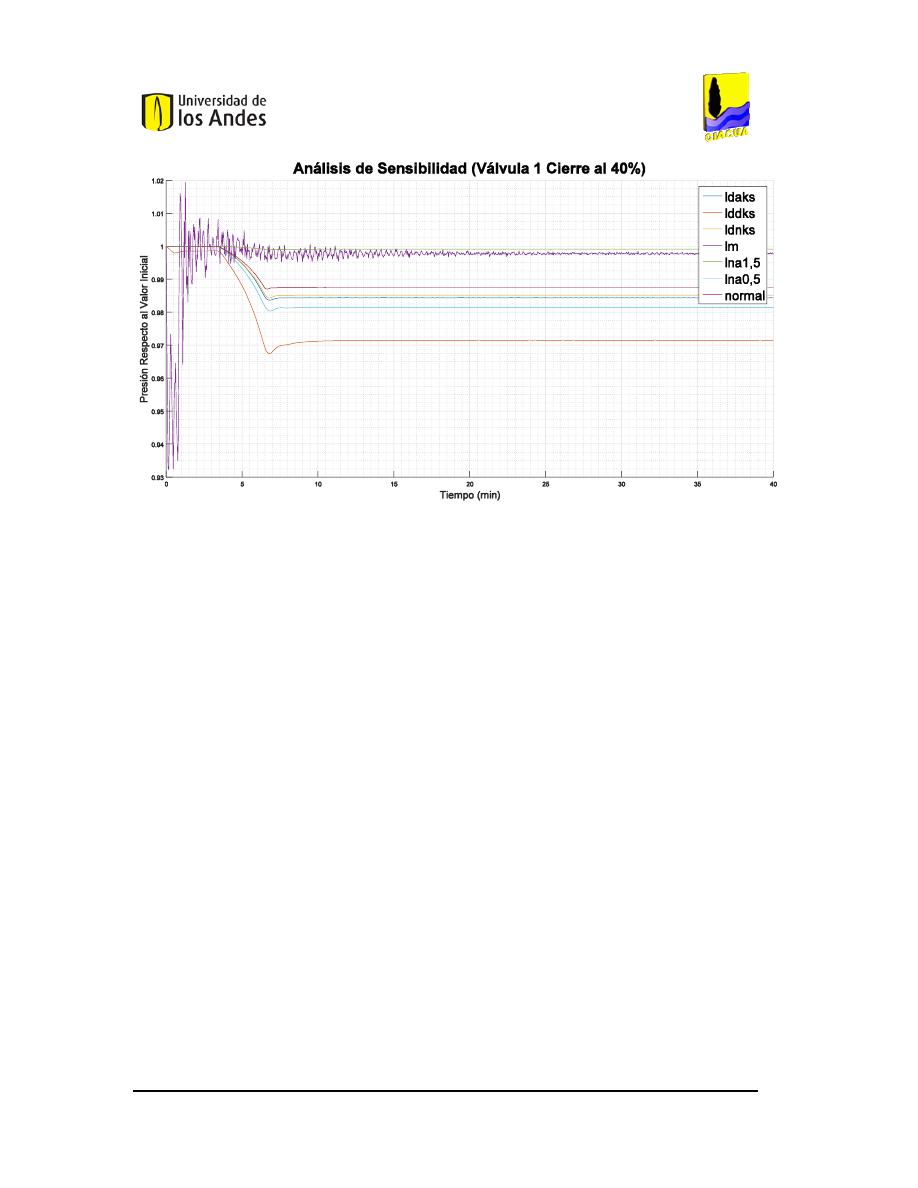
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
72
Figura 78. Comportamiento de la presión para el cierre del 40% de la Válvula 1 en la red matriz de Medellín.
7.2.1.2. Válvula 2
En la presente sección se presentan los resultados obtenidos cuando se realizan cierres de
la válvula 2 en la red matriz de Medellín, mostrando nuevamente el comportamiento del
caudal y la presión.
CAUDAL
En la Figura 79 se puede ver que las perturbaciones que produce el cierre de la válvula 2
a la red son muy bajas. Sin embargo, en el caso que se redujo la longitud de las tuberías a
la mitad hay una mayor perturbación que en los demás casos. A su vez, para todos los
casos, es relevante que el tiempo que requiere la red en sentir la perturbación del cierre de
la válvula es de casi 3 minutos. Una vez que ésta lo siente, su tiempo de estabilización es
de 1 minuto. De esta manera, se encuentra que el tiempo de estabilización de la red
frente a esta operación es de 4 minutos. Sin embargo, se debe tener en cuenta que, salvo
cuando la longitud es la mitad, las perturbaciones a la presión llegan a ser menores al 3%.
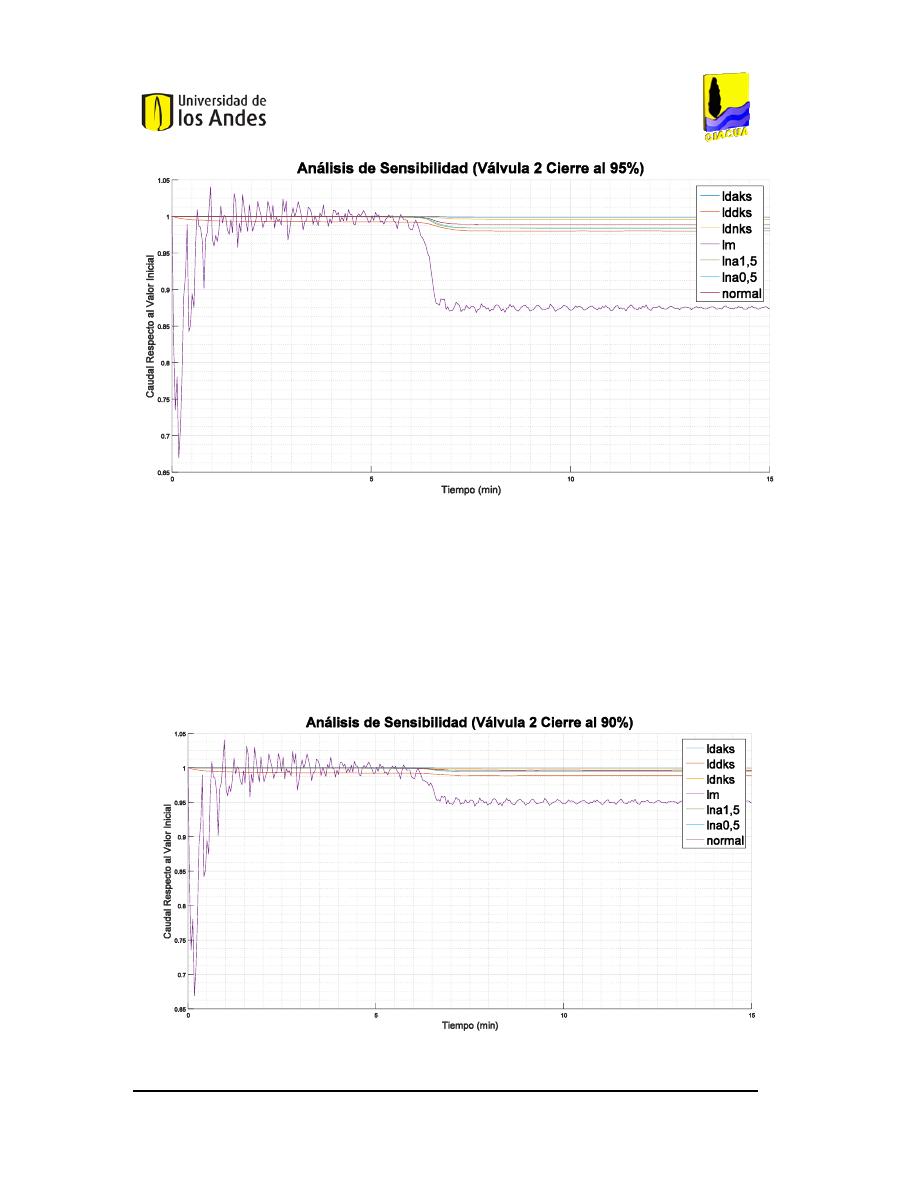
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
73
Figura 79. Comportamiento del caudal para el cierre del 95% de la Válvula 2 en la red matriz de Medellín.
En la Figura 80 se puede ver que al disminuir ligeramente el porcentaje de cierre de la
válvula, la red presenta una perturbación sustancialmente menor. Esto se puede apreciar
en la línea de la red con la mitad de la longitud de las tuberías. Por otra parte, se puede
ver nuevamente que la red se demora en sentir la perturbación que es creada por la
operación de la válvula. Se considera relevante mencionar que los resultados de las
simulaciones de 80%, 60% y 40% presentan variaciones menores al 1% para todos los
casos. Por esta razón, no se mostrarán estas figuras en la presente sección; sin embargo,
se presentan en la sección de anexos para que el lector pueda ver los resultados obtenidos.
Figura 80. Comportamiento del caudal para el cierre del 90% de la Válvula 2 en la red matriz de Medellín.
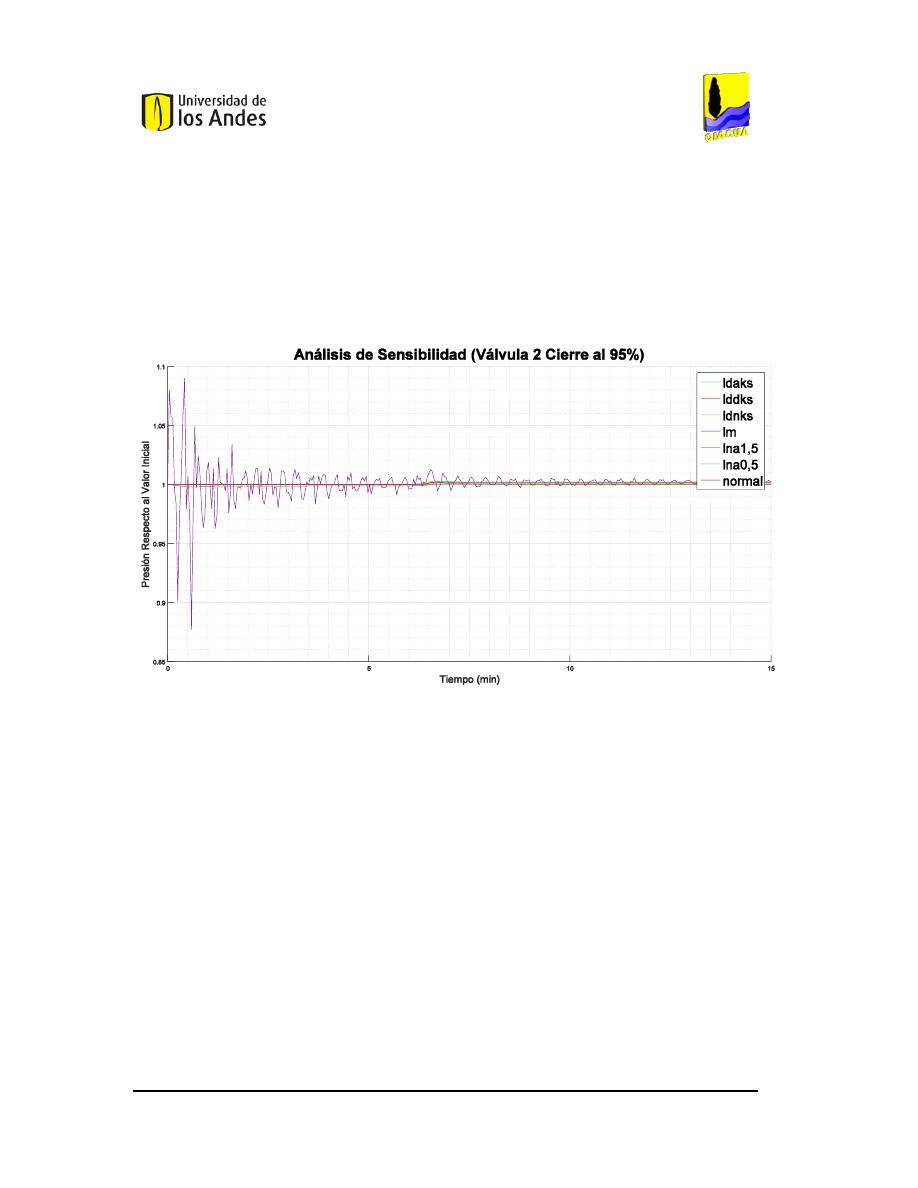
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
74
PRESIÓN
En la Figura 81 se puede ver la baja perturbación que crea la operación de la válvula 2 en
las presiones de la red. Asimismo, se puede ver que hay un ligero incremento de la
presión general de la red, sin embargo, este es menor al 1% del valor inicial. A su vez, se
puede ver que la presión tanto el caudal tiene una demora para sentir el cierre de la
válvula. Nuevamente, dado las bajas perturbaciones que produce esta válvula a la red,
los resultados para los cierres de 90%, 80%, 60% y 40% se presentarán en la sección de
anexos.
Figura 81. Comportamiento de la presión para el cierre del 95% de la Válvula 2 en la red matriz de Medellín.
7.2.1.3. Válvula 3
En la presente sección se muestran los resultados obtenidos para la operación de la
válvula 3. Similar que las secciones anteriores se muestran los comportamientos que
tuvieron los caudales y las presiones.
CAUDAL
En la Figura 82 se puede ver que la operación de esta válvula no genera cambios
drásticos en los caudales de la red. Sin embargo, es relevante que nuevamente para la
simulación en que las tuberías tienen la mitad de la longitud se ve más afectada que las
demás. De esta manera, se puede establecer que las redes cortas son más vulnerables a la
operación de válvulas que aquellas que tengan la distancia de las tuberías más larga.
Adicionalmente, se debe resaltar que la perturbación del caudal es baja dado que, para un
cierre del 95%, se tienen una variación menor al 10% en general para los caudales.
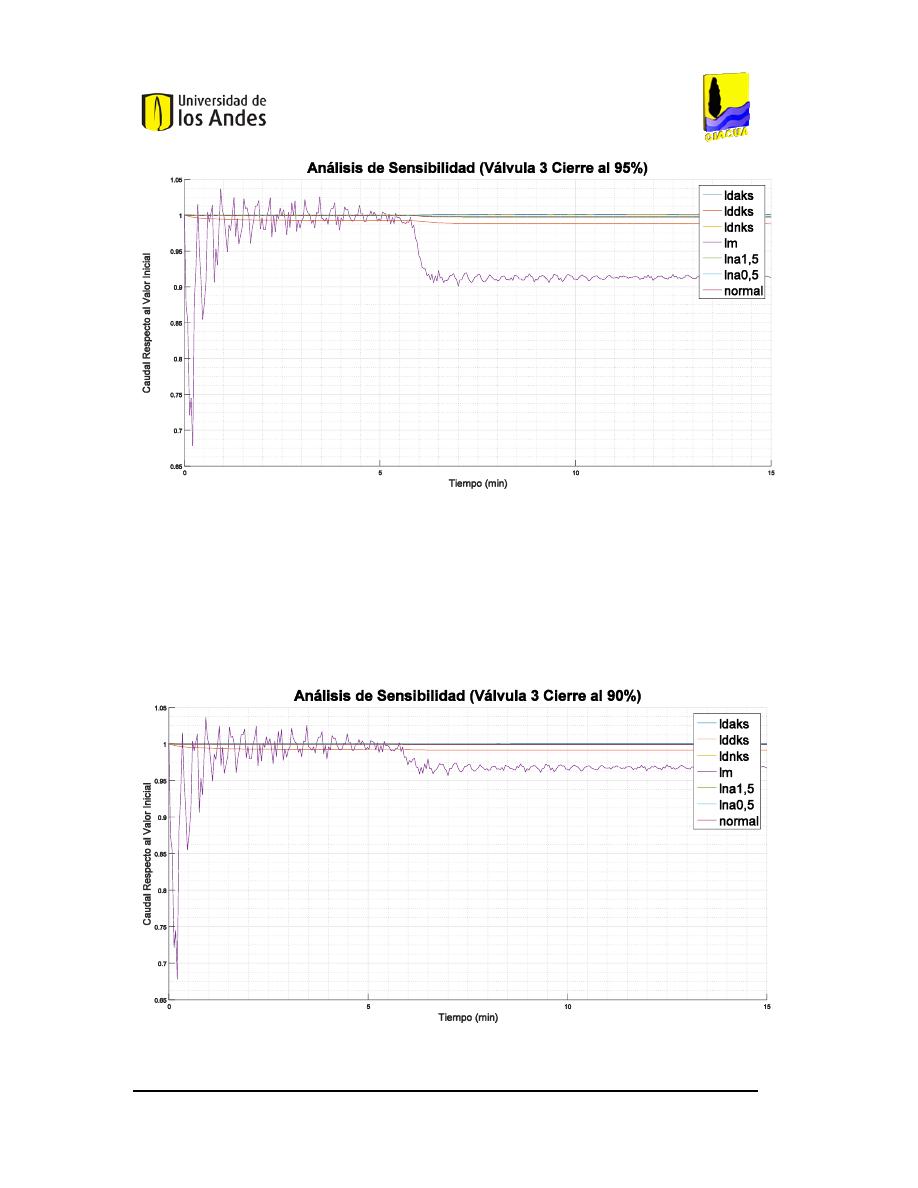
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
75
Figura 82. Comportamiento del caudal para el cierre del 95% de la Válvula 3 en la red matriz de Medellín.
En la Figura 83 se puede que la red más afectada por la operación de la válvula es
nuevamente en la que se redujo la longitud de las tuberías. Por otra parte, si se ven las
diferentes simulaciones realizadas se encuentra que la perturbación realizada a la red es
menor al 5%. De forma similar que la válvula anterior, los cierres de 80%, 60% y 40%
de la válvula generan cambios menores 2%. Por esta razón, estas figuras se presentan en
la parte de anexos y no se consideran relevantes para realizar un análisis de las mismas.
Figura 83. Comportamiento del caudal para el cierre del 90% de la Válvula 3 en la red matriz de Medellín.
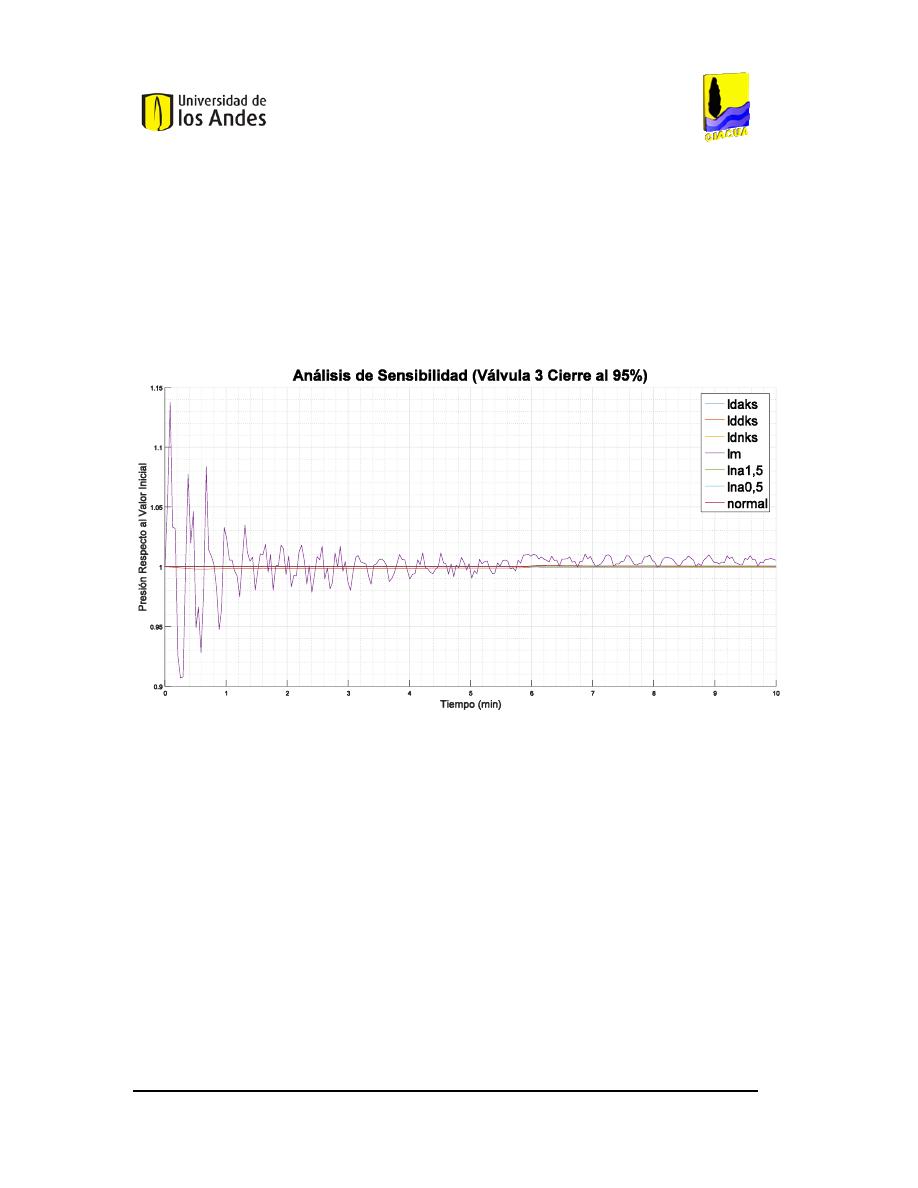
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
76
PRESIÓN
En la Figura 84 se pueden ver las perturbaciones que produce el cierre de la válvula 3 en
las presiones. En ella se encuentra que éstas son muy bajas pues son menores al 1%. Sin
embargo, es llamativo que, similar a los casos presentados anteriormente, el modelo en el
que se reduce la longitud presenta una alta cantidad de ruido. Esto teniendo en cuenta
que antes de los 2 minutos no se presenta ninguna operación en la red y existe una alta
variación de la señal. Por otra parte, si se revisa el comportamiento de las líneas en el
minuto 6, se encuentra que es el punto donde se genera una ligera variación en las
presiones. De esta manera, se puede decir que la red requiere de poco más de 3 minutos
para sentir el efecto generado por la operación del a válvula 3.
Figura 84. Comportamiento de la presión para el cierre del 95% de la Válvula 3 en la red matriz de Medellín.
Nuevamente las figuras del comportamiento de la presión para los cierres del 90%, 80%,
60% y 40% se presentan en la sección de anexos, pues las variaciones que se presentaron
son despreciables.
7.2.1.4. Válvula 4
En la presente sección se muestran los resultados obtenidos por la operación de la válvula
4. Al igual que en las secciones anteriores se muestra inicialmente el comportamiento del
caudal y posteriormente el de la presión.
CAUDAL
En la Figura 85 se puede ver que la válvula 4 genera una mayor perturbación que la
válvula 3, pues la deflexión de las curvas es más notoria. Sin embargo, las variaciones no
superan el 8%. Una vez más, la red que más siente la operación de la válvula es la red en
la que se redujo las longitudes de las tuberías. Adicionalmente, similar al caso anterior se
encuentra que la red requiere de unos 3 minutos para sentir que se está operando una
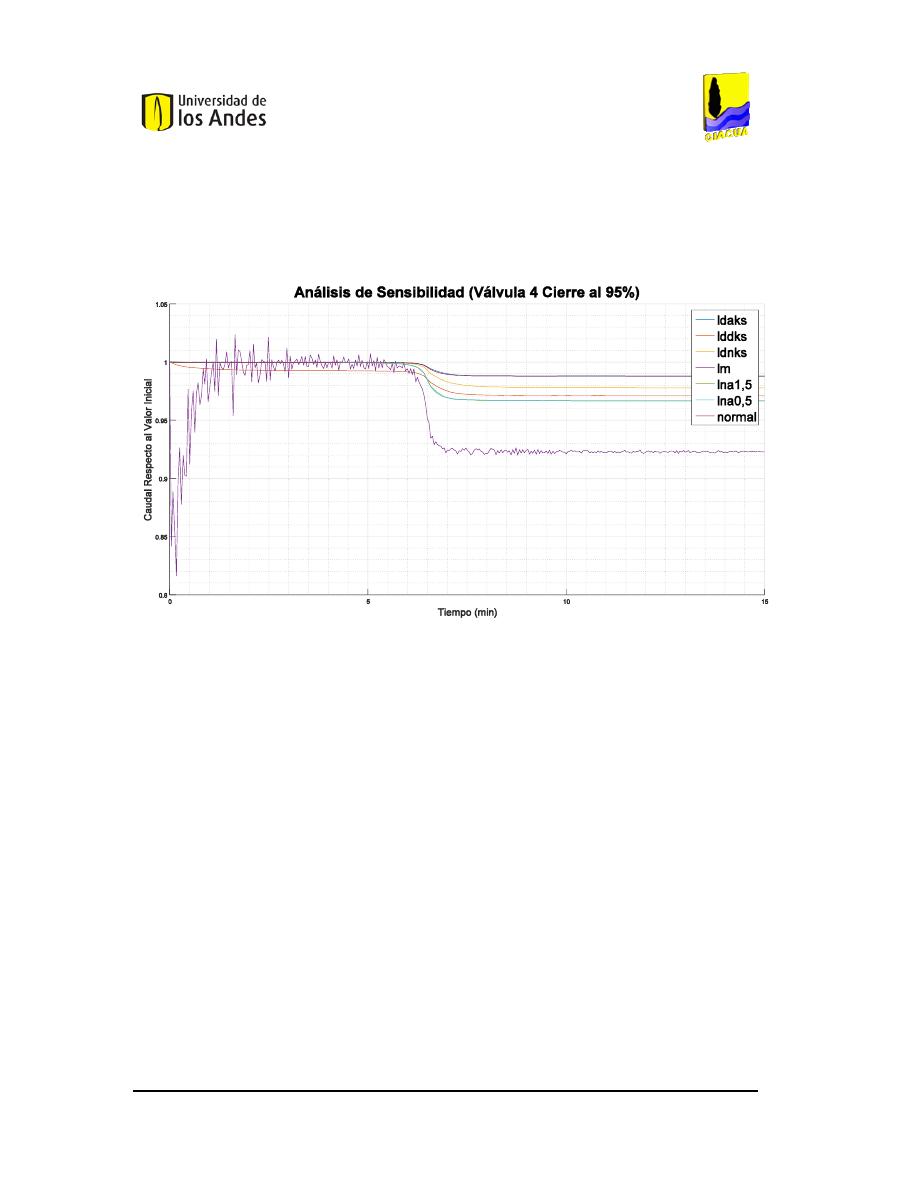
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
77
válvula en el sistema. Por otra parte, se puede ver que el tiempo de respuesta una vez la
red siente la perturbación es tan rápido que en tan solo 1 minuto y medio después, la red
llega a un nuevo estado estable. Adicionalmente, las variaciones realizadas en los
parámetros de longitud, celeridad de la onda y rugosidad no afectan el tiempo de
estabilización.
Figura 85. Comportamiento del caudal para el cierre del 95% de la Válvula 4 en la red matriz de Medellín.
En la Figura 86 se puede ver que el reducir 5% del porcentaje de cierre hace que para el
caso de mayor impacto (lm) se reduzca en 5% la variación del caudal respecto al valor
inicial. A su vez, la reducción del cierre hace que los demás casos simulados tengan un
comportamiento más similar entre ellos. Nuevamente para todas las simulaciones, las
modificaciones de los parámetros iniciales no afectan el tiempo de estabilización. De
esta forma, se encuentra que para todos los casos existe un retraso de 3 minutos en sentir
la perturbación, y una vez se siente ésta, la red requiere de 1 para llegar a un nuevo estado
estable. Por otra parte, se podría decir que al tener variaciones tan pequeñas en la red, no
existe una alteración significativa en la red y, por lo tanto, la estabilización es inmediata.
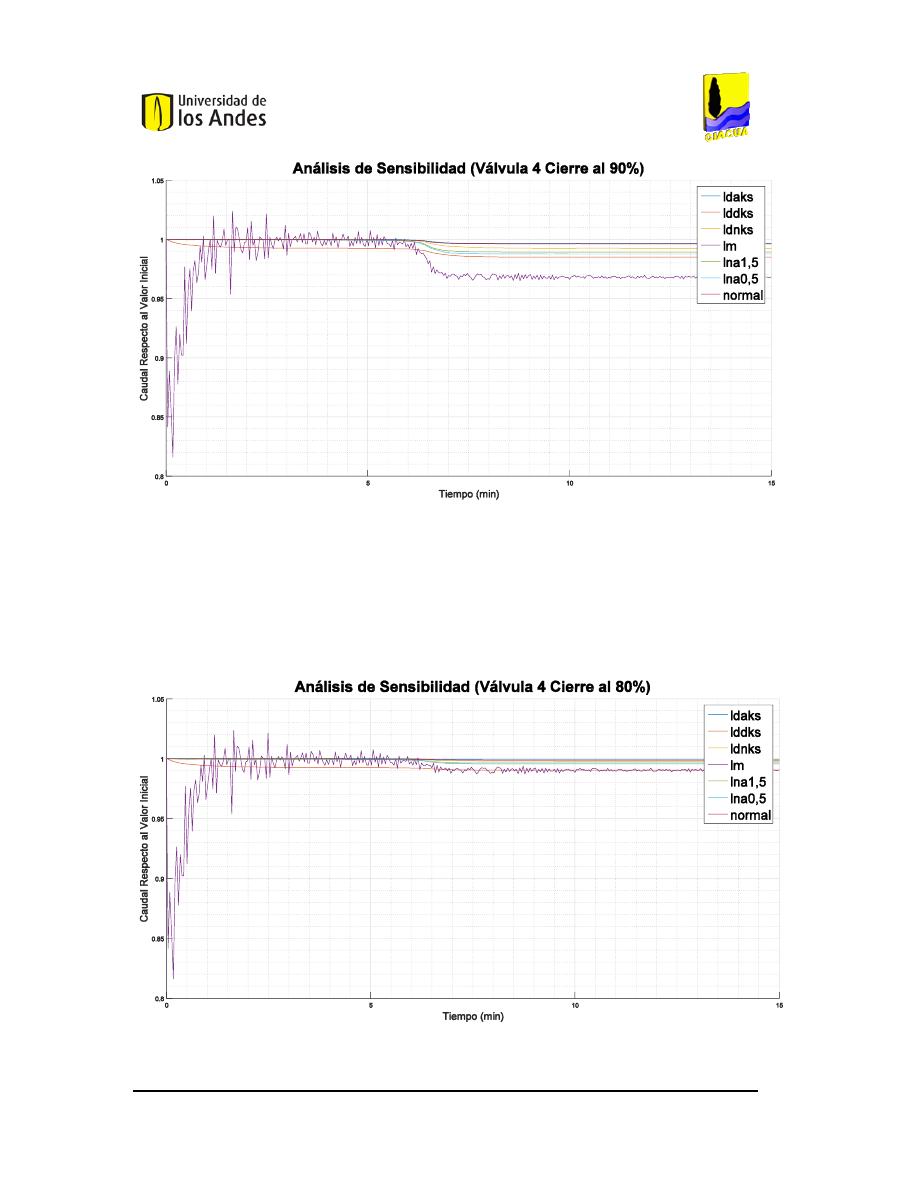
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
78
Figura 86. Comportamiento del caudal para el cierre del 90% de la Válvula 4 en la red matriz de Medellín.
En la Figura 87 se encuentra la baja modificación que es generada si el porcentaje de
cierre de la válvula es de 80%, situación que se ve replicada en los cierres de 60% y 40%.
Por esta razón, las figuras de estos dos últimos cierres se muestran en la parte de anexos.
A partir de los resultados presentados de la Figura 87 se establece que la perturbación a la
red es tan baja, que el tiempo de estabilización es inmediato. Sin embargo, al igual que
los cierres anteriores, existe un retraso de la señal generada por el cierre de la válvula.
Figura 87. Comportamiento del caudal para el cierre del 80% de la Válvula 4 en la red matriz de Medellín.
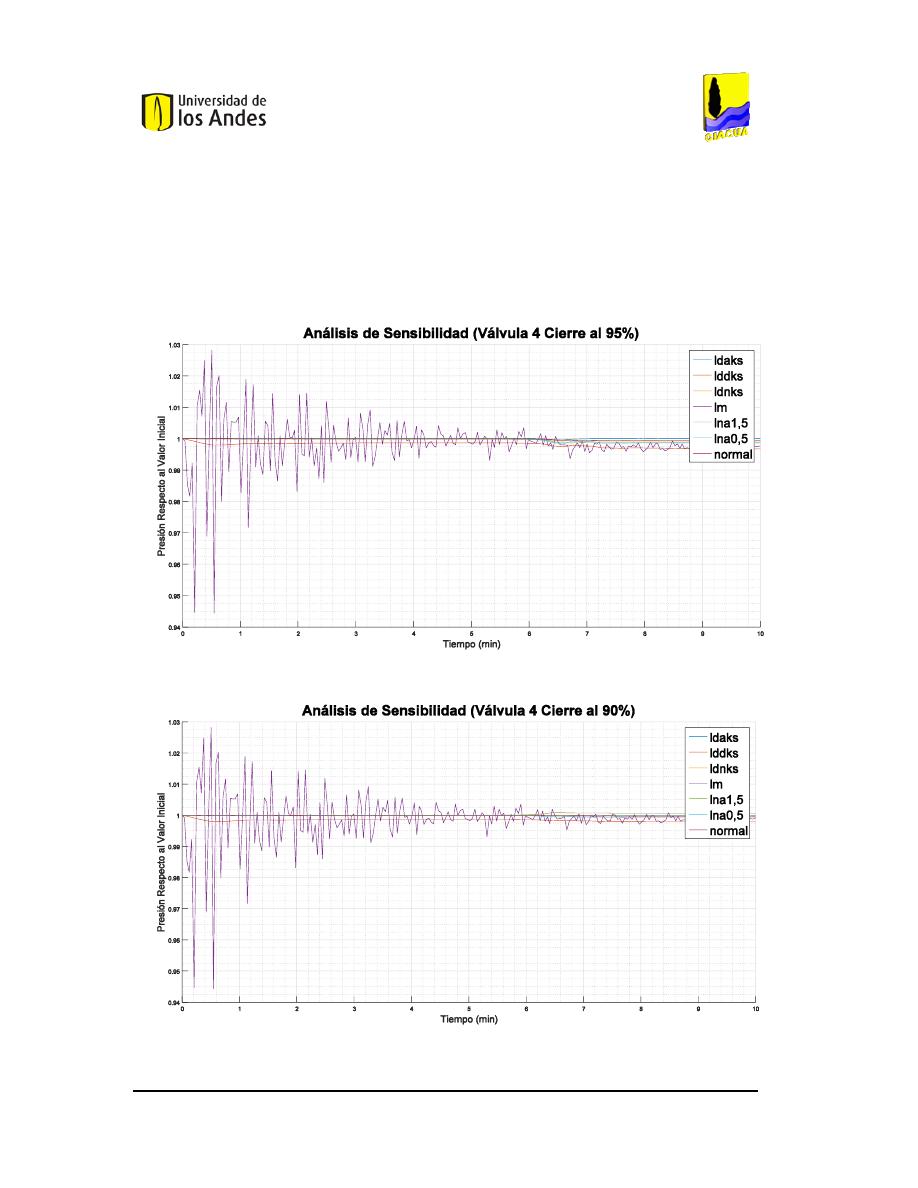
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
79
PRESIÓN
En la Figura 88 se encuentra que las modificaciones de la presión son muy bajas cuando
se presenta un cierre del 95% de la válvula 4. Adicionalmente, similar a lo que ocurría en
las gráficas de los caudales, existe una demora en la reacción de la red frente a la
operación de esta válvula. Por otra parte, llama la atención una vez más la alta presencia
de ruido que tiene el modelo cuando se reducen las longitudes a la mitad. De los
resultados presentados, se encuentra que la red se estabiliza de manera instantánea dado
que las perturbaciones de la presión son muy bajas incluso despreciables.
Figura 88. Comportamiento de la presión para el cierre del 95% de la Válvula 4 en la red matriz de Medellín.
Figura 89. Comportamiento de la presión para el cierre del 90% de la Válvula 4 en la red matriz de Medellín.
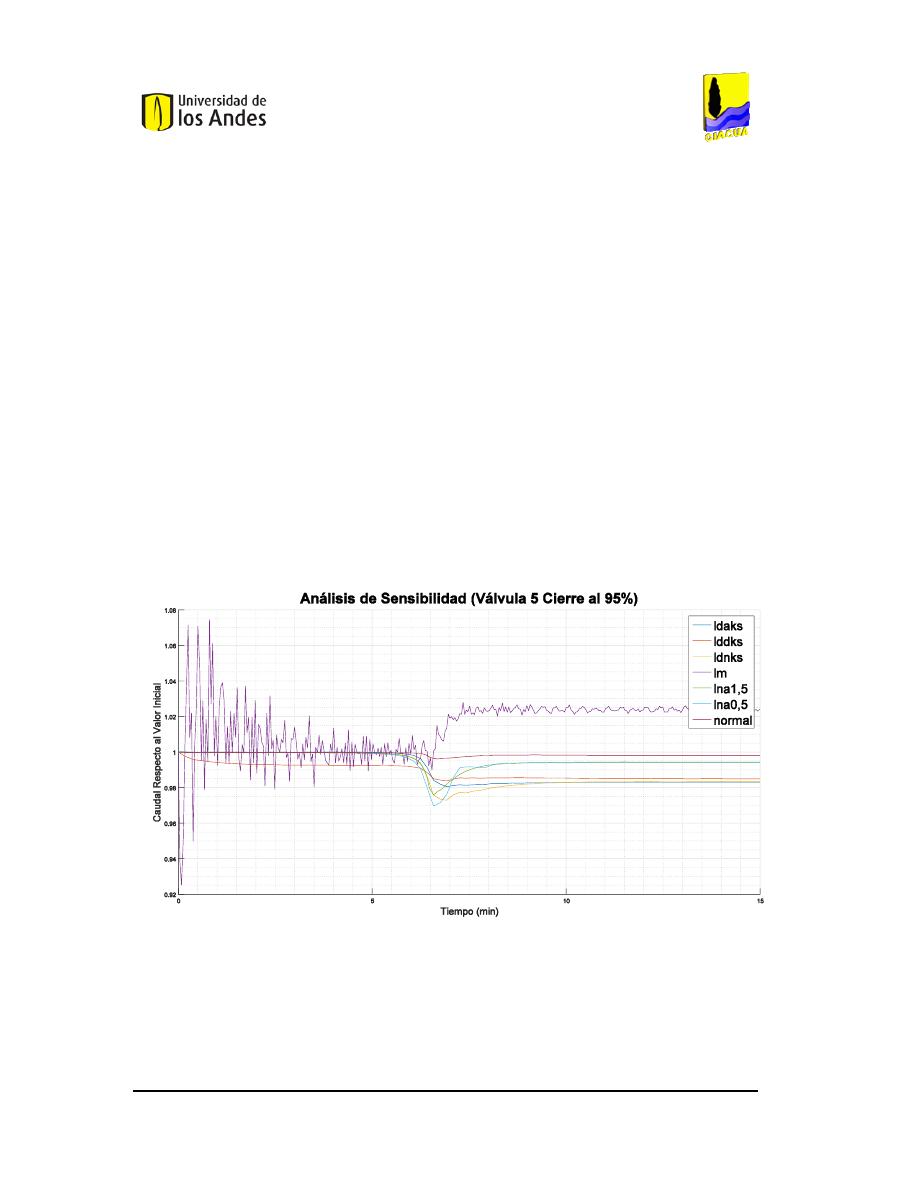
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
80
En la Figura 89 se puede ver las ligeras perturbaciones que genera el cierre del 90% de la
válvula 4 en los sistemas simulados. Se encuentra que las modificaciones son tan bajas
que se puede establecer que la red se estabiliza de manera instantánea. Un aspecto que
vale la pena resaltar es el hecho de que, de todos los casos simulados, el único caso que
tuvo un aumento de la presión en general fue aquel en el que se aumentó la celeridad de
la onda. A pesar de no ser significativo, estos resultados se contraponen frente a los
encontrados cuando se realizó el análisis de sensibilidad del caso simple (ver Sección
7.1.5). Una vez más se presentarán las figuras de los cierres del 80%, 60% y 40% en la
sección de anexos, pues las variaciones encontradas son despreciables.
7.2.1.5. Válvula 5
En la presente sección se muestran los resultados encontrados para los casos en donde se
manipuló el porcentaje de cierre de la válvula 5.
CAUDAL
A partir de la Figura 90 se puede ver que hay una ligera perturbación en los caudales
cuando se cierra al 95% la válvula 5. Es relevante que una vez más el modelo en el que
se reducen las longitudes tiene un comportamiento atípico en comparación con los demás
casos simulados. En esta situación este presenta un ligero incremento de los caudales en
las tuberías de medición. A diferencia de esto, los demás casos tienen una disminución
de los caudales, siendo la más baja para la red que tiene los parámetros iniciales intactos.
Figura 90. Comportamiento del caudal para el cierre del 95% de la Válvula 5 en la red matriz de Medellín.
Nuevamente, al ver la Figura 90 se encuentra que la red siente la perturbación generada
por la válvula a los 3 minutos luego de realizar la operación de ésta. Sin embargo, una
vez que es sentida la alteración en la red, ésta requiere de 3 minutos como máximo para
llegar nuevamente a un estado estable. Al observar la Figura 91 se encuentra que al
disminuir 5% el porcentaje de cierre, hace que se disminuya significativamente la
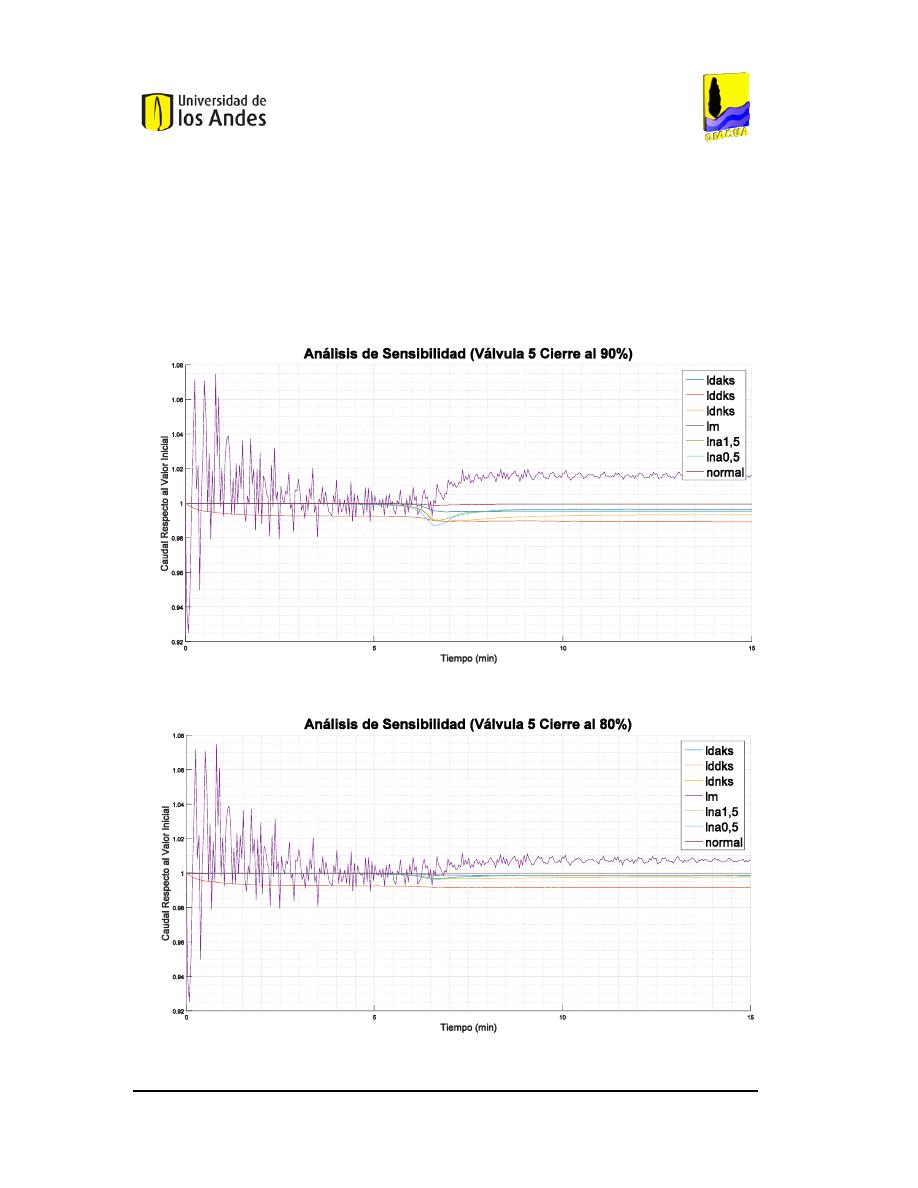
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
81
perturbación en todos los casos a excepción del que se disminuye la longitud. En este
último, la variación de los caudales disminuye en un 0.5%.
Por otra parte, vale la atención resaltar que las curvas que presentan mayor deflexión son
las de los casos en donde se modificó la longitud (ldnks, lm) y la celeridad de la onda
(lna1,5 y lna0,5). Respecto al tiempo de estabilización se encuentra que como máximo la
red requiere de 3 minutos para encontrar un nuevo estado estable. Sin embargo, las
variaciones de caudal son tan pequeñas (menores al 2%) que se puede decir que la red se
estabiliza en un tiempo muy corto; para la práctica de forma instantánea.
Figura 91. Comportamiento del caudal para el cierre del 90% de la Válvula 5 en la red matriz de Medellín.
Figura 92. Comportamiento del caudal para el cierre del 80% de la Válvula 5 en la red matriz de Medellín.
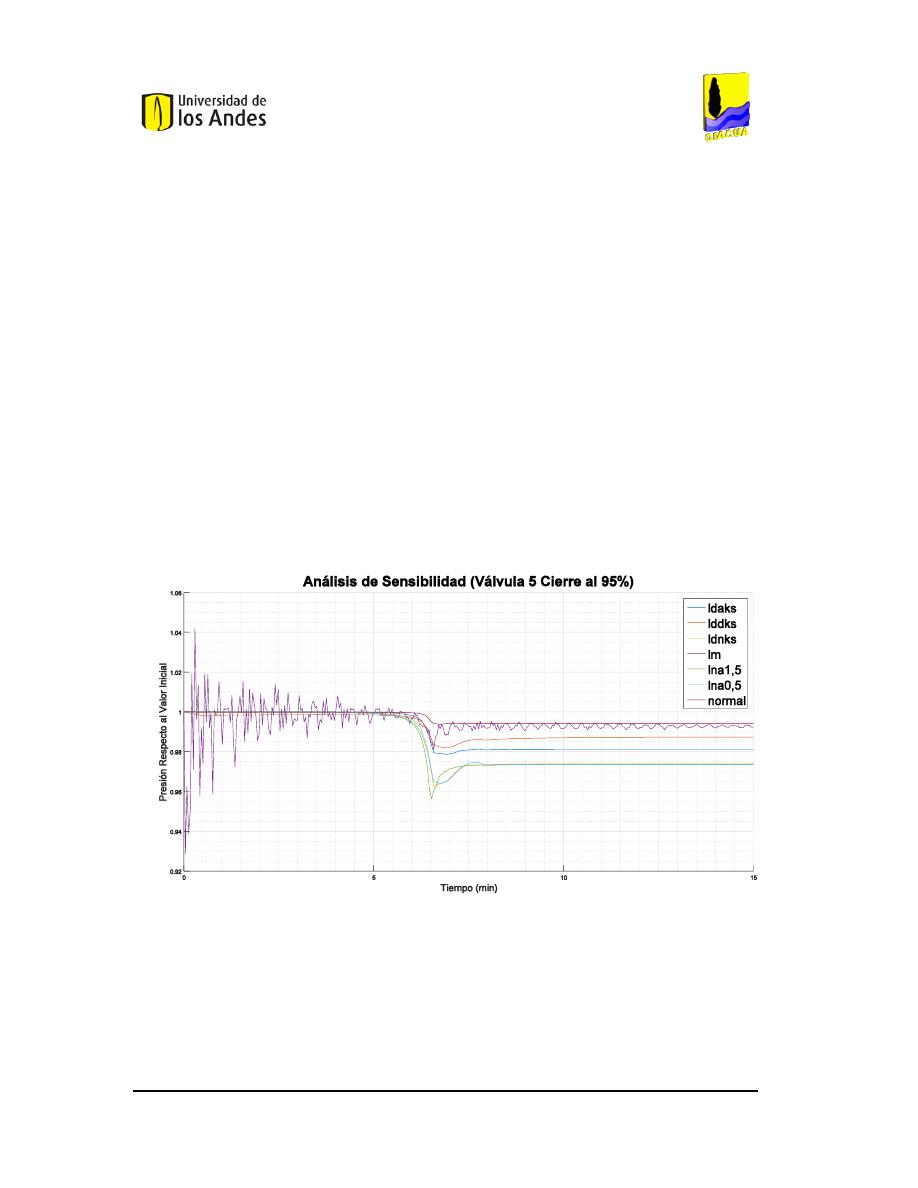
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
82
En la Figura 92 se encuentra que al disminuir el porcentaje de cierre al 80%, las
perturbaciones a la red son menores al 1%. Sin embargo, llama la atención una vez más el
hecho que las simulaciones que presentan la mayor deflexión son aquellas en las que se
modificó la longitud (ldnks, lm) y la celeridad de la onda (lna1,5 y lna0,5). De forma
similar, es recurrente el hecho de que los caudales se incrementen en la red que se
disminuyó la longitud. Respecto al tiempo de estabilización se encuentra que es muy
corto pues las variaciones del caudal son extremadamente bajas para los casos simulados.
Nuevamente, se presentan las figuras de los cierres de 60% y 40% en la parte de anexos,
pues las variaciones son menores al 0.5%.
PRESIÓN
En la Figura 93 se puede ver que la operación de la válvula 5 es capaz de generar
perturbaciones en las presiones de los casos simulados. Al observar las líneas de las
simulaciones en que se aumentó la celeridad de la onda y se duplicó la longitud se
encuentra que tienen una alta similitud. Adicionalmente, estos dos y en la que se
disminuyó la celeridad, son los caso en que más perturbada se encuentra el sistema. Al
igual que en el caudal, la presión se demora cerca de dos minutos en percibir que la
válvula 5 se está operando. Respecto al tiempo de estabilización se encuentra que para
todos los casos oscila entre 4 y 6 minutos. Sin embargo, se debe tener en cuenta que la
máxima variación es de 4.5%.
Figura 93. Comportamiento de la presión para el cierre del 95% de la Válvula 5 en la red matriz de Medellín.
En la Figura 94 se puede ver que el disminuir en 5% el porcentaje de cierre de la válvula
afecta significativamente la respuesta del sistema en términos de presión. Nuevamente,
se encuentra que los caso que se ven más afectados son aquellos en donde se modificó la
celeridad de la onda (lna1,5 y lna0,5) y se incrementó al doble la longitud. Con relación
al tiempo de estabilización se encuentra que para los diferentes casos le red requiere entre
3 y 4 minutos.
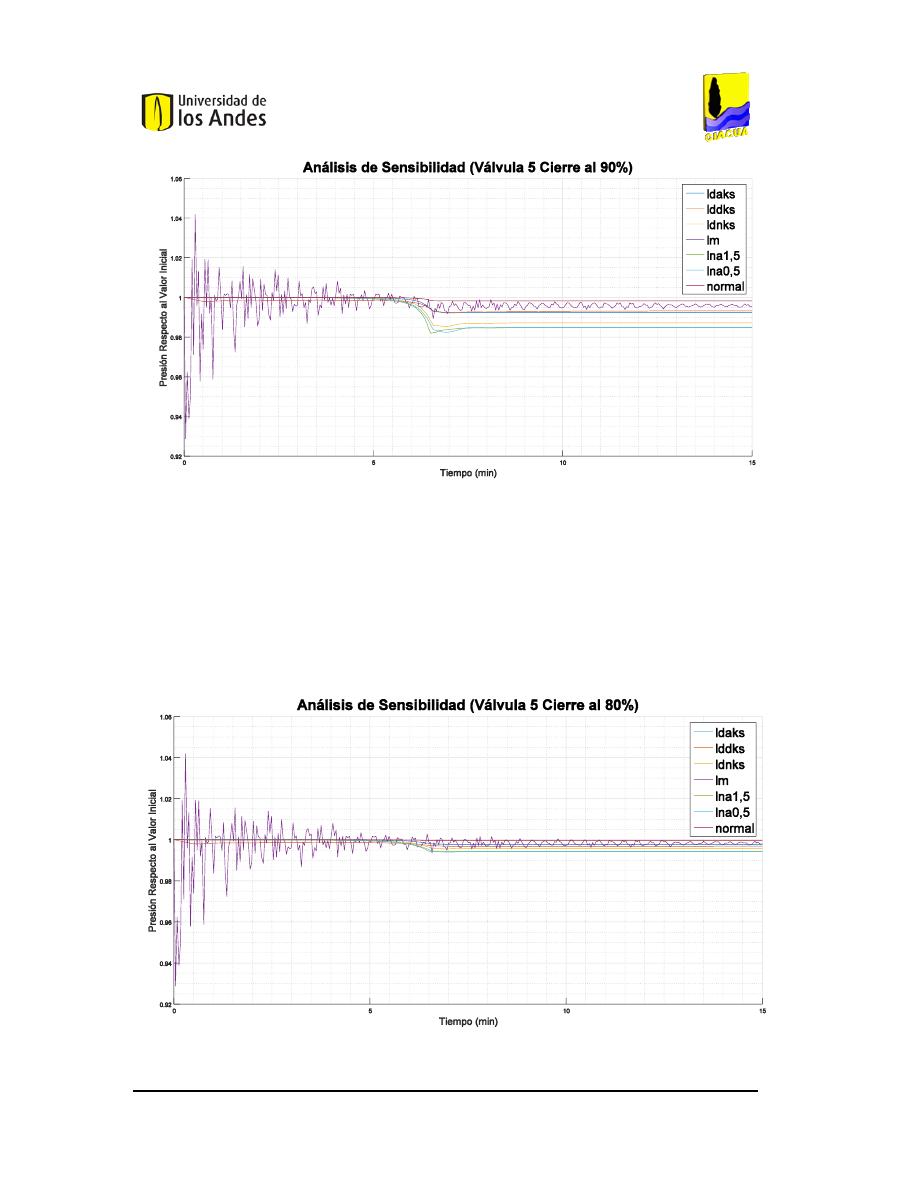
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
83
Figura 94. Comportamiento de la presión para el cierre del 90% de la Válvula 5 en la red matriz de Medellín.
En la Figura 95 se puede ver que al disminuir un 10% más el porcentaje de cierre, las
variaciones del caudal pasan a ser menores al 1%. Por otra parte, la existencia de
diferencias entre los casos se disminuye y todos comienzan a tener gran similitud entre
ellos. Sin embargo, es relevante mencionar que para el caso original (normal), la red
parece no sentir perturbación alguna, pues la línea no tiene ninguna inflexión. Para el
tiempo de estabilización se encuentra que la respuesta de la red requiere de 3 minutos; sin
embargo, la variación es tan baja que se puede considerar que la red se estabiliza en un
tiempo corto.
Figura 95. Comportamiento de la presión para el cierre del 80% de la Válvula 5 en la red matriz de Medellín.
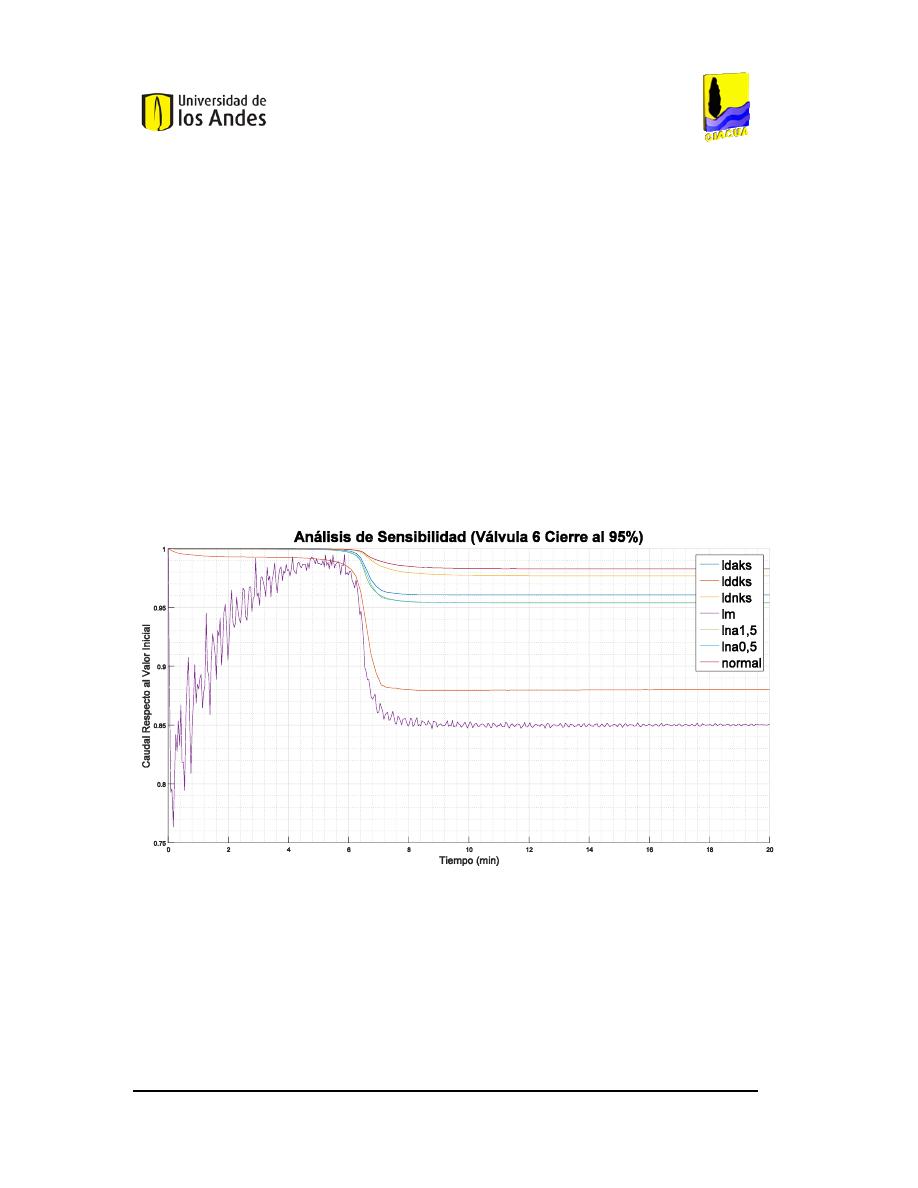
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
84
Las figuras del comportamiento de los porcentajes de cierre del 60% y 40% se presentan
en la sección de anexos.
7.2.1.6. Válvula 6
En la presente sección se muestran los resultados obtenidos cuando se modifica el
porcentaje de apertura de la válvula 6. De esta manera, se presentan las variaciones
obtenidas en términos de caudal y presión.
CAUDAL
En la Figura 96 se encuentra que la válvula 6 tiene una alta capacidad para modificar los
caudales de la red. Adicionalmente, se encuentra que las redes que presentan la mayor
perturbación son la de las longitudes a la mitad y la de la rugosidad más baja. Sin
embargo, a pesar de esto, las deflexiones de las diferentes curvas son muy similares. Por
otra parte, si se analizan las líneas de los casos donde se realizaron modificaciones de la
rugosidad, se encuentra que esta variable es influyente para el cierre de esta válvula. Al
estudiar el tiempo de estabilización se encuentra que para todos los casos está entre 5 y 6
minutos. Sin embargo, es relevante mencionar que las redes requieren de 3 minutos
aproximadamente para sentir la operación de la válvula de la presente sección.
Figura 96. Comportamiento del caudal para el cierre del 95% de la Válvula 6 en la red matriz de Medellín.
Al observar la Figura 96 y la Figura 97 se encuentra que el disminuir el porcentaje de
cierre a 90% hace que la variación de las curvas de mayor afectación, disminuyan 5% en
la variación del caudal de estabilización. Asimismo, al ver la segunda figura se encuentra
que para los demás casos la perturbación de los caudales es menor al 2.5%. Respecto al
tiempo de estabilización se encuentra en 6 minutos. Sin embargo, para los casos de
menor perturbación se puede decir que el tiempo es muy corto, pues la variación respecto
al caudal inicial es casi despreciable.
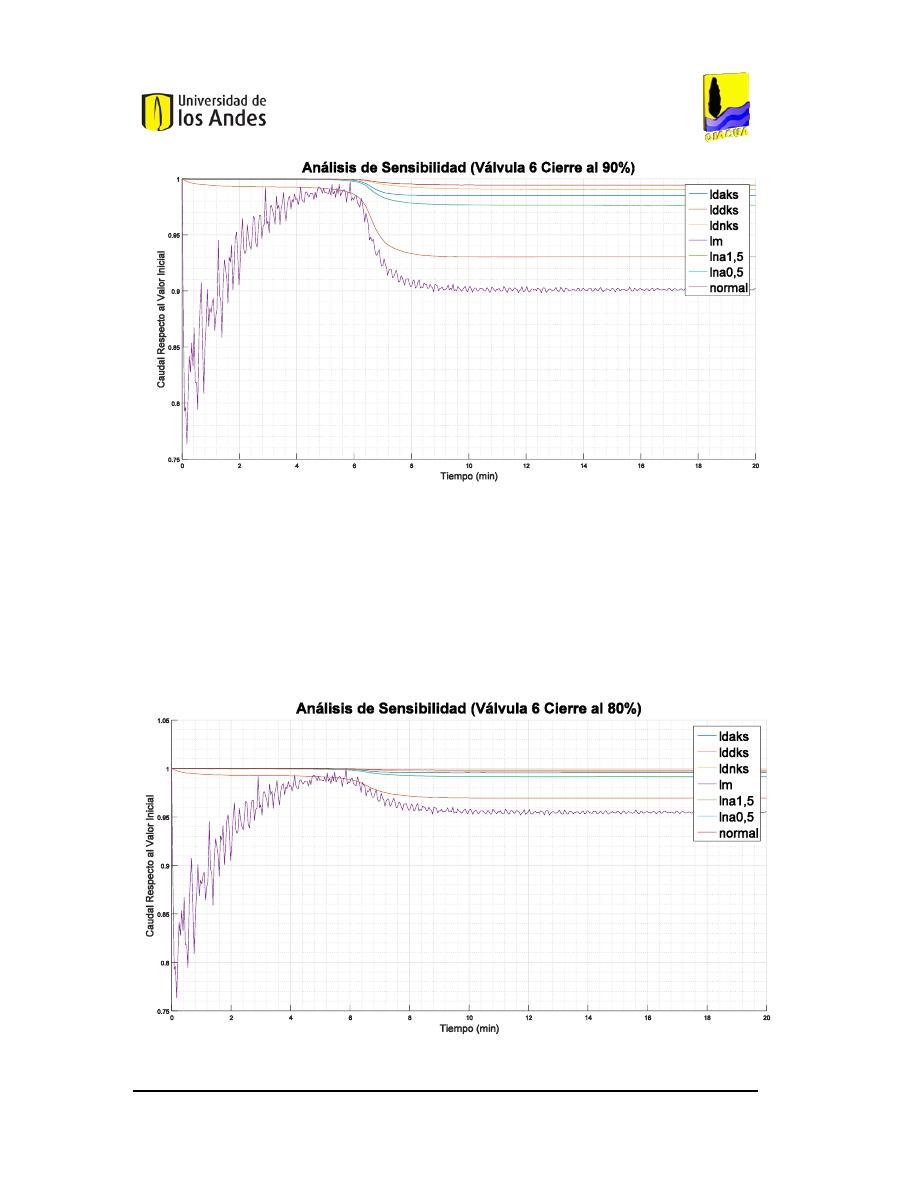
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
85
Figura 97. Comportamiento del caudal para el cierre del 90% de la Válvula 6 en la red matriz de Medellín.
En la Figura 98 se encuentra que el disminuir el porcentaje de cierre al 80% hace que las
variaciones que se produzcan en términos del caudal sean menores al 5%.
Adicionalmente, se encuentra que a medida que se disminuye el porcentaje de cierre de la
válvula, las curvas tienden a tener mayor similitud entre ellas. Sin embargo, al igual que
los cierres anteriores, cuando se reduce la longitud o se disminuye la rugosidad se
presenta una perturbación más fuerte que en los demás casos. Finalmente, para los
tiempos de estabilización se puede decir que es de 5 minutos para los casos con mayor
porcentaje de cierre, y para los demás es aún menor a éste.
Figura 98. Comportamiento del caudal para el cierre del 80% de la Válvula 6 en la red matriz de Medellín.
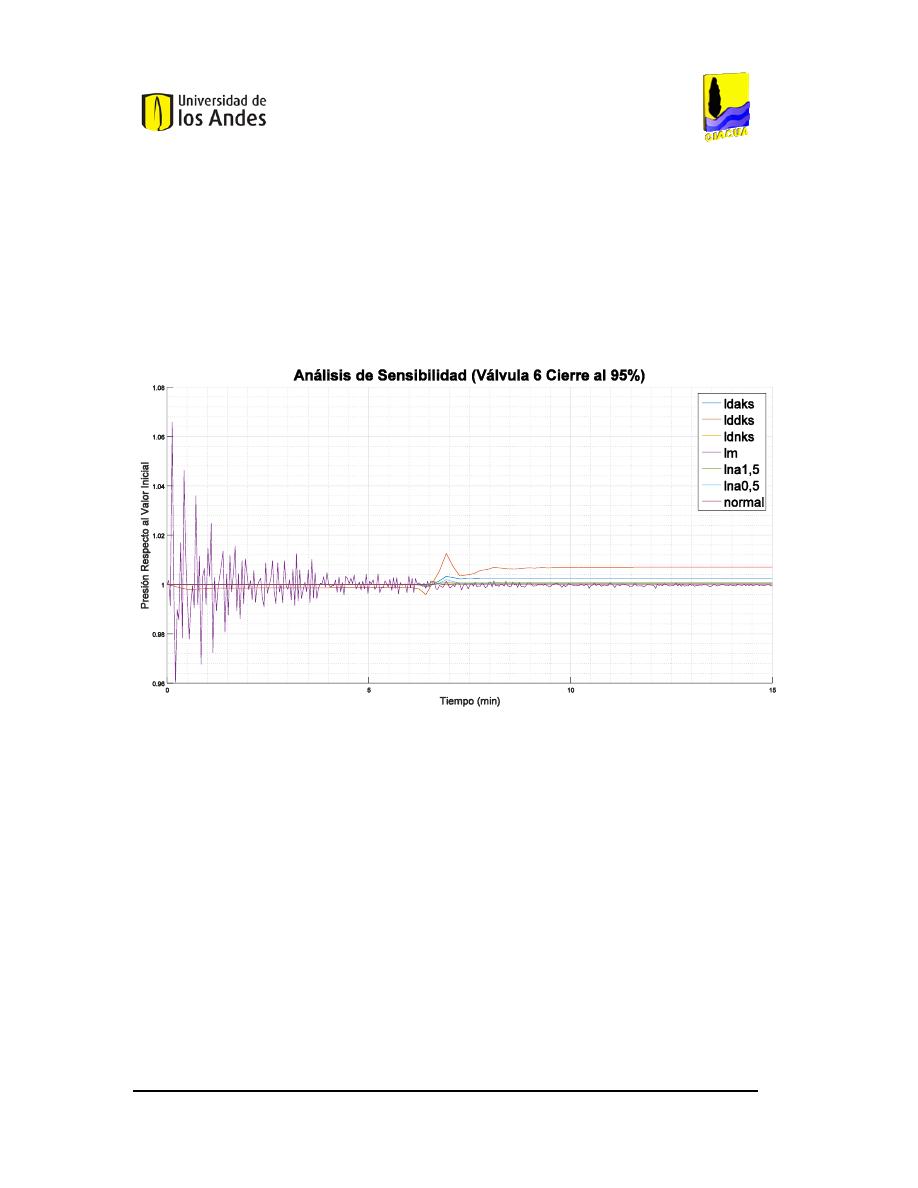
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
86
Respecto a las figuras del 60% y 40% se presentan en la sección de anexos.
PRESIÓN
Al observar la Figura 99 se encuentra que la presión no presenta una perturbación
significativa frente al cierre del 95% de la válvula 6. Sin embargo, resulta llamativo que
para la presión solo la red en donde se disminuyó la rugosidad es la más afectada y no en
conjunto con la que se disminuye la longitud de las tuberías. Respecto al tiempo de
estabilización se encuentra que es inmediato pues las variaciones que se presentan son
menores al 1%. A causa de esto y los resultados que se encuentran en los demás cierres,
se presentan las figuras faltantes en la sección de anexos.
Figura 99. Comportamiento de la presión para el cierre del 95% de la Válvula 6 en la red matriz de Medellín.
7.2.1.7. Válvula 7
En la presente sección se muestran los resultados obtenidos al manipular la válvula 7 en
la red matriz de Medellín.
CAUDAL
En la Figura 100 se encuentran las curvas encontradas para el caudal cuando se realiza un
cierre del 95% de la válvula 7. En ella se puede ver que los casos menos afectados son
cuando la longitud se reduce a la mitad y la red original. Sin embargo, al revisar todas las
curvas se encuentra que tienen una deflexión similar, y ninguna presenta un
comportamiento drástico. Por otra parte, se puede ver que todas las curvas a excepción
de la curva de la red original, sienten la perturbación de la válvula justo al comienzo del
cierre de ésta.
Adicionalmente, se encuentra curioso que el afectar la celeridad de la onda afecta la línea
de respuesta. Sin embargo, es interesante que tanto incrementar o disminuir la celeridad
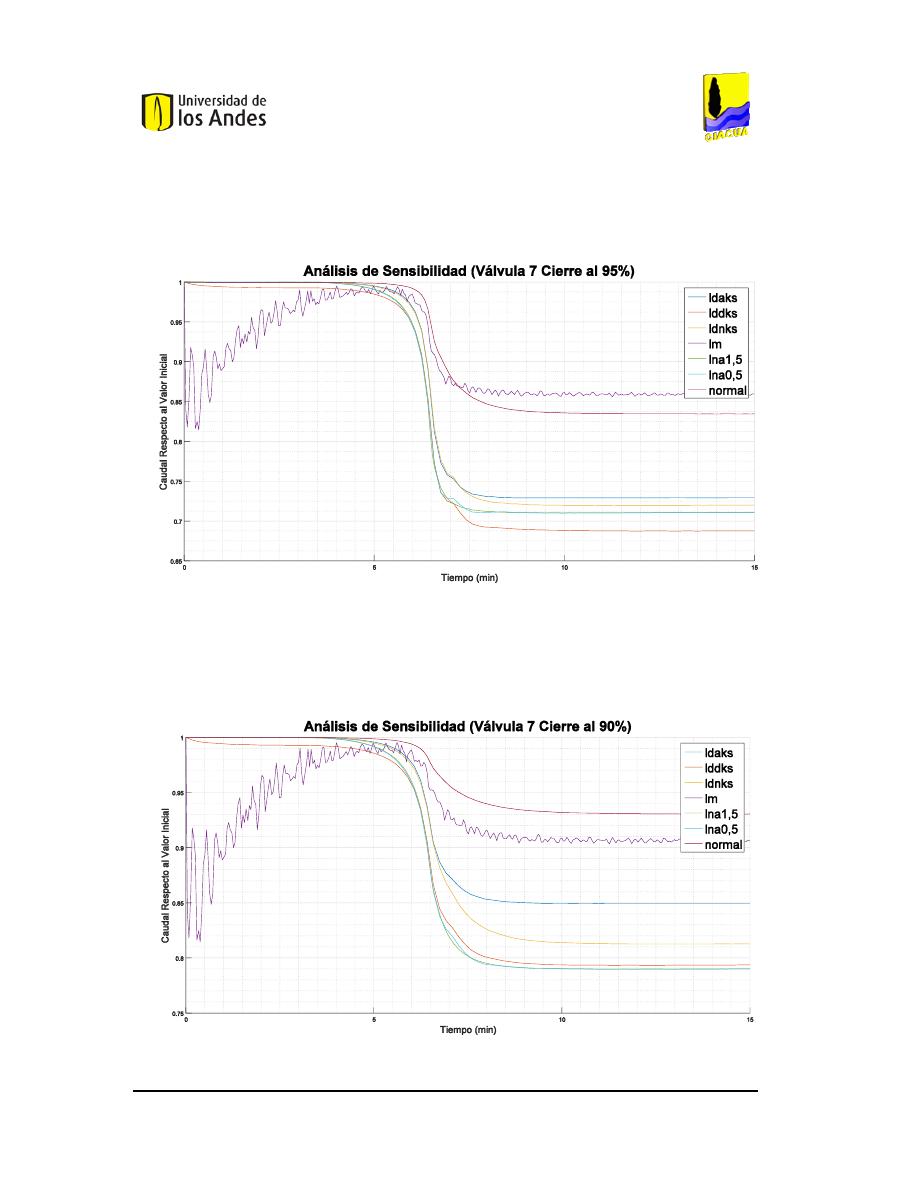
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
87
de la onda, hace que ambas curvas se asemejen. Similar a esto ocurre cuando se modifica
la rugosidad de la tubería. Respecto al tiempo de estabilización se encuentra que todos
los casos se estabilizan a los 6 minutos después de haber iniciado el cierre. Asimismo, se
encuentra que las variaciones de los parámetros iniciales de la red no afectan el tiempo de
estabilización.
Figura 100. Comportamiento del caudal para el cierre del 95% de la Válvula 7 en la red matriz de Medellín.
Al comparar la Figura 100 con la Figura 101 se encuentra que el disminuir el porcentaje
de cierre afecta de manera dramática los casos que son más perturbados, pues estos
disminuyen la variación alrededor de un 10%. Sin embargo, para los casos en donde la
perturbación es baja (normal, lm) se reduce la misma en un 5%.
Figura 101. Comportamiento del caudal para el cierre del 90% de la Válvula 7 en la red matriz de Medellín.

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
88
Un último aspecto que llama la atención es que al disminuir el porcentaje de cierre, la red
más afectada cambio, no siendo ahora la de la disminución de la rugosidad sino aquellas
en donde se varío la celeridad de la onda. Respecto al tiempo que requieren las redes
para llegar a un nuevo estado estable se encuentra que éstas necesitan de 7 minutos. Esto
resulta contradictorio con la lógica, pues la red necesita menor tiempo para encontrar un
nuevo estado estable cuando se realiza un porcentaje de cierre mayor.
Figura 102. Comportamiento del caudal para el cierre del 80% de la Válvula 7 en la red matriz de Medellín.
En la Figura 102 se encuentra que el disminuir el porcentaje de cierre a 80%, hace que la
perturbación se reduzca en 10% de la variación para los casos más drásticos (ldaks, lddks,
ldnks, lna1,5 y lna0,5). Adicionalmente, a medida que se disminuye el porcentaje de
cierre, las líneas del cambio de celeridad se asemejan más y se alejan en mayor medida al
caso que tiene el valor original. Se debe agregar que esos casos son los que son más
perturbados se encuentran, dada la operación de la válvula 7. Respecto al tiempo de
estabilización se encuentra que para el caso en el que se duplica la longitud se incrementa
a 8 minutos y para las demás simulaciones el tiempo de estabilización es de 7 minutos.
En la Figura 103 se encuentra que la perturbación a la red disminuye sustancialmente.
Adicionalmente, las curvas en donde se modificó la celeridad de la onda se sobreponen
entre sí, además, se aleja el punto de estabilización de la red sin modificaciones y él de
éstas. Respecto a la estabilización de las redes se encuentra que para la normal, la que se
aumenta la rugosidad y la que se disminuye la longitud, su punto de estabilización
disminuye y llega a ser de 4 minutos. Para las demás llega a tener un valor de 7 minutos.
Es necesario tener en cuenta que la máxima variación que se presenta es de 3.5%.
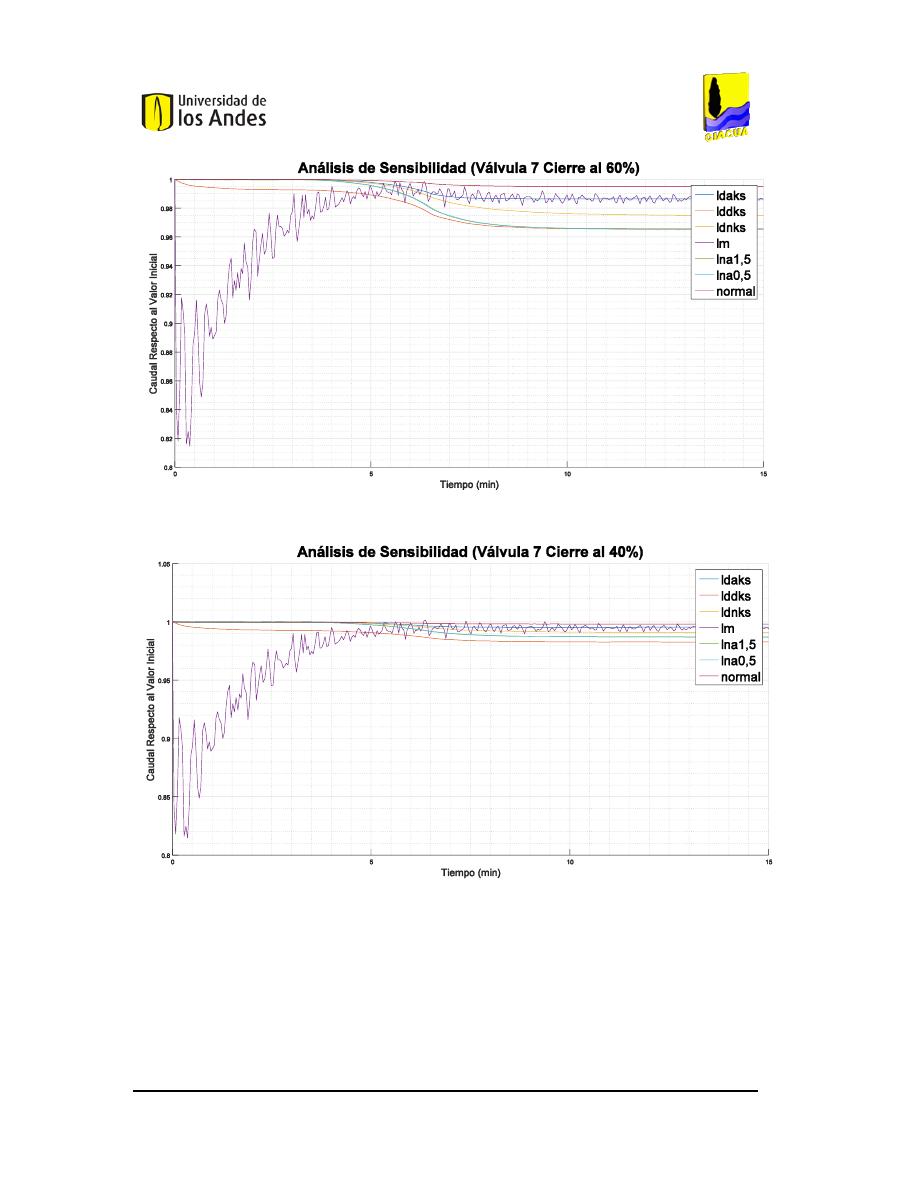
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
89
Figura 103. Comportamiento del caudal para el cierre del 60% de la Válvula 7 en la red matriz de Medellín.
Figura 104. Comportamiento del caudal para el cierre del 40% de la Válvula 7 en la red matriz de Medellín.
En la Figura 104 se encuentra que si el cierre disminuye al 40%, la red no presenta
variaciones de caudal significativas, llegando a ser menores al 2%. Por esta razón se
establece que la red se estabiliza en un tiempo muy corto, llegando a ser despreciable.
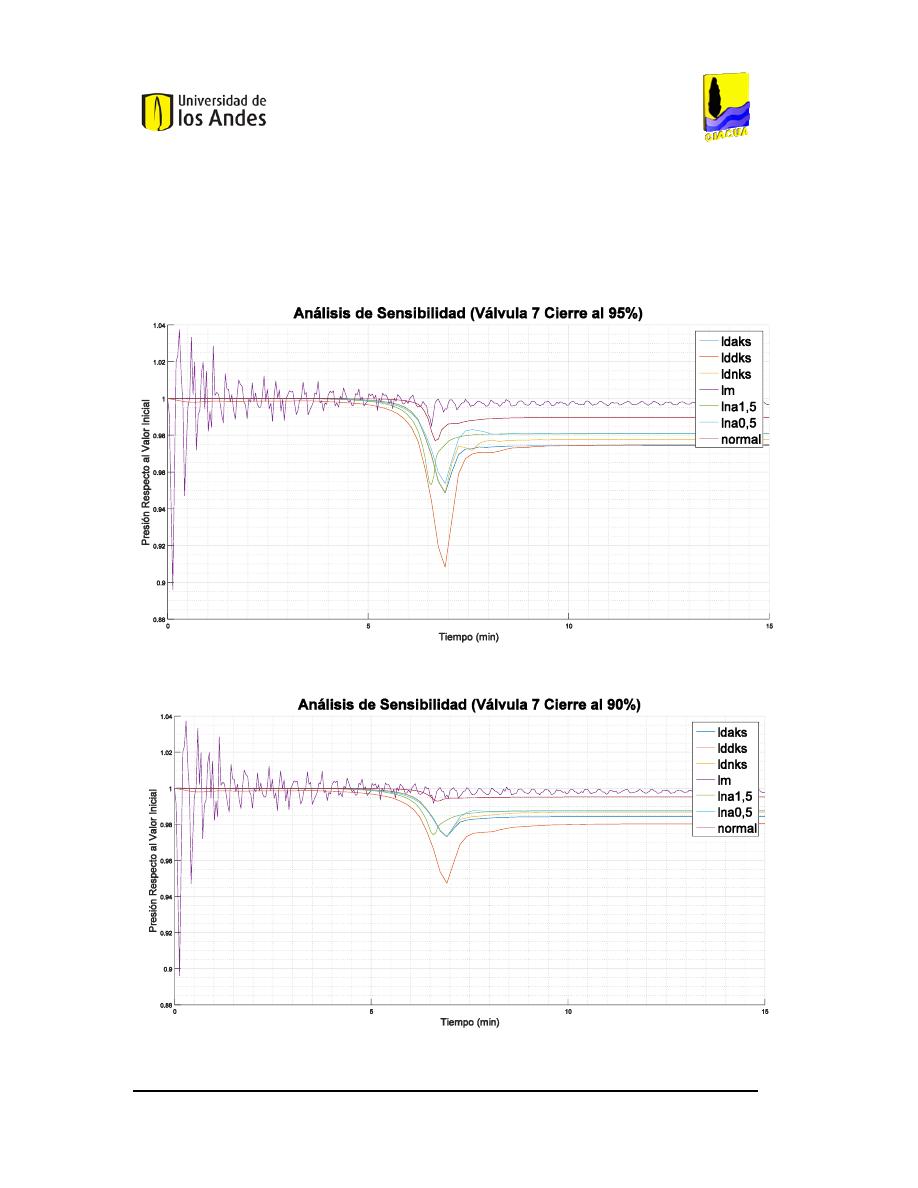
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
90
PRESIÓN
En la Figura 105 se puede ver que la simulación con mayor afectación en las presiones de
la red es en la que se disminuye la rugosidad. Adicionalmente, se puede ver que salvo en
dos casos (lm y normal), la red percibe cuando inicia la operación de la válvula.
Respecto al tiempo de estabilización se establece que todos los casos encuentran un
nuevo estado estable a los 5 minutos después de haber iniciado la operación de la válvula.
Por último es relevante mencionar que las variaciones de la presión son menores al 10%.
Figura 105. Comportamiento de la presión para el cierre del 95% de la Válvula 7 en la red matriz de Medellín.
Figura 106. Comportamiento de la presión para el cierre del 90% de la Válvula 7 en la red matriz de Medellín.

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
91
A partir de la Figura 106 se encuentra que el disminuir el porcentaje de cierre de la
válvula 7 al 90% hace que la perturbación de la presión sea sustancialmente menor. Es
tal el caso que para dos simulaciones (normal y lm) la variación es menor al 1%.
Respecto a la estabilización se encuentra que, para los casos de la mitad de la longitud y
la red original, la variación de las presiones es despreciable y la estabilización es en un
tiempo muy corto. Para los demás casos se requiere de 5 minutos para encontrar un
nuevo estado estable. Las figuras de los porcentajes de cierres restantes se presentan en
la sección de anexos, pues las variaciones de presión fueron menores al 2%.
7.2.2. RED DE BUCARAMANGA (SECTOR ESTADIO)
En la presente sección se presentan los resultados obtenidos en las simulaciones
realizadas en la red de Bucaramanga (Sector Estadio). Es relevante mencionar que dado
el tamaño de la red, las simulaciones requerían una gran cantidad de tiempo. Por esta
razón y teniendo en cuenta los resultados obtenidos en Tesis I, se optó por realizar los
análisis de sensibilidad solo para los cierres (95%, 90%, 80%, 60%, 40%) de las 4
primeras válvulas.
Se encuentra relevante mencionar que en la presente no se realizó el análisis de
sensibilidad de la rugosidad. Sin embargo, si se evaluó los impactos producidos por la
variación de la celeridad de la onda y la longitud de las tuberías. Para la primera
propiedad sólo se realizaron las simulaciones cuando el cierre era de 95%, para la
segunda, todos los cierres de las 5 primeras válvulas. De esta manera, en la Tabla 4 se
muestran los casos simulados. A continuación se presentan los resultados obtenidos en
los análisis de sensibilidad, en conjunto con las simulaciones realizadas para la red con
las propiedades originales.
Tabla 4.
Casos simulados para la red de Bucaramanga.
Caso simulado
Siglas
Red sin cambios
original
Red con las tuberías con dos veces la longitud
ld
Red con las tuberías con la mitad de la longitud
lm
Red con 1.5 veces la celeridad de la onda
lna1,5
Red con 1.2 veces la celeridad de la onda
lna1,2
7.2.2.1. Red Original
En esta sección se presentan los comportamientos de los caudales y las presiones en 8
puntos (Ubicaciones de las válvulas) para los cierres del 95% de las 7 primeras válvulas.
Es relevante mencionar que no se muestran los resultados del cierre de la última válvula,
pues dado los resultados de Tesis I se encontró que ésta no tiene una afectación
significativa en la red.
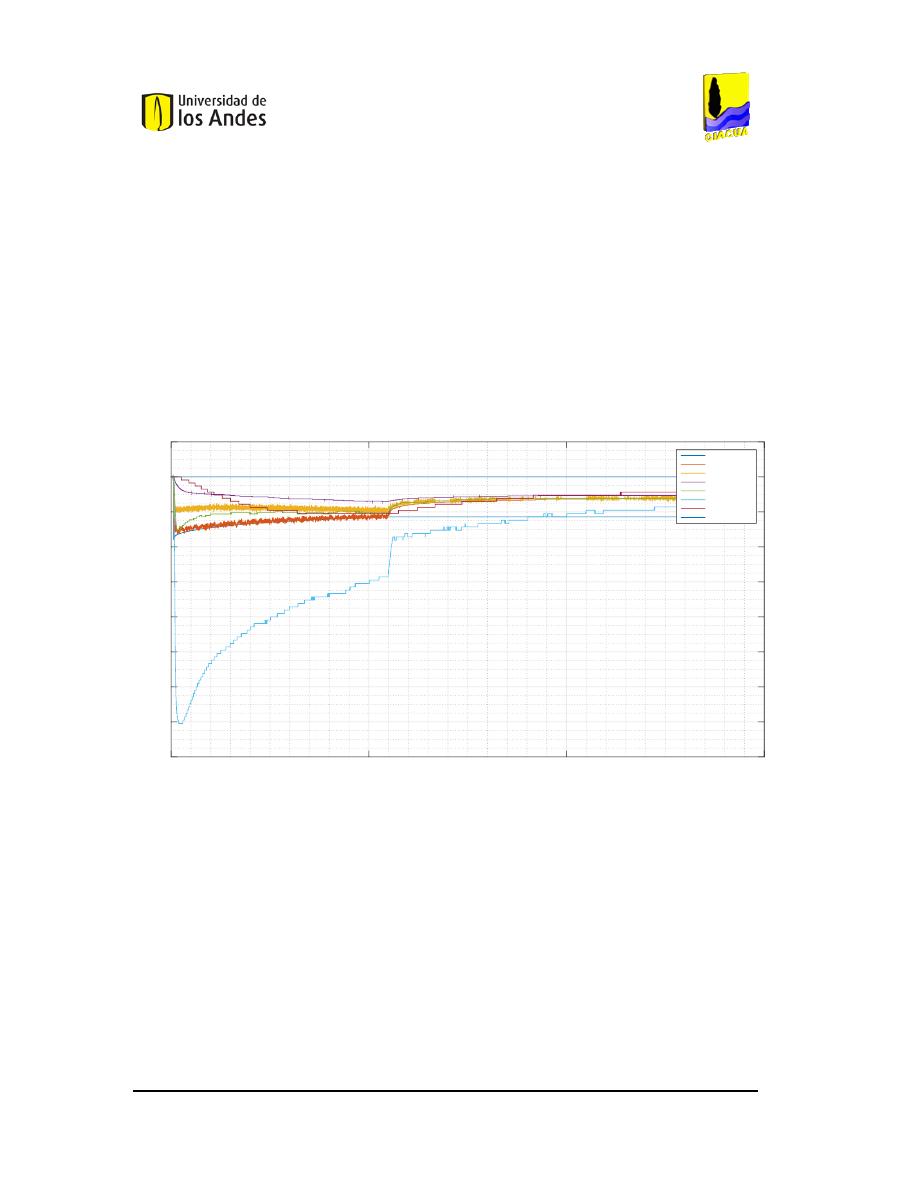
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
92
7.2.2.1.1.
Válvula 1
CAUDAL
En la Figura 107 se puede ver que el cierre de la válvula 1 perturba de una manera
drástica la red. Si se ve el comportamiento de la tubería adyacente a la válvula 6, se
encuentra que la alteración es tan alta que hace que el flujo cambie de dirección. Para las
demás tuberías se encuentra que, salvo la tubería adyacente a la válvula 4, la perturbación
es mayor al 40%. Adicionalmente, cerca de los 550 minutos, las curvas tienen un nuevo
cambio, factiblemente dado al regreso de la onda que es producida por el cierre de la
válvula. Respecto al tiempo de estabilización se encuentra que las tuberías con mayores
caudales (Tuberías adyacentes a las válvulas 1-6) encuentran un nuevo estado estable a
los 800 minutos. Vale la pena establecer que para las válvulas 7 y 8, hasta los 1200
minutos se tienen variaciones del 5%.
Figura 107. Comportamiento de los caudales frente al cierre de la válvula 1 al 95%.
PRESIÓN
Al observar la Figura 108 se encuentra que las presiones de las válvulas de la 1 a la 6,
tienen variaciones mayores al 50%. Sin embargo, es interesante que las señales de la
presión presentan cambios más graduales de los encontrados en el comportamiento del
caudal. A pesar de esto se encuentra que las variaciones que son generadas por la válvula
1 son relevantes, mostrando así que la válvula 1 es de alta relevancia en la red. Respecto
al tiempo de estabilización se encuentra que para todas las válvulas, salvo la válvula 7, se
estabilizan a los 600 minutos. De esta manera, para el cierre de la válvula 1 al 95%, las
presiones se estabilizan en un menor tiempo que los caudales.
Tiempo (min)
0
500
1000
1500
C
a
u
d
a
l
R
e
s
p
e
c
to
a
l
V
a
lo
r
In
ic
ia
l
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
Comportamiento del caudal frente el cierre de la válvula 1
P-7:Válvula 1
P-8:Válvula 2
P-9:Válvula 3
P-10:Válvula 4
P-11:Válvula 5
P-12:Válvula 6
P-13:Válvula 7
P-10:Válvula 8
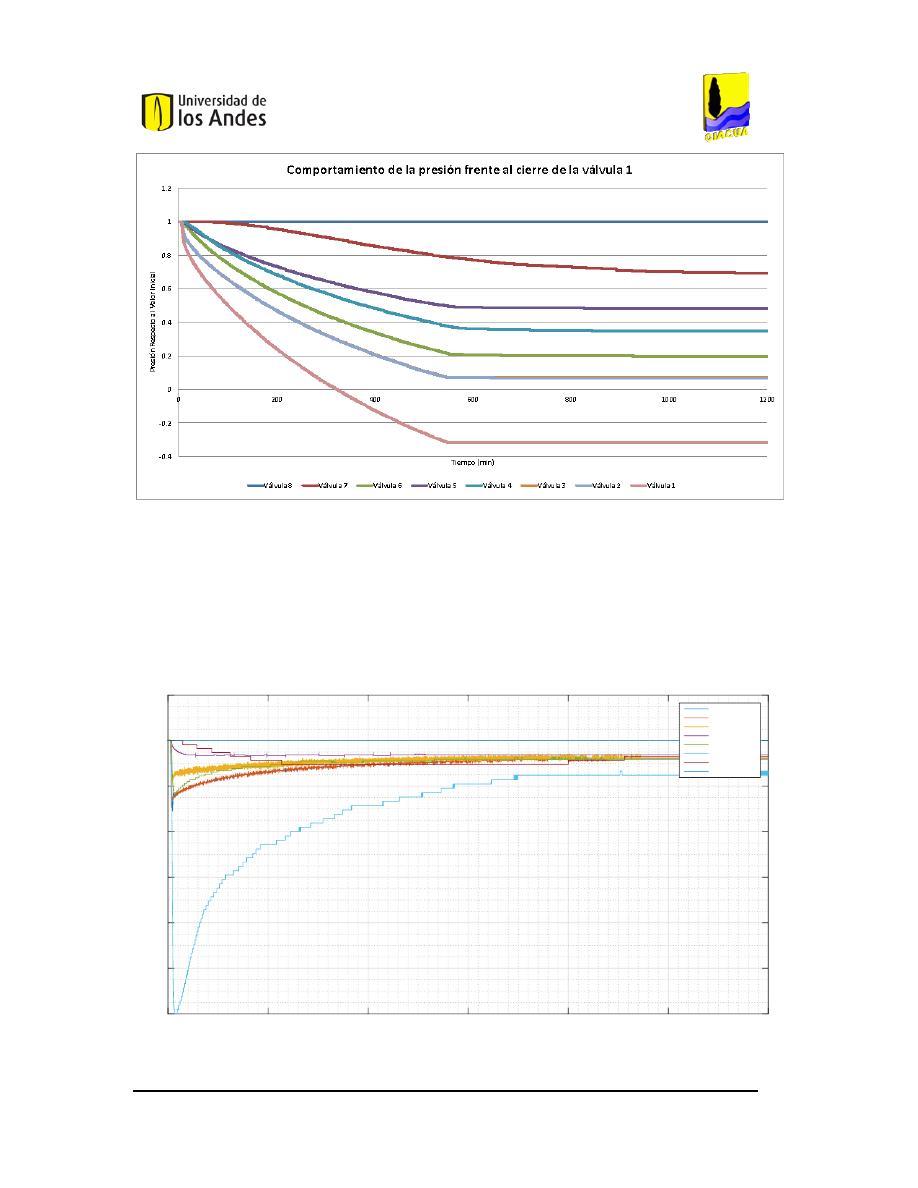
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
93
Figura 108. Comportamiento de las presiones frente al cierre de la válvula 1 al 95%.
7.2.2.1.2.
Válvula 2
CAUDAL
Al observar la Figura 109 se puede ver la alta similitud que tienen las señales generadas
por la operación de la válvula 1 con la 2. Situación que es lógica pues, ésta última se
encuentra aguas abajo de la primera válvula, sobre la tubería que alimenta a toda la red.
Sin embargo, es relevante mencionar que no se da el incremento a los 500 minutos, el
cual se presentaba en la válvula anterior.
Figura 109. Comportamiento de los caudales frente al cierre de la válvula 2 al 95%.
Tiempo (min)
0
200
400
600
800
1000
1200
C
a
u
d
a
l
R
e
s
p
e
c
to
a
l
V
a
lo
r
In
ic
ia
l
-2
-1.5
-1
-0.5
0
0.5
1
1.5
Comportamiento del caudal frente al cierre de la válvula 2
P-7:Válvula 1
P-8:Válvula 2
P-9:Válvula 3
P-10:Válvula 4
P-11:Válvula 5
P-12:Válvula 6
P-13:Válvula 7
P-10:Válvula 8
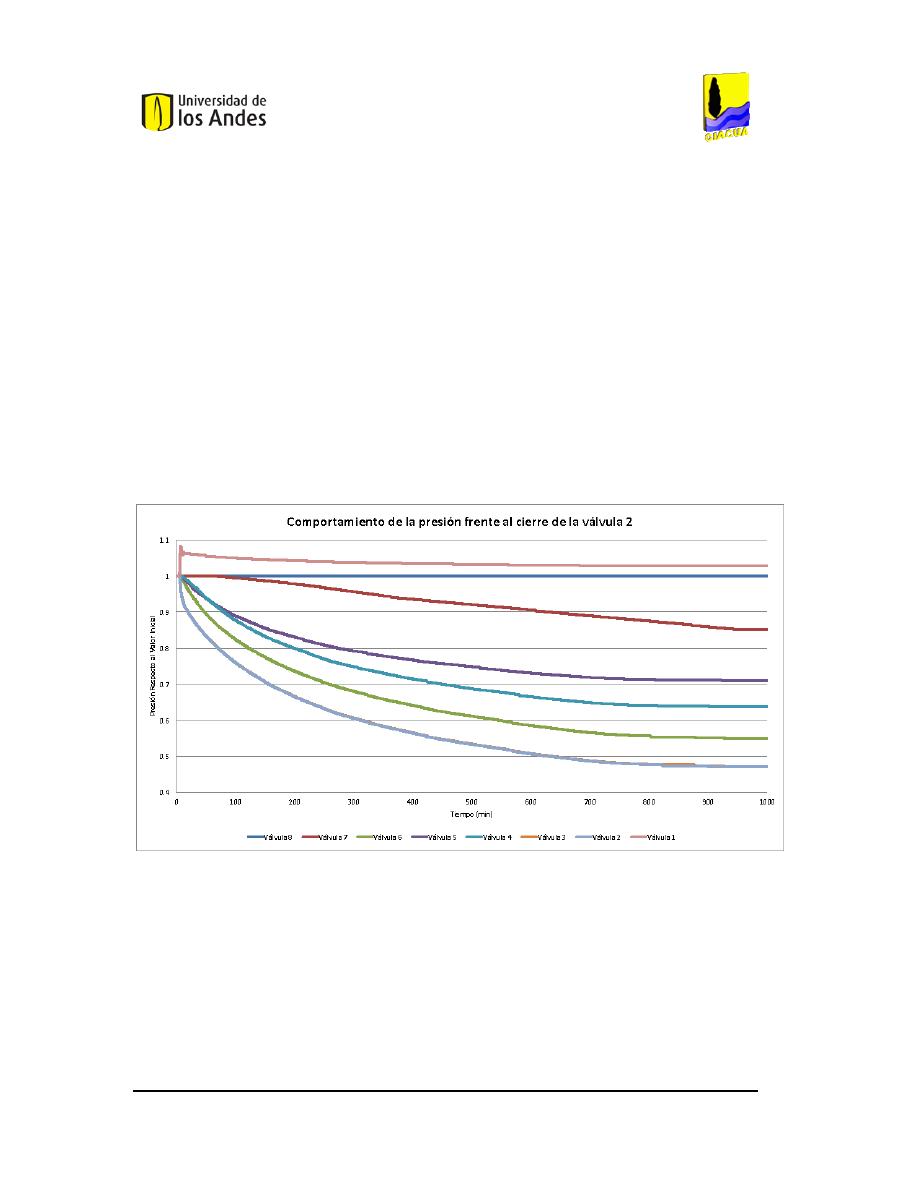
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
94
En la figura anterior se encuentra que a los 750 minutos, la red encuentra nuevamente un
estado estable. Esta situación llama la atención pues entre la válvula 1 y la válvula 2 no
existe ninguna demanda; sin embargo, el tiempo de estabilización se ve disminuido. Por
lo tanto, se podría establecer que entre más aguas abajo se encuentra la válvula, menor es
el tiempo de estabilización después de la operación de ésta.
PRESIÓN
En la Figura 110 se encuentra el comportamiento de las presiones frente al cierre del 95%
de la válvula 2. En ella se puede ver que existe un incremento de la presión en la válvula
1, situación que es coherente pues este punto recibe la onda que viaja aguas arriba. Sin
embargo, a pesar de esto, la sobrepresión que se presenta después del cierre de la válvula
2, es menor al 10% de la presión inicial. Respecto al tiempo de estabilización se
encuentra que la red requiere de 800 minutos para estabilizarse en su mayor parte. Para
que estabilice por completo se requiere de 950 minutos, a causa del comportamiento
encontrado en la válvula 7. Sin embargo, se debe tener en cuenta que ésta última
abastece un caudal de 23 L/s, sustancialmente menor al de las válvulas principales que
distribuyen un caudal de hasta 324 L/s.
Figura 110. Comportamiento de las presiones frente al cierre de la válvula 2 al 95%.
7.2.2.1.3.
Válvula 3
CAUDAL
En la Figura 111 se encuentra que la operación de la válvula 3 perturba
significativamente la red. Sin embargo, es mucho menor que las dos válvulas anteriores
que eran capaces de cambiar la dirección de flujo en un punto. Es relevante mencionar
que a pesar de lo anterior, esta válvula es capaz de incrementar los caudales de las
válvulas 5 y 6 en un 90% y 45%, respectivamente.
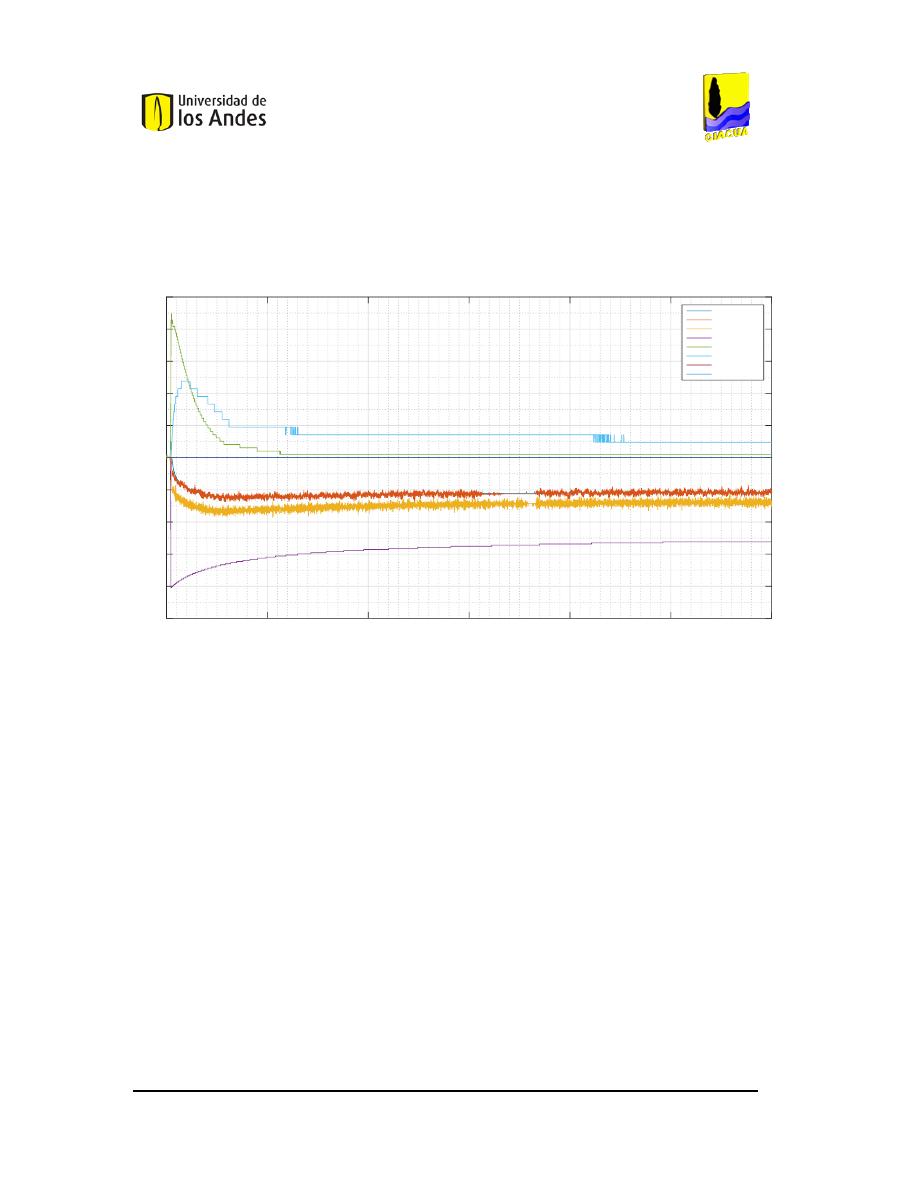
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
95
Respecto al tiempo de estabilización se puede decir que la red requiere de 330 minutos
para su completa estabilización. Este tiempo es establecido principalmente por el
comportamiento que tiene la tubería adyacente a la válvula 4, la cual transporta un caudal
de 147 L/s. De esta manera, a pesar de que las tuberías principales se estabilicen
alrededor de los 150 minutos, la válvula 4 hace que la red se tome una mayor cantidad de
tiempo pues su caudal es considerable.
Figura 111. Comportamiento de los caudales frente al cierre de la válvula 3 al 95%.
PRESIÓN
En la Figura 112 se encuentra que el cierre de la válvula 3 genera un incremento de
presión en la mayoría de la red. Sin embargo, éste es menor al 6% lo cual no presenta
ningún riesgo para el sistema. Por otra parte, se puede ver que las señales de todas las
válvulas, a excepción de la 3, se estabilizan en menos de 45 minutos. Es relevante
mencionar que si se acepta que una variación del 2% se considera que la red es estable, el
tiempo de estabilización para estos puntos no sería de 45 minutos sino de 20 minutos.
Por otra parte, para la presión reportada en el punto de la válvula 3, se encuentra que se
requieren de 500 minutos para que llegue a estabilizarse. Adicionalmente, es llamativo
que la presión en este punto llega a ser del 3% del valor inicial.
Tiempo (min)
0
100
200
300
400
500
600
C
a
u
d
a
l
R
e
s
p
e
c
to
a
l
V
a
lo
r
In
ic
ia
l
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
Comportamiento del caudal frente al cierre de la válvula 3
P-7:Válvula 1
P-8:Válvula 2
P-9:Válvula 3
P-10:Válvula 4
P-11:Válvula 5
P-12:Válvula 6
P-13:Válvula 7
P-10:Válvula 8
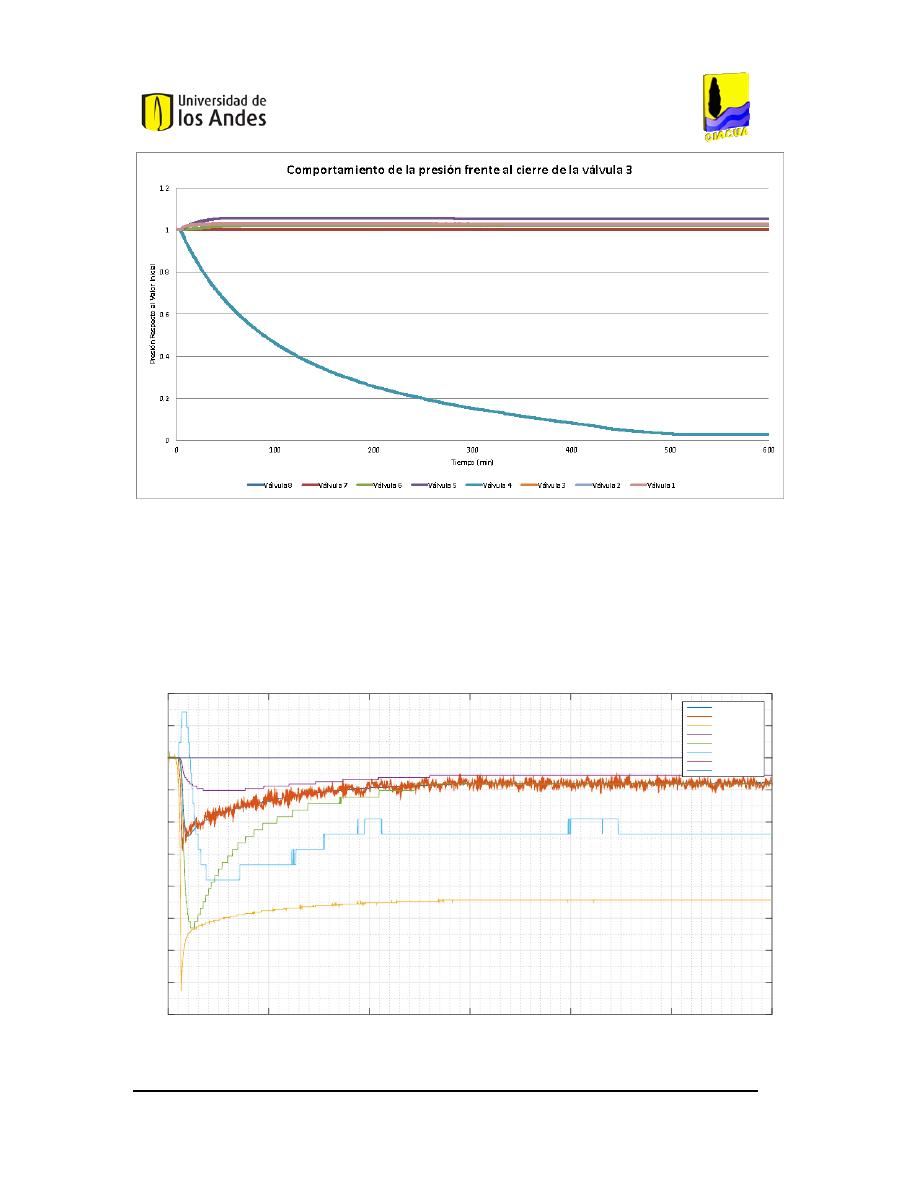
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
96
Figura 112. Comportamiento de las presiones frente al cierre de la válvula 3 al 95%.
7.2.2.1.4.
Válvula 4
CAUDAL
Al observar la Figura 113 se encuentra que la operación de la válvula 4 tiene un menor
efecto que el de las válvulas presentadas anteriormente. Sin embargo, es relevante que la
operación de ésta válvula afecta de manera dramática el comportamiento del caudal de la
válvula 3. Es tal la perturbación que hace que el caudal llegue a ser menor al 30% del
flujo inicial.
Figura 113.Comportamiento de los caudales frente al cierre de la válvula 4 al 95%.
Tiempo (min)
0
50
100
150
200
250
300
C
a
u
d
a
l
R
e
s
p
e
c
to
a
l
V
a
lo
r
In
ic
ia
l
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
Comportamiento del caudal frente al cierre de la válvula 4
P-7:Válvula 1
P-8:Válvula 2
P-9:Válvula 3
P-10:Válvula 4
P-11:Válvula 5
P-12:Válvula 6
P-13:Válvula 7
P-10:Válvula 8
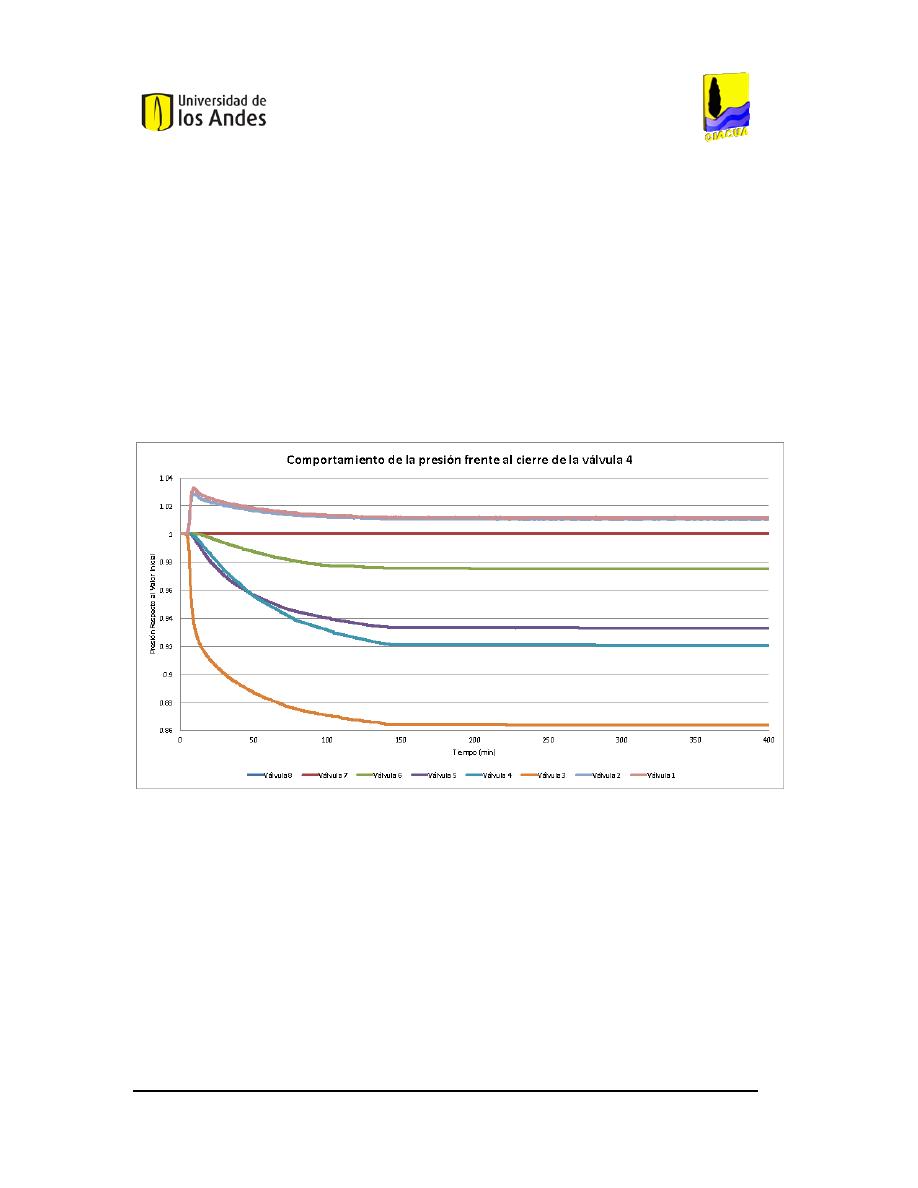
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
97
Respecto al tiempo de estabilización se encuentra una alta disminución en comparación
con el caso anterior. Para este escenario se establece que la red requiere de 100 minutos
para encontrar una nueva situación estable.
PRESIÓN
Al observar el comportamiento de la presión en la Figura 114 se encuentra que la
operación de la válvula 4 hace que exista una sobrepresión en dos puntos de la red. Sin
embargo, se debe tener en cuenta que ésta es menor al 4%. Similar a los caudales, se
encuentra que el operar esta válvula tiene efectos importantes en la válvula 3. Respecto
al tiempo de estabilización se encuentra que la red requiere de 150 minutos para
estabilizarse en su totalidad. De esta manera, se encuentra que para este caso, las
presiones requieren de una mayor cantidad de tiempo para encontrar un nuevo estado
estable.
Figura 114.Comportamiento de las presiones frente al cierre de la válvula 4 al 95%.
7.2.2.1.5.
Válvula 5
CAUDAL
Al observar la Figura 115 se encuentra que para las tuberías principales, la operación de
la válvula 5 no genera una alta variación, pues la variación es menor al 7.5%.
Adicionalmente, la operación de esta válvula solo afecta significativamente (75% de
variación) el caudal que es transportado por la tubería adyacente a la válvula operada.
Respecto al tiempo de estabilización se encuentra que la red requiere de 500 minutos, a
causa de la tubería de la válvula 5. Sin embargo, si se tiene en cuenta solo las tuberías
principales y, además, se asume un estado estable cuando las variaciones son menores al
2%, se encuentra que el tiempo de estabilización es de 20 minutos.
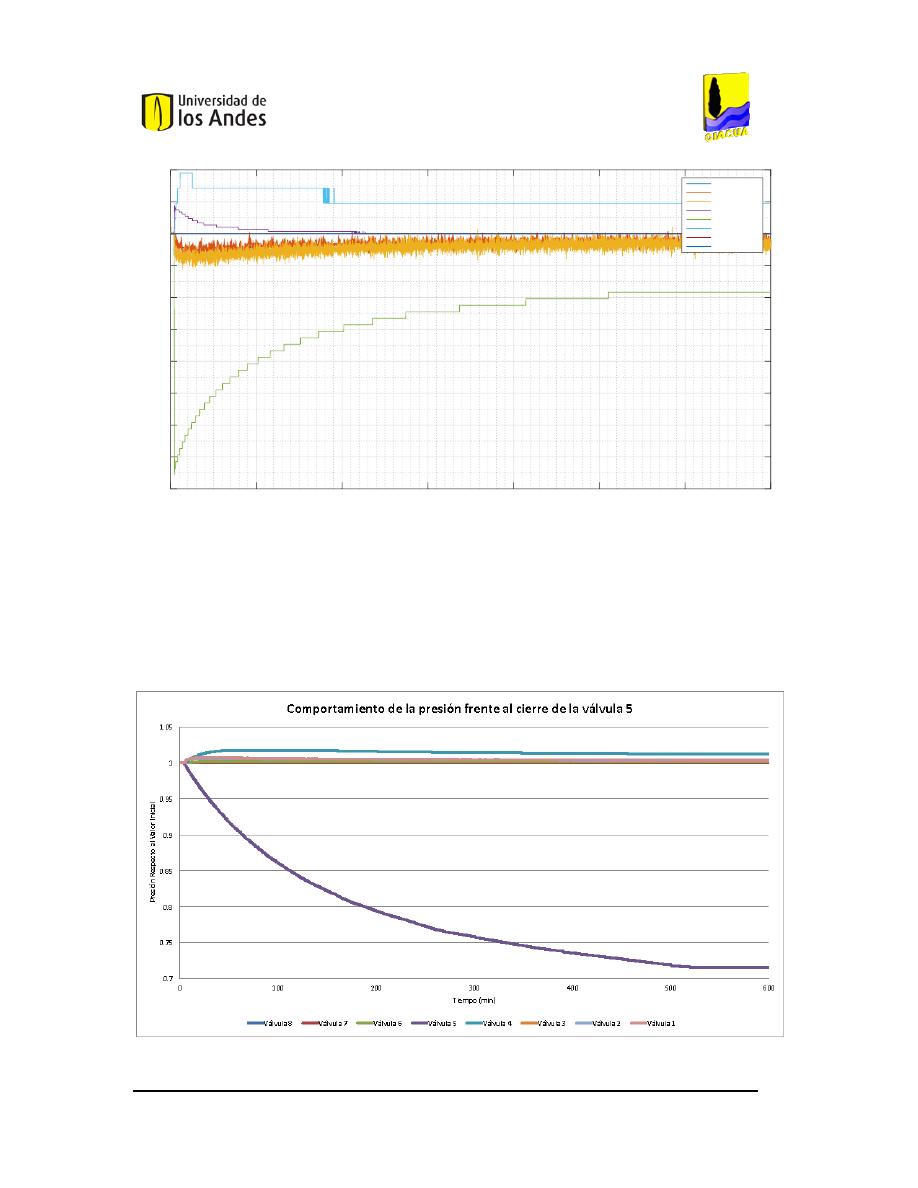
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
98
Figura 115. Comportamiento de los caudales frente al cierre de la válvula 5 al 95%.
PRESIÓN
En la Figura 116 se encuentra que la operación de la válvula 5 genera una sobrepresión
en la mayoría de la red, sin embargo, esta llega a ser menor al 2%. Respecto al tiempo de
estabilización se encuentra que para la mayoría de la red se puede establecer que la red se
estabiliza en un tiempo muy corto. Sin embargo, si se toma en cuenta solo el
comportamiento que tiene la presión en la válvula 5, se encuentra que se requiere de 500
minutos para la estabilización.
Figura 116. Comportamiento de las presiones frente al cierre de la válvula 5 al 95%.
Tiempo (min)
0
100
200
300
400
500
600
700
C
a
u
d
a
l
R
e
s
p
e
c
to
a
l
V
a
lo
r
In
ic
ia
l
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
Comportamiento del caudal frente al cierre de la válvula 5
P-7:Válvula 1
P-8:Válvula 2
P-9:Válvula 3
P-10:Válvula 4
P-11:Válvula 5
P-12:Válvula 6
P-13:Válvula 7
P-10:Válvula 8
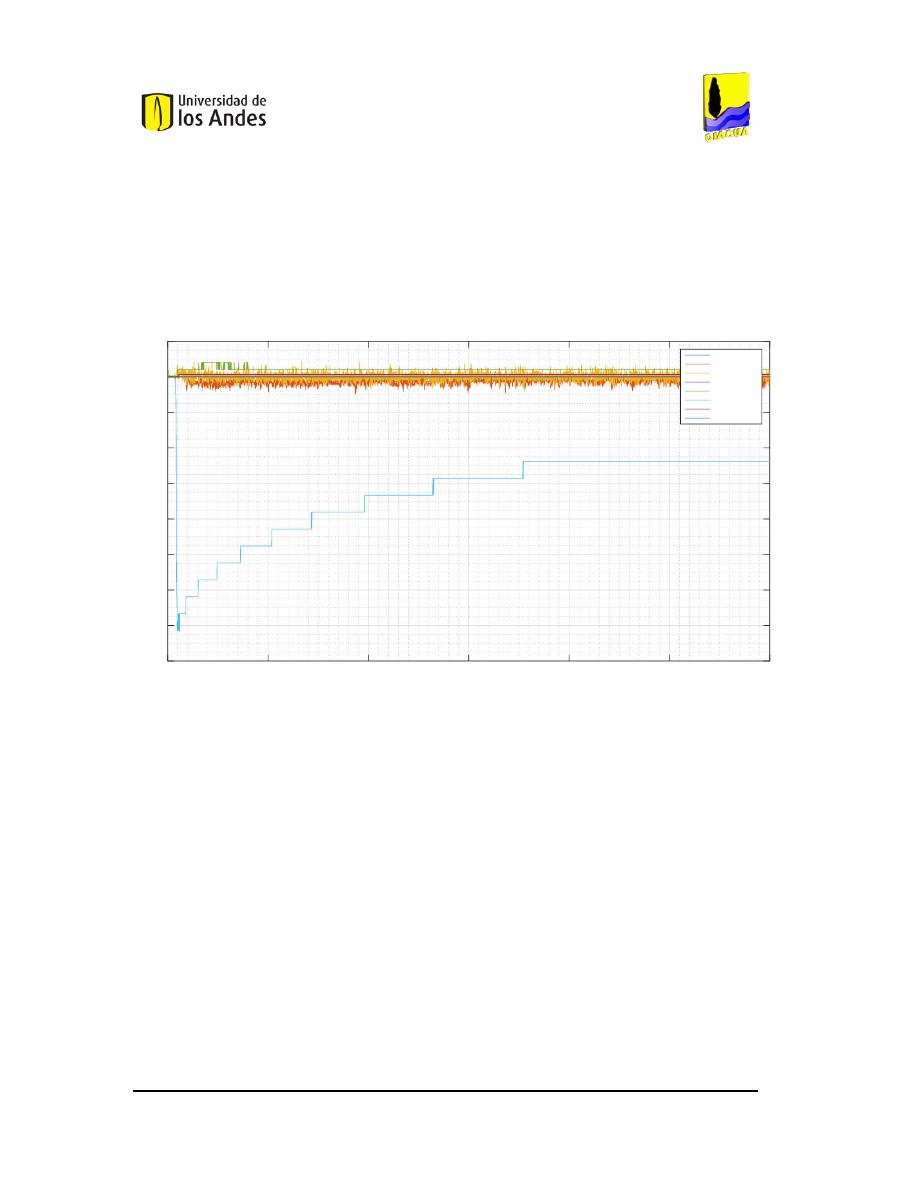
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
99
7.2.2.1.6.
Válvula 6
CAUDAL
A partir de la Figura 117 se encuentra que la operación de la válvula 6 no tiene relevancia
ni genera cambios en los demás puntos de la red. De esta manera, se establece que la red
se estabiliza de manera inmediata. Es relevante mencionar que bajo la operación
realizada, el caudal de la válvula 6 requiere de 170 minutos para encontrar un nuevo
estado estable.
Figura 117. Comportamiento de los caudales frente al cierre de la válvula 6 al 95%.
PRESIÓN
Al revisar la Figura 118 se encuentra que el operar esta válvula genera un aumento de la
presión en el resto de la red; sin embargo, este es despreciable pues es menor al 0.5%.
Adicionalmente, se puede observar que solo se ve afectado la presión de la válvula 6.
Respecto al tiempo de estabilización se encuentra que la red tiene la capacidad de
encontrar un nuevo estado estable inmediatamente, pues la perturbación generada por la
válvula es muy baja.
Tiempo (min)
0
50
100
150
200
250
300
C
a
u
d
a
l
R
e
s
p
e
c
to
a
l
V
a
lo
r
In
ic
ia
l
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
Comportamiento del caudal frente al cierre de la válvula 6
P-7:Válvula 1
P-8:Válvula 2
P-9:Válvula 3
P-10:Válvula 4
P-11:Válvula 5
P-12:Válvula 6
P-13:Válvula 7
P-10:Válvula 8
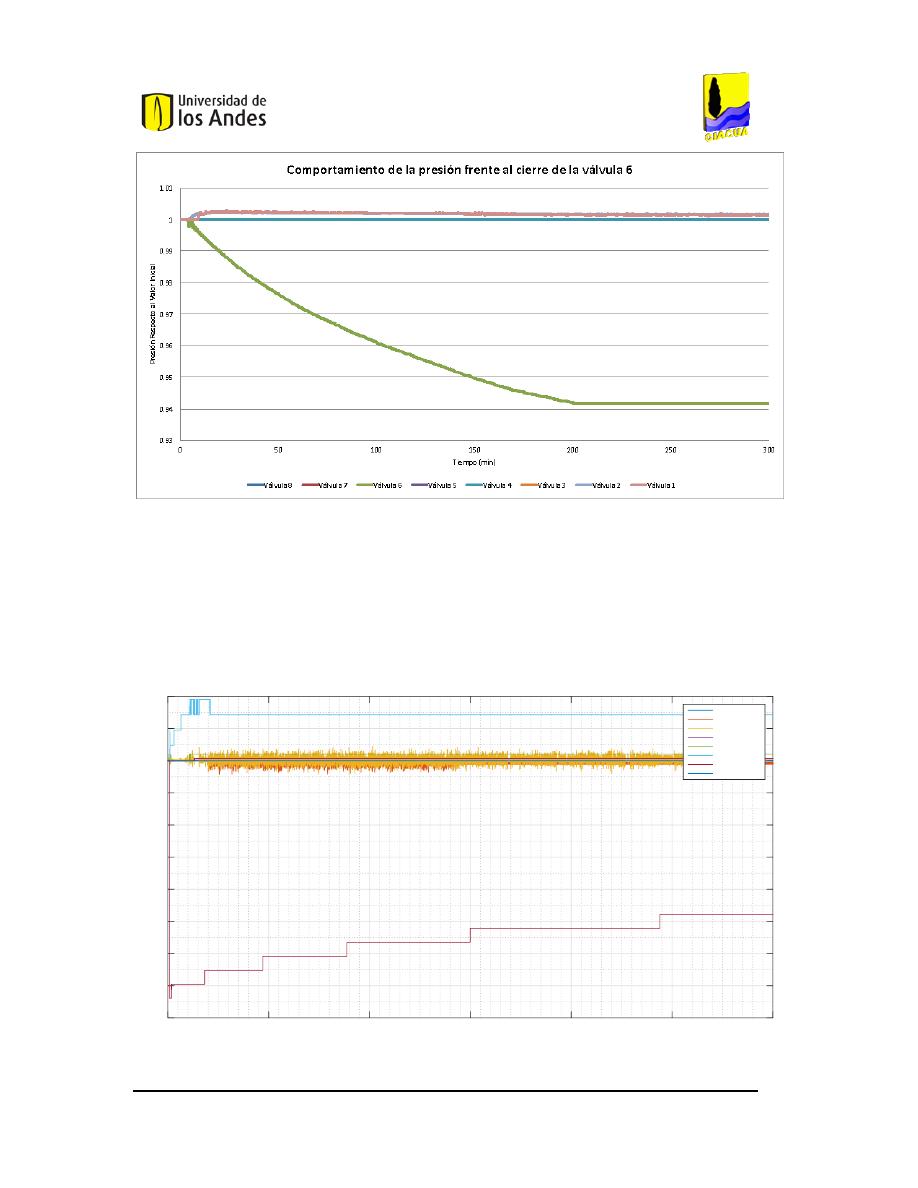
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
100
Figura 118. Comportamiento de las presiones frente al cierre de la válvula 6 al 95%.
7.2.2.1.7.
Válvula 7
CAUDAL
Al observar la Figura 119 se encuentra que la operación de la válvula 7 no genera
cambios drásticos en términos de caudal en la red. Se observa que las tuberías
adyacentes a las válvulas 6 y 7 son las únicas que presentan variación en los caudales.
Teniendo en cuenta los bajos caudales de estas tuberías, y que las demás tuberías no se
ven afectadas por la operación, se establece que la red se estabiliza instantáneamente.
Figura 119. Comportamiento de los caudales frente al cierre de la válvula 7 al 95%.
Tiempo (min)
0
200
400
600
800
1000
1200
C
a
u
d
a
l
R
e
s
p
e
c
to
a
l
V
a
lo
r
In
ic
ia
l
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
Comportamiento del caudal frente al cierre de la válvula 7
P-7:Válvula 1
P-8:Válvula 2
P-9:Válvula 3
P-10:Válvula 4
P-11:Válvula 5
P-12:Válvula 6
P-13:Válvula 7
P-10:Válvula 8
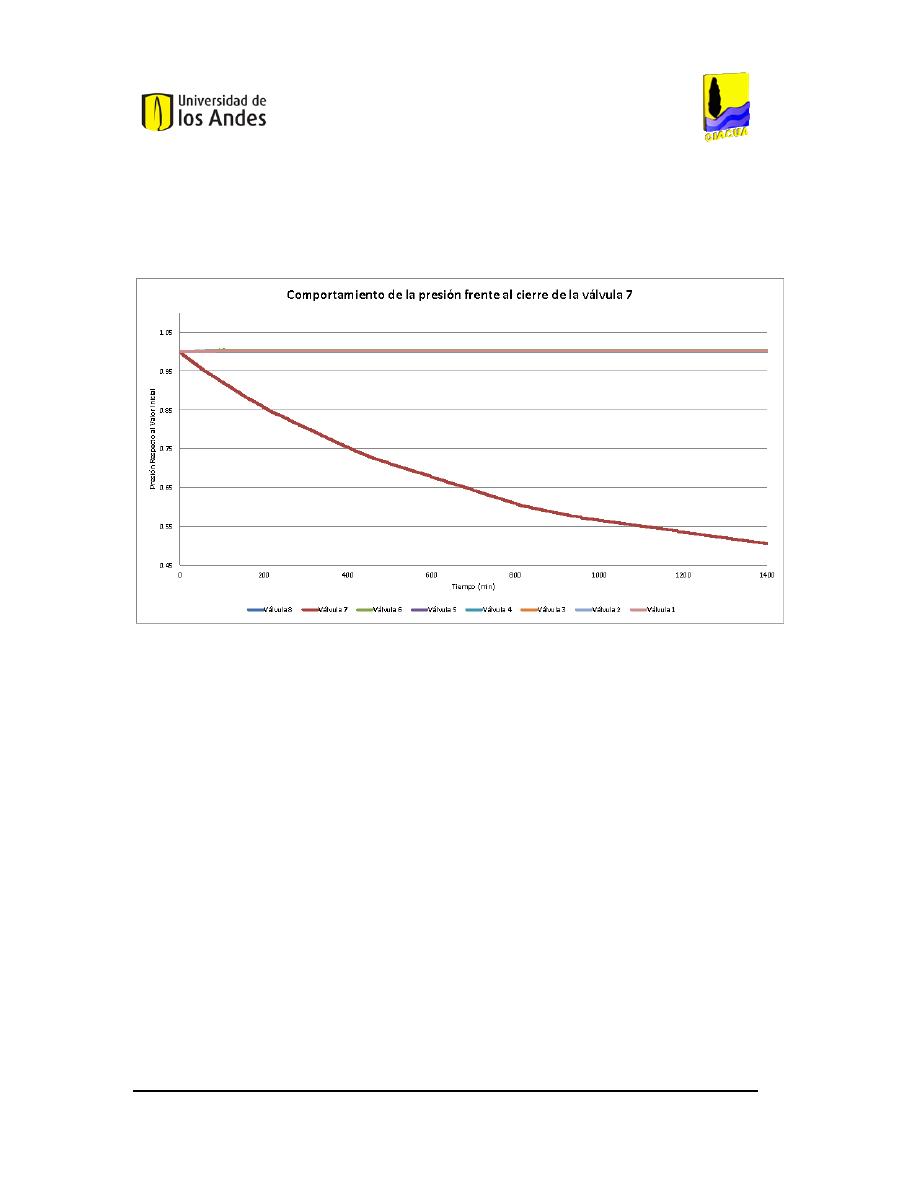
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
101
PRESIÓN
En la Figura 120 se encuentra que el operar la válvula 7 no perturba la red, pues las
presiones en los diferentes puntos de la red son menores al 1%. Sin embargo, la presión
de la válvula 7 se ve altamente afectada. Teniendo en cuenta el comportamiento general
de la red, se establece que la red se estabiliza de manera instantánea.
Figura 120. Comportamiento de las presiones frente al cierre de la válvula 7 al 95%.
7.2.2.2. Análisis de Sensibilidad
En la presente sección se presentan los resultados obtenidos de los análisis de
sensibilidad realizados. Es relevante mencionar que dada la baja relevancia que tienen
las válvulas 5, 6 y 7, se tomó la decisión de no incluirlas en esta sección. Sin embargo,
en la sección de anexos se presentan los resultados obtenidos de estas simulaciones.
7.2.2.2.1.
Válvula 1
En la presente sección se presentan los resultados obtenidos de los cierres realizados en la
válvula 1. Los resultados serán presentados en términos de caudales y presiones.
CAUDAL
En la Figura 121 se encuentran las altas variaciones que se producen al operar la válvula
1. De forma similar, se observa que el variar las longitudes de la red es un factor decisivo
para el comportamiento de la red. Incluso, llega a tener mayor relevancia el variar este
parámetro que la celeridad de la onda. Respecto al tiempo de estabilización, se encuentra
que la red original toma un tiempo de 800 minutos para estabilizarse completamente. A
diferencia, las redes en donde se modificó la longitud se encontró una reducción en los
tiempos para encontrar un nuevo estado estable. Al reducir este parámetro el tiempo de
estabilización fue de 420 minutos, y para la red que se incrementó se redujo a 25 minutos.
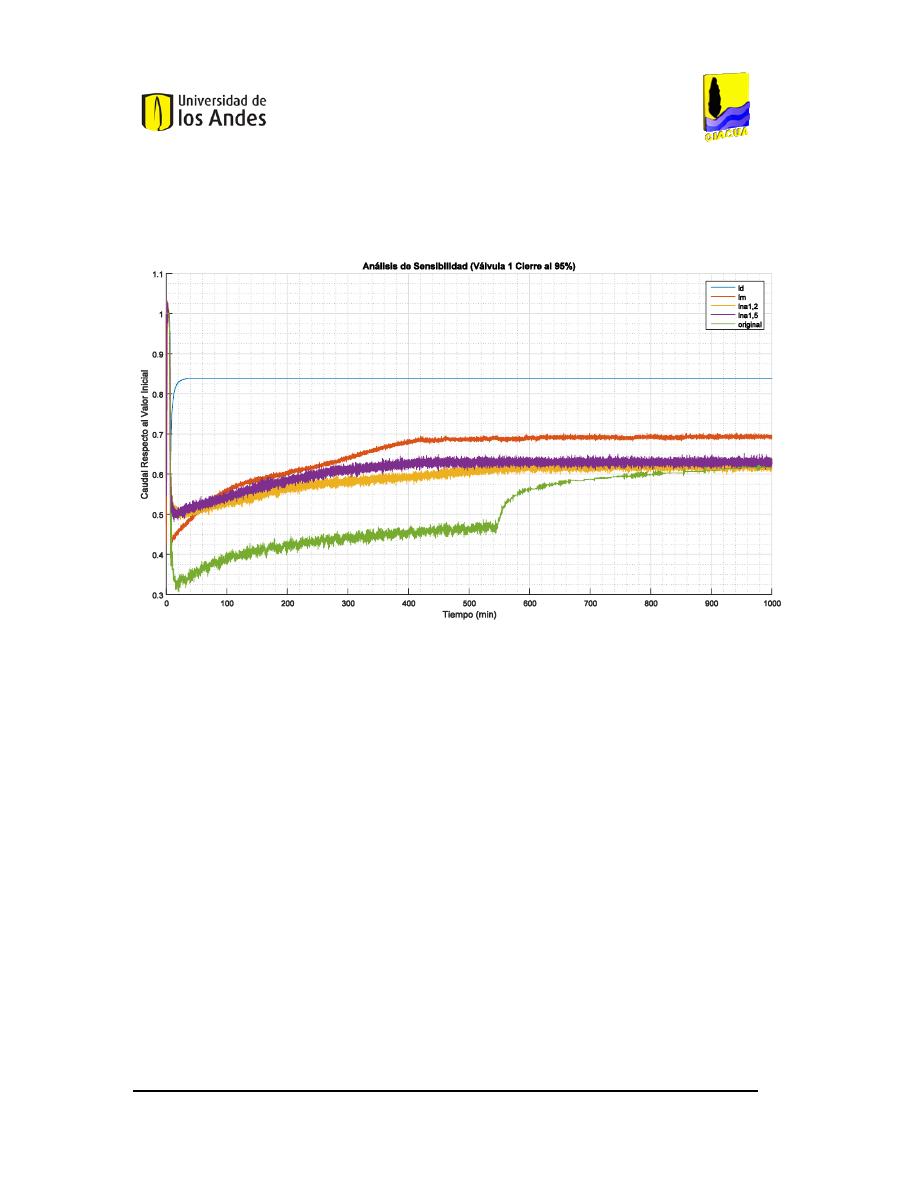
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
102
Por otra parte, si se ve el comportamiento del sistema al incrementar la celeridad de la
onda, se encuentra que a medida que ésta aumenta el tiempo de estabilización disminuye.
De esta manera, cuando la celeridad es de 1.2 veces la inicial el tiempo de estabilización
es de 550 minutos. Para el otro caso el tiempo se redujo hasta 450 minutos.
Figura 121. Análisis de sensibilidad del cierre del 95% de la válvula 1 en la red de Bucaramanga (Caudal).
Al observar la Figura 122 se presenta sólo el análisis de sensibilidad de las longitudes.
Similar al porcentaje de cierre anterior se encuentra que el duplicar la longitud de las
tuberías se disminuye el tiempo de estabilización de la red. Sin embargo, es interesante
encontrar que cuando se disminuye la longitud y se varía el porcentaje de cierre, el
resultado obtenido cambia. Es decir, el punto de estabilización de la red original en el
cierre del 95% era menor al de la red lm, situación que varía cuando el cierre se reduce a
90%.
Al analizar los tiempos de estabilización se encuentra que para la red en la que se duplica
las longitudes, el tiempo es de 16 minutos. Mientras tanto, cuando las longitudes son las
originales éste se incrementa a 220 minutos. Para la situación en que se reduce la
longitud no se puede establecer el tiempo de estabilización, pues el tiempo de simulación
es menor. Sin embargo, se puede establecer que éste es mayor a 133 minutos.
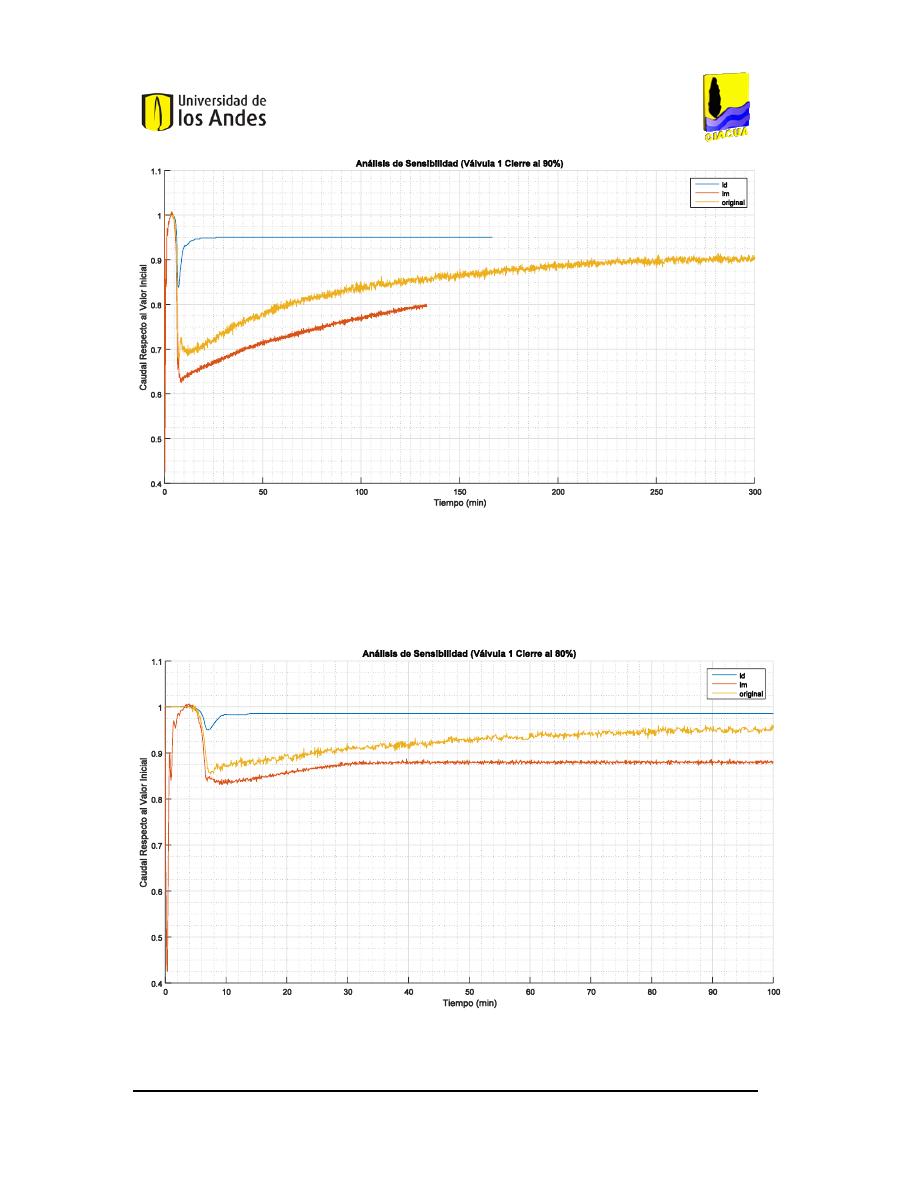
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
103
Figura 122. Análisis de sensibilidad del cierre del 90% de la válvula 1 en la red de Bucaramanga (Caudal).
En la Figura 123 se encuentran las variaciones que produjeron el cierre del 80% de la
válvula 1. En ella se puede ver que las perturbaciones se reducen de manera
significativa, llegando a tener una variación máxima menor a 20%. Respecto a los
tiempos de estabilización se encuentra nuevamente una reducción. Para las redes
original, ld y lm los tiempos fueron de 70, 10 y 30 minutos, respectivamente.
Figura 123. Análisis de sensibilidad del cierre del 80% de la válvula 1 en la red de Bucaramanga (Caudal).
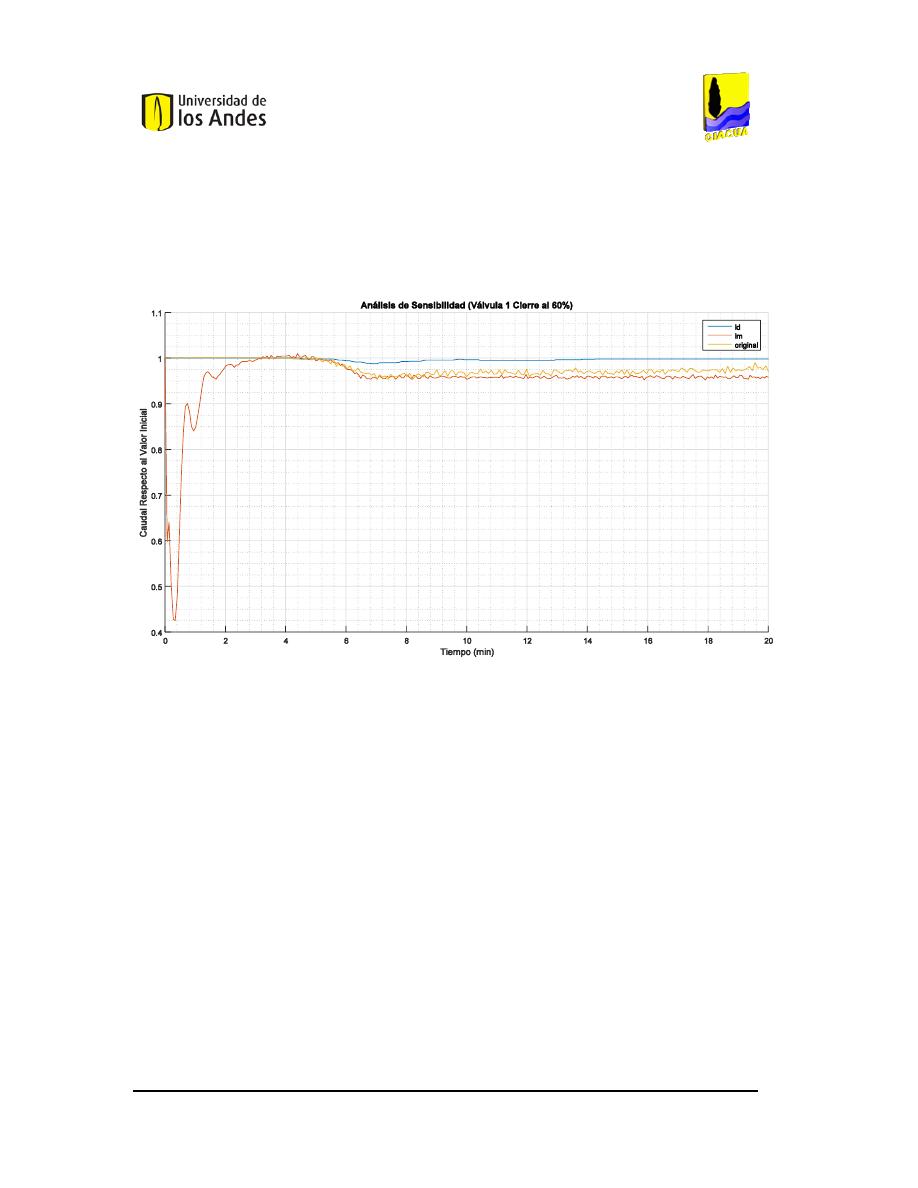
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
104
En la Figura 124 se encuentra que el reducir el porcentaje de cierre a 60%, se reducen las
variaciones del caudal. Adicionalmente, las curvaturas de las señales son menores,
haciendo que éstas sean más suaves. Respecto al tiempo de estabilización, se encuentra
que para los 3 casos es de 4 minutos después del cierre de la válvula. Es relevante
mencionar que no se presenta el cierre de 40% pues las variaciones son despreciables; sin
embargo, esta figura se presenta en la sección de anexos.
Figura 124. Análisis de sensibilidad del cierre del 60% de la válvula 1 en la red de Bucaramanga (Caudal).
PRESIÓN
En la Figura 125 se encuentra que el variar la celeridad de la onda es un parámetro
significativo para el punto de estabilización de la red. Es decir, para la Figura 121 se
puede ver que el punto de estabilización es muy similar entre las redes original, lm y ld.
Sin embargo, al observar la Figura 125 se encuentra una diferencia significativa en el
punto de estabilización de éstas. Al igual que en los caudales, el duplicar la longitud hace
que la presión se estabilice mucho más rápido que los otros casos simulados.
Al observar la estabilización se encuentra que para los casos original, lm y ld, el tiempo
fue de 900, 420 y 30 minutos, respectivamente. Para la red en la que se aumenta la
celeridad de la onda a 1.2 veces del valor original, el tiempo es de 620 minutos.
Finalmente, para el último caso simulado, el tiempo fue de 430 minutos. De esta manera
se encuentra nuevamente que el modificar la longitud es más relevante que la celeridad
de la onda.
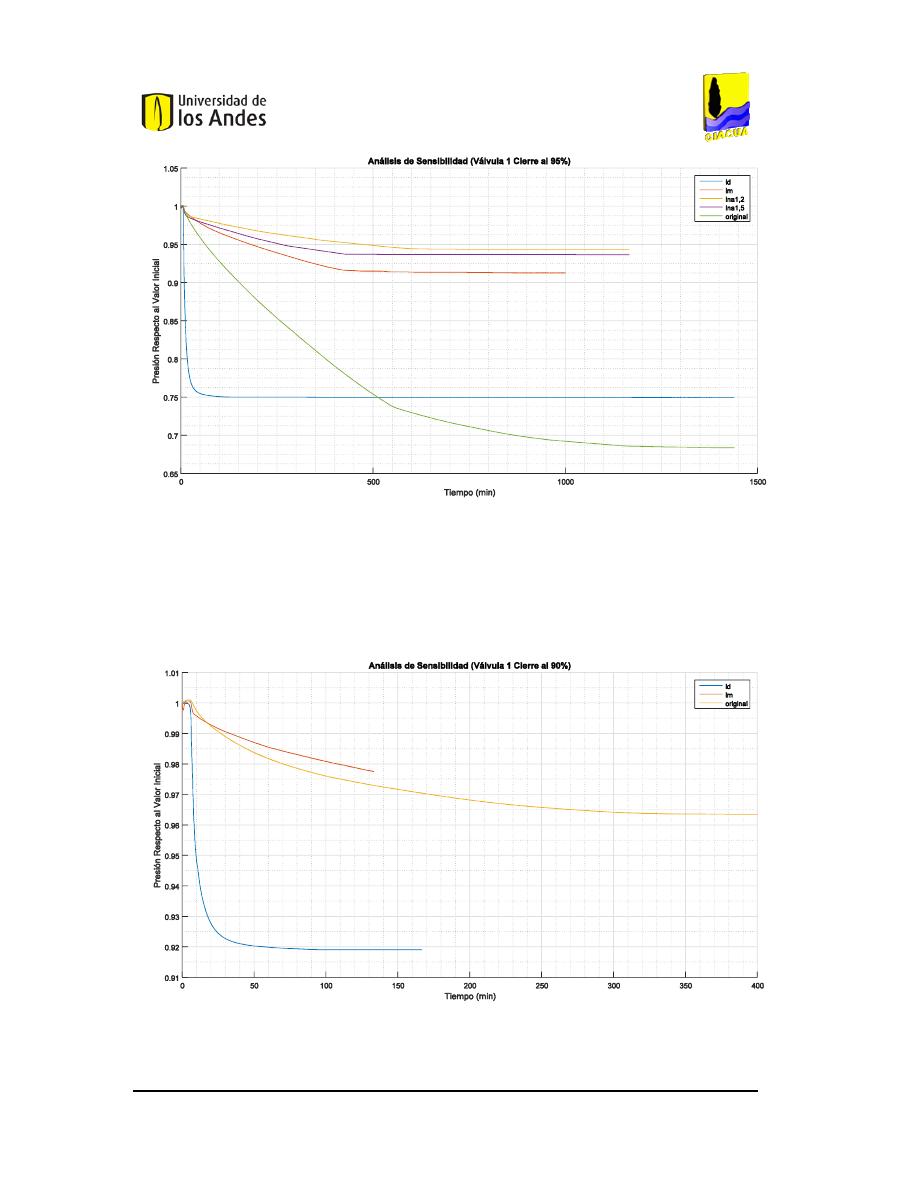
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
105
Figura 125. Análisis de sensibilidad del cierre del 95% de la válvula 1 en la red de Bucaramanga (Presión).
Al observar la Figura 126 se puede ver que para el cierre del 90% de la válvula 1, las
señales de la red original y lm tiene una gran similitud. Por otra parte, se puede ver
nuevamente que el disminuir la longitud ayuda a reducir el tiempo de estabilización.
Respecto a éste último, se encuentra que para la red original y ld, el tiempo es de 250 y
20 minutos, respectivamente. Para el último caso no se puede establecer el tiempo de
estabilización, sin embargo, se encuentra que es mayor a 133 minutos.
Figura 126. Análisis de sensibilidad del cierre del 90% de la válvula 1 en la red de Bucaramanga (Presión).
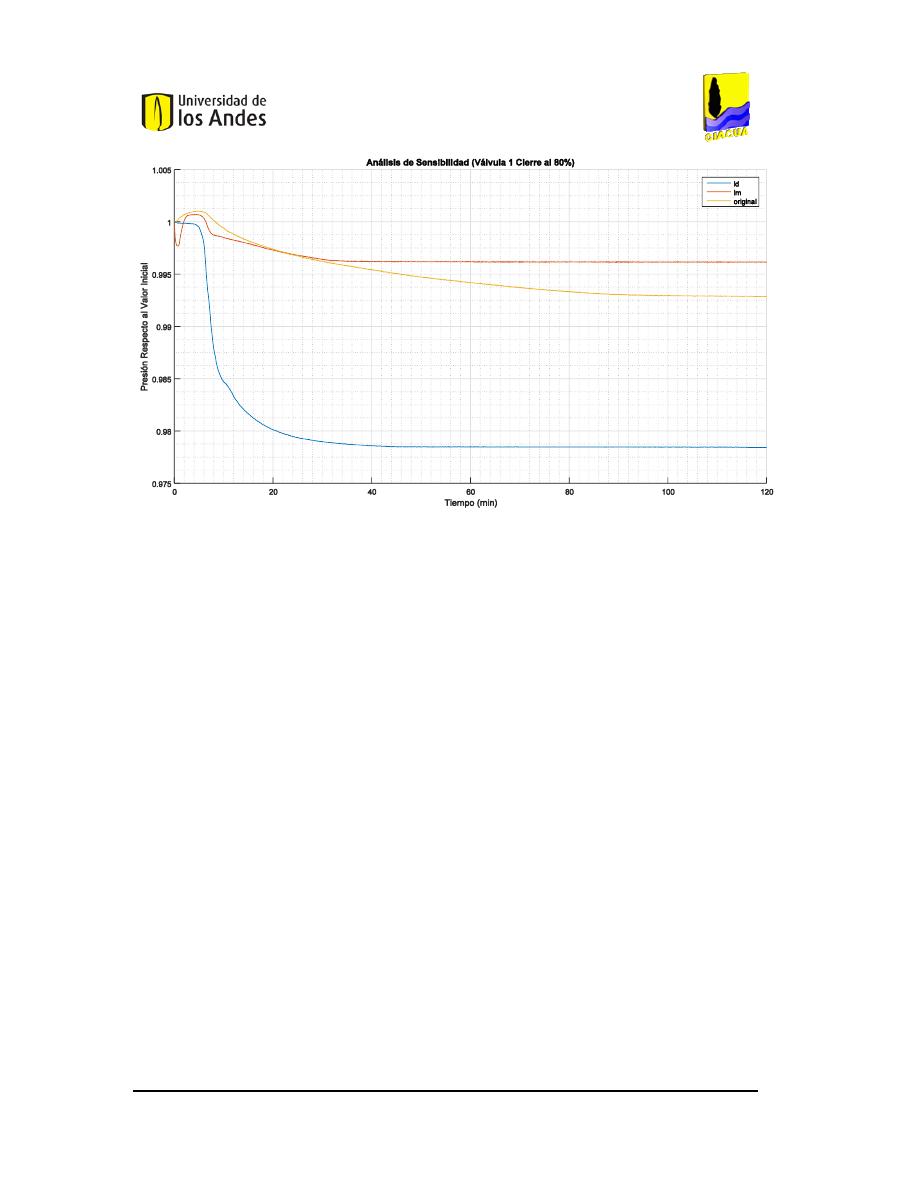
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
106
Figura 127. Análisis de sensibilidad del cierre del 80% de la válvula 1 en la red de Bucaramanga (Presión).
En la Figura 127 se encuentra que cuando el porcentaje de cierre de la válvula 1 es de
80%, la perturbación es muy baja. De tal forma, que si se supone que las variaciones del
2% o menos muestran un estado estable, se encuentra que la red se estabiliza
instantáneamente. Es necesario establecer que los cierres de 60% y 40%, muestran
variaciones menores a éstas. Por tal motivo no se presentan las figuras de éstas en la
presente sección.
7.2.2.2.2.
Válvula 2
En la siguiente sección se muestran los resultados obtenidos después de realizar
diferentes porcentajes de cierres de ésta.
CAUDAL
En la Figura 128 y Figura 121 se puede ver que, el cambiar la posición de la válvula
afecta el tiempo de estabilización y la respuesta del sistema. Se debe tener en cuenta que
las válvulas 1 y 2 están ubicadas sobre una misma serie de tuberías, la cual no tienen
ninguna demanda entre éstas. Teniendo esto en cuenta y al mirar las figuras enunciadas,
se encuentra que los puntos de estabilización de las redes son diferentes y las curvas son
más pronunciadas en el cierre de la válvula 1. Respecto a los puntos de estabilización, se
encuentra que para los casos simulados, los tiempos para encontrar un nuevo estado
estable fueron 20 (ld), 400 (lm), 500 (lna1,2), 270 (lna1,5) y 670 (original) minutos. Por
lo tanto, se encuentra que para el cierre de esta válvula, la celeridad de la onda juega un
papel de mayor relevancia, en comparación con el cierre de la válvula 1. Asimismo, se
muestra nuevamente que el duplicar la longitud de la red, disminuye de manera notoria el
tiempo de estabilización.
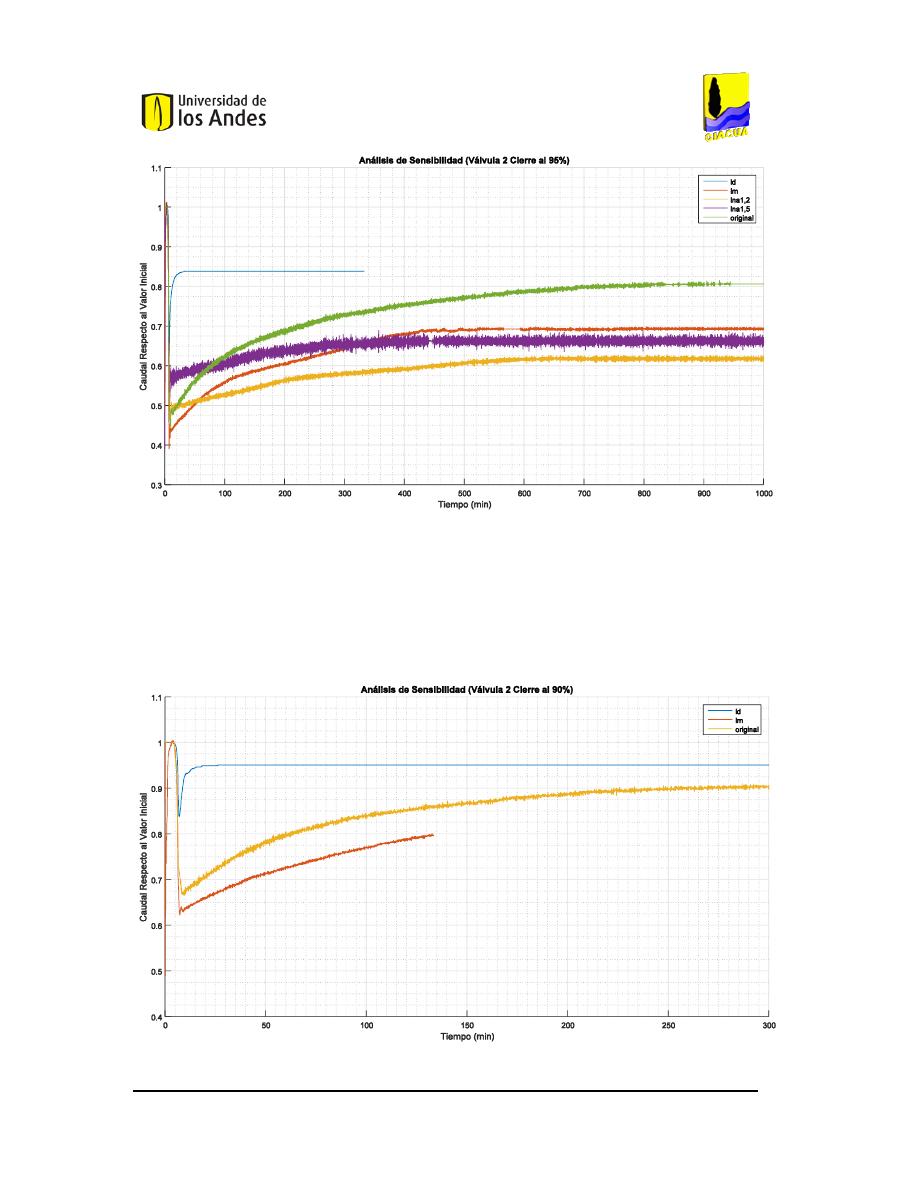
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
107
Figura 128. Análisis de sensibilidad del cierre del 95% de la válvula 2 en la red de Bucaramanga (Caudal).
Al observar la Figura 129 se encuentra que el reducir en 5% el cierre de la válvula, hace
que la perturbación a la red sea notoriamente menor. Una vez más, se encuentra que el
duplicar la longitud ayuda a la red a encontrar un estado estable en una menor cantidad de
tiempo. Los tiempos de estabilización encontrados fueron de 15 (ld) y 220 (original)
minutos. Para el último caso no se puede establecer un tiempo de estabilización pero se
puede argumentar que éste es mayor a 133 minutos.
Figura 129. Análisis de sensibilidad del cierre del 90% de la válvula 2 en la red de Bucaramanga (Caudal).
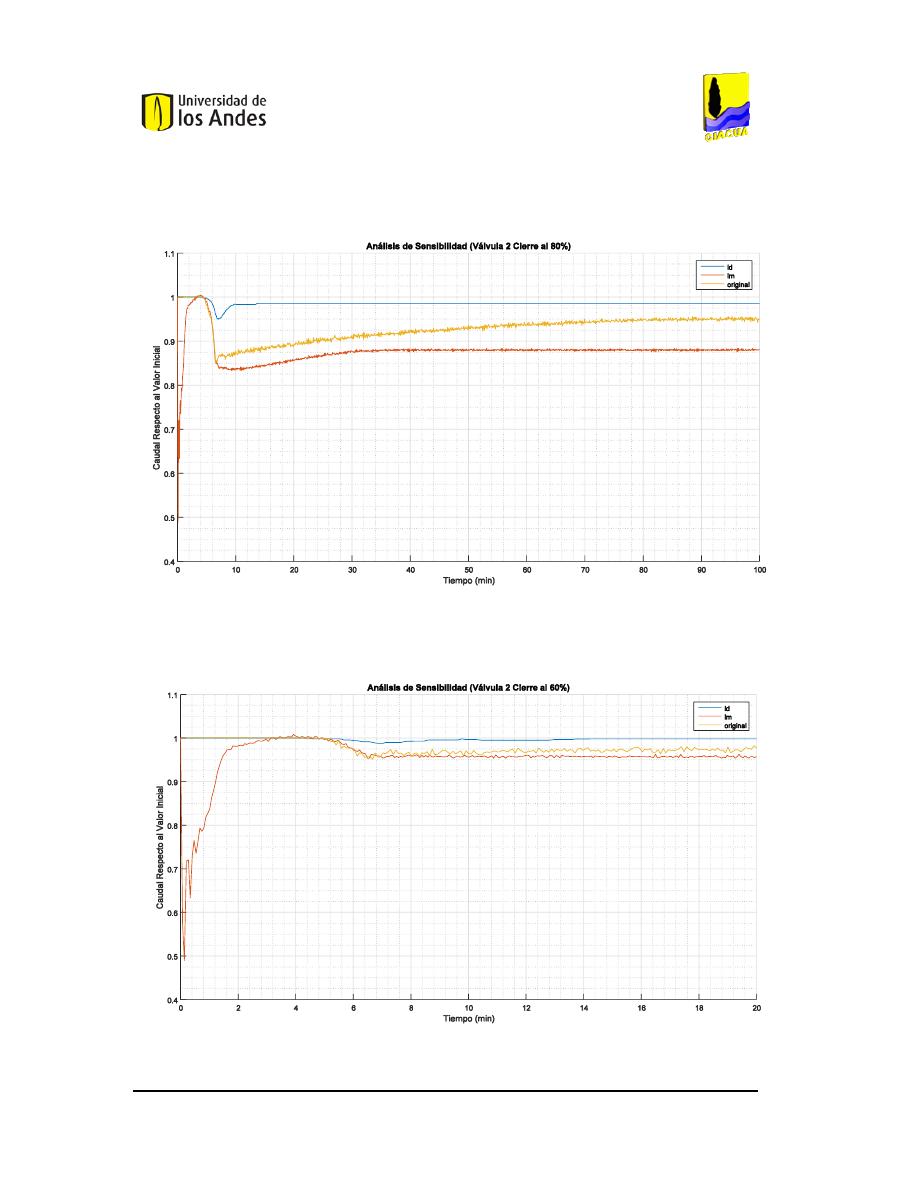
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
108
En la Figura 130, se puede ver que el reducir en 10% en el porcentaje de cierre hace que
la perturbación de la válvula disminuya en casi 20% de las variaciones. Nuevamente, se
encuentra que la estabilización de la red que tiene el doble de la longitud es la menor de
todas. Los tiempo de estabilización fueron de 9 (ld), 32 (lm) y 60 (original) minutos.
Figura 130. Análisis de sensibilidad del cierre del 80% de la válvula 2 en la red de Bucaramanga (Caudal).
En la Figura 131 se encuentra la baja variación producida por el cierre de la válvula 2.
De la misma forma, se encuentra que el tiempo de estabilización es instantáneo, pues las
variaciones encontradas son menores al 2%.
Figura 131. Análisis de sensibilidad del cierre del 60% de la válvula 2 en la red de Bucaramanga (Caudal).
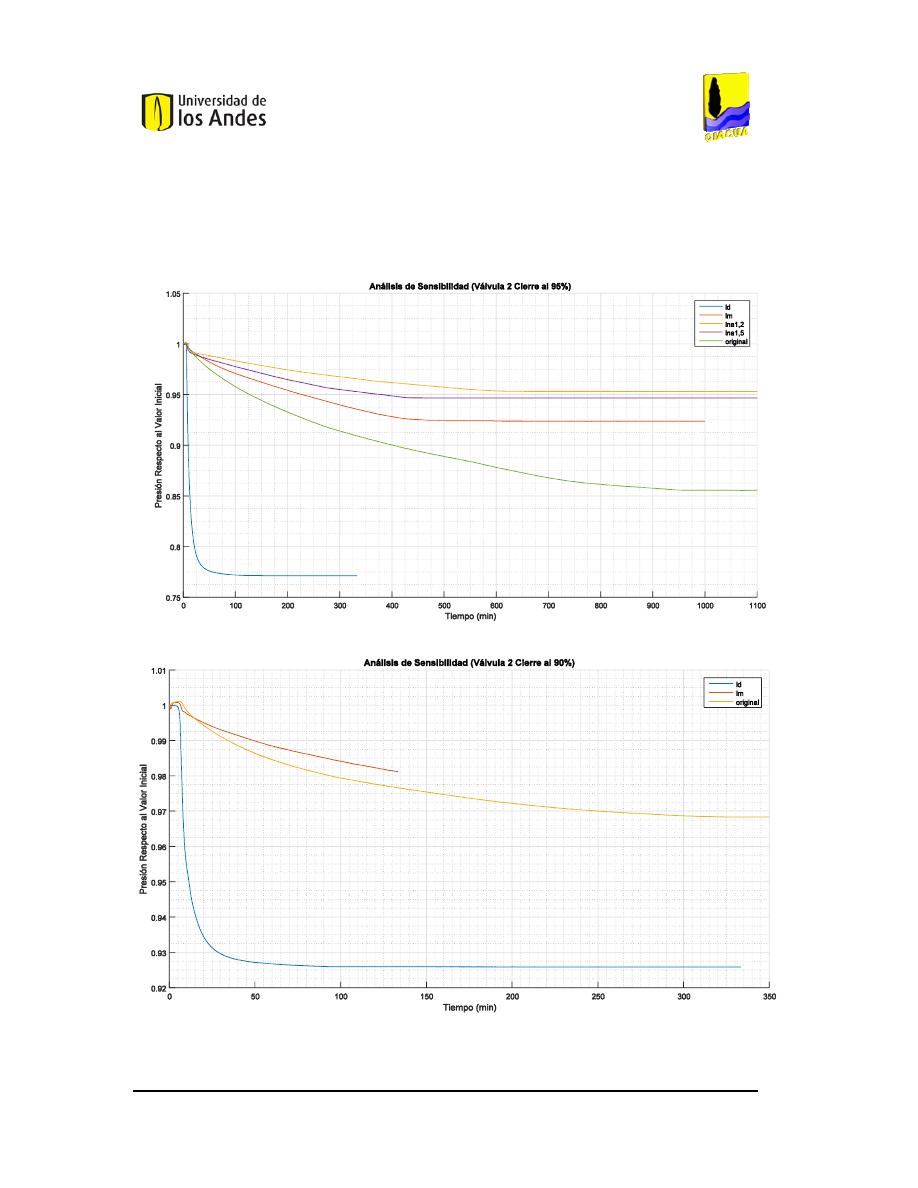
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
109
PRESIÓN
En la Figura 132 se encuentra que todas las variaciones realizadas (longitud y celeridad
de la onda) ayudaron a disminuir el tiempo de estabilización. Asimismo, se encuentra
una vez más que las variaciones en la presión son más suaves en comparación con las
encontradas en los caudales. Los tiempos de estabilización encontrados fueron 30 (ld),
340 (lm), 550 (lna1,2), 400 (lna1,5) y 1050 (original) minutos.
Figura 132. Análisis de sensibilidad del cierre del 95% de la válvula 2 en la red de Bucaramanga (Presión).
Figura 133. Análisis de sensibilidad del cierre del 90% de la válvula 2 en la red de Bucaramanga (Presión).
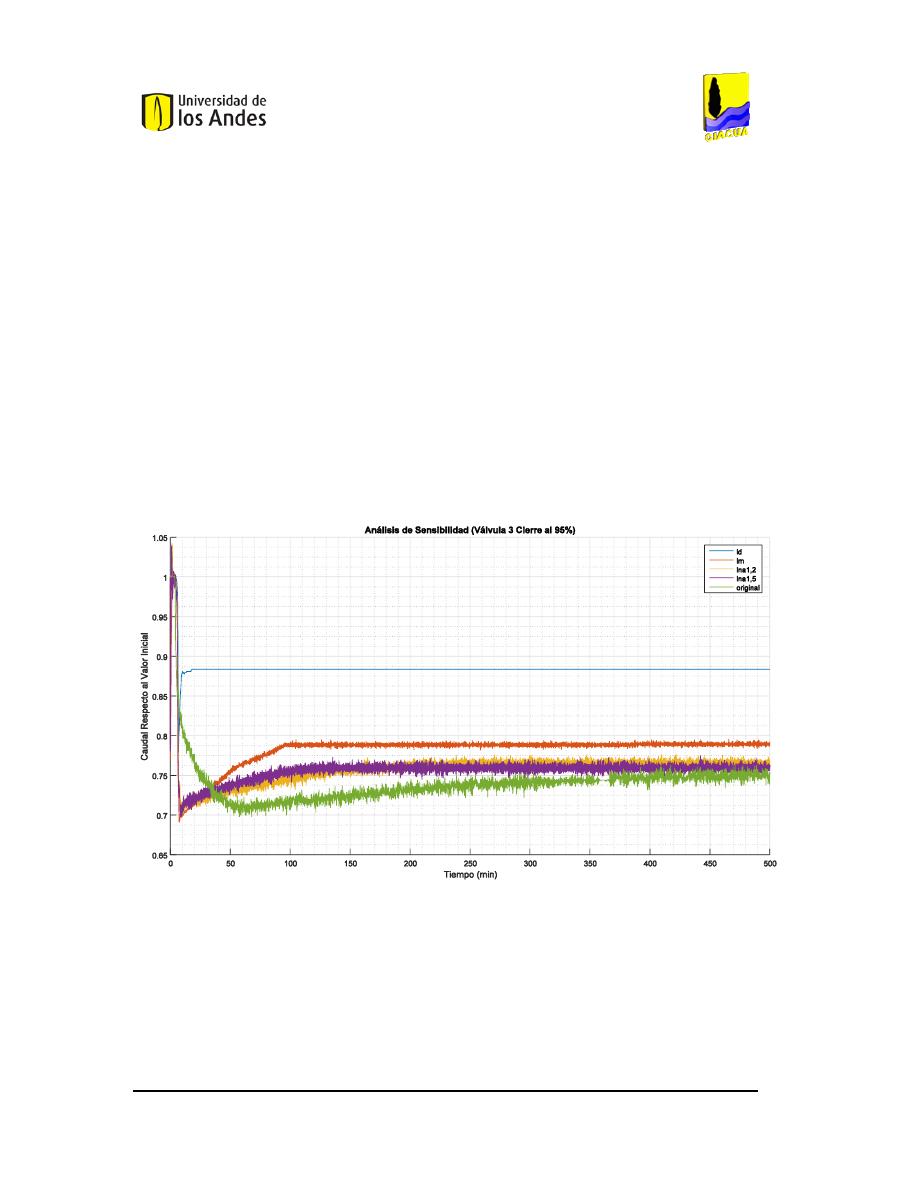
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
110
En la Figura 133 se encuentra que la reducción de 5% en el porcentaje de cierre, hace que
las variaciones se reduzcan en más de 20%. Es relevante mencionar que se genera una
sobrepresión en la red, sin embargo, el valor es menor a 0.2%. Los tiempos de
estabilización encontrados fueron 20 (ld) y 150 (original) minutos. Para el caso faltante
no se pudo establecer el tiempo. Se debe tener en cuenta que las variaciones que se
encuentran son muy bajas y dependiendo del límite que uno establezca para considerar la
estabilización, el resultado cambia.
7.2.2.2.3.
Válvula 3
En la presente sección se muestran los resultados obtenidos cuando se operó la válvula 3.
Los resultados se presentan una vez más en términos de caudal y presión.
CAUDAL
En la Figura 134 se puede ver que la variación de la celeridad de la onda no afecta de
manera drástica la respuesta del sistema frente al cierre del 95% de la válvula 3. Una vez
más se encuentra que el disminuir la longitud de las tuberías acorta el tiempo de
estabilización del sistema. Los tiempos que requirieron los diferentes casos fueron 10
(ld), 90 (lm), 130 (lna1,2), 110 (lna1,5) y 300 (original) minutos.
Figura 134. Análisis de sensibilidad del cierre del 95% de la válvula 3 en la red de Bucaramanga (Caudal).
En la Figura 135 se encuentra que el disminuir en 5% el porcentaje de cierre de la
válvula, genera que las variaciones disminuyan en 10%. Por otra parte, una vez más se
encuentra la alta influencia que tiene el modificar la longitud de las tuberías, pues esto
disminuye el tiempo de estabilización de la red. Para los casos simulados se encontró
que, para la situación original, el sistema necesita de 70 minutos para encontrar un nuevo
estado estable. Al modificar la longitud los tiempos de estabilización fueron de 6 (ld) y
40 (lm) minutos.
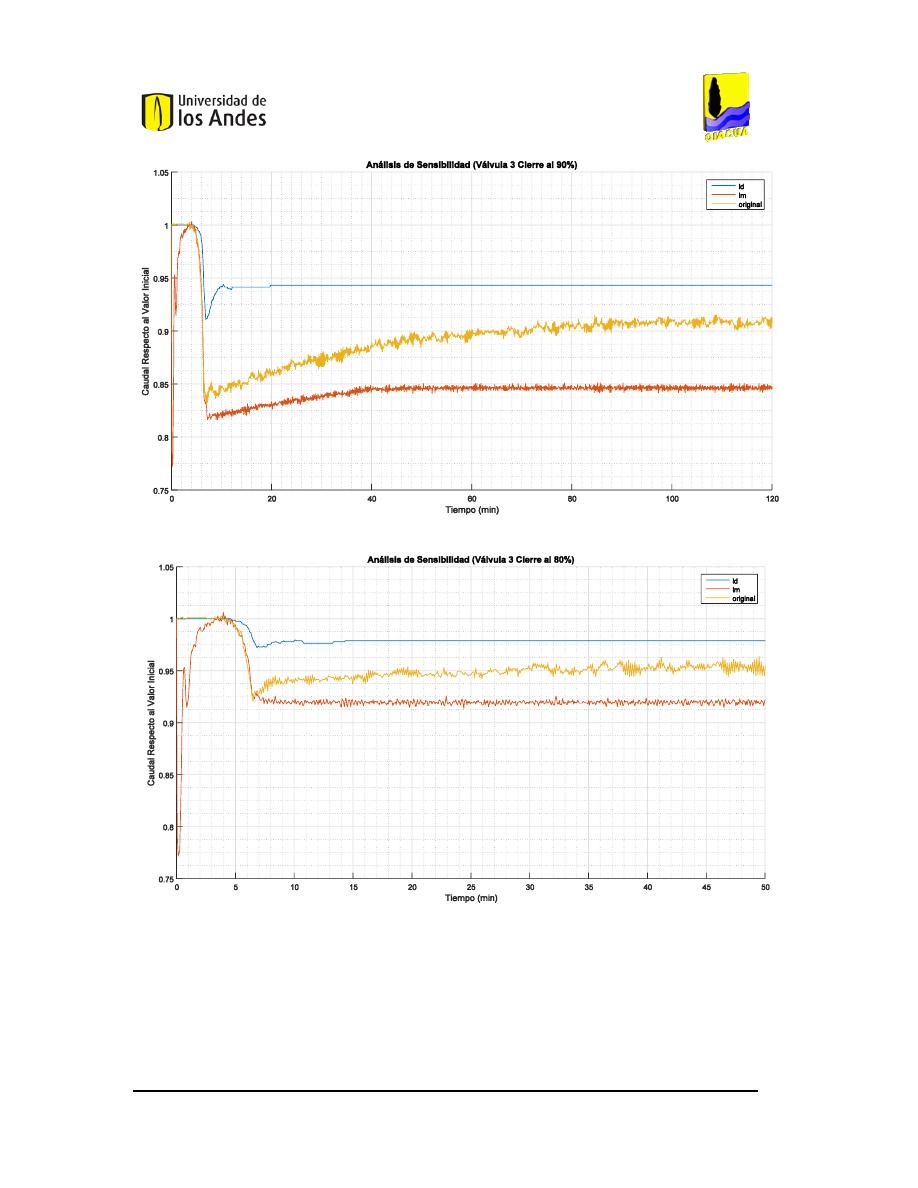
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
111
Figura 135. Análisis de sensibilidad del cierre del 90% de la válvula 3 en la red de Bucaramanga (Caudal).
Figura 136. Análisis de sensibilidad del cierre del 80% de la válvula 3 en la red de Bucaramanga (Caudal).
En la Figura 136 se puede ver que para un cierre del 80%, las variaciones generadas son
menores a 9%. Asimismo, el tiempo de estabilización se reduce drásticamente, llegando
a ser de 4 minutos para todos los casos simulados. De esta manera, se encuentra que al
reducir el porcentaje de cierre, la modificación de la longitud se vuelve irrelevante para la
respuesta del sistema.
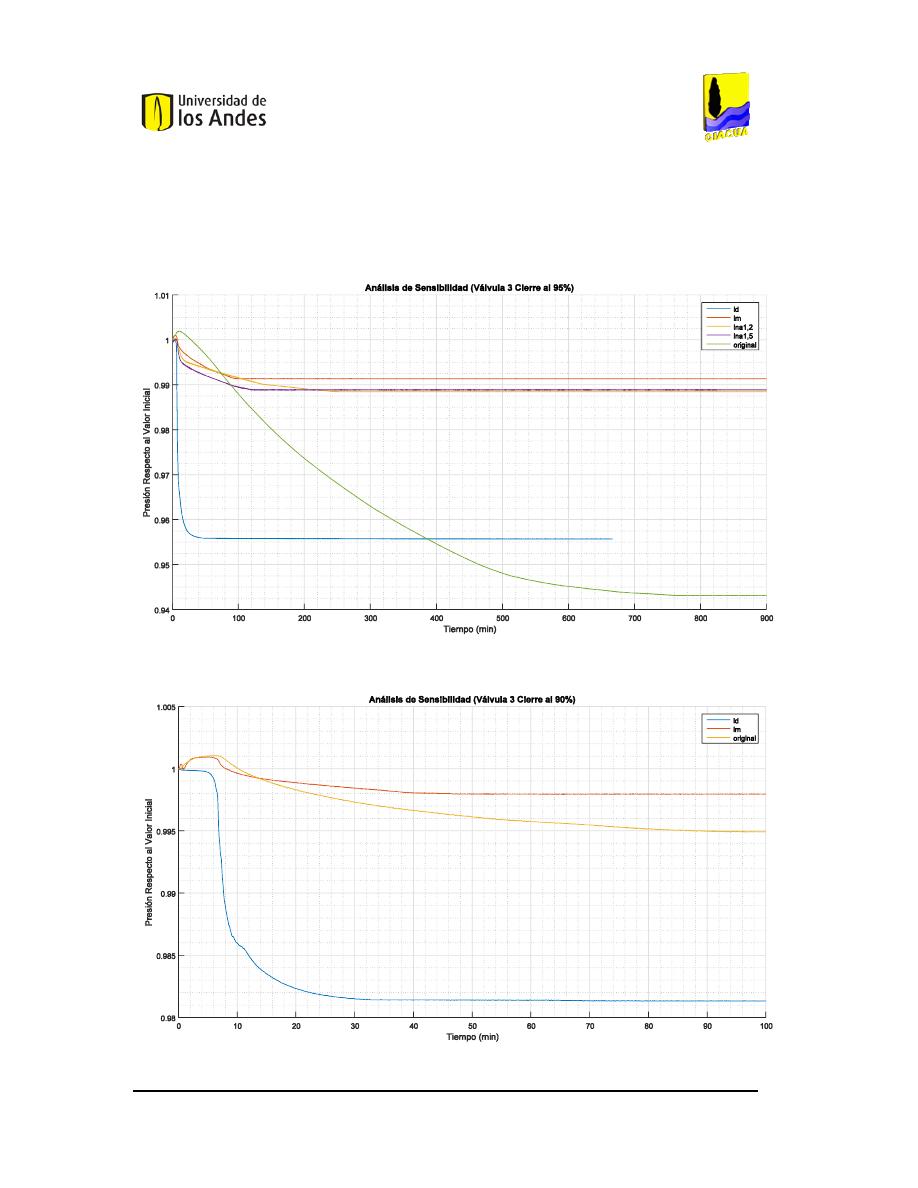
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
112
PRESIÓN
En la Figura 137 se puede ver que para las simulaciones lm, lna1,2 y lna1,5, las
variaciones son de 1.2%. De esta manera, se establece que estos casos se estabilizan de
manera inmediata. Por otra parte, los tiempos encontrados para las otras redes fueron de
10 (ld) y 440 (original) minutos. Se encuentra así que para la presión, el disminuir la
longitud o aumentar la celeridad de la onda ayuda a disminuir el tiempo de estabilización.
Figura 137. Análisis de sensibilidad del cierre del 95% de la válvula 3 en la red de Bucaramanga (Presión).
Figura 138. Análisis de sensibilidad del cierre del 90% de la válvula 3 en la red de Bucaramanga (Presión).
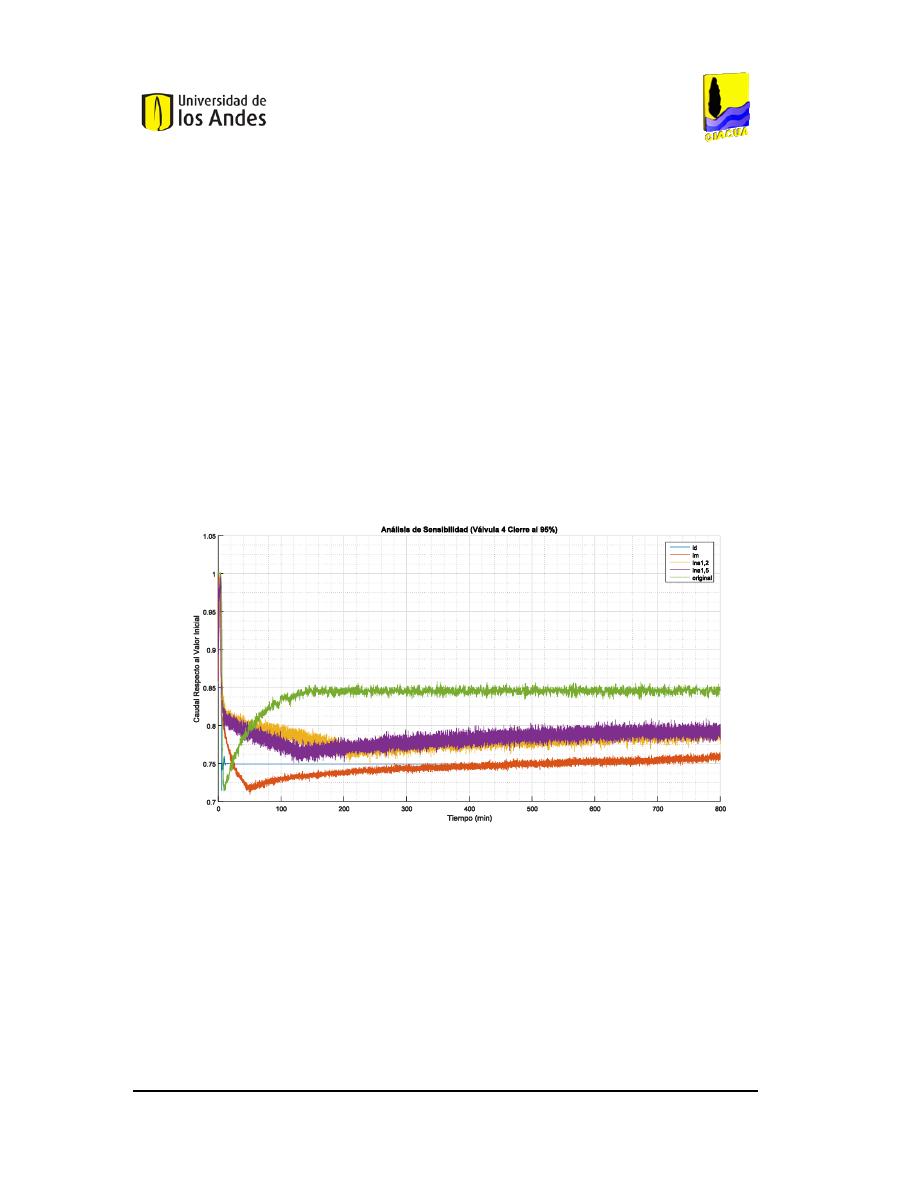
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
113
En la Figura 138 se puede ver que el disminuir un 5% el porcentaje de cierre de la
válvula, hace que las variaciones de la presión se vean disminuidas hasta que sean
menores al 2%. Por lo tanto, para términos de presión, todas las redes se estabilizan
instantáneamente frente al cierre del 90% de la válvula 3.
7.2.2.2.4.
Válvula 4
En la presente sección se muestran los resultados encontrados bajo la operación de la
válvula 4.
CAUDAL
Al observar la Figura 139 se puede ver que, el modificar la celeridad de la onda afecta de
manera significativa la respuesta de la red frente al cierre de la válvula 4.
Adicionalmente, se puede ver que el duplicar la longitud ayuda a disminuir el ruido del
modelo. Respecto a los tiempos de estabilización se encuentra que para el caso original,
la red requiere de 140 minutos. Para los demás casos se necesita de 6 (ld), 600 (lm), 700
(lna1,2) y 500 (lna1,5) minutos. Es relevante mencionar que los últimos tres casos
presentan altos tiempos, pues el ruido de la simulación es considerable.
Figura 139. Análisis de sensibilidad del cierre del 95% de la válvula 4 en la red de Bucaramanga (Caudal).
En la Figura 140 se encuentra que el duplicar la longitud produce una diferencia
significativa en el tiempo de estabilización. Sin embargo, a diferencia que los casos
anteriores, el disminuir la longitud no genera una diferencia significativa con el modelo
original. Los tiempos de estabilización obtenidos fueron de 3 (ld) y 600 (original)
minutos. Para el último caso no se puede establecer el tiempo exacto de estabilización,
sin embargo, éste es mayor a 133 minutos. Un aspecto relevante es que el tiempo de
estabilización haya incrementado para el caso original.
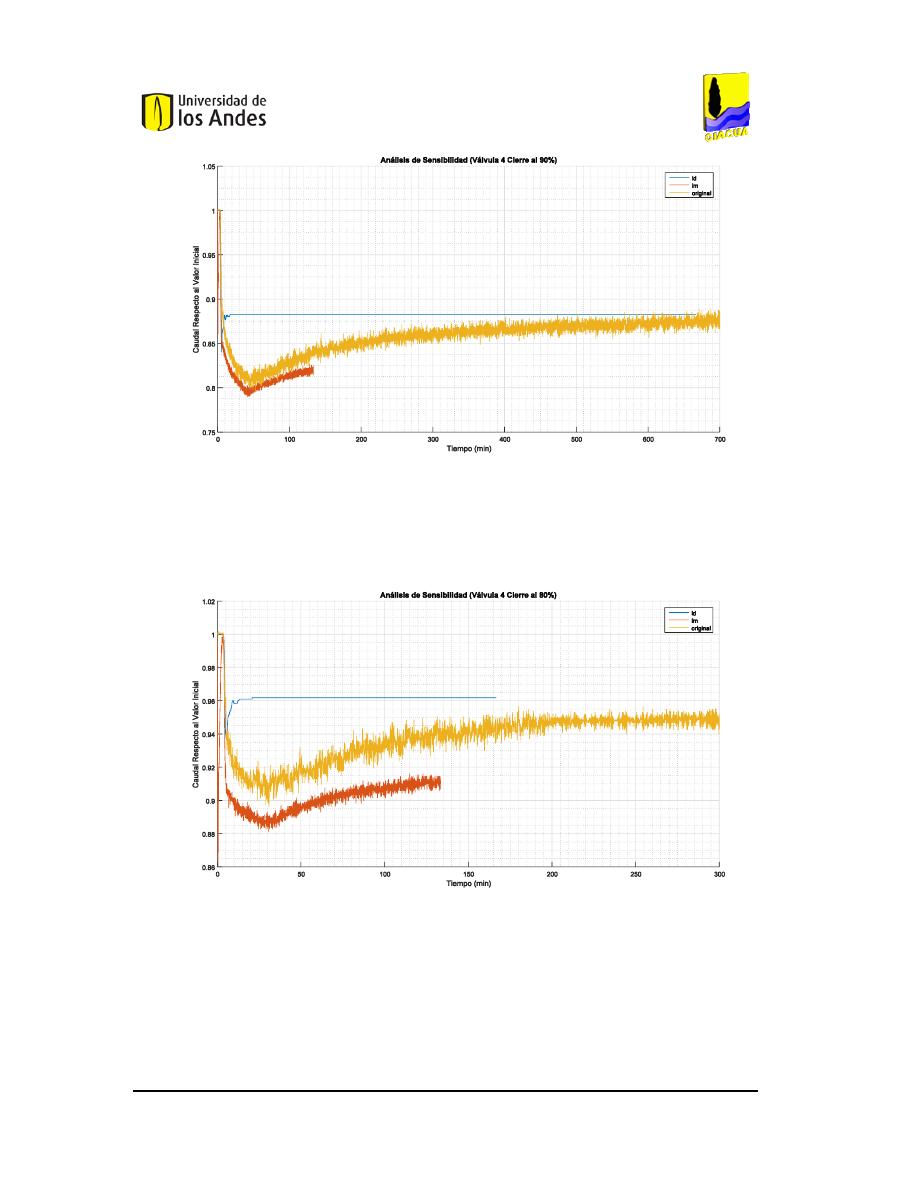
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
114
Figura 140. Análisis de sensibilidad del cierre del 90% de la válvula 4 en la red de Bucaramanga (Caudal).
Finalmente, para el cierre del 80% de la válvula 4, se puede ver que sigue siendo un
cierre que genera perturbaciones significativas en el sistema. Resulta llamativo que para
este cierre parece que el reducir la longitud de las tuberías tiene un efecto más apreciable
que en el cierre anterior. Los tiempos de estabilización encontrados fueron de 6 (ld), 130
(lm) y 150 (original) minutos.
Figura 141. Análisis de sensibilidad del cierre del 80% de la válvula 4 en la red de Bucaramanga (Caudal).
PRESIÓN
Al observar la Figura 142 se encuentra que la única modificación que no favorece el
tiempo de estabilización es al multiplicar por 1.2 la celeridad de la onda. Para los demás
casos se puede ver que el momento de estabilización es antes del de la red original. Los
tiempos de estabilización encontrados fueron 30 (ld), 140 (lm), 1050 (lna1,2), 740
(lna1,5) y 780 (original) minutos.
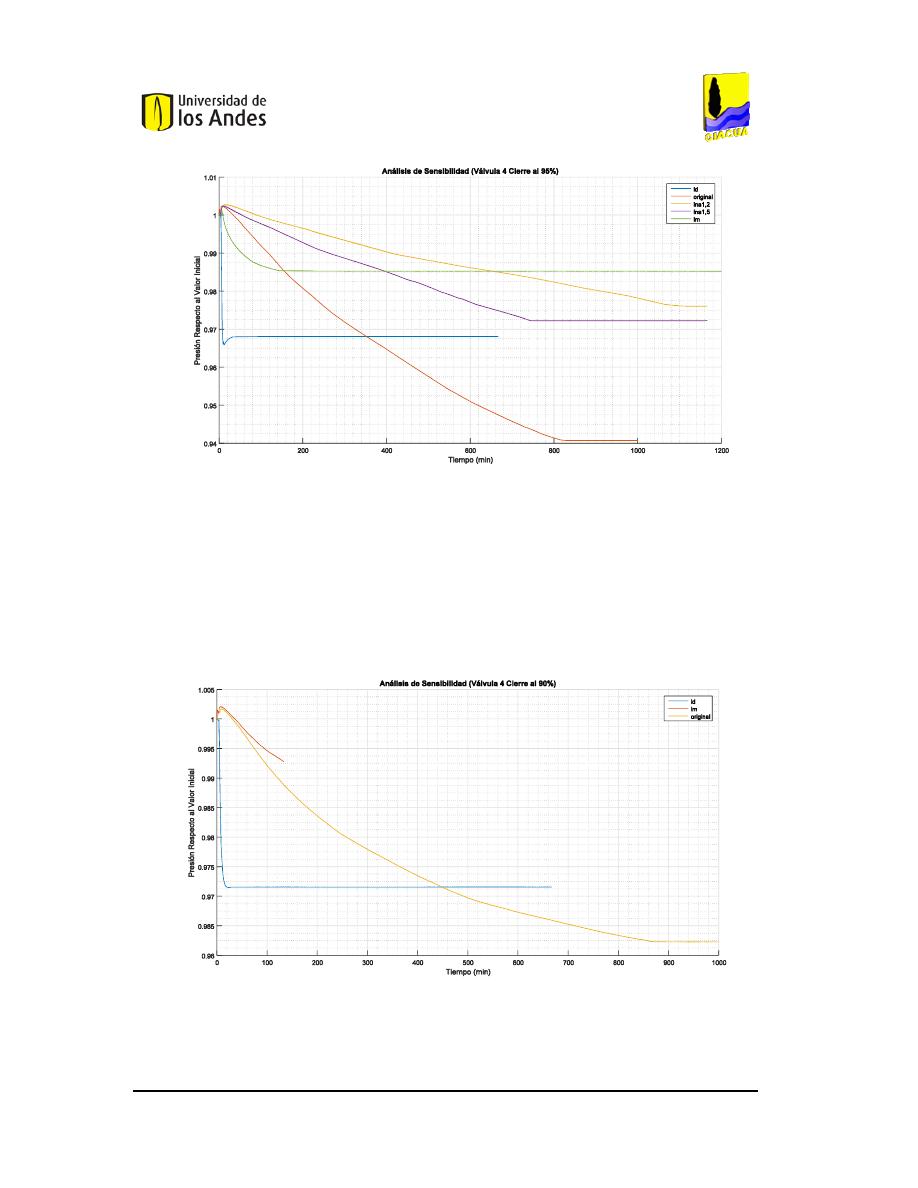
ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
115
Figura 142. Análisis de sensibilidad del cierre del 95% de la válvula 4 en la red de Bucaramanga (Presión).
Finalmente, al observar la Figura 143 se encuentra que, el disminuir 5% el porcentaje de
cierre hace que se reduzca en casi 2% las variaciones. Por otra parte, es curioso que el
disminuir el porcentaje de cierre hace que el tiempo de estabilización aumente. Los
tiempos de estabilización encontrados fueron de 15 (ld) y 860 (original). Sin embargo, si
se toma como 2% el límite de estabilización, se llega a que el tiempo del último caso se
reduzca a 300 minutos. Para cuando se reduce la longitud de las tuberías, no se puede
establecer el tiempo de estabilización; sin embargo, se sabe que es mayor a 133 minutos.
Figura 143. Análisis de sensibilidad del cierre del 90% de la válvula 4 en la red de Bucaramanga (Presión).

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
116
8. Conclusiones y Trabajo Futuro
A partir del trabajo realizado se pueden plantear diferentes conclusiones y trabajos que se
deben realizar para el futuro. De esta manera, en la presente sección se plantean los
resultados de mayor relevancia que se tuvieron. Adicionalmente, se plantearán las ideas
y análisis de sensibilidad que se consideran de gran ayuda para la presente investigación
en una etapa posterior.
8.1. Conclusiones
Después de realizar los análisis pertinentes se pueden establecer algunas conclusiones
acerca del trabajo realizado.
Se encontró de suma relevancia entender de qué forma HAMMER utiliza las
demandas para modelar el flujo transiente. Al conocer que éste las utiliza como si
fueran orificios o emisores, brindó una herramienta de gran ayuda para poder
establecer el estado estable al que llegaría la red. Esto permite entender y poder
cuantificar en que momento la red se estabiliza y se encuentra en su nuevo estado
estable.
Una vez que se entendió la modelación que realizaba HAMMER, se pudo establecer
el error que generaba el uso de los diferentes métodos de cálculo del factor de
fricción. De esta manera, se encontró que el que tiene más error es el método
Unsteady. Por otra parte, al utilizar el método Steady, el cual supone que el factor de
fricción se mantendrá constante en la simulación, no genera errores de gran magnitud
en la red probada. Sin embargo, se debe tener en cuenta que en la presente red todas
las tuberías tenían un flujo considerable. En caso de que esto no hubiera ocurrido, los
ductos que tuvieran un incremento significativo del flujo hubieran estado
subestimando las pérdidas por fricción, y se hubiera llegado a un estado estable
distinto al que debería alcanzar la red.
Al aplicar la metodología planteada para ubicar las válvulas y sectorizar la red, se
encontró que fue un éxito y fue de gran ayuda para establecer los casos de simulación.
Sin embargo, es relevante mencionar que ésta no tiene gran efectividad para redes que
sean completamente cerradas y que tengan varias fuentes de abastecimiento. Esto se
debe a que el cierre de una tubería cualquiera de la red no es capaz de desabastecer a
un sector de la misma.
A partir de la revisión bibliográfica realizada se encontró que hay distintos
parámetros de entrada al modelo de transiente, que pueden generar cambios
considerables en los resultados obtenidos. Un ejemplo de esto es suponer que el
fluido en la red no tiene concentración de aire y, por lo tanto, se tendrá una velocidad
de onda superior a la que se tendría en la realidad. Se debe tener en cuenta que es de
gran dificultad o casi imposible que en una red matriz de abastecimiento se tenga que
la concentración de aire sea 0, dado que es una red extensa y compleja. Sin embargo,
al realizar los análisis de sensibilidad en las redes probadas, se encontró que es un
parámetro influyente pero menos que otros tales como la longitud.
Por otra parte, se encontró en la revisión bibliográfica una constante crítica al análisis
de periodo extendido. Es decir, dependiendo de las variaciones que se tengan en los

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
117
componentes de la red y en las demandas de la misma, se producirá un efecto de
transiente que puede ser de baja o alta relevancia. De esta manera, se plantea que
salvo que los cambios de la red sean graduales y en tiempos largos, el análisis de
periodo extendido tendrá errores considerables en los caudales y en la predicción de
los niveles en los tanques de almacenamiento. Esto generará problemas en el cálculo
de la hidráulica y, en consecuencia, en los modelos de calidad de agua.
A partir de los resultados de la modelación se pudo ver que las válvulas que generan
mayor perturbación a la red, son aquellas que se encuentran más cerca a la fuente.
Sin embargo, cabe resaltar que éstas solo afectan el sistema cuando el porcentaje de
cierre es superior a 60%.
Al ver las distintas figuras realizadas se encuentra que el impacto que tiene el cierre
de ciertas válvulas en la red, no es instantáneo en puntos alejados a ella. Por lo tanto,
se encuentra que las válvulas situadas más alejadas de la fuente, pierden la capacidad
de perturbar puntos aguas arriba de éstas y la red en general.
Por otra parte, al revisar los diferentes puntos que se utilizaron para analizar el cierre
de las válvulas, se encontró que los nudos más alejados de la red no sienten gran
afectación a las operaciones que se realicen. De esta manera, se encuentra que para
perturbar los nudos alejados de la fuente, es necesario ubicar válvulas cercanas a estos
puntos.
Se encontró que la medida de tendencia elegida es de gran ayuda, dado que puede
cuantificar las variaciones grandes y pequeñas que se tengan en las tuberías. Sin
embargo, se considera necesario revisar los límites que se utilizaron como frontera
para establecer si la red se estabilizó o no.
A partir de las simulaciones realizadas se encuentra que para las válvulas que se
sitúan en puntos estratégicos, con cierres superiores a 80%, afectan de manera
drástica la red. De esta manera, los caudales presentan altas variaciones y el tiempo
de estabilización llega a ser mayor a 60 minutos. Es tal la perturbación, que para
cierres del 95% la red pueden llegar a hacer que la red necesite de más de 500
minutos para estabilizarse. Por lo tanto, si realizan cierres de las válvulas mayores al
80%, se encuentra que el análisis de periodo extendido puede conllevar a tener
resultados errados. Asimismo, se encuentra que el tener patrones de consumo con
una alta resolución (menor a 20 minutos) es innecesario e incorrecto, dado que los
tiempos de estabilización del sistema pueden ser mayores que la resolución de estos.
De forma similar, se encontró que el duplicar la longitud de las tuberías ayuda a que
se reduzca significativamente el ruido de las simulaciones. Además, el aumento de
este parámetro hace que el tiempo de estabilización se reduzca considerablemente,
llegando a ser el 10% del tiempo requerido cuando las longitudes son las originales.
De esta manera, es posible justificar el uso de patrones de consumo de alta resolución
y el análisis de periodo extendido para las redes largas y no para las cortas.
Por otra parte, el efecto de la variación de la longitud no es muy claro, pues si ésta se
reduce o se aumenta, ayuda a disminuir el tiempo de estabilización de la red. Esto
hace que cada caso que para cada caso que se vaya a estudiar, sea necesario

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
118
desarrollar las simulaciones pertinentes para, encontrar el comportamiento del tiempo
de estabilización frente a las longitudes de las tuberías.
Se encontró también que la rugosidad es un parámetro que no tiene gran influencia en el
fenómeno. Sin embargo, es llamativo que la importancia de esto es dependiente de los
porcentajes de cierre que se realicen. Es decir, sólo para porcentajes mayores o iguales al
80%, la rugosidad es un parámetro relevante para el tiempo de estabilización.
Finalmente, se encuentra necesario establecer una metodología que pueda definir qué
tan sectorizada es una red. Esto se plantea dado que la red de Medellín, que está más
interconectada, tiene menores tiempos de estabilización que la de Bucaramanga. Esta
última se considera que es una red altamente sectorizada.
A partir de lo enunciado anteriormente, y revisar la resiliencia de la red de Medellín,
se encuentra que puede existir una alta correlación en el tiempo de estabilización y la
resiliencia de la red.
Por otra parte, se considera que es necesario evaluar las variaciones de los caudales,
pues éstas son sustancialmente mayores a las encontradas en la presión. De esta
manera, si se tomaran solo las presiones como parámetro para medir la estabilización,
se encuentra que se podría subestimar el tiempo de estabilización de la red.
8.2. Trabajo Futuro
A partir del trabajo realizado se considera que existen nuevas preguntas para este tema de
estudio. De esta forma, a continuación se presenta el trabajo futuro que debería ser
realizado, basado en los resultados de la presente investigación.
Se deben realizar análisis de sensibilidad más detallados frente a las longitudes de
las tuberías, pues la afectación de esta propiedad tiene una alta relevancia en el
comportamiento del sistema. De esta forma, se tendrá un conocimiento más
amplio sobre el impacto que puede tener esta variable sobre la operación de las
válvulas en el sistema.
Se deben probar otras redes que sean del mismo tamaño y complejidad similar. Sin
embargo, se considera que puede ser de gran ayuda el analizar redes con la mitad del
número de nudos y de tuberías, para poder ver la variación que tienen las señales de
respuesta del sistema. Entre las redes que se estudien, es necesario evaluar si estas son
completamente abiertas o cerradas, o si presenta una combinación de ambas.
Por la razón anterior, se encuentra que es necesario establecer una metodología
que afirme el porcentaje o qué tan sectorizada es una red. Pues con las
simulaciones realizadas se encontró que si el sistema no está muy interconectado,
éste requiere una mayor cantidad de tiempo para encontrar un nuevo estado
estable bajo porcentajes de cierres mayores al 80%.
Se considera de alta relevancia el involucrar tanques de almacenamiento en el
modelo, para poder ver el impacto que tienen estos elementos en el fenómeno de
transiente. Pues a partir de la revisión bibliográfica realizada se encontró que
estos componentes pueden disminuir de manera significativa la perturbación en la
red. Esto haría que las variaciones sean menores y, por lo tanto, el tiempo de
estabilización sea menor.

ICYA 4202 –201510
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Tiempo de Respuesta Típico de Operaciones en Redes de Distribución
de Agua Potable.
_________________________________________________________________________________________________________________________________________________
Juan Pablo Paris Valencia
Tesis de Maestría en Ingeniería Civil
119
9. Referencias
Bohórquez, J. M. (2014). OPTIMIZACIÓN EN LA OPERACIÓN DE VÁLVULAS PARA
MINIMIZAR EFECTOS POR FLUJO TRANSIENTE EN REDES DE
DISTRIBUCIÓN DE AGUA POTABLE. APLICACIÓN EN RED MATRIZ DE
BOGOTÁ D.C. Bogotá: Tesis de Maestría en Ingeniería Civil sin Publicar.
Davis, A. L. (2004). Hydraulic Transients in Distribution Systems. World Water
Congress 2001. Corvallis: ASCE.
Duan, H.-F., Tung, Y.-K., & Ghidaoui, a. M. (2010). Probabilistic Analysis of Transient
Design for Water Supply Systems . JOURNAL OF WATER RESOURCES
PLANNING AND MANAGEMENT , 678-687.
Giustolisi, O., Kapelan, Z., & Savic, a. D. (2008). Extended Period Simulation Analysis
Considering Valve Shutdowns . JOURNAL OF WATER RESOURCES
PLANNING AND MANAGEMENT , 527-537.
Karney, B. W. (2006). ASSESSING THE DEGREE OF UNSTEADINESS IN FLOW
MODELING: FROM PHYSICS TO NUMERICAL SOLUTION . Water
Distribution Systems Analysis Symposium . Ohio: ASCE.
Karney, Y. R. (2002). Extended-Period Analysis with a Transient Model . JOURNAL OF
HYDRAULIC ENGINEERING , 616-524.
Methods, H., Walski, T. M., Chase, D. V., Savic, D. A., Grayman, W., Beckwith, S., &
Koelle, E. (2003). ADVANCED WATER DISTRIBUTION MODELING AND
MANAGEMENT . Waterbury : HAESTAD PRESS .
Saldarriaga, J. (2007). Hidráulica de Tuberías: Abastecimiento de agua, redes, riegos.
Bogotá: Alfaomega.
Silva, G. (1975). Diseño de Acueductos y Alcantarillados. Bogotá: Universidad Santo
Tomás y Universidad Javeriana.
Tanyimboh, C. S. (2010). PRESSURE DEPENDENT EPANET EXTENSION:
EXTENDED PERIOD SIMULATION . Water Distribution System Analysis.
Tucson: ASCE.
Thorley, D. (2004). Fluid Transients in Pipeline Systems. London: Professional
Engineering Publishing.
Tzatchkov, V. G., Alcocer-Yamanaka, V. H., & Buchberger, S. G. (2006).
STOCHASTIC DEMAND GENERATED UNSTEADY FLOW IN WATER
DISTRIBUTION NETWORKS. Water Distribution Systems Analysis Symposium.
Cincinnati: ASCE.
Wood, D. J. (2005). Waterhammer Analysis—Essential and Easy (and Efficient).
JOURNAL OF ENVIRONMENTAL ENGINEERING , 1123-1131.
Wylie, E. B., & Streeter, V. L. (1978). Fluid Transients. New York: McGraw-Hill Inc.
