
IAHR
CIC
XXV CONGRESO LATINOAMERICANO DE HIDRÁULICA
SAN JOSÉ, COSTA RICA, 9 AL 12 DE SETIEMBRE DE 2012
SUPERFICIE DE USO ÓPTIMO DE POTENCIA PARA EL DISEÑO DE
REDES DE DISTRIBUCIÓN DE AGUA POTABLE
Juan Saldarriaga, Felipe Hernández, María A. Escovar y Diego A. Páez
Centro de Investigaciones en Acueductos y Alcantarillados – Universidad de los Andes - Bogotá, Colombia
<jsaldarr , feli-her , ma-escov , da.paez27>@uniandes.edu.co
RESUMEN:
El diseño de mínimo costo para redes de distribución de agua potable (RDAP) es
probablemente el problema de modelación más investigado en la ingeniería hidráulica. En las
últimas décadas, diferentes técnicas de soft computing tales como algoritmos metaheurísticos, han
sido aceptados como los métodos más efectivos para solucionar dicho problema. Sin embargo, dada
su naturaleza estocástica, un alto número de simulaciones hidráulicas son requeridas antes de lograr
hallar resultados aceptables. En este artículo se presenta una metodología alternativa, basada en el
entendimiento del comportamiento hidráulico de los diseños óptimos. Esta metodología pretende
remplazar las búsquedas considerablemente largas de los algoritmos metaheurísticos. Para ello se
concentra en establecer maneras eficientes de disipar energía y distribuir caudal. El algoritmo fue
probado en dos redes de referencia llegando a resultados similares a los encontrados por
investigaciones previas pero con una amplia reducción en el número de iteraciones requeridas. Esta
nueva aproximación al problema muestra un alto potencias para otras aplicaciones relacionadas con
los modelos matemáticos RDAPs.
ABSTRACT:
Water distribution system minimum-cost design is probably the most commonly addressed
modeling problem in hydraulic engineering. In the last decades, soft computing techniques, such as
metaheuristics, have been established as the most effective methods to solve this problem.
However, because of their stochastic nature, a huge number of hydraulic simulations are needed
before adequate results are found. An alternative soft approach, based on the understanding of the
hydraulic behavior of optimal designs, is presented in this paper. It attempts to replace the tiresome
search process undertaken by metaheuristics. The methodology focuses on establishing efficient
ways in which energy is dissipated and flow is distributed. The algorithm was tested on two
benchmark systems reaching similar results to those of previous works but in an amply reduced
number of iterations. This novel approach shows plenty of potential in other water distribution
mathematical modeling applications
PALABRAS CLAVES: Optimización, Diseño, Heurísticas.

INTRODUCCIÓN
La disponibilidad de agua potable es esencial para el desarrollo de las actividades humanas.
Sin embargo, millones de personas todavía no disponen de un adecuado servicio, especialmente en
países en desarrollo. Adicionalmente, los recursos económicos para solucionar dicho problema son
escasos, y es por ello que el problema de diseño optimizado de RDAPs ha sido estudiado por
investigadores de diferentes partes del mundo. Si bien el diseño de una RDAP debe tener en cuenta
otros criterios adicionales a los de costo, tales como la confiabilidad de la red y el impacto
ambiental asociado (Walski, 2001; Todini, 2008), el criterio de mínimo costo continua siendo
utilizado para la comparación de diferentes diseños. De hecho, usualmente, los algoritmos de diseño
multiobjetivo que tienen en cuenta estos otros criterios, son extensiones de un algoritmo exitoso de
diseño de minimización de costos (e.g., Laucelli et al., 2008; Tanyimboh et al., 2009; Wu et al.,
2009).
El problema de diseño de RDAPs consiste en la determinación de los diámetros de las
tuberías, de manera que se satisfagan los caudales demandados en cada nudo con una presión
aceptable haciendo uso de los tamaños de tubería disponibles en el mercado. La formulación
matemática del problema como un problema de optimización donde se minimizan los costos
constructivos, se clasifica como un problema NP-Duro indicando que no se conocen algoritmos con
complejidad de orden polinomial que puedan encontrar una solución exacta del mismo (Yates et al,
1984).
Los primeros intentos de solución del problema incluyeron técnicas de optimización como
enumeración (Gessler, 1985), y programación lineal y no lineal (Alperovits & Shamir, 1977,
Fujiwara & Kang, 1990). Con el paso del tiempo, los investigadores se han concentrado en el uso de
metaheurísticas dada su facilidad de implementación, su amplio espacio de búsqueda, su baja
dependencia de la configuración inicial del modelo y la capacidad de incorporar la restricción de
diámetros discretos disponibles en el mercado.
Los algoritmos metaheurísticos son algoritmos basados en comportamientos observados en
la naturaleza, que generan un gran número de posibles alternativas resultado, evaluando cada una, y
generando muchas otras con base en la evaluación de las alternativas pasadas. La evaluación de
cada alternativa incluye una comprobación de cumplimiento de las restricciones del problema y una
evaluación de la función objetivo. Cada comprobación de las restricciones tiene asociada una
ejecución hidráulica en el caso del problema de diseño de RDAPs, y por lo tanto buena parte del
tiempo computacional requerido por un algoritmo corresponde a ejecuciones hidráulicas. Es por
ello que en la comparación de metodologías no sólo se usa el costo mínimo alcanzado sino también
el número de simulaciones hidráulicas requeridas para llegar a dicho resultado de mínimo costo.
Gracias a implementaciones de las mencionadas metodologías, en la actualidad se dispone
de diseños considerablemente buenos que optimizan de manera aceptable la función objetivo,
permitiendo a nuevos investigadores hacer un análisis de los resultados encontrados buscando y
analizando patrones hidráulicos que siguen dichos diseños. Un análisis de esta naturaleza fue hecho
por I-Pai Wu (1975) para tuberías principales de redes de riego localizado de alta frecuencia. Según
I-Pai Wu, si se conoce la altura piezométrica a la entrada de una tubería en serie (
), y la
altura piezométrica mínima aceptable en los nudos de ésta (
), es posible asignar una altura
piezométrica objetivo a cada nudo de la tubería (
), de manera que el diseño correspondiente a
las perdidas objetivo asignadas y a los caudales que debe transportar cada segmento de la tubería, es
de mínimo costo. Analizando las diferentes posibles asignaciones de alturas piezométricas, I-Pai
Wu encontró que la mejor distribución correspondía a una línea de gradiente hidráulico (LGH)
parabólica como la mostrada en la Figura 1 y cuya ecuación corresponde a la Ecuación 1:
(
)
( )
(
)
[1]
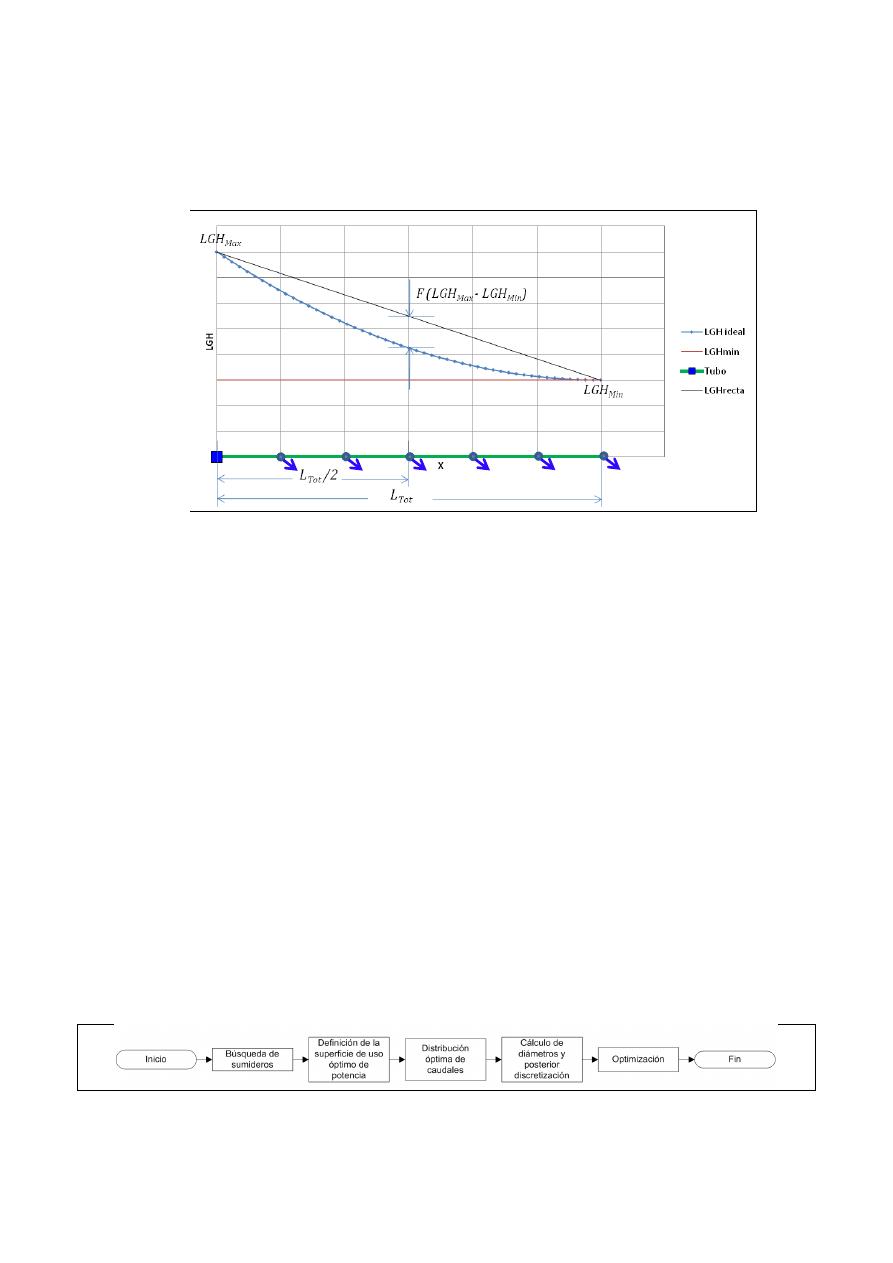
Donde
es la longitud total de la tubería en serie,
es la diferencia relativa entre la
altura piezométrica asignada al punto del medio por una línea recta y por la línea parabólica, y
es
la coordenada longitudinal de cada nudo donde se asignará la altura piezométrica. I-Pai Wu también
encontró que en caso de que los nudos de demanda estén igualmente espaciados y con demanda
igual para todos, la LGH que genera el mínimo costo es la línea parabólica con flecha (
) igual a
15%.
Figura 1.- Criterio de I-Pai Wu para la línea de gradiente hidráulico ideal o de mínimo costo.
En 1983, el profesor Ronald Featherstone de la Universidad de Newcastle en Reino Unido,
propuso una extensión del criterio de I-Pai Wu para redes de acueducto usualmente cerradas. Esta
idea fue planteada e investigada por Saldarriaga (1998) y tuvo grandes avances con los trabajos de
Villalba (2004) y Ochoa (2009). Este artículo describe una metodología de diseño basada en la idea
del profesor Featherstone utilizando algunos resultados de las investigaciones de Villalba y Ochoa,
denominada Superficie de Uso Óptimo de Potencia (OPUS por sus siglas en inglés). Cada paso del
algoritmo es descrito y analizado, y finalmente se presentan los resultados de la aplicación de OPUS
en dos redes de referencia (Two-loop y Hanoi).
DESCRIPCIÓN DE LA METODOLOGÍA
En la Figura 2 se muestran los pasos o subprocesos de la metodología y el orden en que se
realizan. El primer subproceso consiste en convertir la topología de la red, en una estructura de
árbol o red abierta. Después se asigna a cada nudo, su altura piezométrica objetivo con base en la
metodología desarrollada por Ochoa (2009), utilizando para ello, la estructura de árbol generada, y
las características topológicas y de demanda de la red. A continuación se realiza una distribución de
caudales, de manera que para cada nudo se asigna el porcentaje de caudal demandado que
provendrá de cada tubo conectado a dicho nudo. Posteriormente se realiza el diseño, encontrando
diámetros continuos como resultado, y requiriendo que dichos diámetros sean aproximados a algún
diámetro discreto disponible en el mercado. Finalmente se realizan una serie de ejecuciones
hidráulicas con el objetivo de asegurar que no se viole la presión mínima en los nudos y buscando
una reducción en los costos mediante reducción de algunos de los diámetros.
Figura 2.- Descripción de los subprocesos de la metodología OPUS.
Definición de la estructura de árbol (Búsqueda de sumideros):
q
q
q
q
q
q
Este subproceso se basa en dos principios. El primero radica en que un diseño de mínimo
costo debe proveer agua a casa nudo de demanda a través de una única ruta o trayectoria de flujo.
Esto debido a la ineficiencia hidráulica asociada con la redundancia de tuberías (Saldarriaga, 1998).
Así, redes abiertas pueden ser considerablemente menos costosas que redes cerradas (aunque
también resultan menos confiables (Todini, 2000)). De esta manera, este subproceso busca la
manera de transformar la geometría de la red para generar una red abierta (usualmente denominadas
estructuras de árbol por su parecido con las ramificaciones) mediante la identificación de nudos
sumideros (nudos con altura piezométrica menor que todos sus vecinos).
El segundo principio se deriva de las ecuaciones de pérdidas por fricción en tuberías con
flujo presurizado, (Darcy-Weisbach & Colebrooke-White o Hazen-Williams). Suponiendo que
todos las demás variables de la ecuación permanecen constantes, es posible encontrar una relación
biunívoca entre el caudal de diseño (Q) y el diámetro requerido. Además, si se conoce la relación
entre el diámetro de la tubería y el costo por unidad de longitud de la misma, es posible encontrar
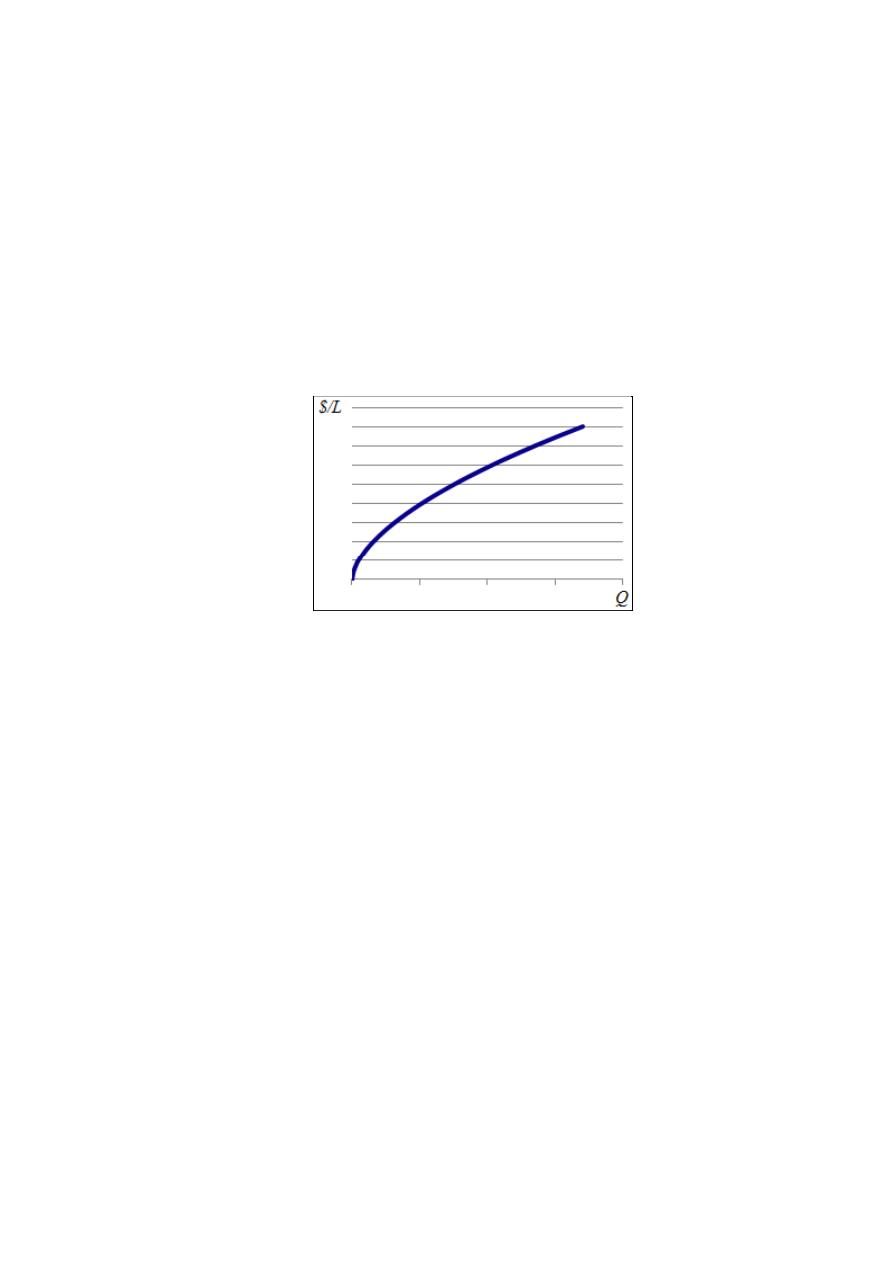
una relación entre Q y el costo por unidad de longitud de la tubería, tal y como se muestra en la
Figura 3.
Figura 3.- Relación esquemática entre el caudal de diseño y el costo por unidad de longitud de la tubería.
De la Figura 3, es posible notar que a medida que aumenta el caudal de diseño, el costo
marginal de la tubería decrece. Es decir que agregar caudales en unos pocos tubos reduce el costo
total de la red. De esta manera, teniendo en cuenta los dos principios analizados, se diseñó un
algoritmo recursivo de definición de la estructura de árbol. Este algoritmo inicia en la fuente o
embalse de la red y recorre las tuberías hacia aguas abajo agregando a la red abierta un tubo y nudo
a la vez. En el momento en que tiene más de una posibilidad de adición de una pareja tubería-nudo
selecciona aquella cuya relación beneficio-costo (cociente entre la demanda del nudo y el costo
marginal de conectarlo a la fuente) es mayor.
En el momento en que se han agregado todos los nudos de la red cerrada a la red abierta, se
definen como sumideros, aquellos nudos son ningún nudo aguas abajo, y la estructura de árbol está
completa. La complejidad computacional del algoritmo es O(NN
2
), donde NN es el número de
nudos de la red, y por lo tanto el tiempo computacional de toda la metodología no se ve
mayormente afecta por este paso.
Definición de la superficie de uso óptimo de potencia:
Este paso, que se considera el más importante de la metodología y le da el nombre a está,
está basado en el trabajo de I-Pai Wu (1975). El subproceso asigna una altura piezométrica a cada
nudo de la red, de manera que las pérdidas totales de las tuberías quedan predefinidas como la
diferencia entre las alturas piezométricas de sus nudos adyacentes. La manera de hacer esta
asignación de alturas piezométricas de manera óptima se basa en los resultados de Ochoa (2009)
para tuberías en serie con caudales y longitudes no homogéneas. Según Ochoa, la flecha
( ) de la
Ecuación 1, que minimiza los costos de la tubería resultante, depende de la distribución longitudinal
de la demanda, del cociente entre los caudales y las longitudes de las tuberías y de la función de

costos. Así un diseño de una red abierta que minimice costos, consistirá en implementar estos
resultados de cálculo de la flecha óptima a cada trayectoria que una los sumideros con la fuente.
Para ello, se define una altura piezométrica mínima en los nudos de la red con base en las
regulaciones que existan en la ciudad de la RDAP. Después se calculan las distancias topológicas
entre cada nudo del sistema y la fuente. Conociendo entonces la altura piezométrica disponible en la
fuente (
), la altura piezométrica mínima en cada sumidero (
) y las distancias de
cada trayectoria entre sumidero y fuente (
), se le asigna una LGH parabólica a cada trayectoria
de flujo. Dado que algunas trayectorias compartirán segmentos aguas arriba, se recalcula la
parábola modificando el valor de la flecha como un promedio ponderado de las flechas de las
trayectorias encontradas, en donde el peso de cada valor será el caudal transportado por cada
trayectoria. Finalmente es necesario revisar que no se violen las presiones mínimas en los nudos
intermedios cuya elevación puede ser suficiente para que la altura piezométrica asignada, no cumpla
con los requisitos. En dado caso, se modificarán las parábolas de las trayectorias aguas arriba de
dicho punto.
Como resultado, cada nudo de la red tiene asignada una altura piezométrica objetivo o ideal
de manera que se generará una superficie de alturas piezométricas sobre la red. Estas alturas
piezométricas definen a su vez las perdidas objetivo o ideales de cada tubería, de manera que al
conocer el caudal de diseño, se puede utilizar una ecuación de fricción para flujo presurizado a fin
de encontrar el diámetro continuo (i.e. diámetro cuyo valor pertenece a
) que corresponde a ese
caudal y a esas pérdidas por fricción.
Distribución óptima de caudales:
Si se supone que el conjunto de diámetros disponibles es
, una misma superficie de
alturas piezométricas puede ser alcanzada con diferentes configuraciones de diámetros cuando la
red es cerrada. Así, este subproceso busca seleccionar una manera de distribuir los caudales
demandados en las tuberías de la red, de manera que se cumpla la conservación de masa en cada
nudo, que se genere la superficie de alturas piezométricas determinada en el subproceso anterior y
que se minimicen los costos asociados al diseño generado con esa combinación de caudales y
pérdidas totales en las tuberías.
En este subproceso se hace uso de la red con geometría cerrada así como de los principios
utilizados en el primer paso de la metodología. El procedimiento consiste en recorrer cada nudo de
la red, desde aguas abajo hasta aguas arriba, asignando a cada tubo inmediatamente aguas arriba del
nudo analizado una cierta fracción del caudal total demandado en el nudo y en sus nudos aguas
abajo. La manera de distribuir ese caudal total entre los tubos aguas arriba puede hacerse de
diferentes maneras, pero el criterio que minimiza costos es el que asigna a una única tubería una
porción significativa del caudal, dejando para los demás tubos sólo el caudal correspondiente al
diámetro mínimo disponible en el mercado.
La selección de la tubería a la cuál será asignada la mayor parte del caudal demandado, se
hace calculando la función
donde
son las pérdidas totales asignadas al tubo y es su
longitud, y seleccionando aquella tubería con mayor valor de la función. Para implementar este
procedimiento se hace uso de un algoritmo recursivo iterativo con complejidad computacional
O(NN).
Cálculo de diámetros y discretización:
Como resultado de los dos pasos anteriores, cada tubería de la red tiene asignadas unas
pérdidas totales objetivo y un caudal de diseño. Así, es posible hacer uso de una ecuación de
fricción para flujo presurizado a fin de calcular el diámetro continuo necesario para transportar ese
caudal con esas pérdidas. En caso de que la ecuación sea la de Hazen-Williams, este cálculo es
explícito. En caso de que la ecuación sea la de Darcy-Weisbach en conjunto con la ecuación de
Colebrooke-White es necesario realizar un proceso iterativo relativamente simple.

Como resultado se tienen diámetros continuos asignados a cada tubería del sistema de
manera que al ejecutar la hidráulica de la RDAP con este diseño, se obtendrían las alturas
piezométricas objetivo en lo nudos y los caudales asignados en los tubos. Sin embargo esta
configuración de diámetros no se considera factible para el problema de optimización, dado que se
están violando las restricciones que aseguran que a cada tubería se le debe asignar únicamente un
diámetro disponible en el mercado local.
Para resolver este problema se requiere en un principio, una discretización de los diámetros
encontrados ajustándolos a uno de los diámetros del conjunto de diámetros disponibles en el
mercado. Dado que se dispone de un diámetro continuo, se debe disponer de dos diámetros
discretos entre los que se encuentra el valor continuo. Así este paso consiste en seleccionar cuál de
esos dos valores de diámetros discretos se asignará al tubo analizado.
El anterior procedimiento de discretización puede ser realizado de diferentes maneras, pero
después de evaluar cuatro posibles alternativas, se encontró que la que produce mejores resultados,
consiste en redondear al caudal equivalente más cercano. Para ello, se eleva el valor del diámetro
continuo y de los diámetros disponibles a una potencia de 2.6 como una estimación de la función
que relaciona el caudal que pasa por una tubería con el diámetro que ésta tiene. Finalmente se
selecciona el diámetro cuya aproximación de caudal es más cercana a la aproximación de caudal del
diámetro continuo.
Sin embargo al finalizar este subproceso, el comportamiento hidráulico de la red puede
diferir significativamente del comportamiento objetivo (caudales y alturas piezométricas asignadas),
y por lo tanto el diseño generado puede estar bastante alejado del óptimo, o inclusive puede no
cumplir con la restricción de presión mínima en algunos de los nudos
Optimización (Reducción de costos y comprobación de diseño):
Este subproceso consiste en ejecutar un cálculo hidráulico de la red resultado del subproceso
anterior, verificando las presiones en los nudos. En caso de que algún nudo presente una presión
inferior a la mínima aceptable, se procede a aumentar diámetros de las tuberías aguas arriba hasta
que se cumpla con la restricción. El orden en el que se aumentan los diámetros de dichas tuberías
puede seleccionarse de diferentes maneras, pero se encontró que, si primero se aumentan los
diámetros de las tuberías con mayor diferencia de pendiente entre la LGH objetivo y la LGH
presente, se llega a diseños finales de menor costo.
Una vez se asegura que en la red no se presentan presiones inferiores a la mínima, se recorre
la red de aguas arriba a aguas abajo y después en sentido contrario, reduciendo los diámetros de las
tuberías, y evaluando las presiones en todos los nudos. En caso de que las presiones se reduzcan por
debajo de la presión mínima, el cambio en los diámetros es reversado y se continúa con los tubos
aguas abajo (o aguas arriba en caso de que ya se haya cambiado el sentido de avance). En caso de
que la presión mínima no sea violada, el nuevo diámetro se mantiene y se continúa con el
procedimiento en los siguientes tubos.
Este proceso de optimización es una heurística por si misma y es similar a la utilizada por
Todini (2000) con la diferencia de que la complejidad computacional del presente algoritmo es
O[NT*O(SH)] en contraste con la complejidad computacional del algoritmo citado
(O[NT
2
*O(SH)]), donde NT es el número de tubos de la red y O(SH) es la complejidad del
algoritmo de simulación hidráulica del sistema.
RESULTADOS Y ANÁLISIS
La metodología OPUS fue implementada en el software REDES desarrollado por CIACUA
a fin de automatizar todos los subprocesos anteriormente mencionados. Esta implementación fue
utilizada para diseñar dos redes de referencia: Two-loop y Hanoi (Alperovits & Shamir, 1977).
Dado que el objetivo es comparar los resultados de la metodología con otros algoritmos de diseño,
fueron utilizados los mismos valores de los diferentes parámetros de simulación hidráulica y
disponibilidad de diámetros que los reportados en otros estudios. Dentro de dichos parámetros se
encuentra el uso de la ecuación de Hazen-Williams para calcular las pérdidas por fricción de un
flujo presurizado, con un coeficiente de rugosidad C=130 (PVC – policloruro de vinilo) y con unos
parámetros de la ejecución hidráulica con el método del gradiente de
y .
Two-loop:
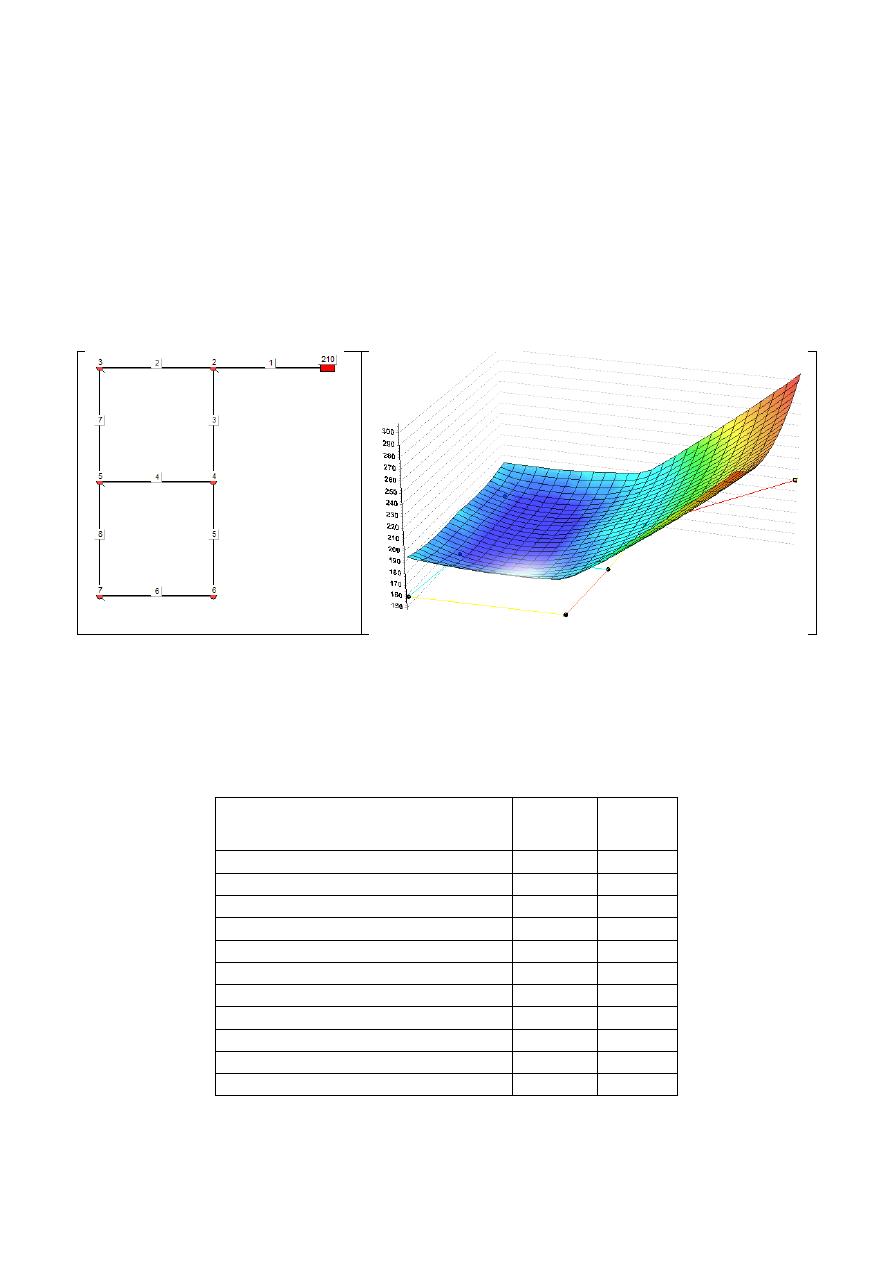
La red de Two-loop es una red de 8 tubos cuya geometría se presenta en la Figura 4. La
presión mínima aceptable en cada nudo es de 30 m.c.a., mientras que la altura piezométrica
disponible en la fuente es de 210 m.c.a. Además tiene un conjunto de 14 posibles diámetros cada
uno con un costo por unidad de longitud conocido. Una descripción completa de la red puede ser
encontrada en Alperovits & Shamir (1977).
Figura 4.- Red de Two-loop. a) Geometría e IDs de los elementos, b) Superficie de uso óptimo de potencia.
Al ejecutar el algoritmo de diseño en esta RDAP hipotética, se alcanzó el costo mínimo
reportado en la literatura para este problema (USD$419.000) con un total de 51 simulaciones
hidráulicas (ver Tabla 1). En la Figura 4 se muestra la superficie de uso óptimo de potencia
encontrada con la metodología.
Tabla 1.- Red de Two-Loop. Comparación de resultados. (Resultados tomados de Geem, 2009).
Algoritmo
Costo de la
red
diseñada
Número
de
iteraciones
Algoritmos genéticos
$419,000
65,000
Algoritmos genéticos
$419,000
10,000
Algoritmos genéticos
$419,000
7,467
Recocido simulado
$419,000
25,000
Salto de rana barajado
$419,000
11,155
Evolución compleja barajada
$419,000
1,091
Búsqueda de armonía
$419,000
1,121
Entropía cruzada
$419,000
35,000
Búsqueda dispersa
$419,000
3,215
Enjambre de partículas con búsqueda de armonía
$419,000
204
OPUS (este estudio)
$419,000
51
Hanoi:
La red de Hanoi es una red con 34 tubos cuya geometría se presenta en la Figura 5. La
presión mínima aceptable en cada nudo también es de 30 m.c.a., mientras que la altura piezométrica
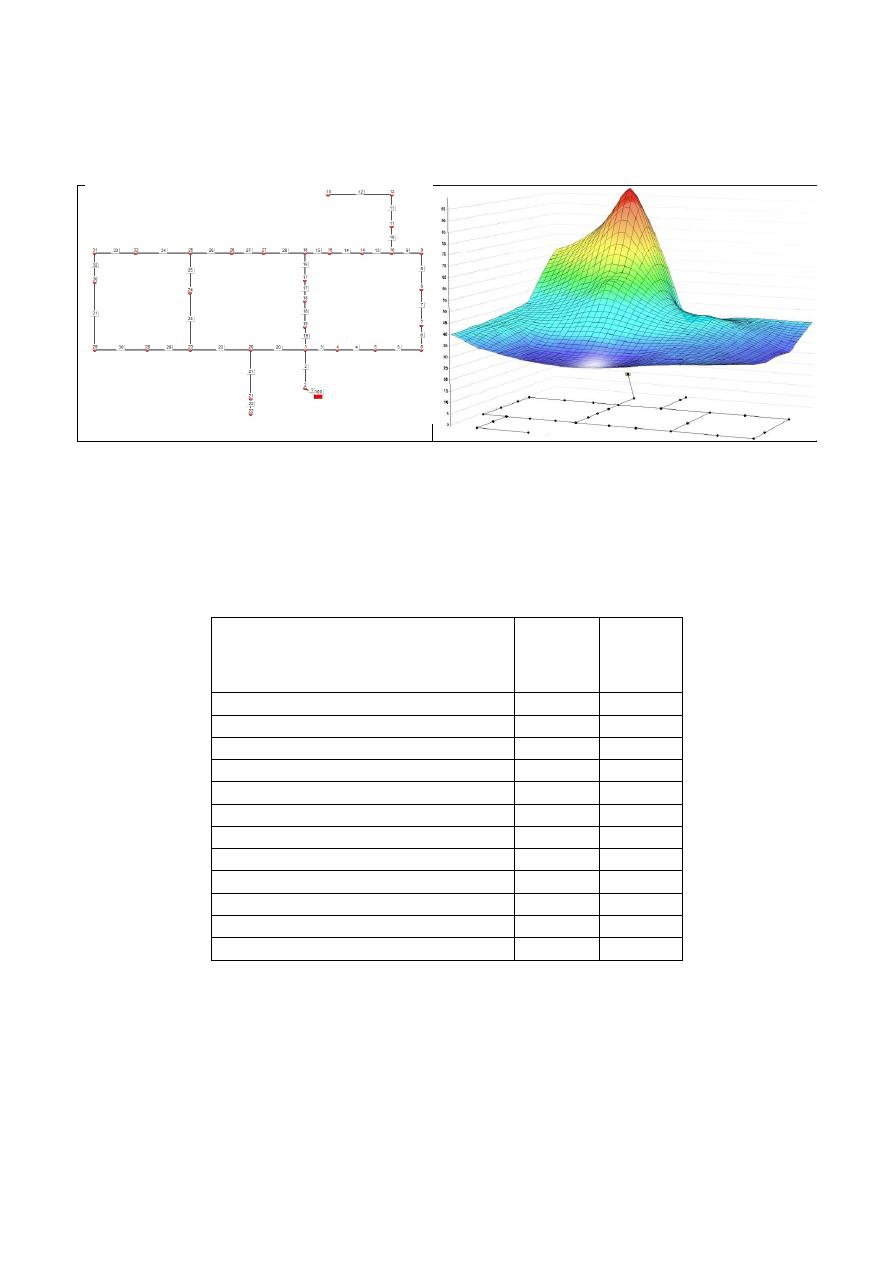
disponible en la fuente es de 100 m.c.a. Además tiene un conjunto de 6 posibles diámetros cada uno
con un costo por unidad de longitud calculable como una función potencial del diámetro con un
coeficiente de USD$1.1/m y un exponente de 1.5. Una descripción completa de la red puede ser
encontrada en Fujiwara & Kang (1990).
Figura 5.- Red de Hanoi. a) Geometría e IDs de los elementos, b) Superficie de uso óptimo de potencia.
El resultado de la ejecución de la metodología fue un diseño de la red con un costo de
USD$6’147,882.45 alcanzado tras 83 ejecuciones hidráulicas. Si bien el costo no iguala al mínimo
reportado en la literatura, el número de iteraciones requeridas es inferior a los demás en tres órdenes
de magnitud (ver Tabla 2). En la Figura 5 se muestra la superficie de uso óptimo de potencia
encontrada con la metodología
Tabla 2.- Red de Hanoi. Comparación de resultados. (Resultados tomados de Geem, 2009).
Algoritmo
Costo de la
red
diseñada
(millones)
Número de
iteraciones
Evolución compleja barajada
$6,220
25,402
Optimización por colonia de hormigas
$6,134
35,433
Algoritmos genéticos
$6,081
50,000
Algoritmos genéticos
$6,173
26,457
Recocido simulado
$6,333
26,457
Recocido simulado con búsqueda tabú
$6,353
26,457
Búsqueda local con recocido simulado
$6,308
26,457
Búsqueda de armonía
$6,081
27,721
Entropía cruzada
$6,081
97,000
Búsqueda dispersa
$6,081
43,149
Enjambre de partículas con búsqueda de armonía
$6,081
17,980
OPUS (este estudio)
$6,148
83
Respecto a los resultados mostrados en la Tabla 2, cabe decir que mediante el análisis de la
superficie de alturas piezométricas, se pudo concluir que los diámetros disponibles para solucionar
el problema de la RDAP de Hanoi representan una restricción considerablemente importante al
notar que las pérdidas totales por unidad de longitud en los tubos de más aguas arriba son mucho
más altas que las asignadas por la superficie de uso óptimo de potencia y que cualquiera de los
demás tubos del sistema. Esto, debido a que el conjunto de diámetros disponibles en el mercado
tiene un máximo de 40” y dicho diámetro genera unas pérdidas mucho más altas que las ideales u
objetivo para los tubos 1 y 2 (ver Figura 5). Dado que en este caso el subproceso Cálculo de
diámetros y discretización, para estos dos tubos, encuentra un diámetro continuo mayor al máximo

disponible, el algoritmo de redondeo sólo dispone de una opción de aproximación y por lo tanto la
metodología se ve limitada, indicando de esta manera que se debe considerar la opción de un
diámetro disponible adicional para el problema, a fin de ajustar la superficie de alturas
piezométricas a la ideal. A fin de sustentar la anterior afirmación, se ejecutó la metodología OPUS
para la red Hanoi, con un diámetro disponible adicional de 50” y con costo por unidad de longitud
correspondiente a la ecuación de costos descrita anteriormente. El costo alcanzado con esta nueva
ejecución fue de USD$5’342,840.13 demostrando así que el costo adicional de poner diámetros
mayores en los tubos de más aguas arriba se ve superado por el beneficio alcanzado al reducir los
costos de las demás tuberías.
Análisis
Los resultados encontrados en las dos RDAPs de referencia, muestran el potencial de la
presente metodología para la solución del problema de diseño de mínimo costo. Por un lado, el
diseño alcanzado para Two-Loop fue el óptimo conocido, y el número de simulaciones requeridas
fue considerablemente menor que los demás estudios con implementación de metaheurísticas. Por
otro lado, la red Hanoi requirió un número de iteraciones con una diferencia mucho más
considerable que en el caso de Two-loop, representando una disminución de tres órdenes de
magnitud y encontrando una solución con un sobrecosto de 1.1% respecto a la solución óptima
reportada.
Estos resultados demuestran la conveniencia del análisis hidráulico de los diseños de
mínimo costo para su posterior aplicación en una metodología de diseño por si misma que resulta
mucho más eficiente que los demás algoritmos metaheurísticos. En este caso particular, la estrategia
de analizar y predeterminar la superficie de alturas piezométricas que genera diseños
aceptablemente buenos es una reducción eficiente del inmenso espacio de solución del problema
que no sacrifica de manera importante la calidad de la solución final. Además esta ventaja se hace
mucho más significativa a medida que la red a diseñar aumenta de tamaño, dado que los algoritmos
metaheurísticos requerirán un aumento mucho mayor del número de simulaciones que la
metodología OPUS.
Otra ventaja que debe ser notada, es el carácter determinístico de la metodología, que
entregará siempre el mismo resultado cuando se usen los mismos parámetros. En contraste, los
algoritmos estocásticos, como su nombre lo indica, generan diferentes resultados para diferentes
ejecuciones, y por lo tanto los mejores resultados, son los mejores entre una serie de ejecuciones del
algoritmo, haciendo que el número de ejecuciones hidráulicas total requerido para replicar los
resultados de estas metodologías sea indeterminado y probablemente mayor que el reportado en las
investigaciones.
Una desventaja de la metodología consiste en la aplicabilidad de la misma. Es posible que
existan redes con condiciones hidráulicas que no permiten la implementación directa de la
metodología y sea necesario ajustar la misma de alguna manera. Estos ajustes, y en general todos
los análisis hidráulicos requeridos para el desarrollo de una metodología de esta naturaleza,
requieren un esfuerzo importante para su desarrollo. Ello contrasta con la aplicabilidad
prácticamente ilimitada de las metaheurísticas, que son aplicables a cualquier problema de
optimización sin requerir un entendimiento específico de las condiciones del problema.
Finalmente es importante mencionar que el entender el comportamiento hidráulico puede
permitir concluir de manera relativamente fácil medidas adicionales de optimización como en el
caso de Hanoi, la inclusión de un diámetro máximo más grande. Adicionalmente en el caso de tener
en cuenta otros términos en la función objetivo, tales como confiablidad del sistema o minimización
de fugas sólo se requiere evaluar el paso de la metodología donde mejor se puede procurar incluir el
criterio adicional y la manera de hacerlo. Por ejemplo Todini (2008), propone que una RDAP que
minimice fugas, debe minimizar las presiones en sus nudos sin violar la mínima aceptable. Así, en
la metodología de OPUS, tener en cuenta un criterio de minimización de fugas sería probablemente
implementado reformulando la manera de calcular la superficie de uso óptimo de potencia,
seguramente afectando el parámetro F.

CONCLUSIONES
Se desarrolló e implementó una metodología de solución del problema de diseño de RDAPs
de mínimo costo, denominada Superficie de Uso Óptimo de Potencia (OPUS). Su principal
característica es su aproximación novedosa basada en el entendimiento de la hidráulica de los
diseños óptimos y específicamente de las superficies de alturas piezométricas que estos generan.
Gracias a esta aproximación de asignación de presiones y caudales de manera óptima, se logró
reducir el espacio de solución considerablemente y sin generar una pérdida de calidad en la solución
significativa. La metodología fue implementada en dos redes de referencia mundial denominadas
Two-loop y Hanoi. Para la primera de ellas se llegó al diseño óptimo conocido en un número de
iteraciones mucho menor que otros estudios de metodologías metaheurísticas. En la segunda red el
costo mínimo reportado no fue alcanzado, llegando a un diseño con un sobrecosto de 1.1%, pero
alcanzado con un número de cálculos hidráulicos menor en tres órdenes de magnitud respecto al
resto de metodologías conocidas.
Los resultados encontrados permiten concluir que la metodología planteada, y en general la
aproximación propuesta puede generar resultados similares a los encontrados mediante el uso de
metaheurísticas, pero con una reducción importante del número de ejecuciones hidráulicas
requeridas para ello. Por ello se considera apropiado estudiar posibles mejoras a cada subproceso de
la metodología así como un posible ajuste de la aproximación para plantear metodologías de
solución de otros problemas relacionados con RDAPs tales como calibración y operación de los
sistemas.
REFERENCIAS
Alperovits, E. and Shamir, U., (1977) Design of Optimal Water Distribution Systems, Water Resources
Research, Vol.13, No.6, pp. 885-900.
Fujiwara, O. and Khang, D., (1990) A two-phase decomposition method for optimal design of looped water
distribution networks, Water Resources Research, Vol.26, No.4, pp. 539-549.
Geem, Z., (2009) Optimal cost design of water distribution networks using harmony search, Engineering
Optimization, Vol.38, No.3, pp. 259-277.
Gessler, J., (1985) Pipe network optimization by enumeration, Proceedings of Special Conference on Computer
Applications in Water Resources (New York), ASCE.
Laucelli, D., Giustolisi, O. and Todini, E., (2008) New concepts and tools for pipe network design, Proceedings
of the 10th Annual WDSA Conference.
Ochoa, S., (2009) Diseño optimizado de redes de distribución de agua potable con base en el concepto energético
de superficie óptima de gradiente hidráulico, Dpto. de Ing. Civil y Ambiental, U. de los Andes.
Saldarriaga, J., (1998 y 2007) Hidráulica de Tuberías. Abastecimiento de Agua, Redes, Riegos, Editorial
Alfaomega, Ediciones Uniandes.
Tanyimboh, T., Ward, K., Prasad, T. Jarvis, E. and Kanyoza, A., (2009) Multiobjective optimization and
multicriteria decision making for water networks, Proceedings of the CCWI 'Integrating Water Systems'.
Todini, E., (2000) Looped water distribution networks design using a resilience index based heuristic approach,
Urban Water, Vol.2, No.2, pp. 115-122.
Todini, E., (2008) Design, expansion and rehabilitation of water distribution networks aimed at reducing water
losses. Where are we?, Proceedings of the 10th Annual WDSA Conference.
Villalba, G., (2004) Algoritmos de optimización combinatoria aplicados al diseño de redes de distribución de
agua potable, Departamento de Ing. de Sistemas y Computación, U. de los Andes.
Walski, T., (2001) The Wrong Paradigm - Why Water Distribution Optimization Doesn’t Work, Journal of Water
Resources Planning and Management, Vol.127, No.4, pp. 203-205.
Wu, I., (1975) Design of drip irrigation main lines, Journal of the Irrigation and Drainage Division, Vol.101,
No.4, pp. 265-278.
Wu, W., Simpson, A. and Maier, H., (2009) Trade-off analysis between cost and reliability of water distribution
systems using genetic algorithms, Proceedings of the CCWI 'Integrating Water Systems'.
Yates, D., Templeman, A. and Boffey, T., (1984) The computational complexity of the problem of determining
least capital cost designs for water supply networks, E. Optimization, Vol.7, No.2, pp. 142-155.
