Revisión del diseño de cámaras de inspección con criterio de empate por línea de energía

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

1 

JORGE MARIO LIZARAZO MARTÍNEZ 

Universidad de los Andes 

Facultad De Ingeniería 

Departamento de Ingeniería Civil y Ambiental 

 
 
 

 

 

TESIS DE ESPECIALIZACIÓN 

INGENIERÍA DE SISTEMAS HÍDRICOS URBANOS 

 
 

REVISIÓN CRÍTICA DEL DISEÑO DE CÁMARAS DE INSPECCIÓN 

UTILIZANDO EL CRITERIO DE EMPATE POR LÍNEA DE ENERGÍA 

 
 

Preparado por: 

Ing. JORGE MARIO LIZARAZO MARTÍNEZ 

 
 
 

Asesor: 

Ing. JUAN SALDARRIAGA VALDERRAMA 

 
 

Informe Final Tesis 

 
 
 
 

Bogotá, 15 de febrero de 2012 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

2 

JORGE MARIO LIZARAZO MARTÍNEZ 

TABLA DE CONTENIDO

 

INTRODUCCIÓN ....................................................................................................................................................... 7

 

1

 

ANTECEDENTES Y OBJETIVOS .................................................................................................................. 8

 

1.1

 

ANTECEDENTES .......................................................................................................................................... 8

 

1.2

 

OBJETIVOS .................................................................................................................................................... 8

 

1.2.1

 

Objetivo General .................................................................................................................................... 8

 

1.2.2

 

Objetivos Específicos ............................................................................................................................. 8

 

2

 

ESTADO DEL ARTE ........................................................................................................................................ 9

 

2.1

 

GENERALIDADES ........................................................................................................................................ 9

 

2.2

 

EL

 

FLUJO

 

A

 

TRAVÉS

 

DE

 

CÁMARAS

 

DE

 

INSPECCIÓN ......................................................................... 11

 

2.2.1

 

Flujo Subcrítico .................................................................................................................................... 11

 

2.2.2

 

Flujo Supercrítico ................................................................................................................................ 11

 

2.3

 

PRINCIPALES

 

ESTUDIOS

 

ACERCA

 

DEL

 

COMPORTAMIENTO

 

DEL

 

FLUJO

 

EN

 

CÁMARAS

 

DE

 

INSPECCIÓN ......................................................................................................................................................... 11

 

2.3.1

 

Comportamiento Hidráulico de Cámaras de Inspección Bajo Flujo Supercrítico .............................. 11

 

2.3.2

 

Estudios de la FHWA ........................................................................................................................... 13

 

2.3.3

 

Otros Estudios ...................................................................................................................................... 17

 

3

 

METODOLOGÍA............................................................................................................................................. 20

 

4

 

EL CRITERIO DE EMPATE POR LÍNEA DE ENERGÍA ........................................................................ 21

 

4.1

 

JUSTIFICACIÓN .......................................................................................................................................... 21

 

4.2

 

CASOS .......................................................................................................................................................... 21

 

4.2.1

 

Flujo Subcrítico .................................................................................................................................... 21

 

4.2.2

 

Flujo Supercrítico ................................................................................................................................ 23

 

5

 

METODOLOGÍAS ALTERNAS DE CÁLCULO ........................................................................................ 29

 

5.1

 

FLUJO

 

SUBCRÍTICO ................................................................................................................................... 29

 

5.2

 

FLUJO

 

SUPERCRÍTICO

 

–

 

METODOLOGÍA

 

DEL

 

CIACUA ..................................................................... 30

 

5.3

 

METODOLOGÍA

 

DE

 

LA

 

FHWA-HEC

 

22

 

TERCERA

 

EDICIÓN ............................................................... 32

 

6

 

REVISIÓN DEL MÉTODO DE EMPATE POR LÍNEA DE ENERGÍA ................................................... 39

 

7

 

CONCLUSIONES ............................................................................................................................................ 45

 

8

 

RECOMENDACIONES .................................................................................................................................. 46

 

9

 

BIBLIOGRAFÍA .............................................................................................................................................. 47

 

10

 

REFERENCIAS ............................................................................................................................................... 48

 

 

 

 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

3 

JORGE MARIO LIZARAZO MARTÍNEZ 

ÍNDICE DE FIGURAS 

F

IGURA 

2-1

 

E

STRUCTURA DE UNIÓN EN ALCANTARILLADO

.

  

T

OMADA DE LA REFERENCIA 

15. ....................................... 9

 

F

IGURA 

2-2

 

M

ONTAJE UTILIZADO POR LA 

FHWA.

  

T

OMADA DE LA REFERENCIA 

12. ................................................... 15

 

F

IGURA 

2-3

 

E

LEVACIÓN DE LA 

L

ÍNEA DE 

E

NERGÍA 

(ELE)

 PARA DIFERENTES 

I

NTENSIDADES DE 

D

ESCARGA

 ............... 16

 

F

IGURA 

4-1

 

E

STRUCTURA DE 

U

NIÓN CON 

P

OZO DE 

I

NSPECCIÓN

.

  

F

UENTE

:

 

RAS

 

2000. ................................................ 24

 

F

IGURA 

4-2A

NÁLISIS DE ESTRUCTURA DE UNIÓN SIN CAÍDA

.

  

F

UENTE

:

 

RAS2000 ........................................................ 25

 

F

IGURA 

4-3

 

C

ONDICIÓN 

N

O 

S

UMERGIDA

.

 

F

UENTE

:

 

RAS

 

2000. .................................................................................... 27

 

F

IGURA 

4-4

 

C

ONDICIÓN 

S

UMERGIDA

.

  

F

UENTE

:

 

RAS

 

2000. ......................................................................................... 28

 

F

IGURA 

5-1

 

C

ONTROL A LA 

E

NTRADA

.

  

F

UENTE 

FHWA. ............................................................................................. 32

 

F

IGURA 

5-2

 

C

ONTROL A LA 

S

ALIDA

.

  

F

UENTE 

FHWA. ................................................................................................. 32

 

F

IGURA 

5-3

 

C

ONFIGURACIONES DE 

C

AÑUELA DE 

F

ONDO

.

  

F

UENTE

:

 

HEC-22

 

–

 

2009. .................................................. 35

 

F

IGURA 

5-4

 

D

EFINICIONES 

P

ARA EL 

N

IVEL DE 

E

NERGÍA EN LA 

C

ÁMARA

.

  

F

UENTE

:

 

HEC

 

22

 

-

 

2009 ............................ 38

 

 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

4 

JORGE MARIO LIZARAZO MARTÍNEZ 

ÍNDICE DE TABLAS 

T

ABLA 

4-1

 

C

OEFICIENTE DE 

P

ÉRDIDA POR 

C

AMBIO DE 

D

IRECCIÓN

 .............................................................................. 22

 

T

ABLA 

4-2

 

M

ÁXIMO 

Á

NGULO DE 

I

NTERSECCIÓN 

P

ARA 

C

OLECTORES 

S

IN 

C

AÍDA

.

  

F

UENTE

:

 

RAS

 

2000. ...................... 23

 

T

ABLA 

4-3

 

V

ALOR DEL 

C

OEFICIENTE 

K

C

.

  

F

UENTE

:

 

RAS

 

2000. ................................................................................... 24

 

T

ABLA 

4-4

 

V

ALOR DEL 

C

OEFICIENTE 

K.

  

F

UENTE

:

 

RAS

 

2000. ..................................................................................... 27

 

T

ABLA 

5-1

 

E

CUACIÓN DE LA 

O

NDA 

P

ARA 

D

IFERENTES 

C

ONFIGURACIONES

.

  

T

OMADA DE LA REFERENCIA 

1. ............. 30

 

T

ABLA 

5-2

 

E

CUACIÓN 

P

ARA LA 

P

ÉRDIDA EN LA 

C

ÁMARA

.

  

T

OMADA DE LA REFERENCIA 

1. ........................................ 31

 

T

ABLA 

5-3

 

V

ALOR DEL 

C

OEFICIENTE 

C

B

.

  

F

UENTE

:

 

HEC

 

22

 

–

 

2009. ............................................................................ 35

 

 

 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

5 

JORGE MARIO LIZARAZO MARTÍNEZ 

ÍNDICE DE FOTOGRAFÍAS 

F

OTOGRAFÍA 

2-1M

ONTAJE EXPERIMENTAL

.

  

T

OMADA DE LA REFERENCIA 

1. ............................................................... 10

 

F

OTOGRAFÍA 

2-2M

ONTAJE EXPERIMENTAL

.

  

T

OMADA DE LA REFERENCIA 

2. ............................................................... 10

 

F

OTOGRAFÍA 

2-3

 

M

ODELO FÍSICO UTILIZADO POR EL 

CIACUA.

  

T

OMADA DE LA REFERENCIA 

1. ................................ 12

 

F

OTOGRAFÍA 

2-4

 

M

ONTAJE UTILIZADO POR LA 

FHWA.

 

T

OMADA DE LA REFERENCIA 

12. ............................................ 14

 

 
 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

6 

JORGE MARIO LIZARAZO MARTÍNEZ 

ÍNDICE DE ECUACIONES 

E

CUACIÓN 

4.2.1

 

E

CUACIÓN DE CONSERVACIÓN DE LA ENERGÍA EN UNA CÁMARA BAJO FLUJO SUBCRÍTICO

. ............... 21

 

E

CUACIÓN 

4.2.2

 

P

ÉRDIDAS POR UNIÓN DE TUBERÍAS

. ................................................................................................... 22

 

E

CUACIÓN 

4.2.3

 

C

ANTIDAD DE MOVIMIENTO PARA FLUJO SUPERCRÍTICO

. ................................................................... 25

 

E

CUACIÓN 

4.2.4

 

V

ALOR DE LA INTENSIDAD DE DESCARGA PARA CONDICIÓN NO SUMERGIDA

. ..................................... 26

 

E

CUACIÓN 

4.2.5

 

C

OEFICIENTE 

H

W CONDICIÓN NO SUMERGIDA

. ................................................................................... 26

 

E

CUACIÓN 

4.2.6

 

C

OEFICIENTE 

H

E

. ............................................................................................................................... 26

 

E

CUACIÓN 

4.2.7

 

V

ALOR DE LA INTENSIDAD DE DESCARGA PARA CONDICIÓN SUMERGIDA

. .......................................... 27

 

E

CUACIÓN 

4.2.8

 

C

OEFICIENTE 

H

W CONDICIÓN SUMERGIDA

. ........................................................................................ 27

 

E

CUACIÓN 

5.2.1

 

C

AÍDA MÁXIMA PERMITIDA EN UNA CÁMARA

..................................................................................... 30

 

E

CUACIÓN 

5.2.2

 

D

IÁMETRO INTERNO REQUERIDO PARA LA CÁMARA

. .......................................................................... 31

 

E

CUACIÓN 

5.2.3

 

L

ONGITUD REQUERIDA DE LA CAÑUELA

. ............................................................................................ 31

 

E

CUACIÓN 

5.3.1

 

E

NERGÍA DE ACCESO A LA CÁMARA CON CONTROL A LA SALIDA

........................................................ 33

 

E

CUACIÓN 

5.3.2

 

E

NERGÍA INICIAL EN LA TUBERÍA DE SALIDA

. ..................................................................................... 33

 

E

CUACIÓN 

5.3.3

 

P

ÉRDIDAS DE ENERGÍA POR ENTRADA A LA TUBERÍA DE SALIDA

. ....................................................... 33

 

ECUACIÓN 

5.3.4

 

I

NTENSIDAD DE DESCARGA

. ................................................................................................................ 33

 

E

CUACIÓN 

5.3.5

 

E

NERGÍA DE ACCESO A LA CÁMARA CON CONTROL A LA ENTRADA 

(

SUMERGIDA

). ............................. 34

 

E

CUACIÓN 

5.3.6

 

E

NERGÍA DE ACCESO A LA CÁMARA CON CONTROL A LA ENTRADA 

(

NO SUMERGIDA

). ....................... 34

 

E

CUACIÓN 

5.3.7

 

E

NERGÍA DE ACCESO CORREGIDA

. ...................................................................................................... 34

 

E

CUACIÓN 

5.3.8

 

P

ÉRDIDA POR CONFIGURACIÓN DE LA CAÑUELA

. ................................................................................ 35

 

E

CUACIÓN 

5.3.9

 

C

OEFICIENTE 



W

. ............................................................................................................................... 36

 

E

CUACIÓN 

5.3.10

 

C

OEFICIENTE 

C



............................................................................................................................... 36

 

E

CUACIÓN 

5.3.11

 

P

ÉRDIDA DE ENERGÍA POR ÁNGULO DE ENTRADA

. ............................................................................ 36

 

E

CUACIÓN 

5.3.12

 

C

OEFICIENTE 

H

K

. ............................................................................................................................. 36

 

E

CUACIÓN 

5.3.13

 

C

OEFICIENTE 

C

P

. .............................................................................................................................. 37

 

E

CUACIÓN 

5.3.14

 

P

ÉRDIDA POR CAÍDA EN LA CÁMARA

. ............................................................................................... 37

 

E

CUACIÓN 

5.3.15

 

E

LEVACIÓN DE LA LÍNEA DE GRADIENTE HIDRÁULICO EN LA CÁMARA

. ............................................ 37

 

E

CUACIÓN 

5.3.16

 

E

LEVACIÓN DE LA LÍNEA DE GRADIENTE HIDRÁULICO EN LA TUBERÍA DE ENTRADA

. ....................... 37

 

E

CUACIÓN 

5.3.17

 

C

OEFICIENTE DE PÉRDIDA POR SALIDA DE LA TUBERÍA DE ENTRADA A LA CÁMARA

. ........................ 37

 

 

 

 

 
 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

7 

JORGE MARIO LIZARAZO MARTÍNEZ 

INTRODUCCIÓN 

 

Dentro  de  las  redes  de  drenaje  las  cámaras  de  unión  e  inspección  constituyen  elementos 
críticos para el adecuado funcionamiento del sistema, debido a las perturbaciones que generan 
en  el  flujo  las  cuales  a  su  vez  inducen  la  aparición  de  fenómenos  como  remansos,  resaltos 
hidráulicos y sobrecarga. 

En consecuencia, las cámaras han sido objeto de estudio y se han desarrollado metodologías 
para  su  dimensionamiento  y  para  el  cálculo  de  las  pérdidas  generadas.    En  Colombia  la 
metodología  tradicionalmente  aceptada  y  utilizada,  plasmada  además  en  el  Reglamento 
Técnico Para el Sector de Agua Potable y Saneamiento (RAS), es la de “empate por línea de 
energía”,  la  cual  busca  determinar  la  pérdida  en  altura  generada  por  la  cámara  y  aplicarla 
como una caída en la cota batea para evitar la formación de un remanso o sobrecarga según el 
tipo de flujo. 

Sin  embargo, recientemente se han publicado importantes investigaciones acerca del  flujo  a 
través  de  cámaras  en  colectores  especialmente  bajo  flujo  supercrítico,  con  un  enfoque 
bidimensional  y  estudio  profundo  de  las  ondas  de  choque  y  otros  fenómenos  presentes,  lo 
cual acerca en mayor medida sus resultados al comportamiento real del flujo en la cámara. 

Es  importante  en  consecuencia  analizar  estos  nuevos  resultados  y  compararlos  con  la 
metodología aplicada en Colombia a fin de determinar si es necesario revaluar este criterio y 
reemplazarlo por un procedimiento más exacto. 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

8 

JORGE MARIO LIZARAZO MARTÍNEZ 

1  ANTECEDENTES Y OBJETIVOS 

1.1  ANTECEDENTES 

Una  revisión  crítica  del  método  de  diseño  de  cámaras  utilizado  en  Colombia  no  registra 
antecedentes propiamente dichos.  Sin embargo el comportamiento del flujo en cámaras si ha 
sido ampliamente tratado a nivel internacional y en los últimos años a nivel nacional.  Dentro 
de la investigación realizada a nivel nacional se destacan los siguientes trabajos: 



 

“Comportamiento  Hidráulico  de  Cámaras  de  Inspección  Bajo  Condiciones  de  Flujo 
Supercrítico”

1

.    Por  Juan  Saldarriaga,  Nataly  Bermúdez,  Eccehomo  Quejada  y  Paula  A. 

Cuero.  Centro  de  Investigaciones  en  Acueductos  y  Alcantarillados  (CIACUA), 
Universidad de los Andes, 2011. 
 



 

“Determinación del  Comportamiento  Hidráulico de Cámaras de Inspección  Plásticas”.  
Mario Moreno,  Daniel Rodríguez  y Fabio Amador. Seminario Nacional De Hidráulica e 
Hidrología, Mayo de 2008, Colombia. 

En  el  Capítulo  2  se  abordan  con  mayor  detalle  los  estudios  realizados  en  los  últimos  años 
acerca del comportamiento del flujo en cámaras. 

 

1.2  OBJETIVOS 

1.2.1  Objetivo General 



  Revisar  la  metodología  de  diseño  de  cámaras  de  inspección  por  empate  de  la  línea  de 

energía,  comparándola con las investigaciones  más recientes  y otros modelos de cálculo 
para  establecer  las  fortalezas  y  debilidades  del  método  y  la  conveniencia  o  no  de  su 
utilización. 

1.2.2  Objetivos Específicos 



  Desarrollar  un  caso  de  estudio  práctico  y  comparar  los  resultados  aplicando  diferentes 

metodologías. 



  Analizar  el  comportamiento  de  un  sistema  diseñado  con  empate  por  línea  de  energía 

cuando se trabaja con caudales diferentes al de diseño. 

 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

9 

JORGE MARIO LIZARAZO MARTÍNEZ 

2  ESTADO DEL ARTE 

 

2.1  GENERALIDADES 

En  el  diseño  de  los  sistemas  de  drenaje  urbano,  uno  de  los  elementos  importantes  que 
componen  el  sistema  son  las  cámaras  o  pozos  de  unión,  las  cuales  se  utilizan  para  realizar 
cambios  en  la  geometría  o  material  de  los  colectores,  así  como  para  propósitos  de 
mantenimiento, aireación, inspección y rehabilitación.   

Las  cámaras  pueden  generar  grandes  pérdidas  que  se  traducen  en  una  pobre  condición 
hidráulica  de  flujo  y  sobrecargas  del  sistema.    Es  por  ello  que  se  requiere  de  un  adecuado 
diseño de las mismas.   

Las  investigaciones  más  extensas  acerca  del  flujo  en  cámaras  han  sido  realizadas  por  el 
profesor  Willi  H.  Hager  del  ETH  en  Zurich  y  por  los  profesores  Gargano,  Del  Giudice  y 
Gisonni  en  Italia,  con  el  inconveniente  de  que  la  mayoría  de  estructuras  estudiadas  son 
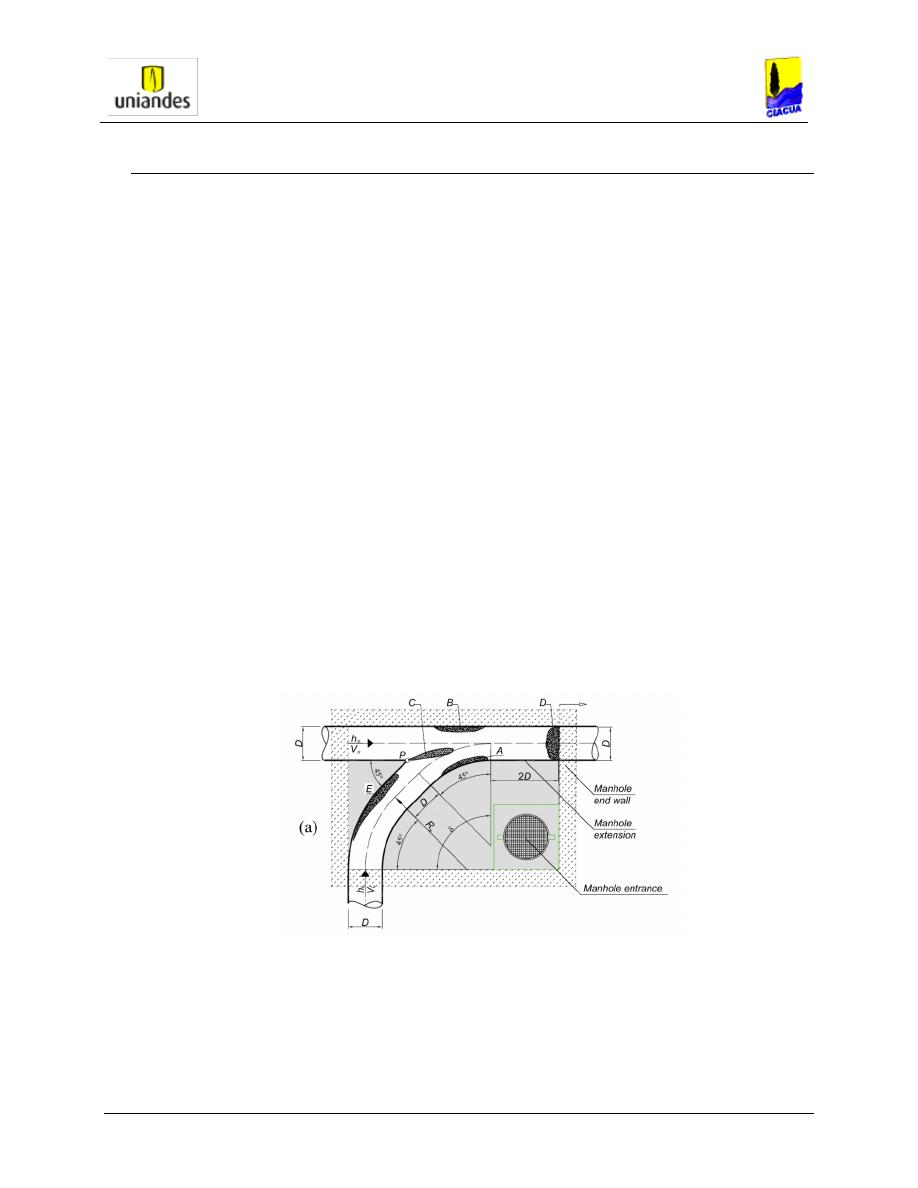
diferentes  a  las  utilizadas  en  Colombia.    Como  se  observa  en  la  Figura  2-1,  lo  que  ellos 
denominan  “junction  manhole”  es  una  estructura  de  unión  bastante  grande  con  un  radio  de 
curvatura usual de 3 veces el diámetro de la tubería de salida y canales de paredes altas, muy 
diferentes  a  las  cámaras  usadas  en  Colombia,  las  cuales  para  tuberías  menores  a  900mm 
tienen diámetro de 1.20m, con un canal semicircular en el fondo o cañuela que generalmente 
no sobrepasa la tercera parte del diámetro de la tubería. 

Figura 2-1 Estructura de unión en alcantarillado.  Tomada de la referencia 15. 

 

Por  otra  parte,  en  el  Centro  de  Investigaciones  en  Acueductos  y  Alcantarillados  (CIACUA) 
de  la  Universidad  de  los  Andes  se  han  desarrollado  investigaciones  importantes  sobre  el 
comportamiento del flujo supercrítico en cámaras utilizando un montaje mucho más cercano 
a  la  realidad  de  los  alcantarillados  en  el  país,  con  una  escala  entre  1:2  y  1:3  respecto  a  la 
estructura convencional. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

10 

JORGE MARIO LIZARAZO MARTÍNEZ 

Fotografía 2-1Montaje experimental.  Tomada de la referencia 1. 

 

Uno  de  los  aspectos  importantes  del  estudio  es  que,  aparte  de  analizar  y  describir  el 
comportamiento del flujo, desarrolló una metodología para el cálculo de las dimensiones de la 
cámara de manera que se logre un funcionamiento adecuado del sistema.  Por esta razón, en 
el  presente  trabajo  se  utilizará  como  referencia  para  el  diseño  de  cámaras  con  flujo 
supercrítico  la  metodología  desarrollada  por  el  CIACUA.    Los  detalles  del  estudio  se 
presentan en el numeral 2.3.1 y la metodología de diseño se explica en el numeral 5.2. 

En Estados Unidos la Federal Highway Administration (FHWA) ha sido la entidad líder en el 
desarrollo de los estudios al respecto.  En el numeral 2.3.2 se detallan los trabajos realizados 
por esta organización. 

En  Canadá  resulta  interesante  el  trabajo

23

  realizado  por  los  investigadores  Zhao,  Zhu  y 

Rajaratnam, los cuales han analizado el fenómeno de sobrecarga en cámaras. 

 

Fotografía 2-2Montaje experimental.  Tomada de la referencia 2. 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

11 

JORGE MARIO LIZARAZO MARTÍNEZ 

2.2  EL FLUJO A TRAVÉS DE CÁMARAS DE INSPECCIÓN 

2.2.1  Flujo Subcrítico 

Se  ha  establecido  que  una  aproximación  unidimensional  es  aceptable  para  flujo  subcrítico

4

.  

Estudios  realizados  en  cámaras  bajo  flujo  subcrítico  indican  que  éstas  se  comportan  como 
tuberías  presurizadas  en  términos  de  pérdidas  de  energía

5

.    En  consecuencia  es  correcto 

aplicar coeficientes de pérdidas en forma similar a las redes de suministro.  La mayoría de los 
métodos  de  diseño  tienen  en  cuenta  las  características  geométricas  de  las  cámaras  para 
determinar un coeficiente global de pérdidas que afecta el valor  de altura de velocidad en la 
tubería de salida o al valor promedio entre la salida y entrada.   El resultado corresponde a la 
pérdida de energía en la estructura, valor que a su vez se utiliza como caída en el fondo de la 
cámara para evitar que bajo ciertas condiciones la línea de energía a la salida resulte más alta 
y pueda generarse un remanso. 

 

2.2.2  Flujo Supercrítico 

En  este  caso  la  suposición  de  flujo  uniforme  pierde  validez  y  el  flujo  pasa  a  ser  en  esencia 
bidimensional.  La superficie libre en un flujo supercrítico es dominada por ondas de choque 
debido a la perturbación del flujo, el cual cambia su perfil de forma circular a uno con forma 
de  U  de  igual  diámetro  de  la  tubería;  sin  embargo  para  profundidades  de  aproximación 
menores  a la mitad del  diámetro, la forma  circular se mantiene  a través  de la cámara.  Para 
flujos  con  número  de  Froude  cercano  a  1,  aparece  en  la  superficie  distorsión  ondular  y 
posibilidad de resaltos hidráulicos, lo cual sumado a relaciones de llenado mayores a 0.5 a la 
salida  de  la  cámara  puede  generar  sobrecarga,  transporte  de  aire,  ahogamiento  o  flujo  a 
presión en la salida. 

Los  experimentos  han  demostrado  que  para  profundidades  de  flujo  menores  al  70%  del 
diámetro, se evitan los  efectos  de pérdida de capacidad, lo  cual  contrasta con la mayoría de 
las normas de diseño que permiten hasta un 85% en la relación de llenado. 

 

2.3  PRINCIPALES  ESTUDIOS  ACERCA  DEL  COMPORTAMIENTO 

DEL FLUJO EN CÁMARAS DE INSPECCIÓN 

2.3.1  Comportamiento  Hidráulico  de  Cámaras  de  Inspección  Bajo  Flujo 

Supercrítico 

Este trabajo  fue realizado por el  Centro de  Investigaciones  en Acueductos  y Alcantarillados 
(CIACUA) de la Universidad de los Andes en el año 2011.   

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

12 

JORGE MARIO LIZARAZO MARTÍNEZ 

El objetivo de la investigación era el de analizar el comportamiento del flujo supercrítico en 
una  cámara  de  inspección  y  con  base  en  ello  establecer  una  metodología  para  el  diseño 
geométrico de la estructura de forma tal que se garantizara un adecuado funcionamiento del 
sistema. 

Para lograrlo se realizó un montaje (ver Fotografía 2-1) en cristal acrílico con dos tuberías de 
entrada  de  0.22m  de  diámetro,  alineadas  a  180°  y  90°  con  la  tubería  de  salida  de  0.28m  de 
diámetro y una cámara cilíndrica en acrílico de 0.85m de diámetro y 0.70m de altura con sus 
canales de conducción interna o cañuelas. El montaje permitía que las tuberías de entrada se 
pudieran ubicar a cuatro diferentes alturas sobre la batea de la cámara. 

Fotografía 2-3 Modelo físico utilizado por el CIACUA.  Tomada de la referencia 1. 

 

El montaje fue instrumentado con un sensor de nivel y medidores de caudal por ultrasonido.  
Se evaluaron tres configuraciones: 



  Cámaras  con  paso  directo  donde  la  tubería  de  entrada  se  encuentra  alineada  con  la  de 

salida. 



  Cámaras con una tubería de entrada y cambio de dirección de 90° respecto a la salida. 



  Cámaras con una tubería  en paso directo y otra con cambio de dirección de 90° respecto a 

la salida. 

Utilizando relaciones de llenado entre el 5% y el 75% se realizaron las mediciones de altura 
del  nivel  del  agua  y  caudal  para  cada  una  de  las  configuraciones  y  las  diferentes  alturas  de 
caída.    El  estudio  encontró  formación  de  cinco  diferentes  tipos  de  ondas  de  acuerdo  con  el 
caudal y la configuración, las cuales se describen a continuación: 



  Onda A: Generada por el choque del flujo de entrada de la tubería con paso directo en la 

cañuela con el final de la pared interna de la cañuela de conducción del flujo de la tubería 
lateral. 



  Onda B: Onda característica de los flujos supercríticos con paso directo sin presencia de 

una tubería de entrada lateral, que se forma a la entrada de la tubería de salida. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

13 

JORGE MARIO LIZARAZO MARTÍNEZ 



  Onda  C:  Generada  por  el  choque  frontal  del  flujo  entrante  por  la  tubería  lateral  con  la 

pared de la cañuela de paso directo. 



  Onda  D:  Generada  por  el  choque  del  flujo  entrante  por  la  tubería  lateral  con  la  pared 

interna de la cañuela por la cual se desplaza. 



  Onda E: Generada cuando se tiene flujo simultáneo en paso directo y lateral, por la unión 

de los flujos en el punto de confluencia de las dos cañuelas. 

Aunque  de  acuerdo  con  las  características  del  flujo  y  de  la  cámara  se  pueden  presentar 
simultáneamente  varios  tipos  de  ondas,  los  resultados  indicaron  que  el  comportamiento  se 
rige por la onda hidráulicamente dominante. 

Con los datos obtenidos de las mediciones, los investigadores encontraron correlaciones entre 
la altura de la onda y las pérdidas de energía en la cámara y procedieron a realizar un análisis 
estadístico  mediante  el  software  Statgraphics  para  obtener  ecuaciones  de  diseño  que 
permitieron definir una metodología de trabajo para encontrar las dimensiones apropiadas de 
la cámara, la cual se presenta en el numeral 5.2 

 

2.3.2  Estudios de la FHWA 

Por muchos años la FHWA desarrolló métodos para la estimación de las pérdidas en cámaras 
de inspección, entre ellos: 



  Método  del  coeficiente  de  corrección  por  pérdida  de  energía,  basado  en  una 

investigación realizada por Chang y Kilgore

6

. 



  Método de la pérdida de energía, presentado en el “HEC 22 Urban Drainage Manual” 

segunda  edición  con  base  en  estudios  realizados  por  la  FHWA.

78

    Este  método  se 

caracterizaba por aplicar un gran número de coeficientes de pérdidas que dependían de las 
características geométricas y constructivas de la cámara.  Tenía la limitante de que no se 
podía  usar  cuando  la  cota  batea  de  la  tubería  de  entrada  se  encontraba  por  encima  del 
nivel del agua en la cámara, o cuando existían muchas tuberías de entrada a la estructura.  
Este además es uno de los métodos disponibles en el programa SewerCad, uno de los más 
utilizados para el cálculo de sistemas de drenaje. 



  Método  de  la  pérdida  de  energía  compuesta,  desarrollado  con  base  en  un  reporte  de 

investigación  de  1994

9

;  se  implementó  en  el  paquete  informático  de  análisis  y  diseño 

HYDRA  (HYDRAIN,  1996)  y  se  incluyó  en  la  segunda  edición  (2001)  del  “HEC  22 
Urban Drainage Manual”, para los casos en los cuales no se podía utilizar el método de la 
pérdida  de  energía.    Este  método  se  caracteriza  al  igual  que  el  anterior  por  utilizar 
coeficientes que dependen de las características geométricas y constructivas de la cámara, 
con la diferencia de que el cálculo de los coeficientes es extremadamente complejo. 

Sin embargo se encontraron limitaciones en éstos métodos que incluían: 



  Representación limitada de diferentes condiciones hidráulicas dentro de las cámaras. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

14 

JORGE MARIO LIZARAZO MARTÍNEZ 



  Resultados  cuestionables  cuando  se  trabajaba  en  sistemas  sobrecargados  o  con  flujo 

supercrítico. 



  Las profundidades de flujo calculadas vs las observadas resultaban subvaloradas. 



  Aplicación inconsistente en el software relacionado. 

Por tal motivo la FHWA, con base en la metodología desarrollada por Roger Kilgore

10,11

, la 

cual  fue  ajustada  por  él  mismo  de  acuerdo  a  un  estudio

12,13

  complementario  realizado  en 

2005,  incluyó  en  la  tercera  edición  (2009)  del  “HEC  22  Urban  Drainage  Manual”  el 
procedimiento de cálculo vigente a la fecha.  

Para el desarrollo de su método, Kilgore utilizó como base los datos obtenidos en sus trabajos 
para la FHWA de 1986 a 1992 separándolos en dos grupos.  En el primer grupo se incluyeron 
los  datos  de  los  montajes  con  la  configuración  más  simple  y  en  el  otro  los  más  complejos, 
para realizar ajustes a las primeras aproximaciones.  Los estudios de 1986-1992 se realizaron 
en  modelos  a  gran  escala  en  una  cámara  de  0.60m  de  diámetro,  con  un  total  de  755 
mediciones.    Para  los  estudios  complementarios    los  investigadores  decidieron  utilizar  un 
modelo  de  pequeña  escala  instrumentado  con  elementos  de  gran  precisión,  en  particular  un 
velocímetro de imagen de partículas (VIP) para visualizar y medir los patrones de flujo, para 
lo cual se requería incluir en el mismo trazadores de partículas. 

Fotografía 2-4 Montaje utilizado por la FHWA. Tomada de la referencia 12. 

 

Se  observan  las  tuberías  verticales  adheridas  al  conducto  horizontal  para  la  medición  de  la  línea  de 
gradiente hidráulico mediante sensores de imagen de contacto (SIC). 

Los  objetivos  de  la  investigación  eran  en  primer  lugar  comparar  los  resultados  de  las 
mediciones anteriores con la nueva metodología propuesta e incluir los rangos de pendientes 
y caídas que no se tuvieron en cuenta en los estudios de 1986-1992, los cuales re realizaron 
con el objeto de obtener aplicaciones para zonas muy planas.   En segundo lugar se buscaba 
caracterizar el nivel de energía en la cámara con varias  configuraciones de entrada  y salida, 
realizando una modelación en tres dimensiones de los datos arrojados por el VIP.  Debido a la 
naturaleza caótica del  flujo  en las cámaras los  investigadores  tuvieron que  suponer  aspectos 
del comportamiento de manera arbitraria con el fin de obtener resultados razonables. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

15 

JORGE MARIO LIZARAZO MARTÍNEZ 

El montaje consistía en tres tanques de agua, uno de entrada, otro de salida y uno principal.  
En el tanque principal se ubicó el modelo en cristal acrílico rodeado de agua para minimizar 
las distorsiones en las medidas del VIP; también se ubicaron dos sensores laser para medir la 
profundidad en las tuberías verticales adheridas a la tubería de entrada y salida, apuntando a 
discos flotantes dentro de las primeras.  Otro dispositivo utilizado para medir la profundidad 
del flujo era un sensor de imagen de contacto (SIC), el cual tiene la ventaja de que escanea las 
columnas de agua arrojando la profundidad en cada una al mismo tiempo.  La cámara tenía 
15cm de diámetro y las tuberías 3.8cm 

 

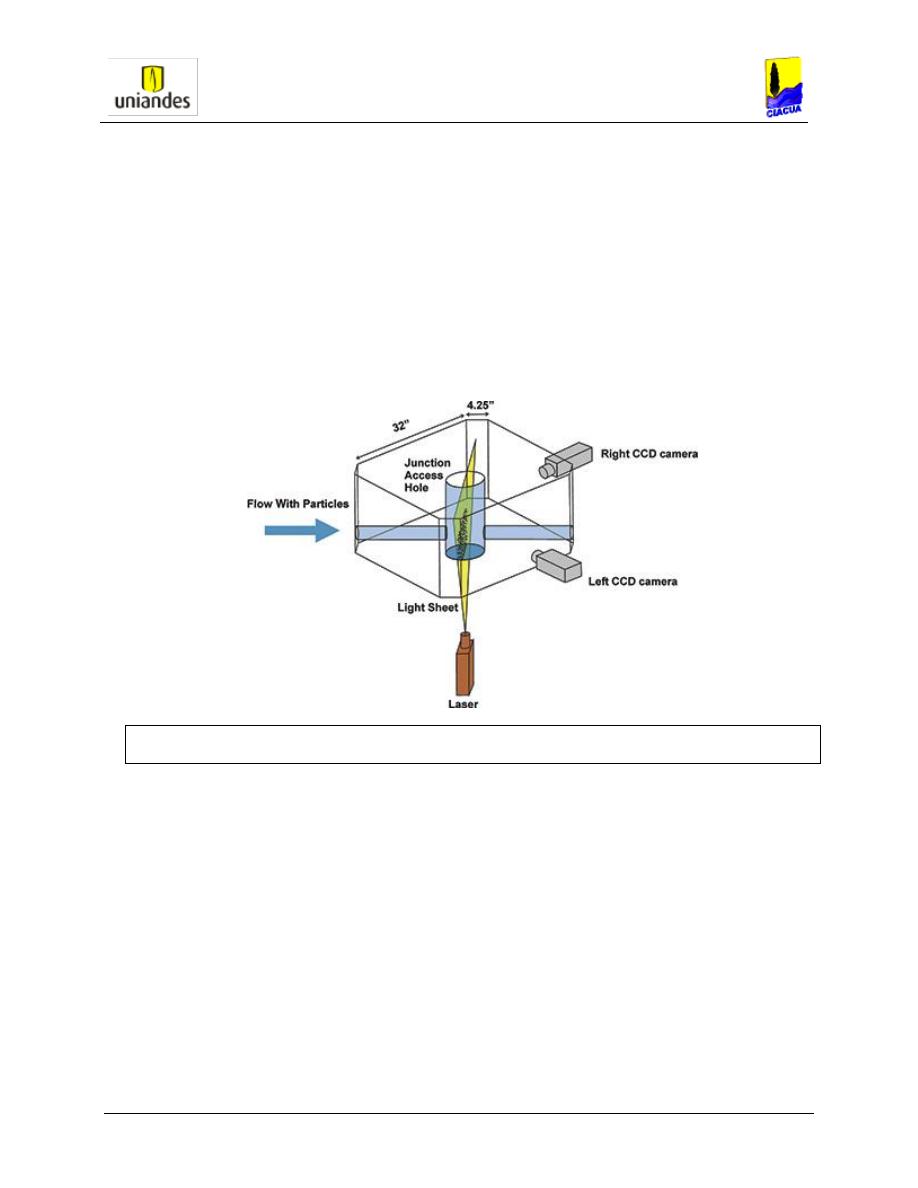
Figura 2-2 Montaje utilizado por la FHWA.  Tomada de la referencia 12. 

 

Se  muestra  el  tanque  central  y  un  arreglo  con  dos  cámaras  digitales  en  ángulo  y  una  lámina  de  luz 
generada por un dispositivo laser. 

Una  vez  verificaron  que  la  escala  no  influía  en  los  resultados  de  los  experimentos,  los 
investigadores  procedieron  a  comparar  y  a  realizar  las  nuevas  mediciones.    Ejecutaron  18 
pruebas  con  flujo  supercrítico  y  tuberías  de  entrada  a  180°  y  90°  con  relación  a  la  salida; 
adicionalmente  18  mediciones  para  bajo  caudal.    Los  resultados  obtenidos  se  ajustaron 
bastante  a  bien  a  los  calculados  utilizando  la  metodología  de  Kilgore  tanto  para  flujo 
subcrítico  como  supercrítico.    Los  valores  obtenidos  con  la  ecuación  propuesta  para  la 
pérdida  adicional  por  flujo  en  caída  coincidieron  con  los  medidos  en  los  ensayos  sólo  para 
relaciones  altura  de  caída/diámetro  del  tubo  de  salida  menores  a  10.    También  encontraron 
una  profundidad  del  flujo  constante  en  el  centro  de  la  cámara  para  diferentes  valores  de  la 
intensidad de descarga. 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

16 

JORGE MARIO LIZARAZO MARTÍNEZ 

 

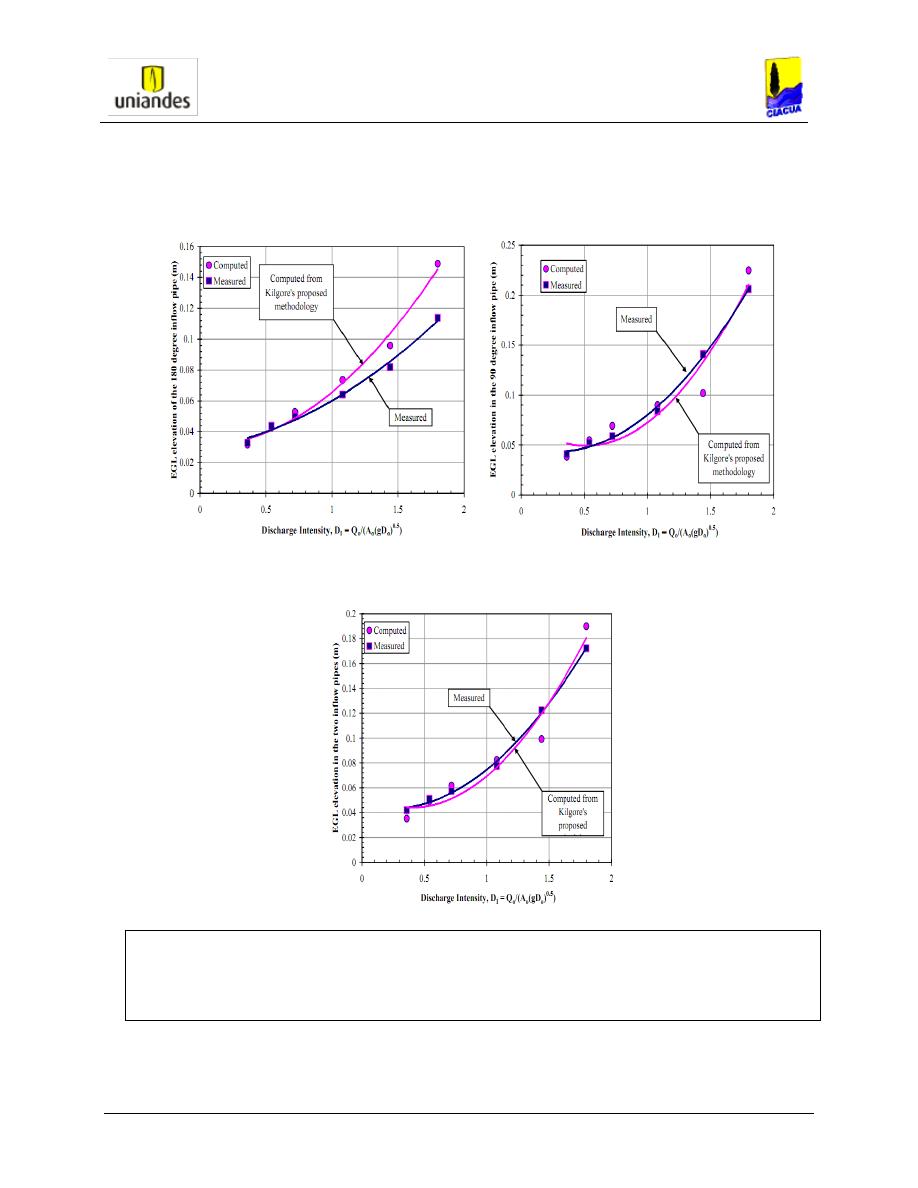
Figura 2-3 Elevación de la Línea de Energía (ELE) para diferentes Intensidades de Descarga 

 

 

 

 

Las gráficas representan la altura de la línea de gradiente hidráulico (eje vertical) contra la intensidad de 
descarga  (ID),  que  es  un  parámetro  similar  al  número  de  Froude  para  tuberías  a  flujo  lleno.    La  línea 
magenta representa el cálculo con la metodología de Kilgore; la línea azul los datos medidos en el modelo.  
Gráfica superior izquierda para flujo a 180°; gráfica superior derecha para flujo a 90° y gráfica inferior  
para flujo combinado. 

 

Resultados para flujo a 180° 

Resultados para flujo a 90° 

Resultados para flujo combinado 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

17 

JORGE MARIO LIZARAZO MARTÍNEZ 

Kilgore señala en su publicación que su metodología no es apropiada para altas intensidades 
de descarga con una tubería de salida en flujo supercrítico, debido a que el agua podría cruzar 
la cámara por el aire y no expandirse y contraerse de acuerdo con lo esperado. 

 

 

2.3.3  Otros Estudios 

A continuación se presenta una breve reseña de  otros estudios importantes realizados en los 
últimos años: 

 

a.  Flujo Supercrítico en Cámaras en Curva

14

 

En  esta  investigación  se  determinaron  las  características  típicas  de  un  flujo  supercrítico  a 
través de un canal en curva con sección transversal en forma de U que comunica dos tubos de 
igual diámetro (modelo físico de la cañuela); Las principales conclusiones del estudio fueron: 



  El comportamiento del flujo en la cámara depende únicamente del número de Froude en 

la entrada de la estructura de conexión, sin importar la relación de llenado y el ángulo de 
desviación de la unión.  



  Para  números  de  Froude  altos  surge  un  aumento  en  el  nivel  de  la  lámina  de  agua  y  se 

origina  un  resalto  hidráulico,  que  después  de  un  choque  frontal  comienza  a  llenar  la 
cámara; el límite del ahogo del flujo es claramente una base importante de diseño.  



  El flujo supercrítico en la curva afecta principalmente la altura de la superficie libre más 

que la distribución de velocidades. 

 

b.  Flujo Supercrítico en Cámaras con Unión a 45° 

15

 

En  este  trabajo  se  describió  la  estructura  principal  de  la  onda  que  se  presenta  en  una  unión 
con sección transversal en forma de U, conformada por dos tuberías de llegada: una tubería 
principal aguas arriba y una tubería lateral con un ángulo de deflexión de 45°. Las principales 
conclusiones del estudio fueron: 



  Se  establecieron  ecuaciones  para  el  cálculo  de  la  localización  y  altura  de  las  ondas 

dominantes identificadas, en función de la relación de llenado y número de Froude. 



  Se  determinó  la  capacidad  hidráulica  de  la  unión  para  cada  caso  posible  según  las 

características  del  flujo  en  los  ramales  de  entrada,  expresada  como  un  valor  límite  del 
número de Froude. 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

18 

JORGE MARIO LIZARAZO MARTÍNEZ 

c.  Flujo Supercrítico en Cámaras con Unión a 90° 

16

 

Este  estudio  se  desarrolló  para  analizar  el  comportamiento  de  un  flujo  supercrítico  en  una 
unión  con  sección  transversal  en  forma  de  U  conformada  por  dos  tuberías  de  llegada:  una 
tubería  principal  aguas  arriba  y  una  tubería  lateral  con  un  ángulo  de  deflexión  de  90°.    Las 
conclusiones  fueron  similares  a  las  de  los  anteriores  trabajos.    Como  datos  interesantes  se 
obtuvieron los siguientes resultados: 

•  Cámaras de unión con dos tuberías de llegada, una aguas arriba y una lateral con ángulos 
de deflexión  entre 30°  y 90°, tienen un comportamiento  hidráulico similar bajo  condiciones 
de flujo supercrítico, siempre y cuando se conserve la modificación geométrica de la cámara 
descrita  en  el  estudio  previo.  Lo  anterior,  crea  una  base  de  diseño  general  sin  importar  el 
ángulo de intersección de la tubería lateral.  

•  Todos  los  parámetros  varían  exclusivamente  con  el  número  de  Froude  y  la  relación  de 
llenado de las tuberías. 

 

d.  Flujo Supercrítico en Cámaras de Alcantarillado

17

 

El propósito de la investigación era el de analizar los datos recolectados en el ETH de Zurich 
y  determinar  el  comportamiento  del  flujo  en  tres  tipos  de  cámaras:  paso  directo,  curva  y 
unión.  Las principales conclusiones del estudio fueron: 



  La  menor  capacidad  de  descarga  la  tienen  las  cámaras  para  cambios  de  dirección, 

seguidas por las cámaras de unión con el doble de capacidad y las cámaras de paso directo 
con el triple de la capacidad.  El efecto del ángulo de la curva resultó ser despreciable. 



  El  flujo  en  la  cámara  es  gobernado  por  la  presencia  de  ondas  que  se  forman  debido  a 

cambios hidráulicos o geométricos en la estructura. 
 

e.  Caída en Cámara de Alcantarillado Combinado para Flujo Supercrítico

18

 

Esta  investigación  identificó  el  efecto  hidráulico  del  flujo  supercrítico  en  cámaras  de 
alcantarillado con caídas, diferenciando entre caídas pequeñas e intermedias. Las principales 
conclusiones del estudio fueron: 



  Las cámaras con  caída no mejoran  el funcionamiento del flujo supercrítico,  y  aunque el 

efecto es mínimo para pequeñas caídas, se generan ondas expansivas, arrastre de aire y se 
llega a un resultado menos económico de diseño.  



  Las  caídas  intermedias  tienen  un  efecto  nocivo  sobre  el  flujo  supercrítico  debido  a  la 

formación excesiva de ondas y la reducción significativa de la capacidad de descarga. Por 
lo tanto, el uso de cámaras con caída no debe ser incorporado para un flujo supercrítico. 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

19 

JORGE MARIO LIZARAZO MARTÍNEZ 

f.  Flujo Supercrítico en Sistemas de Alcantarillado en Una Unión Combinada: Estudio 

de Un Modelo de Unión de Edworthy, Calgary, Alberta

19

 

En  este  estudio  experimental  se  analizó  el  comportamiento  del  flujo  supercrítico  en  una 
cámara de alcantarillado mediante el uso de un modelo físico.  Las principales conclusiones 
del estudio fueron: 



  La unión de la cámara con pequeños ángulos de confluencia ayuda a conservar la energía 

cinética del flujo y reduce el nivel del agua en la cámara sobrecargada.  



  Las  pérdidas  de  energía  generadas  en  la  estructura  de  conexión  se  encuentran  entre  un 

35%  y  un  55%  de  la  energía  de  entrada.    En  las  pérdidas  se  incluyen  los  efectos  de  la 
fricción, desviación del tubo, resalto hidráulico en los conductos aguas arriba, flujo mixto 
aire-agua en la cámara y pérdidas locales en la entrada y la salida de la misma. 

 

 

 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

20 

JORGE MARIO LIZARAZO MARTÍNEZ 

3  METODOLOGÍA 

Para  lograr  los  objetivos  propuestos  se  realizará  una  investigación  bibliográfica  para 
determinar el estado del arte del diseño de cámaras de inspección, se presentará el método de 
empate  por  línea  de  energía  y  se  realizará  la  comparación  con  las  metodologías  propuestas 
por las investigaciones más recientes.   

Estas investigaciones han determinado los patrones de comportamiento del flujo en cámaras y 
han  establecido  correlaciones  entre  los  parámetros  que  lo  definen  con  las  dimensiones 
requeridas  de  la  estructura.    La  revisión  del  método  incluye  el  determinar  si  sus  postulados 
básicos  son  congruentes  con  el  comportamiento  real  del  flujo  y  si  consecuentemente  se 
obtienen las dimensiones requeridas para garantizar el adecuado funcionamiento del sistema. 

Por último se desarrollará un ejercicio práctico utilizando por una parte el criterio de empate 
por  línea  de  energía  y  por  otra  parte  la  metodología  que  el  presente  trabajo  considere  más 
completa y acorde con el caso colombiano. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

21 

JORGE MARIO LIZARAZO MARTÍNEZ 

4  EL CRITERIO DE EMPATE POR LÍNEA DE ENERGÍA

20

 

4.1  JUSTIFICACIÓN 

La  unión  de  colectores  se  realiza  a  través  de  una  estructura  hidráulica  tal  como  un  pozo  o 
cámara.  El paso del flujo a través de dicha estructura genera pérdidas de energía.  Esto puede 
ocasionar  que,  para  ciertas  condiciones,  se  requiera  a  la  salida  (teniendo  en  cuenta  que  la 
salida  genera  una  pérdida  adicional)  una  mayor  energía  que  la  disponible  al  descontar  las 
pérdidas, lo cual generaría un remanso en el sistema.  Para evitar esto se deja una caída en la 
cámara  igual  a  las  pérdidas  calculadas,  de  modo  que  la  energía  total  a  la  salida  sea  igual  o 
menor que la disponible luego de pasar por la cámara. 

 

4.2  CASOS 

4.2.1  Flujo Subcrítico 

Se  calcula  la  pérdida  localizada  de  energía  en  la  cámara  utilizando  coeficientes  “K”  de 
manera análoga a los conductos a presión; utilizando la ecuación de Bernoulli, la pérdida total 
se  obtiene  de  sumar  a  las  pérdidas  localizadas  la  diferencia  entre  los  valores  de  energía 
específica a la salida y a la entrada. 

Planteando la ecuación de energía entre las tuberías de entrada y salida al centro del pozo: 

e

H

g

V

d

Z

g

V

d

Z















2

2

2

2

2

2

2

1

1

1

 

e

H

g

V

d

g

V

d

Z

Z







































2

2

2

1

1

2

2

2

2

1

 

e

H

E

E

Z

Z











1

2

2

1

 

 

dónde: 

Z=  Altura de posición. 

d = Altura de la lámina de agua en la tubería. 

V2/2g=Altura de velocidad. 

ΔHe = Pérdidas en la estructura. 

E = Energía específica. 

Ecuación 4.2.1 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

22 

JORGE MARIO LIZARAZO MARTÍNEZ 

Las pérdidas de energía en la estructura ΔHe se dividen en dos: 

ΔHd = Pérdida por cambio de dirección. 

ΔHt = Pérdida por unión o transición. 

Cuando  existan  varias  tuberías  afluentes,  se  debe  verificar  que  todas  las  cotas  de  energía 
entrantes, después de descontadas las pérdidas de energía correspondientes, sean superiores o 
iguales  a  la  de  la  tubería  efluente.    Al  empatar  con  la  tubería  principal  entrante,  los  demás 
tramos pueden diseñarse nuevamente de tal manera que coincidan con la misma energía de la 
principal entrante (después de descontadas las pérdidas) en el pozo. 

 

Pérdida por Cambio de Dirección ΔHd 

La pérdida de energía por cambio de dirección, para flujo subcrítico o supercrítico, se calcula 
como función de la relación entre el radio de curvatura del pozo, rc y el diámetro de la tubería 
de salida Ds.  En la tabla se presenta el valor de la pérdida de energía k V

2

/2g, siendo “V” la 

velocidad promedio entre la tubería de entrada y la de salida. 

Tabla 4-1 Coeficiente de Pérdida por Cambio de Dirección 

Régimen de flujo

rc/Ds

ΔH

d

1.0-1.5

0.4V2/2g

1.5-3.0

0.2V2/2g

> 3.0

0.05V2/2g

6.0-8.0

0.4V2/2g

8.0-10.0

0.2V2/2g

>10.0

0.05V2/2g

subcrítico

supercrítico

 

 
 
 
Pérdidas Debidas a la Unión de las Tuberías ΔHt 
 
Las  pérdidas  por  la  unión  o  transición  obedecen  al  aumento  o  a  la  disminución  de  la 
velocidad debido a un cambio de diámetro, pendiente o adición de caudal.  La forma general 
de expresión de dichas pérdidas es: 
 



















g

V

g

V

k

H

t

2

2

2

1

2

2

 

 
k = 0.1 para un aumento de velocidad. 
k = 0.2 para una disminución de la velocidad. 
 

Ecuación 4.2.2 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

23 

JORGE MARIO LIZARAZO MARTÍNEZ 

4.2.2  Flujo Supercrítico 

Si  el  flujo  cumple  ciertas  condiciones  y  se  cuenta  con  suficiente  espacio,  se  construye  una 
estructura alargada, con gran radio de curvatura.  El cálculo incluye la ecuación de cantidad 
de movimiento, debido a las altas velocidades.  En caso contrario se utiliza una estructura con 
caída,  a  fin  de  disipar  la  energía  cinética  del  flujo.    El  cálculo  supone  que  se  pierda  la 
totalidad  de  la  energía  cinética  y  el  comportamiento  es  equivalente  al  de  una  masa 
estacionaria de agua en un recipiente con un orificio en la base, que corresponde al colector 
de salida. 

Unión De Colectores Sin Caída En La Estructura De Unión 

En  algunos  casos  es  posible  hacer  la  unión  de  colectores  sin  necesidad  de  proveer  a  la 
estructura de unión de un pozo de caída. Para esto se requiere lo cumplir con los siguientes 
requerimientos hidráulicos: 

a.  La  cota  de  la  superficie  de  agua  en  los  colectores  afluentes  a  la  estructura  debe  ser 

aproximadamente la misma. Contribuciones menores al 10% del caudal principal pueden 
eventualmente  llegar  por  encima  de  la  cota  de  la  superficie  de  agua  en  el  colector  de 
salida. 

b.  La  cota  de  energía  del  colector  de  salida  debe  ser  menor  que  la  de  los  de  entrada  para 

evitar la formación de resaltos hidráulicos en la estructura de conexión. 

c.  El  máximo  ángulo  de  intersección  entre  los  colectores  principales  de  entrada  y  salida 

depende del diámetro del colector de salida según la Tabla 4-2: 

Tabla 4-2 Máximo Ángulo de Intersección Para Colectores Sin Caída.  Fuente: RAS 2000. 

Diámetro del colector de salida Ds (mm)

Ángulo

Ds < 250

90

250 < Ds ≤ 350

75

350 < Ds ≤ 530

60

530 < Ds ≤ 900

45

Ds > 900

15

Máximo ángulo de intersección

 

 

d.  Es  necesario  adecuar  la  unión  en  la  estructura  para  evitar  alteraciones  en  el  flujo  y 

disminuir las pérdidas en la confluencia de los colectores. Para esto puede construirse una 
curva  en  el  sistema  principal  de  recolección  y  evacuación  de  aguas  residuales  o  lluvias 
que  esté  de  acuerdo  con  las  dimensiones  de  los  colectores  principales  y  las  deflexiones 
definidas  en  la  Tabla  4-2.  Dependiendo  de  los  elementos  de  la  curva  (radio,  deflexión, 
tangencia, etc.), ésta puede ser desarrollada en la cañuela dentro de la estructura de unión, 
o  a  lo  largo  de  la  intersección,  entre  las  longitudes  Lpi  y  Lpd,  de  la  Figura  4-1, 
requiriéndose una altura adecuada de la cañuela para las condiciones del caudal de diseño. 
La pendiente del colector en el desarrollo de la curva (Pp), está definida por la pérdida de 

 

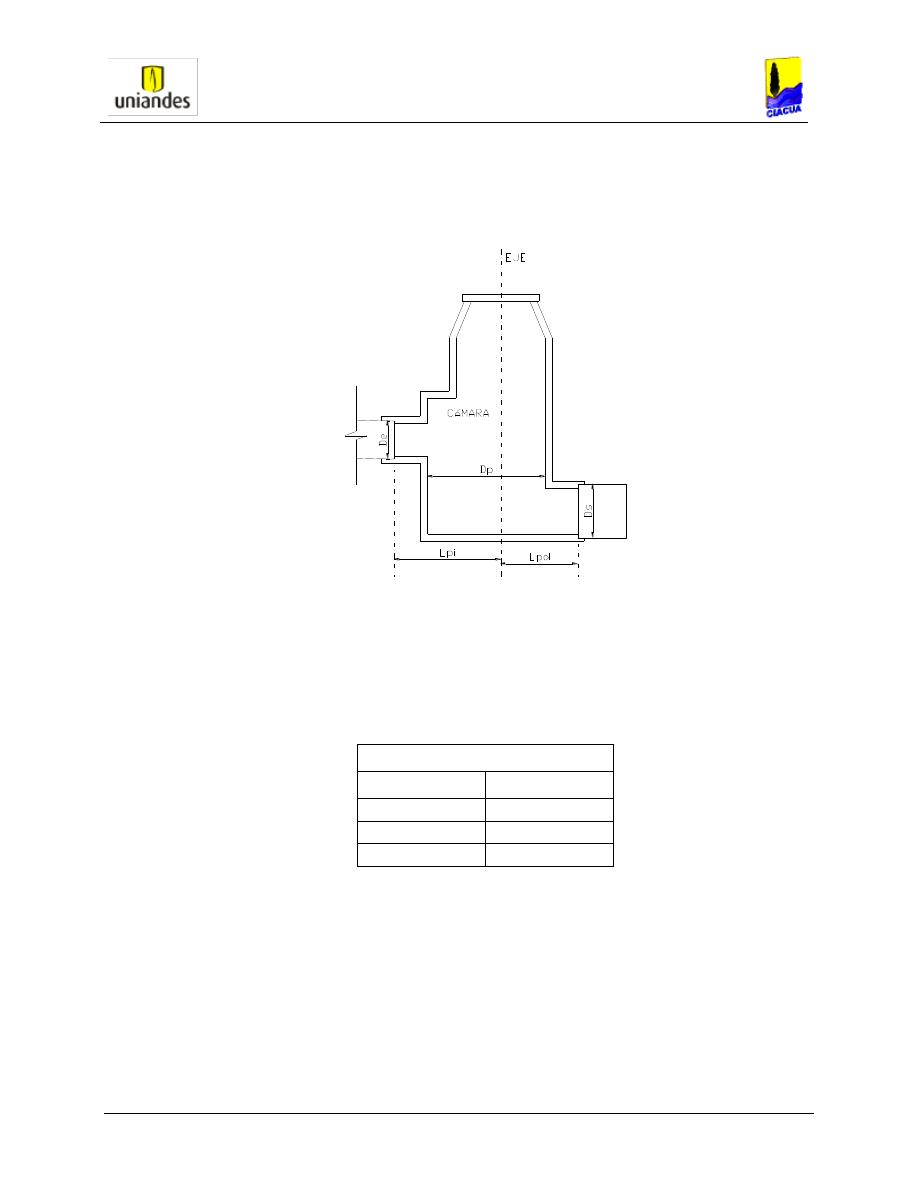
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

24 

JORGE MARIO LIZARAZO MARTÍNEZ 

energía  en  la  estructura  de  unión,  DHc,  la  cual  se  debe  principalmente  al  cambio  de 
dirección en el alineamiento. 

Figura 4-1 Estructura de Unión con Pozo de Inspección.  Fuente: RAS 2000. 

 

En la Tabla 4-3 Valor del Coeficiente Kc, se presentan los valores del coeficiente Kc de 
pérdidas de energía en flujo curvilíneo como función del radio de curvatura y el diámetro 
del  colector  de  salida.    D

HC

  se  calcula  entonces  como  el  producto  de  Kc  y  la  altura  de 

velocidad en el colector de salida. 

Tabla 4-3 Valor del Coeficiente Kc.  Fuente: RAS 2000. 

 

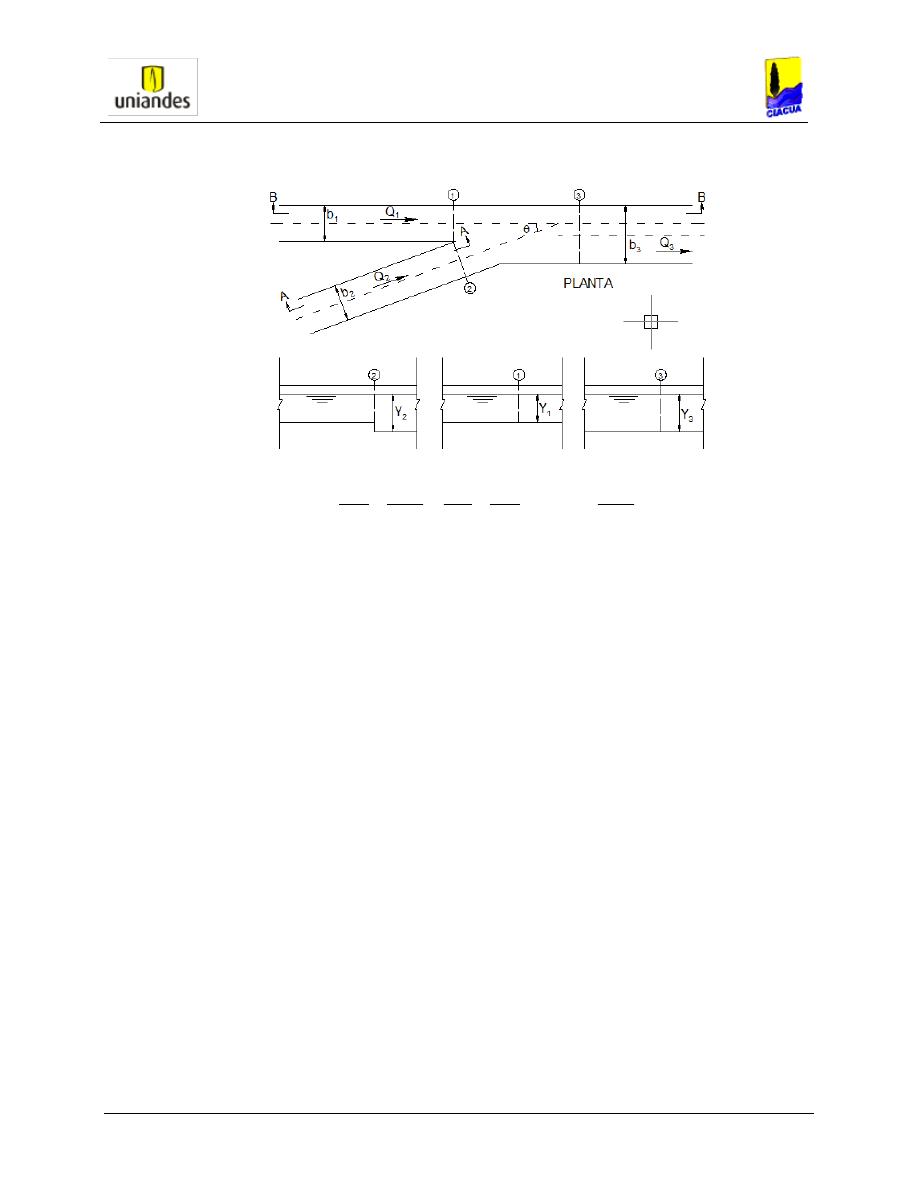
e.  Cuando se unen dos colectores con diámetros mayores a 900 mm, el análisis hidráulico de 

la  estructura  de  conexión  debe  basarse  en  la  ecuación  de  cantidad  de  movimiento,  que 
puede expresarse de la siguiente forma, de acuerdo con las definiciones  mostradas  en la 
Figura 4-2. 
 

Dp/Ds

K

C

6 - 8

1.2

8- 10

1.3

> 10

1.4

Coeficiente K

C 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

25 

JORGE MARIO LIZARAZO MARTÍNEZ 

Figura 4-2Análisis de estructura de unión sin caída.  Fuente: RAS2000 

 

 

2

2

2

1

3

3

2

2

2

1

2

1

2

3

3

3

2

3

Y

b

b

Cos

gA

Q

gA

Q

Y

b

gA

Q











 

En  la  anterior  ecuación  todos  los  valores  son  conocidos  excepto  los  de  b3  y  Y3,  por  lo 
cual  para  su  solución  se  puede  iterativamente  adoptar  valores  de  b3  para  encontrar  el 
correspondiente  valor  de  Y3.    Es  necesario  además,  calcular  el  número  de  Froude  en  la 
sección  3-3  para  garantizar  que  el  régimen  continuo  siendo  supercrítico  y  así  evitar 
posibles resaltos dentro de la estructura. 

Unión De Colectores Con Caída En La Estructura  

Para los casos en los cuales no es justificable o no hay espacio para construir estructuras de 
unión  como  las  anteriores,  en  particular  cuando  los  diámetros  son  mayores  que  900  mm, 
pueden  hacerse  estructuras  de  unión  convencionales,  que  aunque  son  estructuras  más 
compactas requieren en ciertos casos caídas relativamente grandes dentro de la estructura. En 
general,  este  tipo  de  estructura  de  unión  (ver  Figura  4-4)  está  limitada  a  caudales  efluentes 
hasta  de  5  m

3

/s,  con  control  de  velocidades  que  puedan  generar  abrasión  dentro  de  la 

estructura.  En  casos  particulares  y  para  caudales  mayores  al  anterior,  se  deben  diseñar 
estructuras  especiales  de  caída  que  regulen  el  flujo,  como  estructuras  escalonadas  o 
parabólicas, entre otras. 

En  general,  el  análisis  hidráulico  en  estos  casos  considera  que  la  totalidad  de  la  energía 
cinética  del  flujo  se  pierde  en  la  estructura  de  unión  y  por  lo  tanto  el  comportamiento  es 
equivalente al de una masa de agua estacionaria que para salir de la estructura de unión debe 
hacerlo  por  el  orificio  formado  por  el  colector  de  salida.  Esto  corresponde  al  flujo  en  un 
conducto cerrado con control en la entrada, donde la capacidad del colector es mayor que la 
capacidad de entrada de agua a éste. 

Ecuación 4.2.3 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

26 

JORGE MARIO LIZARAZO MARTÍNEZ 

El diseño debe determinar la elevación del agua en la estructura de unión, de tal forma que la 
cota del agua en la estructura de unión no sobrepase las elevaciones de los flujos afluentes, las 
cuales pueden estimarse suponiendo flujo uniforme en la entrada de los colectores afluentes. 

La  entrada  de  agua  al  colector  de  salida  puede  presentarse  de  manera  sumergida  o  no 
sumergida, dependiendo del diámetro del colector y del caudal efluente. 

 

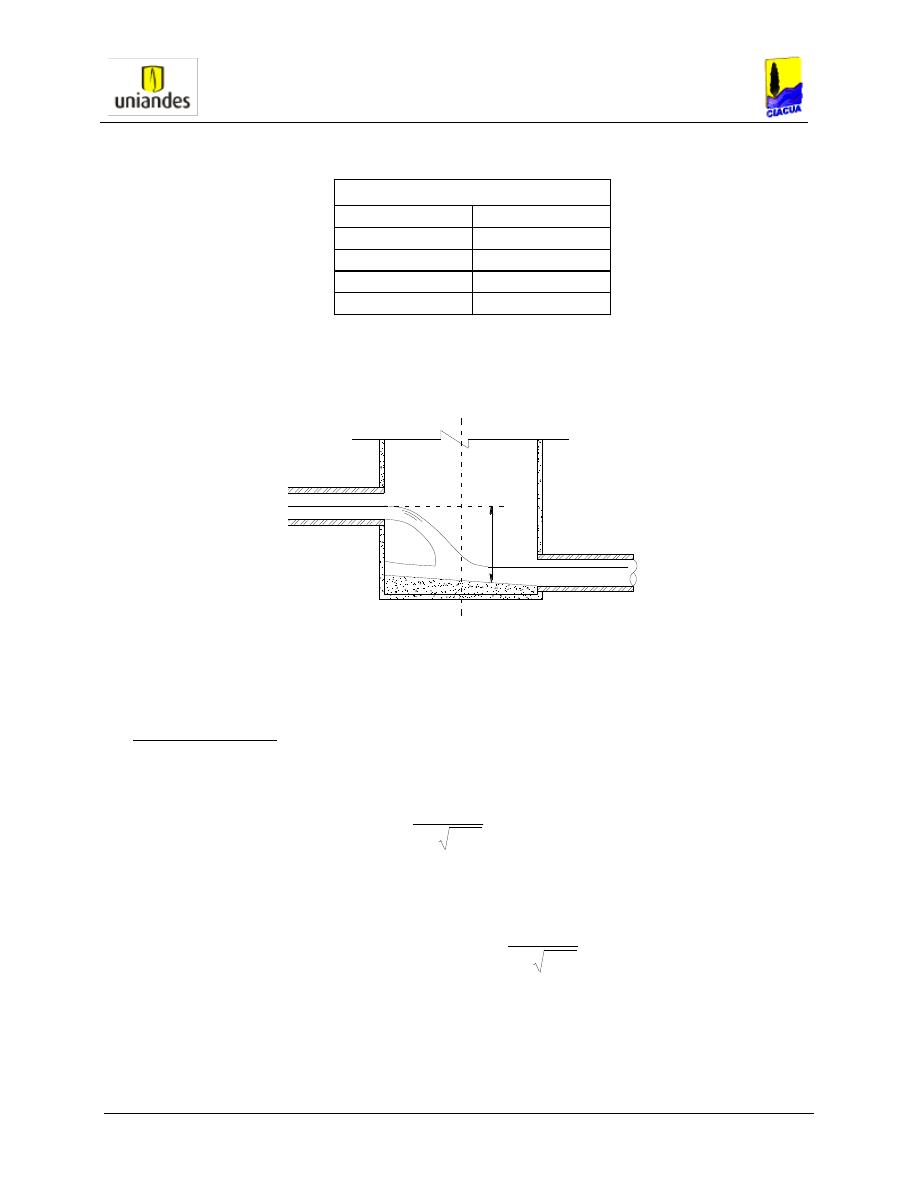
Entrada No Sumergida: 

Se presenta cuando 

62

.

0

2



s

s

gD

D

Q

 

La caída en la estructura de unión (H

w

) se puede estimar con la siguiente ecuación: 

















s

e

s

c

w

D

H

D

H

k

H

 

67

.

2

589

.

0

















s

s

s

e

gD

D

Q

D

H

 

en dónde: 

Q = caudal de salida de la tubería, m

3

/s. 

D

s

= diámetro interno de la tubería de salida, m. 

H

c

 = energía específica para las condiciones de flujo crítico. 

H

e

 = incremento de altura debido a las pérdidas.   

k  =  Coeficiente  que  depende  de  la  relación  entre  el  diámetro  del  pozo  y  el  de  la  tubería 
saliente. 

g = Aceleración de la gravedad. 

 

Ecuación 4.2.4 

Ecuación 4.2.5 

Ecuación 4.2.6 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

27 

JORGE MARIO LIZARAZO MARTÍNEZ 

Tabla 4-4 Valor del Coeficiente K.  Fuente: RAS 2000. 

Dp/Ds

K

> 2.0

1.2

1.6 - 2.0

1.3

1.3 - 1.6

1.4

< 1.3

1.5

Coeficiente K

 

 

Figura 4-3 Condición No Sumergida. Fuente: RAS 2000. 

 

 

 

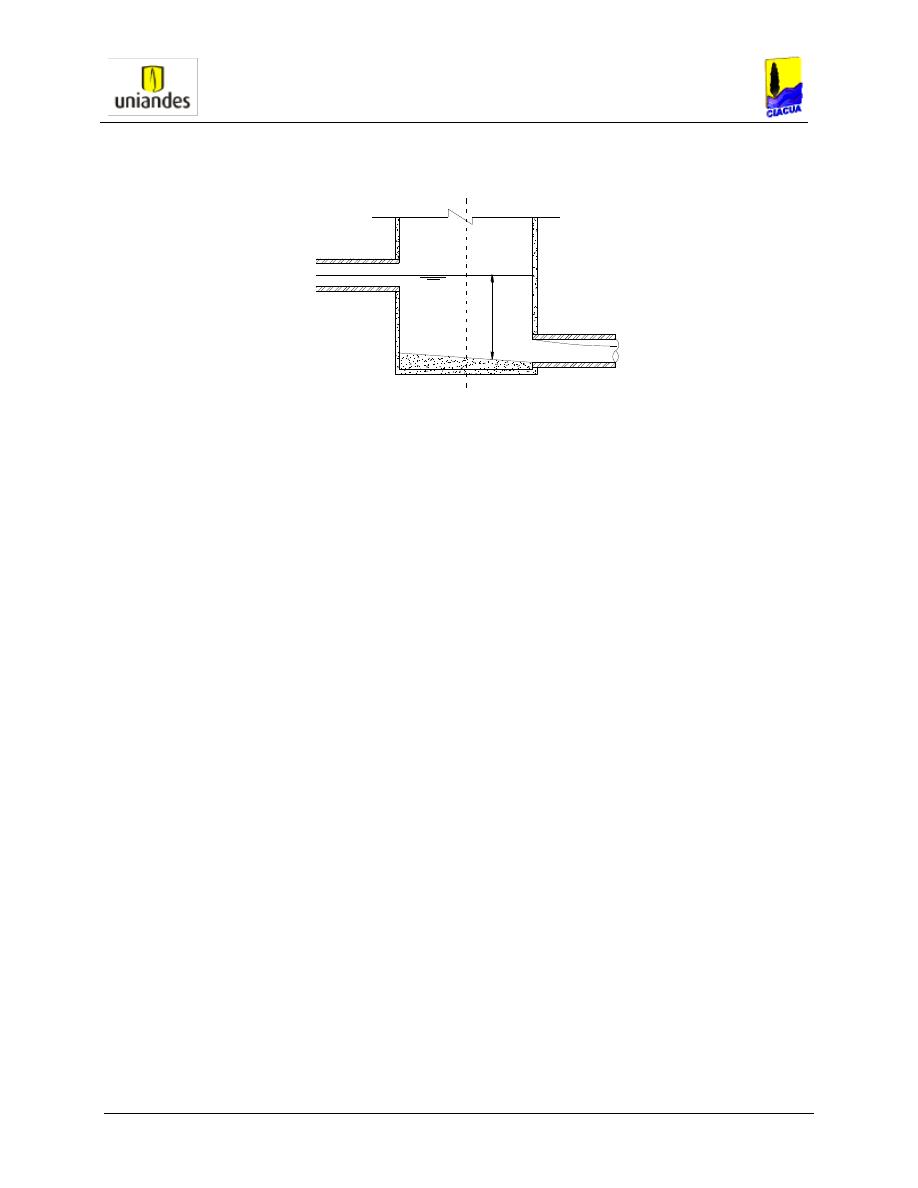
Entrada Sumergida: 

Se presenta cuando: 

62

.

0

2



s

s

gD

D

Q

 

La caída en la estructura de unión (H

w

) se puede estimar con la siguiente ecuación: 

































2

2

91

.

1

70

.

0

s

s

s

w

gD

D

Q

kD

H

 

 

 

H

w

D

s

TUBERÍA DE

ENTRADA

TUBERÍA DE

SALIDA

POZO

Ecuación 4.2.7 

Ecuación 4.2.8 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

28 

JORGE MARIO LIZARAZO MARTÍNEZ 

Figura 4-4 Condición Sumergida.  Fuente: RAS 2000. 

 

 

MEJORA EN LAS CONDICIONES DE ENTRADA 

En algunos casos la caída en las estructuras de unión puede ser lo suficientemente grande para 
resultar en una estructura muy costosa,  ya sea porque es necesario profundizar demasiado o 
porque se  requiere utilizar tuberías con  capacidad mayor que  el  caudal  de diseño.  En  estos 
casos es posible mejorar las condiciones de entrada, las cuales constituyen el punto crítico del 
sistema, haciendo una transición o boquilla en la cual se aumenta el diámetro de entrada a la 
estructura, disminuyendo así la elevación del agua en la estructura y por consiguiente la caída 
H

w

 en el mismo. 

 

 

H

w

D

s

TUBERÍA DE

ENTRADA

TUBERÍA DE

SALIDA

POZO

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

29 

JORGE MARIO LIZARAZO MARTÍNEZ 

5  METODOLOGÍAS ALTERNAS DE CÁLCULO 

 

5.1  FLUJO SUBCRÍTICO 

No existen métodos que hayan sido desarrollados específicamente para condiciones de flujo 
subcrítico; sin embargo teniendo en cuenta que tal como se mencionó en el numeral 2.2.1, se 
ha  establecido  que  cuando  se  trabaja  bajo  esta  condición  resulta  apropiado  el  uso  de 
coeficientes de pérdidas  localizadas al estilo de los conductos a presión;  el uso de  cualquier 
método que aplique estos coeficientes podría ser válido para dicho propósito.   

Gracias  a  la  difusión  del  programa  SewerCad,  en  Colombia  son  conocidos  los  siguientes 
métodos: 



  Método Absoluto 



  Método Estándar 



  Método Genérico 



  Método AASHTO 



  Método de la  pérdida de energía (HEC 22-2001), ver numeral 2.3.2 



  Método de la pérdida de energía compuesta (HEC 22-2001), ver numeral 2.3.2 

El  método  AASHTO  fue  publicado  en  el  “Model  Drainage  Manual”  de  1991;  sin  embargo 
para la versión 2005, la AASHTO declinó en favor de los métodos presentados por la HEC 22 
en su edición 2001.  Los otros son métodos bastante simplificados y mucho más antiguos. 

En principio el procedimiento más completo y con mayor base experimental y teórica es el de 
la  pérdida  de  energía  compuesta.    No  obstante,  un  estudio

21

  realizado  en  cámaras  de 

inspección  plásticas  fabricadas  por  PAVCO  encontró  que  éste  método,  al  igual  que  el  de  la 
pérdida  de  energía,  subestimaban  la  caída  de  energía  y  que  el  método  que  presentaba  la 
mayor correlación con los datos obtenidos experimentalmente era el de la AASHTO. 

Por  tal  motivo  y  teniendo  en  cuenta  que  no  se  justifica  un  procedimiento  tan  complejo  e 
impráctico como el del método de la pérdida de energía para obtener un simple coeficiente de 
pérdida  local,  para  efectos  de  comparación  de  resultados  en  el  caso  práctico  con  flujo 
subcrítico,  se  tomarán  como  referentes  los  métodos  de  la  AASHTO  y  de  la  pérdida  de 
energía.    Por  ser  estos  últimos  bastante  conocidos,  no  se  describen  en  el  presente  trabajo.  
También se pueden consultar en la referencia 1. 

Es conveniente resaltar que los anteriores no son métodos de diseño propiamente dichos, sino 
que permiten determinar la pérdida producida por la cámara de inspección a fin de tenerla en 
cuenta para el cálculo de la línea de energía. 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

30 

JORGE MARIO LIZARAZO MARTÍNEZ 

5.2  FLUJO SUPERCRÍTICO – METODOLOGÍA DEL CIACUA 

La metodología desarrollada en esta investigación se puede resumir de la siguiente manera: 

a.  Determinar la velocidad, profundidad de flujo y el número de Froude en cada una de las 

tuberías de entrada. 

b.  Si hay entrada de flujo a la cámara por más de una tubería, determinar la altura de caída y 

verificar que se encuentre entre los límites que se indican adelante. 

c.  Identificar  el  conducto  hidráulicamente  dominante  y  a  su  vez  establecer  cuál  es  la  onda 

dominante dentro de la cámara. 

d.  Calcular  la  altura  de  la  onda  con  las  ecuaciones  empíricas  encontradas,  las  cuales  son 

función de la relación de llenado, el número de Froude y la altura de caída a la entrada de 
la cámara.  El valor obtenido equivale a la altura necesaria de la cañuela de piso. 

e.  Calcular la longitud requerida de la cañuela de piso. 
f.  Calcular el diámetro requerido de la cámara de inspección. 
g.  Calcular la pérdida de energía. 

La  caída  mínima  en  la  cámara  para  evitar  la  formación  de  un  resalto  es  de  0.25  veces  el 
diámetro de la tubería de entrada.  La caída máxima para evitar el fenómeno de ahogo en la 
cámara está dada por la siguiente ecuación: 

0

max

75

.

0

75

.

0

D

S





 

dónde: 

S

max

 = Caída máxima permitida (m). 

D

0

 = Diámetro interno real de la tubería de entrada (m). 

Para  determinar  el  conducto  hidráulicamente  dominante  se  aplica  uno  de  los  siguientes 
criterios: 



  Conducto con menor ángulo de deflexión. 



  Conducto con mayor altura de velocidad [V

2

/2g]. 



  Conducto con mayor valor resultante al multiplicar el caudal por la velocidad. 

Seguidamente se determina el tipo de onda dominante que se forma al interior de la cámara: 

Tabla 5-1 Ecuación de la Onda Para Diferentes Configuraciones.  Tomada de la referencia 1. 

 

CONFIGURACIÓN

TUBERÍA DOMINANTE

CONDICIÓN

TIPO DE ONDA 

DOMINANTE

ECUACIÓN

Una tubería con paso directo

No aplica

Ninguna

Onda A

h = 2.91Y

1

1.015

F

1

-0.025

S'

1

0.068

Una tubería con giro a 90°

No aplica

Ninguna

Onda C

h = 3.41Y

2

0.84

F

2

0.41

S'

2

0.128

Q

T2 

< 10%Q

T2

Onda A

h = 2.91Y

1

1.015

F

1

-0.025

S'

1

0.068

Q

T2  

> 10%Q

T2

Onda E

h = 3.902Y

1

0.21

Y

2

0.55

F

1

0.11

F

2

0.078

S'

1

0.033

S'

2

0.129

Tubería con giro a 90° (T2)

Ninguna

Onda C

h = 2.66Y

1

0.16

Y

2

0.57

F

1

0.056

F

2

0.42

S'

1

0.0077

S'

2

-0.098

Tubería con paso directo 

(T1)

Una tubería con paso directo 
y otra con giro de 90°

Ecuación 5.2.1 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

31 

JORGE MARIO LIZARAZO MARTÍNEZ 

El diámetro interno de la cámara se obtiene con: 











 



2

Cos

D

D

S

C

 

dónde: 

D

C

 = Diámetro interno real de la estructura de conexión. 

D

S

 = Diámetro externo real de la tubería de salida (m). 

Δ = Ángulo de intersección entre los tramos. 

 

La longitud de la cañuela o trayectoria de flujo se determina con: 

g

h

V

X

c

c

2



 

dónde: 

X

c

 = Trayectoria del flujo. 

V

c

 = Velocidad crítica. 

h = Distancia vertical entre la cota batea de la tubería de entrada y el fondo de la cámara. 

g = Aceleración de la gravedad. 

Se debe verificar que D

C

 ≥ 2X

C

 

Para el cálculo de las pérdidas de energía se cuenta con las siguientes ecuaciones: 

Tabla 5-2 Ecuación Para la Pérdida en la Cámara.  Tomada de la referencia 1. 

 

 

 

CONFIGURACIÓN

TUBERÍA DOMINANTE

ECUACIÓN

Una tubería con paso directo

No aplica

ΔE = 0.368F

1

-0.266

Y

1

-0.469

S'

1

-0.109

Una tubería con giro a 90°

No aplica

ΔE = 0.224F

2

0.533

Y

2

-0.196

S'

2

-0.278

Tubería con paso directo (T1)

ΔE = 0.233F

1

0.084

Y

1

-0.363

S'

1

-0.276

Tubería con giro a 90° (T2)

ΔE = 0.192F

2

0.512

Y

2

-0.161

S'

2

-0.291

Una tubería con paso directo y 
otra con giro a 90°

Ecuación 5.2.2 

Ecuación 5.2.3 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

32 

JORGE MARIO LIZARAZO MARTÍNEZ 

5.3  METODOLOGÍA DE LA FHWA-HEC 22 TERCERA EDICIÓN 

Para  poder  entender  esta  metodología,  es  necesario  primero  aclarar  el  concepto  de  control 
hidráulico. 

Control hidráulico: Es la sección de la tubería que determina el máximo caudal que se puede 
transportar.  Se reconocen dos tipos de control: 

Control a la entrada: Ocurre cuando la sección de control se encuentra a la entrada o cerca a 
la  entrada  de  la  tubería.    En  este  caso  las  características  geométricas  de  la  entrada  y  las 
pérdidas generadas en este punto dificultan el ingreso del flujo en tal forma que este circula y 
sale  de  la  tubería  más  rápido  de  lo  que  puede  entrar.    Una  tubería  con  control  a  la  entrada 
siempre fluye parcialmente llena en régimen supercrítico 

 

Figura 5-1 Control a la Entrada.  Fuente FHWA. 

 

Control a la salida: Ocurre cuando la sección de control se encuentra a la salida o cerca de la 
salida.  En este caso las condiciones de entrada son óptimas y el caudal transportado obedece 
a  las  características  hidráulicas  de  la  tubería  (rugosidad,  pendiente,  diámetro,  etc.).    Las 
tuberías  con  control  a  la  salida  pueden  trabajar  parcial  o  completamente  llenas  bajo  flujo 
subcrítico. 

 

Figura 5-2 Control a la Salida.  Fuente FHWA. 

 

Se debe anotar que los dos controles se pueden dar de forma sumergida o libre. 

La metodología se compone de tres pasos fundamentales: 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

33 

JORGE MARIO LIZARAZO MARTÍNEZ 

a.  PASO 1: DETERMINAR LA ENERGÍA DE ACCESO A LA CÁMARA (Eai) 

Se toma como la máxima calculada bajo tres condiciones posibles, lo cual a su vez determina 
el tipo de control y régimen hidráulico en la estructura: 



  Control a la salida: 

Control a la salida con flujo lleno. 
Control a la salida con flujo parcial. 
 

Eai = Ei + Hi   

Ecuación 5.3.1 

Ei = EGLi – Zi 

Ecuación 5.3.2 

Hi = Ki (V

2

/2g)  

Ecuación 5.3.3 

dónde: 

Ki = Coeficiente de pérdida a la entrada = 0.2. 

EGLi = Altura de la línea de gradiente hidráulico a la salida. 

Zi = Cota batea de la tubería de salida. 

V = Velocidad. 

g = aceleración de la gravedad. 

 



  Control  a  la  entrada  (entrada  sumergida):  Como  las  características  de  la  entrada  a  la 

tubería de salida limitan el flujo, la profundidad del agua en la cámara se incrementa de 
tal forma que la salida puede ser tratada como un orificio. 
 
Se utiliza el parámetro intensidad de descarga: 
 

      

 

[ (  

 

)

   

]

 

 
dónde: 
A = área transversal de la tubería de salida (m

2

). 

g = aceleración de la gravedad (m/s

2

). 

D

0 

= diámetro de la tubería de salida (m). 

Q = Caudal (m

3

/s). 

 
 
Luego: 
 

Ecuación 5.3.4 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

34 

JORGE MARIO LIZARAZO MARTÍNEZ 

 

  

   

 

(  )

 

 

 
 



  Control a la entrada (entrada no sumergida): El mismo caso anterior con la diferencia de 

que la altura del agua en la cámara no es suficiente para el tratamiento como orificio sino 
como vertedero: 

 

  

      

 

(  )

    

 

Según la HEC 22, Los datos experimentales indican que esta condición se presenta para 
intensidades de descarga entre 0 y 0.5, lo cual no limita la validez de la ecuación. 

 

b.  PASO  2:  AJUSTES  POR  CAÑUELA,  ÁNGULO  DE  ENTRADA  Y  FLUJO  EN 

CAÍDA 

El  nivel de energía inicial  calculado en el  paso 1 es  usado como  base para estimar pérdidas 
adicionales por: 



  Cañuela. 



  Tuberías de entrada a la cámara con ángulos diferentes de 180°. 



  Flujos de entrada a la estructura por encima del nivel del agua en la misma. 

Estos efectos pueden ser estimados y aplicados a la energía de entrada usando el principio de 
superposición.    La  energía  de  acceso  corregida  (Ea)  es  igual  a  la  estimada  en  el  paso  1, 
modificada por cada uno de los tres factores: 

Ea = Eai + HB + Hθ+ HP  

Ecuación 5.3.7 

dónde: 

HB = Pérdida en la cañuela. 

Hθ= Pérdida por ángulo de entrada a la cámara. 

HP = Pérdida por caída. 

Ea  =  altura  de  la  línea  de  gradiente  hidráulico  en  el  pozo.    Sin  embargo  si  Ea  resulta  ser 
menor que Ei, entonces Ea debe ser igualado a Ei  

 

Si se quiere conocer la altura de la lámina de agua en el pozo, el método establece como una 
aproximación conservadora usar el valor de Ea. 

 

Ecuación 5.3.6 

Ecuación 5.3.5 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

35 

JORGE MARIO LIZARAZO MARTÍNEZ 



  Pérdida Por Cañuela 

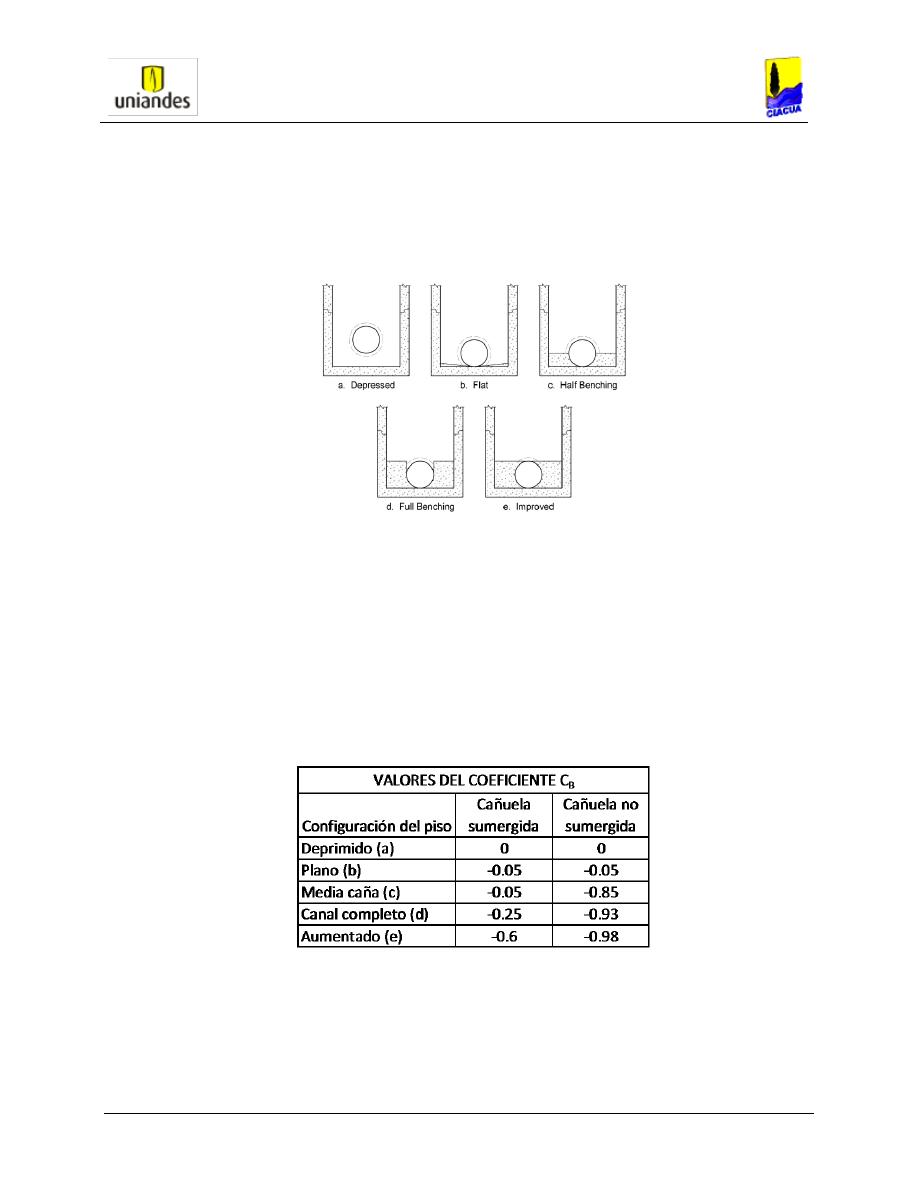
En la Figura 5-3 se muestran las diferentes configuraciones para la cañuela de fondo. 

 

Figura 5-3 Configuraciones de Cañuela de Fondo.  Fuente: HEC-22 – 2009. 

 

La pérdida por cañuela se calcula como: 

HB = CB (Eai - Ei) 

Ecuación 5.3.8 

dónde: 

CB = Coeficiente de pérdida por cañuela; un valor negativo indica que la altura de la lámina 
se reduce.  Se obtiene de la siguiente tabla: 

 

Tabla 5-3 Valor del Coeficiente C

B

.  Fuente: HEC 22 – 2009. 

 

La condición sumergida se da para relaciones E

ai

/D

0

> 2.5  y la condición no sumergida para 

E

ai

/D

0

> 1.0.  Los valores de C

B

 para condiciones intermedias se deben interpolar linealmente. 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

36 

JORGE MARIO LIZARAZO MARTÍNEZ 



  Pérdida Por Ángulo De Entrada 

Primero se calcula el siguiente coeficiente: 

θw = Σ (QJ θJ) / ΣQJ  

 

 

Ecuación 5.3.9 

dónde: 

QJ = Caudal de entrada de la tubería J, m

3

/s. 

θJ = Ángulo de entrada con relación a la tubería de salida (grados). 

La  suma  incluye  únicamente  flujos  sin  caída;  si  todos  los  flujos  se  dan  con  caída    entonces 
θw=180. 

Luego se calcula el coeficiente Cθ: 

Cθ= 4.5 (ΣQJ / Qo) cos (θw / 2)   

Ecuación 5.3.10 

dónde: 

Qo = caudal en la tubería de salida, m

3

/s. 

El  valor  de  Cθ  se  aproxima  a  cero  conforme  θw  se  acerca  a  180°  y  el  caudal  de  entrada  a 
cero. 

Luego la pérdida de energía por ángulo de entrada es igual a: 

Hθ= Cθ( Eai - Ei ) 

 

 

Ecuación 5.3.11 

 



  Pérdida Por Caída 

El flujo en caída se define como el flujo en una tubería con cota batea superior a la cota de la 
lámina de agua en el pozo (la altura de la lámina de agua en el pozo se aproxima como Eai).  
El método define una altura relativa de caída “h” para el tubo “k”: 

hk = (zk – Eai) / Do  

 

 

Ecuación 5.3.12 

dónde: 

Z

k

= Diferencia entre las cotas batea de la tubería de entrada y la cámara. Si Z

k

>10D

0

 entonces 

se toma Z

k

=10D

0

. 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

37 

JORGE MARIO LIZARAZO MARTÍNEZ 

Luego se calcula el coeficiente de flujo en caída (CP): 

CP = Σ (Qkhk) / Qo 

 

 

Ecuación 5.3.13 

Por último la pérdida (HP) por caída se calcula como: 

HP = CP (Eai - Ei) 

 

 

Ecuación 5.3.14 

 

Línea de Gradiente de Energía en la Cámara 

Conociendo la altura de energía a la entrada (Ea) y suponiendo que la cota batea de la cámara 
(za)  es  la  misma  de  la  tubería  de  salida  (zi),  se  puede  determinar  la  altura  de  la  línea  de 
gradiente hidráulico (EGLa) en la cámara: 

EGLa = Ea + Za   

 

 

Ecuación 5.3.15 

 

c.  PASO 3: PÉRDIDAS POR SALIDA EN LAS TUBERÍAS DE ENTRADA 

El paso final es calcular la línea de gradiente hidráulico  (EGLo) en cada tubería de entrada. 



  Tuberías Sin Caída: 

EGLo = EGLa + Ho  

 

 

Ecuación 5.3.16 

Ho = Ko (V2 /2g)  

 

 

Ecuación 5.3.17 

Ko = Coeficiente de pérdida por salida de la tubería de entrada a la cámara = 0.4. 

 



  Tuberías con caída: 

Para  tuberías  con  caída  la  línea  de  gradiente  hidráulico  es  independiente  de  la  altura  de  la 
lámina de agua en la cámara y es calculada según la hidráulica del tubo de entrada. 

 

CONTINUACIÓN DE LOS CÁLCULOS AGUAS ARRIBA 

La  altura  de  la  línea  de  gradiente  hidráulico  obtenida  es  usada  para  continuar  los  cálculos 
aguas arriba hasta la siguiente cámara.  En cada pozo se repiten los tres pasos descritos. 

 

 

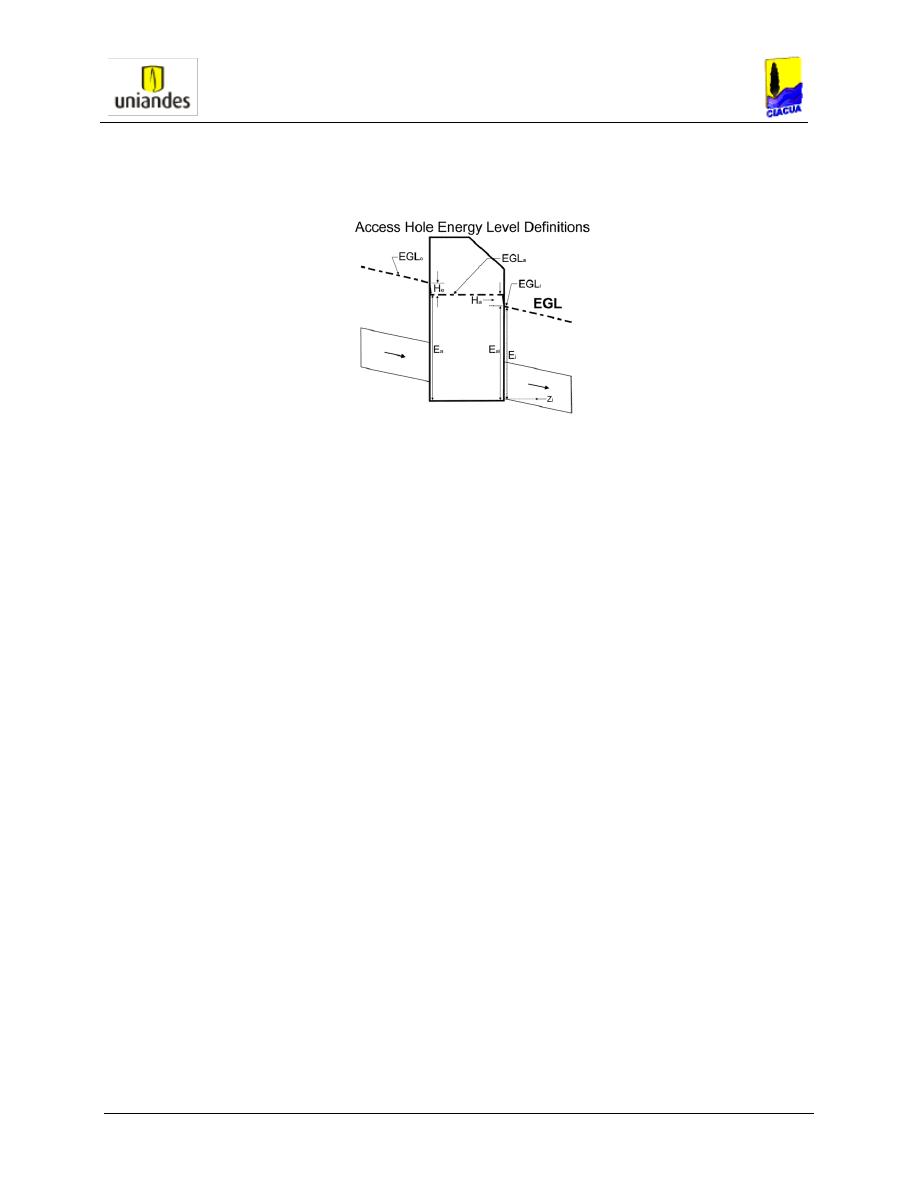
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

38 

JORGE MARIO LIZARAZO MARTÍNEZ 

 

Figura 5-4 Definiciones Para el Nivel de Energía en la Cámara.  Fuente: HEC 22 - 2009 

 

 

 

 

 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

39 

JORGE MARIO LIZARAZO MARTÍNEZ 

6  REVISIÓN  DEL  MÉTODO  DE  EMPATE  POR  LÍNEA  DE 

ENERGÍA 

Con  base  en  las  investigaciones  presentadas  anteriormente,  que  corresponden  al  estado  del 
arte en el análisis del flujo en cámaras de inspección, se puede realizar entonces una crítica a 
los  postulados  del  método  de  empate  por  línea  de  energía,  indicando  cuales  aspectos  del 
comportamiento real en la estructura no se reflejan en los resultados obtenidos. 

 

FLUJO SUBCRÍTICO 

Tal como se presentó en el numeral 2.2.1, un análisis unidimensional y el uso de coeficientes 
de pérdidas es una aproximación válida para el cálculo de las pérdidas en cámaras con flujo 
en  régimen  subcrítico.    El  método  de  empate  por  línea  de  energía  que  en  adelante  se 
denominará “MELE”, utiliza ese enfoque, calculando coeficientes  que tienen en cuenta los 
efectos del cambio de dirección y aumento o disminución de la velocidad. 

Teniendo  en  cuenta  que  el  MELE  tiene  su  origen  en  los  estudios  realizados  en  Estados 
Unidos  para  Culverts  (alcantarillas  para  permitir  el  paso  de  agua  de  escorrentía  bajo 
estructuras de caminos), el método más apropiado para realizar una comparación  es el de la 
HEC 22 tercera edición.  Al respecto, el MELE presenta las siguientes deficiencias: 



  No tiene en cuenta las pérdidas generadas a la entrada y salida de la cámara. 



  No tiene en cuenta las pérdidas en la cañuela y la configuración de la misma. 



  No  tiene  en  cuenta  el  efecto  que  provoca  la  caída  del  flujo  cuando  la  cota  batea  de  las 

tuberías entrantes es superior a la altura de la lámina de agua en la cámara. 



  El  hecho  de  que  existan  uno  o  varios  caudales  de  entrada  a  la  estructura  no  altera  el 

procedimiento de cálculo. 

 

FLUJO SUPERCRÍTICO 

Básicamente en este caso el MELE deja de ser un procedimiento de cálculo para convertirse 
en  uno  que  obliga  al  flujo  a  comportarse  de  una  manera  en  la  cual  sí  pueda  analizarlo, 
estableciendo  un  control  hidráulico  a  la  entrada.    Esto  tampoco  deja  de  tener  sus 
inconvenientes,  ya  que  en  ocasiones  no  es  posible  dejar  la  caída  necesaria  para  disipar  la 
energía del flujo sin tener que recurrir posteriormente a bombeo, aparte de los mayores costos 
en tiempo y dinero por excavaciones y estructuras más profundas.   

Por  tanto  no  es  posible  hacer  una  crítica  diferente  a  la  mencionada,  ya  que  el  MELE  no 
presenta un análisis matemático o experimental para esta condición. 

 

 

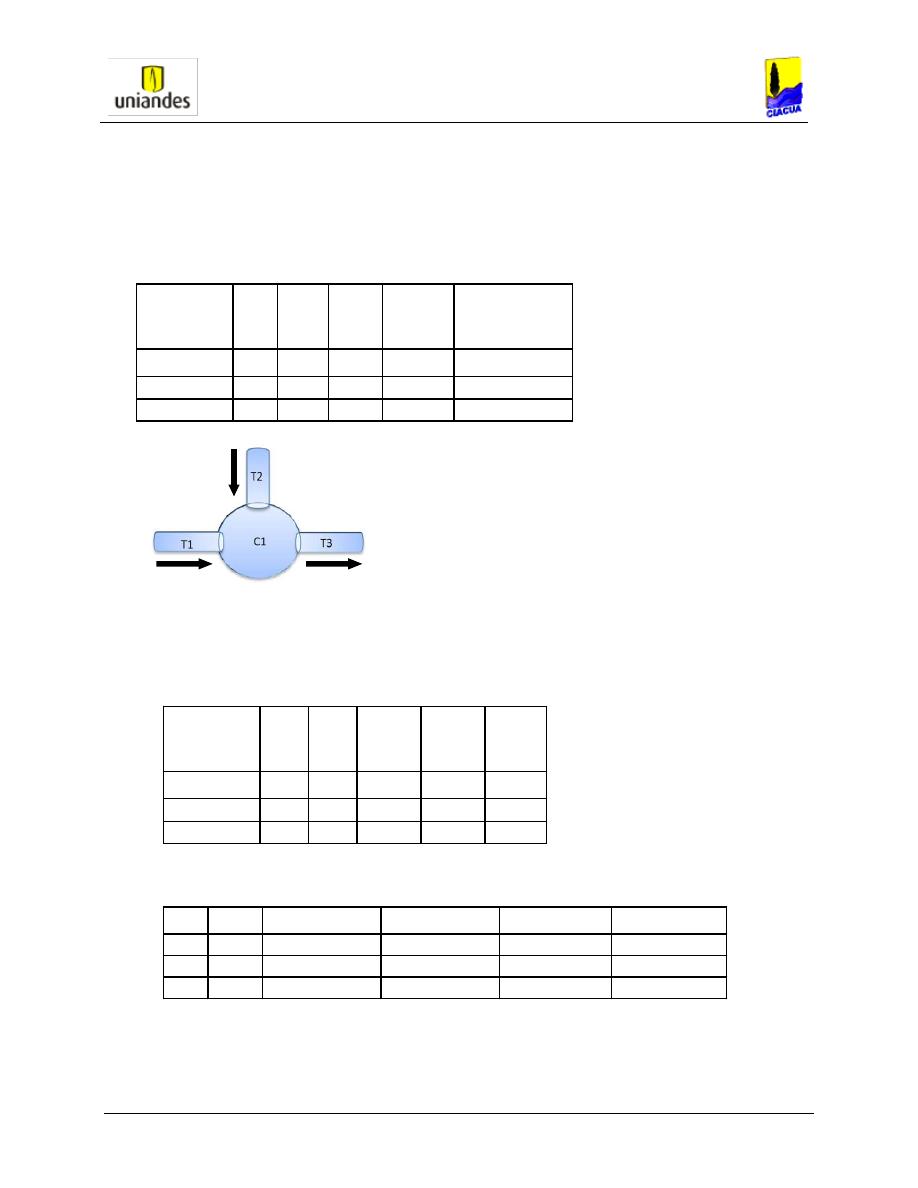
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

40 

JORGE MARIO LIZARAZO MARTÍNEZ 

EJEMPLO PRÁCTICO 

A continuación se desarrolla un ejemplo de cálculo para comparar los resultados siguiendo las 
diferentes metodologías presentadas anteriormente.  Se calculará con el método del CIACUA, 
de  la  HEC  22  y  con  el  MELE  para  posteriormente  presentar  las  conclusiones  a  lugar.    A 
continuación se encuentran los datos de entrada: 

 

 

METODOLOGÍA DEL CIACUA (ver numeral 5.2): 

 

a.  Determinar la velocidad, profundidad y número de Froude en cada tubería: 

 

 

 

b.  Determinar si se cumple con las limitantes en la altura de caída (S’): 

 

 

 
Por tanto se cumple con los requerimientos. 
 
 

TUBERÍA

ID

S

0 

(%) D

0 

(m) Q (m

3

/s)

Caída (m)

Entrada

T1

0.015

0.25

0.05

0.55

Entrada

T2

0.02

0.3

0.15

0.47

Salida

T3

0.02

0.35

0.20

0.00

TUBERÍA

Y

n

Y

n

/D

0

V (m/s)

v2/2g

F

Entrada

0.131 0.522 1.9263

0.1891

1.91

Entrada

0.181 0.603 3.3361

0.5673

2.73

Salida

0.235 0.67

3.7893

0.7318

2.65

ID

D

0 

(m) Cota batea (m)

Caída (m)

Caída min (m) Caída max (m)

T1

0.25

110.95

0.55

0.0625

0.5625

T2

0.3

110.87

0.47

0.075

0.525

T3

0.362

110.40

0.00

 

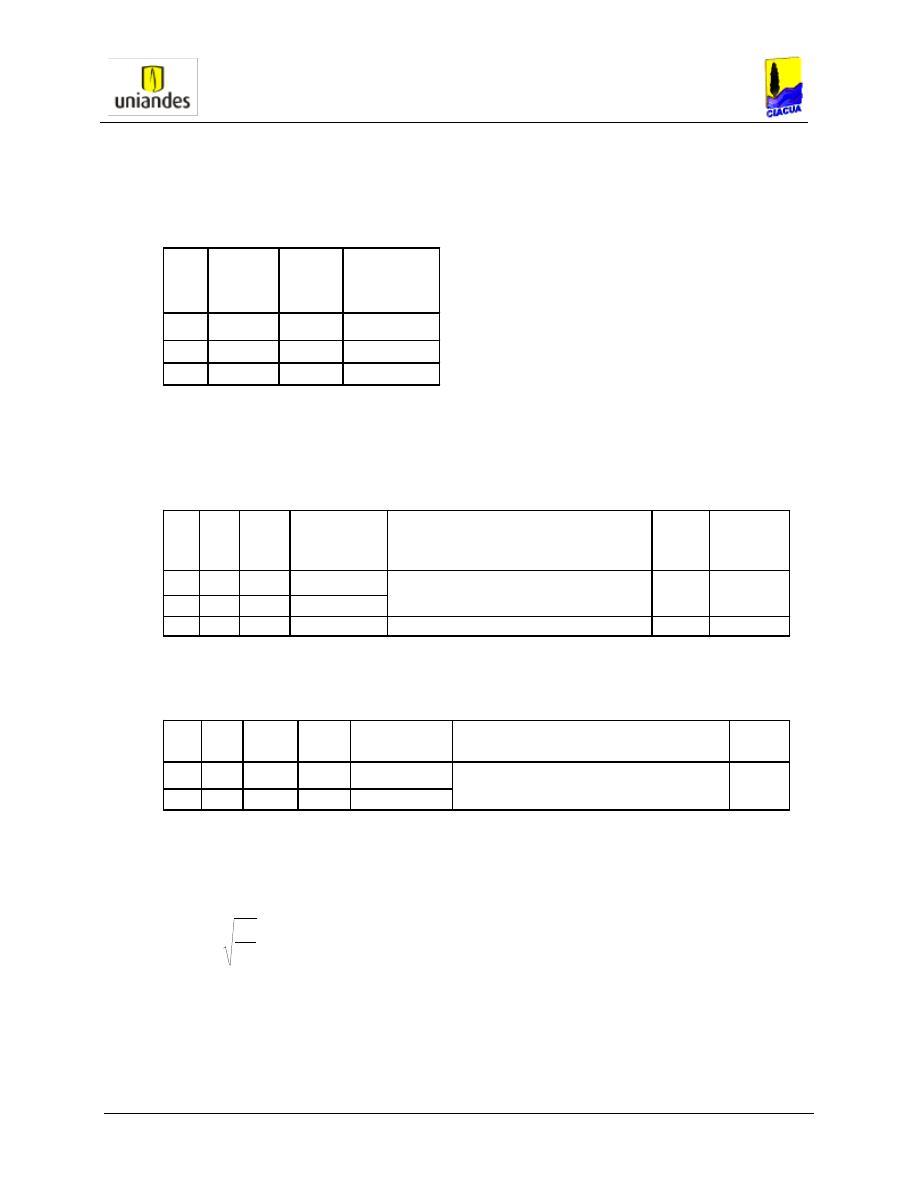
Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

41 

JORGE MARIO LIZARAZO MARTÍNEZ 

c.  Definir el conducto y la onda hidráulicamente dominante: 

 
Se adopta como tubería dominante la que presente el mayor valor resultante de multiplicar 
el caudal por la velocidad, que resulta ser la tubería 2: 
 

 

 
Esto implica que la onda dominante en el sistema será del tipo C. 
 
 

d.  Determinar la altura de la onda 

 

 

 
 

e.  Determinar la pérdida de energía: 

 

 

 
 

f.  Determinar la longitud de la cañuela o trayectoria de flujo para la tubería hidráulicamente 

dominante con la ecuación 5.2.3: 
 

m

g

h

V

X

c

c

82

.

0

2





 

 
 

g.  Determinar el diámetro de la cámara con la ecuación 5.2.2: 

 

ID

Q (m

3

/s) V (m/s)

Q x V

T1

0.05

1.9263

0.096

T2

0.15

3.3361

0.500

T3

0.20

3.7893

0.75786

ID

Y

n

/D

0

F

Caída "S" (m)

Ecuación de la Onda

h/(D

0

/2)

Altura de la 

onda - h (m)

T1

0.522

1.91

0.55

T2

0.603

2.73

0.47

T3

0.67

2.65

0.00

3.04697

0.419

h = 2.66Y

1

0.16

Y

2

0.57

F

1

0.056

F

2

0.42

S'

1

0.0077

S'

2

-0.098

ID

Y

n

/D

0

V (m/s)

F

Caída "S" (m)

Ecuación de la Pérdida



E

T1

0.46

2.6812

2.88

0.55

T2

0.57

4.7668

4.06

0.47

ΔE = 0.192F

2

0.512

Y

2

-0.161

S'

2

-0.291

0.537

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

42 

JORGE MARIO LIZARAZO MARTÍNEZ 

m

Cos

Cos

D

D

S

C

91

.

0

2

4

3

35

.

0

2































 





 

Se  verifica  este  valor  contra  el  doble  de  la  trayectoria  de  flujo  Dc  =  2X

C 

=  2*0.82  = 

1.64m; por tanto el diámetro de diseño para la cámara es de 1.64m. 

Se tiene como resultado entonces una cámara con 1.64m, cañuelas de 0.42m de alto y 0.82m 
de longitud y una pérdida de energía de 0.537m. 

 

 

METODOLOGÍA DE EMPATE POR LÍNEA DE ENERGÍA 

Para  flujo  supercrítico  este  método  sólo  permite  definir  la  altura  de  caída  en  la  cámara.  
Primero se calcula la intensidad de descarga.  

88

.

0

2



s

s

gD

D

Q

 

Cuando el resultado es mayor a 0.6 quiere decir que se presenta entrada sumergida, por lo que 

la caída en la cámara está dada por la ecuación 4.2.8: 

































2

2

91

.

1

70

.

0

s

s

s

w

gD

D

Q

kD

H

 

Suponiendo una cámara tradicional de 1.20m de diámetro, el coeficiente k es igual a 1.2.  Por 
tanto: 

m

H

w

92

.

0

35

.

0

*

81

.

9

35

.

0

20

.

0

91

.

1

70

.

0

35

.

0

*

2

.

1

2

2



































 

Por tanto se tiene una cámara de 1.20m de diámetro, con una caída de 0.92m entre la altura de 
la  lámina  de  agua  del  colector  entrante  más  bajo  y  el  fondo  de  la  cámara;  es  decir  0.92m-
0.181m = 0.739m entre la batea de la tubería lateral y el fondo de la estructura.  Si se tiene en 
cuenta el recubrimiento mínimo de 1m a la clave de la tubería más elevada, la altura total de 
la cámara es de 2.04m.  Aparte según la normatividad vigente se deberá construir una cámara 
de caída. 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

43 

JORGE MARIO LIZARAZO MARTÍNEZ 

 

MÉTODO DE LA HYDRAULIC ENGINEERING CIRCULAR 22 (HEC22-FHWA) 

PASO 1.  Determinar la energía inicial: 

Se toma el mayor valor entre tres cálculos: 



  Condición de control a la salida: 

 

 

 

      

 

 

 

   

 

 

 

 

  

                     

 

 

  

   

 

   

 

                      

 



  Control a la entrada en condición sumergida 

      

 

[ (  

 

)

   

]

   

    

√         

       

 

  

   

 

(  )

 

       (    )

 

        

 



  Control a la entrada en condición no sumergida 

 

  

      

 

(  )

    

           (    )

    

        

En consecuencia la condición hidráulica es control a la entrada en condición sumergida, que 
curiosamente es la misma que busca generar el MELE.  El valor de E

ai

 queda definido como 

1.45m. 

Paso 2.  Ajustes por Cañuela, Ángulo de Entrada y Caída 

 

 

   

  

   

 

   

 

   

 

 

Ajuste por cañuela: 

 

 

     

 

( 

  

   

 

)                          

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

44 

JORGE MARIO LIZARAZO MARTÍNEZ 

Ajustes por ángulo de entrada: 

 

 

         

 

 

        

 

 

     

 

( 

  

   

 

)                        

Ajustes por caída: 

 

 

   

           

    

      

 

 

   

           

    

         

 

 

          

 

 

           

Con esto se obtiene el nivel de energía en el pozo: 

 

 

   

  

   

 

   

 

   

 

                                        

 

Paso 3.  Pérdidas a la entrada 

Debido a que las dos tuberías de entrada tienen flujo en caída, las pérdidas en la entrada a la 
cámara  son  independientes  de  las  pérdidas  en  el  pozo  y  la  salida.    El  cálculo  se  debe  hacer 
entonces de acuerdo con las ecuaciones de la hidráulica.  Para efectos del presente trabajo no 
se requiere hacer dicho cálculo, pues no influye en las pérdidas totales de la estructura. 

 

Se ve entonces que la energía en la tubería de salida es de 0.97m y la energía en el pozo, es de 
1.71m  lo  que  indica  que  la  pérdida  en  la  cámara  es  de  0.74m,  mucho  más  que  los  0.537m 
obtenidos  con  la  metodología  del  CIACUA.    Cabe  resaltar  que  el  método  de  la  HEC  22  se 
comprobó para intensidades de descarga menores a 1.6 y en el presente ejercicio el valor es 
de  2.04;  el  autor  del  método  indica  en  su  estudio  la  posible  falla  del  procedimiento  para 
intensidades de descarga grandes, aunque no define el límite.  Por otra parte la misma FHWA 
reconoce la dificultad en determinar la altura de velocidad al interior de la cámara. 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

45 

JORGE MARIO LIZARAZO MARTÍNEZ 

7  CONCLUSIONES 

El  flujo  en  cámaras  de  inspección,  principalmente  bajo  condición  supercrítica,  es  un 
fenómeno  difícil  de  modelar  incluso  bajo  condiciones  controladas.    La  determinación  de  la 
altura de la lámina de agua dentro del pozo en un flujo altamente turbulento resulta bastante 
problemática. 

En Colombia el método aceptado y plasmado en las normas desde el año 2000 para el cálculo 
de las pérdidas de energía en pozos de inspección es el de Empate por Línea de Energía.  Este 
método,  que  fue  desarrollado  de  acuerdo  con  estudios  realizados  en  Estados  Unidos  en 
alcantarillas  para  drenaje  de  escorrentía  de  aguas  lluvias  bajo  estructuras  de  caminos 
(Culverts)  presenta  serias  falencias  que  llevan  a  estructuras  sobredimensionadas  y  de  difícil 
implementación. 

Para flujo subcrítico se presentan los siguientes inconvenientes: 



  No tiene en cuenta las pérdidas generadas a la entrada y salida de la cámara. 



  No tiene en cuenta las pérdidas en la cañuela y la configuración de la misma. 



  No  tiene  en  cuenta  el  efecto  que  provoca  la  caída  del  flujo  cuando  la  cota  batea  de  las 

tuberías entrantes es superior a la altura de la lámina de agua en la cámara. 



  El  hecho  de  que  existan  uno  o  varios  caudales  de  entrada  a  la  estructura  no  altera  el 

procedimiento de cálculo. 

Para flujo supercrítico el método de ser un procedimiento de cálculo para convertirse en uno 
que obliga al flujo a comportarse de una manera en la cual sí pueda analizarlo, estableciendo 
un control hidráulico a la entrada que implica que el sistema se comporte como una masa de 
agua estacionaria saliendo por un orificio.  Las  caídas de altura necesarias para obtener este 
comportamiento  resultan  imprácticas  pues  se  pierden  valiosos  centímetros  que  incrementan 
los costos  y obligan al bombeo de las aguas antes de lo necesario. 

Por otra parte este método no corresponde al estado del arte para el diseño de Culverts, el cual 
en este momento se encuentra plasmado en el método de la HEC 22 tercera edición (2009). 

El  ejemplo  desarrollado  arrojó  como  resultado  unas  pérdidas  calculadas  según  la  HEC  22 
superiores  en  un  37.8%  a  las  calculadas  con  la  metodología  del  CIACUA;  sin  embargo  se 
debe  anotar  que  en  los  estudios  de  la  FHWA  se  emplearon  intensidades  de  descarga, 
inferiores a las del ejercicio. 

Todo  lo  anterior  desnuda  que  el  diseño  de  cámaras  en  el  país  se  hace  bajo  criterios 
equivocados  que  generan  mal  funcionamiento  hidráulico  de  los  sistemas  de  drenaje,  por  lo 
que es necesario revaluar el método atendiendo a los resultados de las investigaciones de los 
últimos doce años. 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

46 

JORGE MARIO LIZARAZO MARTÍNEZ 

8  RECOMENDACIONES 

Es necesario continuar con la investigación de este fenómeno, rompiendo las limitaciones que 
presentan  los  estudios  para  así  completar  la  descripción  del  comportamiento  del  flujo  en 
cámaras. 

Mientras tanto se hace evidente la necesidad de actualizar el método de cálculo utilizado en el 
país, para lo cual se dispone de varias metodologías desarrolladas en los últimos años, lo cual 
permitirá  a  los  ingenieros  realizar  diseños  más  acordes  a  la  realidad  y  a  las  empresas 
operadoras la reducción de los costos de mantenimiento. 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

47 

JORGE MARIO LIZARAZO MARTÍNEZ 

9  BIBLIOGRAFÍA 



  Hager, Willi.  Wastewater Hydraulics. Berlin, Heidelberg: Springer, 2010. 

 



  Saldarriaga,  Juan,  Nataly  Bermúdez,  Eccehomo  Quejada  y  Paula  A.  Cuero. 

Comportamiento  hidráulico  de  cámaras  de  inspección  bajo  condiciones  de  flujo 
supercrítico.    Centro  de  Investigaciones  en  Acueductos  y  Alcantarillados  CIACUA, 
Universidad de los Andes, 2011. 
 



  Ministerio  de  Desarrollo  Económico.  República  de  Colombia.    Reglamento  técnico  del 

sector de agua potable y saneamiento básico RAS 2000. 
 



  Brown, Schall, Morris, Doherty, Stein y Warner. Urban Drainage Design Manual HEC-

22.  Federal Highway Administration: 2009, tercera edición; 2001 segunda edición. 
 

 

 

 

 

Universidad de los Andes 
Departamento de Ingeniería Civil y Ambiental 
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA 
Revisión Crítica del Diseño de Cámaras de Inspección por Línea de Energía

 

 

 

48 

JORGE MARIO LIZARAZO MARTÍNEZ 

10 REFERENCIAS 

 

                                                 

1

Juan  Saldarriaga,  Nataly  Bermúdez,  Eccehomo  Quejada  y  Paula  A.  Cuero.  Comportamiento  hidráulico  de 

cámaras  de  inspección  bajo  condiciones  de  flujo  supercrítico.    Centro  de  Investigaciones  en  Acueductos  y 
Alcantarillados CIACUA, Universidad de los Andes, 2011. 

2

Can-Hua Zhao, David Z. Zhu y Nallamuthu Rajaratnam.  Experimental Study of Surcharged Flow at Combining 

Sewer Junctions.Journal of Hydraulic Engineering, Vol. 132, No. 12, Diciembre 1, 2006. 

3

Can-Hua Zhao, David Z. Zhu y Nallamuthu Rajaratnam.  Computational and Experimental Study of Surcharged 

Flow at a 90° Combining Sewer Junction.  Journal of Hydraulic Engineering, Vol. 134, No. 6, Junio 1, 2008. 

4

Hager, Willi.Wastewater Hydraulics.2da edición, Capítulo16.1  Springer: 2010, Berlín Heidelberg. 

5

Hager, Willi. WastewaterHydraulics. 2da edición, Capítulo 2.4.1.  Springer: 2010, Berlín Heidelberg. 

6

Federal  Highway  Administration,  1989.Calculation  of  Head  Loss  Coefficients  for  Junction  Manholes, 

unpublished research report by F.M. Chang and R.T. Kilgore. 

7

Normann,  J.  M.,  Houghtalen,  R.  J.  and  Johnston,  W.  J.,  1985.    Hydraulic  Design  of  Highway  Culverts. 

Hydraulic Design Series No. 5, Federal Highway Administration, FHWA-IP-85-15, McLean, VA. 

8

  Federal  Highway  Administration,  Revised  1993.  Urban  Drainage  Design  Participant  Notebook,  Course  No. 

13027.United States Department of Transportation, Federal Highway Administration, National Highway Institute 
Publication No. FHWA HI-89-035, Washington, D.C. 

9

Chang, F.M., Kilgore, R.T. et al., 1994.Energy Losses through Junction Manholes, Volume I: Research Report 

and  Design  Guide,  FHWA-RD-94-080,  U.S.  Department  of  Transportation,  Federal  Highway  Administration, 
McLean, VA. 

10

  Kilgore,  R.T.,  2005.  A  Proposed  Storm  Drain  Energy  Loss  Methodology  for  Access  Holes,  presented  at  the 

Transportation Research Board 84th Annual Meeting, Washington, D.C., Enero 9-13. 

11

 Kilgore, R.T., 2006. A Proposed Storm Drain Energy Loss Methodology for Access Holes, unpublished report 

to FHWA, January. 

12

Kornel Kerenyi y Sterling Jones.  Energy Losses in Storm Drain Access Holes.  FHWA-HRT-07-036 - Marzo, 

2007. 

13

Kornel Kerenyi, Sterling Jones y Stuart Stein.  Junction Loss Experiments: Laboratory Report.  FHWA-HRT-

2006-002 Public Roads Magazine Ene/Feb 2006 Vol. 69 No. 4 

14

Del  Giudice,  Giuseppe,  Corrado  Gisonni  y  Willi  Hager.  Supercritical  Flow  in  Bend  Manhole.    Journal  Of 

Irrigation And Drainage Engineering, 126, 48 (2000) 

15

Del Giudice, Giuseppe y Willi Hager. Supercritical Flow in 45° Junction Manhole.  Journal Of Irrigation And 

Drainage Engineering, 127 No. 2,Marzo/Abril, 2001 

16

CorradoGisonni  y WilliHager.  Supercritical Flow in the 90° Junction Manhole.   Urban Water, Diciembre de 

2002, Pg 363-372. 

17

Hager, Willi y Corrado Gisonni.  Supercritical Flow in Sewer Manholes.  Acqua e città I convegnonazionale di 

idraulica urbana.  Sant’Agnello (NA), Septiembre 2005. 

18

  De  Martino,  Flavio,  Corrado  Gisonni  y  Willi  Hager.    Drop  in  Combined  Sewer  Manhole  for  Supercritical 

Flow.  Journal Of Irrigation And Drainage Engineering, Noviembre/Diciembre 2002/397. 

19

 Can-Hua Zhao, David Z Zhu, Nallamuthu Rajaratnam.  Supercritical sewer flows at a combining junction: A 

model  study  of  the  Edworthy  trunk  junction,  Calgary,  Alberta.    Journal  of  Environmental  Engineering  and 
Science, 2004, 3:(5) 343-353. 

20

 Fuente: RAS 2000 y “Elementos de Diseño Para Acueductos y Alcantarillados”, de Ricardo Lopez Cualla. 

21

  Mario  Moreno,  Daniel  Rodríguez  y  Fabio  Amador.  Determinación  del  Comportamiento  Hidráulico  de 

Cámaras de Inspección Plásticas.  Seminario Nacional de Hidráulica e Hidrología, Mayo de 2008, Colombia.