
Full Terms & Conditions of access and use can be found at
https://www.tandfonline.com/action/journalInformation?journalCode=nurw20
Urban Water Journal
ISSN: 1573-062X (Print) 1744-9006 (Online) Journal homepage: https://www.tandfonline.com/loi/nurw20
Predicting bedload sediment transport of
non-cohesive material in sewer pipes using
evolutionary polynomial regression – multi-
objective genetic algorithm strategy
Carlos Montes, Luigi Berardi, Zoran Kapelan & Juan Saldarriaga
To cite this article:
Carlos Montes, Luigi Berardi, Zoran Kapelan & Juan Saldarriaga (2020)
Predicting bedload sediment transport of non-cohesive material in sewer pipes using evolutionary
polynomial regression – multi-objective genetic algorithm strategy, Urban Water Journal, 17:2,
154-162, DOI: 10.1080/1573062X.2020.1748210
To link to this article: https://doi.org/10.1080/1573062X.2020.1748210
© 2020 The Author(s). Published by Informa
UK Limited, trading as Taylor & Francis
Group.
Published online: 08 Apr 2020.
Submit your article to this journal
Article views: 1195
View related articles
View Crossmark data
Citing articles: 12 View citing articles

RESEARCH ARTICLE
Predicting bedload sediment transport of non-cohesive material in sewer pipes using
evolutionary polynomial regression
– multi-objective genetic algorithm strategy
Carlos Montes
a
, Luigi Berardi
b
, Zoran Kapelan
c
and Juan Saldarriaga
a
a
Department of Civil and Environmental Engineering, Universidad de los Andes, Bogotá, Colombia;
b
Department of Engineering and Geology,
Università degli Studi
“G. d’Annunzio” Chieti, Pescara, Italy;
c
Department of Water Management, Delft University of Technology, Delft, Netherlands
ABSTRACT
Sediment transport in sewer systems is an important issue of interest to engineering practice. Several
models have been developed in the past to predict a threshold velocity or shear stress resulting in self-
cleansing
flow conditions in a sewer pipe. These models, however, could still be improved. This paper
develops three new self-cleansing models using the Evolutionary Polynomial Regression-Multi-Objective
Genetic Algorithm (EPR-MOGA) methodology applied to new experimental data collected on a 242 mm
diameter acrylic pipe. The three new models are validated and compared to the literature models using
both new and previously published data sets. The results obtained demonstrate that three new models
have improved prediction accuracy when compared to the literature ones. The key feature of the new
models is the inclusion of pipe slope as a signi
ficant explanatory factor in estimating the threshold self-
cleansing velocity.
ARTICLE HISTORY
Received 19 November 2019
Accepted 24 March 2020
KEYWORDS
Bedload; EPR-MOGA; non-
cohesive sediment transport;
sediment transport; self-
cleansing sewer pipes
Introduction
Sewer sediments can be de
fined as any settleable particulate
material found in stormwater or wastewater that are able to
form bed deposits in pipes and hydraulic structures (Ackers et
al.
2001
; Butler and Davies
2011
). These solids contain a wide
range of very small to large particles, i.e. ranging from clays
with a mean diameter of 0.0001 to 60 mm gravels (Bertrand-
Krajewski, Luc, and Scrivener
1993
; Ashley et al.
2004
) and may
originate from a variety of sources, such as large fecal and
organic matter, atmospheric fall-out and grit from abrasion of
road surface, among others (Butler and Davies
2011
). These
particles move in the drainage catchment during storm events
and, eventually, enter into the system.
The movement of particles in sewer pipes embodies the
processes of erosion, entrainment, transportation, deposition,
and compaction (Vanoni
2006
). Each of these phases depends
on the water velocity magnitude. For example, deposition
begins when water velocity is low, erosion occurs for higher
velocities and transportation for even higher velocities
(Alvarez-Hernandez
1990
). The movement of these particles
inside sewers depends on several parameters, such as sediment
concentration, mean particle size, the speci
fic gravity of sedi-
ments (Ackers et al.
2001
; Butler, May, and Ackers
2003
), and
flow-hydraulics (Merritt
2009
).
Sediment transport in sewer systems has traditionally been
an important issue in hydraulic engineering. During dry
weather seasons, the risk of sedimentation in sewer pipes
increases, and a permanent deposit of particles in the sewer
may produce changes in the pipes such as the consolidation
and cementation of sediments (Ebtehaj and Bonakdari
2013
).
As a related problem in this
field, these variations may also alter
the hydraulic roughness of the pipes, resulting in an increase of
the
flow resistance, blockage, flooding, surcharge and a pre-
mature over
flow operation, among others (Ab Ghani
1993
;
Ashley
and
Verbanck
1996
;
Mays
2001
;
Bizier
2007
;
Vongvisessomjai, Tingsanchali, and Babel
2010
). To avoid
these problems, minimum velocity and minimum shear stress
values have been proposed in di
fferent design manuals. As an
example, a minimum self-cleansing velocity of 0.6 m s
−1
is
highly used in the United States (ASCE
1970
) and France
(Minister of Interior
1977
), and, according to Montes, Kapelan,
and Saldarriaga (
2019
), minimum shear stress values between
1.0 and 4.0 Pa are recommended in several water utilities
design manuals in the United States, Europe and South
America.
Previous traditional self-cleansing criteria may be unsuitable
if there are variations in particle diameter and sediment con-
centration (Vongvisessomjai, Tingsanchali, and Babel
2010
).
Based on the aforementioned, several experimental investiga-
tions have studied the movement of particles to determine a
critical velocity to prevent sedimentation and particle deposi-
tion in sewers. These studies have developed self-cleansing
equations to predict a minimum velocity or shear stress values,
such as a function of several combination of parameters, e.g.
mean particle diameter, volumetric sediment concentration
and hydraulic radius, amongst others parameters. According
to Safari, Mohammadi, and Ghani (
2018
), these self-cleansing
criteria studies can be classi
fied into two major groups: bed
sediment motion and non-deposition.
Bed sediment motion is a criterion used to calculate the
flow
conditions required to move deposited material at the bottom
of the sewer pipes, i.e. a permanent accumulated material
during low-
flow rates. In this group, minimum velocity or mini-
mum shear stress values are required to allow the initiation of
CONTACT
Juan Saldarriaga
jsaldarr@uniandes.edu.co
URBAN WATER JOURNAL
2020, VOL. 17, NO. 2, 154
–162
https://doi.org/10.1080/1573062X.2020.1748210
© 2020 The Author(s). Published by Informa UK Limited, trading as Taylor & Francis Group.
This is an Open Access article distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives License (
http://creativecommons.org/licenses/by-nc-nd/4.0/
),
which permits non-commercial re-use, distribution, and reproduction in any medium, provided the original work is properly cited, and is not altered, transformed, or built upon in any way.

sediment motion (i.e. incipient motion criterion) or scouring of
existing sediment bed (i.e. scouring criterion) (Vongvisessomjai,
Tingsanchali, and Babel
2010
; Safari et al.
2017
; Safari,
Mohammadi, and Ghani
2018
). Several studies in this group
can be found in the literature of incipient motion (Novak and
Nalluri
1975
,
1984
; Ab Ghani et al.
1999
) and scouring (Camp
1946
). A full review of bed sediment motion studies has been
prepared by Safari, Mohammadi, and Ghani (
2018
).
In contrast, in the second group, non-deposition criterion,
minimum velocity values are required to prevent a permanent
deposit of particles at the bottom of the pipes, i.e. avoiding a
permanent accumulated material during low-
flow rates. This
group can be divided into three sub-groups: non-deposition
without deposited bed (i.e. sediment movement without form-
ing a stationary deposited bed), non-deposition with deposited
bed (i.e. sediment movement forming a stationary deposited
bed but limiting to a certain proportion of the pipe diameter
(May et al.
1989
)) and incipient deposition (i.e. changing from
suspended to bedload transport) (Safari et al.
2017
). Each of
these sub-groups considers di
fferent sediment dynamics and
represents the self-cleansing criteria such as a function of a
particular combination of parameters. As an example, in the
non-deposition transport without deposited bed, all the mate-
rial should be transported in
flume traction along the bottom of
the pipe (Mayerle
1988
; Butler, May, and Ackers
1996
). For the
non-deposition with deposited bed, a depth of sediment is
allowed in the pipe, to increase the transport capacity (El-
Zaemey
1991
; Ab Ghani
1993
; May
1993
; Butler, May, and
Ackers
1996
; May et al.
1996
). Finally, the incipient deposition
criterion is de
fined as the limit where particles in suspension
are deposited at the bottom of the pipes and begin to move
such bedload (Butler, May, and Ackers
1996
; Safari, Aksoy, and
Mohammadi
2015
).
In this paper, the non-deposition without deposited bed
criterion is studied, which is a conservative criterion useful to
the design of self-cleansing sewer pipes, according to Butler,
May, and Ackers (
2003
), Vongvisessomjai, Tingsanchali, and
Babel (
2010
) and Safari, Mohammadi, and Ghani (
2018
). To
apply this criterion, it is necessary to identify several parameters
such as size, concentration and density of the sediments
(Vongvisessomjai, Tingsanchali, and Babel
2010
) and the
mode of transport of the particles inside the pipes, i.e. bedload
or suspended load transport. For bedload transport, several
authors have developed equations to calculate a minimum
self-cleansing velocity to prevent the deposition of particles at
the bottom of the pipes. These equations have been developed
using experimental approaches and data handling. Craven
(
1953
) studied the transport of sands in 152 mm diameter
pipe, using three quartz sands of 0.25 mm, 0.58 mm and
1.62 mm. Robinson and Graf (
1972
) conducted experiments
using 102 mm and 152 mm diameter pipes, varying the mate-
rial concentration and the pipe slope. Novak and Nalluri (
1975
)
evaluated the bedload transport in a 152 mm diameter pipe,
using sand and gravel with mean diameters between 0.6 mm
and 50 mm. Mayerle (
1988
) conducted a series of experiments
for non-deposition without deposited bed, using a circular
channel of 152 mm diameter and a rectangular channel variat-
ing the particle diameter between 0.5 and 5.22 mm. May et al.
(
1989
) carried out experiments in a 300 mm diameter concrete
pipe moving sediments, with a mean particle diameter of
0.72 mm and developed a guideline for the design of self-
cleansing sewers. Other authors (El-Zaemey
1991
; Mayerle,
Nalluri, and Novak
1991
; Perrusquía
1991
; Ab Ghani
1993
; Ota
1999
; Vongvisessomjai, Tingsanchali, and Babel
2010
) studied
the sediment transport of non-cohesive material such as bed-
load movement using several mean particle sizes, pipe dia-
meters, and material concentrations under uniform
flow
conditions.
For suspended load transport, Pulliah (
1978
) carried out 21
experiments, using three uniform particles of 0.027 mm,
0.018 mm and 0.006 mm and varying the volumetric concen-
tration between 170 ppm and 48,542 ppm. Macke (
1982
) stu-
died the suspended load transport in three pipes of 192 mm,
290 mm and 445 mm diameters, and estimated an equation
that provides a good
fit for suspended load particles (Ackers et
al.
2001
). Macke
’s equation has been proposed for self-cleans-
ing sewer systems design (May et al.
1996
; Ackers et al.
2001
).
Arora (
1983
) used three uniform sands of 0.147 mm, 0.106 mm
and 0.082 mm, varying the material concentration from 35 ppm
to 6,562 ppm. Vongvisessomjai, Tingsanchali, and Babel (
2010
)
studied the suspended load transport, using sands with a par-
ticle diameter of 0.2 mm and 0.3 mm and varying the sediment
concentration between 113 ppm and 1,374 ppm.
In this context, Ackers, Butler, and May (
1996
) evaluated the
performance of several self-cleansing equations proposed by
di
fferent authors (Macke
1982
; Mayerle
1988
; May et al.
1989
;
Ab Ghani
1993
; Nalluri, Ghani, and El-Zaemey
1994
; Nalluri and
Ghani
1996
) and proposed three formulas for design sewers
under three typical sediment conditions, i.e. suspended load,
bedload and cohesive sediment erosion. In their study, they
concluded that for bedload transport, the May et al. (
1996
)
equation should be used to design future self-cleansing sewer
systems. Recent studies have collected and used existing
experimental data (Mayerle
1988
; May et al.
1989
; May
1993
;
Ota
1999
; Vongvisessomjai, Tingsanchali, and Babel
2010
) to
develop new self-cleansing equations, using Adaptive Neuro-
Fuzzy Inference System (Azamathulla, Ghani, and Fei
2012
),
Arti
ficial Neuronal Network (Ebtehaj and Bonakdari
2013
),
non-linear regression and the digital analysis in MINITAB
(Ebtehaj, Bonakdari, and Shari
fi
2014
), Group Method of Data
Handling (Ebtehaj and Bonakdari
2016
), Model Tree and
Evolutionary Polynomial Regression (Najafzadeh, Laucelli, and
Zahiri
2017
) and Evolutionary Polynomial Regression Multi-
Objective Genetic Algorithm (EPR-MOGA) tool (Montes et al.
2018
), amongst other approaches.
Usually, the self-cleansing models found in the literature
have been developed as a function of the modi
fied Froude
number (F
R
*):
F
R
¼
v
l
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
gd SG
1
ð
Þ
p
(1)
This parameter allows the estimation of the minimum self-
cleansing velocity (v
l
), using the gravitational acceleration coef-
ficient (g), the mean particle diameter (d) and the specific
gravity of sediments (SG). The di
fferences with traditional self-
cleansing models are the number of parameters required to
estimate v
l
, and the exponents and coe
fficients of each
URBAN WATER JOURNAL
155

equation.
Table 1
presents a review of typical equations used
on sediment transport as bedload, where C
v
is the volumetric
sediment concentration; y the water level; R the hydraulic
radius;
λ the channel friction factor; D the pipe diameter; A
the cross-section area; v
t
the velocity of sediment incipient
motion, de
fined as (Novak and Nalluri
1975
):
v
t
¼ 0:61 g SG 1
ð
ÞR
½
0
:5
R
d
0:23
(2)
D
gr
the dimensionless grain size:
D
gr
¼
SG
1
ð
Þgd
3
#
2
1
3
(3)
β a cross-section shape factor and υ the water kinematic
viscosity.
Each experimental study mentioned above has been carried
out under uniform, steady
flow conditions, and using a specific
hydraulic conditions and particle characteristics. This means
that the self-cleansing equations could be over
fitting certain
datasets resulting in poor performance when applied to other
datasets. As an example, Safari, Mohammadi, and Ghani (
2018
)
showed that the Mayerle, Nalluri, and Novak (
1991
)
’s model has
acceptable performance with the Mayerle (
1988
) data, but it
gives poor results when this equation is used with other data-
sets (May
1982
,
1993
; Ab Ghani
1993
; Vongvisessomjai,
Tingsanchali, and Babel
2010
).
The cohesive properties of sewer sediments have not been
considered in the above-mentioned studies. Higher velocities
are required to move the cohesive material in the deposited
bed (Butler, May, and Ackers
1996
); however, according to
Alvarez-Hernandez (
1990
), who studied the cohesive e
ffects
on sewer sediments using Laponite clay gel and granular
sand, when the threshold of movement is exceeded, cohesive
sediments lose their cohesive properties and move as granular
material. Based on the above, May et al. (
1996
) suggest that the
transport equations developed under well-controlled labora-
tory conditions can be applied to real sewer systems, where
in sewer sediments present cohesive properties.
This paper proposes three new models for predicting self-
cleansing
flow conditions for bedload sediment transport in
sewer pipes for uniformly graded and non-cohesive sediments.
The aim is to improve the prediction accuracy of existing
methods. Evolutionary Polynomial Regression Multi-Objective
Genetic Algorithm methodology (EPR-MOGA) (Giustolisi and
Savic
2009
) implemented in the EPR-MOGA-XL tool (Laucelli
et al.
2012
) is used to develop these predictive self-cleansing
models.
The rest of the paper is organized as follows. Section 2
presents the experimental setup and data collection. Section
3 contains the model development. In section 4 the model
validation is presented. Finally, conclusions are presented in
section 5.
Experimental data
The experimental work is carried out on a 242 mm diameter
acrylic pipe located at the Universidad de los Andes, Colombia.
This pipe has a length of 11.8 m and is supported on a steel
truss, which is sustained on
five hydraulic jacks. These jacks
allow varying the pipe slope (S
o
) between
−1.5% and 1.6%.
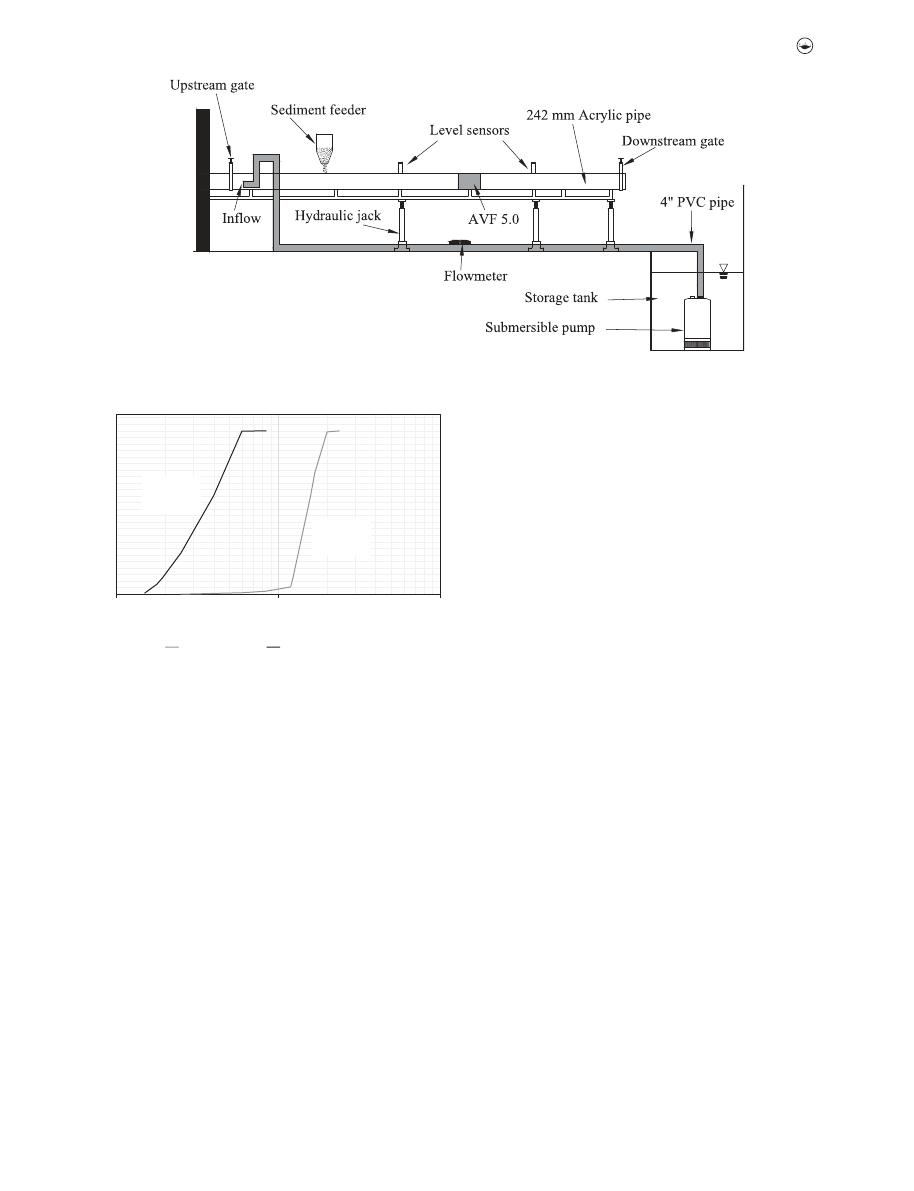
Figure 1
shows the general scheme of the experimental
apparatus.
A submersible pump (10 HP, 60 Hz, 440 V) is used to supply
water to the apparatus. This pump takes water from a 3.5 m
3
tank downstream of the pipe and conducts it through a PVC
pipe upstream. An ABB-Electromagnetic
flowmeter sensor is
installed on this pipe. Flows ranged from 0.82 L s
−1
to 25.93 L
s
−1
were simulated. These
flows are obtained using a variable
frequency drive, which controls the rotation velocity of the
submersible pump motor. Complementarily, the water depth
is measured using two ultrasonic level sensors (see
Figure 1
).
Water velocity is measured with a Greyline Area-Velocity
Flowmeter Doppler E
ffect sensor, model AVFM 5.0. A sediment
feeder controlled by a valve is used to supply the granular
material to the system with particles having a mean diameter
of 0.35 mm and 1.51 mm. The mean particle diameter is calcu-
lated developing a particle size distribution curve, which is
useful to check the uniformity of the sediments. Both sands
showed a poorly graded material (Uniformity Coe
fficient of 2.0
and 1.3, respectively), i.e. well uniformly graded material, as
shown in
Figure 2
. Particle density and speci
fic gravity are
determined by pycnometer method-procedure (Bong
2013
),
according to ASTM D854-10 (ASTM D854-14
2014
). Sediment
Table 1.
Traditional self-cleansing models used to evaluate the bedload sediment transport in sewer pipes.
Self-cleansing models
Reference
d (mm)
D (mm)
Equation
v
l
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
gd SG
1
ð
Þ
p
¼ 6:37C
v
1
=3 d
D
0:5
Craven (
1953
)
0.25
–1.65
152
(4)
v
l
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
gd SG
1
ð
Þ
p
¼ 4:32C
v
0
:23 d
R
0:68
Mayerle (
1988
)
0.50
–5.22
152
(5)
v
l
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
gd SG
1
ð
Þ
p
¼ 3:08D
gr
0:09
C
v
0
:21 d
R
0:53
λ
0:21
Ab Ghani (
1993
)
0.46
–8.30
154, 305 and 450
(6)
C
v
¼ 0:0303
D
2
A
d
D
0
:6
1
v
t
v
l
h
i
4
v
l
2
gD SG
1
ð
Þ
h
i
1
:5
May et al. (
1996
)
0.16
–8.30
77
–450
(7)
v
l
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
gd SG
1
ð
Þ
p
¼ 4:31C
v
0
:226 d
R
0:616
Vongvisessomjai, Tingsanchali, and Babel (
2010
)
0.20
–0.40
100
–150
(8)
v
l
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
gd SG
1
ð
Þ
p
¼ 4:49C
v
0
:21 d
R
0:54
Ebtehaj, Bonakdari, and Shari
fi (
2014
)
Ab Ghani (
1993
) and Vongvisessomjai, Tingsanchali,
and Babel (
2010
) data
(9)
v
l
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
gd SG
1
ð
Þ
p
¼ 0:404
R
d
0
:5
þ 23:25
R
d
0
:5
C
v
0
:5
Najafzadeh, Laucelli, and Zahiri (
2017
)
Ab Ghani (
1993
) data
(10)
v
l
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
gd SG
1
ð
Þ
p
¼ 7:34C
v
0
:13
D
gr
0:12 d
R
0:44
β
0:91
Safari et al. (
2017
)
0.15
–0.83
Trapezoidal channel
(11)
156
C. MONTES ET AL.
supply rate is estimated weighting the amount of material
supplied by the sediment feeder, during the time of the experi-
ment (Ota
1999
).
The sediment transport as bedload in the acrylic pipe is
evaluated under steady uniform
flow conditions. The step-by-
step methodology employed to obtain steady uniform
flow
conditions is as follows. Firstly, the variable frequency drive is
programmed for a speci
fic frequency of operation, and the
water
flow is measured. Secondly, the water level is monitored,
using the two ultrasonic sensors. According to Ab Ghani (
1993
),
when the water level di
fference is less than ± 2 mm, the steady
uniform
flow conditions are obtained. This criterion is evalu-
ated experimentally, and the di
fferences obtained between the
energy gradient line, the water surface slope and the pipe slope
are less than 2.0%. Thirdly, if the previous criterion is unsatis-
fied, the flow in the pipe is controlled using the downstream
gate, which is opened or closed until the steady uniform
flow
conditions are obtained. Fourthly, sediments are supplied to
the system at an increasing rate until deposition occurs. This
condition is achieved by varying the opening area of the sedi-
ment feeder valve and weighing the amount of material during
the experiment. Fifthly, the supplied rate is reduced manually,
using the sediment feeder, until the non-deposition condition
occurs. Finally, this condition is kept for at least 15 min and the
water
flow level, the water flow rate, the water velocity and the
rate of sediment are collected. The above experimental proce-
dure is repeated for di
fferent water flow rates and pipe slopes.
A set of 44 experiments were conducted using the above
procedure. The data collected this way were used to derive new
self-cleansing models (33 experiments) and the remaining data
(11 experiments) were used to validate these models.
Experimental data collected for bedload transport are shown
in
Table 2
.
In addition to the previous data collected experimentally,
four datasets found in the literature have been used to validate
the new models proposed in this study.
Table 3
presents the
characteristics of the data collected. These datasets have a
typical range of variation of conditions commonly found in
real sewer systems, according to Ackers et al. (
2001
).
EPR-MOGA-based model development
Evolutionary Polynomial Regression (EPR) is a hybrid regression
model (Giustolisi and Savic
2004
,
2006
) which combines
Genetic Algorithm, for searching exponents in a symbolic for-
mula, with a regression approach, for parameter estimation on
final models (Giustolisi and Savic
2006
,
2009
). In its original
version, the EPR strategy uses a single-objective genetic algo-
rithm (SOGA) for exploring the space of solution (Giustolisi and
Savic
2009
). Later on (Giustolisi and Savic
2009
) the use of
multi-objective optimization strategy based on genetic algo-
rithm (MOGA) allowed to improve the exploration of the space
of symbolic formulas, providing also few alternative models
which could be suited for di
fferent modelling purposes.
The EPR-MOGA strategy allows pseudo-polynomial expres-
sions such as (Giustolisi and Savic
2009
):
bY ¼ a
0
þ
X
m
j¼1
a
j
X
1
ð Þ
ES j;1
ð Þ
: . . . :ðX
k
Þ
ES j;k
ð Þ
:f ðX
1
Þ
ES j;kþ1
ð
Þ
i: . . . :f ðX
k
Þ
ES j;2k
ð
Þ
(12)
Figure 1.
Experimental apparatus used to collect bedload sediment transport data.
0
20
40
60
80
100
0.1
1
10
)
%(
re
ni
F
e
ga
t
ne
cr
e
P
Particle Size (mm)
d50 = 1.51 mm
d50 = 0.35 mm
d50 = 1.51 mm
d60 = 1.58 mm
d10 = 1.23 mm
d50 = 0.35 mm
d60 = 0.39 mm
d10 = 0.19 mm
CU = 2.0
Figure 2.
Grading curve of material used on experimental setup.
URBAN WATER JOURNAL
157

where b
Y is the vector of model predictions or estimated depen-
dent variable (El-Baroudy et al.
2010
); a
o
the optional bias term;
a
j
the parameters which are estimated through numerical
regression; X
1
. . . X
k
the matrix of the k candidate explanatory
variables; ES the matrix of candidate exponents; f the inner
function selected by the user and m is the maximum number
of additive terms. Full details can be seen in (Giustolisi and
Savic
2006
).
Multi-objective genetic algorithm in EPR-MOGA strategy
explores the space of solutions pursuing two or three objec-
tives simultaneously (Giustolisi and Savic
2009
): maximization
of the model accuracy, i.e. minimization of the Sum of Squared
Errors (as shown in Equation (16)), and minimization of com-
plexity of
final formula in Equation (12), i.e. the number of
pseudo-polynomial additional terms j, the number of inputs
X
k
or both. Using this multi-objective strategy, it is possible to
obtain parsimonious model structures with high
fitting levels.
Recently, Laucelli et al. (
2012
) implemented the EPR-MOGA
strategy as an add-in tool in MS-Excel called EPR-MOGA-XL,
which was used in this work.
To develop new self-cleansing models for sewers three opti-
mization strategies (OS) are used here. Each OS considers a
di
fferent potential group of input parameters to describe the
modi
fied Froude number, as shown in
Table 4
.
Each OS is implemented using the EPR-MOGA-XL and taking
into account several considerations. In this paper, the expression
structure considered is the Case 2 (as shown in Equation (12)),
reported by Giustolisi and Savic (
2006
) with no function f; the
range of exponent values with a step of 0.02 ES = [
−0.60, −0.58,
−0.56, . . ., 0.16] and a maximum number of polynomial terms m
equals to one. In addition, the regression method considered is
Least Squares (Giustolisi and Savic
2006
). Finally, the optimiza-
tion strategy considered aims to minimizing the number of
inputs in the
final formula (i.e. X
i
) in the pseudo-polynomial
structure and the Sum of Squared Error. Such settings allowed
to have a large search space, based on 39 candidate exponents
ES, while seeking for a compact monomial formulas readily
interpretable from hydraulic standpoint.
The models obtained by EPR-MOGA-XL are shown in
Table 5
,
which presents the best
fitting to training data shown in
Table 2
. As shown in
Table 5
, Models (13), (14) and (15) have a
structure that considers the parameters that most a
ffect the
prediction for sediment transport (Nalluri, Ghani, and El-
Zaemey
1994
; May et al.
1996
; Ebtehaj and Bonakdari
2016
),
such as the volumetric sediment concentration, mean particle
diameter, speci
fic gravity of particles and hydraulics radius.
Nevertheless, models (14) and (15) include the pipe slope,
Table 2.
Bedload experiments in the 242 mm acrylic pipe.
Experiment
Model develop-
ment stage
d
(mm)
S
o
(m
m
−1
)
C
v
(ppm)
R
(mm)
F
R
*
v
l
(m
s
−1
)
1
Training
1.510 0.0080
13.0 15.31 1.54
0.24
2
Training
1.510 0.0020
13.2 63.20 3.61
0.56
3
Training
0.351 0.0080
0.5 64.89 5.86
0.46
4
Training
1.510 0.0060
176.8 55.17 5.48
0.85
5
Training
1.510 0.0060
109.7 51.12 5.21
0.81
6
Training
1.510 0.0070
160.2 51.33 5.79
0.90
7
Training
1.510 0.0060
139.0 46.08 4.96
0.77
8
Training
1.510 0.0020
3.2 65.50 3.31
0.52
9
Training
1.510 0.0050
4.0 60.91 2.89
0.45
10
Training
1.510 0.0050
101.2 52.38 5.25
0.82
11
Training
0.351 0.0025
2.2 70.27 6.75
0.53
12
Training
1.510 0.0050
70.1 52.65 5.21
0.81
13
Training
1.510 0.0050
81.1 42.78 4.45
0.69
14
Training
1.510 0.0050
103.1 42.69 4.37
0.68
15
Training
1.510 0.0070
67.3 25.69 3.41
0.53
16
Training
1.510 0.0050
87.0 55.51 5.27
0.82
17
Training
1.510 0.0050
94.0 47.36 4.80
0.75
18
Training
1.510 0.0050
33.4 19.97 2.77
0.43
19
Training
1.510 0.0050
82.8 52.10 5.08
0.79
20
Training
0.351 0.0025
41.4 59.95 9.81
0.77
21
Training
1.510 0.0020
9.8 70.47 3.48
0.54
22
Training
1.510 0.0080
632.3 34.72 5.79
0.90
23
Training
1.510 0.0020
6.4 58.90 2.95
0.46
24
Training
1.510 0.0050
128.9 39.40 4.18
0.65
25
Training
0.351 0.0050
10.1 47.60 7.90
0.62
26
Training
1.510 0.0030
44.7 66.13 4.48
0.70
27
Training
1.510 0.0050
51.3 30.03 3.76
0.59
28
Training
1.510 0.0060
80.6 54.24 5.34
0.83
29
Training
1.510 0.0070
226.4 55.57 6.11
0.95
30
Training
0.351 0.0050
12.1 49.08 8.28
0.65
31
Training
1.510 0.0050
104.8 46.28 4.63
0.72
32
Training
1.510 0.0060
94.2 27.61 3.73
0.58
33
Training
1.510 0.0050
62.5 26.76 3.60
0.56
34
Testing
1.510 0.0070
424.4 43.86 5.60
0.87
35
Testing
1.510 0.0030
24.4 59.83 4.28
0.67
36
Testing
1.510 0.0060
87.6 50.15 5.08
0.79
37
Testing
1.510 0.0030
21.1 57.74 3.99
0.62
38
Testing
0.351 0.0050
20.5 53.97 9.04
0.71
39
Testing
0.351 0.0050
1.8 23.89 3.82
0.30
40
Testing
1.510 0.0050
70.9 38.69 3.99
0.62
41
Testing
1.510 0.0060
100.1 40.23 4.18
0.65
42
Testing
1.510 0.0080
715.0 41.41 6.76
1.05
43
Testing
1.510 0.0050
103.5 44.75 4.67
0.73
44
Testing
1.510 0.0030
32.0 60.51 4.80
0.75
Table 3.
Dataset used to evaluate the performance of self-cleansing models.
Experimental data
Model development stage
No. of runs
D (mm)
d (mm)
S
o
[%]
C
v
(ppm)
v
l
(m s
−1
)
Present study
Training
33
242
0.35
–1.51 0.20–0.80
0.26
–875.62
0.24
–0.95
Present study
Testing
11
242
0.35
–1.51 0.30–0.80
1.77
–715.01
0.30
–1.05
Mayerle (
1988
)
Testing
106
152
0.50
–8.74 0.14–0.56 20.00–1275.00 0.37–1.10
Ab Ghani (
1993
)
Testing
221
154, 305, 450
0.46
–8.30 0.04–2.56
0.76
–1450.00
0.24
–1.22
Ota (
1999
)
Testing
36
305
0.71
–5.61
0.20
4.20
–59.40
0.39
–0.74
Vongvisessomjai, Tingsanchali, and Babel (
2010
)
Testing
36
100, 150
0.20
–0.43 0.20–0.60
4.00
–90.00
0.24
–0.63
Table 4.
Optimization strategies adopted to derive new self-cleansing models.
Optimization
strategy
Group of parameters
Parameters
Functional
relationship
1
Hydraulic characteristics
R, A
F
R
* = f(R, A,
λ, C
v
, d)
Pipe material
λ
Sediment characteristics
C
v
, d
2
Hydraulic characteristics
R, A
F
R
* = f(R, A,
λ, D, S
o
,
C
v
, d)
Pipe material
λ
Pipe characteristics
D, S
o
Sediment characteristics
C
v
, d
3
Hydraulic characteristics
R, A
F
R
* = f(R, A,
λ, D, S
o
,
C
v
, d, D
gr
)
Pipe material
λ
Pipe characteristics
D, S
o
Sediment characteristics
C
v
, d, D
gr
158
C. MONTES ET AL.

which increases the model accuracy for training and testing
dataset, as shown in
Table 6
.
In addition, the symbolic expressions returned by EPR-
MOGA enable direct comparison with existing models. In
more detail, selected explaining variables and relevant expo-
nents allow to validate each single model based on the con-
sistency with technical insight on the phenomenon, thus
promoting the general validity of selected models outside the
training data set.
Evaluation of proposed models
Performance measures
To validate the models obtained by EPR-MOGA-XL, the testing
datasets shown in
Table 3
are used. The models proposed are
evaluated using four performance measures (index): Sum of
Squared Errors (SSE), Coe
fficient of Determination (CoD) and
Akaike Information Criterion (AIC). These expressions are
de
fined as follows:
SSE
¼
1
n
X
n
i
¼1
Y
Y
ð
Þ
2
(16)
CoD
¼ 1
P
n
i
¼1
Y
Y
ð
Þ
2
P
n
i
¼1
Y
Y
m
2
(17)
AIC
¼ n: ln
1
n
X
n
i
¼1
Y
Y
ð
Þ
2
"
#
þ 2k
l
(18)
where Y and Y* are the calculated and observed data, respec-
tively, n the number of data, Y*
m
the mean of observed data
and k
l
the number of parameters included in the model. The
Sum of Squared Errors measures how well the model predic-
tions (Froude numbers) are close to the corresponding obser-
vations. Smaller values of SSE are better with zero value
denoting a perfect match between predictions and observa-
tions. The Coe
fficient of Determination (CoD) estimates the
fraction (i.e. percentage) of model prediction variation that
can be explained by all model input variables together. The
CoD has a value between 0 and 1 with 1 denoting a perfect
match between model predictions and observations. Finally,
the Akaike Information Criterion (AIC) is a measure of trade-o
ff
between the goodness of
fit (i.e. accuracy) and parsimony (i.e.
simplicity) of the model. Generally, the model with the lowest
AIC value is selected as the optimal model. These three perfor-
mance measures were selected here because they are, in addi-
tion to being well known and frequently used, complementary
to each other, i.e. they evaluate di
fferent aspects of model
fitting to observed data.
Self-cleansing model performance comparison
The performance of EPR models and traditional equations is
presented in
Table 6
. As it can be seen from this table, some
traditional models have low correlations with experimental data.
For example, Craven (
1953
) model (Equation (4)) has a CoD value
varying between 0.00 and 0.43, which shows poor performance
of this model applied to all experimental datasets. Another
example is Ab Ghani (
1993
) model (Equation (6)), which presents
better results, CoD = [0.56, 0.95], and high
fitting for the datasets.
Based on the aforementioned, Ab Ghani (
1993
) model consid-
ers
five parameters to predict the modified Froude number:
Volumetric sediment concentration, mean particle diameter,
hydraulic radius, dimensionless grain size, and channel friction
factor. In contrast, Craven (
1953
) considers the volumetric sedi-
ment concentration, mean particle diameter, and pipe diameter, to
predict the modi
fied Froude number. These differences in the
combination of input parameters used can increase or decrease
Table 5.
Models obtained using EPR for di
fferent optimization strategies.
OS
Expression
Equation
1
v
l
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
gd SG
1
ð
Þ
p
¼ 3:35C
v
0
:20 d
R
0:60
(13)
2
v
l
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
gd SG
1
ð
Þ
p
¼ 6:20S
o
0
:15
C
0
:13
v
d
R
0:50
(14)
3
v
l
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
gd SG
1
ð
Þ
p
¼ 5:60S
o
0
:14
C
0
:16
v
D
gR
0
:02 d
R
0:58
(15)
Table 6.
Performance of models returned by EPR-MOGA-XL and literature self-cleansing models/equations. Bolded values show best performing models.
Data source
Stage
Performance
measure
Traditional Models
EPR-MOGA models
Eq. (4)
Eq. (5)
Eq. (6)
Eq. (7)
Eq. (8)
Eq. (9)
Eq.
(10)
Eq.
(11)
Eq. (13)
Eq. (14)
Eq. (15)
Present Study
Training SSE
4.25
0.96
1.21
0.46
0.41
0.98
1.65
0.63
0.61
0.12
0.06
CoD
0.00
0.65
0.56
0.83
0.85
0.64
0.40
0.77
0.78
0.96
0.98
AIC
53.72
4.53
16.41
−15.87
−23.24
5.26
22.62
−5.15 −10.32
−62.57
−82.17
Present Study
Testing
SSE
3.56
0.80
0.91
0.40
0.28
0.88
1.75
0.66
0.55
0.11
0.06
CoD
0.00
0.64
0.59
0.82
0.87
0.60
0.21
0.70
0.75
0.95
0.97
AIC
19.98
3.56
8.98
−0.03
−7.99
4.58
12.15
5.48
−0.50
−16.23
−20.15
Mayerle (
1988
)
Testing
SSE
2.86
0.22
0.46
0.67
0.67
1.23
2.28
0.61
1.09
0.79
0.56
CoD
0.43
0.96
0.91
0.87
0.87
0.76
0.55
0.88
0.78
0.84
0.89
AIC
117.57
−152.47 −72.71
−32.08
−35.74
28.09
93.31
−43.11
15.20
−17.43
−52.24
Ab Ghani (
1993
)
Testing
SSE
2.88
2.55
0.38
0.44
0.32
0.36
0.75
0.84
0.25
0.33
0.18
CoD
0.38
0.45
0.92
0.90
0.93
0.92
0.84
0.82
0.95
0.93
0.96
AIC
239.81
213.22
−202.55 −168.96 −243.61 −221.39 −58.67 −27.49 −300.53 −237.82 −363.39
Ota (
1999
)
Testing
SSE
1.63
0.78
0.09
0.07
0.07
0.13
0.26
0.09
0.07
0.04
0.04
CoD
0.09
0.57
0.95
0.96
0.96
0.93
0.86
0.95
0.96
0.98
0.98
AIC
23.69
−2.97
−76.10
−85.07
−89.09
−66.19 −42.59 −78.11 −90.27 −107.40 −105.57
Vongvisessomjai,
Tingsanchali, and Babel
(
2010
)
Testing
SSE
4.18
2.42
0.16
0.02
0.02
0.59
1.80
0.76
0.15
0.27
0.10
CoD
0.00
0.00
0.93
0.99
0.99
0.75
0.23
0.68
0.93
0.89
0.96
AIC
57.48
37.75
−56.32 −135.57 −134.89
−13.10
27.14
0.02
−61.54
−39.24
−71.42
URBAN WATER JOURNAL
159
the model performance. As several previous studies show (Mayerle
1988
; Ab Ghani
1993
; Nalluri, Ghani, and El-Zaemey
1994
; May et al.
1996
; Ebtehaj and Bonakdari
2016
), the most important para-
meters in the estimation of self-cleansing conditions in sewers
can be classi
fied in dimensionless groups (Ebtehaj and Bonakdari
2016
) related to motion (F
R
*), transport (C
v
), sediment character-
istics (D
gr
, d, SG), transport mode (d/R) and
flow resistance (λ). For
example, models such as F
R
* = aC
v
α
(d/R)
ϴ
(Mayerle
1988
;
Vongvisessomjai,
Tingsanchali,
and
Babel
2010
;
Ebtehaj,
Bonakdari, and Shari
fi
2014
; Najafzadeh, Laucelli, and Zahiri
2017
and EPR-MOGA Equation (13)) tend to represent better the experi-
mental data (CoD = [0.00, 0.99]) for almost all datasets; di
fferences
are represented by the values of the exponents
α and ϴ. Other
models, that are in the form F
R
* = aC
v
α
(d/R)
ϴ
D
gr
γ
β
ω
(Ab Ghani
1993
,
with
ω = 0; Safari et al.
2017
), also show good results (CoD = [0.56,
0.95]) for all the experimental datasets. Finally, EPR-MOGA models
in the form F
R
* = aC
v
α
(d/R)
ϴ
D
gr
γ
S
o
µ
(Equation (14) with
γ = 0 and
Equation (15)) show the highest
fitting for all the experimental
datasets (CoD = [0.84, 0.98]).
As the results in
Table 6
show, the EPR-MOGA models,
especially Equations (14 and 15), have high correlations for all
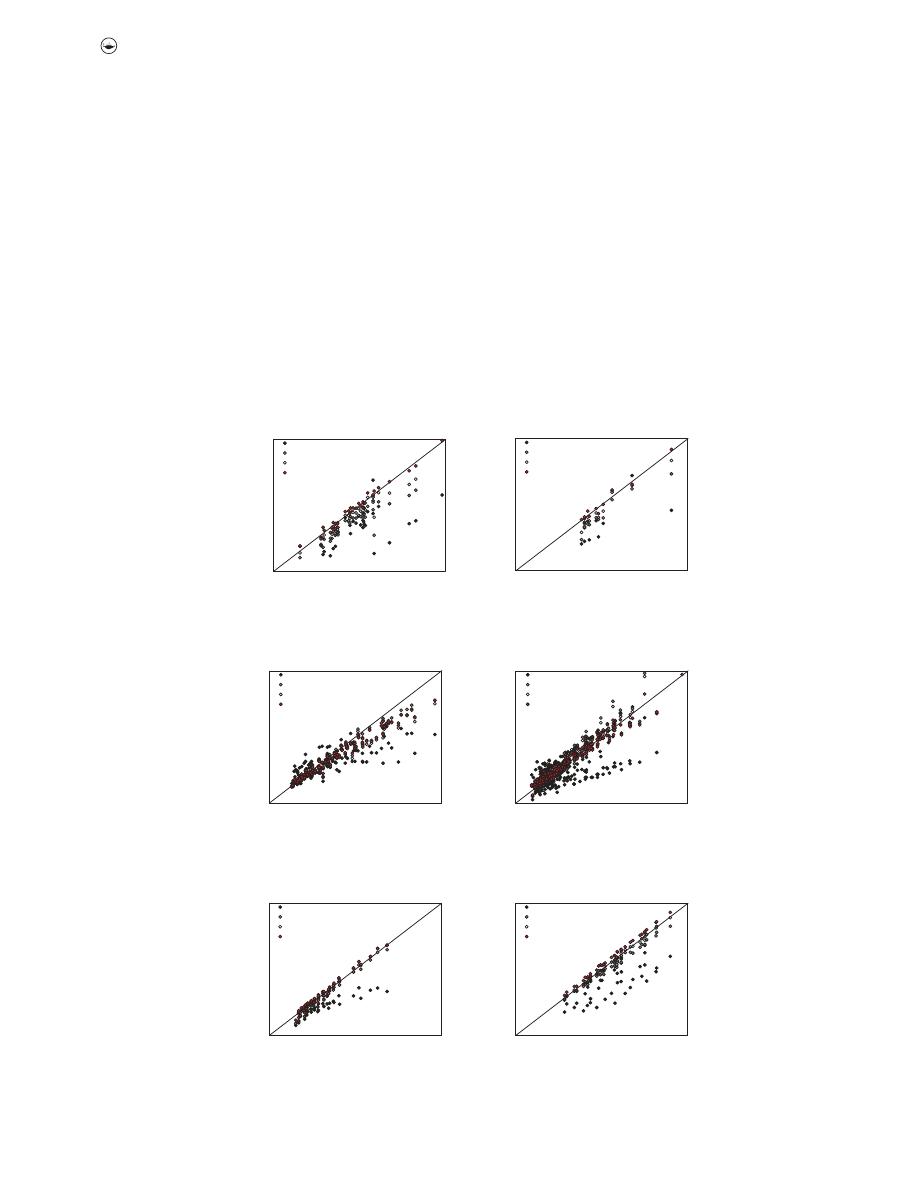
experimental data. Graphically, these results can be seen in
Figure 3
, which shows the
fitting of the self-cleansing equations
for several experimental data. The traditional Craven (
1953
)
equation underestimates the calculation of the modi
fied
Froude number for all experimental datasets. This means that
if this formula is used for the design of self-cleansing sewer
systems, the minimum slope required will be
flatter than that
actually required, increasing the risk to deposit of particles at
the bottom of the pipes.
(a)
(b)
(c) (d)
(e)
(f)
0
2
4
6
8
10
0
2
4
6
8
10
a
ta
D
de
ta
l
uc
la
C-
F
R
*
Experimental Data -
F
R
*
Present Study - Training data
Eq. (4) - Craven (1953)
Eq. (6) - Ab Ghani (1993)
Eq. (8) - Vongvisessomjai et al. (2010)
Eq. (15) - EPR-MOGA
0
2
4
6
8
10
0
2
4
6
8
10
Calculated Data
-
F
R
*
Experimental Data -
F
R
*
Present Study - Testing data
Eq. (4) - Craven (1953)
Eq. (6) - Ab Ghani (1993)
Eq. (8) - Vongvisessomjai et al. (2010)
Eq. (15) - EPR-MOGA
0
2
4
6
8
10
0
2
4
6
8
10
a
ta
D
de
ta
l
uc
la
C-
F
R
*
Experimental Data -
F
R
*
Mayerle (1988) data
Eq. (4) - Craven (1953)
Eq. (6) - Ab Ghani (1993)
Eq. (8) - Vongvisessomjai et al. (2010)
Eq. (15) - EPR-MOGA
0
2
4
6
8
10
12
14
0
2
4
6
8
10
12
14
Calculated Data
-
F
R
*
Experimental Data -
F
R
*
Ab Ghani (1993) data
Eq. (4) - Craven (1953)
Eq. (6) - Ab Ghani (1993)
Eq. (8) - Vongvisessomjai et al. (2010)
Eq. (15) - EPR-MOGA
0
2
4
6
8
10
0
2
4
6
8
10
a
ta
D
de
ta
l
uc
la
C
-
F
R
*
Experimental Data -
F
R
*
Ota (1999) data
Eq. (4) - Craven (1953)
Eq. (6) - Ab Ghani (1993)
Eq. (8) - Vongvisessomjai et al. (2010)
Eq. (15) - EPR-MOGA
0
2
4
6
8
10
0
2
4
6
8
10
Calculated Data
-
F
R
*
Experimental Data -
F
R
*
Vongvisessomjai et al. (2010) data
Eq. (4) - Craven (1953)
Eq. (6) - Ab Ghani (1993)
Eq. (8) - Vongvisessomjai et al. (2010)
Eq. (15) - EPR-MOGA
Figure 3.
Fitting of traditional equations and EPR-MOGA models, using (a) Present study training data; (b) Present study testing data; (c) Mayerle (
1988
) data; (d) Ab
Ghani (
1993
) data; (e) Ota (
1999
) data and (f) Vongvisessomjai, Tingsanchali, and Babel (
2010
) data.
160
C. MONTES ET AL.

The modi
fied Froude number calculated by model (15) cor-
rectly represents the measured experimental data. However, for
Mayerle (
1988
) dataset when F
R
* > 4.0, all the self-cleansing
equations, including the EPR-MOGA models, tend to sub-estimate
the real value. The other experimental datasets can be correctly
represented by EPR-MOGA models. This increase in the model
accuracy can be explained by the inclusion of the pipe slope
parameter in the self-cleansing models. The accuracy increases
in all cases, which means that this parameter can be signi
ficant in
the prediction of self-cleansing capacity in sewer pipes.
Conclusions
The study proposes new self-cleansing models based on data
collected from a set of 44 lab experiments conducted on a
242 mm diameter acrylic pipe with varying steady-state
flow
conditions and sediment characteristics. The data collected this
way were processed using the EPR-MOGA-XL modelling tech-
nique to derive three new self-cleansing models based on
respective optimization strategies. The new self-cleansing mod-
els were validated with collected experimental data but also
the corresponding data found in the literature. A comparison to
eight self-cleansing equations published previously in the lit-
erature was also performed in the process. This was done using
four di
fferent evaluation metrics. Based on the results obtained
the following conclusions are made:
(1) EPR-MOGA-based models showed overall better performance
than traditional self-cleansing models. This is attributed to the
proposed self-cleansing models include the pipe slope para-
meter to calculate the modi
fied Froude number. By including
this parameter in the estimation of self-cleansing in sewer
pipes, a better
fitting is observed in all the experimental
datasets considered.
(2) In addition, the EPR-based new models tend to represent, in a
better way, the experimental data for the whole range of
variation for the existing experimental data (e.g. d = [0.20
–
8.74 mm], v
l
= [0.24
–1.25 m s
−1
], C
v
= [0.27
–1,450 ppm], and
S
o
= [0.04
–2.56%], amongst other parameter variation). The
reason for this is that EPR-MOGA approach trades-o
ff model
prediction accuracy with model generalization capability
ensuring over
fitting is avoided in the model development
process.
Based on the above, new self-cleansing models can be use-
ful for the design of new sewer systems by estimating the
threshold self-cleansing
flow conditions.
It is recommended to continue the experimental investiga-
tion of sediment transport, especially in large sewer pipes and
considering di
fferent flow regimes (e.g. non-steady flow condi-
tions) as self-cleansing conditions are less well understood
under these conditions. In addition, di
fferent sediment charac-
teristics, hydraulic conditions and non-circular cross sections
should be evaluated in the future, including experiments for
cohesive material.
Disclosure Statement
No potential con
flict of interest was reported by the author(s).
References
Ab Ghani, A.
1993
.
“Sediment Transport in Sewers.” PhD diss., University of
Newcastle Upon Tyne. Newcastle Upon Tyne, UK.
Ab Ghani, A., A. Salem, R. Abdullah, A. Yahaya, and N. Zakaria.
1999
.
“Incipient Motion of Sediment Particles over Deposited Loose Beds in
a Rectangular Channels.
” In Proceedings of the 8th International
Conference on Urban Storm Drainage, 157
–163. Sydney, Australia.
Ackers, J., D. Butler, D. Leggett, and R. May.
2001
.
“Designing Sewers to
Control Sediment Problems.
” In Urban Drainage Modeling: Proceedings of
the Specialty Symposium Held in Conjunction with the World Water and
Environmental Resources Congress, edited by Robert W. Brashear and
Cedo Maksimovic, 818
–823. Orlando, FL. doi:
10.1061/9780784405833
Ackers, J., D. Butler, and R. May.
1996
.
“Design of Sewers to Control
Sediment Problems.
” Report 141. London, UK: Construction Industry
Research and Information Association (CIRIA).
Alvarez-Hernandez, E.
1990
.
“The Influence of Cohesion on Sediment
Movement in Channels of Circular Cross-Section.
” PhD diss., University
of Newcastle Upon Tyne. Newcastle Upon Tyne, UK.
American Society of Civil Engineers [ASCE].
1970
.
“Design and Construction
of Sanitary and Storm Sewers.
” Report No. 37. New York, USA: American
Society of Civil Engineers Manuals and Reports on Engineering Practices.
Arora, A.
1983
.
“Velocity Distribution and Sediment Transport in Rigid-Bed
Open Channels.
” PhD diss., University of Roorkee. Roorkee, India.
Ashley, R., J. L. Bertrand-Krajewski, T. Hvitved-Jacobsen, and M. Verbanck.
2004
.
“Solids in Sewers.” Scientific and Technical Report Series. London:
IWA Publishing.
Ashley, R., and M. Verbanck.
1996
.
“Mechanics of Sewer Sediment Erosion
and Transport.
” Journal of Hydraulic Research 34 (6): 753–770.
doi:
10.1080/00221689609498448
.
ASTM D854-14.
2014
. Standard Test Methods for Speci
fic Gravity of Soil Solids
by Water Pycnometer. West Conshohocken, PA: ASTM International.
Azamathulla, H., A. A. Ghani, and S. Fei.
2012
.
“ANFIS-Based Approach for
Predicting Sediment Transport in Clean Sewer.
” Applied Soft Computing
Journal 12 (3): 1227
–1230. doi:
10.1016/j.asoc.2011.12.003
.
Bertrand-Krajewski, J., P. B. Luc, and O. Scrivener.
1993
.
“Sewer Sediment
Production and Transport Modelling: A Literature Review.
” Journal of
Hydraulic Research 31 (4): 435
–460. doi:
10.1080/00221689309498869
.
Bizier, P., Ed.
2007
. Gravity Sanitary Sewer Design and Construction. 2nd ed.
Reston, VA: American Society of Civil Engineers.
Bong, C.
2013
.
“Self-Cleansing Urban Drain Using Sediment Flushing Gate
Based on Incipient Motion.
” PhD diss., Universiti Sains Malaysia. Penang,
Malaysia.
Butler, D., and J. Davies.
2011
. Urban Drainage. 3rd ed. London, UK: Spon
Press.
Butler, D., R. May, and J. Ackers.
1996
.
“Sediment Transport in Sewers Part 1:
Background.
” In Proceedings of the Institution of Civil Engineers - Water,
Maritime and Energy 118 (2): 103
–112. doi:
10.1680/iwtme.1996.28431
.
Butler, D., R. May, and J. Ackers.
2003
.
“Self-Cleansing Sewer Design Based
on Sediment Transport Principles.
” Journal of Hydraulic Engineering 129
(4): 276
–282. doi:
10.1061/(ASCE)0733-9429(2003)129:4(276)
.
Camp, T.
1946
.
“Design of Sewers to Facilitate Flow.” Sewage Works Journal
18 (1): 3
–16.
Craven, J.
1953
.
“The Transportation of Sand in Pipes I. Full-Pipe Flow.” In
Proceedings of the Fifth Hydraulics Conference, 67
–76. Iowa City, IA.
Ebtehaj, I., and H. Bonakdari.
2013
.
“Evaluation of Sediment Transport in
Sewer Using Arti
ficial Neural Network.” Engineering Applications of
Computational
Fluid
Mechanics
7
(3):
382
–392. doi:
10.1080/
19942060.2013.11015479
.
Ebtehaj, I., and H. Bonakdari.
2016
.
“Bed Load Sediment Transport in Sewers
at Limit of Deposition.
” Scientia Iranica 23 (3): 907–917. doi:
10.24200/
sci.2016.2169
.
Ebtehaj, I., H. Bonakdari, and A. Shari
fi.
2014
.
“Design Criteria for Sediment
Transport in Sewers Based on Self-Cleansing Concept.
” Journal of
Zhejiang University SCIENCE A 15 (11): 914
–924. doi:
10.1631/jzus.
A1300135
.
El-Baroudy, I., A. Elshorbagy, S. Carey, O. Giustolisi, and D. Savic.
2010
.
“Comparison of Three Data-Driven Techniques in Modelling the
Evapotranspiration Process.
” Journal of Hydroinformatics 12 (4): 365–
379. doi:
10.2166/hydro.2010.029
.
URBAN WATER JOURNAL
161

El-Zaemey, A.
1991
.
“Sediment Transport over Deposited Beds in Sewers.”
PhD diss., University of Newcastle Upon Tyne. Newcastle Upon Tyne, UK.
Giustolisi, O., and D. Savic.
2004
.
“A Novel Genetic Programming Strategy:
Evolutionary Polynomial Regression.
” In Proceedings of the 6th
International Conference on Hydroinformatics, 787
–794. Singapore.
Giustolisi, O., and D. Savic.
2006
.
“A Symbolic Data-Driven Technique Based
on Evolutionary Polynomial Regression.
” Journal of Hydroinformatics 8
(3): 207
–222. doi:
10.2166/hydro.2006.020b
.
Giustolisi, O., and D. Savic.
2009
.
“Advances in Data-Driven Analyses and
Modelling Using EPR-MOGA.
” Journal of Hydroinformatics 11 (3–4): 225–
236. doi:
10.2166/hydro.2009.017
.
Laucelli, D., L. Berardi, A. Doglioni, and O. Giustolisi.
2012
.
“EPR-MOGA-XL:
An Excel Based Paradigm to Enhance Transfer of Research Achievements
on Data-Driven Modeling.
” In Proceedings of 10th International
Conference on Hydroinformatics HIC, 14
–18. Hamburg, Germany.
Macke, E.
1982
.
“About Sediment at Low Concentrations in Partly Filled
Pipes.
” PhD diss., Technical University of Braunschweig, Germany.
Braunschweig, Germany.
May, R.
1982
.
“Sediment Transport in Sewers.” Report IT 222. Wallingford,
UK: Hydraulics Research Wallingford.
May, R.
1993
.
“Sediment Transport in Pipes and Sewers with Deposited
Beds.
” Report SR 320. Wallingford, UK: Hydraulics Research Wallingford.
May, R., J. Ackers, D. Butler, and S. John.
1996
.
“Development of Design
Methodology for Self-Cleansing Sewers.
” Water Science and Technology
33 (9): 195
–205. doi:
10.2166/wst.1996.0210
.
May, R., P. Brown, G. Hare, and K. Jones.
1989
.
“Self-Cleansing Conditions for
Sewers Carrying Sediment.
” Report SR 221. Wallingford, UK: Hydraulics
Research Wallingford.
Mayerle, R.
1988
.
“Sediment Transport in Rigid Boundary Channels.” PhD
diss., University of Newcastle upon Tyne. Newcastle Upon Tyne, UK.
Mayerle, R., C. Nalluri, and P. Novak.
1991
.
“Sediment Transport in Rigid Bed
Conveyances.
” Journal of Hydraulic Research 29 (4): 475–495.
doi:
10.1080/00221689109498969
.
Mays, L.
2001
. Stormwater Collection Systems Design Handbook. New York:
McGraw-Hill.
Merritt, L.
2009
.
“Tractive Force Design for Sanitary Sewer Self-Cleansing.”
Journal of Hydraulic Engineering 135 (12): 1338
–1348.
Minister of Interior.
1977
. Instruction Technique Relative Aux Réseaux
D
’assainissement Des Agglomerations, IT 77284 I. Paris, France: Minister
of interior: circulaire interministerielle.
Montes, C., L. Berardi, Z. Kapelan, and J. Saldarriaga.
2018
.
“Evaluation of
Sediment Transport in Sewers Using the EPR-MOGA-XL.
” In 1st Water
Distribution Systems Analysis - Computing and Control for the Water
Industry Joint Conference, Kingston, Ontario, Canada.
Montes, C., Z. Kapelan, and J. Saldarriaga.
2019
.
“Impact of Self-Cleansing
Criteria Choice on the Optimal Design of Sewer Networks in South
America.
” Water 11 (6): 1148. doi:
10.3390/w11061148
.
Najafzadeh, M., D. Laucelli, and A. Zahiri.
2017
.
“Application of Model Tree
and Evolutionary Polynomial Regression for Evaluation of Sediment
Transport in Pipes.
” KSCE Journal of Civil Engineering 21 (5): 1956–1963.
doi:
10.1007/s12205-016-1784-7
.
Nalluri, C., A. A. Ghani, and A. El-Zaemey.
1994
.
“Sediment Transport over
Deposited Beds in Sewers.
” Water Science and Technology 29 (1–2): 125–133.
Nalluri, C., and A. A. Ghani.
1996
.
“Design Options for Self-Cleansing Storm
Sewers.
” Water Science and Technology 33 (9): 215–220. doi:
10.2166/
wst.1996.0214
.
Novak, P., and C. Nalluri.
1975
.
“Sediment Transport in Smooth Fixed Bed
Channels.
” Journal of the Hydraulics Division of the American Society of
Civil Engineering 101 (HY9): 1139
–1154.
Novak, P., and C. Nalluri.
1984
.
“Incipient Motion of Sediment Particles over
Fixed Beds.
” Journal of Hydraulic Research 22 (3): 181–197. doi:
10.1080/
00221688409499405
.
Ota, J.
1999
.
“Effect of Particle Size and Gradation on Sediment Transport in
Storm Sewers.
” PhD diss., University of Newcastle Upon Tyne. Newcastle
Upon Tyne, UK.
Perrusquía, G.
1991
.
“Bedload Transport in Storm Sewers: Stream Traction in
Pipe Channels.
” PhD diss., Chalmers University of Technology.
Gothenburg, Sweden.
Pulliah, V.
1978
.
“Transport of Fine Suspended Sediment in Smooth Rigid
Bed Channels.
” PhD diss., University of Roorkee. Roorkee, India.
Robinson, M., and W. Graf.
1972
. Critical Deposit Velocities for Low-
Concentration Sand-Water Mixtures. Atlanta, GA: ASCE National Water
Resources Engineering Meeting.
Safari, M., H. Aksoy, and M. Mohammadi.
2015
.
“Incipient Deposition of
Sediment in Rigid Boundary Open Channels.
” Environmental Fluid
Mechanics 15 (5): 1053
–1068. doi:
10.1007/s10652-015-9401-8
.
Safari, M., H. Aksoy, N. Unal, and M. Mohammadi.
2017
.
“Non-Deposition Self-
Cleansing Design Criteria for Drainage Systems.
” Journal of Hydro-
Environment Research 14 (2017): 76
–84. doi:
10.1016/j.jher.2016.11.002
.
Safari, M., M. Mohammadi, and A. A. Ghani.
2018
.
“Experimental Studies of
Self-Cleansing Drainage System Design: A Review.
” Journal of Pipeline
Systems Engineering and Practice 9 (4): 04018017. doi:
10.1061/(ASCE)
PS.1949-1204.0000335
.
Vanoni, V., Ed.
2006
. Sedimentation Engineering. Reston, VA: American
Society of Civil Engineers.
Vongvisessomjai, N., T. Tingsanchali, and M. Babel.
2010
.
“Non-Deposition
Design Criteria for Sewers with Part-Full Flow.
” Urban Water Journal 7 (1):
61
–77. doi:
10.1080/15730620903242824
.
162
C. MONTES ET AL.
