
IAHR
CIC
XXV CO
GRESO LATI
OAMERICA
O DE HIDRÁULICA
SA
JOSÉ, COSTA RICA, 9 AL 12 DE SETIEMBRE DE 2012
UEVA
METODOLOGÍA
PARA
DISEÑO
DE
REDES
I TER AS
DE
DISTRIBUCIÓ
DE
AGUA
POTABLE
Silvia Takahashi, Pablo Ñáñez
Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA), Departamento de Ingeniería Civil y Ambiental,
Universidad de los Andes, Bogotá, Colombia
<stakahas@uniandes.edu.co>, <pa.nanez49@uniandes.edu.co>
RESUME: Las redes internas de distribución de agua potable (RIDAP), son el componente final del
sistema de distribución de agua potable de cualquier asentamiento urbano. En la actualidad, las
aproximaciones al análisis de estos sistemas son considerablemente obsoletas teniendo en cuenta, por
ejemplo, que las metodologías vigentes de diseño en Colombia y América Latina son basadas en
estudios de hace más de medio siglo (Hunter 1940), que no representan de manera aceptable el
comportamiento real de éstos (Acero 2009, Cruz y Barrios 2001). Ello contrasta con las metodologías
de análisis de las redes de distribución de agua potable (RDAP), en donde constantemente aparecen
nuevos avances para la solución de problemas como el de calibración o el de diseño del sistema,
haciendo uso de herramientas modernas como las técnicas de Inteligencia Artificial, las ecuaciones
físicamente basadas, criterios de optimización multiobjetivo para minimizar costos constructivos y de
operación, e incluso software capaz de implementar todas estas herramientas. Basado en el modelado
de la demanda por medio de procesos de Markov, se presenta un método para el análisis y diseño de
RIDAP. Finalmente se presenta un pseudocódigo del método y muestran los resultados obtenidos con
una red de prueba.
ABSTRACT:
Nowadays, most used analysis methods for internal water distribution systems IWDS are obsolete,
which are based on methods developed in the 40s. Recent studies shown that this previous approaches
didn't fit properly in the dynamical behavior of the IWDS. On the other hand, the water distribution
network WDN analysis methods are well developed, even more this field is very active. In this paper,
we take borrow some succesful concepts in WDN analysis and a novel model for water demand in
IWDS for develop a methodology for IWDS design. Finally, some results are drawn with a test
network.
PALABRAS CLAVE: Redes internas de distribución de agua potable, modelos de demanda de agua
en edificaciones, modelos estocásticos, método de Hunter.

ITRODUCCIÓ
.
El diseño de redes internas de distribución de agua potable (RIDAP) supone un problema de
optimización que busca los diámetros de las tuberías que conforman la red de tal forma que se cumplan
con ciertas restricciones hidráulicas a un bajo costo. Para solucionar este problema primero es
necesario estimar las condiciones de operación del sistema una vez este sea instalado. Estas
condiciones son variantes en el tiempo y siguen procesos estocásticos derivados del comportamiento de
los usuarios del sistema. Por lo tanto, la condición de operación de una RIDAP debe ser modelada
mediante un proceso estocástico que relacione el número de usuarios, el número de aparatos y el tipo
de uso (e.g., residencial, comercial, industrial, etc.). Una vez se establecen las condiciones de operación
y dado un nivel de confiabilidad para el sistema, se seleccionan los diámetros de las tuberías dentro de
un conjunto finito de diámetros disponibles.
Aproximaciones tradicionales hacen uso de modelos estocásticos (o métodos empíricos) para
determinar el caudal máximo probable en las diferentes tuberías del sistema, y luego siguiendo algún
tipo de aproximación se diseñan las tuberías e.g., el método de Hunter (Hunter 1940), el método
británico (García Sosa 2001), el método de Dawson y Bowman (Castro Ladino, Garzón Garzón et al.
2006) el método Alemán o de raíz cuadrada (García Sosa 2001), el método del factor de simultaneidad
(Melguizo 2002), el método racional (Roca Suárez and Carratalá Fuentes). La mayoría de metodologías
siguen el enfoque de Hunter, presentando variaciones con respecto al modelo estocástico para obtener
el caudal máximo probable, la forma de agregar los caudales, o simplemente variando los valores que
relacionan caudal máximo probable por cada tipo de aparato.
Con el objetivo de optimizar el diseño de RIDAP es indispensable conocer las características de la
demanda que se requiere satisfacer. Los métodos de diseño tradicionales tienen en cuenta estimaciones
de la demanda (e.g., método de Hunter) ya sea explícita o implícitamente. Debido a que múltiples
análisis de sensibilidad en su comportamiento muestran que el factor más influyente es la variación de
la demanda, es indispensable contar con modelos lo más acertados posibles para poder estudiar
metodologías de optimización de diseño de RIDAP (García, García-Bartual et al. 2004). En general, las
metodologías tradicionales de diseño de RIDAP involucran cierto conocimiento empírico y algunos
factores probabilísticos a manera de modelos de predicción de demanda. En (Acero 2009), el autor
explica claramente el método británico, el método alemán, el método racional, de la raíz cuadrada y de
Hunter, siendo el último a la fecha el más comúnmente utilizado. Existen además ciertas metodologías
de diseño de redes en general que están basadas en modelos estocásticos de la demanda. En
(Buchberger and Wu 1995), el autor propone el modelado de patrones de consumo como variables
aleatorias. A partir de esta aproximación se ha desarrollado una línea de investigación que busca
mejorar el desempeño de los modelos de demanda. En (García, García-Bartual et al. 2004), los autores
describen la demanda mediante 9 parámetros y 5 funciones estadísticas.
En este trabajo de investigación se propone una nueva metodología que si bien sigue la estructura
clásica de Hunter, hace uso de herramientas computacionales para simulación de RIDAP que le
permiten prescindir de simplificaciones con respecto al modelo estocástico que determina el caudal
máximo probable. Así mismo, hace uso de cadenas de Markov para calcular la probabilidad de
aparición de cualquier configuración de los nudos de consumo en la red, y dado un nivel de
confiabilidad del sistema, permite encontrar un diseño que cumple con las restricciones en cuanto a
presiones mínimas de operación y satisfacción de la demanda. Consecuentemente, en este proyecto de
investigación el modelo de demandas planteado sigue un proceso estocástico (Pulsos Rectangulares no
Homogéneos de Poisson PRNHP) definido de manera similar que en los modelos más aceptados en la
actualidad (Buchberger and Wu 1995; Buchberger and Wells 1996; García, García-Bartual et al. 2004);

y adicionalmente, se propone un modelo basado en cadenas de Markov que define los escenarios de
demanda a los cuales puede ser sometida una RIDAP dado un nivel de servicio.
DESCRIPCIÓ DEL PROBLEMA Y METODOLOGÍA DE AÁLISIS.
En la actualidad, las RIDAPs son redes a las que se conectan un alto número de aparatos de consumo
de agua, cada uno de los cuales tiene un comportamiento diferente tanto hidráulicamente como
respecto a la manera en que las personas lo utilizan. Además, con fenómenos como la conciencia
ambiental de los usuarios, y el encarecimiento del costo del servicio, se puede esperar el desarrollo de
más aparatos sanitarios (Para el resto de este documento, la palabra aparatos, se referirá a aparatos
sanitarios tales como sanitarios, lavamanos, duchas, etc.) que seguramente tendrán un comportamiento
diferente a los ya existentes. Teniendo en cuenta esto, las metodologías de diseño deben buscar la
facilidad de acoplamiento de nuevos aparatos, y en general, nuevas tecnologías que se desarrollen para
el sistema. Está es una de las más notables deficiencias de los métodos tradicionales de diseño, que
hacen de esta tarea algo notablemente impreciso y subjetivo. Si además se adiciona la variabilidad en el
comportamiento de los usuarios, por efectos como el clima, la tarifa del servicio de distribución de
agua o las costumbres de diferentes culturas, se encuentra que estos métodos son aplicables en
situaciones muy específicas y por lo tanto se hace necesaria una metodología que sea de fácil
aplicación para cualquier contexto.
Haciendo uso de un estudio previo sobre patrones de demanda en RIDAPs, se presenta un modelo del
comportamiento de los usuarios en las RIDAPs basado en cadenas de Markov. Para esto se definen los
escenarios de una red como las posibles combinaciones de nudos ocupados y libres. Son representados
por vectores binarios (1/0, demanda/ no demanda). Por medio de los escenarios se describe el espacio
muestral de las posibles situaciones de servicio en los que se puede encontrar la red. Por ejemplo, para
una red de 4 nudos se tienen
= 2
= 2
ସ
= 16 posibles escenarios de consumo. Luego, se definen
estados del sistema como grupos de escenarios que comparten el número de nudos ocupados y libres,
sin importar la forma como se distribuyan en la red. En todo el espacio muestral existen
+ 1 estados,
donde el valor n es igual al número de nudos en la red.
Dado que el uso de los aparatos (nudos de consumo) sigue un proceso estocástico que puede ser
descrito por el modelo de PRNHP, la secuencia de estados (es decir el número de aparatos ocupados en
el tiempo) es también una variable aleatoria. Esta secuencia es una secuencia de Markov y es posible
predecir su comportamiento en estado estacionario utilizando la teoría de cadenas de Markov. Este
proceso aleatorio es estocásticamente estable; por lo tanto se tiene interés en la probabilidad
estacionaria para 0, 1, 2, …
aparatos encendidos simultáneamente. Es decir, dar respuesta a la pregunta
¿cuál es la probabilidad de que m aparatos de n estén ocupados simultáneamente? El modelo planteado
para
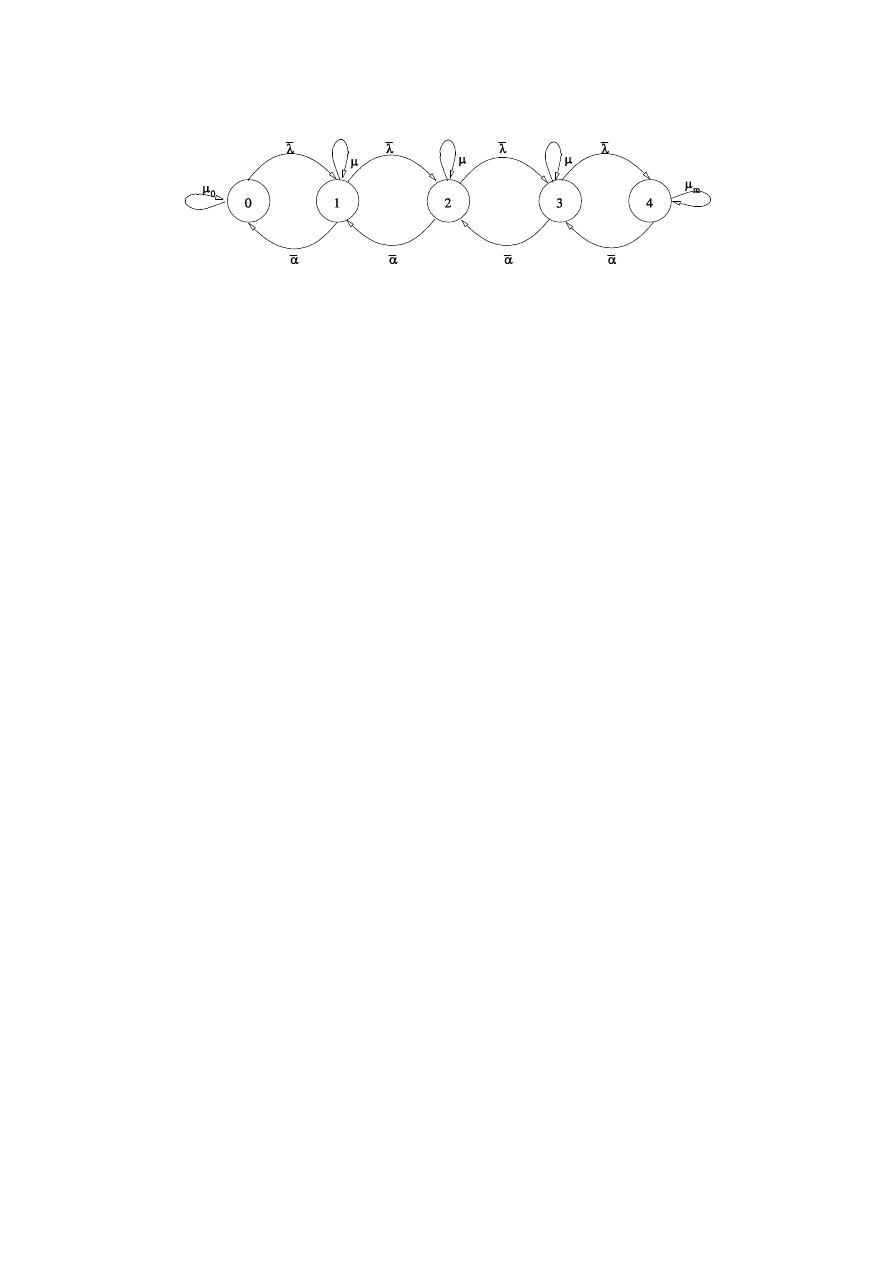
aparatos ( = 4) puede observarse en la Figura 1, en donde los arcos que incrementan el
número del estado están relacionados con la aparición de pulsos de consumo (parámetro
), mientras
que los arcos que disminuyen el número del estado están relacionados con la duración de los pulsos de
demanda (parámetro
), en donde los parámetros , y son parte del modelo de PRNHP.
Cada estado (escenario) tiene asociada una probabilidad de aparición en el tiempo (e.g, la probabilidad
de que ningún aparato esté en uso es del 50%, y de que solo un aparato esté en uso es del 45%).
En la Figura 1 se puede observar un diagrama para una cadena de Markov en particular. En este grafo
se pueden observar los elementos que constituyen una cadena, a saber, i) los estados como círculos
enumerados de 0 a 4; ii) los arcos de transición, que unen los estados. Estos arcos están marcados con
una variable que representa la probabilidad de que el sistema pase de un estado (desde donde sale el
arco) a otro (hacia donde se dirige el arco). Dado que estas variables representan probabilidades, es
claro que todas las probabilidades que salen de un estado deben sumar 1. De esta manera, para el
ejemplo, en el estado cero se puede asegurar que λ + μ
= 1, y en el estado uno λ + μ + α
= 1 y así
sucesivamente. La probabilidad de que el sistema se encuentre en el estado a
୧
en el instante n (x
୬
= a
୧
)
se calcula como:
p
x
୬
= a
୧
x
୬ିଵ
= a
୧
షభ
, … , x
ଵ
= a
୧
భ
= p x
୬
= a
୧
x
୬ିଵ
= a
୧
షభ
,
[1]
que es una secuencia de Markov de tiempo discreto. La probabilidad de transición entre estados está
determinada por:
p
x
୬
= a
୧
= p
୧
n = π
୧୨
n, sp
୨
(s)
୨
[2]
donde p
୧
n es la probabilidad de que la cadena de Markov se encuentre en el estado i en el tiempo n.
Por otra parte, la sumatoria sobre j representa la sumatoria de todos los pares estado arco que llevan a i.
En consecuencia, π
୧୨
n, s es la probabilidad de transición entre el estado j al i en los instantes s y n,
finalmente p
୨
s es la probabilidad de que la cadena de Markov se encuentre en el estado j en el tiempo
s. Así:
π
୧୨
n, s = p x
ୱ
= a
୨
x
୬
= a
୧
[3]
Adicionalmente, como se explicó anteriormente, π
୧୨
al representar probabilidades de transición desde i
a j, l debe mantenerse a siguiente relación:
π
୧୨
n, s = 1,
୨
[4]
Además,
π
୧୨
n, s = π
୧୰
n, n
ଶ
π
୰୨
n
ଶ
, s
୰
[5]
Si el proceso x
୬
es homogéneo, las probabilidades de π
୧୨
n, s dependen únicamente de la diferencia
n − s, es decir, dependen únicamente de m = n − s. Reescribiendo las ecuaciones para m (Papoulis,
Pillai et al. 1965):
π
୧୨
m = p x
୬ା୫
= a
୨
x
୬
= a
୧
[6]
π
୧୨
n + k = ∑ π
୧୰
kπ
୰୨
n
୰
, (Ecuación de Chapman Kolmogoroff)
[7]
Reescribiendo la última ecuación de manera matricial se obtiene,
Π
n + k = ΠkΠn
[8]
Por definición la matriz de la primera transición es Π
1 = Π. Por lo tanto,
Figura 1. Cadena de Markov

Π
n = Π
୬
[9]
Utilizando la notación matricial y la ecuación anterior, se reemplaza en la Ecuación [2]
¡Error! o se
encuentra el origen de la referencia.
y s
e obtiene la ecuación en diferencias recursiva para el vector de
p
୧
n, ó Pn:
P
n = P n − kΠ
୩
= P
0Π
୬
,
[10]
donde P
n = [p
ଵ
n, p
ଶ
n, p
ଷ
n, … p
୫
n]. Si el proceso es estadísticamente estable(Papoulis, Pillai
et al. 1965), después de muchos instantes de tiempo n → ∞, P
n se hace independiente de n, es mas si
P
1 es tal que P 2 = P 1 = P, entonces P n = P para todo n. Si el sistema es estadísticamente
estable el vector de estados en estado estacionario P es la solución del sistema de ecuaciones descrito
por:
PΠ
P
=
[11]
Es decir, P es un eigenvector de Π asociado con el eigenvalor λ = 1. Adicionalmente, si Π
୬
tiende a un
límite cuando n → ∞ entonces el proceso x
୬
es estadísticamente estable (asintóticamente). Para
continuar con el modelado del sistema, es necesario encontrar las probabilidades de transición en
función de los parámetros del modelo PRNHP. La aparición de los pulsos está relacionada con el
incremento en el estado de la cadena de Markov (e.g., Figura 1) ó la probabilidad λ; por otra parte, la
disminución en el estado de la cadena de Markov está relacionado con la duración de los pulsos de
consumo, es decir, que cada vez que un pulso de consumo termina, un aparato se libera, y el estado de
la cadena de Markov cambia (e.g., α
); este proceso es conocido como un birth-dead process en la teoría
de colas. La evolución de las probabilidades para cada uno de los estados de la cadena de Markov de la
Figura 1, es mostrada en la Figura 2.
METODOLOGÍA DE DISEÑO
Una vez las probabilidades de los escenarios son calculadas se procede a diseñar la RIDAP para
aquellos escenarios que acumulen la probabilidad de aparición para la confiabilidad seleccionada. Para
propósitos de diseño, se seleccionó como parámetro de diseño el porcentaje de tiempo en el cuál el
sistema opera correctamente, (e.g., en el 95% del tiempo se cumplen las restricciones hidráulicas), de
esta manera solo interesan los estados (escenarios) que acumulen esa probabilidad de aparición (e.g.,
solamente los escenarios con cero y un aparatos en uso). Finalmente, se diseña exhaustivamente para
los escenarios críticos que cumplan con la confiabilidad requerida (e.g., 95%).
Sin embargo la metodología de análisis descrita anteriormente presenta un reto importante a la hora de
realizar los diseños de las redes. Este consiste en que, el número de soluciones para el modelo
hidráulico necesarios para comprobar que el diseño una red cumpla con E aparatos encendidos es muy
0
20
40
60
80
100
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Iteraciones (n)
Probabilidad para cada estado
p
0
p
1
p
2
p
3
p
4
Figura 2. Evolución de la probabilidad de
aparición de los estados

alto. Por ejemplo, el número de posibles escenarios es del orden de
n
E
(aproximadamente 5 millones)
para una red con N=25 y E=12, y si se tiene en cuenta que en el procedimiento de diseño se requieren
varias soluciones del modelo hidráulico, el número de ejecuciones hacen que el tiempo de diseño no
sea aceptable para el usuario. Por lo tanto se presenta un método que divide la red en subredes más
pequeñas para luego solucionarlas por separado y así disminuir el número de ejecuciones del motor
hidráulico. El método se resume en los siguientes pasos:
1. Se define una línea de gradiente hidráulico LGH recta para todas las ramas de la red, en donde se
cumpla con las restricciones de presión en el nudo más alejado.
2. Se calcula el estado de Markov que cumpla con la confiabilidad seleccionada para toda la red
,
(
= 0).
3. Se identifican las subredes que contienen menos de
nudos de consumo
4. Para estas subredes se calcula un nuevo estado de Markov
, (
= + 1).
5. Para el peor de los casos (sumatoria de los
caudales requeridos en los nudos), revisar si es posible
transportar ese caudal con el diámetro menor dada la LGH calculada en 1.
6. Se regresa al paso 3.
7. Se continua dividiendo las subredes hasta que todas las ramas cumplan con 5
8. Una vez la red es dividida en subredes, cada una de las subredes es analizada como un nudo de
consumo con un modelo de demanda modificado; así cada nivel es diseñado para los casos críticos
siguiendo la LGH descrita en 1.
9. Finalmente se comprueba todo el diseño con simulaciones en tiempo extendido, y con perfiles de
demanda generados a partir del modelo de PRNHP.
•
SUPOSICIOES ECESARIAS E LA METODOLOGÍA
A fin de desarrollar la metodología de solución del problema anteriormente descrito, se hacen
necesarias una serie de suposiciones que se muestran a continuación. La primera suposición necesaria
es que las RIDAPs son redes abiertas. Es decir que, topológicamente, solo existe un camino para unir
cualquier nudo de la red con la conexión de la misma al sistema de acueducto (embalse). Esta
suposición permite prescindir de cálculos hidráulicos de la red durante la etapa de diseño. La segunda
suposición es que la demanda de todo aparato conectado a la red puede ser modelada con pulsos de
Poisson no homogéneos de duración aleatoria que siguen una Distribución Exponencial con media α en
segundos, y de frecuencia tal, que la aparición de un evento sigue un proceso de Poisson con tasa
λ = f(t), donde f(t) es una función del tiempo usualmente periódica con periodo igual a 1 día. La tercera
suposición hecha es que, si bien la mayoría de aparatos conectados a una red interna tienen un
comportamiento que se ajusta idealmente al de un emisor (Acero 2009), para el método presentado se
modelan los estos como nudos de demanda independientes de la presión. Se especifica para cada nudo
el caudal mínimo aceptable como el caudal demandado, y la presión correspondiente a dicho caudal
como la presión mínima de acuerdo con la ecuación del emisor. Finalmente se supone que a lo largo de
la red las propiedades del fluido no cambian (densidad y viscosidad), de manera que el diseño de redes
de distribución de agua fría debe hacerse independiente del diseño de redes de distribución de agua
caliente en caso de querer tener en cuenta los cambios en las propiedades del agua producidos por los
cambios en la temperatura de la misma.
•
PSEUDO ALGORITMO DEL MÉTODO DE DISEÑO
Para resolver el problema de diseño de RIDAP, teniendo en cuenta las suposiciones anteriormente
mencionadas, así como los resultados del análisis del sistema y sus correspondientes consideraciones,
se plantea el siguiente algoritmo de diseño:
1.
Leer la red y calcular atributos de los tubos y los nudos: Dentro de este paso se espera que se
reciba como dato de entrada la red con los parámetros hidráulicos de tubos y nudos así como los

parámetros de caracterización de la demanda de los nudos. Además se calculan datos como la
ruta que toma el agua para llegar a cada nudo, así como la distancia de cada nudo al embalse, el
número de nudos aguas abajo de cada tubo y sus tubos inmediatamente aguas abajo.
2.
Asignar a cada nudo su LGH objetivo: Utilizando criterios de optimización de los costos
constructivos (Wu, 1975; Ochoa, 2009), se asigna una LGH objetivo para cada nudo. De esta
manera el diseño buscará que la red presente dichos valores cuando ocurra el (o los)
escenario(s) de diseño. Dado que Wu (1975) encuentra que la diferencia entre la distribución
óptima de presiones y la distribución de presiones utilizando líneas rectas no es considerable en
términos de costos constructivos, se recomienda el uso de distribuciones de presiones rectas,
dada su facilidad de cálculo.
3.
Dividir la red en ramas de diseño:
i.
Ejecutar el algoritmo de cadenas de Markov para toda la red, conociendo para ello, el
número de nudos de demanda, el promedio de los parámetros α de todos los nudos y el
promedio de los parámetros λ de todos los nudos. Como resultado del proceso se obtiene
el estado de Markov de diseño de la red E
Red
.
ii.
Hacer una comprobación de diseño del tubo principal de la red suponiendo que tiene el
diámetro mínimo, y que la energía disponible es la diferencia entre la LGH objetivo del
nudo aguas arriba y del nudo aguas abajo. En caso de que el caudal que puede
transportar ese tubo sea mayor que la suma de los caudales de los E
Red
nudos con mayor
caudal demandado aguas abajo del tubo (Q
Crítico
), se puede suponer que el resto de tubos
aguas abajo quedarán bien diseñados si se les asigna el diámetro mínimo, de manera que
el diseño hidráulico finalizaría en este punto. Sin embargo si el caudal que puede
transportar la tubería es inferior a Q
Crítico
, entonces es necesario seguir con el paso iii.
iii.
Calcular J como un porcentaje FJ de la diferencia entre N y E
Red
:
J=FJ⋅
N-E
Red
[15]
iv.
Dado que puede llegar a tardarse mucho el procedimiento de diseño evaluando los
N
E
Red
posibles escenarios, se dejan en la rama de nivel 1, solo aquellos tubos con más
de
E
Red
+J
nudos de demanda aguas abajo.
v.
Para cada tubo que esté inmediatamente aguas abajo de la rama recién definida, volver a
ejecutar el algoritmo de cadenas de Markov (paso i) utilizando el número de nudos de
demanda aguas abajo del tubo, y el promedio de los parámetros α y λ de dichos nudos.
Después realizar una comprobación de diseño (paso ii) para verificar si el tubo puede
cumplir con los requerimientos de caudal aguas abajo en caso de ser diseñado con el
diámetro mínimo.
vi.
Repetir el paso v para los tubos inmediatamente aguas abajo de la rama recién definida,
incrementando el nivel de la rama con cada iteración hecha, hasta que todos los tubos de
la red cumplan alguna de los siguientes condiciones: a) Pertenecer a una rama de diseño,
o b) Tener asignado el diámetro mínimo.
4.
Diseñar cada rama de diseño:
i.
Seleccionar todas las ramas con nivel máximo. Para cada rama de dicho nivel contar el
número de nudos de demanda dentro de la rama N
Rama
y ejecutar el algoritmo de
cadenas de Markov para dicho número de nudos y con el promedio de los parámetros α
y λ para ese conjunto de nudos. Como resultado se obtiene el estado de Markov de
diseño para la rama analizada E
Rama
.
ii.
Generar cada posible escenario de E
Rama
nudos encendidos en la rama a diseñar. Dado
que la rama tiene N
Rama
nudos, el total de posibles escenarios es
N
Rama
E
Rama
. Para cada

escenario posible, diseñar todos los tubos de la rama a partir de la diferencia de LGH
objetivo entre el nudo aguas arriba y el nudo aguas abajo del tubo
iii.
Dado que en el paso anterior se generaron
N
Rama
E
Rama
escenarios de demanda, se debe
disponer de
N
Rama
E
Rama
caudales transportados por el tubo padre de la rama en cuestión.
Utilizando los anteriores datos se deben modificar los parámetros de demanda del nudo
inmediatamente aguas arriba del tubo padre de acuerdo con las siguiente ecuaciones:
α
Modificado
=
∑
α
i
N
Rama
i=1
N
Rama
[16]
λ
Modificado
=
∑
λ
i
N
Rama
i=1
N
Rama
[17]
Q
Modificado Alto
= máx.
Q
Nudo
, P
PA
Caudales
Tubo Padre
[18]
Q
Modificado bajo
= mín.
Q
Nudo
, P
PB
Caudales
Tubo Padre
[19]
donde:
Q
Nudo
: Caudal demandado por el aparato conectado al nudo en cuestión.
P
A
B: Función que calcula el percentil A-avo de la lista B de caudales.
Caudales
Tubo Padre
: Lista de los
N
Rama
E
Rama
caudales transportados por el tubo padre
de la rama.
Q
Modificado Alto
: Caudal que demandará el nudo en cuestión cuando se modele
como encendido.
Q
Modificado Bajo
: Caudal que demandará el nudo en cuestión cuando se modele
como apagado.
Con este paso se pretende resumir las demandas de la rama recién diseñada es dos
demandas representativas ubicadas en el nudo aguas arriba de dicha rama.
iv.
Seleccionar todas las ramas de nivel anterior al nivel ya diseñado y repetir los pasos i, ii
y ii
v.
Repetir el paso iv hasta que sea diseñada la rama de nivel 1. Exportar red.
EVALUACIÓ DE RESULTADOS
Dado que los métodos más utilizados hoy en día son variaciones del método de Hunter, a continuación
se presenta una comparación cuantitativa de los resultados obtenidos con el método tradicional de
Hunter y el método aquí propuesto. Esta comparación busca encontrar las diferencias en el desempeño
hidráulico y en los costos constructivos de la red. A continuación se presentan los diseños obtenidos
por ambas metodologías. La metodología de Hunter se puede resumir de la siguiente manera: Primero
se calculan los caudales siguiendo las unidades de Hunter, donde se considera una disminución en el
caudal a medida que el sistema aumenta en complejidad. Posteriormente, se calcula una Línea de
Gradiente Hidráulico (LGH) recta desde el embalse hasta cada nudo de consumo de la red. Esta LGH
se considera ideal, y con ésta es posible obtener las pérdidas totales ideales que tendría cada tubo
perteneciente a la RIDAP. Una vez se tiene las pérdidas de las tuberías, es posible realizar el diseño
tubo a tubo con todos los materiales disponibles y con el conjunto de diámetros comerciales que se
tengan. También es posible utilizar diámetros continuos para una solución tubo a tubo exacta.
Particularmente se utiliza una presión mínima de 7 mca para el cálculo de la LGH ideal.
A continuación se presentan diferentes comparaciones entre los diseños generados por las
metodologías. El primer criterio de comparación es el costo de construcción de cada sistema. Dados los
diseños con diámetros continuos, se utiliza una función de costos de la siguiente forma:
donde:
es el costo constructivo calculado de la red,
்௨
: Longitud del tubo analizado,
்௨
:
Diámetro del tubo analizado.
, : Parámetros de la función de costo. La Ecuación [20] ha sido
utilizada para estimar los costos constructivos de las RDAPs y por lo tanto se está suponiendo que los
costos de las RIDAPs tienen un comportamiento similar. Los parámetros de la función de costos
utilizados para la comparación, fueron
= 0.015 y = 1.46 y (los diámetros de las tuberías en
milímetros). A continuación se presenta una comparación de los valores encontrados para cada red:
Tabla 1. Comparación de costos constructivos para la red de ejemplo
En la Tabla 1 se puede ver que no existe una diferencia clara en los costos constructivos entre las dos
metodologías, siendo más barato el diseño alcanzado por la metodología propuesta. Así, un costos altos
corresponden a escenarios de demanda más exigentes que los utilizados por Hunter, para asegurar una
probabilidad de falla igual o menor a la aceptable, mientras un costo más bajo puede corresponder a un
escenario menos exigente que asegura una probabilidad de falla aceptable, o a un diseño que resulta
minimizando costos por su uso de energía. Por otro lado es posible comparar los diámetros de cada
tubería de la red, lo cual es equivalente a una comparar los caudales de diseño. Teniendo en cuenta que
para ambas metodologías se ajustó una superficie de altura piezométrica objetivo igual. Respecto a esta
última observación, cabe mencionar que el diseño tradicional de Hunter implementado en el ámbito
profesional, difícilmente tiene en cuenta una superficie óptima de alturas piezométricas, y por lo tanto
el diseño tradicional presentado en esta sección es un diseño basado en una metodología tradicional
pero optimizado en su uso de energía y, por lo tanto en los costos constructivos. Es decir que los costos
de las redes diseñadas con la metodología de Hunter, en el ámbito profesional resultarían mayores al no
tener en cuenta ningún criterio de minimización de costos.
0
20
40
60
80
100
120
140
160
0
10
20
30
40
50
60
70
80
90
100
D
iam
e
tr
o
(
m
m
)
Orden decreciente de tuberías según su diámetro por Hunter
Diseño Hunter
Diseño Propuesto
= ⋅
்௨
⋅
்௨
௫
்௨௦
,
[20]
Costo (USD)
Diseño Hunter
Diseño Propuesto
$73,109.68
$60,056.33
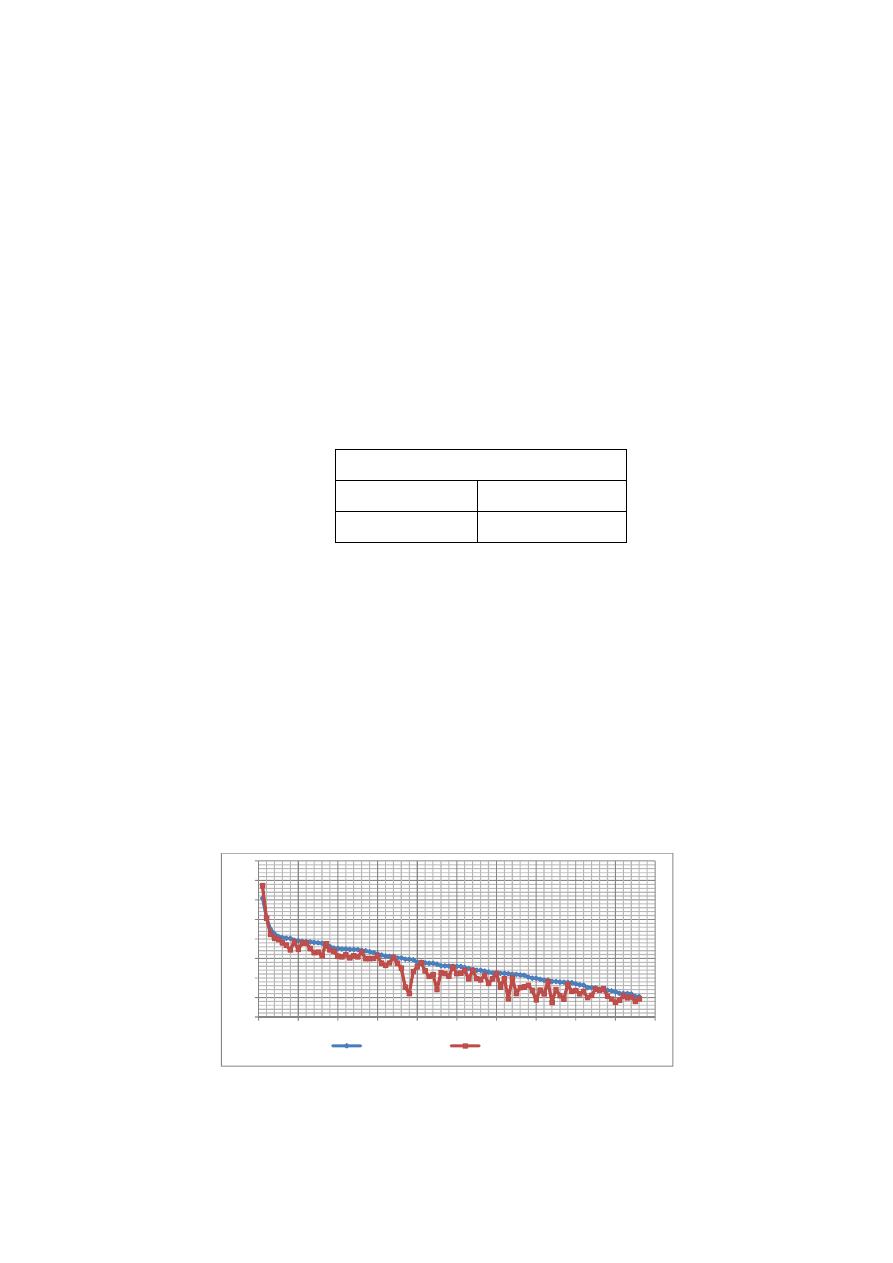
Figura 3. Comparación de diámetros obtenidos en los diseños realizados por Hunter y la
metodología propuesta

Como se puede ver en la Figura 3, los diseños generados por ambas metodologías son relativamente
similares, aunque presentan algunas diferencias que pueden implicar un comportamiento hidráulico
considerablemente diferente. Por otro lado, las diferencias en algunas tuberías responden especialmente
al método de agregación de caudales implementado por ambos métodos. Así, el método propuesto llega
a un caudal acumulado para las tuberías más cercanas al embalse (punto de unión de la RIDAP con la
RDAP), considerablemente mayor que el método de Hunter. Este déficit de capacidad de las tuberías
principales, puede generar comportamientos no aceptables del sistema en condiciones de demanda alta,
como presiones bajas en aparatos como duchas y grifos, o largos tiempos de recarga en el caso de las
cisternas de los inodoros. Además diámetros subestimados para el caso de tuberías principales puede
implicar la necesidad de diámetros más grandes aguas abajo de éstas, y si el número de tuberías y su
longitud, son suficientes.
COCLUSIOES
Se presenta una nueva metodología para el diseño de RIDAP utilizando cadenas de Markov para
modelar las demandas. Usando un método de división de las redes se propone una metodología que
permite aplicar este método a redes de tamaño real. Finalmente se presentan resultados comparativos
con diseños obtenidos con métodos tradicionales.
Los resultados obtenidos con respecto al diseño muestran que es posible mejorar en gran medida los
diseños obtenidos con los métodos tradicionales, ya que estos sobreestiman los caudales máximos
probables. Además al utilizar el método de división por subredes, el tiempo requerido para diseñar
RIDAPs es adecuado.
REFERECIAS BIBLIOGRÁFICAS
Acero, M. F. (2009). Revisión Crítica de los Métodos de Diseño de Abastecimiento de Agua Potable al
Interior de edificaciones. Departamento de Ingeniería Civil y Ambiental. Bogotá, Universidad
de los Andes. Master in Science.
Acero, M. F. (2009). Revisión Crítica de los Métodos de Diseño de Abastecimiento de Agua Potable al
Interior de edificaciones. Bogotá, Universidad de los Andes.
Buchberger, S. G. and G. J. Wells (1996). "Intensity, Duration, and Frequency of Residential Water
Demands." Journal of Water Resources Planning and Management 122(1): 11-19.
Buchberger, S. G. and L. Wu (1995). "Model for Instantaneous Residential Water Demands." Journal
of Hydraulic Engineering 121(3): 232-246.
Castro Ladino, . Y., J. E. Garzón Garzón, et al. (2006). "Aplicación de los métodos para el cálculo
de caudales máximos probables instantáneos, en edificaciones de diferente tipo." Seminario
Iberoamericano sobre Sistemas de Abastecimiento Urbano de Agua, João Pessoa (Brasil).
García Sosa, J. (2001). Intalaciones Hidráulicas y Sanitarias. México D.F., Fernando Cuna Rojas.
García, V. J., R. García-Bartual, et al. (2004). "Stochastic Model to Evaluate Residential Water
Demands." Journal of Water Resources Planning and Management 130(5): 386-394.
Hunter, R. (1940). "Methods of Estimating Loads in Plumbing Systems." Building Materials and
Structures ational Bureau of Standards.
Melguizo, S. (2002). Fundamentos de Hidráulica e Instalaciones de Abasto en Edificaciones.
Papoulis, A., S. U. Pillai, et al. (1965). Probability, random variables, and stochastic processes,
McGraw-hill New York.
Roca Suárez, M. and J. Carratalá Fuentes Manual de fontanería. España, CA.
