
TESIS
MAESTRIA INGENIERÍA CIVIL
MODELO DE OPTIMIZACIÓN MULTIOBJETIVO PARA EL DISEÑO DE
REDES DE DRENAJE URBANO
PRESENTADO POR:
ANDRÉS FELIPE AGUILAR SUÁREZ
ASESOR:
JUAN GUILLERMO SALDARRIAGA VALDERRAMA
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA, Departamento de
Ingeniería Civil y Ambiental, Universidad de los Andes, Bogotá, Colombia
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
BOGOTÁ D.C
DICIEMBRE 2019

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
2
AGRADECIMIENTOS
A Dios,
a mi familia por su apoyo sin condiciones a lo largo de toda mi vida,
a mi asesor Juan Saldarriaga por siempre ayudarme y guiarme durante el desarrollo de este
proyecto,
a Daniel Duque y Natalia Duque, por sus enseñanzas y guía que me permitieron culminar este
trabajo y contribuir a mi formación profesional y personal,
Gracias.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
3
Contenido
1.
INTRODUCCIÓN Y OBJETIVOS
........................................................................................6
1.1 Introducción
.............................................................................................................................6
1.2 Objetivos
..................................................................................................................................8
1.2.1. Objetivo General
..............................................................................................................8
1.2.2. Objetivo Específicos
.........................................................................................................8
2.
ANTECEDENTES Y REVISIÓN DE LITERATURA
.........................................................9
3. MARCO TEÓRICO
..................................................................................................................10
3.1. Redes de drenaje urbano
....................................................................................................10
3.1.1. Tipos de sistemas de alcantarillados
...............................................................................11
3.1.2. Componentes de una red de drenaje urbano:
..................................................................12
3.1.3. Problemas usuales en el sistema de drenaje urbano:
.......................................................13
3.1.4. Servicio de acueducto y alcantarillado en Colombia:
.....................................................14
3.2 Generalidades del diseño optimizado de alcantarillados:
.................................................15
3.2.1. Supuestos del trazado:
....................................................................................................16
3.2.2. Supuestos del diseño hidráulico:
.....................................................................................16
3.2.3. Restricciones hidráulicas:
...............................................................................................17
3.3 Metodología para el diseño optimizado de redes de alcantarillado:
.................................19
3.3.1 Selección de Trazado
.......................................................................................................20
3.3.2 Diseño Hidráulico:
..........................................................................................................21
3.3.3 Función de Costo:
............................................................................................................21
3.4 Eficiencia de Pareto:
............................................................................................................22
4.
DEFINICIÓN DEL PROBLEMA
.........................................................................................23
4.1
Problema de estimación de los costos para la Frontera de Pareto:
.............................24
4.1.1 Estimación de los costos en la selección de trazado según Aguilar (2016):
.....................24
4.1.2
Estimación de los costos en la selección de trazado según Zambrano (2018):
..........27
5.
METODOLOGIA
..................................................................................................................28
5.1
Diseño Hidráulico con Cámaras de Caída:
...................................................................28
5.2
Ecuación de costo:
..........................................................................................................30

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
4
5.2.1
Ecuación: Maurer (2012)
..........................................................................................31
5.3
Estimación de Confiabilidad:
........................................................................................31
5.3.1
Índice de confiabilidad propuesto por Haghighi & Bakhshipour (2016):
.................32
5.3.2
Índice de confiabilidad propuesto Aguilar (2019):
...................................................32
5.4
Construcción de la Frontera de Pareto:
........................................................................33
5.5
Estrategia para reducir tiempos y recursos computacionales:
....................................38
6.
RESULTADOS:
.....................................................................................................................40
6.1
Cedritos 1:
.......................................................................................................................40
6.1.1
Resultados con el índice de confiabilidad de Haghighi & Bakshipour (2016) y
modelo de Zambrano (2018)
....................................................................................................41
6.1.2
Resultados con el índice de confiabilidad de Aguilar (2019) y modelo de Zambrano
(2018)
41
6.1.3
Resultados con el índice de confiabilidad de Aguilar (2019) y modelo de selección
de trazado de Aguilar (2016)
....................................................................................................42
6.1.4
Resultados con el índice de confiabilidad de Haghighi & Bakshipour (2016) y
modelo de selección de trazado de Aguilar (2016)
...................................................................43
6.2
Esmeralda:
......................................................................................................................44
6.2.1
Resultados con el índice de confiabilidad de Haghighi & Bakshipour (2016) y
modelo de Zambrano (2018)
....................................................................................................44
6.2.2
Resultados con el índice de confiabilidad de Aguilar (2019) y modelo de Zambrano
(2018)
45
6.2.3
Resultados con el índice de confiabilidad de Aguilar (2019) y modelo de selección
de trazado de Aguilar (2016)
....................................................................................................45
6.2.4
Resultados con el índice de confiabilidad de Haghighi & Bakshipour (2016) y
modelo de selección de trazado de Aguilar (2016)
...................................................................46
6.3
Tumaco – Sector 2:
.........................................................................................................47
6.3.1
Resultados con el índice de confiabilidad de Haghighi & Bakshipour (2016) y
modelo de Zambrano (2018)
....................................................................................................47
6.3.2
Resultados con el índice de confiabilidad de Aguilar (2019) y modelo de Zambrano
(2018)
48
6.3.3
Resultados con el índice de confiabilidad de Aguilar (2019) y modelo de selección
de trazado de Aguilar (2016)
....................................................................................................49
6.3.4
Resultados con el índice de confiabilidad de Haghighi & Bakshipour (2016) y
modelo de selección de trazado de Aguilar (2016)
...................................................................49

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
5
6.4
Convergencia del ponderador alfa del algoritmo NISE:
.............................................50
7.
ANALISIS DE RESULTADOS
.............................................................................................51
8.
CONCLUSIONES Y RECOMENDACIONES
....................................................................53
9.
BIBLIOGRAFIA:
...................................................................................................................54

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
6
1. INTRODUCCIÓN Y OBJETIVOS
1.1 Introducción
El diseño de redes de drenaje urbano es un problema que requiere de tener en cuenta una gran
cantidad de variables que describen el comportamiento de la red y el cumplimiento de
restricciones hidráulicas que permitan el correcto funcionamiento del sistema. Por tal motivo,
es necesario abordar el problema en dos etapas: Selección de trazado y diseño hidráulico.
En la selección de trazado se tiene como objetivo definir la dirección, tipo (Inicio o continua)
y caudal que transita por cada tubería, teniendo como parámetros la topología de la red y los
caudales de entrada a cada uno de los pozos. De esta manera, se debe conservar la masa y
todo el agua que entra por los pozos de inspección debe fluir hacia un punto de descarga
definido previamente. Tradicionalmente, en la práctica este problema se soluciona
empíricamente y según el criterio del ingeniero, es decir, la dirección y el caudal de las
tuberías se determina de tal manera que el agua fluya a favor de la pendiente del terreno, bajo
el principio que los volúmenes de excavación y por ende los costos de construcción van a
resultar mucho menores si se tienen demasiados tramos en contra pendiente.
Posteriormente, en el diseño hidráulico se pretende seleccionar el diámetro y la profundidad
de excavación de cada una de las tuberías que componen la red. Sujeto a restricciones
hidráulicas proporcionadas por el reglamento técnico que se aplique. Comúnmente, los
ingenieros civiles diseñan este tipo de redes de una manera iterativa verificando que se
cumplan las especificaciones dadas ante la prueba de los diferentes diámetros comerciales
disponibles.
En los países en vías de desarrollo no solo es indispensable proporcionar el servicio de
alcantarillado a la mayor cantidad de población posible, sino que a la vez se deben construir
las redes con el menor costo posible. Por tal motivo, en la literatura es posible encontrar
diferentes metodologías, tanto heurísticas como exhaustivas, que tratan de encontrar un
diseño con un costo mínimo.
En este trabajo se pretende trabajar con la metodología para el diseño optimizado de redes de
drenaje urbano propuesta por Duque (2015), la cual aborda el problema de la selección del
trazado mediante un modelo de Programación Entera Mixta (MIP en inglés) y

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
7
consecuentemente mediante Programación Dinámica y el algoritmo de ruta más corta
Bellman-Ford resuelve el problema del diseño hidráulico.
Por otra parte, a la hora de diseñar una red de alcantarillado al igual que minimizar el costo
de construcción es importante maximizar su confiabilidad, en otras palabras, se debe velar
para que en caso del daño u obstrucción de una tubería resulte la menor cantidad de población
o área afectada aguas arriba de la zona critica. Para garantizar esta confiabilidad normalmente
se tienen restricciones de autolimpieza para el modelo de diseño hidráulico, es decir, el flujo
debe tener una velocidad mínima que permita garantizar un esfuerzo cortante que evite la
sedimentación y la obstrucción en las tuberías. Sin embargo, Haghighi & Bakhshipour (2016)
sugiere que la confiabilidad puede considerarse desde la definición del trazado al calcular los
caudales de diseño de las tuberías y de esta manera distribuir el agua de tal manera que se
cumpla con la premisa del concepto.
De este modo, en este trabajo se quiere proponer una metodología multiobjetivo que
simultáneamente permita optimizar los costos de construcción de la red y la confiabilidad,
destacando que es un problema que debe ser abordado desde la selección misma del trazado
de la red, y por tal motivo va a ser posible determinar diferentes escenarios en los que se
pueda construir una frontera de Pareto, con un algoritmo de ponderación de funciones
objetivo (NISE en inglés) propuesto por Medrano et al. (2015). Esta frontera tendrá como
ejes fundamentales el costo del diseño hidráulico y la confiabilidad de la red en cuestión.
Para poner a prueba esta metodología se aplica en tres casos de estudio, para cada uno de los
cuales se proponen varias fronteras de Pareto, las cuales se diferencian en el criterio (Función
objetivo) utilizado para minimizar los costos desde el modelo de selección de trazado y la
función de costo del diseño hidráulico.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
8
1.2 Objetivos
1.2.1. Objetivo General
Implementar una metodología de optimización multiobjetivo que permita diseñar
redes de drenaje urbano, donde sea posible minimizar el costo de construcción y
maximizar la confiabilidad del sistema simultáneamente, y de esta manera construir
una frontera de Pareto para cada uno de los casos de estudio y bajo diferentes
escenarios planteados.
1.2.2. Objetivo Específicos
• Realizar una búsqueda bibliográfica que permita encontrar criterios e índices que
permitan calcular la confiabilidad de una red de drenaje urbano.
• Implementar el modelo de selección de trazado propuesto por Duque (2015) en
Gurobi-Python.
• Evaluar la viabilidad de los criterios para minimizar los costos de construcción de una
red desde la selección de trazado propuestos por Zambrano (2018) y Aguilar (2016).
• Implementar la metodología “Non-Inferior Set Estimation” (NISE) con el fin de
construir una frontera de Pareto entre el costo de construcción y la confiabilidad de
una red.
• Validar la metodología propuesta en el presente trabajo con varios casos de estudio
usados tradicionalmente en las investigaciones del CIACUA.
• Realizar un análisis de sensibilidad de la metodología en la que se implementen los
diferentes casos de estudio con cada uno de los criterios de minimización de costo y
de confiabilidad, y de este modo construir una frontera de Pareto para cada escenario.
• Ampliar el espacio de solución del diseño hidráulico creando un módulo que permita
diseñar cámaras de caída y de esta manera tener redes de alcantarillado en terrenos
de alta pendiente.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
9
2. ANTECEDENTES Y REVISIÓN DE LITERATURA
En el Centro de Investigaciones de Acueductos y Alcantarillados de la Universidad de los
Andes (CIACUA) se han desarrollado diferentes trabajos de investigación referente a la
optimización del diseño de alcantarillados, que intentan dar una solución factible al problema
desde diferentes puntos de vista tanto hidráulicos como económicos. Sin embargo, la mayoría
de trabajos se ha enfocado en el diseño hidráulico, siempre asumiendo un trazado dado.
Inicialmente, (López Sabogal, 2011) plantea una metodología que involucra aspectos
económicos y técnicos, garantizando el cumplimiento de las restricciones hidráulicas con
costos de construcción bajos, por lo que plantea el desarrollo de los conceptos de potencia
unitaria, que es un índice de confiabilidad que ayuda al sistema a reducir las probabilidades
de que se presente algún problema que afecte a la infraestructura, o a la comunidad
circundante (López Sabogal, 2011), y el de pendiente lógica que se refiere a la discretización
de la pendiente en múltiplos de 0.001, y se le atribuye esta característica a aquella pendiente
que permite que el valor del diámetro de la tubería se reduzca al inmediatamente anterior
variando su relación de llenado (López Sabogal, 2011). Teniendo en cuenta esto concluye
que existe una relación inversa entre los costos de la red y la potencia unitaria, la
discretización de la pendiente permite un mejor manejo de los recursos computacionales y
que para obtener el diseño optimizado de la red se debe maximizar la potencia unitaria.
Posteriormente, (Copete Rivera, 2012) continuando con la metodología de (López Sabogal,
2011) diseñó un gran número de redes verificando que se cumplieran todos los
requerimientos exigidos por el RAS, y así establecer relaciones entre los costos constructivos
y los criterios de confiabilidad como el de la potencia unitaria. De esta manera, se pudo
confirmar que los costos mínimos se dan cuando se maximiza la potencia unitaria de la red.
Por otro lado, alrededor del mundo se han realizado investigaciones que están más
relacionadas con lo propuesto por (Duque, 2015). Por ejemplo, (Li y Mathew, 1990) utilizan
modelos de programación no lineal (PNL) con el fin de determinar los factores topográficos
como flujo, diámetros y pendientes de las tuberías de la red. En este planteamiento los autores
dividen el problema en dos etapas. La primera corresponde a la optimización de los diámetros
y pendientes de las tuberías, junto a la ubicación de las estaciones de bombeo, si aplica el
caso. En segunda instancia, se mantienen todas las variables constantes y se modifica
gradualmente la tasa de flujo y así se busca tuberías que minimicen la función objetivo que
depende de la velocidad de flujo, la cota de corona de las tuberías y la presencia de estaciones
de bombeo, a través de una búsqueda utilizando el algoritmo de ruta más corta de Dijkstra.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
10
Sin embargo, el método que más se ha desarrollado y popularizado por muchos autores son
los Algoritmos Genéticos (AG). Por ejemplo (Haghighi A. y Bakhshipour A., 2012) utilizan
estos algoritmos para el diseño hidráulico, donde determinan los diámetros de las tuberías y
las cotas de excavación. Además, se han combinado diferentes metodologías con los AG
como (Cisty M., 2010) que propone una alternativa que utiliza AG y programación lineal,
(Pan y Kao, 2009) combinan los AG con programación cuadrática. También se han utilizado
otras metodologías heurísticas para el diseño optimizado de alcantarillados como el
algoritmo de colonia de hormigas (Afshar 2010, Moeini & Afshar 2012, Moeini & Afshar
2017), recocido simulado y búsqueda Tabú (Yeh et al. 2011, Yeh et al. 2013, Haghighi &
Bakhshipour 2015).
3. MARCO TEÓRICO
3.1. Redes de drenaje urbano
La existencia de sistemas de alcantarillado es fundamental para que la evolución y el
desarrollo de una sociedad se dé en una interacción beneficiosa entre el ser humano y el ciclo
del agua, es decir, el objetivo de estas redes se resume en dar un correcto manejo a los dos
tipos de aguas: residuales y pluviales, con el fin de minimizar los problemas causados a los
seres humanos y al medio ambiente (Butler & Davies, 2011). De esta manera, resulta
necesario buscar metodologías que permitan determinar diseños ejecutables en los que se
minimicen los costos de construcción y que cumplan con los requisitos hidráulicos
establecidos.
Para llevar a cabo lo anterior es necesario entender cómo funciona un sistema de drenaje
urbano convencional y como es su interacción con el ciclo del agua. Normalmente esta
interacción se da de dos maneras. En primer lugar, el ser humano se vale del ciclo del agua
para abastecerse y realizar sus actividades y en segundo lugar esta interacción se da en un
sentido contrario a través de las precipitaciones y escorrentías que van a dar a las redes de
alcantarillado.
Ahora, las aguas residuales y pluviales surgen como consecuencia de las interacciones
nombradas anteriormente. Las aguas residuales, también llamadas aguas servidas, se
caracterizan porque ya han sido utilizadas como recurso para abastecer las actividades vitales
y productivas de los seres humanos, por lo tanto, dentro de su composición contienen
diversos materiales solidos de diversos tamaños, y por lo tanto el alcantarillado debe tener la
capacidad de conducirlos hasta el punto de descarga. Por su parte, el agua pluvial se refiere

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
11
básicamente a aquella proveniente de la precipitación sobre el área de interés, y que resulta
un fenómeno natural dentro del ciclo del agua. Sin embargo, sino se tienen presupuestadas
de manera correcta en el diseño para ser evacuadas, pueden causar problemas de
inundaciones y salud pública.
3.1.1. Tipos de sistemas de alcantarillados
En el drenaje urbano existen tres tipos de sistema: El combinado, el Separado y el Híbrido,
siendo importante esta diferenciación debido a que según el tipo de sistema que se vaya a
diseñar los requerimientos pueden variar.
El primero de estos se caracteriza por transportar tanto las aguas residuales como las lluvias
por la misma tubería, siendo el destino final de estas la planta de tratamiento. En las épocas
secas del año, por la tubería combinada solamente fluirán las aguas residuales, pero una vez
empieza la época invernal las aguas lluvias dominarán el flujo generado. Por esta razón, es
evidente que no es factible económicamente dimensionar una tubería que tenga la capacidad
total requerida en toda la longitud de esta dado que la mayoría del tiempo solo fluirá una
pequeña proporción del caudal para el cual fue diseñada (Salcedo, 2012).
El sistema separado de drenaje urbano se caracteriza porque transporta las aguas residuales
y las aguas lluvias en tuberías diferentes, pero que suelen ir en paralelo. En este tipo de
sistema se diseña una tubería que transporte el flujo máximo de aguas residuales que deberá
ser entregado a la planta de tratamiento, mientras que en el caso de aguas lluvias,
nuevamente, se va a tener una tubería de mayor tamaño que puede ser descargada en
cualquier punto que sea conveniente del cuerpo receptor (Butler & Davies, 2011). La
principal desventaja de este sistema corresponde al aumento en los costos al instalar otra
tubería, ya que a pesar que el conducto de aguas residuales será más pequeño que el de aguas
lluvias, y que ambas se instalen en paralelo utilizando la misma zanja, este sistema resultará
más costoso que el combinado.
Finalmente, los sistemas híbridos o mixtos se caracterizan por ser una mezcla entre sistemas
combinados y separados. Estos sistemas buscan tener redes separadas cuando haya cuerpos
de agua que sirvan para el vertimiento de las aguas lluvias, y que por otro lado permitan el
paso de las aguas residuales provenientes de la urbanización hacia las plantas de tratamiento.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
12
3.1.2. Componentes de una red de drenaje urbano:
Independiente del lugar y el tipo de sistema de alcantarillado que se quiera construir, una red
de drenaje urbano generalmente siempre debe tener los siguientes componentes que se
describen a continuación (Salcedo, 2012):
• Sumideros, Canaletas y Bajantes:
El principal objetivo de estas estructuras es la recolección de los líquidos y fluidos que viajan
por la superficie, como las aguas lluvias. Los sumideros, ubicados en los bordes de los
andenes, se encargan de captar la escorrentía y transportarla hacia las tuberías de la red. En
cambio, las canaletas y bajantes son elementos complementarios entre si y tienen el propósito
también de captar aguas lluvias de los tejados de las edificaciones para transportarlas hacia el
sistema de alcantarillado de la ciudad.
• Tuberías:
Son las estructuras cuyo principal objetivo es transportar el agua que entra a la red de drenaje
urbano. Por lo tanto, significa que ocupan el mayor porcentaje del área de la red de
alcantarillado.
• Cámaras de Inspección:
Estas estructuras permiten el acceso del personal especializado a la red de drenaje para
realización de labores de mantenimiento e inspección. También su principal uso es a nivel
hidráulico, pues permite el cambio de dirección del flujo, cambios de diámetro entre dos
tuberías y conexión con otras redes.
• Cámaras de Caída:
En caso que el flujo llegue a la cámara de inspección con mucha energía, la estructura se
encarga de disipar el exceso de esta con el fin de proteger la infraestructura del sistema.
Además, permiten la conexión entre tuberías que se encuentren en cotas muy diferentes.
• Aliviaderos:
Se encargan de evacuar las aguas cuando estas sobrepasan un determinado nivel con el fin de
reducir los costos de conducción. El tipo de aguas que evacua este elemento va a depender
del tipo de sistema que se tenga.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
13
• Sifones Invertidos:
Son estructuras cuyo principal propósito es sobrepasar obstáculos en el trazado de la red
cuando estos son inevitables. Su funcionamiento se basa en la presurización de las tuberías.
• Sistemas de Almacenamiento Temporal:
Se encargan de retener el agua con el propósito de disminuir los picos de caudal y de
contaminación que se presentan cuando ocurre un evento de lluvia. De este modo, su función
se resume en homogenizar el caudal y la concentración de los contaminantes del agua.
• Canales Abiertos:
Su función principal es la de conducir aguas lluvias provenientes de las vías y andenes.
• Estructura de Disipación de Energía:
Se encuentran ubicadas en los puntos de donde se entrega el agua, y se encargan de disipar
energía para que el flujo pase de ser supercrítico a ser subcrítico.
3.1.3. Problemas usuales en el sistema de drenaje urbano:
Las fallas y problemas en la estructura de una red de alcantarillado resultan normales debido
a la exposición química y física que tiene las tuberías y otros componentes del sistema a los
contaminantes y otros fenómenos externos durante su larga vida útil. Los inconvenientes más
comunes están relacionados con defectos constructivos como malas conexiones entre
tuberías que pueden llevar a fugas, grietas y facturas que deterioran rápidamente el sistema
de drenaje. También, se debe tener en cuenta que inadecuadas técnicas de
impermeabilización son causantes de infiltraciones o exfiltraciones que pueden llevar a la
contaminación de las aguas subterráneas.
A nivel interno, las causas de las fallas pueden ser estar relacionadas con el tamaño y el
material de las tuberías, es decir, hay materiales que debido a su composición resultan más
reactivos debido a los contaminantes del agua, lo que los hace más propensos a los procesos
de oxidación y corrosión. Además, el tiempo que lleva en uso la red puede ser causa del
colapso del sistema. Otra posibilidad para que se dé un daño en la red se puede dar por el
taponamiento de grasas y sedimentación de partículas que disminuyen la capacidad
hidráulica. Sin embargo, las anteriores fallas siempre se pueden evitar con un cuidado y
mantenimiento riguroso (Torres Dueñas, 2013).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
14
Las fallas externas, se derivan de la intrusión de raíces de plantas a las tuberías que
disminuyen su sección transversal y por lo tanto la capacidad de mover un caudal. Y también
está asociado los daños por actividad sísmica o la inestabilidad del terreno que provocan
afectación en la estructura.
Debido a las causas nombradas anteriormente se puede deducir que hay una disminución de
la capacidad hidráulica de las tuberías, y adicionalmente hay un aumento en la tasa de
infiltración en los sistemas que lleva a que se produzcan sobrecargas en las tuberías que
sobrepasan el caudal para el que fue diseñada la tubería. De esta manera, la sobrecarga es un
proceso en el que la tubería se presuriza y en ciertos momentos puede ser causante del
rebosamiento de las cámaras de inspección, que posteriormente puede llevar a inundaciones.
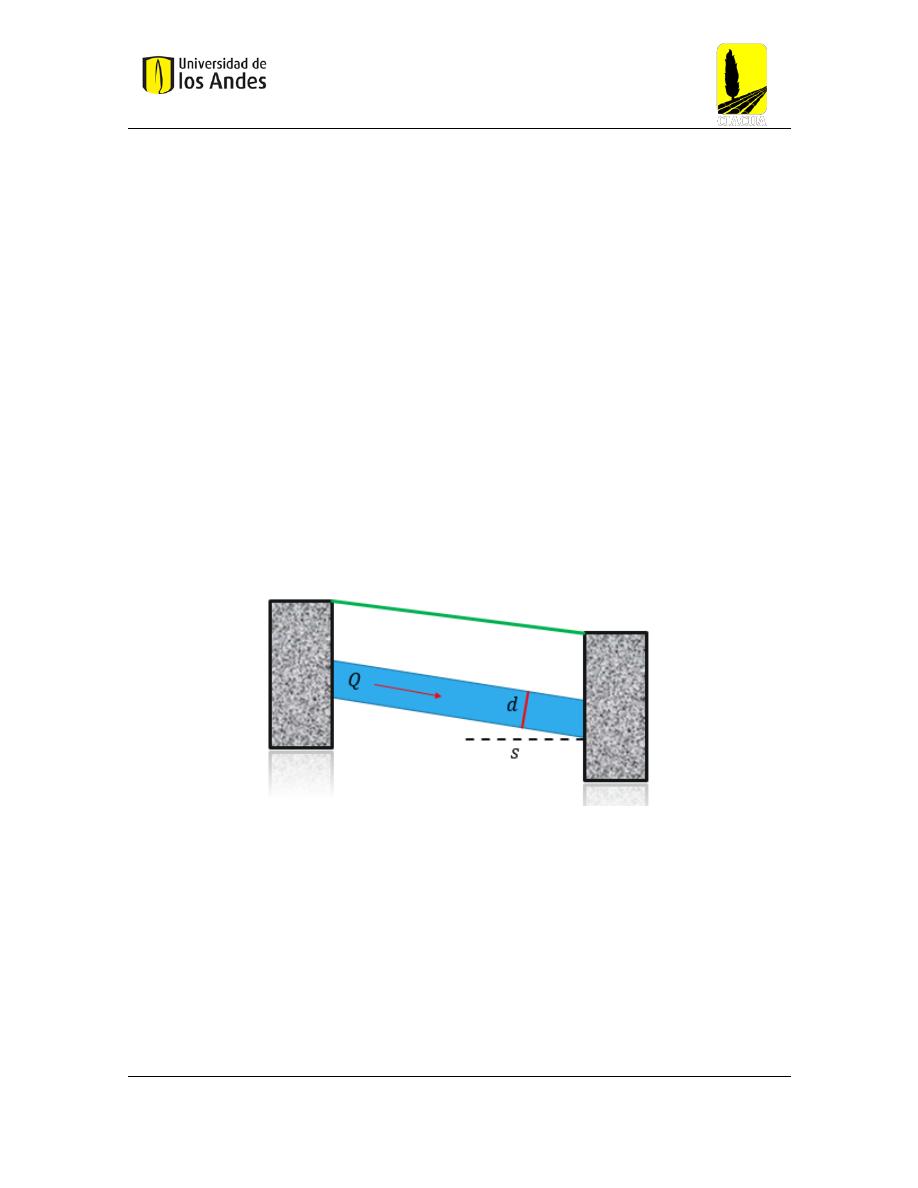
Figura 1 Funcionamiento de un pozo cuando existe una obstrucción aguas abajo
3.1.4. Servicio de acueducto y alcantarillado en Colombia:
En la actualidad, la prestación del servicio de acueducto y alcantarillado en todos los
municipios de Colombia es una cuenta que no se ha podido saldar, debido a diferentes
factores económicos, sociales y políticos que no han permitido que se cumpla con este
objetivo. Según datos del 2015, la cobertura urbana de estos servicios alcanza el 97% para el
acueducto y el 92% para el alcantarillado, siendo las metas propuestas de 99% y 97%
respectivamente. Por otro lado, en el área rural el nivel de cobertura es del 72% en el
acueducto y del 69% para el alcantarillado, muy lejana a la meta propuesta del 81% y el 75%.
De este modo, es posible deducir que todavía es necesario emprender una inversión y
esfuerzos para compensar el déficit que se tiene en esta materia (Salinas, 2015).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
15
Ahora, a lo que se refiere netamente al servicio de alcantarillado, el indicador del tratamiento
de aguas residuales es preocupante en todo el país, por lo que es un ítem que requiere una
gran inversión y gestión hacia el futuro. En la actualidad, solo el 25% de las aguas que se
vierten a los cuerpos receptores son tratados, lo que conlleva una gran afectación ambiental
al liberar toda la carga contaminante, y luego se presenta un aumento en los costos acueductos
que captan el agua de estas fuentes. Exactamente el 30% de los municipios en Colombia
cuentan con sistemas de tratamiento de aguas residuales, concentrados en zonas de más de
10 mil habitantes. Así, en los centros urbanos se trata cerca del 41% de las aguas residuales
(Salinas, 2015).
3.2 Generalidades del diseño optimizado de alcantarillados:
El diseño de alcantarillados es un problema complejo que debe ser resuelto en dos etapas: la
selección del trazado y el diseño hidráulico. Esto debido a que la gran cantidad de variables
que se deben determinar y el que carácter de las mismas es muy diferente en cada uno de los
problemas. Además, el hecho de solucionar el problema en una sola sección puede implicar
un alto costo computacional.
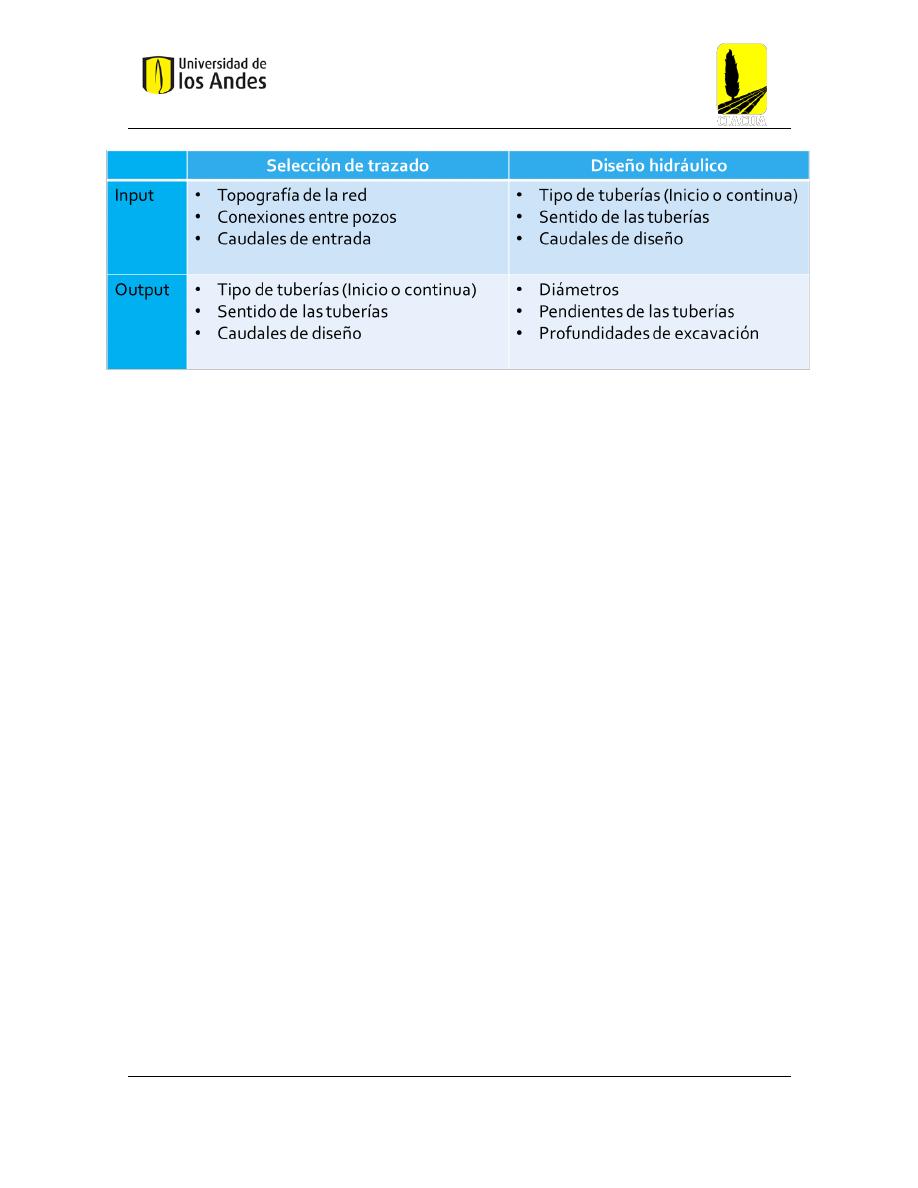
En la selección del trazado se define el recorrido del agua en la red, es decir, se determina el
sentido de las tuberías, el tipo de las tuberías y los caudales de diseño correspondientes para
cada una de los conductos. Para dicho proceso es necesario tener como parámetros de entrada
la topología de la red, la cual permite tener una descripción del relieve del terreno, las
conexiones entre pozos, que indican las posibles configuraciones que pueden tener las
tuberías entre pozos, y los caudales sanitarios por cada uno de los pozos, que representan las
entradas externas a la red y van a definir los caudales de diseño para cada una de las tuberías.
Luego de obtener los resultados de la selección del trazado que sirven como parámetro para
la etapa de diseño hidráulico, donde se define los diámetros, pendientes y profundidades de
excavación de las tuberías en cada uno de los tramos de la red de interés, siempre cumpliendo
con las restricciones hidráulicas impuestas por la reglamentación de cada país. De esta
manera, al final se obtiene un sistema de drenaje capaz de captar las descargas de aguas
residuales de un área de influencia, y llevarlas hasta un punto de descarga previamente
determinado.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
16
3.2.1. Supuestos del trazado:
• Con el fin de que haya una cobertura total y que se preste el servicio de alcantarillado
a cada una de las edificaciones que se encuentren dentro del área de influencia de la
red es necesario la instalación de una tubería por cada calle.
• En cada intersección de tuberías hay un pozo de inspección, debido a que en las
conexiones entre conductos es necesario un cambio de pendiente, diámetro o de
dirección del flujo.
• La red de drenaje capta toda el agua que es descargada en las cámaras de inspección,
y debe ser llevada hasta un punto de descarga que es determinado previamente por el
diseñador.
• Se asume que el agua residual que entra a la red lo hace por cada uno de los pozos de
inspección, donde se distribuye a cada una de las tuberías dispuestas en el sistema.
3.2.2. Supuestos del diseño hidráulico:
En la naturaleza, los flujos pueden clasificarse según dos criterios: Su variación en el espacio
siendo éste variado o uniforme, y su variación en el tiempo siendo éste permanente o no
permanente. Al combinar las condiciones previamente mencionadas se da origen a 3 tipos de
flujo: Flujo Uniforme – Permanente, Flujo Uniforme - No Permanente, Flujo Variado –
Permanente y Flujo Variado – No Permanente (Saldarriaga, 2014). Generalmente, a la hora
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
17
de diseñar sistemas de drenaje urbano se plantea bajo las condiciones del Flujo Uniforme, ya
que este no cambia sus condiciones en tiempo ni en espacio, siendo que esto es un supuesto
adecuado ya que asume que el nivel de agua es constante en toda la longitud de la tubería y
permite tener una mayor precisión al momento de realizar cálculos y estimaciones de caudal.
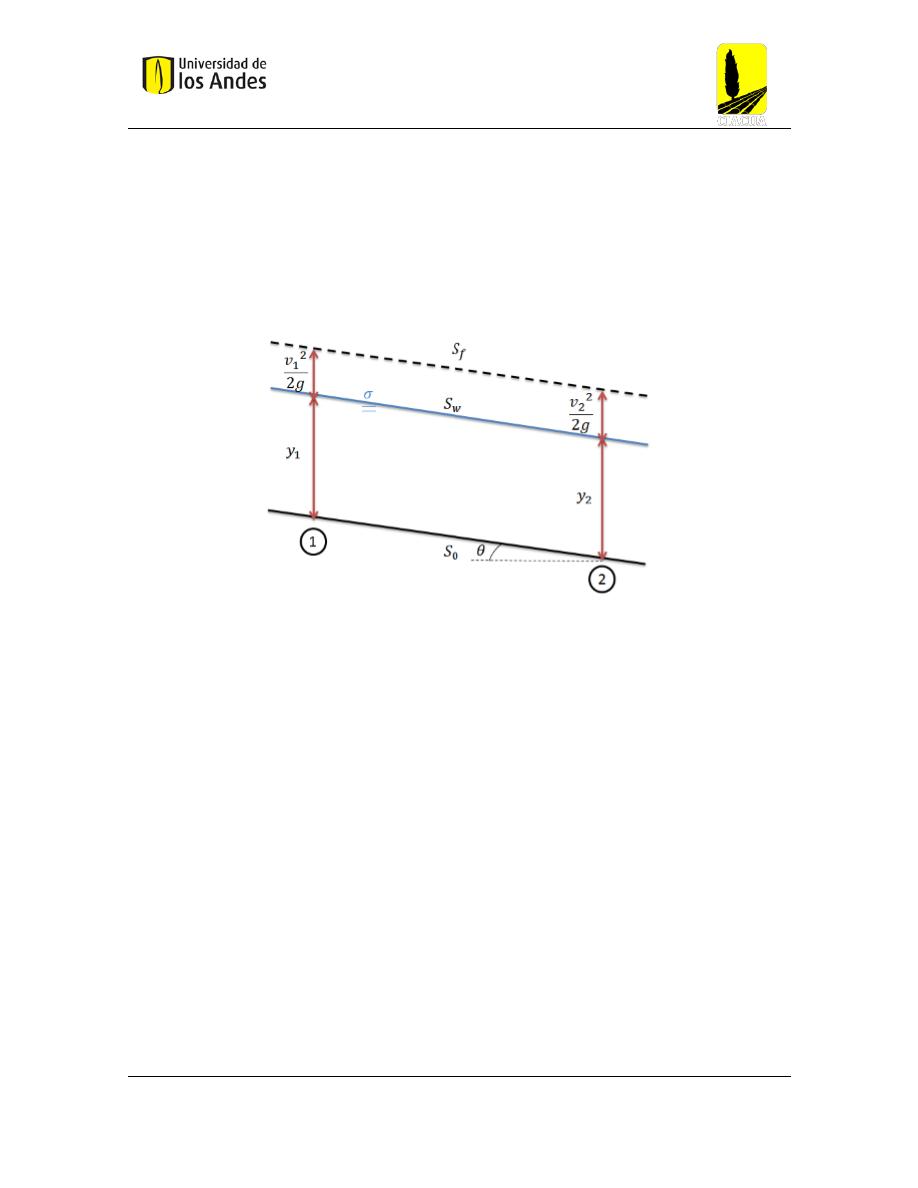
En otras palabras, en condiciones de flujo uniforme las pendientes de energía (
𝑆
𝑓
), lámina de
agua (
𝑆
𝑤
) y el canal (
𝑆
0
) son siempre iguales a lo largo de todo el espacio y tiempo.
Figura 2 Condiciones de un flujo uniforme
3.2.3. Restricciones hidráulicas:
Para que haya un correcto funcionamiento del sistema de alcantarillado, el Reglamento
Técnico del Sector de Saneamiento Básico y Agua Potable – RAS 2000 establece algunas
restricciones de diseño. En esa sección se describe algunas de las recomendaciones que se
deben tener en cuenta a la hora de establecer el diseño de la red (Salcedo, 2012).
• Diámetro Interno Real Mínimo:
Se define un diámetro interno real mínimo con el fin de prevenir la obstrucción de las tuberías
causada por entrada objetos de gran tamaño. Para las tuberías que transportan aguas residuales
el diámetro interno real mínimo es de 200 mm, y para las tuberías que transportan aguas
lluvias este diámetro es de 250 mm ya que hay mayor riesgo que entren objetos que obstruyan
la red.
• Velocidad Mínima:
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
18
Para un alcantarillado sanitario, esta velocidad mínima debe ser de 0.6 m/s, mientras que para
sistemas pluviales esta debe ser de 0.75 m/s. Se define con el fin de evitar la sedimentación
de partículas en el fondo de las tuberías que obstruyan el paso del agua y que disminuya la
capacidad hidráulica de la red, además para que en las tuberías se dé el proceso de auto
limpieza.
• Esfuerzo Cortante Mínimo:
Para el caso de aguas residuales, este esfuerzo cortante debe ser de 1.5 Pa, y de 2.0 Pa para
aguas lluvias. Está relacionado directamente con el proceso de auto limpieza de las tuberías
pues garantiza la remoción de las partículas sedimentadas en la superficie.
• Velocidad Máxima:
Con el fin de proteger las paredes internas de las tuberías se debe garantizar una velocidad
máxima del agua transportada, y esta depende fundamentalmente del material de la red. Sin
embargo, como valor promedio limite se es de 5 m/s, pero para materiales lisos como el PVC
este es de 10 m/s.
• Pendiente Mínima y Máxima:
Los límites de las pendientes están en función directamente de las velocidades permitidas.
De esta manera, la pendiente máxima corresponderá a aquella con la que se presente la
velocidad máxima, y de la misma manera sucede con la velocidad mínima, todo con el fin de
garantizar las condiciones de auto limpieza.
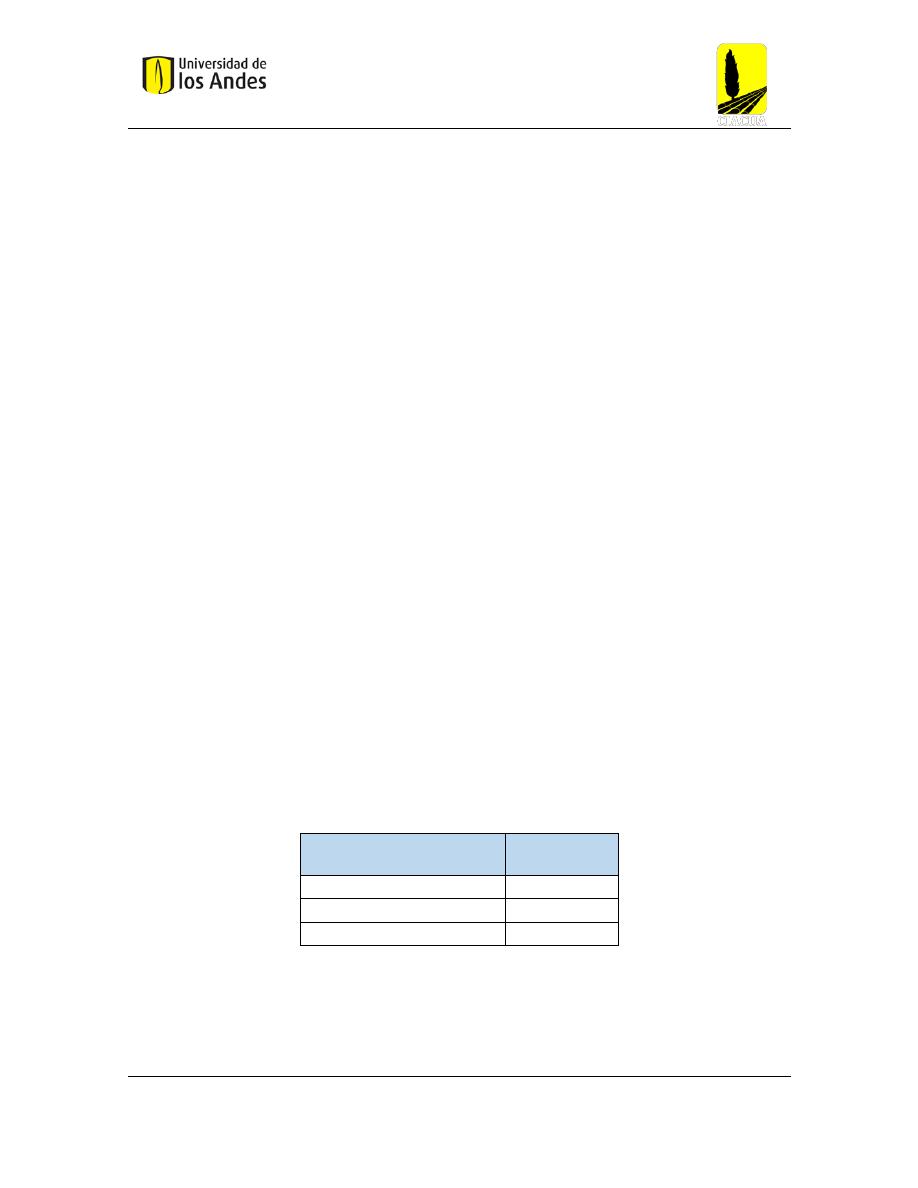
• Relación de Llenado Máxima:
Se debe garantizar la existencia de un flujo de aire en la superficie de la tubería con el fin de
que no exista sobrecarga ni presurización. Para esto el RAS 2000 recomienda que la relación
de llenado máxima se encuentre en el intervalo de 70% a 85% (Copete Rivera, 2012). De este
modo, la relación de llenado debe ser dependiente del diámetro de la tubería.
Relación de llenado
máxima
Diámetro
(m)
70%
0.2 - 0.5
80%
0.5 - 1.0
85%
> 1.0
• Profundidad de la Cota Clave de la Tubería:
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
19
El RAS 2000 sugiere que la cota clave de las tuberías se encuentren mínimo a 0.75 metros
cuando este se encuentre en zonas verdes o en vías peatonales, y que se encuentren mínimo a
1.20 metros cuando este se encuentre bajo vías vehiculares. Esto con el fin de brindar
protección a los conductos, y favorecer el drenaje por gravedad.
• Profundidad Máxima a la Cota Clave:
El RAS 2000 recomienda que la profundidad máxima a la cota clave sea de 5 metros. Esta
profundidad puede ser mayor siempre y cuando se garanticen las condiciones geotécnicas para
este fin.
3.3 Metodología para el diseño optimizado de redes de alcantarillado:
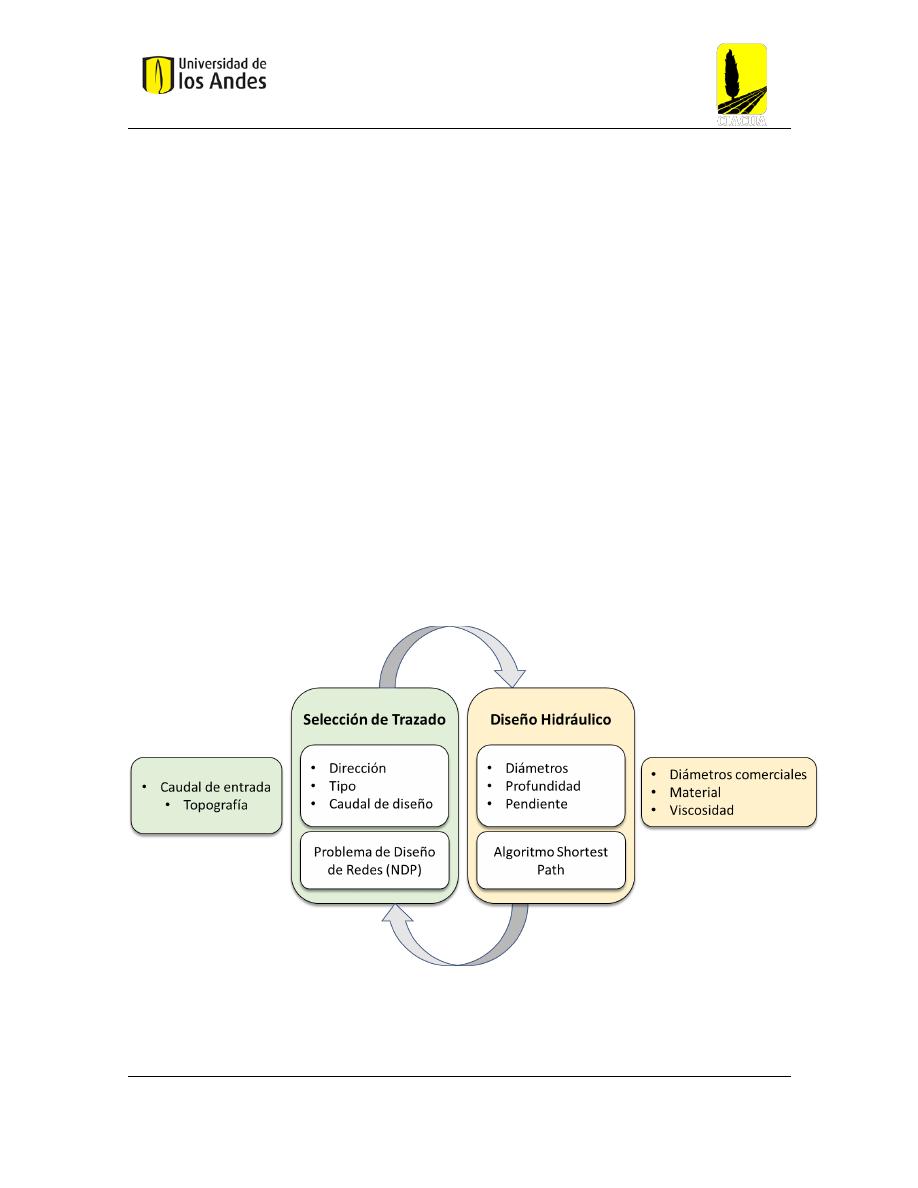
Para el problema de diseñar un alcantarillado desde su trazado hasta su topología, Duque
(2015) propone una metodología exhaustiva en el que al igual que estudios realizados
previamente, intenta solucionar esta situación a través de la división del proceso en dos
etapas: La selección del trazado y el diseño hidráulico. En donde siempre se garantiza que la
solución proporcionada cumple con los requisitos y recomendaciones dadas por el RAS 2000,
y enunciadas en la sección 3.2.
Figura 3 Diagrama de flujo de la metodología para el diseño optimizado de alcantarillados propuesta por Duque(2015)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
20
3.3.1 Selección de Trazado
Para la selección de trazado Duque (2015) propone un modelo de programación entera mixta
que se conoce en la literatura como problema de diseño de redes (NDP en inglés). Este
necesita como parámetros de entrada: un grafo no dirigido
𝒢 = (ℳ, ℰ), donde ℳ =
{𝑚
1
, … , 𝑚
𝐾
} es el conjunto de pozos y ℰ ⊂ {(𝑚
𝑖
, 𝑚
𝑗
): 𝑚
𝑖
∈ ℳ; 𝑚
𝑗
∈ ℳ; 𝑖 < 𝑗 }
es el conunto de
arcos no dirigidos que unen los pozos, la topografía de la red, que se refiere a las coordenadas
de cada uno de los pozos de inspección, los caudales de entrada (
𝑄
𝑖
) de cada pozo
𝑚
𝑖
∈ ℳ
.
Así, es posible definir los sentidos de flujo del agua, el tipo (Inicio o continua)
𝒯 = {𝑡
1
, 𝑡
2
}
y
el caudal de diseño de cada una de las tuberías que interconectan los pozos de inspección.
Todo con el propósito de captar al agua que ingresa a la red por cada uno de los pozos y
depositarla en el único punto de descarga. De esa manera, Duque (2015) plantea la creación
de una variable binaria
𝑥
𝑖𝑗𝑡
que toma el valor de uno si la dirección de flujo desde los pozos
𝑚
𝑖
y
𝑚
𝑗
es desde
𝑚
𝑖
hasta
𝑚
𝑗
y es de tipo
𝑡, y una variable continua 𝑞
𝑖𝑗𝑡
que representa el
caudal de diseño que transita desde el pozo
𝑚
𝑖
al
𝑚
𝑗
de tipo
𝑡.
Por otro lado, esta metodología entiende los sistemas de alcantarillado como redes abiertas,
a pesar de que todos los pozos están interconectados por tuberías. Al ser de esta manera se
evita recirculación del agua en el sistema. Teniendo en cuenta esto, se debe definir el tipo de
tubería entre inicio y continua, como se mencionaba anteriormente. Las tuberías de inicio
son aquellas que no están conectadas a otras aguas arriba, es decir, solo reciben el agua que
entra por el pozo de inspección adyacente. Por el contrario, las tuberías continuas se
encuentran en los tramos intermedios de la red, en otras palabras, estas están conectadas con
otras tuberías aguas arriba (Duque, 2015).
A partir de lo anterior, es posible observar que de cada pozo de inspección puede salir
máximo una tubería continua o tantas tuberías de inicio como pozos adyacentes tenga dicho
pozo, es decir, que cuando hay más de una tubería de inicio en un pozo, el caudal de entrada
se debe distribuir entre dichas tuberías, pero no necesariamente de manera proporcional.
Además, todos los pozos de inspección aportan un caudal sanitario o pluvial que solo puede
salir por el punto de descarga y no se puede almacenar dentro del sistema (Duque, 2015).
Finalmente, resulta importante destacar que la solución de este modelo de programación
entera mixta se resuelve mediante una implementación en el software de optimización lineal
XPRESS-MP. Donde el objetivo es minimizar los costos asociados al caudal y el tipo de las
tuberías.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
21
3.3.2 Diseño Hidráulico:
Luego de definir el trazado es posible determinar el diseño hidráulico de la red, donde el
principal objetivo es encontrar la combinación diámetro-pendiente para cada tubería que
tiene el sistema, siempre teniendo en cuenta que se quiere minimizar el costo de construcción
de la red y asegurar el correcto funcionamiento de la misma. De este modo, el diseño
hidráulico obtenido siempre cumple con las reglamentaciones vigentes en cada país.
De esta manera, partiendo de un trazado determinado, donde se conoce el caudal de diseño
𝑄
𝑑
, el sentido de flujo y el tipo de tubería para cada tramo, es posible determinar el diámetro
𝑑 y la pendiente 𝑠 de la tubería que se debe instalar para que el caudal pueda ser transportado.
Adicionalmente, en el diseño hidráulico se debe garantizar que todas las conexiones de la red
sean consistentes. En otras palabras, siempre se debe tener un flujo a favor de la gravedad,
que las tuberías estén conectadas a la altura de su cota de batea y que todas las tuberías de
inicio estén conectadas a la descarga. Sin embargo, debido a la cantidad de alternativas
factibles en el diseño se define un algoritmo de ruta más corta, conocido en la literatura como
Bellman Ford, donde el principal objetivo es minimizar los costos de construcción del
alcantarillado.
Figura 4 Diseño hidráulico de un tramo de una red
3.3.3 Función de Costo:
A lo largo de las diferentes metodologías que existen para solucionar el problema de diseño
de redes de alcantarillado se han propuesto diferentes ecuaciones que intentan estimar los
costos de construcción (
𝑐
𝑖𝑗
), las cuales son funciones principalmente dependientes del
diámetro de las tuberías (
𝑑
𝑖𝑗
) y las profundidades de excavación (
ℎ
𝑖𝑗
) de cada uno de los
tramos que ocupa la red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
22
𝑐
𝑖𝑗
= 𝑓(𝑑
𝑖𝑗
, ℎ
𝑖𝑗
)
Estas ecuaciones son de diferente naturaleza, pues se han utilizado diferentes metodologías
y herramientas como regresiones lineales, análisis estadísticos y otras estrategias con el fin
de encontrar expresiones que permitan calcular los costos asociados a la construcción de un
alcantarillado.
Por otra parte, gracias a la revisión bibliográfica realizada se puede deducir que la mayoría
de las ecuaciones solo tienen en cuenta los costos de instalación de las tuberías, que dependen
netamente del material y la longitud del tramo, y los costos de excavación de cada sección.
Esto debido a que representan en promedio el 70% de los costos totales de construcción de
una red.
3.4 Eficiencia de Pareto
:
Cuando se tiene un problema de optimización multiobjetivo se puede hablar de un problema
de optimización que tiene presente dos o más funciones objetivo. La complejidad de este tipo
de problemas es que se tiene que apelar a la subjetividad para seleccionar una solución única,
pues se debe tener en cuenta que un modelo de optimización multiobjetivo no proporciona
una única solución óptima, sino que por el contrario genera un conjunto de soluciones que
no pueden ser comparadas mutuamente. De esta manera, el conjunto de soluciones óptimas
es denominado Frontera de Pareto. De esta frontera se puede decir que contiene soluciones
que no pueden ser superadas en todos los objetivos por alguna otra solución, y de ahí nace el
concepto de dominancia. Por lo tanto, los puntos que componen la frontera de Pareto son
soluciones no dominadas. Una solución domina a otra si y solo si, es al menos es igual que
la otra en todos sus objetivos y es mejor en al menos uno. (Baesler et al. 2006)
Ahora la decisión de cuál de las soluciones de la frontera de Pareto se va a ejecutar va a
depender netamente del diseñador, es decir, se tendrá en cuenta el grado de importancia que
se le quiera dar a cada uno de los objetivos y el análisis que se haga alrededor.
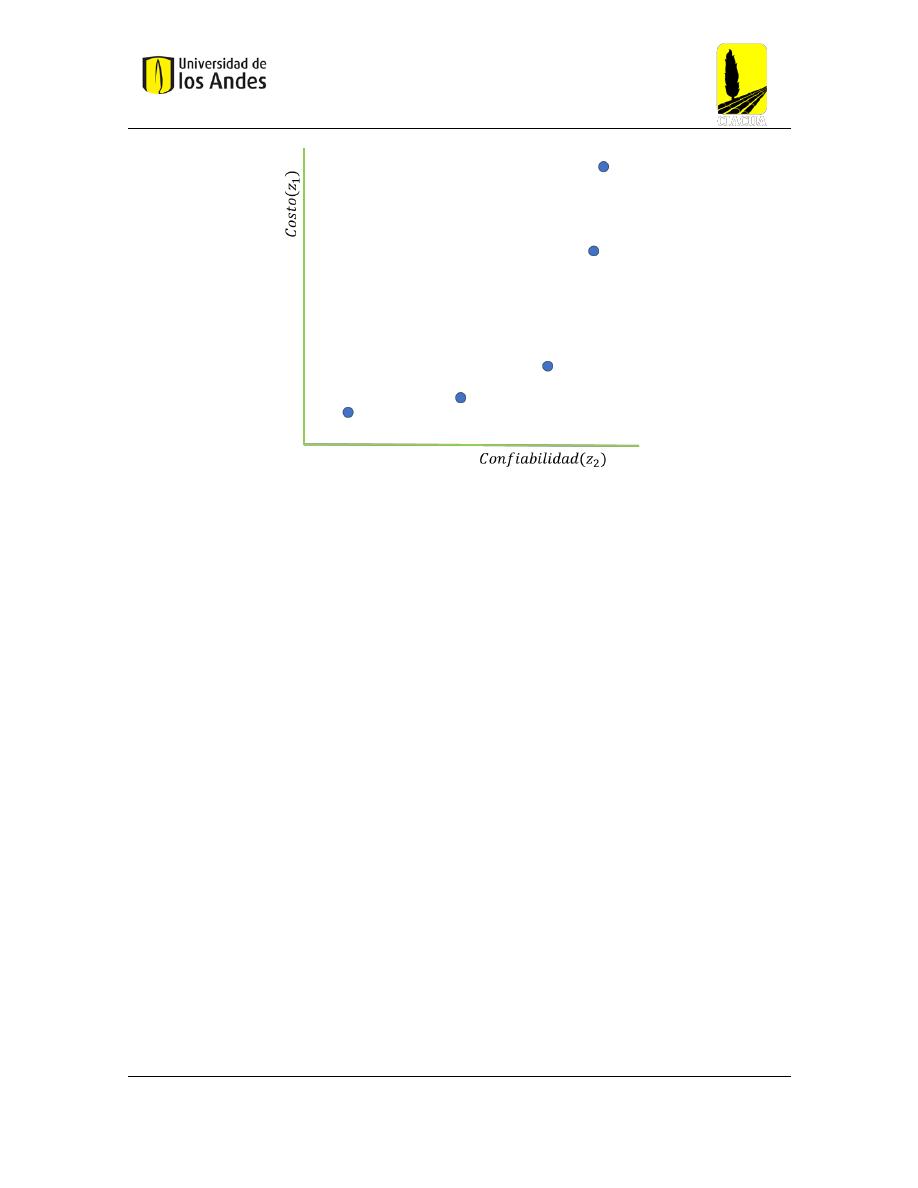
Para el caso particular de este trabajo la frontera de Pareto van a estar conformadas por
diseños de una red que van a tener asociados un costo de construcción que quiere ser
minimizado y una confiabilidad de la misma que debe ser maximizado, los cuales más
adelante van a ser detallados, y por lo tanto se pretenderá tener idealmente gráficas como las
de la
Figura 5
.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
23
Figura 5 Frontera de Pareto Ideal
4. DEFINICIÓN DEL PROBLEMA
En el presente proyecto se quiere continuar con el trabajo realizado por Duque (2015) en el
que se propone una metodología para el diseño optimizado de alcantarillados, la cual se
explicó en la sección 3.3. Ahora, se quiere hacer una extensión de la metodología que permita
por un lado realizar diseños de redes que se encuentren en terrenos de alta pendiente mediante
la construcción de cámaras de caída. De esta manera, es posible ampliar el espacio de
solución de la metodología original teniendo en cuenta que se puede diseñar redes, tanto
pluviales como sanitarias, con terrenos en todo tipo de pendiente.
Por otra parte, cuando se diseña una red de alcantarillado al ingeniero no solo le debe interesar
minimizar los costos de construcción y tener un modelo con un solo objetivo, sino que
también debe tener en cuenta maximizar la confiabilidad de la red, es decir, tener un diseño
en donde en caso de que haya un daño en una tubería esta afecte la menor población posible
que se encuentre aguas arriba, y que adicionalmente cumpla con las restricciones hidráulicas
de autolimpieza. De esta manera, el modelo que se tendría que plantear ya no sería mono-
objetivo con el costo como única función objetivo, sino multiobjetivo donde el costo y la
confiabilidad son funciones objetivo que se deben optimizar simultáneamente.
Se debe tener en cuenta que con el modelo mono-objetivo propuesto por Duque (2015) solo
se puede obtener una solución que tiene que ser mejor o igual al resto de las alternativas que
se encuentran en el espacio de solución. Cuando se involucra la confiabilidad como un
segundo objetivo y opuesto al primero, aunque no hay cambio en el espacio de solución, ya

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
24
no hay una sola solución que optimice simultáneamente las funciones objetivo y por el
contrario se podrá obtener un conjunto de soluciones que las consideren. Las soluciones de
dicho conjunto deben ser dominante frente al resto de alternativas que se encuentren en el
espacio de solución. En otras palabras, una solución que pertenezca a este conjunto debe
tener como principal característica, que para un nivel de confiabilidad que se tenga no hay
ninguna otra solución que tenga un menor costo, o viceversa, para una solución con un costo
determinado no hay otra que tenga una mayor confiabilidad. De esta manera, este conjunto
de soluciones dominantes se les conoce como frente de Pareto.
Finalmente, el resultado principal de esta metodología será la construcción de una frontera
de Pareto de cada caso de estudio, que contemple los costos y la confiabilidad en cada uno
de sus ejes, y que va a brindar diferentes alternativas de diseño para una sola red y ya
dependerá del ingeniero encargado la decisión de que prioridad le va a asignar a cada uno de
los objetivos del modelo. Sin embargo, para llegar a este producto se debe tener en cuenta
que el modelo de selección de trazado en su función objetivo no estima directamente los
costos de la red, sino que se establece uno de los criterios propuestos por Aguilar (2016)
como función objetivo del modelo y el propuesto por Zambrano (2018), que serán explicados
en la sección 4.2, y seguido de esto con el modelo del diseño hidráulico es posible estimar
los costos de construcción precisos para cada uno de los trazados generados con la
metodología.
4.1 Problema de estimación de los costos para la Frontera de Pareto:
La frontera de Pareto debe estar conformada en uno de sus ejes por un índice de confiabilidad,
que será explicado en la sección 5, y en el otro eje debe considerar el costo de construcción
estimado con la ecuación de costo utilizada en el modelo del diseño hidráulico. Sin embargo,
para llegar a obtener el diseño hidráulico óptimo de una red es necesario tener una estrategia
desde el modelo MIP de selección de trazado que permita implícitamente minimizar dichos
costos. Por tal motivo, en este trabajo se utilizan dos criterios que permiten realizar una
aproximación de los costos reales, pero utilizando las variables propias del modelo MIP.
4.1.1 Estimación de los costos en la selección de trazado según Aguilar (2016):
Para la selección de trazado se propone un modelo basado en un problema de diseño de redes,
el cual es solucionado como un problema de Programación Entera Mixta en el que se
involucran variables de decisión que modelan el flujo y otras que determinan el sentido de
este y el tipo de la tubería.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
25
Para resolver el problema se plantea un modelo de Flujo de Costo Mínimo, en el cual se
busca la forma más económica de enviar cierta cantidad de flujo a través de la red. De esta
manera, el modelo se concentra en conocer cuánto caudal pasa por cada tubería, y el tipo de
cada una de estas (Inicio o continua), pero tratando de priorizar los costos del diseño
hidráulico.
Aguilar (2016) propone una metodología que permite establecer una función objetivo del
modelo de selección de trazado basado en una aproximación de los costos del diseño
hidráulico a través de una transformación de la función de costo usada en este modelo, es
decir, la idea es expresar la función de costo, que depende del diámetro
𝑑
𝑖𝑗
y la profundidad
de excavación
ℎ
𝑖𝑗
, en términos de las variables del trazado como lo es el caudal de diseño
𝑞
𝑖𝑗𝑡
, el sentido y tipo de tubería
𝑥
𝑖𝑗𝑡
.
Ahora, cuando se hace dicha transformación con ayuda de una ecuación de resistencia fluida
(Darcy-Weisbach y Colebrook-White o Manning), se puede concluir que la relación de costo
frente a caudal de diseño no es lineal, lo que presenta una dificultad para la implementación
de la función objetivo del modelo de selección de trazado. De esta manera, Aguilar (2016)
propone una serie de cambios a modelo, el cual permite mediante la creación de nuevas
variables y restricciones realizar una aproximación mediante rectas de la función objetivo, y
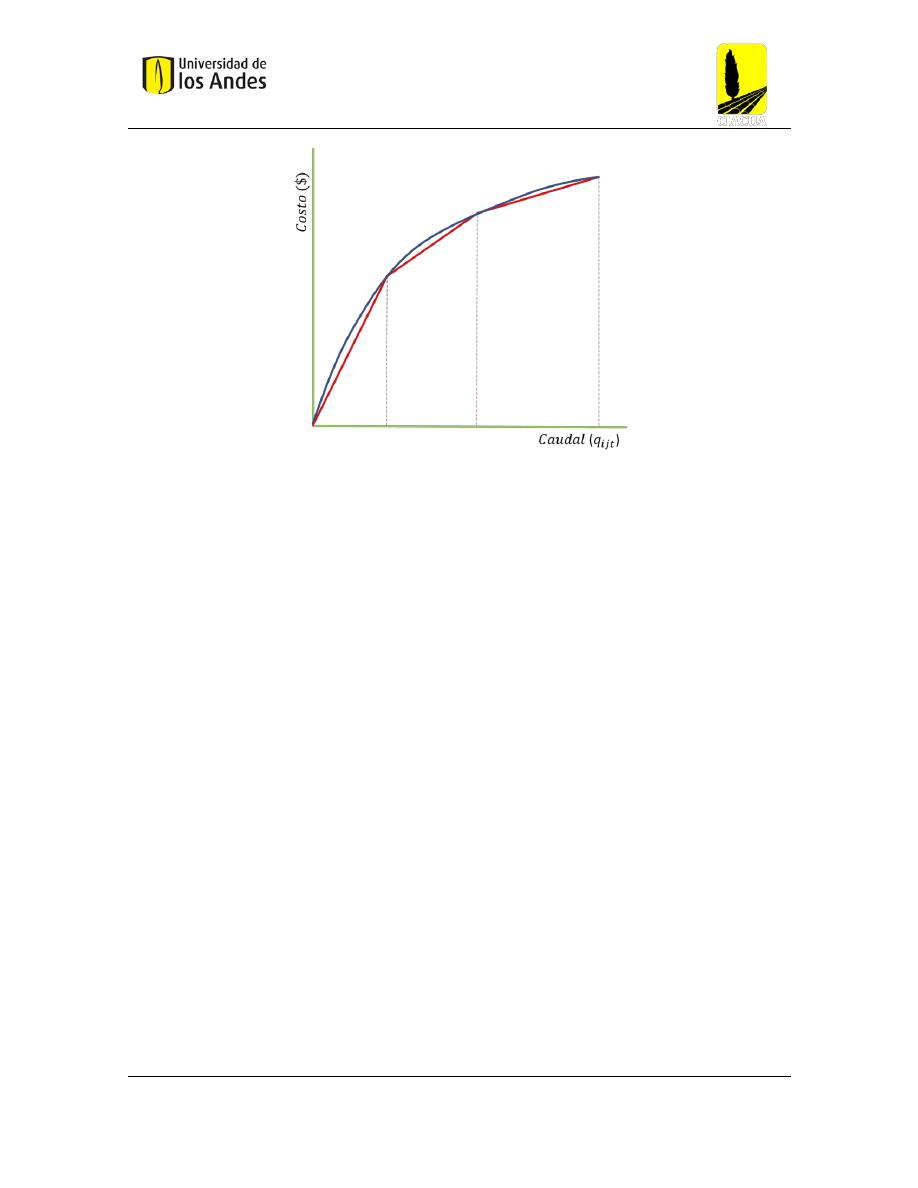
de ese modo permitir la implementación del modelo MIP. En la
Figura 6
se puede notar como
la relación entre el costo y el caudal de diseño de un tramo no muestra una tendencia lineal,
por lo que ese necesario realizar una aproximación lineal (3 segmentos de recta roja), donde
se puede anotar que entre mayor cantidad de rectas se implementen para representar el
comportamiento de la función se van a describir los costos con un mejor ajuste, pero teniendo
en cuenta que esto conlleva la creación de un mayor número de variables y posiblemente de
un mayor tiempo computacional requerido para la solución del modelo. Para mayor detalle
de las variables y restricciones del modelo se debe referir al trabajo de Aguilar (2016).
Por otra parte, se debe tener en cuenta que la función objetivo antes de ser linealizada requiere
de parámetros como la profundidad de excavación
ℎ
𝑖𝑗
y la pendiente del terreno
𝑠
𝑖𝑗
, Pero
como es de conocimiento estos pertenecen al diseño hidráulico, por lo tanto Aguilar (2016)
propone un algoritmo donde en cada iteración estos parámetros van siendo actualizados con
cada diseño hidráulico que se realizan y por lo tanto se ajustan mejor a los costos reales. Así
es posible que los resultados en el trazado que se vayan obteniendo a través de las iteraciones
favorezcan los resultados de diseño hidráulico, y que ocurra lo mismo en sentido contrario.
Haciendo que se vuelva un ciclo de retroalimentación continua.
Aguilar (2016) propone lo siguiente:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
26
A continuación, se presenta las ecuaciones utilizadas para estimar las profundidades
promedio y las pendientes de cada uno de los tramos de la red:
ℎ
𝑖𝑗
𝑡
= 𝛼ℎ
𝑖𝑗
𝑡−1
+ (1 − 𝛼)ℎ
𝑖𝑗
𝐽𝐴𝑉𝐴
ℎ
𝑗𝑖
𝑡
= (𝛼ℎ
𝑗𝑖
𝑡−1
+ (1 − 𝛼)ℎ
𝑖𝑗
𝑡
)𝜙
Para el caso de la profundidad, específicamente se propone realizar una ponderación
entre la profundidad que se obtiene con el diseño hidráulico (
ℎ
𝑖𝑗
𝐽𝐴𝑉𝐴
) y la profundidad
obtenida en la iteración anterior (
ℎ
𝑖𝑗
𝑡−1
), a través de la asignación de una constante
𝛼 que permite darle mayor importancia a una u otra dimensión dependiendo el criterio
del diseñador. Adicionalmente, se tiene en cuenta que se debe penalizar aquellos
tramos que no pertenecen al trazado, para eso se asigna un factor de penalización que
debe ser mayor que 1, y de esta manera se favorece las profundidades que pertenecen
al trazado y se puede mejorar de cierto modo la solución del modelo.
𝑠
𝑖𝑗
𝑡
= 𝛼𝑠
𝑖𝑗
𝑡−1
+ (1 − 𝛼)𝑠
𝑖𝑗
𝐽𝐴𝑉𝐴
𝑠
𝑗𝑖
𝑡
= 𝛼𝑠
𝑗𝑖
𝑡−1
+ (1 − 𝛼)𝑠
𝑖𝑗
𝑡
Para el caso de las pendientes, se realiza una ponderación similar que con las
profundidades donde se tiene en cuenta la pendiente de la iteración anterior (
𝑠
𝑖𝑗
𝑡−1
) y
la pendiente que permite calcular el diseño hidráulico de la red (
𝑠
𝑖𝑗
𝐽𝐴𝑉𝐴
). Igualmente
se asigna la constante
𝛼 que permite dicha ponderación, y tiene como única condición
es que debe estar en el intervalo entre 0 y 1.
Ahora para la inicialización de la estrategia se asume que todas las profundidades
promedio (
ℎ
𝑖𝑗
0
) de la red son de 3.1 metros, pues resulta de un promedio entre las
profundidades mínimas y máximas permitidas por el RAS 2000. Y para el caso de las
pendientes se asume que inicialmente son las mismas del terreno.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
27
Figura 6 Aproximación mediante rectas del costo de un tramo en el modelo de selección de trazado
Finalmente, para la construcción de la frontera de Pareto va a ser posible en primera instancia
construir una entre los costos calculados con la función objetivo del modelo de selección de
trazado y un índice de confiabilidad propuesto en la sección 5, posterior a esto si se podrá
construir una frontera de Pareto de costos del diseño hidráulico de una red y la respectiva
confiabilidad.
4.1.2 Estimación de los costos en la selección de trazado según Zambrano (2018):
Zambrano (2018) en su trabajo propone una nueva función objetivo para el modelo MIP
propuesto por Duque (2015) en el que se maximicen la cantidad de tuberías que fluyen a
favor de la pendiente del terreno, con la premisa de que esta manera los volúmenes y por
ende los costos de excavación resultaran ser mucho menores que si se tiene tramos en
contrapendiente, los cuales requerirán de un mayor volumen de excavación.
max
∑
𝑚
𝑖𝑗
𝑥
𝑖𝑗𝑡
(𝑚
𝑖
,𝑚
𝑗
)∈𝒜
𝐿
,𝑡∈𝒯
Donde
𝐴
𝐿
es el conjunto de arcos que tienen en cuenta de la dirección de tuberías y el tipo
de la misma. Recordando que
𝑥
𝑖𝑗𝑡
es la variable binaria que indica la dirección y el tipo de
tubería. El coeficiente
𝑚
𝑖𝑗
con este criterio se calcula la pendiente entre los pozos
pertenecientes al arco
(𝑖, 𝑗, 𝑡). De esta manera, las pendientes positivas indicaran un descenso
en el terreno entre un pozo y otro, y las negativas indicaran un ascenso en el terreno. Donde
𝑍
𝑖
y
𝑍
𝑗
son las cotas del terreno de los pozos y
𝐿
𝑖𝑗
es la longitud horizontal entre pozos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
28
𝑚
𝑖𝑗
=
𝑍
𝑖
− 𝑍
𝑗
𝐿
𝑖𝑗
Posteriormente, a determinar los trazados con alguno de los criterios se podrá estimar el
diseño hidráulico de cada uno de estos, y por lo tanto conocer el costo con ayuda de las
funciones de costo, para posteriormente conformar la frontera de Pareto que se quiere como
producto final.
5. METODOLOGIA
En términos generales, cualquier metodología de diseño optimizado de alcantarillados se
basa en determinar una serie de variables de decisión referentes al trazado y diseño hidráulico
de la red, en el que según sea el caso se tiene un criterio de decisión, que puede ser de costos
económicos, beneficios hidráulicos. Para este caso, el principal objetivo es minimizar los
costos de construcción de la red y a la misma vez tratar de maximizar la confiabilidad, que
específicamente se resume en optimizar de manera ponderada las funciones objetivo del
modelo de la selección de trazado y el diseño hidráulico.
Adjunto a lo anterior se propone la extensión al modelo del diseño hidráulico que permita la
creación de cámaras de caída en redes de alta pendiente mediante la modificación del grafo
planteado por Duque (2015) y la formulación presentada por Marú (2017).
5.1 Diseño Hidráulico con Cámaras de Caída:
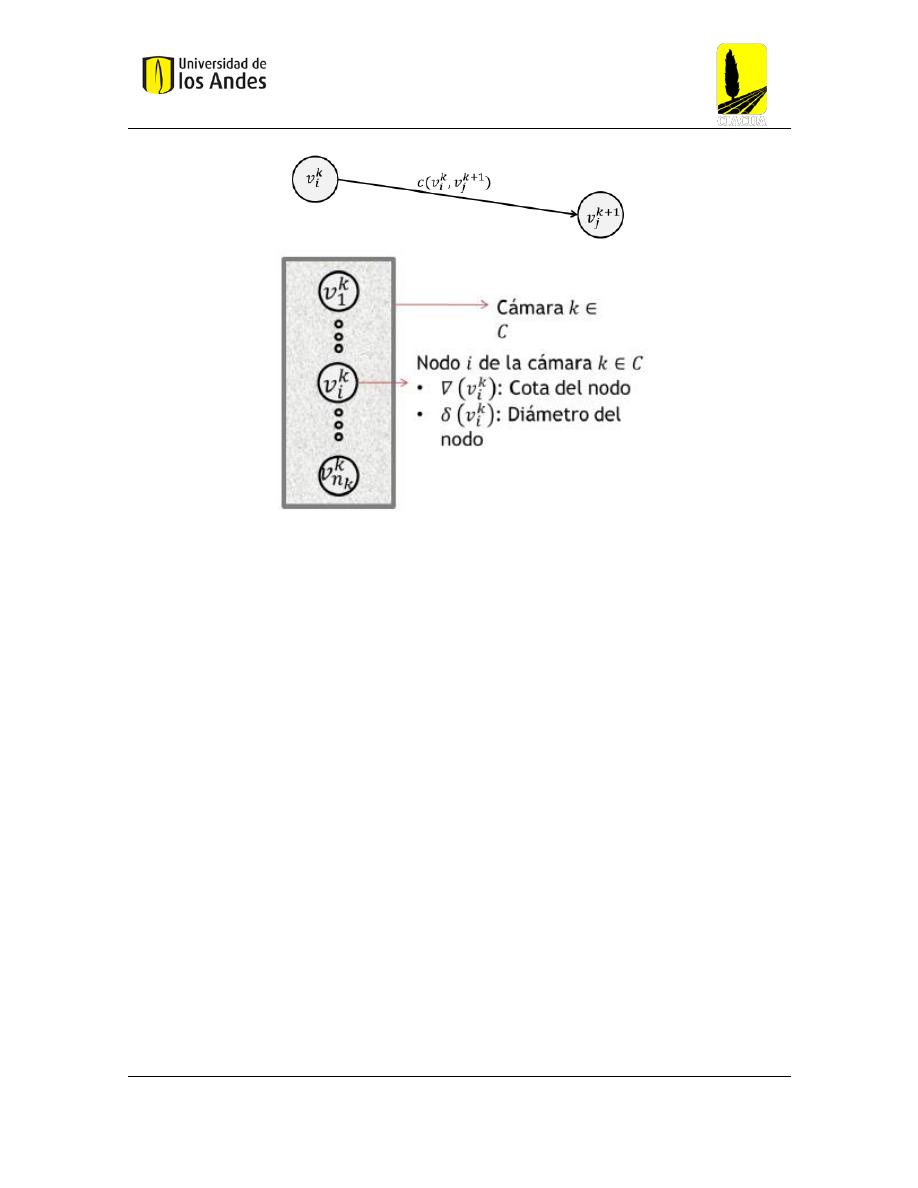
El modelaje del grafo del diseño hidráulico propuesto por Duque (2015) plantea que cada
uno de las cámaras que constituyen la red de alcantarillado se puede representar como un
grupo de nodos. Donde cada uno de los nodos representa una profundidad de excavación o
cota batea de una posible tubería, y un diámetro comercial disponible. Por otro lado, los arcos
representan la conexión entre dos nodos que sería la existencia de una posible tubería y esta
tendría un costo asociado calculado con una función de costo determinada.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
29
Figura 7 Arcos y nodos del grafo de diseño hidráulico. Tomado de Marú(2017)
Ahora, Marú (2017) propone una modificación para la metodología del diseño de tuberías en
serie que será aplicable al diseño de redes a partir de la creación de arcos que permitan
representar las cámaras de caída en un pozo de inspección. De esta manera, en el grafo van a
existir arcos tipo 1, los cuales están relacionados con las tuberías y van a tener un costo
asociado a la instalación de las mismas, y arcos tipo 2 (Figura 2) que representan las cámaras
de caída y tendrán también un costo asociado que debe ser calculado con una función de
costo diferente a las utilizadas para las tuberías.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
30
Figura 8 Arcos que representan las cámaras de caída. Tomado de Marú (2017)
De este modo, el algoritmo de ruta más corta implementado por Duque (2015) funcionará de
la misma manera recorriendo el grafo de manera exhaustiva partiendo desde la descarga hacia
cada uno de los arranques de las series de tuberías que componen la red. La diferencia ahora
radica en que el espacio de solución va a ser mayor pues va a ser necesario explorar tanto los
arcos tipo 1 y tipo 2 lo que aumenta la cantidad de diseños factibles.
Se debe destacar que la presencia de cámaras de caída va a depender directamente de la
restricción de velocidad máxima, pues cuando se tienen terrenos de alta pendiente, es decir
mayores al 10%, las tuberías van a tender a tener pendientes similares lo que produce altas
velocidades y condiciones super críticas, y lo que va a suceder es que cuando esas
velocidades superen las velocidad máxima permitida será necesario construir una cámara de
caída que permita disminuir la pendiente de la tubería aguas abajo y de ese modo también
reducir la velocidad de flujo. Ahora, la longitud de la caída va a depender directamente de la
función de costo que se tenga y de las condiciones de la red.
5.2 Ecuación de costo:
Las ecuaciones de costo son funciones que permiten calcular los costos de construcción de
un tramo de alcantarillado, a través del conocimiento del diámetro, las pendientes y las

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
31
profundidades de excavación de las tuberías. Así para la metodología de Duque (2015) estas
ecuaciones son de vital importancia ya que permiten determinar el criterio de selección de
las alternativas tanto en el diseño hidráulico como en la selección de trazado.
En la literatura internacional se encuentran diferentes tipos de ecuaciones que pretender
explicar de diferentes maneras los costos de construcción, haciendo uso de herramientas
estadísticas y diferentes tipos de análisis.
5.2.1 Ecuación: Maurer (2012)
Es una ecuación propuesta en el artículo “Quantifying costs and lengths of urban drainage
systems with a simple static sewer infrastructure model” por Maurer et al. (2012) en el que
se realiza un modelo de economías a escala en una zona de la ciudad de Dubendorf en Suiza
en el que se quiere emular de manera más precisa los costos y dimensiones de un sistema de
drenaje urbano en donde se tenga en cuenta un análisis hidrológico, densidad poblacional y
el área de la zona. Y de esta manera realizar una comparación con otras alternativas de diseño
que se han realizado a lo largo de la historia en la zona.
De esta manera, se propone esta ecuación que tiene en cuenta los costos de instalación de las
tuberías y los costos de excavación de cada uno de los tramos. A continuación, se presenta la
ecuación:
𝐶
𝑖𝑗
= 𝛼ℎ
𝑖𝑗
+ 𝛽
𝛼 = 𝑚
𝛼
𝑑
𝑖𝑗
+ 𝑛
𝛼
𝛽 = 𝑚
𝛽
𝑑
𝑖𝑗
+ 𝑛
𝛽
𝐶
𝑖𝑗
= (𝑚
𝛼
𝑑
𝑖𝑗
+ 𝑛
𝛼
)ℎ
𝑖𝑗
+ 𝑚
𝛽
𝑑
𝑖𝑗
+ 𝑛
𝛽
Donde
𝐶
𝑖𝑗
es el costo de construcción del tramo en dólares por metro lineal de tubería,
ℎ
𝑖𝑗
es
la profundidad de excavación promedio de la tubería,
𝑑
𝑖𝑗
es el diámetro en metros de la
tubería en un tramo determinado y
𝑚
𝛼
,
𝑛
𝛼
,
𝑚
𝛽
y
𝑛
𝛽
son constantes propias de las regresiones
que tratan de explicar la dependencia de las variables frente al costo.
5.3 Estimación de Confiabilidad:
Según Haghighi & Bakhshipour (2016) una red con un trazado que tenga la mayor
confiabilidad es aquella que genera la menor área afectada ante la obstrucción de alguna de
las tuberías que componen la red, en otras palabras, si hay un mínimo de población afectada
por el daño de una tubería esa red va a resultar muy confiable
.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
32
5.3.1 Índice de confiabilidad propuesto por Haghighi & Bakhshipour (2016):
Según Haghighi & Bakhshipour (2016) una red con un trazado que tenga la mayor confiabilidad es
aquella que genera la menor área afectada ante la obstrucción de alguna de las tuberías que componen
la red, en otras palabras, si hay un mínimo de población afectada por el daño de una tubería esa red
va a resultar muy confiable.
La confiabilidad por cada tubería se calcula de la siguiente manera:
𝑅
𝑖𝑗𝑡
= 1 −
𝑞
𝑖𝑗𝑡
𝑄
𝑂𝑈𝑇
Donde
𝑞
𝑖𝑗𝑡
es el caudal de diseño de la tubería
(𝑚
𝑖
, 𝑚
𝑗
) ∈ 𝒜
𝐿
, 𝑡 ∈ 𝒯
y
𝑄
𝑂𝑈𝑇
es el caudal en la
descarga. De esta manera, se puede interpretar que una tubería va a resultar más confiable si
por esta transita la menor cantidad de agua posible.
Para toda una red la confiabilidad promedio se puede calcular de la siguiente manera, donde
𝑛 es el número de tramos de la red:
𝑅̅ = 1 −
∑
𝑞
𝑖𝑗𝑡
(𝑚
𝑖
,𝑚
𝑗
)∈𝒜
𝐿
,𝑡∈𝒯
𝑛𝑄
𝑂𝑈𝑇
A partir de lo anterior se puede decir que la metodología propuesta va a maximizar la anterior
expresión, con el fin de tener un trazado confiable que lleve a un diseño que permita distribuir
el agua a lo largo de la red de manera equitativa de tal manera que sea bastante útil en redes
con una topografía plana.
5.3.2 Índice de confiabilidad propuesto Aguilar (2019):
Basado en lo anterior, en esta tesis se plantea un indicador que se calcula de la siguiente
manera:
𝑅̅ = 1 −
∑
𝑒
𝑖𝑗𝑡
𝑥
𝑖𝑗𝑡
(𝑚
𝑖
,𝑚
𝑗
)∈𝒜
𝐿
,𝑡∈𝒯
𝑛
Donde
𝑛 es el número de tramos de la red y 𝑒
𝑖𝑗𝑡
es un coeficiente que indica el porcentaje
del caudal total de descarga que podría potencialmente transitar por la tubería, es decir, es la
suma de los caudales de entrada de los pozos que se podrían encontrar aguas arriba de la
tubería en cuestión. Para el caso de las tuberías de inicio solo se tiene en cuenta el caudal de
entrada del pozo adyacente aguas arriba. En la
Figura 9
se muestra un ejemplo para calcular
la confiabilidad para un tramo en una red de 9 pozos, donde se asume que el caudal de entrada
a cada pozo es de 1
𝑚
3
𝑠
y que se va a calcular el coeficiente
𝑒
69𝐶
, que corresponde al tramo
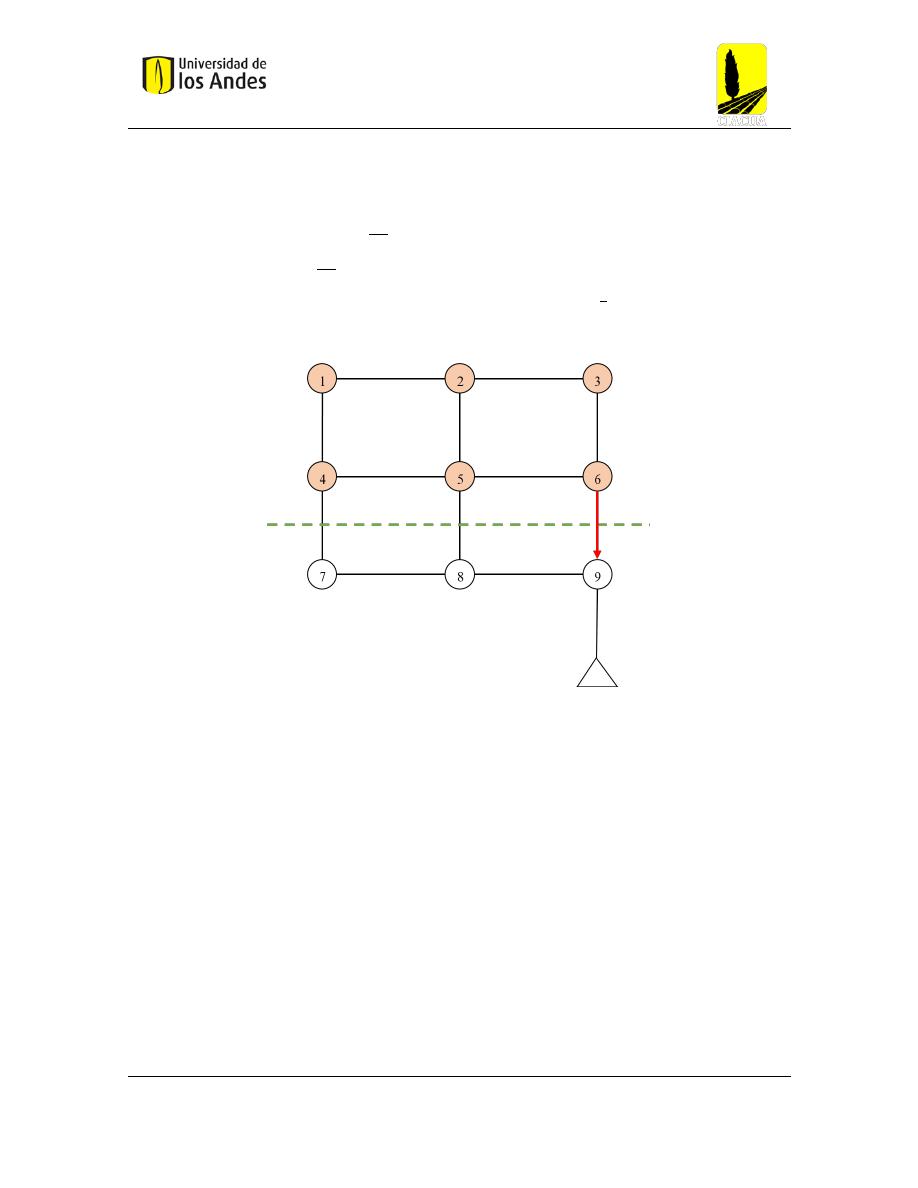
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
33
del pozo 6 al 9 de tipo continuo. Para eso se traza una recta perpendicular al tramo de interés
(línea punteada en verde), y de esa manera se suma el caudal de entrada de cada uno de los
pozos que se encuentra aguas arriba de dicha recta, en este caso se sumaria el caudal de los
pozos 1 al 6, danto un total de 6
𝑚
3
𝑠
. Posteriormente, esta suma se divide por el caudal total
en la descarga que seria 9
𝑚
3
𝑠
, lo que daría que
𝑒
69𝐶
= 0.66. Si se quisiera calcular 𝑒
69𝐼
, solo
se tendría en cuenta el caudal del pozo 6, lo que daría que
𝑒
69𝐼
=
1
9
.
Figura 9 Estimación de la confiabilidad de un tramo para una red de 9 pozos
5.4 Construcción de la Frontera de Pareto:
Para llegar a una frontera de Pareto como producto final que considere los costos reales
(estimados con la ecuación de costo del diseño hidráulico) y la confiabilidad de una red en
cada uno de sus ejes y que contenga las soluciones eficientes que optimizan cada uno de estos
objetivos, previamente se debe construir una frontera de Pareto aproximada con la función
objetivo del modelo MIP y el índice de confiabilidad escogido. Teniendo en cuenta, que esta
función objetivo depende del criterio de estimación de costos que se utilice, ya sea el de
Aguilar (2016) o el de Zambrano (2018), y que indirectamente van a intentar minimizar los
costos del diseño hidráulico.
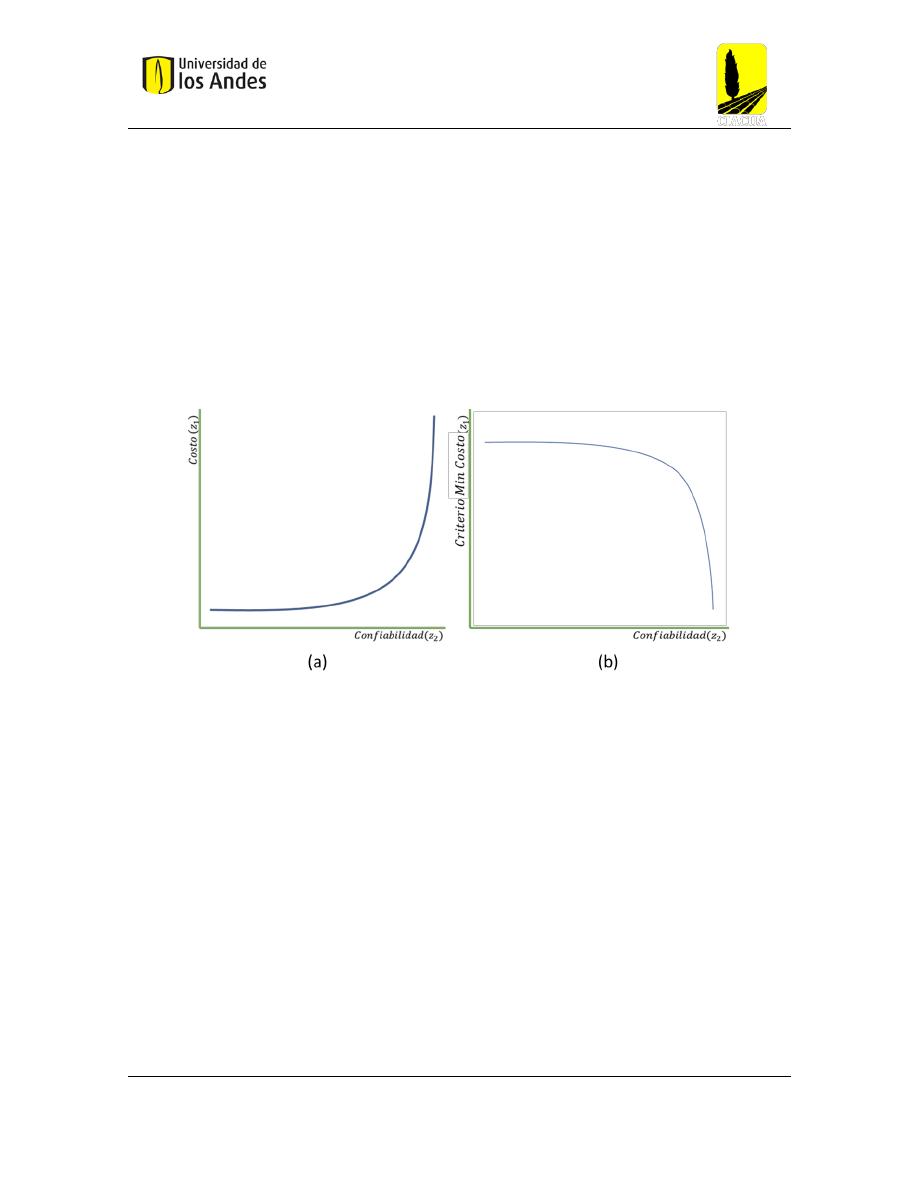
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
34
Esta frontera de Pareto aproximada va estar conformada por un conjunto de trazados
eficientes, que en el caso de que se implemente el modelo MIP de Aguilar (2016) la frontera
tendrá la forma de la
Figura 10
(a), la cual tiene esa concavidad debido a que las dos funciones
son opuestas (minimización y maximización), mientras que si se utiliza el modelo MIP de
Zambrano (2018) se tendrá una gráfica como la de la
Figura 10
(b) con una concavidad
diferente debido a que las dos funciones son de maximización. Para conformar la frontera de
Pareto con los costos reales el procedimiento que se debe seguir es realizar el diseño
hidráulico de cada uno de los trazados de la frontera de Pareto aproximada, de esta manera
se va a tener soluciones que van a tener asociado un costo real y un nivel de confiabilidad
que van a poder ser graficadas y se podrá observar si pertenecen o no a la frontera de Pareto
real, dependiendo de su dominancia con respecto al resto de soluciones.
Figura 10 a) Frontera de Pareto del modelo de Selección de Trazado con el criterio de Aguilar (2016). b) Frontera de
Pareto del modelo de Selección de Trazado con el criterio de Zambrano (2018)
En la
Figura 11
se presenta el algoritmo para construir la frontera de Pareto aproximada, luego
la frontera de Pareto real cuando se utiliza el modelo en la selección de trazado propuesto por
Aguilar (2016). En una primera etapa la idea es encontrar el diseño hidráulico y trazado de
la red de interés que minimice los costos de construcción de la red luego determinadas
iteraciones del modelo (
𝑡
𝑚𝑎𝑥
), para que seguido de esto se implemente el algoritmo que va a
permitir encontrar los trazados eficientes (
𝑛
𝑚𝑎𝑥
) que conforman la frontera de Pareto
aproximada los cuales se les realiza el diseño hidráulico correspondiente para que entren a
componer la frontera de Pareto con los costos reales.
En el caso del modelo de Zambrano (2018) este procedimiento no es necesario en su totalidad
debido a que este es un modelo explicito y no requiere de las iteraciones mencionadas para
obtener un diseño con el costo mínimo para determinada red.
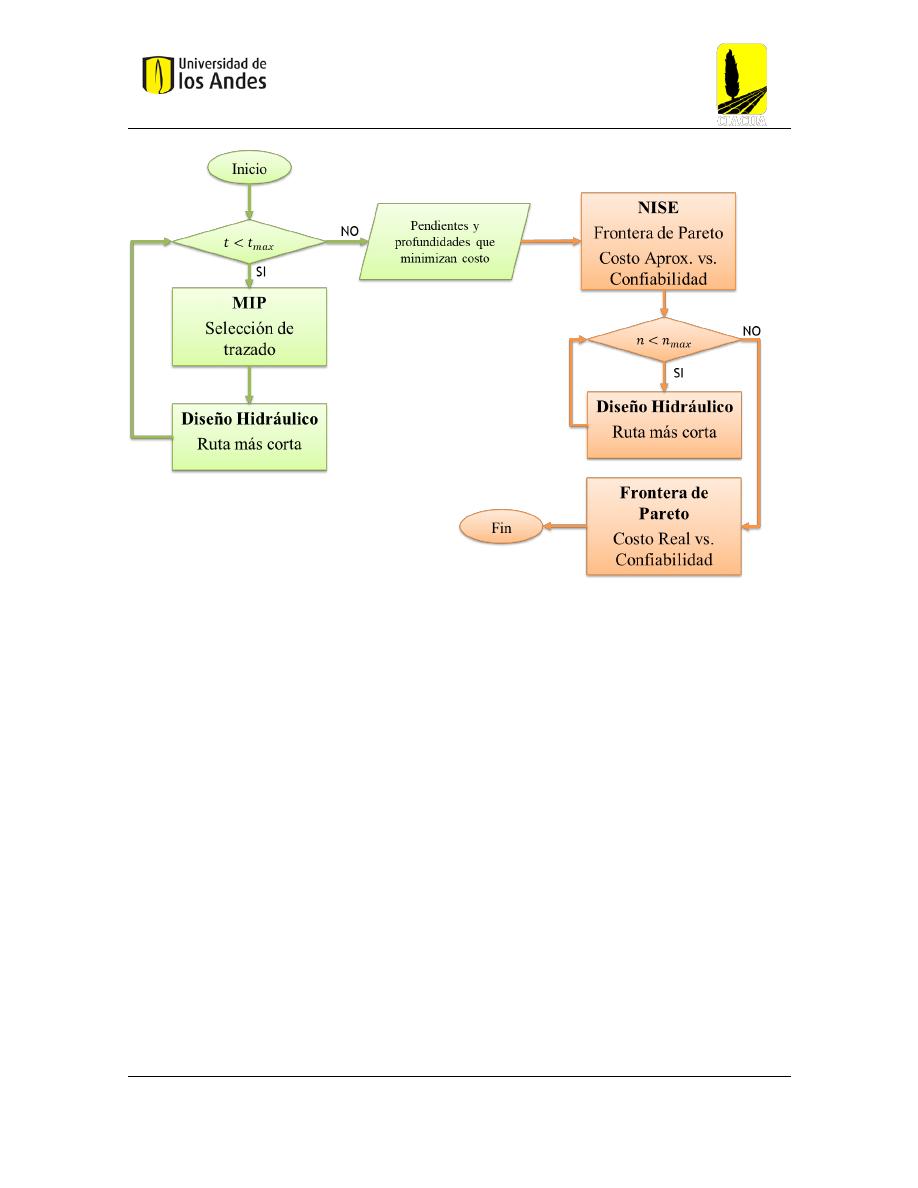
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
35
Figura 11 Algoritmo para la construcción de la frontera de Pareto con el modelo de Aguilar (2016)
Ahora, exactamente para construir frontera de Pareto aproximada de una red se implementa
un algoritmo de ponderación de funciones objetivo propuesto por Medrano et al. (2015) que
lo denomina “Non-Inferior Set Estimation” (NISE en inglés), el cual permite ir encontrando
de manera recursiva las soluciones de un modelo MIP que pertenecen a la frontera.
El algoritmo en primera medida consiste en modificar la función objetivo del modelo MIP,
para que ahora esta sea una ponderación de las dos funciones objetivo de interés, es decir,
del criterio de minimización de costos (
𝑍
1
) y del índice de confiabilidad promedio (
𝑍
2
), y
que a depender de un coeficiente
𝛼 que determina la importancia que se le da a cada uno de
las funciones en cada solución del modelo.
𝑧
𝑐
= 𝛼𝑧
1
+ (1 − 𝛼)𝑧
2
Ahora, el algoritmo resulta ser iterativo porque en cada paso es posible actualizar el valor de
𝛼, lo que modifica la función objetivo 𝑍
𝑐
y por lo tanto es posible obtener un trazado diferente
cada vez pero que siempre pertenece a la frontera de Pareto. El valor del coeficiente
𝛼 se
calcula de la siguiente manera, donde
𝜎
𝑖
y
𝜎
𝑗
son soluciones al modelo MIP encontradas en
cada iteración del algoritmo:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
36
𝛼 =
𝑧
2
(𝜎
𝑖
) − 𝑧
2
(𝜎
𝑗
)
𝑧
2
(𝜎
𝑖
) − 𝑧
2
(𝜎
𝑗
) + 𝑧
1
(𝜎
𝑗
) − 𝑧
1
(𝜎
𝑖
)
En la
Figura 12
se muestra un ejemplo de la construcción de la frontera de Pareto. Donde para
inicializar el algoritmo se comienza asignando
𝛼 = 1 y se soluciona el MIP para obtener un
trazado
𝜎
1
, posteriormente se asigna un
𝛼 = 0 para obtener un trazado 𝜎
2
. Dadas esas dos
soluciones es posible calcular un valor de
𝛼 con la anterior ecuación para así tener una
función objetivo
𝑧
𝑐
con la que se puede solucionar el modelo MIP y obtener un trazado
𝜎
3
.
Para obtener la solución
𝜎
4
, se realiza el procedimiento anterior, pero con las soluciones
𝜎
1
y
𝜎
3
y de la misma manera para la solución
𝜎
5
pero con
𝜎
3
y
𝜎
2
.
Figura 12 Frontera de Pareto con el algoritmo NISE
A continuación, se muestra un algoritmo general que permite la conformación de la frontera
de Pareto, Duque & Peña (2017):
Algoritmo 1: Función Principal
Requerimientos: Modelo MIP de selección de trazado que requiere un coeficiente
𝛼,
1.
𝛹 = ∅: Conjunto de soluciones de la frontera de Pareto
2.
𝛼 = 1
3.
𝜎
𝑖
𝑀𝐼𝑃(𝛼)
4.
𝛼 = 0
5.
𝜎
𝑗
𝑀𝐼𝑃(𝛼)
6.
𝛹 𝛹 𝑈 𝜎
𝑖
7.
𝛹 𝛹 𝑈 𝑅𝑒𝑐𝑢𝑟𝑠𝑖𝑣𝑜𝑁𝐼𝑆𝐸(𝜎
𝑖
, 𝜎
𝑗
, 𝛹)
8. Retornar
𝛹

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
37
Algoritmo 2: Recursivo NISE
1. Actualizar el valor del coeficiente
𝛼.
2.
𝜎
𝑘
𝑀𝐼𝑃(𝛼)
3. If
𝑧
2
(𝜎
𝑘
) > 𝑧
2
(𝜎
𝑖
) and 𝑧
1
(𝜎
𝑘
) > 𝑧
1
(𝜎
𝑗
) then
4. If
𝑧
2
(𝜎
𝑘
) = 𝑧
2
(𝜎
𝑗
) then
5.
𝑅𝑒𝑐𝑢𝑟𝑠𝑖𝑣𝑜𝑁𝐼𝑆𝐸(𝜎
𝑖
, 𝜎
𝑘
, 𝛹)
6. Else If
𝑧
1
(𝜎
𝑘
) = 𝑧
1
(𝜎
𝑖
) then
7.
𝛹
𝛹 𝑈 𝜎
𝑖
8.
𝑅𝑒𝑐𝑢𝑟𝑠𝑖𝑣𝑜𝑁𝐼𝑆𝐸(𝜎
𝑘
, 𝜎
𝑗
, 𝛹)
9. Else
10.
𝑅𝑒𝑐𝑢𝑟𝑠𝑖𝑣𝑜𝑁𝐼𝑆𝐸(𝜎
𝑖
, 𝜎
𝑘
, 𝛹)
11.
𝑅𝑒𝑐𝑢𝑟𝑠𝑖𝑣𝑜𝑁𝐼𝑆𝐸(𝜎
𝑖
, 𝜎
𝑘
, 𝛹)
12. Else
13.
𝛹 𝛹 𝑈 𝜎
𝑗
14. Retornar
𝜎
𝑗
Como es posible observar, al ser un algoritmo iterativo no tiene un criterio de para
predefinido. El algoritmo va a detenerse cuando encuentre todas las soluciones factibles que
pertenezcan a la frontera de Pareto. De esta manera, el tiempo computacional que se requiera
va a depender directamente de la cantidad de variables del modelo MIP, es decir, del número
de tuberías que tenga la red de caso de estudio.
Posteriormente, luego de obtener esta primera frontera de Pareto que contiene los trazados
que optimizan tanto el criterio de costos como el índice de confiabilidad, se procede a realizar
el diseño hidráulico de cada uno de estos. De ese modo, ahora para cada trazado se va a tener
un costo de construcción asociado, y un índice de confiabilidad que ya estaba dado desde
antes, lo que permite conformar la frontera de Pareto final de costo real vs. Confiabilidad
como se muestra en la
Figura 13
.
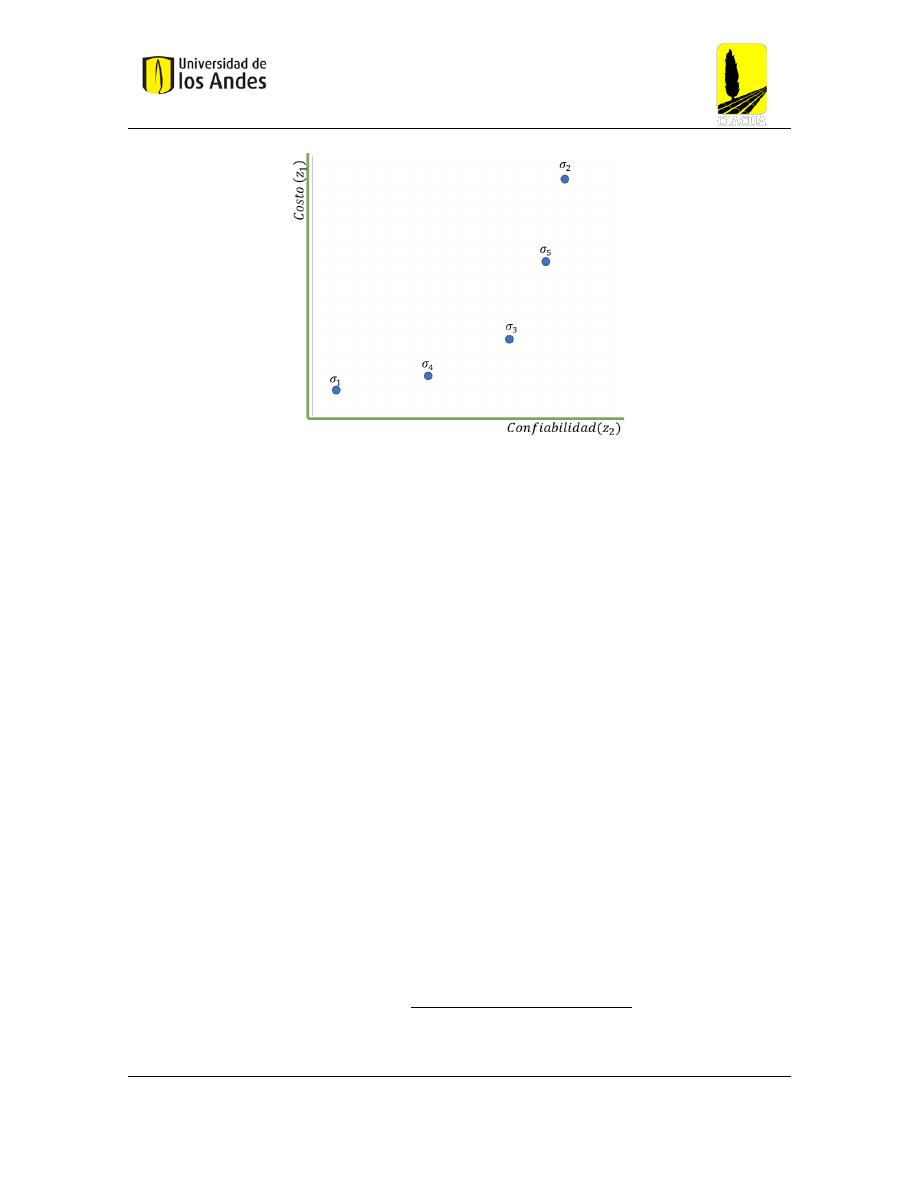
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
38
Figura 13 Frontera de Pareto costo vs. confiabilidad con NISE
5.5 Estrategia para reducir tiempos y recursos computacionales:
Durante la implementación de los casos de estudio se pudo notar que cuando se utilizaba el
modelo MIP propuesto por Aguilar (2016) los tiempos computacionales aumentaban
considerablemente en comparación a los que requería el modelo de Zambrano (2018) para
obtener la frontera de Pareto aproximada, requiriendo de varias horas para llegar a la
conclusión del algoritmo NISE, o en su defecto de agotar la memoria RAM disponible del
computador.
Para darle solución a este problema se implementaron tres estrategias que permitieron reducir
los tiempos computacionales y obtener soluciones correctas a los modelos. La primera
estrategia consistió en asignar un criterio de parada al modelo MIP con el fin de obtener un
trazado muy cercano al óptimo en cuanto a su función objetivo, que requería de menor tiempo
computacional para ser encontrado. Para esto se decide aumentar la tolerancia relativa del
gap del modelo MIP, anotando que el valor por default que asume el software de
optimización utilizado es de 0.00001. Recordando que en el algoritmo de Branch-and-bound
el gap corresponde a la diferencia porcentual entre una frontera superior, que en el caso de
un problema de minimización correspondería al valor de la función objetivo de la mejor
solución encontrada hasta el momento, y una frontera inferior, que correspondería al valor
mínimo de la función objetivo cuando el modelo MIP está totalmente relajado cuando el
problema es de minimización. Gurobi (n.d).
𝑔𝑎𝑝 𝑟𝑒𝑙𝑎𝑡𝑖𝑣𝑜 =
|𝑏𝑒𝑠𝑡 𝑏𝑜𝑢𝑛𝑑 − 𝑏𝑒𝑠𝑡 𝑖𝑛𝑡𝑒𝑔𝑒𝑟|
𝑏𝑒𝑠𝑡 𝑖𝑛𝑡𝑒𝑔𝑒𝑟

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
39
Como segunda estrategia, aprovechando la aproximación lineal mediante segmentos de recta
que se realiza a la función objetivo se propone un análisis de sensibilidad para cada uno de
los casos de estudio donde se cambia el número de segmentos utilizados para hacer la
aproximación y finalmente escoger el número que permite disminuir el tiempo
computacional, pero encontrando el mayor número de soluciones posibles.
La tercera estrategia básicamente consiste establecer un inicio en caliente para cada una de
las iteraciones del modelo MIP cuando se ejecuta el algoritmo NISE, es decir, lo que se
realiza es asignar un valor inicial de las variables del modelo (
𝑥
𝑖𝑗𝑡
y
𝑞
𝑖𝑗𝑡
) en determinada
iteración basadas en la solución dada por la corrida del modelo en la anterior iteración.
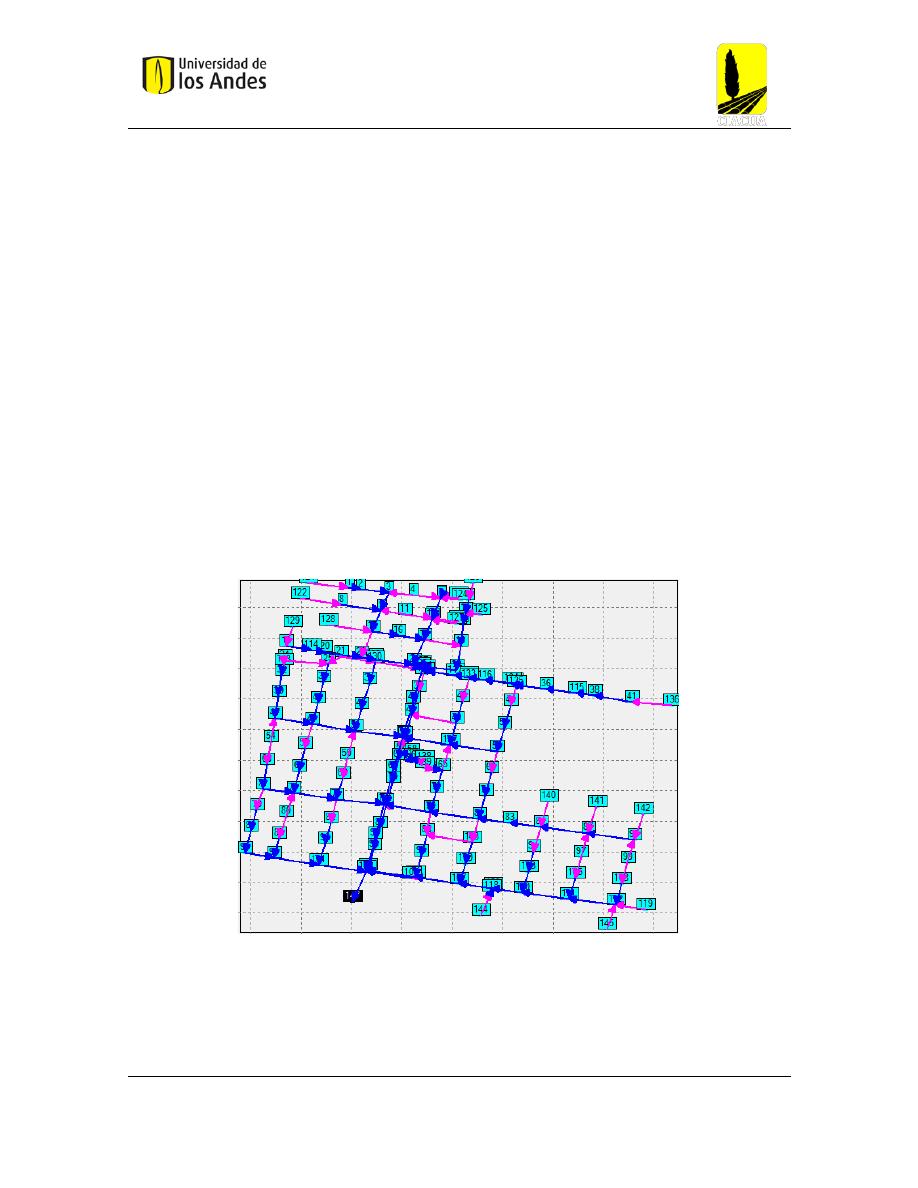
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
40
6. RESULTADOS:
Para poner a prueba la presente metodología de optimización multiobjetivo se va a
implementar tres redes de diferente naturaleza y tamaño con el fin de observar el
funcionamiento y el comportamiento del algoritmo. Para cada una de las redes se va a
analizar varios escenarios para determinar la frontera de Pareto, estos consisten en utilizar
cada uno de los criterios de minimización de costo del trazado (Modelos de Aguilar (2016)
y Zambrano (2018)) y la función de costo de Maurer (2012)
Para el diseño hidráulico de las redes se utilizó la ecuación de Manning (
𝑛 = 0.009 𝑃𝑉𝐶)
con restricciones de velocidad máxima de 10 m/s y esfuerzo cortante mínimo de 2Pa.
Los
diámetros
comerciales
en
metros
disponibles
son
los
siguientes:
0.227,0.284,0.327,0.362,0.407,0.452,0.595,0.670,0.747,0.824,0.9,0.9776,1.054,1.127.
6.1 Cedritos 1:
Esta red consiste en 110 pozos y 160 tramos con topografía plana y el alcantarillado es
combinado.
Figura 14 Ejemplo de Trazado de la red Cedritos 1
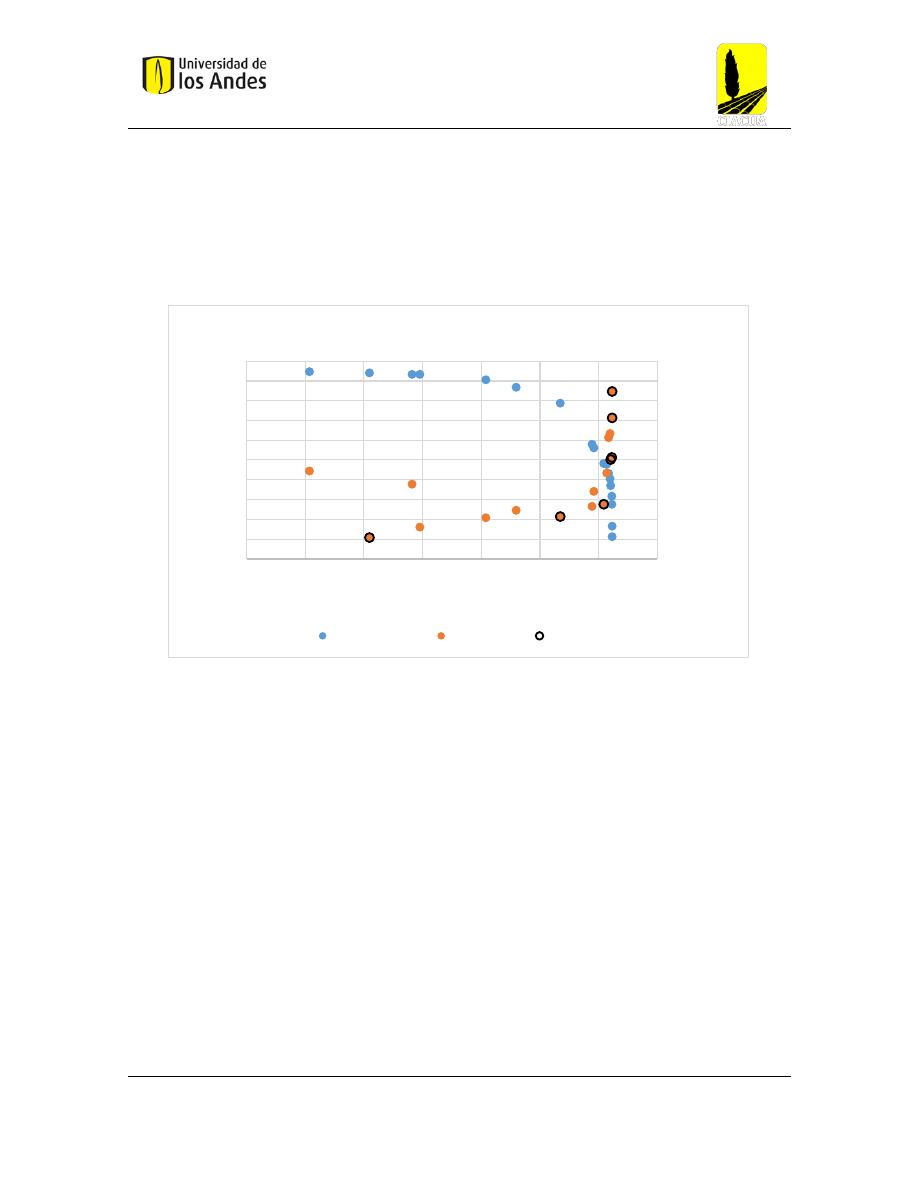
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
41
6.1.1 Resultados con el índice de confiabilidad de Haghighi & Bakshipour (2016) y
modelo de Zambrano (2018)
Las fronteras de Pareto obtenidas con el modelo MIP de la selección de trazado pripuesto por
Zambrano (2018) y con un índice de confiabilidad de
Haghighi & Bakshipour (2016)
fue la
siguiente:
Figura 15 Fronteras de Pareto para Cedritos 1
En la Figura 15 se puede observar la frontera de Pareto aproximada (Azul) con los trazados eficientes
la cual requirió un tiempo computacional de 27 segundos para ser construida. También se observan
los diseños de los trazados (Naranja) nombrados anteriormente que requirieron 6.3 minutos para ser
realizados. Además, es posible identificar los diseños que se encuentran no dominados y que por lo
tanto conforman la frontera de Pareto real (Negro).
6.1.2 Resultados con el índice de confiabilidad de Aguilar (2019) y modelo de Zambrano
(2018)
Las fronteras de Pareto obtenidas con el modelo MIP de la selección de trazado propuesto
por Zambrano (2018) y con un índice de confiabilidad presentado en este trabajo
fue la
siguiente (Aguilar (2019)):
$6.30
$6.40
$6.50
$6.60
$6.70
$6.80
$6.90
$7.00
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
95.00
95.10
95.20
95.30
95.40
95.50
95.60
95.70
Real
C
o
st
H
D
(U
SD
)x
1
0
6
Ob
je
ct
iv
e
M
IP
Reliability(%)
PA R E TO F RO N T - C E D R I TO S 1
Layout Solutions
HD Solutions
HD Pareto
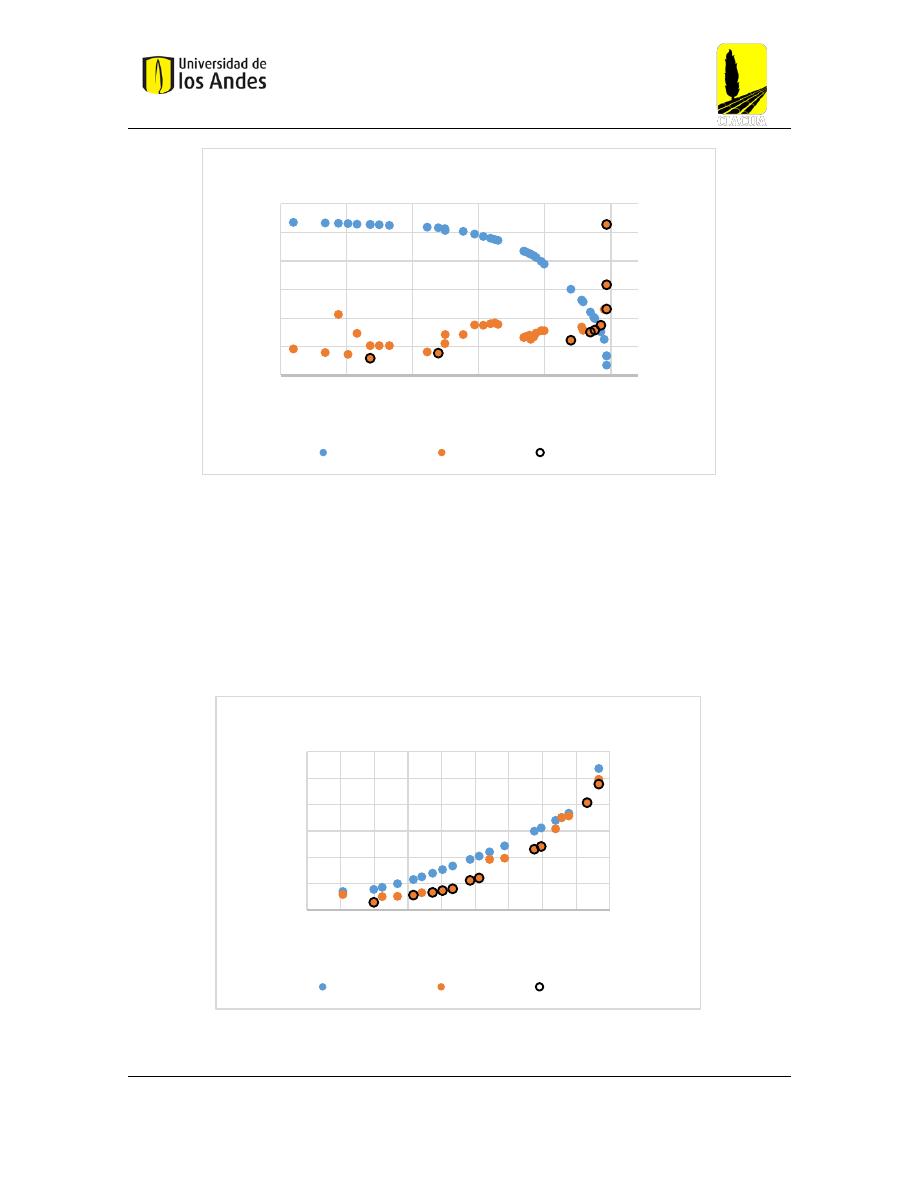
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
42
Figura 16 Frontera de Pareto de Cedritos 1
La frontera de Pareto aproximada (Azul) con sus respectivos trazados requirió de 28 segundos para
ser construida, mientras que realizar los diseños hidráulicos (Naranja) requirió de 9.1 minutos.
6.1.3 Resultados con el índice de confiabilidad de Aguilar (2019) y modelo de selección
de trazado de Aguilar (2016)
Las fronteras de Pareto obtenidas con el modelo MIP de la selección de trazado propuesto
por Aguilar (2016) y con un índice de confiabilidad presentado en este trabajo
fue la siguiente
(Aguilar (2019)):
Figura 17 Frontera de Pareto de Cedritos 1
6.45
6.50
6.55
6.60
6.65
6.70
6.75
6.80
6.85
6.90
6.95
7.00
0.05
0.15
0.25
0.35
0.45
0.55
0.65
51.0
56.0
61.0
66.0
71.0
76.0
Real
C
o
st
H
D
(U
SD
)x
1
0
6
Ob
je
ct
iv
e
M
IP
Reliability(%)
PA R E TO F RO N T - C E D R I TO S 1
Layout Solutions
HD Solutions
HD Pareto
$6.75
$6.80
$6.85
$6.90
$6.95
$3.80
$3.85
$3.90
$3.95
$4.00
$4.05
$4.10
67.00 68.00 69.00 70.00 71.00 72.00 73.00 74.00 75.00 76.00
R
eal
C
o
st
H
D
(
U
SD
)x
10
6
Ap
ro
x.
. C
o
st
(U
SD
)x
1
0
6
Reliability (%)
PA R E TO F RO N T - C E D R I TO S 1
Layout Solutions
HD Solutions
HD Pareto
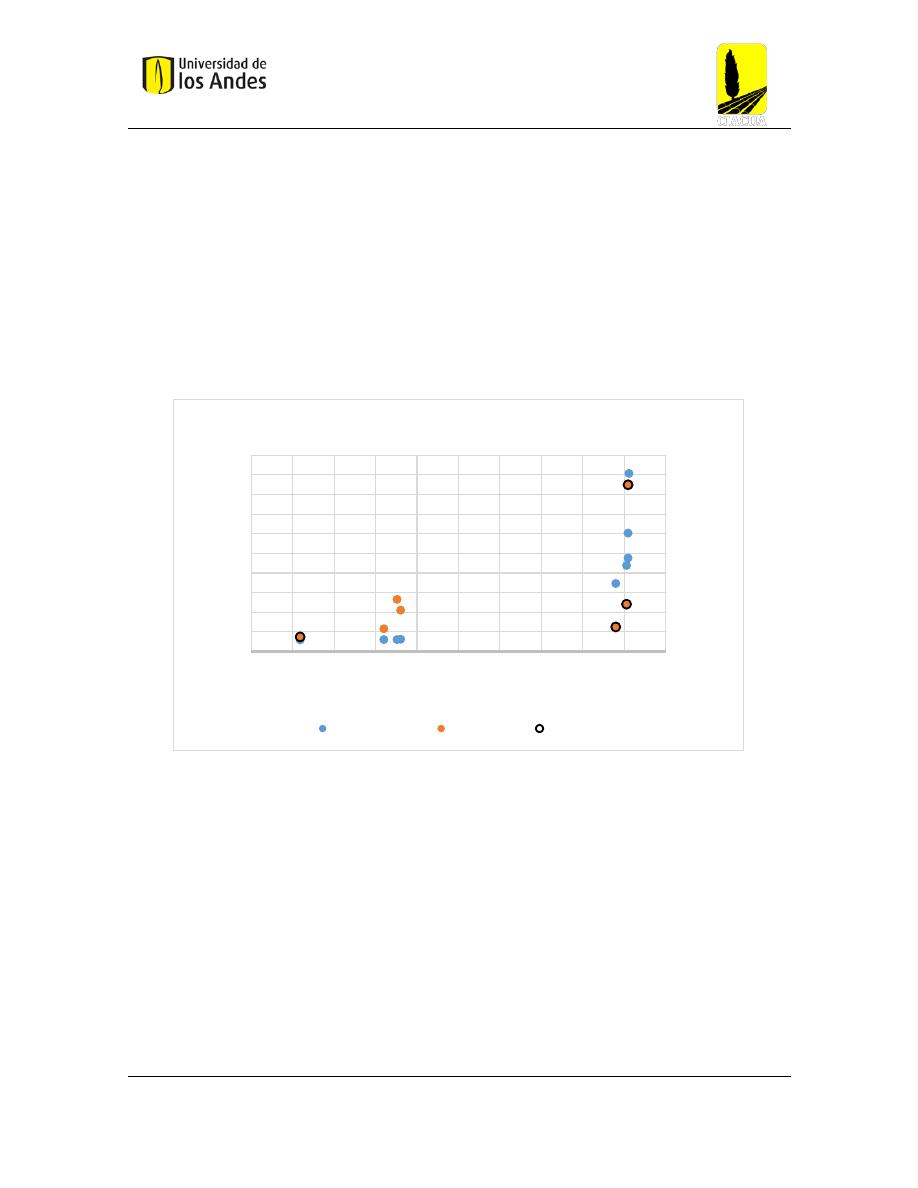
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
43
La frontera de Pareto aproximada (Azul) con sus respectivos trazados requirió de 2.2 horas para ser
construida, donde se usaron 4 segmentos de recta para aproximar la función de costo y una tolerancia
relativa del gap del 1%, mientras que realizar los diseños hidráulicos (Naranja) requirió de 10.3
minutos.
6.1.4 Resultados con el índice de confiabilidad de Haghighi & Bakshipour (2016) y
modelo de selección de trazado de Aguilar (2016)
Las fronteras de Pareto obtenidas con el modelo MIP de la selección de trazado pripuesto por
Aguilar (2016) y con un índice de confiabilidad de
Haghighi & Bakshipour (2016)
fue la
siguiente:
Figura 18 Frontera de Pareto de Cedritos 1
La frontera de Pareto aproximada (Azul) con sus respectivos trazados requirió de 1.4 horas para ser
construida, donde se usaron 4 segmentos de recta para aproximar la función de costo y una tolerancia
relativa del gap del 1%, mientras que realizar los diseños hidráulicos (Naranja) requirió de 6.3
minutos.
6.7
6.75
6.8
6.85
6.9
3.98
4
4.02
4.04
4.06
4.08
4.1
4.12
4.14
4.16
4.18
93.80 94.00 94.20 94.40 94.60 94.80 95.00 95.20 95.40 95.60 95.80
Real
C
o
st
H
D
(U
SD
)x
1
0
6
Ap
ro
x.
. C
o
st
(U
SD
)x
1
0
6
Reliability (%)
PA R E TO F RO N T - C E D R I TO S 1
Layout Solutions
HD Solutions
HD Pareto
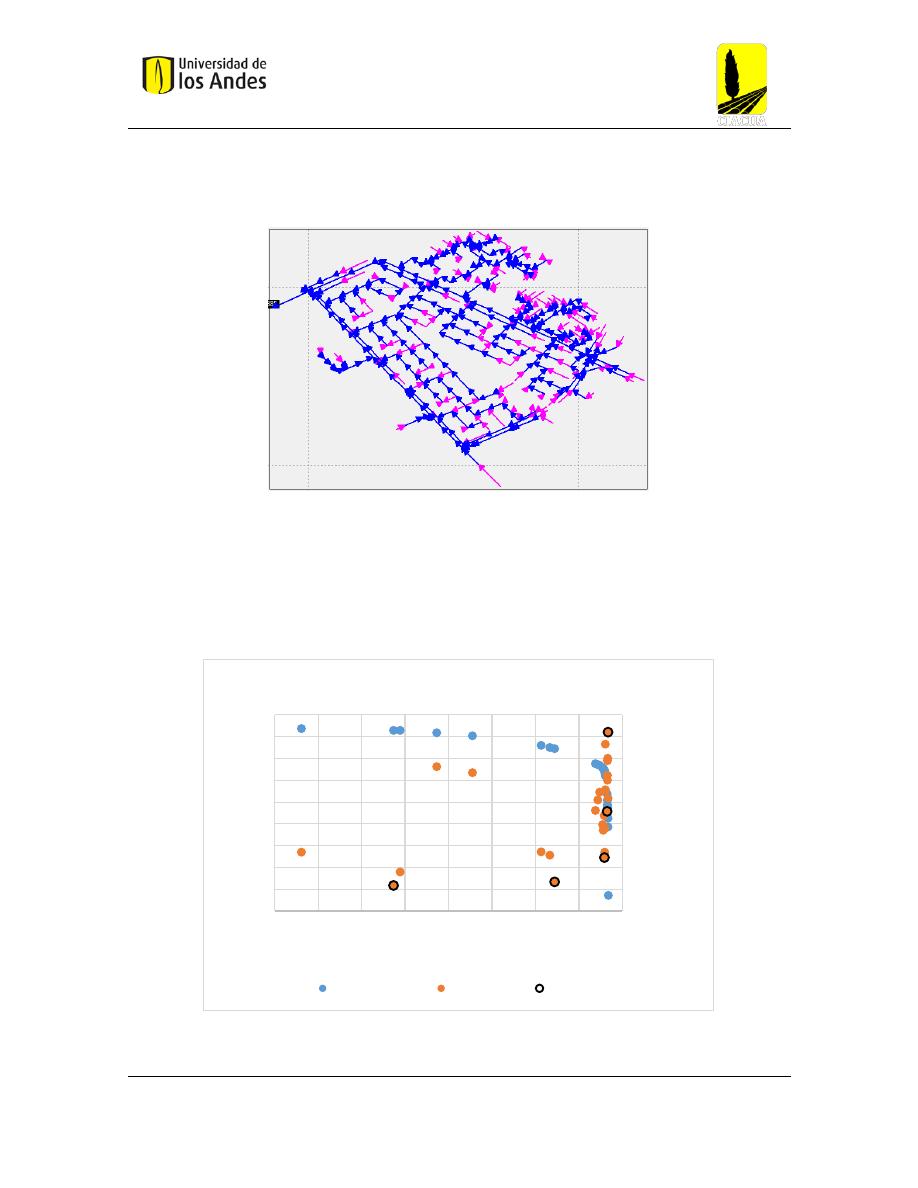
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
44
6.2 Esmeralda:
Esta red consiste en 385 pozos y 413 tramos con topografía plana y el alcantarillado es
sanitario.
Figura 19 Ejemplo de Trazado de la red Esmeralda
6.2.1 Resultados con el índice de confiabilidad de Haghighi & Bakshipour (2016) y
modelo de Zambrano (2018)
Las fronteras de Pareto obtenidas con el modelo MIP de la selección de trazado propuesto
por Zambrano (2018) y con un índice de confiabilidad de
Haghighi & Bakshipour (2016)
fue la
siguiente:
Figura 20 Frontera de Pareto de Esmeralda
$2.03
$2.05
$2.07
$2.09
$2.11
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
95.40 95.50 95.60 95.70 95.80 95.90 96.00 96.10 96.20
Real
C
o
st
H
D
(U
SD
)x
1
0
7
Ob
je
ct
iv
e
M
IP
Reliability (%)
PA R E TO F RO N T - ES M E R A L DA
Layout Solutions
HD Solutions
HD Pareto
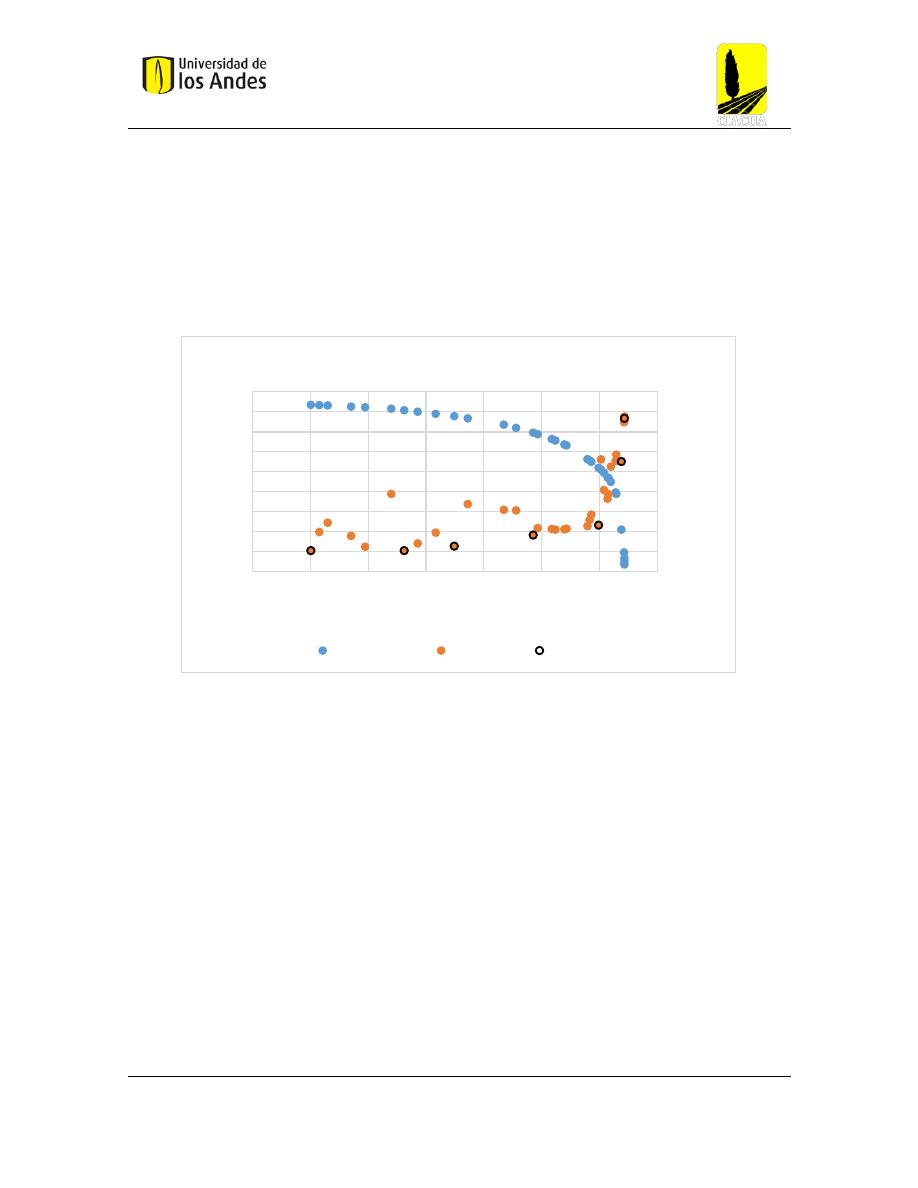
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
45
La frontera de Pareto aproximada (Azul) con sus respectivos trazados requirió de 51 segundos para
ser construida, mientras que realizar los diseños hidráulicos (Naranja) requirió de 11.1 minutos.
6.2.2 Resultados con el índice de confiabilidad de Aguilar (2019) y modelo de Zambrano
(2018)
Las fronteras de Pareto obtenidas con el modelo MIP de la selección de trazado propuesto
por Zambrano (2018) y con un índice de confiabilidad de
Aguilar (2019)
fue la siguiente:
Figura 21 Frontera de Pareto de Esmeralda
6.2.3 Resultados con el índice de confiabilidad de Aguilar (2019) y modelo de selección
de trazado de Aguilar (2016)
Las fronteras de Pareto obtenidas con el modelo MIP de la selección de trazado propuesto
por Aguilar (2016) y con un índice de confiabilidad presentado en este trabajo
fue la siguiente
(Aguilar (2019)):
2.08
2.10
2.12
2.14
2.16
2.18
2.20
2.22
2.24
2.26
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
53.00
54.00
55.00
56.00
57.00
58.00
59.00
60.00
Real
C
o
st
H
D
(U
SD
)x
1
07
Ob
je
ct
iv
e
M
IP
Reliability (%)
PARETO FRONT - ESMERALDA
Layout Solutions
HD Solutions
HD Pareto
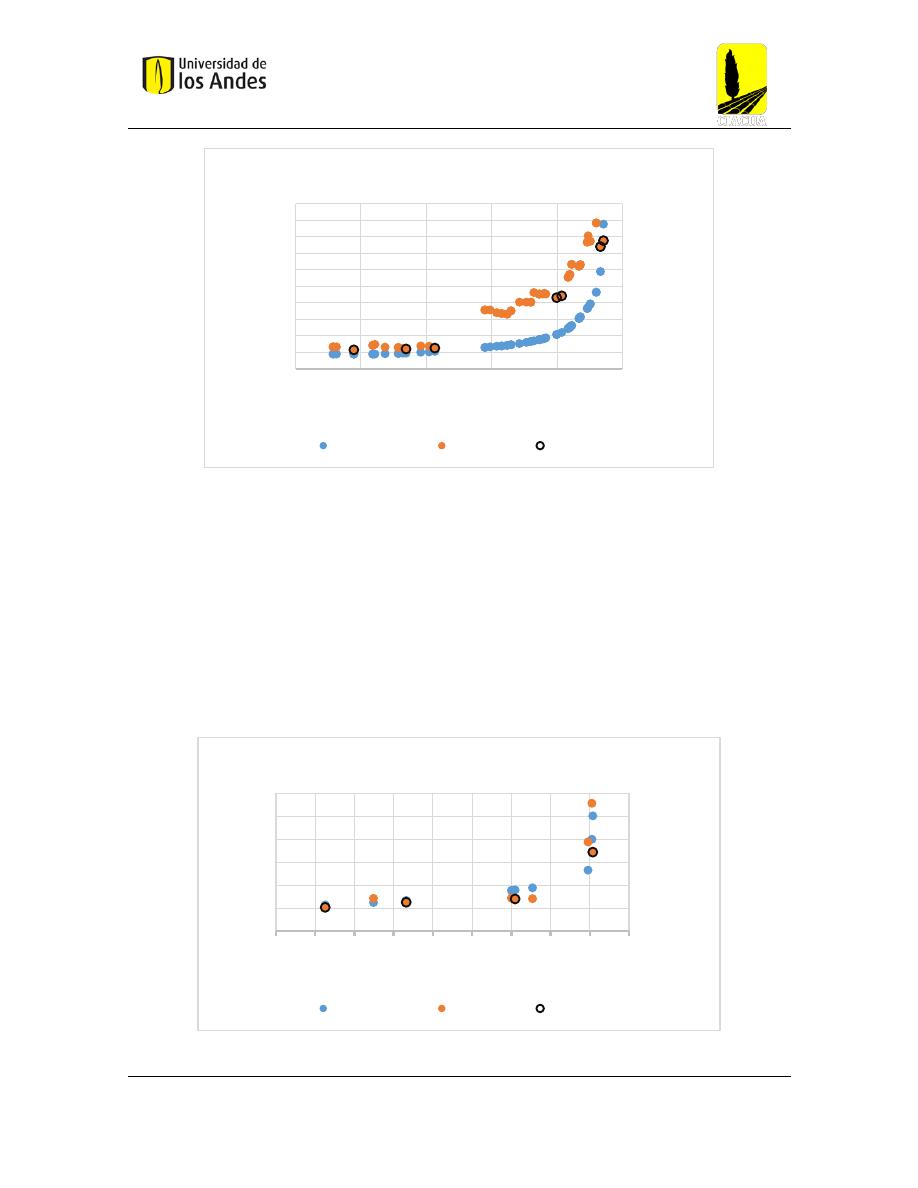
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
46
Figura 22 Frontera de Pareto de Esmeralda
La frontera de Pareto aproximada (Azul) con sus respectivos trazados requirió de 22.2 horas
para ser construida, donde se usaron 7 segmentos de recta para aproximar la función de costo
y una tolerancia relativa del gap del 3%, mientras que realizar los diseños hidráulicos
(Naranja) requirió de 46.3 minutos.
6.2.4 Resultados con el índice de confiabilidad de Haghighi & Bakshipour (2016) y
modelo de selección de trazado de Aguilar (2016)
Las fronteras de Pareto obtenidas con el modelo MIP de la selección de trazado propuesto
por Aguilar (2016) y con un índice de confiabilidad de
Haghighi & Bakshipour (2016)
fue la
siguiente:
$2.00
$2.05
$2.10
$2.15
$2.20
$2.25
$2.30
$1.20
$1.22
$1.24
$1.26
$1.28
$1.30
$1.32
$1.34
$1.36
$1.38
$1.40
50
52
54
56
58
60
Real
C
o
st
H
D
(U
SD
)x
1
0
7
Ap
ro
x.
. C
o
st
(U
SD
)x
1
0
7
Reliability (%)
PA R E TO F RO N T - ES M E R A L DA
Layout Solutions
HD Solutions
HD Pareto
$2.02
$2.04
$2.06
$2.08
$2.10
$2.12
$2.14
1.28
1.3
1.32
1.34
1.36
1.38
1.4
95.75 95.8 95.85 95.9 95.95
96
96.05 96.1 96.15 96.2
Real
C
o
st
H
D
(U
SD
)x
1
0
7
Ap
ro
x.
. C
o
st
(U
SD
)x
1
0
7
Reliability (%)
PA R E TO F RO N T - ES M E R A L DA
Layout Solutions
HD Solutions
HD Pareto
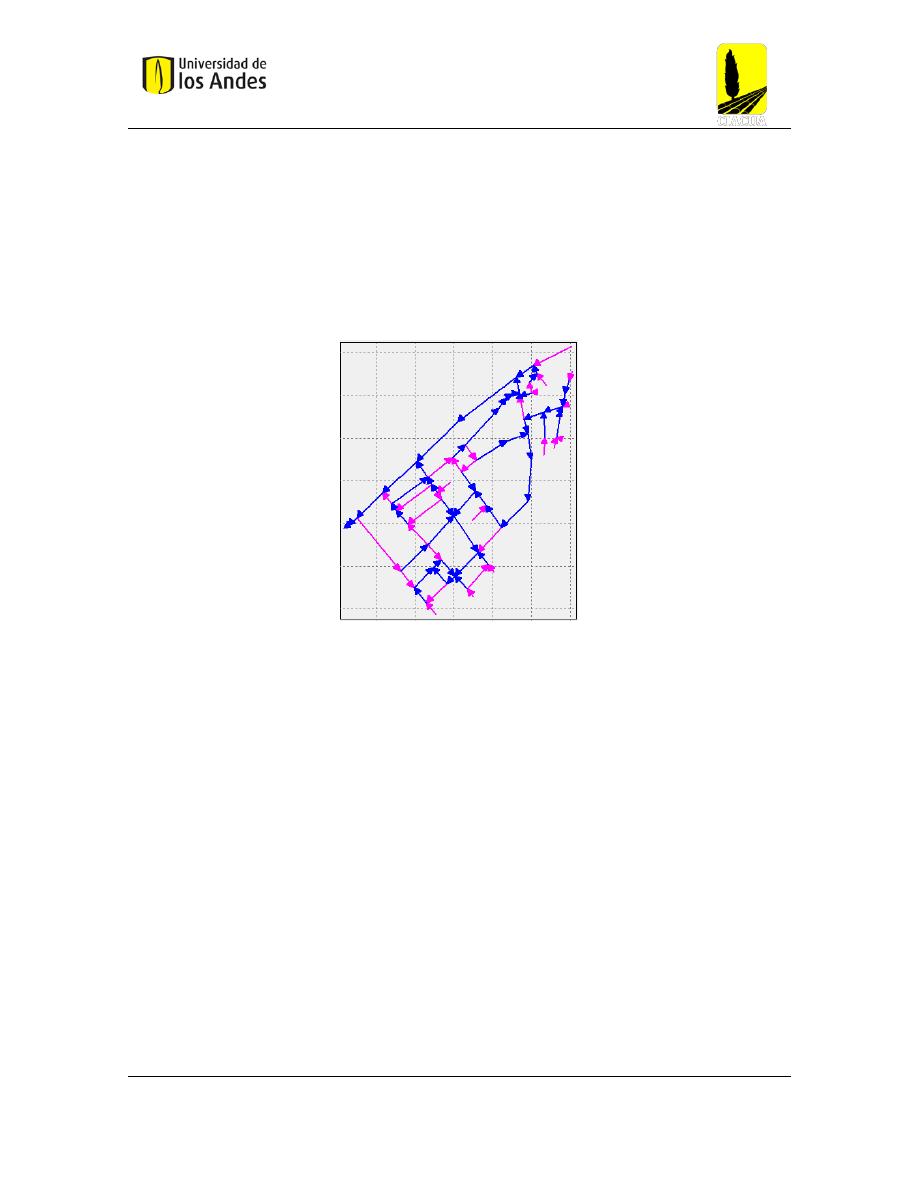
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
47
La frontera de Pareto aproximada (Azul) con sus respectivos trazados requirió de 13.2 horas
para ser construida, donde se usaron 7 segmentos de recta para aproximar la función de costo
y una tolerancia relativa del gap del 3%, mientras que realizar los diseños hidráulicos
(Naranja) requirió de 31.8 minutos.
6.3 Tumaco – Sector 2:
Esta red consiste en 67 pozos y 83 tramos con topografía plana y el alcantarillado es sanitario.
Figura 23 Red de Tumaco - Sector 2
6.3.1 Resultados con el índice de confiabilidad de Haghighi & Bakshipour (2016) y
modelo de Zambrano (2018)
Las fronteras de Pareto obtenidas con el modelo MIP de la selección de trazado propuesto
por Zambrano (2018) y con un índice de confiabilidad de
Haghighi & Bakshipour (2016)
fue la
siguiente:
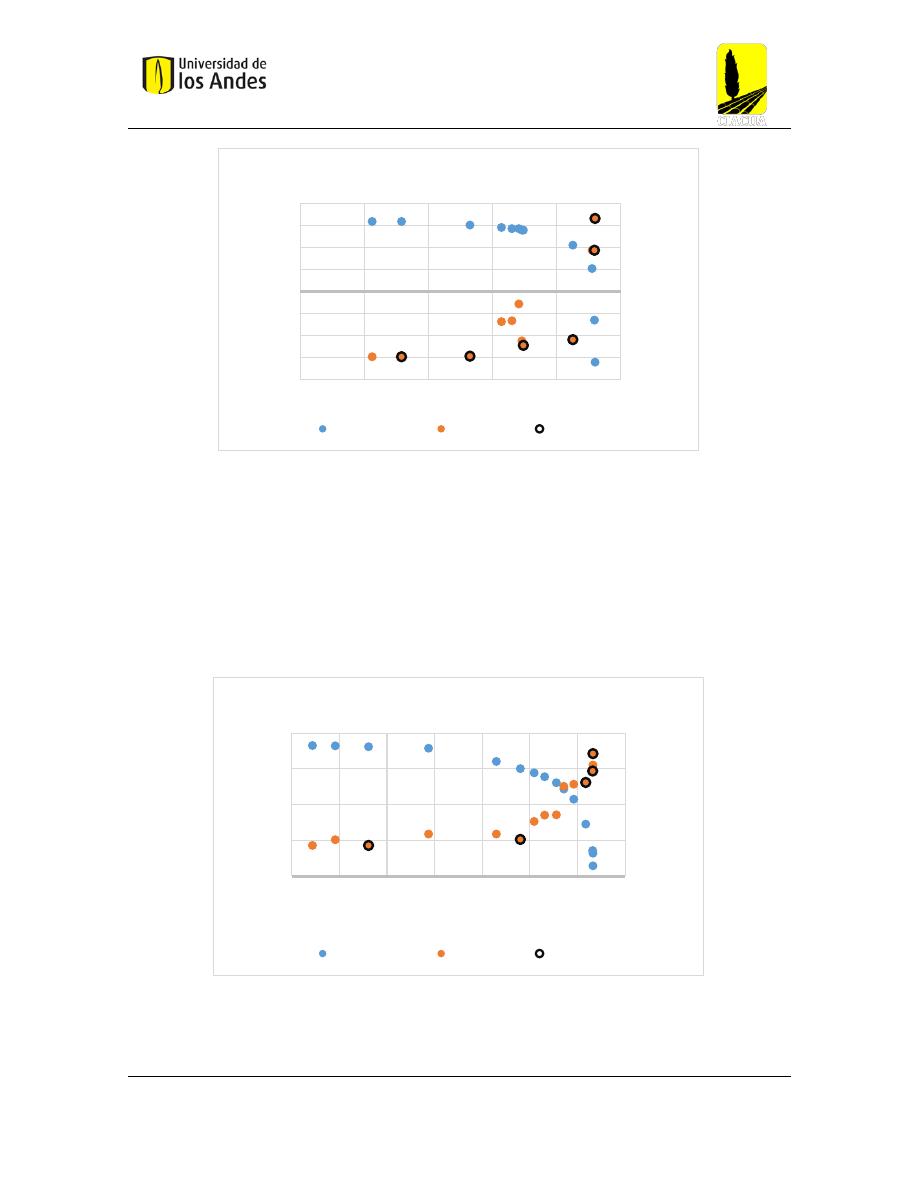
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
48
Figura 24 Frontera de Pareto de Tumaco
La frontera de Pareto aproximada (Azul) con sus respectivos trazados requirió de 14
segundos para ser construida, mientras que realizar los diseños hidráulicos (Naranja) requirió
de 7.1 minutos.
6.3.2 Resultados con el índice de confiabilidad de Aguilar (2019) y modelo de Zambrano
(2018)
Las fronteras de Pareto obtenidas con el modelo MIP de la selección de trazado propuesto
por Zambrano (2018) y con un índice de confiabilidad de Aguilar (2019) fue la siguiente:
Figura 25 Frontera de Pareto Tumaco
3.15
3.2
3.25
3.3
3.35
3.4
3.45
3.5
3.55
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
89.60
89.80
90.00
90.20
90.40
90.60
R
eal
C
o
st
H
D
(
U
SD
)x
10
7
Ob
je
ct
iv
e
M
IP
Reliability (%)
PA R E TO F RO N T - T U M ACO
Layout Solutions
HD Solutions
HD Pareto
3.1
3.15
3.2
3.25
3.3
3.35
0
0.05
0.1
0.15
0.2
35.0
40.0
45.0
50.0
55.0
60.0
65.0
70.0
R
eal
C
o
st
H
D
(
U
SD
)x
10
7
Ob
je
ct
iv
e
M
IP
Realiability (%)
PA R E TO F RO N T - T U M ACO
Layout Solutions
HD Solutions
HD Pareto
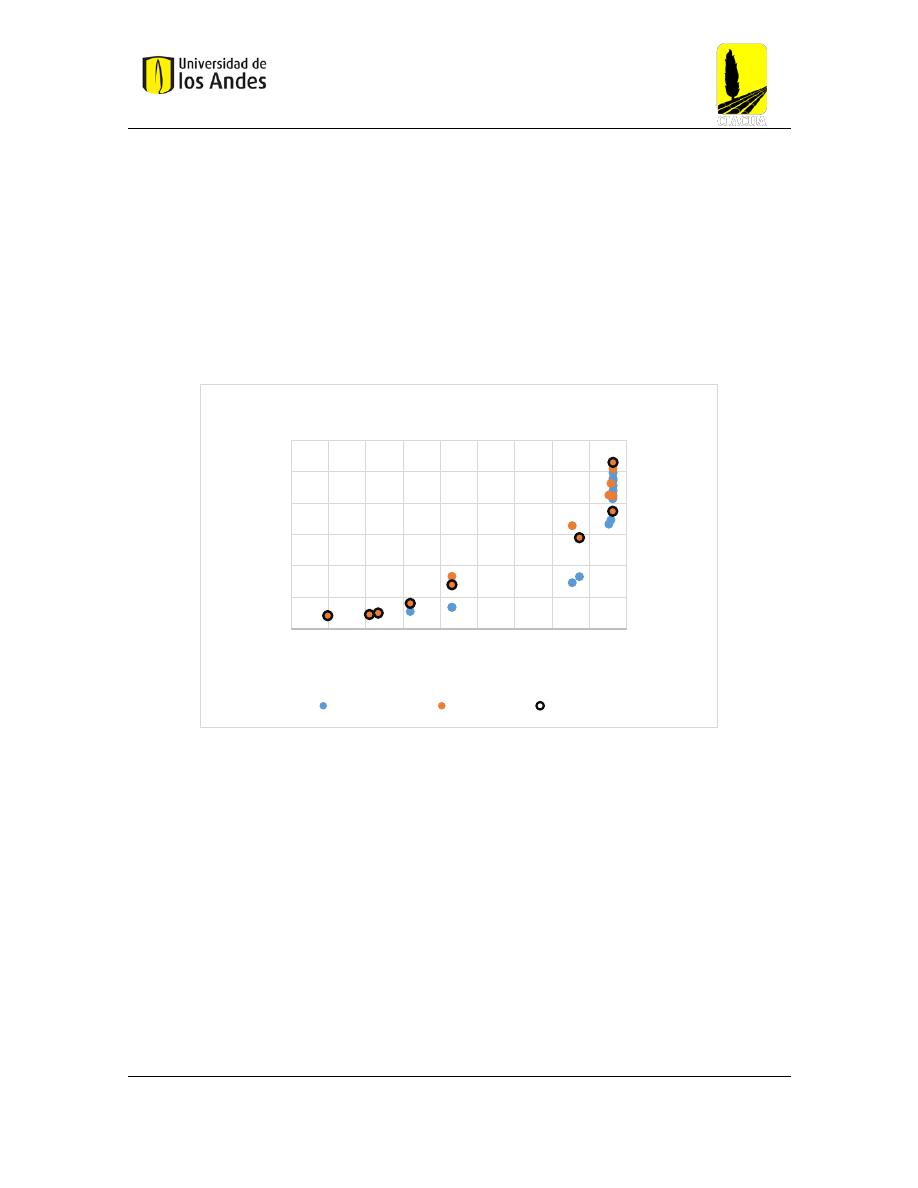
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
49
La frontera de Pareto aproximada (Azul) con sus respectivos trazados requirió de 14
segundos para ser construida, mientras que realizar los diseños hidráulicos (Naranja)
requirió de 7.1 minutos
.
6.3.3 Resultados con el índice de confiabilidad de Aguilar (2019) y modelo de selección
de trazado de Aguilar (2016)
Las fronteras de Pareto obtenidas con el modelo MIP de la selección de trazado propuesto
por Aguilar (2016) y con un índice de confiabilidad presentado en este trabajo
fue la siguiente
(Aguilar (2019)):
Figura 26 Frontera de Pareto Tumaco
La frontera de Pareto aproximada (Azul) con sus respectivos trazados requirió de 1.2 horas
para ser construida, donde se usaron 10 segmentos de recta para aproximar la función de
costo y una tolerancia relativa del gap del 0.001%, mientras que realizar los diseños
hidráulicos (Naranja) requirió de 34.2 minutos.
6.3.4 Resultados con el índice de confiabilidad de Haghighi & Bakshipour (2016) y
modelo de selección de trazado de Aguilar (2016)
$3.20
$3.22
$3.24
$3.26
$3.28
$3.30
$3.32
$3.34
$2.15
$2.20
$2.25
$2.30
$2.35
$2.40
$2.45
58.0 59.0 60.0 61.0 62.0 63.0 64.0 65.0 66.0 67.0
Real
C
o
st
H
D
(U
SD
)x
1
0
6
Ap
ro
x.
C
o
st
(U
SD
)x
1
0
6
Reliability (%)
PA R E TO F RO N T - T U M ACO
Layout Solutions
HD Solutions
HD Pareto
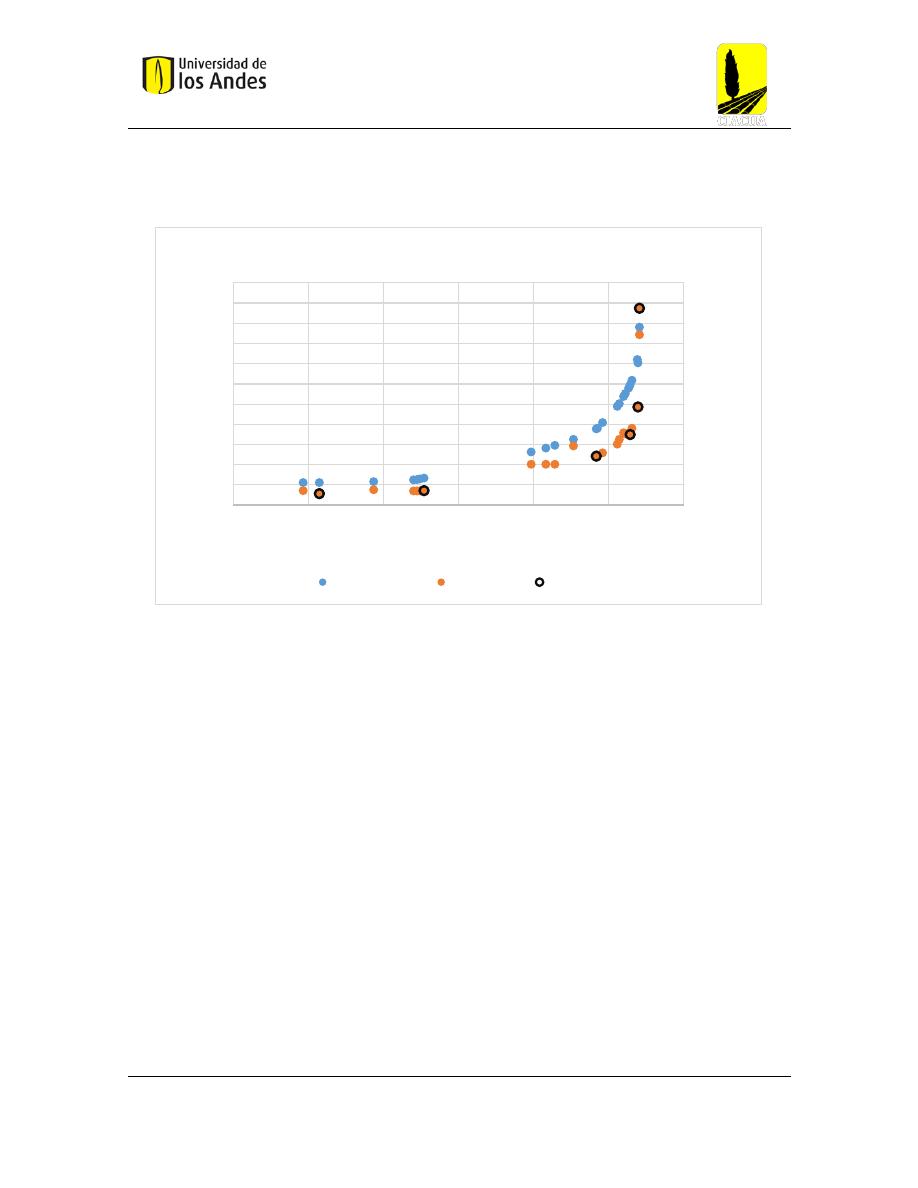
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
50
Las fronteras de Pareto obtenidas con el modelo MIP de la selección de trazado propuesto
por Aguilar (2016) y con un índice de confiabilidad de
Haghighi & Bakshipour (2016)
fue la
siguiente:
La frontera de Pareto aproximada (Azul) con sus respectivos trazados requirió de 55 minutos
para ser construida, donde se usaron 10 segmentos de recta para aproximar la función de
costo y una tolerancia relativa del gap del 0.001%, mientras que realizar los diseños
hidráulicos (Naranja) requirió de 40.4 minutos.
6.4 Convergencia del ponderador alfa del algoritmo NISE:
Adicionalmente, se hizo un análisis del comportamiento del ponderador alfa en el algoritmo
NISE con el fin de ver el impacto que tiene el tamaño y naturaleza de la red sobre la cantidad
de iteraciones, el valor de alfa y la velocidad de convergencia. En la Figura 27 se muestra el
comportamiento del alfa a través de las iteraciones de cada uno de los casos de estudio
mencionados anteriormente cuando fueron implementados con el modelo MIP propuesto por
Zambrano (2018) y con el índice de confiabilidad de Haghighi y Bakshipour (2016). Sin
embargo, se logró identificar la misma tendencia para todos los escenarios planteados en este
trabajo.
3.10
3.15
3.20
3.25
3.30
3.35
2.3
2.32
2.34
2.36
2.38
2.4
2.42
2.44
2.46
2.48
2.5
2.52
90.25
90.3
90.35
90.4
90.45
90.5
90.55
Real
C
o
st
H
D
(U
SD
)x
1
0
6
Ap
ro
x.
C
o
st
(U
SD
)x
1
0
6
Reliability (%)
PA R E TO F RO N T - T U M ACO
Layout Solutions
HD Solutions
HD Pareto
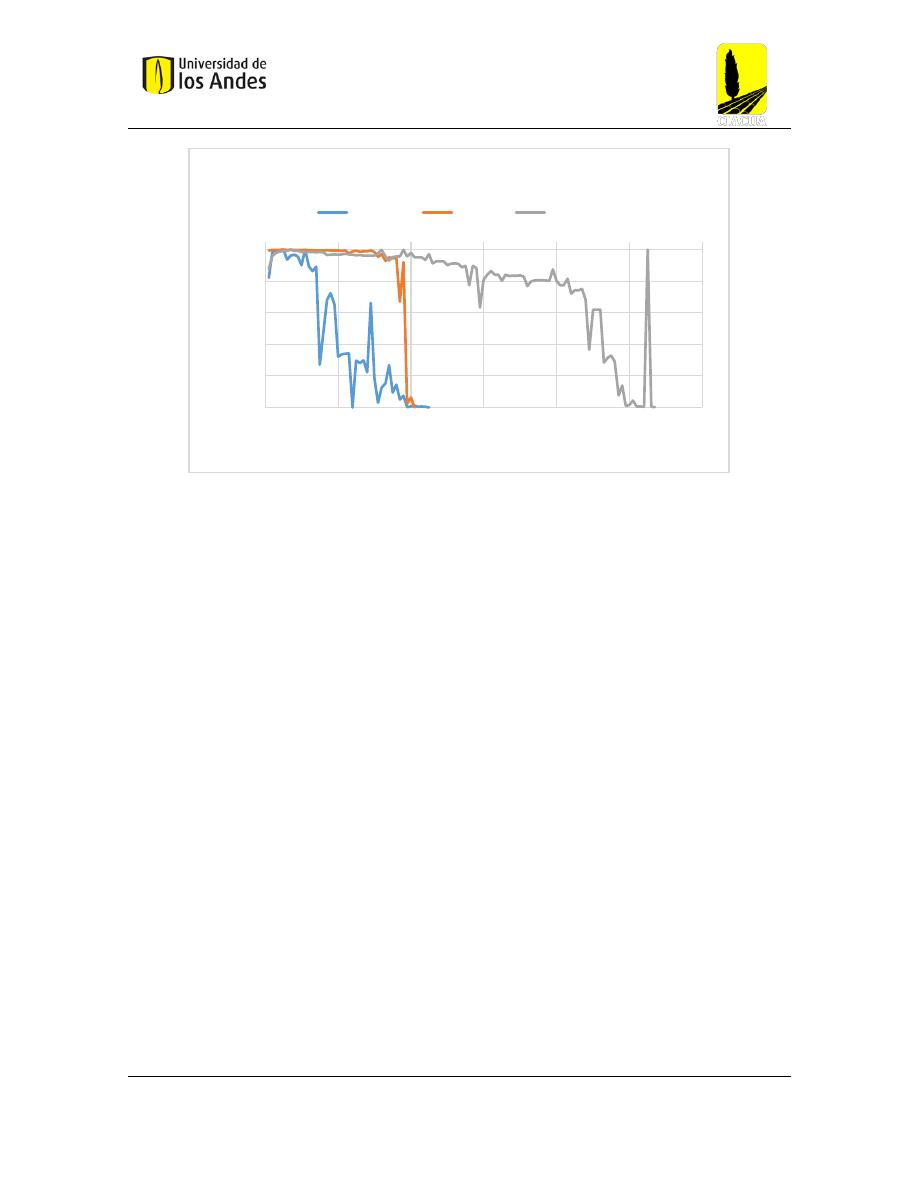
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
51
Figura 27 Convergencia de alfa en los tres casos de estudio
7. ANALISIS DE RESULTADOS
La construcción de una Frontera de Pareto permite tener un conjunto de diseños de una red
determinada que cumplen con la optimización de los costos de construcción y la confiabilidad
de su trazado de manera ponderada, dependerá del ingeniero y de las condiciones técnicas y
económicas cuál de estos diseños va a ser el que se va a ejecutar.
De los resultados mostrados en la sección 6 es posible decir que la metodología NISE en
todos los casos de estudio permite construir una primera Frontera de Pareto que contiene las
dos funciones objetivo, consideradas para el modelo de selección de trazado MIP, que son el
uno de los criterios para minimizar el costo y el índice de confiabilidad promedio. La
construcción de esta frontera se hace de manera eficiente y en tiempos computacionales
aceptables, pues se debe tener en cuenta que se está resolviendo en repetidas ocasiones el
modelo MIP donde lo único que se cambia es la ponderación de las funciones objetivo. Sin
embargo, se debe anotar que cuando la metodología se resuelve con el modelo MIP propuesto
por Aguilar (2016) el tiempo computacional requerido es mucho mayor que cuando se utiliza
el modelo de Zambrano (2019), lo cual resulta lógico si se tiene en cuenta que en este modelo
se tienen un mayor número de variables y restricciones que se deben cumplir, lo que vuelve
más complejo el problema y requiere de mayores recursos computacionales para encontrar
una solución óptima. Por lo que se puede decir que las estrategias mencionadas de modificar
el valor inicial de las variables del modelo MIP, el número de rectas para la aproximación
lineal de las función objetivo y la tolerancia relativa del gap fueron aptas y permitieron la
reducción del tiempo computacional en promedio en un 50%.
0
0.2
0.4
0.6
0.8
1
0
2 0
4 0
6 0
8 0
1 0 0
1 2 0
ALP
HA
ITERACIONES
CONVERGENCE ALPHA
Cedritos 1
Tumaco
Esmeralda

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
52
En términos generales, se puede deducir que el número de trazados que conforman la frontera
de Pareto puede depender en parte del tamaño de la red, pero más que este factor, se puede
concluir que depende directamente de la cantidad de circuitos que se puedan formar según la
naturaleza de cada red, De igual manera sucede con las iteraciones pues se puede observar
en la
Figura 27
que la red de Esmeralda, la cual tiene el mayor número de pozos y tuberías,
requiere de más iteraciones para construir la frontera de Pareto, seguido de las redes de
Cedritos 1 y Tumaco.
En cuanto al efecto que tiene el índice de confiabilidad utilizado sobre la frontera de Pareto,
en primera instancia se puede decir que el índice propuesto en este trabajo considera un
mayor espacio de solución que el propuesto por Haghighi y Bakshipour (2016), en otras
palabras la diferencia promedio en todos los casos de estudio entre el valor mínimo de
confiabilidad y el máximo es mayor en el caso del índice de Aguilar (2019), lo que genera
como principal impacto que la frontera de Pareto aproximada construida con el índice de
confiabilidad de Aguilar (2019) tenga en promedio un mayor número de trazados que la
construida con el índice de Haghighi y Bakshipour (2016).
Con respecto a las funciones objetivo de minimización de costos se puede decir que ambas
son alternativas que permiten aproximar de manera correcta los costos del diseño hidráulico
pues permiten tener diseños con similares características. Sin embargo, se debe destacar que
el modelo propuesto por Aguilar (2016), aunque requiere de mayores tiempos y recursos
computacionales, permite obtener fronteras de Pareto reales que se ajustan de mejor manera
a una frontera de Pareto ideal, es decir, los puntos que componen la frontera de Pareto con
este modelo presentan menos dispersión y variabilidad que las fronteras con el modelo de
Zambrano (2018), y por lo tanto se ajustan de mejor manera a la concavidad ideal de la
frontera de Pareto.
Por otra parte, cuando se construye la frontera de Pareto real, que contempla costo y
confiabilidad, se puede concluir que no todos los trazados que se obtienen de la primera etapa
de la metodología resultan ser factibles. Esto se debe a que no cumplen con algunas de las
restricciones impuestas en el diseño hidráulico por lo que no se grafican en las fronteras
definitivas. Sin embargo, lo más importante que se puede destacar es que también no todos
los trazados cuando son diseñados van a conformar la frontera de Pareto, esto se debe a que
se convierten a soluciones dominadas o con dominancia débil, es decir, existen otras
soluciones que para un mismo costo permiten tener una mayor confiabilidad, o viceversa,
permiten obtener un menor costo con un mismo nivel de confiabilidad.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
53
Finalmente, se puede decir que el modelo de selección de trazado propuesto por Aguilar
(2016) permite hacer una buena estimación de los costos indirectamente de una red sin
importar su naturaleza, pero reconociendo que funciona mejor en el caso de las redes
sanitarias, donde la diferencia entre diseños radica generalmente en las profundidades de
excavación, pues los diámetros de las tuberías son muy similares. Esto se concluye porque
las fronteras obtenidas tienen una forma esperada, donde el costo aumenta a medida que
aumenta la confiabilidad de la red y la mayoría de las soluciones resultan no dominadas.
8. CONCLUSIONES Y RECOMENDACIONES
• La metodología NISE de ponderación de funciones que permite la optimización
multiobjetivo permite encontrar las fronteras de Pareto de una manera eficiente y
exhaustiva al permitir encontrar todas las soluciones que pertenecen a esta.
• Se debe proponer en el futuro un índice de confiabilidad que permita comparar de
mejor manera la confiabilidad entre las redes, lo que permita concluir mejor acerca de
la red que se debe construir.
• La metodología propone un conjunto de diseños que pertenecen a una frontera de
Pareto, por lo que la elección de una sola solución es netamente subjetiva.
• Con el fin de que todas las soluciones propuestas en el modelo de selección de trazado
pertenezcan posteriormente a la frontera de Pareto definitiva se debe proponer
modificaciones a los criterios para minimizar el costo que contemplen de una mejor
manera las variables o los costos del diseño hidráulico.
• El tiempo y los recursos computacionales requeridos dependen directamente y
proporcionalmente del tamaño de la red de estudio.
• El uso de estos criterios de minimizar costos no garantiza obtener el menor costo en
el diseño pero si permiten obtener fronteras de Pareto en donde la forma de esta va
acorde a la teoría, en la que el costo asciende a media que la confiabilidad aumenta.
• En todos los casos de estudio se observa que el trazado que tiene la mayor
confiabilidad, a su vez es el diseño que tiene el mayor costo lo cual tiene sentido dentro
de los principios de la optimización multiobjetivo.
• El índice de confiabilidad de Aguilar (2016) permite realizar un mejor análisis del
nivel de confiabilidad de cada uno de los diseños y un mejor apoyo en la toma de
decisiones que el otro índice utilizado en este trabajo.
• El modelo de selección de trazado de Aguilar (2016) permite una mejor descripción
implícita de los costos del diseño hidráulico al generar fronteras de Pareto reales mas
ajustados a lo que se quiere idealmente, a pesar de requerir un tiempo computacional
mayor.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
54
9. BIBLIOGRAFIA:
Aguilar, A. (2016). Evaluación de Funciones Objetivo en una Metodología para el Diseño
Optimizado de Alcantarillados. Bogotá, Colombia: Universidad de los Andes.
Baesler, F., Ceballos, L., & Ramírez, M. (2006). MULTIOBJECTIVE MOLDING
MACHINE SCHEDULING USING MEMETIC ALGORITHMS.
Copete Rivera, D. (2012). Diseño Hidráulico Optimizado de Redes de Alcantarillado
Usando los Conceptos de Potencia Unitaria y Pendiente Lógica. Bogotá, Colombia:
Universidad de los Andes.
Duque, N. (2015). Metodología para el diseño optimizado de alcantarillados. Bogotá,
Colombia: Uniandes.
Duque, N., Duque , D., & Saldarriaga, J. (2015). A new methodology for the optimal
design of series fo pipes on sewer systems. Journal of Hydroinformatics.
Haghighi, A., & Bakhshipour, A. (2016). Reliability-based layout design of sewage
collection systems in flat areas.
Lopes, N., Marchionni , V., Mamouros, L., & Covas, D. (junio de 2014). Modelling Sewer
Systems Costs with Multiple Linear Regression. Portugal: Water Resour Manage .
López Sabogal, D. (2011). Diseño optimizado de redes de drenaje urbano usando el
concepto de potencia unitaria. Bogotá, Colombia: Universidad de los Andes.
Maurer, Scheidegger, & Herlyn. (12 de septiembre de 2012). Quantifying costs and lengths
of urban drainage systems with a simple static sewer. Dubendorf, Suiza: Taylor &
Francis.
Navarro, I. (2009). Diseño Optimizado de Redes de Drenaje Urbano. Bogotá: Universidad
de los Andes.
PAVCO. (2012). Manual Tecnico para Alcantarillados NOVALOC y NOVAFORT.
Salcedo, C. A. (diciembre de 2012). Diseño optimizado de alcantarillados utilizando los
conceptos de resiliencia y potencia unitaria. Bogotá DC.
Saldarriaga, J. (2014). Metodología de selección de trazado de una red de drenaje urbano
optimizado, usando concemto de mínima masa-longitud transportada. Santiago,
Chile.
Salinas, J. M. (2015). Retos a futuro del sector de acueducto y alcantarillado en Colombia.
Obtenido de http://www.cepal.org/publicaciones/xml/3/42733/lcw379e.pdf

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Modelo de Optimización Multiobjetivo para el Diseño de Redes de Drenaje
Urbano
Andrés Felipe Aguilar Suárez
Proyecto de Grado
55
Torres Dueñas, L. F. (2013). Métodos de diseño en redes de alcantarillado: ¿Que se usa hoy
en día? Bogotá: Uniandes.
Zambrano, J. (2018). Diseño Optimizado de Redes de Drenaje Urbano. Casos de Estudio
variando la topografia del terreno. Tesis de Mestría .
Afshar, M. H. (2010) A parameter free Continuous Ant Colony Optimization Algorithm for
the optimal design of storm sewer networks: Constrained and unconstrained
approach. Advances in Engineering Software, 41(2), pp. 188-195, doi:
10.1016/j.advengsoft.2009.09.009.
Moeini, R. and Afshar, M. H. (2012) Layout and size optimization of sanitary sewer network
using intelligent ants. Advances in Engineering Software, 51, pp. 49-62, doi:
10.1016/j.advengsoft.2012.05.003.
Moeini, R. and Afshar, M. H. (2017) Arc Based Ant Colony Optimization Algorithm for
optimal design of gravitational sewer networks. Ain Shams Engineering Journal,
8(2), pp. 207-223, doi: 10.1016/j.asej.2016.03.003.
Yeh, S.-F., Chang, Y.-J. and Lin, M.-D. (2013) Optimal design of sewer network by tabu
search and simulated annealing. in 2013 IEEE International Conference on
Industrial Engineering and Engineering Management. pp. 1636-1640.
Yeh, S.-F., Chu, C.-W., Chang, Y.-J. and Lin, M.-D. (2011) Applying tabu search and
simulated annealing to the optimal design of sewer networks. Engineering
Optimization, 43(2), pp. 159-174, doi: 10.1080/0305215x.2010.482989.
Haghighi, A. and Bakhshipour, A. E. (2015) Deterministic Integrated Optimization Model
for Sewage Collection Networks Using Tabu Search. Journal of Water Resources
Planning and Management, 141(1), pp. 04014045, doi: Artn 04014045
