
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y
Alcantarillados
CIACUA
Modelación numérica del flujo supercrítico en cámaras de
inspección para sistemas de alcantarillado.
Proyecto de grado
Ingeniería Civil
Santiago Arango de Larrañaga
Bogotá, Julio 2012

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
i
ICIV 201210 01
RESUMEN
Esta investigación busca estudiar los mecanismos numéricos disponibles para
resolver el flujo supercrítico que se presenta en las cámaras de inspección de
los sistemas de alcantarillado. Debido a la complejidad del flujo y su entorno
es necesario incluir el fenómeno de la turbulencia en los modelos
matemáticos. De manera que se hace uso de la Dinámica de Fluidos
Computacional (CFD) y de tres modelos de turbulencia para simular
escenarios de flujo que han sido previamente modelados experimentalmente.
Los resultados obtenidos demuestran que el uso de la CFD puede ser muy útil
para los procesos de estudio y diseño de cámaras de inspección en sistemas de
alcantarillado, aunque quedan aspectos por mejorar en cuanto a los procesos
de experimentación y de análisis numérico de estos componentes hidráulicos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
ii
ICIV 201210 01
TABLA DE CONTENIDO
1. INTRODUCCIÓN ................................................................................................................. 1
1.1.
Objetivos ............................................................................................................................. 2
1.1.1.
Objetivo general .......................................................................................................... 2
1.1.2.
Objetivos específicos ................................................................................................... 2
2. ANTECEDENTES ................................................................................................................. 3
2.1.
Dinámica de fluidos computacional .................................................................................... 3
2.2.
Ecuaciones que gobiernan el flujo ...................................................................................... 4
2.2.1.
Ecuación de conservación de la masa ......................................................................... 4
2.2.2.
Ecuación de conservación de momentum .................................................................. 4
2.2.3.
Ecuación de conservación de la energía ..................................................................... 5
2.3.
Flujo multifásico .................................................................................................................. 5
2.4.
El fenómeno de la turbulencia ............................................................................................ 6
2.4.1.
Consideraciones matemáticas sobre el fenómeno de la turbulencia ......................... 6
2.4.2.
Modelación del fenómeno turbulento ........................................................................ 9
2.5.
Investigación de cámaras de inspección bajo condiciones de flujo supercrítico .............. 12
2.5.1.
Modelo hidráulico ..................................................................................................... 12
2.5.2.
Instrumentación del modelo y procedimiento de medición .................................... 15
2.5.3.
Pruebas sobre el modelo hidráulico.......................................................................... 17
2.6.
Clasificación de flujos en canales abiertos: ....................................................................... 19
3. SIMULACIÓN Y MODELO COMPUTACIONAL ..................................................................... 20
3.1.
Diseño a computador del modelo hidráulico: ................................................................... 20
3.2.
Enmallado de la geometría ............................................................................................... 22
3.3.
Selección de escenarios de modelación............................................................................ 24
3.4.
Definición de las condiciones de frontera ......................................................................... 27
4. RESULTADOS ................................................................................................................... 30
4.1.
Escenarios de modelación para Unión de flujos (UF) ....................................................... 30
4.2.
Escenarios de modelación para Flujo Directo (FD) y Flujo a 90° (FN) ............................... 36
4.3.
Comportamiento de los residuos de las ecuaciones fundamentales ............................... 41

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
iii
ICIV 201210 01
5. ANÁLISIS DE RESULTADOS ............................................................................................... 45
5.1.
Perfiles de flujo ................................................................................................................. 45
5.2.
Fenómeno de recirculación ............................................................................................... 48
5.3.
Tiempos de simulación ...................................................................................................... 55
6. CONCLUSIONES ............................................................................................................... 56
7. ANEXOS .......................................................................................................................... 58
7.1.
Escenario de modelación UF-2 .......................................................................................... 58
7.2.
Escenario de modelación UF-3 .......................................................................................... 62
7.3.
Escenario de modelación UF-4 .......................................................................................... 67
7.4.
Escenario de modelación UF-5 .......................................................................................... 72
7.5.
Escenario de modelación FD-3 .......................................................................................... 77
7.6.
Escenario de modelación FD-4 .......................................................................................... 80
7.7.
Escenario de modelación FD-6 .......................................................................................... 84
7.8.
Escenario de modelación FD-8 .......................................................................................... 88
7.9.
Escenario de modelación FN-7 .......................................................................................... 91
7.10.
Escenario de modelación FN-8 ...................................................................................... 94
8. BIBLIOGRAFÍA ................................................................................................................. 99

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
iv
ICIV 201210 01
ÍNDICE DE TABLAS
Tabla 1: Tuberías de entrada y salida a la cámara de inspección. .................................................... 25
Tabla 2: Pruebas a simular, escenario Unión de flujos (UN). ............................................................ 25
Tabla 3: Pruebas a simular, escenario Flujo Directo (FD).. ................................................................ 26
Tabla 4: Pruebas a simular, escenario Flujo a 90° (FN).. ................................................................... 26
Tabla 5: Variables de entrada y variables de salida para los modelos conceptuales. ...................... 27
Tabla 6: Parámetros temporales de simulación. ............................................................................... 30
Tabla 7: Tiempos de simulación para cada escenario. ...................................................................... 30
Tabla 8: Condiciones de flujo para UF-2. .......................................................................................... 31
Tabla 9: Condiciones de flujo para UF-3 ........................................................................................... 31
Tabla 10: Condiciones de flujo para UF-4. ........................................................................................ 32
Tabla 11: Condiciones de flujo para UF-5. ........................................................................................ 32
Tabla 12: Condiciones de flujo para FD-3. ......................................................................................... 37
Tabla 13: Condiciones de flujo para FD-4. ......................................................................................... 37
Tabla 14: Condiciones de flujo para FD-6. ......................................................................................... 37
Tabla 15: Condiciones de flujo para FD-8. ......................................................................................... 37
Tabla 16: Condiciones de flujo para FN-7. ........................................................................................ 37
Tabla 17: Condiciones de flujo para FN-8. ........................................................................................ 37

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
v
ICIV 201210 01
ÍNDICE DE GRÁFICAS
Gráfica 1: Perfil recto de flujo por la línea central para UF-2. .......................................................... 33
Gráfica 2: Perfil recto de flujo por la línea derecha para UF-2. ......................................................... 34
Gráfica 3: Perfil recto de flujo por la línea de flujo izquierda para UF-2........................................... 34
Gráfica 4: Perfil curvo de flujo por la línea central para UF-2. .......................................................... 35
Gráfica 5: Perfil curvo de flujo por la línea derecha para UF-2. ........................................................ 35
Gráfica 6: Perfil curvo de flujo por la línea izquierda para UF-2. ...................................................... 36
Gráfica 7: Perfil recto de flujo por la línea central para FD-4. .......................................................... 39
Gráfica 8: Perfil recto de flujo por línea derecha para FD-4 ............................................................. 39
Gráfica 9: Perfil recto de flujo por línea izquierda para FD-4. ........................................................... 40

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
vi
ICIV 201210 01
ÍNDICE DE FIGURAS
Figura 1: Variaciones en la velocidad. ................................................................................................. 7
Figura 2: Montaje experimental de la cámara de inspección. .......................................................... 13
Figura 3: Forma de la cañuela.. ......................................................................................................... 13
Figura 4: Configuraciones de caídas. ................................................................................................. 14
Figura 5: Estructura de medición.. .................................................................................................... 16
Figura 6: Estructura de medición al interior de la cámara. ............................................................... 16
Figura 7: Resultados para escenario UF-6 (Dinámica del flujo). ....................................................... 18
Figura 8: Modelo computacional de la cámara de inspección. ......................................................... 21
Figura 9: Vista lateral de tubería de entrada principal y tubería de salida. ...................................... 22
Figura 10: Vista lateral de tubería de entrada lateral. ...................................................................... 22
Figura 11: Cañuela del modelo computacional. ................................................................................ 22
Figura 12: Superficie del enmallado de la cámara de inspección. .................................................... 23
Figura 13: Elementos internos del enmallado. ................................................................................. 23
Figura 14: Inflación al interior del dominio. ...................................................................................... 24
Figura 15: Inflación en tubería de entrada principal ......................................................................... 24
Figura 16: Relaciones geométricas para tubería parcialmente llena. ............................................... 26
Figura 17: Perfiles recto y curvo de flujo en UF-2. ............................................................................ 28
Figura 18: Plano de corte para perfil recto de flujo por línea central ............................................... 31
Figura 19: Planos de corte para perfil curvo de flujo por línea central ............................................. 31
Figura 20: Superficie del flujo en UF-2. Modelo k-ε estándar. .......................................................... 32
Figura 21: Superficie del flujo en UF-2. Modelo k-ε RNG. ................................................................. 32
Figura 22: Superficie del flujo en UF-2. Modelo k-ω. ........................................................................ 33
Figura 23: Superficie del flujo en FD-4. Modelo k-ε estándar. .......................................................... 38
Figura 24: Superficie del flujo en UFD-4. Modelo k-ε RNG. .............................................................. 38
Figura 25: Superficie del flujo en FD-4. Modelo k-ω. ........................................................................ 38
Figura 26: Residuos para FN-8, modelo k-ε estándar. ...................................................................... 42

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
vii
ICIV 201210 01
Figura 27: Residuos para FN-8, modelo k-ε RNG. ............................................................................. 42
Figura 28: Residuos para FN-8, modelo k-ω. ..................................................................................... 42
Figura 29: Residuos para FD-4, modelo k-ε estándar. ...................................................................... 43
Figura 30: Residuos para FD-4, modelo k-ε RNG. ............................................................................. 43
Figura 31: Residuos para FD-4, modelo k-ω. ..................................................................................... 43
Figura 32: Residuos para FD-6, modelo k-ε estándar. ...................................................................... 44
Figura 33: Residuos para FD-6, modelo k-ε RNG. ............................................................................. 44
Figura 34: Residuos para FD-6, modelo k-ω. ..................................................................................... 44
Figura 35: Formación de onda C en UF-2. Modelo k-ω de turbulencia. ........................................... 47
Figura 36: Zonas de formación de ondas estacionarias. ................................................................... 48
Figura 37: Vórtices i recirculación en escenario FN-7. ...................................................................... 49
Figura 38: Vórtices o recirculación en escenario FN-8. ..................................................................... 49
Figura 39: Vórtices o recirculación en escenario FD-3. ..................................................................... 50
Figura 40: Vórtices o recirculación en escenario FD-4. ..................................................................... 51
Figura 41: Vórtices o recirculación en escenario FD-6. ..................................................................... 51
Figura 42: Vórtices o recirculación en escenario FD-8. ..................................................................... 52
Figura 43: Vórtices o recirculación en escenario UF-2. ..................................................................... 53
Figura 44: Vórtices o recirculación en escenario UF-3. ..................................................................... 53
Figura 45: Vórtices o recirculación en escenario UF-4. ..................................................................... 54

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
viii
ICIV 201210 01
ÍNDICE DE FOTOS
Foto 1: Formación de una Onda C en el punto de confluencia de los flujos, para el escenario UF-2
................................................................................................................................................... 47

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
ix
ICIV 201210 01
ÍNDICE DE GRÁFICAS EN ANEXOS
Gráfica anexa 1: Perfil recto de flujo por línea central para UF-2. .................................................... 60
Gráfica anexa 2: Perfil recto de flujo por línea derecha para UF-2. .................................................. 60
Gráfica anexa 3: Perfil recto de flujo por línea izquierda para UF-2. ................................................ 61
Gráfica anexa 4: Perfil curvo de flujo por la línea central para UF-2. ............................................... 61
Gráfica anexa 5: Perfil curvo de flujo por línea derecha para UF-2. ................................................. 62
Gráfica anexa 6: Perfil curvo de flujo por línea izquierda para UF-2. ............................................... 62
Gráfica anexa 7: Perfil recto de flujo por línea central para UF-3. .................................................... 65
Gráfica anexa 8: Perfil recto de flujo por línea derecha para UF-3. .................................................. 65
Gráfica anexa 9: Perfil recto de flujo por línea izquierda para UF-3. ................................................ 66
Gráfica anexa 10: Perfil curvo de flujo por la línea central para UF-3. ............................................. 66
Gráfica anexa 11: Perfil curvo de flujo por línea derecha para UF-3. ............................................... 67
Gráfica anexa 12: Perfil curvo de flujo por línea izquierda para UF-3. ............................................. 67
Gráfica anexa 13: Perfil recto de flujo por línea central para UF-4. .................................................. 70
Gráfica anexa 14: Perfil recto de flujo por línea derecha para UF-4. ................................................ 70
Gráfica anexa 15: Perfil recto de flujo por línea izquierda para UF-4. .............................................. 71
Gráfica anexa 16: Perfil curvo de flujo por línea central para UF-4. ................................................. 71
Gráfica anexa 17: Perfil curvo de flujo por línea derecha para UF-4. ............................................... 72
Gráfica anexa 18: Perfil curvo de flujo por línea izquierda para UF-4. ............................................. 72
Gráfica anexa 19: Perfil recto de flujo por línea central para UF-5. .................................................. 75
Gráfica anexa 20: Perfil recto de flujo por línea derecha para UF-5. ................................................ 75
Gráfica anexa 21: Perfil recto de flujo por línea izquierda para UF-5. .............................................. 76
Gráfica anexa 22: Perfil curvo de flujo por línea central para UF-5. ................................................. 76
Gráfica anexa 23: Perfil curvo de flujo por línea derecha para UF-5. ............................................... 77
Gráfica anexa 24: Perfil curvo de flujo por línea izquierda para UF-5. ............................................. 77
Gráfica anexa 25: Perfil recto de flujo por la línea central para FD-3. .............................................. 80
Gráfica anexa 26: Perfil recto de flujo por línea izquierda para FD-3. .............................................. 80

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
x
ICIV 201210 01
Gráfica anexa 27: Perfil recto de flujo por línea central para FD-4. .................................................. 83
Gráfica anexa 28: Perfil recto de flujo por línea derecha para FD-4. ................................................ 83
Gráfica anexa 29: Perfil recto de flujo por línea izquierda para FD-4. .............................................. 84
Gráfica anexa 30: Perfil recto de flujo por línea central para FD-6. .................................................. 86
Gráfica anexa 31: Perfil recto de flujo por línea derecha para FD-6. ................................................ 87
Gráfica anexa 32: Perfil recto de flujo por línea izquierda para FD-6. .............................................. 87
Gráfica anexa 33: Perfil recto de flujo por línea central para FD-8. .................................................. 90
Gráfica anexa 34: Perfil recto de flujo por línea derecha para FD-8. ................................................ 90
Gráfica anexa 35: Perfil recto de flujo por línea izquierda para FD-8. .............................................. 91
Gráfica anexa 36: Perfil curvo de flujo por línea central para FN-7. ................................................. 93
Gráfica anexa 37: Perfil curvo de flujo por línea derecha para FN-7. ............................................... 94
Gráfica anexa 38: Perfil curvo de flujo por línea izquierda para FN-7. ............................................. 94
Gráfica anexa 39: Perfil curvo de flujo por línea central para FN-8. ................................................. 97
Gráfica anexa 40: Perfil curvo de flujo por línea derecha para FN-8. ............................................... 97
Gráfica anexa 41: Perfil curvo de flujo por línea izquierda para FN-8. ............................................. 98

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
xi
ICIV 201210 01
ÍNDICE DE FIGURAS EN ANEXOS
Figura anexa 1: Superficie del flujo en UF-2. Modelo k-ε estándar. ................................................. 58
Figura anexa 2: Superficie del flujo en UF-2. Modelo k-ε RNG. ........................................................ 58
Figura anexa 3: Superficie del flujo en UF-2. Modelo k-ω. ............................................................... 59
Figura anexa 4: Patrón de flujo tridimensional para UF-2. ............................................................... 59
Figura anexa 5: Superficie del flujo en UF-3. Modelo k-ε estándar. ................................................. 63
Figura anexa 6: Superficie del flujo en UF-3. Modelo k-ε RNG. ........................................................ 63
Figura anexa 7: Superficie del flujo en UF-3. Modelo k-ω ................................................................ 64
Figura anexa 8: Patrón de flujo tridimensional para UF-3. ............................................................... 64
Figura anexa 9: Superficie del flujo en UF-4. Modelo k-ε estándar. ................................................. 68
Figura anexa 10: Superficie del flujo en UF-4. Modelo k-ε RNG. ...................................................... 68
Figura anexa 11: Superficie del flujo en UF-4. Modelo k-ω .............................................................. 69
Figura anexa 12: Formación de un resalto en la tubería principal. ................................................... 69
Figura anexa 13: Superficie del flujo en UF-5. Modelo k-ε estándar. ............................................... 73
Figura anexa 14: Superficie del flujo en UF-5. Modelo k-ε RNG. ...................................................... 73
Figura anexa 15: Superficie del flujo en UF-5. Modelo k-ω. ............................................................. 74
Figura anexa 16: Formación de un resalto en la tubería principal. ................................................... 74
Figura anexa 17: Superficie del flujo en FD-3. Modelo k-ε estándar. ............................................... 78
Figura anexa 18: Superficie del flujo en FD-3. Modelo k-ε RNG. ...................................................... 78
Figura anexa 19: Superficie del flujo en FD-3. Modelo k-ω. ............................................................. 79
Figura anexa 20: Patrón de flujo tridimensional para FD-3. ............................................................. 79
Figura anexa 21: Superficie del flujo en FD-4. Modelo k-ε estándar. ............................................... 81
Figura anexa 22: Superficie del flujo en FD-4. Modelo k-ε RNG. ...................................................... 81
Figura anexa 23: Superficie del flujo en FD-4. Modelo k-ω. ............................................................. 82
Figura anexa 24: Patrón de flujo tridimensional para FD-4. ............................................................. 82
Figura anexa 25: Superficie del flujo en FD-6. Modelo k-ε estándar. ............................................... 84
Figura anexa 26: Superficie del flujo en FD-6. Modelo k-ε RNG ....................................................... 85

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
xii
ICIV 201210 01
Figura anexa 27: Superficie del flujo en FD-6. Modelo k-ω. ............................................................. 85
Figura anexa 28: Patrón de flujo tridimensional para FD-6. ............................................................. 86
Figura anexa 29: Superficie del flujo en FD-8. Modelo k-ε estándar. ............................................... 88
Figura anexa 30: Superficie del flujo en FD-8. Modelo k-ε RNG ....................................................... 88
Figura anexa 31: Superficie del flujo en FD-8. Modelo k-ω. ............................................................. 89
Figura anexa 32: Patrón de flujo tridimensional para FD-8. ............................................................. 89
Figura anexa 33: Superficie del flujo en FN-7. Modelo k-ε estándar. ............................................... 91
Figura anexa 34: Superficie del flujo en FN-7. Modelo k-ε RNG ....................................................... 92
Figura anexa 35: Superficie del flujo en FN-7. Modelo k-ω .............................................................. 92
Figura anexa 36: Patrón de flujo tridimensional. .............................................................................. 93
Figura anexa 37: Superficie del flujo en FN-8. Modelo k-ε estándar. ............................................... 95
Figura anexa 38: Superficie del flujo en FN-8. Modelo k-ε RNG. ...................................................... 95
Figura anexa 39: Superficie del flujo en FN-8. Modelo k-ω. ............................................................. 96
Figura anexa 40: Patrón de flujo tridimensional. .............................................................................. 96

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
1
ICIV 201210 01
1. INTRODUCCIÓN
Las cámaras de inspección son estructuras hidráulicas utilizadas para unir, ventilar, inspeccionar y
darle mantenimiento a las tuberías de un sistema de alcantarillado (Centro de Investigaciones de
Acueductos y Alcantarillados - CIACUA, 2010), por lo que estudiar y modelar el comportamiento
hidráulico en este tipo de elementos es fundamental para asegurar un diseño de sistemas de
alcantarillado eficientes y de bajo costo, evitando problemas de desbordamiento y afloramiento del
agua a la superficie.
El flujo de entrada a una cámara de inspección puede ser subcrítico o supercrítico. Cuando el
régimen del flujo en la unión o entrada de la cámara es subcrítico existen ecuaciones analíticas que
permiten estudiar el comportamiento del fluido en interacción con su entorno. Pero, cada vez es más
común encontrar condiciones de flujo supercrítico a la entrada de la cámara debido a las crecientes
demandas y a la baja rugosidad de los materiales poliméricos que se utilizan en la actualidad para la
construcción de estas estructuras. Además, en la actualidad, el diseño de cámaras de inspección no
tiene en cuenta la presencia de flujo supercrítico debido a que no existe una función analítica que
correlaciones los distintos parámetros involucrados en el estudio de este tipo de flujos (Centro de
Investigaciones de Acueductos y Alcantarillados - CIACUA, 2010).
La complicación en estos flujos se debe a la turbulencia, un fenómeno físico y matemático de gran
complejidad ocasionado por el efecto de la viscosidad y las altas velocidades, que le confiere al
fluido un estado de movimiento caótico y aleatorio que a la fecha solo ha podido ser modelado de
manera exacta en casos sencillos, que no tienen la complejidad geométrica de los problemas que
normalmente se enfrentan en ingeniería. En consecuencia, se debe recurrir a distintos modelos
numéricos de turbulencia que han sido desarrollados para geometría y condiciones de flujo
particulares.
En el año 2010, el Centro de Investigación en Acueductos y Alcantarillados de la Universidad de
los Andes (CIACUA) realizó una investigación experimental con el fin de “explicar el
comportamiento hidráulico de las cámaras de inspección de un sistema de alcantarillado bajo
condiciones de flujo supercrítico, y así poder establecer ecuaciones que permitan una metodología
de diseño adecuada de estas estructuras” (Centro de Investigaciones de Acueductos y
Alcantarillados - CIACUA, 2010).
En la actualidad, la manera más común de estudiar y caracterizar el comportamiento hidráulico de
cámaras de inspección bajo condiciones de flujo supercrítico es a través de la experimentación, pero
este tipo de aproximación resulta muy costosa. En consecuencia, dado que no existen ecuaciones
analíticas que permitan modelar el comportamiento hidráulico de cámaras de inspección bajo
condiciones de flujo supercrítico teniendo en cuenta el fenómeno de la turbulencia, una
aproximación matemática requiere utilizar modelos numéricos y herramientas computacionales a
fin de lograr un análisis adecuado que permita estudiar la dinámica del flujo a la vez que se
economiza en recursos humanos, temporales y técnicos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
2
ICIV 201210 01
Este proyecto de grado busca entonces utilizar algunos de los mecanismos numéricos y
computacionales disponibles en la actualidad para simular el flujo con superficie libre que se
presenta en las cámaras de inspección de los sistemas de drenaje y alcantarillado de la ciudad de
Bogotá y comparar los resultados obtenidos con mediciones experimentales a fin de evaluar
distintos modelos computacionales y establecer la validez de los mismos. En primera instancia, se
realiza una aproximación a los conceptos básicos de la Mecánica de Fluidos, incluyendo el
fenómeno de la turbulencia y las ecuaciones y conceptos físicos de cada uno de los modelos de
turbulencia que se utilizarán para llevar a cabo las simulaciones. A continuación, se procede con
una introducción al proyecto experimental desarrollado por el CIACUA (Centro de Investigación en
Acueductos y Alcantarillados de la Universidad de los Andes) sobre el comportamientos hidráulico
de cámaras de inspección bajo condiciones de flujo supercrítico, que llevó al desarrollo de este
proyecto, junto con una descripción de la geometría de la cámara de inspección trabajada por el
CIACUA y la selección de los escenarios experimentales que se estudiaron y simularon con el uso
de la Mecánica de Fluidos Computacional (CFD). Posteriormente, se realiza un descripción detalla
del proceso de simulación, incluyendo la geometría y malla, los parámetros utilizados, las
condiciones de frontera y demás. Finalmente, se procede con el análisis de los resultados obtenidos
y conclusiones sobre los mismos.
1.1. Objetivos
1.1.1. Objetivo general
Desarrollar un modelo matemático que corrobore los resultados obtenidos por el CIACUA a partir
de los modelos físicos de cámaras de inspección, de manera que se pueda establecer una
metodología de diseño confiable para este tipo de estructuras hidráulicas.
1.1.2. Objetivos específicos
Simulación de un flujo con superficie libre a través de una cámara de inspección de aguas
residuales con CDF para relaciones de llenado superiores al 20% en las tuberías de entrada
a la cámara.
Validación, uso y calibración del modelo computacional implementado a partir de un
estudio realizado en el 2010 por la Universidad de los Andes que reporta mediciones
realizadas sobre un modelo físico de una cámara de inspección de aguas residuales.
Comparación de 3 modelos computacionales de turbulencia bajo la evaluación de diferentes
parámetros tales como costo computacional, errores respecto a los resultados
experimentales, perfiles de flujo, el comportamiento de la capa límite turbulenta en las
paredes de la cámara, etc. a fin de establecer cual modelo de turbulencia es más adecuado
para la simulación de flujo libre a través de cámaras de inspección.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
3
ICIV 201210 01
2. ANTECEDENTES
2.1. Dinámica de fluidos computacional
Dinámica de Fluidos Computacional o CFD (por sus siglas en inglés) se refiere al análisis de
sistemas que involucran el flujo de fluidos, la transferencia de calor o fenómenos asociados a estos
mediante el uso de simulaciones desarrolladas por computador (H. K. Versteeg, 2007). A pesar de
ser una herramienta relativamente reciente, ha demostrado ser de gran utilidad para el desarrollo de
la ingeniería. Dentro de sus numerosas aplicaciones se cuenta el diseño de componentes de uso
aeroespacial, náutico, aeronáutico y terrestre; el estudio de distintos fenómenos tales como la
cavitación, la turbulencia, la combustión y los procesos químicos de mezclado; el estudio y
desarrollo de tecnologías para distintas disciplinas como la bioingeniería, la hidráulica, la
meteorología y la ingeniería aeroespacial, entre otras.
Como lo explica H. K. Versteeg en su texto sobre CFD (H. K. Versteeg, 2007), la mayoría de
códigos comerciales se componen de tres etapas o módulos principales. La primera etapa consiste
en el Pre-procesamiento del problema, donde se define la geometría del volumen de control, se
lleva a cabo una subdivisión de la geometría en subdominios y/o elementos muy pequeños, se
seleccionan los fenómenos físicos y químicos a modelar, se definen las propiedades del fluido y se
especifican las condiciones de frontera. La segunda etapa o segundo módulo consiste en la solución
del sistema de ecuaciones expresadas de manera algebraica para cada uno de los puntos del dominio
generados por la subdivisión en elementos pequeños mediante algún método numérico, como
diferencias finitas, elementos finitos o volúmenes finitos. A esta etapa se la conoce como
Solucionador. Finalmente, en el último módulo, comúnmente llamado Post-procesamiento, se lleva
a cabo la visualización y manipulación de la información producida durante las etapas previas.
Para el desarrollo de este proyecto se hace uso de un programa computacional llamado ANSYS
CFX, desarrollado por ANSYS Inc., y que se basa en el método de los volúmenes de control finitos,
el método más utilizado en programas de CFD de gran reputación. El profesor Y. Niño de la
Universidad de Chile ilustra el método de manera muy adecuada (Niño, 2002):
“Consideremos una malla de discretización del espacio fluido. En torno a cada
punto de esta malla se construye un volumen de control que no se traslapa con los
de los puntos vecinos. De esta forma el volumen total de fluido resulta ser igual a la
suma de los volúmenes de control considerados. La ecuación diferencial a resolver
se integra sobre cada volumen de control, lo cual entrega como resultado una
versión discretizada de dicha ecuación. Para realizar la integración se requiere
especificar perfiles de variación de la variable dependiente entre los puntos de la
malla, de modo de poder evaluar las integrales resultantes. La principal propiedad
del sistema de ecuaciones discretizadas resultante, es que la solución obtenida
satisface en forma exacta las ecuaciones de conservación consideradas,
independientemente del tamaño de la malla.”

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
4
ICIV 201210 01
2.2. Ecuaciones que gobiernan el flujo
Las ecuaciones fundamentales de la Mecánica de Fluidos se conocen como la ecuación de
continuidad, la ecuación de energía y las ecuaciones de momentum, que aplicadas al caso de flujos
incompresibles se denominan como "ecuaciones de Navier-Stokes" (Panton, 2005). A continuación
se presenta una descripción general de cada una de estas ecuaciones fundamentales.
2.2.1. Ecuación de conservación de la masa
La ecuación de continuidad, también conocida como ecuación de conservación de la masa, se deriva
del balance de masa en un elemento del flujo, y establece que la tasa de incremento de masa en el
elemento debe ser igual a la tasa neta de flujo de masa que sale del elemento. La ecuación general,
en notación vectorial, para un punto cualquiera de un fluido es la siguiente.
𝜕𝜌
𝜕𝑡
+ ∇ ∙ (𝜌𝑼) = 0
(1.1)
donde ρ es la densidad del fluido en el punto y U es el vector de velocidades.
2.2.2. Ecuación de conservación de momentum
La ley de conservación de momentum se deriva de la segunda ley de Newton y establece que la tasa
de incremento de momentum de una partícula debe ser igual a la suma de las fuerzas sobre la
partícula. Mediante la aproximación de Euler se obtiene la siguiente expresión vectorial.
𝜕(𝜌𝑼)
𝜕𝑡
+ ∇ ∙ (𝜌𝑼⨂𝑼) = −∇𝑝 + ∇ ∙ 𝜏 + 𝑺
𝑴
(1.2)
donde el operador
⨂ corresponde al producto tensorial, p es la presión, S
M
es la fuente de
momentum por unidad de volumen por unidad de tiempo debido a fuerzas ejercidas sobre el cuerpo,
y τ representa el tensor de esfuerzos viscosos que se relaciona con la tasa de deformación del fluido
mediante la ecuación que sigue.
𝜏 = 𝜇 (∇𝑼 + (∇𝑼)
𝑇
−
2
3
𝛿∇ ∙ 𝑼)
(1.3)
En la Ecuación 1.3 µ hace referencia a la viscosidad dinámica y δ es la matriz identidad definida
por:
𝛿 = [
1 0 0
0 1 0
0 0 1
]

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
5
ICIV 201210 01
2.2.3. Ecuación de conservación de la energía
La ecuación de conservación de la energía es fundamental pues todo escenario de flujo debe
cumplir con la primera ley de la termodinámica. Lo anterior quiere decir que la tasa de cambio de
la energía de una partícula de un fluido debe ser igual a la tasa de calor añadido a la partícula más la
tasa de trabajo realizado sobre la partícula. Lo anterior, mediante la aproximación de Euler, se
resume en la siguiente ecuación vectorial:
𝜕𝜌
𝜕𝑡
+ ∇ ∙ (𝜌𝑼) = ∇ ∙ (𝜆∇𝑇) + ∇ ∙ (𝑈 ∙ 𝜏) + 𝑺
𝑬
+ 𝑼 ∙ 𝑺
𝑴
(1.4)
donde λ corresponde a la conductividad térmica, U∙S
M
representa el trabajo debido a fuentes
externas de momentum y S
E
son las fuentes de energía por unidad de volumen por unidad de
tiempo.
2.3. Flujo multifásico
El flujo multifásico se presenta cuando hay interacción de dos o más fluidos en el dominio de
estudio. Un ejemplo claro son las cámaras de inspección de los sistemas de alcantarillado, pues los
sistemas alcantarillado están diseñados para trabajar parcialmente llenos, generalmente bajo
relaciones de llenado menores al 75%. Se presenta entonces flujo de agua y aire, tanto en las
tuberías de entrada y salida como en la cámara misma. Ambos fluidos están divididos por una
interfaz claramente definida. Esto es lo que se conoce como flujo con superficie libre.
El flujo con superficie libre es un caso específico de flujo estratificado en tuberías, pero existe una
gran variedad de flujos multifásicos tales como la lluvia, un aerosol o el transporte de sedimentos.
Estos últimos se conocen como flujo disperso. La modelación de flujos multifásicos puede ser
aproximada mediante varios modelos, pero para el caso específico de flujo segregado, como lo es el
flujo con superficie libre, el modelo generalmente utilizado es el Modelo Euleriano-Euleriano
(EEM), ya que permite lo siguiente (Bakker, 2002):
Mezcla y separación de fases.
Resuelve las ecuaciones de momentum, de continuidad y energía para cada una de las fases
y realiza un seguimiento de la fracción de volumen de cada una de las fases.
Utiliza un único campo de presión para todas las fases.
Permite transferencia de calor y masa entre las fases.
Permite resolver las ecuaciones de turbulencia para cada fase.
Como lo explica la guía de modelación de ANSYS CFX (ANSYS Inc., 2010), cada fase tiene un
campo de flujo propio e interactúan entre ellos mediante términos de transferencia por la interfaz,
como el arrastre. Pero cuando la tasa de transferencia a través de la interfaz es muy alta, las fases en
contacto comparten un campo único de flujo, además de otras propiedades como la temperatura y la
turbulencia. Este caso particular de flujo se conoce como flujo multifásico homogéneo y permite

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
6
ICIV 201210 01
realizar simplificaciones importantes sobre el modelo original. Algunas de las aplicaciones del
Modelo Homogéneo son las siguientes:
Flujo bajo el efecto de la gravedad donde las fases están completamente segregadas. Por
ejemplo el flujo con superficie libre, donde la interfaz está bien definida.
Flujo dominado por el arrastre, donde el campo de velocidades de ambas fases se igualan en
escalas espaciales muy pequeñas.
En consecuencia, para flujo con superficie libre, como el que se presenta en cámaras de inspección
de sistemas de alcantarillado, es adecuado utilizar el Modelo Homogéneo. En la guía teórica de
ANSYS CFX (ANSYS Inc., 2010) se puede encontrar información detallada sobre el tratamiento
matemático que realiza el Modelo Homogéneo EEM a las ecuaciones fundamentales para
problemas de flujo multifásico.
2.4. El fenómeno de la turbulencia
Como lo explica White en su texto Fluid Mechanics (White, 2008), en el campo de la Mecánica de
Fluidos solo existen unas pocas soluciones particulares conocidas que se derivan de no tener en
cuenta fenómenos como la viscosidad o compresibilidad, pero en la realidad son pocas las
situaciones en que se presentan flujos bajo estas condiciones ideales. Es más común encontrarse con
situaciones en que el efecto de la viscosidad y las altas velocidad producen fenómenos turbulentos
que deben ser tenidos en cuenta durante el análisis a fin de obtener resultados coherentes. Ahora,
aunque las ecuaciones de Navier-Stokes contemplan el fenómeno de la turbulencia, aún no se sabe
si exista una solución o no se conoce la solución analítica de las mismas, y en la actualidad no se
cuenta con los recursos computacionales necesarios para intentar resolverlas mediante modelos
numéricos. Es entonces necesario recurrir a herramientas computacionales que permiten obtener
soluciones aproximadas de las ecuaciones de Navier-Stokes. Pero se debe tener cuidado al
manipular estas herramientas, pues debido a la complejidad del fenómeno de la turbulencia los
modelos computacionales han sido desarrollados para geometrías y condiciones de flujo
particulares, por lo que pueden ser muy precisos en ciertas ocasiones pero en otras pueden resultar
inadecuados (White, 2008). De manera que es una práctica común probar varios modelos de
turbulencia al estudiar una condición de flujo particular. Algunos de los modelos de turbulencia que
existen en la actualidad, en particular aquellos que se utilizan durante el desarrollo de este proyecto
son: el modelo k-ε estándar, el modelo k-ε RNG y el modelo Wilcox k-ω.
2.4.1. Consideraciones matemáticas sobre el fenómeno de la turbulencia
En su libro sobre flujo viscoso, White realiza una descripción muy adecuada sobre las
características físicas que presenta un flujo turbulento:
Fluctuaciones en la presión, en las tres componentes del campo de velocidades y en la
temperatura cuando hay transferencia de calor.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
7
ICIV 201210 01
Remolinos en un amplio rango de escalas espaciales que se mezclan con y llenan la capa de
corte.
Variación aleatoria en forma particular de las propiedades de un fluido.
La turbulencia es un fenómeno autónomo, ya que general remolinos para remplazar
aquellos que se disipan por mecanismos como la viscosidad.
Los remolinos turbulentos se mueven en las tres direcciones del flujo, ocasionando una
rápida difusión de masa, momentum y energía. En consecuencia es un fenómeno de mezcla
mucho más fuerte que el que ocurre por acción molecular.
Y explica que es común, en el análisis de la turbulencia, realizar una diferenciación entre el valor
promedio en el tiempo y las fluctuaciones de cualquier propiedad de un flujo, a fin de poder estimar
los promedios en el tiempo de las propiedades primarias. A continuación se muestra una imagen de
variaciones en la velocidad en la dirección de flujo (Dirección X) debido a la turbulencia:
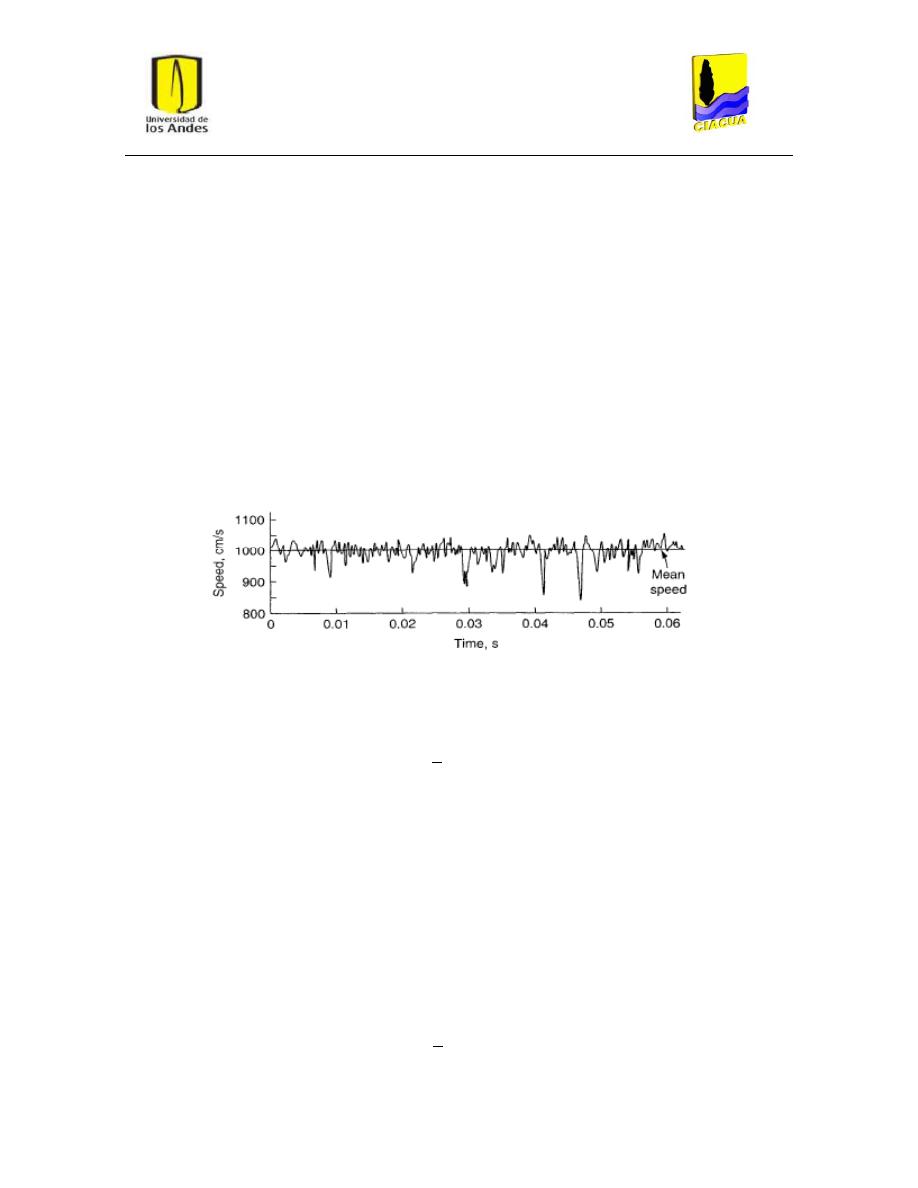
Figura 1: Variaciones en la velocidad. Tomado de (White F. M., 2006).
De
la Figura 1, se puede definir la velocidad promedio como:
𝑢̅ =
1
𝑇
∫
𝑈 𝑑𝑡
𝑡
𝑜
+𝑇
𝑡
𝑜
(1.5)
donde U es la velocidad es cualquier punto y T equivale a un intervalo mayor a cualquier periodo
significante de fluctuaciones en u. Adicionalmente, se define que las fluctuaciones u’ son el residuo
de restar la velocidad media en cualquier instante de tiempo.
𝑢
′
= 𝑈 − 𝑢̅
(1.6)
El promedio de las fluctuaciones en el tiempo debe ser igual a cero,
𝑢′
̅ = 0. Pero en general el
producto del promedio de fluctuaciones en direcciones diferentes (
𝑢′𝑣′
̅̅̅̅̅,…) no es cero, como
tampoco lo es el promedio del cuadrado de las fluctuaciones, que se define por la siguiente
ecuación.
𝑢′
2
̅̅̅̅ =
1
𝑇
∫
𝑢′
2
𝑑𝑡
𝑡
𝑜
+𝑇
𝑡
𝑜
(1.7)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
8
ICIV 201210 01
Se dice que las fluctuaciones son estáticamente estacionarias cuando las Ecuaciones 1.5 y 1.7 no
dependen de t
0
.
De lo anterior es posible definir la energía cinética k debida a la turbulencia y la “Intensidad de la
turbulencia” T
i
. La primera corresponde a la energía cinética total por unidad de masa contenida en
las respectivas fluctuaciones de velocidad, mientras que la segunda se refiere a la cantidad relativa
de intensidad de la turbulencia en cada una de las direcciones del flujo respecto a una velocidad de
referencia denominada U
ref
. La energía cinética debida a la turbulencia en cualquier punto del flujo
se define como:
𝑘 =
1
2
(𝑢′
2
̅̅̅̅ + 𝑣′
2
̅̅̅̅ + 𝑤′
2
̅̅̅̅̅)
(1.8)
donde v corresponde al componente del campo de velocidades en la dirección Y y w corresponde a
la velocidad en la dirección Z, dado que el vector de velocidades está definido por
𝑼 = (𝑈, 𝑉, 𝑊).
Y la intensidad de la turbulencia se relaciona con la energía cinética k mediante la Ecuación 1.9.
𝑇
𝑖
=
√
2
3
𝑘
𝑈
𝑟𝑒𝑓
(1.9)
En 1895, Osborne Reynolds replanteó las ecuaciones fundamentales para flujo incompresible en
términos de las propiedades primarias promediadas en el tiempo, como lo indican las Ecuaciones
1.10.
𝒖 = 𝑼 + 𝒖
′
𝑢 = 𝑈 + 𝑢
′
𝑣 = 𝑉 + 𝑣
′
𝑤 = 𝑊 + 𝑤
′
𝑝 = 𝑃 + 𝑝
′
𝜑 = 𝚽 + 𝜑′
(1.10)
El resultado de son las ecuaciones de Navier-Stokes promediadas en el tiempo, o ecuaciones RANS
(Reynolds-Averaged Navier-Stokes equations). Las ecuaciones RANS eliminan las escalas de
pequeña resolución y reducen significativamente el costo computacional, pero debido a la no
linealidad de las ecuaciones de Navier-Stokes, al promediar las propiedades fundamentales del flujo
en el tiempo y reemplazarlas en las ecuaciones fundamentales surgen incógnitas adicionales que
deben ser modeladas mediante ecuaciones adicionales, como se verá más adelante. Los términos
adicionales se denominan esfuerzos de Reynolds o esfuerzos turbulentos. Se componen de tres
esfuerzos normales (Ecuación 1.11) y de tres esfuerzos cortantes (Ecuación 1.12), y son los
responsables de las variaciones de la velocidad en cada una de las direcciones del flujo, en
consecuencia son los términos responsables de la turbulencia.
𝜏
𝑥𝑥
= −𝜌𝑢′
2
̅̅̅̅ 𝜏
𝑦𝑦
= −𝜌𝑣′
2
̅̅̅̅ 𝜏
𝑧𝑧
= −𝜌𝑤′
2
̅̅̅̅̅
(1.11)
𝜏
𝑥𝑦
= 𝜏
𝑦𝑥
= −𝜌𝑢′𝑣′
̅̅̅̅̅ 𝜏
𝑥𝑧
= 𝜏
𝑧𝑥
= −𝜌𝑢′𝑤′
̅̅̅̅̅̅ 𝜏
𝑦𝑧
= 𝜏
𝑧𝑦
= −𝜌𝑣′𝑤′
̅̅̅̅̅̅
(1.12)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
9
ICIV 201210 01
Para mayor detalle sobre las ecuaciones RANS, el proceso matemático que lleva al desarrollo de
estas, las funciones de correlación para tiempo y espacio o la función de probabilidad de la
densidad, referirse al texto de (H. K. Versteeg, 2007).
2.4.2. Modelación del fenómeno turbulento
Existen tres maneras de aproximarse a la modelación de la turbulencia. La primera se denomina
Simulación Numérica Directa (DNS por sus siglas en inglés) y no es propiamente un modelo ya que
resuelve las ecuaciones fundamentales del flujo sin utilizar promedios. De manera que simulaciones
de este tipo requieren procesos de enmallados dispendiosos, pues se deben asegurar elementos tan
pequeños que puedan resolver las escalas pequeñas de la turbulencia, además de recursos
computacionales enormes. La segunda aproximación se denomina LES (Large Eddy Simulation) y
consiste en filtrar las ecuaciones que gobiernan el flujo de manera que se resuelve el movimiento
turbulento de remolinos de gran escala, mientras que para escalas pequeñas que utiliza un modelo
que recrea de manera aproximada la influencia de los pequeños remolinos sobre las variaciones de
los parámetros primarios del flujo. Esta aproximación es computacionalmente menos costosa que la
DNS, pero aun así requiere muchos recursos para almacenamiento y desarrollo de cálculos en zonas
cercanas a las paredes. Finalmente, la aproximación más común en la actualidad y la menos costosa
computacionalmente, son los modelos de turbulencia desarrollados en torno a las ecuaciones
RANS. Esta aproximación resuelve las ecuaciones de Navier-Stokes promediadas en el tiempo y
modela los términos adicionales, conocidos como esfuerzos de Reynolds, mediante diferentes
modelos que pueden ser de una, dos o más ecuaciones, dependiendo de la cantidad de ecuaciones
diferenciales parciales que se utilicen para resolver estas incógnitas adicionales.
Debido a que la mayoría de modelos computacionales modernos se desarrollan con base en las
ecuaciones RANS, y a que el costo computacional de estos modelos es significativamente menor al
de las demás aproximaciones, para la simulación de la turbulencia en cámaras de inspección bajo
condiciones de flujo supercrítico se seleccionaron
los tres modelos de turbulencia de dos ecuaciones que
se explican a continuación.
a) Modelo k-ε estándar:
Este modelo de turbulencia permite introducir efectos tales como el transporte de propiedades de
turbulencia por convección y difusión, y la generación y destrucción de la misma. En consecuencia,
es sofisticado y general, razón por la cual es el modelo más validado en la actualidad y presenta
muy buen desempeño en muchas aplicaciones industriales (Cebeci, 2004) (H. K. Versteeg, 2007).
El modelo k-
ε se enfoca en los mecanismo que afectan la energía cinética turbulenta k, a través de
dos ecuaciones diferenciales parciales que modelan el transporte de k y la tasa de disipación de la
energía cinética turbulenta ε. El análisis matemático que lleva al desarrollo de las dos ecuaciones
para k y ε parte de la suposición que la energía cinética del flujo dada por
𝒌
𝒄
= 𝐾 + 𝑘, donde K
corresponde a la energía cinética promedio, definida por
𝐾 =
1
2
(𝑼
𝟐
+ 𝑽
𝟐
+ 𝑾
𝟐
), y k corresponde a

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
10
ICIV 201210 01
la energía cinética turbulenta, como se vio anteriormente, puede expresarse matemáticamente a
partir de las ecuaciones RANS y de las ecuaciones instantáneas de Navier-Stokes (H. K. Versteeg,
2007).
Las ecuaciones resultantes para la energía cinética turbulenta k (Ecuación 1.13) y para la tasa de
disipación de la energía cinética turbulenta ε (Ecuación 1.14) son:
𝜕(𝜌𝑘)
𝜕𝑡
+ ∇ ∙ (𝜌𝑘𝑼) = ∇ ∙ [
𝜇
𝑡
𝜎
𝑘
∇𝑘] + 2𝜇
𝑡
𝑆
𝑖𝑗
∙ 𝑆
𝑖𝑗
− 𝜌𝜀
(I) (II) (III) (IV) (V)
(1.13)
𝜕(𝜌𝜀)
𝜕𝑡
+ ∇ ∙ (𝜌𝜀𝑼) = ∇ ∙ [
𝜇
𝑡
𝜎
𝜀
∇𝜀] + 𝐶
1𝜀
𝜀
𝑘
2𝜇
𝑡
𝑆
𝑖𝑗
∙ 𝑆
𝑖𝑗
− 𝐶
2𝜀
𝜌
𝜀
2
𝑘
(I) (II) (III) (IV) (V)
(1.14)
donde el término (I) de ambas ecuaciones corresponde a la tasa de cambio de k o ε (k en la
Ecuación 1.1 y ε en la Ecuación 1.2), el término (II) corresponde al transporte de k o ε por el
fenómeno de convección, el término (III) corresponde al transporte de k o ε por difusión, (IV) es la
tasa de producción de k o ε y (V) es la tasa de destrucción de k o ε. C
µ
, σ
k
, σ
ε
, C
1ε
y C
2ε
son
constantes ajustables.
b) Modelo k-ε RNG:
El modelo k-ε tradicional, da buenos resultados al trabajar con flujos simples pero presenta
problemas de desempeño cuando se enfrenta a flujos con bajo número de Reynolds, flujos
altamente variables en el tiempo, fuertes gradientes de presión adversos y otros. Este modelo, a
diferencia del modelo k-ε estándar, utiliza una aproximación estadística avanzada conocida como
RNG (Renormalization Group) a las ecuaciones de k y ε, logrando representar los efectos de la
turbulencia a pequeña escala a través de una función aleatoria forzada en las ecuaciones de Navier-
Stokes. Esto permite al modelo ser sensible a deformaciones adicionales causadas por fenómenos
tales como curvatura de líneas de flujo y rotaciones, que no pueden ser capturadas por el modelo
estándar (H. K. Versteeg, 2007). Lo anterior resulta muy útil en la simulación de cámaras de
inspección debido a que se puede presentar recirculación. Las 2 ecuaciones de transporte de este
modelo son:
𝜕(𝜌𝑘)
𝜕𝑡
+ ∇ ∙ (𝜌𝑘𝑼) = ∇ ∙ [𝛼
𝑘
𝜇
𝑒𝑓𝑓
∇𝑘] + 𝜏
𝑖𝑗
∙ 𝑆
𝑖𝑗
− 𝜌𝜀
(1.15)
𝜕(𝜌𝜀)
𝜕𝑡
+ ∇ ∙ (𝜌𝜀𝑼) = ∇ ∙ [𝛼
𝑘
𝜇
𝑒𝑓𝑓
∇𝜀] + 𝐶
1𝜀
𝜀
𝑘
𝜏
𝑖𝑗
∙ 𝑆
𝑖𝑗
− 𝐶
2𝜀
𝜌
𝜀
2
𝑘
(1.16)
donde:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
11
ICIV 201210 01
𝜏
𝑖𝑗
= −𝜌𝑢′
𝑖
𝑢′
𝑗
̅̅̅̅̅̅̅ = 2𝜇
𝑡
𝑆
𝑖𝑗
−
2
3
𝜌𝑘𝛿
𝑖𝑗
y
𝜇
𝑒𝑓𝑓
= 𝜇 + 𝜇
𝑡
𝜇
𝑡
= 𝜌𝐶
𝜇
𝑘
2
𝜀
Nuevamente, C
µ
, α
k
, α
ε
, C
1ε
y C
2ε
son constantes ajustables.
c) Modelo Wilcox k-ω:
Otro problema muy común en la CFD es la simulación aerodinámica, que incluye geometrías
complejas y efectos locales a pequeña escala que pueden alterar fuertemente el comportamiento de
todo el flujo. Los modelos antes mencionados, en general, son inadecuados para este tipo de
situaciones ya que en presencia de gradientes adversos de presión predice niveles muy altos de
esfuerzo cortante turbulento que, a su vez, predice niveles excesivos de transferencia de calor en
regiones de reacomplamiento de flujo (H. K. Versteeg, 2007). Para abarcar este tipo de problemas
Wilcox plantea el uso de una variable distinta a ε, denominada frecuencia turbulenta ω. La relación
entre la frecuencia turbulenta y la tasa de disipación de la energía cinética turbulenta es ω=ε/k, por
lo que la viscosidad de remolino está dada por la siguiente relación:
𝜇
𝑡
= 𝜌
𝑘
𝜔
Los esfuerzos de Reynolds se calculan mediante la aproximación de Boussinesq y las ecuaciones de
transporte del modelo son:
𝜕(𝜌𝑘)
𝜕𝑡
+ ∇ ∙ (𝜌𝑘𝑼) = ∇ ∙ [(𝜇 +
𝜇
𝑡
𝜎
𝑘
) ∇𝑘] + 𝑃
𝑘
− 𝛽
∗
𝜌𝑘𝜔
(1.17)
𝜕(𝜌𝜔)
𝜕𝑡
+ ∇ ∙ (𝜌𝜔𝑼)
= ∇ ∙ [(𝜇 +
𝜇
𝑡
𝜎
𝜔
) ∇𝜔] + 𝛾
1
(2𝜌𝑆
𝑖𝑗
∙ 𝑆
𝑖𝑗
−
2
3
𝜌𝜔
𝜕𝑈
𝑖
𝜕𝑥
𝑗
𝛿
𝑖𝑗
)
− 𝛽
1
𝜌𝜔
2
(1.18)
donde
𝑃
𝑘
= (2𝜇
𝑡
𝑆
𝑖𝑗
∙ 𝑆
𝑖𝑗
−
2
3
𝜌𝑘
𝜕𝑈
𝑖
𝜕𝑥
𝑗
𝛿
𝑖𝑗
)
σk, σω, γ1, β1 y β* son constantes ajustables. Para las Ecuaciones 1.17 y 1.18 es posible realizar un
análisis por términos, como con las Ecuaciones 1.13 y 1.14. El resultado es muy similar ya que (I)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
12
ICIV 201210 01
corresponde a la tasa de cambio de k o ω, el término (II) corresponde al transporte de k o ω por el
fenómeno de convección, el término (III) corresponde al transporte de k o ω por difusión, (IV) es la
tasa de producción de k o ω y (V) es la tasa de destrucción de k o ω.
2.5.
Investigación de cámaras de inspección bajo condiciones de flujo supercrítico
A pesar de que la aproximación numérica o matemática a los fenómenos físicos sea de gran
importancia para el estudio y entendimiento de los mismos, la experimentación es fundamental para
observar, entender y corroborar la teoría que se desarrolla en torno a cualquier fenómeno físico.
Esto es especialmente cierto en el caso de la Mecánica de Fluidos, ya que la complejidad de los
fenómenos físicos que ocurren al interior de un flujo son poco fáciles de entender o visualizar. De
hecho, en varias circunstancias sucede que la aproximación experimental al fenómeno establece el
antecedente a la teoría y la formulación matemática.
En el año 2010, el grupo de investigación CIACUA de la Universidad de los Andes desarrollo una
investigación experimental a fin de explicar el comportamiento hidráulico de cámaras de inspección
bajo condiciones de flujo supercrítico y poder establecer una metodología de diseño adecuada y de
bajo costo para estas estructuras. En primer lugar se desarrolló un modelo físico a escala de una
cámara de inspección convencional a fin de describir los fenómenos hidráulicos que se presentan en
la cámara para distintos escenarios de flujo supercrítico. Posteriormente se identificaron los
parámetros hidráulicos de mayor importancia y se correlacionaron con patrones característicos
observados. Luego, se calcularon las pérdidas de energía que se presentaban en cada escenario de
modelación y, finalmente, se establecieron ecuaciones y recomendaciones para el diseño de cámaras
de inspección bajo flujo supercrítico (Centro de Investigaciones de Acueductos y Alcantarillados -
CIACUA, 2010).
2.5.1. Modelo hidráulico
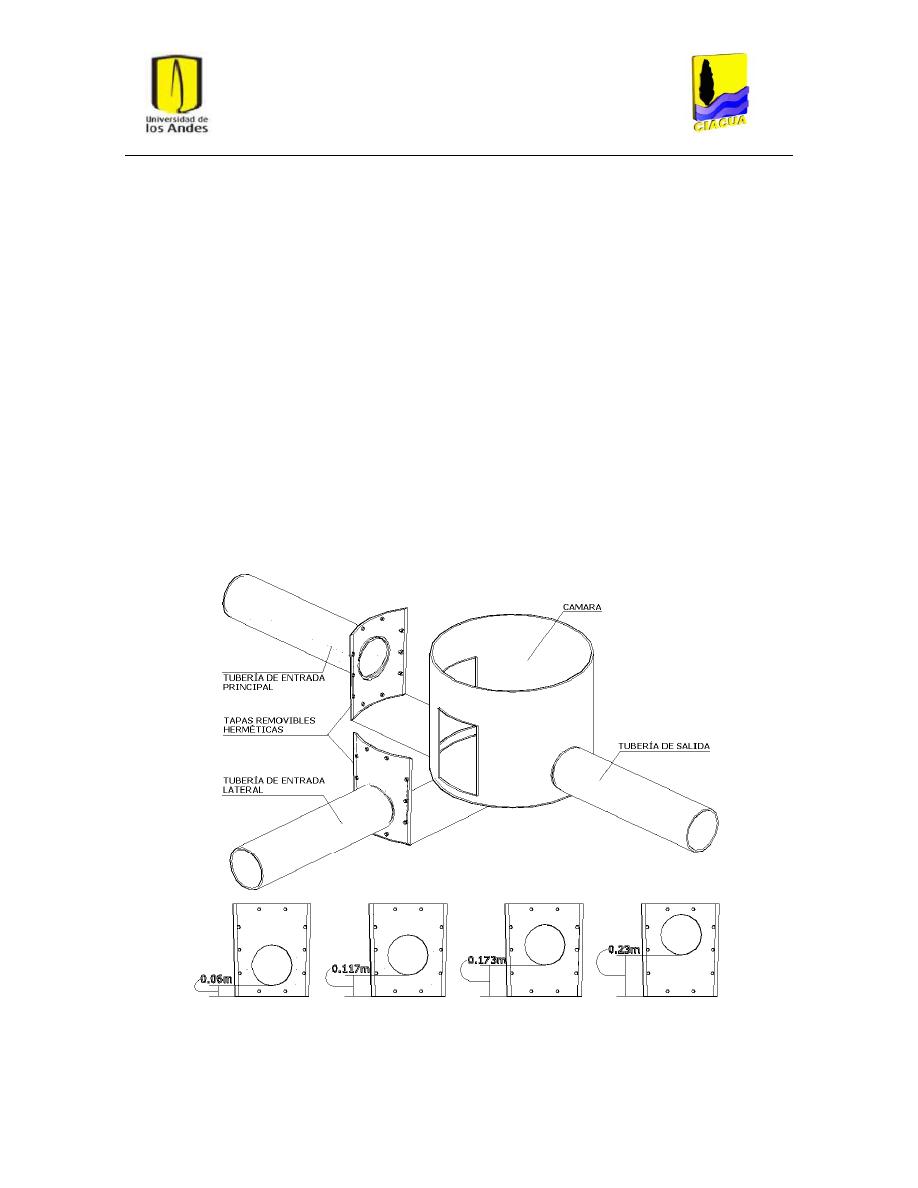
El modelo utilizado en la investigación era una representación a escala 1:2 o 1:3 de un prototipo
convencional y consistió en una estructura de conexión conformada por dos tuberías de entrada
aguas arriba y una tubería de salida aguas abajo, además de un canal de conducción al interior de la
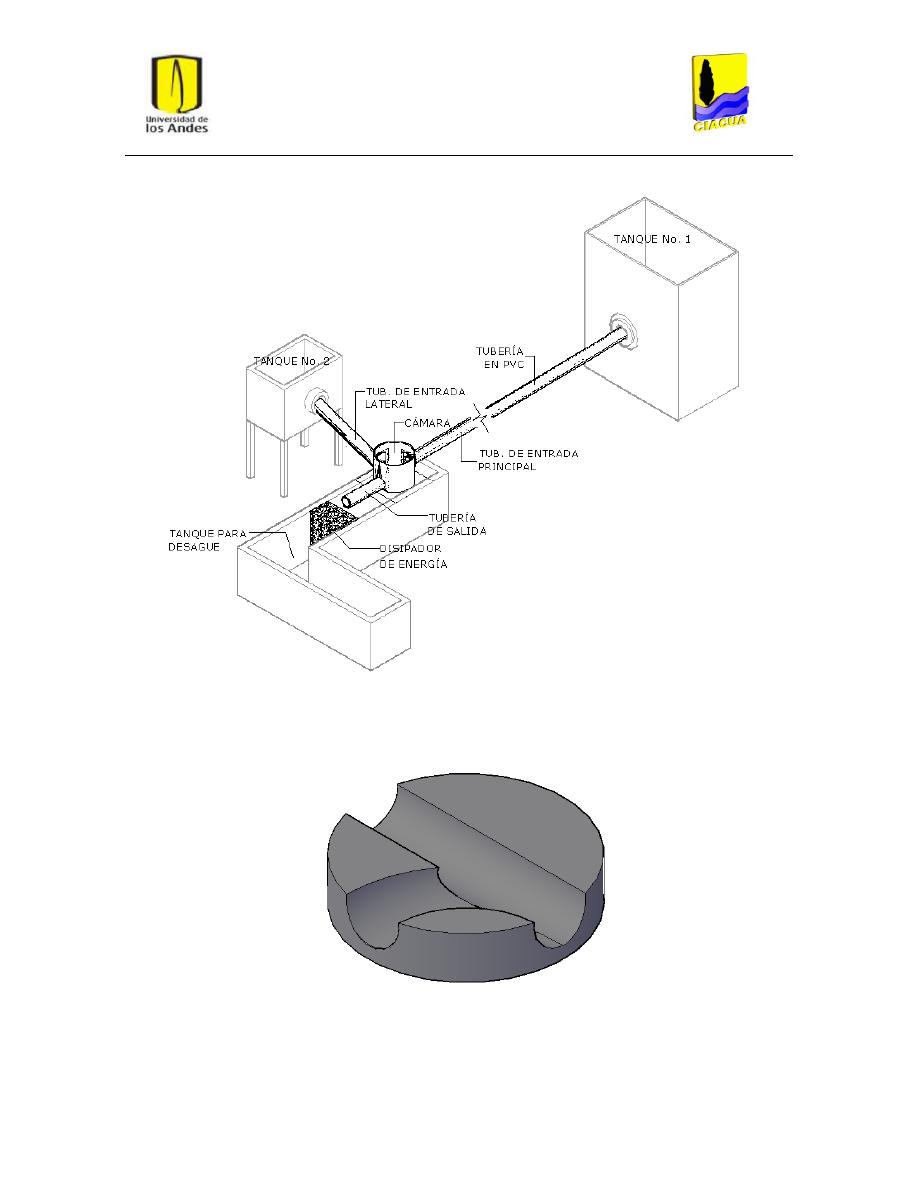
cámara, comúnmente llamado cañuela (ver Figura 3). A continuación se muestra un diagrama del
modelo a escala.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
13
ICIV 201210 01
Figura 2: Montaje experimental de la cámara de inspección. Tomado de la ref. (Centro de Investigaciones de
Acueductos y Alcantarillados - CIACUA, 2010).
Figura 3: Forma de la cañuela. Tomado de la ref. (Centro de Investigaciones de Acueductos y Alcantarillados - CIACUA,
2010).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
14
ICIV 201210 01
Como se observa en la Figura 2, el montaje contaba con dos tanque para el suministro de agua
(TANQUE No.1 y TANQUE No.2) a las tuberías de entrada y que permitían el control del caudal
en cada una de las tuberías a través de vertederos previamente calibrados. Adicionalmente contaba
con una tubería de PVC de 250 mm de diámetro de conectaba la tubería de entrada principal con el
-Tanque No. 1, una estructura de disipación de energía aguas abajo y un tanque de desagüe.
La tubería de entrada principal a la cámara tenía un diámetro de 223 mm, una longitud de 1.00 m y
una pendiente inferior de 2.83%. La tubería de entrada lateral a la cámara estaba ubicada a un
ángulo de 90° respecto a la tubería principal y tenía un diámetro de 223 mm, una longitud de 1.40 m
y una pendiente inferior de15.07%. Ambas tuberías tenían la posibilidad de variar su altura de
entrada a la cámara, medida desde la parte inferior del tubo con respecto al fondo de la cámara, a
cualquiera de las cuatro configuraciones que se indican en la Figura 4. Para el presente proyecto
solo es de interés la configuración más baja (0.06 m) que implicaba una condición similar a que no
hubiera caída, ya que el fondo de las tuberías de entrada casaba casi perfecto con el fondo del canal
de conducción ubicado dentro de la cámara de inspección. La tubería de salida tenía un diámetro de
280 mm, una longitud de 1.00 m y una pendiente inferior de 12.7%. La cámara o estructura de
conexión consistió en un cilindro de 850 mm de diámetro y una altura de 0.7 m.
Figura 4: Configuraciones de caídas. Tomado de la ref. (Centro de Investigaciones de Acueductos y Alcantarillados -
CIACUA, 2010).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
15
ICIV 201210 01
Tanto la estructura de la cámara como la cañuela y las tuberías de entrada y salida a la cámara
fueron construidas con lámina de acrílico transparente para poder observar el comportamiento del
flujo dentro de las tuberías y la cámara, a la vez que se aseguraba una condición de pared lisa.
2.5.2. Instrumentación del modelo y procedimiento de medición
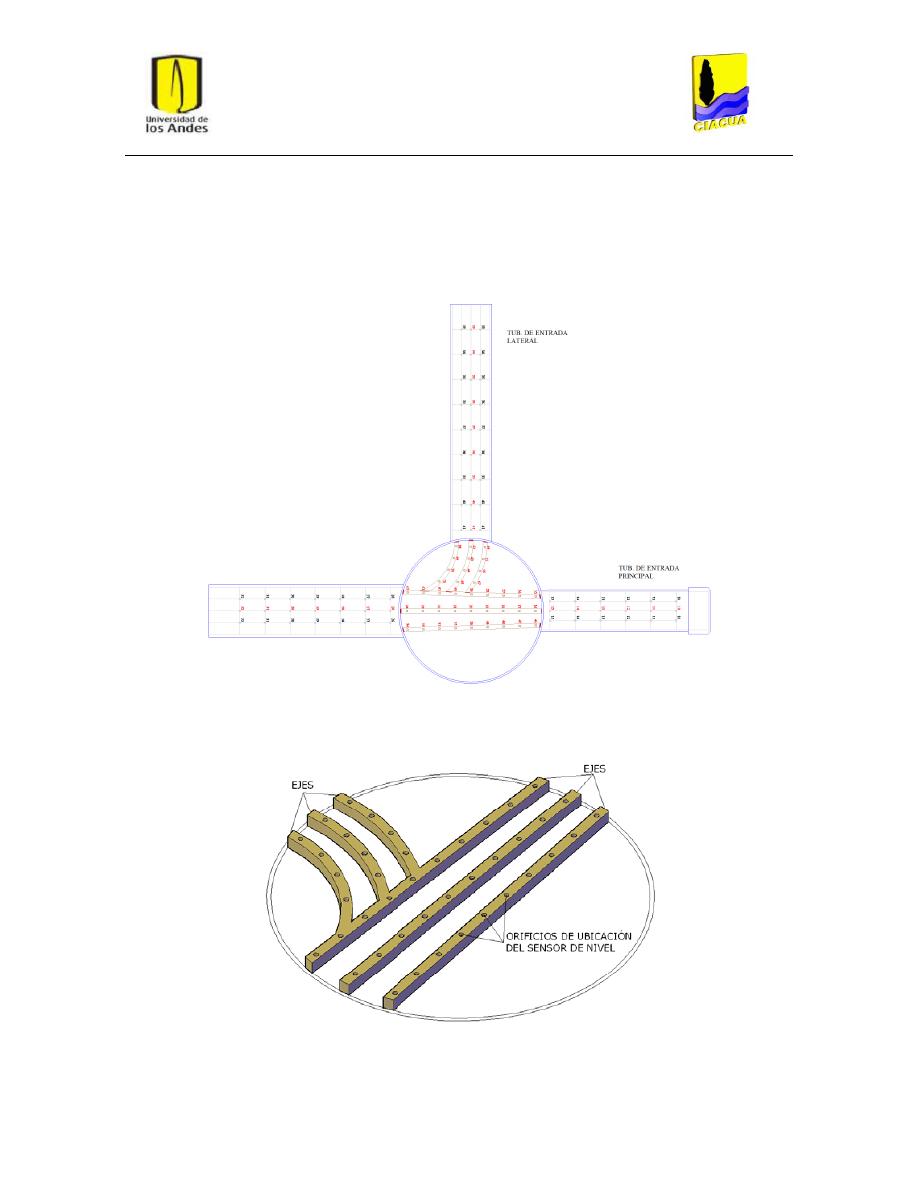
En cuanto a la instrumentación del modelo, se utilizaron dispositivos de medición de nivel para
hacer seguimiento de la altura de la superficie del agua a lo largo de las tuberías de entrada y salida
y en distintos puntos dentro de la cámara, a fin de poder estimar las pérdidas de energía que
ocurrían al interior de la cámara. También se hizo uso de una cámara fotográfica para registrar las
zonas de formación de ondas y las zonas de recirculación. Adicionalmente se utilizaron dispositivos
de medición de caudal para calibrar los vertederos y poder asegurar un control adecuado sobre las
condiciones del flujo a la entrada de la tubería lateral y principal.
Los dispositivos de medición de nivel eran sensores ultrasonido de alta precisión que traducen
señales eléctricas a un programa de computador que convierte estas señales en mediciones de nivel.
Las especificaciones de estos sensores son las siguientes (Centro de Investigaciones de Acueductos
y Alcantarillados - CIACUA, 2010):
Rango de detección: 30 - 400 mm.
Rango de ajuste: 50 - 400 mm.
Zona ciega: 0 - 50 mm.
Estándar: 100 mm * 100 mm.
Frecuencia del transductor: aproximada de 310 kHz.
Retardo de respuesta: aproximada de 50 m.
Los sensores ultrasonido se ubicaron dentro de la cámara y a lo largo de las tuberías de entrada y
salida. A lo largo de las tuberías de entrada y salida se ubicaron sobre tres ejes, en puntos de
medición cada 0.15 m a lo largo de las tuberías, como se enseña en la Figura 5. Y al interior de la
cámara se ubicaron sobre una estructura de medición, también de tres ejes, que simulaba el
recorrido del flujo (ver Figura 6).
En cuanto a la instrumentación para la medición de caudales, consistió en un caudalímetro
ultrasonido no invasivo que permite realizar mediciones de caudal con una precisión de hasta 0.5%,
de manera que se aseguró que los vertederos estuvieran adecuadamente calibrados. A continuación
se muestran las especificaciones técnicas del caudalímetro.
Precisión típica: 0,5%.
Sistema de medición: bidireccional.
Tiempo de resolución: 0,1 ns.
Opción de unidades: desde 1 l/d hasta 100 m³/s.
Medición de volumen: desde 10 ml hasta 100 m³.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
16
ICIV 201210 01
Tuberías multicapas: hasta 3 materiales.
No provoca pérdidas de presión.
No implica daños a la tubería.
Opciones de las sondas en instalación: modo V, N y W.
Figura 5: Estructura de medición. Tomado de la ref. (Centro de Investigaciones de Acueductos y Alcantarillados -
CIACUA, 2010).
Figura 6: Estructura de medición al interior de la cámara. Tomado de la ref. (Centro de Investigaciones de Acueductos
y Alcantarillados - CIACUA, 2010).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
17
ICIV 201210 01
2.5.3. Pruebas sobre el modelo hidráulico
El modelo de cámara implementado por el CIACUA permitió evaluar condiciones de flujo por la
tubería de entrada principal, para la tubería de entrada lateral o por ambas tuberías funcionando al
tiempo. De manera que se pudo evaluar el comportamiento hidráulico de la cámara para las
siguientes condiciones de flujo:
Flujo de entrada a la cámara por la tubería principal (Flujo directo o FD).
Flujo de entrada a la cámara por la tubería lateral (Flujo a 90° o FN).
Flujo de entrada a la cámara por la tubería principal y por la tubería lateral (Unión de flujos
o UF).
Adicionalmente, para cada condición existía la posibilidad de variar la altura de caída de la tubería
de entrada, o de las tuberías de entrada según sea el caso.
Entonces, por cada escenario (combinación entre la condición de flujo y la configuración de caída
en las tuberías de entrada) se evaluó el comportamiento de la cámara para relaciones de llenado
entre el 5% y el 75% (rango habitual de operación de un sistema de alcantarillado) y para caudales
que aseguraran condiciones de flujo supercrítico en las tuberías de entrada a la cámara. Para cada
escenario se estableció el número de Froude en las tuberías de entrada y se llevó el flujo a un estado
estable, esperando por periodos de 10 a 15 minutos hasta que se observara que ninguna de las
propiedades medidas variara significativamente en el tiempo. Posteriormente, se procedió a
registrar la altura de la superficie en los distintos puntos de medición y se tomaron fotos de los
fenómenos relevantes observados.
El resultado fue un total de 188 pruebas en que se registró o calculó el número de Froude (Fr) y la
relación de llenado en cada una de las tuberías del modelo, donde la relación de llenado está dada
por
𝑌 = 𝑌
𝑛
/𝐷
𝑜
(donde Y es la relación de llenado de la tubería, Y
n
es la profundidad del flujo y D
0
es el diámetro interno de la tubería). Se registraron las alturas de caída s
1
y s
2
de cada una de las
tuberías de entrada, se registró la atura de la superficie en distintos puntos y se calcularon las
pérdidas de energía. De todas la pruebas, 23 pruebas se realizaron para condición de Flujo Directo,
otras 23 pruebas se realizaron para la condición de Flujo a 90° y, finalmente, se realizaron 142
pruebas para la condición de Unión de Flujos.
A continuación se muestra un escenario de flujo junto con la información registrada y calculada por
el CIACUA.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
18
ICIV 201210 01
Figura 7: Resultados para escenario UF-6 (Dinámica del flujo). Tomado de la ref. (Centro de Investigaciones de
Acueductos y Alcantarillados - CIACUA, 2010).
PRUEBA UF-6
Parámetros
Comportamiento Hidráulico
Se observó la formación de una onda típica de un flujo a
90° ubicada en la pared externa del canal principal de la
cañuela, con las sigientes características:
Inicio de la onda = 73% del diámetro de la cámara.
Fin de la onda = 100% del diámetro de la cámara.
Altura máxima de la Onda = 197% de la altura de la
cañuela.
Aunque no se desarrolla un resalto hidráulico si se
observó un incremento en el nivel de la lámina de agua
de la tubería de entrada principal.
Patrón de flujo tridimensional
Tubería Principal
h= 135.32mm Y = 61%.
Tubería Lateral
h=63.92mm. Y = 29%.
Cámara: Formación de una onda
típica de un flujo a 90°.
Cámara: Onda en la pared externa
del canal principal de la cañuela
Perfil de flujo de la línea lateral derecha para el flujo directo
Perfil de flujo de la línea lateral derecha para el flujo a 90°

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
19
ICIV 201210 01
2.6. Clasificación de flujos en canales abiertos:
Por último cabe resaltar que en ductos y canales abiertos el flujo se puede clasificar en los
siguientes regímenes:
Laminar - Subcrítico: 𝑅𝑒 < 1000; 𝐹𝑟 < 1
Laminar - Supercrítico: 𝑅𝑒 < 1000; 𝐹𝑟 > 1
Turbulento - Subcrítico: 𝑅𝑒 > 3000; 𝐹𝑟 < 1
Turbulento - Supercrítico: 𝑅𝑒 > 3000; 𝐹𝑟 > 1
El número de Reynolds (Re) es la relación entre las fuerzas inerciales y las fuerzas viscosas del
flujo, de manera que para flujo en ductos y canales abiertos con valores de Re < 1000, las fuerzas
viscosas predominan forzando a un régimen de flujo laminar. Pero si Re > 1000, las fuerzas
inerciales priman sobre las fuerzas viscosidad y comienza a generarse turbulencia. Para Re > 3000
el régimen de flujo es completamente turbulento. La ecuación de Re es la siguiente.
𝑅𝑒 =
𝜌𝑈𝐷
𝐻
𝜇
=
𝑄𝐷
𝐻
𝜈𝐴
(1.19)
donde ρ es la densidad del fluido, U es la velocidad del flujo de aproximación, D
H
es el diámetro
hidráulico de la tubería, µ es la viscosidad dinámica del fluido, ν es la viscosidad cinemática y A es
el área de flujo.
El número de Froude (Fr) es la relación entre las fuerzas inerciales y las fuerzas de gravedad que
actúan sobre un fluido y permite determinar si el flujo es supercrítico o subcrítico. Está dado por la
siguiente ecuación:
𝐹𝑟 =
𝑈
√𝑔𝐷
= √
𝑇
𝑔𝐴
3
(1.20)
donde g es la aceleración debida a la gravedad, D es la profundidad hidráulica, T es el ancho
superficial y Q es el caudal.
En condiciones de flujo subcrítico, las fuerzas de gravedad tienen mayor importancia que las
fuerzas inerciales sobre el comportamiento del flujo, por lo que el número de Froude debe ser
menor a 1 (Fr < 1). Mientras que en condiciones de flujo supercrítico las fuerzas inerciales
predominan sobre las fuerzas gravitacionales, en consecuencia se debe cumplir que
𝐹𝑟 > 1.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
20
ICIV 201210 01
3. SIMULACIÓN Y MODELO COMPUTACIONAL
A fin de desarrollar un modelo computacional capaz de simular adecuadamente el flujo con
superficie libre, se inicia un diseño asistido por computador de la cámara de inspección estudiada
por el CIACUA. Posteriormente, se realiza una subdivisión del dominio en un número muy
pequeño de elementos de flujo, lo que se conoce como enmallado. Luego, se introducen las
condiciones de flujo investigadas en el informe del CIACUA y que son de interés para este proyecto
y, finalmente, se definen los parámetros o características del flujo que se desean medir y evaluar
contra la información experimental con que se cuenta.
En general, la simulación de dominios de flujo de gran tamaño, como es el caso del modelo
hidráulico, requiere una gran cantidad de nodos y, en consecuencia, una gran cantidad de elementos
de volumen para poder lograr resultados adecuados. El problema de subdividir el dominio de flujo
en un número de elementos de volumen elevado es que los costos computacionales para resolver el
dominio de flujo serán igualmente elevados. Aún más elevados si se requiere simular periodos
físicos de 10 a 15 minutos. En consecuencia, por restricciones de tiempo y recursos
computacionales, se utilizó una única configuración de flujo. Esto quiere decir que se desarrolló un
único diseño por computador de la cámara de inspección del CIACUA para la condición de caída
más baja en ambas tuberías de entrada, pues para poder simular cada una de las 142 pruebas habría
sido necesario realizar diseños a computador de cada una de las posibles configuraciones de caída.
La configuración seleccionada permitió desarrollar un número adecuado de simulaciones y permitió
establecer la validez de utilizar un modelo computacional como aproximación para el diseño y/o
estudio de cámaras de inspección.
3.1. Diseño a computador del modelo hidráulico:
Seleccionar adecuadamente el dominio de flujo que se resolverá a través de la CFD es de vital
importancia para lograr una aproximación confiable a la realidad. En general, se ha demostrado que
una simulación mejora su precisión a medida que se aumenta el número de elementos de volumen
en que se subdivide el dominio en estudio, pero también se ha demostrado que los recursos
computacionales que se requieren para resolver el dominio es proporcional al número de elementos
de volumen. De manera que entre menor sea el dominio, menor será el número de elementos y los
recursos computacionales necesarios para asegurar resultados adecuados. Pero, si el dominio
seleccionado para simular es muy pequeño en relación al dominio original es posible que se
observen resultados sesgados ya que se pueden estar excluyendo fenómenos o regiones de flujo
determinantes para el dominio en estudio.
Entonces, a fin de modificar en la menor medida el modelo hidráulico y lograr modelar
adecuadamente los fenómenos que ocurren al interior de la cámara de inspección, se seleccionó
como dominio de flujo a resolver el conjunto comprendido por la cámara de inspección y las
tuberías de entrada y salida en configuración de caída más baja. No se realizó ningún tipo de
modificación sobre las medidas originales del modelo hidráulico con excepción de la tubería de
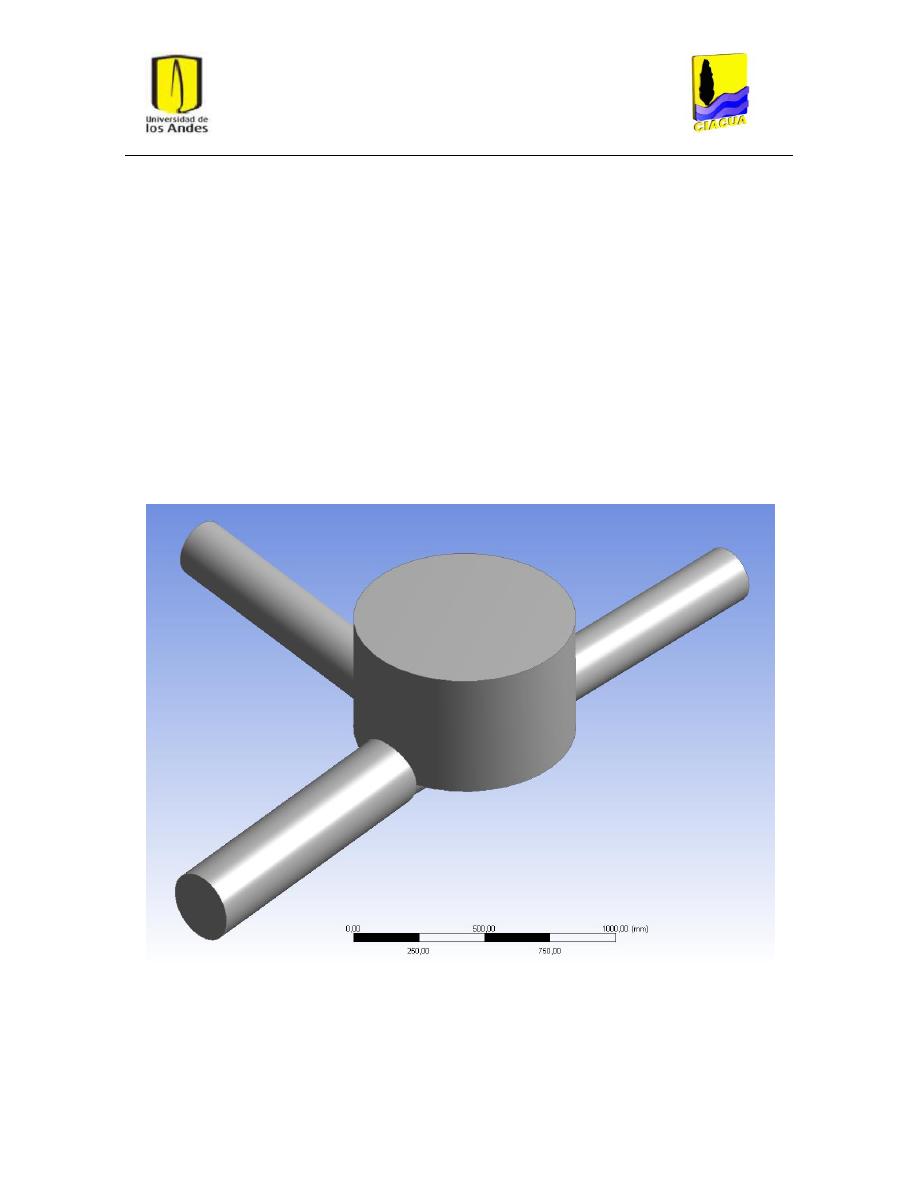
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
21
ICIV 201210 01
entrada lateral, que se recortó de 1.40 m a 1.00 m de longitud. En resumen, el diseño a computador
de la cámara de inspección consiste en:
Una tubería de entrada principal sin caída, con una longitud de 1.00 m, un diámetro de 223
mm y una pendiente inferior del 2.83%.
Una tubería de entrada lateral sin caída, a 90° de la tubería de entrada principal, con una
longitud de 1.00 m, un diámetro de 223 mm y una pendiente inferior del 15.07%.
Una tubería de salida con una longitud de 1.00 m, un diámetro de 280 mm y una pendiente
inferior del 12.7%.
Una cámara de inspección con un diámetro de 850 mm, una altura de 0.7 m y una cañuela
en el fondo para dirigir el flujo que entra por las tuberías principal y lateral.
Una cañuela similar a la que se muestra en la Figura 3.
A continuación se enseñan imágenes del diseño computacional de la cámara de inspección.
Figura 8: Modelo computacional de la cámara de inspección.
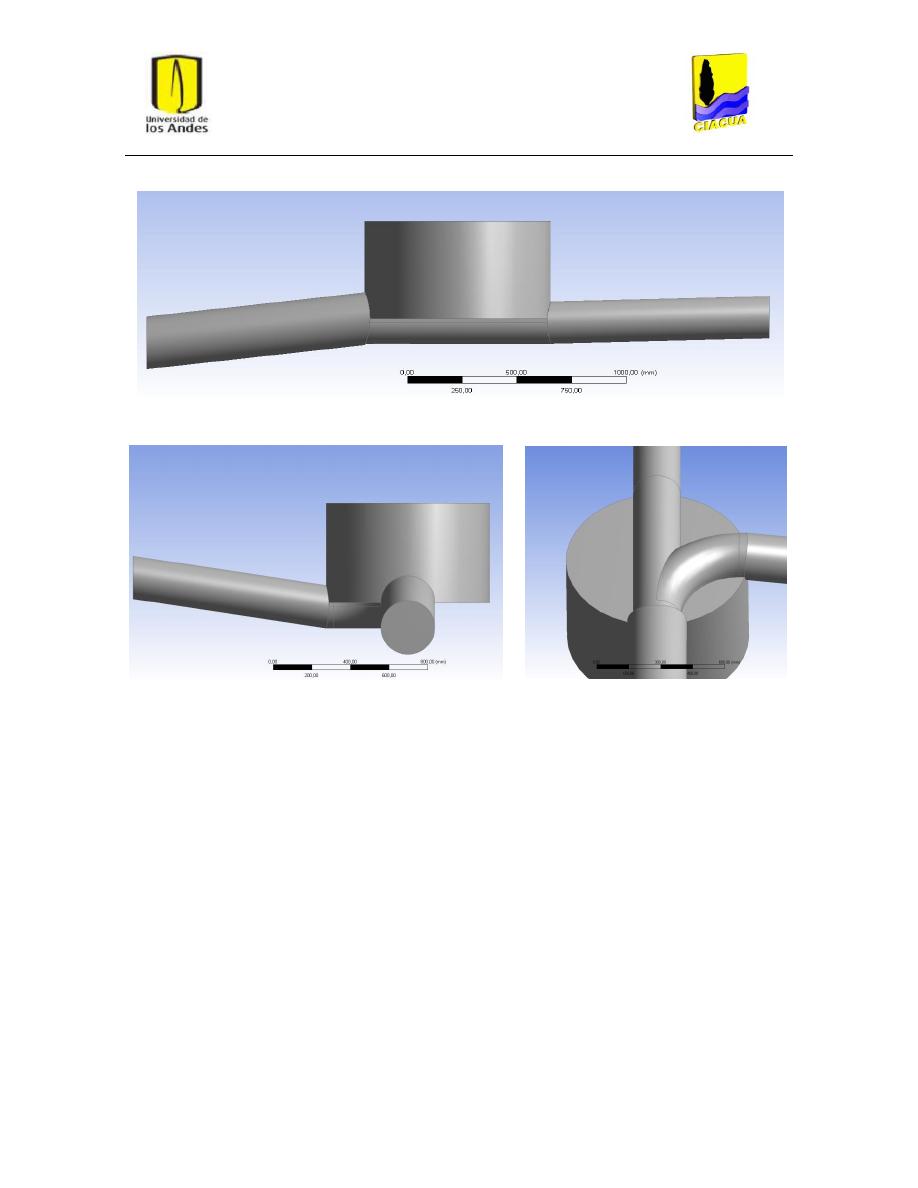
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
22
ICIV 201210 01
Figura 9: Vista lateral de tubería de entrada principal y tubería de salida.
Figura 10: Vista lateral de tubería de entrada lateral.
Figura 11: Cañuela del modelo computacional.
Este modelo computacional de la cámara de inspección se desarrolló con el módulo Geometry del
programa ANSYS 13.0 Workbench.
3.2. Enmallado de la geometría
La subdivisión del dominio en pequeños elementos de volumen es lo que se conoce como creación
de la malla o enmallado y es fundamental en el proceso de modelación pues la precisión de los
resultados obtenidos depende de la resolución de la malla.
Para realizar el enmallado de la cámara de inspección computacional se hizo uso del módulo Mesh
del programa ANSYS 13.0 Workbench. En el proceso se utilizó una función automática de
enmallado que contiene el programa y que realiza una partición del dominio en elementos de
volumen tetraédricos y elementos de superficie triangulares a partir de cierto parámetros definidos
por el usuario. Adicionalmente, se utilizó una función de inflación a partir de las paredes de la
cámara y que aumenta la resolución de la malla en las regiones cercanas a la pared, como se
muestra en las figuras a continuación.
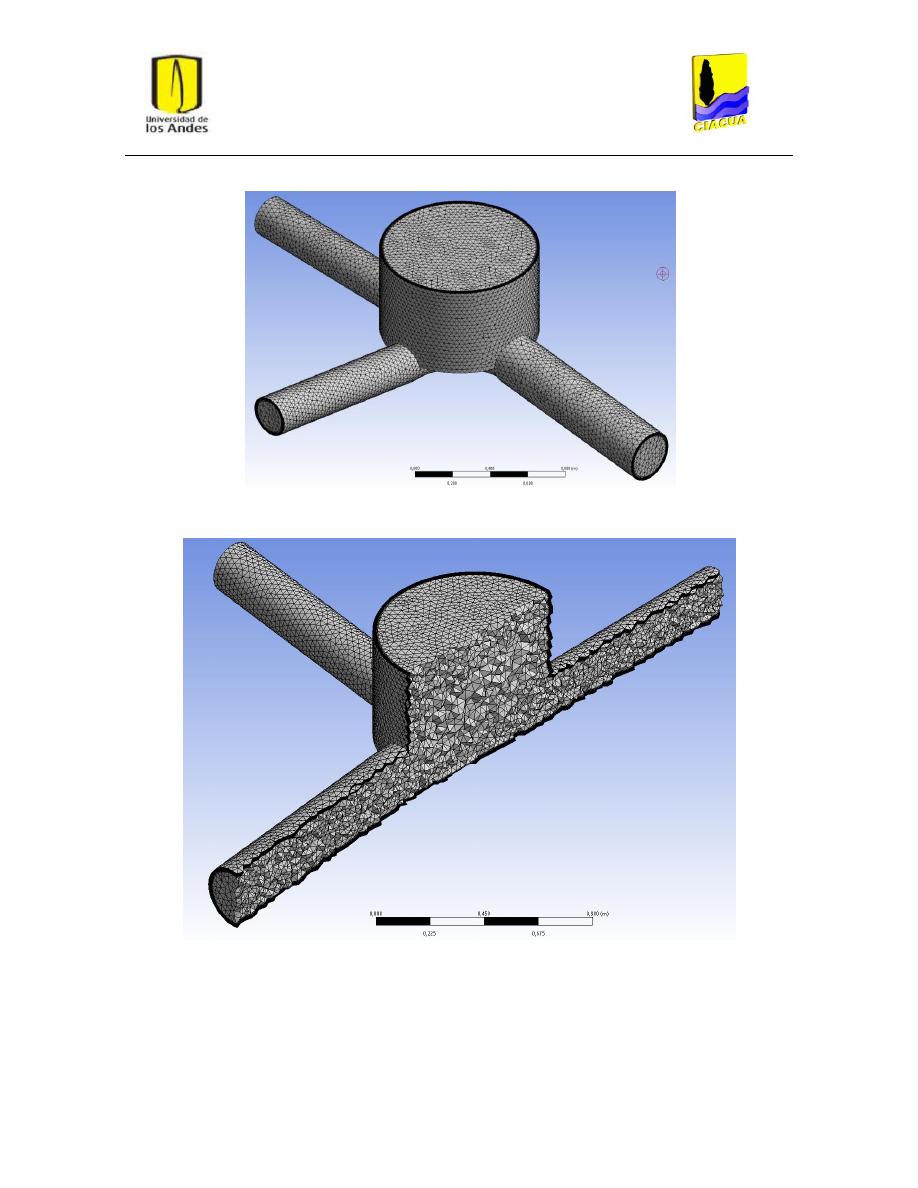
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
23
ICIV 201210 01
Figura 12: Superficie del enmallado de la cámara de inspección.
Figura 13: Elementos internos del enmallado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
24
ICIV 201210 01
Figura 14: Inflación al interior del dominio.
Figura 15: Inflación en tubería de entrada principal
Esta malla cuenta con 199'671 nodos y 495'586 elementos de volumen. En promedio, los elementos
tienen un volumen de 2.32 cm
3
, con un máximo de 78.12 cm
3
y un mínimo de 1.47*10
-3
cm
3
. No ha
sido posible desarrollar una malla de mayor resolución debido a la licencia disponible para realizar
las simulaciones, pero la ventaja de esta malla es que permite simular en periodos relativamente
cortos, dadas las características del dominio.
3.3. Selección de escenarios de modelación
Como se explicó anteriormente las pruebas que pueden ser simuladas a partir del modelo
computacional de la cámara de inspección son aquellas realizadas para la condición de caída más
baja en las tuberías de entrada a la cámara. De esta manera el número de pruebas a modelar se
reduce a 24 (8 pruebas pasa escenario de FD, 8 pruebas para escenario de FN y 8 pruebas para
escenario de UF). Pero, como parte del proyecto es comparar el desempeño de tres modelos de
turbulencia a fin de definir cuál es el adecuado para este tipo de simulaciones, cada prueba o
escenario de modelación se debe simular tres veces. Lo que quiere decir que se requeriría un total
de 72 simulaciones. Entonces, de las 24 pruebas posibles se seleccionaron 10 escenarios de
modelación o pruebas a resolver computacionalmente (4 pruebas para escenario de UF, 4 pruebas
para escenario de FD y 2 prueba para escenario de FN), para un total de 30 simulaciones.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
25
ICIV 201210 01
Nuevamente, las condiciones geométricas de las tuberías de entra y salida son:
Tabla 1: Tuberías de entrada y salida a la cámara de inspección. Tomado de la ref. (Centro de Investigaciones de
Acueductos y Alcantarillados - CIACUA, 2010).
Tubería
Diámetro
[mm]
Longitud
[mt]
Pendiente
[%]
Caída
PRINCIPAL
223
1
2.83%
0Do
LATERAL
223
1.45
15.07%
0Do
SALIDA
280
1
12.70%
0Do
La Tabla 1 es tomada del informe del CIACUA, por lo que aparece una longitud de 1.45 m para la
tubería lateral. Aun así se simula con una tubería lateral de 1.00 m.
En las Tablas 2, 3 y 4 mostradas a continuación se enumeran los escenarios de modelación tomados
de las pruebas realizadas por el CIACUA. En cada tabla aparecen los parámetros de entrada y
condiciones de frontera.
Tabla 2: Pruebas a simular, escenario Unión de flujos (UN). Tomado de la ref. (Centro de Investigaciones de
Acueductos y Alcantarillados - CIACUA, 2010).
El tipo de flujo hace referencia a los cuatro regímenes explicados en el Numeral 3.6, donde Sup-
Turb corresponde a flujo en régimen Supercrítico-Turbulento y Sub-Turb corresponde a flujo en
régimen Subcrítico-Turbulento.
UF-2
Caudal
[L/s]
Profundidad
de flujo [mm]
Relación de
llenado [%]
Ѳ
[Rad]
Área Mojada
[mm]
Prof.
Hidráulica [mm]
Velocidad
[m/s]
No. De
Froude
No. De
Reynolds
Tipo de
Flujo
24.75
82.28
37%
2.61
13086.91
60.812
1.89
2.45
1.01E+06
Sup-Turb
13.03
52.19
23%
2.02
6956.37
36.838
1.87
3.12
1.29E+06
Sup-Turb
37.78
95.11
-
2.49
18436.66
69.516
2.05
2.48
1.44E+06
Sup-Turb
UF-3
Caudal
[L/s]
Profundidad
de flujo [mm]
Relación de
llenado [%]
Ѳ
[Rad]
Área Mojada
[mm]
Prof.
Hidráulica [mm]
Velocidad
[m/s]
No. De
Froude
No. De
Reynolds
Tipo de
Flujo
50
104.19
47%
3.01
17899.52
80.440
2.79
3.14
1.29E+06
Sup-Turb
1.7
49.87
22%
1.97
6521.93
35.093
0.26
0.44
1.84E+05
Sub-Turb
51.70
81.39
-
2.28
14869.60
58.477
3.48
4.59
2.67E+06
Sup-Turb
UF-4
Caudal
[L/s]
Profundidad
de flujo [mm]
Relación de
llenado [%]
Ѳ
[Rad]
Área Mojada
[mm]
Prof.
Hidráulica [mm]
Velocidad
[m/s]
No. De
Froude
No. De
Reynolds
Tipo de
Flujo
13.03
125.54
56%
3.39
22651.54
102.392
0.58
0.57
2.36E+05
Sub-Turb
13.03
51.14
23%
2.00
6758.98
36.047
1.93
3.24
1.35E+06
Sup-Turb
26.06
77.59
-
2.22
13909.67
55.497
1.87
2.54
1.48E+06
Sup-Turb
UF-5
Caudal
[L/s]
Profundidad
de flujo [mm]
Relación de
llenado [%]
Ѳ
[Rad]
Área Mojada
[mm]
Prof.
Hidráulica [mm]
Velocidad
[m/s]
No. De
Froude
No. De
Reynolds
Tipo de
Flujo
13
193.00
87%
4.78
35920.76
236.035
0.36
0.24
1.06E+05
Sub-Turb
25
132.28
59%
3.52
24135.54
110.161
1.04
1.00
4.11E+05
Sub-Turb
38.00
105.98
-
2.65
21357.66
78.634
1.78
2.03
1.17E+06
Sup-Turb
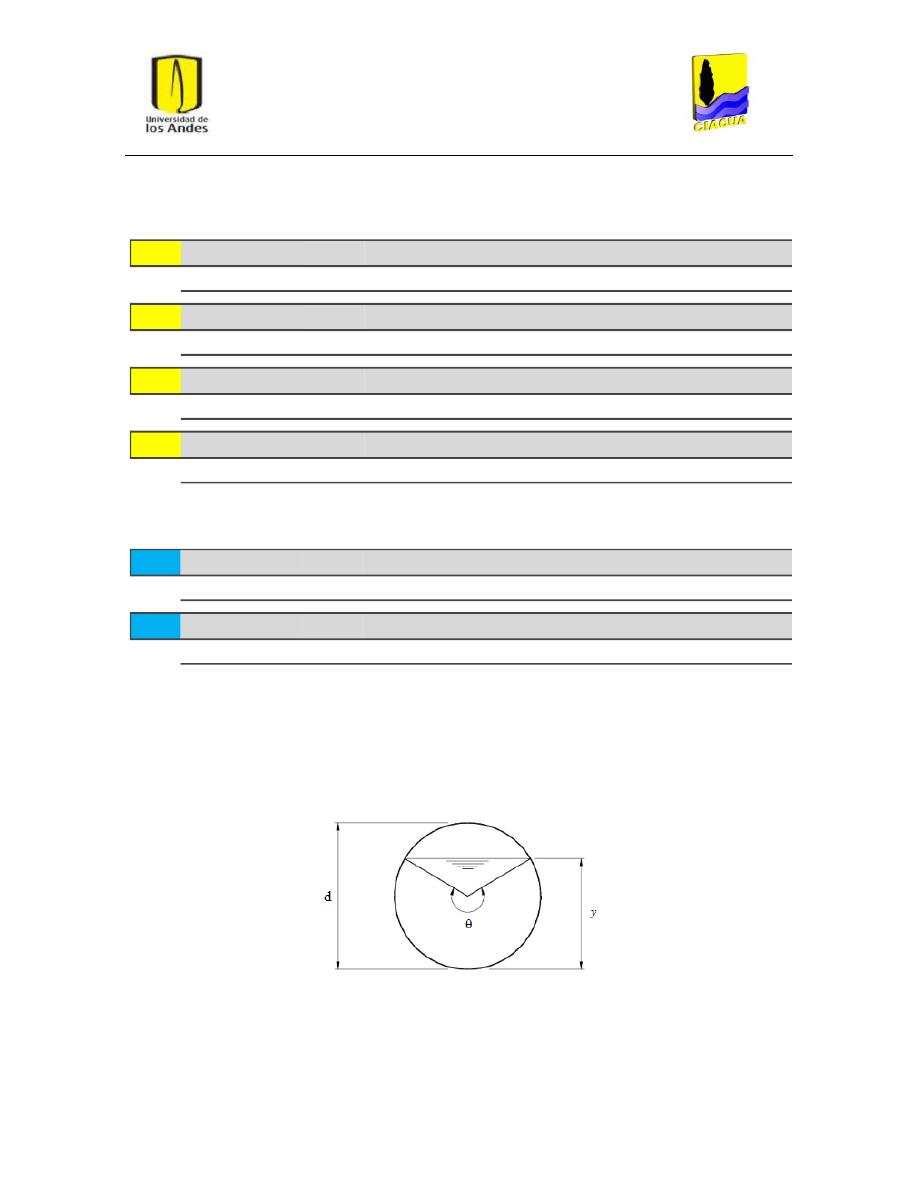
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
26
ICIV 201210 01
Tabla 3: Pruebas a simular, escenario Flujo Directo (FD). Tomado de la ref. (Centro de Investigaciones de Acueductos y
Alcantarillados - CIACUA, 2010).
Tabla 4: Pruebas a simular, escenario Flujo a 90° (FN). Tomado de la ref. (Centro de Investigaciones de Acueductos y
Alcantarillados - CIACUA, 2010).
La profundidad del flujo o y normal (y
n
) corresponde al promedio de las últimas dos mediciones de
la altura de la superficie antes de entrar a la cámara, θ es el ángulo en radianes formado desde la
superficie el agua hasta el centro de la tubería (ver Figura 16), el área mojada A
m
está dada por la
Ecuación 1.21, la profundidad hidráulica D está dada por la Ecuación 1.22 y la velocidad está dada
por la relación
𝑈 = 𝑄/𝐴
𝑚
, donde Q es el caudal.
Figura 16: Relaciones geométricas para tubería parcialmente llena.
FD-3
Caudal
[L/s]
Profundidad
del flujo [mm]
Relación de
llenado [%]
Ѳ
[Rad]
Área Mojada
[mm]
Prof. Hidráulica
[mm]
Velocidad
[m/s]
No. de
Froude
No. De
Reynolds
Tipo de Flujo
25.51
67.21
30%
2.32
9918.66
48.47
2.57
3.73
1.54E+06
Sup-Turb
25.51
55.40
-
1.84
8633.75
38.70
2.95
4.80
2.81E+06
Sup-Turb
FD-4
Caudal
[L/s]
Profundidad
del flujo [mm]
Relación de
llenado [%]
Ѳ
[Rad]
Área Mojada
[mm]
Prof. Hidráulica
[mm]
Velocidad
[m/s]
No. de
Froude
No. De
Reynolds
Tipo de Flujo
47.38
96.61
43%
2.87
16217.78
73.38
2.92
3.44
1.42E+06
Sup-Turb
47.38
74.38
-
2.17
13111.11
53.01
3.61
5.01
2.92E+06
Sup-Turb
FD-6
Caudal
[L/s]
Profundidad
del flujo [mm]
Relación de
llenado [%]
Ѳ
[Rad]
Área Mojada
[mm]
Prof. Hidráulica
[mm]
Velocidad
[m/s]
No. de
Froude
No. De
Reynolds
Tipo de Flujo
73.84
127.59
57%
3.43
23105.01
104.71
3.20
3.15
1.30E+06
Sup-Turb
73.84
93.39
-
2.46
17981.00
68.10
4.11
5.02
2.92E+06
Sup-Turb
FD-8
Caudal
[L/s]
Profundidad
del flujo [mm]
Relación de
llenado [%]
Ѳ
[Rad]
Área Mojada
[mm]
Prof. Hidráulica
[mm]
Velocidad
[m/s]
No. de
Froude
No. De
Reynolds
Tipo de Flujo
52.22
92.50
41%
2.7992
15312.611
69.685
3.41026
4.125
1.699E+06
Sup-Turb
52.22
58.30
-
1.8954
9286.975
40.843
5.62293
8.883
5.193E+06
Sup-Turb
FN-7
Caudal
[L/s]
Profundidad
del flujo [mm]
Relación de
llenado [%]
Ѳ
[Rad]
Área Mojada
[mm]
Prof. Hidráulica
[mm]
Velocidad
[m/s]
No. de
Froude
No. De
Reynolds
Tipo de Flujo
50.5
143.77
64%
3.73
26622.41
124.72
1.90
1.71
7.09E+05
Sup-Turb
50.5
184.19
-
3.78
42952.64
161.67
1.18
0.93
5.44E+05
Sub-Turb
FN-8
Caudal
[L/s]
Profundidad
del flujo [mm]
Relación de
llenado [%]
Ѳ
[Rad]
Área Mojada
[mm]
Prof. Hidráulica
[mm]
Velocidad
[m/s]
No. de
Froude
No. De
Reynolds
Tipo de Flujo
40
89.06
40%
2.74
14559.24
66.65
2.75
3.40
1.40E+06
Sup-Turb
40
101.69
-
2.59
20196.77
74.99
1.98
2.31
1.34E+06
Sup-Turb

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
27
ICIV 201210 01
𝐴
𝑚
=
1
8
(𝜃 − sin 𝜃) ∗ 𝑑
2
(1.21)
𝐷 =
1
8
(
𝜃 − sin 𝜃
sin 𝜃/2
) ∗ 𝑑
(1.22)
donde d es el diámetro de la tubería y θ está en radianes.
Entonces, para cada una de las pruebas enseñadas en las Tablas 2 a 4 (UF-2, UF-3, UF4, UF5,
FD3,…) se realizan tres simulaciones, una por cada modelo de turbulencia utilizado.
3.4. Definición de las condiciones de frontera
Ya se definió la geometría y malla del modelo computacional y se definieron los escenarios o
pruebas simular. Solo queda por definir las variables de entrada y las variables de salida. Como
variables de entrada se entiende los parámetros y condiciones de frontera que se toman de las
pruebas experimentales y se aplican al modelo computacional en la etapa de Pre-procesamiento,
mientras que las variables de salida se refieren a la información arrojada por la solución del modelo
computacional y que se quiere comparar con la información experimental. De esta manera es
posible realizar un análisis cualitativo y cuantitativo del modelo computacional desarrollado y
establecer la validez del mismo.
Las variables de entrada para el modelo en cada uno de los escenarios de modelación son la
velocidad y la altura de la superficie en cada una de las tuberías de entrada, la altura de la superficie
en la tubería de salida, la escala física de tiempo por iteración, el número de iteraciones a realizar y,
por último, el modelo de turbulencia a utilizar. En cuanto a las variables de salida, se requieren los
perfiles de flujo en los planos establecidos en el informe experimental (ver Figura 17), el tiempo de
simulación, e información cualitativa como el comportamiento de los residuos durante el proceso de
solución, imágenes de la superficie al final de la simulación, o remolinos en la cámara de
inspección. En la tabla a continuación se enumeran las variables de análisis.
Tabla 5: Variables de entrada y variables de salida para los modelos conceptuales.
Variables
de
entrada
Escenario
UF
FD
FN
U, h
superficie
,
Δt, #
iteraciones
U, h
superficie
,
Δt, #
iteraciones
U, h
superficie
,
Δt, #
iteraciones
k - ε
k - ε rng
k - ω k - ε
k - ε rng
k - ω k - ε
k - ε rng
k - ω
Variables
de salida
Perfiles de flujo,
Tiempo de simulación
Información cualitativa
Perfiles de flujo,
Tiempo de simulación
Información cualitativa
Perfiles de flujo,
Tiempo de simulación
Información cualitativa
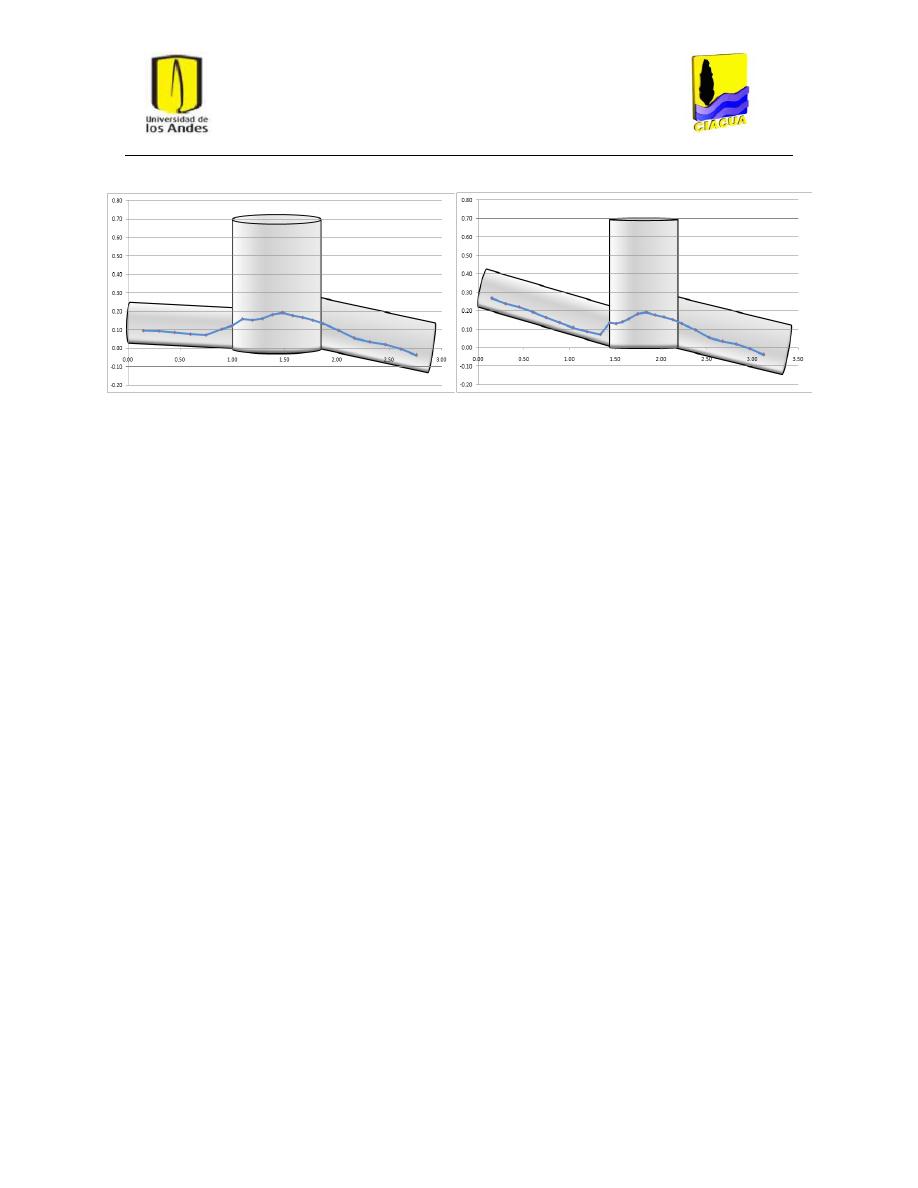
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
28
ICIV 201210 01
Perfil recto de flujo por línea central.
Perfil curvo de flujo por línea central.
Figura 17: Perfiles recto y curvo de flujo en UF-2.
Las curvas que se observan en la Figura 17 son los perfiles recto y curvo de flujo o altura de la
superficie a lo largo de la estructura de medición, que van desde el inicio de las tuberías de entrada
principal y lateral y llegan hasta el final de la tubería de salida, pasando por la cámara de
inspección. Perfil recto de flujo se refieren a las líneas de medición que recorren la tubería de
entrada principal y terminan en la tubería de salida, mientras que perfil curvo de flujo se refieren a
las líneas de medición que inician en la tubería lateral, doblan a la derecha dentro de la cámara y se
dirigen hacia el final de la tubería de salida. "Línea central" hace referencia al eje de medición
utilizado. Como se mencionó anteriormente, la estructura de medición consiste en tres ejes de
medición para cada una de las tuberías, como lo muestra la Figura 5. De manera que los tres ejes se
diferencian mediante "línea central", "línea derecha" y "línea izquierda". Las abscisas corresponden
al recorrido del agua por las tuberías de entrada, la cámara y la tubería de salida, de manera que a
1.00 m sobre la gráfica de perfil recto de flujo y a 1.45 m sobre la gráfica de perfil curvo de flujo
ingresa el perfil de flujo a la cámara de inspección. Las ordenadas corresponden a la medida de la
altura de la superficie o del perfil de flujo relativo al fondo de la cámara; es por esta razón que se
observan valores negativos hacia el final de la tubería de salida (el nivel del fondo del canal se
encuentra a 0.135 m aproximadamente por encima del punto más bajo de la tubería de salida).
En cuanto a las fronteras, el dominio está constituido por cinco. Dos entradas de velocidad (tubería
de entrada lateral y tubería de entrada principal) que permiten entrada de flujo de masa, restringen
salida de flujo de masa y requieren de la velocidad de entrada del flujo en cada una de las
coordenadas cartesianas y de la altura de la superficie para calcular las fracciones de volumen de
cada una de las fases a la entrada. Una salida de presión (tubería de salida) que permite el flujo libre
de masa hacia afuera del dominio a una condición de presión atmosférica y requiere el perfil de
presiones de la lámina de agua en función de la altura, además de la altura de la superficie para
calcular las fracciones de volumen de cada una de las fases y el perfil de presiones a la salida. Otra
salida abierta a la atmósfera (hueco superior de la cámara) que permite circulación libre de aire, o
sea que permite tanto que entre como que salga flujo sin ningún tipo de restricción. Y, finalmente,
las paredes de la cámara de inspección son lisas y operan bajo condición de no deslizamiento
debido a que el material original del modelo físico es acrílico. Para todos los escenarios de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
29
ICIV 201210 01
modelación se utilizó una intensidad de turbulencia media (Intensidad de turbulencia del 5% y
relación de viscosidad
𝜇
𝑡
𝜇
= 10) como condición inicial ya que es la condición recomendable para
ductos y sistemas de ventilación (ANSYS Inc., 2010).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
30
ICIV 201210 01
4. RESULTADOS
En esta sección se presentan los resultados obtenidos de las simulaciones llevadas a cabo para cada
uno de los escenarios de flujo seleccionados en el capítulo anterior. Se enseñan las variables de
entrada de todos los escenarios y algunos de los resultados obtenidos a partir de las simulaciones. El
conjunto de resultados analizados en cada escenario de modelación consiste en imágenes de la
superficie del flujo según cada modelo de turbulencia y los perfiles de flujo sobre cada uno de los
planos establecidos por los ejes de medición del modelo hidráulico experimental.
Las gráficas e imágenes que no se enseñan en esta sección se encuentran en Anexos, pero se
realizarán comentarios de todo lo observado en el análisis de los resultados.
Tabla 6: Parámetros temporales de simulación.
UF-2
UF-3
UF-4
UF-5
FD-3
FD-4
FD-6
FD-8
FN-7
FN-8
Paso de tiempo,
Δt (s): 0.2
0.2
0.2
0.2
0.6
0.6
0.6
0.6
0.6
0.6
# iteraciones: 1500
1500
1500
1500
400
400
400
400
400
400
Tiempo físico (min):
5.00
5.00
5.00
5.00
4.00
4.00
4.00
4.00
4.00
4.00
En la Tabla 6 se enseñan los pasos de tiempo de cada iteración, el número total de iteraciones
realizadas en cada simulación y el tiempo físico simulado. Adicionalmente, en la Tabla 7 se indica
el costo computacional o tiempo que las simulaciones en un computador de escritorio con
procesador Intel i7 de 3.60Hz y memoria RAM de 16.0Gb.
Tabla 7: Tiempos de simulación para cada escenario.
TIEMPO REAL DE SIMULACIÓN (h)
Escenario: UF-2
UF-3
UF-4
UF-5
FD-3
FD-4
FD-6
FD-8
FN-7
FN-8
Modelo k - ε:
8.06
8.22
8.11
8.14
1.96
1.99
2.00
1.99
1.99
1.99
Modelo k - ε rng:
8.21
8.27
8.15
8.18
1.99
2.04
1.99
2.04
1.98
2.04
Modelo k - ω:
8.37
8.33
8.35
8.25
2.04
2.00
2.01
1.99
1.96
1.99
4.1. Escenarios de modelación para Unión de flujos (UF)
Los perfiles de flujo se obtuvieron de graficar la superficie del flujo sobre planos de corte que
corren en la dirección de los ejes de medición, de manera que para graficar los perfiles de flujo que
se observan en las Gráficas 1 a 3 se trazó un plano como el que se muestra en la Figura 18 y se
graficaron los puntos de la superficie del agua sobre este plano. En cuanto a los perfiles a 90°
(Gráficas 4 a 6), como no es posible fabricar un plano que se curve y siga la trayectoria de los ejes
de medición que se observan en la Figura 5, se cruzaron dos planos de corte como se indica en la
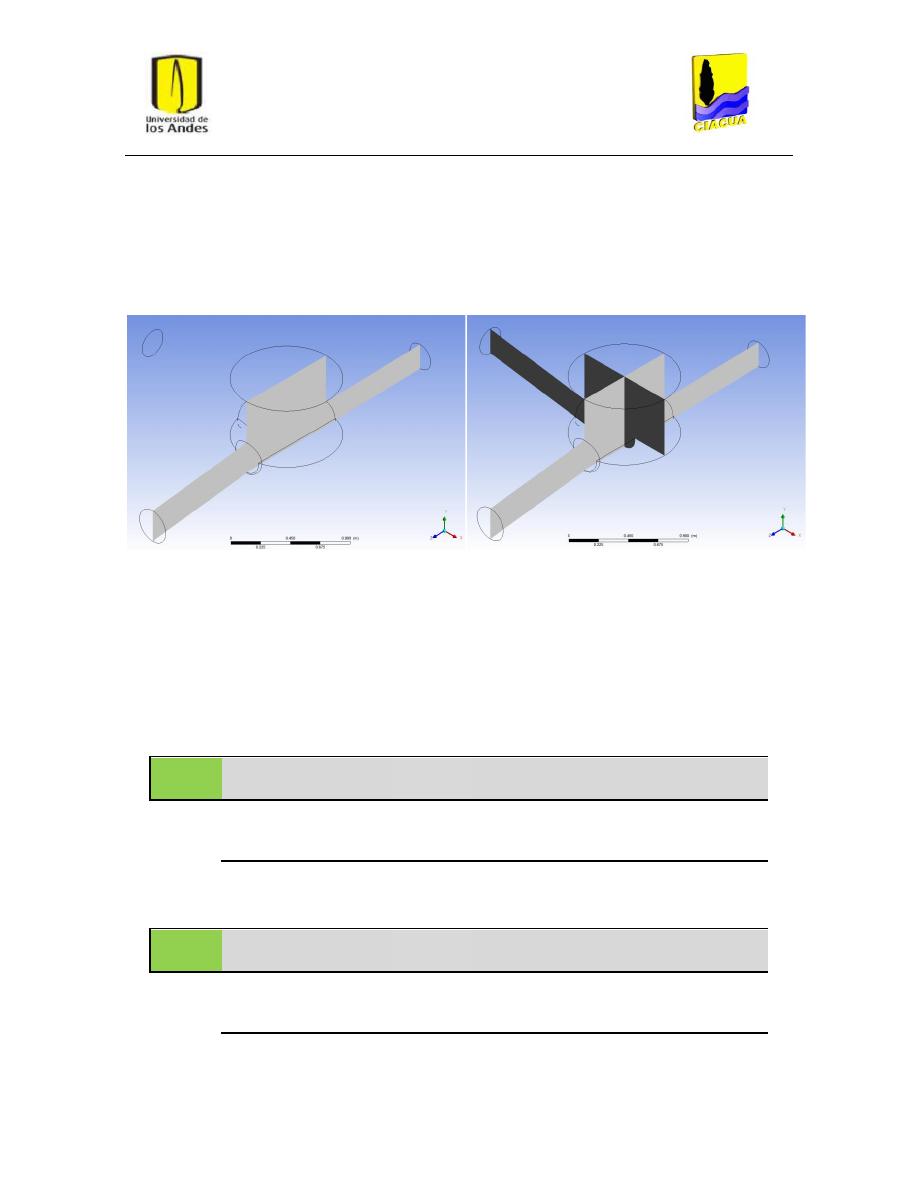
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
31
ICIV 201210 01
Figura 19. Esto permite hacer un seguimiento adecuado del perfil del flujo a lo largo de la tubería
de entrada lateral y a lo largo de la tubería de salida pero presentan inconvenientes en cierta zona al
interior de la cámara. Esto se ve reflejado en los cambios bruscos que ocurren en la abscisa 1.65 m,
en las gráficas de perfiles curvos de flujo, y por lo tanto no se espera que la predicción de CFD sea
correcta en esta zona.
Figura 18: Plano de corte para perfil recto de flujo por
línea central
Figura 19: Planos de corte para perfil curvo de flujo por
línea central
A continuación se presentan los parámetros de modelación para los escenarios en condición de
Unión de Flujos, junto con el tupo de flujo que se presenta en cada una de las tuberías de la cámara.
En las Tablas 8 a 11 es claro que el flujo supercrítico es predominante en estos escenarios de
modelación, por lo que es necesario tener en cuenta los efectos de la turbulencia debido al valor del
número de Reynolds.
Tabla 8: Condiciones de flujo para UF-2.
UF-2
Caudal
[L/s]
Profundidad
de flujo [mm]
Relación de
llenado [%]
Velocidad
[m/s]
No. De
Froude
No. De
Reynolds
Tipo de
Flujo
24.75
82.28
37%
1.89
2.45
1.01E+06
Sup-Turb
13.03
52.19
23%
1.87
3.12
1.29E+06
Sup-Turb
37.78
95.11
-
2.05
2.48
1.44E+06
Sup-Turb
Tabla 9: Condiciones de flujo para UF-3
UF-3
Caudal
[L/s]
Profundidad
de flujo [mm]
Relación de
llenado [%]
Velocidad
[m/s]
No. De
Froude
No. De
Reynolds
Tipo de
Flujo
50
104.19
47%
2.79
3.14
1.29E+06
Sup-Turb
1.7
49.87
22%
0.26
0.44
1.84E+05
Sub-Turb
51.70
81.39
-
3.48
4.59
2.67E+06
Sup-Turb
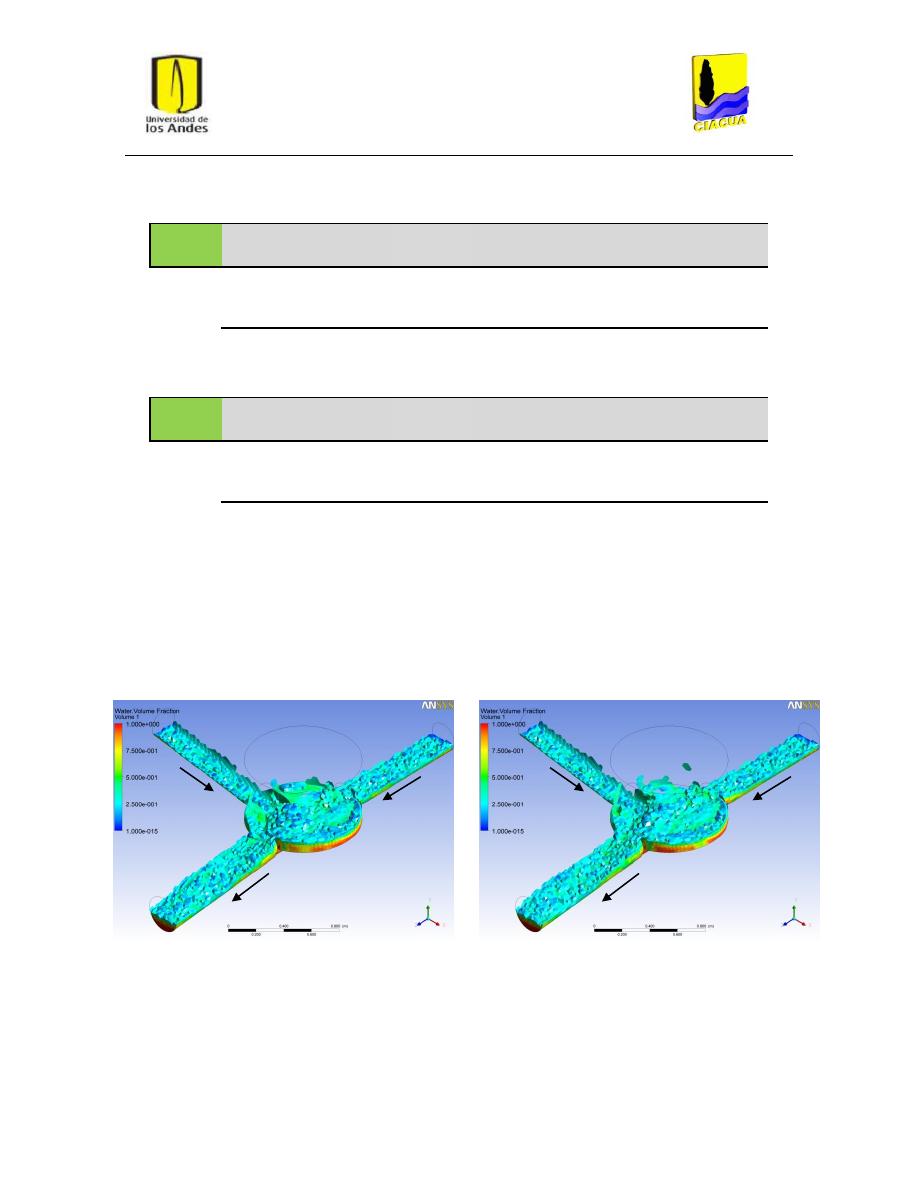
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
32
ICIV 201210 01
Tabla 10: Condiciones de flujo para UF-4.
UF-4
Caudal
[L/s]
Profundidad
de flujo [mm]
Relación de
llenado [%]
Velocidad
[m/s]
No. De
Froude
No. De
Reynolds
Tipo de
Flujo
13.03
125.54
56%
0.57
0.57
2.36E+05
Sub-Turb
13.03
51.14
23%
1.93
3.24
1.34E+06
Sup-Turb
26.06
77.59
-
1.87
2.54
1.48E+06
Sup-Turb
Tabla 11: Condiciones de flujo para UF-5.
UF-5
Caudal
[L/s]
Profundidad
de flujo [mm]
Relación de
llenado [%]
Velocidad
[m/s]
No. De
Froude
No. De
Reynolds
Tipo de
Flujo
13
193.00
87%
0.36
0.24
1.06E+05
Sub-Turb
25
132.28
59%
1.04
1.00
4.11E+05
Sub-Turb
38.00
105.98
-
1.78
2.03
1.17E+06
Sup-Turb
Las siguientes figuras y gráficas son el conjunto de resultados de un escenario tipo para escenarios
de modelación UF. Como se mencionó anteriormente, se compone de la superficie del flujo y de los
perfiles de flujo.
Las figuras a continuación enseñan la superficie del flujo al final de la simulación según cada
modelo de turbulencia utilizado. En estas figuras y en todas las que siguen las flechas hacen
referencia a la dirección del flujo en cada una de las tuberías de la cámara de inspección.
Figura 20: Superficie del flujo en UF-2. Modelo k-ε estándar.
Figura 21: Superficie del flujo en UF-2. Modelo k-ε RNG.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
33
ICIV 201210 01
Figura 22: Superficie del flujo en UF-2. Modelo k-ω.
En las Figuras 20 a 22 no es posible resaltar diferencias importantes entre los modelos de
turbulencia utilizados. De hecho, es un comportamiento común entre los distintos escenarios de
modelación observar que la superficie del flujo no varíe significativamente entre los distintos
modelos de turbulencia utilizados.
En las Gráficas 1 a 6 se observan los perfiles de flujo a través de la tubería de entrada principal y los
perfiles de flujo a través de la tubería de entrada lateral. Las curvas continuas corresponden a cada
uno de los modelos de turbulencia utilizados en la modelación de este escenario de flujo.
Gráfica 1: Perfil recto de flujo por la línea central para UF-2.
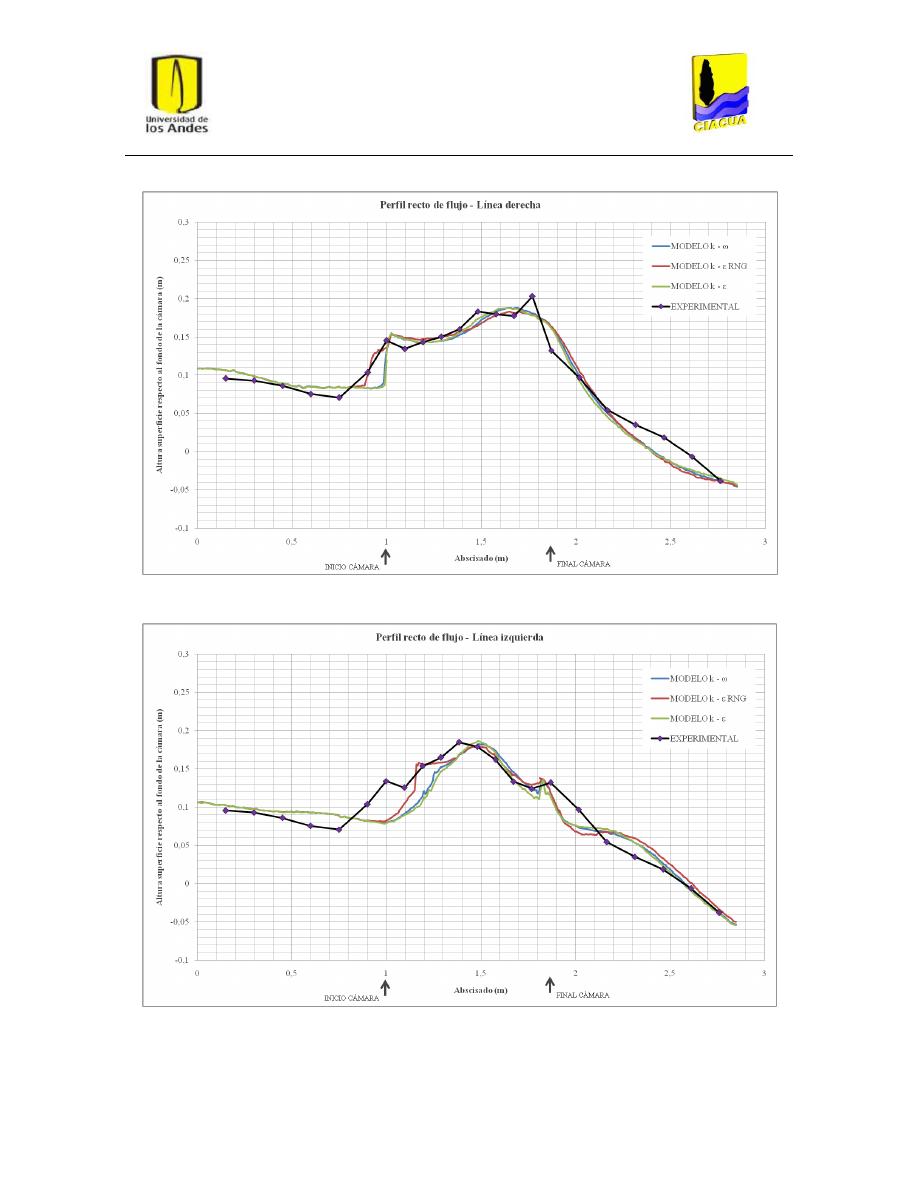
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
34
ICIV 201210 01
Gráfica 2: Perfil recto de flujo por la línea derecha para UF-2.
Gráfica 3: Perfil recto de flujo por la línea de flujo izquierda para UF-2.
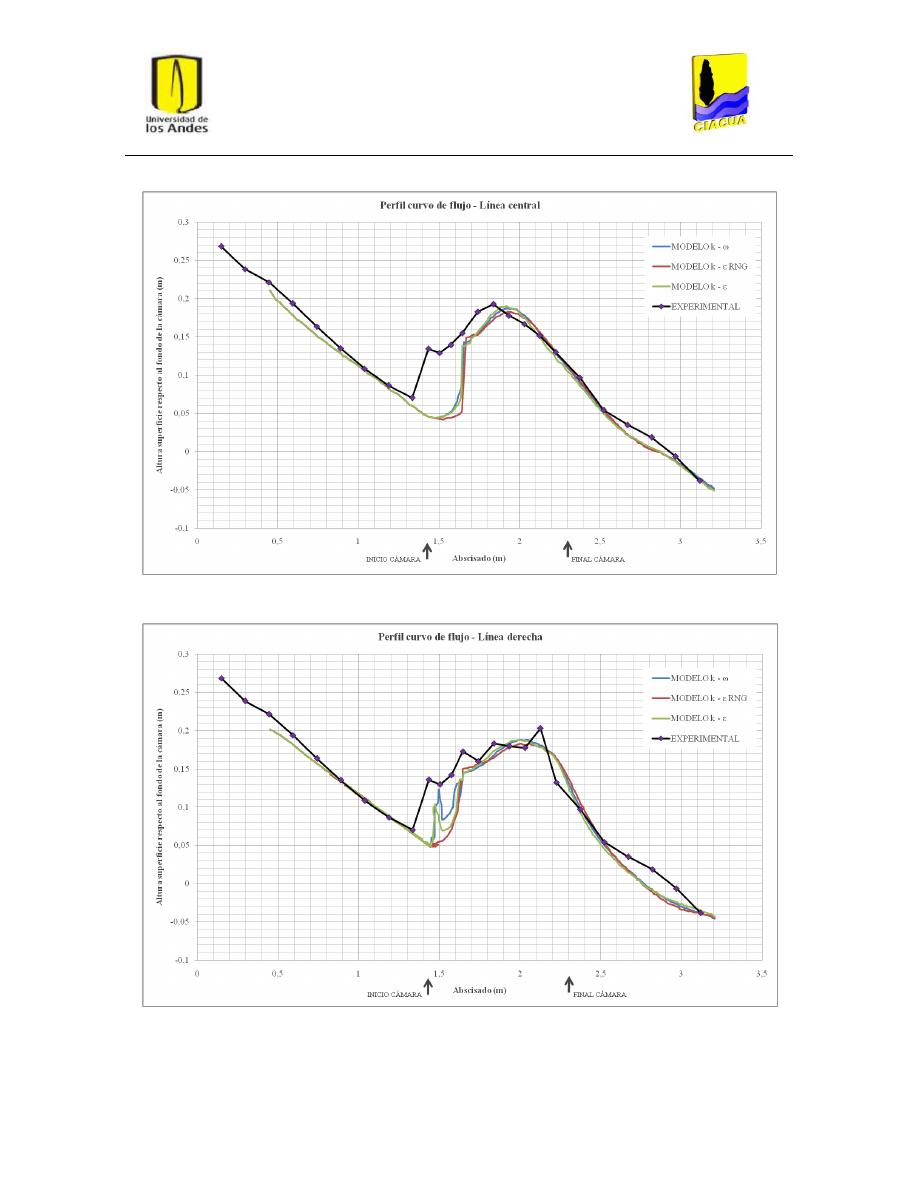
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
35
ICIV 201210 01
Gráfica 4: Perfil curvo de flujo por la línea central para UF-2.
Gráfica 5: Perfil curvo de flujo por la línea derecha para UF-2.
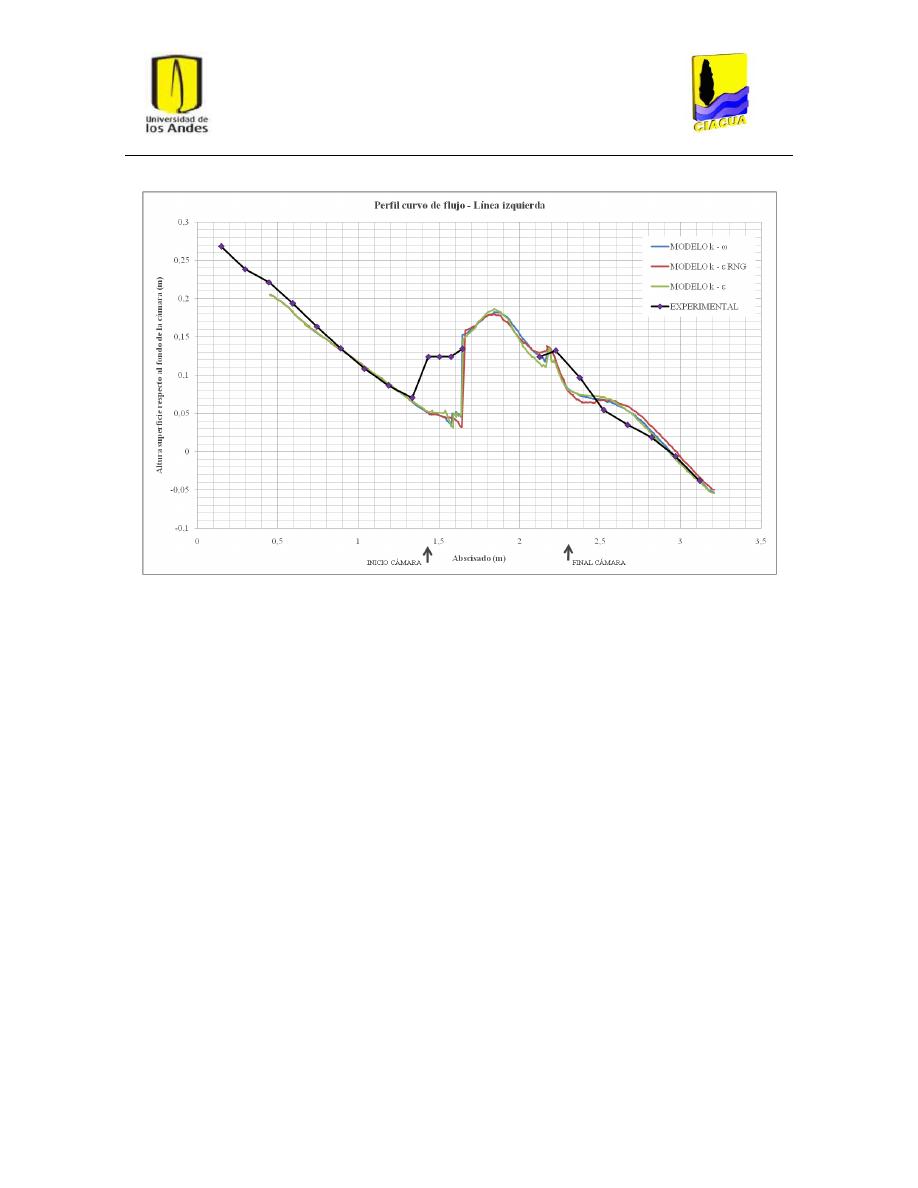
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
36
ICIV 201210 01
Gráfica 6: Perfil curvo de flujo por la línea izquierda para UF-2.
Usando las gráficas anteriores se establece que el modelo computacional desarrollado predice
adecuadamente los perfiles de flujo medidos por el CIACUA para UF-2. Los perfiles rectos de flujo
enseñan mejor comportamiento que lo perfiles curvos de flujo, pero esto se debe al cambio brusco
por la intersección entre planos de corte perpendiculares. Aunque los resultados de algunos
escenarios de modelación no se acoplen adecuadamente la información experimental, el
comportamiento generalizado es bastante bueno. Además es importante recordar que no se cuenta
con las incertidumbres de los perfiles experimentales.
4.2. Escenarios de modelación para Flujo Directo (FD) y Flujo a 90° (FN)
Los escenarios de modelación indicados por las Tablas 12 a 15 corresponden a la condición de
Flujo Directo, (FD). Esto quiere decir que solo se presenta flujo de agua por la tubería de entrada
principal, razón por la cual solo se presentan los perfiles de flujo en la dirección de la tubería de
entrada principal. Mientras que los escenarios de modelación indicados por las Tablas 16 y 17
corresponden a la condición FN, donde solo se presenta flujo a través de la tubería de entrada
lateral, de manera que solo se grafican los perfiles de flujo que inician en la tubería de entrada
lateral.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
37
ICIV 201210 01
Tabla 12: Condiciones de flujo para FD-3.
FD-3
Caudal
[L/s]
Profundidad
del flujo [mm]
Relación de
llenado [%]
Velocidad
[m/s]
No. de
Froude
No. De
Reynolds
Tipo de
Flujo
25.51
67.21
30%
2.57
3.73
1.54E+06
Sup-Turb
25.51
55.40
-
2.95
4.80
2.81E+06
Sup-Turb
Tabla 13: Condiciones de flujo para FD-4.
FD-4
Caudal
[L/s]
Profundidad
del flujo [mm]
Relación de
llenado [%]
Velocidad
[m/s]
No. de
Froude
No. De
Reynolds
Tipo de
Flujo
47.38
96.61
43%
2.92
3.44
1.42E+06
Sup-Turb
47.38
74.38
-
3.61
5.01
2.92E+06
Sup-Turb
Tabla 14: Condiciones de flujo para FD-6.
FD-6
Caudal
[L/s]
Profundidad
del flujo [mm]
Relación de
llenado [%]
Velocidad
[m/s]
No. de
Froude
No. De
Reynolds
Tipo de
Flujo
73.84
127.59
57%
3.19
3.15
1.30E+06
Sup-Turb
73.84
93.39
-
4.11
5.02
2.92E+06
Sup-Turb
Tabla 15: Condiciones de flujo para FD-8.
FD-8
Caudal
[L/s]
Profundidad
del flujo [mm]
Relación de
llenado [%]
Velocidad
[m/s]
No. de
Froude
No. De
Reynolds
Tipo de
Flujo
52.22
92.50
41%
3.41026
4.125
1.699E+06
Sup-Turb
52.22
58.30
-
5.62293
8.883
5.193E+06
Sup-Turb
Tabla 16: Condiciones de flujo para FN-7.
FN-7
Caudal
[L/s]
Profundidad
del flujo [mm]
Relación de
llenado [%]
Velocidad
[m/s]
No. de
Froude
No. De
Reynolds
Tipo de
Flujo
50.5
143.77
64%
1.90
1.71
7.09E+05
Sup-Turb
50.5
184.19
-
1.18
0.93
5.44E+05
Sub-Turb
Tabla 17: Condiciones de flujo para FN-8.
FN-8
Caudal
[L/s]
Profundidad
del flujo [mm]
Relación de
llenado [%]
Velocidad
[m/s]
No. de
Froude
No. De
Reynolds
Tipo de
Flujo
40
89.06
40%
2.75
3.40
1.40E+06
Sup-Turb
40
101.69
-
1.98
2.31
1.34E+06
Sup-Turb
A continuación se presentan los resultados de un escenario tipo para escenarios de modelación FD y
FN. Estos se componen de la superficie del flujo y de los perfiles de flujo en cada uno de los planos
por lo que corren los ejes de medición utilizados por el CIACUA. La única diferencia entre los
resultados de un escenario FD y un escenario FN es que en el primero se enseñan perfiles rectos de
flujo mientras que en el segundo se enseñan perfiles curvos de flujo.
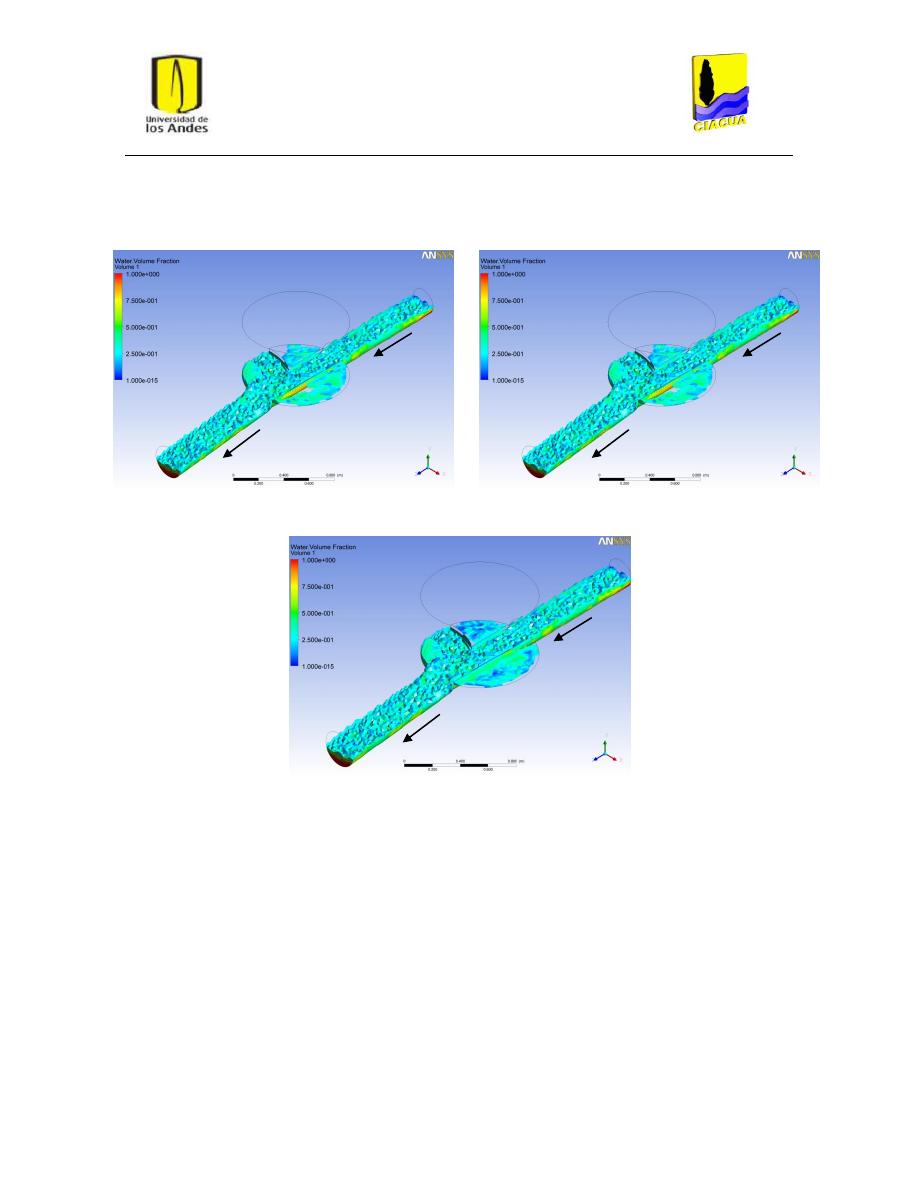
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
38
ICIV 201210 01
Para el escenario de modelación FD-4, la superficie de flujo por cada modelo de turbulencia se
enseña en las Figuras 23 a 25, mientras que los perfiles de flujo se muestran en las Gráficas 7 a 9.
Figura 23: Superficie del flujo en FD-4. Modelo k-ε estándar.
Figura 24: Superficie del flujo en UFD-4. Modelo k-ε RNG.
Figura 25: Superficie del flujo en FD-4. Modelo k-ω.
Como se observa en las Gráficas 7 a 9 y en el resto de gráficas en Anexos, los perfiles de flujo de
los escenario FD presentan un comportamiento muy similar a pesar de que los parámetros de
entrada sea distintos. En general, se observa que el nivel de flujo se mantiene constante o que
disminuye muy poco hasta casi el final de la cámara. A partir de este punto, el nivel cae de manera
pronunciada hasta que el flujo sale por la tubería de salida.
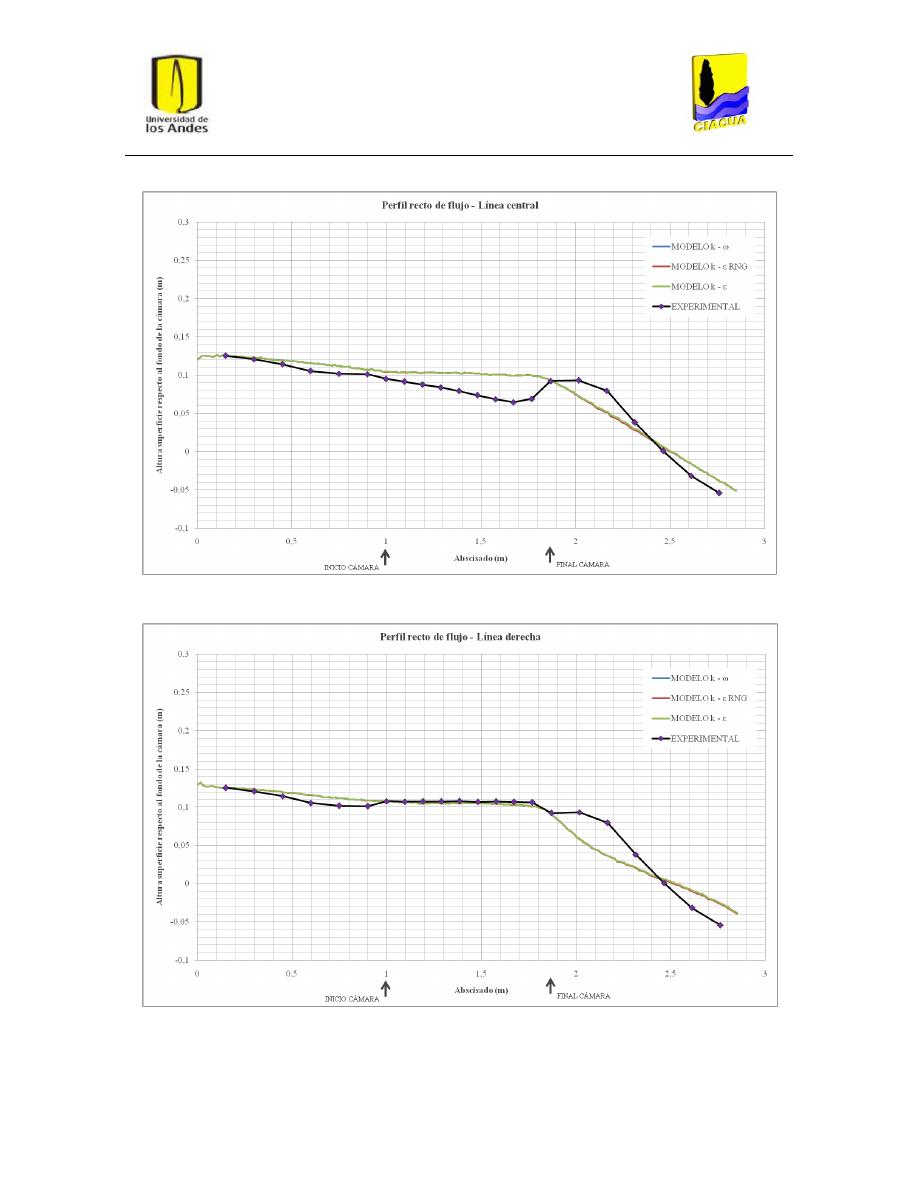
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
39
ICIV 201210 01
Gráfica 7: Perfil recto de flujo por la línea central para FD-4.
Gráfica 8: Perfil recto de flujo por línea derecha para FD-4
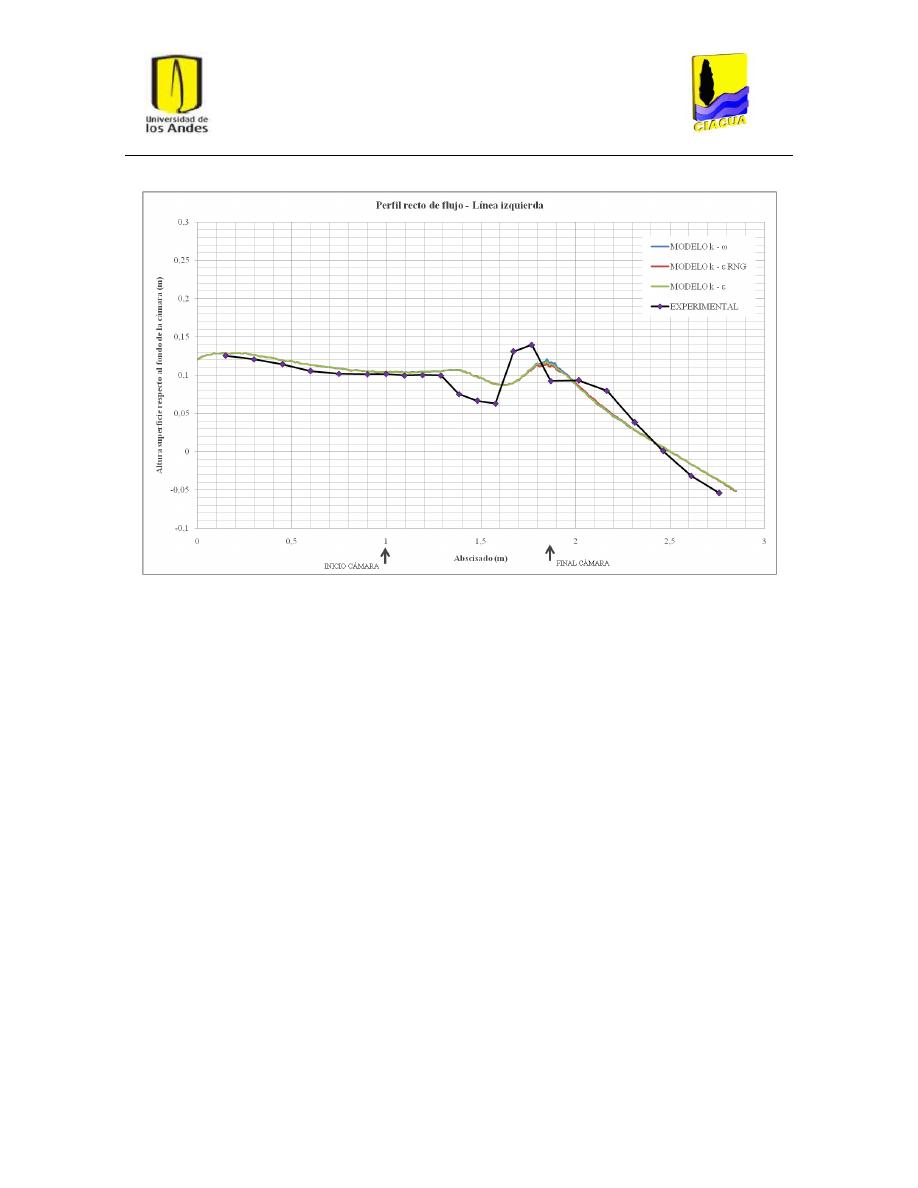
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
40
ICIV 201210 01
Gráfica 9: Perfil recto de flujo por línea izquierda para FD-4.
En cuanto a los resultados en Anexos para los escenario FN, se puede establecer que los modelos
computacionales simulan adecuadamente el perfil de flujo en la tubería de entrada lateral y al inicio
de la cámara de inspección, pero se alejan significativamente de los datos experimentales a medida
que el flujo avanza hacía la tubería de salida. Este comportamiento es más marcado en el escenario
FN-8 que en el escenario FN-7.
Es importante notar que en todas las figuras de perfiles de flujo se indica la ubicación sobre las
abscisas del inicio y final de la cámara. Lo anterior permite establecer relaciones entre cambios
relevantes en el perfil de flujo y su ubicación relativa a la cámara de inspección.
De FD-3 solo se incluyen 2 gráficas de perfiles de flujo en Anexos, para la línea central y para la
línea izquierda. No se anexa gráfica de la línea derecha debido a que no se cuenta con información
experimental sobre el perfil del flujo a lo largo de este plano de medición.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
41
ICIV 201210 01
4.3. Comportamiento de los residuos de las ecuaciones fundamentales
En todas las simulaciones realizadas, el comportamiento de todos los residuos (residuos de las
ecuaciones de momentum en cada dirección: azul oscuro (en X), amarillo (en Y), azul claro (en Z);
residuos de las ecuaciones de continuidad de cada fase: verde (agua), rojo (aire); residuos de las
ecuaciones de adicionales para modelar la turbulencia) es muy similar: Primero se observa un
periodo en que los residuos disminuyen de manera asintótica desde 1*10
-2
, aproximadamente, hasta
un valor en el que desaparece la tendencia a disminuir y se estabiliza el comportamiento. A partir de
este punto aparece la segunda zona que va hasta el final de la simulación, donde se observa que los
residuos oscilan alrededor de un valor suficientemente pequeño (entre 10
-3
y 10
-6
). Aunque el
análisis del flujo a través de la cámara de inspección se realiza para un sistema estabilizado, en la
realidad existen variaciones latentes de las velocidades y presiones en todo el dominio, pero estas
son tan pequeñas que se permiten tratar el fenómeno como flujo en estado estable. Estas variaciones
son las causantes del comportamiento oscilatorio de los residuos.
A continuación se enseñan gráficas de residuos de los escenarios en que se presentaron las
diferencias más marcadas entre modelos de turbulencias. En el resto de escenarios se excluyeron
pues no es posible establecer diferencias relevantes.
Las primeras gráficas (Gráficas 10 a 12), son residuos de las ecuaciones de momentum y
continuidad para los tres modelos de turbulencia en la simulación del escenarios FN-8. Se observa
que el modelo k-ε estándar es más estable que los otros dos en cuanto al comportamiento de las
ecuaciones de momentum, aunque los modelos RNG y k-ω resuelven las ecuaciones de continuidad
con mayor precisión que el primero. El comportamiento del modelo k-ε RNG en relación con las
ecuaciones de momentum es más estable que el del modelo k-ω.
Posteriormente (Gráficas 13 a 15), se enseñan los residuos de las ecuaciones fundamentales para
cada uno de los modelos de turbulencia en el escenario de modelación FD4. El comportamiento es
muy similar para todos los modelos. En general las variaciones presentadas por el modelo RNG son
menores, pero los valores de los residuos de las ecuaciones de continuidad para el modelo k-ω son
menores.
Y, finalmente, se enseña el comportamiento de los residuos de las ecuaciones fundamentales para el
escenario de modelación FD-6. En general, para este escenario de modelación, el modelo de
turbulencia k-ω se comporta mejor que los otros dos modelos. Las variaciones de los residuos son
más pequeñas y oscilan alrededor de valores muchos menores.
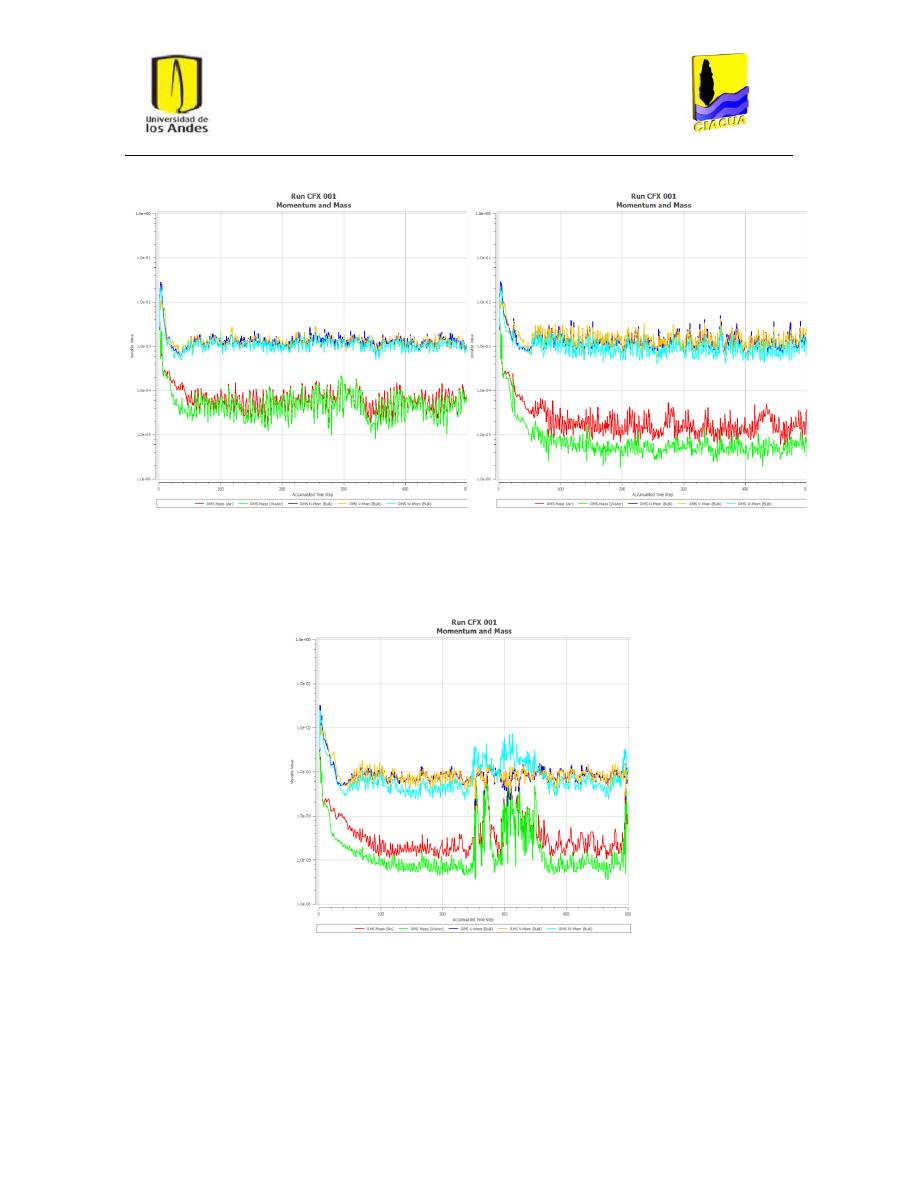
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
42
ICIV 201210 01
Figura 26: Residuos para FN-8, modelo k-ε estándar.
Figura 27: Residuos para FN-8, modelo k-ε RNG.
Figura 28: Residuos para FN-8, modelo k-ω.
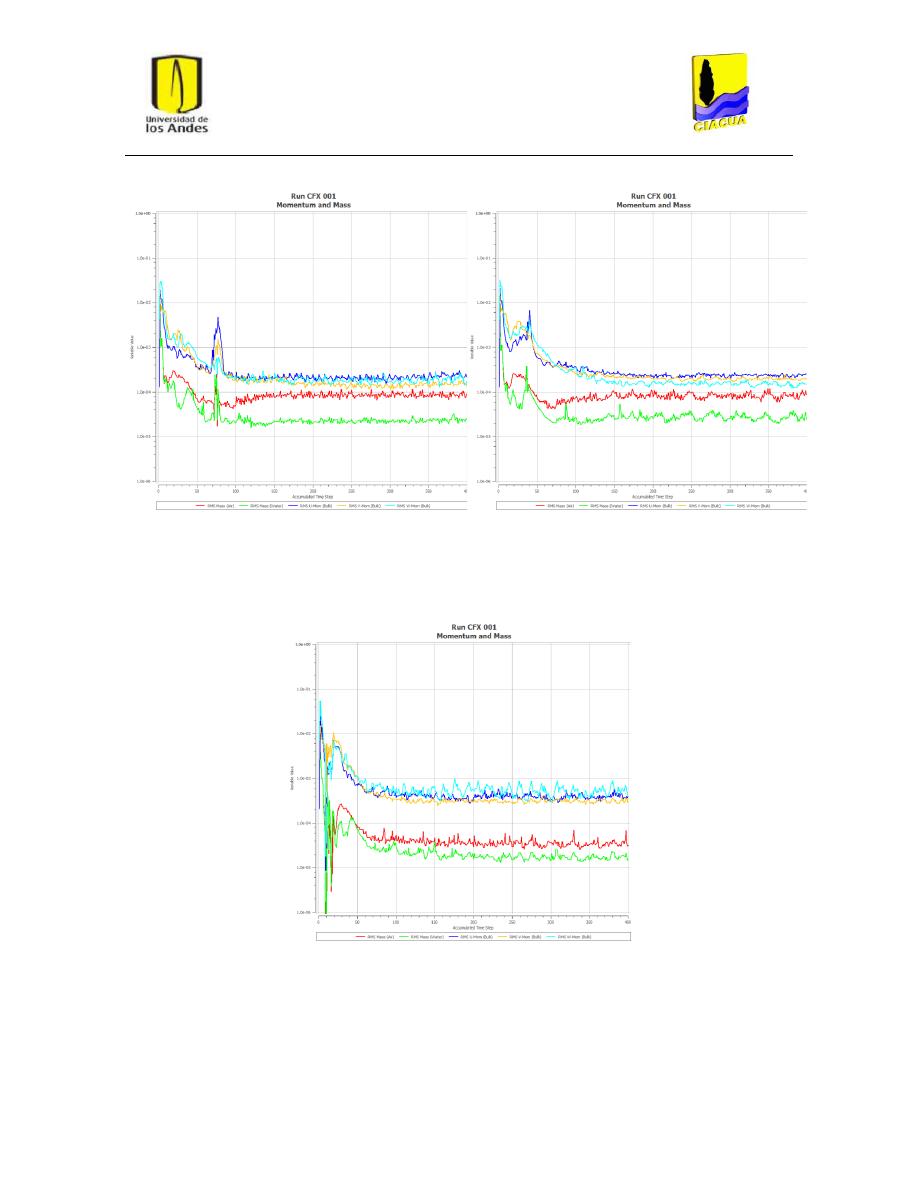
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
43
ICIV 201210 01
Figura 29: Residuos para FD-4, modelo k-ε estándar.
Figura 30: Residuos para FD-4, modelo k-ε RNG.
Figura 31: Residuos para FD-4, modelo k-ω.
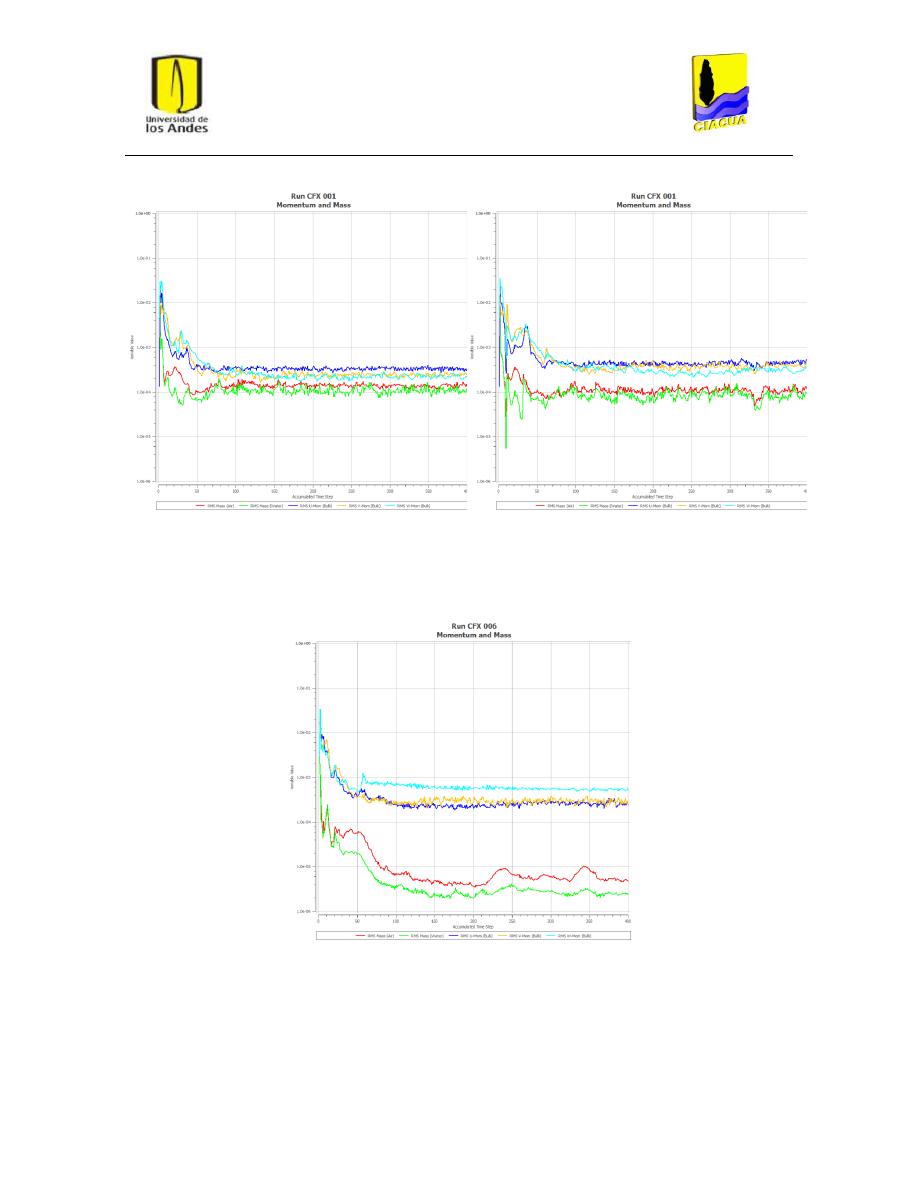
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
44
ICIV 201210 01
Figura 32: Residuos para FD-6, modelo k-ε estándar.
Figura 33: Residuos para FD-6, modelo k-ε RNG.
Figura 34: Residuos para FD-6, modelo k-ω.
De lo anterior es posible establecer que los residuos oscilan alrededor de valores adecuados (<10
-3
)
por periodos prolongados; en consecuencia los modelos tratados logran estabilizarse y alcanzan
resultados deseables.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
45
ICIV 201210 01
5. ANÁLISIS DE RESULTADOS
5.1. Perfiles de flujo
Según los perfiles enseñados en la sección anterior y en Anexos, las simulaciones se comportan
adecuadamente y, en la mayoría de los casos, predicen los resultados medidos por el CIACUA
(Centro de Investigaciones de Acueductos y Alcantarillados - CIACUA, 2010). UF-4, FN-8 y UF-5,
no dan tan buenos resultados como los demás escenarios de modelación. En UF-4 se presentan
variaciones significativas en la tubería de entrada principal y en la tubería de salida mientras que en
UF- 5 se observan variaciones significativas dentro de la cámara. También es común encontrar en
los perfiles curvos de flujo (para UF-2, UF-3, UF-4, UF-5, FN-7 y FN-8) cambios bruscos en el
nivel del agua a la altura de la entrada a la cámara. Esto se debe, como se mencionó anteriormente,
a que este perfil de flujo está compuesto por dos planos de corte que se intersecan. Adicionalmente
se observa en perfiles curvos de flujo por la línea izquierda que los datos experimentales presentan
una discontinuidad a falta de puntos de medición entre 1.7 m y 2.1 m (zona al interior de la cámara).
Esto puede ser un problema ya que no hay curva de referencia en esta región.
Es importante resaltar que en general se observa un pequeño retraso en los perfiles de flujo
obtenidos respecto a las mediciones experimentales, pero no existe información experimental que
permita establecer cuál es el rango de variación de los valores experimentales, por lo que no es
posible establecer si los perfiles de los modelos computacionales están dentro de un rango
adecuado, aunque si se observa buena proximidad entre los resultados de las simulaciones y los
valores experimentales.
En UF-2 y UF--5 se presentan variaciones significativas en el perfil curvo de flujo a la entrada de la
cámara, pero es importante resaltar nuevamente que los planos de corte ocasionan cambios bruscos
en el perfil de flujo. En ambos se observan pequeños retrasos en los perfiles obtenidos de la
simulación respecto a las mediciones experimentales. Se observa un aumento fuerte en el nivel de
agua a la entrada de la cámara que, posteriormente, cae gradualmente, tanto en el perfil lateral
(perfil curvo de flujo) como en el perfil principal (perfil recto de flujo).
Las simulaciones de UF-3 enseñan perfiles rectos de flujo que se asemejan mucho a la curva
experimental. Los perfiles curvos de flujo no se enseñan en su totalidad debido a problemas de
visualización de resultados. Todos los modelos predicen los mismos perfiles de flujo, sobre todo en
la tubería de entrada principal y al interior de la cámara; al recorrer la tubería de salida se observa
una pequeña variación en los perfiles de cada modelo de turbulencia. No se observan cambios de
altura significativos en la altura de la superficie durante el recorrido.
En cuanto a UF-4, los resultados experimentales indican que ocurre un fuerte cambio de nivel del
agua a la entrada de la cámara tanto sobre los perfiles principales como sobre los perfiles laterales.
Los perfiles laterales se comportan adecuadamente, pero los perfiles principales son
significativamente distintos a los resultados experimentales. En el interior de la cámara hay

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
46
ICIV 201210 01
similitud entre la experimentación y los perfiles principales, pero a lo largo de la tubería de entrada
y de salida los resultados divergen en gran medida. Los resultados de las simulaciones predicen que
sobre los perfiles principales debe presentarse una altura de la lámina de agua constante en la
tubería de entrada. Según el estudio del CIACUA, para este escenario de flujo se presenta una
sobrecarga al interior de la cámara que obliga al flujo de agua de la tubería de entrada principal a
aumentar gradualmente su altura. Es posible que el dominio de la tubería de entrada sea muy corto
y, en consecuencia, las simulaciones no puedan recrear el aumento de nivel progresivo debido al
fenómeno de sobrecarga adecuadamente. De ser el caso sería necesario ampliar la longitud de la
tubería de entrada y verificar que la simulación mejore.
Los escenarios de Flujo Directo (FD-3, FD-4, FD-6 y FD-8) muestran comportamientos similares
en cuanto los perfiles de flujo obtenidos de las simulaciones. Las simulaciones del escenario FD-4
enseñan mejor comportamiento que las simulaciones realizadas para los otros escenarios FD, pero
se observa un pequeño retraso respecto a la curva experimental. En cuanto a FD-3, las simulaciones
predicen el aumento pronunciado de nivel que ocurre hacia el final de la cámara pero se presenta un
sesgo importante en relación al valor máximo de nivel de agua medido experimentalmente. Esto
puede deberse a un error en las mediciones experimentales de este punto, pues la diferencia en
alturas entre este punto y los puntos vecinos es muy grande.
FN-8 y FN-7 son los únicos escenarios de modelación para Flujo a 90°, lo que puede ser poco
apropiado ya que no suministran información suficiente sobre el comportamiento de las
simulaciones para escenarios de Flujo a 90°. En ambos casos se predicen adecuadamente los niveles
de agua en la tubería de entrada lateral y al inicio de la cámara. Las predicciones para FN-7
presentan menos diferencias con la curva experimental al interior de la cámara y a lo largo de la
tubería de salida que las predicciones para FN-8. En FN-8 los perfiles sobre la línea central caen
repentinamente hacia el final de la cámara y se alejan sustancialmente de la curva experimental y
los perfiles sobre la línea derecha indican retraso respecto a los datos experimentales y niveles de
superficie mayores a los medidos.
La malla es gruesa y a falta de resolución se pueden estar omitiendo mejores resultados en los
perfiles de flujo, entre otras cosas. Pero de las imágenes recolectadas se pueden ver fenómenos que
se describen en el informe experimental, como la formación de ondas o la elevación de la
superficie. De hecho existe una tendencia al resalto o formación de una onda estacionaria para
escenarios UF y FN en la zona indicada en la Figura 36. Según CIACUA, este tipo de onda se
denomina onda C (Centro de Investigaciones de Acueductos y Alcantarillados - CIACUA, 2010).
Del informe se extrae que para relaciones de llenado y velocidades altas en la tubería lateral
(conducto hidráulicamente dominante) se presenta formación de la onda C, que se ocasiona por el
choque de flujo en la tubería lateral contra la pared de la cañuela. A continuación se presenta este
fenómeno en el escenario de simulación UF-2.
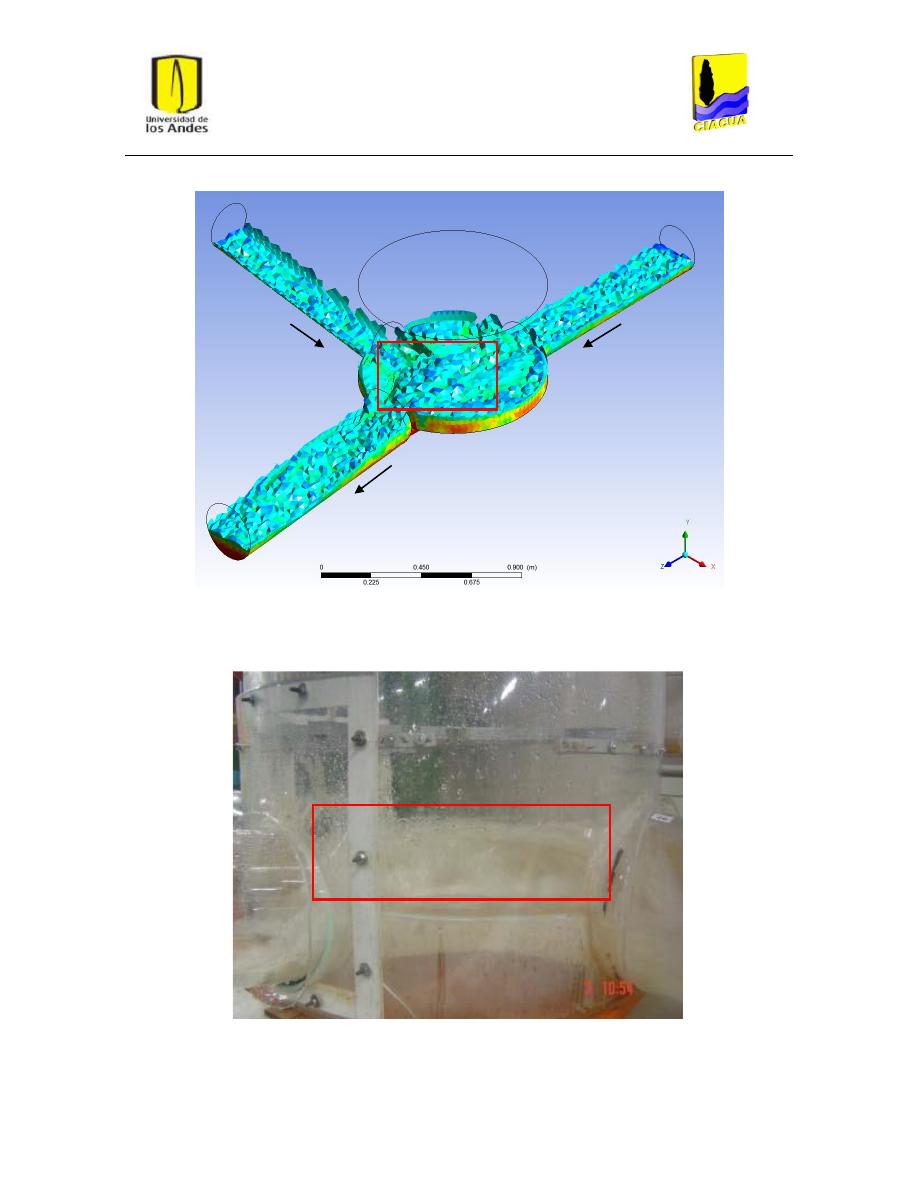
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
47
ICIV 201210 01
Figura 35: Formación de onda C en UF-2. Modelo k-ω de turbulencia.
Foto 1: Formación de una Onda C en el punto de confluencia de los flujos, para el escenario UF-2. Tomado de la ref.
(Centro de Investigaciones de Acueductos y Alcantarillados - CIACUA, 2010).
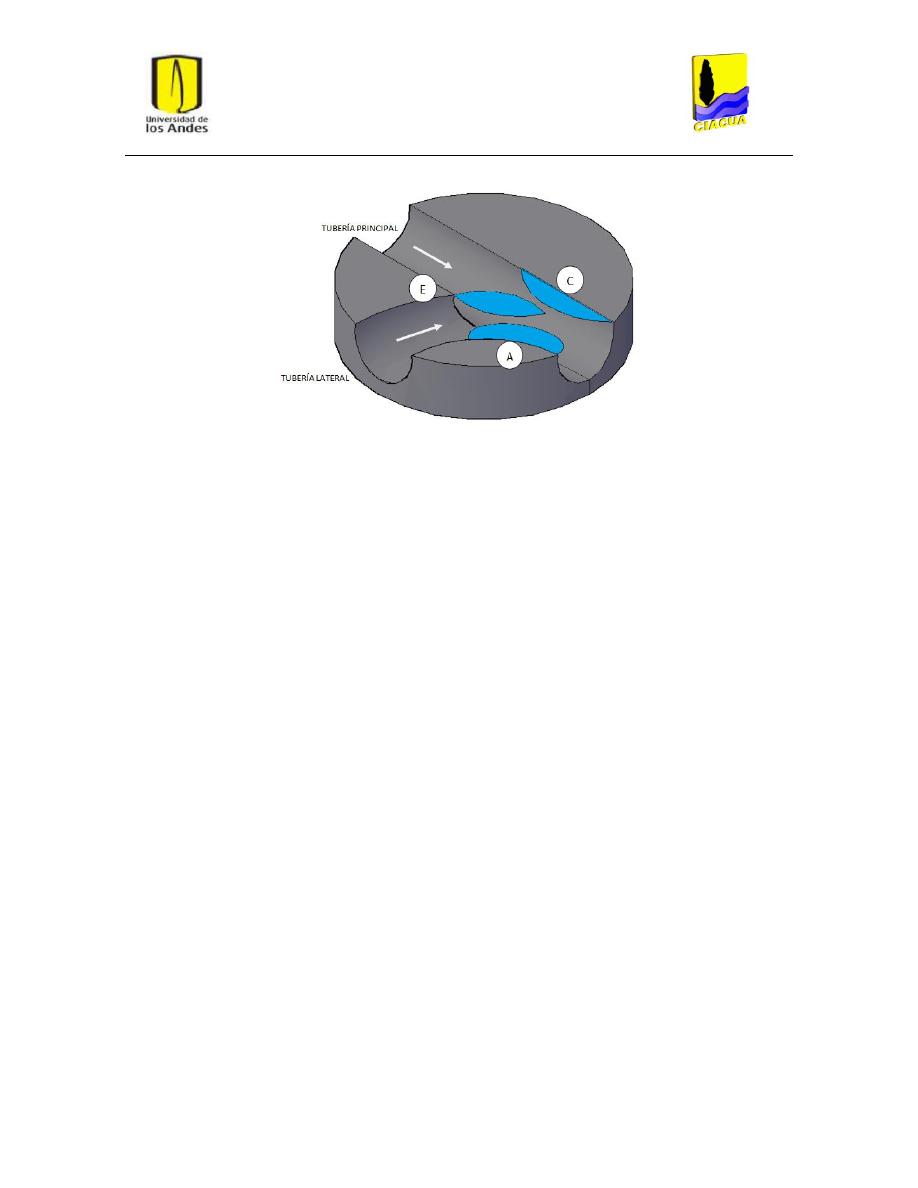
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
48
ICIV 201210 01
Figura 36: Zonas de formación de ondas estacionarias. Tomado de la ref. (Centro de Investigaciones de Acueductos y
Alcantarillados - CIACUA, 2010).
Usando la Figura 35 y la Foto 1, extraídas del informe del CIACUA, es posible concluir que los
perfiles apuntan a que las simulaciones funcionan adecuadamente, a pesar del tamaño de la malla.
Aunque en varios casos se observan variaciones en relación a la experimentación, la mayoría de
diferencias son pequeñas y los perfiles muestran los resaltos, elevaciones y caídas esperadas.
5.2. Fenómeno de recirculación
Según el CIACUA existe la formación de zonas de recirculación debido a que:
"El comportamiento del flujo en una cámara de alcantarillado con flujo
supercrítico está descrito por dos zonas; una zona de ondas aguas abajo del punto
de unión entre los canales de conducción de la cañuela y una zona no perturbada o
sin presencia de ondas aguas arriba del mismo punto, en donde el agua se almacena
o represa y para grandes caudales forma un movimiento de vórtice, el flujo
sobrepasa el canal de conducción o banca formando una recirculación del flujo en
esta zona" (Centro de Investigaciones de Acueductos y Alcantarillados - CIACUA,
2010) .
Por lo que debería observarse este tipo de fenómeno en los resultados de las simulaciones. Al
generar un plano de corte paralelo al fondo y ubicado cerca al fondo de la tubería y dibujar vectores
de velocidad sobre este plano se observan los siguientes comportamientos.
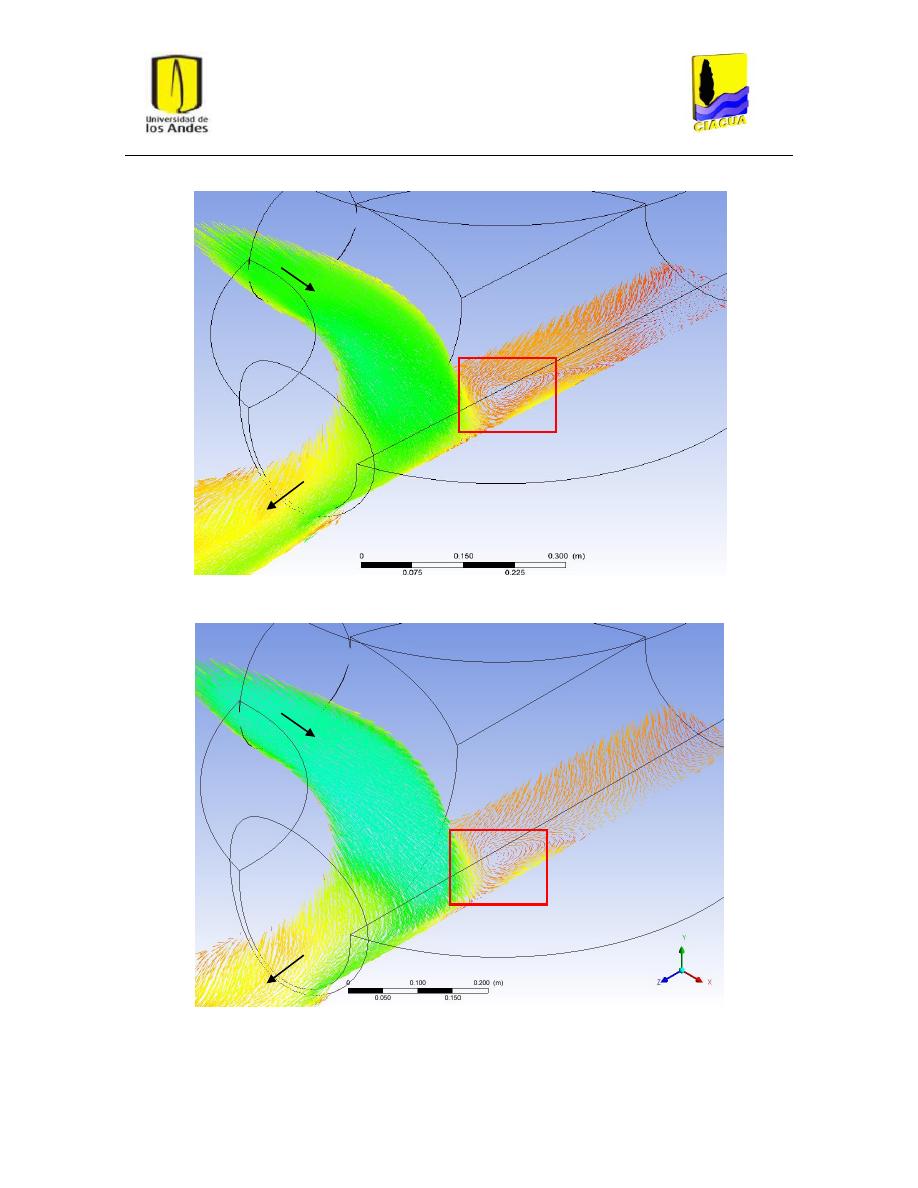
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
49
ICIV 201210 01
Figura 37: Vórtices i recirculación en escenario FN-7.
Figura 38: Vórtices o recirculación en escenario FN-8.
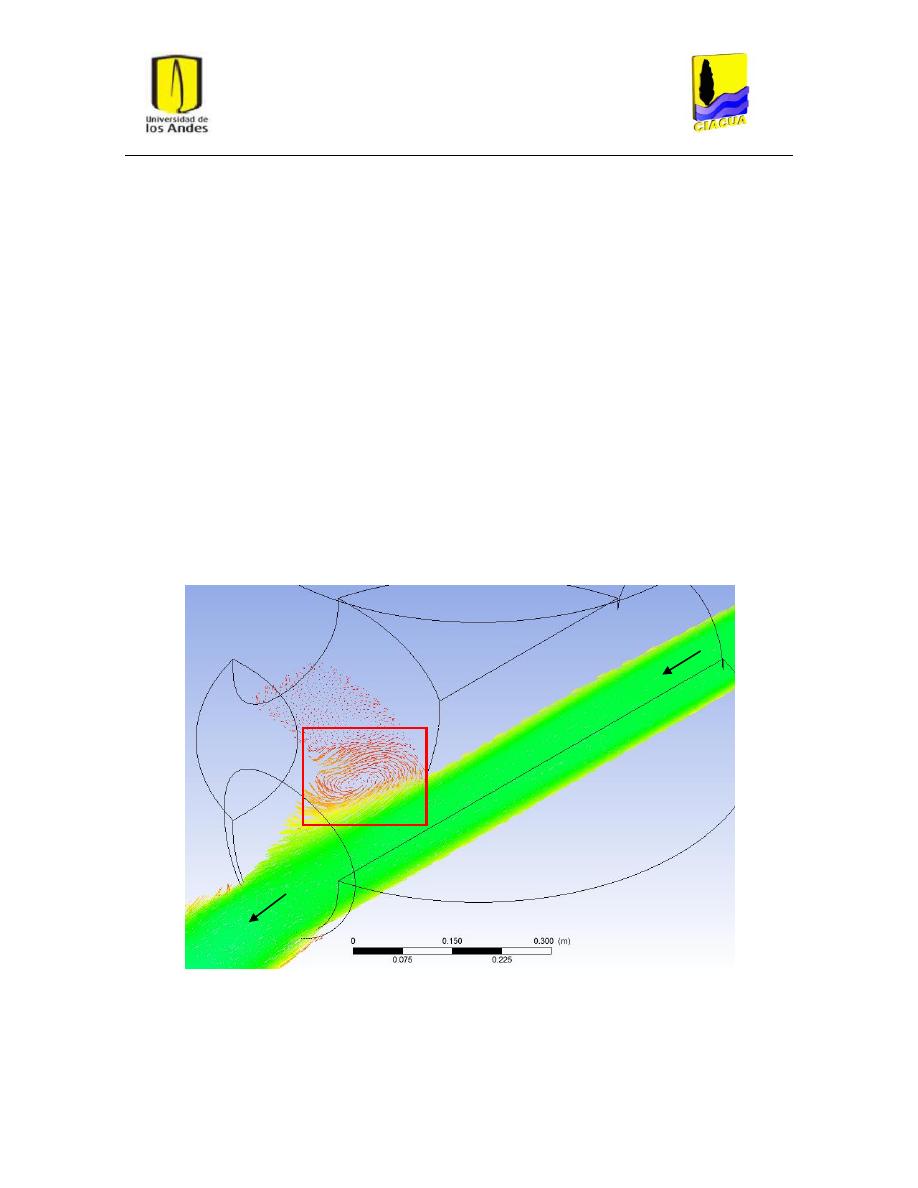
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
50
ICIV 201210 01
En estos escenarios es claro el fenómeno de recirculación documentado por CIACUA en escenarios
de Flujo a 90°. Se observa un flujo continuo por la tubería de entrada lateral y, aguas arriba de la
conexión entre las tuberías de entrada, se observa una zona de almacenamiento o represamiento que
genera los vórtices y se denomina zona de recirculación.
Los escenarios de Flujo Directo a continuación indican también zonas de recirculación, como era
esperado. Se presenta un flujo continuo a través de la tubería de entrada principal y en la zona de la
cañuela, aguas arriba de la conexión; por la tubería de entrada lateral, se presenta represamiento de
flujo y generación de vórtices. Este fenómeno se presenta en ambas figuras a continuación y
corrobora los fenómenos observados por el CIACUA:
"El comportamiento del flujo supercrítico en una cámara de inspección con
entrada únicamente por la tubería principal se caracteriza por seguir su trayectoria
recta, sin tener mayor efecto en el canal de conducción lateral de la cañuela.
Aunque en este canal se observa un almacenamiento de agua con movimiento en
forma de vórtice, […] este almacenamiento es mínimo en comparación al caudal
total que circula por el canal principal." (Centro de Investigaciones de Acueductos
y Alcantarillados - CIACUA, 2010).
Figura 39: Vórtices o recirculación en escenario FD-3.
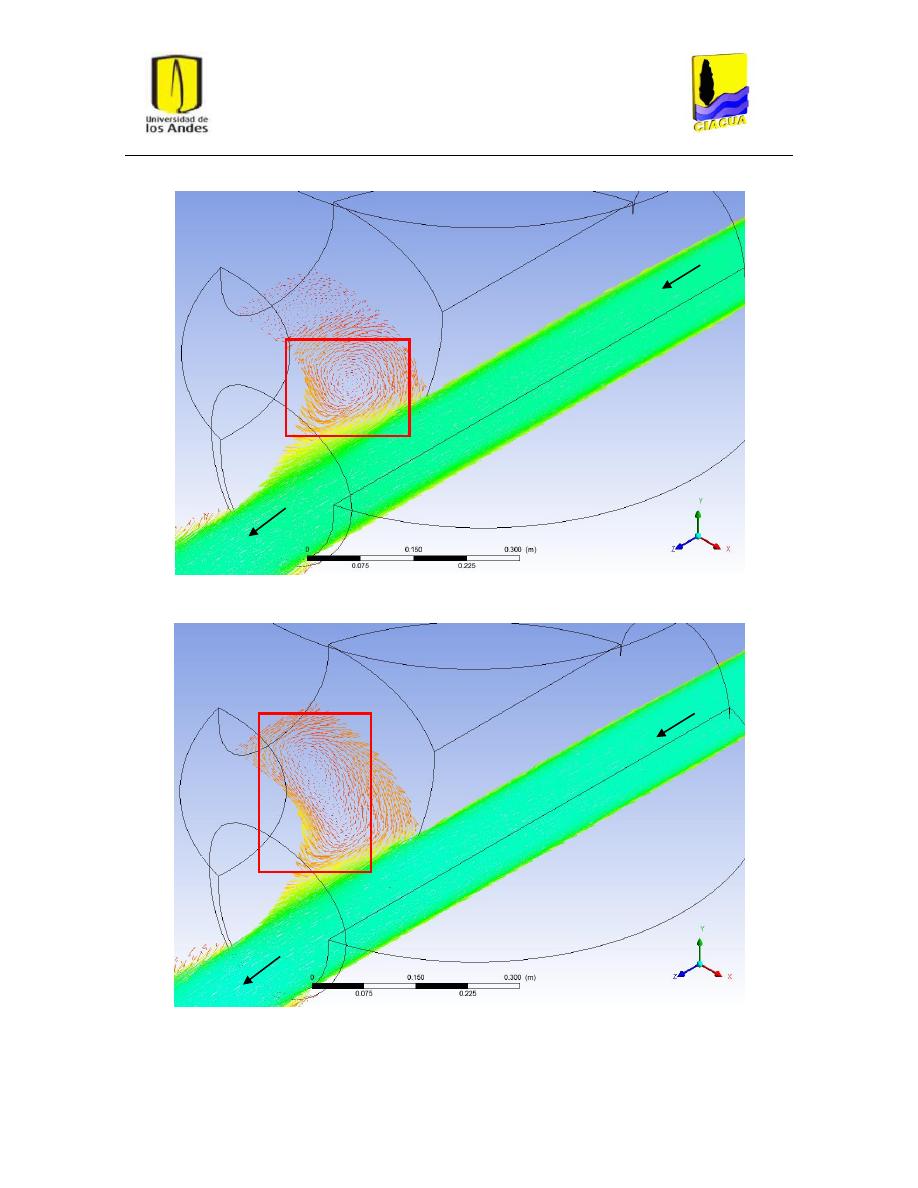
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
51
ICIV 201210 01
Figura 40: Vórtices o recirculación en escenario FD-4.
Figura 41: Vórtices o recirculación en escenario FD-6.
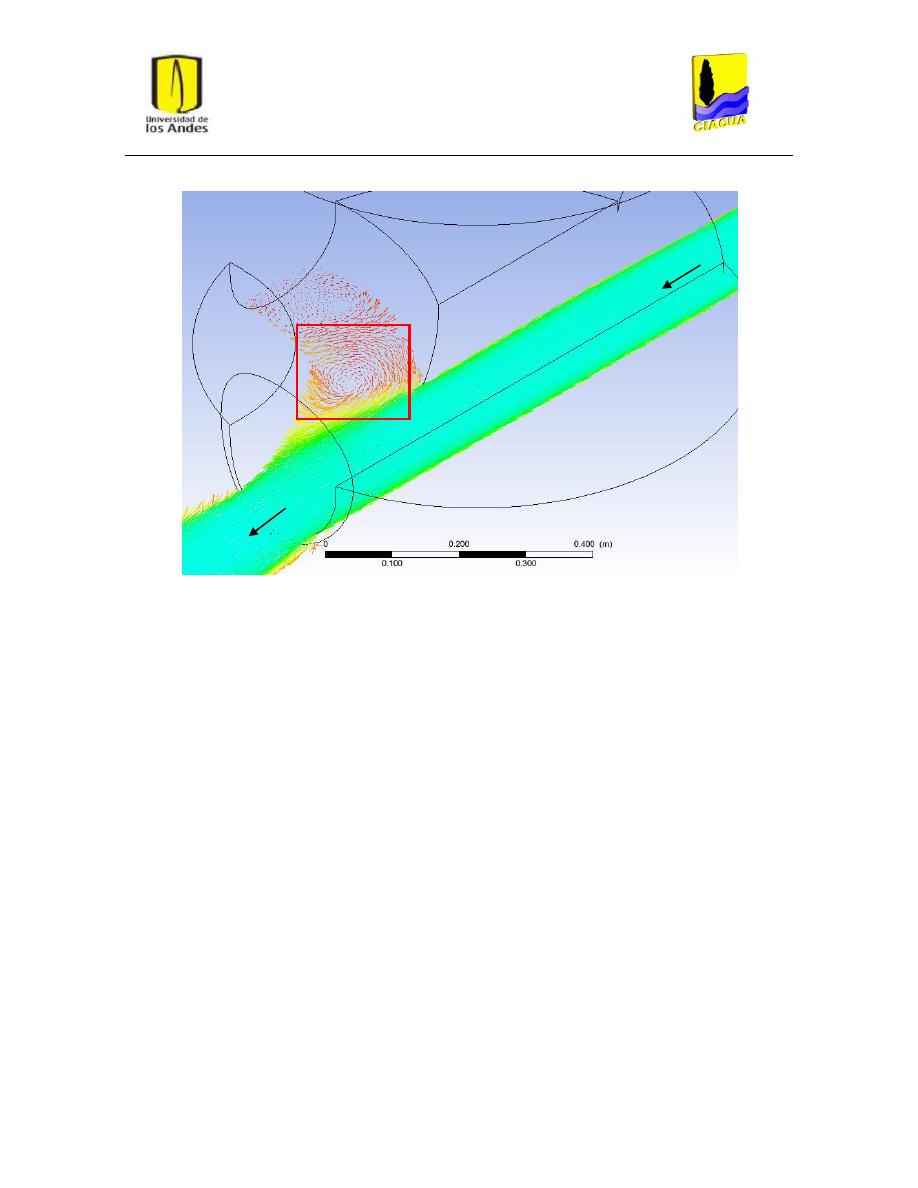
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
52
ICIV 201210 01
Figura 42: Vórtices o recirculación en escenario FD-8.
Se realizó el mismo estudio para escenarios de Unión de Flujos. Aunque el CIACUA no reporta
formación de zonas de recirculación en la superficie, se obtuvieron los siguientes resultados. UF-2 y
UF-3 indican recirculación aguas arriba de la conexión por la tubería de entrada lateral, mientras
que UF-4 muestra una leve recirculación en la llegada de la tubería principal a la conexión.
En UF-3 y UF-2, el ducto dominante es el principal y, en el caso de UF-3, la velocidad del agua en
la tubería lateral es el 10%, aproximadamente, de la velocidad del agua en la tubería principal, por
lo que se observa un fenómeno similar al descrito para escenario de flujo directo. En UF-4 y UF-5,
el conducto dominante es el lateral y la velocidad a través de este es aproximadamente 3 veces
mayor a la velocidad por la tubería principal. El fenómeno de recirculación se presenta en la misma
zona que para los escenarios FN, aunque la recirculación no es tan clara. Puede que estas zonas de
recirculación no se observen a simple vista sobre la superficie, como si sucede en escenarios de
Flujo Directo o Flujo a 90°, pero puede que el fenómeno si esté presente debido a que la velocidad y
caudal del flujo a través de la tubería dominante es mucho mayor en 3 de 4 casos.
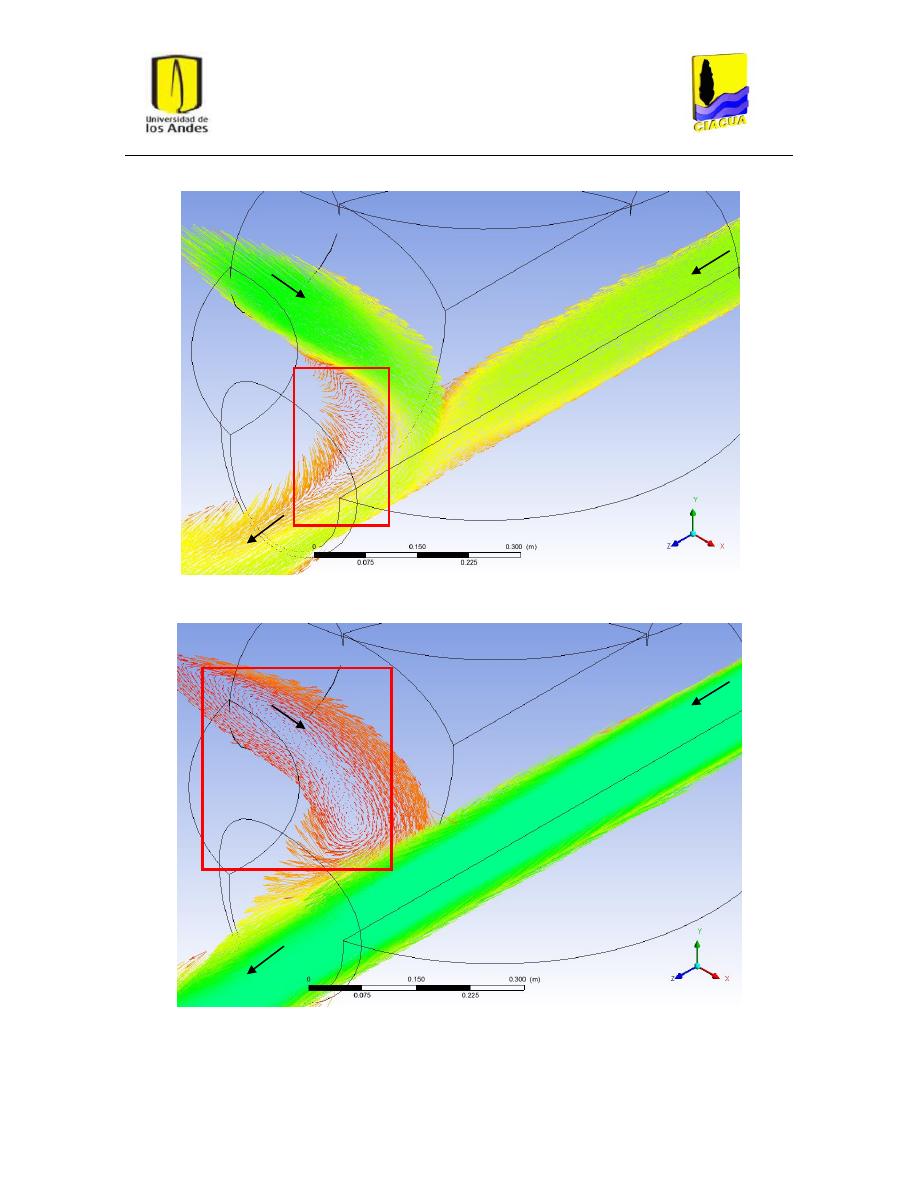
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
53
ICIV 201210 01
Figura 43: Vórtices o recirculación en escenario UF-2.
Figura 44: Vórtices o recirculación en escenario UF-3.
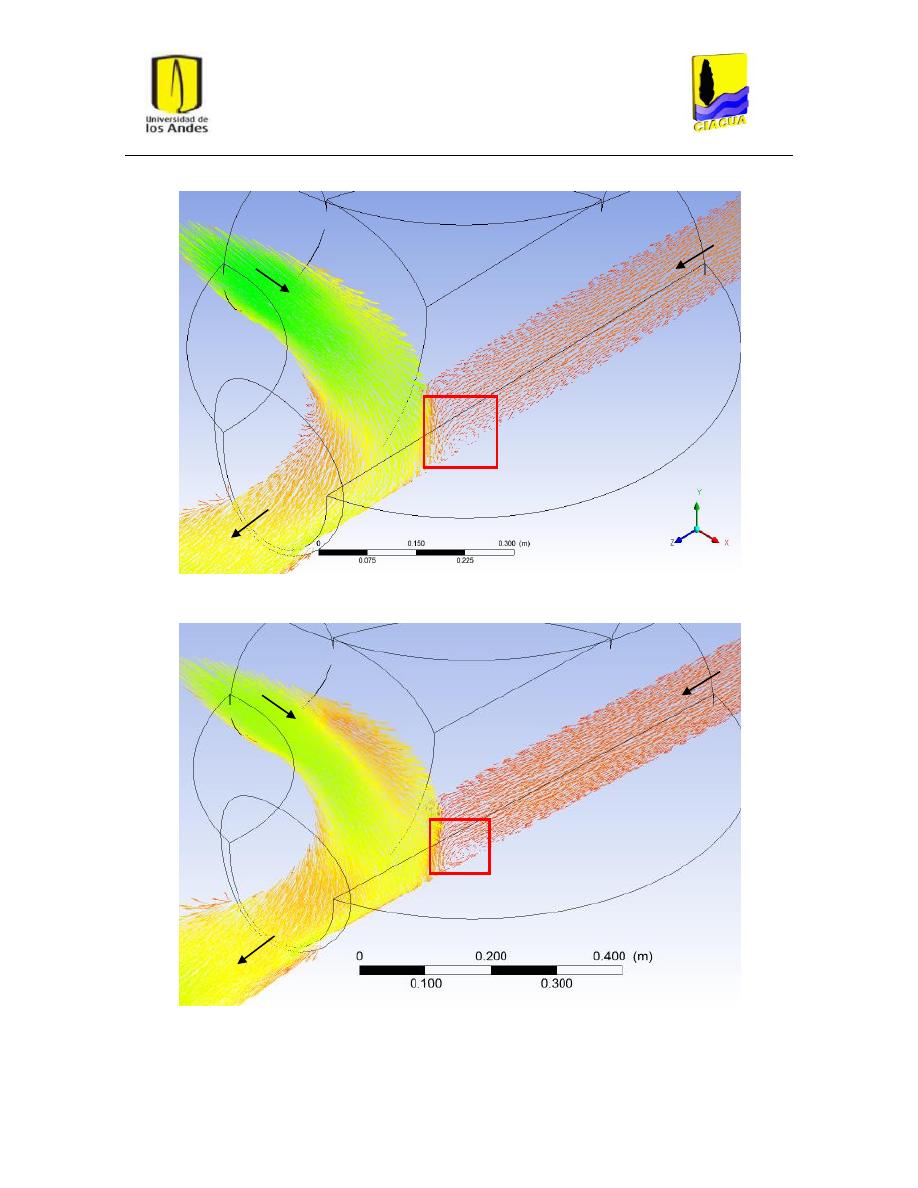
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
54
ICIV 201210 01
Figura 45: Vórtices o recirculación en escenario UF-4.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
55
ICIV 201210 01
Según el reporte del CIACUA, los patrones de Ondas A, C y E que se observan en Figura 36, se
deben a:
" […] choque del flujo de entrada por la tubería principal con el final de la
pared interna del canal de conducción lateral de la cañuela; comportamiento típico
de la onda hidráulicamente dominante de un flujo directo (Onda A). […] choque del
flujo de entrada por la tubería lateral con la pared del canal de conducción
principal de la cañuela, comportamiento típico de la onda hidráulicamente
dominante de un flujo a 90° (Onda C). […] la onda, definida como Onda E se forma
debido a la unión de los flujos en el punto de confluencia de los canales de
conducción principal y lateral."
No existe un estudio detallado sobre la relación entre este tipo de ondas y la turbulencia, pero puede
que las zonas de recirculación estén relacionadas con la formación de ondas estacionarias, en
especial las Ondas A, ya que la ubicación aparente es arriba de la zona de recirculación observada
en los escenarios UF-2 y UF-3. El mismo informe del CIACUA establece que existe la formación
de una Onda A para el escenario de flujo UF-3, lo que puede corroborar la suposición, pero se
requiere de un estudio formal para poder arrojar conclusiones al respecto.
5.3. Tiempos de simulación
Los tiempos físicos que se enseñan en la Tabla 6 se seleccionaron a fin de permitir que el flujo
dentro de la cámara se estabilizara. Entonces, si la velocidad mínima a simular es de 0.26 m/s
(escenario UF-3) y se supone que la longitud máxima dentro del dominio que puede recorrer la
partícula es de 3.5 m, el paso de tiempo máximo debe ser de 0.9 segundos. De manera que,
inicialmente, se utilizaron pasos de tiempo menores para asegurar precisión. Entonces, para los
escenarios de Unión de flujos (UF), debido a que modelar convergencia de flujos puede ser
complicado se utilizó un paso de tiempo de 0.2 segundos (
∆𝑡 = 0.2 𝑠) y 1500 iteraciones para un
tiempo físico de modelación de 5 minutos. Posteriormente, se aumentó el paso de tiempo para los
escenarios de Flujo directo (FD) y Flujo a 90° (FN); se modelaron con
∆𝑡 = 0.6 𝑠 y 400 iteraciones
para asegurar un tiempo físico de modelación de 4 minutos. Como lo demuestran los resultados,
estos parámetros de entrada son suficientes para asegurar que el escenario de modelación alcanzara
estabilidad. Dado que los resultados obtenidos en los escenarios FD y FN son, en general, buenos,
lo anterior establece que es posible aumentar el paso de tiempo para los escenarios de UF. De
manera que se reduzca sustancialmente el número de iteraciones necesarias para lograr la
estabilidad del sistema, reduciendo en tiempo de simulación y en recursos computacionales.
En general los tiempos de simulación requeridos por cada modelo son muy similares. La diferencia
máxima es de 18.6 minutos entre el modelo k-ε estándar y el modelo k-ω para el escenario UF-2,
equivalente al 3.7% del tiempo promedio de simulación del escenario UF-2 (el tiempo promedio de
simulación es de 8.213 horas). En consecuencia las diferencias en tiempo de simulación son muy
pequeñas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
56
ICIV 201210 01
6. CONCLUSIONES
De los resultados observados no fue posible establecer un parámetro cualitativo o cuantitativo que
permitiera determinar qué modelo de turbulencia se comporta mejor y es más adecuado para
modelar cámaras de inspección bajo condiciones de flujo supercrítico. En todas las aproximaciones
realizadas para evaluar el desempeño de los modelos de turbulencia utilizados se observaron
situaciones en que el modelo k-ε estándar presentaba mejor desempeño que los otros dos, o que el
modelo k-ε RNG presentaba mejor desempeño, o que el modelo k-ω presentaba mejor desempeño,
pero no fue posible establecer un desempeño persistentemente superior para alguno de los modelos.
Es necesario entonces utilizar mejores modelos de turbulencia, como el de Esfuerzos de Reynolds
(RSM), que puede mejorar las predicciones por ser un modelo más completo.
A pesar de que el análisis sea mayoritariamente cualitativo, es posible concluir que el
comportamiento de los modelos de turbulencia y los resultados obtenidos de las simulaciones son
buenos. La malla con que se cuenta tiene un tamaño de elementos relativamente grande que no
permite tener un número suficiente de puntos dentro de la capa límite turbulenta y los tres modelos
de turbulencia no difieren significativamente en ninguno de los parámetros evaluados, pero para la
mayoría de los escenarios se observaron perfiles de flujo muy similares a las curvas experimentales.
Aunque no se hayan logrado resultados de gran precisión, las simulaciones desarrolladas y
analizadas permiten al usuario predecir características muy relevantes para el análisis y diseño de
cámaras de inspección bajo condiciones de flujo supercrítico, tales como una forma aproximada de
los perfiles de flujo esperados, aumentos pronunciados en los niveles de agua (resaltos hidráulicos y
ondas estacionarias) y fenómenos como la recirculación.
De los tiempo de simulación que se analizaron es posible concluir que los recursos computacionales
necesarios para llevar a cabo las simulaciones realizadas son relativamente pocos, en especial para
los escenarios FD y FN. Pero si se realiza un enmallado de mayor resolución y se utilizan pasos de
tiempo muy pequeños para asegurar precisión en los resultados, los recursos aumentarán
significativamente. Aun así, es importante notar que el estudio realizado a partir de la modelación
numérica redujo los recursos humanos, temporales y técnicos sustancialmente.
Aunque no se enseñó ninguna escenario simulado sin el uso de modelos de turbulencia, es evidente
que el fenómeno de la turbulencia es fundamental en el desarrollo del flujo supercrítico a través de
cámaras de inspección. Algunos ejemplos claros de los efectos de la turbulencia son las zonas de
recirculación y los cambios bruscos en el nivel de la superficie. Por esta razón es fundamental
utilizar modelos de turbulencia que permitan simular adecuadamente este fenómeno, en especial en
regiones cercanas a la pared.
Se recomienda seguir realizando simulaciones de los diferentes escenarios de estudio que propone
el informe del comportamiento hidráulico de cámaras de inspección bajo condiciones de flujo
supercrítico, a fin de contar con mayor información sobre el comportamiento de la simulación de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
57
ICIV 201210 01
Flujo a 90° (FN) y flujo con caídas en las tuberías de entrada, el cual no fue estudiando en este
proyecto. Si se cuenta con mayor cantidad de escenarios simulados, es posible concluir con mayor
certeza sobre la validez de esta aproximación al estudio de cámaras supercríticas.
Nuevamente, es importante resaltar que no se tiene conocimiento de la incertidumbre de las
variables experimentales y que puede que en la realidad los rangos de variación sean
suficientemente amplios para que todos los resultados obtenidos sean satisfactorios. De manera que
se recomienda tener en cuenta desarrollar mediciones experimentales que contemplen la
incertidumbre para investigaciones experimentales posteriores.
Finalmente, el estudio de sistemas de flujo a través de métodos numéricos es cada vez más común,
ya que si se manejan estas herramientas adecuadamente los resultados obtenidos pueden ser
excelentes. De los resultados obtenidos en este estudio es posible es posible establecer que el
estudio del comportamiento hidráulico de cámaras de inspección o de sistemas de flujo similares a
través de métodos numéricos puede ser muy útil para los procesos de estudio y diseño de estos
elementos hidráulicos y para el análisis de problemas de superficie libre.
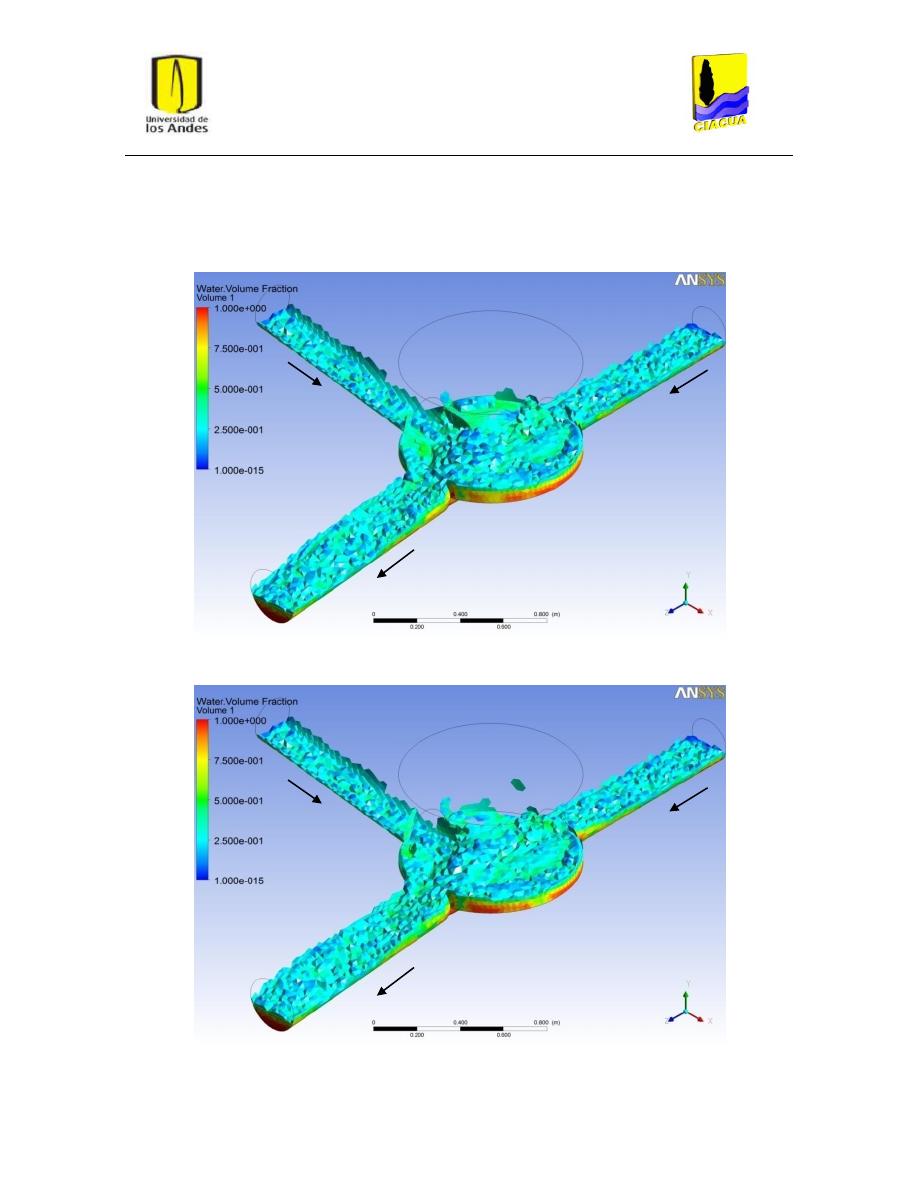
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
58
ICIV 201210 01
7. ANEXOS
7.1. Escenario de modelación UF-2
Figura anexa 1: Superficie del flujo en UF-2. Modelo k-ε estándar.
Figura anexa 2: Superficie del flujo en UF-2. Modelo k-ε RNG.
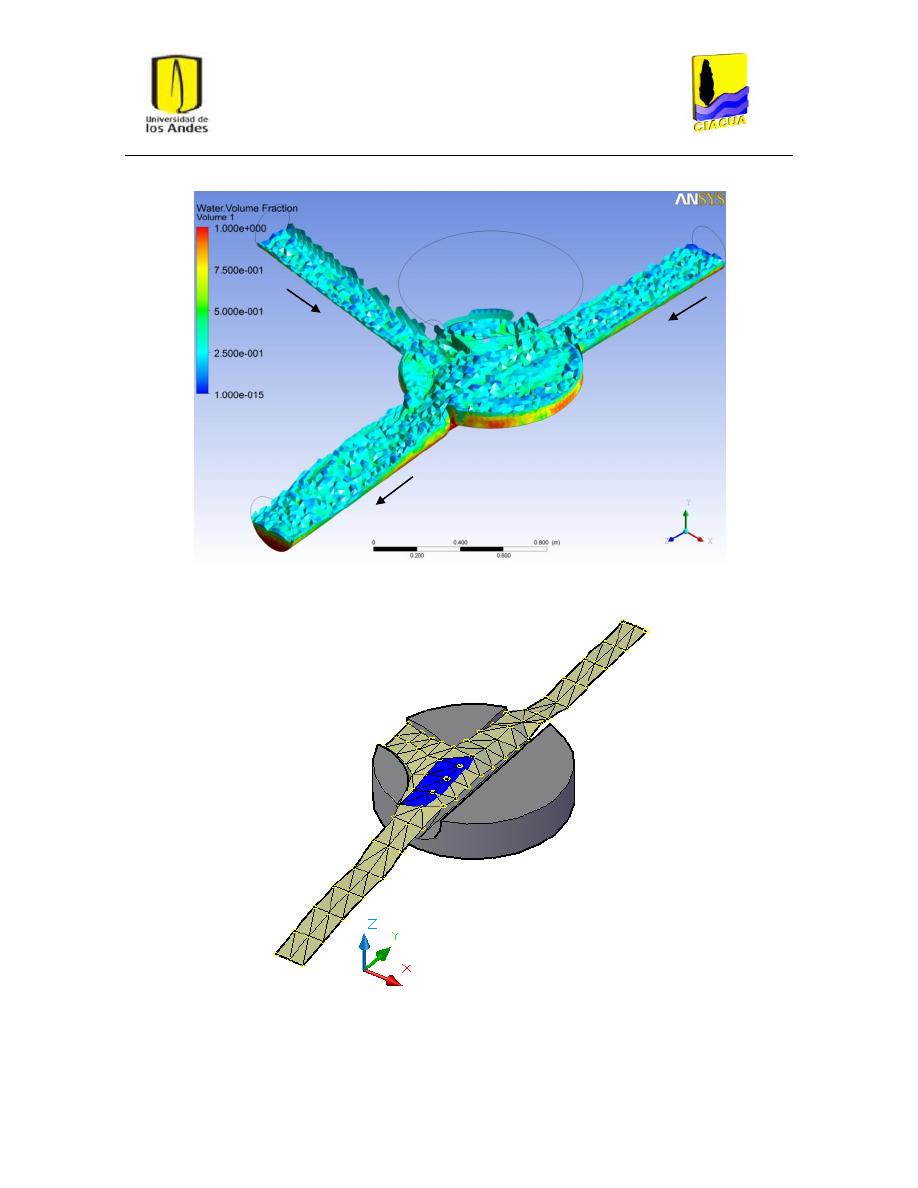
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
59
ICIV 201210 01
Figura anexa 3: Superficie del flujo en UF-2. Modelo k-ω.
Figura anexa 4: Patrón de flujo tridimensional para UF-2. Tomado de (Centro de Investigaciones de Acueductos y
Alcantarillados - CIACUA, 2010).
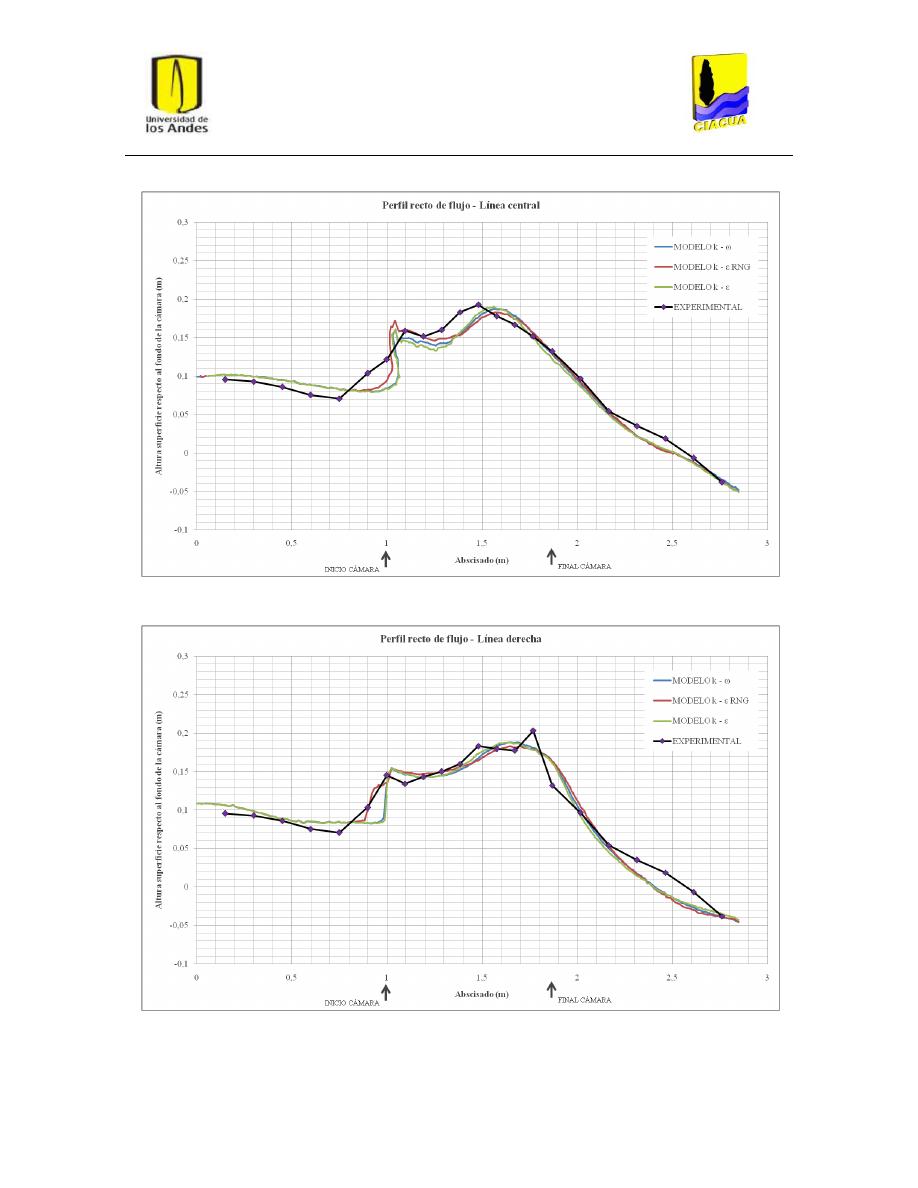
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
60
ICIV 201210 01
Gráfica anexa 1: Perfil recto de flujo por línea central para UF-2.
Gráfica anexa 2: Perfil recto de flujo por línea derecha para UF-2.
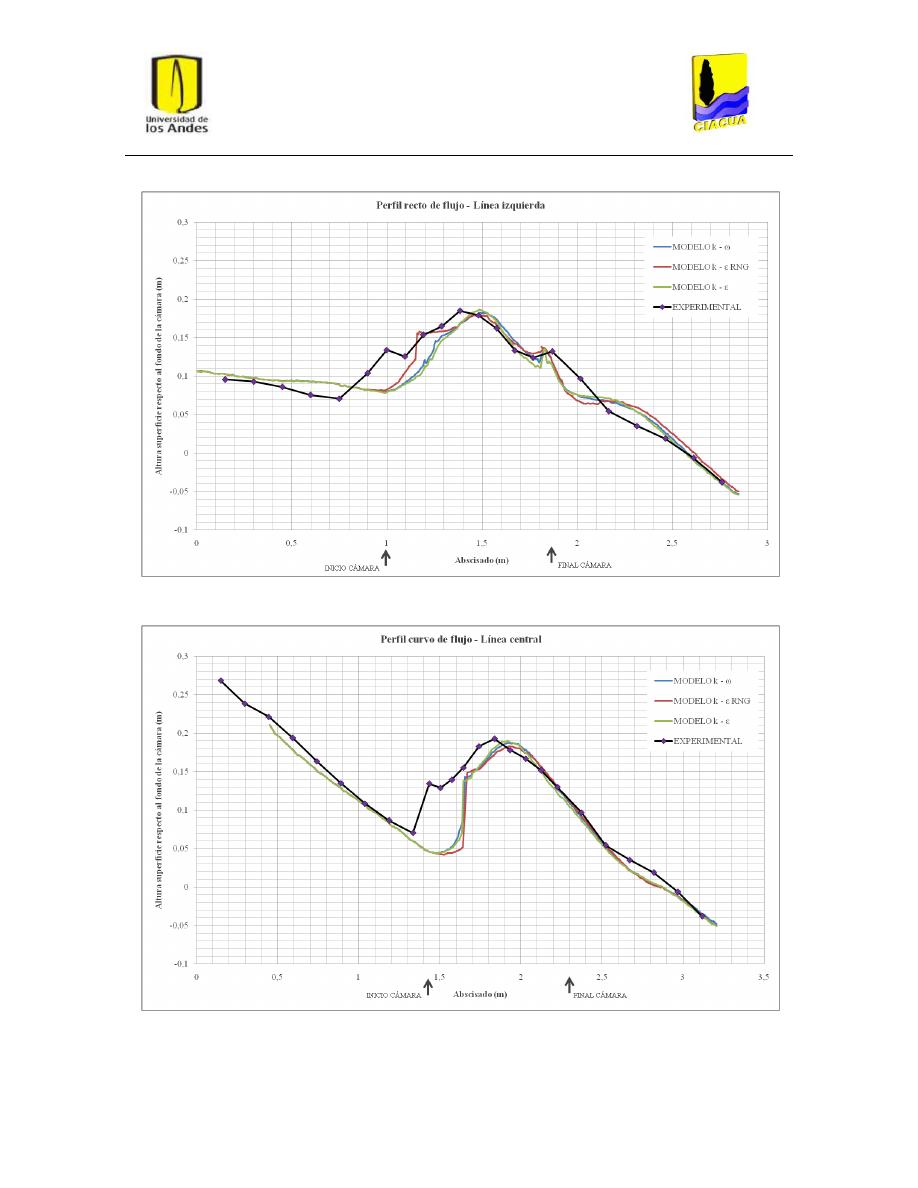
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
61
ICIV 201210 01
Gráfica anexa 3: Perfil recto de flujo por línea izquierda para UF-2.
Gráfica anexa 4: Perfil curvo de flujo por la línea central para UF-2.
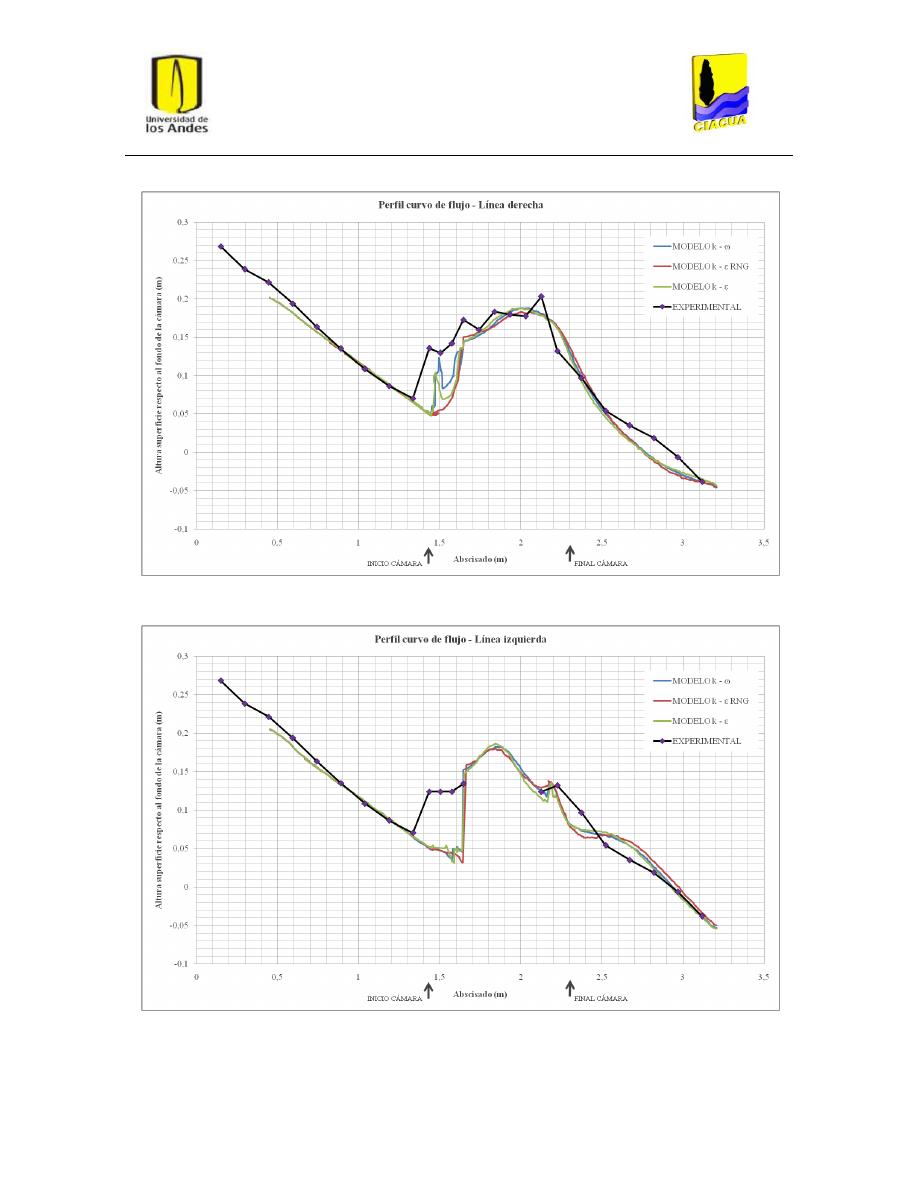
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
62
ICIV 201210 01
Gráfica anexa 5: Perfil curvo de flujo por línea derecha para UF-2.
Gráfica anexa 6: Perfil curvo de flujo por línea izquierda para UF-2.
7.2. Escenario de modelación UF-3
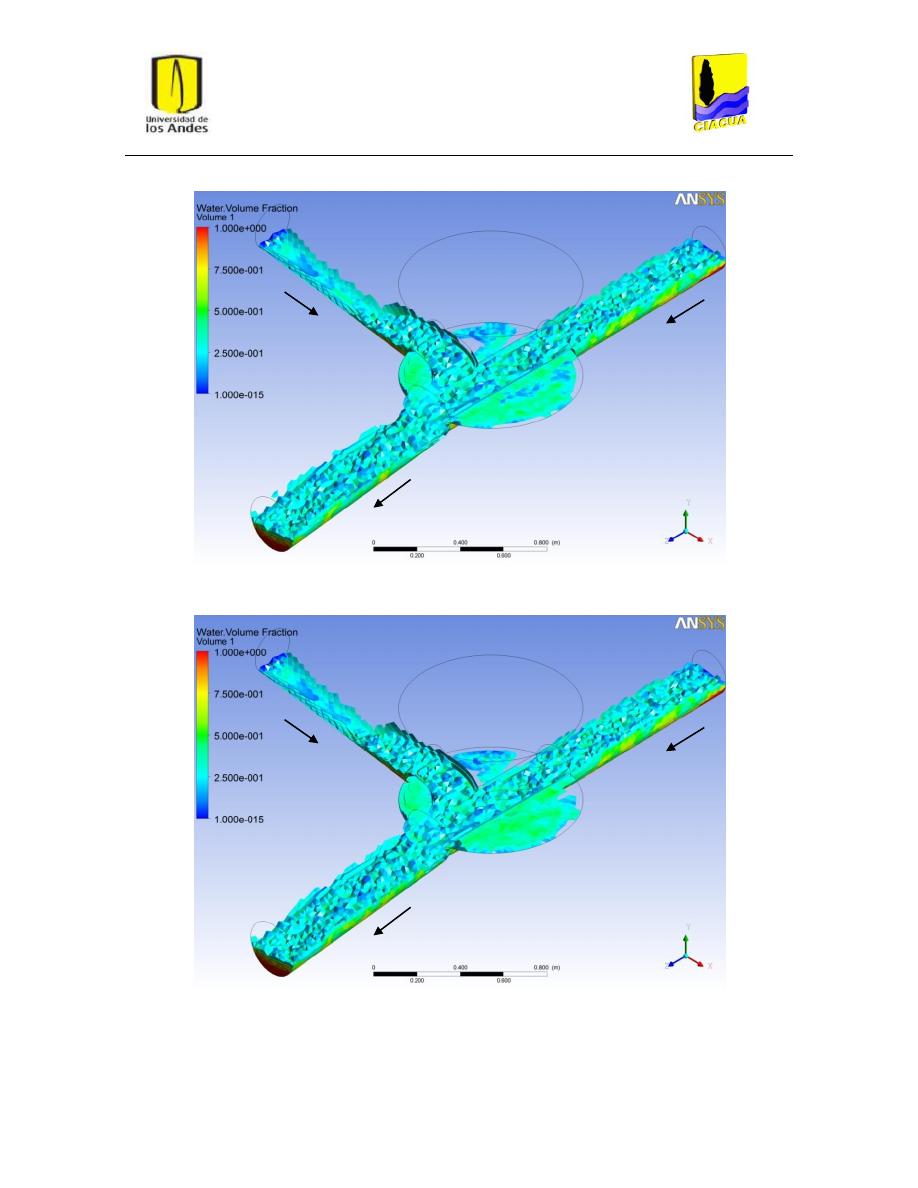
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
63
ICIV 201210 01
Figura anexa 5: Superficie del flujo en UF-3. Modelo k-ε estándar.
Figura anexa 6: Superficie del flujo en UF-3. Modelo k-ε RNG.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
64
ICIV 201210 01
Figura anexa 7: Superficie del flujo en UF-3. Modelo k-ω
Figura anexa 8: Patrón de flujo tridimensional para UF-3. Tomado de (Centro de Investigaciones de Acueductos y
Alcantarillados - CIACUA, 2010).
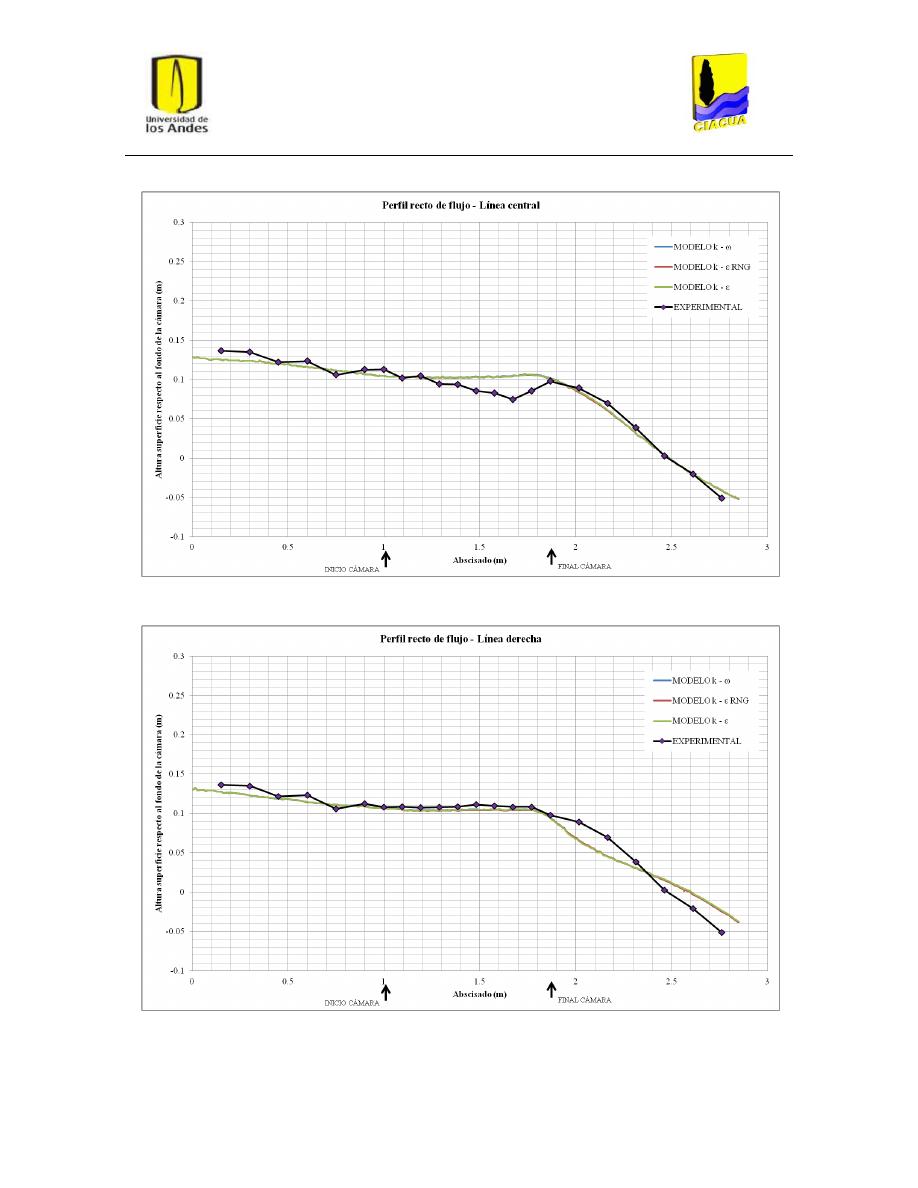
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
65
ICIV 201210 01
Gráfica anexa 7: Perfil recto de flujo por línea central para UF-3.
Gráfica anexa 8: Perfil recto de flujo por línea derecha para UF-3.
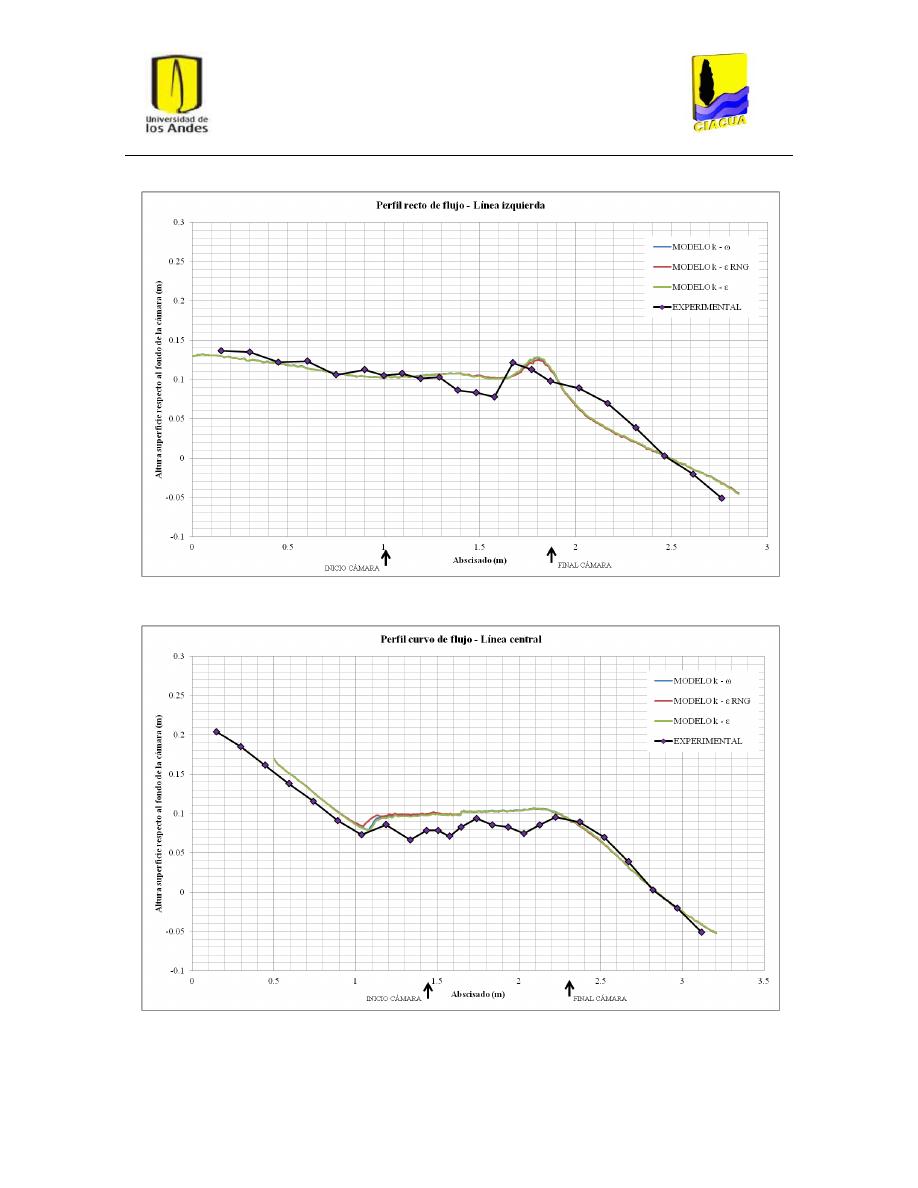
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
66
ICIV 201210 01
Gráfica anexa 9: Perfil recto de flujo por línea izquierda para UF-3.
Gráfica anexa 10: Perfil curvo de flujo por la línea central para UF-3.
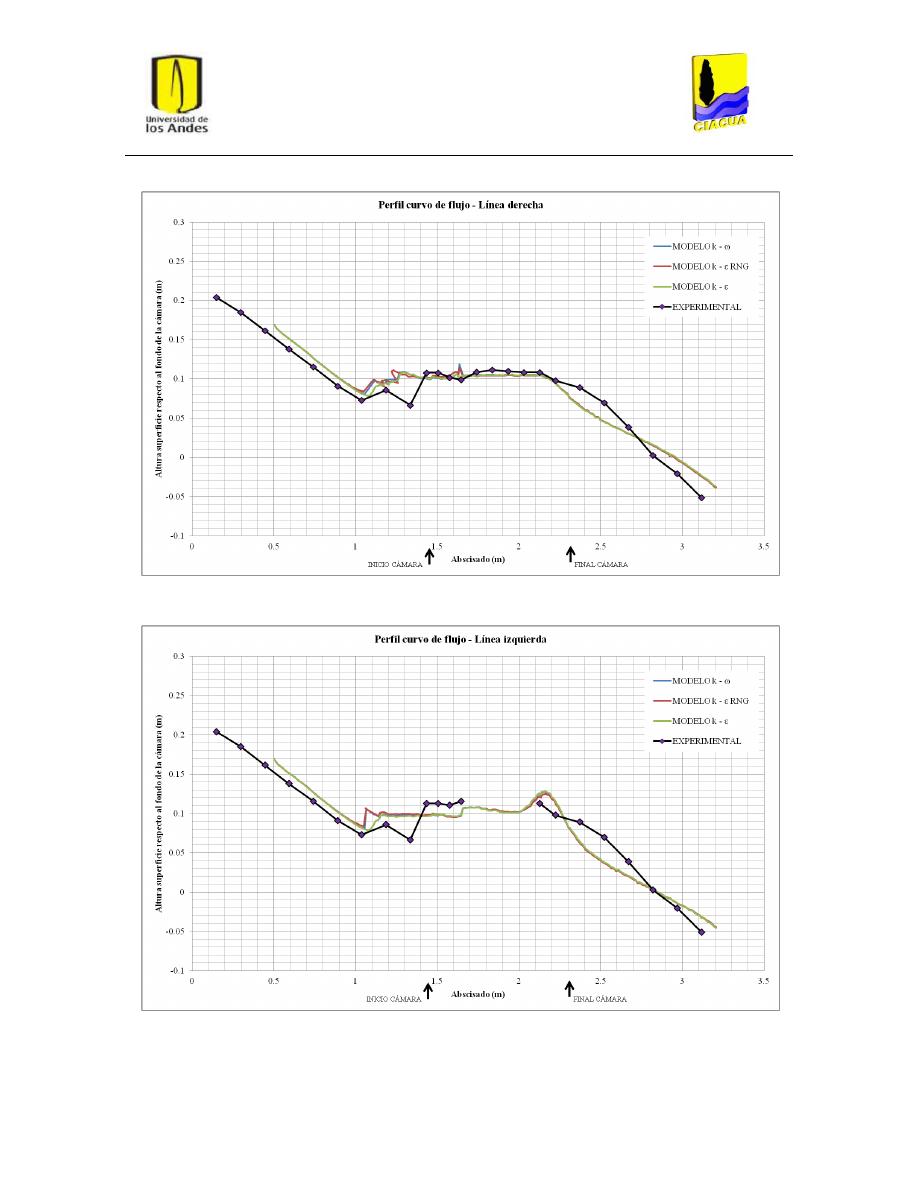
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
67
ICIV 201210 01
Gráfica anexa 11: Perfil curvo de flujo por línea derecha para UF-3.
Gráfica anexa 12: Perfil curvo de flujo por línea izquierda para UF-3.
7.3. Escenario de modelación UF-4
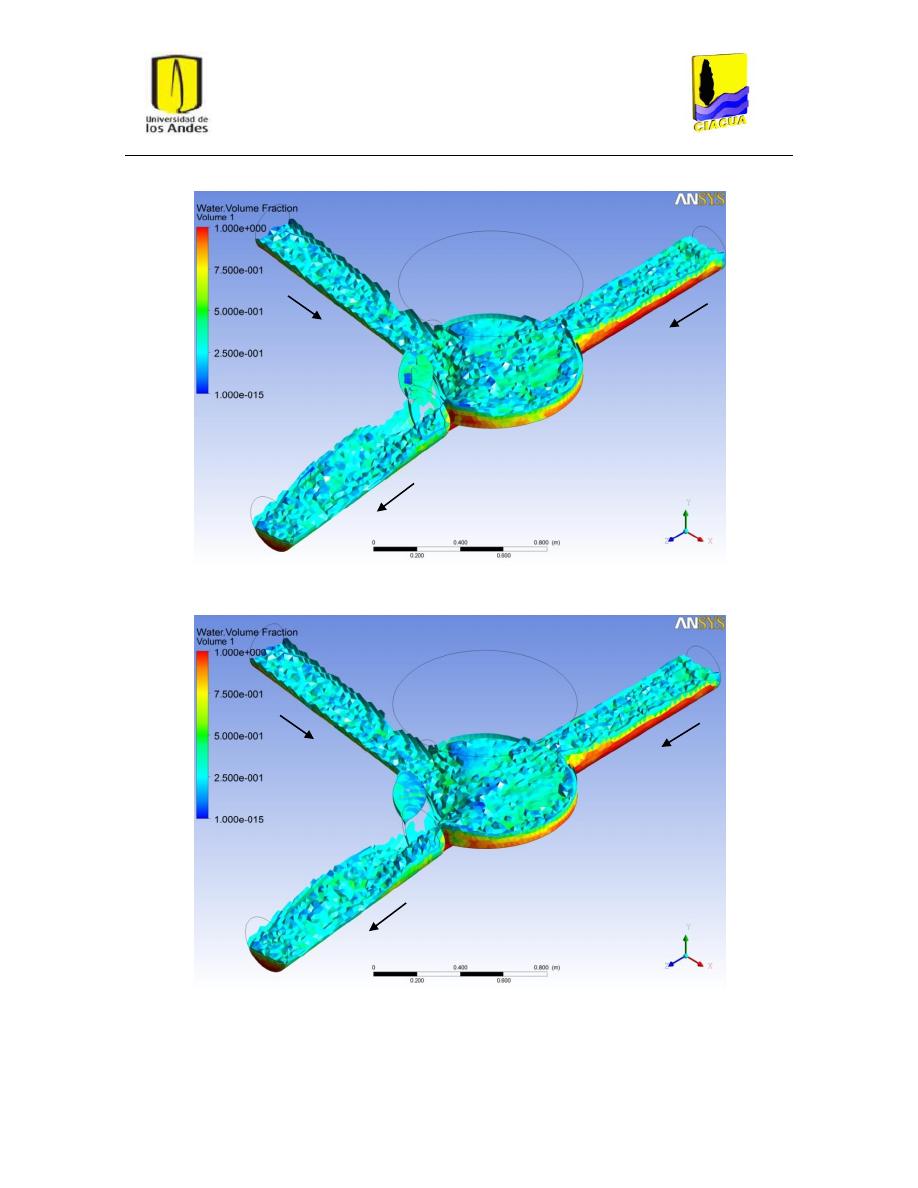
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
68
ICIV 201210 01
Figura anexa 9: Superficie del flujo en UF-4. Modelo k-ε estándar.
Figura anexa 10: Superficie del flujo en UF-4. Modelo k-ε RNG.
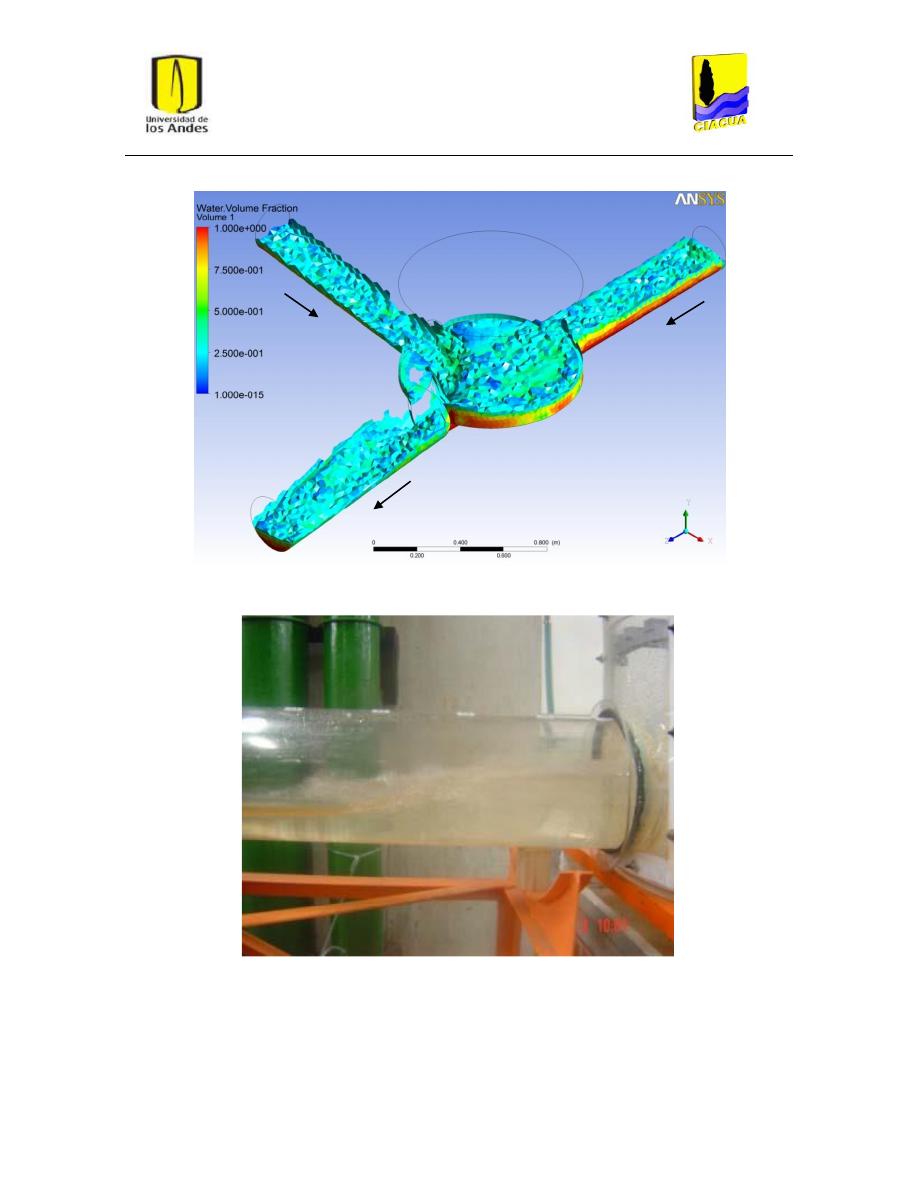
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
69
ICIV 201210 01
Figura anexa 11: Superficie del flujo en UF-4. Modelo k-ω
Figura anexa 12: Formación de un resalto en la tubería principal. Tomado de (Centro de Investigaciones de
Acueductos y Alcantarillados - CIACUA, 2010).
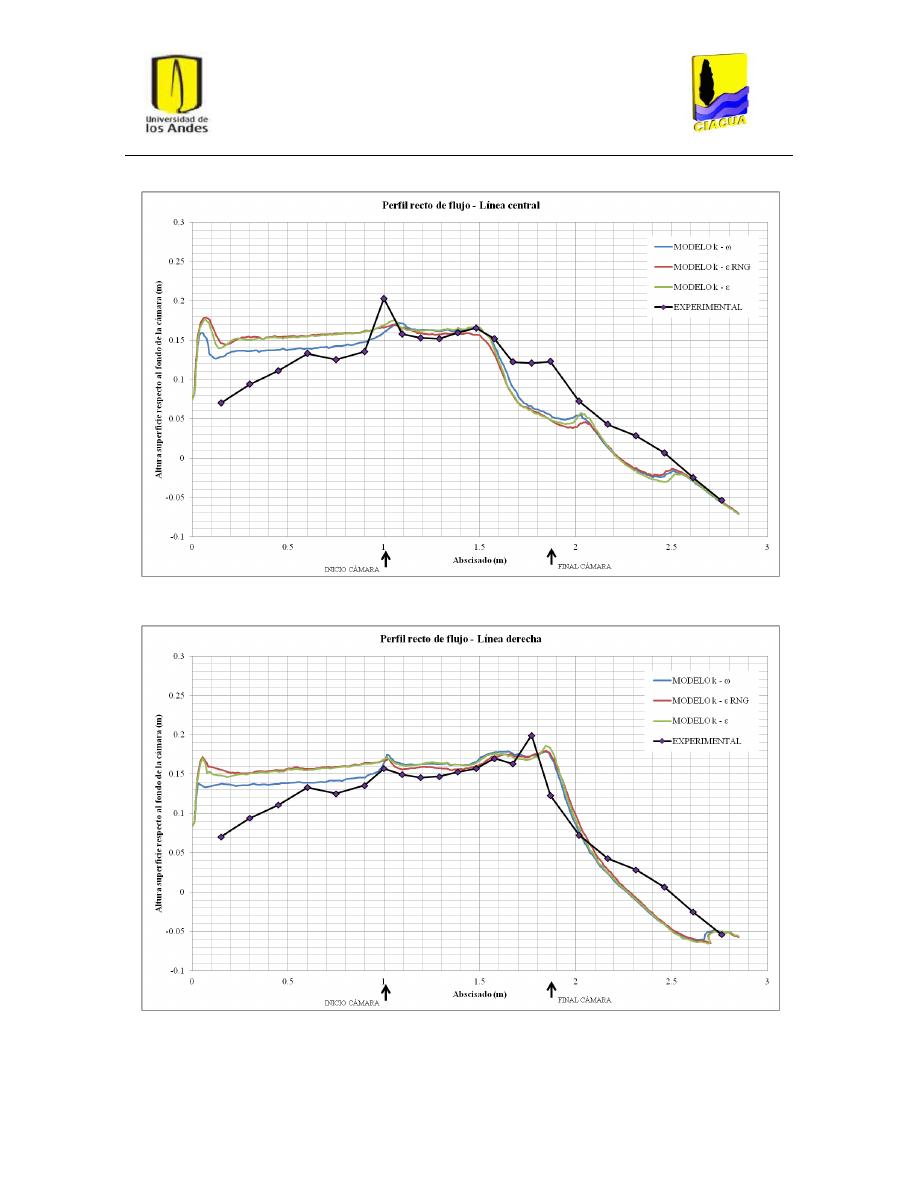
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
70
ICIV 201210 01
Gráfica anexa 13: Perfil recto de flujo por línea central para UF-4.
Gráfica anexa 14: Perfil recto de flujo por línea derecha para UF-4.
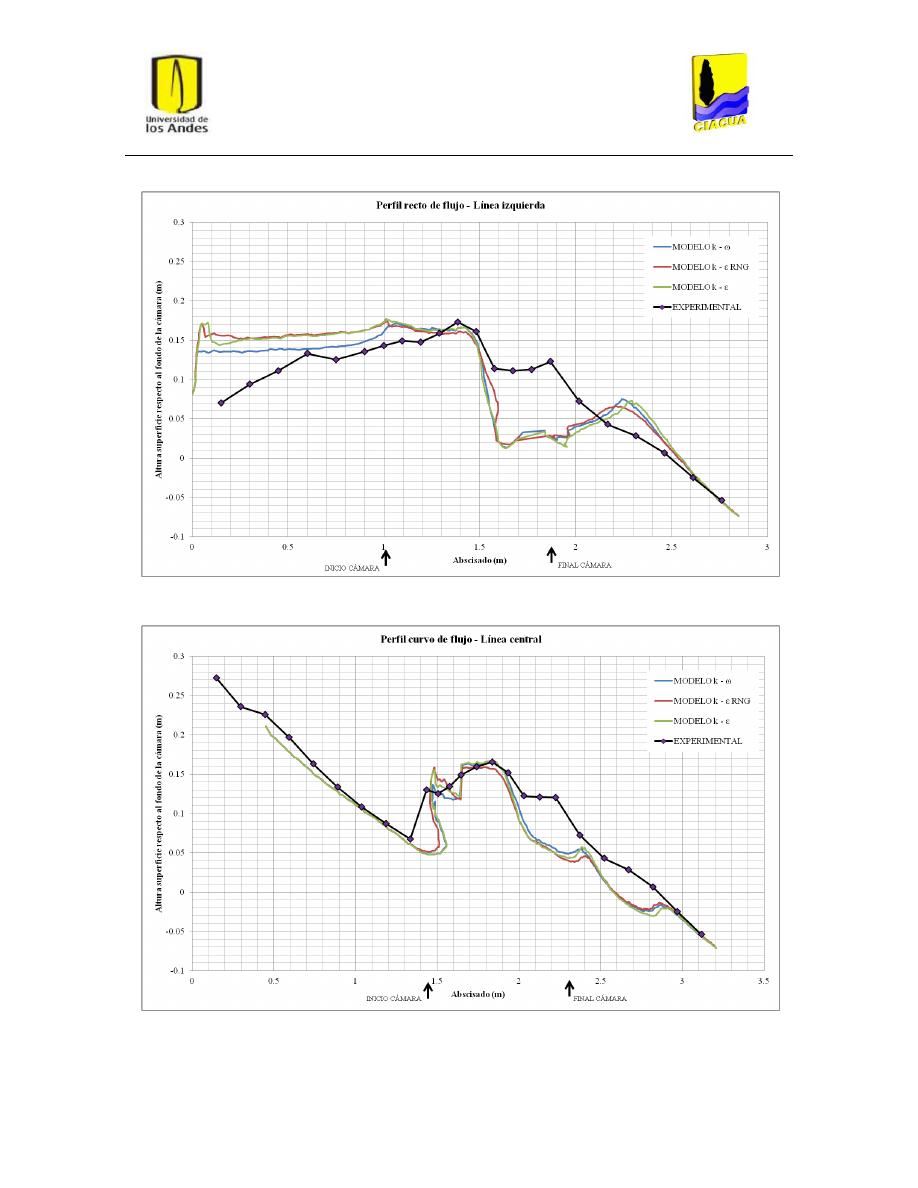
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
71
ICIV 201210 01
Gráfica anexa 15: Perfil recto de flujo por línea izquierda para UF-4.
Gráfica anexa 16: Perfil curvo de flujo por línea central para UF-4.
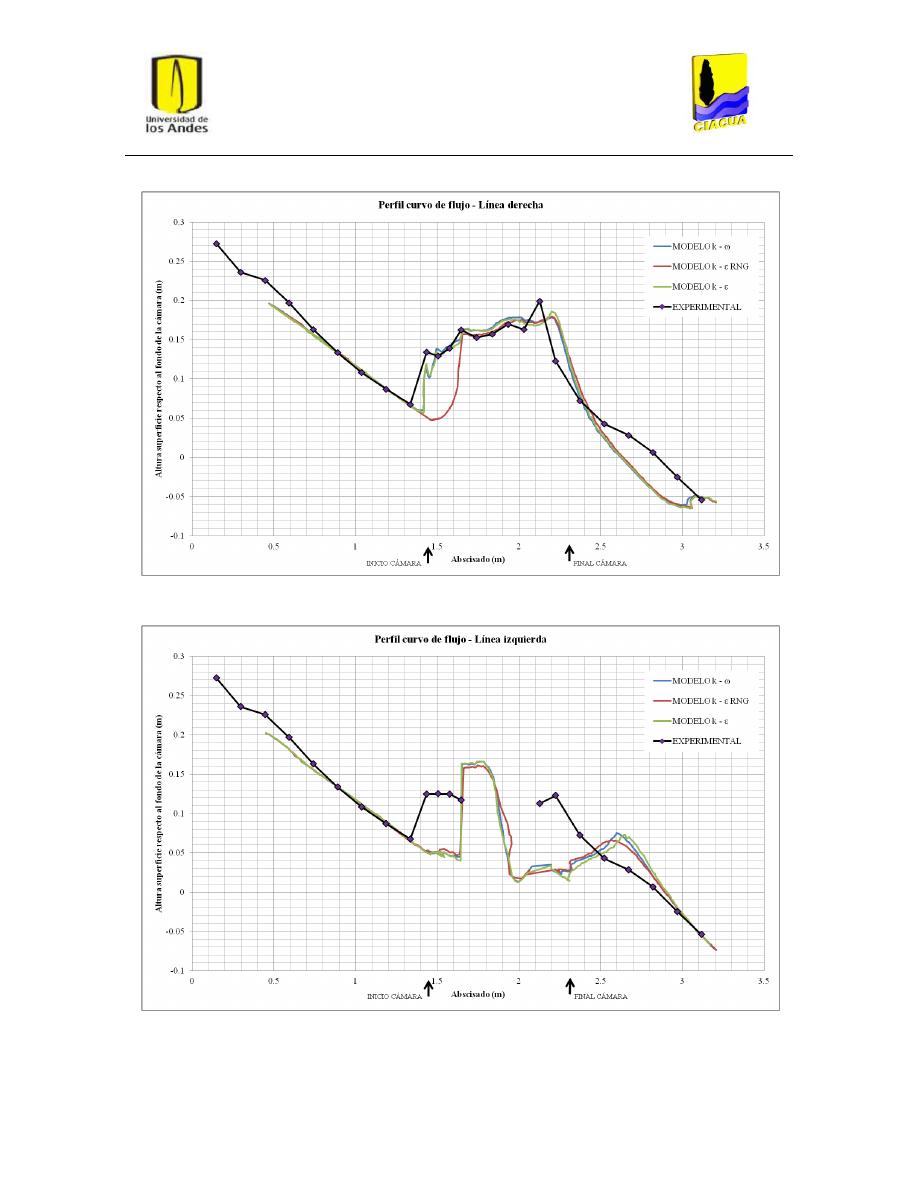
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
72
ICIV 201210 01
Gráfica anexa 17: Perfil curvo de flujo por línea derecha para UF-4.
Gráfica anexa 18: Perfil curvo de flujo por línea izquierda para UF-4.
7.4. Escenario de modelación UF-5
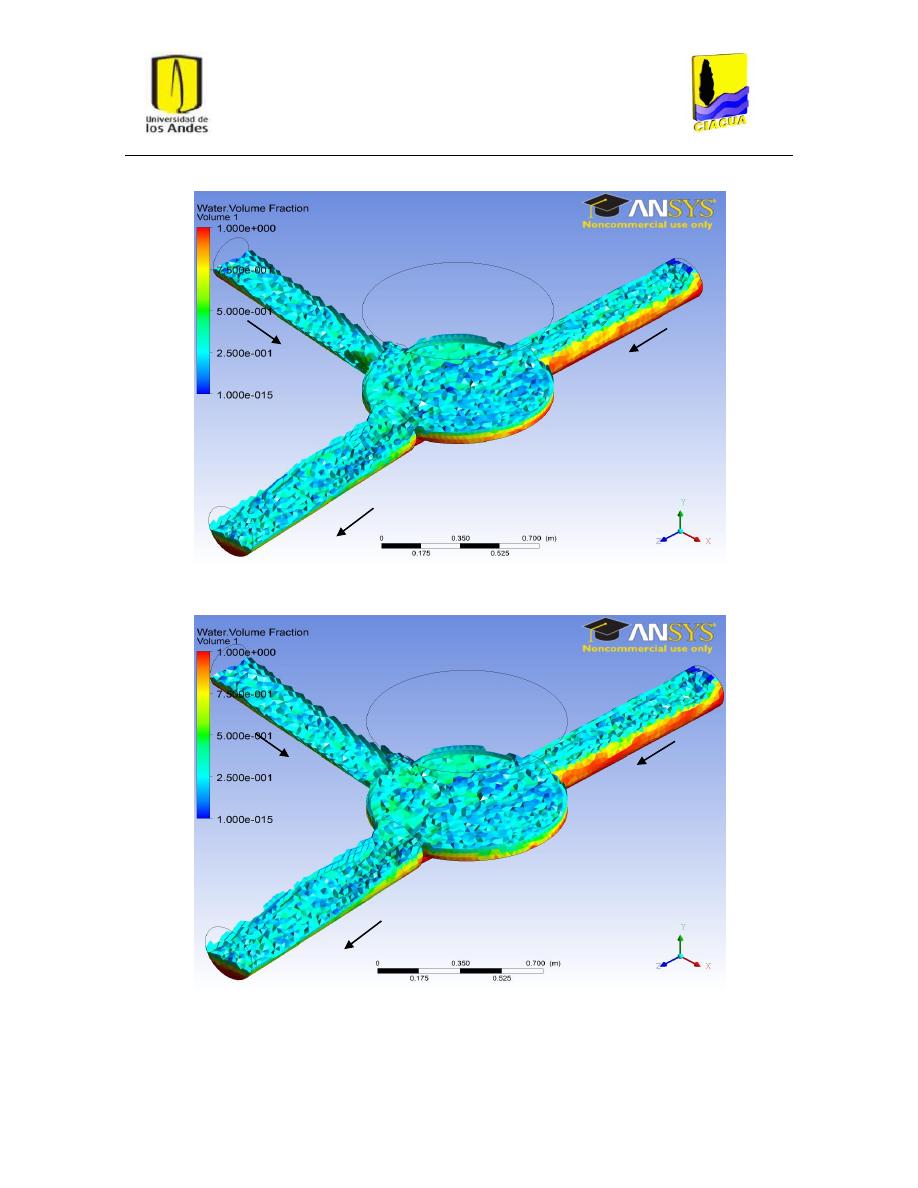
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
73
ICIV 201210 01
Figura anexa 13: Superficie del flujo en UF-5. Modelo k-ε estándar.
Figura anexa 14: Superficie del flujo en UF-5. Modelo k-ε RNG.
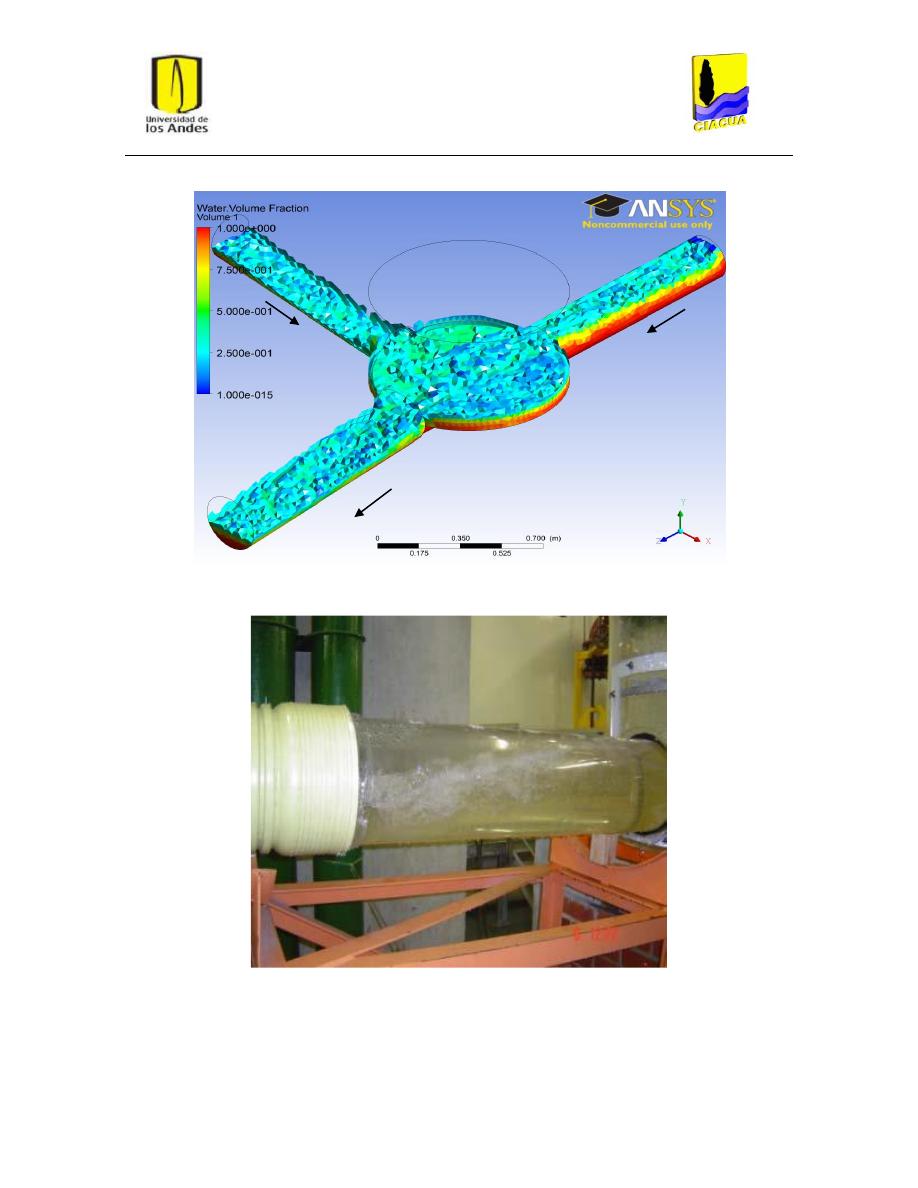
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
74
ICIV 201210 01
Figura anexa 15: Superficie del flujo en UF-5. Modelo k-ω.
Figura anexa 16: Formación de un resalto en la tubería principal. Tomado de (Centro de Investigaciones de
Acueductos y Alcantarillados - CIACUA, 2010).
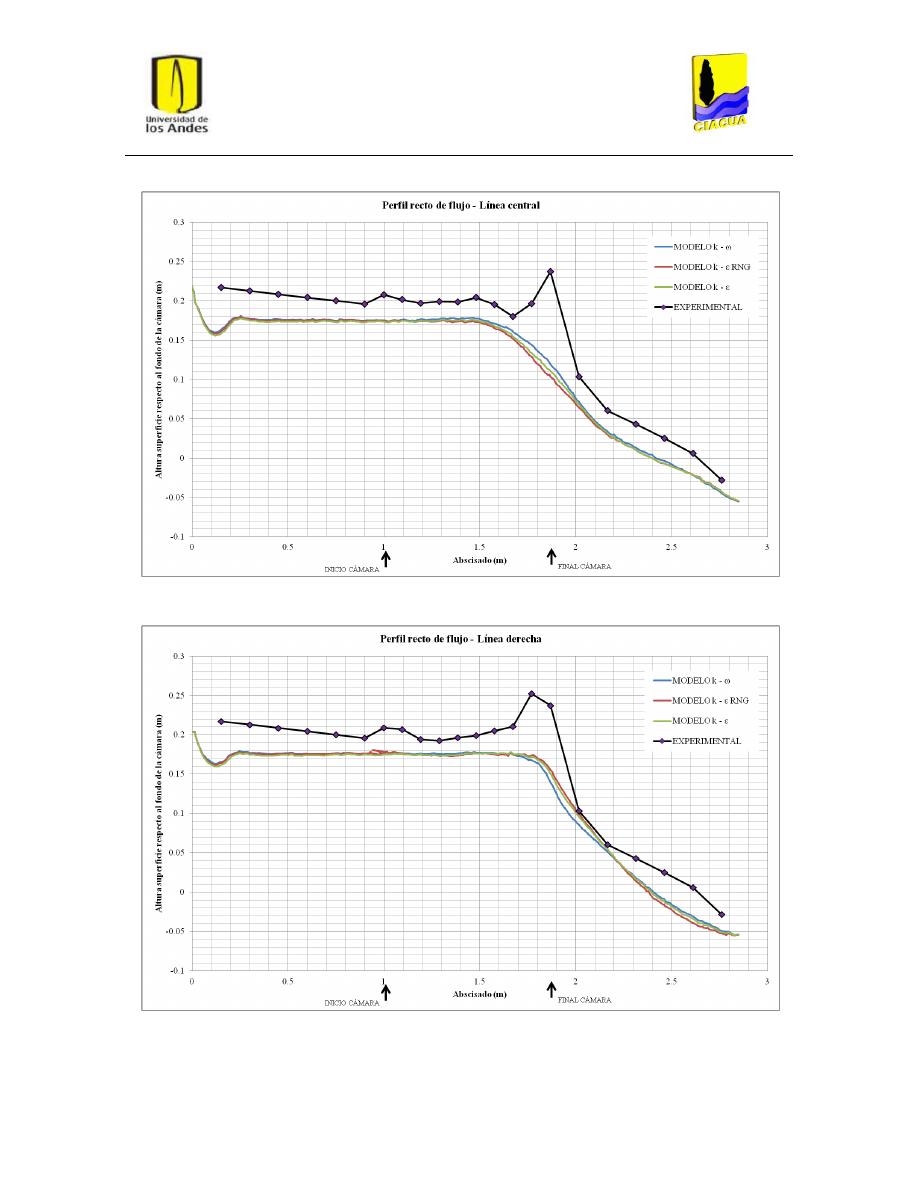
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
75
ICIV 201210 01
Gráfica anexa 19: Perfil recto de flujo por línea central para UF-5.
Gráfica anexa 20: Perfil recto de flujo por línea derecha para UF-5.
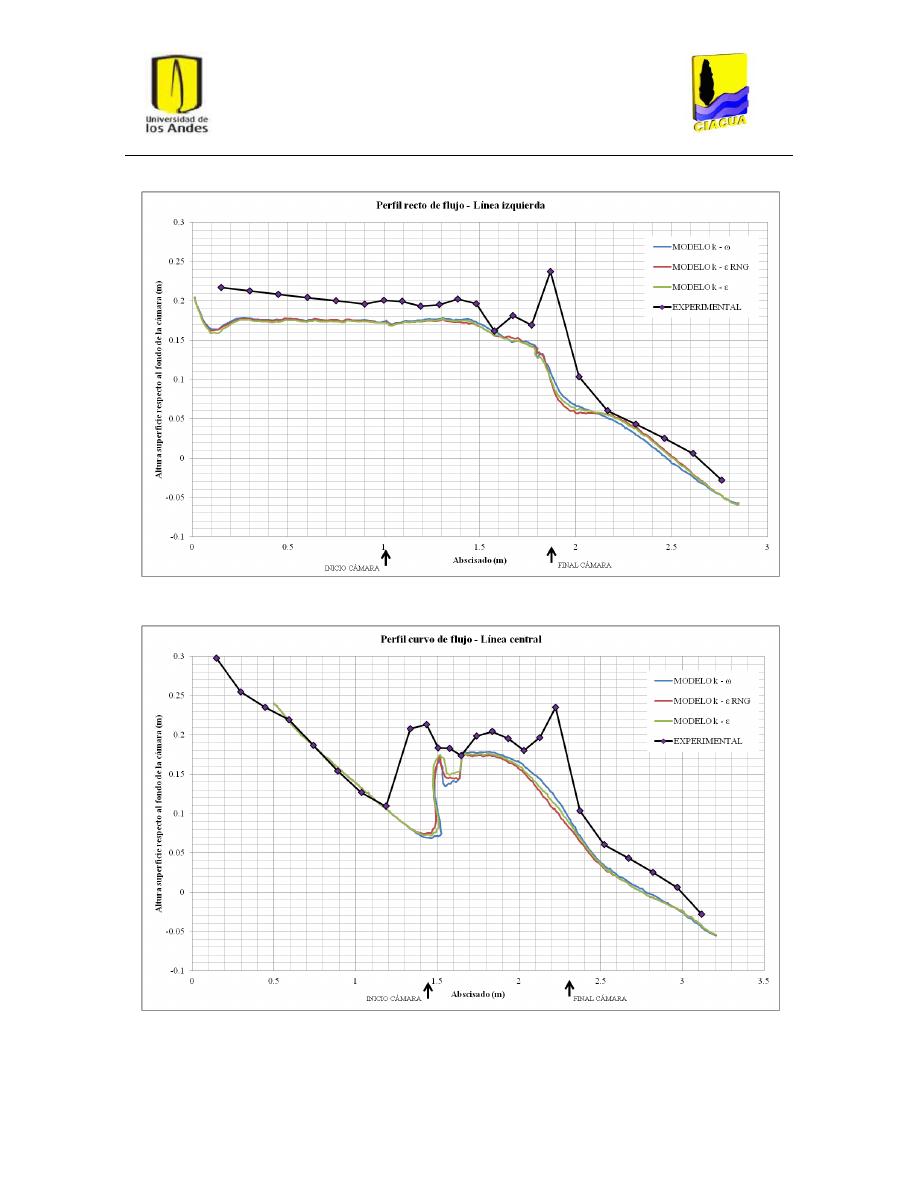
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
76
ICIV 201210 01
Gráfica anexa 21: Perfil recto de flujo por línea izquierda para UF-5.
Gráfica anexa 22: Perfil curvo de flujo por línea central para UF-5.
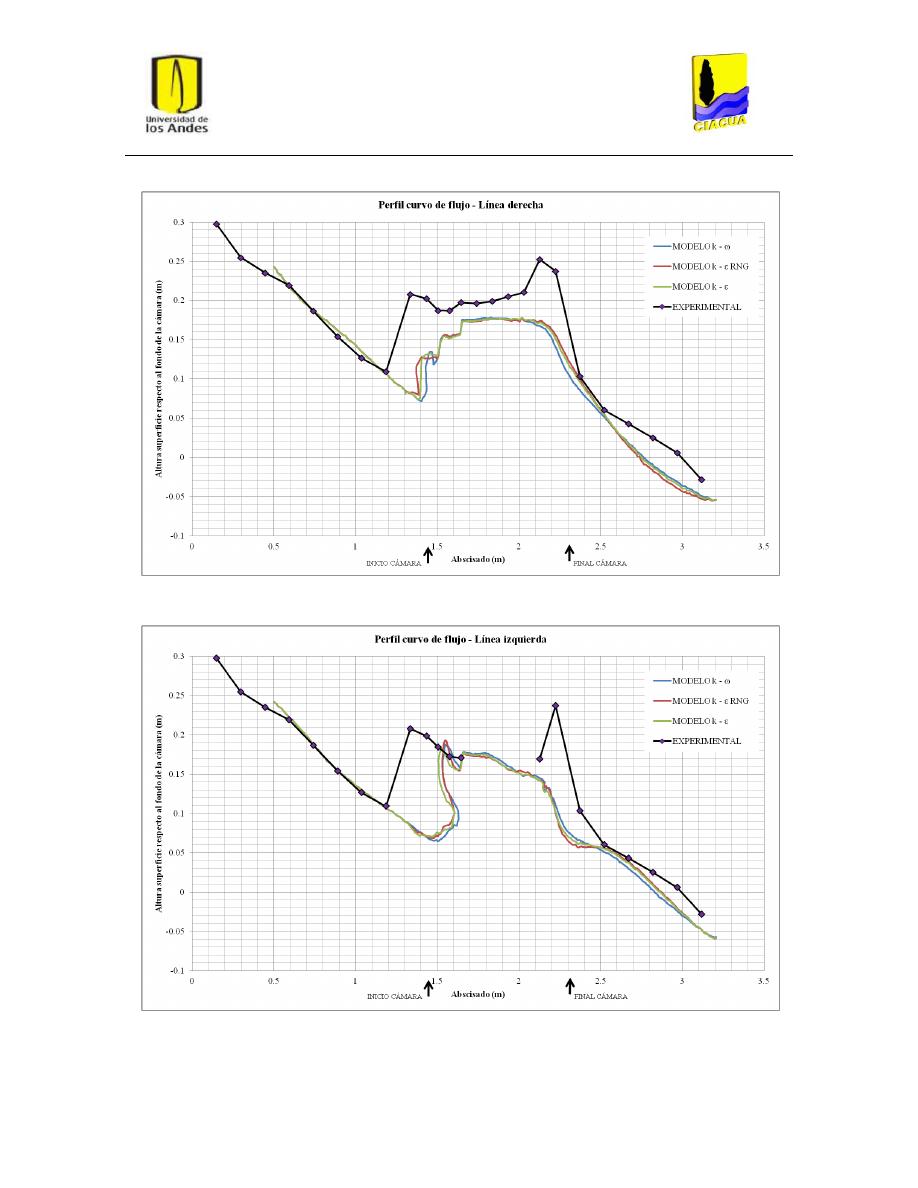
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
77
ICIV 201210 01
Gráfica anexa 23: Perfil curvo de flujo por línea derecha para UF-5.
Gráfica anexa 24: Perfil curvo de flujo por línea izquierda para UF-5.
7.5. Escenario de modelación FD-3

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
78
ICIV 201210 01
Figura anexa 17: Superficie del flujo en FD-3. Modelo k-ε estándar.
Figura anexa 18: Superficie del flujo en FD-3. Modelo k-ε RNG.
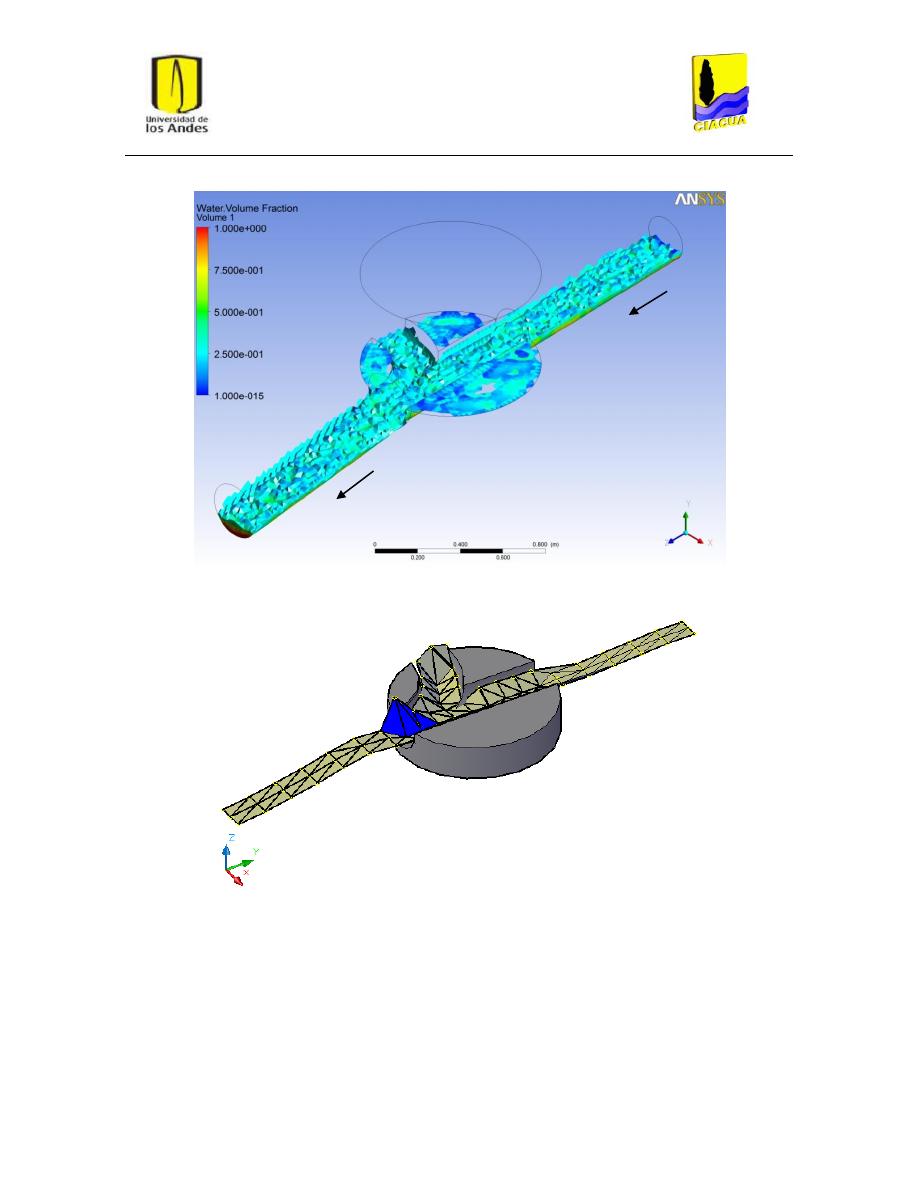
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
79
ICIV 201210 01
Figura anexa 19: Superficie del flujo en FD-3. Modelo k-ω.
Figura anexa 20: Patrón de flujo tridimensional para FD-3. Tomado de (Centro de Investigaciones de Acueductos y
Alcantarillados - CIACUA, 2010).
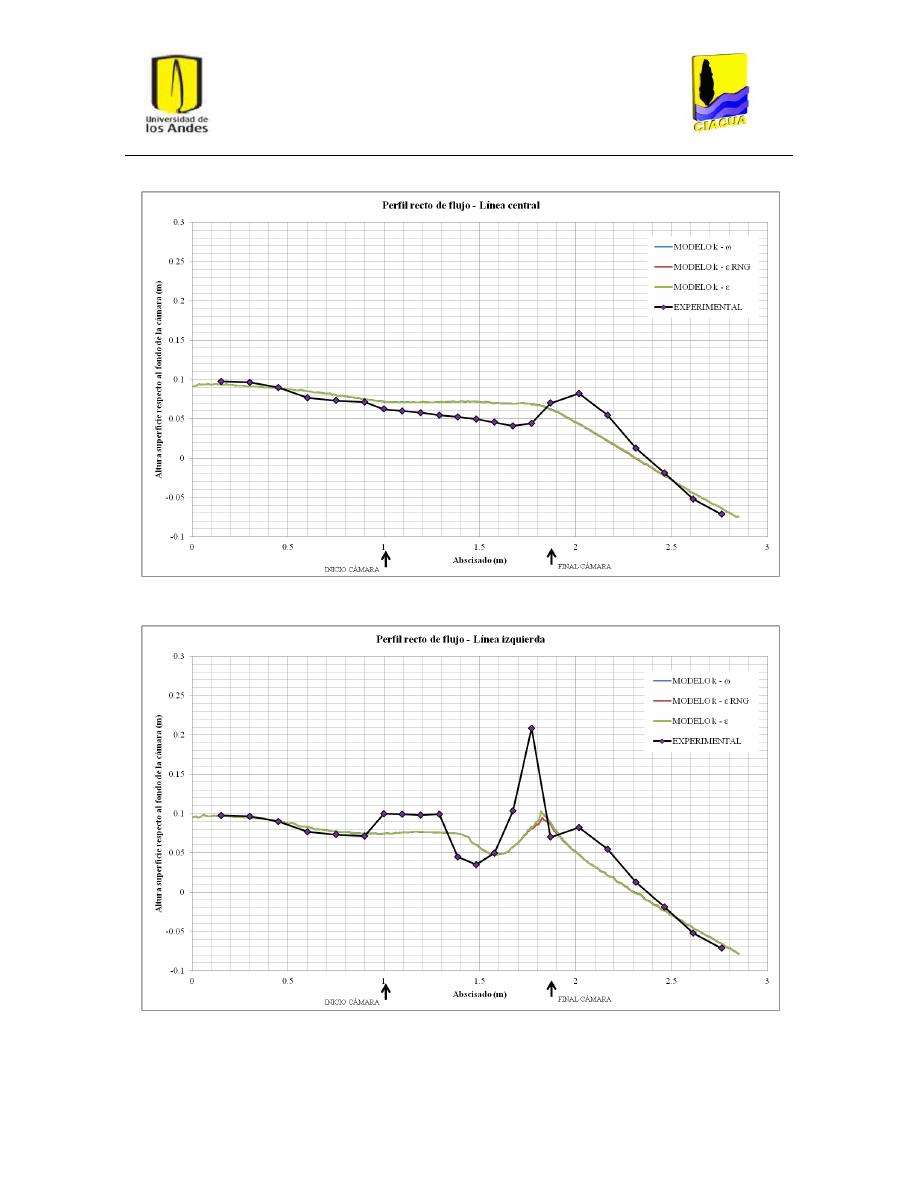
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
80
ICIV 201210 01
Gráfica anexa 25: Perfil recto de flujo por la línea central para FD-3.
Gráfica anexa 26: Perfil recto de flujo por línea izquierda para FD-3.
7.6. Escenario de modelación FD-4
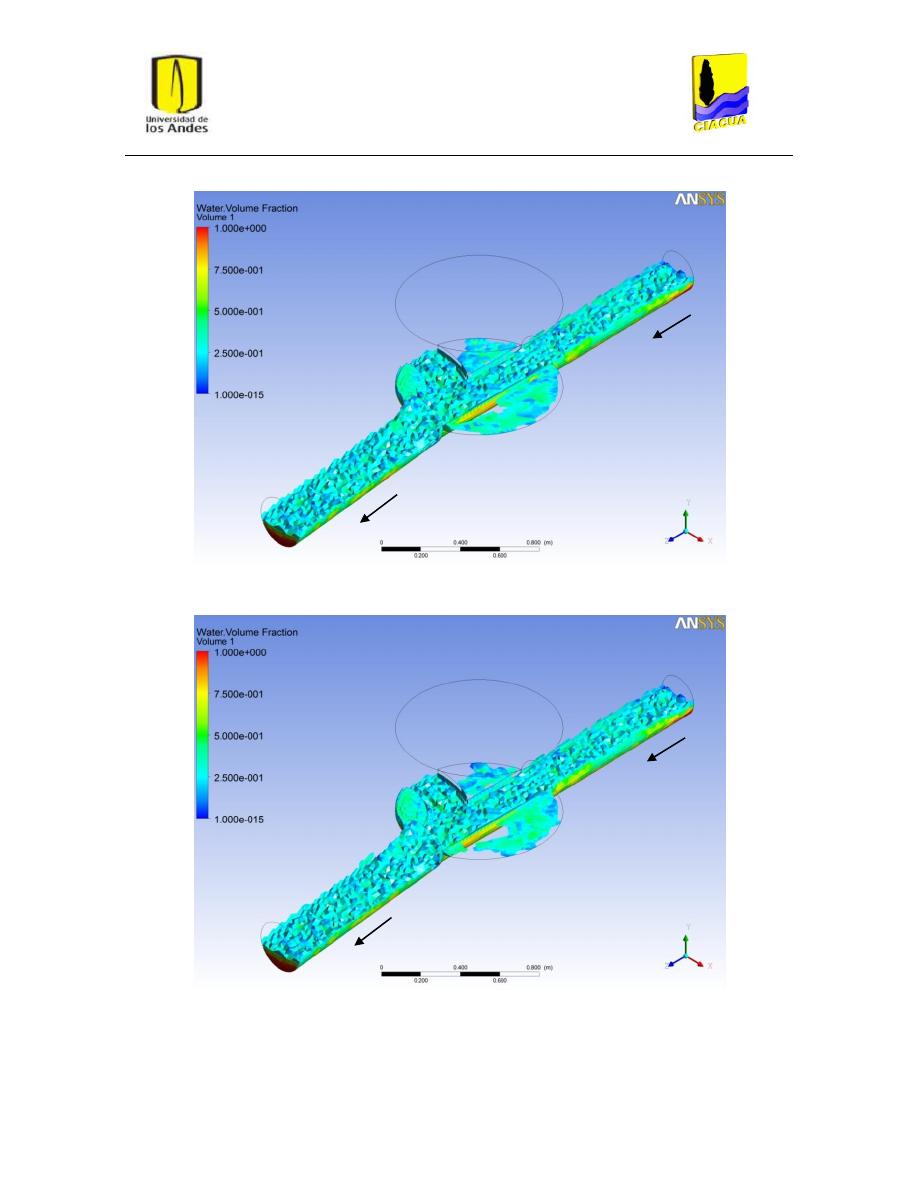
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
81
ICIV 201210 01
Figura anexa 21: Superficie del flujo en FD-4. Modelo k-ε estándar.
Figura anexa 22: Superficie del flujo en FD-4. Modelo k-ε RNG.
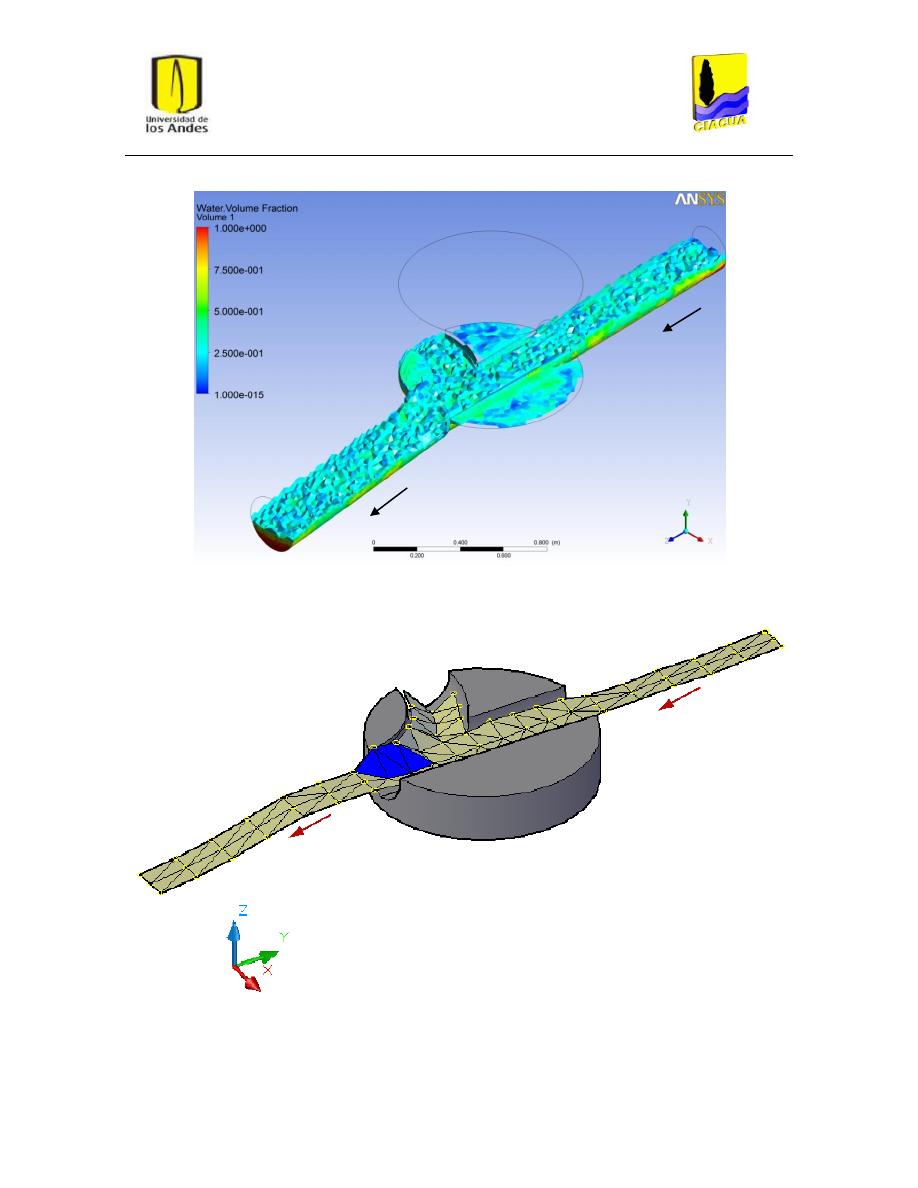
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
82
ICIV 201210 01
Figura anexa 23: Superficie del flujo en FD-4. Modelo k-ω.
Figura anexa 24: Patrón de flujo tridimensional para FD-4. Tomado de (Centro de Investigaciones de Acueductos y
Alcantarillados - CIACUA, 2010).
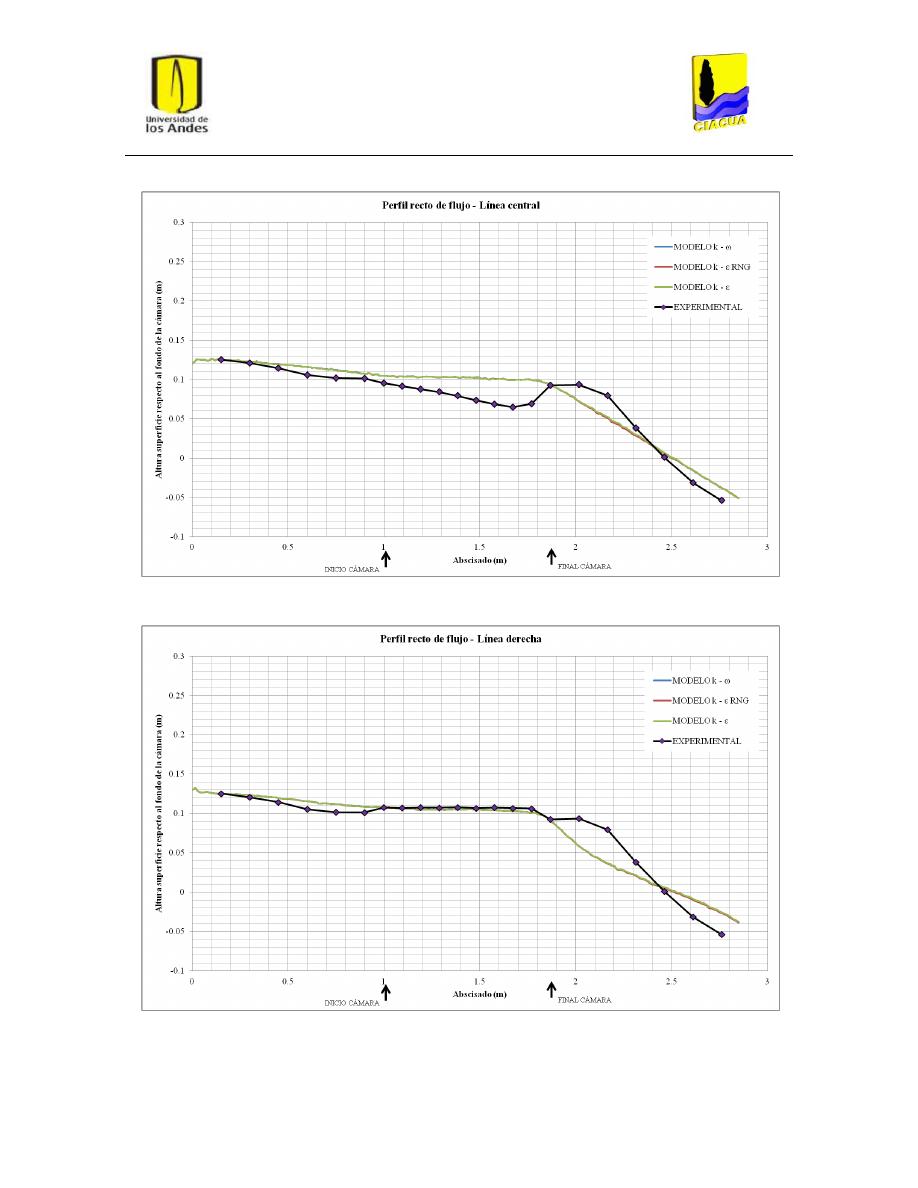
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
83
ICIV 201210 01
Gráfica anexa 27: Perfil recto de flujo por línea central para FD-4.
Gráfica anexa 28: Perfil recto de flujo por línea derecha para FD-4.
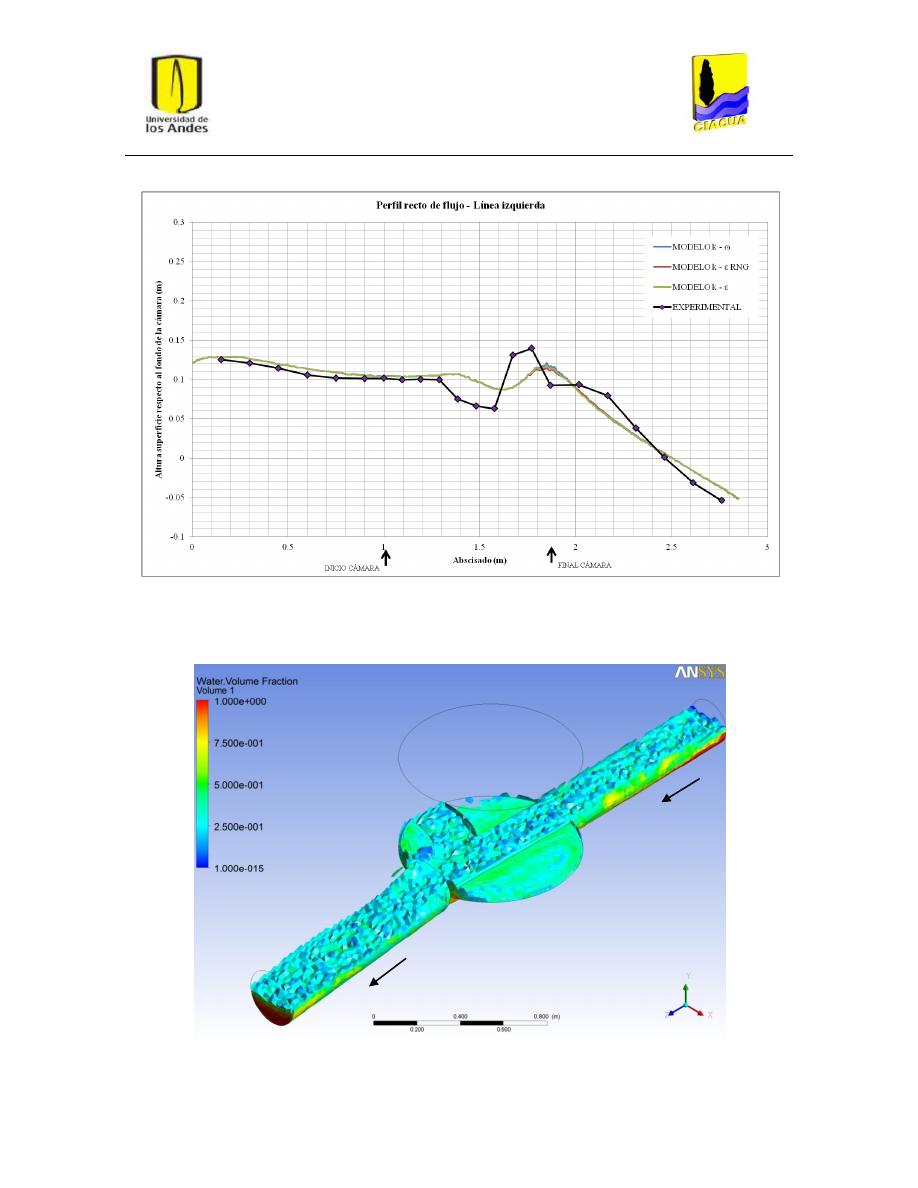
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
84
ICIV 201210 01
Gráfica anexa 29: Perfil recto de flujo por línea izquierda para FD-4.
7.7. Escenario de modelación FD-6
Figura anexa 25: Superficie del flujo en FD-6. Modelo k-ε estándar.
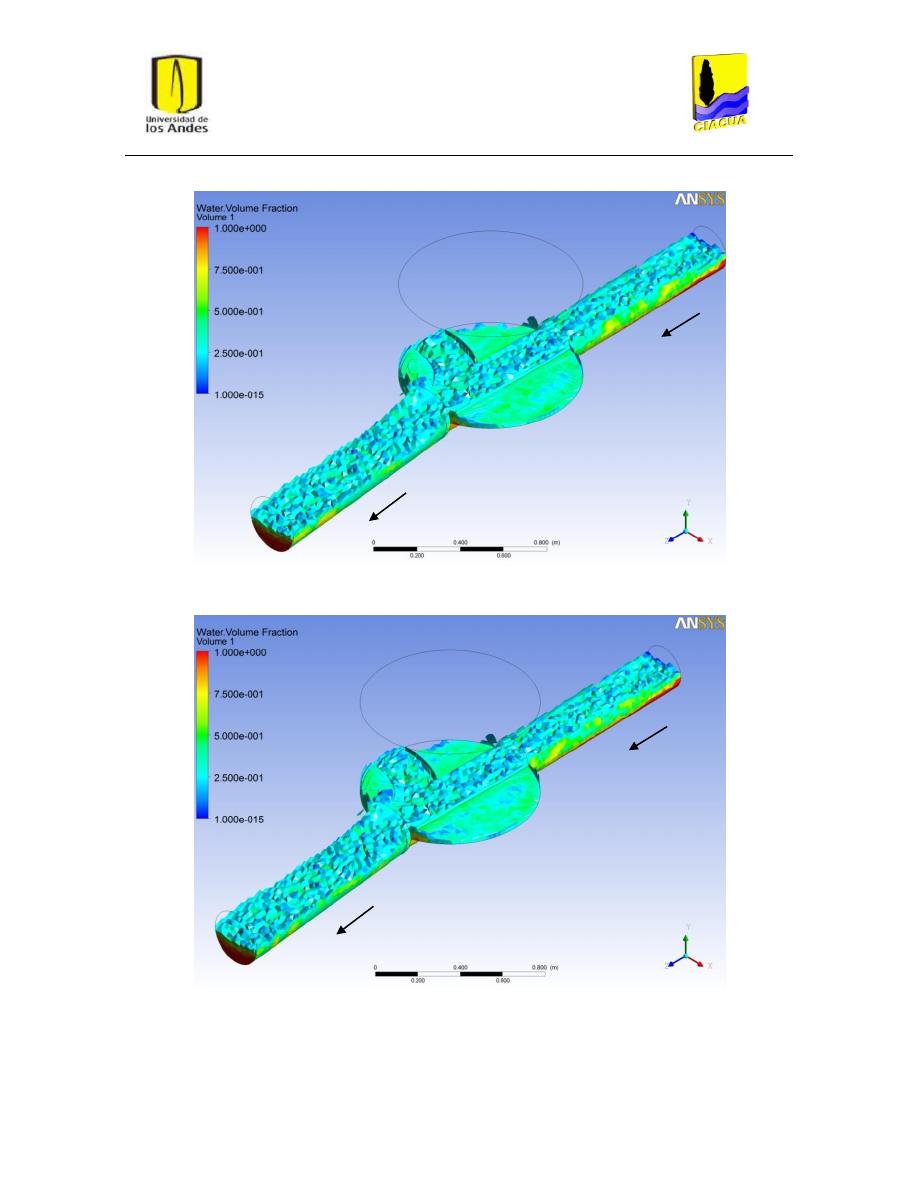
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
85
ICIV 201210 01
Figura anexa 26: Superficie del flujo en FD-6. Modelo k-ε RNG
Figura anexa 27: Superficie del flujo en FD-6. Modelo k-ω.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
86
ICIV 201210 01
Figura anexa 28: Patrón de flujo tridimensional para FD-6. Tomado de (Centro de Investigaciones de Acueductos y
Alcantarillados - CIACUA, 2010).
Gráfica anexa 30: Perfil recto de flujo por línea central para FD-6.
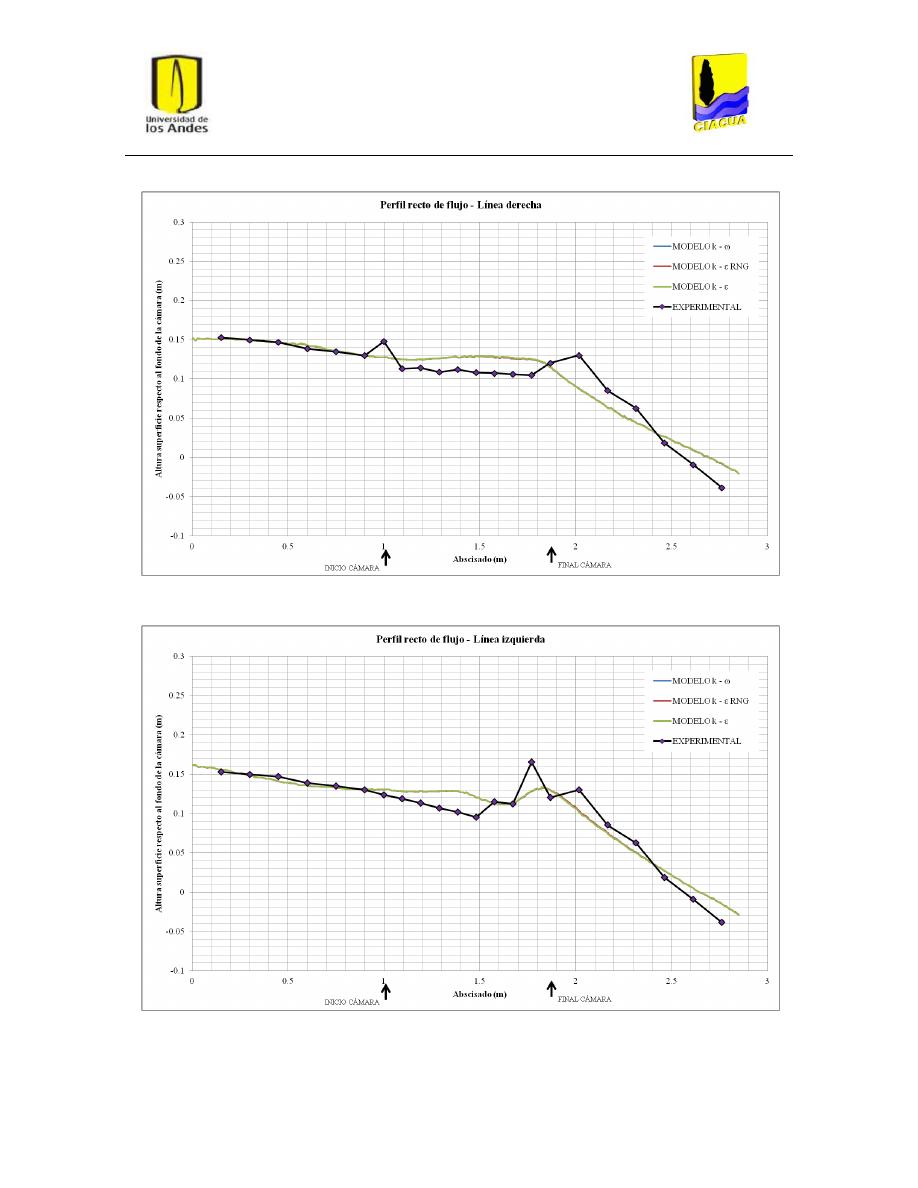
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
87
ICIV 201210 01
Gráfica anexa 31: Perfil recto de flujo por línea derecha para FD-6.
Gráfica anexa 32: Perfil recto de flujo por línea izquierda para FD-6.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
88
ICIV 201210 01
7.8. Escenario de modelación FD-8
Figura anexa 29: Superficie del flujo en FD-8. Modelo k-ε estándar.
Figura anexa 30: Superficie del flujo en FD-8. Modelo k-ε RNG
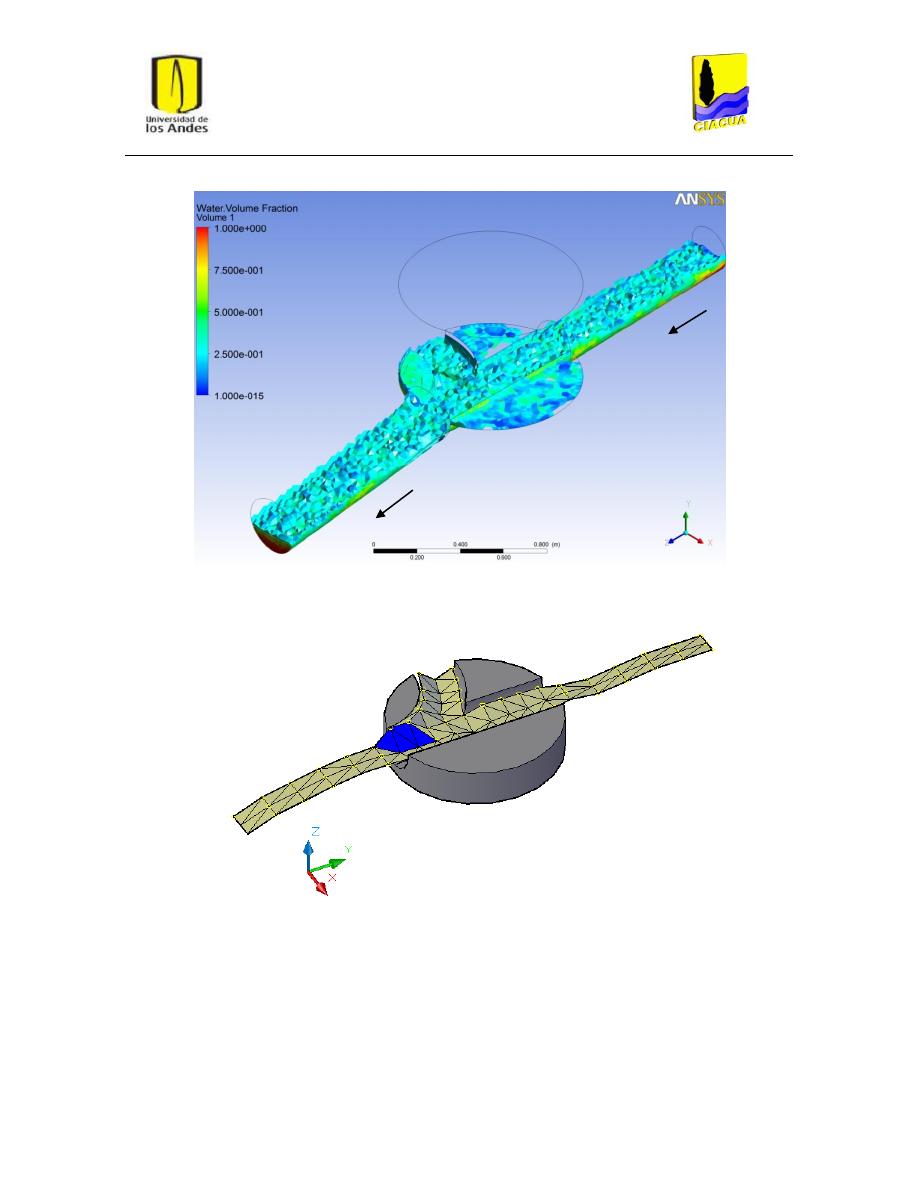
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
89
ICIV 201210 01
Figura anexa 31: Superficie del flujo en FD-8. Modelo k-ω.
Figura anexa 32: Patrón de flujo tridimensional para FD-8. Tomado de (Centro de Investigaciones de Acueductos y
Alcantarillados - CIACUA, 2010).
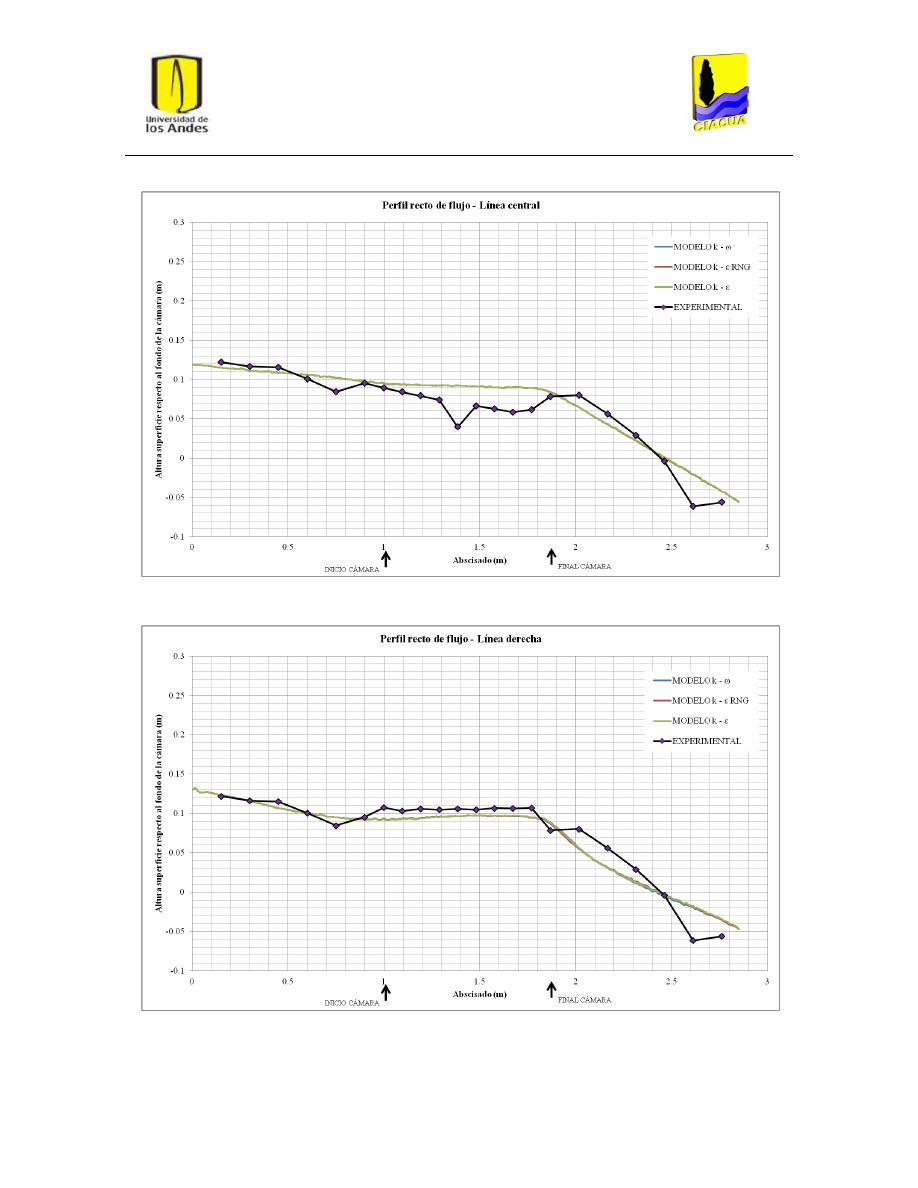
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
90
ICIV 201210 01
Gráfica anexa 33: Perfil recto de flujo por línea central para FD-8.
Gráfica anexa 34: Perfil recto de flujo por línea derecha para FD-8.
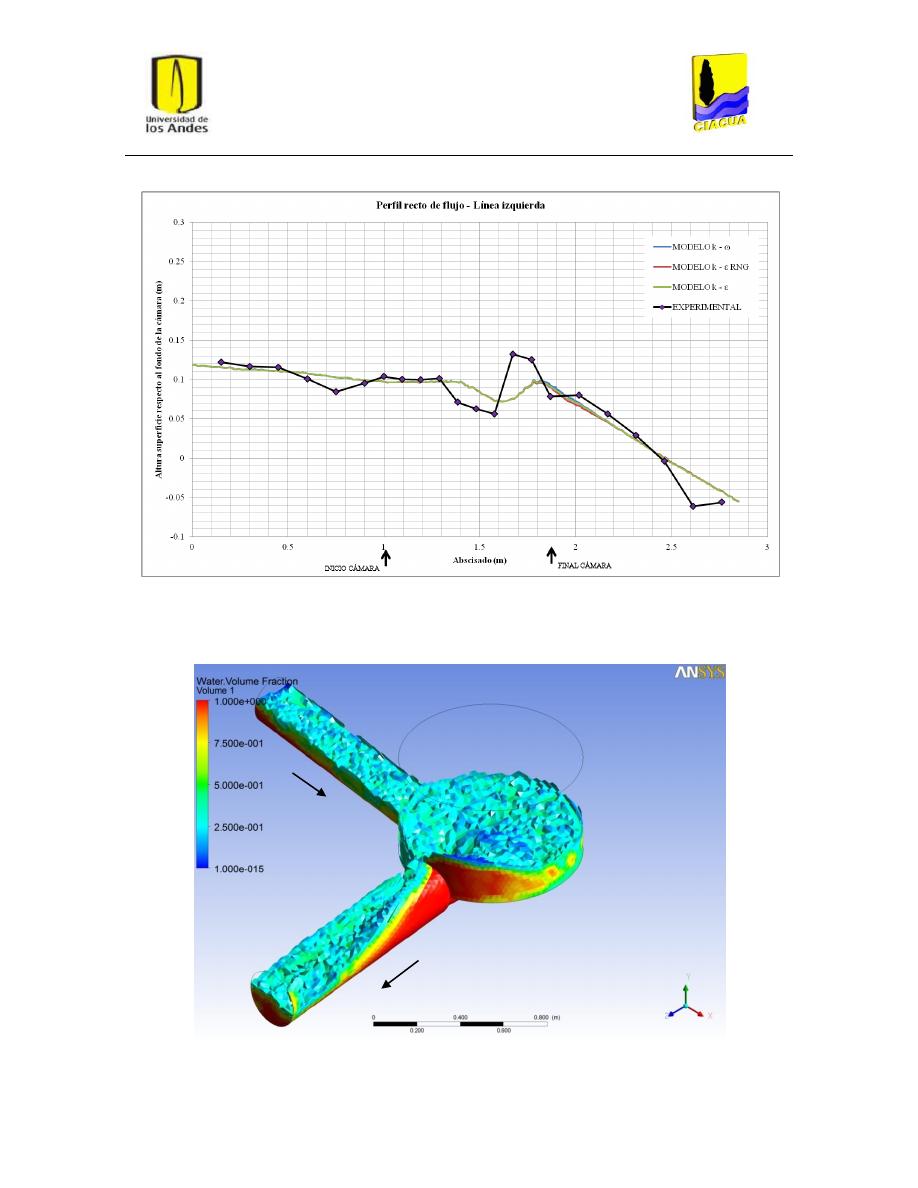
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
91
ICIV 201210 01
Gráfica anexa 35: Perfil recto de flujo por línea izquierda para FD-8.
7.9. Escenario de modelación FN-7
Figura anexa 33: Superficie del flujo en FN-7. Modelo k-ε estándar.
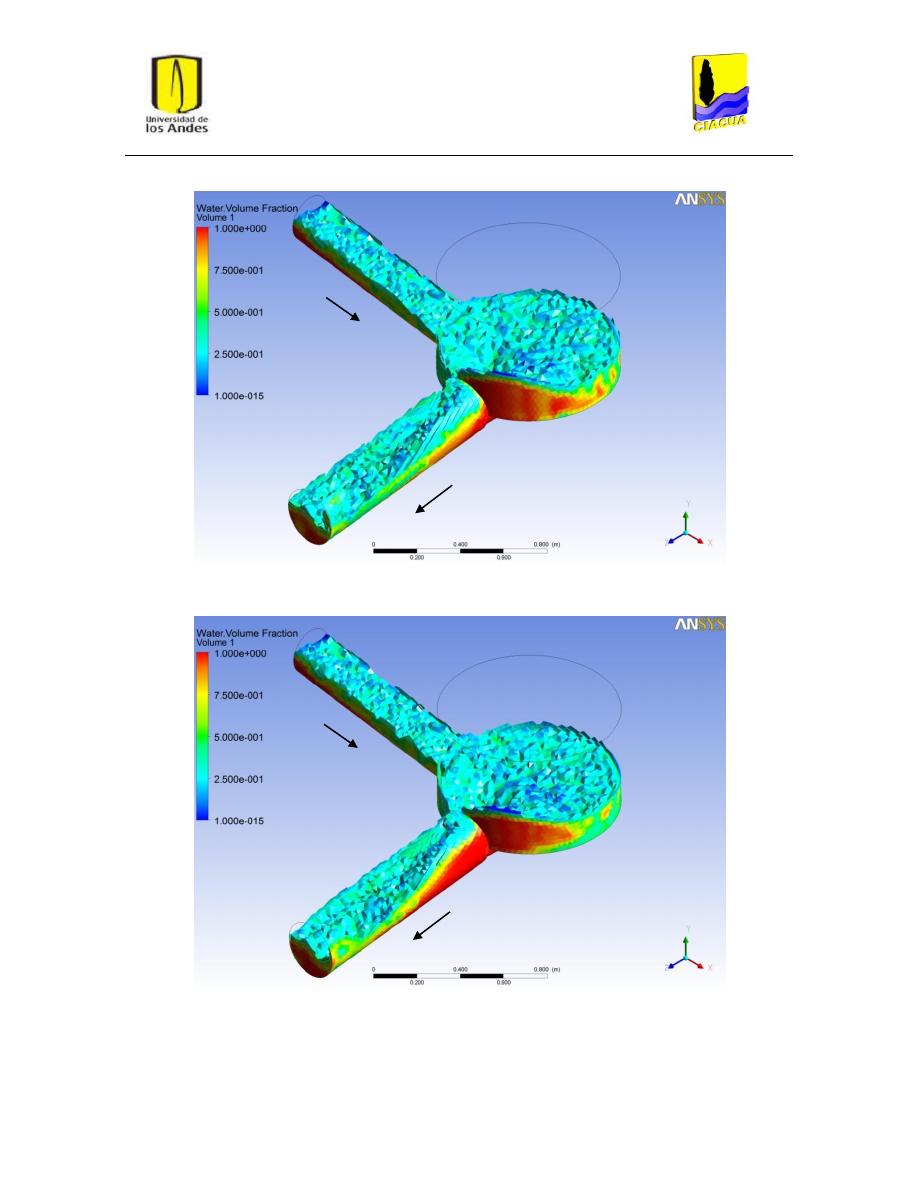
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
92
ICIV 201210 01
Figura anexa 34: Superficie del flujo en FN-7. Modelo k-ε RNG
Figura anexa 35: Superficie del flujo en FN-7. Modelo k-ω
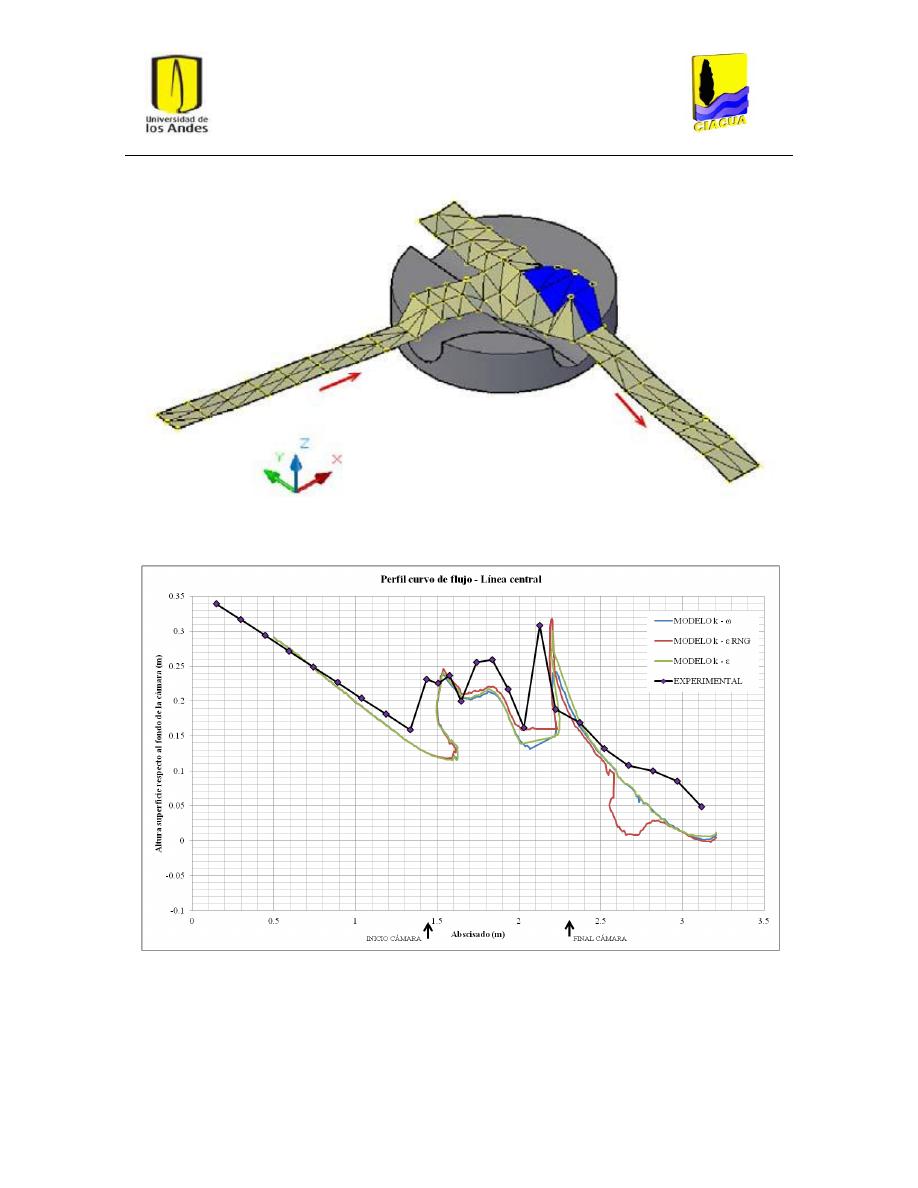
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
93
ICIV 201210 01
Figura anexa 36: Patrón de flujo tridimensional. Tomado de (Centro de Investigaciones de Acueductos y
Alcantarillados - CIACUA, 2010).
Gráfica anexa 36: Perfil curvo de flujo por línea central para FN-7.
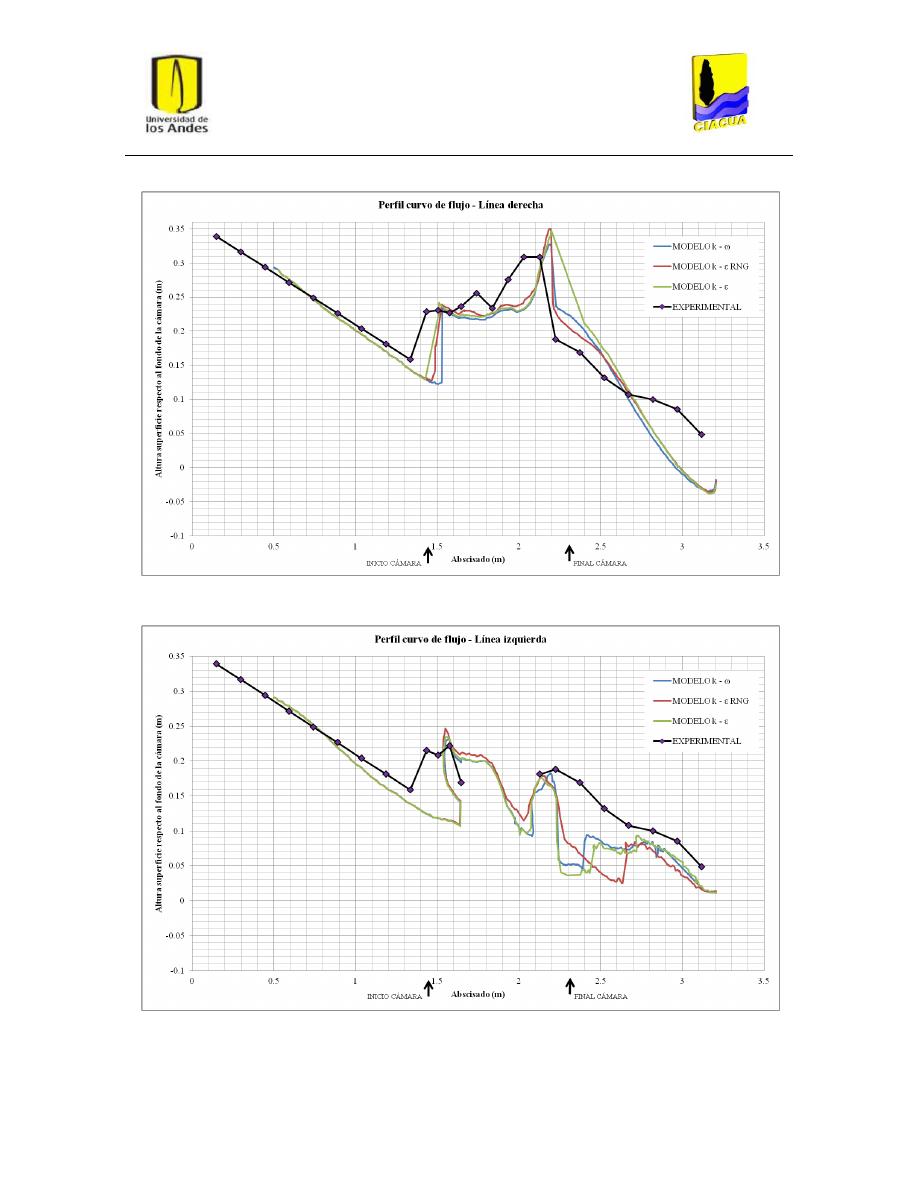
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
94
ICIV 201210 01
Gráfica anexa 37: Perfil curvo de flujo por línea derecha para FN-7.
Gráfica anexa 38: Perfil curvo de flujo por línea izquierda para FN-7.
7.10.
Escenario de modelación FN-8

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
95
ICIV 201210 01
Figura anexa 37: Superficie del flujo en FN-8. Modelo k-ε estándar.
Figura anexa 38: Superficie del flujo en FN-8. Modelo k-ε RNG.
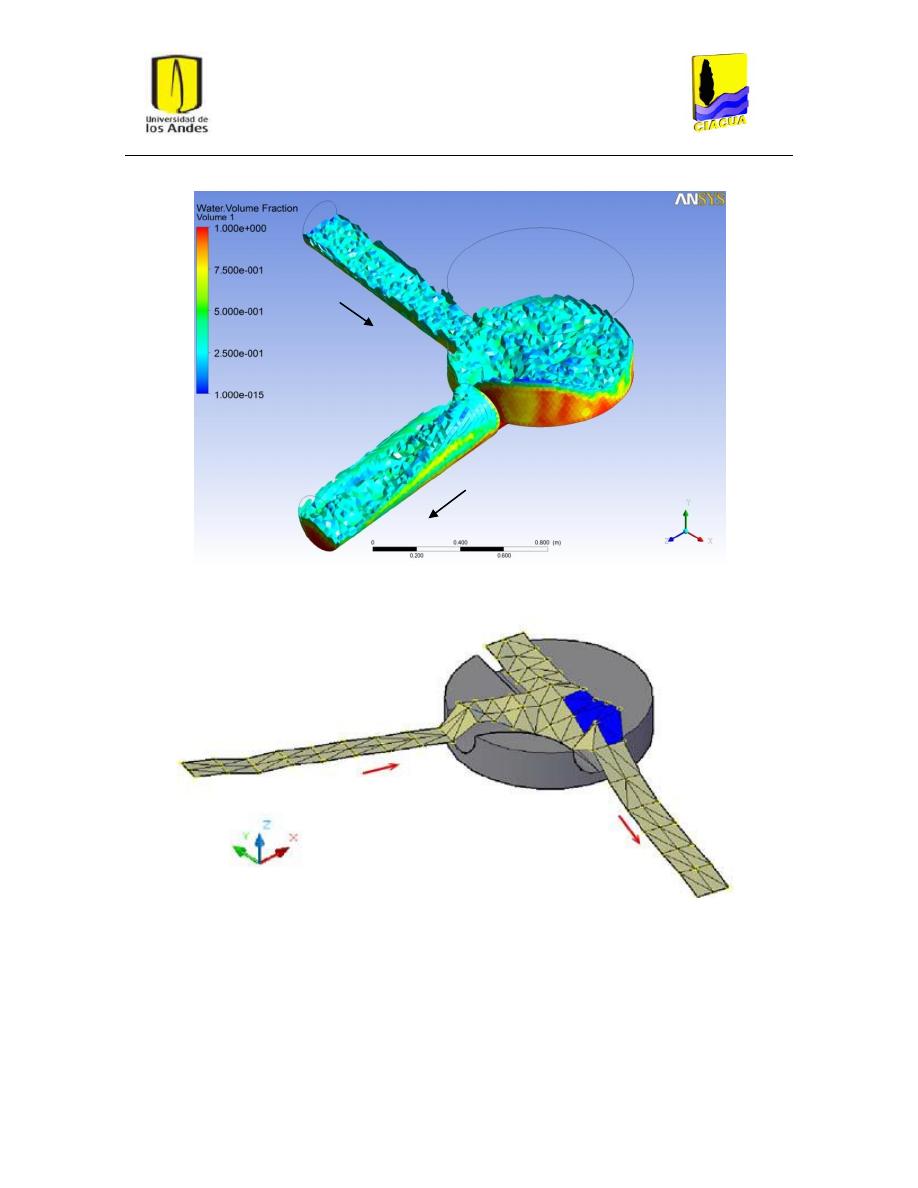
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
96
ICIV 201210 01
Figura anexa 39: Superficie del flujo en FN-8. Modelo k-ω.
Figura anexa 40: Patrón de flujo tridimensional. Tomado de (Centro de Investigaciones de Acueductos y
Alcantarillados - CIACUA, 2010).
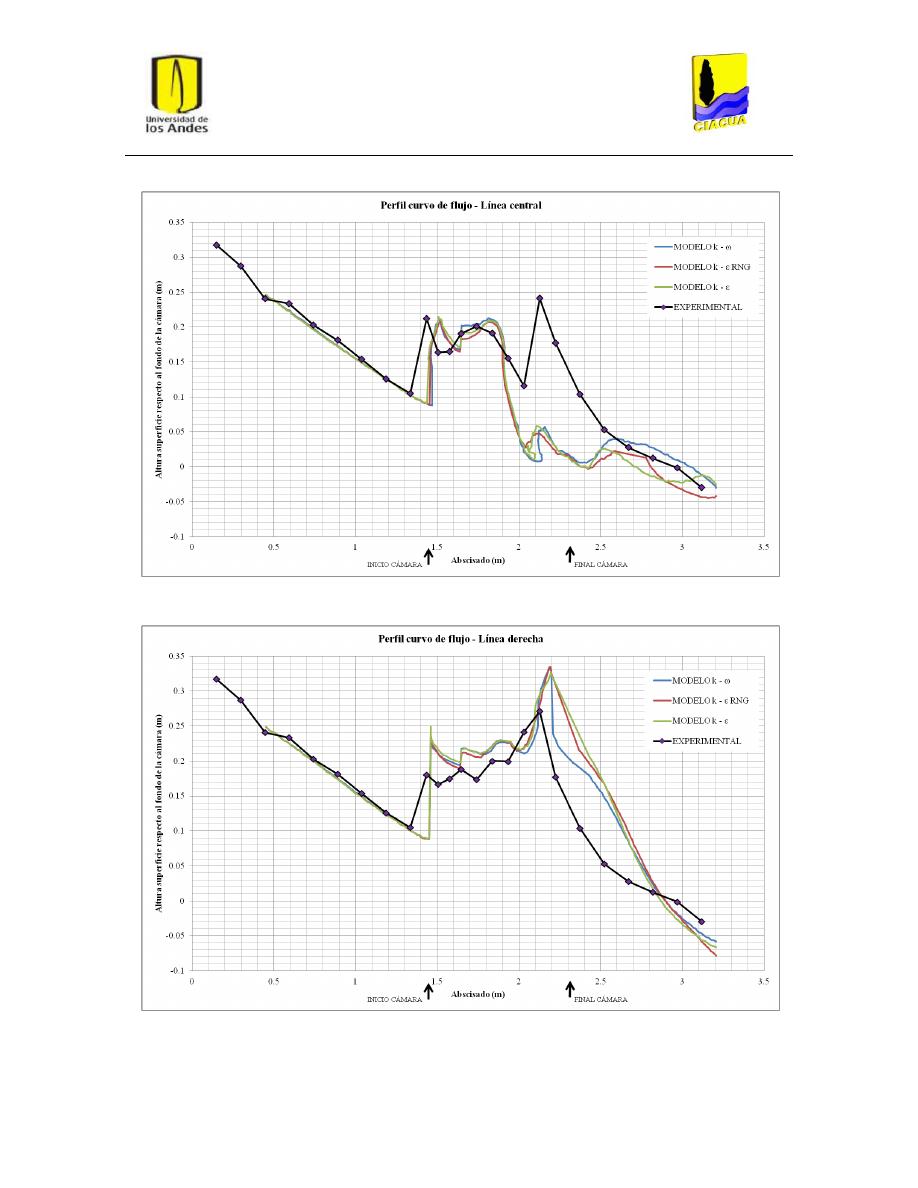
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
97
ICIV 201210 01
Gráfica anexa 39: Perfil curvo de flujo por línea central para FN-8.
Gráfica anexa 40: Perfil curvo de flujo por línea derecha para FN-8.
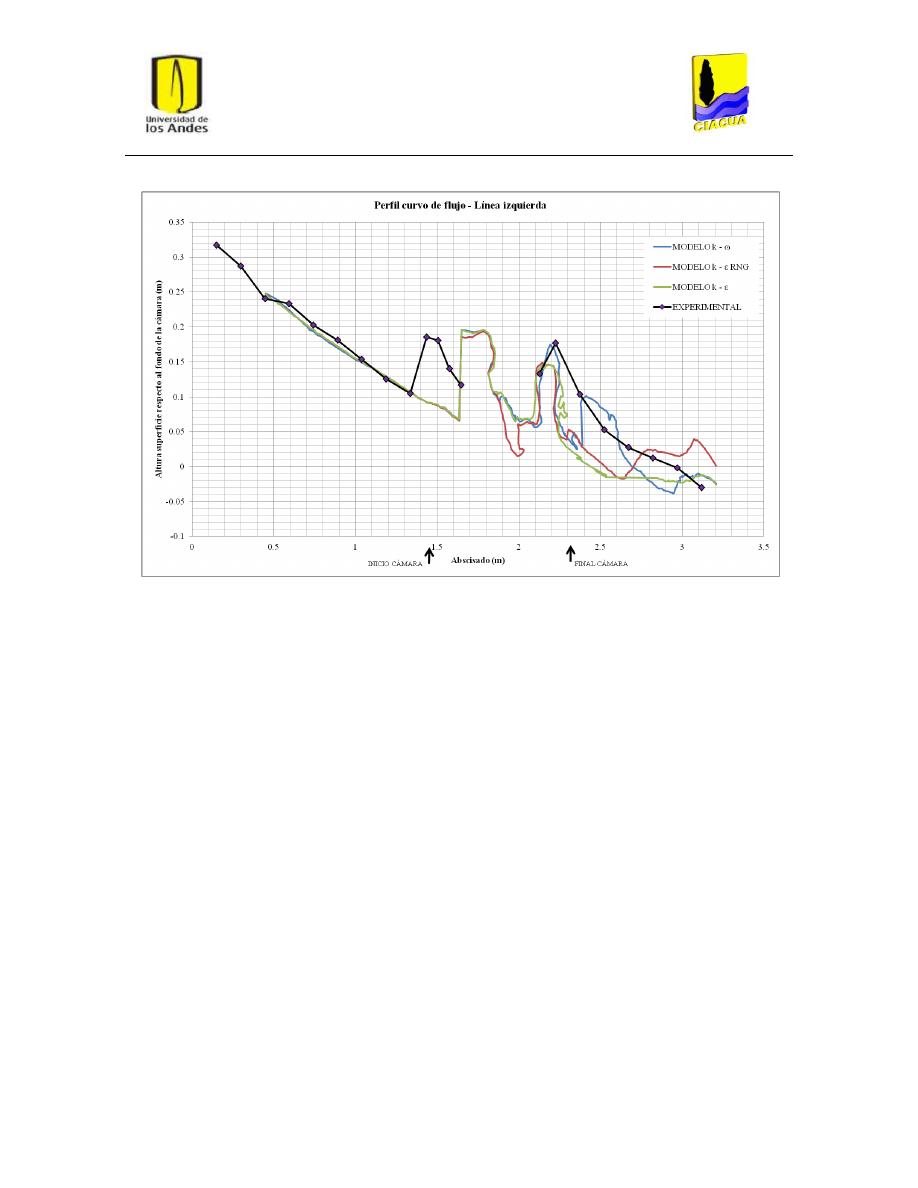
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
98
ICIV 201210 01
Gráfica anexa 41: Perfil curvo de flujo por línea izquierda para FN-8.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Modelación numérica del flujo supercrítico en cámaras de inspección
para sistemas de alcantarillado
99
ICIV 201210 01
8. BIBLIOGRAFÍA
ANSYS Inc. (2010). ANSYS CFX-Solver Modeling Guide. Canonsburg, United States.
Cebeci, T. (2004). Analysis of Turbulent Flows. Boston, United States: Elsevier.
Centro de Investigaciones de Acueductos y Alcantarillados - CIACUA. (2010). Comportamiento hidráulico
de cámaras de inspección bajo condiciones de flujo supercrítico. Bogotá, Colombia: Universidad de los
Andes.
H. K. Versteeg, W. M. (2007). An Introduction to Computational Fluid Dynamics - The Finite Volume
Method. Harlow, England: Pearson Education Limited.
White, F. M. (2008). Fluid Mechanics. New York, United States: McGraw-Hill.
Niño, Yarko. (2002). Método de los Volúmenes Finitos. Notas de Clase. Chile. Universidad de Chile.
Panton, R. L. (2005). Incompressible Flow. New Jersey, United States: John Wiley & Sons Inc.
Bakker, André. (2002). Applied Computational Fluid Dynamics, Lecture 18: Eulerian Flow Modeling.
ANSYS Inc.
ANSYS Inc. (2010). ANSYS CFX-Solver Theory Guide. Canonsburg, United States.
White, F. M. (2006). Viscous Fluid Flow. Singapore: McGraw-Hill
