
METODOLOGÍA DE SELECCIÓN DEL TRAZADO DE UNA RED DE
DRENAJE URBANO OPTIMIZADA, USANDO EL CONCEPTO DE
MÍNIMA MASA-LONGITUD TRANSPORTADA
“XII Simposio Iberoamericano sobre planificación de sistemas de
abastecimiento y drenaje”
Juan Saldarriaga (1), Paula Cuero (2), Laura Montaño (3), Emilio Corrales (4), Daniel
Luna (5)
(1) Profesor Titular, Departamento de Ingeniería Civil y director del Centro de Investigaciones
en Acueductos y Alcantarillados de la Universidad de Los Andes (CIACUA), Carrera 1ª N° 18A
-12, Bogotá, Colombia, (+571) 3394949 Ext: 3521, jsaldarr@uniandes.edu.co
(2) – (5) Investigador(a), Centro de Investigaciones en Acueductos y Alcantarillados de la
Universidad de Los Andes (CIACUA), Carrera 1ª N° 18A -12, Bogotá, Colombia, (+571)
3394949
Ext:
3520,
pa.cuero38@uniandes.edu.co;
le.montano110@uniandes.edu.co;
e.corrales61@uniandes.edu.co; de.luna123@uniandes.edu.co
RESUMEN
El presente documento muestra la formulación y aplicación de dos nuevas metodologías para elegir la
topología de una red de drenaje urbano; la primera metodología consiste en transformar la red
inicialmente cerrada en una red abierta basándose en una relación beneficio - costo orientada a
minimizar el transporte de masa y optimizar el gasto de potencia disponible. La segunda se basa en el
criterio de minimizar el costo hidráulico de la red. Las metodologías fueron evaluadas en diferentes
escenarios. El costo del trazado generado al usar las metodologías en cada red se comparó con el
mejor costo de los diseños exhaustivos, demostrando que conducen a diseños con costos cercanos al
mínimo global.
Palabras claves: Sistemas de drenaje urbano, topología, minimización de transporte de masa,
programación por restricciones.
ABSTRACT
The present paper describes the formulation and application of a two new methodologies for sewer
systems layout selection. The first methodology consist in transformed the looped network in an open
network based in a benefit cost relation oriented to minimize the mass transport and an optimal use of
power. The second one is based on minimize the hydraulic cost. The algorithms were evaluated in
different study cases showing that generates costs near to the global minimum.
Key words: Sewer systems, layout, minimizing of mass transport, constraint programming.
SOBRE EL AUTOR PRINCIPAL
Juan Saldarriaga
: Profesor Titular de la Facultad de Ingeniería de la Universidad de los Andes. Área de
Recursos Hidráulicos, Departamento de Ingeniería Civil y Ambiental. Coordinador del Centro de
Investigación Estratégica del Agua (CIE-AGUA) de la Facultad de Ingeniería de la Universidad de los
Andes. Director del Centro de Investigaciones en Acueductos y Alcantarillados CIACUA del
Departamento de Ingeniería Civil y Ambiental de la Universidad de los Andes.

INTRODUCIÓN
En la actualidad, aún existen algunas ciudades
pequeñas e intermedias, especialmente en países
en vía de desarrollo que no cuentan con acceso a
los sistemas de drenaje urbano. La razón
primordial por la cual no se da acceso, es el bajo
presupuesto con el que se cuenta para realizar su
construcción. Esto motiva a generar una
metodología por medio de la cual se obtenga una
red de drenaje urbano de bajos costos
constructivos y buenas condiciones hidráulicas de
operación.
Uno de los aspectos de mayor impacto en los
costos de una red de drenaje urbano es la
selección del trazado o topología de la red, es
decir cómo están conectados los tubos y las
cámaras de unión correspondientes. Lo anterior,
considerando que para una red determinada
pueden existir gran cantidad de alternativas
posibles de trazado y está comprobado que la
diferencia en costos entre elegir un trazado y otro
puede llegar a significar una diferencia de hasta
un 50%.
El número de alternativas de trazado crece de
manera exponencial con el tamaño de la red, lo
que hace que encontrar el trazado de mínimo
costo se convierta en un problema NP-Duro, es
decir que no tiene solución polinomial. Por tal
razón, diferentes autores han abordado el
problema de optimización de diseño de las redes
de
drenaje
urbano
haciendo
uso
de
methaeurísticas. Por ejemplo, Argaman et al.
(1973), utilizaron programación dinámica para
resolver el problema; Li y Matthew (1990)
implementaron DDDP (Discrete Differential
Dynamic Programming); Weng y Liaw (2005),
establecieron un modelo de optimización (SSOM
– Sewer System Optimization Model), basado en
la combinación de los principios de Algoritmos
Genéticos; Diogo y Graveto (2006) hicieron uso
de la técnica de búsqueda estocástica Simulated
Annealing Model. Recientemente, Moeini y
Afshar (2012) trataron este problema utilizando
un algoritmo de hormigas inteligentes y Haghighi
(2012) desarrolló un método denominado Loop by
Loop Cutting Algorithm.
Heurísticas como las mencionadas, pueden llevar
a buenos resultados; sin embargo el costo
computacional es alto y no se obtienen resultados
explícitos. Por tal razón este trabajo presenta dos
metodologías para la selección del trazado
basadas en criterios hidráulicos y programación
por restricciones, de manera tal que se obtenga un
resultado
de
bajo
costo
con
un
costo
computacional reducido usando una metodología
explícita.
La primer metodología adecúa un algoritmo
utilizado para el diseño de Redes de Distribución
de Agua Potable (RDAP) presentado por
Saldarriaga et al. (2010) donde uno de los pasos
determinantes consiste en convertir la red cerrada
en una abierta haciendo uso de criterios
hidráulicos para identificar los sumideros de la
red. Del mismo modo se convierte la red de
drenaje urbano inicialmente cerrada en una red
abierta para cumplir con las restricciones del
problema.
La segunda metodología combina criterios
utilizados actualmente por los diseñadores, como
elegir la ruta de mayor pendiente como la ruta
principal que transporta mayor caudal, mientras
que para las rutas secundarias se utilizan criterios
para reducir el transporte de masa, lo que se
llamará costo hidráulico; la metodología se llevó a
cabo haciendo uso de la herramienta de sistemas
de información geográfica ArcGIS 10.1(ESRI,
2012).
BASE CIENTÍFICO – TEÓRICA
Dimensionamiento del problema
La selección del trazado de una red consiste en
indicar como se conectan los tubos entre sí, dónde
están ubicadas las cámaras de unión y en cada
cámara hacia dónde fluye el agua.
Los parámetros de entrada para elegir el trazado
de la red son: la distribución urbanística de las
calles, la ubicación del punto de descarga y la
contribución de caudales en cada cámara de
unión. Por cada calle pasa un tubo y en cada
intersección de calles hay una cámara de unión
que conecta los tubos, lo que sucede únicamente
en el caso de sistemas de drenaje sanitario o
combinado.
El desafío al determinar el trazado de una red con
estas características consiste en encontrar los
sentidos de flujo de cada uno de esos tubos, es
decir hacia donde drenan, y determinar en cada
cámara cuál de los tubos conectados transportará
el agua que llega desde aguas arriba. El tubo que
no la transporte es lo que se considera como un
arranque.

Bajo
estas
condiciones,
considerando
los
conceptos de conteo presentados por Walpole et
al. (1999), el número de alternativas posibles de
trazado se puede calcular con la siguiente
ecuación:
(1)
donde, ‘n’ es el número de filas de la grilla y ‘m’
es el número de columnas de la grilla. El hecho
que las variables se encuentren en el exponente
hace que el número de alternativas crezca de
manera exponencial y por tal razón se puede
considerar como un problema NP – Duro.
Restricciones del problema
Las restricciones a seguir para determinar el
trazado son las siguientes:
En cada calle hay una tubería.
En cada intersección de las calles debe existir
una cámara de unión o nudo.
Cada cámara de unión recibe un caudal de
aporte por caudal sanitario y un caudal de las
tuberías que llegan a ésta.
Una cámara de unión sólo puede drenar hacia
un tubo.
La ubicación del punto de descarga debe estar
definida previamente.
La ruta principal es el camino que se debe
recorrer sin la presencia de arranques, desde
el nudo o cámara más alejada hasta el punto
de descarga.
Costos
El costo de elegir un trazado, se puede determinar
únicamente luego de realizar el diseño hidráulico
de cada uno de los tubos que componen la red.
Según Navarro y Saldarriaga (2009) estos costos
tienen dos componentes; el costo por excavación
que se determina con la Ecuación 2 y el costo de
la tubería que depende del diámetro y la longitud
del tubo y se determina por medio de la Ecuación
3. El costo total corresponde a la suma del costo
por excavación y por tubería como se muestra en
la Ecuación 4.
(2)
(3)
donde, K
d
es el coeficiente de costo por diámetros,
K
e
es el coeficiente de costo por excavación, l es
la longitud, d es el diámetro de la tubería y V es el
volumen excavado.
(4)
donde, C
d
es el costo por diámetro, C
e
es el costo
por excavación y k es un coeficiente.
Para realizar el diseño hidráulico que consiste en
determinar el diámetro y la pendiente de cada uno
de los tubos con los caudales asignados según el
trazado definido, se utiliza la metodología
planteada por Corrales et al. (2013).
METODOLOGÍA
I.
Metodología
de
selección
del
trazado haciendo uso de una relación de
beneficio - costo en base a criterios
hidráulicos – (Árbol):
Como se revisó en la sección anterior, la selección
del trazado consiste en indicar que tubos son
puntos de arranque, es decir que no transportan el
caudal de aguas arriba de la cámara de unión y
que tubos son continuos.
Para esto, se evaluaron los factores que más
influían en el costo de la red realizando pruebas
exhaustivas en redes con diferentes distribuciones
urbanísticas, con caudales y topografías variadas;
se llegó a la conclusión de que los dos factores
determinantes en los costos, son la manera en la
que se realiza el gasto de potencia en la red y el
producto masa longitud, lo que se refiere al
transporte de masa.
Se determinó que las redes de menor costo son
aquellas para las cuales las rutas que transportan
mayor caudal, pasan por la ruta de mayor
pendiente del terreno, disminuyendo así el costo
por excavación; por otra parte el trazado que
minimice el producto caudal - longitud estará
minimizando el transporte de masa por lo que los
costos tanto por tubería como por excavación
disminuyen.
Para convertir la red inicialmente cerrada en una
red abierta se adecúa un algoritmo presentado por
Saldarriaga et al. (2010) para convertir una red
cerrada de abastecimiento de agua potable en una
red abierta. Para el caso de redes de drenaje
urbano, el objetivo es entonces determinar los
puntos de arranque de la red, utilizando una
metodología que convierte la red por medio de
una estructura de árbol. La Figura 1 muestra una
red de drenaje con sus nudos como círculos
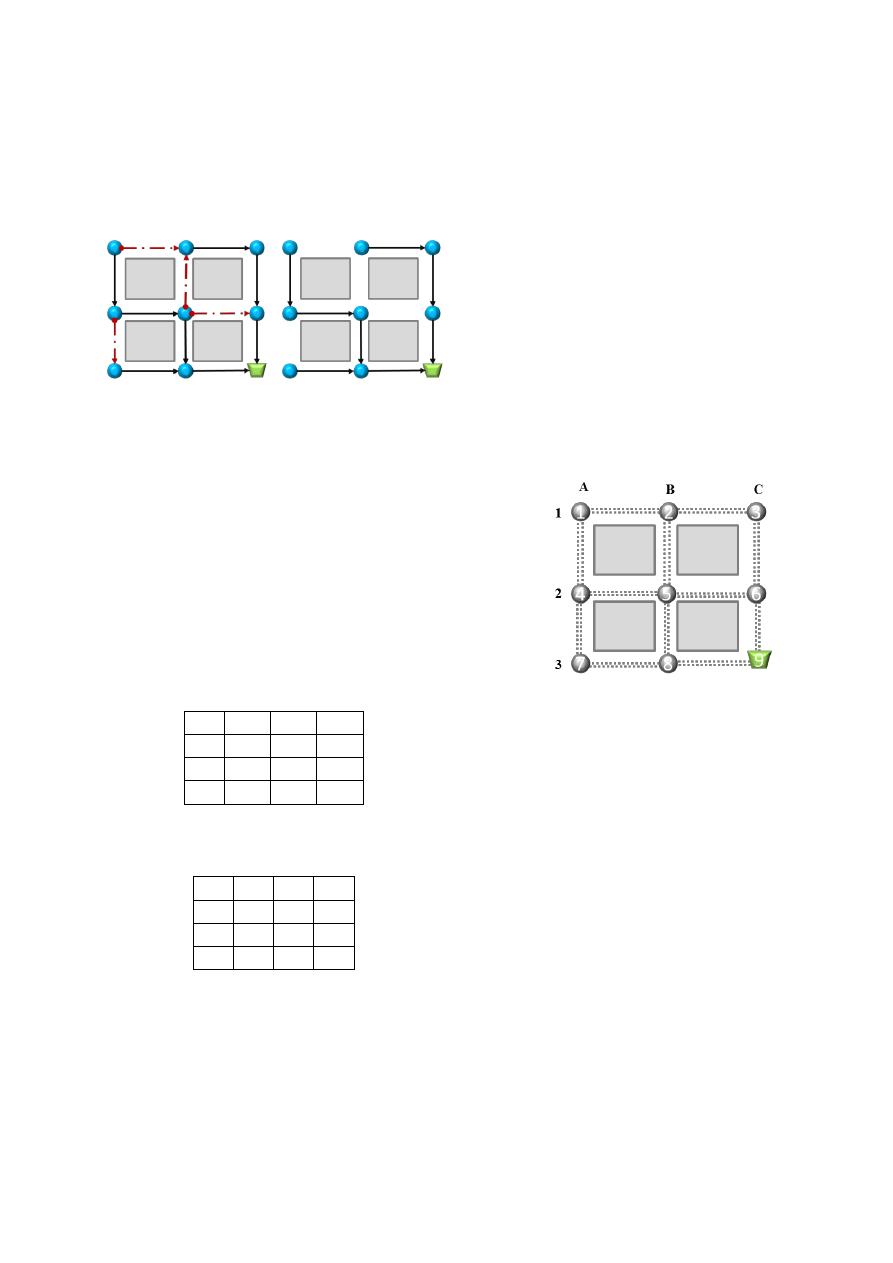
azules, los puntos de arranque como flechas
discontinuas en rojo, los tubos que no son
arranques como flechas continuas negras y el
punto de descarga como un trapecio verde. Si se
eliminan de la red los puntos de arranque, la red
toma la forma de un árbol donde la raíz es el
punto de descarga.
(a)
(b)
Figura 1. Conversión de una red cerrada a
una abierta.
Para explicar la metodología utilizada se
realizarán los cálculos para una red de dos
manzanas por dos manzanas, sus características se
muestran en las siguientes tablas, donde se
especifica el caudal de entrada en cada nudo y la
topografía de la red. La distancia entre todos los
nudos es de 100 m en planta, por lo que se puede
decir que es una red cuadrada de dos bloques; por
dos bloques, cuenta con 8 nudos y un punto de
descarga ubicado en la parte inferior derecha.
Tabla 1. Caudal en cada nudo de la red de
ejemplo en (m
3
/s).
Q
A
B
C
1
0.04
0.036
0.03
2
0.036
0.044
0.04
3
0.036
0.034
PD
Tabla 2 Cota en cada nudo de la red de
ejemplo en (m).
A
B
C
1
100
99.5
98.7
2
99
98.8
98.6
3
98.5
98.5
98
La metodología consiste en: (1) añadir al árbol el
punto de descarga como la raíz, (2) buscar los
frentes de avance, (3) calcular la relación
beneficio - costo para cada frente de avance, (4)
añadir al árbol el tubo que genere mayor
beneficio, (5) seguir el proceso hasta que todos los
tubos necesarios para drenar las cámaras de la red
se encuentren dentro del árbol, (6) determinar los
sentidos de flujo de los puntos de arranque.
1. Añadir el punto de descarga como raíz
al árbol.
De manera semejante a la metodología propuesta
por Saldarriaga et al. (2010) en Redes de
Distribución de Agua Potable (RDAP) en lugar
de considerar el embalse como la raíz del árbol, se
considera el punto de descarga. En caso tal que
exista más de un punto de descarga, se realizaría
todo
el
proceso
como
si
fueran
redes
independientes y los nudos agregados a cada
punto de descarga serán aquellos que generen
mayor relación beneficio - costo.
Para la red del ejemplo se cuenta con un único
punto de descarga por lo que el árbol hasta ahora
solo tienen un nudo que corresponde a ese punto,
como se observa en la Figura 2.
Figura 2. Añadir el punto de descarga al
árbol.
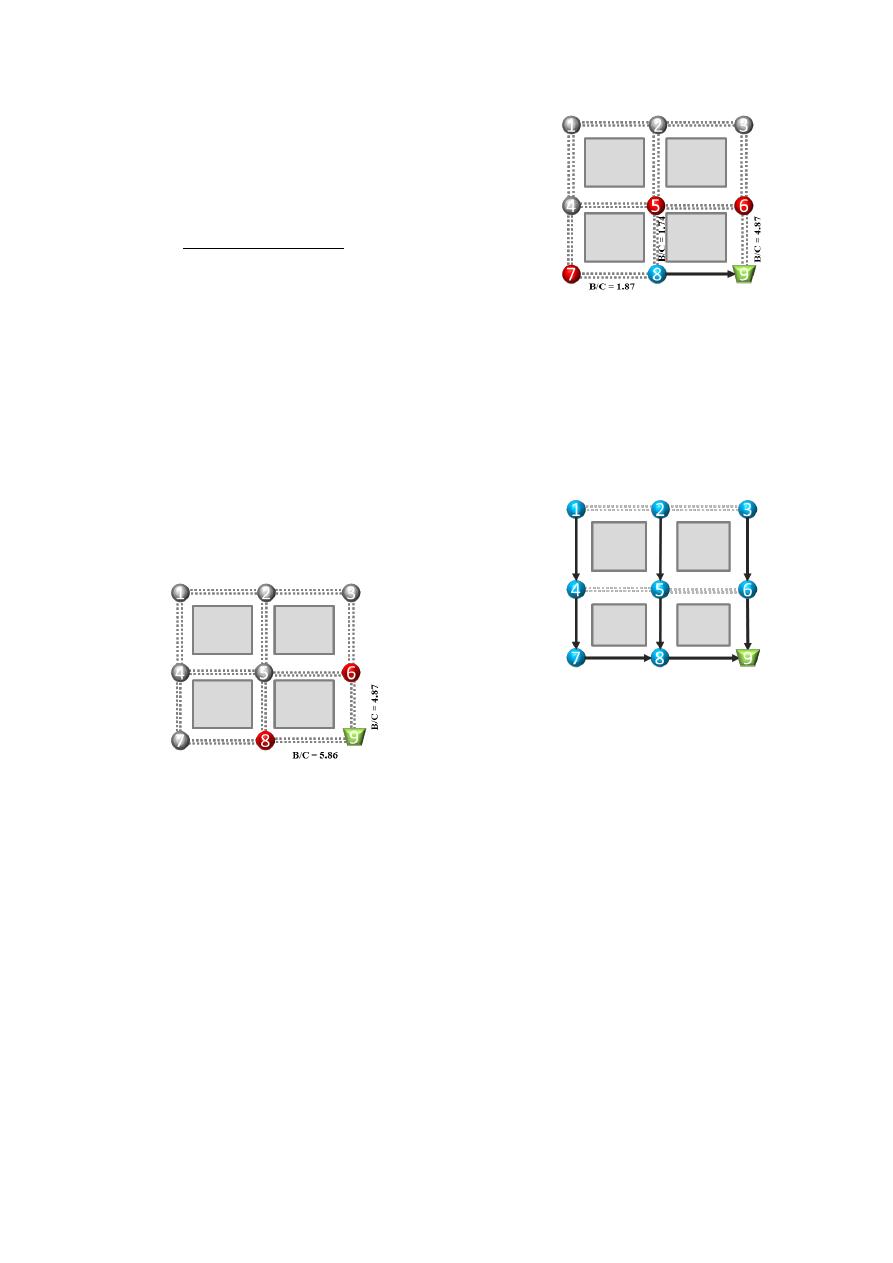
2. Buscar los frentes de avance.
Los frentes de avance son aquellos nudos que
pueden drenar hacia algún otro nudo o cámara que
haga parte del árbol, es decir que pueden
conectarse directamente. Para este caso los frentes
de avance son los que se muestran en la Figura 3
en rojo; qué son los únicos que se pueden conectar
al punto de descarga.
3. Calcular la relación beneficio - costo
para cada frente de avance.
Para cada uno de los tubos que permitan conectar
los frentes de avance actuales con el árbol, se debe
calcular la relación de beneficio - costo. Para ésta
relación el beneficio es el producto de caudal por
longitud marginal, lo que indica que será la suma
de caudal por longitud del árbol si se incluyera el
nuevo tubo menos ese producto antes de incluir el
tubo al árbol. El costo es el costo marginal
calculado con la Ecuación 4, por lo que es claro
que se debe realizar el diseño hidráulico de la red
haciendo uso de la metodología presentada por
Corrales et al. (2013) para poder evaluar cada
alternativa. La relación beneficio - costo se
muestra en la Ecuación 5:
∑
∑
(5)
donde,
BC es el beneficio/costo asociado al frente de
avance.
es el caudal que transporta cada tramo
es la longitud de cada tramo.
es el costo de la red calculada con la Ecuación 4.
es el subíndice que indica que se considera la red
incluyendo el nuevo frente de avance.
es el subíndice que indica que se considera la red
sin el nuevo frente de avance.
Aplicando esta ecuación para los dos frentes de
avance de la red tomada por ejemplo se obtienen
las relaciones beneficio/costo de la siguiente
figura:
Figura 3. Cálculo del beneficio - costo
para los tubos que conectan los frentes
de avance.
4. Añadir al árbol el tubo que genere
mayor relación beneficio - costo.
El tubo que conecte al nudo de mayor relación
beneficio - costo es añadido al árbol, en este caso
se elige el tubo que une al nudo 8 con el punto de
descarga, es importante aclarar que al árbol es
añadido el tubo no el nudo, como se muestra en la
Figura 4.
Figura 4. Añadir el tubo de mayor
beneficio/costo al árbol.
5. Realizar los pasos 2 al 4 hasta que todos
los tubos necesarios para drenar las
cámaras de la red se encuentren dentro
del árbol.
Una vez realizado este proceso, se obtiene el
siguiente árbol para la red tomada como ejemplo.
Figura 5. Árbol generado para la red
tomada por ejemplo.
Los tubos que no aparecen en el árbol son
aquellos considerados como arranques y por tanto
no transportarán el caudal de aguas arriba de la
cámara. Es importante resaltar que estos tubos son
aquellos que generan menor beneficio, por lo que
se busca que transporten la menor cantidad de
caudal posible.
6. Determinar los sentidos de flujo de los
puntos de arranque.
Para cada punto de arranque se calcula la relación
beneficio - costo de transportar el agua en una
dirección u otra utilizando la Ecuación 5, de
manera tal que se elegirá el sentido de flujo que
genere mayores beneficios, como se muestra para
el tubo que une los nudos 1 y 2; se calcula en
ambas direcciones y se elige finalmente que el
agua drene del nudo 1 al nudo 2 ya que ese
sentido genera una mayor relación beneficio -
costo, lo que se muestra en la Figura 6. Luego de
realizar el mismo procedimiento para todos los
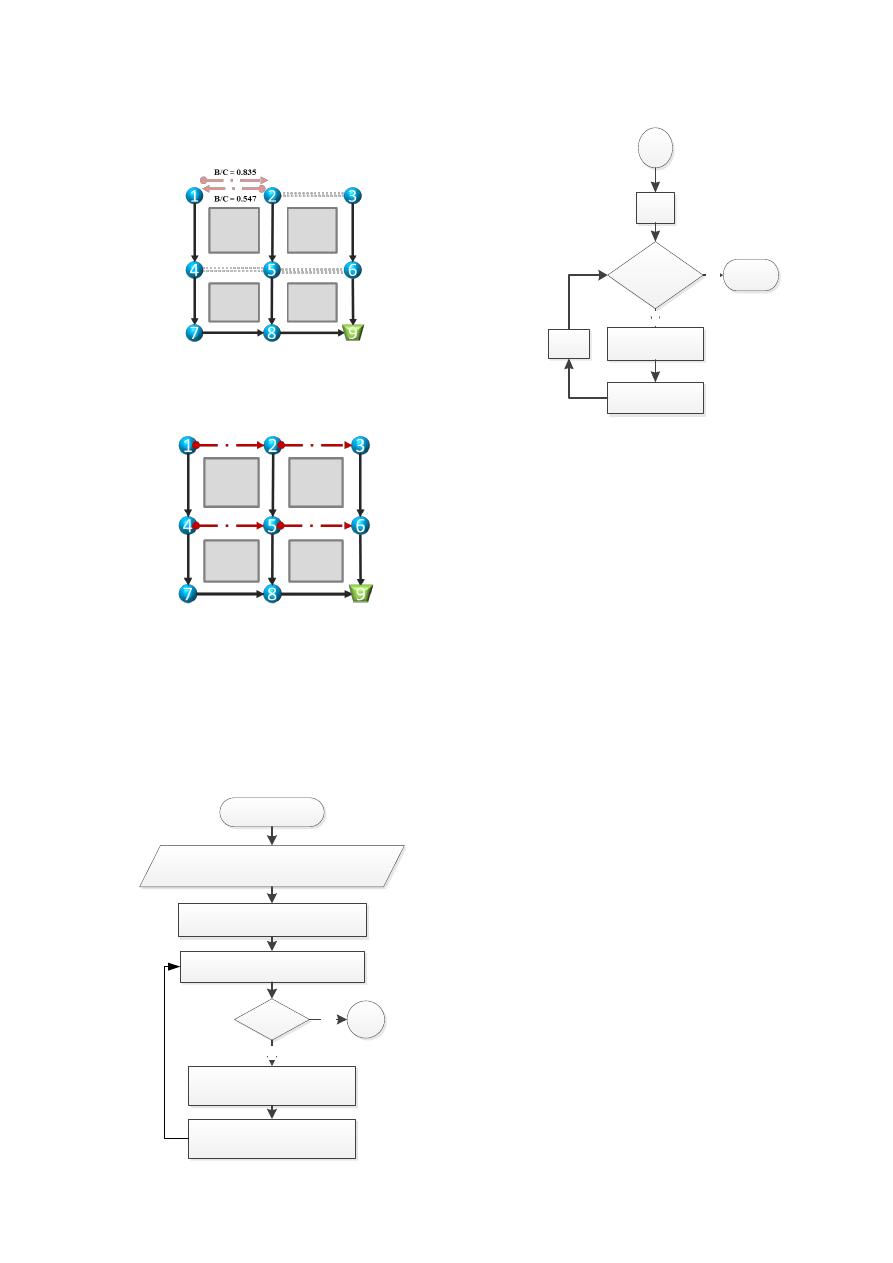
puntos de arranque se obtiene el trazado que se
muestra en la Figura 7.
Figura 6. Cálculo del beneficio/costo para
los sentidos de flujo del primer punto de
arranque.
Figura 7. Trazado de la red tomada por
ejemplo.
En el Diagrama de Flujo 1 se muestra el
procedimiento a seguir para llevar a cabo la
metodología planteada y sobre la cual se basan los
resultados mostrados a continuación.
INICIO
Qi, ubicación punto de descarga
Topología y Topografía de la
red.
Agregar al árbol, el punto de descarga
Buscar frentes de avance (FA)
N
o
FA >0
Calcular la relación beneficio/
costo con la Ecuación 5.
Añadir al árbol el tubo que une al
nudo que genera mayor B/C
SI
NO
A
J<= N
o
Tubos
Inicio?
J=1
Calcular B/C en cada
sentido de flujo
SI
Elegir sentido de
flujo de mayor B/C
J = j+1
FIN
NO
A
Diagrama de Flujo 1. Metodología para la
selección del trazado
– criterio
beneficio/costo.
II.
Metodología
de
selección
del
trazado
haciendo
utilizando
criterios
hidráulicos para asignar costos a las
tuberías y obtener la ruta de menor costo
hidráulico.
La siguiente metodología, tiene como objetivo
obtener un trazado de bajo costo para la red,
utilizando el algoritmo de Dijakstra (Dijakstra,
1959) para encontrar la ruta de menor costo
hidráulico desde un punto hasta otro. En este caso
el costo es un criterio topográfico o hidráulico,
que permite minimizar el transporte de masa y
optimizar el gasto de potencia en la red.
La metodología consiste en los siguientes pasos:
(1) determinar lo sentidos de flujo en la red, (2)
calcular el costo hidráulico de cada tubo, (3)
determinar la ruta principal de máxima pendiente
paso a paso, (4) determinar las rutas secundarias
y/o terciarias.
1. Determinar lo sentidos de flujo en la
red:
Los sentidos de flujo son determinados netamente
por criterios topográficos y de ubicación hacia el
punto de descarga; hasta el momento, con
propósito de ilustrar la metodología, las redes
evaluadas deben tener según estos criterios
sentidos de flujo únicamente hacia la derecha y
hacia abajo.

2. Calcular el costo hidráulico de cada
tubo.
Para cada tubo en la red, se debe estimar cual es
la pendiente del terreno, como se muestra en la
Ecuación 5.
(6)
donde,
es la longitud en planta del tramo,
es la cota del terreno donde encuentra la cámara
de salida y
la de la cámara de llegada.
Adicionalmente se calcula el producto caudal -
longitud para cada tubo, de la siguiente manera:
(7)
donde, el producto caudal - longitud es el caudal
que ingresa cada tubo por la longitud del tubo.
3. Determinar la ruta
principal
de
máxima pendiente paso a paso.
La ruta principal se define como la ruta que debe
seguir sin ningún punto de arranque desde el nudo
más alejado de la red hasta el punto de descarga.
Esa ruta se caracteriza por ser la de mayor
diámetro ya que será la que transporte la mayor
cantidad de caudal.
La ruta principal se determina desde el punto más
alejado, donde se decida hacia que tubos drenar
según la pendiente éstos. Una vez se ha elegido el
tubo por el cual drenan y se llega a la cámara
siguiente el proceso se repite eligiendo el tubo de
mayor pendiente, hasta finalmente llegar al punto
de descarga. Lo que indica que los tubos que eran
de menor pendiente en cada cámara serán los
arranques.
4. Determinar las rutas secundarias y
terciarias.
Los nudos que no se encuentren sobre la ruta
principal, serán los iniciales para determinar las
rutas secundarias, utilizando el algoritmo de
Dijakstra (Dijakstra, 1959) implementado en
ArcGis 10.1 (ESRI, 2012); se calcula la ruta de
menor producto caudal - longitud hasta el punto
de descarga, hasta que todos los nudos tengan una
manera de drenar. Los tubos que no se encuentren
en ninguna de las rutas principales o secundarias,
serán los puntos de arranque.
PRESENTACIÓN DE RESULTADOS
Para evaluar los resultados se probaron redes de
diferente magnitud, distribución urbanística y de
caudales. A continuación se presentarán dos casos
de estudio representativos, el primero de ellos
consiste en una red ficticia llamada la red R-16, la
cual cuenta con 16 ciclos; y la segunda red se
trata de la red R-9 con nueve ciclos, con
modificación en los caudales y las longitudes de
los tubos.
Red R-16.
La red 4X4 cuenta con una distribución
urbanística de cuatro manzanas por cuatro
manzanas, con una distancia entre todos los nudos
de 100 m, por lo que se puede decir que se trata de
una red cuadrada. El caudal que ingresa a cada
nudo es de 40 L/s y se distribuye equitativamente
entre los dos tubos adyacentes. El terreno es
escarpado y toma los valores de cotas presentados
en la Tabla 3.
Tabla 3. Cota en cada nudo de la red de
ejemplo en (m).
A
B
C
D
E
1
100
99.5
99
97.5
96
2
99
98
98
96
93
3
98
97
96.5
95
94
4
97
96.5
95
94
93.5
5
96
95
94.5
93
92
El material es PVC por lo que se utiliza una
rugosidad absoluta 1.5*10
-6
m; la ecuación de
costos a utilizar, es la Ecuación 4 donde K es
igual a 7.0*10
-4
K
e
es 9579.31 y K
d
1163.77. La
lista de diámetros comerciales disponibles en
milímetros es: 150, 200, 250, 300, 350, 400, 450,
500, 600, 675, 750, 825, 900 y 1000.
La restricción principal para el diseño hidráulico
es que hacia aguas abajo de un tramo el diámetro
puede ser mayor o igual al anterior pero nunca
menor.
Adicionalmente
las
restricciones
hidráulicas de diseño se muestran en la siguiente
tabla:
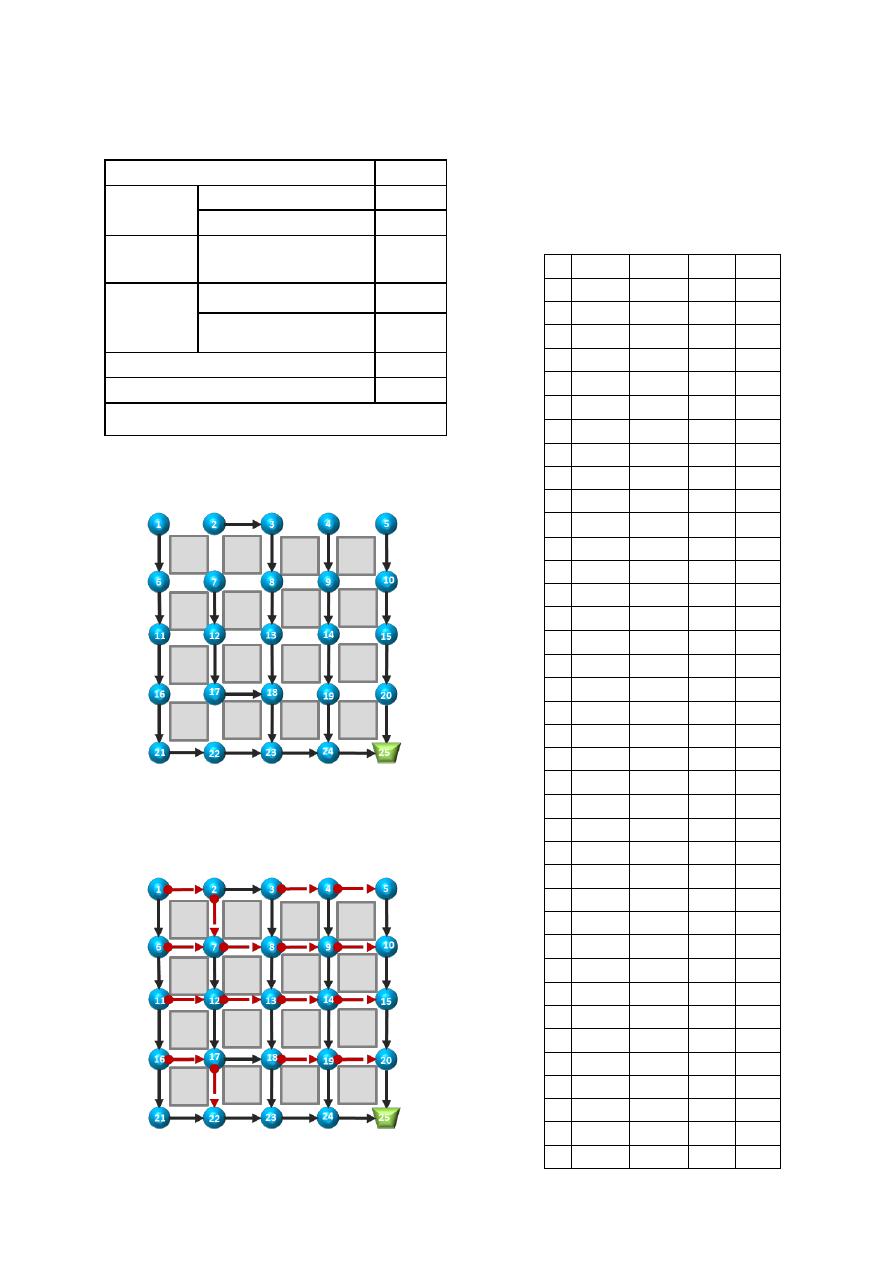
Tabla 4. Restricciones hidráulicas para el
diseño de la red R-16.
Restricción
valor
Velocidad
Mínima
0.75 (m/s)
Máxima
10 (m/s)
Esfuerzo
cortante
Diámetro nominal > 450mm
2 (Pa)
Porcentaje
de llenado
máximo
Flujo cuasi crítico *
70%
Otro régimen de flujo
85%
Profundidad mínima a cota clave
1.2 (m)
Profundidad máxima a cota batea
10 (m)
*
Se presenta cuando el número de Froude está entre 0.7 y
1.3.
Una vez aplicada la metodología para esta red se
obtiene el siguiente árbol:
Figura 8. Árbol generado para la red R-16.
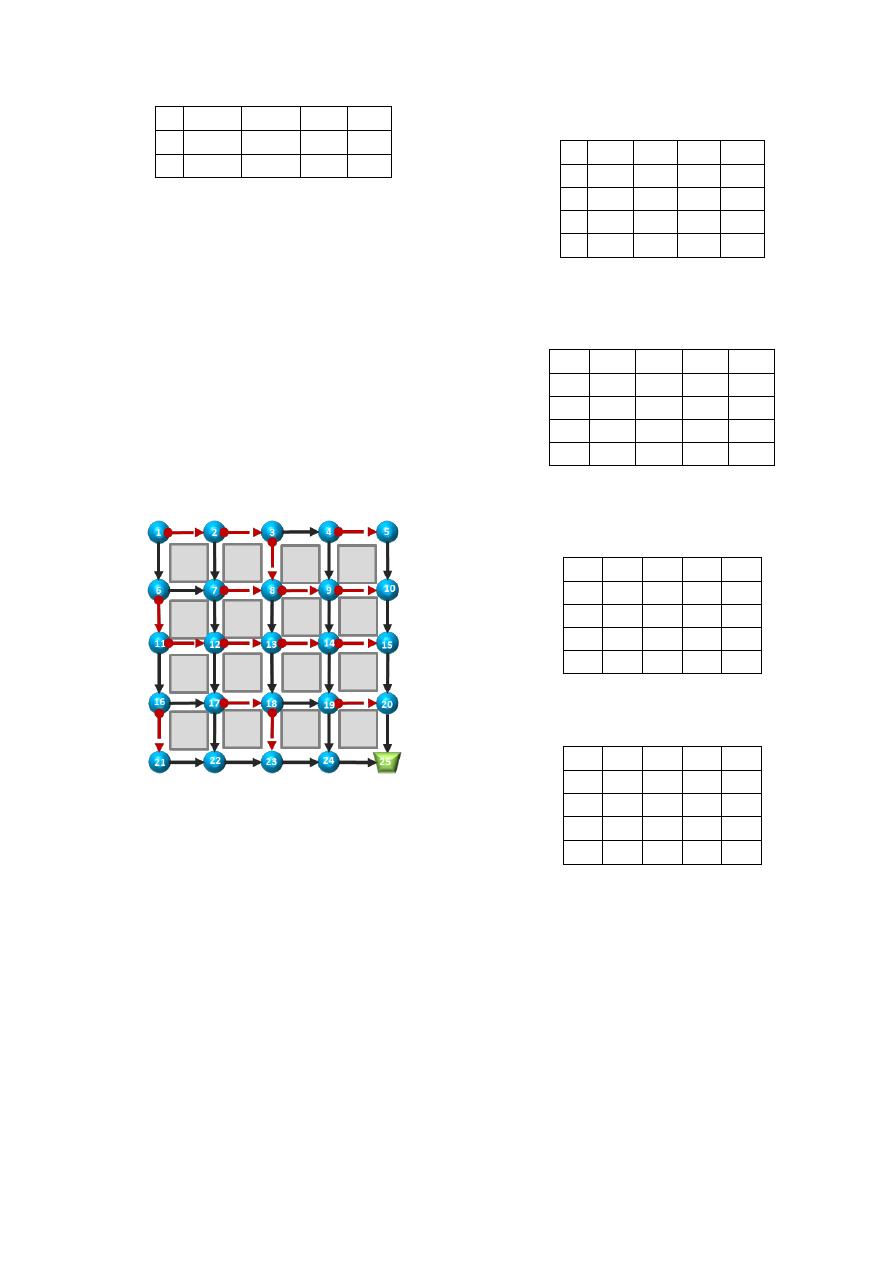
Después de determinar los sentidos de flujo de los
puntos de arranque se obtiene el siguiente trazado
para la red.
Figura 9. Trazado generado para la red R-
16 con la metodología del árbol.
Luego de utilizar la metodología de diseño de
series de drenaje urbano presentada por Corrales
et al. (2013) se obtiene la siguiente configuración
de diámetros y pendientes para cada tubo.
Tabla 5. Resultados del diseño para la red
R-16.
ID Nudo-i Nudo-f d (m) s (-)
1
1
2
0.2
0.005
2
2
3
0.2
0.009
3
3
4
0.15 0.017
4
4
5
0.15 0.017
5
5
10
0.2
0.032
6
1
6
0.15 0.012
7
6
7
0.15 0.012
8
2
7
0.15 0.016
9
7
8
0.2
0.003
10
3
8
0.25 0.007
11
8
9
0.15 0.022
12
4
9
0.2
0.015
13
9
10
0.15 0.032
14
10
15
0.35 0.003
15
6
11
0.2
0.012
16
11
12
0.15
0.01
17
7
12
0.25 0.012
18
12
13
0.15
0.01
19
8
13
0.25 0.016
20
13
14
0.15 0.017
21
9
14
0.25 0.011
22
14
15
0.15
0.01
23
15
20
0.35 0.005
24
11
16
0.25 0.007
25
16
17
0.15
0.01
26
12
17
0.3
0.007
27
17
18
0.3
0.013
28
13
18
0.3
0.016
29
18
19
0.15
0.01
30
14
19
0.3
0.01
31
19
20
0.15
0.01
32
20
25
0.35 0.008
33
16
21
0.25 0.011
34
21
22
0.3
0.011
35
17
22
0.15 0.017
36
22
23
0.35 0.006
37
18
23
0.5
0.005
38
23
24
0.5
0.015
ID Nudo-i Nudo-f d (m) s (-)
39
19
24
0.35
0.01
40
24
25
0.5
0.012
De esta manera se genera un costo total de
$31,169.06 (USD). Para comparar este resultado
con
el
diseño
exhaustivo,
considerando
únicamente sentidos de flujo como derecha abajo,
se obtiene que el diseño es solo 6.18% más
costoso que el diseño óptimo y se ubica en la
posición 19,026 de 65,536 alternativas totales. Es
importante aclarar que el tiempo de cálculo para
encontrar el mejor diseño exhaustivo es de 31
horas, mientras que utilizando la metodología
planteada en éste trabajo, se tarda menos de un
minuto.
Para el caso de la metodología del trazado de
mínimo costo hidráulico, se obtiene el siguiente
trazado para la red.
Figura 10. Trazado generado para la red
R-16 con la metodología de menos costo
hidráulico.
De esta manera se genera un costo de $ 30,251.57
(USD), solo 2.96% más costoso que el diseño de
menor costo exhaustivo.
Red R-9.
La red R-9 cuenta con la misma topografía que se
muestra en la Tabla 6, los caudales de ingreso en
cada cámara son los que se muestran en la Tabla 7
las coordenadas de las cámaras para el cálculo de
las longitudes se muestran en las Tablas 8 y 9.
Tabla 6. Cota de los nudos para la red R-9.
A
B
C
D
1
100.0
99.0
98.5
98.0
2
98.5
96.5
95.8
95.0
3
97.5
95.0
94.0
92.5
4
95.5
94.5
93.0
90.0
Tabla 7. Caudales para la red R-16
modificada en (m
3
/s).
Q
A
B
C
D
1
0.1
0.1
0.1
0.1
2
0.1
0.1
0.1
0.1
3
0.04
0.04
0.04
0.04
4
0.04
0.04
0.04
0.04
Tabla 8. Coordenadas en x para las
cámaras de la red R-16 modificada.
X
A
B
C
D
1
0
100
250
350
2
0
50
250
300
3
0
50
150
300
4
0
60
180
300
Tabla 9. Coordenadas en y para las
cámaras de la red R-16 modificada.
Y
A
B
C
D
1
0
0
0
0
2
80
80
80
80
3
180
180
180
180
4
260
260
260
260
Una vez aplicada la metodología el árbol que se
obtiene para esta red con caudales y longitudes
variables se muestra en la Figura 11; luego de
elegir los sentidos de flujo de los puntos de
arranque se obtiene el trazado de la red mostrado
en la Figura 12.
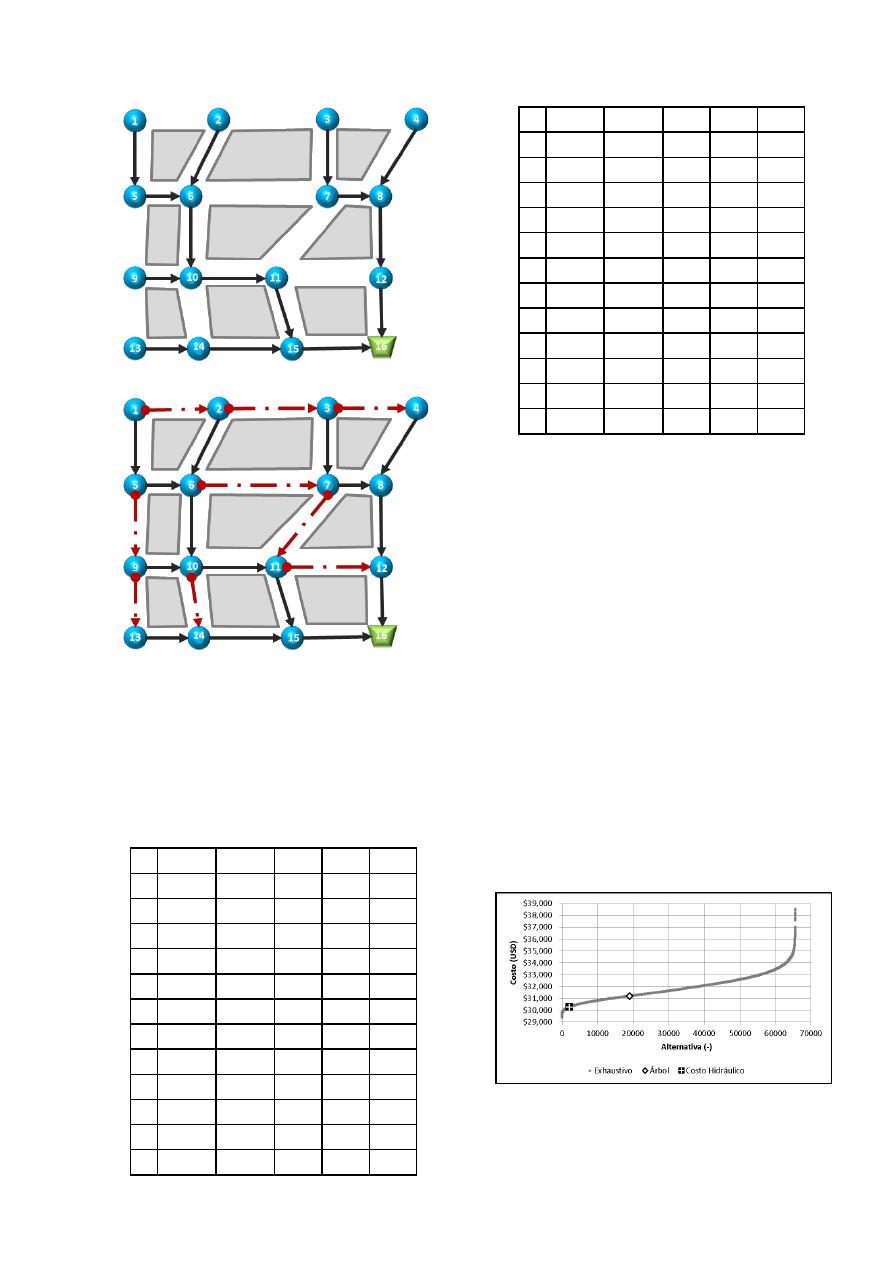
Figura 11. Árbol generado para la red R-9.
Figura 12. Trazado generado para la red
R-9.
Los diámetros y pendientes asignados a cada
tubería, se muestras en la Tabla 10; la longitud de
los tubos mostrada es la longitud real del tubo
incluyendo la pendiente de diseño.
Tabla 10. Resultados del diseño
Hidráulico para la red R-9.
ID Nudo-i Nudo-f d (m) s (-) L (m)
1
1
2
0.2
0.014 100.01
2
2
3
0.3
0.009 150.01
3
3
4
0.2
0.005 100.00
4
4
8
0.2
0.0318 94.39
5
1
5
0.2
0.022
80.02
6
5
6
0.2
0.047
50.06
7
2
6
0.2
0.0265 94.37
8
6
7
0.25
0.005 200.00
9
3
7
0.3
0.02
80.02
10
7
8
0.35
0.019
50.01
11
8
12
0.35
0.028 100.04
12
5
9
0.2
0.014 100.01
ID Nudo-i Nudo-f d (m) s (-) L (m)
13
9
10
0.2
0.047
50.06
14
6
10
0.35
0.012 100.01
15
10
11
0.45
0.01
100.00
16
7
11
0.15
0.0127 141.43
17
11
12
0.15
0.01
150.01
18
12
16
0.35
0.027
80.03
19
9
13
0.2
0.028
80.03
20
13
14
0.25
0.016
60.01
21
10
14
0.25
0.009
80.63
22
14
15
0.35
0.012 120.01
23
11
15
0.45
0.012
85.45
24
15
16
0.45
0.026 120.04
De éste modo el costo total de la red calculado
con la Ecuación 4 y después de realizar el diseño
hidráulico utilizando la metodología de Corrales
et al. (2013), es de $ 18,437.09 (USD), mientras
que el mejor diseño exhaustivo es de 18,338.25
(USD), tan solo 0.54% más económico.
Después de seleccionar el trazado de la red por
medio de la metodología del menor costo
hidráulico, se llega casualmente al mismo trazado
obtenido con la metodología del árbol, por lo que
el trazo elegido por esa segunda metodología es el
que se muestra en la Figura 12.
ANÁLISIS DE RESULTADOS
La siguiente gráfica muestra cómo se comportan
los costos totales para todas las alternativas; el
rombo indica la alternativa de trazado generada
por el árbol y la cruz blanca el trazado generado
por la metodología de menor costo hidráulico,
para la red R-16.
Gráfica 1. Costo total para las alternativas
exhaustivas de diseño para la red R-16.
Para la Red R-16 la metodología del árbol
planteada muestra una cercanía con el diseño

exhaustivo, lo que muestra su eficacia. Sin
embargo la metodología que utiliza el costo
hidráulico para estimar el trazado muestra un
mejor resultado. Cabe resaltar que esta red está
considerada para que los sentidos de flujo sean
hacia la derecha y hacia abajo, lo que permite
reducir el número de alternativas totales y permite
realizar la evaluación exhaustiva. Otro aspecto
relevante indica que algunas alternativas de
trazado no cumplen con las restricciones de
diseño establecidas, mientras que la metodología
del árbol es capaz de llegar siempre a una
alternativa viable y de bajo costo con una
disminución en el tiempo de cálculo, lo que no
sucede con la metodología de menor costo
hidráulico que puede llevar a trazados que
incumplan en su diseño hidráulico algunas
restricciones.
En el caso de la red R-9, la metodología tiene
mayor efectividad debido a que el criterio
utilizado como beneficio depende del producto
caudal - longitud y para ésta red ese parámetro es
diferente en todos los nudos; por esa razón la
diferencia en costos con el mejor diseño
exhaustivo es del 0.54%, un porcentaje menor al
obtenido para la red R-16. La siguiente gráfica
muestra el costo en dólares de todas las
alternativas exhaustivas y con un rombo se
muestra el trazado elegido por medio de las dos
metodologías, dado que para este caso las dos
metodologías obtuvieron el mismo trazado solo se
logra visualizar el resultado de una de éstas en la
Grafica 2.
Gráfica 2. Costo total para las alternativas
exhaustivas de diseño para la red R-9
modificada.
La metodología muestra una buena aproximación
al diseño exhaustivo, especialmente si se
considera que la reducción en el tiempo de cálculo
es relevante y que con las dos metodologías
propuestas el diseño es explícito, es decir sin
importar el número de veces que se aplique la
metodología siempre obtendrá el mismo resultado
para unos parámetros de entrada dados, por lo que
se espera que la metodología propuesta permita
llegar a resultados cercanos al mínimo costo con
bajo tiempo computacional para redes de mayor
tamaño y complejidad.
Considerando las Figuras 9 y 12, se puede
observar que la selección del trazado de la red
depende de la distribución de caudales; para el
caso de R-16, cuando los caudales son iguales en
todas las cámaras las rutas más largas es decir que
no contienen ningún arranque tienden a dirigirse
rápidamente hacia una ruta principal, que pasa por
las cámaras (1-6-11-16-21-25). Mientras que para
el caso de la red R-9 modificada, se observa la
presencia de redes secundarias de menor longitud
que tienden a llegar a la ruta en cámaras cercanas
al punto de descarga.
CONCLUSIONES,
RECOMENDACIONES, Y TRABAJO
FUTURO
Se puede concluir que la selección del trazado
para una red de drenaje urbano es un aspecto
determinante en los costos constructivos de la red,
por lo que se requiere realizar una evaluación
costo efectiva de todas las posibles soluciones,
usando una metodología basada en la hidráulica,
en lugar de evaluar solo algunas de ellas
considerando principalmente la topografía de la
red.
Por otra parte, es claro que las metodologías
planteadas presentan una buena aproximación
para llegar a un trazado de bajo costo,
especialmente cuando la red a considerar cuenta
con tubos de longitudes variables y aportes de
caudal diferentes en cada tubo.
Entre las dos metodologías planteadas, la
selección del trazado por medio de la relación de
beneficio - costo es más intuitiva y permite a los
diseñadores seleccionar el trazado de la red en
base a criterios hidráulicos sin descuidar la
importancia de la topografía del terreno, la
metodología de menor costo hidráulico a pesar de
genera bueno resultados resulta engorrosa y
complicada de entender al momento de aplicarla.
La selección de un trazado óptimo de la red de
drenaje se explica principalmente en gasto óptimo
de la potencia en red, lo que es función de la
topología de la grilla, la topografía y la
distribución de caudales aportados a la red.

El beneficio generado por disminuir el producto
caudal - longitud se ve representado en que se
disminuye el transporte de masa en la red es decir
que la mayor cantidad de masa recorre la menor
distancia posible dentro del sistema.
Como trabajo futuro se espera reducir los tiempos
de cálculo para la metodología, debido a que se
espera tener una ecuación que pueda predecir el
costo de la relación utilizada para generar el árbol
sin tener la necesidad de realizar el diseño
hidráulico.
Este trabajo pretende motivar a los diseñadores de
sistemas de drenaje urbano a considerar mayores
posibilidades en el momento de elegir el trazado
de la red, especialmente si se trata de
urbanizaciones nuevas donde las restricciones
debidas al cruce con tuberías de otros servicios
son reducidas.
BIBLIOGRAFÍA
Argaman, Yerachmiel., Shamir, Uri., y Eldad
Spivak. (1973). "Design of Optimal
Sewerage
Systems".
Journal
of
Environmental Engineering Division.
Corrales, Emilio., Cuero, Paula., Montaño, Laura.,
Luna, Daniel., y Juan Saldarriaga. (2013).
Metodología de diseño optimizado de
series de tramos de alcantarillado,
utilizando los conceptos de pendiente
propia y pendiente intermedia. Artículo
presentado
en
el
XII
Simposio
Iberoamericano sobre planificación de
sistemas de abastecimiento y drenaje,
Buenos Aires, Argentina.
Dijkstra, E. (1959). “ A Note on Two Problems
inConexxion with Graphs”. Journal of
Numerische Mathematic, 1(1), pp. 269-
271.
Diogo, Freire., y Victor Graveto. (2006). "Optimal
Layout
of
Sewer
Systems:
A
Deterministic versus a Stochastic Model".
Journal of Hydraulic Engineering, 132(9),
pp. 927-943.
ESRI, 2012. ArcGIS Desktop: version 10.1
Redlands, CA: Environmental Systems
Research Institute.
Haghighi, A. (2012). "Loop by Loop Cutting
Algorithm to Generate Urban Drainage
Systems Layout". Journal of Water
Resources Planning and Management.
Li, G., y R. Matthew. (1990). "New Approach for
Optimization
of
Urban
Drainage
Systems". Journal of Environmental
Engineering, 116(5), pp. 927-944.
Moeini, R., y M. H. Afshar. (2012). "Layout and
size optimization of sanitary sewer
network using intelligent ants". Advances
in Engineering Software, 51, pp. 49-62.
Navarro, I., y Juan Saldarriaga. (2009). Diseño
optimizado de redes de drenaje urbano.
Bogotá: Uniandes.
Saldarriaga, Juan., Takahashi, Silvia., Hernéndez,
Felipe., Díaz, D., y Susana Ochoa. (2010).
An Energy Methodology for the Design
of Water Distribution Systems World
Environmental and Water Resources
Congress
2010
(pp.
4303-4313):
American Society of Civil Engineers.
Walpole, Ronald., Myers, Raymond., y Sharon
Myers. (1999). Probabilidad y estadística
para ingenieros, 6a ed, México : Prentice-
Hall Hispanoamericana.
Weng, H. T., y S. L. Liaw. (2005). "Establishing
an Optimization Model for Sewer System
Layout with Applied Genetic Algorithm".
Journal of Environmental Informatics,
5(1), pp. 26 - 35.
