
EXTENSIÓN DE LA METODOLOGÍA DE DISEÑO DE REDES DE
DISTRIBUCIÓN DE AGUA POTABLE CON PROGRAMACIÓN LINEAL
ENTERA PARA REDES CON CIRCUITOS
“XII Simposio Iberoamericano sobre planificación de sistemas de
abastecimiento y drenaje”
Juan Saldarriaga (1), Diego Páez (2), Laura Lopez (3), Natalia León (4)
(1) Profesor Titular, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de
los Andes (CIACUA), Carrera 1 Este No. 19ª-40, Bogotá, Colombia. Email: jsaldarr@uniandes.edu.co.
Teléfono: 3394949 Ext: 2810
(2) Profesor Instructor, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad
de
los
Andes
(CIACUA),
Carrera
1
Este
No.
19ª-40,
Bogotá,
Colombia.
Email:
da.paez27@uniandes.edu.co. Teléfono: 3394949 Ext: 2810
(3, 4) Investigador, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de los
Andes (CIACUA), Carrera 1 Este No. 19ª-40, Bogotá, Colombia. Email: ll.lopez28@uniandes.edu.co,
n.leon40@uniandes.edu.co, Teléfono: 3394949 Ext: 2819
RESUMEN
El problema de diseño optimizado de redes de distribución de agua potable (RDAPs) ha sido estudiado desde
hace más de 40 años. Para redes con topología abierta y un único embalse, el óptimo global puede ser
alcanzado mediante Programación Lineal Entera (PLE). Dado que las RDAP típicas no cumplen con dichas
condiciones, se desarrolló una metodología de diseño basada en la división de redes cerradas en redes
abiertas que puedan ser diseñadas con PLE para después ajustar las demás tuberías de la red haciendo uso de
criterios hidráulicos. La metodología fue probada en tres redes benchmark presentando resultados de bajo
costo en un tiempo de cálculo significativamente menor respecto a otras aproximaciones.
Palabras claves: Diseño optimizado, Redes de distribución, Programación lineal entera.
ABSTRACT
Optimized design of water distribution systems (WDS) has been studied for over 40 year now. When the
system has an open topology and only one reservoir, the global optimum can be reached with Integer Linear
Programming (ILP). Considering that typical WDS don’t fulfill those conditions, a new design methodology
was developed, based on the decomposition of looped networks into open networks that can be designed
with ILP and then adjust the other pipes of the network using hydraulic criteria. The methodology was tested
in three benchmark networks reaching results of low cost with a significantly reduced computational time in
regard to other approximations.
Key words: Optimized design, Water distribution systems, Integer Linear Programming.
SOBRE EL AUTOR PRINCIPAL
Juan Saldarriaga: Profesor Titular de la Facultad de Ingeniería de la Universidad de los Andes. Área de
Recursos Hidráulicos, Departamento de Ingeniería Civil y Ambiental. Coordinador del Centro de Investigación
Estratégica del Agua (CIE-AGUA) de la Facultad de Ingeniería de la Universidad de los Andes. Director del
Centro de Investigaciones en Acueductos y Alcantarillados CIACUA del Departamento de Ingeniería Civil y
Ambiental de la Universidad de los Andes.

INTRODUCCIÓN
El problema de diseño optimizado de redes de
distribución de agua potable (RDAPs) es uno de los
problemas más estudiados a nivel mundial en
relación con los sistemas de abastecimiento de agua.
Esto, a razón de que el agua es un recurso esencial
para la vida y el desarrollo humano y que los
recursos para proveer del servicio a la población son
usualmente escasos.
Si bien el diseño de RDAP puede involucrar
diferentes
criterios
además
de
los
costos
constructivos (e.g. resiliencia, impacto ambiental y
calidad de agua), es este criterio el más utilizado y
usualmente del cual se parte para proponer
metodologías que incluyan algún otro criterio. De
esta manera el planteamiento formal del problema
es:
∑( (
)
)
(1)
(2)
(3)
donde
= conjunto de tuberías de la red;
=
diámetro asignado a la tubería
;
= longitud de la
tubería
; = costo por unidad de longitud
de una tubería con diámetro
;
= valor de una
variable de interés
en el nudo bajo la condición
de demanda
;
= valor mínimo admisible de la
variable
bajo la condición de demanda ; =
conjunto de nudos de la red;
= conjunto de
escenarios de demanda a ser analizados; y
=
conjunto de diámetros disponibles en el mercado.
Usualmente la variable de interés
es la presión en
el nudo aunque para algunos casos se ha incluido
algún término de calidad como cloro residual
(Dandy & Hewitson, 2004) y
sólo tiene
escenarios de demanda extremos (e.g. hora pico o
caudales de incendio).
Yates et al. (1984) demuestran que dicho problema
es NP-DURO y por lo tanto solo puede ser resuelto
de manera aproximada en un tiempo computacional
aceptable. Es por ello que investigaciones resientes
han hecho uso de metaheurísticas para encontrar
soluciones aceptables al problema dada la facilidad
de implementación de dichas técnicas, la robustez
que han presentado en otros problemas de
optimización y la capacidad de considerar la
restricción de diámetros discretos. Algunos ejemplos
de estos algoritmos son Algoritmos Genéticos (Savic
& Walters, 1997), Búsqueda de Armonía (Geem,
2006), Scatter Search (Lin et al., 2007), Entropía
Cruzada (Perelman & Ostfeld, 2007), Recocido
Simulado (Reca et al., 2007), Enjambre de Partículas
(Geem, 2009) entre otros.
Todas estas metodologías metaheurísticas son
algoritmos
inspirados
en
comportamientos
observados en la naturaleza a partir de los cuales se
generan un gran número de posibles soluciones al
problema de manera aleatoria, cada una de las cuales
es evaluada tanto con la función objetivo como con
todas las restricciones del problema. Esto implica
que para el caso de diseño de RDAP cada posible
solución es una configuración de diámetros de la red
que debe ser revisada mediante una ejecución
hidráulica, para asegurar que se cumplan con las
restricciones y, dada la cantidad de ejecuciones
hidráulicas que llegan a ser necesarias, el tiempo
computacional requerido por estas metodologías
llega a ser considerable.
Como alternativa a este tipo de soluciones se han
considerado criterios hidráulicos basados en el
trabajo de I-Pai Wu (1975), según el cual, para una
tubería en serie con demandas homogéneas en todos
sus nudos, el diseño óptimo del sistema genera un
línea de gradiente hidráulico (LGH) parabólica
separada de una LGH recta un valor equivalente al
15% de la energía disponible entre el embalse y el
nudo más alejado, en el punto medio de la
trayectoria. Así, dicho concepto fue extendido por
Villalba (2004) y Ochoa (2009) llegando a proponer
la metodología OPUS (Optimal Power Use Surface)
de uso de criterios hidráulicos para diseño de RDAP
(Takahashi et al., 2010).
Así, este trabajo presenta los resultados del continuo
perfeccionamiento que se hace a la metodología
OPUS, esta vez haciendo uso de los pasos iniciales
de separación de las redes cerradas en redes abiertas
para después aplicar Programación Lineal Entera
(PLE) que, como ya lo describen Alperovits &
Shamir (1977), encuentra los óptimos globales del
problema para redes abiertas con un único embalse.
METODOLOGÍA
La metodología de diseño propuesta puede ser
dividida en 5 subprocesos independientes según lo
presentado en la Figura 1. Los pasos Búsqueda de
Sumideros y Optimización de la metodología
propuesta son pasos heredados de la metodología
OPUS mencionada anteriormente (Takahashi et al.,
2010). Sin embargo los pasos
intermedios
representan una variación importante en el algoritmo
especialmente el Diseño con PLE.
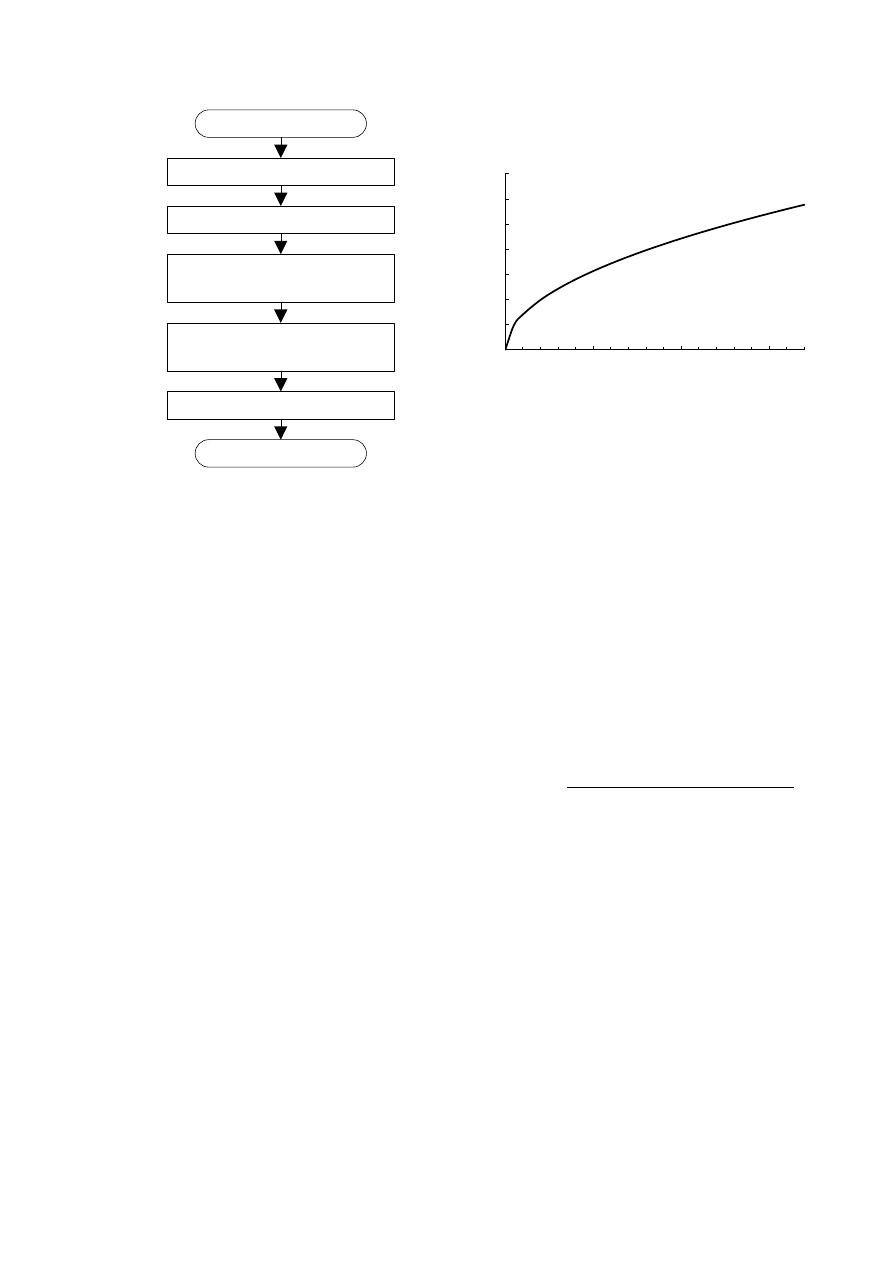
Figura 1. Diagrama de flujo de la
metodología propuesta.
Búsqueda de sumideros
En este subproceso se toma la red cerrada original y,
haciendo uso de dos principios hidráulicos y de
minimización de costos, se genera una red abierta
(i.e., entre dos puntos cualesquiera de la red existe
un único camino que los una) adjunta a cada fuente
de agua de la red original. El primer principio indica
que un diseño de mínimo costo debe proveer agua a
cada nudo de demanda a través de una única ruta o
trayectoria de flujo. Esto debido a la ineficiencia
hidráulica asociada con la redundancia de tuberías
(Saldarriaga, 1998). Así, redes abiertas pueden ser
considerablemente menos costosas que redes
cerradas (aunque también resultan menos confiables
(Todini, 2000)). De esta manera, este subproceso
busca la manera de transformar la geometría de la
red para generar una red abierta (usualmente
denominadas estructuras de árbol por su parecido
con las ramificaciones) mediante la identificación de
nudos sumideros (nudos con altura piezométrica
menor que todos sus vecinos).
El segundo principio se deriva de las ecuaciones de
pérdidas por fricción en tuberías con flujo
presurizado (Darcy-Weisbach & Colebrooke-White
o Hazen-Williams). Suponiendo que todas las demás
variables de la ecuación permanecen constantes, es
posible encontrar una relación biunívoca entre el
caudal de diseño (Q) y el diámetro requerido.
Además, si se conoce la relación entre el diámetro
de la tubería y el costo por unidad de longitud de la
misma, es posible encontrar una relación entre Q y
el costo por unidad de longitud de la tubería, tal y
como se muestra en la Figura 2.
Figura 2. Relación esquemática entre el
caudal de diseño (Q) y el costo por unidad
de longitud de tubería ($/L).
En la Figura 2, es posible notar que a medida que
aumenta el caudal de diseño, el costo marginal de la
tubería decrece. Es decir que agregar caudales en
unos pocos tubos reduce el costo total de la red. De
esta manera, teniendo en cuenta los dos principios
analizados, se diseñó un algoritmo recursivo de
definición de la estructura de árbol. Este algoritmo
inicia en cada fuente o embalse de la red y recorre
las tuberías hacia aguas abajo agregando a la red
abierta un tubo y nudo a la vez. El conjunto de
parejas tubo-nudo que pueden ser agregados en cada
iteración se denomina ‘frente de avance’, y cada una
de dichas parejas se le asigna un valor de una
función Beneficio/Costo (Ecuación 4) que permite
seleccionar la pareja más conveniente para ser
agregada a la red.
⁄
∑
(4)
donde
⁄ = función Beneficio/Costo
evaluada para el nudo
y para el tubo ;
= caudal demandado en el nudo
;
=
costo de mover el caudal
por la tubería
(es
igual al producto de la longitud de
y el valor de
costo por unidad de longitud de acuerdo a la
evaluación numérica de la función de la Figura 2); y
= costo adicional o marginal de mover el
caudal
por cada tubería aguas arriba del nudo
.
A manera de ejemplo se puede tomar la red
benchmark Hanoi (Figura 3) y ver los primeros
pasos de la metodología. Iniciando desde el embalse
(ID=1), la única pareja tubo-nudo que puede ser
agregada es la del tubo 1 y el nudo 2 (<1,2>).
Después la pareja <2,3> es agregada.
Inicio
Búsqueda de sumideros
Diseño con PLE
Adición de tuberías
faltantes
Asignación de diámetros
a tuberías faltantes
Optimización
Fin
$/L
Q
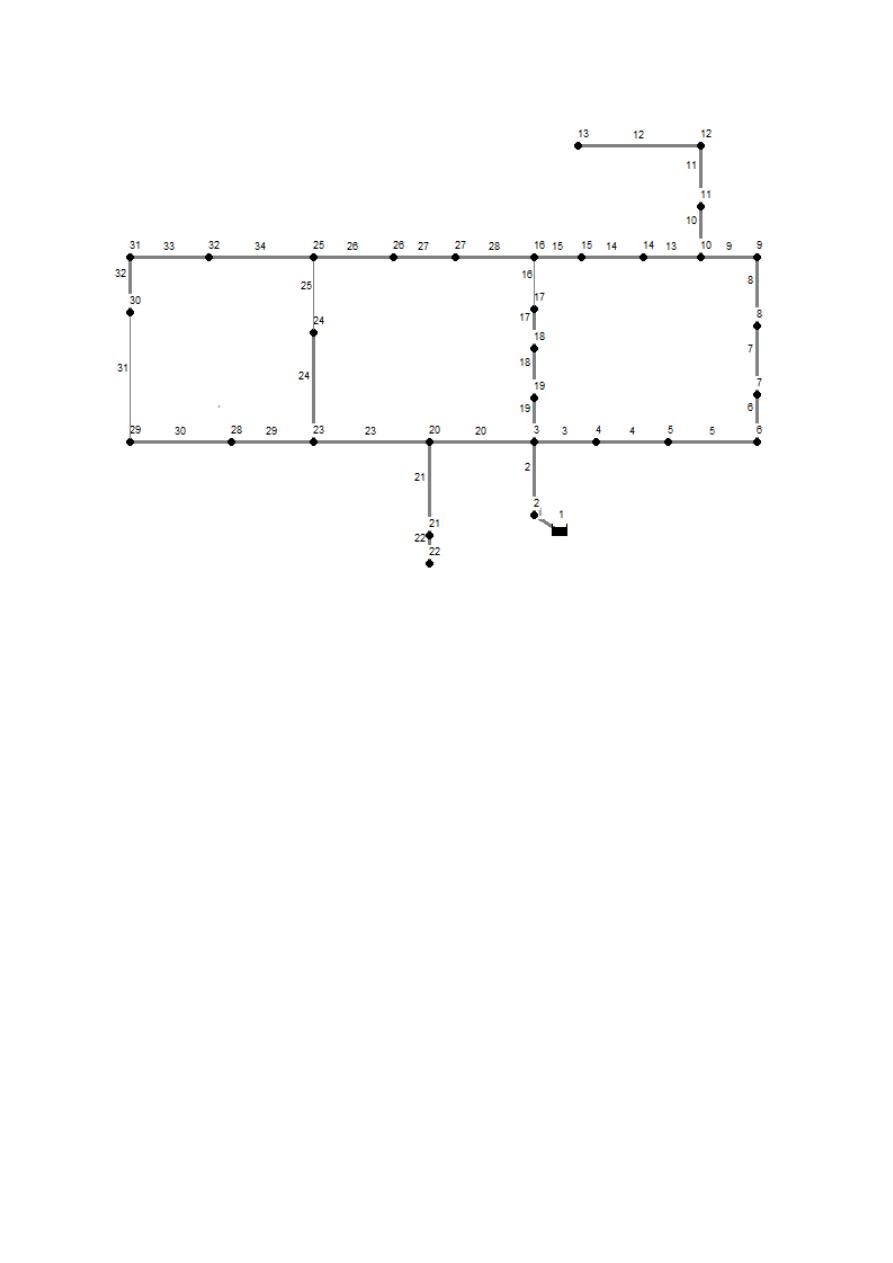
Figura 3. Geometría de la RDAP Hanoi. Etiquetas con ID de tubos y nudos de la red.
En esta iteración, el Frente de Avance se compone
de las parejas <3,4>, <19,19> y <20,20>, y por lo
tanto la función Beneficio/Costo debe ser evaluada
para cada una de las tres. Como resultado de dicha
evaluación se selecciona la pareja <19,19> dado su
mayor Beneficio/Costo. De nuevo se redefine el
Frente de Avance, que ahora tiene a las parejas
<3,4>, <18,18> y <20,20> y se continúa el mismo
procedimiento. En la Figura 3 se presentan
resaltadas las tuberías que al final de procedimiento
fueron agregadas a la red abierta, siendo entonces las
tuberías finas aquellas que no hacen parte de la
misma (Tuberías 16, 25 y 31).
Diseño con PLE
En este procedimiento se plantea el diseño de cada
red abierta generada en el proceso anterior, como un
problema de optimización lineal para después
resolver el problema mediante el software Xpress
IVE el cual implementa métodos de solución como
Simplex y Branch and Bound.
El problema linealizado tiene entonces las siguientes
variables de decisión binarias:
{
de manera que
representa la decisión de poner o
no el diámetro
en la tubería que va del nudo al
nudo
.
Por otro lado, las restricciones del problema son
formuladas de manera lineal respecto a
como se
presenta en la Ecuación 5 y la Ecuación 6 para el
caso de la restricción de presión mínima en los
nudos y la Ecuación 7 para asegurar que la solución
del problema asigne un único diámetro a cada
tubería:
(5)
donde
= altura piezométrica total mínima
admisible en el nudo
(corresponde a la suma de la
presión mínima del problema y la cota del nudo); y
= altura piezométrica total en el nudo
que es
calculada mediante la Ecuación 6:
∑
(6)
donde
= pérdidas totales de energía en el tubo
que va del nudo
al nudo cuando éste tiene el
diámetro
; y = función que asegura que la

restricción únicamente aplique cuando el nudo
esta inmediatamente aguas abajo del nudo
. Y
finalmente:
∑
(7)
que asegura que solo una de las variables de decisión
tome el valor de
para cada tramo de tubería
existente.
Asimismo, la función objetivo se escribe de manera
linealizada respecto a
, calculando a priori los
costos de poner cada posible diámetro en cada
posible tubería de la red abierta:
∑ ∑ ∑
(8)
donde
= costo de poner el diámetro
en la
tubería que va del nudo
al nudo .
Los parámetros de la formulación lineal
y
generan matrices de
que para el caso de las
pérdidas totales de altura piezométrica en cada tubo
pueden ser calculados mediante una ejecución
hidráulica de la red abierta por cada diámetro
disponible en
. Por otro lado los valores de la
matriz de costos pueden ser calculados como el
producto de los costos por unidad de longitud de
cada diámetro disponible en
y la longitud de cada
tubo
.
Una vez conocidos todos los parámetros de la
formulación lineal, el programa Xpress IVE
soluciona
el
problema
de
manera
óptima,
determinando así los valores de
que minimizan
los costos constructivos.
Adición de tuberías faltantes y asignación de
diámetros a éstas
Dado que la red a diseñar es una red cerrada a la
cual no se le pueden quitar tuberías (i.e. el diámetro
cero no pertenece a
), es necesario volver a incluir
las tuberías no consideradas en el procedimiento
anterior para entregar un diseño completo del
sistema.
Si se considera una red con un único embalse, que
ya ha pasado por lo anteriores subprocesos de la
metodología, se tendría una red abierta ya diseñada
que cumple con las restricciones de presiones en
cada nudo del sistema. Si a esta red se le agregan las
demás tuberías con un diámetro mínimo, las
presiones en la red serán mayores o iguales dada la
mayor capacidad hidráulica de la red.
Teniendo esto en cuenta, en este procedimiento se
agregan
las
tuberías
no
diseñadas
en
el
procedimiento anterior con un diámetro igual al
mínimo disponible. Sin embargo, dado que existen
redes con más de un embalse y en las cuales agregar
una tubería que conecte dos redes abiertas puede
generar problemas con las presiones, se hace
necesaria una revisión de las presiones posterior a
este paso.
Optimización
El objetivo de este procedimiento es, por un lado
asegurar que el diseño final cumpla efectivamente
con la restricción de presión mínima en cada nudo
de la red, y por otro lado, buscar una minimización
adicional de los costos mediante una búsqueda local
con
un
Algoritmo
Semivoraz
(Semigreedy
Algorithm).
El primer objetivo es alcanzado mediante una
primera ejecución hidráulica de la red para revisar
las presiones con el diseño obtenido mediante los
anteriores procedimientos. Solo en caso de que
algún nudo presente déficit de presión se ejecutará el
algoritmo de aumento de diámetros mostrado en la
Figura 4.
Los posibles criterios hidráulicos
que pueden ser
seleccionados en el subprocedimeinto de aumento de
diámetros son
;
;
(
);
;
; y
(
); donde
= pendiente de fricción;
= pérdidas
por fricción;
= Caudal en el tubo; y el operador
= diferencia entre el valor con el diámetro actual de
la tubería y el valor con el diámetro siguiente.
Respecto al segundo objetivo del procedimiento,
éste se consigue mediante un doble barrido por la
red reduciendo diámetros. Así, el algoritmo se ubica
en la tubería más aguas arriba de la red, reduce el
diámetro al inmediatamente anterior y ejecuta la
hidráulica revisando la restricción de presión
mínima. En caso de que no cumpla, se reversa el
cambio. Después se avanza a la siguiente tubería
aguas abajo y se continúa el procedimiento hasta
llegar a la totalidad de las tuberías. Una vez
recorrida la red en dicho sentido, se vuelve a
ejecutar el procedimiento pera esta vez iniciando por
las tuberías más aguas abajo y finalizando con las
tuberías más aguas arriba.
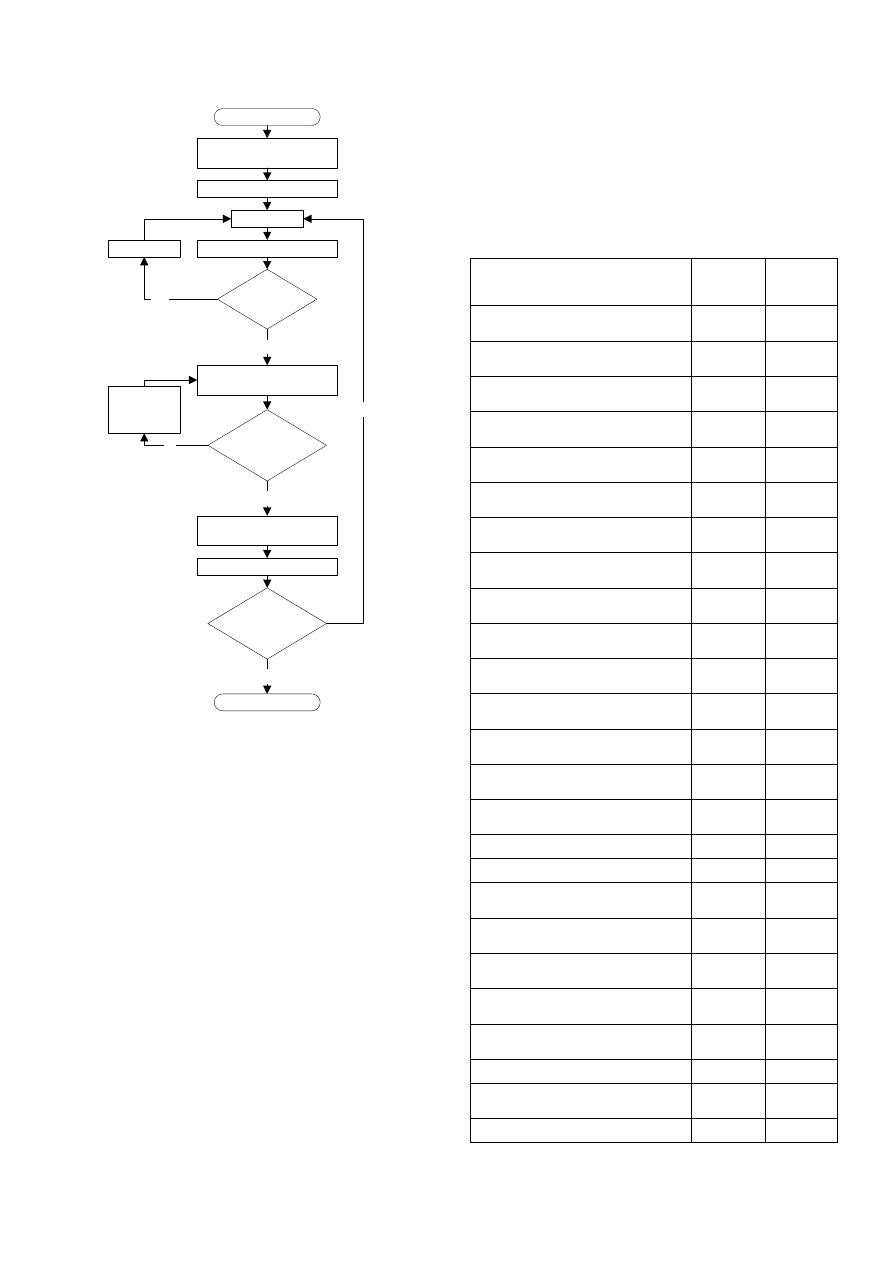
Figura 4. Diagrama de flujo del
subprocedimiento para aumentar diámetros.
RESULTADOS
La metodología presentada es utilizada en tres
RDAP benchmark: Hanoi, Balerma y Taichung.
Hanoi
La red de Hanoi fue presentada por primera vez por
Fujiwara y Khang (1990) y al igual que Two-Loop
(Alperovits & Shamir, 1977), se ha convertido en
una de las más conocidas y utilizadas RDAP para el
problema de diseño. La ecuación de pérdidas por
fricción típicamente utilizada es Hazen-Williams
con un C=130. La presión mínima requerida en
todos los nudos es de 30 m y los costos por unidad
de longitud de cada diámetro puede ser hallado con
un coeficiente de $1.1/m y exponente para el
diámetro en pulgadas de 1.5.
Al aplicar la metodología propuesta se llega a un
diseño con un costo de $6’163 754 requiriendo 119
ejecuciones hidráulicas. A pesar de que este no es el
menor costo alcanzado a nivel mundial, el número
de ejecuciones hidráulicas necesario para llegar a
este resultado es tres órdenes de magnitud menor
que la mayoría de las demás aproximaciones como
se puede ver en la Tabla 1.
Tabla 1. Resultados reportados para Hanoi.
Algoritmo
Costo
(millones)
E.H.*
Algoritmos Genéticos (Savic &
Walters, 1997)
$6.073
1,000,000
Recosido Simulado (Cunha &
Sousa, 1999)
$6.056
53,000
Búsqueda de Armonía (Geem,
2002)
$6.056
200,000
Salto de Rana Barajado (Eusuff
& Lansey, 2003)
$6.073
26,987
Evolución Compleja Barajada
(Liong & Atiquzzaman, 2004)
$6.220
25,402
Algoritmos Genéticos
(Vairavamoorthy, 2005)
$6.056
18,300
Colonia de Hormigas (Zecchin et
al., 2006)
$6.134
35,433
Algoritmos Genéticos (Reca &
Martínez, 2006)
$6.081
50,000
Algoritmos Genéticos (Reca et
al., 2007)
$6.173
26,457
Recosido Simulado (Reca et al.,
2007)
$6.333
26,457
Recosido Simulado con búsqueda
Tabú (Reca et al., 2007)
$6.353
26,457
Búsqueda Local con Recosido
Simulado (Reca et al., 2007)
$6.308
26,457
Búsqueda de Armonía (Geem,
2006)
$6.081
27,721
Entropía Cruzada (Perelman &
Ostfeld, 2007)
$6.081
97,000
Búsqueda Dispersa (Lin et al.,
2007)
$6.081
43,149
AG Modificados 1 (Kadu, 2008)
$6.056
18,000
AG Modificados 2 (Kadu, 2008)
$6.190
18,000
Enjambre de Partículas y B. de
Armonía (Geem, 2009)
$6.081
17,980
Aproximación Heurística (Mohan
S. a., 2009)
$6.701
70
Evolución Diferencial (Suribabu
C. , 2010)
$6.081
48,724
Honey-bee mating optimization
(Mohan S. a., 2010)
$6.117
15,955
Aproximación Heurística
(Suribabu C. , 2012)
$6.232
259
SOGH (Ochoa, 2009)
$6.337
94
OPUS (Saldarriaga, Páez, Cuero,
& León, 2012)
$6.173
83
Esta metodología
$6.163
119
E.H.: Ejecuciones Hidráulicas de la red
Inicio
Seleccionar algún
criterio hidráulico H
Ejecutar Hidráulica
p = 1
Calcular H
p
Ejecutar Hidráulica
Fin
p=|P|
p = p + 1
NO
Seleccionar p tal que
H
p
= max
k
ϵP
(H
k
)
SI
Aumentar al siguiente el
diámetro de p
No
considerar
p en P
SI
Cumple toda la
red con P
min
SI
NO
d
p
= d
max
NO
Los diámetros asignados a las tuberías fueron: 40,
40, 40, 40, 40, 40, 40, 40, 40, 30, 30, 24, 20, 16, 12,
12, 16, 20, 20, 40, 20, 12, 40, 30, 30, 20, 12, 12, 16,
16, 12, 12, 16 y 24 pulgadas (diámetros presentados
en el orden de los ID de las tuberías).
Dentro del proceso de análisis de resultados se
observó cómo la lista de diámetros disponible para
el problema tiene un límite superior altamente
restrictivo que no permite una reducción de costos
considerable. Así, se realizó el mismo ejercicio de
diseño pero agregando a la lista un diámetro de 50”
que de acuerdo con la función de costos tendría un
costo unitario de $388.91/m. Al resolver el problema
nuevamente, se encuentra la siguiente configuración
de diámetros: 40, 50, 40, 40, 40, 40, 30, 30, 30, 24,
24, 20, 16, 12, 12, 12, 16, 16, 20, 40, 16, 12, 30, 30,
30, 20, 12, 12, 16, 12, 12, 12, 16, y 20; que implica
un costo constructivo de $5’414 077, mostrando así
lo inconveniente de la lista real de diámetros
disponibles para Hanoi.
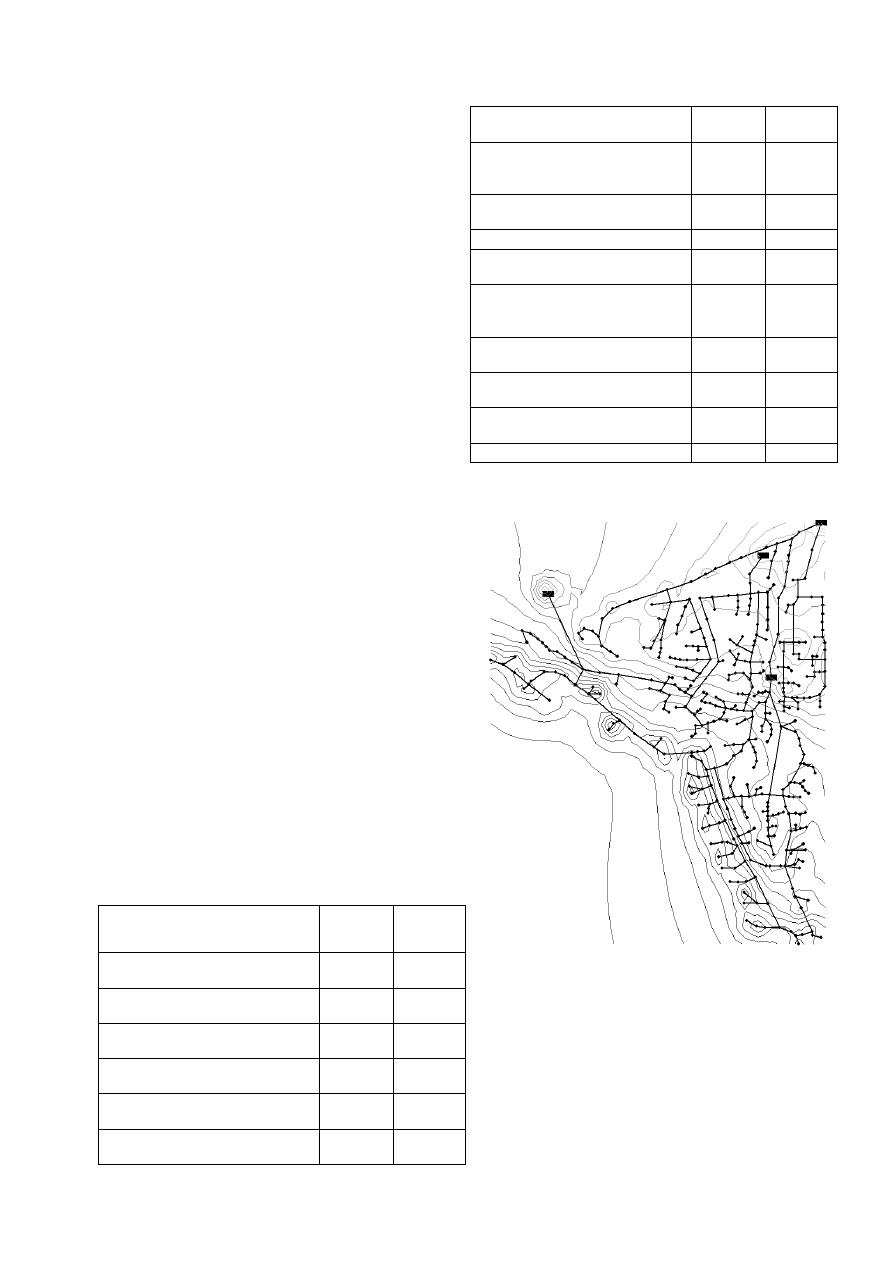
Balerma
La RDAP de Balerma representa un distrito de
irrigación en Almería, España. Dentro de la
definición
del
problema
se
especifica
la
disponibilidad de diámetros de PVC con un
coeficiente de rugosidad absoluta de 0.0025 mmm, y
por lo tanto la ecuación de fricción debe ser Darcy-
Weisbach, una presión mínima de 20 m y una
función de costos potencial con un exponente de
2.06. La topología de la red es mostrada en la Figura
5.
Al aplicar la metodología propuesta se llega a un
diseño con un costo constructivo de €2.148 millones
el cual es comparado con los resultados de otras
aproximaciones en la Tabla 2.
Tabla
2.
Resultados
reportados
para
Balerma.
Algoritmo
Costo
(millones)
E.H.*
Algoritmos Genéticos (Reca &
Martínez, 2006)
€2.302
1.0E07
Búsqueda de Armonía (Geem,
2006)
€2.601
45,400
Búsqueda de Armonía (Geem,
2006)
€2.018
1.0E07
Algoritmos Genéticos (Reca et
al., 2007)
€3.738
45,400
Recosido Simulado (Reca et al.,
2007)
€3.476
45,400
Recosido Simulado con B. Tabú
(Reca et al., 2007)
€3.298
45,400
Búsqueda Local con Recosido
Simulado (Reca et al., 2007)
€4.310
45,400
Hybrid discrete dynamically
dimensioned search (Tolson,
2009)
€1,940
3.9E07
Búsqueda de Armonía with
particle swarm (Geem, 2009)
€2.633
45,400
SOGH (Ochoa, 2009)
€2.100
1,779
Algoritmo Memético (Baños,
2010)
€3,120
45,400
Genetic heritage evolution by
stochastic transmission
(Bolognesi, 2010)
€2,002
250,000
Evolución Diferencial (Zheng,
2012)
€1,998
2,400,000
Evolución Diferencial
Autoadaptativa (Zheng, 2012)
€1,983
1,300,000
OPUS (Saldarriaga, Páez, Cuero,
& León, 2012)
€2.040
957
Esta metodología
€2.148
826
E.H.: Ejecuciones Hidráulicas de la red
Figura 5. Topología y topografía de la RDAP
Balerma.
En este caso resulta más evidente la ventaja de la
metodología en términos del tiempo computacional
requerido, que es considerablemente menor que las
aproximaciones
metaheurísticas,
y
con
un
sobrecosto constructivo respecto al record mundial
de cerca de 10%.
Taichung
Sung, Lin, Lin & Liu (2007) presentan por primera
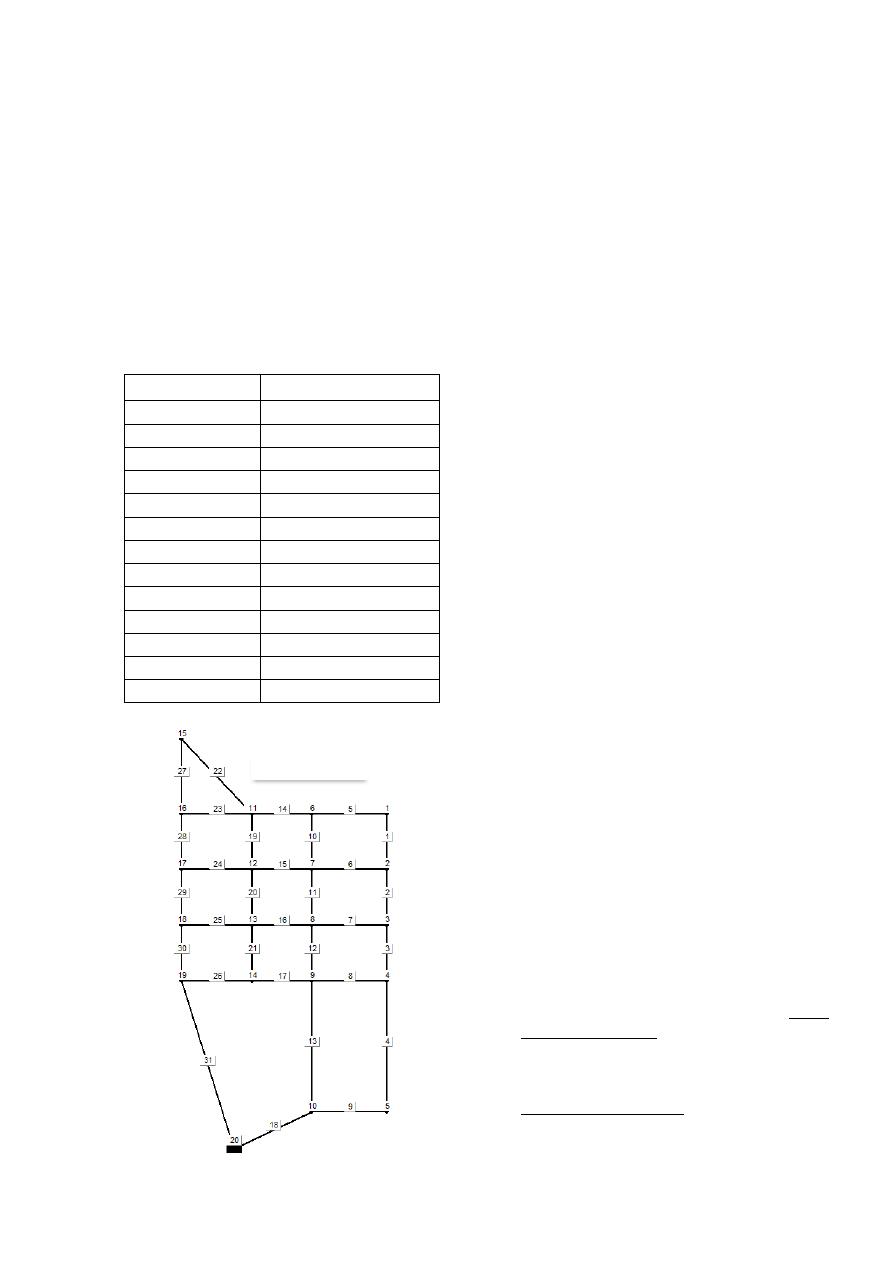
vez la RDAP de Taichung, Taiwan. La red se
compone de 20 nudos y 31 tuberías organizados en
12 circuitos. La red tiene una lista de diámetros
disponibles presentada en la Tabla 3. La ecuación de
fricción a utilizar es Hazen-Williams con una
rugosidad C=100 para todos los tubos. La presión
mínima es 15 m y la topología es mostrada en la
Figura 6.
Tabla 3. Costos Unitarios para la red de
Taichung.
Diámetro (mm)
Costo (NT Dollar m
-1
)
100
860
150
1160
200
1470
250
1700
300
2080
350
2640
400
3240
450
3810
500
4400
600
5580
700
8360
800
10400
900
12800
Figura 6. Topología de la RDAP de Taichung
La metodología propuesta alcanza, para este caso, un
costo constructivo de $8’966 900 en 48 ejecuciones
hidráulicas. La configuración de diámetros final es:
250, 100, 150, 100, 100, 200, 100, 200, 150, 100,
250, 300, 350, 100, 100, 100, 100, 400, 150, 100,
100, 100, 100, 200, 100, 150, 100, 200, 250, 250, y
300 milímetros (diámetros presentados en el orden
de los ID de las tuberías).
Para este caso de estudio no existen diseños
adicionales al reportado por Sung, Lin, Lin & Liu
(2007) de $8’774 900 en un número no reportado de
ejecuciones hidráulicas haciendo uso de la
metaheurística Búsqueda Tabú. Esto implica que la
metodología propuesta llega a un resultado solo un
2.2% por encima del actual record.
CONCLUSIONES
Se presentó una metodología de diseño optimizado
de RDAP que hace uso de criterios hidráulicos para
redefinir el problema como un problema de PLE.
Esta metodología es una modificación de la
metodología OPUS (Takahashi et al., 2010)
anteriormente desarrollada por el Centro de
Investigaciones en Acueductos y Alcantarillados
(CIACUA)..
Los
resultados
de
aplicar
la
metodología
desarrollada en redes benchmark, muestran cómo el
uso de criterios hidráulicos permite llegar a diseños
de alta calidad en términos de minimización de
costos constructivos, con un número de ejecuciones
significativamente
menor
que
aproximaciones
metaheurísticas tradicionales que además incluyen
un componente estocástico importante.
Se recomienda utilizar esta metodología para llegar a
un primer diseño de calidad el cual pueda ser
mejorado mediante una posible postoptimización
con metaheurísticas. Esto podría permitir reducir aún
más la diferencia, en términos de costos, con los
record mundiales.
REFERENCIAS
Alperovits, E., and Shamir, U. (1977) Design of
optimal water distribution systems. Water
Resources Research, Vol.13, No.6, pp. 885-
900.
Baños, C. G. (2010). A memetic algorithm applied
to the design of water distribution networks.
Applied Soft Computing, 261-266.
Bolognesi, A. e. (2010). Genetic Heritage Evolution
by Stochastic Transmission in the optimal
Etiquetas con IDs.

design of water distribution networks.
Advances in Engineering Software, 792-801.
Cunha, M. a. (1999). Water distribution network
design optimization: Simulated annealing
approach. J. Water Resour. Plan. Manage. ,
215-221.
Dandy, G. and Hewitson, C. (2000) Optimizing
Hydraulics and Water Quality in Water
Distribution
Networks
Using
Genetic
Algorithms. Building Partnerships: pp. 1-10.
Eusuff, M. a. (2003). Optimization of water
distribution network design using the shuffled
frog leaping algorithm. J. Water Resour. Plan.
Manage. , 210-225.
Fujiwara, O. and Khang, D. (1990). A two phase
decomposition methods for optimal design of
looped water distribution networks. Water
Resources Research, Vol.26, No. 4, pp. 539-
549.
Geem, Z. K. (2002). Harmony search optimization:
Application to pipe network design. Int. J.
Model. Simulat. , 125-133.
Geem, Z. K. (2006). Optimal cost design of water
distribution networks using harmony search.
Engineering Optimization, Vol.38, No.3, pp.
259-277.
Geem, Z. K. (2009). Particle-swarm harmony search
for water network design. Engineering
Optimization, Vol.41, No.4, pp. 297-311.
Kadu, M. R. (2008). Optimal design of water
networks using a modified genetic algorithm
with reduction in search space. J. Water
Resour. Plan. Manage. , 147-160.
Lin, M., Liu, G. and Chu, C., (2007) Scatter search
heuristic for least-cost design of water
distribution
networks,
Engineering
Optimization, Vol.39, No.7, pp. 857-876.
Liong, S. and Atiquzzaman, M. (2004) Optimal
design of water distribution network using
shuffled complex evolution. Journal of the
Institution of Engineers, Vol.44, No.1, pp. 93-
107.
Mohan, S. a. (2009). Water distribution network
design using heuristics-based algorithm. J.
Comput.Civ. Eng., 249-257.
Mohan, S. a. (2010). Optimal water distribution
network design with Honey-Bee mating
optimization. J. Water Resour. Plan. Manage.,
117-126.
Ochoa, S. (2009). Optimal design of water
distribution systems based on the optimal
hydraulic gradient surface concept. MSc
Thesis, dept. of Civil and Environmental
Engineering, Universidad de los Andes,
Bogotá, Col.
Perelman, L. and Ostfeld, A. (2007). An adaptive
heuristic cross entropy algorithm for optimal
design
of
water
distribution
systems.
Engineering Optimization, Vol.39, No.4, pp.
413-428.
Reca, J. & Martínez, J. (2006). Genetic algorithms
for the design of looped irrigation water
distribution
networks.
Water
Resources
Research, Vol.44, W05416.
Reca, J., Martínez, J., Gil, C. and Baños, R. (2007).
Application
of
several
meta-heuristic
techniques to the optimization of real looped
water distribution networks. Water Resources
Management, Vol.22, No.10, pp. 1367-1379.
Reca, J., Martínez, J., Gil, C. and Baños, R. (2007).
Application
of
several
meta-heuristic
techniques to the optimization of real looped
water distribution networks. Water Resources
Management, Vol.22, No.10, pp. 1367-1379.
Saldarriaga, J. (1998 and 2007). Hidráulica de
Tuberías. Abastecimiento de Agua, Redes,
Riegos. Ed. Alfaomega. Ed. Uniandes. ISBN:
978-958-682-680-8.
Saldarriaga, J., Páez, D., Cuero, P., & León, N.
(2012). Optimal power use surface for design
of water distribution systems. XIV Water
Distribution Systems Analysis Conference.
Tucson, Arizona, USA.
Savic, D. and Walters, G. (1997). Genetic
algorithms for least cost design of water
distribution networks. J. Water Resour. Plan.
Manage., 67-77.
Sung, Y.-H., Lin, M.-D., Lin, Y.-H. L., & Liu, Y.-L.
(2007). Tabu search solution of water
distribution network optimization. Journal of
Environmental Engineering and Management,
177-187.
Suribabu,
C.
(2010).
Differential
evolution
algorithm for optimal design of water
distribution networks. J. of Hydroinf., 66-82.
Suribabu, C. (2012). Heuristic Based Pipe
Dimensioning Model for Water Distribution
Networks. Journal of Pipeline Systems
Engineering and Practice, 45 p.
Takahashi, S., Saldarriaga, S., Hernández, F., Díaz,
D. and Ochoa, S. (2010). An energy
methodology for the design of water
distribution systems. In Proceedings of the
World Environmental and Water Resources
Congress 2010, ASCE.
Todini, E. (2000). “Looped water distribution
networks design using a resilience index
based heuristic approach”. Urban Water, 2(2),
115-122.
Tolson, B. A. (2009). Hybrid discrete dynamically
dimensioned search (HD-DDS) algorithm for

water distribution system design optimization.
Water Resources Research, 45 p.
Vairavamoorthy, K. a. (2005). Pipe index vector: A
method to improve genetic-algorithm-based
pipe optimization. J. Hydraul. Eng., 1117-
1125.
Villalba, G. (2004). Optimal combinatory algorithms
applied to the design of water distribution
systems. MSc Thesis, dept. of Systems and
Computation Engineering, Universidad de los
Andes.
Wu, I. (1975). Design of drip irrigation main lines.
Journal of Irrigation and Drainage Division,
Vol.101, No.4, pp. 265-278.
Yates, D., Templeman, A. and Boffey, T. (1984).
The computational complexity of the problem
of determining least capital cost designs for
water
supply
networks.
Engineering
Optimization, Vol. 7, No.2, pp. 142-155.
Zecchin, A., Simpson, A., Maier, H., Leonard, M.,
Roberts, A., and Berrisfors, M. (2006)
Application of two ant colony optimization
algorithms to water distribution system
optimization. Mathematical and Computer
Modeling, Vol.44, No. 5-6, pp. 451-468.
Zheng, F. e. (2012). A Self
‐Adaptive Differential
Evolution Algorithm Applied to Water
Distribution System Optimization. Journal of
Computing in Civil Engineering, 45 p.
