
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y
Alcantarillados
CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs
la ecuación de Darcy-Weisbach en tuberías de gran
diámetro (Sistemas Matrices) y en tuberías primarias de
bombeo.
Tesis 2
Juan David Uribe Rojas

i
AGRADECIMIENTOS
Agradezco a Dios por darme la fortaleza para llevar a feliz término esta investigación.
Agradezco a mis padres por todo el apoyo y animo que han brindado durante este año de
investigación; sin ellos nunca hubiera logrado avanzar tanto en mi vida profesional. También
agradezco profundamente al Ingeniero Juan Saldarriaga por asesorarme en mi trabajo de
pregrado y durante este año con la Tesis de maestría, ya que fue una fuente de aprendizaje y
de asesoramiento única y soy de los pocos afortunados que la tiene. Así mismo le quiero
agradecer al Ingeniero Diego Páez por toda su ayuda y recomendaciones durante este año de
trabajo. Agradecer a mi jurado externo Rafael Alejandro Flechas por evaluarme y por ser una
fuente de información vital al haber el trabajado en este tema antes de esta investigación.
Finalmente agradecer a mis compañeros de Tesis de Maestría: Daniela Rincón, Gloria Moscote,
Diego Copéte y Andrés López pues sus sugerencias y aportes me ayudaron a culminar este
proyecto.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
ii
CONTENIDO
Capítulo 1: Introducción y Objetivos .................................................................................................................... 1
1.1 Introducción ....................................................................................................................................................... 1
1.2 Objetivos............................................................................................................................................................... 2
1.2.1 Objetivo General ....................................................................................................................................... 2
1.2.2 Objetivos Específicos .............................................................................................................................. 2
Capítulo 2 Marco Teórico .......................................................................................................................................... 3
2.1 Ecuaciones y fórmulas utilizadas en los diseños de RDAP. ............................................................. 3
2.2 Ecuación de Hazen y Williams .................................................................................................................... 4
2.3 Ecuación de Darcy-Weisbach ...................................................................................................................... 5
2.4 Antecedentes Históricos ............................................................................................................................. 10
2.5 Trabajos de Fabián Bombardelli y Marcelo García .......................................................................... 15
2.6 Investigaciones Posteriores ...................................................................................................................... 17
2.7 Programas Utilizados ................................................................................................................................... 18
Capítulo 3. Metodología .......................................................................................................................................... 21
3.1 Rugosidades Absolutas y Coeficientes de Hazen-Williams .......................................................... 21
3.2 Redes trabajadas: .......................................................................................................................................... 24
3.2.1 Red Matriz de Bogotá: ......................................................................................................................... 24
3.2.2 Red Matriz de Medellín: ...................................................................................................................... 25
3.2.3 Red Ginebra Longitudes x 100 Caudales demandados x10 ................................................. 26
3.2.4 Red Andalucía Caudales x100 .......................................................................................................... 27
3.2.5 Red Dtown ................................................................................................................................................ 28
3.2.6 Red La Cumbre ....................................................................................................................................... 29
3.3 Procedimiento ................................................................................................................................................. 30
3.3.1 Procedimiento detallado .................................................................................................................... 30
3.3.2 Adquisición de la información ......................................................................................................... 31
Capitulo 4. Resultados ............................................................................................................................................. 35
4.1 Cálculos matemáticos .................................................................................................................................. 35
4.1.1 Ecuación de los emisores ................................................................................................................... 35
4.1.2 Cálculo del Coeficiente de Hazen-Williams ................................................................................ 36

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
iii
4.1.3 Cálculo de la diferencias de Presión .............................................................................................. 37
4.2 Patrones de las Redes Trabajadas .......................................................................................................... 37
4.2.1 Red Matriz de Bogotá .......................................................................................................................... 37
4.2.2 Red Matriz de Medellín ....................................................................................................................... 39
4.2.3 Red Ginebra ............................................................................................................................................. 40
4.2.4 Red Andalucía ......................................................................................................................................... 42
4.3 Analisis de emisores ..................................................................................................................................... 44
4.3.1 Red Matriz de Bogotá .......................................................................................................................... 44
4.3.2 Red Matriz de Medellín ....................................................................................................................... 58
4.3.3 Red Ginebra ............................................................................................................................................. 72
4.3.4 Red Andalucía ......................................................................................................................................... 86
4.4 Depositos reales, red de bombeo y análisis de la hidráulica del sistema ............................... 99
4.4.1 Red Matriz de Bogotá ....................................................................................................................... 100
4.4.2 Red Matriz de Medellín .................................................................................................................... 117
4.4.3 Red Ginebra .......................................................................................................................................... 146
4.4.4 Red Andalucía ...................................................................................................................................... 172
4.4.5 Red de bombeo DTown ................................................................................................................... 194
4.4.6 Red La Cumbre .................................................................................................................................... 209
5. Conclusiones y trabajo futuro ....................................................................................................................... 216
Bibliografía ................................................................................................................................................................ 219
Anexos ......................................................................................................................................................................... 221
Localización de los emisores ......................................................................................................................... 221
Emisores Bogotá ............................................................................................................................................ 221
Emisores Ginebra .......................................................................................................................................... 226
Emisores Andalucía ...................................................................................................................................... 233
Emisores Medellín ........................................................................................................................................ 238
Resultados Adicionales .................................................................................................................................... 243

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
iv
GLOSARIO DE TÉRMINOS
Análisis de la hidráulica: Consiste en simular la red utilizando alguno de los
programas existentes con el fin de estudiar las presiones, números de Reynolds,
pérdidas por fricción y el comportamiento general de un sistema.
Coeficiente de Hazen-Williams (C): Coeficiente a dimensional que busca representar
la rugosidad interna de las tuberías, entre más alto su valor, se presume que la tubería
tiene una pared interna más lisa.
Diagrama de Moody: Diagrama desarrollado con el fin de encontrar el factor de
fricción de manera visual sin la necesidad de solucionar la ecuación implícita de
Colebrook-White.
Ecuación de Colebrook-White: Ecuación físicamente basada aplicable en todo el
rango de flujo turbulento para hallar de manera implícita los factores de fricción que
se presentaban en las tuberías.
Ecuación de Darcy-Weisbach: Ecuación física y experimentalmente basada que
permite cuantificar las pérdidas por fricción.
Ecuación de Hazen-Williams: Ecuación empírica desarrollad a principios del siglo
XX, para cuantificar de manera explícita las pérdidas por friccion en tuberías
presurizadas con agua.
EPANET: Programa gratuito desarrollado
Emisor: similar a un nudo, pero con la gran diferencia de que su funcionamiento se
basa en que el caudal que sale de él depende de la presión.
Factor de Fricción: valor adimensional que permite relacional las pérdidas por
fricción con el número de Reynolds y la rugosidad absoluta de la tubería.
Flujo: es el movimiento de partículas con respecto a un plano.
Flujo Lamina: Flujo caracterizado por tener números de Reynolds menores a 2000 y
en donde no se presentan intercambio de partículas entre las capas del flujo.
Flujo Turbulento: Flujo caracterizado por presentar números de Reynolds superiores
a 4000, donde existe un intercambio de partículas entre las diferentes capas de flujo.
Flujo Turbulento Hidráulicamente Rugoso (FTHR): Flujo turbulento donde la
subcapa laminar viscosa es 6.1 veces menor a la rugosidad absoluta de la tubería.
Flujo Turbulento Hidráulicamente Liso (FTHL): Flujo turbulento donde la subcapa
laminar viscosa es 30% mayor a la rugosidad absoluta de la tubería.
Número de Reynolds: número adimensional que relaciona el diámetro, la velocidad y
la viscosidad cinemática. Determina el tipo de flujo que se está presentando en un
sistema.
Pérdidas por fricción (Hf): Perdidas de energía que se generan a causa del contacto
entre el fluido y la pared de una estructura hidráulica.
REDES: Programa desarrollado por el centro de investigación en acueducto y
alcantarillado de la Universidad de los Andes (CIACUA), con el fin de estudiar redes y
tuberías a presión.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
v
Redes Matrices: Redes compuestas por captación, transporte desde y hacia las
plantas de tratamiento, tanques de almacenamiento, estaciones de bombeo y tramos
de tubería con gran diámetro.
Subcapa laminar viscosa (δ): Componente de la capa límite turbulenta, localizada
cerca de la pared de la estructura hidráulica. Dentro de esta capa el flujo se comporta
como flujo laminar.
Viscosidad cinemática : Característica del flujo que permite relacionar la
densidad del fluido con su viscosidad dinámica.
INDICE DE ECUACIONES
Ecuación 1 Ecuación de Bernulli. ........................................................................................................................... 3
Ecuación 2 Ecuación de Hazen-Williams ............................................................................................................ 4
Ecuación 3 Ecuación de Chézy. ................................................................................................................................ 5
Ecuación 4 Ecuación de Darcy ................................................................................................................................. 6
Ecuación 5 Ecuación de Darcy forma 2. ............................................................................................................... 6
Ecuación 6 Ecuación de Darcy-Weisbach moderna. ....................................................................................... 7
Ecuación 7 Ecuación de Hagen-Poiseuille. ......................................................................................................... 7
Ecuación 8 Ecuación de Blasius. ............................................................................................................................. 8
Ecuación 9 Ecuación de Prandl. .............................................................................................................................. 8
Ecuación 10 Ecuación de Colebrook-White para todo el rango de Flujo Turbulento. .................. 10
Ecuación 11 Ecuación de Swamee. ..................................................................................................................... 10
Ecuación 12 Ecuación Modificada de Liu. ........................................................................................................ 11
Ecuación 13 Ecuación que relaciona el coeficiente De Hazen-Williams y El Factor de Fricción.
........................................................................................................................................................................................... 11
Ecuación 14 Ecuación final que describe la relación entre f de Darcy y Coeficiente de Hazen-
Williams. ........................................................................................................................................................................ 14
INDICE DE ILUSTRACIONES
Ilustración 1 Rugosidades Absolutas (Saldarriaga, 2007). ....................................................................... 21
Ilustración 2 Rugosidades Absolutas de acuerdo al RAS (Ministerio de Desarrollo Económico,
2013) ............................................................................................................................................................................... 22
Ilustración 3 Coeficientes de Hazen-Williams de acuerdo a las normas técnicas de EPM
(Empresas Públicas de Medellín, 2006-2009). .............................................................................................. 22
Ilustración 4 Coefcientes de Hazen-Williams del libro Hidráulica de Tuberías (Saldarriaga,
2007). .............................................................................................................................................................................. 23
Ilustración 5 Diferentes Coeficientes de Hazen-Williams. ........................................................................ 23
Ilustración 6 Red matriz de Bogotá. ................................................................................................................... 24
Ilustración 7 Red Matriz de Medellín. ............................................................................................................... 25

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
vi
Ilustración 8 Red Ginebra. ...................................................................................................................................... 26
Ilustración 9 Red Andalucía. ................................................................................................................................. 27
Ilustración 10 Red de bombeo DTOWN. .......................................................................................................... 28
Ilustración 11 Red La Cumbre. ............................................................................................................................. 29
Ilustración 12 Se ejecuta el cálculo hidráulico............................................................................................... 32
Ilustración 13 Se escoge la Hora en la que se desean obetner los datos de la tubería o los
Nudos. ............................................................................................................................................................................. 32
Ilustración 14 Se eligen los parámetros relevantes..................................................................................... 33
Ilustración 15 Se copian los datos en portapapeles y se pegan en un archivo de Excel. .............. 34
Ilustración 16 Patrón 1 de Red Bogotá. ............................................................................................................ 38
Ilustración 17 Patrón 2. ........................................................................................................................................... 38
Ilustración 18 Patrón 3. ........................................................................................................................................... 39
Ilustración 19 Patrón de la red matriz de Medellín. .................................................................................... 40
Ilustración 20 Patrón Tanque_Viejo. .................................................................................................................. 41
Ilustración 21 Patrón Tanque_Nuevo. ............................................................................................................... 41
Ilustración 22 Patrón Promedio. ......................................................................................................................... 42
Ilustración 23 Patrón findesemana. ................................................................................................................... 43
Ilustración 24 Patrón días ordinarios. .............................................................................................................. 43
Ilustración 25 Patrón todos los días. ................................................................................................................. 44
Ilustración 26 Resultados emisor 905 .............................................................................................................. 45
Ilustración 27 Resultados Emisor 1521 ........................................................................................................... 45
Ilustración 28 Resultados emisor 2189 ............................................................................................................ 46
Ilustración 29 Resultados emisor 1036........................................................................................................... 47
Ilustración 30 Resultados emisor 905. ............................................................................................................. 48
Ilustración 31 Resultados Emisor 2437. .......................................................................................................... 48
Ilustración 32 Resultados emisor 1702. ........................................................................................................... 49
Ilustración 33 Resultados emisor TUval. ......................................................................................................... 50
Ilustración 34 Gráfica de Reynolds vs Caudal emisor en emisor 1702. .............................................. 51
Ilustración 35 Gráfica del número de Reynolds vs caudal emisor en emisor TUval. .................... 51
Ilustración 36 Variación del Coeficiente de Hazen-Williams respecto al número de Reynolds
para el caudal medio................................................................................................................................................. 52
Ilustración 37 Variación del Coeficiente de Hazen-Williams frente al número de Reynolds para
el caudal mínimo. ....................................................................................................................................................... 53
Ilustración 38 Variación del Coeficiente de Hazen-Williams frente al número de Reynolds para
el caudal máximo. ...................................................................................................................................................... 53
Ilustración 39 Variación del Coeficiente de Hazen-Williams frente a los diámetros de la red
para el caudal medio................................................................................................................................................. 54
Ilustración 40 Variación del coeficiente de Hazen-Williams frente a los diámetros de la red
para el caudal Mínimo. ............................................................................................................................................. 54
Ilustración 41 Variación del coeficiente de Hazen-Williams frente a los diámetros de la red
para el caudal Máximo. ............................................................................................................................................ 55
Ilustración 42 Diferencia de presiones para el caudal mínimo. ............................................................. 56

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
vii
Ilustración 43 Diferencia de Presiones para el caudal medio. ................................................................ 57
Ilustración 44 Diferencia de presiones para el caudal máximo. ............................................................. 57
Ilustración 45 Resultados emisor 225. ............................................................................................................. 58
Ilustración 46 Resultdos Emisor 46 ................................................................................................................... 59
Ilustración 47 Resultados emisor 369. ............................................................................................................. 59
Ilustración 48 Resultados emisor 529. ............................................................................................................. 60
Ilustración 49 Resultados emisor 540. ............................................................................................................. 60
Ilustración 50 Resultados emisores 532. ......................................................................................................... 61
Ilustración 51 Caudal emisor vs número de Reynolds Emisor 529. ..................................................... 62
Ilustración 52 Caudal emisor vs número de Reynolds Emisor 540. ..................................................... 62
Ilustración 53 Caudal Emisor vs Número de Reynolds Emisor 532. .................................................... 63
Ilustración 54 Resultados Emisor 72................................................................................................................. 64
Ilustración 55 Resultados Emisor 495 .............................................................................................................. 64
Ilustración 56 Resultados Emisor 663. ............................................................................................................. 65
Ilustración 57 Variación del Coeficiente de Hazen-Williams frente al número de Reynolds para
el caudal mínimo. ....................................................................................................................................................... 66
Ilustración 58 Variación del Coeficiente de Hazen-Williams frente al número de Reynolds para
el caudal Medio. .......................................................................................................................................................... 66
Ilustración 59 Variación del Coeficiente de Hazen-Williams frente al número de Reynolds para
el caudal Máximo. ...................................................................................................................................................... 67
Ilustración 60 Variación del coeficiente de Hazen-Williams frente a los diámetros de la red
para el caudal medio................................................................................................................................................. 67
Ilustración 61 Variación del coeficiente de Hazen-Williams frente a los diámetros de la red
para el caudal Mínimo. ............................................................................................................................................. 68
Ilustración 62 Variación del coeficiente de Hazen-Williams frente a los diámetros de la red
para el caudal Máximo. ............................................................................................................................................ 68
Ilustración 63 Diferencia de presiones con caudales medios. ................................................................ 70
Ilustración 64 Diferencia de presiones con caudales Mínimos............................................................... 70
Ilustración 65 Diferencia de presiones con caudales Máximos. ............................................................. 71
Ilustración 66 Resultados Emisor 369. ............................................................................................................. 72
Ilustración 67 Resultados emisor 365. ............................................................................................................. 73
Ilustración 68 Resultados emisor 6. ................................................................................................................... 73
Ilustración 69 Características de los emisores pequeños. ........................................................................ 74
Ilustración 70 Resultados emisor 476. ............................................................................................................. 74
Ilustración 71 Resultados emisor 411. ............................................................................................................. 75
Ilustración 72 Rersultados emisor 458. ........................................................................................................... 75
Ilustración 73 Caudal emisor vs número de Reynolds emisor 476. ..................................................... 76
Ilustración 74 Caudal emisor vs número de Reynolds emisor 411. ..................................................... 77
Ilustración 75 Caudal emisor vs número de Reynolds emisor 458. ..................................................... 77
Ilustración 76 Resultados emisor 392. ............................................................................................................. 78
Ilustración 77 Resultados emisor 464 .............................................................................................................. 79
Ilustración 78 Resultados emisor 457. ............................................................................................................. 79

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
viii
Ilustración 79 Variación del coeficiente de Hazen-Williams vs el número de Reynolds para el
caudal medio. ............................................................................................................................................................... 80
Ilustración 80 Variación del coeficiente de Hazen-Williams vs el número de Reynolds para el
caudal mínimo. ............................................................................................................................................................ 81
Ilustración 81 Variación del coeficiente de Hazen-Williams vs el número de Reynolds para el
caudal máximo. ........................................................................................................................................................... 81
Ilustración 82 Variación del coeficiente de Hazen-Williams vs los diámetros de la red para el
caudal medio. ............................................................................................................................................................... 82
Ilustración 83 Variación del coeficiente de Hazen-Williams vs los diámetros de la red para el
caudal mínimo. ............................................................................................................................................................ 82
Ilustración 84 Variación del coeficiente de Hazen-Williams vs los diámetros de la red para el
caudal Máximo. ........................................................................................................................................................... 83
Ilustración 85 Diferencias de presiones para el caudal mínimo. ........................................................... 85
Ilustración 86 Diferencias de presión para el caudal máximo. ............................................................... 85
Ilustración 87 Diferencias de presión para el caudal máximo. ............................................................... 86
Ilustración 88 Resultados emisor 317. ............................................................................................................. 87
Ilustración 89 Resultados emisor 13. ................................................................................................................ 87
Ilustración 90 Resultados emisor 102. ............................................................................................................. 88
Ilustración 91 Resultados emisor 298. ............................................................................................................. 89
Ilustración 92 Resultados emisor 279. ............................................................................................................. 89
Ilustración 93 Resultados emisor 267. ............................................................................................................. 90
Ilustración 94 Resultados emisor 278. ............................................................................................................ 91
Ilustración 95 Resultados emisor 269. ............................................................................................................. 92
Ilustración 96 Caudal emisor vs número de Reynolds emisor 278. ..................................................... 92
Ilustración 97 Caudal emisor vs número de Reynolds emisor 269. ..................................................... 93
Ilustración 98 Variación del coeficiente de Hazen-Williams vs número de Reynolds para el
caudal medio. ............................................................................................................................................................... 94
Ilustración 99 Variación del coeficiente de Hazen-Williams vs número de Reynolds para el
caudal Mínimo. ............................................................................................................................................................ 94
Ilustración 100 Variación del coeficiente de Hazen-Williams vs número de Reynolds para el
caudal Máximo. ........................................................................................................................................................... 95
Ilustración 101 Variación del coeficiente de Hazen-Williams vs diámetros de la red para el
caudal Medio. ............................................................................................................................................................... 95
Ilustración 102 Variación del coeficiente de Hazen-Williams vs diámetros de la red para el
caudal Mínimo. ............................................................................................................................................................ 96
Ilustración 103 Variación del coeficiente de Hazen-Williams vs diámetros de la red para el
caudal Máximo. ........................................................................................................................................................... 96
Ilustración 104 Diferencia de presiones para el caudal medio. ............................................................. 98
Ilustración 105 Diferencia de presiones para el caudal mínimo. .......................................................... 98
Ilustración 106 Diferencia de presiones para el caudal máximo. .......................................................... 99
Ilustración 107 Nivel del tanque Cazucá. ...................................................................................................... 100
Ilustración 108 Nivel tanque NuevoSuba. .................................................................................................... 101

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
ix
Ilustración 109 Nivel tanque San Diego. ....................................................................................................... 101
Ilustración 110 Nivel Tanque Vitelma. .......................................................................................................... 102
Ilustración 111 Mapa con tramos a la salida de los embalses analizados. ...................................... 103
Ilustración 112 Diferencias en el cáulculo de ls pérdidas por fricción. ............................................ 104
Ilustración 113 Diferencias en el número de Reynolds. ......................................................................... 104
Ilustración 114 Diferencias en el cálculo de las pérdidas por fricción. ............................................ 105
Ilustración 115 Diferencia en el número de Reynolds. ........................................................................... 105
Ilustración 116 Diferencia en el cálculo de las pérdidas por fricción. .............................................. 106
Ilustración 117 Diferencia en el número de Reynolds. ........................................................................... 106
Ilustración 118 Diagrama de Moody para la tubería 3701. .................................................................. 113
Ilustración 119 Diagrama de Moody para la tubería 4172. .................................................................. 114
Ilustración 120 Diagrama de Moody para la tubería 75. ........................................................................ 115
Ilustración 121 Ubicación de los Tanques en la red matriz de Medellín. ........................................ 118
Ilustración 122 Nivel tanque 691 Medellín.................................................................................................. 119
Ilustración 123 Nivel tanque 692 Medellín.................................................................................................. 119
Ilustración 124 Nivel tanque 689 Medellín.................................................................................................. 120
Ilustración 125 Nivel Tanque 690 Medellín. ............................................................................................... 120
Ilustración 126 Nivel tanque 690 red Medellín con 2 tanques ............................................................ 121
Ilustración 127 Nivel Tanque 689 red Medellín con 2 tanques........................................................... 122
Ilustración 128 Diferencias en pérdidas por fricción tubería 78 red matriz de Medellín. ....... 123
Ilustración 129 Diferencia en el número de Reynolds tubería 78 red matriz de Medellín. ..... 123
Ilustración 130 Diferencias en pérdidas por fricción tubería 395 red matriz de Medellín. .... 124
Ilustración 131 Diferencia en el número de Reynolds tubería 395 red matriz de Medellín. .. 124
Ilustración 132 Diagrama de Moody 1 red matriz de Medellín Caudal Mínimo. .......................... 134
Ilustración 133 Diagrama de Moody 2 red matriz de Medellín Caudal Mínimo. .......................... 135
Ilustración 134 Diagrama de Moody 1 red matriz de Medellín Caudal Máximo. ......................... 139
Ilustración 135 Diagrama de Moody 2 red matriz de Medellín Caudal Máximo. ......................... 140
Ilustración 136 Diagrama de Moody 3 red matriz de Medellín Caudal Máximo. ......................... 140
Ilustración 137 Diagrama de Moody 1 red matriz de Medellín Caudal Medio. ............................. 144
Ilustración 138 Diagrama de Moody 2 red matriz de Medellín Caudal Medio. ............................. 144
Ilustración 139 Nivel tanque 350 red Ginebra. .......................................................................................... 147
Ilustración 140 Nivel tanque 481 red Ginebra. .......................................................................................... 147
Ilustración 141 Nivel tanque 359 red Ginebra. .......................................................................................... 148
Ilustración 142 Nivel tanque 372 red Ginebra. .......................................................................................... 148
Ilustración 143 Nivel tanque 355 red Ginebra con solo 2 depositos. ............................................... 149
Ilustración 144 Nivel tanque 359 red Ginebra con solo 2 depositos. ............................................... 150
Ilustración 145 Diferencia en las pérdidas por fricción tubería 1. ..................................................... 151
Ilustración 146 Diferencia en el número de Reynolds tubería 1. ....................................................... 151
Ilustración 147 Difrerencia en la pérdidas por fricción tubería 496. ............................................... 152
Ilustración 148 Diferencia en el número de Reynolds tubería 496. .................................................. 152
Ilustración 149 Difrerencia en la pérdidas por fricción tubería 528. ............................................... 153
Ilustración 150 Diferencia en el número de Reynolds tubería 528. .................................................. 153

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
x
Ilustración 151 Diagrama de Moody red Ginebra tramos con Hazen-Williams mayor Caudal
Medio. .......................................................................................................................................................................... 162
Ilustración 152 Diagrama de Moody red Ginebra con Darcy-Weisbach mayor y caudal medio.
........................................................................................................................................................................................ 163
Ilustración 153 Diagrama de Moody red Ginebra con Hazen-Williams mayor y caudal mínimo.
........................................................................................................................................................................................ 165
Ilustración 154 Diagrama de Moody red Ginebra con Darcy-Weisbach mayor y caudal mínimo.
........................................................................................................................................................................................ 166
Ilustración 155 Diagrama de Moody red Ginebra con Hazen-Williams mayor y caudal máximo.
........................................................................................................................................................................................ 168
Ilustración 156 Diagrama de Moody red Ginebra con Darcy-Weisbach mayor y caudal máximo.
........................................................................................................................................................................................ 169
Ilustración 157 Nivel tanque 362 de la red de Andalucía. ..................................................................... 173
Ilustración 158 Nivel tanque 222 de la red de Andalucía. ..................................................................... 173
Ilustración 159 Nivel tanque 343 de la red de Andalucía. ..................................................................... 174
Ilustración 160 Nivel tanque 361 de la red de Andalucía. ..................................................................... 174
Ilustración 161 Nivel tanque 343 de la red de Andalucía con 2 tanques. ...................................... 175
Ilustración 162 Nivel tanque 222 de la red de Andalucía con 2 tanques. ....................................... 176
Ilustración 163 Diagrama de Moody de la tubería 65 Red de Andalucía. ....................................... 177
Ilustración 164 Diagrama de Moody de la tubería 137 Red de Andalucía. ..................................... 177
Ilustración 165 Diagrama de Moody de la tubería 78 Red de Andalucía. ....................................... 178
Ilustración 166 Diagrama de Moody de red de Andalucía tramos con Hazen-Williams mayor
para el caudal mínimo........................................................................................................................................... 185
Ilustración 167 Diagrama de Moody de red de Andalucía tramos con Hazen-Williams mayor
para el caudal medio.............................................................................................................................................. 188
Ilustración 168 Diagrama de Moody de red de Andalucía tramos con Hazen-Williams mayor
para el caudal máximo1. ...................................................................................................................................... 190
Ilustración 169 Diagrama de Moody de red de Andalucía tramos con Hazen-Williams mayor
para el caudal máximo2. ...................................................................................................................................... 191
Ilustración 170 Diagrama de Moody de red de Andalucía tramos con Darcy-Weisbach mayor
para el caudal máximo. ......................................................................................................................................... 191
Ilustración 171 Nivel Tanque 1 red Dtown. ................................................................................................. 196
Ilustración 172 Nivel tanque 2 red Dtown. .................................................................................................. 196
Ilustración 173 Nivel tanque 3 red Dtown. .................................................................................................. 197
Ilustración 174 Nivel tanque 4 red Dtown. .................................................................................................. 197
Ilustración 175 Nivel tanque 5 red Dtown. .................................................................................................. 198
Ilustración 176 Nivel tanque 6 red Dtown. .................................................................................................. 198
Ilustración 177 Nivel tanque 7 red Dtown. .................................................................................................. 199
Ilustración 178 Patrones 1 y 5 de la red de Dtown con sus horarios de diferencia hidráulica.
........................................................................................................................................................................................ 204
Ilustración 179 Patrones 2 y 3 de la red Dtown con sus horarios de diferencia hidráulica. ... 204
Ilustración 180 Patrón 4 de la red Dtown con sus horarios de diferencia Hidráulica. .............. 204

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
xi
Ilustración 181 Diagrama de Moody red Dtown tramos con Hazen-Williams MAYOR para el
caudal medio 1. ........................................................................................................................................................ 205
Ilustración 182 Diagrama de Moody red Dtown tramos con Hazen-Williams MAYOR para el
caudal medio 2. ........................................................................................................................................................ 206
Ilustración 183 Diagrama de Moody red Dtown tramos con Darcy-Weisbach MAYOR para el
caudal medio. ............................................................................................................................................................ 206
Ilustración 184 Localización de los tanques de la red La Cumbre. .................................................... 209
Ilustración 185 Diagrama de Moody red La Cumbre tramos con Hazen-Williams MAYOR para
el caudal mínimo. .................................................................................................................................................... 210
Ilustración 186 Diagrama de Moody red La Cumbre tramos con Darcy-Weisbach MAYOR para
el caudal mínimo. .................................................................................................................................................... 210
Ilustración 187 Diagrama de Moody red La Cumbre tramos con Hazen-Williams MAYOR para
el caudal medio. ....................................................................................................................................................... 212
Ilustración 188 Diagrama de Moody red La Cumbre tramos con Darcy-Weisbach MAYOR para
el caudal medio. ....................................................................................................................................................... 212
Ilustración 189 Diagrama de Moody red La Cumbre tramos con Hazen-Williams MAYOR para
el caudal máximo. ................................................................................................................................................... 214
Ilustración 190 Diagrama de Moody red La Cumbre tramos con Darcy-Weisbach MAYOR para
el caudal máximo. ................................................................................................................................................... 214
Ilustración 191 Emisor 905 red matriz de Bogotá ................................................................................... 221
Ilustración 192 Emisor 1521 red matriz de Bogotá ................................................................................. 222
Ilustración 193 Emisor 2437 red matriz de Bogotá. ................................................................................ 222
Ilustración 194 Emisor 3758 red matriz de Bogotá. ................................................................................ 223
Ilustración 195 Emisor 1045 red matriz de Bogotá. ................................................................................ 223
Ilustración 196 Emisor 1036 red matriz de Bogotá. ................................................................................ 224
Ilustración 197 Emisor 2189 red matriz de Bogotá. ................................................................................ 224
Ilustración 198 Emisor TUval red matriz de Bogotá................................................................................ 225
Ilustración 199 Emisor 1702 red matriz de Bogotá. ................................................................................ 225
Ilustración 200 Emisor 369 red Ginebra. ..................................................................................................... 226
Ilustración 201 Emisor 365 red Ginebra. ..................................................................................................... 227
Ilustración 202 Emisor 6 red Ginebra. ........................................................................................................... 227
Ilustración 203 Emisor 398 red Ginebra. ..................................................................................................... 228
Ilustración 204 Emisor 476 red Ginebra. ..................................................................................................... 228
Ilustración 205 Emisor 455 red Ginebra. ..................................................................................................... 229
Ilustración 206 Emisor 456 red Ginebra. ..................................................................................................... 229
Ilustración 207 Emisor 392 red Ginebra. ..................................................................................................... 230
Ilustración 208 Emisor 458 red Ginebra. ..................................................................................................... 230
Ilustración 209 Emisor 476 red Ginebra. ..................................................................................................... 231
Ilustración 210 Emisor 411 red Ginebra. ..................................................................................................... 231
Ilustración 211 Emisor 464 red Ginebra. ..................................................................................................... 232
Ilustración 212 Emisor 457 red Ginebra. ..................................................................................................... 232
Ilustración 213 Emisor 102 red Andalucía. ................................................................................................. 233

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
xii
Ilustración 214 Emisor 13 red Andalucía. .................................................................................................... 234
Ilustración 215 Emisor 317 red Andalucía. ................................................................................................. 234
Ilustración 216 Emisor 278 red Andalucía. ................................................................................................. 235
Ilustración 217 Emisor 269 red Andalucía. ................................................................................................. 235
Ilustración 218 Emisor 298 red Andalucía. ................................................................................................. 236
Ilustración 219 Emisor 279 red Andalucía. ................................................................................................. 236
Ilustración 220 Emisor 267 red Andalucía. ................................................................................................. 237
Ilustración 221 Emisor 286 red Andalucía. ................................................................................................. 237
Ilustración 222 Emisor 225 red matriz de Medellín. ............................................................................... 238
Ilustración 223 Emisor 46 red matriz de Medellín. .................................................................................. 239
Ilustración 224 Emisor 369 red matriz de Medellín. ............................................................................... 239
Ilustración 225 Emisor 529 red matriz de Medellín. ............................................................................... 240
Ilustración 226 Emisor 540 red matriz de Medellín. ............................................................................... 240
Ilustración 227 Emisor 72 red matriz de Medellín. .................................................................................. 241
Ilustración 228 Emisor 663 red matriz de Medellín. ............................................................................... 241
Ilustración 229 Emisor 495 red matriz de Medellín. ............................................................................... 242
Ilustración 230 Emisor 532 red matriz de Medellín. ............................................................................... 242
Ilustración 231 Emisor 3758 ............................................................................................................................. 243
Ilustración 232 Emisor 1045 ............................................................................................................................. 243
Ilustración 233 Emisor 455 ................................................................................................................................ 244
Ilustración 234 Emisor 456 ................................................................................................................................ 244
Ilustración 235 Emisor 398 ................................................................................................................................ 245
Ilustración 236 Reynolds vs Diámetro caudal medio Darcy-Weisbach. .......................................... 245
Ilustración 237 Reynolds vs Diámetro caudal medio Hazen-Williams ............................................ 246
Ilustración 238 Reynolds vs Diámetro caudal Máximo Darcy-Weisbach ........................................ 246
Ilustración 239 Reynolds vs Diámetro caudal máximo Hazen-Williams. ........................................ 247
Ilustración 240 Reynolds vs Diámetro caudal mínimo Darcy-Weisbach. ....................................... 247
Ilustración 241 Reynolds vs Diámetro caudal mínimo Hazen-Williams. ........................................ 248
Ilustración 242 Reynolds vs Diámetro caudal Medio Darcy-Weisbach. .......................................... 249
Ilustración 243 Reynolds vs Diámetro caudal medio Hazen-Williams. ........................................... 250
Ilustración 244 Reynolds vs Diámetro caudal Máximo Darcy-Weisbach ........................................ 250
Ilustración 245 Reynolds vs Diámetro caudal Máximo Hazen-Williams ......................................... 251
Ilustración 246 Reynolds vs Diámetro caudal Mínimo Darcy-Weisbach ........................................ 251
Ilustración 247 Reynolds vs Diámetro caudal Mínimo Hazen-Williams ......................................... 252
Ilustración 248 Reynolds vs Diámetro caudal Medio Darcy-Weisbach. .......................................... 252
Ilustración 249 Reynolds vs Diámetro caudal Medio Hazen-Williams ............................................ 253
Ilustración 250 Reynolds vs Diámetro caudal Mínimo Darcy-Weisbach. ....................................... 253
Ilustración 251 Reynolds vs Diámetro caudal mínimo Hazen-Williams. ........................................ 254
Ilustración 252 Reynolds vs Diámetro caudal Máximo Darcy-Weisbach ........................................ 254
Ilustración 253 Reynolds vs Diámetro caudal máximo Hazen-Williams ......................................... 255
Ilustración 254 Reynolds vs Diámetro caudal Medio Darcy-Weisbach. .......................................... 255
Ilustración 255 Reynolds vs Diámetro caudal medio Hazen ................................................................ 256

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
xiii
Ilustración 256 Reynolds vs Diámetro caudal Máximo Darcy-Weisbach. ....................................... 256
Ilustración 257 Reynolds vs Diámetro caudal máximo Hazen-Williams. ........................................ 257
Ilustración 258 Reynolds vs Diámetro caudal Mínimo Darcy-Weisbach. ....................................... 258
Ilustración 259 Reynolds vs Diámetro caudal mínimo Hazen-Williams ......................................... 258
INDICE DE FIGURAS
Figura 1 Salida de embalse Tibitoc Caudal Medio. .................................................................................... 108
Figura 2 Salida del Embalse Tibitoc Caudal Máximo. .............................................................................. 108
Figura 3 Salida del Embalse Tibitoc Caudal Mínimo. ............................................................................... 109
Figura 4 Salida del embalse de Wiesner caudal medio. .......................................................................... 109
Figura 5 Salida del embalse de Wiesner caudal máximo. ...................................................................... 110
Figura 6 Salida del embalse de Wiesner caudal mínimo. ....................................................................... 110
Figura 7 Entramado interno de la red matriz de Bogotá Caudal Medio........................................... 111
Figura 8 Entramado interno de la red matriz de Bogotá caudal Máximo. ...................................... 111
Figura 9 Entramado interno red matriz de Bogotá Caudal Mínimo. ................................................. 112
Figura 10 Diferencias Hidráulicas en la red matriz de Medellín (1). ................................................ 126
Figura 11 Diferencias Hidráulicas en la red matriz de Medellín (2). ................................................ 126
Figura 12 Diferencias Hidráulicas en la red matriz de Medellín (3). ................................................ 127
Figura 13 Diferencias Hidráulicas en la red matriz de Medellín (4). ................................................ 128
Figura 14 Diferencias Hidráulicas en la red matriz de Medellín (5). ................................................ 128
Figura 15 Tuberías con Altas diferencias red matriz de Medellín caudal medio. ........................ 129
Figura 16 Tuberías con Altas diferencias red matriz de Medellín caudal medio
(ACERCAMIENTO). ................................................................................................................................................. 130
Figura 17 Tuberías con altas diferencias red Matriz de Medellín caudal máximo. ..................... 130
Figura 18 Tuberías con altas diferencias red Matriz de Medellín caudal máximo
(Acercamiento). ....................................................................................................................................................... 131
Figura 19 Tuberías con altas diferencias red Matriz de Medellín caudal mínimo. ...................... 132
Figura 20 Tuberías con altas diferencias red Matriz de Medellín caudal mínimo
(Acercamiento). ....................................................................................................................................................... 133
Figura 21 Red Ginebra con la localizacion de los depositos y algunas tuberías analizadas. ... 146
Figura 22 Salida del primer embalse red Ginebra. ................................................................................... 154
Figura 23 Diferencia en algunos tramos de la red Ginebra. .................................................................. 155
Figura 24 Salida de los otros embalses de la red Ginebra. .................................................................... 155
Figura 25 Diferencias de los entramados internos de la red Ginebra 1. .......................................... 156
Figura 26 Diferencias de los entramados internos de la red Ginebra 2. .......................................... 156
Figura 27 Diferencias de los entramados internos de la red Ginebra 3. .......................................... 157
Figura 28 Diferencias en las ramificaciones de la red Ginebra. ........................................................... 157
Figura 29 Tramos de la red Ginebra con diferencias significativas en el número de Reynolds
con la demanda media del sistema. ................................................................................................................. 158
Figura 30 Tramos internos de la red Ginebra con diferencias significativas en el número de
Reynolds con la demanda media del sistema. ............................................................................................. 159

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
xiv
Figura 31 Tramos de la red Ginebra con diferencias significativas en el número de Reynolds
con la demanda máxima del sistema. ............................................................................................................. 159
Figura 32 Tramos internos de la red Ginebra con diferencias significativas en el número de
Reynolds con la demanda máxima del sistema. ......................................................................................... 160
Figura 33 Tramos de la red Ginebra con diferencias significativas en el número de Reynolds
con la demanda mínima del sistema. .............................................................................................................. 160
Figura 34 Tramos internos de la red Ginebra con diferencias significativas en el número de
Reynolds con la demanda mínima del sistema. .......................................................................................... 161
Figura 35 Localización de los tanques y de algunos tramos analizados de la red de Andalucía.
........................................................................................................................................................................................ 172
Figura 36 Salida del embalse red Andalucía. ............................................................................................... 179
Figura 37 Principales tramos a la salida del embalse red Andalucía. ............................................... 179
Figura 38 Entramado interno de la red de Andalucía 1. ......................................................................... 180
Figura 39 Entramado interno de la red de Andalucía 2. ......................................................................... 180
Figura 40 Ramificaciones de la red Andalucía. ........................................................................................... 181
Figura 41 Ramificaciones con altas diferencias red de andalucía Caudal Medio. ........................ 182
Figura 42 Entramados internos con altas diferencias red Andalucía caudal medio................... 182
Figura 43 Ramificaciones con altas diferencias red Andalucía caudal máximo. .......................... 183
Figura 44 Entramados internos con altas diferencias red Andalucía caudal máximo. .............. 183
Figura 45 Ramificaciones con altas diferencias red Andalucía caudal mínimo. ........................... 184
Figura 46 Entramados internos con altas diferencias red Andalucía caudal mínimo................ 184
Figura 47 Esquema de la red en la hora de la demanda media de la red Dtown. ......................... 200
Figura 48 Esquema de la red en la hora de la demanda máxima de la red Dtown. ..................... 200
Figura 49 Esquema de la red en la hora de la demanda mínima de la red Dtown. ...................... 201
Figura 50 Tuberías con als diferencias en el número de Reynolds. ................................................... 202
Figura 51 Sectores con las principales diferencias hiráulicas en Dtown. ........................................ 203
INDICE DE TABLAS
Tabla 1 Rugosidades absolutas de acuerdo a las normas tecnicas de EPM (Empresas Públicas
de Medellín, 2006-2009). ....................................................................................................................................... 22
Tabla 2 Tiempos de los horarios medios, máximos y mínimos. ............................................................. 39
Tabla 3 Horarios de Caudales mínimo, medio y máximo. ......................................................................... 40
Tabla 4 Horarios de Caudales mínimo, medio y máximo. ......................................................................... 42
Tabla 5 Horarios de caudal mínimo, máximo y medio. .............................................................................. 44
Tabla 6 Características de los emisores pequeños. ..................................................................................... 46
Tabla 7 Coeficientes emisores de los nudos. .................................................................................................. 47
Tabla 8 Coeficientes de emisores grandes. ..................................................................................................... 76
Tabla 9 IOnformación de los emisores pequeños. ....................................................................................... 88
Tabla 10 Coeficientes de emisión para emisores grandes. ....................................................................... 90
Tabla 11 Resumen de Resultados para tuberías con altas diferencias para el caudal mínimo
demandado de la red matriz de Medellín. .................................................................................................... 136

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
xv
Tabla 12 Resumen de resultados par Tuberías con altas diferencias para el caudal mínimo
demandado de la red matriz de Medellín ..................................................................................................... 136
Tabla 13 Tabla resumen de altas diferencias red Matriz Medellín caudal máximo 1. ............... 141
Tabla 14 Tabla resumen de altas diferencias red Matriz Medellín caudal máximo 2. ............... 142
Tabla 15 Tabla resumen de altas diferencias red Matriz Medellín caudal máximo 3. ............... 142
Tabla 16 Tabla resumen de altas diferencias red Matriz Medellín caudal medio 1. ................... 145
Tabla 17 Tabla resumen de altas diferencias red Matriz Medellín caudal medio 2. ................... 145
Tabla 18 Resumen de tuberías red Ginebra caudal medio 1. ............................................................... 164
Tabla 19 Resumen de tuberías red Ginebra caudal medio 2. ............................................................... 164
Tabla 20 Resumen de tuberías red Ginebra caudal mínimo 1. ............................................................ 167
Tabla 21 Resumen de tuberías red Ginebra caudal mínimo 2. ............................................................ 167
Tabla 22 Resumen de tuberías red Ginebra caudal máximo 1. ........................................................... 170
Tabla 23 Resumen de tuberías red Ginebra caudal máximo 2. ........................................................... 170
Tabla 24 Resumen de tramos de la red Andalucía para el caudal mínimo. .................................... 186
Tabla 25 Resumen de tramos de la red Andalucía para el caudal medio. ....................................... 189
Tabla 26 Resumen de tramos de la red Andalucía para el caudal máximo 1. ................................ 192
Tabla 27 Resumen de tramos de la red Andalucía para el caudal máximo 2. ................................ 192
Tabla 28 Resumen de tramos de la red Andalucía para el caudal máximo 3. ................................ 193
Tabla 29 Tiempos en los que la hidráulica de la red Dtown cambia significativamente. ......... 203
Tabla 30 Resumen de tramos de la red Dtown para el caudal medio 1. .......................................... 207
Tabla 31 Resumen de tramos de la red Dtown para el caudal medio 2. .......................................... 207
Tabla 32 Resumen de tramos de la red Dtown para el caudal medio 3. .......................................... 207
Tabla 33 Resumen de tramos de la red La Cumbre para el caudal mínimo 1. .............................. 211
Tabla 34 Resumen de tramos de la red La Cumbre para el caudal mínimo 2. .............................. 211
Tabla 35 Resumen de tramos de la red La Cumbre para el caudal medio 1. ................................. 213
Tabla 36 Resumen de tramos de la red La Cumbre para el caudal medio 2. ................................. 213
Tabla 37 Resumen de tramos de la red La Cumbre para el caudal máximo 1. .............................. 215
Tabla 38 Resumen de tramos de la red La Cumbre para el caudal máximo 2. .............................. 215

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
1
CAPÍTULO 1: INTRODUCCIÓN Y OBJETIVOS
1.1 INTRODUCCIÓN
Los sistemas de distribución de agua potable se han convertido en una prioridad para los
asentamientos urbanos en los últimos años; esto se debe al crecimiento de las grandes urbes,
la demanda por agua adecuada para el consumo humano y para el desarrollo económico de las
ciudades. Estos se encuentran divididos en sistemas Matrices, que son compuestos por
tuberías de gran diámetro y las redes secundarias que son las que distribuyen internamente el
agua a los usuarios. Todo lo anterior obliga a generar diseños y condiciones de operaciones
adecuadas de tal forma que se logren los mejores estándares hidráulicos y de calidad de agua.
Para todo esto, se han utilizado ecuaciones para representar las pérdidas por fricción. Dentro
de estas se encuentran 2 grandes grupos; las ecuaciones físicamente basadas y las ecuaciones
empíricas, estas últimas utilizadas ampliamente por su rápida y sencilla solución, pese a
contar con limitaciones en su uso debido a su naturaleza. Dentro del grupo de ecuaciones se
encuentran la ecuación de Darcy-Weisbach en conjunto con la ecuación de Colebrook-White
(o Hagen-Poiseuille) como máximo representante de las ecuaciones físicamente basadas y la
ecuación de Hazen-Williams, siendo la ecuación empírica más utilizada al ser explícita para
encontrar las perdidas por fricción.
Las diferencias conceptuales y de metodología en que se fundamentan estas dos ecuaciones
para su uso práctico, constituyen el motivo principal de la presente Tesis, la cual se enfocará
en estudiar los efectos hidráulicos que generan utilizar la ecuación de Hazen-Williams en la
operación de redes matrices y redes primarias de bombeo frente a los efectos de utilizar la
ecuación de Darcy-Weisbach. La primera parte presentará la introducción a este estudio; la
segunda parte expondrá los objetivos tanto general como específicos que se plantearon; la
tercera parte contiene el marco teórico de este estudio el cual plantea los fundamentos
conceptuales, metodologías y principales aplicaciones derivados del usos de estas dos
ecuaciones; la cuarta parte mostrará la metodología utilizada en este trabajo de investigación ,
la cual incluye el procedimiento, los escenarios trabajados y las rugosidades y coeficientes de
Hazen-Williams reportados por fabricantes y por la literatura. En la quinta sección se
mostrarán los resultados encontrados en esta primera fase, así como su análisis. Y finalmente
en
la
sexta
sección
las
conclusiones.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
2
1.2 OBJETIVOS
1.2.1 OBJETIVO GENERAL
Establecer y cuantificar el efecto hidráulico que se presenta al operar redes matrices y redes
primarias de bombeo utilizando la ecuación de Hazen-Williams y la ecuación de Darcy-
Weisbach.
1.2.2 OBJETIVOS ESPECÍFICOS
Analizar el efecto de los diferentes materiales de tuberías comerciales para el diseño
de redes matrices y redes primarias de bombeo.
Establecer la magnitud de la diferencia entre la hidráulica de una red operada
utilizando la ecuación de Hazen-Williams y la ecuación de Darcy-Weisbach.
Realizar una aproximación teórica a los trabajos realizados por Bombardelli y García,
y a su vez verificar la similitud entre ese estudio y el realizado en este trabajo.
Establecer si la normativa actual de Colombia es adecuada para los diseñadores y
operadores al utilizar las ecuaciones estudiadas durante esta investigación.
Establecer si los coeficientes de Hazen-Williams reportados en la literatura y en los
catálogos de los diferentes fabricantes son adecuados para las diferentes condiciones
de operación de redes matrices.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
3
CAPÍTULO 2 MARCO TEÓRICO
El marco teórico utilizado durante este trabajo fue tomado de la Tesis de pregrado realizada
por este mismo autor, ya que es la continuación de una investigación se consideró de la mayor
conveniencia y utilidad mantener este marco teórico realizándole solo unas ligeras
modificaciones. La tesis de pregrado de la que se tomó este marco Teórico es “Efecto del uso de
ecuaciones empíricas vs físicamente basadas sobre los costos de diseños optimizados en
acueductos.”, desarrollada por Juan David Uribe en el año 2012 y asesorada por Juan
Guillermo Saldarriaga. Todo el contenido de este marco Teórico fue extraído de este trabajo y
citado en esta Tesis, realizándole ligeras modificaciones teniendo en cuenta que hay
variaciones entre los dos estudios
(Uribe, 2012)
.
2.1 ECUACIONES Y FÓRMULAS UTILIZADAS EN LOS DISEÑOS DE RDAP.
En las tuberías a presión existen pérdidas de energía causadas por la fricción que existe entre
el fluido y la tubería, y las pérdidas menores asociadas con cambios de dirección y a la
instalación de diferentes accesorios. Estas pérdidas pueden ser calculadas utilizando la
ecuación de conservación de la energía de Bernoulli (Uribe, 2012).
ECUACIÓN 1 ECUACIÓN DE BERNOULLI.
donde:
y
= presiones en los dos puntos.
y
= velocidad del flujo.
z= altura topográfica o con respecto a una cota.
g= gravedad
ρ= densidad del fluido.
HF= pérdidas de energía entre el tramo 1 y 2.
Hm=pérdidas de energía causadas por accesorios.
De acuerdo con lo anterior, puede observarse que para el cálculo de las pérdidas por fricción
se tienen limitaciones ya que se requeriría de una medición de la velocidad o el caudal y de la
presión en la tubería, lo que no es aplicable ya que como es evidente, la tubería aún no está
diseñada (Uribe, 2012).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
4
Las anteriores limitaciones exigieron estudiar a fondo la relación que existía entre las
características de la tubería (diámetro, material, longitud), las características del fluido
(densidad y viscosidad) y las pérdidas por fricción a través de los tramos de tubería. Como
resultado de estas investigaciones surgieron diversas ecuaciones para el cálculo de estas
pérdidas. Estas ecuaciones se dividen en dos grupos: empíricas y físicamente basadas. De las
primeras, la que en la actualidad tiene mayor importancia para los sistemas de acueducto, es
la ecuación de Hazen-Williams, desarrollada a principios del siglo XX por Allan Hazen y
Gardner Williams, que es la ecuación empírica más utilizada. Finalmente la ecuación más
representativa del segundo grupo es la ecuación de Darcy-Weisbach desarrollada por Henry
Darcy (1803-1858) y Julius Weisbach (1806 -1871). Ambas ecuaciones han sido ampliamente
utilizadas en el diseño de redes de distribución de agua potable; sin embargo, la primera
(Hazen-Williams) al ser una ecuación explícita para la velocidad y el caudal, presentaba una
solución rápida y sencilla pero con límites de aplicabilidad en contraste con la ecuación de
Darcy-Weisbach que es una ecuación implícita y requiere de iteraciones o un método
numérico para su solución pero aplicable para cualquier condición de flujo (Uribe, 2012).
2.2 ECUACIÓN DE HAZEN Y WILLIAMS
Ecuación empírica desarrollada por Allan Hazen y Gardner Williams a principios de 1900.
Esta ecuación tuvo la peculiaridad de no tener en cuenta los análisis hidráulicos de la ecuación
de Darcy –Weisbach, ya que se basó en análisis estadísticos de diferentes redes de
distribución con materiales que no fueron ni muy lisos, ni muy rugosos. La forma original de
la ecuación se muestra a continuación en el sistema internacional de unidades (Uribe, 2012).
ECUACIÓN 2 ECUACIÓN DE HAZEN-WILLIAMS
donde:
v= Velocidad del flujo
R= Radio hidráulico (Área/ Perímetro mojado de la tubería)
S= Pendiente de la línea de gradiente de energía.
C= Coeficiente de Hazen-Williams (adimensional).
Es importante resaltar que el 0.849 es una contante utilizada y puede ser cambiada a 1.318
para el Sistema Inglés de Unidades (Liou, 1998).
Esta ecuación es de rápida solución y es explícita para la velocidad del flujo, lo que la hacía
extremadamente útil para diseñar antes de la llegada de los medios de cálculo
computacionales.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
5
Estos estudios fueron realizados principalmente para adaptar la ecuación de Chézy a sistemas
de distribución en vez de su uso en sistemas basados en canales. La ecuación de Chézy se
muestra a continuación.
ECUACIÓN 3 ECUACIÓN DE CHÉZY.
En la ecuación de Chézy, el cálculo del factor de fricción depende del radio hidráulico,
rugosidad (Coeficiente de Chézy) y pendiente de fricción del canal. Es importante resaltar que
esta ecuación fue la más utilizada para el cálculo de la velocidad en tuberías para el año de
1903 (Uribe, 2012).
En su momento, Gardner Williams y Allan Hazen publicaron una serie de valores de C
(coeficiente de Hazen-Williams) para diversos materiales. De tal forma que era posible
calcular la velocidad (comprobación de diseño), las pérdidas por fricción (en caso de que se
tuviera una tubería con diámetro establecido) o el diámetro con el que se quisiera diseñar la
tubería.
Los coeficientes definidos por Hazen-Williams, aplicaban solo para las condiciones “comunes
o normales de la práctica” por lo que desde su misma creación, esta ecuación contaba con
limitaciones que debían ser tenidas en cuenta a la hora de realizar los diseños de RDAP.
Las limitaciones establecidas por los creadores son:
-Solo es aplicable para agua
-Debe estar en condiciones normales (cercanas a 20 grados centígrados)
-Velocidades inferiores a
-Diámetros superiores a 75 mm o 3 pulgadas.
Así mismo, resulta necesario resaltar que estos coeficientes no son constantes, ya que como se
explica en la literatura y por los mismos Gardner Williams y Allan Hazen, pueden variar por la
edad de la tubería (aumento de la rugosidad) o cuando los diámetros de la tubería son
demasiado pequeños. Estos coeficientes son representados en la actualidad con valores entre
80 y 150, donde 80 es un material rugoso y 150 para un material especialmente liso (PVC o
PEAD) (Uribe, 2012).
2.3 ECUACIÓN DE DARCY-WEISBACH
La ecuación de Darcy-Weisbach es la ecuación físicamente basada más utilizada para diseños
de RDAP, redes pluviales y de alcantarillado. Esta ecuación fue inicialmente desarrollada por

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
6
Henry Darcy (1803-1858) mediante el uso de experimentos de flujo en tuberías, realizados
cerca a París (Saldarriaga, 2007).
Los experimentos se llevaron a cabo utilizando un rango de diámetros que iba desde los 12
mm (0.0122 m) hasta los 500 mm (0.5 m), y los materiales utilizados para la experimentación
incluían vidrio, hierro, plomo, hierro recubierto con bitumen, hierro fundido y latón. Para los
experimentos se incluyeron tuberías con paredes recién construidas y tuberías con cierto
tiempo de ser utilizadas, llevando a resultados con velocidades ente 0.03 y
. Los caudales
fueron medidos con tanques de aforo y las longitudes de las tuberías siempre fueron
superiores a los 100 metros (excepción de vidrio y plomo que tuvieron tramos más cortos).
(Saldarriaga, 2007)
A partir de los resultados obtenidos, Henry Darcy concluyó que estos podían ser expresados
mediante la siguiente ecuación:
ECUACIÓN 4 ECUACIÓN DE DARCY
Donde:
R= Radio Hidráulico de la tubería.
= Pendiente de Fricción.
v= Velocidad media dentro de la tubería.
= Coeficientes que describen la edad y el material de la tubería.
De sus experimentos y trabajos llego a la siguiente expresión:
ECUACIÓN 5 ECUACIÓN DE DARCY FORMA 2.
Donde:
Q= caudal
d= diámetro de la tubería.
Esta ecuación fue utilizada posteriormente por Fanning (1837-1911) para combinarla junto
con la ecuación desarrollada por Julius Weisbach (1806-1871), formando una ecuación
físicamente basada que se ajustaba de gran forma a los diferentes datos experimentales
(Saldarriaga, 2007).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
7
Julius Weisbach, desarrolló una ecuación que ayudaría a predecir las pérdidas por fricción
dentro de las tuberías. Esta ecuación requería estar en función del tipo de fluido, el diámetro,
el material de la tubería y la velocidad así como un factor de fricción. Así llego a la siguiente
expresión:
ECUACIÓN 6 ECUACIÓN DE DARCY-WEISBACH MODERNA.
donde:
l= Longitud de la tubería.
f= Factor de fricción adimensional.
Esta ecuación incluyó únicamente las pérdidas por fricción con las paredes de la tubería. La
ecuación anterior puede ser obtenida, así mismo, mediante análisis dimensional considerando
los principales elementos físicos que influyen en el movimiento del fluido en una tubería
(Uribe, 2012).
Sin embargo, la obtención del factor de fricción presentaba un problema complejo, en primera
instancia por que dependía del tipo de flujo que se podía presentar (flujo laminar o flujo
turbulento) y porque en caso de presentarse flujo turbulento se requería de un método
implícito para determinarlo, por lo que se desarrollaron diferentes ecuaciones para su
obtención. Una de ellas fue la ecuación para el flujo laminar de Hagen-Poiseuille que Julius
Weisbach utilizó (Uribe, 2012).
ECUACIÓN 7 ECUACIÓN DE HAGEN-POISEUILLE.
donde:
Re= Número de Reynolds en flujo laminar (2000 o menores en tramos de tuberías).
Sin embargo, estas condiciones raramente se presentaban en las RDAP, por lo que se
requerían ecuaciones adicionales para hallar el factor de fricción en flujos turbulentos
hidráulicamente rugosos y lisos (Uribe, 2012).
En 1911 Blasius, alumno de Prandl von Karman (Saldarriaga, 2007), desarrolló una ecuación
mediante experimentos empíricos para hallar el factor de fricción en flujos con números de
Reynolds entre (5000-100000). La ecuación a la que llegó fue (Uribe, 2012):

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
8
ECUACIÓN 8 ECUACIÓN DE BLASIUS.
Por su parte, Prandl desarrolló una ecuación para hallar el factor de fricción, pero dada su
complejidad de solución, el buen cumplimiento de la ecuación de Blasius y el hecho de que la
ecuación de Colebrook-White aplica para todos los flujos, esta ecuación no fue ampliamente
utilizada.
ECUACIÓN 9 ECUACIÓN DE PRANDL.
Más adelante, se desarrollaron los trabajos de los Ingenieros Johann Nikuradse y de Lewis
Moody. El primero de ellos realizó diversos experimentos para diferentes diámetros, con el
ánimo de entender la naturaleza del factor de fricción, variando el caudal, de tal forma que
incluyera un rango importante de números de Reynolds y abarcara los 4 tipos de flujo (Flujo
Laminar, Flujo Transicional, Flujo Turbulento Hidráulicamente Liso (FTHL) y Flujo
Turbulento Hidráulicamente Rugoso (FTHR)) (Saldarriaga, 2007).
De los experimentos realizados logró concluir:
Cuando el número de Reynolds es inferior a 2000, el factor de fricción es
independiente de la rugosidad relativa de la tubería
.
Al entrar en el flujo Liso, tanto el número de Reynolds como la rugosidad relativa de la
tubería juegan un papel fundamental dentro del cálculo del factor de fricción.
Finalmente, a medida que se aumentan los números de Reynolds, Nikuradse notó que
las curvas en su gráfica se volvían prácticamente horizontales, llevando a que el factor
de fricción dejara de ser una función del número de Reynolds y pasara a ser
únicamente una función de la rugosidad relativa de la tubería, en otras palabras el
numero de Reynolds deja de ser un factor importante para la obtención del factor de
fricción.
Prosiguiendo su investigación, Moody en 1940, avanzó en la determinación de las pérdidas
por fricción en tuberías con rugosidades reales y no artificiales. Desarrolló un trabajo,
combinando el trabajo del ingeniero alemán y de Colebrook (Saldarriaga, 2007). De sus
investigaciones, los resultados más destacables son:
Para el flujo hidráulicamente rugoso, el factor de fricción dependía exclusivamente de
la rugosidad relativa de la tubería.
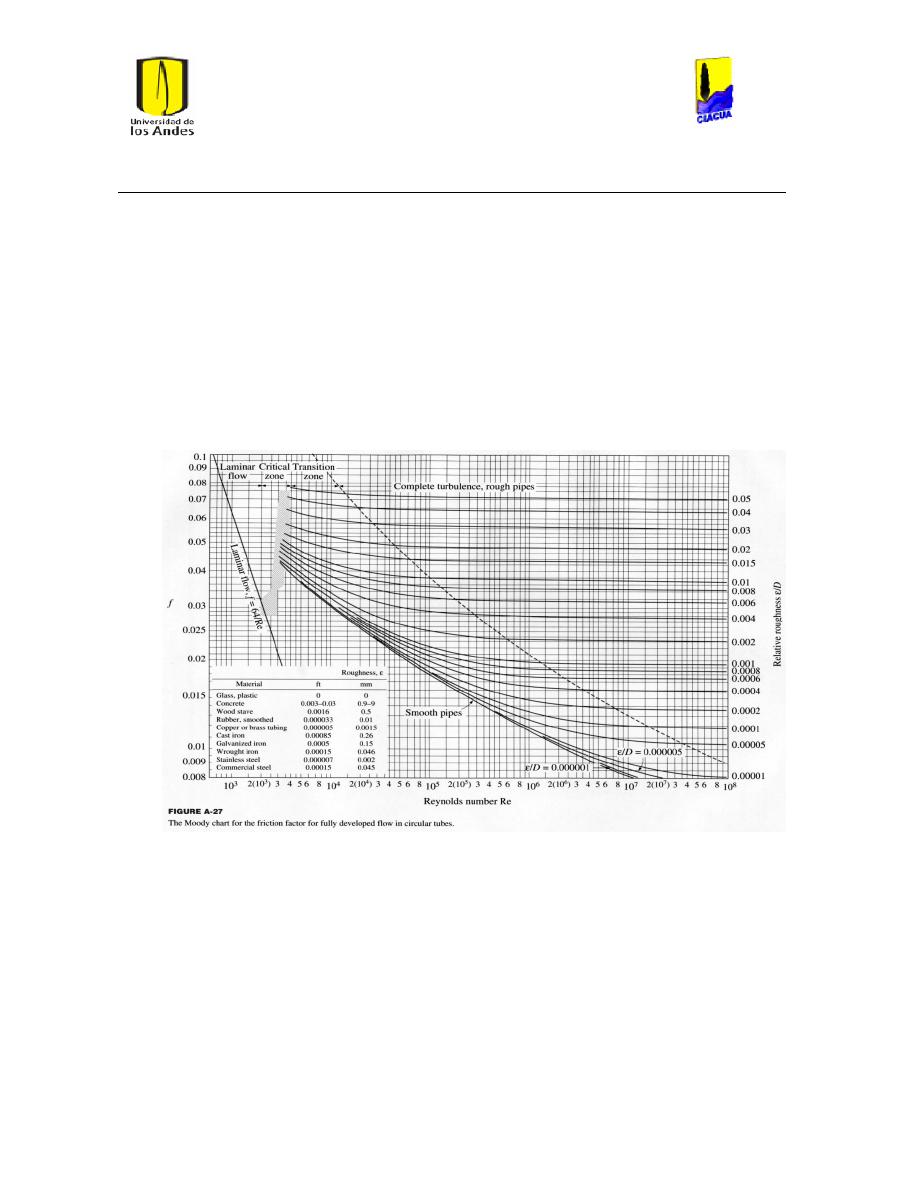
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
9
Con lo anterior Moody, amplió su experimento y mediante la adquisición de tuberías
de diferentes materiales y diámetros comerciales el factor de fricción (sólo para
FTHR). Con estos resultados encontró la rugosidad relativa y con esta y la gráfica de
factor de fricción vs Rugosidad relativa, pudo determinar las diferentes rugosidades
absolutas de las tuberías (Saldarriaga, 2007).
Con esto Moody llegó a la conclusión que para cada tipo de material, había una
rugosidad asociada y que esta representaba el comportamiento hidráulico de cada una
de las tuberías.
Con toda la información y la ecuación de Colebrook, Moody pudo desarrollar un
diagrama donde se podía ver el tipo de flujo y determinar el factor de fricción para
diferentes tuberías comerciales (ver Ilustración 1).
GRÁFICA 1 DIAGRAMA DE MOODY.
Esta gráfica fue ampliamente utilizada antes de la aparición de los métodos computacionales
ya que como se verá más adelante, encontrar el factor de fricción matemáticamente era de
una complejidad importante para la época.
Para el flujo hidráulicamente rugoso, las investigaciones de Colebrook y White en 1939,
utilizando las investigaciones de Prandl, von Karman y Nikuradse, permitieron establecer una
ecuación para hallar el factor de fricción para el flujo de transición. Ellos notaron sin embargo,
que los resultados encontrados solo representaban los extremos, y decidieron que el
comportamiento en tuberías reales debería de estar descrito por una única ecuación
(Saldarriaga, 2007), llegando a obtener:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
10
ECUACIÓN 10 ECUACIÓN DE COLEBROOK-WHITE PARA TODO EL RANGO DE FLUJO TURBULENTO.
Esta última ecuación aplica para todos los tipos de flujo turbulento (para los laminares se
utiliza la Ecuación 2.1.2-3). Sin embargo y como se mencionó anteriormente, esta es una
ecuación de difícil solución si no se cuenta con un método computacional o una calculadora,
por 2 motivos:
-El logaritmo incluido es de difícil solución manual.
-Es una ecuación implícita para despejar el factor de fricción.
Posteriormente, Swamee y Jain desarrollarían en 1976 otra ecuación para el cálculo del factor
de fricción, de tal forma que fuera más simple y fácil de resolver. La ecuación a la que llegaron
fue:
ECUACIÓN 11 ECUACIÓN DE SWAMEE.
Como se puede observar, esta ecuación es explícita y no requiere de métodos numéricos para
su solución. Sin embargo tiene rangos de cumplimiento para rugosidad relativa y números de
Reynolds (Liou, 1998).
La gran ventaja es que sus rangos de cumplimiento solo presenta un error máximo del 5%
con respecto a la ecuación de Colebrook-White.
2.4 ANTECEDENTES HISTÓRICOS
Varios investigadores han realizado trabajos para estudiar ambas ecuaciones de diseño. En
1998 Chyr Pyng Liou publicó un trabajo en el cual demostró las falencias y rangos de validez
de la ecuación de Hazen-Williams, así como la alta variabilidad de su coeficiente respecto al
número de Reynolds, su diámetro y su rugosidad relativa (Uribe, 2012).
Liou empezó su trabajo relacionando el coeficiente de Hazen-Williams con la ecuación
físicamente basada de Darcy-Weisbach. Primero, reorganizó la ecuación de tal forma que la

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
11
pendiente del gradiente hidráulico quedara expresada en términos de la altura de velocidad
. Al realizar esto, dejaba la velocidad expresada en el lado derecho como un denominador
elevado a la 0.1841 (Liou, 1998) . Luego, al introducir la viscosidad cinemática *
es
combinada con
para formar el número de Reynolds elevado a la 0.1841.
Posteriormente, expresó el radio hidráulico como
, combinando esto con
,
resultaba en el diámetro elevado a la 1.0185. Luego siendo ε la rugosidad absoluta de la
tubería, Liou dividió el diámetro encontrado en el paso anterior de tal forma que este quedara
, y reescribirlo para obtener la expresión
Finalmente, expresando
la pendiente como
, manipuló la ecuación expresándola de esta forma (Uribe, 2012):
ECUACIÓN 12 ECUACIÓN MODIFICADA DE LIU.
Luego, reemplazando el lado derecho de la ecuación de Hazen-Williams con la ecuación de
Darcy – Weisbach se obtiene:
ECUACIÓN 13 ECUACIÓN QUE RELACIONA EL COEFICIENTE DE HAZEN-WILLIAMS Y EL FACTOR DE
FRICCIÓN.
donde:
C: Coeficiente adimensional de Hazen-Williams.
R: Número de Reynolds
ε= Rugosidad absoluta del material
v= Diámetro de la tubería
ν= Viscosidad cinemática.
Al llegar a esta expresión Liou pudo concluir que en efecto, el coeficiente de Hazen-Williams
es dependiente del número de Reynolds, de la rugosidad relativa de la tubería
, de la
rugosidad absoluta y de la viscosidad cinemática (ν) así como del factor de fricción de la
ecuación de Darcy, convirtiendo a la ecuación de Hazen-Williams en un caso específico de la
ecuación de Darcy-Weisbach.
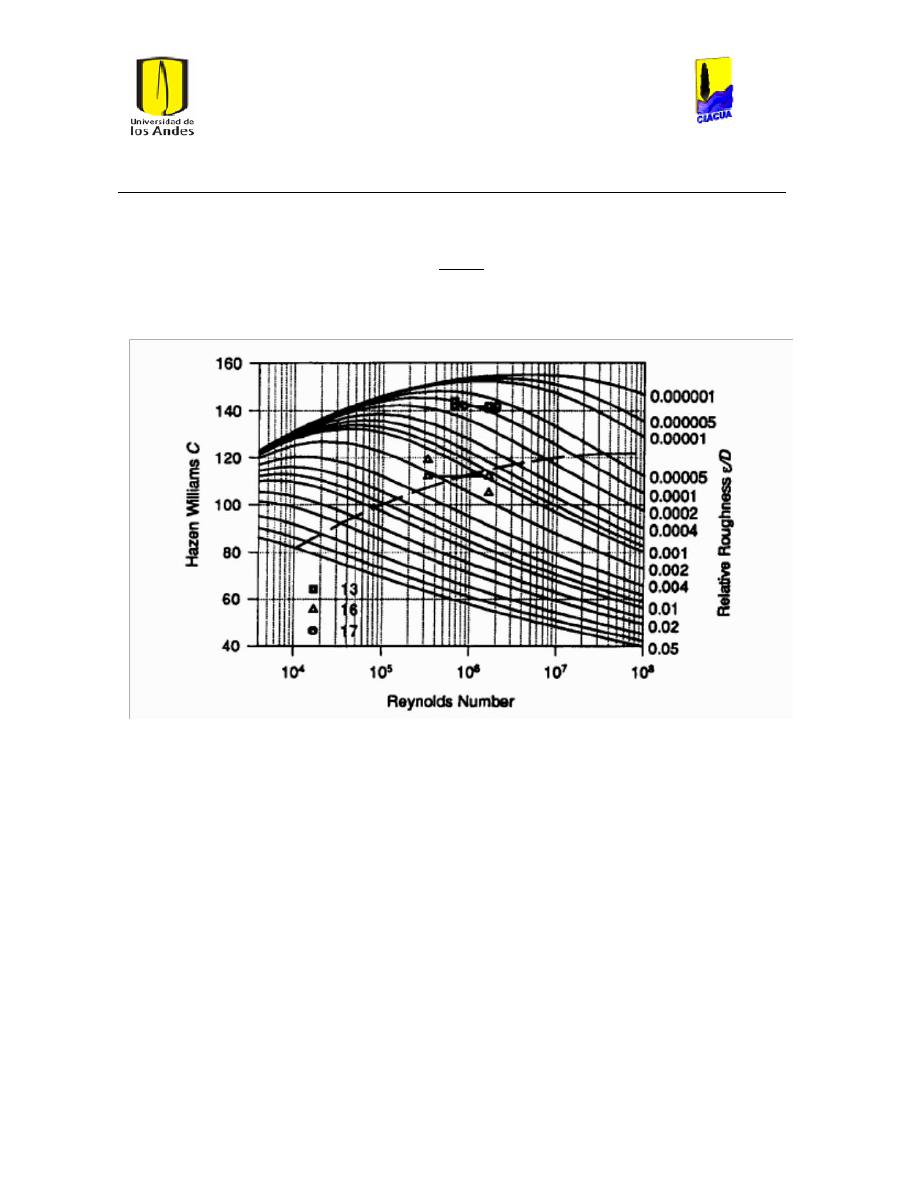
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
12
Posteriormente, Liou varió los números de Reynolds y los diámetros para ver cómo se
comportaban los coeficientes de Hazen-Williams, dejando una rugosidad absoluta de 0.0003
m y una viscosidad cinemática de
(agua a 15.56 grados centígrados) (Liou,
1998). Generó la siguiente gráfica que muestra la variación del coeficiente de Hazen–Williams
con respecto al diámetro y al número de Reynolds.
GRÁFICA 2 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS CON RESPECTO AL NÚMERO DE
REYNOLDS Y EL DIÁMETRO ENCONTRADO POR LIOU (LIOU, 1998).
Como se puede observar, el coeficiente de Hazen y Williams varía relativamente poco en la
zona de transición, pero presenta cambios severos fuera de esta (Línea punteada). Esto
permitió establecer que la ecuación de Hazen-Williams tiene unos rangos de cumplimiento
limitados y fuertemente dependientes del número de Reynolds y del diámetro (Uribe, 2012).
Para finalizar, Liou decidió mostrar los errores que se pueden cometer al calcular el error de
la pendiente de gradiente hidráulico con la ecuación de Hazen-Williams y comparándolos con
la pendiente calculada con la ecuación de Darcy-Weisbach. Los resultados que obtuvo fueron
de gran importancia, no solo debido a que por fuera de la zona de cumplimiento la ecuación
de Hazen-Williams presentaba un error de hasta el 40% sino porque su rango de validez se
limitaba exclusivamente a la zona de transición en el diagrama de Moody (Uribe, 2012).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
13
Ese mismo año, Hosam El-Din Moghazi (M.Moghazi, 1998), realizó experimentos para
determinar el coeficiente de Hazen-Williams para tuberías de Polietileno, encontrando una
vez más que el coeficiente de Hazen-Williams presentaba variaciones con respecto a su
diámetro y también que al realizar un cálculo entre el factor de fricción medido y el calculado
(por el investigador) se encontraba un error no superior al 14%. Sin embargo, al comparar los
valores calculados por el autor y los calculados por los valores recomendados, estos
presentaron diferencias en el cálculo de las pérdidas por ficción con un máximo del 27%
(Uribe, 2012).
En el año 2000, surge una discusión respecto al artículo de Liou (Liou, 1998). Los tres autores
participantes concluyen que el uso de la ecuación de Hazen-Williams debe de ser limitado o
abandonado. En la primera parte, Christensen concuerda con Liou en el sentido de que se
debe dejar de utilizar la ecuación de Hazen-Williams con excepción de la zona dentro del
rango de validez (Uribe, 2012).
Christensen plantea que los rangos de valides de la ecuación de Hazen-Williams deben de ser:
donde:
R es el número de Reynolds.
A su vez, especificó que esta no es la única limitación y que además, la ecuación debe estar
regulada igualmente por el diámetro de la tubería, estableciendo que el diámetro mínimo
debe estar regulado por donde ε es la rugosidad absoluta de la tubería.
Resaltando que es posible que en tuberías de considerable edad, se pueden presentar valores
de ε cercanos a 1 mm, lo que llevaría a que el diámetro mínimo de la tubería fuera de 1.44 m
(B.A. Christensen, 2000).
Concluyen y resaltan que en la actualidad muchos ingenieros y diseñadores no tienen en
cuenta las restricciones y están diseñando por fuera del número de Reynolds reglamentario y
con diámetros muchos menores a los que se deberían utilizar (Uribe, 2012).
El segundo autor Frederick Locher, concuerda con Liou en que el uso de la ecuación de Hazen-
Williams debe de ser abandonado o solo aplicado en sus rangos de cumplimiento, pero
plantea que Liou a la hora de realizar sus cálculos, no debe de introducir una dependencia de
la rugosidad absoluta, ya que esto obscurece la verdadera naturaleza de la ecuación de Hazen-
Williams. Resalta Locher que se debe analizar tal y cómo lo realizó Diskin en 1960, que se
debe relacionar el factor de fricción, el C de Hazen-Williams, Reynolds y la rugosidad relativa,
sin la introducción artificial de la rugosidad absoluta (Uribe, 2012). De tal forma que quede:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
14
ECUACIÓN 14 ECUACIÓN FINAL QUE DESCRIBE LA RELACIÓN ENTRE F DE DARCY Y COEFICIENTE DE
HAZEN-WILLIAMS.
Y teniendo en cuenta que para la ecuación de Hazen-Williams el único fluido válido es el agua,
Locher establece que se puede usar un
, llegando a que para un diámetro
establecido y una rugosidad absoluta de material, surge una constante que representa estos
dos parámetros. De esta manera, concluye que los coeficientes de Hazen-Williams sean
graficados como líneas rectas en el diagrama de Moody (B.A. Christensen, 2000), como se
muestra a continuación:
GRÁFICA 3 DIAGRAMA DE MOODY REALIZADO POR DISKIN 1960 DONDE SE MUESTRAN
VARIACIONES Y REPRESENTACIONES DE LOS COEFICIENTES DE HAZEN-WILLIAMS(CHRISTENSEN,
LOCHER, & SWAMEE, 2000)
De acuerdo con Locher, el trabajo de Diskin permite llegar a las siguientes conclusiones:
1) Los datos estadísticos utilizados para el desarrollo de la ecuación de Hazen-Williams
se encontraban en la zona de transición del diagrama de Moody. Esto lleva a que la

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
15
validez de esta ecuación se encuentre cuando la línea del Coeficiente de Hazen-
Williams se encuentre aproximadamente paralela con las curvas de la constante
en el diagrama de Moody (B.A. Christensen, 2000).
2) La ecuación de Hazen-Williams es inválida para materiales demasiado rugosos
(Cuando C es menor a 100, la ecuación no se debe utilizar), por lo que al diseñar con
valores cercanos o menores a 100 no solo se están encontrando resultados
equivocados en las pérdidas por fricción, sino que al suponer que es un valor
constante se comete el error de hacer al material más liso de lo que realmente
representa (B.A. Christensen, 2000).
Finalmente, Locher concluye que en la actualidad y con métodos computacionales es
inapropiado seguir utilizando una ecuación empírica y no una ecuación físicamente basada
que puede ser resuelta rápidamente por medios computacionales.
Para finalizar, el tercer autor Swamee, felicita a Liou por mostrar las falencias de la ecuación
de Hazen-Williams y considerando irónico que esta sea la ecuación más utilizada, mientras
que la ecuación de Darcy-Weisbach, físicamente basada, sea utilizada casi exclusivamente por
los académicos.
2.5 TRABAJOS DE FABIÁN BOMBARDELLI Y MARCELO GARCÍA
En 2003 Fabián A. Bombardelli y Marcelo H. García realizaron un estudio sobre los diseños de
redes con tuberías de gran diámetro. El caso de estudio utilizado por los autores fue el de una
zona de una metrópolis que a tan solo 5 años de haberse puesto en servicio, era inadecuada
para proveer la cantidad de agua necesaria (Uribe, 2012).
El análisis se realizó consultando la literatura con respecto a los límites y validez de la
ecuación de Hazen-Williams. Una vez realizada la recopilación bibliográfica, procedieron a
revisar la información sobre la red que presentó los problemas (Uribe, 2012).
Lo primero que lograron evidenciar fue que la red fue diseñada con concreto, con un
coeficiente de Hazen-Williams de 120, y con una variación de diámetros de hasta 2.29 m.
Como se mencionó anteriormente, en este caso se vio que una red de tan solo 5 años de
operación presentó problemas en cuanto a requerimientos de presión y al caudal entregado
por lo que se realizó un análisis hidráulico utilizando 2 firmas consultoras. Durante este
análisis se realizaron mediciones en las velocidades del flujo y las presiones en los nudos para
analizar el comportamiento real de la red frente al que se esperaba con el diseño original
(Fabián Bombardelli, 2003).
Con base a los resultados obtenidos, se procedió a obtener los valores de los coeficientes de
Hazen-Williams para los tramos de estudio. Los resultados que se obtuvieron de la primera
firma consultora fueron sorpresivos ya que en las tuberías de 2.29 m de diámetro se encontró
que el coeficiente de Hazen-Williams presentaba valores entre 85 y 95. Esto quería decir que

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
16
la tubería presentaba una rugosidad mucho mayor a la que se había esperado (se diseñó con
un coeficiente de Hazen-Williams de 120), lo que llevaba a que las pérdidas por fricción
fueran mucho mayores y que los cálculos realizados con la ecuación de Hazen-Williams
subestimaban estas pérdidas. Los autores concluyeron que si estos valores eran correctos, en
el futuro la red no podría suplir de forma correcta las crecientes demandas de agua, debido a
que las pérdidas por fricción iban a ser mucho mayores con los nuevos coeficientes (Fabián
Bombardelli, 2003).
Esta situación causó gran sorpresa en el personal y se plantearon si el problema era de la
ecuación de diseño (Hazen-Willams) o si era debido a un incremento real en la rugosidad de la
tubería, por lo que la comisión se enfocó en ver si las medidas que se habían tomado
presentaban algún tipo de error en la toma de los datos. Para verificar esta situación, se llamó
a una segunda firma consultora para tomar una segunda muestra de datos exclusivamente en
la tubería de 2.29 m de diámetro. Esta segunda muestra se realizó de forma más cuidadosa,
teniendo especial cuidado de registrar mejor las pérdidas y los lugares donde se tomaron las
muestras, es decir, el coeficiente de la tubería era menor (y por ende más rugoso) al
coeficiente utilizado para el diseño. Estos resultados mostraron resultados similares a los
encontrados en la primera toma de datos (Uribe, 2012).
Bombardelli y García, después de realizar sus análisis, llegaron a la conclusión de que tuberías
de gran diámetro presentaban un comportamiento bastante peculiar. De una parte, el hecho
de ser tuberías de gran tamaño en diámetro estaría más expuesto a flujos turbulentos que
estarían más relacionadas con altos números de Reynolds. Pero, de otra parte, dado el gran
diámetro, la relación entre
puede llegar a ser muy pequeña y por ende tener condiciones
de trabajo en flujo de transición, lo que llevaría a pensar que se presentan las condiciones
ideales para aplicar la ecuación de Hazen-Williams (Fabián Bombardelli, 2003). Sin embargo,
un análisis detenido de los datos, permitió identificar que era precisamente el constante
aumento de la demanda y por ende de los caudales, los que llevaron al flujo a la zona de Flujo
Turbulento, quitándole toda validez al diseño realizado con la ecuación de Hazen-Williams.
Con estos resultados se concluyó y recomendó que la mejor y más correcta opción era el uso
de la ecuación de Darcy-Weisbach para diseñar las redes de distribución de agua potable
(Uribe, 2012).
Lo interesante de esta investigación es que los autores lograron mostrar sus resultados
basándose en otras tuberías aisladas de la tubería estudiada en el caso de estudio específico.
Debido a que en el caso de estudio descrito por los autores, la tubería si había presentado un
cambio importante en su rugosidad debido a un incremento en la calidad del agua por las
condiciones de crecimiento de la población a la que era suministrada el servicio. La gráfica en
la que se muestran los resultados más significativos de esta investigación se muestra a
continuación:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
17
GRÁFICA 4 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS CON RESPECTO AL NÚMERO DE
REYNOLDS(FABIÁN A.BOMBARDELLI, 2003).
De la gráfica anterior se puede ver que al igual que en las investigaciones de Liou (Liou, 1998),
el coeficiente de Hazen-Williams presenta grandes variaciones al variar el número de
Reynolds; así mismo, se puede observar que esta variación puede llegar a ser de hasta una
magnitud de 60, lo que llevaría a que se estén subestimando o sobrestimando las pérdidas por
fricción en las tuberías. Lo más interesante de esta gráfica es que está en números de
Reynolds bastante altos, que suelen estar asociados a tuberías de gran diámetro y estas
tuberías suelen transportar la mayor cantidad del caudal (redes matriz); en consecuencia, las
redes operadas o diseñadas con la ecuación de Hazen-Williams corren el riesgo de dejar sin
abastecimientos a una población o a una gran ciudad.
2.6 INVESTIGACIONES POSTERIORES
En 2007 Quentin B. Travis y Larry W. Mays, desarrollaron una investigación en la que
reproducían una relación entre el coeficiente de Hazen-Williams y las rugosidades absolutas
en la ecuación de Colebrook-White, lo que permitió a los ingenieros sacar fácilmente los
valores de rugosidades absolutas y a visualizar de forma rápida y sencilla los límites de
aplicabilidad de la ecuación de Hazen-Williams (Quentin B. Travis, 2007).
Posteriores investigaciones como la de John D Valiantzas (2008) permitieron reescribir la
ecuación de Darcy-Weisbach de tal forma que fuera explícita en su solución y solo
presentando una diferencia con respecto a la ecuación original del 5% (Valiantzas, 2008).
Finalmente, en 2011 David Bennett y Rebecca Glaser publican un artículo donde enfatizan las
principales complicaciones que se presentan en los diseños de tuberías con grandes

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
18
diámetros, donde incluyen varios fenómenos físicos como sedimentos, efectos biológicos
dentro de las tuberías (biopelículas), no tener en cuenta el envejecimiento de las diversas
tuberías, mala ubicación de válvulas, mal mantenimiento de las tuberías y finalmente el
extensivo y más generalizado uso de la ecuación de Hazen-Williams al ser ampliamente
utilizada por fuera de los límites de cumplimiento o con Coeficientes de Hazen-Williams que
subestiman las pérdidas y llevan al incumplimiento de las presiones mínimas dentro de las
tuberías (Uribe, 2012).
2.7 PROGRAMAS UTILIZADOS
2.7.1 PROGRAMA REDES
El programa REDES fue desarrollado en la Universidad de los Andes por el grupo de
investigación CIACUA (Centro de Investigaciones en Acueductos y Alcantarillados) en el
Departamento de Ingeniería Civil y Ambiental. Es una herramienta computacional para la
simulación de redes de acueducto y tuberías a presión (Saldarriaga, 2007). Este programa ha
sido modificado y actualizado desde su nacimiento en 1998 hasta el presente año, por
numerosas tesis de pregrado, investigaciones y tesis de magíster, bajo la supervisión del
ingeniero Juan Guillermo Saldarriaga. Así mismo, el programa ha sido utilizado en numerosas
tesis de grado e investigaciones realizadas dentro del grupo de investigación CIACUA.
Las características que ofrece este programa para el usuario son:
- Permite al usuario utilizar dos (2) ecuaciones de diseño: Ecuación de Hazen-Williams y la
ecuación de Darcy-Weisbach.
-Edita o crea redes desde el comienzo, permitiendo al usuario ingresar nudos, bombas,
válvulas, tuberías, tanques y embalses. Adicionalmente, le permite al usuario escoger por
defecto la viscosidad con la que se desea trabajar, escoger el material de la tubería y si el
usuario lo desea, asignar los coeficientes de pérdidas menores y fugas dependiendo del tipo
de investigación que se desee (Uribe, 2012).
-Permite el cálculo hidráulico estático: Permite obtener alturas piezométricas, velocidades,
caudales, factores de fricción, pérdidas menores, pérdidas por fricción, pérdidas totales y las
presiones en cada nudo de la red utilizando el método del gradiente hidráulico.
- Realiza el cálculo hidráulico en período extendido: A diferencia del cálculo estático, esta
opción permite evaluar los resultados en una hora deseada del día, lo que permite ver el
comportamiento de la red durante el día y ver si cumple con los requerimientos deseados por
el usuario (Uribe, 2012).
-Genera el cálculo de calidad del agua
- Permite la calibración de redes de distribución de agua potable.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
19
-Diseño Optimizado: En esta sección hay diferentes opciones para diseñar, dentro de las que
se encuentran:
1) Diseño Rápido: Una solución rápida teniendo en cuenta un mínimo costo y cumplimiento
de la presión mínima.
2) Algoritmos Genéticos: Mediante la utilización de Algoritmos Genéticos, encuentra
soluciones óptimas locales para los diseños, cumpliendo los parámetros de costos e
hidráulicos establecidos por el usuario.
3) Superficie Óptima: Utiliza una superficie óptima de presiones asociadas con una función, ya
sea cuadrática, elipsoidal, catenaria, gaussiana, lineal y recíproca. Estas funciones cuentan con
una flecha que permite aproximar el diseño a una curva de LGH óptima. De las funciones
nombradas anteriormente, la función cuadrática es la que es comúnmente utilizada con una
flecha del 15 % (Criterio de I Pai wu).
4) Metodología SOGH: esta metodología fue utilizada durante la tesis y será explicada más
adelante con mayor detalle. Fue implementada en el programa REDES en 2009 por Susana
Ochoa en su tesis de Maestría.
5) Búsqueda de armonía.
El programa de REDES es compatible con los archivos .INP generados en el programa de
EPANET y con archivos propios .RED. Además de contar con una interfaz gráfica que permite
visualizar los resultados en 2D y 3D, y exportar los mismos a portapapeles y posteriormente a
Excel.
Los archivos .RED al igual que los archivos generados por el programa de EPANET, permiten
su modificación en Excel, de tal forma que el cambio de parámetros se haga de una forma
amistosa para el usuario. Esta es una gran ventaja que presentan los dos programas (EPANET
y REDES); dicha ventaja se ve reflejada en que es bastante sencillo pasar de un programa a
otro con rapidez, facilitando los análisis, los cálculos hidráulicos y las comparaciones de los
resultados.
2.7.2 PROGRAMA EPANET 2.0
El programa de EPANET, es una herramienta computacional desarrollada por la Agencia de
Protección Ambiental de los Estados Unidos de América (EPA). Este programa fue
desarrollado para estudiar el comportamiento hidráulico de una red de distribución de agua
potable (Saldarriaga, 2007).
El programa, dentro de sus múltiples funciones, incluye realizar el análisis hidráulico
utilizando las ecuaciones de Hazen-Williams, Darcy-Weisbach y Chezy-Manning.
Adicionalmente y al igual que el programa REDES, utiliza de la metodología del gradiente

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
20
hidráulico para la solución matemática de la red (a diferencia de otros programas que utilizan
el método de Hardy-Cross) (Uribe, 2012).
El programa cuenta adicionalmente con un módulo para seguir la calidad de las aguas en una
red, permitiendo al usuario seguir el decaimiento o comportamiento de una sustancia en una
red (Saldarriaga, 2007). Esto puede ser de gran importancia en el análisis de cloro residual en
redes, o el comportamiento de manganeso o hierro en los sistemas de distribución al salir de
las plantas de tratamiento. Esto lo realiza utilizando reacciones químicas del agua, o en las
paredes de la tubería y de los tanques. Para ello utiliza reacciones de primer orden (Uribe,
2012).
Además, el programa permite visualizar los resultados en tablas y gráficas y los archivos que
utiliza son compatibles para su modificación con Excel. Lo que lo convierte en un programa
amigable para el usuario (Uribe, 2012).
Al igual que el programa de REDES, EPANET también permite correr la hidráulica en estado
estable y en períodos extendidos (Uribe, 2012).
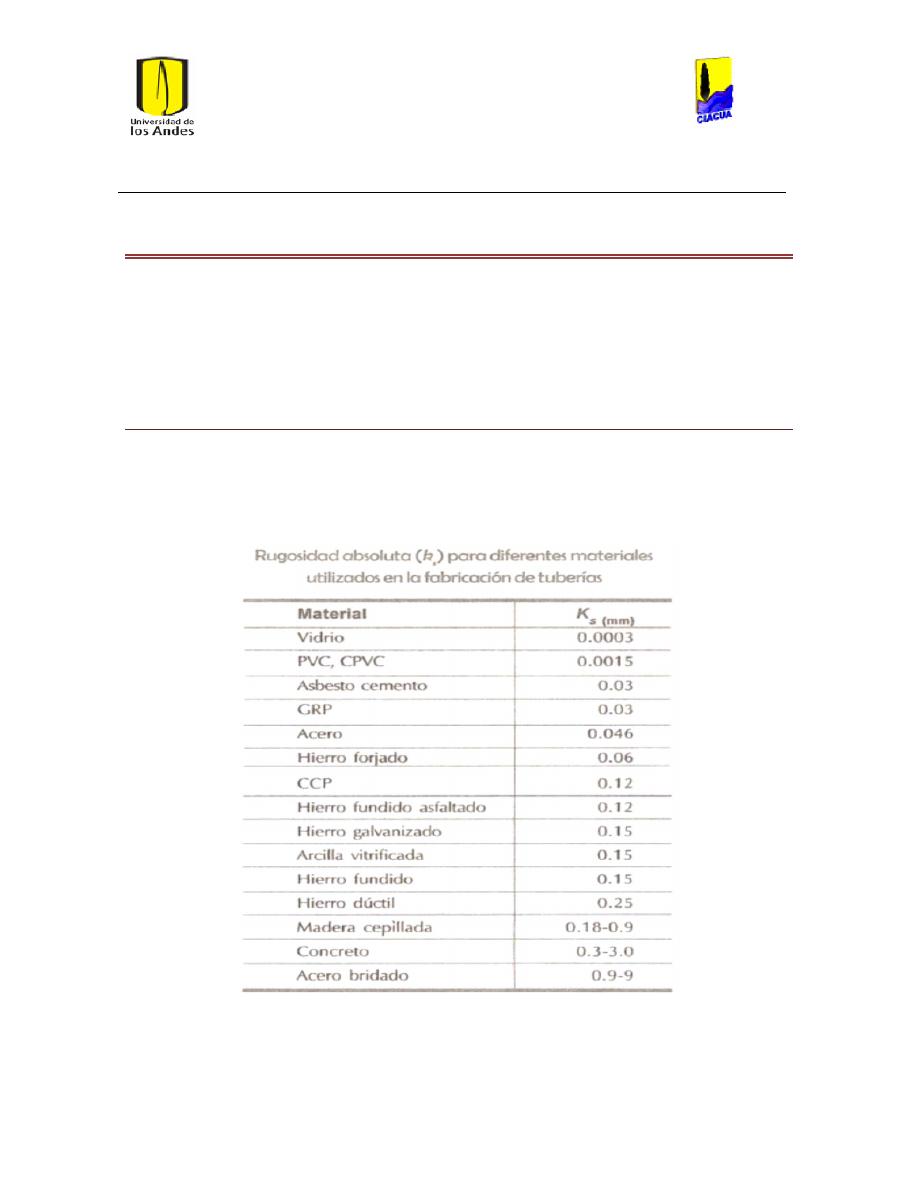
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
21
CAPÍTULO 3. METODOLOGÍA
En esta sección se presentarán los pasos de la investigación. Esto incluye las rugosidades
absolutas y coeficientes de Hazen-Williams utilizados durante la investigación, las redes
trabajadas con sus características más relevantes para el estudio. Posteriormente se
describirá el procedimiento realizado paso por paso y el enfoque que utilizó la investigación,
es decir, cuáles fueron los cálculos realizados para encontrar los resultados.
3.1 RUGOSIDADES ABSOLUTAS Y COEFICIENTES DE HAZEN-WILLIAMS
Los coeficientes de Hazen-Williams y rugosidades absolutas fueron consultados utilizando la
información de la literatura y de libros de hidráulica. Para la primera parte de este estudio se
trabajó esencialmente con Hierro Dúctil y con PVC. En la siguiente tabla se mostrarán las
rugosidades y respectivos Coeficientes de Hazen-Williams:
ILUSTRACIÓN 1 RUGOSIDADES ABSOLUTAS (SALDARRIAGA, 2007).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
22
RUGOSIDAD ABSOLUTA
MATERIAL
mm
HIERRO DÚCTIL
0.1
PVC
0.0015
TABLA 1 RUGOSIDADES ABSOLUTAS DE ACUERDO A LAS NORMAS TECNICAS DE EPM (EMPRESAS
PÚBLICAS DE MEDELLÍN, 2006-2009).
ILUSTRACIÓN 2 RUGOSIDADES ABSOLUTAS DE ACUERDO AL RAS (MINISTERIO DE DESARROLLO
ECONÓMICO, 2013)
Con base en estas tablas se decidió trabajar con una rugosidad absoluta del Hierro dúctil de
0.25 o 0.3 mm; sin embargo, algunos proveedores y el RAS (Reglamento de Agua y
Saneamiento) afirman que se debe tomar la rugosidad del recubrimiento de la tubería. Con
base en esto muchos proveedores recomiendan para sus productos rugosidad de tubería
nueva de 0.1 mm o incluso rugosidades extremadamente lisas como 0.003 mm (Saint-Gobain-
PAM).
A continuación se muestran los coeficientes de Hazen-Williams:
COEFICIENTES DE HAZEN-WILLIAMS
MATERIAL
COEFICENTE
HIERRO DÚCTIL
140-150
PVC
150
ILUSTRACIÓN 3 COEFICIENTES DE HAZEN-WILLIAMS DE ACUERDO A LAS NORMAS TÉCNICAS DE EPM
(EMPRESAS PÚBLICAS DE MEDELLÍN, 2006-2009).
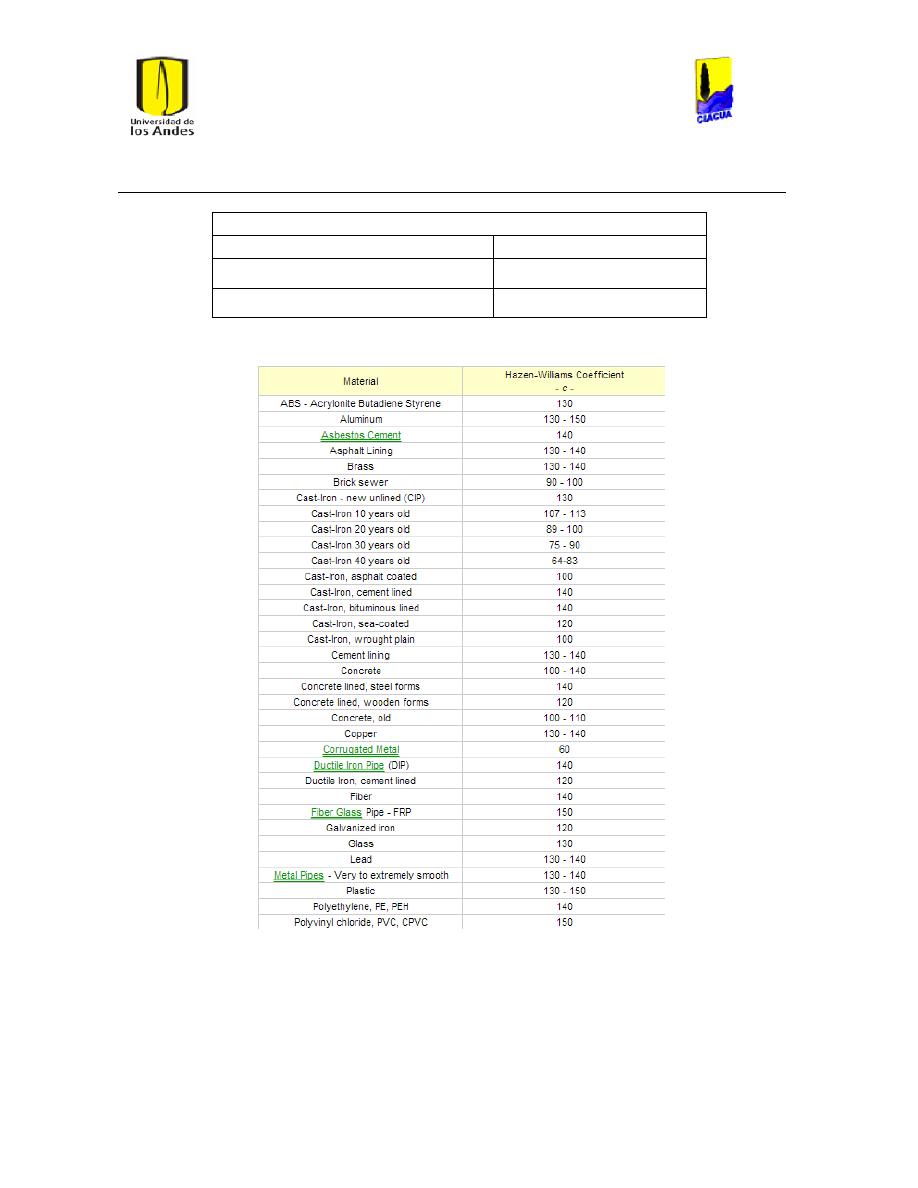
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
23
COEFICIENTES DE HAZEN-WILLIAMS
MATERIAL
COEFICENTE
HIERRO DÚCTIL
130
PVC
150
ILUSTRACIÓN 4 COEFCIENTES DE HAZEN-WILLIAMS DEL LIBRO HIDRÁULICA DE TUBERÍAS
(SALDARRIAGA, 2007).
ILUSTRACIÓN 5 DIFERENTES COEFICIENTES DE HAZEN-WILLIAMS.
Con base en estos valores, se decidió trabajar con los valores de PVC de 0.0015 mm para la
rugosidad absoluta y un coeficiente de Hazen-Williams de 150. Para el hierro dúctil se decidió
trabajar con un valor de 0.1 mm como rugosidad absoluta debido a que, si bien la literatura
sugiere valores entre 0.25 y 0.3 mm, los proveedores comerciales están sugiriendo valores
ente 0.003 mm y 0.15 mm, por lo que en este estudio se decidió trabajar con un valor de 0.1

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
24
mm. Por otro lado el Coeficiente de Hazen-Williams se tomó como 140, que es el valor
sugerido por la literatura, sino además porque el rango sugerido por los proveedores para
tuberías nuevas coincidía con estos valores (Tata Kubota) (AMIANTIT).
3.2 REDES TRABAJADAS:
Durante la tesis se trabajaron 4 redes de estudio. De las redes, dos (2) eran originalmente
redes matrices y las otras dos (2) fueron redes adaptadas, de tal forma que se comportaran
como redes matrices. Las cuatro redes se muestran a continuación:
3.2.1 RED MATRIZ DE BOGOTÁ:
ILUSTRACIÓN 6 RED MATRIZ DE BOGOTÁ.
La red matriz de Bogotá cuenta con las siguientes características:
2601 nudos de demanda
Demandas ente 1.4 y 400 L/s
4 Embalses ( Wiesner, El Dorado, Tibitóc y Tibitóc Alto)
15 Tanques distribuidos en la red.
Elevaciones de la red entre 2540 y 3000 metros.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
25
Longitud total de la red de 514000 metros de tuberías.
4480 tramos de tubería que incluyen valvular de operación.
Diámetros de las tuberías entre 101 mm y 2000 mm.
70 patrones de demanda distribuidos en diferentes sectores de la ciudad.
La red presentó grandes retos debido al gran número de tuberías que poseía así como
identificar las horas de caudal medio, máximo y mínimo de la red. Y dada la alta variabilidad
de diámetros, y propósitos de algunos tramos de tuberías, convirtió a esta red matriz en el
caso más complejo de estudio.
3.2.2 RED MATRIZ DE MEDELLÍN:
ILUSTRACIÓN 7 RED MATRIZ DE MEDELLÍN.
La red Matriz de Medellín cuenta con las siguientes características:
56 nudos de demanda.
Demandas de los nudos entre 10 y 916 L/s.
3 Embalses.
Elevaciones de la red entre 1350 y 1750 metros.
Longitud de la red es de 202000 metros de tuberías.
736 tramos de tuberías.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
26
Diámetros de las tuberías entre 152 mm y 1500 mm.
Para el caso de estudio la red se trabajó con un (1) solo patrón de demanda.
El propósito de tener tan pocos nudos de demandas es que ellos representarán los tanques
que distribuyen el agua a la ciudad de Medellín. Más adelante se explicará el por qué esto fue
tan importante para esta investigación.
3.2.3 RED GINEBRA LONGITUDES X 100 CAUDALES DEMANDADOS X10
ILUSTRACIÓN 8 RED GINEBRA.
La red de Ginebra incorporó una serie de modificaciones para comportarse como una red
matriz; esto se logró modificando las demandas de los nudos y longitudes de las tuberías en el
archivo .INP y posteriormente realizando un diseño simple con la ayuda del programa REDES.
Cuenta con las siguientes características:
368 nudos de demanda.
Demanda de los nudos entre 0.2 y 78 L/s.
3 embalses.
Las elevaciones de la red se encuentran entre 1026 y 1100 metros.
La longitud de la red es de 495500 metros de tuberías.
545 Tramos de tuberías.
Los diámetros de la red se encuentran entre 300 mm y 3000 mm.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
27
La red trabajó con 3 patrones de demanda.
Lo más resaltable de esta red es que la mayoría de los nudos se comportó con 1 solo patrón de
demanda, y aun los que no contaban con este patrón, tenían horas muy similares para el
cálculo de los caudales mínimos, máximos y medios de la red. Con la modificación de los
caudales y las distancias se logró obtener una red que presentaba un comportamiento similar
a una red primaria de bombeo o a una red matriz.
3.2.4 RED ANDALUCÍA CAUDALES X100
ILUSTRACIÓN 9 RED ANDALUCÍA.
La red de Andalucía también fue modificada de tal forma que presentara un comportamiento
similar al comportamiento de una red matriz; el procedimiento fue igual al que se explicó en
la red Ginebra con la excepción de que en esta red no fue necesaria la modificación de las
longitudes. Las características de esta red son expuestas a continuación:
293 nudos de demanda.
Caudales demandados se encuentran entre 0.12 y 91 L/s.
1 embalse.
elevaciones de la red se encuentran entre 916 y 961 metros.
La longitud de la red es de 48150 metros de tuberías.
Cuenta con 394 tramos de tuberías.
Los diámetros de la red se encuentran entre 300 mm y 3000 mm.
La red cuenta con 3 patrones de demanda, pero trabaja con un único patrón.
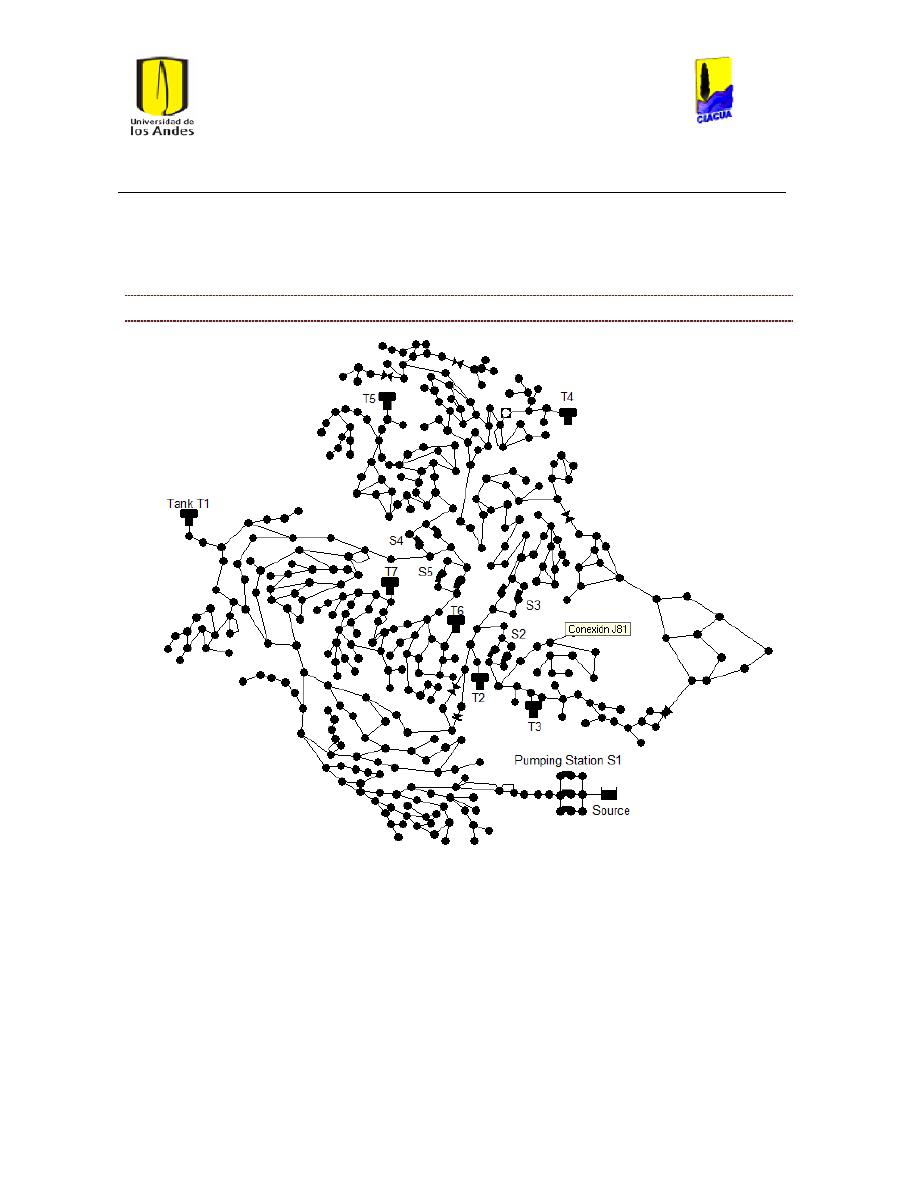
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
28
Esta red, pese a no tener tramos extremadamente largos de tuberías, con los caudales
demandados y las diferentes cotas de sus puntos, presentó el comportamiento de una red
matriz.
3.2.5 RED DTOWN
ILUSTRACIÓN 10 RED DE BOMBEO DTOWN.
La red Dtown fue la red escogida para estudiar el efecto hidráulico que genera la ecuación de
Hazen-Williams frente a la ecuación de Darcy-Weisbach. La red se escogió basándose en el
hecho de que es una red que cuenta con una seria de sectores que funcionan con bombas,
adicionalmente posee patrones en cada uno de los sectores y una diversidad importante de
tanques. Si bien no es una red que cuente con tuberías de gran diámetro, es una red de gran
interés por todas las características anteriormente nombradas. Las características de la red
son mostradas a continuación:
348 nudos de demanda

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
29
Caudales demandados entre 0.5 L/s y 6.3 L/s
1 embalse para alimentar el sistema
Elevaciones entre 0 y 105 metros.
La longitud total de la red es de 62316 metros de tuberías.
Cuenta con 454 tramos de tuberías.
Diámetros de la red entre 51 mm y 616 mm.
La red cuenta con 5 patrones, uno para cada sector.
La red cuenta con 11 bombas con sus respectivas curvas y eficiencias.
Esta red ha sido utilizada mundialmente para investigaciones y eventos internacionales como
lo es la “Batalla de Redes”. Esto último es una competencia internacional que busca analizar
las formas de optimizar una red existente de tal forma que se encuentre el menor costo y se
cumplan con todas las restricciones hidráulicas.
3.2.6 RED LA CUMBRE
ILUSTRACIÓN 11 RED LA CUMBRE.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
30
Esta red fue utilizada con el fin de ver si los resultados hidráulicos encontrados en las redes
trabajadas anteriormente se presentaban en esta red o si en la red se encontraba algún tipo de
fenómeno nuevo. Los resultados de esta red se enfocaron principalmente en ver los
desbalances de masa, factores de fricción de la red y solución de la hidráulica del sistema. Las
características de la red se muestran a continuación:
338 nudos de demanda.
Caudales demandados entre 0.3 L/s y 124 L/s (la mayoría de los caudales se
encuentran en 45 L/s).
1 embalse de alimentación para la red.
Elevaciones entre 823 y 1033 metros.
La longitud total de la red es de 266650 metros.
Cuenta con 378 tramos de tuberías.
Diámetros de la red entre 300 mm y 1800 mm (donde predominan los diámetros de
300 y 350 mm).
1 patrón de demanda para todos los nudos.
3.3 PROCEDIMIENTO
3.3.1 PROCEDIMIENTO DETALLADO
Esta tesis se enfocó inicialmente en el estudio de emisores que simularan tanques en puntos
estratégicos de la red, de tal forma que se pudieran analizar de manera detallada los efectos
hidráulicos que se podían presentar al utilizar la ecuación de Hazen-Williams frente a la
ecuación de Darcy-Weisbach.
A continuación se muestran los pasos que se realizaron:
1. Recopilación bibliográfica de artículos e información relacionada con la investigación,
incluidos diámetros, rugosidades, coeficientes y precedentes de la investigación.
2. Una vez se contaba con la información, se procedió a seleccionar las redes de trabajo,
para lo cual en algunos casos se modificaron redes de tal forma que estas presentaran
un comportamiento y características de una red primaria de bombeo o red matriz
(grandes diámetros).
3. Para el estudio de emisores se escogió el PVC y el Hierro Dúctil como los materiales
con los que se realizaría el primer análisis hidráulico, principalmente porque son
materiales comunes en el contexto colombiano.
4. Con base en esto, se analizaron los diámetros comerciales disponibles y se decidió que
para tuberías con diámetros menores a 14 pulgadas, el material de estas tuberías sería
PVC y para mayores, sería Hierro Dúctil.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
31
5. Utilizando los programas de REDES y EPANET 2.0 se analizó la hidráulica en periodo
extendido, de tal forma que se obtuvieran los datos hidráulicos necesarios.
6. Una vez realizados estos cambios en las redes, se procedió a realizar una comparación
inicial de las presiones de las redes en los 3 momentos claves; cuando se presentaba el
caudal mínimo, el caudal medio y el caudal máximo. Para ello fue necesario analizar
los patrones de demandas y determinar las horas del día en que se presentaban estos
caudales.
7. Se decidió cambiar algunos nudos de la red de tal forma que se comportaran como si
fueran tanques o tanques, con la característica de que no se quería que devolvieran el
agua en la red. Para ello se utilizaron emisores para simular el comportamiento de un
tanque.
8. Se volvió a correr la hidráulica de la red que utilizaba la ecuación de Hazen-Williams y
la que utilizaba la ecuación de Darcy-Weisbach, y se adquirían los caudales que
arrojaban los emisores en el periodo de análisis. Dado que los patrones de las redes
estaban configurados en 24 horas, el tiempo de cálculo hidráulico fue de 24 horas.
9. Se compararon los resultados de los 2 emisores, graficando simultáneamente el
comportamiento del emisor y comparando los resultados.
10. Los emisores iniciales se calcularon con base a la presión mínima exigida por el RAS
que es de 20 metros de columna de agua y la demanda base del emisor; sin embargo
después se decidió estudiar el comportamiento con caudales mayores de emisión por
lo que se asignaron altos coeficientes emisores a los diferentes emisores.
11. Así mismo, con las herramientas computacionales de EPANET y REDES se obtuvieron
los datos de los números de Reynolds, diámetros de la red, velocidades, factores de
fricción y caudales que circulaban por la red.
12. Con base en esto, se explican las diferencias o similitudes entre los resultados,
calculando los coeficientes de Hazen-Williams con base a la hidráulica de la ecuación
de Darcy-Weissbach. Esta fase de la investigación, será explicada con más detalle en la
sección de resultados.
13. Finalmente, se analizaron los resultados de las diferentes redes.
3.3.2 ADQUISICIÓN DE LA INFORMACIÓN
En esta sección se mostrará mediante imágenes el procedimiento realizado para la obtención
de la información:
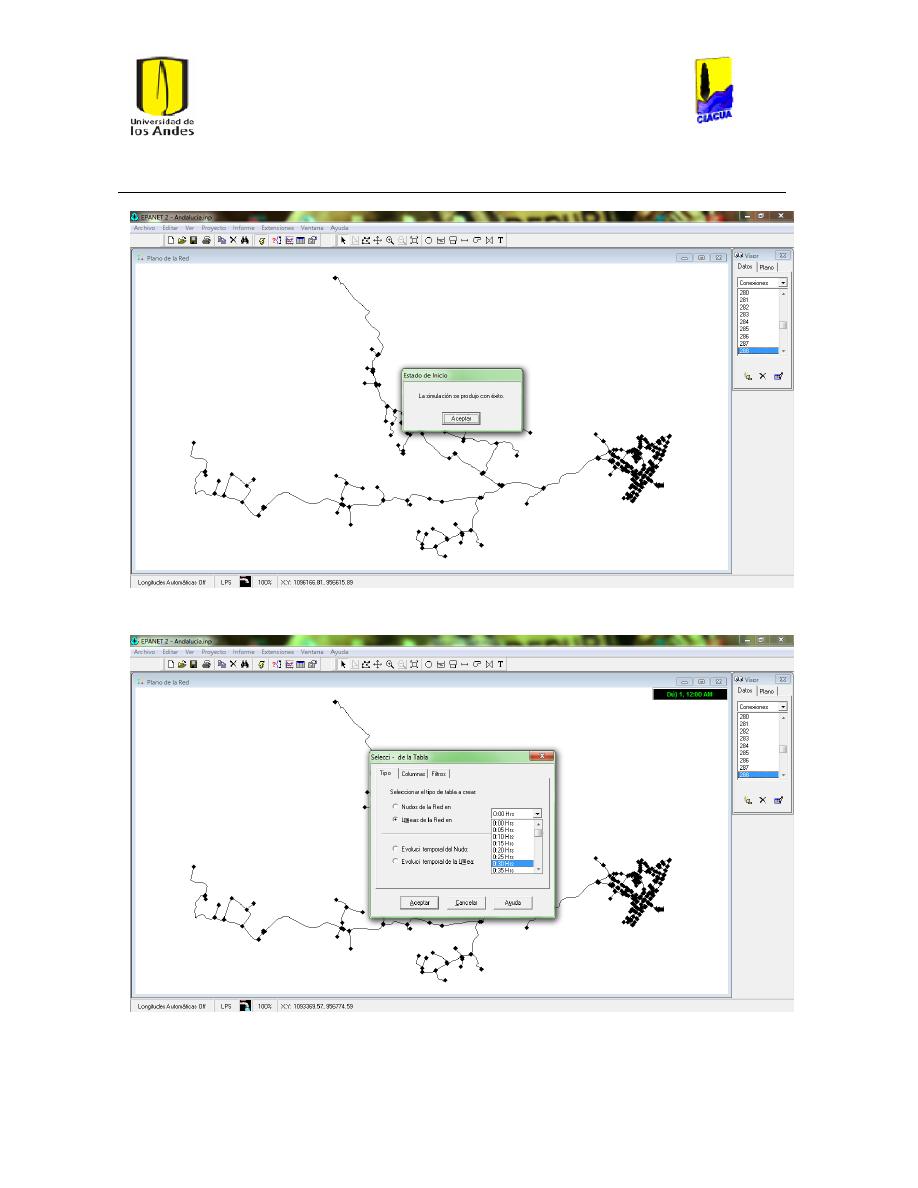
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
32
ILUSTRACIÓN 12 SE EJECUTA EL CÁLCULO HIDRÁULICO.
ILUSTRACIÓN 13 SE ESCOGE LA HORA EN LA QUE SE DESEAN OBETNER LOS DATOS DE LA TUBERÍA O
LOS NUDOS.
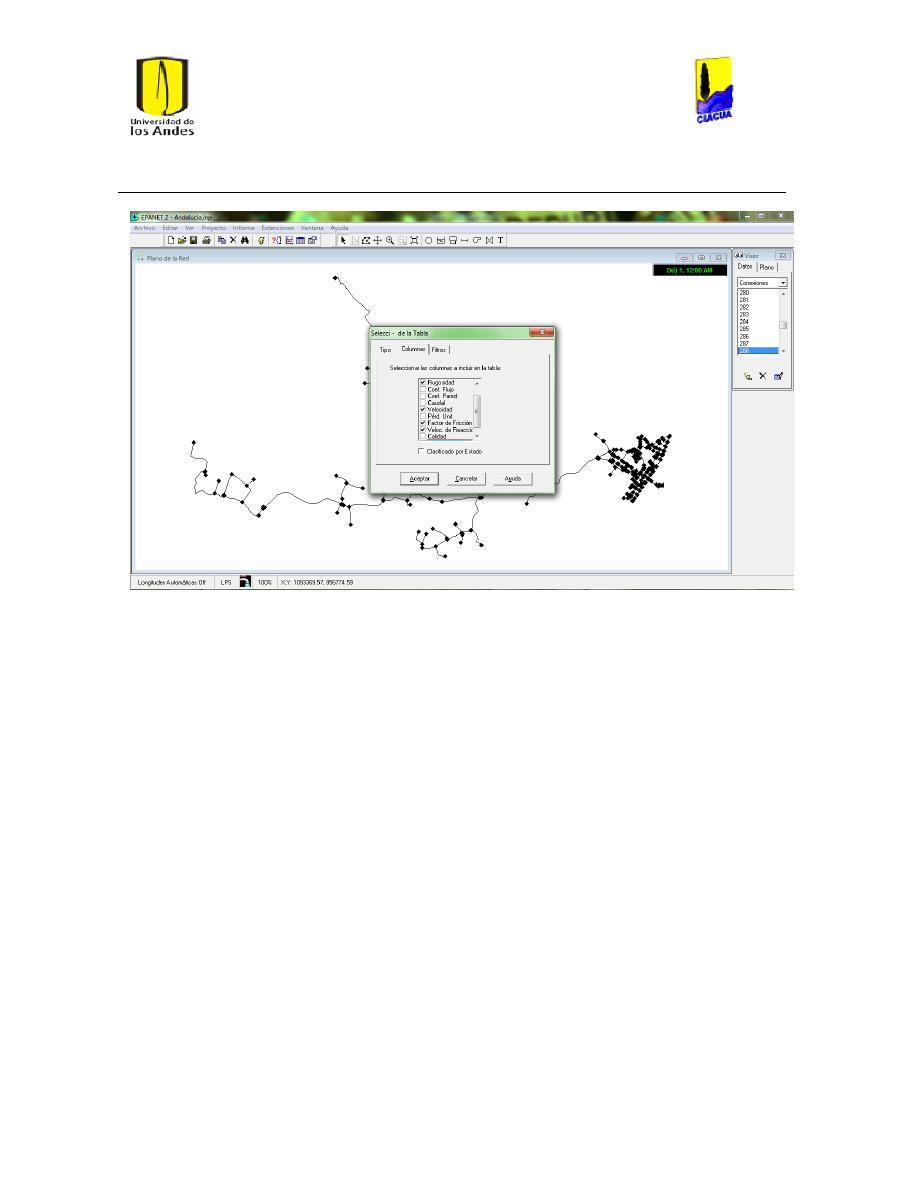
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
33
ILUSTRACIÓN 14 SE ELIGEN LOS PARÁMETROS RELEVANTES.
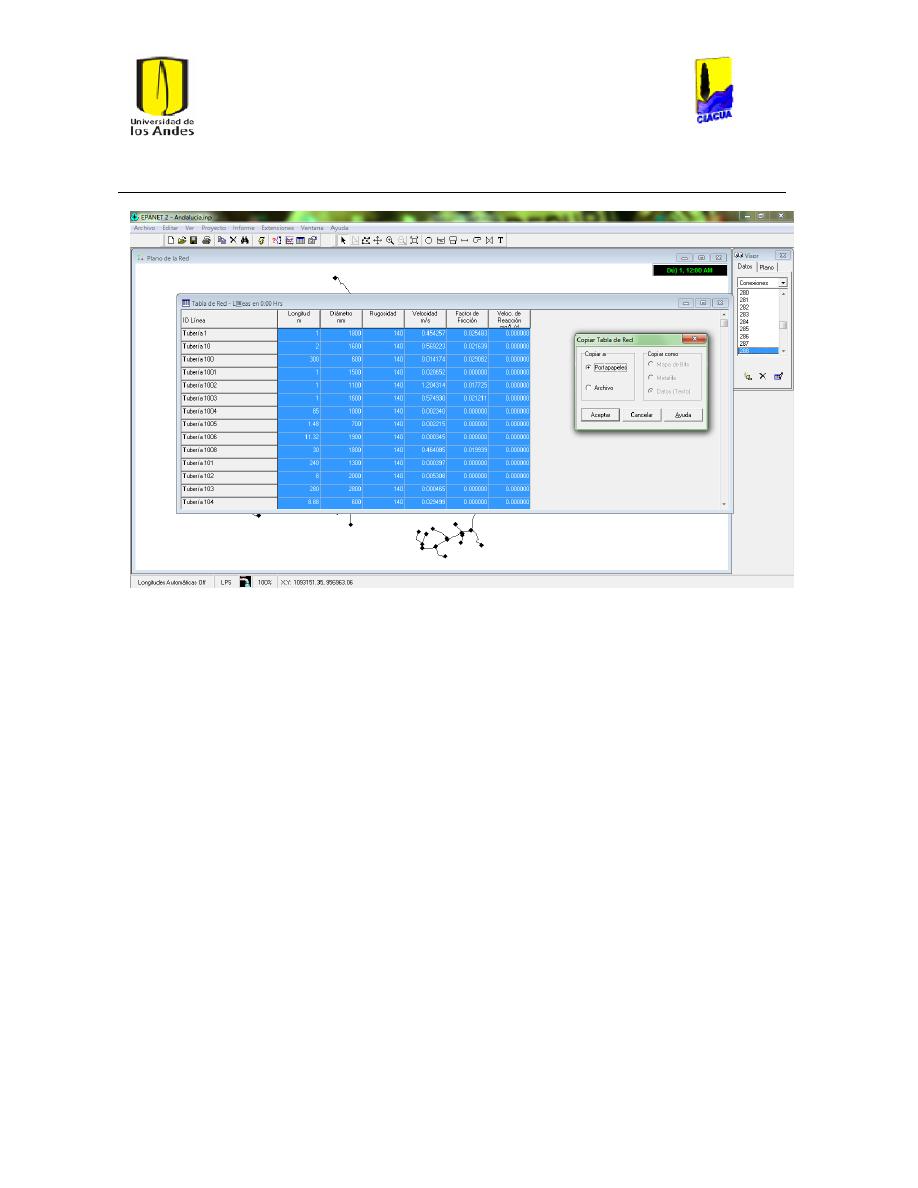
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
34
ILUSTRACIÓN 15 SE COPIAN LOS DATOS EN PORTAPAPELES Y SE PEGAN EN UN ARCHIVO DE EXCEL.
Como muestran las ilustraciones anteriores, el procedimiento para la adquisición de los datos
es muy sencillo. Lo anterior muestra el procedimiento realizado con EPANET. Se resalta
también que la adquisición de los datos, usando el programa REDES, es muy similar. El
procesamiento de los datos se realizó utilizando Microsoft EXCEL 2010.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
35
CAPÍTULO 4. RESULTADOS
En esta sección se mostrarán los principales resultados, así como los procedimientos
matemáticos que se utilizaron. Así mismo, se mostrarán los principales Patrones con los que
se definieron los períodos de caudal mínimo, medio y máximo.
Esta sección se encuentra dividida en 3 sub secciones. La primera presenta los cálculos
matemáticos para el procesamiento de la información obtenida utilizando EPANET o REDES.
La segunda parte expone los principales patrones en los que el autor se basó para tomar los
caudales mínimos, medios y máximos. Y finalmente, la tercera sección detalla los resultados
encontrados en esta investigación y realiza los análisis correspondientes.
4.1 CÁLCULOS MATEMÁTICOS
4.1.1 ECUACIÓN DE LOS EMISORES
Los emisores suelen ser mecanismos en los que se trabaja ya sea una fuga de una tubería o en
los que se puede determinar el caudal dejando fija una presión. En otras palabras, el caudal
que se emite o se extrae de un nudo es dependiente de la presión (en contraste con el
comportamiento de un nudo normal, donde la presión varia por diferentes condiciones y el
caudal que le llega es constante).
La ecuación de los emisores se muestra a continuación:
donde:
Q= Caudal del emisor
k= Coeficiente Emisor
H= Presión del emisor
x=Exponente emisor
Cabe resaltar que este exponente emisor oscila entre 0 y 1, donde 0 es un emisor perfecto, 1
es cuando el flujo se encuentra en régimen laminar y 0.5 cuando se tiene régimen turbulento.
Si bien, es posible que en algunos momentos del tiempo se obtenga flujo laminar en redes de
distribución de agua potable, dicho caso es bastante raro; por ende en esta tesis se trabajó con
un exponente emisor de 0.5.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
36
4.1.2 CÁLCULO DEL COEFICIENTE DE HAZEN-WILLIAMS
El procedimiento seguido para el cálculo del coeficiente de la ecuación de Hazen-Williams a
partir de los datos obtenidos corriendo la hidráulica con la ecuación de Darcy-Weisbach se
basó en la combinación de la ecuación de Darcy y la ecuación de Hazen-Williams. Este
procedimiento fue muy similar al realizado por Liou en 1998 (Liou, 1998). Dicho proceso se
muestra a continuación:
Se tiene la ecuación de Hazen-Williams.
Así mismo se tiene la ecuación de Darcy-Weisbach:
Contando con las relaciones:
es posible expresar la ecuación de Hazen-Williams de la siguiente forma:
Ahora ya se puede igualar la ecuación de Hazen-Williams con la ecuación de Darcy-Weisbach
y dividiendo por la viscosidad elevada a la 0.15 se obtiene la siguiente ecuación:
Al despejar el coeficiente de Hazen-Williams de esta ecuación se obtiene la ecuación que se
utilizó.
Donde:
f= Factor de fricción adimensional
d=Diámetro de la tubería (m)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
37
ν = Viscosidad cinemática
Re= Número de Reynolds adimensional.
4.1.3 CÁLCULO DE LA DIFERENCIAS DE PRESIÓN
Para calcular las diferencias de presión entre la red operada con la ecuación de Darcy-
Weisbach y la ecuación empírica de Hazen-Williams se utilizó el concepto de error relativo.
Es importante mencionar que para resultados donde las presiones eran bajas, los errores
relativos magnificaban las diferencias, generando valores porcentualmente muy altos y de
difícil interpretación; para estos casos se decidió utilizar el error absoluto.
Teniendo en cuenta que la ecuación que representa de mejor forma la hidráulica, es la
ecuación de Darcy-Weisbach, esta fue la que se utilizó para representar los resultados reales.
La ecuación por ende queda formulada de la siguiente forma:
donde:
Presión Hw= Presión corriendo la hidráulica con la ecuación de Hazen-Williams.
Presión Dw= Presión corriendo la hidráulica con la ecuación de Darcy-Weisbach.
El numerador de la ecuación el error absoluto de las presiones.
4.2 PATRONES DE LAS REDES TRABAJADAS
4.2.1 RED MATRIZ DE BOGOTÁ
En esta investigación, la red matriz de Bogotá es la que cuenta con mayor cantidad de
patrones. A partir del análisis realizados a estos patrones se determinaron los tiempos en que
se presentaban los caudales mínimos, medios y máximos.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
38
ILUSTRACIÓN 16 PATRÓN 1 DE RED BOGOTÁ.
ILUSTRACIÓN 17 PATRÓN 2.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
39
ILUSTRACIÓN 18 PATRÓN 3.
Como se puede observar, los patrones son muy similares. Si bien existen otros patrones con
diferencias importantes, la mayoría de los nudos de la ciudad se rige por los patrones
anteriores. De esto se determinaron las horas como se muestra en la siguiente tabla:
Q máximo 10:30 am
Q mínimo 4:00 am
Q medio
7:00 pm
TABLA 2 TIEMPOS DE LOS HORARIOS MEDIOS, MÁXIMOS Y MÍNIMOS.
4.2.2 RED MATRIZ DE MEDELLÍN
La red matriz de Medellín fue más sencilla de trabajar pues contaba únicamente con un patrón
de demanda y por tanto, cumple con el propósito de trabajar con nudos limitados para el
análisis hidráulico. El patrón con el que contaba esta red se muestra a continuación:
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
40
ILUSTRACIÓN 19 PATRÓN DE LA RED MATRIZ DE MEDELLÍN.
Q máximo 11:00 am
Q mínimo 3:30 am
Q medio
7:00 pm
TABLA 3 HORARIOS DE CAUDALES MÍNIMO, MEDIO Y MÁXIMO.
4.2.3 RED GINEBRA
La red de Ginebra cuenta con 3 patrones, muy similares entre ellos, por lo que fue
relativamente sencillo identificar las horas de los caudales. Los 3 patrones se muestran a
continuación:
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
41
ILUSTRACIÓN 20 PATRÓN TANQUE_VIEJO.
ILUSTRACIÓN 21 PATRÓN TANQUE_NUEVO.
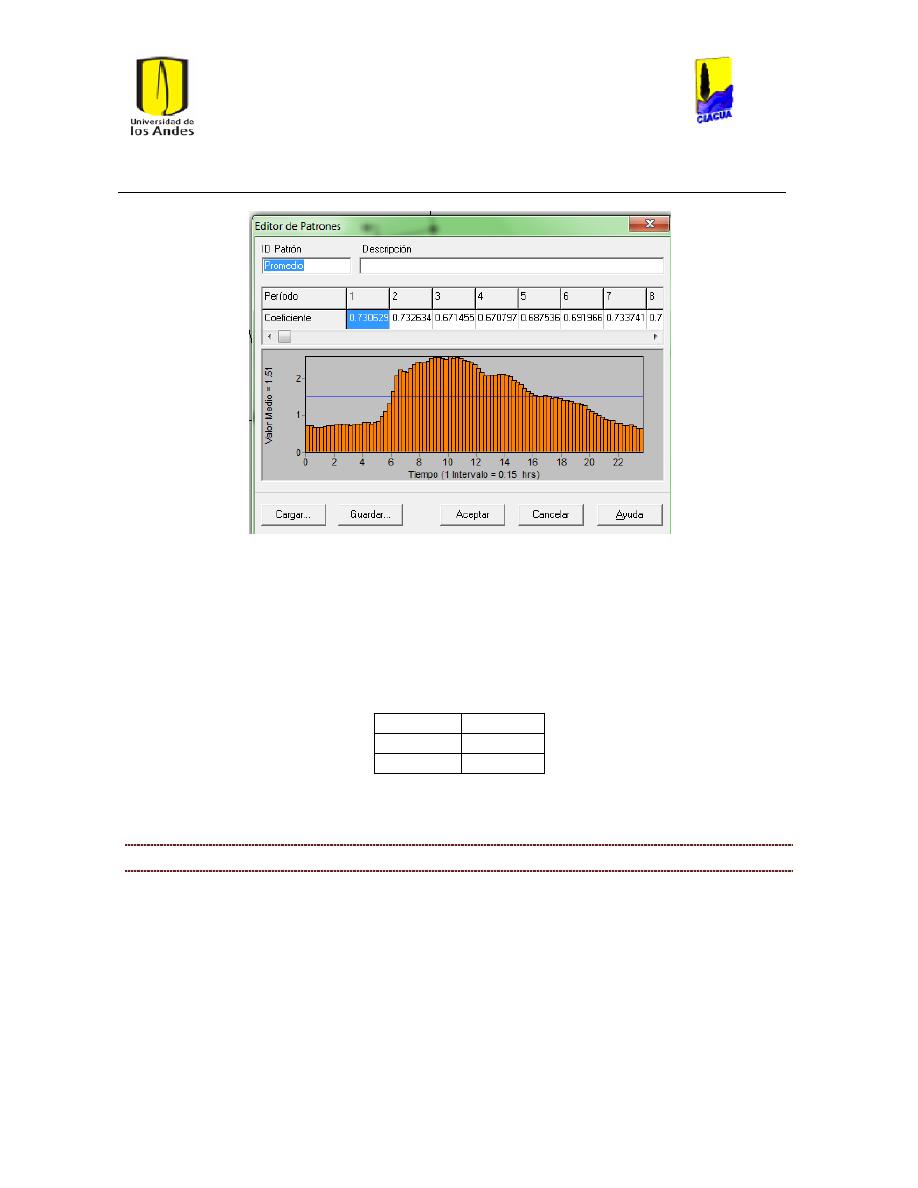
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
42
ILUSTRACIÓN 22 PATRÓN PROMEDIO.
De las ilustraciones anteriores es posible ver que si bien existen diferencias entre los 3
patrones, la mayoría de la red trabaja con el patrón de Tanque_Nuevo seguido por el patrón
Promedio. A partir de los resultados que arrojan estos patrones, se determinaron los horarios
de los 3 caudales.
La tabla con los tres horarios de caudales se muestra a continuación:
Q máximo 10:15 am
Q mínimo 3:30 am
Q medio
7:15 pm
TABLA 4 HORARIOS DE CAUDALES MÍNIMO, MEDIO Y MÁXIMO.
4.2.4 RED ANDALUCÍA
La red de Andalucía también cuenta con 3 patrones de demanda de caudal; sin embargo, en
este caso los tres patrones eran muy similares entre ellos. Adicionalmente, la mayor parte de
los nudos de demanda de la red trabajan con el patrón, todos los días. Los patrones
nombrados se muestran a continuación:
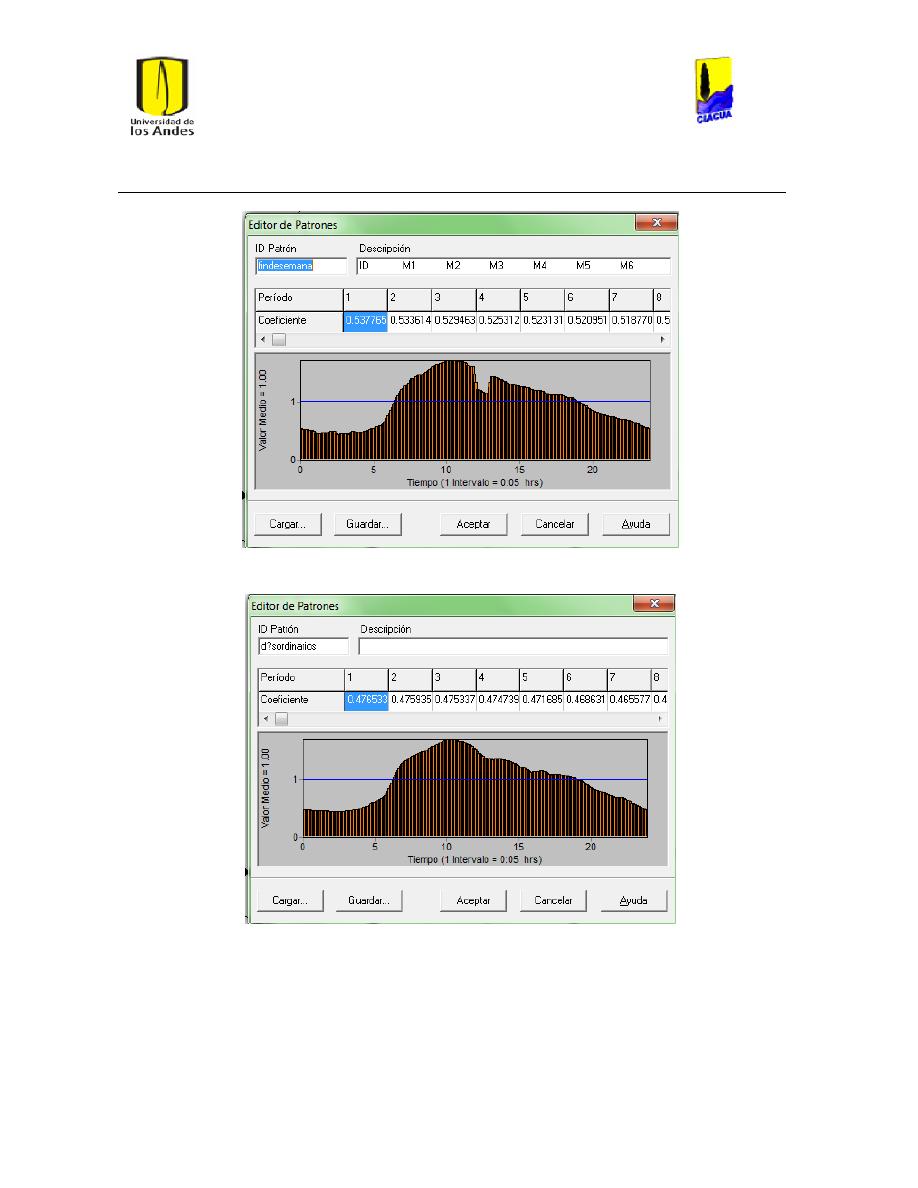
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
43
ILUSTRACIÓN 23 PATRÓN FINDESEMANA.
ILUSTRACIÓN 24 PATRÓN DÍAS ORDINARIOS.
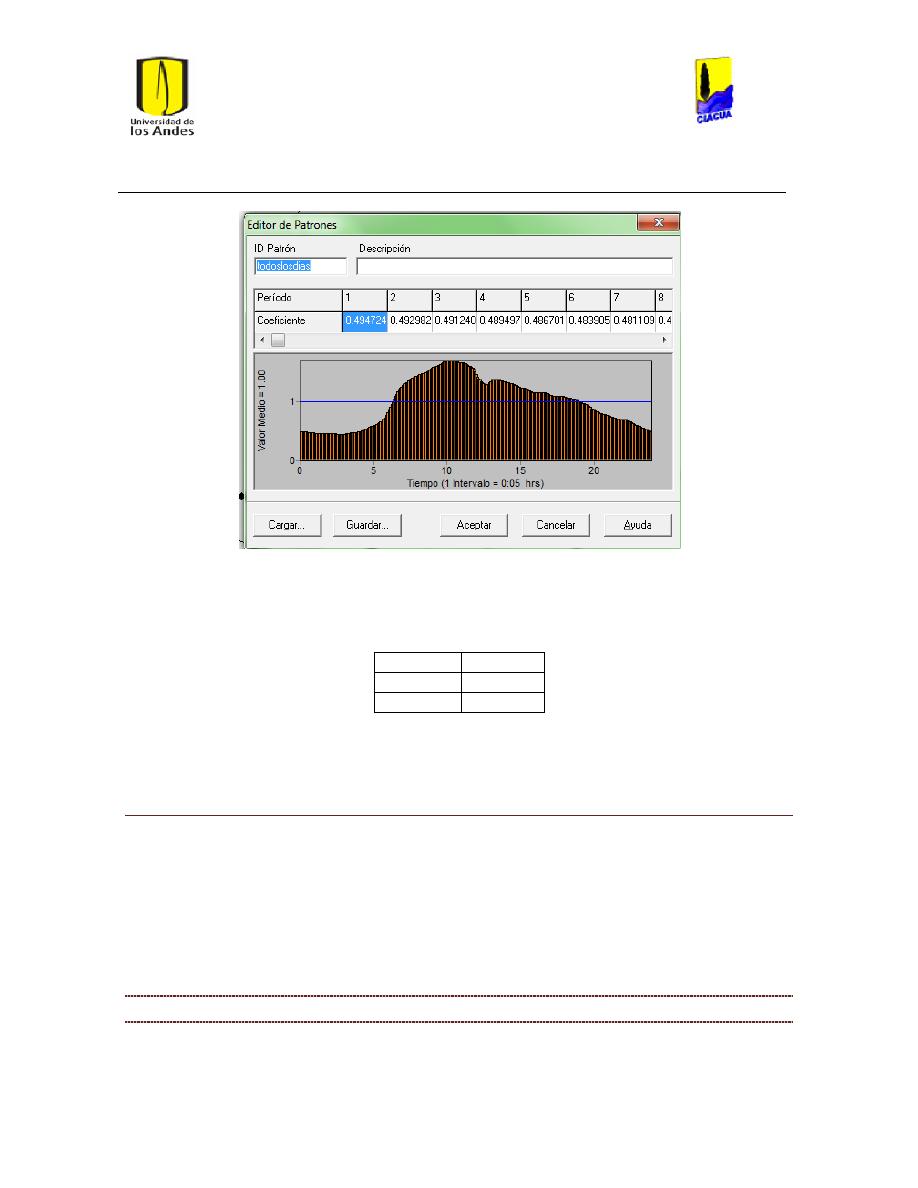
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
44
ILUSTRACIÓN 25 PATRÓN TODOS LOS DÍAS.
Con base en esto, se determinaron las horas de caudal mínimo, medio y máximo, estas se
muestran en la tabla a continuación:
Q máximo 10:00 am
Q mínimo 2:30 am
Q medio
6:20 pm
TABLA 5 HORARIOS DE CAUDAL MÍNIMO, MÁXIMO Y MEDIO.
4.3 ANÁLISIS DE EMISORES
En esta sección se exponen los resultados y su respectivo análisis de los datos recopilados tras
correr la red con diferentes emisores. Los resultados se muestran por casos, es decir, están
divididos en cada una de las redes; adicionalmente en esta sección se presentan y analizan los
resultados más relevantes y que ilustren mejor los objetivos del estudio, los demás resultados
pueden ser visualizados si es deseado en la sección de Anexos; esto incluye las imágenes con
las localizaciones de los emisores, resultados de las diferencias de los números de Reynolds
que se presentaban entre la ecuación de Hazen-Williams y la ecuación de Darcy-Weisbach.
4.3.1 RED MATRIZ DE BOGOTÁ
En esta sección se muestran los resultados de la red matriz de Bogotá. El orden será: Primero
los emisores pequeños, posteriormente los emisores grandes, las gráficas del caudal del
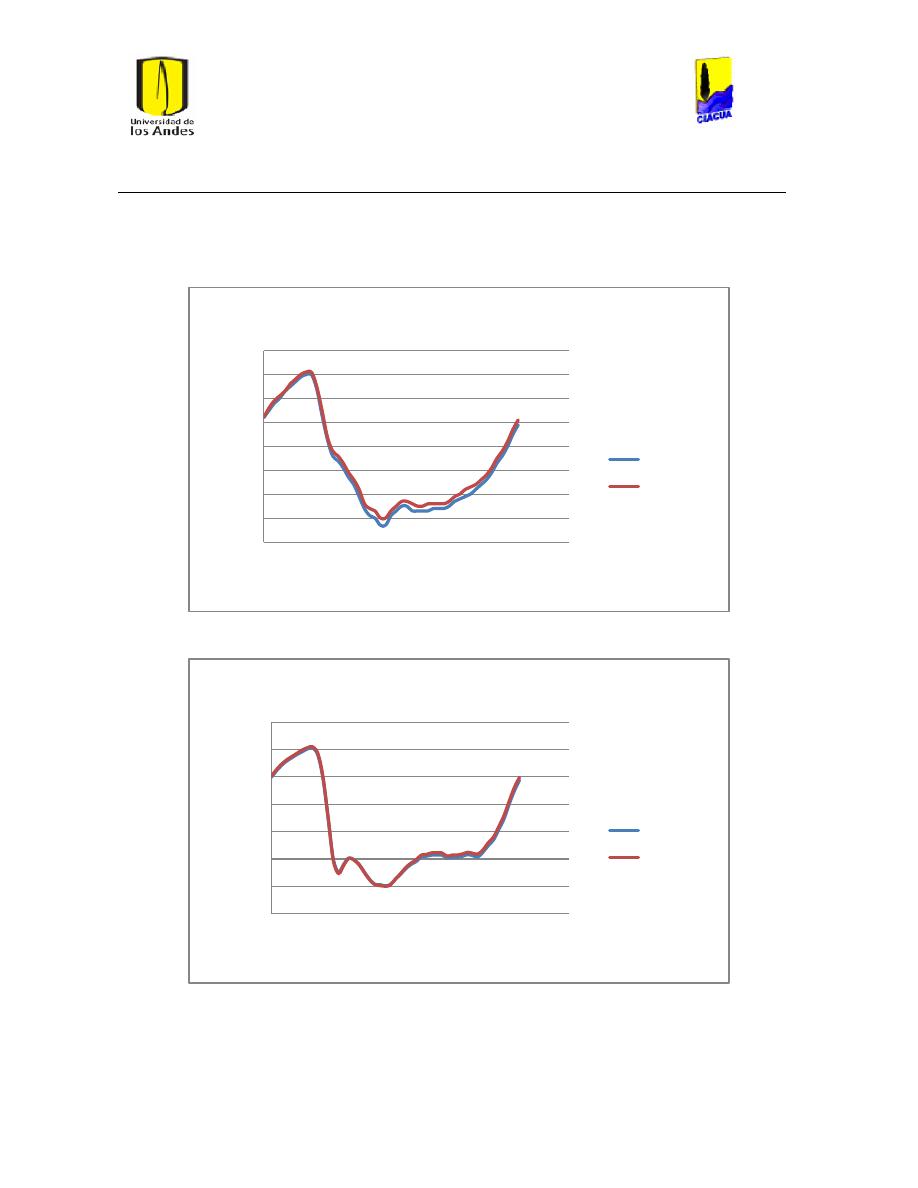
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
45
emisor frente al número de Reynolds, las variaciones del coeficiente de Hazen-Williams frente
al número de Reynolds y frente a los diámetros presentes en la red en los 3 momentos del día
(Qmax, Qmin y Qmed) y finalmente las presiones de la red en los momentos establecidos.
ILUSTRACIÓN 26 RESULTADOS EMISOR 905
ILUSTRACIÓN 27 RESULTADOS EMISOR 1521
Estos dos resultados representan los emisores pequeños de la red. Una revisión detenida del
comportamiento de los datos que arrojan la ecuación de Hazen-Williams como la ecuación de
7.6
7.7
7.8
7.9
8
8.1
8.2
8.3
8.4
00:00 04:48 09:36 14:24 19:12 00:00 04:48
L/s.
Tiempo (h)
Diferencia Emisor 905 Bogotá
Emisor H-W
Emisor D-W
16
16.5
17
17.5
18
18.5
19
19.5
00:00 04:48 09:36 14:24 19:12 00:00 04:48
L/s.
Tiempo (h)
Diferencia Emisor 1521 Bogotá
Emisor H-W
Emisor D-W
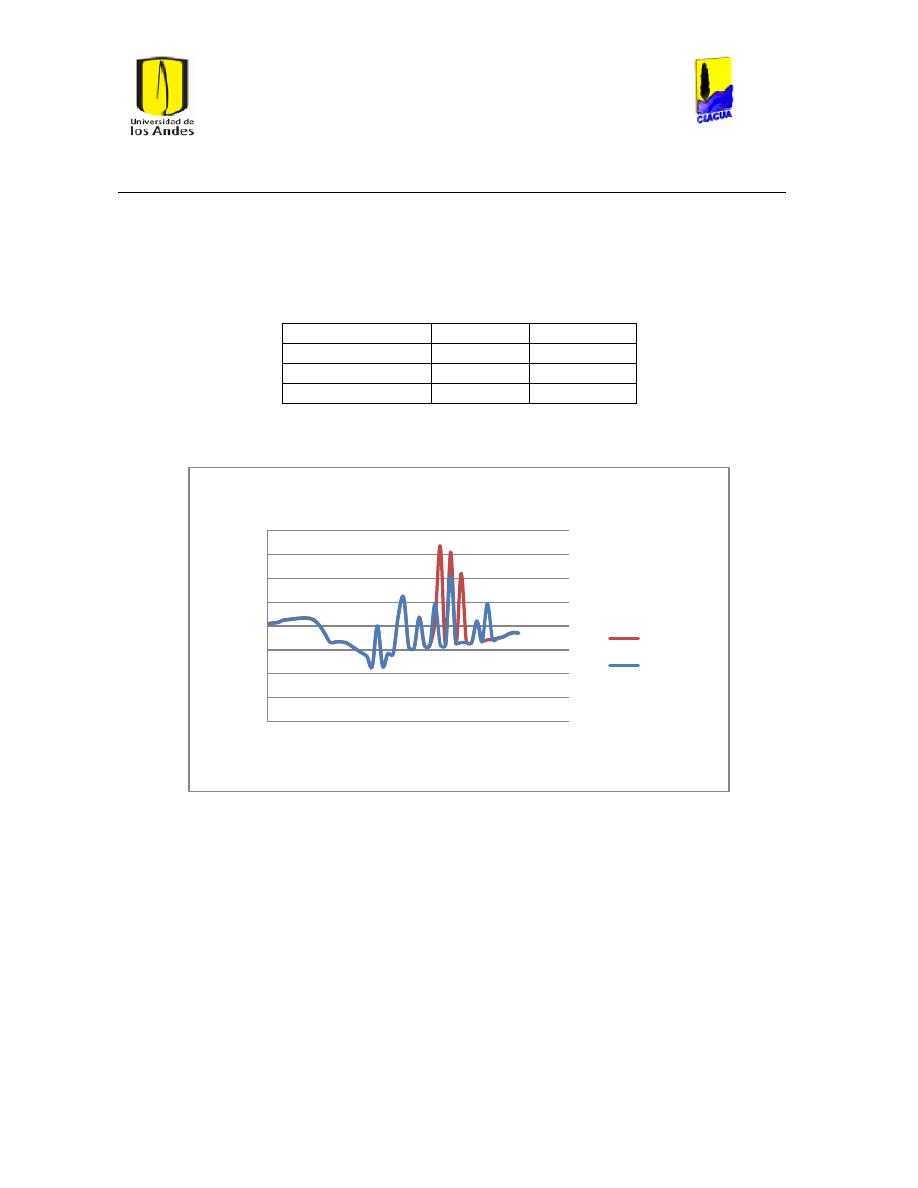
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
46
Darcy-Weisbach indica que su comportamiento es similar y no presenta diferencias evidentes.
Las curvas parecen seguir el mismo patrón y no existen diferencias de caudal significativas
entre la simulación con la ecuación de Hazen-Williams y la ecuación de Darcy-Weisbach.
Las características de estos dos emisores se trabajaron como:
Emisor 905 Emisor 1521
Presión(m)
20
20
Caudal Base(L/s)
4.5076
11.119
Coeficiente Emisor
1.0079
2.486417
TABLA 6 CARACTERÍSTICAS DE LOS EMISORES PEQUEÑOS.
ILUSTRACIÓN 28 RESULTADOS EMISOR 2189
100
105
110
115
120
125
130
135
140
00:00 04:48 09:36 14:24 19:12 00:00 04:48
L/s.
Tiempo (h)
Diferencia Emisor 2189 Bogotá
Emisor D-W
Emisor H-W
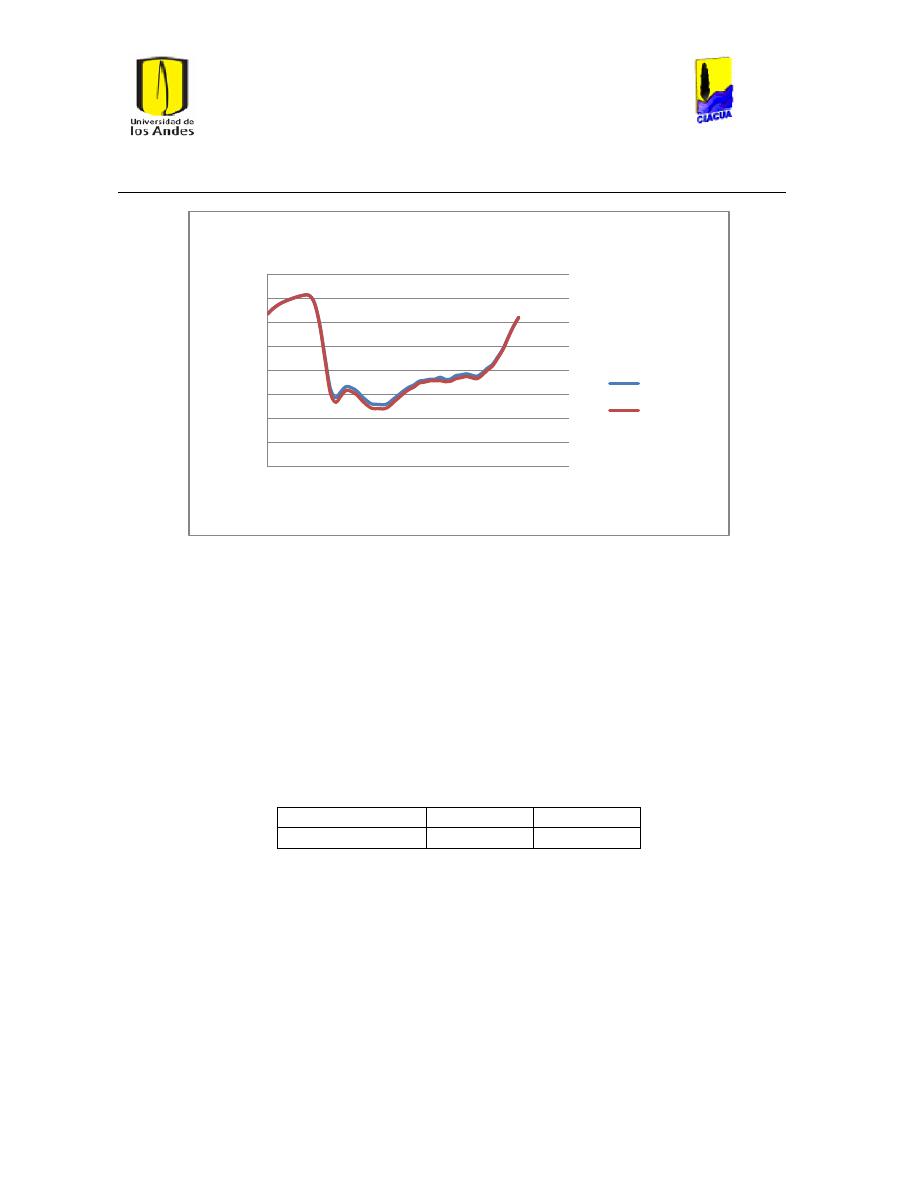
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
47
ILUSTRACIÓN 29 RESULTADOS EMISOR 1036.
Por el contrario, cuando se trabaja con emisores mayores fue posible evidenciar diferencias
significativas entre los valores que arrojan la hidráulica con la ecuación de Darcy-Weisbach y
la ecuación de Hazen-Williams. Si bien, solo se vio en un caso particular, es importante ver que
la ecuación de Hazen-Williams subestima en este caso el caudal del emisor; esta diferencia se
encuentra entre 5 y 10 L/s.
En este caso, como se deseaba aumentar los emisores, se modificó directamente el coeficiente
emisor de tal forma que se comportara más como un tanque grande que no devolvía el caudal,
es decir que funcionara como si se llenara un tanque de gran tamaño.
Emisor 2189 Emisor 1036
Coeficiente Emisor
16.09
18.33
TABLA 7 COEFICIENTES EMISORES DE LOS NUDOS.
100
105
110
115
120
125
130
135
140
00:00 04:48 09:36 14:24 19:12 00:00 04:48
L/s
Tiempo (h)
Diferencia Emisor 1036 Bogotá
Emisor H-W
Emisor D-W
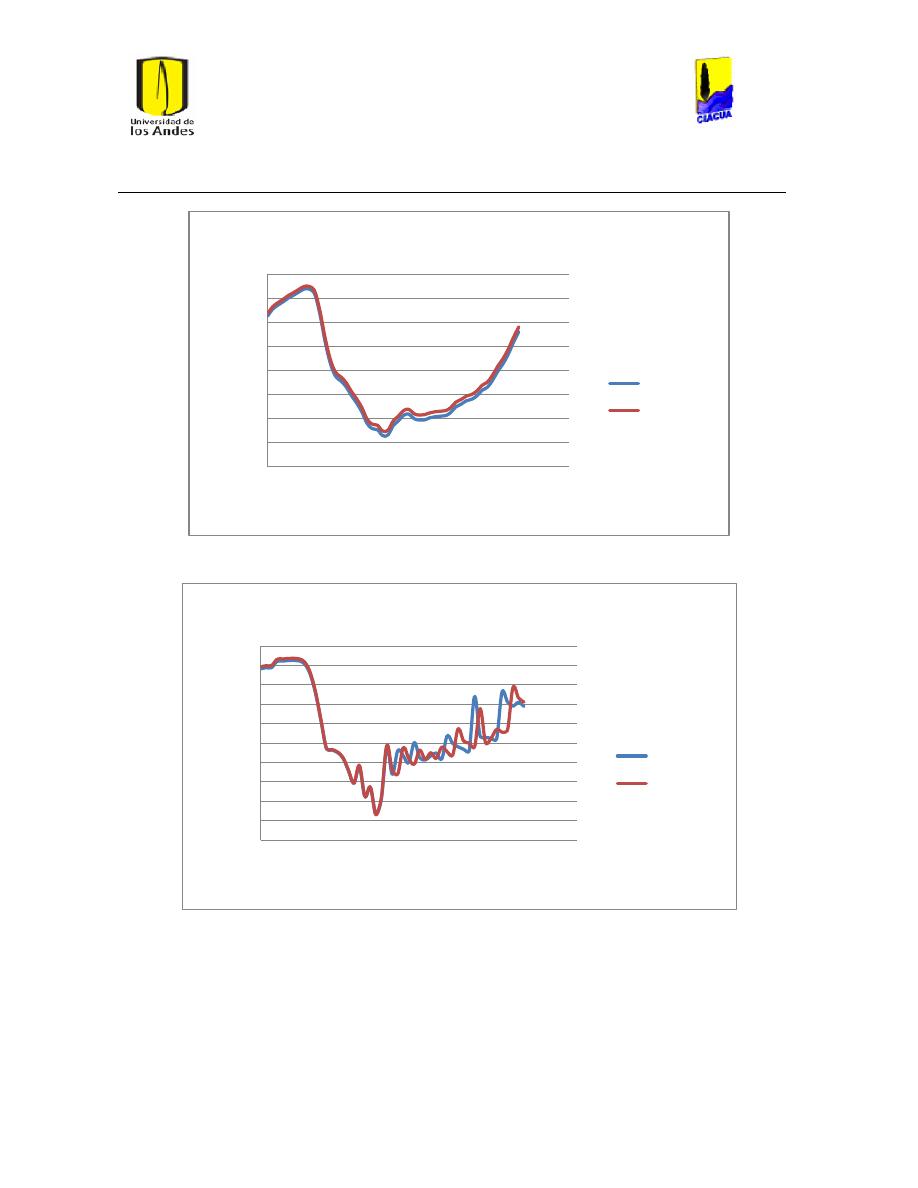
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
48
ILUSTRACIÓN 30 RESULTADOS EMISOR 905.
ILUSTRACIÓN 31 RESULTADOS EMISOR 2437.
El proceso prosiguió trabajando con coeficientes emisores aún más grandes. Como se puede
ver, no se vieron diferencias importantes en estos emisores, ya que los resultados arrojan
diferencias de máximo 2 litros en algunos horarios del día. Se concluye que en esta red se está
presentando un comportamiento similar entre las dos ecuaciones, es decir, el
comportamiento entre la ecuación de Hazen-Williams y la ecuación de Darcy-Wesibach no
presentan grandes diferencias, con la sola excepción de las diferencias que se detectaron en
225
230
235
240
245
250
255
260
265
00:00 04:48 09:36 14:24 19:12 00:00 04:48
L/s.
Tiempo(h)
Bogotá Emisor 905
Emisor H-W
Emisor D-W
292
294
296
298
300
302
304
306
308
310
312
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s.
Tiempo(h)
Bogotá Emisor 2437
Emisor H-W
Emisor D-W
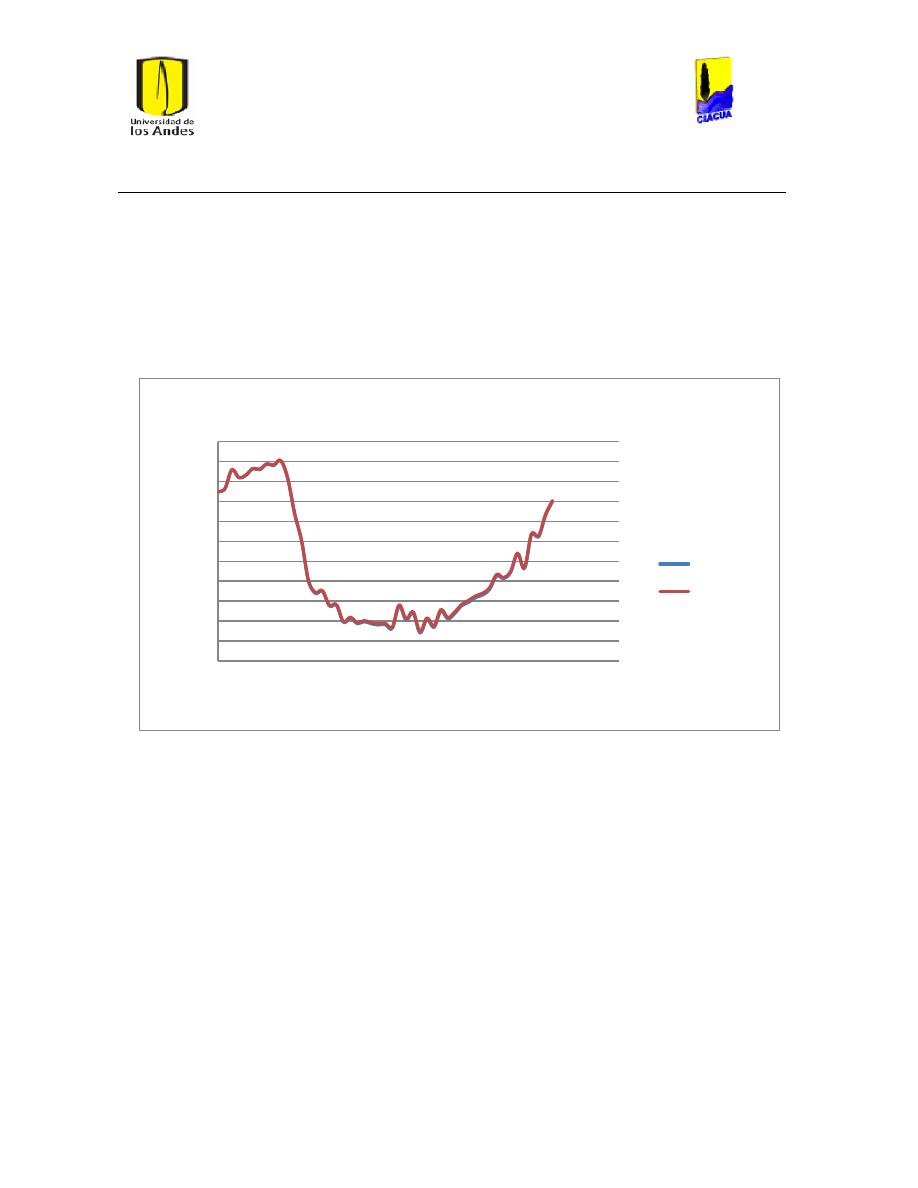
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
49
algunos horas del día y que no superan, con los valores de emisores caudales en esta fase de la
investigación, los tres litros por segundo.
Sin embargo, se decidió seguir probando escenarios con coeficientes de emisión mayores para
ver si se presentaba algún tipo de diferencias entre la hidráulica de las dos ecuaciones. Estos
resultados se muestran a continuación:
ILUSTRACIÓN 32 RESULTADOS EMISOR 1702.
300
310
320
330
340
350
360
370
380
390
400
410
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s.
Tiempo(h)
Diferencia Emisor 1702 Bogotá
Emisor H-W
Emisor D-W
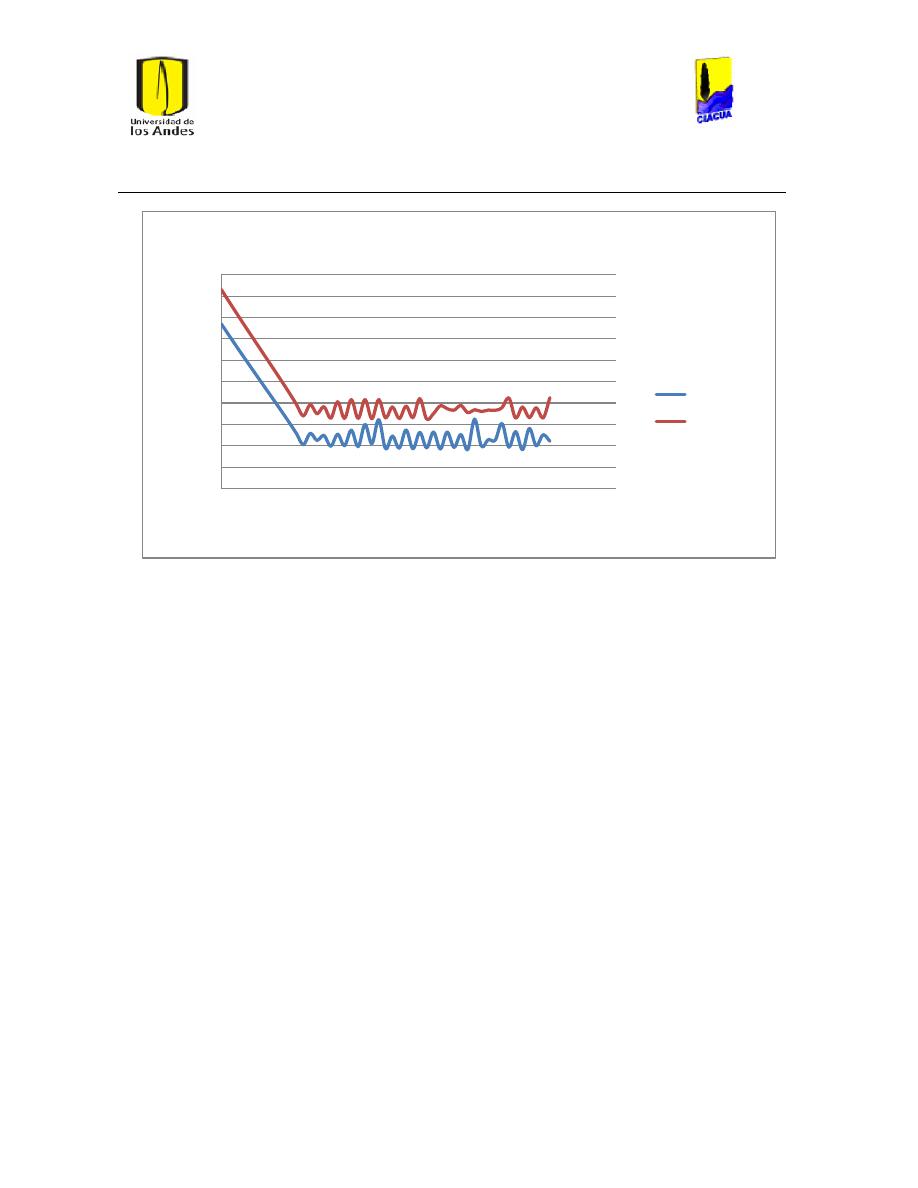
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
50
ILUSTRACIÓN 33 RESULTADOS EMISOR TUVAL.
Así mismo, se decidió estudiar qué posible relación podía tener el número de Reyolds de
llegada frente al caudal emisor: El número de Reynolds utilizado fue el encontrado con la
ecuación físicamente basada. Los resultados para estos dos emisores se muestran a
continuación:
350
352
354
356
358
360
362
364
366
368
370
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s.
Tiempo (h)
Diferencia Emisor TUval Bogotá
Emisor D-W
Emisor H-W
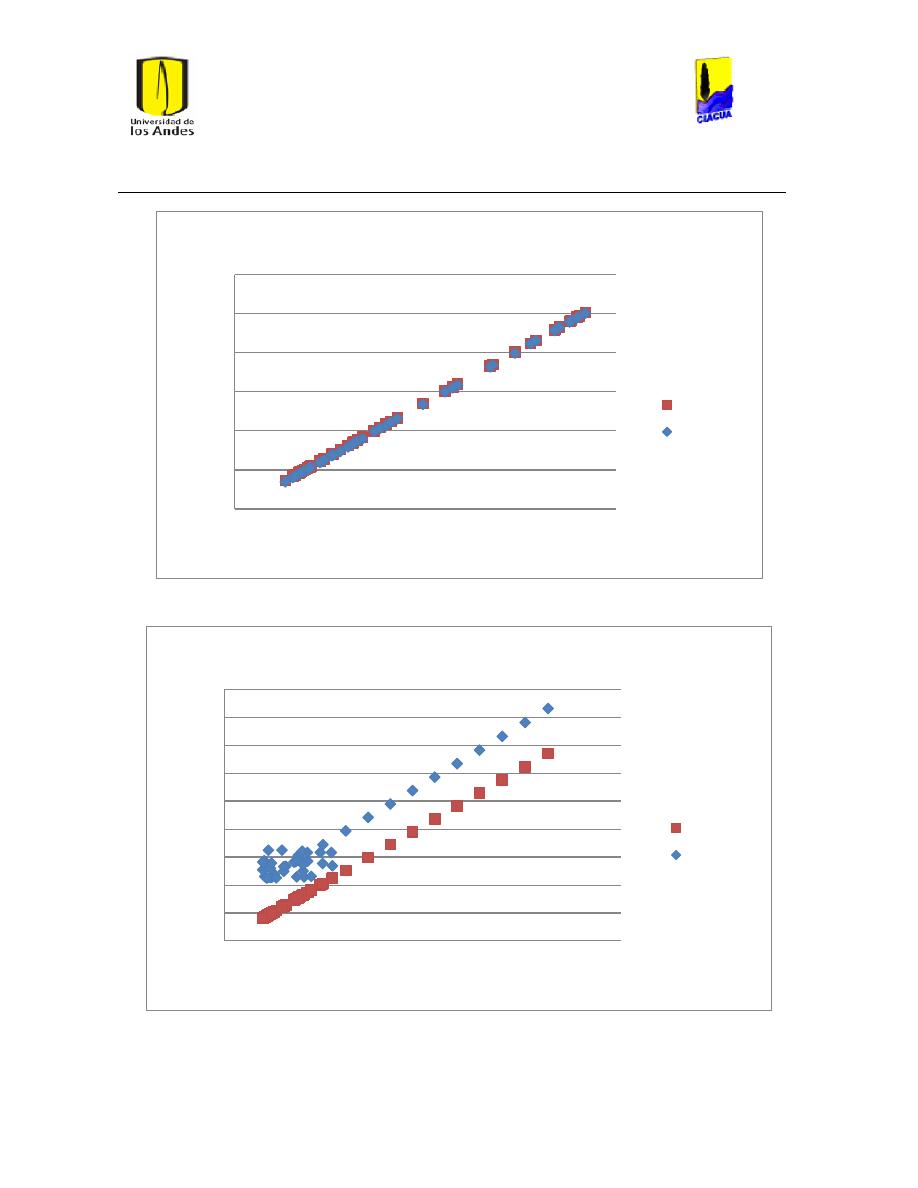
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
51
ILUSTRACIÓN 34 GRÁFICA DE REYNOLDS VS CAUDAL EMISOR EN EMISOR 1702.
ILUSTRACIÓN 35 GRÁFICA DEL NÚMERO DE REYNOLDS VS CAUDAL EMISOR EN EMISOR TUVAL.
300
320
340
360
380
400
420
550000
600000
650000
700000
750000
L/s.
Número de Reynolds
Bogotá Emisor 1702
Emisor D-W
Emisor H-W
352
354
356
358
360
362
364
366
368
370
1290000 1300000 1310000 1320000 1330000 1340000 1350000
L/s
Número de Reynolds
Bogotá Emisor TUval
Emisor D-W
Emisor H-W
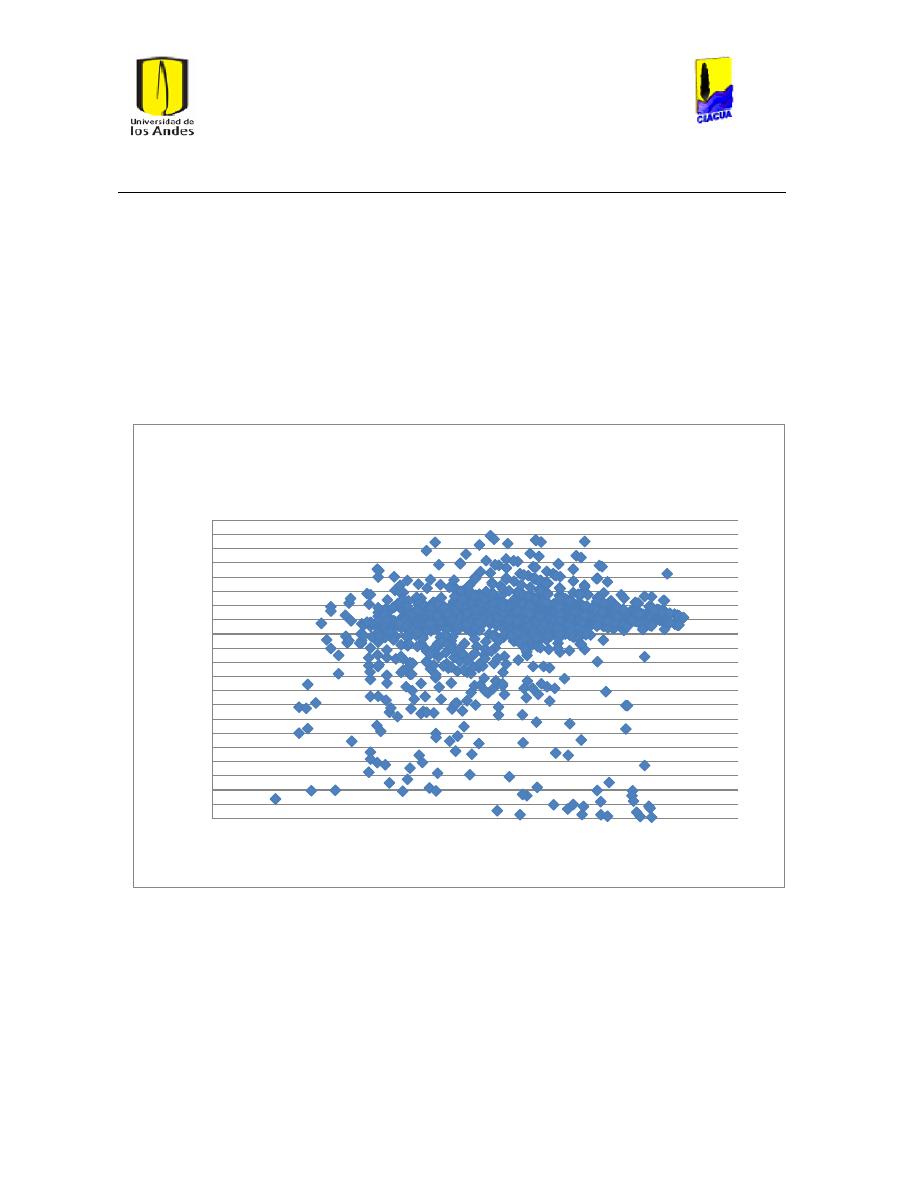
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
52
Estos resultados son bastante interesantes ya que si bien en el primer emisor no se presentan
diferencias significativas, en el segundo emisor, las diferencias resultan evidentes,
especialmente cuando se visualizan los litros por segundo en relación con el número de
Reynolds con la red que utiliza la ecuación de Hazen-Williams frente a la ecuación que utiliza
la ecuación de Darcy-Weisbach. Más adelante cuando se muestren los resultados para las
otras redes, se verán con más detalle estas diferencias.
La investigación avanzó en el análisis del comportamiento del coeficiente de Hazen-Williams
en la red que trabajó con la ecuación de Darcy-Weisbach. Los resultados de esto se muestran a
continuación:
ILUSTRACIÓN 36 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS RESPECTO AL NÚMERO DE
REYNOLDS PARA EL CAUDAL MEDIO.
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
1000
10000
100000
1000000
10000000
Coe
fi
cient
e
H
azen
-W
ill
iam
s
Número de Reynolds
Bogotá Coeficientes Hazen-Williams Caudal
Medio
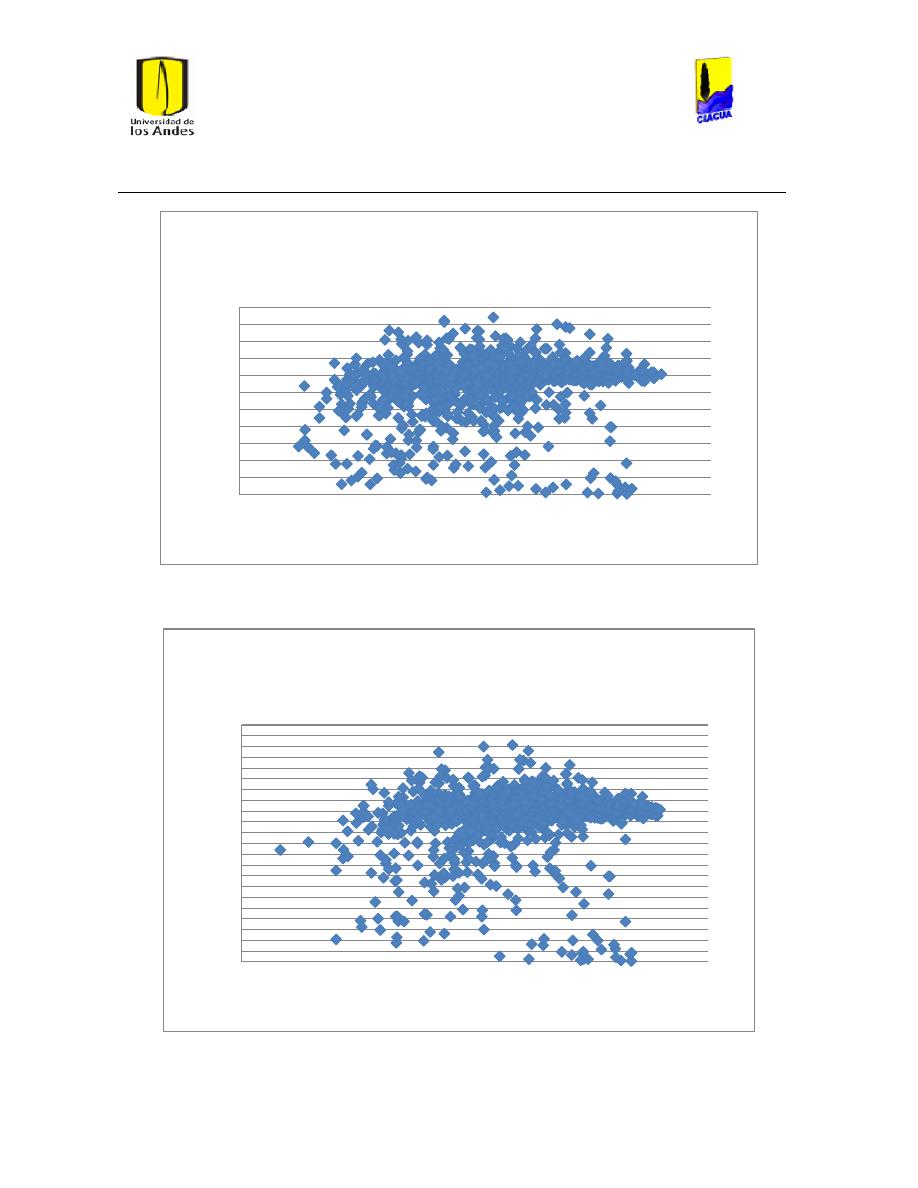
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
53
ILUSTRACIÓN 37 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS FRENTE AL NÚMERO DE
REYNOLDS PARA EL CAUDAL MÍNIMO.
ILUSTRACIÓN 38 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS FRENTE AL NÚMERO DE
REYNOLDS PARA EL CAUDAL MÁXIMO.
0
20
40
60
80
100
120
140
160
180
200
220
1000
10000
100000
1000000
10000000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Número de Reynolds
Bogotá Coeficientes Hazen-Williams
Caudal Mínimo
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
220
1000
10000
100000
1000000
10000000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Número de Reynolds
Bogotá Coeficientes Hazen-Williams
Caudal Máximo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
54
ILUSTRACIÓN 39 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS FRENTE A LOS DIÁMETROS DE
LA RED PARA EL CAUDAL MEDIO.
ILUSTRACIÓN 40 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS FRENTE A LOS DIÁMETROS DE
LA RED PARA EL CAUDAL MÍNIMO.
0
20
40
60
80
100
120
140
160
180
200
220
0
500
1000
1500
2000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Diametro (mm)
Bogotá Caudal Medio
0
20
40
60
80
100
120
140
160
180
200
220
0
500
1000
1500
2000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Diametro (mm)
Bogotá Caudal Mínimo
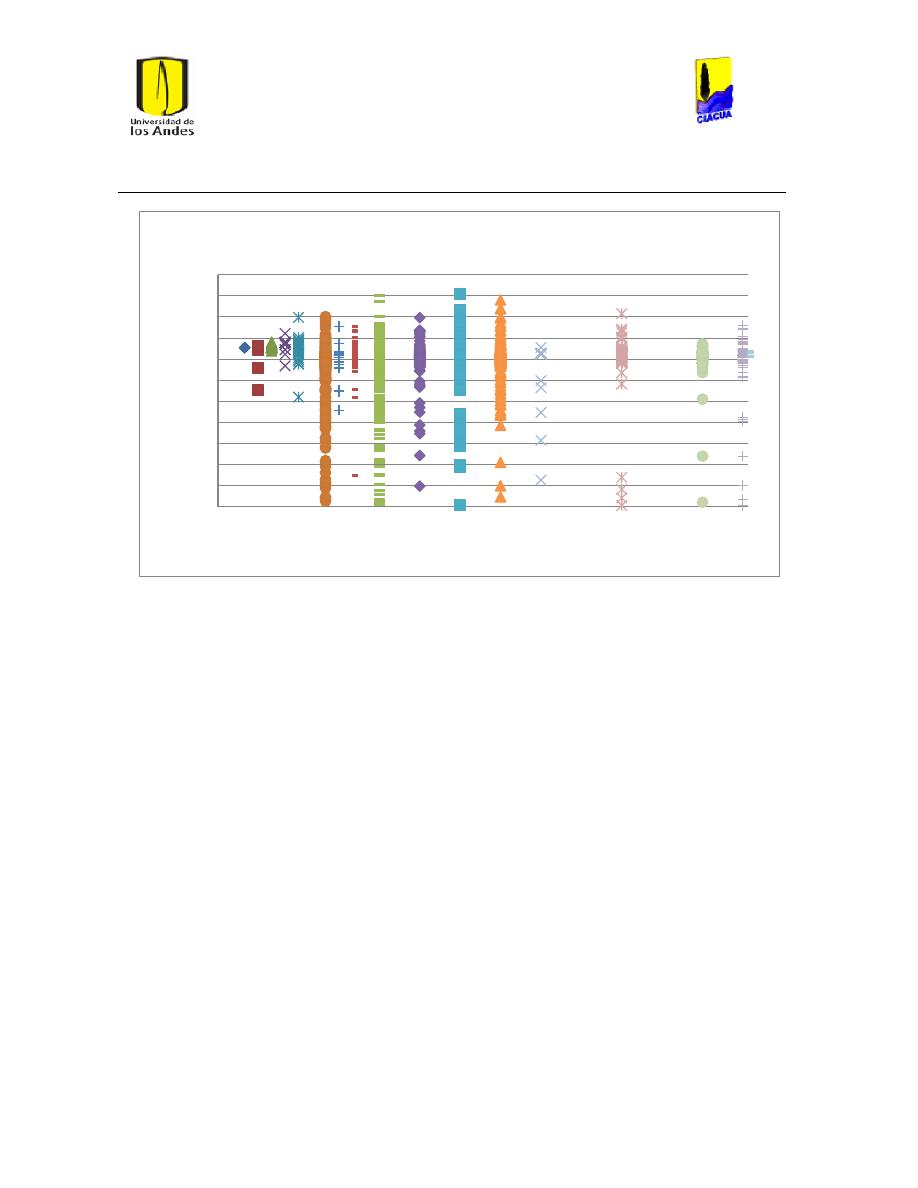
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
55
ILUSTRACIÓN 41 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS FRENTE A LOS DIÁMETROS DE
LA RED PARA EL CAUDAL MÁXIMO.
De las gráficas anteriores es importante resaltar el hecho de que la red presenta variaciones
significativas de los coeficientes de Hazen-Williams. Se destaca que si bien hay resultados muy
por encima o muy por debajo de la franja de coeficientes entre 130 y 160, la mayoría de los
datos se encuentran entre estos valores. Lo anterior puede ser explicado en virtud a que las
tuberías empleadas no tenían como propósito representar las condiciones reales, a lo cual
conviene agregar que las pruebas realizadas representan tramos muy cortos que se utilizaron
para intentar representar de mejor manera la hidráulica de la red y que pueden llegar a
presentar pérdidas por fricción muy pequeñas. Adicionalmente conviene señalar que, en otros
casos, se trataba de tramos en los que pasaba muy poco caudal por un diámetro muy grande,
lo que reducía notablemente la velocidad que se presentaba y por ende las pérdidas por
fricción, llegando incluso a presentarse flujo laminar, cambiando de manera significativa el
comportamiento del coeficiente de Hazen-Williams.
Los resultados de las gráficas constituyen que la red se está comportando de una forma
relativamente parecida a los coeficientes teóricos establecidos que son de 140 y 150.
Retomando la franja principal donde se encuentran los coeficientes, es posible decir que la
diferencia entre los emisores es muy baja debido a que la red operada con la ecuación de
Hazen-Williams se está comportando de manera muy similar a la red operada con la ecuación
de Darcy-Weisbach. Esto se concluye al analizar las diferencias de presión en la red como se
mostrara más adelante y con base a que los coeficientes de Hazen-Williams teóricos se
comportaron de manera similar a los hallados a partir de la red que estaba siendo operada
con la ecuación de Darcy-Weisbach (lo que implica números de Reynolds similares al igual
0
20
40
60
80
100
120
140
160
180
200
220
0
200
400
600
800
1000
1200
1400
1600
1800
2000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Diametro (mm)
Bogotá Caudal Máximo
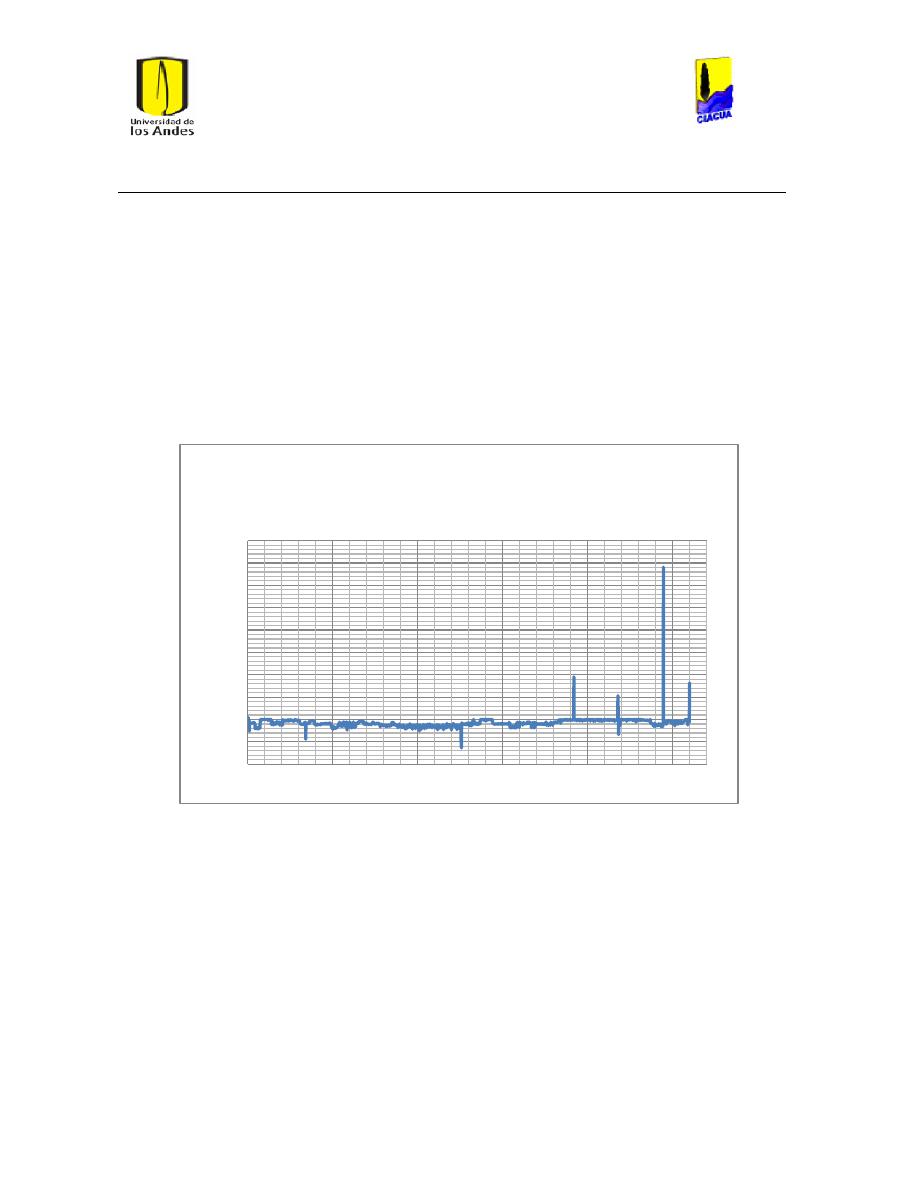
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
56
que factores de fricción similares en los tramos de interés); por otro lado también se
estudiaron diferentes condiciones de los emisores (mayor y menor caudal emisor) y no existió
una diferencia significativa. Así mismo, cabe resaltar que si bien en la mayoría de los casos se
presentó un comportamiento similar, también se presentaron casos donde se presentaban
diferencias; si bien estas se encontraban entre un rango de 5 y 15 L/s, son diferencias que
deben ser tenidas en cuenta a la hora de operar redes matrices, ya que como se señaló atrás, la
ecuación de Hazen-Williams puede llegar a dar un falso sentido de alerta y como se verá más
adelante, puede considerar un excesivo sentido de seguridad al operario.
A continuación se muestran los resultados encontrados para las diferencias de presión en la
red.
ILUSTRACIÓN 42 DIFERENCIA DE PRESIONES PARA EL CAUDAL MÍNIMO.
-2
-1
0
1
2
3
4
5
6
7
8
0
500
1000
1500
2000
2500
(H
w
-D
w)
/D
w
*100
Nudos
Diferencia de presiones Caudal
Mínimo Bogotá
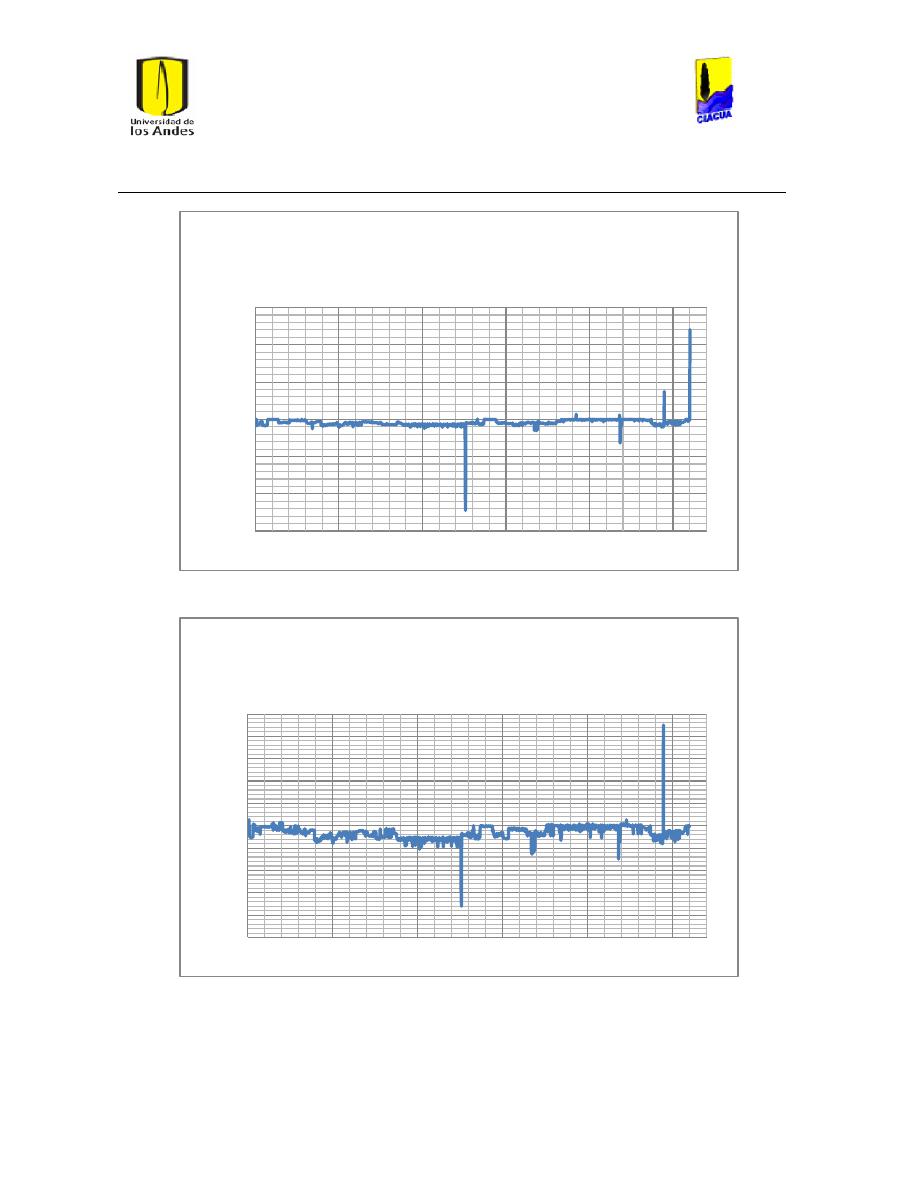
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
57
ILUSTRACIÓN 43 DIFERENCIA DE PRESIONES PARA EL CAUDAL MEDIO.
ILUSTRACIÓN 44 DIFERENCIA DE PRESIONES PARA EL CAUDAL MÁXIMO.
Estos resultados concuerdan con lo analizado anteriormente, y es que en términos generales
los valores de presión que arrojan las dos ecuaciones son relativamente similares. Sin obviar
-15
-10
-5
0
5
10
15
0
500
1000
1500
2000
2500
(H
w
-D
w)
/D
w
*100
Nudos
Diferencia de presiones Caudal Medio
Bogotá
-5
-4
-3
-2
-1
0
1
2
3
4
5
0
500
1000
1500
2000
2500
(H
w
-D
w)
/D
w
*100
Nudos
Diferencia de presiones Caudal
Máximo Bogotá
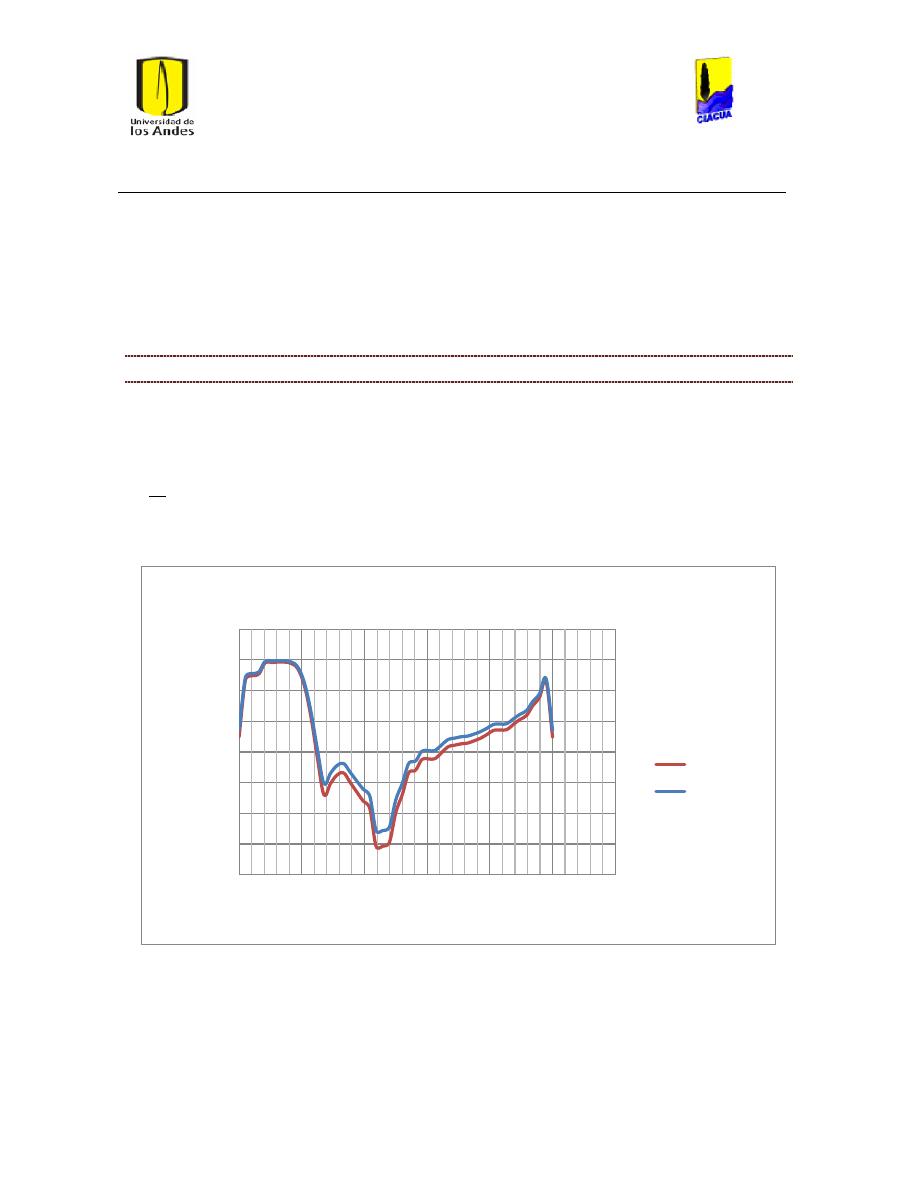
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
58
el hecho de que si se están presentando diferencias que pueden llegar a un máximo diferencial
del 12% entre las presiones; dicha situación sin embargo, se presenta en muy pocos nudos de
la red. Todo esto indica que el cálculo de las pérdidas por fricción en la red matriz de Bogotá
usando la ecuación de Hazen-Williams no presenta diferencias considerables frente al cálculo
realizado utilizando la ecuación de Darcy-Weisbach y que las diferencias presentadas, que son
de máximo el 12%, se presentan sólo en algunos nudos de la red.
4.3.2 RED MATRIZ DE MEDELLÍN
A continuación se mostrarán de los resultados de la red matriz de Medellín. La diferencia
entre esta red y la mostrada previamente es que en este caso no se mostrarán los resultados
para emisores bajos, esto se debió a que en el momento de realizar estos cálculos la red tenía
mal establecidas las unidades de los caudales demandados en los nudos (estaban en L/s y no
en
) y por ende no estaba representando de manera verídica la hidráulica de la red. Por lo
que se procedió a corregir esto y se empezó a trabajar con los caudales reales de la red y con
emisores de gran tamaño en diferentes puntos de la red.
ILUSTRACIÓN 45 RESULTADOS EMISOR 225.
415.00
420.00
425.00
430.00
435.00
440.00
445.00
450.00
455.00
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia emisor 225 Medellín
Emisor D-W
Emisor H-W
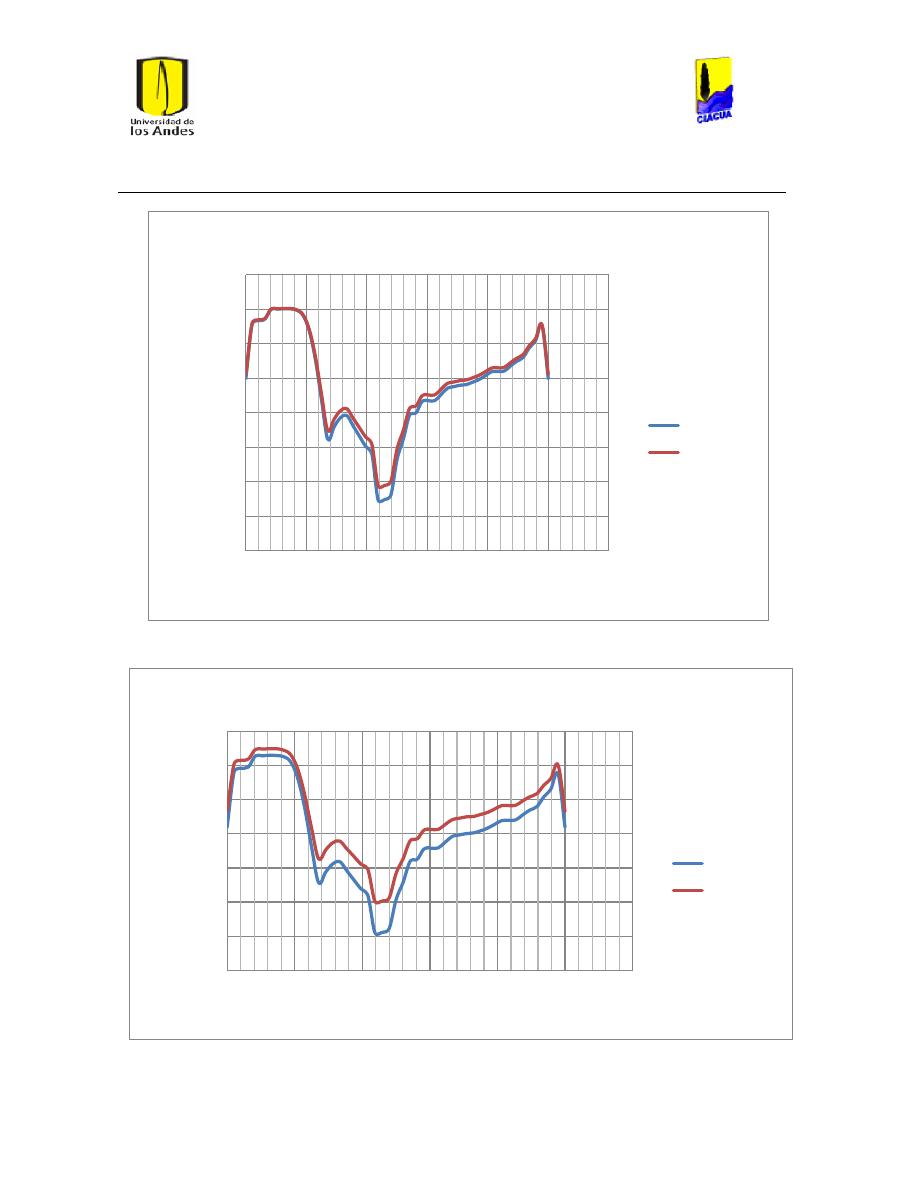
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
59
ILUSTRACIÓN 46 RESULTDOS EMISOR 46
ILUSTRACIÓN 47 RESULTADOS EMISOR 369.
80.00
85.00
90.00
95.00
100.00
105.00
110.00
115.00
120.00
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia emisor 46 Medellín
Emisor D-W
Emisor H-W
137.00
138.00
139.00
140.00
141.00
142.00
143.00
144.00
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 369 Medellín
Emisor D-W
Emisor H-W
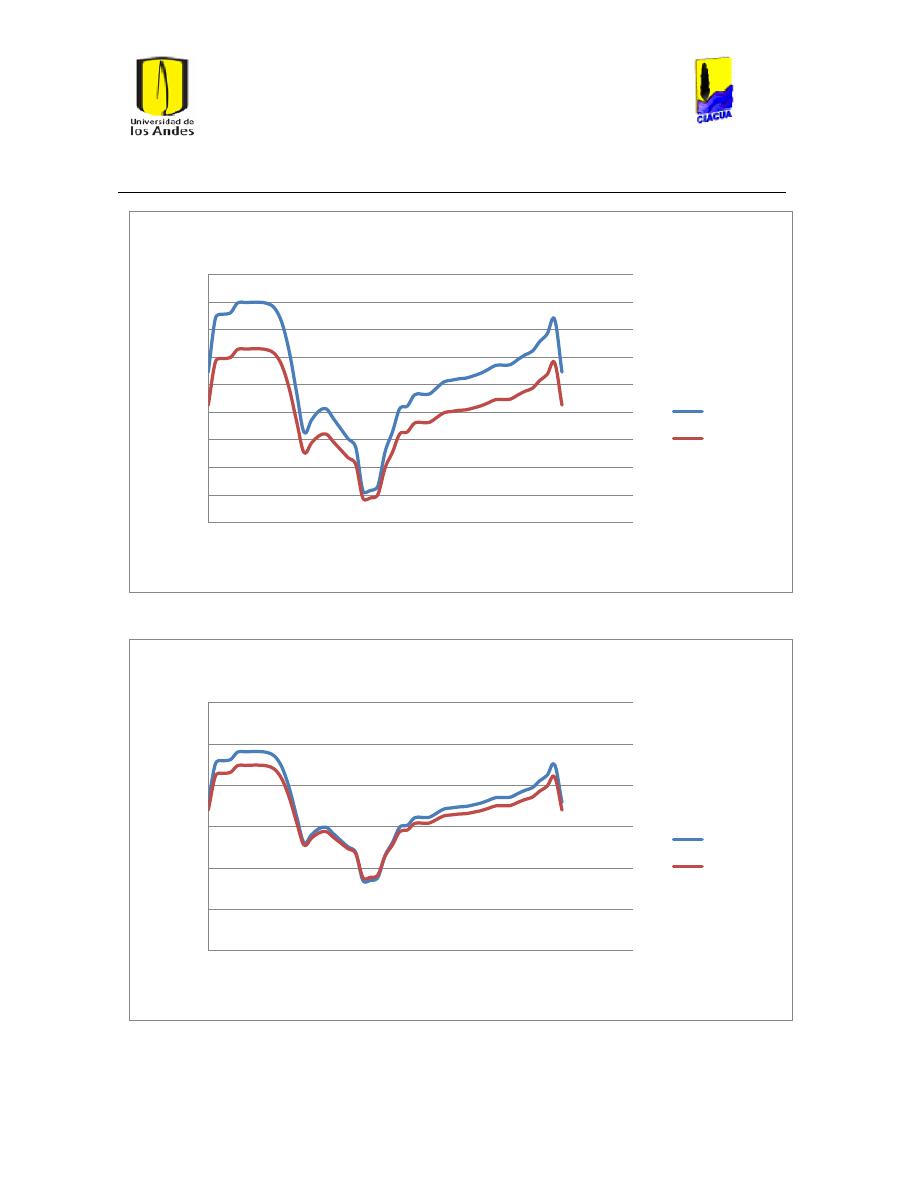
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
60
ILUSTRACIÓN 48 RESULTADOS EMISOR 529.
ILUSTRACIÓN 49 RESULTADOS EMISOR 540.
112
114
116
118
120
122
124
126
128
130
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 529 Medellín
Emisor D-W
Emisor H-W
150
170
190
210
230
250
270
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 540 Medellín
Emisor D-W
Emisor H-W
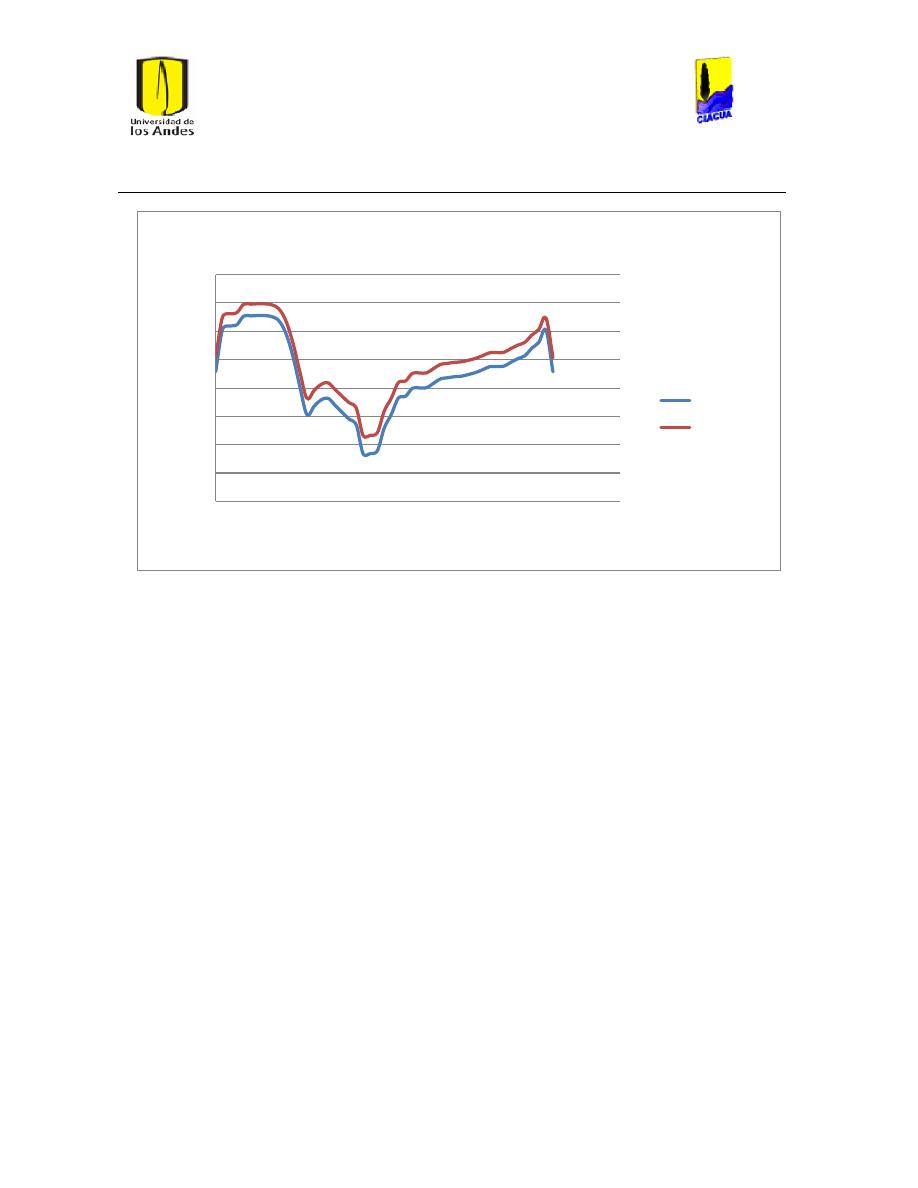
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
61
ILUSTRACIÓN 50 RESULTADOS EMISORES 532.
Se pueden evidenciar diferencias importantes entre los emisores usando la ecuación de
Hazen-Williams y la ecuación de Darcy-Weisbach. Para empezar, se puede ver que cuando la
hora de máximo caudal (alrededor de las 10 am) se está aproximando, estas diferencias se ven
acrecentadas sustancialmente, como es el caso en los emisores 369 y 332 donde se llegan a
presentar diferencias de hasta 30 L/s. Es decir, en este caso la ecuación de Hazen-Williams
está entregando un caudal de emisor 30 litros mayor al que entrega la ecuación físicamente
basada, lo que implica que en el caso de la red que utiliza la ecuación de Hazen-Williams está
dando un falso sentido de la seguridad pues el operador observa que el tanque contiene un
volumen de agua mayor al que realmente puede llegar a tener. Lo anterior representa una
condición preocupante, ya que estas diferencias no se presentan en todos los emisores, lo cual
puede conducir a los operarios de la red a confundirse y cometer errores de estimación del
caudal emisor, al suponer que los valores que arroja la ecuación de Hazen-Williams está
representando de forma verídica la hidráulica de la red.
Con base en esto, se decidió analizar qué diferencias podían ocurrir con respecto al número de
Reynolds de llegada y el caudal emisor. Los resultados de esto se muestran a continuación:
300
350
400
450
500
550
600
650
700
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 532 Medellín
Emisor D-W
Emisor H-W
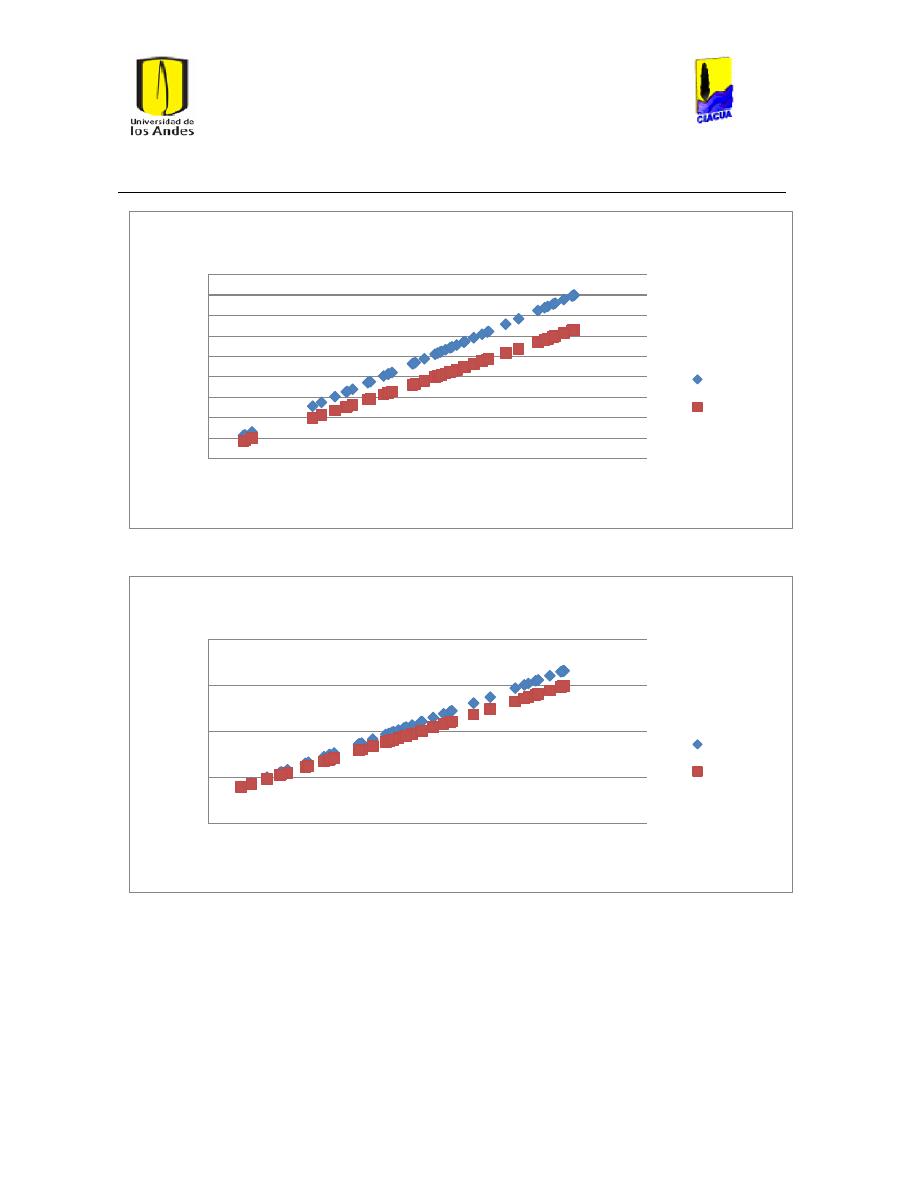
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
62
ILUSTRACIÓN 51 CAUDAL EMISOR VS NÚMERO DE REYNOLDS EMISOR 529.
ILUSTRACIÓN 52 CAUDAL EMISOR VS NÚMERO DE REYNOLDS EMISOR 540.
112
114
116
118
120
122
124
126
128
130
620000
640000
660000
680000
700000
720000
L/s
Número de Reynolds
Emisor 529 Medellín
Emisor D-W
Emisor H-W
180
200
220
240
260
700000
750000
800000
850000
900000
950000
L/s
Número de Reynolds
Emisor 540 Medellín
Emisor D-W
Emisor H-W

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
63
ILUSTRACIÓN 53 CAUDAL EMISOR VS NÚMERO DE REYNOLDS EMISOR 532.
Estas gráficas muestran un comportamiento hidráulicamente interesante; esto puede
observar el comportamiento de la red cuando se analiza el número de Reynolds. Esto último
se puede ver cuando el caudal emisor con un mismo número de Reynolds es diferente para las
dos ecuaciones. Otro resultado importante es que las diferencias parecen ser menos
significativas cuando el número de Reynolds es menor, según se aprecia en las ilustraciones
52, 53 y 54. Lo anterior parece soportar lo que se analizó anteriormente y es que utilizar la
ecuación de Hazen-Williams para la operación de redes implica un riesgo importante, en
especial si se utilizan coeficientes constantes para la ecuación, ya que lo que genera el emisor
utilizando la ecuación de Hazen-Williams es mayor a lo que se presenta en la realidad; lo
anterior tiene dos implicaciones importantes. La primera, en caso de que se esté simulando un
tanque, este está presentando una taza de llenado mayor a la que se presenta en la realidad.
Segundo, en el caso en que se desee trabajar redes con emisores que representen las fugas de
un sistema, se corre el grave riesgo de estar subestimando o sobrestimando los valores de las
fugas, generando problemas como la instalación inadecuada de válvulas, o controles erróneos
de los sistemas de bombeo.
A continuación se presentaran más resultados de emisores junto con las variaciones del
coeficiente de Hazen-Williams:
360
380
400
420
440
460
480
500
520
540
560
580
600
620
640
660
680
700000
900000
1100000
1300000
1500000
1700000
1900000
L/s
Número de Reynolds
Emisor 532 Medellín
Emisor D-W
Emisor H-W
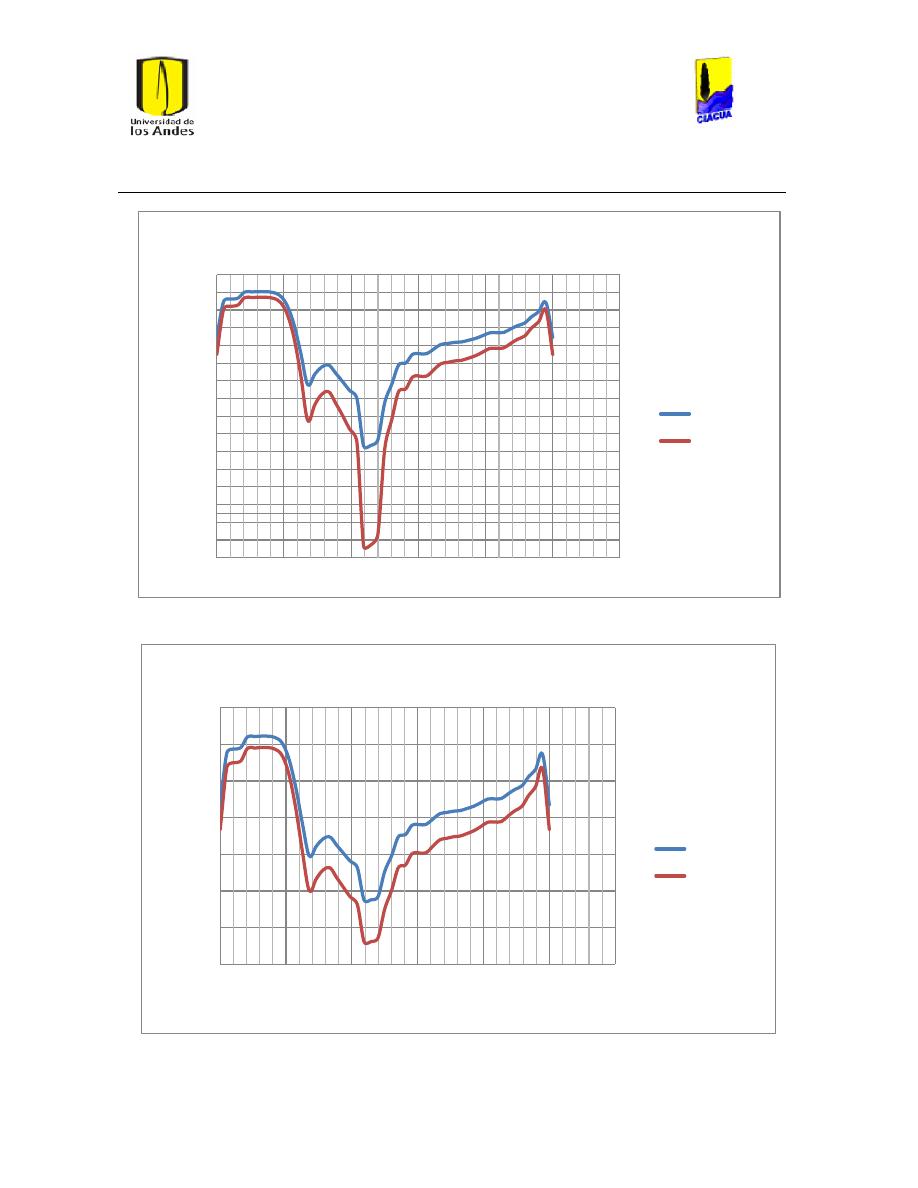
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
64
ILUSTRACIÓN 54 RESULTADOS EMISOR 72
ILUSTRACIÓN 55 RESULTADOS EMISOR 495
-50
-30
-10
10
30
50
70
90
110
130
150
170
190
210
230
250
270
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 72 Medellín
Emisor H-W
Emisor D-W
204
206
208
210
212
214
216
218
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 495 Medellín
Emisor H-W
Emisor D-W
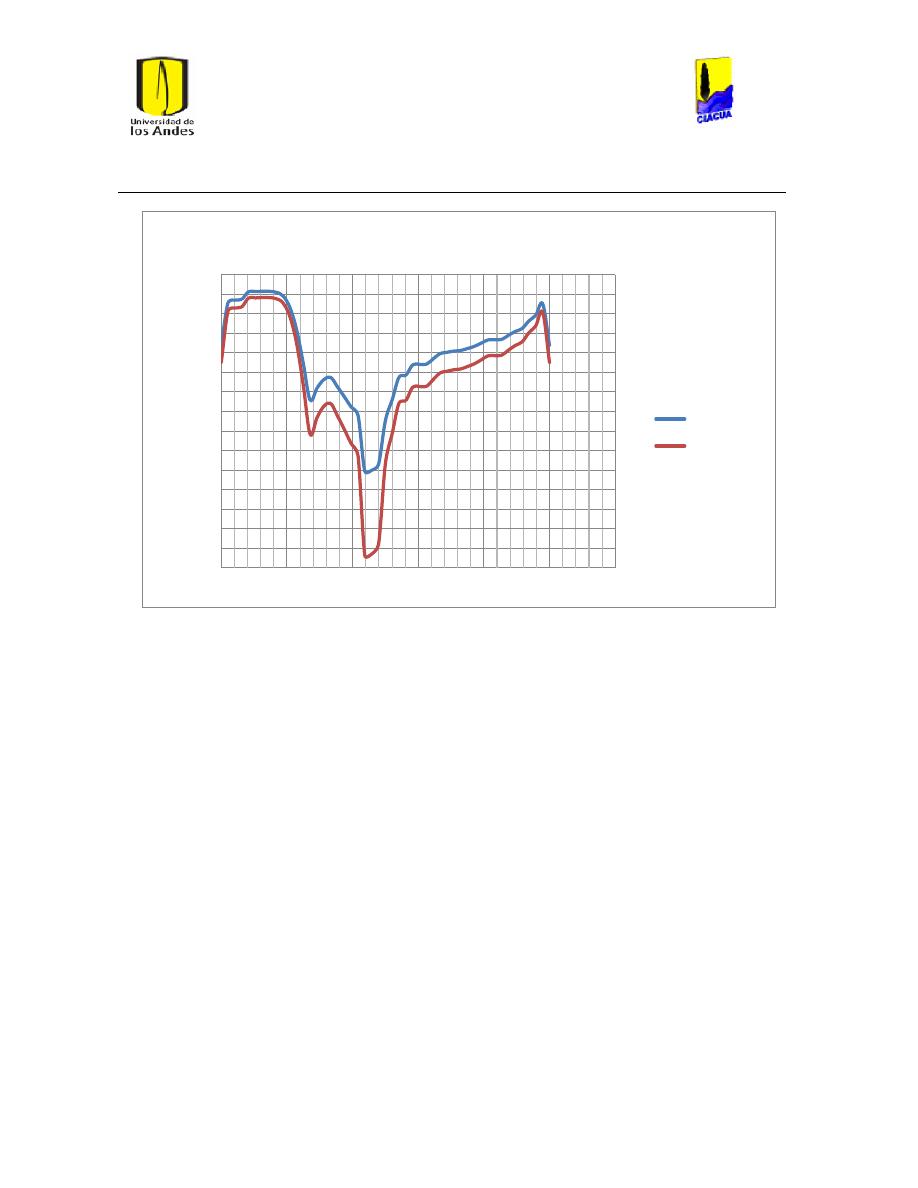
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
65
ILUSTRACIÓN 56 RESULTADOS EMISOR 663.
-40
-20
0
20
40
60
80
100
120
140
160
180
200
220
240
260
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 663 Medellín
Emisor H-W
Emisor D-W
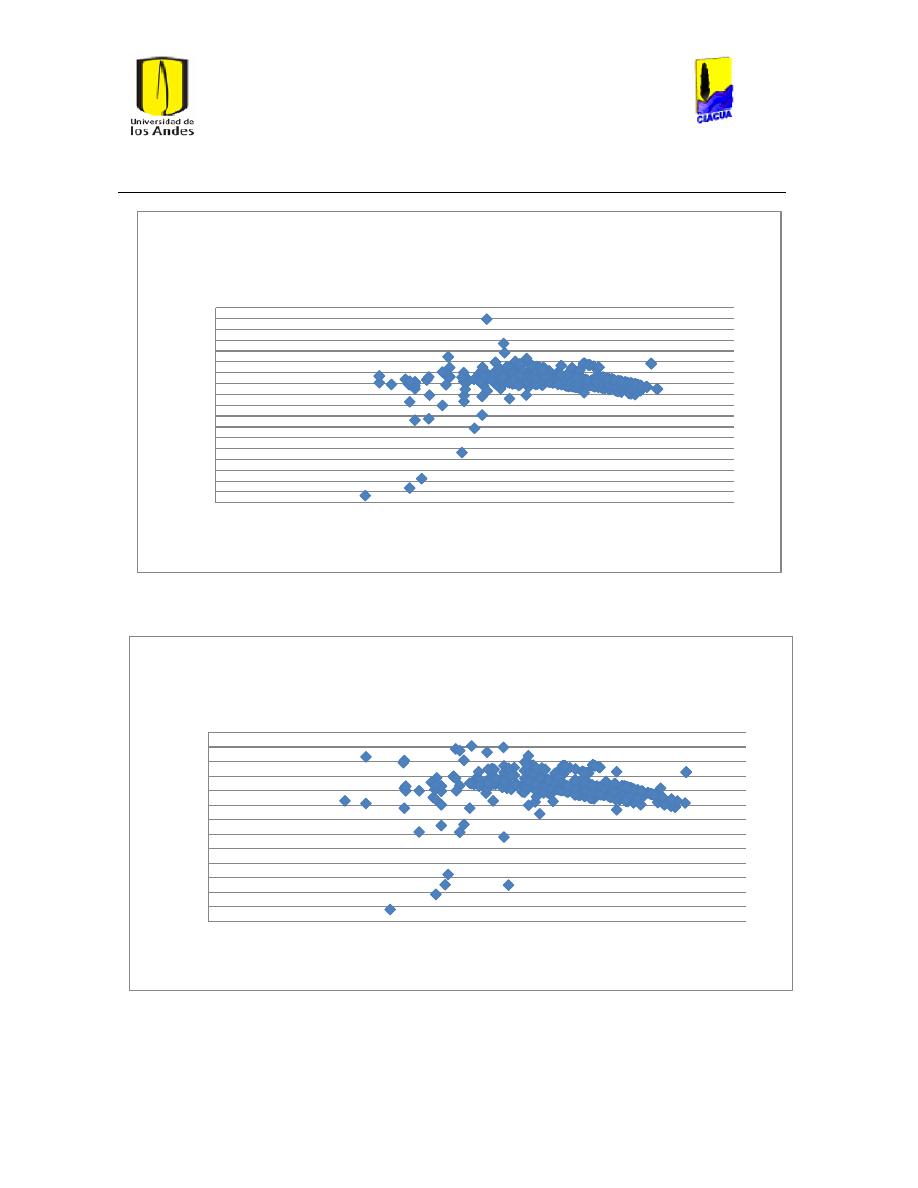
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
66
ILUSTRACIÓN 57 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS FRENTE AL NÚMERO DE
REYNOLDS PARA EL CAUDAL MÍNIMO.
ILUSTRACIÓN 58 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS FRENTE AL NÚMERO DE
REYNOLDS PARA EL CAUDAL MEDIO.
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
1000
10000
100000
1000000
10000000
Co
e
fi
ci
e
n
te
s Ha
ze
n
-Wi
lli
am
s
Número de Reynolds
Medellín Caudal Mínimo Coeficientes Hazen-
Williams
50
60
70
80
90
100
110
120
130
140
150
160
170
180
1000
10000
100000
1000000
10000000
Co
e
fi
ci
e
n
te
s Ha
ze
n
-Wi
lli
am
s
Número de Reynolds
Medellín Caudal Medio Coeficientes Hazen-
Williams
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
67
ILUSTRACIÓN 59 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS FRENTE AL NÚMERO DE
REYNOLDS PARA EL CAUDAL MÁXIMO.
ILUSTRACIÓN 60 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS FRENTE A LOS DIÁMETROS DE
LA RED PARA EL CAUDAL MEDIO.
60
70
80
90
100
110
120
130
140
150
160
170
180
190
1000
10000
100000
1000000
10000000
Co
e
fi
ci
e
n
te
s Ha
ze
n
-Wi
lli
am
s
Número de Reynolds
Medellín Caudal Máximo Coeficientes
Hazen-Williams
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
0
100 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 1600
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Díametro (mm)
Medellín Caudal Medio
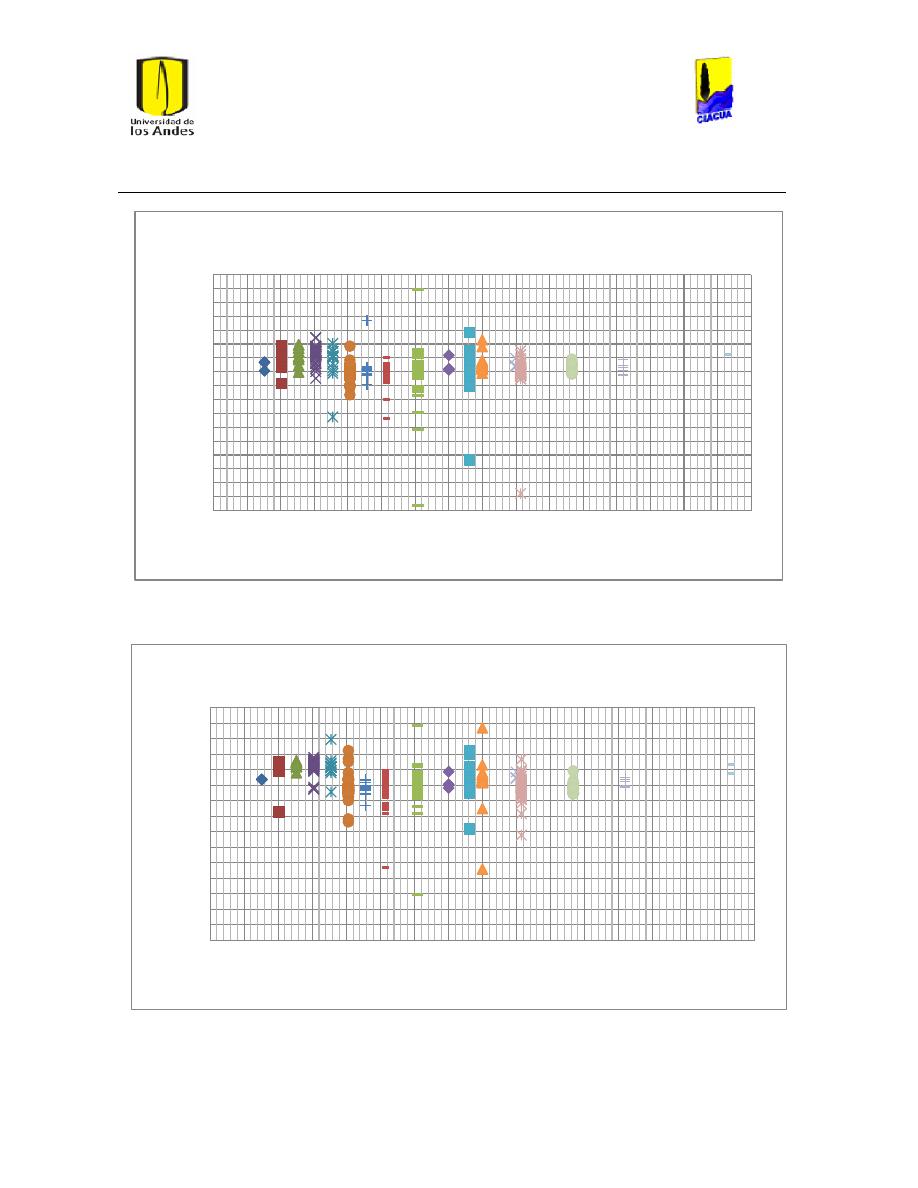
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
68
ILUSTRACIÓN 61 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS FRENTE A LOS DIÁMETROS DE
LA RED PARA EL CAUDAL MÍNIMO.
ILUSTRACIÓN 62 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS FRENTE A LOS DIÁMETROS DE
LA RED PARA EL CAUDAL MÁXIMO.
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
0
100 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 1600
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Díametro (mm)
Medellín Caudal Mínimo
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
0
100 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 1600
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Díametro (mm)
Medellín Caudal Máximo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
69
Las ilustraciones anteriores muestran resultados relevantes debido a que las diferencias en
los emisores son aun más importantes. Conviene señalar que algunos resultados arrojan
caudales con valores negativos, lo cual teóricamente no tiene mucho sentido, pero evidencia
en la práctica la condición de algunos emisores localizados en sitios críticos de la red, que se
ven sometidos en ciertos momentos del día a presentar presiones negativas, que coinciden
con los períodos donde el caudal es máximo.
Lo interesante de esto último es que existen casos en los cuales mientras la ecuación de Darcy-
Weisbach arroja caudales negativos (en la realidad el caudal emisor sería 0 o si es un tanque
empezaría a vaciarse) causado por que el nudo emisor tiene altas demandas y presenta
presiones negativas; en contraparte el emisor que utiliza la ecuación de Hazen-Williams sigue
arrojando valores positivos. Esto puede ser un problema de gran magnitud para una empresa
que desee controlar de forma eficiente la distribución de agua en una ciudad, ya que estos
resultados le dan un falso sentido de seguridad al operario. En este caso, el operario observará
con la ecuación de Hazen-Williams que el tanque se está llenando con un caudal relativamente
bajo pero se está llenando, mientras que la realidad es que el tanque está presentando una
salida importante de caudal y está disminuyendo su nivel de agua, así mismo si se esta
analizando el problema desde un punto de vista de fugas, el operario estará viendo que con la
ecuación de Hazen-Williams se está presentando un alto índice de fugas que realmente no
existen o no se encuentran en la magnitud que observa. Las consecuencias de estos dos
problemas pueden llegar a tener implicaciones catastróficas; disminuyendo las presiones de
un sector o lo que es aún peor, dejando sin abastecimiento a un sector de la ciudad. Puede ser
de tal magnitud la diferencia presentada, que en el caso de esta investigación se encontraron
diferencias entre los caudales de los emisores de hasta 120 L/s.
Pasando a las gráficas de variación de los coeficientes de Hazen-Williams, se ve que la red se
está comportando hidráulicamente entre valores de 130 y 140. Si bien la red está trabajando
con un coeficiente de 140 para tuberías mayores a 14 pulgadas (350 mm), no hay que obviar
el hecho de que la red también tiene un conjunto importante de tuberías que trabajan con un
coeficiente de 150, lo que lleva a pensar que la red se está comportando con mayores pérdidas
por fricción que las simuladas con la ecuación de Hazen-Williams; adicionalmente si se ve la
variación del coeficiente de Hazen-Williams para diámetros mayores a 14 pulgadas se ve que
hay tuberías donde se llega a comportar con valores de hasta 80. Por otro lado, las tuberías de
diámetros menores parecen comportarse de manera adecuada para los 3 momentos claves
del estudio.
Cabe resaltar de estos resultados que para los horarios en que se presentan los caudales
medios y caudales mínimos, las diferencias de los emisores no parecen ser tan grandes,
mientras que a medida que se acerca la hora de máximo consumo de la red, las diferencias de
los emisores parecen volverse mayores, en especial si el emisor se encuentra localizado en un
punto crítico de la red como se puede observar en las gráficas de los diferentes emisores.
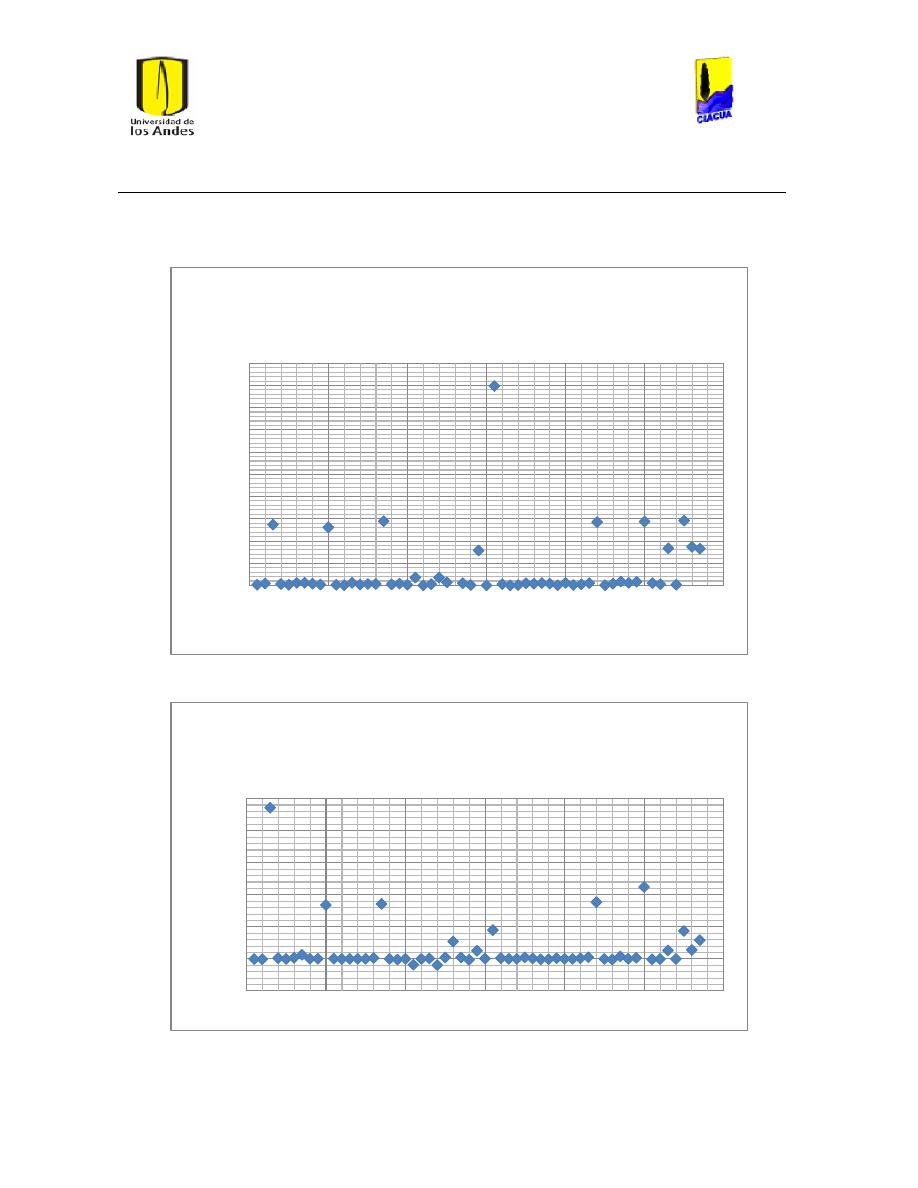
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
70
A continuación presentaremos finalmente las presiones encontradas en los tres horarios
claves de la red matriz de Medellín:
ILUSTRACIÓN 63 DIFERENCIA DE PRESIONES CON CAUDALES MEDIOS.
ILUSTRACIÓN 64 DIFERENCIA DE PRESIONES CON CAUDALES MÍNIMOS.
0
10
20
30
40
50
60
70
80
90
100
0
10
20
30
40
50
60
(H
w
-D
w/
D
w)
*100
Nudo
Diferencia de Presiones Medellín Caudal
Medio
-10
0
10
20
30
40
50
0
10
20
30
40
50
60
(H
w
-D
w/
D
w)
*100
Nudo
Diferencia de Presiones Medellín Caudal
Mínimo
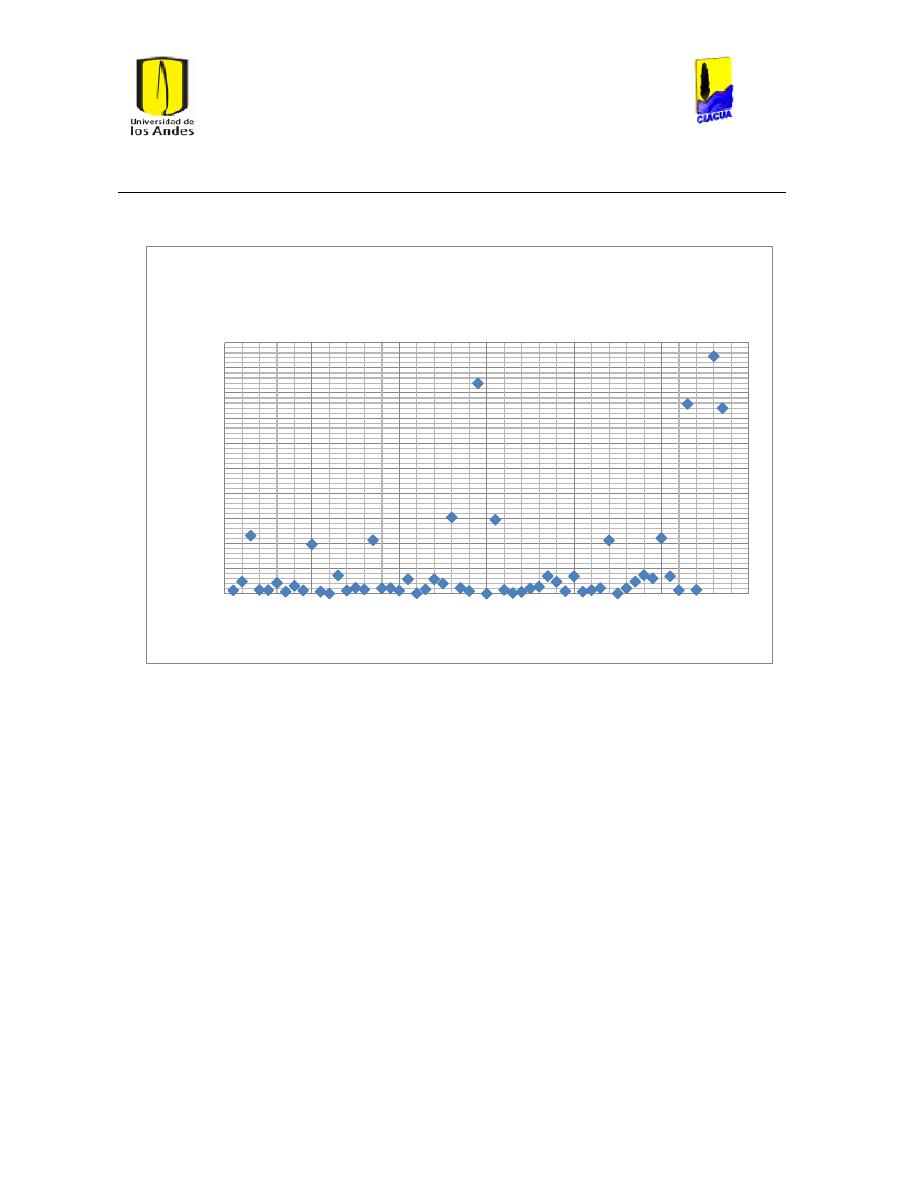
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
71
ILUSTRACIÓN 65 DIFERENCIA DE PRESIONES CON CAUDALES MÁXIMOS.
Los resultados son consistentes con lo encontrado en el análisis de los emisores y en la
variación de coeficiente de Hazen-Williams. Si bien existen diferencias en las presiones
cuando se tiene el caudal mínimo y el caudal medio, los valores más amplios y de por sí más
relevantes se pueden observar cuando se tiene la hora de máximo consumo. Las diferencias
observables en algunos casos alcanzan diferencias superiores al 90%, esto se debe a que en
algunos escenarios las presiones con la ecuación de Darcy-Weisbach son inferiores a uno, o
muy cercanas a cero elevando considerablemente el error relativo. Este es un error común
cuando se realizan análisis con valores de presión tan bajos. Sin embargo, lo más importante
de estos resultados es que queda una vez más demostrado que la ecuación de Hazen-Williams
es una ecuación que puede presentar grandes divergencias con respecto a los resultados de la
ecuación de Darcy-Weisbach que es físicamente basada y considera todos los parámetros
físicos relevantes para el cálculo de las pérdidas por fricción. Lo anterior también implica que
en la red operada con la ecuación de Hazen-Williams está sobrestimando y/o subestimando la
pérdidas por fricción que se presentan en la red. En la próxima sección se va a mostrar con
más claridad que parte de estos efectos es causado por un desbalance de masa en la red a
causa de tanques o emisores y a que la solución hidráulica entre las dos ecuaciones es
diferente (caudal que pasa por cada una de las tuberías de la red).
0
10
20
30
40
50
60
70
80
90
100
0
10
20
30
40
50
60
(H
w
-D
w/
D
w)
*100
Nudo
Diferencia de Presiones Medellín Caudal
Máximo
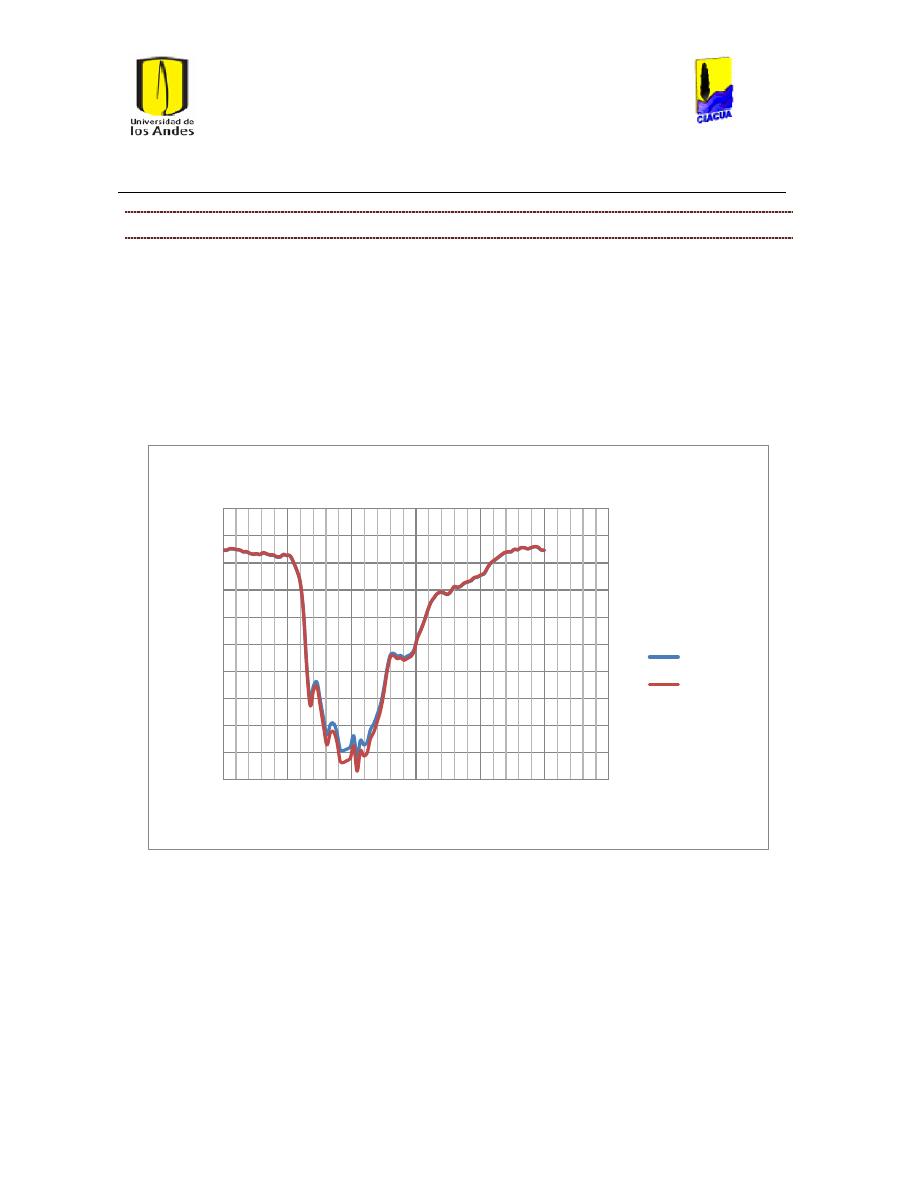
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
72
4.3.3 RED GINEBRA
Al igual que en el caso de la red matriz de Bogotá, la red Ginebra se analizó con emisores
pequeños y grandes. Cabe resaltar que el comportamiento de esta red fue excepcional debido
a que el comportamiento de esta al utilizar la ecuación de Hazen-Williams fue prácticamente
igual al comportamiento hidráulico utilizando la ecuación de Darcy-Weisbach en algunos de
los escenarios; sin obviar el hecho de que más adelante se muestran los resultados con
tanques y de que algunos emisores si presentaron diferencias significativas. Los resultados de
los emisores pequeños se muestran a continuación.
ILUSTRACIÓN 66 RESULTADOS EMISOR 369.
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 369 Ginebra
Emisor H-W
Emisor D-W
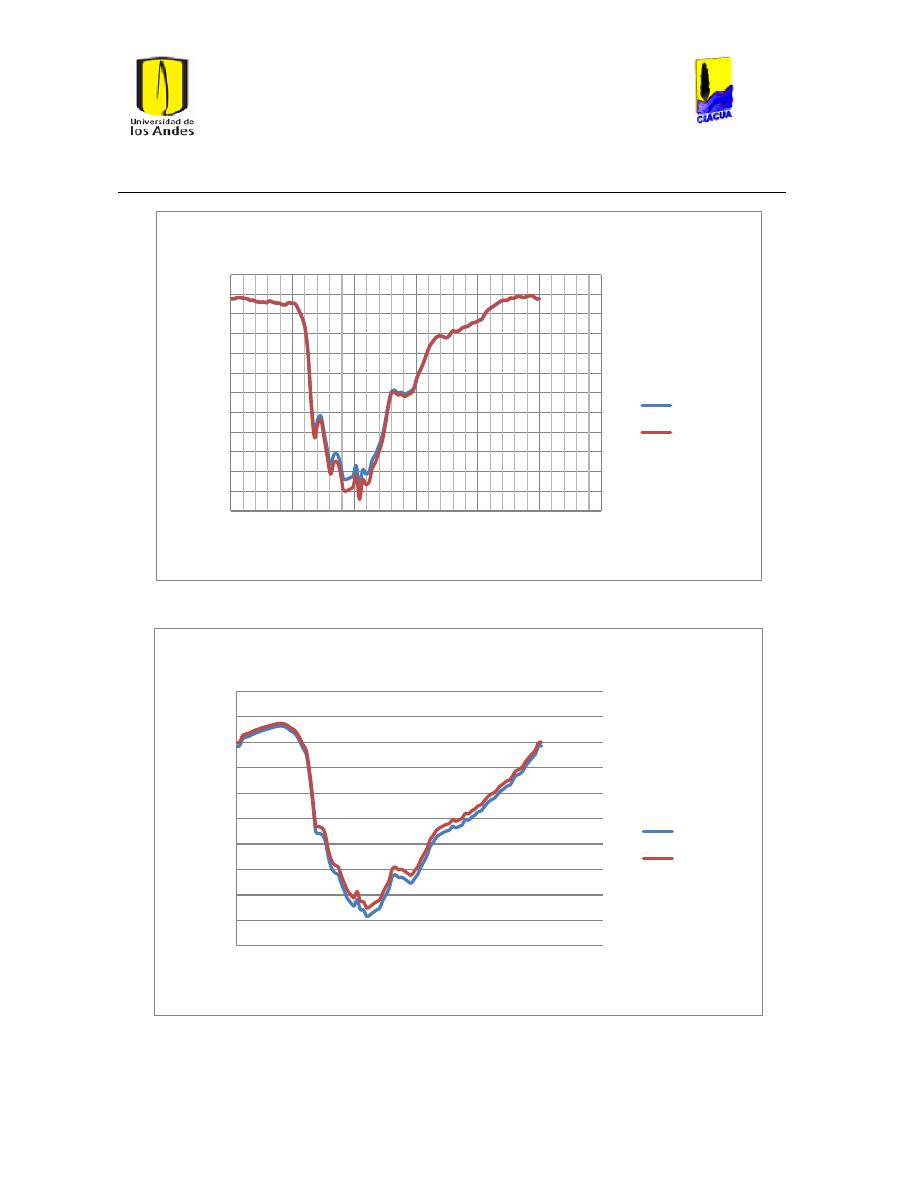
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
73
ILUSTRACIÓN 67 RESULTADOS EMISOR 365.
ILUSTRACIÓN 68 RESULTADOS EMISOR 6.
3
3.5
4
4.5
5
5.5
6
6.5
7
7.5
8
8.5
9
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 365 Ginebra
Emisor H-W
Emisor D-W
4.5
4.55
4.6
4.65
4.7
4.75
4.8
4.85
4.9
4.95
5
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 6 Ginebra
Emisor H-W
Emisor D-W
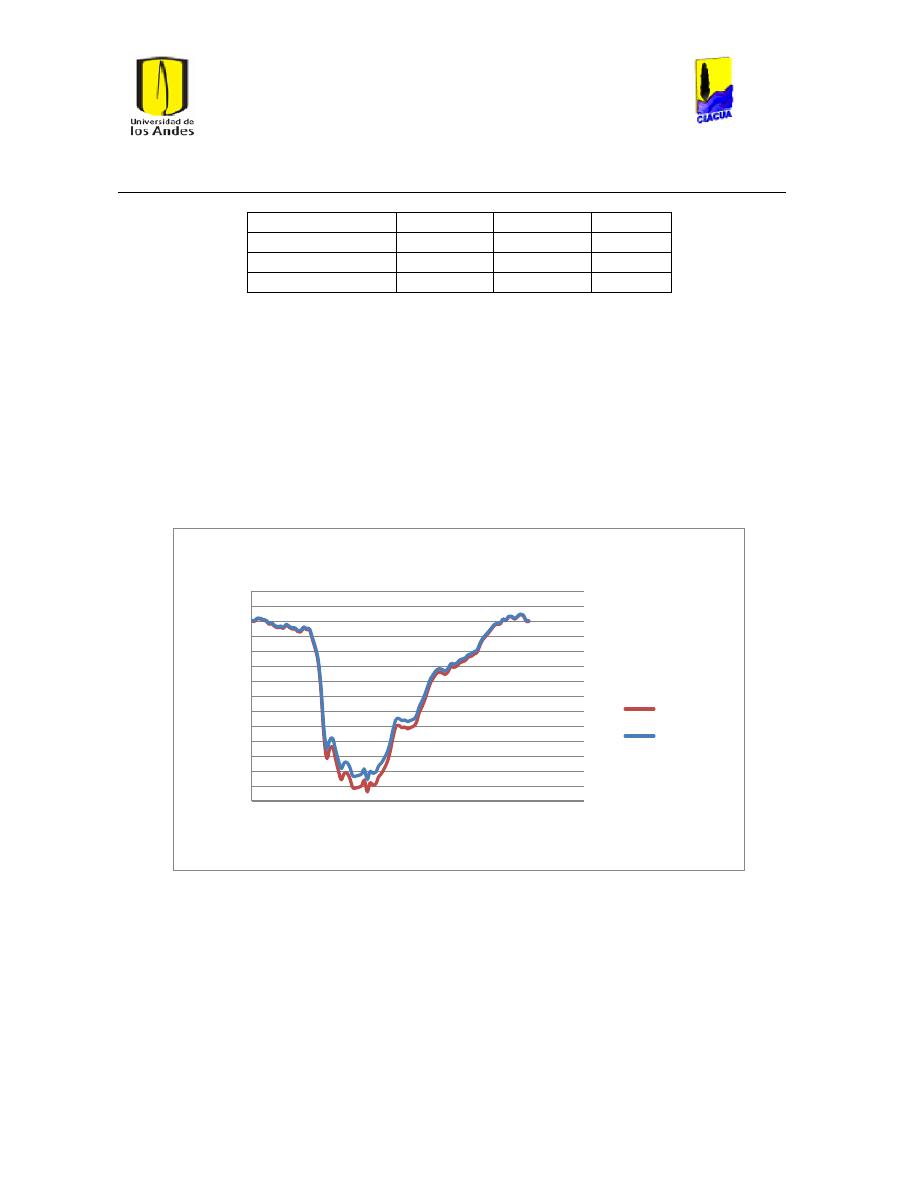
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
74
Emisor 369 Emisor 365 Emisor 6
Presión(m)
20
20
20
Caudal Base(L/s)
0.7704
4.522
2.4049
Coeficiente Emisor
0.1722
1.011
0.5377
ILUSTRACIÓN 69 CARACTERÍSTICAS DE LOS EMISORES PEQUEÑOS.
Al igual que en el caso de la red matriz de Bogotá, es posible ver en las gráficas anteriores que
la diferencia entre la red simulada con la ecuación empírica y la ecuación físicamente basada
es muy poca. Más adelante se mostrarán los resultados con emisores más grandes; si bien los
resultados fueron muy similares y no presentaron grandes diferencias, si se empezó a ver que
el caudal emisor iba en aumento y existían puntos con diferencias importantes.
Prosiguiendo con los emisores, a continuación se muestran los emisores con coeficientes de
emisión mayores:
ILUSTRACIÓN 70 RESULTADOS EMISOR 476.
200
215
230
245
260
275
290
305
320
335
350
365
380
395
410
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Ginebra Emisor 476
Emisor D-W
Emisor H-W
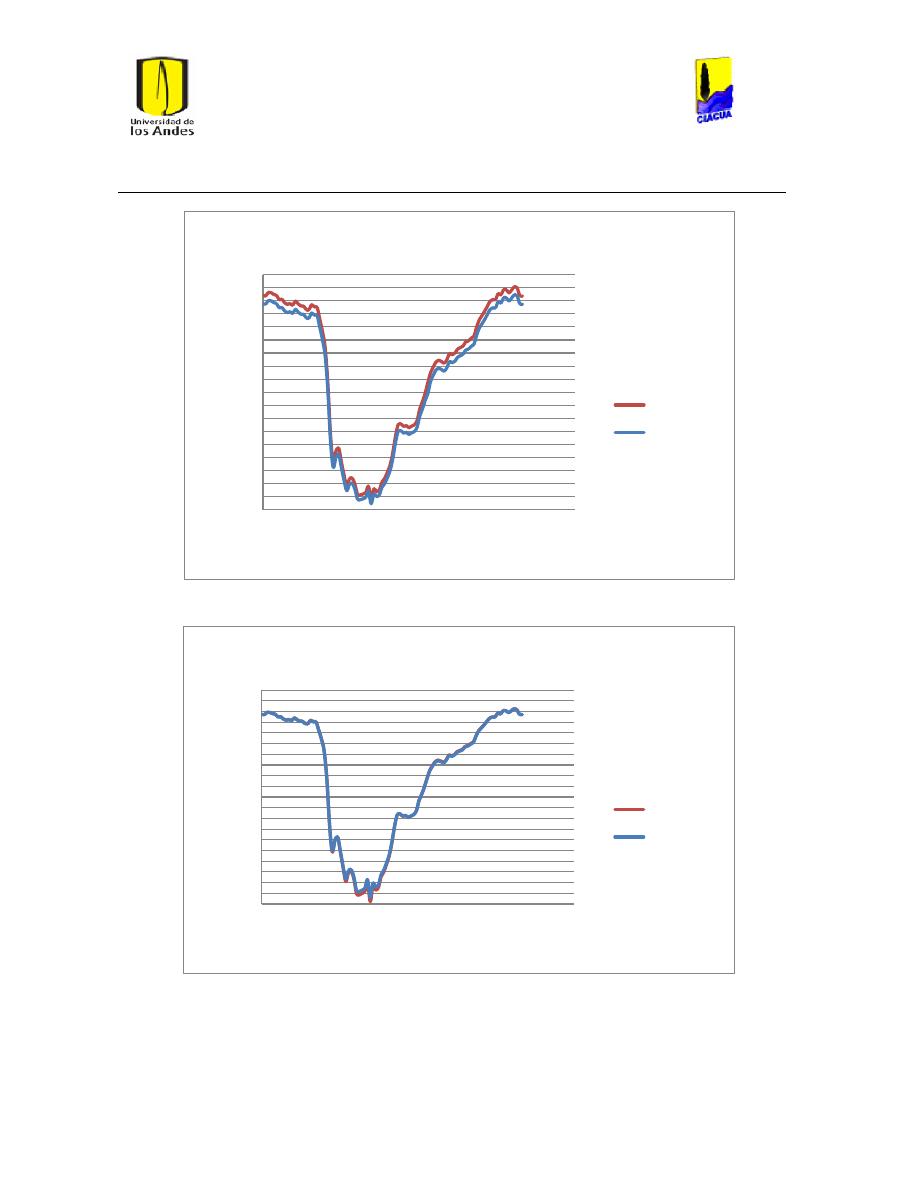
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
75
ILUSTRACIÓN 71 RESULTADOS EMISOR 411.
ILUSTRACIÓN 72 RESULTADOS EMISOR 458.
90
100
110
120
130
140
150
160
170
180
190
200
210
220
230
240
250
260
270
00:00 04:48 09:36 14:24 19:12 00:00 04:48
L/s
Tiempo(h)
Ginebra Emisor 411
Emisor D-W
Emisor H-W
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
220
230
240
00:00 04:48 09:36 14:24 19:12 00:00 04:48
L/s
Tiempo(h)
Ginebra Emisor 458
Emisor D-W
Emisor H-W
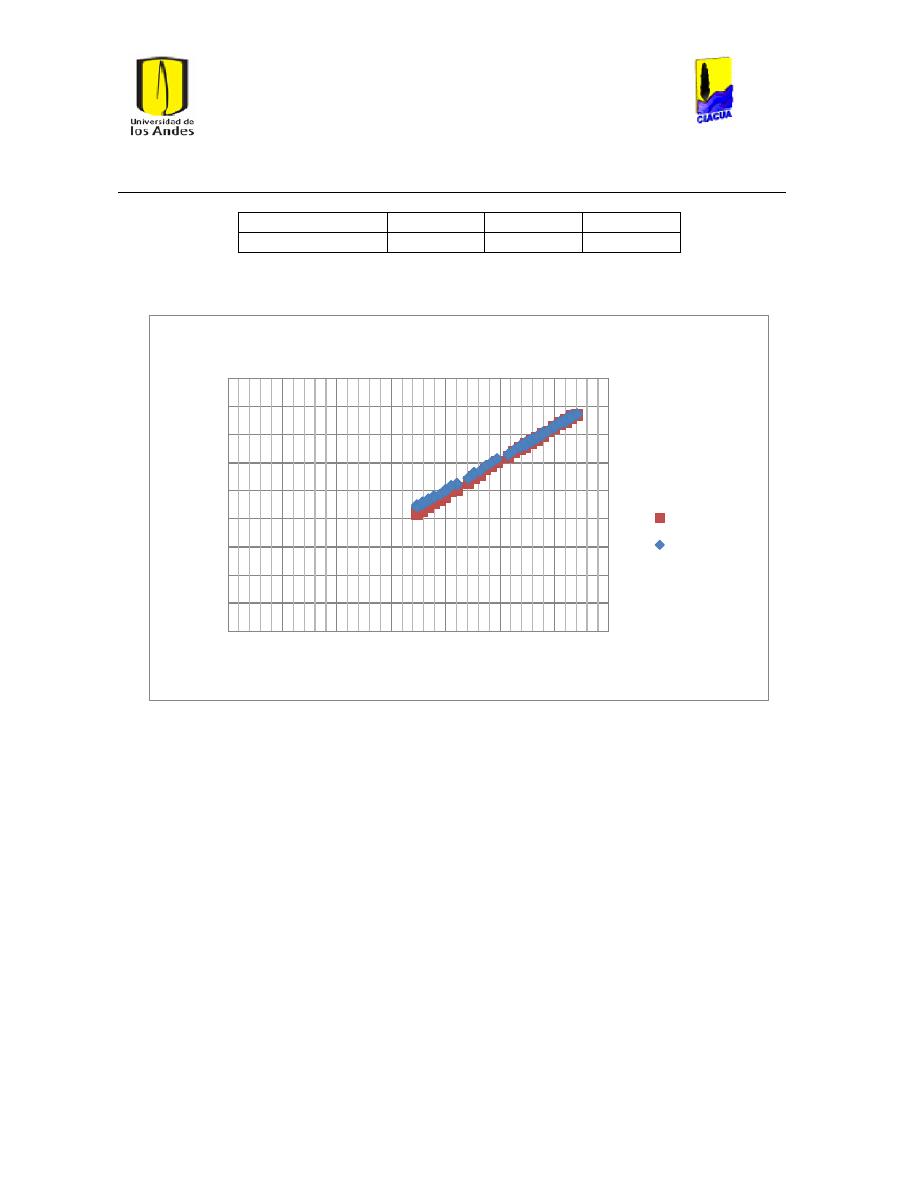
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
76
Emisor 458 Emisor 411 Emisor 476
Coeficiente Emisor
12.74
14.53
11.18
TABLA 8 COEFICIENTES DE EMISORES GRANDES.
ILUSTRACIÓN 73 CAUDAL EMISOR VS NÚMERO DE REYNOLDS EMISOR 476.
0
50
100
150
200
250
300
350
400
450
0
75000 150000 225000 300000 375000 450000 525000
L/s
Número de Reynolds
Emisor 476 Ginebra
Q emisor D-W
Q Emisor H-W
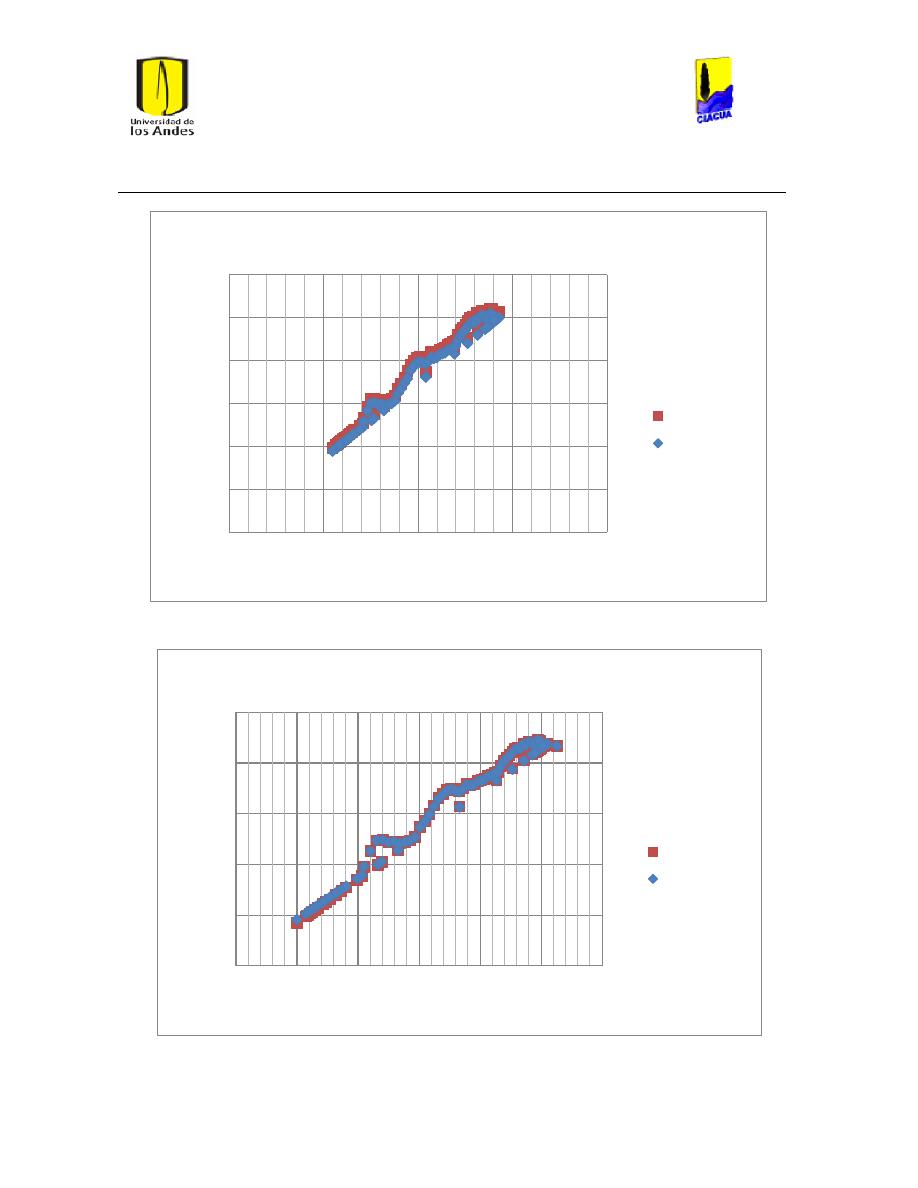
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
77
ILUSTRACIÓN 74 CAUDAL EMISOR VS NÚMERO DE REYNOLDS EMISOR 411.
ILUSTRACIÓN 75 CAUDAL EMISOR VS NÚMERO DE REYNOLDS EMISOR 458.
0
50
100
150
200
250
300
0
50000
100000
150000
200000
L/s
Número de Reynolds
Emisor 411 Ginebra
Q emisor D-W
Q Emisor H-W
0
50
100
150
200
250
0
20000
40000
60000
80000
100000 120000
L/s
Número de Reynolds
Emisor 458 Ginebra
Q emisor D-W
Q Emisor H-W
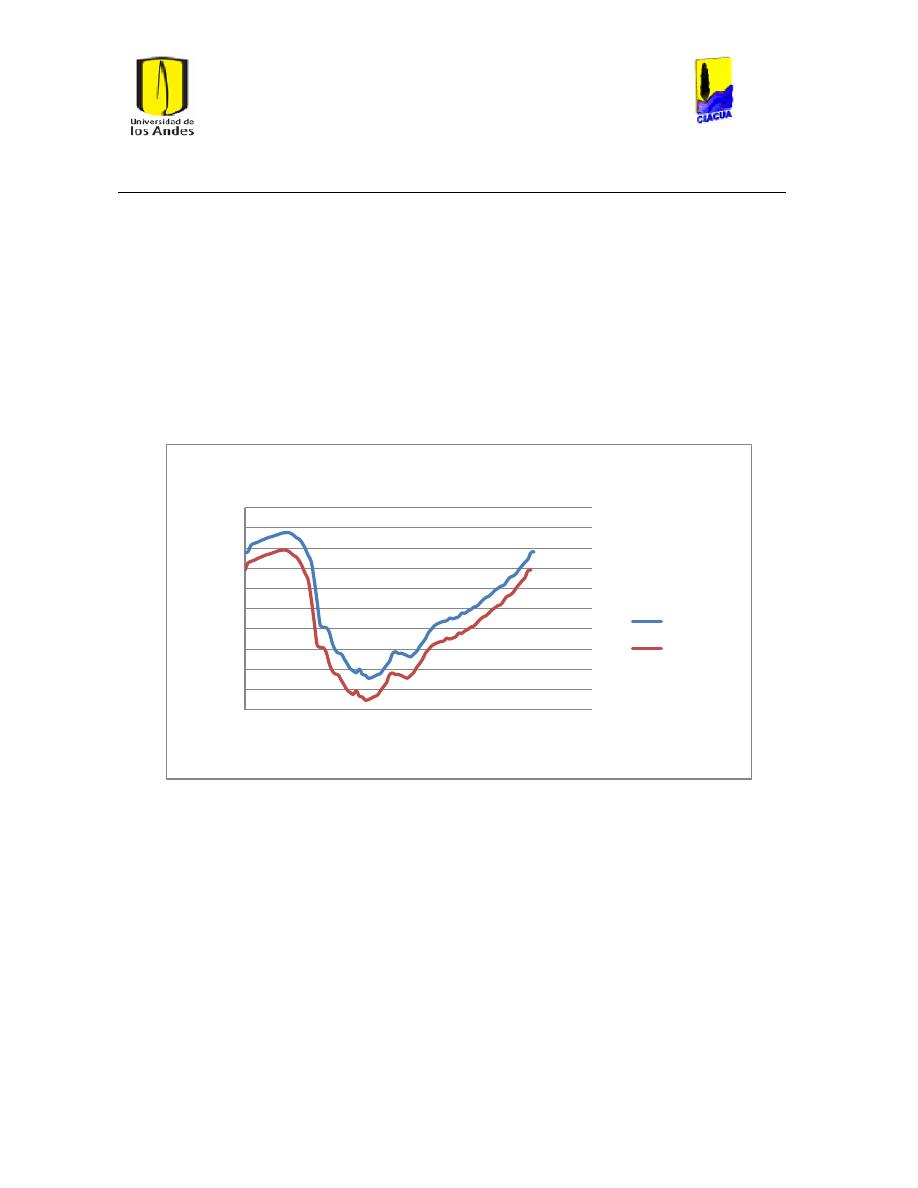
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
78
Los resultados con emisores grandes dieron tendencias similares a las encontradas con los
emisores pequeños; es decir la diferencia de los caudales de los emisores no fue muy
diferente. Este efecto es interesante teniendo en cuenta que no se usaron los mismos emisores
en cada una de las pruebas y dentro del análisis; algunos de estos emisores estaban
localizados en puntos críticos de la red (donde se presentaban las presiones más pequeñas).
Por otro lado, si se ven las gráficas de caudal emisor vs número de Reynolds, se confirma una
vez más lo que se logra observar en las gráficas de los 2 emisores, y es que el comportamiento
entre las dos ecuaciones es casi idéntico, con diferencias mínimas, no superiores a 2 L/s.
La investigación avanzó en la obtención de información corriendo las ecuaciones mediante el
uso de emisores grandes. Los resultados se muestran a continuación:
ILUSTRACIÓN 76 RESULTADOS EMISOR 392.
200
210
220
230
240
250
260
270
280
290
300
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 392 Ginebra
Emisor H-W
Emisor D-W
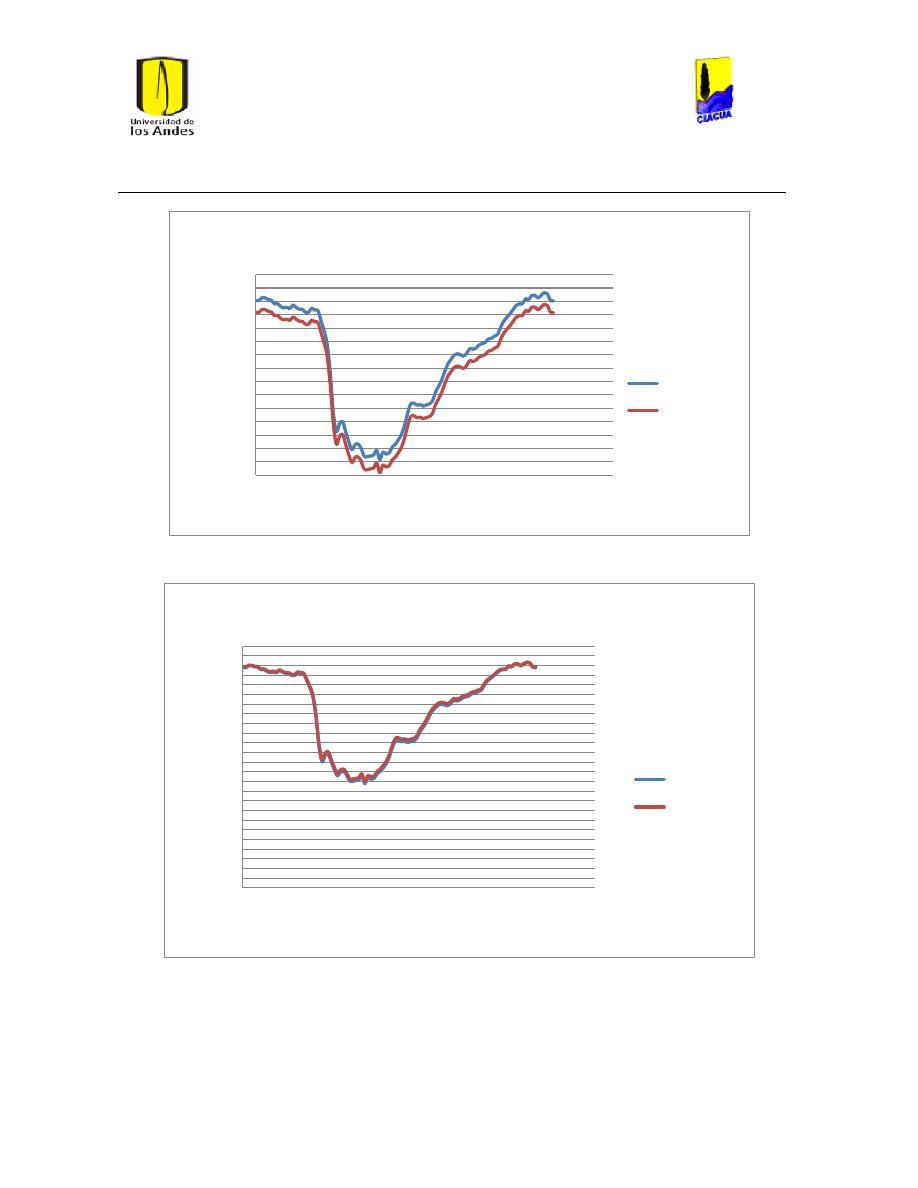
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
79
ILUSTRACIÓN 77 RESULTADOS EMISOR 464
ILUSTRACIÓN 78 RESULTADOS EMISOR 457.
270
320
370
420
470
520
570
620
670
720
770
820
870
920
970
1020
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(Hr)
Diferencia Emisor 464 Ginebra
Emisor H-W
Emisor D-W
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
220
230
240
250
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(Hr)
Diferencia Emisor 457 Ginebra
Emisor H-W
Emisor D-W
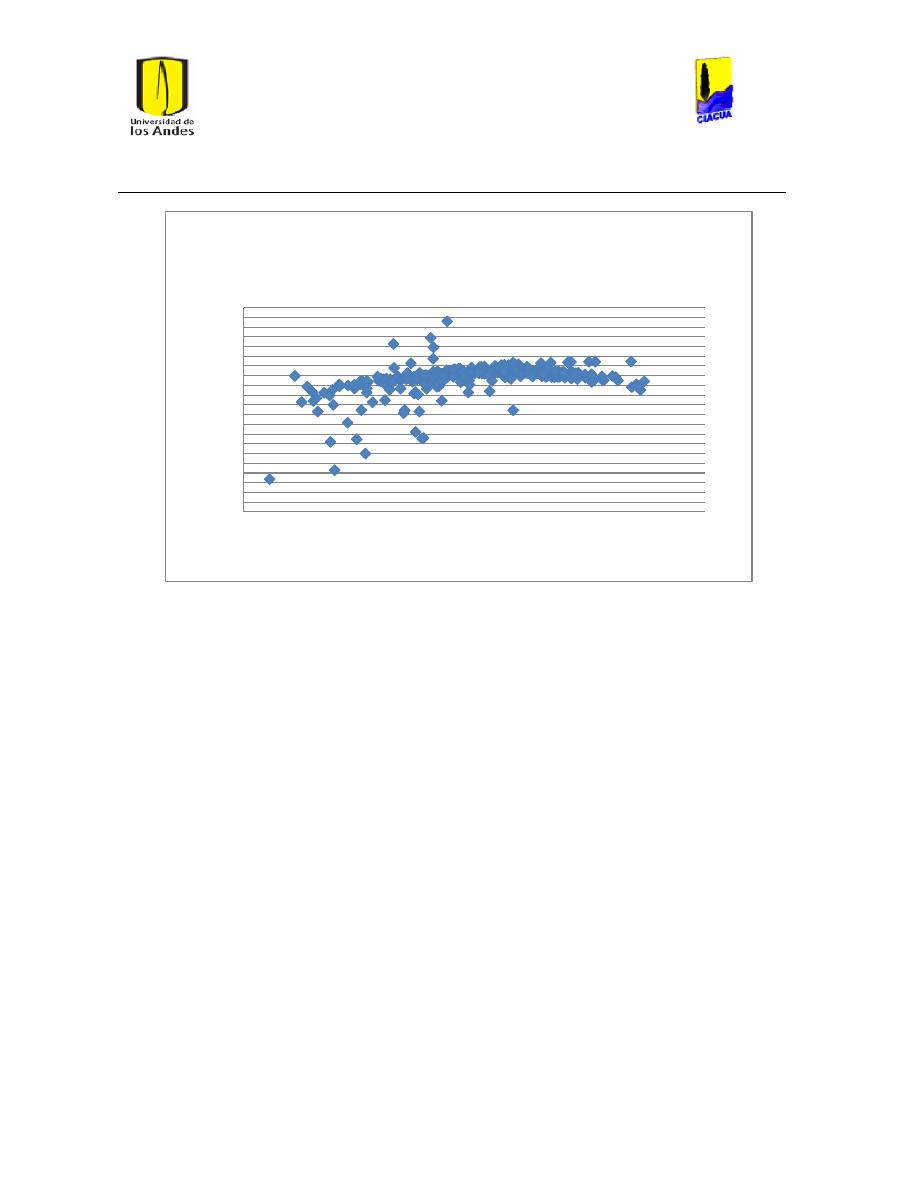
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
80
ILUSTRACIÓN 79 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS VS EL NÚMERO DE REYNOLDS
PARA EL CAUDAL MEDIO.
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
1000
10000
100000
1000000
10000000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Número de Reynolds
Ginebra Coeficiente de Hazen-Williams
Caudal Medio
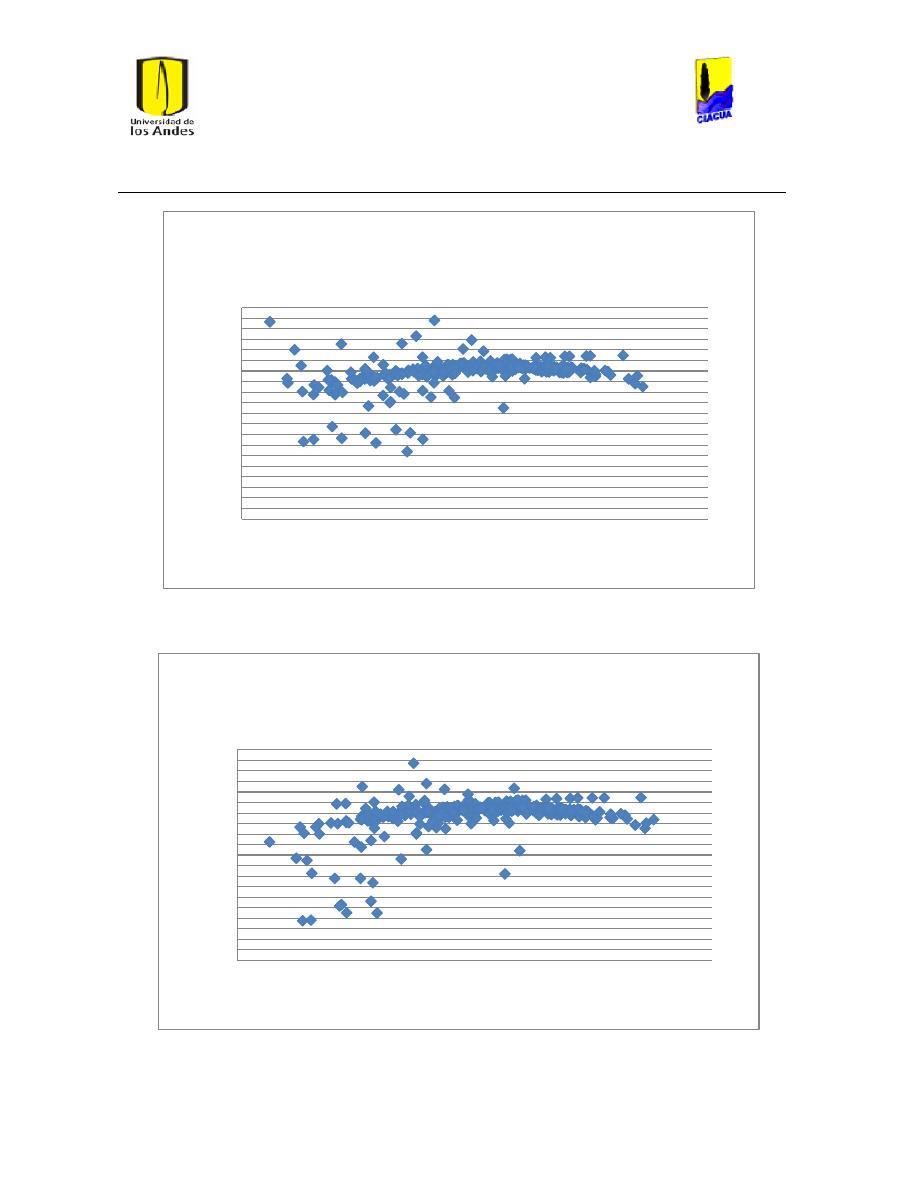
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
81
ILUSTRACIÓN 80 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS VS EL NÚMERO DE REYNOLDS
PARA EL CAUDAL MÍNIMO.
ILUSTRACIÓN 81 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS VS EL NÚMERO DE REYNOLDS
PARA EL CAUDAL MÁXIMO.
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
1000
10000
100000
1000000
10000000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Número de Reynolds
Ginebra Coeficiente de Hazen-Williams
Caudal Mínimo
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
1000
10000
100000
1000000
10000000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Número de Reynolds
Ginebra Coeficiente de Hazen-Williams
Caudal Máximo
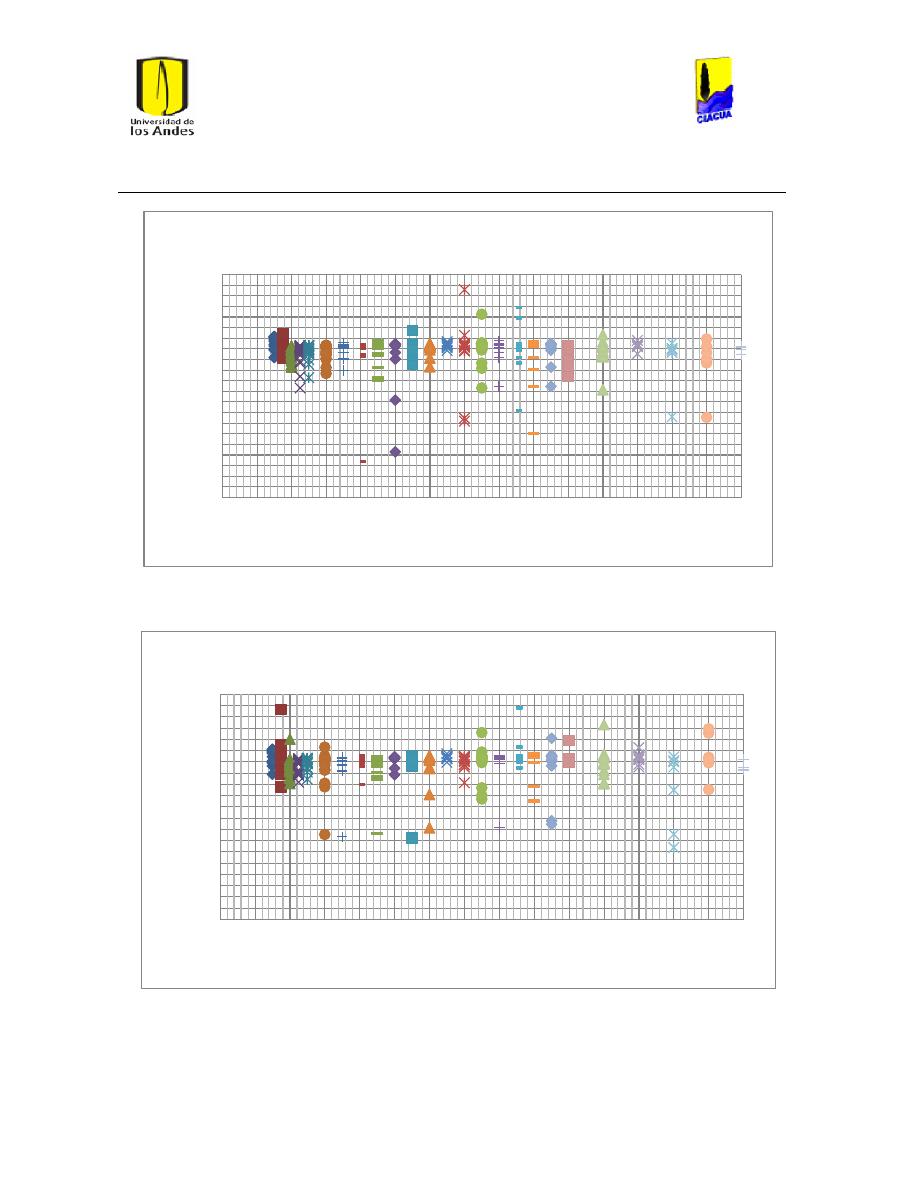
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
82
ILUSTRACIÓN 82 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS VS LOS DIÁMETROS DE LA RED
PARA EL CAUDAL MEDIO.
ILUSTRACIÓN 83 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS VS LOS DIÁMETROS DE LA RED
PARA EL CAUDAL MÍNIMO.
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
0
200 400 600 800 1000 1200 1400 1600 1800 2000 2200 2400 2600 2800 3000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Diametro (mm)
Ginebra Caudal Medio
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
0
200 400 600 800 1000 1200 1400 1600 1800 2000 2200 2400 2600 2800 3000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Diametro (mm)
Ginebra Caudal Mínimo
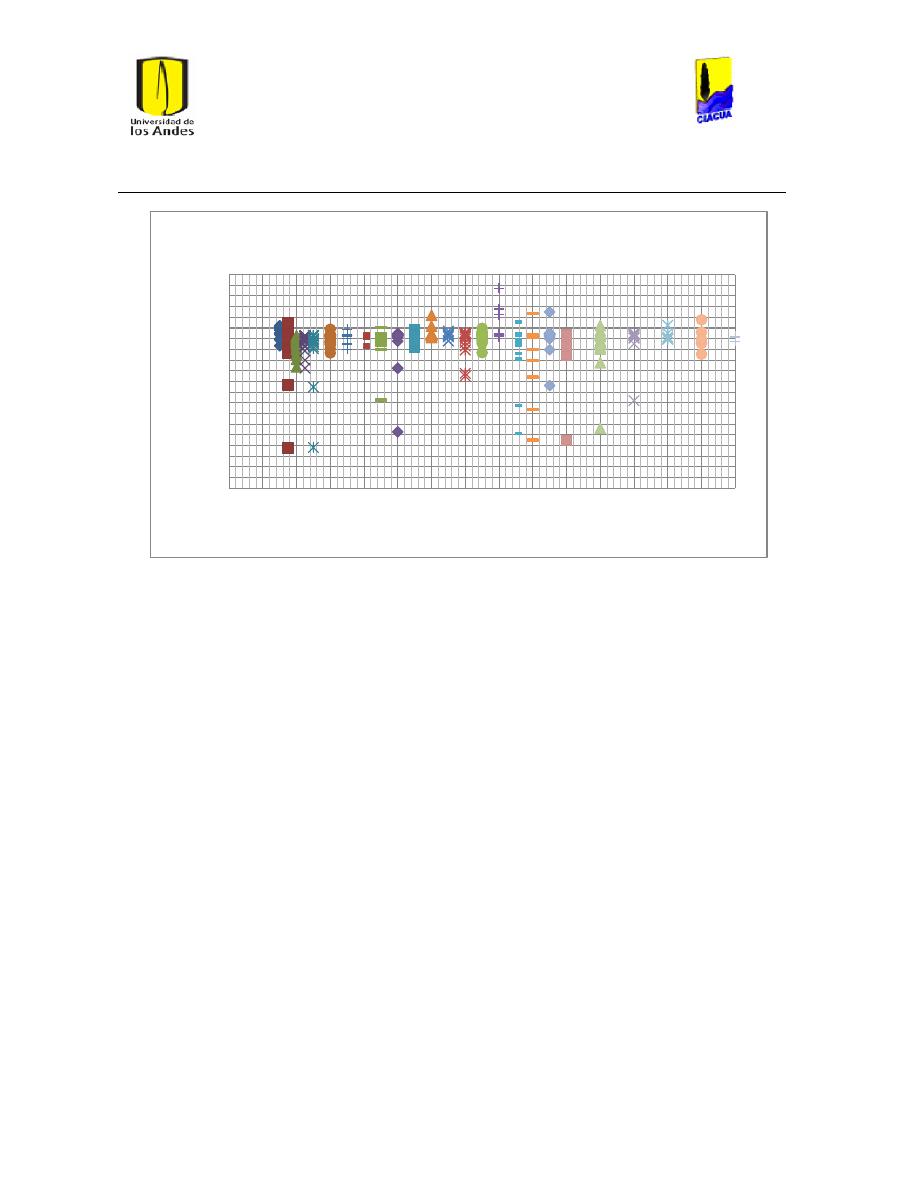
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
83
ILUSTRACIÓN 84 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS VS LOS DIÁMETROS DE LA RED
PARA EL CAUDAL MÁXIMO.
Estos últimos resultados muestran una tendencia interesante; el hecho de que se presenten
diferencias entre los emisores utilizando la ecuación de Darcy-Weisbach y la ecuación de
Hazen-Williams, demuestra lo analizado en la red de Medellín, y es que le hecho de que en
algunos emisores la ecuación de Hazen-Williams cumpla o se comporte similar que el emisor
con la ecuación físicamente basada, no implica que el comportamiento de toda la red sea igual
a lo largo de los nudos. Si bien las diferencias con respecto a los caudales emitidos parecen
relativamente pequeñas, 10 L/s entre un máximo de 300 L/s demandados, existen otros casos
en que llega a ser de hasta 80 L/s; estas diferencias siguen representando una cantidad
importante de agua, y demuestra una vez más que existen diferencias importantes entre la
ecuación de Hazen-Williams y la ecuación de Darcy-Weisbach. Por otro lado, cabe resaltar que
estas diferencias repiten la tendencia vista en la red matriz de Medellín, en el sentido que
tienden a presentarse presiones negativas cuando llegan las horas de máximos caudales
demandados (ver 4.2 Patrones de las Redes Trabajadas); esto puede ser una complicación
importante, especialmente cuando se considera que en estos momentos algunos puntos de la
red pueden llegar a presentar escasés de agua o presiones inferiores a la exigida por la
normativa("RAS Título B: Sistemas de Acueducto," 2012). Considerando lo anterior, es
importante mencionar que esta fue la red que menores diferencias presentó entre las dos
ecuaciones. Si se observan los emisores con respecto a las otras redes, se puede evidenciar
que las diferencias fueron mínimas y se presentaron exclusivamente en un par de emisores.
Lo anterior es consistente con lo que se puede observar en las gráficas de variación del
coeficiente de Hazen-Williams vs el número de Reynolds. En estas gráficas se puede ver que la
gran mayoría de los coeficientes de Hazen-Williams se encuentran entre 135 y 150. Esto en
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
0
200 400 600 800 1000 1200 1400 1600 1800 2000 2200 2400 2600 2800 3000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Diametro (mm)
Ginebra Caudal Máximo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
84
comparación con los valores teóricos de la red que fueron tomados como 140 y 150, se puede
decir que la red se está comportando relativamente bien con respecto a los valores supuestos
del coeficiente de Hazen-Williams. Así mismo cuando se analizan las gráficas de variación del
coeficiente de Hazen-Willliams vs los diámetros de las redes, se puede ver que la mayoría de
estos se encuentran en los rangos ya nombrados anteriormente, en especial los diámetros
analizados en este estudio (tuberías de más de 900 mm).
A pesar de lo anterior, es importante notar que si bien la red se comporta muy bien, existen un
conjunto de tuberías que presentan coeficientes de Hazen-Williams bajos (valores de 70 y 60),
y otros bastante altos (considerando que un coeficiente de 150 es alto y por ende muy liso).
Quizás estas tuberías que presentan estos comportamientos tan diferentes puedan influir de
alguna manera en la hidráulica general de la red y estén generando que las caudales emitidos
por el emisor, diverjan entre las dos ecuaciones. Este caso también se observó en la red matriz
de Medellín, donde existían diferencias importantes entre los coeficientes de Hazen-Williams
y estas se vieron claramente reflejadas en el comportamiento de los emisores de la ecuación
físicamente basada frente a la ecuación empírica. Lo anterior se verificó y más adelante,
cuando se muestren los resultados de tanques, se va a evidenciar que el comportamiento de la
red se ve afectado por un desbalance de masa en las tuberías causado por el uso de la
ecuación de Hazen-Williams; adicionalmente se va a mostrar que la hidráulica de la red se
soluciona de manera diferente entre las dos ecuaciones (caudales que pasan por las tuberías)
causando que las pérdidas por fricción y números de Reynolds entre tramos de tuberías
iguales sean distintos, generando 2 efectos importantes: 1) Los Coeficientes de Hazen-
Williasm calculados a partir de los resultados de la ecuación de Darcy-Weisbach van a ser
diferentes a los trabajados teóricamente ya que estos dependen del flujo, 2) La hidráulica de la
red va a cambiar radicalmente al existir diferencias importantes en las perdidas por fricción
que existen en todas las tuberías del sistema ( unas en mayor magnitud que otras).
Todo esto parece confirmar lo que se ha encontrado en las redes anteriores, y es que a pesar
de que la red se comporte relativamente bien en cuanto a coeficientes de Hazen-Williams
teóricos y calculados, las pequeñas diferencias pueden llevar a que se presenten diferencias
en los caudales que simulan los tanques (emisores), llevando a un operador a tener una falsa
sensación de confianza (al ver que el tanque se está llenando más rápidamente de lo que
realmente está ocurriendo).
En cuanto a los resultados de diferencias de presión de la red, no se presentaron grandes
diferencias; los resultados de estas presiones se muestran a continuación, para los 3 tiempos
establecidos:
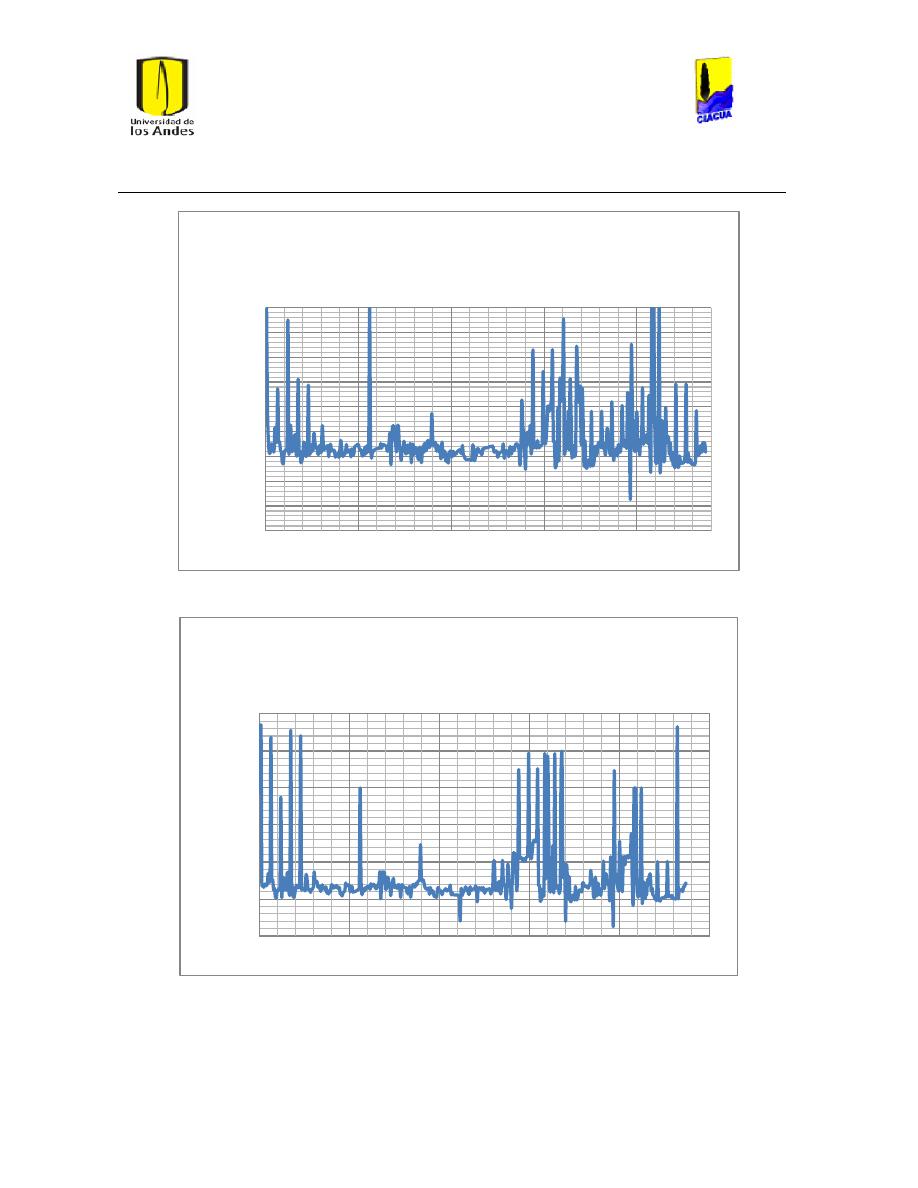
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
85
ILUSTRACIÓN 85 DIFERENCIAS DE PRESIONES PARA EL CAUDAL MÍNIMO.
ILUSTRACIÓN 86 DIFERENCIAS DE PRESIÓN PARA EL CAUDAL MEDIO.
-0.45
-0.4
-0.35
-0.3
-0.25
-0.2
-0.15
-0.1
-0.05
0
0
100
200
300
400
(H
w
-D
w)
/(Dw)*
100
Nudos
Diferencia de presiones Ginebra
Caudal Mínimo
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0
100
200
300
400
500
(H
w
-D
w)
/(Dw)*
100
Nudos
Diferencia de presiones Ginebra
Caudal Medio

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
86
ILUSTRACIÓN 87 DIFERENCIAS DE PRESIÓN PARA EL CAUDAL MÁXIMO.
Las gráficas muestran que para caudales medios y mínimos las diferencias de presión entre la
red simulada con la ecuación de Hazen-Williams frente a la red simulada con la ecuación de
Darcy-Weisbach presentan diferencias mínimas. Sin embargo para el caudal máximo, se llegan
a presentar diferencias importantes en algunos de los nudos de la red; si bien estas
diferencias son relativamente bajas (máximo 15%) con respecto a los errores encontrados en
la red matriz de Medellín y la red de Andalucía que será mostrada posteriormente, estos
errores son considerables teniendo en cuenta que una diferencia de las presiones del 15%
puede dejar generar una insuficiencia y desabastecimiento de la red en ciertos nodos críticos,
afectando la disponibilidad de agua por la población, además que se está incumpliendo la
normativa de presiones mínimas.
4.3.4 RED ANDALUCÍA
Finalmente, se mostrarán los resultados de la red de Andalucía; esta red presentó diferencias
bastante importantes en aspectos de presiones y en el comportamiento de los emisores. Los
resultados de emisores pequeños se muestran a continuación:
-5
0
5
10
15
20
0
50
100
150
200
250
300
350
400
450
500
(H
w
-D
w)
/(Dw)*
100
Nudos
Diferencia de presiones Ginebra Caudal
Máximo
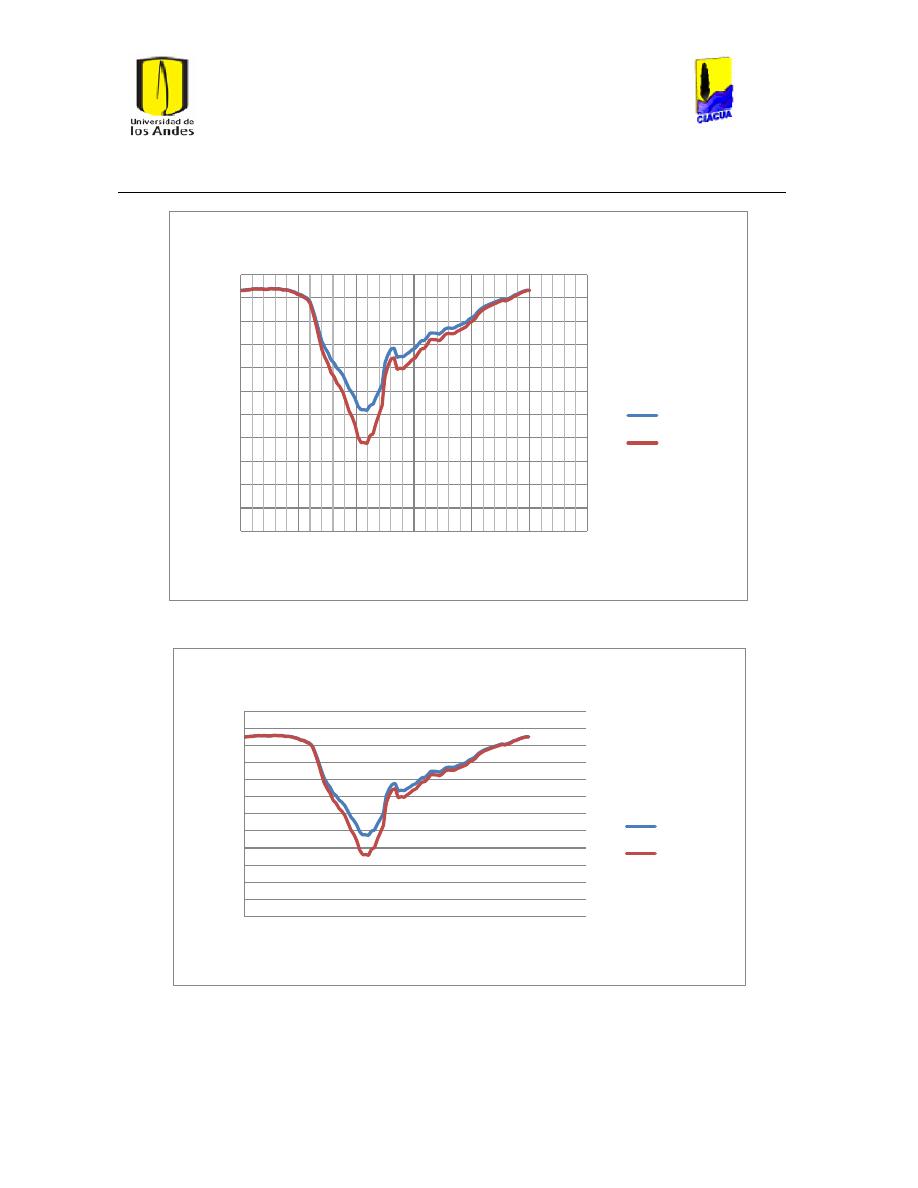
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
87
ILUSTRACIÓN 88 RESULTADOS EMISOR 317.
ILUSTRACIÓN 89 RESULTADOS EMISOR 13.
0
2
4
6
8
10
12
14
16
18
20
22
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 317 Andalucía
Emisor H-W
Emisor D-W
0
2
4
6
8
10
12
14
16
18
20
22
24
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 13 Andalucía
Emisor H-W
Emisor D-W
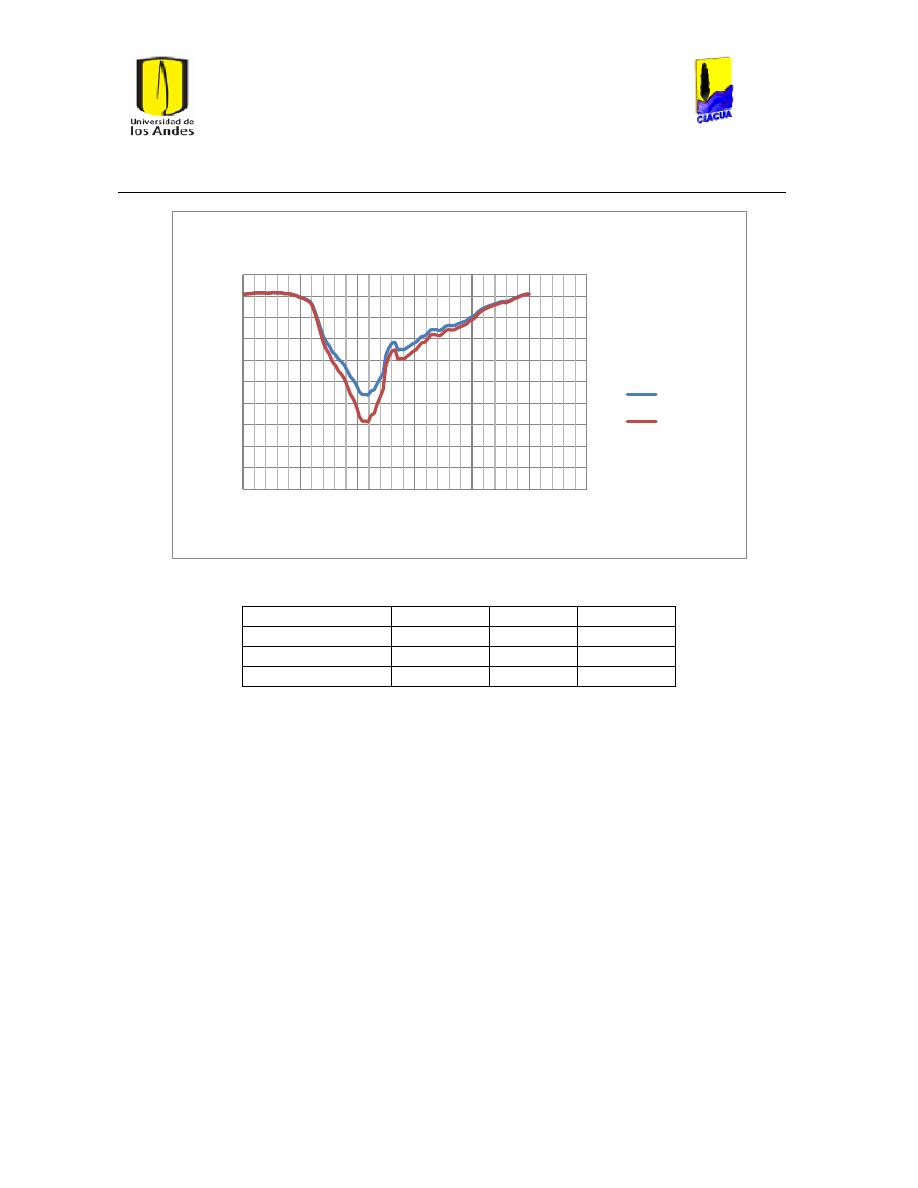
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
88
ILUSTRACIÓN 90 RESULTADOS EMISOR 102.
Emisor 102 Emisor 13 Emisor 317
Presión(m)
20
20
20
Caudal Base(L/s)
31.08
12.34
14.93
Coeficiente Emisor
6.95
2.76
3.33
TABLA 9 INFORMACIÓN DE LOS EMISORES PEQUEÑOS.
Los resultados que aquí se presentan, muestran un comportamiento hidráulicamente
interesante, como se puede evidenciar en las 3 gráficas de los emisores, donde se aprecian
diferencias entre los dos emisores. Si bien las diferencias son de bajos caudales (ente 5 y 10
L/s), hay que considerar que los caudales máximos que se pueden presentar en estos 3
emisores alcanzan un máximo de 45 L/s (en el caso del tercer emisor), lo que representaría
diferencias de hasta el 20% entre el cálculo de las dos ecuaciones. Estas diferencias de
caudales pueden ser bastante importantes cuando se aumentan los exponentes de emisión.
Adicionalmente, es importante notar que estas diferencias se presentan en las horas de
máximo consumo, es decir cuando el patrón de consumo alcanza las 10 de la mañana.
A continuación se muestran los resultados para emisores de mayor tamaño, donde se vieron
de mejor forma las diferencias de la red.
0
5
10
15
20
25
30
35
40
45
50
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 102 Andalucía
Emisor H-W
Emisor D-W

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
89
ILUSTRACIÓN 91 RESULTADOS EMISOR 298.
ILUSTRACIÓN 92 RESULTADOS EMISOR 279.
80
95
110
125
140
155
170
185
200
215
230
245
260
275
290
305
320
335
350
365
380
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencias Emisor 298 Andalucía
Emisor H-W
Emisor D-W
180
190
200
210
220
230
240
250
260
270
280
290
300
310
320
330
340
350
360
370
380
390
400
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencias Emisor 279 Andalucía
Emisor H-W
Emisor D-W
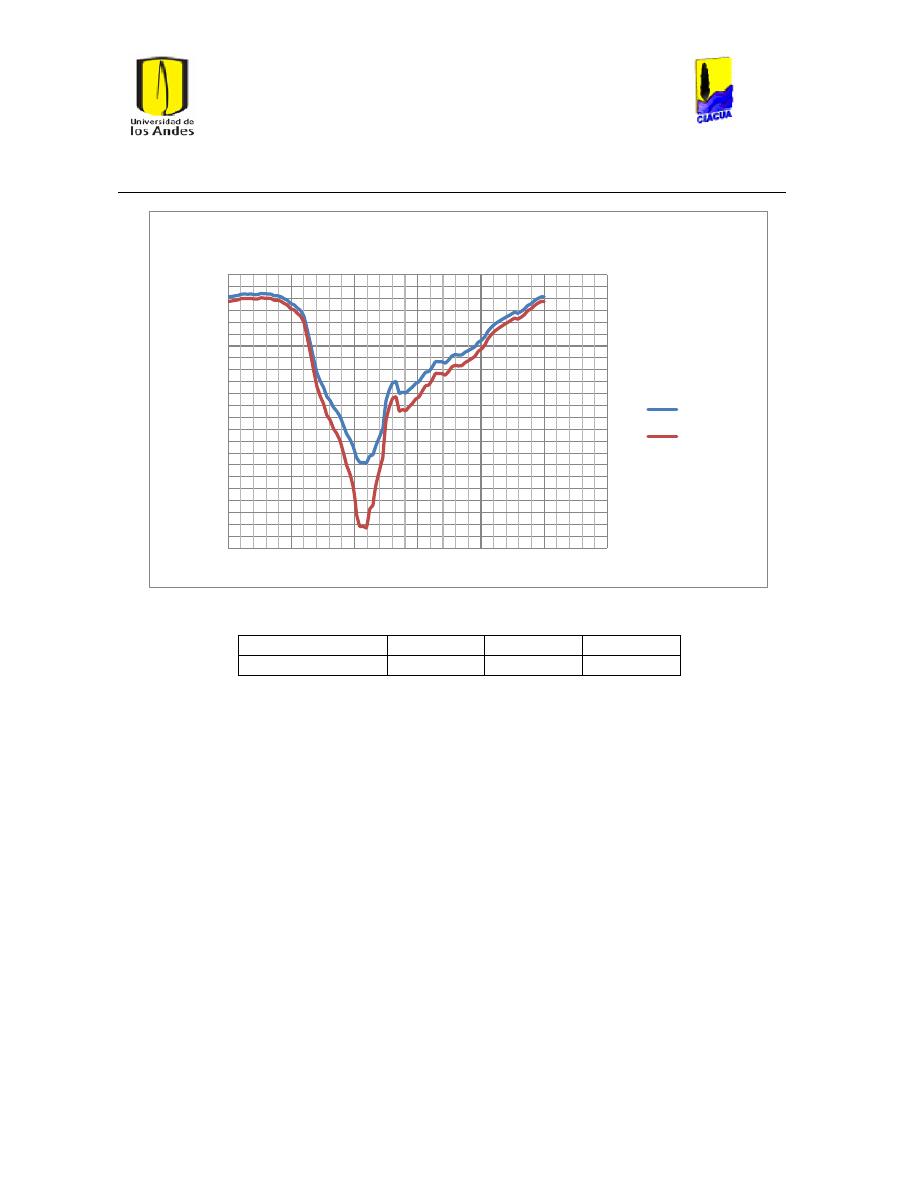
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
90
ILUSTRACIÓN 93 RESULTADOS EMISOR 267.
Emisor 267 Emisor 279 Emisor 298
Coeficiente Emisor
72
65
62
TABLA 10 COEFICIENTES DE EMISIÓN PARA EMISORES GRANDES.
Los resultados coinciden con lo encontrado con los emisores pequeños, es decir, se puede
observar en las ilustraciones anteriores que las diferencias entre los emisores son bastante
grandes; en algunos casos pueden a llegar a presentar diferencias de 100 L/s como se
presenta en el caso del emisor 267(que ocurre un fenómeno similar al que se presentó en
emisores de la red de Medellín, es decir es un nudo en el que se presentan presiones negativas
al utilizar la ecuación de Darcy-Weisbach). Así mismo se presentan diferencias importantes en
los otros dos emisores (de 20 L/s para el emisor 279 y de cerca de 50 L/s para el emisor 298).
También es interesante observar que después de la hora máxima de caudales, el
comportamiento de los emisores presenta una tendencia paralela, es decir, después de
alcanzar su máxima diferencia, las dos curvas de los emisores parecieran comportarse como si
fueran una función paralela y siguiendo una misma tendencia.
En cuanto a cómo afecta esto una situación de operación real, está claro que el operario que
está trabajando con la ecuación de Hazen-Williams está subestimando las pérdidas por
fricción que se presentan en la red, y está encontrando que el emisor que simula el tanque
-60
-40
-20
0
20
40
60
80
100
120
140
160
180
200
220
240
260
280
300
320
340
360
380
400
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencias Emisor 267 Andalucía
Emisor H-W
Emisor D-W
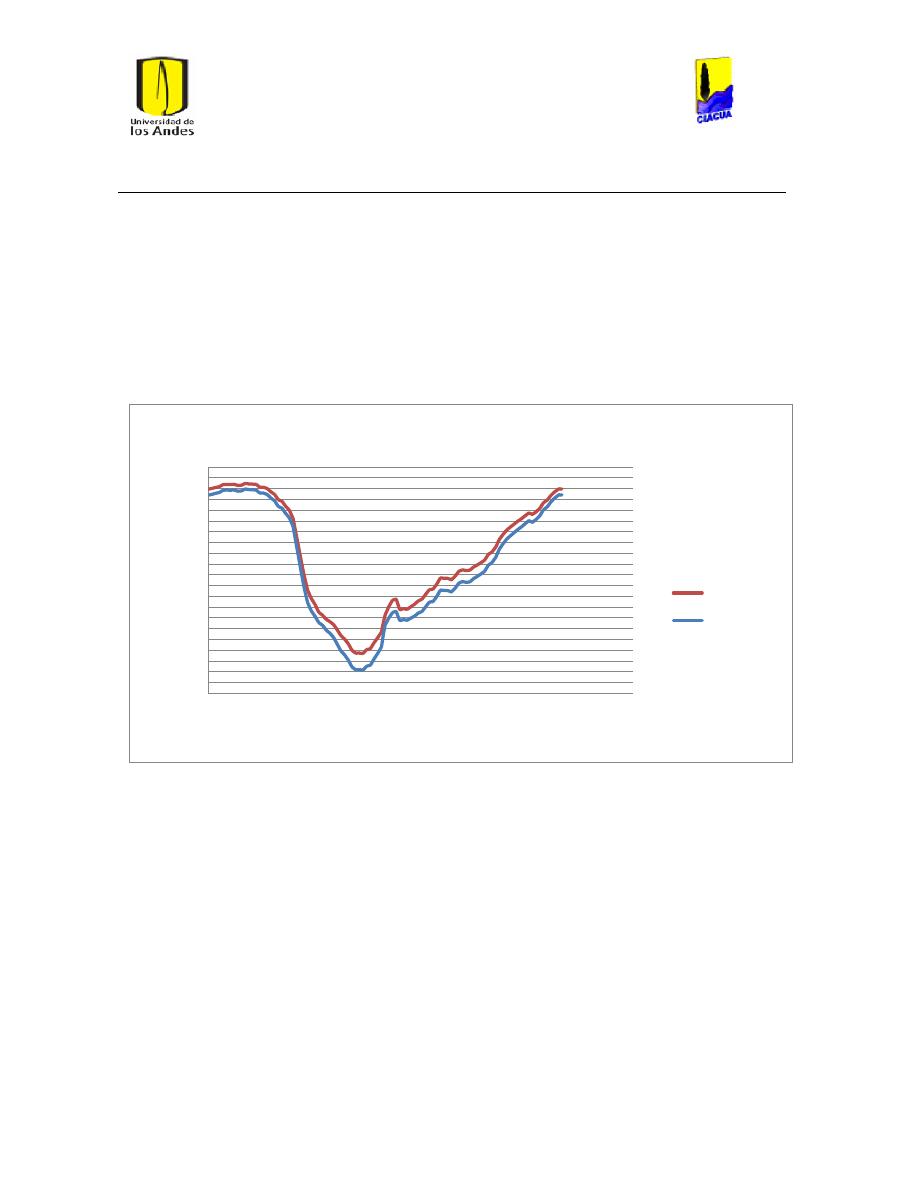
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
91
está extrayendo caudal mayor al que se presenta en la realidad (es decir el encontrado con la
ecuación físicamente basada de Darcy-Weisbach); estas diferencias, como ya se mencionó en
las redes pasadas, pueden significar un problema de entrega de presiones insuficientes ( a la
hora de operar los tanques) o incluso de dejar desabastecido un sector de la población por la
insuficiencia de caudales.
El análisis prosiguió con otros emisores, y se analizó detalladamente la variación de los
coeficientes de Hazen-Williams en los períodos más relevantes del día. Los resultados de esto
se muestran a continuación:
ILUSTRACIÓN 94 RESULTADOS EMISOR 278.
300
320
340
360
380
400
420
440
460
480
500
520
540
560
580
600
620
640
660
680
700
720
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 278 Andalucía
Emisor H-W
Emisor D-W
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
92
ILUSTRACIÓN 95 RESULTADOS EMISOR 269.
ILUSTRACIÓN 96 CAUDAL EMISOR VS NÚMERO DE REYNOLDS EMISOR 278.
0
100
200
300
400
500
600
700
800
900
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 269 Andalucía
Emisor D-W
Emisor H-W
300
320
340
360
380
400
420
440
460
480
500
520
540
560
580
600
620
640
660
680
700
720
0
50000
100000
150000
200000
250000
300000
L/s
Número de Reynolds
Andalucía Emisor 278
Emisor H-W
Emisor D-W

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
93
ILUSTRACIÓN 97 CAUDAL EMISOR VS NÚMERO DE REYNOLDS EMISOR 269.
0
30
60
90
120
150
180
210
240
270
300
330
360
390
420
450
480
510
540
570
600
630
660
690
720
750
780
810
840
870
0
100000
200000
300000
400000
500000
600000
L/s
Número de Reynolds
Andalucía Emisor 269
Emisor H-W
Emisor D-W
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
94
ILUSTRACIÓN 98 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS VS NÚMERO DE REYNOLDS
PARA EL CAUDAL MEDIO.
ILUSTRACIÓN 99 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS VS NÚMERO DE REYNOLDS
PARA EL CAUDAL MÍNIMO.
0
20
40
60
80
100
120
140
160
180
1000
10000
100000
1000000
10000000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Número de Reynolds
Andalucía Caudal Medio Coeficientes
Hazen-Williams
0
20
40
60
80
100
120
140
160
180
1000
10000
100000
1000000
10000000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Número de Reynolds
Andalucía Caudal Mínimo Coeficientes
Hazen-Williams
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
95
ILUSTRACIÓN 100 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS VS NÚMERO DE REYNOLDS
PARA EL CAUDAL MÁXIMO.
ILUSTRACIÓN 101 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS VS DIÁMETROS DE LA RED
PARA EL CAUDAL MEDIO.
0
20
40
60
80
100
120
140
160
180
1000
10000
100000
1000000
10000000
100000000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Número de Reynolds
Andalucía Caudal Máximo Coeficientes
Hazen-Williams
0
20
40
60
80
100
120
140
160
180
0
500
1000
1500
2000
2500
3000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Diámetro (mm)
Andalucía Caudal Medio
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
96
ILUSTRACIÓN 102 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS VS DIÁMETROS DE LA RED
PARA EL CAUDAL MÍNIMO.
ILUSTRACIÓN 103 VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS VS DIÁMETROS DE LA RED
PARA EL CAUDAL MÁXIMO.
0
20
40
60
80
100
120
140
160
180
0
500
1000
1500
2000
2500
3000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Diámetro (mm)
Andalucía Caudal Mínimo
0
20
40
60
80
100
120
140
160
180
0
500
1000
1500
2000
2500
3000
Co
e
fi
ci
e
n
te
H
aze
n
-Wi
lli
am
s
Diámetro (mm)
Andalucía Caudal Máximo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
97
Los resultados de estos últimos emisores mantienen la tendencia presentada en esta red y en
general con muchos emisores de esta tesis, es decir, existen grandes diferencias entre los
caudales del emisor utilizando la ecuación empírica y la ecuación físicamente basada. Para el
emisor 278 se llegaron a presentar diferencias de hasta 40 L/s y para el emisor 269 se
presentaron diferencias de gran importancia, siendo la máxima de 150 L/s. Estas diferencias
se vienen analizando a lo largo de este trabajo en las otras redes, pero es especialmente
relevante en este caso ya que es la primera vez que se presentan diferencias entre las dos
ecuaciones con esta magnitud de error.
Por otro lado, revisando los datos del caudal emisor frente al número de Reynolds de la
tubería de llegada se puede apreciar que para números de Reynolds menores, las diferencias
suelen ser mucho mayores. Esta es una observación interesante, considerando que para otros
casos ocurría lo opuesto, es decir, las diferencias entre los emisores ocurrían cuando el
número de Reynolds era más alto. Esto lleva a pensar a que la ecuación de Hazen-Williams
puede llegar a presentar diferencias en los caudales de los emisores para diferentes rangos de
números de Reynolds, ya sea para rangos muy altos o para rangos relativamente bajos.
Continuando con el análisis de los resultados es importante mostrar, para este caso particular,
la variación del coeficiente de Hazen-Williams con respecto a los diámetros y con respecto al
número de Reynolds. Se puede observar que los coeficientes de la red se están comportando
en un rango de 100 y 120 en contraste con los rangos teóricos de 140 y 150. Esto implica que
la red de Andalucía se está comportando en la realidad como una red mucho más rugosa de lo
que realmente representa y por ende la ecuación de Hazen-Williams está subestimando en
gran medida las pérdidas por fricción que se presenta en la misma. Todo esto es consistente
con los resultados encontrados en los emisores, que al subestimar las pérdidas de la red, los
caudales que arroja el emisor son mucho mayores a los que se presentan en la realidad (es
decir con la ecuación de Darcy-Weisbach).
Así mismo, cuando se analizan los resultados de la variación del coeficiente de Hazen-
Williams vs los diámetros de la red, se puede ver que en tuberías de gran diámetro que juegan
un papel fundamental en la hidráulica de la red, la variación del coeficiente puede llegar a
tener valores de hasta 60, frente al coeficiente teórico de 140 para tuberías mayores a 350
mm. Estas consecuencias se verán más adelante cuando se analizan las presiones de la red,
pues las diferencias fueron bastante importantes. Adicionalmente conviene señalar que que la
red incluso llega a presentar diferencias en el número de Reynolds de la ecuación de Hazen-
Williams frente a la ecuación de Darcy-Weisbach, como se aprecia en los anexos y que esta
condición no es exclusiva de la Red Andalucía sino que se evidencia en la mayoría de redes
trabajadas. Estos resultados son una señal de alerta y una situación extremadamente
preocupante por el hecho de que la ecuación empírica está entregando, de manera errada, los
caudales que realmente están circulando en la red, que evidentemente cambiará de acuerdo
con el comportamiento de los emisores, las presiones y la hidráulica en general.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
98
ILUSTRACIÓN 104 DIFERENCIA DE PRESIONES PARA EL CAUDAL MEDIO.
ILUSTRACIÓN 105 DIFERENCIA DE PRESIONES PARA EL CAUDAL MÍNIMO.
-1
0
1
2
3
4
5
6
7
0
50
100
150
200
250
300
350
400
(H
w
-D
w)
/D
w
*100
Nudo
Diferencia de presiones Caudal Medio
Andalucía
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
0.25
0.3
0
50
100
150
200
250
300
350
400
(H
w
-D
w)
/D
w
*100
Nudo
Diferencia de presiones Caudal Mínimo
Andalucía

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
99
ILUSTRACIÓN 106 DIFERENCIA DE PRESIONES PARA EL CAUDAL MÁXIMO.
Como se mencionó anteriormente, se puede ver que las diferencias que se presentan entre la
red simulada con la ecuación de Hazen-Williams y la ecuación de Darcy-Weisbach son
importantes. Si bien en caudales mínimos las diferencias son despreciables, para el caudal
medio ya se presentan errores en la mayoría de los nudos del 5% y diferencias mucho más
grandes con el caudal máximo, que exigió plasmarlas con diferencias de presiones y no con el
error relativo. Esto último se pude observar en la Ilustración 106, donde se presentan
diferencias de hasta 6 metros. Para ponerlo en contexto, si en un nudo que trabaja con la
ecuación de Hazen-Williams se tiene una presión de 20 metros, en la realidad se puede estar
presentando una presión de 14 metros, y el caso alarmante es cuando hay presiones cercanas
a 2 o 3 metros con la ecuación de Hazen-Williams y en la realidad se puedan llegar a presentar
presiones negativas que significan un mayor y más rápido vaciado del tanque, que se puede
traducir en desabastecimiento del sector, afectando enormemente a la población usuaria del
servicio de agua.
4.4 TANQUES REALES, RED DE BOMBEO Y ANÁLISIS DE LA HIDRÁULICA
DEL SISTEMA
En esta sección se van a mostrar los resultados más relevantes de cada una de las redes
trabajadas; esto incluye los niveles de los tanques, diagramas de Moody con los factores de
fricción de toda la red y los tramos que presentaron las diferencias más significativas entre la
-6
-5
-4
-3
-2
-1
0
0
50
100
150
200
250
300
350
400
D
ifer
e
n
ci
a e
n
m
Nudo
Diferencia de presiones Caudal Máximo
Andalucía

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
100
ecuación de Hazen-Williams y la ecuación de Darcy-Weisbach. Así mismo, se realizó un
análisis comparativo con base a los resultados de las investigaciones de Bombardelli y García
(Fabián Bombardelli, 2003) y se analizaron los rangos de números de Reynolds de ambas
investigaciones.
4.4.1 RED MATRIZ DE BOGOTÁ
El estudio con tanques reales continuó con la red matriz de Bogotá, que a diferencia de las
otras redes estudiadas, estaba compuesta por una gran cantidad de circuitos, la llegada a los
tanques de almacenamiento estaban conectados a 2 o más tuberías y en raras ocasiones
terminaban en ramificaciones. Lo anterior es bastante importante ya que como se mencionó
en los análisis anteriores, esta red fue la que presentó menores diferencias en comparación
con los otros casos de estudio. A continuación se muestran los resultados encontrados para
los niveles de los tanques en la red matriz de Bogotá:
ILUSTRACIÓN 107 NIVEL DEL TANQUE CAZUCÁ.
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
00:00 04:48 09:36 14:24 19:12 00:00 04:48
N
iv
e
l (
m
)
Tiempo (h)
Bogotá Tanque Cazucá
Tanque Cazucá D-W
Tanque Cazucá H-W
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
101
ILUSTRACIÓN 108 NIVEL TANQUE NUEVOSUBA.
ILUSTRACIÓN 109 NIVEL TANQUE SAN DIEGO.
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
00:00
12:00
00:00
12:00
A
ltu
ra(m
)
Tiempo(h)
Tanque NuevoSuba Bogotá
Tanque NuevoSuba D-W
Tanque NuevoSuba H-W
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
00:00
12:00
00:00
12:00
N
iv
e
l (
m
)
Tiempo (h)
Bogotá Tanque San Diego
Tanque San Diego D-W
Tanque San Diego H-W
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
102
ILUSTRACIÓN 110 NIVEL TANQUE VITELMA.
Las ilustraciones mostradas anteriormente representan los niveles de los tanques en la red
matriz de Bogotá. Como se puede observar, las diferencias en los niveles de los tanques son
bastante bajas y si bien en la Ilustración 108 existe una pequeña diferencia a la hora del
vaciado del tanque, esta es una diferencia poco significativa. Esto es coherente con lo
encontrado en los análisis realizados anteriormente; en el sentido que la red matriz de
Bogotá parece estar representando, de manera similar, la hidráulica cuando se utiliza la
ecuación empírica de Hazen-Williams en comparación con la hidráulica evaluada con la
ecuación de Darcy-Weisbach.
El análisis siguiente tuvo como objetivo observar si las redes llegaban a presentar algún tipo
de diferencias en otros aspectos hidráulicos, los cuales se muestran a continuación:
2.5
3
3.5
4
4.5
5
00:00
12:00
00:00
12:00
N
iv
e
l (
m
)
Tiempo (h)
Tanque Vitelma Bogotá
Tanque Vitelma D-W
Tanque Vitelma H-W
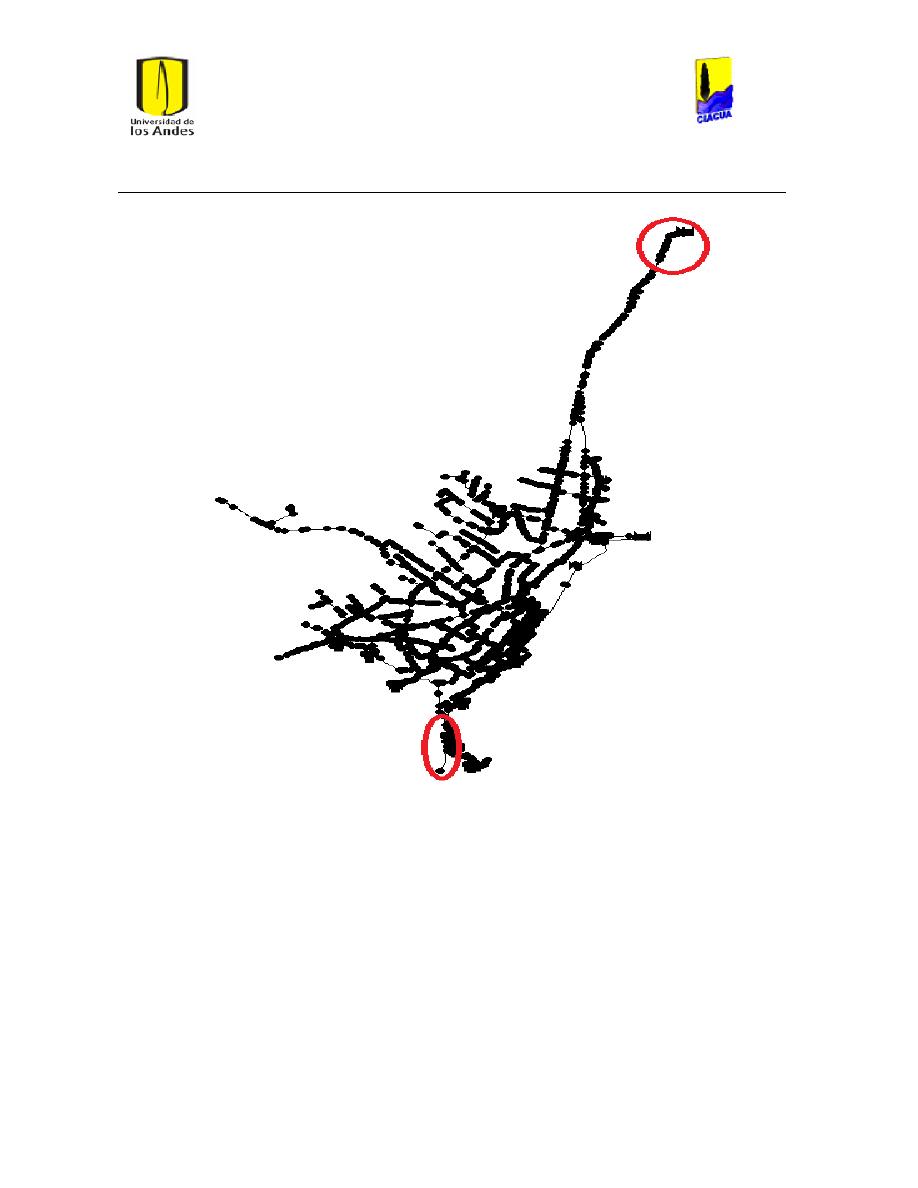
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
103
ILUSTRACIÓN 111 MAPA CON TRAMOS A LA SALIDA DE LOS EMBALSES ANALIZADOS.
El análisis se decidió enfocar en las tuberías de gran diámetro y en las tuberías que estaban
transportando la mayor cantidad del caudal en la red. Este análisis incluyó buscar diferencias
en los números de Reynolds y pérdidas por fricción asociadas con las tuberías nombradas. A
continuación se van a mostrar los resultados:
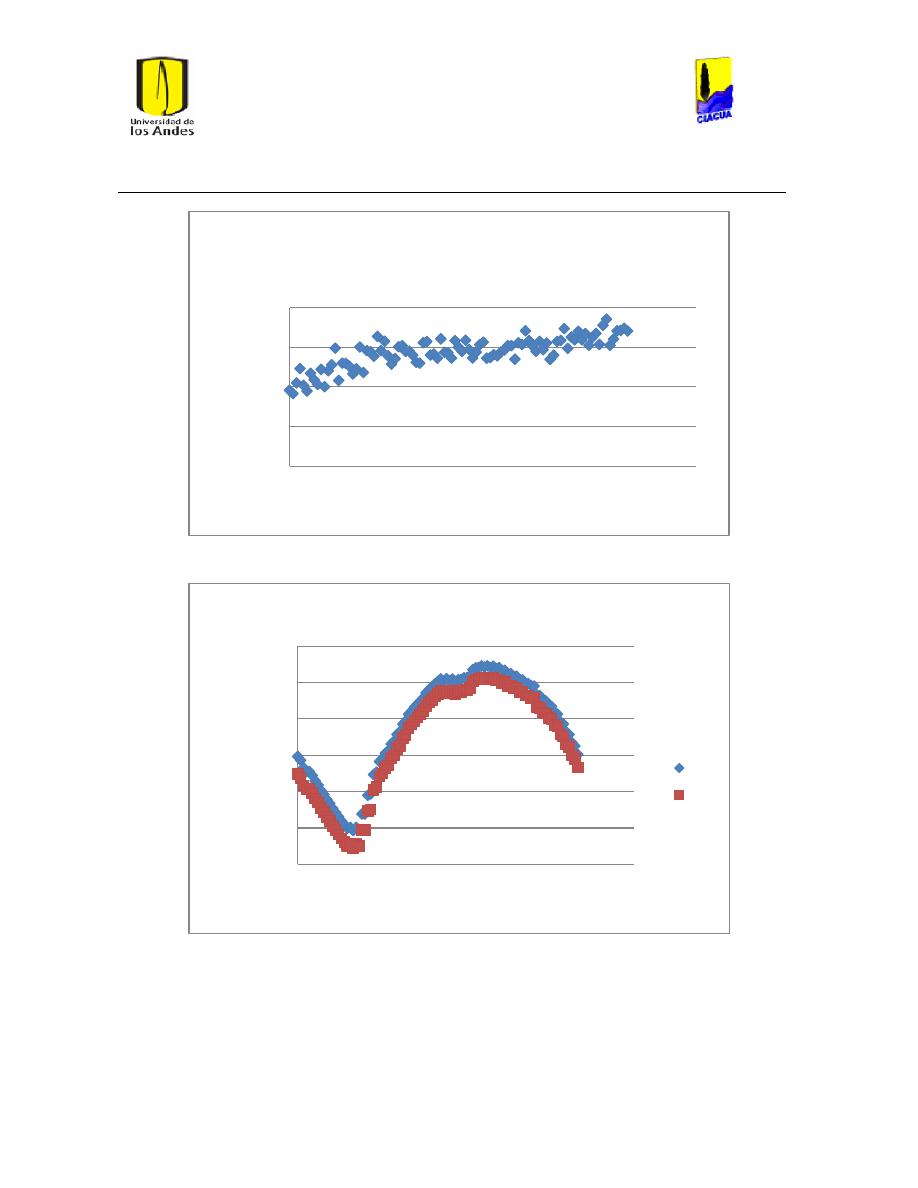
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
104
ILUSTRACIÓN 112 DIFERENCIAS EN EL CÁULCULO DE LAS PÉRDIDAS POR FRICCIÓN.
ILUSTRACIÓN 113 DIFERENCIAS EN EL NÚMERO DE REYNOLDS.
0.000%
0.500%
1.000%
1.500%
2.000%
00:00
04:48
09:36
14:24
19:12
00:00
04:48
(H
W
-D
W)/DW
Tiempo (h)
Diferencia de hf en tubería 927
Bogotá
1550000
1600000
1650000
1700000
1750000
1800000
1850000
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Tiempo (h)
Bogotá Tubería 927
D-W
H-W
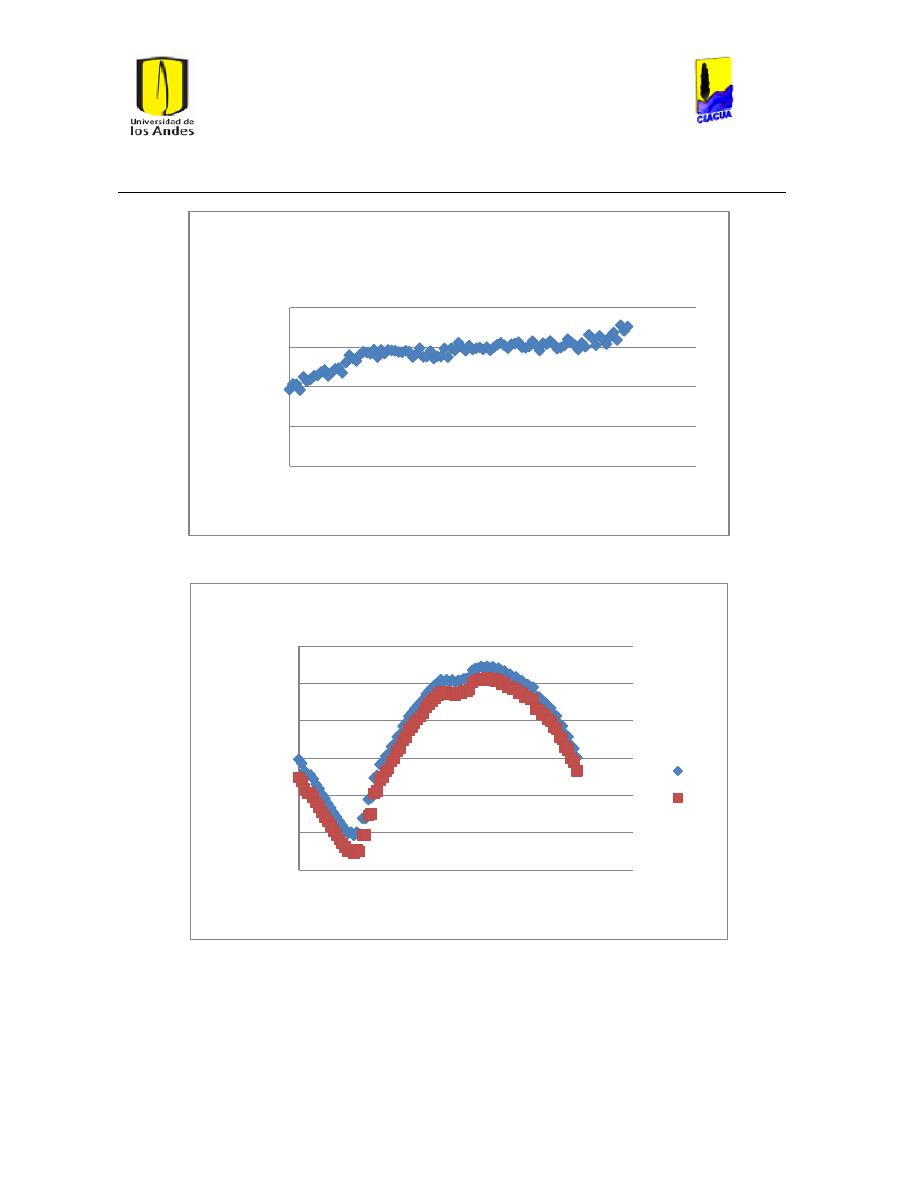
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
105
ILUSTRACIÓN 114 DIFERENCIAS EN EL CÁLCULO DE LAS PÉRDIDAS POR FRICCIÓN.
ILUSTRACIÓN 115 DIFERENCIAS EN EL NÚMERO DE REYNOLDS.
0.000%
0.500%
1.000%
1.500%
2.000%
00:00
04:48
09:36
14:24
19:12
00:00
04:48
(H
W
-D
W)/DW
Tiempo (h)
Diferencia de hf en tubería 933
Bogotá
1550000
1600000
1650000
1700000
1750000
1800000
1850000
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Tiempo (h)
Bogotá Tubería 933
D-W
H-W
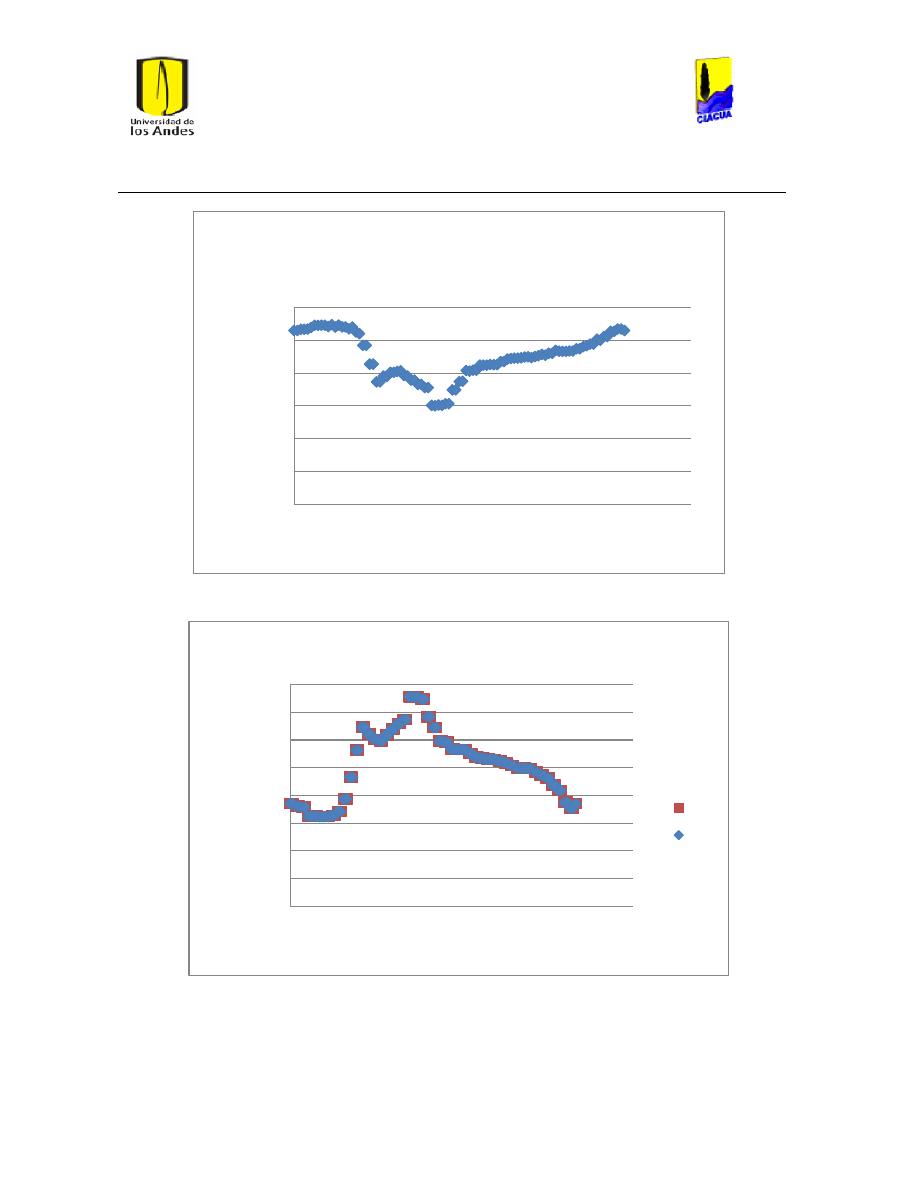
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
106
ILUSTRACIÓN 116 DIFERENCIAS EN EL CÁLCULO DE LAS PÉRDIDAS POR FRICCIÓN.
ILUSTRACIÓN 117 DIFERENCIAS EN EL NÚMERO DE REYNOLDS.
Los resultados anteriores muestran que si bien existen diferencias en los números de
Reynolds en las tuberías, estas diferencias suelen ser muy bajas (aunque no despreciables).
Así mismo al analizar las ilustración es se puede observar que las diferencias en el cálculo de
0.000%
1.000%
2.000%
3.000%
4.000%
5.000%
6.000%
00:00
04:48
09:36
14:24
19:12
00:00
04:48
(H
W
-D
W)/DW
Tiempo (h)
Diferencia de hf en tubería 2616
Bogotá
0
50000
100000
150000
200000
250000
300000
350000
400000
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Tiempo (h)
Bogotá Tubería 2616
H-W
D-W

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
107
las pérdidas por fricción en ningún momento exceden el 7%; se puede concluir que en
términos generales la red que está siendo operada con la ecuación de Hazen-Williams está
funcionando de manera muy similar a lo que se esperaría en la realidad.
Sin embargo, no hay que obviar el hecho que la diferencia en los números de Reynolds, en
especial en estas tuberías que salen de los embalses implica que la red operada con la
ecuación de Hazen-Williams está sobrestimando en algunos casos y en otros subestimando, la
cantidad de masa o de agua que está saliendo de los embalses. Tal efecto genera como
consecuencia que la hidráulica de toda la red esté cambiando (pérdidas por fricción, factores
de fricción, presiones de la red, llenado de los tanques); y aunque en este caso las diferencias
sean bastante bajas, este efecto va a tener consecuencias importantes a la hora de operar
redes primarias de bombeo o redes matrices, como se mostrará más adelante.
Una vez identificados estos efectos, se procedió a generar los diagramas de Moody y construir
un mapa con las diferentes redes, identificando en qué tuberías era mayor el número de
Reynolds al utilizar la ecuación de Hazen-Williams, en qué tuberías era mayor con la ecuación
de Darcy-Weisbach y en qué escenarios eran iguales. El análisis se realizó en los momentos
del día donde se presentaba la demanda de caudal promedio, mínima y máxima.
Con el fin de entender los resultados que se muestran a continuación es necesario aclarar que
en aquellos tramos donde la tubería presenta color VERDE, el número de Reynolds es mayor
al utilizar la ecuación de Darcy-Weisbach, el color ROJO para las tuberías en las que el número
de Reynolds es mayor con la ecuación de Hazen-Williams y finalmente, en AMARILLO, las
tuberías en las que no existe ninguna diferencia entre las dos ecuaciones.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
108
FIGURA 1 SALIDA DE EMBALSE TIBITOC CAUDAL MEDIO.
FIGURA 2 SALIDA DEL EMBALSE TIBITOC CAUDAL MÁXIMO.
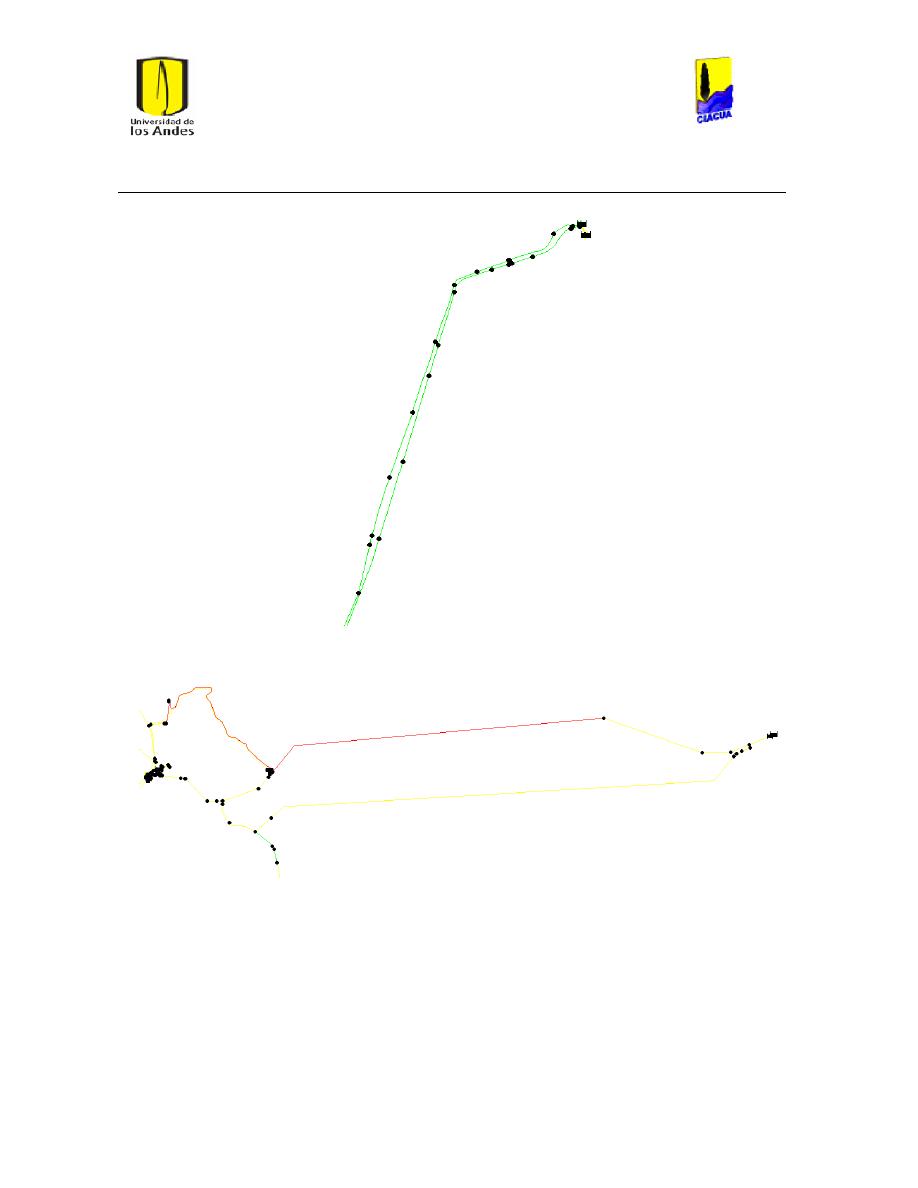
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
109
FIGURA 3 SALIDA DEL EMBALSE TIBITOC CAUDAL MÍNIMO.
FIGURA 4 SALIDA DEL EMBALSE DE WIESNER CAUDAL MEDIO.
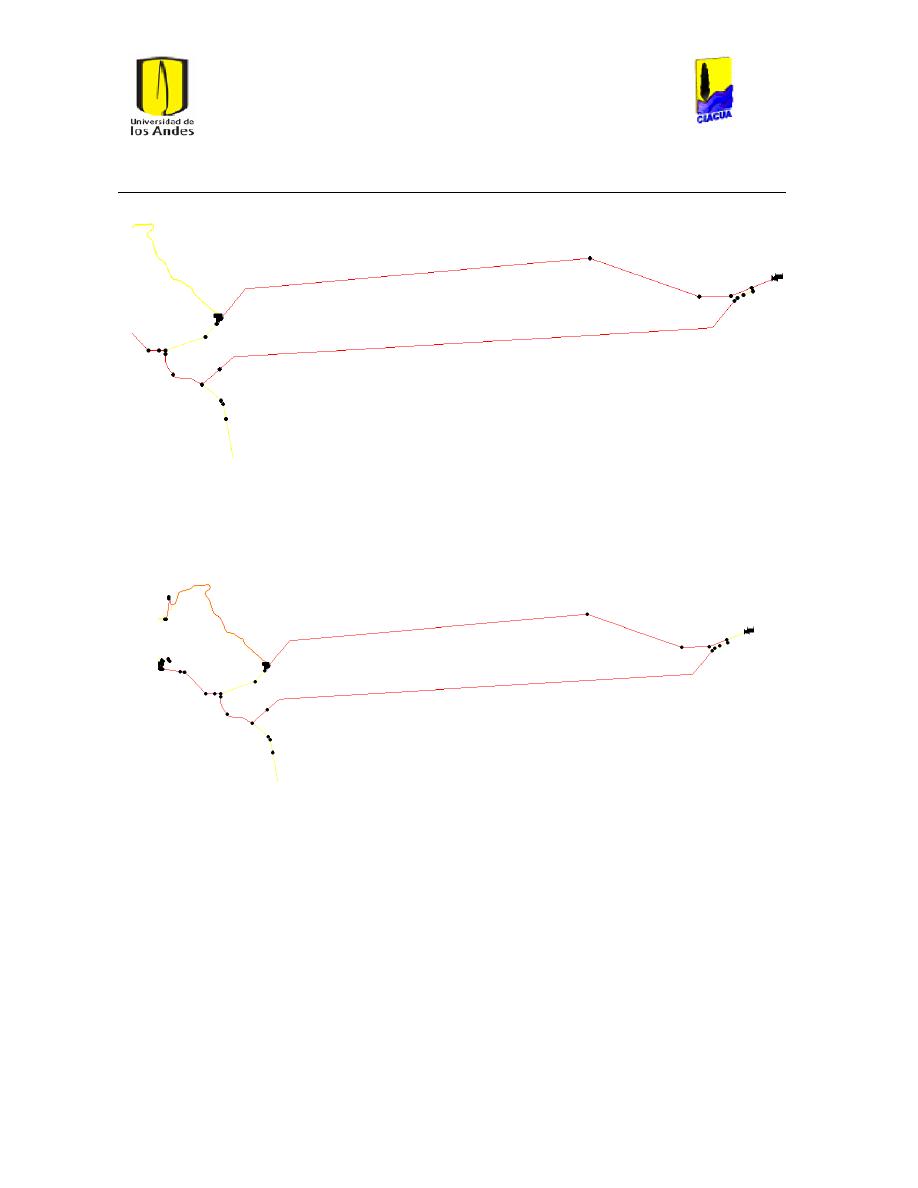
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
110
FIGURA 5 SALIDA DEL EMBALSE DE WIESNER CAUDAL MÁXIMO.
FIGURA 6 SALIDA DEL EMBALSE DE WIESNER CAUDAL MÍNIMO.
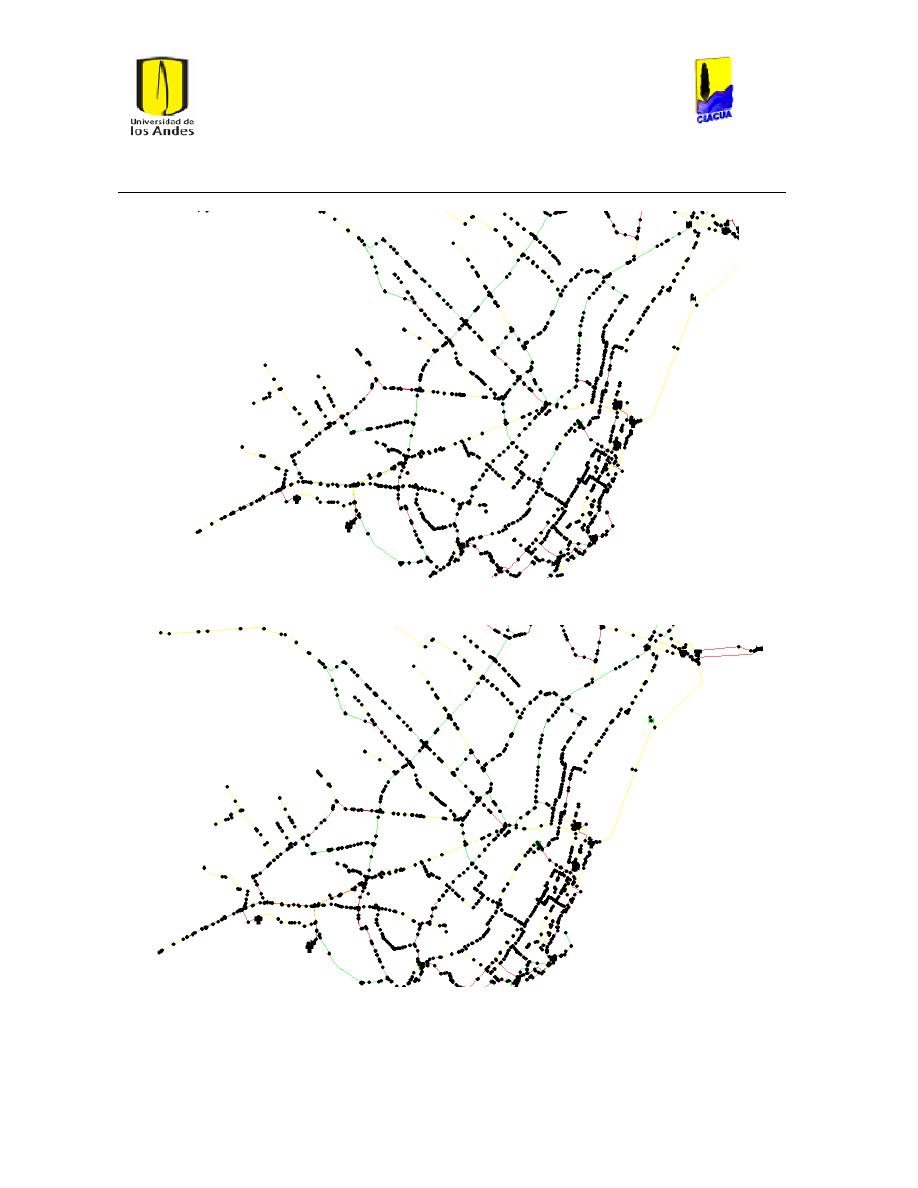
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
111
FIGURA 7 ENTRAMADO INTERNO DE LA RED MATRIZ DE BOGOTÁ CAUDAL MEDIO.
FIGURA 8 ENTRAMADO INTERNO DE LA RED MATRIZ DE BOGOTÁ CAUDAL MÁXIMO.
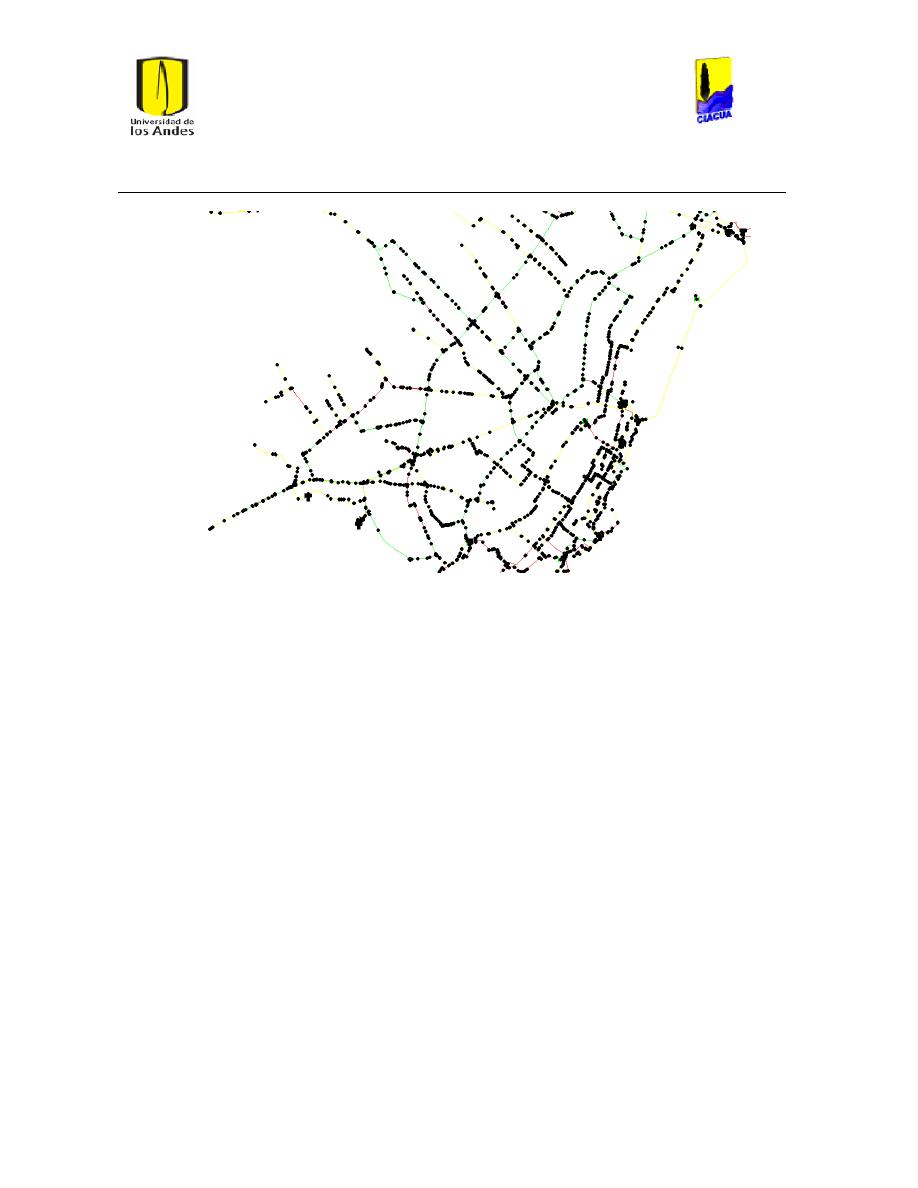
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
112
FIGURA 9 ENTRAMADO INTERNO RED MATRIZ DE BOGOTÁ CAUDAL MÍNIMO.
Las figuras anteriores muestran que en efecto las diferencias en la solución hidráulica de la
red son bastante evidentes. Está claro que desde el inicio de los embalses, el caudal que está
saliendo de los mismos es diferente entre las dos ecuaciones, llevando a que no sólo por la
naturaleza empírica de la ecuación se estén subestimando y/o sobrestimando las pérdidas
por fricción, sino que por causa de esta ecuación (empírica) la red está transportando una
cantidad de masa diferente a la que se simula utilizando la ecuación físicamente basada de
Darcy-Weisbach. Los resultados de estos análisis mostraron que las diferencias máximas que
se llegaron a presentar en la red fueron de números de Reynolds de 40000, entre un número
de Reynolds de la red máximo de
, lo que no es una diferencia significativa y que por
consiguiente no cambiaba de manera radical la hidráulica de la red. Para confirmar estos
análisis se decidió hacer diagramas de Moody de algunas tuberías con el fin de ver que ocurría
con ellas al aplicar las dos ecuaciones y si de alguna forma se podía ver alguna tendencia de lo
que estaba pasando con el flujo. Estos resultados de se muestran a continuación:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
113
ILUSTRACIÓN 118 DIAGRAMA DE MOODY PARA LA TUBERÍA 3701 CON DIÁMETRO DE 508 MM Y
CAUDAL MEDIO DE 37 L/S.
0.01
0.1
1.00E+05
1.00E+06
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Tubería 3701 D-W
Tubería 3701 H-W
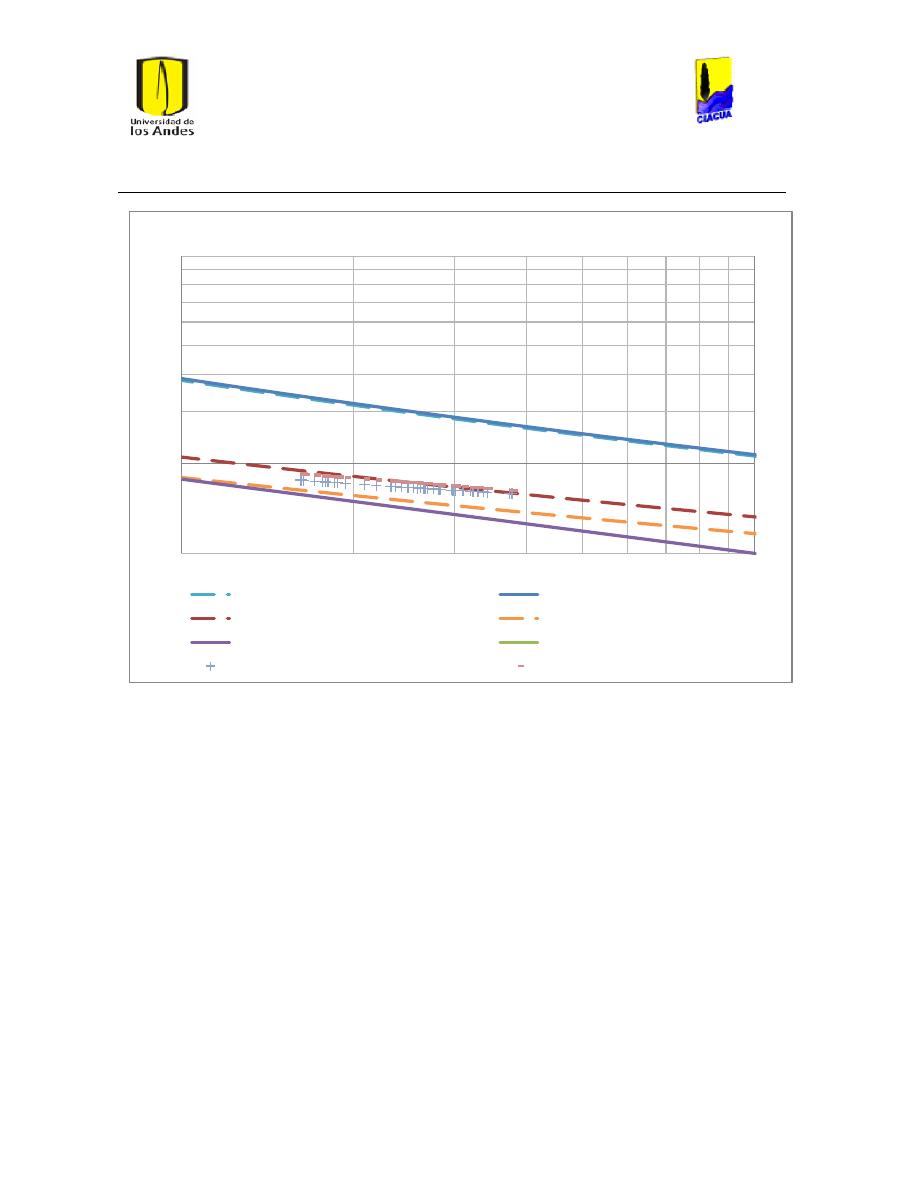
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
114
ILUSTRACIÓN 119 DIAGRAMA DE MOODY PARA LA TUBERÍA 4172 CON DIÁMETRO DE 508 MM Y
CAUDAL MEDIO DE 37 L/S.
0.01
0.1
1.00E+05
1.00E+06
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Tubería 4172 D-W
Tubería 4172 H-W
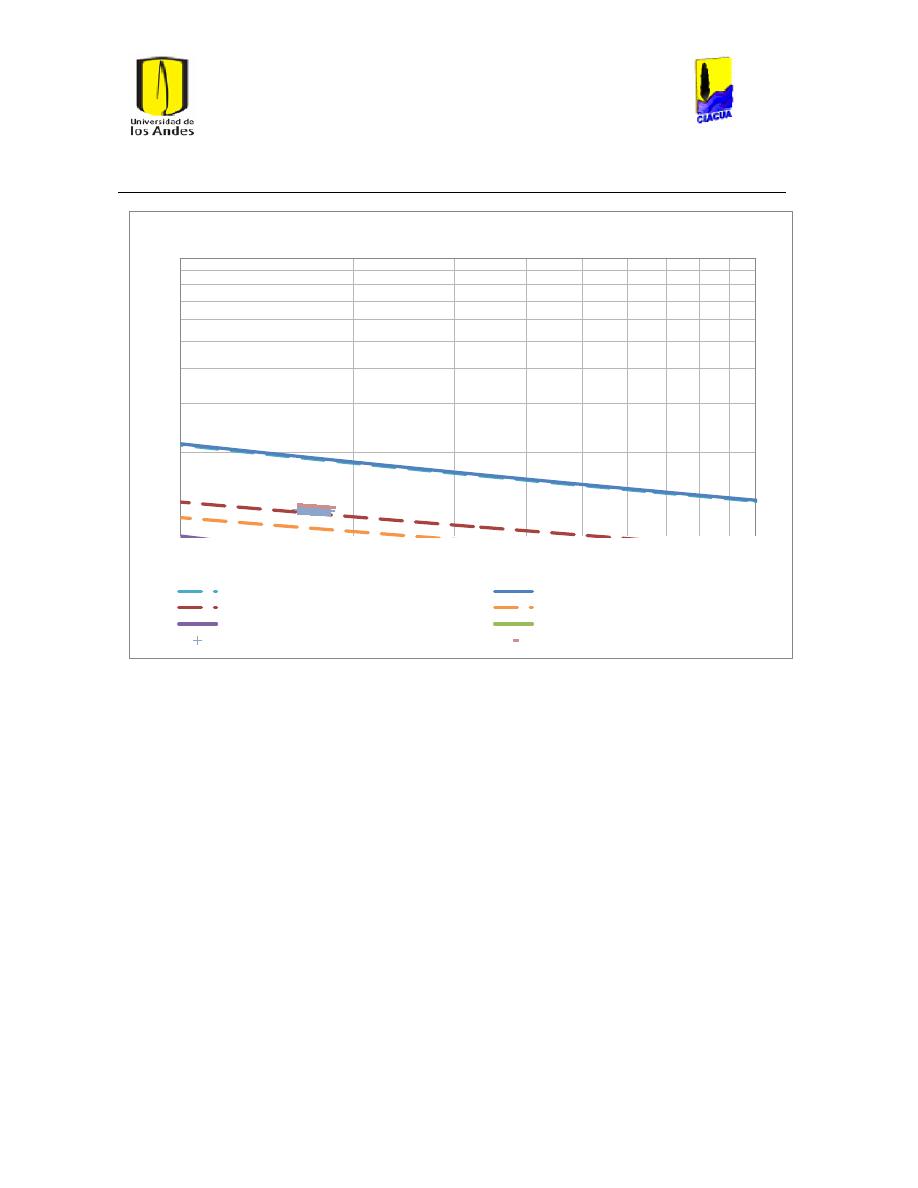
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
115
ILUSTRACIÓN 120 DIAGRAMA DE MOODY PARA LA TUBERÍA 75 CON DIÁMETRO DE 1524 MM Y
CAUDAL MEDIO DE 700 L/S.
Como se puede ver en los Diagramas de Moody, las diferencias entre las dos ecuaciones son
bastante pequeñas, si bien en algunos casos parece que existiera un desfase en el número de
Reynolds y valores mayores en el factor de fricción cuando se calcula con la ecuación de
Hazen-Williams. Estos resultados son coherentes teniendo en cuenta que hay 2 causas: La
primera se relaciona con el hecho que la ecuación de Hazen-Williams suele subestimar o
sobrestimar las pérdidas por fricción en las tuberías (e intrínsecamente los factores de
fricción que se encuentran en las redes), según lo reporta la literatura y se ha confirmado en
esta tesis. La segunda causa que se evidenció de manera más clara en esta investigación es la
subestimación o sobrestimación de la masa de agua que está circulando en la red, lo que en
efecto está causando que toda la hidráulica de la red esté cambiando.
Otro análisis importante de resaltar en la red matriz de Bogotá es que al comparar las gráficas
que muestran la variación del coeficiente de Hazen-Williams con respecto al número de
Reynolds (Ilustraciones 36, 37 y 38) en la Sección 4.3.1 Red Matriz de Bogotá con las gráficas
generadas a partir de la investigación de Fabián Bombardelli y Marcelo García (Gráfica 4)
(Fabián Bombardelli, 2003), se observa que las tendencias son bastante similares lo que
significa que el coeficiente de Hazen-Williams presenta variaciones importantes en un
0.01
0.1
1.00E+06
1.00E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Tubería 75 D-W
Tubería 75 H-W

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
116
espectro amplio de números de Reynolds . Sin embargo se puede ver que para la red Bogotá,
la media del coeficiente de Hazen-Williams se encontró muy cercana al valor de 140, que fue
el valor teórico con el que se trabajó, concluyendo de manera preliminar que la red
efectivamente se está comportando de manera muy similar a lo que se presenta en la realidad.
Por otro lado, al comparar estos resultados con los que arrojan la investigación de Liou (Liou,
1998), se observa una tendencia muy similar que se aprecian mejor en las ilustraciones
anteriores y los datos de la Gráfica 2. Esto ratifica el hecho que el trabajar con un coeficiente
constante de Hazen-Williams puede llegar a ser peligroso dada la alta variabilidad presentada,
en especial entre números de Reynolds entre
y
. Esto significa que si bien la
hidráulica de la red se está comportando de manera similar con las dos ecuaciones y
muestran pocas diferencias, existen sectores específicos en que la variación del coeficiente
presenta diferencias a tener en cuenta que si bien no tienen un impacto relevante en la
hidráulica de esta red en particular, no implica que esto sea un problema menor o que pueda
ser obviado, especialmente porque los rangos de números de Reynolds anteriormente
nombrados son típicos de redes matrices y redes primarias de bombeo, es decir, redes que
suministran los caudales a poblaciones.
Por su parte, los resultados encontrados con tanques y emisores, parecen indicar que el riesgo
en que se incurre al utilizar la ecuación empírica no se limita a una diferencia de presiones de
la red; también puede llegar a estar vinculado en la operación inadecuada de tanques, que
afectaría la calidad del agua que se está entregando en la red por los tiempos de permanencia
del agua en estos. Así mismo, las consecuencias de sobrestimar o subestimar caudales de la
red, puede llegar a afectar la toma de decisiones a la hora de asignar válvulas para el control
de fugas, sin mencionar los efectos negativos que se pueden llegar a tener al analizar de
manera errónea la distribución de caudales con la ecuación de Hazen-Williams, dado el
comportamiento divergente con respecto a la ecuación de Darcy-Weisbach que puede
presentarse en determinados tramos de la red.
Para finalizar, es importante mencionar que si bien los resultados de la red Matriz de Bogotá
no arrojan diferencias significativas en los indicadores hidráulicos considerados en esta
investigación (salvo en algunos puntos y en muy baja magnitud), esto no implica que la
ecuación de Hazen-Williams sea adecuada para operar las redes de distribución de agua
potable. Lo que sí parece ser un factor relevante, es que esta red es bastante redundante,
presenta múltiples entradas a los tanques de almacenamiento y rara vez se encontraron
ramificaciones. Esas características parecieron ejercer un efecto de amortiguación en los
indicadores hidráulicos generados al correr la ecuación empírica de Hazen-Williams; esto se
ve en las bajas diferencias en presiones, pérdidas por fricción y números de Reynolds, todo lo
cual influye en los coeficientes teóricos de Hazen-Williams que se aproximaron relativamente
bien a los que se hallaron simulando la red con la ecuación de Darcy-Weisbach. Esto último es
muy importante, ya que como se verá más adelante, cuando se probaron redes con otras
características, se presentaron resultados significativamente diferentes. Así mismo, cuando
se probó una red con bombeo que presentaba características similares, los resultados

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
117
arrojaron iguales resultados en algunos momentos del tiempo pero otros radicalmente
divergentes en tiempos específicos del día.
4.4.2 RED MATRIZ DE MEDELLÍN
Los resultados de la red matriz de Medellín serán mostrados y analizados de manera similar a
lo expuesto en la red matriz de Bogotá.
A diferencia de la red mostrada anteriormente, la red matriz de Medellín presentó diferencias
hidráulicas bastante más significativas por lo que el análisis y los resultados que se
encontraron fueron más extensos y con un análisis más profundo, según se aprecia a
continuación.
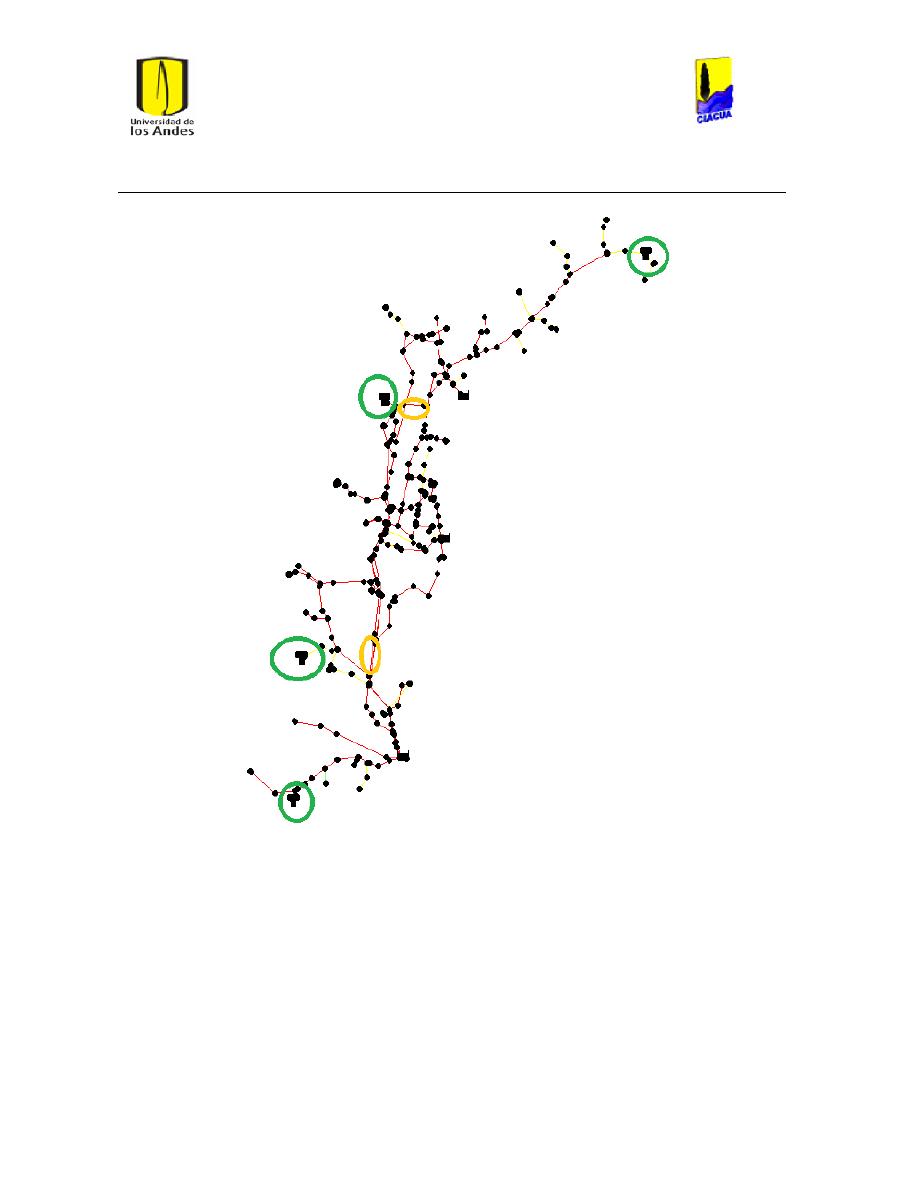
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
118
ILUSTRACIÓN 121 UBICACIÓN DE LOS TANQUES EN LA RED MATRIZ DE MEDELLÍN.
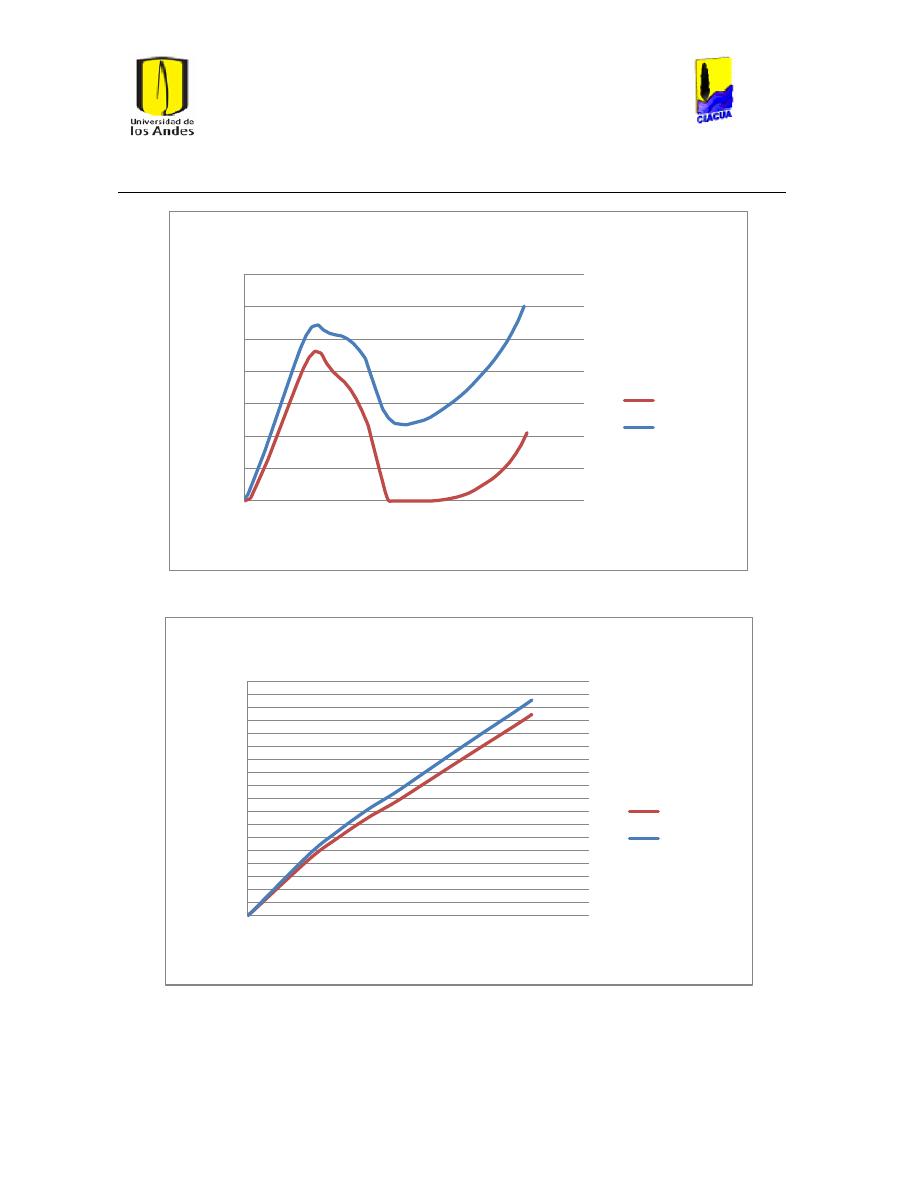
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
119
ILUSTRACIÓN 122 NIVEL TANQUE 691 MEDELLÍN.
ILUSTRACIÓN 123 NIVEL TANQUE 692 MEDELLÍN.
0
0.5
1
1.5
2
2.5
3
3.5
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
iv
e
l (
m
)
Tiempo (h)
Tanque 691 Medellín
Tanque D-W
Tanque H-W
0
1.5
3
4.5
6
7.5
9
10.5
12
13.5
15
16.5
18
19.5
21
22.5
24
25.5
27
00:00
04:48
09:36
14:24
19:12
00:00
04:48
A
ltu
ra(m
)
Tiempo (h)
Tanque 692 Medellín
Tanque D-W
Tanque H-W
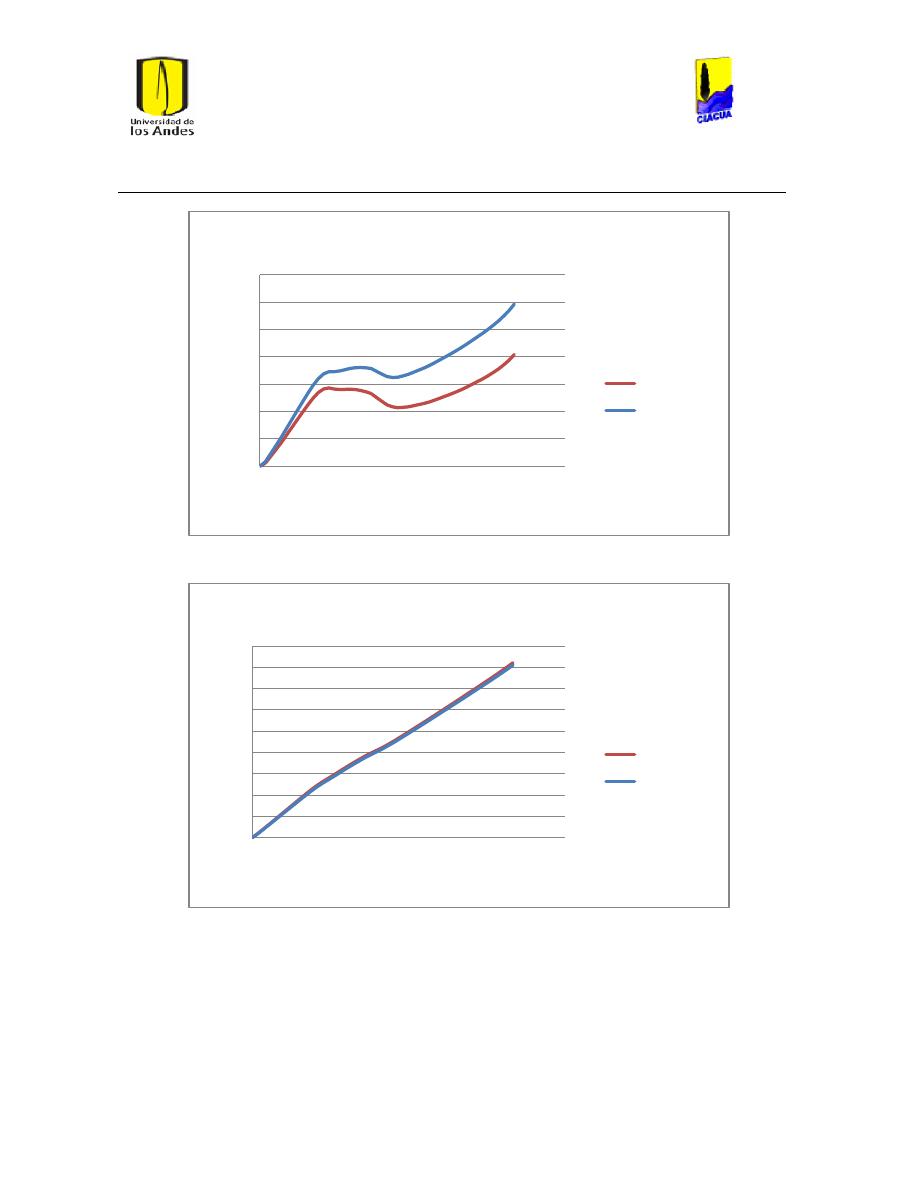
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
120
ILUSTRACIÓN 124 NIVEL TANQUE 689 MEDELLÍN.
ILUSTRACIÓN 125 NIVEL TANQUE 690 MEDELLÍN.
Las ilustraciones anteriores muestran unos efectos hidráulicos importantes debido a que los
patrones de llenado de los tanques en la red matriz de Medellín presentan altas diferencias
entre las dos ecuaciones. Algo que se observó durante esta investigación es que el efecto de
que sea una red con tuberías grandes, con tanques localizados en terminaciones altamente
ramificadas y con altos caudales demandados, pareciera magnificar las diferencias hidráulicas
entre la ecuación físicamente basada y la ecuación empírica.
0
2
4
6
8
10
12
14
00:00 04:48 09:36 14:24 19:12 00:00 04:48
A
ltu
ra(m
)
Tiempo (h)
Tanque 689 Medellín
Tanque D-W
Tanque H-W
0
1
2
3
4
5
6
7
8
9
00:00 04:48 09:36 14:24 19:12 00:00 04:48
A
ltu
ra(m
)
Tiempo(h)
Tanque 690 Medellín
Tanque D-W
Tanque H-W
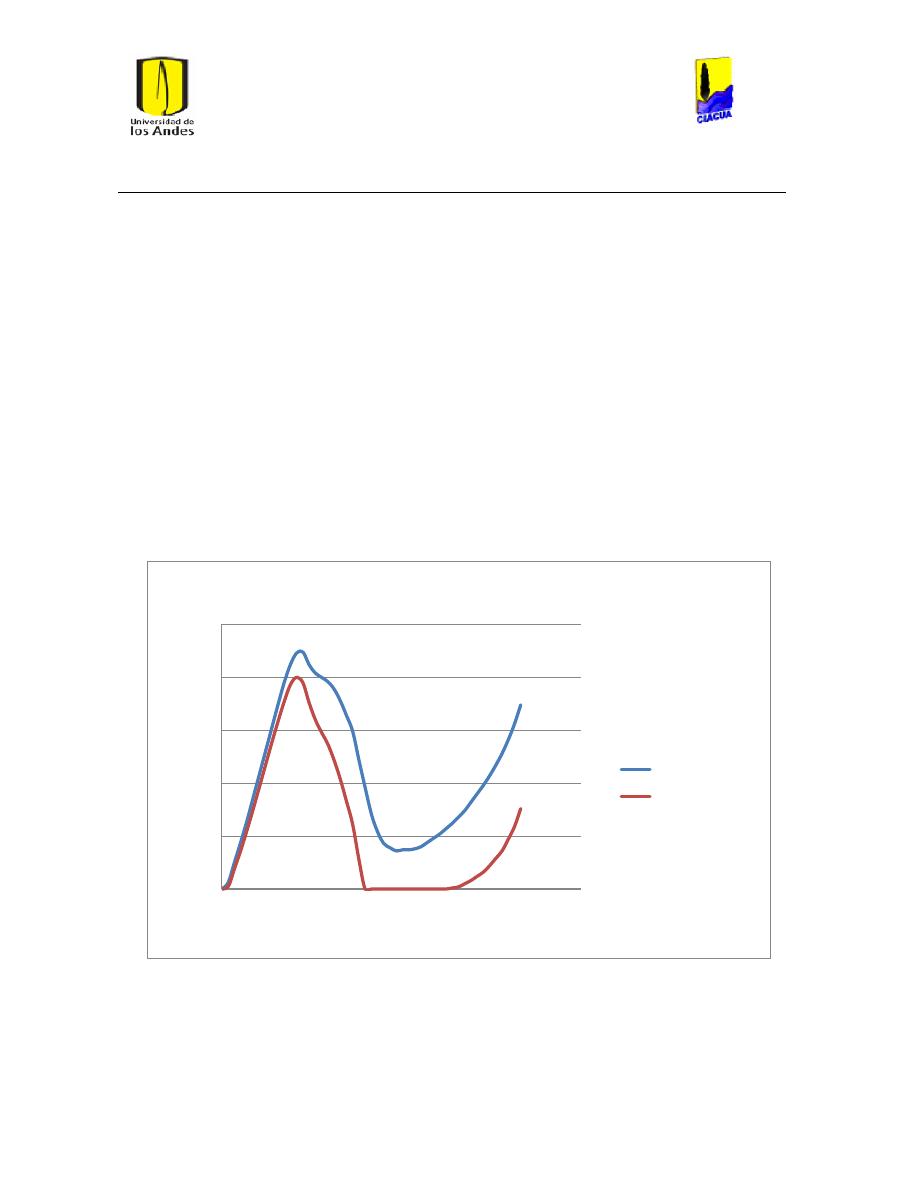
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
121
Las consecuencias de estos efectos, son que de acuerdo con la ecuación de Hazen-Williams, los
tanques 689, 691 y 692 tienen más cantidad de agua en el tiempo, siendo menor cuando la
simulación se realiza con la ecuación de Darcy-Weisbach. Esto revalida lo que se observó y
analizó en el análisis de emisores; es decir, el operario que está trabajando con la ecuación de
Hazen-Williams creerá que el nivel del tanque puede ser suficiente para satisfacer las
necesidades de un sector de la ciudad, cuando en la realidad el tanque puede no tener el nivel
suficiente o estar completamente vacío.
Así mismo, el hecho de que los patrones de llenado de los tanques registren tantas diferencias
entre las dos ecuaciones, implica que la hidráulica del sistema presenta un serio desbalance
de masa en la red, que conlleva a que las presiones de la misma se vean afectadas; más
adelante se mostrará una serie de resultados encontrados que soportan la afirmación acá
mencionada.
Con el fin de evaluar si este efecto se repetía en escenarios diferentes, se probó a su vez, la red
Matriz de Medellín pero con la presencia de solo 2 tanques y no 4 como se vio anteriormente.
Los resultados se muestran a continuación:
ILUSTRACIÓN 126 NIVEL TANQUE 690 RED MEDELLÍN CON 2 TANQUES
0
0.5
1
1.5
2
2.5
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
iv
e
l (
m
)
Tiempo (h)
Tanque 690 Medellín
Tanque 690 H-W
Tanque 690 D-W
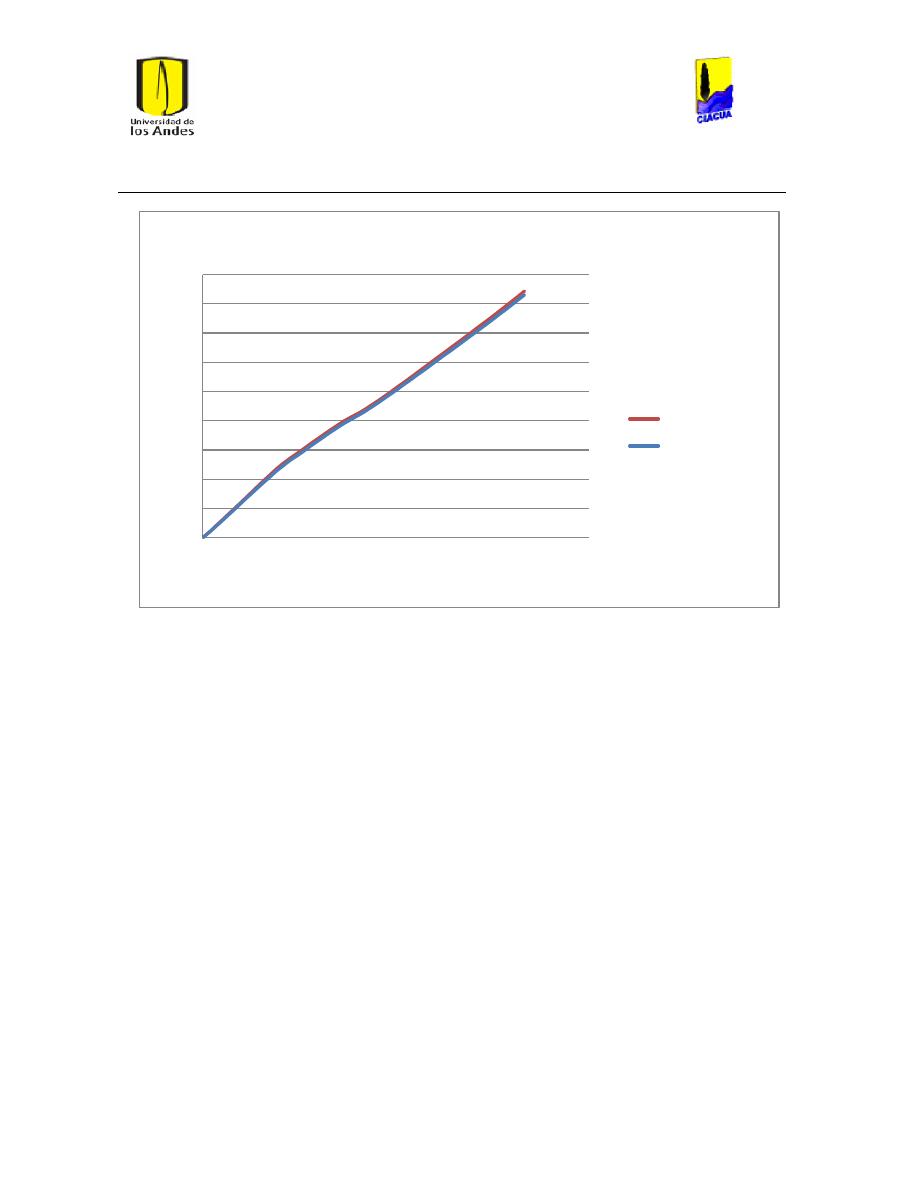
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
122
ILUSTRACIÓN 127 NIVEL TANQUE 689 RED MEDELLÍN CON 2 TANQUES.
Los resultados son bastante interesantes debido a que en uno de los tanques se presentó una
diferencia importante, mientras que en el otro, las dos ecuaciones se comportaron de manera
similar. Lo anterior era un resultado esperado teniendo en cuenta el análisis de emisores que
se realizó anteriormente y el hecho de que en algunos puntos de la ciudad, las dos ecuaciones
se están comportando de manera similar. Así mismo es revelador observar que el desbalance
de masa en la red con 4 tanques y la red con sólo 2 parece afectar de manera similar a los
tanques, con lo cual las tasas de llenado resultan ser mayores al utilizar la ecuación de Hazen-
Williams. A partir de estos resultados, se decidió realizar un análisis de algunos tramos de
interés de la red con el fin de analizar qué es lo que estaba ocurriendo con la hidráulica
(número de Reynolds y pérdidas por fricción).
A continuación se muestran los resultados para algunas de las tuberías probadas:
0
1
2
3
4
5
6
7
8
9
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
iv
e
l (
m
)
Tiempo (h)
Tanque 689 Medellín
Tanque 689 D-W
Tanque 689 H-W
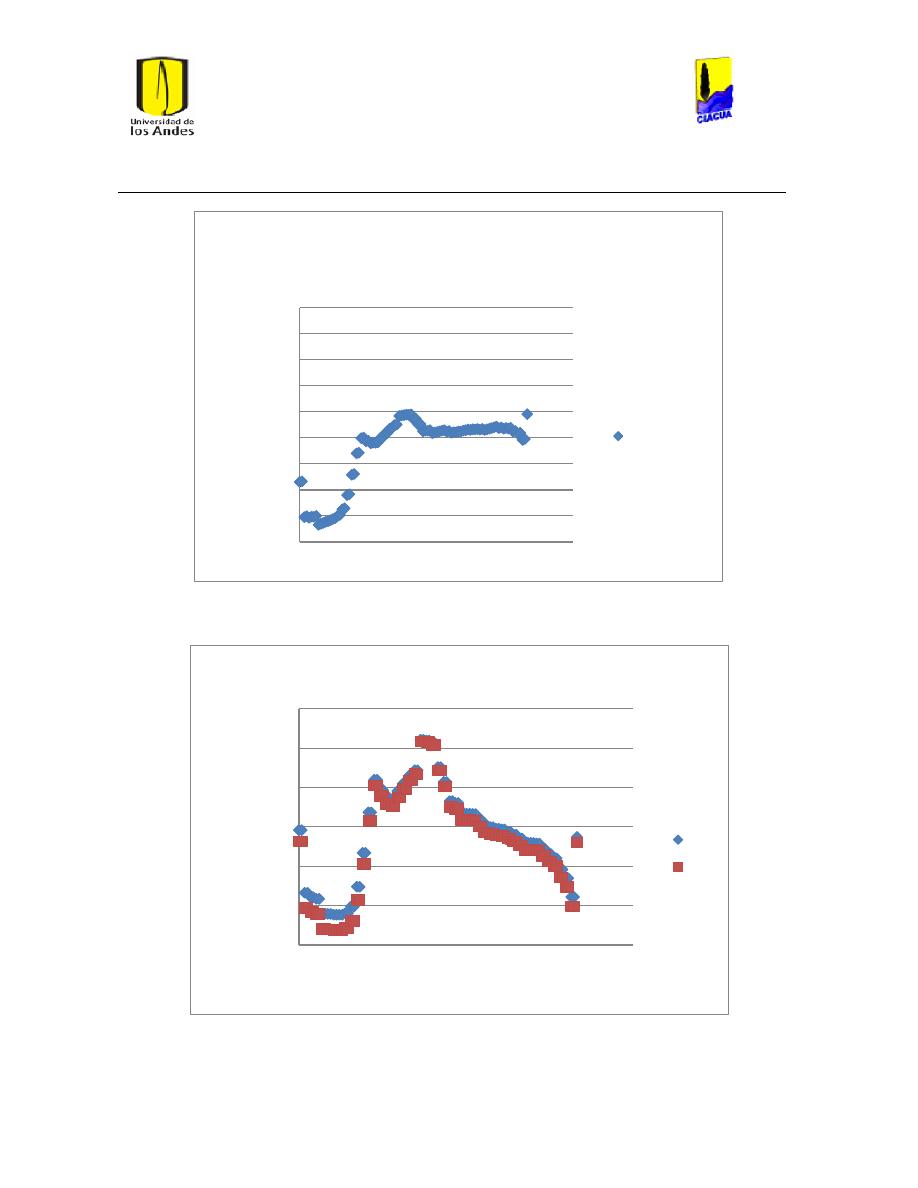
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
123
ILUSTRACIÓN 128 DIFERENCIAS EN PÉRDIDAS POR FRICCIÓN TUBERÍA 78 RED MATRIZ DE
MEDELLÍN CON DIÁMETRO DE 1066 MM Y CAUDAL MEDIO DE 600 L/S.
ILUSTRACIÓN 129 DIFERENCIA EN EL NÚMERO DE REYNOLDS TUBERÍA 78 RED MATRIZ DE
MEDELLÍN CON DIÁMETRO DE 1066 MM Y CAUDAL MEDIO DE 600 L/S.
-9.000%
-8.000%
-7.000%
-6.000%
-5.000%
-4.000%
-3.000%
-2.000%
-1.000%
0.000%
00:00 04:48 09:36 14:24 19:12 00:00 04:48
HW
-D
W/DW
Tiempo (h)
Diferencia de hf en tubería 78
Medellín
Diferencia HF
1500000
1700000
1900000
2100000
2300000
2500000
2700000
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Tiempo (h)
Medellín Tubería 78
D-W
H-W
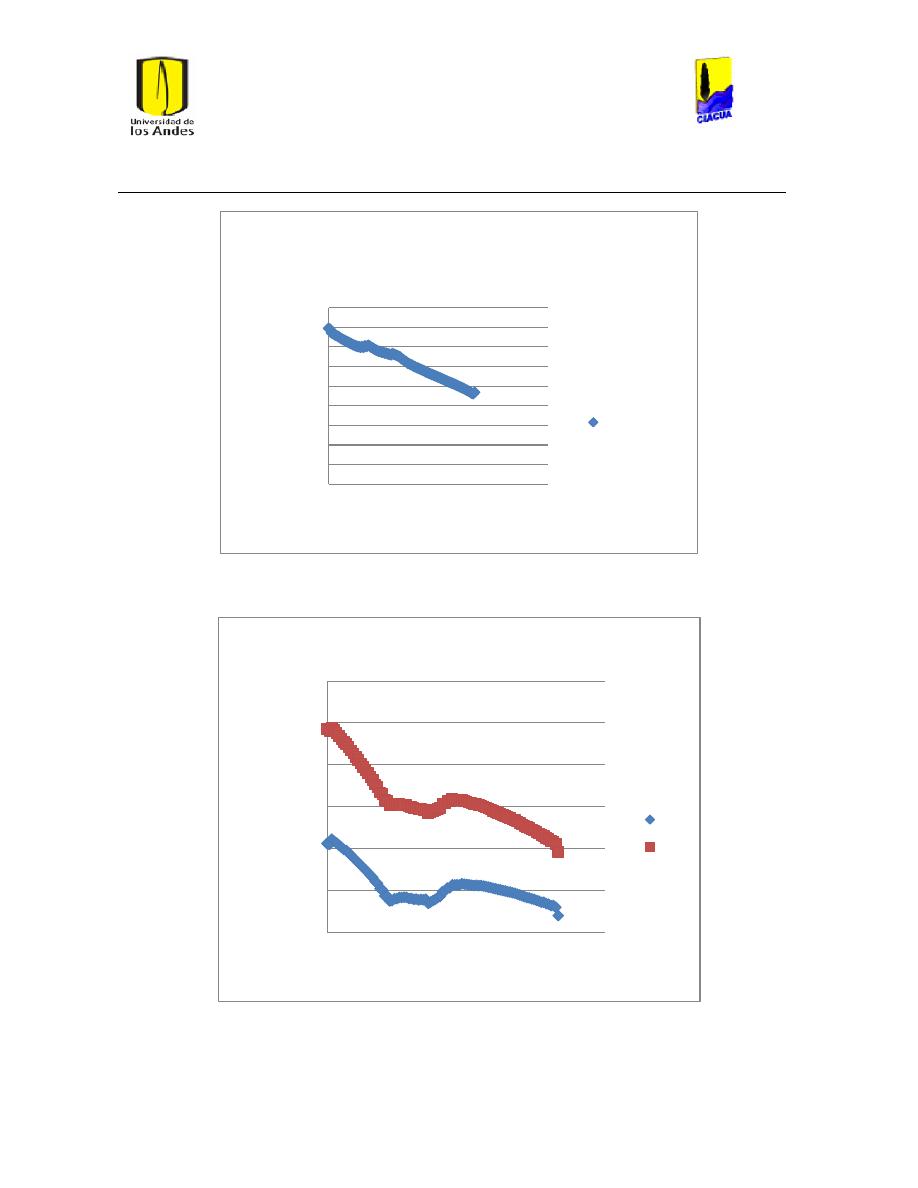
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
124
ILUSTRACIÓN 130 DIFERENCIAS EN PÉRDIDAS POR FRICCIÓN TUBERÍA 395 RED MATRIZ DE
MEDELLÍN CON DIÁMETRO DE 914 MM Y CAUDAL MEDIO DE 390 L/S.
ILUSTRACIÓN 131 DIFERENCIA EN EL NÚMERO DE REYNOLDS TUBERÍA 395 RED MATRIZ DE
MEDELLÍN CON DIÁMETRO DE 914 MM Y CAUDAL MEDIO DE 390 L/S.
0.000%
2.000%
4.000%
6.000%
8.000%
10.000%
12.000%
14.000%
16.000%
18.000%
00:00
12:00
00:00
12:00
HW
-D
W/DW
Tiempo (h)
Diferencia de HF en tubería 395
Medellín
Diferencia HF
1450000
1500000
1550000
1600000
1650000
1700000
1750000
00:00 04:48 09:36 14:24 19:12 00:00 04:48
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Tiempo (h)
Medellín Tubería 395
D-W
H-W

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
125
En el desarrollo de esta investigación se simularon varios escenarios para toda la red y para
diferentes tramos de tubería. Las 4 gráficas anteriores muestran los resultados que resultan
más relevantes en tanto representan bien lo que está ocurriendo internamente en la red. Se
aprecia claramente que las pérdidas por fricción entre las dos ecuaciones pueden alcanzar
diferencias de hasta 16% lo que es coherente con el estudio de Rafael Flechas (Flechas, 2011) .
Como se verá más adelante, estas diferencias resultan ser mayores en otras redes. Así mismo,
se puede ver que los números de Reynolds que arrojan las simulaciones presentan grandes
diferencias, al punto que el número de Reyolds que arroja una tubería simulada con la
ecuación empírica se vuelve una paralela casi perfecta comparándola con la misma tubería
simulada con la ecuación físicamente basada, lo anterior implica que pese a que su
comportamiento es similar, existe un desfase considerable en el caudal que está
transportando la tubería.
Así mismo, cuando se utiliza la ecuación de Darcy Weisbach, resulta revelador que la
diferencia en el número de Reynolds que se aprecia en la ilustración 130 esté decayendo de
manera casi lineal; éste fenómeno probablemente esté causado porque el caudal que está
circulando por la tubería es menor, y por ende la magnitud de los errores que se presentan en
la misma esté decayendo. Este mismo resultado se presentó en varias de las tuberías de la
red.
A continuación, la investigación avanzó tratando identificar las diferencias en la hidráulica de
la red entre las dos ecuaciones, por lo que se procedió a ver cuáles tuberías presentaban
mayores números de Reynolds al utilizar la ecuación de Hazen-Williams, cuales tuberías con
la ecuación de Darcy-Weisbach y finalmente que tuberías no presentaban ninguna diferencia.
Los resultados se muestran empleando las mismas convenciones de colores utilizados en la
red matriz de Bogotá, es decir, ROJO las tuberías que tienen números de Reynolds mayores al
utilizar la ecuación de Hazen-Williams, VERDE las tuberías que tienen mayor número de
Reynolds con la ecuación de Darcy-Weisbach y finalmente en AMARILLO los tramos con
hidráulica igual entre las dos ecuaciones.
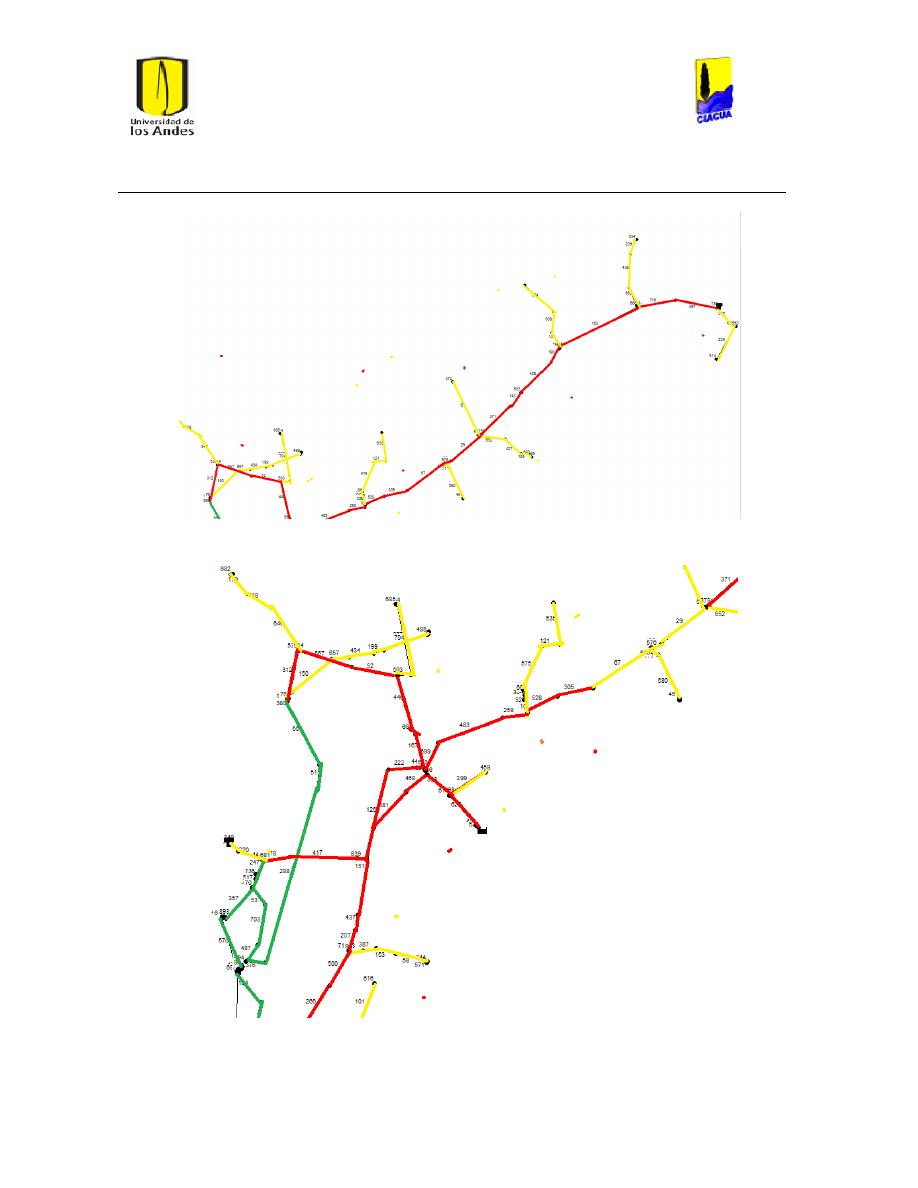
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
126
FIGURA 10 DIFERENCIAS HIDRÁULICAS EN LA RED MATRIZ DE MEDELLÍN (1).
FIGURA 11 DIFERENCIAS HIDRÁULICAS EN LA RED MATRIZ DE MEDELLÍN (2).
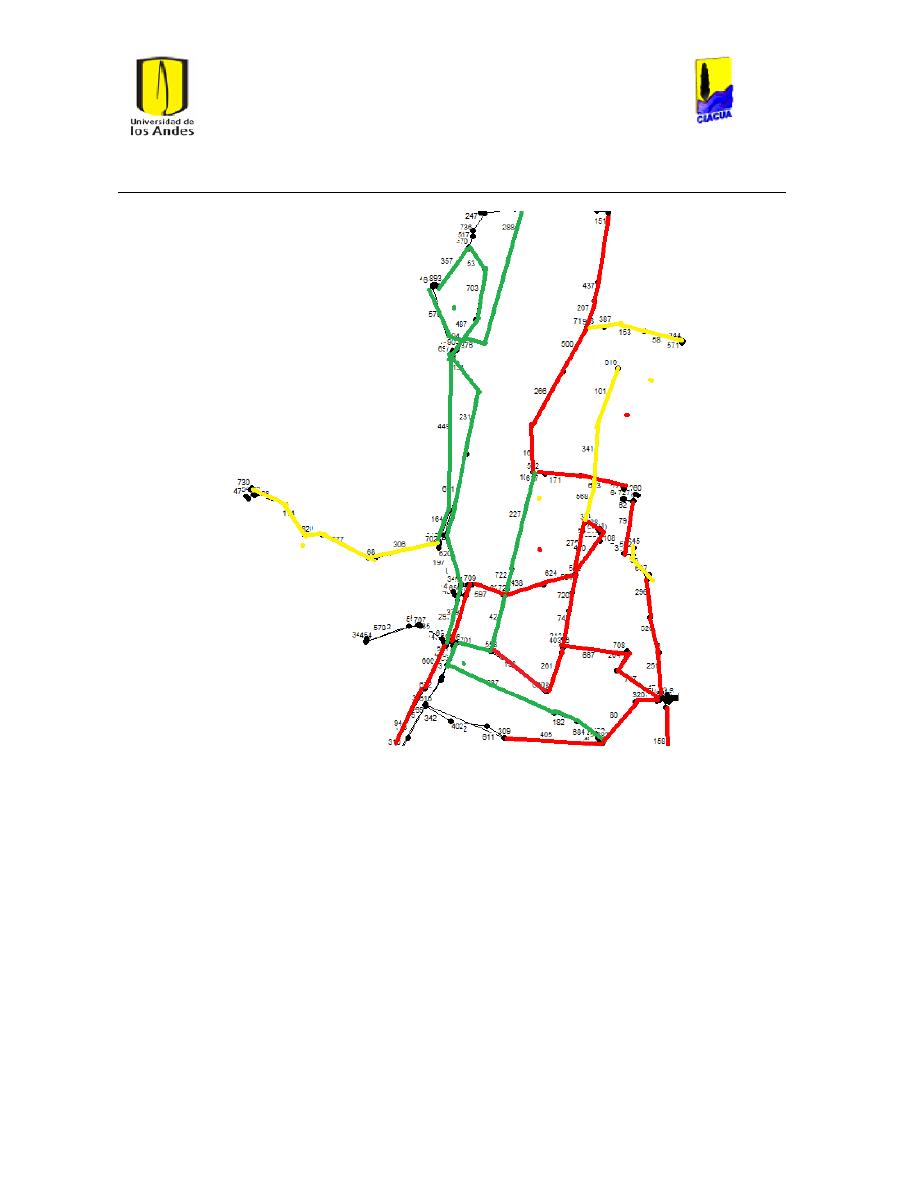
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
127
FIGURA 12 DIFERENCIAS HIDRÁULICAS EN LA RED MATRIZ DE MEDELLÍN (3).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
128
FIGURA 13 DIFERENCIAS HIDRÁULICAS EN LA RED MATRIZ DE MEDELLÍN (4).
FIGURA 14 DIFERENCIAS HIDRÁULICAS EN LA RED MATRIZ DE MEDELLÍN (5).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
129
Las gráficas anteriores muestran claramente que existen diferencias en la solución hidráulica
entre las dos ecuaciones del estudio. Así mismo, se puede observar que a la salida de los
embalses se están presentando números de Reynolds diferentes en las dos ecuaciones, lo que
implica que en efecto los balances de masa de ambas ecuaciones presentan diferencias
significativas que afectan la hidráulica y el funcionamiento de todo el sistema. Otro efecto
importante a mencionar es que en las horas de mayor caudal, las diferencias se ven altamente
magnificadas y en horarios de menor consumo el número de tuberías que presentan altas
diferencias es menor; sin embargo, viendo los resultados y analizando a las demás redes, se
concluye que existen una serie de tuberías que presentan diferencias permanentemente.
A partir de estos resultados se avanzó en identificar estas tuberías y determinar las
características de las mismas. Los resultados de esto se muestran a continuación:
Las tuberías que presentan color azul son las tuberías que presentan las diferencias más
importantes en términos del número de Reynolds y el caudal transportado.
FIGURA 15 TUBERÍAS CON ALTAS DIFERENCIAS RED MATRIZ DE MEDELLÍN CAUDAL MEDIO.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
130
FIGURA 16 TUBERÍAS CON ALTAS DIFERENCIAS RED MATRIZ DE MEDELLÍN CAUDAL MEDIO
(ACERCAMIENTO).
FIGURA 17 TUBERÍAS CON ALTAS DIFERENCIAS RED MATRIZ DE MEDELLÍN CAUDAL MÁXIMO.
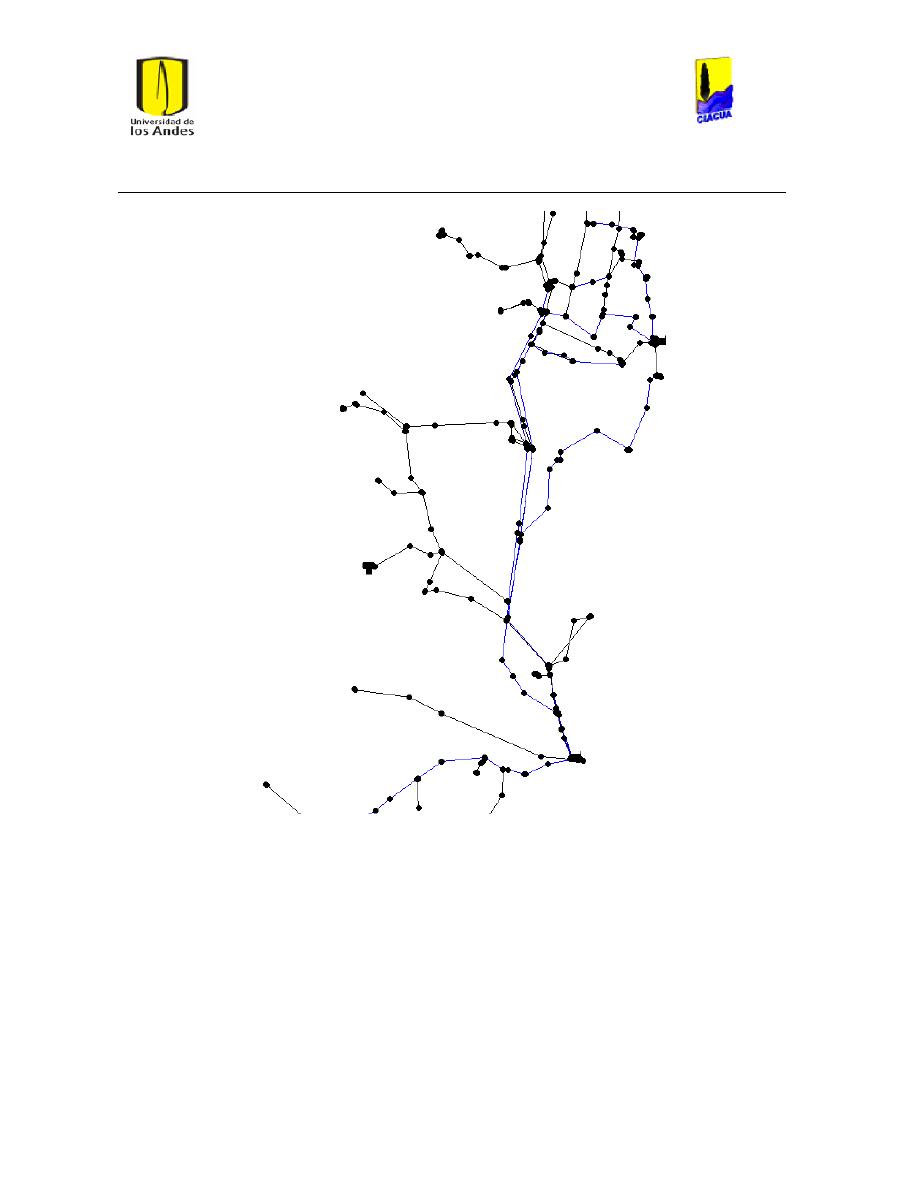
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
131
FIGURA 18 TUBERÍAS CON ALTAS DIFERENCIAS RED MATRIZ DE MEDELLÍN CAUDAL MÁXIMO
(ACERCAMIENTO).
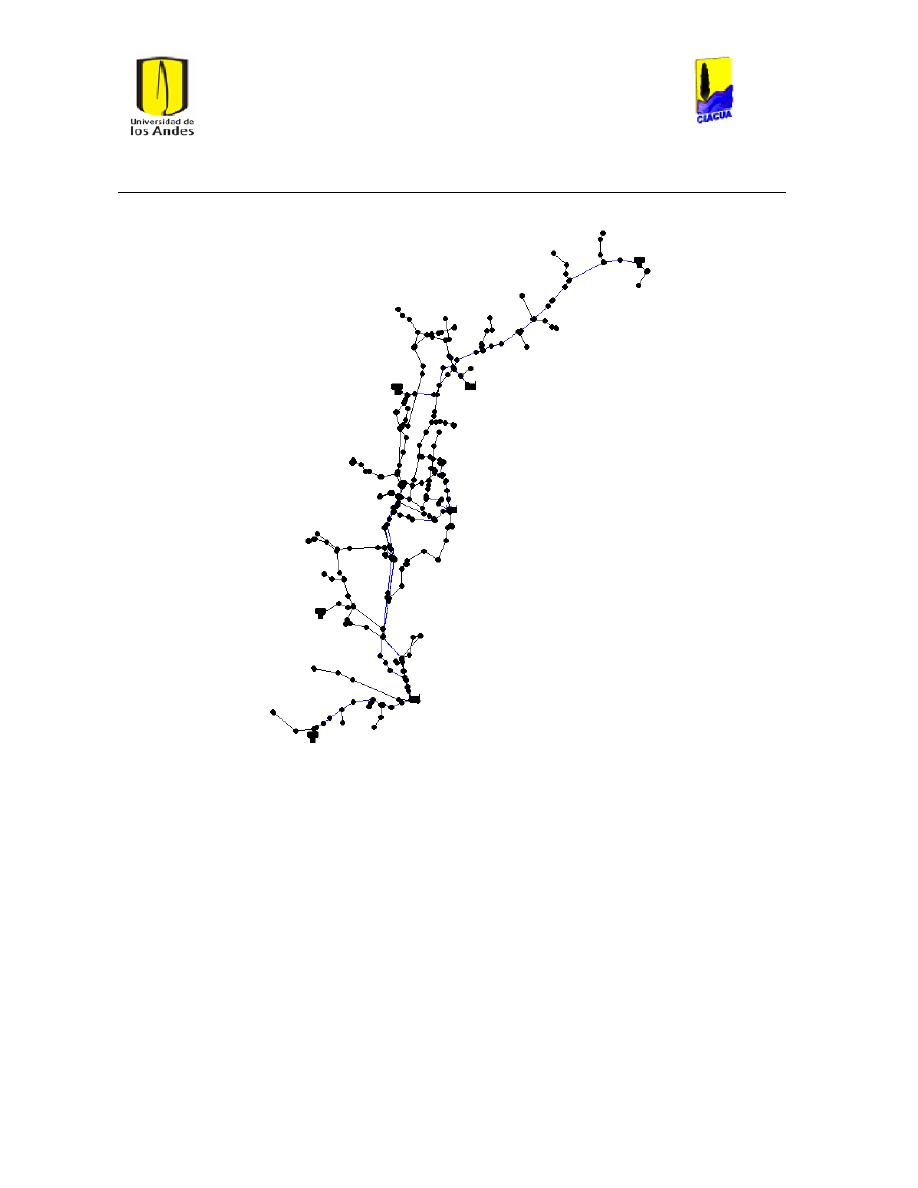
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
132
FIGURA 19 TUBERÍAS CON ALTAS DIFERENCIAS RED MATRIZ DE MEDELLÍN CAUDAL MÍNIMO.
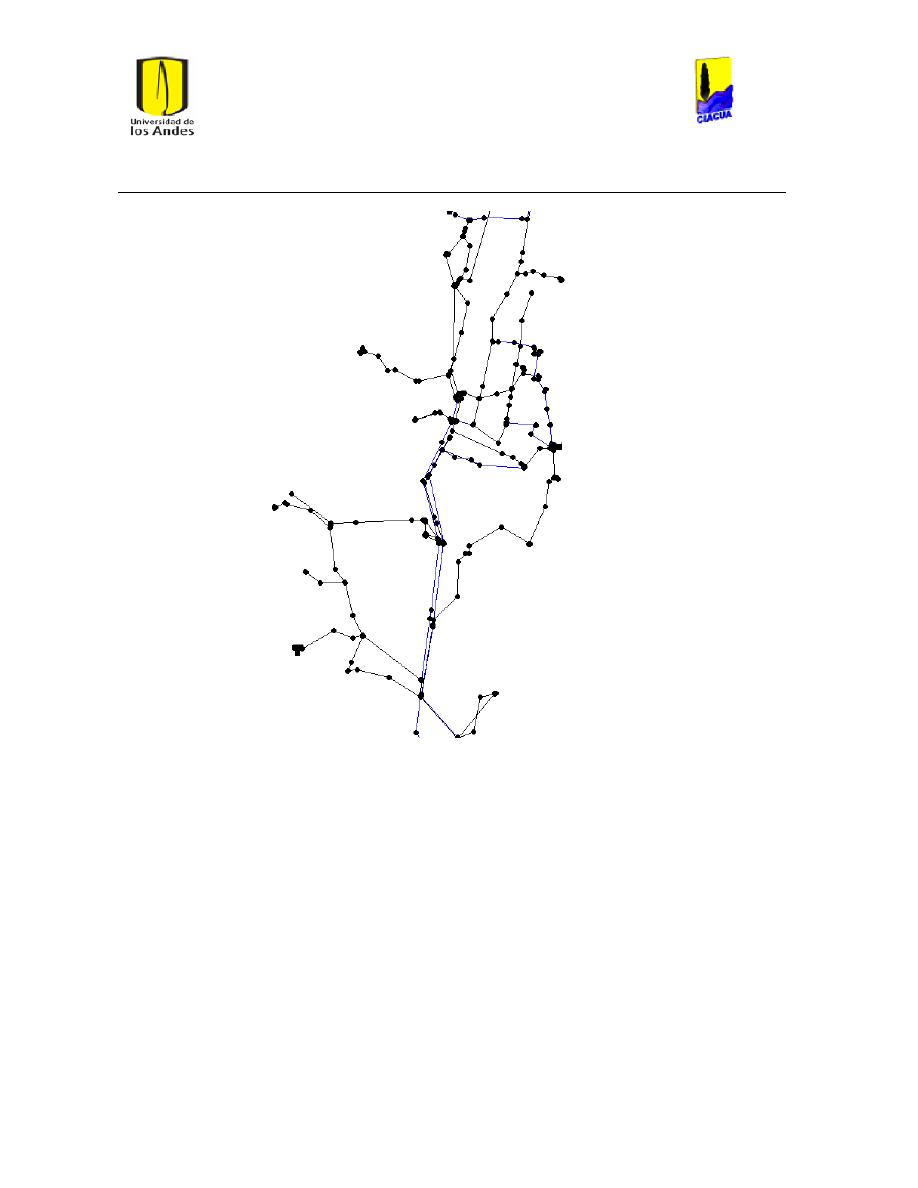
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
133
FIGURA 20 TUBERÍAS CON ALTAS DIFERENCIAS RED MATRIZ DE MEDELLÍN CAUDAL MÍNIMO
(ACERCAMIENTO).
Las gráficas anteriores muestran comportamientos interesantes en cada una de las tuberías.
En primer lugar se confirma que en algunas tuberías se presentan de manera continua las
diferencias en términos del caudal transportado y pérdidas por fricción. Son precisamente
estas tuberías las que cuentan con las características que afectan la solución hidráulica entre
la ecuación físicamente basada y la ecuación empírica. Lo segundo y quizás lo más relevante
de esta investigación, es que son tramos de tubería que se dirigen a las ramificaciones de la
red y son los tramos que transportan la cantidad de caudal más significativa asociados con
tuberías de gran diámetro. Esto es bastante importante considerando el hecho de que en
Bogotá no se presentó este fenómeno a causa de ser una red poco ramificada y altamente
redundante. Así mismo, en el caso de la Red Medellín este fenómeno se presentó cuando solo
existía una tubería única de llegada a los tanques, cosa que no ocurrió en la red matriz de
Bogotá.
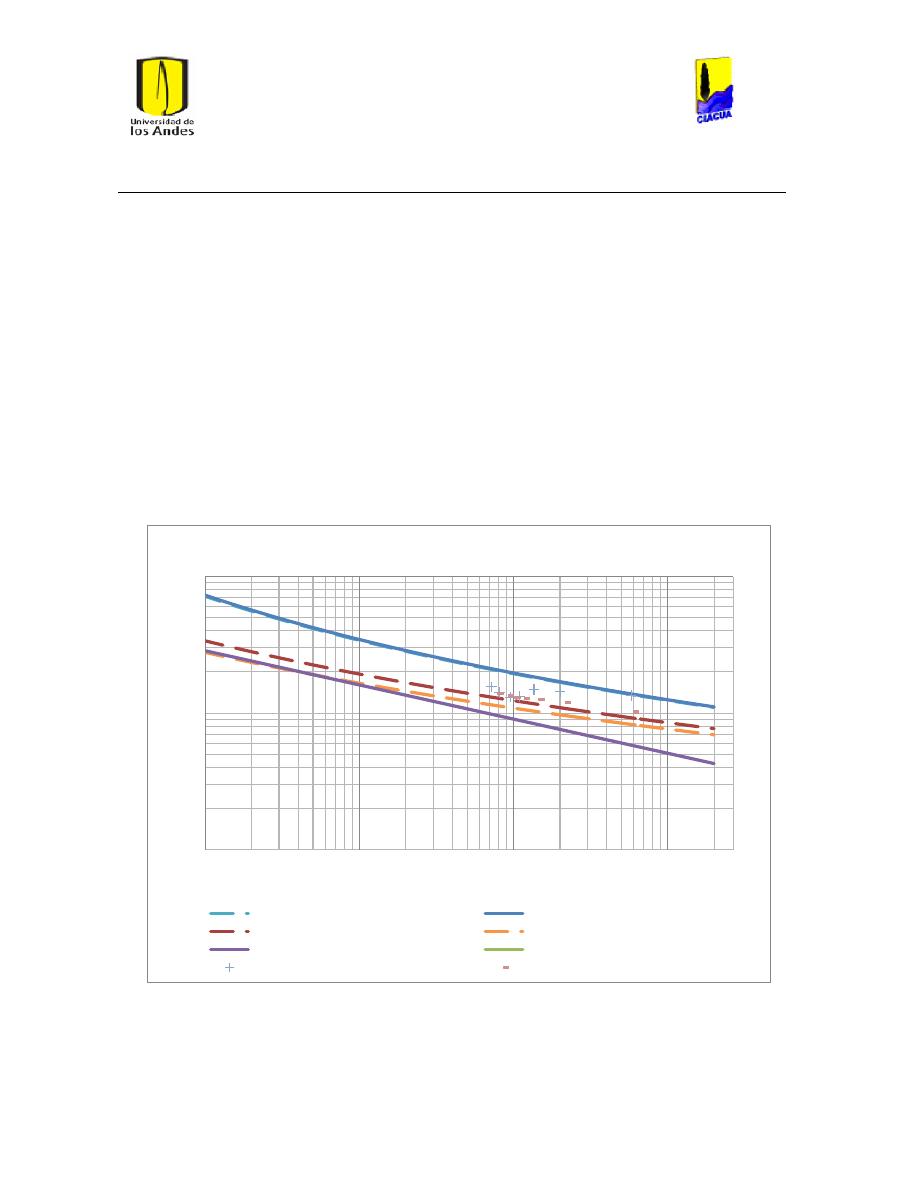
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
134
Al continuar con las demás redes, estos efectos hidráulicos se vieron replicados, confirmado
que lo encontrado en la red Matriz de Medellín no fue una simple coincidencia o un caso
aislado. Es más, con los resultados que se mostrarán más adelante con la red de Bombeo de
Dtown, que es una red con alta redundancia pero con algunas terminaciones ramificadas
importantes, se confirman las diferencias más importantes que ocurren en la hidráulica del
sistema.
Se muestran a continuación los efectos hidráulicos de las tuberías destacadas en las figuras
anteriores. Esto incluye un análisis en el diagrama de Moody donde se verán claras diferencias
entre la ecuación de Hazen-Williams y la ecuación de Darcy-Weisbach, así como unas tablas
resúmenes donde se va a identificar claramente que las tuberías que transportan la mayor
cantidad del caudal están causando un efecto significativo al sistema a tal punto que los
caudales que están circulando por las tuberías o por tramos específicos de la misma son
diferentes y están cambiando de manera drástica el comportamiento entre la red simulada
con la ecuación de Hazen-Williams y la ecuación de Darcy-Weisbach.
ILUSTRACIÓN 132 DIAGRAMA DE MOODY 1 RED MATRIZ DE MEDELLÍN CAUDAL MÍNIMO.
0.001
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Medellín Qmin (Diferencia Número de
Reynolds 100000-300000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
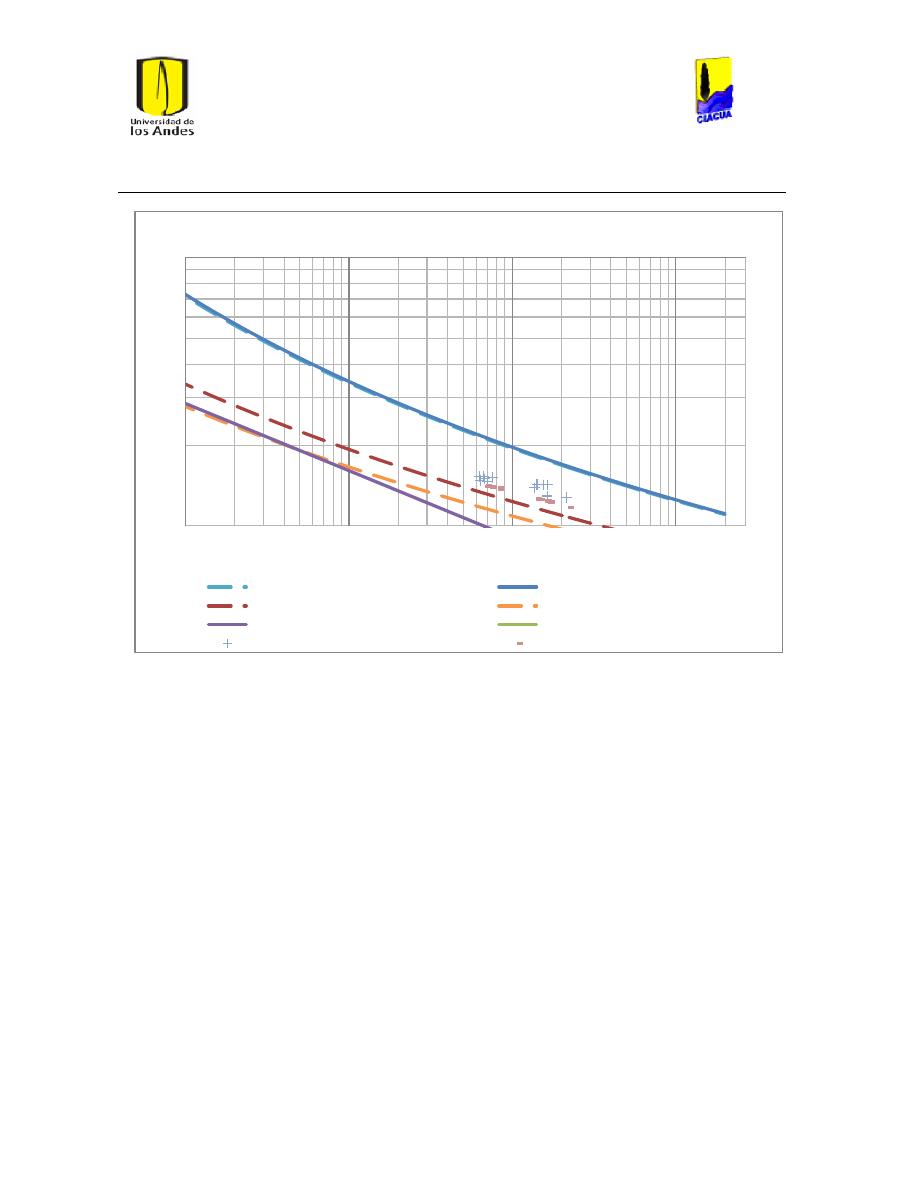
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
135
ILUSTRACIÓN 133 DIAGRAMA DE MOODY 2 RED MATRIZ DE MEDELLÍN CAUDAL MÍNIMO
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Medellín Qmin (Diferencia Número de
Reynolds 50000-100000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
136
TABLA 11 RESUMEN DE RESULTADOS PARA TUBERÍAS CON ALTAS DIFERENCIAS PARA EL CAUDAL MÍNIMO DEMANDADO DE LA RED MATRIZ DE
MEDELLÍN.
TABLA 12 RESUMEN DE RESULTADOS PAR TUBERÍAS CON ALTAS DIFERENCIAS PARA EL CAUDAL MÍNIMO DEMANDADO DE LA RED MATRIZ DE
MEDELLÍN 2.
Las primeras dos columnas de las tablas representan el caudal transportado con cada una de las ecuaciones, la tercera columna es la
diferencia en el número de Reynolds entre las ecuaciones, la cuarta y sexta corresponden a los números de Reynolds de cada ecuación, la
quinta y séptima columna corresponden a los factores de fricción de cada ecuación y finalmente la columna final equivale a la diferencia
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/355.6
0.377880187
0.344344902
1.05E+05
1.08E+06
0.015532
1.19E+06
0.013839
9.74%
Tramo 1/406.4
0.7977993
0.740523097
1.57E+05
2.04E+06
0.014836
2.19E+06
0.012605
7.73%
Tramo1/457.2
1.330562902
1.233351668
2.37E+05
3.01E+06
0.014375
3.25E+06
0.011865
7.88%
Tramo1/609.6
4.894837055
4.741772157
2.80E+05
8.69E+06
0.013381
8.97E+06
0.010155
3.23%
Tramo2/609.6
0.759477589
0.662266318
1.78E+05
1.21E+06
0.014191
1.39E+06
0.013377
14.68%
Tramo 1/914.1
1.439873374
1.342661812
1.19E+05
1.64E+06
0.013182
1.76E+06
0.012824
7.24%
Tramo 1/1066.8
1.463411236
1.366199856
1.02E+05
1.43E+06
0.013044
1.53E+06
0.013051
7.12%
Medellín Qmín (Diferencias número de Reynolds 100000-300000) Hazen Mayor
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
0.448275497
0.41474012
9.22E+04
1.14E+06
0.015156
1.23E+06
0.013728
8.09%
0.377880224
0.344344847
9.22E+04
9.46E+05
0.015286
1.04E+06
0.014083
9.74%
0.39742535
0.363890103
9.22E+04
1.00E+06
0.015244
1.09E+06
0.013976
9.22%
0.448275479
0.414740143
8.19E+04
1.01E+06
0.014961
1.23E+06
0.013938
21.60%
1.093523789
1.059988469
7.37E+04
2.33E+06
0.014208
2.40E+06
0.012382
3.16%
0.467676815
0.434141496
7.37E+04
9.54E+05
0.014777
1.03E+06
0.014041
7.72%
1.150619791
1.117084471
7.37E+04
2.46E+06
0.014208
2.53E+06
0.012289
3.00%
0.999968563
0.966784696
7.30E+04
2.13E+06
0.014264
2.20E+06
0.012563
3.43%
0.504120231
0.480915663
5.10E+04
1.06E+06
0.014682
1.11E+06
0.013884
4.83%
1.150619928
1.11708452
6.14E+04
2.05E+06
0.013851
2.11E+06
0.012581
3.00%
2.698456168
2.634410223
7.82E+04
3.22E+06
0.012763
3.30E+06
0.011685
2.43%
2.0528187
2.009605024
5.28E+04
2.45E+06
0.012919
2.51E+06
0.012181
2.15%
Medellín Qmín (Diferencias número de Reynolds 50000-100000) Hazen Mayor

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
137
porcentual del número de Reynolds entre las dos ecuaciones. Estas tablas se presentan en todos los casos de estudio, por lo que la
descripción
de
las
mismas
solo
se
va
realizar
en
esta
parte.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
138
Los diagramas de Moody y las tablas resumen mostradas, representan los tramos de la red
que registran diferencias considerables en el número de Reynolds (entre 50000 y 300000).
Estos resultados muestran claramente que las tuberías que presentan diferencias se
encuentran en números de Reynolds mayores a
; estos números de Reynolds están
asociados con tuberías de gran diámetro y por ende a tuberías que están diseñadas para
transportan gran cantidad de caudal. Ahora, al analizar los diagramas de Moody, se puede
indentificar un claro desfase entre los números de Reynolds entre la ecuación empírica y la
ecuación físicamente basada, así mismo se puede ver claramente que hay diferencias
importantes entre los factores de fricción entre las dos ecuaciones.
Por otro lado, si se centra la atención en las tablas resumen se puede evidenciar
cuantitativamente que el caudal que están transportando las tuberías diverge de manera
importante, por lo que es evidente que el cálculo de las pérdidas por fricción y por ende del
factor de fricción va a variar de manera considerable entre la red simulada con la ecuación de
Darcy-Weisbach y la ecuación de Hazen-Williams. Como se mencionó atrás, se encontró que
con la ecuación de Hazen-Williams el caudal que salía de los embalses podía ser mayor o
menor al que se encontraba con la red que utilizó la ecuación físicamente basada, lo cual se
confirma con estos resultados, ya que se logró cuantificar que la diferencia de caudal que se
puede presentar en esta red es de 184 L/s, lo que es una diferencia bastante importante a la
hora de calcular las pérdidas de energía en la red. Por supuesto, el efecto de este exceso de
caudal va más allá de lo que se acaba de nombrar ya que al observar las cifras de las tablas
resumen resulta evidente que este exceso de caudal está generando que la distribuciones del
caudal cambie de manera drástica en casi toda la red.
De esta manera, con la ecuación de Darcy-Weisbach, algunas tuberías están transportando un
caudal porcentualmente muy inferior que el mismo tramo trabajado con la ecuación de
Hazen-Williams, lo cual implica que la distribución de caudales en toda la red está
desbalanceado al utilizar esta ecuación. Esto es coherente con lo mostrado en las Figuras 10,
11, 12, 13 y 14, es decir, hay tramos que transportan más caudal con la ecuación de Hazen-
Williams y otros con la ecuación de Darcy-Weisbach.
Estos análisis conllevan muchas consecuencias hidráulicas y operacionales de gran
importancia. La primera es que al tener caudales diferentes, los coeficientes teóricos de
Hazen-Williams van a divergir de manera considerable con los coeficientes calculados a partir
del funcionamiento de la red operada con la ecuación de Darcy-Weisbach, que es consecuente
con lo analizado por Bombardelli y García (Fabián Bombardelli, 2003) y por Liou (Liou, 1998),
es decir, se presenta una gran variabilidad del coeficiente de Hazen-Williams y este depende
profundamente del flujo que esté circulando por la tubería; precisando que en este estudio las
condiciones fueron influenciadas por el desbalance de masa que se presentó en la red causado
por la solución hidráulica que arroja la ecuación de Hazen-Williams. En segunda instancia, si
la red tuviera algún tipo de fugas, la cuantificación de las mismas y los impactos que podrían
generar al utilizar la ecuación de Hazen-Williams podrían ser de magnitud, al subestimar la
medida de control necesaria y como consecuencia empeorar el problema y dejar a sectores de
la red con presiones inferiores a las exigidas en las normativas. En tercera instancia y de
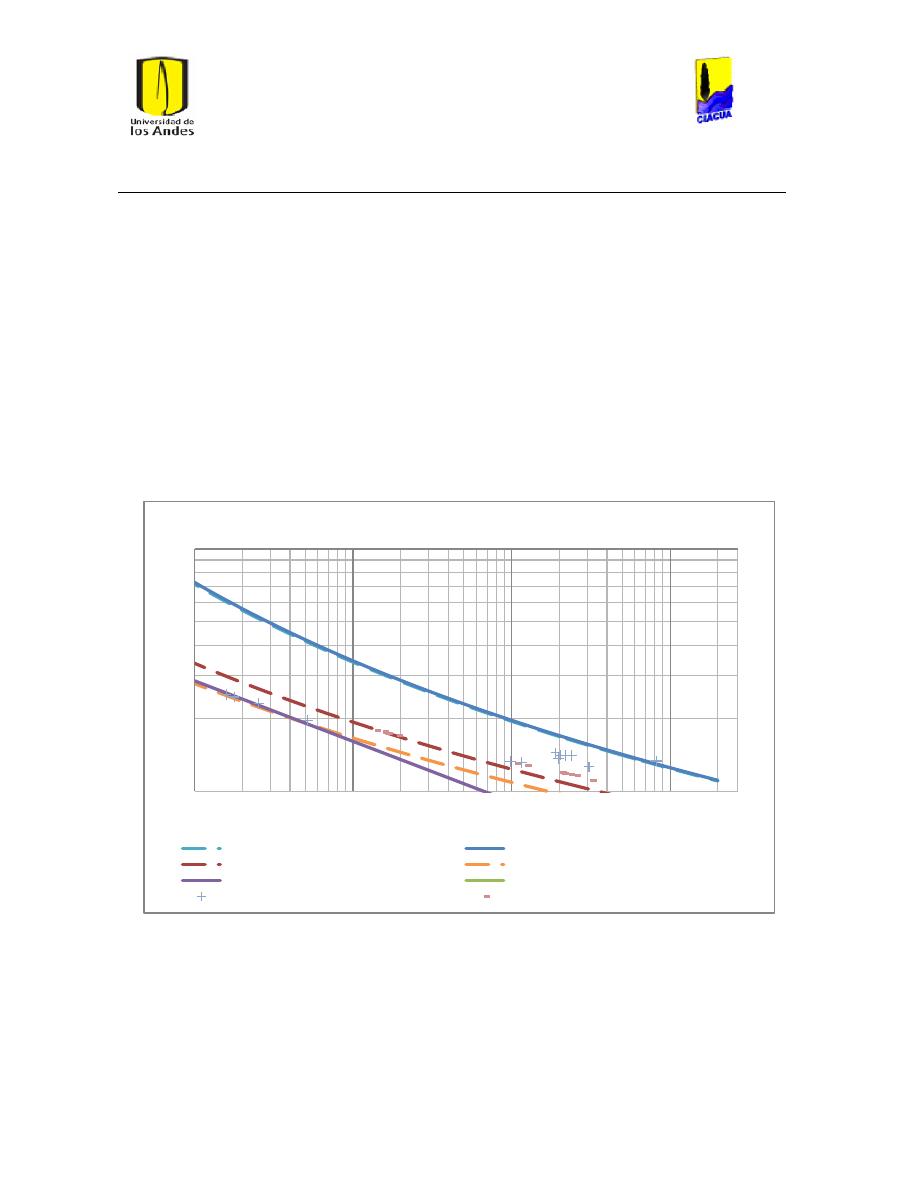
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
139
acuerdo con lo mencionado desde el principio de la investigación, los llenados de los tanques
son diferentes; en ciertos momentos, algunos de ellos presentan un vaciado total con la
ecuación de Darcy-Weisbach y no con la ecuación de Hazen-Williams, lo que de por sí también
tiene un efecto hidráulico importante en las presiones y en el funcionamiento general de la
red (direcciones de flujo, caudal que pasa por las tuberías y presiones de la red).
La consecuencia final es que estos efectos se vieron presentes en una red con presencia de
tanques en sectores ramificados, en tuberías de gran diámetro y que transportaban
cantidades de agua considerable, lo que pareciera indicar que este tipo de sistemas matrices
son especialmente vulnerables a efectos negativos cuando se utiliza la ecuación de Hazen-
Williams con respecto a lo que se presentaría en una red con la hidráulica real del sistema
(Darcy-Weisbach).
A continuación se muestran los resultados para el caudal máximo:
ILUSTRACIÓN 134 DIAGRAMA DE MOODY 1 RED MATRIZ DE MEDELLÍN CAUDAL MÁXIMO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Medellín Qmax (Diferencia Número de
Reynolds 100000-300000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
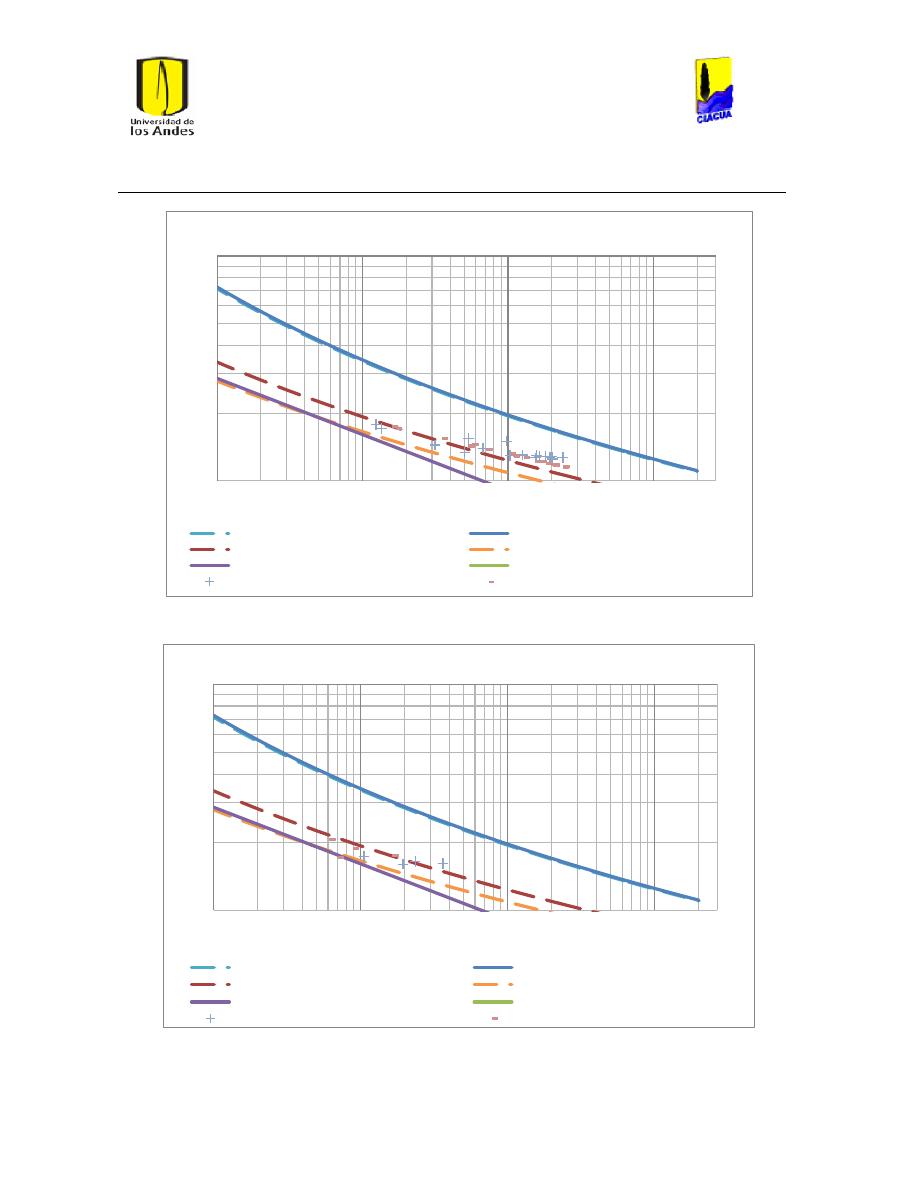
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
140
ILUSTRACIÓN 135 DIAGRAMA DE MOODY 2 RED MATRIZ DE MEDELLÍN CAUDAL MÁXIMO.
ILUSTRACIÓN 136 DIAGRAMA DE MOODY 3 RED MATRIZ DE MEDELLÍN CAUDAL MÁXIMO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fa
ct
or
d
e
Fr
icc
ión
Número de Reynolds
Diagrama de Moody Medellín Qmax(Diferencia Número de
Reynolds 50000-100000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Medellín Qmax(Diferencia Número de
Reynolds 50000-100000 Darcy Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
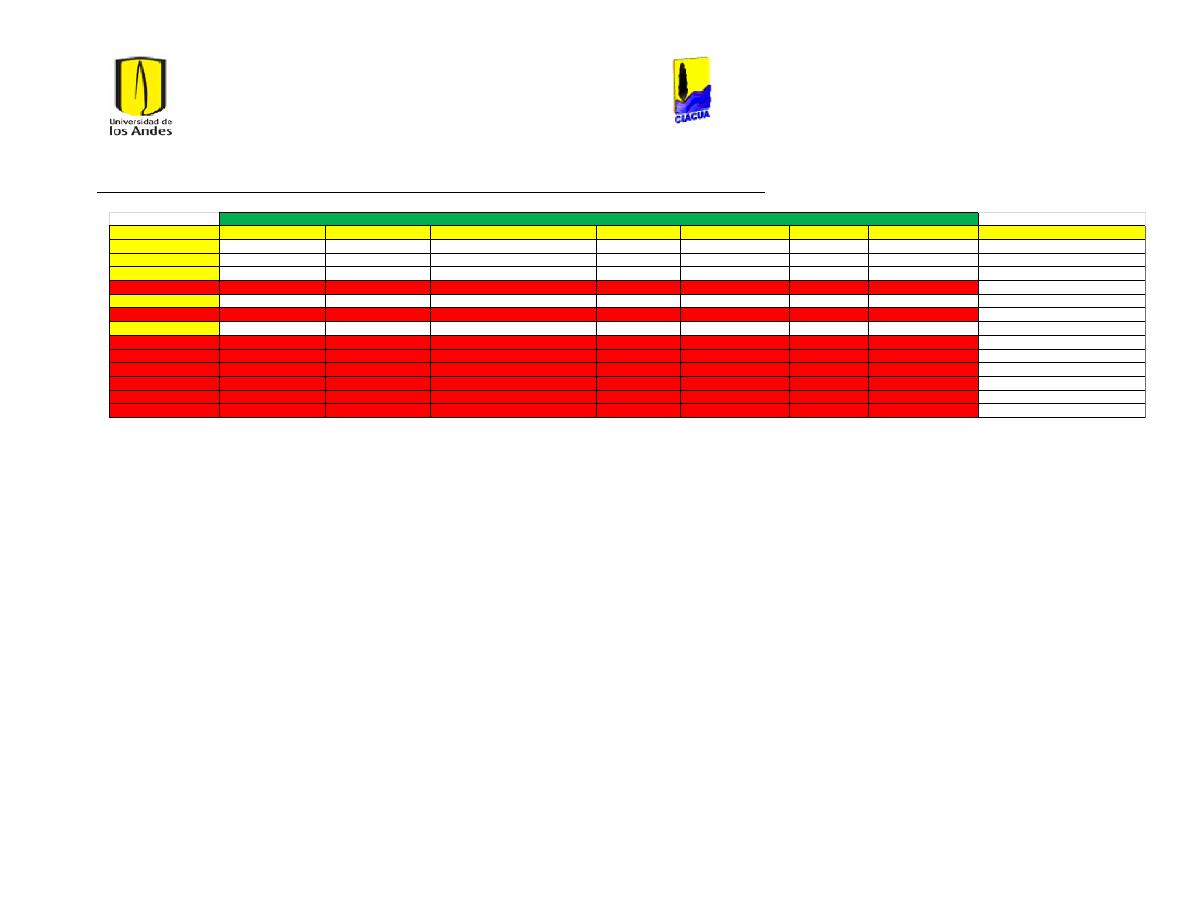
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
141
TABLA 13 TABLA RESUMEN DE ALTAS DIFERENCIAS RED MATRIZ MEDELLÍN CAUDAL MÁXIMO 1 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS
ENTRE 100000 Y 300000.
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/406.4
0.084857823
0.009738642
2.06E+05
2.68E+04
0.024496
2.33E+05
0.017563
771.35%
Tramo 1/457.2
1.258401382
1.172251484
2.10E+05
2.86E+06
0.014393
3.07E+06
0.011964
7.35%
Tramo2/457.2
0.084857691
0.009738591
1.84E+05
2.38E+04
0.025134
2.07E+05
0.017825
771.35%
Tramo 1/508
1.722426817
1.627830003
2.08E+05
3.58E+06
0.014048
3.79E+06
0.011577
5.81%
Tramo 2/508
0.1300937
0.035496886
2.08E+05
7.80E+04
0.019639
2.86E+05
0.01697
266.49%
Tramo 3/508
1.589303007
1.494706396
2.08E+05
3.29E+06
0.014075
3.49E+06
0.011716
6.33%
Tramo 4/508
0.111998973
0.017402767
2.08E+05
3.83E+04
0.022973
2.46E+05
0.01735
543.57%
Tramo 5/508
1.453840235
1.393323958
1.33E+05
3.06E+06
0.014099
3.20E+06
0.011871
4.34%
Tramo1/609.6
6.938926482
6.756240356
3.35E+05
1.24E+07
0.013331
1.27E+07
0.009644
2.70%
Tramo 2/609.6
1.722426655
1.627829898
1.73E+05
2.98E+06
0.013667
3.16E+06
0.011853
5.81%
Tramo 1/914.4
3.895558716
3.789505441
1.30E+05
4.63E+06
0.012613
4.76E+06
0.011068
2.80%
Tramo 2/914.4
1.30430832
1.212321406
1.05E+05
1.48E+06
0.013266
1.59E+06
0.013022
7.11%
Tramo 3/914.4
1.513267342
1.427117115
1.05E+05
1.74E+06
0.013138
1.85E+06
0.01273
6.04%
Medellín Qmáx (Diferencias número de Reynolds 100000-300000) Hazen Mayor
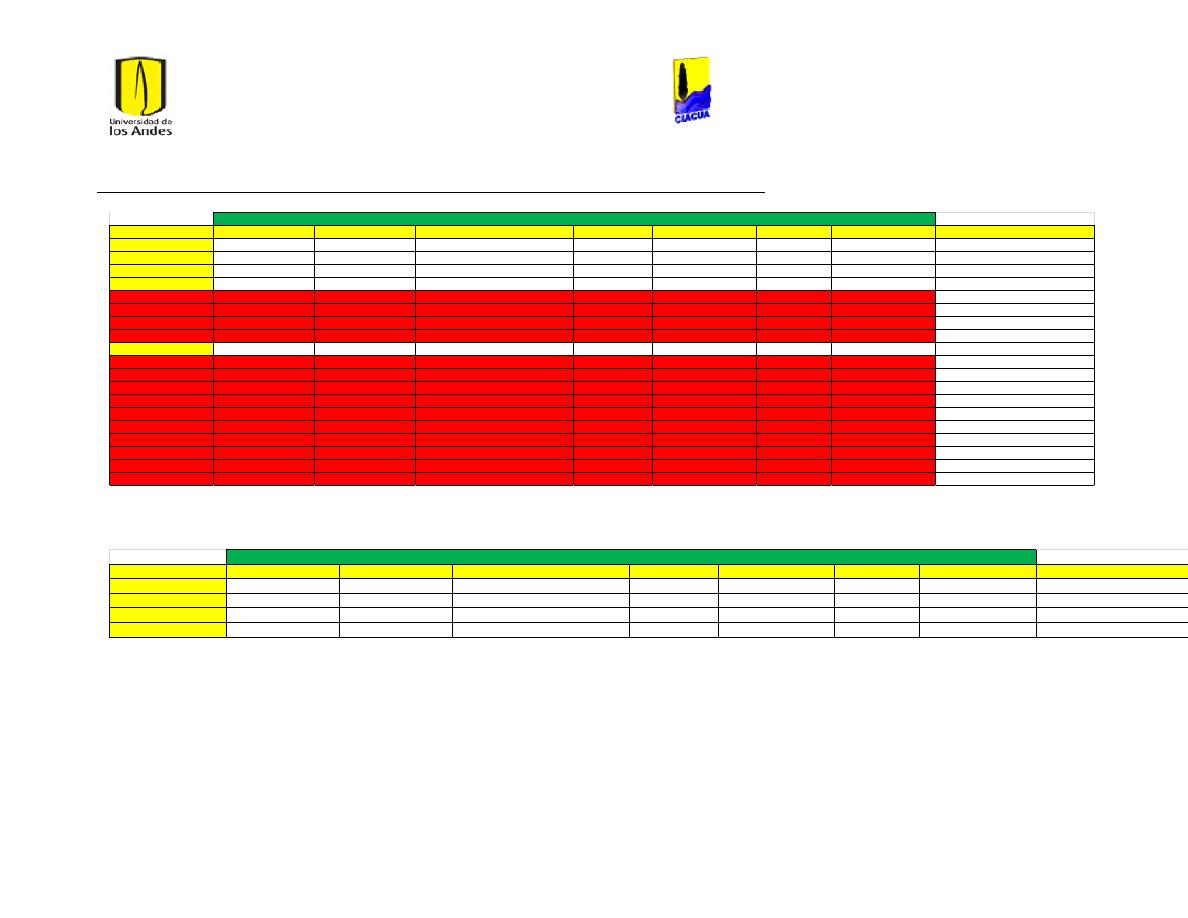
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
142
TABLA 14 TABLA RESUMEN DE ALTAS DIFERENCIAS RED MATRIZ MEDELLÍN CAUDAL MÁXIMO 2 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS
ENTRE 50000 Y 100000.
TABLA 15 TABLA RESUMEN DE ALTAS DIFERENCIAS RED MATRIZ MEDELLÍN CAUDAL MÁXIMO 3 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS
ENTRE 50000 Y 100000.
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/355.6
0.07685674
0.059267417
5.52E+04
1.86E+05
0.017823
2.41E+05
0.017511
29.68%
Tramo 1/406.4
0.567917613
0.534669689
9.14E+04
1.47E+06
0.014998
1.56E+06
0.013256
6.22%
Tramo 2/406.4
0.313034379
0.293936777
5.25E+04
8.08E+05
0.015424
8.60E+05
0.014478
6.50%
Tramo 1/508
0.117172254
0.092333656
5.46E+04
2.03E+05
0.017056
2.58E+05
0.017133
26.90%
Tramo 1/914.4
2.972526947
2.908707561
7.80E+04
3.55E+06
0.012744
3.63E+06
0.011525
2.19%
Tramo 2/914.4
0.883612465
0.828882366
6.68E+04
1.01E+06
0.013973
1.08E+06
0.013771
6.60%
Tramo 3/914.4
2.993133313
2.940336518
6.45E+04
3.59E+06
0.012715
3.66E+06
0.011536
1.80%
Tramo 4/914.4
2.272625632
2.223289608
6.03E+04
2.72E+06
0.012864
2.78E+06
0.011987
2.22%
Tramo 5/914.4
0.436581256
0.388173139
5.91E+04
4.74E+05
0.014441
5.33E+05
0.015445
12.47%
Tramo 6/914.4
2.441718798
2.396181743
5.56E+04
2.93E+06
0.01276
2.98E+06
0.011825
1.90%
Tramo 7/914.4
2.518327277
2.472790222
5.56E+04
3.02E+06
0.012793
3.08E+06
0.011805
1.84%
Tramo 8/914.4
1.977192633
1.93205616
5.51E+04
2.36E+06
0.012932
2.42E+06
0.012237
2.34%
Tramo 9/914.4
2.067744673
2.022948367
5.47E+04
2.47E+06
0.012841
2.53E+06
0.012154
2.21%
Tramo 10/914.4
1.594049761
1.551377857
5.21E+04
1.89E+06
0.013019
1.95E+06
0.012694
2.75%
Tramo 1/1066.8
1.568147787
1.481997578
9.02E+04
1.55E+06
0.012966
1.64E+06
0.012914
5.81%
Tramo 2/1066.8
1.588139233
1.501989024
9.02E+04
1.57E+06
0.012961
1.66E+06
0.012885
5.74%
Tramo 3/1066.8
2.972526783
2.908707178
6.68E+04
3.05E+06
0.012499
3.11E+06
0.011751
2.19%
Tramo 4/1066.8
2.272625942
2.223289097
5.17E+04
2.33E+06
0.012661
2.38E+06
0.012227
2.22%
Tramo 1/1219.2
0.883612101
0.828883023
5.01E+04
7.59E+05
0.013425
8.09E+05
0.0143
6.60%
Medellín Qmáx (Diferencias número de Reynolds 50000-100000) Hazen Mayor
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/355.6
0.079274158
0.173870484
-2.97E+05
5.46E+05
0.016122
2.49E+05
0.017438
-54.41%
Tramo 1/406.4
0.033702971
0.128299436
-2.60E+05
3.53E+05
0.016386
9.26E+04
0.02057
-73.73%
Tramo 1/609.6
0.073127278
0.159277213
-1.58E+05
2.92E+05
0.015995
1.34E+05
0.018679
-54.09%
Tramo 1/1066.8
0.101640317
0.151339164
-5.20E+04
1.58E+05
0.017317
1.06E+05
0.017063
-32.84%
Medellín Qmáx (Diferencias número de Reynolds 50000-100000) Darcy Mayor

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
143
Los resultados con caudal máximo muestran tendencias similares, pero como se mencionó
con anterioridad, los efectos están magnificados; no sólo porque es el momento donde más se
está presentando el desbalance de masa en la red, sino porque el número de tramos que
presentan altas diferencia se vio incrementado. Adicionalmente se identifican diferencias
importantes en aquellos tramos cuyas tuberías están transportando más caudal cuando se
emplea la ecuación de Darcy-Weisbach respecto a lo encontrado con la ecuación de Hazen-
Williams. En resumen, cuando en esta red se presenta el caudal máximo demandado, las más
altas diferencias en el número de Reynolds se registran en un mayor número de tramos
cuando se emplea la ecuación de Hazen-Williams respecto a la ecuación de Darcy-Weisbach.
Este resultado soporta una vez más que la red presenta una hidráulica radicalmente
diferente entre las dos ecuaciones, advirtiendo de paso los peligros de utilizar la ecuación de
Hazen-Williams en sistemas matrices ramificados y con la presencia de emisores y tanques.
En cuanto al diagrama de Moody, se puede observar que las diferencias entre las dos
ecuaciones se vieron severamente magnificadas; es decir, el desfase en los números de
Reynolds y las diferencias entre los factores de fricción son realmente importantes. Así
mismo, la magnitud de la diferencia en cuanto a los números de Reynolds parecen
incoherentes, pero se presentan de este modo ya que la diferencia de caudal que circula por
cada tubería es considerable. Un detalle curioso que se puede ver es que cuando la diferencia
es mayor en los tramos con la ecuación de Darcy-Weisbach, los números de Reynolds están
más cercanos al
que a
, y casualmente se presentan en tramos con diámetros
menores, mientras que con la ecuación de Hanzen-Williams las grandes diferencias se
presentan en tramos con diámetros mayores. .
Finalmente, se presentan los resultados para el caudal medio:
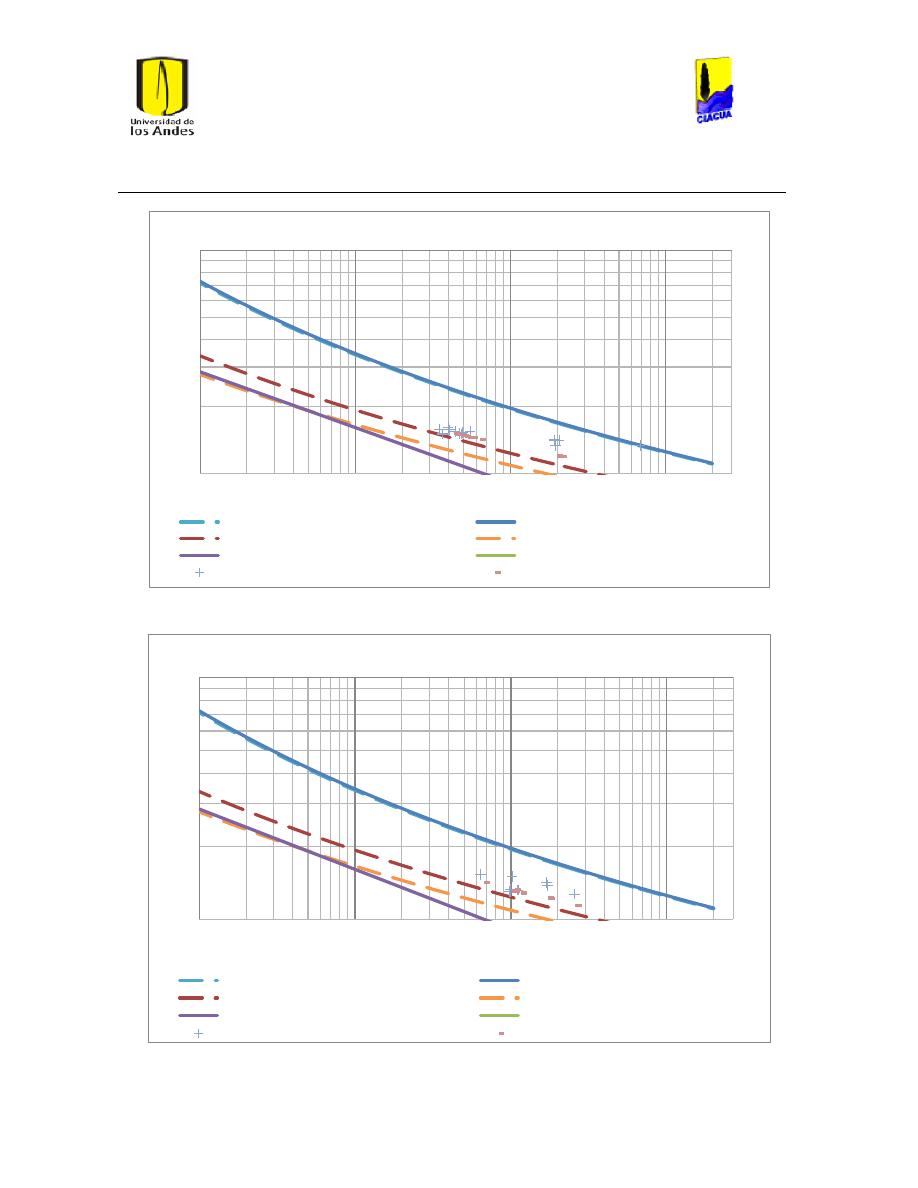
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
144
ILUSTRACIÓN 137 DIAGRAMA DE MOODY 1 RED MATRIZ DE MEDELLÍN CAUDAL MEDIO.
ILUSTRACIÓN 138 DIAGRAMA DE MOODY 2 RED MATRIZ DE MEDELLÍN CAUDAL MEDIO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Medellín Qmed Diferencia Número de Reynolds
100000-300000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Medellín Qmed Diferencia Número de Reynolds
50000-100000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
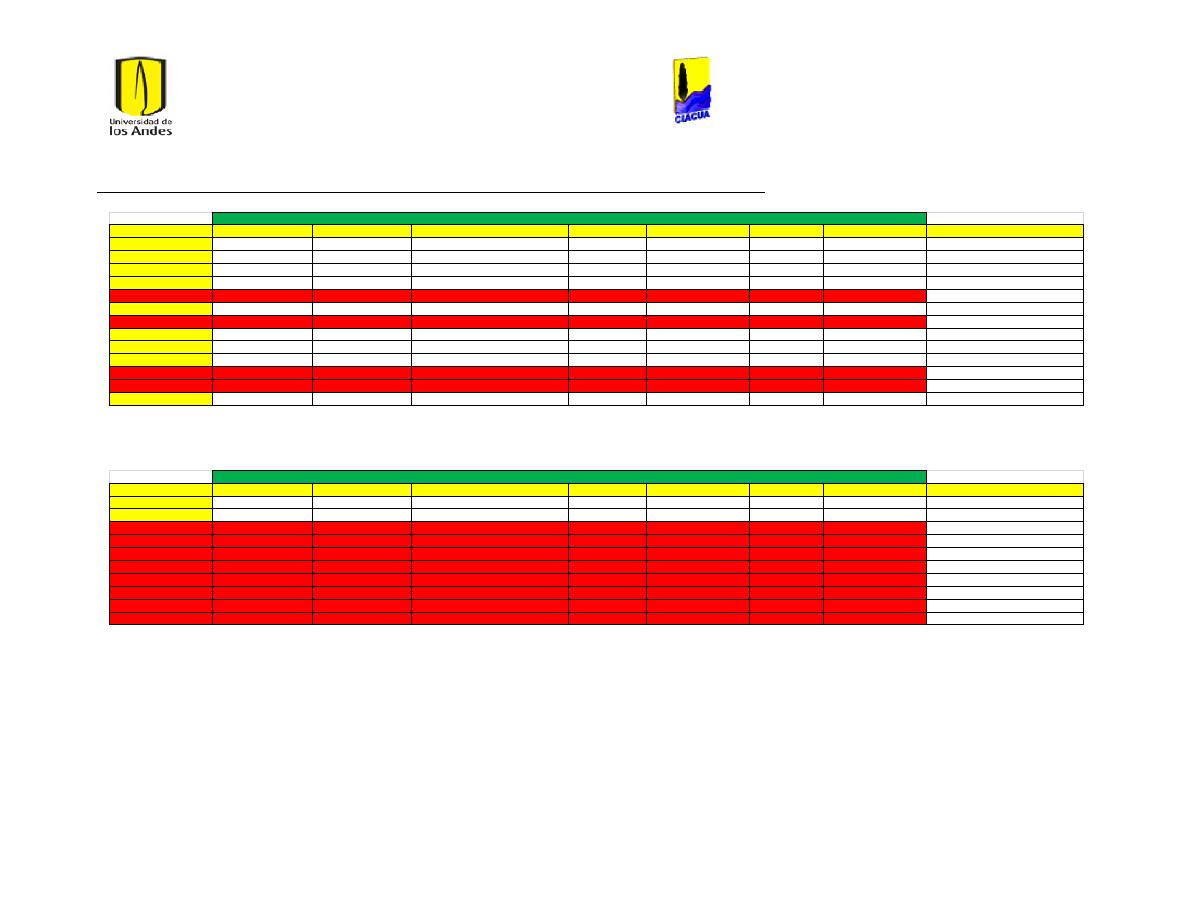
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
145
TABLA 16 TABLA RESUMEN DE ALTAS DIFERENCIAS RED MATRIZ MEDELLÍN CAUDAL MEDIO 1 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS
ENTRE 100000 Y 300000.
TABLA 17 TABLA RESUMEN DE ALTAS DIFERENCIAS RED MATRIZ MEDELLÍN CAUDAL MEDIO 2 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS
ENTRE 50000 Y 100000.
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/355.6
0.237910566
0.189845645
1.51E+05
5.96E+05
0.016034
7.47E+05
0.01482
25.32%
Tramo 1/406.4
0.237910528
0.189845667
1.32E+05
5.22E+05
0.015784
6.54E+05
0.015076
25.32%
Tramo 2/406.4
0.268626243
0.220561383
1.32E+05
6.06E+05
0.015704
7.38E+05
0.014809
21.79%
Tramo 3/406.4
0.348538342
0.300473611
1.32E+05
8.26E+05
0.015399
9.58E+05
0.014248
16.00%
Tramo 1/457.2
1.26688569
1.195643541
1.74E+05
2.92E+06
0.013355
3.09E+06
0.011952
5.96%
Tramo 2/457.2
0.34853844
0.300473609
1.17E+05
7.34E+05
0.015248
8.51E+05
0.014467
16.00%
Tramo 1/508
1.45228971
1.404224857
1.06E+05
3.09E+06
0.014097
3.19E+06
0.011873
3.42%
Tramo 2/508
0.366832096
0.318767243
1.06E+05
7.01E+05
0.01507
8.07E+05
0.01455
15.08%
Tramo 3/508
0.379027937
0.330963084
1.06E+05
7.28E+05
0.015038
8.33E+05
0.014484
14.52%
Tramo 4/508
0.348538334
0.300473481
1.06E+05
6.61E+05
0.01544
7.66E+05
0.014638
16.00%
Tramo 5/508
1.362561949
1.314497097
1.06E+05
2.89E+06
0.014121
3.00E+06
0.011986
3.66%
Tramo 1/609.6
5.744988755
5.61182603
2.44E+05
1.03E+07
0.013355
1.05E+07
0.009917
2.37%
Tramo 2/609.6
0.369411058
0.298168927
1.31E+05
5.46E+05
0.015027
6.77E+05
0.014914
23.89%
Medellín Qmed (Diferencias número de Reynolds 100000-300000) Hazen Mayor
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/406.4
0.581948335
0.557428557
6.74E+04
1.53E+06
0.014975
1.60E+06
0.013208
4.40%
Tramo 2/406.4
0.368149624
0.349940844
5.00E+04
9.62E+05
0.01528
1.01E+06
0.014135
5.20%
Tramo 1/508
1.192732249
1.160050022
7.19E+04
2.55E+06
0.01417
2.62E+06
0.012225
2.82%
Tramo 1/609.6
1.452289758
1.4042248
8.81E+04
2.57E+06
0.013735
2.66E+06
0.012155
3.42%
Tramo 1/914.4
1.293893827
1.222651186
8.70E+04
1.49E+06
0.01326
1.58E+06
0.013028
5.83%
Tramo 2/914.4
1.438669656
1.367427671
8.70E+04
1.67E+06
0.013169
1.76E+06
0.012826
5.21%
Tramo 3/914.4
3.20947225
3.152687358
6.94E+04
3.85E+06
0.012684
3.92E+06
0.01139
1.80%
Tramo 1/1066.8
1.48913572
1.417892841
7.46E+04
1.48E+06
0.012999
1.56E+06
0.013013
5.02%
Tramo 2/1066.8
1.475660309
1.404418324
7.46E+04
1.47E+06
0.013021
1.54E+06
0.013033
5.07%
Tramo 3/1066.8
1.499167197
1.427925212
7.46E+04
1.49E+06
0.013008
1.57E+06
0.013016
4.99%
Medellín Qmed (Diferencias número de Reynolds 50000-100000) Hazen Mayor
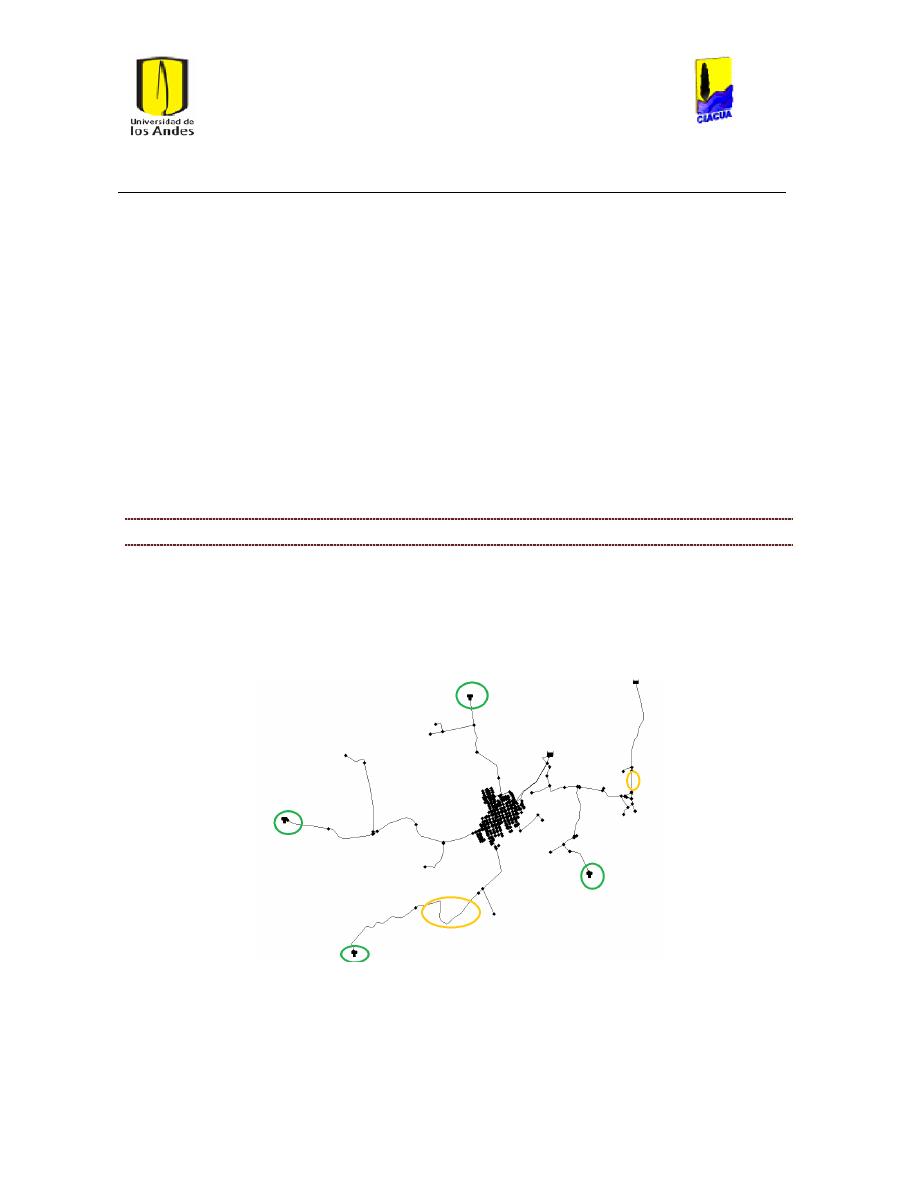
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
146
Los resultados que arrojan los dos modelos en la hora de consumo medio, son similares a los
que se han estado observando a lo largo de análisis de esta red. Sin embargo, resulta de
particular importancia resaltar un hallazgo de esta investigación que ha sido objeto de
discusión, ampliamente documentada en la literatura, según la cual la ecuación de Hazen-
Williams al haber sido desarrollada en un tiempo en el que existían materiales de rugosidad
intermedia (no muy rugosos ni muy lisos), y dado que la mayoría de los datos fueron
recolectados en flujo transicional, teóricamente estas deberían ser condiciones de
aplicabilidad aceptable de la ecuación. Los resultados que arrojaron los diagramas de Moody
para los 3 caudales demandados de la red, permiten apreciar que en una cantidad
considerable de casos, los datos recolectados durante esta investigación se encuentran
localizados en la zona de transición y presentan diferencias importantes. Esto permite
concluir que la aplicabilidad de la ecuación de Hazen-Williams, aun en las zonas donde se
supone que debería funcionar relativamente bien, muestra por el contrario inconsistencias
con respecto a los resultados con la red simulada mediante la ecuación de Darcy-Weisbach.
4.4.3 RED GINEBRA
Al igual que en la dos redes anteriores, se muestran a continuación los resultados para la red
de Ginebra. Los resultados que se encontraron en esta red presentan una tendencia similar a
lo que se encontró en la red Matriz de Medellín. La siguiente figura muestra las localizaciones
de los 4 tanques de la red, así como las ilustraciones donde se ven los niveles de los tanques
en el tiempo de ejecución hidráulica.
FIGURA 21 RED GINEBRA CON LA LOCALIZACION DE LOS TANQUES Y ALGUNAS TUBERÍAS
ANALIZADAS.
Al igual que en la red matriz de Medellín, la red Ginebra es una red que tiene importantes
ramificaciones y terminaciones en tanques ubicados en cuatro puntos de la red. Esta
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
147
característica es de gran importancia, ya que como se verá más adelante, presenta diferencias
en la hidráulica de la red, en los niveles de los tanques y un desbalance de masa en la red, que
ocasiona que las pérdidas por fricción y factores de fricción de toda la red se vean afectadas. A
continuación se van a mostrar los resultados para los niveles de los tanques:
ILUSTRACIÓN 139 NIVEL TANQUE 350 RED GINEBRA.
ILUSTRACIÓN 140 NIVEL TANQUE 481 RED GINEBRA.
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
iv
e
l (
m
)
Tiempo(h)
Tanque 350 Ginebra
Tanque D-W
Tanque H-W
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
iv
e
l (
m
)
Tiempo(h)
Tanque 481 Ginebra
Tanque D-W
Tanque H-W
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
148
ILUSTRACIÓN 141 NIVEL TANQUE 359 RED GINEBRA.
ILUSTRACIÓN 142 NIVEL TANQUE 372 RED GINEBRA.
Los resultados tienen dos detalles bastante interesantes de analizar. El primero es que
pareciera que no existiera una diferencia notable entre los patrones de llenado entre la
ecuación empírica y la ecuación físicamente basada, salvo en los tanques 481 y 359 donde al
0
1
2
3
4
5
6
7
8
9
10
11
12
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
iv
e
l (
m
)
Tiempo(h)
Tanque 359 Ginebra
Tanque D-W
Tanque H-W
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
iv
e
l (
m
)
Tiempo(h)
Tanque 372 Ginebra
Tanque D-W
Tanque H-W
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
149
final del tiempo de ejecución se puede ver que las líneas de llenado se empiezan a separar. Lo
segundo es que en los dos tanques donde se vieron diferencias, los patrones de llenado son
diferentes. Conviene recordar acá que en la red Matriz de Medellín se había visualizado que el
nivel del tanque con la ecuación de Hazen-Williams siempre se encontraba por encima del
nivel respecto de lo encontrado con la ecuación de Darcy-Weisbach; en contraste, lo que se
encontró en la red Ginebra es que hay tanques que se están llenado más rápido con la
ecuación de Darcy-Weisbach que con la ecuación de Hazen-Williams. Esto es un
descubrimiento bastante significativo ya que se encuentra que no solo la ecuación de Hazen-
Williams puede subestimar o sobrestimar el caudal que sale de los embalses, sino también
los caudales que están entrando en los tanques de la red. .
La consecuencia de esto es que evidentemente la hidráulica del sistema va a cambiar de
manera radical, al existir un tanque con más nivel del que realmente se presenta y otro con un
nivel menor, con lo cual el operario que busca solucionar un problema podría adoptar
soluciones inadecuadas dado a que en los dos casos los resultados son claramente
divergentes respecto de lo que realmente se está presentando en la red.
Con el fin de determinar si las diferencias se seguían presentando bajo otros escenarios, se
decidió probar la red con solo 2 tanques. Los resultados de este escenario se presentan a
continuación:
ILUSTRACIÓN 143 NIVEL TANQUE 355 RED GINEBRA CON SOLO 2 TANQUES.
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
7
7.5
8
8.5
9
9.5
10
00:00 04:48 09:36 14:24 19:12 00:00 04:48
N
iv
e
l (
m
)
Tiempo (h)
Tanque 355 Ginebra
Tanque 350 H-W
Tanque 350 D-W

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
150
ILUSTRACIÓN 144 NIVEL TANQUE 359 RED GINEBRA CON SOLO 2 TANQUES.
Los resultados con solo dos tanques son mucho más evidentes que los encontrados
anteriormente. Las ilustraciones permiten apreciar claramente las diferencias entre el
patrón de llenado con la ecuación de Hazen-Williams y la ecuación de Darcy-Weisbach. No
obstante, a diferencia de los hallazgos encontrados cuando la red cuenta con los 4 tanques, en
este modelo no se detectó que uno de los dos tanques se llenara a mayor velocidad que el
otro, al aplicar la ecuación de Darcy-Weisbach. A pesar de esto, ya queda sentado el
antecedente de que esta situación si puede llegar a ocurrir y que definitivamente existe un
desbalance de masa y un desbalance de caudales que circula por la red cuando se compara la
hidráulica de las dos ecuaciones.
A continuación se muestran los resultados con tuberías de la Red Ginebra en cuanto al
número de Reynolds y las pérdidas por fricción, cuando se emplea la ecuación físicamente
basada y la ecuación empírica:
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
00:00 04:48 09:36 14:24 19:12 00:00 04:48
N
iv
e
l (
m
)
Tiempo (h)
Tanque 359 Ginebra
Tanque 359 H-W
Tanque 359 D-W
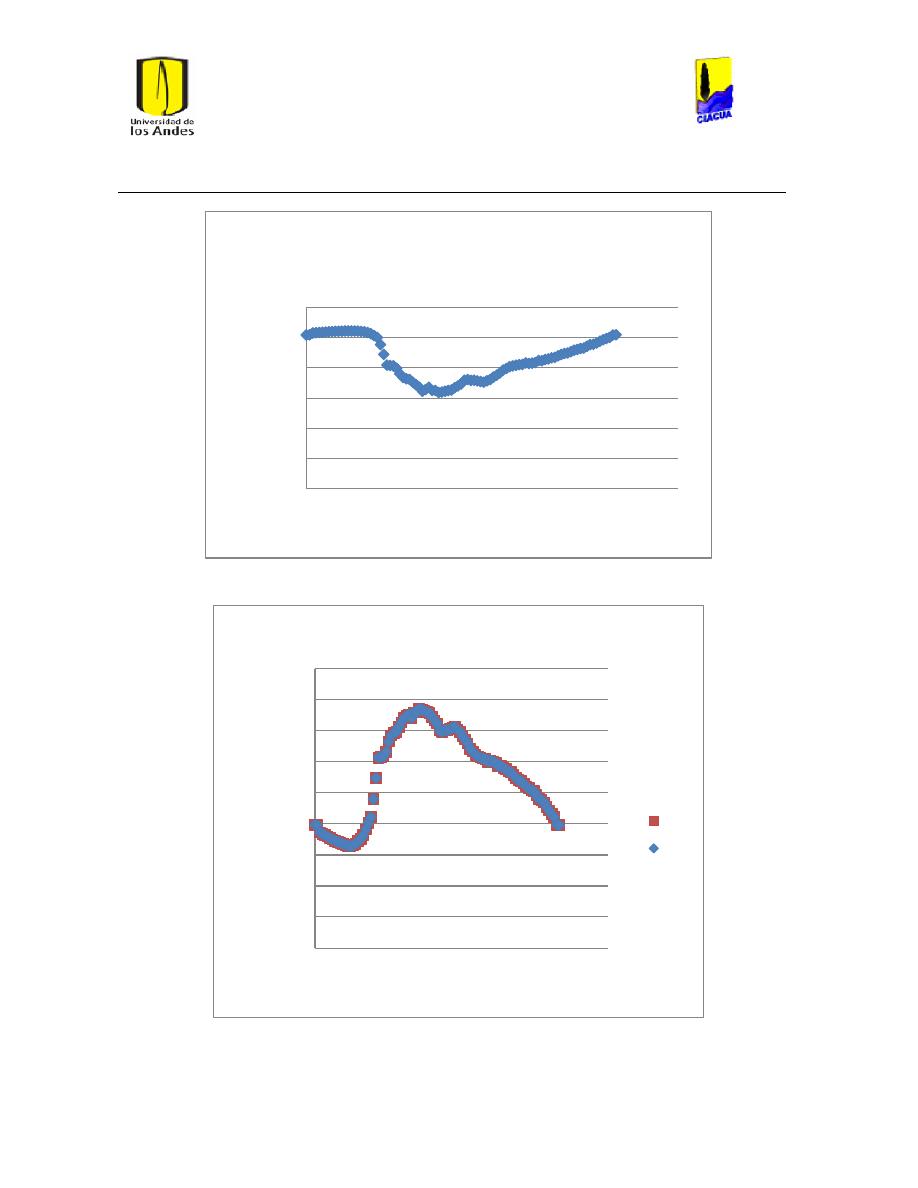
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
151
ILUSTRACIÓN 145 DIFERENCIA EN LAS PÉRDIDAS POR FRICCIÓN TUBERÍA 1.
ILUSTRACIÓN 146 DIFERENCIA EN EL NÚMERO DE REYNOLDS TUBERÍA 1.
0.000%
1.000%
2.000%
3.000%
4.000%
5.000%
6.000%
00:00
04:48
09:36
14:24
19:12
00:00
04:48
HW
-D
W/DW
Tiempo (h)
Diferencia de hf en Tubería 1
Ginebra
0
50000
100000
150000
200000
250000
300000
350000
400000
450000
00:00 04:48 09:36 14:24 19:12 00:00 04:48
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Tiempo (h)
Ginebra Tubería 1
H-W
D-W
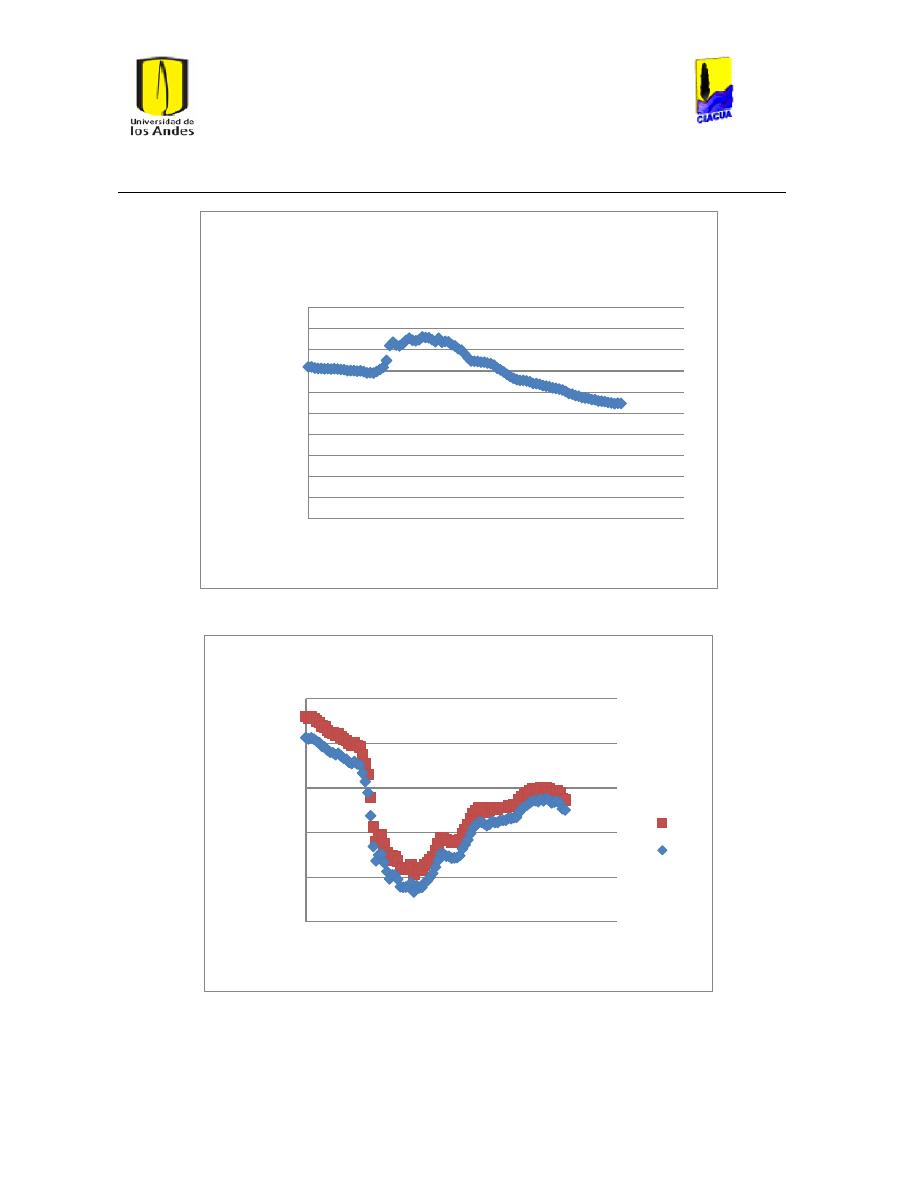
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
152
ILUSTRACIÓN 147 DIFRERENCIA EN LA PÉRDIDAS POR FRICCIÓN TUBERÍA 496.
ILUSTRACIÓN 148 DIFERENCIA EN EL NÚMERO DE REYNOLDS TUBERÍA 496.
0.000%
2.000%
4.000%
6.000%
8.000%
10.000%
12.000%
14.000%
16.000%
18.000%
20.000%
00:00
04:48
09:36
14:24
19:12
00:00
04:48
HW
-D
W/DW
Tiempo (h)
Diferencia de hf en Tubería 496
Ginebra
350000
400000
450000
500000
550000
600000
00:00 04:48 09:36 14:24 19:12 00:00 04:48
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Tiempo (h)
Ginebra Tubería 496
H-W
D-W
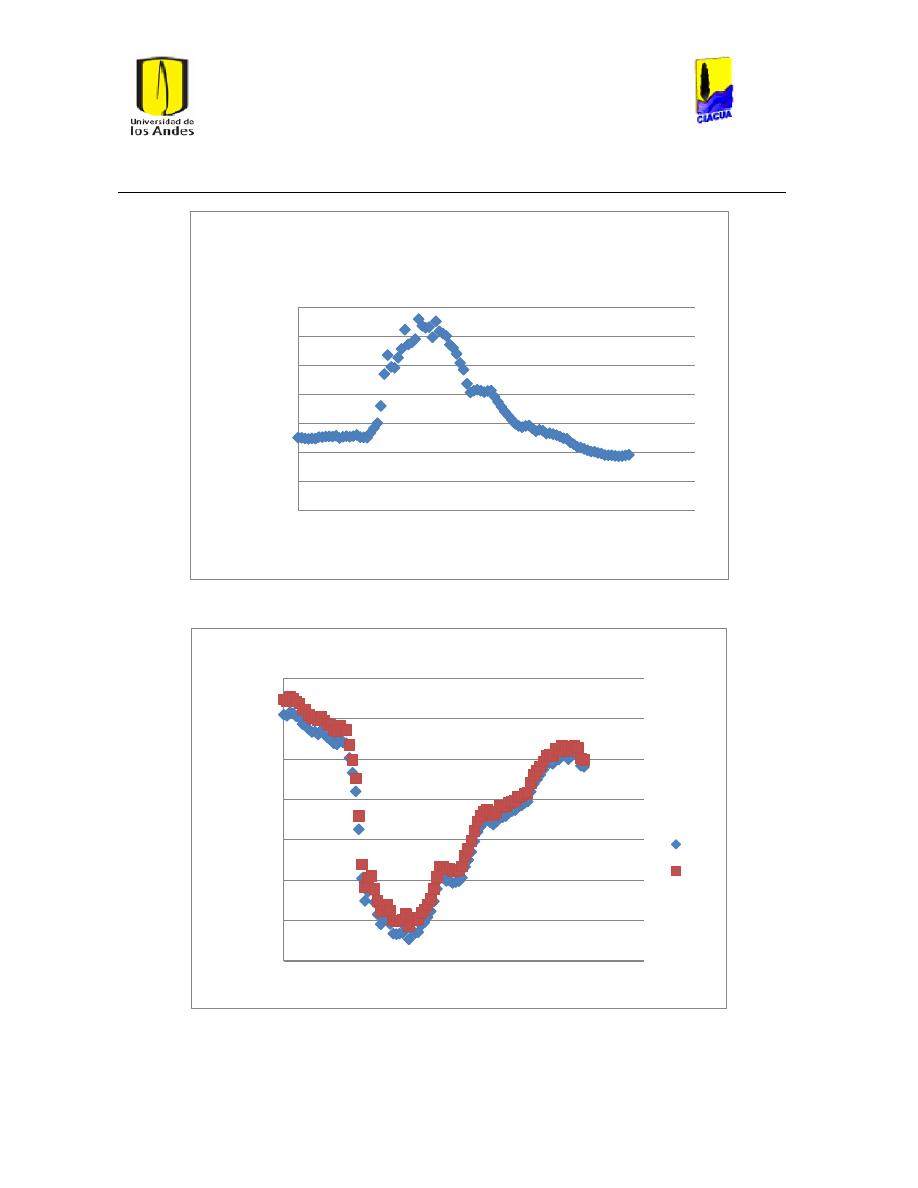
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
153
ILUSTRACIÓN 149 DIFRERENCIA EN LA PÉRDIDAS POR FRICCIÓN TUBERÍA 528.
ILUSTRACIÓN 150 DIFERENCIA EN EL NÚMERO DE REYNOLDS TUBERÍA 528.
0.000%
5.000%
10.000%
15.000%
20.000%
25.000%
30.000%
35.000%
00:00
04:48
09:36
14:24
19:12
00:00
04:48
HW
-D
W/DW
Tiempo (h)
Diferencia de Hf en tubería 528
Ginebra
200000
300000
400000
500000
600000
700000
800000
900000
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Tiempo (h)
Ginebra Tubería 528
D-W
H-W
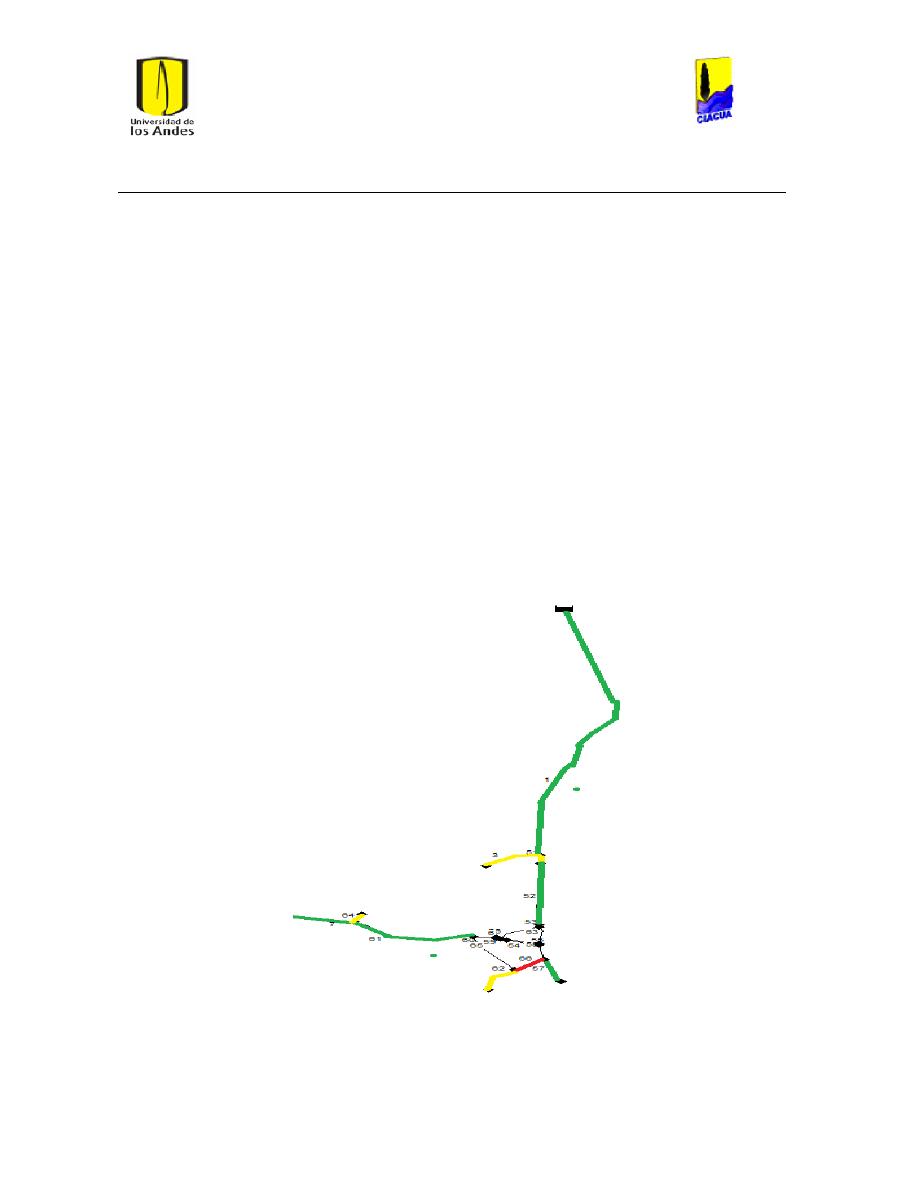
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
154
Los resultados demuestran una vez más lo que se ha estado observando a partir de la red
Matriz de Medellín y en general en toda la investigación: La red que opera con la ecuación de
Hazen-Williams está presentando caudales diferentes a la salida de los embalses y el caudal
que pasa por los tramos de las tuberías es diferente con respecto a lo que ocurre en la red que
es operada mediante la ecuación de Darcy-Weisbach. Por otro lado, se puede ver que en este
caso, los desbalances que resultan característicos por la naturaleza empírica de la ecuación
Hanzen-Williams, están generando unas diferencias considerables en las pérdidas por fricción
en las tuberías, lo que condiciona en gran medida las presiones que va a tener la red en todo
su conjunto.
Lo anterior genera nuevas preguntas que sería bastante interesante seguir a futuro en otras
tesis o investigaciones y es: ¿cuántas de estas diferencias están causadas por el balance de
masa de la red? Y ¿cuántas son atribuibles a la naturaleza empírica de la ecuación y al uso
indiscriminado de coeficientes constantes en la ecuación de de Hazen-Williams?
Prosiguiendo con los resultados, se muestran a continuación aquellos tramos de las tuberías
que tienen números de Reynolds mayores al utilizar la ecuación de Hazen-Williams (Rojo), las
que tienen mayor con la ecuación de Darcy-Weisbach (Verde) y las tuberías que no presentan
ningún tipo de diferencias (Amarillo):
FIGURA 22 SALIDA DEL PRIMER EMBALSE RED GINEBRA.
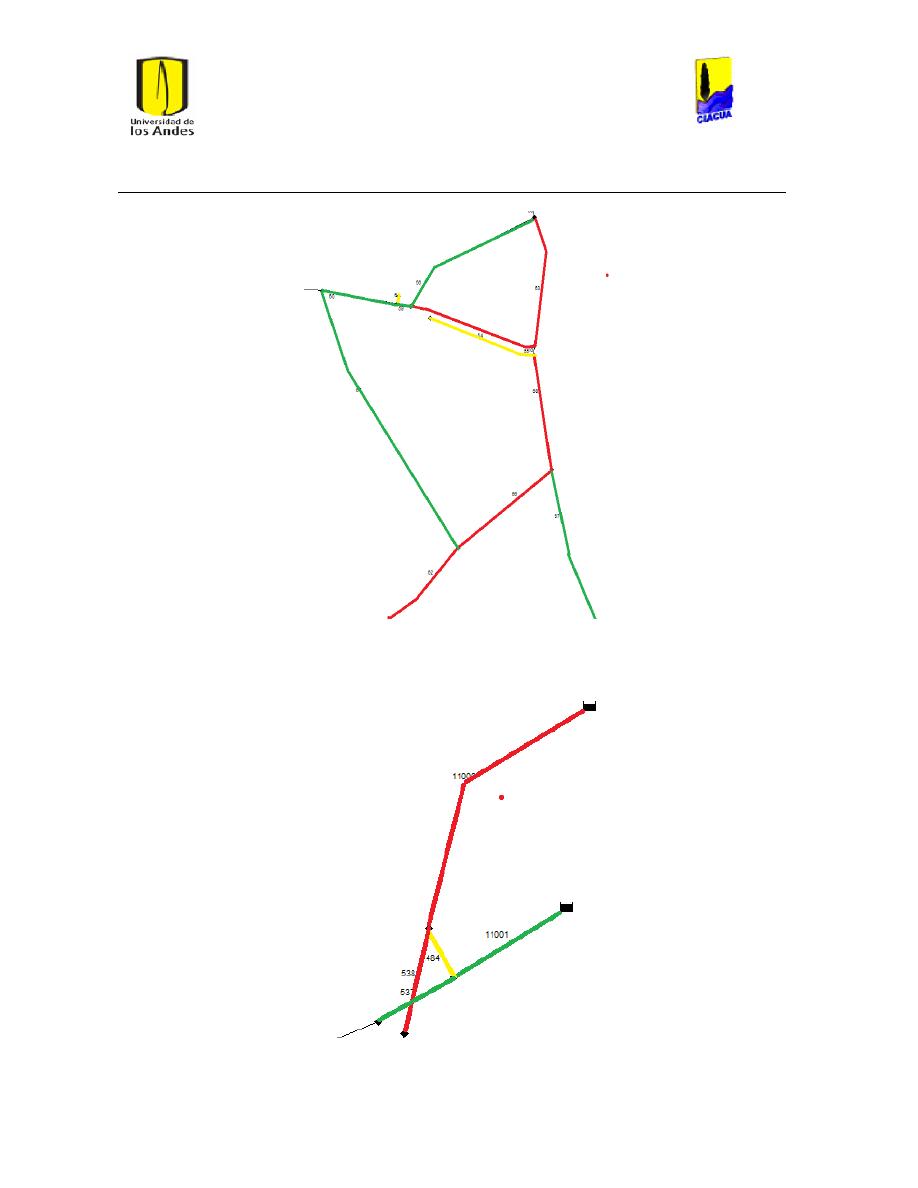
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
155
FIGURA 23 DIFERENCIA EN ALGUNOS TRAMOS DE LA RED GINEBRA.
FIGURA 24 SALIDA DE LOS OTROS EMBALSES DE LA RED GINEBRA.
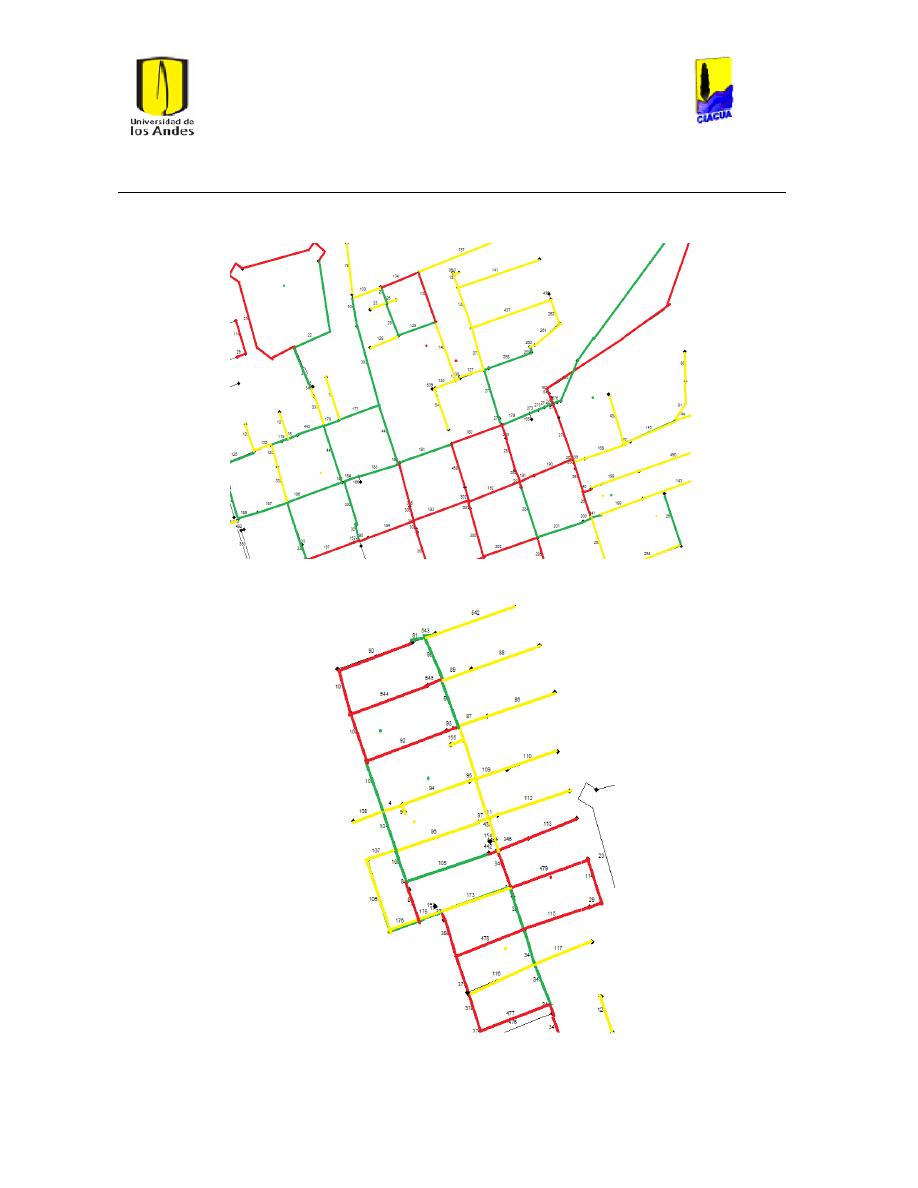
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
156
FIGURA 25 DIFERENCIAS DE LOS ENTRAMADOS INTERNOS DE LA RED GINEBRA 1.
FIGURA 26 DIFERENCIAS DE LOS ENTRAMADOS INTERNOS DE LA RED GINEBRA 2.
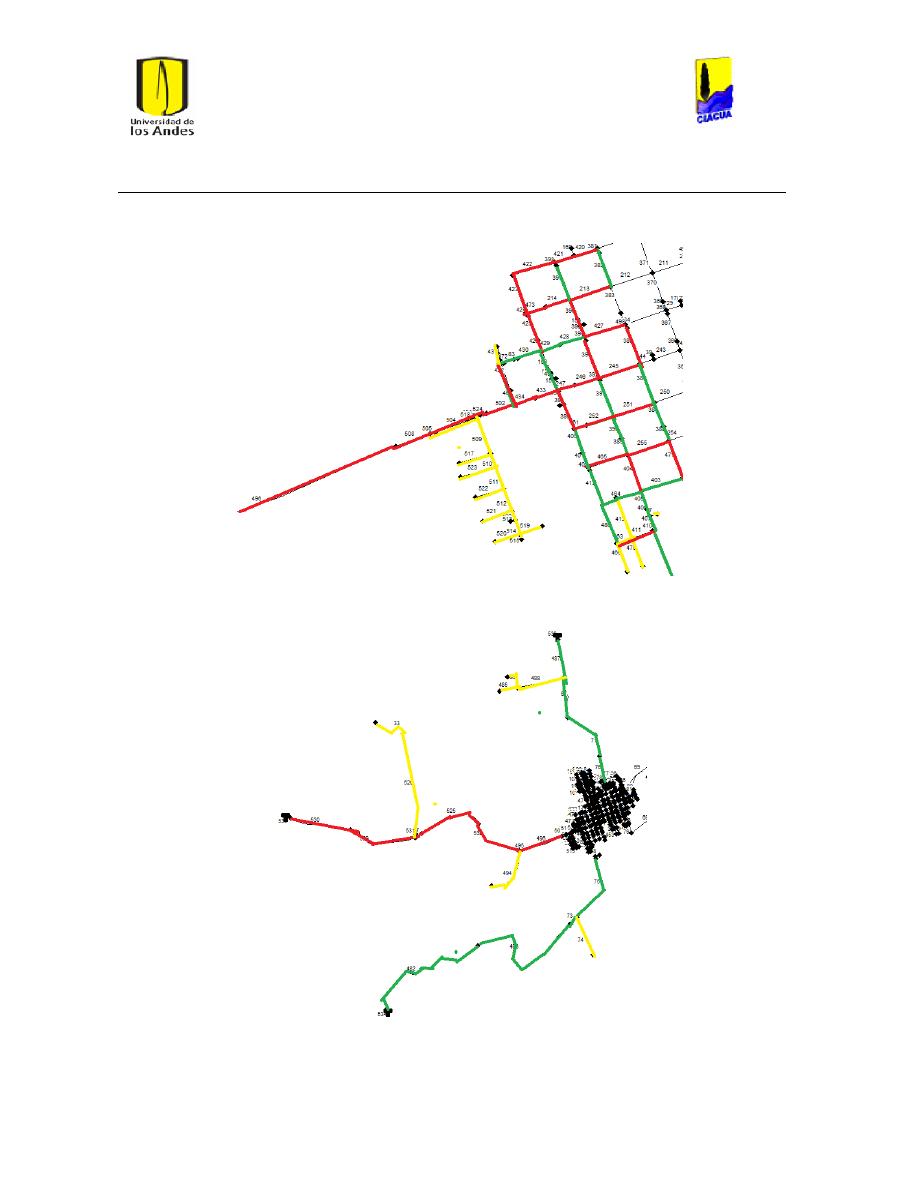
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
157
FIGURA 27 DIFERENCIAS DE LOS ENTRAMADOS INTERNOS DE LA RED GINEBRA 3.
FIGURA 28 DIFERENCIAS EN LAS RAMIFICACIONES DE LA RED GINEBRA.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
158
Las figuras anteriores muestran nuevamente que la hidráulica entre la ecuación de Hazen-
Williams y la ecuación de Darcy-Wesibach es bastante diferente. De las figuras se identifican
2 patrones importantes: primero, se puede ver que para 2 tanques, el número de Reynolds es
mayor utilizando la ecuación de Darcy-Weisbach, lo que implica que el tiempo de llenado es
menor en la realidad (el llenado es más rápido) que en la simulación basada en la ecuación
de Hazen-Williams. Lo segundo, la presencia de diferencias en la salida de los embalses
implica que en efecto se está presentando un desbalance de masa en la red; este desbalance
fue cuantificado y se encontró que en esta red se presenta un desbalance de masa máximo de
44 L/s.
Esta cantidad resulta ser bastante más baja en comparación con la cantidad de caudal
encontrada en la red matriz de Medellín; sin embargo hay que considerar que la red de
Medellín maneja en conjunto con sus 3 embalses una demanda de cerca de 8.5
, en
contraste con los casi 1.5
que maneja la red de Ginebra. Aun así y pese a que el
desbalance de masa parece ser muy bajo en comparación con el caudal total, es este
desbalance el que está causando que los tanques se llenen más rápido cuando se aplica la
ecuación de Darcy-Weisbach y más lentamente con la ecuación de Hazen-Williams. A su vez
es uno de los causantes de que se presenten diferencias en las pérdidas por fricción en la red,
sin mencionar que está causando que la hidráulica de toda la red se esté solucionando de
manera diferente a la realidad cuando se utiliza la ecuación empírica.
A continuación se muestran los resultados en aquellos tramos de tubería de la red que
presentaron las diferencias hidráulicas más amplia (tramos con números de Reynolds
considerablemente mayores con la ecuación de Hazen-Williams.):
FIGURA 29 TRAMOS DE LA RED GINEBRA CON DIFERENCIAS SIGNIFICATIVAS EN EL NÚMERO DE
REYNOLDS CON LA DEMANDA MEDIA DEL SISTEMA.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
159
FIGURA 30 TRAMOS INTERNOS DE LA RED GINEBRA CON DIFERENCIAS SIGNIFICATIVAS EN EL
NÚMERO DE REYNOLDS CON LA DEMANDA MEDIA DEL SISTEMA.
FIGURA 31 TRAMOS DE LA RED GINEBRA CON DIFERENCIAS SIGNIFICATIVAS EN EL NÚMERO DE
REYNOLDS CON LA DEMANDA MÁXIMA DEL SISTEMA.
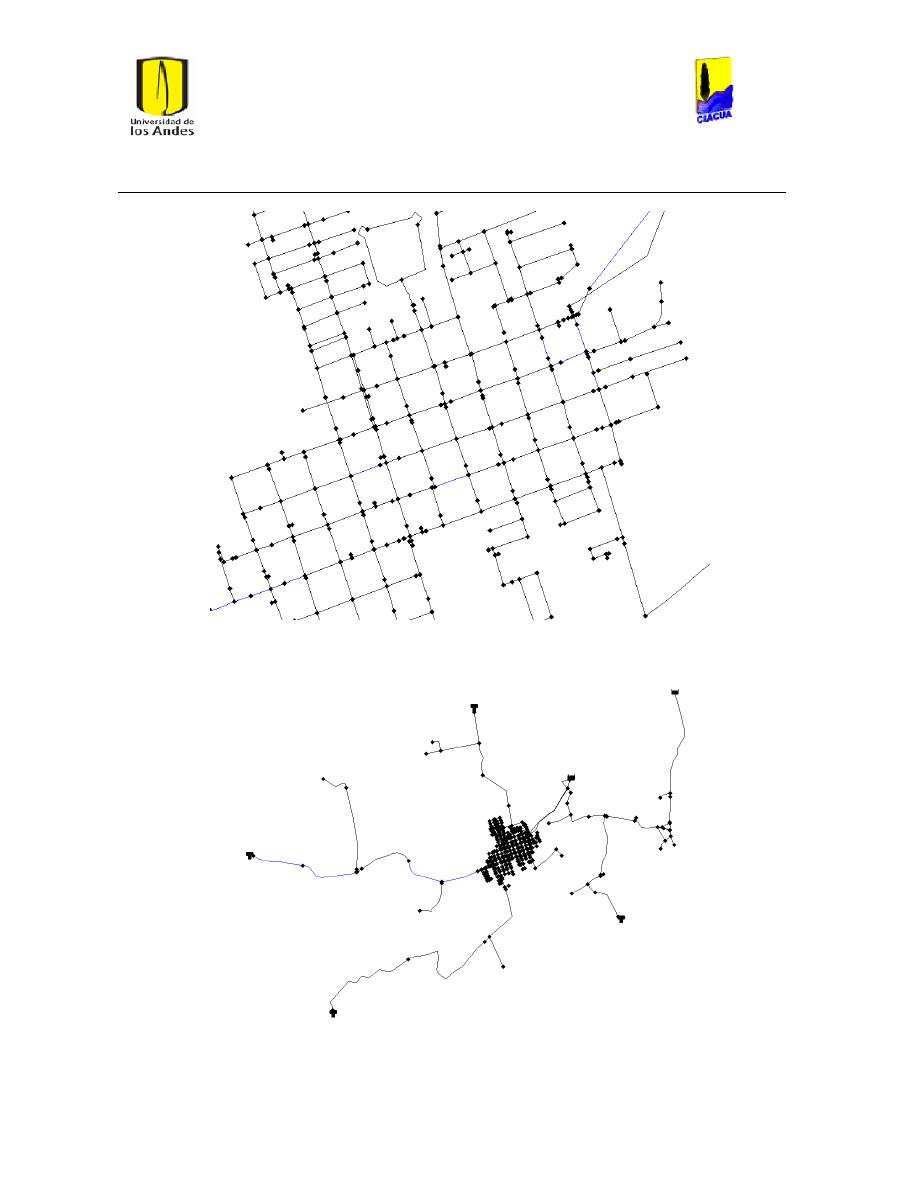
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
160
FIGURA 32 TRAMOS INTERNOS DE LA RED GINEBRA CON DIFERENCIAS SIGNIFICATIVAS EN EL
NÚMERO DE REYNOLDS CON LA DEMANDA MÁXIMA DEL SISTEMA.
FIGURA 33 TRAMOS DE LA RED GINEBRA CON DIFERENCIAS SIGNIFICATIVAS EN EL NÚMERO DE
REYNOLDS CON LA DEMANDA MÍNIMA DEL SISTEMA.
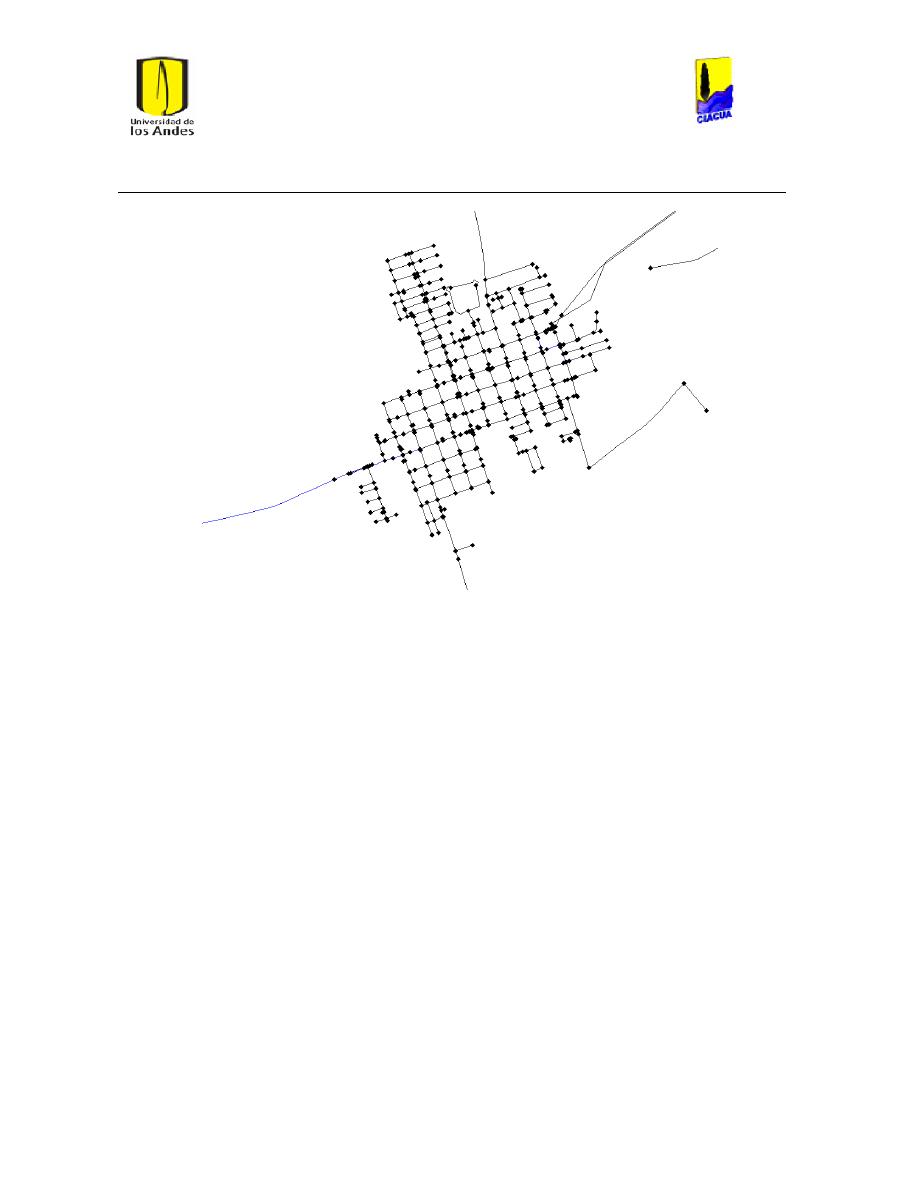
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
161
FIGURA 34 TRAMOS INTERNOS DE LA RED GINEBRA CON DIFERENCIAS SIGNIFICATIVAS EN EL
NÚMERO DE REYNOLDS CON LA DEMANDA MÍNIMA DEL SISTEMA.
Los resultados que se aprecian en las figuras anteriores son nuevamente un testimonio de lo
que se ha venido presentando en esta investigación en cuanto a que las diferencias
significativas tienen una tendencia a dirigirse a los tanques que se encuentran localizados en
las ramificaciones de la red. En la Figura 31 se observa con claridad que se presentan
diferencias significativas a la salida de dos de los embalses del sistema, siendo
considerablemente mayor el caudal que está circulando cuando se emplea la ecuación de
Hazen-Williams que cuando se emplea la ecuación de Darcy-Weisbach. Así mismo, durante la
investigación se pudo ver el comportamiento que se genera, al desbalancear la masa del
sistema y dirigirse hacia las ramificaciones, cuando se emplea la ecuación de Hazen-Williams
está cambiando de manera considerable el comportamiento de la red; es decir, el flujo sigue
una dirección diferente con la ecuación empírica que con la ecuación físicamente basada y
como se vio en los análisis previos de los emisores, una causa importante para esto es el hecho
de que el coeficiente teórico de 140 (la mayor parte de la red) es inadecuado y el agua se
dirige por un camino que de acuerdo con la ecuación de Hazen-Williams parece ser el más
viable, pero que con la ecuación de Darcy-Weisbach revela que no es el adecuado para ese
caudal específico. Lo anterior se suma con lo que se ha venido discutiendo y es el hecho de que
al existir una subestimación y/o sobrestimación de la masa del sistema, la hidráulica de los
dos sistemas arroja resultados radicalmente distintos.
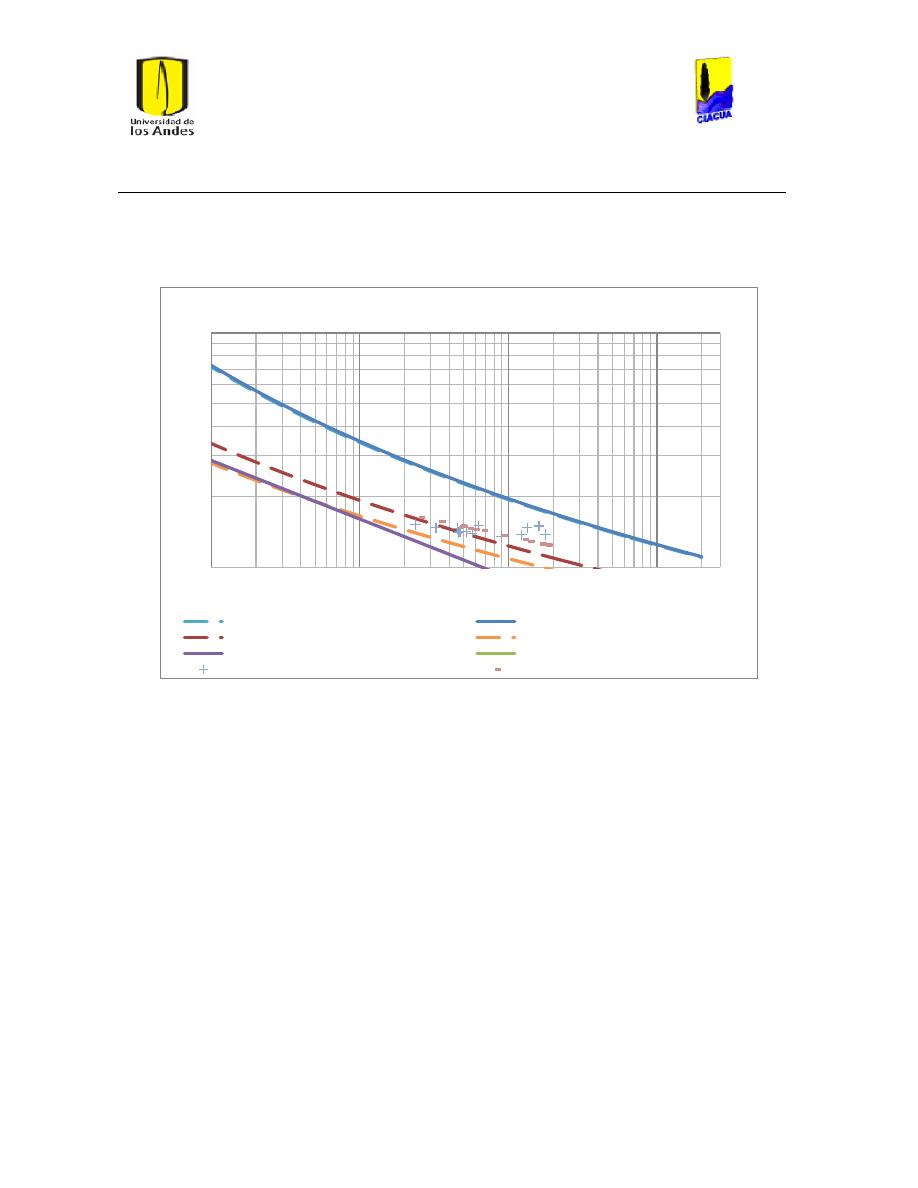
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
162
Adicionalmente, se graficaron en el diagrama de Moody los tramos de tuberías con
diferencias significativas y se elaboró una tabla resumen con las principales características de
estos tramos. Dichos resultados se muestran a continuación:
ILUSTRACIÓN 151 DIAGRAMA DE MOODY RED GINEBRA TRAMOS CON HAZEN-WILLIAMS MAYOR
CAUDAL MEDIO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Ginebra Qmed (Diferencia Número de Reynolds
20000-100000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
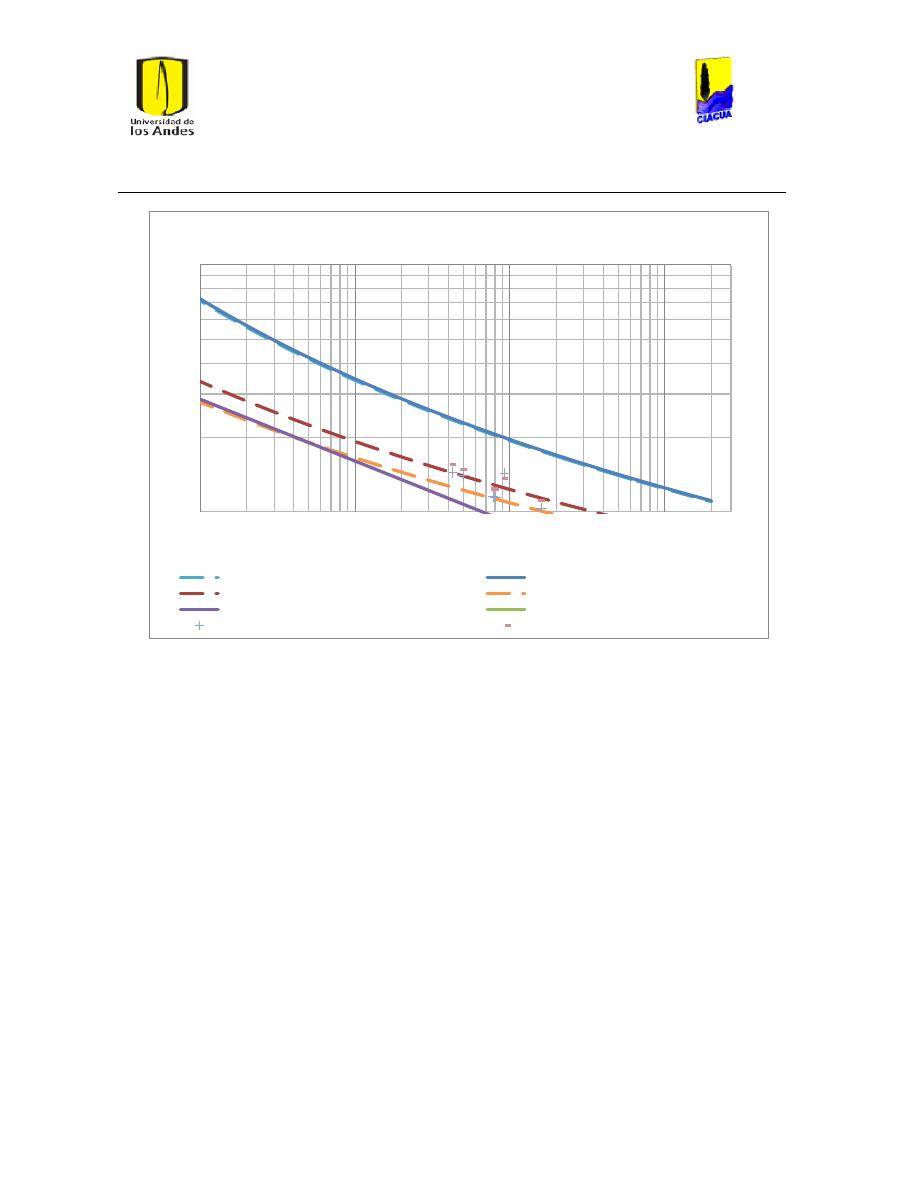
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
163
ILUSTRACIÓN 152 DIAGRAMA DE MOODY RED GINEBRA CON DARCY-WEISBACH MAYOR Y CAUDAL
MEDIO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Ginebra Qmed (Diferencia Número de Reynolds
20000-100000 Darcy Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
164
TABLA 18 RESUMEN DE TUBERÍAS RED GINEBRA CAUDAL MEDIO 1 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE 20000 Y 100000.
TABLA 19 RESUMEN DE TUBERÍAS RED GINEBRA CAUDAL MEDIO 2 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE 20000 Y 100000.
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/400
0.886178194
0.862266527
6.68E+04
2.41E+06
0.014994
2.47E+06
0.012568
2.77%
Tramo 1/450
0.831258153
0.807395481
5.92E+04
2.00E+06
0.014715
2.06E+06
0.012831
2.96%
Tramo 1/500
0.44836614
0.42473724
5.28E+04
9.49E+05
0.015015
1.00E+06
0.0143
5.56%
Tramo 1/700
1.701775796
1.665451807
5.80E+04
2.66E+06
0.013764
2.72E+06
0.012443
2.18%
Tramo 1/800
0.51657585
0.487614387
4.04E+04
6.81E+05
0.014654
7.21E+05
0.015013
5.94%
Tramo 2/800
1.349101924
1.320827088
3.95E+04
1.84E+06
0.01374
1.88E+06
0.013122
2.14%
Tramo 1/900
0.652497971
0.628654862
2.96E+04
7.80E+05
0.014228
8.10E+05
0.014659
3.79%
Tramo 1/1000
0.790535453
0.76668134
2.66E+04
8.56E+05
0.01399
8.83E+05
0.014477
3.11%
Tramo 2/1000
0.657719911
0.633876794
2.66E+04
7.08E+05
0.014239
7.35E+05
0.014868
3.76%
Tramo 1/1100
0.51017041
0.481209049
2.94E+04
4.89E+05
0.014734
5.18E+05
0.015651
6.02%
Tramo 2/1100
1.349128055
1.320852833
2.87E+04
1.34E+06
0.013498
1.37E+06
0.013702
2.14%
Tramo 1/1300
0.827664138
0.803804181
2.05E+04
6.91E+05
0.014047
7.11E+05
0.014954
2.97%
Tramo 1/1500
0.507591445
0.478631458
2.16E+04
3.56E+05
0.01525
3.78E+05
0.016302
6.05%
Ginebra Qmed (Diferencias número de Reynolds 20000-100000) Hazen Mayor
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/300
0.314627952
0.326242129
-4.32E+04
1.21E+06
0.011468
1.17E+06
0.012332
-3.56%
Tramo1/350
0.359975159
0.366814049
-2.18E+04
1.17E+06
0.011575
1.15E+06
0.012394
-1.86%
Tramo2/350
0.725253099
0.751855805
-8.49E+04
2.40E+06
0.010359
2.31E+06
0.01114
-3.54%
Tramo1/600
0.72148777
0.748090243
-4.95E+04
1.39E+06
0.0143
1.34E+06
0.013632
-3.56%
Tramo1/1100
0.714592477
0.741195114
-2.70E+04
7.53E+05
0.014064
7.26E+05
0.014898
-3.59%
Tramo1/1300
0.72162033
0.748222535
-2.29E+04
6.43E+05
0.014461
6.20E+05
0.015546
-3.56%
Ginebra Qmed (Diferencias número de Reynolds 20000-100000) Darcy Mayor
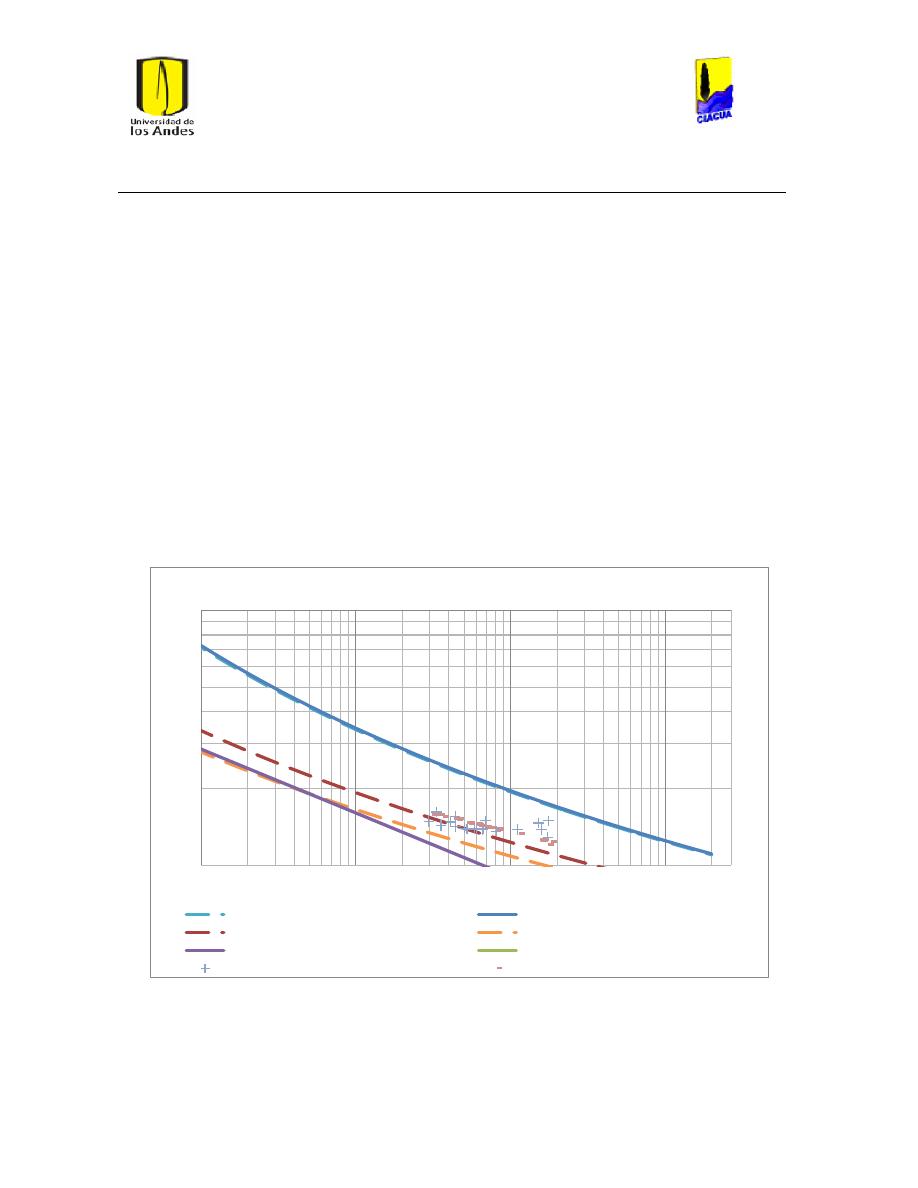
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
165
Los resultados de los diagramas de Moody y las tablas resumen muestran que si bien las
diferencias no son tan significativas como en la red matriz de Medellín, si se mantienen las
conclusiones que se han sacado hasta ahora, es decir, la presencia de caudales mayores con la
ecuación de Hazen-Williams se presenta en tuberías de gran diámetro que transportan gran
cantidad de caudal y viceversa en tuberías de menor diámetro cuando se emplea la ecuación
de Darcy-Weisbach (salvo algunas excepciones en las que aparecen tramos pequeños en
Hazen-Williams y de gran diámetro en la de Darcy-Weisbach). Así mismo, se puede ver que el
efecto hidráulico se está presentando nuevamente en números de Reynolds entre
y
que está generalmente asociado con tuberías de gran diámetro como lo ilustran en su
artículo Bombardelli y García (Fabián Bombardelli, 2003). Otro detalle importante es que, si
bien el desfase en el número de Reynolds no es tan significativo según se observa en los
diagramas y en las tablas resumen, sí se puede ver con claridad que el desfase del factor de
fricción entre las dos ecuaciones puede tener implicaciones considerables a la hora de evaluar
la hidráulica del sistema.
A continuación se muestran los resultados para el caudal mínimo de la red así como su
respectivo análisis:
ILUSTRACIÓN 153 DIAGRAMA DE MOODY RED GINEBRA CON HAZEN-WILLIAMS MAYOR Y CAUDAL
MÍNIMO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Ginebra Qmin (Diferencia Número de Reynolds
20000-100000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
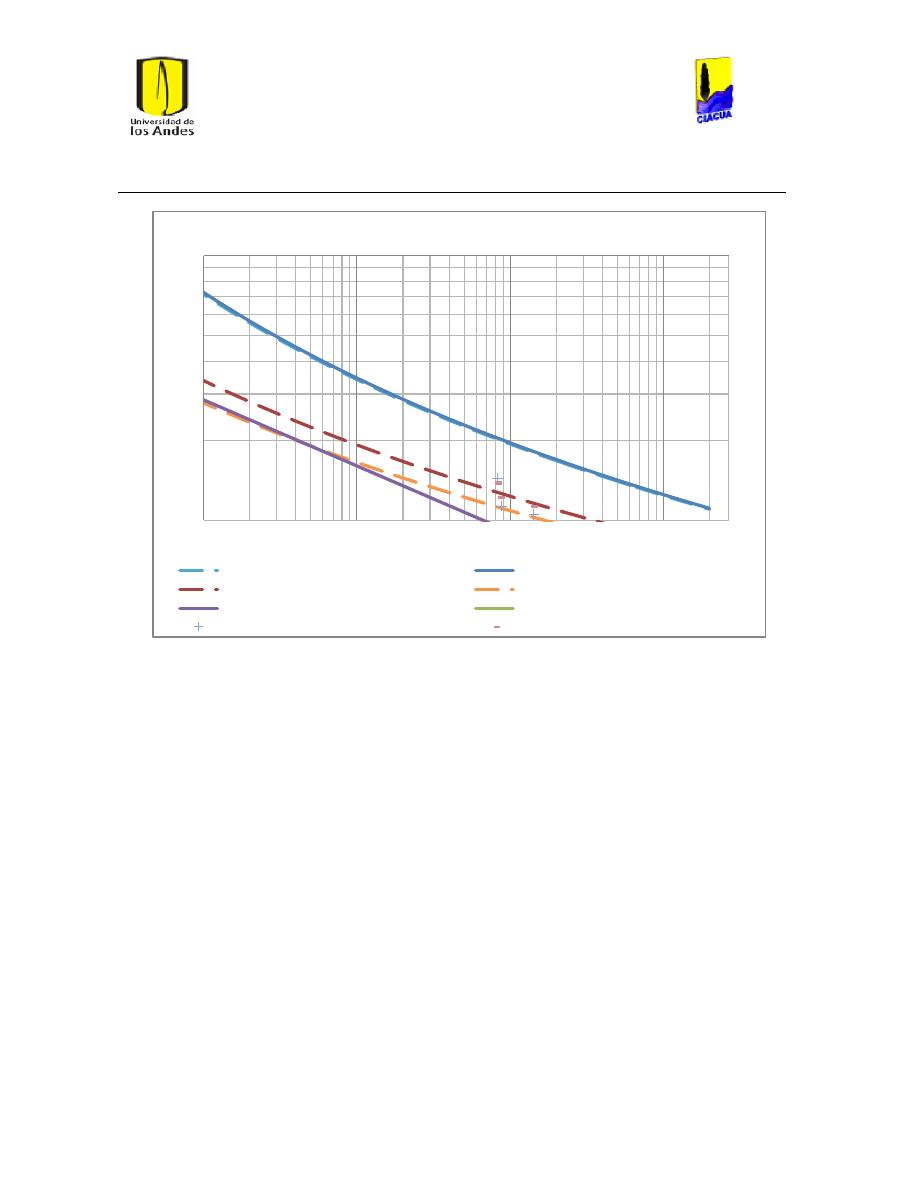
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
166
ILUSTRACIÓN 154 DIAGRAMA DE MOODY RED GINEBRA CON DARCY-WEISBACH MAYOR Y CAUDAL
MÍNIMO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Ginebra Qmin (Diferencia Número de Reynolds
20000-100000 Darcy Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
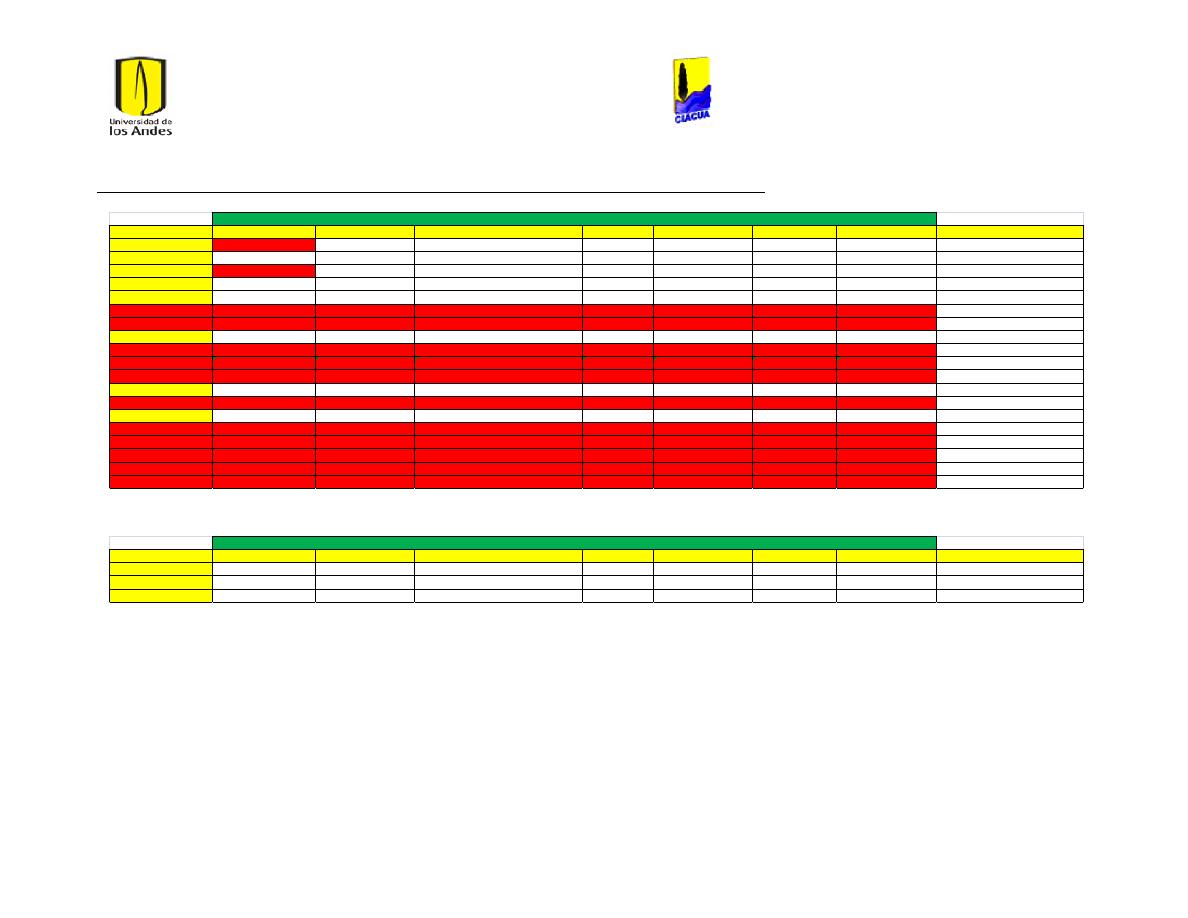
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
167
TABLA 20 RESUMEN DE TUBERÍAS RED GINEBRA CAUDAL MÍNIMO 1 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE 20000 Y 100000.
TABLA 21 RESUMEN DE TUBERÍAS RED GINEBRA CAUDAL MÍNIMO 2 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE 20000 Y 100000.
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/400
0.985769571
0.949498125
1.01E+05
2.65E+06
0.01496
2.75E+06
0.012374
3.82%
Tramo 2/400
0.185409007
0.17824228
2.00E+04
4.98E+05
0.016185
5.18E+05
0.015831
4.02%
Tramo 1/450
0.951802666
0.915589659
8.99E+04
2.27E+06
0.01466
2.36E+06
0.012579
3.96%
Tramo 2/450
0.273641336
0.265373161
2.05E+04
6.59E+05
0.015573
6.79E+05
0.015144
3.12%
Tramo 1/500
0.496994853
0.464789208
7.19E+04
1.04E+06
0.01494
1.11E+06
0.014086
6.93%
Tramo 1/700
1.52909503
1.491191636
6.05E+04
2.38E+06
0.013819
2.44E+06
0.012636
2.54%
Tramo 1/800
1.223768462
1.194131431
4.14E+04
1.67E+06
0.013811
1.71E+06
0.013308
2.48%
Tramo 2/800
0.46807167
0.441692847
3.68E+04
6.17E+05
0.014787
6.53E+05
0.015232
5.97%
Tramo 1/900
0.841537906
0.805348596
4.49E+04
9.99E+05
0.013939
1.04E+06
0.014127
4.49%
Tramo 2/900(10m)
2.128923957
2.109213424
2.45E+04
2.62E+06
0.012904
2.64E+06
0.012079
0.93%
Tramo 1/1000
0.926680297
0.890477369
4.04E+04
9.95E+05
0.013814
1.03E+06
0.014148
4.07%
Tramo 2/1000
0.844762484
0.808572122
4.04E+04
9.03E+05
0.013926
9.43E+05
0.014339
4.48%
Tramo 1/1100
1.223795449
1.194158402
3.01E+04
1.21E+06
0.013598
1.24E+06
0.013893
2.48%
Tramo 2/1100
0.464115431
0.437736121
2.68E+04
4.44E+05
0.014888
4.71E+05
0.015855
6.03%
Tramo 1 /1200
0.980285858
0.944021198
3.38E+04
8.79E+05
0.013894
9.12E+05
0.014542
3.84%
Tramo 2 /1200
0.8455383
0.809346022
3.37E+04
7.53E+05
0.013982
7.87E+05
0.01474
4.47%
Tramo 1/1300
0.94958671
0.913376014
3.11E+04
7.85E+05
0.013861
8.16E+05
0.014662
3.96%
Tramo 1/1600
0.986868249
0.950596677
2.53E+04
6.64E+05
0.014161
6.89E+05
0.015227
3.82%
Tramo 1/1900
0.943487237
0.907277782
2.13E+04
5.33E+05
0.014318
5.55E+05
0.015572
3.99%
Ginebra Qmín (Diferencias número de Reynolds 20000-100000) Hazen Mayor
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/300
0.341147651
0.355331047
-5.28E+04
1.32E+06
0.011318
1.27E+06
0.012187
-3.99%
Tramo 1/350
0.653872607
0.672552988
-5.96E+04
2.15E+06
0.010525
2.09E+06
0.01131
-2.78%
Tramo 1/600
0.651522931
0.670202935
-3.48E+04
1.25E+06
0.014383
1.21E+06
0.013839
-2.79%
Ginebra Qmín (Diferencias número de Reynolds 20000-100000) Darcy Mayor
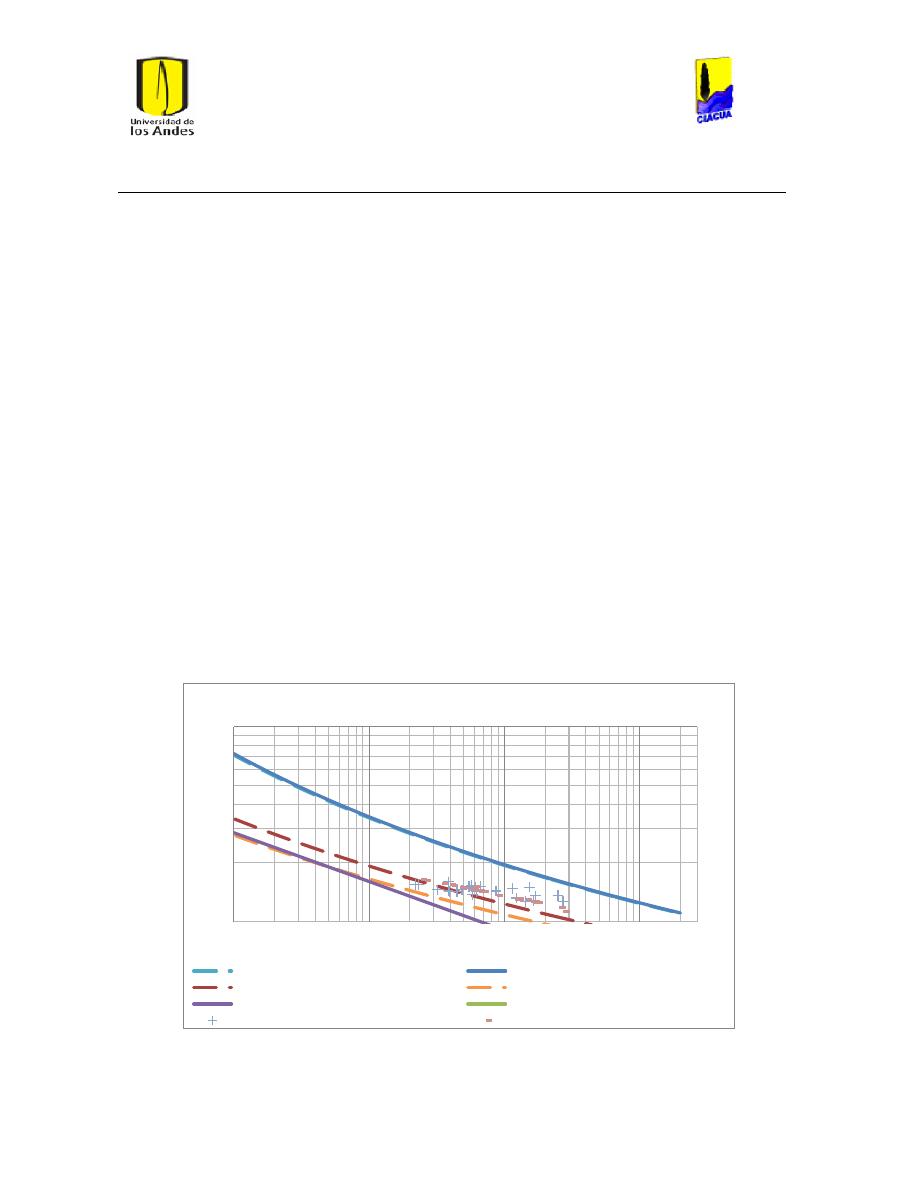
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
168
Los resultados que se encontraron en el caudal mínimo no presentaron grandes diferencias
según se aprecia en el diagrama de Moody y porcentualmente en la tablas de resumen; esto
es coherente con lo que se encontró en el análisis de emisores y en la red matriz de Medellín,
donde se puede ver claramente que incluso en el análisis de presiones este es el momento de
ejecución hidráulica que presenta menores diferencias entre las dos ecuaciones. Sin embargo
vale la pena resaltar que si bien son diferencias pequeñas, hay repetición en las tendencias de
la red, es decir, hay desfases entre los factores de fricción de las dos ecuaciones. Por lo demás,
el efecto se está presentando en diámetros de gran tamaño (ver Tablas 20 y 21) y los rangos
de números de Reynolds donde estas tuberías presentan las diferencias, son similares a lo
observado en las tuberías con el caudal medio y en los tramos analizados en la red matriz de
Medellín.
Lo anterior reafirma lo que se viene analizando y es que efectivamente las tuberías que están
transportando la mayor cantidad de caudal son las que están presentando estas grandes
diferencias; así mismo, al mirar los mapas de la redes también se puede ver que el efecto es
bastante importante en las tuberías que se dirigen a las ramificaciones con terminaciones en
tanques. Es de resaltar finalmente que al examinar los datos de presiones que aparecen en la
Sección 4.3.3 Red Ginebra y lo registrado en las Figuras 22, 23, 24, 25, 26, 27 y 28, se concluye
que estas diferencias están cambiando de manera significativa la hidráulica de la red,
generando resultados divergentes entre la ecuación físicamente basada y la ecuación empírica
de Hazen-Williams.
Por último, se muestran los resultados para la hora de máximo consumo en la red:
ILUSTRACIÓN 155 DIAGRAMA DE MOODY RED GINEBRA CON HAZEN-WILLIAMS MAYOR Y CAUDAL
MÁXIMO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Ginebra Qmax (Diferencia Número de Reynolds
20000-100000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
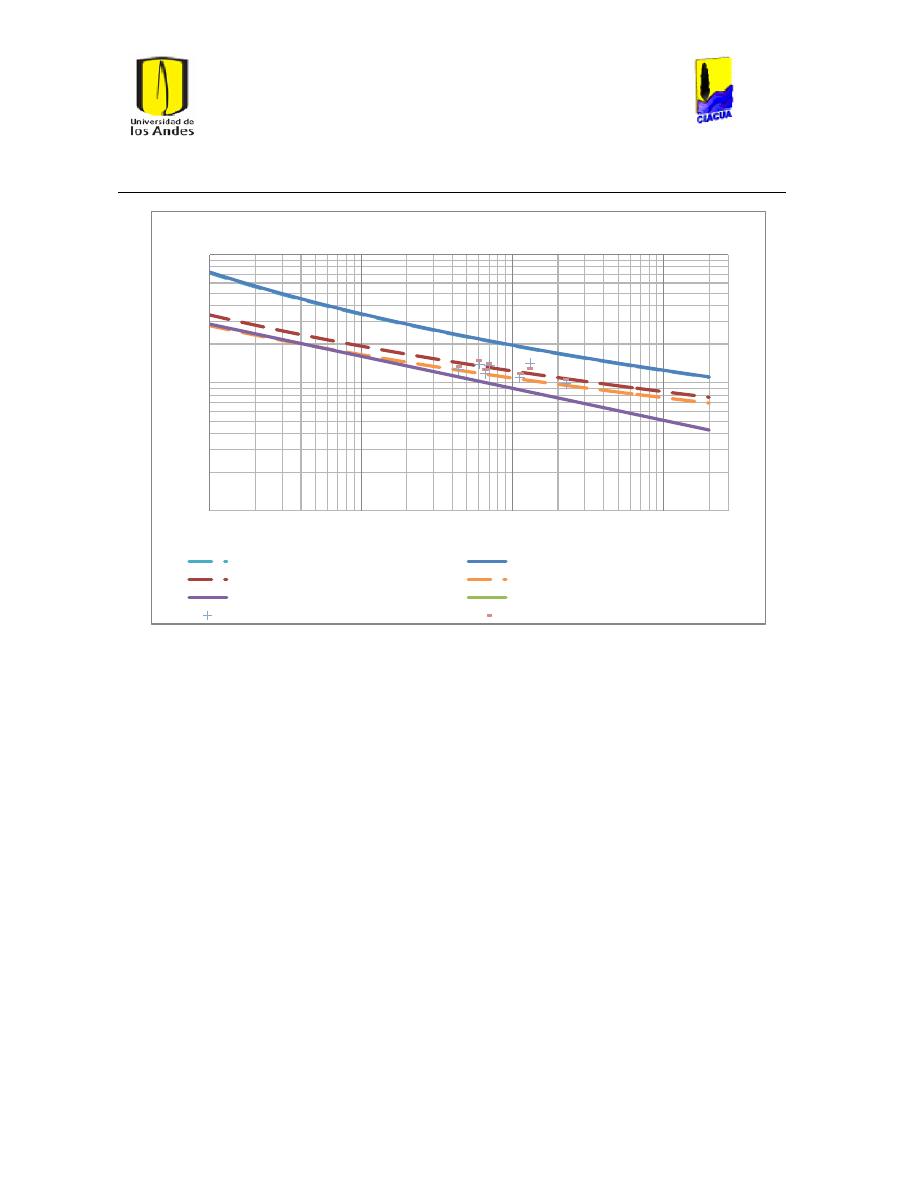
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
169
ILUSTRACIÓN 156 DIAGRAMA DE MOODY RED GINEBRA CON DARCY-WEISBACH MAYOR Y CAUDAL
MÁXIMO.
0.001
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Ginebra Qmax (Diferencia Número de Reynolds
20000-100000 Darcy Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
170
TABLA 22 RESUMEN DE TUBERÍAS RED GINEBRA CAUDAL MÁXIMO 1 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE 20000 Y 100000.
TABLA 23 RESUMEN DE TUBERÍAS RED GINEBRA CAUDAL MÁXIMO 2 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE 20000 Y 100000.
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/400
0.855668428
0.821648121
9.50E+04
2.29E+06
0.015013
2389190.526
0.012632
4.14%
Tramo 2/400
0.214688148
0.206816825
2.20E+04
5.77E+05
0.01601
599450.5263
0.015497
3.81%
Tramo 1/450
0.729701641
0.695725894
8.43E+04
1.73E+06
0.014788
1811081.842
0.013078
4.88%
Tramo 2/450
0.353687583
0.344002493
2.40E+04
8.54E+05
0.015321
877834.3421
0.014586
2.82%
Tramo 3/450
0.419230847
0.404677923
3.61E+04
1.00E+06
0.015185
1040509.342
0.014228
3.60%
Tramo 1/500
0.438097255
0.410053632
6.26E+04
9.16E+05
0.015045
978601.3158
0.014348
6.84%
Tramo 2/500
0.377434476
0.367914861
2.13E+04
8.22E+05
0.015098
843095.614
0.014615
2.59%
Tramo 1/600
0.713216114
0.699241242
2.60E+04
1.30E+06
0.014351
1327624.211
0.013657
2.00%
Tramo 1/700
2.414230294
2.344037241
1.12E+05
3.74E+06
0.013621
3851996.842
0.011833
2.99%
Tramo 1/800
1.877102113
1.821462245
7.77E+04
2.54E+06
0.013546
2620614.737
0.012515
3.05%
Tramo 2/800
0.719910785
0.667302931
7.34E+04
9.32E+05
0.014281
1005064.561
0.014315
7.88%
Tramo 3/800
0.537068584
0.522515722
2.03E+04
7.29E+05
0.014557
749799.2982
0.014908
2.79%
Tramo 1/900(10m)
3.321460504
3.278810226
5.29E+04
4.07E+06
0.012694
4121846.842
0.011309
1.30%
Tramo 2/900
0.316100126
0.282152688
4.21E+04
3.50E+05
0.015497
392272.1053
0.016288
12.03%
Tramo 1/1000
0.635544194
0.601577294
3.79E+04
6.72E+05
0.014311
709824.5614
0.014943
5.65%
Tramo 2/1000
0.328166056
0.294218791
3.79E+04
3.29E+05
0.015544
366521.0526
0.016447
11.54%
Tramo 1/1100
1.877121937
1.821481912
5.65E+04
1.85E+06
0.013216
1905921.754
0.013068
3.05%
Tramo 2/1100
0.705100563
0.652493047
5.34E+04
6.63E+05
0.014247
715918.5965
0.014925
8.06%
Tramo 1/1300
2.923951644
2.881826397
3.62E+04
2.48E+06
0.012811
2512072.105
0.012604
1.46%
Tramo 2/1300
0.721407958
0.687433801
2.92E+04
5.91E+05
0.01429
619787.5439
0.015257
4.94%
Tramo 1/1500
0.699141221
0.646533289
3.92E+04
4.81E+05
0.014556
520569.7368
0.01566
8.14%
Tramo 1/1600
0.859742823
0.825721133
2.37E+04
5.76E+05
0.014392
600141.7544
0.015518
4.12%
Tramo 1/1700
3.321456098
3.278806543
2.80E+04
2.15E+06
0.012687
2182151.316
0.012956
1.30%
Tramo 1/3000
2.414211067
2.344020033
2.61E+04
8.73E+05
0.013793
898792.1053
0.01508
2.99%
Ginebra Qmáx (Diferencias número de Reynolds 20000-100000) Hazen Mayor
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/300
0.257876628
0.266503127
-3.21E+04
9.92E+05
0.011838
9.60E+05
0.012698
-3.24%
Tramo 1/350
0.200476396
0.206990188
-2.08E+04
6.61E+05
0.012649
6.40E+05
0.013455
-3.15%
Tramo 2/350
0.512478112
0.527357185
-4.75E+04
1.68E+06
0.010953
1.64E+06
0.01177
-2.82%
Tramo 3/350
1.0220822
1.065028027
-1.37E+05
3.40E+06
0.009877
3.26E+06
0.010593
-4.03%
Tramo 1/600
1.013464093
1.056409413
-7.99E+04
1.97E+06
0.014082
1.89E+06
0.012973
-4.07%
Tramo 1/1100
0.997552813
1.040498306
-4.36E+04
1.06E+06
0.013639
1.01E+06
0.014196
-4.13%
Tramo 1/1300
1.013737553
1.056683085
-3.69E+04
9.08E+05
0.013938
8.71E+05
0.01482
-4.06%
Ginebra Qmáx (Diferencias número de Reynolds 20000-100000) Darcy Mayor

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
171
Los resultados con caudal máximo muestran que, al igual que en la red matriz de Medellín, un
mayor número de tramos se vieron afectados con respeto a las demás horas del día. Se
observa también que las diferencias porcentuales aumentaron de manera considerable, a
pesar de que en esta red no se vio un efecto tan claro del desfase del número de Reynolds, sí
se aprecia que en muchos casos se presentaba una diferencia considerable cuando se
comparaban los factores de fricción con las dos ecuaciones. Otro detalle de resaltar es que
con el caudal máximo de la red o en mejores términos, en la hora de máximo consumo, los
rangos de número de Reynolds de los tramos con las principales diferencias se mantuvo
también entre
que suelen corresponder a los tramos con diámetros de gran
diámetro y por ende a los tramos que están transportando la mayor cantidad de caudal.
Otro detalle importante es el hecho de que el flujo que se está presentando en las tuberías
oscila entre flujo turbulento hidráulicamente liso y flujo transicional (este último
predominando en la mayoría de los escenarios), lo que en principio llevaría a pensar que la
ecuación de Hazen-Williasm está en un punto de aplicación aceptable. Sin embargo, al mirar
los resultados, está claro que pese a ser una red que no presentó las diferencias que se vieron
en la red matriz de Medellín y las que se verán a continuación en las redes de Dtown y
Andalucía, es una red que también presentó divergencias importantes en la hidráulica, en
cuanto a los niveles de los tanques, presiones de los nudos de demanda, números de Reynolds
del sistema y pérdidas por fricción en los tramos de las tuberías.
La explicación de por qué es posible que las diferencias sean bajas entre la red Ginebra
simulada con la ecuación de Hazen-Williams y la ecuación de Darcy-Weisbach se encuentra en
la sección dedicada a emisores, en el análisis de las ilustraciones (Ilustración 79, Ilustración
80, Ilustración 81) y en la comparación realizada en los estudios de Bombardelli y García
(Fabián Bombardelli, 2003), específicamente en la Gráfica 4 (Sección 2.5 Trabajos de Fabián
Bombardelli y Marcelo García). Al comparar estas gráficas, se puede ver que aunque en los
estudios de los autores hay gran variación de los coeficientes de Hazen-Williams para un
mismo material, en los resultados de la presente investigación los coeficientes encontrados
con la ecuación empírica coinciden con los coeficientes teóricos tomados en esta
investigación (140 para hierro dúctil y 150 para PVC). Esto último implica que en este caso, la
hidráulica entre las dos ecuaciones es muy similar; lo que no quiere decir que la ecuación de
Hazen-Williams sea indicada para este tipo de redes, ya que como se ha visto a través de los
análisis de esta red y de toda investigación, existen diferencias que cambian radicalmente la
hidráulica, y adicionalmente se registra un desbalance de masa entre las dos ecuaciones,
diferencias en las pérdidas por fricción en las tuberías, diferencias en los llenados en los
tanques y por ende diferencias a la hora de establecer criterios para una operación indicada o
búsqueda de soluciones a la red.
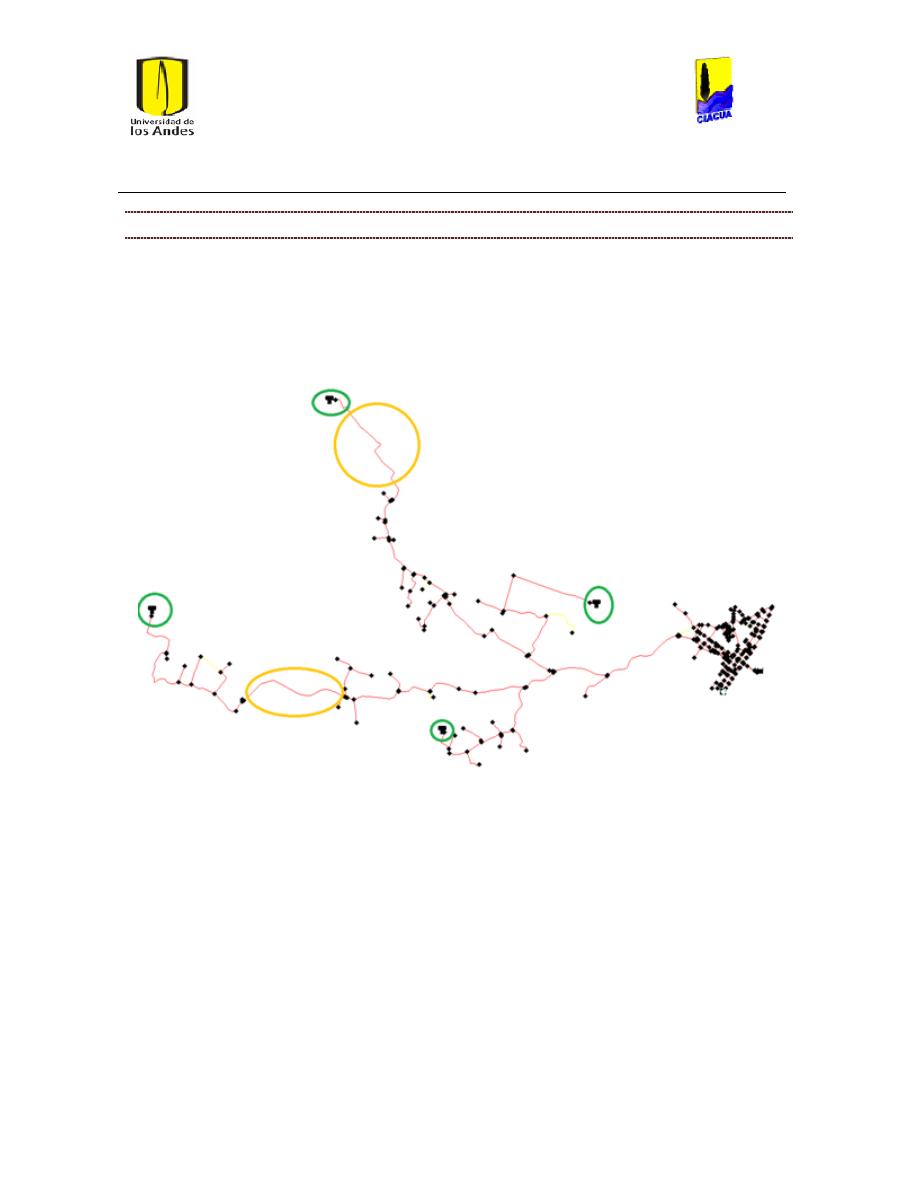
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
172
4.4.4 RED ANDALUCÍA
Los resultados de la red de Andalucía se muestran de manera similar a la redes presentadas a
anteriormente. Hay que resaltar que después de la red matriz de Medellín esta fue la red que
presentó las mayores diferencias hidráulicas entre la ecuación de Hazen-Williams y la
ecuación de Darcy-Weisbach.
A continuación se muestran los tanques y el esquema de su localización:
FIGURA 35 LOCALIZACIÓN DE LOS TANQUES Y DE ALGUNOS TRAMOS ANALIZADOS DE LA RED DE
ANDALUCÍA.
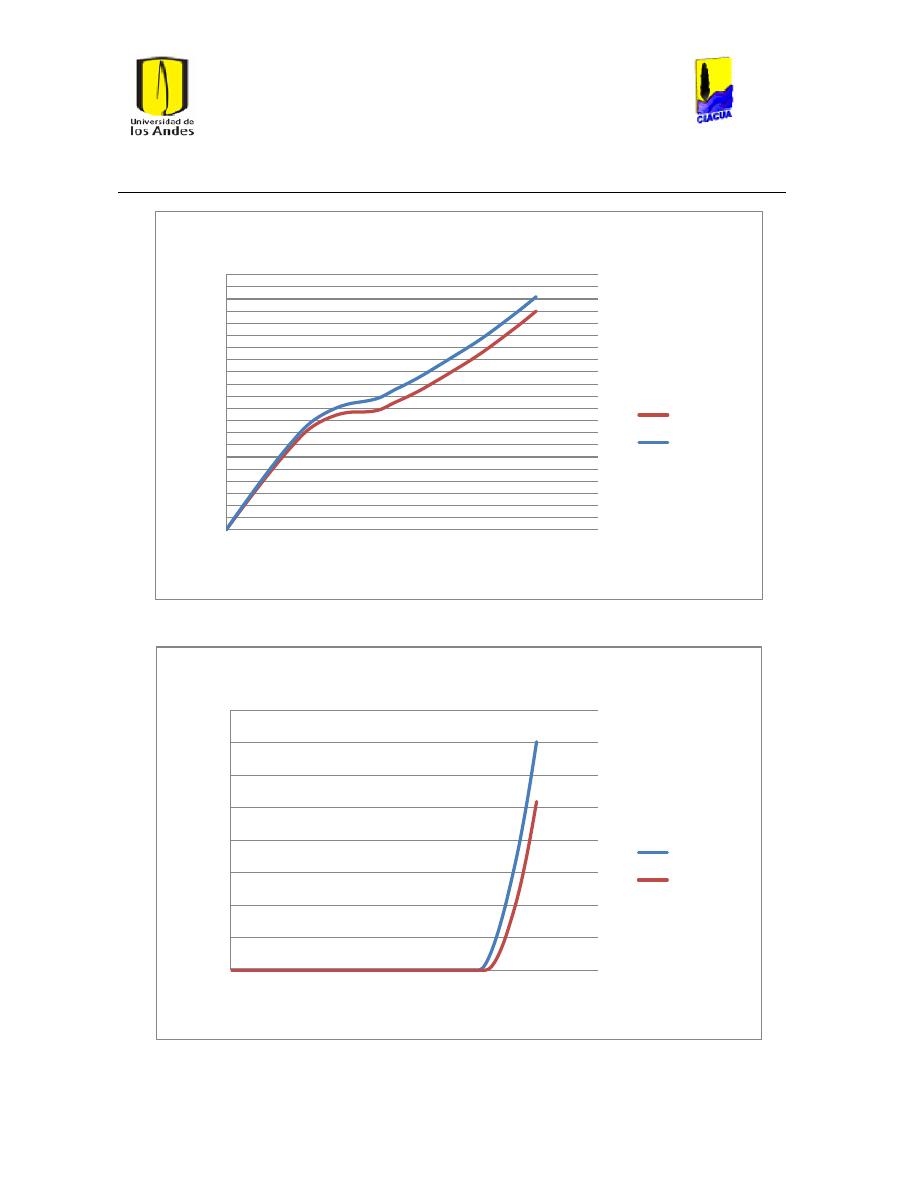
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
173
ILUSTRACIÓN 157 NIVEL TANQUE 362 DE LA RED DE ANDALUCÍA.
ILUSTRACIÓN 158 NIVEL TANQUE 222 DE LA RED DE ANDALUCÍA.
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
00:00
04:48
09:36
14:24
19:12
00:00
04:48
Ni
vel
(m
)
Tiempo (h)
Tanque 362 Andalucía
Tanque D-W
Tanque H-W
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
iv
e
l (
m
)
Tiempo (h)
Tanque 222 Andalucía
Tanque H-W
Tanque D-W
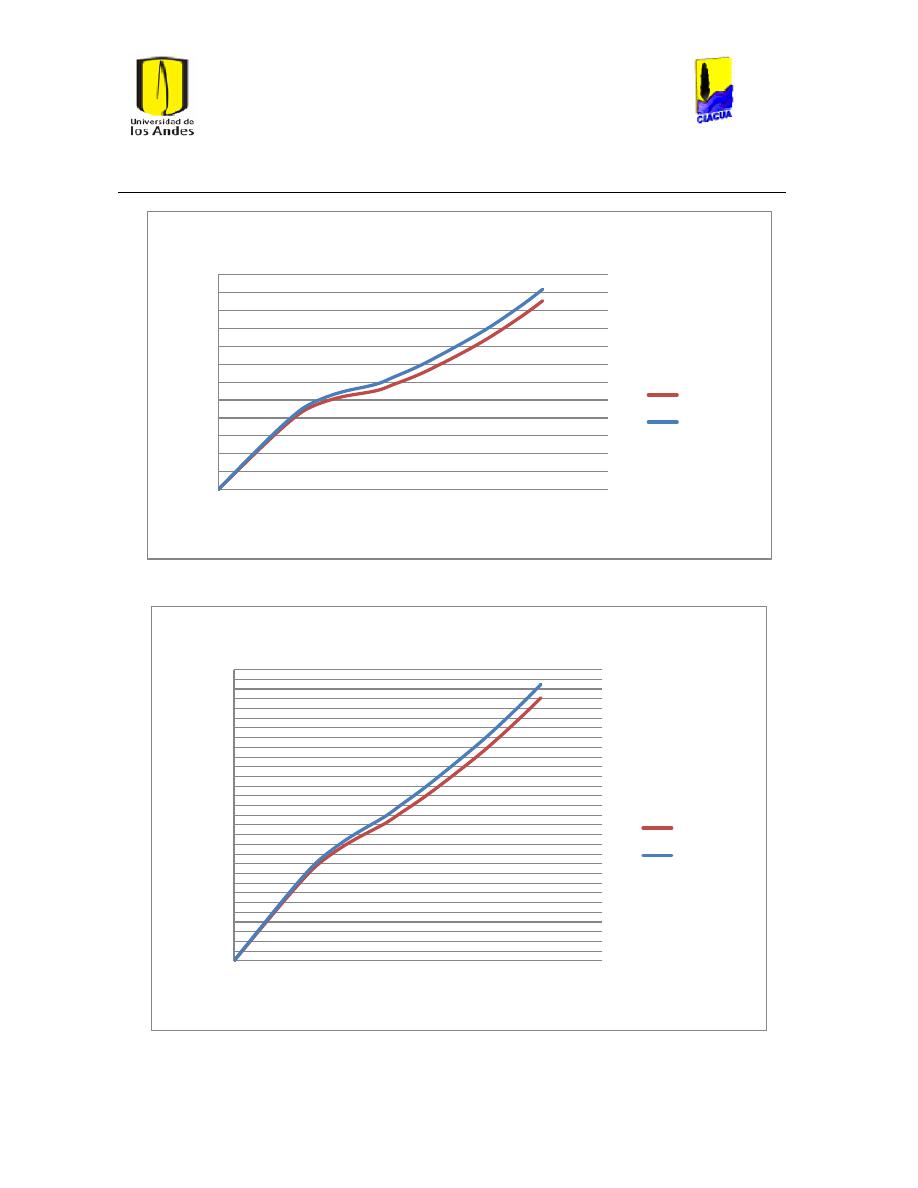
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
174
ILUSTRACIÓN 159 NIVEL TANQUE 343 DE LA RED DE ANDALUCÍA.
ILUSTRACIÓN 160 NIVEL TANQUE 361 DE LA RED DE ANDALUCÍA.
0
1
2
3
4
5
6
7
8
9
10
11
12
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
iv
e
l (
m
)
Tiempo(h)
Tanque 343 Andalucía
Tanque D-W
Tanque H-W
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
7
7.5
8
8.5
9
9.5
10
10.5
11
11.5
12
12.5
13
13.5
14
14.5
15
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
iv
e
l (
m
)
Tiempo(h)
Tanque 361 Andalucía
Tanque D-W
Tanque H-W
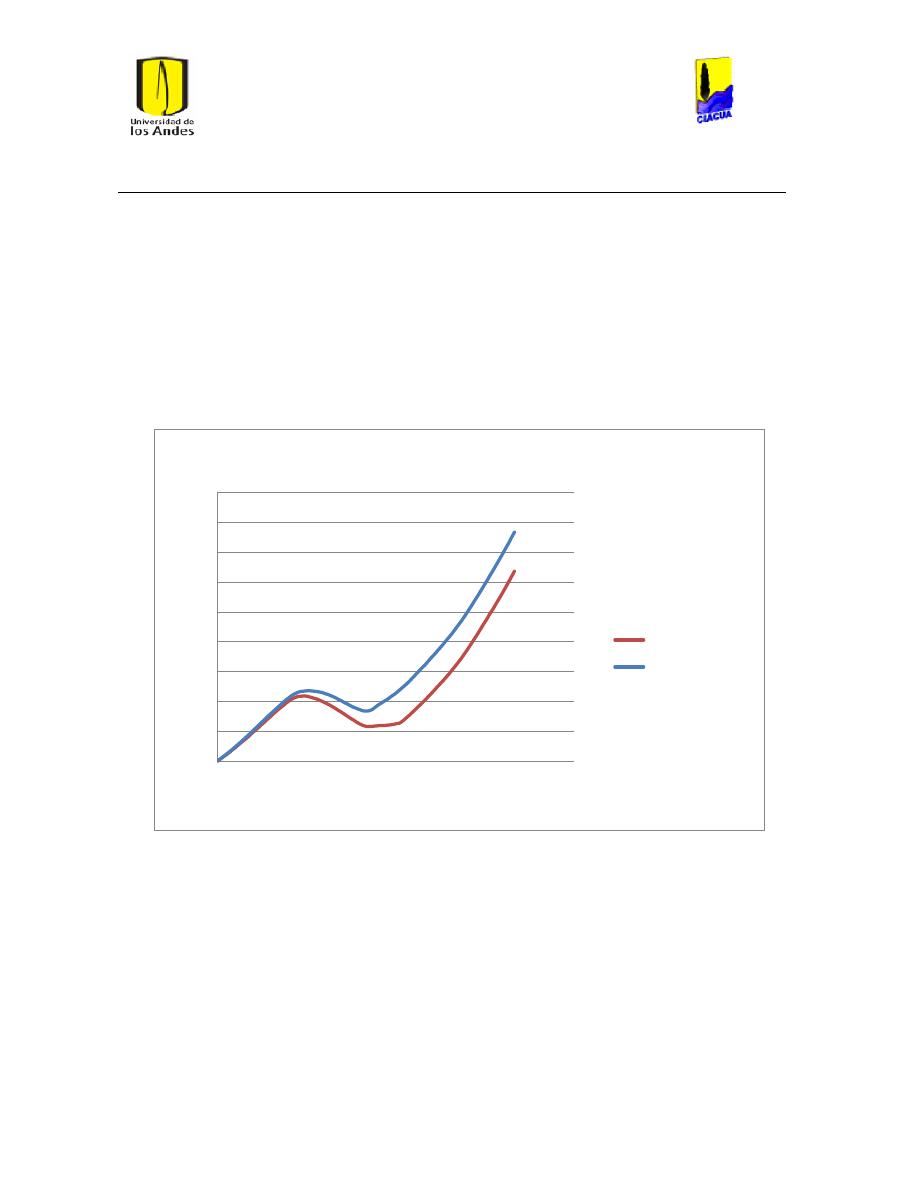
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
175
Los resultados con los 4 tanques en la red de Andalucía muestran un comportamiento muy
similar a lo que se encontró inicialmente en la red de Ginebra. Al inicio del día los tanques
parecen estar llenándose de manera muy similar en las dos redes; sin embargo, si se
observan las ilustraciones, se puede ver que existe una clara separación en los patrones de
llenado de los tanques en los últimos horarios del día o más precisamente cuando se
presentan los tiempos de demanda media y máxima del día, con diferencias que alcanzan
hasta 1 metro. Esto se presenta ya que como se ha venido analizando a lo largo de esta
investigación, existe un desbalance de masa causado por operar la red utilizando la ecuación
de Hazen-Williams con respecto a la hidráulica. Por tales motivos se decidió investigar el
efecto con 2 tanques en la red.
ILUSTRACIÓN 161 NIVEL TANQUE 343 DE LA RED DE ANDALUCÍA CON 2 TANQUES.
0
1
2
3
4
5
6
7
8
9
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
iv
e
l (
m
)
Tiempo (h)
Tanque 343 Andalucía
Tanque 343 D-W
Tanque 343 H-W
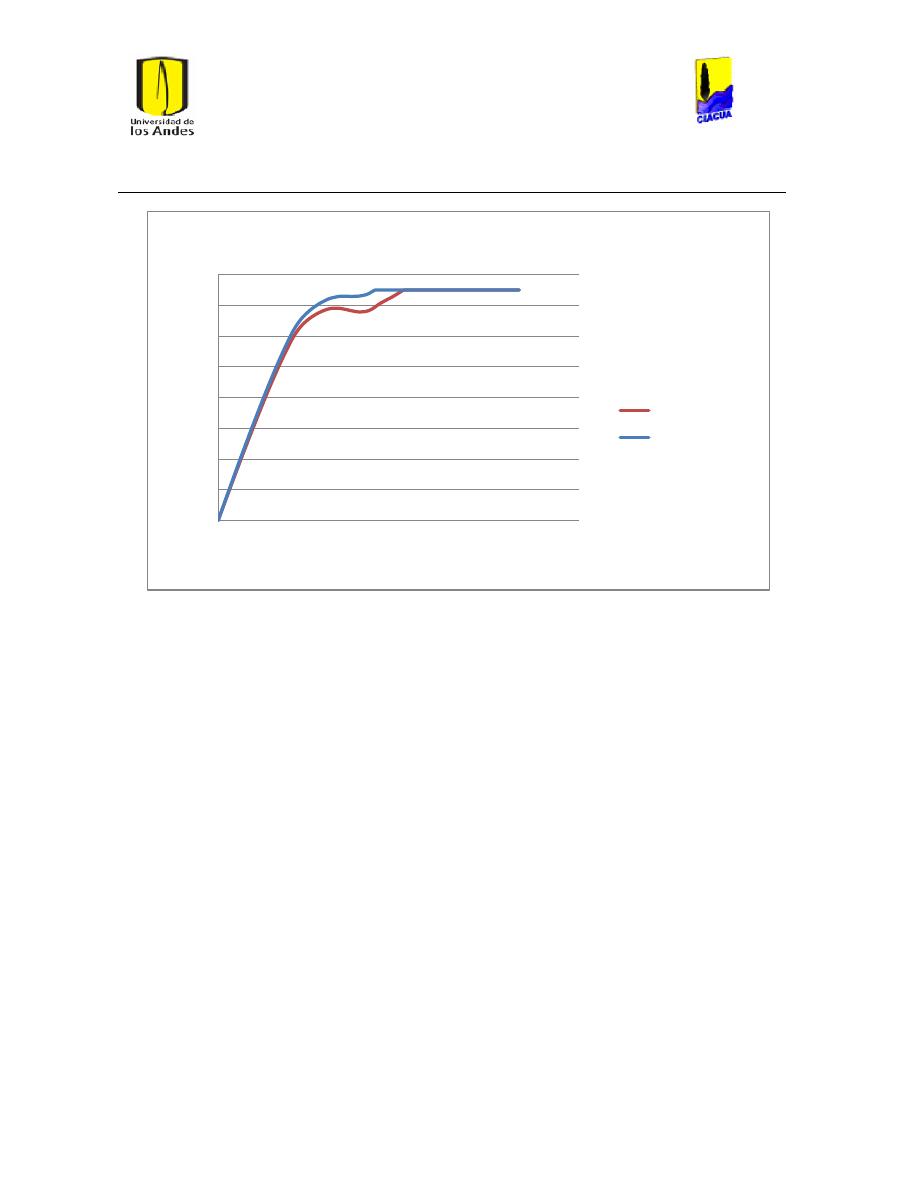
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
176
ILUSTRACIÓN 162 NIVEL TANQUE 222 DE LA RED DE ANDALUCÍA CON 2 TANQUES.
Los resultados con 2 tanques no muestran una diferencia significativa con respecto a lo que
se encontró cuando se trabajó con los cuatro tanques; sin embargo, debido a que los niveles
de los tanques no fueron tan altos como cuando se tenían los cuatro tanques, se puede ver con
mucha más claridad que hay diferencias significativas entre las dos ecuaciones. Para
comenzar, se observa que en el momento en que se produce un vaciado de tanque, está claro
que con la ecuación de Hazen-Williams el vaciado del tanque 222 es mucho más lento.
Adicionalmente, cuando se ven los tanques en el análisis de esta red, se identifica una
diferencia casi constante, como si se mantuviera una distancia entre los llenados, al aplicar las
dos ecuaciones.
Estas diferencias, como se verá más adelante, van a jugar un papel vital en la hidráulica de la
red, y al recopilar los resultados con emisores en la red se identifica claramente que los
emisores presentan diferencias bastante grandes en el caudal emisor y en las presiones de la
red. Así mismo, cuando se llegue a los análisis de los diagramas de Moody y las diferencias en
las tuberías de la red con respecto al número de Reynolds, se va a observar que lo que está
ocurriendo internamente en la red es bastante interesante ya que las consecuencias
operacionales al emplear la ecuación de Hazen-Williams van a ser preocupantes.
A continuación se muestran los análisis realizados a un grupo de tuberías con el fin de
determinar lo que ocurría en el tiempo y si los hallazgos eran similares a lo encontrado en las
otras redes probadas durante esta tesis. Los resultados que arroja esta red ratifican los
0
2
4
6
8
10
12
14
16
00:00
04:48
09:36
14:24
19:12
00:00
04:48
N
iv
e
l (
m
)
Tiempo (h)
Tanque 222 Andalucía
Tanque 222 D-W
Tanque 222 H-W
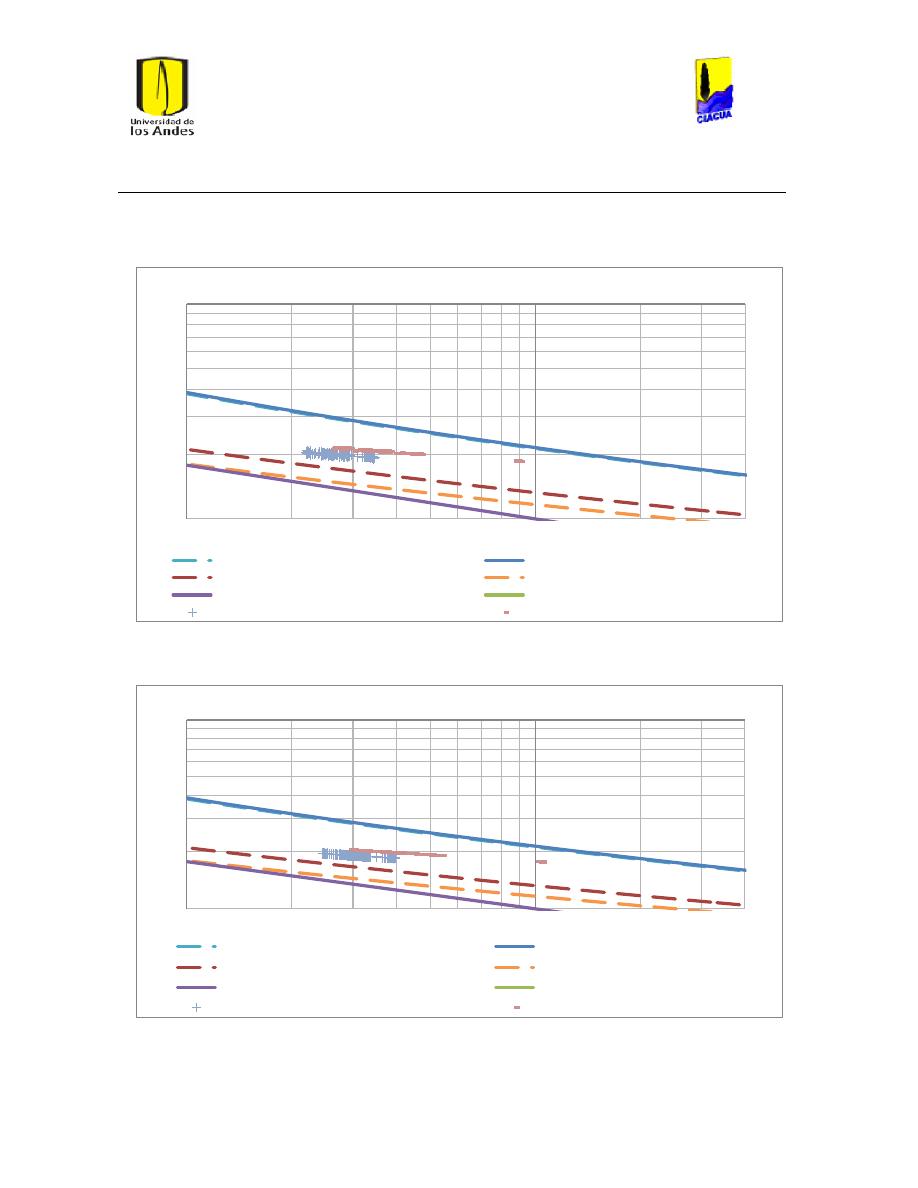
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
177
hallazgos encontrados en la red matriz de Medellín y la red de Ginebra, según se aprecia en el
diagrama de Moody donde se aprecian claramente las diferencias entre las dos ecuaciones.
ILUSTRACIÓN 163 DIAGRAMA DE MOODY DE LA TUBERÍA 65 RED DE ANDALUCÍA, CON DIÁMETRO DE
1500 MM Y CAUDAL MEDIO DE 110 L/S.
ILUSTRACIÓN 164 DIAGRAMA DE MOODY DE LA TUBERÍA 137 RED DE ANDALUCÍA, CON DIÁMETRO
DE 1300 MM Y CAUDAL MEDIO DE 110 L/S.
0.01
0.1
1.00E+05
1.00E+06
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Tubería 65 D-W
Tubería 65 H-W
0.01
0.1
1.00E+05
1.00E+06
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Tubería 137 D-W
Tubería 137 H-W
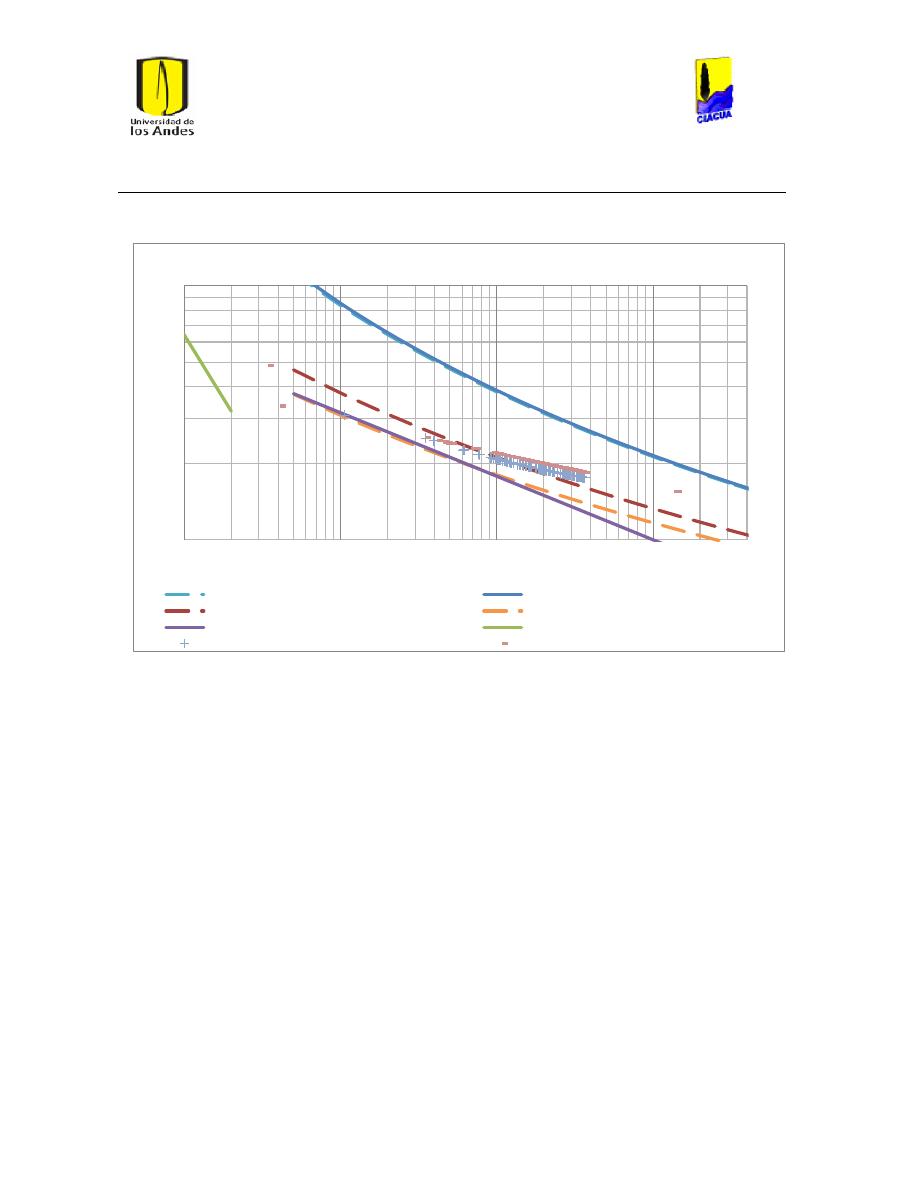
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
178
ILUSTRACIÓN 165 DIAGRAMA DE MOODY DE LA TUBERÍA 78 RED DE ANDALUCÍA, CON DIÁMETRO DE
700 MM Y CAUDAL MEDIO DE 408 L/S.
Conviene precisar que los diagramas de Moody realizados para esta red se basaron en
tuberías que se dirigían a los tanques y que a su vez eran pertenecientes a las ramificaciones
de la red. Como se mencionó atrás, los resultados que se observan en estos diagramas
permiten ver con total claridad que hay una diferencia considerable en los números de
Reynolds que se presentan en las tuberías. Al igual que en los casos anteriores este desfase es
causado por un desbalance de masa entre la red simulada con la ecuación empírica y la
ecuación físicamente basada. Posteriormente se realizó un análisis para determinar cuáles
fueron las tuberías que presentaron mayores diferencias y se identificó que los efectos
hidráulicos en la red fueron bastante considerables.
Una vez identificadas las diferencias de nivel en los tanques de la red (al igual que
anteriormente se habían identificado las diferencias en los emisores) y que también se estaba
presentando un desbalance importante en el caudal que estaba circulando por la red, se trazó
un mapa para determinar cuáles eran las tuberías que presentaban números de Reynolds
mayores con la ecuación de Hazen-Williams (Rojo), cuales presentaban diferencias mayores
con la ecuación de Darcy-Weisbach (Verde) y las tuberías que no presentaron ningún tipo de
diferencias (Amarillo).
0.01
0.1
1.00E+03
1.00E+04
1.00E+05
1.00E+06
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Tubería 78 D-W
Tubería 78 H-W
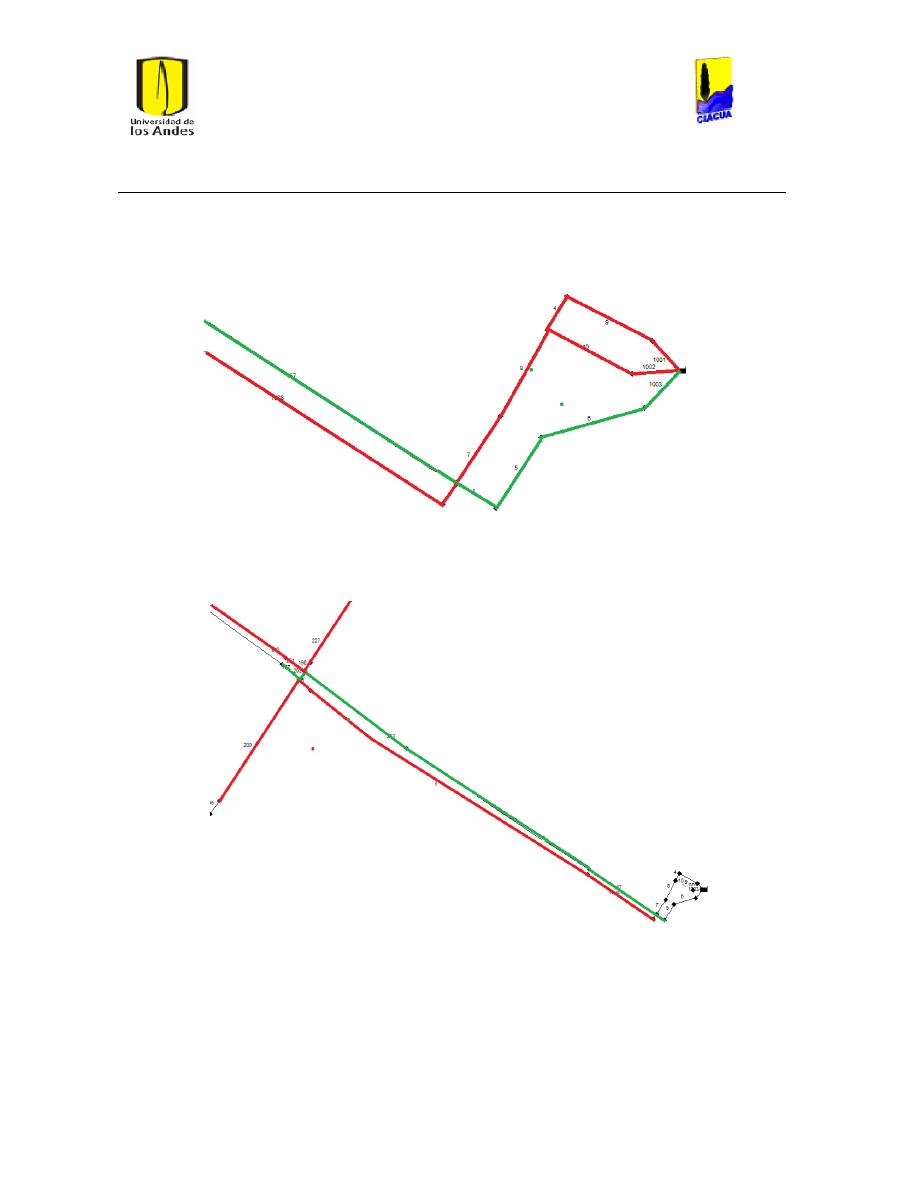
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
179
FIGURA 36 SALIDA DEL EMBALSE RED ANDALUCÍA.
FIGURA 37 PRINCIPALES TRAMOS A LA SALIDA DEL EMBALSE RED ANDALUCÍA.
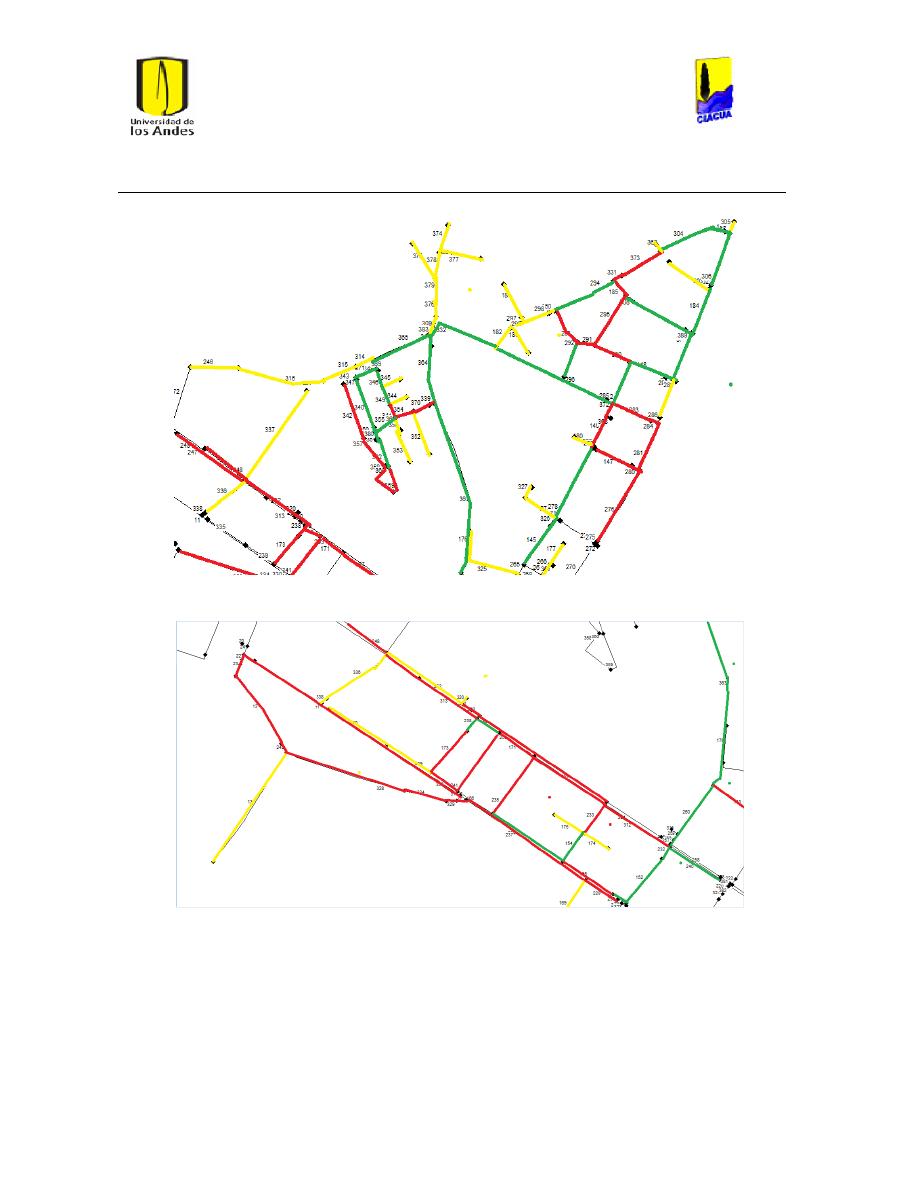
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
180
FIGURA 38 ENTRAMADO INTERNO DE LA RED DE ANDALUCÍA 1.
FIGURA 39 ENTRAMADO INTERNO DE LA RED DE ANDALUCÍA 2.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
181
FIGURA 40 RAMIFICACIONES DE LA RED ANDALUCÍA.
De las figuras anteriores se puede ver que la solución de la hidráulica utilizando la ecuación de
Hazen-Williams es considerablemente diferente a la ecuación de Darcy-Weisbach. Este no es
un efecto nuevo, teniendo en cuenta que es algo que se ha observado en todas las redes del
sistema.
Así mismo, los resultados que se observan en las figuras anteriores permiten concluir una vez
más que los tramos que presentan diferencias entre las dos ocasiones suelen seguir la
dirección de las ramificaciones con tanques y también que hay tanques a los que les está
entrando más caudal cuando se emplea la ecuación de Hazen-Williams que con la ecuación de
Darcy-Weisbach.
Hay quienes argumentan que las diferencias de llenado en estos tanques son bajas o poco
significativas y que esta no es una razón suficiente para dejar de utilizar la ecuación de Hazen-
Williams. Sin embargo, si se vuelve al análisis de los emisores y a las ilustraciones con los
niveles de los tanques en las otras redes, se puede ver que, al utilizar la ecuación de Hanzen-
Williams, los patrones de vaciado de los tanques tienen a ser subestimados y/o
sobrestimados. El efecto que esto tiene en la red es que si se utiliza la ecuación de Darcy-
Weisbach y la lectura arroja que el tanque ya no tenga agua, esta será suministrada por el
embalse, mientras que al operar la misma red con la ecuación empírica, el resultado
mostrará erróneamente que el tanque todavía tiene agua almacenada, lo cual genera un nuevo
desbalance de masa en la red y direcciones de flujo distintas, cambiando la forma en que se
están simulando las pérdidas por fricción, las presiones en la red e incluso las velocidades que
se presentan en las tuberías.
Con base a lo expuesto anteriormente, se procedió a identificar las tuberías que presentaban
las mayores diferencias entre las dos ecuaciones y se crearon nuevos mapas resaltando las
tuberías que presentaban diferencias importantes en términos del número de Reynolds.
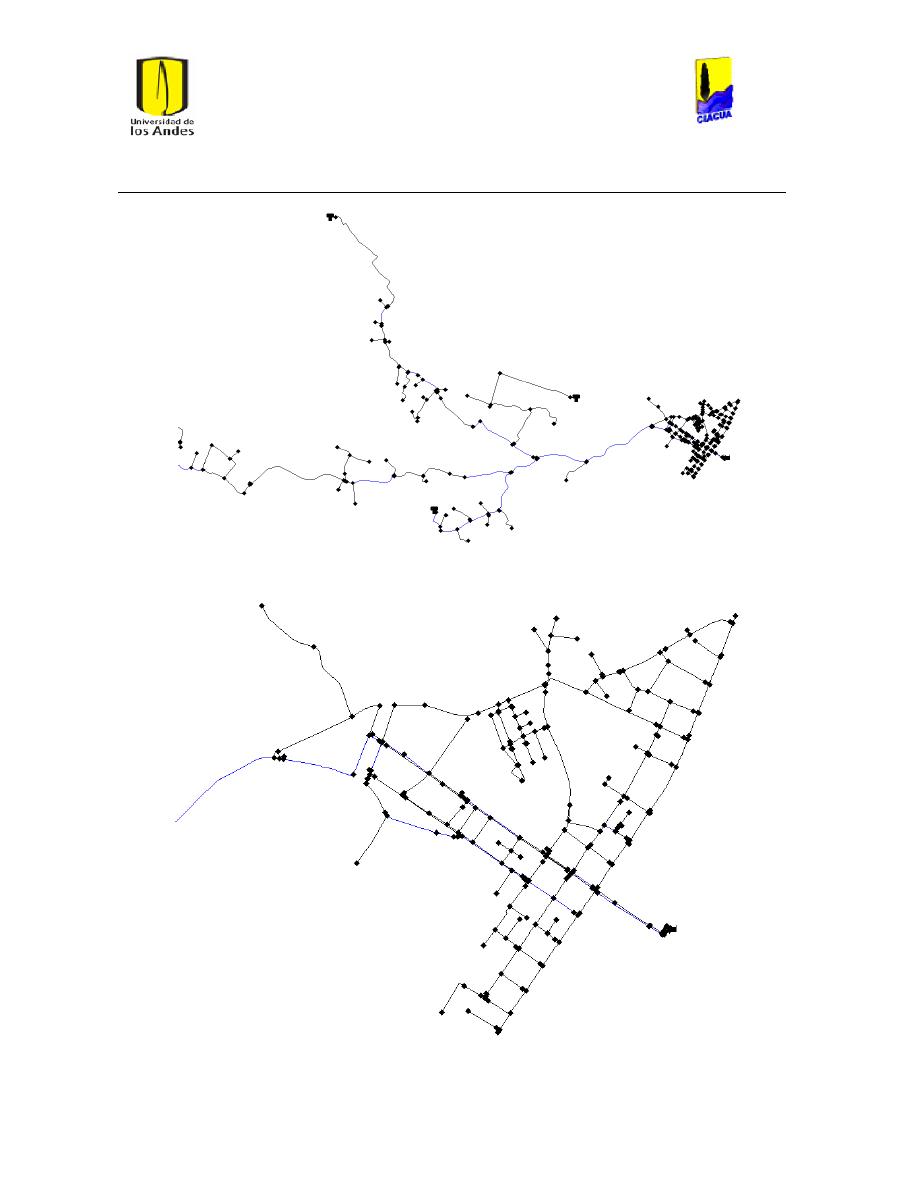
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
182
FIGURA 41 RAMIFICACIONES CON ALTAS DIFERENCIAS RED DE ANDALUCÍA CAUDAL MEDIO.
FIGURA 42 ENTRAMADOS INTERNOS CON ALTAS DIFERENCIAS RED ANDALUCÍA CAUDAL MEDIO.
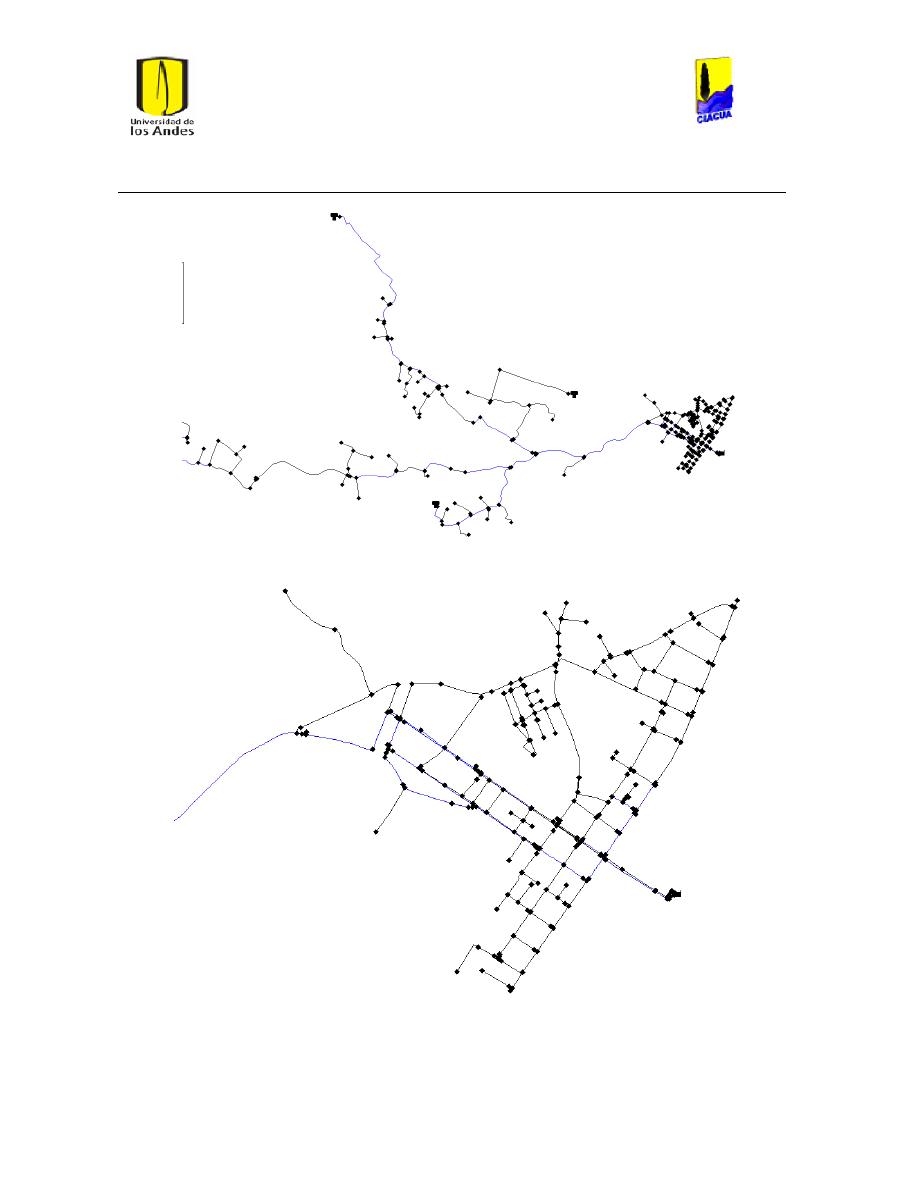
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
183
FIGURA 43 RAMIFICACIONES CON ALTAS DIFERENCIAS RED ANDALUCÍA CAUDAL MÁXIMO.
FIGURA 44 ENTRAMADOS INTERNOS CON ALTAS DIFERENCIAS RED ANDALUCÍA CAUDAL MÁXIMO.
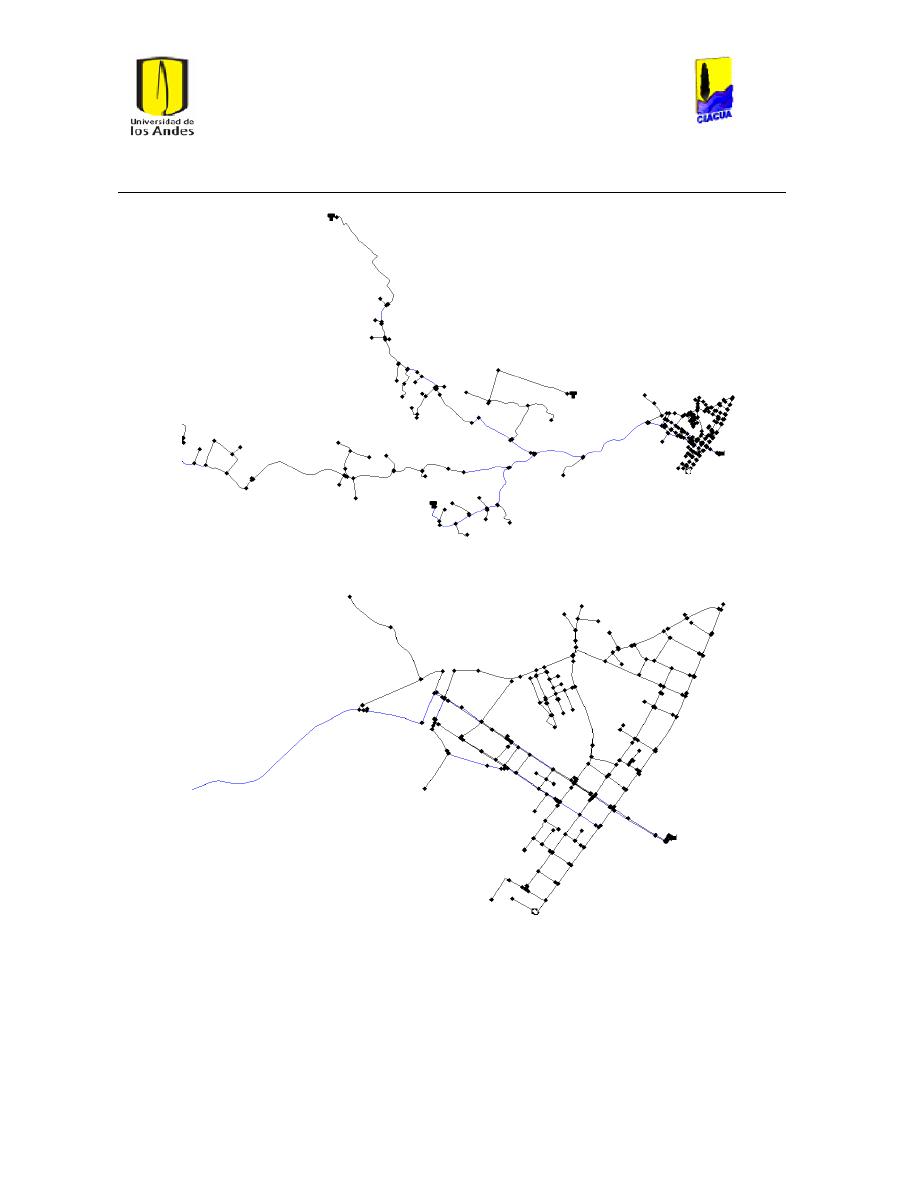
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
184
FIGURA 45 RAMIFICACIONES CON ALTAS DIFERENCIAS RED ANDALUCÍA CAUDAL MÍNIMO.
FIGURA 46 ENTRAMADOS INTERNOS CON ALTAS DIFERENCIAS RED ANDALUCÍA CAUDAL MÍNIMO.
Se observa una vez más que los tramos de tuberías que presentan altas diferencias en cuanto
al número de Reynolds son tramos que salen de los embalses (es decir se está presentando
una diferencia de caudal entre la red que trabaja con la ecuación empírica y la ecuación
físicamente basada) y en los tramos que conducen a las ramificaciones que tienen
terminaciones en tanques. Si bien las figuras podrían interpretarse en que sólo son estas
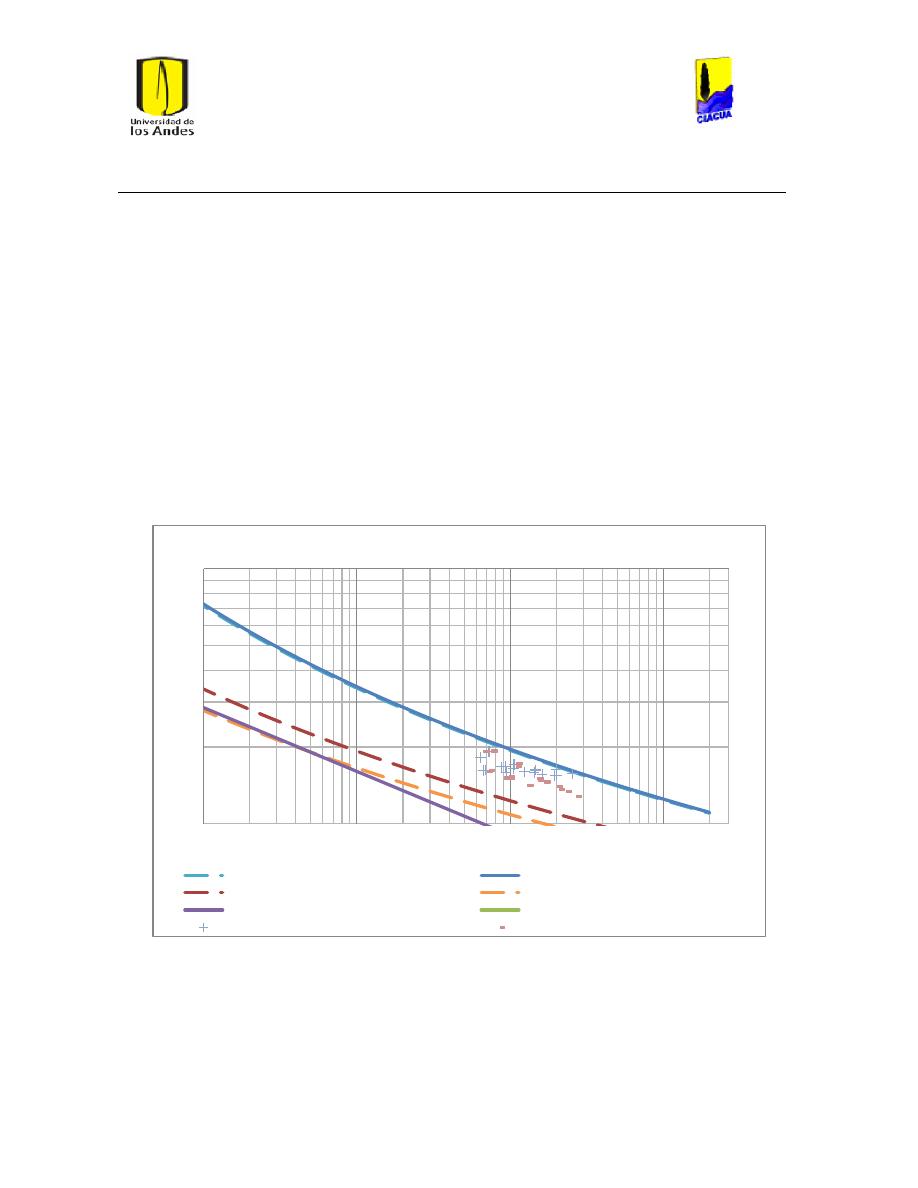
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
185
ramas los que se ven afectadas, la realidad es que al estar transportando caudales diferentes,
toda la hidráulica de la red se está viendo comprometida, ya que de estos tramos se
subdividen nuevos tramos que a su vez están transportando una cantidad de caudal diferente
a la que transportarían si se operara con la ecuación de Darcy-Weisbach. Otro efecto que se
puede observar en las figuras es que el número de tramos con diferencias en el número de
Reynolds se ve incrementado cuando se presenta la hora de máximo consumo por lo que es el
momento en que la hidráulica de la red está más vulnerable a presentar diferencias entre las
dos ecuaciones. Al observar más detalladamente las figuras, se puede ver que en los 3
momentos claves del estudio hay tramos que permanentemente presentan diferencias
significativas; estos tramos, como se verá más adelante, son aquellos que presentan grandes
diámetros y que están transportando la mayor cantidad de caudal.
A continuación se presentan los resultados cuantitativos de estos tramos; esto incluye, los
diagramas de Moody de los tramos, al igual que las tablas resumen con la información más
relevante.
ILUSTRACIÓN 166 DIAGRAMA DE MOODY DE RED DE ANDALUCÍA TRAMOS CON HAZEN-WILLIAMS
MAYOR PARA EL CAUDAL MÍNIMO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Andalucía Qmin (Diferencia Número de Reynolds
50000-200000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
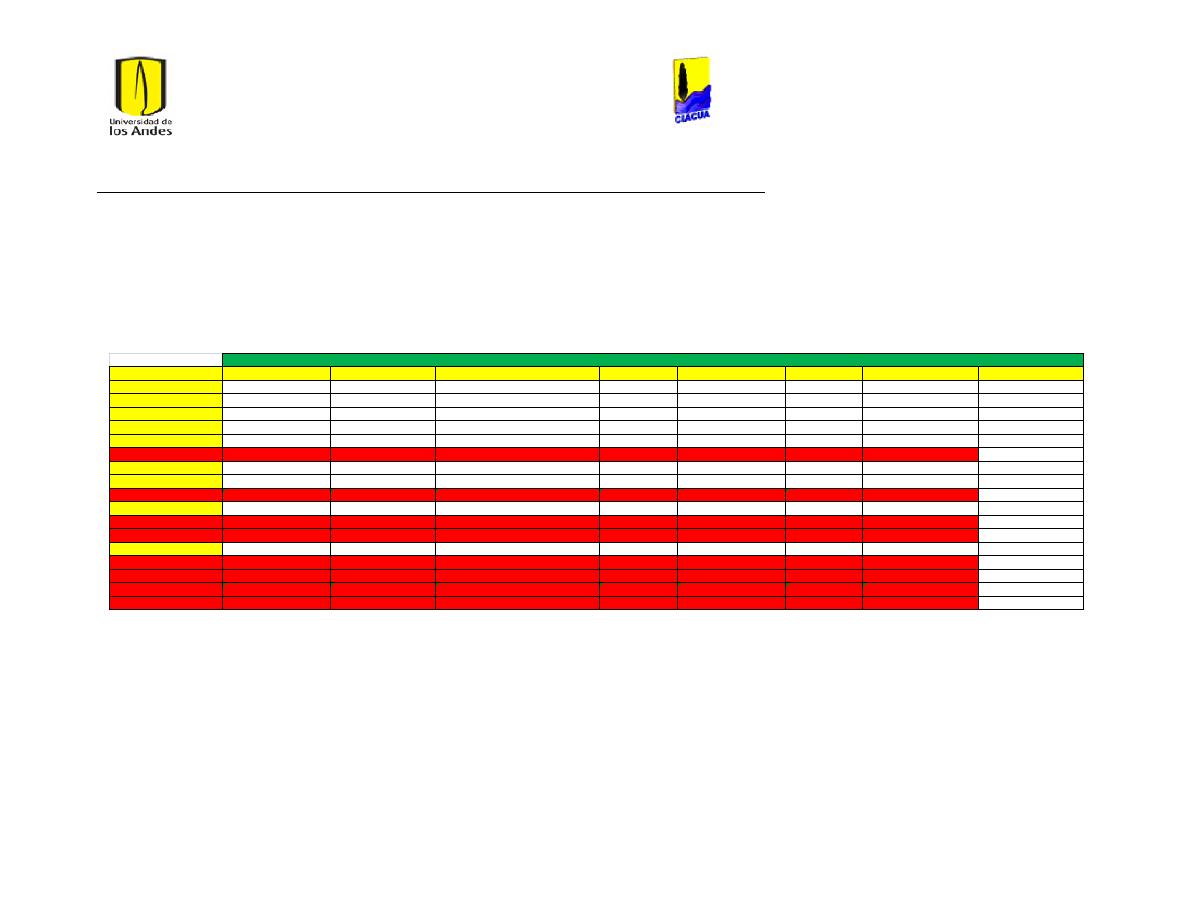
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
186
TABLA 24 RESUMEN DE TRAMOS DE LA RED ANDALUCÍA PARA EL CAUDAL MÍNIMO PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE 50000
Y 200000.
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Porcentual
Tramo 1/400(1 m)
1.255457833
1.208021166
1.32E+05
3.01E+06
0.016299
3.51E+06
0.013364
16.33%
Tramo 2/400
0.492057604
0.473851698
5.08E+04
1.32E+06
0.016718
1.37E+06
0.015112
3.84%
Tramo 1/450(14 m)
1.633116866
1.546938234
2.14E+05
3.84E+06
0.015684
4.05E+06
0.012828
5.57%
Tramo 2/450
0.789886582
0.752138173
9.37E+04
1.87E+06
0.015963
1.96E+06
0.014141
5.02%
Tramo 3/450
0.597988802
0.561470273
9.06E+04
1.39E+06
0.016753
1.48E+06
0.015306
6.50%
Tramo 1/600
1.694455383
1.618881764
1.41E+05
3.01E+06
0.015501
3.15E+06
0.013657
4.67%
Tramo 2/600
1.232868682
1.185431984
8.83E+04
2.21E+06
0.016241
2.29E+06
0.014828
4.00%
Tramo 3/600
0.798179922
0.760431707
7.03E+04
1.42E+06
0.01591
1.49E+06
0.015054
4.96%
Tramo 1/700
1.917299443
1.846180069
1.13E+05
2.95E+06
0.01546
3.06E+06
0.013975
3.85%
Tramo 2/700
0.668146127
0.631627405
5.83E+04
1.01E+06
0.01618
1.07E+06
0.015967
5.78%
Tramo 1/800
1.632515805
1.546337646
1.20E+05
2.16E+06
0.015905
2.28E+06
0.015029
5.57%
Tramo 2/800
1.812858303
1.74173918
9.93E+04
2.43E+06
0.015575
2.53E+06
0.014583
4.08%
Tramo 3/800
0.785671608
0.747923236
5.27E+04
1.04E+06
0.016217
1.10E+06
0.016187
5.05%
Tramo 1/1100 (1 m)
1.641815987
1.56855301
7.44E+04
1.59E+06
0.017104
1.67E+06
0.017227
4.67%
Tramo 1/1300(8 m)
1.917301996
1.84618138
6.11E+04
1.59E+06
0.016471
1.65E+06
0.016726
3.85%
Tramo 1/1600(1 m)
1.641815422
1.568552476
5.11E+04
1.09E+06
0.0192
1.15E+06
0.019277
4.67%
Tramo 1/1800
1.634192316
1.548013842
5.35E+04
9.61E+05
0.018209
1.01E+06
0.019143
5.57%
Andalucía Qmín (Diferencias número de Reynolds 50000-200000) Hazen Mayor

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
187
En la hora de menor consumo de la red, los resultados muestran las mismas tendencias que
se han estado observados a lo largo de esta investigación. Es decir, tanto en el diagrama de
Moody como en la tabla de resumen se puede ver que las tuberías que están teniendo este
efecto son tuberías con números de Reynolds entre
. Así mismo, los
diámetros de la red que presentan divergencias considerables en los números de Reynolds
son los mayores a los 600 mm. Si bien, las diferencias porcentuales no parecen ser de gran
magnitud, estas juegan un papel significativo por el hecho de que simplemente no se está
representando de manera correcta la hidráulica del sistema, al utilizar la ecuación de Darcy-
Weisbach. Así mismo, cuando se presenten los resultados para la hora en que se consume el
caudal medio y el caudal máximo de esta red se observará que las diferencias porcentuales
se amplían. .
Se destaca también el hecho que la mayoría de los datos mostrados se encuentran dentro de
la zona de transición, acercándose al flujo turbulento hidráulicamente rugoso. Esto es
bastante interesante porque como se ha estado mencionando anteriormente, estas
condiciones deberían ser las adecuadas para la aplicación de la ecuación de Hazen-Williams.
Sin embargo, al identificar los puntos en el diagrama de Moody (cada uno representa un
tramo de la red), se puede ver que hay divergencia considerable a la hora de evaluar el factor
de fricción y también un desfase en los números de Reynolds. Todo lo anterior permite
concluir que incluso dentro de ciertos rangos históricamente aceptables (B.A. Christensen,
2000) de la ecuación de Hazen-Williams, esta sigue presentando divergencias considerables
con respecto a la ecuación de Darcy-Weisbach en términos de la masa que circula en el
sistema, el cálculo de las pérdidas por fricción y las presiones de la red. Ver Sección 4.2.4 Red
Andalucía.
Otro aspecto que no se ha mencionado de la red es que se cuantificó el desbalance de masa
que la ecuación de Hazen-Williams está enviando al sistema con respecto a lo que se presenta
con la ecuación de Darcy-Weisbach. La red está presentando un desbalance de masa de 170
L/s, que se constituye en el desbalance de masa más grande de todas las redes probadas
hasta el momento; una vez más, 170 L/s dentro de un caudal total de la red de
no
parece ser tan significativo, pero con lo que se ha mostrado y analizado, en conjunto con los
resultados que se van a mostrar más adelante, se concluye que el efecto que puede tener este
desbalance es bastante considerable.
A continuación se muestran los resultados para la hora en que se presenta el caudal medio
demandado:
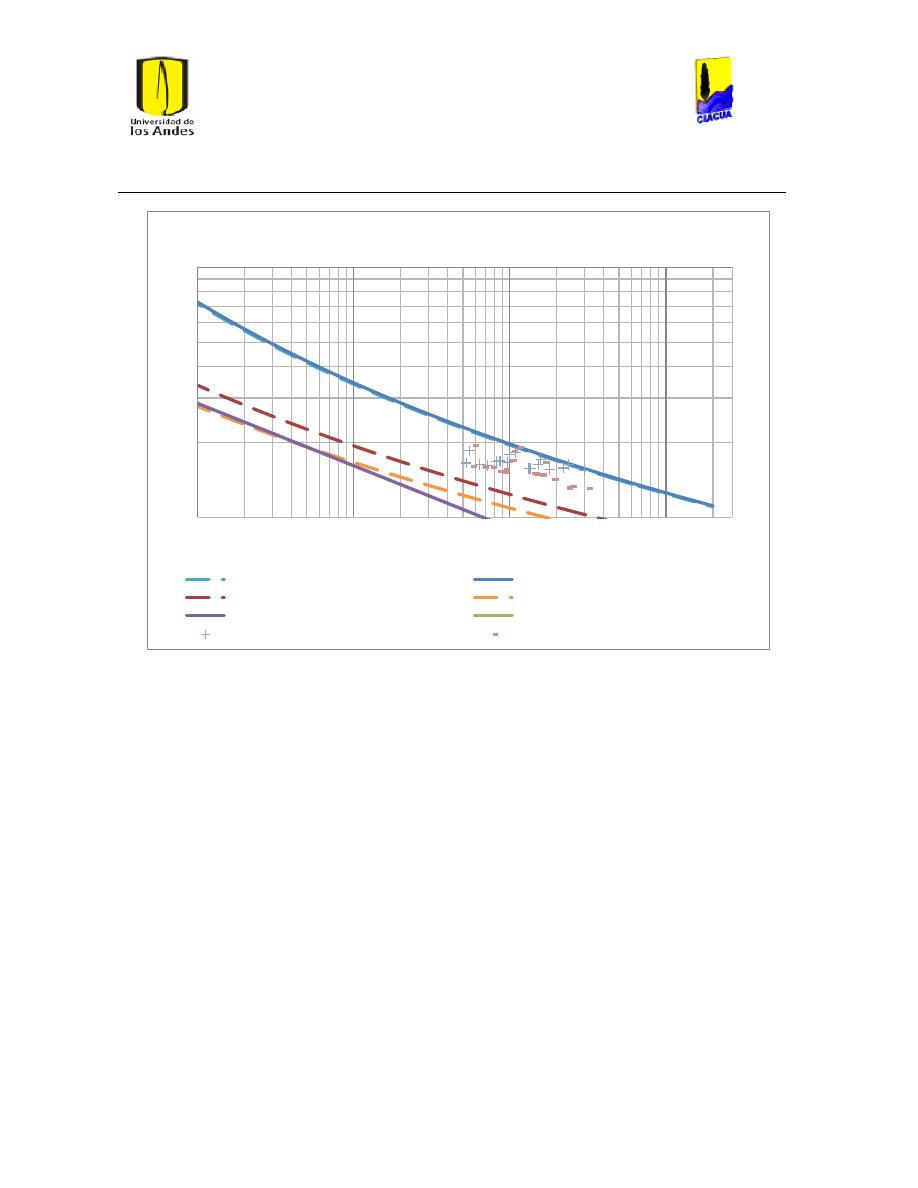
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
188
ILUSTRACIÓN 167 DIAGRAMA DE MOODY DE RED DE ANDALUCÍA TRAMOS CON HAZEN-WILLIAMS
MAYOR PARA EL CAUDAL MEDIO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Andalucía Qmed (Diferencia Número de Reynolds
100000-200000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
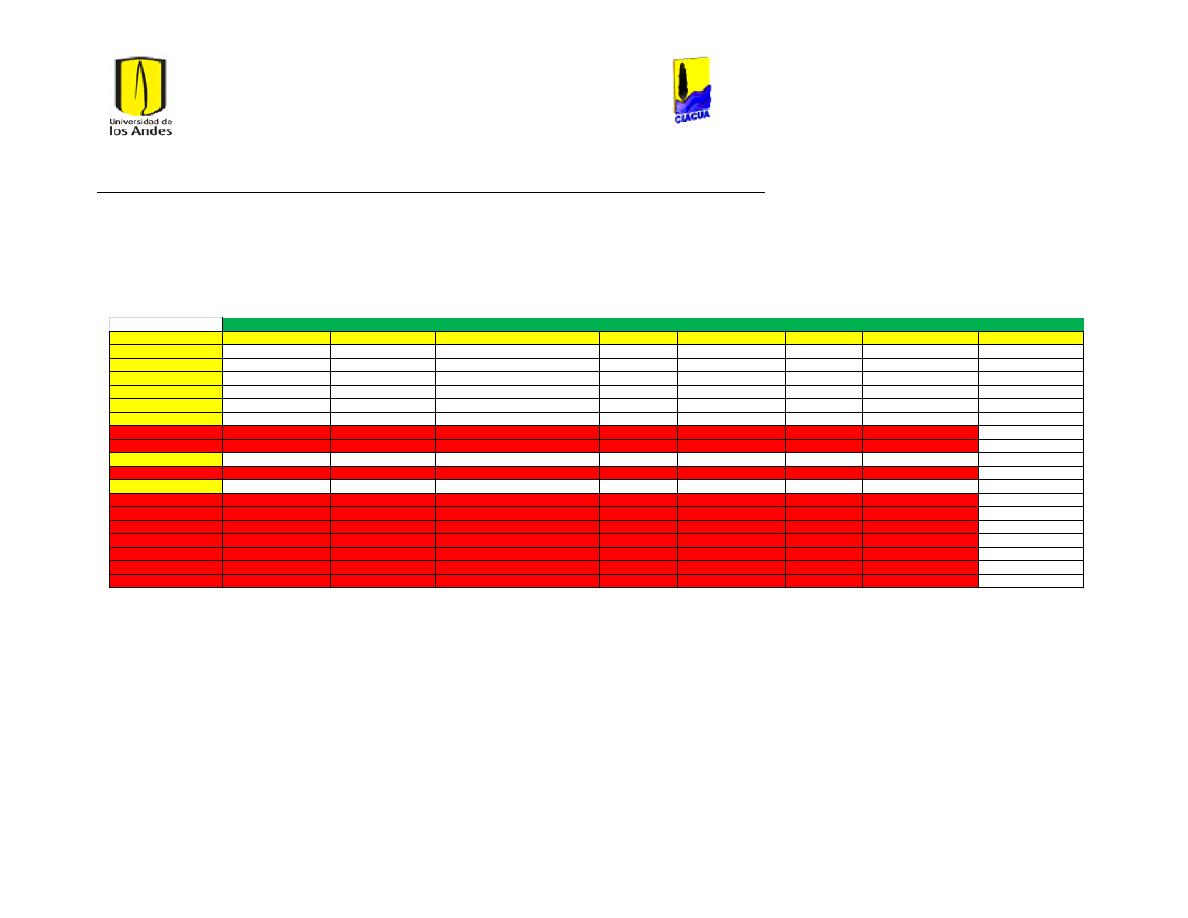
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
189
TABLA 25 RESUMEN DE TRAMOS DE LA RED ANDALUCÍA PARA EL CAUDAL MEDIO PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE 100000
Y 200000.
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Porcentual
Tramo 1/400(1m)
1.3246161
1.2731166
1.44E+05
3.55E+06
0.016286
3.70E+06
0.013267
4.05%
Tramo 2/400
0.486968475
0.468815599
5.07E+04
1.31E+06
0.016706
1.36E+06
0.015133
3.87%
Tramo 3/400
0.457533009
0.439380133
5.07E+04
1.23E+06
0.016747
1.28E+06
0.015258
4.13%
Tramo 1/450(14 m)
1.4152378
1.329811601
2.12E+05
3.30E+06
0.015729
3.51E+06
0.013074
6.42%
Tramo 2/450
0.556147736
0.518839081
9.26E+04
1.29E+06
0.016804
1.38E+06
0.01545
7.19%
Tramo 1/500
0.382239542
0.352280529
6.69E+04
7.87E+05
0.016488
8.54E+05
0.015937
8.50%
Tramo 1/600
2.51929687
2.41194912
2.00E+05
4.49E+06
0.015366
4.69E+06
0.012981
4.45%
Tramo 2/600
1.274045443
1.222546571
9.59E+04
2.28E+06
0.016226
2.37E+06
0.014768
4.21%
Tramo 3/600
0.547248601
0.517153966
5.60E+04
9.63E+05
0.016224
1.02E+06
0.015816
5.82%
Tramo 1/700(26 m)
1.772082763
1.696207088
1.21E+05
2.71E+06
0.015499
2.83E+06
0.014115
4.47%
Tramo 2/700
0.713206485
0.675897677
5.95E+04
1.08E+06
0.016111
1.14E+06
0.015838
5.52%
Tramo 1/800(15m)
1.538275062
1.462399819
1.06E+05
2.04E+06
0.015678
2.15E+06
0.014882
5.19%
Tramo 2/800
1.501440014
1.425564771
1.06E+05
1.99E+06
0.015694
2.10E+06
0.014927
5.32%
Tramo 1/1100(1m)
2.440539436
2.334931916
1.07E+05
2.37E+06
0.017034
2.48E+06
0.016567
4.52%
Tramo 1/1300(8m)
1.772084907
1.696208493
6.52E+04
1.46E+06
0.016592
1.52E+06
0.016904
4.47%
Tramo 1/1600(2m)
2.440537959
2.334932191
7.37E+04
1.63E+06
0.018196
1.70E+06
0.019035
4.52%
Tramo 1/1800
2.519296587
2.411951382
6.66E+04
1.50E+06
0.017755
1.56E+06
0.01833
4.45%
Tramo 2/1800
1.417644282
1.332219037
5.30E+04
8.27E+05
0.01845
8.80E+05
0.019417
6.41%
Andalucía Qmed (Diferencias número de Reynolds 100000-200000) Hazen Mayor
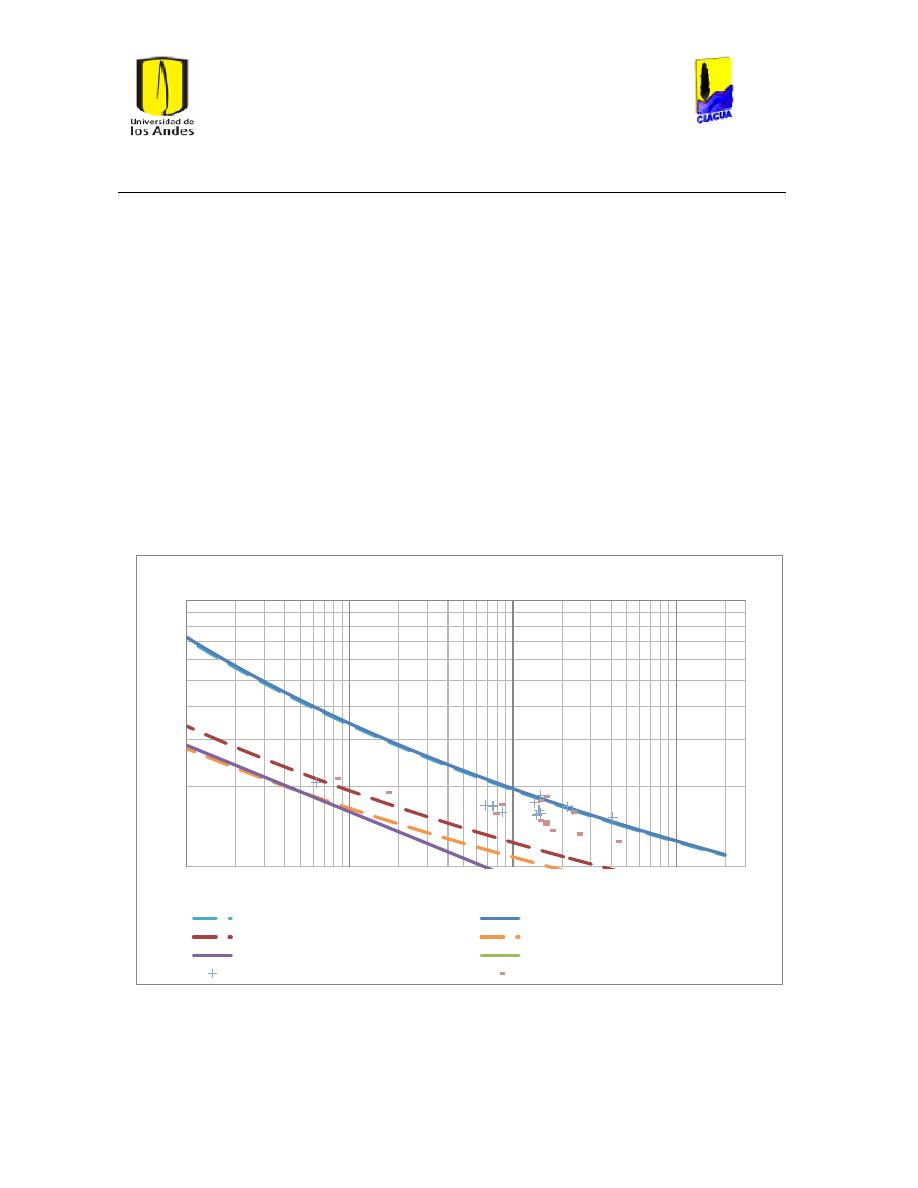
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
190
Como se mencionó anteriormente, los resultados del caudal medio son muy similares a lo
encontrado con el caudal mínimo y con los resultados encontrados en la red Ginebra y la red
matriz de Medellín. Se puede ver que existe un desbalance de masa, una diferencia importante
en el diagrama de Moody, donde se ve claramente un desfase en el número de Reynolds y
también diferencias considerables a la hora de calcular el factor de fricción. Así mismo, se
observó que el efecto se vio agravado, tanto en el número de tramos afectados, como en la
magnitud de los errores.
Un detalle a mencionar es que no se deben subestimar la magnitud de los errores en los
factores de fricción ni en los caudales, teniendo en cuenta que la hidráulica de la red se está
solucionando de manera diferente y lo que es más importante, las pérdidas por fricción en la
red están directamente relacionadas con el factor de fricción y directamente relacionadas con
el cuadrado de la velocidad.
Finalmente se van a presentar los resultados de la red en la hora de máximo consumo:
ILUSTRACIÓN 168 DIAGRAMA DE MOODY DE RED DE ANDALUCÍA TRAMOS CON HAZEN-WILLIAMS
MAYOR PARA EL CAUDAL MÁXIMO1.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Andalucía Qmax (Diferencia Número de Reynolds
100000-300000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
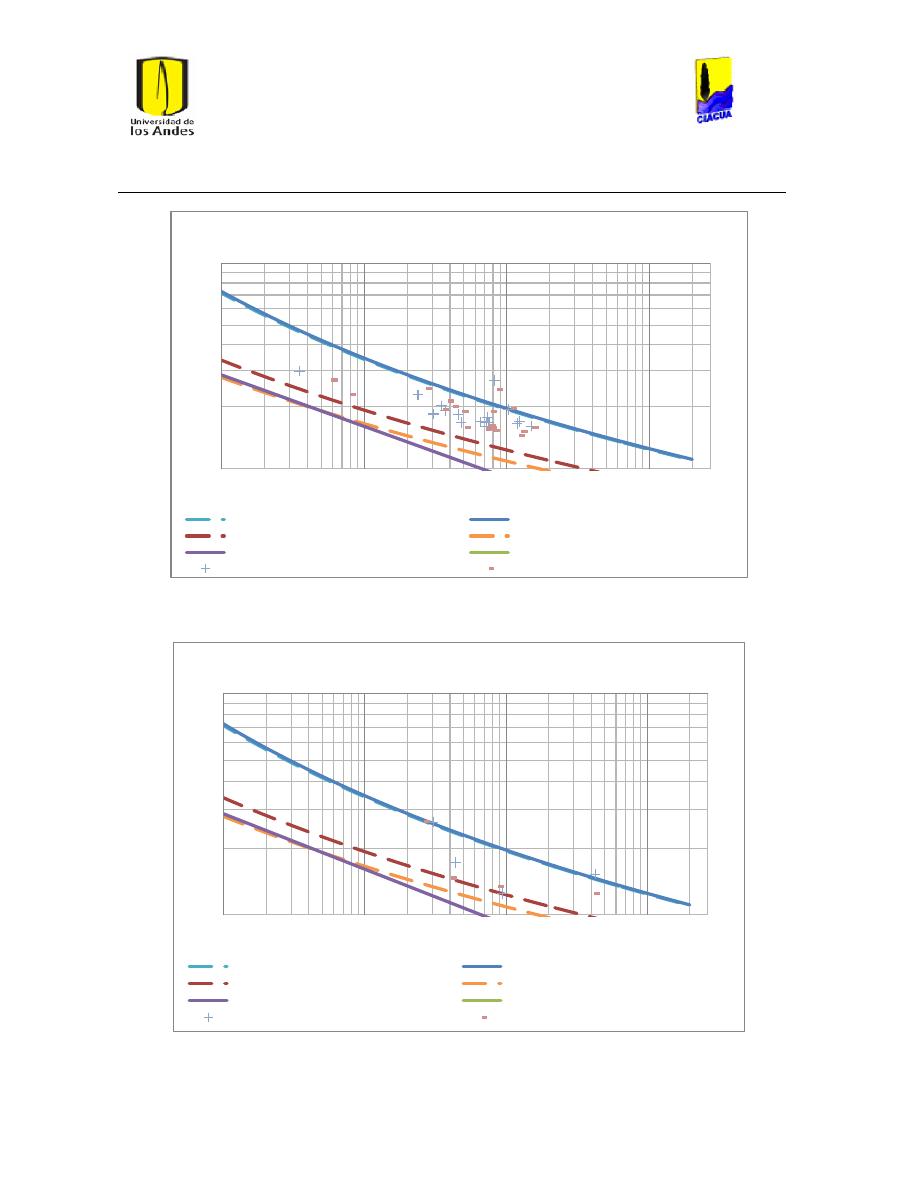
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
191
ILUSTRACIÓN 169 DIAGRAMA DE MOODY DE RED DE ANDALUCÍA TRAMOS CON HAZEN-WILLIAMS
MAYOR PARA EL CAUDAL MÁXIMO2.
ILUSTRACIÓN 170 DIAGRAMA DE MOODY DE RED DE ANDALUCÍA TRAMOS CON DARCY-WEISBACH
MAYOR PARA EL CAUDAL MÁXIMO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Andalucía Qmax (Diferencia Número de
Reynolds 50000-100000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Andalucía Qmax (Diferencia Número de
Reynolds 50000-100000 Darcy Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
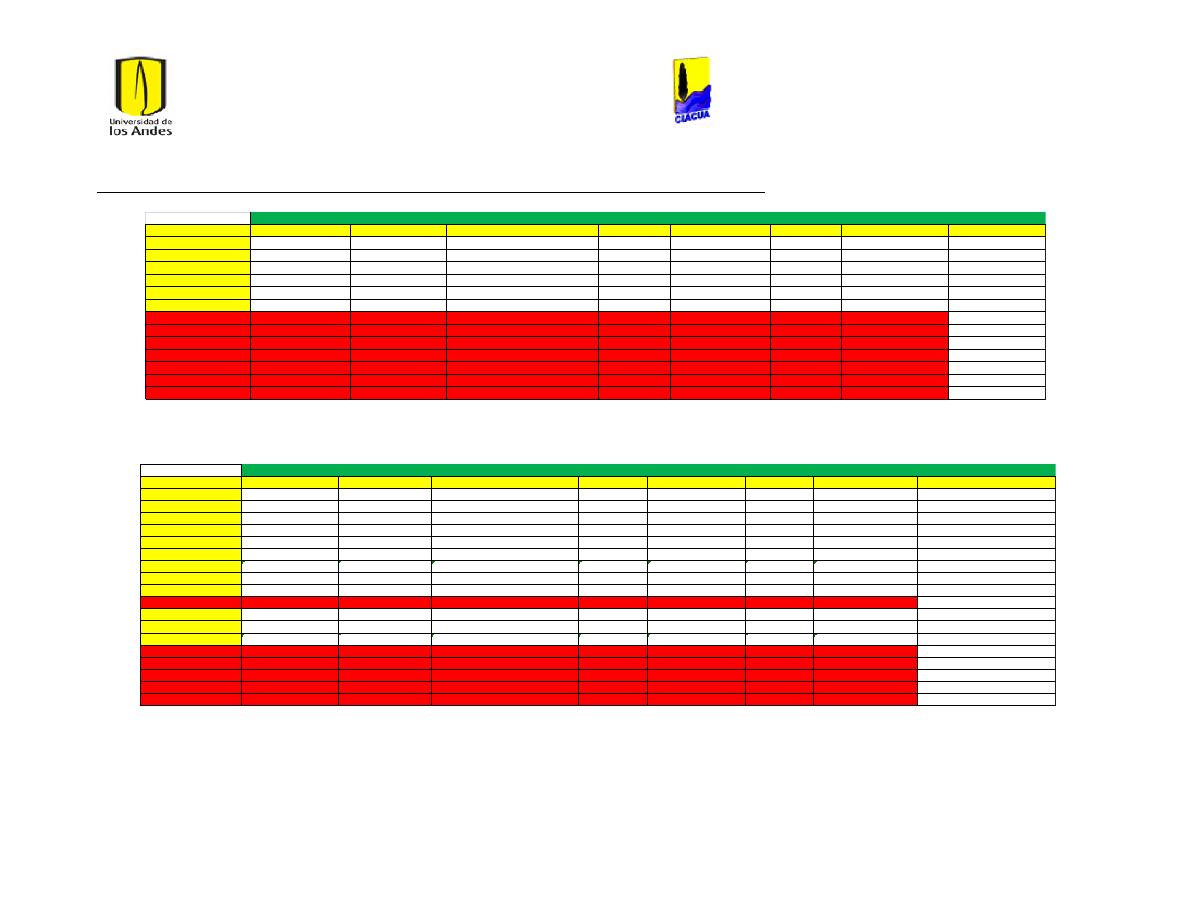
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
192
TABLA 26 RESUMEN DE TRAMOS DE LA RED ANDALUCÍA PARA EL CAUDAL MÁXIMO 1 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE
100000 Y 300000.
TABLA 27 RESUMEN DE TRAMOS DE LA RED ANDALUCÍA PARA EL CAUDAL MÁXIMO 2 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE
50000 Y 100000.
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Porcentual
Tramo 1/400 (1m)
1.336721285
1.251016627
2.39E+05
3.49E+06
0.016295
3.73E+06
0.013255
6.85%
Tramo 1/450(14m)
1.022125493
0.893315668
3.20E+05
2.22E+06
0.015874
2.54E+06
0.013652
14.42%
Tramo 2/450(13m)
0.463505432
0.410747645
1.31E+05
1.02E+06
0.016965
1.15E+06
0.015818
12.84%
Tramo 1/600
3.473507572
3.301068065
3.21E+05
6.14E+06
0.015287
6.47E+06
0.012462
5.22%
Tramo 2/600
1.25140986
1.165704982
1.60E+05
2.17E+06
0.01625
2.33E+06
0.0148
7.35%
Tramo 3/600
0.135378642
0.050535
1.58E+05
9.41E+04
0.020735
2.52E+05
0.019026
167.89%
Tramo 1/700
1.453820098
1.319000393
2.15E+05
2.10E+06
0.01563
2.32E+06
0.014472
10.22%
Tramo 1/800
1.059387768
0.92456921
1.88E+05
1.29E+06
0.016019
2.15E+06
0.014882
66.38%
Tramo 2/800
0.088147058
0.003303448
1.18E+05
4.61E+03
0
1.23E+05
0.021442
2568.34%
Tramo 1/1100(1 m)
3.364344602
3.193374214
1.74E+05
3.24E+06
0.016791
3.42E+06
0.016025
5.35%
Tramo 1/1300(8m)
1.45382075
1.319001909
1.16E+05
1.13E+06
0.016902
1.25E+06
0.017165
10.22%
Tramo 1/1600(2m)
3.364345144
3.193372132
1.19E+05
2.23E+06
0.01853
2.35E+06
0.018364
5.35%
Tramo 1/1800
3.473507007
3.30106863
1.07E+05
2.05E+06
0.017395
2.16E+06
0.017686
5.22%
Andalucía Qmáx (Diferencias número de Reynolds 100000-300000) Hazen Mayor
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/400
0.437297634
0.404428658
9.18E+04
1.13E+06
0.016802
1.22E+06
0.015351
8.13%
Tramo 2/400
0.387639861
0.354771011
9.18E+04
9.91E+05
0.016895
1.08E+06
0.015598
9.26%
Tramo 3/400
0.660977397
0.637131578
6.66E+04
1.78E+06
0.016545
1.85E+06
0.014539
3.74%
Tramo 4/400
0.276631182
0.258013224
5.20E+04
7.20E+05
0.016766
7.72E+05
0.015914
7.22%
Tramo 1/450(5m)
0.773151269
0.742804409
7.53E+04
1.84E+06
0.016959
1.92E+06
0.015175
4.09%
Tramo 1/600
0.615466935
0.582596891
6.12E+04
1.08E+06
0.016718
1.15E+06
0.016173
5.64%
Tramo 1/700(25m)
0.728463284
0.675704484
8.42E+04
1.08E+06
0.016107
1.16E+06
0.015793
7.81%
Tramo 1/1100
0.728462569
0.67570395
5.36E+04
6.86E+05
0.018354
7.40E+05
0.019005
7.81%
Tramo 1/1200
0.096001542
0.011158183
7.90E+04
1.04E+04
0
8.94E+04
0.02703
760.37%
Tramo 2/1200
2.465549058
2.397585476
6.33E+04
2.23E+06
0.016092
2.29E+06
0.015868
2.83%
Tramo 1/1400
0.680851018
0.578302114
8.18E+04
4.61E+05
0.018463
5.43E+05
0.019339
17.73%
Tramo 2/1400
0.151213337
0.066370386
6.77E+04
5.29E+04
0.029795
1.21E+05
0.02296
127.83%
Tramo 1/1600
0.837071079
0.751368432
5.98E+04
5.24E+05
0.020228
5.84E+05
0.021339
11.41%
Tramo 1/1700(6m)
1.780161557
1.679770542
6.60E+04
1.10E+06
0.017807
1.17E+06
0.018904
5.98%
Tramo 1/1800
1.026184433
0.897374767
7.99E+04
5.57E+05
0.019158
6.37E+05
0.020108
14.35%
Tramo 1/2400
3.473508703
3.301066934
8.02E+04
1.54E+06
0.019433
1.62E+06
0.019658
5.22%
Tramo 1 /2800
1.027801191
0.898991996
5.14E+04
3.59E+05
0.022885
4.10E+05
0.024512
14.33%
Tramo 1/3000(3m)
3.473508986
3.301070892
6.42E+04
1.23E+06
0.02679
1.29E+06
0.024196
5.22%
Andalucía Qmáx (Diferencias número de Reynolds 50000-100000) Hazen Mayor
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
193
TABLA 28 RESUMEN DE TRAMOS DE LA RED ANDALUCÍA PARA EL CAUDAL MÁXIMO 3 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE
50000 Y 100000.
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
0.193565348
0.207216669
-4.36E+04
6.61E+05
0.017206
6.18E+05
0.014661
-6.59%
0.41481193
0.440925305
-8.33E+04
1.41E+06
0.012501
1.32E+06
0.013388
-5.92%
3.405600123
3.443189868
-1.20E+05
1.10E+07
0.00956
1.09E+07
0.009828
-1.09%
3.405598277
3.443189004
-7.00E+04
6.41E+06
0.015278
6.34E+06
0.012493
-1.09%
0.637332891
0.737308674
-6.20E+04
4.57E+05
0.026208
3.95E+05
0.026306
-13.56%
Andalucía Qmáx (Diferencias número de Reynolds 50000-100000) Darcy Mayor

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
194
Los resultados con máximo caudal muestran que la magnitud de las diferencias aumentó de
manera considerable; esto se puede ver en el diagrama de Moody donde es más evidente el
desfase en los números de Reynolds y las altas diferencias entre los factores de fricción
calculados. Por otro lado, al mirar las tablas de resumen, se puede ver que las diferencias en
estos casos alcanzaron unas magnitudes altas que confirman una vez más que la solución de la
hidráulica con la ecuación empírica, para este tipo de escenarios o redes (con tanques o
emisores y ramificaciones) pueden presentar diferencias radicales en aspectos como las
pérdidas por fricción, factores de fricción de las tuberías y números de Reynolds en cada uno
de los tramos.
En cuanto al funcionamiento de la red, las razones para que se presenten tantas diferencias
hidráulicas entre la ecuación de Hazen-Williams y la ecuación de Darcy-Weisbach, están
fundamentadas en lo que se ha documentado a lo largo de esta sección. Pero así mismo
también se basa en lo que los autores Liou (Liou, 1998) y Bombardelli (Fabián Bombardelli,
2003) describen en sus investigaciones. Al igual que estos autores, durante esta investigación
también se compararon los coeficientes teóricos de Hazen-Williams reportados en la
literatura, con los coeficientes hallados analizando los resultados de una red que utilizó la
ecuación de Darcy-Weisbach. Estos resultados se pueden ver en la Sección 4.3.4 Red
Andalucía, en donde se encontró que en efecto, la variabilidad del coeficiente de Hazen-
Williams es bastante significativa, demostrando una vez más que utilizar un coeficiente
constante es un riesgo de suma importancia. Otro aspecto relevante es el análisis realizado a
partir de los diámetros de la red que permitió concluir que incluso en grandes diámetros de
presentaban variaciones drásticas del coeficiente.
Al comparar los resultados del estudio de Bombardelli con lo encontrado en esta y las dos
redes anteriores, se puede ver con claridad que existe una variación para números de
Reynolds grandes (entre
estando estos números de Reynolds asociados
con tuberías de gran diámetro, o como en este caso de estudio, asociados con tuberías de
redes matrices. Conviene precisar también que, a pesar de que no siempre se presenten estos
rangos del número de Reynolds en tuberías de gran diámetro, durante esta investigación se
ha venido demostrando que las tuberías que están presentando las principales variaciones e
inconsistencias entre la ecuación de Hazen-Williams y la ecuación de Darcy-Weisbach, son las
tuberías de mayor diámetro, que transportan la cantidad más importante de caudal en la red
y también las tuberías de las ramificaciones que se dirigen a los diferentes tanques.
4.4.5 RED DE BOMBEO DTOWN
La red de Dtown, se trabajó con el fin de observar los efectos que podía tener en la hidráulica
el utilizar la ecuación de Hazen-Williams con coeficientes constantes. Esta red a diferencia de
las anteriores, tiene unas características únicas, estas son: La presencia de bombas para
entregar el caudal, los diámetros de las tuberías no superan los 600 mm y al ser tan pequeños,
la red estaba compuesta principalmente por tuberías de PVC.
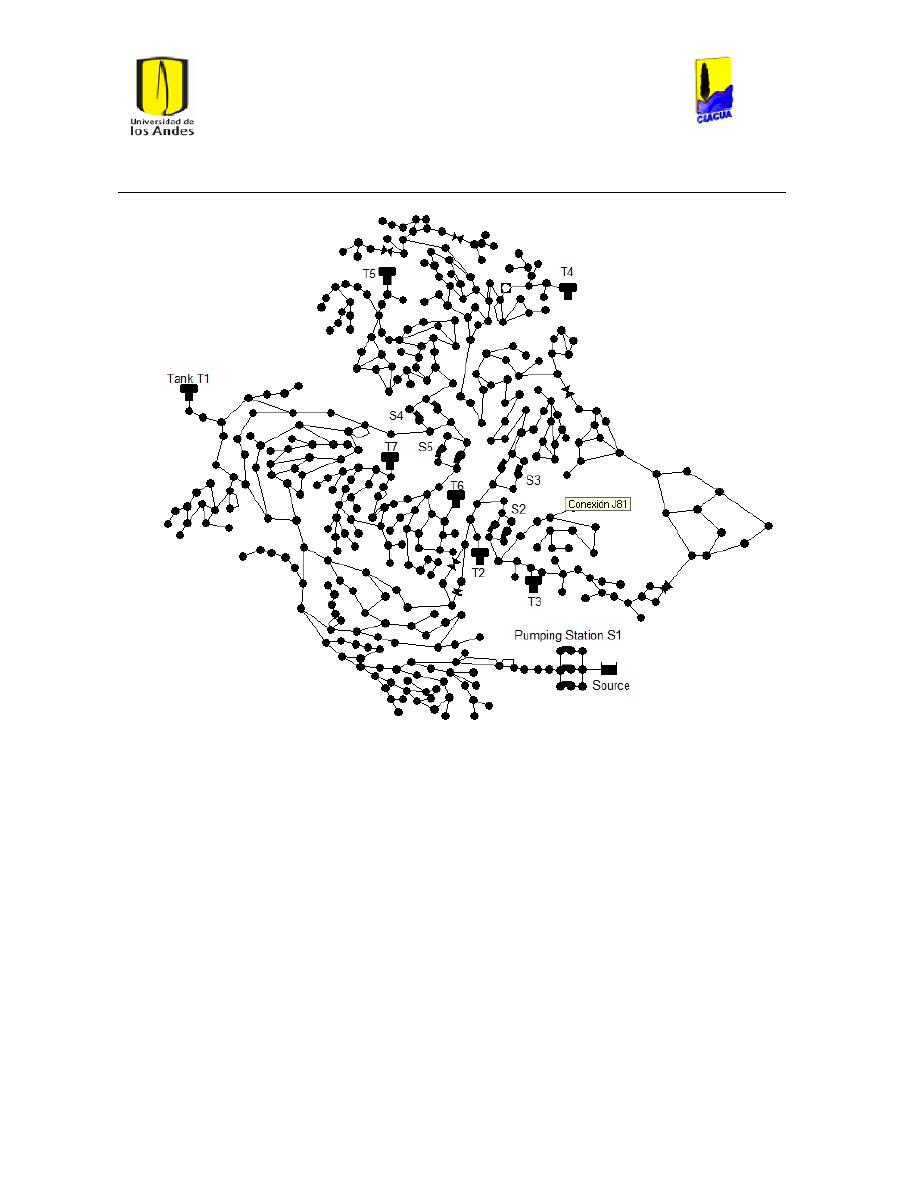
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
195
ILUSTRACIÓN 171 RED DTOWN CON SUS RESPECTIVOS TANQUES.
Antes de comenzar, hay que aclarar que si bien muchos de los resultados arrojaron
similitudes con lo que se ha encontrado hasta el momento, esta red presentó diferencias
importantes ya que los momentos en que se presentaron las diferencias más significativas
fueron en una serie de horas específicas del día y estas serán detalladas más adelante. A
continuación se muestran los resultados para los tanques de esta red; sin embargo no se
analizaron tuberías específicas como en los demás casos ya que está más que demostrado que
existen diferencias en los números de Reynolds del sistema; lo que si se realizó fue identificar
aquellas tuberías que presentaban las diferencias más significativas y en que horarios
específicos.
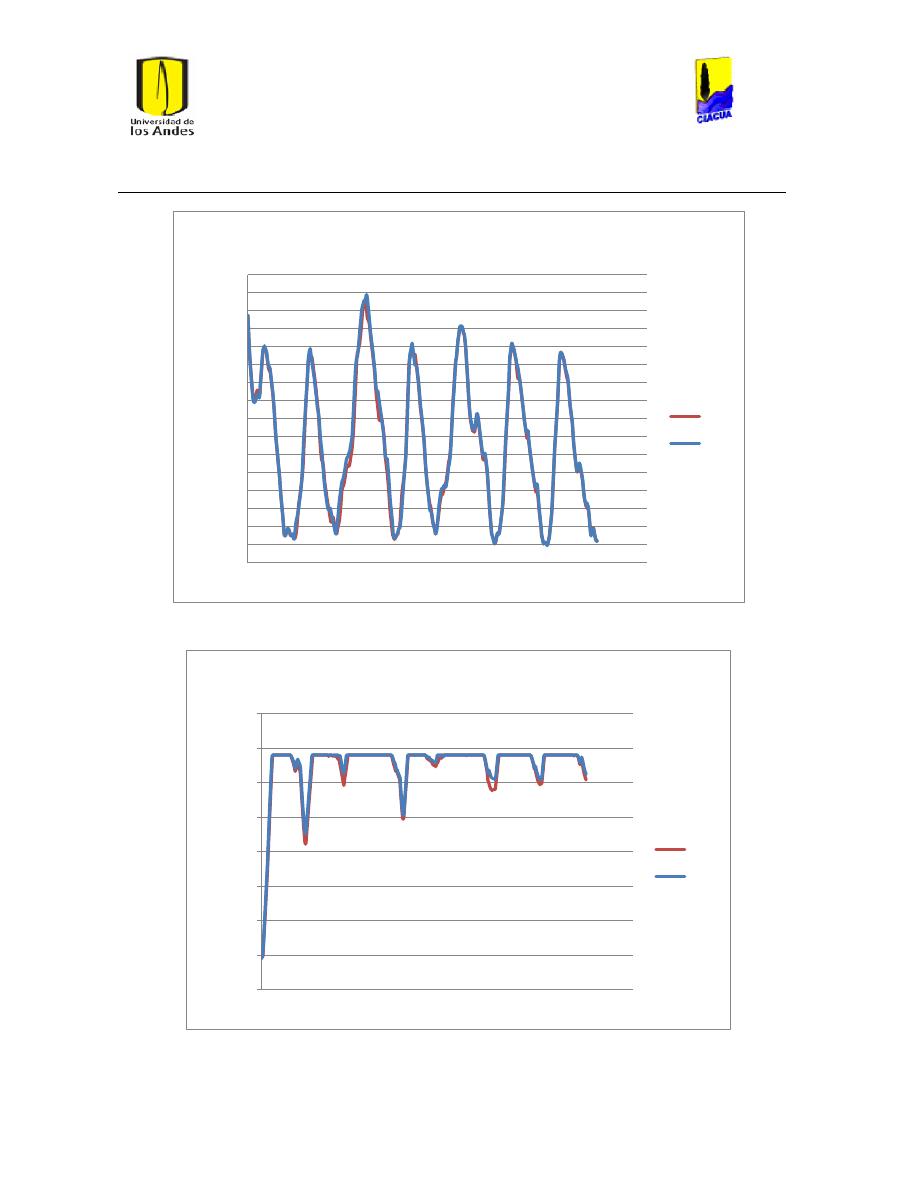
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
196
ILUSTRACIÓN 172 NIVEL TANQUE 1 RED DTOWN.
ILUSTRACIÓN 173 NIVEL TANQUE 2 RED DTOWN.
0.5
0.7
0.9
1.1
1.3
1.5
1.7
1.9
2.1
2.3
2.5
2.7
2.9
3.1
3.3
3.5
3.7
Ni
vel
(m
)
Tiempo (h)
Tanque 1 Dtown
H-W
D-W
2.5
3
3.5
4
4.5
5
5.5
6
6.5
N
iv
e
l (
m
)
Tiempo (h)
Tanque 2 Dtown
H-W
D-W
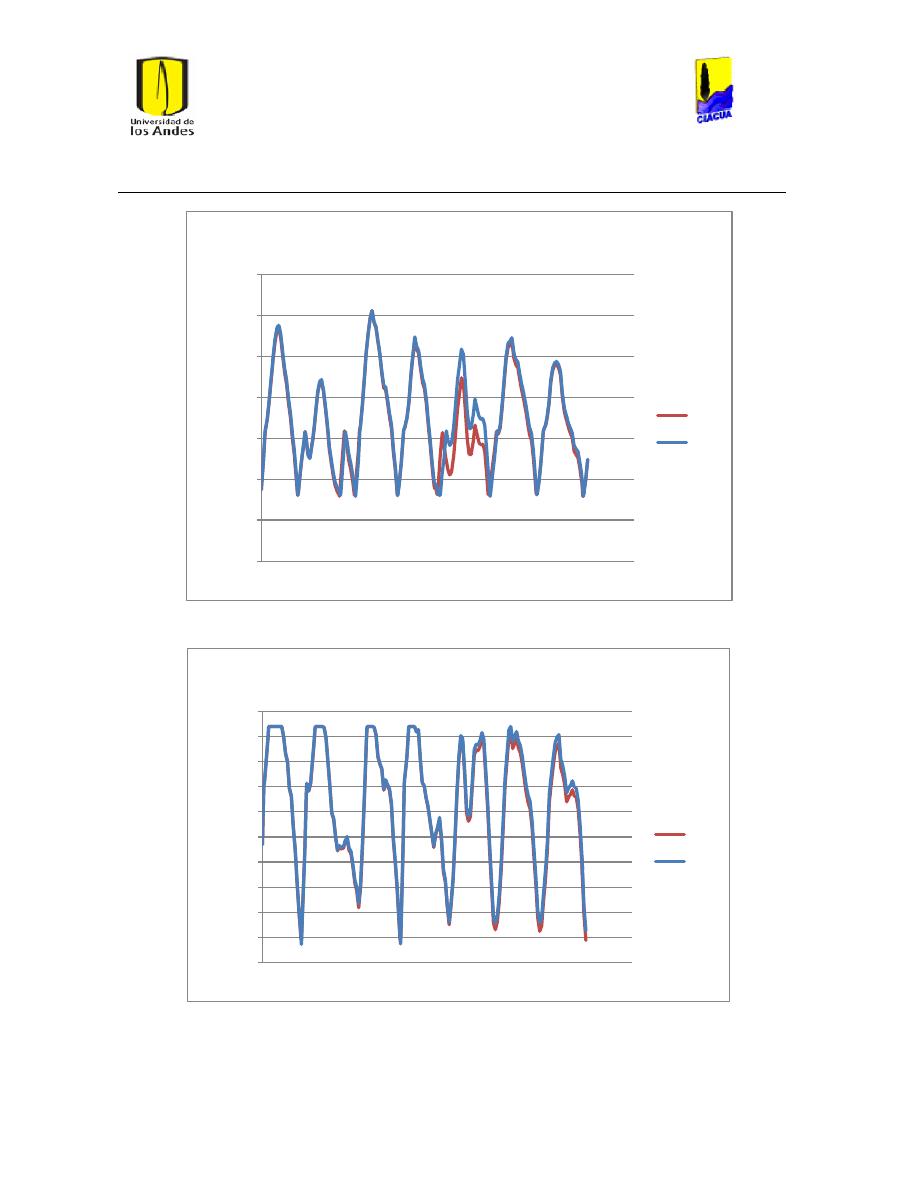
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
197
ILUSTRACIÓN 174 NIVEL TANQUE 3 RED DTOWN.
ILUSTRACIÓN 175 NIVEL TANQUE 4 RED DTOWN.
2.5
3
3.5
4
4.5
5
5.5
6
N
iv
e
l (
m
)
Tiempo (h)
Tanque 3 Dtown
H-W
D-W
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
N
iv
e
l (
m
)
Tiempo (h)
Tanque 4 Dtown
H-W
D-W
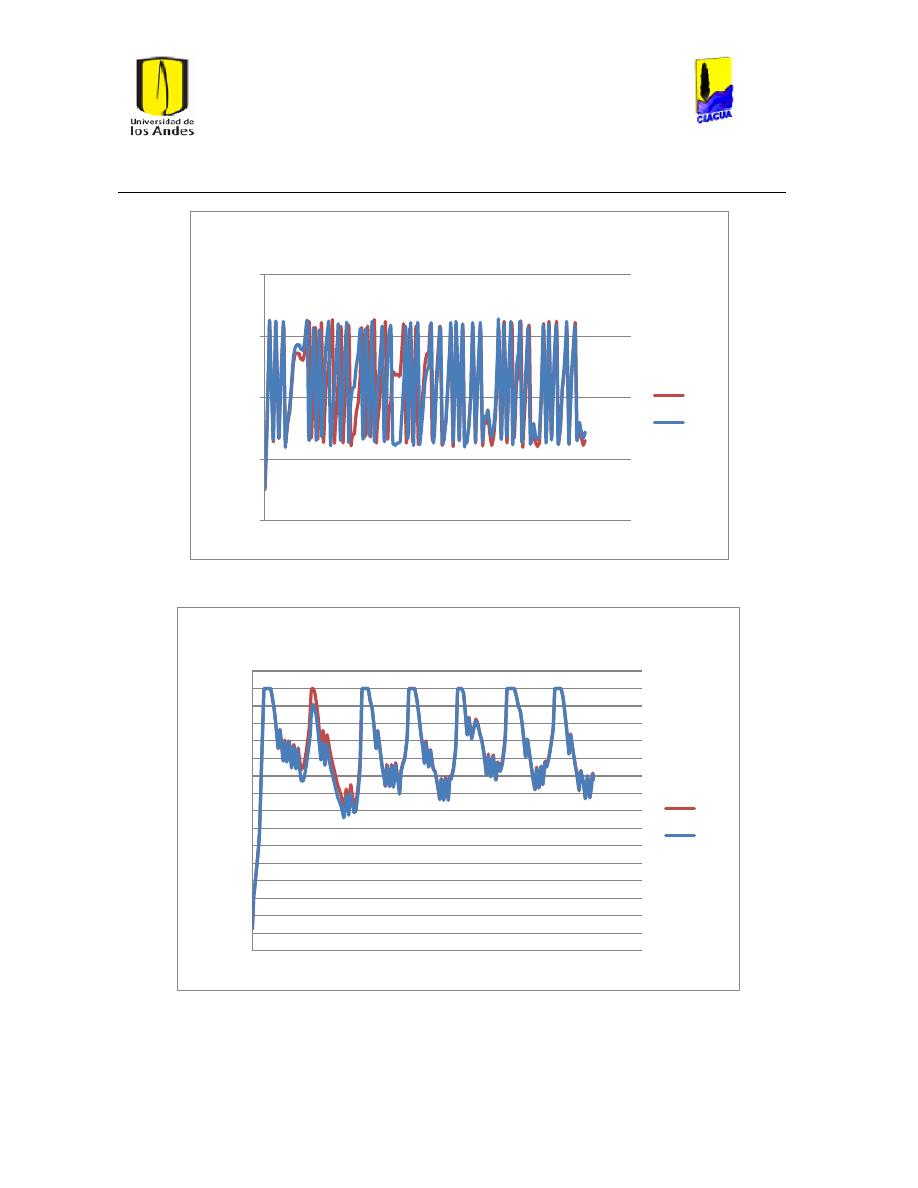
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
198
ILUSTRACIÓN 176 NIVEL TANQUE 5 RED DTOWN.
ILUSTRACIÓN 177 NIVEL TANQUE 6 RED DTOWN.
2
2.5
3
3.5
4
N
iv
e
l (
m
)
Tiempo (h)
Tanque Dtown
H-W
D-W
2.5
2.7
2.9
3.1
3.3
3.5
3.7
3.9
4.1
4.3
4.5
4.7
4.9
5.1
5.3
5.5
5.7
Ni
vel
(m
)
Tiempo (h)
Tanque 6 Dtown
H-W
D-W
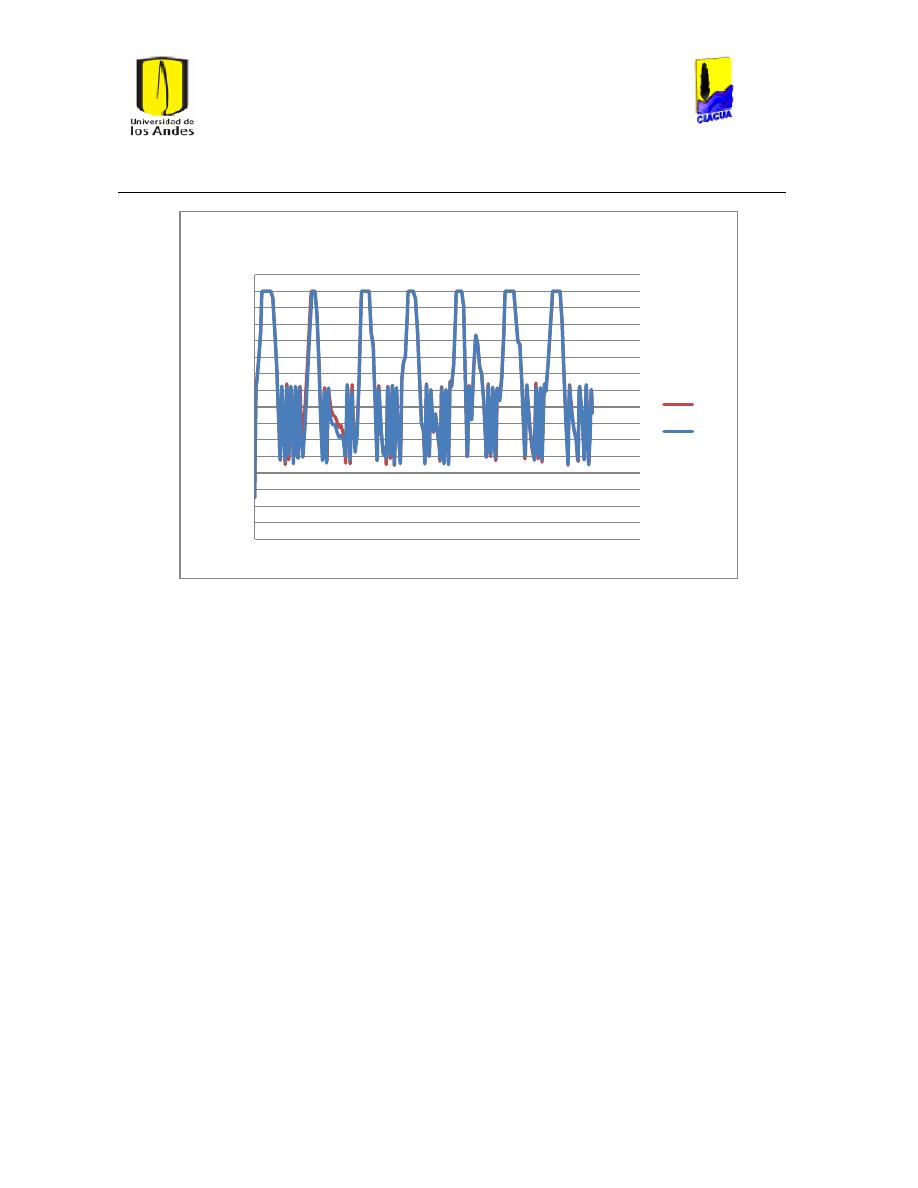
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
199
ILUSTRACIÓN 178 NIVEL TANQUE 7 RED DTOWN.
Los resultados que arroja el estudio de los tanques de la red de bombeo de Dtown son
bastante reveladores ya que pese a ser una red con diámetros más bajos que las redes
trabajadas anteriormente, estos muestran una gran similitud. Si se analizan los tanques 3 y 5
de esta red, se puede ver que tienen diferencias en los patrones de llenado de los tanques así
como en los tiempos de vaciado. En el tanque 3 se puede ver que en un período de tiempo, el
llenado con la ecuación de Hazen-Williams es menor que con la ecuación de Darcy-Weisbach.
Sin embargo, si se observa el tanque 5 se puede ver que en más de un período de tiempo, el
llenado del tanque es mayor con la ecuación de Hazen-Williams y lo que es más importante
aún, hay momentos donde se ve claramente que el tanque se está vaciando a una gran
velocidad con la ecuación de Darcy-Weisbach, mientras que en esos tiempos el tanque se sigue
llenado o su vaciado es muy poco con la ecuación de Hazen-Williams.
Lo anterior parece coincidir con lo que se encontró inicialmente en la red de Ginebra; es decir,
la ecuación de Hazen-Williams tiende a subestimar o sobrestimar los niveles de los tanques en
la red; considerando además que esto ocurre bajo un mismo escenario, lo que implica que las
hidráulica al ejecutar la ecuación de Hazen-Williams es diferente a la hidráulica con la
ecuación de Darcy-Weisbach. Si bien, los resultados que arroja esta red muestran tendencias
similares a los de las redes estudiadas anteriormente, cabe resaltar que las diferencias
hidráulicas en los tramos de esta red fueron las más grandes en términos de magnitud del
desbalance de masa, números de Reynolds de las tuberías y por ende cálculo del factor de
fricción y pérdidas por fricción en la red. A continuación se van a mostrar las figuras de las
redes en los 3 períodos más significativos (horarios de consumo medio, máximo y mínimo).
2
2.2
2.4
2.6
2.8
3
3.2
3.4
3.6
3.8
4
4.2
4.4
4.6
4.8
5
5.2
N
iv
e
l (
m
)
Tiempo (h)
Tanque 7 Dtown
H-W
D-W
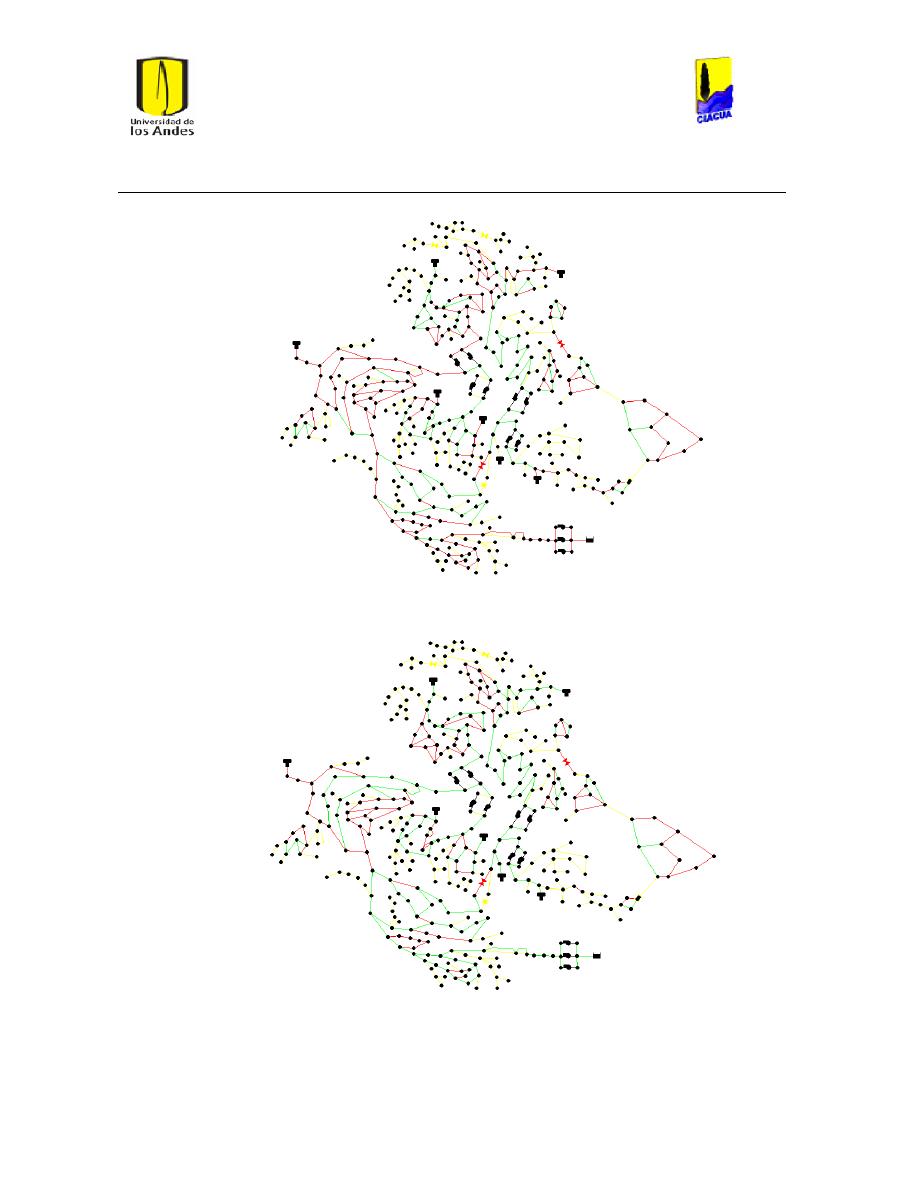
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
200
FIGURA 47 ESQUEMA DE LA RED EN LA HORA DE LA DEMANDA MEDIA DE LA RED DTOWN.
FIGURA 48 ESQUEMA DE LA RED EN LA HORA DE LA DEMANDA MÁXIMA DE LA RED DTOWN.
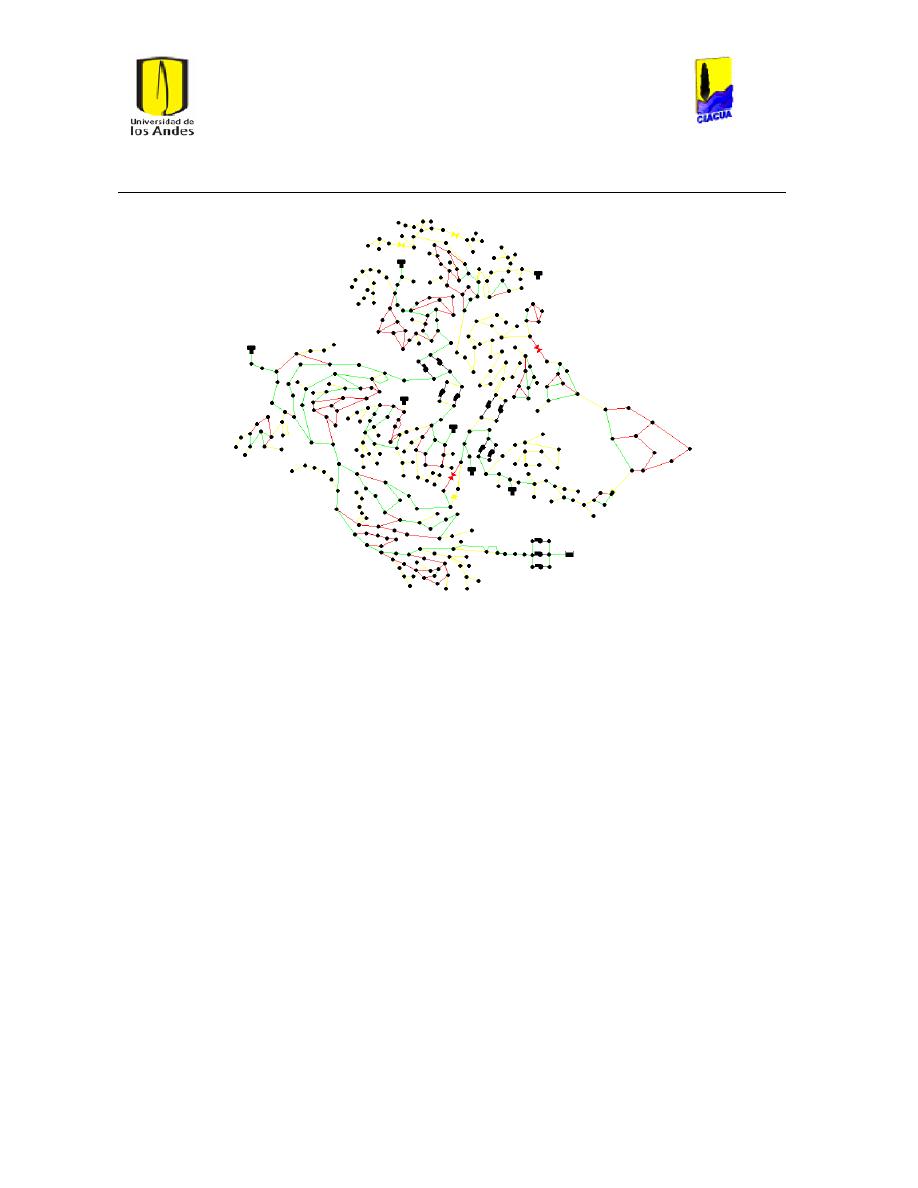
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
201
FIGURA 49 ESQUEMA DE LA RED EN LA HORA DE LA DEMANDA MÍNIMA DE LA RED DTOWN.
Después de sacar estas gráficas y analizar los resultados, se encontró que las hidráulicas de la
red en la hora de máximo y mínimo consumo no presentaban diferencias significativas entre
la ecuación físicamente basada y la ecuación empírica, mientras que en la hora de consumo
medio, la hidráulica cambiaba de manera radical. Este resultado fue bastante extraño
considerando lo que se había analizado anteriormente y es que el efecto hidráulico que
generaba la ecuación de Hazen-Williams frente a la ecuación de Darcy-Weisbach se veía
magnificado cuando se llegaba al horario de máximo consumo. Este fenómeno se estudiará
más en detalle al examinar lo que ocurre internamente en la red, en cada fracción de tiempo
(cada 15 minutos para 168 horas). Con base en esto, se identificaron las tuberías y sectores de
la red que estaban presentando las diferencias más significativas; el esquema de la red se
muestra a continuación:
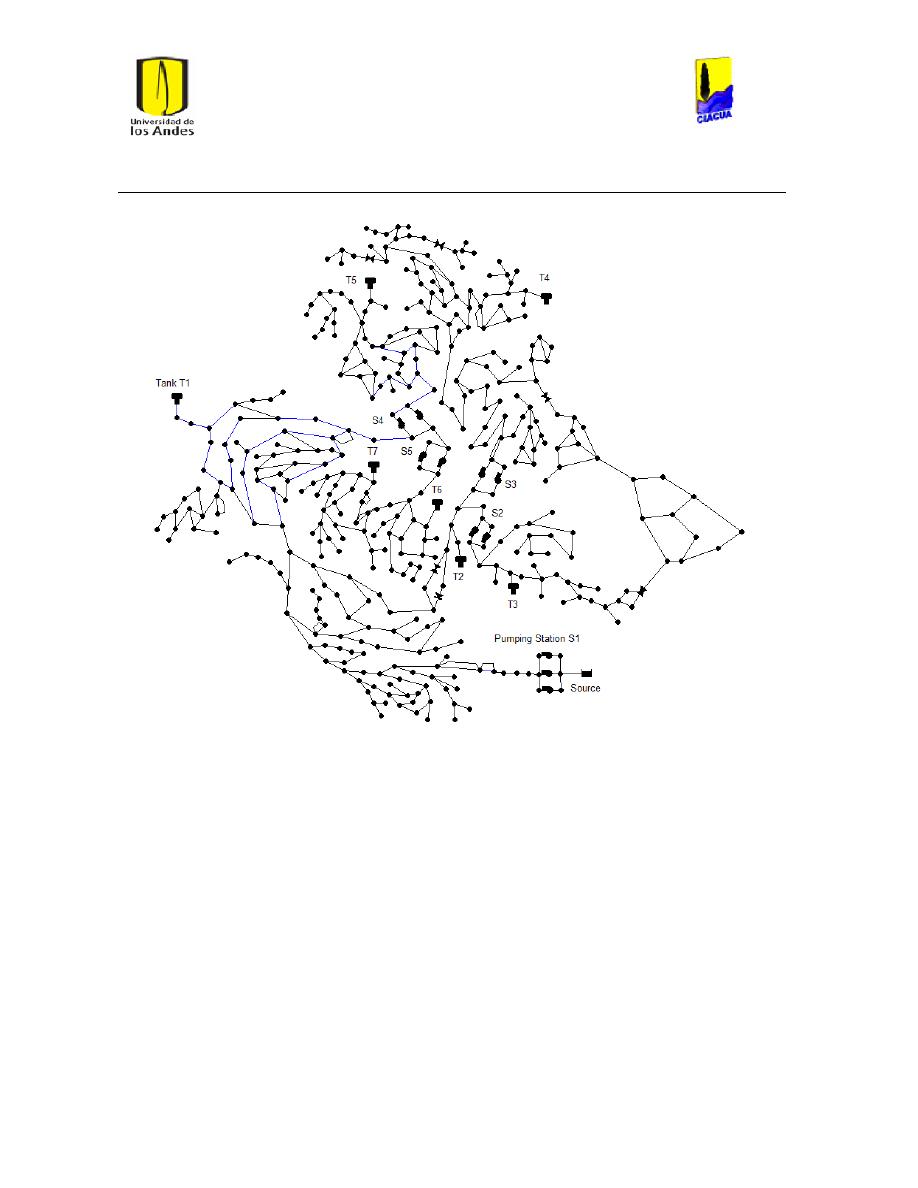
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
202
FIGURA 50 TUBERÍAS CON LAS DIFERENCIAS EN EL NÚMERO DE REYNOLDS.
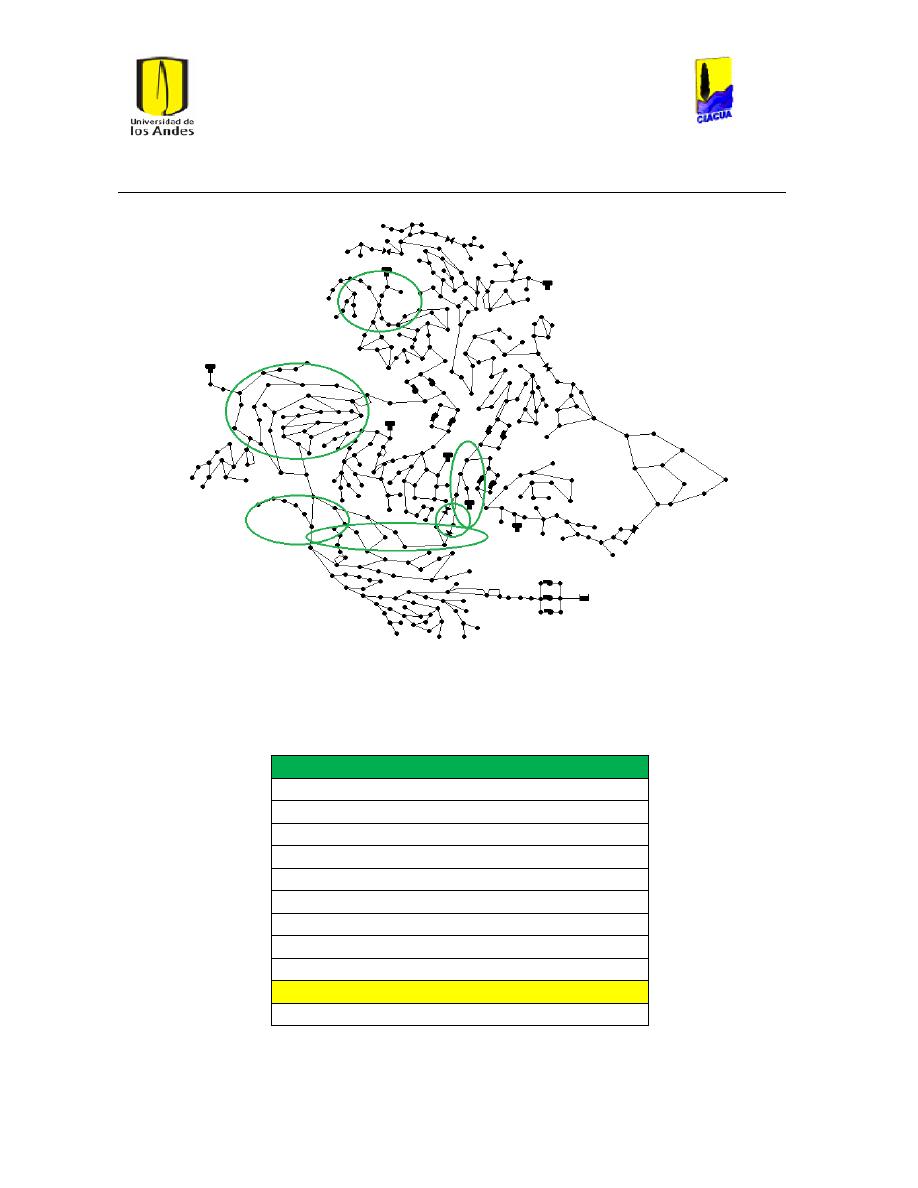
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
203
FIGURA 51 SECTORES CON LAS PRINCIPALES DIFERENCIAS HIRÁULICAS EN DTOWN.
Una vez identificados los sectores, se procedió a analizar los horarios en que se estaban
presentando las diferencias hidráulicas más significativas.
TABLA 29 TIEMPOS EN LOS QUE LA HIDRÁULICA DE LA RED DTOWN CAMBIA SIGNIFICATIVAMENTE.
Momentos con hidráulica diferente
05:45
10:45
17:30-24:15
26:00-31:00
35:00-38:45
43:00-56:00
73:00-76:45
79:15-81:15
93:45-95:15
Tiempo total de ejecución de la red
168:00:00

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
204
ILUSTRACIÓN 179 PATRONES 1 Y 5 DE LA RED DE DTOWN CON SUS HORARIOS DE DIFERENCIA
HIDRÁULICA.
ILUSTRACIÓN 180 PATRONES 2 Y 3 DE LA RED DTOWN CON SUS HORARIOS DE DIFERENCIA
HIDRÁULICA.
ILUSTRACIÓN 181 PATRÓN 4 DE LA RED DTOWN CON SUS HORARIOS DE DIFERENCIA HIDRÁULICA.
La tabla y las ilustraciones muestran que las principales diferencias entre la ecuación de
Hazen-Williams y la ecuación de Darcy-Weisbach se están presentando en los momentos del
día en los que se está pasando del caudal máximo al caudal mínimo. Si bien, cuando se llegan a
estos puntos ya la hidráulica parece igualarse entre las dos ecuaciones, las diferencias en
estos momentos del tiempo son bastante significativas. En las tablas que se muestran más
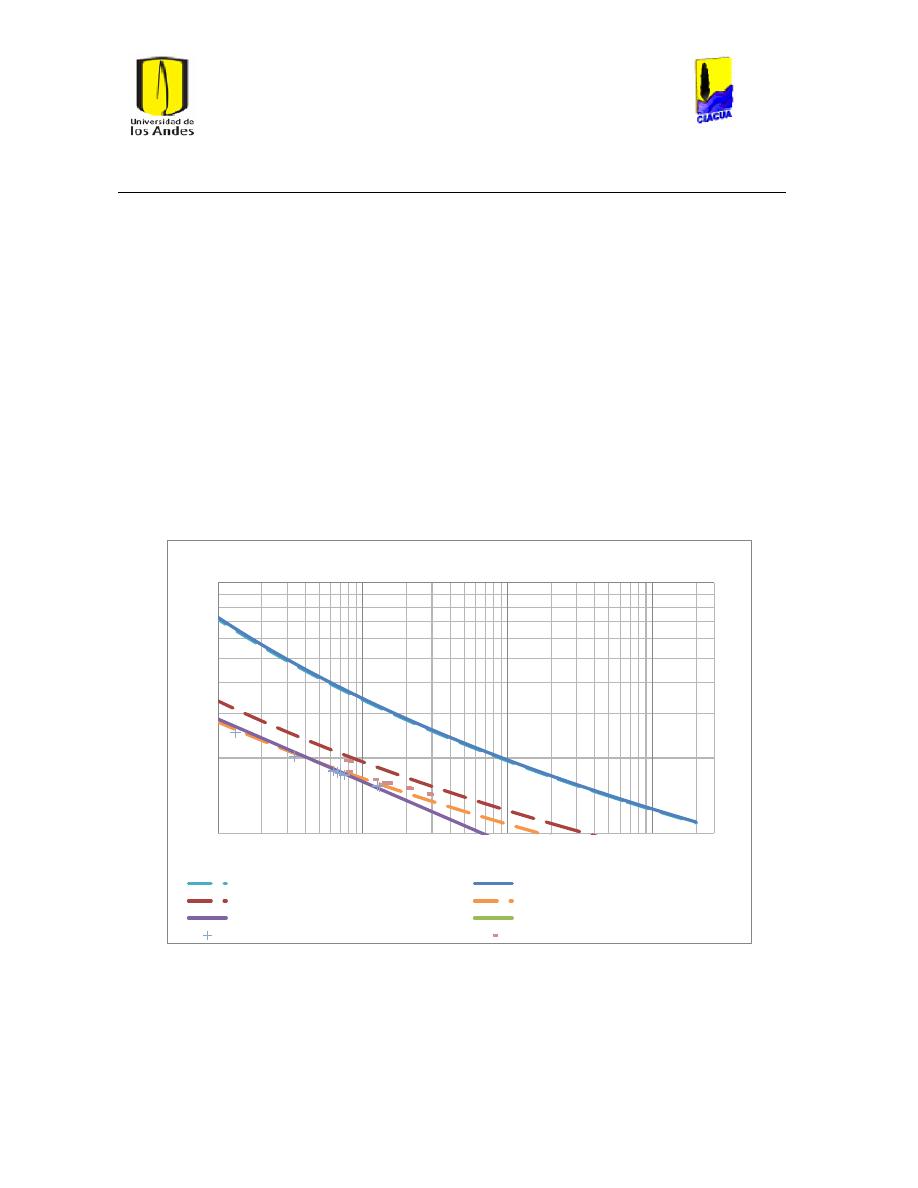
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
205
adelante se van a mostrar las altas diferencias que se presentan en los tramos de la red
identificados, así como los diagramas de Moody donde se va a evidenciar la magnitud de la
diferencia con respecto al número de Reynolds y el factor de fricción.
Todo lo anterior parece reforzar los análisis de la redes anteriores y prenden una nueva
alarma, ya que al limitarse el análisis del problema a solo tres momentos del día o de la
ejecución hidráulica, se pueden estar obviando efectos significativos de la ecuación de Hazen-
Williams; infortunadamente, estos cálculos y estos resultados se encontraron al final del
estudio, pues el enfoque de trabajar en tantas redes consumió una cantidad considerable de
tiempo. A futuro, se recomienda que se trabaje con solo un par de redes y se pueda estudiar
todo lo que se realizó durante esta investigación, pero analizando períodos de tiempo con
separación menor y de manera más detallada.
A continuación se presentan los resultados de los diagramas de Moody con los tramos de
tuberías que presentaron las diferencias hidráulicas más significativas, así como las tablas
resumen de la red.
ILUSTRACIÓN 182 DIAGRAMA DE MOODY RED DTOWN TRAMOS CON HAZEN-WILLIAMS MAYOR PARA
EL CAUDAL MEDIO 1.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Dtown Qmed (Diferencia Número de
Reynolds 100000-300000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
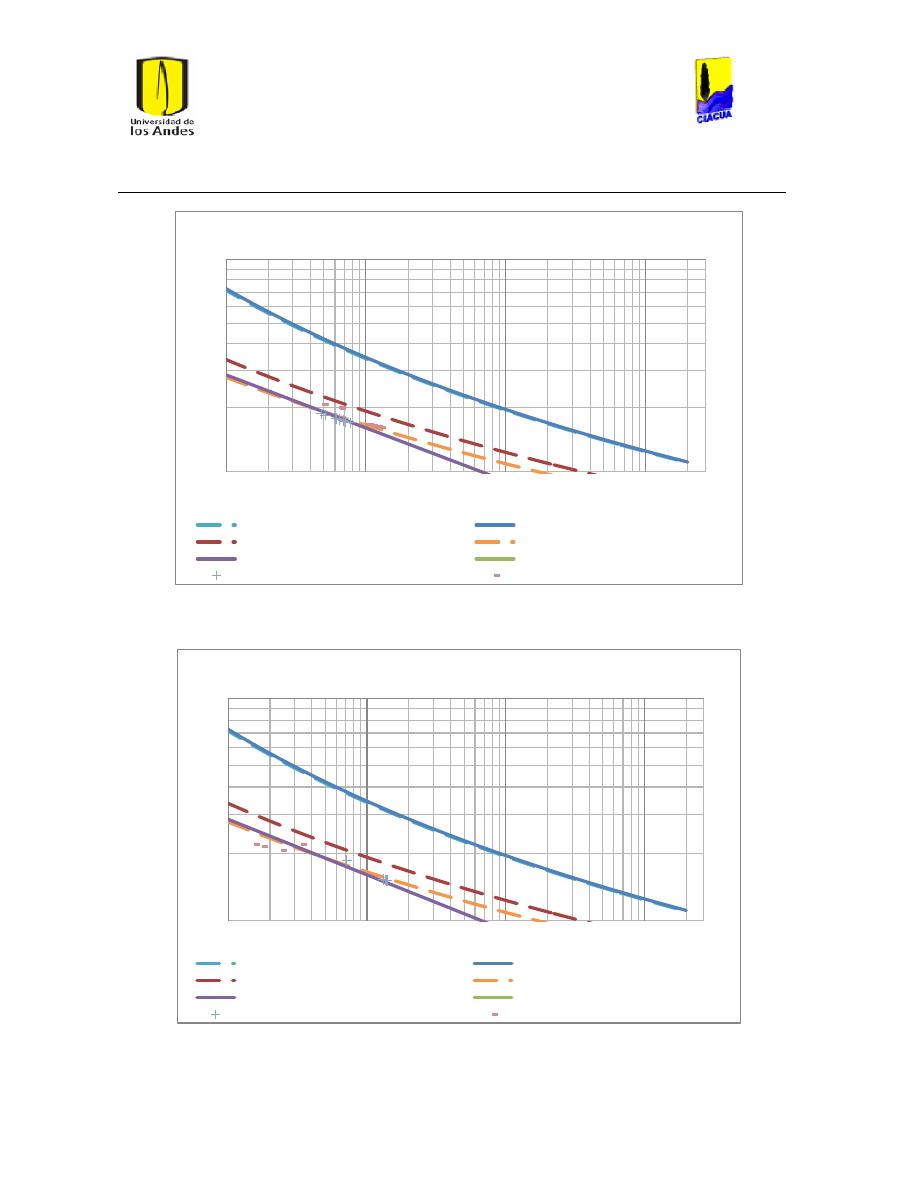
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
206
ILUSTRACIÓN 183 DIAGRAMA DE MOODY RED DTOWN TRAMOS CON HAZEN-WILLIAMS MAYOR PARA
EL CAUDAL MEDIO 2.
ILUSTRACIÓN 184 DIAGRAMA DE MOODY RED DTOWN TRAMOS CON DARCY-WEISBACH MAYOR PARA
EL CAUDAL MEDIO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Dtown Qmed(Diferencia Número de
Reynolds 50000-100000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Dtown Qmed (Diferencia Número de
Reynolds 50000-100000 Darcy Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
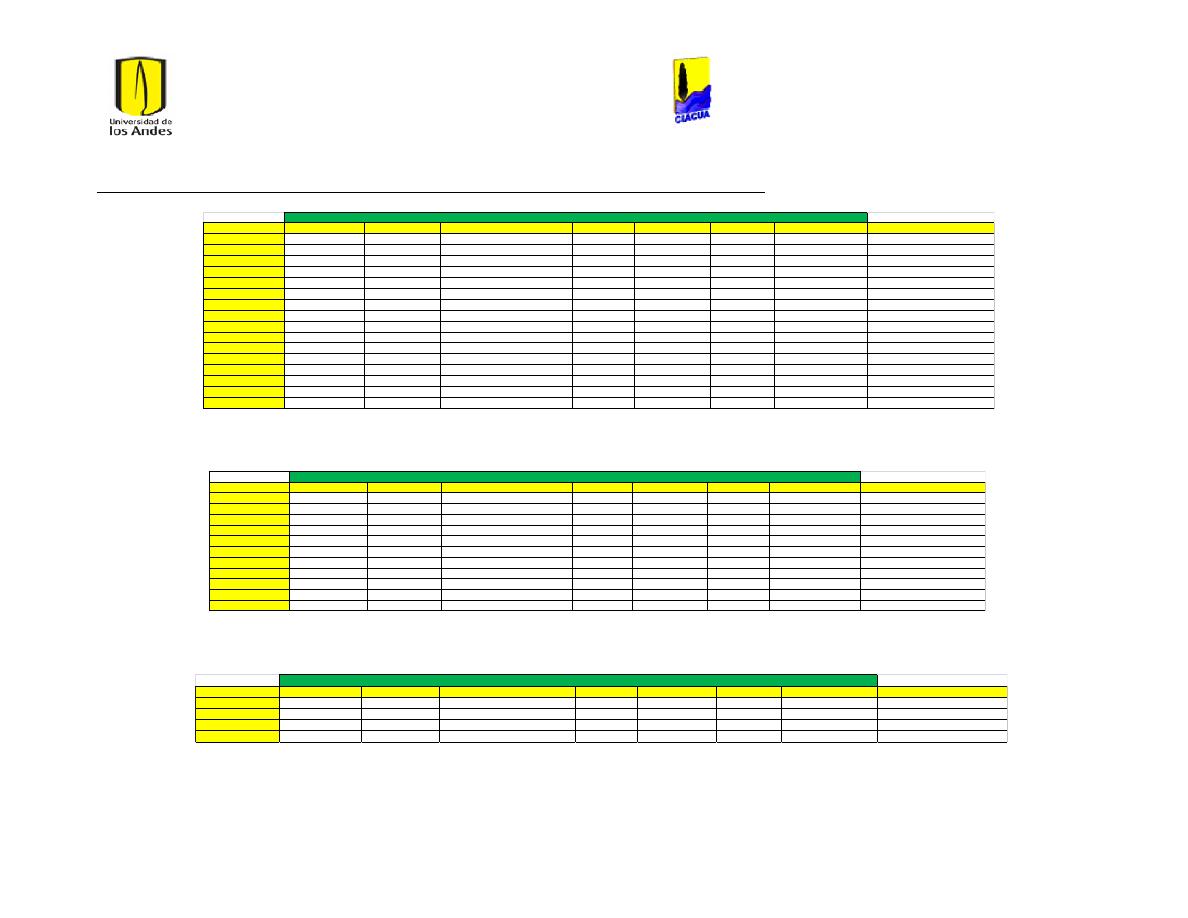
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
207
TABLA 30 RESUMEN DE TRAMOS DE LA RED DTOWN PARA EL CAUDAL MEDIO 1 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE 100000 Y
300000.
TABLA 31 RESUMEN DE TRAMOS DE LA RED DTOWN PARA EL CAUDAL MEDIO 2 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE 50000 Y
100000.
TABLA 32 RESUMEN DE TRAMOS DE LA RED DTOWN PARA EL CAUDAL MEDIO 3 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE 50000 Y
100000.
Tramo/Diametro(mm) Caudal Hazen(m^3/s) Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/102
0.010621605
0.000268181
1.13E+05
2.94E+03
0.037296
1.16E+05
0.017588
3860.60%
Tramo 1/152
0.042245765
3.64829E-08
3.10E+05
2.67E-01
0.00E+00
3.10E+05
0.0151
115795850.00%
Tramo 2/152
0.04224571
5.47244E-08
3.10E+05
4.01E-01
0.00E+00
3.10E+05
0.0151
77197100.00%
Tramo 3/152
0.040837433
0.001408333
2.89E+05
1.03E+04
0.029787
2.99E+05
0.015176
2799.70%
Tramo 4/152
0.030032108
0.001860239
2.07E+05
1.37E+04
0.027663
2.21E+05
0.015877
1514.42%
Tramo 5/152
0.029199432
0.002692915
1.95E+05
1.98E+04
0.025193
2.15E+05
0.015943
984.31%
Tramo 6/152
0.02412075
0.006909631
1.26E+05
5.06E+04
0.020238
1.77E+05
0.016406
249.09%
Tramo 1/203
0.077389244
0.035727728
2.29E+05
1.97E+05
0.015329
4.26E+05
0.014326
116.61%
Tramo 2/203
0.076061025
0.034399487
2.29E+05
1.89E+05
0.015443
4.18E+05
0.014365
121.11%
Tramo 3/203
0.040396674
0.01904543
1.17E+05
1.05E+05
0.017342
2.22E+05
0.015773
112.11%
Tramo 4/203
0.038645022
0.018334749
1.12E+05
1.01E+05
0.01748
2.13E+05
0.015877
110.77%
Tramo 5/203
0.03745284
0.017142567
1.12E+05
9.43E+04
0.017722
2.06E+05
0.015951
118.48%
Tramo 6/203
0.038745517
0.020444881
1.01E+05
1.12E+05
0.017097
2.13E+05
0.015871
89.51%
Tramo 1/406
0.043311994
0.002287462
1.13E+05
6.29E+03
0.035439
1.19E+05
0.019397
1793.45%
Tramo 2/406
0.042183604
0.001159202
1.13E+05
3.19E+03
0.027483
1.16E+05
0.019474
3539.02%
Tramo 3/406
0.040838883
0.000185519
1.12E+05
5.10E+02
1.25E-01
1.12E+05
0.019564
21913.33%
Dtown Qmed (Diferencias número de Reynolds 100000-300000) Hazen Mayor
Tramo/Diametro(mm) Caudal Hazen(m^3/s) Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/152
0.021392938
0.009893753
8.43E+04
7.25E+04
0.018728
1.57E+05
0.0167
116.23%
Tramo 1/203
0.027720769
0.014102349
7.49E+04
7.76E+04
0.018455
1.53E+05
0.016677
96.57%
Tramo 2/203
0.030359364
0.016828104
7.44E+04
9.26E+04
0.01779
1.67E+05
0.016454
80.41%
Tramo 3/203
0.03312331
0.019592051
7.44E+04
1.08E+05
0.017246
1.82E+05
0.016243
69.07%
Tramo 4/203
0.034770842
0.021239615
7.44E+04
1.17E+05
0.016967
1.91E+05
0.016128
63.71%
Tramo 1/254
0.040517597
0.022216944
8.05E+04
9.77E+04
0.017586
1.78E+05
0.016229
82.37%
Tramo 2/254
0.039175683
0.020875031
8.05E+04
9.18E+04
0.017813
1.72E+05
0.01631
87.67%
Tramo3/254
0.041800225
0.023499573
8.05E+04
1.03E+05
0.017384
1.84E+05
0.016154
77.88%
Tramo 1/406
0.035851623
0.003163142
8.99E+04
8.70E+03
0.030592
9.86E+04
0.019947
1033.42%
Tramo 2/406
0.035255451
0.003759444
8.66E+04
1.03E+04
0.02924
9.70E+04
0.019996
837.78%
Tramo 1/508
0.033667672
0.00534698
6.23E+04
1.18E+04
0.02877
7.40E+04
0.020737
529.66%
Dtown Qmed (Diferencias número de Reynolds 50000-100000) Hazen Mayor
Tramo/Diametro(mm) Caudal Hazen(m^3/s) Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/203
0.006571227
0.035674551
-1.60E+05
1.96E+05
0.015334
3.62E+04
0.020636
-81.58%
Tramo 2/203
0.004791708
0.03745407
-1.80E+05
2.06E+05
0.015193
2.64E+04
0.021633
-87.21%
Tramo 3/203
0.004229973
0.038015805
-1.86E+05
2.09E+05
0.01515
2.33E+04
0.022029
-88.87%
Tramo 1/406
0.018336335
0.039050497
-5.70E+04
1.07E+05
0.018681
5.04E+04
0.022028
-53.04%
Dtown Qmed (Diferencias número de Reynolds 50000-100000) Darcy Mayor

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
208
Los resultados que se muestran solo corresponden al caudal medio, ya que colocar los
resultados en cada uno de los tiempos en que se presentaba la hidráulica radicalmente
diferente entre las dos ecuaciones era muy extenso y los resultados con el caudal medio
representan de manera muy similar lo que ocurre en los tiempos de alta diferencia hidráulica.
Lo primero que se puede observar en los diagramas de Moody es que se presentan unas
diferencias en los números de Reynolds de una magnitud superior a las redes de Andalucía y
Medellín. Como se mencionó con anterioridad, estas diferencias son tan grandes que por
momentos la magnitud de la diferencia del caudal que pasa por los mismos tramos de
tuberías, utilizando las dos ecuaciones, es enorme. Con base en esto, se cuantificó cuanto era
la cantidad de caudal que se podía estar desbalanceando a causa del uso de la ecuación de
Hazen-Williasm y se encontró que era de 80 L/s. Esta es una cantidad considerable de masa
teniendo en cuenta que la demanda base de la red es de 360 L/s.
Lo anterior fortalece todo lo que se ha venido estudiando en esta investigación solo que a una
mayor escala; es decir, en redes con terminaciones en tanques y que operan con coeficientes
constantes de Hazen-Williams, se están presentando desbalances de masa en instantes claves
del tiempo; así mismo, gracias a los resultados encontrados en la red de Dtown, se puede ver
que el problema no se limita a tiempos de máximo, mínimo y consumo medio, sino que es un
problema en varios períodos, lo que lo hace todavía más preocupante. Por otro lado, y al
existir este desbalance de masa, también se puede ver que la solución de la hidráulica de la
red está cambiando de manera radical, el agua está seleccionando una ruta para suplir la red
con la ecuación de Darcy-Weisbach y una distinta al utilizar la ecuación empírica.
Otro punto clave que también se vio en la red de la Cumbre, que se analiza a continuación, es
que pese a tener predominantemente tuberías en PVC, presentó los mayores errores de
magnitud en los números de Reynolds de todas las tuberías evaluadas. Este resultado parece
mostrar que las diferencias en redes con este material si pueden a llegar a ser de gran
importancia, en contraste con lo que se había estudiado previamente. Por otro lado, un detalle
interesante es que si bien las tuberías que presentaban diferencias tenían números de
Reynolds con rangos más bajos que las otras redes estudiadas (principalmente entre
, las grandes diferencias se siguieron presentando en las tuberías que
transportaban la mayor cantidad de caudal y en los tramos que se dirigían hacia las
ramificaciones con tanques (siendo la red Dtown una red con mucha redundancia y ciclos
pero con la presencia de terminaciones ramificada pequeñas).
Todo lo anterior permite decir que la ecuación de Hazen-Williams presenta más problemas de
los que se habían analizado anteriormente en la literatura. Al ser esta una red de bombeo, la
sobrestimación y/o subestimación del caudal del sistema generara evidentemente que los
costos del bombeo de la red se vean afectados en gran medida, sin mencionar la posibilidad de
que se comentan graves equivocaciones, al seleccionar la bomba adecuada para operar el
sistema. A lo anterior se le suman las consecuencias que se observaron en las redes
anteriores: 1) Diferencias de presiones en los nudos, al calcular de manera diferente la
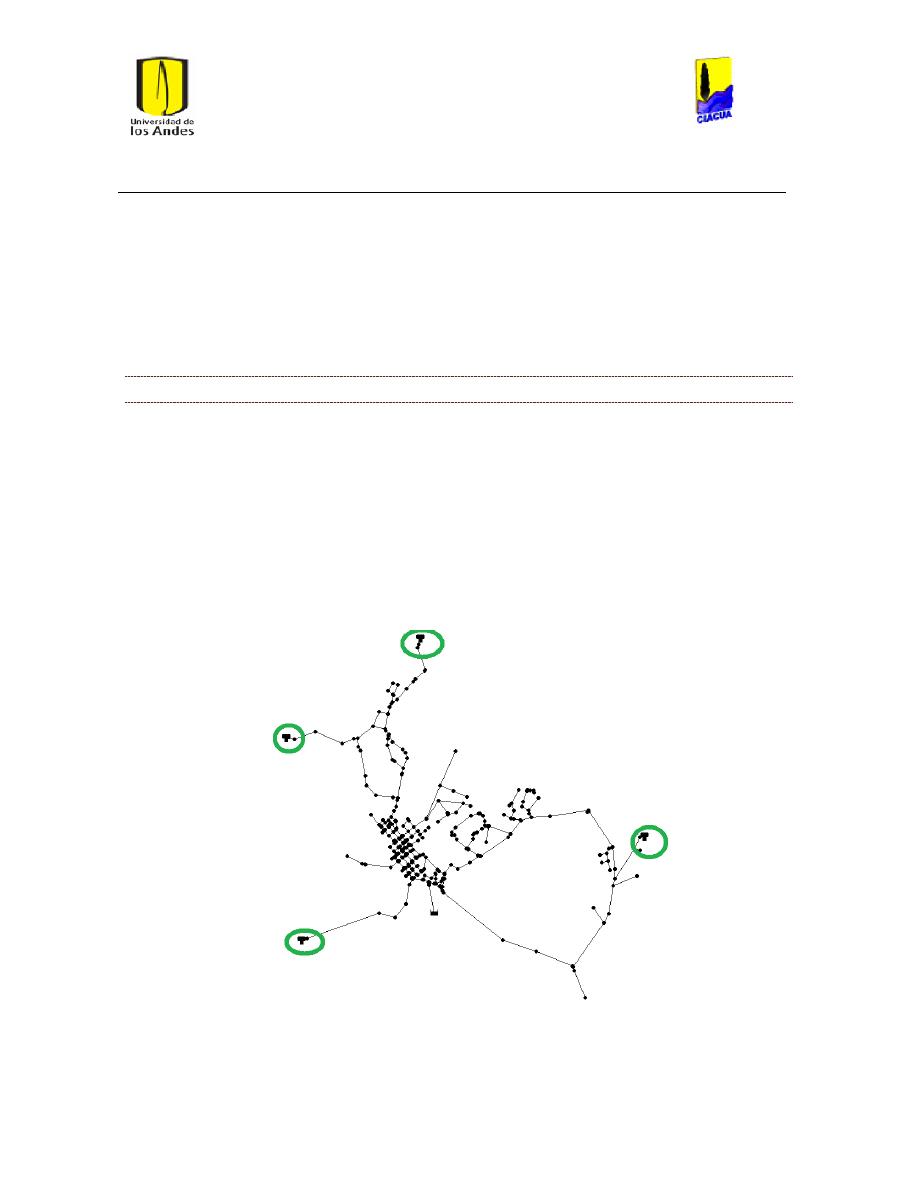
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
209
hidráulica del sistema utilizando la ecuación de Hazen-Williams con coeficientes estáticos. 2)
Subestimación o sobrestimación de las fugas del sistema al evaluar de forma incorrecta el
caudal de los emisores. 3) Posibles errores de los operarios de la red al plantear las soluciones
al tener hidráulicas del sistema diferentes entre las dos ecuaciones. 4) En algunas condiciones
del día, la hidráulica del sistema entre las dos ecuaciones es bastante similar, lo que puede
conllevar a pensar que el sistema siempre se va a comportar de manera correcta y sin
falencias, lo que puede llevar a tener consecuencias de desabastecimiento considerables.
4.4.6 RED LA CUMBRE
En esta sección solo se van a mostrar los resultados más relevantes de esta red, pues se utilizó
exclusivamente para determinar si en esta red también se presentaban las diferencias más
representativas entre las dos ecuaciones. Esto con el fin de no volver a mencionar lo que se ha
estado mencionado con las cuatro redes anteriores.
Pese a ser una red con bajo caudal base (800 L/s) y en la cual predominan los diámetros de
300 mm, presentó las mismas diferencias encontradas en las redes de Ginebra, Medellín y
Andalucía., solo que a una menor escala (debido a que el caudal era más bajo) pero con
órdenes de magnitud porcentual importantes. A continuación se muestran los resultados de
esta red:
ILUSTRACIÓN 185 LOCALIZACIÓN DE LOS TANQUES DE LA RED LA CUMBRE.
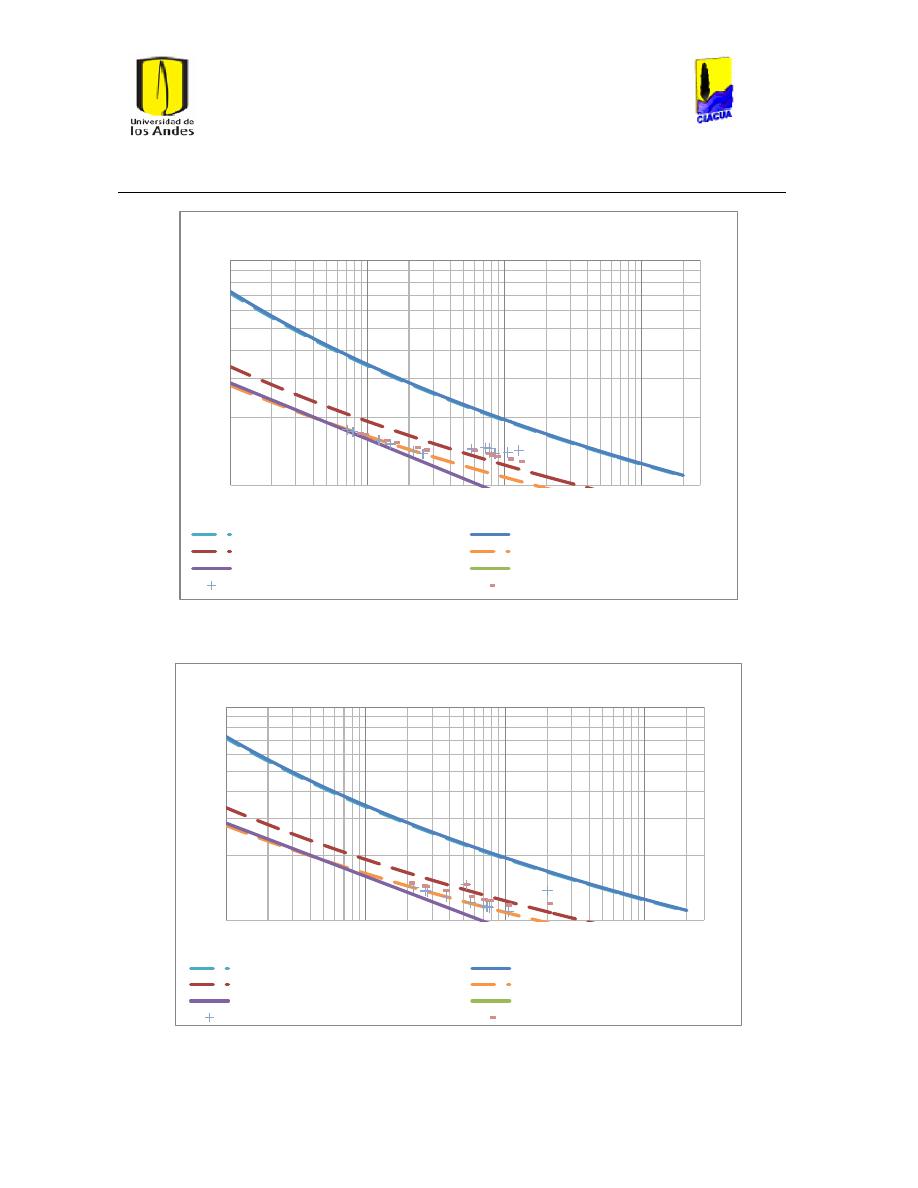
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
210
ILUSTRACIÓN 186 DIAGRAMA DE MOODY RED LA CUMBRE TRAMOS CON HAZEN-WILLIAMS MAYOR
PARA EL CAUDAL MÍNIMO.
ILUSTRACIÓN 187 DIAGRAMA DE MOODY RED LA CUMBRE TRAMOS CON DARCY-WEISBACH MAYOR
PARA EL CAUDAL MÍNIMO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Cumbre Qmin (Diferencia Número de
Reynolds 10000-20000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Cumbre Qmin (Diferencia Número de
Reynolds 20000-50000 Darcy Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
211
TABLA 33 RESUMEN DE TRAMOS DE LA RED LA CUMBRE PARA EL CAUDAL MÍNIMO 1 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE
10000 Y 20000.
TABLA 34 RESUMEN DE TRAMOS DE LA RED LA CUMBRE PARA EL CAUDAL MÍNIMO 2 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE
10000 Y 20000.
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Porcentual
Tramo 1/300
0.010935968
0.009129038
2.11E+04
1.07E+05
0.017672
1.28E+05
0.016989
19.79%
Tramo 2/300
0.011853743
0.010046813
2.11E+04
1.18E+05
0.017328
1.39E+05
0.016796
17.99%
Tramo 3/300
0.017065913
0.015547163
1.78E+04
1.82E+05
0.015875
2.00E+05
0.015908
9.77%
Tramo 4/300
0.02014164
0.01880145
1.57E+04
2.20E+05
0.015303
2.36E+05
0.015523
7.13%
Tramo 5/300
0.028760378
0.027891
1.02E+04
3.26E+05
0.014213
3.36E+05
0.014725
3.12%
Tramo 6/300
0.03346398
0.032594603
1.02E+04
3.81E+05
0.013819
3.91E+05
0.014398
2.67%
Tramo1/500
0.158064438
0.155465313
1.82E+04
1.09E+06
0.014701
1.11E+06
0.013889
1.67%
Tramo 2/500
0.272526625
0.270998375
1.07E+04
1.90E+06
0.014344
1.91E+06
0.012812
0.56%
Tramo 3/500
0.167425
0.165482875
1.36E+04
1.16E+06
0.014653
1.17E+06
0.013771
1.17%
Tramo 1/600
0.1498725
0.14793039
1.14E+04
8.65E+05
0.014529
8.76E+05
0.01433
1.31%
Tramo 2/600
0.27248247
0.27063756
1.08E+04
1.58E+06
0.014034
1.59E+06
0.013118
0.68%
Tramo 1/700
0.236649788
0.23327724
1.69E+04
1.17E+06
0.013951
1.19E+06
0.013663
1.45%
Tramo 2/700
0.257234443
0.254712045
1.26E+04
1.28E+06
0.013877
1.29E+06
0.013496
0.99%
Cumbre Qmin (Diferencias número de Reynolds 10000-20000) Hazen Mayor
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Porcentual
Tramo 1/300
0.0710019
0.07273017
-20213.68421
850645.2632
0.012043
830431.5789
0.012882
-2.38%
Tramo 2/300
0.032684715
0.034412985
-20213.68421
402491.0526
0.013685
382277.3684
0.014449
-5.02%
Tramo 3/300
0.046622745
0.048476363
-21679.73684
566975
0.012885
545295.2632
0.01371
-3.82%
Tramo 4/300
0.0338886
0.035742218
-21679.73684
418037.6316
0.013588
396357.8947
0.014372
-5.19%
Tramo 5/300
0.02643165
0.028285268
-21679.73684
330821.8421
0.014171
309142.1053
0.014911
-6.55%
Tramo 6/300
0.093625155
0.095656433
-23757.63158
1118788.684
0.011527
1095031.053
0.012366
-2.12%
Tramo 7/300
0.087315435
0.089346713
-23757.63158
1044990.789
0.011651
1021233.158
0.012493
-2.27%
Tramo 8/300
0.09672264
0.098753918
-23757.63158
1155016.579
0.011468
1131258.947
0.012306
-2.06%
Tramo 9/300
0.131488695
0.13591683
-51791.05263
1589670.526
0.010918
1537879.474
0.011759
-3.26%
Tramo 1/350
0.108997897
0.111029192
-20363.85965
1113074.605
0.011516
1092710.746
0.012333
-1.83%
Tramo1/600
0.51298551
0.51739281
-25773.68421
3025688.947
0.0137
2999915.263
0.011945
-0.85%
Tramo 2/600
0.13057092
0.13499901
-25895.26316
789467.8947
0.014622
763572.6316
0.014627
-3.28%
Cumbre Qmin(Diferencias número de Reynolds 20000-50000) Darcy Mayor
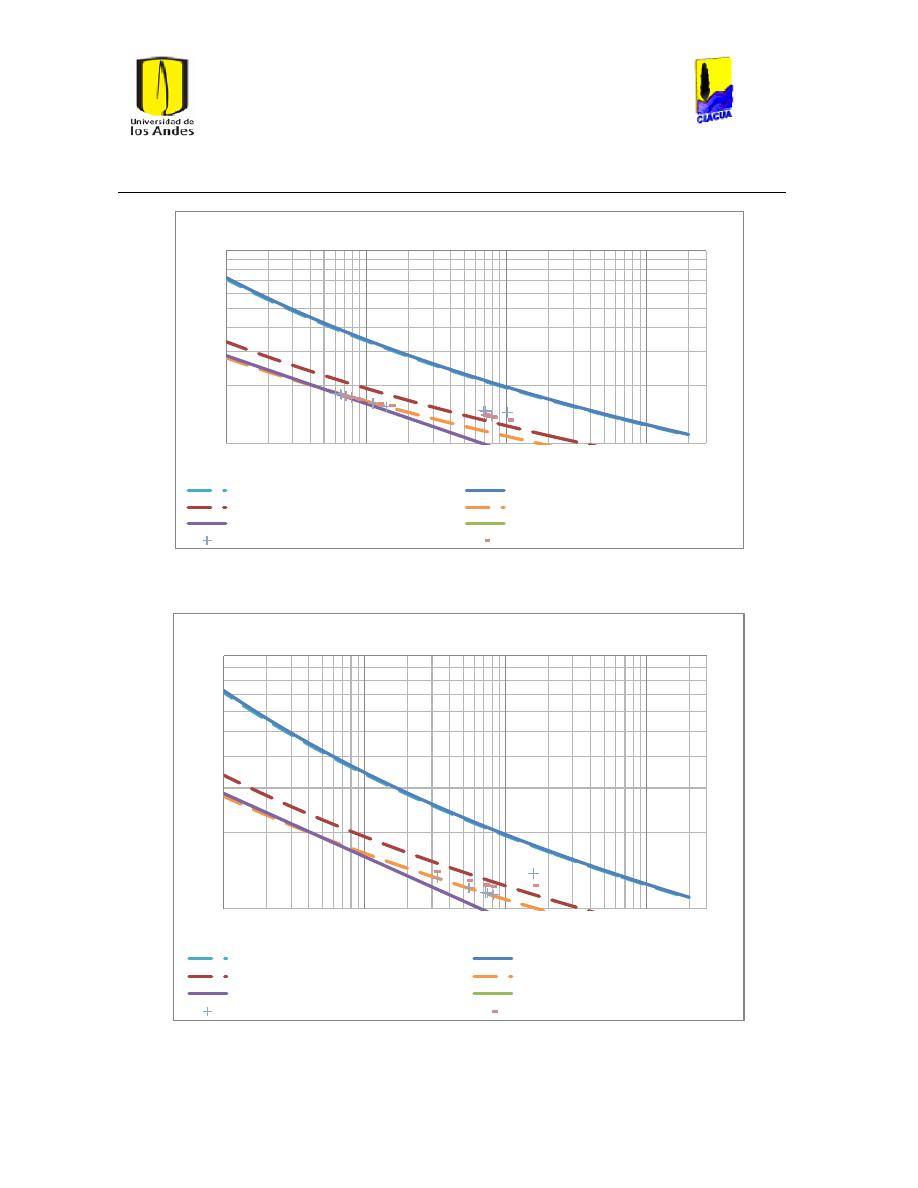
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
212
ILUSTRACIÓN 188 DIAGRAMA DE MOODY RED LA CUMBRE TRAMOS CON HAZEN-WILLIAMS MAYOR
PARA EL CAUDAL MEDIO.
ILUSTRACIÓN 189 DIAGRAMA DE MOODY RED LA CUMBRE TRAMOS CON DARCY-WEISBACH MAYOR
PARA EL CAUDAL MEDIO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Cumbre Qmed (Diferencia Número de Reynolds
10000-20000 Hazen-Williams Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Cumbre Qmed (Diferencia Número de Reynolds
20000-50000 Darcy-Weisbach Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
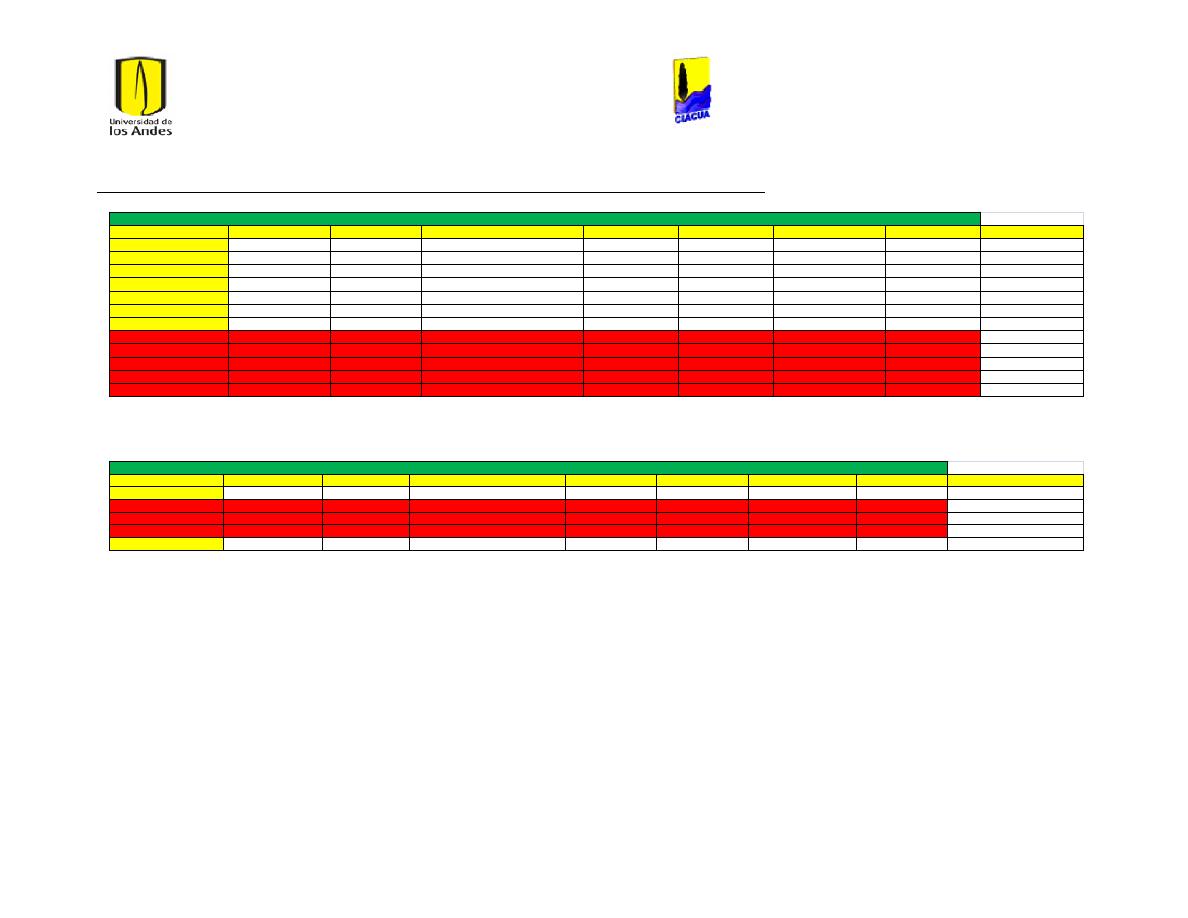
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
213
TABLA 35 RESUMEN DE TRAMOS DE LA RED LA CUMBRE PARA EL CAUDAL MEDIO 1 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE 10000
Y 20000.
TABLA 36 RESUMEN DE TRAMOS DE LA RED LA CUMBRE PARA EL CAUDAL MEDIO 2 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE 20000
Y 50000.
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Porcentual
Tramo 1/300
0.010796873
0.009233393
1.83E+04
1.08E+05
0.017633
1.26E+05
0.017021
16.93%
Tramo 2/300
0.009959603
0.008396123
1.83E+04
9.82E+04
0.017983
1.16E+05
0.017226
18.62%
Tramo 3/300
0.015702368
0.014386928
1.54E+04
1.68E+05
0.016118
1.84E+05
0.016105
9.14%
Tramo 4/300
0.018998798
0.017831003
1.37E+04
2.09E+05
0.015461
2.22E+05
0.015657
6.55%
Tramo 5/300
0.011186168
0.01013661
1.23E+04
1.19E+05
0.017246
1.31E+05
0.016933
10.35%
Tramo 6/300
0.009616275
0.00856674
1.23E+04
1.00E+05
0.017845
1.12E+05
0.017318
12.25%
Tramo 7/300
0.008779005
0.00772947
1.23E+04
9.04E+04
0.01823
1.03E+05
0.01755
13.58%
Tramo 1/500
0.221013813
0.218273125
1.92E+04
1.53E+06
0.014466
1.55E+06
0.013216
1.26%
Tramo 2/500
0.14833175
0.146261688
1.45E+04
1.03E+06
0.01475
1.04E+06
0.014019
1.42%
Tramo 3/500
0.15442325
0.152837125
1.11E+04
1.07E+06
0.014714
1.08E+06
0.013936
1.04%
Tramo 1/700
0.21860664
0.215865948
1.37E+04
1.08E+06
0.014022
1.10E+06
0.013825
1.27%
Tramo 2/700
0.237702308
0.235671258
1.02E+04
1.18E+06
0.013943
1.19E+06
0.013654
0.86%
Cumbre Qmed (Diferencias número de Reynolds 10000-20000) Hazen Mayor
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Número Reynolds(%)
Tramo 1/300
0.091793475
0.093991163
-2.57E+04
1.10E+06
0.011558
1.07E+06
0.012401
-2.34%
Tramo 2/300
0.121291043
0.125235428
-4.61E+04
1.46E+06
0.011054
1.42E+06
0.0119
-3.15%
Tramo 1/350
0.107178282
0.109375993
-2.20E+04
1.10E+06
0.011544
1.07E+06
0.012364
-2.01%
Tramo 1/600
0.12045375
0.12439818
-2.31E+04
7.27E+05
0.014712
7.04E+05
0.014802
-3.17%
Tramo 1/600
0.47415555
0.47822625
-2.38E+04
2.80E+06
0.013732
2.77E+06
0.012085
-0.85%
Cumbre Qmed (Diferencias número de Reynolds 20000-50000) Darcy Mayor
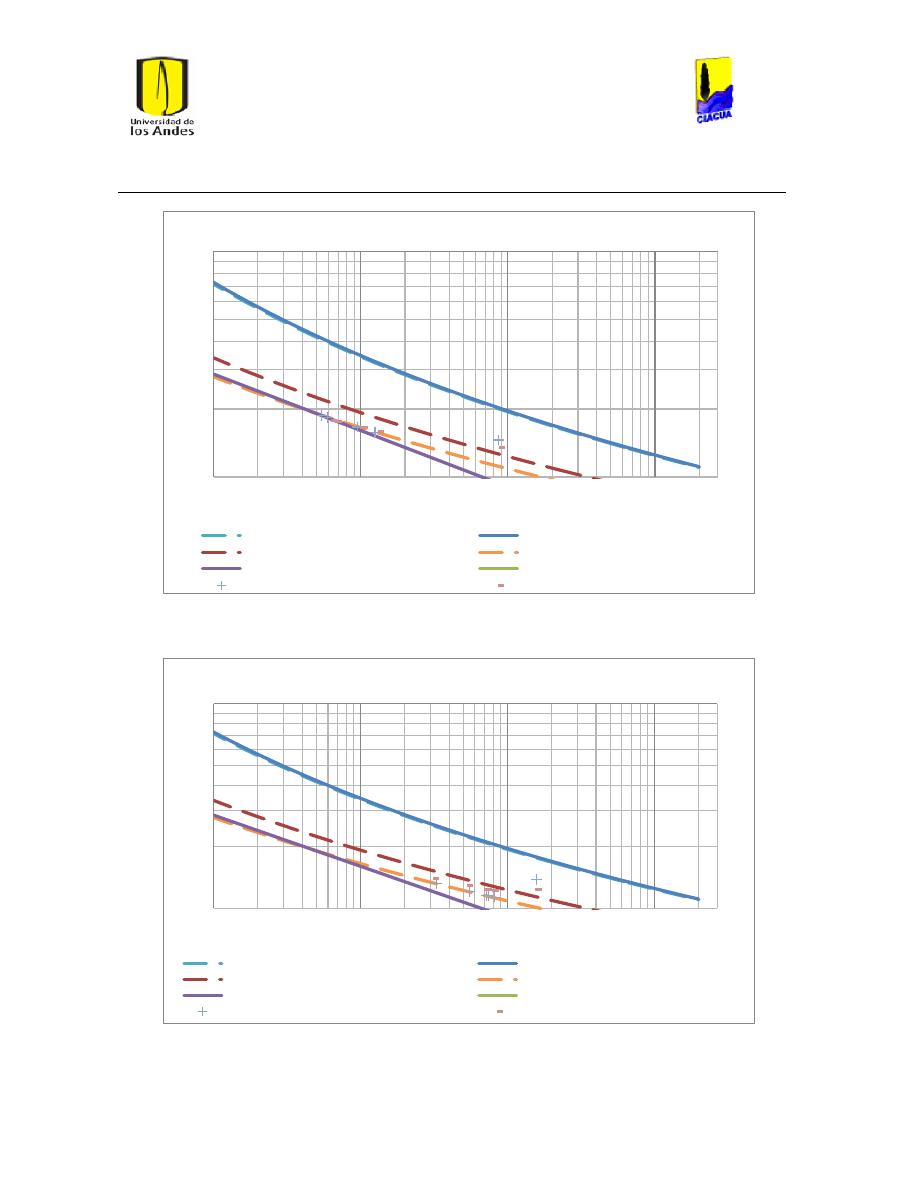
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
214
ILUSTRACIÓN 190 DIAGRAMA DE MOODY RED LA CUMBRE TRAMOS CON HAZEN-WILLIAMS MAYOR
PARA EL CAUDAL MÁXIMO.
ILUSTRACIÓN 191 DIAGRAMA DE MOODY RED LA CUMBRE TRAMOS CON DARCY-WEISBACH MAYOR
PARA EL CAUDAL MÁXIMO.
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Cumbre Qmax (Diferencia Número de
Reynolds 10000-20000 Hazen Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
0.01
0.1
1.50E+04
1.50E+05
1.50E+06
1.50E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody Cumbre Qmax (Diferencia Número de
Reynolds 20000-50000 Darcy Mayor)
Límite FTHR (Colebrook-White) 0
Límite FTHR (Prantdl-Von Kármán) 0
Límite FTHL (Colebrook-White) 0
Límite FTHL (Prantdl-Von Kármán) 0
Límite FTHL (Blasius) 0
Flujo laminar
Red Darcy
Red Hazen
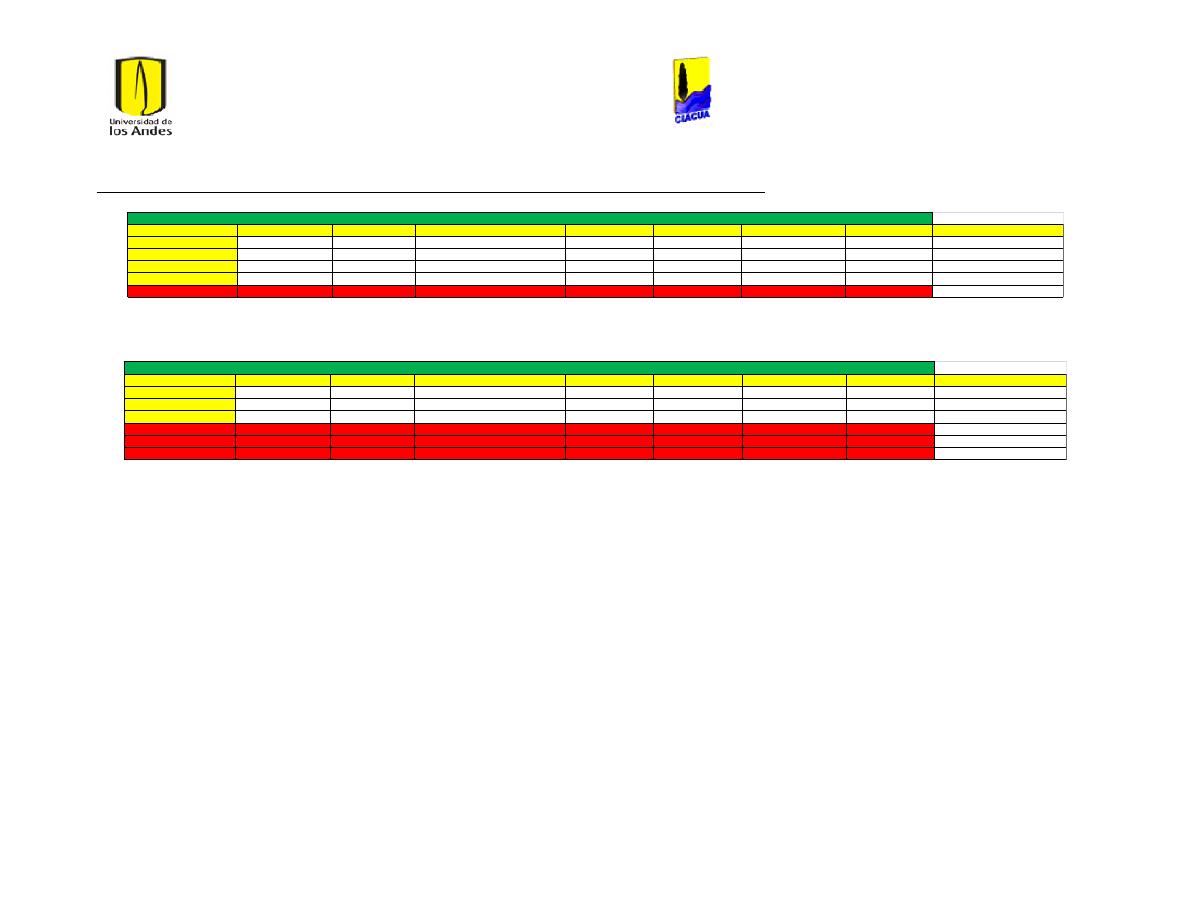
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
215
TABLA 37 RESUMEN DE TRAMOS DE LA RED LA CUMBRE PARA EL CAUDAL MÁXIMO 1 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE
10000 Y 20000.
TABLA 38 RESUMEN DE TRAMOS DE LA RED LA CUMBRE PARA EL CAUDAL MÁXIMO 2 PARA DIFERENCIAS EN EL NÚMERO DE REYNOLDS ENTRE
20000 Y 50000.
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Porcentual
Tramo 1/300
0.008785328
0.007652025
1.33E+04
8.95E+04
0.018343
1.03E+05
0.017539
14.81%
Tramo 2/300
0.008100743
0.00696744
1.33E+04
8.15E+04
0.018683
9.47E+04
0.017764
16.27%
Tramo 3/300
0.013135658
0.012180465
1.12E+04
1.42E+05
0.016654
1.54E+05
0.016534
7.84%
Tramo 4/300
0.01693602
0.016069928
1.01E+04
1.88E+05
0.015767
1.98E+05
0.015926
5.39%
Tramo 1/500
0.1867995
0.185204875
1.12E+04
1.30E+06
0.014572
1.31E+06
0.013549
0.86%
Cumbre Qmax (Diferencias número de Reynolds 10000-20000) Hazen Mayor
Tramo/Diametro(mm)
Caudal Hazen(m^3/s)
Caudal Darcy(m^3/s)
Diferencia en Número de Reynolds
Reynolds Darcy
Factor Fricción Darcy
Reynolds Hazen
Factor Fricción Hazen
Diferencia Porcentual
Tramo 1 /300
0.040413938
0.042159578
-2.04E+04
4.93E+05
0.013204
4.73E+05
0.014002
-4.14%
Tramo 2/300
0.068824665
0.070570305
-2.04E+04
8.25E+05
0.012102
8.05E+05
0.012941
-2.47%
Tramo 3/300
0.092250113
0.094805393
-2.99E+04
1.11E+06
0.011541
1.08E+06
0.012392
-2.70%
Tramo 4/300
0.102138098
0.105232613
-3.62E+04
1.23E+06
0.011354
1.19E+06
0.012207
-2.94%
Tramo 1/350
0.104829559
0.107384848
-2.56E+04
1.08E+06
0.011577
1.05E+06
0.012404
-2.38%
Tramo 1/600
0.40170321
0.40522131
-2.06E+04
2.37E+06
0.013806
2.35E+06
0.012385
-0.87%
Cumbre Qmax (Diferencias número de Reynolds 20000-50000) Darcy Mayor

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
216
5. CONCLUSIONES Y TRABAJOS FUTUROS
El estudio con emisores demostró que operar una red matriz utilizando la ecuación de
Hazen-Williams conlleva el riesgo de que se esté sobrestimando el caudal que pueda
ser emitido.
Las diferencias de los caudales de emisores trabajados con la ecuación de Darcy-
Weisbach frente a uno operando con la ecuación de Hazen-Williams pueden ser de 5
hasta más de 100 L/s, lo que implica un volumen considerable, teniendo en cuenta que
la red debe funcionar 24 horas.
Pese a que en el caso de la Red Ginebra ésta se comportó con coeficientes de Hazen-
Williams similares a los valores teóricos establecidos durante este estudio, se pudo
evidenciar que en las otras redes la variación del coeficiente es bastante importante,
llegando a presentarse valores de 80 e incluso 200, que pueden llevar a subestimar o
sobrestimar en gran medida las pérdidas por fricción.
Pese a que se utilizó una rugosidad absoluta menor para el hierro dúctil a los valores
utilizados en la literatura clásica (debido a que los proveedores de la tubería sugieren
este valor), y teniendo en cuenta que una rugosidad de 0.1 mm debería asemejarse
más a un coeficiente de Hazen-Williams de 140 (que es un coeficiente relativamente
liso), las redes siguieron presentando variaciones importantes, incluso alcanzando
coeficientes con valores de 100 o 120, demostrando una vez más los riesgoso que
puede llegar a ser el diseñar o en este caso, operar una red matriz con coeficientes
constantes de Hazen-Williams, como también se concluye en las investigaciones
adelantadas por Bombardelli.
Una conclusión importante es que se logró establecer que la red que trabajaba con la
ecuación de Hazen-Williams presentaba valores diferentes en los números de
Reynolds que la red trabajada con la ecuación de Darcy-Weisbach, lo que permite
concluir que para una tubería específica, el caudal que circula en ella no es el mismo
para las dos ecuaciones, cambiando así la hidráulica de todo el sistema.
En cuanto a las presiones, se encontraron resultados similares a los que se han
encontrado en las tesis que precedieron a este trabajo, es decir, que la ecuación de
Hazen-Williams puede subestimar o sobrestimar las pérdidas por fricción, entregando
presiones que realmente no se presentan en la realidad.
Adicionalmente, es aconsejable trabajar con controles de bombas, de tal forma que se
optimice el comportamiento de la misma, para una red que opere con la ecuación de
Hazen-Williams y posteriormente analizar el comportamiento con la ecuación de
Darcy-Weisbach y analizar las diferencias hidráulicas y consecuencias económicas.
Los trabajos futuros también deben tener en cuenta la variación en la operación de
válvulas, para analizar que ocurre con la hidráulica en caso de que se presente alguna
situación inesperada en la red, es decir analizar que tan robusta se comporta la red
con las dos ecuaciones y ver si las diferencias hidráulicas de las mismas se ven
afectadas por una situación como esta.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
217
Es recomendable extender los análisis que se realizaron en esta parte, para otros tipos
de materiales como lo son el CCP (Concreto con revestimiento interno de acero) y
materiales modernos como lo es el GRP (Poliester reforzado con fibra de vidrio), ya
que estos materiales o se usan ya ampliamente o van a convertirse en el futuro de las
redes de distribución de agua potable.
En las redes estudiadas, está claro que la ecuación de Hazen-Williams presenta un
desbalance de masa con respecto a la red en la que se emplea la ecuación de Darcy-
Weisbach; esto implica que se presenten llenados de los tanques diferentes entre las
dos ecuaciones.
Así mismo, las 2 ecuaciones (Hazen-Williams y Darcy-Weisbach) están presentando
diferencias considerables en los caudales que transportan las tuberías; como
consecuencia, la hidráulica de la red utilizando las 2 ecuaciones es diferente. Esto
último conlleva a que se presenten diferencias en las presiones, en los números de
Reynolds en las tuberías y en las pérdidas por fricción.
Si bien, en términos porcentuales las mayores diferencias en el número de Reynolds
se presentan en tuberías de diámetros pequeños, esto se debe a que el caudal
transportado es más bajo que en tuberías de gran diámetro y se ve “magnificada” esta
diferencia.
En consecuencia, las tuberías que transportan gran cantidad de caudal (las de mayor
diámetro de la red) presentan diferencias porcentuales menores; pero el efecto de
estos tramos es grande en la hidráulica de toda la red, considerando que el caudal que
se dejó de transportar en las otras tuberías está cambiando radicalmente el
comportamiento hidráulico; este efecto se presentó principalmente y en mayor grado
en las redes que tienen ramificaciones y terminaciones en tanques.
En el caso de estudio de Dtown, éste presento altas diferencias en la solución de la
hidráulica de la red entre las dos ecuaciones; esto debido a que ciertos tramos de
tubería se calculó más caudal utilizando la ecuación de Hazen-Williasm en contraste a
lo encontrado usando la ecuación de Darcy-Weisbach y viceversa
Esto último se presentó en momentos específicos del día y en 2 de los 5 sectores de la
red Dtown. Las diferencias implican que el fluido debe recorrer diferentes rutas para
satisfacer las demandas de los nudos.
En la red Dtown las grandes diferencias parecen presentarse en instancias cuando el
patrón de consumo está pasado de máximo consumo, a horarios de menor consumo,
es decir cuando el patrón está presentando una especie de “valle”.
Se puede concluir que al evaluar la hidráulica de manera diferente en este tipo de
redes, el análisis de fugas o de selección de puntos para la colocación de válvulas va a
ser radicalmente distinto entre un operario que maneje la red utilizando la ecuación
de Hazen-Williams que otro que utilice la ecuación de Darcy-Weisbach. El primero
corre el riesgo de agravar o dejar de solucionar el problema al utilizar una hidráulica
que no se presenta en la realidad.
El desbalance de masa en las redes con sistemas de bombeo también causará que los
costos del mismo y la selección de bombas del sistema sea diferente entre las dos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
218
ecuaciones, corriendo el riesgo de que se sobrestime la bomba que se necesite o en un
escenario más grave, que se seleccione una bomba con capacidad insuficiente para el
sistema.
El análisis realizado en la red Dtown en varios momentos del día (cada 15 minutos)
permitió detectar efectos significativos de la ecuación de Hazen-Williams. A futuro, se
recomienda que se trabaje con solo un par de redes y se pueda estudiar todo lo que se
realizó durante esta investigación, pero analizando períodos de tiempo con separación
menor y de manera más detallada.
Para finalizar, está claro que la ecuación de Hazen-Williams subestima o sobrestima el
caudal que circula en las redes; como consecuencia, la ecuación empírica está
resolviendo de manera diferente la hidráulica de la red. Así mismo, es importante
mencionar que el efecto se ve aseverado en redes con ramificaciones, tanques, y a
mayor demanda de caudal las diferencias en los números de Reynolds de las tuberías
se ven magnificados.
Los resultados de esta tesis pueden ser utilizados para la calibración de redes, de tal
forma que los operarios apunten siempre a las tuberías de gran diámetro.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
219
BIBLIOGRAFÍA
AMIANTIT. (s.f.). http://www.amiantit.com/. Obtenido de http://www.amiantit.com/:
http://www.amiantit.com/media/pdf/brochures/Ductile_Iron_Pipe_Co._Ltd/final%20
sadip%20ductile%20iron%20pipe_FINAL_LR_WS_HIDD.pdf
B.A. Christensen, F. A. (2000). Discussion Limitations and proper use of the Hazen-Williams
Ecuation. Journal of hidraulics engineering , 167-170.
Empresas Públicas de Medellín. (2006-2009). http://es.scribd.com. Obtenido de
http://es.scribd.com: http://es.scribd.com/doc/35115401/Normas-Acueducto-
Version-Final
Engineering Tool Box. (s.f.). Engineering Tool Box. Obtenido de Engineering Tool Box:
http://www.engineeringtoolbox.com/hazen-williams-coefficients-
d_798.html#.UpDEFsRLNy0
Fabián A.Bombardelli, M. H. (2003). Hydraulic Design of Large-Diameter Pipes. Journal of
Hydraulic Engineering, 839-846.
Gardner Williams, A. H. (1905). Hydraulic Tables . Library of the University of California.
Hernández, R. A. (Diciembre de 2011). Efecto del Uso de la ecuación de Hazen-Williams vs la
ecuación de Darcy-Weisbach en tuberías de gran diámetro (Redes matrices). Bogotá,
Colombia.
Liou, C. P. (1998). LIMITATIONS AND PROPER USE OF THE HAZEN-WILLIAMS EQUATION.
Journal of hydraulics Engineering, 951-954.
M.Moghazi, H. E.-D. (1998). Estimating Hazen-Williams Coefficient for Polyethylene Pipes.
Journal of Transportation Engineering, 197-199.
Ministerio de Desarrollo Económico. (01 de Febrero de 2013). DOCUMENTACIÓN TÉCNICO
NORMATIVA DEL SECTOR DE AGUA . DOCUMENTACIÓN TÉCNICO NORMATIVA DEL
SECTOR DE AGUA . Bogotá.
Quentin B. Travis, L. W. (2007). Relationship between Hazen-Williams and Colebrook-White
Roughness Values. Journal of Hydraulic Engineering, 1270-1273.
Saint-Gobain-PAM. (s.f.). http://www.saint-gobain-pam.co.uk/. Obtenido de http://www.saint-
gobain-pam.co.uk/: http://www.saint-gobain-
pam.co.uk/assets/docs/ws/Water_Sewer_Design_Guide.pdf

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
220
Saldarriaga, J. G. (2007). Hidráulica de Tuberias Abastecimiento de agua, redes, riesgos. Bogotá:
Alfaomega.
Tata Kubota. (s.f.). http://tatametalikskubota.com/. Obtenido de
http://tatametalikskubota.com/: http://tatametalikskubota.com/products/ductile-
iron-pipes.asp
Uribe, J. D. (Junio de 2012). Efecto del uso de ecuaciones empíricas vs físicamente basadas
sobre los costos de diseños optimizados en acueductos. Bogotá: Universidad de los
Andes.
Valiantzas, J. D. (2008). Explicit Power Formula for the Darcy-Weisbach Pipe Flow Equation:
Application in Opimal Pipeline Design. Journal of Irrigation and Drainage Engineering,
454-461.
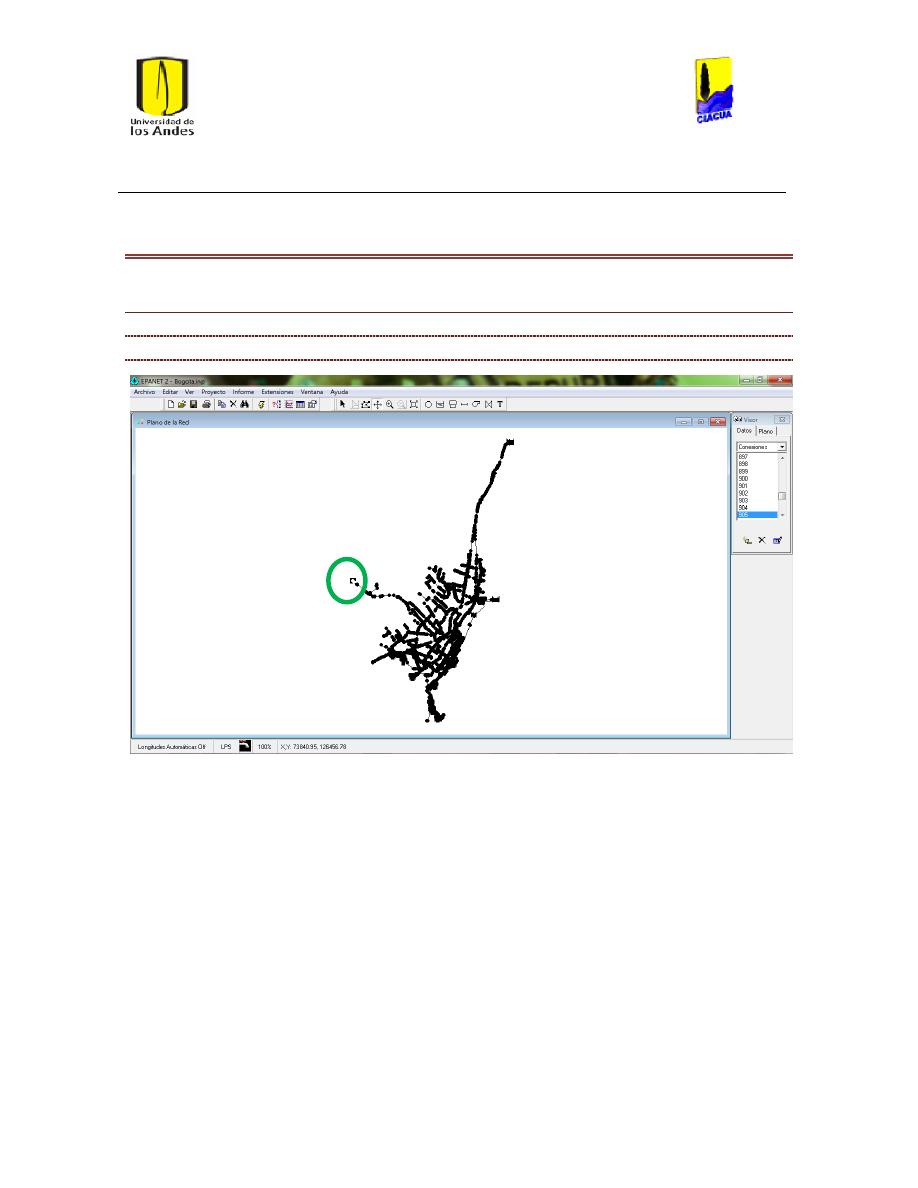
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
221
ANEXOS
LOCALIZACIÓN DE LOS EMISORES
EMISORES BOGOTÁ
Ilustración 192 Emisor 905 red matriz de Bogotá.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
222
Ilustración 193 Emisor 1521 red matriz de Bogotá.
Ilustración 194 Emisor 2437 red matriz de Bogotá.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
223
Ilustración 195 Emisor 3758 red matriz de Bogotá.
Ilustración 196 Emisor 1045 red matriz de Bogotá.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
224
Ilustración 197 Emisor 1036 red matriz de Bogotá.
Ilustración 198 Emisor 2189 red matriz de Bogotá.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
225
Ilustración 199 Emisor TUval red matriz de Bogotá.
Ilustración 200 Emisor 1702 red matriz de Bogotá.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
226
EMISORES GINEBRA
Ilustración 201 Emisor 369 red Ginebra.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
227
Ilustración 202 Emisor 365 red Ginebra.
Ilustración 203 Emisor 6 red Ginebra.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
228
Ilustración 204 Emisor 398 red Ginebra.
Ilustración 205 Emisor 476 red Ginebra.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
229
Ilustración 206 Emisor 455 red Ginebra.
Ilustración 207 Emisor 456 red Ginebra.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
230
Ilustración 208 Emisor 392 red Ginebra.
Ilustración 209 Emisor 458 red Ginebra.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
231
Ilustración 210 Emisor 476 red Ginebra.
Ilustración 211 Emisor 411 red Ginebra.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
232
Ilustración 212 Emisor 464 red Ginebra.
Ilustración 213 Emisor 457 red Ginebra.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
233
EMISORES ANDALUCÍA
Ilustración 214 Emisor 102 red Andalucía.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
234
Ilustración 215 Emisor 13 red Andalucía.
Ilustración 216 Emisor 317 red Andalucía.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
235
Ilustración 217 Emisor 278 red Andalucía.
Ilustración 218 Emisor 269 red Andalucía.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
236
Ilustración 219 Emisor 298 red Andalucía.
Ilustración 220 Emisor 279 red Andalucía.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
237
Ilustración 221 Emisor 267 red Andalucía.
Ilustración 222 Emisor 286 red Andalucía.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
238
EMISORES MEDELLÍN
Ilustración 223 Emisor 225 red matriz de Medellín.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
239
Ilustración 224 Emisor 46 red matriz de Medellín.
Ilustración 225 Emisor 369 red matriz de Medellín.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
240
Ilustración 226 Emisor 529 red matriz de Medellín.
Ilustración 227 Emisor 540 red matriz de Medellín.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
241
Ilustración 228 Emisor 72 red matriz de Medellín.
Ilustración 229 Emisor 663 red matriz de Medellín.
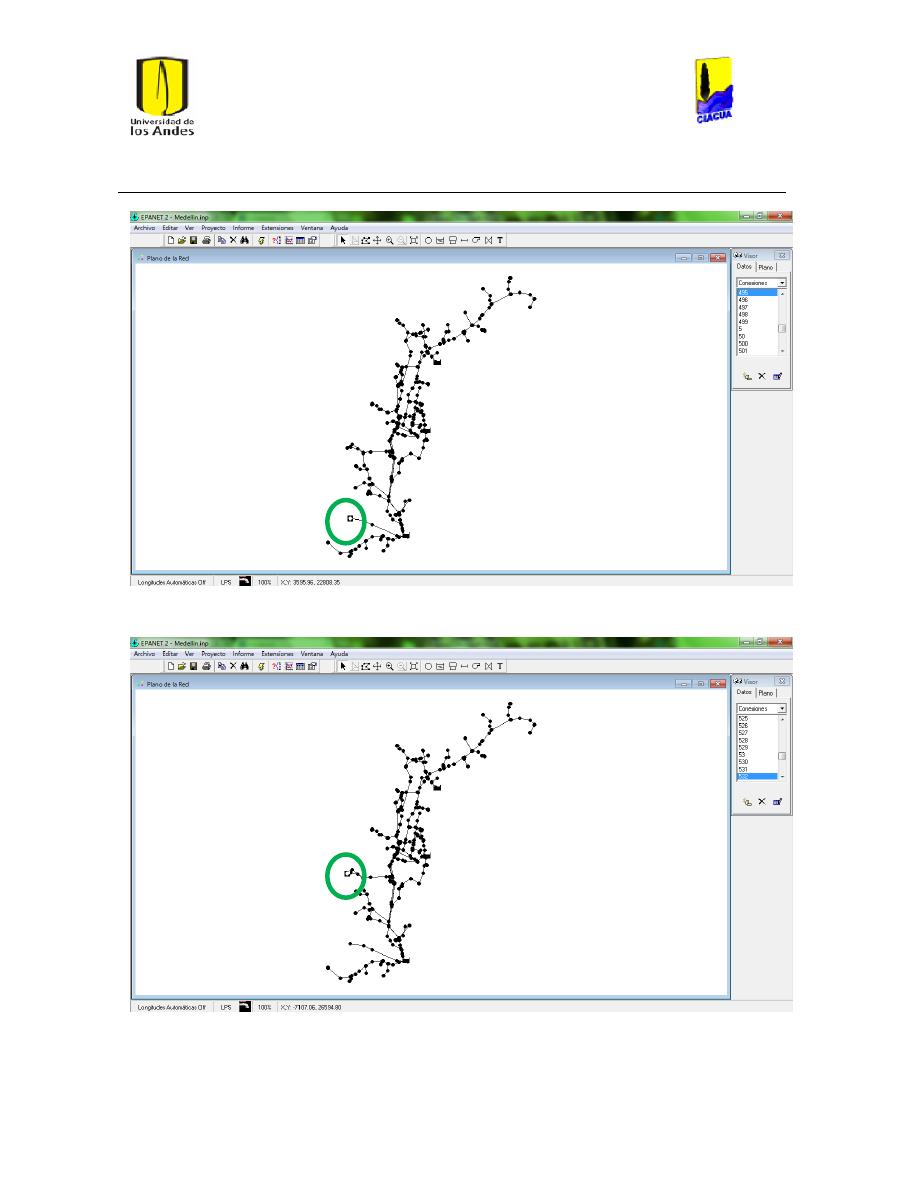
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
242
Ilustración 230 Emisor 495 red matriz de Medellín.
Ilustración 231 Emisor 532 red matriz de Medellín.
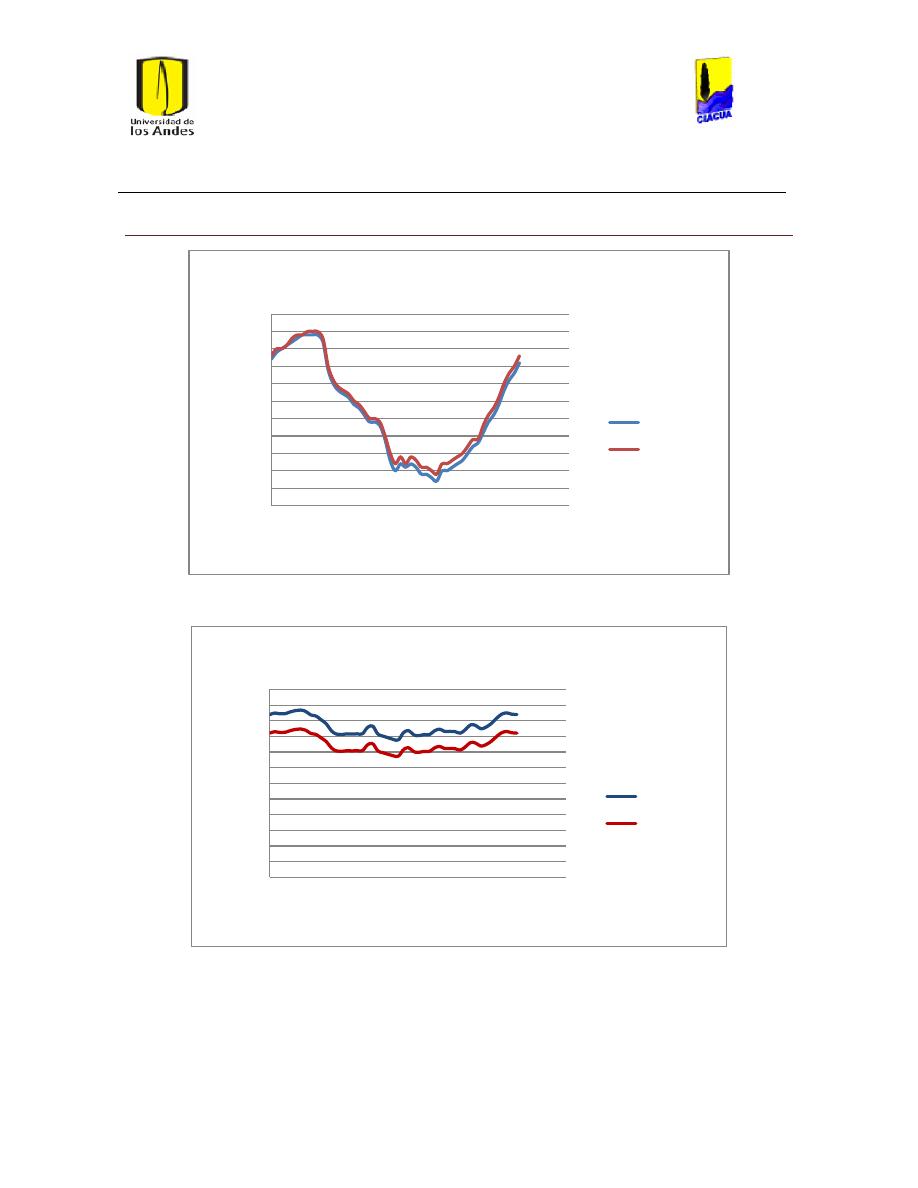
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
243
RESULTADOS ADICIONALES
Ilustración 232 Emisor 3758.
Ilustración 233 Emisor 1045.
4.2
4.25
4.3
4.35
4.4
4.45
4.5
4.55
4.6
4.65
4.7
4.75
00:00 04:48 09:36 14:24 19:12 00:00 04:48
L/s
Tiempo(h)
Diferencia Emisor 3758 Bogotá
Emisor H-W
Emisor D-W
150
155
160
165
170
175
180
185
190
195
200
205
210
00:00 04:48 09:36 14:24 19:12 00:00 04:48
L/s
Tiempo (h)
Bogotá Emisor 1045
Emisor D-W
Emisor H-W
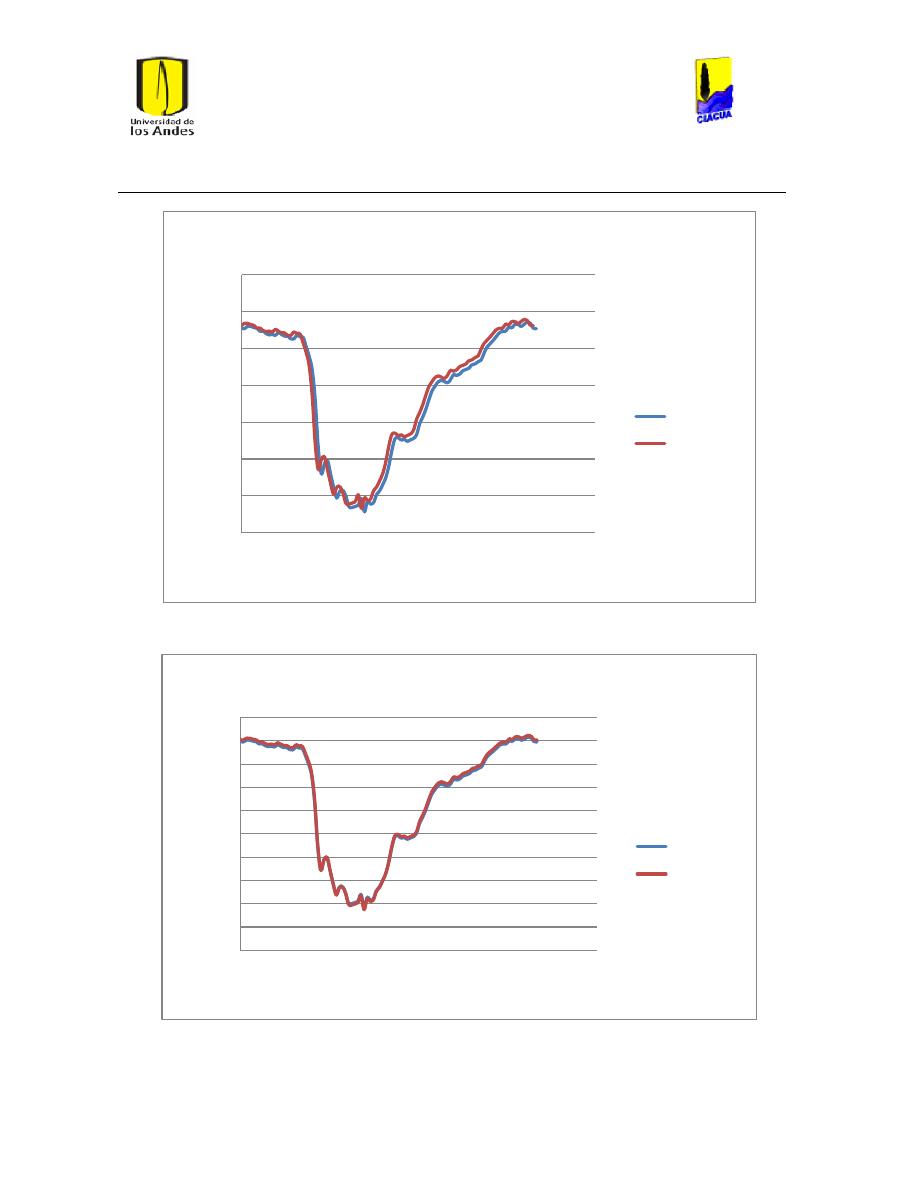
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
244
Ilustración 234 Emisor 455.
Ilustración 235 Emisor 456.
80
90
100
110
120
130
140
150
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 455 Ginebra
Emisor H-W
Emisor D-W
50
55
60
65
70
75
80
85
90
95
100
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s
Tiempo(h)
Diferencia Emisor 456 Ginebra
Emisor H-W
Emisor D-W
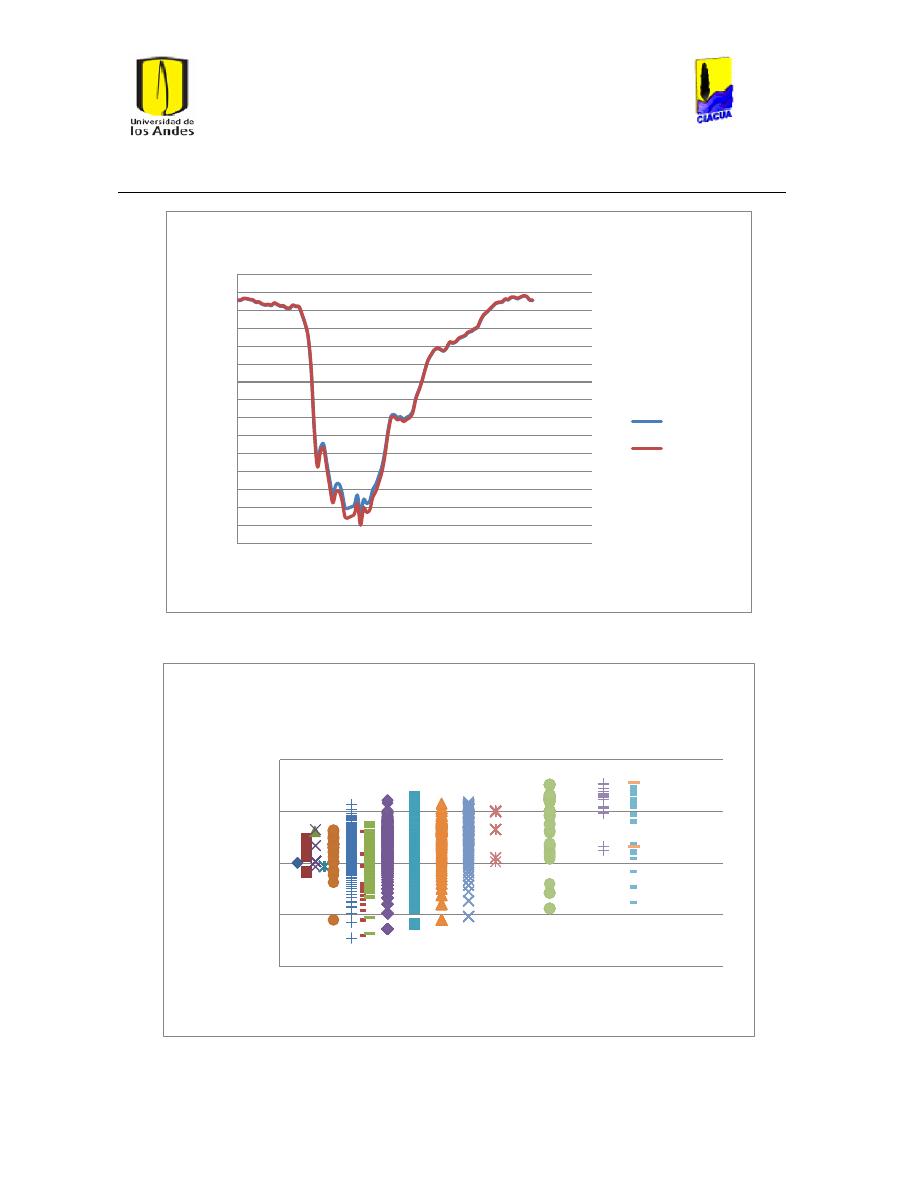
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
245
Ilustración 236 Emisor 398.
Ilustración 237 Reynolds vs Diámetro caudal medio Darcy-Weisbach.
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
00:00
04:48
09:36
14:24
19:12
00:00
04:48
L/s.
Tiempo(h)
Diferencia Emisor 398 Ginebra
Emisor H-W
Emisor D-W
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Bogotá número Reynolds vs Diámetro
Darcy-Weisbach Caudal Medio
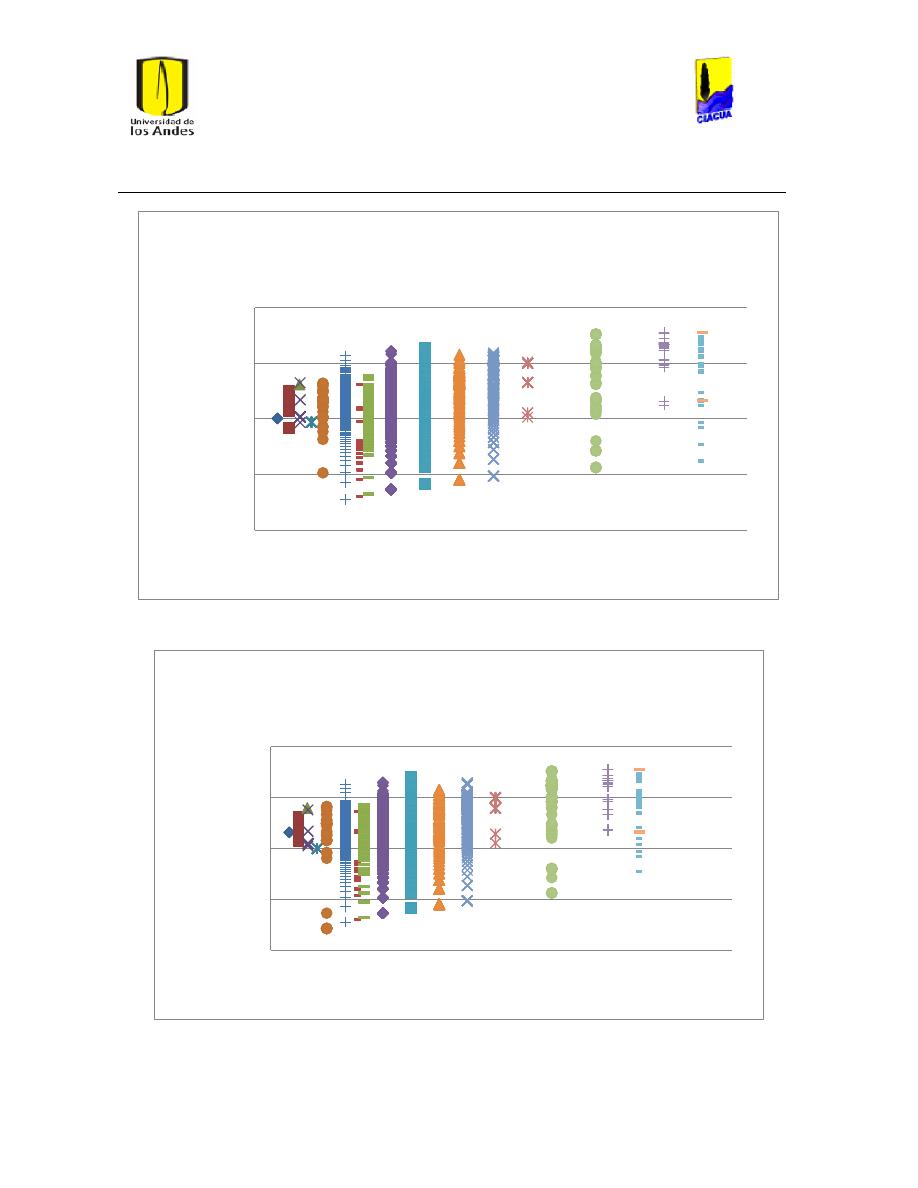
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
246
Ilustración 238 Reynolds vs Diámetro caudal medio Hazen-Williams.
Ilustración 239 Reynolds vs Diámetro caudal Máximo Darcy-Weisbach.
1000
10000
100000
1000000
10000000
0
200
400
600
800
1000 1200 1400 1600 1800 2000 2200
Nú
m
er
o
d
e
Re
yn
olds
Diámetro (mm)
Bogotá número de Reynolds vs Diámetro
Hazen-Williams Caudal Medio
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Bogotá número Reynolds vs Diámetro
Darcy-Weisbach Caudal Máximo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
247
Ilustración 240 Reynolds vs Diámetro caudal máximo Hazen-Williams.
Ilustración 241 Reynolds vs Diámetro caudal mínimo Darcy-Weisbach.
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Bogotá número Reynolds vs Diámetro
Hazen-Williams Caudal Máximo
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Bogotá número de Reynolds vs Diámetro
Darcy-Weisbach Caudal Mínimo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
248
Ilustración 242 Reynolds vs Diámetro caudal mínimo Hazen-Williams.
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Bogotá número de Reynolds vs Diámetro
Hazen-Williams Caudal Mínimo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
249
Ilustración 243 Reynolds vs Diámetro caudal Medio Darcy-Weisbach.
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
3000
3500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Ginebra número de Reynolds Darcy-
Weisbach Caudal Medio

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
250
Ilustración 244 Reynolds vs Diámetro caudal medio Hazen-Williams.
Ilustración 245 Reynolds vs Diámetro caudal Máximo Darcy-Weisbach.
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
3000
3500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Ginebra número de Reynolds Hazen-
Williams Caudal Medio
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
3000
3500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Ginebra número de Reynolds Darcy-
Weisbach Caudal Máximo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
251
Ilustración 246 Reynolds vs Diámetro caudal Máximo Hazen-Williams.
Ilustración 247 Reynolds vs Diámetro caudal Mínimo Darcy-Weisbach.
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
3000
3500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Ginebra número de Reynolds Hazen-
Williams Caudal Máximo
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
3000
3500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Ginebra número de Reynolds Darcy-
Weisbach Caudal Mínimo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
252
Ilustración 248 Reynolds vs Diámetro caudal Mínimo Hazen-Williams.
Ilustración 249 Reynolds vs Diámetro caudal Medio Darcy-Weisbach.
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
3000
3500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Ginebra número de Reynolds Hazen-
Williams Caudal Mínimo
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
3000
3500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Andalucía número de Reynolds Darcy-
Weisbach Caudal Medio
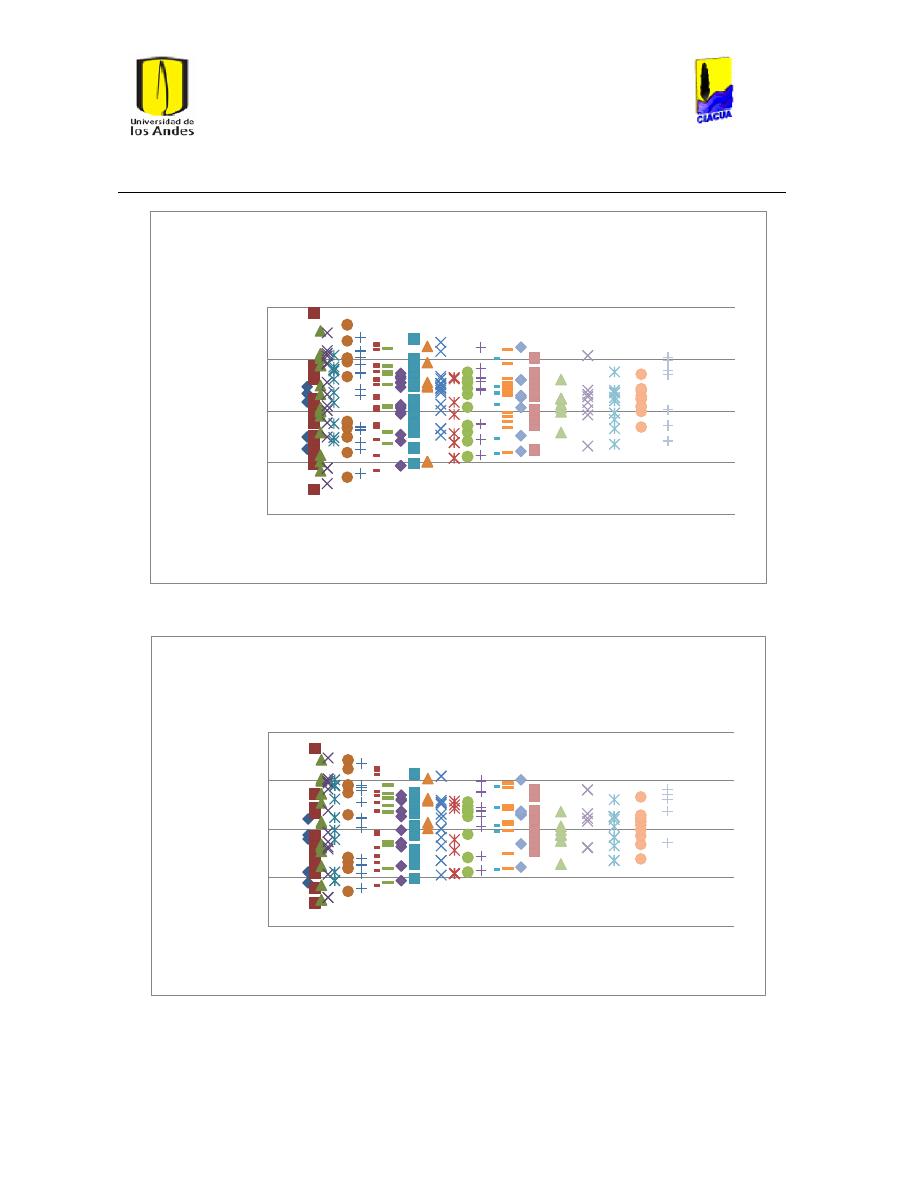
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
253
Ilustración 250 Reynolds vs Diámetro caudal Medio Hazen-Williams.
Ilustración 251 Reynolds vs Diámetro caudal Mínimo Darcy-Weisbach.
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
3000
3500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Andalucía número de Reynolds Hazen-
Williams Caudal Medio
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
3000
3500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Andalucía número de Reynolds Darcy-
Weisbach Caudal Mínimo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
254
Ilustración 252 Reynolds vs Diámetro caudal mínimo Hazen-Williams.
Ilustración 253 Reynolds vs Diámetro caudal Máximo Darcy-Weisbach
1000
10000
100000
1000000
10000000
0
500
1000
1500
2000
2500
3000
3500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Andalucía número de Reynolds Hazen-
Williams Caudal Mínimo
1000
10000
100000
1000000
10000000
100000000
0
500
1000
1500
2000
2500
3000
3500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Andalucía número de Reynolds Darcy-
Weisbach Caudal Máximo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
255
Ilustración 254 Reynolds vs Diámetro caudal máximo Hazen-Williams.
Ilustración 255 Reynolds vs Diámetro caudal Medio Darcy-Weisbach.
1000
10000
100000
1000000
10000000
100000000
0
500
1000
1500
2000
2500
3000
3500
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Andalucía número de Reynolds Hazen-
Williams Caudal Máximo
1000
10000
100000
1000000
10000000
0
200
400
600
800
1000
1200
1400
1600
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Medellín número de Reynolds Darcy-
Weisbach Caudal Medio

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
256
Ilustración 256 Reynolds vs Diámetro caudal medio Hazen-Williams.
Ilustración 257 Reynolds vs Diámetro caudal Máximo Darcy-Weisbach.
1000
10000
100000
1000000
10000000
100000000
0
200
400
600
800
1000
1200
1400
1600
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Medellín número de Reynolds Hazen-
Williams Caudal Medio
1000
10000
100000
1000000
10000000
100000000
0
200
400
600
800
1000
1200
1400
1600
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Medellín número de Reynolds Darcy-
Weisbach Caudal Máximo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
257
Ilustración 258 Reynolds vs Diámetro caudal máximo Hazen-Williams.
1000
10000
100000
1000000
10000000
100000000
0
200
400
600
800
1000
1200
1400
1600
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Medellín número de Reynolds Hazen-
Williams Caudal Máximo
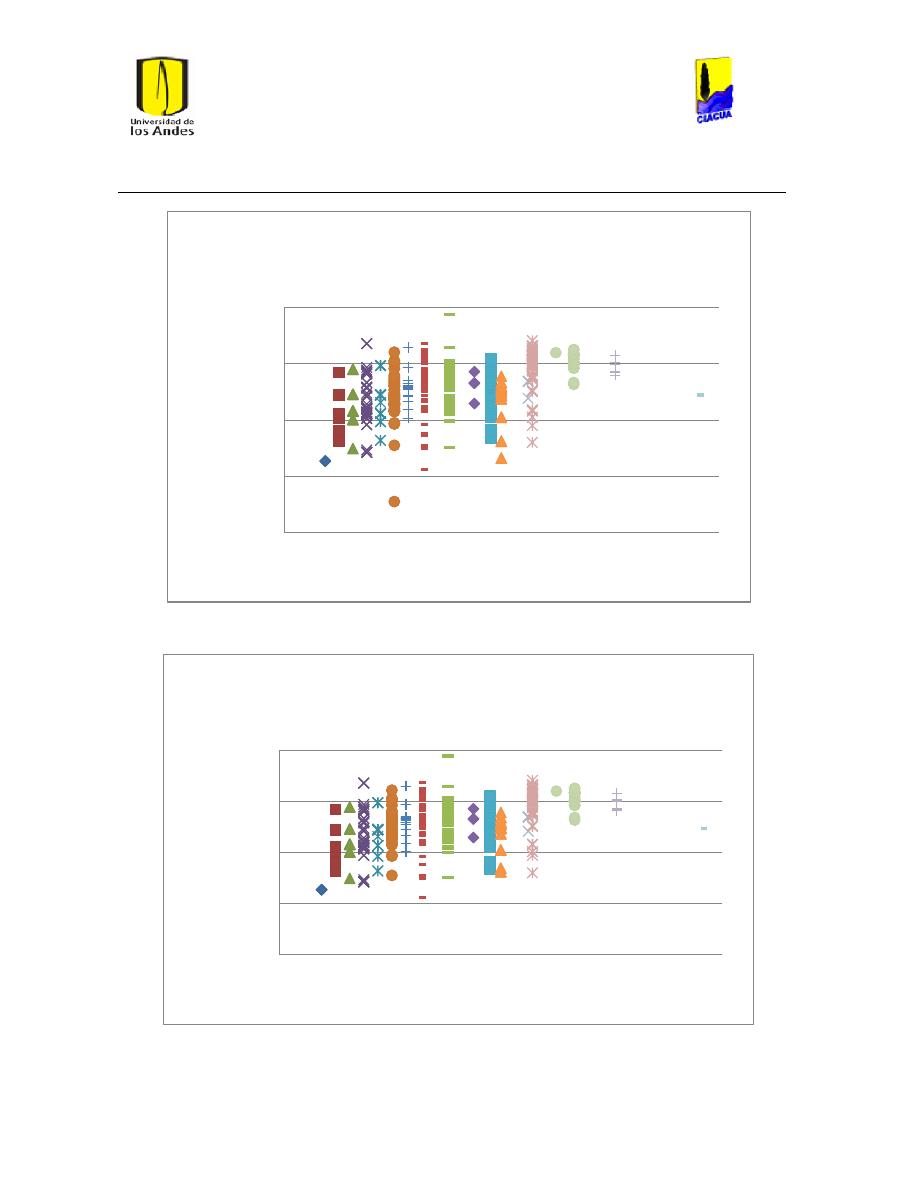
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
258
Ilustración 259 Reynolds vs Diámetro caudal Mínimo Darcy-Weisbach.
Ilustración 260 Reynolds vs Diámetro caudal mínimo Hazen-Williams.
1000
10000
100000
1000000
10000000
0
200
400
600
800
1000
1200
1400
1600
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro (mm)
Medellín número de Reynolds Darcy
Caudal Mínimo
1000
10000
100000
1000000
10000000
0
200
400
600
800
1000
1200
1400
1600
N
ú
m
e
ro
d
e
R
e
yn
o
ld
s
Diámetro(mm)
Medellín número de Reynolds Hazen-
Williams Caudal Mínimo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Estudio sobre el uso de la ecuación de Hazen-Williams vs la ecuación
de Darcy-Weisbach en tuberías de gran diámetro (Sistemas Matrices) y
en tuberías primarias de bombeo.
.
259
