
ESTUDIO DEL COMPORTAMIENTO DE RESALTOS HIDRÁULICOS EN
TUBERÍAS FLUYENDO PARCIALMENTE LLENAS
“XII Simposio Iberoamericano sobre planificación de sistemas de
abastecimiento y drenaje”
Laura Montaño (1), Juan Saldarriaga (2), Diego Páez (3)
(1) Investigadora, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de Los
Andes (CIACUA), Carrera 1ª N° 18ª – 10, Bogotá, Colombia, (+571) 3394949 Ext: 3520,
le.montano110@uniandes.edu.co
(2) Profesor Titular, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de
Los Andes (CIACUA), Carrera 1ª N° 18ª – 10, Bogotá, Colombia, (+571) 3394949 Ext: 1744,
jsaldarr@uniandes.edu.co
(3) Profesor Instructor, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad
de Los Andes (CIACUA), Carrera 1ª N° 18ª – 10, Bogotá, Colombia, (+571) 3394949 Ext: 1744,
da.paez27@uniandes.edu.co
RESUMEN
El resalto hidráulico es un fenómeno generado cuando existe un cambio de flujo supercrítico a flujo
subcrítico causado por un obstáculo aguas abajo. Éste estudio analiza el comportamiento de los resaltos
hidráulicos en tuberías a partir del análisis del comportamiento de las profundidades subsecuentes, la
longitud del resalto, las pérdidas de energía y la distribución de velocidades mediante datos experimentales
obtenidos en un modelo construido en laboratorio. El análisis realizado permite predecir la generación del
fenómeno de sobrecarga, y confirma que los parámetros más influyentes en la generación del resalto son la
pendiente, el caudal y el Número de Froude.
Palabras claves: Resalto hidráulico, profundidades subsecuentes, sistemas de alcantarillado, disipación de
energía, distribución de velocidades.
ABSTRACT
Hydraulic jumps are generated when the flow regime suffers a transition from supercritical to subcritical
usually result from downstream-located obstruction. This study analyzes the subsequent depths, length,
energy dissipation and velocity behavior in the hydraulic jump. We used a Plexiglass pipe to physically
model the hydraulic jump behavior. The results of this study let predict the overflow generation, and the
importance of the slope, flow and Froude Number in the analysis of the hydraulic jump.
Key words: Hydraulic jump, subsequent depths, sewer systems, energy dissipation, velocity distribution.
SOBRE EL AUTOR PRINCIPAL
Autor 1: Ingeniera Ambiental y estudiante de maestría en recursos hídricos e hidroinformática de la
Universidad de los Andes. Asistente Graduada del Centro de Investigaciones en Acueductos y
Alcantarillados CIACUA del Departamento de Ingeniería Civil y Ambiental de la Universidad de los Andes.
Investigadora del Centro de Investigación Estratégica del Agua (CIE-AGUA) de la Facultad de Ingeniería de
la Universidad de los Andes.

INTRODUCCIÓN
El resalto hidráulico es un fenómeno generado
cuando existe un cambio de flujo supercrítico a
subcrítico. Este fenómeno ocurre por la presencia de
altas pendientes u obstáculos (como las compuertas)
que generan un aumento importante del flujo aguas
abajo, afectando las condiciones del flujo aguas
arriba. Es importante tener en cuenta que a medida
que el flujo sea más supercrítico, la profundidad
subsecuente del resalto será mayor disipando más
energía; por el contrario, cuando la profundidad
subsecuente aguas arriba del resalto es mayor (flujo
menos supercrítico), la profundidad subsecuente será
muy similar y en algunos casos, no se forma resalto.
Los principales parámetros de un resalto hidráulico
son: las pérdidas de energía, la longitud del resalto,
la localización y el comportamiento de la
distribución de velocidades. Las pérdidas de energía
son causadas por la turbulencia generada en el
resalto, y se calculan como la diferencia de la
energía específica entre el flujo aguas arriba y el
flujo aguas abajo. La longitud del resalto se mide
desde el lugar donde inicia la turbulencia hasta el
lugar donde finaliza; según la literatura encontrada,
existen relaciones empíricas que permiten encontrar
la longitud del resalto hidráulico dependiendo del
número de Froude y de la altura del flujo aguas
arriba del resalto en canales rectangulares,
trapeciales, triangulares y en el caso de tuberías
circulares
existen
ecuaciones
empíricas
que
dependen del Número de Froude y las profundidades
subsecuentes; sin embargo es un parámetro con alta
incertidumbre, dada la dificultad de medir resaltos
cuando la tubería se presuriza. Por otra parte, la
localización del resalto varía de acuerdo con el
impacto que genere el obstáculo que se encuentre
aguas abajo; por lo tanto, es una variable que en
estudios del resalto en el laboratorio puede ser
modificada.
Por
último,
la
distribución
de
velocidades es un parámetro difícil de identificar
dada la turbulencia que se presenta en la zona del
resalto y no hay estudios previos realizados para
resaltos hidráulicos en tuberías circulares.
ANTECEDENTES Y BASE TEÓRICA
El estudio de resaltos hidráulicos en tuberías inició
en 1938 bajo la dirección del investigador
Kindsvater (1938), quien mediante un modelo
experimental analizaba el comportamiento del
resalto. Su modelo se basaba en una tubería de 6
pulgadas, 6 m de longitud, y con tres obstrucciones
diferentes que generaban el resalto: la primera
ocupaba el 40% de la tubería, la segunda el 60% y la
tercera el 80%. A partir del estudio realizado por
Kindsvater, varios investigadores desarrollaron
ecuaciones, análisis y criterios para estudiar el
comportamiento de los resaltos hidráulicos en las
tuberías.
Uno de estos investigadores que a partir de la
investigación
de
Kindsvater
analizó
el
comportamiento de resaltos hidráulicos en tuberías
fue Silvester (1964). Silvester evaluó ecuaciones
para calcular la profundidad subsecuente del resalto
y su respectiva longitud. En cuanto al cálculo de la
profundidad subsecuente aguas abajo del resalto
hidráulico (
), planteó dos ecuaciones diferentes
para su cálculo: la primera se usa cuando
es
menor al diámetro, y la segunda se usa para
mayores al diámetro:
[
] (1)
[
] (2)
donde
equivale a un factor de proporción del flujo
respecto al centro de masa,
representa el nivel del
flujo,
es el diámetro de la tubería, el área
mojada del flujo y
el Número de Froude. Es
importante aclarar que las dos ecuaciones mostradas
anteriormente, son ecuaciones implícitas, por lo cual,
para resolverlas se requiere de un método numérico;
en el caso de éste estudio, se usó el método de la
bisección para todos los casos evaluados.
Por otro lado, para calcular la longitud del resalto
hidráulico, Silvester propuso una general para todos
los tipos de secciones:
(
)
(3)
donde
es la longitud del resalto hidráulico, y y
son constantes determinadas según la sección del
canal. Para canales circulares, los resultados que se
observaban para los datos obtenidos por Kindsvater
permiten inferir que a medida que aumenta la
relación de llenado aguas arriba del resalto, la
longitud del resalto es menor, es decir, a menor
Número de Froude menor longitud.
Otro investigador en el tema de resaltos hidráulicos
fue Straub (1978), quien propuso ecuaciones
semiempíricas para calcular las profundidades
subsecuentes en el resalto. Esta ecuación se basa en
calcular la profundidad crítica a partir de la siguiente
ecuación:
(
) (
)
(4)
donde
es el caudal, es el diámetro y g es la
gravedad. Para usar la anterior ecuación, se debe
cumplir que 0.02
. Posteriormente, si
la anterior restricción se cumple, entonces se calcula
el Número de Froude a partir de la siguiente
ecuación:
(
)
(5)
Finalmente, la profundidad subsecuente del resalto
hidráulico se calcula dependiendo del valor del
Número de Froude, como se muestra en la Tabla 1:
Tabla 1. Ecuaciones para el cálculo de las
profundidades subsecuentes del resalto.
Condición
Ecuación
(6)
(7)
Posteriormente, French (1988) propone un método
iterativo para el cálculo de la profundidad
subsecuente en el resalto hidráulico en tuberías,
igualando el momento aguas arriba y aguas abajo del
resalto hidráulico:
(
)
̅
(
)
̅
(8)
donde
̅ es la distancia desde la superficie de agua
hasta el centroide de masa,
el área mojada, el
caudal y
la gravedad (Akan, 2006).
En 1999 el investigador Hager (1999) realizó un
proyecto en un nuevo modelo, con un diámetro de
240 mm, pendiente de 0.5%, y una longitud de 6 m
(25 veces el diámetro de la tubería). Éste nuevo
modelo lo planteó para comprobar la Ecuación 9 y la
Ecuación
10,
las
cuales
fueron
deducidas
matemáticamente:
(9)
la cual para F > 2 se puede simplificar a:
(10)
Posteriormente, el modelo experimental permitió
concluir que la Ecuación 10 se representaba mejor
con la Ecuación 11:
(11)
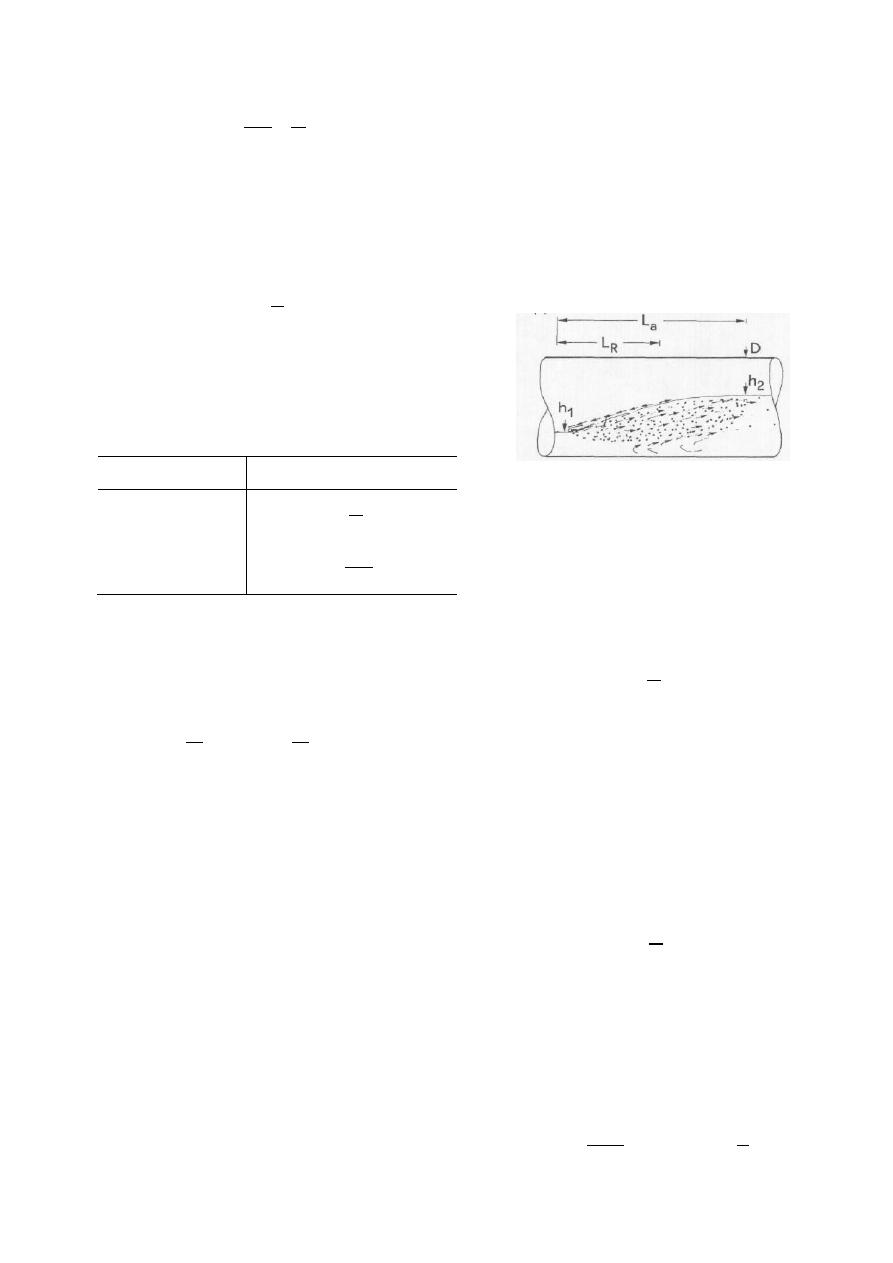
También pudo identificar la longitud del resalto,
estudiada desde dos perspectivas: longitud de
aireación (
) y longitud de recirculación (
) como
se observa en la Figura 1:
Figura 1. Longitudes del resalto hidráulico
en tuberías. (Hager, 1999)
La longitud de recirculación (
) se mide desde el
extremo aguas arriba de los remolinos hasta el punto
de estancamiento. Por lo tanto, para expresar una
ecuación que determine la longitud de recirculación
del resalto hidráulico, Hager y Stahl determinan una
relación entre longitud y altura del flujo aguas abajo
del resalto:
(12)
(13)
La longitud de aireación se mide desde el extremo
aguas arriba del resalto dónde comienzan los
remolinos hasta el lugar dónde no hay burbujas de
aire (Esta longitud es base para encontrar la longitud
del resalto). Para determinarla, Hager y Stahl
nuevamente calcularon una relación entre la longitud
del resalto y la profundidad aguas abajo del resalto y
encontraron una ecuación en función del número de
Froude:
(14)
(15)
En el 2006, la FHWA (Federal Highway
Administration) replantea la ecuación planteada por
Silvester, modificando las relaciones de área que se
muestran anteriormente, por un nuevo coeficiente
(C):
(
)
(16)

(
)
(
)
(17)
También se muestra una aproximación para el
cálculo de la longitud en el resalto, la cual depende si
la profundidad aguas abajo del resalto es mayor o
menor al diámetro de la tubería:
(18)
(
) (19)
DESCRIPCIÓN DEL MODELO Y
METODOLOGÍA
El
modelo
experimental
desarrollado
está
conformado por una tubería de acrílico de 242 mm
de diámetro interno, 13 m de longitud, los cuales se
dividen en 6 tuberías de 2 m y una tubería de 1 m
conectados mediante bridas en acrílico; además la
tubería se encuentra sobre un soporte de acero de 12
m de longitud, el cual se divide en 4 secciones de 3
m; por otra parte, la pendiente de la tubería puede
variar entre 0 % y 2.5 %, y el caudal puede variar
entre 5 L/s y 80 L/s. El resalto se genera por una
compuerta aguas abajo de la tubería, la cual permite
ubicar el resalto en la posición deseada mediante la
apertura o el cierre de la misma.
Adicionalmente, para la medición del resalto, se
modificaron tres tubos del montaje; dos tubos
presentan una modificación en la parte superior, para
ubicar los sensores de nivel, los cuales requieren una
zona muerta para medir el nivel de 15 cm; el tercer
tubo presenta una apertura en la parte superior de la
tubería para ubicar un sensor de velocidad, el cual se
usó para medir el comportamiento y la distribución
de velocidades en el resalto hidráulico. La variación
de la pendiente se realiza mediante unos gatos
hidráulicos ubicados en las uniones del soporte y en
la compuerta, y se facilita su uso gracias a la
ubicación de una diferencial. A continuación se
presenta el esquema para mostrar el montaje
realizado:
Figura 2. Montaje para el análisis de resaltos
hidráulicos en tuberías.
Adicionalmente, cuando el nivel de la tubería aguas
abajo del resalto hidráulico se presurizaba, el nivel
del flujo se midió mediante piezómetros ubicados
cada 20 cm.
Los instrumentos de medición usados en el montaje
fueron: Sensor de nivel ultrasónico U – GAGE T30,
el cual requiere de una zona muerta de 15 cm y tiene
una precisión de 0.25% respecto a la distancia
medida; el segundo instrumento es el velocímetro
Doppler acústico (ADV), el cual es un sensor que
mide la velocidad en las tres dimensiones y tiene una
precisión de 0.01 cm/s; para su medición se realizó
un montaje que permite variar puntualmente la
posición del ADV en las 3 dimensiones; y
finalmente el último instrumento es un caudalímetro
electromagnético ABB que permite conocer el
caudal que entra a la tubería y su precisión es de
0.3% respecto al caudal medido.
Se realizaron dos tipos de pruebas, la primera
analizaba el comportamiento de las profundidades
subsecuentes del resalto hidráulico y la longitud; la
segunda prueba analizaba el comportamiento de la
velocidad en el resalto hidráulico. En las dos pruebas
se realizó variación de pendiente y caudal; sin
embargo, en la primera prueba las pendientes
evaluadas se encontraban en el rango de 0.5% y
2.5%, con caudales entre 5 L/s y 80 L/s. En la
segunda prueba las pendientes variaron entre 1.2% y
2.5% con caudales entre 19 L/s y 26 L/s. El rango de
variación se disminuye dado que para analizar el
comportamiento de la velocidad, se requería que el
resalto hidráulico se ubicara en un solo lugar, para lo
cual, se necesitaban condiciones que generaran un
resalto hidráulico estable.
RESULTADOS
Comparación con los autores previos
Con el fin de comprobar los resultados que se
obtendrían en el montaje, se analizaron cada una de

las
ecuaciones
planteadas
por
los
autores
mencionados en antecedentes, y así observar cuál
debe ser el comportamiento esperado en el montaje
(la solución de las ecuaciones implícitas se realizó
mediante el método de la bisección). Las
condiciones iniciales evaluadas son las que se
encuentran en el montaje:
,
, ,
y
la pendiente evaluada fue de 1.9%, la cual equivale a
la pendiente promedio esperada en el montaje.
Los resultados obtenidos con las ecuaciones
planteadas por Silvester, Straub, French, Hager y la
FHWA, se muestran en las siguientes gráficas:
Figura 3. Comportamiento de las
profundidades subsecuentes en el resalto
hidráulico.
En la Figura 3 se muestra el comportamiento de la
relación entre las profundidades subsecuentes con
respecto al Número de Froude. Se observa
claramente que existe una tendencia a que aumenta
la diferencia entre la profundidad aguas abajo y la
profundidad aguas arriba cuando aumenta el Número
de Froude. El autor que está por debajo de todos los
valores es Straub, teniendo en cuenta que su
ecuación
no
es
físicamente
basada,
sino
semiempírica. Y los valores más altos se obtienen
con las ecuaciones planteadas por Silvester y la
FHWA.
Figura 4. Longitudes en el resalto hidráulico.
En la Figura 4 se observa que a medida que aumenta
el Número de Froude, aumenta la longitud del resalto
hidráulico. Además se observa que cuando se
alcanzan valores del Número de Froude superiores a
2.5, aumenta el rango de variación de la longitud.
Resultados de las pruebas
Los ensayos realizados se basaron en diferentes
pendientes. El primer ensayo se realizó para una
pendiente del 0.5% y el último ensayo realizado fue
para una pendiente del 2.5%. La pendiente del 0.5%
presentó en general resaltos muy débiles que no
permitían inferir fácilmente cuál era la longitud total
del resalto, mientras que en la pendiente del 1.9%, y
con caudales mayores a 0.02 m
3
/s, se pueden
observar resaltos hidráulicos más estables.
En general, para todas aquellas pendientes menores a
1%, la estabilidad del resalto es muy baja
independientemente del caudal analizado; para
pendientes mayores a 1% y caudales menores a 10
L/s el resalto también es débil. Para caudales
mayores a 50 L/s y cualquier pendiente evaluada, el
resalto generaba mucho oleaje, lo que impedía la
localización del resalto en un solo sitio. El resalto
hidráulico era estable para caudales mayores a 10 L/s
y menores a 50 L/s con pendientes mayores a 1%.
Figura 5. Resalto hidráulico débil para S =
0.007 y Q = 34 L/s.
Figura 6. Resalto hidráulico débil para S =
0.011 y Q = 5 L/s.

Figura 7. Resalto hidráulico con oleaje para
S = 0.013 y Q = 50 L/s.
Figura 8. Resalto hidráulico estable para S =
0.011 y Q = 30 L/s.
Figura 9. Resalto hidráulico estable para S =
0.019 y Q = 30 L/s.
A partir de todos los escenarios evaluados, se
graficaron los diferentes comportamientos de la
profundidad del resalto hidráulico y la longitud del
mismo.
A continuación se presenta el comportamiento de las
profundidades subsecuentes y de la longitud del
resalto hidráulico para una pendiente de 2.1%:
Figura 10. Comportamiento profundidades
subsecuentes.
Se puede observar que a medida que aumenta el
caudal, aumenta la profundidad subsecuente del
resalto hidráulico, sin afectar la diferencia que existe
entre la profundidad subsecuente aguas arriba y
aguas abajo del resalto.
Figura 11. Longitudes en el resalto
hidráulico.
En cuanto a la longitud del resalto hidráulico, se
puede observar en la Figura 11 que existe cierta
tendencia a que aumente ésta a medida que aumenta
el Número de Froude. Sin embargo, respecto a los
otros escenarios, no es una tendencia general.
Adicionalmente, se graficó el perfil del resalto
hidráulico para todos los escenarios evaluados
obtenidos a partir de la medición realizada con los
piezómetros. A continuación se muestra el perfil
para una pendiente de 1.1% y diferentes caudales:
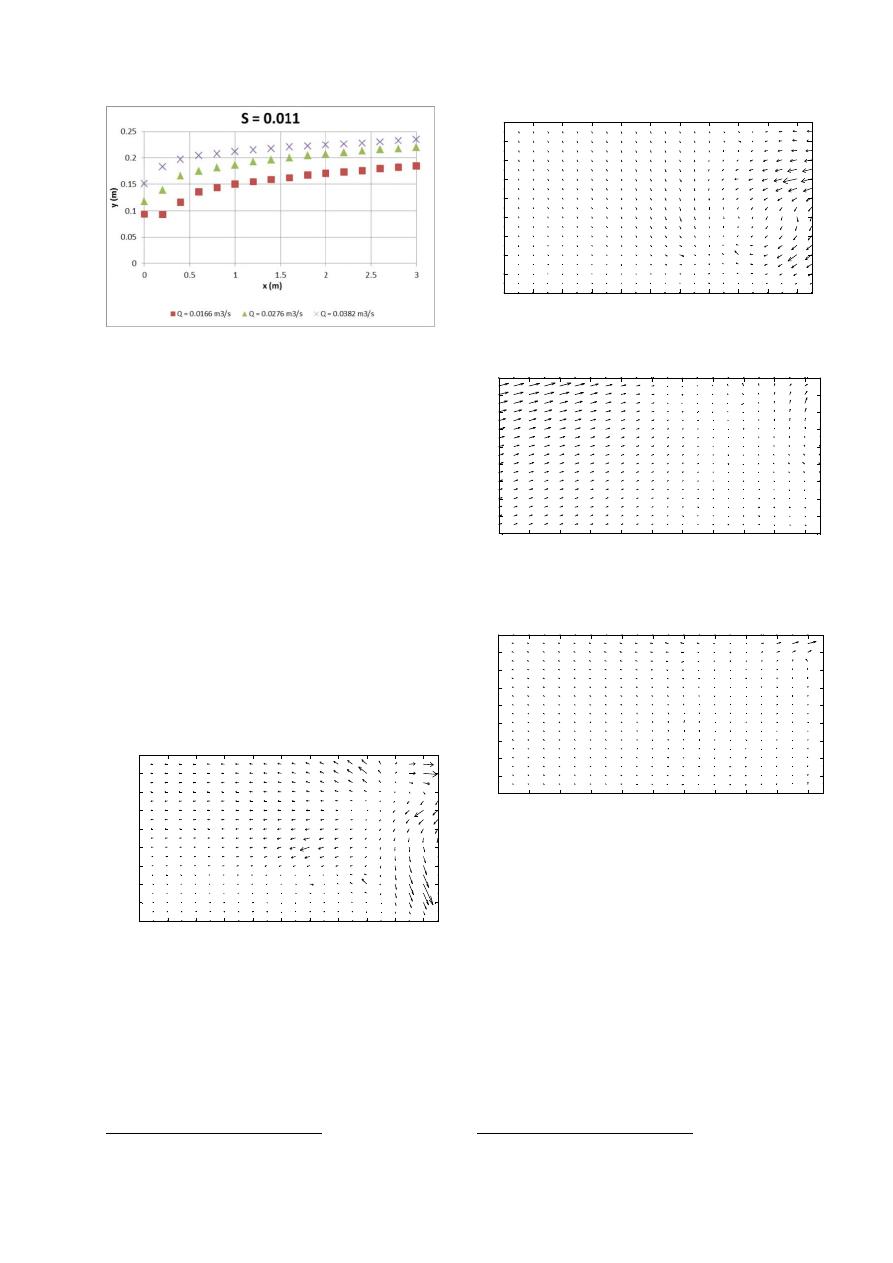
Figura 12. Perfil de altura en el resalto
hidráulico.
Se puede observar que a mayor caudal, mayor nivel
en el flujo. Es importante resaltar, que a pesar de que
la variación entre los 3 caudales mostrados es la
misma, existe mayor distancia entre los datos
tomados con el caudal más bajo (0.0166 m
3
/s) con
respecto al caudal medio, que la distancia existente
entre el caudal medio y el caudal más alto medido
(0.0382 m
3
/s). Con éste resultado se podría inferir
que a medida que aumenta el caudal, las
profundidades subsecuentes aguas abajo del resalto
tienden a ser más parecidas entre sí.
Por otra parte, para analizar el comportamiento de la
distribución de las velocidades en el resalto
hidráulico, se realizó un campo vectorial de los
diferentes escenarios evaluados. A continuación se
muestran los resultados obtenidos para una pendiente
de 1.6 % y un caudal de 24 L/s.
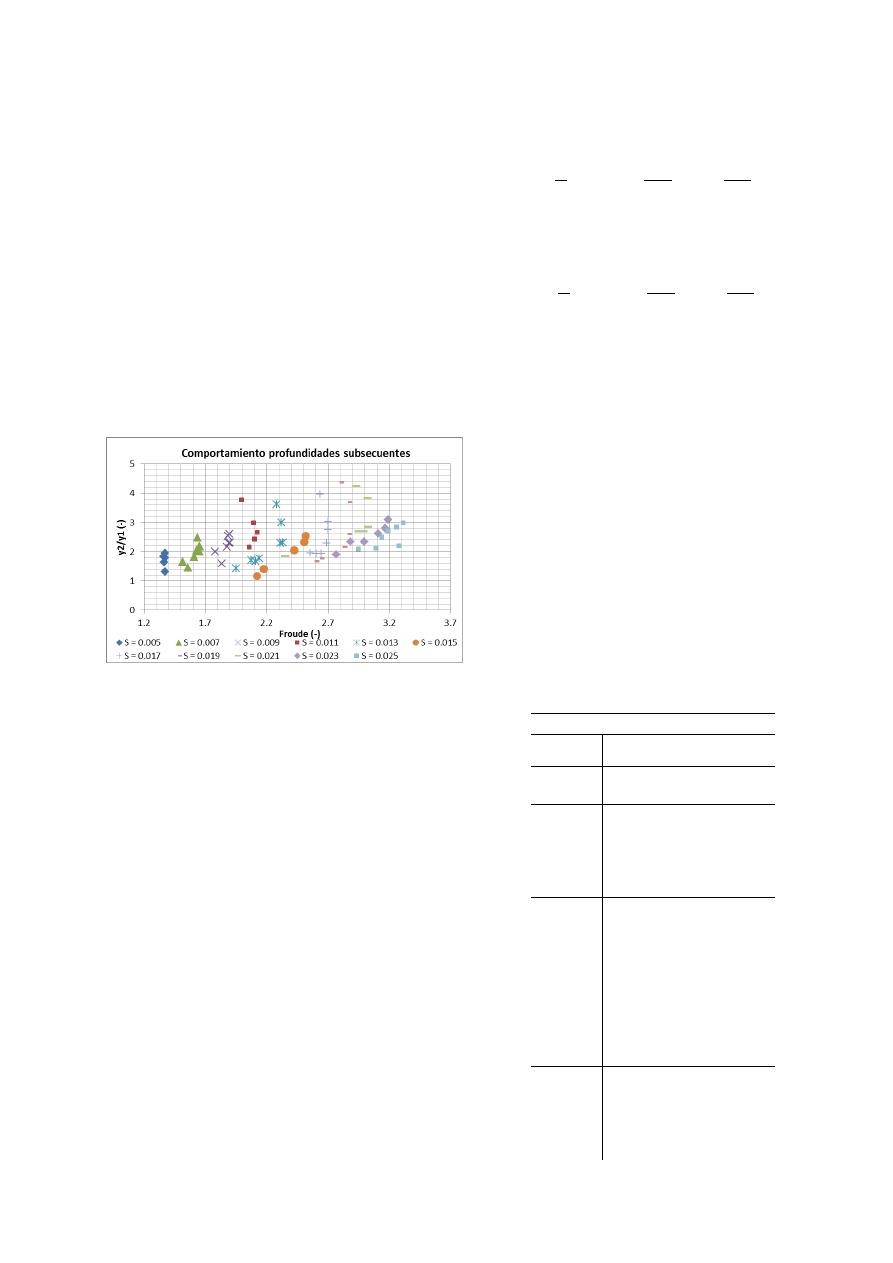
Figura 13. Distribución velocidades resalto
hidráulico para Py
1
= 0 m
– Vista Perfil.
1
Py corresponde a la posición medida en la coordenada y
(Sección transversal de la tubería).
Figura 14. Distribución velocidades resalto
hidráulico para Py = 0.04 m
– Vista Perfil.
Figura 15. Distribución velocidades resalto
hidráulico para Pz
2
= 0.01 m
– Vista en
Planta.
Figura 16. Distribución velocidades resalto
hidráulico para Pz = 0.02 m
– Vista en Planta.
El campo vectorial representa la dirección de la
velocidad del flujo en diferentes puntos de medición;
y en las ilustraciones anteriores se puede observar
como varía la dirección de estas partículas
independientemente si se realiza un análisis vista en
perfil o vista en planta. Es decir, este análisis permite
observar los remolinos presentes en un resalto
hidráulico, los cuales se generan en el eje vertical de
la tubería y en el eje transversal.
2
Pz corresponde a la posición medida en la coordenada z
(Sección vertical de la tubería).
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
x (m) - Sección Longitudinal
z
(
m
)
-
S
e
c
c
ió
n
V
e
rt
ic
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.016 y Q = 0.024 m3/s) Py = 1
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
x (m) - Sección Longitudinal
z
(
m
)
-
S
e
c
c
ió
n
V
e
rt
ic
a
l
PERFIL VELOCIDAD RESALTO HIDRÁULICO (S = 0.016 y Q = 0.024 m3/s) Py = 3
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
x (m) - Sección Longitudinal
y
(
m
)
-
S
e
c
c
ió
n
T
ra
n
s
v
e
rs
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.016 y Q = 0.024 m3/s) Pz = 1
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
x (m) - Sección Longitudinal
y
(
m
)
-
S
e
c
c
ió
n
T
ra
n
s
v
e
rs
a
l
PERFIL DE VELOCIDAD RESALTO HIDRÁULICO (S = 0.016 y Q = 0.024 m3/s) Pz = 2
ANÁLISIS DE RESULTADOS
A partir de los datos obtenidos, se realizaron 4
análisis
diferentes:
comportamiento
de
las
profundidades subsecuentes en el resalto hidráulico,
longitud del mismo, comportamiento de la disipación
de energía y el comportamiento de la velocidad del
resalto.
Análisis del comportamiento entre las
profundidades subsecuentes
El
comportamiento
de
las
profundidades
subsecuentes del resalto hidráulico se analizó
mediante la comparación entre estas y el Número de
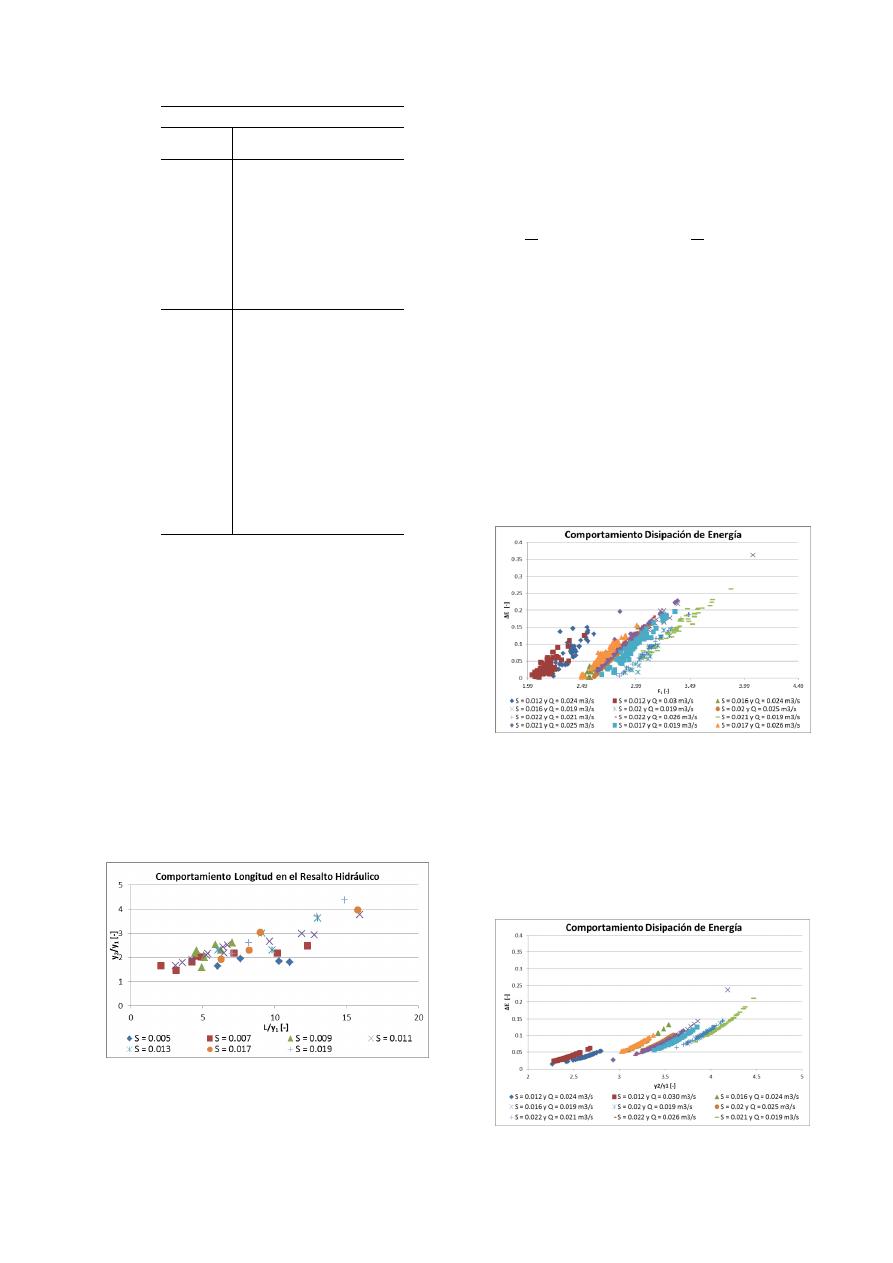
Froude, como se observa en la Figura 17:
Figura 17. Comportamiento de las
profundidades subsecuentes.
En la Figura 17 se observa un comportamiento
similar para los 8 tipos de pendiente evaluados.
Además existe cierta tendencia a que cuando la
relación entre las profundidades de flujo alcanza el
máximo Número de Froude, la gráfica presenta una
variación en el sentido de la curva. Por lo tanto, para
aquellas relaciones entre las profundidades de flujo
que se encuentran por debajo del máximo Número
de Froude, a mayor Número de Froude, existe mayor
diferencia entre la profundidad aguas abajo del
resalto y la profundidad aguas arriba; mientras que
cuando los valores son superiores al máximo valor
del Número de Froude, este disminuye a medida que
la relación entre las profundidades subsecuentes del
resalto aumenta. Adicionalmente, aquellos puntos en
los cuales se encuentra el máximo Número de
Froude corresponden a relaciones de llenado
cercanas al 30%. Por ésta razón, se puede determinar
que el comportamiento de las profundidades
subsecuentes depende de la pendiente, del Número
de Froude y del caudal. Por consiguiente se realizó
una regresión multivariable con éstos tres parámetros
y se obtuvo que la aproximación que describe mejor
el comportamiento empírico de las profundidades
subsecuentes del resalto hidráulico depende de las
dos ecuaciones mostradas a continuación:
(
)
(
)
(20)
el R
2
de la ecuación 20 es de 85.3%.
(
)
(
)
(21)
el R
2
de la ecuación 21 es de 90.7%.
Se observa que cuando la profundidad subsecuente
aguas abajo del resalto es menor el diámetro, el
parámetro más relevante es la pendiente con un
porcentaje de 63 %, mientras que el caudal tiene un
peso de 37%. Para
mayor al diámetro, el peso del
caudal pasa a ser de 75.2% y la pendiente tiene un
peso 24.8%, lo que permite inferir la importancia
que adquiere el caudal de entrada cuando la altura
subsecuente aguas abajo del resalto es mayor al
diámetro.
Adicionalmente, al usar esta ecuación en otros
escenarios (variación en el diámetro, la pendiente y
el caudal), se establece una limitación en el rango de
validez de las ecuaciones para los siguientes casos:
Tabla 2. Ecuaciones para el cálculo de las
profundidades subsecuentes del resalto.
Rango de validez
d
(m)
y/d
(-)
S
(-)
0.150
0.47 - 0.70
0.200
0.35 - 0.38
0.300
0.200
0.29 - 0.38
0.01
0.33 - 0.35
0.015
0.26 - 0.28
0.02
0.33 - 0.36
0.2
0.27 - 0.28
0.3
0.250
0.21 - 0.26
0.01
0.20 - 0.25
0.015
0.20 - 0.24
0.02
0.19 - 0.23
0.025
0.19 - 0.23
0.03
0.19 - 0.2
0.04
0.25 - 0.69
0.08
0.44 - 0.70
0.09
0.41 - 0.47
0.1
0.300
0.16 - 0.20
0.01
0.16 - 0.19
0.015
0.15 - 0.19
0.015
0.15 - 0.19
0.02
0.15 - 0.18
0.025
Rango de validez
d
(m)
y/d
(-)
S
(-)
0.15 - 0.18
0.03
0.15 - 0.18
0.04
0.15 - 0.17
0.05
0.15 - 0.70
0.06
0.14 - 0.7
0.07
0.38 - 0.43
0.08
0.35 - 0.39
0.09
0.33 - 0.36
0.1
0.350
0.13 - 0.16
0.01
0.13 - 0.15
0.015
0.13 - 0.15
0.02
0.13 - 0.15
0.025
0.13 - 0.15
0.03
0.12 - 0.15
0.04
0.12 - 0.7
0.05
0.12 - 0.43
0.06
0.12 - 0.38
0.07
0.12 - 0.35
0.08
0.12 - 0.32
0.09
0.12 - 0.30
0.1
En la Tabla 2 se observa que el rango de validez de
los resultados obtenidos con la Ecuación 20 y la
Ecuación 21 se encuentra para parámetros de entrada
similares a los del montaje evaluado; es decir,
diámetros cercanos a 250 mm y pendientes bajas.
Análisis del comportamiento de la longitud
del resalto hidráulico
La longitud en el resalto hidráulico se analiza
respecto a la pendiente y a la relación entre las
profundidades subsecuentes. Éste análisis se realizó
también comparando el Número de Froude, sin
embargo el coeficiente de determinación calculado
no era tan alto respecto a un análisis sin el Número
de Froude.
Figura 18. Comportamiento de la longitud en
el Resalto Hidráulico.
En la Figura 18 se observa cierta tendencia a que con
el aumento de la pendiente en el modelo
experimental, la pendiente de cada curva va
aumentando. Por lo tanto, se puede establecer que la
longitud del resalto hidráulico está relacionada con la
relación entre las profundidades subsecuentes y la
pendiente, por lo cual, usando la función cftool de
Matlab se obtiene la siguiente ecuación:
(
)
(22)
La ecuación 22 tiene un coeficiente de determinación
de 70.7% y un EMC de 1.974.
Análisis del comportamiento de disipación de
energía
Para analizar la eficiencia del resalto hidráulico, se
desarrolla el análisis de disipación de energía en el
cual se compara la variación del Número de Froude
y la relación entre las profundidades subsecuentes
respecto a la disipación de Energía para diferentes
caudales, obteniendo las siguientes gráficas:
Figura 19. Comportamiento Disipación de
Energía.
En la Figura 19 se observa que la relación entre el
Número de Froude y la disipación de Energía es
lineal y directamente proporcional. El aumento de la
pendiente y del caudal afectan el valor del Número
de Froude pero no afectan el valor de la disipación
de Energía.
Figura 20. Comportamiento Disipación de
Energía.
En la Figura 20 se observa que el comportamiento
entre la relación de las profundidades subsecuentes y
la disipación de energía también es directamente
proporcional; sin embargo el crecimiento no es
lineal, sino que tiende a aumentar lento al inicio
(para valores de la disipación de energía bajos) y
aumentar más rápido para valores de la disipación de
energía más altos.
Con las gráficas anteriores se puede establecer una
clara relación entre la disipación de energía, el
Número de Froude y la relación entre las
profundidades subsecuentes; por lo tanto usando la
función cftool de Matlab se obtiene la siguiente
regresión potencial:
(
)
(
(
)
(
)
)
(23)
La ecuación obtenida tiene un coeficiente de
determinación de 84.5%, con lo cual se establece que
la Ecuación 22 representa de manera apropiada el
comportamiento de la disipación de energía.
Análisis
del
comportamiento
de
la
distribución de velocidades
Para entender el comportamiento de la velocidad en
la zona de un resalto hidráulico en la tubería, se
realizaron dos tipos de análisis; el primer análisis se
basa en determinar la importancia de los diferentes
componentes de la velocidad (v
x
, v
y
, v
z
) respecto a la
magnitud total de la velocidad, con lo cual se puede
definir si la dirección de cada partícula se ve
afectada por los remolinos generados en el resalto. El
segundo análisis evalúa si existe mayor varianza en
la toma de datos medidos cerca al fondo del canal o a
la superficie del resalto.
La importancia de cada uno de los componentes de
la velocidad se observa en la Figura 21:
Tabla 3. Escenarios evaluados para la
distribución de las velocidades.
# Escenario
S
(-)
Q
(m³/s)
1
0.012
0.024
2
0.012
0.030
3
0.016
0.019
4
0.016
0.024
5
0.017
0.019
6
0.017
0.026
7
0.020
0.020
8
0.020
0.025
9
0.021
0.019
10
0.021
0.025
# Escenario
S
(-)
Q
(m³/s)
11
0.022
0.021
12
0.022
0.026
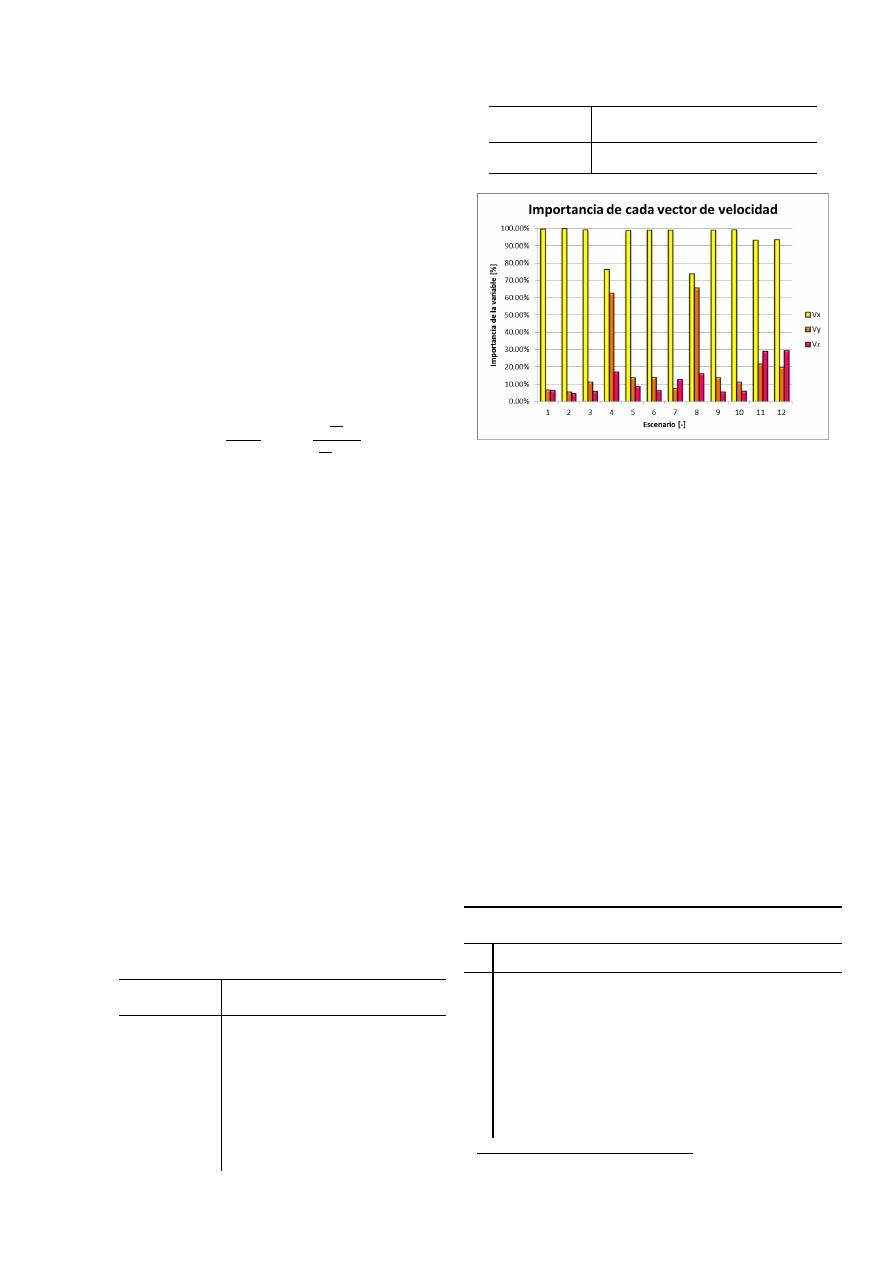
Figura 21. Importancia de los diferentes
componentes de la velocidad.
3
En la Figura 21 se observa que en la mayoría de
casos, el vector de la velocidad en el eje x
corresponde a más del 90% de la magnitud total de
la velocidad, es decir, que a pesar de los remolinos
generados en el resalto hidráulico, la velocidad que
rige el comportamiento de las partículas es la
velocidad en x.
Para determinar cómo era el comportamiento de la
distribución de velocidades en el resalto hidráulico
se realizó un análisis de varianza de datos respecto a
la posición de los puntos medidos. El análisis se
realizó comparando la desviación estándar de cada
uno de los puntos de medición en el perfil vertical y
en el perfil transversal; sin embargo, la tendencia
solo se presentó en el análisis de los datos realizado
en el perfil vertical.
Tabla 4. Análisis de la distribución de
velocidad en resaltos hidráulicos en
tuberías.
Comportamiento de la Distribución de
Velocidades
ID
Desviación
(cm/s)
Media
(cm/s)
Per 20
(cm/s)
Per 80
(cm/s)
Diferencia
(cm/s)
F/S
1
116.754
20.14
-114.922
127.328
242.25
S
7
106.422
55.754
-104.07
131.95
236.02
S
11
15.079
0.458
-10.468
8.344
18.812
F
12
12.006
1.373
-8.554
10.902
19.456
F
19
26.988
12.844
-4.16
31.53
35.69
F
21
75.603
-81.099
-124.214
-83.952
40.262
S
22
113.024
0.34
-106.296
126.696
232.992
S
3
Cada ID del escenario se explica en la Tabla 3.

Comportamiento de la Distribución de
Velocidades
ID
Desviación
(cm/s)
Media
(cm/s)
Per 20
(cm/s)
Per 80
(cm/s)
Diferencia
(cm/s)
F/S
25
41.805
46.208
18.716
80.218
61.502
F
26
29.425
61.574
36.064
84.764
48.7
F
29
77.229
-52.719
-108.232
32.742
140.974
S
30
113.509
-10.516
-110.51
127.55
238.06
S
En la Tabla 4 se observan dos letras diferentes; F
hace referencia a aquellos puntos medidos cerca al
fondo de la tubería y S hace referencia a aquellos
puntos que fueron medidos lejos del fondo de la
tubería. Además existen 6 columnas; la primera
columna hace referencia al ID del punto de
medición; la segunda columna a la desviación
estándar de todos los datos tomados en cada punto de
medición; la tercera columna hace referencia a la
media de todos los datos tomados en cada punto de
medición; la cuarta y quinta columna representan los
percentiles 20 y 80 de la muestra respectivamente,
para lo cual se organizaron los datos de menor a
mayor. Por último la sexta columna hace referencia a
la diferencia que hay entre el percentil 80 y el
percentil 20. Con éstos resultados se puede observar
que aquellos puntos que se encuentran cercanos al
fondo del canal presentan menor desviación estándar
y menor diferencia entre el percentil 20 y 80,
mientras que aquellos puntos que se encuentran lejos
del fondo de la tubería tienen desviaciones y
diferencias mayores. Por lo tanto, se puede concluir
que aquellos puntos cercanos al fondo de la tubería
presentan menor variación de datos, es decir, menor
turbulencia, y menor variación en la dirección de las
partículas, mientras que los puntos medidos lejos del
fondo de la tubería presentan mayor variación en la
dirección de las partículas. Esto es consistente con la
teoría de distribución de velocidades en tuberías a
presión, en dónde la variación de la velocidad en el
fondo de la tubería es cero.
CONCLUSIONES
En todas las metodologías estudiadas de resaltos
hidráulicos en tuberías, se observa que siempre
que aumente el valor en el Número de Froude, la
relación entre las profundidades subsecuentes
será mayor.
El valor del Número de Froude para pendientes
más altas es mayor, lo cual también aumenta la
relación entre las profundidades subsecuentes en
el resalto.
Según las metodologías estudiadas de resaltos
hidráulicos en tuberías, a mayor Número de
Froude, la longitud del resalto será mayor.
Para las pendientes del montaje menores a 0.010,
la estabilidad del resalto es muy baja, y no se
puede ubicar exactamente en la zona requerida
para la medición; además los resaltos hidráulicos
son muy inestables y no se puede identificar
claramente cuál es la longitud del resalto, ya que
no existe una clara diferencia entre la profundidad
aguas arriba y aguas abajo del resalto hidráulico.
Esto ocurre ya que el Número de Froude aguas
arriba del resalto es muy bajo, y no permite
generar la fuerza suficiente para presentar un
resalto hidráulico estable.
Cuando las pendientes en el resalto son mayores a
0.010, pero el caudal es menor o igual a 0.01
m³/s, el resalto también es débil y no se puede
identificar la longitud ni las profundidades
subsecuentes en el resalto claramente.
Para caudales mayores a 0.05 m³/s, el perfil del
resalto hidráulico empieza a generar muchas
ondas en la zona subcrítica; y el resalto deja de
ser estable ya que la profundidad aguas abajo del
resalto se acerca a la zona de flujo cuasicrítico.
A mayor pendiente, aumenta el valor en los
Números de Froude, y la longitud del resalto
aumenta con un aumento muy leve en este
número.
El comportamiento de la profundidad subsecuente
aguas abajo del resalto hidráulico en tuberías
depende del caudal, de la pendiente y de la
profundidad subsecuente aguas arriba.
La longitud del resalto hidráulico en tuberías
depende de las profundidades subsecuentes del
resalto y de la pendiente medida.
La disipación de energía depende del Número de
Froude y de la relación entre las profundidades
subsecuentes, lo cual sucede en los resaltos
hidráulicos que ocurren en canales rectangulares.
La velocidad principal que rige la dirección de las
partículas ubicadas en los remolinos del resalto
hidráulico es la velocidad en x.
La distribución de velocidades cercana al fondo
del canal es más estable que la presentada en
puntos cercanos a la superficie del resalto, dónde
se presenta mayor turbulencia.
RECOMENDACIONES
Recomendaciones de diseño
A
continuación
se
presentarán
algunas
recomendaciones para el diseño de tuberías de
alcantarillado de 250 mm de diámetro y que

presenten el riesgo de la formación de un resalto
hidráulico, con el fin de evitar el fenómeno de
sobrecarga en la tubería:
Para un diámetro de 250 mm y cualquier
pendiente, se deben evitar caudales mayores
a 50 L/s.
Para pendientes menores a 1.5 %, se pueden
permitir caudales menores a 50 L/s.
Para pendientes entre 1.5 % y 1.9 %, no se
deben permitir caudales mayores a 20 L/s.
Para pendientes mayores a 2 %, la tubería se
presuriza con caudales iguales o mayores a
20 L/s.
Con pendientes superiores a 2%, se debe
evitar cualquier obstáculo en el flujo aguas
abajo de la tubería, ya que la velocidad del
flujo
hace
que
se
generen
resaltos
hidráulicos con caudales bajos.
Se deben evitar Números de Froude
superiores a 2.0 para evitar resaltos
hidráulicos que generen sobrecarga en la
tubería.
BIBLIOGRAFÍA
Akan,
A.
O.
(2006).
OPEN
CHANNEL
HYDRAULICS. Canada: ELSEVIER.
FHWA. (2006), “Hydraulic Design of Energy
Dissipators for Culverts and Channels”,
Hydraulic Engineering Circular, 6-1 a 6-14.
French, R. H. (2007). Open Channel Hydraulics.
Colorado, USA: Copyright.
Ghamry, H. K., Shames, A., & Branch, F. (2002).
“Hydraulic Jumps in Circular Conduits.”
Québec: CSCE.
Gonzales
Rodríguez,
M.
(1992).
“Estudio
Experimental de Flujos Disipativos: I.
Resalto Hidráulico.” Cantabria: Universidad
de Cantabria.
Hager, W. H. (1990). “CRITICAL FLOW.”
Wastewater Hydraulics (pp. 137 - 172).
Kindsvater, E. W. (1938). “Hydraulic Jump In
Enclosed Conduits”. Engineering News
Record, 815 - 817.
Rajaratnam, N. (1965). “Hydraulic Jump in
Horizontal Conduits.” WATER POWER, 80
- 83.
Silvester, R. (1964). “HYDRAULIC JUMP IN ALL
SHAPES
OF
HORIZONTAL
CHANNELS.” Proceedings of the American
Society of Civil Engineers, 23 - 55.
SMITH, C. D., & CHEN, W. (1989). “The hydraulic
jump in a steeply sloping square conduit.”
JOURNAL OF HYDRAULIC RESEARCH,
385 - 399.
Stahl, H., & Hager, W. H. (1999). “Hydraulic jump
in circular pipes.” Canadian Journal of Civil
Engineering, 368 -373.
Sturm, T. W. (2010). Open Channel Hydraulics.
Singapore: McGraw-Hill.
