
IAHR
CIC
XXV CONGRESO LATINOAMERICANO DE HIDRÁULICA
SAN JOSÉ, COSTA RICA, 9 AL 12 DE SETIEMBRE DE 2012
ERRORES EN EL DISEÑO DE TUBERÍAS DE DRENAJE URBANO
CAUSADOS POR EL USO DE LA ECUACIÓN DE MANNING
Diana Martínez , Juan Ossa
Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA), Departamento de Ingeniería Civil y Ambiental,
Universidad de los Andes, Bogotá, Colombia
de.martinez56@uniandes.edu.co
,
js.ossa117@uniandes.edu.co
RESUMEN:
Desde su aparición original en 1889, la ecuación de Manning ha sido la más popular a la hora de
diseñar redes de drenaje urbano. Sin embargo, no siempre se conoce la historia completa de su
aparición, sus coautores, sus limitaciones y los errores que origina cuando las variables de entrada
se salen de su rango de aplicación. El presente estudio hace un repaso del proceso investigativo que
siguieron distintos científicos, para permitir que el ingeniero Irlandés Robert Manning llegara a
definir su metodología. Se presentan también las limitaciones que tiene este acercamiento, muchas
conocidas por el propio Manning, y algunos procedimientos por medio de los cuales distintos
autores han tratado de corregir el coeficiente n. Finalmente, se desarrolla un programa que permite
realizar una gran cantidad de diseños, variando las distintas condiciones de entrada, usando esta
ecuación y la de Darcy-Weisbach en conjunto con la ecuación de Colebrook-White. De esta forma
se evalúa la diferencia de los resultados entre ambas, y teniendo en cuenta que la segunda es más
precisa, se halla evidencia de la magnitud de los errores de la primera.
ABSTRACT:
Manning’s equation has been very popular since it was first conceived in 1889. It is used for the
design of urban drainage networks. However, there are aspects—limitations, co-authors, and
errors—that remain unknown. This paper reviews the investigation that scientists carried out prior
to the development of the Irish engineer’s methodology. It specifically points out the limitations
that this methodology brings, which have been acknowledged by Manning himself. The paper also
describes how researchers have attempted to correct the n coefficient. Finally, a computer program
that uses both the Manning and the Darcy-Weisbach equation is developed to change input values
(and solve design problems as a result). The later one is widely recognized for being more accurate,
reason why both equations are compared.
PALABRAS CLAVES:
Errores en el diseño, n de Manning, Redes de Drenaje Urbano

INTRODUCCIÓN
En la visión integral de sistemas de drenaje urbano, se conceptualizan tres componentes
importantes que son: las redes de alcantarillado, las plantas de tratamiento de aguas residuales
(PTAR) y el cuerpo receptor. En la práctica, la primera se entiende como el conjunto de tuberías y
estructuras usadas para transportar, en forma segura, las aguas residuales, pluviales, o la
combinación de las mismas, hasta un lugar donde sean tratadas o se les permita seguir el ciclo
hidrológico. El origen de esto se puede encontrar en civilizaciones como Grecia y Roma, donde se
construyeron canales para drenar las ciudades, y así evitar inundaciones, o problemas de salud
pública. Por mucho tiempo, para realizar estas obras fue suficiente el conocimiento básico de los
ingenieros. Sin embargo, cuando el crecimiento acelerado de la población y las urbes aumentó la
complejidad del problema, se requirieron soluciones óptimas que usaran fórmulas teóricas en el
diseño de las redes.
En Williams (1970), el autor menciona que uno de los primeros trabajados conocidos fue el
de Chézy en 1769; él realizó un estudio empírico y llegó a una ecuación que describe la velocidad
en canales abiertos, como función del radio hidráulico, la pendiente y la rugosidad del suelo. En
1845, Weisbach basándose en estudios de Darcy, propuso la hasta ahora muy célebre ecuación de
Darcy – Weisbach, que relaciona las mismas variables que su predecesor. Actualmente, este
acercamiento es el más aceptado por los versados en el tema; sin embargo, para su época resultaba
tedioso por lo complejo de estimar implícitamente el factor f. Teniendo en cuenta esta dificultad,
surgieron fórmulas explícitas como la propuesta por Manning en 1889, que se asemejaban bastante
a la de Chézy y solo incluían algunos exponentes dentro del cálculo (fueron varios los
investigadores los que propusieron fórmulas similares, pero solo la de Manning logró tal acogida).
El resultado de estas era suficientemente bueno para las necesidades de la época, y dadas ciertas
condiciones, puede llegar a ser aceptable para los requerimientos del mundo contemporáneo.
Sin embargo, desde hace varias décadas se sabe que cuando se busca mayor exactitud, esta
no es la mejor opción pues se ha comprobado la dependencia del coeficiente n de Manning, en otros
factores además de la rugosidad de la tubería. En Chrisolm & Tsang (1970) por ejemplo, los autores
despejan el n de la ecuación, y al comparar este resultado con otros acercamientos, encuentran que
es función del radio hidráulico, diámetro, pendiente, velocidad y viscosidad. En Yen (1992) el autor
conluye que esta metodología sólo es válida para los casos en los que una precisión del 20% sea
aceptable para el proyecto. A consecuencia de esto, a nivel internacional se ha cuestionado el uso de
la ecuación de Manning en el diseño de redes de drenaje urbano y se recomienda el uso de la de
Darcy–Weisbach (American Society of Civil Engineers, 2007).
Esta última ecuación aunque un poco más vieja, está basada en principios físicos, y no tiene
un rango restrictivo de aplicación; no obstante, a pesar de su idoneidad muchos diseñadores son
renuentes a cambiar el acercamiento que tradicionalmente se había usado. Algunos de ellos
argumentan que a pesar de las imperfecciones e inexactitudes, prefieren la primera pues no contiene
funciones matemáticas complejas que dificulten su uso. Este comentario sin embargo, resulta
ilógico desde hace mucho tiempo, si se tiene en cuenta que con la llegada de las calculadoras y los
computadores personales, la operación de logaritmos o ecuaciones no explícitas no representa un
obstáculo considerable para llevar a cabo un cálculo.
En el presente estudio, se espera evaluar la magnitud de los errores en un diseño de redes de
drenaje, derivados del uso de la ecuación de Manning. Se busca definir ciertas recomendaciones,
para que los diseñadores sean conscientes de la precisión y exactitud de su trabajo usando esta
metodología. Para conseguir esto, se genera un programa de diseño y tablas de datos en hojas de
cálculo, donde se muestra la variación de los resultados al usar coeficientes n de Manning supuestos
tradicionalmente vs coeficientes de Manning calculados utilizando la relación de la ecuación de
Darcy- Weisbach. Por último, teniendo en cuenta que habrá diseñadores que desearán seguir
utilizando la ecuación de Manning, con base en el análisis de los diseños realizados, se recomiendan
valores n de Manning, de acuerdo con la rugosidad, el diámetro, y otras de las características
hidráulicas que influyen en él.

OBJETIVOS
El objetivo principal del presente trabajo, es estimar la precisión y magnitud de los errores
inducidos en un diseño de redes de drenaje urbano por el uso de la ecuación de Manning vs. la
ecuación de Darcy- Weisbach. Se espera en primer lugar revisar el desarrollo histórico de la
ecuación de Manning, junto con las restricciones bajo las cuales fue propuesta. Esto incluye estudiar
los resultados previos que le permitieron desarrollar su metodología, los acercamientos
contemporáneos a su época, y las correcciones que se han hecho desde su publicación, tratando de
disminuir las inexactitudes implícitas a las que conlleva. Posteriormente se desea generar un motor
de cálculo, para comparar los valores de coeficientes de rugosidad n utilizados tradicionalmente,
con los calculados según la relación de las ecuaciones de Darcy-Weisbach y la de Manning.
Se busca también establecer los errores porcentuales en el diseño, teniendo como variable a
comparar, la velocidad calculada por medio de ambas metodologías. Teniendo en cuenta la
evidencia encontrada, se espera revisar las tendencias internacionales en cuanto al diseño de
sistemas de alcantarillado, para poder comparar la información y generar recomendaciones, que
justifiquen por qué los diseñadores deberían cambiar de ecuación a la hora de realizar su labor.
Finalmente, se desea recomendar valores del coeficiente de rugosidad n de Manning, que tengan en
cuenta las distintas características de las cuales depende.
ANTECEDENTES
La ecuación de Manning, ampliamente usada para estimar las pérdidas de energía en canales
y tuberías, recibe su nombre de uno de sus desarrolladores, el ingeniero irlandés Robert Manning,
quien en 1889 la publicó por primera vez; en la Ecuación 1 y Ecuación 2 se encuentra en su forma
original y en la Ecuación 3 se puede ver la versión comúnmente usada. Esta ecuación fue deducida
con base en múltiples experimentos, especialmente en canales; se reportan 104 pruebas de Bazin, 40
de Kutter y 15 de Ftely y Stearms (Powell, 1968). El factor de rugosidad n de Manning, suele
suponerse como adimensional. Pero al realizar un análisis, se encuentra que las dimensiones son
s/m
1/3
. Los rangos usuales del n de Manning para tuberías pueden consultarse en textos de
hidráulica como (Chow, 1994) y (Butler & Davies, 2004).
[1] (Dooge, Walsh, Ackers & Powell,1958)
[2] (Dooge, Walsh, Ackers & Powell,1958)
[3]
donde V es la velocidad en el canal, R es el radio hidráulico, S es la pendiente, K es una corrección
por el tipo de unidades y n es el comúnmente llamado coeficiente de Manning. Algunos autores han
tratado de relacionar esta ecuación con la de Chézy (1769), hasta el punto de replantear su nombre
como Chézy-Manning; sin embargo, ambas metodologías tienen diferencias estructurales, que se
deben al hecho de que fueron obtenidas de formas diversa (Wunderlich, 1970).
El desarrollo histórico de esta metodología es bastante interesante, pues por lo menos 10
investigadores llegaron a un resultado similar (Williams, 1970). Para empezar se puede cuestionar
cómo llegó la ecuación de Manning a ser nombrada como tal, al parecer A.A. Flamant en 1891 fue
la primera persona que empezó a denominarla de esa manera, dejando de lado la forma extensa
propuesta por el ingeniero irlandés. Posteriormente, Willcoks y Holt en 1899 fueron las primeras
personas en referirse a ella de esta forma en un libro, luego Church en 1900 continúa con tal
denominación y hace referencia a los escritos de Flamant. Para 1918 múltiples textos y artículos lo
continuaban llamado de esta forma, de esta forma se consolidó y llegó a ser conocida así en los
países de habla inglesa.
En cuanto al coeficiente de rugosidad, antes de 1896 ninguno de los investigadores los había
relacionado con el n de Kutter y mucho menos había recibido el nombre de n de Manning. De
hecho este último, tal como explica Williams (1970), en la página 205 de su artículo definitivo
publicado en 1891, parece ser consciente de las limitaciones de estos coeficientes. Citando a
Williams: “Es meritorio notar que el valor del recíproco de la variable C por él propuesta es muy
cercana al n de Kutter y Ganguillet. Pero según aparece en una traducción publicada por Hering y
Trautwine, con la autorización de los autores…, el n no es constante como lo habían determinado
ellos, éste varía en el mismo canal, ya sea grande o pequeño, con el radio medio, con los
sedimentos que transporte, con la velocidad, con la superficie de inclinación, así como decrece en
canales lisos y regulares y aumenta cuando ellos son rugosos e irregulares”. Esto quiere decir que
ya en su época, Manning conocía las limitaciones de estos valores y aparentemente advertía los
riesgos de su generalización.
Y si la advertencia de la variabilidad de la constante n de Kutter no es suficiente, es
importante agregar que Manning también alertó sobre las inconsistencias en las dimensiones de su
fórmula. Tras la publicación original de su artículo en 1889, Manning propuso en 1895 un
complemento donde mostraba una segunda ecuación (Ver Ecuación 2). Aunque en él no detalla la
forma cómo la derivó, según Powell (1962) en la discusión del texto un investigador llamado J.P.
Griffith, preguntó por qué la presión barométrica fue introducida en la segunda fórmula. La
respuesta del irlandés fue que la primera no producía resultados correctos para tuberías de pequeños
diámetros, y que además las dimensiones de sus variables no eran homogéneas. Asimismo agregó
que para la época era algo tedioso la extracción de una raíz cúbica, y por ende su primera
metodología podría llegar a ser bastante difícil de calcular. Teniendo en cuenta todo esto, se puede
afirmar que Manning definitivamente no fue quien recomendó usar 1/ n en vez de C, y que además
trataba de advertir de sus imperfecciones.
A pesar de su esfuerzo, tal parece que sus comentarios nos fueron escuchados y con el
tiempo se supuso que el n era constante. Se cree que fue también a causa del trabajo de A.A.
Flamant en 1891, que se empezó a referenciar al Irlandés como el autor del coeficiente n. Sin
embargo, solo se tiene evidencia escrita de que en 1916 M.J. Orbeck menciona el coeficiente n de
Manning. Desde entonces se siguió denotando de esta forma y hoy en día muchos lo consideran
como el autor original. Su trabajo tiene gran acogida en el medio contemporáneo, pero en muchos
casos se ignora totalmente el legado de investigadores como Gauckler y Kutter, quienes fueron
fundamentales para que se llegara a estos resultados.
Entre aquellos que conocen sus falencias, ha habido recientes esfuerzos para mejorar los
resultados a los que se puede llegar actualmente. Algunos como Wong y Zhou (2003), Zaghloul
(1993), Akgiray (2005) y Yen (1992), han intentado extrapolar los resultados conseguidos en
condiciones específicas, para ser usados sin importar las condiciones. Teniendo en cuenta que el
trabajo original fue ideado para grandes canales rectangulares, con flujo turbulento hidráulicamente
rugoso, se intenta tener en cuenta otros factores como el radio hidráulico, la rugosidad efectiva y el
número de Reynolds. Para lograr esto calculan la relación entre el valor de n real y los valores
constantes, como función de los otros parámetros. A continuación se muestran algunos ejemplos de
estos avances, para el caso de estudio específico de esta investigación, las tuberías fluyendo
parcialmente llenas;
[4] Zaghloul (1993)
[5] Wong y Zhou (2003)
[6] Akgiray (2005)
[7] Akgiray (2005)
donde
es el ángulo de la superficie del agua y
es la relación de llenado de la tubería. Para el
mismo tipo de conductos, existe un gráfico realizado por Zaghloul (1997) que relaciona las mismas
variables, pero facilita calcular los valores. Este se muestra a continuación;
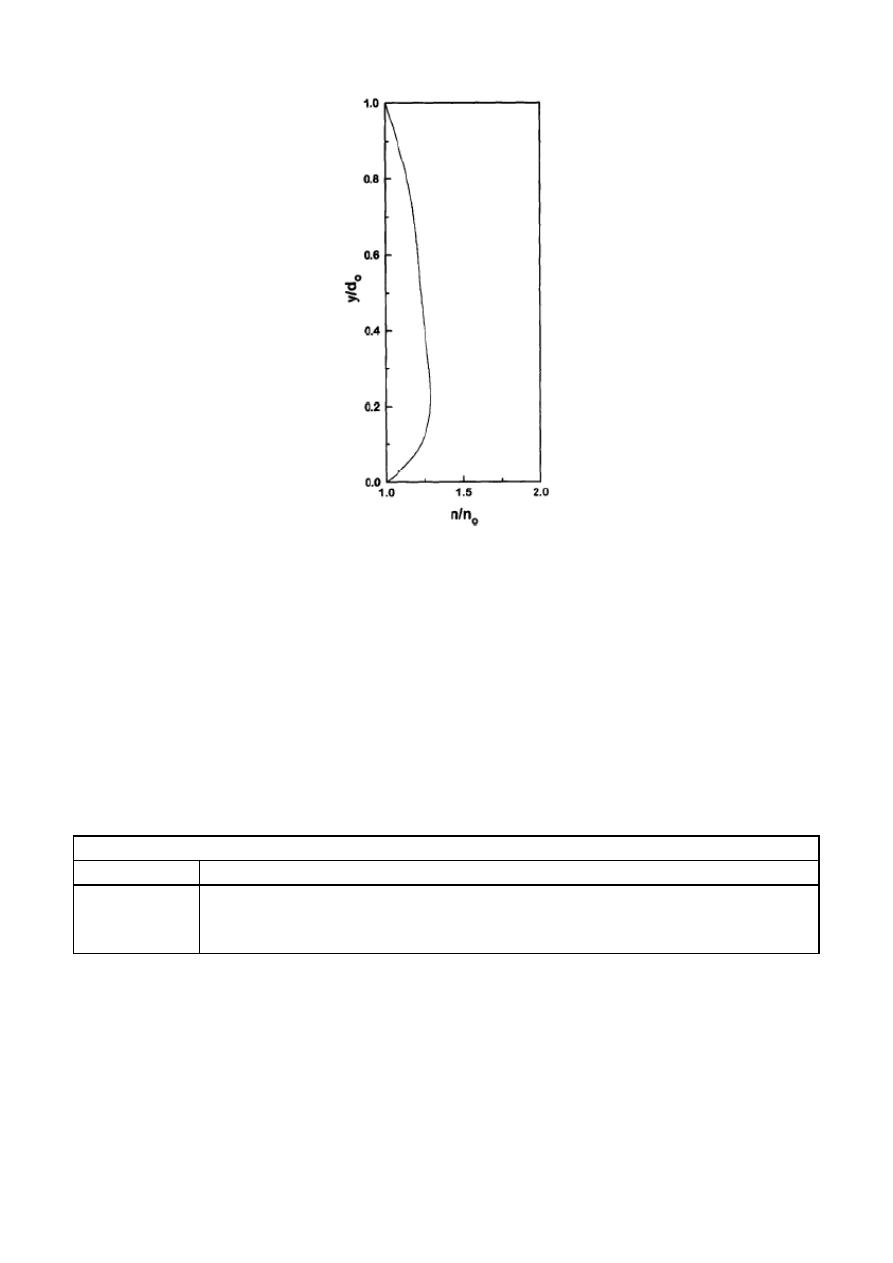
Figura 1.- Relación entre n real y n constante, en función de la relación de llenado Zaghloul (1997).
Por último, la ASCE (2007) sugiere algunos valores a la hora de diseñar alcantarillados
sanitarios (Ver Tabla 1). Ellos no distinguen el tipo de material, es decir utilizan un único valor para
cualquier tipo de tubería, debido a que la capa que se forma alrededor de las mismas en
alcantarillados sanitarios, hace que independientemente del material se comporten de manera
similar. Además afirma que valores altos del n de Manning, pueden llegar a cubrir posibles flujos de
retardo significativos causados por mal alineamiento de la tubería, irregularidades de juntas,
corrosión interior ó acumulación en las paredes, grietas, roturas, protuberancias o interferencias
laterales, sedimentos, entre otros. Si bien estos factores causan grandes valores de n de operación,
cuando son moderados, causan menos incremento que el valor comúnmente supuesto de 0.013.
Finalmente, afirma que los diseñadores deberían reconocer que de la mano de una buena instalación
y mantenimiento, las capacidades reales de la tubería serían más grandes que los valores calculados,
y por ende vale la pena contemplar el proceso constructivo a la hora de escoger los coeficientes.
Tabla 1.- Valores sugeridos de n de Manning para diseño de alcantarillados sanitarios.
Diámetro en Pulgadas
Condición
6
8
10
12
15
18
24
30
36
48
60
Extra cuidadoso
0.0092 0.0093 0.0095 0.0096 0.0097 0.0098 0.0100 0.0102 0.0103 0.0105 0.0107
Típico
0.0106 0.0107 0.0109 0.0110 0.0112 0.0113 0.0115 0.0117 0.0118 0.0121 0.0123
Conservador
0.0120 0.0121 0.0123 0.0125 0.0126 0.0127 0.0130 0.0133 0.0134 0.0137 0.0139
METODOLOGÍA
Aunque las condiciones de flujo en alcantarillados varían espacial y temporalmente, el
diseño de una tubería parcialmente llena se hace bajo condiciones de flujo uniforme y permanente.
Gracias a estas suposiciones, surge la necesidad de diseñar los sistemas tramo a tramo para verificar
condiciones de capacidad y autolimpieza. La primera se chequea calculando las propiedades
geométricas de la sección y corriendo la hidráulica del conducto; de esta forma se estima si este
puede transportar el caudal de diseño, sin violar la restricción de profundidad de flujo máxima. Las
condiciones de autolimpieza por su parte, se verifican revisando los valores del esfuerzo cortante en

la pared y la velocidad media del flujo, para el caso en que se transporta exactamente la descarga
requerida.
Para llevar a cabo ambos procesos, diseño y verificación, se definieron dos rutinas que
entregan el diámetro mínimo requerido y la profundidad de flujo exacta. Como datos de entrada se
requiere la pendiente del terreno, algunas propiedades del fluido (densidad y viscosidad dinámica),
propiedades de la tubería a utilizar (material, ks), el caudal requerido y el rango de los tamaños de
las tuberías disponibles. Como se quería tener evidencia robusta del comportamiento de la ecuación
de Manning ante pequeñas variaciones de las variables de entrada, se decidió generar un motor de
diseño en una hoja de cálculo, que permitiera el procesamiento de un gran número de
combinaciones. La idea era diseñar cada grupo de datos tanto con la ecuación de Darcy-Weisbach,
como con la de Manning, y al final comparar los valores de salida como el caudal total
transportado, la velocidad media, la altura de flujo y el n de Manning usado en cada situación.
Con la segunda metodología el coeficiente n sólo variaba en función del material, mientras
que con la primera dependía de todas las características posibles. La forma de hallarlo en este
último caso requería asociarlo con el factor de fricción f de Darcy; para esto se usaban ambas
ecuaciones y al relacionar algunos factores se llegaba a la siguiente expresión;
[8]
donde R es el radio hidráulico y f es el factor de fricción de Darcy. Gracias a la Ecuación 8, se
puede hallar el valor del n de Manning que correspondería para cada situación, teniendo en cuenta
la combinación de los distintos factores que influyen en ella. De esta forma se corrige la
imperfección que tradicionalmente entiende el coeficiente, como una constante que depende
únicamente de la rugosidad del material.
Una vez definido el procedimiento para realizar y comparar los distintos diseños, se define
el rango de valores que pueden tomar las variables de entrada. Para empezar se determinó el de las
rugosidades, ks y su equivalente coeficiente de rugosidad n de Manning constante:
• ks
m → n 0.015. Rugosidad alta.
• ks
m → n 0.013. Rugosidad equivalente a concreto.
• ks
m → n 0.013. Rugosidad intermedia recomendada por la ASCE para
diseños de alcantarillados sanitarios.
• ks
m→ n 0.010. Rugosidad equivalente a material PVC.
En cuanto a los tamaños de las tuberías, se decidió trabajar con diámetros que cubrieran todo
tipo de casos en las redes de drenaje. El menor de ellos se podría encontrar a la salida de un
conjunto de casas o de un pequeño sector residencial, el más grande podría servir para evacuar el
agua de un área urbana considerable, y entre ellos se pueden encontrar diámetros para todo tipo de
propósitos; el listado completo se puede ver en la Tabla 2. Para las pendientes se decidió trabajar
con valores desde 0.1% hasta 10% con un ΔS= 0.1%; de esta manera se garantizan mínimos reales
y máximos que no excedan la distribución de presiones hidrostática. En total para cada ciclo de
diseño (1 rugosidad y 1 diámetro), se evalúan 100 pendientes.
Tabla 2.- Diámetros utilizados para el diseño de las tuberías.
Diámetro
(pul)
Diámetro (m)
Diámetro
(pul)
Diámetro (m)
Diámetro
(pul)
Diámetro (m)
Diámetro
(pul)
Diámetro (m)
6
0,152
12
0,305
24
0,610
48
1,219
8
0,203
15
0,381
30
0,762
60
1,524
10
0,254
18
0,457
36
0,914
Para determinar el rango de caudales se definieron 3 grupos; en el primero estaban los bajos
(1.5 - 50 L/s con un cambio de 0.5 L/s), los medios (50 - 500 L/s con un cambio de 10 L/s) y los
altos (500 - 2500 L/s con un cambio de 50 L/s). Las propiedades del fluido siempre fueron las
mismas, agua a una temperatura de 15ºC cuya viscosidad cinemática (ν) es de 1.14E-6 (m
2
/s). En
total cada una de las metodologías debía resolver 73200 combinaciones distintas, lo que equivale a
146400 datos a comparar.
RESULTADOS
Con base en los diseños realizados a través de las metodologías planteadas, se presentan a
continuación los resultados obtenidos. Los parámetros establecidos para comparar las distintas
rugosidades, fueron; variación del coeficiente n de Manning según Darcy – Weisbach, error
porcentual del n de Manning vs. n según Darcy – Weisbach y error porcentual de la velocidad
calculada usando la ecuación de Manning vs. velocidad calculada usando la ecuación Darcy –
Weisbach. Para cada uno de estos casos se calculó el diámetro, el caudal, la velocidad y la altura de
flujo, como función de la rugosidad, la pendiente y la relación de llenado. Teniendo en cuenta el
volumen de información, sólo se presentan los resultados para los diámetros de 8 pulgadas y un
resumen de los diámetros extremos, 6 y 60 pulgadas.
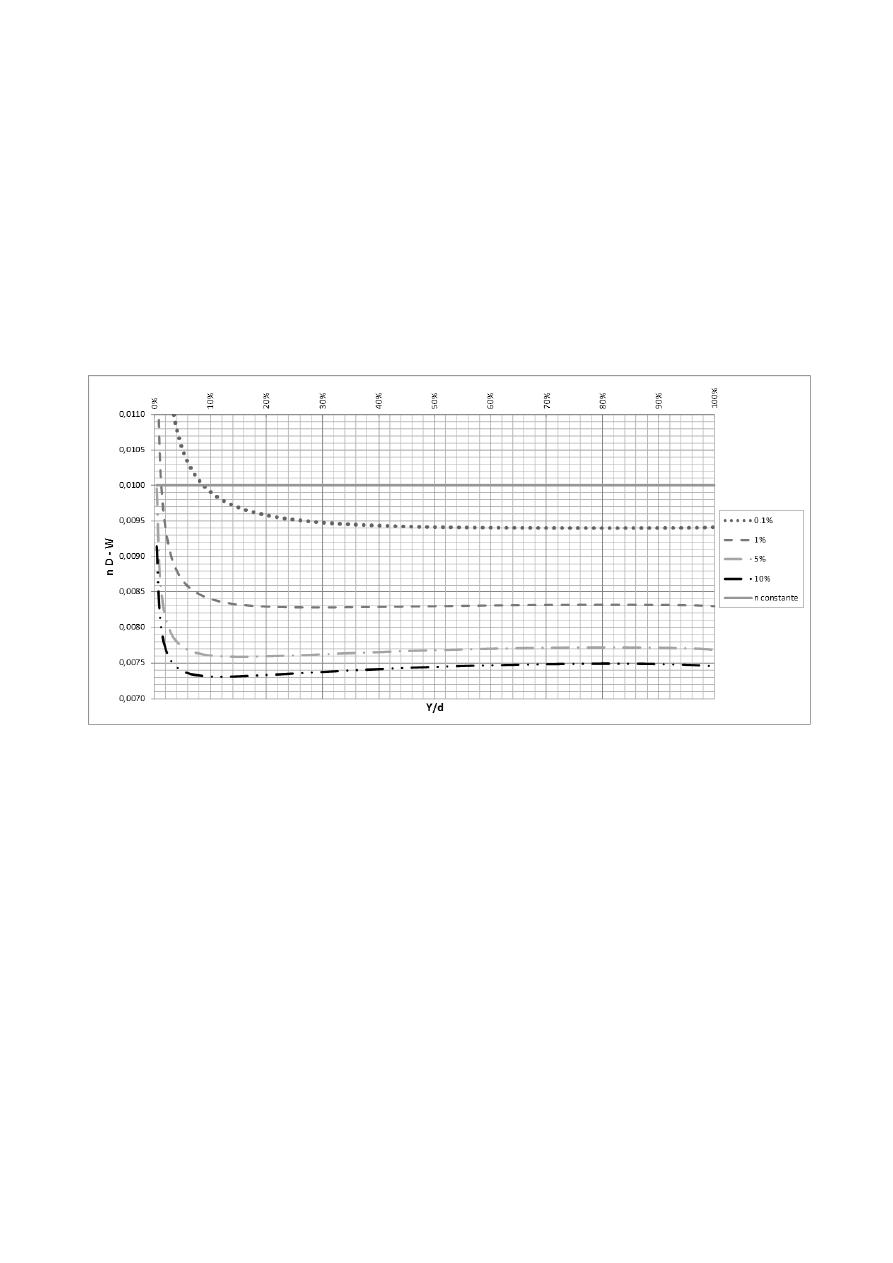
Figura 2.- Variación del n de Manning respecto a los resultados de D-W en tuberías de PVC de 8”,
para distintas pendientes y relaciones de llenado.
Lo primero que muestran los resultados es la forma como varía el n de Manning, en función
de las propiedades que se sospechaba tenían relación con él, y que la metodología tradicional ignora
(Ver Figura 2). En ella se puede ver que el valor constante siempre es mayor que los reales
(Calculados a partir de la Ecuación 8), y sucede lo mismo para más del 95% de las combinaciones
totales. Vale la pena mencionar que en la mayoría de los casos, para relaciones de llenado (y/d)
menores al 20%, los valores resultan ser atípicos por ser una condición de flujo inestable. De ahí
que estos valores anómalos no se tengan en cuenta en los análisis respectivos, por ser bastante
grande la incertidumbre de los mismos.
Entrando en el análisis, para las pendientes se puede decir que mientras más grandes son
éstas, más tiende diferir el n constante del valor real. Esta variación no es claramente lineal, pero
parece que a medida que aumenta el grado de inclinación, las líneas parecen acercarse unas a otras.
Los diámetros, en cambio, muestran una relación inversa en el rango de análisis; los diseños con
tuberías de 6” para la mayoría de los casos analizados, presentan mayores imprecisiones que las
tuberías de 60” (Ver Figura 3). Y si se analizan ambas variables al mismo tiempo, cuando las
pendientes aumentan se sienten mucho más sus efectos en las tuberías pequeñas. Esto se encuentra
no solo para los casos mostrados, sino en general para todas las condiciones estudiadas. La relación
de llenado por su parte presenta un comportamiento particular, excepto para valores menores al
20%, donde inicialmente los n de Manning superan considerablemente el valor constate, para
después ser muy inferiores a él. Los coeficientes n aumentan gradualmente hasta el 50-60 %, donde
parecen tomar un valor constante hasta el final de la curva.
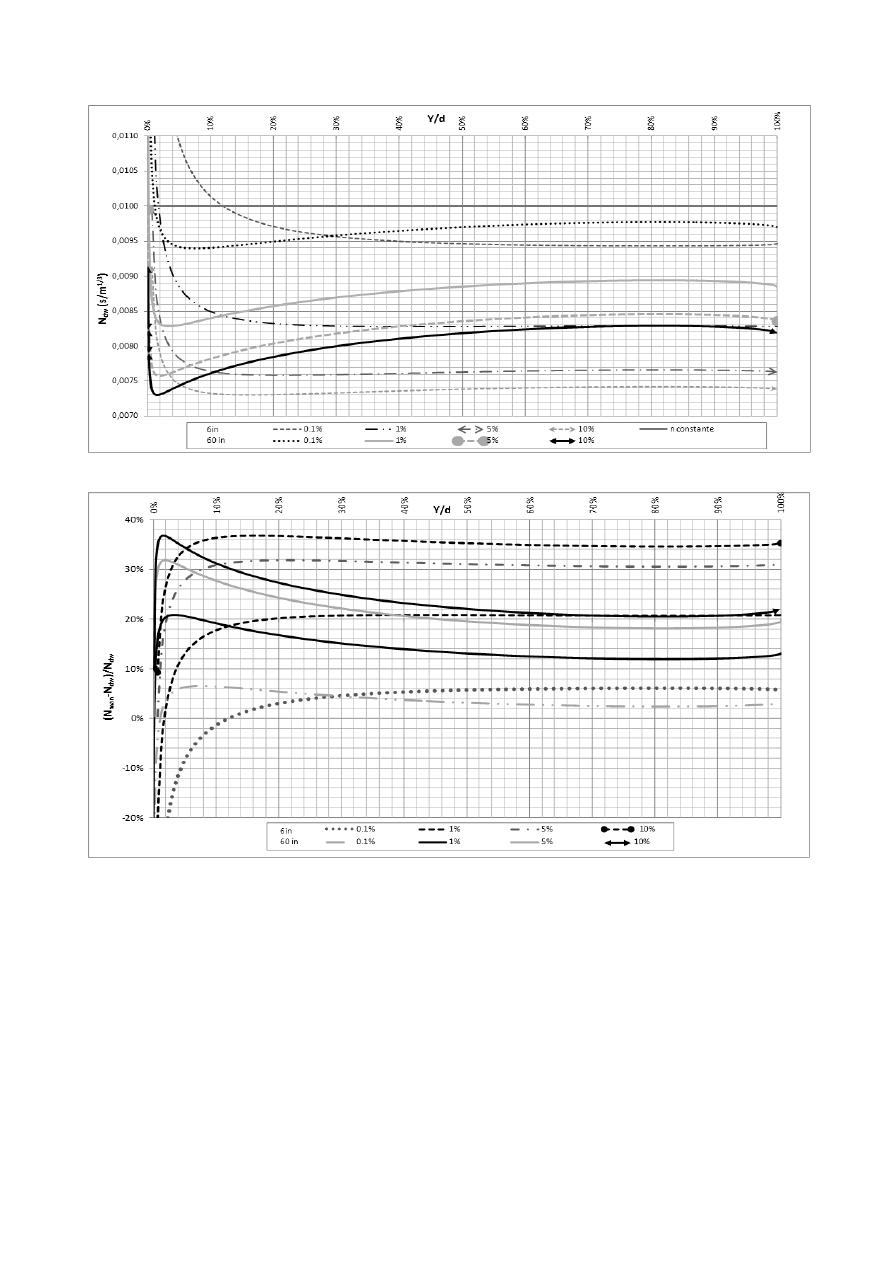
Figura 3.- Variación del
n de Manning
respecto a los resultados de D-W con un
en
tub ría d ” y ”, para distintas pendientes y relaciones de llenado.
Figura 4.- Error Porcentual en el cálculo del
n de Manning
vs el
n
según Darcy Weisbach con un
tub ría d ” y ”
En la Figura 4 se muestran los errores generados al usar los coeficientes constantes; como era de
esperarse, se encuentran curvas opuestas a las presentadas anteriormente. Lo que resulta
sorprendente, es que más de la mitad de las combinaciones presentan errores relativos mayores al
20%, y que la cuarta parte de ellas supera el 30%. Estas imperfecciones no dicen nada
explícitamente; sin embargo, teniendo en cuenta su relación con el cálculo de la velocidad se
pueden estudiar las consecuencias reales. En la Figura 5 se encuentran los errores porcentuales en el
cálculo de las velocidades; en ella se puede ver que las calculadas con la metodología tradicional de
Manning, son mucho menores que las calculadas con la metodología de Darcy-Weisbach. Esto era
obvio teniendo en cuenta que los n constantes siempre fueron mayores. El significado de esto es que
siempre que se use este procedimiento, las condiciones reales serán mucho más rápidas que las que
se esperaban en el diseño, por ende se podrá transportar caudales mayores a los que se tenía
planeado. La magnitud de estos errores llega a ser del -23%, lo que querría decir que en la realidad
se transporta una quinta parte más de lo que se diseña. En el mejor de los casos la diferencia es del -
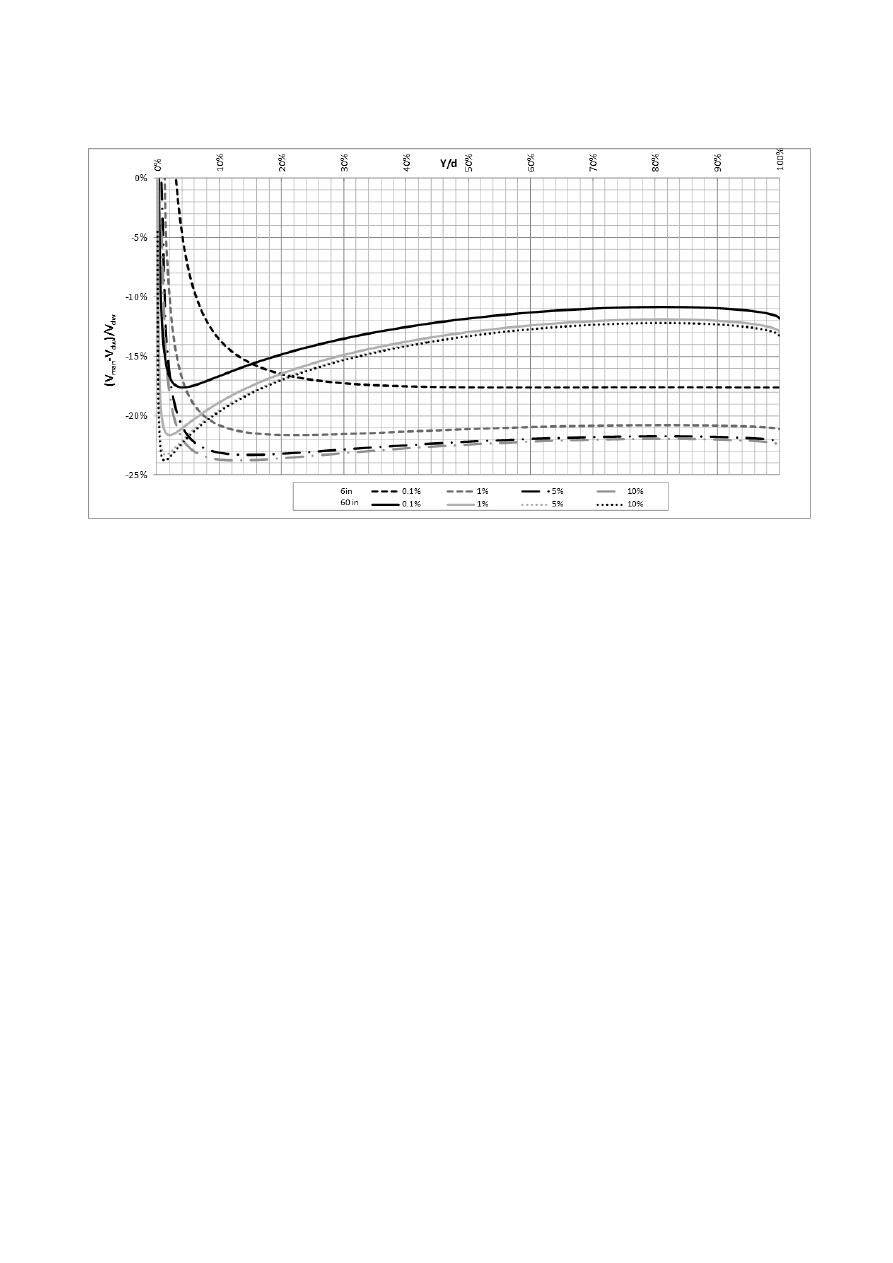
10%, que sigue siendo un valor bastante grande y dado que en esta gráfica se trabaja con una
rugosidad mayor, si se hablara de PVC u otro material más liso, seguramente los resultados serían
mucho peores.
Figura 5.- Error Porcentual en el cálculo de v con la ecuación de
Manning
vs el cálculo con
Darcy Weisbach.
tub ría d ” y .
CONCLUSIONES Y RECOMENDACIONES
A partir del estudio del desarrollo de la ecuación de Manning, se puede ver que esta ha tenido
cambios significativos, y el procedimiento actual no corresponde específicamente al planteado por
el ingeniero irlandés. De hecho han sido varios los investigadores que han aportado a su desarrollo.
Al menos 10 que propusieron una ecuación de la misma forma antes de su presentación formal, y
mucho otros que desde entonces han tratado de corregir los distintos errores encontrados. Es claro
que existe otra metodología que a menos que se demuestre lo contrario, presenta un mejor
desempeño y debería ser usada en todo caso. Las limitaciones que alguna vez impidieron su
procesamiento no se presentan más y no hay razón para ignorarlas. Es evidente también que muchas
personas a pesar de la evidencia, continúan usando la ecuación tradicional. Estas personas deberían
ser conscientes de las limitaciones para evitar así sorpresas en la vida real, mientras se trabaje
dentro de los rangos se obtendrán resultados aceptables; en caso contrario se debería usar valores
del coeficiente variables.
En cuanto al coeficiente n de Manning, se ve que para rugosidades menores a 0.003 m, los
coeficientes constantes para alcantarillados nuevos, están sobrestimados desde el 10% hasta el 60%.
Es importante mencionar que la ASCE (2007) advierte de este incremento en esta variable,
alegando que la mayoría de los valores recomendados tradicionalmente, están basados en
observaciones y estimaciones hechas hace cerca de 100 años. Los resultados hallados en la presente
investigación, basada en tuberías modernas, confirman que el rango real de n es bastante diferente
al estimado originalmente. Esto significa que los cálculos de las velocidades y caudales también
están erróneos, y en la vida real serán mayores a los estimados en el diseño. En primera instancia se
podría pensar que esto es una ventaja, y que solamente consiste en un criterio conservador, sin
embargo para ciertas relaciones de llenado puede significar un peligro.
Tal es el caso de una relación de llenado de 0.85; en ella el riesgo de presentar fenómenos de
sobrecarga es muy alto, y al no tener certeza de la velocidad del flujo se aumenta esta posibilidad.
Por otro lado, el hecho de disminuir la capacidad real de transporte de la red obliga a aumentar el
tamaño de los tubos, o en su defecto requiere de mayores pendientes. Todo esto significa un
aumento considerable en los costos de construcción. Al sobrediseñar sectores de la red de drenaje,

en países donde los recursos son tan limitados, un error de esto puede generar grandes costos de
oportunidad para la sociedad. Eso sin contemplar que cuando se dan sobrediseños innecesarios, se
pone en riesgo las condiciones de autolimpieza. Al disminuir la velocidad de flujo se reducen los
esfuerzos cortantes, y esto permite un menor transporte de sedimentos y limita la capacidad de
limpiar las paredes con la misma fuerza generada por el agua
Observando las distintas figuras, se ve que la pendiente del 0.1% es la que presenta menores errores
en la estimación del n y por ende de la velocidad, si importar las rugosidades, diámetros y
relaciones de llenado. Teniendo esto en cuenta, si se opta por utilizar en el diseño la ecuación de
Manning, se deberían tener en cuenta valores recalculados que de alguna forma incluyan la
variabilidad. En la Tabla 3 se muestra un ejemplo para estas pendientes; se presentan los valores
como función de la rugosidad, el diámetro y una relación de llenado alta. Se presentan 3 valores por
combinación: el primero es el hallado en este trabajo y los otros representan bandas de confianza de
15%. Finalmente se recomienda que estudios posteriores se encaminen a estimar los coeficientes
n de Manning para alcantarillados con edades altas (> 10 años), a estudiar el efecto de condiciones
reales de flujo como flujo gradualmente variado, no permanente y a estudiar otros valores de las
pendientes.
Tabla 3.- Valores sugeridos de n de Manning según Rugosidades y Diámetros. Pendiente de 0.1%.
Rugosidad (m)
Condición
Diámetro en Pulgadas
6
8
10
12
15
18
24
30
36
48
60
3.0 e-4
Cuidadoso
0.0108
0.0108
0.0108
0.0109
0.0109
0.0110
0.0111
0.0112
0.0113
0.0115
0.0116
Típico
0.0124
0.0124
0.0124
0.0125
0.0126
0.0126
0.0128
0.0129
0.0130
0.0132
0.0134
Conservador
0.0140
0.0140
0.0141
0.0141
0.0142
0.0143
0.0144
0.0146
0.0147
0.0149
0.0151
3.0 e-3
Cuidadoso
0.0145
0.0145
0.0144
0.0144
0.0144
0.0144
0.0145
0.0146
0.0146
0.0148
0.0149
Típico
0.0167
0.0166
0.0166
0.0166
0.0166
0.0166
0.0167
0.0167
0.0168
0.0170
0.0171
Conservador
0.0189
0.0188
0.0187
0.0187
0.0187
0.0188
0.0188
0.0189
0.0190
0.0192
0.0193
BIBLIOGRAFÍA
Akgiray, Ö. (2005). Explicit solutions of the Manning equation for partially filled circular pipes.
Canadian Journal of Civil Engineering , 32 (3), 490-499.
American Society of Civil Engineers. (2007). Gravity Sanitary Sewer Design and Construction
(ASCE Manuals and Reports on Engineering Practice No. 60) (2nd ed.). Reston, Virginia:
American Society of Civil Engineers.
Butler, D., & Davies, J. (2004). Urban Drainage (2nd Edition ed.). London and New York: E&FN
SPON.Taylor &Francis.
Chrisolm, P., & Tsang, G. (1970). The Manning Equation And Boundary Resistance. Journal
WPCF (Water Pollution Control Federation) , 42 (5), 753-757.
Chow, V. T. (1994). Hidráulica de canales abiertos. (J. G. Saldarriaga, Trad.) Santafé de Bogotá:
McGraw-Hill Interamericana S.A.
Powell, R. (1962). Another Note on Manning's Formula. Journal of Geophysical Research , 67 (9),
3634-3635.
Powell, R. (1968). The Origin of Manning's Formula. Journal of the Hydraulics Division , 94
(HY4), 1179-1181.
Williams, G. (1970). Manning Formula - A Misnomer? Journal of the Hydraulics Division , 96
(HY1), 193-200.
Wong, T.S.W., and Zhou, M.C. (2003). “Kinematic wave parameters and time of travel in circular
channel revisited”. Advances in Water Resources, 26(4): 417–425.
Wunderlich, W. (1970). Universal Formula for Uniform Flow. Civil Engineering , 40 (1), 51-52.
Yen, B. C. (1992). Dimensionally Homogeneos Manning's Formula. Journal of Hydraulic
Engineering , 118 (9), 1326-1332.
Zaghloul, N. (1997). Unsteady gradually varied flow in circular pipes with variable roughness.
Advances in Engineering Software , 28 (2), 115-131.
