
IAHR
CIC
XXV CONGRESO LATINOAMERICANO DE HIDRÁULICA
SAN JOSÉ, COSTA RICA, 9 AL 12 DE SETIEMBRE DE 2012
EL MÉTODO DE FLUJO EN REDES APLICADO AL CASO DEL LAVADO
DE SISTEMAS DE DISTRIBUCIÓN DE AGUA POTABLE
Diva P. Rubio, Eric Rothstein, Silvia Takahashi
Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA), Departamento de Ingeniería Civil y Ambiental,
Universidad de los Andes, Bogotá, Colombia
<dp.rubio50@uniandes.edu.co>, <e-rothst@uniandes.edu.co>, <stakahas@uniandes>
RESUMEN:
Muchos problemas de optimización en ingeniería pueden resolverse haciendo uso de diseño
de algoritmos. Estor problemas generalmente son dirigidos por profesionales en el campo de acción
específico del problema quienes no tienen conocimientos suficientes de teoría de algoritmos. Por
otro lado, los informáticos muchas veces solucionan problemas teóricos que no pueden ser
fácilmente aplicados en la vida real. El mejor enfoque es tener equipos interdisciplinarios que
aborden los problemas del mundo real y tratar de resolverlos mediante la aplicación de técnicas
algorítmicas conocidas. Uno de los campos en los que se ha demostrado que esta colaboración
prueba ser fructífera es en los problemas relacionados con sistemas de distribución de agua. En este
trabajo se aborda el problema de lavado unidireccional para garantizar la calidad del agua mediante
modelación como la suma de subconjuntos de problemas NP-difícil. El problema de lavado
unidireccional (UDFP) indica que válvulas e hidrantes deben ser operados para llevar a cabo un
lavado de la red de distribución de agua potable (RDAP).
ABSTRACT:
Several optimization problems in engineering can be solved when applying algorithm
design. These problems, however, are addressed by professionals who know little regarding the
theory of algorithms. Computer scientists know about algorithms, but most of them focus on
theoretical problems that cannot be applied to real-world situations. Having interdisciplinary teams
is probably the best approach, teams in which algorithm techniques are applied to all kinds of
situations. This approach has been applied to water distribution system (WDS) problems, and the
results obtained are fruitful. This paper addressed the problem of unidirectional flushing in systems.
It also seeks to ensure water quality, modeling it as the subset sum NP-hard problem. Unidirectional
flushing problem, or UDFP, shows which valves and hydrants should be operated to perform a
better WDS flushing.
PALABRAS CLAVES: lavado, hidrantes, válvulas, algoritmo de aproximación, sistema de
distribución de agua potable

INTRODUCCIÓN
En las redes de distribución de agua potable (RDAP) es importante garantizar la calidad del
agua suministrada para el consumo. Se deben mantener las propiedades físico-químicas adecuadas a
lo largo del recorrido de la red y hasta llegar a los usuarios. La calidad del agua se ve afectada por
diversos factores como: la entrada de material orgánico e inorgánico desde la fuente de
abastecimiento, el desprendimiento de capas minerales y biopelículas en las tuberías, depósitos de
sedimentos en puntos específicos, entre otros.
El lavado de tuberías es uno de los métodos más empleados en el mantenimiento y
mejoramiento de la calidad del agua en las RDAP. La técnica de lavado para la red de distribución
que presente problemas de calidad de agua debe ser seleccionada mediante la consideración del tipo
de tubería, el tamaño de la tubería, el tipo de problema específico a solucionar, o combinaciones de
ellos. Adicionalmente cada técnica presenta un tiempo estimado de beneficio debido al impacto que
ésta tiene sobre la tubería y así mismo presenta una relación de costos distinta. Entre las distintas
técnicas o métodos existentes para la limpieza de tuberías se presentan lavados hidráulicos que
requieren de un aumento de la velocidad para aumentar el esfuerzo cortante y así limpiar el
conducto de la tubería; este lavado puede ser convencional o unidireccional y no requiere de una
suspensión del servicio; lavados, que requieren el vaciado de las tuberías, por medio del flujo de
aire a presión o por medio de sistemas mecánicos que incluyen la conducción de esponjas o
émbolos que limpian el conducto; limpieza química o manual y revestimiento de tuberías (Gómez,
2010).
El lavado unidireccional en RDAP es una estrategia económicamente viable que ha venido
siendo empleada en la solución de problemas tanto operativos como de calidad del agua. El lavado
unidireccional tiene las siguientes ventajas para la RDAP: incremento en la velocidad, remoción de
depósitos minerales y biológicos, control de sabor y olor, reducción de la turbidez, reducción de la
frecuencia de lavado, ahorro de agua usada en el lavado y reducción de costos en comparación con
el lavado tradicional. En la actualidad existen diferentes metodologías y software para obtener y
simular planes de lavado unidireccional (UDFP), pero estas metodologías presentan limitaciones
como la necesidad de expertos que conozcan la red para tener una mejor solución, la falta de
garantías para encontrar la solución óptima y/o la necesidad del uso sistemas más complejos como
los SIGs. En el presente trabajo se propone un algoritmo que evita o minimiza estos problemas
permitiendo desarrollar el plan de lavado unidireccional siguiendo restricciones hidráulicas
únicamente.
ANTECEDENTES
El lavado de RDAP es una estrategia económicamente viable que ha venido siendo
empleada en la solución de problemas tanto operativos como de calidad del agua. Entre los
problemas operativos asociados a la implementación de lavados están: el cambio de rugosidad,
pérdidas de presión y el mantenimiento de válvulas. En cuanto a problemas de calidad se
encuentran: crecimiento bacteriano, biopelículas, acumulación de sedimentos, corrosión y eventos
de coloración. Adicionalmente, en la última década se han incrementado las investigaciones acerca
de cómo sacar contaminantes rápidamente de la red, en parte, por el temor a ataques terroristas. El
presente trabajo se enfoca en la parte operativa y de mantenimiento de la red empleando lavado
hidráulico unidireccional.
En 1998 la American Association Research Foundation (AWWARF) presentó el estudio de
como mantener la calidad del agua en un sistema de distribución a partir del programa de cuatro
pasos de lavado: (1) Determinar la conveniencia del lavado como parte del programa de
mantenimiento del sistema, (2) Planear y manejar el programa de lavado, (3) Implementar el
programa de lavado y recolección de datos y (4) Evaluar y revisar el proceso. El lavado con flujo
unidireccional surgió a principios de los 90´s como un refinamiento al lavado convencional; Antoun

(1999) presenta un resumen del lavado unidireccional en tuberías, de las técnicas claves, de los
potenciales beneficios y explora como UDF encaja en los esfuerzos para controlar la calidad del
agua de sistema de distribución de agua. Friedman (2002) proporciona una justificación y
directrices para la evaluación de programas de lavado, así mismo, suministra consejos para
identificar si el lavado es apropiado y en caso de que lo sea como debe ser su planeación,
implementación y manejo del programa. Reyes (2005) evalúa la eficiencia de remoción de lavados
y el comportamiento de pérdidas de energía a través del tiempo. En los trabajos de Boxal (2005) y
Vreeburg (2007) se evidencia la necesidad de un modelo de calidad de la red para evitar manejar el
lavado únicamente como una buena práctica de gerencia de RDAP y aprovechar sus beneficios para
obtener resultados óptimos de calidad. Poullin (2008) propone una aproximación heurística que
hace uso de la topología de la red para aislar áreas contaminadas e identificar que válvulas cerrar.
Preis (2008) desarrolla un modelo multiobjetivo que incluye como minimizar la masa contaminada
y como a su vez minimizar el número de actividades operacionales para contener y lavar los
contaminantes del sistema. Alfonso (2010) presenta una metodología para encontrar grupos de
intervenciones operacionales en redes de distribución para minimizar el impacto en la población al
tener eventos de contaminación.
Como se puede ver, en la actualidad existen diferentes metodologías y software para obtener
y simular planes de lavado unidireccional UDFP, entre los que se encuentran: El modulo de UDF
del programa WaterGEMS; la metodología propuesta por Álvarez (2009) que hace uso de
algoritmos genéticos (AG); y el software InfoWater UDF. Entre los problemas asociados con las
metodologías existentes está la necesidad de expertos que conozcan la red para tener una mejor
solución, la falta de garantías para encontrar la solución óptima y/o la necesidad del uso sistemas
más complejos como SIG y costos de obtención de software. En el presente trabajo se propone un
algoritmo que evita estos problemas permitiendo desarrollar el plan de lavado siguiendo
restricciones hidráulicas.
MODELO DE LA RED DE DISTRIBUCIÓN DE AGUA
Es necesario modelar correctamente la RDAP para dar una definición formal al problema de
planeación de lavado unidireccional (UDFP). El modelo debe incluir los elementos necesarios y
suficientes, debe ser claro y reflejar una buena abstracción de la realidad.
Se define la RDAP como un conjunto de nudos, tuberías, válvulas, hidrantes, aperturas de
válvulas y aperturas de hidrantes mediante la siguiente 6-tupla (N, T, V, H, Pv, Ph) y cada uno de
estos elementos requieren características específicas para la modelación.
Nudos – N: Los nudos se clasifican en dos categorías fuentes y puntos de demanda. Las
fuentes son nudos donde no hay consumo de agua y se necesita para su modelación conocer
sus coordenadas y altura piezométrica. Los puntos de demanda o de consumo se caracterizan
mediante sus coordenadas y demanda de agua.
Tubos – T: Los son arcos que conectan los nudos de la RDAP. Para el modelo se requiere
conocer el diámetro, la rugosidad, el coeficiente de fricción y el coeficiente de pérdidas
menores.
Válvulas – V: Son accesorios agregados al tubo para regular el flujo de agua. Este elemento
se modela mediante dos características: el tubo donde se ubica y una función de
comportamiento.
Hidrantes – H: Elementos que se ubican en un nudo y permiten generar diferencia de
presiones en la red y por lo tanto aumento de velocidad en tubos cercanos. Los hidrantes se
representan en el modelo mediante el nudo en donde se ubican, el coeficiente del emisor y el
exponente del emisor.
Apertura de válvulas Pv: Es el conjunto de las posibles aperturas de las válvulas.
Apertura de hidrantes Ph: Es el conjunto de las posibles aperturas de los hidrantes.

Adicionalmente, para la modelación se emplean diferentes configuraciones de la red. Cada
configuración corresponde a un cambio en los estados de las válvulas o los hidrantes por lo que,
cada configuración tiene dos conjuntos: el primero de cada válvula con su respectiva apertura y el
segundo de cada hidrante con su respectiva apertura.
FORMULACIÓN DEL PROBLEMA
Se formula el problema de lavado unidireccional (UDFP) como un problema de decisión, en
el cuál dada una RDAP, un conjunto de tubos, un conjunto de hidrantes, un conjunto de válvulas y
algunas restricciones se decide si es posible o no lavar un/unos tubos dados modificando el estado
de válvulas e hidrantes del sistema y asegurando que las restricciones se cumplan.
Los parámetros de entrada al problema son: la red de distribución de agua modelada como la
6-tupla antes mencionada, un valor mínimo de velocidad de agua en los tubos, un valor máximo de
velocidad de agua en los tubos, la presión mínima de los nudos de la red, el mínimo número de
válvulas a operar, el mínimo número de hidrantes a operar, el conjunto de aperturas que se
evaluarán para las válvulas y el conjunto de aperturas que se evaluarán para los hidrantes. También
se debe considerar que el plan de lavado sea físicamente posible para reproducirlo en campo. En
primer lugar, la RDAP siempre debe proveer agua a todos los nudos, se debe evitar situaciones en
las que se presente desconexión de nudos por cierre de válvulas. No se debe reducir la presión por
debajo de una presión mínima permitida y finalmente la velocidad no debe ser mayor a la máxima
establecida para evitar daños en el sistema.
El UDFP por ser un problema de decisión tiene como respuesta si se puede o no realizar el
lavado, pero para esta investigación a esta respuesta se le asocia un conjunto de válvulas e hidrantes
que al ser operados generan el lavado deseado en la RDAP. En conclusión el UDFP responde si
existe una configuración de válvulas e hidrantes (V
*
a
. H
*
a
) de manera que al configurar la RDAP la
velocidad en todos los tubos este acotada entre un valor mínimo y máximo dados, y además, en
ningún momento un nudo presente presiones menores a la mínima establecida ni este desconectado
del resto de la red.
METODOLOGÍA DE SOLUCIÓN DEL PROBLEMA
En primer lugar se identificó la dificultad del problema como un NP-Completo, lo que
permite identificar qué algoritmos pueden darle solución. Según esta complejidad el problema de
UDFP puede resolverse de forma exacta haciendo uso de un algoritmo exacto exponencial; sin
embargo, esta solución no es eficiente ya que requiere una cantidad exponencial de tiempo para ser
calculado, lo que implica que puede superar una cantidad de tiempo aceptable. El algoritmo
propuesto en este trabajo es un algoritmo de aproximación de orden polinomial que pretende
encontrar una configuración (V
+
a
. H
+
a
) similar a la que se obtendría si se hiciera uso del algoritmo
exacto exponencial (V
*
a
. H
*
a
), donde una configuración se refiere a un estado particular de cada una
de las válvulas e hidrantes de la red. Para poder hacer esta aproximación al problema de lavado
unidireccional UDFPA se requiere optimizar el conjunto de configuraciones.
Optimización: Se crea una función de influencia que sirve para medir que tanto afecta la
configuración la RDAP; esta función hace uso de los valores de las velocidades en los tubos a lavar,
donde la solución óptima (V
*
a
. H
*
a
) tiene un alto valor de influencia, y por lo tanto se busca una
configuración (V
+
a
. H
+
a
) con una influencia similar.
Zona de influencia: La función de influencia tiene una desventaja y es que no tiene en cuenta
los rangos de velocidad mínima y máxima; por lo tanto pueden existir configuraciones con el valor
de influencia adecuado pero que no sean solución. Para corregir esto se agregó una medida de
comparación que permite asegurar sin error que dos configuraciones son similares. Esta medida
realiza una comparación de la velocidad de los tubos de la red entre dos configuraciones haciendo

uso de un parámetro de precisión
∈, permitiendo conocer si las dos configuraciones generan o no
cambios similares en la RDAP.
Reducción del espacio de búsqueda: Para que el espacio de búsqueda de la solución sea de
orden polinomial, el algoritmo de aproximación debe podar (quitar) algunos elementos que de
antemano se sabe que no satisfacen el lavado. Las condiciones tenidas en cuenta para realizar estas
podas fueron:
Poda por déficit de presión: Se eliminan las configuraciones con déficit de presión y las que
se deriven de esta.
Poda por velocidad máxima: Por la forma del algoritmo si una configuración excede la
velocidad máxima todas las que se derivan de ella serán aun mayores por lo tanto también se
eliminan esos elementos.
Poda por desconexión: Con esta poda se pretende descartar las configuraciones en las que
algún nudo quedaría desconectado por el cierre de válvulas.
Algoritmo: A partir de las condiciones anteriores se planteó el algoritmo que evalúa un
número de orden polinomial de configuraciones diferentes y encuentra la mejor configuración que
sea similar a la que se obtendría con un espacio de búsqueda exponencial.
El algoritmo tiene como datos de entrada velocidad mínima, velocidad máxima, presión
mínima, número mínimo de válvulas a operar, número máximo de válvulas a operar, posibles
aperturas de válvulas, la red y el parámetro
∈.
Luego, el algoritmo genera diferentes configuraciones según el número de hidrantes,
válvulas y aperturas de válvulas que se tienen y va ordenando las diferentes configuraciones según
el valor de influencia, realiza la reducción del espacio de búsqueda y finalmente retorna la
configuración con el mayor valor de influencia.
El UDFPA explorará el conjunto de posibles configuraciones. Tendría que evaluar |
|
| |
|
|
| |
configuraciones diferentes; este número es exponencial, por esto se introducen podas en el
algoritmo para poder reducir el espacio de búsqueda a uno polinomial; para esto se hace uso del
factor de aproximación
∈. El objetivo de UDFPA es entonces encontrar una configuración (V
+
a
.
H
+
a
) para la cual se cumpla:
( | ∈
( )
)
( | ∈
( )
)
((
))
((
))
∈
Sea R = (N, P, V, H, Pv, Ph) la RDAP,
∈ el valor de aproximación (un valor real entre 0 y 1)
y
las restricciones de velocidad mínima, velocidad máxima y presión
mínima el siguiente algoritmo se emplea para darle solución al UDFPA.
UDFPA
( (
)
∈)
1.
〈({( )| ∈ } {( )| ∈ })〉
2.
j
3. ( ∈
∈
)
4.
( (
))
5.
( )
6.
(
∈
(| ||
| | ||
|)
)
7.
8.
( ∈
∈
)
9.
( (
))
10.
( )
11.
(
∈
(| ||
| | ||
|)
)
12.
13. ( )
Este algoritmo hace uso de las siguientes funciones:
1. Unir: Esta función combina dos listas.
2. OrdenaryFiltrar: Esta función ordena las configuraciones de forma ascendente con respecto
al orden Influencia, (2) eliminar las configuraciones que no cumplen con las restricciones de
velocidad máxima y presión mínima y (3) remplazar las configuraciones que desconecten
nodos por configuraciones similares que no los desconectan y de no ser posible el cambio se
elimina la configuración.
3. Max: Retorna la configuración con mayor valor de Influencia de la lista de configuraciones.
4. Podar: Esta función almacena cada nudo que se pode, separa las configuraciones que
pertenezcan a una misma zona de influencia de las configuraciones que únicamente tienen
valores similares de influencia y elimina las configuraciones similares de la lista.
Para realizar la eliminación de configuraciones si una configuración C
i
es similar a una
configuración C
i+1
, significa que la influencia de C
i+1
es menor o igual a la influencia de (C
i
)(1+δ)
entonces la configuración Ci es podada de la lista, donde
es el factor que determina la zona de
influencia y depende de
∈. Para el caso de este artículo caso
se define como
:
∈
(
|
||
|
|
||
|
)
CASO DE ESTUDIO
El algoritmo se implementó en el software REDES desarrollado por el Centro de
Investigaciones en Acueductos y Alcantarillados CIACUA de la Universidad de los Andes, Bogotá,
Colombia. Se desarrolló el Módulo de Software para planeación de lavado unidireccional en
REDES y para evaluar la funcionalidad del algoritmo se usó la Red R28; esta es una red de
distribución teórica creada por el CIACUA. La red tiene 67 tuberías de PVC, 39 nudos, un embalse
y una longitud total de 9750 m. Para este ejemplo se emplearon 12 válvulas, un hidrante, una
rugosidad de 0.0015 mm y un coeficiente de pérdidas menores de 0 en todos los tubos. Se buscaba
realizar el lavado de dos tuberías y se utilizaron tres aperturas de las válvulas: abierta, cerrada y
abierta a la mitad.
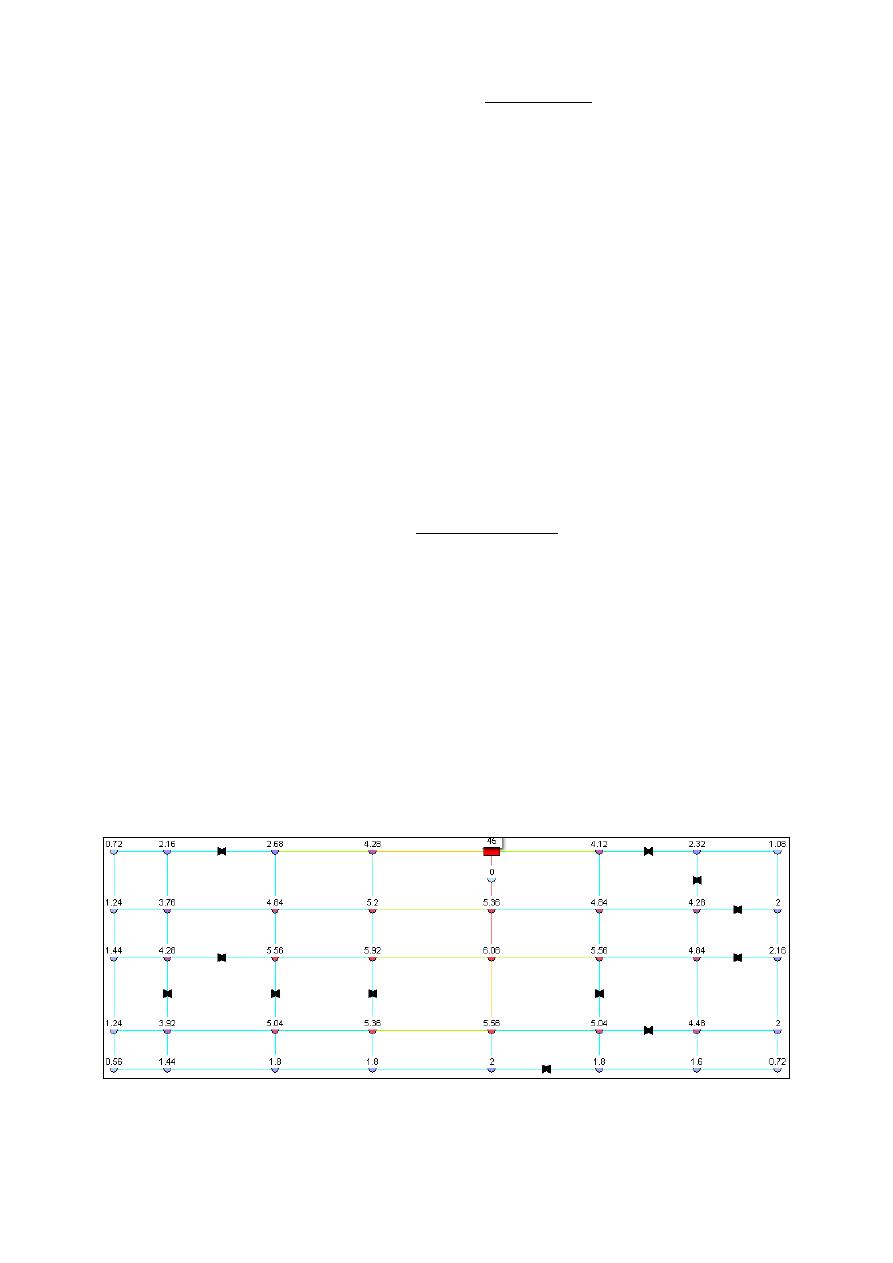
Figura 1. - RDAP R28. Un tanque con su línea de gradiente hidráulico (m), 39 nudos con su demanda de caudal (L/s),
12 válvulas y un hidrante.
A continuación se presentan las características de cada una de las tuberías del sistema (Tabla
1). Las características de localización espacial para cada nudo se muestran en la Tabla 2. Las
tuberías a lavar son la 33 y la 37 con unas velocidades de 1m/s y 1.4 m/s respectivamente.
Tabla 1.- Características de las tuberías de la red R28.
ID
Tubo
Longitud
(m)
Diámetro
(mm)
Nudo
Inicial
Nudo
Final
ID
Tubo
Longitud
(m)
Diámetro
(mm)
Nudo
Inicial
Nudo
Final
1
80
50
2
1
35
150
50
34
35
2
150
50
3
2
36
120
50
35
36
3
100
50
4
3
37
100
50
36
37
4
120
50
5
4
38
150
50
37
38
5
100
50
6
5
39
80
50
38
39
6
120
50
6
7
40
150
50
30
39
7
100
50
7
8
41
200
50
21
29
8
150
50
8
9
42
220
50
20
21
9
80
50
9
10
43
180
50
11
20
10
200
50
15
6
44
100
50
1
10
11
120
50
15
14
45
200
50
10
11
12
100
50
14
13
46
180
50
29
30
13
150
50
13
12
47
100
50
2
9
14
80
50
12
11
48
150
50
31
38
15
180
100
16
15
49
200
50
9
12
16
120
75
16
17
50
180
50
28
31
17
100
50
17
18
51
180
75
12
19
18
150
50
18
19
52
200
75
22
28
19
80
50
19
20
53
220
100
19
22
20
220.51
150
40
16
54
100
50
3
8
21
60.93
200
40
41
55
150
50
32
37
22
100
200
24
23
56
200
50
8
13
23
150
150
23
22
57
180
50
27
32
24
80
75
22
21
58
180
75
13
18
25
200.56
100
40
25
59
200
100
23
27
26
120
50
25
26
60
220
100
18
23
27
100
50
26
27
61
100
50
4
7
28
150
50
27
28
62
150
50
33
36
29
80
50
28
29
63
200
75
7
14
30
180
75
25
34
64
180
50
26
33
31
120
50
34
33
65
180
75
14
17
32
100
50
33
32
66
200
75
24
26
33
150
50
32
31
67
220
100
17
24
34
80
50
31
30
68
60
200
41
24

Tabla 2.- Características de los nudos e hidrante de la red R28. Hidrante señalizado (nudo 41).
ID Nudo Demanda (lps) X (m) Y (m)
ID Nudo Demanda (lps) X (m) Y (m)
1
0.56
0
0
21
2
700
0
2
1.24
0
80
22
5.56
700
80
3
1.44
0
230
23
6.08
700
230
4
1.24
0
330
24
5.36
700
330
5
0.72
0
450
25
4.12
900
450
6
2.16
100 450
26
4.84
900
330
7
3.76
100 330
27
5.56
900
230
8
4.28
100 230
28
5.04
900
80
9
3.92
100
80
29
1.8
900
0
10
1.44
100
0
30
1.6
1080
0
11
1.8
300
0
31
4.48
1080
80
12
5.04
300
80
32
4.84
1080 230
13
5.56
300 230
33
4.28
1080 330
14
4.84
300 330
34
2.32
1080 450
15
2.68
300 450
35
1.08
1230 450
16
4.28
480 450
36
2
1230 330
17
5.2
480 330
37
2.16
1230 230
18
5.92
480 230
38
2
1230
80
19
5.36
480
80
39
0.72
1230
0
20
1.8
480
0
41
0
700.4 393
En la tabla anterior el nudo 41 representa el hidrante que será utilizado para el lavado. Se
plantearon dos escenarios, uno con un parámetro de aproximación
∈ de 99.99% y el otro de 1%.
Esto a fin de ver la importancia de este parámetro en la obtención de la solución. Este parámetro
define la calidad de la solución pero a la vez aumenta el número de escenarios a evaluar, siendo 1%
el parámetro de aproximación con mejor calidad pero con mayor número de escenarios a evaluar.
Figura 2. – RDAP R28. Se muestran los ID de cada nudo y tubería. El hidrante esta ubicado en el nudo 41 y se indica
en el rectángulo. Las tuberías a lavar son la 33 y la 37 y se señalan con círculos.
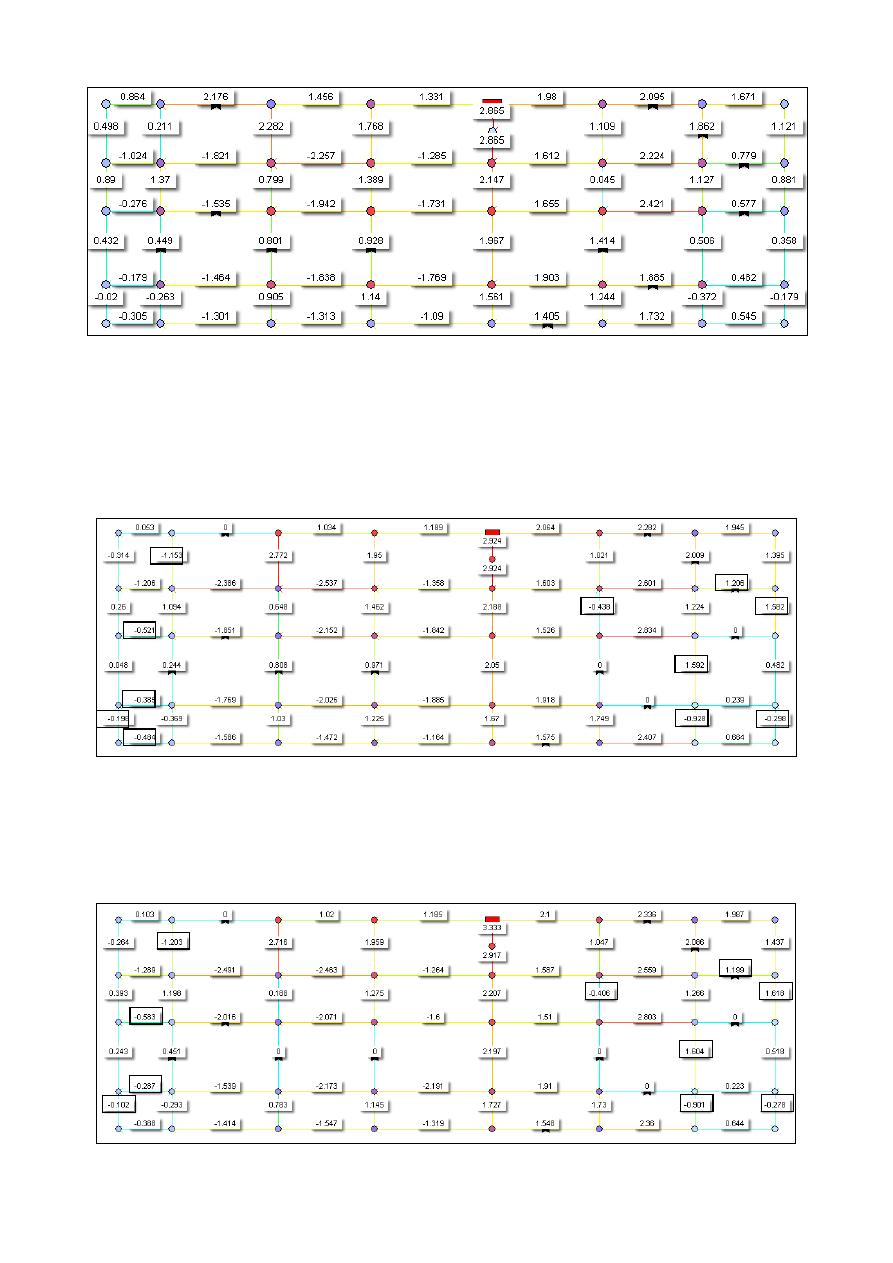
Figura 3. –RDAP R28. Velocidades iniciales (m/s).
Resultados con 99.99%
Usando el parámetro de aproximación con un valor del 99.99% se encontró una solución
evaluando 260 escenarios con un valor de influencia de 4.175. Las velocidades obtenidas en los
tuberías a lavar fueron de 1.59 m/s para la tubería 33 y de 1.58 m/s para la tubería 37. El
procedimiento de lavado consiste en abrir la válvula 30 a la mitad, cerrar las válvulas 55, 28, 50 y
10. Y esto genera cambios de velocidad en las tuberías 1, 27, 33, 34, 37, 39, 44, 47, 54, 6, y 62.
Figura 4. –RDAP R28. Velocidades obtenidas con un parámetro de aproximación de 99.99% (m/s).
Resultados con 1%
Usando el parámetro de aproximación con un valor del 1% se encontró una solución
evaluando 10664 escenarios con un valor de influencia de 4.221.
Figura 5. –RDAP R28. Velocidades obtenidas con un parámetro de aproximación de 1% (m/s).

Las velocidades obtenidas en los tuberías a lavar fueron de 1.60 m/s para la tubería 33 y de
1.62 m/s para la tubería 37. El procedimiento de lavado consiste en cerrar las válvulas 55, 18, 13,
28, 50 y 10 y abrir el hidrante 41. Esto genera cambios de velocidad en las tuberías 1, 27, 33, 34,
37, 39, 44, 47, 54, 6, y 62.
Comparación de resultados
El escenario de 1% se obtuvo un mejor valor de influencia pero el número de escenarios
evaluados aumentó de 260 a 10664. Por esta razón aunque se tiene un mejor escenario de solución
con la aproximación del 1% el aumento de los escenarios a evaluar puede ser excesivo y además
con la aproximación de 99.99% se llaga también a una solución factible y similar. Por lo tanto, con
los resultados se comprobó que el parámetro de aproximación define la calidad de la solución.
CONCLUSIONES
Se determinó la dificultad del problema lo que permite ahorros en tiempo, ya que esto
permite identificar que tipos de algoritmos dan solución al problema planteado.
Se probó que UDFP es un problema NP-Completo y se propuso un algoritmo de
aproximación de orden polinomial que brinda garantías sobre la solución que calcula con respecto a
la óptima.
Se desarrolló de manera óptima un algoritmo que determinará si es posible encontrar un plan
de lavado para una RDAP.
Se desarrolló el módulo de planeación de lavado en el software REDES lo que permite
evaluar la funcionalidad del algoritmo para diferentes casos de estudio.
Es posible automatizar el planeado de lavado unidireccional para así evitar las decisiones
subjetivas que se toman cuando el plan se realiza con la necesidad de la opinión de un experto o
alguien que conozca la red.
REFERENCIAS
Ahuja, R. K., Magnanti, T.L. and Orlin, J.B. (1993). “Network Flows: Theory, Algorithms, and
Applications”. 1st edition. Prentice Hall.
Álvarez, L.M. (2009). “Propuesta de una metodología para el diseño optimizado de lavados hidráulicos
unidireccionales en redes de distribución de agua potable”. Msc.Tesis. Universidad de los Andes. Bogotá,
Colombia
Cormen, T. H., Leiserson, C. E., Rivest, R.L. and Stein, C. (2009) Third Edition. Introduction to
Algorithms. The MIT Press.
Friedman, M. (2002). “Distribution system. Flushing program”. Journal AWWA. vol. 94, num. 7, pp. 48-56.
Gómez, D.M. (2010). “Técnicas para el Lavado de Redes de Distribución de Agua Potable”. Tesis de
grados. Universidad de los Andes. Bogotá, Colombia
Garey, M.R. and Johnson, D.S. (1979). “Computers and Intractability: A Guide to the Theory of NP-
Completeness”. W.H. Freeman.
Rothstein, E.G. (2011). “Planeación de Lavado Unidireccional en Redes de Distribución de Agua: Una
Aproximación”. Msc.Tesis. Universidad de los Andes. Bogotá, Colombia
Saldarriaga, J.G. (2002). “Hidráulica de tuberías. Edición especial”. McGraw-Hill. ISBN: 9586008312
Todini, E. and Pilati, S. (1987). “A gradient method for the analysis of pipe networks, International
Conference on Computer Applications for Water Supply and Distribution”, Leicester Polytechnic, UK.
