
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y
Alcantarillados
CIACUA
Efecto del uso de ecuaciones empíricas vs físicamente
basadas sobre los costos de diseños optimizados en
acueductos.
Proyecto de Grado
Ingeniería Ambiental
Juan David Uribe Rojas

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
II
Bogotá, Junio de 2012
Agradecimientos
Un especial agradecimiento al Ingeniero Juan Guillermo Saldarriaga Valderrama, asesor de
esta tesis, por la gran ayuda, guía y asistencia proporcionada sin la cual este proyecto de grado
no hubiera sido posible desarrollar. A su vez un agradecimiento especial a Diego Alejandro
Páez, Paula Andrea Cuero, Claudia Stella Solano, Rafael Alejandro Flechas y Daniela Rincón
Romero por su apoyo y aportes con los cuales el proyecto avanzó y se realizó de forma
exitosa.
Así mismo un agradecimiento a todo el personal del Centro de investigaciones de Acueducto y
Alcantarillado (CIACUA) por la ayuda suministrada en la realización de este proyecto de
grado.
Gracias a Dios, a mis amados Padres Álvaro Francisco Uribe Cálad y Martha Dolly Rojas
Ospina, a mi familia en Medellín y a todos los que han creído en mí y siempre me han
brindado su apoyo y estímulo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
III
Resumen
En los diseños optimizados de Redes de Distribución de Agua Potable (RDAP) se han utilizado
comúnmente ecuaciones empíricas o físicamente basadas, para el cálculo de las pérdidas por
fricción. Dentro de las más destacables se encuentra la ecuación empírica de Hazen-Williams y
la ecuación físicamente basada de Darcy-Weisbach. Siendo la primera una ecuación explícita
en la solución de las pérdidas por fricción, por lo que su uso en el contexto internacional y en
el marco colombiano es extenso. Sin embargo al ser una ecuación empírica, se encuentra
sujeta a restricciones de uso y a un número importante de limitaciones, las cuales en muchos
casos no son tenidas en cuenta por los ingenieros a la hora de realizar los diseños de las RDAP.
Por este motivo, en este proyecto se realizaron análisis en cuanto a costos en el momento de
diseñar con la ecuación de Hazen-Williams comparándolos con los costos de diseñar con la
Ecuación de Darcy-Weisbach para los materiales: hierro dúctil, PVC y polietileno de alta
densidad (PEAD).
En este trabajo se simularon, se diseñaron y se analizaron redes como la red Balerma, San
Vicente, R28, Bogotá-Cazucá y tres redes hipotéticas diseñadas por el autor. Con los
resultados obtenidos se van a mostrar los riesgos y serias limitaciones que puede tener la
ecuación de Hazen-Williams y porqué su uso debe ser restringido y seriamente vigilado por la
normativa colombiana.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
IV
CONTENIDO
Tabla de Ilustraciones ........................................................................................................................................... VI
Tablas .......................................................................................................................................................................... XIII
Capítulo 1 Introducción .......................................................................................................................................... 1
1.1
Objetivos ...................................................................................................................................................... 2
Capítulo 2 Marco Teórico....................................................................................................................................... 3
2.1 Ecuaciones y fórmulas utilizadas En los diseños de RDAP. ................................................... 3
2.1.1 Ecuación de Hazen y Williams ....................................................................................................... 4
2.1.2 Ecuación de Darcy-Weisbach ......................................................................................................... 5
2.1.3 Antecedentes Históricos ................................................................................................................ 10
2.2 Diseños Optimizados ................................................................................................................................ 16
2.3 Programas Utilizados durante el Proyecto .................................................................................. 17
2.3.1 Programa REDES ................................................................................................................................ 17
2.3.3 Programa EPANET 2.0 ..................................................................................................................... 20
2.4 Materiales utilizados y sus características .................................................................................. 21
2.4.1 Rugosidades absolutas ................................................................................................................... 21
2.4.2 Coeficientes de Hazen-Williams ................................................................................................ 23
2.4.3 Diámetros comerciales y Curvas de costo .......................................................................... 24
2.4.3.1 PVC ......................................................................................................................................................... 24
2.4.3.2 PEAD ..................................................................................................................................................... 26
2.4.3.3 HIERRO DÚCTIL .............................................................................................................................. 29
Capítulo 3. Metodología ....................................................................................................................................... 33
3.1 Red San Vicente ........................................................................................................................................... 33
3.2 Red Balerma .................................................................................................................................................. 34
3.3 Red Bogotá-Cazucá .................................................................................................................................... 35
3.4 Red R28 ............................................................................................................................................................ 36
3.5 Red Tesis 1 ..................................................................................................................................................... 36
3.6 Red Tesis 2 ..................................................................................................................................................... 37
3.7 Red Tesis 3 ..................................................................................................................................................... 38
3.8 Procedimiento para la obtención de los diseños ...................................................................... 39
Capítulo 4. Resultados .......................................................................................................................................... 48

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
V
4.1 Red San Vicente ........................................................................................................................................... 49
4.2 Red Balerma .................................................................................................................................................. 54
4.3 Red Bogotá-Cazucá .................................................................................................................................... 58
4.4 Red R28 ............................................................................................................................................................ 62
4.5 Red Tesis 1 ..................................................................................................................................................... 66
4.6 Red Tesis 2 ..................................................................................................................................................... 70
4.7 Red Tesis 3 ..................................................................................................................................................... 74
Capítulo 5 Análisis de resultados ................................................................................................................... 78
5.1 Red San Vicente ........................................................................................................................................... 78
5.2 Red Balerma .................................................................................................................................................. 79
5.3 Red Bogotá-Cazucá .................................................................................................................................... 83
5.4 Red R28 ............................................................................................................................................................ 86
5.5 Red Tesis 1 ..................................................................................................................................................... 89
5.6 Red Tesis 2 ..................................................................................................................................................... 92
5.7 Red Tesis 3 ..................................................................................................................................................... 95
5.8 Resumen de resultados ........................................................................................................................... 98
Capítulo 6 Concusiones ........................................................................................................................................ 99
Capítulo 7 Recomendaciones ........................................................................................................................ 100
Bibliografía .............................................................................................................................................................. 101
Anexos ........................................................................................................................................................................ 102

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
VI
TABLA DE ILUSTRACIONES
Ilustración 1. Diagrama de Moody.
9
Ilustración 2. Variación del coeficiente de Hazen-Williams con respecto al número de
Reynolds y el diámetro encontrado por Liou (Liou, 1998).
12
Ilustración 3. Diagrama de Moody realizado por Diskin 1960 donde se muestran
variaciones y representaciones de los coeficientes de Hazen-Williams (B.A. Christensen,
2000).
14
Ilustración 4. Diagrama de flujo de la metodologia sogh desarrollada por susana ochoa
(Ochoa, 2009).
20
Ilustración 5. Tabla de rugosidades absolutas del libro de hidráulica de tuberías
(Saldarriaga, 2007).
22
Ilustración 6. Rugosidades absolutas del RAS (Ministerio de Desarrollo Economico, 2000).
23
Ilustración 7. Lista de diámetros comerciales disponibles para PVC (PAVCO, 2011).
24
Ilustración 8. Curva de costos para PVC.
26
Ilustración 9.Curva de costos para PEAD.
29
Ilustración 10. Curva de costos para hierro dúctil.
32
Ilustración 11. Red San Vicente.
33
Ilustración 12. Red Balerma.
34
Ilustración 13. Red Bogotá-Cazucá.
35
Ilustración 14. Red R28.
36
Ilustración 15. Red Tesis 1.
37
Ilustración 16. Red Tesis 2.
38
Ilustración 17. Red Tesis 3.
39
Ilustración 18. Interfaz del Programa REDES.
40
Ilustración 19. Cargar la Red a Trabajar.
40
Ilustración 20. Verificación de los parámetros.
41
Ilustración 21. Prueba inicial para correr la Hidráulica en estado Estable.
41
Ilustración 22. Parametros de diseño: Curva de Costos, Diámetros y Ecuacion que se
desea utilizar.
42
Ilustración 23. Ventana de Diseño con Metodología SOGH.
43
Ilustración 24. Cálculo de la Flecha.
43
Ilustración 25. Diseño exitoso de la red.
44
Ilustración 26. Mensaje de error.
45
Ilustración 27. Resultados en REDES.
45
Ilustración 28 Exportar los resultados.
46
Ilustración 29. Costos de la red.
46
Ilustración 30. Gráfica de costos red San Vicente caudales normales.
50
Ilustración 31. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
51
Ilustración 32. Presiones de la red diseñada con Hazen-Williams despues de Correr la
hidráulica con la ecuacion de Darcy-Weisbach para hierro dúctil.
51
Ilustración 33. Presiones con la ecuación de Hazen-Williams para PVC.
52

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
VII
Ilustración 34. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
52
Ilustración 35. Presiones con la ecuación de Hazen-Williams para PEAD.
53
Ilustración 36.Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
53
Ilustración 37. Gráfica de costos Red Balerma con caudales normales.
54
Ilustración 38. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
55
Ilustración 39. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
55
Ilustración 40. Presiones con la ecuación de Hazen-Williams para PVC.
56
Ilustración 41. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
56
Ilustración 42. Presiones con la ecuación de Hazen-Williams para PEAD.
57
Ilustración 43. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
57
Ilustración 44. Gráfica de costos de la Red Bogotá-Cazucá con caudales normales.
58
Ilustración 45. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
59
Ilustración 46. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
59
Ilustración 47. Presiones con la ecuación de Hazen-Williams para PVC.
60
Ilustración 48. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
60
Ilustración 49. Presiones con la ecuación de Hazen-Williams para PEAD.
61
Ilustración 50. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
61
Ilustración 51. Gráfica de costos de la Red R28 con caudales normales.
62
Ilustración 52. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
63
Ilustración 53. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para Hierro dúctil.
63
Ilustración 54. Presiones con la ecuación de Hazen-Williams para PVC.
64
Ilustración 55. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
64
Ilustración 56. Presiones con la ecuación de Hazen-Williams para PEAD.
65
Ilustración 57. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
65
Ilustración 58. Gráfica de costos de la Red Tesis 1 con caudales normales.
66
Ilustración 59. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
67
Ilustración 60. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
67
Ilustración 61. Presiones con la ecuación de Hazen-Williams para PVC.
68
Ilustración 62. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
68
Ilustración 63. Presiones con la ecuación de Hazen-Williams para PEAD.
69

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
VIII
Ilustración 64. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
69
Ilustración 65. Gráfica de costos para la Red Tesis 2 con caudales normales.
70
Ilustración 66. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
71
Ilustración 67. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
71
Ilustración 68. Presiones con la ecuación de Hazen-Williams para PVC.
72
Ilustración 69. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
72
Ilustración 70. Presiones con la ecuación de Hazen-Williams para PEAD.
73
Ilustración 71. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
73
Ilustración 72. Gráfica de costos de la Red Tesis 3 con caudales normales.
74
Ilustración 73. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
75
Ilustración 74. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
75
Ilustración 75. Presiones con la ecuación de Hazen-Williams para PVC.
76
Ilustración 76. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
76
Ilustración 77. Presiones con la ecuación de Hazen-Williams para PEAD.
77
Ilustración 78. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
77
Ilustración 79. Comparación entre el diseño y su comprobación.
79
Ilustración 80. Comparación entre el diseño y su comprobación.
80
Ilustración 81. Comparación entre el diseño y su comprobación.
84
Ilustración 82. Comparación entre el diseño y su comprobación.
87
Ilustración 83.Comparación entre el diseño y su comprobación.
90
Ilustración 84.Comparación entre el diseño y su comprobación.
93
Ilustración 85 Comparación entre el diseño y su comprobación.
96
Ilustración 86. Gráfica de costos red San Vicente caudales duplicados.
102
Ilustración 87. presiones con la ecuación de hazen-Williams para hierro dúctil.
103
Ilustración 88. Presiones de la red diseñada con Hazen-Williams despues de Correr la
hidráulica con la ecuacion de Darcy-Weisbach para hierro dúctil.
103
Ilustración 89. Presiones con la ecuación de Hazen-Williams para PVC.
104
Ilustración 90. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
104
Ilustración 91. Presiones con la ecuación de Hazen-Williams para PEAD.
105
Ilustración 92. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
105
Ilustración 93. Gráfica de costos Red San Vicente con caudales Cuadruplicados.
106
Ilustración 94. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
107
Ilustración 95. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
107
Ilustración 96. Presiones con la ecuación de Darcy-Weisbach para hierro dúctil.
108

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
IX
Ilustración 97. Presiones con la ecuación de Hazen-Williams con PVC.
108
Ilustración 98. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach.
109
Ilustración 99. Presiones con la ecuación de Darcy-Weisbach para PVC.
109
Ilustración 100. Presiones con la ecuación de Hazen-Williams para PEAD.
110
Ilustración 101. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
110
Ilustración 102. Presiones con la ecuación de Darcy-Weisbach para PEAD.
111
Ilustración 103. Gráfica de los costos de la Red Balerma con caudales duplicados.
112
Ilustración 104. Presiones con la ecuación de Hazen-Williams con hierro dúctil.
112
Ilustración 105. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
113
Ilustración 106. Presiones con la ecuación de Hazen-Williams para PVC.
113
Ilustración 107. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
114
Ilustración 108. Presiones con la ecuación de Hazen-Williams para PEAD.
114
Ilustración 109. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
115
Ilustración 110. Gráfica de costos de la Red Balerma con caudales cuadruplicados. 116
Ilustración 111. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
116
Ilustración 112. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
117
Ilustración 113. Presiones con la ecuación de Darcy-Weisbach para hierro dúctil.
117
Ilustración 114. Presiones con la ecuación de Hazen-Williams para PVC.
118
Ilustración 115. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
118
Ilustración 116. Presiones con la ecuación de Darcy-Weisbach para pvc.
119
Ilustración 117. Presiones con la ecuación de Hazen-Williams para PEAD.
119
Ilustración 118. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
120
Ilustración 119. Presiones con la ecuación de Darcy-Weisbach para PEAD.
120
Ilustración 120. Gráfica de costos de la Red Bogotá-Cazucá con caudales duplicados. 121
Ilustración 121. Presiones con al ecuación de Hazen-Williams para hierro dúctil.
122
Ilustración 122. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
122
Ilustración 123. Presiones con la ecuación de Hazen-Williams para PVC.
123
Ilustración 124. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
123
Ilustración 125. Presiones con la ecuación de Hazen-Williams para PEAD.
124
Ilustración 126. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
124
Ilustración 127. Gráfica de costos de la Red Bogotá-Cazucá con caudales
cuadruplicados.
125
Ilustración 128. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
126

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
X
Ilustración 129. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
126
Ilustración 130. Presiones con la ecuación de Darcy-Weisbach para hierro dúctil.
127
Ilustración 131. Presiones con la ecuación de Hazen-Williams para PVC.
127
Ilustración 132. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
128
Ilustración 133. Presiones con la ecuación de Darcy-Weisbach para PVC.
128
Ilustración 134. Presiones con la ecuación de Hazen-Williams para PEAD.
129
Ilustración 135. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
129
Ilustración 136. Presiones con la ecuación de Darcy-Weisbach para PEAD.
130
Ilustración 137. Gráfica de costos para la Red R28 con caudales duplicados.
131
Ilustración 138 Presiones con la ecuación de Hazen-Williams para hierro dúctil.
131
Ilustración 139. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
132
Ilustración 140. Presiones con la ecuación de Hazen-Williams para PVC.
132
Ilustración 141. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
133
Ilustración 142. Presiones con la ecuación de Hazen-Williams para PEAD.
133
Ilustración 143. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
134
Ilustración 144. Gráfica de costos de la Red R28 con caudales cuadruplicados.
135
Ilustración 145. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
135
Ilustración 146. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
136
Ilustración 147. Presiones con la ecuación de Darcy-Weisbach para hierro dúctil.
136
Ilustración 148. Presiones con la ecuación de Hazen-Williams para PVC.
137
Ilustración 149. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
137
Ilustración 150. Presiones con la ecuación de Darcy-Weisbach para PVC.
138
Ilustración 151. Presiones con la ecuación de Hazen-Williams para PEAD.
138
Ilustración 152. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
139
Ilustración 153. Presiones con la ecuación de Darcy-Weisbach para PEAD.
139
Ilustración 154. Gráfica de costos de la Red Tesis 1 para caudales duplicados.
140
Ilustración 155. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
141
Ilustración 156. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
141
Ilustración 157. Presiones con la ecuación de Hazen-Williams para PVC.
142
Ilustración 158. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
142
Ilustración 159. Presiones con la ecuación de Hazen-Williams para PEAD.
143
Ilustración 160. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
143

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
XI
Ilustración 161. Gráfica de costos para la Red Tesis 1 con caudales cuadruplicados. 144
Ilustración 162. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
145
Ilustración 163. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
145
Ilustración 164. Presiones con la ecuación de Darcy-Weisbach para hierro dúctil.
146
Ilustración 165. Presiones con la ecuación de Hazen-Williams para PVC.
146
Ilustración 166. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
147
Ilustración 167. Presiones con la ecuación de Darcy-Weisbach para PVC.
147
Ilustración 168. Presiones con la ecuación de Hazen-Williams para PEAD.
148
Ilustración 169. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
148
Ilustración 170. Presiones con la ecuación de Darcy-Weisbach para PEAD.
149
Ilustración 171. Gráfica de costos para la Red Tesis 2 con caudales duplicados.
150
Ilustración 172. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
150
Ilustración 173. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
151
Ilustración 174. Presiones con la ecuación de Hazen-Williams para PVC.
151
Ilustración 175. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
152
Ilustración 176. Presiones con la ecuación de Hazen-Williams para PEAD.
152
Ilustración 177. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
153
Ilustración 178. Gráfica de costos de la Red Tesis 2 con caudales cuadruplicados.
154
Ilustración 179. Presiones con la ecuación de Hazen-Williams para Hierro Dúctil.
154
Ilustración 180. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
155
Ilustración 181. Presiones con la ecuación de Darcy-Weisbach para hierro dúctil.
155
Ilustración 182. Presiones con la de Hazen-Williams para pvc.
156
Ilustración 183. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
156
Ilustración 184. Presiones con la ecuación de Darcy-Weisbach para PVC.
157
Ilustración 185. Presiones con la ecuación de Hazen-Williams para PEAD.
157
Ilustración 186. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
158
Ilustración 187. Presiones con la ecuación de Darcy-Weisbach para PEAD.
158
Ilustración 188. Gráfica de costos para la Red Tesis 3 con caudales Duplicados.
159
Ilustración 189. Presiones con la ecuación de Hazen-Williams para hierro dúctil.
160
Ilustración 190. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
160
Ilustración 191. Presiones con la ecuación de Hazen-Williams para PVC.
161
Ilustración 192. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
161
Ilustración 193. Presiones con la ecuacion de Hazen-Williams para PEAD.
162

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
XII
Ilustración 194. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
162
Ilustración 195. Gráfica de costos de la Red Tesis 3 con caudales cuadruplicados.
163
Ilustración 196. Presiones de la ecuación de Hazen-Williams para hierro dúctil.
164
Ilustración 197. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para hierro dúctil.
164
Ilustración 198. Presiones para la ecuación de Darcy-Weisbach para hierro dúctil. 165
Ilustración 199. Presiones con la ecuación de Hazen-Williams para PVC.
165
Ilustración 200. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PVC.
166
Ilustración 201. Presiones con la ecuación de Darcy-Weisbach para PVC.
166
Ilustración 202. Presiones CON la ecuaciÓn de Hazen-Williams PARA PEAD.
167
Ilustración 203. Presiones de la red diseñada con Hazen-Williams después de correr la
hidráulica con la ecuación de Darcy-Weisbach para PEAD.
167
Ilustración 204. Presiones con la ecuación de Darcy-Weisbach para PEAD.
168
Ilustración 205. Diagrama de Moody con factores de fricción de redes con caudales
normales utilizando PEAD.
169
Ilustración 206. Diagrama de Moody con factores de fricción de redes con caudales
normales utilizando PEAD.
170
Ilustración 207. Diagrama de Moody con factores de fricción de redes con caudales
cuadruplicados utilizando PEAD.
171

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
XIII
TABLAS
Tabla 1. Rugosidades absolutas de las normas tecnicas de epm 2009 (Empresas Públicas
de Medellín, 2006-2009) ........................................................................................................................................ 22
Tabla 2. Tabla de coeficientes de Hazen-Williams de la EPM (Empresas Públicas de
Medellín, 2006-2009). ............................................................................................................................................. 23
Tabla 3. Costos por 6 metros de tubería de pvc (PAVCO, 2012). .................................................... 25
Tabla 4. Tabla de costos por metro y extensión de diámetros. ..................................................... 25
Tabla 5. Tabla de diámetros para PEAD de PAVCO (PAVCO, 2011). ............................................. 27
Tabla 6. Tabla de costos para PEAD suministrada por PAVCO (PAVCO, 2012). ..................... 27
Tabla 7. Costos por metro para PEAD. ......................................................................................................... 28
Tabla 8. Parte 1 de la lista de Diámetros de hierro dúctil (Saint-Gobain PAM , 2012). ....... 30
Tabla 9. Parte 2 de la lista de diámetros de hierro dúctil (Saint-Gobain PAM , 2012). ....... 30
Tabla 10. Costos con sus respectivos diámetros internos para Hierro Dúctil. ..................... 31
Tabla 11. Costos de la Red San Vicente con caudales normales.................................................... 50
Tabla 12. Costos de la Red Balerma con caudales normales. ......................................................... 54
Tabla 13. Costos de la Red Bogotá-Cazucá con caudales normales. ............................................ 58
Tabla 14. Costos de la Red R28 con caudales normales. ................................................................... 62
Tabla 15. Costos de la Red Tesis 1 con caudales normales. ............................................................. 66
Tabla 16. Costos de la Red Tesis 2 con caudales normales. ............................................................. 70
Tabla 17. Costos de la Red Tesis 3 con caudales normales. ............................................................. 74
Tabla 18. Resumen de resultados encontrados en el proyecto. ................................................... 98
Tabla 19. Costos de la Red San Vicente con caudales duplicados ............................................. 102
Tabla 20. Costos de la Red San Vicente con caudales cuadruplicados. .................................. 106
Tabla 21. Costos de la Red Balerma con caudales duplicados. ................................................... 111
Tabla 22. Costos de la Red Balerma con caudales cuadruplicados. ......................................... 115
Tabla 23. Costos de la Red Bogotá-Cazucá con caudales duplicados. ..................................... 121
Tabla 24. Costos de la red Bogotá-Cazucá con caudales cuadruplicados. ............................ 125
Tabla 25. Costos de la Red R28 con caudales duplicados. ............................................................. 130
Tabla 26. Costos de la Red R28 con caudales cuadruplicados. ................................................... 134
Tabla 27.Costos de la red con caudales duplicados. ......................................................................... 140
Tabla 28 Costos de la Red Tesis 1 con caudales cuadruplicados. ............................................. 144
Tabla 29. Costos de la Red Tesis 2 con caudales duplicados. ...................................................... 149
Tabla 30. Costos de la Red Tesis 2 con caudales cuadruplicados. ............................................ 153
Tabla 31. Costos de la Red Tesis 3 con caudales duplicados. ...................................................... 159
Tabla 32. Costos de la Red Tesis 3 con caudales cuadruplicados. ............................................ 163

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
1
CAPÍTULO 1 INTRODUCCIÓN
En el diseño de redes de distribución de agua potable (RDAP), se han utilizado a través de la
historia dos ecuaciones. La primera, la ecuación empírica conocida como la ecuación de
Hazen-Williams desarrollada por Allen Hazen y Gardner Steward Williams. La segunda, la
ecuación físicamente basada de Darcy-Weisbach, desarrollada por Henry Darcy y Julius
Weisbach. Pese a que esta última es una ecuación físicamente basada y tiene un cumplimiento
de diseño prácticamente ilimitado (Tipo de flujo, velocidad del flujo, diámetros, gravedad y
longitud de la tubería), su uso no es tan extendido como el de la ecuación de Hazen-Williams
debido a su complejidad de solución; esto se debe a que no es una ecuación explícita y
requiere de iteraciones o de un método numérico para su solución. Por el contrario, la
ecuación de Hazen-Williams es una ecuación de solución directa y no requiere de iteraciones
o métodos numéricos para su solución. Sin embargo, esta ecuación tiene serias e importantes
limitaciones que por lo general no son tenidas en cuenta actualmente por los ingenieros.
Adicionalmente, por ser una ecuación empírica, tiene limitaciones serias en su rango de
cumplimiento (Diámetros, Velocidad, Temperatura, Factores de Fricción y Números de
Reynolds que deben estar en el rango de flujo de transición).
En la actualidad, y en especial en el contexto colombiano, la ecuación de Hazen-Williams se
utiliza de forma generalizada e indiscriminada, con riesgos de diversa naturaleza, pese a
contar con métodos computacionales que facilitan y promueven el uso de la ecuación de
Darcy-Weisbach. Considerando los puntos fuertes y las desventajas de cada ecuación, se
debería poder establecer cual debe de ser la ecuación ideal para el diseño de RDAP.
Por ende el enfoque de este trabajo es diseñar y evaluar 7 RDAP a partir de las dos ecuaciones
existentes, con tres materiales diferentes (Hierro Dúctil, PEAD y PVC), con base a la
normativa colombiana (Presión mínima, rugosidad absoluta y coeficientes de Hazen-
Williams) y analizarlas desde el punto de vista hidráulico (presiones mínimas para esta tesis)
y desde el punto de vista de costos para concluir cual debe ser la ecuación más indicada a ser
utilizada.
Por tal motivo este trabajo de grado estará organizado de la siguiente forma. En el Capítulo 1
se realiza la introducción del proyecto y se definen los objetivos que se esperan alcanzar.
El Capítulo 2 desarrolla el marco teórico en el que se explicarán las características básicas de
las ecuaciones de diseño, antecedentes e investigaciones sobre las ecuaciones de Hazen-
Williams y Darcy-Weisbach. Adicionalmente, se mostrarán los materiales, valores para las
rugosidades de las tuberías, coeficientes de Hazen-Williams, lista de precios (incluyendo la
curva de costo para el diseño de la red), los programas que se utilizaron para el diseño
(REDES y EPANET) y diámetros que se utilizaron durante el proyecto.
El Capítulo 3 explicará la metodología que fundamenta este trabajo de investigación, lo cual
incluye las redes que se utilizaron, los parámetros de diseño y el procedimiento que se realizó
para la obtención de los resultados.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
2
En el Capítulo 4 se exponen los resultados obtenidos en cuanto a costos y presiones para cada
una de las redes diseñadas, con sus diferentes parámetros.
En el Capítulo 5 se encuentran los análisis de los resultados obtenidos para cada una de las
redes y materiales.
Finalmente los Capítulos 6 y 7 se mostrarán las conclusiones y las recomendaciones que se
sacaron de todo el trabajo semestral que se realizó.
1.1 OBJETIVOS
-Entender el efecto hidráulico (presiones en los Nudos de la red) que causa utilizar ecuaciones
empíricas en contraste con las ecuaciones físicamente basadas.
-Establecer la magnitud del efecto que tiene la hidráulica al utilizar las ecuaciones empíricas y
físicamente basadas en los costos de diseños de redes de distribución de agua potable (RDAP).
- Analizar y plantear cambios en la legislación actualmente vigente para el diseño de redes de
acueducto, estableciendo cuales deben ser las ecuaciones a utilizar y qué tipo de
restricciones tienen a la hora de aplicarlas en diferentes modelos de diseños.
-Identificar los materiales con los cuales hay que tener especial precaución al utilizar la
ecuación empírica de Hazen-Williams y nombrar los efectos que conlleva diseñar con estos
materiales, utilizando esta ecuación.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
3
CAPÍTULO 2 MARCO TEÓRICO
2.1 ECUACIONES Y FÓRMULAS UTILIZADAS EN LOS DISEÑOS DE RDAP.
En las tuberías a presión existen pérdidas de energía causadas por la fricción que existe entre
el fluido y la tubería, y las pérdidas menores que son por cambios de dirección del flujo e
instalación de accesorios. Estas pérdidas pueden ser calculadas utilizando la ecuación de
conservación de la energía de Bernoulli.
ECUA CIÓN 2.1 -1
siendo:
-p= presión.
-v= velocidad del flujo.
-z= altura topográfica o con respecto a una cota.
-g= gravedad
-ρ= Densidad del fluido.
-HF= pérdidas de energía entre el tramo 1 y 2.
De acuerdo con lo anterior, puede observarse que para el cálculo de las pérdidas por fricción
se tienen limitaciones ya que se requeriría de una medición de la velocidad o el caudal y de la
presión en la tubería. Lo que no es aplicable ya que como es evidente, la tubería aún no está
diseñada.
Las anteriores limitaciones exigieron estudiar a fondo la relación que existía entre las
características de la tubería (diámetro, material, longitud), las características del fluido
(densidad y viscosidad) y las pérdidas por fricción a través de los tramos de tubería. Como
resultado de estas investigaciones surgieron diversas ecuaciones para la realización de este
cálculo. Estas ecuaciones se dividen en dos grupos: empíricas y físicamente basadas. De las
primeras, la que en la actualidad tiene mayor importancia para los sistemas de acueducto, es
la ecuación de Hazen-Williams, desarrollada a principios del siglo XX por Allan Hazen y
Gardner Williams. Finalmente la ecuación más representativa del segundo grupo es la
ecuación de Darcy-Weisbach desarrollada por Henry Darcy (1803-1858) y Julius Weisbach

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
4
(1806 -1871). Ambas ecuaciones han sido ampliamente utilizadas en el diseño de redes de
distribución de agua potable; sin embargo, la primera (Hazen-Williams) al ser una ecuación
explícita para la velocidad y el caudal, presentaba una solución rápida y sencilla en contraste
con la ecuación de Darcy-Weisbach que es una ecuación implícita y requiere de iteraciones o
un método numérico para su solución.
2.1.1 ECUACIÓN DE HAZEN Y WILLIAMS
Ecuación empírica desarrollada por Allan Hazen y Gardner Williams a principios de 1900.
Esta ecuación tuvo la peculiaridad de no tener en cuenta los análisis hidráulicos de la ecuación
de Darcy –Weisbach. La forma original de la ecuación se muestra a continuación en el sistema
internacional de unidades.
ECUA CIÓN 2.1 .1 -1
donde:
v= Velocidad del flujo
R= Radio hidráulico (Área/ Perímetro mojado de la tubería)
S= Pendiente de la línea de gradiente de energía.
C= Coeficiente de Hazen-Williams (adimensional).
Es importante resaltar que el 0.849 es una contante utilizada y puede ser cambiada a 1.318
para el sistema inglés de unidades (Liou, 1998).
Esta ecuación es de rápida solución y es explícita para la velocidad del flujo, lo que la hacía
extremadamente útil para diseñar, antes de la llegada de los medios de cálculo
computacionales. Su desarrollo se realizó mediante el análisis estadístico de estudios de flujos
en sistemas de distribución de agua potable que más se presentaban en la ingeniería.
Estos estudios fueron realizados principalmente para modificar la ecuación de Chezy que se
muestra a continuación.
ECUA CIÓN 2.1 .1 -2
En la ecuación de Chezy, el cálculo del factor de fricción dependía del radio, rugosidad y
pendiente de fricción de la tubería, lo que la hacía extremadamente compleja de utilizar. Es

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
5
importante resaltar que esta ecuación fue la más utilizada para el cálculo de la velocidad en
tuberías para el año de 1903 (Gardner Williams, 1905).
En su momento, Gardner Williams y Allan-Hazen publicaron una serie de valores de C
(coeficiente de Hazen-Williams) para diversos materiales (Gardner Williams, 1905). De tal
forma que era posible calcular la velocidad (comprobación de diseño), las pérdidas por
fricción (en caso de que se tuviera una tubería con diámetro establecido) o el diámetro con el
que se quisiera diseñar la tubería (teniendo las pérdidas por fricción calculadas de la
Ecuación 2.1-1).
Los coeficientes definidos por Hazen-Williams, aplicaban solo para las condiciones “comunes
o normales de la práctica” por lo que desde su misma creación, esta ecuación contaba con
limitaciones que debían ser tenidas en cuenta a la hora de realizar los diseños de RDAP.
Las limitaciones establecidas por los creadores son:
-Solo es aplicable para Agua
-Debe estar en condiciones normales (20 grados centígrados)
-Velocidades inferiores a
-Diámetros superiores a 100 mm o 4 pulgadas.
Así mismo, resulta necesario resaltar que estos coeficientes no son constantes, ya que como
se explica en la literatura y por los mismos Gardner Williams y Allan Hazen, pueden variar por
la edad de la tubería (aumento de la rugosidad) o cuando los diámetros de la tubería son
demasiado pequeños. Estos coeficientes son representados en la actualidad con valores entre
80 y 150, donde 80 es un material rugoso y 150 para un material especialmente liso (PVC o
PEAD).
2.1.2 ECUACIÓN DE DARCY-WEISBACH
La ecuación de Darcy Weisbach es la ecuación físicamente basada más utilizada para diseños
de RDAP, redes pluviales y de alcantarillado. Esta ecuación fue inicialmente desarrollada por
Henry Darcy (1803-1858) mediante el uso de experimentos de flujo en tuberías, realizados
cerca a Paris. (Saldarriaga, 2007).
Los experimentos se llevaron a cabo utilizando un rango de diámetros que iba desde los 12
mm (0.0122 m) hasta los 500 mm (0.5 m), y los materiales utilizados para la experimentación
incluían vidrio, hierro, plomo, hierro recubierto con bitumen, hierro fundido y latón. Para los
experimentos se incluyeron tuberías con paredes recién construidas y tuberías con cierto
tiempo de ser utilizadas, llevando a resultados con velocidades ente 0.03 y
. Los caudales
fueron medidos con tanques de aforo y las longitudes de las tuberías siempre fueron

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
6
superiores a los 100 metros (excepción de vidrio y plomo que tuvieron tramos más cortos).
(Saldarriaga, 2007)
A partir de los resultados obtenidos, Henry Darcy concluyó que estos podían ser expresados
mediante la siguiente ecuación:
ECUA CIÓN 2.1 .2 -1
donde
R= Radio Hidráulico de la tubería.
= Pendiente de Fricción.
v= Velocidad media dentro de la tubería.
= Siendo coeficientes que describen la edad y el material de la tubería.
Llegando finalmente a la ecuación:
ECUA CIÓN 2.1 .2 -2
Donde
Q= Caudal
d= diámetro de la tubería.
Esta ecuación fue utilizada posteriormente por Fanning( 1837-1911) para combinarla junto
con la ecuación desarrollada por Julius-Weisbach ( 1806-1871), formando una ecuación
físicamente basada que se ajustaba de gran forma a los diferentes datos experimentales
(Saldarriaga, 2007).
Julius Weisbach, desarrolló una ecuación que ayudaría a predecir las pérdidas por fricción
dentro de las tuberías. Esta ecuación requería estar en función del tipo de fluido, el diámetro,
el material de la tubería y la velocidad. Llegando a la siguiente expresión:
ECUA CIÓN 2.1 .2 -3

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
7
donde
l= longitud de la tubería.
f= factor de fricción adimensional.
Esta ecuación incluyó únicamente las pérdidas por fricción con las paredes de la tubería. Más
adelante se desarrolló una forma de calcular las pérdidas menores causadas por el uso de
accesorios y por cambios de dirección dentro de las tuberías. La ecuación anterior (2.1.2-2)
puede ser obtenida mediante análisis dimensional.
Sin embargo, la obtención del factor de fricción seguía presentando una complicación, por lo
que se desarrollaron diferentes ecuaciones para su obtención. Una de ellas fue la ecuación
para el flujo laminar de Hagen-Poiseuille que Julius Weisbach utilizó:
ECUA CIÓN 2.1 .2 -4
donde:
Re= Número de Reynolds en flujo laminar (2000 o menores en tramos de tuberías).
Sin embargo, estas condiciones raramente se presentaban en las RDAP, por lo que se
requerían ecuaciones adicionales para hallar el factor de fricción en flujos turbulentos
hidráulicamente rugosos y lisos.
En 1911 Blasius, alumno de Prandl von Karman (Saldarriaga, 2007), desarrolló una ecuación
mediante experimentos empíricos para hallar el factor de fricción en flujos con números de
Reynolds entre (5000-100000). La ecuación a la que llegó fue:
ECUA CIÓN2.1 .2 -5
Por su parte, Prandl desarrolló una ecuación para hallar el factor de fricción, pero dada su
complejidad de solución, el buen cumplimiento de la ecuación de Blasius y el hecho de que la
ecuación de Colebrook-White aplica para todos los flujos, esta ecuación no es ampliamente
utilizada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
8
ECUA CIÓN 2.1 .2 -6
Más adelante, se desarrollaron los trabajos de los Ingenieros Johann Nikuradse y de Lewis
Moody. El primero de ellos con el ánimo de entender la naturaleza del factor de fricción,
realizó diversos experimentos para diferentes diámetros, variando el caudal, de tal forma que
incluyera un rango importante de números de Reynolds y abarcara los 4 tipos de flujo (Flujo
Laminar, Flujo Transicional, Flujo Turbulento Hidráulicamente Liso (FTHL) y Flujo
Turbulento Hidráulicamente Rugoso (FTHR)) (Saldarriaga, 2007).
De los experimentos logró concluir:
Cuando el número de Reynolds es inferior a 2000, el factor de fricción es
independiente de la rugosidad relativa de la tubería
.
Al entrar en el flujo Liso, tanto el número de Reynolds como la rugosidad relativa de la
tubería juegan un papel fundamental dentro del cálculo del factor de fricción.
A medida que el número Reynolds se va alejando del flujo liso, y entra en la zona de
transición, se vuelve una función compleja tanto de Reynolds como de la rugosidad
relativa.
Finalmente, a medida que se aumentan los números de Reynolds, Nikuradse notó que
las curvas en su gráfica se volvían prácticamente horizontales, llevando a que el factor
de fricción dejara de ser una función del número de Reynolds y pasara a ser
únicamente una función de la rugosidad relativa de la tubería, en otras palabras el
numero de Reynolds deja de ser un factor importante para la obtención del factor de
fricción.
Prosiguiendo su investigación Moody en 1940, con la intención de investigar las pérdidas por
fricción en tuberías con rugosidades reales y no artificiales. Desarrolló un trabajo combinando
el trabajo del ingeniero alemán y de Colebrook. (Saldarriaga, 2007). De sus resultados lo más
destacable es:
Para el flujo hidráulicamente rugoso, el factor de fricción dependía exclusivamente de
la rugosidad relativa de la tubería.
Con lo anterior Moody, amplió su experimento y mediante la adquisición de tuberías
de diferentes materiales y diámetros comerciales realizo experimentos, en los que
hallaba las pérdidas por fricción, posteriormente calculaba el factor de fricción (sólo
para FTHR). Con estos resultados hallo la rugosidad relativa y con esta y la gráfica de
factor de fricción vs Rugosidad relativa, pudo determinar las diferentes rugosidades
absolutas de las tuberías (Saldarriaga, 2007).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
9
Con esto Moody llego a la conclusión que para cada tipo de material había una
rugosidad asociada y que esta representaba el comportamiento hidráulico de cada una
de las tuberías.
Con toda la información y la ecuación de Colebrook, Moody pudo desarrollar un
diagrama donde se podía ver el tipo de flujo y determinar el factor de fricción para
diferentes tuberías comerciales (ver Ilustración 1).
ILUSTRACIÓN 1. DIAGRAMA DE MOODY.
Esta gráfica fue ampliamente utilizada hasta la aparición de los métodos computacionales ya
que como se verá más adelante, encontrar el factor de fricción matemáticamente era de una
complejidad importante para la época.
Para el flujo hidráulicamente rugoso, las investigaciones de Colebrook y White en 1939,
utilizando las investigaciones de Prandl, von Karman y Nikuradse, permitieron establecer una
ecuación para hallar el factor de fricción para el flujo de transición. Ellos notaron sin embargo,
que los resultados encontrados solo representaban los extremos, y decidieron que el
comportamiento en tuberías reales debería de estar descrito por una única ecuación
(Saldarriaga, 2007). Llegando a obtener:
ECUA CIÓN 2.1 .2 -7

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
10
Esta última ecuación aplica para todos los tipos de flujo turbulento (para los laminares se
utiliza la Ecuación 2.1.2-3). Sin embargo y como se mencionó anteriormente, esta es una
ecuación de difícil solución si no se cuenta con un método computacional o una calculadora,
por 2 motivos:
-El logaritmo incluido es de difícil solución manual.
-Es una ecuación implícita para despejar el factor de fricción.
Posteriormente, Swamee y Jain desarrollarían en 1976 otra ecuación para el cálculo del factor
de fricción, de tal forma que fuera más simple y fácil de resolver. La ecuación a la que llegaron
fue:
ECUA CIÓN 2.1 .2 -8
Como se puede observar, esta ecuación es explícita y no requiere de métodos numéricos para
su solución. Sin embargo tiene rangos de cumplimiento para rugosidad relativa y números de
Reynolds (Liou, 1998).
La gran ventaja es que sus rangos de cumplimiento solo presenta un error máximo con
respecto a la ecuación de Colebrook-White del 5%.
2.1.3 ANTECEDENTES HISTÓRICOS
Varios investigadores han realizado trabajos para estudiar ambas ecuaciones de diseño. En
1998 Chyr Pyng Liou publicó un trabajo en el cual demostró las falencias y rangos de validez
de la ecuación de Hazen-Williams, así como la alta variabilidad de su Coeficiente respecto al
número de Reynolds, su diámetro y su rugosidad relativa.
Liou empezó su trabajo relacionando el coeficiente de Hazen-Williams con la ecuación
físicamente basada de Darcy-Weisbach. Primero, reorganizó la ecuación de tal forma que la
pendiente del gradiente hidráulico quedara expresada en términos de la cabeza de velocidad
. Al realizar esto, dejaba la velocidad expresada en el lado derecho como un denominador
elevado a la 0.1841 (Liou, 1998). Luego, al introducir la viscosidad cinemática ,
es

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
11
combinada con
para formar el número de Reynolds elevado a la 0.1841.
Posteriormente, expresó el radio hidráulico como
, combinando esto con
,
resultaba en el diámetro elevado a la 1.0185. Luego siendo ε la rugosidad absoluta de la
tubería, Liou dividió el diámetro encontrado en el paso anterior de tal forma que este quedara
, y reescribirlo para obtener la expresión
(Liou, 1998). Finalmente,
expresando la pendiente como
, manipuló la ecuación expresándola de esta forma:
ECUA CIÓN 2.1 .3 -1
Luego, reemplazando el lado derecho de la ecuación con la ecuación de Darcy – Weisbach se
obtiene:
ECUA CIÓN 2.1 .3 -2
donde:
C: Coeficiente adimensional de Hazen-Williams.
R: Número de Reynolds
ε= Rugosidad Absoluta del material
v= Diámetro de la tubería
ν= Viscosidad Cinemática.
Al llegar a esta expresión Liou pudo concluir que en efecto, el coeficiente de Hazen-Williams
es dependiente del número de Reynolds, de la rugosidad relativa de la tubería
, de la
rugosidad absoluta y de la viscosidad cinemática (ν).
Posteriormente Liou varió los números de Reynolds y los diámetros para ver cómo se
comportaban los Coeficientes de Hazen-Williams, dejando una rugosidad absoluta de 0.0003
m y una viscosidad cinemática de
(agua a 15.56 grados centígrados) (Liou,
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
12
1998). Generó la siguiente tabla que muestra la variación del coeficiente de Hazen –Williams
con respecto al diámetro y al número de Reynolds.
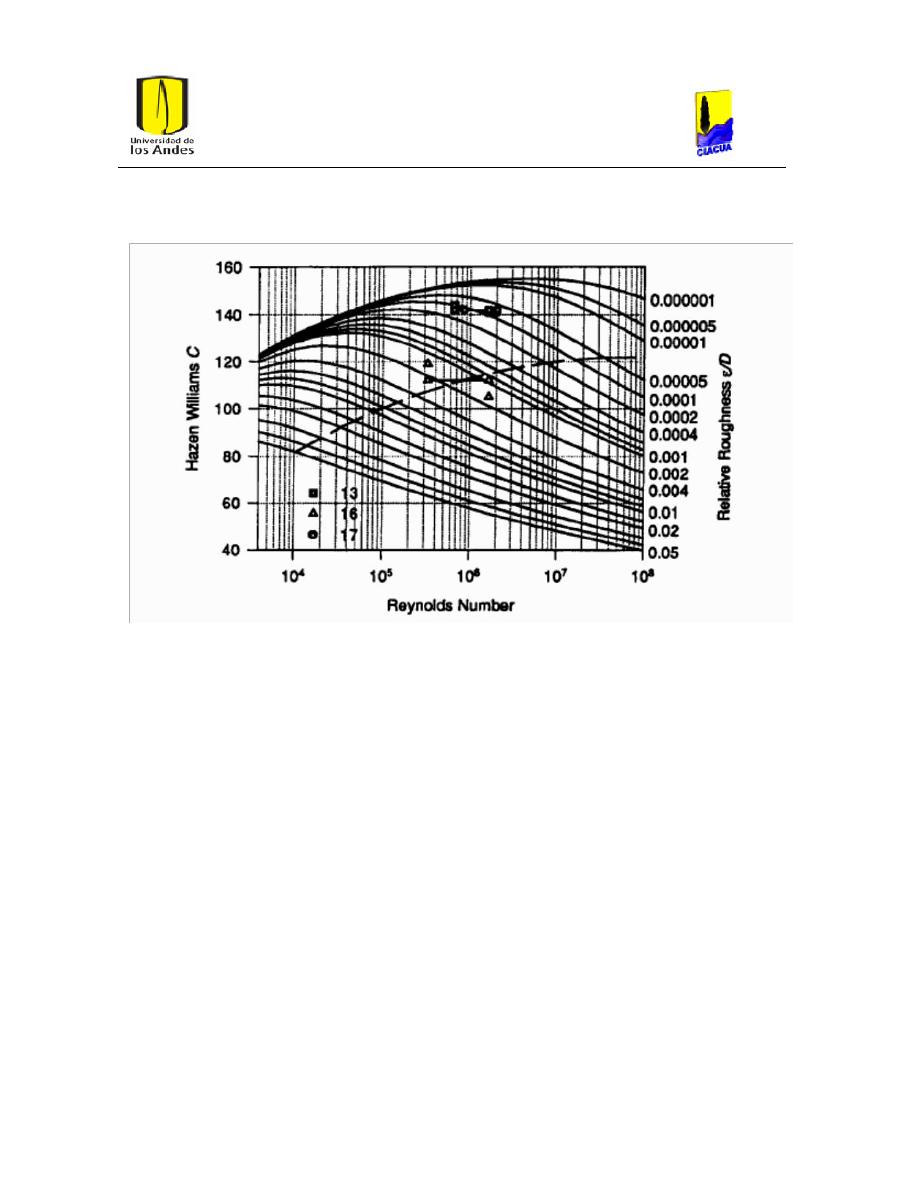
ILUSTRACIÓN 2. VARIACIÓN DEL COEFICIENTE DE HAZEN-WILLIAMS CON RESPECTO AL NÚMERO
DE REYNOLDS Y EL DIÁMETRO ENCONTRADO POR LIOU (LIOU, 1998).
Como se puede observar, el coeficiente de Hazen y Williams varía relativamente poco en la
zona de transición, pero presenta cambios severos fuera de esta (Línea punteada). Esto
permitió establecer que la ecuación de Hazen-Williams tiene unos rangos de cumplimiento
limitados y fuertemente dependientes del número de Reynolds y del Diámetro.
Para finalizar Liou decidió mostrar los errores que se pueden cometer al calcular el error de la
pendiente de gradiente hidráulico con la ecuación de Hazen-Williams y comparándolos con la
pendiente calculada con la ecuación de Darcy-Weisbach. Los resultados que obtuvo fueron de
gran importancia, no solo debido a que por fuera de la zona de cumplimiento la ecuación de
Hazen-Williams presentaba un error de hasta el 40% sino porque su rango de validez se
limitaba exclusivamente a la zona de transición en el diagrama de Moody.
Ese mismo año, Hosam El-Din Moghazi (M.Moghazi, 1998), realizó experimentos para
determinar el coeficiente de Hazen-Williams para tuberías de Polietileno, encontrando una
vez más que el coeficiente de Hazen y Williams presentaba variaciones con respecto a su
diámetro y también que al realizar un cálculo entre el factor de fricción medido y el calculado
(por el investigador) se encontraba un error no superior al 14%. Sin embargo, al comparar los
valores calculados por el autor y los calculados por los valores recomendados estos
presentaron diferencias en el cálculo de las pérdidas por ficción con un máximo del 27%.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
13
En el año 2000, surge una discusión respecto al artículo de Liou (Liou, 1998). Los tres autores
participantes concluyen que el uso de la ecuación de Hazen-Williams debe de ser limitada o
abandonado. En la primera parte, Christensen concuerda con Liou en el sentido de que se
debe dejar de utilizar la ecuación de Hazen-Williams con excepción de la zona dentro del
rango de validez.
Christensen plantea que los rangos de valides de la ecuación de Hazen y Williams deben de
ser:
donde R es el número de Reynolds.
A su vez, específica que no es la única limitación y que la ecuación debe estar regulada
igualmente por el diámetro de la tubería, estableciendo que el diámetro mínimo debe estar
regulado por donde ε es la rugosidad absoluta de la tubería. Resaltando que es
posible que en tuberías de considerable edad, se pueden presentar valores de ε cercanos a 1
mm, lo que llevaría a que el diámetro mínimo de la tubería fuera de 1.44 m (B.A. Christensen,
2000). Concluyen y resaltan que en la actualidad muchos ingenieros y diseñadores no tienen
en cuenta las restricciones y están diseñando por fuera del número de Reynolds
reglamentario y con diámetros muchos menores a los que se deberían utilizar.
El segundo autor Frederick Locher, concuerda con Liou en que el uso de la ecuación de Hazen-
Williams debe de ser abandonado o solo aplicado en sus rangos de cumplimiento, pero
plantea que Liou a la hora de realizar sus cálculos, no debe de introducir una dependencia de
la rugosidad absoluta, ya que esto obscurece la verdadera naturaleza de la ecuación de Hazen-
Williams. Resalta Locher que se debe analizar tal y cómo lo realizo Diskin en 1960, que se
debe relacionar el factor de fricción, el C de Hazen-Williams, Reynolds y la rugosidad relativa,
sin la introducción artificial de la rugosidad absoluta (B.A. Christensen, 2000). De tal forma
que quede:
ECUA CIÓN 2.1 .3 -3
Y teniendo en cuenta que para la ecuación de Hazen-Williams el único fluido valido es el agua,
Locher establece que se puede usar un
, llegando a que para un diámetro
establecido y una rugosidad absoluta de material, surge una constante que representa estos
dos parámetros. De esta manera, concluye que los coeficientes de Hazen-Williams sean
graficados como líneas rectas en el diagrama de Moody. (B.A. Christensen, 2000), como se
muestra a continuación:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
14
ILUSTRACIÓN 3. DIAGRAMA DE MOODY REALIZADO POR DISKIN 1960 DONDE SE MUESTRAN
VARIACIONES Y REPRESENTACIONES DE LOS COEFICIENTES DE HAZEN-WILLIAMS (B.A.
CHRISTENSEN, 2000).
De acuerdo con Locher, el trabajo de Diskin permite llevar a las siguientes conclusiones:
1) Los datos estadísticos utilizados para el desarrollo de la ecuación de Hazen-Williams
se encontraban en la zona de transición del diagrama de Moody. Llevando a que la
validez de esta ecuación se encuentre cuando la línea del Coeficiente de Hazen-
Williams se encuentre aproximadamente paralela con las curvas de la constante
en el diagrama de Moody (B.A. Christensen, 2000).
2) La ecuación de Hazen-Williams es inválida para materiales demasiado rugosos (C
menores a 100 nunca se debería de utilizar). Por lo que al diseñar con valores
cercanos o menores a 100 no solo se están encontrando resultados equivocados en las
pérdidas por fricción, sino que al suponer que es un valor constante se comete el error
de hacer al material más liso de lo que realmente representa (B.A. Christensen, 2000).
Finalmente, Locher concluye que en la actualidad y con métodos computacionales es
inapropiado seguir utilizando una ecuación empírica y no una ecuación físicamente basada
que puede ser resuelta rápidamente por medios computacionales.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
15
Para finalizar, el tercer autor Swamee, felicita a Liou por mostrar las falencias de la ecuación
de Hazen y Williams y considerando irónico que esta sea la ecuación más utilizada, mientras
que la ecuación de Darcy-Weisbach, físicamente basada, sea utilizada casi exclusivamente por
los académicos.
En 2003 Fabián A. Bombardelli y Marcelo H. García realizaron un estudio sobre los diseños
con diámetros de gran tamaño. El caso de estudio utilizado por los autores fue el de una zona
de una metrópolis que a tan solo 5 años de haberse puesto en servicio, era inadecuada para
proveer la cantidad de agua necesaria.
El análisis se realizó consultando la literatura con respecto a los límites y validez de la
ecuación de Hazen-Williams. Una vez realizada la recopilación bibliográfica, procedieron a
revisar la información sobre la red que presentó los problemas.
Lo primero que lograron evidenciar fue que la red fue diseñada con concreto, con un
coeficiente de Hazen-Williams de 120, y con una variación de diámetros de hasta 2.29 m.
Como se mencionó anteriormente, en este caso se vio que una red de tan solo 5 años de
operación presentó problemas y se le realizó un análisis hidráulico por 2 firmas consultoras.
Durante este análisis se realizaron mediciones en las velocidades del flujo y las presiones en
los Nudos (Fabián A.Bombardelli, 2003).
Con base a los resultados obtenidos, se procedió a obtener los valores de los Coeficientes de
Hazen-Williams. Los resultados que se obtuvieron de la primera firma consultora fueron
sorprendentes ya que en las tuberías de 2.29 m de diámetro se encontró que el coeficiente de
Hazen-Williams presentaba valores entre 85 y 95. Esto quería decir que la tubería presentaba
una rugosidad mucho mayor a la que se había esperado (se diseñó con un coeficiente de
Hazen-Williams de 120). Los autores concluyeron que si estos valores eran correctos, en el
futuro la red no podría suplir de forma correcta las crecientes demandas de agua, debido a
que las pérdidas por fricción iban a ser mucho mayores con los nuevos coeficientes (Fabián
A.Bombardelli, 2003).
Esta situación causó gran sorpresa en el personal y se plantearon si el problema era de la
ecuación de diseño (Hazen-Willams) o si era debido a un incremento real en la rugosidad de la
tubería, por lo que la comisión se enfocó en ver si las medidas que se habían tomado
presentaban algún tipo de error en la toma de los datos. Para verificar esta situación, se llamó
a una segunda firma consultora para tomar una segunda muestra de datos exclusivamente en
la tubería de 2.29 m de diámetro. Esta segunda muestra se realizó de forma más cuidadosa,
teniendo especial cuidado de registrar mejor las pérdidas y los lugares donde se tomaron las
muestras. Estos resultados mostraron resultados similares a los encontrados en la primera
toma de datos.
Bombardelli y García, después de realizar sus análisis, llegaron a la conclusión de que tuberías
de gran diámetro presentaban un comportamiento bastante peculiar. De una parte, el hecho
de ser tuberías de gran tamaño en diámetro estaría más expuesto a flujos turbulentos que
estarían más relacionadas con altos números de Reynolds. Pero, de otra parte, dado el gran

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
16
diámetro, la relación entre
puede llegar a ser muy pequeña y por ende tener condiciones
de trabajo en flujo de transición, lo que llevaría a pensar que se presentan las condiciones
ideales para aplicar la ecuación de Hazen-Williams (Fabián A.Bombardelli, 2003). Sin
embargo un análisis de los datos, permitió concluir que era precisamente el constante
aumento de la demanda y por ende de los caudales, los que llevaron al flujo a la zona de Flujo
Turbulento, quitándole toda validez al diseño realizado con la ecuación de Hazen-Williams.
Llevando a concluir y recomendar que la mejor y más correcta opción era el uso de la
ecuación de Darcy-Weisbach para diseñar las redes de distribución de agua potable.
En 2007 Quentin B. Travis y Larry W. Mays, desarrollaron una investigación en la que
reproducían una relación entre el coeficiente de Hazen-Williams y las rugosidades absolutas
en la ecuación de Colebrook-White, lo que permitió a los ingenieros a sacar fácilmente los
valores de rugosidades absolutas y a visualizar de forma rápida y sencilla los límites de
aplicabilidad de la ecuación de Hazen-Williams (Quentin B. Travis, 2007).
Posteriores investigaciones como la de John D Valiantzas| (2008) permitieron reescribir la
ecuación de Darcy-Weissbach de tal forma que fuera explícita en su solución y solo
presentando una diferencia con respecto a la ecuación original del 5% (Valiantzas, 2008).
Finalmente, en 2011 David Bennett y Rebecca Glaser publican un artículo donde enfatizan las
principales complicaciones que se presentan en los diseños de tuberías con grandes
diámetros, donde incluyen varios fenómenos físicos como sedimentos, efectos biológicos
dentro de las tuberías (biopelículas), no tener en cuenta el envejecimiento de las diversas
tuberías, mala ubicación de válvulas, mal mantenimiento de las tuberías y finalmente el
extensivo y más generalizado uso de la ecuación de Hazen-Williams al ser ampliamente
utilizada por fuera de los límites de cumplimiento o con Coeficientes de Hazen-Williams que
subestiman las pérdidas y llevan al incumplimiento de las presiones mínimas dentro de las
tuberías.
2.2 DISEÑOS OPTIMIZADOS
Los diseños de redes de distribución de agua potable han estado regidos por una serie de
restricciones importantes. Dentro de las principales, está el adecuado suministro de agua a
poblaciones, industrias o sectores comerciales. Estas restricciones están plasmadas
principalmente en la presión mínima de cada uno de los Nudos de la red. Si bien, parece un
problema sencillo de solucionar, la verdad es que la complejidad aumenta ya que se aplica una
segunda restricción a los diseños y es los costos de diseño. No solo es necesario cumplir con
los requerimientos de presión mínima dentro de la red, sino que el costo de diseño de la
misma sea el menor posible. Lo anterior llevó al desarrollo de técnicas que permitieran
diseñar de forma óptima RDAP.
Las RDAP poseen varias características importantes para sus diseños. Dentro de estas
características, se destacan la captación, tratamiento, conducción, almacenamiento y
distribución del agua. Esto exige tener en cuenta muchos factores para el diseño (las pérdidas

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
17
en cada uno de estos procesos). Adicionalmente, las RDAP están regidas por las demandas de
las poblaciones bajo un periodo de tiempo, lo que lleva a diseñar sistemas que puedan suplir a
la población en estos periodos de diseño sin ningún problema. Lo anterior obliga a que los
diseños tengan que ser precisos y cuidadosos. Por este motivo y por las restricciones
nombradas anteriormente, se han desarrollado innumerables metodologías para el diseño
óptimo.
Dentro de las metodologías más importantes se encuentra la de Algoritmos Genéticos (AG),
que si bien ofrecían la opción de comparar diferentes generaciones de diseños, el excesivo uso
de memoria computacional solo permitía arrojar óptimos locales. Adicionalmente, existen
diseños con superficie óptima, búsqueda de armonía y superficie optima de gradiente
hidráulico. Esta última fue la que se utilizó durante este trabajo de grado y será explicada
adelante.
Con base en lo anterior, muchos ingenieros han aplicado estas metodologías junto con las
ecuaciones de diseño nombradas anteriormente, para diseñar de forma efectiva redes de
distribución. Sin embargo y en muchas ocasiones muchos de los diseños creados fueron
aplicando la ecuación de Hazen-Williams sin verificar si se encontraba dentro de sus rangos
de cumplimiento. Lo que en muchas ocasiones generaba redes con bajos costos de diseño pero
que incumplían las presiones mínimas exigidas por las normativas.
Por este motivo, se realizó este proyecto a fin de contribuir a ilustrar sobre los efectos que
conlleva utilizar una ecuación físicamente basada o una ecuación empírica en los costos y en
el cumplimiento de la presión mínima.
2.3 PROGRAMAS UTILIZADOS DURANTE EL PROYECTO
2.3.1 PROGRAMA REDES
El programa REDES fue desarrollado en la Universidad de los Andes por el grupo de
investigación CIACUA (Centro de investigaciones en Acueductos y Alcantarillados) en el
Departamento de Ingeniería Civil y Ambiental, es una herramienta computacional para la
simulación de redes de acueducto y tuberías a presión. (Saldarriaga, 2007). Este programa ha
sido modificado y actualizado desde su nacimiento en 1998 hasta el presente año, por
numerosas tesis de pregrado, investigaciones y magíster, bajo la supervisión del ingeniero
Juan Guillermo Saldarriaga. Así mismo, el programa ha sido utilizado en numerosas tesis de
grado e investigaciones realizadas dentro del grupo de investigación CIACUA.
Las características que ofrece este programa para el usuario son:
- Permite al usuario utilizar dos (2) ecuaciones de diseño: Ecuación de Hazen-Williams y la
ecuación de Darcy-Weisbach.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
18
-Edita o crea redes desde el comienzo, permitiendo al usuario ingresar Nudos, bombas,
válvulas, tuberías, tanques y embalses. Adicionalmente, le permite al usuario escoger por
defecto la viscosidad con la que se desea trabajar, escoger el material de la tubería y si el
usuario lo desea, asignar los coeficientes de pérdidas menores y fugas dependiendo del tipo
de investigación que se desee.
-Permite el cálculo hidráulico estático: Permite obtener alturas piezométricas, velocidades,
caudales, factores de fricción, pérdidas menores, pérdidas por fricción, pérdidas totales y las
presiones en cada nudo de la red utilizando el método del gradiente hidráulico.
- Realiza el cálculo hidráulico en periodo extendido: A diferencia del cálculo estático, esta
opción permite evaluar los resultados en una hora deseada del día, lo que permite ver el
comportamiento de la red durante el día y ver si cumple con los requerimientos deseados por
el usuario.
-Genera el cálculo de Calidad del Agua
- Permite la calibración de Redes de distribución de agua potable.
-Diseño Optimizado: En esta sección hay diferentes opciones para diseñar, dentro de las que
se encuentran:
1) Diseño Rápido: Una solución rápida teniendo en cuenta un mínimo costo y cumplimiento
de la presión mínima.
2) Algoritmo Genético: Mediante la utilización de algoritmos genéticos, encontrar soluciones
óptimas locales para los diseños, cumpliendo los parámetros de costos e hidráulicos
establecidos por el usuario.
3) Superficie Óptima: Utiliza una superficie óptima, ya sea cuadrática, elipsoidal, catenaria,
gaussiana, lineal y recíproca. Siendo la cuadrática la más utilizada, utilizando una flecha del
15%.
4) Metodología SOGH: esta metodología fue utilizada durante la tesis y será explicada más
adelante con mayor detalle. Esta metodología fue implementada en el programa REDES en
2009 por Susana Ochoa en su tesis de Maestría.
5) Finalmente, la metodología de búsqueda de armonía.
El programa de redes es compatible con los archivos .INP generados en el programa de
EPANET y con archivos propios .RED. Además de contar con una interfaz gráfica que permite
visualizar los resultados en 2D y 3D, y exportar los mismos a portapapeles y posteriormente a
Excel.
Los archivos .RED al igual que los archivos generados por el programa de EPANET, permiten
su modificación en Excel, de tal forma que el cambio de parámetros se haga de una forma
amistosa para el usuario. Esta es una gran ventaja que presentan los dos programas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
19
En la actualidad, el programa se encuentra sujeto a actualizaciones bajo la supervisión del
Ingeniero Juan Guillermo Saldarriaga, sobre todo en lo que concierne a la nueva metodología
de OPUS.
2.3.2 METODOLOGIA SOGH
La metodología de Superficie Óptima del Gradiente Hidráulico (SOGH) fue desarrollada por
Susana Ochoa en el año 2009 y fue el resultado de su proyecto de Maestría supervisado por el
Ingeniero Juan Guillermo Saldarriaga. Esta metodología, es muy similar a la de Superficie
Óptima, utiliza las mismas funciones (siendo la cuadrática la más recomendable al ser la que
mejores resultados arroja) para optimizar el diseño, pero a diferencia de la metodología de
superficie óptima, no utiliza una flecha establecida del 15%, sino que calcula una flecha con
base a la distribución de las demandas de la RDAP, la demanda total, la longitud de la red y la
función de costos que se le asigne.
Para la utilización de esta metodología, el usuario debe de establecer los siguientes
parámetros:
-Cargar la red que se desea trabajar.
-Presión mínima que se desea en la red.
-Conjunto de diámetros con los que se desea diseñar (Diámetros comerciales).
-Curva de Costos.
-Ecuación de diseño con que se desea trabajar.
Una vez especificados estos diámetros, la metodología SOGH se ejecuta con base al siguiente
diagrama de flujo, donde se describen los pasos:
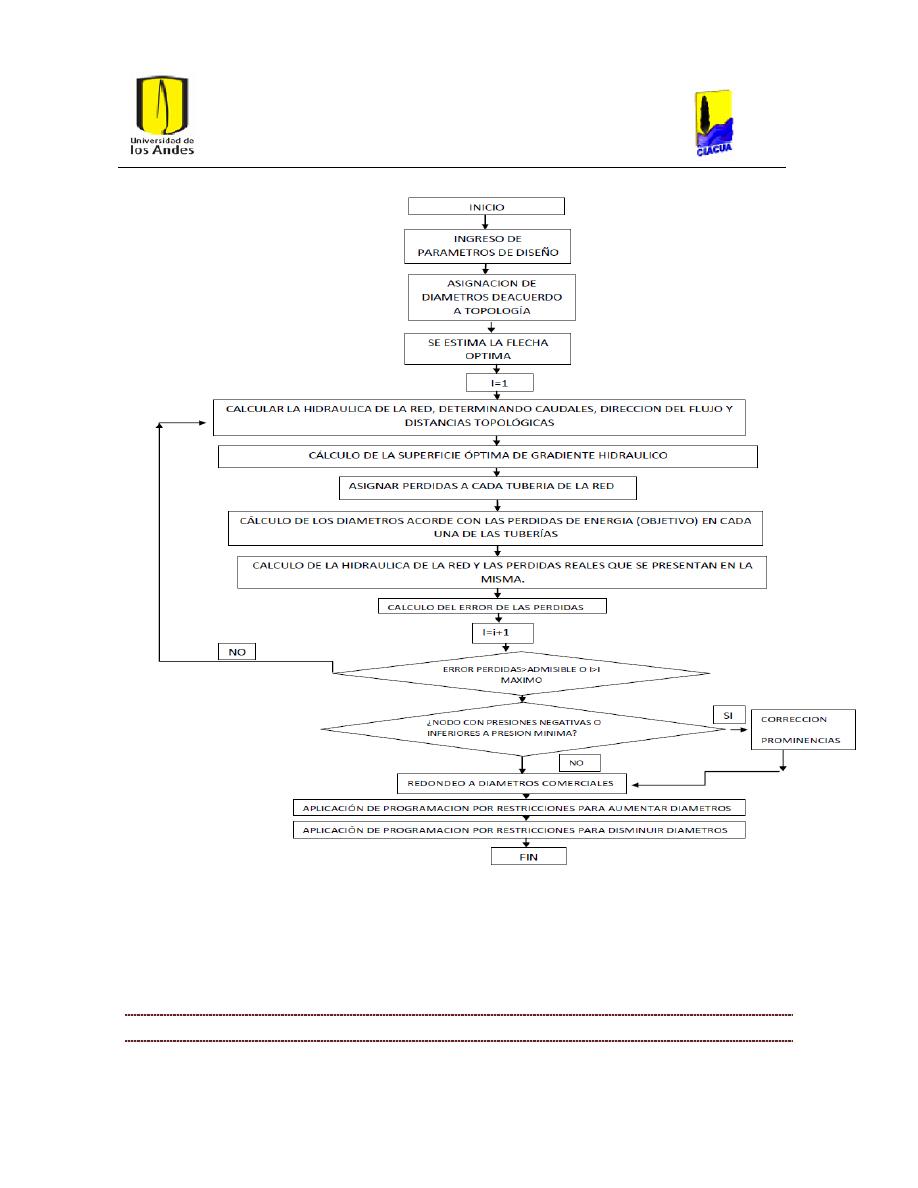
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
20
ILUSTRACIÓN 4. DIAGRAMA DE FLUJO DE LA METODOLOGIA SOGH DESARROLLADA POR SUSANA
OCHOA (OCHOA, 2009).
El diagrama de flujo presentado es similar al presentado por Susana Ochoa en su proyecto de
Maestría., y muestra todos los pasos que realiza la metodología para encontrar el diseño
óptimo de la red.
2.3.3 PROGRAMA EPANET 2.0

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
21
El programa de EPANET, es una herramienta computacional desarrollada por la Agencia de
Protección Ambiental de los Estados Unidos de América (EPA). Este programa fue
desarrollado para estudiar el comportamiento hidráulico de una red de distribución de agua
potable (Saldarriaga, 2007).
Este programa, dentro de sus múltiples funciones, incluye realizar el análisis hidráulico
utilizando las ecuaciones de Hazen-Williams, Darcy-Weisbach y Chezy-Manning.
Adicionalmente y al igual que el programa REDES utiliza de la metodología del gradiente
hidráulico para la solución matemática de la red (a diferencia de otros programas que utilizan
el método de Hardy-Cross).
El programa cuenta adicionalmente con un módulo para seguir la calidad de las aguas en una
red, permitiendo al usuario seguir el decaimiento o comportamiento de una sustancia en una
red (Saldarriaga, 2007). Esto puede ser de gran importancia en el análisis de cloro residual en
redes, o el comportamiento de manganeso o hierro en los sistemas de distribución al salir de
las plantas de tratamiento. Esto lo realiza utilizando reacciones químicas del agua, o en las
paredes de la tubería y de los tanques. Para ello utiliza reacciones de primer orden.
Además, el programa permite visualizar los resultados en tablas y gráficas y los archivos que
utiliza son compatibles para su modificación con Excel. Lo que lo convierte en un programa
amigable para el usuario.
Al igual que el programa de REDES, EPANET también permite correr la hidráulica en estado
estable y en periodos extendidos.
2.4 MATERIALES UTILIZADOS Y SUS CARACTERÍSTICAS
Los materiales utilizados en esta tesis de grado fueron PVC (Policloruro de vinilo), PEAD
(Polietileno de alta densidad) y Hierro Dúctil. Estos materiales fueron escogidos por su amplia
aplicabilidad en los diseños de RDAP. Por lo tanto, en esta sección se mostrarán sus
correspondientes rugosidades absolutas de la normativa y literatura que se aplicaron para el
desarrollo del proyecto, sus diámetros comerciales disponibles y sus correspondientes curvas
de costo.
2.4.1 RUGOSIDADES ABSOLUTAS
A continuación se presentan las rugosidades absolutas de los materiales utilizados en esta
tesis de grado. Los valores de rugosidad fueron sacados de las normas técnicas de las
Empresas Públicas de Medellín (EPM) del año 2006 y su versión final actualizada en 2009 y
del libro de hidráulica de tuberías del ingeniero Juan Saldarriaga. Adicionalmente, se incluye
la tabla de rugosidades absolutas que maneja el RAS, que es la normativa vigente en
acueductos y alcantarillados de Colombia.
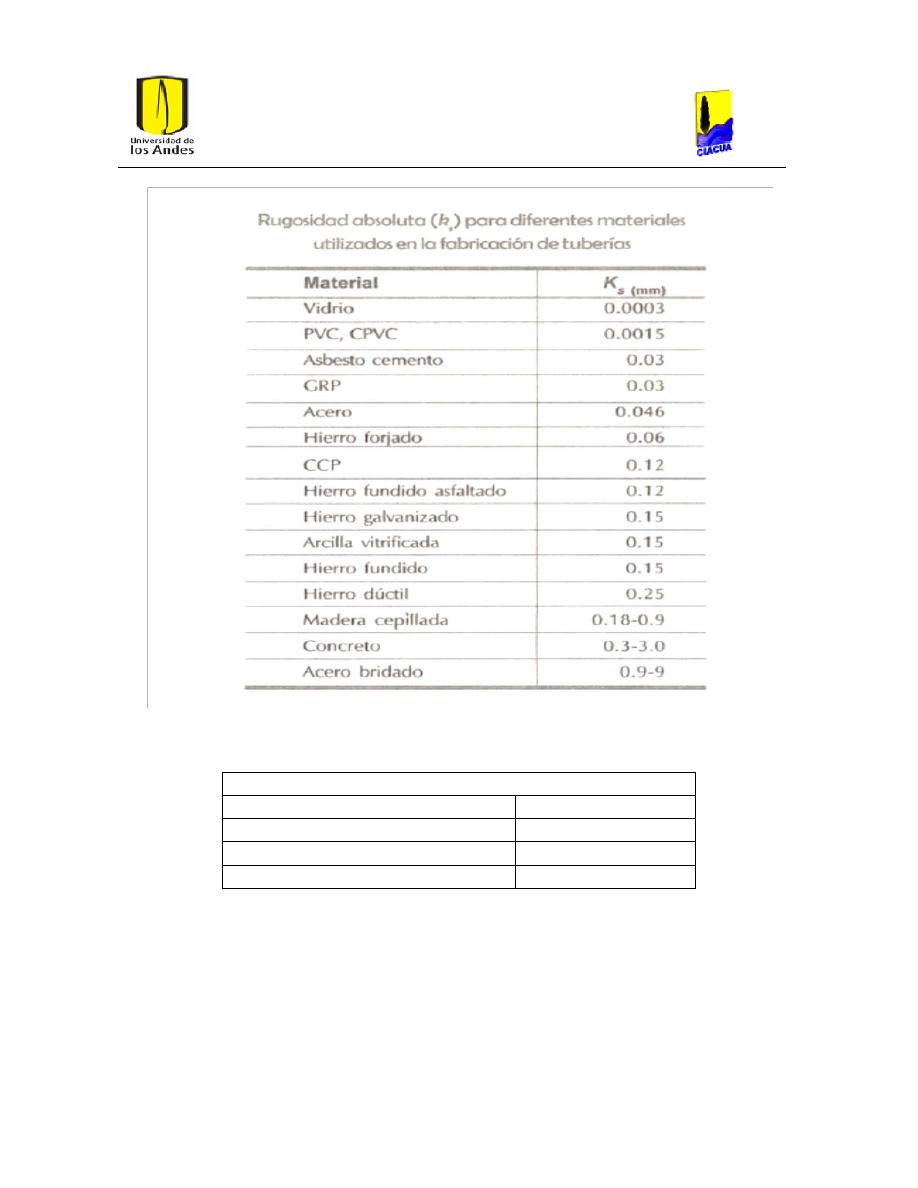
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
22
ILUSTRACIÓN 5. TABLA DE RUGOSIDADES ABSOLUTAS DEL LIBRO DE HIDRÁULICA DE TUBERÍAS
(SALDARRIAGA, 2007).
RUGOSIDAD ABSOLUTA
MATERIAL
mm
HIERRO DÚCTIL
0.25
PVC
0.0015
PEAD*
0.007
TABLA 1. RUGOSIDADES ABSOLUTAS DE LAS NORMAS TECNICAS DE EPM 2009 (EMPRESAS
PÚBLICAS DE MEDELLÍN, 2006-2009)
*El valor del PEAD fue complementado con la información del manual técnico para PEAD de
PAVCO (PAVCO, 2011).
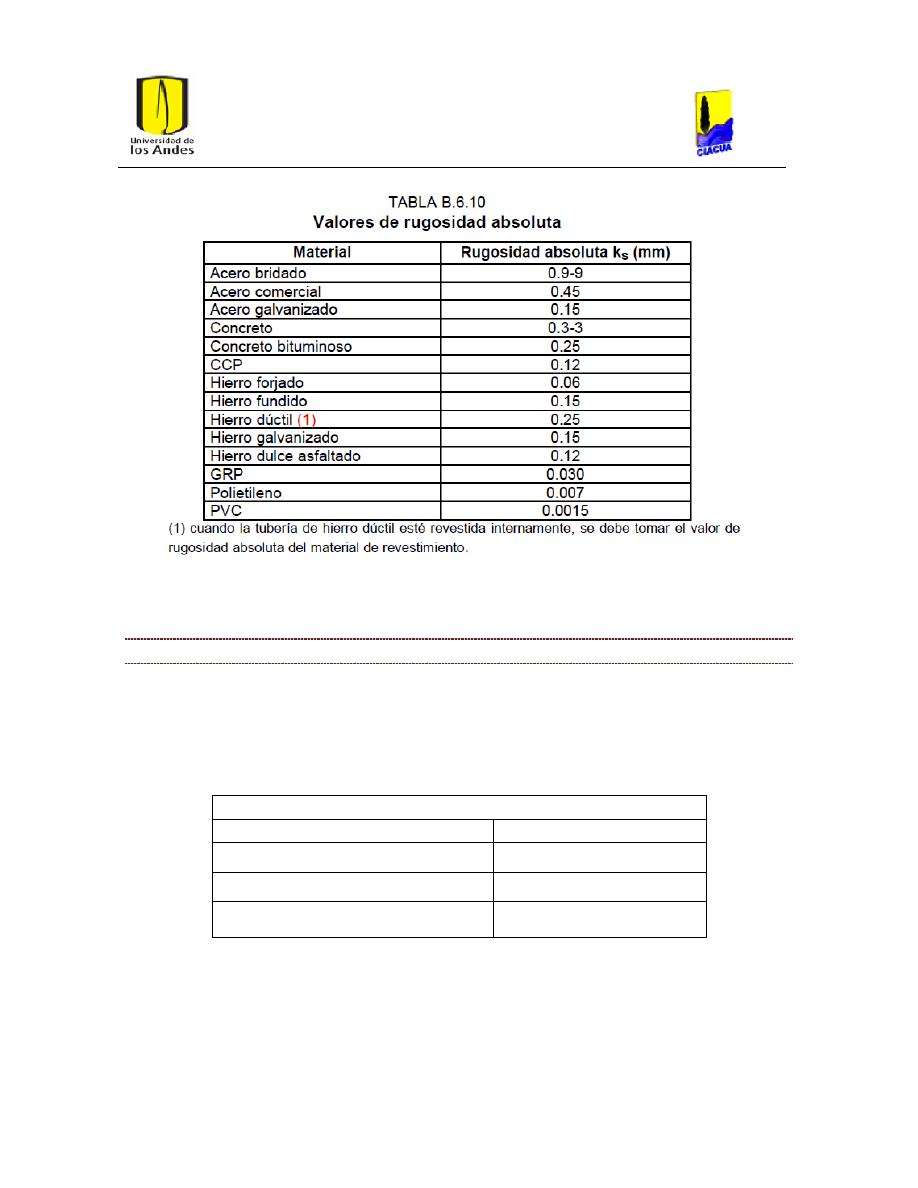
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
23
ILUSTRACIÓN 6. RUGOSIDADES ABSOLUTAS DEL RAS (MINISTERIO DE DESARROLLO ECONOMICO,
2000).
2.4.2 COEFICIENTES DE HAZEN-WILLIAMS
Ya que en este trabajo de grado se empleará la ecuación de Hazen-Williams, es necesario
consultar los Coeficientes para cada uno de los materiales. Y dado a que uno de los objetivos
de este trabajo es el de analizar la normativa colombiana, es necesario utilizar los Coeficientes
de Hazen-Williams de la normativa colombiana y por ello se consultaron las normas técnicas
de la EPM.
COEFICIENTES DE HAZEN-WILLIAMS
MATERIAL
COEFICENTE
HIERRO DÚCTIL
140-150
PVC
150
PEAD
150
TABLA 2. TABLA DE COEFICIENTES DE HAZEN-WILLIAMS DE LA EPM (EMPRESAS PÚBLICAS DE
MEDELLÍN, 2006-2009).
Para propósitos de esta tesis y con base a la literatura el valor del Coeficiente de Hazen-
Williams para Hierro dúctil fue de 140, teniendo en cuenta que es con revestimiento interior.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
24
2.4.3 DIÁMETROS COMERCIALES Y CURVAS DE COSTO
Los diámetros comerciales son de gran importancia a la hora de diseñar las redes de
distribución de agua potable. Por lo que se consultaron los diámetros comerciales y para el
diseño los diámetros Internos y sus respectivas curvas de costos.
2.4.3.1 PVC
Para el PVC se consultó con la empresa PAVCO. La lista de diámetros se muestra a
continuación. La referencia (RED 21 PVC Tipo 1, Grado1) utilizada fue es cogida ya que es a
que presenta la mejor resistencia a presión y una lista bastante amplia de diámetros.
ILUSTRACIÓN 7. LISTA DE DIÁMETROS COMERCIALES DISPONIBLES PARA PVC (PAVCO, 2011).
Los costos también fueron suministrados por PAVCO y fueron resumidos en las siguientes
tablas.
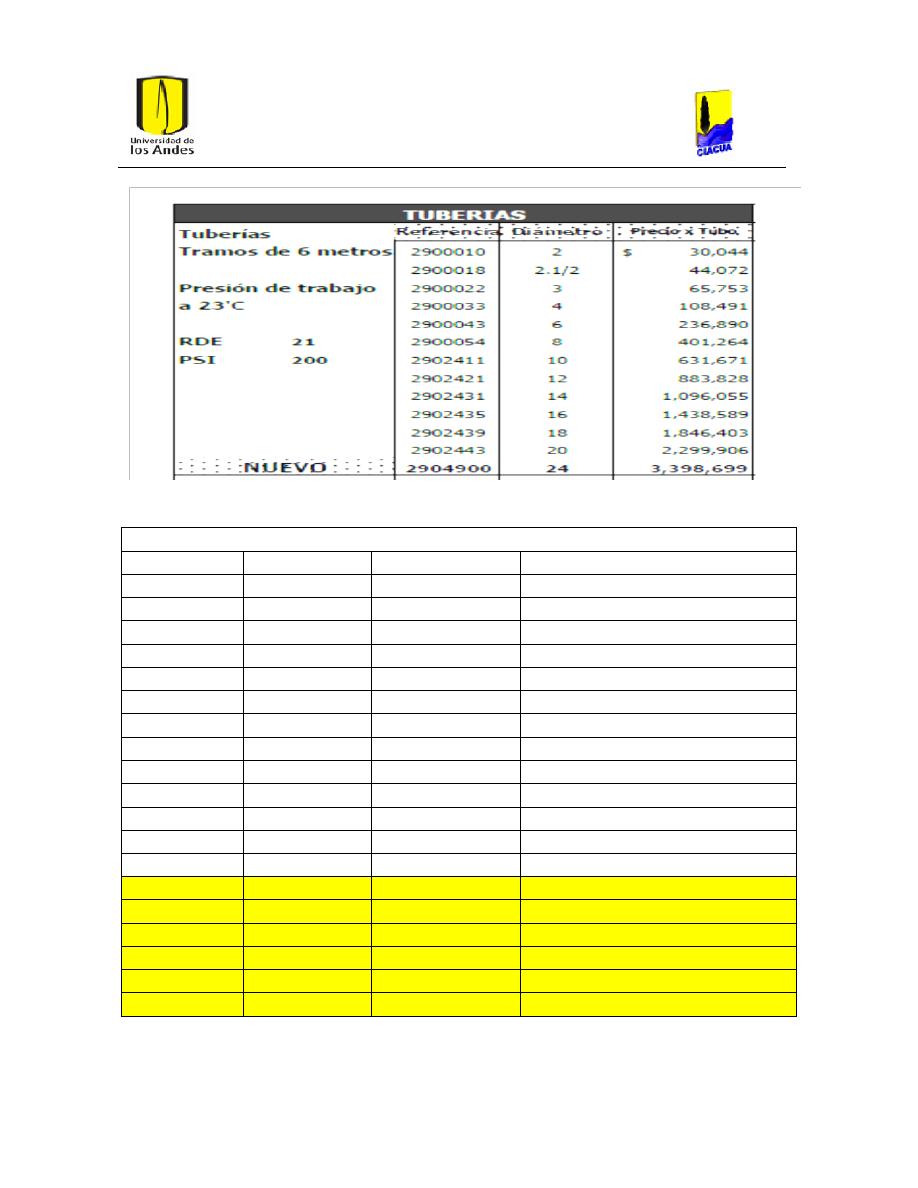
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
25
TABLA 3. COSTOS POR 6 METROS DE TUBERÍA DE PVC (PAVCO, 2012).
RDE 21 PVC Tipo 1 Grado 1
DN (in)
DI (mm)
Costo( 6 metros)
Costo (metro)
2
54.58
$ 30 044.00
$ 5 007.33
2 1/2
66.07
$ 44 072.00
$ 7 345.33
3
80.42
$ 65 753.00
$ 10 958.83
4
103.42
$ 108 491.00
$ 18 081.83
6
152.22
$ 236 890.00
$ 39 481.67
8
198.21
$ 401 264.00
$ 66 877.33
10
247.09
$ 631 671.00
$ 105 278.50
12
293.07
$ 883 828.00
$ 147 304.67
14
321.76
$ 1 096 055.00
$ 182 675.83
16
367.7
$ 1 438 589.00
$ 239 764.83
18
413.66
$ 1 846 403.00
$ 307 733.83
20
459.54
$ 2 299 906.00
$ 383 317.67
24
551.54
$ 3 398 699.00
$ 566 449.83
*
600
$ 3 910 086.74
$ 651 681.12
*
700
$ 5 352 504.03
$ 892 084.00
*
800
$ 7 025 651.42
$ 1 170 941.90
*
900
$ 8 930 675.04
$ 1 488 445.84
*
1000
$ 11 068 589.86
$ 1 844 764.98
*
1400
$ 21 966 208.61
$ 3 661 034.77
TABLA 4. TABLA DE COSTOS POR METRO Y EXTENSIÓN DE DIÁMETROS.
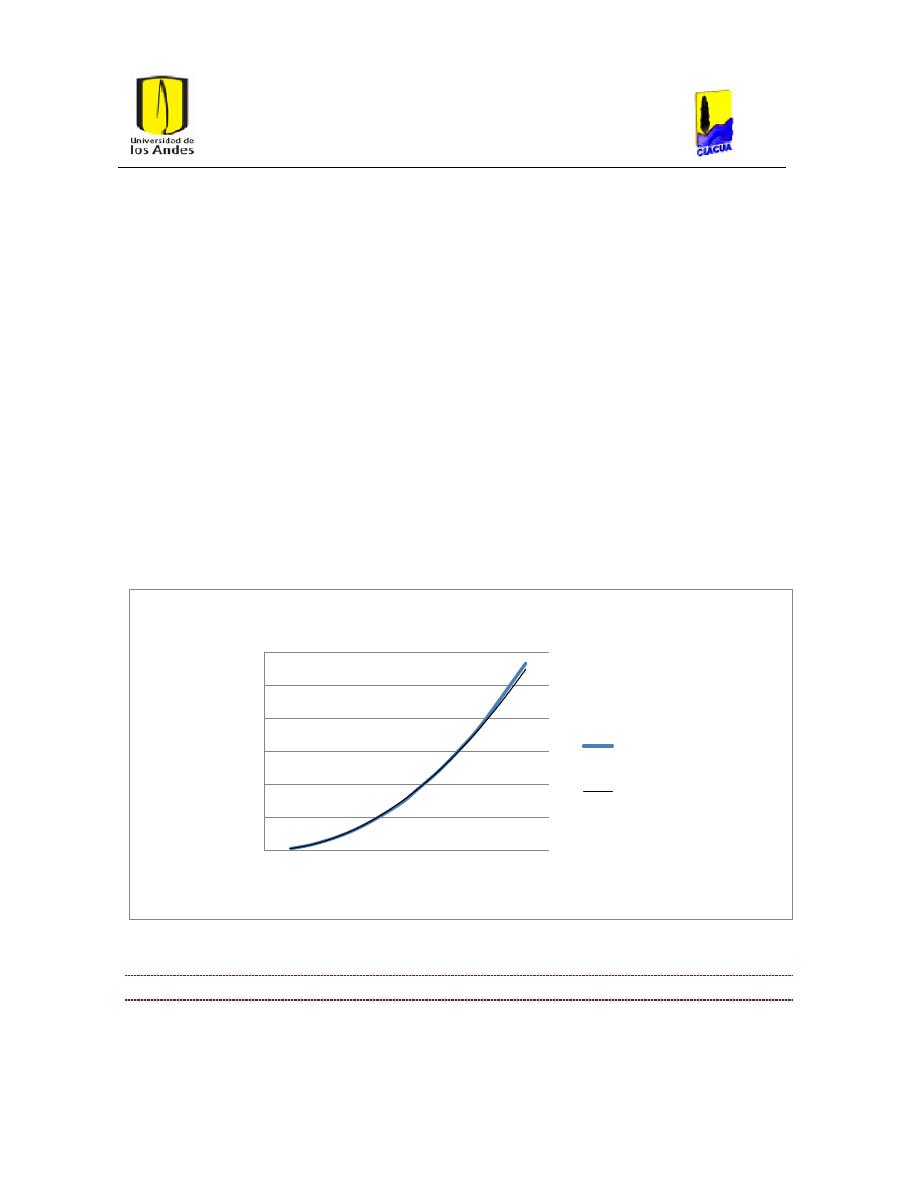
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
26
En las tablas anteriores se pueden evidenciar los diámetros con los que se trabajó durante la
tesis. Los que están con el * y resaltados en amarillo fueron diámetros que se adicionaron
artificialmente con fines investigativos (para los diseños que incluían el caudal inicial
aumentado 4 veces), y los costos fueron ajustados con la curva de costos.
La curva de costos resultante fue:
ECUA CIÓN 2.4 .3.1 -1
en donde:
C= Costo en pesos colombianos
L= Longitud del tramo de la tubería
D= Diámetro de la tubería en mm.
A continuación se muestra la gráfica con la que se obtuvo la Curva de Costos:
ILUSTRACIÓN 8. CURVA DE COSTOS PARA PVC.
2.4.3.2 PEAD
El siguiente material fue el Polietileno de alta densidad (PEAD). Para este material también se
consultaron los diámetros y costos de PAVCO y la referencia seleccionada se realizó con los
mismos criterios que el PVC. A continuación se muestras los diferentes diámetros.
y = 1.4287x
2.037
R² = 0.9999
$ 0.00
$ 100 000.00
$ 200 000.00
$ 300 000.00
$ 400 000.00
$ 500 000.00
$ 600 000.00
0
100
200
300
400
500
600
Co
sto
s
e
n
Peso
s
co
lo
m
b
ian
o
s
Diámetros en Milimetros
Curva de Costos PVC
Curva de Costos PVC
Potencial (Curva de Costos
PVC)
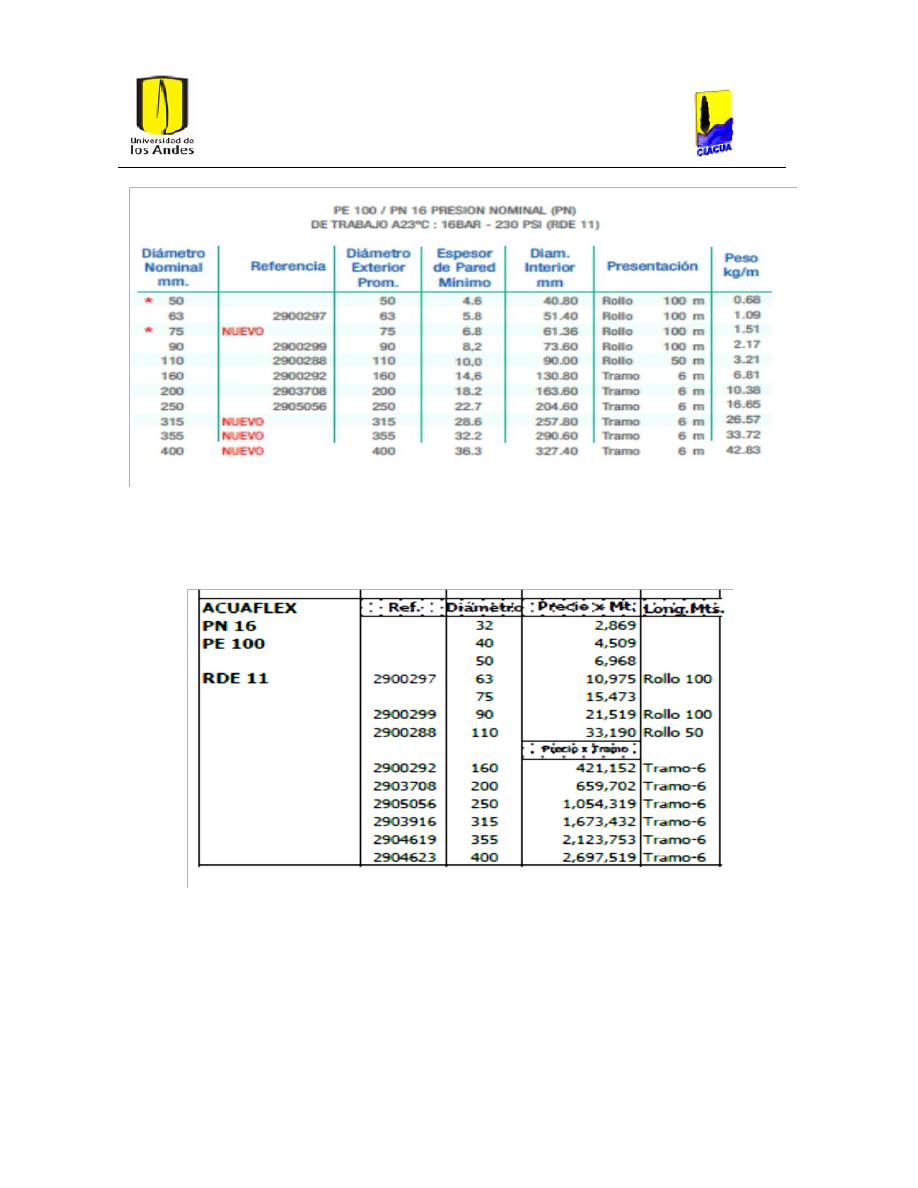
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
27
TABLA 5. TABLA DE DIÁMETROS PARA PEAD DE PAVCO (PAVCO, 2011).
Al igual que con el PVC los costos también fueron suministrados por PAVCO como se muestra
a continuación:
TABLA 6. TABLA DE COSTOS PARA PEAD SUMINISTRADA POR PAVCO (PAVCO, 2012).
Con lo anterior, se sacaron los costos por metro y por diámetro como se ilustra en la siguiente
tabla.
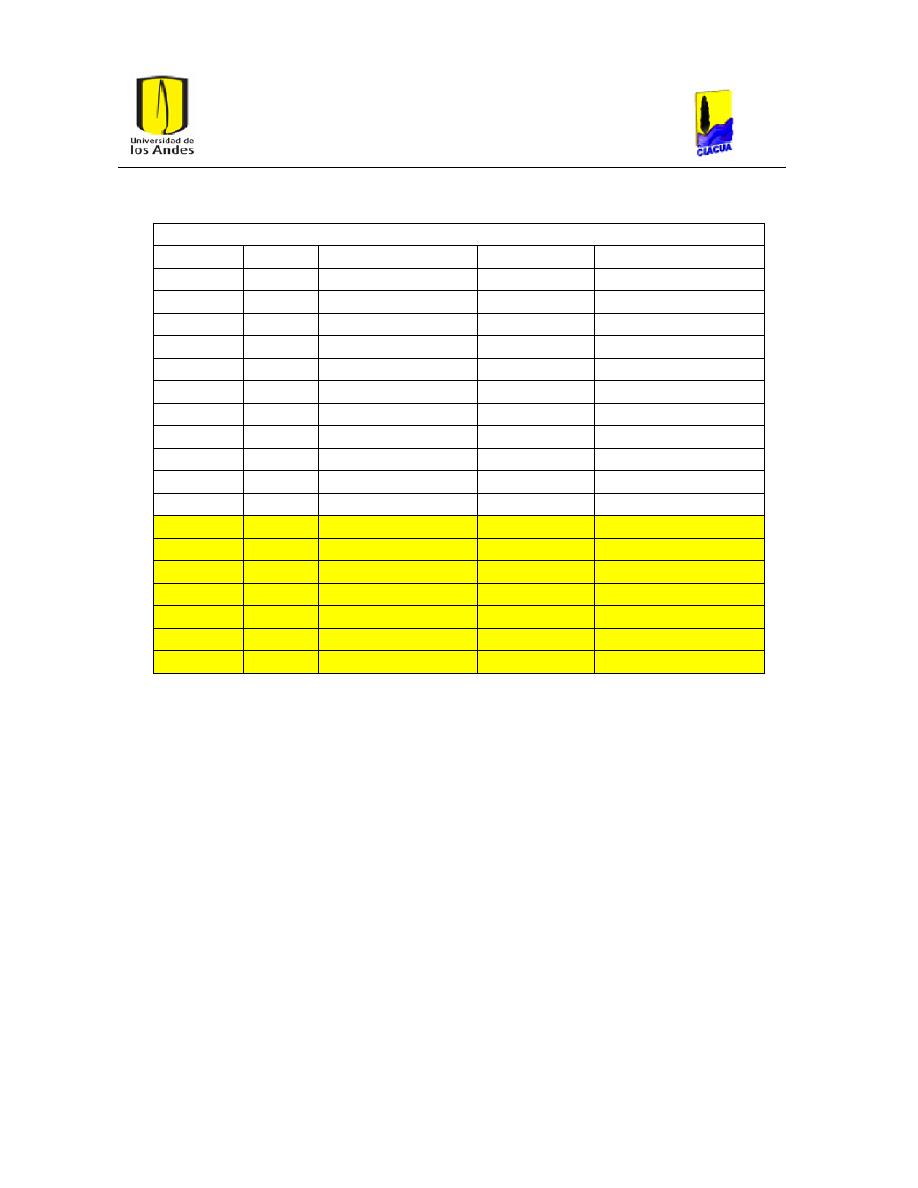
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
28
RDE11 PEAD
DN(mm)
DI(mm)
Costo
Presentación
Costo(Metro)
50
40.8
$ 6 968.00
Rollo 100 m
$ 6 968.00
63
51.4
$ 10 975.00
Rollo 100 m
$ 10 975.00
75
61.36
$ 15 473.00
Rollo 100 m
$ 15 473.00
90
73.6
$ 21 519.00
Rollo 100 m
$ 21 519.00
110
90
$ 33 190.00
Rollo 50 m
$ 33 190.00
160
130.8
$ 421 152.00
Tramo 6 m
$ 70 192.00
200
163.6
$ 659 702.00
Tramo 6 m
$ 109 950.33
250
204.6
$ 1 054 319.00
Tramo 6 m
$ 175 719.83
315
257.8
$ 1 673 432.00
Tramo 6 m
$ 278 905.33
355
290.6
$ 2 123 753.00
Tramo 6 m
$ 353 958.83
400
327.4
$ 2 697 519.00
Tramo 6 m
$ 449 586.50
*
400
$ 4 016 503.08
Tramo 6 m
$ 669 417.18
*
450
$ 5 089 137.84
Tramo 6 m
$ 848 189.64
*
500
$ 6 289 244.33
Tramo 6 m
$ 1 048 207.39
*
600
$ 9 072 377.21
Tramo 6 m
$ 1 512 062.87
*
700
$ 12 366 800.85
Tramo 6 m
$ 2 061 133.48
*
1000
$ 25 324 935.39
Tramo 6 m
$ 4 220 822.56
*
1400
$ 49 797 466.32
Tramo 6 m
$ 8 299 577.72
TABLA 7. COSTOS POR METRO PARA PEAD.
Como se puede ver, se encuentran los costos normalizados por metro de tubería. Al igual que
con el PVC los diámetros que están marcados con * y delineados en amarillo son diámetros
que fueron agregados de manera artificial con fines investigativos (para los diseños que
incluían el caudal inicial aumentado 4 veces). Y estos diámetros nuevos fueron ajustados en la
curva de costos.
La curva de costos resultante fue:
ECUA CION 2.4 .3.2 -1
Con los mismos parámetros del PVC.
En la siguiente grafica se muestra la curva de costos:
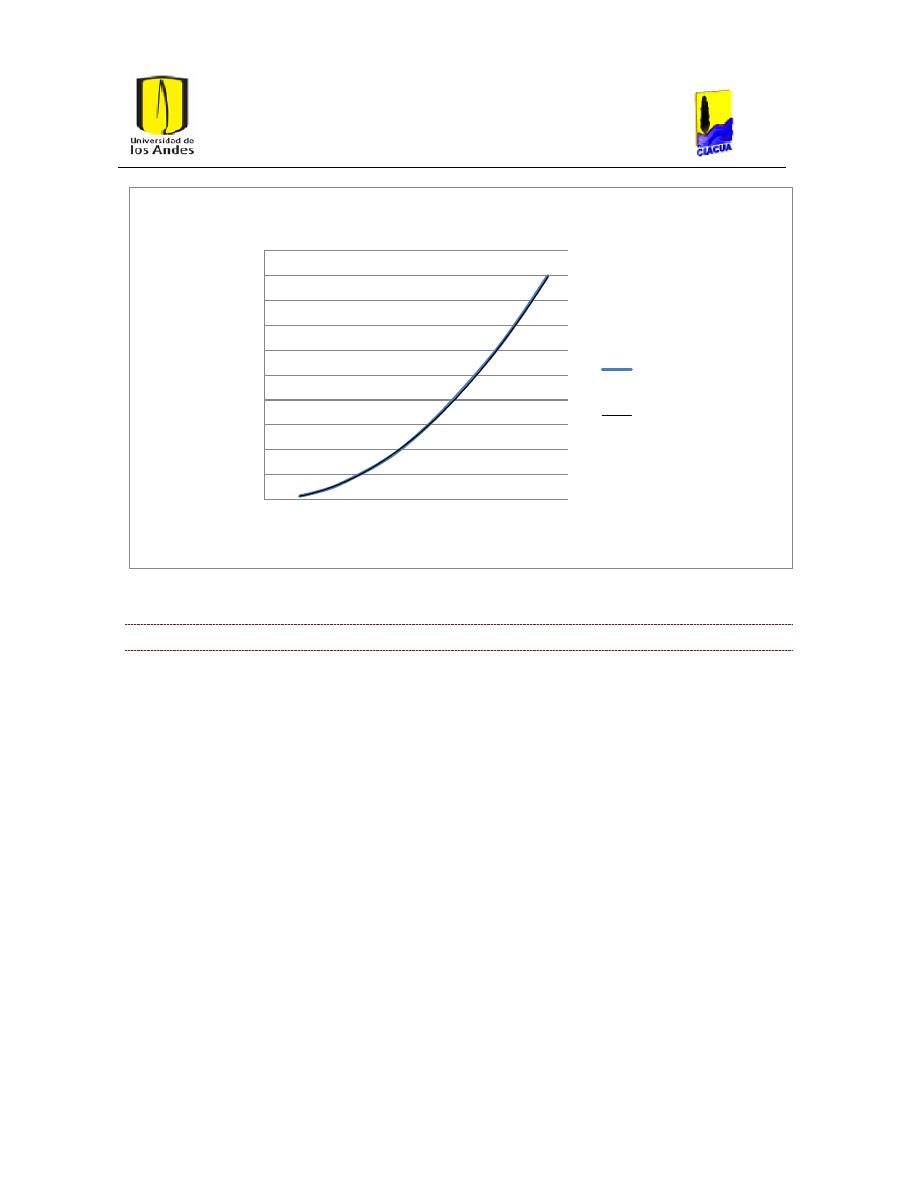
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
29
ILUSTRACIÓN 9.CURVA DE COSTOS PARA PEAD.
2.4.3.3 HIERRO DÚCTIL
Para la información de Hierro Dúctil se consultó con la empresa Saint-Gobain PAM Colombia,
la cual tiene una lista de diámetros comerciales e internos. Sin embargo solo especificaban
que el precio de tramo de tubería era de 750 Dólares por Kg-Metro de tubería. A continuación
se muestra la tabla de diámetros que se utilizaron.
y = 3.95x
2.0096
R² = 0.9999
$ 0.00
$ 50 000.00
$ 100 000.00
$ 150 000.00
$ 200 000.00
$ 250 000.00
$ 300 000.00
$ 350 000.00
$ 400 000.00
$ 450 000.00
$ 500 000.00
0
50
100
150
200
250
300
350
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Diámetros en Milimetros
Curva Costos PEAD
Curva Costos PEAD
Potencial (Curva Costos
PEAD)
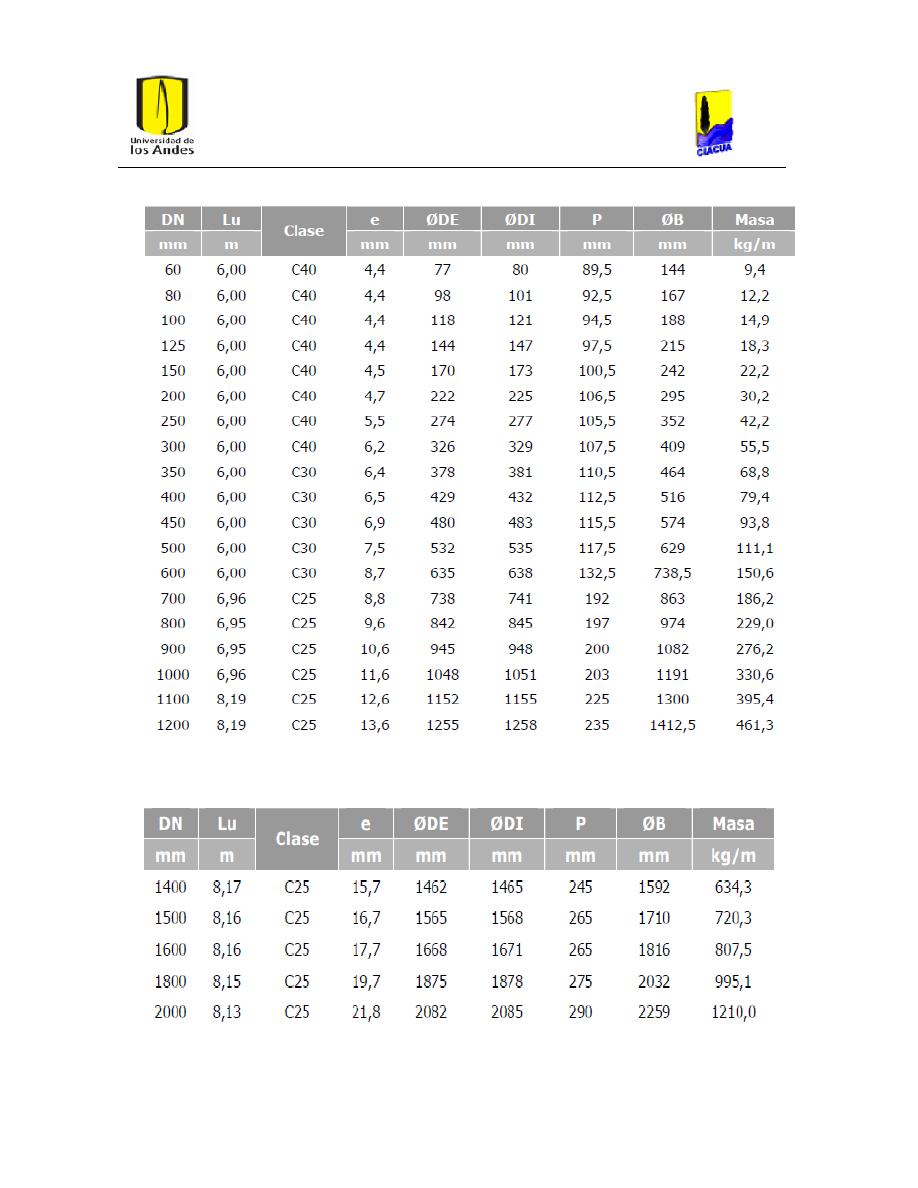
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
30
TABLA 8. PARTE 1 DE LA LISTA DE DIÁMETROS DE HIERRO DÚCTIL (SAINT-GOBAIN PAM , 2012).
TABLA 9. PARTE 2 DE LA LISTA DE DIÁMETROS DE HIERRO DÚCTIL (SAINT-GOBAIN PAM , 2012).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
31
Con estos diámetros y la información suministrada para los costos se procedió a calcular el
costo de la tubería. Los resultados se muestran en la siguiente tabla.
TABLA 10. COSTOS CON SUS RESPECTIVOS DIÁMETROS INTERNOS PARA HIERRO DÚCTIL.
Con lo anterior se obtuvo la siguiente curva de Costos:
ECUA CIÓN 2.4 .3.3 -1
Los parámetros e la ecuación son los mismos que los aplicados a PVC y PEAD.
La gráfica con la que se obtuvo la curva de costos se muestra a continuación.
DN
LONGITUD
DI
MASA Costo Tonelada/Metro Costo kg/m Costo /m
Costo/m
mm
m
mm
kg/m
Dólares$
Dólares$
$ Dólares
Pesos$
60
6
80
9.4
750.00
$
0.75
$
7.05
$
12 478.50
$
80
6
101
12.2
750.00
$
0.75
$
9.15
$
16 195.50
$
100
6
121
14.9
750.00
$
0.75
$
11.18
$
19 779.75
$
125
6
147
18.3
750.00
$
0.75
$
13.73
$
24 293.25
$
150
6
173
22.2
750.00
$
0.75
$
16.65
$
29 470.50
$
200
6
225
30.2
750.00
$
0.75
$
22.65
$
40 090.50
$
250
6
277
42.2
750.00
$
0.75
$
31.65
$
56 020.50
$
300
6
329
55.5
750.00
$
0.75
$
41.63
$
73 676.25
$
350
6
381
68.8
750.00
$
0.75
$
51.60
$
91 332.00
$
400
6
432
79.4
750.00
$
0.75
$
59.55
$
105 403.50
$
450
6
483
93.8
750.00
$
0.75
$
70.35
$
124 519.50
$
500
6
535
111.1
750.00
$
0.75
$
83.33
$
147 485.25
$
600
6
638
150.6
750.00
$
0.75
$
112.95
$
199 921.50
$
700
6.96
741
186.2
750.00
$
0.75
$
139.65
$
247 180.50
$
800
6.95
845
229
750.00
$
0.75
$
171.75
$
303 997.50
$
900
6.95
948
276.2
750.00
$
0.75
$
207.15
$
366 655.50
$
1000
6.96
1051 330.6
750.00
$
0.75
$
247.95
$
438 871.50
$
1100
8.19
1155 395.4
750.00
$
0.75
$
296.55
$
524 893.50
$
1200
8.19
1258 461.3
750.00
$
0.75
$
345.98
$
612 375.75
$
1400
8.17
1465 634.3
750.00
$
0.75
$
475.73
$
842 033.25
$
1500
8.16
1568 720.3
750.00
$
0.75
$
540.23
$
956 198.25
$
1600
8.16
1671 807.5
750.00
$
0.75
$
605.63
$
1 071 956.25
$
1800
8.15
1878 995.1
750.00
$
0.75
$
746.33
$
1 320 995.25
$
2000
8.13
2085
1210
750.00
$
0.75
$
907.50
$
1 606 275.00
$
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
32
ILUSTRACIÓN 10. CURVA DE COSTOS PARA HIERRO DÚCTIL.
y = 12.702x
1.5103
R² = 0.9929
$ -
$ 200 000.00
$ 400 000.00
$ 600 000.00
$ 800 000.00
$ 1 000 000.00
$ 1 200 000.00
$ 1 400 000.00
$ 1 600 000.00
$ 1 800 000.00
0
500
1000
1500
2000
2500
COS
TOS
E
N
PE
SOS
COLOMB
IA
N
OS
Diámetros en Milimietros
Curva Costos Hierro Dúctil
Curva Costos Hierro Dúctil
Potencial (Curva Costos
Hierro Dúctil)
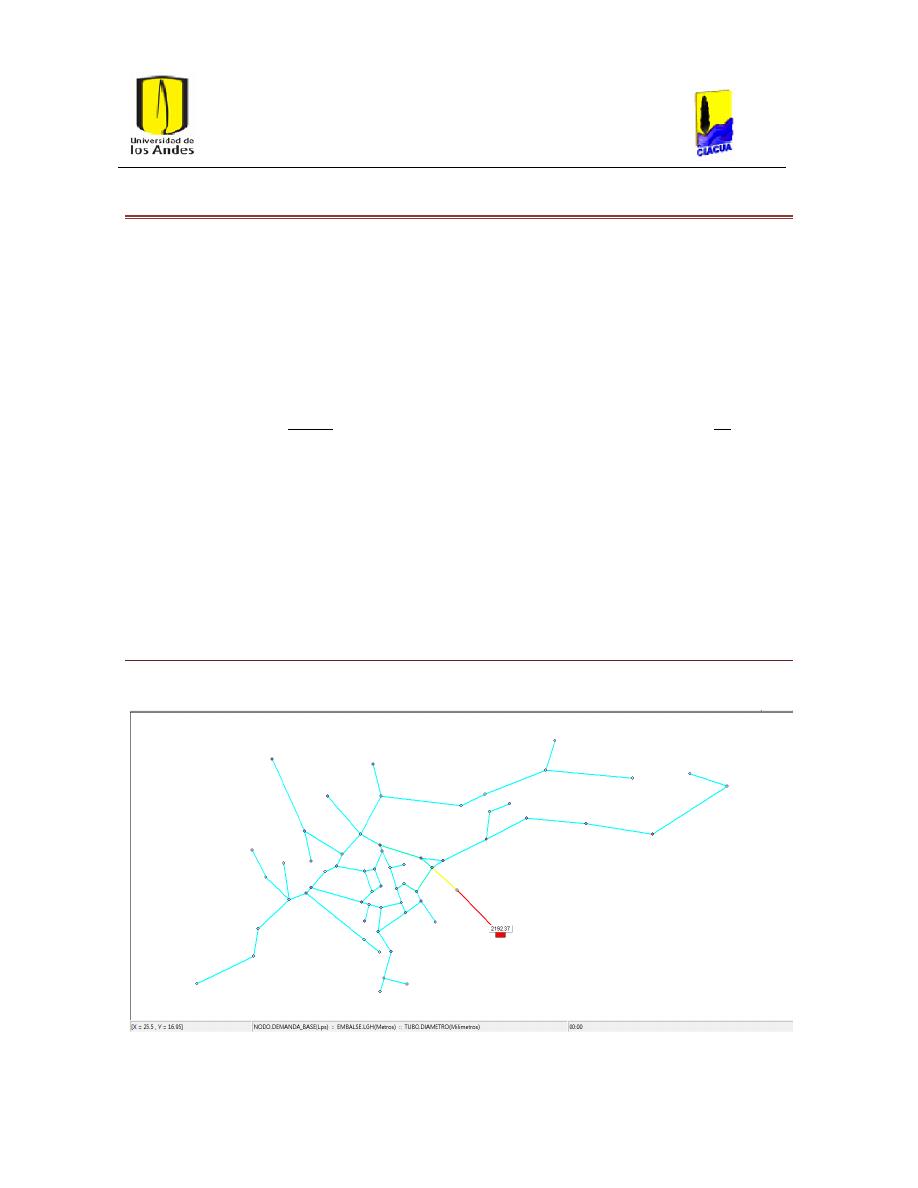
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
33
CAPÍTULO 3. METODOLOGÍA
En esta sección se muestran las redes que se utilizaron con sus respectivas características.
Adicionalmente, se presentan los parámetros de diseño utilizados y los procedimientos que se
llevaron a cabo en el programa REDES y EPANET para obtener los resultados.
Todas las redes estuvieron sujetas a la normativa colombiana; esto se refiere a las
rugosidades absolutas mostradas en la Sección 2.4.1 y a los coeficientes de Hazen-Williams de
la Sección 2.4.2. La presión mínima fue la exigida por el RAS 2000 Título B (Ministerio de
Desarrollo Economico, 2000) de 15 metros de cabeza de agua. Adicionalmente, para este
trabajo se utilizó una temperatura de agua de 15 grados centígrados y una viscosidad
cinemática de
. La gravedad se trabajó con el valor estándar de
. Se tuvo
especial cuidado en seleccionar redes que no presentaran ningún tipo de fugas, con rugosidad
única para toda la tubería (al igual que mismo coeficiente de Hazen-Williams). En cuanto a
fuentes de abastecimiento, se trabajó con un máximo de 4 fuentes de abastecimiento. Las
demandas base de cada una de las redes serán mostradas más adelante cuando se presenten
las características de la red, sin embargo la metodología se trabajó de tal forma que las redes
fueran diseñadas con el caudal original que tenían establecido, dos veces el caudal y cuatro
veces el caudal. Esto se realizó para analizar si el aumento del caudal en cada uno de los
Nudos tenía algún efecto sobre los diseños con la ecuación de Hazen-Williams.
3.1 RED SAN VICENTE
ILUSTRACIÓN 11. RED SAN VICENTE.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
34
La red San Vicente es una red que cuenta con las siguientes características:
- 62 Nudos
- Alturas de la red varían entre un mínimo de 2192 msnm y 2176 msnm
- Una fuente de abastecimiento con una LGH de 2192.37 msnm
- 71 tramos de tubería
- Demandas en los Nudos que van desde demanda nula (solo 2 Nudos en la red) hasta
los .
Esta red no tuvo ningún tipo de variación en las simulaciones de 2 veces y 4 veces el caudal.
Cabe resaltar que esta es una red ubicada en el departamento de Antioquia, Colombia, con una
temperatura promedio de 18 grados centígrados.
3.2 RED BALERMA
ILUSTRACIÓN 12. RED BALERMA.
Esta fue la red más grande que se trabajó en este proyecto de grado. Las características de la
misma se presentan a continuación:
- 443 Nudos
- Las alturas en la red varían entre los 1.3 y 104 msnm.
- Cuenta con 4 Fuentes de abastecimiento. Y las LGH que se trabajaron fueron las
siguientes: Grupo 1: (117, 127,122 y 112) M.C.A estos LGH se utilizaron en la mayoría
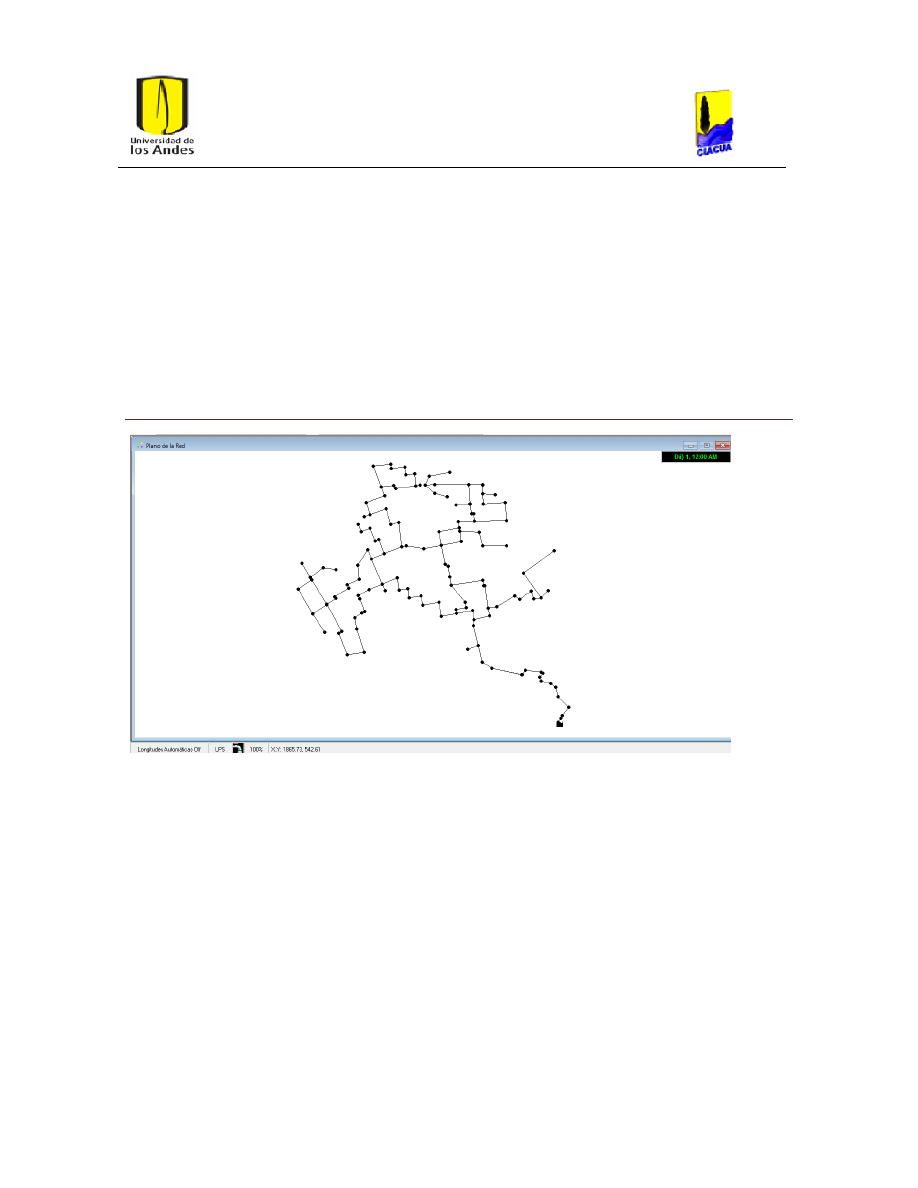
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
35
de los diseños. Grupo 2: (200, 200,220 y 240) Estas LGH se utilizaron únicamente para
el diseño de Balerma con PEAD con caudal base, sin caudal x2 y sin caudal x4.
- 454 tramos de tubería.
- La demanda fue igual en todos los Nudos de 5.5 L/s
Las LGH Grupo 2 fue un caso especial, ya que la introducción de diámetros artificiales se
realizó en la etapa final del proyecto cuando los cálculos y los diseños de esta red ya se
encontraban realizados. Sin embargo, la mayoría de las simulaciones se realizó con el Grupo 1
y no presentó ningún tipo de inconvenientes.
3.3 RED BOGOTÁ-CAZUCÁ
ILUSTRACIÓN 13. RED BOGOTÁ-CAZUCÁ.
Esta es la tercera red que se trabajó en este proyecto. Como lo dice su nombre es una red
ubicada en Cazucá. Las Características de la red se muestran acá:
- 145 Nudos
- Alturas de la red varían entre 2605 y 2825 msnm.
- Cuenta con una única fuente de abastecimiento con la LGH de 2850 M.C.A para todas
las simulaciones.
- 150 tramos de tubería.
- Demandas base varían entre los Nudos, con un mínimo de 1 L/s y un máximo de 58,1
L/s.
Esta red no presentó ningún tipo de inconveniente en sus diseños y al igual que con las demás
redes la metodología fue trabajar con caudal base normal, duplicado y cuadruplicado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
36
3.4 RED R28
ILUSTRACIÓN 14. RED R28.
Esta red a diferencia de las redes anteriores, no es una red real. Esta red fue trabajada y es
trabajada en el CIACUA de la Universidad de los Andes en diferentes proyectos y Tesis. Las
características de esta red se muestran a continuación:
- 40 Nudos.
- Topografía plana (todos los Nudos a 0 metros).
- Cuenta con una única fuente de abastecimiento con una LGH de 40 m.
- Cuenta con 67 tramos de Tubería.
- Demandas Base varían entre los Nudos. Con un mínimo de 3 L/s y un máximo de 34
L/s.
Esta fue una red extremadamente útil para el desarrollo de este proyecto, no solo por su
facilidad de manejo sino por los resultados arrojados. Se trabajó con la misma metodología de
demanda base normal, duplicada y cuadruplicada. Y no presentó ningún inconveniente con los
diseños en ninguno de los 3 materiales trabajados.
3.5 RED TESIS 1

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
37
ILUSTRACIÓN 15. RED TESIS 1.
Esta red fue diseñada por el autor de la tesis y aprobada por el asesor ingeniero Juan
Saldarriaga. Las características que se utilizaron durante esta tesis de grado se presentan a
continuación:
- 43 Nudos.
- Alturas en la red que varían entre 5 y 32 metros.
- Cuenta con una única fuente de abastecimiento y una LGH de 55 metros.
- Presente 78 tramos de tubería.
- Y una demanda base fija de 3 L/s.
La metodología utilizada para esta red fue igual a las anteriores trabajando la demanda base,
de tal forma que se realizaran los diseños con la demanda base estándar, duplicada y
cuadruplicada para cada uno de los 3 materiales utilizados en este proyecto de grado.
3.6 RED TESIS 2
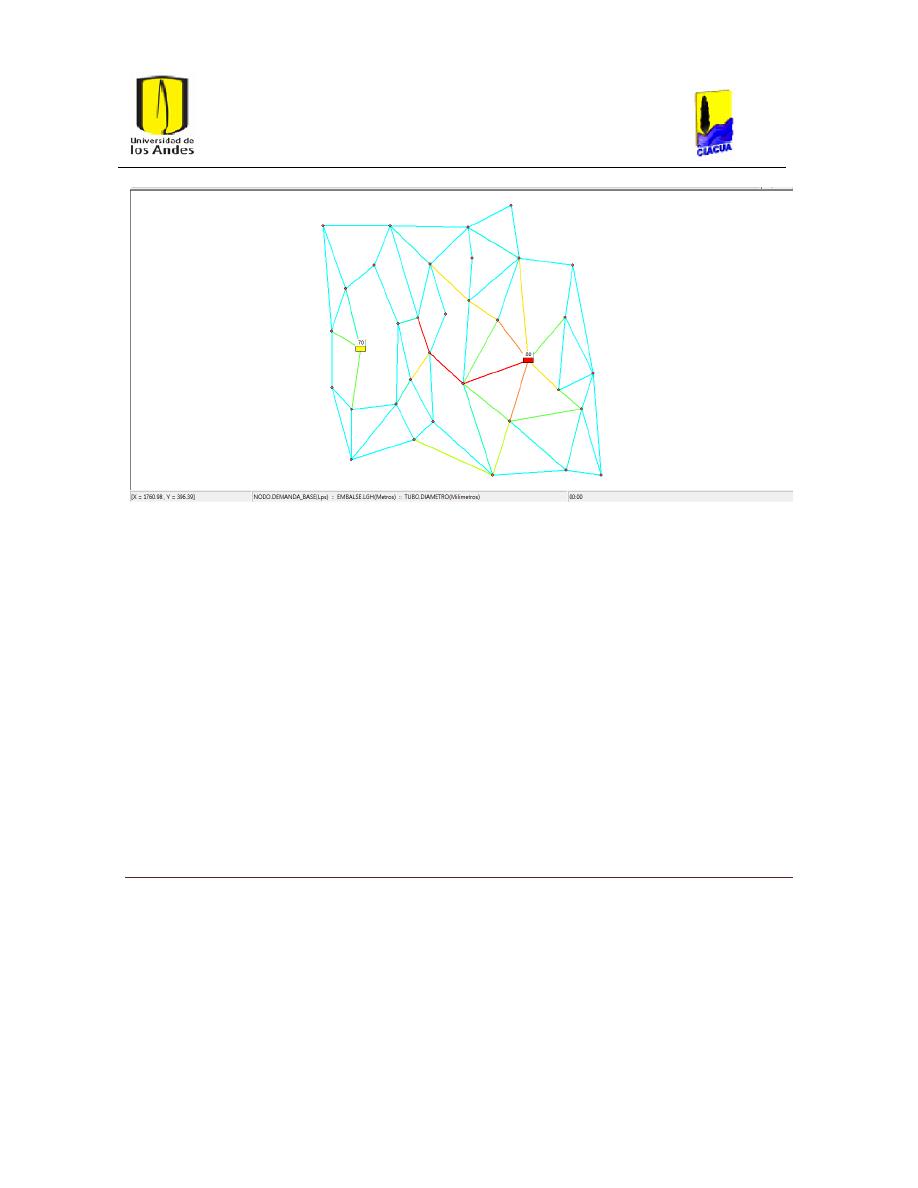
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
38
ILUSTRACIÓN 16. RED TESIS 2.
Al igual que en la red anterior, esta red fue diseñada por el autor y autorizada por el asesor de
este trabajo. Las características con las que se trabajó esta red se van a mostrar a
continuación:
- 33 Nudos
- Alturas en la red que varían entre los 7 y los 56 m.
- La red cuenta con 2 fuentes de abastecimiento con las LGH de 70 y 80 m
respectivamente.
- La red cuenta con 72 tramos de tubería.
- Y una demanda base de 15 L/s para todos los Nudos de la tubería.
Al igual que las redes anteriores, se trabajó con la demanda base estándar, duplicada y
cuadruplicada, y no presentó ningún problema al diseñarla con los materiales seleccionados
para este trabajo.
3.7 RED TESIS 3

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
39
ILUSTRACIÓN 17. RED TESIS 3.
Última red que se trabajó en este proyecto de grado, al igual que las 2 redes anteriores
también fue creada para la realización de este proyecto de grado. Las características de esta
red se mostrarán a continuación:
- 67 Nudos
- Alturas en la red se encuentran entre los 4 y 56 m.
- Cuenta con una única fuente de abastecimiento. La LGH se modificó por los mismos
motivos que los nombrados en Balerma. LGH: 75 m se utilizó en la mayoría de las
simulaciones, LGH: 90 m se utilizó en el diseño con PVC con demanda duplicada y
PEAD con demanda estándar y finalmente LGH: 130 m se utilizó únicamente en el
diseño de PEAD para demanda duplicada.
- La demanda base que se trabajó para esta red fue de 7 L/s para todos los Nudos de la
red.
Como se nombró en la red Balerma, el único inconveniente que esta red presentó fue en 3
diseños, en los cuales aún no se había implementado los diámetros artificiales.
3.8 PROCEDIMIENTO PARA LA OBTENCIÓN DE LOS DISEÑOS
El procedimiento a seguir consistió en los siguientes pasos:
- Abrir el Programa REDES
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
40
ILUSTRACIÓN 18. INTERFAZ DEL PROGRAMA REDES.
- Cargar la red que se desea trabajar.
ILUSTRACIÓN 19. CARGAR LA RED A TRABAJAR.
- Revisar que los parámetros establecidos en la metodología sean correctos.
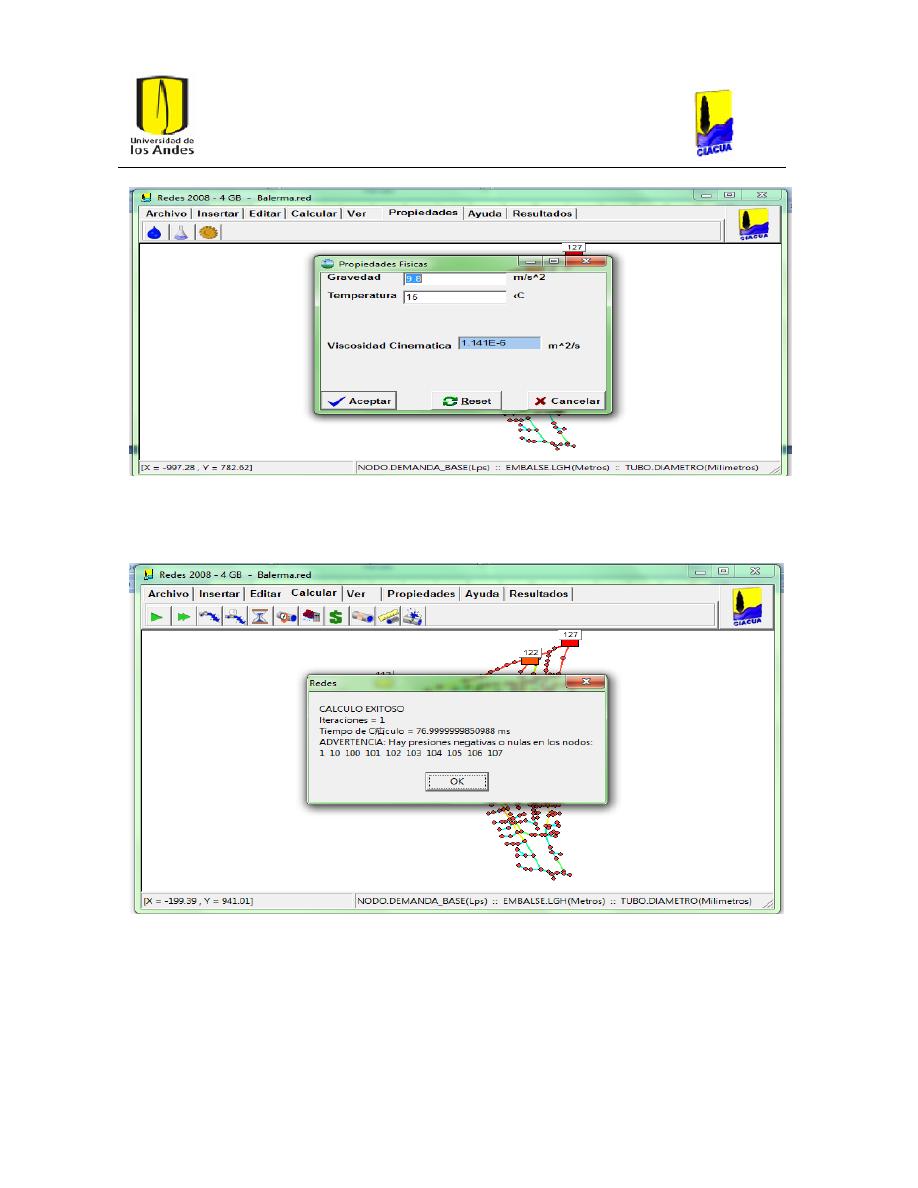
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
41
ILUSTRACIÓN 20. VERIFICACIÓN DE LOS PARÁMETROS.
- Se realiza una comprobación hidráulica inicial para ver el estado de la red.
ILUSTRACIÓN 21. PRUEBA INICIAL PARA CORRER LA HIDRÁULICA EN ESTADO ESTABLE.
- Se establece la curva de costos, los diámetros comerciales que se desean utilizar y la
ecuación de diseño.
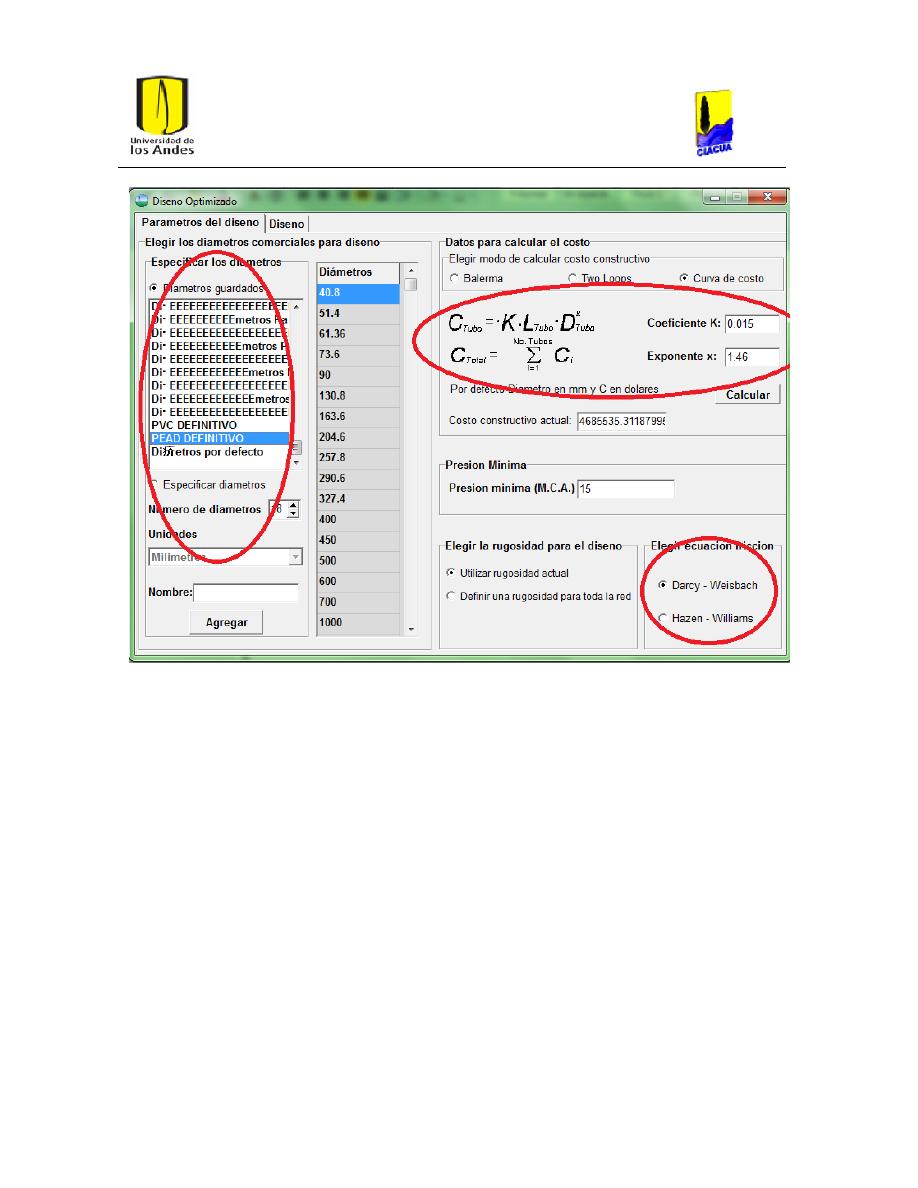
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
42
ILUSTRACIÓN 22. PARAMETROS DE DISEÑO: CURVA DE COSTOS, DIÁMETROS Y ECUACION QUE SE
DESEA UTILIZAR.
- Entrar a la ventana de Diseño y seleccionar SOGH, verificando que los parámetros sean
los correctos.
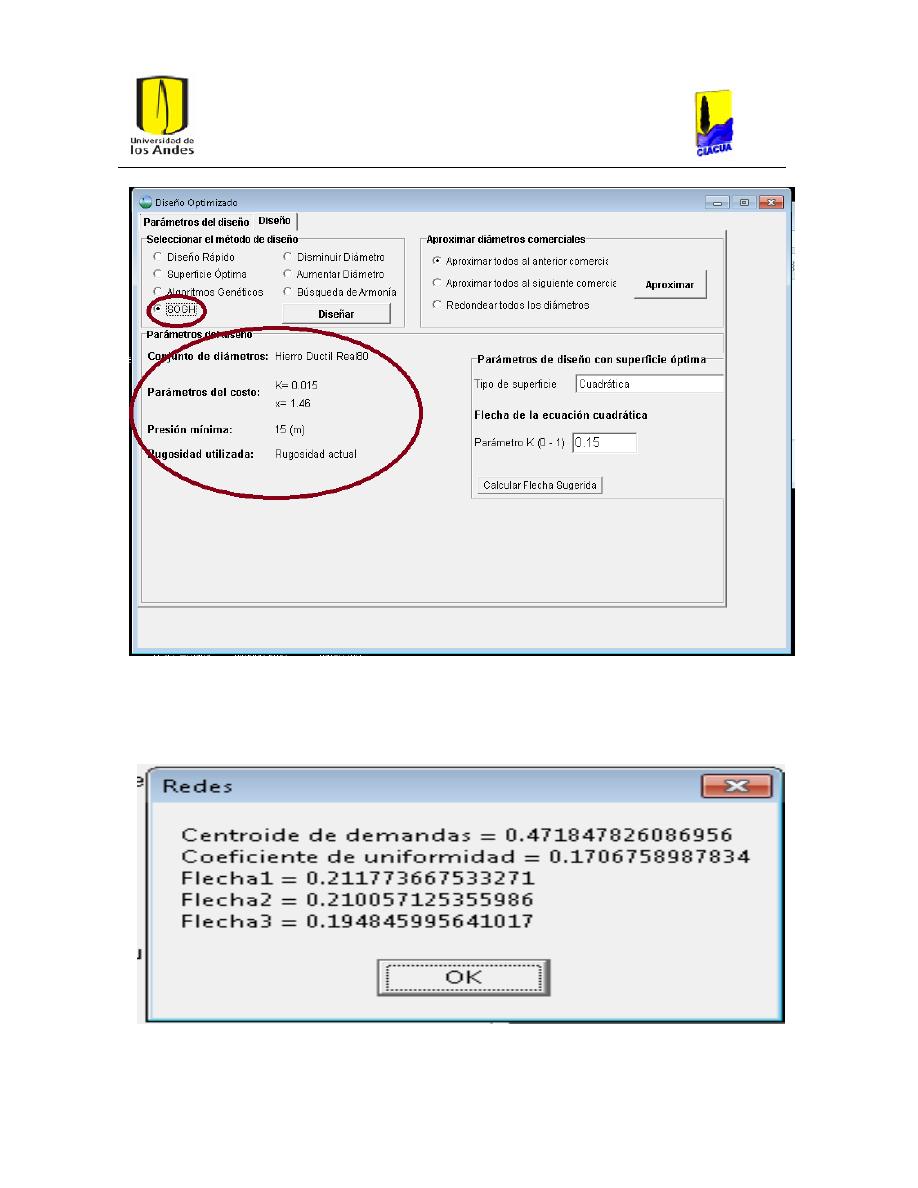
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
43
ILUSTRACIÓN 23. VENTANA DE DISEÑO CON METODOLOGÍA SOGH.
- Como se muestra en el marco teórico específicamente en la sección 2.3.1.1, se calcula
la flecha óptima que será utilizada para el diseño de la red. Seleccionando la flecha 3
para que cumpla tanto con requerimientos hidráulicos como de costos mínimos.
ILUSTRACIÓN 24. CÁLCULO DE LA FLECHA.
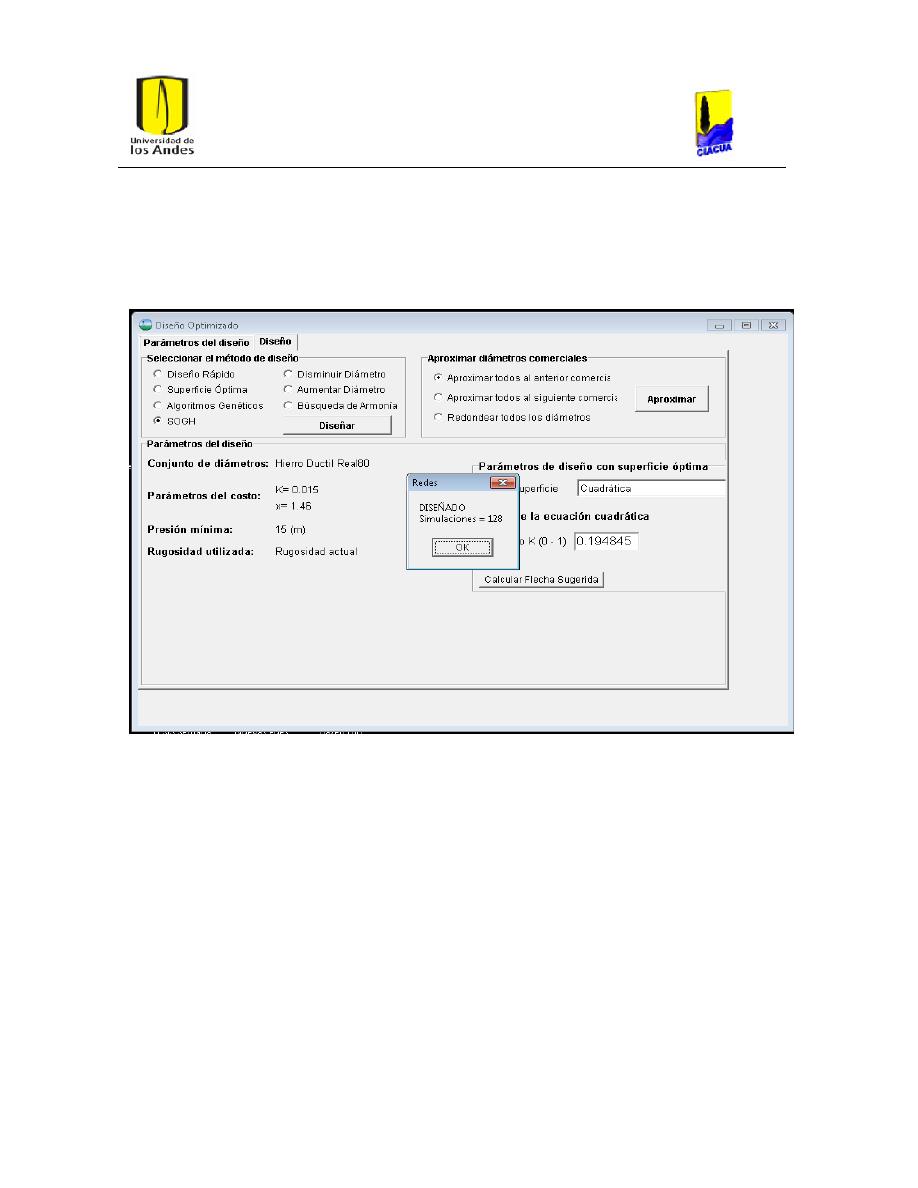
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
44
- Una vez asignada la flecha, se procede a diseñar la red. El programa finalizará cuando
haya concluido el diseño o presente algún mensaje de error que puede ser causado
por que los diámetros escogidos son muy pequeños, o la presión mínima es demasiado
grande o la LGH de los embalses no tiene un valor lo suficientemente alto para suplir
las demandas.
ILUSTRACIÓN 25. DISEÑO EXITOSO DE LA RED.
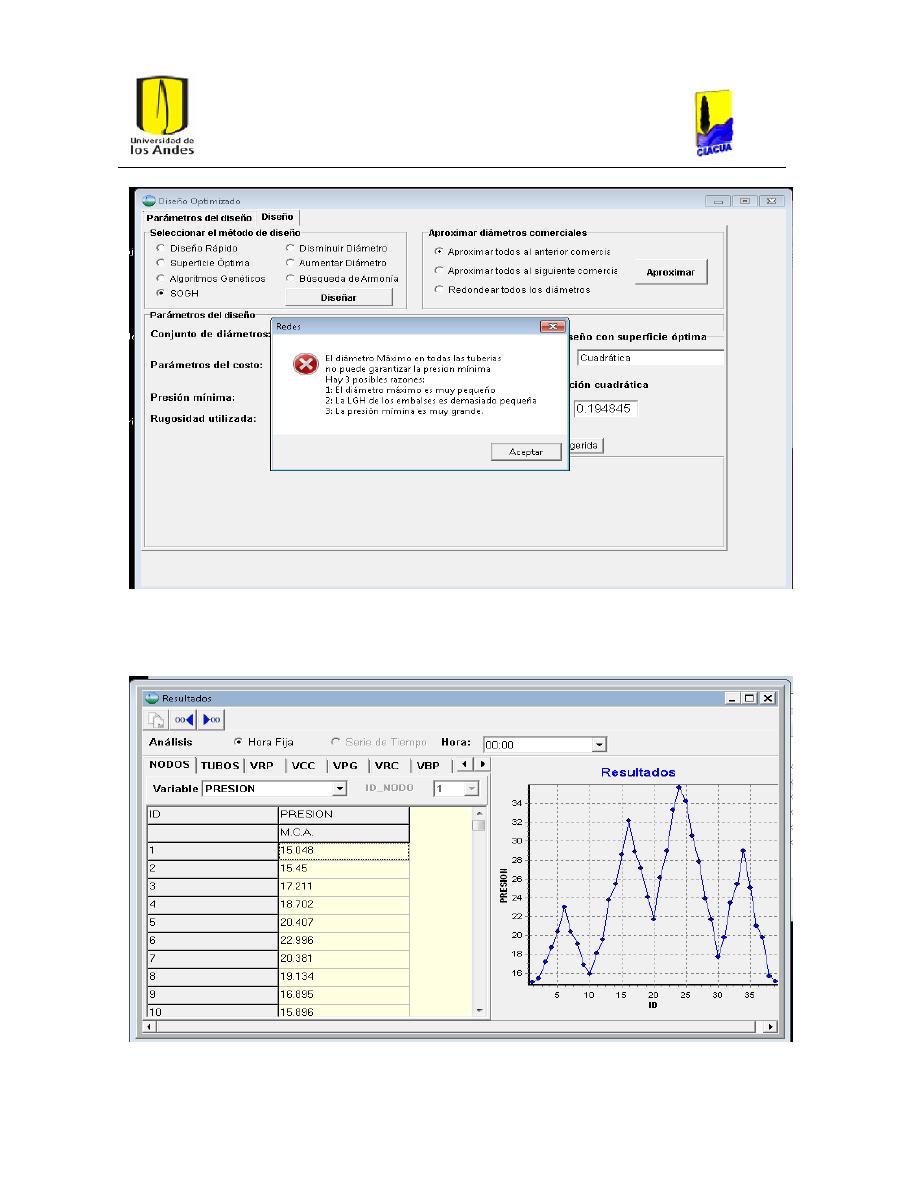
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
45
ILUSTRACIÓN 26. MENSAJE DE ERROR.
- Obtención de los resultados:
ILUSTRACIÓN 27. RESULTADOS EN REDES.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
46
- Exportar los resultados para su análisis.
ILUSTRACIÓN 28 EXPORTAR LOS RESULTADOS.
- Para el caso de este proyecto de Tesis, se realizó una segunda comprobación de los
datos con el programa de EPANET.
- Se observaron los costos, utilizando la herramienta de REDES.
ILUSTRACIÓN 29. COSTOS DE LA RED.
- Y ya que el proyecto desea analizar los efectos de la ecuación empírica de Hazen-
Williams frente a la ecuación físicamente basada de Darcy-Weisbach, la comparación

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
47
se realizó diseñando con la ecuación de Hazen-Williams. Posteriormente, se abrió una
nueva ventana de redes y se corrió la hidráulica en estado estable, ya que por defecto
el Programa REDES corre la hidráulica con la ecuación de Darcy-Weisbach. Y con estos
resultados se exportan para su posterior análisis.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
48
CAPÍTULO 4. RESULTADOS
Los resultados de este proyecto se realizaron analizando los efectos hidráulicos de la ecuación
de Hazen-Williams. Para este propósito, se utilizó la herramienta computacional de REDES.
Como se nombró en la metodología, se diseñó la red con la ecuación y el coeficiente de Hazen-
Williams y posteriormente se corrió la hidráulica de esta red con rugosidad absoluta en la
ecuación de Darcy-Weisbach, de tal forma que el C de Hazen-Williams y
coincidieran para el
mismo material. Con este procedimiento, se lograban obtener las presiones al correr la
hidráulica con la ecuación físicamente basada de Darcy-Weisbach y observar el efecto
hidráulico que causaba el uso de la ecuación de Hazen-Williams en los diseños optimizados.
Por lo cual se diseña con la ecuación de Hazen-Williams:
ECUA CIÓN 2.1 .1 -1
De esta ecuación se obtiene el diámetro de diseño. Posteriormente realizamos una especie de
comprobación de diseño con la ecuación de Darcy-Weisbach:
- Se halla el factor de fricción con la ecuación de Colebrook-White :
ECUA CIÓN 2.1 .2 -5
- Ya que se cuenta con todos los parámetros, se puede hallar el factor de fricción con
algún método numérico o de forma iterativa.
- Posteriormente, encontramos las verdaderas pérdidas por fricción, con la ecuación de
Darcy-Weisbach:
ECUA CIÓN 2.1 .2 -2
- Finalmente, con las pérdidas reales (ya que es una ecuación físicamente basada), se
procede a aplicar la ecuación de Bernoulli y encontrar la presión en cada uno de los
Nudos después de realizada la comprobación:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
49
ECUA CIÓN 2.1-1
- Como se puede observar, los parámetros del lado izquierdo de la ecuación se conocen,
por lo que solo la presión del lado derecho de la ecuación termina como incógnita.
Sin embargo como no es una tubería única, sino una red cerrada, para hallar la presión en
Nudos, se utilizo el método del gradiente hidráulico desarrollado por E.Todini y E.P.O’Connell
entre 1982 y 1983 (Saldarriaga, 2007) para el cálculo de las alturas piezometricas finales en
cada uno de los Nudos.
- Como paso final, se graficaron las presiones diseñadas con la ecuación de Hazen-
Williams y las comprobaciones con la ecuación de Darcy-Weisbach. Y para el caso del
caudal cuadruplicado, también se graficaron las presiones con la ecuación de Darcy-
Weisbach. Eso permitió ilustrar el efecto hidráulico que causan los diseños con la
ecuación de Hazen-Williams.
4.1 RED SAN VICENTE
A continuación se mostraran los resultados de la Red San Vicente.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
50
- Costos
TABLA 11. COSTOS DE LA RED SAN VICENTE CON CAUDALES NORMALES
La tabla anterior se obtuvo después de diseñar la red con los diferentes materiales utilizando
caudales normales y al aplicar la curva de costos correspondiente. Una vez se obtuvieron los
costos, estos se graficaron para intentar evidenciar alguna diferencia entre los diseños con la
ecuación empírica y la ecuación físicamente basada. Los resultados de caudales duplicados y
cuadruplicados se encuentran en los anexos de este trabajo.
ILUSTRACIÓN 30. GRÁFICA DE COSTOS RED SAN VICENTE CAUDALES NORMALES.
RED SAN VICENTE CAUDALES NORMALES
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
HAZEN-WILLIAMS
102 988 343.00
$
151 328 039.00
$
DIFERENCIA
-
$
(289 499.59)
$
(496 800.44)
$
380 323 515.62
$
DARCY-WEISBACH
102 988 343.00
$
151 617 538.59
$
380 820 316.06
$
$ 0.00
$ 50 000 000.00
$ 100 000 000.00
$ 150 000 000.00
$ 200 000 000.00
$ 250 000 000.00
$ 300 000 000.00
$ 350 000 000.00
$ 400 000 000.00
COSTO
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red San Vicente
DARCY-WEISBACH HIERRO
DÚCTIL
HAZEN-WILLIAMS HIERRO
DÚCTIL
DARCY-WEISBACH PVC
HAZEN-WILLIAMS PVC
DARCY-WEISBACH PEAD
HAZEN-WILLIAMS PEAD
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
51
- Resultados de presiones con Hierro Dúctil:
ILUSTRACIÓN 31. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
Estos fueron los resultados de diseñar la red utilizando la ecuación de Hazen-Williams con un
coeficiente de 140 para hierro dúctil.
ILUSTRACIÓN 32. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUES DE CORRER
LA HIDRÁULICA CON LA ECUACION DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
Esta ilustración muestra las presiones después de correr la hidráulica con la ecuación de
Darcy-Weisbach del diseño realizado utilizando la ecuación de Hazen-Williams. La rugosidad
absoluta que se trabajo es la que se mostro en metodología, es decir, una rugosidad absoluta
de 0.25 mm.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS SAN VICENTE
HIERRO DÚCTIL
PRESIONES CON HAZEN-
WILLIAMS SAN VICENTE HIERRO
DÚCTIL
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES SAN VICENTE
HIERRO DÚCTIL
COMPROBACIÓN DE
PRESIONES SAN
VICENTE HIERRO …
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
52
- Resultados de presiones con PVC:
ILUSTRACIÓN 33. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
El procedimiento es similar al realizado con el hierro dúctil, solo que en esta ocupación se
utilizo un coeficiente de Hazen-Williams de 150.
ILUSTRACIÓN 34. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
Al igual que en el hierro dúctil, también se corrió la hidráulica para comprobar las presiones
reales de la red que fue diseñada con la ecuación de Hazen-Williams. La rugosidad absoluta
trabajada fue de 0.0015 mm.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
250
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS SAN VICENTE
PVC
PRESIONES CON HAZEN-
WILLIAMS SAN VICENTE PVC
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
250
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES SAN VICENTE PVC
COMPROBACIÓN DE PRESIONES
SAN VICENTE PVC
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
53
- Resultados de presiones PEAD:
ILUSTRACIÓN 35. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
Al igual que en el caso del PVC esta red fue diseñada utilizando la ecuación de Hazen-Williams
y un coeficiente de 150.
ILUSTRACIÓN 36.PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
Utilizando el mismo procedimiento de los materiales anteriores fue posible realizar esta
grafica. Para este caso la rugosidad absoluta de la red fue de 0.007 mm como corresponde al
PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
250
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS SAN VICENTE
PEAD
PRESIONES CON
HAZEN-WILLIAMS SAN
VICENTE PEAD
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
250
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES SAN VICENTE PEAD
COMPROBACIÓN DE
PRESIONES SAN
VICENTE PEAD
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
54
4.2 RED BALERMA
Los resultados de la Red Balerma:
Los procedimientos de esta red fueron exactamente iguales a los que se utilizaron durante la
red San Vicente para todos los materiales. Los resultados para caudales duplicados y
cuadruplicados se encuentran en los anexos de este trabajo.
- Costos,
TABLA 12. COSTOS DE LA RED BALERMA CON CAUDALES NORMALES.
ILUSTRACIÓN 37. GRÁFICA DE COSTOS RED BALERMA CON CAUDALES NORMALES.
RED BALERMA CAUDALES NORMALES
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
DIFERENCIA
(245 917 212.00)
$
500 243 338.23
$
1 055 579 818.54
$
HAZEN-WILLIAMS
4 956 143 781.00
$
10 712 044 076.81
$
20 662 508 943.83
$
DARCY-WEISBACH
5 202 060 993.00
$
10 211 800 738.58
$
19 606 929 125.29
$
$ 0.00
$ 5 000 000 000.00
$ 10 000 000 000.00
$ 15 000 000 000.00
$ 20 000 000 000.00
$ 25 000 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Balerma
DARCY-WEISBACH HIERRO
DÚCTIL
HAZEN-WILLIAMS HIERRO
DÚCTIL
DARCY-WEISBACH PVC
HAZEN-WILLIAMS PVC
DARCY-WEISBACH PEAD
HAZEN-WILLIAMS PEAD
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
55
- Resultados de presiones con Hierro Dúctil
ILUSTRACIÓN 38. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
ILUSTRACIÓN 39. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
0
100
200
300
400
500
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BALERMA
HIERRO DÚCTIL
PRESIONES
CON HAZEN-
WILLIAMS
BALERMA
HIERRO DÚCTIL
-20
-10
0
10
20
30
40
50
60
70
0
100
200
300
400
500
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BALERMA HIERRO
DÚCTIL
COMPROBACIÓN DE
PRESIONES
BALERMA HIERRO …
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
56
- Resultados de presiones con PVC.
ILUSTRACIÓN 40. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
ILUSTRACIÓN 41. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
0
100
200
300
400
500
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BALERMA PVC
PRESIONES
CON HAZEN-
WILLIAMS
BALERMA PVC
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
0
100
200
300
400
500
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BALERMA PVC
COMPROBACIÓN
DE PRESIONES
BALERMA PVC
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
57
- Resultados de presiones con PEAD.
ILUSTRACIÓN 42. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
ILUSTRACIÓN 43. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
115
120
125
130
0
100
200
300
400
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BALERMA PEAD
PRESIONES CON
HAZEN-
WILLIAMS
BALERMA PEAD
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
0
50
100
150
200
250
300
350
400
450
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BALERMA PEAD
COMPROBACIÓN
DE PRESIONES
BALERMA PEAD
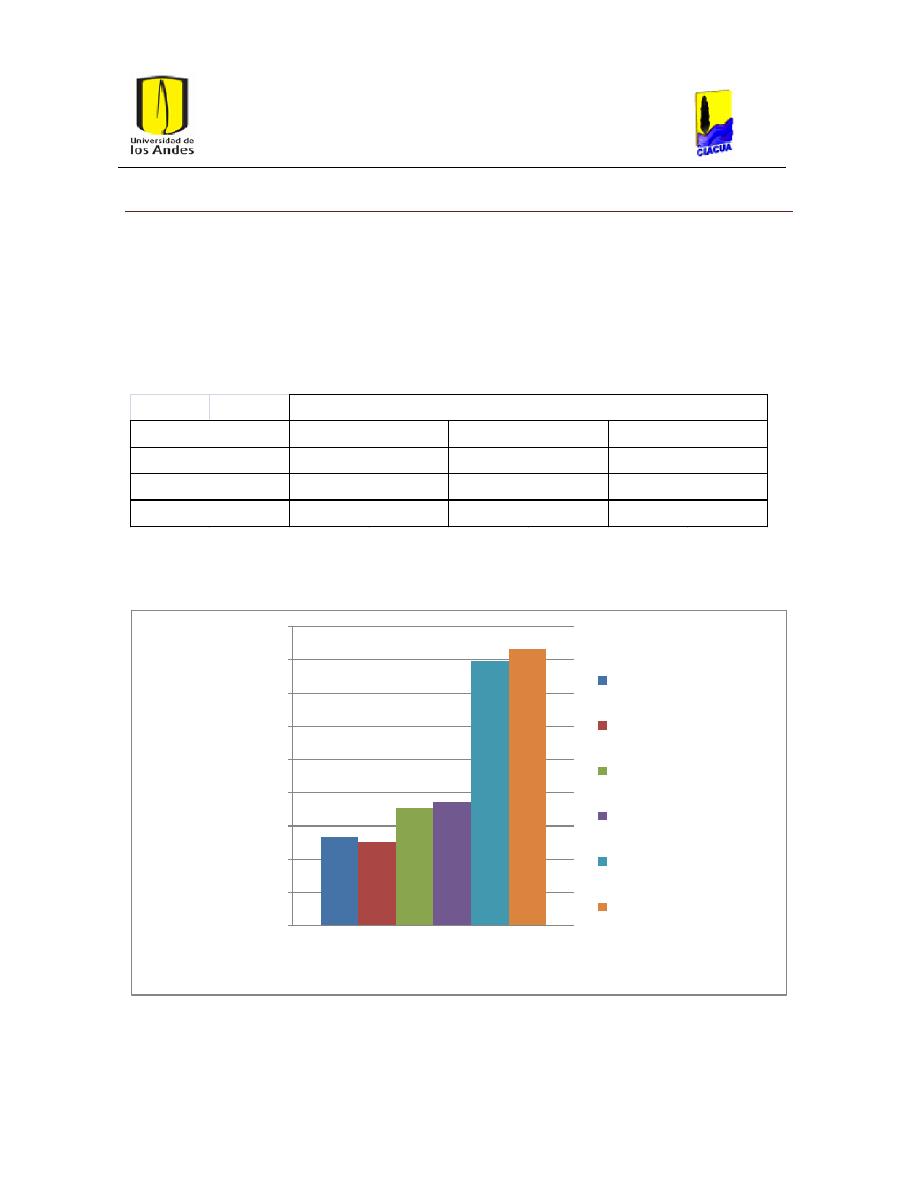
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
58
4.3 RED BOGOTÁ-CAZUCÁ
A continuación se mostraran los resultados obtenidos para los costos y para las presiones de
esta red:
Los procedimientos de esta red fueron exactamente iguales a los que se utilizaron durante las
redes anteriores para todos los materiales. Los resultados para caudales duplicados y
cuadruplicados se encuentran en los anexos de este trabajo.
- Costos.
TABLA 13. COSTOS DE LA RED BOGOTÁ-CAZUCÁ CON CAUDALES NORMALES.
ILUSTRACIÓN 44. GRÁFICA DE COSTOS DE LA RED BOGOTÁ-CAZUCÁ CON CAUDALES NORMALES.
RED BOGOTÁ-CAZUCÁ CAUDALES NORMALES
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
DIFERENCIA
(15 576 804.00)
$
17 628 436.92
$
36 317 586.47
$
HAZEN-WILLIAMS
252 069 725.00
$
371 437 472.44
$
831 932 111.78
$
DARCY-WEISBACH
267 646 529.00
$
353 809 035.52
$
795 614 525.31
$
$ 0.00
$ 100 000 000.00
$ 200 000 000.00
$ 300 000 000.00
$ 400 000 000.00
$ 500 000 000.00
$ 600 000 000.00
$ 700 000 000.00
$ 800 000 000.00
$ 900 000 000.00
costos
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Bogotá-Cazucá
DARCY-WEISBACH HIERRO
DÚCTIL
HAZEN-WILLIAMS HIERRO
DÚCTIL
DARCY-WEISBACH PVC
HAZEN-WILLIAMS PVC
DARCY-WEISBACH PEAD
HAZEN-WILLIAMS PEAD
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
59
- Resultados de presiones con Hierro Dúctil.
ILUSTRACIÓN 45. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
ILUSTRACIÓN 46. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
15
30
45
60
75
90
105
120
135
150
165
180
195
210
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BOGOTÁ-
CAZUCÁ HIERRO DÚCTIL
PRESIONES CON
HAZEN-
WILLIAMS
BOGOTÁ-
CAZUCÁ HIERRO
DÚCTIL
-10
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
0
20
40
60
80
100
120
140
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BOGOTÁ-CAZUCÁ
HIERRO DÚCTIL
COMPROBACIÓN
DE PRESIONES
BOGOTÁ-CAZUCÁ
HIERRO DÚCTIL
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
60
- Resultados de presiones con PVC.
ILUSTRACIÓN 47. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
ILUSTRACIÓN 48. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
115
120
125
0
20
40
60
80
100
120
140
160
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BOGOTÁ-
CAZUCÁ PVC
PRESIONES
CON HAZEN-
WILLIAMS
BOGOTÁ-
CAZUCÁ PVC
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
115
120
125
130
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BOGOTÁ-CAZUCÁ
PVC
COMPROBACIÓN
DE PRESIONES
BOGOTÁ-
CAZUCÁ PVC
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
61
- Resultados para PEAD.
ILUSTRACIÓN 49. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
ILUSTRACIÓN 50. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN WILLIAMS BOGOTÁ-
CAZUCÁ PEAD
PRESIONES CON
HAZEN
WILLIAMS
BOGOTÁ-…
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BOGOTÁ-CAZUCÁ
PEAD
COMPROBACIÓN
DE PRESIONES
BOGOTÁ-CAZUCÁ
PEAD
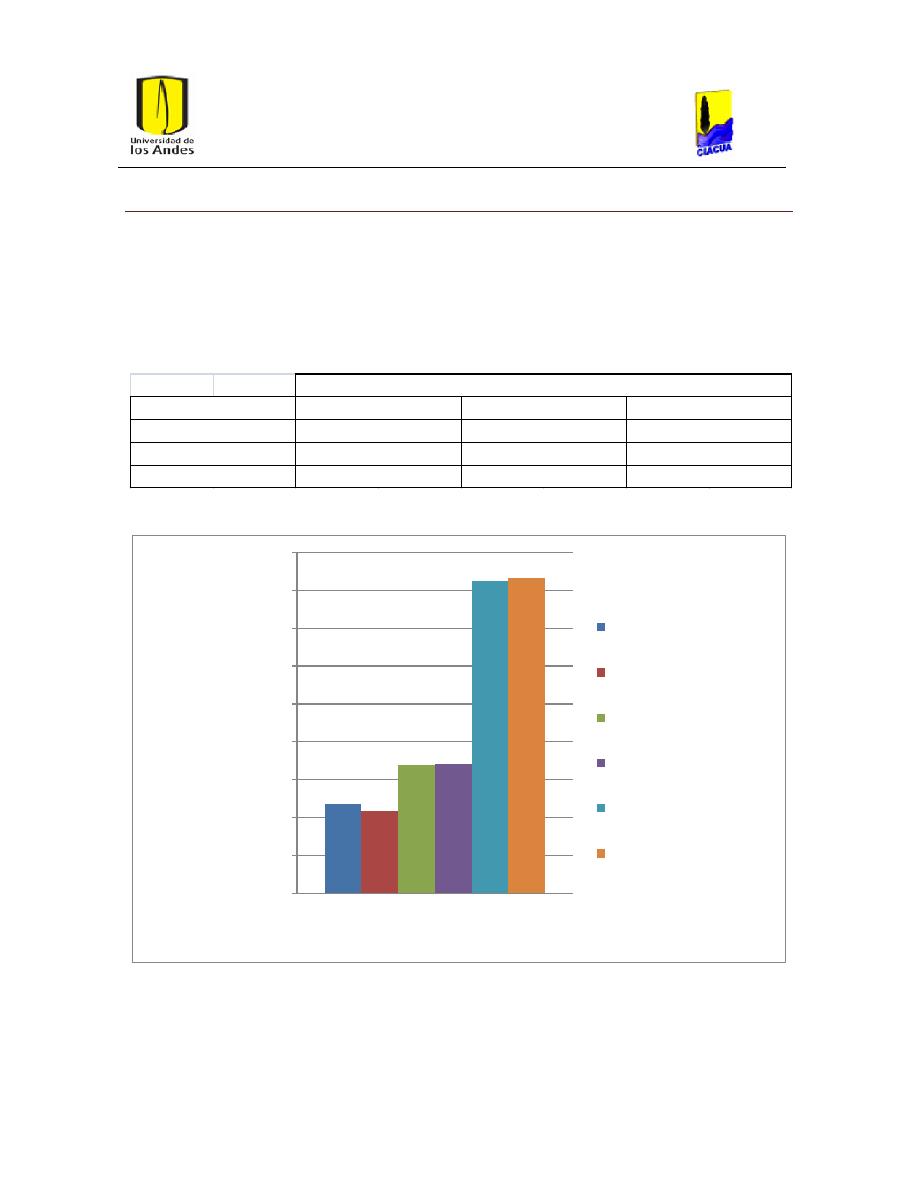
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
62
4.4 RED R28
Los resultados de esta red se mostraran a continuación:
Los procedimientos de esta red fueron exactamente iguales a los que se utilizaron durante las
redes anteriores para todos los materiales. Los resultados para caudales duplicados y
cuadruplicados se encuentran en los anexos de este trabajo.
- Costos.
TABLA 14. COSTOS DE LA RED R28 CON CAUDALES NORMALES.
ILUSTRACIÓN 51. GRÁFICA DE COSTOS DE LA RED R28 CON CAUDALES NORMALES.
DIFERENCIA
(19 367 515.00)
$
2 550 857.00
$
7 199 259.00
$
HAZEN-WILLIAMS
216 741 724.00
$
341 717 974.00
$
831 216 362.00
$
DARCY-WEISBACH
236 109 239.00
$
339 167 117.00
$
824 017 103.00
$
RED R28 CAUDALES NORMALES
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
$-
$100 000 000.00
$200 000 000.00
$300 000 000.00
$400 000 000.00
$500 000 000.00
$600 000 000.00
$700 000 000.00
$800 000 000.00
$900 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red R28
DARCY-WEISBACH HIERRO
DÚCTIL
HAZEN-WILLIAMS HIERRO
DÚCTIL
DARCY-WEISBACH PVC
HAZEN-WILLIAMS PVC
DARCY-WEISBACH PEAD
HAZEN-WILLIAMS PEAD
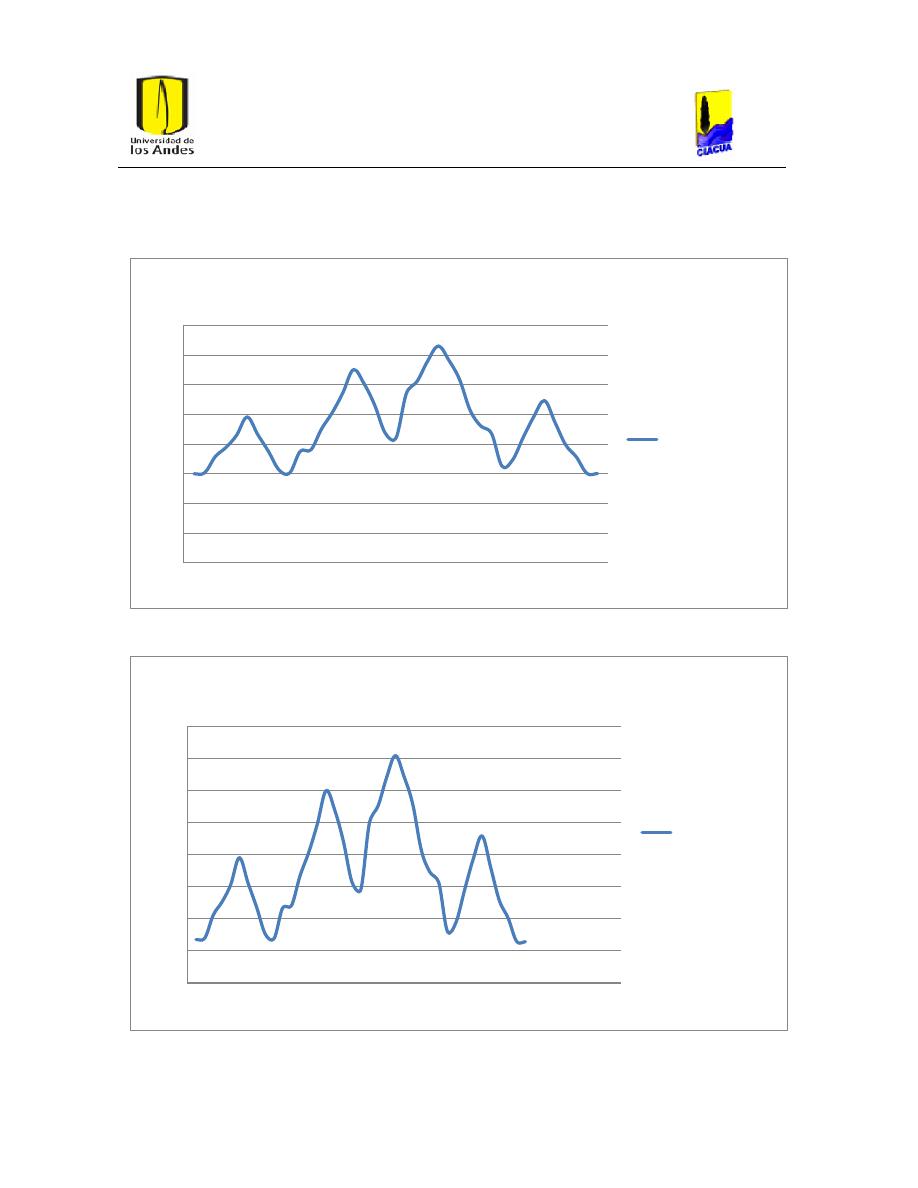
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
63
- Resultados de presiones con Hierro Dúctil
ILUSTRACIÓN 52. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
ILUSTRACIÓN 53. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
5
10
15
20
25
30
35
40
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS R28 HIERRO
DÚCTIL
PRESIONES CON
HAZEN-WILLIAMS
R28 HIERRO DÚCTIL
0
5
10
15
20
25
30
35
40
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES R28 HIERRO
DÚCTIL
COMPROBACIÓN
DE PRESIONES
R28 HIERRO
DÚCTIL
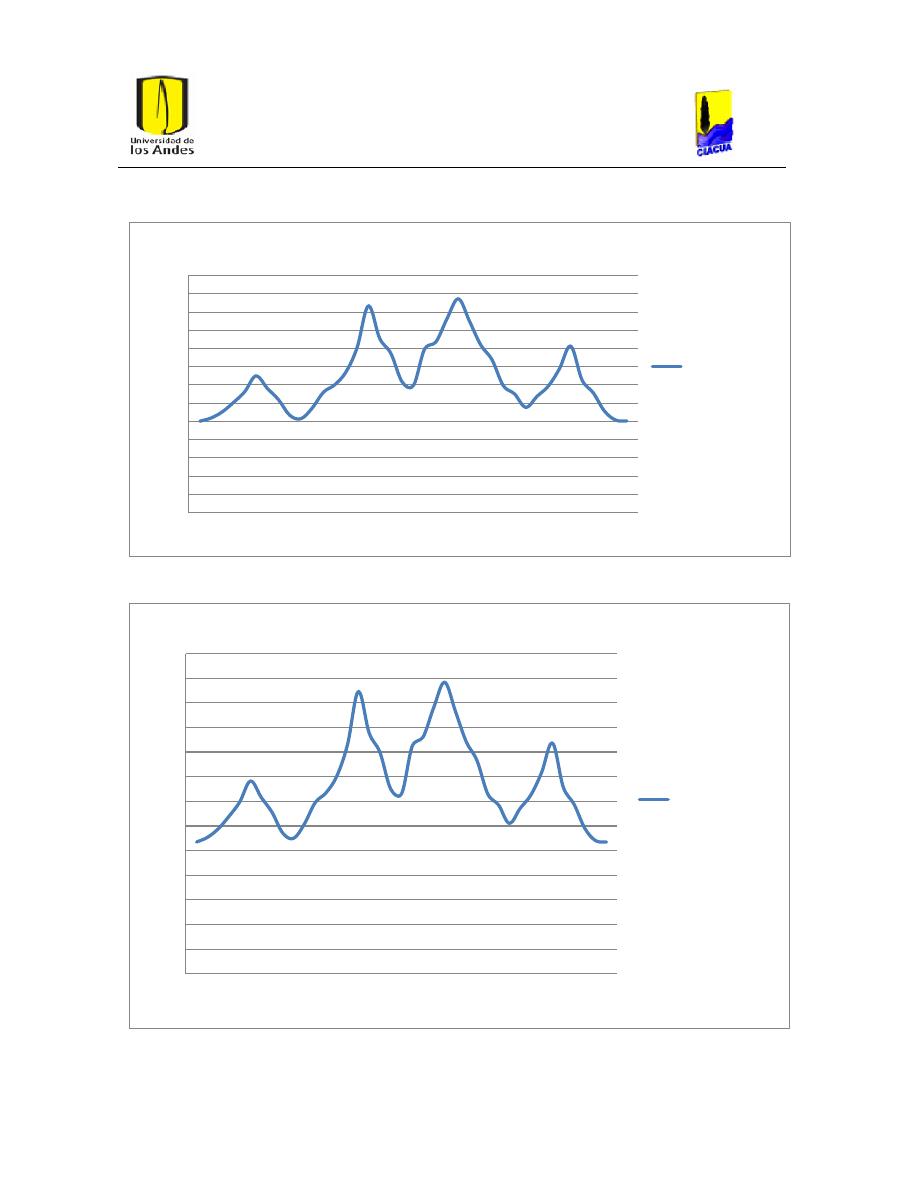
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
64
- Resultados de presiones para PVC.
ILUSTRACIÓN 54. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
ILUSTRACIÓN 55. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
3
6
9
12
15
18
21
24
27
30
33
36
39
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS R28 PVC
PRESIONES CON
HAZEN-
WILLIAMS R28
PVC
0
3
6
9
12
15
18
21
24
27
30
33
36
39
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES R28 PVC
COMPROBACIÓN
DE PRESIONES R28
PVC
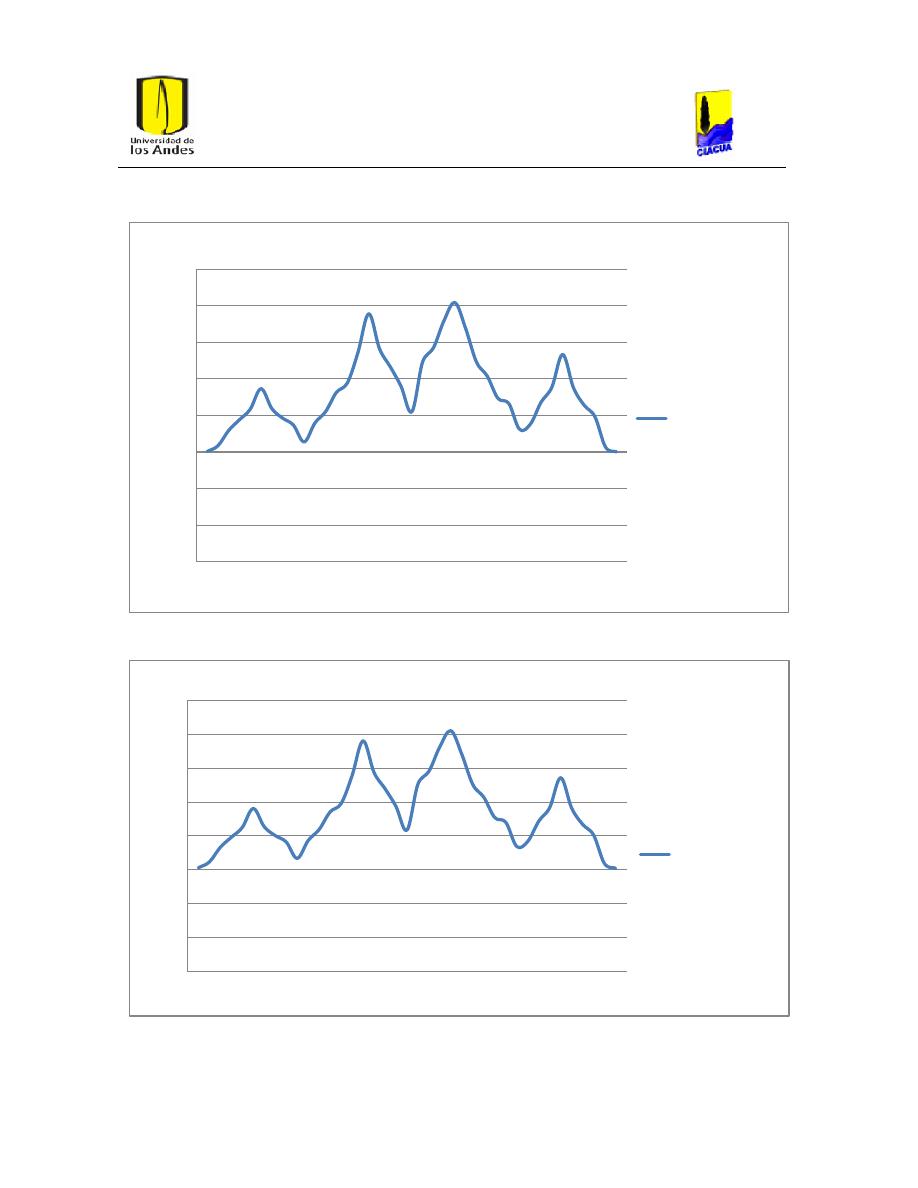
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
65
- Resultados de presiones para PEAD.
ILUSTRACIÓN 56. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
ILUSTRACIÓN 57. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS R28 PEAD
PRESIONES CON
HAZEN-WILLIAMS
R28 PEAD
0
5
10
15
20
25
30
35
40
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES R28 PEAD
COMPROBACIÓN
DE PRESIONES
R28 PEAD

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
66
4.5 RED TESIS 1
Los resultados de esta red se muestran a continuación:
Los procedimientos de esta red fueron exactamente iguales a los que se utilizaron durante las
redes anteriores para todos los materiales. Los resultados para caudales duplicados y
cuadruplicados se encuentran en los anexos de este trabajo.
- Costos.
TABLA 15. COSTOS DE LA RED TESIS 1 CON CAUDALES NORMALES.
ILUSTRACIÓN 58. GRÁFICA DE COSTOS DE LA RED TESIS 1 CON CAUDALES NORMALES.
DIFERENCIA
(2 778 010.00)
$
6 989 360.00
$
21 530 105.00
$
HAZEN-WILLIAMS
185 978 041.00
$
260 763 825.00
$
558 250 289.00
$
DARCY-WEISBACH
188 756 051.00
$
253 774 465.00
$
536 720 184.00
$
RED TESIS1 CAUDALES NORMALES
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
$-
$100 000 000.00
$200 000 000.00
$300 000 000.00
$400 000 000.00
$500 000 000.00
$600 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Tesis1
HAZEN-WILLIAMS HIERRO
DÚCTIL
DARCY-WEISBACH HIERRO
DÚCTIL
HAZEN-WILLIAMS PVC
DARCY-WEISBACH PVC
HAZEN-WILLIAMS PEAD
DARCY-WEISBACH PEAD
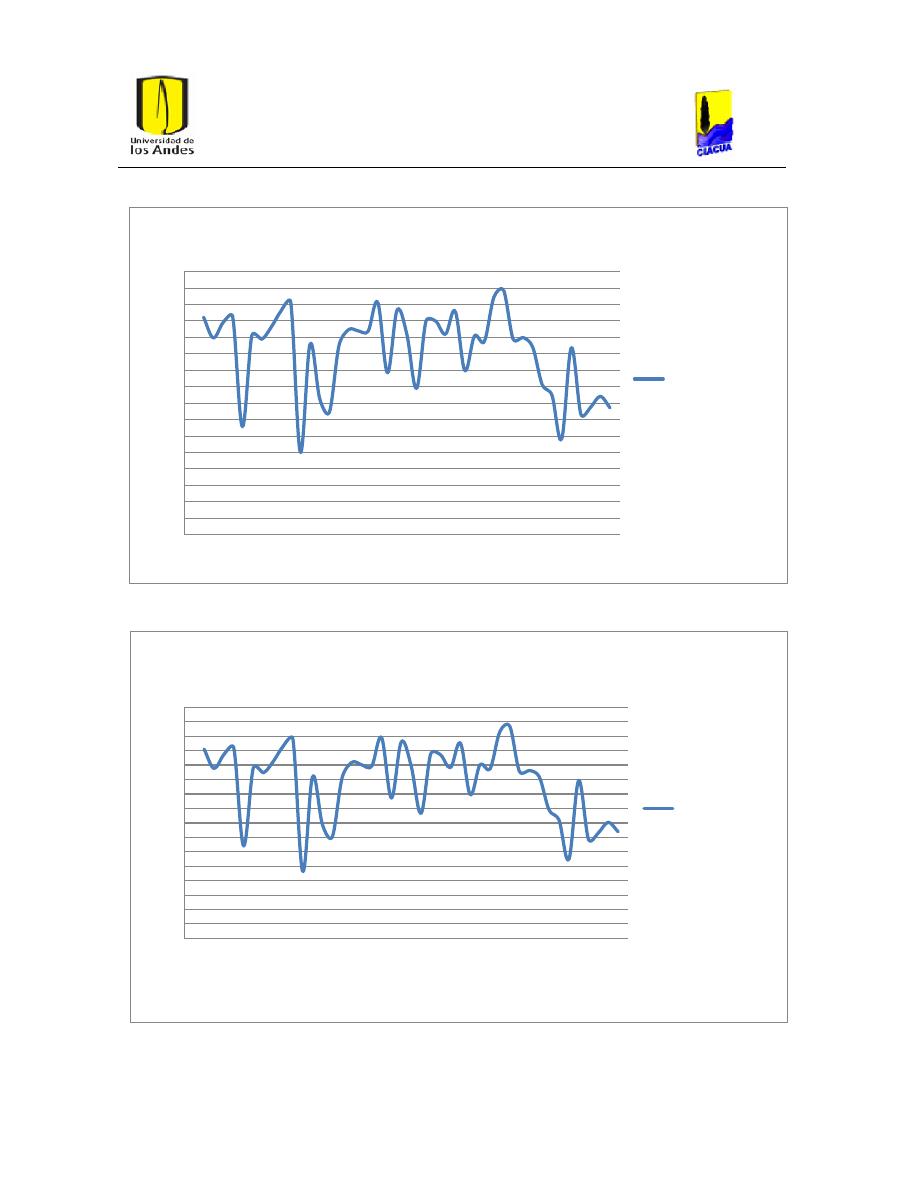
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
67
- Resultados de presiones para Hierro Dúctil.
ILUSTRACIÓN 59. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
ILUSTRACIÓN 60. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
3
6
9
12
15
18
21
24
27
30
33
36
39
42
45
48
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 1 HIERRO
DÚCTIL
PRESIONES CON
HAZEN-WILLIAMS
TESIS1 HIERRO
DÚCTIL
0
3
6
9
12
15
18
21
24
27
30
33
36
39
42
45
48
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 1 HIERRO
DÚCTIL
COMPROBACIÓN
DE PRESIONES
TESIS1 HIERRO
DÚCTIL
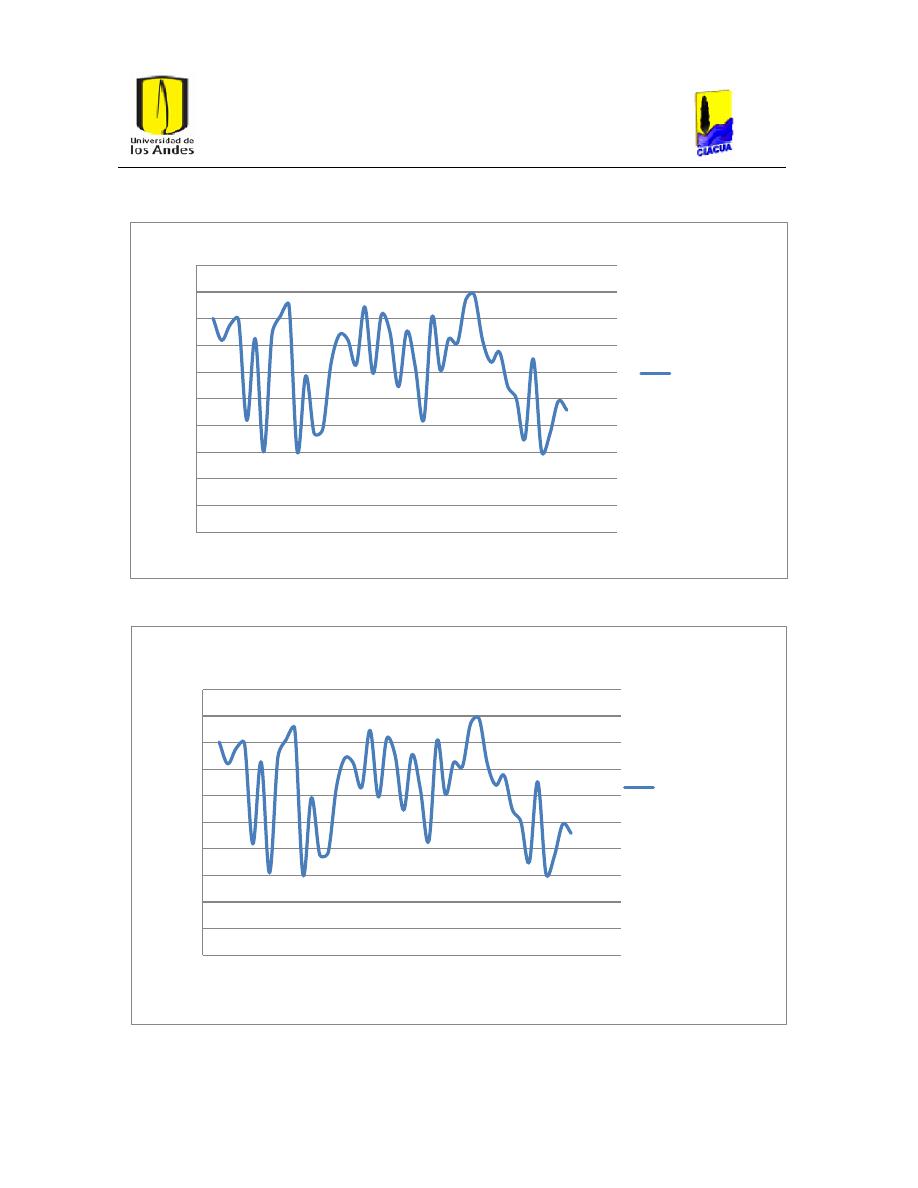
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
68
- Resultados de presiones para PVC.
ILUSTRACIÓN 61. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
ILUSTRACIÓN 62. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 1 PVC
PRESIONES CON
HAZEN-WILLIAMS
TESIS1 PVC
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 1 PVC
COMPROBACIÓN
DE PRESIONES
TESIS1 PVC
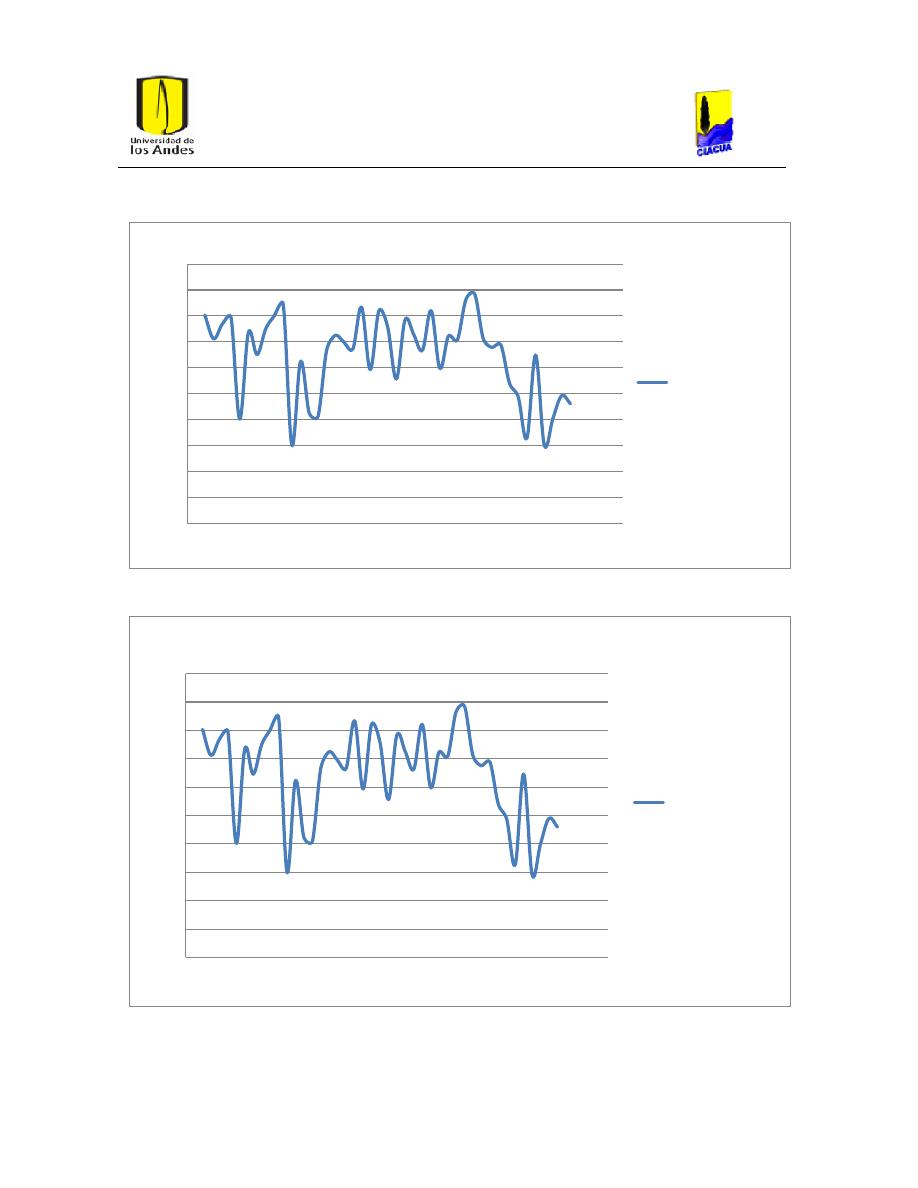
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
69
- Resultados de presiones para PEAD
ILUSTRACIÓN 63. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
ILUSTRACIÓN 64. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 1 PEAD
PRESIONES CON
HAZEN-WILLIAMS
TESIS1 PEAD
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 1 PEAD
COMPROBACIÓN
DE PRESIONES
TESIS1 PEAD
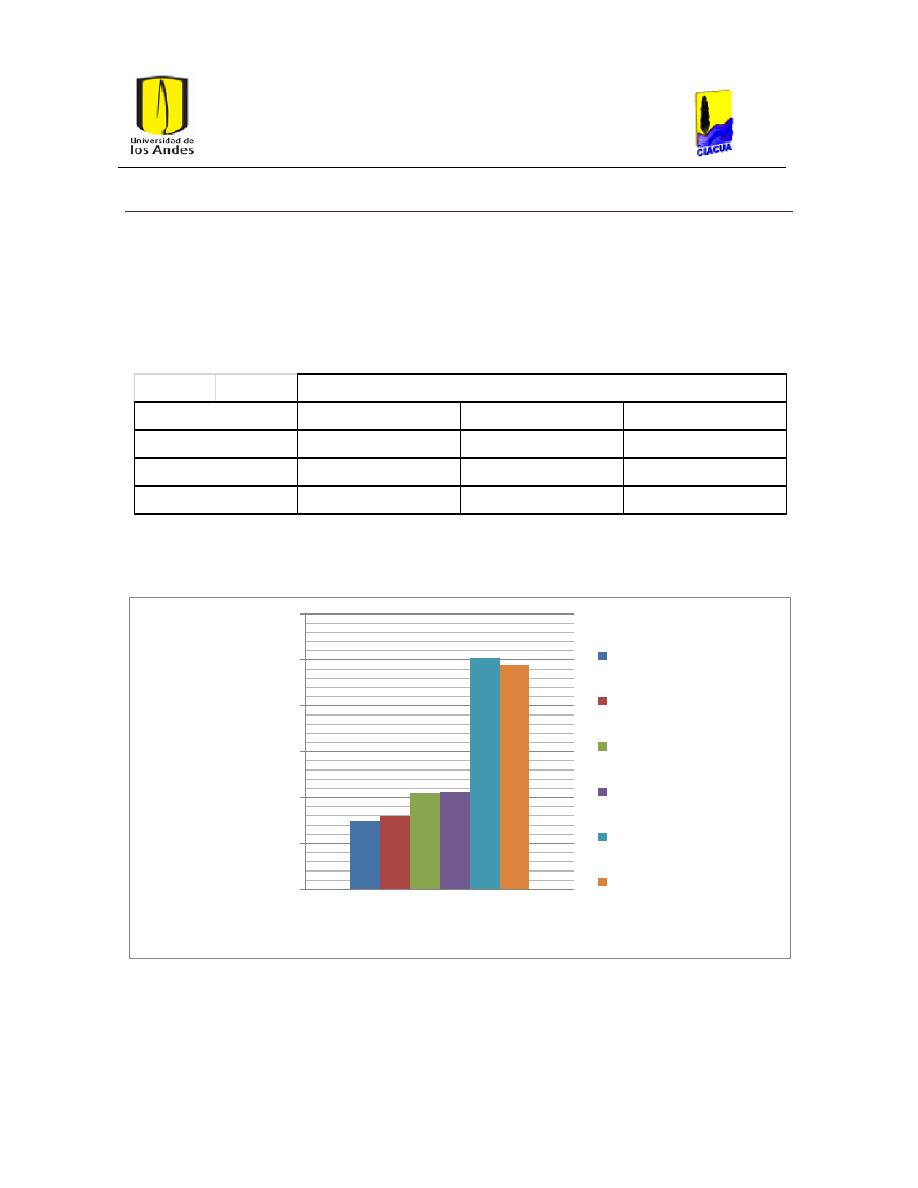
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
70
4.6 RED TESIS 2
Los resultados de esta res se muestran a continuación:
Los procedimientos de esta red fueron exactamente iguales a los que se utilizaron durante las
redes anteriores para todos los materiales. Los resultados para caudales duplicados y
cuadruplicados se encuentran en los anexos de este trabajo.
- Costos.
TABLA 16. COSTOS DE LA RED TESIS 2 CON CAUDALES NORMALES.
ILUSTRACIÓN 65. GRÁFICA DE COSTOS PARA LA RED TESIS 2 CON CAUDALES NORMALES.
DIFERENCIA
(24 014 430.00)
$
(6 940 016.20)
$
27 081 938.00
$
HAZEN-WILLIAMS
296 340 611.00
$
418 048 066.34
$
1 006 033 833.00
$
DARCY-WEISBACH
320 355 041.00
$
424 988 082.54
$
978 951 895.00
$
RED TESIS2 CAUDALES NORMALES
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
$-
$200 000 000.00
$400 000 000.00
$600 000 000.00
$800 000 000.00
$1 000 000 000.00
$1 200 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Tesis2
HAZEN-WILLIAMS HIERRO
DÚCTIL
DARCY-WEISBACH HIERRO
DÚCTIL
HAZEN-WILLIAMS PVC
DARCY-WEISBACH PVC
HAZEN-WILLIAMS PEAD
DARCY-WEISBACH PEAD
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
71
- Resultados de presiones para Hierro Dúctil.
ILUSTRACIÓN 66. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
ILUSTRACIÓN 67. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
3
6
9
12
15
18
21
24
27
30
33
36
39
42
45
48
51
54
57
60
63
0
5
10
15
20
25
30
35
P
resi
ón
en
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 2 HIERRO
DÚCTIL
PRESIONES CON
HAZEN-WILLIAMS
TESIS 2 HIERRO
DÚCTIL
0
3
6
9
12
15
18
21
24
27
30
33
36
39
42
45
48
51
54
57
60
63
0
5
10
15
20
25
30
35
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 2 HIERRO
DÚCTIL
COMPROBACIÓN
DE PRESIONES
TESIS2 HIERRO
DÚCTIL
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
72
- Resultados de presiones para PVC.
ILUSTRACIÓN 68. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
ILUSTRACIÓN 69. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 2 PVC
PRESIONES
CON HAZEN-
WILLIAMS
TESIS2 PVC
0
5
10
15
20
25
30
35
40
45
50
55
60
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 2 PVC
COMPROBACIÓN
DE PRESIONES
TESIS2 PVC
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
73
- Resultados de presiones para PEAD
ILUSTRACIÓN 70. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
ILUSTRACIÓN 71. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 2 PEAD
PRESIONES CON
HAZEN-WILLIAMS
TESIS2 PEAD
0
5
10
15
20
25
30
35
40
45
50
55
60
65
0
10
20
30
40
Pr
e
si
ó
o
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 2 PEAD
COMPROBACIÓN
DE PRESIONES
TESIS2 PEAD

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
74
4.7 RED TESIS 3
Los resultados de esta red se muestran a continuación:
Los procedimientos de esta red fueron exactamente iguales a los que se utilizaron durante las
redes anteriores para todos los materiales. Los resultados para caudales duplicados y
cuadruplicados se encuentran en los anexos de este trabajo.
- Costos.
TABLA 17. COSTOS DE LA RED TESIS 3 CON CAUDALES NORMALES.
ILUSTRACIÓN 72. GRÁFICA DE COSTOS DE LA RED TESIS 3 CON CAUDALES NORMALES.
DIFERENCIA
(22 944 745.00)
$
28 454 053.00
$
(18 490 731.00)
$
HAZEN-WILLIAMS
671 672 311.00
$
1 258 134 919.00
$
2 306 476 242.00
$
DARCY-WEISBACH
694 617 056.00
$
1 229 680 866.00
$
2 324 966 973.00
$
RED TESIS 3 CAUDALES NORMALES
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
$-
$500 000 000.00
$1 000 000 000.00
$1 500 000 000.00
$2 000 000 000.00
$2 500 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Tesis 3
HAZEN-WILLIAMS
HIERRO DÚCTIL
DARCY-WEISBACH
HIERRO DÚCTIL
HAZEN-WILLIAMS PVC
DARCY-WEISBACH PVC
HAZEN-WILLIAMS PEAD
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
75
- Resultados de presiones para Hierro Dúctil.
ILUSTRACIÓN 73. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
ILUSTRACIÓN 74. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
3
6
9
12
15
18
21
24
27
30
33
36
39
42
45
48
51
54
57
60
63
66
69
72
0
10
20
30
40
50
60
70
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 3 HIERRO
DÚCTIL
PRESIONES CON
HAZEN-WILLIAMS
TESIS 3 HIERRO
DÚCTIL
0
3
6
9
12
15
18
21
24
27
30
33
36
39
42
45
48
51
54
57
60
63
66
69
0
10
20
30
40
50
60
70
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 3 HIERRO
DÚCTIL
COMPROBACIÓN
DE PRESIONES
TESIS 3 HIERRO
DÚCTIL
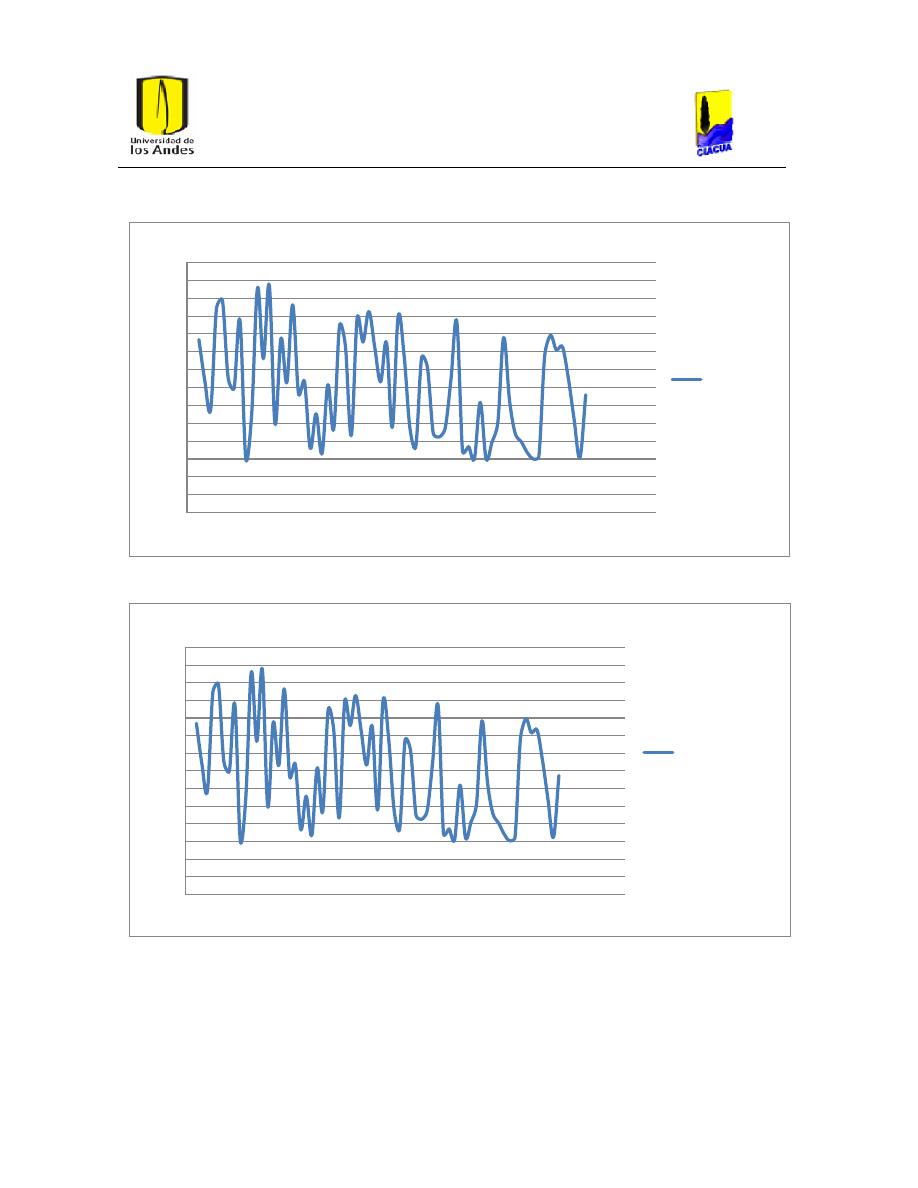
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
76
- Resultados de presión para PVC.
ILUSTRACIÓN 75. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
ILUSTRACIÓN 76. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
10
20
30
40
50
60
70
80
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN WILLIAMS TESIS 3 PVC
PRESIONES
CON HAZEN
WILLIAMS
TESIS3 PVC
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 3 PVC
COMPROBACIÓN
DE PRESIONES
TESIS3 PVC
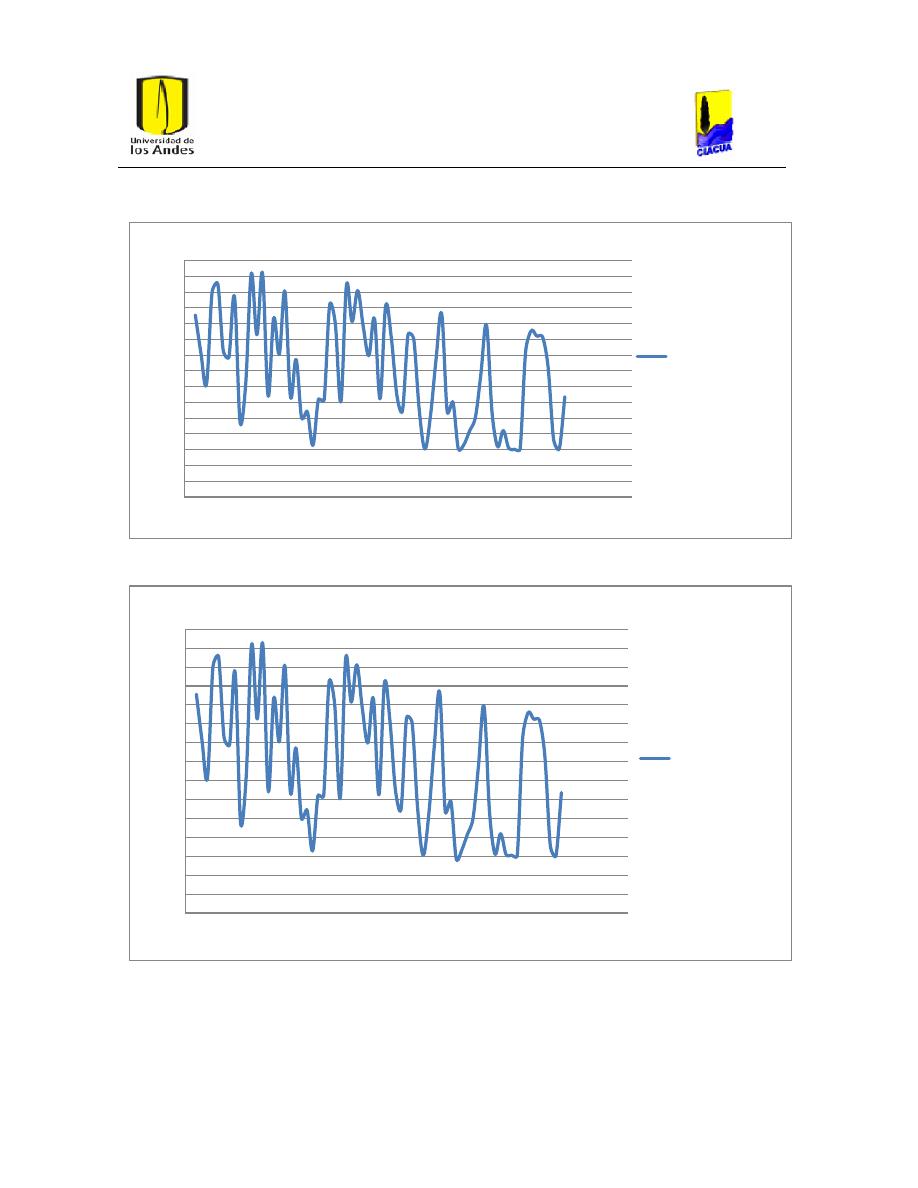
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
77
- Resultados de presiones para PEAD
ILUSTRACIÓN 77. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
ILUSTRACIÓN 78. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 3 PEAD
PRESIONES CON
HAZEN-WILLIAMS
TESIS3 PEAD
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 3 PEAD
COMPROBACIÓN
DE PRESIONES
TESIS3 PEAD

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
78
CAPÍTULO 5 ANÁLISIS DE RESULTADOS
En esta sección, se analizarán los resultados obtenidos en este proyecto. Esto se refiere al
análisis hidráulico de la red y al análisis de costos que presentaron las ecuaciones de Darcy-
Weisbach y Hazen-Williams. El análisis se realizará red por red, mostrando cuales fueron los
efectos de las ecuaciones en la hidráulica y en los costos de diseños con diferentes caudales y
diferentes materiales. Adicionalmente en anexos se pueden encontrar diagramas de Moody
con los factores de fricción de las redes diseñadas para mostrar los resultados del PEAD que
no presento una tendencia clara al diseñar con la ecuación de Darcy-Weisbach frente a la
ecuación de Hazen-Williams. Estos diagramas muestran que la mayoría de los factores de
fricción se encuentran dentro del rango sugerido por Christensen (B.A. Christensen, 2000), es
decir, se encuentran entre
.
5.1 RED SAN VICENTE
Los resultados para caudales normales que presentó esta red fueron bastante inusuales. En
cuanto a los costos de diseño no se vio ninguna tendencia claramente diferencial. Las dos
ecuaciones presentaban costos similares para los 3 materiales de diseño. Esto se debió
principalmente a que en ambos diseños, la mayoría de los diámetros coincidían por lo que el
costo resultaba muy similar al diseñar. Por este mismo motivo, no se pudo observar ningún
efecto hidráulico para la ecuación de Hazen-Williams para ninguno de los materiales, como se
puede observar en la Sección 3.1 Red San Vicente. La causa principal es que si bien en
algunos tramos de tuberías se presentaba una variación de diámetros entre los diseños con la
ecuación de Hazen-Williams y la de Darcy-Weisbach, los tramos más largos y más cercanos a
la fuente de abastecimiento presentaron el mismo diámetro, y dado a que este era el diámetro
más grande y más relevante de la red, es normal que se presente una hidráulica similar entre
ambas ecuaciones.
Para los caudales duplicados ocurrió algo muy similar, el efecto en los costos fue mínimo. Al
igual que con los caudales normales, el efecto de los costos fue insignificante y las
características hidráulicas dentro de la red no presentaron variación significativa entre las
ecuaciones de Hazen-Williams y la ecuación de Darcy-Weisbach. Los resultados obtenidos no
permiten decidir cuál debe ser la ecuación ideal para el diseño de RDAP.
Por el contrario, para los caudales cuadruplicados se notó una variación importante en los
costos, lo cual fue especialmente visible en los costos con el PEAD, que presentaron una
variación extrema. Un análisis detenido de los resultados que arrojaron las dos ecuaciones
muestran que en tramos muy largos de tubería se presentaron diámetros mayores con la
ecuación de Darcy-Weisbach que con la ecuación de Hazen-Williams lo cual repercute de
manera determinante en los costos.
En consideración a que los costos por diámetro-metros de PEAD son los más altos de los tres
materiales, el aumento de los diámetros en un tramo largo de tubería con la ecuación de
Darcy-Weisbach, generó una elevación en los costos de una forma desproporcionada. No
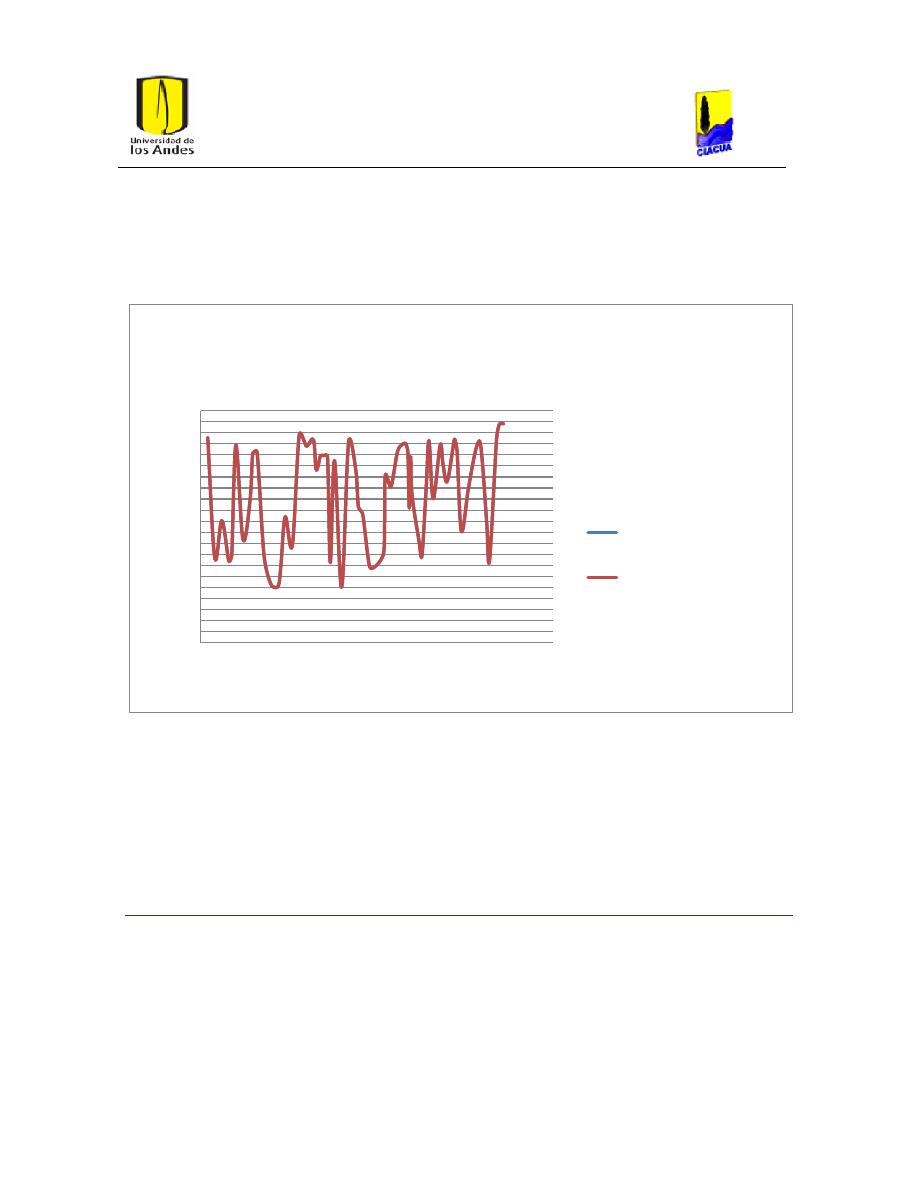
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
79
obstante lo anterior, no se pudo observar una variación dramática en las presiones con este
material para las ecuaciones de Hazen-Williams y Darcy-Weisbach, con excepción de un par
de Nudos que presentaban presiones mayores con la ecuación de Darcy-Weisbach. Sin
embargo, estas presiones no superaban el 7% de diferencia con respecto a la ecuación de
Hazen-Williams.
ILUSTRACIÓN 79. COMPARACIÓN ENTRE EL DISEÑO Y SU COMPROBACIÓN.
Pese a que en PEAD con caudales cuadruplicados se presentó una diferencia de costos
importante y favorable al diseño de Hazen-Williams, sin embargo esto no tuvo ningún efecto
en las presiones de la red a pesar de esto no es recomendable tomar como base este único
resultado, ya que con caudales normales y duplicados para esta red y al observar la tendencia
con las otras redes, es más probable pensar que este fue un caso particular y aislado.
5.2 RED BALERMA
La Red Balerma, fue una de las redes que presentó resultados más relevantes para este
trabajo de tesis. En primera instancia, para caudales normales se vio que los costos
presentaron variación significativa para los tres materiales (Ver Tabla 12) Para el hierro
dúctil, se pudo observar que los costos de diseño resultaban ser mucho más económicos con
la ecuación de Hazen-Williams que con la ecuación de Darcy-Weisbach. Para PVC y PEAD esta
tendencia cambió y se presentaron sobrecostos al diseñar la red con este tipo de materiales al
emplear la ecuación de Hazen-Williams. Estos resultados muestran que aun cuando la
0
3
6
9
12
15
18
21
24
27
30
33
36
39
42
45
48
51
54
57
60
63
0
50
100
150
200
250
Pr
e
si
ó
n
e
n
m
Nudos
Comparación entre diseño y comprobación
para PEAD con caudales cuadruplicados San
Vicente.
Diseño con la ecuación de
Hazen-Williams
Comprobación hidráulica
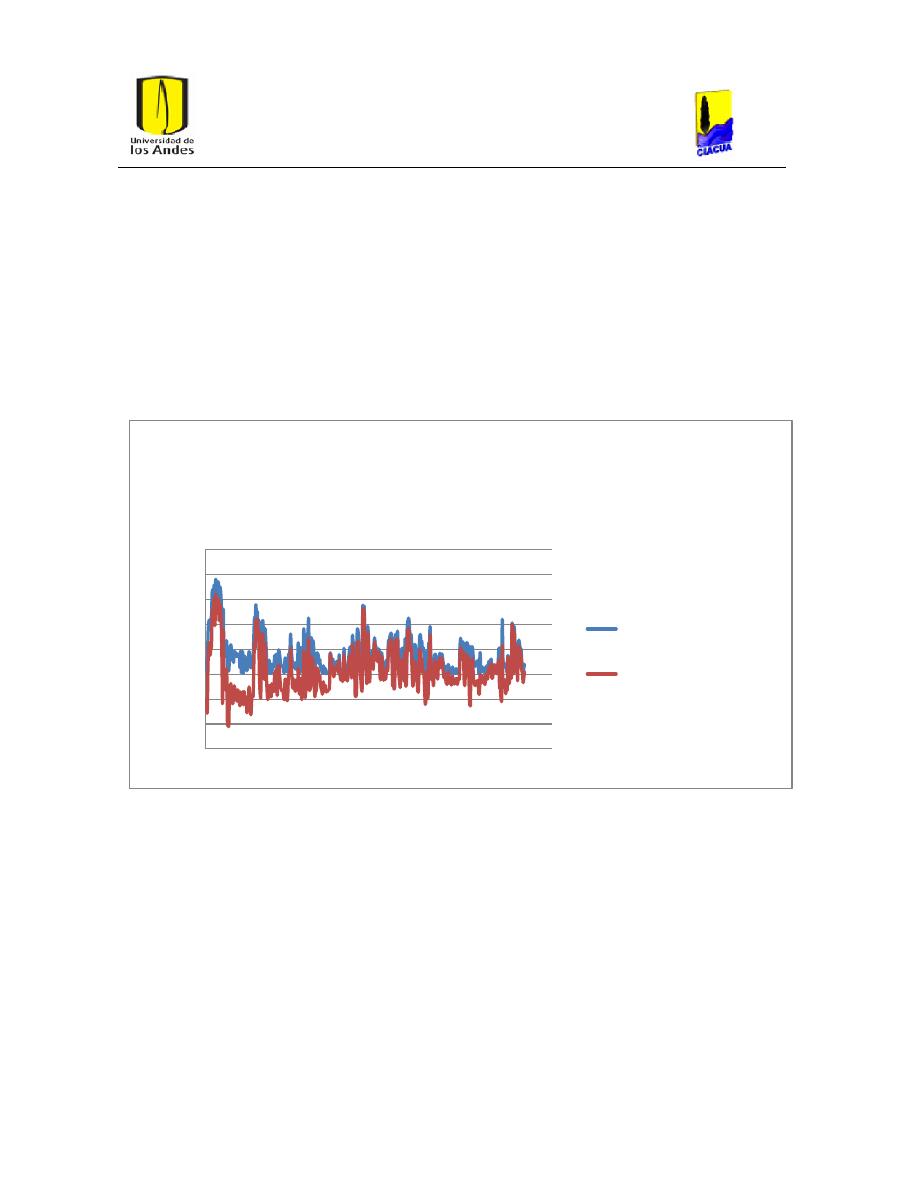
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
80
ecuación de Hazen-Williams presenta una facilidad para obtener las pérdidas por fricción
frente a la ecuación de Darcy-Weisbach, no siempre se obtienen costos más bajos.
El análisis hidráulico de los caudales normales arrojó resultados importantes para hierro
dúctil y para PVC. Para el primero de estos materiales, al realizar la comprobación hidráulica
de la red diseñada con la se ecuación de Hazen-Williams se pudo observar que en muchos de
los Nudos (más del 50%) presentaba incumplimiento en la presión mínima de los Nudos
(presión mínima de la red era de 15 m), llegando a presentar en varios nudos presiones
negativas (Ilustración 39). Reflejando que el diseño con la ecuación con Hazen-Williams
pese a que se obtiene un diseño más económico, no cumple con los requerimientos legales de
presión.
ILUSTRACIÓN 80. COMPARACIÓN ENTRE EL DISEÑO Y SU COMPROBACIÓN.
Para el PVC se presentó resultado opuesto al encontrado en el hierro dúctil. Al realizar la
comprobación del diseño de Hazen-Williams se presentó una sobrestimación de las presiones
en muchos de los nudos llegando a alcanzar una sobrestimación cercana al 25% trabajando
con el mismo programa y utilizando la misma flecha de diseño (Ver Ilustración 41).Este
comportamiento no fue único, y se presentó en esta red con los diferentes caudales y en otras
redes como se va a observar más adelante. Para este caso, esta sobrestimación de las
presiones en los Nudos se vio reflejada en los sobrecostos con respecto a la ecuación de
Darcy-Weisbach. Si bien, este problema de la sobrestimación de las presiones no presenta un
riesgo para la población abastecida, si constituye un problema serio para el diseñador del
proyecto, ya que se incurre en un sobrecosto para el diseño de la red y por lo tanto deja de ser
un diseño optimizado que es quizás el segundo objetivo más importante al diseñar una red de
distribución de agua potable.
-30
-15
0
15
30
45
60
75
90
0
100
200
300
400
500
Pr
e
si
ó
n
e
n
m
Nudos
Comparación entre diseño y su respectiva
comprobación hidráulica con hierro dúctil
para Balerma utilizando caudales normales
Diseño con la ecuación de
Hazen-Williams
Comprobación hidráulica

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
81
El comportamiento del PEAD presentó una leve sobreestimación de presiones cuando se
realizó la comprobación hidráulica de la red diseñada con la ecuación de Hazen-Williams (Ver
Ilustración 43).Si bien, no fue un efecto tan notorio como el que se pudo observar en PVC, si
se vio reflejado en un sobrecosto en el diseño realizado con la ecuación empírica.
Para el comportamiento con los caudales duplicados, la tendencia que se presentaran costos
más altos con la ecuación de Hazen-Williams se mantuvo para los materiales de PVC y PEAD
(Ver Tabla 21). En el caso del hierro dúctil se registra un comportamiento anómalo ya que
también sus costos se vieron incrementados con lo cual todos los costos fueron más altos
para la ecuación de Hazen-Williams. A pesar de esto y al igual que en el caso particular de la
Red San Vicente, los sobrecostos de la ecuación de Hazen-Williams con hierro dúctil fueron un
caso particular y como se podrá observar más adelante con otras redes, es un sobrecosto que
no se repite.
Para el análisis hidráulico se presentaron resultados similares a los que se presentaron con
caudales normales. El diseño de la red con la ecuación de Hazen-Williams con hierro dúctil,
volvió a presentar presiones inferiores a la presión mínima trabajada durante el proyecto.
Este efecto puede deberse a que la ecuación de Hazen-Williams esté subestimando las
pérdidas por fricción, confirmando lo estipulado por Liou en 1998 o que el coeficiente de
Hazen-Williams que se está trabajando sea equivocado y esté representando las
características del material mucho más lisas de lo que realmente son. Por lo anterior, podría
afirmarse que es un error trabajar únicamente con un coeficiente de Hazen-Williams, ya que
como mostró Liou (Liou, 1998) en sus investigaciones, este coeficiente presenta una variación
dependiendo del número de Reynolds y la rugosidad relativa de la tubería.
En el caso del hierro dúctil, la relación de costos que genera el modelo se debió a que en
algunos tramos de las tuberías se presentaron diámetros mayores que los que se presentaban
con la ecuación de Darcy-Weisbach. A pesar de que se presentaban diámetros mayores, estos
no se encontraban localizados en los tramos vitales de la tubería, por lo que se seguían
presentando presiones inferiores a la mínima establecida en el proyecto.
Por su parte, para el PVC se presentó la misma tendencia que con los caudales normales. Es
decir, se presentó una sobrestimación de las presiones en muchos de los Nudos de las tuberías
con la ecuación de Hazen-Williams (Ver Ilustración 107). Esta sobrestimación se hizo más
evidente con los caudales duplicados, llegando a alcanzar una sobrestimación de las presiones
cercana al 30%. Al igual que con los caudales normales esta sobrestimación de las presiones
se vio reflejada en un sobrecosto, llevando a que los diseños realizados con la ecuación de
Darcy-Weisbach resultaran más económicos y por lo tanto más eficientes.
Finalmente en el caso del material PEAD se presentaron prácticamente las mismas tendencias
que las encontradas con los caudales normales. Es decir, se encontró que existía una pequeña
sobrestimación de presiones, pero no tan evidente ni con la misma magnitud que la que es
posible observar en el PVC (Ver Ilustración 109) y se volvió a observar que los costos con
caudales duplicados mostraban diseños más costosos con la ecuación de Hazen-William.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
82
Para los caudales cuadruplicados se volvió a evidenciar un diseño mucho más económico en
hierro dúctil al utilizar la ecuación de Hazen-Williams (Ver Tabla 22) y se mantuvo la
tendencia de obtener diseños más costosos con la ecuación de Hazen-Williams para PVC y
PEAD.
En cuanto a la hidráulica de la red, se pudo observar que para hierro dúctil la tendencia de
presiones inferiores a la presión mínima se seguía presentando cuando se realizaba la
comprobación hidráulica de la red diseñada con la ecuación de Hazen-Williams. Al observar
la gráfica de presiones con Hazen-Williams contra la gráfica de su comprobación (Ver
Ilustración 111 e Ilustración 112), es muy evidente observar que los diseños con la
ecuación de Hazen-Williams están subestimando las pérdidas por fricción ya sea por utilizar
un coeficiente de Hazen-Williams incorrecto o por la naturaleza empírica de la ecuación
(trabajada por fuera de sus rangos de cumplimiento). En cualquiera de los casos, queda
evidenciado que en la red Balerma no es justificable utilizar la ecuación de Hazen-Williams
para diseños con hierro dúctil solo por su facilidad de manejo y sus bajos costos constructivos,
ya que como quedó evidenciado con los resultados, los diseños no son apropiados e
incumplen con las presiones mínimas que la normatividad exige.
Para PVC se mantuvo el comportamiento visto con los caudales normales y los caudales
duplicados. Los registros muestran que en algunos Nudos de la red se están presentando
sobrepresiones, en contraste con las que arrojaba originalmente el diseño utilizando la
ecuación de Hazen-Williams. Esto significa que en este caso, la ecuación de Hazen-Williams
está sobrestimando las pérdidas por fricción en la tubería, lo que lleva a que se obtengan
diámetros más grandes a los que se obtendrían con la ecuación de Darcy-Weisbach y con ello,
se genere un sobrecosto al utilizar la ecuación de Hazen-Williams, como se puede observar en
las tablas de costos de Balerma.
Lo anterior permite concluir que por lo menos para la red Balerma, utilizar la ecuación de
Hazen-Williams es un error ya que genera un sobre costo con respecto a los diseños de la
ecuación de Darcy-Weisbach.
En el caso del PEAD, se repitió la tendencia que se presentaba en los caudales normales y
duplicados. Se presenta una pequeña sobrestimación de las presiones por parte de la ecuación
de Hazen-Williams; sin embargo esta no representa una diferencia hidráulica demasiado
relevante. En los costos, si bien el diseño con la ecuación con Darcy-Weisbach resulta más
económico, el efecto no tiene la misma magnitud que el observado en hierro dúctil y en PVC.
Con base a los análisis de este material, es difícil afirmar o rechazar la ventaja de una ecuación
frente a la otra en cuanto a los diseños de esta red.
Para finalizar, los resultados en los diseños de la red Balerma muestran que el diseño con
ambas ecuaciones resulta en una variación importante de la hidráulica y de los costos. Los
efectos más importantes se vieron con el hierro dúctil y el PVC, siendo el primer material más
económico en sus diseños pero incumpliendo los requerimientos de presión y el segundo
entregando redes sobre diseñadas. Mientras que con el PEAD se vieron efectos de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
83
sobrestimación de pérdidas muy leves y las desventajas o ventajas de una ecuación frente a la
otra no fueron evidentes para este material.
5.3 RED BOGOTÁ-CAZUCÁ
Los resultados obtenidos para esta red fueron similares a los que se obtuvieron con la red
Balerma, con lo cual se empieza a evidenciar que el uso de la ecuación de Hazen-Williams si
tiene un efecto indeseado en los costos y en la hidráulica de las redes de acueducto.
Para caudales normales, esta red presentó un costo menor cuando se diseñó con hierro dúctil,
utilizando la ecuación de Hazen-Williams, respecto de los costos que arrojó la ecuación Darcy-
Weisbach. Por su parte los costos más económicos para los diseños con PVC y PEAD se
encontraron al utilizar la ecuación de Darcy-Weisbach (ver Tabla 13). En cuanto a la
hidráulica de la red, los resultados presentaron comportamientos similares para los tres
materiales respecto de los encontrados en la Red Balerma.
Para la red diseñada con hierro dúctil y caudales normales, se presentaron diferencias
importantes de costos con la ecuación de Darcy-Weisbach y con la ecuación de Hazen-
Williams, siendo esta última mucho más económica. Hidráulicamente la red presentó el
mismo comportamiento que la red Balerma. Al realizar la comprobación de presiones de la
red diseñada con la ecuación de Hazen-Williams, quedó evidenciada una vez más que pese a
que el diseño resulta más económico con esta ecuación, los resultados revelan un
incumplimiento con el requerimiento de presión mínima (Ver Ilustración 46).Esto confirma
la tendencia de que los diseños con la ecuación de Hazen-Williams al utilizar hierro dúctil,
presentan un incumplimiento en las presiones mínimas, y que a pesar de que presenta
menores costos no es una razón válida para ignorar la normatividad hidráulica vigente.
Para el diseño con PVC, los costos muestran que el diseño con la ecuación de Darcy-Weisbach
es más económico que el diseño con la ecuación de Hazen-Williams (para caudales normales).
Hidráulicamente las tendencias que se presentaron en la red Balerma se repitieron en el
diseño de la Red Bogotá-Cazucá. Los resultados para esta red mostraron que los diseños con
la ecuación de Hazen-Williams al ser comprobados hidráulicamente con la ecuación de Darcy-
Weisbach están sobre diseñando la red, es decir, las presiones de la red eran mayores en la
comprobación que en el diseño original (Ver Ilustración 50). Si bien, no se incumple con las
presiones mínimas, se está sobre diseñando la red lo cual tiene un impacto en los costos con
un sobredimensionamiento de los mismos, al ser el diseño con la ecuación de Hazen-William
más costoso que el diseño realizado con la ecuación de Darcy-Weisbach.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
84
ILUSTRACIÓN 81. COMPARACIÓN ENTRE EL DISEÑO Y SU COMPROBACIÓN.
Para PEAD, no se vio un efecto evidente en los diseños con los caudales normales. Al realizar
la comprobación hidráulica del diseño realizado con la ecuación de Hazen-Williams las
presiones no variaron demasiado, con un máximo del 5 % frente a los diseños originales. En
cuanto a costos, se evidenció que el diseño con la ecuación de Hazen-Williams presentaba un
mayor costo que el diseño realizado con la ecuación de Darcy-Weisbach. Lo que lleva a pensar
que la ventaja de solución rápida de la ecuación de Hazen-Williams se ve más que
compensada por el diseño económico que presentó la ecuación de Darcy-Weisbach, sin
embargo es importante mencionar que esta diferencia de costos no es tan grande.
Para los caudales duplicados y pese a que los costos aumentaron, se presentó el mismo
comportamiento que en caudales normales. En otras palabras, al comparar los diseños con
hierro dúctil se puede ver que el diseño realizado con la ecuación de Hazen-Williams es
mucho más económico que el diseño que se realizó con la ecuación de Darcy-Weisbach. A su
vez se puede ver que para PVC la diferencia de costos favorece al diseño con Darcy-Weisbach
mientras que para PEAD la diferencia es tan pequeña entre los 2 diseños que no muestra un
predomino real cuando se enfrentan los costos.
La hidráulica conservó las características vistas en los caudales normales, en otras palabras, el
diseño con hierro dúctil utilizando la ecuación de Hazen-Williams presentó presiones
inferiores a las exigidas por este trabajo (ver Ilustración 122) (Al realizar la comprobación
0
20
40
60
80
100
120
140
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
Comparación entre el diseño y su
comprobación hidráulica con PVC para
Bogotá-Cazucá.
Diseño con la ecuación de
Hazen-Williams
Comprobación hidráulica

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
85
hidráulica con la ecuación de Darcy-Weisbach). Estos resultados permiten confirmar lo visto
en la red Balerma con hierro dúctil, es decir, los diseños con la ecuación de Hazen-Williams
para hierro dúctil presentan costos muy inferiores a los diseños con la ecuación de Darcy-
Weisbach; sin embargo estos diseños no cumplen con los requerimientos hidráulicos mínimos
establecidos por el autor por lo que el diseño debe de ser descartado.
Para PVC se repitió la tendencia que se había visto anteriormente con los caudales normales
de esta red y con la red Balerma. Se presentaron sobrepresiones al realizar la comprobación
hidráulica del diseño realizado con la ecuación de Hazen-Williams (ver Ilustración 123 e
Ilustración 124). Lo que se puede analizar es que la ecuación de Hazen-Williams está
sobrestimando las pérdidas por fricción, es decir el opuesto del caso del hierro dúctil. Esto a
su vez está repercutiendo en los costos de diseño de esta red, causando que los diseños con la
ecuación de Hazen-Williams presente costos más elevados que los generados al diseñar con la
ecuación de Darcy-Weisbach.
En el caso del PEAD no se logró evidenciar una sobrestimación o subestimación de presiones
por parte de la ecuación de Hazen-Williams. Así mismo no se logró ver que la diferencia de
precios fuera demasiado grande entre el diseño realizado con la ecuación de Darcy-Weisbach
y la ecuación de Hazen-Williams. En otras palabras no se pudo evidenciar un efecto negativo
o positivo por parte de la ecuación de Hazen-Williams al diseñar esta red con PEAD,
concordando con los resultados obtenidos en la red Balerma, que presentó solo una leve
sobrestimación de las presiones y una leve diferencia en los costos de diseño.
Para finalizar se va a analizar el último caso de esta red que fue el de los caudales
cuadruplicados. En lo que a costos se refiere, se mantuvo la tendencia observada para hierro
dúctil, es decir, la red diseñada con la ecuación de Hazen-Williams presento un diseño más
económico que la red diseñada con la ecuación de Darcy-Weisbach. Para el caso del PVC y el
PEAD se presentaron unas pequeñas variaciones con respecto a los resultados obtenidos
hasta el momento. Para ambos materiales los diseños con la ecuación de Hazen-Williams
resultaron más baratos que los diseños realizados con la ecuación de Darcy-Weisbach.
En la parte hidráulica los resultados de hierro dúctil continuaron con el comportamiento
presentado hasta el momento. En otras palabras, pese a que el diseño resultante con la
ecuación de Hazen-Williams resulto bastante más barato que el realizado con la ecuación de
Darcy-Weisbach, al realizar la comprobación hidráulica del mismo se evidenció que este no
cumplía con las presiones mínimas de la red, llegando incluso a presentar Nudos con
presiones negativas (ver Ilustración 129). Sin embargo y a diferencia de los casos con
caudales normales y duplicados, en este caso se vio mucho más agravado el problema,
presentando presiones debajo de la reglamentaria en muchos más Nudos y presiones
negativas en por lo menos 10 Nudos más con respecto a los caudales duplicados y normales.
Esto lleva en principio a pensar que la demanda en cada uno de los Nudos juega un rol
importante a la hora de mostrar los efectos hidráulicos causados por el uso de la ecuación de
Hazen-Williams para el caso de hierro dúctil.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
86
En el caso del PVC cuando se ven los resultados con caudales cuadruplicados, es posible
evidenciar una vez más que los diseños con la ecuación de Hazen-Williams al ser evaluados
con la ecuación de Darcy-Weisbach, presentan presiones más elevadas a las que normalmente
arrojaba el modelo original ( ver Ilustración 132). Extrañamente esta sobrestimación de las
pérdidas no se vio reflejada en los costos de la red, siendo un poco más económica la red
diseñada con la ecuación de Hazen-Williams, resaltando que esta diferencia de costos es tan
baja que es prácticamente insignificante. No obstante, si bien desde los costos no representa
una ventaja o una desventaja, desde el punto de vista hidráulico se logra evidenciar una vez
más que la ecuación de Hazen-Williams está sobrestimando las presiones en muchos de los
Nudos y el uso de la misma para diseñar debe realizarse con sumo cuidado.
Para el último material PEAD, la hidráulica se comportó de forma muy similar a lo que se
podía evidenciar con caudales normales y duplicados, es decir, no se logra observar un efecto
hidráulico claro por parte de la ecuación de Hazen-Williams cuando se evalúa su hidráulica
con la ecuación de Darcy-Weisbach. Si bien se presentó una diferencia de precios entre los
diseños con la ecuación de Darcy-Weisbach y la ecuación de Hazen-Williams, esta diferencia
de precios era insignificante cuando se observan los costos totales para este material, en otros
términos la magnitud de la diferencia no es relevante a la hora de escoger una ecuación frente
a la otra. Esta evidencia junto con la observada en las redes anteriores parece indicar que no
hay un efecto positivo o negativo al diseñar con la ecuación de Hazen-Williams para el PEAD,
independiente del caudal demandado en cada uno de los Nudos.
5.4 RED R28
Los resultados de esta red al poseer menos Nudos fue más fácil de analizar y de evidenciar los
cambios. Los comportamientos observados continuaron con las tendencias vistas en las redes
anteriores (con excepción de la red San Vicente, que como se nombró anteriormente presente
resultados anómalos).
Cuando se observaban los resultados con caudales normales es posible evidenciar que los
costos con hierro dúctil siguen presentando el mismo comportamiento que con las redes
Balerma y Bogotá-Cazucá, presentando un costo menor en el diseño con la ecuación de Hazen-
Williams que con la ecuación de Darcy-Weisbach. Para PVC y PEAD si bien los diseños con la
ecuación de Darcy-Weisbach presentaron costos menores que los diseñados con la ecuación
de Hazen-Williams, esta diferencia fue bastante pequeña, en especial para el caso del PEAD
donde la magnitud de la diferencia fue prácticamente despreciable.
Para hierro dúctil, cuando se realiza su comprobación hidráulica se evidencia claramente que
la ecuación de Hazen-Williams no entrega diseños que cumplan con los requerimientos
mínimos de presión (ver Ilustración 53). En otros términos, se están subestimando las
pérdidas por fricción con la tubería. Este comportamiento no es único y como se ha observado
anteriormente se ha presentado en la red Balerma y en la red Bogotá-Cazucá. Demostrando
una vez más que pese a que esta ecuación empírica arroja diseños considerablemente más
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
87
económicos que la ecuación físicamente basada, sus diseños incumplen con los
requerimientos hidráulicos y por lo tanto sus diseños no deben tomarse en consideración.
ILUSTRACIÓN 82. COMPARACIÓN ENTRE EL DISEÑO Y SU COMPROBACIÓN.
El caso del PVC continuó con la tendencia observada en las redes anteriores, presentando
sobrestimación de presiones con el diseño de la ecuación de Hazen-Williams para caudales
normales (ver Ilustración 55); aunque esta sobrestimación no fue de la misma magnitud que
la que se presentó en las redes Balerma y Bogotá-Cazucá, sirve para evidenciar un efecto de
sobrestimación de presiones por parte de la ecuación de Hazen-Williams. Si bien los costos de
esta red fueron bastante similares cuando se compararon la ecuación empírica y la
físicamente basada, este sobrecosto por parte de la primera, puede explicar la sobrestimación
presentada en las presiones.
En el PEAD, al analizar los resultados con caudales normales es posible ver que
hidráulicamente no se evidencia un comportamiento negativo cuando se comprueba la
ecuación de Hazen-Williams (ver Ilustración 57).Esto quiere decir que no se presentan
presiones por debajo de la mínima establecida en este trabajo, ni tampoco se presenta un
sobrestimación importante de las presiones. A su vez, cuando se observan los costos entre la
ecuación empírica y la ecuación físicamente basada, tampoco se ve una diferencia importante
en los costos. Este comportamiento parece mostrar que no hay una diferencia importante en
los diseños con la ecuación empírica frente a la ecuación físicamente basada.
0
5
10
15
20
25
30
35
40
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
Comparación entre el diseño y su
comprobación hidráulica con hierro dúctil
para R28 utilizando caudales normales.
Diseño con la ecuación
de Hazen-Williams
Comprobación
hidráulica

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
88
Los resultados con caudales duplicados muestran una vez más que los costos con hierro dúctil
presentan una diferencia importante, siendo otra vez el diseño con la ecuación de Hazen-
Williams mucho más económico. Para PVC se presentó un diseño más económico cuando se
utilizó la ecuación de Darcy-Weisbach; sin embargo es una diferencia de costos relativamente
pequeña, que va a ser relevante cuando se analice la hidráulica. Finalmente en el PEAD no se
evidencia una diferencia importante de costos (ver Tabla 25), lo que indica junto con los
resultados de Balerma, Bogotá-Cazucá y esta red con caudales normales, que los diseños para
PEAD con las ecuaciones de Hazen-Williams y Darcy-Weisbach no presentan diferencias
significativas.
Hidráulicamente, el resultado con hierro dúctil presentó el mismo comportamiento que se ha
ido evidenciando en la mayoría de las redes, es decir, la comprobación hidráulica del diseño
con la ecuación de Hazen-Williams arroja presiones inferiores a la mínima que se ha
establecido (ver Ilustración 139). Aunque para este caso duplicar el caudal no causó que se
amplificara este efecto, es importante mostrar que el efecto de diseñar con hierro dúctil
utilizando la ecuación de Hazen-Williams, produce efectos negativos en la hidráulica e
incumple con los requerimientos mínimos para diseñar una red.
El PVC mostró sobrestimación de la presiones en diferentes Nudos al utilizar el diseño con la
ecuación de Hazen-Williams (ver Ilustración 141); estas presiones fueron un poco más
elevadas que cuando se utilizaron caudales normales, y como se nombró anteriormente, esta
sobrestimación de las presiones fue producto de que se seleccionaran diámetros mayores a
los que realmente se necesitaban, causando que se elevaran los costos de la red. Esta
tendencia no es única y como se puede observar en retrospectiva, esta no es la única red que
presenta este tipo de comportamiento; esto lleva a que los diseños con Hazen-Williams
utilizando PVC, no incumplen con la presión mínima de la red pero la sobre diseñan y pueden
ser descartados como diseños óptimos de RDAP.
Con el PEAD pese a que se duplicaron los caudales de los Nudos, la tendencia no cambio. Esto
implica que no se vio ningún efecto hidráulico al realizar la comprobación hidráulica del
diseño con la ecuación de Hazen-Williams. A su vez, no se pudo evidenciar una diferencia
notoria de los costos al comparar los diseños con ambas ecuaciones. Si bien en este caso
resultó ser más económico diseñar con la ecuación de Hazen-Williams la diferencia fue tan
pequeña que es prácticamente igual al costo con la ecuación de Darcy-Weisbach (ver Tabla
25).
Para caudales cuadruplicados los costos presentaron un comportamiento similar que el
observado en todo este trabajo, hierro más barato con el diseño de Hazen-Williams, PVC más
económico para la ecuación de Darcy-Weisbach y PEAD no presentó una variación
importante. Como es evidente al aumentar tanto los caudales de los Nudos esto hace que los
costos con respecto a caudales normales y duplicados sean mayores; sin embargo como se
acaba de nombrar la tendencia de los mismos se mantuvo.
Hidráulicamente el hierro dúctil no cambio demasiado con respecto a los resultados con
caudales normales y duplicados. Si bien se siguió presentando la subestimación de presiones

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
89
al realizar la comprobación hidráulica del diseño con la ecuación de Hazen-Williams, este
efecto no se vio incrementado al cuadruplicar los caudales como se había visto en las otras
redes de este trabajo (ver Ilustración 146). Aun cuando no hubo una diferencia hidráulica
entre el análisis de los diferentes caudales para este material, los costos si se vieron
modificados, y resultó ser mucho más económico diseñar con la ecuación de Hazen-Williams,
y a diferencia de la hidráulica, la variación de costos en los diseños fue bastante importante.
Al igual que con el hierro dúctil, para el caso del PVC no se presentaron diferencias
significativas en cuando a las presiones con respecto a los caudales normales y duplicados
(ver Ilustración 149). A pesar de esto se pudo seguir evidenciando la sobrestimación de
presiones en algunos Nudos al realizar la comprobación hidráulica el diseño realizado con la
ecuación de Hazen-Williams. Cuando se comparan estos resultados con los costos para este
material, se hace notorio que el sobre diseño de la red R28 por parte de la ecuación de Hazen-
Williams causa que se aumenten estos costos (pues utiliza diámetros mayores a los que un
diseño con la ecuación de Darcy-Weisbach utiliza), llevando a que el diseño con esta ecuación
empírica deje de ser óptimo y sea descartable frente al diseño realizado con la ecuación
físicamente basada de Darcy-Weisbach.
Para el PEAD no se profundizara demasiado en el análisis, ya que repitió el mismo
comportamiento en costos y en hidráulica que con caudales normales y duplicados. Es decir,
no se vio una diferencia grande entre los costos cuando se compararon las dos ecuaciones, e
hidráulicamente la ecuación de Hazen-Williams tampoco incumplió con los requerimientos
mínimos ni con sobrepresiones cuando se realizó su comprobación hidráulica con la ecuación
de Darcy-Weisbach.
5.5 RED TESIS 1
Los resultados de esta red mostraron un cambio en el comportamiento hidráulico con los
diseños del PVC con respecto a lo observado en las redes anteriores. A su vez esta red hizo
evidente que el aumento de la demanda base (caudal) en cada uno de los Nudos si repercute
en los efectos hidráulicos cuando se diseña con la ecuación de Hazen-Williams para el caso del
hierro dúctil. El efecto del PEAD se mantuvo para todos los caudales.
En los resultados con caudales normales se logró evidenciar que los costos presentaron la
tendencia de las otras redes con excepción de PEAD, es decir, para hierro dúctil la red Tesis 1
presentó un diseño más económico cuando se diseñó con la ecuación de Hazen-Williams; a su
vez el diseño con PVC resultó ser más económico con la ecuación de Darcy-Weisbach, aunque
no tanto como en otras redes con los caudales normales; finalmente vino el caso de PEAD que
presentó costos mucho más económicos al diseñar con Darcy-Weisbach.
Hidráulicamente la comprobación del diseño realizado con la ecuación de Hazen-Williams
para hierro dúctil presentó incumplimiento de presión en un solo nudo y fue de menos de 1 m
(ver Ilustración 60). Este resultado es extraño si se compara con los resultados obtenidos en
otras redes, ya que el efecto de subestimación de las presiones no resultó tan evidente. Aun
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
90
así, el hecho de que se presente incumplimiento indica que los diseños con la ecuación de
Hazen-Williams para hierro dúctil son peligrosos de utilizar.
El PVC cambio bastante con respecto a los resultados obtenidos en Balerma, Bogotá-Cazucá y
R28, ya que en este caso no se evidenció una sobrestimación de las presiones en la
comprobación hidráulica del diseño realizado con la ecuación de Hazen-Williams.
Curiosamente los costos de la red mantuvieron la constante del trabajo y resultaron ser más
económicos cuando se trabajó con la ecuación de Darcy-Weisbach, aun cuando no fue una
diferencia tan grande.
En el PEAD para caudales normales se pudo evidenciar que aunque los costos resultaron
mucho más baratos al utilizar la ecuación de Darcy-Weisbach, la hidráulica con la ecuación de
Hazen-Williams no presente sobrestimación o incumplimiento de las presiones (ver
Ilustración 64); estos resultados permiten concluir que aunque la hidráulica para las dos
ecuaciones cumple con la normativa y no causa sobrepresiones dentro de la red, la
distribución de diámetros entre los diseños es diferente, causando que el diseño con la
ecuación de Hazen-Williams resulto más costoso que el de la ecuación de Darcy-Weisbach.
ILUSTRACIÓN 83.COMPARACIÓN ENTRE EL DISEÑO Y SU COMPROBACIÓN.
Los resultados con caudales duplicados mostraron que los costos para los 3 materiales
presentaron un comportamiento inusual. Esto se ve reflejando en que la diferencia de costos
entre las ecuaciones de diseño fue muy pequeña e insignificante (ver Tabla 27). Sin embargo,
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
Comparación entre el diseño y su
comprobación hidráulica con PEAD para Tesis
1 con caudales normales.
Diseño con la ecuación de
Hazen-Williams
Comprobación hidráulica

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
91
este comportamiento pareció aislado dentro de este estudio y no representa una tendencia
normal en los diseños de esta red.
Extrañamente al analizar el comportamiento hidráulico del hierro dúctil, se hizo mucho más
evidente la subestimación de las presiones por parte de la ecuación de Hazen-Williams (ver
Ilustración 156); en este caso se vio que el aumento de los caudales base de cada nudo si
ejerció un efecto, y si se comparan las presiones que arroja el diseño original con la ecuación
de Hazen-Williams frente a su comprobación hidráulica, se puede ver que esta ecuación está
subestimando de forma alarmante las presiones en los Nudos, especialmente en los Nudos
críticos de la red.
El PVC siguió el comportamiento de esta red con caudales normales, es decir, cuando se
realizó la comprobación hidráulica del diseño que utilizó la ecuación de Hazen-Williams no se
pudo evidenciar incumplimiento de las presiones mínimas o sobrestimación de presiones
importantes (ver Ilustración 158). Y como se nombró anteriormente, para caudales
duplicados tampoco se logró evidenciar una diferencia importante en los costos cuando se
comparó la ecuación de Darcy-Weisbach con la ecuación de Hazen-Williams.
Los diseños con PEAD no presentaron sobrestimación de las pérdidas o incumplimiento de la
presión mínima establecida cuando se realizó la comprobación hidráulica del diseño que
utilizó la ecuación de Hazen-Williams (ver Ilustración 160). Los costos tampoco presentaron
una gran diferencia entre los diseños con ambas ecuaciones. Todos estos resultados, junto con
los resultados que se han obtenido de las otras redes corroboran el hecho de que no se
evidencia un efecto negativo o benéfico al utilizar la ecuación de Hazen-Williams para PEAD.
Finalmente para caudales cuadruplicados, los costos presentaron una variación importante.
Para empezar se hizo evidente que para hierro dúctil y PVC los diseños con la ecuación de
Hazen-Williams resultaron más económicos que los diseños que utilizaron la ecuación de
Darcy-Weisbach. Mientras que para los diseños del PEAD no se vio una diferencia grande en
los diseños de las 2 ecuaciones, (Ver Tabla 28).
En el análisis hidráulico del hierro dúctil, se pudo ver que el aumento de los caudales causó
que el efecto de la ecuación de Hazen-Williams se hiciera evidente, al revisar la comprobación
hidráulica del diseño que utilizó la ecuación de Hazen-Williams (ver Ilustración 163); no
solo se presentó en varios Nudos la subestimación de presiones, sino que varios de ellos
incumplieron con la presión mínima que se estableció en la metodología de este proyecto.
Adicionalmente en los costos se vio que el diseño con la ecuación de Hazen-Williams resultaba
más tentador al presentar menores costos. Todo esto se ha venido repitiendo en las demás
redes, lo que muestra una vez más que no es casualidad que la ecuación de Hazen-Williams
arroje diseños más baratos pero que incumplen con los requerimientos hidráulicos
establecidos. A su vez se confirma que un aumento importante en las demandas bases de los
nudos causa que este efecto se vea incrementado.
Para el PVC se vio evidenciado que el diseño con la ecuación de Hazen-Williams resultó ser
considerablemente más económico que el homólogo con la ecuación de Darcy-Weisbach. Pese

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
92
a obtener estos resultados en costos, hidráulicamente se observo que la ecuación de Hazen-
Williams no presentó incumplimiento en la presión mínima de este trabajo, ni presento
sobrepresiones en sus nudos. Es claro que al igual que en un caso anterior, la distribución de
diámetros en la red entre las dos ecuaciones sea la causante de la diferencia de costos.
Finalmente, y como se viene presentando en todo este trabajo de grado, los resultados para
PEAD no presentaron ninguna diferencia en costos para las dos ecuaciones. Hidráulicamente
tampoco se pudo establecer un efecto de subestimación o sobrestimación de las presiones al
utilizar la ecuación de Hazen-Williams (ver Ilustración 169). Esto parece estar demostrando
que no existe un efecto entre diseñar con la ecuación de Hazen-Williams o la ecuación de
Darcy-Weisbach utilizando PEAD, salvo una pequeña diferencia de precios que no resulta
significativa si se compara con el costo total de la red.
5.6 RED TESIS 2
Los resultados de la red Tesis 2 mostraron un comportamiento parecido al que se obtuvo con
la red Tesis 1. Los costos para los tres caudales siempre mostraron un diseño más económico
por parte de la ecuación de Hazen-Williams; el comportamiento del PVC y el PEAD fueron
variables. La hidráulica de la red continúo su comportamiento con el hierro dúctil. Mientras
que lo observado en red Balerma, Bogotá-Cazucá y R28 no se presentó para PVC y en el caso
de PEAD los costos presentaron una variabilidad entre los diferentes caudales.
Los costos con caudales normales mostraron que el diseño de la red utilizando hierro dúctil
con la ecuación de Hazen-Williams resultaba más económico que el diseño con la ecuación de
Darcy-Weisbach. El PVC mostró un costo ligeramente más económico para la ecuación
empírica que para la ecuación físicamente basada. Finalmente para PEAD se presentó una
diferencia de costos entre las dos ecuaciones; sin embargo aunque el valor numérico de la
diferencia parezca alto (ver Tabla 16), si se observa con detenimiento se ve que es una
diferencia mínima con respecto a la magnitud global del costo de la red.
Hidráulicamente el hierro dúctil presentó la tendencia que se ha visto a lo largo de este
proyecto de grado. Cuando se realizó la comprobación hidráulica del diseño que utilizó la
ecuación de Hazen-Williams, se puede observar que un par de Nudos se encuentran por
debajo de la presión mínima establecida en este trabajo (ver Ilustración 67). Al presentarse
este comportamiento, es posible afirmar que la ecuación de Hazen-Williams está
subestimando las pérdidas por fricción ya sea porque su coeficiente de 140 está
representando al material más liso de lo que realmente es o por que al ser una ecuación
empírica se está saliendo de sus rangos óptimos de cumplimiento ( zona de transición del
flujo turbulento). Este comportamiento parece estar relacionado con el bajo costo de la red,
ya que al calcular erróneamente las pérdidas en la tubería asigna un diámetro más pequeño
que el que asignaría la ecuación físicamente basada de Darcy-Weisbach, llevando a que los
costos con la ecuación empírica sean menores.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
93
El PVC presentó un comportamiento diferente al que se observó en red Balerma, Bogotá-
Cazucá y R28, pero presentó un comportamiento similar al observado en San Vicente y Tesis
1. Cuando se realizó la comprobación hidráulica al diseño de Hazen-Williams, no se puede
observar un incumplimiento de la normativa o una sobrestimación de las presiones. Este
comportamiento variable entre las diferentes redes parece indicar que las características de la
red parecen incidir en la sobrestimación de las pérdidas por parte del PVC cuando se utiliza la
ecuación de Hazen-Williams.
ILUSTRACIÓN 84.COMPARACIÓN ENTRE EL DISEÑO Y SU COMPROBACIÓN.
El PEAD presenta resultados similares a los que se han observado en todo este trabajo;
cuando se realiza la comprobación hidráulica, no se logra evidenciar una sobrestimación de
presiones o un incumplimiento de los diferentes requerimientos hidráulicos establecidos.
Curiosamente es posible ver que se presenta una diferencia de costos entre los dos diseños;
sin embargo esta se debe a que en algunos tramos no críticos de la red se presentaron
diámetros mayores, esto combinado con el hecho de que los costos del PEAD sean los más
altos causan que se genere una diferencia notoria entre los dos diseños sin que se afecte la
hidráulica de forma dramática.
Cuando se analizaron los costos con los caudales duplicados fue posible observar que una vez
más los costos para hierro dúctil seguían siendo más económicos cuando se utiliza la ecuación
de Hazen-Williams para sus diseños. Para PVC se presentó un cambio importante; el diseño
que se realizó con la ecuación de Hazen-Williams presentó un costo considerablemente más
alto que el arrojado por el diseño con la ecuación de Darcy-Weisbach (ver Tabla 29).
Finalmente el PEAD presentó un costo mayor para el diseño con la ecuación de Darcy-
Weisbach.
0
10
20
30
40
50
60
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
Comparación entre el diseño y su
comprobación hidráulica con PVC para Tesis 2
con caudales normales.
Diseño con la ecuación de
Hazen-Williams
Comprobación hidráulica

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
94
La hidráulica para el hierro dúctil con los caudales duplicados presentó un cambio, cuando se
comprobó la hidráulica del diseño que utilizo la ecuación de Hazen-Williams; se evidenció que
más Nudos presentaron subestimación en las presiones, en otras palabras, más nudos en la
red presentaron presiones menores a las que el diseño original con la ecuación de Hazen-
Williams arrojaba (ver Ilustración 173 e Ilustración 172). Esto parece apoyar el hecho de
que al aumentar las demandas base de los Nudos se esté haciendo más evidente el efecto
negativo de aplicar la ecuación de Hazen-Williams con hierro dúctil.
El caso del PVC fue bastante peculiar, ya que al duplicar los caudales base no implicó que se
presentara una sobrestimación importante de las presiones (un máximo del 4 % con respecto
al diseño original utilizando la ecuación de Hazen-Williams). Esto significa que al realizar la
comprobación hidráulica del diseño de Hazen-Williams, no se logró ver ningún efecto
hidráulico frente a lo que arrojaba el diseño original con esta ecuación (ver Ilustración 174 e
Ilustración 175). Sorpresivamente este efecto hidráulico no repercutió en los costos; todo se
debió a que en los tramos largos, pero no críticos de la red se presentaron diámetros mayores
con la ecuación de Hazen-Williams que con la ecuación de Darcy-Weisbach; esto llevó a que
los costos se elevaran de gran forma dentro de la red sin que esto afectara la hidráulica de la
misma.
Para PEAD no parecen haber efectos evidentes al utilizar la ecuación empírica de Hazen-
Williams (ver Ilustración 176 e Ilustración 177), las presiones que arroja el diseño con la
ecuación de Hazen-Williams frente a la comprobación del mismo utilizando la ecuación de
Darcy-Weisbach no muestran una diferencia significativa. Los costos como se ha visto a través
de esta tesis parecen no mostrar un diferencia importante cuando se comparan con el costo
global de la red; sin embargo estas pequeñas diferencias están dadas por los altos costos
(diámetro-metro de tubería) del PEAD, que al ser aumentados en tramos largos y no críticos
de la red, aumentan significativamente el costo sin afectar la hidráulica de la misma.
Al realizar el análisis con los caudales cuadruplicados se puede observar que para los 3
materiales los diseños con la ecuación de Hazen-Williams resultaron más económicos. El
fenómeno de que en tramos largos pero no críticos de la tubería se estén presentando
diámetros más grandes con la ecuación de Darcy-Weisbach es el que está explicando este
comportamiento de los costos.
La hidráulica en el diseño con el hierro dúctil cambió con respecto a los caudales duplicados;
si bien se siguen presentando la subestimación de presiones en los nudos (al analizar la
comprobación de la hidráulica del diseño que utilizó la ecuación de Hazen-Williams), en este
caso en particular se presentó en más Nudos que cuando se analizaron los caudales normales
y los caudales duplicados (ver Ilustración 180). Esto parece una vez más apoyar lo
evidenciado en otras redes con caudales cuadruplicados, y es que este aumento de las
demandas base de los nudos este agudizando el efecto de subestimación por parte de la
ecuación de Hazen-Williams.
En el caso del PVC se vio una pequeña sobrestimación de las presiones cuando se realizó la
comprobación hidráulica de la red diseñada con la ecuación de Hazen-Williams (ver

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
95
Ilustración 183). Este hecho es importante resaltarlo principalmente porque este efecto no
se había presentado en lo absoluto con los caudales normales ni con los caudales duplicados
en esta red, si bien la sobrestimación de las pérdidas solo alcanzo un máximo del 12% frente a
lo que arrojó originalmente la ecuación de Hazen-Williams; esto muestra que en efecto la
ecuación empírica puede sobrestimar la presiones en varios Nudos de la red. Aun en
presencia de este efecto, los costos con la ecuación de Darcy-Weisbach resultaron más
elevados, y es por el fenómeno que se nombró al principio de este análisis con caudales
cuadruplicados.
Parece ser que el caso del PEAD no presenta cambios con respecto a las demás redes, cuando
se compara la comprobación hidráulica del diseño realizado utilizando la ecuación de Hazen-
Williams no se puede evidenciar un efecto de sobrepresiones o de subestimación de las
mismas (ver Ilustración 186). Por otro lado los altos costos presentados con el diseño de
Darcy-Weisbach, están asociados con ligero aumento de los diámetros en tramos largos y no
críticos sumados con los altos costos del PEAD.
5.7 RED TESIS 3
Esta red presentó tendencias muy similares a las de red Tesis 1 y red Tesis 2 para el PVC en
cuanto a la hidráulica de la red. El PEAD siguió con su comportamiento, es decir, se comportó
como en la mayoría de las redes de este trabajo. El hierro dúctil siguió presentando diseños
más económicos cuando se utilizó la ecuación de Hazen-Williams, presentando a su vez la
misma subestimación de presiones.
Los caudales normales presentaron que el diseño utilizando la ecuación de Hazen-Williams
para hierro dúctil arrojaba costos menores. Sin embargo al ver los costos con PVC y PEAD, se
ve que esta tendencia desaparece y la diferencia entre ambos diseños no es evidente.
La hidráulica de la red para el material hierro dúctil presentó el mismo comportamiento de las
otras redes. Al analizar la comprobación de diseño (de la red diseñada con Hazen-Williams),
está presentó subestimación de las presiones en algunos Nudos de la red. Esto termina de
corroborar lo visto en las otras redes, y es que la ecuación de Hazen-Williams que trabaja con
un coeficiente constante de 140 subestima las pérdidas por fricción, generando diseños más
económicos pero que incumplen con la presión mínima establecida.
En el caso del PVC se presentó una sobrestimación no superior al 7% cuando se comprobó la
hidráulica de la red diseñada con Hazen-Williams. En esta ocasión este resultado se ve en
reflejado en los costos, ya que estos no presentaron una variación significativa entre la
ecuación empírica y la físicamente basada. Parece ser que al diseñar redes como Tesis 1, Tesis
2 y Tesis 3 con caudales normales, la ecuación de Hazen-Williams está operando dentro de sus
rangos de cumplimiento presentando diferencias mínimas cuando se compara con la
ecuación de Darcy-Weisbach.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
96
ILUSTRACIÓN 85 COMPARACIÓN ENTRE EL DISEÑO Y SU COMPROBACIÓN.
El PEAD no presenta subestimación o sobrestimación de las presiones cuando se comprueba
la hidráulica del diseño de Hazen-Williams. Esto muestra que los diseños con este material,
independientemente del caudal demandado, se encuentran dentro de los rangos de
cumplimiento de la ecuación empírica. Esto implica que no es relevante la ecuación que se
utilice para diseñar ya que ambas cumplen con los requerimientos hidráulicos.
Cuando se analizan los caudales duplicados se puede ver que solo se presenta una diferencia
de costos importante en PEAD con respecto a los costos con caudales normales. El hierro
dúctil presentó igualmente un diseño más económico cuando se utilizó la ecuación de Hazen-
Williams aunque no fue my significativa. Así mismo el PVC presentó costos similares al
comparar las dos ecuaciones.
En el análisis hidráulico se puede ver que para hierro dúctil, se presenta una subestimación de
presiones cuando se comprueba el diseño de Hazen-Williams (ver Ilustración 190). Si bien
esta subestimación se presenta en un nudo, este nudo excede por mucho la presión mínima de
la red; la presión que se presenta es de 12 m en comparación con la presión mínima de 15 m.
Esta subestimación se ve reflejada en menores diámetros que causa que en efecto se reduzcan
los costos de la red pero que se incumplan con las necesidades hidráulicas de la misma.
El caso del PVC no muestra resultados concluyentes; cuando se analiza la comprobación
hidráulica de la red diseñada con Hazen-Williams, se puede ver que no se incumple ni se
sobrestima con las presiones de la red. Si bien este resultado contrasta con lo encontrado en
0
10
20
30
40
50
60
70
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
Comparación entre el diseño y su
comprobación hidráulica con PVC para Tesis 3
con caudales normales.
Diseño con la ecuación de
Hazen-Williams
Comprobación hidáulica

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
97
red Balerma, Bogotá-Cazucá y R28, no está muy alejado de los resultados con estos mismos
caudales para Tesis 1 y Tesis2.
El PEAD presentó una hidráulica similar cuando se comprobó la red diseñada con Hazen-
Williams. Sin embargo, cuando se vieron los costos finales de la red, se vio que la diferencia
entre el diseño con la ecuación de Hazen-Williams y Darcy-Weisbach era abismal siendo este
ultimo casi 230 millones de pesos más económico. Este sobrecosto se debió a que en los
tramos más largos de la tubería se presentaron diferencias importantes de diámetros, esto
causó que el costo se elevara bastante sin incumplir con los requerimientos hidráulicos. Sin
embargo la ecuación de Darcy-Weisbach utilizando diámetros menores, logró obtener un
diseño optimo (presiones cercanas 15 m) y no tan conservador como el de la ecuación
empírica.
Cuando se cuadruplicaron los caudales solo se presentó un ahorro de recursos en hierro dúctil
al utilizar la ecuación de Hazen-Williams. Para los otros dos materiales no fue evidente una
diferencia importante en los costos de diseños (ver Tabla 32).
El análisis hidráulico con los caudales cuadruplicados mostró que para hierro dúctil el efecto
de subestimación de las presiones por parte de la ecuación de Hazen-Williams se
incrementara notoriamente (ver Ilustración 197). A su vez, esta subestimación de las
presiones y las pérdidas por fricción causó que los diseños resultaran más económicos y que
incumplieran en más de un 40% de los Nudos con la presión mínima establecida.
Hidráulicamente el PVC no mostró subestimaciones de las presiones y un máximo de 8% en
las sobrestimaciones de las presiones de la red cuando se analizaron los caudales
cuadruplicados (ver Ilustración 200). Esta diferencia tan pequeña a su vez se vio plasmada
en los costos, que si bien arrojaban un diseño más económico con la ecuación de Darcy-
Weisbach, no era significativa y resultaba prácticamente igual diseñar con la ecuación
físicamente basada o con la ecuación empírica.
Finalmente el PEAD mostró costos e hidráulica similares a los que se presentaron en caudales
normales y duplicados; así mismo el comportamiento que se logró evidenciar en los
resultados demuestra lo que se ha venido mostrando en todas las redes de este trabajo, y es
que el PEAD no tiene un efecto claro de subestimación o de sobrestimación de las presiones
en los Nudos de la red (ver Ilustración 203). Esto lleva a que tampoco se vea una diferencia
clara en los costos de diseño de la red Tesis 3, ya que tanto la ecuación de Hazen-Williams
como la ecuación de Darcy-Weisbach están evaluando las pérdidas por fricción de manera
similar , sus diseños no son tan diferente y solo presentan cambios en algunos tramos poco
importantes de la red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
98
5.8 RESUMEN DE RESULTADOS
TABLA 18. RESUMEN DE RESULTADOS ENCONTRADOS EN EL PROYECTO.
Normales
Duplicados
Cuadruplicados
Hierro Dúctil
Se obtienen menores costos con la
ecuación de Hazen-Williams pero
no cumplen los requerimientos de
presiones. Los números de
Reynolds de estas redes oscilaban
entre los 7000 y un máximo de
1'750.000.
Al igual que en caudales normales
se ve el mismo fenómeno. Los
números de Reynolds aumentaron
considerablemente frente a los
caudales normales se encontraron
entre los 20000 y lo 2'800.000
La tendencia permaneció en todo el
trabajo de que se incumplieran las
presiones con la ecuación empírica
pese a que presentara costos
menores. Los rangos de Reynolds
que se presentaron estuvieron
entre los 70000 y los 5'000000.
PVC
El PVC no mostro una diferencia
clara entre los dos diseños. Sin
embargo algunas redes diseñadas
con la ecuación empírica
presentaron sobrestimación de las
presiones lo que implicaba una
diferencia entre los costos de
diseños. Los rangos de Reynolds
estaban entre los 5000 y los
2'300.000.
Con los caudales duplicados la
sobrestimación de las presiones se
hizo más evidente. A pesar de esto
no todas las redes presentaron este
fenómeno y las que lo presentó
solo una leve diferencia de costos
no superior al 20%. Los números de
Reynolds asociados a estos caudales
rondaron entre 12000 y los
4'750.000.
Los caudales cuadruplicados
incrementaron aun más la
tendencia de sobrestimación de las
presiones. Si bien no todas las
redes lo presentaron, el fenómeno
se hizo presente en varios de los
diseños causando que en los que se
presentó se encontraran costos
mayores al utilizar la ecuación de
Hazen-Williams. Los números de
Reynolds encontrados oscilaron
entre 15000 y los 4'000000.
PEAD
El PEAD no presento ningún tipo de
diferencia en su comportamiento
hidráulico o en sus costos al
comparar ambas ecuaciones salvo
en 2 excepciones donde los costos
se aumentaron debido a una leve
sobrestimación de las presiones
por parte de la ecuación de Hazen-
Williams. Los rangos del número
de Reynolds oscilaron entre 4000 y
2'800000. Aunque existieron un par
de tuberías aisladas en 2 redes que
presentaron Reynolds inferiores a
2000.
Siguiendo la tendencia de los
caudales normales, estos diseños
tampoco presentaron una
diferencia clara cuando se
compararon las dos ecuaciones
tanto en la parte hidráulica como en
los costos. Los números de
Reynolds oscilaron entre los 5000 y
3'200000. Una vez más se volvieron
a presentar algunos tramos de
tubería con números de Reynolds
inferiores a los 2000 lo que llevaría a
que el flujo fuera laminar.
Finalmente con los caudales
cuadruplicados tampoco se
evidenciaron diferencias notorias
entre los diseños al comparar las
dos ecuaciones. Sus números de
Reynolds variaron entre los 3000 y
los 3'700000. Con un par de nodos
con valores cercanos a los 2000.La
mayoría de estos resultados
parecen encontrarse dentro del
rango sugerido por Christensen
(B.A. Christensen, 2000). En los
anexos se encuentran diagramas de
Moody donde se pueden ver los
factores de fricción de las
comprobaciones de diseño.
Caudales
M
a
t
e
r
i
a
l
e
s
Resultados Obtenidos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
99
CAPÍTULO 6 CONCUSIONES
Los resultados permiten concluir que las redes diseñadas con la ecuación de Hazen-
Williams utilizando hierro dúctil resultaban más económicos que los diseños con la
ecuación de Darcy-Weisbach para esta ecuación. A pesar de esto, también fue evidente
que la reducción de costos fue consecuencia de una subestimación de las presiones
por parte de la ecuación empírica.
El PEAD no mostró ningún efecto importante. Esto se vio reflejado en que los costos
con PEAD variaron para la mayoría de las redes, y el utilizar una ecuación sobre otra
no implicaba tener un diseño más económico ni más optimo. Así mismo la hidráulica
tampoco arrojó resultados que diferenciaran el efecto de utilizar la ecuación de Hazen-
Williams frente a la ecuación de Darcy-Weisbach.
Los resultados para el PVC en todas las redes muestran resultados contradictorios. Si
bien se pueden presentar sobrestimaciones por parte de la ecuación de Hazen-
Williams en algunos diseños (redes: Balerma, Bogotá-Cazucá y R28), este
comportamiento no fue generalizado, y en otras redes no se pudo observar esta
tendencia.
El efecto de los caudales en los resultados solo se hizo evidente en el caso del hierro
dúctil donde se hacía más evidente la subestimación de las pérdidas y las presiones en
la red (caso de la ecuación de Hazen-Williams) al aumentar las demandas bases de los
Nudos. Para el caso del PVC, solo con caudales cuadruplicados se pudo observar un
cambio en las sobrestimaciones de las presiones.
Con base a los resultados del hierro dúctil y del PVC, es posible afirmar que utilizar la
ecuación de Hazen-Williams genera resultados hidráulicos indeseados en la práctica
de la ingeniería. No solo porque todas las redes presentaron falencia de presiones
cuando se diseñaron con la ecuación de Hazen-Williams en hierro dúctil, sino porque
se presentaron sobrestimaciones de presiones por parte de esta ecuación cuando se
utilizó el PVC en 3 redes de este trabajo.
Los métodos computacionales permiten una solución rápida a la obtención del factor
de fricción de la ecuación de Colebrook-White. Adicionalmente la iteración necesaria
para la ecuación de Darcy-Weisbach deja de ser un problema, ya que existen nuevas
tecnologías y equipos de cómputo que lo solucionan en segundos, haciendo
innecesario el uso de la ecuación de Hazen-Williams, y ahorrarse el trabajo de
verificar si su coeficiente de Hazen-Williams es el indicado o si el diseño se encuentra
dentro de los rangos de cumplimiento.
Se concluye que la normativa colombiana es muy laxa en la regulación de los diseños
con Hazen-Williams. Si bien el RAS especifica que esta ecuación solo se debe de
utilizar para sus límites establecidos, esta normativa no especifica cuáles son los
rangos de cumplimiento.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
100
CAPÍTULO 7 RECOMENDACIONES
Los resultados de este trabajo debe de ser verificados con datos de campo para
asegurar su validez como investigación; en otras palabras, es recomendable trabajar
una red que se halla diseñado con la ecuación de Hazen-Williams, con caudales reales
y comparar sus resultados para el modelo computacional y los datos en campo.
Si se desea utilizar la ecuación de Hazen-Williams para los diseños de acueductos, es
importante tener en cuenta sus rangos de validez y tener una lista de coeficientes de
Hazen-Williams en vez de solo uno, ya que como se mostró en los resultados y en el
análisis de este trabajo, utilizar un único valor para este coeficiente puede representar
erróneamente las características del material y llevar a errores de subestimación de
las pérdidas por fricción.
Tal como lo recomendó Rafael Alejandro Flechas en su tesis, el autor también
recomienda que se utilicen otras metodologías para la validación de los datos; esta
puede ser la Búsqueda de Armonía, Algoritmos Genéticos e inclusive el diseño rápido
para ver si los efectos vistos en esta tesis se repiten.
Se recomienda endurecer la normativa colombiana en cuanto al uso de la ecuación de
Hazen-Williams, ya que existe suficiente evidencia científica para mostrar los riesgos
si se usa por fuera de sus rangos de cumplimiento.
Estudiar más a fondo el coeficiente del hierro dúctil ya que los resultados de este
trabajo parecen mostrar que está representando al material mucho más liso de lo que
en la realidad es.
En el caso del PVC, es importante verificar si la sobrestimación de las presiones en los
Nudos se repite en redes reales. Como se mostró en este trabajo varias redes
diseñadas con PVC utilizando la ecuación de Hazen-Williams presentaron este
fenómeno y es idóneo verificarlo con alguna red real o con datos de campo.
Continuar esta investigación con redes que presenten más de 3 años de edad sería
ideal, ya que se podría estudiar más afondo la hidráulica de las mismas, en especial
para redes que hayan sido con la ecuación empírica de Hazen-Williams y un solo
coeficiente.
Se recomienda verificar los resultados del PEAD con algún otro método, ya que como
se mostró en el análisis y en los resultados, los diseños con este material no parecen
mostrar un efecto adverso ni en los costos al utilizar la ecuación de Hazen-Williams
para sus diseños.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
101
BIBLIOGRAFÍA
B.A. Christensen, F. A. (2000). Discussion Limitations and proper use of the Hazen-Williams
Ecuation. Journal of hidraulics engineering , 167-170.
Empresas Públicas de Medellín. (2006-2009). http://es.scribd.com. Recuperado el 10 de
Febrero de 2012, de http://es.scribd.com: http://es.scribd.com/doc/35115401/Normas-
Acueducto-Vesion-Final
Fabián A.Bombardelli, M. H. (2003). Hydraulic Design of Large-Diameter Pipes. Journal of
Hydraulic Engineering , 839-846.
Gardner Williams, A. H. (1905). Hydraulic Tables . Library of the University of California.
Liou, C. P. (1998). LIMITATIONS AND PROPER USE OF THE HAZEN-WILLIAMS EQUATION.
Journal of hydraulics Engineering , 951-954.
M.Moghazi, H. E.-D. (1998). Estimating Hazen-Williams Coefficient for Polyethylene Pipes.
Journal of Transportation Engineering , 197-199.
Ministerio de Desarrollo Economico. (2000). Reglamento Técnico del Sector de Agua Potable y
Saneamiento Basico Titulo B. Bogotá: Ministro de desarrollo Economico.
Ochoa, S. (2009). DISEÑO OPTIMIZADO DE REDES DE DISTRIBUCIÓN DE AGUA POTABLE CON
BASE EN EL CONCEPTO ENERGÉTICO DE SUPERFICIE ÓPTIMA DE GRADIENTE HIDRÁULICO.
Bogota: Uniandes.
PAVCO. (2012). LISTA DE PRECIOS. Bogota: PAVCO.
PAVCO. (2011). Manual Tecnico Tubosistemas para ACUEDUCTO Union de Platino y Alta
presion Acometidas Domiciliarias PF+UAD. Bogota: PAVCO.
PAVCO. (2011). Manual Tecnico Tubosistemas PEAD para Conduccion de Agua Potable
ACUFLEX. Bogota: PAVCO.
Quentin B. Travis, L. W. (2007). Relationship between Hazen-Williams and Colebrook-White
Roughness Values. Journal of Hydraulic Engineering , 1270-1273.
Saint-Gobain PAM . (2012). Tuberías, válvulas y accesorios en hierro dúctil para sistemas de
acueducto, alcantarillado,riego e industrial Hydroclass. Bogota: PAM.
Saldarriaga, J. G. (2007). Hidráulica de Tuberias Abastecimiento de agua, redes, riesgos. Bogotá:
Alfaomega.
Valiantzas, J. D. (2008). Explicit Power Formula for the Darcy-Weisbach Pipe Flow Equation:
Application in Opimal Pipeline Design. Journal of Irrigation and Drainage Engineering , 454-
461.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
102
ANEXOS
En esta sección se encuentran los resultados para caudales duplicados y cuadruplicados para
todas las redes que se trabajaron durante el proyecto.
- Costos
TABLA 19. COSTOS DE LA RED SAN VICENTE CON CAUDALES DUPLICADOS
ILUSTRACIÓN 86. GRÁFICA DE COSTOS RED SAN VICENTE CAUDALES DUPLICADOS.
RED SAN VICENTE CAUDALES X2
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
HAZEN-WILLIAMS
139 187 498.00
$
328 624 925.00
$
DIFERENCIA
(540 567.00)
$
-
$
250 548.00
$
607 495 979.00
$
DARCY-WEISBACH
139 728 065.00
$
328 624 925.00
$
607 245 431.00
$
$ 0.00
$ 50 000 000.00
$ 100 000 000.00
$ 150 000 000.00
$ 200 000 000.00
$ 250 000 000.00
$ 300 000 000.00
$ 350 000 000.00
$ 400 000 000.00
$ 450 000 000.00
$ 500 000 000.00
$ 550 000 000.00
$ 600 000 000.00
$ 650 000 000.00
COSTO
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red San Vicente(x2)
DARCY HIERRO DUCTIL SAN
VICENTE
HAZEN HIERRO DUCTIL SAN
VICENTE
DARCY PVC SAN VICENTE
HAZEN PVC SAN VICENTE
DARCY PEAD SAN VICENTE
HAZEN PEAD SAN VICENTE
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
103
- Resultado de presiones con Hierro Dúctil
ILUSTRACIÓN 87. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
ILUSTRACIÓN 88. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUES DE CORRER
LA HIDRÁULICA CON LA ECUACION DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS SAN
VICENTE HIERRO DÚCTIL(X2)
PRESIONES CON
HAZEN-WILLIAMS
SAN VICENTE
HIERRO
DÚCTIL(X2)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
250
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES SAN VICENTE
HIERRO DÚCTIL(X2)
COMPROBACIÓN DE
PRESIONES SAN
VICENTE HIERRO
DÚCTIL(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
104
- Resultados de presiones con PVC.
ILUSTRACIÓN 89. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
ILUSTRACIÓN 90. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS SAN
VICENTE PVC(X2)
PRESIONES CON
HAZEN-WILLIAMS
SAN VICENTE
PVC(X2)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES SAN VICENTE
PVC(X2)
COMPROBACIÓN
DE PRESIONES
SAN VICENTE
PVC(X2)
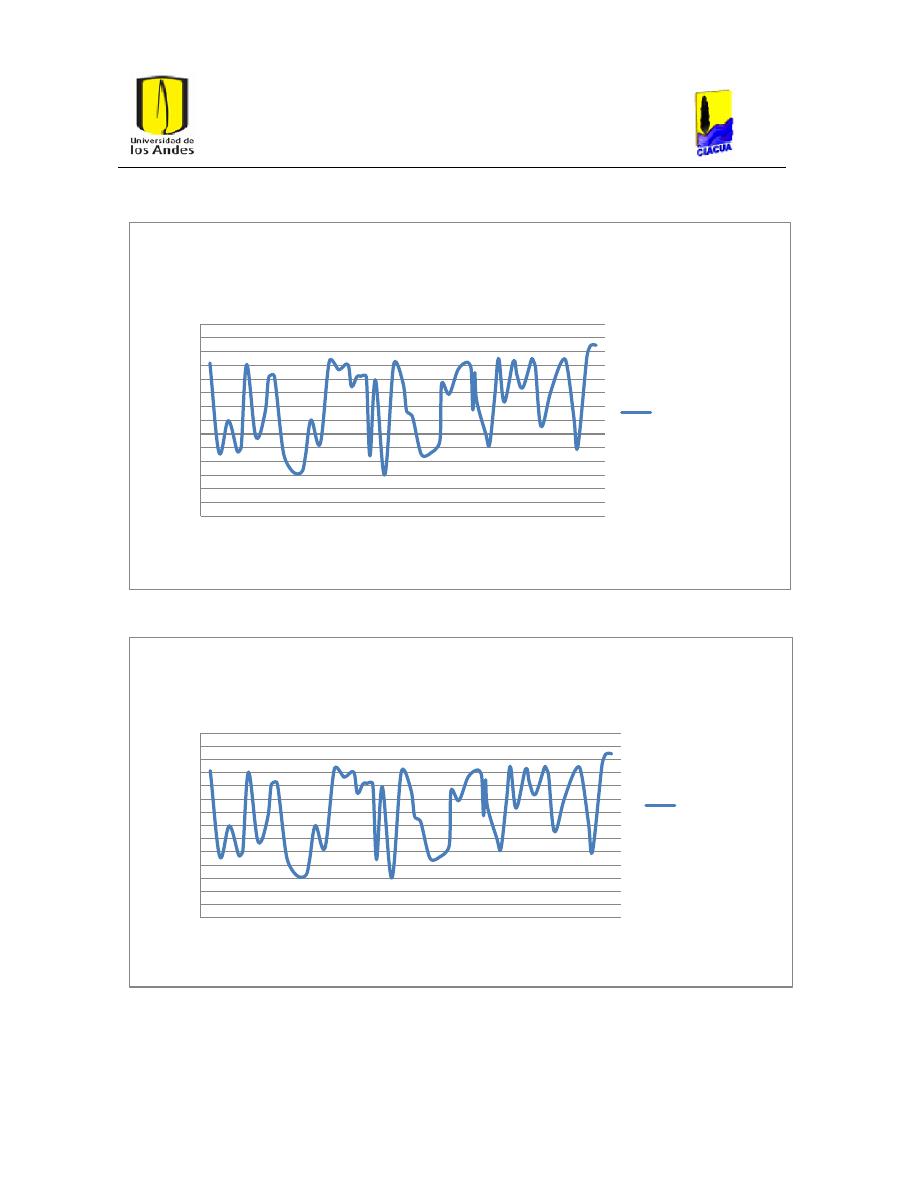
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
105
- Resultados de presiones para PEAD.
ILUSTRACIÓN 91. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
ILUSTRACIÓN 92. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS SAN
VICENTE PEAD(X2)
PRESIONES CON HAZEN-
WILLIAMS SAN VICENTE
PEAD(X2)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES SAN VICENTE
PEAD(X2)
COMPROBACIÓN
DE PRESIONES SAN
VICENTE PEAD(X2)
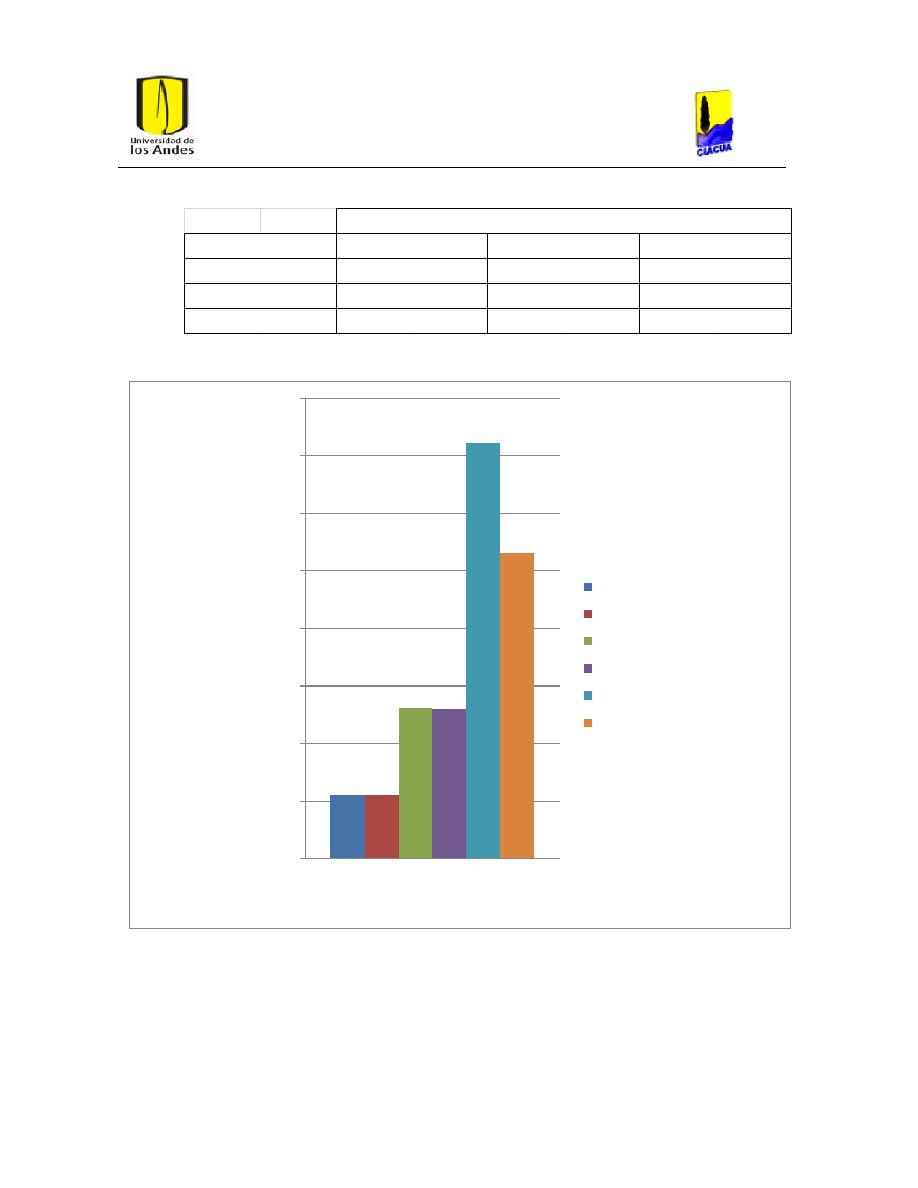
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
106
- Costos.
TABLA 20. COSTOS DE LA RED SAN VICENTE CON CAUDALES CUADRUPLICADOS.
ILUSTRACIÓN 93. GRÁFICA DE COSTOS RED SAN VICENTE CON CAUDALES CUADRUPLICADOS.
DARCY-WEISBACH
222 059 591.00
$
522 339 619.00
$
1 443 096 528.00
$
DIFERENCIA
(171 711.00)
$
(870 817.00)
$
(380 484 440.00)
$
HAZEN-WILLIAMS
221 887 880.00
$
521 468 802.00
$
1 062 612 088.00
$
RED SAN VICENTE CAUDALES X4
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
$-
$200 000 000.00
$400 000 000.00
$600 000 000.00
$800 000 000.00
$1 000 000 000.00
$1 200 000 000.00
$1 400 000 000.00
$1 600 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red San Vicente (x4)
Darcy-Weisbach Hierro Dúctil
Hazen-Williams Hierro Dúctil
Darcy-Weisbach PVC
Hazen-Wiliams PVC
Darcy-Weisbach PEAD
Hazen-Williams PEAD
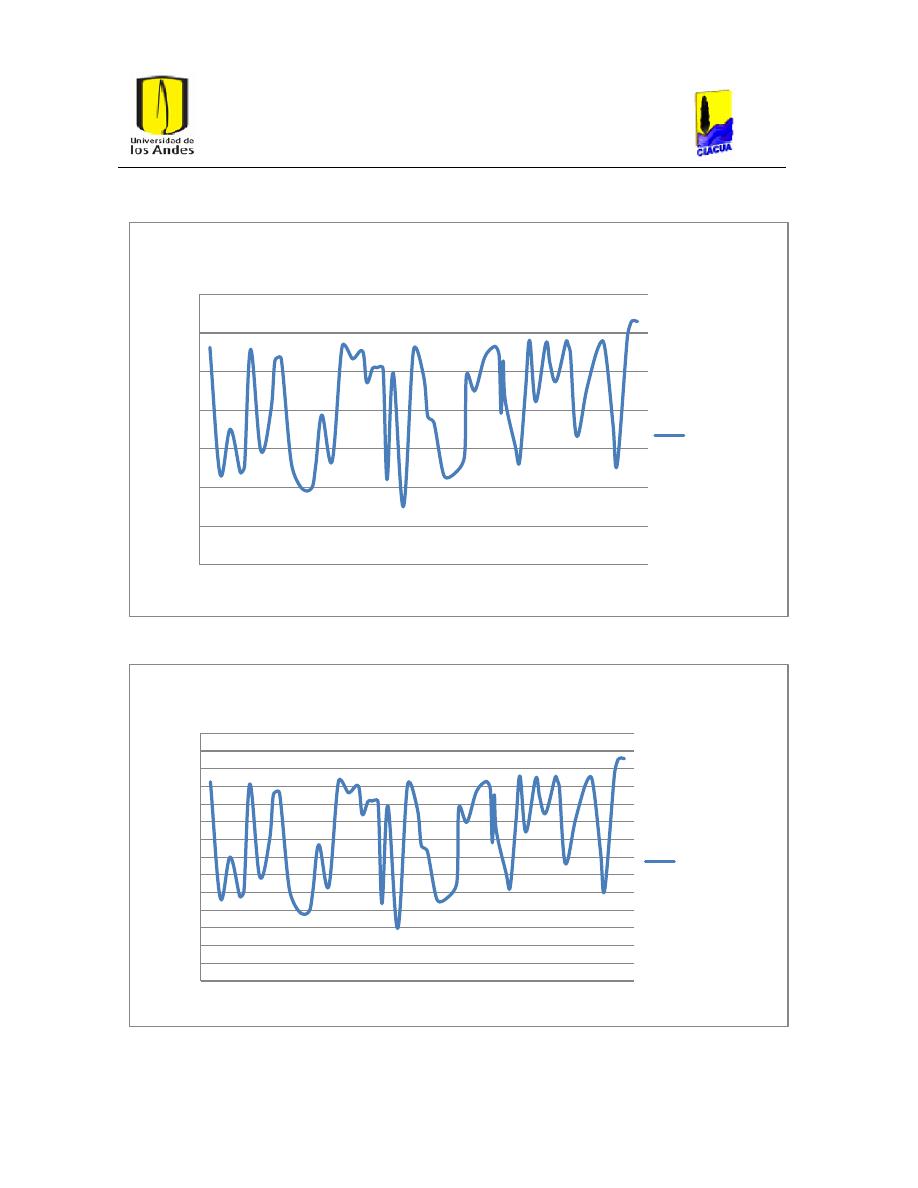
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
107
- Resultados de presiones para Hierro Dúctil
ILUSTRACIÓN 94. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
ILUSTRACIÓN 95. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
10
20
30
40
50
60
70
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS SAN
VICENTE HIERRO DÚCTIL(X4)
PRESIONES CON
HAZEN-WILLIAMS
SAN VICENTE
HIERRO …
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
P
resi
ón
en
m
Nudos
COMPROBACIÓN DE PRESIONES SAN VICENTE
HIERRO DÚCTIL (X4)
COMPROBACIÓN DE
PRESIONES SAN
VICENTE HIERRO …
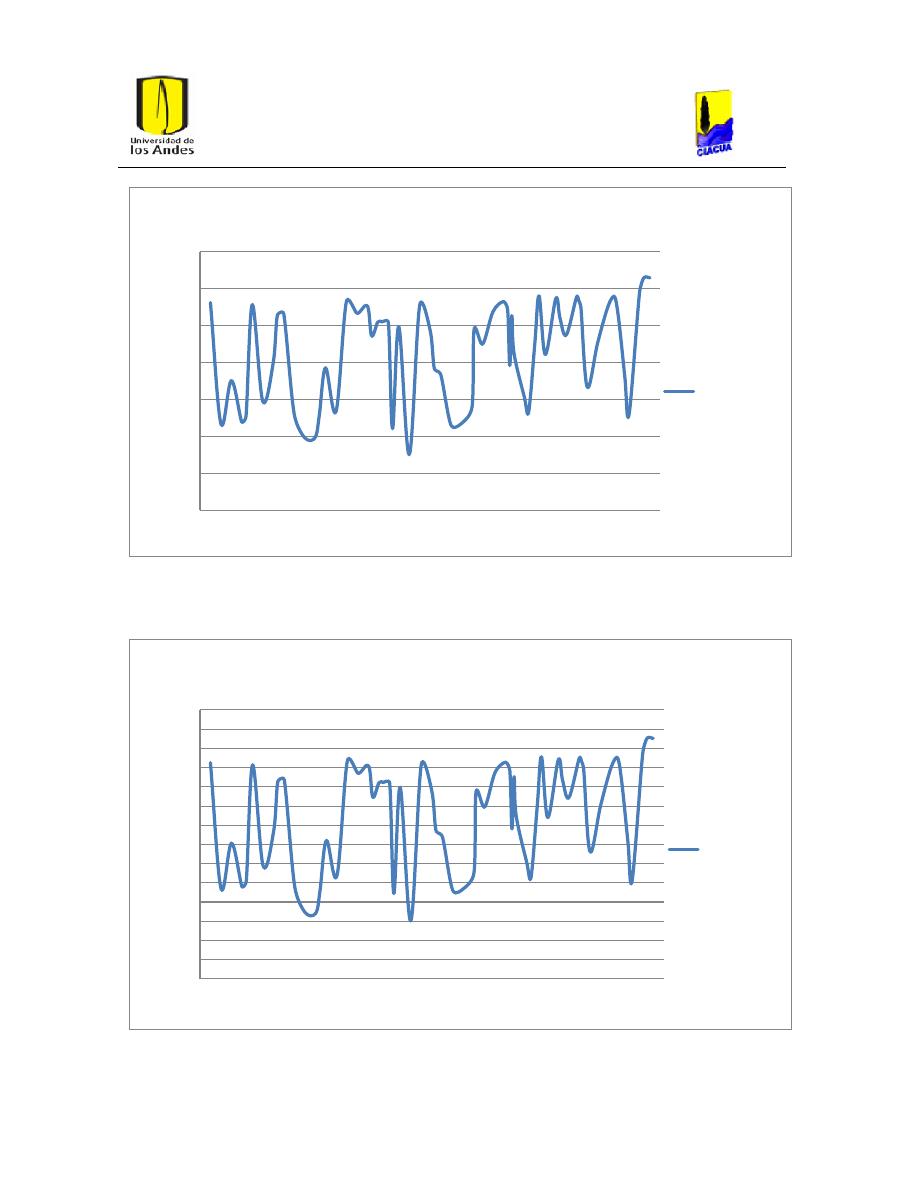
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
108
ILUSTRACIÓN 96. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
- Resultados para PVC
ILUSTRACIÓN 97. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS CON PVC.
0
10
20
30
40
50
60
70
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH SAN
VICENTE HIERRO DÚCTIL(X4)
PRESIONES CON
DARCY-WEISBACH
SAN VICENTE …
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS SAN
VICENTE PVC(X4)
PRESIONES CON
HAZEN-WILLIAMS
SAN VICENTE
PVC(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
109
ILUSTRACIÓN 98. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE CORRER
LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH.
ILUSTRACIÓN 99. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES SAN VICENTE
PVC(X4)
COMPROBACIÓN DE
PRESIONES SAN VICENTE
PVC(X4)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH SAN
VICENTE PVC(X4)
PRESIONES CON
DARCY-WEISBACH
SAN VICENTE …
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
110
- Resultados para PEAD.
ILUSTRACIÓN 100. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
ILUSTRACIÓN 101. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS SAN
VICENTE PEAD(X4)
PRESIONES
CON HAZEN-
WILLIAMS SAN
VICENTE …
0
5
10
15
20
25
30
35
40
45
50
55
60
65
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES SAN VICENTE
PEAD(X4)
COMPROBACIÓN DE
PRESIONES SAN
VICENTE PEAD(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
111
ILUSTRACIÓN 102. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
- Costos:
TABLA 21. COSTOS DE LA RED BALERMA CON CAUDALES DUPLICADOS.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
0
50
100
150
200
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH SAN
VICENTE PEAD(X4)
PRESIONES CON
DARCY-WEISBACH
PEAD(X4)
RED BALERMA CAUDALES X2
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
DIFERENCIA
50 621 107.00
$
1 308 024 691.00
$
1 456 641 182.00
$
HAZEN-WILLIAMS
7 612 855 286.00
$
15 839 378 398.00
$
45 262 861 878.00
$
DARCY-WEISBACH
7 562 234 179.00
$
14 531 353 707.00
$
43 806 220 696.00
$
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
112
ILUSTRACIÓN 103. GRÁFICA DE LOS COSTOS DE LA RED BALERMA CON CAUDALES DUPLICADOS.
- Resultados de presiones con Hierro Dúctil.
ILUSTRACIÓN 104. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS CON HIERRO DÚCTIL.
$ 0.00
$ 5 000 000 000.00
$ 10 000 000 000.00
$ 15 000 000 000.00
$ 20 000 000 000.00
$ 25 000 000 000.00
$ 30 000 000 000.00
$ 35 000 000 000.00
$ 40 000 000 000.00
$ 45 000 000 000.00
$ 50 000 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Balerma(x2)
DARCY-WEISBACH HIERRO
DÚCTIL
HAZEN-WILLIAMS HIERRO
DÚCTIL
DARCY-WEISBACH PVC
HAZEN-WILLIAMS PVC
DARCY-WEISBACH PEAD
HAZEN-WILLIAMS PEAD
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
0
100
200
300
400
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BALERMA
HIERRO DÚCTIL(X2)
PRESIONES CON
HAZEN-WILLIAMS
BALERMA HIERRO
DÚCTIL(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
113
ILUSTRACIÓN 105. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
- Resultados de presiones con PVC.
ILUSTRACIÓN 106. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
-25
-20
-15
-10
-5
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
0
100
200
300
400
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BALERMA
HIERRO DÚCTIL(X2)
COMPROBACIÓN DE
PRESIONES BALERMA
HIERRO DÚCTIL(X2)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
0
100
200
300
400
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BALERMA
PVC(X2)
PRESIONES CON
HAZEN-WILLIAMS
BALERMA PVC(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
114
ILUSTRACIÓN 107. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
- Resultados de presiones con PEAD.
ILUSTRACIÓN 108. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
0
100
200
300
400
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BALERMA
PVC(X2)
COMPROBACIÓN
DE PRESIONES
BALERMA PVC(X2)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
0
100
200
300
400
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BALERMA
PEAD(X2)
PRESIONES CON
HAZEN-
WILLIAMS
BALERMA
PEAD(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
115
ILUSTRACIÓN 109. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
- Costos.
TABLA 22. COSTOS DE LA RED BALERMA CON CAUDALES CUADRUPLICADOS.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
0
100
200
300
400
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BALERMA
PEAD(X2)
COMPROBACIÓN
DE PRESIONES
BALERMA
PEAD(X2)
DIFERENCIA
(983 776 829.00)
$
290 053 904.00
$
753 042 776.00
$
32 856 752 197.00
$
79 250 492 943.00
$
11 289 412 631.00
$
32 566 698 293.00
$
78 497 450 167.00
$
HAZEN-WILLIAMS
DARCY-WEISBACH
10 305 635 802.00
$
RED BALERMA CAUDALES X4
HIERRO DÚCTIL
PVC
PEAD
COSTOS $
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
116
ILUSTRACIÓN 110. GRÁFICA DE COSTOS DE LA RED BALERMA CON CAUDALES CUADRUPLICADOS.
- Resultados de presiones para Hierro Dúctil.
ILUSTRACIÓN 111. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
$-
$10 000 000 000.00
$20 000 000 000.00
$30 000 000 000.00
$40 000 000 000.00
$50 000 000 000.00
$60 000 000 000.00
$70 000 000 000.00
$80 000 000 000.00
$90 000 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Balerma(x4)
Darcy-Weisbach Hierro Dúctil
Hazen-Williams Hierro Dúctil
Darcy-Weisbach PVC
Hazen-Williams PVC
Darcy-Weisbach PEAD
Hazen-Williams PEAD
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
0
100
200
300
400
500
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BALERMA
HIERRO DÚCTIL (X4)
PRESIONES CON
HAZEN-WILLIAMS
BALERMA HIERRO
DÚCTIL (X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
117
ILUSTRACIÓN 112. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
ILUSTRACIÓN 113. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
-35
-30
-25
-20
-15
-10
-5
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
0
100
200
300
400
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BALERMA
HIERRO DÚCTIL (X4)
COMPROBACIÓN
DE PRESIONES
BALERMA HIERRO
DÚCTIL (X4)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
0
100
200
300
400
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH BALERMA
HIERRO DÚCTIL(X4)
PRESIONES
CON DARCY-
WEISBACH
BALERMA
HIERRO
DÚCTIL(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
118
- Resultados de presiones con PVC.
ILUSTRACIÓN 114. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
ILUSTRACIÓN 115. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
0
100
200
300
400
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BALERMA
PVC(X4)
PRESIONES CON
HAZEN-WILLIAMS
BALERMA PVC(X4)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
0
100
200
300
400
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BALERMA
PVC(X4)
COMPROBACIÓN DE
PRESIONES BALERMA
PVC(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
119
ILUSTRACIÓN 116. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
- Resultados de presiones para PEAD.
ILUSTRACIÓN 117. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
0
100
200
300
400
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH BALERMA
PVC(X4)
PRESIONES CON
DARCY-
WEISBACH
BALERMA
PVC(X4)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
0
100
200
300
400
500
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BALERMA
PEAD(X4)
PRESIONES CON
HAZEN-WILLIAMS
BALERMA
PEAD(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
120
ILUSTRACIÓN 118. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
ILUSTRACIÓN 119. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
0
100
200
300
400
500
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BALERMA
PEAD(X4)
COMPROBACION
DE PRESIONES
BALERMA
PEAD(X4)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
0
100
200
300
400
500
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH BALERMA
PEAD(X4)
PRESIONES
CON DARCY-
WEISBACH
BALERMA
PEAD(X4)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
121
- Costos.
TABLA 23. COSTOS DE LA RED BOGOTÁ-CAZUCÁ CON CAUDALES DUPLICADOS.
ILUSTRACIÓN 120. GRÁFICA DE COSTOS DE LA RED BOGOTÁ-CAZUCÁ CON CAUDALES
DUPLICADOS.
RED BOGOTÁ-CAZUCÁ CAUDALES X2
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
DIFERENCIA
(80 085 318.00)
$
37 728 075.00
$
13 737 214.00
$
HAZEN-WILLIAMS
339 485 347.00
$
805 009 939.00
$
1 400 998 498.00
$
DARCY-WEISBACH
419 570 665.00
$
767 281 864.00
$
1 387 261 284.00
$
$ 0.00
$ 200 000 000.00
$ 400 000 000.00
$ 600 000 000.00
$ 800 000 000.00
$ 1 000 000 000.00
$ 1 200 000 000.00
$ 1 400 000 000.00
$ 1 600 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Bogotá-Cazucá (x2)
HAZEN-WILLIAMS HIERRO
DÚCTIL
DARCY-WEISBACH HIERRO
DÚCTIL
HAZEN-WILLIAMS PVC
DARCY-WEISBACH HIERRO
DÚCTIL
HAZEN-WILLIAMS PEAD
DARCY-WEISBACH PEAD
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
122
- Resultados de presiones con Hierro Dúctil.
ILUSTRACIÓN 121. PRESIONES CON AL ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
ILUSTRACIÓN 122. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BOGOTÁ-
CAZUCÁ HIERRO DÚCTIL(X2)
PRESIONES CON
HAZEN-WILLIAMS
BOGOTÁ-CAZUCÁ
HIERRO
DÚCTIL(X2)
-25
-20
-15
-10
-5
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BOGOTÁ-CAZUCÁ
HIERRO DÚCTIL(X2)
COMPROBACIÓN
DE PRESIONES
BOGOTÁ-CAZUCÁ
HIERRO
DÚCTIL(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
123
- Resultados de presiones para PVC
ILUSTRACIÓN 123. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
ILUSTRACIÓN 124. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
0
20
40
60
80
100
120
140
160
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BOGOTÁ-
CAZUCÁ PVC(X2)
PRESIONES CON
HAZEN-WILLIAMS
BOGOTÁ-CAZUCÁ
PVC(X2)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
115
0
20
40
60
80
100
120
140
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BOGOTÁ-CAZUCÁ
PVC(X2)
COMPROBACIÓN
DE PRESIONES
BOGOTÁ-CAZUCÁ
PVC(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
124
- Resultados de presiones para PEAD.
ILUSTRACIÓN 125. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
ILUSTRACIÓN 126. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN WILLIAMS BOGOTÁ-
CAZUCÁ PEAD(X2)
PRESIONES CON
HAZEN WILLIAMS
BOGOTÁ-CAZUCÁ
PEAD(X2)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
115
120
125
130
135
140
145
150
155
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BOGOTÁ-CAZUCÁ
PEAD(X2)
COMPROBACIÓN DE
PRESIONES BOGOTÁ-CAZUCÁ
PEAD(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
125
- Costos.
TABLA 24. COSTOS DE LA RED BOGOTÁ-CAZUCÁ CON CAUDALES CUADRUPLICADOS.
ILUSTRACIÓN 127. GRÁFICA DE COSTOS DE LA RED BOGOTÁ-CAZUCÁ CON CAUDALES
CUADRUPLICADOS.
DARCY-WEISBACH
632 444 331.00
$
1 599 529 400.00
$
3 477 459 602.00
$
DIFERENCIA
(19 323 314.00)
$
(12 734 090.00)
$
(93 988 898.00)
$
HAZEN-WILLIAMS
613 121 017.00
$
1 586 795 310.00
$
3 383 470 704.00
$
RED BOGOTÁ-CAZUCÁ CAUDALES X4
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
$-
$500 000 000.00
$1 000 000 000.00
$1 500 000 000.00
$2 000 000 000.00
$2 500 000 000.00
$3 000 000 000.00
$3 500 000 000.00
$4 000 000 000.00
Costos
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Bogotá-Cazucá ( x4)
Darcy-Weisbach Hierro Dúctil
Hazen-Williams Hierro Dúctil
Darcy-Weisbach PVC
Hazen-Williams PVC
Darcy-Weisbach PEAD
Hazen-Williams PEAD
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
126
- Resultados de presiones para Hierro Dúctil.
ILUSTRACIÓN 128. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
ILUSTRACIÓN 129. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH BOGOTÁ-
CAZUCÁ HIERRO DÚCTIL(X4)
PRESIONES CON DARCY-
WEISBACH BOGOTÁ-CAZUCÁ
HIERRO DÚCTIL(X4)
-40
-35
-30
-25
-20
-15
-10
-5
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BOGOTÁ-CAZUCÁ
HIERRO DUCTIL (X4)
COMPROBACIÓN DE
PRESIONES
BOGOTÁ-CAZUCÁ
HIERRO DUCTIL (X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
127
ILUSTRACIÓN 130. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
- Resultados de presiones con PVC.
ILUSTRACIÓN 131. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
0
20
40
60
80
100
120
140
160
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH BOGOTÁ-
CAZUCÁ HIERRO DÚCTIL(X4)
PRESIONES CON
DARCY-
WEISBACH
BOGOTÁ-
CAZUCÁ HIERRO
DÚCTIL(X4)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
115
120
125
130
135
140
145
150
155
160
165
0
20
40
60
80
100
120
140
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BOGOTÁ-CAZUCÁ
PVC(X4)
PRESIONES
CON HAZEN-
WILLIAMS
BOGOTÁ-
CAZUCÁ
PVC(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
128
ILUSTRACIÓN 132. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
ILUSTRACIÓN 133. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
115
120
125
130
135
140
145
150
155
160
165
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BOGOTÁ-CAZUCÁ
PVC(X4)
COMPROBACIÓN
DE PRESIONES
BOGOTÁ-CAZUCÁ
PVC(X4)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
115
120
125
130
135
140
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH BOGOTÁ-
CAZUCÁ PVC(X4)
PRESIONES CON
DARCY-
WEISBACH
BOGOTÁ-CAZUCÁ
PVC(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
129
- Resultados de presiones para PEAD.
ILUSTRACIÓN 134. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
ILUSTRACIÓN 135. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
15
30
45
60
75
90
105
120
135
150
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS BOGOTÁ-
CAZUCÁ PEAD(X4)
PRESIONES CON
HAZEN-WILLIAMS
BOGOTÁ-CAZUCÁ
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
115
120
125
130
135
140
145
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES BOGOTÁ-CAZUCÁ
PEAD(X4)
COMPROBACIÓN
DE PRESIONES
BOGOTÁ-CAZUCÁ
PEAD(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
130
ILUSTRACIÓN 136. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
- Costos.
TABLA 25. COSTOS DE LA RED R28 CON CAUDALES DUPLICADOS.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
115
120
125
130
135
140
145
150
0
50
100
150
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH BOGOTÁ-
CAZUCÁ PEAD(X4)
PRESIONES CON
DARCY-WEISBACH
BOGOTÁ-CAZUCÁ
RED R28 CAUDALES X2
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
DIFERENCIA
(30 309 850.00)
$
6 100 327.00
$
(1 548 962.00)
$
HAZEN-WILLIAMS
323 226 773.00
$
587 029 233.00
$
1 458 785 597.00
$
DARCY-WEISBACH
353 536 623.00
$
580 928 906.00
$
1 460 334 559.00
$
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
131
ILUSTRACIÓN 137. GRÁFICA DE COSTOS PARA LA RED R28 CON CAUDALES DUPLICADOS.
- Resultados de presiones con Hierro Dúctil.
ILUSTRACIÓN 138 PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
$-
$200 000 000.00
$400 000 000.00
$600 000 000.00
$800 000 000.00
$1 000 000 000.00
$1 200 000 000.00
$1 400 000 000.00
$1 600 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red R28(x2)
DARCY-WEISBACH HIERRO
DÚCTIL
HAZEN-WILLIAMS HIERRO
DÚCTIL
DARCY-WEISBACH PVC
HAZEN-WILLIAMS PVC
DARCY-WEISBACH PEAD
HAZEN-WILLIAMS PEAD
0
5
10
15
20
25
30
35
40
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS R28 HIERRO
DÚCTIL(X2)
PRESIONES CON
HAZEN-WILLIAMS
R28 HIERRO
DÚCTIL(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
132
ILUSTRACIÓN 139. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
- Resultados de presiones para PVC.
ILUSTRACIÓN 140. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
0
5
10
15
20
25
30
35
40
0
10
20
30
40
p
re
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES R28 HIERRO
DÚCTIL(X2)
COMPROBACIÓN
DE PRESIONES
R28 HIERRO
DÚCTIL(X2)
0
5
10
15
20
25
30
35
40
0
10
20
30
40
P
resi
ón
en
m
Nudos
PRESIONES CON HAZEN-WILLIAMS R28
PVC(X2)
PRESIONES CON
HAZEN-WILLIAMS
R28 PVC(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
133
ILUSTRACIÓN 141. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
- Resultados de presiones para PEAD.
ILUSTRACIÓN 142. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES R28 PVC(X2)
COMPROBACIÓN
DE PRESIONES R28
PVC(X2)
0
5
10
15
20
25
30
35
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS R28 PEAD(X2)
PRESIONES CON
HAZEN-WILLIAMS
R28 PEAD(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
134
ILUSTRACIÓN 143. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
- Costos.
TABLA 26. COSTOS DE LA RED R28 CON CAUDALES CUADRUPLICADOS.
0
5
10
15
20
25
30
35
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES R28 PEAD(X2)
COMPROBACIÓN
DE PRESIONES R28
PEAD(X2)
DARCY-WEISBACH
522 773 934.00
$
969 144 343.00
$
2 347 982 702.00
$
DIFERENCIA
(42 085 769.00)
$
27 600 993.00
$
4 829 572.00
$
HAZEN-WILLIAMS
480 688 165.00
$
996 745 336.00
$
2 352 812 274.00
$
RED R28 CAUDALES X4
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
135
ILUSTRACIÓN 144. GRÁFICA DE COSTOS DE LA RED R28 CON CAUDALES CUADRUPLICADOS.
- Resultados de presiones con Hierro Dúctil
ILUSTRACIÓN 145. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
$-
$500 000 000.00
$1 000 000 000.00
$1 500 000 000.00
$2 000 000 000.00
$2 500 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red R28 (x4)
Darcy-Weisbach Hierro Dúctil
Hazen-Williams Hierro Dúctil
Darcy-Weisbach PVC
Hazen-Wiliams PVC
Darcy-Weisbach PEAD
Hazen-Williams PEAD
0
5
10
15
20
25
30
35
40
0
10
20
30
40
P
resi
ón
en
m
Nudos
PRESIONES CON HAZEN-WILLIAMS R28 HIERRO
DÚCTIL(X4)
PRESIONES CON
HAZEN-WILLIAMS
R28 HIERRO
DÚCTIL(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
136
ILUSTRACIÓN 146. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
ILUSTRACIÓN 147. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
5
10
15
20
25
30
35
40
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES R28 HIERRO
DÚCTIL(X4)
COMPROBACIÓN DE
PRESIONES R28 HIERRO
DÚCTIL(X4)
0
5
10
15
20
25
30
35
40
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH R28 HIERRO
DÚCTIL(X4)
PRESIONES CON
DARCY-
WEISBACH R28
HIERRO
DÚCTIL(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
137
- Resultados de presiones para PVC.
ILUSTRACIÓN 148. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
ILUSTRACIÓN 149. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
3
6
9
12
15
18
21
24
27
30
33
36
39
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS R28 PVC(4X)
PRESIONES CON
HAZEN-WILLIAMS
R28 PVC(4X)
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
0
10
20
30
40
Pr
e
si
ó
n
e
n
M
.C.A
Nudos
COMPROBACIÓN DE PRESIONES R28 PVC(X4)
COMPROBACIÓN DE
PRESIONES R28
PVC(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
138
ILUSTRACIÓN 150. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
- Resultados de presiones para PEAD.
ILUSTRACIÓN 151. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
0
3
6
9
12
15
18
21
24
27
30
33
36
39
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH R28 PVC(4X)
PRESIONES CON
DARCY-WEISBACH
R28 PVC(4X)
0
5
10
15
20
25
30
35
40
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS R28 PEAD(X4)
PRESIONES CON
HAZEN-WILLIAMS
R28 PEAD(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
139
ILUSTRACIÓN 152. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
ILUSTRACIÓN 153. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES R28 PEAD(X4)
COMPROBACIÓN
DE PRESIONES
R28 PEAD(X4)
0
5
10
15
20
25
30
35
40
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH R28 PEAD(X4)
PRESIONES CON
DARCY-
WEISBACH R28
PEAD(X4)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
140
- Costos.
TABLA 27.COSTOS DE LA RED CON CAUDALES DUPLICADOS.
ILUSTRACIÓN 154. GRÁFICA DE COSTOS DE LA RED TESIS 1 PARA CAUDALES DUPLICADOS.
RED TESIS 1 CAUDALES X2
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
DIFERENCIA
(8 442 303.00)
$
(1 675 051.00)
$
6 759 605.00
$
HAZEN-WILLIAMS
261 767 444.00
$
413 528 622.00
$
972 139 777.00
$
DARCY-WEISBACH
270 209 747.00
$
415 203 673.00
$
965 380 172.00
$
$-
$200 000 000.00
$400 000 000.00
$600 000 000.00
$800 000 000.00
$1 000 000 000.00
$1 200 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Tesis 1(x2)
HAZEN-WILLIAMS HIERRO
DÚCTIL
DARCY-WEISBACH HIERRO
DÚCTIL
HAZEN-WILLIAMS PVC
DARCY-WEISBACH PVC
HAZEN-WILLIAMS PEAD
DARCY-WEISBACH PEAD
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
141
- Resultados de presiones para Hierro Dúctil
ILUSTRACIÓN 155. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
ILUSTRACIÓN 156. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
3
6
9
12
15
18
21
24
27
30
33
36
39
42
45
48
51
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 1 HIERRO
DÚCTIL(X2)
PRESIONES CON
HAZEN-WILLIAMS
TESIS1 HIERRO
DÚCTIL(X2)
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
42
44
46
48
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 1 HIERRO
DÚCTIL(X2)
COMPROBACIÓN
DE PRESIONES
TESIS1 HIERRO
DÚCTIL(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
142
- Resultados de presiones para PVC.
ILUSTRACIÓN 157. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
ILUSTRACIÓN 158. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 1 PVC(X2)
PRESIONES
CON HAZEN-
WILLIAMS
TESIS1
PVC(X2)
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 1 PVC(X2)
COMPROBACIÓN
DE PRESIONES
TESIS 1 PVC(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
143
- Resultados de presiones para PEAD
ILUSTRACIÓN 159. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
ILUSTRACIÓN 160. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 1
PEAD(X2)
PRESIONES CON
HAZEN-
WILLIAMS TESIS1
PEAD(X2)
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 1 PEAD(X2)
COMPROBACIÓN
DE PRESIONES
TESIS1 PEAD(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
144
- Costos.
TABLA 28 COSTOS DE LA RED TESIS 1 CON CAUDALES CUADRUPLICADOS.
ILUSTRACIÓN 161. GRÁFICA DE COSTOS PARA LA RED TESIS 1 CON CAUDALES
CUADRUPLICADOS.
DARCY-WEISBACH
387 561 043.00
$
803 469 384.00
$
1 864 532 255.00
$
DIFERENCIA
(12 006 197.00)
$
(25 050 043.00)
$
5 615 149.00
$
HAZEN-WILLIAMS
375 554 846.00
$
778 419 341.00
$
1 870 147 404.00
$
RED TESIS 1 CAUDALES X4
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
$-
$200 000 000.00
$400 000 000.00
$600 000 000.00
$800 000 000.00
$1 000 000 000.00
$1 200 000 000.00
$1 400 000 000.00
$1 600 000 000.00
$1 800 000 000.00
$2 000 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Tesis 1(x4)
Darcy-Weissbach Hierro Dúctil
Hazen-Williams Hierro Dúctil
Darcy-Weisbach PVC
Hazen-Wiliams PVC
Darcy-Weisbach PEAD
Hazen-Williams PEAD
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
145
- Resultados de presiones para Hierro Dúctil.
ILUSTRACIÓN 162. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
ILUSTRACIÓN 163. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 1 HIERRO
DÚCTIL(X4)
PRESIONES CON
HAZEN-WILLIAMS
HIERRO
DÚCTIL(X4)
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
42
44
46
48
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 1 HIERRO
DÚCTIL(X4)
COMPROBACIÓN
DE PRESIONES
TESIS 1 HIERRO
DÚCTIL(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
146
ILUSTRACIÓN 164. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
- Resultados de presiones para PVC.
ILUSTRACIÓN 165. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH TESIS 1 HIERRO
DÚCTIL(X4)
PRESIONES CON
DARCY-WEISBACH
HIERRO
DÚCTIL(X4)
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
P
resi
ón
en
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 1 PVC(X4)
PRESIONES CON
HAZEN-
WILLIAMS
TESIS1 PVC(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
147
ILUSTRACIÓN 166. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
ILUSTRACIÓN 167. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 1 PVC(X4)
COMPROBACIÓN
DE PRESIONES
TESIS1 PVC(X4)
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH TESIS 1 PVC(X4)
PRESIONES
CON DARCY-
WEISBACH
TESIS1 PVC(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
148
- Resultado de presiones para PEAD.
ILUSTRACIÓN 168. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
ILUSTRACIÓN 169. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 1
PEAD(4X)
PRESIONES CON
HAZEN-WILLIAMS
TESIS1 PEAD(4X)
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 1 PEAD(X4)
COMPROBACIÓN
DE PRESIONES
TESIS1 PEAD(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
149
ILUSTRACIÓN 170. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
- Costos.
TABLA 29. COSTOS DE LA RED TESIS 2 CON CAUDALES DUPLICADOS.
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
50
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH TESIS 1
PEAD(4X)
PRESIONES CON
DARCY-WEISBACH
TESIS1 PEAD(4X)
RED TESIS 2 CAUDALES X2
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
DIFERENCIA
(23 603 078.00)
$
84 138 817.00
$
(54 605 070.00)
$
HAZEN-WILLIAMS
408 116 612.00
$
751 731 271.00
$
1 579 203 765.00
$
DARCY-WEISBACH
431 719 690.00
$
667 592 454.00
$
1 633 808 835.00
$
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
150
ILUSTRACIÓN 171. GRÁFICA DE COSTOS PARA LA RED TESIS 2 CON CAUDALES DUPLICADOS.
- Resultados de presiones para Hierro Dúctil.
ILUSTRACIÓN 172. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
$-
$200 000 000.00
$400 000 000.00
$600 000 000.00
$800 000 000.00
$1 000 000 000.00
$1 200 000 000.00
$1 400 000 000.00
$1 600 000 000.00
$1 800 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Tesis 2(x2)
HAZEN-WILLIAMS HIERRO
DÚCTIL
DARCY-WEISBACH HIERRO
DÚCTIL
HAZEN-WILLIAMS PVC
DARCY-WEISBACH PVC
HAZEN-WILLIAMS PEAD
DARCY-WEISBACH PEAD
0
5
10
15
20
25
30
35
40
45
50
55
60
65
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 2 HIERRO
DÚCTIL(X2)
PRESIONES CON
HAZEN-WILLIAMS
TESIS2 HIERRO
DÚCTIL(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
151
ILUSTRACIÓN 173. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
- Resultados de presiones para PVC.
ILUSTRACIÓN 174. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
0
10
20
30
40
Pr
e
si
ó
n
e
n
M
.C.A
Nudos
COMPROBACIÓN DE PRESIONES TESIS2 HIERRO
DÚCTIL(X2)
COMPROBACIÓN
DE PRESIONES
TESIS2 HIERRO
DÚCTIL(X2)
0
5
10
15
20
25
30
35
40
45
50
55
60
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 2 PVC(X2)
PRESIONES CON
HAZEN-
WILLIAMS TESIS
2 PVC(X2)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
152
ILUSTRACIÓN 175. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
- Resultados de presiones para PEAD.
ILUSTRACIÓN 176. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 2 PVC(X2)
COMPROBACIÓN
DE PRESIONES
TESIS2 PVC(X2)
0
5
10
15
20
25
30
35
40
45
50
55
60
0
5
10
15
20
25
30
35
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 2 PEAD(2X)
PRESIONES CON
HAZEN-
WILLIAMS
TESIS2
PEAD(2X)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
153
ILUSTRACIÓN 177. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
- Costos.
TABLA 30. COSTOS DE LA RED TESIS 2 CON CAUDALES CUADRUPLICADOS.
0
5
10
15
20
25
30
35
40
45
50
55
60
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 2 PEAD(X2)
COMPROBACIÓN
DE PRESIONES
TESIS2 PEAD(X2)
DARCY-WEISBACH
576 904 087.00
$
1 303 913 585.00
$
2 732 550 411.00
$
DIFERENCIA
(18 158 838.00)
$
(46 666 212.00)
$
(91 997 712.00)
$
HAZEN-WILLIAMS
558 745 249.00
$
1 257 247 373.00
$
2 640 552 699.00
$
RED TESIS 2 CAUDALES X4
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
154
ILUSTRACIÓN 178. GRÁFICA DE COSTOS DE LA RED TESIS 2 CON CAUDALES CUADRUPLICADOS.
- Resultados de presiones para Hierro Dúctil.
ILUSTRACIÓN 179. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
$-
$500 000 000.00
$1 000 000 000.00
$1 500 000 000.00
$2 000 000 000.00
$2 500 000 000.00
$3 000 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Tesis 2(x4)
Darcy-Weissbach Hierro Dúctil
Hazen-Williams Hierro Dúctil
Darcy-Weisbach PVC
Hazen-Wiliams PVC
Darcy-Weisbach PEAD
Hazen-Williams PEAD
0
5
10
15
20
25
30
35
40
45
50
55
60
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 2 HIERRO
DÚCTIL(X4)
PRESIONES CON
HAZEN-WILLIAMS
HIERRO
DÚCTIL(X4)
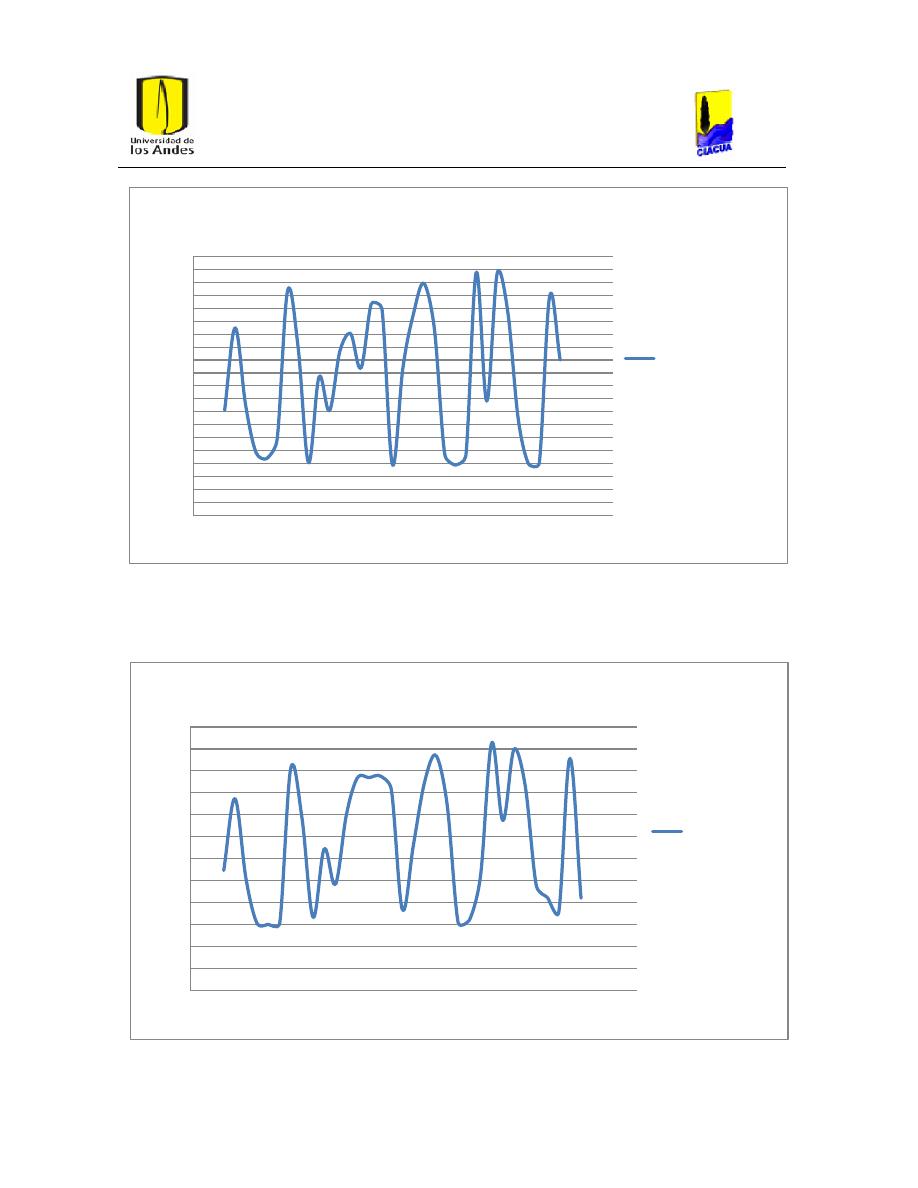
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
155
ILUSTRACIÓN 180. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
ILUSTRACIÓN 181. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
3
6
9
12
15
18
21
24
27
30
33
36
39
42
45
48
51
54
57
60
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACION PRESIONES TESIS 2 HIERRO
DÚCTIL(X4)
COMPROBACION
PRESIONES TESIS 2
HIERRO DÚCTIL(X4)
0
5
10
15
20
25
30
35
40
45
50
55
60
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH TESIS 2 HIERRO
DÚCTIL(X4)
PRESIONES CON
DARCY-
WEISBACH
HIERRO
DÚCTIL(X4)
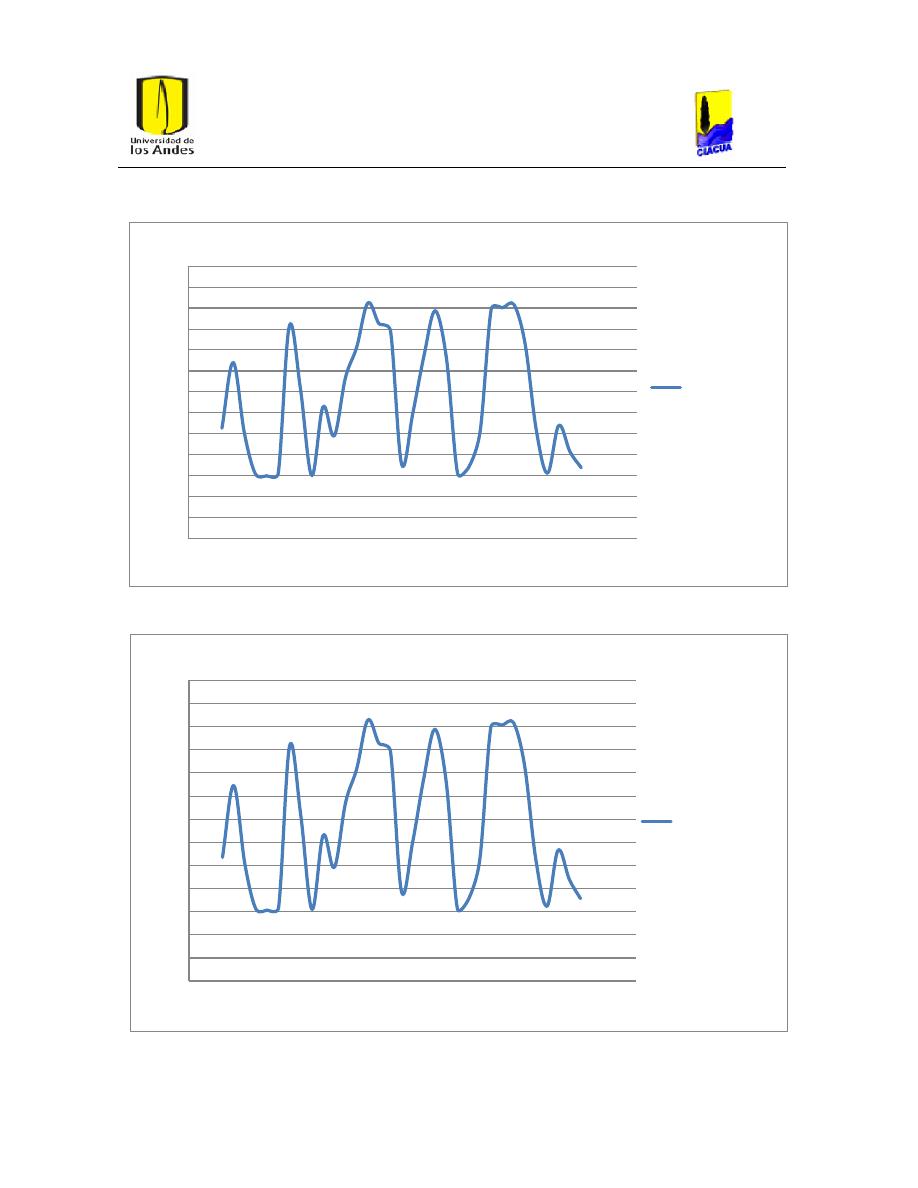
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
156
- Resultados de presiones para PVC.
ILUSTRACIÓN 182. PRESIONES CON LA DE HAZEN-WILLIAMS PARA PVC.
ILUSTRACIÓN 183. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 2 PVC(X4)
PRESIONES CON
HAZEN-
WILLIAMS
TESIS2 PVC(X4)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 2 PVC(X4)
COMPROBACIÓN
DE PRESIONES
TESIS2 PVC(X4)
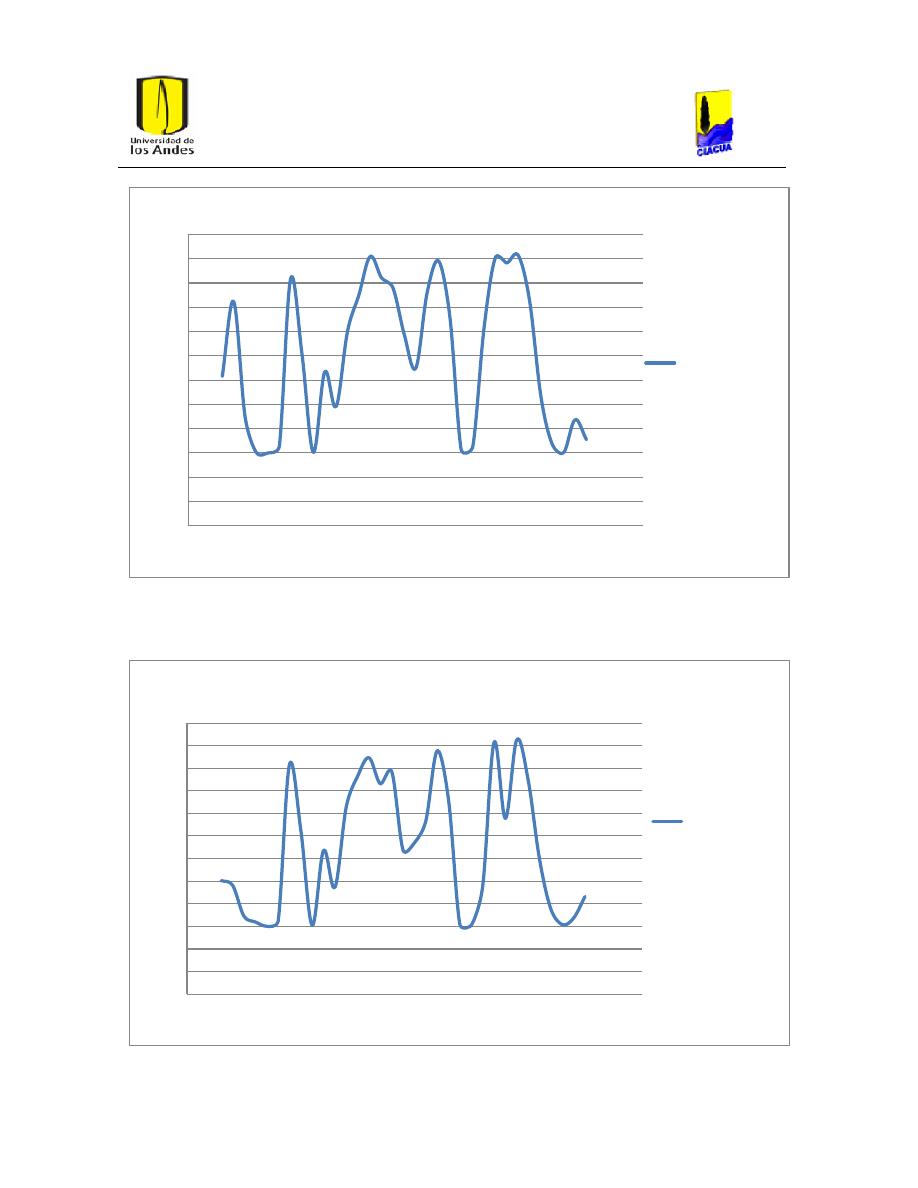
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
157
ILUSTRACIÓN 184. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
- Resultados de presiones para PEAD.
ILUSTRACIÓN 185. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH TESIS 2 PVC(X4)
PRESIONES CON
DARCY-
WEISBACH
TESIS2 PVC(X4)
0
5
10
15
20
25
30
35
40
45
50
55
60
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 2
PEAD(X4)
PRESIONES CON
HAZEN-
WILLIAMS
TESIS2 PEAD(X4)
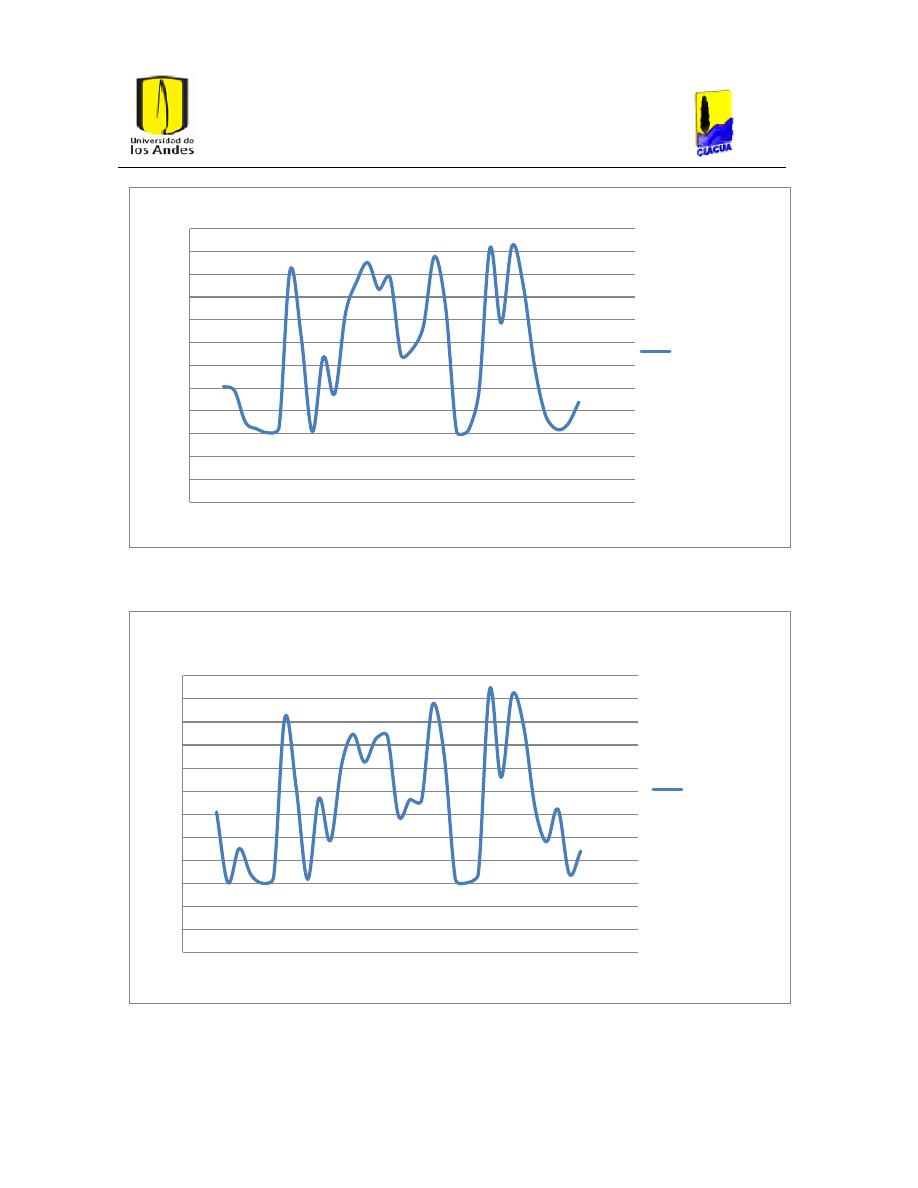
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
158
ILUSTRACIÓN 186. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
ILUSTRACIÓN 187. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 2 PEAD(X4)
COMPROBACIÓN
DE PRESIONES
TESIS2 PEAD(X4)
0
5
10
15
20
25
30
35
40
45
50
55
60
0
10
20
30
40
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH TESIS 2
PEAD(X4)
PRESIONES CON
DARCY-
WEISBACH
TESIS2 PEAD(X4)
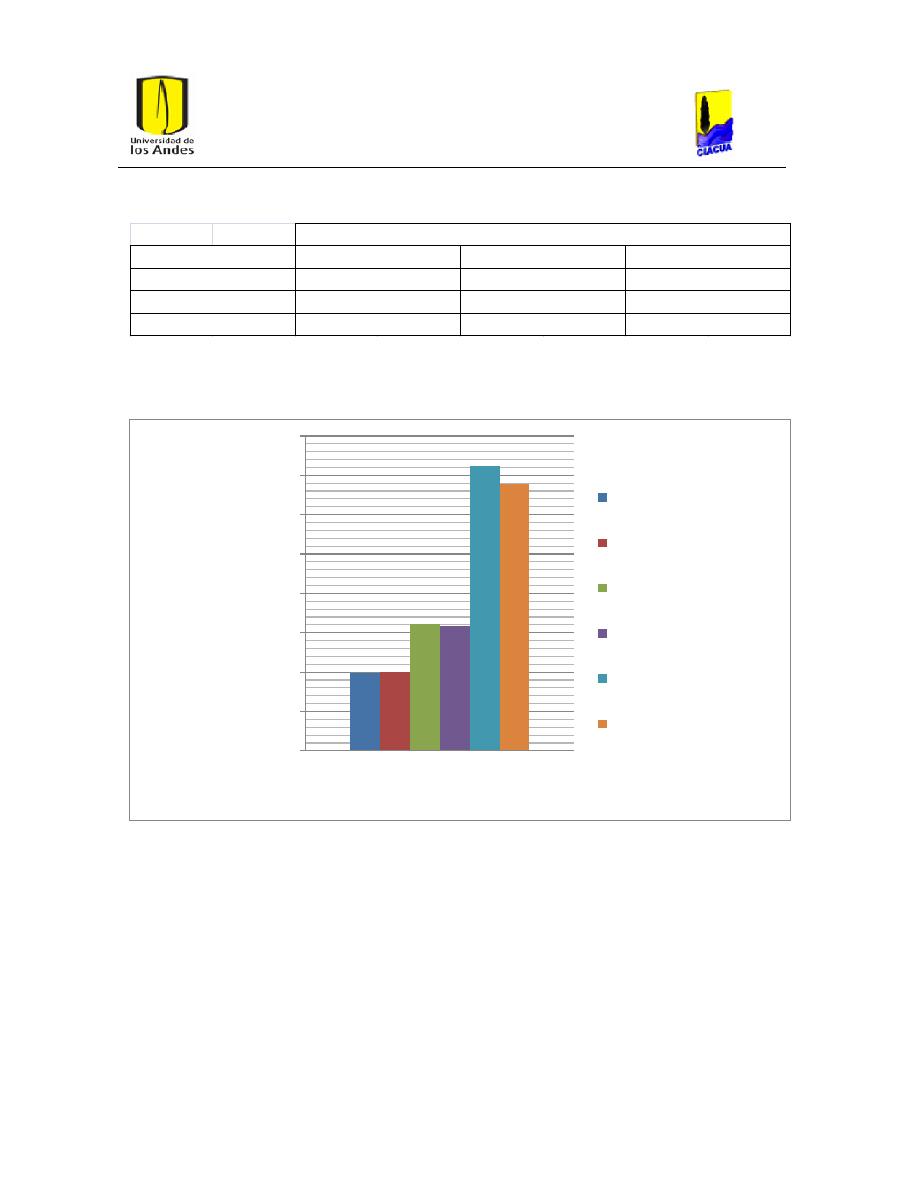
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
159
- Costos.
TABLA 31. COSTOS DE LA RED TESIS 3 CON CAUDALES DUPLICADOS.
ILUSTRACIÓN 188. GRÁFICA DE COSTOS PARA LA RED TESIS 3 CON CAUDALES DUPLICADOS.
DIFERENCIA
(12 696 878.00)
$
24 646 880.00
$
228 104 364.00
$
HAZEN-WILLIAMS
983 747 748.00
$
1 612 342 648.00
$
3 617 739 194.00
$
DARCY-WEISBACH
996 444 626.00
$
1 587 695 768.00
$
3 389 634 830.00
$
RED TESIS 3 CAUDALES X2
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
$-
$500 000 000.00
$1 000 000 000.00
$1 500 000 000.00
$2 000 000 000.00
$2 500 000 000.00
$3 000 000 000.00
$3 500 000 000.00
$4 000 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Tesis 3(x2)
HAZEN-WILLIAMS HIERRO
DÚCTIL
DARCY-WEISBACH HIERRO
DÚCTIL
HAZEN-WILLIAMS PVC
DARCY-WEISBACH PVC
HAZEN-WILLIAMS PEAD
DARCY-WEISBACH PEAD
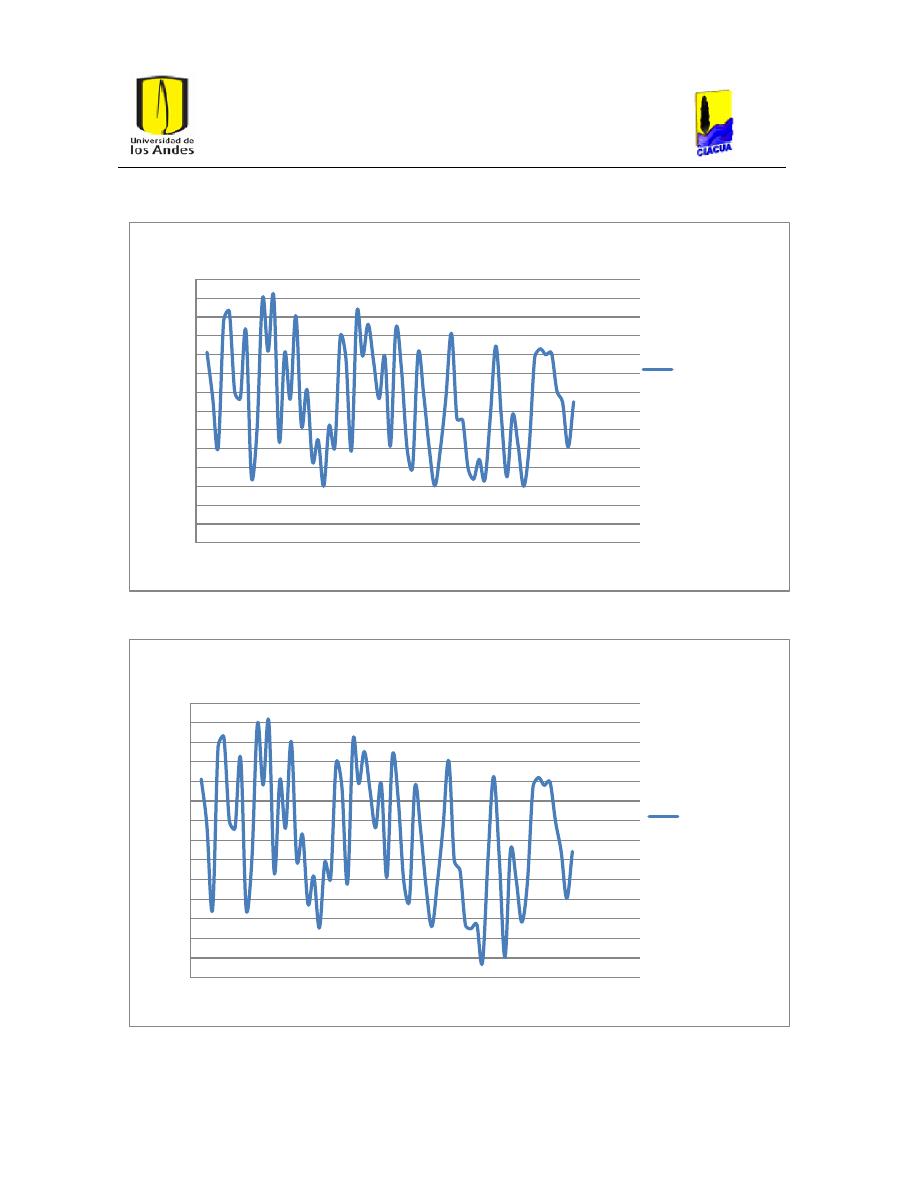
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
160
- Resultados de presiones para Hierro Dúctil.
ILUSTRACIÓN 189. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
ILUSTRACIÓN 190. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 3 HIERRO
DÚCTIL(X2)
PRESIONES CON
HAZEN-WILLIAMS
TESIS3 HIERRO
DÚCTIL(X2)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 3 HIERRO
DÚCTIL(X2)
COMPROBACIÓN
DE PRESIONES
TESIS3 HIERRO
DÚCTIL(X2)
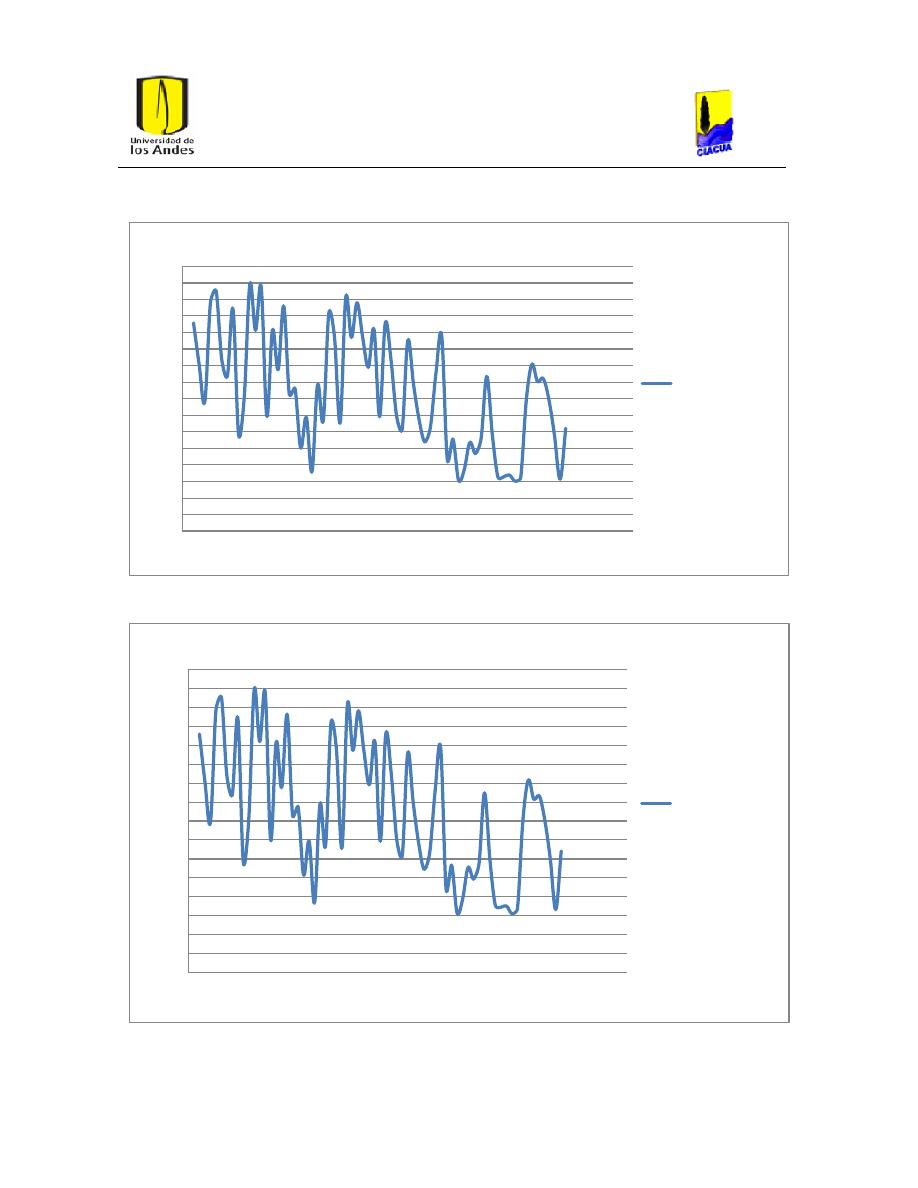
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
161
- Resultados de presiones para PVC.
ILUSTRACIÓN 191. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
ILUSTRACIÓN 192. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 3 PVC(X2)
PRESIONES CON
HAZEN-WILLIAMS
TESIS3 PVC(X2)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 3 PVC(X2)
COMPROBACIÓN
DE PRESIONES
TESIS3 PVC(X2)
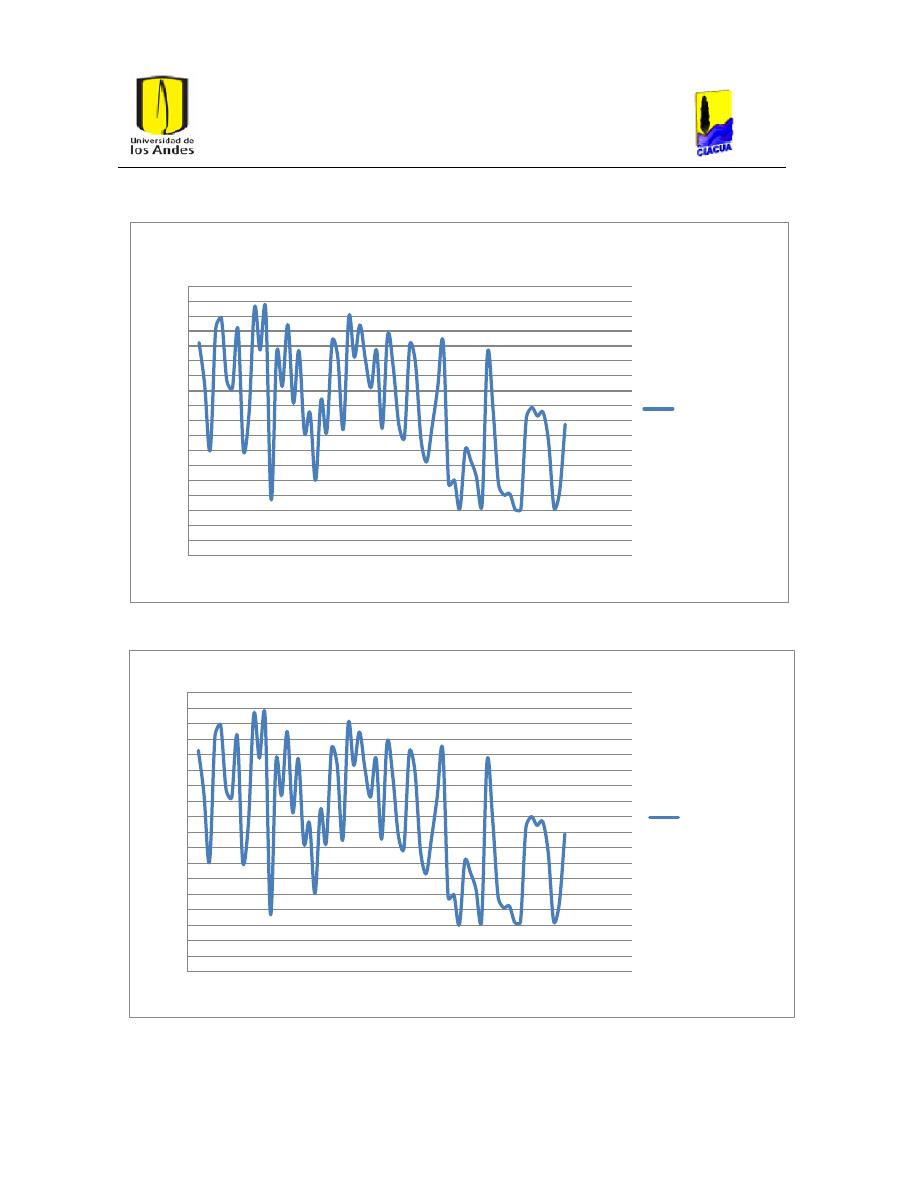
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
162
- Resultados de presiones para PEAD.
ILUSTRACIÓN 193. PRESIONES CON LA ECUACION DE HAZEN-WILLIAMS PARA PEAD.
ILUSTRACIÓN 194. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 3
PEAD(X2)
PRESIONES CON
HAZEN-WILLIAMS
TESIS3 PEAD(X2)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 3 PEAD(X2)
COMPROBACIÓN
DE PRESIONES
TESIS3 PEAD(X2)
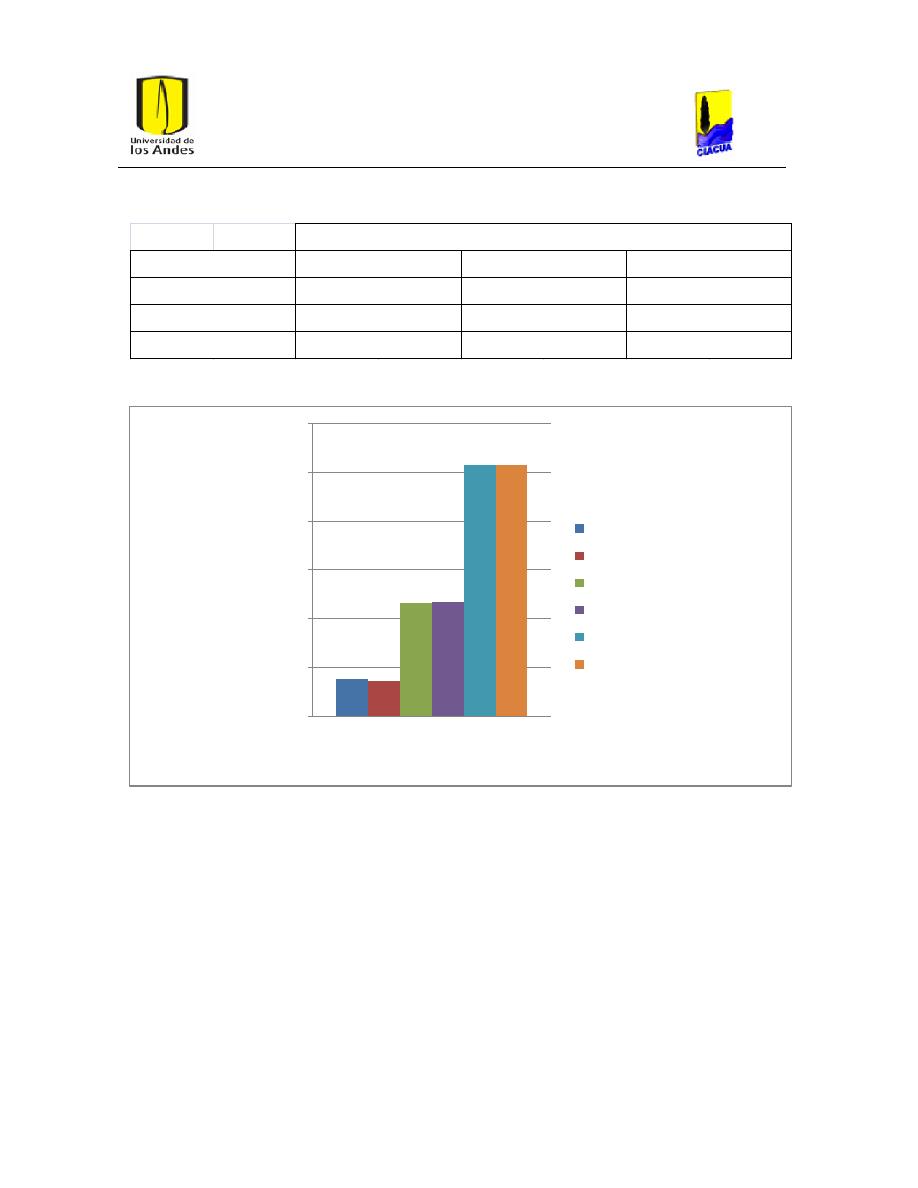
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
163
- Costos.
TABLA 32. COSTOS DE LA RED TESIS 3 CON CAUDALES CUADRUPLICADOS.
ILUSTRACIÓN 195. GRÁFICA DE COSTOS DE LA RED TESIS 3 CON CAUDALES CUADRUPLICADOS.
DARCY-WEISBACH
1 540 521 729.00
$
4 642 152 360.00
$
10 298 405 339.00
$
DIFERENCIA
(65 035 806.00)
$
32 641 022.00
$
(28 042 950.00)
$
HAZEN-WILLIAMS
1 475 485 923.00
$
4 674 793 382.00
$
10 270 362 389.00
$
RED TESIS 3 CAUDALES X4
COSTOS $
HIERRO DÚCTIL
PVC
PEAD
$-
$2 000 000 000.00
$4 000 000 000.00
$6 000 000 000.00
$8 000 000 000.00
$10 000 000 000.00
$12 000 000 000.00
COSTOS
Co
sto
s
e
n
Peso
s
Co
lo
m
b
ian
o
s
Red Tesis 3(x4)
Darcy-Weissbach Hierro Dúctil
Hazen-Williams Hierro Dúctil
Darcy-Weisbach PVC
Hazen-Wiliams PVC
Darcy-Weisbach PEAD
Hazen-Williams PEAD
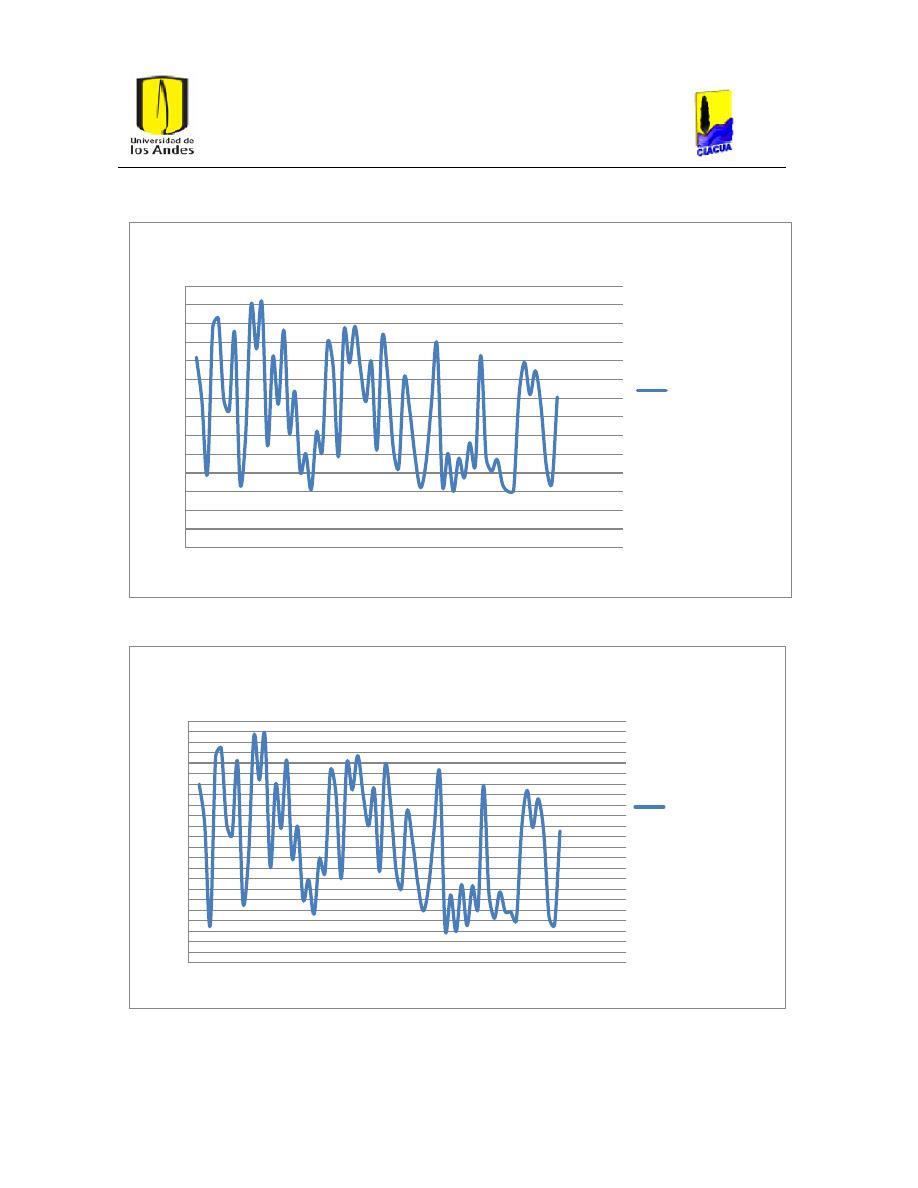
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
164
- Resultados de presiones para Hierro Dúctil.
ILUSTRACIÓN 196. PRESIONES DE LA ECUACIÓN DE HAZEN-WILLIAMS PARA HIERRO DÚCTIL.
ILUSTRACIÓN 197. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 3 HIERRO
DÚCTIL(X4)
PRESIONES CON
HAZEN-WILLIAMS
TESIS3 HIERRO
DÚCTIL(X4)
0
3
6
9
12
15
18
21
24
27
30
33
36
39
42
45
48
51
54
57
60
63
66
69
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 3 HIERRO
DÚCTIL(X4)
COMPROBACIÓN
DE PRESIONES
TESIS 3 HIERRO
DÚCTIL(X4)
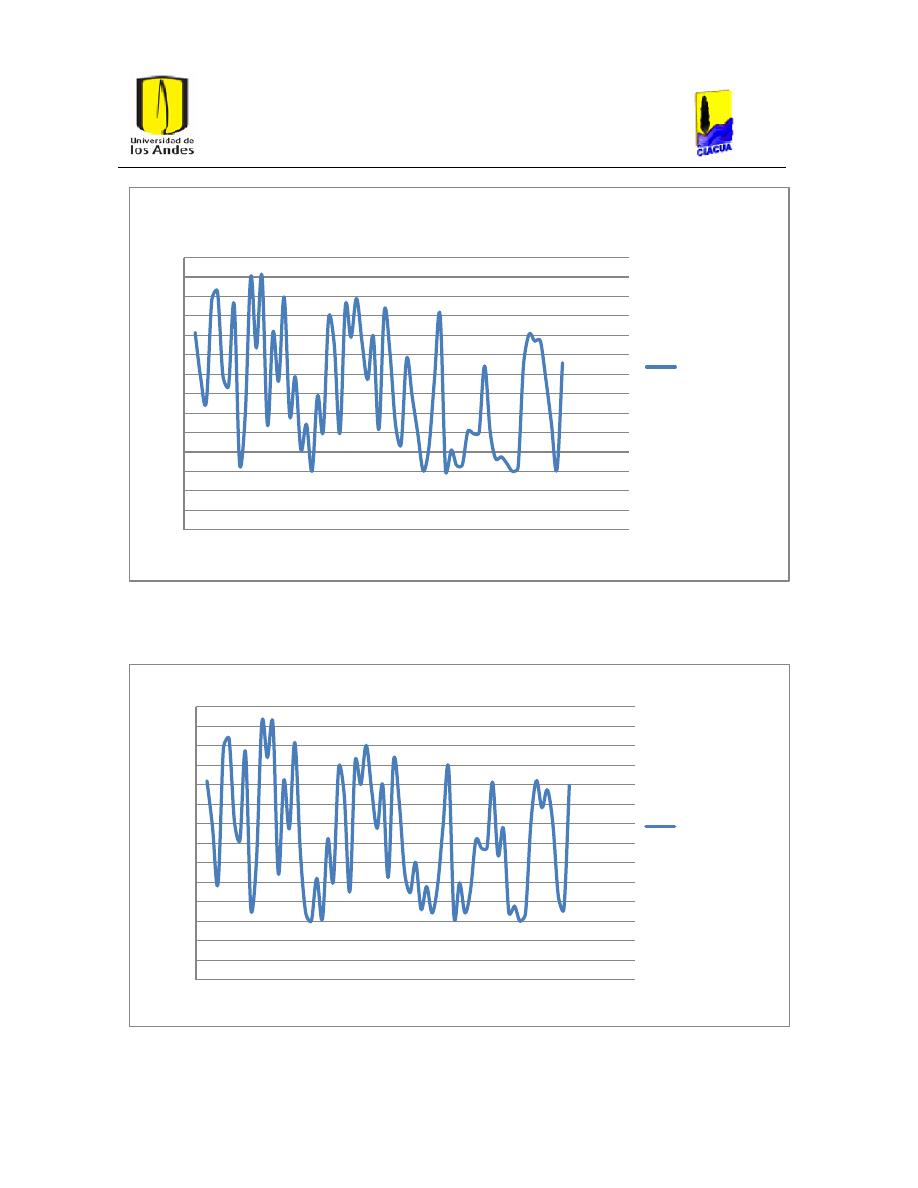
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
165
ILUSTRACIÓN 198. PRESIONES PARA LA ECUACIÓN DE DARCY-WEISBACH PARA HIERRO DÚCTIL.
- Resultados de presiones para PVC.
ILUSTRACIÓN 199. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH TESIS 3 HIERRO
DÚCTIL(X4)
PRESIONES CON
DARCY-
WEISBACH
TESIS3 HIERRO
DÚCTIL(X4)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 3 PVC(X4)
PRESIONES CON
HAZEN-
WILLIAMS TESIS3
PVC(X4)
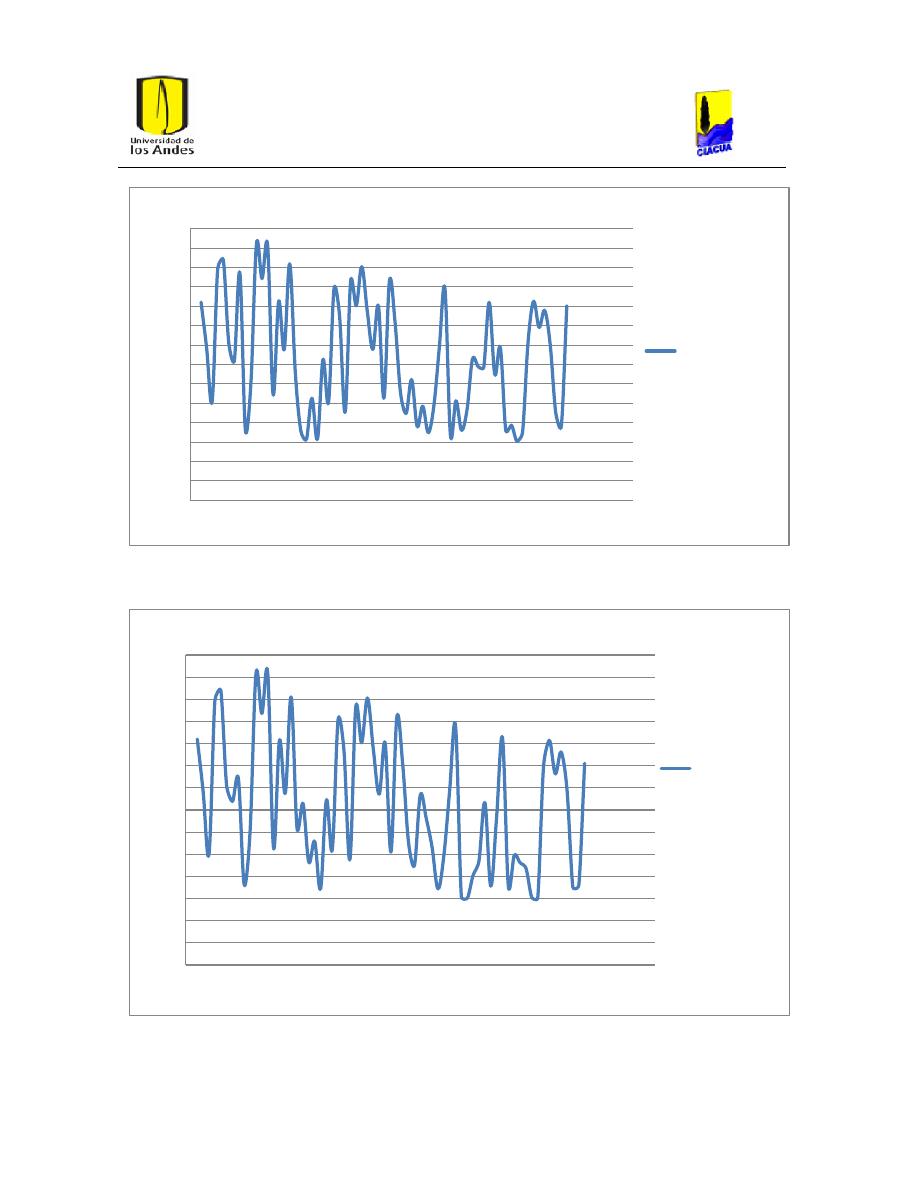
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
166
ILUSTRACIÓN 200. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
ILUSTRACIÓN 201. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA PVC.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 3 PVC(X4)
COMPROBACIÓN
DE PRESIONES
TESIS3 PVC(X4)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
10
20
30
40
50
60
70
80
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH TESIS 3 PVC(X4)
PRESIONES
CON DARCY-
WEISBACH
TESIS3 PVC(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
167
- Resultados de presiones para PEAD.
ILUSTRACIÓN 202. PRESIONES CON LA ECUACIÓN DE HAZEN-WILLIAMS PARA PEAD.
ILUSTRACIÓN 203. PRESIONES DE LA RED DISEÑADA CON HAZEN-WILLIAMS DESPUÉS DE
CORRER LA HIDRÁULICA CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
10
20
30
40
50
60
70
80
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON HAZEN-WILLIAMS TESIS 3 PEAD(X4)
PRESIONES
CON HAZEN-
WILLIAMS
TESIS3
PEAD(X4)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
20
40
60
80
P
resi
ón
en
m
Nudos
COMPROBACIÓN DE PRESIONES TESIS 3 PEAD(X4)
COMPROBACIÓN
DE PRESIONES
TESIS3 PEAD(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
168
ILUSTRACIÓN 204. PRESIONES CON LA ECUACIÓN DE DARCY-WEISBACH PARA PEAD.
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0
20
40
60
80
Pr
e
si
ó
n
e
n
m
Nudos
PRESIONES CON DARCY-WEISBACH TESIS 3
PEAD(X4)
PRESIONES
CON DARCY-
WEISBACH
TESIS3
PEAD(X4)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
169
ILUSTRACIÓN 205. DIAGRAMA DE MOODY CON FACTORES DE FRICCIÓN DE REDES CON CAUDALES NORMALES UTILIZANDO PEAD.
0.001
0.01
0.1
1
1.00E+00 1.00E+01 1.00E+02 1.00E+03 1.00E+04 1.00E+05 1.00E+06 1.00E+07 1.00E+08 1.00E+09 1.00E+10
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody para PEAD con caudales normales
Comprobación Balerma
Comprobación San Vicente
Comprobación R28
Comprobación Tesis 1
Comprobación Tesis 2
Comprobación Tesis 3
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
170
ILUSTRACIÓN 206. DIAGRAMA DE MOODY CON FACTORES DE FRICCIÓN DE REDES CON CAUDALES NORMALES UTILIZANDO PEAD.
0.001
0.01
0.1
1
1.00E+00
1.00E+01
1.00E+02
1.00E+03
1.00E+04
1.00E+05
1.00E+06
1.00E+07
Fact
o
r
d
e
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody para PEAD con caudales duplicados
Comprobación Balerma
Comprobación San Vicente
Comprobación R28
Comprobación Tesis 1
Comprobación Tesis 2
Comprobación Tesis 3
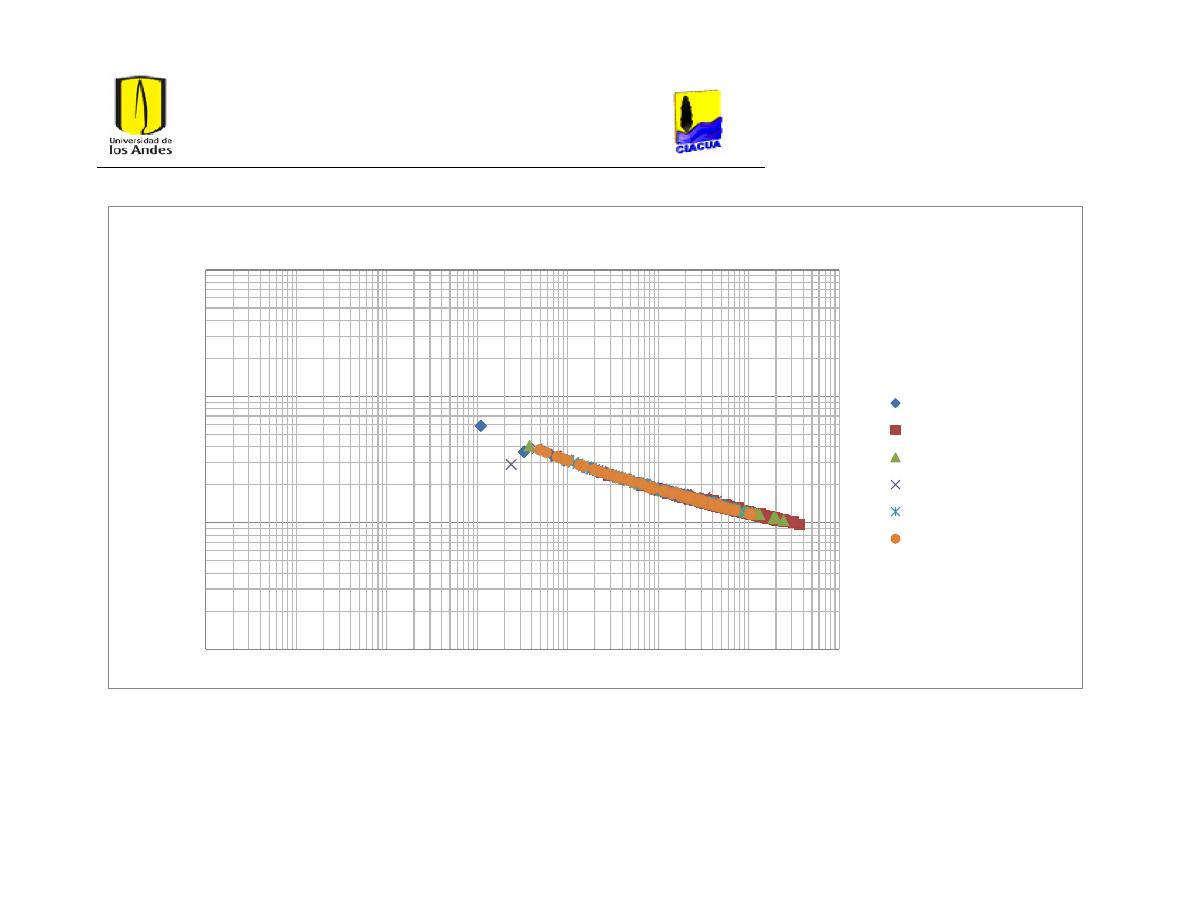
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
171
ILUSTRACIÓN 207. DIAGRAMA DE MOODY CON FACTORES DE FRICCIÓN DE REDES CON CAUDALES CUADRUPLICADOS UTILIZANDO PEAD.
0.001
0.01
0.1
1
1.00E+00
1.00E+01
1.00E+02
1.00E+03
1.00E+04
1.00E+05
1.00E+06
1.00E+07
Far
cto
r
Fr
ic
ci
ó
n
Número de Reynolds
Diagrama de Moody para PEAD con caudales cuadruplicados
Comprobación San Vicente
Comprobación Balerma
Comprobación R28
Comprobación Tesis 1
Comprobación Tesis 2
Comprobación Tesis 3

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Efecto del uso de ecuaciones empíricas vs ecuaciones físicamente
basadas sobre los costos de diseños optimizados en acueductos.
IAMB 201210 29
172
