
Efecto de la redundancia de redes de distribución en el cloro residual y en
la vida media del agua en la red.
“XII Simposio Iberoamericano sobre planificación de sistemas de
abastecimiento y drenaje”
Daniela Rincón (1), Juan Saldarriaga (2)
(1) Investigador, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de los
Andes (CIACUA), Carrera 1 No. 18ª-10, Bogotá, Colombia, Teléfono: 3394949 Ext:2819, Email:
d.rincon52@uniandes.edu.co.
Teléfono: 3394949 Ext: 3521
(2) Profesor Titular, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de
los Andes (CIACUA), Carrera 1 No. 18ª-10, Bogotá, Colombia, Teléfono: 3394949 Ext:3521, Email:
jsaldarr@uniandes.edu.co. Teléfono: 3394949 Ext: 3282
RESUMEN
Esta investigación tuvo como objetivo analizar el efecto que tiene la redundancia de redes de distribución, la
variabilidad en longitudes de los tubos, los cambios de demandas y los cambios de presión en los parámetros
de calidad del agua medidos a través de la concentración de cloro residual. Para la modelación de ésta
calidad se hizo uso del modelo tradicional y el modelo moderno de flujo bidimensional.
Se encontró que al aumentar la redundancia de las redes la concentración de cloro promedio disminuye, la
vida media del agua aumenta y las tuberías tienden hacia la región de Supuesto de Mezcla Completa
Quebrantado del modelo bidimensional.
Palabras claves: Redes de distribución, redundancia, calidad del agua, vida media del agua, flujo
bidimensional.
ABSTRACT
This research project aims to analyze the effect of the water distribution network redundancy, variability of
lengths of pipelines, changes in demands at the nodes and pressure changes in water quality parameters
measured with the chlorine concentration. This was obtained by the traditional model and the modern model
of two-dimensional flow, including the water age.
When the water distribution network redundancy increases the average chlorine concentration decreases, the
half-life of water increases and the pipelines tends toward the region where the Well-Mixedness Assumption
is not valid.
Key words: Water distribution systems, water distribution network redundancy, Water quality Chlorine
residuals, water age, two-dimensional flow
SOBRE EL AUTOR PRINCIPAL
Daniela Rincón: Actualmente se encuentra realizando maestría en Ingeniería Civil en el área de Recursos
Hídricos e Hidroinformática en la Universidad de los Andes, Colombia. Obtuvo su título de pregrado en la misma
universidad en Ingeniería Ambiental en el año 2012. Trabaja como investigadora en el Centro de Investigación
en Acueductos y Alcantarillados (CIACUA) del Departamento de Ingeniería Civil y Ambiental de la Universidad
de los Andes.

ANTECEDENTES E INTRODUCCIÓN
En el proceso de potabilización del agua en las
Plantas de Tratamiento de Agua Potable (PTAP), el
cloro es el agente desinfectante más utilizado. Una
de las razones se debe a su característica de
permanecer en el agua como cloro residual a través
de un sistema de distribución. Adicionalmente, las
concentraciones del cloro permiten determinar la
calidad del agua en su recorrido, desde que deja la
planta de tratamiento hasta que llega a los usuarios,
y controlar que estas concentraciones estén dentro
unos rangos establecidos. Sin embargo, durante el
recorrido del agua en la red de distribución, se puede
presentar un deterioro de la calidad de ésta, ya que
existe un decaimiento del cloro residual al
reaccionar con la pared de las tuberías, tanques y
con el agua en sí.
En ese sentido, es necesario mantener un cierto nivel
de desinfección en las redes de distribución. Para
garantizar que esto se cumpla, se emplean modelos
computacionales de simulación de calidad del agua,
los cuales han venido adquiriendo cada vez mayor
importancia por su aproximación a la realidad sin
tener que realizar monitoreos periódicos del
desinfectante en cada punto de la red, lo que
resultaría bastante costoso e imposible de realizar.
La mayoría de los modelos computacionales, entre
ellos el programa REDES (CIACUA, 2009), usados
comúnmente para modelar la tasa de reacción o
decaimiento del cloro (K) debido a la demanda de
pared (
), suponen una mezcla completa a través
de la sección transversal del fluido en las tuberías,
con flujo unidimensional al considerar las tuberías
como objetos unidimensionales y un decaimiento
exponencial del soluto. No obstante, el suponer
cada tubería como elemento unidimensional puede
resultar en cambios en la tasa de decaimiento del
soluto, ya que los perfiles de velocidad y de difusión
turbulenta pueden variar en cualquier dirección en el
caso de presentarse flujos turbulentos. Asimismo el
suponer una mezcla completa del fluido también
puede conducir a errores en la modelación, ya que
dicha suposición, no tiene en cuenta el efecto de la
capa límite turbulenta en la tasa de transferencia de
masa ni las variaciones en concentraciones del
soluto que se pueden presentar a lo largo de la
sección transversal de la tubería.
Estudios recientes plantean un flujo bidimensional
(método moderno) para lograr establecer un rango
de parámetros en donde el sistema turbulento tiene
un supuesto de mezcla completa y en donde la
influencia de las capas límite y la falta de
uniformidad en el perfil de concentración a través de
la sección transversal son insignificantes (Sookhak,
Reeuwijk, & Maksimovic, 2010).
De otro lado, la redundancia (cantidad de tuberías en
las redes de distribución) y características de las
redes tienen efecto sobre la tasa de reacción del
cloro (K). Para ello, este parámetro se calcula
utilizando el método moderno y tradicional de
modelación del decaimiento o crecimiento del cloro.
El primero, tiene en cuenta el efecto de la capa
límite turbulenta por lo que se plantea un flujo
bidimensional para establecer un rango de
parámetros en donde el sistema turbulento tiene un
supuesto de mezcla completa, mientras que el
método tradicional supone una mezcla completa en
las tuberías con flujo unidimensional y un
decaimiento exponencial del soluto.
En este artículo se analiza el efecto que tiene la
redundancia de redes de distribución, los cambios de
longitudes de los tubos de las redes y cambios de
demandas base, en la concentración de cloro
residual, en la vida media del agua y en el modelo de
flujo bidimensional a partir de simulaciones llevadas
a cabo en tres redes hipotéticas (Red Tipo 1, Red
Tipo 2 y Red Tipo 3).
BASE CIENTÍFICO - TEÓRICA
Modelo Tradicional de Calidad del Agua:
Modelación unidimensional del flujo
La forma tradicional de modelar la calidad del agua,
incluyendo la forma en que modela el programa
REDES (CIACUA, 2009) que se utiliza en el
presente proyecto, es suponiendo una mezcla
completa del soluto (caso del cloro) a través de su
transporte por las tuberías de la red, de forma que las
tuberías se modelan como objetos unidimensionales.
Por lo tanto, las tasas de decaimiento son deducidas
empíricamente y se da un decaimiento exponencial
del soluto.
Las ecuaciones que gobiernan las variaciones de
tiempo y espacio se basan en el principio de
conservación de la masa (teniendo en cuenta la
mezcla en los nudos, el transporte convectivo de
tuberías y mezclas en tanques) acoplado con la
cinética de reacción.

Desarrollo del modelo matemático de decaimiento
de cloro en tuberías
Las reacciones químicas son función de la
concentración de cloro (para este caso), de la tasa de
reacción y del número de orden de la reacción. La
forma general de expresar la tasa de reacción es:
(1)
donde, es la concentración de cloro, es el tiempo,
es la tasa de reacción global y es el orden de la
reacción. El cloro y otros desinfectantes están
gobernados por un decaimiento de primer orden.
(2)
Reordenando se tiene:
(3)
Integrando se tiene:
(4)
Resolviendo
(5)
Despejando para la concentración en cualquier
tiempo se tiene:
(6)
Adicionalmente
depende del coeficiente de
reacción de la pared
, de la velocidad media del
agua
y del diámetro de la tubería (
como se
expresa en la siguiente ecuación (Sookhak,
Reeuwijk, & Maksimovic, 2009):
(7)
La modelación tradicional de la calidad del agua se
realizó tomando como constantes el coeficiente de
reacción en la pared
con un valor de
y el coeficiente de reacción en el
cuerpo de agua
con un valor de
.
Las reacciones en la pared de la tubería ocurren
porque las sustancias disueltas que fluyen en las
tuberías, pueden tener contacto con la pared de las
mismas y reaccionar con los materiales. Para una
reacción de primer orden, la velocidad de reacción
de pared se puede expresar de la siguiente forma:
(8)
donde es la velocidad de reacción en la pared de la
tubería,
es la constante de reacción en la pared
(longitud/tiempo),
es la concentración de cloro
(masa/volumen), es el radio de la tubería y
es
el
coeficiente
de
transferencia
de
masa
(longitud/tiempo) el cual se puede expresar en
función del número dimensional de Sherwood (
de la siguiente forma:
(9)
donde
es el número de Sherwood (adimensional),
es el diámetro de la tubería (longitud) y es la
difusividad
molecular
del
reactivo
(longitud
2
/tiempo). El número de Sherwood
es
empleado para procesos de transferencia de masa,
simbolizando el cociente entre la transferencia de
masa por convección y difusión. Su valor depende
del régimen en que se encuentre el flujo y se expresa
de la siguiente forma (Rossman et al., 1994; Haas et
al., 2002):
En régimen estacionario
En régimen turbulento
(11)
En régimen laminar
(12)
(10)
Modelo Moderno de Calidad del Agua:
Modelación bidimensional del flujo
Los modelos existentes de demanda en la pared
suponen una mezcla completa del flujo, y es por esto
que no consideran ninguna variación en la
concentración, a lo largo de toda la sección
transversal de la tubería. Sin embargo la forma
moderna de modelar la calidad del agua en las redes
de distribución, a diferencia del la forma tradicional,
sí tiene en cuenta el efecto de la capa límite
turbulenta, por lo que se plantea un flujo
bidimensional para establecer un rango de
parámetros en donde el sistema turbulento tiene un
supuesto de mezcla completa. Al no tener en cuenta
el efecto de la capa límite turbulenta en la derivación
de las tasas de transferencia de masa, se puede
afectar el supuesto de mezcla completa y en
consecuencia los resultados de la modelación
también se pueden ver afectados. Por tal razón, es
que se desarrolla el estudio en cuanto al modelo
moderno de calidad del agua presentado por
Sookhak, Reeuwijk, & Maksimovic en el año 2009.
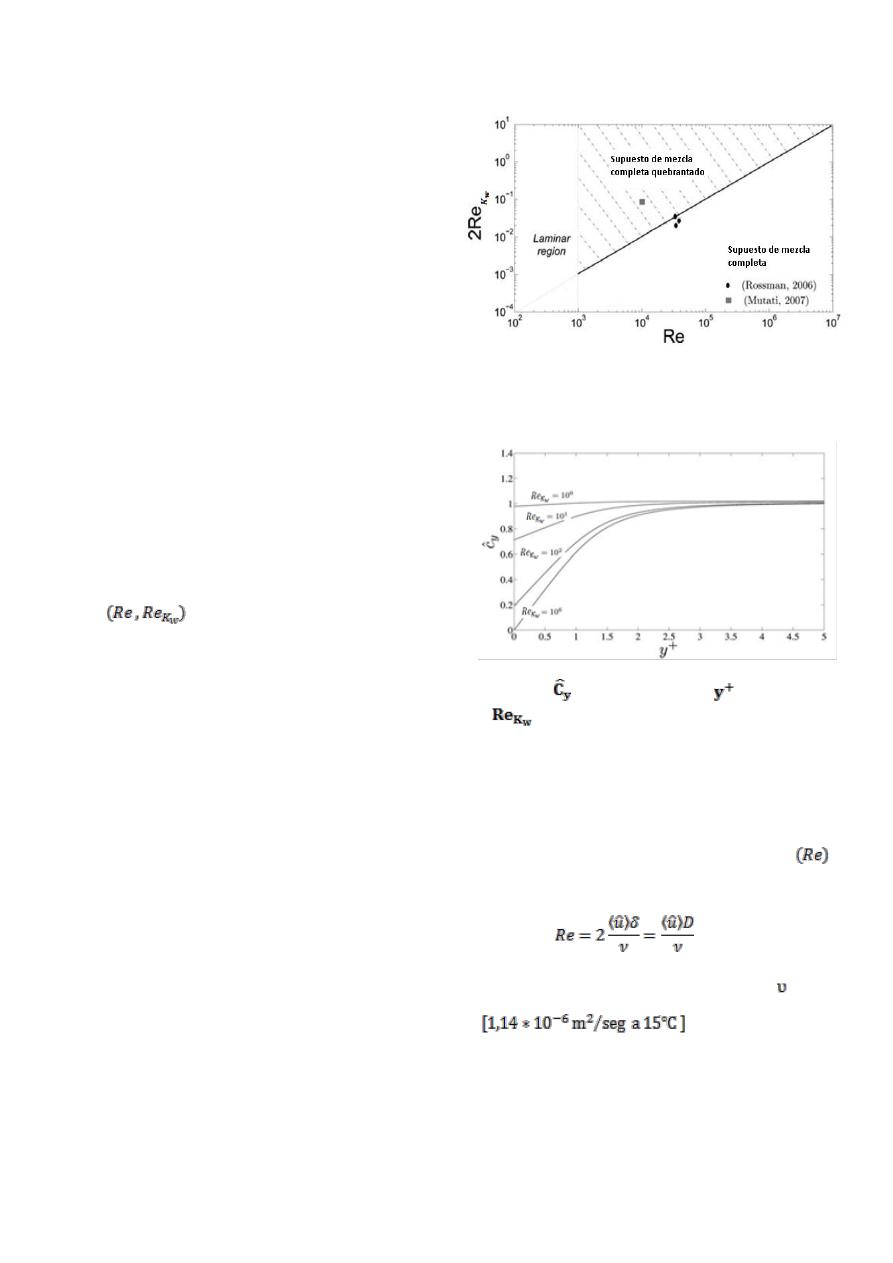
En la Figura 1 se presenta un diagrama de
, en el cual se indica la región en la cual
el supuesto de mezcla completa es válido y también
se observa algunas mediciones de Rossman (2006) y
Mutati et al. (2007) para el decaimiento de cloro.
Los resultados de esta gráfica muestran que el
supuesto de mezcla completa enfrenta algunas
situaciones críticas en el decaimiento del cloro
debido a la demanda en la pared (Sookhak et al.
2009).
Adicionalmente mediante la Figura 1, se puede
verificar fácilmente en que situaciones se aplica el
modelo tradicional de calidad de agua o si se debe
tener en cuenta la modificación presentada por
Sookhak et al. 2009. Incluso, esta gráfica enfatiza la
importancia de las desviaciones en los perfiles de
concentración. Los perfiles de concentración son
importantes en aquellos fenómenos que se
encuentran directamente relacionados con la
concentración local, como son formación de
biopelícula y corrosión.
Si los parámetros del problema se ecuentran en la
región donde el supuesto de mezcla no es válido, el
modelo de equilibrio puede definir las desviaciones
de concentración en el corte transversal mediante la
Figura 2.
Figura 1. Región de validez para modelo de
calidad de agua (Sookhak, Reeuwijk, &
Maksimovic, 2010).
Figura 2.
Como función de
para varios
(Sookhak, Reeuwijk, & Maksimovic,
2010).
El procedimiento para realizar la gráfica de región
de validez para cada tubería se muestra a
continuación.
Primero se haya el número de Reynolds
mediante la siguiente ecuación:
(13)
donde, D es el diámetro de la tubería y es la
viscosidad
cinemática
del
agua
.
Luego se haya Re
Kw
el cual, como se había dicho
anteriormente, puede ser interpretado como un valor
adimensional que representa la demanda en la pared
de una tubería con radio y características del fluido
fijas.
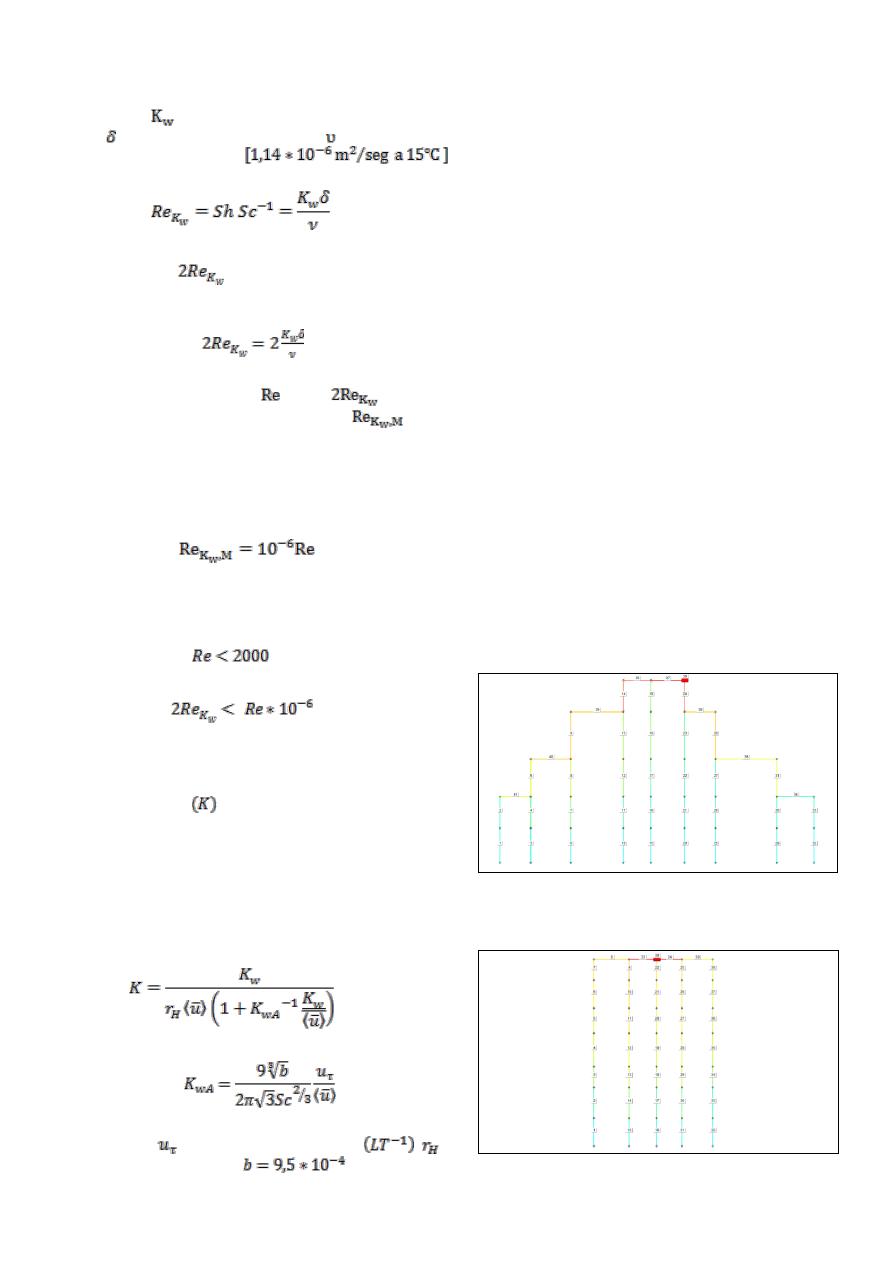
donde
es el coeficiente de demanda en la pared ,
es el radio de la tubería y es la viscosidad
cinemática del agua
.
Se calcula
simplemente multiplicado por 2 el
valor obtenido en la ecuación anterior.
(15)
Ahora bien, se grafica
contra
y se dibuja
la línea que define el límite superior
para el
cual el flujo puede ser considerado como
completamente mezclado y también se dibuja una
línea vertical que establece el límite en que el flujo
se comporta con régimen laminar.
Por lo tanto, las tuberías se encuentran en el
supuesto de mezcla completa cuando:
Dependiendo de la región en que se encuentren las
tuberías (región de validez o quebrantada) se utiliza
una ecuación diferente para calcular el coeficiente de
decaimiento
. Para las tuberías que se encuentran
en la región de supuesto de mezcla completa se usa
la Ecuación 7.
Para las tuberías que se encuentran en la región de
supuesto de mezcla completa quebrantado se usa la
ecuación del coeficiente de decaimiento del método
moderno como se expresa a continuación:
(19)
(20)
donde,
es la velocidad de fricción
,
es
el radio hidráulico y
.
METODOLOGÍA
Se utilizó el programa REDES, programa creado en
la Universidad de los Andes, Bogotá, Colombia
(1988), para la simulación hidráulica, utilizando el
método del gradiente hidráulico, y la simulación de
la calidad de agua, basándose en ecuaciones de
conservación de la masa y cinética de reacciones del
cloro. Estas simulaciones se llevaron a cabo en tres
redes hipotéticas (Red Tipo 1, Red Tipo 2 y Red
Tipo 3) con las siguientes características:
Se supuso una densidad de población de 450
habitantes por hectárea y un consumo de
250 litros por habitante por día.
Se utilizó PVC (ks=0.0015 mm) como
material de las tuberías.
Presión mínima de 10 mca.
Temperatura de 20°C.
Altura del tanque de suministro de 30 m.
La estimación de las demandas en los nodos
se determinó mediante el método de las
áreas.
El funcionamiento de la red es por gravedad.
Topografía completamente plana.
Figura 3. Red Tipo 1.
Figura 4. Red Tipo 2.
(14)
(16)
(17)
(18)
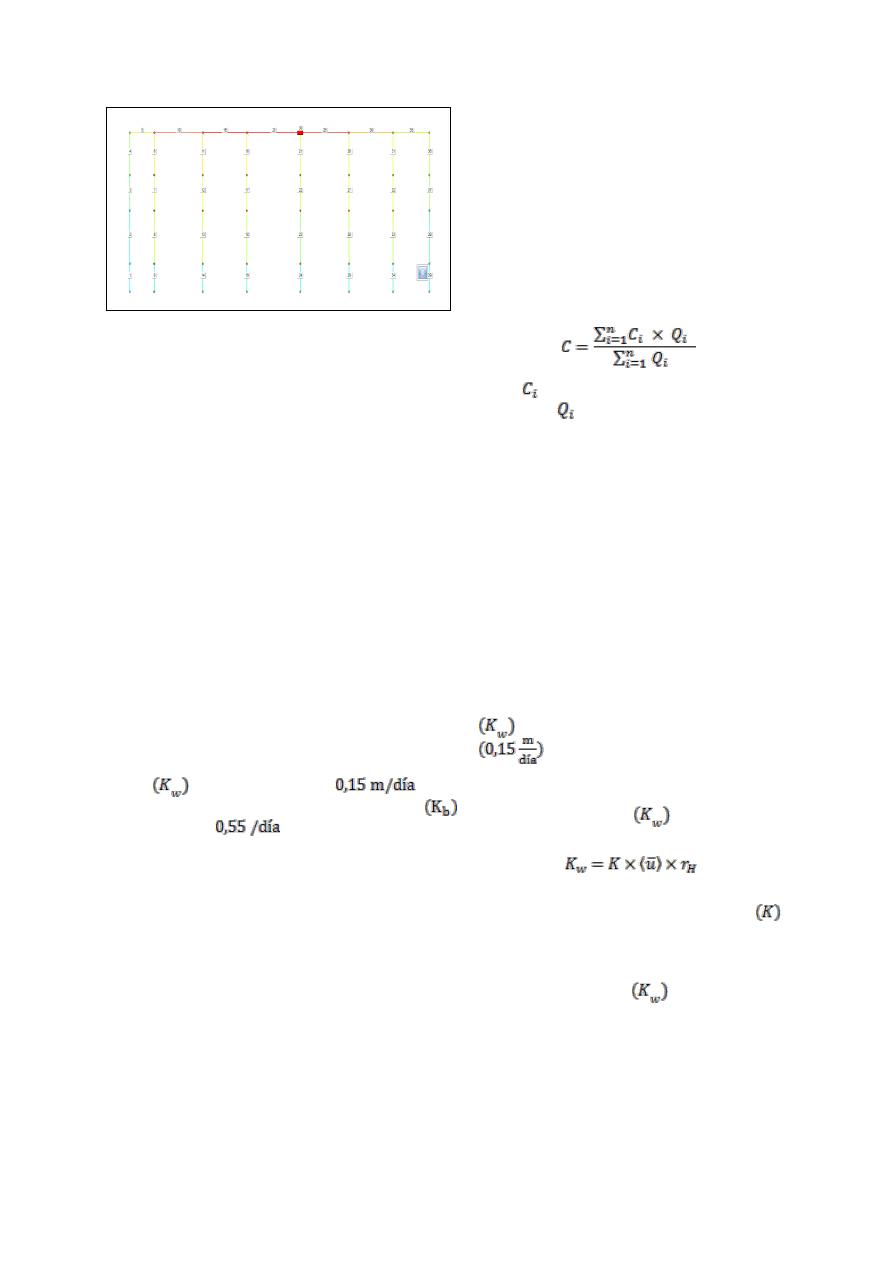
Figura 5. Red Tipo 3.
Cada una de las redes presenta 10 modelos
diferentes
que
corresponden
a
diferentes
redundancias (número de tuberías). Adicionalmente,
se realizaron modificaciones para cada red y sus
respectivos modelos en las longitudes de las tuberías
(multiplicando cada longitud por 10), en las
demandas de los nudos (multiplicando cada
demanda por 10) y en la combinación de longitudes
y demandas aumentadas por 10. Por último, fue
necesario volver a diseñar las redes con una presión
mínima de 15 mca (metros de columna de agua) ya
que al aumentar las longitudes y demandas las
presiones pueden ser negativas.
Modelo Tradicional de Calidad del Agua:
Modelación unidimensional del flujo
La modelación tradicional de la calidad del agua se
realizó mediante el programa REDES, tomando
como constantes el coeficiente de reacción en la
pared
con un valor de
y el
coeficiente de reacción en el cuerpo de agua
con un valor de
. Estos valores son valores
típicos en la modelación tradicional de la calidad del
agua.
Adicionalmente, en el análisis de calidad del agua en
las redes de distribución de agua potable, es de gran
importancia determinar los nudos que presentan la
concentración máxima y la concentración mínima.
Por esta razón se calcula la diferencia entre la
concentración máxima y mínima de cada nudo para
así evidenciar los efectos que tiene el cambio de
redundancias en la sensibilidad de este parámetro.
Para cada red se obtienen las concentraciones
obtenidas con las presiones originales y las
obtenidas al modificar las presiones en los casos de
longitudes y demandas aumentadas, ya que al
establecer las presiones con un mínimo de 15 mca
(para que no den negativas) y manteniendo el mismo
caudal, el programa REDES aumenta el diámetro de
las tuberías por lo que las concentraciones asimismo
se ven modificadas.
A fin de evaluar el comportamiento que tiene la
calidad del agua dentro de las redes de distribución
en relación con la redundancia de las redes, es
necesario además introducir el cálculo de la calidad
promedio mediante la siguiente ecuación:
(21)
donde
corresponde a la concentración en el nudo i
de la red y
corresponde al caudal demandado en
el nudo i.
Modelo Moderno de Calidad del Agua:
Modelación bidimensional del flujo
Con el objetivo de verificar en que situaciones se
aplica el modelo tradicional de calidad de agua o si
se debe tener en cuenta la modificación presentada
por Sookhak et al. 2009, se realizan las gráficas de
región de validez (ver Figura 1) para las tres redes.
Ahora bien, a las tuberías que se encuentran en la
región de supuesto de mezcla completa se les
conserva el
coeficiente de reacción de la pared
establecido para el presente proyecto
, mientras que a las que se encuentran en
la región de supuesto de mezcla completa
quebrantado se les calcula el nuevo coeficiente de
reacción de la pared
mediante la siguiente
expresión:
donde el coeficiente de decaimiento
es el
calculado mediante la Ecuación 19.
Una vez se tienen los nuevos coeficientes de
reacción de la pared
de las tuberías de las
redes, éstos se ingresan al programa REDES para
calcular las concentraciones obtenidas por el modelo
moderno y estas se comparan con las
concentraciones
obtenidas
por
el
modelo
tradicional.
A fin de comparar las concentraciones obtenidas por
el método moderno y por el método tradicional, se
calcula el porcentaje de error entre estas mediante la
siguiente ecuación:
(22)

(23)
donde,
corresponde a la concentración de cloro
obtenida por el método tradicional y
corresponde a la concentración de cloro obtenida por
el método moderno.
Edad media del agua (Tiempo de retención)
La edad media del agua en las redes se define como
el tiempo de retención del agua, es decir el tiempo
en que el agua permanece en la red de distribución
de agua potable.
Mediante la siguiente ecuación se calcula el tiempo
de retención promedio para así evaluar el efecto que
tiene sobre este la redundancia de las redes.
(24)
donde,
es el tiempo de retención en el nudo i de
la red y
es el caudal demandado en el nudo i.
Densidad de población por nudos
Dentro del procedimiento general de diseño de los
sistemas de distribución de agua potable, es
fundamental estimar la población urbana para definir
el nivel de complejidad del sistema y determinar los
caudales que se deben emplear para lograr abastecer
a toda la población. Igualmente es importante
determinar la densidad de población por nudos ya
que debe verificarse que estas densidades no superen
las densidades de saturación previstas en el
momento del diseño de las redes de distribución.
En el presente artículo se calcula la densidad
poblacional para cada área aferente de los nudos de
las redes. El procedimiento para dicho cálculo es el
siguiente:
Cálculo de la demanda promedio
Se halla el caudal demandado promedio
en los
nudos a partir del caudal demandado máximo
(obtenido en el programa REDES) y un
factor de mayoración de 1.8 como se expresa a
continuación:
(25)
Cálculo del volumen diario
(26)
Cálculo del número de habitantes
Para calcular el número de habitantes se debe
establecer una dotación per cápita, por lo tanto se
utiliza una dotación de
.
(27)
Cálculo de áreas aferentes
El cálculo de las áreas aferentes se realiza en el
programa Arcview a partir de polígonos de Thiessen
creados internamente por el programa. Para esto fue
necesario crear polígonos alrededor de las redes ya
que al ser hipotéticas no tienen áreas establecidas.
Para pasar las redes del programa REDES a Arcview
se realizaron los siguientes pasos:
Cálculo de densidad poblacional
Con las áreas aferentes de cada nodo obtenidas en
Arcview, se calcula la densidad poblacional para
cada área mediante la siguiente expresión:
(28)
RESULTADOS Y ANÁLISIS DE
RESULTADOS
Modelo Tradicional de Calidad del Agua:
Modelación unidimensional del flujo
Al obtener y comparar los promedios de las
diferencias entre las concentraciones máximas y
mínimas de las redes, con sus variaciones de
demandas y longitudes, se puede observar que al
aumentar las longitudes de las tuberías, estas
diferencias aumentan debido a que la velocidad del
agua en las redes disminuye, por lo que las
concentraciones de cloro se vuelven más variables.
Por el contrario, al aumentar las demandas en los
nudos la velocidad del agua aumenta y por lo tanto
las concentraciones se hacen más estables,
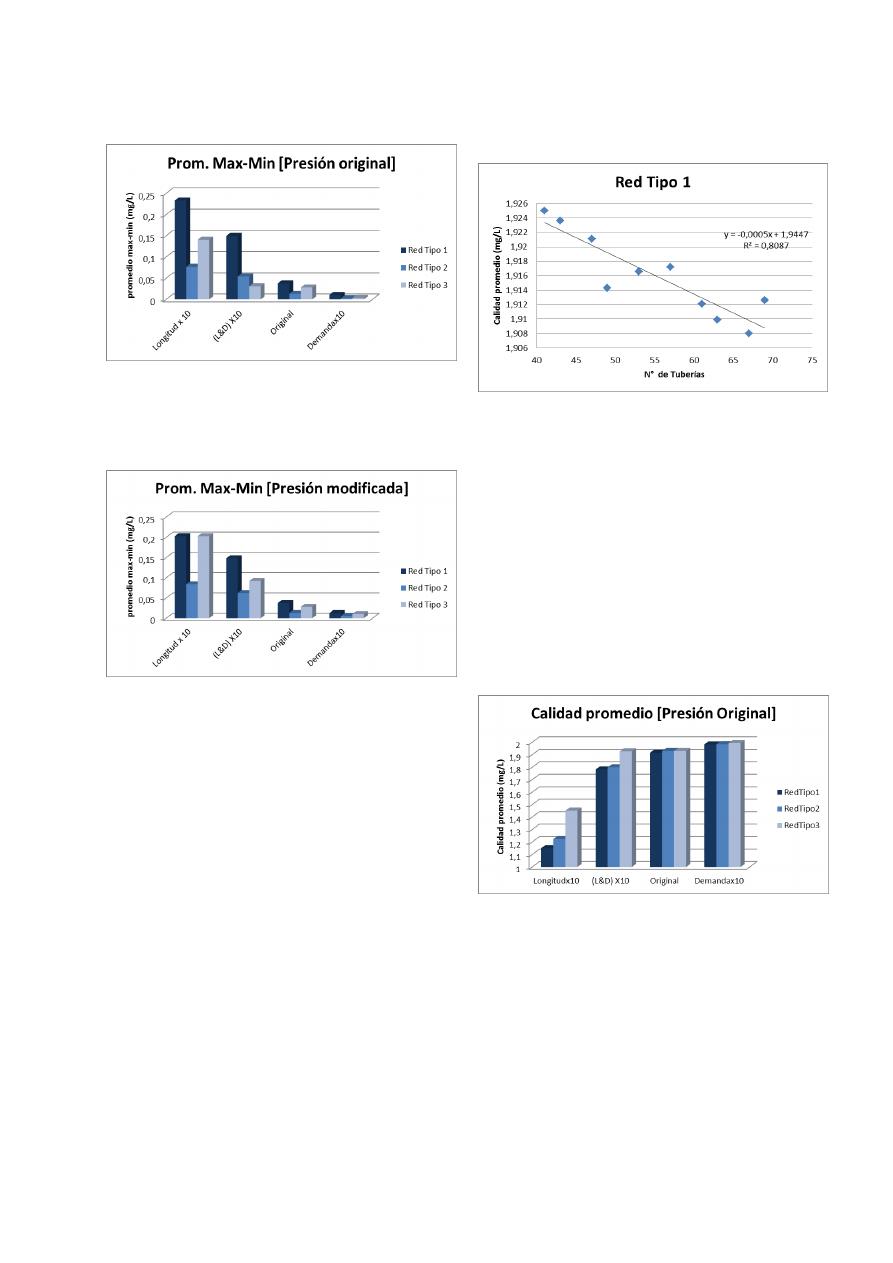
disminuyendo así su variabilidad (Ver Figura 6 y
Figura 7).
Figura 6. Promedio de diferencias entre la
concentración máxima y mínima para las
diferentes modificaciones de las redes con
presión original.
Figura 7. Promedio de diferencias entre la
concentración máxima y mínima para las
diferentes modificaciones de las redes con
presión modificada.
Por otro lado, a fin de mostrar el efecto que tiene la
redundancia en la concentración promedio de las
redes, en la Figura 8 se presenta la gráfica de calidad
promedio vs. número de tuberías para la Red Tipo 1.
Los resultados obtenidos indican una disminución en
la calidad promedio del agua al aumentar la
redundancia de la red, es decir al aumentar el
número de tuberías (los mismos efectos se
evidenciaron en la Red Tipo 2 y en la Red Tipo 3).
Esto se debe a que al aumentar el número de tuberías
y conservando el mismo caudal, la velocidad del
flujo de agua disminuye aumentando así las
reacciones del cloro en las paredes de las tuberías y
en la masa de agua. Sin embargo, existen nudos en
los que la concentración aumenta en vez de
disminuir con la redundancia. Por lo tanto es de gran
importancia analizar el comportamiento de la
calidad del agua nudo a nudo y determinar los nudos
que presentan la máxima y la mínima concentración.
Figura 8. Calidad promedio vs. N°
tuberías Red Tipo 1.
Adicionalmente se encontró que al aumentar las
demandas base de los nodos, la calidad promedio
aumenta y, por el contrario, al aumentar las
longitudes de los tubos la calidad promedio
disminuye (Ver Figura 9). Esto se debe igualmente
al efecto que tiene la velocidad en la calidad del
agua. Por un lado, al aumentar las demandas base de
los nudos la velocidad del agua aumenta, mientras
que al aumentar la longitud de las tuberías la
velocidad del agua disminuye.
Figura 9. Calidad promedio para las
diferentes modificaciones de la Red
Tipo 1, la Red Tipo 2 y la Red Tipo 3
con presión original.
Ahora bien, comparando los resultados obtenidos
con las presiones originales (negativas) y con las
presiones modificadas (presión mínima de 15 mca),
se encontró que la calidad promedio disminuye al
modificar las presiones ya que la velocidad también
disminuye.
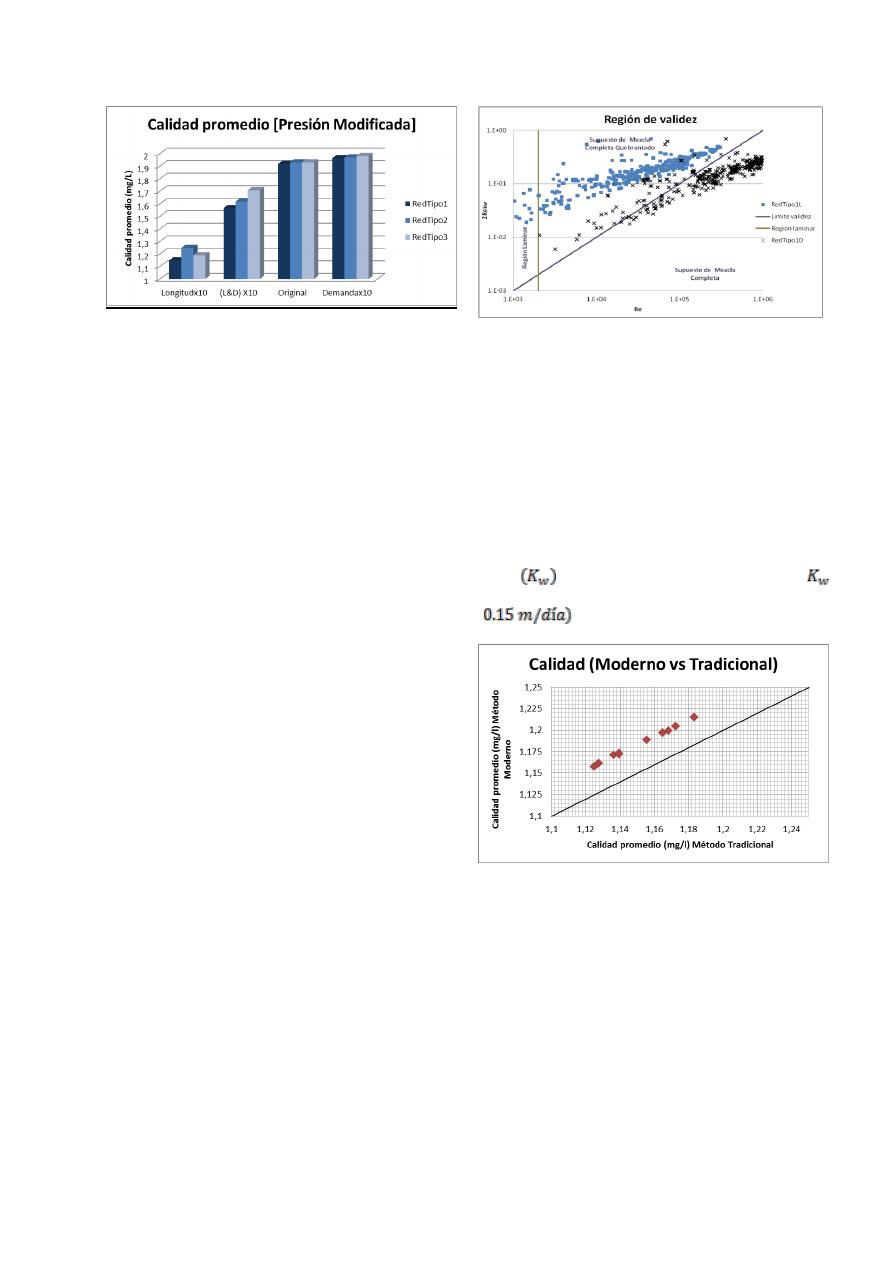
Figura 10. Calidad promedio para las
diferentes modificaciones de la Red
Tipo 1, la Red Tipo 2 y la Red Tipo 3
con presión modificada.
Modelo Moderno de Calidad del Agua:
Modelación bidimensional del flujo
Una vez caracterizadas las redes de estudio a partir
de la Figura 1, se obtuvo que al aumentar la
redundancia en las redes y las longitudes de las
tuberías, estas muestran mayor tendencia hacia la
región
de
Supuesto
de
Mezcla
Completa
Quebrantado (Método moderno), mientras que al
aumentar las demandas base de los nodos las
tuberías muestran mayor tendencia hacia la región
de Supuesto de Mezcla Completa (Método
Tradicional). La Figura 11 corresponde a los
resultados obtenidos en la Red Tipo 1. Los mismos
efectos se evidenciaron en la Red Tipo 2 y en la Red
Tipo 3. La razón de este efecto que tiene la
redundancia y el aumento en las longitudes de las
tuberías es que, al disminuir la velocidad con el
aumento de tuberías y aumento de sus longitudes
respectivamente, el flujo tiende más a comportase
con régimen laminar que turbulento por lo que se
dificultan las mezclas completas de sustancias en el
fluido.
Adicionalmente se encontró que con las presiones
modificadas (aumentadas) el porcentaje de tuberías
que violan el Supuesto de Mezcla Completa es
mucho mayor que con las presiones originales, ya
que al aumentar las presiones la velocidad
disminuye.
Figura 11. Región de validez para RedTipo1
con longitudes y demandas aumentadas.
Al comparar la calidad del agua obtenida mediante
el modelo moderno y el modelo tradicional, se
observa que a medida que aumenta la redundancia
de las redes el error porcentual, calculado mediante
la Ecuación 23, tiende a aumentar. Adicionalmente
se puede evidenciar que bajo el modelo moderno la
concentración es mayor a la obtenida por el modelo
tradicional (Ver Figura 12). Esto se debe a que con
el método moderno el consumo de cloro es menor,
ya que los nuevos coeficientes de demanda en la
pared
son menores en comparación con el
establecido
para
el
modelo
tradicional
(
.
Figura 12. Comparación de la concentración
de Cloro para cada configuración de
redundancia, entre el método tradicional y
moderno de Calidad de Agua de la Red Tipo
1L con presión original.
Edad media del agua (Tiempo de retención)
En relación con el tiempo de retención, se obtuvo un
aumento de este al aumentar la redundancia de la red
(Ver Figura 13). Este comportamiento se debe a que
al aumentar el número de tuberías el agua debe
recorrer una mayor longitud para llegar a ciertos
nudos de la red, por lo que el agua permanecerá
mayor tiempo en la red. Adicionalmente, se encontró

que al aumentar las demandas base de los nudos el
tiempo de retención disminuye y, por el contrario, al
aumentar las longitudes de los tubos el tiempo de
retención aumenta (Ver Figura 14). Esto se debe a
que al aumentar las demandas base de los nudos la
velocidad del agua aumenta por lo que ésta
permanece menos tiempo en la red, mientras que al
aumentar la longitud de las tuberías la velocidad del
agua disminuye aumentando así el tiempo de
retención del agua en la red.
Figura 13. Tiempo de retención vs. N°
tuberías Red Tipo 1.
Ahora bien, comparando los resultados obtenidos
con las presiones originales (negativas) (Ver Figura
14) y con las presiones modificadas (presión mínima
de 15 mca) (Ver Figura 15), se puede observar que
el tiempo de retención promedio aumenta al
modificar las presiones ya que la velocidad del agua
disminuye (la relación velocidad y tiempo de
retención es inversamente proporcional).
Figura 14. Tiempo de retención promedio
para las diferentes modificaciones de la Red
Tipo 1, la Red Tipo 2 y la Red Tipo 3 con
presión original.
Figura 15. Tiempo de retención promedio
para las diferentes modificaciones de la Red
Tipo 1, la Red Tipo 2 y la Red Tipo 3 con
presión modificada.
Densidad de población por nudos
Se obtuvo que al aumentar las longitudes de las
tuberías la densidad poblacional promedio de los
nudos disminuye ya que el área aumenta. Por el
contrario, al aumentar las demandas base de los
nudos la densidad poblacional promedio de los
nudos aumenta; asimismo aumenta el volumen
diario de agua y por lo tanto el número de habitantes
por nudo. Adicionalmente se encontró que la
redundancia no tiene efectos sobre las áreas
aferentes de los nudos, por lo tanto se puede concluir
que la redundancia de una red de distribución no
afecta la densidad poblacional estimada para cada
área aferente de los nudos de las redes.
CONCLUSIONES Y
RECOMENDACIONES
Aunque se evidencia una tendencia en el
decrecimiento de la calidad del agua con el aumento
de la redundancia, en ciertos nudos de las redes no
se cumple con esta disminución debido a que el
posicionamiento de las nuevas tuberías influye de
manera significativa en las variaciones de
concentraciones. De igual manera ocurre con el
tiempo de retención, que aunque es evidente una
tendencia en el aumento de éste a medida que
aumenta la redundancia de la red, en ciertas tuberías
hay variaciones que no cumplen con esta tendencia.
Es necesario que se realice un análisis nudo a nudo
de la calidad del agua, cuando se hacen aumentos en
redundancias de las redes, para evitar disminuciones
significativas de las concentraciones de cloro. El
análisis mencionado es necesario ya que no
necesariamente en los diseños más redundantes se
presentan las mínimas concentraciones para cada

nodo y no necesariamente en los diseños menos
redundantes
se
presentan
las
máximas
concentraciones.
Las diferencias entre las concentraciones máximas y
mínimas por cada nudo de los diferentes diseños de
redundancias de las redes, aumentan al aumentar las
longitudes de las tuberías, por el contrario al
aumentar las demandas en los nudos estas
diferencias disminuyen. Esto se debe a que la
velocidad del agua influye en la variabilidad de las
concentraciones de cada nudo.
Se puede concluir que a mayor redundancia de las
redes y un aumento de longitudes de las tuberías,
éstas muestran mayor tendencia hacia la región de
Supuesto de Mezcla Completa Quebrantado.
Mientras que al aumentar las demandas de los
nudos, las tuberías muestras mayor tendencias hacia
la región de validez del supuesto de mezcla
completa.
En general se puede observar que, al aumentar las
longitudes de las tuberías la densidad poblacional
promedio de los nodos disminuye, mientras que al
aumentar las demandas base de los nudos la
densidad poblacional promedio de los nudos
aumenta.
El método moderno del decaimiento del cloro
demuestra que el Supuesto de Mezcla Completa no
rige para un alto coeficiente de demanda de la pared
de la tubería o para bajos números de Reynolds (Re).
Por lo tanto al aumentar la redundancia en las redes,
los números de Re disminuyen y las tuberías
muestran mayor tendencia hacia la región de
Supuesto de Mezcla Completa Quebrantado.
BIBLIOGRAFÍA
Baldrich, L.F. (2010) Efecto de la redundancia de
redes de distribución en el cloro residual y
en la vida media del agua en la red. Bogotá:
Universidad de los Andes. Bogotá D.C:
Proyecto de grado, Universidad de los
Andes.
Facultad
de
Ingeniería.
Departamento de Ing. Civil y Ambiental.
Chapra, S. (1997) Surface water-quality modeling.
United States: McGraw-Hill.
Cortés Rivero, O. J. (2007). Modelación de la
calidad de agua en sistemas de distribución de
agua potable en período extendido. Bogotá
D.C.: Trabajo de grado, Universidad de los
Andes.
Prieto, C. M. (2008). Comparación de los módulos
de calidad de agua de REDES y EPANET en
período extendido. Bogotá D.C.: Proyecto de
grado, Universidad de los Andes.
Ramírez, A.P. (2010). Calidad del Agua en Redes
de
Distribución
de
Agua
Potable:
Comparación
entre
una
Modelación
Unidimensionl
Vs.
una
Modelación
Bidimensional del Flujo. Bogotá D.C:
Proyecto de grado, Universidad de los Andes.
Facultad de Ingeniería. Departamento de Ing.
Civil y Ambiental.
RAS Titulo b (2000). Reglamento técnico del sector
de agua potable y saneamiento básico. Bogotá
D.C : Ministerio de Desarrollo Económico.
Sanchez Orozco, C. A. (2001). Análisis de
confiabilidad y costos en el diseño de redes de
distribución de agua potable. Bogotá D.C.:
Proyecto de grado, Universidad de los Andes.
Sookhak, K., Reeuwijk, M. v., Maksimovic, C., &
Sharifan, S. (2010). Combined bulk and wall
reactions in turbulent pipe flow: decay
coefficients and concentration. Editorial
Manager(tm) for Journal of Hydroinformatics
Manuscript Draft . London: Imperial College.
Saldarriaga Valderrama, J. G. (2007). Hidráulica de
tuberías: abastecimiento de agua, redes, riegos
. Bogotá, D.C.: Alfaomega: Uniandes. ISBN:
978-958-682-680-8.
