
IAHR
CIC
XXV CONGRESO LATINOAMERICANO DE HIDRÁULICA
SAN JOSÉ, COSTA RICA, 9 AL 12 DE SETIEMBRE DE 2012
D
ISEÑO
Ó
PTIMO DE
S
UBMÓDULOS EN
S
ISTEMAS DE
R
IEGO
L
OCALIZADO DE
A
LTA
F
RECUENCIA
David A. Hernández, Nataly Bermúdez y Juan G. Saldarriaga
Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA), Departamento de Ingeniería Civil y Ambiental,
Universidad de los Andes, Bogotá, Colombia
<da.hernandez39@uniandes.edu.co>, <n.bermudez87@uniandes.edu.co>, <jsaldarr@uniandes.edu.co>
RESUMEN:
El presente artículo describe el desarrollo de una metodología para el diseño hidráulico de
submódulos de Riego Localizado de Alta Frecuencia, la cual parte de una metodología para el
diseño optimizado de Redes de Distribución de Agua Potable que se basa en el concepto energético
de Superficie Óptima de Gradiente Hidráulico. La metodología propuesta está conformada de una
sub rutina que determina la Presión Óptima a la Entrada del Submódulo, es decir no existe un
superávit de energía. El objetivo principal del trabajo consistió en determinar la Presión de Entrada
al Submódulo (PES) que asegurara el cumplimiento del Coefciente de Uniformidad (CU)
establecido por el díselo agronómico. Para obtener el resultado final se realizó un diseño exhaustivo
de diferentes submódulos de riego, cambiando el valor de las variables de entrada al problema y
determinando cuales de estas afectaban la curva que relaciona el Coeficiente de Uniformidad
resultante y la presión a la entrada del submódulo.
ABSTRACT:
This paper shows the development of a methodology for the hydraulic design of a sub-module in a
high frequency located irrigation system. This methodology is based in a previous methodology for
the optimized hydraulic design in water distribution networks using the energetic concept of
Hydraulic Head Optimum Surface. The proposed methodology calculates the optimum pressure at
the entry of the sub-module; in others words a surplus of energy does not exist. The main objective
of the study was to determine the inlet pressure to the submodule to ensure the Uniformity
Coefficient established by the agronomic recommendations. Finally, an exhaustive design was
carried for different irrigation submodules, changing theinput data and looking which of this
variables affect the relation curve of the Uniformity Coefficient and the inlet pressure.
PALABRAS CLAVES: Submódulos de riego, diseño óptimo, presión de entrada al submódulo.

INTRODUCCIÓN
El agua es un bien cada vez más escaso no sólo en cantidad sino también en calidad y como
tal, sus principales usuarios, los agricultores, se ven obligados a usarla con la mayor eficiencia
posible dentro de las consideraciones económicas que toda actividad productiva conlleva. En
Colombia, según el Estudio Nacional del Agua, se calcula que la demanda de agua por concepto de
grandes irrigaciones es del 32.2% y para riegos pequeños del 6.5%.
La falta de conocimiento y de datos para un adecuado diseño de riego es la principal causa
de diseños sobredimensionados, los cuales conllevan a un inadecuado uso del agua. Es por esto que
la presente investigación, tiene como objetivo establecer una metodología de diseño hidráulico para
submódulos de sistemas de Riego Localizado de Alta Frecuencia RLAF.
La idea surge de los importantes avances que se han logrado en el campo del diseño
optimizado de Redes de Distribución de Agua Potable RDAP, en conjunto con la facilidad que
brinda el uso de las herramientas computacionales. El concepto inicial para el uso de una
metodología de RDAP en el diseño optimizado de sistemas RLAF, es que cada planta o árbol del
cultivo pueda tratarse como un usuario independiente, en forma similar a cada uno de los usuarios
de un sistema de abastecimiento de agua potable. De esta forma, y entendiendo que los sistemas de
riego son redes abiertas, debido a que sólo durante parte del tiempo los sistemas se encuentran
operando (por consiguiente no se necesitan circuitos para garantizar un uso permanente del agua),
es posible conocer la presión y el caudal en cada uno de los árboles del cultivo.
EMISORES
Los emisores son tal vez los elementos más importantes de las instalaciones de RLAF y
desde luego los más delicados. Estos elementos se modelan mediante una ecuación que relaciona el
caudal y la presión; la relación es del tipo:
[1]
donde, Q es el caudal del emisor, h es la presión en el punto donde se encuentra éste y K y x
hacen representan el coeficiente y el exponente del emisor, respectivamente. El exponente de
descarga x se puede considerar como una medida de la sensibilidad de los emisores a la variación de
presión, entre mayor sea el exponente más sensible es el caudal a la presión. Por el contrario un
emisor con exponente 0 representa un emisor autocompensante donde el caudal es independiente de
la presión.
UNIFORMIDAD DE RIEGO
La uniformidad de riego es una magnitud que caracteriza todo sistema de riego e interviene
definitivamente en su diseño. El objetivo de un sistema de RLAF es tratar de obtener la mayor
uniformidad posible, de tal manera que todas las plantas del cultivo reciban la misma cantidad de
agua y nutrientes.
Según (López, 1992) es muy frecuente el uso del Coeficiente de Uniformidad (CU) que
compara la media del 25% de observaciones de caudal más bajo con la media total de caudales de
emisor. Esta media se considera como estricta, ya que al mejorar las técnicas de manejo de riego
preocupan más las plantas que puedan recibir menos agua.
Si se consideran los factores de los que depende la Uniformidad de Riego, suponiendo que
los efectos de la temperatura actúan normalmente en favor de la uniformidad, y que los problemas
inherentes a las obturaciones deben estar controlados, quedan como las más importantes causas de
la variación de caudal de los emisores a efectos del diseño hidráulico, la variabilidad de fabricación
y la diferencias de presiones. Teniendo en cuenta lo anterior, se puede definir estadísticamente CU
como:
[2]

Donde CU corresponde al Coeficiente de Uniformidad en el submódulo, n
e
al número de
emisores por planta, Q
mp
al caudal del emisor de menor presión del submódulo, y Q
m
es el caudal
medio de todo el submódulo.
TOLERANCIA DE CAUDALES Y PRESIONES
Suponiendo que al inicio de cada submódulo de riego hay un mecanismo que sirve para
regular la presión de entrada, de tal forma que en todos ellos los emisores proporcionen un caudal
medio Q
m
, el problema se reduce a conseguir en cada submódulo la Uniformidad de Riego que se
ha fijado para el diseño.
La relación entre el caudal de mínima presión y el caudal medio es la tolerancia de caudales,
la cual se calcula a partir de la Ecuación (3).
[3]
Una vez conocida la tolerancia de caudales (i.e. el caudal de mínima presión y el caudal
medio), mediante la ecuación del emisor escogido se puede calcular la presión media y la presión
mínima:
[4]
donde h puede ser de acuerdo con el caudal utilizado en la ecuación, la presión media o
mínima en el submódulo de riego.
La diferencia máxima de presiones permitida en el submódulo de riego ΔH, compatible con
el CU elegido, será proporcional a la diferencia entre la presión media que produce el caudal medio
y la presión mínima, de modo que:
[5]
siendo M un factor empírico que depende del número de diámetros que se vayan a emplear
en una misma tubería.
[6]
H
max
es la altura máxima para todo el submódulo. Usualmente, aunque no siempre, se
encuentra a la entrada de éste.
M depende de las características topográficas del terreno y del número de diámetros que se
usen en una misma tubería, ya sea terciaria o lateral
1
; no obstante, como en la fase de diseño es
difícil saber el número de diámetros, se recomienda un valor de 2.5. Una vez obtenido el valor de
ΔH deberá repartirse esta tolerancia entre los laterales y la tubería terciaria.
DISEÑO HIDRÁULICO DE SISTEMAS DE RLAF
El primer paso es calcular la tolerancia de caudales y presiones; estos cálculos son comunes
para toda la instalación de riego. Posteriormente, el cálculo se desarrolla en forma independiente
para cada uno de los submódulos que conforman el cultivo, el cual corresponde a la superficie del
cultivo dominado por un regulador de presión.
1
Lateral de riego son las tuberías de último orden de un submódulo de riego en las cuales se conectan los emisores
finales. La tubería terciaria es la tubería que alimenta directamente los laterales de riego.
EVALUACIÓN DEL DESEMPEÑO DE LA METODOLOGÍA SOGH APLICADO AL
DISEÑO DE UN SUBMÓDULO DE RLAF
El primer paso de esta investigación consistió en verificar si la metodología de diseño
SOGH es aplicable al diseño de sistemas de Riego Localizado de Alta frecuencia (RLAF). Para lo
anterior, se realizó el diseño óptimo de diferentes submódulos mediante la metodología de
Superficie Óptima de Gradiente Hidráulico implementada en el programa REDES. A cada uno de
los submódulos se le variaba el factor M para la determinación de la Presión a la Entrada del
Submódulo (PES) y la flecha óptima de diseño. Esto permitió llegar a importantes resultados, los
cuales se trataran de forma independiente y se presentan a continuación.
VARIACIÓN DEL FACTOR M PARA LA DETERMINACIÓN DE LA PES
El diseño de cada submódulo se realizó para diferentes valores del factor M, lo cual, daba
como resultado diferentes presiones a la entrada del submódulo. Se encontró que existe una relación
inversamente proporcional entre el Coeficiente de Uniformidad Resultante (CU
R
) y la Presión a la
Entrada del Submódulo (PES), descrita por una función polinómica de segundo orden, la cual
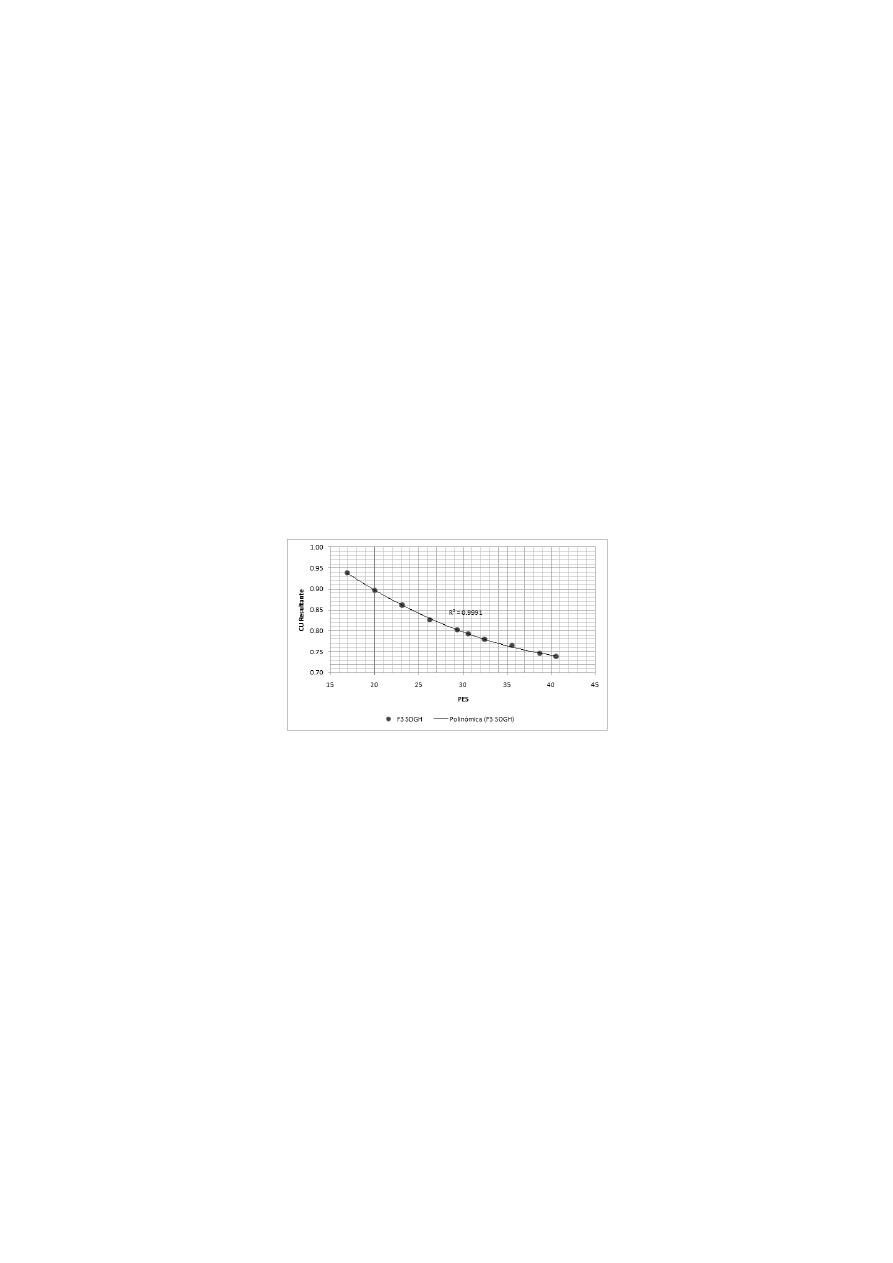
representa el mejor ajuste (Figura 2).
Figura 2. -Coeficiente de Uniformidad Resultante vs. Presión a la Entrada del Submódulo.
Saber que la relación entre estos dos parámetros (CU
R
y PES) es descrita por este tipo de
ecuación representa un resultado importante, ya que se podría determinar con exactitud la PES (o el
valor del Factor de M) necesaria para cumplir con el CU exigido por el agrónomo desde la fase de
diseño. Lo anterior, aparte de optimizar la energía disponible para el submódulo, proporciona el
dato de entrada (LGH de la fuente de abastecimiento) necesario para la metodología de diseño
propuesta.
DETERMINACIÓN DE LA PRESIÓN A LA ENTRADA DEL SUBMÓDULO PES
La PES representa la energía necesaria para cumplir con el CU del diseño agronómico, dada
la topología de la red y las características del emisor. Como se dijo anteriormente, la relación entre
el CU
R
y la Presión a la Entrada del Submódulo se representa con gran exactitud mediante una
función polinómica de segundo orden; es decir, se puede expresar mediante la siguiente ecuación:
[7]
2
y
x
x
donde CU
R
es el Coeficiente de Uniformidad final de la red diseñada, es decir el valor que
comprueba el cumplimiento de la tolerancia de caudales y presiones; PES es la Presión a la Entrada
del Submódulo o presión inmediatamente aguas abajo del regulador de presión; α, β y γ son
coeficientes que describen la forma de la curva.
Se tiene que para un diseño con un M = 1, la PES se traduce en la presión media de
operación del emisor, lo que indica que el espacio de desarrollo de la curva CU
R
vs. PES en la
abscisa es cerca a este valor. A partir de lo anterior, se analizó el comportamiento de la curva CU
R
vs. PES con función de las características del emisor (coeficiente del emisor K y exponente del
emisor x) para una determinada presión media de operación del emisor.
VARIACION DEL EXPONENTE DEL EMISOR (x)
El primer paso consistió realizar el diseño exhaustivo de un submódulo de RLAF para una
presión y caudal de operación del emisor determinado (el término exhaustivo se refiere al diseño del
submódulo para cada valor del factor de M posible), en el cual se variaba el exponente del emisor.
El primer submódulo analizado fue una red con una distribución simétrica en planta. Los datos del
diseño agronómico fueron: CU = 0.8, n
e
= 2, CV = 0.04. La presión media de operación del emisor
H
m
= 10 m y el caudal medio de operación del emisor Q
m
= 20 L/s. La variación del exponente del
emisor x fue 0.25, 0.35, 0.5 y 0.75.
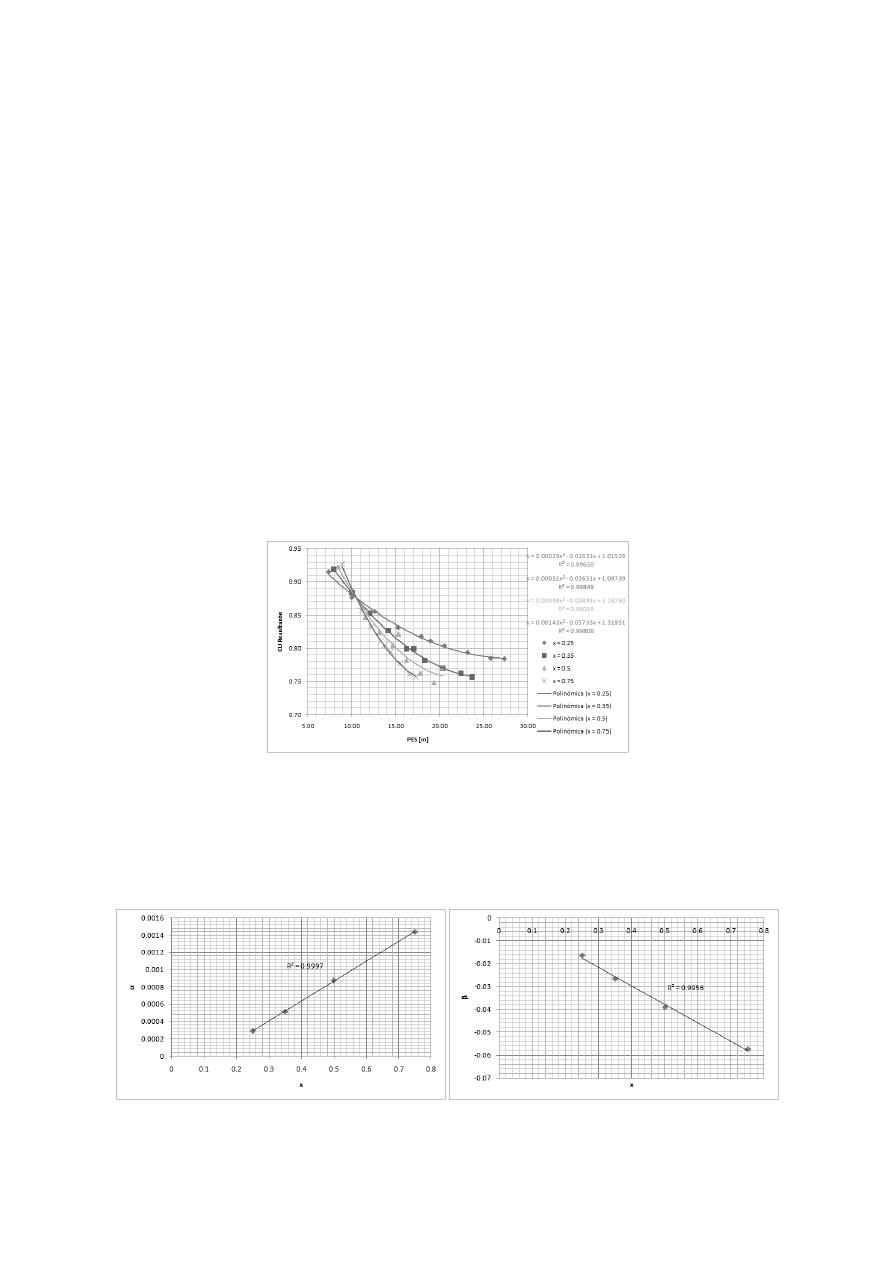
La Figura 5 muestra los resultados obtenidos. Se observa claramente que el espacio de
desarrollo de la curva CU
R
vs. PES está determinado por la presión media de operación del emisor;
sin embargo la forma de la curva está dada por el exponente.
Figura 5. - CU
R
vs. PES para un submódulo simétrico de RLAF con H
m
=10 m y Q
m
=20 L/h.
Se encontró un comportamiento de rotación de la curva sobre el punto que representa la
presión media de operación del emisor, la cual desciende a medida que aumenta el valor del
exponente del emisor. De igual forma, se encontró un patrón en el comportamiento de los
coeficientes de las ecuaciones cuadráticas (α, β y γ) que describen cada curva de acuerdo con el
exponente del emisor.
Figura 6.- Coeficiente α y β vs. Exponente del emisor con H
m
=10m y Q
m
=20 L/h.

Figura 7. - Coeficiente
vs. Exponente del emisor con H
m
=10m y Q
m
=20 L/h.
La función que mejor se ajustó para las relaciones anteriores fue una de tipo lineal. Estos
resultados plantean que: dado el exponente de la ecuación del emisor es posible determinar los
coeficientes de la ecuación cuadrática que representa la curva CU
R
vs. PES.
VARIACIÓN DEL COEFICIENTE DEL EMISOR (K)
Para analizar si el anterior comportamiento era independiente al coeficiente del emisor (K),
se realizaron nuevos diseños exhaustivos del submódulo anterior modificando el caudal medio de
operación del emisor; es decir, no se modificaron los datos del diseño agronómico, la presión media
de operación del emisor ni la variación utilizada para el exponente del emisor.
Se obtuvo como resultado relaciones muy similares a la del submódulo anterior; se puede
concluir que la forma de la curva CU
R
vs. PES depende de la presión media de operación y del
exponente del emisor e independiente del caudal medio de operación.
VARIACIÓN DE LA TOPOLOGÍA DE LA RED
Para analizar si el comportamiento descrito hasta el momento era independiente de la
topología, se realizaron diseños exhaustivos de una red totalmente diferente, con una distribución en
planta asimétrica y para diferentes caudales medios de operación. Los datos del diseño agronómico
son los mismos de los submódulos anteriores al igual que la presión media de operación del emisor.
Se observó que los resultados, aunque no son exactos, se consideran similares dados los cambios
tan significativos de las variables (Q
m
y topología).
En este punto se puede llegar a un valor aproximado de los coeficientes (α, β y γ) dada una
presión de operación igual a 10 m y cualquier valor del exponente del emisor, para unos
requerimientos agronómicos iguales a CU = 0.8, n
e
= 2, CV = 0.04.
DETERMINACIÓN DE LOS VALORES DE LOS COEFICIENTES DE LA ECUACIÓN
CUADRÁTICA PARA DIFERENTES VALORES DE PRESIÓN MEDIA DE OPERACIÓN.
Los resultados hasta el momento sólo funcionan cuando la presión media de operación del
emisor es igual a 10 m y los requerimientos agronómicos iguales a CU = 0.8, n
e
= 2, CV = 0.04. Sin
embargo, estos últimos no afectan como tal la forma de la curva (como si lo hace H
m
) si no el
espacio de desarrollo de la misma.
Para determinar los valores de los coeficientes de la ecuación cuadrática ajustada para
cualquier valor de presión media de operación, se realizó el mismo procedimiento desarrollado para
H
m
= 10 m. A continuación se presenta el compendio de resultados para cada coeficiente de la
ecuación cuadrática variando la presión media de operación.

Figura 8. - Coeficiente
y β vs. Exponente del Emisor para Caudales Altos.
Figura 9. - Coeficiente γ vs. Exponente del Emisor para Caudales Altos.
Lo anterior da como resultado las siguientes ecuaciones para la determinación de los
coeficientes α, β y γ de la ecuación cuadrática ajustada, en donde se pretende que para cualquier
valor de presión media de operación, caudal medio de operación y exponente del emisor, se pueda
obtener el resultado deseado mediante interpolación lineal.
Tabla 1. Ecuaciones para la determinación de los coeficientes α, β y γ.
Dado que las ecuaciones anteriores son válidas para unas condiciones de CU = 0.8, n
e
= 2 y
CV = 0.04, se identificó de que manera afectan estas variables el espacio de desarrollo de la curva
CU
R
vs. PES.
VARIACIÓN DEL COEFICIENTE DE UNIFORMIDAD (CU
I
)
Con el objetivo de analizar de qué manera afecta el Coeficiente de Uniformidad impuesto
por el diseño agronómico, el cual se denominó CU
I
(I de inicial), la curva CU
R
vs. PES, se
realizaron diseños exhaustivo de submódulos de RLAF con n
e
= 2 y CV = 0.04 para diferentes CU
I
.
Figura 10. - CU
R
vs. PES. Para CU
I
variable.

Se encontró que el CU
I
no afecta la forma de la curva CU
R
vs. PES, pero si su espacio de
desarrollo; es decir, el coeficiente γ de la ecuación cuadrática ajustada. Sí se toma la ecuación
cuadrática que describe el diseño exhaustivo para un CU
I
= 0.8 (el cual representa las condiciones
iniciales para la deducción de las ecuaciones de los coeficientes α, β y γ), y se le suma un valor de
0.03 (valor que representa la magnitud de desplazamiento de la curva), se obtiene como resultado la
curva que describe el diseño exhaustivo para un CU
I
= 0.85 (Figura 18); de manera similar si se
suma un valor de 0.06, se obtiene como resultado la curva que describe el diseño exhaustivo para un
CU
I
= 0.9.
Se encontró que la ecuación que representa de manera confiable la variación en la curva
CU
R
vs. PES debido al CU
I
impuesto por el diseño agronómico es:
[8]
donde γ
[CU]
es el coeficiente que representa la variación debido al CU
I
.
Se puede concluir que el coeficiente de variación γ
[CU]
es independiente de la presión y
caudal medio de operación del emisor y topología de la red. Este coeficiente representa una tasa de
cambio igual a un valor de 0.03 por cada diferencia del 5% en el CU
I
con respecto a un CU del
80%. Lo anterior da como resultado:
[9]
CAMBIOS DEBIDOS AL COEFICIENTE DE VARIACIÓN POR FABRICACIÓN DEL
EMISOR (CV)
Con el objetivo de verificar de qué manera afecta el Coeficiente por Variación (CV) de
Fabricación del Emisor la curva CU
R
vs. PES, se realizaron diseños exhaustivos de submódulos de
RLAF con CU = 0.8 y n
e
= 2 para diferentes CV.
Figura 11. - CU
R
vs. PES. Para CV variable.
Se encontró que el CV no afecta la forma de la curva CU
R
vs. PES, pero si su espacio de
desarrollo; es decir, el coeficiente γ de la ecuación cuadrática ajustada. Sí se toma la ecuación
cuadrática que describe el diseño exhaustivo para un CV = 0.04 (el cual representa las condiciones
iniciales para la deducción de las ecuaciones de los coeficientes α, β y γ), y se le suma un valor de
0.006, se obtiene como resultado la curva que describe el diseño exhaustivo para un CV = 0.025
(Figura 19). De manera similar si se resta un valor de 0.004, se obtiene como resultado la curva que
describe el diseño exhaustivo para un CV = 0.05; y si se resta un valor de 0.016, se obtiene como
resultado la curva que describe el diseño exhaustivo para un CV = 0.08.
Se encontró que la ecuación que representa de manera confiable la variación en la curva
CU
R
vs. PES debido al CV es:
[10]
donde γ
[CV]
es el Coeficiente que representa la variación debido al CV.
Se puede concluir que el coeficiente γ
[CV]
es independiente de la presión y caudal medio de
operación del emisor y topología de la red. Este coeficiente representa una tasa de cambio igual a un
valor de 0.004 por cada diferencia del 0.01 en el CV con respecto a un CV de 0.04. Lo anterior da
como resultado:
[11]
VARIACIÓN DEL NÚMERO DE EMISORES POR PLANTA
Con el objetivo de verificar de qué manera afecta el número de emisores (n
e
) por planta la
curva CU
R
vs. PES, se realizaron diseños exhaustivos de submódulos de RLAF con CU = 0.8, CV =
0.04 para diferentes n
e
. Se encontró que el número de emisores por planta no afecta la forma de la
curva CU
R
vs. PES ni su espacio de desarrollo, y que este comportamiento es independiente de la
presión y caudal medio de operación del emisor y topología de la red.
Finalmente, la ecuación que describe la curva CU
R
vs. PES para cualquier Uniformidad de
Riego y características de emisor es:
[12]
A continuación se muestra el diagrama de flujo de la metodología propuesta para la
determinación de la PES (Figura 21).
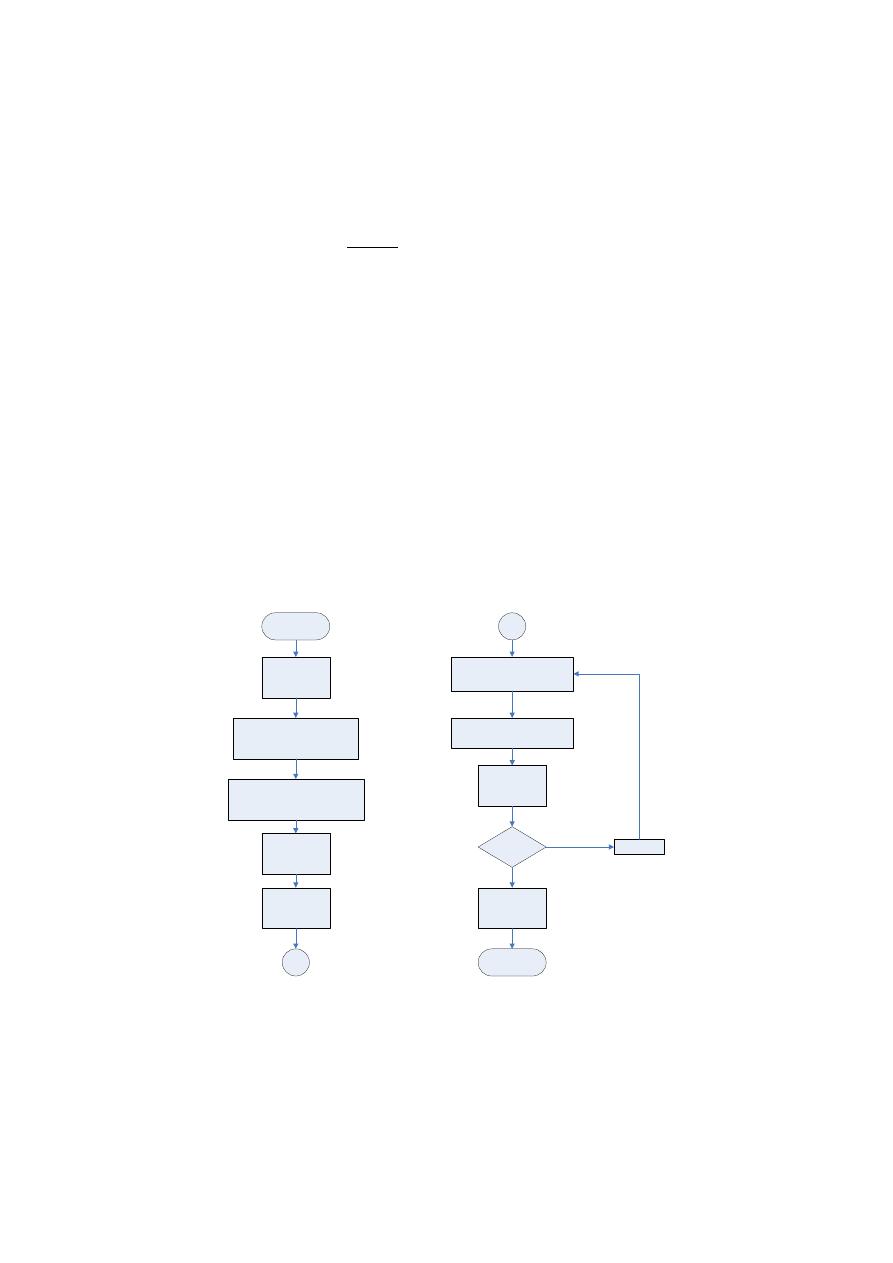
INICIO
Leer Hm y x
Calcular α, β y γ usando
la Tabla 1
Calcular γ
(CU)
y γ
(CV)
según
ecuaciones
i = 1
Mi = 0.5
B
B
Leer H
mp
Calcular PES mediante
ecuación 6.
Calcular CU
R
mediante
la ecuación 12
M = M + 0.1
Mi > 4.5 ?
Escoger PES
óptima
FIN
i = i +1
Figura 12. - Diagrama de flujo de la metodología propuesta para la determinación de la PES.
CONCLUSIONES Y RECOMENDACIONES
La presente investigación desarrolló una metodología de diseño de sistemas de Riego
Localizado de Alta Frecuencia (RLAF), basada en una metodología para el de diseño óptimo de
Redes de Distribución de Agua Potable (RDAP). Esta metodología se denominó “Superficie
Óptima de Gradiente Hidráulico Ajustada”.

Para el desarrollo de la metodología “SOGH Ajustada” fue necesario crear una metodología
interna que permitiera el cálculo óptimo de la Presión a la Entrada del Submódulo (PES). Esta
presión determina la energía necesaria aguas abajo del regulador de presión para cumplir con los
requerimientos impuestos en el diseño agronómico, sin generar déficit de energía en el submódulo.
La metodología para la determinación de la PES partió de la relación encontrada entre el CU
del submódulo de riego diseñado y la PES, descrita por una función polinómica de segundo orden,
la cual representó el mejor ajuste. Se encontró que la forma de la curva CU
R
vs. PES depende de la
presión de operación y del exponente del emisor a utilizar en el submódulo de riego, ya que la PES
es cercana a la presión de operación del emisor e inversamente proporcional al exponente del
mismo. A partir de lo anterior, fue posible plantear ecuaciones para la determinación aproximada de
cada uno de los coeficientes de la ecuación cuadrática ajustada de la curva CU
R
vs. PES dado
cualquier exponente del emisor y una presión de operación del emisor determinada. De igual forma,
se encontró que la curva CU
R
vs. PES es independiente del caudal medio de operación del emisor y
de la topología de la red.
Se concluyó que el CU
I
y CV afectan de manera significativa el espacio de desarrollo de la
curva CU
R
vs. PES; es decir, el coeficiente γ de la ecuación cuadrática ajustada. Por el contrario el
n
e
no representó un efecto significativo. Los anteriores resultados son independientes de la presión y
caudal medio de operación del emisor, y de la topología de red.
La metodología propuesta para la determinación de la PES fue puesta a prueba en diferentes
submódulos de RLAF, comprobando el buen desempeño de la metodología planteada.
Aunque se partió de una metodología para el diseño óptimo de RDAP, se encontró que esta
no asegura el diseño de la red mínimo costo. Lo anterior, se debe a que la línea de gradiente
hidráulico que genera la red óptima es determinada en diámetros continuos; al aplicar el proceso de
redondeo esta se afecta, alejándose de la red de mínimo costo.
La metodología planteada, aparte de asegurar una red con diseño hidráulico cercano al
óptimo económico, asegura un incremento en el CU
R
de la red, ya que al determinar la PES
necesaria para cumplir con el CU exigido por el diseño agronómico y optimizar en gran parte los
diámetros de la red, regula la distribución de presiones en el submódulo.
BIBLIOGRAFÍA
Bos, M. G., & Nugteren, J. (1982). On irrigation efficiencies. ILRI. Pobox 45, 6700 AA Wageningen , 138.
Centro de Investigaciones en Acueductos y Alcantarillados, C. (2007). Manual Programa RIEGOS. Bogotá:
Universidad de Los Andes.
Centro de Investigaciones en Acueductos y Alcantarillados, C. (2008). Programa REDES. Bogotá: Universidad de los
Andes.
Centro de Investigaciones en Acueductos y Alcantarillados, C. (2007). Programa RIEGOS. Bogotá: Universidad de Los
Andes.
De Paco, J. L. (1993). Fundamentos del Cálculo Hidráulico en los Sistema de Riego y de Drenaje. Madrid: Mundi-
Prensa.
IDEAM. (2011). Estudio Nacional del Agua. Bogotá, Colombia.
Kelle, J., & Karmeli. (1974). Trickle irrigation design. Rainbird Sprinkler Manufacturing Corporation .
López, J. R. (1992). Riego Localizado. Madrid: Mundi-Prensa.
Ochoa, S. (2009).Diseño Optimizado de Redes de Distribución de Agua Potable con Base en el Concepto Energético de
Superficie Óptima de Gradiente Hidráulico . Bogota: Univresidad de los Andes.
Pizarro, F. (1996). Riegos Localizados de Alta Frecuencia. Goteo, microaspersión, exudación. Madrid: Mundi-Prensa.
Saldarriaga, J. (2007). Hidráulica de Tuberías. Abastecimiento de Agua, Redes, Riego. Bogotá: Alfaomega.
Solomon, K. H. (1985). Global uniformity of trickle irrigation system. ASAE , 1151-1158.
Villalba, G. (2004). Algoritmos de optimización combinatoria aplicados al diseño de redes de distribución de agua
potable. Bogotá: Universidad de Los Andes.
Wu, I. (1975). Design of Drip Irrigation Main Lines. Journal of the Irrigatio
