
IAHR
CIC
XXV CONGRESO LATINOAMERICANO DE HIDRÁULICA
SAN JOSÉ, COSTA RICA, 9 AL 12 DE SETIEMBRE DE 2012
DISEÑO OPTIMIZADO DE TUBERÍAS EN SERIE:
UNA APROXIMACIÓN EXPLÍCITA
Juan G. Saldarriaga
1
, Susana Ochoa
2
, Claudia S. Solano
3
Universidad de los Andes-Departamento de Ingeniería Civil y Ambiental-CIACUA; Colombia;
e-mail: jsaldarr@uniandes.edu.co, ochoa-rodriguez@imperial.ac.uk,
cs.solano133@uniandes.edu.co
RESUMEN:
Este trabajo presenta una nueva metodología de diseño optimizado de tuberías en serie,
denominada Superficie Óptima de Gradiente Hidráulico (SOGH). La metodología es explícita y se
basa en el conocimiento de la topología de la serie de tuberías y en la distribución geométrica de los
caudales demandados en los nudos, es decir en la forma en que la serie entrega la masa de agua con
respecto a la distancia recorrida. SOGH se basa en predeterminar la línea de gradiente hidráulico
(LGH) que produce un diseño de mínimo costo, en forma explícita. Una vez se establece esa línea,
el cálculo de los diámetros continuos es directo; posteriormente se hace un redondeo a los diámetros
comerciales. El desempeño de la metodología propuesta fue evaluado mediante el diseño de 1200
series de tuberías, simultáneamente mediante Algoritmos Genéticos (AG) y SOGH, las cuales
tenían diferentes características topológicas y de demanda de agua.
ABSTRACT:
This paper introduces a new methodology for the optimal design of pipes in series, known as
Optimal Hydraulic Grade Line (OHGL). This methodology is explicit and is based on the
knowledge of the series topology and the geometrical distribution of water demands on nodes, i.e.
the way in which the pipe in series delivers water mass as a function of the distance from the
entrance. OHGL consists in the pre-determination of that hydraulic grade line which results in the
minimum construction cost, in an explicit way. The shape of the HGL that leads to an optimal
design depends on system topography, demands allocation, demands magnitudes, available energy,
and pipelines cost function. Once this line has been established, calculation of the pipe’s continuous
diameters is direct; after a round up to commercial diameters is developed. To validate the
proposed methodology, several pipes in series were designed both using GA and OHGL. One
thousand two hundred series were used in total, each with different topological characteristics and
demands.
PALABRAS CLAVES: Tuberías en serie; diseño optimizado; línea de gradiente hidráulico.

1. INTRODUCCIÓN
El presente documento se basa en el diseño optimizado de tuberías en serie para obtener los
costos mínimos de construcción. Una tubería en serie es un sistema de tuberías conectadas entre sí
de tal manera que uno o varias de sus características varían: diámetro, rugosidad absoluta y caudal;
además es posible que exista o no demanda de agua en los nudos del sistema. Las tuberías en serie
son muy comunes en los sistemas de riego, pero pueden ser encontradas también en los sistemas de
distribución de agua potable. El criterio de I-Pai Wu (1975) es probablemente el método más
importante de diseño de las tuberías principales en los sistemas de riego por goteo. Consiste en
asignar un valor a la presión mínima del nudo más alejado del distrito de riego y, a continuación,
calcular la LGH en las tuberías aguas arriba. Wu utilizó distritos de riego compuestos de tuberías en
serie cuyas longitudes eran iguales o muy similares; la demanda de agua en los nudos también era
uniforme. Wu concluyó que el diseño de menor costo es el que genera una LGH con forma de
parábola y con una flecha ubicada en el centro de la serie de tuberías, correspondiente al 15% de las
perdidas totales del sistema. Este documento utiliza la metodología de Wu y trata de ajustarla de tal
forma que no existan restricciones en los valores de longitudes de tuberías y demandas en los
nudos. De esta manera se introduce una nueva alternativa para el diseño optimizado de tuberías en
serie. La investigación demostró que la LGH tenía forma de parábola. La flecha de la parábola
depende de la distribución de los nudos (topología de las series) y de la demanda de agua en cada
uno de los nudos, además es fácil de obtener empleando la distribución geométrica de la demanda
de agua. Una vez que se conoce el valor de la flecha, el diseño optimizado se hace de manera
explícita y se obtiene directamente independientemente de la configuración de la serie de tuberías.
La metodología propuesta se verificó con un gran número de series de tuberías generadas
aleatoriamente con diferentes valores de nivel de entrada, longitudes de tuberías y demandas en los
nudos. Las series fueron diseñadas inicialmente utilizando AG con muchas generaciones e
iteraciones, luego fueron diseñadas utilizando la nueva metodología. Los resultados obtenidos
favorecieron la nueva metodología ya que los diseños con costos mínimos se obtuvieron sin
necesidad de realizar iteraciones.
2. ANTECEDENTES
Como se mencionó anteriormente, I-Pai Wu (1975) desarrolló una metodología para el
diseño optimizado de las tuberías principales en los sistemas de riego por goteo; dichas tuberías
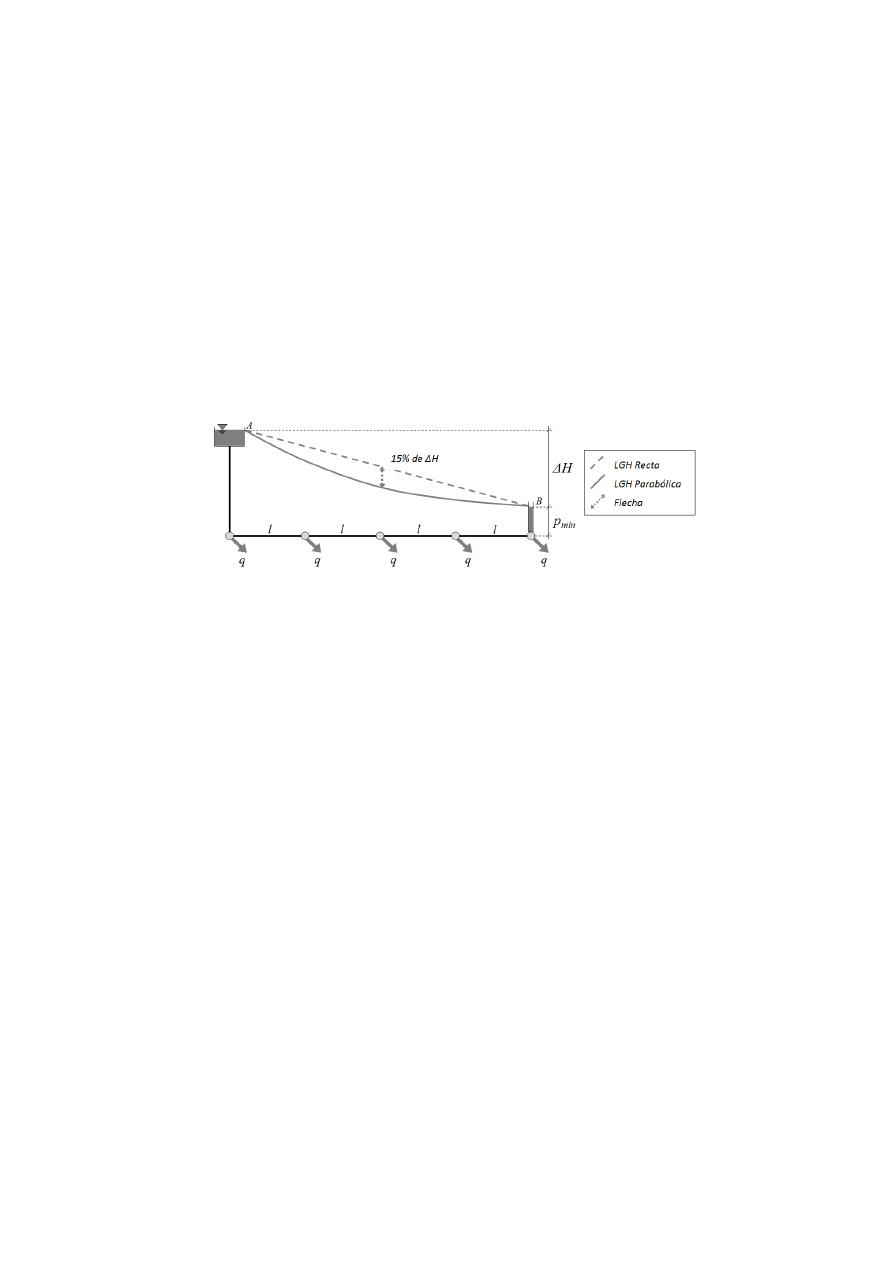
funcionan como tuberías en serie. Wu estableció que la forma y la pendiente de la LGH puede ser
calculada de tal manera que se procure el costo mínimo de la red, teniendo en cuenta los costos de
las tuberías en función del diámetro y garantizando que la presión en cada punto del sistema sea la
mínima requerida para la operación del distrito de riego. Wu encontró que la forma óptima de la
LGH describe una curva parabólica que pasa un poco más abajo que la línea recta de energía que
conecta los puntos de entrada y salida en la serie de tuberías; la curva óptima que genera el costo
mínimo tiene una flecha correspondiente al 15% de la diferencia total de energía entre la entrada y
la salida de la serie; dicha flecha se mide exactamente en la mitad de la serie. También encontró que
la diferencia de costos usando la LGH recta y la LGH óptima es de aproximadamente 2% (Ver
Figura 1). El criterio de Wu fue creado para ser empleado en el diseño de las tuberías iniciales de
los distritos de riego, los cuales se caracterizan por tener demandas iguales y constantes en los
nudos con casi la misma separación entre ellas. A pesar que el problema de tuberías en serie se
encuentra en muchos sistemas de ingeniería hidráulica, como redes de distribución de agua, plantas
de tratamiento de agua, estaciones de extinción de incendios, etc., es en el campo de la ingeniería de
riego donde se han llevado a cabo la mayoría de investigaciones. Martin (1990) aplicó una
metodología computacional para establecer el costo mínimo aproximado de diseño para la
construcción inicial y posterior ampliación de la capacidad de una línea de distribución de agua a
través de una ruta específica. El problema de encontrar el mínimo costo de diseño y ampliación de

la capacidad de la red fue formulado como un problema de programación matemática de costo
mínimo. Martin encontró que utilizando programación dinámica, la solución aproximada era el
diseño de mínimo costo si las adiciones de tubería paralela no permitían opciones de expansión.
Valiantzas (2002) presentó un estudio analítico del caudal de salida continuo y uniforme que toma
en cuenta el efecto del número de salidas en los laterales para calcular la longitud óptima de cada
tubería de la serie. Se describe la altura piezométrica a lo largo de los tubos de la serie mediante una
función analítica simple de cálculo directo de la presión a la salida de los emisores. Valiantzas
concluyó que las longitudes óptimas de diseño de las tuberías pueden ser calculadas directamente
usando una ecuación simple, asegurando que la variación de la presión máxima sea menor o igual a
la admisible. En un documento relacionado con el diseño de tuberías en serie, González (2011)
propone el uso de un algoritmo de asignación de la ubicación de hidrantes para una red de riego
abierta, usando sistemas de información geográfica (SIG) y programas de optimización matemática
con AG para reducir al mínimo los costos de construcción instalando únicamente los hidrantes que
sean estrictamente necesarios, pero teniendo en cuenta que la asignación de éstos debe ser aprobada
por los consumidores.
3. FORMULACIÓN DEL PROBLEMA
Una vez se ha establecido que la presente investigación se basa en el análisis de tuberías sin
ciclos, se define el diseño optimizado de tuberías en serie como: Dado un sistema hidráulico (se
incluye la longitud e inclinación de cada tubería) y las demandas de agua en los nudos, se requiere
encontrar la combinación de diámetros que genere el mínimo costo constructivo. Esta combinación
debe obedecer a las restricciones impuestas por la conservación de masa en los nudos, la
conservación de la energía en las tuberías, y la presión mínima en los nudos. La disponibilidad de
los diámetros comerciales debe tenerse en cuenta también. Matemáticamente, el problema objetivo
puede expresarse como:
[1]
donde C es el costo constructivo de las tuberías en serie, el cual es calculado en función del
diámetro:
[2]
donde NT es el número de tuberías en la serie, L
i
es la longitud de la tubería i, D
i
es el diámetro de
la tubería i, y a, b son parámetros de una regresión que toma en cuenta los costos de las tuberías.
Las restricciones del problema son:
Conservación de la Masa:
[3]
donde Q
T
es el caudal total (en la serie es el de la primera tubería), Q
α
es el caudal en la tubería i,
Q
Li
es el caudal lateral (demanda) al final de la tubería i.
Conservación de la Energía (ver Figura 1):
[4]
donde m es el número de accesorios que generan las pérdidas menores, hf
i
es la pérdida por fricción
en la tubería i, hm
i
es la perdida menor en el accesorio i. Las pérdidas por fricción son calculadas
con la ecuación de Darcy-Weisbach en conjunto con la de Colebrook-White.
Presión mínima en los nudos:
[5]
donde H
j
es la altura piezométrica en el nudo j y H
jmin
es la presión mínima requerida en el nudo j.
b
i
NT
i
i
D
L
a
C
1
1
1
i
L
T
i
Q
Q
Q
m
i
mi
NT
i
fi
h
h
H
1
1
min
j
j
H
H
Los diámetros de la tubería pueden ser solamente valores discretos y se redondean a valores
comerciales mediante
D
:
[6]
4. ANÁLISIS DE LA LÍNEA ÓPTIMA DE GRADIENTE HIDRÁULICO PARA
TUBERIAS EN SERIE
Inicialmente se analizaron las formas de las LGH correspondientes a los diseños de mínimo costo
de muchas tuberías en serie. El primer investigador que sugirió que la LGH de los diseños de
mínimo costo tiene una forma particular fue I-Pai Wu (1975). Wu estableció que las series de
mínimo costo (considerando solo los costos de mano de obra y materiales) usualmente tienen una
LGH que es cóncava hacia arriba y es muy cercana a la línea recta entre el nivel de gradiente
hidráulico a la entrada de la serie (punto A, Figura 1) y el nivel de gradiente hidráulico al final de la
serie (punto B). Wu también estableció que la LGH en la sección de la mitad de la serie, tiene una
flecha que corresponde al 15% de ΔH, donde ΔH is la pérdida total de energía en toda la serie.
Figura 1.- Criterio de I-Pai Wu.
El criterio de Wu es una metodología para el diseño de sistemas de riego y es aplicable solo a
tuberías en serie con demandas y longitudes uniformes, entonces se realizó una investigación para
encontrar la forma de la LGH óptima para series de tuberías con demandas y longitudes no
uniformes. Fueron generadas 120 series con demandas, topografía, nivel de entrada y longitudes de
tuberías variables. Cada una de las series fue diseñada optimizadamente (empleando AG), y se
encontró que siempre las LGH eran curvas cuadráticas (se obtuvieron siempre valores de R
2
mayores al 98%).
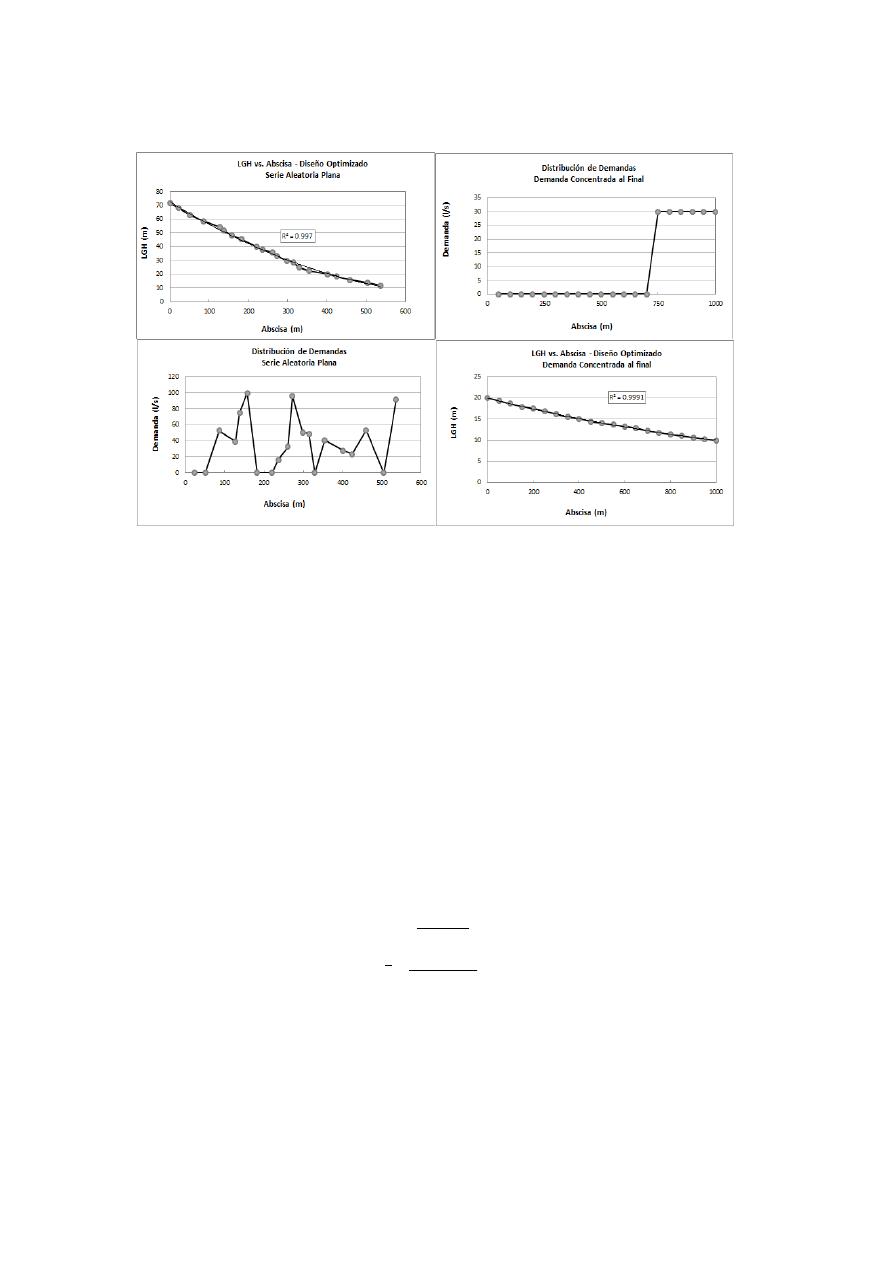
La Figura 2 muestra las LGH de mínimo costo para dos series con demandas no uniformes, las
cuales son realmente parábolas; sin embargo, la forma de estas curvas es diferente para cada serie.
Como se ilustró en el análisis, la LGH óptima es función de tres factores: distribución de la
demanda, relación entre la longitud de las series y el caudal de demanda y la función de costos.
Además, se observó que la pérdida total de energía en todo el sistema (ΔH) no afecta de forma
significativa la forma de la LGH. Para determinar la ecuación de la LGH óptima es necesario
conocer solamente tres puntos, ya que ésta tiene forma de parábola. Para cualquier serie de tuberías,
se conocen los puntos inicial y final de la LGH:
En el nudo inicial de la serie, la abscisa cero, la LGH tiene una altura piezométrica igual al nivel
del tanque, lo que significa que se conocen sus coordenadas: P
inicial
(0, LGH
entrada
).
En el nudo final, la abscisa igual a toda la longitud de la serie, la LGH es mínima y es igual a la
presión mínima requerida en el último nudo (LGH
mín
= Z + P
min
); por consiguiente se conocen
sus coordenadas: P
final
(L
total
, LGH
mín
).
Cuando se determina la ecuación de la LGH se requiere un tercer punto. Un punto fácilmente
identificable con abscisa conocida es el máximo de la curva de LGH , el cual se ubica en la mitad
de la longitud total de la serie. Analizando 120 series se estableció la forma en la que los tres
factores mencionados anteriormente (distribución de la demanda, relación entre el caudal y la
i
D
i
D
,
longitud total de la serie y el exponente de la función de costos) afectan la flecha de la curva de
LGH. Los resultados obtenidos se muestran a continuación. Es importante resaltar que la flecha
máxima se da como un porcentaje de la pérdida total de energía (ΔH).
(A) (B)
Figura 2. -(A) LGH Óptima y Distribución de la Demanda para series con concentración de la demanda al
final (y=0.0001x
2
-0.1747x+72.67) (B) LGH Óptima y Distribución de la Demanda para series con
concentración de la demanda aleatoria (y=0.000004x
2
-0.0135x+19.967).
4.1.Efecto de la distribución de la demanda sobre la flecha máxima de la LGH óptima
Para analizar el efecto de la distribución de la demanda en la magnitud de la flecha de la LGH, se
generaron 50 series de tuberías con la misma longitud total (1000 m), el mismo nivel en el tanque
de entrada (50 m) and demandas totales iguales (1 m
3
/s) pero con diferentes patrones de demandas;
de esta manera, es posible analizar el efecto de la demanda sobre la magnitud de la flecha óptima.
Para medir la distribución de demandas en las tuberías en serie se desarrollaron dos indicadores:
Centroide de Demandas (
̅) y Coeficiente de Uniformidad (CU). El primero es una medida de la
localización general de las demandas a lo largo de la serie de tuberías y el segundo es la medida de
la dispersión de las demandas con respecto a
̅. Para calcularlos se establecieron las siguientes
expresiones:
- Centroide de Demandas ( ̅):
[7]
donde NN es el número de nudos con demanda, q
i
es el caudal de demanda en el nudo i, d
i
es la
distancia desde el nudo i a la entrada de la serie, Q
total
es el caudal total demandado por el sistema y
L
total
es la longitud total de la serie. En general, si el
̅ es grande, la magnitud de la flecha es
pequeña. La dispersión de las demandas que afecta este valor, se explica mediante el CU.
- Coeficiente de Uniformidad (CU): Para calcular el CU es necesario calcular de forma
independiente el centroide de demandas para cada una de las dos secciones en las que se divide la
serie gracias al
̅ general; es necesario recordar que estos dos centroides son calculados con
total
total
NN
i
i
i
L
Q
d
q
x
0

respecto al
̅ general. Una vez se ha calculado cada centroide, se calcula un promedio equilibrado
de ambos basado en la longitud de cada una de las secciones:
̅̅̅ (
)
̅̅̅ (
)
[8]
donde
̅
es el centroide de demandas de la Sección 1,
̅
es el centroide de demandas para la
Sección 2, L
sección1
es la longitud de la primera sección y L
sectción2
la de la Sección 2. El centroide de
cada sección se calcula con la siguiente ecuación:
̅̅̅
∑
∑
[9]
donde NN
t
es el número de nudos en la sección t, d
nudoi-centroide
es la distancia desde el nudo i al
̅
general. Realizando un ajuste estadístico empleando el programa DataFit®, se obtuvo la siguiente
expresión para estimar la flecha óptima basada en
̅ y CU.
̅
[10]
Los valores de los coeficientes requeridos en la Ecuación 10 se presentan a continuación:
Tabla 1.- Valores de los Coeficientes de la Ecuación 10 obtenidos mediante una regresión.
Resultados de las Variables de la Regresión
Variable
Valor
Error Estándar
Relación-t
Probabilidad (t)
a
0.435521465
3.64E-02
11.96423962
0
b
-0.176612805
2.08E-02
-8.49833046
0
c
-0.977366227
0.252627675
-3.868801108
0.00034
d
0.906254447
0.459064981
1.974131079
0.05439
4.2 Efecto de la Relación entre la Demanda Total y la Longitud Total sobre la Flecha Máxima
de SOGH
Para analizar el efecto de la relación entre la demanda total y la longitud total sobre la Flecha
Máxima de SOGH, se analizaron 5 patrones diferentes de demanda; para cada uno de ellos se
generaron 24 series de tuberías con el mismo nivel de entrada (50 m), el mismo exponente de la
función de costos (1.46) y la misma distribución de demandas, pero con diferente magnitud de
demandas y longitudes de tuberías (en cada una de las series generadas, las demandas y longitudes
fueron multiplicadas por diferentes factores, y de acuerdo con el patrón de demandas,
̅ y CU
siguen siendo los mismos, a pesar de las diferencias entre la magnitud de las demandas y la longitud
total). El análisis estadístico determinó que la flecha de la LGH como función de la descarga (Q) y
la longitud total (L) es:
[11]
Para cada uno de los 5 patrones analizados, se obtuvieron 24 series en total. El valor de esta función
fue calculado para cada una de las series, (Ecuación 11). En la Figura 3, es evidente que la función f
(Q, L) tiene una relación logarítmica con respecto a la flecha óptima de la LGH de las series de
tuberías probadas. Los coeficientes de determinación múltiple obtenidos en todos los casos superan
el 99%, lo que significa que la función definida f (Q, L) describe en un 99% la variación de la
flecha óptima (si la distribución de las demandas y la altura de entrada a la serie se mantienen
constantes). Los resultados de los valores de las flechas óptimas en cada caso se muestran a
continuación (ver Figura 3).
3
2
,
L
Q
L
Q
f

Figura 3.- Efecto de la combinación de la Longitud Total y la Demanda Total sobre la Flecha Óptima de la
LGH vs. Abscisa
Figura 4.- A) Coeficientes de las Ecuaciones Logarítmicas vs. Flecha Óptima con Q
2
/L
3
= 1 x 10
-9
m
3
/s
2
(y=0.00868x+0.00066) B) Interceptos de las ecuaciones logarítmicas vs. Flecha Óptima con Q
2
/L
3
= 1 x 10
-9
m
3
/s
2
(y=1.18069x+0.01345).
En la Figura 4 se muestra una relación lineal entre la Flecha Óptima para un valor determinado de
Q
2
/L
3
= 1 x 10
-9
m
3
/s
2
y los parámetros de las ecuaciones logarítmicas ajustadas. La razón para
desarrollar estas gráficas para un valor de la función f (Q, L) = 1 x 10
-9
m
3
/s
2
es que todas las series
que emplean el análisis estadístico para explicar la flecha optima en función del
̅ y CU tienen una
longitud total de 1000 m y una demanda total de 1 m
3
/s; evaluando la función f para estos valores se
obtiene lo siguiente:
[12]
Conociendo el
̅ y CU para las series de tuberías, la Ecuación 10 se utiliza para obtener la flecha
óptima para un valor de la función f (Q, L) = 1 x 10
-9
m
3
/s
2
, la cual es la condición bajo la cual se
desarrolló dicha ecuación. Con este valor, se emplea la Figura 5 para determinar el coeficiente y el
intercepto para la function logarítmica que describe la variación de la flecha óptima en términos de
Q
2
/L
3
; después esta ecuación puede ser usada para calcular la flecha óptima para la relación Q
2
/L
3
actual en la serie de tuberías que se están analizando. Este procedimiento se explica a continuación:
4.3. Efecto del Exponente de la Función de Costos sobre la Flecha Máxima de la LGH Óptima
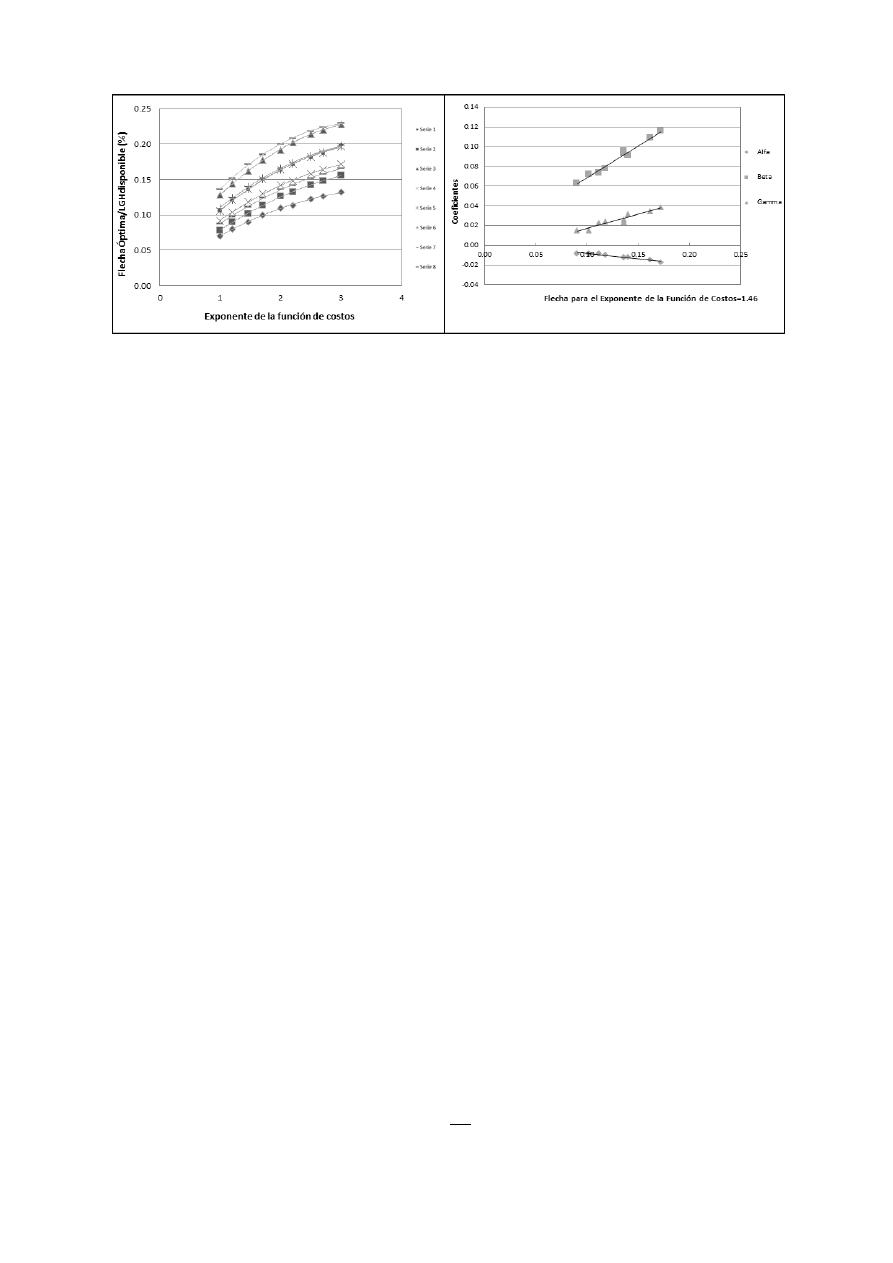
Los costos que se generaron en las series anteriores fueron calculados con una función de costos
similar a la Ecuación 2, con un exponente de 1.46 y un coeficiente de 0.015. Para analizar el efecto
del exponente de la función de costos sobre la flecha óptima de la LGH, se generaron 9 series; para
cada una se calculó la flecha óptima para valores del exponente de la función de costos entre 1 y 3.
Los resultados obtenidos se muestran en la siguiente figura:
2
3
9
-
3
2
3
3
2
/s
m
10
1
1000
/
1
,
m
s
m
L
Q
L
Q
f
(A) (B)
Figura 5.- A) Análisis del efecto del exponente de la función de costos en la Flecha Óptima. B) Coeficientes
de las ecuaciones cuadráticas en la Figura 5-A vs. Flecha Óptima para el exponente de costos de 1.46.
En las Figuras 5-A y 5-B, la relación entre la flecha óptima y el exponente de la función de costos
describe de manera perfecta una parábola. Además, todas las curvas son aproximadamente paralelas
y los valores de los coeficientes son grandes si el valor de la flecha es grande para un exponente de
costos dado. Para verificar lo anterior, existe una gráfica de la flecha óptima para un exponente de
costos dado vs. los coeficientes α, β and γ de las ecuaciones cuadráticas obtenidas anteriormente. La
Figura 5-B muestra la gráfica obtenida para 1.46 como el valor del exponente de la función de
costos; este fue el valor utilizado para estimar los costos de las tuberías. La relación entre la flecha
óptima (para un exponente de costos determinado) y el valor de los coeficientes de la ecuación
cuadrática ajustada es lineal. De este modo, si se conoce la flecha óptima para un exponente de
1.46, las ecuaciones obtenidas de la Figura 5 pueden ser utilizadas para determinar la flecha óptima
para cualquier valor de exponente de la función de costos.
A partir del análisis de los factores para determinar la flecha óptima de la LGH, se estableció un
procedimiento para estimar esta flecha para un sistema de tuberías en serie con características
topológicas, hidráulicas y comerciales variables; el procedimiento se describe a continuación:
5. METODOLOGÍA DE DISEÑO SOGH
Los pasos a seguir para estimar el valor de la flecha óptima son:
1. Calcular el Centroide de Demandas usando la Ecuación 7.
2. Calcular el Coeficiente de Uniformidad (CU) usando la Ecuación 8.
3. Usando la Ecuación 10 se estima el valor de la flecha óptima de acuerdo con
̅ y CU. La
flecha calculada con esta ecuación corresponde a la relación Q
2
/L
3
= 1 x 10
-9
m
3
/s
2
y a un
exponente de la función de costos de 1.46.
4. De la flecha obtenida en el paso 3, se estima la flecha óptima para el exponente de la
función de costos (n) que se tiene, empleando la siguiente expresión:
[13]
donde n es el exponente de la function de costos, α es igual a -0.1134 + 0.0032 * F
1.46
(de Figura 5),
β es igual a 0.6443 * F
1.46
- 0.0043 (de Figura 5), γ es igual a 0.2835 + 0.0111 * F
1.46
(de Figura 5),
y F
1.46
es la flecha óptima para un exponente de 1.46 (obtenida en el paso 3).
5. De la flecha obtenida en el paso 4, correspondiente a la relación Q
2
/L
3
= 1 x 10
-9
, se calcula
la flecha en términos de Q
2
/L
3
. Para esto se emplea la siguiente expresión (de Figura 4):
(
)
[14]

donde a es igual a 0.00868 * F
1x10-9
+ 0.00066 (de Figura 4-A), b es igual 1.18069 * F
1x10-9
+
0.01345 (de Figura 4-B) y F
1x10-9
es la flecha óptima para una relación Q
2
/L
3
= 1 x 10
-9
(del paso 4).
Conociendo la magnitud de la deflexión máxima de la LGH óptima, se puede conocer el tercer
punto de la curva y es posible determinar la ecuación cuadrática que describe esta trayectoria.
[15]
donde LGH(x) es la LGH ideal en el punto x y los coeficientes α, β y γ dependen del nivel de la
LGH a la entrada, la LGH mínima, la longitud máxima de la serie de tuberías y la flecha óptima. La
metodología para diseñar tuberías en serie determinando previamente la LGH óptima se describe a
continuación:
1. Ajustar los parámetros de diseño, las características topológicas e hidráulicas de las tuberías
en serie (es decir la presión mínima requerida, la longitud de las tuberías, la rugosidad de las
tuberías, la elevación del nivel del tanque de entrada, las demandas base y la función de
costos).
2. Estimar el valor de la flecha óptima de la LGH.
3. Calcular la LGH ideal en cada uno de los nudos de la serie de tuberías utilizando la
Ecuación 15.
4. A cada sección de la serie se le asigna una pérdida de energía objetivo como la diferencia
entre la LGH ideal en los nudos aguas arriba y aguas abajo de dicha sección, estimada en el
paso 3.
[16]
donde i es el nudo aguas arriba y j es el nudo aguas abajo de la tubería. Con la pérdida de energía
objetivo y el caudal en cada tubería, se calcula el diámetro optimizado empleando la ecuación de
Darcy-Weisbach en conjunto con la de Colebrook-White. Es importante resaltar que el resultado
obtenido resulta más bien una configuración preliminar de la tubería en serie que cumple con las
restricciones hidráulicas del problema de diseño; sin embargo, dado que los diámetros son valores
continuos, los requerimientos comerciales no se cumplen. A fin de redondear los diámetros a los
disponibles comercialmente, se implementaron unas restricciones mediante procedimientos de
programación de baja complejidad y que requieren un pequeño número de simulaciones hidráulicas.
6. METODOLOGÍA PROPUESTA VS. DISEÑO CON AG
A fin de verificar la metodología de diseño SOGH, se utilizaron un total de 1.200 series con
características topológicas aleatorias (demandas en los nudos, longitudes de tuberías y niveles de
entrada) y 4 tipos de topografías diferentes. Las series fueron generadas mediante el uso de una
función de generación aleatoria de valores en Excel y se clasificaron en tres tipos: 160 series con
demandas en los nudos y longitudes de tuberías uniformes (Tipo 1), 120 series con demandas
uniformes y longitudes de los tubos aleatorias (Tipo 2) y 120 series con demandas y longitudes
aleatorias (Tipo 3). Cada una de las series fue diseñada usando los 4 topografías: Horizontal, una
sección horizontal y la otra inclinada descendente, dos secciones inclinada y la sección central
horizontal y toda la sección inclinada descendente. En total, se diseñaron 640 series Tipo 1, 480
series Tipo 2, y 480 series Tipo 3. Las series se diseñaron utilizando SOGH y AG. Los AG
utilizados en este diseño tienen las siguientes características: operadores de cruce simple,
probabilidad de crear inversamente proporcional a la función de costos, y selección al azar en donde
el número real de descendientes de un individuo varía considerablemente y no es igual al número
esperado. Las características topológicas y topográficas uniformes o al azar de las series tuvieron
los siguientes rangos: número de tubos en cada serie (t): entre 3 y 30; longitud de las tuberías (l):
entre 10 y 100 m; demanda base en los nudos (q): entre 5 y 150 L/s; nivel del tanque de entrada (h):
entre 20 y 50 m. Para el proceso de diseño se estableció una presión mínima de 15 m. El material de
las tuberías seleccionado fue PVC, con rugosidad absoluta de 0.0000015 m; y los diámetros
comerciales disponibles fueron: 50, 75, 100, 150, 200, 250, 300, 350, 400, 450, 500, 600, 750, 800,
1000, 1200, 1400, 1500 y 1800 mm. Otros parámetros de diseño fueron la viscosidad cinemática
igual a 1.141 * 10
-6
m
2
/s; el coeficiente y exponente de la función de costos fueron 0.015 y 1.46,
respectivamente (Ver Ecuación 2).
(A) (B) (C) (D)
Figura 6.- A) Topografía A con 5 % de pendiente. (B) Topografía B con una sección horizontal seguida de
una sección inclinada (5%). (C) Topografía C con dos secciones inclinadas (5%) y una sección horizontal en
la mitad. (D) Topografía D con toda la sección horizontal.
7. RESULTADOS
Los resultados mostraron que para todos los tipos de series de tuberías, SOGH obtuvieron los
mismos resultados que los AG. En muy pocos casos los costos con AG resultaron más bajos en los
diseños, además las diferencias son menores al 2% en comparación con SOGH. Por otro lado,
cuando los diseños con AG resultaron más costosos, las diferencias estaban alrededor del 10%. A
continuación se describen los resultados:
- Series Tipo 1: 80.46% (515 series) de las 640 diseñadas obtuvieron el mismo costo con SOGH y
AG, un 15.93% (102 series) obtuvieron un costo menor con SOGH. Finalmente, un 3.59% (23
series) obtuvieron costos menores con AG. La diferencia de costos fue siempre menor al 10%,
demostrando las bondades del diseño explicito propuesto.
- Series Tipo 2: 71.66% (344 series) de las 480 series diseñadas obtuvieron el mismo costo con
SOGH y AG, 22.5% (108 series) obtuvieron un costo menor con SOGH y 5.83% (28 series)
obtuvieron un costo menor con AG. En este tipo de series, se presentó el mismo patrón de
comportamiento en la función de costos que en las series Tipo 1.
- Series Tipo 3: 74.16% (356 series) de las 480 series diseñadas obtuvieron el mismo costo con
SOGH y AG, 21.45% (103 series) obtuvieron un costo menor con SOGH, and 4.38% (21 series)
obtuvieron un costo menor con AG.
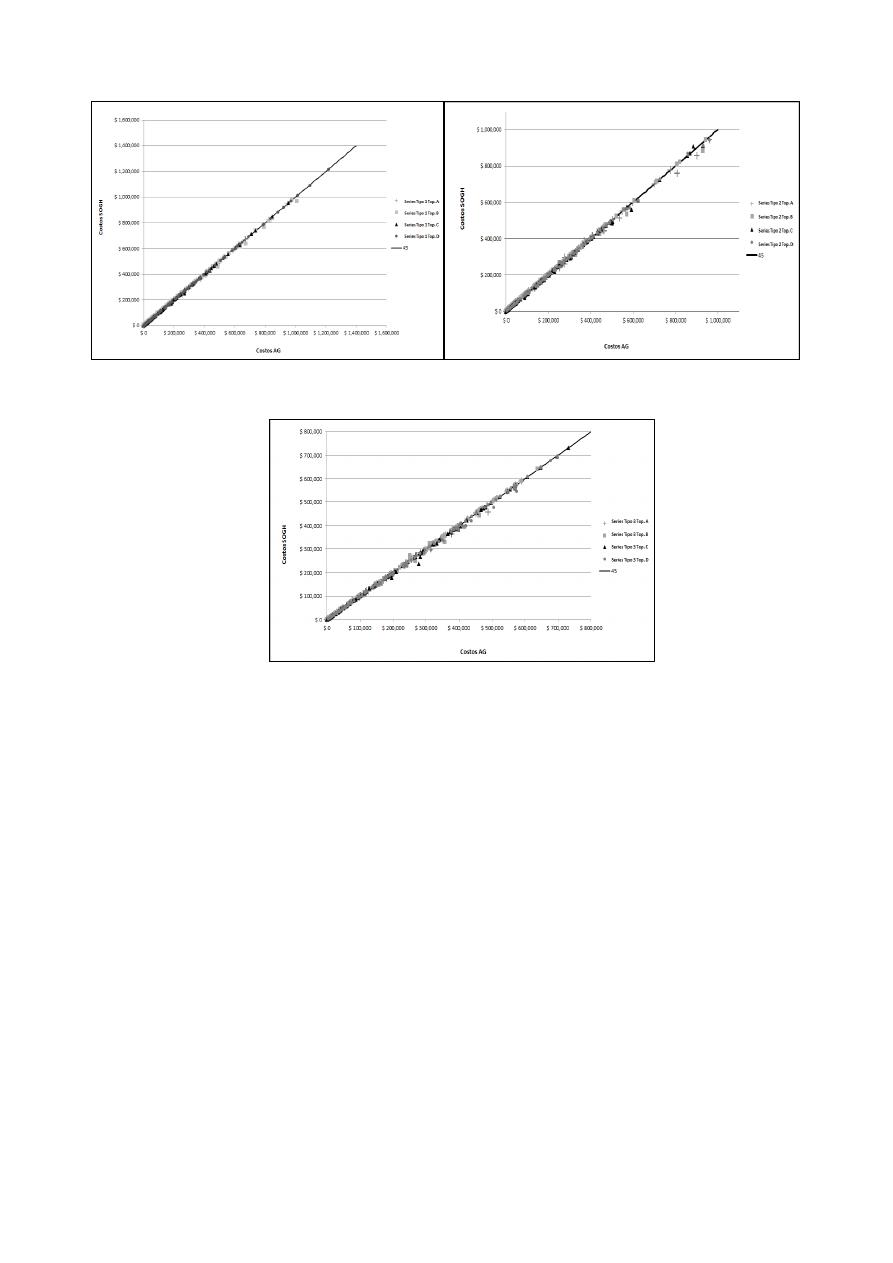
La Tabla 2 muestra la comparación de costos para 1200 series de tuberías diseñadas con ambas
metodologías. Las Figuras 7, y 8 muestran la comparación grafica de los costos de diseño. En ellas
se puede observar que la mayoría de puntos están sobre la línea de 45°. El número de puntos por
debajo de la línea de 45 es mayor que la de puntos por encima de ella; esto quiere decir que los
diseños con AG son más costosos.
Tabla 2.- Resultados de la comparación de costos para las dos metodologías.
TIPO
TOTAL DE
SERIES
No. DE
SERIES
%
COMPARACIÓN
1
640
617
96,40
SOGH≤AG
23
3,59
SOGH>AG
2
480
452
94,17
SOGH≤AG
28
5,83
SOGH>AG
3
480
459
95,63
SOGH≤AG
21
4,38
SOGH>AG
A) B)
Figura 7.- A) Comparación de costos de diseño para las tuberías en serie Tipo 1. B) Comparación de costos
de diseño para las tuberías en serie Tipo 2.
Figura 8.- Comparación de costos de diseño para las tuberías en serie Tipo 3.
8. CONCLUSIONES
Se desarrolló y evaluó de manera exitosa la metodología explícita de diseño optimizado de
tuberías en serie denominada Superficie Óptima de Gradiente Hidráulico (SOGH). A diferencia
de la mayoría de metodologías de diseño (AG, búsqueda de armonía, colonia de hormigas, etc.)
SOGH se basa en la imitación de fenómenos naturales y físicos y en el entendimiento de la
hidráulica y la topología del sistema.
Se comprobó que es posible diseñar series de mínimo costo si la LGH óptima se conoce
previamente. Este consiste en un conjunto de puntos (X, Y, LGH
ideal
), donde X y Y son las
coordenadas planas de cada uno de los nudos de la serie y LGH
ideal
es la presión que cada nudo
debe tener para lograr el menor costo constructivo de toda la serie. La forma de ésta línea
describe una función cuadrática cuya curvatura depende de las características hidráulicas,
topológicas y de las restricciones comerciales tales como la distribución espacial de la demanda,
la relación existente entre el caudal total de los tubos y su longitud total junto con la función de
costos.
La relación entre LGH y las características de las series de tuberías fue establecida mediante la
proposición de una metodología que permitiera estimar la ecuación de la parábola de LGH, la
cual describe la forma como se comporta la energía disponible en las tuberías en serie.
La LGH óptima depende de la topografía del sistema, de la asignación y magnitud de las
demandas, de la energía disponible en la entrada de la serie, y de la función de costos de las
tuberías. La forma de la LGH óptima es muy fácil de calcular, ya que no tiene restricciones con

respecto a la topografía, a la magnitud de las demandas y/o su localización ni a la energía
disponible.
Los porcentajes de tuberías en serie que fueron más económicas al diseñarlas con AG no
superan el 10 %. Las diferencias de costos entre las series diseñadas, donde los costos con AG
estaban por debajo de los costos de SOGH, son bastante bajos; no superan el 1% para las series
Tipo 1. Además, las diferencias en los costos para las series Tipo 2 y 3 son menores al 5 %.
Cuando los diseños con SOGH son más económicos que los diseños con AG, las diferencias en
costos pueden llegar hasta un 33 %. Las series que se diseñaron y obtuvieron costos iguales o
menores con AG son aquellas en las que la demanda de agua se localiza aguas abajo, lo que
hace que centroide de demandas se desplace hacia aguas abajo también.
En general, para todos los tipos de series analizadas con diferentes topografías, es posible
concluir que el método SOGH presenta un comportamiento muy similar (en términos de costo)
comparado con los AG.
Con base en los resultados encontrados, se puede concluir que la metodología SOGH es eficaz y
eficiente en el diseño optimizado de tuberías en serie. La baja complejidad y eficiencia son las
principales ventajas de SOGH sobre los AG; por otra parte, SOGH tiene un carácter explícito y
no depende de la configuración inicial de los diámetros de las tuberías.
La metodología SOGH se puede ampliar al caso de diseño optimizado de redes de distribución
de agua potable, donde los AG empleados tienen un componente aleatorio relevante y requieren
un gran número de simulaciones hidráulicas para obtener un diseño aproximado y que sea el de
menor costo. Además, debido a su carácter aleatorio, los resultados alcanzados en cada
ejecución no son siempre los mismos, razón por la cual debe hacerse un número considerable de
simulaciones hasta que se obtenga un buen diseño.
9. BIBLIOGRAFÍA
Afshar, M.H. 2006. Application of a max–min ant system to joint layout and size optimization of
pipe networks. Engineering Optimization, 38(3): 299 - 317.
CIACUA, 2008. Programa REDES. Universidad de Los Andes. Bogotá D.C., Colombia. Research
program for analysis and design of water distribution networks.
Goldberg, D.E. & Kuo, C.H. 1987. Genetic algorithm in pipeline optimization. Journal of
Computing in Civil Engineering, 1 (2): 128–141.
Kadu, S.M., Gupta, R. & Bhave, P.R. 2008. Optimal design of water networks using a modified
genetic algorithm with reduction in search space. Journal of Water Resources Planning and
Management, 134 (2): 147 - 160.
Martin, Q. W. 1990. Linear water supply pipeline capacity expansion model. Journal of Hydraulic
Engineering: 116, 675 - 691.
Montalvo, I., Izquierdo, J., Pérez, R. & Tung, M.M. 2008. Particle swarm optimization applied to
the design of water supply systems. Computers & Mathematics with Applications: 56, 769 - 776.
Perelman, L. & Ostfeld, A. 2007. An adaptive heuristic cross-entropy algorithm for optimal design
of water distribution systems. Engineering Optimization, 39(4): 413 - 428.
Saldarriaga, J.G. 2007. Hidráulica de Tuberías: abastecimiento de agua, redes, riegos. Bogotá:
Editorial Alfaomega. ISBN: 978-958-682-680-8.
Simpson, A.R., Dandy, G.C., & Murphy, L.J. 1994. Genetic algorithms compared to other
techniques for pipe optimization. Journal of Water Resources Planning and Management, 120
(4): 423 - 443.
Wu, I.-p. 1975. Design of drip irrigation main lines. Journal of the Irrigation and Drainage
Division, 101 (4): 265 - 278.
Wu, Z.Y. & Simpson, A.R. 2001. Competent genetic-evolutionary optimization of water
distribution systems. Journal of Computing in Civil Engineering, 15 (2): 89 – 101.
Yildirim, G. 2006. Analytical relationships for designing multiple outlet pipelines. Journal of
Irrigation and Drainage Division, 133 (2): 140-155.
