
Metodología de diseño optimizado de series de tramos de alcantarillado,
utilizando los conceptos de pendiente propia y pendiente intermedia
“XII Simposio Iberoamericano sobre planificación de sistemas de
abastecimiento y drenaje”
Emilio Corrales (1), Paula Cuero (2), Laura Montaño (3),
Daniel Luna (4), Juan Saldarriaga (5).
(1,2,3,4) Investigador(a), Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad
de Los Andes (CIACUA), Carrera 1ª Este N° 19A -40, Bogotá, Colombia, (+571) 3394949 Ext: 3520,
e.corrales61@uniandes.edu.co;
pa.cuero38@uniandes.edu.co;
le.montano110@uniandes.edu.co;
de.luna123@uniandes.edu.co
(5) Profesor Titular, Departamento de Ingeniería Civil y Ambiental, Director Centro de
Investigaciones en Acueductos y Alcantarillados de la Universidad de Los Andes (CIACUA), Carrera
1ª Este N° 19A -40, Bogotá, Colombia, (+571) 3394949 Ext: 3520, jsaldarr@uniandes.edu.co
RESUMEN
El diseño de las redes de alcantarillado tiene dos componentes básicos: la topología de la red y el diseño
hidráulico. En esta investigación, con el objetivo minimizar costos, partiendo de una topología definida, se
desarrolló un método exhaustivo para el diseño hidráulico de una serie de tramos de alcantarillado, que
cumple con las restricciones constructivas y los parámetros hidráulicos y garantiza la selección del óptimo
global, dentro del espacio solución al realizar una comparación de los costos constructivos de todas las
alternativas posibles. Para esto fue necesario introducir los conceptos de Pendiente Propia y Pendiente
Intermedia de cada tramo.
Palabras claves: Pendientes propias, Diseño de alcantarillados, Optimización.
ABSTRACT
The sewer networks’ design has two basic components: the network layout and the hydraulic design. To
achieve the objective of this research, which is to minimize the costs of designs that have a defined layout, an
exhaustive method was developed to determine the hydraulic design of a series of sewer’s stretch, within the
constructive restrictions and hydraulic parameters, ensuring the selection of the global optimum inside search
space after comparing the construction costs among all possible alternatives. The new methodology
introduces the concepts of “Eigen Slopes” and “Intermediate Slopes”.
Key words: Eigen Slopes, Sewer design, Optimization.
SOBRE EL AUTOR PRINCIPAL
Autor 1:
Ingeniero Civil de la Universidad del Valle (Colombia). Estudiante de la Maestría en Recursos Hídricos de la
Universidad de los Andes (Colombia). Asistente Graduado del Centro de Investigaciones en Acueductos y
Alcantarillados CIACUA del Departamento de Ingeniería Civil y Ambiental de la Universidad de los Andes.

INTRODUCCIÓN
En la práctica de la ingeniería, uno de los factores
más importantes para la aprobación y ejecución de
un proyecto es la valoración de sus costos globales,
razón por la cual la búsqueda de la alternativa más
económica que satisfaga a cabalidad todas las
necesidades del proyecto, se convierte en un proceso
primordial dentro de su desarrollo. Esta condición
no es ajena al diseño de sistemas de drenaje urbano.
El diseño de las redes de alcantarillado tiene dos
componentes básicos: topología de la red y el diseño
hidráulico de la misma. En esta investigación, con el
objetivo minimizar costos, partiendo de una
topología definida, se desarrolló un método
exhaustivo para el diseño hidráulico de una serie de
tramos de alcantarillado, (entendiéndose como tramo
la serie de tuberías que conectan dos cámaras de
inspección) que cumple con las restricciones
constructivas y los parámetros hidráulicos y
garantiza la selección del óptimo global, dentro del
espacio de solución al realizar una comparación de
los costos constructivos de todas las alternativas
posibles. Para esto fue necesario introducir los
conceptos de Pendiente Propia y Pendiente
Intermedia de cada tramo.
En la metodología propuesta, primero se diseñan los
tramos que componen la serie, realizando una
búsqueda de la combinación diámetro - pendiente
con la cual se pueda transportar el caudal de diseño
con la máxima relación de llenado posible, es decir,
aprovechando de la mejor manera la capacidad
hidráulica de las tuberías.
Una vez definidos estos diseños, se procede a
realizar todas las combinaciones posibles de diseños
por tramo, con el fin de excluir aquellos diseños que
incumplan con las restricciones inherentes a las
series de alcantarillado e identificar las alternativas
que sí cumplan con estas. Posteriormente se realiza
una comparación usando una ecuación de costos y se
selecciona la más económica.
ANTECEDENTES
A finales del siglo XIX, las ecuaciones de Bazin y
de Ganguillet y Kutter eran las más utilizadas para el
cálculo de la velocidad en canales abiertos bajo la
suposición de flujo uniforme; no obstante, ésta
última empleaba métodos tediosos para su solución
y presentaba problemas dimensionales. Debido a
esto Robert Manning, partiendo de un ajuste
realizado a 7 ecuaciones aproximadas para la
velocidad en canales abiertos bajo la suposición de
flujo uniforme (ecuaciones de Du Buat (1786),
Eytelwein (1814), Weisbach (1845), St. Venant
(1851), Neville (1860), Darcy y Bazin (1865) y
Ganguillet y Kutter (1869)) llevó a cabo un cálculo
de la velocidad para cada fórmula con un rango del
radio hidráulico entre 0.35 y 30 m para una
pendiente dada. Con los resultados obtenidos,
concluyó que la velocidad era proporcional a la
pendiente elevada a la 1/2 y al radio hidráulico
elevado a la 4/7. Sin embargo, con el objetivo de
obtener una ecuación más general, Manning analizó
los
resultados
de
algunos
experimentos
seleccionados de Bazin en canales semicirculares
revestidos de cemento y con una mezcla de arena y
cemento, a partir de los cuales concluyó que el
exponente para el radio hidráulico en ambos casos
era muy cercano a 2/3, dando lugar a la siguiente
ecuación (Chie, 1991):
⁄
⁄
(1)
Cabe aclarar que el C
1
mostrado en la Ecuación 1 se
refiere a un coeficiente propuesto por Manning, el
cual difiere del coeficiente propuesto por Chezy.
Adicionalmente, el exponente del radio hidráulico
(2/3) fue sugerido en primera instancia por el
Ingenierio Francés Gauckler en 1867, el cual, al
igual que Manning, basó su estudio en los
experimentos desarrollados por Darcy y por Bazin.
Por esta razón la fórmula de Manning también es
conocida como la fórmula de Gauckler-Manning.
Finalmente, Alfred Flamant sugirió que el C
1
propuesto por Manning podría expresarse como el
recíproco del n de Kutter en unidades simétricas,
afirmación
que
fue
presentada
en
textos
subsecuentes y en 1918 el hidráulico americano
King denominó éste coeficiente como el n de
Manning, resultando la ecuación que se conoce hoy
en día como tal.
(2)
donde,
-
K
n
es igual a 1 en el Sistema Internacional y
1.49 para el Sistema Inglés.
A pesar de que la ecuación de Manning ha sido
ampliamente utilizada en el diseño de tuberías
fluyendo parcialmente llenas, diferentes estudios
demuestran que, debido a que es una formulación
empírica, ésta ecuación pierde validez para el diseño
de alcantarillados que usan materiales modernos, los
cuales, debido a su baja rugosidad, presentan Flujo
Turbulento Hidráulicamente Liso (FTHL), mientras
la ecuación de Manning solo es válida para Flujo
Turbulento Hidráulicamente Rugoso (FTHR). Por lo
tanto, usar la ecuación de Manning con régimen de
FTHL genera el sobredimensionamiento de la
tubería hasta en un 20%, lo cual incurre en un
aumento de los costos del diseño.
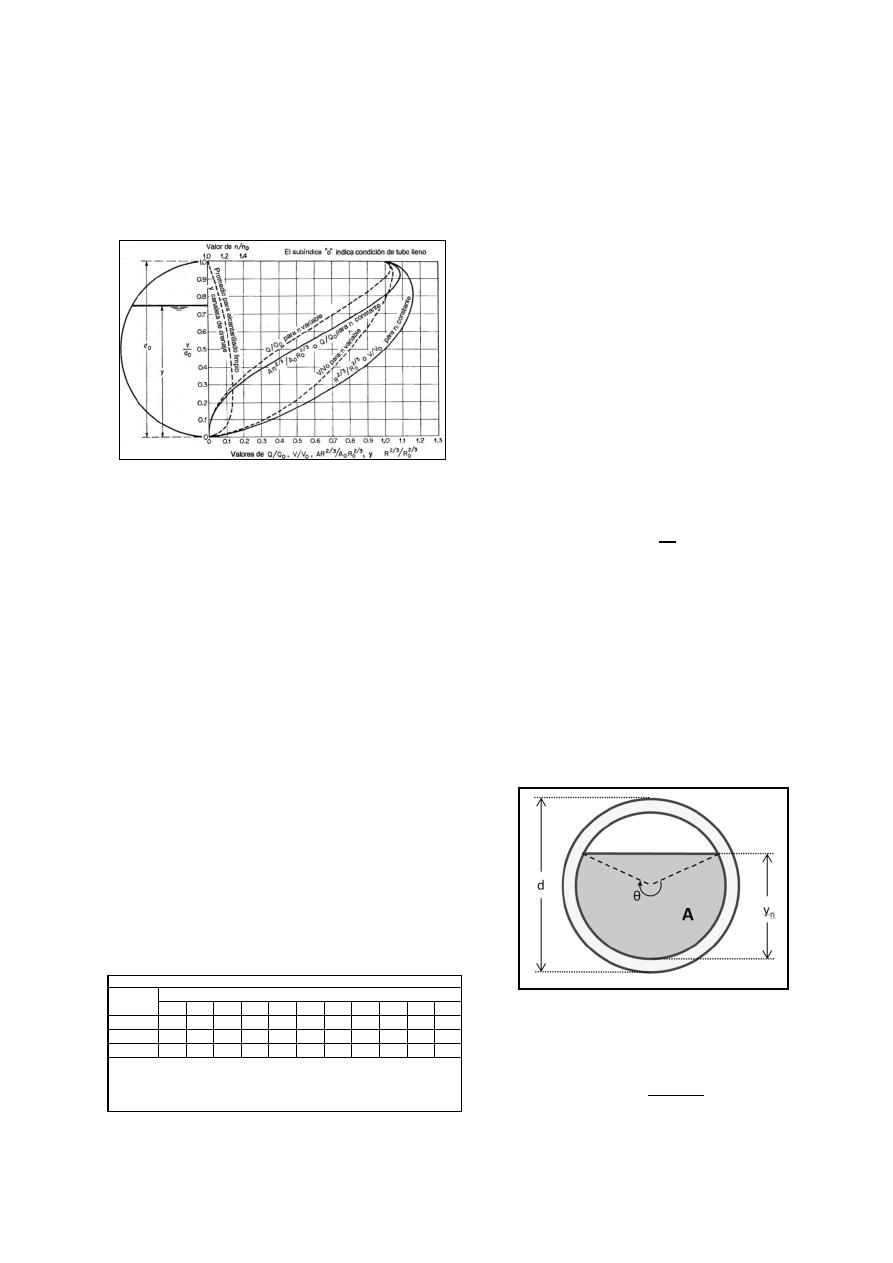
Figura 1.- Características del flujo para una
sección circular con n de Manning
constante y variable (T.R. Camp, s.f.).
En la Figura 1, se observa que para los diseños
generados con valores del coeficiente de n de
Manning variable, el caudal máximo se encuentra
para una profundidad ligeramente superior al 90%
del diámetro interno y tiene una magnitud total de
1.07 veces el caudal a tubería llena. Mientras que al
utilizar el n de Manning constante el caudal máximo
se encuentra a la misma profundidad, pero su
magnitud es de 1.18 veces el caudal de la tubería
llena.
Por esta razón, la Sociedad Americana de Ingenieros
Civiles (ASCE – American Society of Civil
Engineers) planteó una tabla en la cual, dependiendo
del diámetro de la tubería, adopta un rango válido
para el coeficiente de Manning (mostrando 3 valores
por cada diámetro, para diseños conservadores,
diseños menos conservadores, y los valores típicos).
Tabla 1.
– Valores recomendados del n
de Manning para cálculos en el diseño de
alcantarillados (ASCE , 2007).
BASE CIENTÍFICO - TEÓRICA
El primer paso que se debe dar en el diseño de un
sistema de drenaje urbano de mínimo costo,
involucra el diseño de un tramo de alcantarillado. Se
entiende por tramo de alcantarillado a la secuencia
de tuberías que va desde una cámara de inspección a
otra. Éstas se caracterizan por tener el mismo
diámetro, el mismo material y estar instaladas con la
misma pendiente. Para esto es necesario variar el
diámetro de diseño al igual que la pendiente hasta
que se cumpla con el caudal de diseño, como se
explicará en la metodología.
Ecuaciones utilizadas en el proceso de diseño
Las variables geométricas de la tubería de sección
circular dependen de la relación de llenado que se
tenga. Ésta se relaciona con el diámetro y la
profundidad de flujo de la siguiente manera:
(3)
dónde:
-
es la altura de agua dentro de la tubería.
-
es la relación de llenado de la
tubería.
-
es el diámetro de la tubería.
Teniendo esto, es posible calcular el ángulo que
forma la superficie libre de flujo con respecto al
centro de la tubería, como se muestra en la Figura 2.
Figura 2.- Propiedades geométricas de una
tubería circular fluyendo parcialmente llena.
(
)
(4)
TABLE 5-2 Suggested Values of Manning for sewer Design Calculations
Condition
Pipe Diameters in inches
6
8
10
12
15
18
24
30
36
48
60
Extra Care
0.0092 0.0093 0.0095 0.0096 0.0097 0.0098 0.0100 0.0102 0.0103 0.0105 0.0107
Typical
0.0106 0.0107 0.0109 0.0110 0.0112 0.0113 0.0115 0.0117 0.0118 0.0121 0.0123
Substandard
0.0120 0.0121 0.0123 0.0125 0.0126 0.0127 0.0130 0.0133 0.0134 0.0137 0.0139
Note: Extra care values are calculated from the Darcy-Weisbach equation for 60 °F, 2 fps velocity, ε = 0.001 ft.
Typical values are 15% higer than Extra Care values; Substandard values are 30% higers thatn Extra Care values.
After Haestad, M. et al. (2004). Wastewater colletion system modeling and design, Haestad Press, Waterbury.
Conn, with permission
donde:
-
θ es el ángulo que forma la superficie libre
de flujo con respecto al centro de la tubería.
El ángulo ayuda a definir fácilmente las propiedades
geométricas que describen la zona de la tubería que
contiene agua, como se observa en las Ecuaciones 5
a 7.
( )
(5)
donde:
-
A es el área mojada que fluye dentro de la
tubería.
(6)
donde:
-
P es el perímetro mojado presente en la
tubería.
( )
(7)
donde:
-
R es el radio hidráulico.
Con estas propiedades geométricas es posible
calcular la velocidad de flujo, haciendo uso de la
ecuación de resistencia fluida de Darcy-Weisbach.
√
(
√
)
(8)
donde:
-
es la velocidad de flujo dentro de la
tubería.
-
S es la pendiente de la tubería.
-
es la rugosidad absoluta de la tubería.
-
es la viscosidad cinemática del agua.
Teniendo la velocidad, es posible calcular el caudal
que pasa por la tubería, usando la Ecuación 9.
(9)
donde:
-
Q es el caudal que fluye dentro de la tubería.
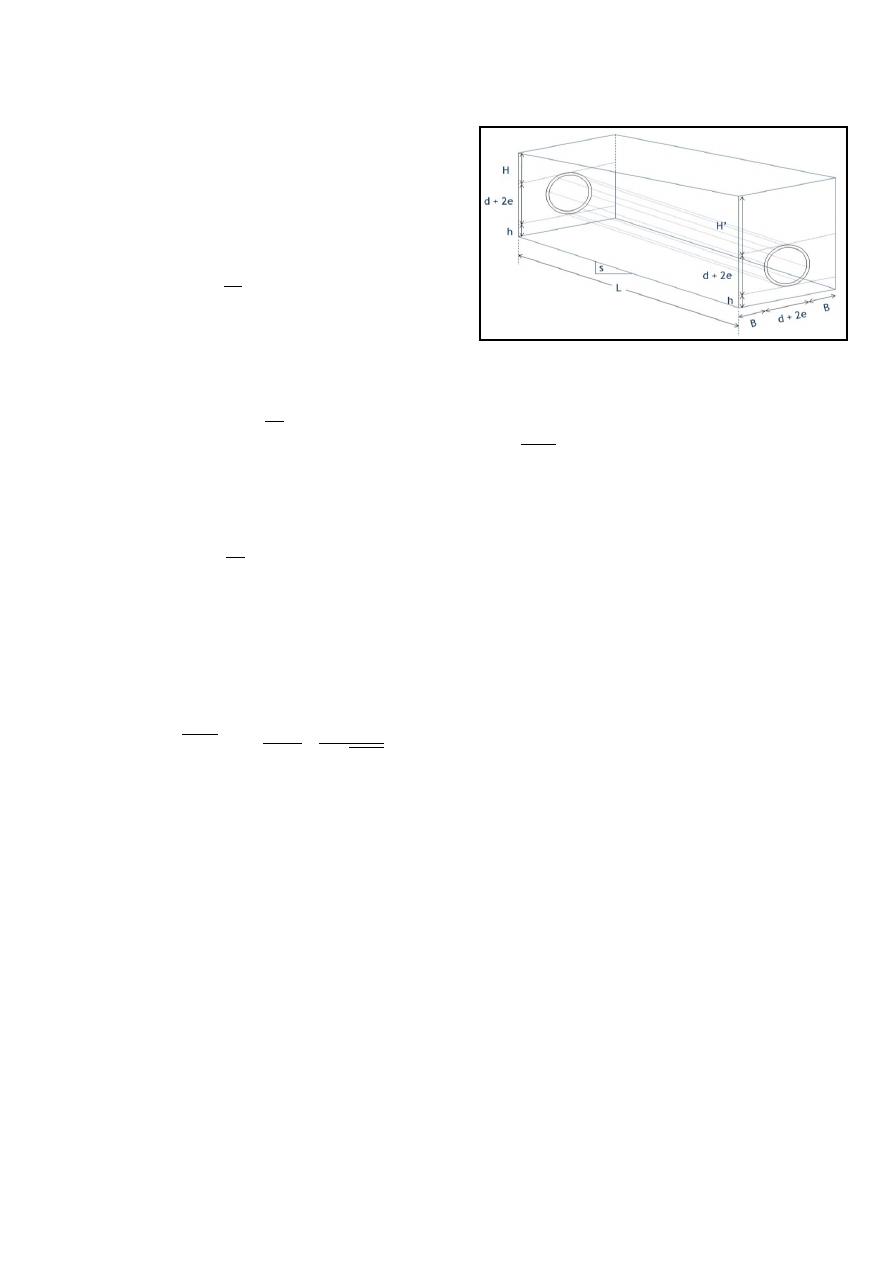
También es de gran importancia saber el volumen
excavado requerido para la disposición de una
tubería en el lugar indicado. En la Ecuación 10 se
muestra una ecuación de volumen de acuerdo con el
análisis de la Figura 3, en donde se muestra la
proyección de un trapecio a lo ancho de la zanja
resultante.
Figura 3.- Proyección del trapecio que
produce el área excavada para una tubería
de alcantarillado.
([
] ) ( ) ( [
])
(10)
donde:
-
V es el volumen excavado para poner la
tubería.
-
H es la profundidad de excavación hasta la
cota clave aguas arriba de la tubería.
-
H´ es la profundidad de excavación hasta la
cota clave aguas abajo de la tubería.
-
d es el diámetro interno de la tubería
-
e es el espesor de la pared de la tubería.
-
h es el relleno que debe disponerse bajo la
tubería. Depende de la reglamentación del
lugar donde se lleve a cabo el diseño. Para
los
ejemplos
se
siguieron
las
recomendaciones
del
Reglamento
Colombiano de Agua y Saneamiento (RAS):
h=15cm.
-
B es el espacio lateral que debe dejarse a
ambos lados de la tubería para ponerla.
-
s es la pendiente en la que se dispone la
tubería.
-
L es la longitud de la tubería.
Con el fin de verificar el cumplimiento de algunas
restricciones es importante calcular el esfuerzo
cortante y el número de Froude, usando la Ecuación
11 y la Ecuación 12, respectivamente.
(11)
donde:
-
τ es el esfuerzo cortante en la pared.
-
es la aceleración de la gravedad.
-
es la densidad del fluido dentro de la
tubería. En este caso es agua.

√
(12)
donde:
-
Fr es el número de Froude.
-
T es el ancho de la superficie libre que se
produce dentro de la tubería.
La superficie libre de flujo se calcula siguiendo la
Ecuación 13.
(
)
(13)
Es de importancia central calcular la Potencia
Unitaria, con el fin de ser usada como herramienta
de análisis para hallar criterios de optimización en el
diseño. La PU se define como:
(14)
donde:
-
PU es la Potencia Unitaria del flujo debido
al paso a través de la tubería.
-
son las pérdidas de energía por fricción
que ocurren dentro de la tubería.
Ya que el diseño se realiza bajo condiciones de flujo
uniforme, la Ecuación 14 se puede simplificar como
se presenta en la Ecuación 15.
(15)
Para terminar, también se tiene la diferencia de
pendientes promedio entre el terreno y la tubería,
como criterio de optimización en el diseño. Esto se
describe en la Ecuación 16.
( )
∑|
|
(16)
donde:
-
( ) es la diferencia de pendientes
promedio.
-
es la pendiente del terreno en el tramo i-
ésimo.
-
es la pendiente de la tubería del tramo i-
ésimo.
-
es el número total de tramos.
METODOLOGÍA
Selección de un diámetro mínimo de diseño,
dada una pendiente
Los datos que se conocen para realizar cada diseño
son: material de la tubería, una pendiente y el caudal
de diseño. El proceso que se sigue para encontrar el
diámetro comienza por tomar el menor valor de una
lista de diámetros discretos dada por los fabricantes.
Para cada diámetro interno se establece el máximo
porcentaje de llenado posible según la normatividad.
Con esta relación de llenado es posible calcular la
profundidad de flujo, usando la Ecuación 3.
Teniendo esto, se calcula el ángulo que forma la
superficie libre con el centro de la tubería, con la
Ecuación 4, para luego calcular el área mojada
(Ecuación 5), el perímetro mojado (Ecuación 6) y el
radio hidráulico (Ecuación 7). Teniendo esto, se
calcula la velocidad de flujo con la Ecuación 8 y el
caudal máximo que fluye por la tubería (Ecuación
9).
En caso de que este caudal máximo no sea mayor al
caudal de diseño, se escoge un diámetro más grande,
recorriendo la lista ordenada de diámetros de menor
a mayor, y se repite el proceso hasta encontrar un
diámetro que tenga capacidad suficiente para
transportar el caudal de diseño.
En este momento, es necesario calcular la
profundidad de flujo producida cuando por esa
tubería fluye el caudal de diseño. Para esto se hace
un proceso iterativo, haciendo uso de la Ecuación
17.
(
)
(17)
El exponente usado en la relación fue hallado
revisando el comportamiento hidráulico de la
relación de llenado con respecto al caudal de diseño.
En todos los casos se encontró que el exponente que
hace que la relación de llenado se aproxime a la
relación de llenado objetivo es 0.65.
Este proceso se resume en el diagrama de flujo
presentado en la Figura 4.
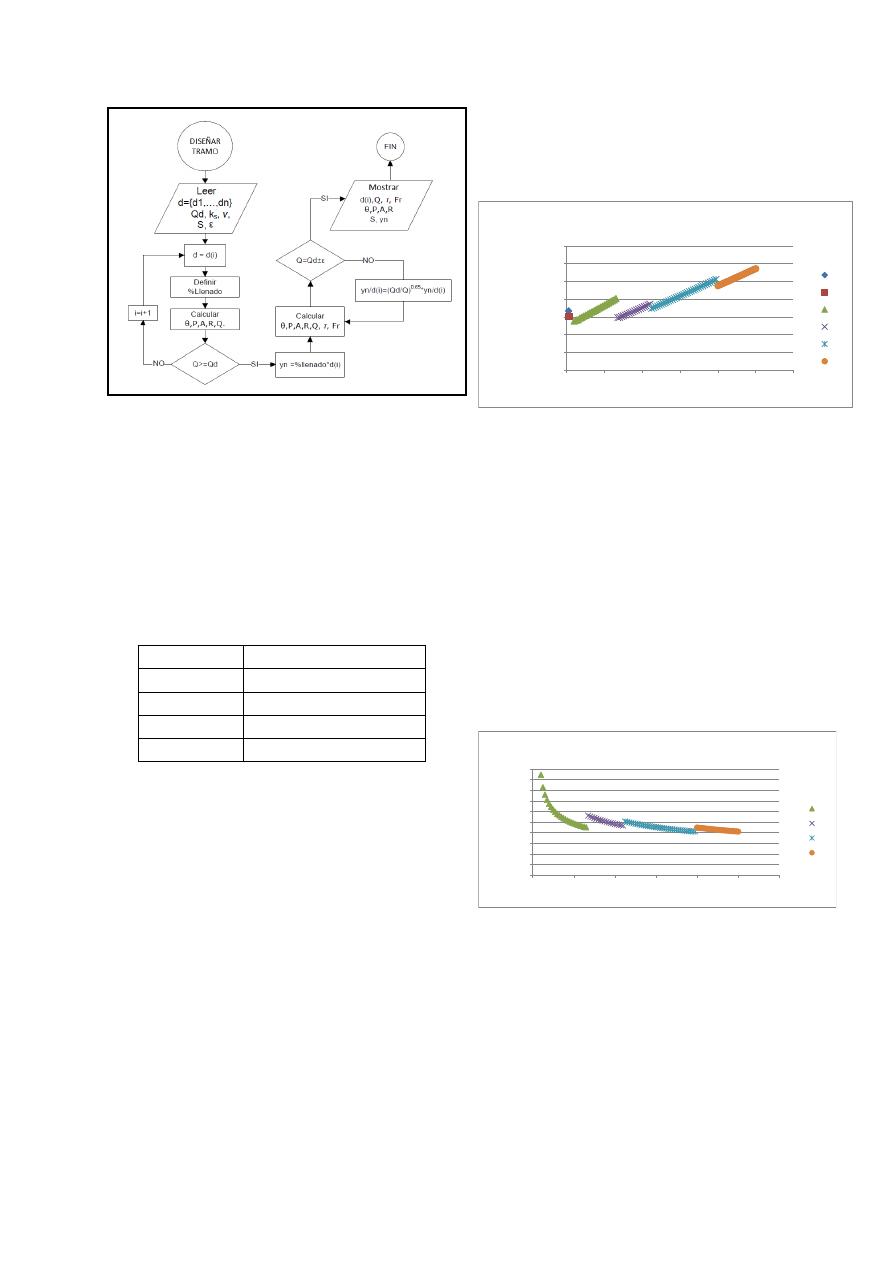
Figura 4.- Búsqueda de un diámetro de
diseño dada una pendiente.
Cabe resaltar que luego de repetidos cálculos, la
función de convergencia resultó más rápida que los
métodos numéricos tradicionales usados en la
búsqueda de raíces, como se resume en la Tabla 2.
Esto se debe a que el método tiene en cuenta la
naturaleza hidráulica del problema, y se centra en
ello para encontrar rápidamente el resultado.
Tabla 2. Iteraciones promedio para la
convergencia del y
n
/d.
Método
Iteraciones Promedio
Hidráulico
3.07
Secante
3.45
Falsa posición
3.57
Bisección
8.20
Una vez finalizado este cálculo se realiza una
verificación de restricciones. En muchas ciudades es
común encontrar una serie de restricciones que son
necesarias a la hora de diseñar una red de
alcantarillado. Estas consisten en limitar los tamaños
de diámetro, los valores de las pendientes, las
velocidades de flujo y los regímenes de flujo que se
pueden presentar dentro del sistema, con el fin de
facilitar el mantenimiento, garantizar autolimpieza
(velocidad mínima y/o esfuerzo cortante mínimo),
evitar
daños
por
abrasión,
minimizar
la
presurización por oleaje en las tuberías, entre otras
situaciones.
Búsqueda de la pendiente de diseño
Para encontrar las pendientes adecuadas para el
diseño, es necesario hacer un análisis de costos sobre
diferentes diseños realizados para una tubería. Si se
lleva a cabo el proceso de diseño descrito en la
Figura 4, para todas las pendientes que son múltiplos
de 1/1000, y se calculan los costos del diseño, se
obtiene la gráfica de la Figura 5. Los diseños se
hicieron para un caudal de 460 Litros por segundo,
en PVC. Los costos se calcularon usando la
Ecuación 22.
Figura 5.-
Comportamiento del costo de un
tramo, según la pendiente de diseño.
Se puede observar que a medida que aumenta la
pendiente usada para el diseño, los diámetros
resultantes disminuyen. De igual manera, se observa
que cada vez que se puede usar un diámetro menor,
el costo se reduce. Esto ocurre porque, en estos
puntos, el costo adicional de la excavación es menor
que el ahorro en la reducción del diámetro de la
tubería.
En la Figura 6 se puede observar el efecto de la
selección de una tubería nueva, según la pendiente
de diseño. Es evidente que, a medida que aumenta
ésta, el nivel del agua dentro de la tubería se reduce.
Figura 6. Comportamiento del nivel del agua
de un tramo, según la pendiente de diseño.
El efecto de la reducción del nivel del agua dentro
de la tubería es un indicador claro de que, para ese
diámetro, la mayoría de pendientes hacen que la
tubería fluya parcialmente libre. Entonces, si se
busca aprovechar al máximo una tubería, se
recomienda usar la pendiente que haga que la
profundidad de llenado sea la máxima posible. Esto
no solo permite aprovechar el diámetro al máximo,
también reduce el costo de diseño al mínimo, tal
como se observó en la Figura 5.
$ 0
$ 1.000.000
$ 2.000.000
$ 3.000.000
$ 4.000.000
$ 5.000.000
$ 6.000.000
$ 7.000.000
0
0,02
0,04
0,06
0,08
0,1
0,12
Co
sto
s To
tales (
COP)
Pendiente de Diseño
Comportamiento del costo de un tramo
30"
27"
24"
20"
18"
14"
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,45
0,5
0
0,02
0,04
0,06
0,08
0,1
0,12
Por
u
n
d
id
ad
d
e
Fl
u
jo
(m
)
Pendiente de Diseño
Comportamiento de y
n
en el diseño de un tramo
24"
20"
18"
14"

Estas pendientes son muy importantes para el diseño
optimizado, y se denominan Pendientes Propias.
Para buscarlas se debe hacer el proceso inverso que
se llevaba a cabo en la búsqueda del diámetro de
diseño. Se sabe que para cada diámetro discreto debe
existir una Pendiente Propia, por lo tanto se
comienza recorriendo la lista de diámetros de menor
a mayor. Usando la Ecuación 3 se encuentra el nivel
del agua para la máxima relación de llenado.
Teniendo esto, se calcula el ángulo que forma la
superficie libre con el centro de la tubería, con la
Ecuación 4, para luego calcular el área mojada
(Ecuación 5), el perímetro mojado (Ecuación 5) y el
radio hidráulico (Ecuación 7). En este punto se
calcula la pendiente que resuelva la siguiente
expresión.
√
(
√
)
(18)
Búsqueda de pendientes intermedias
Después de llevar a cabo una gran cantidad de
diseños para series de tramos, fue claro que el
concepto de Pendiente Propia no era suficiente para
garantizar que los costos se reducirían en todos los
casos.
Esto ocurre ya que el concepto de Pendiente Propia
es muy efectivo reduciendo el costo de las tuberías,
pero descuida bastante el costo asociado con la
excavación. El hecho de que un diámetro sólo pueda
ser dispuesto de una forma (una pendiente) hace que
se limiten las posibilidades, desembocando en un
sobrecosto innecesario de la red. Un buen ejemplo es
el caso en el que las Pendientes Propias sean muy
diferentes a la pendiente del terreno. En este caso las
tuberías serán dispuestas siempre con la Pendiente
Propia que supere la pendiente del terreno.
Cabe preguntarse ¿El sobrecosto de la excavación es
mayor que el sobrecosto de disponer una tubería de
menor diámetro a una pendiente más alta? La
respuesta depende del tipo de situación en la que se
esté. Si la profundidad ya es muy alta, la función de
costos hace que el costo de excavar unos centímetros
más sea tan alto que no valga la pena diseñar con la
Pendiente Propia.
Es por esto que nació el concepto de Pendiente
Intermedia, como una opción de diseño de un tramo.
La Pendiente Intermedia (
) es el promedio
ponderado de un par de pendientes propias, que hace
que se reduzca la diferencia de pendientes promedio
(Ecuación 16).
( )
(19)
El cálculo de la Pendiente Intermedia se hace con las
Pendientes Propias exactas, sin aproximar.
De esta manera, se tiene que entre dos pendientes
propias
y
, si se cumple que
se lleve
a cabo el siguiente análisis, involucrando la
pendiente del terreno
:
1. En caso de que
entonces el factor
de ponderación
2. En caso de que
entonces el factor
de ponderación
La variable β se encuentra en el intervalo [0; 0.5) y
permite una variación leve en las pendientes, con el
fin de encontrar el mejor diseño posible. Fue
pensada para fines investigativos; sin embargo, es
posible introducirla como variable externa del
problema, con el fin de permitir al diseñador obtener
mejores resultados.
Se ha observado que para la mayoría de diseños, un
β=0.3 es un buen valor para reducir los costos de
excavación. Análisis de casos han demostrado que la
reducción de costos mejora aún más cuando se
incluye la pendiente del terreno como una de las
pendientes de diseño posibles.
Diseño exhaustivo de series de alcantarillado
Hasta el momento se tiene un conjunto de diseños
posibles para cada uno de los tramos que harán parte
de la serie que se desea diseñar. Con el fin de
garantizar la exhaustividad del proceso, se deben
hacer todas las combinaciones posibles de diseños
por tramo, con el fin de excluir aquellos diseños que
incumplan con las restricciones inherentes a las
series de alcantarillado. Una alternativa es aquella
combinación de diseños propios hecha en los tramos
que conforman la línea principal de una red de
alcantarillado. De esta manera se tiene que el
número total de alternativas es:
∏
(19)
donde:
-
es el número de tramos que conforman la
serie.
-
es el número de diseños del tramo i-
ésimo.
Este planteamiento implica que se está tratando con
un problema de decisión que crece de manera
exponencial. Este
tipo de problemas están
catalogados dentro del conjunto de problemas NP-
Duros, y no existen algoritmos que puedan
resolverlos de manera práctica. Es por esta razón que
estos son abordados siempre con números pequeños,
donde los algoritmos funcionan correctamente; de
otro modo, el proceso podría tardar tanto tiempo
que, para sentidos prácticos, no se encontraría nunca
una solución.
La idea de realizar un análisis de forma exhaustiva
de un problema NP-Duro es un reto interesante. En
realidad es necesario conocer el funcionamiento
interno de las herramientas computacionales, incluso
más a fondo que el comportamiento hidráulico y la
naturaleza del problema. De este modo se aplicaron
un conjunto de técnicas para acelerar el proceso y
permitir la realización de análisis de forma veloz y
cómoda: reducción del almacenamiento de datos en
memoria secundaria (en el disco de la máquina) a la
menor cantidad de veces posible, reducción del
espacio a explorar mediante la eliminación de
alternativas que, antes de ser analizadas, se puede
saber que no constituyen un camino válido y,
finalmente, reducción de información retenida en
memoria principal a lo largo del procedimiento, al
mínimo posible.
PRESENTACIÓN DE RESULTADOS
Diseño de la rama principal de Alcantarillado
Se muestra el diseño de una línea principal de
alcantarillado que consta de 8 tramos en serie,
hechos en PVC, con los datos que se muestran en la
Tabla 3.
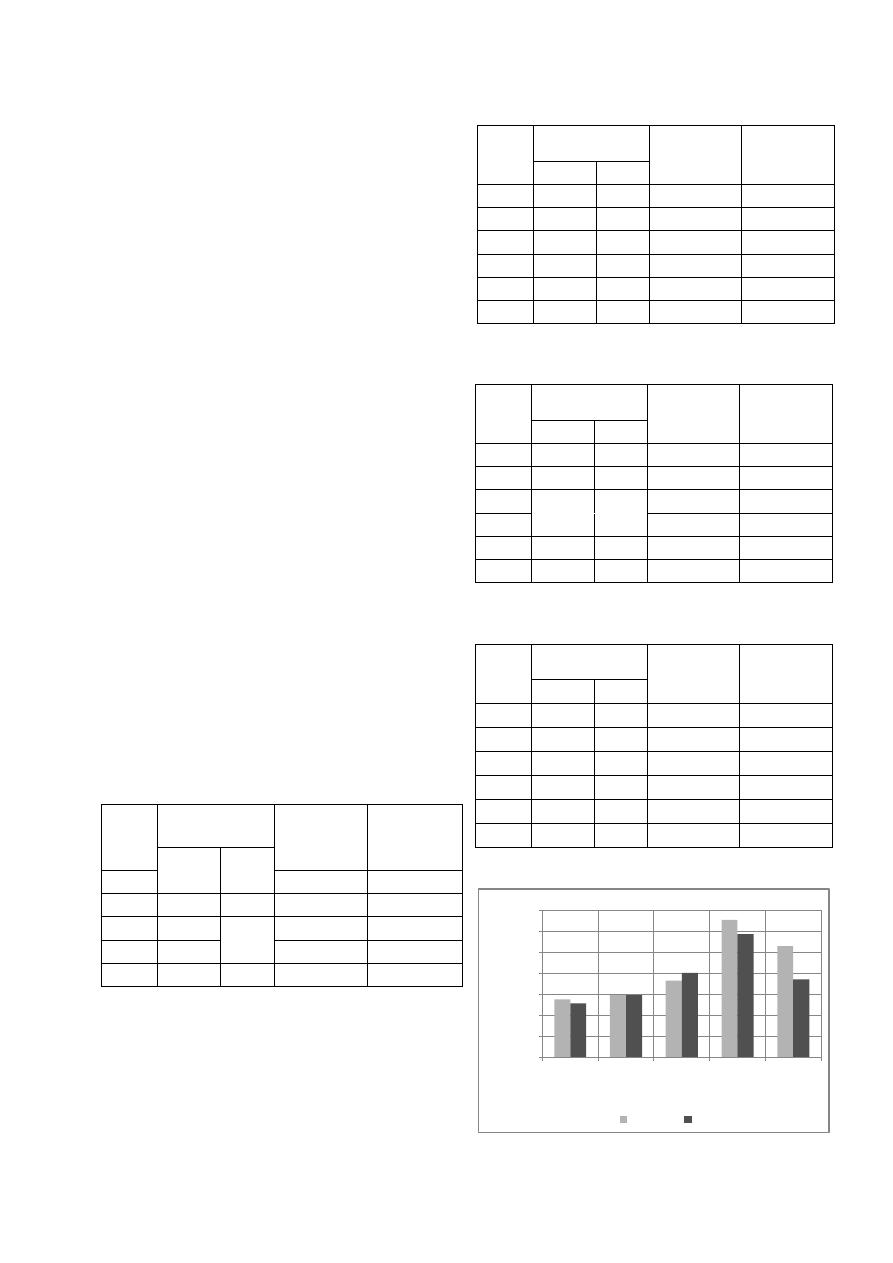
Para este diseño existen 76.8 millones de
combinaciones posibles, de las cuales se obtienen
más de 4500 alternativas válidas cuando se tienen en
cuenta todos los grupos de pendientes en el diseño.
La rutina que realizó la evaluación de las 76.8
millones de alternativas de forma exhaustiva, tardó
18 segundos en finalizar de manera exitosa la tarea.
Tabla 3. Datos utilizados para el diseño de la
línea principal de alcantarillado (serie
Limonar 4x4).
Tramo
Cota terreno
(m)
Longitud
(m)
Caudal
(m
3
/s)
N°
Diseños
Inicial Final
1
1000
998
100
0.04022
8
2
998
997
100
0.04762
10
3
997
997
100
0.05481
10
4
997
995
100
0.06438
12
5
995
994
100
0.07382
10
6
994
992
100
0.08536
8
7
992
991
100
0.09903
10
8
991
990
100
0.11471
10
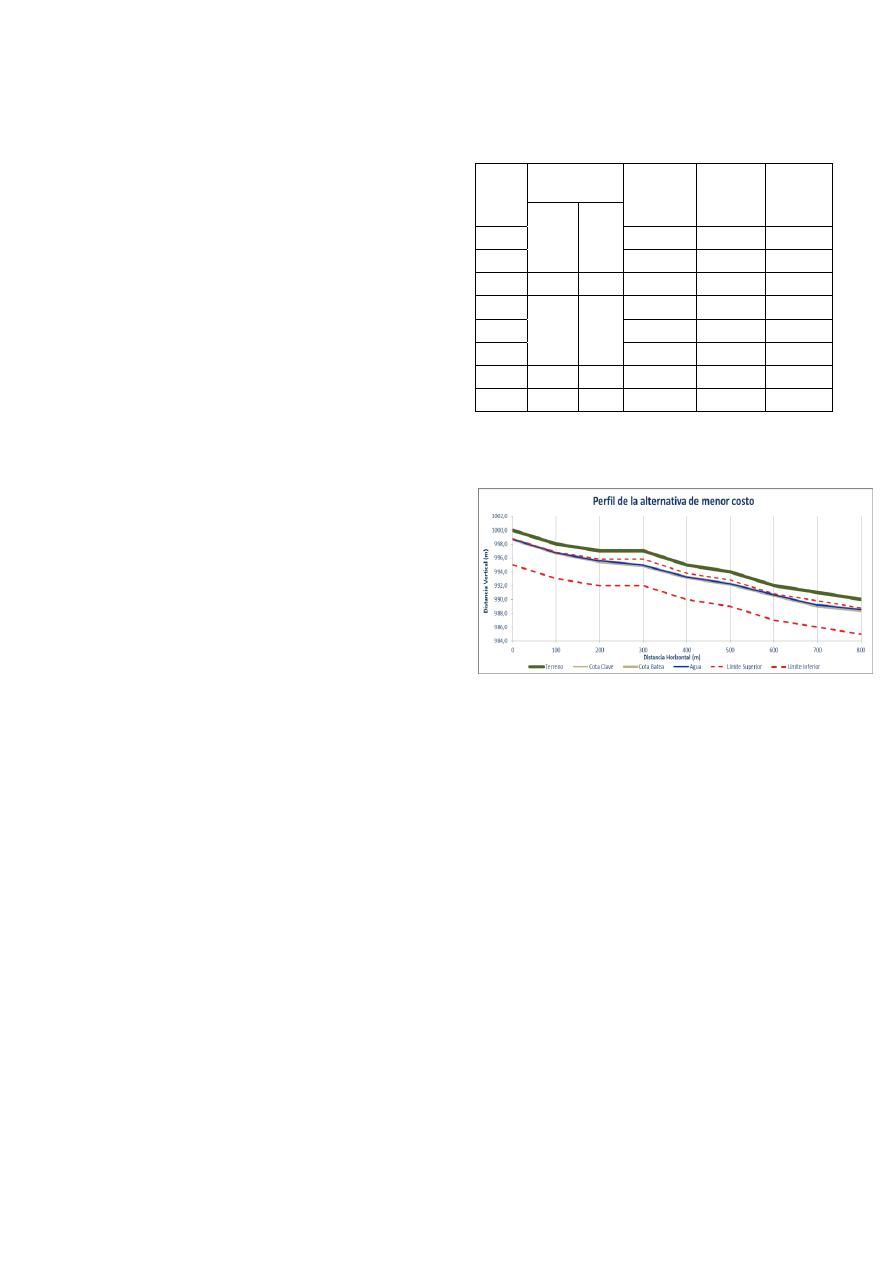
La Figura 7 representa el perfil de la alternativa de
costo mínimo.
Figura 7. Perfil de la alternativa de menor
costo.
Costos del diseño
La evaluación de costos de cada una de las redes
validas tiene dos componentes; el costo por
excavación que se determina con la Ecuación 21 y el
costo de la tubería que depende del diámetro y la
longitud del tubo y se determina por medio de la
Ecuación 20. El costo total corresponde a la suma
del costo por excavación y por tubería como se
muestra en la Ecuación 22.
(20)
(21)
donde:
-
Kd es el coeficiente de costo por diámetros.
-
Ke es el coeficiente de costo por
excavación.
-
L es la longitud.
-
d es el diámetro de la tubería.
-
V es el volumen excavado.
(
)
(22)
donde:
-
Cd es el costo por diámetro.
-
Ce es el costo por excavación
-
k es un coeficiente.
Comparación con otros programas de diseño
Con el objetivo de probar la metodología propuesta,
se realizó una serie de pruebas con ésta, y con el
programa de diseño SEDAL Plus, utilizando
diferentes escenarios, en los cuales se varió la
cantidad de tramos en la serie, los caudales de
diseño, los materiales de las tuberías y las
características del terreno.
El programa SEDALplus es descrito por su creador,
el Ingeniero Rafael Paredes, como un Sistema
Experto, creado para diseñar diferentes tipos de
redes de drenaje urbano. Este programa es capaz de
elegir la topología de la red de forma automática, es
decir puede elegir como se interconectan los tramos
de la red. Una vez definida esta topología por el
usuario o por el programa, SEDAL es capaz de
realizar el diseño hidráulico que incluye la elección
de diámetros y pendientes de cada uno de los tubos
que satisfagan las restricciones técnicas.
Los datos de las serias utilizadas para realizar esta
evaluación, se presentan en las Tablas 3 a 7. Para los
casos de “Pendiente Alta” y “Pendiente Media”, se
consideró realizar el diseño con tuberías con
rugosidad de 3.0x10
-4
m; mientras que para los otros
tres, se utilizó una rugosidad de 1.5x10
-6
m.
Tabla 4. Datos serie Pendiente Alta.
Tramo
Cota terreno
(m)
Longitud
(m)
Caudal
(m
3
/s)
Inicial Final
1
100
98.8
120
0.1518
2
98.8
97.75
105
0.28504
3
97.75
96.7
105
0.41124
4
96.7
95.65
105
0.53424
5
95.65
94.45
120
0.655
En las Figuras 8 a 10, se presenta la comparación de
costos de cada uno de los diseños obtenidos, tanto al
implementar la metodología propuesta (CIE - Disc)
como el programa SEDAL Plus. Se presentan los
costos totales, los costos por tuberías y los costos
por excavación.
Tabla 5. Datos serie Pendiente Media.
Tramo
Cota terreno
(m)
Longitud
(m)
Caudal
(m
3
/s)
Inicial Final
1
100
99.76
120
0.1518
2
99.76
99.55
105
0.28504
3
99.55
99.34
105
0.41124
4
99.34
99.13
105
0.53424
5
99.13
98.89
120
0.655
6
98.89
98.65
120
0.74448
Tabla 6. Datos serie Pendiente Combinada.
Tramo
Cota terreno
(m)
Longitud
(m)
Caudal
(m
3
/s)
Inicial Final
1
1000
999.5
100
0.10984
2
999.5
999
100
0.20625
3
999
998.5
100
0.29795
4
998.5
996.5
100
0.38651
5
996.5
994.5
100
0.47306
6
994.5
992.5
100
0.55826
Tabla 7. Datos serie Baluarte 3x3.
Tramo
Cota terreno
(m)
Longitud
(m)
Caudal
(m
3
/s)
Inicial Final
1
1000
999
100
0.05244
2
999
998
100
0.0807
3
998
997
100
0.11697
4
997
995
100
0.13901
5
995
994
100
0.14767
6
994
992
100
0.16452
Figura 8. Comparación de costos totales.
$
$ 2000
$ 4000
$ 6000
$ 8000
$ 10000
$ 12000
$ 14000
Baluarte
(3x3)
Limonar
(4x4)
Pendiente
Alta
Pendiente
Media
Pendiente
Combinada
C
o
st
o
T
o
ta
l (U
SD
)
Serie de Tuberías
SEDAL
CIE-Disc

Figura 9. Comparación de costos de
tuberías.
Figura 10. Comparación de costos de
excavación.
Los siguientes son los perfiles de los diseños
obtenidos tanto por CIE, como por SEDAL, para dos
de los escenarios evaluados:
Figura 11. Serie Limonar diseñada por
SEDAL Plus.
Figura 12. Serie Limonar diseñada con la
metodología propuesta (CIE).
Figura 13. Serie Pendiente Alta diseñada
con SEDAL Plus.
Figura 14. Serie Pendiente Alta diseñada
con la metodología propuesta (CIE).
ANÁLISIS DE RESULTADOS
El uso de un método hidráulico para la convergencia
de la profundidad normal de flujo permite hacer
diseños de una manera más eficiente, en
comparación con el uso de otros métodos numéricos.
Esto ocurre ya que el método está basado en un
análisis hidráulico del problema, la cual corresponde
a la filosofía que hay detrás de los métodos
modernos de optimización en hidráulica, pues hacen
uso de funciones objetivo y restricciones que
obedecen principios netamente hidráulicos.
El problema de diseño de líneas principales de
alcantarillado
se
simplifica
enormemente
al
establecer al introducir los conceptos de Pendiente
Propia y Pendiente Intermedia. Este planteamiento
permite evaluar alternativas finitas de diseño, lo que
abre la posibilidad de hacer análisis exhaustivos en
la evaluación de alternativas. A partir de los
resultados de este proceso, es posible encontrar un
costo mínimo global que resulta ser un diseño que
cumple con todas las restricciones. El uso de
estructuras de datos que permitan evaluar el
cumplimiento de restricciones a través de múltiples
caminos, resulta fundamental a la hora de establecer
metodologías eficientes para realizar cálculos
exhaustivos.
$
$ 500
$ 1000
$ 1500
$ 2000
$ 2500
$ 3000
$ 3500
$ 4000
Baluarte
(3x3)
Limonar
(4x4)
Pendiente
Alta
Pendiente
Media
Pendiente
Combinada
C
o
st
o
p
o
r
Tu
b
e
ría
s
(U
SD
)
Serie de Tuberías
SEDAL
CIE-Disc
$
$ 2000
$ 4000
$ 6000
$ 8000
$ 10000
Baluarte
(3x3)
Limonar
(4x4)
Pendiente
Alta
Pendiente
Media
Pendiente
Combinada
C
o
st
o
p
o
r
Ex
ca
va
ció
n
(U
SD
)
Serie de Tuberías
SEDAL
CIE-Disc

Al realizar comparaciones de diseños con el
programa SEDAL Plus, el cual es una excelente
herramienta, la metodología a pesar de obtener
diseños con costos de tuberías un poco más altos,
tiene unos costos globales menores. SEDAL Plus,
generó diseños más económicos que CIE, solo en
dos casos: serie “Limonar” y serie “Pendiente Alta”,
pero como se puede apreciar en las Figuras 11 y 13,
los diseños obtenidos por SEDAL Plus, no cumplen
con la restricción de profundidad mínima, mientras
que CIE sí lo hace.
CONCLUSIONES Y
RECOMENDACIONES
La idea de realizar diseños exhaustivos cobra gran
validez a través del uso de herramientas y técnicas
computacionales
modernas,
que
al
ser
implementadas de manera adecuada, reducen
notoriamente los tiempos de cálculo.
Los procesos de optimización son muy importantes
ya que por medio de éstos se puede realizar una
valoración exhaustiva de alternativas en un tiempo
corto, lo que se ve reflejado en una reducción tanto
de
tiempos
operacionales
como
de
costos
constructivos.
El uso de estructuras de datos para llevar a cabo la
evaluación de las alternativas a partir de
restricciones de diseño, alcanza niveles de eficiencia
satisfactorios, teniendo en cuenta que el problema de
optimización se está solucionando de manera
exhaustiva.
Es necesario añadir a los diseños en los tramos,
Pendientes Intermedias que minimicen la diferencia
entre la pendiente del terreno y la pendiente de la
tubería. Esto permite que, cuando se lleve a cabo la
evaluación de series de tramos, los costos de
excavación se reduzcan de forma importante.
La exhaustividad del proceso de selección de la serie
de tramos de menor costo se logra con relativa
rapidez para series considerablemente largas (de más
de 13 tramos). Esto, en conjunto con la ausencia de
un criterio para la selección de los tramos que
formen la mejor serie posible, lleva a concluir que lo
más indicado para diseñar series es proceder de
manera exhaustiva.
El aprovechamiento de la capacidad hidráulica de las
tuberías, le permite al programa CIE obtener muy
buenos diseños, ya que lleva los tubos a su máximo
porcentaje de llenado mientras
cumpla las
restricciones, esto haciendo uso de Pendientes
Propias para terrenos planos y en el caso de terrenos
inclinados haciendo uso de Pendientes Intermedias y
Propias para lograr ajustarse a éste.
Al realizar el diseño de redes de alcantarillado,
existen muchas variables que pueden influir sobre la
definición del diseño de la red, tales como
decisiones políticas, localización de la obra,
afectación de la infraestructura existente, entre otras
que no se tuvieron en cuenta dentro de la ecuación
de costos, quedando abierta la opción, para
investigaciones
futuras,
de
vincularlas
para
complementar
el
proceso
de
selección
de
alternativas.
BIBLIOGRAFÍA
American Society of Civil Engineers. (2007).
Gravity
Sanitary
Sewer
Design
and
Construction.
Chie, B. (1991). Gravity Sanitary Sewer Design and
Construction, LLC, 5-8. Colorado, Water
Resources Publications.
López, A. (2012), Diseño Optimizado de Redes de
Drenaje Urbano Usando el Concepto de
Potencia Unitaria. Bogotá: Tesis de Grado
20112021 Universidad de Los Andes.
Salcedo, C. (2012). Diseño optimizado de sistemas
de alcantarillado utilizando los conceptos de
resiliencia y potencia unitaria. Bogotá: Tesis
de Grado Universidad de Los Andes.
