
TESIS DE MAESTRÍA
DISEÑO OPTIMIZADO DE SUBMÓDULOS DE SISTEMAS DE RIEGO
LOCALIZADO DE ALTA FRECUENCIA.
David Hernández Benítez
Asesor: Juan G. Saldarriaga Valderrama
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
MAESTRÍA EN INGENIERÍA CIVIL
BOGOTÁ D.C.
2012

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
i
TABLA DE CONTENIDO
ÍNDICE DE FIGURAS ............................................................................................................................. iii
ÍNDICE DE GRÁFICAS ........................................................................................................................... v
1.
INTRODUCCIÓN Y OBJETIVOS ..................................................................................................... 1
1.1.
Introducción. ....................................................................................................................... 1
1.2.
Objetivo General. ................................................................................................................ 3
1.3.
Objetivos Específicos. .......................................................................................................... 3
2.
MARCO TEÓRICO ......................................................................................................................... 5
2.1.
Características de un sistema de riego localizado de alta frecuencia. ................................ 5
2.1.1.
Emisores. ..................................................................................................................... 7
2.1.2.
Uniformidad del riego. .................................................................................................. 13
2.2.
Diseño hidráulico de sistemas de RLAF. ............................................................................ 17
2.2.1.
Ecuaciones básicas de la hidráulica de redes. ........................................................... 17
Para flujo laminar, el factor de fricción se calcula mediante: ................................................... 18
2.2.2.
Diseño de sistemas de RLAF. ..................................................................................... 19
2.2.3.
Resultados y análisis de trabajo de Bermúdez (2011). ............................................. 32
2.3.
Programas. ........................................................................................................................ 38
2.3.1.
Programa REDES. ....................................................................................................... 38
2.3.2.
Optimizador Xpress. .................................................................................................. 40
3.
RESULTADOS Y ANÁLISIS PRIMERA FASE .................................................................................. 41
3.1.
Análisis metodología SOGH. .............................................................................................. 41
3.1.1.
Análisis etapa 2, metodología SOGH. ........................................................................ 41
3.1.2.
Flecha mínima y máxima para el diseño de sistemas de riego. ................................ 42
3.2.
Casos de estudio metodología SOGH. ............................................................................... 46
3.2.1.
Diseño de los submódulos de riego. ......................................................................... 49
3.2.2.
Resultados diseños. ................................................................................................... 54
3.3.
Análisis de la metodología propuesta por Bermúdez. ...................................................... 74
3.3.1.
Red Asimétrica 1, con emisores de exponente 0.3. .................................................. 74

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
ii
3.4.
Diseño de submódulos de riego usando programación lineal. ......................................... 79
3.4.1.
Formulación matemática del problema de diseño de redes abiertas. ..................... 79
3.4.2.
Aplicación de programación lineal al diseño de submódulos de riego. .................... 86
3.4.3.
Metodología para el diseño de submódulos de riego usando programación lineal en
conjunto con SOGH. .................................................................................................................. 94
3.4.4.
Resultados de la metodología planteada en el diseño de submódulos de sistemas de
RLAF………. ............................................................................................................................... 100
4.
CONCLUSIONES ....................................................................................................................... 119
5.
RECOMENDACIONES ............................................................................................................... 121
6.
REFERENCIAS ........................................................................................................................... 123
7.
ANEXOS ................................................................................................................................... 124
7.1.
Programa para el cálculo de PES y generar archivo de Xpress. ...................................... 124

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
iii
ÍNDICE DE FIGURAS
Figura 1. Esquema común de un sistema de riego, Adaptado de (Saldarriaga, 2007). ...................... 6
Figura 2. Clasificación de emisores en sistemas de RLAF, Adaptado de (Saldarriaga, 2007). ............. 8
Figura 3. Tipos de curva caudal-altura, Tomado de Bermúdez (2010) y Adaptado de De Paco
(1993). ................................................................................................................................................. 9
Figura 4. Secuencia del diseño hidráulico de un sistema de RLAF. Adaptado de Pizarro (1996). .... 19
Figura 5. Esquema de cálculo de los caudales en un lateral de riego. Tomado de Bermúdez (2011).
Adoptado de Saldarriaga (2007). ...................................................................................................... 21
Figura 6. Esquema de un submódulo de riego. Tomado de Saldarriaga (2007). .............................. 22
Figura 7. Etapas de la metodología SOGH. Tomando de Saldarriaga y Ochoa (2009). ..................... 31
Figura 8. Diagrama de flujo de la metodología SOGH ajustada propuesta por Bermúdez (2011). .. 37
Figura 9. Mapa de un submódulo de RLAF en el programa REDES con altura piezométrica en los
nudos de acuerdo a una escala de colores. ...................................................................................... 39
Figura 10. LGH objetivo, basada en tres puntos conocidos. ............................................................. 42
Figura 11. Red Asimétrica 1. Modelo de REDES. ............................................................................... 46
Figura 12. Red Simétrica. Modelo de REDES. .................................................................................... 47
Figura 13. Red Asimétrica 2. Modelo de REDES. ............................................................................... 47
Figura 14. Curva Costo vs. Diámetro de tubería. .............................................................................. 48
Figura 15. Curva exponente del emisor vs. Coeficiente, para un caudal de 120 l/h. ........................ 49
Figura 16. Rutas posibles para la Red Asimétrica 1. .......................................................................... 55
Figura 17. Red abierta de ejemplo para establecer la formulación matemática del problema de
optimización lineal. ........................................................................................................................... 80
Figura 18. Pérdidas de altura piezométrica que se presentarían en la red ejemplo si se utiliza el
Diámetro d
1
en cada tubería, unidades de presión en metros de columna de agua. ...................... 81
Figura 19. Pérdidas de altura piezométrica que se presentarían en la red ejemplo si se utiliza el
Diámetro d
2
en cada tubería, unidades de presión en metros de columna de agua. ...................... 81
Figura 20. Pérdidas de altura piezométrica que se presentarían en la red ejemplo si se utiliza el
Diámetro d
3
en cada tubería, unidades de presión en metros de columna de agua. ...................... 81
Figura 21. Submódulo Asimétrico 2. ................................................................................................. 86
Figura 22. Superficie de gradiente hidráulico definida a partir de metodología SOGH, Submódulo
Asimétrico 2. ..................................................................................................................................... 88
Figura 23A. Diagrama de flujo, metodología para el diseño de submódulos de riego usando
programación lineal en conjunto con SOGH. Parte A. ...................................................................... 98
Figura 24. Caso de Estudio 1, Submódulo Asimétrico 2 Plano. ....................................................... 101
Figura 25. Caso de estudio 3, Submódulo Simétrico Plano. ............................................................ 105
Figura 26. Caso de Estudio 3, Submódulo Asimétrico 2 con Topografía Variable. ......................... 106

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
iv
Figura 27. Caso de Estudio 3, Submódulo Asimétrico 3 con Topografía Variable, vista en planta. 111
Figura 28. Caso de Estudio 4, Submódulo Asimétrico 3 con Topografía Variable, vista en perfil. . 111
Figura 29. Caso de Estudio 5, Submódulo con Emisores Autocompensantes, vista en planta. ...... 115
Figura 30. Hoja “INICIO”. Programa para el cálculo de PES y la generación de matrices de Xpress.
......................................................................................................................................................... 124
Figura 31. Red ejemplo para mostrar uso de programa. ................................................................ 127
Figura 32. Vista general de la hoja “Matriz” para la generación del archivo con las matrices de
entrada a Xpress. ............................................................................................................................. 128
Figura 33. Ventana para seleccionar el archivo de EPANET que se desea importar, Red Ejemplo. 129
Figura 34. Generación del rótulo de las matrices de costos y pérdidas totales, Red Ejemplo. ...... 130
Figura 35. Ventana para ingresar el valor del coeficiente de la curva de costos, Red Ejemplo. ..... 130
Figura 36. Ventana para ingresar el valor del exponente de la curva de costos, Red Ejemplo. ..... 130
Figura 37. Matriz de Costos, Red Ejemplo. ..................................................................................... 131
Figura 38. Matriz de pérdidas totales, Red Ejemplo. ...................................................................... 133
Figura 39. Ventana para ingresar la presión mínima deseada, Red Ejemplo.................................. 134
Figura 40. Ventana para guardar el archivo *.DAT de entrada a Xpress. ....................................... 135
Figura 41. Interfaz Xpress. ............................................................................................................... 136
Figura 42A. Código de formulación lineal, problema de diseño de tuberías. ................................. 136
Figura 43. Resultados del diseño generado por Xpress, Red Ejemplo. ........................................... 138

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
v
ÍNDICE DE GRÁFICAS
Gráfica 2-1. Coeficiente de uniformidad resultante vs. Presión de entrada al submódulo. Tomado
de Bermúdez (2011). ......................................................................................................................... 32
Gráfica 2-2. Costo total de la red vs. Presión a la entrada del submódulo. Tomado de Bermúdez
(2011). ............................................................................................................................................... 33
Gráfica 3-1. LGH objetivo vs. Distancia topológica, para diferentes flechas de diseño. ................... 43
Gráfica 3-2. Costos vs. Flecha, Red Asimétrica 1. Emisores con exponente 0.3. .............................. 54
Gráfica 3-3. Presión en los nudos correspondientes a la ruta crítica (Ruta 8), Flecha 0. .................. 56
Gráfica 3-4. Presión en los nudos correspondientes a la Ruta 7, Flecha 0. ...................................... 56
Gráfica 3-5. Presión en los nudos correspondientes a la Ruta 6, Flecha 0. ...................................... 57
Gráfica 3-6. Presión en los nudos correspondientes a la Ruta 5, Flecha 0. ...................................... 57
Gráfica 3-7. Presión en los nudos correspondientes a la Ruta 4, Flecha 0. ...................................... 57
Gráfica 3-8. Presión en los nudos correspondientes a la Ruta 3, Flecha 0. ...................................... 58
Gráfica 3-9. Presión en los nudos correspondientes a la Ruta 2, Flecha 0. ...................................... 58
Gráfica 3-10. Presión en los nudos correspondientes a la Ruta 1, Flecha 0. .................................... 58
Gráfica 3-11. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la
tubería, Tubería múltiple, Flecha 0. .................................................................................................. 59
Gráfica 3-12. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la
tubería, Lateral ruta 8 (crítica), Flecha 0. .......................................................................................... 60
Gráfica 3-13. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la
tubería, Lateral ruta 7, Flecha 0. ....................................................................................................... 60
Gráfica 3-14. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la
tubería, Lateral ruta 6, Flecha 0. ....................................................................................................... 60
Gráfica 3-15. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la
tubería, Lateral ruta 5, Flecha 0. ....................................................................................................... 61
Gráfica 3-16. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la
tubería, Lateral ruta 4, Flecha 0. ....................................................................................................... 61
Gráfica 3-17. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la
tubería, Lateral ruta 3, Flecha 0. ....................................................................................................... 61
Gráfica 3-18. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la
tubería, Lateral ruta 2, Flecha 0. ....................................................................................................... 62
Gráfica 3-19. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la
tubería, Lateral ruta 1, Flecha 0. ....................................................................................................... 62
Gráfica 3-20. Costos vs. Flecha, Red Asimétrica 1. Emisores con exponente 0.5. ............................ 64
Gráfica 3-21. Costos vs. Flecha, Red Asimétrica 1. Emisores con exponente 1.0. ............................ 64
Gráfica 3-22. Línea de presiones para diferentes flechas, Flecha 0, 0.14, 0.25. ............................... 65

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
vi
Gráfica 3-23. Pendiente de fricción vs distancia topológica, Red Asimétrica 1, exponente del emisor
0.3. ..................................................................................................................................................... 67
Gráfica 3-24. Flecha vs. Coeficiente de uniformidad resultante. Red Asimétrica 1, exponente del
emisor 0.3. ......................................................................................................................................... 68
Gráfica 3-25. Flecha vs. Coeficiente de uniformidad resultante. Red Asimétrica 1, exponente del
emisor 0.5. ......................................................................................................................................... 68
Gráfica 3-26. Flecha vs. Coeficiente de uniformidad resultante. Red Asimétrica 1, exponente del
emisor 1.0. ......................................................................................................................................... 69
Gráfica 3-27. Costos vs. Flecha, Red Simétrica. Emisores con exponente 0.3. ................................. 70
Gráfica 3-28. Costos vs. Flecha, Red Simétrica. Emisores con exponente 0.5. ................................. 70
Gráfica 3-29. Costos vs. Flecha, Red Simétrica. Emisores con exponente 1.0. ................................. 71
Gráfica 3-30. Costos vs. Flecha, Red Asimétrica 2. Emisores con exponente 0.3 ............................. 72
Gráfica 3-31. Costos vs. Flecha, Red Asimétrica 2. Emisores con exponente 0.5. ............................ 72
Gráfica 3-32. Costos vs. Flecha, Red Asimétrica 2. Emisores con exponente 1.0. ............................ 73
Gráfica 3-33. Curva PES vs. Coeficiente de uniformidad resultante, Red Asimétrica 1, exponente
0.3. ..................................................................................................................................................... 76
Gráfica 3-34. Curva Costo-Flecha, Red Asimétrica 1, exponente del emisor 0.3. Metodología de
Bermúdez. ......................................................................................................................................... 77
Gráfica 3-35. Coeficiente de Uniformidad resultante vs. Flecha, Red Asimétrica 1, exponente del
emisor 0.3. Metodología de Bermúdez. ............................................................................................ 77
Gráfica 3-36. Curva Coeficiente de Uniformidad vs. PES, Submódulo Asimétrico 2. ........................ 87
Gráfica 3-37. Relación Costo-Flecha obtenida mediante la metodología SOGH para el diseño del
Submódulo Asimétrico 2, variando el valor de la flecha y utilizando 4 criterios de redondeo de
diámetros. ......................................................................................................................................... 90
Gráfica 3-38. Costo del diseño del Submódulo Asimétrico 2 partiendo de diferentes flechas
iniciales, usando programación lineal. .............................................................................................. 91
Gráfica 3-39. Coeficientes de uniformidad resultantes, variando flecha de inicio, Submódulo
Asimétrico 2. ..................................................................................................................................... 92
Gráfica 3-40. Presiones mínimas resultantes, variando flecha de inicio, Submódulo Asimétrico 2. 92
Gráfica 3-41. Número de nudos por debajo de la presión mínima resultantes, variando flecha de
inicio, Submódulo Asimétrico 2. ....................................................................................................... 93
Gráfica 3-42. Curva Costo vs. Diámetro de tubería. ........................................................................ 100
Gráfica 3-43. Curva CU vs PES. Caso de estudio 1, Submódulo Asimétrico 2 Plano. ...................... 102
Gráfica 3-44. Comparación de la relación Costo-Flecha usando SOGH y utilizando 4 criterios de
redondeo, con el costo del diseño obtenido mediante la metodología propuesta. Submódulo
Asimétrico 2 Plano. ......................................................................................................................... 104

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
vii
Gráfica 3-45. Comparación de la relación Costo-Flecha usando SOGH y utilizando 4 criterios de
redondeo, con el costo del diseño obtenido mediante la metodología propuesta. Submódulo
Simétrico Plano. .............................................................................................................................. 105
Gráfica 3-46. Curva CU vs PES. Submódulo Asimétrico 2 con Topografía. ..................................... 107
Gráfica 3-47. Comparación de la relación Costo-Flecha usando SOGH y utilizando 4 criterios de
redondeo, con el costo del diseño obtenido mediante la metodología propuesta. Submódulo
Asimétrico 2 con Topografía Variable. ............................................................................................ 110
Gráfica 3-48. Curva CU vs PES. Caso de estudio 3, Submódulo Asimétrico 3 con Topografía Variable.
......................................................................................................................................................... 112
Gráfica 3-49. Comparación de la relación Costo-Flecha usando SOGH y utilizando 4 criterios de
redondeo, con el costo del diseño obtenido mediante la metodología propuesta. Submódulo
Asimétrico 3 con Topografía Variable. ............................................................................................ 114
Gráfica 3-50. Comparación de la relación Costo-Flecha usando SOGH y utilizando 4 criterios de
redondeo, con el costo del diseño obtenido mediante programación lineal. , Submódulo con
Emisores Autocompensantes. ......................................................................................................... 116
Gráfica 3-51. Comparación de la relación Costo-Flecha usando SOGH y utilizando 4 criterios de
redondeo, con el costo del diseño obtenido mediante programación lineal. Caso de estudio 5
usando la curva de costos C
2
. .......................................................................................................... 117
Gráfica 3-52. Comparación de la relación Costo-Flecha usando SOGH y utilizando 4 criterios de
redondeo, con el costo del diseño obtenido mediante programación lineal. Caso de estudio 5
usando la curva de costos C
3
. .......................................................................................................... 118
Gráfica 7-1. Curva CU vs PES, Hoja “Cálculo PES”. .......................................................................... 126

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
1
1. INTRODUCCIÓN Y OBJETIVOS
1.1. Introducción.
En 1992 la Conferencia Internacional sobre el Agua y Medio Ambiente (CIAMA), en Dublín
estableció como Principio N
úmero 1 que “el agua dulce es un recurso finito y vulnerable, esencial
para sostener la vida, el desarrollo y el medio ambiente”. Lo que esto implica es que el agua es
indispensable para la vida y por lo tanto se requiere de una gestión eficaz de los recursos hídricos
(CIAMA, 1992). A partir de éste principio fundamental del agua se deriva un segundo principio, el
cual establece que “el aprovechamiento y la gestión del agua debe inspirarse en un planteamiento
basado en la participación de los usuarios, los planificadores y los responsables de las decisiones
a todos los niveles”. De éste último principio, vale la pena resaltar la referencia a la participación
de los planificadores dentro del uso eficaz y sostenible del agua. Dentro del grupo de
planificadores se encuentran una serie de entidades (e.g. Departamento Nacional de Planeación,
Empresas Prestadoras de Servicio de agua potable, Gobernaciones, Ministerios) que tienen como
función armonizar una serie de variables de tal manera que se maximice el beneficio
socioeconómico. Dentro de las variables que intervienen en la toma de decisiones están los
diseños de obras civiles. Teniendo en cuenta los principios de la Conferencia de Dublín, la
relevancia de los diseños de obras civiles y la necesidad de optimizar el uso del agua de riego,
éste trabajo busca la manera de realizar diseños de sistemas de Riego Localizado a Alta
Frecuencia (RLAF) con el fin de alcanzar un aprovechamiento máximo de los recursos hídricos y
económicos, y que a su vez permitan una adecuada producción agropecuaria.
Según estudios realizados por la Organización Económica para la Cooperación y el Desarrollo
(OECD) en el año 2006, el 70% del agua extraída de fuentes naturales es usada para la irrigación
de zonas agrícolas. Éste valor representa una importante cantidad de agua si se tiene en cuenta
que el volumen de agua dulce consumida, en total, es de 2500 km³ anuales. Adicional a esto, la
cantidad de agua que es extraída y consumida ha venido creciendo. En 1990, la cantidad de agua
extraída de las fuentes hídricas para uso agrícola en el mundo era apenas de 500 km³ anuales. Se
estima que para el año 2025 esta misma variable crezca a 3200 km³ anuales (OECD, 2006).
Como bien muestran los datos del estudio de la OECD, el consumo anual para agricultura es muy
importante; por esta razón, es necesario lograr que éste proceso sea eficiente. En varias partes
del mundo, como por ejemplo en India y algunos países de Latinoamérica, la irrigación de cultivos
se realizaba tradicionalmente por inundación del área de cultivo. Esta manera de regar los
cultivos, según el mismo estudio de la OECD, presenta apenas un 40% de eficiencia, lo cual no
sólo se traduce en un desperdicio del recurso, sino que además, saliniza el suelo e implica
problemas de exudación en acuíferos. Por esta razón aparece (en la segunda mitad del siglo XX)
el riego por medio de tuberías a presión. Lo que se busca con éste tipo de sistemas de
abastecimiento de agua para plantas, es que a través de emisores (orificios en tuberías que
emiten un caudal en función de la presión) se lleve a cada planta la cantidad exacta de agua que
necesita para lograr su desarrollo eficiente.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
2
Con la introducción del abastecimiento de áreas agropecuarias, por medio de tuberías a presión,
aparece el concepto de sistemas de Riego Localizado a Alta Frecuencia. Tal como su nombre lo
indica, éste tipo de sistemas se basan en dos hechos fundamentales, la localización y la
frecuencia. La localización obedece al hecho que sólo se humedece parte del volumen del suelo
del cultivo en la zona de las raíces de la planta; por otro lado, la frecuencia hace referencia a la
necesidad continua de agua por parte de la planta (Goldemberg, 1976). Este tipo de sistemas
fueron desarrollados inicialmente en los países netamente agrícolas, pioneros en la realización de
grandes proyectos. De estos sistemas es importante decir que deben ser diseñados para
optimizar la utilización del recurso agua, teniendo en cuenta que día a día éste es un recurso más
escaso (Saldarriaga, 2009).
Partiendo del crecimiento en la extracción del agua y el crecimiento en la cantidad de áreas
cultivadas, resulta importante buscar una manera de realizar los diseños de RLAF lo más
económicos posibles. En el caso de Colombia, según estudios del Departamento Nacional de
Planeación, en 1999 existían en Colombia 3’759,174 hectáreas de cultivos; años después, en el
2008, éste número se había incrementado en 152,594 hectáreas. Estos valores implican una alta
inversión en rehabilitación de redes existentes y en inversión para construcción de nuevos
sistemas de riego; además, si se tiene presente que los sistemas de abastecimiento de agua
presentan una vida útil de alrededor de 30 años, será necesario hacer inversiones de renovación
de redes de riego existentes. En un informe presentado por Manuel Ramírez (Asesor de la Unidad
de Desarrollo Agraria, 1998), se estima que en Colombia, de acuerdo con los recursos asignados
en el Presupuesto General de la Nación para proyectos que se van a ejecutar y sobre los cuales
existe certeza de construcción, la parte que financia el Estado por hectárea oscila alrededor de los
6,500 dólares. Para optimizar éste presupuesto y hacer un mejor uso de los recursos públicos, se
debe procurar concebir sistemas de Riego Localizado a Alta Frecuencia que sean económicos.
Actualmente, el diseño de los sistemas de Riego Localizado a Alta Frecuencia se hace mediante
las metodologías clásicas basadas en la comprobación de diseño. Esto último quiere decir que se
prueban diferentes diámetros de tuberías para cada uno de los tubos que conforman el sistema y
se escoge alguna de las múltiples soluciones que cumplen con los requisitos hidráulicos
(Saldarriaga, 2007). Algunos ejemplos de estas maneras de diseño se pueden encontrar en los
trabajos de Goldemberg (1976), Rodríguez (1982) y Pizarro (1987). Muchas veces la escogencia
del conjunto de diámetros de las tuberías se basa en la experiencia del diseñador, y por lo tanto
no existe ningú
n proceso exhaustivo como heurísticas de “Colonia de Hormigas” (Ostfled &
Tubaltzev, 2008) o metodologías de diseño basadas en la hidráulica (Ochoa & Saldarriaga, 2009)
que permitan llegar a un diseño óptimo. Éste trabajo compara los resultados obtenidos al diseñar
submódulos de riego haciendo uso de la metodología de Superficie Óptima de Gradiente
Hidráulico (SOGH) (Ochoa & Saldarriaga, 2009) y una metodología planteada con base en
optimización lineal. Los resultados finales muestran que la metodología planteada, que hace uso
de los conceptos de optimización lineal, SOGH y el programa Xpress presentan diseños más
económicos que la metodología SOGH planteada originalmente por Ochoa y cumplen con todas
las restricciones hidráulicas y agronómicas. Adicionalmente, al final de este documento se
presentan algunas recomendaciones para seguir estudiando metodologías basadas en
optimización lineal en diferentes problemas de hidráulica.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
3
1.2. Objetivo General.
Desarrollar una metodología para realizar diseños óptimos de submódulos de sistemas de riego
localizado de alta frecuencia.
1.3. Objetivos Específicos.
Los objetivos específicos planteados, que permitirán lograr el objetivo general, consisten en el
análisis de metodologías actuales para el diseño de redes de distribución, su aplicación en el
diseño de submódulos de riego y a partir de esto formular una metodología para la optimización
del diseño de estos sistemas. Adicionalmente, los objetivos específicos consisten en el desarrollo
de toda herramienta informática y análisis comparativos que permitan plantear, generar y evaluar
una metodología nueva para el diseño de submódulos de riego.
Generar la formulación matemática del problema de diseño de redes abiertas, usando
conceptos de optimización lineal e implementando su formulación en el programa Xpress
para realizar de forma eficiente el diseño de submódulos de riego localizado de alta
frecuencia.
Realizar comparaciones entre los resultados de la metodología propuesta y la metodología
SOGH planteada por Ochoa, para evaluar el desempeño del nuevo algoritmo de diseño
que se propone.
Realizar análisis de sensibilidad del desempeño de la metodología planteada respecto a
cambios en diferentes variables de entrada al problema de diseño. Adicional a esto, se
realizará la evaluación de la metodología planteada en diferentes casos de estudio con
características topográficas, agronómicas y topológicas diferentes.
Desarrollar un programa informático que permita facilitar al usuario el proceso de diseño
mediante la metodología propuesta, presentando su correspondiente manual de usuario y
haciendo de este una herramienta fácil para el diseñador..
Analizar la metodología para el diseño hidráulico de submódulos de sistemas de RLAF,
definida como “Superficie Óptima de Gradiente Hidráulico Ajustada” (SOGH Ajustada),
propuesta por Bermúdez (2011), con el fin de aplicar sus conceptos en la nueva
metodología propuesta.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
4
Desarrollar un programa informático para realizar de forma automática el procedimiento
propuesto por Bermúdez (2011) para el cálculo de la presión de entrada al submódulo de
riego, que permita realizar el diseño del submódulo por medio de la nueva metodología
que se propone.
Presentar un análisis de los costos resultantes de los diferentes casos de estudio, y el
efecto de las diferentes flechas utilizadas para establecer la superficie de gradiente
hidráulico de diseño.
Establecer los límites de las flechas que pueden utilizarse para el diseño de sistemas de
tuberías, realizando un análisis matemático de la ecuación establecida por Ochoa que
permita determinar las restricciones de la metodología SOGH al diseño de tuberías.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
5
2. MARCO TEÓRICO
2.1. Características de un sistema de riego localizado de alta
frecuencia.
Un sistema de riego localizado de alta frecuencia (RLAF) se caracteriza, tal como su nombre lo
indica, por la localización óptima del riego y la utilización de alta frecuencia. La localización hace
referencia al hecho de que solo se humedece la parte del volumen del suelo donde se encuentra
ubicada la raíz de las plantas, de tal manera que los cultivos obtengan el agua y los nutrientes
necesarios para su correcto desarrollo, evitando el riego de áreas que no lo requieren. Por su
parte, la frecuencia implica que el suelo se mantiene húmedo una mayor cantidad de tiempo en
comparación a un riego convencional. Estas dos características se encuentran relacionadas porque
la localización del riego obliga a que sea necesario aplicarlo con mayor frecuencia. Esta necesidad
obedece a que el volumen del suelo humedecido es reducido y, por lo tanto, se tiene una baja
capacidad de almacenamiento, siendo preciso aplicar con frecuencia pequeñas dosis de agua y
nutrientes (Saldarriaga, 2007).
El objetivo primordial del diseño de una RLAF es lograr una alta eficiencia, entendiendo por ésta,
que el área humedecida por el sistema de riego se limite únicamente a la zona radicular. Esto se
hace con el objetivo de conseguir un ahorro importante de agua y entregar a la planta únicamente
la cantidad que ésta necesita para su correcto desarrollo. Adicional al objetivo de no desperdiciar
agua se requiere que cada uno de los cultivos reciba como mínimo, un caudal superior al que
establece el diseño agronómico.
Para poder realizar el diseño de los sistemas de RLAF es necesario tener en cuenta que estos
presentan un esquema diferente al conocido para las redes de distribución de agua potable. Un
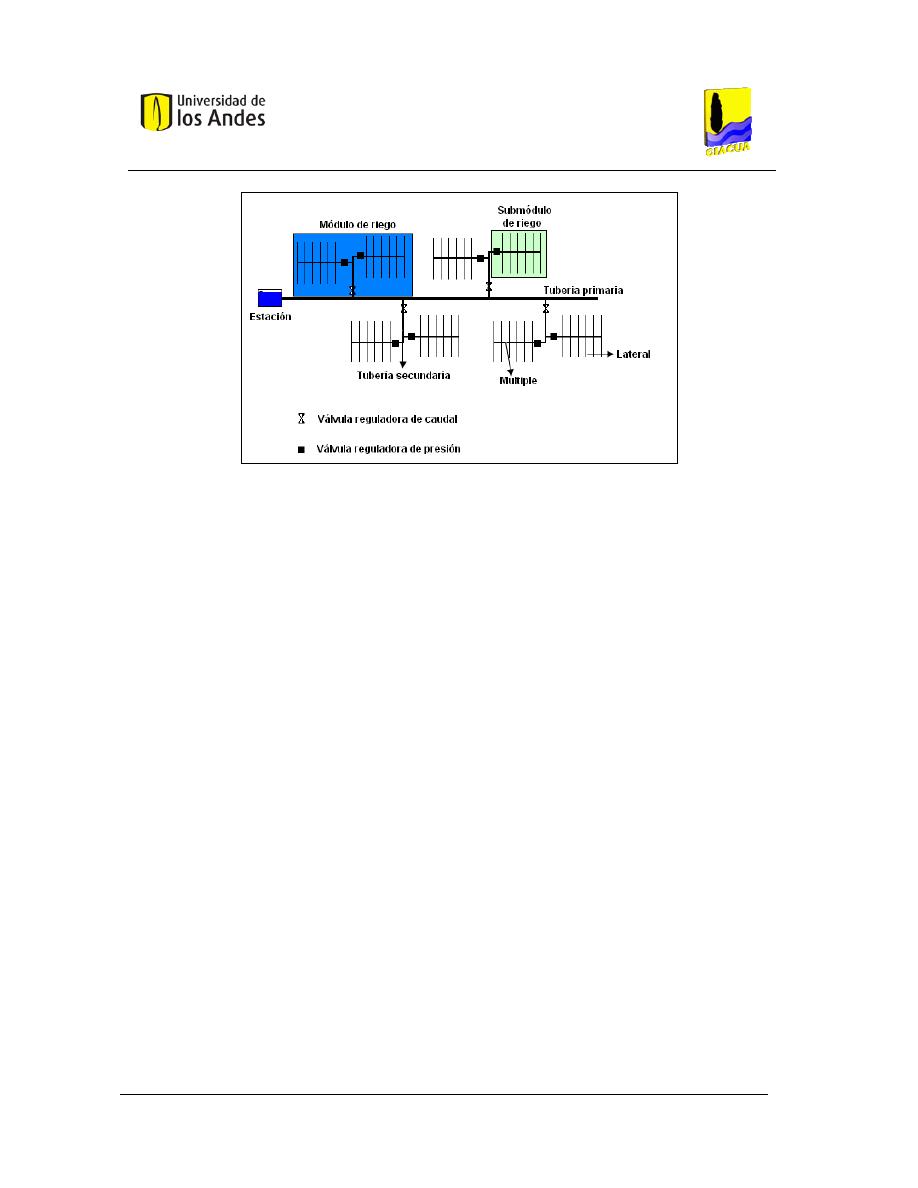
esquema común se presenta en la Figura 1.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
6
Figura 1. Esquema común de un sistema de riego, Adaptado de (Saldarriaga, 2007).
En la Figura 1 se observan los componentes de un sistema de RLAF típico. De acuerdo con
Saldarriaga (2007), cada uno de los componentes se define de la forma que se presenta a
continuación:
Estación de riego: conjunto de elementos que permiten el bombeo, tratamiento, filtrado y control
de la presión del agua de riego. En algunos casos permite también la fertilización y la medición
integral de los caudales que se envían hacia el cultivo.
Tubería primaria: Tubería que parte de la estación y llega a todos los módulos de riego del cultivo.
Tubería secundaria: Tubería que parte del tubo principal y lleva el caudal a uno solo de los
módulos de riego.
Tubería múltiple: Tubería que alimenta directamente los laterales de riego.
Laterales de riego: Tuberías de último orden en donde se conectan los emisores que suministrarán
agua a las plantas.
Regulador de presión: Por lo general, este elemento se encuentra ubicado al inicio de cada tubería
terciaria. El objetivo del regulador de presión es controlar la presión de entrada a los submódulos
de riego.
Regulador de caudal: Elemento que controla la cantidad de agua que entra en una tubería
secundaria y por lo tanto a un módulo de riego.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
7
Además de la diferencia esquemática que existe entre un sistema de riego localizado de alta
frecuencia y una red de distribución de agua potable, se presenta una diferencia importante en la
hidráulica de los nudos de consumo. Ésta última es tal vez una de las características hidráulicas
más importante de un sistema RLAF, y es que los nudos de consumo funcionan con emisores. A
diferencia de una red de distribución de agua potable donde la demanda es constante e
independiente de la presión, en un sistema de riego el caudal que recibe cada uno de los emisores
se verá afectado por la presión en el punto de llegada al emisor.
Como se mencionó en el párrafo anterior, los emisores representan los nudos de consumo de
agua en un sistema de riego localizado de alta frecuencia. Por esta razón es necesario entender
adecuadamente su comportamiento para comprender la hidráulica de los submódulos de riego. En
la siguiente sección se presenta una descripción detallada de las características de los emisores.
2.1.1. Emisores.
De acuerdo con Pizarro (1996), los emisores son la parte más delicada de un RLAF, debido a que
son los encargados de suministrar el caudal y los nutrientes necesarios para el adecuado
desarrollo de cada planta. El problema principal en el diseño con emisores, es la contradicción
presente en los criterios que deben tener en cuenta los fabricantes. Los tres criterios que se deben
tener en cuenta son bajo caudal, alta presión y diámetros de entrega máximos. El primer criterio
hace referencia a que los emisores deben proporcionar un bajo caudal, con el objetivo de que los
diámetros de las tuberías (laterales y múltiples) sean bajos. Por su parte, una alta presión en los
emisores, es deseable para minimizar el efecto de los desniveles del terreno y las pérdidas de
energía sobre la uniformidad del riego. Finalmente, el tercer criterio es que el diámetro de entrega
de los emisores sea lo más grande posible, con el fin de evitar posibles obstrucciones del emisor,
que son el principal problema en el manejo de los sistemas RLAF.
De acuerdo con el caudal que se requiera por planta y la presión normal de trabajo, los emisores
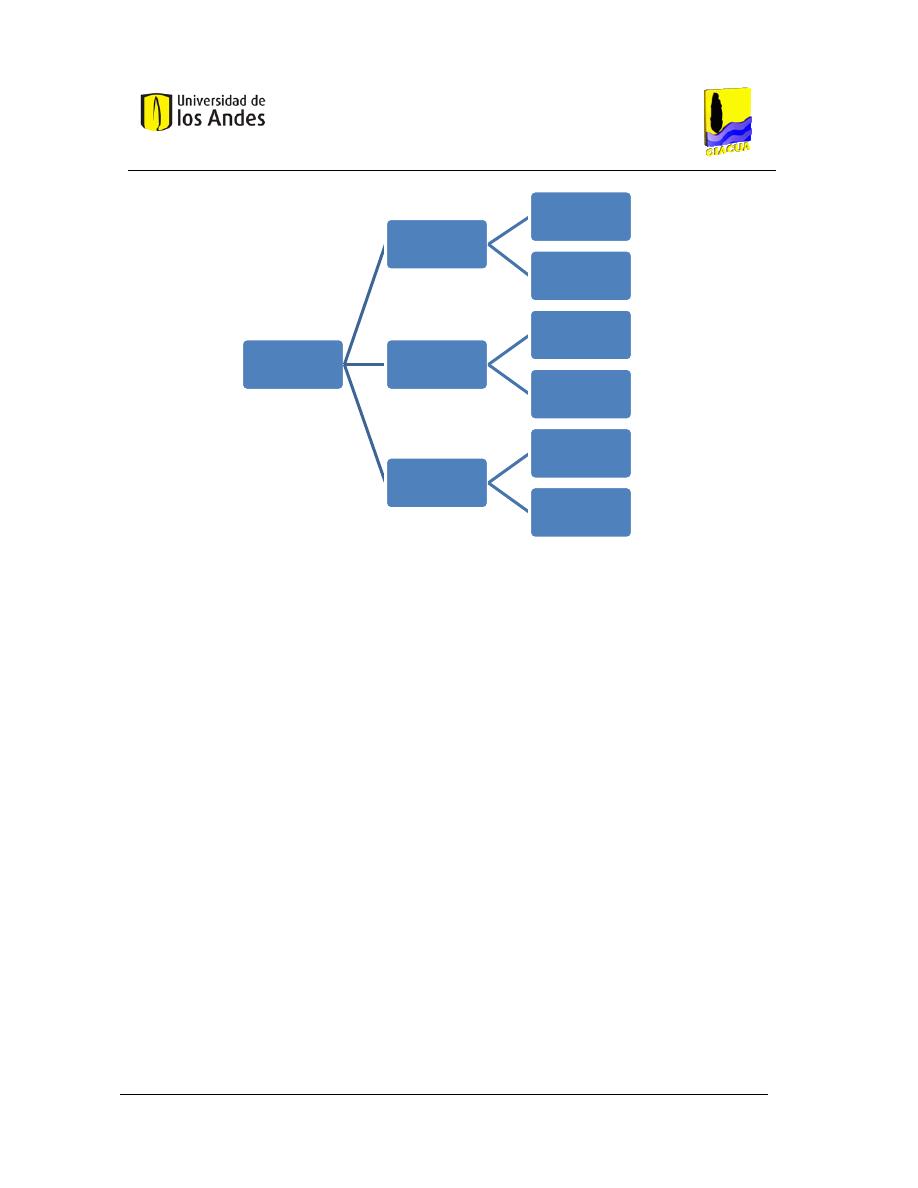
se pueden caracterizar en tres grandes grupos. Estos grupos son, emisores de alto caudal,
emisores de bajo caudal y cintas de exudación. Las características de cada uno de estos grupos se
presentan en la siguiente figura.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
8
Figura 2. Clasificación de emisores en sistemas de RLAF, Adaptado de (Saldarriaga, 2007).
Esta caracterización es una muestra inicial de los tipos de emisores que existen. Para poder
clasificarlos con un mayor detalle, es necesario entender las ecuaciones y conceptos hidráulicos
que permiten modelar y determinar sus características cuando están presentes en un sistema de
riego.
2.1.1.1.
Hidráulica de Emisores.
Para describir el funcionamiento de un emisor presente en un sistema de riego, es necesario
empezar diciendo que el caudal resultante es función de la presión observada en el punto de
ubicación del emisor. La relación que describe el comportamiento de un emisor es la que se
presenta a continuación:
Ecuación 2.1
donde Q hace referencia al caudal del emisor y h a la presión en el mismo. Por su parte, k y x
corresponden al coeficiente y el exponente de descarga del emisor respectivamente. Es
importante decir que la ecuación no es dimensionalmente homogénea, por lo que k y x dependen
del sistema de unidades utilizado. De estos dos parámetros resulta muy importante el exponente
x, que mide la sensibilidad del emisor con respecto a la altura de presión.
Tanto k como x pueden variar de acuerdo con el tipo de emisor. Pero resulta muy importante
hacer énfasis en el exponente del emisor, dado que este determinará la forma de la curva que
Emisores en
sistemas RLAF
Alto caudal
Presión nominal
20 mca
Caudal nominal,
16 - 150 l/h
Bajo Caudal
Presión nominal
10 mca
Caudal nominal,
2 - 16 l/h
Cintas de
exudación
Presión nominal
1 - 3 mca
Caudal nominal,
0.5 - 3 l/h
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
9
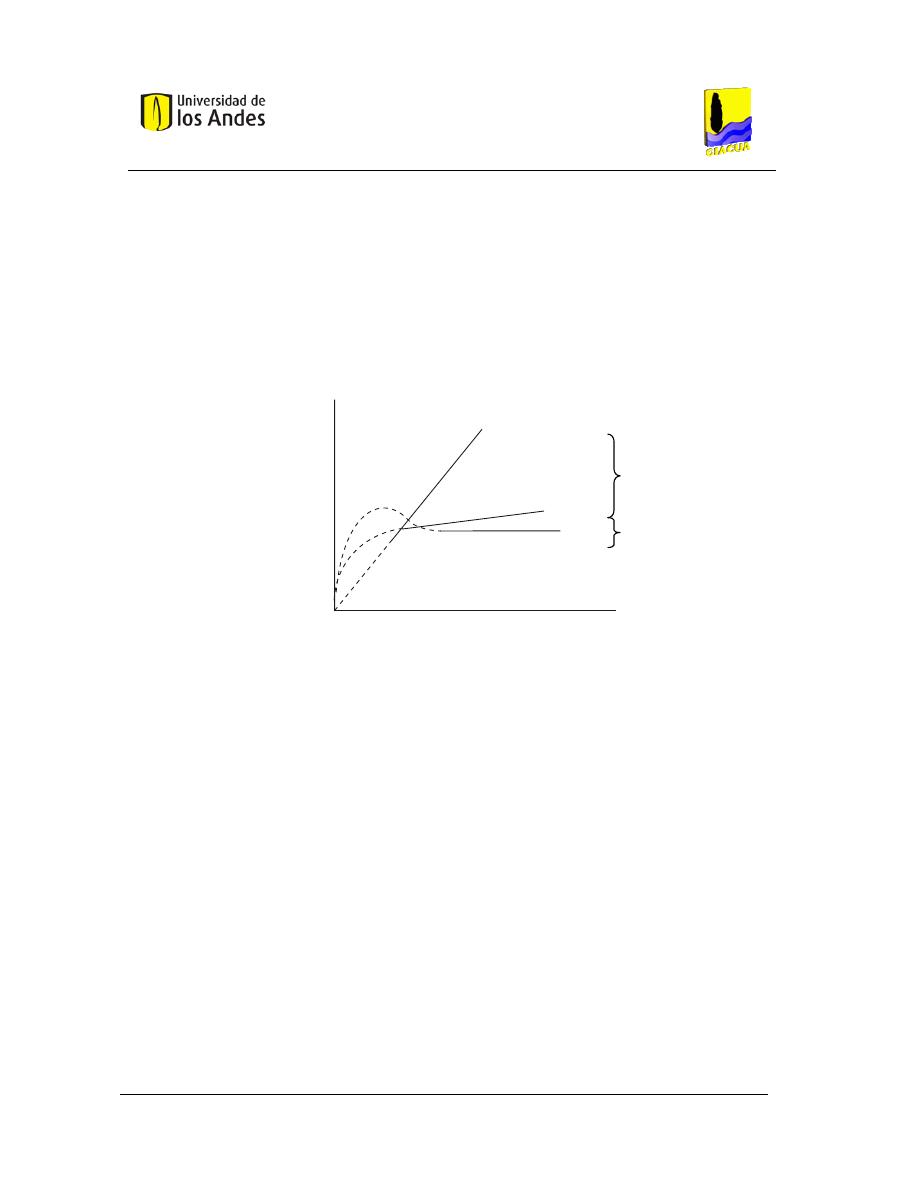
relaciona el caudal del emisor con la altura de presión y permite establecer si se presenta un flujo
laminar o turbulento. Este comportamiento se puede apreciar gráficamente en la Figura 3, que
presenta un esquema de varios tipos de curvas correspondientes a la ecuación que relaciona
caudal-altura. En la figura se observa el caso en que el exponente del emisor (x), es igual a 1 y se
presenta un flujo laminar; también se presenta el caso en que x=0.5 y existe plena turbulencia,
representado en la zona 1 de regímenes hidráulicos. Finalmente se presenta el caso teórico en que
el exponente del emisor es cero (zona 2) y el emisor se comporta como un emisor
autocompensante o con limitaciones de caudal.
Figura 3. Tipos de curva caudal-altura, Tomado de Bermúdez (2010) y Adaptado de De Paco (1993).
Es importante tener en cuenta que la ecuación del emisor final es válida, solo a partir de cierto
rango de presiones, que este rango no es suministrado por los fabricantes de emisores y que debe
ser determinado de forma empírica por el diseñador del sistema de riego.
Ahora bien, una vez se han identificado las posibles curvas caudal-altura que pueden existir en los
emisores finales de un sistema de riego, se debe entender por qué no es recomendado que exista
un flujo laminar en los emisores finales y se requiere asegurar la turbulencia en los ductos de estos
accesorios. De acuerdo con Pizarro (1996), el régimen laminar en los emisores, es inconveniente
porque:
En régimen laminar las pérdidas de energía a lo largo de una conducción dependen de la
viscosidad y por lo tanto de la temperatura. De esta manera, para una misma presión, los
emisores en donde el agua se encuentre a una mayor temperatura tendrán un mayor
caudal. Este problema resulta importante si se tiene en cuenta que los materiales de estos
sistemas están conformados de aditivos que según mediciones, hacen que la temperatura
a lo largo de un lateral llegue a variar hasta 20°C (Saldarriaga, 2007). Este fenómeno puede
a veces compensar las pérdidas de energía a lo largo del lateral, pero su comprensión a la
h ( )
m
Q (l/h)
Laminar
= 1.0
x
Turbulento
= 0.5
x
x = 0.0
Zona 1
Zona 2

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
10
hora de diseñar un sistema de riego resulta difícil y además se recomienda considerarlo
como un factor de pérdida de uniformidad del riego.
La relación entre el caudal que sale del emisor y la presión en el punto, es una relación
lineal para flujo laminar. Esta relación implica una mayor dependencia por parte del caudal
y puede llevar a una menor uniformidad en el riego.
Finalmente, en flujo laminar, el riesgo de sedimentación puede ser alto. Esto se debe a
que en este tipo de flujos se requiere que el área de salida de los emisores sea mayor y a
su vez conlleve a una menor velocidad en los conductos.
Una vez definidas las causas por las cuales no es recomendable un flujo laminar en los emisores
finales, vale anotar que en principio el valor del exponente de los emisores estaría comprendido
entre 0.5 y 1; sin embargo, debido a la existencia actualmente de emisores autocompensantes, el
valor de x puede ser incluso inferior a 0.5. Lo que interesa en el diseño es que los emisores tengan
un exponente de descarga bajo, esto con el objetivo de que una variación en la presión no
conlleve a cambios importantes en el caudal de los emisores y mantener la uniformidad del riego.
De esta manera, y teniendo en cuenta la ecuación de los emisores se puede definir la siguiente
ecuación que, a partir de la tolerancia de caudales y el exponente del emisor, permitirá fijar una
tolerancia de presiones:
Ecuación 2.2
Más adelante se explicará, en más detalle, los conceptos de tolerancia de caudales y tolerancia de
presiones a partir de la definición de uniformidad de riego.
2.1.1.2.
Clasificación y tipos de emisores.
De acuerdo con la investigación desarrollada por Bermúdez (2011), existen una gran variedad de
emisores en el mercado. Este tipo de accesorios pueden clasificarse de diferentes maneras,
atendiendo a sus características hidráulicas, forma de inserción en laterales, riesgo de
obturaciones, etc. A continuación se describen algunos emisores considerados en el trabajo de
Bermúdez (2011), con base en los trabajos de Pizarro (1996) y López (1992).
Goteros: Hacen parte del grupo de emisores de bajo caudal. Los goteros pueden
clasificarse según la configuración de los conductos de paso del agua. Estos pueden ser de
largo conducto, de orificio, vortex y autocompensantes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
11
-
De largo conducto: El flujo dentro del emisor es laminar y en ellos la pérdida de
energía tiene lugar en un largo conducto de pequeño diámetro. A este grupo
pertenecen los emisores helicoidales, microtubos y de laberinto. En la Tabla 1 se
observan las características de cada uno de estos tipos de goteros de largo
conducto:
Tabla 1. Características de goteros de largo conducto, Tomado de Bermúdez (2011).
Emisor
Características
Esquema
Microtubos
Diámetro interior: 2mm – 0.6mm.
Coeficiente de variación: 0.02 – 0.05.
Exponente del emisor: 0.55 – 0.80.
Constante del emisor: 4 – 8.
Helicoidales
[Prácticamente en desuso
por problemas de
obturaciones]
Caudales nominales: 2 – 4 L/h.
Coeficiente de variación: 0.02 – 0.13.
Exponente del emisor: 0.65 – 0.85.
Constante del emisor: 0.4 – 0.8.
De laberinto
Caudales nominales: 2 – 8 L/h.
Coeficiente de variación: <0.05.
Exponente del emisor: 0.5 – 0.6.
-
De orificio: Son emisores que se caracterizan por tener un diámetro inferior a 0.4
mm, un coeficiente de variación entre 0.07 y 0.11 y el exponente del emisor es de
0.5.
-
Vortex: Este tipo de emisores tipo gotero de largo conducto cuenta con una
cámara de vórtice donde se genera una fuerza centrífuga que se opone a la
dirección del flujo y genera pérdidas adicionales de energía. Este tipo de emisor
surgió como un intento de solucionar el problema del diámetro pequeño de los
goteros de orificio (Saldarriaga, 2007).
-
Autocompensante: Como se ha mencionado anteriormente, un emisor
autocompensante tiene el objetivo de lograr que el caudal sea independiente de
la presión. La autorregulación del caudal se consigue mediante una pieza móvil y
flexible de caucho o algún elastómero sintético que se deforma bajo el efecto de
la presión, disminuyendo la sección de paso del agua y limitando así el caudal de
salida.
Mangueras: Al igual que los goteros, este tipo de accesorios hacen parte de los emisores
de bajo caudal. El exponente de descarga x para este tipo de emisores varía entre 0.4 y
0.8, lo cual corresponde a un flujo en régimen turbulento. Sus principales características se
pueden observar en la siguiente tabla.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
12
Tabla 2. Características de emisores tipo manguera, Tomada de Bermúdez (2011).
Emisor
Características
Esquema
Mangueras
Presiones de operación: < 10 mca.
Coeficiente de variación: 0.10 – 0.20.
Exponente del emisor: 0.4 – 0.8.
Cintas de exudación: Hacen parte del grupo de emisores de bajo caudal, y se caracterizan
por su fabricación a partir de un geotextil compuesto de microfibras de polietileno
entrecruzadas que forman una malla en la cual los poros tienen un tamaño medio de 4 a 5
micras y ocupan el 50% de la superficie (Saldarriaga, 2007). Este tipo de emisores no
cumplen con la Ecuación 2.1.
Microaspersores y difusores: A diferencia de los emisores presentados anteriormente,
este tipo de emisores forman parte del grupo de emisores de alto caudal. Al hacer parte
de los emisores de alto caudal, este tipo de accesorios conlleva a tener un diámetro de los
laterales y los múltiples mayor al de los emisores de bajo caudal. La ventaja de los
microaspersores y los difusores es que, a pesar de tener diámetros pequeños, son poco
sensibles a las obturaciones debido a la velocidad del agua. Este tipo de emisores se
pueden clasificar en cuatro grupos, de acuerdo con el exponente de descarga del emisor
(ver Tabla 3 ).
Tabla 3. Características de microaspersores y difusores, tomado de Bermúdez (2011).
Tipo de Emisor
Exponente del Emisor
Esquema
De largo conducto
0.45 – 0.5.
Micro aspersor
De orificio
0.45 – 0.85.
Vortex
0.35 – 0.45.
Autocompensantes
0.0 – 0.25.
Microtubos de alto caudal: como su nombre lo dice, son microtubos que operan como
emisores de alto caudal. No obstante, son poco empleados como emisores de alto caudal
porque presentan los inconvenientes característicos de los emisores de alto caudal

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
13
(grandes diámetros en las tuberías laterales y múltiples) sin tener la ventaja de mojar
grandes superficies.
2.1.2. Uniformidad del riego.
En la sección anterior se presentaron algunas características de los emisores, tales como sus
características hidráulicas (regímenes de flujo y ecuación de los accesorios) y su clasificación. En
esta sección se va a entender una de las características más importantes de un sistema de riego, la
uniformidad del riego. Esta característica esencial de un sistema de riego localizado de alta
frecuencia, va a estar dada por el diseño agronómico e influenciará directamente los resultados
sobre el diseño de las tuberías que componen este tipo de sistemas. De esta manera, el diseñador
debe buscar que el sistema de tuberías sea tal que el diseño sea económico y que todas las plantas
reciban la misma cantidad de agua y nutrientes necesarios para alcanzar su correcto desarrollo y
producción.
Como se mencionó anteriormente, este tipo de sistemas utilizan emisores como nudos de
consumo. El uso de emisores implica que el caudal que recibe cada una de las plantas va a
depender de la presión en el punto de llegada y por esta razón debe entenderse correctamente la
hidráulica. Antes de hacer mención a la hidráulica de este tipo de sistemas es necesario definir el
coeficiente de uniformidad como la variable que dará inicio y afectará todo el proceso de diseño.
Como se dijo anteriormente, la uniformidad del riego es una de las variables más importantes del
diseño de los sistemas RLAF. La uniformidad del riego se caracteriza mediante el coeficiente de
uniformidad (CU) que se define según la Ecuación 2.3:
Ecuación 2.3
donde:
-
CU: Coeficiente de uniformidad del riego; éste es un dato de entrada y es suministrado por
el diseño agronómico
-
n
e
: Número de emisores por planta.
-
Q
mp
: Caudal del emisor sometido a la mínima presión. Este caudal será calculado a partir
de la Ecuación 2.3 y será uno de los datos de entrada para el proceso de diseño.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
14
-
Q
m
: Caudal medio por planta. Este dato es dado por el diseño agronómico y corresponde
al caudal que se espera que cada planta reciba.
-
CV: Coeficiente de variación por fabricación de los emisores finales. Éste se determina
sobre una muestra mínima de 25 emisores y se calcula haciendo uso de las siguientes
ecuaciones:
Ecuación 2.4
donde σ corresponde a la desviación estándar y se calcula como:
Ecuación 2.5
y corresponde al caudal promedio de la muestra de n emisores.
Ecuación 2.6
Como se puede observar el coeficiente de uniformidad (CU) depende tanto de factores
constructivos como de factores hidráulicos. Los factores constructivos se incluyen en el coeficiente
de variación (CV) y tienen en cuenta las diferencias que causan los procesos de fabricación y los
materiales utilizados en los caudales finales. Por su parte, los factores hidráulicos tienen en
cuenta las pérdidas de energía (altura) ocurridas a lo largo de todas las tuberías que conforman el
sistema de riego y la topografía del terreno. Además de los factores hidráulicos y constructivos,
que afectan la uniformidad del riego, existen otros factores como el envejecimiento del sistema,
las obturaciones que ocurran en los emisores y las diferencias de temperatura que se presentan
en los diferentes laterales del sistema. Estos últimos factores no se tienen en cuenta en el proceso
de diseño debido a la alta incertidumbre que existe con relación a estos.
El coeficiente de uniformidad, también puede calcularse aplicando la siguiente ecuación:
Ecuación 2.7
donde Q
25
representa el caudal medio de los emisores que constituyen el 25 % de caudal más bajo,
y Q
m
representa el caudal medio de todos los emisores de la instalación.
Esta última ecuación (Ecuación 2.7), aunque es útil para definir el coeficiente de uniformidad por
parte del diseño agronómico, no resulta útil a la hora de comenzar el proceso de diseño hidráulico
del sistema de RLAF. Para realizar el diseño se hace uso de la Ecuación 2.3 la cual permitirá, como
se muestra a continuación, establecer la tolerancia de caudales y la tolerancia de presiones.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
15
2.1.2.1.
Cálculo de la tolerancia de caudales.
Con el objetivo de cumplir con el coeficiente de uniformidad impuesto por el diseño agronómico,
es necesario que los caudales que emite cada uno de los emisores, no resulten muy diferentes
entre ellos. Para esto es necesario asegurarse que el rango de caudales se encuentre entre un
máximo y un mínimo. Para determinar el caudal de mínima presión que puede presentarse en un
submódulo de riego se parte de la Ecuación 2.3.
Ecuación 2.3
En esta ecuación, se conocen todas las variables a excepción del caudal de mínima presión (Q
mp
).
El Coeficiente de Uniformidad es un dato de entrada, dado por el diseño agronómico. También se
conocen el número de emisores (n
e
) que llegará a cada planta, el coeficiente de variación (CV) y el
caudal medio. De esta manera, despejando la única incógnita se puede establecer la siguiente
ecuación que permite determinar el caudal de mínima presión.
Ecuación 2.8
Una vez obtenido el caudal de mínima presión que se puede presentar en un submódulo de riego,
se establece la tolerancia de caudales como la relación entre el caudal de mínima presión y el
caudal medio.
2.1.2.2.
Cálculo de la tolerancia de presiones.
Para poder cumplir con la tolerancia de caudales, es necesario establecer la presión
correspondiente para que se cumpla con el requerimiento de uniformidad. De esta manera, es
lógico establecer una presión mínima que puede presentarse en un submódulo de riego y la
presión máxima. Para poder determinar la presión mínima, se hace uso de la ecuación del emisor
tal como se muestra a continuación:
Ecuación 2.9
Como se observa en la Ecuación 2.9, para determinar la altura de mínima presión, solo es
necesario conocer el caudal de mínima presión que fue determinado a partid de CU, CV, Q
m
y n
e
;

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
16
además de conocer el coeficiente (k) y el exponente (x) del emisor. Esta misma ecuación puede
utilizarse para determinar la presión correspondiente al caudal medio.
Una vez conocidas la presión media y la presión mínima, se puede determinar la tolerancia de
presiones tal como se observa en la Ecuación 2.10.
Ecuación 2.10
En esta última ecuación hace referencia a la tolerancia de presiones, h
m
a la presión media, h
mp
a la presión mínima y M es un factor empírico que depende del número de diámetros que se
vayan a emplear en una misma tubería, ya sea un múltiple o un lateral. El problema para
determinar M, es que durante esta etapa no se han definido el número de diámetros que tendrá
un lateral, por esta razón para realizar los diseños se recomienda un valor de M=2.5 (Saldarriaga,
2007).
Finalmente, conociendo la tolerancia de presiones, se puede determinar la presión de entrada al
submódulo de riego. Para esto se hace uso de los resultados obtenidos en la Ecuación 2.9 y
Ecuación 2.10 y se determina la presión máxima (presión de entrada) en el submódulo de riego:
Ecuación 2.11
Una vez se han definido las características que componen un sistema de riego localizado de alta
frecuencia, tales como su esquema, la hidráulica de emisores, clasificación de emisores,
uniformidad de riego, tolerancia de caudales y presiones, el siguiente paso es entender como es el
proceso de diseño de los sistemas de riego, en qué consiste la metodología de superficie óptima
de gradiente hidráulico (Saldarriaga y Ochoa, 2009) y como puede aplicarse esta para el diseño
optimizado de submódulos de riego.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
17
2.2. Diseño hidráulico de sistemas de RLAF.
Para entender la hidráulica de tuberías es necesario tener claras algunas definiciones y leyes que
se utilizarán a la hora de hacer los diseños de estas redes por medio del método de Superficie
Óptima de Gradiente Hidráulico. Las leyes base del diseño de redes son la conservación de la masa
y energía. Una vez se han entendido las ecuaciones básicas, se puede hacer usos de estas a nivel
macro para analizar los diferentes sistemas hidráulicos que existen.
2.2.1. Ecuaciones básicas de la hidráulica de redes.
Como se mencionó anteriormente, las ecuaciones básicas para analizar sistemas como los de
riego, son las ecuaciones de conservación de la energía, conservación de masa, y pérdidas de
energía.
2.2.1.1.
Ley de conservación de la masa.
La ley de conservación de la masa es aplicable en cada uno de los nudos de la red. La Ecuación
2.12 es la ecuación de conservación de la masa para toda la red.
Ecuación 2.12
NT
i
=
número de tuberías que llegan al nudo i.
Q
ij
=
Caudal que pasa por la tubería ij al nudo i desde el nudo j.
Q
Di
=
Caudal demandado en el nudo i.
La convención adoptada por la ingeniería hidráulica es que el caudal Q
ij
es positivo si el flujo va
hacia el nudo i, o negativo si el caudal sale de este nudo.
2.2.1.2.
Ley de conservación de la energía.
La ecuación de conservación de energía se establece para dos puntos en la red de agua potable
(Ecuación 2.13).
Ecuación 2.13

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
18
H
j
=
Altura en el nudo j.
H
i
=
Altura en el nudo i.
Q
i,j
=
Caudal transportado por el tramo comprendido entre los nudos i y j.
A
i,j
=
Área transversal de la tubería entre el nudo i y j.
Km
i,j
= Coeficiente de perdidas menores.
f
i,j
=
Factor de fricción en la tubería.
En esta ecuación se establece que la diferencia de energía entre un punto j y un punto i es igual a
las pérdidas que se presentan en el tramo comprendido entre los dos puntos. Las pérdidas que
generan esa diferencia de energía corresponden a las pérdidas por fricción y las pérdidas por
accesorios.
2.2.1.3.
Pérdidas por fricción.
Las pérdidas por fricción en un tramo de tuberías se pueden calcular haciendo uso de la ecuación
deducida por los ingenieros Henry Darcy y Julius Weisbach. Estas pérdidas son función de la
longitud y diámetro de la tubería, la velocidad del flujo a través de esta y el factor de fricción (ver
Ecuación 2.14).
Ecuación 2.14
donde f se calcula por medio de una ecuación no explícita, para flujos no laminares (ver Ecuación
2.15).
Ecuación 2.15
Para flujo laminar, el factor de fricción se calcula mediante:
Ecuación 2.16
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
19
2.2.2. Diseño de sistemas de RLAF.
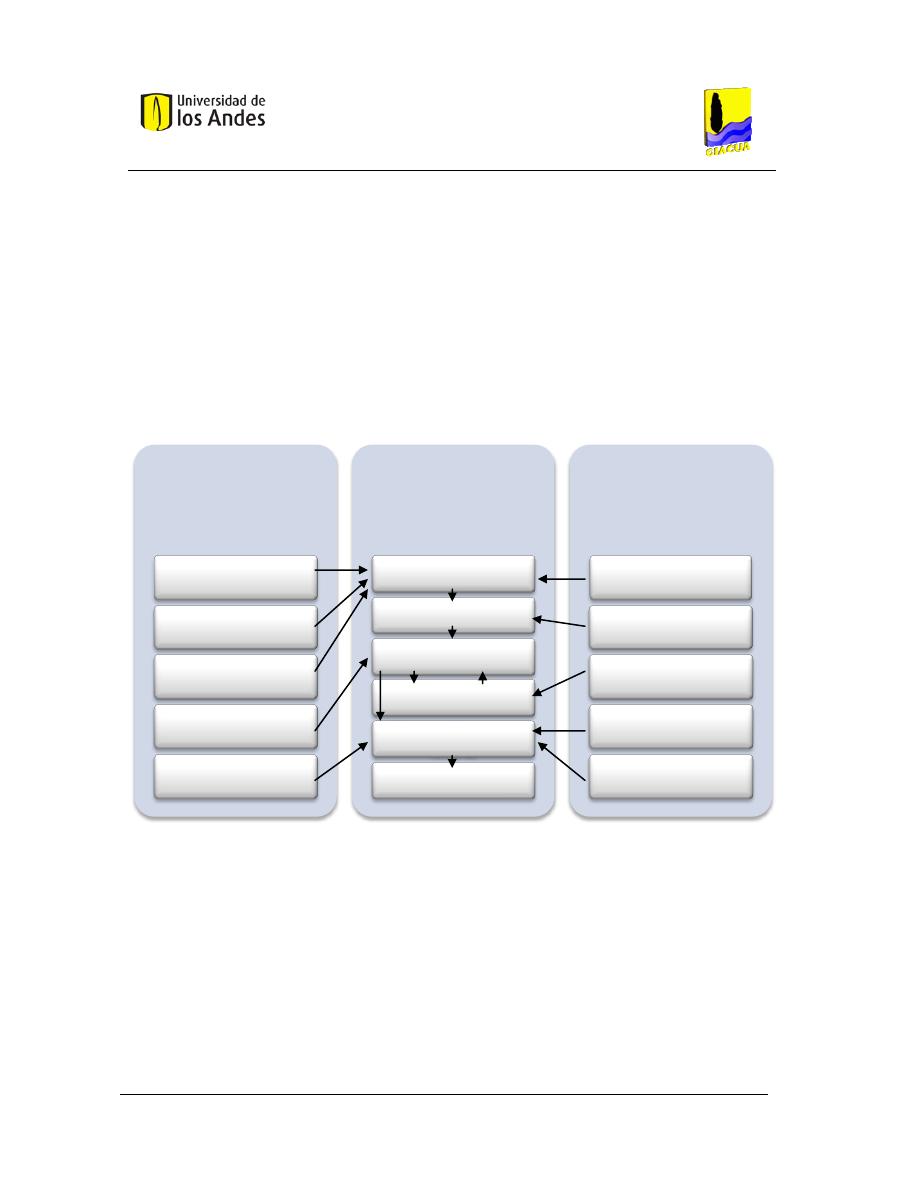
El diseño de un sistema de riego localizado de alta frecuencia, es un proceso que depende de una
serie de datos de entrada que se pueden dividir en agronómicos y no agronómicos. Dentro de los
datos de entrada agronómicos se encuentran el coeficiente de uniformidad (CU), el número de
emisores por planta (n
e
), el caudal medio del emisor, la dosis de riego, tiempo de riego y el
espaciamiento entre emisores. Dentro de los datos no agronómicos, se encuentran el coeficiente
de variación (CV), la ecuación del emisor, el plano topográfico, las ecuaciones de diseño de
tuberías y la conexión emisor-lateral. En la siguiente figura, tomada del trabajo de Bermúdez
(2011), se muestra la secuencia de diseño de un sistema RLAF.
Figura 4. Secuencia del diseño hidráulico de un sistema de RLAF. Adaptado de Pizarro (1996).
Como puede observase en la Figura 4 el proceso de diseño comienza con la determinación de la
tolerancia de caudales (ver Sección 2.1.2.1), seguido por el cálculo de la tolerancia de presiones
(ver Sección 2.1.2.2). Una vez se tienen los datos de presión mínima, presión máxima y caudal
mínimo, los siguientes pasos corresponden a un diseño basado en una comprobación de diseño,
donde el diseñador conociendo los caudales que se esperan en cada lateral prueba diferentes
combinaciones de diámetros hasta encontrar una que satisfaga las condiciones de uniformidad de
Datos del Diseño
Agronómico
Coeficiente de Uniformidad
CU
Número de Emisores por
Planta (ne)
Caudal Medio del Emisor
(Qm)
Dosis y Tiempo de Riego
Espaciamiento entre
Emisores
Diseño Hidráulico
Tolerancia de Caudales
Tolerancia de Presiones
Caudal de Laterales y
Terciarias
Distribución de la Red de
Riego
Diámetros y Régimenes de
Presiones en Laterales y
Terciarias
Secundaria, Primaria,
Cabezal
Otros Datos
Coeficiente de variación de
Fabricación del Emisor (CV)
Ecuación del Emisor (Q-h)
Plano Topográfico
Ecuaciones de Diseño de
Tuberías
Conexión Emisor - Lateral

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
20
riego, tolerancia de presiones y tolerancia de caudales. El procedimiento para realizar el cálculo
hidráulico de un submódulo de riego se presenta a continuación.
2.2.2.1.
Cálculo hidráulico de los submódulos.
Con base en el Capítulo 9 del libro Hidráulica de Tuberías de Juan Saldarriaga (2007), a
continuación se presentan una serie de pasos que se requiere llevar a cabo para realizar el diseño
hidráulico de los sumbódulos de riego. Esto incluye únicamente el cálculo de la tubería múltiple y
los laterales de riego. El diseño no puede realizarse de forma directa y requiere de un proceso
iterativo en el que el diseñador prueba diferentes diámetros de tuberías hasta satisfacer las
condiciones impuestas por el diseño agronómico y los resultados del cálculo de tolerancia de
caudales y presiones. Al colocar los diámetros correspondientes, el diseñador conoce únicamente
las propiedades de las tuberías que utilizarán (tales como el diámetro, la rugosidad absoluta, la
longitud y los coeficientes de pérdidas menores) y el caudal que sale por el emisor de mínima
presión. El proceso de cálculo de un submódulo de RLAF se describe a continuación y fue tomado
de Saldarriaga (2007):
1. Escoger los diámetros de las tuberías que van a conformar los laterales de riego, utilizando
los disponibles en el mercado local. Escoger el diámetro del múltiple, el cual debe permitir
una conexión adecuada con los laterales de riego.
2. Escoger el emisor con las condiciones más adversas de presión. Este emisor puede ser el
emisor más alejado del punto de entrada al submódulo o el emisor que se encuentre
ubicado en el punto más elevado. A este emisor se le asigna la presión mínima permisible.
3. A partir, del emisor de mínima presión, se procede a calcular el lateral que lo contiene. En
este punto vale la pena aclarar que se conoce el diámetro del lateral (este fue asignado
por el diseñador) y siempre se conocen los caudales aguas abajo, del emisor que se va a
analizar. Para realizar el cálculo hidráulico es necesario hacer uso de las ecuaciones de
pérdidas por fricción (ver Ecuación 2.14 y Ecuación 2.15).
Ecuación 2.14
Ecuación 2.15
Si el flujo es laminar utilizar
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
21
Ecuación 2.16
Por su parte, el caudal que debe utilizarse para calcular el número de Reynolds y las
pérdidas por fricción corresponde a la suma de los caudales de los emisores localizados
inmediatamente aguas abajo del emisor que está siendo calculado. De esta manera,
conociendo la presión en el nudo aguas abajo del emisor de análisis y el caudal que corre
aguas abajo del nudo de análisis se puede determinar la presión en este punto como se
muestra en la siguiente ecuación:
Ecuación 2.17
El caudal de salida del emisor de análisis se encuentra utilizando la ecuación del emisor:
Ecuación 2.1
Se debe tener en cuenta que cada uno de los términos de pérdidas de fricción de la
Ecuación 2.14 tiene un caudal diferente, el cual se calcula mediante la siguiente ecuación:
Ecuación 2.18
donde los
son los caudales individuales de los emisores. En la siguiente figura se
muestra un esquema del cálculo de los caudales para cada uno de los tramos del lateral
entre los emisores finales.
Figura 5. Esquema de cálculo de los caudales en un lateral de riego. Tomado de Bermúdez (2011). Adaptado
de Saldarriaga (2007).
Q
1
+Q
2
+Q
3
+Q
4
Q
1
+Q
2
+Q
3
Q
1
+Q
2
Q
1
Q
1
Q
2
Q
3
Q
4
Q
5
Q
i
Lateral

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
22
4. Mediante las ecuaciones anteriores se llega al cálculo de la presión en el punto en que se
unen el lateral de análisis y la tubería múltiple (punto m1 de la Figura 6).
Figura 6. Esquema de un submódulo de riego. Tomado de Saldarriaga (2007).
5. Conociendo la presión en el punto m1 se procede a calcular el siguiente lateral. En este
caso, el proceso debe hacerse por tanteo ya que no se conoce el caudal que pasa por el
lateral. Este proceso implica:
-
Se debe suponer una presión en el último emisor del nuevo lateral de análisis
(e
21
).
-
Calcular el lateral de la misma manera como se hizo en el caso anterior (pasos 1 a
4).
-
Comparar la presión en el múltiple (
) con la encontrada en el paso 4. Si son
diferentes se debe volver a calcular la presión en el último emisor del lateral que
está siendo determinado, utilizando el siguiente criterio.
en donde el Δh es un dato que debe ser suministrado por el diseñador. El proceso se
detiene cuando:
Es decir, cuando la diferencia en dos iteraciones sucesivas del valor de la presión en el
múltiple sea menor que un cierto error (E) definido por el diseñador.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
23
6. Con la presión calculada en el punto m
1
se determina la presión en el punto m
2
mediante
la Ecuación 2.19.
Ecuación 2.19
donde la pérdida de energía debida a la fricción entre los puntos m
1
y m
2
se calcula de
acuerdo con la Ecuación 2.20.
Ecuación 2.20
7. Con la presión m
2
se repite todo el proceso del paso 5 para los laterales y después la
presión en m3 y m4 y así sucesivamente.
8. El proceso sigue hasta llegar al punto de entrada al submódulo de riego.
9. Una vez se han determinado las presiones en todos los puntos, se verifica que en ningún
punto, es decir en ninguno de los emisores o grupos de emisores de alguna de las plantas
del cultivo, la presión sea menor que la presión mínima permisible. De ocurrir esto, se
debe reiniciar el proceso asignando la presión mínima al emisor o punto de emisión donde
el proceso haya dado esa presión menor que la mínima permisible.
10. Finalmente se verifica la tolerancia de presiones.
El proceso de diseño descrito en esta sección hace referencia al proceso de diseño clásico. En este
trabajo se propone hacer uso de una metodología que hace uso de programación lineal en
conjunto con los primeros pasos del método de Superficie Óptima de Gradiente Hidráulico (SOGH)
con el objetivo de obtener un diseño económico de forma rápida. En la siguiente sección se
comienza por describir la metodología SOGH, más adelante se mostrará la formulación
matemática de la metodología planteada y el algoritmo final para el diseño de submódulos.
2.2.2.2.
Método de Superficie Óptima de Gradiente Hidráulico.
En el año 2009 y consientes del problema que implica obtener un diseño de redes de agua potable
óptimo, Juan Saldarriaga y Susana Ochoa de la Universidad de los Andes, propusieron este método
con el objetivo de tener de manera rápida y óptima, los diseños de redes de agua potable.
El objetivo de esta metodología es minimizar el costo de la red. Este costo incluye el costo
comercial de las tuberías y el costo de instalación. Los costos constructivos se pueden calcular de
la siguiente manera:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
24
Ecuación 2.21
donde NT es el número de tuberías que forman parte de la red, L
i
es la longitud de la i-ésima
tubería, D
i
es el diámetro de la i-ésima tubería, α y b son parámetros que se determinan mediante
una regresión de costos comercial y de instalación de las tuberías en función de su diámetro. Esta
función de costos es la que se pretende minimizar teniendo en cuenta las restricciones hidráulicas
y comerciales que se tienen al momento de diseñar la red.
Como se mencionó en el párrafo anterior el objetivo es minimizar el costo de la red. Esto se logra a
partir de la línea de gradiente hidráulico (LGH) que implique los menores costos. Esta LGH
conocida como la línea de gradiente hidráulico, depende de tres factores que son la distribución
de las demandas, la relación entre el caudal total demandado y la longitud total de la serie de
tuberías y del exponente de la función de costos.
La LGH óptima presenta una forma parabólica; de esta manera es necesario conocer tres puntos
de la curva para encontrar la ecuación que describe su trayectoria. Estos tres puntos son el inicio
de la LGH (LGH de la fuente de abastecimiento), la LGH del nudo topológicamente más alejado de
la fuente y el punto de máxima curvatura.
Las etapas que conforman la metodología se describen a continuación:
1. Asignación inicial de diámetros.
Con el fin de determinar la distancia topológica de un nudo a la fuente (distancia que
recorre el agua desde un punto de almacenamiento antes de llegar a un nudo) es
necesario conocer una hidráulica previa de la red, por lo que es importante asignar
inicialmente un diámetro a cada tubería. Se recomienda asignar el menor diámetro
disponible a todas las tuberías, lo cual garantiza que la distribución de caudales sea lo más
independiente posible del diseño y hace que el agua fluya de las fuentes de
abastecimiento hacia los nudos y no en sentido contrario. Después de conocer la
hidráulica de la red, es decir, qué caminos toma el agua antes de llegar a un nudo, se
calcula la distancia topológica de cada nudo.
Conociendo la distancia topológica se puede asignar a cada tubería un diámetro
inversamente proporcional a esa distancia, es decir entre más lejos se encuentren la
tubería de la fuente de abastecimiento, menor debe ser su diámetro.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
25
2. Estimación de la flecha óptima de la curva LGH vs abscisa.
La flecha óptima se calcula de la misma manera que en el caso de una serie de tuberías;
sin embargo, debido a que se tiene una red y no una serie de tuberías, la manera en la cual
se calcula el centroide de demandas, varía y se calcula como se explica a continuación.
Calcular el centroide de demandas:
Ecuación 2.22
Donde:
NN = número de nudos.
q
i
= caudal demandado en el nudo i.
d
i Topológica
= distancia del nudo i con respecto a las fuentes de abastecimiento.
Q
total
= Caudal total demandado en la red.
d
topológica máxima
= Distancia topológica del nudo más alejado de las fuentes de
abastecimiento.
El Coeficiente de Uniformidad 7 (CU
7
) es un indicador de la localización de las
demandas, considerando tanto su ubicación espacial como su magnitud, con
respecto al Centroide de Demandas. Para estimar el CU
7
se supone que el
Centroide de Demandas divide la red en dos subconjuntos: el primero
corresponde a los nudos cuya distancia topológica es inferior a la distancia a la
que se encuentra localizado con respecto a la fuente de abastecimiento; el
segundo está conformado por los nudos con mayor distancia topológica. Para
cada uno de los dos subconjuntos se debe calcular su Centroide de Demandas con
respecto al centroide general y luego se hace un promedio ponderado de
estos dos centroides, así:
Ecuación 2.23

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
26
donde
es el centroide de demandas del subconjunto 1,
es el centroide de
demandas del subconjunto 2,
es la longitud del primer subconjunto y
la del
segundo.
es igual a la distancia a la que se encuentra localizado con
respecto a la fuente de abastecimiento y
corresponde a la diferencia entre la
distancia topológica máxima y
:
Ecuación 2.24
Ecuación 2.25
Los centroides
y
se calculan con respecto al centroide general y la
expresión para su estimación es la siguiente:
Ecuación 2.26
donde NNs corresponde al número de nudos del subconjunto s.
-
Cálculo de la flecha óptima en función del centroide de demandas y el
coeficiente de uniformidad 7:
Ecuación 2.27
donde:
a = 0.435521465
b = -0.176612805
c = -0.977366227
d = 0.906254447

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
27
La flecha calculada con esta ecuación corresponde a una relación Q
2
/L
3
= 1 x 10
-9
y
a un exponente de la función de costos de 1,46, dado que estos fueron los
parámetros considerados en la derivación de dicha ecuación.
-
Cálculo de la flecha óptima para el exponente de la función de costo (n) que se
tenga:
Ecuación 2.28
donde:
n = Exponente de la función de costos.
1
F
1.46
= Flecha óptima para un exponente de 1.46.
-
Cálculo de la flecha óptima para la relación real de Q
2
/L
3
:
Ecuación 2.29
donde:
F
n
= Flecha óptima para una relación de Q
2
/L
3
= 1 x 10
-9
.
Q corresponde al caudal total demandado en el sistema y L a la longitud total del
mismo. Para el cálculo de la relación Q
2
/L
3
la longitud debe corresponder al
recorrido total del agua en el sistema; por lo tanto, en el caso de redes de
distribución esta longitud total se calcula como la sumatoria de las longitudes de
los tubos, así:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
28
Ecuación 2.30
donde NT es número total de tubos de la red y L
i
es la longitud total del tubo
i
3. Con los diámetros asignados, realizar una simulación hidráulica para determinar caudales,
sentidos de flujo y las distancias topológicas de los nudos.
4. Cálculo de la superficie óptima de gradiente hidráulico:
Consiste en calcular la LGH ideal para cada nudo de la red; la superficie óptima de gradiente
hidráulico está conformada por un conjunto de puntos con coordenadas (X, Y, LGH). Para calcular
la SOGH se deben seguir los siguientes pasos.
Iniciar el LGH de todos los nudos en cero.
Determinar y asignar la fuente de abastecimiento de cada nudo. Esto se hace
inyectando un trazador y simulando la hidráulica de la red. Si un nudo es abastecido
por más de una fuente se le asigna aquella con mayor LGH.
Detectar los sumideros de la red, es decir aquellos nudos que no alimentan a ningún
otro nudo de la red.
Ordenar los sumideros de mayor a menor distancia topológica.
Recorrer los sumideros en el orden establecido en el paso 4 y para cada uno realizar
los procedimientos descritos del paso 6 al 10.
Iniciar el número de sumideros en 1.
Asignar a cada sumidero una LGH ideal que cumpla con la presión mínima y considere
la altura topográfica de cada nudo.
Ecuación 2.31
Identificar el embalse asignado al sumidero i.
Ajustar los coeficientes de la ecuación cuadrática que se utilizará para calcular la LGH
óptima. Esta ecuación se puede reescribir de la siguiente manera para el caso de
redes.
Ecuación 2.32
donde:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
29
5. Asignación de las pérdidas de energía objetivo a cada tramo de tubería.
6. Cálculo del diámetro ideal de cada tubería para las pérdidas objetivo fijadas en la etapa 5 y
para los caudales obtenidos en la simulación hidráulica del paso 3.
7. Realizar una simulación hidráulica para estimar las pérdidas reales de energía que se
presentan en cada tubería para los nuevos diámetros calculados.
8. Cálculo del error entre las pérdidas de energía objetivo obtenidas en la etapa 5 y las reales
obtenidas en la etapa 7.
9. Si el error calculado en la etapa 8 es menor al error admisible o si el número de interacciones
realizadas es superior al máximo se continúa con la etapa 10, de lo contrario se regresa a la
etapa 3.
10. Realizar una simulación hidráulica con los diámetros obtenidos en la etapa 9, para determinar
los caudales en las tuberías y las presiones en los nudos de la red.
11. Si en algún nudo de la red, la presión es inferior a la mínima, se realizan correcciones de las
prominencias para poder continuar con la etapa 12.
12. Aproximación de todos los diámetros al siguiente diámetro comercial.
13. Aplicación de programación por restricciones para aumentar diámetros hasta que se satisfaga
el requisito de presión mínima en todos los nudos.
14. Aplicación de programación por restricciones para disminuir los diámetros de algunas
tuberías, teniendo en cuenta el requisito de presión mínima en todos los nudos.
Respecto a esta metodología es importante recalcar que tuvo sus inicios en el diseño de redes de
distribución de agua potable. Para este tipo de redes, la metodología ha probado llevar a

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
30
resultados muy económicos y rápidos. Su uso para el diseño de sistemas de riego localizado de alta
frecuencia comenzó en el 2010 con el trabajo realizado por Bermúdez y donde se probó la
aplicabilidad de esta metodología para este tipo de sistemas. Existen algunas variaciones y puntos
de esta metodología que no se han tomado en cuenta a la hora de hacer los diseños. Por ejemplo,
en el paso 2 de la metodología (Cálculo de la flecha óptima), en sistemas de riego no es posible
hablar de un centroide de demandas que lleve a determinar la flecha óptima. No se puede hablar
de un centroide de demandas, dado que las demandas en los nudos no son constantes o no
corresponden a una demanda base (La demanda base en los nudos es cero). Por el contrario, la
demanda en los nudos de un sistema de RLAF son demandas que dependerán de las presiones en
los nudos y por ende, de la línea de gradiente hidráulico objetivo que se tenga. De esta manera, la
demanda en cada uno de los nudos, va a depender de la LGH objetivo, la cual a su vez depende de
la flecha que el diseñador defina. Finalmente, en la Figura 7 se resumen los pasos de la
metodología SOGH haciendo uso de un diagrama de flujo tomado del trabajo de Ochoa (2009).
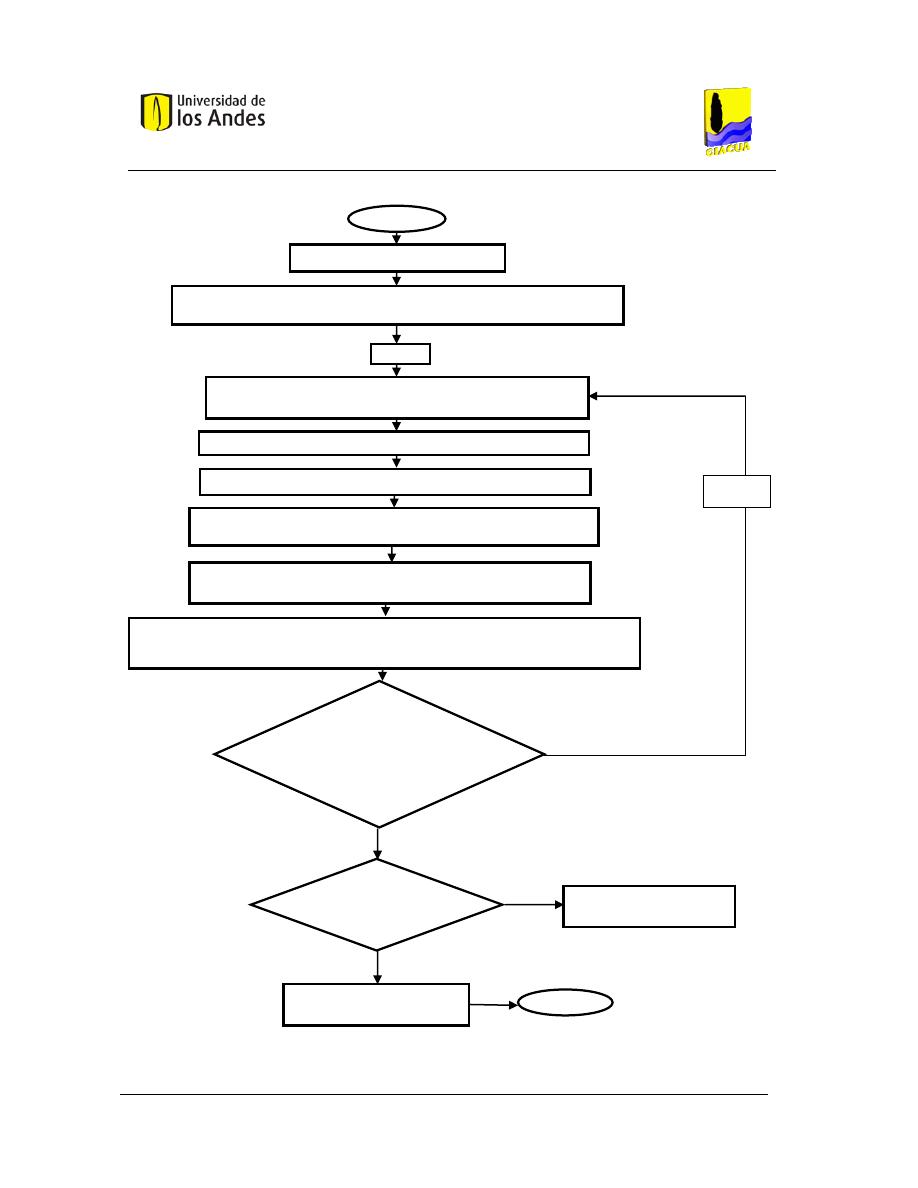
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
31
Figura 7. Etapas de la metodología SOGH. Tomando de Saldarriaga y Ochoa (2009).
Inicio
Fijar parámetros de diseño
Asignación de diámetros proporcionales a la distancia topológica
i=1
Calcular la hidráulica de la red, determinar caudales, sentidos de
flujo y distancias topológicas.
Calcular la superficie óptima de gradiente hidráulico.
Asignar pérdidas de energía objetivo a cada tubería.
Calcular y asignar los diámetros ideales correspondientes a las pérdidas de
energía objetivo.
Calcular la hidráulica de la red y las pérdidas reales de energía
objetivo.
¿Error pérdidas < Ɛ?
¿i > Num Iteraciones?
¿Hay nudos con
déficit de presión?
Corrección de
prominencias
Asignación de diámetros
comerciales
SI
SI
NO
NO
FIN
i = i+1
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
32
2.2.3. Resultados y análisis de trabajo de Bermúdez (2011).
Para realizar el trabajo de diseño de submódulos de riego localizado de alta frecuencia, Bermúdez
hiso uso del programa REDES, desarrollado en el Centro de Investigaciones en Acueductos y
Alcantarillados (CIACUA). El producto final de este trabajo consiste en una metodología para
determinar la presión de entrada al submódulo de riego, de tal forma que el coeficiente de
uniformidad resultante (después del diseño) sea igual o superior al mismo que suministra el diseño
agronómico.
Para comenzar este proceso, vale la pena recordar que el diseño de submódulos de riego
comienza determinando la tolerancia de caudales y la tolerancia de presiones. A partir de estos
cálculos se determina, la presión mínima y la presión máxima que se puede presentar en los
submódulos. El problema que presentaba esta metodología es que el cálculo de la presión máxima
se obtiene mediante la Ecuación 2.11.
Ecuación 2.33
donde
Ecuación 2.34
y M, es un valor que se no se conoce de antemano y se sugiere usar un valor de 2.5. De esta
manera, el primer paso en el trabajo de Bermúdez consistió en observar la manera en que
variaban los resultados de coeficiente de uniformidad (CU) y costos, si este valor M cambiaba.
Para esto, se varió el valor de M entre 0.5 y 4.3. Una vez hecho esto, Bermúdez encontró los
siguientes resultados:
Gráfica 2-1. Coeficiente de uniformidad resultante vs. Presión de entrada al submódulo. Tomado de Bermúdez (2011).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
33
En la Gráfica 2-1 se observa que el coeficiente de uniformidad resultante y la presión de entrada al
submódulo, presentan una relación cuadrática. En la medida en que la presión de entrada
disminuye (valores de M pequeños) el coeficiente de uniformidad resultante es mayor; por otro
lado, para valores muy altos (superiores a 2.5) el coeficiente de uniformidad es inferior al deseado
por el diseño agronómico. Respecto a este resultado de Bermúdez, vale la pena decir que los
resultados son consistentes con lo que se esperaría. Resulta claro que si se mantiene la presión
mínima fija y se varía la presión de entrada únicamente, a medida que el rango de presiones
dentro del submódulo se reduce, la variación entre los caudales de salida de los emisores que
componen el submódulo, será menor. Por otro lado, aunque un menor rango entre las presiones,
resulta en un coeficiente de uniformidad más alto, también conlleva a una red más costosa (ver
Gráfica 2-2).
Gráfica 2-2. Costo total de la red vs. Presión a la entrada del submódulo. Tomado de Bermúdez (2011).
Como se observa en la Gráfica 2-2 al tener una menor presión de entrada al submódulo, se tienen
mayores costos. Esto se debe a que, al tener un menor rango entre la presión mínima y la presión
máxima, se tiene menos energía para perder a lo largo del submódulo. El hecho de tener menos
energía disponible para perder a lo largo del sistema, implica mayores diámetros de tuberías con
el objetivo de reducir velocidades y lograr disminuir las pérdidas por fricción y pérdidas menores.
A partir de estos resultados, Bermúdez decidió establecer de qué depende esta curva. Para esto
empezó a variar diferentes variables tales como el exponente de los emisores, el coeficiente de los
emisores, la topología de la red, el coeficiente de variación (CV), la presión media, el coeficiente de
uniformidad del diseño agronómico y el número de emisores por planta. A partir de los resultados
obtenidos, Bermúdez planteó una metodología de diseño que es la que se resume a continuación.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
34
2.2.3.1.
Descripción de la metodología de diseño de propuesta por Bermúdez.
La metodología propuesta por Bermúdez consta de 5 pasos que se describen a continuación. Vale
aclarar, que antes de comenzar con el proceso es necesario contar con los parámetros de diseño,
topología de la red, la uniformidad de riego, las características del emisor a emplear y los
diámetros comerciales disponibles. Una vez se tiene esto se procede así:
1. Cálculo de tolerancia de caudales y presiones.
Este procedimiento se hace de forma exacta a como se describió en la Sección 2.1.2.1 y
Sección 2.1.2.2. Este procedimiento para determinar el caudal de mínima presión, la presión
mínima, la tolerancia de presiones, resulta exactamente igual a como se hace el diseño
actualmente. En este paso lo único que cambia es el cálculo de la presión de entrada al
submódulo de riego. Esta presión se calcula como se muestra en el siguiente paso.
2. Cálculo de la presión de entrada del submódulo.
La presión a la entrada del submódulo corresponde a la energía necesaria, inmediatamente
después de la válvula reguladora de presión para cumplir con la uniformidad de riego. Como
se mencionó anteriormente, Bermúdez determinó que la relación entre la presión de entrada
al submódulo y el coeficiente de uniformidad resultante es una ecuación cuadrática de la
siguiente forma:
Ecuación 2.35
donde CU
R
es el coeficiente de uniformidad resultante, PES es la presión de entrada del
submódulo; y α, β y
son coeficientes que describen la forma y ubicación de la curva. El valor
de
se calculó como se muestra en la Ecuación 2.36.
Ecuación 2.36
donde
Ecuación 2.37
y
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
35
Ecuación 2.38
Los valores de α, β y γ se calculan como se muestra en la Tabla 4. En esta tabla resulta claro que
estos tres parámetros dependen de la presión nominal de trabajo y del exponente del emisor.
Tabla 4. Ecuaciones para la determinación de los coeficientes α, β y γ. Tomado de Bermúdez (2011).
Tipo de
Emisor
Caudal
Nominal
[L/h]
Presión
Nominal
[mca]
α
β
γ
Bajo
Caudal
2 – 16
1
[
5
[
Alto
Caudal
16 – 150
10
[
15
[
20
[
Conociendo los valores de α, β y
se procede a conformar la Ecuación 2.35 y determinar la
presión de entrada al submódulo, que llevará a tener el coeficiente de uniformidad resultante
deseado.
3. Aplicar la metodología de Superficie Óptima de Gradiente Hidráulico (SOGH).
Esta metodología fue desarrollada para redes de distribución de agua potable; por esta razón,
según Bermúdez, fue necesario realizar algunas modificaciones en ciertas etapas para poder hacer
uso de la metodología. Primero es necesario definir la altura del tanque o fuente de
abastecimiento, ya no corresponde a un parámetro de diseño o dato de entrada; este valor será
tomado del paso anterior; es decir, la LGH del tanque es igual a la PES calculada más la cota
topográfica correspondiente.
Bermúdez recomienda realizar algunos cambios en el cálculo de la flecha óptima. El cambio que se
requeriría hacer en la metodología SOGH, corresponde a la etapa 2, en el cálculo del centroide de
demandas. Bermúdez propone calcular este centroide de acuerdo con la siguiente ecuación.
Ecuación 2.39
donde
es el caudal medio de operación del emisor,
el número de emisores por planta, NN
corresponde al número de nudos que representan un punto de emisión en la red,
es
la distancia topológica del nudo i con respecto a la válvula reguladora de presión,
corresponde al caudal total demandado en la red y
es la distancia topológica

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
36
máxima (i.e. la distancia topológica del punto de emisión más alejado de la válvula reguladora de
presión).
Finalmente, Bermúdez propone que el mejor proceso de aproximación de diámetros continuos a
discretos, corresponde a un redondeo al diámetro comercial más cercano.
4. Cálculo del coeficiente de uniformidad resultante del submódulo diseñado.
El coeficiente de uniformidad resultante corresponde al calculado con los datos finales de la red.
Para esto se debe conocer el caudal de mínima presión resultante y el caudal medio resultante. A
partir de estos resultados se puede calcular el CU
R
de la siguiente manera:
Ecuación 2.3
5. Si CU
R
es menor que CU impuesto por el diseño agronómico volver al paso 2.
Si el Coeficiente de Uniformidad Resultante CU
R
del submódulo diseñado es menor al Coeficiente
de Uniformidad CU
I
impuesto por el diseño agronómico se debe rediseñar. Lo anterior se puede
presentar porque el valor calculado de la Presión a la Entrada del Submódulo corresponde a una
aproximación.
Si se presenta lo anterior, es necesario volver al paso 2 de la metodología de diseño SOGH
ajustada y reducir la Presión a la Entrada del Submódulo, de lo contrario finaliza el proceso.
Estos son los 5 pasos que conforman la metodología propuesta por Bermúdez y la cual será
analizada en secciones siguientes de este trabajo. Esta metodología puede resumirse en el
diagrama de flujo presentado en la Figura 8.
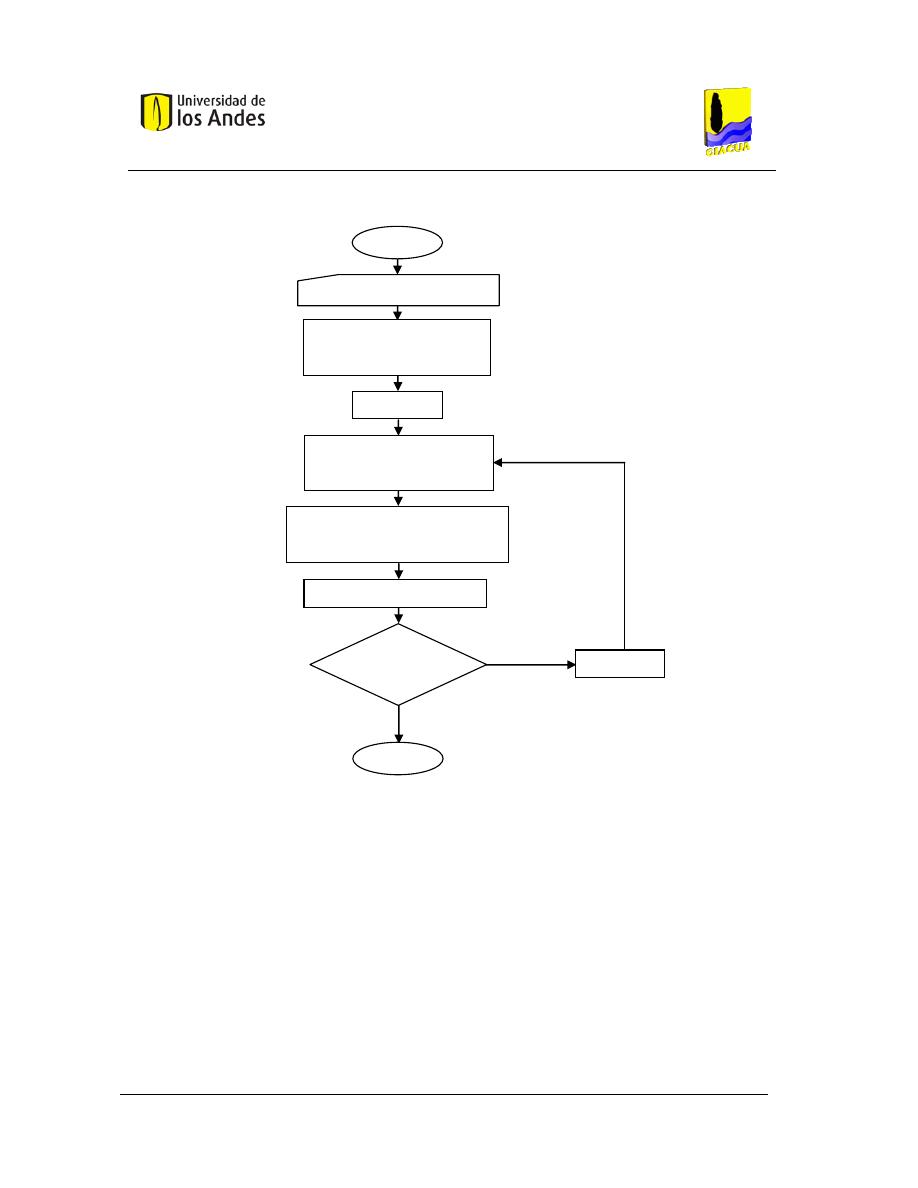
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
37
Figura 8. Diagrama de flujo de la metodología SOGH ajustada propuesta por Bermúdez (2011).
SI
NO
INICIO
Calcular la Tolerancia de
Caudales y Presiones
Calcular la Presión a la
Entrada del Submódulo
Leer parámetros de diseño
Diseño mediante la metodología
“SOGH Ajustada”
Calcular CU
R
CU
R
<
CU
i
?
FIN

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
38
2.3. Programas.
Para el desarrollo de este trabajo se hiso uso de varios programas que permitieron diseñar
diferentes submódulos de riego y calcular las características hidráulicas resultantes. Los programas
que permitieron la realización de este trabajo fueron el programa REDES (desarrollado en el
Centro de Investigaciones en Acueductos y Alcantarillados, CIACUA), EPANET (desarrollado por la
Enviromental Protection Agency, EPA) y el optimizador Xpress (desarrollado por Dash Associates
Ltda.). A continuación se presenta una breve descripción del programa REDES y el optimizador
Xpress.
2.3.1. Programa REDES.
El programa REDES, desarrollado en el Centro de
Investigaciones en Acueductos y Alcantarillados
CIACUA de la Universidad de Los Andes, Bogotá,
Colombia, es una herramienta de simulación de
sistemas de tuberías con flujo a presión.
El desarrollo del programa REDES está basado en
criterios de optimización de Redes de Distribución de
Agua Potable (RDAP) a los que se ha llegado a través
de investigaciones en diferentes universidades de
Estados Unidos y Europa. Entre los criterios más
importantes se encuentran los de optimización económica de diámetros de tuberías en redes
cerradas de distribución de agua, desarrollados por Ronald Featherstone y Karim El-Jumaily
(basados en el criterio de Wu), el método del gradiente para el cálculo de redes cerradas de
distribución de agua, desarrollado por Ezio Todini y Enda O´Connell y el método de Superficie
Óptima de Gradiente Hidráulico, desarrollado por Susana Ochoa como tesis de magíster. Este
último, corresponde a la metodología que se aplicará para el diseño de submódulos de RLAF.
A diferencia de otros programas comerciales, el programa REDES permite el diseño optimizado de
redes de distribución de agua, tanto de redes nuevas como de ampliaciones de redes existentes.
En su módulo de diseño incluye las opciones para diseñar con diferentes métodos: Algoritmos
Genéticos aplicados al diseño de redes, Superficie Óptima de Presiones (SOP), Programación por
Restricciones y Superficie Óptima de Gradiente Hidráulico (SOGH).
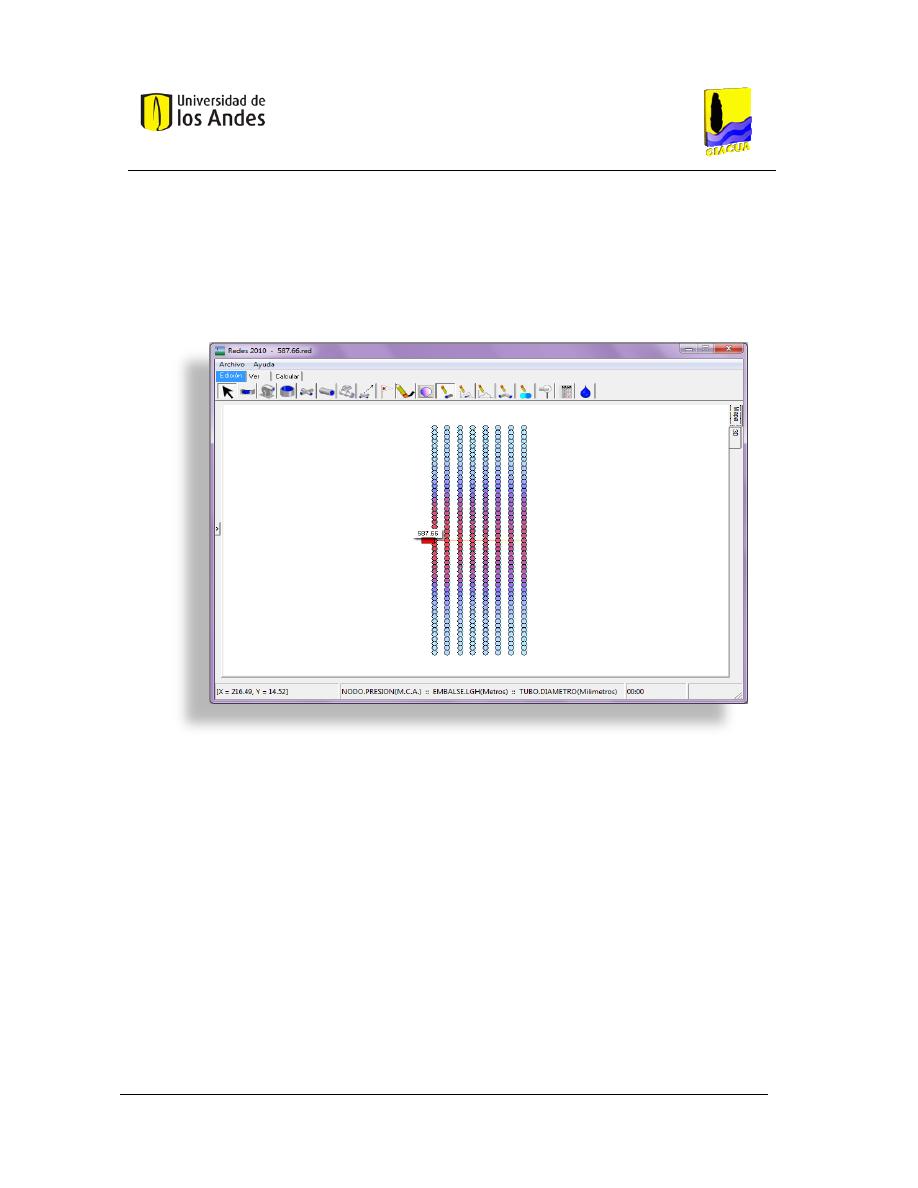
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
39
2.3.1.1.
Características del Programa.
La interfaz gráfica de REDES consiste en un mapa de la red en la cual es posible visualizar los
valores de diferentes variables de los elementos; de igual forma se pueden apreciar a través de
curvas de nivel y de superficies, de manera que el usuario pueda tener una idea global de lo que
ocurre en la red.
Figura 9.
Mapa de un submódulo de RLAF en el programa REDES con altura piezométrica en los nudos de acuerdo con
una escala de colores.
2.3.1.2.
Elementos.
Hasta la red más simple está compuesta por al menos una fuente de agua, un tubo y un nudo de
demanda; sin embargo, redes más complejas pueden tener diferentes accesorios, como emisores,
válvulas o bombas hidráulicas. El programa REDES maneja siete tipos de elementos diferentes,
presentados a continuación:
Embalses; son fuentes de agua cuya altura piezométrica es fija.
Tanques; fuente de agua cuya altura piezométrica es variable, ya que pueden tener un
caudal de entrada y alimentar la red o pueden ser alimentados por la red y tener un
caudal de salida.
Nudos; puntos donde hay demanda de caudal.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
40
Tuberías; tuberías de la red.
Emisores; elementos hidráulicos de los nudos que permiten simular fugas y emisores en
sistemas de riego.
Válvulas; accesorios de las tuberías que combinan la relación entre altura piezométrica y
el caudal, se pueden modelar válvulas reductoras de presión, válvulas reguladoras de
presión, válvulas de control de caudal, válvulas de propósito general, válvulas de
regulación de cierre y válvulas de cheque.
Bombas; accesorios de las tuberías que proporcionan energía a la red.
2.3.1.3.
Capacidades del Programa.
El programa REDES ofrece múltiples opciones de cálculos al usuario; entre estas se encuentra el
cálculo hidráulico estático (cálculo de alturas piezométricas y presiones), cálculo hidráulico en
periodo extendido (cálculo hidráulico a diferentes horas del día), cálculo de la calidad de agua
(concentraciones, edad, trazadores y porcentaje de procedencia), diseño de RDAP con métodos
modernos, calibración de redes y cálculo del índice de resiliencia.
2.3.2. Optimizador Xpress.
El programa Xpress es un optimizador que cuenta con sofisticados subprocesos y múltiples
algoritmos con capacidad de resolver con rapidez y precisión diferentes problemas de
optimización. Los algoritmos de optimización de Xpress tienen la capacidad de resolver problemas
lineales (LP), problemas lineales usando variables enteras, problemas cuadráticos (QP), problemas
cuadráticos usando variables enteras y problemas lineales convexos, entre otros.
Este optimizador proporciona implementaciones rápidas y fiables de los métodos simplex primal y
dual para resolver problemas de programación lineal e integra algoritmos de solución previa para
reducir el tamaño y el tiempo del problema. Realiza ajustes automáticos para un mejor
rendimiento y tiene una amplia gama de parámetros configurables para un control avanzado del
proceso de optimización. El programa cuenta también con el optimizador MIP que hace uso del
algoritmo Branch and Bound para resolver problemas que utilizan variables enteras; este
algoritmo elimina de forma efectiva las soluciones no factibles y reduce considerablemente el
espacio y tiempo de solución en busca de la solución óptima.
En secciones siguientes de este documento se mostrará el uso que se le dio al programa Xpress
para realizar diseños de submódulos. Para este trabajo se formuló el problema de diseño como un
problema de optimización lineal y la formulación se implemento en Xpress dejando claro la
función objetivo del problema y sus diferentes restricciones.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
41
3. RESULTADOS Y ANÁLISIS PRIMERA FASE
Este proyecto, tiene como objetivo principal, determinar la forma óptima de realizar el diseño de
submódulos de sistemas de riego localizado de alta frecuencia. Para cumplir con este objetivo se
diseñó una metodología basada en programación lineal, la cual fue evaluada respecto a la
metodología de Superficie Óptima de Gradiente Hidráulico. Los Numerales 3.1 y 3.2 hacen un
análisis de la metodología SOGH y los resultados obtenidos en su aplicación para el diseño de
submódulos de RLAF. En el Numeral 3.3 se hace un análisis de la metodología propuesta por
Bermúdez para determinar la presión de entrada al submódulo de riego. Finalmente a partir de la
página 79 el Capítulo 3.4 explica la metodología final propuesta para el diseño de submódulos de
riego.
3.1. Análisis metodología SOGH.
Sobre esta metodología propuesta en el año 2009, hay que decir que es una metodología bastante
adecuada a la hora de hacer diseños rápidos y económicos de redes de distribución de agua
potable (RDAP). Los pasos propuestos por la metodología SOGH que fueron resumidos en la Figura
7, parecen en principio simples de aplicar al diseño de submódulos de sistemas de riego; sin
embargo, esta metodología no puede ser aplicada de forma directa ya que presenta algunas
restricciones que deben ser tenidas en cuenta.
3.1.1. Análisis etapa 2, metodología SOGH.
En la etapa 2 de la metodología SOGH Ochoa y Saldarriaga proponen encontrar la flecha óptima de
diseño. La flecha óptima para el diseño de RDAP es función de varios parámetros y variables, tales
como el caudal total demandado por el sistema, la longitud total del sistema, el exponente de
función de costos, el centroide de demandas ( ) y el coeficiente de uniformidad 7 (CU
7
). El primer
problema que se tiene en sistemas de RLAF, con respecto a la estimación de la flecha óptima,
consiste en que para un submódulo de riego no se conocen a priori los caudales de los emisores.
Cuando se está diseñando un submódulo de riego, el diseñador no conoce los caudales que
saldrán por cada uno de los emisores. En una RDAP, por ejemplo, los caudales demandados son
conocidos en cada uno de los nudos y a partir de estos, el diseñador puede estimar el caudal total
demandado en la red, el centroide de demandas y el coeficiente de uniformidad 7 (CU
7
). Por el
contrario en el diseño de los sistemas de RLAF, la demanda de cada uno de los nudos va a
depender de la presión. Esta presión a su vez, es definida por el diseñador y hace referencia a la
línea de gradiente hidráulico (LGH) objetivo, que el mismo diseñador asigna.
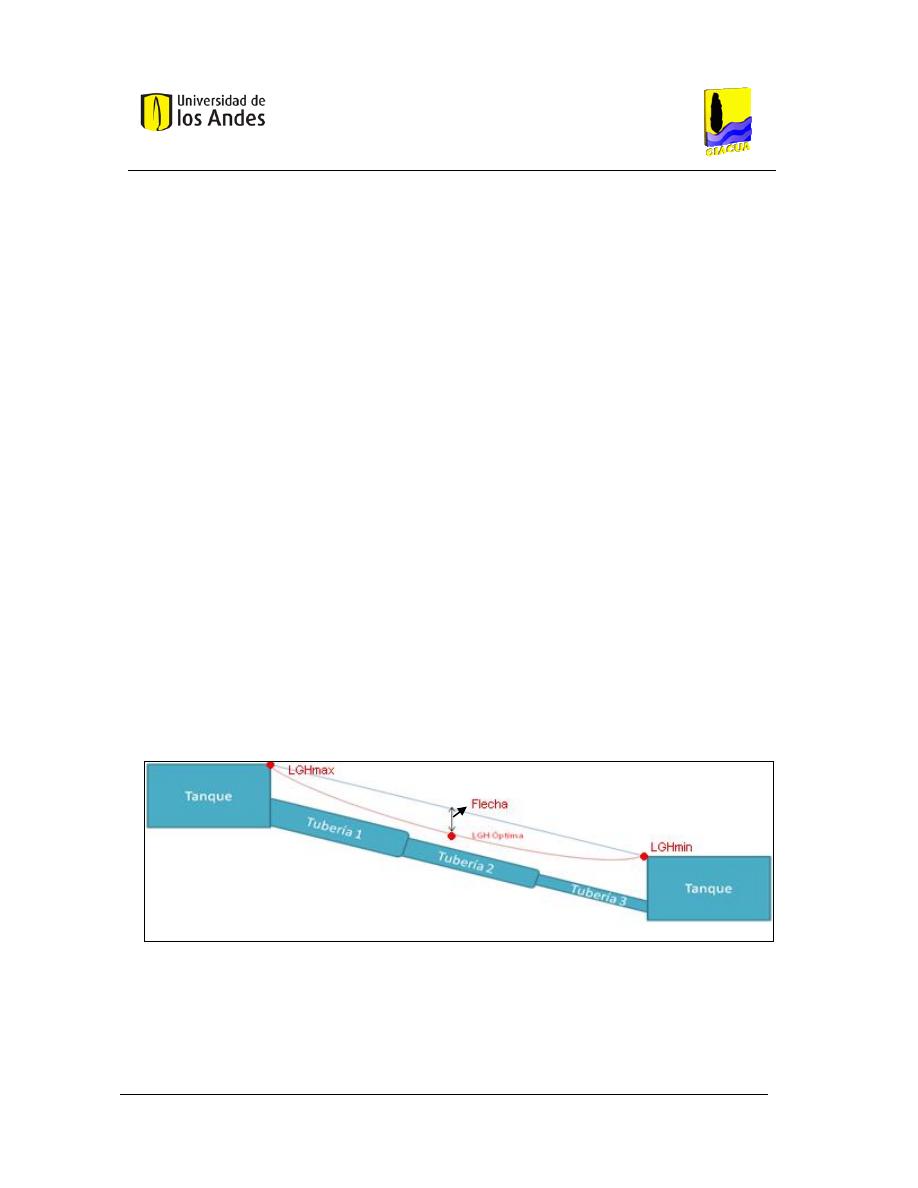
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
42
Teniendo en cuenta lo mencionado en el párrafo anterior, no es posible establecer una flecha
óptima de diseño sin antes conocer la presión en cada uno de los nudos. Esto se debe, a que la
LGH objetivo depende de la flecha escogida. De esta manera, como primer paso vale la pena variar
la flecha de diseño para cada una de las redes de caso de estudio, y determinar el comportamiento
de los costos en relación con la flecha. Antes de proceder a mostrar los resultados de la variación
de la flecha, se presenta otra de las restricciones presentes en la metodología SOGH.
3.1.2. Flecha mínima y máxima para el diseño de sistemas de riego.
Como bien lo estableció I-pai Wu (1975) y posteriormente Ochoa y Saldarriaga (2009), la red de
mínimo costo puede corresponder a aquel diseño que se desarrolla a partir de una línea de
gradiente hidráulico parabólica. En el caso del diseño de submódulos de riego, el punto
correspondiente a la LGH máxima, será la cota de entrada al submódulo más la presión de entrada
(ver Ecuación 3.1).
Ecuación 3.1
El punto correspondiente al gradiente hidráulico mínimo, corresponde al sumidero que presente
las condiciones más adversas topográficamente y que se encuentre más alejado de la válvula
reguladora de presión. La presión mínima, es la correspondiente al caudal de mínima presión
obtenido en el cálculo de tolerancia de caudales. Finalmente, para poder describir una parábola,
se requiere de un tercer punto. Este tercer punto, corresponde al lugar donde se presenta la
máxima curvatura en la LGH; y se puede determinar mediante la flecha.
Figura 10. LGH objetivo, basada en tres puntos conocidos.
La Figura 10, muestra un esquema de los tres puntos requeridos para determinar la LGH objetivo
cuando se va a diseñar un sistema de tuberías. A partir de esta figura, se puede establecer la
ecuación propuesta por la metodología SOGH para determinar la línea de gradiente hidráulico.
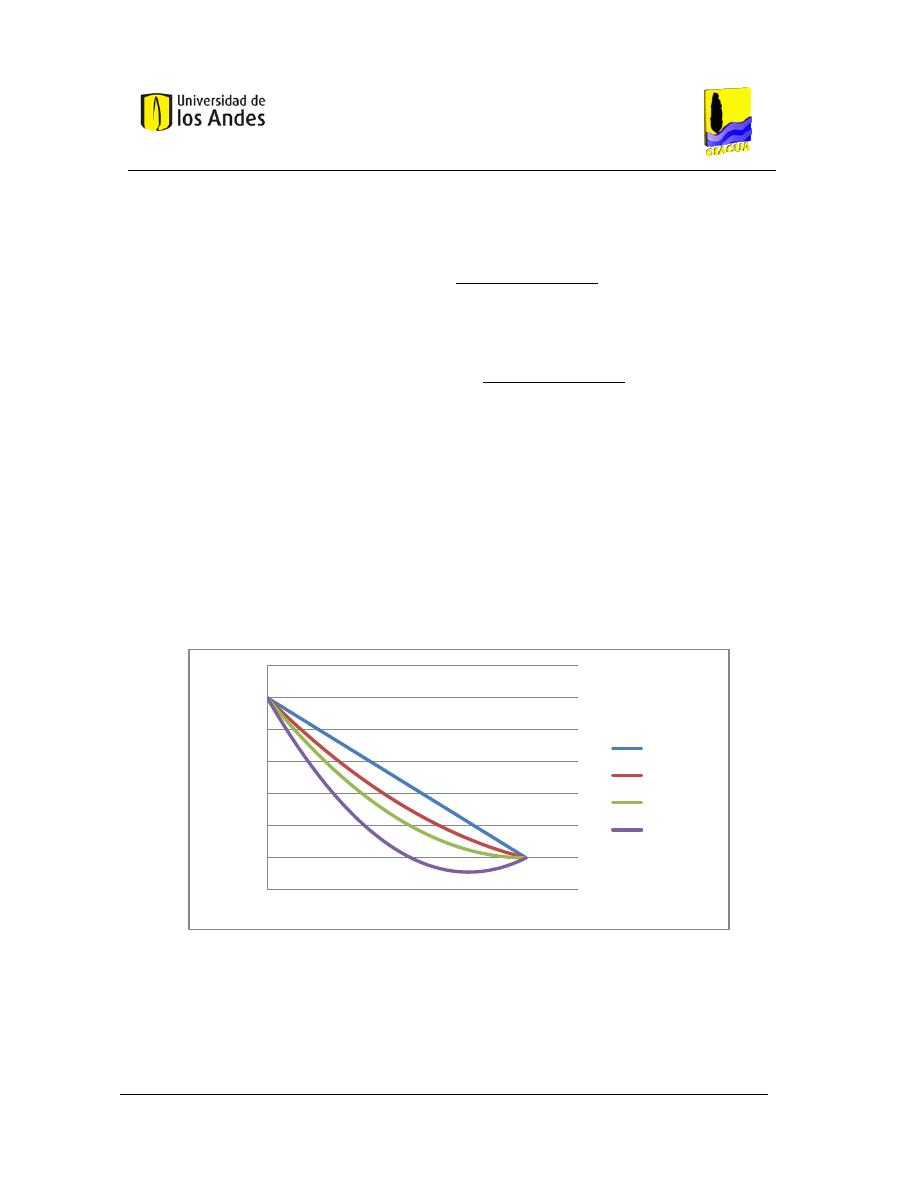
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
43
Ecuación 2.32
donde:
Como puede observarse claramente, la línea de gradiente hidráulico en cada uno de los puntos del
sistema de tuberías, depende de la flecha seleccionada (F) y de su distancia topológica al punto de
alimentación del sistema. Teniendo en cuenta esta ecuación y la Figura 10, surgió la pregunta
sobre cuál es el rango en que es físicamente válida la flecha de diseño. Para responder esta
pregunta, se creó un sistema de tuberías en serie y se varió la flecha de diseño, observando los
siguientes resultados.
Gráfica 3-1. LGH objetivo vs. Distancia topológica, para diferentes flechas de diseño.
Aunque se probaron diferentes flechas, la Gráfica 3-1 se concentra en solo 4 de estas. Los
resultados que se obtuvieron de esta gráfica, muestran que a pesar de que Ochoa (2009) permitía
variar el rango de la flecha entre -0.5 y 0.5, existen valores de flecha para los cuales esta pierde su
sentido físico. Antes de entrar en detalle a analizar la Gráfica 3-1, vale la pena decir que un diseño
-20
0
20
40
60
80
100
120
0
20
40
60
80
100
120
LGH
(m)
Distancia topológica al nodo (m)
Flecha 0
Flecha 0.15
Flecha 0.25
Flecha 0.35

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
44
óptimo nunca va a corresponder a flechas entre -0.5 y 0; esto debido a que este tipo de flechas
conlleva a un menor gasto de energía objetivo por tubería e implicarían mayores costos. De esta
manera, el estudio se concentra en flechas entre 0 y 0.5. Dicho esto, y observando la Gráfica 3-1,
resulta claro que para flechas como la de 0.35, existe un punto a partir del cual, el sistema estaría
creando energía. Si se tiene en cuenta que para producir unas pérdidas objetivo de cero, en un
tramo de tubería, se requeriría de un diámetro infinito, no tendría ningún sentido físico hablar de
diseñar un sistema de tuberías en el cual se requiere la creación de energía a partir de cierto
punto.
Teniendo en cuenta lo dicho anteriormente, el siguiente paso consistió en determinar la flecha
máxima de diseño. Esta flecha corresponde a aquella en la cual, en el último tramo de tubería, la
curva de la LGH tenga una pendiente cero. Esto último quiere decir, que en esta curva se
presentarán pérdidas objetivo en toda la trayectoria, excepto en el último punto del sistema. Para
lograr esto, se llevó a cabo el siguiente procedimiento:
Partiendo de la ecuación planteada por Ochoa y Saldarriaga (2009):
Ecuación 2.32
donde
Se obtiene la siguiente expresión para determinar la LGH objetivo en cada uno de los nudos que
componen el sistema de tuberías.
Si esta ecuación se deriva con respecto a x, donde x corresponde a la distancia topológica de cada
nudo al punto de alimentación del sistema, se tiene:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
45
Si esta última ecuación, se iguala a cero y la variable x se remplaza por la longitud total (L
total
) del
sistema, se obtiene una expresión para determinar el valor de la flecha (F) que implica tener unas
pérdidas de energía iguales a cero en el último punto del sistema.
Como se puede observar en este resultado, la flecha máxima teórica, corresponde a una flecha de
0.25. Con la flecha de 0.25, ocurrirá que en el último punto del sistema se requieran unas pérdidas
objetivo de cero. Si se hace uso de flechas mayores a esta, se estaría pidiendo realizar un diseño
en el cual se cree energía en ciertos puntos. Ahora bien, este resultado de una flecha máxima de
0.25 corresponde al caso en que la última tubería del sistema es de longitud infinitesimal, cosa que
no sucede nunca. Por esta razón, resultaba de interés determinar cuál es la flecha máxima en los
casos en que la última tubería del sistema tenga una longitud considerable. Esta pregunta fue
respondida por Páez (2011) y su ecuación final para la flecha máxima es la que se muestra a
continuación:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
46
Ecuación 3.2
donde L
Tot
es la longitud total del sistema,
es la longitud de la última tubería y F es el es la
flecha máxima.
3.2. Casos de estudio metodología SOGH.
Para poner a prueba la metodología SOGH en el diseño de sistemas de riego localizado de alta
frecuencia, se tomaron tres casos de estudio, que han mostrado algunos resultados que se
consideran importantes para entender la hidráulica resultante del diseño con SOGH. Las redes de
análisis, son las que se muestran a continuación:
1. Red Asimétrica 1
El primer submódulo de análisis se presenta en la Figura 11. Este cuenta con una tubería múltiple,
que alimenta 8 tuberías laterales; cada una de ellas con 25 nudos. Cada uno de los nudos
corresponde a una planta a la que es necesario suministrarle agua. Para cada planta se requieren
dos emisores, pero dado que en el programa REDES no es posible colocar dos emisores en el
mismo punto, fue necesario modelar esto, multiplicando el coeficiente del emisor por 2.
Figura 11. Red Asimétrica 1. Modelo de REDES.
Como todo submódulo de riego, éste se compone de un punto de entrada regulado donde la
presión cambiará de acuerdo con las especificaciones del problema. Por su parte, la distancia
entre los laterales es de 10 metros y la distancia entre cada planta es de 5 metros. De esta manera
el submódulo se compone de 200 plantas (400 emisores) y 208 tuberías. La topografía de la red es
totalmente plana.
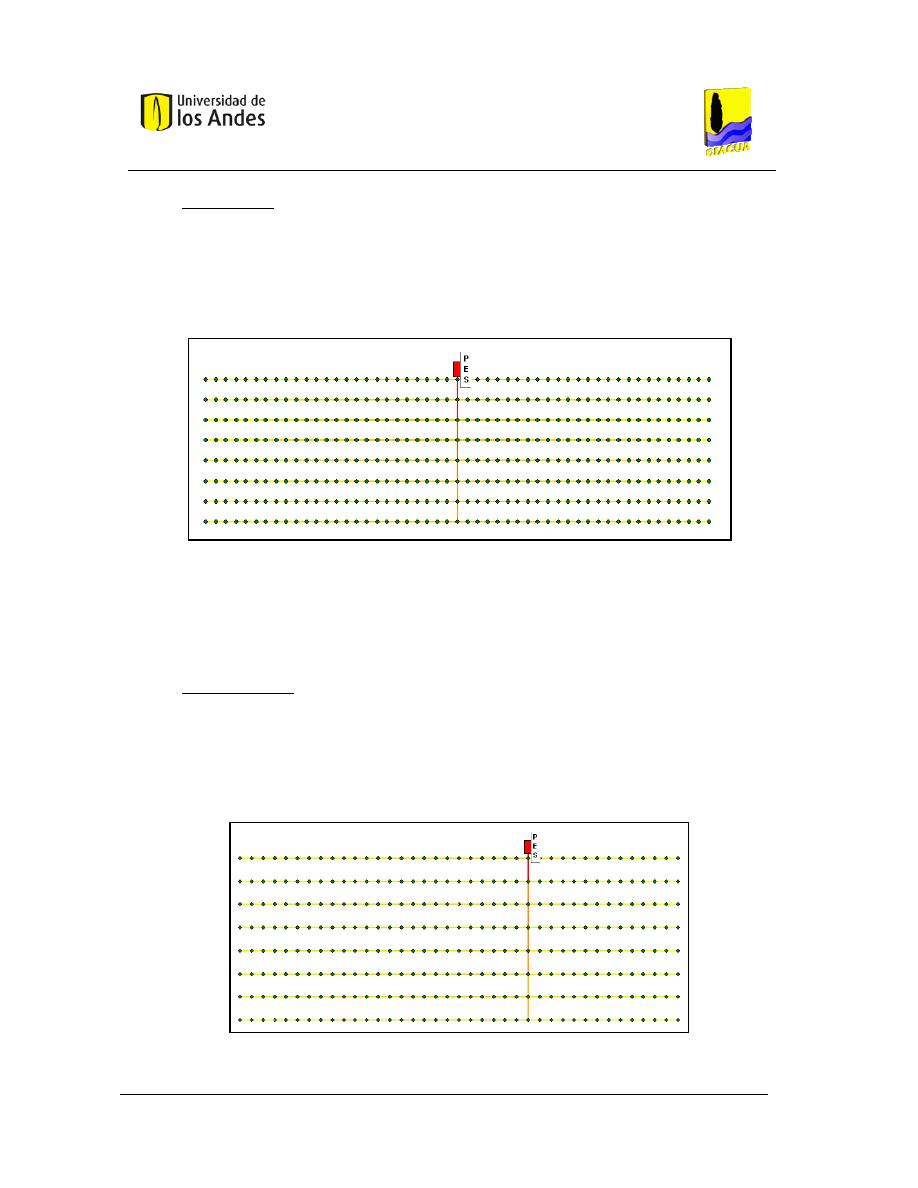
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
47
2. Red Simétrica
El segundo submódulo de riego, consta del doble de laterales y emisores que el primer
submódulo. Como puede observarse en la Figura 12, esta red es similar a la asimétrica 1 solo que
el múltiple alimenta laterales por ambos lados. Este submódulo cuenta con 408 tuberías, 400
plantas (800 emisores) y un punto de entrada.
Figura 12. Red Simétrica. Modelo de REDES.
En este submódulo de análisis, la distancia entre laterales también es de 10 metros y la distancia
entre las plantas es de 5 metros. Al igual que el primer submódulo de análisis, la topografía en esa
red, también es plana.
3. Red Asimétrica 2
Esta última red presenta las mismas características de las anteriores (distancia entre laterales de
10 metros y distancia entre nudos de 5 metros), la principal diferencia es que la tubería múltiple,
entrega agua a un mayor número de nudos al lado izquierdo, que al lado derecho. El submódulo
consta de 312 tuberías y 304 plantas (608 emisores).
Figura 13. Red Asimétrica 2. Modelo de REDES.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
48
Para estas tres redes se realizaron diseños variando el exponente del emisor. Para esto, primero se
determinó la ecuación de costos de las tuberías disponibles, ofrecidas por PAVCO. Los diámetros
de tubos ofrecidos por PAVCO para sistemas de riego se muestran en la siguiente tabla.
Tabla 5. Diámetros comerciales y su costo, ofrecidos por PAVCO.
Diámetro
Costo tramo de 6 m
(in)
(mm)
(COP)
0.5
12.7
9394
0.75
19.05
11637
1
25.4
16332
1.25
31.75
29418
1.5
38.1
38412
2
50.8
58902
2.5
63.5
95460
3
76.2
127452
4
101.6
217392
6
152.4
448128
A partir de esta lista de diámetros se pudo obtener la ecuación de costos mediante una regresión
como la que se muestra a continuación, donde la curva azul representa los valores de costo
correspondientes a los diámetros ofrecidos por PAVCO y la curva negra la línea de tendencia.
Figura 14. Curva Costo vs. Diámetro de tubería.
y = 16.871x
1.647
R² = 0.985
0
10000
20000
30000
40000
50000
60000
70000
80000
0
50
100
150
200
Costo
de metro
lineal
de tubería
(COP)
Diámetro de tubería (mm)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
49
Ecuación 3.3
La Ecuación 3.3, representa la curva final de costos. En esta ecuación se observa que cada una de
las tuberías, presentará un costo igual a la longitud de la tubería, multiplicado por 16.871 y el
diámetro que tenga el tubo elevado a un exponente de 1.647. Si se suman los costos de todas las
tuberías, el resultado final será el costo de la red.
3.2.1. Diseño de los submódulos de riego.
Una vez se tiene la curva de costos y se ha definido la topología de cada uno de los submódulos de
riego que se van a analizar, se procede a realizar los diseños. Como se mencionó anteriormente,
para cada una de las redes, se realizaron varios diseños. Para cada red se varió el exponente del
emisor buscando que el caudal medio requerido por emisor no variara. El caudal medio por emisor
deseado, fue un caudal de 120 litros por hora (l/h) y adicional a esto se utilizó una presión media
de 18 mca.
Figura 15. Curva exponente del emisor vs. Coeficiente, para un caudal de 120 l/h.
En la Figura 15 se observa el coeficiente del emisor que se debe utilizar si se varía el exponente del
emisor. La curva mostrada corresponde a la relación exponente-coeficiente del emisor, que
mantiene un caudal de 120 l/h y a su vez corresponde a una presión media de 18 mca. Como se
mencionó en la Sección 2.1.1.1 lo deseable es que el exponente del emisor corresponda a
emisores de régimen turbulento. Un emisor de exponente 1 corresponderá a un emisor de
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0
0.5
1
1.5
2
2.5
K
(l/s/
m^x)
x
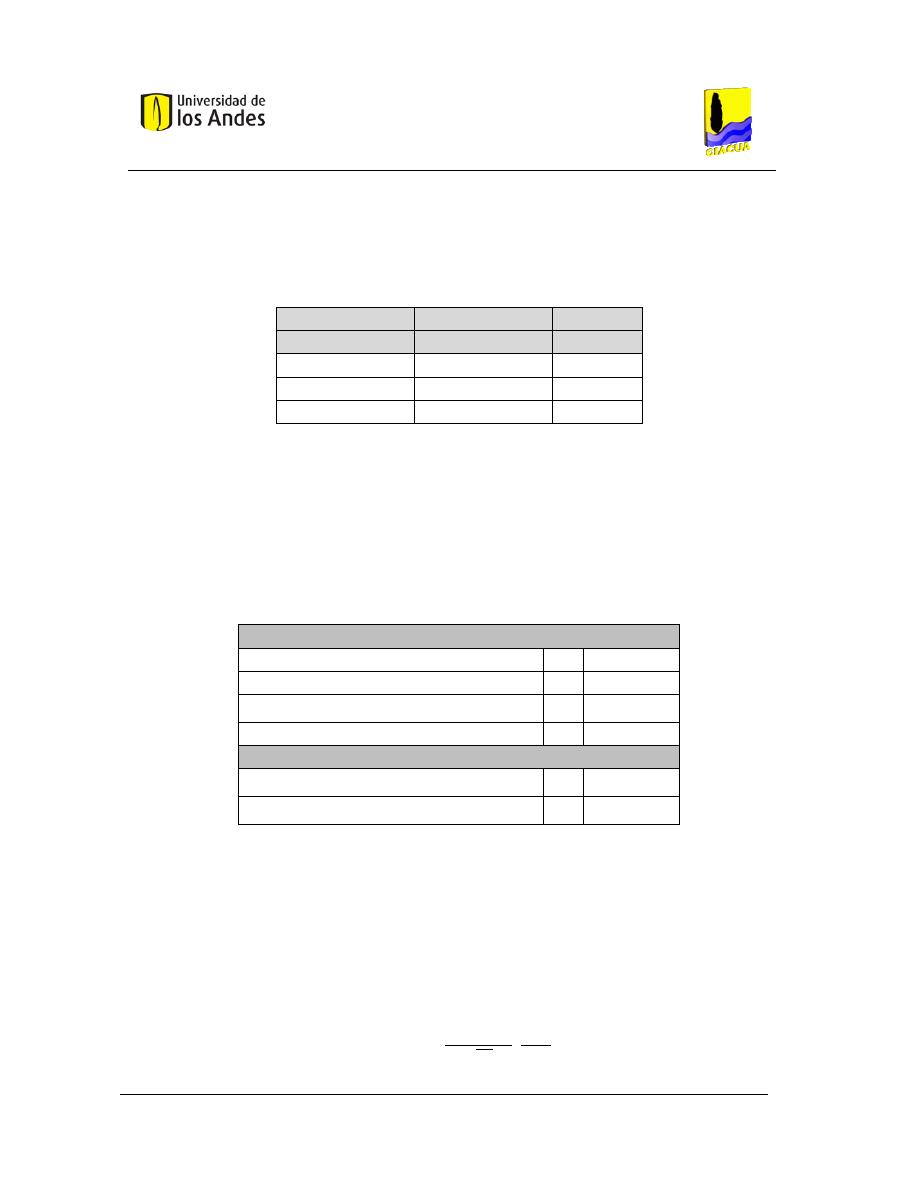
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
50
régimen de flujo laminar. Teniendo en cuenta esto, los diseños para los tres submódulos de riego
se concentraron en los exponentes de 0.3, 0.5 y 1.0. Para cada uno de estos exponentes
corresponde el coeficiente del emisor mostrado en la siguiente tabla:
Tabla 6. Coeficiente del emisor para los exponentes de diseño.
Coeficiente
Coeficiente
Exponente
l/s/m
l/h/m
0.014005448
50.420
0.3
0.007856742
28.284
0.5
0.001851852
6.667
1
El programa REDES no puede modelar dos emisores en un solo punto; por esta razón, para
modelar dos emisores por nudo, es necesario multiplicar el coeficiente que se tiene por dos. Dicho
esto y teniendo los diferentes emisores que se van a utilizar, se puede proceder a realizar los
diseños. Para esto, el primer paso es el cálculo de la tolerancia de presiones y tolerancia de
caudales. Los datos de entrada para los tres submódulos son los que se presentan en la Tabla 7.
Tabla 7. Datos de entrada para el diseño de los submódulos de estudio.
Uniformidad del Riego
Coeficiente de Uniformidad (CU)
0.8
Coeficiente de Variación (CV)
0.04
Número de Emisores por Planta (n
e
)
2 Emisores
Temperatura
15 °C
Características del Emisor
Caudal Promedio del Emisor (Q
m
)
120 Litros/hora
Presión Media de Operación (H
m
)
18 mca.
A partir de estos datos, se calcularon la tolerancia de caudales y de presiones como se muestra a
continuación.
3.2.1.1.
Cálculo tolerancia de caudales y presiones, exponente del emisor de 0.3.
Determinación del caudal de mínima presión:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
51
Determinación de la presión mínima:
Determinación de la presión media:
Cálculo de la tolerancia de presiones:
3.2.1.2.
Cálculo tolerancia de caudales y presiones, exponente del emisor de 0.5.
Determinación del caudal de mínima presión:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
52
Determinación de la presión mínima:
Determinación de la presión media:
Cálculo de la tolerancia de presiones:
3.2.1.3.
Cálculo tolerancia de caudales y presiones, exponente del emisor de 1.0.
Determinación del caudal de mínima presión:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
53
Determinación de la presión mínima:
Determinación de la presión media:
Cálculo de la tolerancia de presiones:
A partir de los resultados de tolerancia de caudales y presiones para cada uno de los emisores, se
puede observar que a medida que aumenta el exponente del emisor, el diseño se vuelve más
exigente. Esto quiere decir, que entre un diseño con exponente de 0.3 y un diseño con exponente
del emisor de 1.0, el diseño de 1.0 presentará un mayor costo debido a que la tolerancia de
presiones es menor. Al tenerse una tolerancia de presiones menor, el sistema cuenta con menor
energía disponible para gastar y por esta razón, los diámetros de las tuberías tienen que ser
mayores con el objetivo de reducir la velocidad del flujo y reducir las pérdidas por fricción.
Al tener la tolerancia de presiones, presión máxima (correspondiente a la presión de entrada al
submódulo) y la presión mínima, se puede proceder a hacer uso del programa REDES y la
metodología SOGH para realizar los diseños finales de los tres casos de estudio.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
54
3.2.2. Resultados diseños.
Una vez se ingresaron en el programa REDES cada uno de los submódulos de estudio, se procedió
a diseñar cada uno de ellos variando el exponente del emisor como se mencionó anteriormente.
Para cada grupo submódulo-exponente del emisor, se realizaron diferentes diseños, variando la
flecha de diseño. Las flechas que se probaron correspondían a números entre 0 (LGH
completamente recta) y 0.25; utilizando intervalos de 0.02 para probar un alto número de flechas
de diseño.
3.2.2.1.
Resultados Red Asimétrica 1.
Como se mostró en la Figura 11, este submódulo cuenta con 8 laterales, que se componen cada
uno de ellos de 25 puntos de alimentación a plantas (cada punto con 2 emisores de riego).
Habiendo establecido la tolerancia de presiones y caudales, se realizaron los diseños para
diámetros continuos y discretos, con criterio de aproximación al diámetro comercial más cercano.
Los resultados obtenidos se presentan en las siguientes gráficas.
Gráfica 3-2. Costos vs. Flecha, Red Asimétrica 1. Emisores con exponente 0.3.
En la Gráfica 3-2 se observa el costo del submódulo de riego, para diferentes flechas. Este caso
corresponde a la Red Asimétrica 1 usando emisores con exponente 0.3. Como se puede observar
en la gráfica, al realizar el diseño con diámetros continuos, existe un patrón. Es claro que la flecha
de mínimo costo es la flecha de 0.14 y que las flechas de máximo costo son las flechas 0 y de 0.25.
Por otro lado, se observa que al discretizar los diámetros este comportamiento Costo-Flecha se ve
totalmente afectado y no existe un patrón claro. Para analizar estos resultados y el
4050000
4100000
4150000
4200000
4250000
4300000
4350000
4400000
4450000
4500000
0
0.05
0.1
0.15
0.2
0.25
0.3
Costo
Sub
mód
ulo
(COP)
Flecha
Diámetros continuos
Diámetros discretos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
55
comportamiento de la curva para diámetros continuos, se muestran a continuación los resultados
de las presiones en los nudos de la red. Los resultados que se mostrarán corresponden
únicamente a las flechas 0, 0.14 y 0.25. Para hacer esto de forma clara, se van a definir 8 rutas que
puede tomar el agua; cada una de ellas correspondiente a cada lateral (Ver Figura 16).
En la Figura 16 se puede ver que existen ocho rutas posibles que puede tomar el agua, cada una de
ellas correspondiente a cada lateral. Como puede observarse en la figura, la ruta 8 corresponde a
la ruta crítica. La ruta crítica se define como la ruta 8, debido a que es el camino más largo que
debe tomar el agua (distancia topológica máxima).
Figura 16. Rutas posibles para la Red Asimétrica 1.
Una vez se han definido las rutas, a continuación se presentan las presiones en cada uno de los
puntos de cada ruta, para diámetros discretos y continuos. En cada gráfica se mantienen las
siguientes convenciones:
Presión Diámetros Continuos
Presión Diámetros Discretos
Presión Mínima
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
56
Gráfica 3-3. Presión en los nudos correspondientes a la ruta crítica (Ruta 8), Flecha 0.
En la Gráfica 3-3, se observa la presión en cada uno de los nudos que corresponden a la ruta
crítica, al haber diseñado con una flecha de 0. La gráfica muestra los resultados para diámetros
continuos (correspondientes a la LGH objetivo), diámetros discretos y la presión mínima (calculada
en la tolerancia de presiones). Como puede observarse la línea correspondiente a la presión en
diámetros continuos es una línea recta perfecta. Esta línea se traza desde su punto inicial en la
abscisa 0 (correspondiente a la entrada al submódulo), donde la presión es la presión máxima;
hasta llegar al punto más alejado topológicamente, donde la presión deseada es la presión
mínima. La pregunta que surge es cómo se ve la línea de presiones para las otras rutas. A
continuación se presentan las líneas de presiones correspondientes a las otras rutas posibles:
Gráfica 3-4. Presión en los nudos correspondientes a la Ruta 7, Flecha 0.
0
5
10
15
20
25
30
35
0
50
100
150
200
250
Presión
(mca)
Distancia topológica (m)
0
5
10
15
20
25
30
35
0
50
100
150
200
Presión
(mc
a)
Distancia topológica (m)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
57
Gráfica 3-5. Presión en los nudos correspondientes a la Ruta 6, Flecha 0.
Gráfica 3-6. Presión en los nudos correspondientes a la Ruta 5, Flecha 0.
Gráfica 3-7. Presión en los nudos correspondientes a la Ruta 4, Flecha 0.
0
5
10
15
20
25
30
35
0
50
100
150
200
Presión
(mca)
Distancia topológica (m)
0
5
10
15
20
25
30
35
0
50
100
150
200
Presión
(mca)
Distancia topológica (m)
0
5
10
15
20
25
30
35
0
50
100
150
200
Presión
(mca)
Distancia topológica (m)
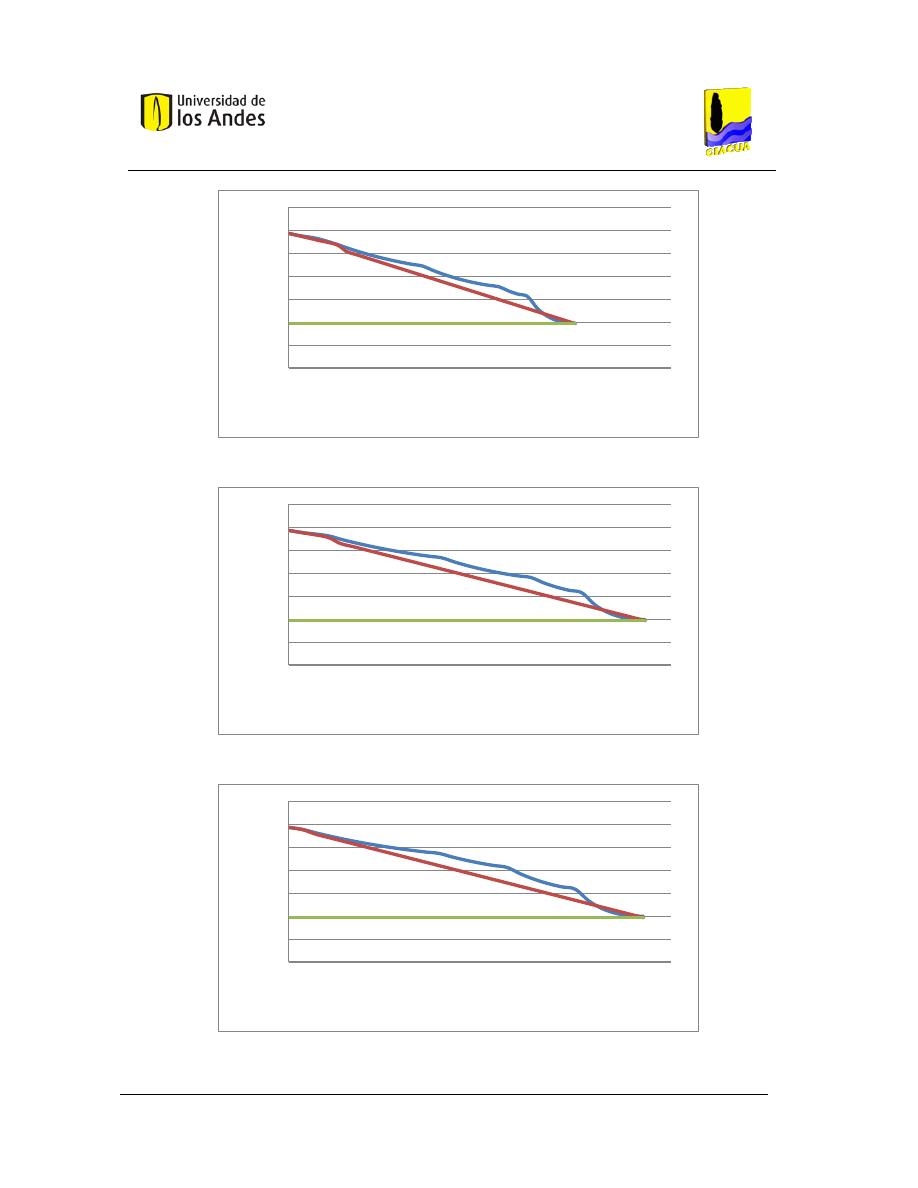
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
58
Gráfica 3-8. Presión en los nudos correspondientes a la Ruta 3, Flecha 0.
Gráfica 3-9. Presión en los nudos correspondientes a la Ruta 2, Flecha 0.
Gráfica 3-10. Presión en los nudos correspondientes a la Ruta 1, Flecha 0.
0
5
10
15
20
25
30
35
0
50
100
150
200
Presión
(mca)
Distancia topológica (m)
0
5
10
15
20
25
30
35
0
50
100
150
Presión
(mca)
Distancia topológica (m)
0
5
10
15
20
25
30
35
0
20
40
60
80
100
120
140
Presión
(mc
a)
Distancia topológica (m)
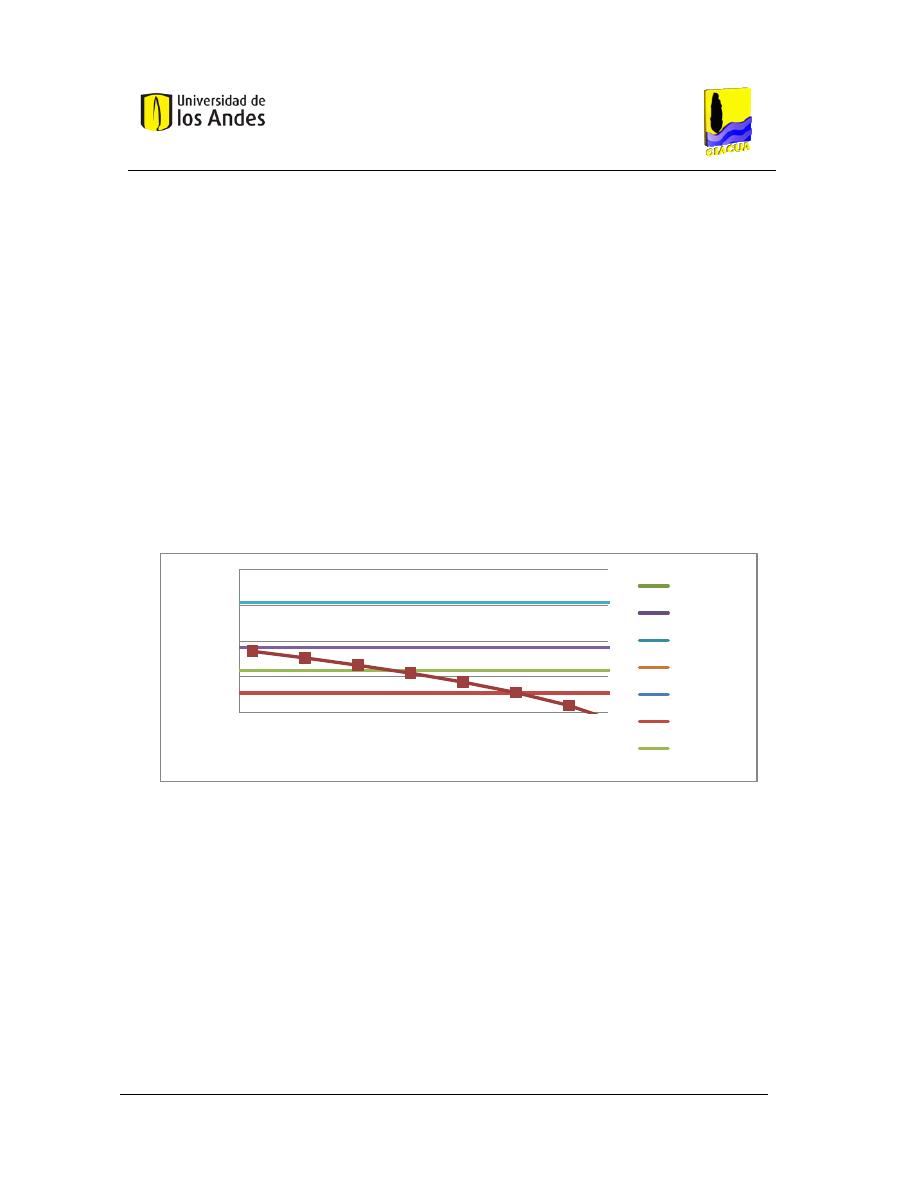
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
59
Las gráficas comprendidas entre la Gráfica 3-4 y la Gráfica 3-10 corresponden a las líneas de
presión de cada una de las rutas. Sobre estas gráficas hay que anotar, que a medida que el lateral
está más cerca del punto de entrada al submódulo, la deformación de la LGH objetivo es mayor
cuando se hace el redondeo. Adicionalmente se observa que a partir de la ruta 7 hasta la ruta 1, la
línea de presiones en los nudos se compone de dos líneas rectas. La primera de ellas corresponde
a los nudos ubicados sobre la tubería múltiple y la segunda línea recta corresponde al lateral. Si se
observa, por ejemplo la ruta 6, se observará que en una distancia topológica de 45 metros del
punto de entrada, existe un salto en la línea de presiones. Este salto ocurre porque la tubería
múltiple presenta unas presiones que permiten llevar el agua hasta el punto más distante del
lateral más lejano; de esta manera, las presión que tiene la tubería múltiple a una distancia de 45
metros del punto de entrada, son más que suficientes para poder llevar el agua al punto más
alejado del lateral 6 (en este caso). Si se analizan los diámetros continuos de diseño, en cada una
de las rutas se observa el siguiente comportamiento que explicaría lo que hace la metodología
SOGH. De esta manera, se grafica la distancia topológica al centro de cada una de las tuberías vs el
diámetro correspondiente. Para la tubería múltiple se obtiene el siguiente resultado:
Gráfica 3-11. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la tubería, Tubería múltiple,
Flecha 0.
En la Gráfica 3-11, se observan una serie de líneas horizontales, correspondientes a los diámetros
discretos ofrecidos por PAVCO; adicional a esto, se observa que existe una relación cuadrática
entre el diámetro de cada una de las tuberías y la distancia topológica del centro del tubo al punto
de entrada al submódulo. Esta misma gráfica se puede hacer para cada uno de los laterales de
riego, tal como se observa a continuación:
40
60
80
100
120
0
10
20
30
40
50
60
70
Dia
metro
(mm)
Distancia topológica (m)
D=12.7 mm
D=19.05
D=25.4
D=31.75
D=38.1
D=50.8
D=63.5
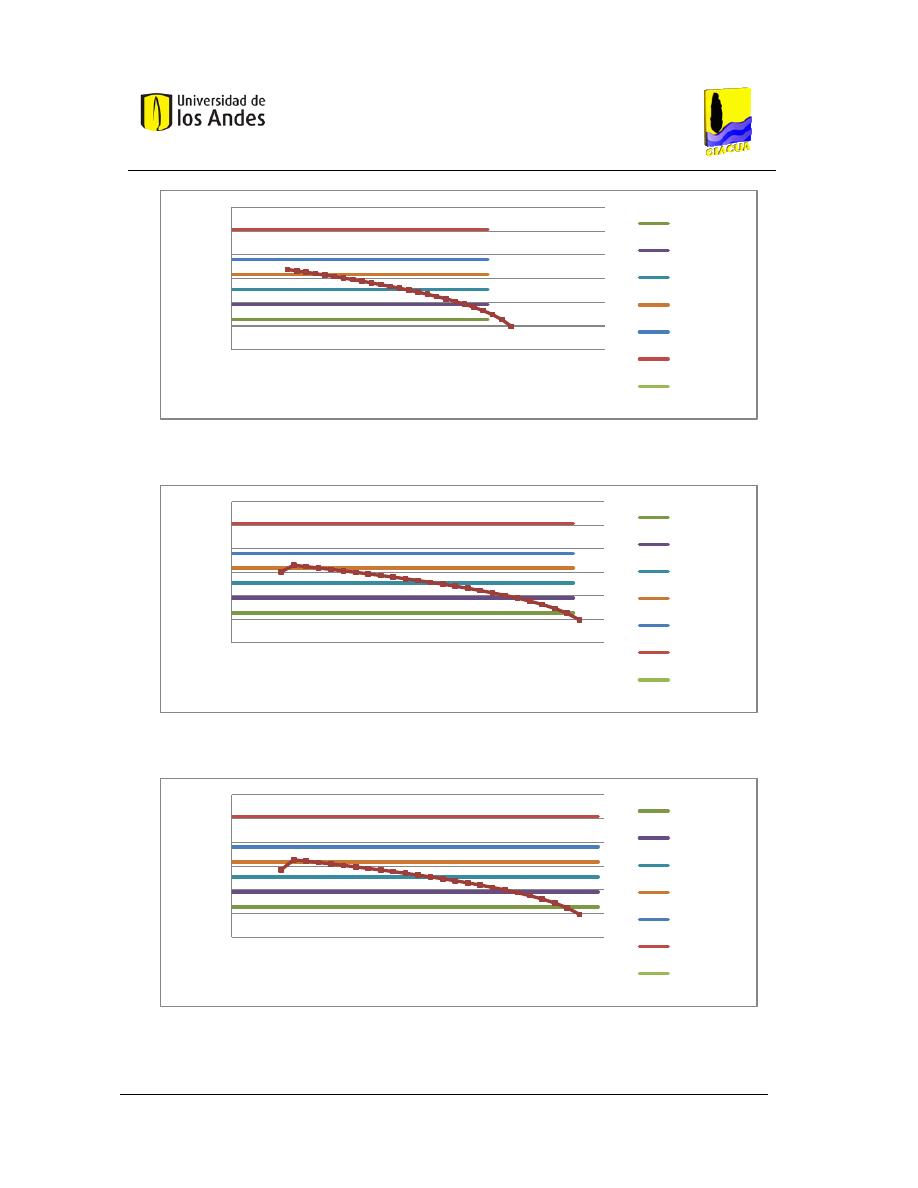
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
60
Gráfica 3-12. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la tubería, Lateral ruta 8
(crítica), Flecha 0.
Gráfica 3-13. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la tubería, Lateral ruta 7,
Flecha 0.
Gráfica 3-14. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la tubería, Lateral ruta 6,
Flecha 0.
0
10
20
30
40
50
60
50
100
150
200
250
Dia
metro
(mm)
Distancia topológica al centro de la tubería (m)
D=12.7 mm
D=19.05
D=25.4
D=31.75
D=38.1
D=50.8
D=63.5
0
10
20
30
40
50
60
50
100
150
200
Dia
metro
(mm)
Distancia topológica al centro de la tubería (m)
D=12.7 mm
D=19.05
D=25.4
D=31.75
D=38.1
D=50.8
D=63.5
0
10
20
30
40
50
60
40
90
140
190
Dia
metro
(mm)
Distancia topológica al centro de la tubería (m)
D=12.7 mm
D=19.05
D=25.4
D=31.75
D=38.1
D=50.8
D=63.5
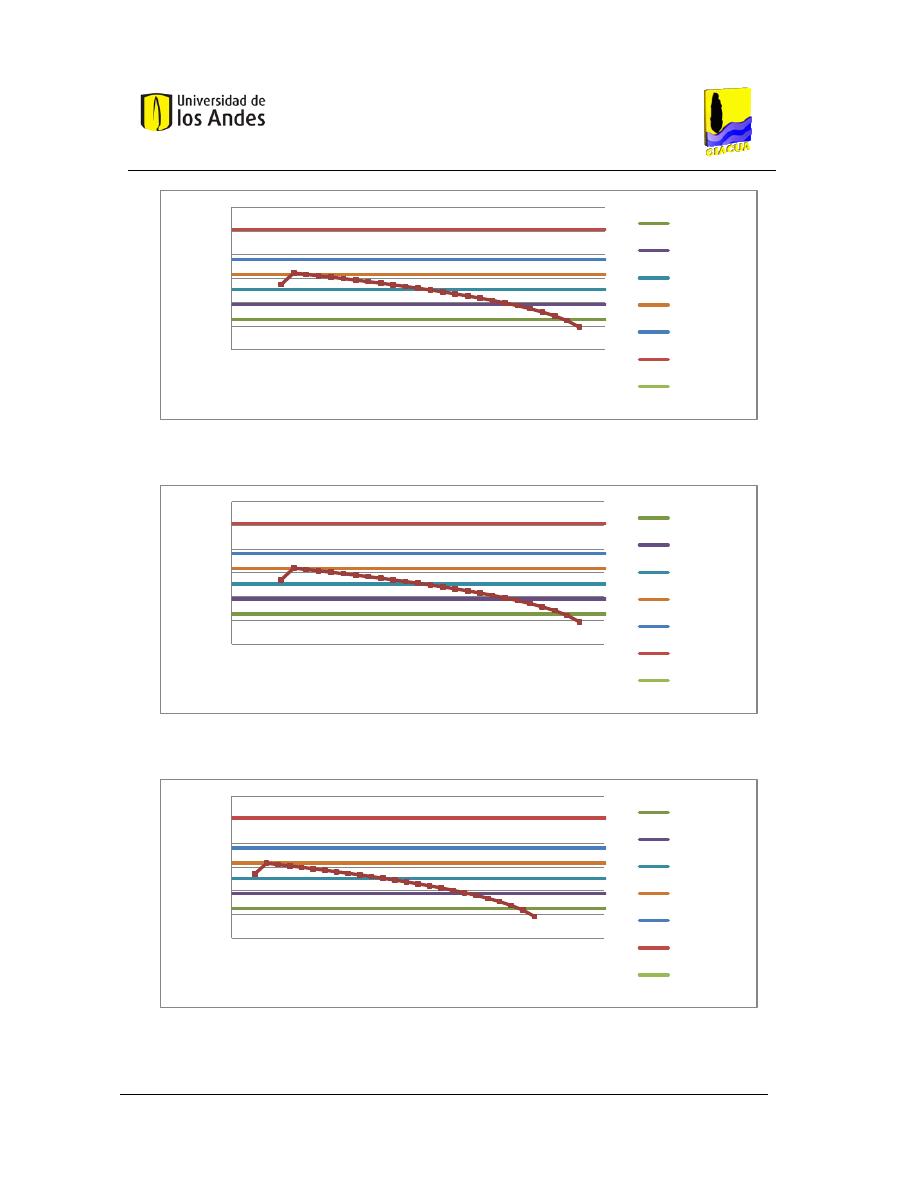
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
61
Gráfica 3-15. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la tubería, Lateral ruta 5,
Flecha 0.
Gráfica 3-16. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la tubería, Lateral ruta 4,
Flecha 0.
Gráfica 3-17. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la tubería, Lateral ruta 3,
Flecha 0.
0
10
20
30
40
50
60
30
80
130
180
Dia
metro
(mm)
Distancia topológica al centro de la tubería (m)
D=12.7 mm
D=19.05
D=25.4
D=31.75
D=38.1
D=50.8
D=63.5
0
10
20
30
40
50
60
20
70
120
170
Dia
metro
(mm)
Distancia topológica al centro de la tubería (m)
D=12.7 mm
D=19.05
D=25.4
D=31.75
D=38.1
D=50.8
D=63.5
0
10
20
30
40
50
60
20
70
120
170
Dia
metro
(mm)
distancia topológica al centro de la tubería (m)
D=12.7 mm
D=19.05
D=25.4
D=31.75
D=38.1
D=50.8
D=63.5
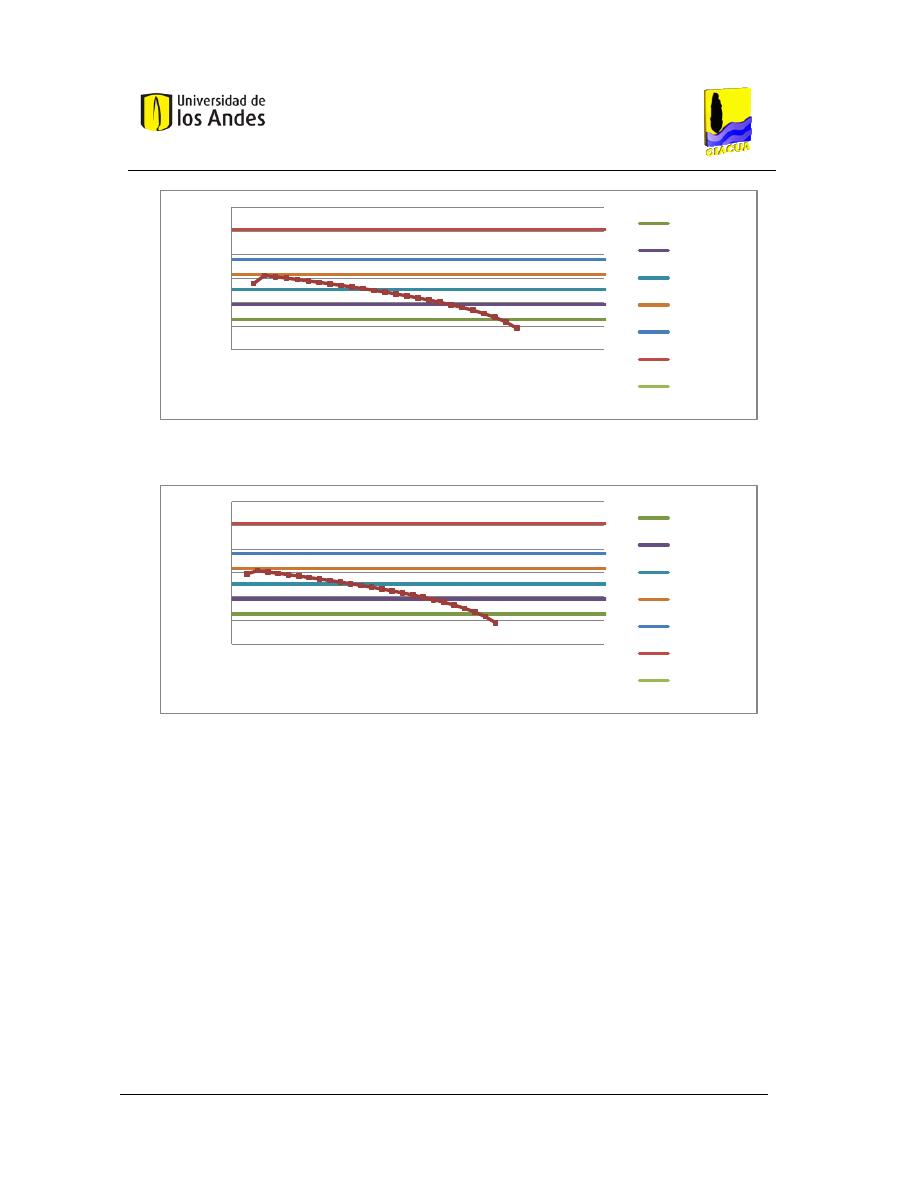
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
62
Gráfica 3-18. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la tubería, Lateral ruta 2,
Flecha 0.
Gráfica 3-19. Curva Distancia topológica al centro de la tubería vs. Diámetro continúo de la tubería, Lateral ruta 1,
Flecha 0.
Como puede observarse en las gráficas comprendidas entre la Gráfica 3-12 y la Gráfica 3-19, todos
los laterales de riego también presentan una relación cuadrática entre la distancia topológica al
centro de cada tubería y su diámetro. A partir de estas gráficas es posible explicar el salto que se
presenta en las líneas de presión presentadas anteriormente para cada una de las rutas. Si se
observa, por ejemplo la Gráfica 3-19 se observará que la curva se comporta como una cuadrática,
excepto por el primer punto. Este primer punto corresponde al diámetro de la primera tubería que
comprende el lateral. Si se observan todas las gráficas de diámetros de laterales, se aprecia que
este primer punto se presenta en todas ellas, menos en la correspondiente al lateral de la ruta
crítica.
La razón para que se presente el comportamiento descrito en el párrafo anterior, es que, como ya
se mencionó, para todos los laterales excepto el lateral crítico, antes de que el agua entre al
lateral, ésta presenta una energía más que suficiente para llevar el agua al punto final del lateral.
0
10
20
30
40
50
60
10
60
110
160
Dia
metro
(mm)
Distancia topológica al centro de la tubería (m)
D=12.7 mm
D=19.05
D=25.4
D=31.75
D=38.1
D=50.8
D=63.5
0
10
20
30
40
50
60
0
50
100
150
Dia
metro
(mm)
Distancia topológica al centro de la tubería (m)
D=12.7 mm
D=19.05
D=25.4
D=31.75
D=38.1
D=50.8
D=63.5

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
63
Lo anterior implica que la metodología SOGH reduzca drásticamente el diámetro de la tubería
inicial del lateral buscando que le presión en el último punto sea la mínima. Por esta razón se tiene
que en diámetros continuos, la primera tubería de los laterales 1 al 7 tenga un diámetro inferior al
del segundo tubo. Si se observa la Gráfica 3-12 (correspondiente a la ruta crítica), en esta no se
presenta la reducción del diámetro del primero tubo. Esto se debe a que el lateral 8 es el crítico.
Este comportamiento presentado para la flecha 0 sucede en todas las flechas. Esto quiere decir,
que en todas las líneas de presión para todas las flechas que se probaron, se presenta una relación
cuadrática entre los diámetros de las tuberías y la distancia topológica al centro de las tuberías.
Adicionalmente, en todas las flechas ocurre el salto que se mostró para las diferentes rutas entre
la 1 y la 7. También vale la pena decir que este comportamiento se mantiene inclusive para
diferentes exponentes de emisor.
Sobre lo anterior se puede decir que sí existe una curva cuadrática que relaciona el diámetro de las
tuberías con su distancia topológica, y adicionalmente se tienen unas ecuaciones lineales que
definen los diámetros comerciales suministrados por PAVCO, es posible que exista una manera de
hacer uso de estos resultados para realizar un proceso de redondeo que mantenga un
comportamiento como el que se presenta para la curva Costo-Flecha mostrado para diámetros
continuos.
Ahora bien, una vez se inicia el análisis de cómo se comportan las líneas de presión en lo nudos y
la relación de los diámetros por tuberías en cada una de las rutas, vale la pena observar qué
sucede con el coeficiente de uniformidad en cada uno de los diseños y qué sucede con la curva
Costo-Flecha para los diferentes exponentes de emisor y para los otros casos de estudio.
En este punto vale la pena retomar la Gráfica 3-2, y recordar que para un exponente de los
emisores de 0.3 en la Red Asimétrica 1, se tenía que la flecha de diseño de mínimo costo (para
diámetros continuos) era la flecha de 0.14. Tal como se observará en las siguientes gráficas, esta
flecha se mantiene para el caso de emisores con exponente 0.5 y 1.0.
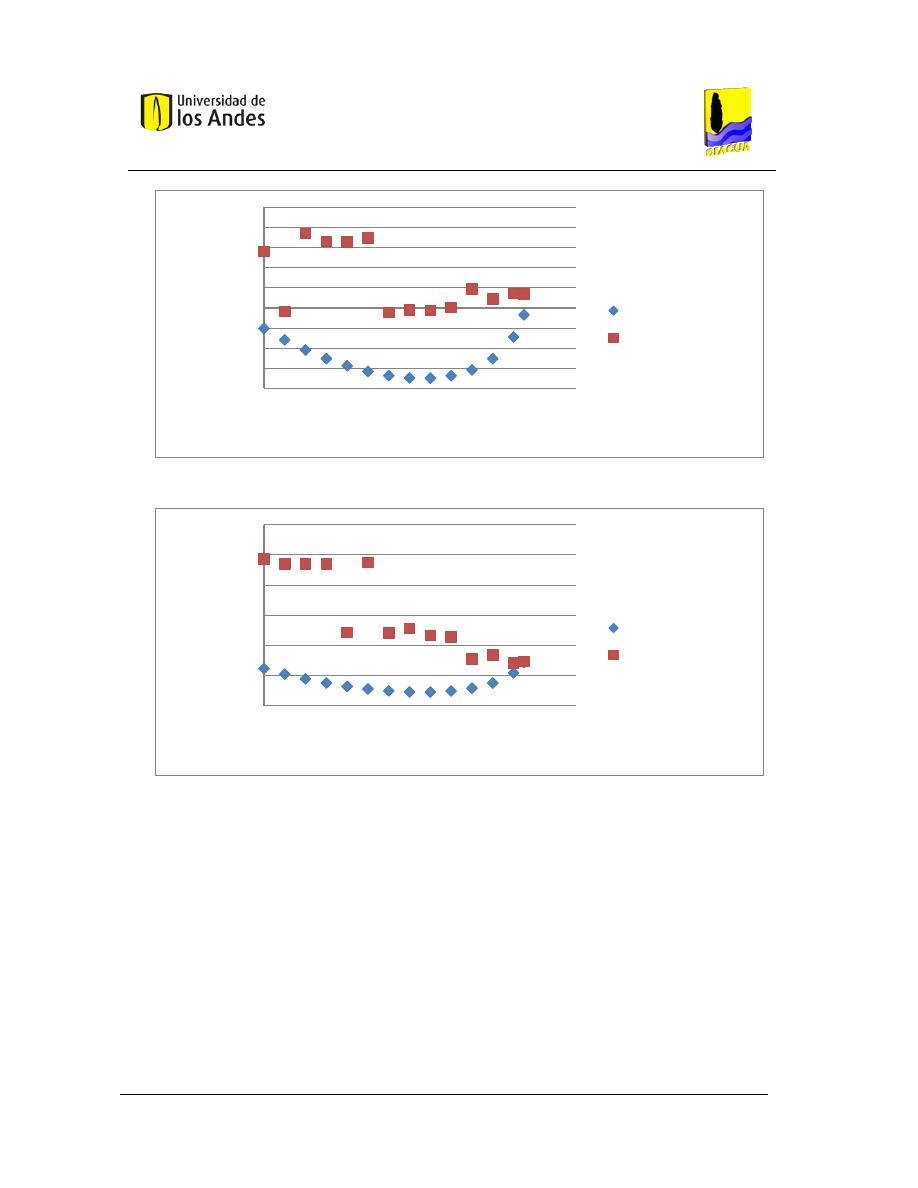
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
64
Gráfica 3-20. Costos vs. Flecha, Red Asimétrica 1. Emisores con exponente 0.5.
Gráfica 3-21. Costos vs. Flecha, Red Asimétrica 1. Emisores con exponente 1.0.
Como se observa en la Gráfica 3-20 y la Gráfica 3-21, la flecha de mínimo costo correspondiente
para éste submódulo, independientemente del exponente de los emisores, es una flecha de 0.14.
Este resultado aunque no resulta claro si permite plantear la hipótesis de que la flecha de mínimo
costo corresponderá a una flecha intermedia. Para entender, el por qué de esta hipótesis, se debe
observar la siguiente gráfica:
4600000
4650000
4700000
4750000
4800000
4850000
4900000
4950000
5000000
5050000
0
0.05
0.1
0.15
0.2
0.25
0.3
Costo
(COP)
Flecha
Diámetros continuos
Diámetros discretos
5600000
5800000
6000000
6200000
6400000
6600000
6800000
0
0.05
0.1
0.15
0.2
0.25
0.3
Costo
del
Sub
mód
ulo
(COP)
Flecha
Diámetros continuos
Diámetros discretos
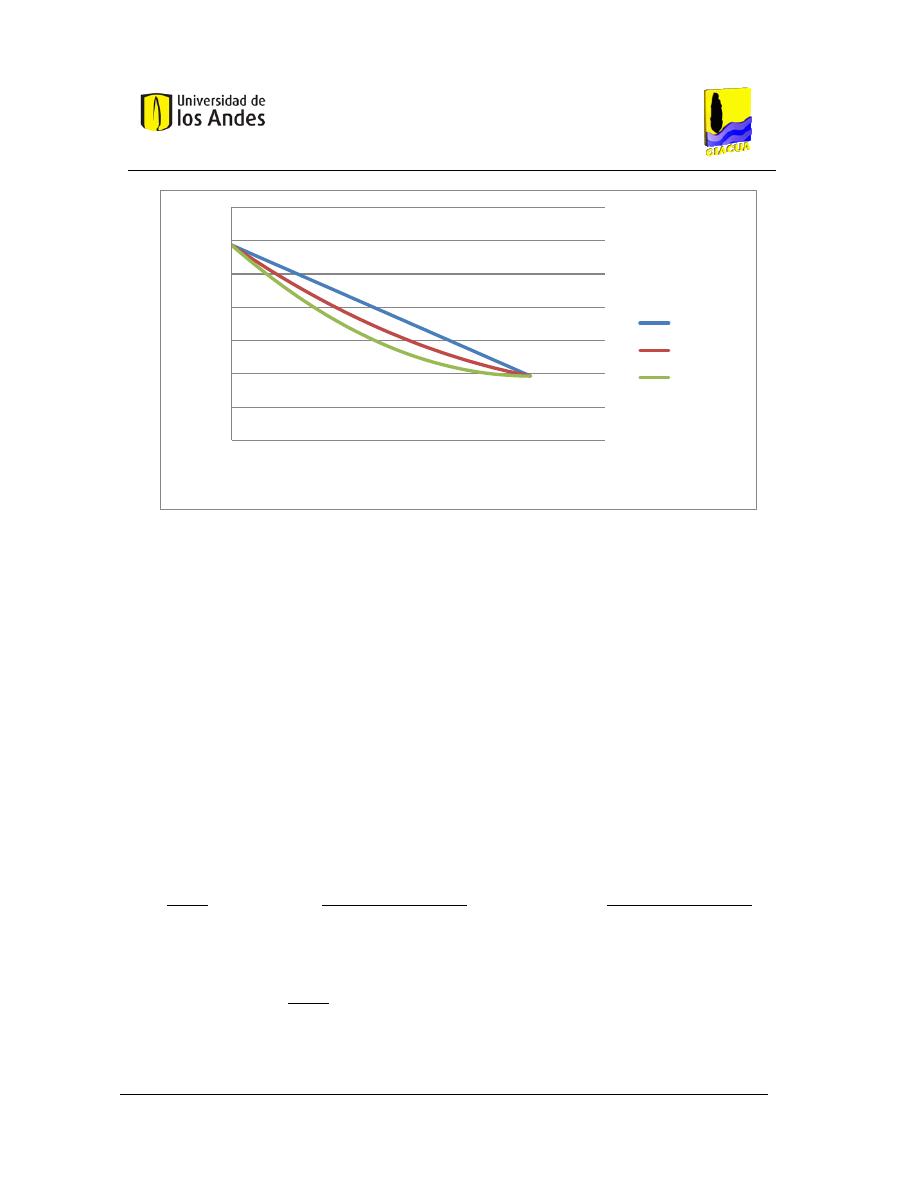
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
65
Gráfica 3-22. Línea de presiones para diferentes flechas, Flecha 0, 0.14, 0.25.
En la gráfica anterior se puede ver que la pendiente de la línea de presiones no es igual para
ninguna de las flechas. Se puede observar, que la flecha 0 mantiene una pendiente constante y
que las líneas de presión de las flechas 0.14 y 0.25 tienen una pendiente variable a lo largo de la
curva. De esta manera, la pregunta que surge es cómo se comportan las pendientes de fricción
objetivo. Estas son las que determinarán el diámetro final de las tuberías.
Si se tiene una alta pendiente en la línea de presiones, esto implicará que el sistema está en
capacidad de gastar mayor energía y por lo tanto puede hacer uso de diámetros menores.
Teniendo en cuenta lo anterior, se realizó el siguiente procedimiento para observar cómo se
comportan las pendientes de las líneas de presión a lo largo de la ruta crítica, en el que se hizo uso
de la derivada de la ecuación de la LGH objetivo para cada una de las flechas que se están
analizando (Flechas 0, 0.14 y 0.25).
Para el caso de la flecha 0 se parte de:
0
5
10
15
20
25
30
35
0
50
100
150
200
250
Presión
(mca)
Distancia topológica (m)
Flecha 0
Flecha 0.14
Flecha 0.25

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
66
Obteniendo, que para el caso de la Red Asimétrica 1 con emisores de exponente 0.3, la pendiente
de la línea de presiones es de 0.098395. Esto quiere decir que para la flecha de 0, se está teniendo
como objetivo, una pérdida de energía de 9.83 centímetros por cada metro que se recorre en la
ruta crítica. Este mismo procedimiento se puede realizar para las flechas de 0.14 y 0.25, tal como
se muestra a continuación. Para la flecha de 0.14 se tiene:
Y para la flecha de 0.25:
Como se puede observar en los anteriores procedimientos, y como es de esperarse, la pendiente
de la línea de presiones (igual a la pendiente de la LGH objetivo para el caso de topografías
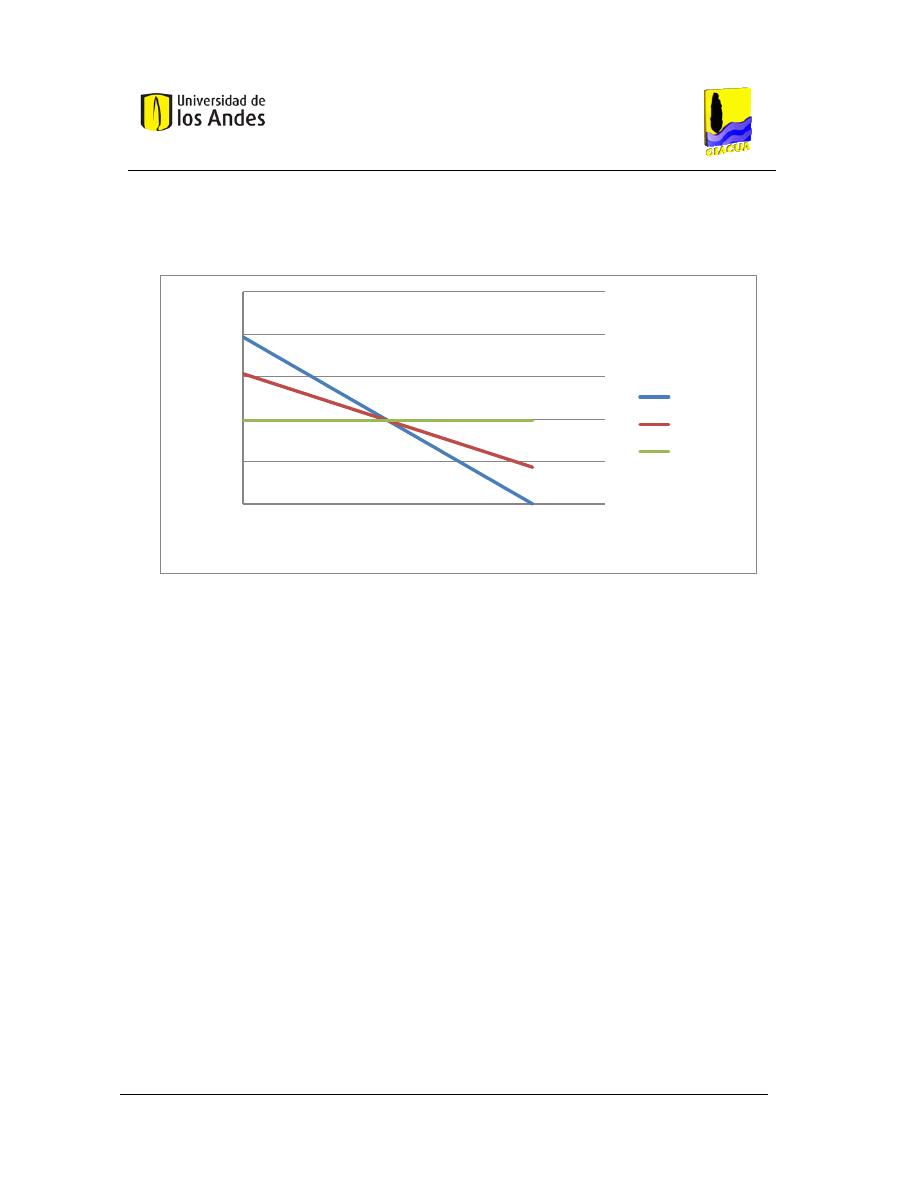
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
67
planas), corresponde a una ecuación lineal para los casos de las flechas de 0.14 y 0.25. Si se realiza
la gráfica de cada una de las ecuaciones obtenidas para estas tres flechas de análisis, se observan
los siguientes resultados:
Gráfica 3-23. Pendiente de fricción vs distancia topológica, Red Asimétrica 1, exponente del emisor 0.3.
Los resultados presentados en la Gráfica 3-23 resultan claves para entender el comportamiento de
la curva Costo-Flecha. La hipótesis planteada anteriormente hacía referencia a que las redes de
mínimo costo corresponderán a las flechas intermedias. Lo que se puede deducir de la Gráfica
3-23, es que a medida que la flecha de diseño crece, los diámetros de las tuberías iniciales irán
reduciéndose; contrario a esto, las tuberías finales irán aumentando su diámetro. Si se comparan
las tres pendientes de fricción de las tres flechas, se observa que entre la abscisa 0 y la abscisa
100, la flecha de 0.25 tiene una mayor pendiente de fricción y por lo tanto conllevará a diámetros
menores que las flechas 0 y 0.14. Por el contrario, entre la abscisa 100 y la abscisa 200, la flecha
de 0.25 pasa a ser la que tiene una menor pendiente de fricción y por lo tanto será la que lleve a
tener mayores diámetros en las tuberías ubicadas entre estas dos últimas abscisas. En la gráfica
puede verse que la flecha intermedia (la de 0.14) siempre se encuentra en un punto medio; esto
quiere decir que, a diferencia de las flechas de 0 y 0.25, esta flecha no representa los mayores
costos en ninguno de los tramos de la ruta crítica. De esta manera, queda demostrado que aunque
una flecha extrema como la de 0 o la 0.25 conlleven a tener diámetros menores en ciertos puntos
del sistema, solo una flecha intermedia es capaz de llevar a tener los costos globales del sistema
en un mínimo. Es posible que la flecha intermedia no sea exactamente el promedio entre la flecha
0 y 0.25, pero si es claro que se encuentra en un rango intermedio entre estos dos valores.
0
0.05
0.1
0.15
0.2
0.25
0
50
100
150
200
250
Pend
iente
de fri
cción
Distancia topológica (m)
Flecha 0.25
Flecha 0.14
Flecha 0
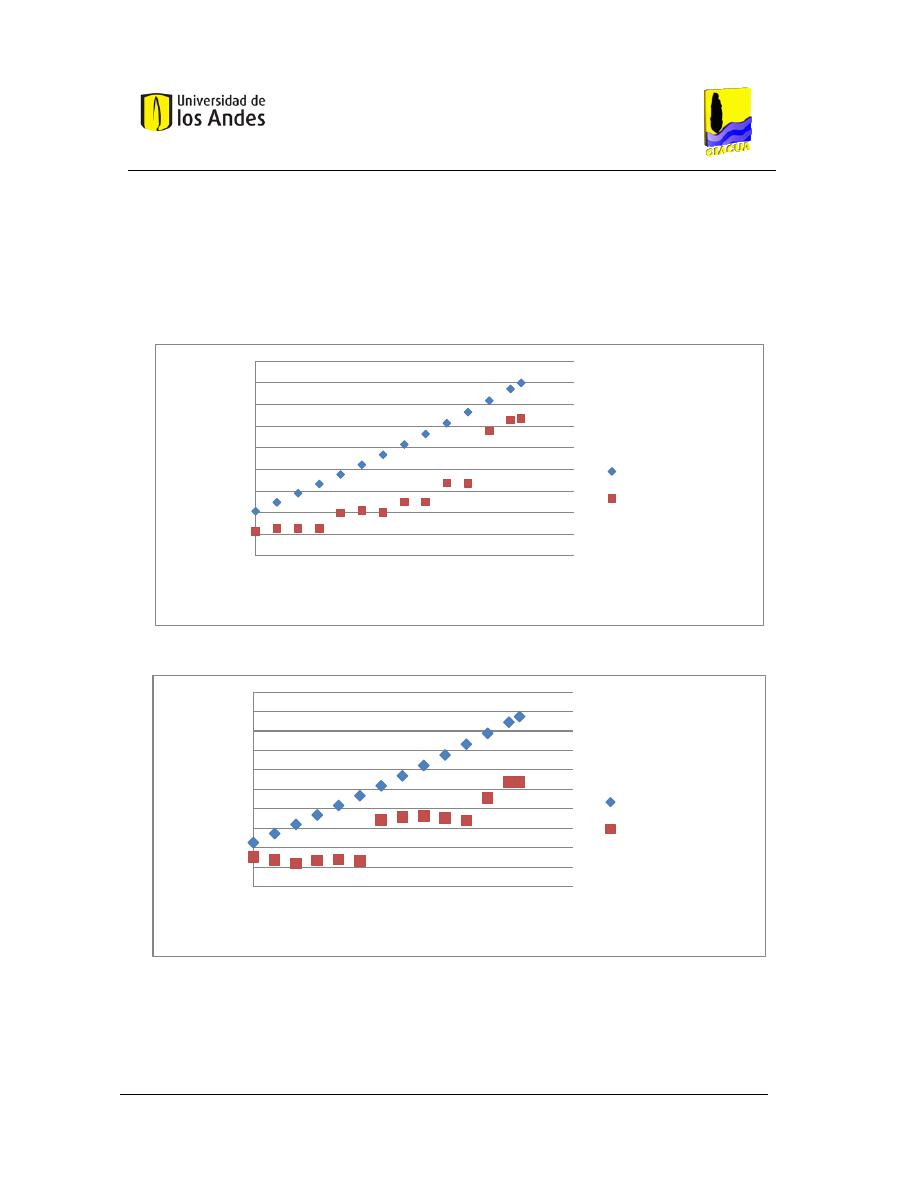
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
68
Por último y para concluir el análisis y obtención de resultados de la Red Asimétrica 1, se puede
decir que todos los diseños condujeron a un coeficiente de uniformidad superior al establecido por
el diseño agronómico. En las siguientes figuras se observan los resultados para el coeficiente de
uniformidad final de la Red Asimétrica 1, variando el exponente del emisor. En las figuras se puede
observar el coeficiente de uniformidad resultante después de realizar los diseños variando las
flechas y usando diámetros continuos y discretos.
Gráfica 3-24. Flecha vs. Coeficiente de uniformidad resultante. Red Asimétrica 1, exponente del emisor 0.3.
Gráfica 3-25. Flecha vs. Coeficiente de uniformidad resultante. Red Asimétrica 1, exponente del emisor 0.5.
0.8
0.81
0.82
0.83
0.84
0.85
0.86
0.87
0.88
0.89
0
0.05
0.1
0.15
0.2
0.25
0.3
Coeficiente
de Uniformidad
Fin
al
(CU)
Flecha
Diámetros Continuos
Diámetros Discretos
0.79
0.8
0.81
0.82
0.83
0.84
0.85
0.86
0.87
0.88
0.89
0
0.05
0.1
0.15
0.2
0.25
0.3
Coe
fic
ie
n
te
d
e Un
if
or
m
id
ad
Fin
al
(CU
)
Flecha
Diámetros Continuos
Diámetros Discretos
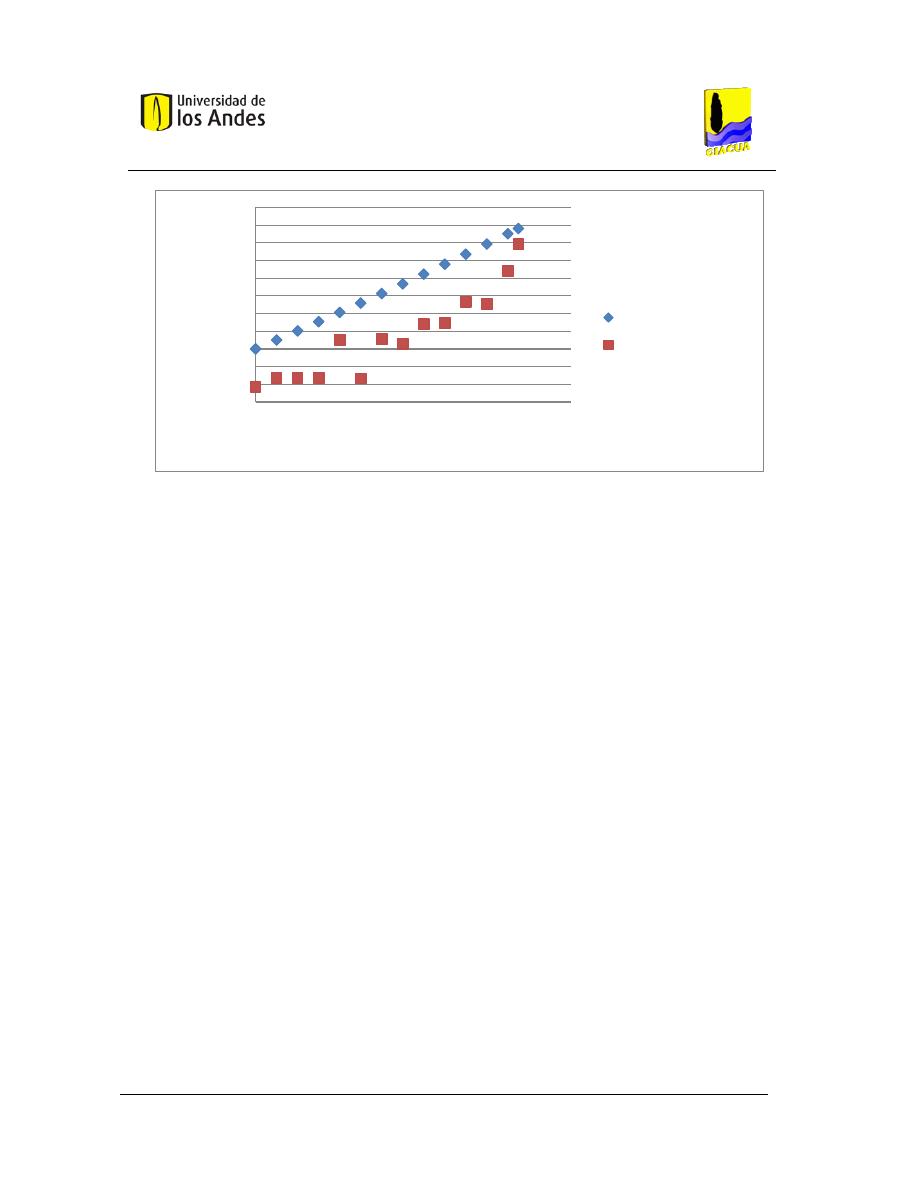
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
69
Gráfica 3-26. Flecha vs. Coeficiente de uniformidad resultante. Red Asimétrica 1, exponente del emisor 1.0.
Respecto a los resultados correspondientes al coeficiente de uniformidad final, se puede observar
que en diámetros continuos, todos los diseños para los diferentes exponentes de emisor, cumplen
con el coeficiente de uniformidad del diseño agronómico. Por otro lado, de los 84 diseños
presentados en las gráficas de coeficiente de uniformidad, solo 5 de ellos no cumplen con éste.
Corresponden a los diseños con emisores de exponente 1.0.
3.2.2.2.
Resultados Red Simétrica .
Para la Red Simétrica, se realizaron los mismos análisis que se hicieron para la Red Asimétrica 1.
Los resultados encontrados fueron básicamente los mismos. Esto quiere decir:
-
Existe una relación cuadrática entre el diámetro de diseño continuo de cada una de las
tuberías y su distancia topológica al punto de entrada.
-
La primera tubería de cada uno de los laterales, a excepción del lateral crítico, presenta un
diámetro inferior al del segundo tubo, con el objeto de reducir la energía disponible en el
lateral y llegar al último nudo con la presión mínima.
-
La discretización de diámetros, al diámetro comercial más cercano, no presenta ningún
tipo de patrón y adicionalmente, deteriora completamente la línea de gradiente hidráulico
objetivo del diseño.
-
Todos los diseños realizados con diámetros continuos cumplen con el coeficiente de
uniformidad establecido por el diseño agronómico.
Por otro lado, respecto a la curva Costo-Flecha, aunque se mantuvo una forma de la curva muy
parecida, la flecha que conlleva el mínimo costo cambió. Los resultados de las curvas Costo-Flecha
0.78
0.79
0.8
0.81
0.82
0.83
0.84
0.85
0.86
0.87
0.88
0.89
0
0.05
0.1
0.15
0.2
0.25
0.3
Coeficiente
de Uniformidad
Fin
al
(CU)
Flecha
Diámetros Continuos
Diámetros Discretos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
70
para la red simétrica y los tres tipos de emisores (con exponente 0.3, 0.5 y 1.0) se muestran a
continuación:
Gráfica 3-27. Costos vs. Flecha, Red Simétrica. Emisores con exponente 0.3.
Gráfica 3-28. Costos vs. Flecha, Red Simétrica. Emisores con exponente 0.5.
7600000
7800000
8000000
8200000
8400000
8600000
8800000
9000000
9200000
9400000
0
0.05
0.1
0.15
0.2
0.25
0.3
Costo
d
el
Sub
mód
ulo
(COP)
Flecha
Diámetros continuos
Diámetros Discretos
8800000
9000000
9200000
9400000
9600000
9800000
10000000
10200000
0
0.05
0.1
0.15
0.2
0.25
0.3
Costo
del
su
bm
ódu
lo
(COP)
Flecha
Diámetros continuos
Diámetros Discretos
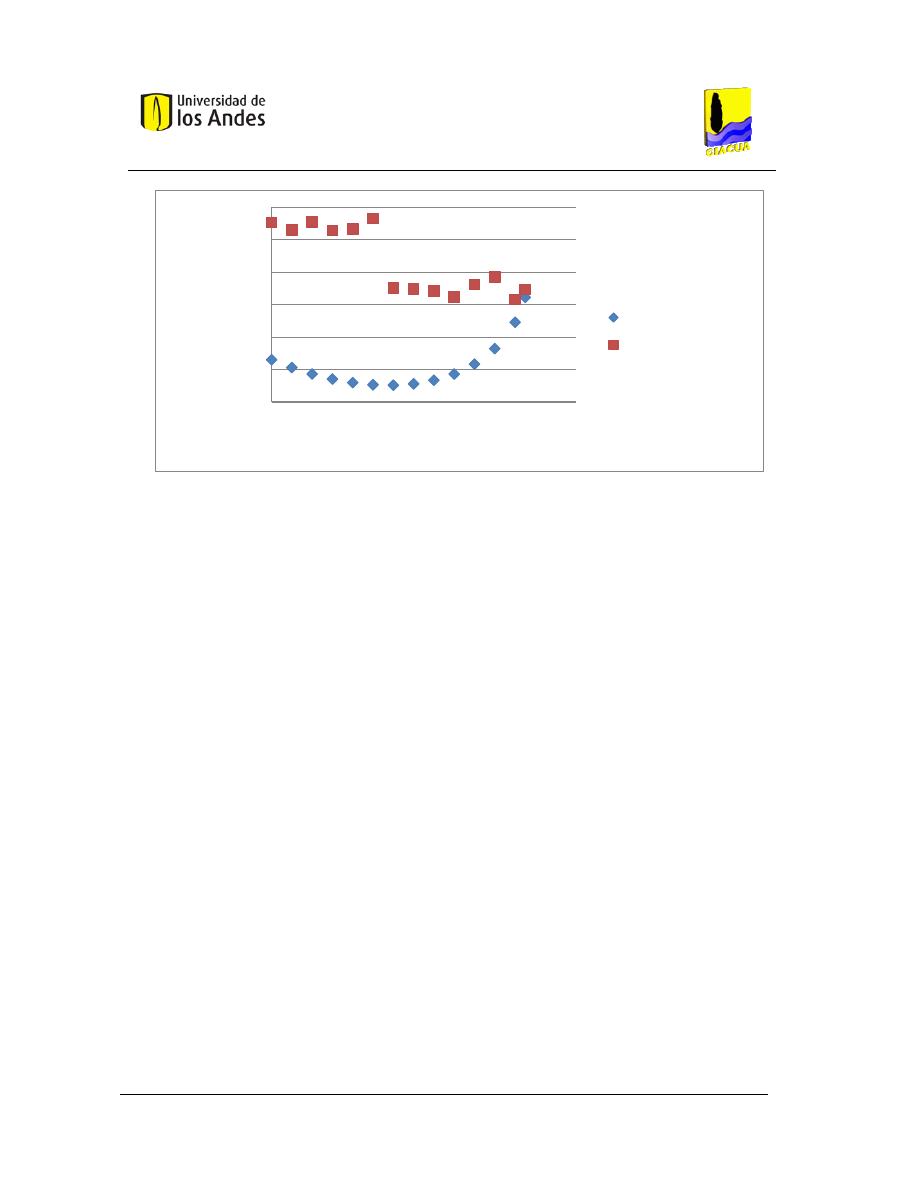
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
71
Gráfica 3-29. Costos vs. Flecha, Red Simétrica. Emisores con exponente 1.0.
Como es posible observar en las gráficas anteriores, para la Red Simétrica se cumple que la flecha
de mínimo costo corresponde a una flecha de 0.12. También se observa que, al igual que sucedió
con la Red Asimétrica 1, la discretización de diámetros afecta completamente la curva Costo-
Flecha respecto a la que se tiene inicialmente para diámetros continuos. Y adicional a esto, y
aunque ya se ha explicado la razón, entre mayor es el exponente de los emisores en el submódulo,
mayor es el costo del sistema; esto se debe en principio a que para los mayores exponentes, la
tolerancia de presiones es menor y por lo tanto se tiene menor energía disponible para ser
gastada.
3.2.2.3.
Resultados Red Asimétrica 2.
Finalmente, y para concluir con la parte de resultados que deja una serie de preguntas abiertas
para la segunda fase de este trabajo, se presentan los resultados obtenidos para la Red Asimétrica
2. A continuación se pueden apreciar los resultados para las curvas Costo-Flecha de este
submódulo usando los tres tipos de emisores analizados para los otros casos.
11000000
11200000
11400000
11600000
11800000
12000000
12200000
0
0.05
0.1
0.15
0.2
0.25
0.3
Costo
del
Sub
mód
ulo
(COP)
Flecha
Diámetros continuos
Diámetros Discretos
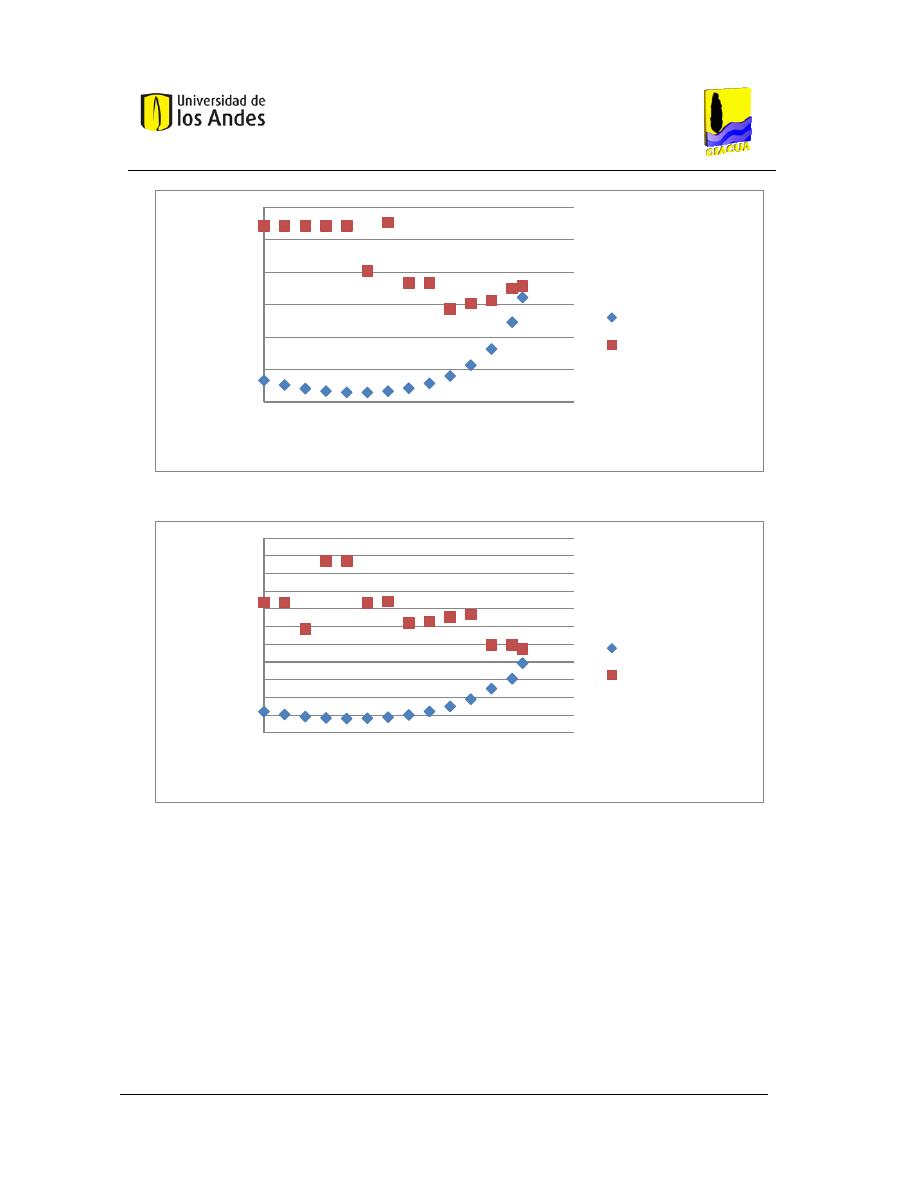
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
72
Gráfica 3-30. Costos vs. Flecha, Red Asimétrica 2. Emisores con exponente 0.3
Gráfica 3-31. Costos vs. Flecha, Red Asimétrica 2. Emisores con exponente 0.5.
4800000
4900000
5000000
5100000
5200000
5300000
5400000
0
0.05
0.1
0.15
0.2
0.25
0.3
Costo
del
Sub
mód
ulo
(COP)
Flecha
Diámetros Continuos
Diámetros discretos
5400000
5500000
5600000
5700000
5800000
5900000
6000000
6100000
6200000
6300000
6400000
6500000
0
0.05
0.1
0.15
0.2
0.25
0.3
Costo
del
Sub
mód
ulo
(COP)
Flecha
Diámetros Continuos
Diámetros Discretos
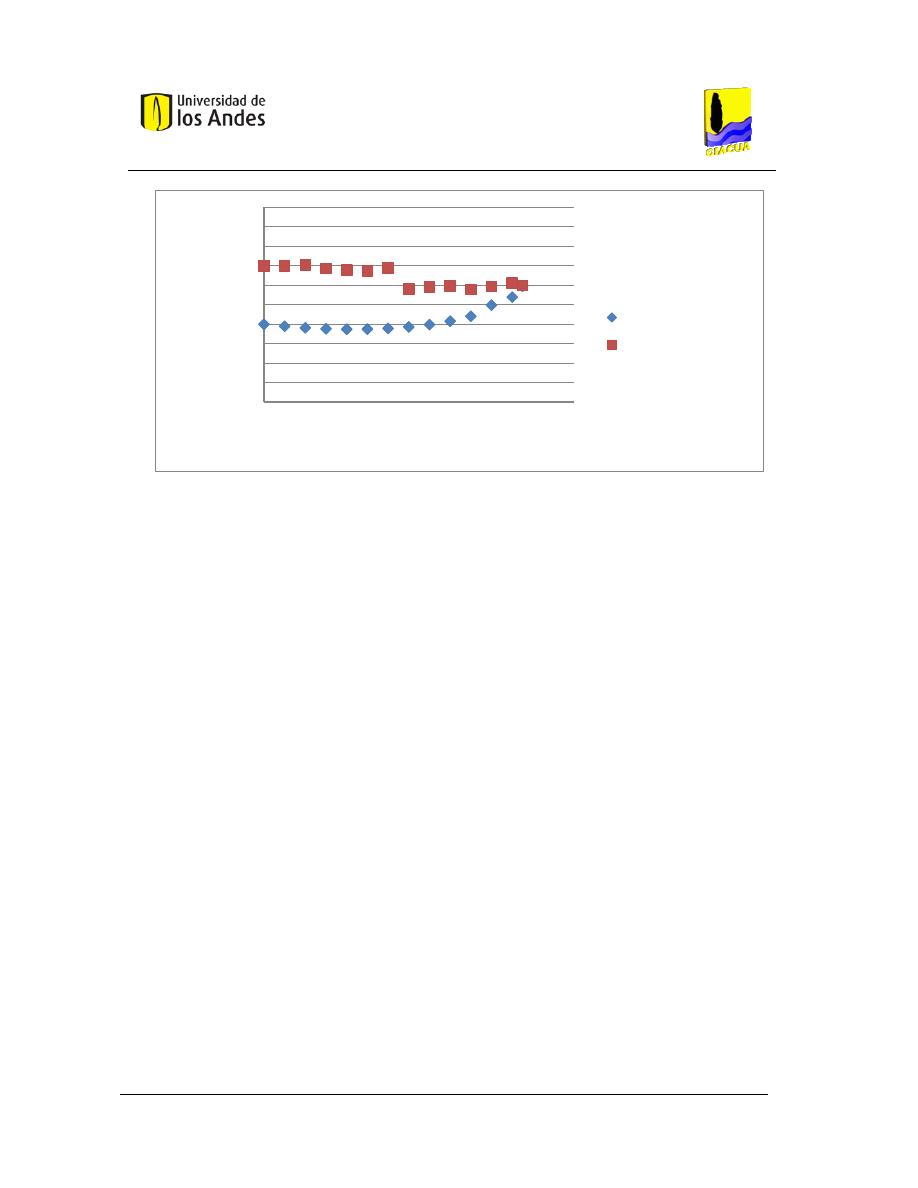
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
73
Gráfica 3-32. Costos vs. Flecha, Red Asimétrica 2. Emisores con exponente 1.0.
En los resultados mostrados en las gráficas anteriores se observa que para esta red, la flecha de
mínimo costo no se encuentra dentro de las flechas intermedias. La flecha de mínimo costo para
esta red es la flecha de 0.08. De esta manera se aprecia, que la topología de la red tiene alguna
implicación sobre la flecha de mínimo costo. Esto se puede afirmar debido a que las tres redes
analizadas presentan exactamente las mismas características topográficas (redes planas), mismos
exponentes de emisor, mismo coeficiente de uniformidad (CU) y misma tolerancia de presiones y
caudales.
6000000
6200000
6400000
6600000
6800000
7000000
7200000
7400000
7600000
7800000
8000000
0
0.05
0.1
0.15
0.2
0.25
0.3
Costo
del
Sub
mód
ulo
(COP)
Flecha
Diámetros Continuos
Diámetros Discretos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
74
3.3. Análisis de la metodología propuesta por Bermúdez.
Para llevar a cabo un análisis de la metodología propuesta por Bermúdez (2011), se decidió hacer
una prueba para la Red Asimétrica 1 y el emisor del exponente de 0.3. El procedimiento para llevar
a cabo esto se presenta a continuación.
3.3.1. Red Asimétrica 1, con emisores de exponente 0.3.
Teniendo en cuenta el procedimiento propuesto por Bermúdez, se realizó el siguiente proceso con
el objetivo de determinar la presión de entrada óptima al submódulo de riego:
1. Determinación de los coeficientes
y de la ecuación cuadrática ajustada.
Para determinar los parámetros α, β y γ correspondientes a una presión media (Hm) de 18 mca y
un exponente del emisor de 0.3, se hacen uso de las ecuaciones planteadas por Bermúdez y
mediante interpolación lineal, se obtienen estos parámetros. Según se explica a continuación:
Para determinar α se tiene que:
Para determinar β:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
75
Para determinar γ:
2. Determinación de coeficiente de variación total
.
Para la determinación de este coeficiente se hace uso de la Ecuación 2.36.
Ecuación 2.36
donde
corresponde al coeficiente de variación debido al Coeficiente de Uniformidad
impuesto por el diseño agronómico (CU
I
), que calcula se de la siguiente forma:
y
corresponde al coeficiente de variación debido al Coeficiente de Variación de Fabricación
del emisor. Se calcula de la siguiente forma:
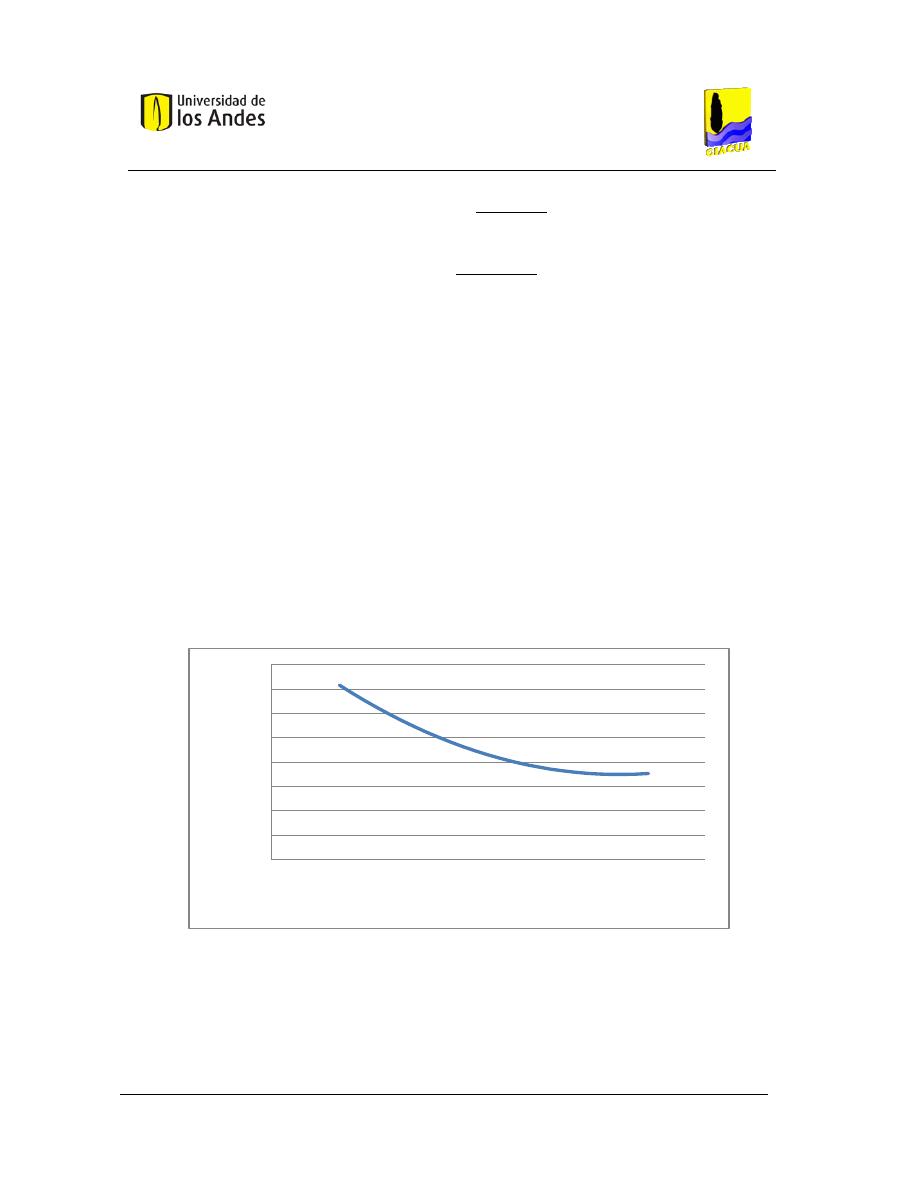
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
76
De esta forma, se obtiene que el coeficiente de variación total es:
3. Determinación de la curva CU
R
vs. PES.
Para la determinación de la curva CU
R
vs. PES se debe tener como dato de entrada la presión
mínima de operación del submódulo (h
mp
), determinada mediante la tolerancia de caudales y
presiones (Numeral 3.2.1.1). Con estos resultados, se obtiene la Ecuación 2.35 y mediante la cual
se obtiene la Gráfica 3-33.
Ecuación 2.35
Gráfica 3-33. Curva PES vs. Coeficiente de uniformidad resultante, Red Asimétrica 1, exponente 0.3.
De acuerdo con los resultados obtenidos por Bermúdez, en este caso se debe escoger una presión
de entrada al submódulo igual a 33.74 mca. Esta presión corresponde a un valor del parámetro M
de 2.88. Como se puede observar este valor de M es superior al que se utilizó en la Sección 3.2.1.1
en la página 50 de este documento, donde el valor utilizado es de 2.5. Antes de mostrar los
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
0
10
20
30
40
50
60
CU
resultante
PES (mca)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
77
resultados obtenidos, es claro que al haber aumentado la presión de entrada y haber mantenido la
presión mínima, se tendrá mayor energía disponible para gastar y por lo tanto el diseño obtenido,
de acuerdo con la metodología de Bermúdez, será más económico. Para hacer un análisis más
detallado es necesario analizar cómo se comporta la curva Costo-Flecha y el coeficiente de
uniformidad resultantes. Estos resultados se muestran en las siguientes dos gráficas.
Gráfica 3-34. Curva Costo-Flecha, Red Asimétrica 1, exponente del emisor 0.3. Metodología de Bermúdez.
Gráfica 3-35. Coeficiente de Uniformidad resultante vs. Flecha, Red Asimétrica 1, exponente del emisor 0.3.
Metodología de Bermúdez.
En las gráficas anteriores se puede observar que los diseños son más económicos para este caso
en que se utilizó una mayor presión de entrada, dada una mayor tolerancia de presiones. Por otro
lado se puede ver que el diseño con la flecha de 0 lleva a un coeficiente de uniformidad igual al
3880000
3900000
3920000
3940000
3960000
3980000
4000000
4020000
4040000
0
0.05
0.1
0.15
0.2
0.25
0.3
cos
to
del
su
bm
ódu
lo
(COP)
Flecha
0.79
0.8
0.81
0.82
0.83
0.84
0.85
0.86
0.87
0.88
0
0.05
0.1
0.15
0.2
0.25
0.3
Coeficiente
de Uniformidad
Resu
lta
nte
Flecha

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
78
deseado por el diseño agronómico, pero este no es el diseño más económico de todas las flechas
posibles. La flecha más económica es la flecha de 0.16 y este diseño representa un coeficiente de
uniformidad muy superior (de 0.84) sobre el deseado por el diseño agronómico. De esta manera,
se puede decir que hacer uso de la metodología de Bermúdez no resulta muy adecuado para la
selección de un diseño óptimo, ya que ésta determina una presión de entrada al submódulo que,
claramente, entre mayor sea llevará a menores costos del sistema, pero no es determinante ya
que el diseño de mínimo costo estará determinado por la línea de gradiente hidráulico objetivo
que se trace. Lo que si permite establecer esta metodología, y que resulta importante, es que
ayuda al diseñador a determinar una presión máxima de entrada al submódulo que logre
mantener el coeficiente de uniformidad impuesto por el diseño agronómico. Esto se puede
evidenciar en la Gráfica 3-33, donde se observa que para presiones de entrada muy altas, el
coeficiente de uniformidad resultante, no cumplirá con el establecido por el diseño agronómico.
Esta metodología propuesta por Bermúdez será la que se utilizará para determinar la PES en la
metodología que se propone en este trabajo para el diseño de submódulos de riego. En la
siguiente sección se presenta la metodología planteada que hace uso de programación lineal.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
79
3.4. Diseño de submódulos de riego usando programación lineal.
En esta sección se hace una descripción detallada de la metodología propuesta para el diseño de
submódulos de sistemas RLAF. La primera parte de esta sección presenta la formulación
matemática del problema para un sistema de tuberías que tiene demanda constante en sus nudos
de consumo. Una vez se haya establecido la formulación matemática se procede a explicar y hacer
un análisis de las variaciones necesarias para su aplicación en submódulos de riego, donde la
demanda en los nudos es función de la presión. Como paso siguiente se presenta el algoritmo
propuesto para obtener un diseño óptimo de submódulos de riego; y finalmente mediante
diferentes casos de estudio, se presentará una comparación entre los resultados obtenidos con la
metodología propuesta y la metodología SOGH.
3.4.1. Formulación matemática del problema de diseño de redes abiertas.
Antes de presentar la formulación matemática, es importante mencionar que la formulación
propuesta únicamente funciona para sistemas de tuberías abiertas con demanda constante en sus
nudos de consumo. La razón por la cual la formulación únicamente funciona para este tipo de
sistemas es que existen algunas variables que se pueden parametrizar y de esta manera el
problema se puede linealizar. La parametrización de algunas variables se logra porque en una red
abierta con demanda constante en sus nudos, se conoce la trayectoria del fluido y los caudales
que pasan por cada una de las tuberías.
Para poder formular el problema lineal se tiene en cuenta que el diseño de un sistema de tuberías
ramificadas consiste en determinar los diámetros de cada una de las tuberías que componen la
red, de manera que no se violen presiones mínimas en los nudos de consumo del sistema. Para
esto, el diseñador cuenta con un conjunto de diámetros comerciales disponibles que pueden ser
asignados a cada tubería. Existen diferentes diseños que pueden cumplir con la restricción de
presiones mínimas, de manera que el diseñador también debe buscar que el costo de su diseño
sea mínimo.
La presión en la entrada de la red es un dato conocido por el diseñador y cada diámetro tiene
asociadas unas pérdidas de energía, que implican que la altura piezométrica en el nudo al que
entrega el agua es menor a la altura piezométrica del nudo del que sale el agua. Dichas pérdidas
de presión son conocidas para cada combinación de Tubo-Diámetro. Teniendo en cuenta lo
anterior, a continuación se presenta un ejemplo simple que permite explicar la formulación
matemática utilizada.
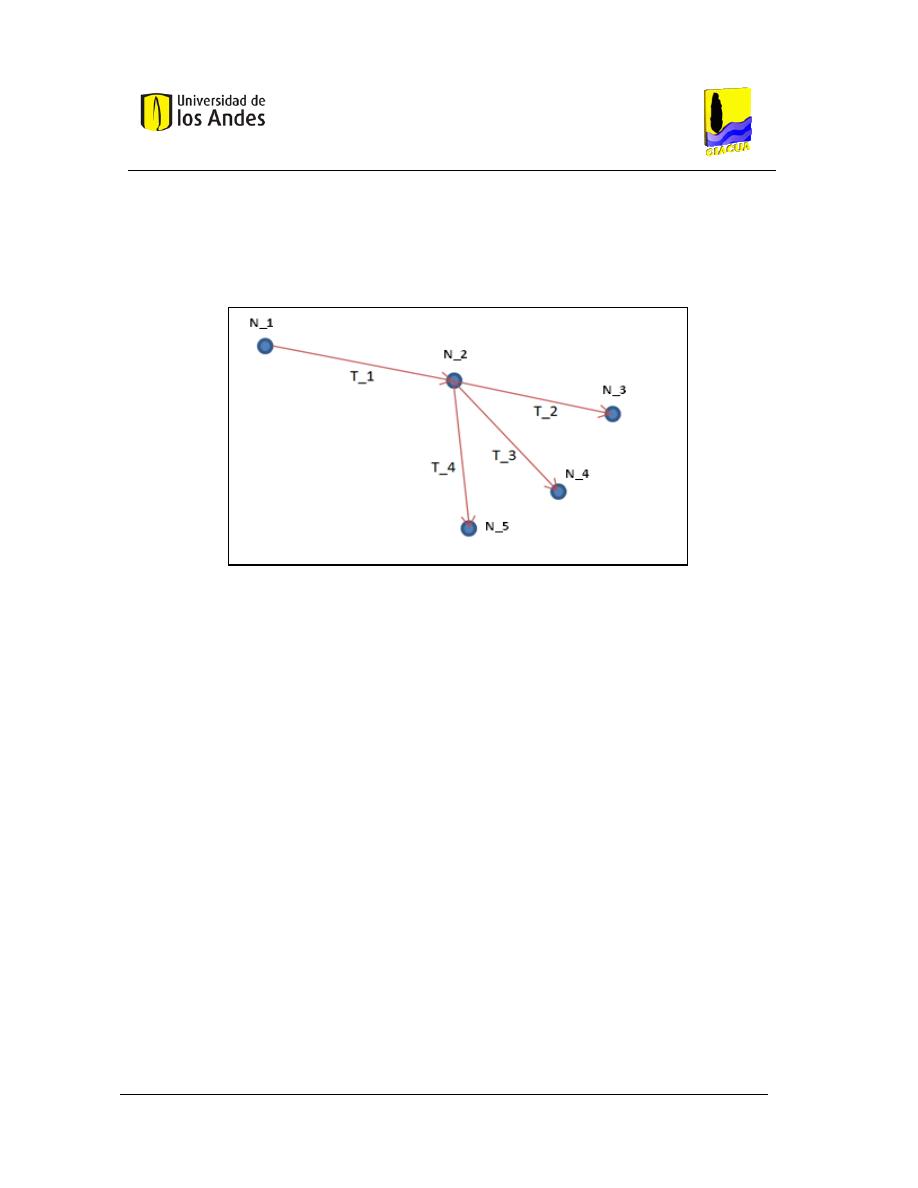
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
80
3.4.1.1.
Ejemplo.
En la siguiente figura se muestra una red compuesta por 4 tramos (T_1, T_2, T_3 y T_4) y 5 nudos
(4 nudos de consumo y el nudo correspondiente a la fuente de agua).
Figura 17. Red abierta de ejemplo para establecer la formulación matemática del problema de optimización lineal.
Suponiendo que se tienen 3 diámetros comerciales disponibles que pertenecen al conjunto D, y
teniendo en cuenta que se conoce la rugosidad absoluta de cada uno de los materiales que se
utilizarán en cada tubería y que por ser una red abierta se conocen los caudales, se pueden
determinar las pérdidas totales para cada combinación Tramo-Diámetro, haciendo uso de la
ecuación de Darcy-Weisbach en conjunto con la ecuación de Colebrook-White, las cuales son
función del caudal en la tubería, la rugosidad absoluta, la longitud de la tubería (que se conoce a
priori) y el diámetro de la tubería.
En la Figura 18 se presenta el caso en que en cada uno de los tramos del sistema se utiliza una
tubería de diámetro d
1
. En la figura se observa que la presión a la entrada es de 100 metros de
columna de agua, y que las pérdidas correspondientes a la combinación (T_1, d
1
) son de 20 mca,
para la combinación (T_2, d
1
) son de 10 mca, en la combinación (T_3, d
1
) son de 5 mca y para la
combinación (T_4, d
1
) son de 10 mca. Es importante mencionar que para cada tramo se conoce la
longitud, rugosidad y coeficiente de pérdidas menores. En la Figura 19 se presentan las pérdidas
correspondientes para las combinaciones (T_i,d
2
) y en la Figura 20 para las combinaciones (T_i,d
3
).
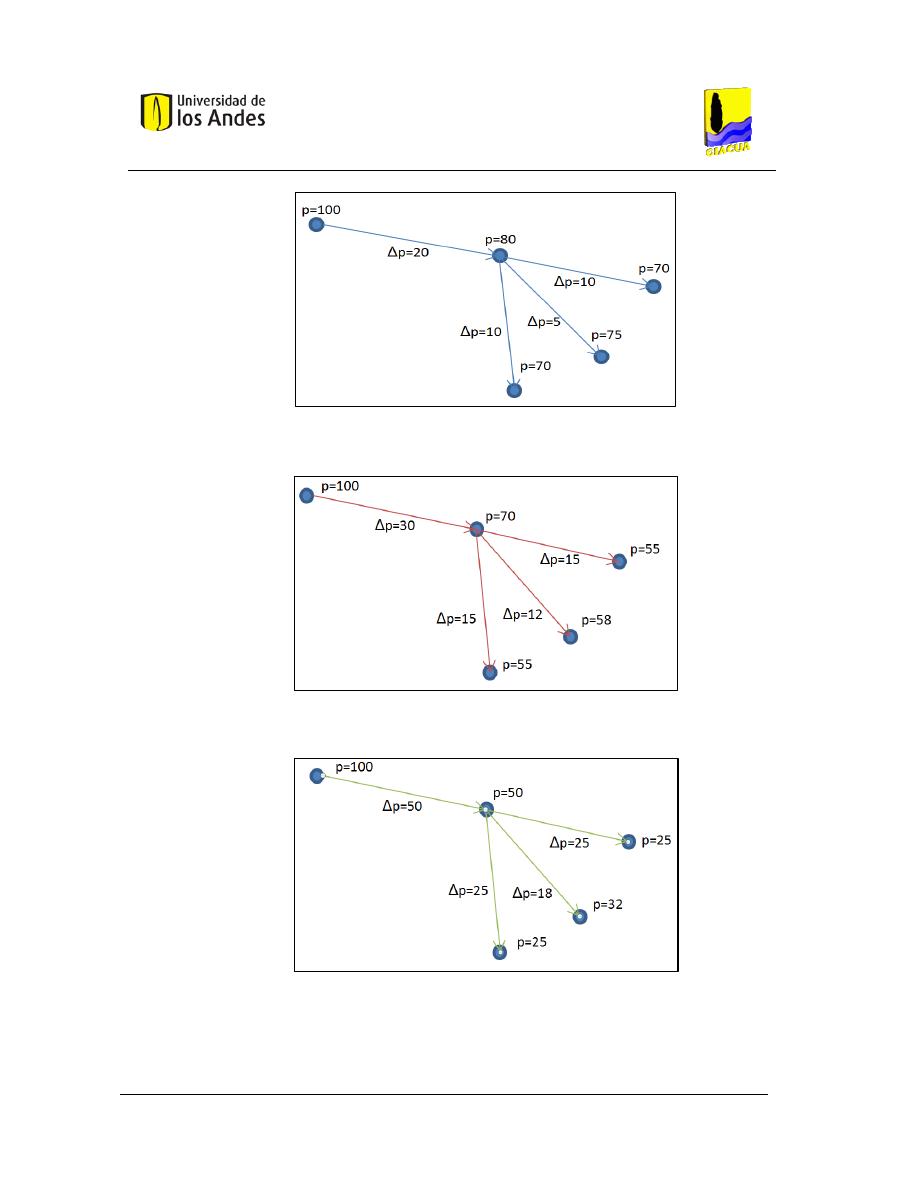
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
81
Figura 18. Pérdidas de altura piezométrica que se presentarían en la red ejemplo si se utiliza el Diámetro d
1
en cada
tubería, unidades de presión en metros de columna de agua.
Figura 19. Pérdidas de altura piezométrica que se presentarían en la red ejemplo si se utiliza el Diámetro d
2
en cada
tubería, unidades de presión en metros de columna de agua.
Figura 20. Pérdidas de altura piezométrica que se presentarían en la red ejemplo si se utiliza el Diámetro d
3
en cada
tubería, unidades de presión en metros de columna de agua.
Los resultados de las figuras anteriores se pueden resumir en la siguiente tabla.
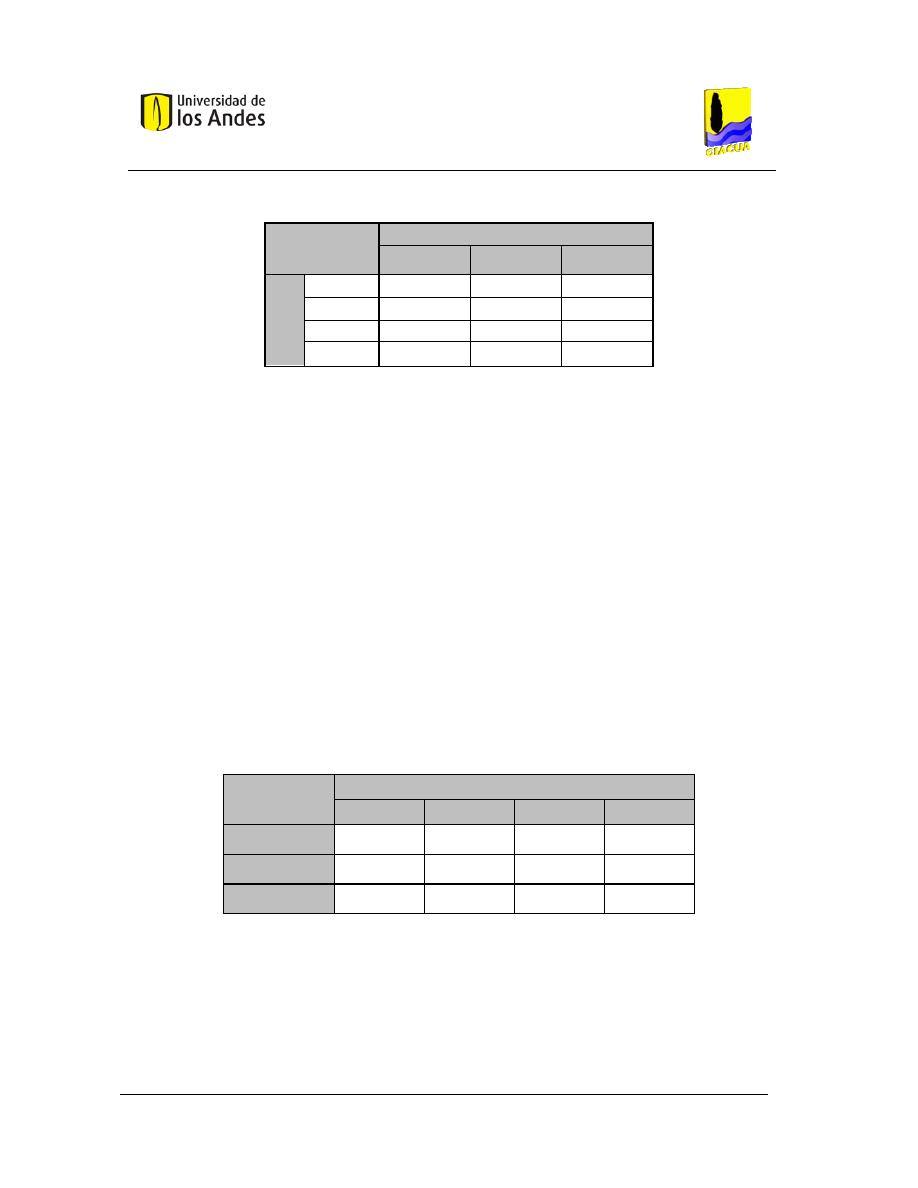
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
82
Tabla 8. Matriz (dp) de pérdidas totales para las diferentes combinaciones Tramo-Diámetro, Red Conceptual.
Pérdidas
Totales (mca)
Diámetro
d
1
d
2
d
3
Tramo
N_1,N_2
20
30
50
N_2,N_3
10
15
25
N_2,N_4
5
12
18
N_2,N_5
10
15
25
Una vez que se obtiene la matriz de pérdidas totales, se desea encontrar el diseño (combinación
de diámetros en todo el sistema) que conlleve al mínimo costo y cumpla con que la presión en
todos los nudos sea mayor a 50 mca. De esta manera el siguiente paso consiste en determinar los
costos asociados con cada combinación Tramo-Diámetro. Para esto se tiene en cuenta que la
función para calcular el costo de una tubería de determinado diámetro es la siguiente
Ecuación 3.4
donde C corresponde al costo de la tubería, L a la longitud del tramo donde se colocará la tubería,
D es el diámetro que se utilizará y K y x son el coeficiente y el exponente asociado con la curva de
costos. Haciendo uso de la Ecuación 3.4 y conociendo la longitud de cada tramo, el coeficiente y el
exponente de la ecuación, se pueden determinar los costos asociados con cada combinación
Tramo-Diámetro. En la Tabla 9 se presenta la matriz de costos asociada con cada combinación
Tramo-Diámetro.
Tabla 9. Matriz (c) de Costos para las diferentes combinaciones Tramo-Diámetro, Red Conceptual.
Costos (USD)
Tramo
N_1,N_2
N_2,N_3
N_2,N_4
N_2,N_5
Diámetro d
1
360
320
300
332
Diámetro d
2
270
250
220
255
Diámetro d
3
200
175
150
180
Teniendo la matriz de costo y la matriz de pérdidas totales, el siguiente paso consiste en definir
una matriz de conectividad que permita conocer qué nudos están conectados con que nudos. La
matriz de conectividad para este ejemplo conceptual quedaría de la siguiente manera:
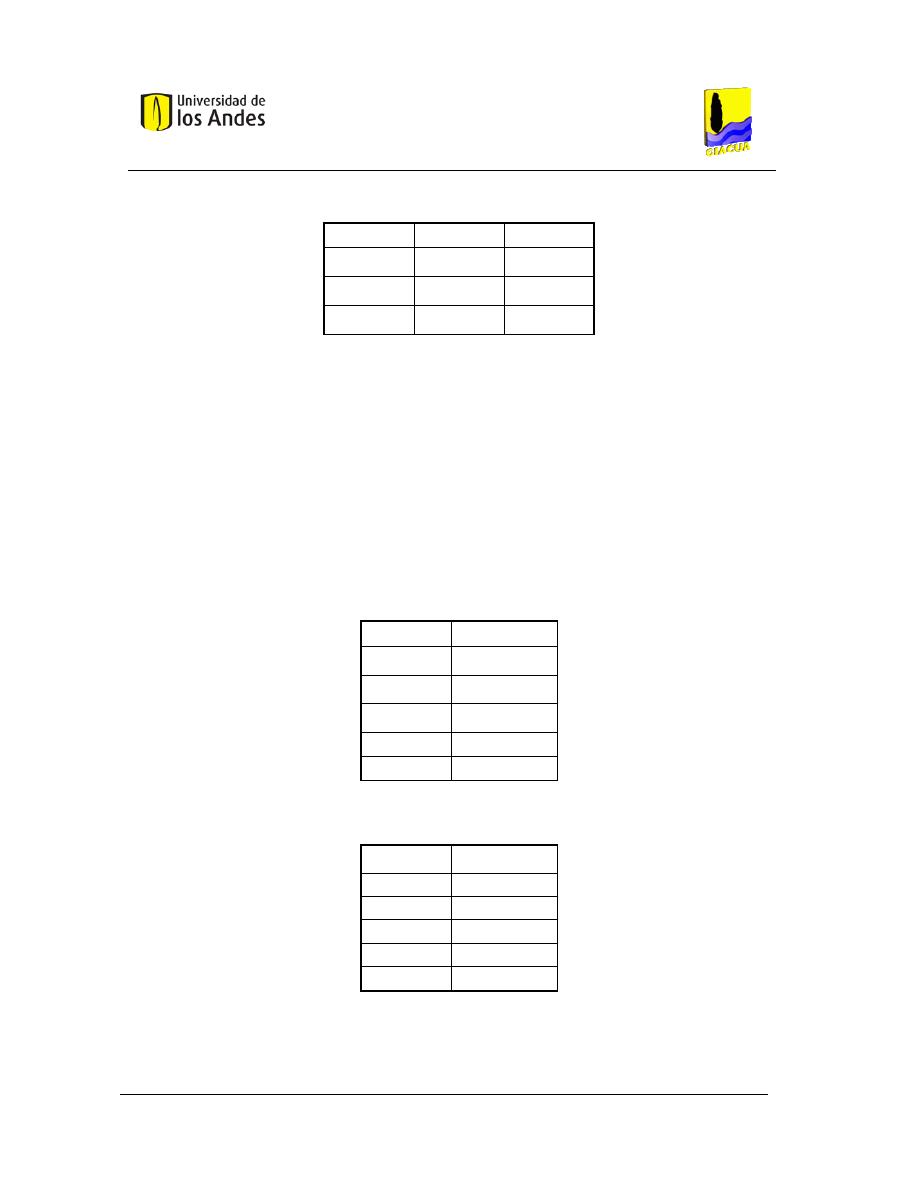
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
83
Tabla 10. Matriz (w) de conectividad entre nudos, Red Conceptual.
N_1
N_2
1
N_2
N_3
1
N_2
N_4
1
N_2
N_5
1
En la Tabla 10 se puede observar que la matriz de conectividad entre nudos contiene 3 columnas.
En la primera se ubican los nudos aguas arriba de cada tramo existente, en la segunda columna se
ubican los nudos aguas abajo de cada tramo y en la tercera se asigna el valor de 1 a los tramos
existentes.
Una vez que se tiene la matriz de conectividad, y conociendo la presión mínima deseada (50 mca)
en cada uno de los nudos del sistema, se puede establecer la LGH mínima en cada nudo. Para este
ejemplo y suponiendo una elevación en los nudos como la que se muestra en la siguiente tabla
(Tabla 11) se puede obtener la matriz de LGH mínimas (ver Tabla 12).
Tabla 11. Elevación de los nudos, Red Conceptual.
Nudo
Elevación (m)
N_1
10
N_2
9
N_3
8
N_4
7
N_5
6
Tabla 12. Matriz (LGH
min
) de LGH mínimas en los nudos, Red Conceptual.
Nudo
LGH
mínima
(m)
N_1
60
N_2
59
N_3
58
N_4
57
N_5
56
En la Tabla 12 se observa que a diferencia de la presión mínima deseada, la LGH mínima es
diferente para cada uno de los nudos; lo anterior se debe a que cada nudo tiene una elevación

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
84
diferente. De esta manera se obtienen para este problema las 4 matrices que se necesitarán para
implementar el modelo en Xpress, estas matrices son:
-
Matriz de Costos (c)
-
Matriz de pérdidas totales (dp)
-
Matriz de Conectividad (w)
-
Matriz de LGH mínimas (LGH
min
)
Además de tener las matrices es necesario estructurar su formulación matemática. Que teniendo
en cuenta el ejemplo conceptual, se plantea a continuación
3.4.1.1.1.
Formulación matemática del modelo de optimización para el diseño de
redes abiertas.
El primer paso dentro de una formulación matemática de un modelo de optimización lineal
consiste en definir los conjuntos que componen el problema. Una vez se han definido éstos, se
definen las variables de decisión, las restricciones del problema y la función objetivo. De esta
manera, para el problema de diseño de una red abierta la formulación matemática quedaría:
Conjuntos
N: Conjunto que contiene todos los nudos del submódulo.
D: Conjunto que contiene todos los diámetros comerciales disponibles.
Variables de decisión
X
ijd
Variable binaria
Como puede observarse la variable de decisión X
ijd
solo puede tomar valores de 1 o 0. Y tendrá un
valor igual a 1 si el modelo asigna para el tramo comprendido entre el nudo i y el nudo j un
diámetro igual a d. Adicional a la variable de decisión binaría X
ijd
es necesario definir una variable
auxiliar que contenga la altura piezométrica en cada nudo del sistema.
p
i
variable de decisión auxiliar que define la altura piezométrica en el nudo i.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
85
Restricciones del problema
Restricción de LGH
min
: Restricción que se asegura que para todos los nudos se tenga una LGH
superior a la LGH mínima correspondiente al nudo.
Restricción de LGH en nudos aguas abajo: Restricción que se asegura que la LGH en el nudo j N
aguas abajo de un nudo i N sea igual a la LGH aguas arriba menos las pérdidas (dp) ocasionadas
en el tramo de tubería que comprenden el nudo i N y el nudo j N siempre que exista una
conexión entre el nudo i y el nudo j.
,
donde LGHj corresponde a la línea de gradiente hidráulico o altura piezométrica en el nudo j N
aguas abajo del nudo i N. Por otro lado dp
ijd
corresponderá a las pérdidas totales de altura
piezométrica que se presentarán en el tramo entre los nudos i y j si se utiliza una tubería de
diámetro d. Por su parte X
ijd
corresponde a la variable de decisión. Es importante anotar que los
valores de dp
ijd
corresponden a las pérdidas totales de altura piezométrica obtenidas como
parámetros del problema, en la matriz de pérdidas totales.
Restricción de único diámetro en cada tramo: Esta restricción se encarga de asegurar que en cada
tramo se asigne un solo diámetro.
,
Función Objetivo
donde C
ijd
es el Costo de utilizar un diámetro d D en el tramo comprendido entre el nudo i N y
el nudo j N. X
ijd
corresponde a la variable de decisión. El objetivo es minimizar esta función
objetivo. Las restricciones presentadas anteriormente se encargarán de cumplir con los requisitos
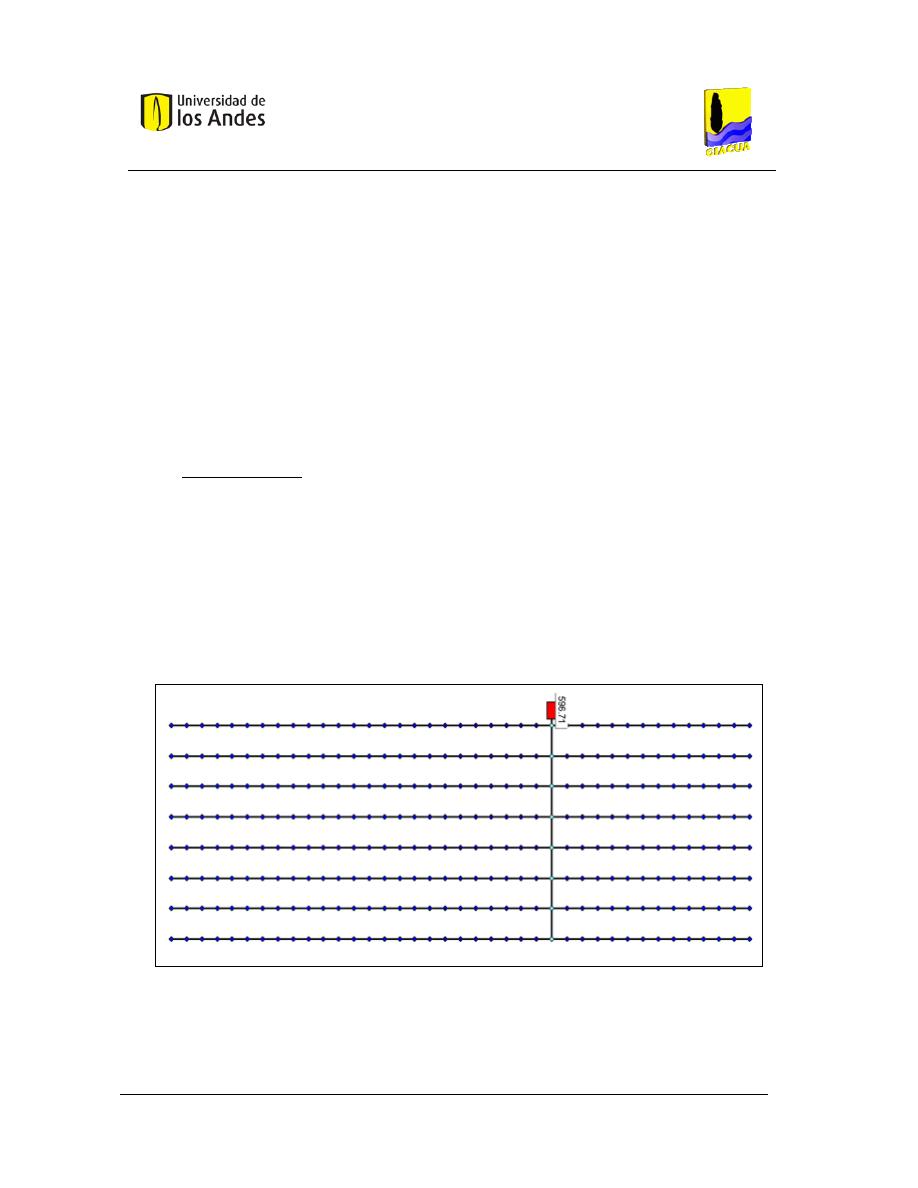
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
86
hidráulicos de presión mínima. Es importante notar que los valores de C
ijd
corresponden a
parámetros de la función objetivo que se obtienen de la matriz de costos.
3.4.2. Aplicación de programación lineal al diseño de submódulos de riego.
En la sección anterior se construyó la formulación matemática para realizar el diseño de redes
abiertas, utilizando programación lineal. Para realizar la formulación se hizo uso de un ejemplo
conceptual de una red abierta con demanda constante en sus nudos de consumo. Esta
metodología permite obtener el diseño óptimo global en el diseño de redes abiertas con nudos de
demanda constante, pero a la hora de utilizarlo para realizar diseños de submódulos de riego se
encontraron algunos problemas que fue necesario solucionar para poder obtener un diseño
óptimo. Estos problemas son dos:
-
Uso de Emisores: Como se ha mencionado durante este trabajo, los sistemas de riego
utilizan emisores en sus nudos de demanda. Lo anterior implica que el caudal que se
consume en cada planta depende de la presión que se tenga en ese punto. Teniendo en
cuenta lo anterior, se puede afirmar que el caudal que se emitirá a cada planta no se
conocerá a priori. Por esta razón para realizar el diseño de un submódulo de riego la
primera idea que se viene a la cabeza es definir una superficie de gradiente hidráulico,
para de esta manera conocer una presión en cada emisor y finalmente determinar el
caudal correspondiente a la presión establecida en el nudo. De esta manera, se puede
suponer que se tiene el siguiente submódulo de riego que se muestra en la Figura 21.
Figura 21. Submódulo Asimétrico 2.
El submódulo mostrado en la Figura 21 se desea diseñar usando programación lineal.
Antes de realiza el diseño es necesario establecer la presión de entrada al submódulo (PES)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
87
y la presión mínima. Lo anterior se obtiene haciendo uso de la metodología de Bermúdez
(2011) y en las siguientes tablas se presentan los datos de entrada del problema y los
resultados que arroja la metodología propuesta en el 2011.
Tabla 13. Datos de entrada para el diseño del Submódulo Asimétrico 2.
DATOS AGRONÓMICOS
Coeficiente
de
uniformidad
(CU)
Número de
emisores por
planta (n
e
)
Presión
media de
operación
(h
m
)
Caudal
medio por
emisor (Q
m
)
()
()
(mca)
(l/h)
0.8
2
18.00
120
Coeficiente de variación del emisor (CV)
0.04
Exponente del emisor
1.0
Coeficiente del emisor (l/s)/(m
x
)
0.00185185
En la Tabla 13 se observa que el coeficiente de uniformidad (CU) deseado por el diseño
agronómico es de 0.8, el número de emisores por planta será de 2, el caudal medio por
emisor es de 120 litros por hora, la presión media de operación es de 18 mca, el
exponente del emisor es 1.0, el coeficiente de los emisores es 0.00185185 (l/s/m
x
) y el
coeficiente de variación (CV) es de 0.04. A partir de estos valores y haciendo uso de la
metodología propuesta por Bermúdez se obtienen los siguientes resultados (Ver Gráfica
3-36):
Gráfica 3-36. Curva Coeficiente de Uniformidad vs. PES, Submódulo Asimétrico 2.
0.5
0.6
0.7
0.8
0.9
1
10
15
20
25
30
Co
efic
ie
n
te
de
U
nif
o
rm
ida
d
()
Presión de Entrada al Submódulo (mca)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
88
A partir de la Gráfica 3-36 y sabiendo que el CU deseado es de 0.8, se obtiene que la PES es
21.71 mca.
Tabla 14. Resultados de presión mínima y PES, para ejemplo de Submódulo Asimétrico 2.
Presión mínima en el Submódulo (mca)
14.94
Presión de Entrada al Submódulo (PES), (mca)
21.71
Conociendo la PES y la presión mínima se puede proceder a buscar el conjunto de tuberías
que representarían el diseño final. Para comenzar este proceso es necesario definir una
superficie de gradiente hidráulico tal como se muestra en la siguiente figura:
Figura 22. Superficie de gradiente hidráulico definida a partir de metodología SOGH, Submódulo Asimétrico 2.
La superficie mostrada en la Figura 22 corresponde a una superficie de gradiente
hidráulico obtenida a partir de una flecha 0. Una vez se ha definido la superficie de
gradiente hidráulico y conociendo la altura topográfica de cada uno de los nudos que se
modelarán con emisores, se puede determinar la presión correspondiente en cada nudo.
La presión se determina simplemente como la diferencia entre la altura piezométrica en
cada nudo y la altura topográfica. De esta manera, conociendo la presión en cada punto
del submódulo se puede determinar el caudal que se emitirá en el emisor
correspondiente, para esto se hace uso de la ecuación del emisor. Finalmente, conociendo
el caudal correspondiente a la superficie de gradiente planteada, se puede asignar este
caudal como constante en los nudos que componen el submódulo y modelarse como
caudales constantes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
89
Teniendo en cuenta lo anterior, en este punto del problema se tiene un submódulo de
riego con una presión de entrada (PES=21.71 mca), una presión mínima deseada
(P
min
=14.94 mca) y un caudal constante en cada nudo obtenido a partir de la superficie de
gradiente y la ecuación de los emisores; de esta manera, y aprovechando que un
submódulo de riego es una red abierta, es posible hacer uso de la formulación lineal
planteada en la Sección 3.4.1.1.1 y diseñar. Para diseñar es necesario crear las 4 matrices
(Matriz de costos, pérdidas totales, conectividad y LGH mínimas) necesarias que se
ingresarán en el programa Xpress. Para crear las matrices de forma automática se hiso uso
de un programa creado para este trabajo, que permite obtener a partir del archivo *.INP el
archivo *.DAT que lee Xpress
2
.
Una vez se obtuvieron las matrices, y se realizó el diseño mediante programación lineal
(usando Xpress) es necesario que el diseño obtenido se modele con emisores para verificar
que se cumpla con las restricciones de presión mínima y coeficiente de uniformidad
deseado. Para este caso se obtuvo como presión mínima en el submódulo una presión de
15.04 mca y un coeficiente de uniformidad de 0.84, que como puede observarse cumplen
con los requerimientos. Dado que el diseño cumple con los requerimientos hidráulicos y
agronómicos, el siguiente paso consiste en determinar que tan buenos resultan los costos
de esta metodología. Para esto se realizó el diseño del mismo submódulo mediante la
metodología SOGH, variando el valor de la flecha de diseño y utilizando cuatro criterios de
redondeo de diámetros. Los cuatro criterios de redondeo fueron:
-
Aproximación al anterior diámetro.
-
Aproximación al siguiente diámetro.
-
Redondeo Potencial.
-
Redondeo al diámetro comercial más cercano.
Los resultados obtenidos utilizando la metodología SOGH se observan en Gráfica 3-37. En
esta gráfica se observa en el eje de las abscisas, el valor de la flecha utilizada para obtener
la superficie óptima de gradiente hidráulico y en el eje de las ordenadas se observa el
costo que se obtiene después del diseño. Aunque en secciones anteriores a este
documento se demostró que la flecha máxima de diseño (con valides física) es la flecha de
0.25, en la gráfica se presentan los resultados para flechas superiores a la flecha máxima.
2
El archivo *.DATA para este ejemplo del Submódulo Asimétrico 2, resulta en un archivo de 7499
líneas que por razón de espacio no es posible anexar al documento de este trabajo. En el CD Anexo,
se puede abrir el archivo “Submódulo Asimétrico 2, Flecha 0, X=1.dat” para observar las 4 matrices
obtenidas para este ejemplo.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
90
Gráfica 3-37. Relación Costo-Flecha obtenida mediante la metodología SOGH para el diseño del Submódulo
Asimétrico 2, variando el valor de la flecha y utilizando 4 criterios de redondeo de diámetros.
De la gráfica mostrada es importante decir que mediante la metodología SOGH, para éste
caso de estudio, se obtuvo que el diseño de mínimo costo corresponde a un diseño
obtenido mediante la Flecha 0.24 y el criterio de redondeo de aproximación al siguiente
diámetro para un costo mínimo de $ 7,913,646. Por otro lado, el costo del diseño obtenido
mediante la metodología propuesta es de $ 7,838,949 (más económico). Lo anterior
muestra que la metodología propuesta conlleva, para este caso, a un diseño que cumple
con las restricciones hidráulicas y agronómicas y además presenta un costo de 74 mil
pesos por debajo del mas económico obtenido mediante la metodología SOGH.
Ahora bien, como se mencionó al inicio de la Sección 3.4.2 existían dos problemas de la
formulación lineal aplicada al diseño de submódulo de riego. El primer problema, quedó resuelto
al definir una superficie de gradiente hidráulico que permitiera establecer unos caudales
constantes en los nudos de consumo y de esta manera poder diseñar. El segundo problema surge
de la pregunta ¿Qué pasa con el diseño usando formulación lineal si la superficie de gradiente
hidráulico parte de una flecha diferente a la Flecha 0?, esta pregunta se responde a continuación.
7700000
7900000
8100000
8300000
8500000
8700000
8900000
9100000
9300000
9500000
9700000
0
0.1
0.2
0.3
0.4
0.5
0.6
Costo
Sub
mód
ulo
(COP)
Flecha
Aprox. Anterior
Aprox. Siguiente
Red. Potencial
Redondeo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
91
-
Sensibilidad del diseño a la flecha utilizada: En el ejemplo presentado anteriormente se
observó que se puede obtener un diseño más económico mediante el uso programación
lineal. Lo que se pretende en esta sección es observar las variaciones que se presentarán
en los resultados si se cambia la flecha a partir de la cual se define la superficie de
gradiente hidráulico inicial. De esta manera, se realizaron diferentes diseños tal como se
mostró en el ejemplo anterior, solo que ahora la superficie de gradiente hidráulico varía.
En las siguientes figuras se presentan los resultados obtenidos para diseños partiendo de
flechas 0, 0.02, 0.04, 0.06, 0.10, 0.12, 0.13, 0.15, 0.20 y 0.25, que a partir de ahora se
denominarán diseño(F0), diseño(F0.02), diseño(F0.04), diseño(F0.06), diseño(F0.10),
diseño(F0.12), diseño(F0.13), diseño(F0.15), diseño(F0.20), diseño(F0.25).
Gráfica 3-38. Costo del diseño del Submódulo Asimétrico 2 partiendo de diferentes flechas iniciales, usando
programación lineal.
En la Gráfica 3-38 se observan los costos que se tendrían haciendo uso de programación
lineal para el diseño del submódulo Asimétrico 2. En la gráfica se observa que a medida
que la flecha para determinar la superficie de gradiente aumenta, el costo final del
submódulo se reduce; sin embargo, no todos los diseños obtenidos son factibles, para el
caso presentado, únicamente el diseño(F0) y el diseño(F0.02) son factibles. En este caso,
un diseño es factible si la presión en todos los nudos es superior a 14.94 mca y
adicionalmente se cumple con el coeficiente de uniformidad deseado (CU = 0.8). En las
siguientes gráficas se presentan los resultados de coeficiente de uniformidad, presión
mínima y número de nudos por debajo de la presión mínima en el submódulo.
7550000
7600000
7650000
7700000
7750000
7800000
7850000
7900000
0
0.1
0.2
0.3
Costo
(COP)
Flecha de inicio
Diseños Factibles
Diseños no Factibles
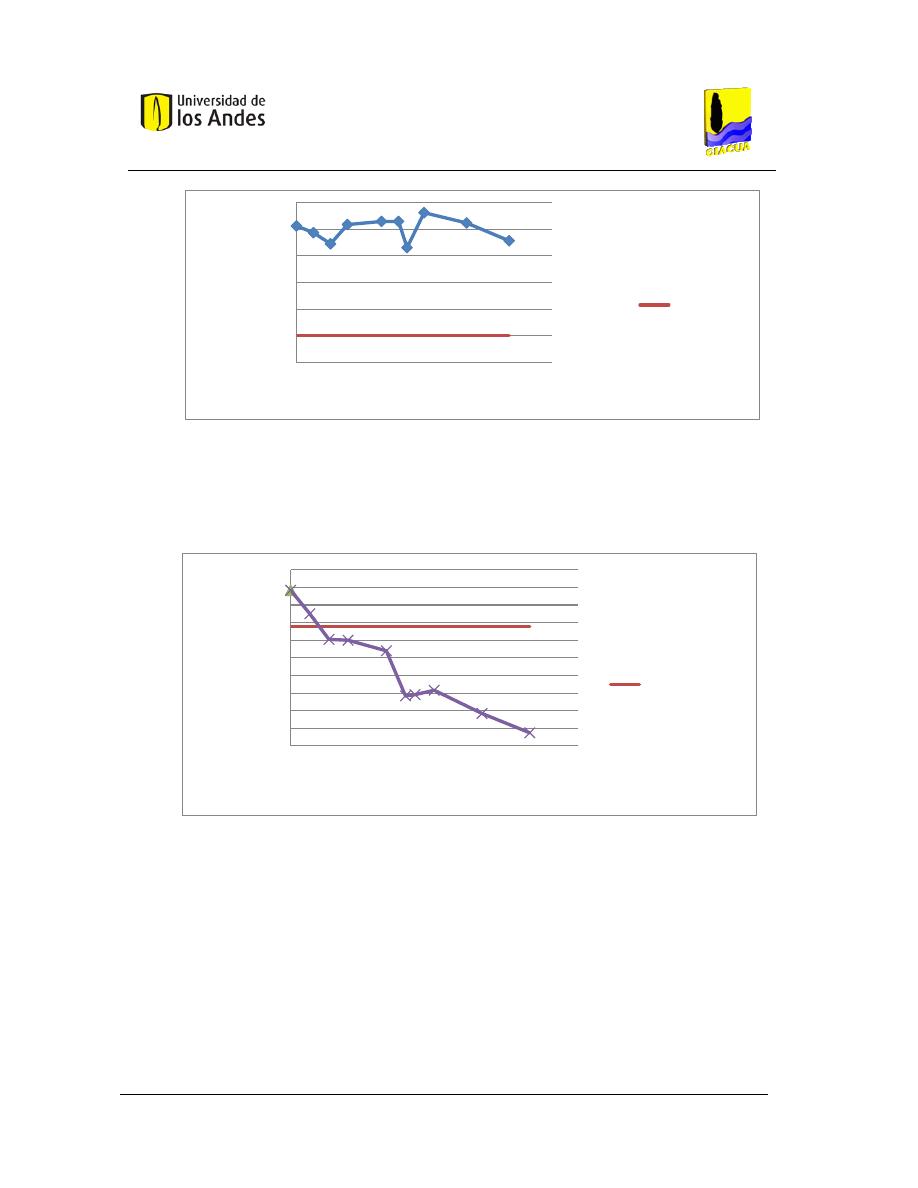
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
92
Gráfica 3-39. Coeficientes de uniformidad resultantes, variando flecha de inicio, Submódulo Asimétrico 2.
En la Gráfica 3-39 se observa que todos los diseños cumplen con el coeficiente de
uniformidad deseado, esto se debe a que el trabajo realizado por Bermúdez se asegura de
cumplir con el coeficiente de uniformidad.
Gráfica 3-40. Presiones mínimas resultantes, variando flecha de inicio, Submódulo Asimétrico 2.
A diferencia del coeficiente de uniformidad y los resultados presentados en la Gráfica 3-39,
las presiones mínimas en el submódulo únicamente se cumplen para el diseño(F0) y el
diseño(F0.02). En la Gráfica 3-40 se puede observar la razón por la cual algunos diseños se
consideran no factibles (presión en 1 o más nudos por debajo de la presión mínima). Al
analizar el número de nudos por debajo de la presión mínima se observaron los resultados
que se muestran en la siguiente gráfica:
0.79
0.8
0.81
0.82
0.83
0.84
0.85
0
0.1
0.2
0.3
CU Re
su
lt
ant
e
()
Flecha de inicio
CU deseado
14.6
14.65
14.7
14.75
14.8
14.85
14.9
14.95
15
15.05
15.1
0
0.05
0.1
0.15
0.2
0.25
0.3
Presión
mínim
a
en el
su
bm
ódulo
resultante
(mca)
Flecha de inicio
Presión Mínima
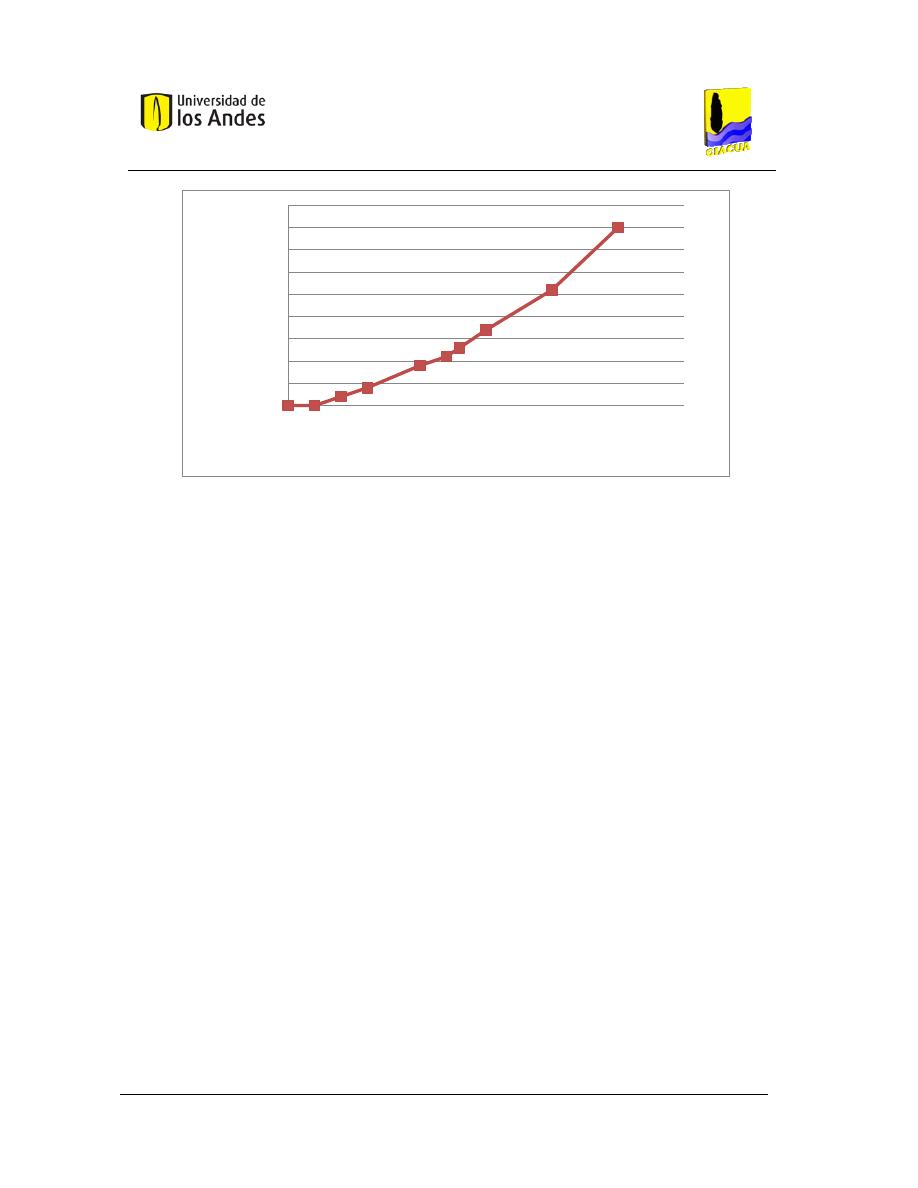
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
93
Gráfica 3-41. Número de nudos por debajo de la presión mínima resultantes, variando flecha de inicio, Submódulo
Asimétrico 2.
Finalmente, en la Gráfica 3-38 y en la Gráfica 3-41 se podrá notar que a medida que
aumenta la flecha inicial de diseño se reducen los costos pero también se corre el riesgo
de no cumplir con la restricción hidráulica de presión mínima. Adicional a esto, resulta
claro que entre mayor sea la flecha de partida, el número de nudos por debajo de la
presión mínima tiende a aumentar. Teniendo en cuenta los resultados anteriores se
realizaron diferentes pruebas para establecer un criterio para diseñar submódulos de riego
sabiendo que existe una sensibilidad en los resultados respecto a la flecha de inicio. A
continuación se presenta el criterio que finalmente se adoptó y los resultados obtenidos
para diferentes casos de estudio.
0
5
10
15
20
25
30
35
40
45
0
0.05
0.1
0.15
0.2
0.25
0.3
Número
de nud
os
por
deb
ajo
de l
a
presión
mínim
a
Flecha de inicio

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
94
3.4.3. Metodología para el diseño de submódulos de riego usando programación
lineal en conjunto con SOGH.
Con base en lo presentado en la Sección 3.4.2 fue necesario plantear una metodología para el
diseño de submódulos de riego. Es importante recordar que los dos problemas presentados al usar
programación lineal en el diseño de submódulos, se refieren a que estos hacen uso de emisores y
que existe una sensibilidad de los resultados respecto a la flecha inicial para establecer la
superficie de gradiente. En esta sección se presentará el algoritmo final que se utilizará para el
diseño de submódulos de sistemas RLAF. Los pasos a seguir son:
1. Datos de entrada: Para iniciar el proceso de diseño es necesario conocer la topología del
submódulo de riego, el Coeficiente de Uniformidad (CU), el caudal medio por planta, el
número de emisores por planta (n
e
), la ecuación de los emisores (su exponente y
coeficiente) y el Coeficiente de Variación (CV).
2. Cálculo de la PES y presión mínima: Conociendo los valores de entrada establecidos por el
diseño agronómico, se debe hacer uso de la metodología planteada por Bermúdez (2011)
para determinar la presión de entrada al submódulo (PES) y la presión mínima aceptable
en los emisores
3
.
3. Cálculo de superficies de gradiente: Una vez se han determinado la presión de entrada
(PES) y la presión mínima deseada, se procede a hacer uso de la metodología SOGH. La
metodología SOGH en conjunto con el programa REDES, permite establecer de forma
rápida la superficie de gradiente hidráulico deseado. En este caso, el diseñador debe
determinar la superficie de gradiente hidráulico correspondiente a la Flecha 0 y Flecha
0.25.
4. Cálculo de caudales de diseño: Conociendo la altura piezométrica en cada nudo del
sistema (tanto para la Flecha 0 como para la Flecha 0.25) y su altura topográfica, se
obtienen las presiones en cada nudo. Al utilizar la ecuación del emisor, se obtienen los
caudales correspondientes que recibiría cada planta. El caudal calculado mediante la
ecuación del emisor, se asigna como un caudal de demanda base del nudo y se modelará
como constante. De esta manera, en este punto se tienen dos submódulos
topológicamente iguales pero con caudales en sus nudos diferentes. El primero
corresponde al submódulo partiendo de la Flecha 0 y el segundo al submódulo partiendo
de la Flecha 0.25.
3
En este trabajo, se hace entrega de un programa en el cual el usuario únicamente ingresa los datos
de entrada del paso 1 de la metodología, y de forma automática se calcula la curva CU vs PES para
establecer la presión de entrada al submódulo; adicionalmente el programa entrega al usuario la
presión mínima que debe existir en el submódulo de riego. Más adelante se mostrará el uso de este
programa en la sección de Anexos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
95
Es importante anotar que en la medida que se aumenta la flecha de inicio la suma de los
caudales que se emitirían en todo el sumódulo se reduce. De esta manera, el caudal que
saldrá de la fuente de alimentación de un submódulo con caudales en sus nudos
correspondientes a una superficie de gradiente de Flecha 0 será mayor al caudal total que
se obtiene a partir de una Flecha 0.25. Por esta razón, al usar programación lineal el
diseño obtenido a partir de la Flecha 0 resulta más costoso que el diseño obtenido a partir
de la Flecha 0.25.
5. Diseñar usando programación lineal: Habiendo asignado los caudales emitidos como
caudales de demanda constante en los nudos, se procede a calcular las matrices de costo,
pérdidas totales, conectividad y LGH
mínimas
. Teniendo en cuenta que se tienen dos
submódulos a diseñar (el que contiene los caudales a partir de la Flecha 0 y el que tiene
los caudales a partir de la Flecha 0.25), se obtendrán 2 diseños diferentes. Estos diseños se
obtienen usando la formulación lineal implementada en el programa Xpress
4
. De esta
manera se obtienen lo que se denominará de ahora en adelante como D
1
y D
2
. D
1
corresponde al diseño más costoso (diseño a partir de Flecha 0) y D
2
(diseño a partir de
Flecha 0.25) al diseño más económico.
6. Modelar diseños con emisores: Como bien se sabe, los diseños D
1
y D
2
fueron obtenidos a
partir de demandas constantes en sus nudos; por esta razón es necesario verificar el
comportamiento del sistema cuando se hacen funcionar los diseños con emisores.
Respecto al diseño D
1
obtenido en el paso 5 es importante aclarar que este diseño siempre
será factible; por otro lado, el diseño D
2,
obtenido en el paso 5, por lo general no será
factible. Si en algún caso el diseño D
2
obtenido a partir de la flecha 0.25 resultara factible,
entonces el proceso de diseño terminaría y el diseño D2 sería el definitivo.
Al modelar los diseños D
1
y D
2
con emisores se obtendrá para cada nudo i el caudal
emitido. De esta manera se conocerá para cada nudo i un caudal que para el caso del
diseño D
1
se denominará CaudalE
1i
y para el caso del diseño D
2
se llamará CaudalE
2i
5
.En
este punto el diseñador también debe calcular la suma de caudales emitidos en el
submódulo para D
1
y D
2
(ver Ecuación 3.5 y Ecuación 3.6).
Ecuación 3.5
Ecuación 3.6
4
El programa de Xpress se entregará en el CD anexo a este documento.
5
En el término CaudalE
ji
el primer subíndice corresponde al subíndice del diseño (D
j
) y el segundo
subíndice corresponde al Id del nudo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
96
7. Promedio de Caudales: Una vez se tienen los caudales CaudalE
1i
y CaudalE
2i
estos se
promedian en cada nudo i para obtener lo que se denominará Caudal
ji
que se asignará
como un caudal constante en cada uno de los nudos del sistema. De esta manera se tiene
un nuevo submódulo, que aunque tiene las mismas características topológicas del original,
comprende caudales obtenidos del promedio de caudales de 2 diseños anteriores (D
1
y
D
2
).
8. Diseñar promedio usando programación lineal: Con los caudales en cada nudo (Caudal
ji
)
obtenidos en el paso 7 se obtienen las matrices de costo (c), pérdidas totales (dp),
conectividad (w) y LGH
minimas
. Con estas matrices y usando la formulación implementada
en Xpress se diseña el submódulo y se obtiene el diseño D
j
.
9. Modelar el nuevo diseño con emisores: Teniendo el diseño D
j
éste debe ser modelado
con emisores. De esta manera se conoce el caudal que cada nudo i emite. El resultado de
esta etapa es obtener lo que se denominará CaudalE
ji
(Caudales emitidos en el diseño j en
cada nudo i).
10. Comprobación de suma de caudales, presiones y CU: Una vez se ha modelado el diseño Dj
usando emisores, se puede establecer si este diseño es factible (CU mayor al establecido
por el diseño agronómico y todos los nudos con presión mayor a la mínima) o no factible.
Adicional a esto el diseñador debe determinar la suma de caudal total emitido en el diseño
D
j
calculado como se muestra en la siguiente ecuación:
Ecuación 3.7
De esta manera, si el diseño Dj es factible y
el
diseño termina y se obtiene como diseño final Dj. Si por otro lado el diseño Dj resulta no
factible y/o
se debe seguir al paso 11.
11. Restablecer D
1
o D
2
: Dado que el diseño D
j
no resultó factible y/o la diferencia deseada en
la suma de caudales fue mayor a la establecida, en este paso el diseñador debe observar el
número de nudos por debajo de la presión mínima que se obtuvieron mediante el diseño
D
j
. De esta manera:
En el anterior condicional se puede observar que comienza un algoritmo de bisección, en
el cual, si el número de nudos que incumplen la presión mínima es mayor a 0 entonces el

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
97
diseño denominado D
j
pasa a remplazar el diseño D
2
; y por el contrario, si ningún nudo
incumple con la presión mínima el diseño D
j
pasa a remplazar D
1
. De igual forma el
o el
será remplazado por el
. Teniendo en cuenta lo anterior
el diseñador debe volver al paso 7 y seguir con el proceso hasta que finalmente se cumpla
que D
j
sea factible y
.
Los 11 pasos que comprenden el algoritmo planteado, permiten al diseñador obtener un diseño
óptimo de submódulos de riego. En la siguiente página se resume el algoritmo mediante un
diagrama de flujo que hace más fácil entender su procedimiento (Ver Figura 23). Respecto al
algoritmo hay que decir que como se pudo observar el diseño parte de caudales obtenidos a partir
de una Flecha 0 y una Flecha 0.25. La Flecha 0.25 se escogió por ser la flecha máxima teórica, pero
es importante dejar abierta la pregunta de qué pasa si se parte de una flecha mayor.
Adicionalmente, es posible que exista un proceso de convergencia al diseño óptimo de forma más
rápida, aunque como se mostrará en la solución de casos de estudio, el algoritmo de bisección
logra finalizar el algoritmo en el quinto o sexto diseño.
En las próximas secciones se presentarán los resultados obtenidos para 5 casos de estudio de
submódulos de sistemas RLAF en donde se realizaron variaciones en la topología, topografía,
ecuación del emisor y Coeficiente de Uniformidad deseado. Posterior a esto se mostrará el uso de
los programas desarrollados para este trabajo. Con los programas que se mostrarán se entregará
el manual del usuario para el programa que permite determinar la presión de entrada al
submódulo (PES) y crear las matrices necesarias para realizar el diseño en Xpress. También se
mostrará la estructura del código en Xpress que contiene toda la formulación matemática del
problema.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
98
INICIO
Leer Topología del submódulo, CU, Ecuación
del emisor, Caudal medio por planta,
Coeficiente de variación
Calcular presión mínima y presión de
entrada al submódulo (PES)
Usando SOGH, calcular LGH y presión
resultante en cada planta partiendo de la
flecha 0 y flecha 0.25
Calcular el caudal resultante en cada planta
para la Superficie de Gradiente obtenida a
partir de la flecha 0
Asignar el caudal obtenido como la
demanda base en el nudo
correspondiente
Calcular el caudal resultante en cada planta
para la Superficie de Gradiente obtenida a
partir de la flecha 0.25
Asignar el caudal obtenido como la
demanda base en el nudo
correspondiente
Usando programación
lineal y Xpress diseñar el
submódulo
Se obtiene el
Diseño (F0) = D1
Se obtiene el Diseño
(F 0.25) = D2
Modelar el D1 con emisores y obtener las
presiones y caudales en cada nudo (i)
Modelar el D2 con emisores y obtener las
presiones y caudales en cada nudo (i)
Print:
CaudalE_1i,
Print:
CaudalE_2i,
Usando programación
lineal y Xpress diseñar el
submódulo
B
Figura 23A. Diagrama de flujo, metodología para el diseño de submódulos de riego usando programación lineal en
conjunto con SOGH. Parte A.
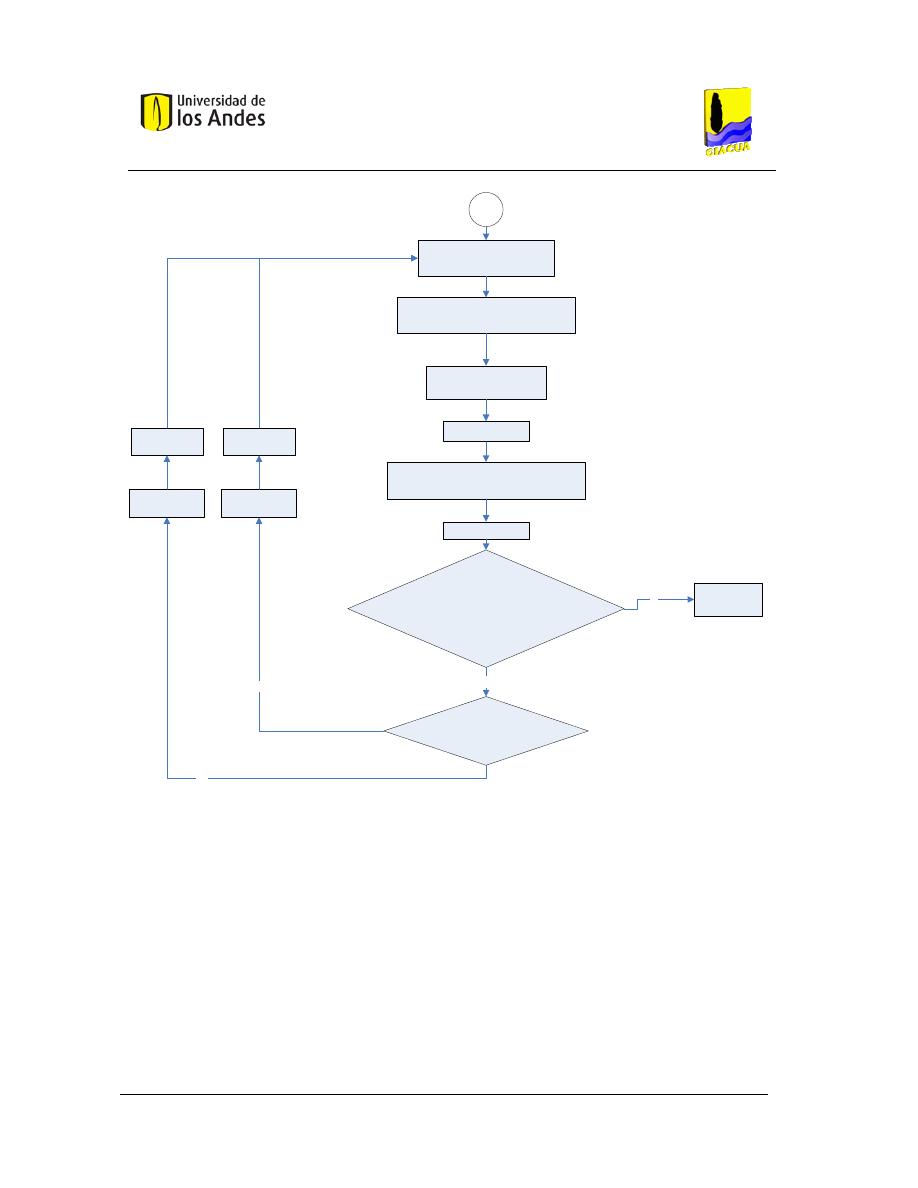
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
99
Caudal_ji = (CaudalE_1i +
CaudalE_2i )/2
Asignar el caudal obtenido como la
demanda base en el nudo
correspondiente
Usando programación
lineal y Xpress diseñar el
submódulo
Modelar el Dj con emisores y obtener las
presiones y caudales en cada nudo
Si el número de nudos con presión por
debajo de la mínima es > 0
Print: Diseño
Promedio j = Dj
Si
CaudalE_1i =
CaudalE_ji
Print: CaudalE_ji
CaudalE_2i =
CaudalE_ji
Si ∑CaudalE_ji - ∑CaudalE_j-1i < Diferencia
Deseada y todos los nudos tienen presión mayor a
la mínima y CU> CU requerido
No
No
Si
FIN
D2 = Dj
D1 = Dj
B
Figura 23B. Diagrama de flujo, metodología para el diseño de submódulos de riego usando programación lineal en
conjunto con SOGH. Parte B.
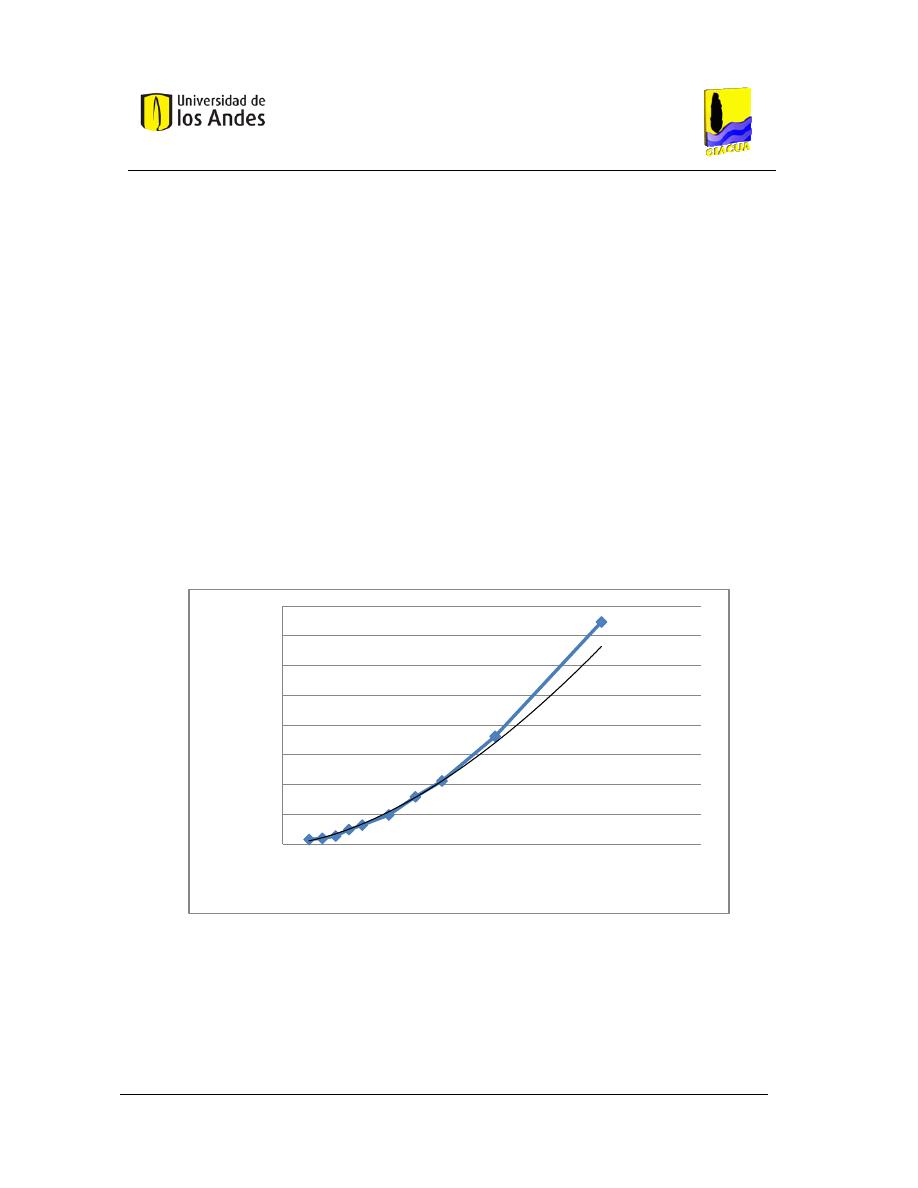
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
100
3.4.4. Resultados de la metodología planteada en el diseño de submódulos de
sistemas de RLAF.
A continuación se presentan los resultados obtenidos para 5 casos de estudio de submódulos de
riego que se diseñaron usando la metodología basada en programación lineal en conjunto con
SOGH. Para evaluar el desempeño de esta metodología se utilizó como punto de comparación la
metodología SOGH, planteada por Ochoa y Saldarriaga (2011). De esta manera, para cada uno de
los casos de estudio que se presentarán, se realizó el diseño usando la metodología SOGH,
partiendo de diferentes flechas de diseño y utilizando los cuatro criterios de redondeo de
diámetros que plantea esta metodología, estos son:
-
Aproximación al diámetro comercial anterior.
-
Aproximación al diámetro comercial siguiente.
-
Redondeo Potencial.
-
Redondeo al diámetro más cercano.
La curva de costos que se utilizó para el diseño de todos los submódulos de riego fue exactamente
la misma y corresponde a la que se muestra a continuación (ver Gráfica 3-42 y Ecuación 3.3):
Gráfica 3-42. Curva Costo vs. Diámetro de tubería.
Ecuación 3.8
y = 16.871x
1.647
R² = 0.985
0
10000
20000
30000
40000
50000
60000
70000
80000
0
50
100
150
200
Costo
de metro
lineal
de tubería
(COP)
Diámetro de tubería (mm)
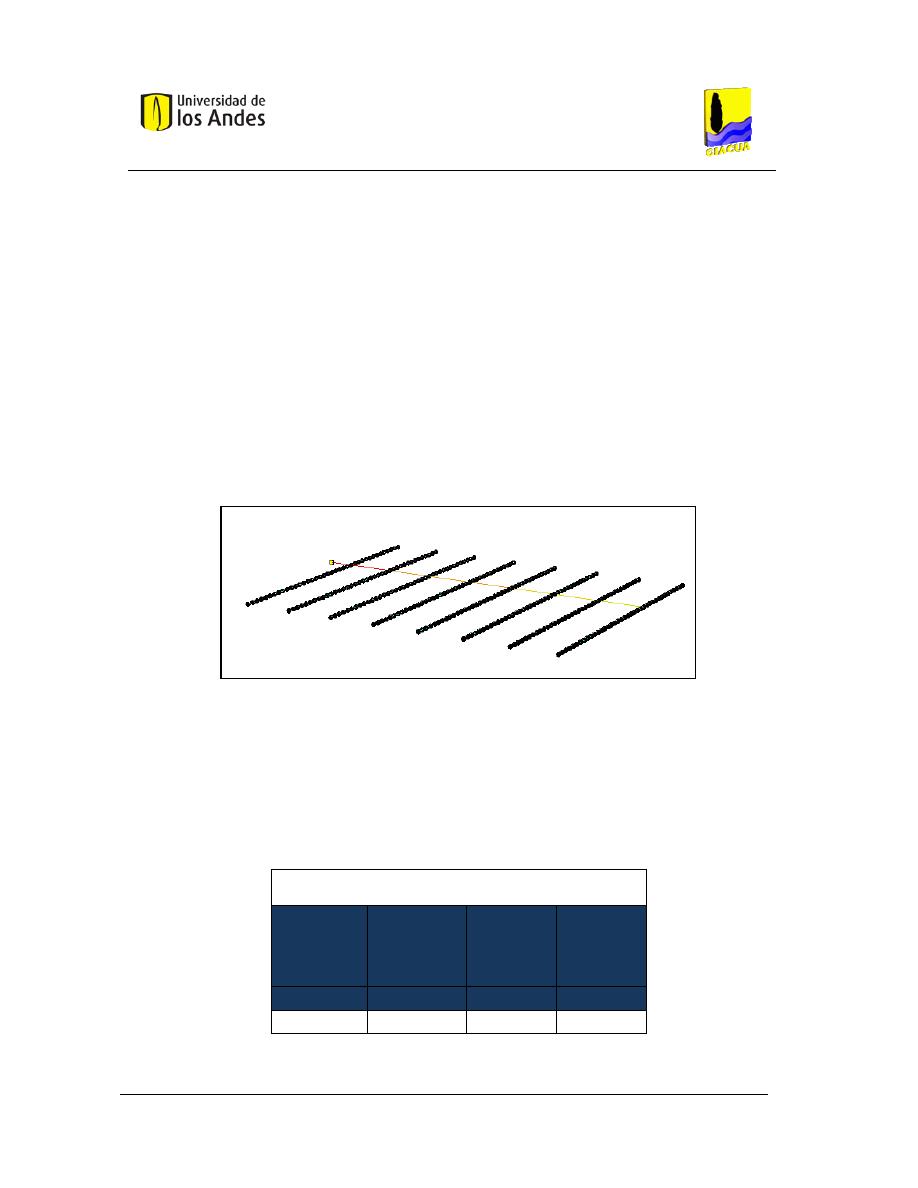
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
101
3.4.4.1.
Submódulos de riego planos.
La presente sección muestra los resultados obtenidos para dos submódulos de riego con
topografía plana. Los dos submódulos de riego se diseñaron usando la metodología planteada en
este trabajo, que hace uso de programación lineal en conjunto con SOGH. Una vez se presenten
los resultados de los submódulos de riego planos, se procederá a mostrar los casos de estudio de
submódulos de riego con topografía variable.
3.4.4.1.1.
Caso de Estudio 1, Submódulo Asimétrico 2 Plano.
Este caso de estudio corresponde al ejemplo mostrado en la Sección 3.4.2. En la siguiente figura se
observa la topología correspondiente del submódulo de estudio:
Figura 24. Caso de Estudio 1, Submódulo Asimétrico 2 Plano.
Este submódulo se compone de 1 tubería múltiple, 16 laterales de riego, 312 plantas y tramos y,
es un submódulo de topografía plana. A continuación se presentan los datos de entrada para
empezar el diseño.
Tabla 15. Datos agronómicos de entrada, Submódulo Asimétrico 2 Plano.
DATOS AGRONÓMICOS
Coeficiente
de
uniformidad
(CU)
Número de
emisores
por planta
(n
e
)
Presión
media de
operación
(h
m
)
Caudal
medio por
emisor
(Q
m
)
()
()
(mca)
(lph)
0.8
2
18.00
120

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
102
Tabla 16. Datos de entrada de los emisores, Submódulo Asimétrico 2 Plano.
Coeficiente de variación del emisor (CV)
0.04
Exponente del emisor
1
Coeficiente del emisor (l/s)/(m
x
)
0.00185185
Teniendo en cuenta los datos de entrada presentados en la Tabla 15 y Tabla 16 y haciendo uso de
la metodología de Bermúdez (2011), se obtiene la siguiente curva para determinar la presión de
entrada al submódulo (PES).
Gráfica 3-43. Curva CU vs PES. Caso de estudio 1, Submódulo Asimétrico 2 Plano.
Por medio de la Gráfica 3-43 y teniendo en cuenta que el Coeficiente de Uniformidad deseado es
de 0.8 se tiene que la PES a utilizar en el diseño es de 21.71 mca. Por otro lado y a partir de la
tolerancia de presiones se obtiene que la presión mínima en el submódulo debe ser de 14.94 mca.
Teniendo estos resultados se procede a realizar el diseño del submódulo usando la metodología
planteada en el diagrama de flujo que se presentó en la Figura 23. Para esto, el primer paso es
realizar los diseños del submódulo partiendo de la Flecha 0 y la Flecha 0.25. Estos diseños
corresponden a lo que se denomina diseño D
1
y diseño D
2
. En la siguiente tabla se observan los
resultados obtenidos para estos dos primeros diseños:
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
10
12
14
16
18
20
22
24
26
28
30
Co
eficien
te
de Unif
orm
idad
()
Presión de Entrada al Submódulo (mca)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
103
Tabla 17. Resultados diseños D
1
y D
2
, Submódulo Asimétrico 2 Plano.
CU
Presión
Mínima
Nudos con
Presión < P
min
6
Costo
Diseños
(l/s)
()
(mca)
()
(COP)
D
1
19.3434
0.8412
14.949
0
7838950
D
2
18.89113
0.8356
14.637
40
7590520
En la Tabla 17 se puede observar que el diseño D
1
(diseño obtenido a partir de la Flecha 0) es un
diseño factible, donde todos sus nudos cumplen con la presión mínima (14.94 mca) y el
Coeficiente de Uniformidad resulta mayor al deseado. Por el contrario, el diseño D
2
(diseño
obtenido a partir de la Flecha 0.25) aunque cumple con el CU deseado, presenta 40 nudos con
presión por debajo de la presión mínima, y por esta razón aunque D
2
sea un diseño más
económico que D
1
, resulta no factible hidráulicamente. Haciendo uso de estos dos primeros
diseños, se pueden obtener los caudales promedio en cada nudo i de manera que se pueda
proceder a calcular un tercer diseño (D
j
)
7
, con el cual se puede obtener un cuarto diseño y así
sucesivamente hasta que finalmente se cumpla que D
j
sea factible y
. Los resultados obtenidos finalmente se presentan en la siguiente tabla:
Tabla 18. Resultados de los diseños promedio D
j,
Submódulo Asimétrico 2 Plano.
Diseño
Promedio (D
j
)
CU
Presión
Mínima
Nudos con
Presión < P
min
Costo
(l/s)
()
(mca)
()
(COP)
1
19.22514969
0.8391
14.862
9
7747716
2
19.28909043
0.8397
14.915
1
7785937
3
19.29083858
0.8412
14.95
0
7787082
Como puede verse en la Tabla 18 fue necesario realizar 3 diseños adicionales para llegar al
resultado definitivo. El primer diseño promedio (D
j
) sigue siendo no factible pero el número de
nudos por debajo de la presión mínima deseada pasó de ser 40 en D
2
a tan solo 9. De esta manera,
siguiendo el algoritmo de la Figura 23, el primer diseño D
j
pasaría a ser el diseño D
2
y sus caudales
se promedian con los del diseño D
1
original; de esta manera se obtuvo el segundo diseño
promedio (D
j
), el cual no es factible, pero únicamente presenta 1 nudo por debajo de la presión
mínima. El proceso continúa, y se realiza un tercer diseño promedio. Como se observa en la Tabla
18 el tercer diseño promedio es un diseño factible (CU mayor a 0.8 y ningún nudo con presión
6
P
min
corresponde a la presión mínima deseada.
7
Es importante recordar al lector que el diseño D
j
corresponde en cada iteración al diseño obtenido
mediante programación lineal, a partir de los caudales promedio de los dos diseños anteriores.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
104
menor a 14.94 mca) y presenta un costo de $ 7, 787,082. Al comparar este costo final con los
obtenidos mediante la metodología SOGH se observa el siguiente resultado:
Gráfica 3-44. Comparación de la relación Costo-Flecha usando SOGH y utilizando 4 criterios de redondeo, con el costo
del diseño obtenido mediante la metodología propuesta. Submódulo Asimétrico 2 Plano.
Mediante los resultados obtenidos, que se presentan en la Gráfica 3-44, se puede evaluar el
desempeño de la metodología planteada en este trabajo. Se aprecia el costo final del submódulo
obtenido a partir de diferentes flechas de diseño y utilizando los 4 criterios de redondeo
planteados por Ochoa (2009). Para el caso de la metodología SOGH el diseño más económico
corresponde a un diseño obtenido mediante la Flecha 0.24 y el criterio de redondeo de
aproximación al siguiente diámetro, para un costo mínimo de $ 7, 913,646. Por otro lado el costo
del diseño obtenido mediante la metodología planteada es de de $ 7, 787,082, que representa una
reducción del 1.6 % (COP$ 126,563.0) en el costo total del submódulo.
Como se pudo observar, en esta sección, la metodología planteada que hace uso de programación
lineal en conjunto con SOGH, permite obtener un diseño factible de forma rápida y conlleva a un
diseño más económico que la metodología SOGH planteada por Ochoa (2009). En las siguientes
secciones se presentarán los resultados obtenidos para otros casos de estudio.
7700000
7900000
8100000
8300000
8500000
8700000
8900000
9100000
9300000
9500000
9700000
0
0.1
0.2
0.3
0.4
0.5
0.6
Costo
Sub
mód
ulo
(COP)
Flecha
Aprox. Siguiente
Aprox. Anterior
Redondeo Pot.
Redondeo
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
105
3.4.4.1.2.
Caso de Estudio 2, Submódulo Simétrico Plano.
En esta sección se presentan los resultados obtenidos para un submódulo de riego plano, donde la
longitud de los laterales a ambos lados de la tubería múltiple es igual. Los datos de entrada para
este submódulo corresponden exactamente a los mismos utilizados para el caso de estudio 1 (ver
Tabla 15, Tabla 16 y Gráfica 3-35). En la siguiente figura se presenta un esquema del submódulo:
Figura 25. Caso de estudio 3, Submódulo Simétrico Plano.
Al igual que en el caso de estudio 1, en este submódulo se realizó el diseño usando la metodología
planteada en este trabajo y se compararon sus resultados con los diseños obtenidos mediante la
metodología planteada por Ochoa. En la Gráfica 3-45 se presentan los resultados finales obtenidos
para este submódulo, donde se puede observar que nuevamente la metodología planteada resulta
más económica que los diseños realizados utilizando SOGH.
Gráfica 3-45. Comparación de la relación Costo-Flecha usando SOGH y utilizando 4 criterios de redondeo, con el costo
del diseño obtenido mediante la metodología propuesta. Submódulo Simétrico Plano.
12000000
12500000
13000000
13500000
14000000
0
0.1
0.2
0.3
0.4
0.5
0.6
Costo
Sub
mód
ulo
(COP)
Flecha
Aprox. Anterior
Aprox. Siguiente
Redondeo Pot.
Redondeo
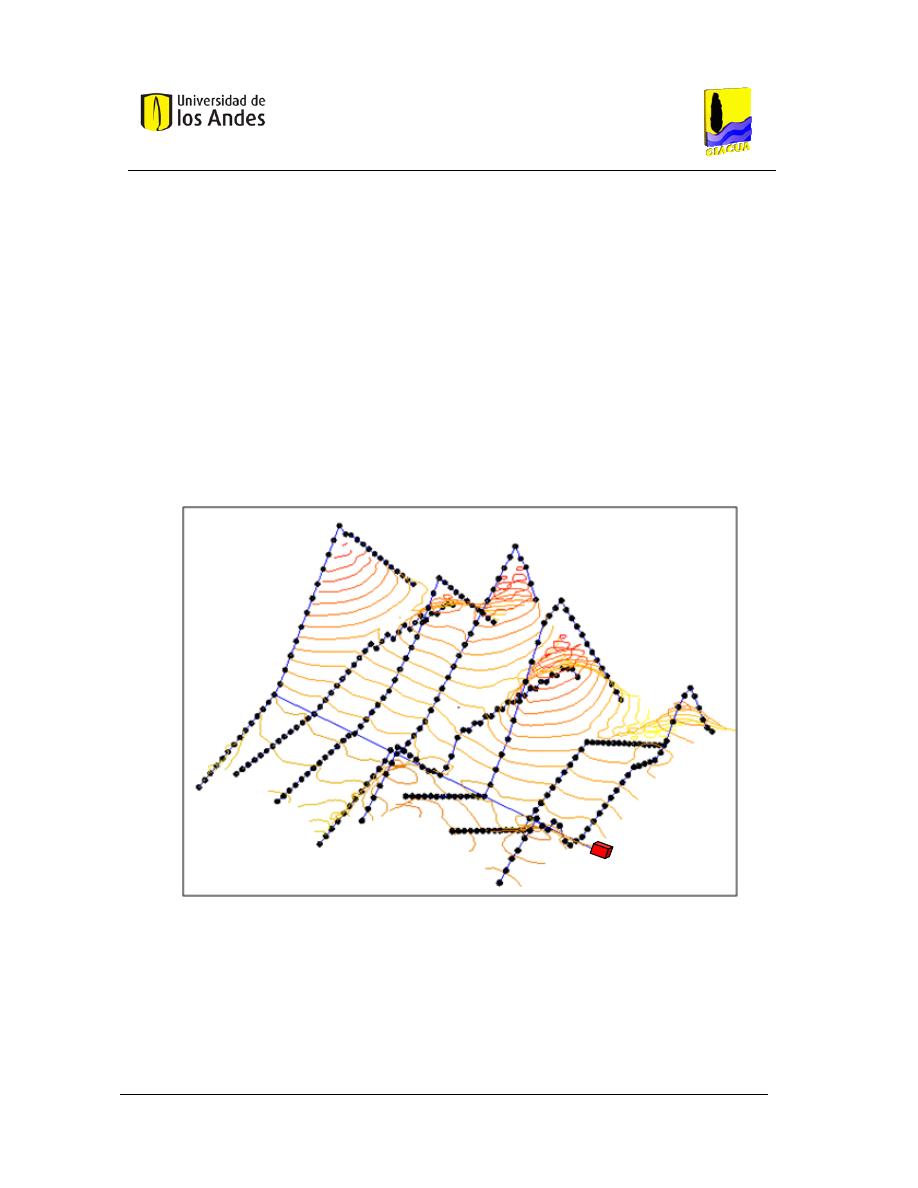
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
106
Para el caso de la metodología SOGH el diseño más económico corresponde a un diseño obtenido
mediante la Flecha 0.24 y el criterio de redondeo de aproximación al diámetro comercial más
cercano, para un costo mínimo de COP $ 12, 334,934. Por otro lado el costo del diseño obtenido
mediante la metodología planteada es de de COP $ 12, 168,800, que representa una reducción del
1.36 % (COP$ 166,134) en el costo total del submódulo.
3.4.4.2.
Caso de Estudio 3, Submódulo Asimétrico 2 con Topografía Variable.
En esta sección se presenta el tercer caso de estudio que resulta de gran importancia debido a que
permite evaluar la metodología planteada, en submódulos de riego con topografía variable. En la
práctica resulta poco común encontrar submódulos de riego en los cuales la topografía sea plana
como los presentados en los casos de estudio 1 y 2. De esta manera, para el caso de estudio 3 se
planteó un submódulo teórico con topografía variable tal como se muestra en la siguiente figura:
Figura 26. Caso de Estudio 3, Submódulo Asimétrico 2 con Topografía Variable.
Como se observa en la Figura 26 el submódulo de riego correspondiente al caso de estudio 3, es
un submódulo en donde la topografía es completamente variada. De esta manera, el nudo crítico
(nudo donde se presentará la presión más baja) puede encontrarse en cualquier punto del
sistema; contrario a lo que sucede en submódulos de riego planos donde el nudo crÍtico estará

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
107
ubicado en el punto más alejado de la fuente de abastecimiento de agua. A continuación se
presentan los datos de entrada utilizados para empezar el diseño.
Tabla 19. Datos agronómicos de entrada, Submódulo Asimétrico 2 con Topografía Variable.
DATOS AGRONÓMICOS
Coeficiente
de
uniformidad
(CU)
Número de
emisores
por planta
(n
e
)
Presión
media de
operación
(h
m
)
Caudal
medio por
emisor
(Q
m
)
()
()
(mca)
(l/h)
0.85
2
14.32
80
Tabla 20. Datos de entrada de los emisores, Submódulo Asimétrico 2 con Topografía.
Coeficiente de variación del emisor (CV)
0.04
Exponente del emisor
0.3
Coeficiente del emisor (l/s)/(m
x
)
0.01
A partir de los datos de entrada presentados en la Tabla 19 y Tabla 20 y haciendo uso de la
metodología de Bermúdez (2011), se obtiene la siguiente curva para determinar la presión de
entrada al submódulo (PES).
Gráfica 3-46. Curva CU vs PES. Submódulo Asimétrico 2 con Topografía.
Con base en la Gráfica 3-46 obtenida a partir del algoritmo planteado por Bermúdez (2011) y
teniendo en cuenta que el Coeficiente de Uniformidad deseado es de 0.85 se tiene que la PES a
0.55
0.65
0.75
0.85
0.95
1.05
0
5
10
15
20
25
30
35
Co
eficien
te
de Unif
orm
idad
R
es
ult
an
te
()
Presión de Entrada al Submódulo (mca)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
108
utilizar es de 22.57 mca. Por otro lado y a partir de la tolerancia de presiones se obtiene que la
presión mínima en el submódulo debe ser de 9.41 mca. Teniendo estos resultados se procede a
realizar el diseño del submódulo usando la metodología planteada. Para esto, el primer paso es
realizar los diseños del submódulo partiendo de la Flecha 0 y la Flecha 0.25. Estos diseños
corresponden a lo que se denomina diseño D
1
y diseño D
2
. En la siguiente tabla se observan los
resultados obtenidos para estos dos primeros diseños:
Tabla 21. Resultados diseños D
1
y D
2
, Submódulo Asimétrico 2 con Topografía.
CU
Presión Mínima
Nudos con
Presión < P
min
Costo
Diseños
(l/s)
()
(mca)
()
(COP)
D
1
13.0838176
0.8820
9.56
0 5129056
D
2
13.0465654
0.8655
8.89
20
5083611
Tal como se muestra en la tabla superior, los diseños D
1
y D
2
cumplen con el Coeficiente de
Uniformidad deseado de 0.85, pero únicamente el diseño D
1
(diseño obtenido a partir de la Flecha
0) no presenta nudos con presión por debajo de la mínima. El diseño D
2
(diseño obtenido a partir
de la Flecha 0.25) presenta 20 nudos con déficit de presión, con una presión en el nudo crítico de
8.89 mca (52 cm de columna de agua por debajo de la presión mínima). Usando los resultados de
los caudales emitidos en los diseños D
1
y D
2
se pueden obtener caudales promedio en cada nudo i
de manera que se proceda a calcular un tercer diseño (D
j
), con el cual se puede obtener un cuarto
diseño y así sucesivamente hasta que finalmente se cumpla que D
j
sea factible y
. Los resultados obtenidos finalmente se presentan en la siguiente
tabla:
Tabla 22. Resultados de los diseños promedio D
j,
Submódulo Asimétrico 2 con Topografía Variable.
Diseño
Promedio (D
j
)
CU
Presión Mínima
Nudos con
Presión < P
min
Costo
(l/s)
()
(mca)
()
(COP)
1
13.0652
0.8764
9.37
3
5100632
2
13.0559
0.8826
9.498
0 5098791
3
13.0457
0.8828
9.5
0 5098791
De la Tabla 22 se puede concluir que fue necesario realizar dos diseños promedio a fin de obtener
un diseño factible. En esta tabla se puede ver que en el primer diseño promedio, el número de
nudos por debajo de la presión mínima pasó de ser 20 en D
2
a tan solo 3. De esta manera,
siguiendo el algoritmo de la Figura 23 el primer diseño D
j
pasaría a ser el diseño D
2
y sus caudales

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
109
se promedian con el diseño D
1
original, para de esta manera obtener el segundo diseño promedio
(D
j
), el cual resulta factible. Observando los resultados presentados en la Tabla 22 queda
establecido que el segundo diseño promedio es un diseño factible de manera que éste pasa a
reemplazar el diseño D
1
y sus caudales se promediaron con los caudales del diseño D
2
, que para
esta iteración corresponden a los del primer diseño promedio. Al realizar el tercer diseño
promedio, se observa que nuevamente, el número de nudos con déficit de presión es cero y dado
que D
j
es factible y
se decide terminar el proceso de
diseño. Es importante hacer notar al lector que el costo del segundo diseño promedio y el tercero,
son iguales; pero esto no quiere decir que el diseño sea exactamente igual en cuanto a la
distribución de diámetros. Los diseños promedio 2 y 3 tienen 304 tuberías con el mismo diámetro
asignado, únicamente 8 tubos presentan un diámetro diferente entre los dos diseños. En la
siguiente tabla se presentan los diámetros asignados a las 8 tuberías en las que los diámetros
difieren entre los dos diseños:
Tabla 23. Diámetros asignados por Xpress en las 8 tuberías diferentes entre el segundo y el tercer diseño promedio.
Submódulo Asimétrico 2 con Topografía.
ID
Tubería
Longitud
Tubería
(m)
Diámetro Asignado en el
diseño promedio (mm)
Costo del tubo (COP)
D
j
2
D
j
3
D
j
2
D
j
3
73
5.009
25.4
19.05
17404.16
10836.25
74
5.009
19.05
25.4
10836.25
17404.16
99
5.001
19.05
25.4
10818.94
17376.36
101
5.001
25.4
19.05
17376.36
10818.94
151
5.004
19.05
25.4
10825.43
17386.78
152
5.004
25.4
19.05
17386.78
10825.43
162
5.001
25.4
31.75
17376.36
25093.98
163
5.001
31.75
25.4
25093.98
17376.36
Suma (COP $)
127118.3
127118.3
En la Tabla 23 se muestran los diámetros, longitudes y costo de las 8 tuberías en los que difieren el
segundo y tercer diseño promedio. Como se puede observar aunque los 8 tubos presentan un
diámetro diferente entre un diseño y otro, la suma de los costos de los 8 tubos es exactamente
igual, pero como se dijo anteriormente esto es únicamente una coincidencia. De esta manera y
habiendo aclarado los resultados obtenidos en la Tabla 22, se escoge como diseño final el tercer
diseño promedio, el cual presenta un costo de COP $ 5, 098,791 y que en comparación con la
metodología SOGH, resulta más económico, como se observa en la Gráfica 3-47.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
110
Gráfica 3-47. Comparación de la relación Costo-Flecha usando SOGH y utilizando 4 criterios de redondeo, con el costo
del diseño obtenido mediante la metodología propuesta. Submódulo Asimétrico 2 con Topografía Variable.
Como puede verse en la Gráfica 3-47 la metodología propuesta para el diseño de submódulos de
riego resulta en un diseño más económico que al emplear la metodología propuesta por Ochoa. Al
diseñar haciendo uso de la metodología SOGH variando el valor de la flecha de diseño y utilizando
los cuatro criterios de redondeo (Aproximación al siguiente, Aproximación al anterior, Redondeo
potencial y Redondeo al diámetro más cercano) mostrados en la Gráfica 3-47, se obtiene que el
diseño del submódulo que presenta el menor costo es el de la Flecha 0.25 con criterio de
aproximación al diámetro comercial siguiente, para un costo total de COP $ 5, 246,523. Si se
compara el costo del diseño más económico de la metodología SOGH con respecto al costo
obtenido mediante la metodología propuesta, se observa que la nueva metodología conlleva a un
costo 2.9% por debajo del mas económico de SOGH, y esto corresponde a una reducción de COP $
147,732.
De esta manera y habiendo visto los resultados obtenidos para este caso de estudio, en el cual se
tienen variaciones en la topografía a lo largo del submódulo, se observa que el desempeño de la
metodología propuesta para submódulos de riego utilizando programación lineal en conjunto con
SOGH resulta bastante buena y permite obtener una reducción en los cotos finales del submódulo.
5000000
5100000
5200000
5300000
5400000
5500000
5600000
5700000
0
0.1
0.2
0.3
0.4
0.5
0.6
Costo
Sub
mód
ulo
(COP)
Flecha
Aprox. Anterior
Aprox. Siguiente
Redondeo Pot.
Redondeo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
111
3.4.4.3.
Caso de Estudio 4, Submódulo Asimétrico 3 con Topografía Variable.
En esta sección se estudia un nuevo submódulo en el cual los laterales de riego no son rectos y
todos presentan longitudes diferentes. Adicionalmente, el submódulo presenta una topografía
generada mediante números aleatorios y de esta manera, ningún nudo del sistema tiene la misma
elevación de otro nudo (ver Figura 27 y Figura 28).
Figura 27. Caso de Estudio 3, Submódulo Asimétrico 3 con Topografía Variable, vista en planta.
Figura 28. Caso de Estudio 4, Submódulo Asimétrico 3 con Topografía Variable, vista en perfil.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
112
Como puede observarse en la Figura 27 y la Figura 28 los nudos del sistema presentan diferentes
alturas topográficas, pero el sistema en sí tiene una tendencia a aumentar su elevación a medida
que se aleja de la fuente de abastecimiento; de esta manera, los laterales más alejados de la
entrada al submódulo presentan la mayor elevación y por lo tanto serán los que presentarán
presiones más críticas, al estar más alejados y presentar un altura topográfica superior a la de la
entrada. Para este caso de estudio los valores de entrada al problema de diseño fueron:
Tabla 24. Datos agronómicos de entrada, Submódulo Asimétrico 3 con Topografía Variable.
DATOS AGRONÓMICOS
Coeficiente
de
uniformidad
(CU)
Número de
emisores
por planta
(n
e
)
Presión
media de
operación
(h
m
)
Caudal
medio por
emisor
(Q
m
)
()
()
(mca)
(l/h)
0.85
2
10.00
80
Tabla 25. Datos de entrada de los emisores, Submódulo Asimétrico 3 con Topografía Variable.
Coeficiente de variación del emisor (CV)
0.04
Exponente del emisor
0.2
Coeficiente del emisor (l/s)/(m
x
)
0.01402127
de donde se obtiene la curva CU vs PES establecida por Bermúdez (2011):
Gráfica 3-48. Curva CU vs PES. Caso de estudio 3, Submódulo Asimétrico 3 con Topografía Variable.
0.75
0.8
0.85
0.9
0.95
1
0
5
10
15
20
25
30
Co
eficien
te
de
Unif
orm
idad
()
Presión de Entrada al Submódulo (mca)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
113
Con base en la Gráfica 3-48 obtenida a partir del algoritmo planteado por Bermúdez (2011) y
teniendo en cuenta que el Coeficiente de Uniformidad deseado es de 0.85 se tiene que la PES a
utilizar es de 18.69 mca. Por otro lado y a partir de la tolerancia de presiones se obtiene que la
presión mínima en el submódulo debe ser de 5.33 mca. Teniendo estos resultados se procede a
realizar el diseño del submódulo usando la metodología planteada. Para esto, el primer paso es
realizar los diseños del submódulo partiendo de la Flecha 0 y la Flecha 0.25. Estos diseños
corresponden a lo que se denomina diseño D
1
y diseño D
2
. En la siguiente tabla se observan los
resultados obtenidos para estos dos primeros diseños:
Tabla 26. Resultados diseños D
1
y D
2
, Submódulo Asimétrico 3 con Topografía Variable.
CU
Presión Mínima
Nudos con
Presión < P
min
Costo
Diseños
(l/s)
()
(mca)
()
(COP)
D
1
5.05644
0.88285
5.366
0 1756991
D
2
5.03981
0.87810
5.137
5
1735176
Tal como se muestra en la tabla superior, los diseños D
1
y D
2
cumplen con el Coeficiente de
Uniformidad deseado de 0.85, pero únicamente el diseño D
1
no presenta nudos con presión por
debajo de la mínima, por su parte el diseño D
2
presenta 5 nudos con déficit de presión. Usando los
resultados de los caudales emitidos en los diseños D
1
y D
2
se pueden obtener caudales promedio
en cada nudo i de manera que se proceda a calcular el siguiente diseño (D
j
), con el cual se puede
obtener un tercer diseño, del cual se presentan sus resultados en la siguiente tabla:
Tabla 27. Resultados del diseño promedio D
j,
Submódulo Asimétrico 3 con Topografía Variable.
Diseño
Promedio (D
j
)
CU
Presión Mínima
Nudos con
Presión < P
min
Costo
(lps)
()
(mca)
()
(COP)
1
5.05644
0.88285
5.366
0
1756991
Si se observa con cuidado la Tabla 27 en conjunto con la Tabla 26 se puede ver que el primer
diseño promedio dio exactamente el mismo resultado del diseño D
1
. Cuando sucede esto, el
algoritmo termina y se obtiene como resultado el primer diseño promedio. Es importante
mencionar que el proceso de convergencia en los diseños de submódulos de riego, será más
rápido en la medida en que el exponente de los emisores disminuya. Los resultados obtenidos en
el diseño del caso de estudio 4 muestran que tarde o temprano el algoritmo tiene que converger a
un mismo diseño, pero como se dijo, este proceso tardará más entre mayor sea el exponente del

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
114
emisor. De esta manera, el caso más sencillo en el diseño de submódulos de riego usando la
metodología propuesta corresponde al de emisores autocompensantes (exponente de emisor
x=0); este caso se presentará en la Sección 3.4.4.4.
Finalmente y volviendo al caso de estudio que corresponde a esta sección, se obtuvo que el costo
del submódulo mediante la metodología planteada es de COP $ 1, 756,991. Si se compara el costo
obtenido a partir de la metodología propuesta, con los costos que se obtienen utilizando la
metodología SOGH se tiene la siguiente gráfica comparativa:
Gráfica 3-49. Comparación de la relación Costo-Flecha usando SOGH y utilizando 4 criterios de redondeo, con el costo
del diseño obtenido mediante la metodología propuesta. Submódulo Asimétrico 3 con Topografía Variable.
De la misma manera como sucedió para los casos de estudio 1, 2 y 3, en este caso el diseño
obtenido mediante la metodología propuesta resultó más económico que los diseños obtenidos
mediante la metodología SOGH. El menor costo (COP $ 1, 767,447) mediante la metodología SOGH
corresponde al diseño con la Flecha 0.24 y un criterio de redondeo al diámetro comercial más
cercano; la diferencia entre este costo y el obtenido mediante la metodología propuesta es de diez
mil quinientos pesos (COP $ 10,456) que corresponde a una diferencia del 0.6 %.
Teniendo los resultados presentados en las secciones 3.4.4.1, 3.4.4.2 y 3.4.4.3 se puede concluir
que la metodología planteada conlleva a diseños óptimos. Es importante anotar que los cuatro
casos de estudios presentados hasta ahora corresponden a submódulos con características
completamente diferentes. Los cuatro casos de estudio difieren en su topografía, ecuación del
emisor, topología, caudal medio por planta, Coeficiente de Uniformidad, PES y Presión mínima.
1760000
1770000
1780000
1790000
1800000
1810000
1820000
1830000
1840000
1850000
0
0.1
0.2
0.3
0.4
Costo
Sub
mód
ulo
(COP)
Flecha
Redondeo
Redondeo Pot.
Aprox. Anterior
Aprox. Siguiente
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
115
3.4.4.4.
Caso de Estudio 5, Submódulo con Emisores Autocompensantes.
En esta sección se presenta un submódulo de riego en el cual se tienen emisores
autocompensantes. Es importante recordar al lector que un emisor autocompensante es aquel en
el que el exponente de la ecuación del emisor es cero (0), implicando que el caudal que sale por
cada nudo es independiente de la presión que se tenga en el punto. El submódulo que se utilizó
como ejemplo para este caso es un ejemplo teórico con una pendiente del 100%, como se puede
ver en la siguiente figura:
Figura 29. Caso de Estudio 5, Submódulo con Emisores Autocompensantes, vista en planta.
En la Figura 29 se puede ver que el submódulo presenta una pendiente topográfica en la cual
entre más alejado se encuentre el lateral de riego, menor elevación topográfica tendrá. Este tipo
de submódulo se asemeja a los submódulos de riego utilizados en los cultivos de café.
Para este caso de estudio y al hacer uso de emisores autocompensantes, el diseñador debe definir
por sí mismo, la presión de entrada al submódulo que desea tener o la presión que las condiciones
hidráulicas aguas arriba de la entrada le permiten alcanzar. Adicional a esto, el diseñador definirá
una presión mínima deseada en el submódulo y asignará el caudal que desee que se emita a cada
planta. En el caso que se presenta en esta sección se escogió una presión de entrada al submódulo
de 17 mca y una presión mínima de 5 mca; por su parte, el caudal que se asignó a cada nudo fue
de 0.045 l/s. Teniendo en cuenta que se tienen emisores autocompensantes no es necesario
seguir el diagrama de flujo presentado en la Figura 23, esto quiere decir que no es necesario
definir ninguna superficie de gradiente hidráulico y únicamente se requiere realizar el diseño
directamente usando programación lineal para obtener los diámetros del submódulo, que por ser
de emisores autocompensantes se comporta como una red abierta con demanda constante en sus
nudos de consumo. Teniendo en cuenta lo anterior en la siguiente gráfica se presentan los
resultados de comparación entre el diseño usando programación lineal y el diseño que se
obtendría usando diferentes flechas de diseño y la metodología SOGH:
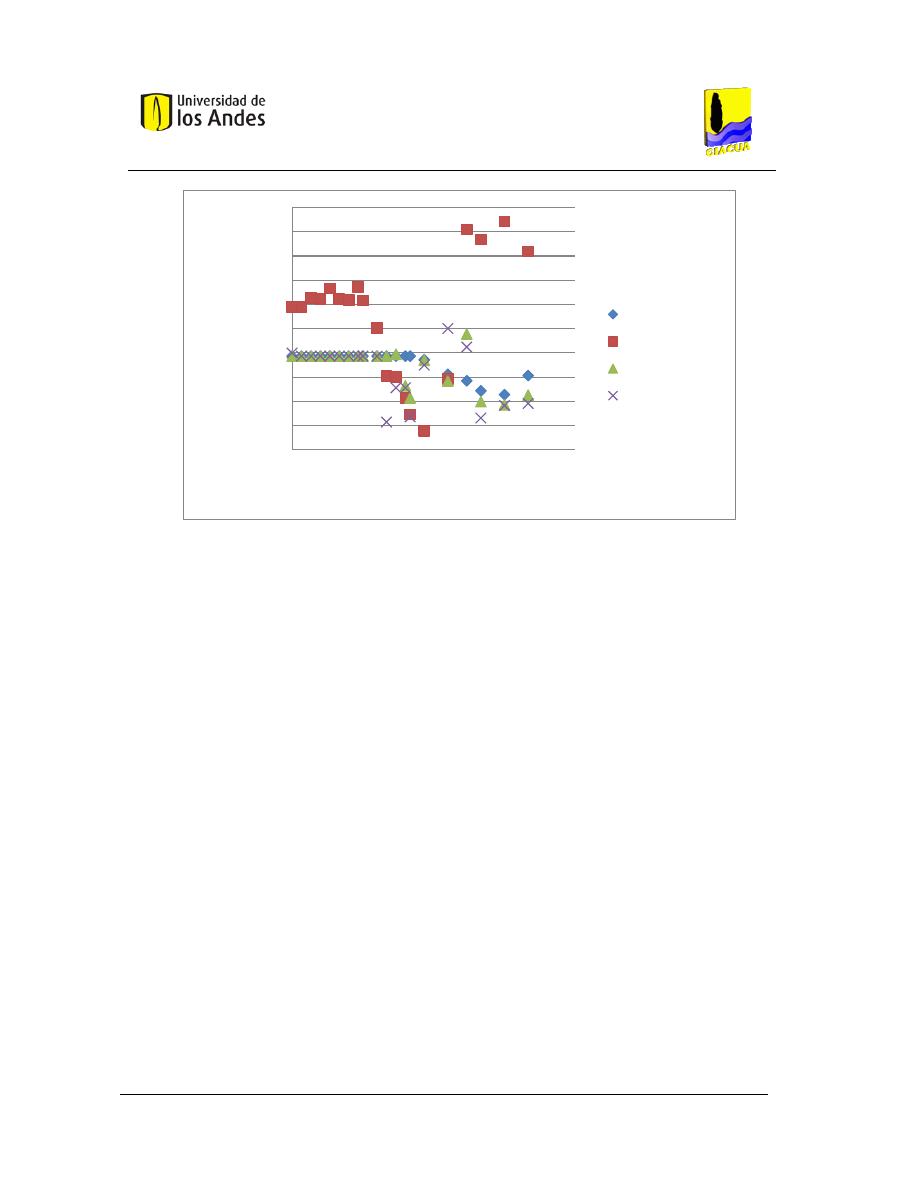
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
116
Gráfica 3-50. Comparación de la relación Costo-Flecha usando SOGH y utilizando 4 criterios de redondeo, con el costo
del diseño obtenido mediante programación lineal. , Submódulo con Emisores Autocompensantes.
Como era de esperarse, el diseño haciendo uso de programación lineal resultó más económico que
los diseños obtenidos mediante SOGH. El diseño más económico mediante la metodología SOGH
corresponde a una flecha de 0.28 y un criterio de redondeo de aproximación al siguiente diámetro
comercial y su costo es de COP $ 5, 778,819. Por su parte el costo del diseño obtenido con
programación lineal es de COP $ 5, 666,668 implicando una diferencia de COP $ 112,151. Es
importante aclarar que para este caso de estudio todos los diseños de SOGH y el diseño mediante
programación lineal cumplieron con el coeficiente de uniformidad y la presión mínima en todos
sus nudos.
Este caso de estudio resulta importante debido a que para éste se realizó un análisis de
sensibilidad. El objetivo era determinar que implicaciones tenía sobre el resultado final del
submódulo, una variación en el coeficiente (K) o el exponente de la curva de costos (x) (ver
Ecuación 3.9).
Ecuación 3.9
Aunque ya se ha mencionado anteriormente, es importante recordar que en la Ecuación 3.9 NT
hace referencia al número de tubos en el sistema, K corresponde al coeficiente de la curva de
costos, L
i
es la longitud de la tubería i, D
i
el diámetro de la tubería i y x es el exponente de la curva
5700000
5800000
5900000
6000000
6100000
6200000
6300000
6400000
6500000
6600000
6700000
0
0.1
0.2
0.3
0.4
0.5
0.6
Costo
Sub
mód
ulo
(COP)
Flecha
Aprox. Anterior
Aprox. Siguiente
Redondeo Pot.
Redondeo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
117
de costos. De esta manera, se plantearon diferentes curvas de costos a la original en donde el
Coeficiente K es de 16.871 y el exponente x es de 1.647; en la siguiente tabla se presentan los
valores de K y x que se utilizaron:
Tabla 28. Valores de K y x utilizados para crear diferentes curvas de costos.
Curva de
Costo
K
x
C
1
16.871
1.647
C
2
16.871
0.7
C
3
3
1.647
En la Tabla 28 se observan 3 curvas de costos utilizadas para el análisis de sensibilidad realizado.
Se puede ver que la curva de costos C
1
corresponde a la que se utilizó para todos los casos de
estudio mostrados anteriormente y corresponde a la curva de costos obtenida a partir de las
tuberías que suministra la empresa PAVCO S.A., las demás curvas mostradas son variaciones
teóricas de la curva original. Los resultados comparativos entre SOGH y programación lineal con la
curva de costos C
1
son los que se presentaron en la Gráfica 3-50 en las siguientes gráficas se
observa la comparación entre ambas metodologías usando C
2
y C
3
.
Gráfica 3-51. Comparación de la relación Costo-Flecha usando SOGH y utilizando 4 criterios de redondeo, con el costo
del diseño obtenido mediante programación lineal. Caso de estudio 5 usando la curva de costos C
2
.
285000
290000
295000
300000
305000
310000
315000
320000
0
0.2
0.4
0.6
Costo
Sub
mód
ulo
(COP)
Flecha
Aprox. Anterior
Aprox. Siguiente
Redondeo Pot.
Redondeo
Diseño - Programación
Lineal
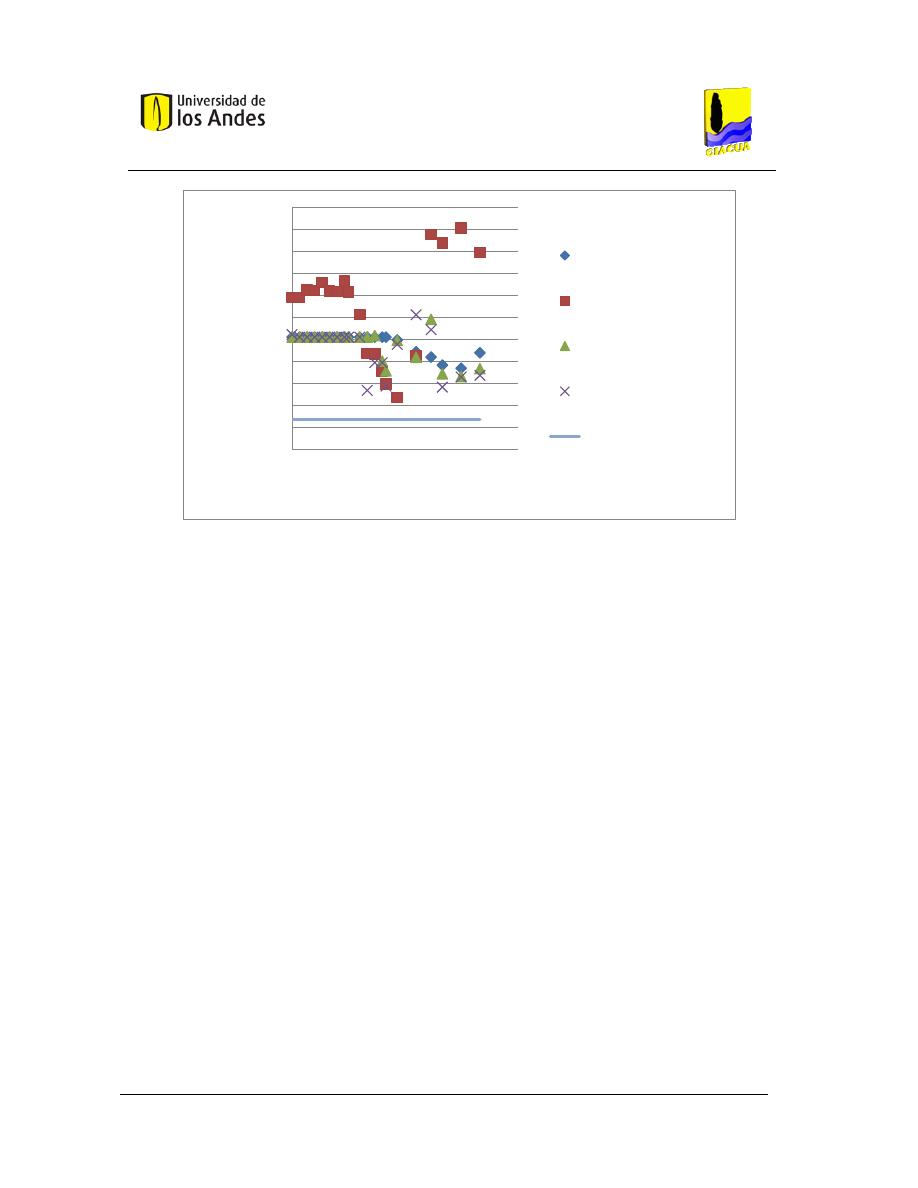
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
118
Gráfica 3-52. Comparación de la relación Costo-Flecha usando SOGH y utilizando 4 criterios de redondeo, con el costo
del diseño obtenido mediante programación lineal. Caso de estudio 5 usando la curva de costos C
3
.
Como puede observarse en la Gráfica 3-51 y la Gráfica 3-52, el diseño usando programación lineal
siempre resulta más económico que los diseños de SOGH, independiente de la curva de costos
utilizada. Lo que se puede esperar es que el único caso en que el diseño de SOGH y el diseño
mediante programación lineal tengan el mismo costo es en un caso hipotético en el que el
exponente de la curva de costos sea igual a cero (0). En el caso en que el exponente de la curva de
costos sea 0 el costo del sistema únicamente será función de la longitud de las tuberías y del
coeficiente de la curva de costos. Para este caso, la metodología SOGH establecerá un diseño igual
al obtenido en el caso inicial, ya que la forma en que SOGH asigna los diámetros es independiente
de la curva de costos. Por otro lado la formulación lineal presentará una gran cantidad de
soluciones factibles, donde una de ellas será un diseño en el que todos los tubos del sistema
tengan el diámetro máximo; sin embargo, a pesar de que se asigne el máximo diámetro
disponible, dado que el exponente de la curva de costos es 0 entonces el diseño tendrá el mismo
costo establecido por la metodología SOGH.
980000
1000000
1020000
1040000
1060000
1080000
1100000
1120000
1140000
1160000
1180000
1200000
0
0.2
0.4
0.6
Costo
Sub
mód
ulo
(COP)
Flecha
Aprox. Anterior
Aprox. Siguiente
Redondeo Pot.
Redondeo
Diseño - Programación
Lineal

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
119
4. CONCLUSIONES
A lo largo de este trabajo se presentaron diferentes análisis, diseños, metodologías y
comparaciones. Primero se presentó un resumen de lo que se conoce de sistemas de riego
localizado de alta frecuencia, después se realizó un análisis de la metodología SOGH y su aplicación
al diseño de submódulos de riego y finalmente se presentó una nueva metodología para el diseño
de sistemas de submódulos de riego. Teniendo en cuenta lo mostrado a lo largo de este
documento se puede concluir:
El uso de programación lineal en conjunto con la metodología SOGH permitió
obtener una metodología de diseño de submódulos de riego que conlleva a
diseños que cumplen con las restricciones hidráulicas y agronómicas y que a su vez
resulta en diseños más económicos que los obtenidos por la metodología SOGH
originalmente planteada por Ochoa (2011).
La metodología planteada requiere de un proceso iterativo basado en el algoritmo
de bisección para poder llegar a un diseño óptimo. Esto se debe a que existe una
sensibilidad de los diseños obtenidos, respecto a la flecha a partir de la cual se
plantea la superficie de gradiente hidráulico que permite establece los caudales
que se emitirán en los nudos del sistema.
La metodología de diseño se probó para diferentes casos de estudio, donde cada
caso de estudio presentó parámetros de entrada diferentes. En los diferentes
diseños se cambiaron los caudales medios por emisor, la ecuación del emisor, la
topología, CU y la topografía y se observó que siempre la metodología planteada
presentaba menores costos que la metodología SOGH del 2009.
Entre menor sea el exponente de la curva de los emisores en el submódulo, el
proceso de convergencia del algoritmo será más rápido. Esto ocurre debido a que
entre menor sea el exponente del emisor, se presentará una menor sensibilidad
del caudal emitido con respecto a la presión en el punto de emisión.
En los casos en que el submódulo presente emisores autocompensantes el
diseñador debe definir la PES, la presión mínima y los caudales que desea en cada
emisor del submódulo. En este caso la metodología planteada por Bermúdez no
puede aplicarse dado que el exponente de la ecuación del emisor es 0 y resulta
matemáticamente inviable.
Cuando el submódulo de riego tiene emisores autocompensantes, el algoritmo
planteado resulta innecesario y únicamente se requiere realizar un diseño
mediante programación lineal en Xpress, que resultará en el diseño óptimo del
sistema. Este diseño resulta ser el diseño óptimo global ya que al ser un problema

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
120
lineal no se presentan óptimos locales y solo se presenta un diseño óptimo que
cumple con todas las restricciones establecidas en la formulación. Adicionalmente
es importante mencionar que el tiempo que Xpress tarda en realizar un diseño es
inferior a 1 segundo.
La metodología SOGH es aplicable al diseño de submódulos de riego, llevando a
diseños cuyo costo no es superior al 2% del óptimo obtenido mediante la
metodología planteada.
La flecha máxima de diseño de la metodología SOGH para el caso en que la última
tubería tiene una longitud infinitesimal, es la flecha de 0.25. En este caso, la
pendiente de la línea de gradiente hidráulico presenta una pendiente cero en el
último punto del sistema y esto significaría hacer uso de una tubería de diámetro
infinito con el fin de cumplir con las pérdidas objetivo de cero. Por otro lado, este
caso es solo un caso teórico, y dado que la última tubería del sistema presentará
una longitud no diferencial, el valor de la flecha máxima puede aumentar en
función de la última tubería de la ruta crítica.
En el caso de submódulos de riego, no es posible determinar la flecha óptima
propuesta por Ochoa; esto ocurre porque en un submódulo de riego, con
emisores no autocompensantes, no se conocen a priori los caudales emitidos en
los nudos que componen el sistema.
Al aplicar la metodología SOGH al diseño de submódulos de riego, La curva Costo-
Flecha del diseño de diámetros continuos, presenta un patrón donde la flecha de
mínimo costo es una flecha intermedia entre la flecha 0 y 0.25. Este patrón se
mantiene para un mismo submódulo de riego, independientemente de las
características de los emisores que se utilicen; sin embargo, la flecha que lleva al
mínimo costo con diámetros continuos varía dependiendo de la topología de la
red.
Los resultados encontrados por Bermúdez, aunque no llevan a un diseño óptimo
de forma directa, permiten determinar la relación que existe entre la presión de
entrada al submódulo de riego y el coeficiente de uniformidad, de tal manera que
se pueda establecer la presión a la entrada del submódulo, a partir de la cual no se
cumplirá con el requerimiento agronómico de uniformidad.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
121
5. RECOMENDACIONES
Con este trabajo surgió una nueva forma de diseñar submódulos de sistemas de riego localizado
de alta frecuencia, que como bien es sabido, la metodología hace uso de programación lineal y su
formulación surgió de un ejemplo sencillo de redes abiertas con demanda constante en sus nudos.
De esta manera la formulación implementada en el programa Xpress se puede utilizar para realizar
el diseño de cualquier sistema de tuberías en donde se conozca el camino que toma el fluido y el
caudal que pasará por cada una de las tuberías que componen el sistema, permitiendo obtener de
forma rápida el diseño óptimo global del sistema. Teniendo en cuenta lo mencionado y lo
presentado a lo largo de este trabajo a continuación se presentan las siguientes recomendaciones
para futuros estudios:
Dado que la formulación matemática planteada en este trabajo es aplicable a redes
abiertas con demanda constante, su uso para el diseño diferentes sistemas hidráulicos
podría presentar resultados muy parecidos a los mostrados en este trabajo. A
continuación se dan algunos ejemplos para futuras investigaciones:
-
Diseño de redes de distribución de agua potable (RDAP): En los últimos años se ha
venido desarrollando en el Centro de Investigaciones en Acueductos y
Alcantarillados (CIACUA) la metodología OPUS que busca obtener el diseño
óptimo de RDAP. Esta metodología, que ha obtenido importantes resultados en
sus investigaciones, presenta dentro de su algoritmo, una etapa en la cual la red
cerrada se convierte en un árbol (red abierta). Al tenerse una red abierta y los
caudales de diseño en cada tubería se puede proceder a utilizar la formulación
planteada en este trabajo de tal forma que se tenga un diseño óptimo del árbol
que se generó mediante la metodología OPUS. Una vez se tiene el diseño óptimo
del árbol es necesario diseñar las tuberías que no se incluyeron en éste. Para esto
es recomendable probar diferentes criterios de diseño de las tuberías faltantes de
forma que se pueda obtener un diseño óptimo de una RDAP. Actualmente y con
base en los resultados y programas del presente trabajo se han venido realizando
los diseños de diferentes redes, y hasta la fecha se ha encontrado que para las
redes R28 y Balerma se puede obtener un diseño óptimo.
-
Diseño de alcantarillados: Como bien es conocido, el conjunto de tuberías que
conforman un sistema de drenaje urbano presenta una topología abierta.
Teniendo una topología abierta y conociendo los caudales que pasan por cada
unas de las tuberías se puede hacer uso de la formulación lineal presentada en
este trabajo, de manera que se obtenga un diseño óptimo. Es importante aclarar
que se deben hacer algunas modificaciones en las restricciones de la formulación
matemática, dado que el flujo en alcantarillados no es un flujo a presión.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
122
Adicionalmente se deben agregar restricciones que se presentan en estos tipos de
sistemas; por ejemplo, cuando se tiene flujo cuasicrítico la relación de llenado de
las tuberías no puede ser mayor al 70% y que en cada tubería se debe cumplir con
una velocidad mínima (para asegurar la autolimpieza) y velocidad máxima (por
seguridad).
-
Diseño de tuberías en serie: El diseño con programación lineal, de tuberías en
serie con demanda constante en los nudos de consumo es un problema resuelto.
La formulación lineal permitirá obtener el diseño óptimo del problema de forma
rápida y eficiente. Teniendo en cuenta lo anterior, se recomienda estudiar las
líneas de gradiente hidráulico resultantes en diferentes sistemas de tuberías en
serie al aplicar programación lineal. Estas investigaciones permitirán conocer de
forma exacta las características de la LGH óptima y sus variaciones respecto a las
características del sistema de tuberías que se plantee.
En el presente trabajo se pudo observar que se obtuvo el diseño óptimo de submódulos
de riego. Ahora es necesario investigar la manera en que se debe diseñar todo el sistema
que se encuentra aguas arriba de la entrada a los diferentes submódulos de riego. Para
esto se debe definir la manera en que se operará todo el sistema de riego en sí, es decir el
orden en que se operarán los diferentes submódulos de riego que componen el sistema
en su totalidad, de forma que se optimice el diseño de los sistemas de tuberías principales
y la aplicación de los nutrientes que se agregan al fluido en la estación que alimenta todo
el sistema de riego.
Mediante los resultados obtenidos al verificar el trabajo de Bermúdez, se puede
establecer que existe una presión de entrada máxima que cumpla con el coeficiente de
uniformidad. Pero es posible que en campo esta presión no pueda lograrse a la entrada
del submódulo y se requiera de alguna bomba para lograr tener esa presión. En este caso
se recomienda un análisis de costos que determine si es mejor colocar una bomba que
permita tener la PES establecida por Bermúdez, logrando minimizar los costos de las
tuberías o si es mejor no colocar la bomba y tener una PES menor pero con diámetros de
tuberías mayores.
La metodología SOGH presenta resultados muy buenos en el diseño de submódulos de
sistemas de riego, pero es necesario realizar algunas modificaciones en algunos pasos
como en el de la determinación de la flecha óptima. Para el caso de Submódulos de RLAF,
no es posible establecer la flecha óptima mediante lo propuesto por Ochoa debido a que
no es posible establecer un centroide de demandas. Se recomienda hacer uso de
programación lineal para poder determinar la LGH óptima en este tipo de sistemas y sus
variaciones respecto a variaciones en los parámetros de entrada al problema de diseño.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
123
6. REFERENCIAS
-
Centro de Investigaciones en Acueductos y Alcantarillados, C. (2008). Programa REDES.
Bogotá: Universidad de los Andes.
-
De Paco, J. L. (1993). Fundamentos del Cálculo Hidráulico en los Sistema de Riego y de
Drenaje. Madrid: Mundi-Prensa.
-
IDEAM. (2011). Estudio Nacional del Agua. Bogotá, Colombia.
-
Kelle, J., & Karmeli. (1974). Trickle irrigation design. Rainbird Sprinkler Manufacturing
Corporation .
-
López, J. R. (1992). Riego Localizado. Madrid: Mundi-Prensa.
-
Ochoa, S. (2009). Diseño Optimizado de Redes de Distribución de Agua Potable con Base
en el Concepto Energético de Superficie Óptima de Gradiente Hidráulico . Bogota:
Universidad de los Andes.
-
Pizarro, F. (1996). Riegos Localizados de Alta Frecuencia. Goteo, microaspersión,
exudación. Madrid: Mundi-Prensa.
-
Saldarriaga, J. (2007). Hidráulica de Tuberías. Abastecimiento de Agua, Redes, Riego.
Bogotá: Alfaomega.
-
Solomon, K. H. (1985). Global uniformity of trickle irrigation system. ASAE , 1151-1158.
-
Villalba, G. (2004). Algoritmos de optimización combinatoria aplicados al diseño de redes
de distribución de agua potable. Bogotá: Universidad de Los Andes.
-
Wu, I. (1975). Design of Drip Irrigation Main Lines. Journal of the Irrigation and Drainage
Division , 265 - 278.
-
Bermúdez, N. (2011). Desarrollo de una metodología de diseño hidráulico para
submódulos de sistemas de riego localizado de alta frecuencia. Bogotá: Universidad de los
Andes.
-
Paez, D. (2011). Análisis de redes internas de distribución de agua potable utilizando
simulación de eventos discretos. Bogotá: Universidad de los Andes.
-
OECD 2006, The impacts of Change on the Long-term Future Demand for Water Sector
infrastructure.
-
Departamento Nacional de Planeación. (1998). Recuperado el 9 de Junio de 2011, de
http://www.dnp.gov.co/PortalWeb/Portals/0/archivos/documentos/DDRS/Publicaciones_
Estudios/ProductividadMR.pdf
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
124
7. ANEXOS
En esta sección se presenta una breve descripción del uso de los programas que fue necesario
desarrollar con el objetivo de realizar los diseños mediante la metodología planteada. Se
mostrarán dos programas sin entrar en detalle en las subrutinas y la formulación detrás de estos,
únicamente se mostrará su manera de uso y los resultados que producen.
7.1. Programa para el cálculo de PES y generar archivo de Xpress.
El programa que se presenta a continuación es un programa en Microsoft Excel con Visual Basic
para aplicaciones. El programa permite determinar la presión de entrada al submódulo usando la
metodología planteada por Bermúdez y adicionalmente permite generar las 4 matrices (en el
formato de Xpress) necesarias para realizar el diseño de una red abierta mediante programación
lineal. De esta manera al abrir el programa el usuario se encontrará con la hoja “INICIO” la cual se
ve como se muestra a continuación:
Figura 30. Hoja “INICIO”. Programa para el cálculo de PES y la generación de matrices de Xpress.
Como se observa en la Figura 30, la hoja “INICIO” es una hoja bastante sencilla, donde el usuario
solo tiene dos opciones, hacer click en el botón que lo llevará a la hoja para realizar el cálculo de la
presión de entrada al submódulo (PES) o hacer click en el botón para generar el archivo con las
matrices de entrada a Xpress. Al hacer click en el botón para cálculo de presión a la entrada, el
usuario será llevado a la hoja “Cálculo PES” donde se encontrará con una tabla para ingresar los
datos de entrada. La primera parte de la tabla permite al usuario ingresar los valores de la
viscosidad cinemática del fluido que se moverá por el sistema de tuberías y adicionalmente
permite asignar el valor de la aceleración de la gravedad (Ver Tabla 29).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
125
Tabla 29. Tabla para ingresar la gravedad y la viscosidad cinemática del fluido, Hoja “Cálculo PES”.
CONSTANTES
Gravedad (g)
Viscosidad cinemática
(m/s
2
)
(m
2
/s)
9.81
1.14E-06
Como se puede observar en la Tabla 29, las celdas de los datos de entrada son azules, de esta
manera en todo el programa los valores que el usuario debe ingresar presentarán un color azul. La
segunda parte de la tabla principal permite al usuario ingresar los valores correspondientes al
diseño agronómico y las propiedades de los emisores (ver Tabla 30).
Tabla 30. Tabla para ingresar los datos agronómicos y las propiedades de los emisores, Hoja “Cálculo PES”.
DATOS AGRONÓMICOS
Coeficiente
de
uniformidad
(CU)
Número de
emisores
por planta
(n
e
)
Presión
media de
operación
(h
m
)
Caudal
medio por
emisor
(Q
m
)
()
()
(mca)
(l/h)
0.85
2
10.00
80
Coeficiente de variación del emisor (CV)
0.04
Exponente del emisor
0.2
Coeficiente del emisor (l/s)/(m
x
)
0.01402127
En la Tabla 30 se puede ver que el usuario debe ingresar el Coeficiente de Uniformidad (CU)
deseado, el número de emisores que utilizará por planta, el caudal medio por cada emisor, el
coeficiente de variación (CV) y los valores del exponente y coeficiente de la ecuación que
caracteriza los emisores. Se puede ver que la presión media de operación en cada emisor no es un
dato que el diseñador asigne, sino que es calculado (En color verde se presentan los resultados); el
cálculo de la presión media se obtiene a partir del caudal medio del emisor y la ecuación de éste.
Una vez el usuario ha ingresado todos los datos de entrada (Celdas en azul), debe hacer click en el
botón:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
126
Al hacer click en el botón “Calcular Presión de Entrada al Submódulo” el programa calculará la
tolerancia de caudales y presiones para determinar la presión mínima aceptable en el submódulo
de riego, adicionalmente se generará la curva de Coeficiente de Uniformidad vs PES establecida en
el trabajo de Bermúdez (ver Gráfica 7-1).
Gráfica 7-1. Curva CU vs PES, Hoja “Cálculo PES”.
Como se mencionó anteriormente, el programa calcula internamente la presión mínima aceptable
y haciendo uso de los resultados de la Gráfica 7-1 establece la presión de entrada al submódulo de
riego. Los resultados de la presión mínima y la PES se muestran en la tercera tabla que comprende
la hoja “Cálculo PES” (ver Tabla 31).
Tabla 31. Resultados de presión mínima y PES. Hoja “Cálculo PES”.
Presión mínima en el Submódulo (mca)
5.33
Presión de Entrada al Submódulo (PES), (mca)
18.69
Habiendo calculado la presión mínima y la presión de entrada al submódulo el siguiente paso
consiste en generar el archivo de entrada a Xpress. Para esto se debe generar un modelo del
submódulo de riego en REDES o EPANET, donde se establezca la topología del submódulo, asigne
las propiedades a cada una de las tuberías, establezca el caudal demandado en cada nudo y asigne
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
0
5
10
15
20
25
30
Co
eficien
te
de Unif
orm
idad
()
Presión de Entrada al Submódulo (mca)
Curva PES vs CU
R
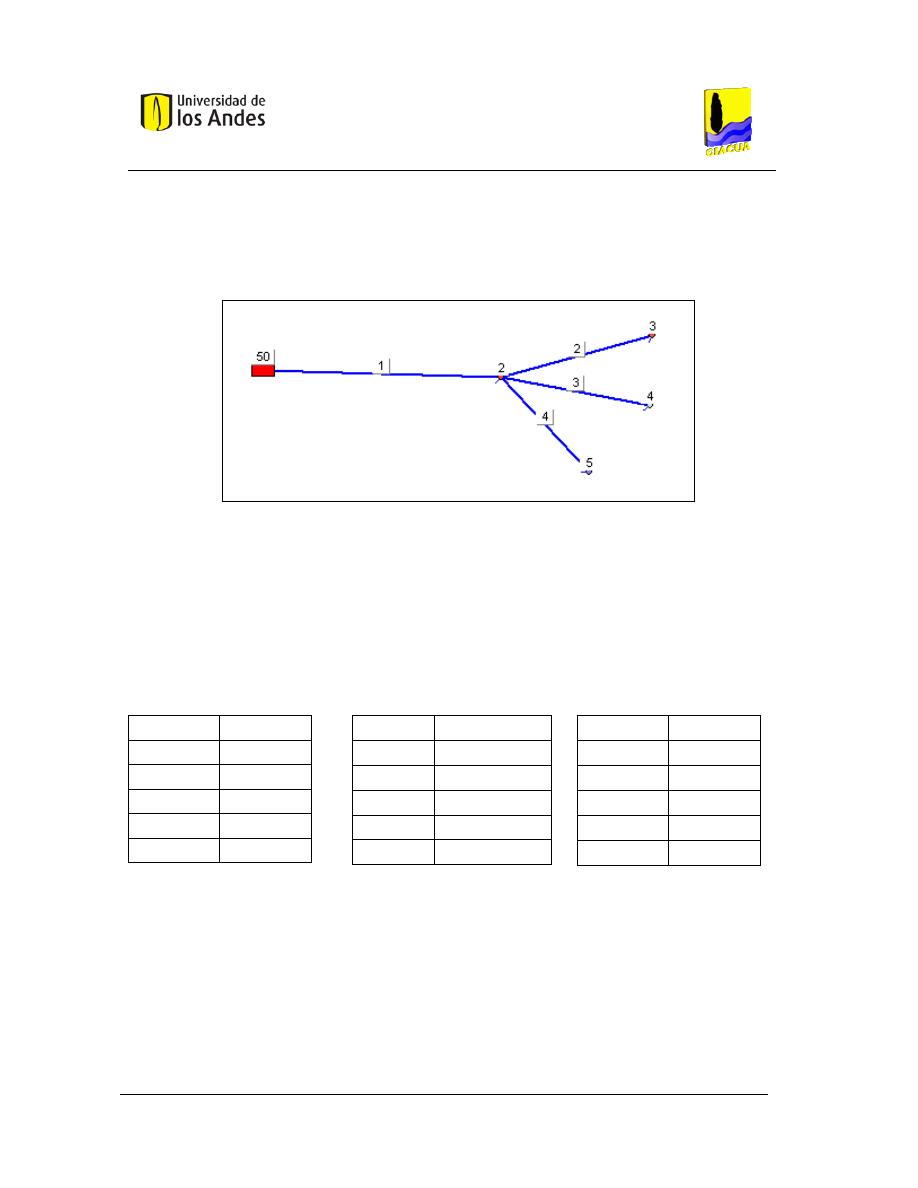
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
127
a la entrada del submódulo la PES calculada. Si el usuario generó el modelo en REDES debe
exportarlo a EPANET debido a que el programa lee archivos *.INP que corresponden al formato de
EPANET. Para mostrar el funcionamiento de esta parte del programa se utilizará una pequeña red
de ejemplo que es la que se muestra a continuación:
Figura 31. Red ejemplo para mostrar uso de programa.
La red ejemplo para mostrar el uso del programa con el fin de generar las matrices de entrada a
Xpress se observa en la Figura 31, donde se puede ver que existen 4 tuberías (1, 2, 3 y 4), 4 nudos
de consumo (1, 2, 3 y 4) y una fuente de abastecimiento con LGH de 50 mca. En la siguiente tabla
se presentan la altura topográfica y demanda base de cada uno de los nudos y la longitud de cada
una de las tuberías. La rugosidad utilizada para este ejemplo es de 0.0000015 m.
Tabla 32. Elevación y demanda base en los nudos y longitud de las tuberías.
ID Nudo
Elevación
()
(m)
2
4
3
0
4
4
5
3
ID Nudo Demanda_Base
()
(l/s)
2
10
3
5
4
8
5
7
ID Tubo
Longitud
()
(m)
1
170.514
2
122.788
3
113.893
4
148.037
Una vez se tiene el modelo del submódulo en EPANET, el usuario debe hacer click en el botón
“Generación de Archivo de Entrada a Xpress” de la hoja “INICIO” y este botón llevará al usuario a la
hoja “Matriz” que se ve como se muestra a continuación:
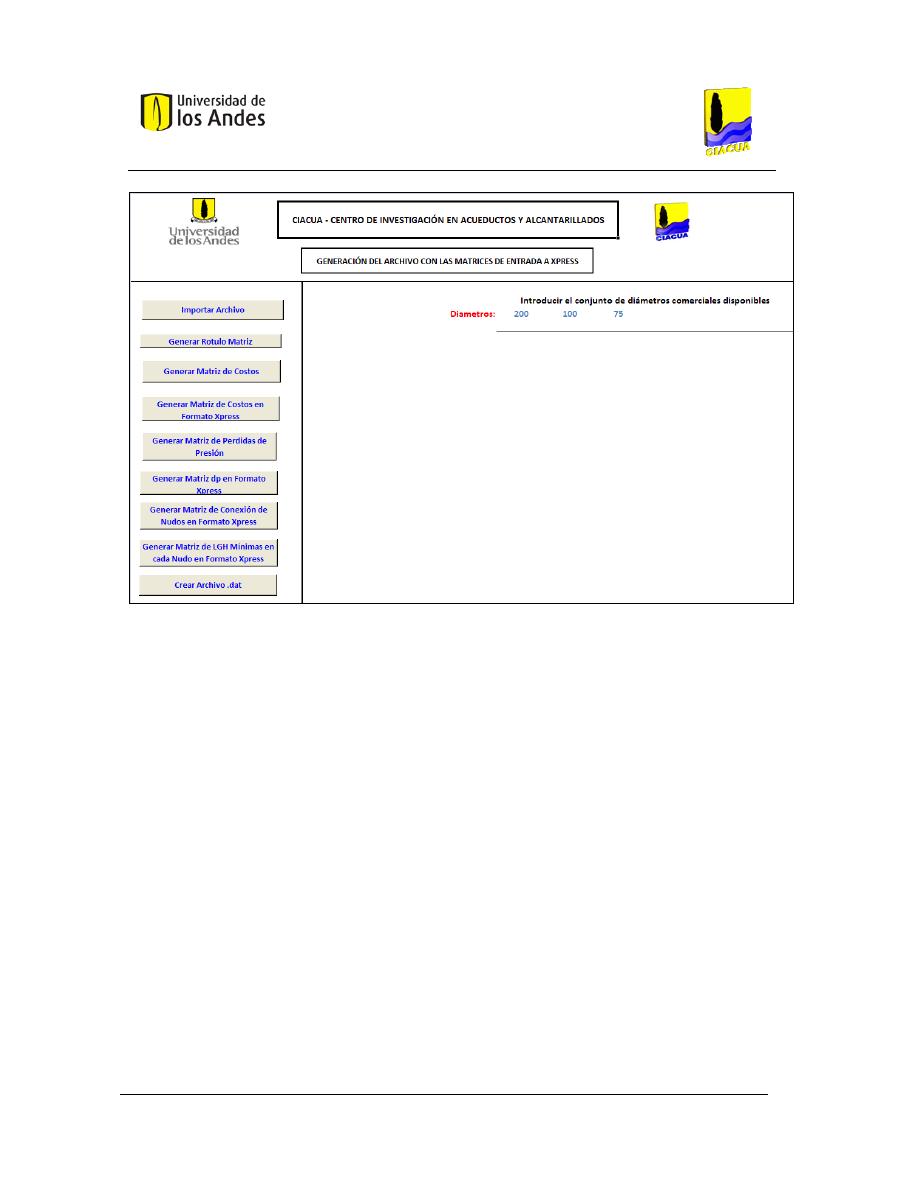
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
128
Figura 32. Vista general de la hoja “Matriz” para la generación del archivo con las matrices de entrada a Xpress.
Como se puede ver en la figura superior, la hoja “Matriz” cuenta con 9 botones que el usuario
debe utilizar de manera secuencial de arriba hacia abajo. Adicionalmente en la parte derecha se
observa que existe una espacio donde se le pide al usuario introducir el conjunto de diámetros
comerciales disponibles; y para el correcto funcionamiento del programa el usuario debe
introducir en las celdas adjuntas a la palabra “Diámetros:” todos los diámetros que tiene
disponibles para diseñar. Para la red ejemplo mostrada suponga que únicamente se tienen 3
diámetros comerciales disponible (200 mm, 100 mm y 75 mm) como se muestra en la Figura 32.
Una vez el usuario ha introducido los diámetros comerciales, puede empezar a hacer uso de los
botones que se describen a continuación
1. Importar Archivo: Este es el primer botón que el usuario debe utilizar. Este botón
permitirá importar el archivo *.INP de EPANET para que el programa pueda leer la
topología de la red y adicionalmente permitirá que el programa haga uso del Toolkit de
EPANET con Excel para poder realizar los cálculos hidráulicos requeridos para calcular la
matriz de pérdidas totales. Cuando el usuario hace click en este botón aparecerá una
ventana como la que se muestra a continuación, donde el usuario debe seleccionar el
archivo *.INP que se desea importar.
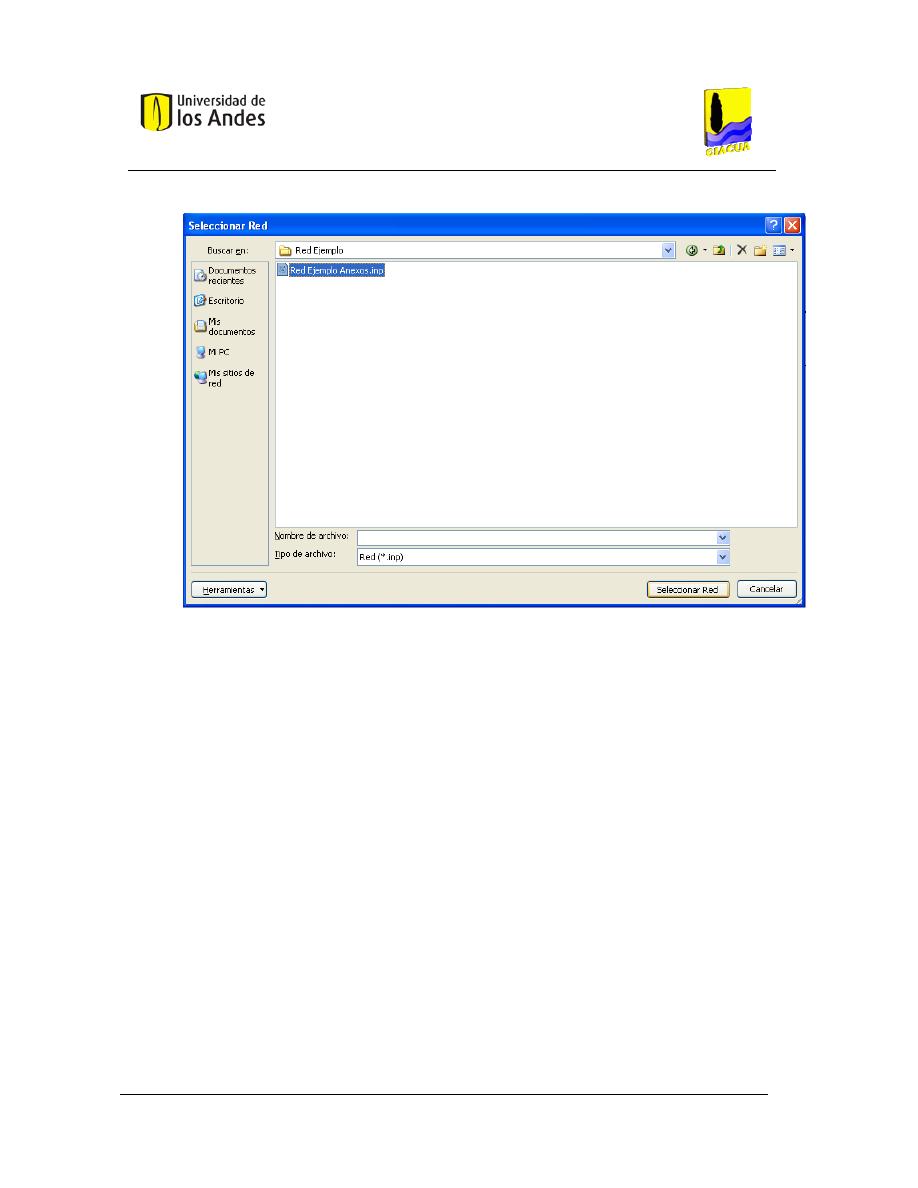
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
129
Figura 33. Ventana para seleccionar el archivo de EPANET que se desea importar, Red Ejemplo.
Al seleccionar el archivo *.INP deseado el programa colocará en una hoja aparte todas las
características de la red y guardará en una celda oculta la dirección del archivo
seleccionado. De esta manera se tiene ubicado el archivo para poder hacer uso del Toolkit
de EPANET con Microsoft Excel para los procedimientos posteriores. De esta manera,
habiendo importado el archivo (en este caso Red Ejemplo Anexos.inp) exitosamente el
usuario puede proceder al siguiente botón.
2. Generar Rótulo Matriz: Este botón es el encargado de leer el archivo importado y generar
el rótulo de la matriz de costos y la matriz de pérdidas totales. Al hacer click en el botón se
generará el rótulo tal como se puede observar en la siguiente figura para el caso de la red
de ejemplo:
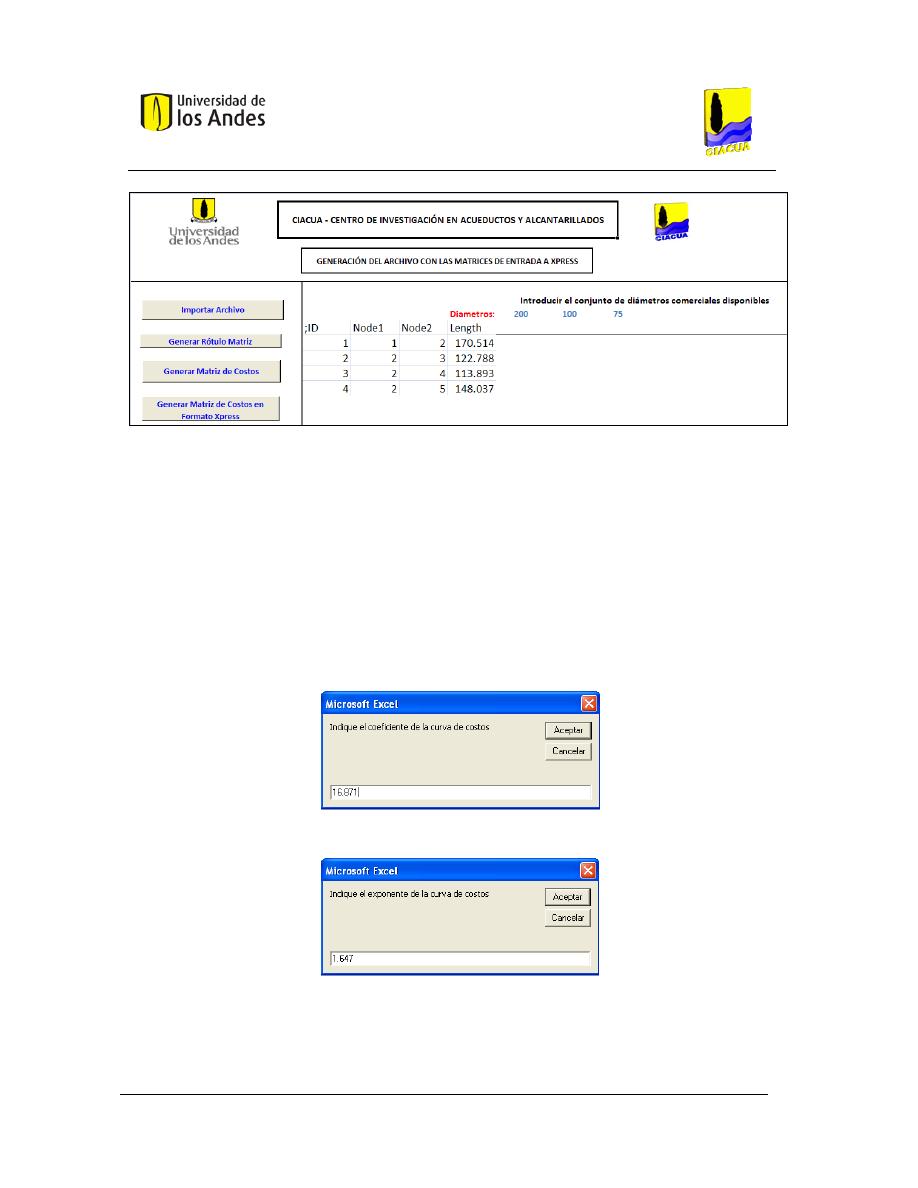
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
130
Figura 34. Generación del rótulo de las matrices de costos y pérdidas totales, Red Ejemplo.
Si se observa la Figura 34 se puede notar que al seleccionar el botón “Generar Rótulo Matriz” se
llenan 4 columnas con la información correspondiente al ID de la tubería, el nudo 1 (nudo aguas
arriba del tubo), nudo 2 (nudo aguas abajo del tubo) y la longitud del tubo en metros. Para esta
red de ejemplo se puede observar que existen las 4 tuberías mostradas en la Figura 31 y que a
cada una le corresponde la longitud que se mostró inicialmente en la Tabla 32. Haciendo uso de
este rotulo se procede a hacer click en el siguiente botón.
3. Generar Matriz de Costos: Al hacer click sobre este botón al usuario le saldrán las
siguientes ventanas:
Figura 35. Ventana para ingresar el valor del coeficiente de la curva de costos, Red Ejemplo.
Figura 36. Ventana para ingresar el valor del exponente de la curva de costos, Red Ejemplo.
En la primera ventana que aparece (ver Figura 35) se ingresa el valor del coeficiente de la
curva de costos, que para este caso se asignó un valor de 16.871. Cuando el usuario hace

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
131
click en aceptar, aparece inmediatamente la ventana donde se ingresa el exponente de la
curva de costos (ver Figura 36). Al aceptar el valor del exponente asignado se crea la
matriz de costos que para el caso de la red de ejemplo quedaría así:
Figura 37. Matriz de Costos, Red Ejemplo.
Al observar la Figura 37 se puede ver que se generó la matriz de costos. Si se desea
verificar que los resultados mostrados son correctos, se puede determinar el costo de
asignarle a la tubería con ID 1 el diámetro de 200 mm; para esto se utiliza la siguiente
ecuación
Ecuación 7.1
De esta manera, habiendo establecido la matriz de costos, se puede proceder a
transformar la matriz mostrada al formato que lee el programa Xpress (Siguiente botón).
4. Generar Matriz de Costos en Formato Xpress: Hacer click en este botón únicamente
guardará en la hoja “datos.txt” la matriz de costos en el formato que lee Xpress. En el
formato creado por Xpress se asigna en un paréntesis los parámetros que identifican la
tubería y fuera del paréntesis el valor del costo al utilizar el diámetro que se muestra
dentro de los parámetros. El formato de cada línea correspondiente a la matriz de costos
en formato Xpress es el siguiente:
(Nudo Aguas Arriba, Nudo Aguas Abajo, Diámetro)Costo Asociado
De esta manera para el caso de la red de ejemplo, el formato quedará como se muestra a
continuación:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
132
Formato Xpress 1. Matriz de costos.
c:[
(1,2,200)17729539.0235421
(2,3,200)12767151.3322971
(2,4,200)11842222.2772582
(2,5,200)15392397.3391019
(1,2,100)5661102.7962649
(2,3,100)4076595.33683489
(2,4,100)3781262.30799107
(2,5,100)4914845.41712585
(1,2,75)3524738.82118234
(2,3,75)2538186.34974677
(2,4,75)2354304.89954064
(2,5,75)3060101.02011986
]
Si se observan la matriz de costos en formato de archivo de entrada a Xpress se podrá ver
que por ejemplo en la segunda línea, se indica que el costo asociado al tramo
comprendido entre el nudo 1 y el nudo 2, usando un diámetro de 200 mm es de COP $ 17,
729,539.
5. Generar Matriz de Pérdidas de Presión: Una vez se ha generado la primera matriz en
formato Xpress se procede a calcular la matriz de pérdidas totales. Para poder calcular las
pérdidas que ocurren en un tramo del sistema utilizando un diámetro determinado se
hace uso del Toolkit de EPANET con Excel, el cual permite que únicamente haciendo click
en el botón “Generar Matriz de Pérdidas de Presión”, se calcule la matriz de pérdidas de
forma automática. Si el usuario desea entrar en detalle de cómo se realiza este proceso de
forma automática, puede encontrar la subrutina correspondiente en el Módulo “Llenar
Datos” y la subrutina “Matrizdp”.
Dicho lo anterior si se hace click en este botón se generará la matriz de pérdidas tal como
se muestra a continuación (ver Figura 38). Si se observa la siguiente figura se podrá ver,
por ejemplo, que si en la tubería de ID 1 se utiliza un diámetro de 100 mm, las pérdidas
totales serán de 18.153 mca, si por el contrarío se utiliza un diámetro de 75 mm las
pérdidas totales serán mayores y representarán un gasto de 73.180 mca de la energía
total.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
133
Figura 38. Matriz de pérdidas totales, Red Ejemplo.
6. Generar Matriz dp en Formato Xpress: Este botón permite que, habiendo calculado la
matriz de pérdidas totales, se pase la información al formato que se requiere por Xpress.
Este formato para el caso de la matriz de pérdidas totales se presenta a continuación:
Formato Xpress 2. Matriz de pérdidas totales.
dp:[
(1,2,200)0.642143368721008
(2,3,200)1.89556125551462E-02
(2,4,200)4.03186343610287E-02
(2,5,200)4.13717590272427E-02
(1,2,100)18.1530704498291
(2,3,100)0.517597138881683
(2,4,100)1.11126124858856
(2,5,100)1.137322306633
(1,2,75)73.1820068359375
(2,3,75)2.05202221870422
(2,4,75)4.4234676361084
(2,5,75)4.52198696136475
]
Si se observa el Formato Xpress 2 se podrá ver (penúltima línea) que en el tramo
comprendido entre el nudo 2 y el nudo 5, si se utiliza un diámetro de 75 mm se generarán
unas pérdidas totales de 4.521 mca.
7. Generar Matriz de Conexión en Nudos en Formato Xpress: Una vez se han creado las
matrices de costo y pérdidas totales, es necesario establecer una matriz de conectividad
que permitirá a Xpress conocer la forma en que se conectan los nudos que componen el
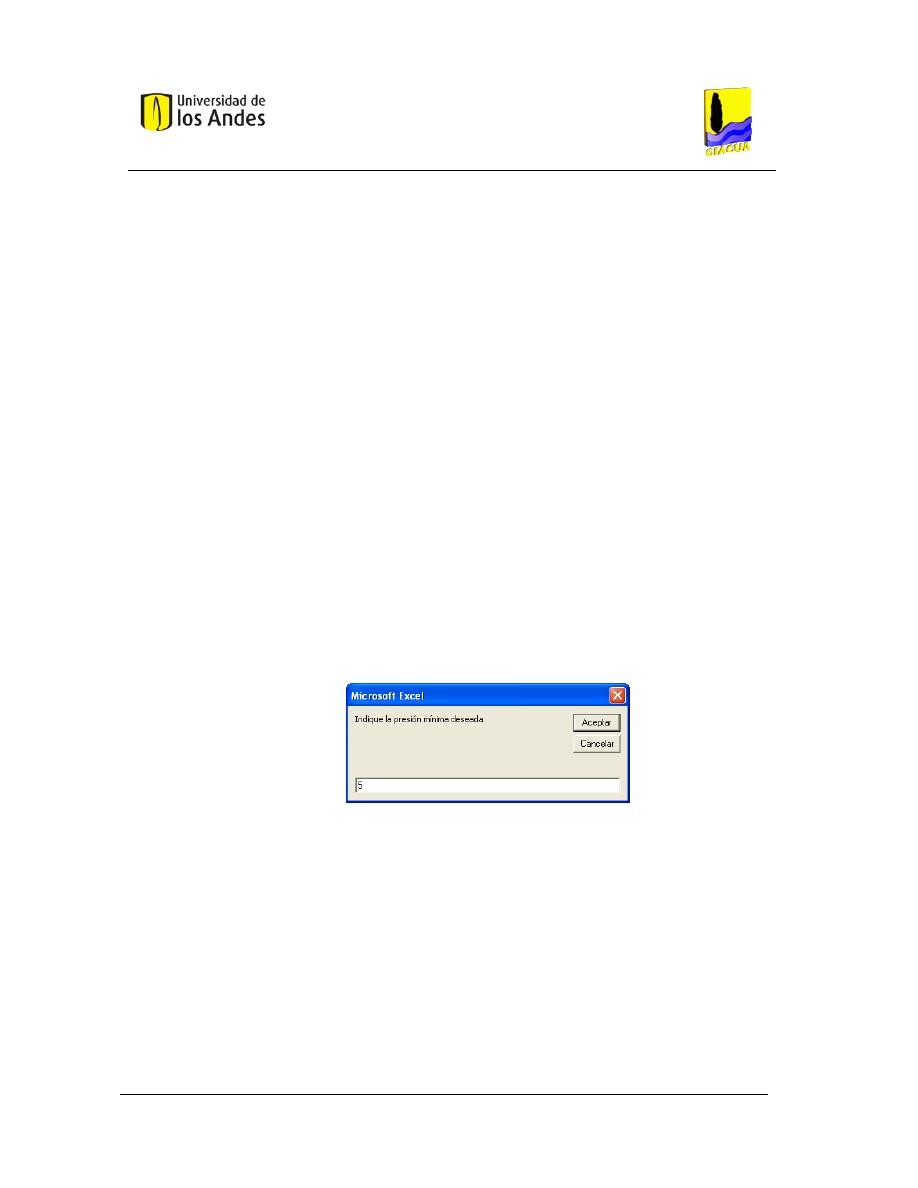
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
134
sistema. Al hacer click en este botón se generará automáticamente la matriz de
conectividad en formato de entrada a Xpress. A continuación se muestra la forma en que
quedó para el caso de la red de ejemplo:
Formato Xpress 3. Matriz de Conectividad de los nudos.
w:[
(1,2)1
(2,3)1
(2,4)1
(2,5)1
]
Como se observa en el Formato Xpress 3 la matriz de conectividad asigna un valor de 1 a
los nudos que se encuentran conectados. Por ejemplo, dado que el nudo 1 (nudo aguas
arriba) y el nudo 2 (nudo aguas abajo) están conectados, se asigna un valor de 1 para
establecer en Xpress que estos nudos están conectados con una tubería.
8. Generar Matriz de LGH Mínimas en cada Nudo en Formato Xpress: Este botón permite
generar finalmente la matriz donde se establece la LGH mínima en cada uno de los nudos.
Al hacer click saldrá la siguiente ventana:
Figura 39. Ventana para ingresar la presión mínima deseada, Red Ejemplo.
En la ventana mostrada en la Figura 39 el usuario debe ingresar la presión mínima que
desea, y al hacer click en aceptar se generará la matriz de LGH mínima en formato Xpress:
Formato Xpress 4. Matriz de LGH mínima en los nudos.
LGHmin:[
(2)9
(3)5
(4)9
(5)8
]
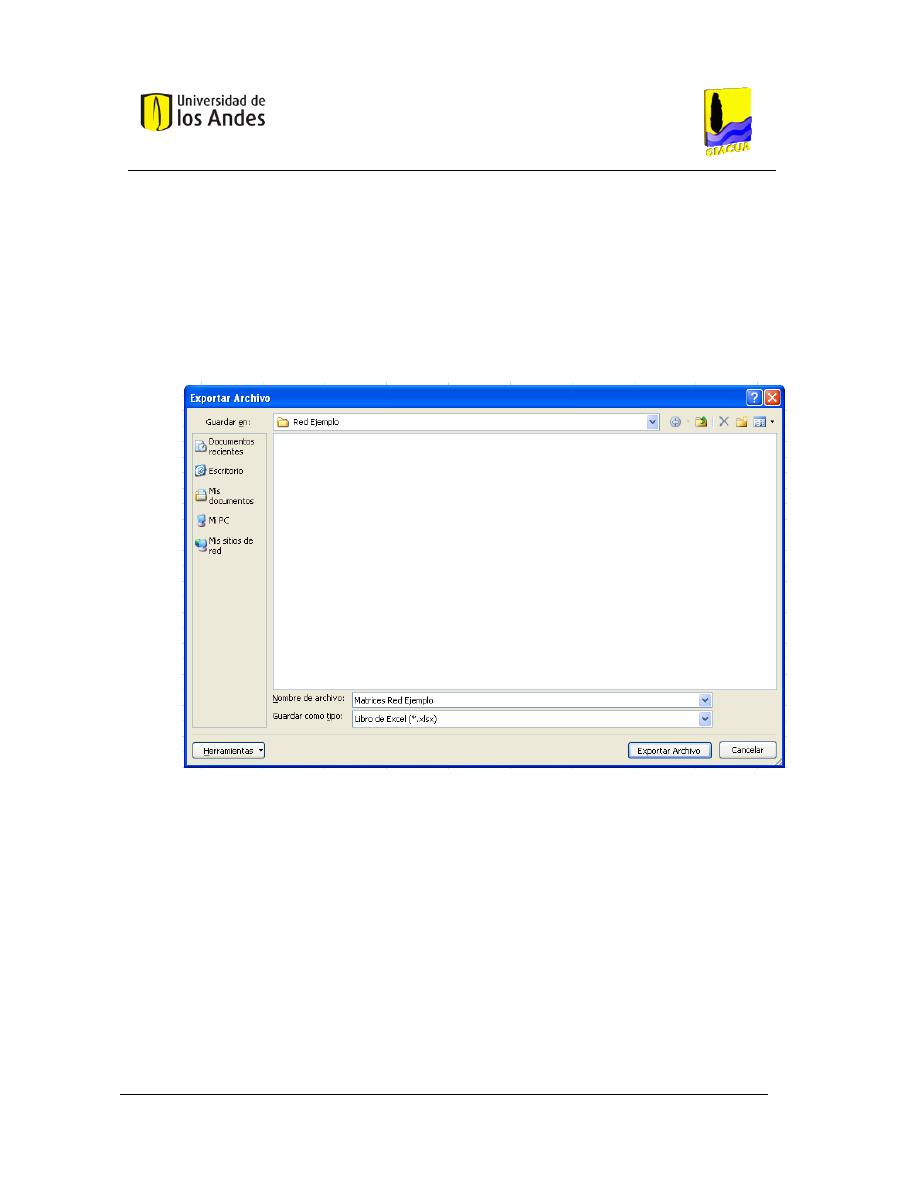
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
135
Observando el Formato Xpress 4 se puede ver que la LGH mínima en el nudo 2 es igual a 9
mca, que corresponden a los 5 metros de presión mínima sumados a su elevación
topográfica de 4 metros. Una vez se tienen las cuatro matrices que entran a Xpress, el
siguiente paso es generar el archivo *.DAT.
9. Crear Archivo .dat: Al hacer click en este botón saldrá una ventana (ver Figura 40) donde
el usuario debe ubicar la dirección donde desea ubicar el archivo que entrará a Xpress y
que contiene las cuatro matrices requeridas para realizar el diseño:
Figura 40. Ventana para guardar el archivo *.DAT de entrada a Xpress.
Si se observa la Figura 40 se podrá ver que el archivo que se guarda debe guardarse como
un archivo tipo *.XLSX, el programa automáticamente convertirá el archivo guardado
como *.XLSX a *.DAT.
De esta manera, una vez el usuario ha creado el archivo *.DAT el siguiente paso consiste en utilizar
Xpress. Cuando el usuario abre Xpress se encontrará con la siguiente interfaz:
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
136
Figura 41. Interfaz Xpress.
Al entrar a Xpress el usuario puede abrir la formulación del problema de diseño y en la parte
derecha de la interfaz aparecerá el código correspondiente a la formulación creada:
Figura 42A. Código de formulación lineal, problema de diseño de tuberías.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
137
Figura 42B. Código de formulación lineal, problema de diseño de tuberías, continuación.
En la Figura 42 se presenta el código de Xpress para el problema de diseño de tuberías de redes
abiertas. En el código se encuentran definidas todas las restricciones del problema, la función
objetivo y el tipo de variable que se utiliza (para ver la formulación matemática del problema ir a
la Sección 3.4.1.1.1 en la página 84). Para poder diseñar el usuario únicamente debe cambiar 2
cosas en el código de acuerdo con la red que desee diseñar.
1. Leer archivo de entrada con las matrices: Para poder diseñar se le debe indicar a Xpress el
nombre del archivo que contiene las 4 matrices (costos, pérdidas totales, conectividad y
LGH
mínimas
). Para esto en la parte del código donde se define el archivo de entrada se debe
colocar el nombre, tal como se muestra a continuación:
En este caso se observa que el archivo de entrada (inputFile) se llamó data.dat. El ejemplo
que se muestra corresponde al de la red ejemplo que se ha utilizado en la sección Anexos.
Es importante recordar que el archivo data.dat contiene las cuatro matrices que se
presentaron anteriormente.
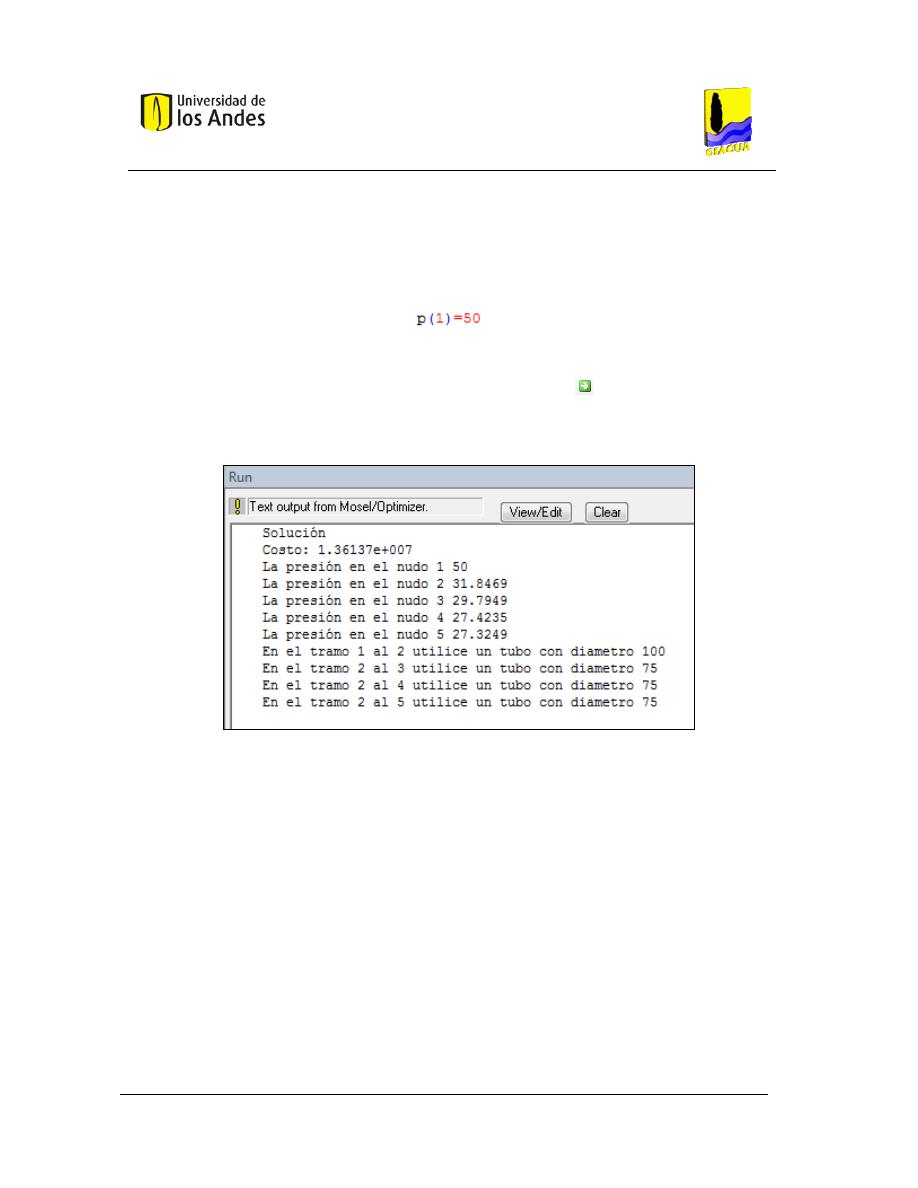
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Diseño optimizado de submódulos de sistemas de riego localizado de
alta frecuencia.
MIC 201210-11
David Hernández
Tesis II
138
2. LGH y ID del nudo de abastecimiento: Para el caso de la red ejemplo se debe indicar a
Xpress que el ID del embalse es 1 y que su altura piezométrica es de 50 mca. Para esto se
debe cambiar en el código la línea donde se define esto, que es la que se muestra a
continuación:
Habiendo indicado a Xpress el archivo de entrada y el ID y la altura piezométrica del embalse, se
procede a diseñar. Para diseñar se debe hacer click en el botón
de Xpress y de esta manera
Xpress generará el resultado del diseño, entregando un archivo de Salida, que para el caso de la
red ejemplo resulta:
Figura 43. Resultados del diseño generado por Xpress, Red Ejemplo.
En la Figura 43 se observa que Xpress entrega como solución un diseño que cuesta COP $ 13,
613,700 y que consiste en colocar una tubería de 100 mm y las otras tres de 75 mm. De esta
manera, se ha diseñado usando formulación lineal y el siguiente paso consiste en pasar los
resultados al modelo en EPANET donde se podrá verificar el adecuado funcionamiento del diseño
resultante.
