IAHR
CIC
XXV CONGRESO LATINOAMERICANO DE HIDRÁULICA
SAN JOSÉ, COSTA RICA, 9 AL 12 DE SETIEMBRE DE 2012
D
ISEÑO DE
S
UBMÓDULOS DE
R
IEGO POR
G
RAVEDAD
U
SANDO
S
UPERFICIE
Ó
PTIMA
DE
G
RADIENTE
H
IDRÁULICO
David A. Hernández
2
, Nataly Bermúdez
2
, Juan Saldarriaga
1
1
Director, Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA), Profesor Titular,
Departamento de Ingeniería Civil y Ambiental, Universidad de los Andes, Bogotá, Colombia
2
Investigador, Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA),Universidad
de los Andes, Bogotá, Colombia
<da.hernandez39@uniandes.edu.co>, <n.bermudez87@uniandes.edu.co>, <jsaldarr@uniandes.edu.co>
RESUMEN:
El presente trabajo se desarrolló teniendo en cuenta la importancia y el alto crecimiento en
proyectos de riego que se viene dando actualmente en Colombia. El artículo presenta los resultados
obtenidos para diferentes diseños de submódulos de sistemas de riego localizado de alta frecuencia
(RLAF) haciendo uso de la metodología de Superficie Óptima de Gradiente Hidráulico (SOGH)
planteada en sus inicios para el obtener diseños de mínimo costo en Redes de Distribución de Agua
Potable (RDAP). Los diseños realizados se hicieron mediante la metodología SOGH variando el
valor de la flecha que compone la línea de gradiente hidráulico objetivo. Para esto, primero se
determinó el valor máximo de la flecha de diseño y se procedió a determinar el comportamiento de
los costos de diferentes submódulos respecto a la flecha. Se encontró que el uso de la metodología
SOGH en el diseño de submódulos de sistemas de riego permite encontrar diseños de mínimo costo
y adicionalmente cumplir con los requisitos establecidos por el diseño agrónomo. Finalmente se
determinó que la flecha de mínimo costo para el diseño con diámetros continuos corresponde a una
flecha intermedia entre la flecha máxima y la mínima; y que el mejor criterio para el redondeo de
diámetros corresponde al redondeo al diámetro comercial más cercano.
ABSTRACT:
This work was developed taking into account the importance and high growth in irrigation
projects that has been going on actually in Colombia. The article presents the results for
different designs of submodules of Localized Irrigation Systems of High Frequency (RLAF)
using the methodology of Optimal Surface Hydraulic Gradient (OSHG) made for Water
Distribution Systems design.
The designs were done using the OSHG methodology by varying the
arrow that makes up the target hydraulic grade line. For this, we first determined the maximum
value of the arrow design and the behavior of the submodules different costs with respect to the
arrow. It was found that the use of the OSHG methodology in the design of irrigation submodules
allows to find the least-cost and additionally meet the agricultural desgind requirements. Finally it
was determined that the minimum cost arrow for designs with continuous diameters corresponds to
an intermediate arrow between the maximum and minimum arrow, and the best approach to obtain
the discrete diameters is the rounding to nearest.
PALABRAS CLAVES: Sistemas de riego localizado, Submódulos de riego, diseño óptimo,
presión de entrada al submódulo.

INTRODUCCIÓN
En Colombia, según estudios del Departamento Nacional de Planeación, en 1999 existían
en Colombia 3’759,174 hectáreas de cultivos; años después, en el 2008, éste número se había
incrementado en 152,594 hectáreas. Estos valores implican una alta inversión en rehabilitación de
redes existentes y en inversión para construcción de nuevos sistemas de riego; además, si se tiene
presente que los sistemas de abastecimiento de agua presentan una vida útil de alrededor de 30
años, será necesario hacer inversiones de renovación de redes de riego existentes. En un informe
presentado por Manuel Ramírez (Asesor de la Unidad de Desarrollo Agraria, 1998), se estima que
en Colombia, de acuerdo con los recursos asignados en el Presupuesto General de la Nación para
proyectos que se van a ejecutar y sobre los cuales existe certeza de construcción, la parte que
financia el Estado por hectárea oscila alrededor de los 6,500 dólares. Para reducir éste presupuesto
y hacer un mejor uso de los recursos públicos, se debe procurar concebir sistemas de Riego
Localizado a Alta Frecuencia (RLAF) que sean económicos.
Actualmente el diseño de los sistemas de RLAF se hace mediante las metodologías clásicas
basadas en la comprobación de diseño. Esto último quiere decir que se prueban diferentes
diámetros de tuberías para cada uno de los tubos que conforman el sistema y se escoge alguna de
las múltiples soluciones que cumplen con los requisitos hidráulicos (Saldarriaga, 2007). Algunos
ejemplos de estas formas de diseño se pueden encontrar en los trabajos de Goldemberg (1976),
Rodríguez (1982) y Pizarro (1987). Muchas veces la escogencia del conjunto de diámetros de las
tuberías se basa en la experiencia del diseñador, y por lo tanto no existe ningún proceso exhaustivo
como heurísticas de “Colonia de Hormigas” (Ostfled & Tubaltzev, 2008) o metodologías de diseño
basadas en la hidráulica (Ochoa & Saldarriaga, 2009) que permitan llegar a un diseño óptimo. Éste
trabajo busca hacer uso de las metodologías como Superficie Óptima de Gradiente Hidráulico
(SOGH) (Ochoa & Saldarriaga, 2009), planteadas para redes de distribución de agua potable, a fin
de utilizar sus bases teóricas para obtener diseños de sistemas de riego de mínimo costo.
UNIFORMIDAD DE RIEGO
La uniformidad del riego es característica esencial de un sistema de riego localizado de alta
frecuencia, que va a estar dada por el diseño agronómico e influenciará directamente los resultados
sobre el diseño de las tuberías que componen este tipo de sistemas. De esta manera, el diseñador
debe buscar que el sistema de tuberías sea tal que el diseño sea económico y que todas las plantas
reciban la misma cantidad de agua y nutrientes necesarios para alcanzar su correcto desarrollo y
producción.
Este tipo de sistemas utilizan emisores como nudos de consumo. El uso de emisores implica
que el caudal que recibe cada una de las plantas va a depender de la presión en el punto de llegada y
por esta razón se establece el criterio de uniformidad. La uniformidad del riego se caracteriza
mediante el coeficiente de uniformidad (CU) que se define como se muestra en la Ecuación 1:
[1]
donde:
- CU: Coeficiente de uniformidad del riego; éste es un dato de entrada y es suministrado por
el diseño agronómico
- n
e
: Número de emisores por planta.
- Q
mp
: Caudal del emisor sometido a la mínima presión. Este caudal será uno de los datos de
entrada para el proceso de diseño.

- Q
m
: Caudal medio por planta. Este dato es dado por el diseño agronómico y corresponde al
caudal que se espera que cada planta reciba.
- CV: Coeficiente de variación por fabricación de los emisores finales.
-
corresponde al caudal promedio de la muestra de emisores.
Como se puede observar el coeficiente de uniformidad (CU) depende tanto de factores
constructivos como de factores hidráulicos. Los factores constructivos se incluyen en el coeficiente
de variación (CV) y tienen en cuenta las diferencias que causan los procesos de fabricación y los
materiales utilizados en los caudales finales. Por su parte, los factores hidráulicos tienen en cuenta
las pérdidas de energía (altura) ocurridas a lo largo de todas las tuberías que conforman el sistema
de riego y la topografía del terreno. Además de los factores hidráulicos y constructivos, que afectan
la uniformidad del riego, existen otros factores como el envejecimiento del sistema, las
obturaciones que ocurran en los emisores y las diferencias de temperatura que se presentan en los
diferentes laterales del sistema. Estos últimos factores no se tienen en cuenta en el proceso de
diseño debido a la alta incertidumbre que existe con relación a estos.
CÁLCULO DE LA TOLERANCIA DE CAUDALES
Con el objetivo de cumplir con el coeficiente de uniformidad impuesto por el diseño
agronómico, es necesario que los caudales que entrega cada uno de los emisores, no resulten muy
diferentes entre ellos. Para esto es necesario asegurarse que el rango de caudales se encuentre entre
un máximo y un mínimo. Para determinar el caudal de mínima presión que puede presentarse en un
submódulo de riego se parte de la Ecuación 1 y de esta manera, resolviendo para el caudal de
mínima presión se obtiene:
[2]
Una vez obtenido el caudal de mínima presión que se puede presentar en un submódulo de
riego, se establece la tolerancia de caudales como la relación entre el caudal de mínima presión y el
caudal medio.
CÁLCULO DE LA TOLERANCIA DE PRESIONES
Para poder cumplir con la tolerancia de caudales, es necesario establecer la presión
correspondiente para que se cumpla con el requerimiento de uniformidad. De esta manera, es lógico
establecer una presión mínima que puede presentarse en un submódulo de riego y la presión
máxima. Para poder determinar la presión mínima, se hace uso de la ecuación del emisor tal como
se muestra a continuación:
[3]
donde h
mp
es la presión mínima y Q
mp
es el caudal correspondiente a la presión mínima. Una
vez conocidas la presión media y la presión mínima, se puede determinar la tolerancia de presiones
(ΔH)..
[4]
donde h
m
es la presión media, h
mp
a la presión mínima y M es un factor empírico que
depende del número de diámetros que se vayan a emplear en una misma tubería, ya sea un múltiple

o un lateral. El problema para determinar M, es que durante esta etapa no se han definido el número
de diámetros que tendrá un lateral, por esta razón para realizar los diseños se recomienda un valor
de M=2.5 (Saldarriaga, 2007).
Finalmente, conociendo la tolerancia de presiones, se puede determinar la presión de entrada
al submódulo de riego (h
max
).
[5]
Una vez se han definido las características que componen un sistema de RLAF, tales como
su esquema, la hidráulica de emisores, clasificación de emisores, uniformidad de riego, tolerancia
de caudales y presiones, el siguiente paso consiste en realizar diseños haciendo uso de la
metodología de SOGH (Saldarriaga y Ochoa, 2009).
DISEÑO DE UN SISTEMA RLAF
El primer paso del diseño consiste en calcular la tolerancia de caudales y presiones; estos
cálculos son comunes para toda la instalación de riego. Posteriormente, el cálculo de los diámetros
de diseño se desarrolla en forma independiente para cada uno de los submódulos que conforman el
cultivo, el cual corresponde a la superficie del cultivo dominado por un regulador de presión.
DISEÑO OPTIMIZADO DE REDES DE DISTRIBUCIÓN DE AGUA POTABLE CON
BASE EN EL CONCEPTO ENERGÉTICO DE SOGH
La metodología de Superficie Óptima de Gradiente Hidráulico SOGH, nace para darle
solución al problema del diseño óptimo de una Red de Distribución de Agua Potable (RDAP). Este
es un problema bastante complejo ya que existe una enorme cantidad de configuraciones de
diámetros de tuberías que satisfacen las restricciones hidráulicas (i.e. caudales de consumo y
presión mínima), pero sólo una de éstas es la más económica.
La metodología SOGH fue elegida para aplicar en el diseño de sistemas de RLAF, por ser
una metodología que se basa netamente en la comprensión de la hidráulica y la topología del
sistema; esto la diferencia de la mayoría de metodologías de diseño existentes, las cuales se
fundamentan en la imitación de otros fenómenos físicos y naturales (e.g. Algoritmos Genéticos
(AG), búsqueda de armonía, enjambre de partículas, colonia de hormigas) para explorar el espacio
de solución del problema de diseño.
La metodología SOGH comprobó que es posible llegar al diseño de mínimo costo de una red
si se conoce previamente la forma de la SOGH del sistema, la cual está conformada por un conjunto
de puntos (X, Y, LGH
ideal
), donde X y Y corresponden a las coordenadas planas de cada nudo de la
red y LGH
ideal
es la altura piezométrica que debería tener cada nudo para lograr una configuración
de mínimo costo. La forma de esta superficie se ajusta a una función cuadrática cuya curvatura
depende características hidráulicas, topológicas y comerciales del sistema.
La metodología de SOGH se basa en la determinación de una flecha que describe la forma
de la línea de gradiente hidráulico en función de las características anteriormente mencionadas,
después establece un procedimiento que estima la forma de la SOGH de cada red de distribución.
Con base en esta superficie se obtiene una pre-configuración de la red que cumple con las
restricciones hidráulicas del problema del diseño de redes, pero no con las restricciones
comerciales, dado que los diámetros de las tuberías de esta pre-configuración son continuos. Para
redondear dichos diámetros a valores discretos contenidos dentro del conjunto de diámetros
comerciales disponibles, la metodología implementa un procedimiento de Programación por
Restricciones (PR) que son de baja complejidad y requieren un número pequeño de simulaciones
hidráulicas, lo cual constituye una gran ventaja para el diseño de redes grandes.
Como bien, lo estableció I-pai Wu (1975) y posteriormente Ochoa y Saldarriaga (2009), la
red de mínimo costo puede corresponde a aquel diseño que se desarrolla a partir de una línea de
gradiente hidráulico parabólica. En el caso del diseño de submódulos de riego, el punto
correspondiente a la LGH máxima, será la cota de entrada al submódulo más la presión de entrada
(ver Ecuación 6).
[6]
El punto correspondiente a la línea de gradiente hidráulico mínimo, corresponde al sumidero
que presente las condiciones más adversas topográficamente y que se encuentre más alejado de la
válvula reguladora de presión. La presión mínima, es la correspondiente al caudal de mínima
presión obtenido en el cálculo de tolerancia de caudales. Finalmente, para poder describir una
parábola, se requiere de un tercer punto. Este tercer punto, corresponde al lugar donde se presenta la
máxima curvatura en la LGH; y se puede determinar mediante la flecha.
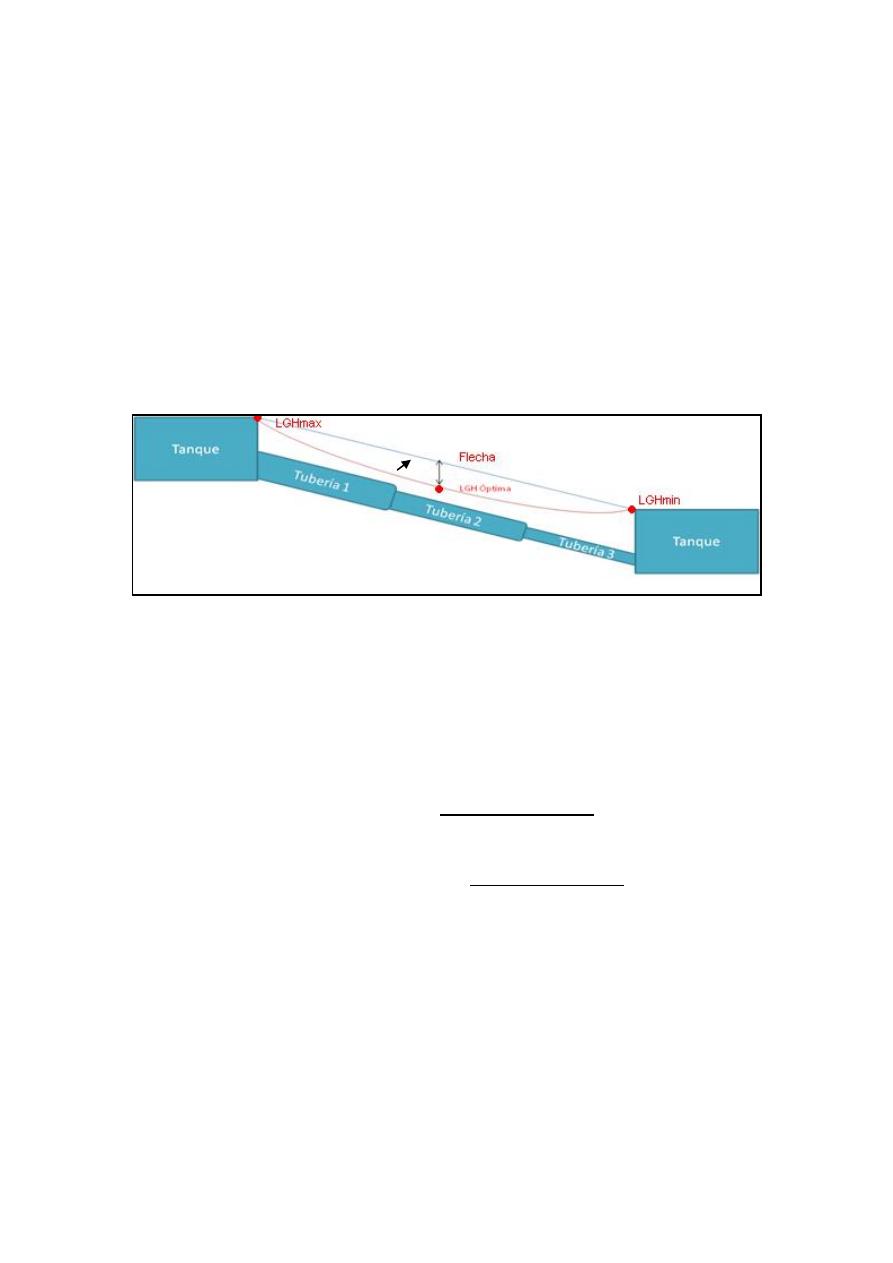
Figura 1.- LGH objetivo, basada en tres puntos conocidos
.
La Figura 1, muestra un esquema de los tres puntos requeridos para determinar la LGH
objetivo a la hora de diseñar un sistema de tuberías. A partir de esta figura, se puede establecer la
ecuación propuesta por la metodología SOGH para la línea de gradiente hidráulico.
[7]
donde:
donde α,β, y γ son parámetros de la ecuación cuadrática que define la superfice de gradiente
hidráulico objetivo, LGH
max
es la altura piezométrica a la entrada del submódulo de riego, LGH
min
es la altura piezométrica correspondiente a la suma de la presión mínima y la altura topográfica en
el punto en que ésta ocurre, F es la flecha que define la curva cuadrática de la línea de gradiente
hidráulico y d es la distancia topológica desde la fuente de abastecimiento a cada uno de los puntos
que componen el sistema.
Como puede observarse, claramente la línea de gradiente hidráulico en cada uno de los puntos del
sistema de tuberías, depende de la flecha seleccionada y de su distancia topológica al punto de
alimentación del sistema. Vale la pena decir que un diseño óptimo nunca va a corresponder a
flechas entre -0.5 y 0; esto debido a que este tipo de flechas conlleva a un menor gasto de energía
objetivo por tubería e implicarían mayores costos. De esta manera, el estudio se concentra en
flechas entre 0 y 0.5. Dicho esto, y después de observar las líneas de gradiente hidráulico para
flechas altas (por ejemplo la flecha 0.45), se observó que existía un punto (nudo de mínima LGH) a
partir del cual, el sistema estaría creando energía. Si se tiene en cuenta que para producir unas
pérdidas objetivo de cero, en un tramo de tubería, se requiere de un diámetro infinito, no tendría
ningún sentido físico hablar de diseñar un sistema de tuberías en el cual se requiere la creación de
energía a partir de cierto punto.
De esta manera, teniendo en cuenta la Ecuación 7 y la Figura 1 surgió la pregunta, sobre
cuál es el rango en que tiene una valides física la flecha de diseño y no se presentan zonas del
sistema en donde se requiere una creación de energía. Después de realizar el proceso matemático
correspondiente sobre la Ecuación 7, se encontró que la flecha máxima de diseño es de 0.25.
Con la flecha de 0.25, ocurrirá que en el último punto del sistema se requieran unas
pérdidas objetivo de cero. Si se hace uso de flechas mayores a esta, se estaría pidiendo realizar un
diseño en el cual se cree energía en ciertos puntos. Ahora bien, este resultado de una flecha máxima
de 0.25 corresponde al caso en que la última tubería del sistema es de longitud infinitesimal, cosa
que no sucede nunca. Por esta razón resultaba de interés determinar cuál es la flecha máxima en los
casos en que la última tubería del sistema tenía una longitud considerable. La ecuación que
responde esta pregutna corresponde a la Ecuación 8:
[8]
donde L
Tot
es la longitud total del sistema,
es la longitud de la última tubería y F es el es la
flecha máxima.
EVALUACIÓN DEL DESEMPEÑO DE LA METODOLOGÍA SOGH APLICADO AL
DISEÑO DE UN SUBMÓDULO DE RLAF
Una vez se había establecido la flecha máxima de diseño, el siguiente paso consistió en
realizar múltiples diseños para diferentes submódulos de riego. Para lo anterior, se realizó el diseño
óptimo de diferentes submódulos mediante la metodología de SOGH implementada en el programa
REDES (software de cálculo hidráulico creado en el Centro de Investigaciones en Acueductos y
Alcantarillados (CIACUA)). A cada uno de los submódulos se le variaba la flecha óptima de diseño
y finalmente se verificaba que los requisitos de caudal mínimo, uniformidad del riego y mínimo
costo se cumplieran. Los submódulos de análisis utilizados son los que se muestran a continuación:
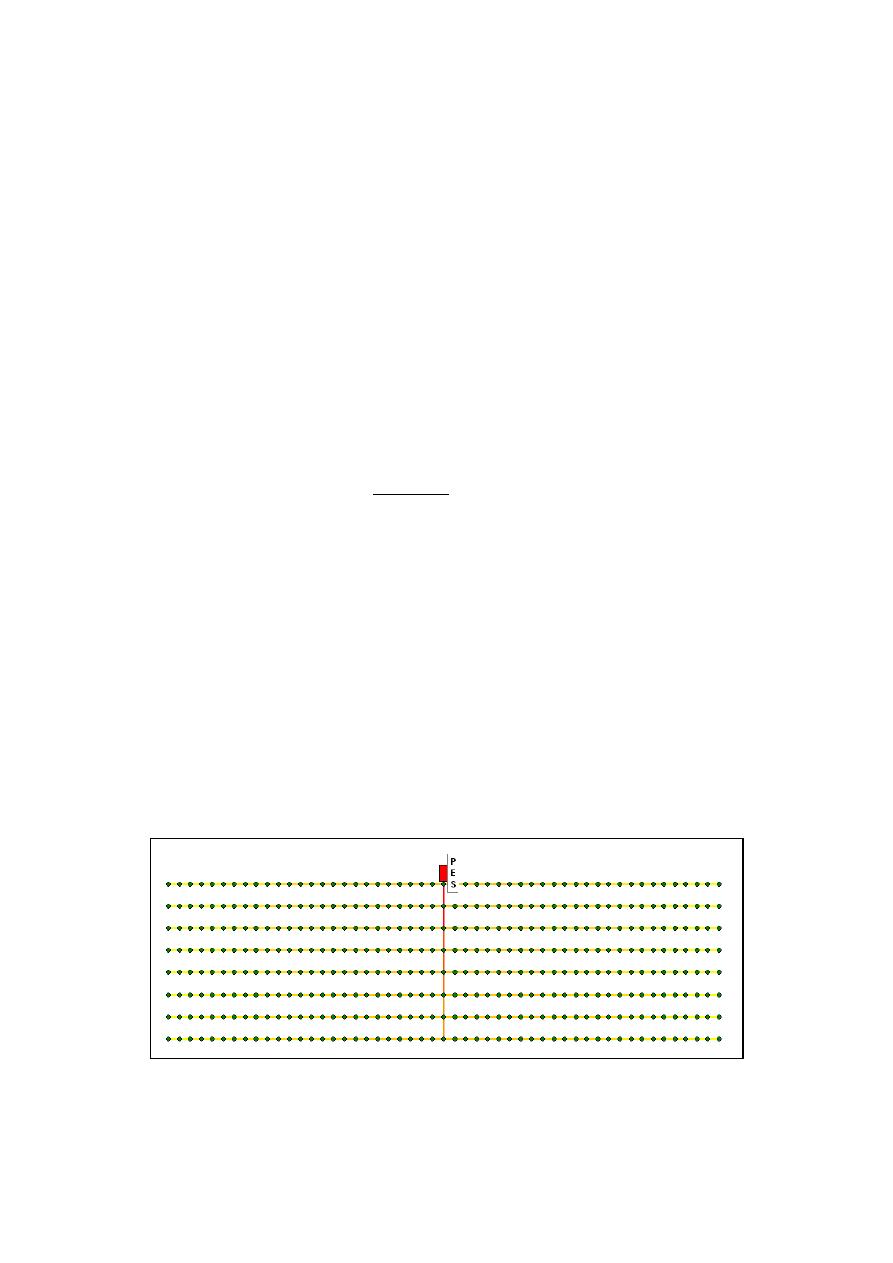
Figura 2 .- Submódulo Simétrico. Modelo de REDES.
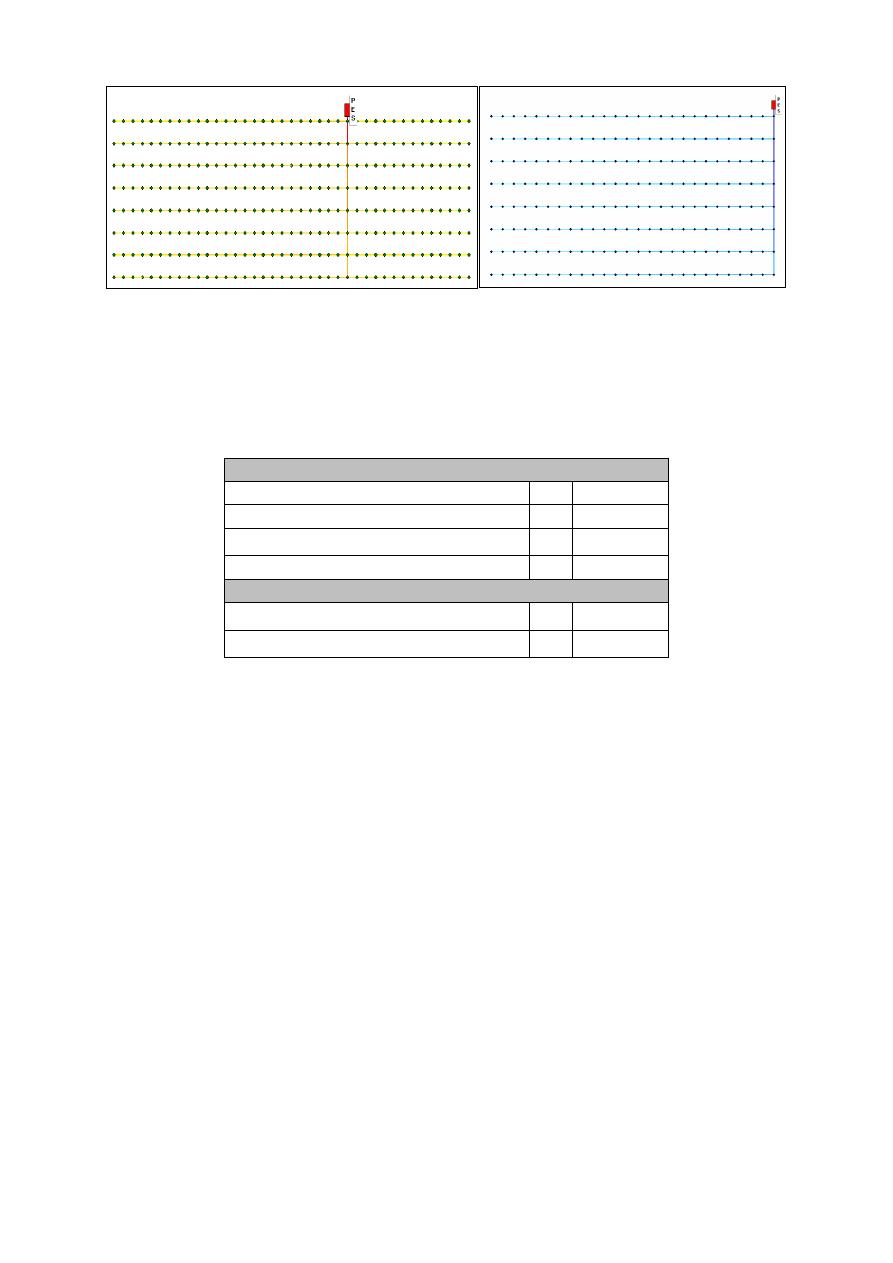
Figura 3.- Submódulos Asimétricos 1 y 2. Modelo de REDES.
Para cada uno de estos sobmódulos de riego se realizaron diferentes diseños usando la
metodología SOGH y variando las ecuaciones de los emisores que conformaban sus laterales de
riego. Los datos de entrada del diseño agronómico que se utilizaron para obtener los resultados
finales fueron los que se muestran en la siguiente tabla:
Tabla 1.- Datos de entrada para el diseño de los submódulos de estudio.
Uniformidad del Riego
Coeficiente de Uniformidad (CU)
0.8
Coeficiente de Variación (CV)
0.04
Número de Emisores por Planta (n
e
)
2 Emisores
Temperatura
15 °C
Características del Emisor
Caudal Promedio del Emisor (Q
m
)
120 Litros/hora
Presión Media de Operación (H
m
)
18 mca
De esta manera y después de hacer uso del programa REDES para realizar los diferentes
diseños se obtuvieron resultados similares para cada una de las configuraciones de submódulos
presentadas anteriormente.
RESULTADOS DEL DISEÑO DE SUBMÓDULOS USANDO LA METODOLOGÍA SOGH
Como se mostró en la Figura 2, el Submódulo Asimétrico 1 cuenta con 8 laterales, que se
componen cada uno de ellos de 25 puntos de alimentación a plantas (cada punto con 2 emisores de
riego). Habiendo establecido la tolerancia de presiones y caudales, se realizaron los diseños para
diámetros continuos y discretos, con criterio de aproximación al diámetro comercial más cercano.
Lo que se pudo observar para este primer tipo de submódulo es que la flecha de mínimo costo es la
misma independientemente de la ecuación del emisor utilizado. En la Figura 4 se observa el costo
del submódulo de riego, para diferentes flechas. Este caso corresponde a la Submódulo Asimétrico
1 usando emisores con exponente 0.3. Como se puede observar en la gráfica, al realizar el diseño
con diámetros continuos, existe un patrón. Es claro que la flecha de mínimo costo es la flecha de
0.14 y que las flechas de máximo costo son las flechas 0 y de 0.25. Por otro lado, se observa que al
discretizar los diámetros al diámetro comercial más cercano, este comportamiento Costo-Flecha se
ve totalmente afectado y no existe un patrón claro.
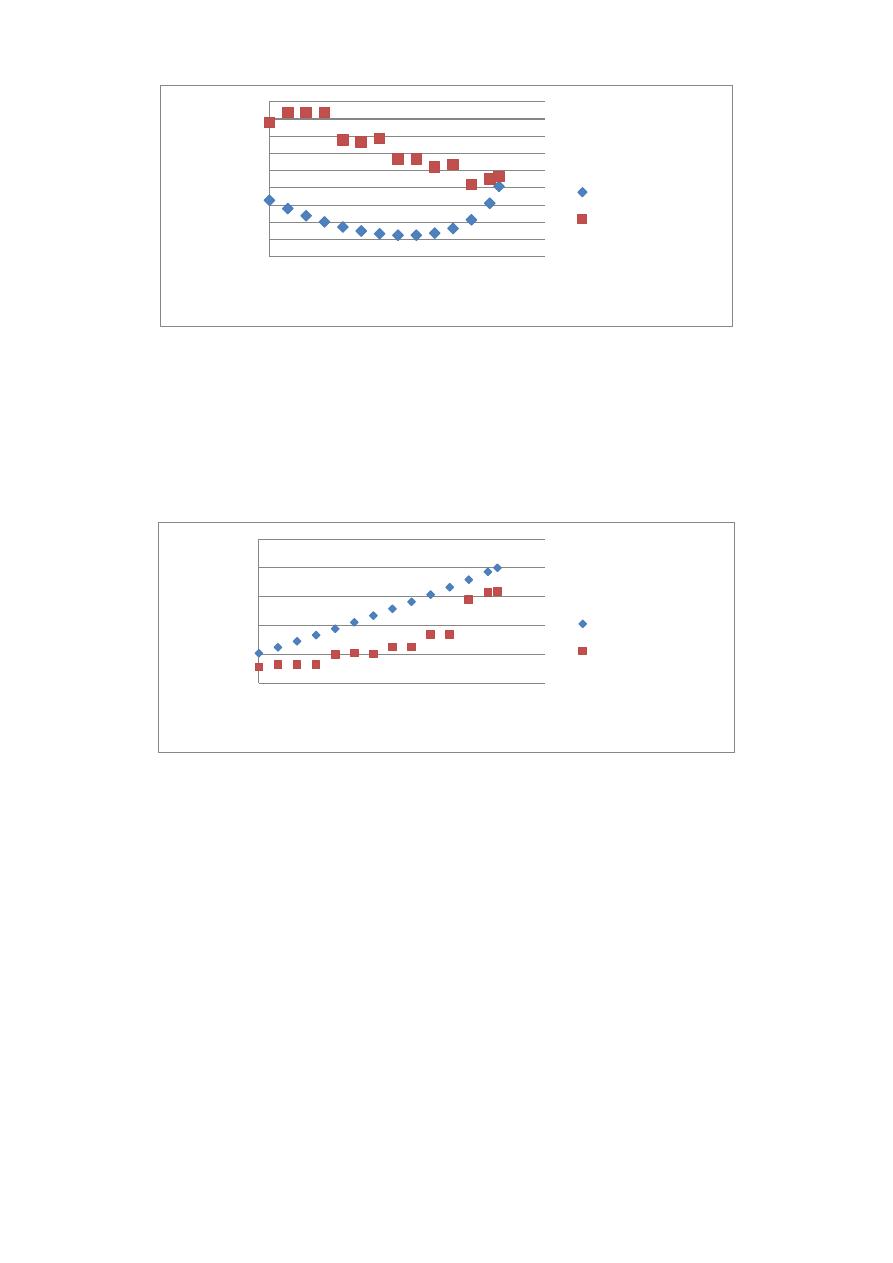
Figura 4.- Costos vs. Flecha, Submódulo Asimétrico 1. Emisores con exponente 0.3.
Por otro lado se observó para cada uno de estos diseños, el valor del Coeficiente de
Uniformidad después del diseño y se observó que tanto los diseños con diámetros discretos como
los diseños con diámetros continuos cumplían con el coeficiente de uniformidad. En la Figura 5 se
puede ver que a medida que aumenta el valor de la flecha de diseño aumenta el valor del
Coeficiente de Uniformidad (CU). Adicional a esto se observa que para todas las flechas de diseño,
al momento de discretizar los diámetros el CU se reduce.
Figura 5.- Flecha vs. Coeficiente de uniformidad resultante. Submódulo Asimétrico 1, exponente del emisor 0.3.
Estos mismos resultados se observaron para los otros dos sumódulos donde se obtuvo una
curva Costo-Flecha con un comportamiento muy similar y una alteración en la esta relación al
discretizar los diámetros; adicional a esto, los submódulos cumplen con el Coeficiente de
Uniformidad establecido en el diseño agronómico para todos los diseños. Obtenidos estos
resultados se pudo concluir que la metodología SOGH resulta bastante buena para determinar el
diseño de mínimo costo de forma rápida y cumpliendo con los requisitos agronómicos. La pregunta
que surgió a partir de los resultados presentados, es por qué la flecha de mínimo costo para el
diseño con diámetros continuos, corresponde a una flecha intermedia.
Al observar diferentes línea de gradiente hidráulico para diferentes flechas se observó, que
por ejemplo, la flecha 0 mantiene una pendiente constante y que las líneas de presiones de flechas
como la de 0.14 y 0.25 tienen una pendiente variable a lo largo de la curva. Para responder la
anterior pregunta y entender este comportamiento, se determinó, a partir de la ecuación de la LGH,
la ecuación de la pendiente de fricción en diferentes submódulos y sus correspondientes rutas
críticas.
Si se tiene una alta pendiente en la línea de presiones, esto implicará que el sistema está en
capacidad de gastar mayor energía y por lo tanto puede hacer uso de diámetros menores. Teniendo
en cuenta lo anterior, se realizó el siguiente procedimiento para observar cómo se comportan las
pendientes de las líneas de presión a lo largo de la ruta crítica. Para esto se hizo uso de la derivada
4050000
4100000
4150000
4200000
4250000
4300000
4350000
4400000
4450000
4500000
0
0.05
0.1
0.15
0.2
0.25
0.3
Costo
Sub
mód
ulo
(COP)
Flecha
Diámetros continuos
Diámetros discretos
0.8
0.82
0.84
0.86
0.88
0.9
0
0.1
0.2
0.3
Coeficiente
de Uniformidad
Fin
al
(CU)
Flecha
Diámetros Continuos
Diámetros Discretos
de la ecuación de la LGH objetivo para cada una de las flechas que se están analizando (Flechas 0,
0.14 y 0.25).
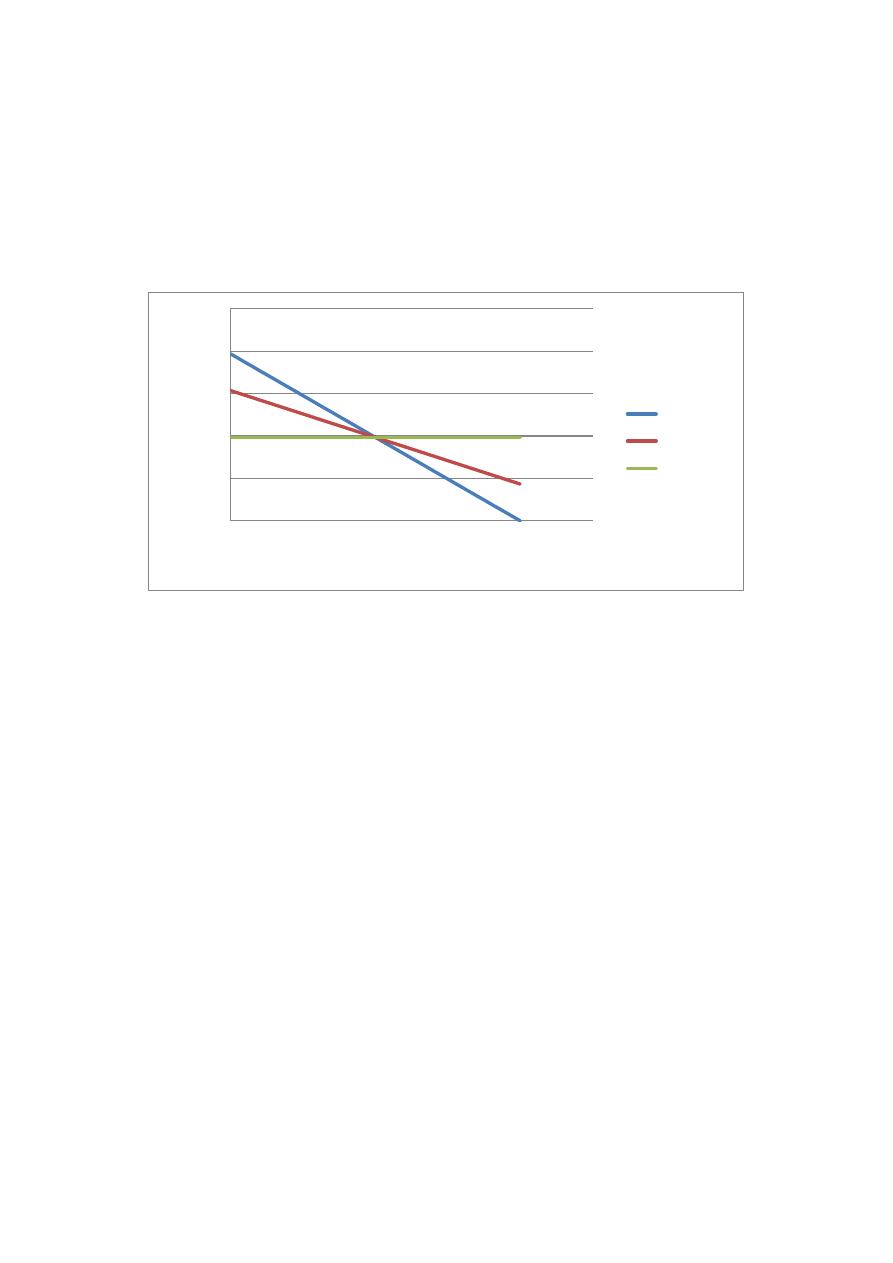
Graficando los valores de la pendiente de fricción en diferentes abscisas de los sistemas se
obtuvieron resultados como el que se muestra a continuación. En la Figura 6 se observa, como era
de esperarse, que la relación entre la pendiente de fricción para la flecha 0 y la distancia topológica
es una ecuación lineal de pendiente 0. Por otro lado, la relación entre la pendiente de fricción y la
distancia topológica de los nodos a la fuente de abastecimiento, en las flechas 0.14 y 0.25 es una
ecuación lineal con una pendiente diferente a cero. El valor de la pendiente crecerá a medida que el
valor de flecha sea mayor (Ver Figura 6).
Figura 6.- Pendiente de fricción vs distancia topológica, Submódulo Asimetrico 1, exponente del emisor 0.3.
Los resultados presentados en la Figura 5 resultan claves para entender el comportamiento
de la curva Costo-Flecha. La hipótesis planteada anteriormente hacía referencia a que las redes de
mínimo costo corresponderán a las flechas intermedias. Lo que se puede deducir de la Figura 6, es
que a medida que la flecha de diseño crece, los diámetros de las tuberías iniciales irán reduciéndose;
contrario a esto, las tuberías finales irán aumentando su diámetro. Si se comparan las tres
pendientes de fricción de las tres flechas, se observa que entre la abscisa 0 y la abscisa 100, la
flecha de 0.25 tiene una mayor pendiente de fricción y por lo tanto conllevará a diámetros menores
que las flechas 0 y 0.14. Por el contrario, entre la abscisa 100 y la abscisa 200, la flecha de 0.25
pasa a ser la que tiene una menor pendiente de fricción y por lo tanto será la que lleve a tener
mayores diámetros en las tuberías ubicadas entre estas dos últimas abscisas. En la gráfica puede
verse que la flecha intermedia (la de 0.14) siempre se encuentra en un punto medio; esto quiere
decir que, a diferencia de las flechas de 0 y 0.25, esta flecha no representa los mayores costos en
ninguno de los tramos de la ruta crítica. De esta manera, queda demostrado que aunque una flecha
extrema como la de 0 o la 0.25 conlleven a tener diámetros menores en ciertos puntos del sistema,
solo una flecha intermedia es capaz de llevar a tener los costos globales del sistema en un mínimo.
Es posible que la flecha intermedia no sea exactamente el promedio entre la flecha 0 y 0.25, pero si
es claro que se encuentra en un rango intermedio.
CONCLUSIONES
La presente investigación desarrolló una metodología de diseño de sistemas de Riego
Localizado de Alta Frecuencia (RLAF), basada en una metodología para el de diseño óptimo de
Redes de Distribución de Agua Potable (RDAP). Esta metodología se denominó “Superficie
Óptima de Gradiente Hidráulico (SOGH)”.
0
0.05
0.1
0.15
0.2
0.25
0
50
100
150
200
250
Pend
iente
de fri
cción
Distancia topológica (m)
Flecha 0.25
Flecha 0.14
Flecha 0

La curva Costo-Flecha obtenida a partir del diseño de diámetros continuos, presenta un
patrón donde la flecha de mínimo costo es una flecha intermedia entre la flecha 0 y 0.25. Este
patrón se mantiene para un mismo submódulo de riego, independientemente de las características de
los emisores que se utilicen.
Es necesario entender por qué la flecha que lleva al mínimo costo con diámetros continuos
varía dependiendo de la topología de la red. Para esto es necesario hacer un análisis detallado de las
líneas de gradiente hidráulico objetivo de cada una las rutas que toma el agua y buscar la manera de
determinar cómo se puede seleccionar la flecha óptima sin necesidad de probar todas las flechas
posibles. Para esto se puede también hacer uso de la pendiente de fricción de las diferentes rutas.
La flecha máxima de diseño para el caso en que la última tubería presenta una longitud
infinitesimal, es la flecha de 0.25. En este caso, se la pendiente de la línea de gradiente hidráulico
presenta una pendiente cero en el último punto y esto significaría hacer uso de una tubería de
diámetro infinito a fin de cumplir con las pérdidas objetivo de cero. Por otro lado, este caso es solo
un caso teórico, y dado que la última tubería del sistema presentará una longitud no diferencial, el
valor de la flecha máxima puede aumentar.
BIBLIOGRAFÍA
- Centro de Investigaciones en Acueductos y Alcantarillados, C. (2008). Programa REDES.
Bogotá: Universidad de los Andes.
- De Paco, J. L. (1993). Fundamentos del Cálculo Hidráulico en los Sistema de Riego y de
Drenaje. Madrid: Mundi-Prensa.
- IDEAM. (2011). Estudio Nacional del Agua. Bogotá, Colombia.
- Kelle, J., & Karmeli. (1974). Trickle irrigation design. Rainbird Sprinkler Manufacturing
Corporation .
- López, J. R. (1992). Riego Localizado. Madrid: Mundi-Prensa.
- Ochoa, S. (2009). Diseño Optimizado de Redes de Distribución de Agua Potable con Base
en el Concepto Energético de Superficie Óptima de Gradiente Hidráulico . Bogota:
Universidad de los Andes.
- Pizarro, F. (1996). Riegos Localizados de Alta Frecuencia. Goteo, microaspersión,
exudación. Madrid: Mundi-Prensa.
- Saldarriaga, J. (2007). Hidráulica de Tuberías. Abastecimiento de Agua, Redes, Riego.
Bogotá: Alfaomega.
- Solomon, K. H. (1985). Global uniformity of trickle irrigation system. ASAE , 1151-1158.
- Villalba, G. (2004). Algoritmos de optimización combinatoria aplicados al diseño de redes
de distribución de agua potable. Bogotá: Universidad de Los Andes.
- Wu, I. (1975). Design of Drip Irrigation Main Lines. Journal of the Irrigation and Drainage
Division , 265 - 278.
- Bermúdez, N. (2011). Desarrollo de una metodología de diseño hidráulico para
submódulos de sistemas de riego localizado de alta frecuencia. Bogotá: Universidad de los
Andes.
- OECD 2006, The impacts of Change on the Long-term Future Demand for Water Sector
infrastructure.
- Departamento Nacional de Planeación. (1998). Recuperado el 9 de Junio de 2011, de
http://www.dnp.gov.co/PortalWeb/Portals/0/archivos/documentos/DDRS/Publicaciones_Est
udios/ProductividadMR.pdf

