
Diseño de redes de distribución de agua potable por medio de la metodología
OPUS e inicio en caliente
“XII Simposio Iberoamericano sobre planificación de sistemas de
abastecimiento y drenaje”
López, L. (1), Cuero, P. (2), Díaz, O. (3), Páez, D. (4), Saldarriaga, J. (5)
(1,2,3) Investigador(a), Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad
de Los Andes (CIACUA), Carrera 1 Este N° 19ª-40, Bogotá, Colombia, (+571) 3394949 Ext: 3520,
ll.lopez28@uniandes.edu.co; pa.cuero38@uniandes.edu.co; or.diaz56@uniandes.edu.co
(4) Profesor Instructor, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad
de Los Andes (CIACUA), Carrera 1 Este N° 19ª-40, Bogotá, Colombia, (+571) 3394949 Ext: 3717,
da.paez27@uniandes.edu.co
(5) Profesor Titular, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de
Los Andes (CIACUA), Carrera 1 Este N° 19ª-40, Bogotá, Colombia, (+571) 3394949 Ext: 3520,
jsaldarr@uniandes.edu.co
RESUMEN
Este documento describe una extensión de la metodología de Superficie de Uso Óptimo de Potencia (OPUS),
que consiste en la post-optimización del diseño de una red previamente diseñada por OPUS por medio de un
método meta-heurístico. Las metaheurísticas probadas fueron Algoritmos Genéticos (GA), Búsqueda de
Armonía (HS) y Recocido Simulado (SA). La metodología propuesta es probada en tres problemas de
referencia (Hanoi, Balerma, Taichung) y una cuarta de red denominada R28. Esta extensión de la
metodología OPUS demuestra que tener en cuenta los principios hidráulicos en el proceso de diseño permite
obtener resultados cercanos al óptimo, cuya mejora exige un considerable número de iteraciones,
proporcionando un beneficio mínimo como la reducción en el costo solo del 1%.
Palabras claves: OPUS, inicio en caliente, algoritmos metaheurísticos, redes Benchmark.
ABSTRACT
This paper describes an extension to the Optimal Power Use Surface (OPUS) methodology, which consists
in applying a metaheuristic post-optimization process to a network previously designed by OPUS. The
metaheuristic tested were Genetic Algorithms (GAs), Harmony Search (HS) and Simulated Annealing (SA).
The proposed methodology is tested on three benchmark problems (Hanoi, Balerma, Taichung) and fourth
network called R28. This extension to the OPUS methodology proves that following hydraulic principles
allows obtaining near-optimal results, whose improvement demands a considerable number of iterations,
providing minimum benefit as the reduction in cost is only of 1% at the most.
Key words: OPUS, warm start, metaheuristic algorithms, Benchmark network.
SOBRE EL AUTOR PRINCIPAL
Laura López:
Ingeniera Ambiental de la Universidad de Los Andes, investigadora del Centro de Investigaciones en
Acueductos y Alcantarillados (CIACUA) y estudiante de Maestría en Ingeniería de Sistemas de la
Universidad de los Andes, Bogotá, Colombia.

ANTECEDENTES E INTRODUCCIÓN
El problema de diseño óptimo de RDAPs ha ganado
mucha importancia en las últimas décadas. Esto se
debe a la limitación de fondos para resolver este
asunto, el hecho de que el suministro de agua sea
esencial para la vida humana y el rápido incremento
de la demanda de este servicio, ya que la población
mundial está creciendo cada vez a mayor velocidad.
Por más de 40 años, muchos investigadores han
estudiado el problema, dando como resultado
diversas metodologías que ofrecen soluciones
viables a este.
Uno de los criterios más comunes de comparación y
validación de las diferentes metodologías de diseño
es el costo de construcción, incluso si otros criterios
como la confiabilidad, el impacto ambiental y la
calidad del agua también son de gran importancia.
Este tipo de diseño consiste en la determinación del
conjunto de tamaños de diámetro de las tuberías que
ofrezca el costo de capital mínimo, cumpliendo con
las demandas de caudal y con una presión mínima
requerida. No obstante el hecho de que los tubos se
fabrican normalmente en tamaños de diámetro
discreto, la cantidad de posibles configuraciones de
tuberías es inmenso, lo que hace que el problema sea
altamente indeterminado. Yates et al. (1984)
demostró que es un problema NP-duro, lo que
implica que sólo se puedan utilizar métodos
aproximados exitosamente.
Las primeras aproximaciones al problema utilizaron
técnicas de optimización tradicionales, como la
enumeración, la programación lineal y no lineal. Sin
embargo con el paso del tiempo diferentes
algoritmos metaheurísticos comenzaron a ganar
popularidad, debido a su facilidad de aplicación y
ventajas adicionales como una búsqueda más amplia
en el espacio de solución, una dependencia
relativamente pequeña de la configuración inicial del
sistema, y su capacidad de incorporar la restricción
de diámetros discretos. Algunos intentos exitosos
incluyen Algoritmos Genéticos por Savic y Walters
(1997), Búsqueda de Armonía por Geem (2006),
Búsqueda Dispersa por Lin et al. (2007), Entropía
Cruzada por Perelman y Ostfeld (2007), recocido
simulado por Reca et al. (2007), y el enjambre de
partículas por Geem (2009).
Estas metaheurísticas consisten en la imitación de
fenómenos o algoritmos evolutivos que generan al
azar un gran número de posibles soluciones y
evalúan su desempeño en términos de costos de
calidad y de capital. Los resultados se mejoran
progresivamente debido a la utilización de funciones
de aprendizaje genéricos. En el contexto de diseño
de RDAPs, cada solución representa un diseño
alternativo, es decir un conjunto diferente de
tamaños de diámetro de las tuberías. Cada vez que
un diseño alternativo se genera, una simulación
hidráulica estática se debe realizar con el fin de
evaluar su viabilidad; por lo tanto se requiere un
gran número de iteraciones para llegar a la
convergencia. Esto hace que las metaheurísticas sean
muy
exigentes
en
términos
de
esfuerzo
computacional,
independientemente
de
su
flexibilidad y capacidad de lograr resultados casi
óptimos.
Debido a esto, además del costo de la solución final,
el
número
de
simulaciones
hidráulicas
(o
iteraciones) debe ser tomado en cuenta al medir y
comparar
la
eficiencia
de
las
diferentes
metodologías. A pesar de las funciones de
aprendizaje
utilizadas
en
los
algoritmos
metaheurísticos, ninguno de estos hace uso de
criterios hidráulicos lo que implica probar el
rendimiento hidráulico de cada una de las posibles
soluciones.
Como respuesta a los problemas de los algoritmos
estocásticos,
más
recientemente
algunos
investigadores han utilizado nuevos enfoques
hidráulicos en el diseño de RDAPs, basados en el
uso de la energía disponible a lo largo del sistema.
Mientras las metaheurísticas tienen la intención de
optimizar una función objetivo, tratando las
variables de decisión simplemente como una serie de
números que deben seguir cierta lógica, sin la
comprensión de la maquinaria detrás de ésta; los
nuevos
enfoques
tratan
de
caracterizar
el
comportamiento
de
las
diferentes
variables
hidráulicas y entender su dinámica subyacente,
enfocándose en la distribución óptima de la energía
utilizada en la red.
En este sentido, I-Pai Wu (1975) analizó el
comportamiento de la función objetivo, la cual es la
suma individual de los costos de cada tubería. Este
análisis se llevó a cabo para sistemas simples, es
decir sistemas compuestos por series de tubos con
una demanda uniforme conocida en los nudos.
Como resultado Wu encontró que la distribución de
la altura de presión (carga) a lo largo de la red que
minimiza los costos constructivos sigue una curva
cuadrática, que es cóncava hacia arriba, y se separa
de la línea recta que conecta la línea de gradiente
hidráulico (LGH) en un valor del 15% del total de la
pérdida de altura (H). Por lo tanto, los diseños
óptimos pueden obtenerse por medio del cálculo de

unos valores de perdida de altura objetivo para cada
tubería, los cuales son derivados de la LGH obtenida
haciendo uso del criterio de Wu.
La extensión del concepto básico de Wu fue
propuesta por Ronald Featherstone en 1983,
sugiriendo su aplicación a sistemas más complejos
que los estudiados por Wu, como lo son las redes en
circuito. Este concepto ha sido utilizado en modelos
con demandas independientes de la presión en
topologías abiertas y cerradas, y más recientemente
en sistemas abiertos con demandas dependientes de
la presión. La metodología de Superficie de Uso
Óptimo de Potencia (OPUS) introducido por
Takahashi et al. (2010), propone un enfoque
hidráulico neto que sigue el criterio mencionado
anteriormente, lo que demuestra que los criterios
hidráulicos podrían ser utilizados como base en el
diseño de RDAPs con el fin de sustituir la iteración
intensiva requerida por las metaheurísticas.
Por otra parte, la aplicación de estos principios
hidráulicos
junto
con
formulaciones
de
programación lineal (programación lineal entera o
ILP) se han utilizado en otros estudios presentados
por Saldarriaga et al. (2012). Los resultados
obtenidos
utilizando
estas
metodologías
son
excepcionales no sólo en términos de la función
objetivo, demostrando llegar a soluciones casi
óptimas con pequeñas diferencias en comparación
con los registros mundiales, sino también en
términos del esfuerzo computacional requerido, el
cual siempre es varios órdenes de magnitud menor
que la mayoría de las soluciones comparables
alcanzadas a través de diferentes metodologías.
Además, este enfoque ofrece una visión más clara de
la mecánica interna que rige el diseño RDAPs, lo
que hace que sea fácil de entender y muy versátil
para ser implementado, permitiendo su acoplamiento
con herramientas tales como ILP con el fin de
acelerar el proceso.
Teniendo en cuenta estos resultados y haciendo un
análisis detallado de las diferencias entre los
modelos
obtenidos
por
medio
de
criterios
hidráulicos y diseños óptimos globales, se encontró
que estas diferencias son una consecuencia de la
restricción de diámetro comercial. Esta restricción
normalmente plantea dificultades en el diseño de
RDAPs para metodologías hidráulicamente basadas
como OPUS, que tienen pasos intermedios que
calculan diseños continuos teóricamente óptimos,
que luego son completamente afectados por la
posterior aproximación de los diámetros continuos a
diámetros comerciales (redondeo). Esto sucede
porque la hidráulica del sistema puede cambiar
drásticamente después de las modificaciones en los
diámetros de las tuberías. En este sentido, esta
investigación implementa diseños obtenidos en la
etapa final de la metodología OPUS como un "Inicio
en Caliente" para las metodologías metaheurísticas
típicamente utilizadas en el diseño de RDAPs, tales
como Algoritmos Genéticos, Búsqueda de Armonía
y Recocido Simulado. Esto se propone con el
objetivo de mejorar los resultados ya alcanzados con
criterios hidráulicos. Los resultados obtenidos en
esta nueva etapa del desarrollo de metodologías
basadas en el uso de energía para el diseño de
RDAPs, se presentan en las tablas comparativas que
representan los costos obtenidos, las ejecuciones
hidráulicas (medición del esfuerzo computacional)
para obtener dichos costos, y el Índice de Resiliencia
de las soluciones de los diseños. La metodología
propuesta se ha probado en diferentes problemas de
referencia (Hanoi, Balerma y Taichung) y una cuarta
red denominada R28, dando resultados muy
cercanos a los registros globales, pero con una
diferencia poco significativa en relación con la
metodología OPUS. Además, el número de
iteraciones aumenta sustancialmente con respecto a
la metodología de OPUS, lo que implica que la
mejora de los diseños hidráulicamente basados
requiere un gran esfuerzo computacional adicional
para una reducción mínima en los costos.
BASE TEÓRICA: METODOLOGÍA OPUS
La metodología de diseño OPUS está compuesta por
seis pasos diferentes. Estos se presentan en la Figura
1 en el orden en que deben ser ejecutadas. Cada uno
de los procesos que se describen a continuación y el
algoritmo detallado que cada uno de ellos sigue se
explica en el trabajo desarrollado por Saldarriaga et
al. (2012).
Figura 1. Metodología OPUS.
Búsqueda de Sumideros o Estructura de
Árbol
Este paso se basa en dos principios: el primero es
que el diseño de menor costo debe abastecer la
demanda de cada nudo mediante una única ruta
desde la fuente de agua. La segunda, establece que a
medida que aumenta el caudal de diseño de un tubo,
su costo marginal disminuye. El primer principio
viene del hecho de que la redundancia, aunque
favorece la seguridad, es hidráulicamente ineficiente
y por lo tanto las redes abiertas son mucho más
baratas que las redes cerradas. El segundo principio
proviene de la representación del caudal derivada de
las ecuaciones de Colebrook-White y Darcy-
Weisbach, en la cual al dejar constantes todos los
demás parámetros, el caudal (Q) presenta una
relación aproximadamente proporcional con el
diámetro a una potencia de 2,6. Suponiendo una
ecuación estándar del costo de la tubería y
remplazando el diámetro de acuerdo con esta
proporción, el costo por unidad de longitud de un
tubo como una función de su caudal de diseño se
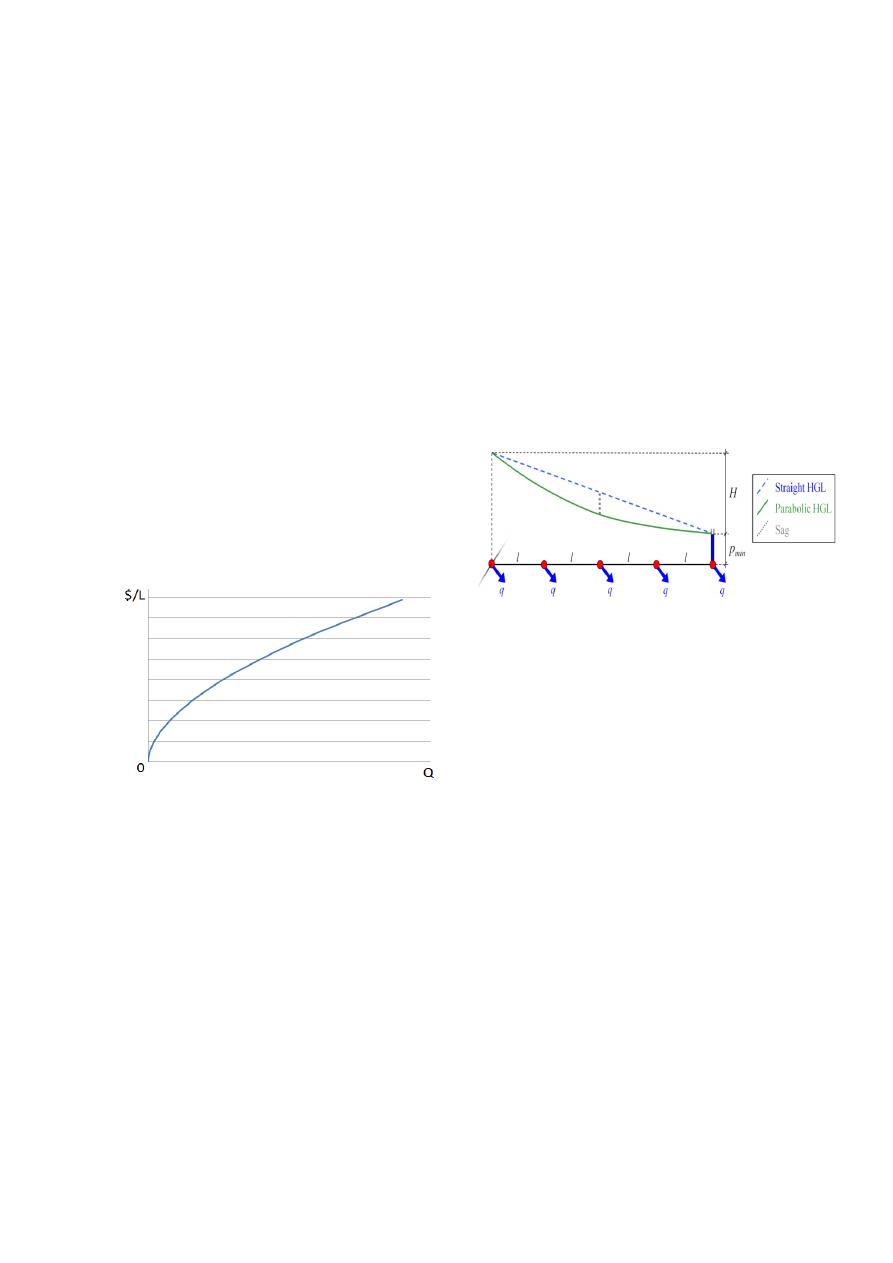
comporta como se muestra en la Figura 2.
Figura 2. Relación esquemática entre el
costo por metro de la tubería y el caudal.
Por lo tanto, el objetivo de este sub-proceso es
descomponer una red cerrada en una estructura
abierta (es decir, el agua sólo puede ser transportada
a través de un camino desde la fuente a cualquier
nudo en el sistema) con el fin de identificar los
nudos sumideros, que son nudos con una altura de
energía más baja a la de todos sus vecinos y por lo
cual al convertirse en una red abierta son los nudos
sin nudos aguas abajo. Una función de costo-
beneficio se utiliza para establecer la red abierta, y
una vez hecho esto, el paso del Uso de Energía de
Superficie Óptima puede iniciar.
Uso de Superficie Óptima de Energía
Esta etapa consiste en la asignación de una altura
hidráulica objetivo a todos los nudos de la red y
predefinir las pérdidas de altura de cada tubo. Este
sub-proceso le da el nombre a toda la metodología,
ya que es aquí donde se aplica el concepto I-Pai Wu
de Línea Óptima de Gradiente de Energía. Mediante
la asignación a todos los nudos sumideros de la
presión mínima permitida, y conociendo la altura en
el embalse, la altura de los nudos intermedios de
cada ruta se calcula suponiendo una LGH parabólica
como se muestra en la Figura 3. El valor óptimo de
pandeo se puede estimar usando una metodología
sugerida por Ochoa (2009), quien encontró que este
depende de la distribución de la demanda, la tasa
entre la demanda de caudal y la longitud de la
tubería, y la función de costo. Como resultado del
sub-proceso se ha asignado una altura objetivo a
cada uno de los nudos de la red y por lo tanto se
necesita un caudal de diseño para poder determinar
el diámetro de cada uno de los tubos de la red.
Figura 3. Criterio de I-Pai Wu para predefinir
la altura en cada nudo.
Distribución óptima del caudal
Teniendo en cuenta que en una red en circuito una
misma superficie de gradiente hidráulico se puede
obtener a través de muchas configuraciones de
diámetros, cuando el conjunto de diámetros
permitidos es de R
+
(números reales positivos), es
necesario predefinir también el caudal objetivo para
cada tubería con el fin de obtener una configuración
de diámetros que minimice los costos. Por lo tanto,
este sub-proceso pretende encontrar un esquema
único de distribución de caudales que respete la
conservación de la masa y se ajuste al uso de energía
de superficie óptima previamente establecido. Para
llevar a cabo esta tarea de manera que el resultado
final minimice los costos, los principios utilizados
en la primera etapa se utilizan una vez más y, como
resultado, la metodología decide para cada nudo qué
tubo de aguas arriba (en la red en circuito) es el
principal, es decir, el tubo que transportará la mayor
parte del caudal. Esto implica que el resto de los
tubos transportarán el caudal correspondiente al
diámetro mínimo. Para determinar la tubería
principal, se evalúa la función h
f
2
/L (donde h
f
son las
perdidas por fricción y L es la longitud de la tubería)
por cada tubo y se selecciona el que tenga el valor
máximo. Al final de este paso, cada tubería del

sistema debe haber sido asignada con un caudal de
diseño.
Cálculo del diámetro
Este subproceso calcula diámetros continuos para
cada tubo con el resultado de los pasos anteriores.
Como ya se conocen las pérdidas de altura objetivo
y el caudal de diseño para cada tubo, el diámetro
continuo necesario se puede obtener fácilmente a
partir de un cálculo directo. Este cálculo es explícito
cuando se utiliza la ecuación de Hazen-Williams e
iterativo cuando se emplean la ecuaciones de Darcy-
Weisbach y Colebrook-White. El diseño continuo
resultante es, en teoría, una RDAP completamente
operacional, con un costo muy cerca del mínimo.
Debido a la limitada disponibilidad de tamaños de
diámetro comerciales, se requiere un siguiente paso
para transformar este diseño "óptimo" en uno
factible.
Redondeo de Diámetros
Esta etapa consiste en la aproximación de cada
diámetro continuo a un valor discreto de la lista de
tamaños de diámetros disponibles comercialmente.
Se encontró que el redondeo del valor de caudal
equivalente más cercano ofrece los mejores
resultados, a pesar de que se puede obtener después
de varios criterios. La mejor manera de lograr esto
es mediante la elevación de los valores de diámetro a
una potencia de 2,6 y redondeando estos valores, tal
como se explica en el paso de la estructura de árbol.
Desafortunadamente, este paso afecta drásticamente
el comportamiento hidráulico del sistema, sobre todo
si todos los diámetros se redondean hacia arriba o
hacia abajo.
Optimización
Este paso final tiene dos objetivos principales: el
primero es para asegurar que cada nudo tiene una
presión mayor o igual a la mínima permitida. El
segundo, es la búsqueda de posibles reducciones de
costos. El primer objetivo se alcanza incrementando
los diámetros (si es necesario) a partir de los que
tienen mayor diferencia de pérdidas de altura entre
los valores reales y objetivos, hasta que todo el
sistema cumple con la restricción de presión. El
segundo objetivo se alcanza a través de un doble
recorrido a partir de las fuentes hasta los sumideros
en la dirección del flujo, y luego hacia atrás. La
reducción del diámetro de cada tubo se considera
dos veces, y el diámetro se reduce de forma
permanente si no se viola alguna restricción después
del cambio. Para asegurarse que no se está violando
la presión mínima se requieren numerosas
simulaciones hidráulicas, ya que es necesario
ejecutar una simulación hidráulica por cada
modificación del diámetro de cada tubo individual.
La metodología de OPUS fue probada por
Saldarriaga et al. (2012) en tres sistemas de
referencia conocidos: Hanoi, Balerma y Taichung,
así como en la red R28 que se presenta en este
artículo. Los resultados alcanzaron costos cercanos a
los óptimos con un número de iteraciones alrededor
de tres órdenes de magnitud más pequeño que otros
enfoques. Para la red de Hanoi, la metodología
OPUS alcanzó un costo de $ 6.147 millones después
de 83 iteraciones, que es sólo un 1,5% por encima
del récord mundial de $ 6.056 millones obtenidos a
través de diferentes metaheurísticas por Cunha y
Sousa (1999), Geem (2002), Vairavamoorthy
(2005), Kadu (2008), entre otros. En adición a esto,
la solución conseguida por OPUS para Hanoi se
obtuvo con un número de iteraciones de 3 órdenes
de magnitud por debajo al de estas. En el caso de la
red de Balerma, se obtuvo un costo de € 2.040
millones después de 677 iteraciones. Este resultado
presenta una diferencia de 5,1% en comparación con
el costo más bajo reportado en trabajos anteriores,
que es de € 1.940 millones, con 30'000.000
iteraciones obtenidos por Tolson (2009). La
discrepancia en el número de iteraciones en este
caso es de 5 órdenes de magnitud, lo que representa
un esfuerzo computacional importante. En cuanto a
la red de Taichung, la metodología OPUS dio un
diseño con un costo de $ 8.935 millones requiriendo
98 iteraciones. Este costo presenta una diferencia de
2,03% en comparación con el resultado reportado
por Sung et al. (2007) obtenido a través de la
Búsqueda Tabú de $ 8.774 millones con 74.500
iteraciones.
Estos resultados se hacen más valiosos cuando se
informa que la metodología de OPUS es
determinística y por lo tanto un diseño idéntico
puede ser encontrado por cualquier usuario después
emplear
el
mismo
número
de
iteraciones,
contrariamente
a
otros
algoritmos
con
un
componente estocástico. Esta metodología es más
eficiente que las técnicas heurísticas y los esfuerzos
realizados
para
comprender
los
principios
hidráulicos están bien recompensados. La solución
obtenida a través de OPUS ofrecerá una muy buena
configuración
inicial
a
los
algoritmos
no
deterministicos, una reducción del número de
iteraciones necesarias para llegar a resultados casi
óptimos a través de los métodos iterativos y una
búsqueda más amplia del espacio de soluciones. Este
es el motivo conveniente para ser utilizado como un
inicio en caliente para las metodologías meta
heurísticas, con el objetivo de mejorar los resultados

obtenidos mediante la aplicación de los principios
hidráulicos.
METODOLOGÍA DE INCIO EN CALIENTE
La metodología de Inicio en Caliente que se
introduce en este documento combina el algoritmo
hidráulicamente
basado
OPUS
con
uno
metaheurístico. El conjunto de diámetros obtenidos a
través de OPUS se utiliza como la configuración
inicial de la red para ser post-optimizada usando una
técnica estocástica. Las metaheurísticas analizadas
en esta investigación han sido adaptadas para el caso
del diseño de RDAPs y se llevaron a cabo utilizando
diferentes
programas
informáticos:
REDES,
MATLAB y GANetXL. REDES es un programa de
modelación de RDAPs desarrollado en el CIACUA
de la Universidad de los Andes, Colombia.
MATLAB es un conocido software de alto nivel y
entorno interactivo para el cálculo numérico, la
visualización de superficies y la programación,
desarrollado por MathWorks. Y por último
GANetXL, es una herramienta de optimización
programada sobre Microsoft Excel, que utiliza
algoritmos genéticos para resolver problemas de
optimización complejos y de búsqueda, desarrollado
en el CWS (Center for Water Systems) de la
Universidad de Exeter, Reino Unido. A continuación
se describen las principales características de los
algoritmos incluidos en este trabajo.
REDES Algoritmos Genéticos
El AG implementado en REDES utiliza la
reproducción generacional con recombinación
estándar, y selección rueda de ruleta como el
método de reproducción. Además, REDES utiliza
serie de restricciones para evitar el estancamiento en
mínimos locales, así como un algoritmo para reducir
el error estocástico. Este software califica cada una
de las soluciones y guarda un número limitado de las
mejores soluciones de todas las generaciones. Esta
lista de soluciones se guarda y reordena mediante el
algoritmo SHAKE cada vez que se crea una nueva
generación, de modo que cada nueva solución se
pueda comparar con las soluciones en la lista, y por
lo tanto se pueda actualizar correctamente. La
calificación de cada solución y el reordenamiento de
la lista realizado por REDES es una función inversa
del costo y de penalizaciones por infringir la
restricción de presión mínima. Esto causa que el
número de simulaciones hidráulicas aumente en
comparación con otro AGs. Es fundamental definir
el tamaño de la población (PS), el número de
generaciones (NG), la probabilidad de mutación
(PMUT), el ajuste de probabilidad constante (PAC),
que define una limitación para el número de
descendientes para una solución dominante, y la
pena de déficit de presión (DPP), como parámetros
iniciales del algoritmo.
GANetXL Algoritmos Genéticos
El software GANetXL permite al usuario elegir
entre un AG multiobjetivo o un mono-objetivo.
Para este caso, se elige la segunda opción y la
función a ser optimizada corresponde a la ecuación
del costo de la red. El algoritmo de reproducción
puede ser uno de los siguientes: generacional,
donde todos los individuos de la población son
producto de mutaciones aleatorias producidas en los
individuos de la población anterior, selección
elitista, similar al anterior algoritmo pero con la
diferencia de que un número específico de mejores
individuos (EL, el cual es elegido por el usuario) es
perpetuado sin ninguna mutación a la siguiente
generación, y el estado de equilibrio, donde sólo
unos pocos individuos mutan antes de ser copiados
en la nueva generación. Por último, la forma en que
se realiza la recombinación debe ser seleccionada de
alguna de las siguientes tres opciones: punto
simple, que asigna los diámetros de uno de los
padres a la mitad de los tubos de la red y los
diámetros del segundo padre al resto a la otra mitad;
multi-puntos simples, que divide la red en
diferentes secciones y asigna de manera aleatoria los
diámetros de uno de los padres a algunas de estas y
los diámetros del otro padre al resto de secciones, y
al azar en el que se decide aleatoriamente tubo por
tubo el padre del cual va a transferir su tamaño del
diámetro al nuevo individuo. La probabilidad de
recombinación se define por el parámetro (pcross).
Antes de ser asignados, los diámetros de los padres
mutan de acuerdo con una probabilidad de mutación
(PMUT), definido por el usuario.
Algoritmo Genético MATLAB
El AG implementado en MATLAB hace una
selección elitista generación por generación. Esto
significa que la población en una generación no
interactúa con la población en el siguiente. La única
información que se comparte entre las generaciones
posteriores es la de los mejores individuos, ya que
ésta se copia de una generación a la otra sin ser
modificada. El número de individuos copiados se
determina por el parámetro individuos élite (el
mismo EL anteriormente mencionado). El inicio en
caliente puede estar dispuesto de dos maneras:
tomando como la población inicial la configuración
exacta de diámetros obtenidos a través de OPUS, o
la asignación de un rango inicial de posibles
diámetros de cada tubería en la red. El rango
utilizado en este caso incluye 3 diámetros: el
diámetro original asignado por OPUS, el diámetro

discreto inmediatamente por debajo y el diámetro
discreto inmediatamente por encima, de la lista de
diámetros disponibles de la red. Esta opción se
seleccionó ya que evita que el algoritmo se atasque
en un óptimo local. El proceso de mutación se
realiza utilizando una función uniforme.
Búsqueda de Armonía (HS) REDES
HS es un algoritmo evolutivo que imita el proceso
de improvisación seguida por los músicos para crear
una "fantástica" armonía. Se compone de tres pasos
básicos, que se describen a continuación.
Preparar una Memoria Armónica
La memoria armónica (HM) es una matriz que
almacena las mejores armonías. En el contexto de
diseño de redes presurizadas, cada fila en HM es una
configuración de diámetros de la red y cada columna
indica el diámetro discreto que ha sido seleccionado
para cada tubo de ella. El tamaño de la memoria
Armónica (HMS), que se define por el usuario,
determina el número de configuraciones que se
guardan en el HM. Cada uno de los posibles diseños
son evaluados mediante la siguiente función
objetivo:
(1)
donde,
(
) es el valor de la función objetivo para
la configuración de diámetros
, es el número
total de tubos en el sistema,
es el costo por unidad
de longitud de la tubería
,
es la longitud de la
tubería
,
es el número de nudos que tienen
un déficit de presión,
es la presión en el nudo
;
por último
y son parámetros de la función de
penalización, que puede tomar valores del orden de
magnitud de 1.000 y 100.000, respectivamente. Para
la metodología de inicio en caliente, el HM se
inicializa con la configuración de diámetros
obtenido a través de la metodología de OPUS. A
continuación, se generan una serie de soluciones,
hasta que el HMS se ocupe. Esto se hace mediante la
asignación al azar a cada tubo de un diámetro cerca
de la asignada por OPUS.
Improvisar una nueva Armonía
Las nuevas armonías se seleccionan basándose en el
conjunto de configuraciones almacenadas en la HM.
Por esta razón, el diámetro de una tubería se
selecciona al azar de las configuraciones en la HM, a
fin de crear nuevos diseños.
Actualización de la Memoria de Armonía
Si de acuerdo con la función objetivo de la última
armonía generada ésta es mejor que el peor diseño
en el HM, el diseño anterior se sustituye por el
nuevo.
Recocido simulado (SA) MATLAB
SA es un algoritmo metaheurístico introducido por
Kirkpatrick et al. (1983), que fue diseñado para
evitar el estancamiento en óptimos locales, como
sucede con los enfoques tradicionales de ascenso.
Consiste en una técnica de relajación estocástica
inspirada por el proceso físico del recocido de un
metal. En contraste con los AGs, SA utiliza una
única solución durante el proceso de optimización.
En SA, las mejores soluciones se aceptan en todos
los casos, mientras que la aceptación de las
soluciones en decadencia depende de un parámetro
denominado
temperatura,
que
indica
la
probabilidad de que esto ocurra. La temperatura
inicial
(Tini)
disminuye
en
las
siguientes
interacciones a una tasa dada por el factor
denominado tasa de enfriamiento (Tcr). La
temperatura está incluida en la función de
Metropolis introducida por Metropolis et al. (1953),
controlando el número de iteraciones del algoritmo
al mismo tiempo que define de la probabilidad de
que una cierta solución sea aceptada. El proceso
finaliza
cuando
la
temperatura
alcanza
un
determinado umbral, Tstop, que por lo general es
cercano a cero. MATLAB permite dos formas
diferentes de generar nuevos individuos para la
siguiente iteración: recocido rápido y recocido
Boltzmann. La primera de ellas genera una nueva
población tomando medidas aleatorias, con tamaño
proporcional a la temperatura. La segunda, toma
medidas al azar con tamaño proporcional a la raíz
cuadrada de la temperatura. La manera en la que
disminuye la temperatura se limita a una de las
siguientes: de manera exponencial, que disminuye
en
; logarítmica, que disminuye en
,
y
lineal,
la
temperatura
disminuye en
, donde iteración se
refiere al n
úmero de iteración correspondiente.
ANALISIS DE RESULTADOS
Toda la metodología propuesta se validó con la
ayuda de 3 redes de referencia: Hanoi, Balerma y
Taichung, además de una cuarta red conocida como
R28, que será presentada a continuación. Cada una
de estas RDAPs fueron diseñadas utilizando todas
las 5 metaheurísticas explicadas anteriormente, una
vez que se aplicó la metodología OPUS.
Hanoi
La red de Hanoi fue presentada por primera vez por
Fujiwara y Khang (1990). La ecuación de la pérdida
de altura es la de Hazen-Williams con un coeficiente
de rugosidad (C) de 130, la presión mínima para el
escenario de diseño es de 30 m y los costos de las
tuberías pueden ser calculados usando una función
potencial del diámetro con un coeficiente de unidad
de $1,1 / m, y un exponente de 1,5. Los tubos
disponibles comercialmente son: 12, 16, 20, 24, 30 y
40 pulgadas. La red está formada por 34 tubos y 31
nudos configurados en 3 circuitos. Todo el caudal
del sistema es suministrado por 1 embalse con una
altura constante de 100 m. La topología de la red se
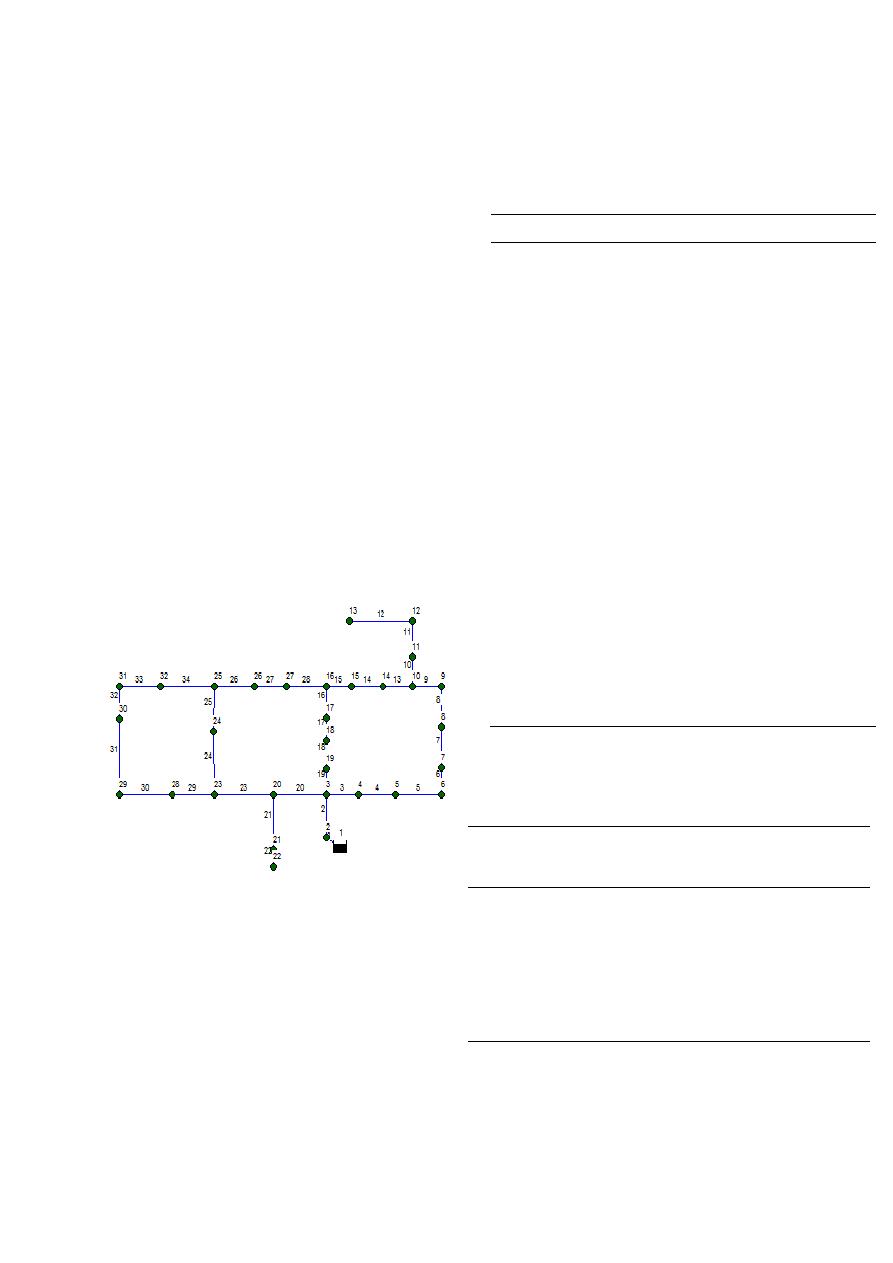
presenta en la Figura 4
Figura 4. Topología de la red Hanoi. Las
etiquetas muestran los ids de las tubería y
nudos.
En la Tabla 1 se presentan los todos los parámetros
utilizados para cada una de las metaheurísticas, así
como los valores específicos con las que se
encontraron las soluciones de costo mínimo. Los
resultados obtenidos para esta red se presentan en la
Tabla 2 donde se hace una comparación de los
costos obtenidos a través de OPUS y en el récord
mundial; adicionalmente se muestra el Índice de
Resiliencia (Todini, et al., 2000) de cada diseño
como valor de comparación en términos de la
confiabilidad de la red.
Tabla 1. Parámetros
usados para la red
Hanoi.
Tabla 2. Resultados obtenidos para la red
Hanoi.
Balerma
Balerma corresponde a una red un distrito de riego
en Almería, España. Fue introducido por primera
vez por Reca y Martínez (2006). Se hace uso de la
ecuación de pérdida de altura de Darcy-Weisbach.
Los
diámetros
de
tubería
disponibles
Metaheurísticas
Parámetros
Valores
probados
Valores(costo
mínimo)
GA REDES
PS
50, 100, 500,
1000, 2000
500
NG
50, 200, 600,
1000
600
Pmut
0.0001, 0.0005,
0.001, 0.1, 0.5
0.01
PAC
1, 2, 4, 10, 50
2
DPP
100, 1000, 5000,
10000, 100000
1000
GA GANetXL
PS
100, 200, 300,
400, 500
200
NG
10000
10000
Pcross
0.75, 0.85, 0.95
0.85
Pmut
0.85
0.85
EL
2
2
GA MATLAB
PS
50, 100, 200
200
Pcross
0.8
0.8
Pmut
0.1, 0.2, 0.3,
0.35, 0.4
0.2
EL
10% del tamaño
de la población
20
HS REDES
HMS
5, 10, 30, 50
N/A
a
1000
N/A
b
100000
N/A
SA MATLAB
Tini
50, 100
50
Tstop
0.001
0.001
Función de
recocido
Rápido,
Boltzman
Recocido rápido
Costo
(M)
Iteraciones
Presión
mínima
(m)
IR
Diferen
cia de
costo
con
Record
Diferencia
de costo
con OPUS
Record
Kadu (2008)
$6.056
18,000
30.01
0.180
N/A
N/A
OPUS
$6.147
83
30.04
0.205
1.52%
N/A
GA REDES
$6.121
399,001
30.11
0.192
1.08%
-0.43%
GA
GANetXL
$6.097
50,683
30.06
0.192
0.68%
-0.82%
GA
MATLAB
$6.081
5,083
30.01
0.192
0.41%
-1.09%
HS REDES
$6.120
10,083
30.33
0.189
1.07%
-0.44%
SA
MATLAB
$6.123
3,083
30.08
0.199
1.12%
-0.39%

comercialmente para su diseño se fabrican
exclusivamente en PVC, con una rugosidad absoluta
de 0,0025 mm. La presión mínima permitida es de
20 metros y cuenta con 10 tubos disponibles en el
mercado cuyos costos unitarios se indican en pares
(diámetro en mm, costo en € / m): 113, 7.22; 126.6,
9.1; 144.6, 11.92; 162.8, 14.84; 180.8, 18.38; 226.2,
28.6; 285, 45.39; and 361.8, 76.32. Cuenta con un
total de 454 tubos y 443 nudos de consumo que son
abastecidos por 4 embalses. La topología de la red
se presenta en la Figura 5
Figura 5. Topología de la red Balerma.
En la Tabla 3 se presentan todos los parámetros
probados para cada una de las metaheurísticas
presentadas, así como los valores específicos con las
que se encontraron las soluciones de costo mínimo
para Balerma. Los resultados obtenidos para esta red
se presentan en la Tabla 4 y se comparan con los
costos obtenidos a través de OPUS y el menor costo
reportado en la red Balerma en trabajos anteriores.
Taichung
La red Taichung fue presentada por primera vez por
Sung et al. (2007) y corresponde a una RDAP
ubicada en Taichung, Taiwán. La topología de la red
se compone de 12 circuitos formados por 31 tubos y
20 nudos, que son abastecidos por un único embalse
con una altura de 113,98 m. Por su diseño hay 13
diámetros de tubería disponibles comercialmente,
cuyos costos unitarios se indican en pares (diámetro
en mm, el costo en dólares / m): 100, 860; 150,
1160; 200, 1470; 250, 1700; 300, 2080; 350, 2640;
400, 3240; 450, 3810; 500, 4400; 600, 5580; 700,
8360; 800, 10400; y 900, 12800. La ecuación de la
pérdida de altura utilizada es la de Hazen-Williams
con un coeficiente de rugosidad (C) de 100 y la
presión mínima para el escenario de diseño es de 15
m. La topología de la red se presenta en la Figura 6.
Tabla 3. Parámetros usados para la red
Balerma.
Tabla 4. Resultados obtenidos para la red
Balerma.
Metaheurísticas
Parámetros
Valores probados
Valores(costo
mínimo)
GA REDES
PS
50, 100, 500, 1000,
2000
N/A
NG
50, 200, 600, 1000
N/A
Pmut
0.0001, 0.0005, 0.001,
0.1, 0.5
N/A
PAC
1, 2, 4, 10, 50
N/A
DPP
100, 1000, 5000,
10000, 100000
N/A
GA MATLAB
PS
50, 100, 200
200
Pcross
0.8
0.8
Pmut
0.1, 0.2, 0.3, 0.35, 0.4
0.2
EL
10% del tamaño de la
población
20
HS REDES
HMS
5, 10, 30, 50
N/A
a
1000
N/A
b
100000
N/A
SA MATLAB
Tini
50, 100
50
Tstop
0.001
0.001
Función
Recocido
Rápido, Boltzman
Recocido
Boltzman
Costo
( M)
Iteraciones
Presión
mínima
(m)
RI
Diferenc
ia costo
con
Record
Diferencia
costo con
OPUS
World
Record by
Tolson
(2009)
€ 1.940
30'000,000
N/A
0.308
N/A
N/A
OPUS
€ 2,040
677
20.00
0.306
5.17%
N/A
OPUS 2
€ 2,015
833
20.07
0.357
3.89%
N/A
GA REDES
(con
OPUS2)
€ 2,015
22,334
20.07
0.357
3.89%
0.00%
GA
MATLAB
(con
OPUS2)
€ 2,000
20,677
20.05
0.336
3.07%
-1.99%
HS REDES
€ 2,015
22,334
20.07
0.357
3.89%
0.00%
SA
MATLAB
€ 2,018
5,677
20.07
0.317
4.03%
-1.08%
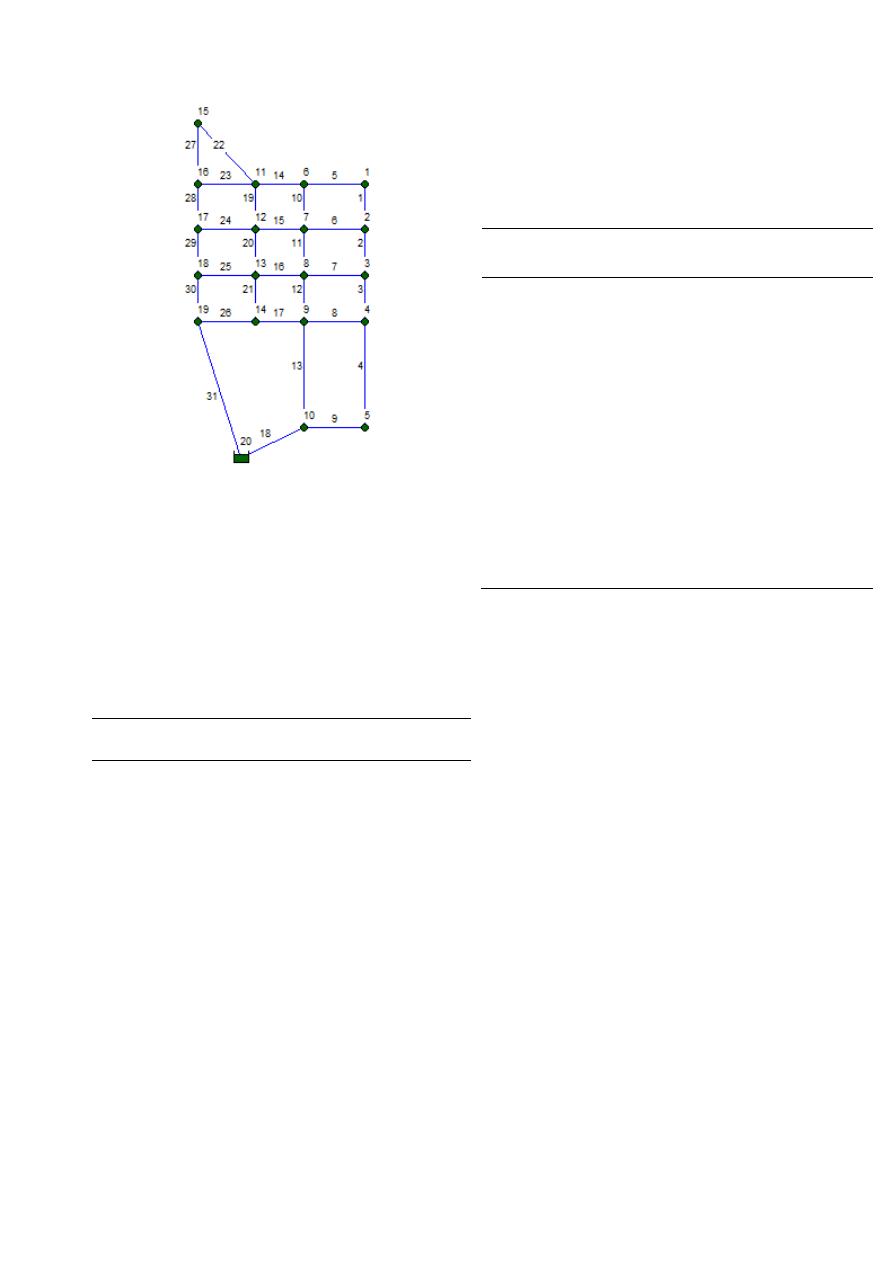
Figura 6. Topología de la red Taichung.
En la Tabla 5 se presentan todos los parámetros de la
prueba para cada una de las metaheurísticas, así
como los valores específicos con los que se
encontraron las soluciones de costo mínimo. Los
resultados obtenidos para la red Taichung se
presentan en la Tabla 6 y se comparan los costos
obtenidos a través de OPUS y el menor costo
reportado para la red Taichung en trabajos
anteriores.
Tabla 5. Parámetros para la red Taichung
.
Metaheurísticas
Parámetros
Valores probados
Valores
(costo
mínimo)
GA REDES
PS
50, 100, 500, 1000,
2000
500
NG
50, 200, 600, 1000
600
Pmut
0.0001, 0.0005, 0.001,
0.1, 0.5
0.01
PAC
1, 2, 4, 10, 50
2
DPP
100, 1000, 5000,
10000, 100000
100
GA GANetXL
PS
100, 200, 300, 400,
500
500
NG
10000
10000
Pcross
0.75, 0.85, 0.95
0.75
Pmut
0.85
0.85
EL
2
2
GA MATLAB
PS
50, 100, 200
200
Pcross
0.8
0.8
Pmut
dxdxd
0.2
EL
10% del tamaño de la
población
20
HS REDES
HMS
5, 10, 30, 50
N/A
a
1000
N/A
b
100000
N/A
SA MATLAB
Tini
50, 100
50
Tstop
0.001
0.001
Tabla 6. Resultados obtenidos para la red
Taichung.
R28
R28 es una red hipotética creada con fines de
investigación en el Centro de Investigación de
Acueducto y Alcantarillado (CIACUA) de la
Universidad de Los Andes en Bogotá, Colombia. La
topología de la red se compone de 28 circuitos
formados por 67 tubos y 39 nudos que son
abastecidos por un solo embalse, con una altura de
40 m. Todos los nudos están a la misma altura
topográfica a excepción del embalse, el cual está 15
m sobre el nivel de estos. Esta red tiene la
característica de tener una demanda con demandas
de alta magnitud en el centro de la red y menor en la
periferia. Las pérdidas por fricción se calculan con la
ecuación de Darcy-Weisbach y el material de la
tubería para toda la red es de PVC, con una
rugosidad absoluta de 0,0015 mm. La presión
mínima para el escenario de diseño es de 15 m. El
sistema cuenta con 19 diámetros disponibles, que
son: 50, 75, 100, 150, 200, 250, 300, 350, 400, 450,
500, 600, 750, 800, 1.000, 1.200, 1.400, 1.500 y
1.800 mm. El costo de las tuberías en millones de
dólares por metro ($ / m) se puede calcular
utilizando una función potencial del diámetro (mm)
con un coeficiente de 1,5 y un exponente de 1,45.
Las demandas de esta red se enumeran en orden de
número de identificación de nudo 3, 7, 8, 7, 4, 12,
21, 24, 22, 8, 10, 28, 31, 27, 15, 24, 29, 33, 30, 10,
Costo
( M)
Iteracio
nes
Presión
mínima
(m)
IR
Diferenc
ia costo
con
Record
Diferencia
costo con
OPUS
World
Record by
Sung et al.
(2007)
$ 8.774
74,500
N/A
0.212
N/A
N/A
OPUS 1
$ 8.952
74
15.42
0.282
2.03%
N/A
OPUS 2
$ 8.935
98
15.16
0.282
1.85%
N/A
GA REDES
$ 8.877
399,001
15.02
0.238
1.16%
-0.84%
GA
GANetXL
$ 8.844
10,074
15.18
0.238
0.80%
-1.02%
GA
MATLAB
(con
OPUS2)
$ 8.842
10,098
15.02
0.253
0.78%
-1.23%
HS REDES
$ 8.952
10,098
15.42
0.282
2.03%
0.00%
SA
MATLAB
(con
OPUS2)
$ 8.844
10,098
15.17
0.238
0.80%
-1.21%
11, 31, 34, 30, 23, 27, 31, 28, 10, 9, 25, 27, 24, 13, 6,
11, 12, 11, 4 L/s.
La longitud de los tubos se enumeran en orden de
tubo de número de identificación: 80, 150, 100, 120,
100, 120, 100, 150, 80, 200, 120, 100, 150, 80, 180,
120, 100, 150, 80, 220, 120, 100, 150, 80, 200, 120,
100, 150, 80, 180, 120, 100, 150, 80, 150, 120, 100,
150, 80, 150, 200, 220, 180, 100, 200, 180, 100, 150,
200, 180, 180, 200, 220, 100, 150, 200, 180, 180,
200, 220, 100, 150, 200, 180, 180, 200, 220 metros.
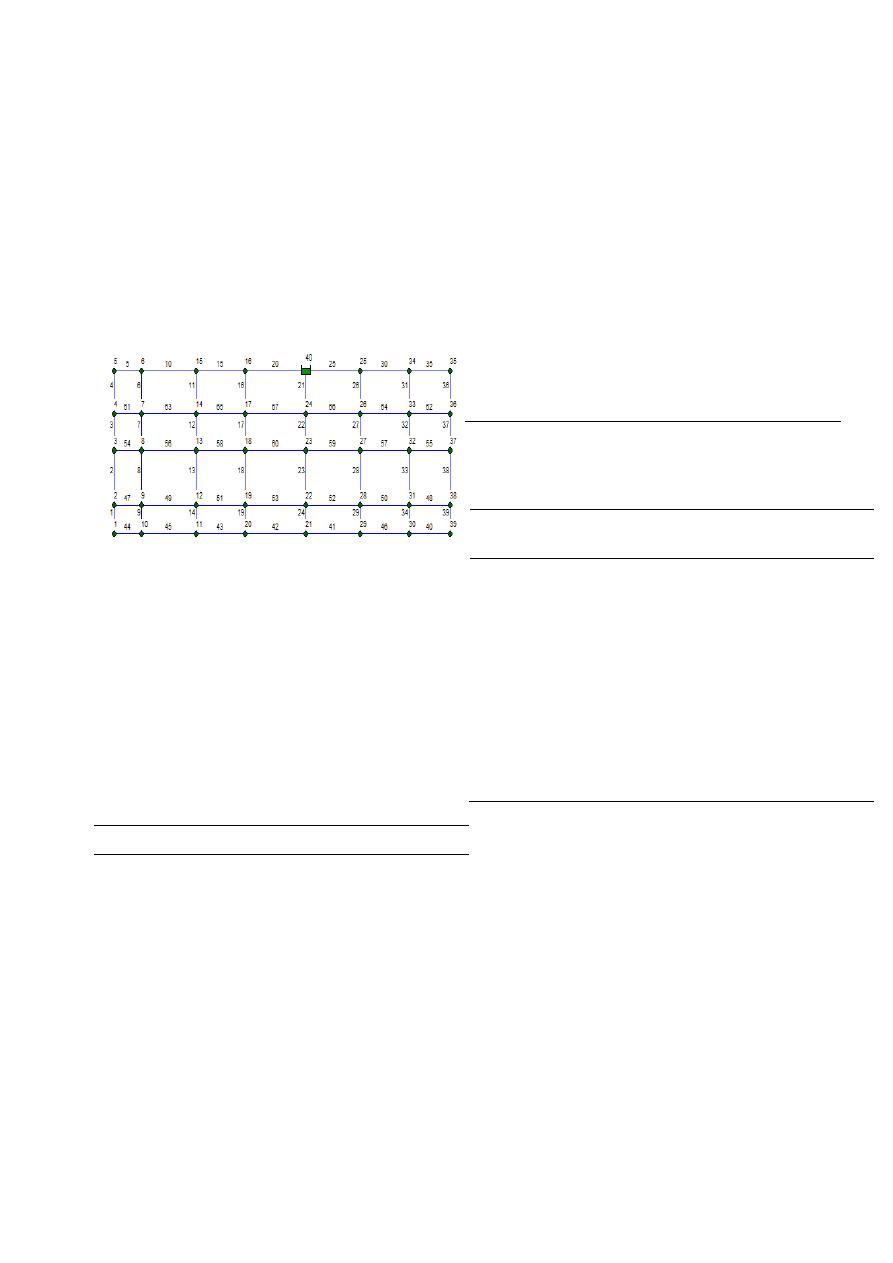
La topología de la red se presenta en la Figura 7.
Figura 7. Topología de la red R28. Las
etiquetas muestran la identificación
numérica de tuberías y nudos.
En la Tabla 7 se presentan todos los parámetros de la
prueba para cada una de las metaheurísticas, así
como los valores específicos con los que se
encontraron las soluciones de costo mínimo. Los
resultados obtenidos para la red R28 se presentan en
la Tabla 8 y se comparan con los costos obtenidos a
través de la metodología OPUS y con el menor costo
alcanzado para la red mediante AG MATLAB sin
Inicio en Caliente.
Tabla 7. Parámetros usados para la red R28.
Metaheurísticas
Parámetros
Valores
probados
Valores (costo
mínimo)
GA REDES
PS
50, 100,
500, 1000,
2000
N/A
NG
50, 200,
600, 1000
N/A
Pmut
0.0001,
0.0005,
0.001, 0.1,
0.5
N/A
PAC
1, 2, 4, 10,
50
N/A
DPP
100, 1000,
5000,
10000,
100000
N/A
GA GANetXL
PS
100, 200,
300, 400,
500
200
NG
10000
10000
Pcross
0.75, 0.85,
0.95
0.85
Pmut
0.85
0.85
EL
2
2
GA MATLAB
PS
50, 100,
200
200
Pcross
0.8
0.8
Pmut
0.1, 0.2,
0.3, 0.35,
0.4
0.2
EL
10% del
tamaño de
la
población
20
HS REDES
HMS
5, 10, 30,
50
N/A
a
1000
N/A
b
100000
N/A
SA MATLAB
Tini
50, 100
50
Tstop
0.001
0.001
F. Recocido
Rápido,
Boltzman
Recocido Boltzman
Tabla 8. Resultados obtenidos para la red
R28.
CONCLUSIONES
La metodología de Inicio en Caliente introducida en
este documento hace uso del algoritmo de OPUS,
que se basa enteramente en principios hidráulicos.
Los diseños obtenidos a través de este algoritmo se
utilizan como un Inicio en Caliente para la
aplicación de un enfoque metaheurístico. En otras
palabras, la red es re-diseñada después de que se ha
aplicado la metodología de OPUS, pero la segunda
vez haciendo uso de un algoritmo metaheurístico
que
utiliza
la
solución
anterior
como
la
configuración inicial de la red. La metodología
Inicio en Caliente combina el uso de principios de la
hidráulica para obtener eficientemente diseños casi
óptimos, con una búsqueda más amplia del espacio
Costo
( M)
Iteraciones
Presión
mínima
(m)
IR
Diferenc
ia costo
con
Record
Diferencia
costo con
OPUS
GA
MATLAB
sin Inicio en
Caliente
$14.792
180,000
15.00
0.341
N/A
N/A
OPUS
$14.978
78
15.10
0.385
1.26%
N/A
GA REDES
$14.978
10,751
15.14
0.385
1.26%
0.00%
GA
GANetXL
$14.978
20,078
15.00
0.385
1.26%
0.00%
GA
MATLAB
$14.825
10,078
15.20
0.345
0.23%
-0.01%
HS REDES
$14.978
10,078
15.00
0.385
1.26%
0.00%
SA
MATLAB
$14.870
10,078
15.01
0.378
0.53%
-0.72%

de solución propuesta por diferentes enfoques
estocásticos.
De acuerdo con los resultados obtenidos, la
metodología reduce consistentemente los costos
obtenidos a través del algoritmo de OPUS en un
porcentaje muy pequeño, hasta del 1%. En cuanto al
número
de
iteraciones,
estas
aumentan
sustancialmente en todos los casos, alrededor de 3
órdenes de magnitud. Además, los Índices de
Resiliencia de las soluciones alcanzadas por el
método de Inicio en Caliente son más pequeños en la
mayoría de los casos en comparación con los
requeridos por OPUS.
Esta metodología demuestra
claramente que
teniendo en cuenta las bases hidráulicas se logra la
optimización del diseño de RDAPs reduciendo
significativamente
el
número
de
iteraciones
necesarias en comparación con los enfoques
metaheurísticos y dando soluciones casi óptimas.
Los resultados obtenidos a través de la metodología
de Inicio en Caliente son significativamente
cercanos a los registros, pero no presentan una
mejora considerable con respecto a la metodología
de OPUS. Además, el esfuerzo computacional
requerido aumenta considerablemente, lo que
implica que no vale la pena tratar de mejorar una
solución que ya está muy cerca del mínimo óptimo y
requiere un esfuerzo computacional y humano
mínimo para ser alcanzada; teniendo en cuenta que
el uso del conocimiento hidráulico para el diseño de
RDAPs permite obtener excelentes resultados sin
necesidad de un conocimiento experto en técnicas de
optimización.
BIBLIOGRAFÍA
Cunha, M., 1999. Water distribution network design
optimization: Simulated annealing approach. J.
Water Resour. Plan. Manage. , 215-221.
Fujiwara, O. and Khang, D., 1990. A two phase
decomposition methods for optimal design of
looped water distribution networks. Water
Resources Research, Vol.26, No. 4, pp. 539-549.
Geem, Z. K., 2002. Harmony search optimization:
Application to pipe network design. Int. J.
Model. Simulat. , 125-133.
Geem, Z. K., 2006. Optimal cost design of water
distribution networks using harmony search.
Engineering Optimization, Vol.38, No.3, pp.
259-277.
Geem, Z. K., 2009. Particle-swarm harmony search
for
water
network
design.
Engineering
Optimization, Vol.41, No.4, pp. 297-311.
Kadu, M. R., 2008. Optimal design of water
networks using a modified genetic algorithm
with reduction in search space. J. Water Resour.
Plan. Manage. , 147-160.
Kirkpatrick S, Gelatt CD, Vecchi MP, 1983.
Optimization by simulated annealing. Science
220:671
Lin, M., Liu, G. and Chu, C., 2007. Scatter search
heuristic
for
least-cost
design
of
water
distribution networks, Engineering Optimization,
Vol.39, No.7, pp. 857-876.
Metropolis N, Rosenbluth A, RosenbluthM, Teller
A, Teller E, 1953. Equation of state calculations
by fast computing machines. Chem Phys
21(6):1087–1092
Ochoa, S., 2009. Optimal design of water
distribution systems based on the optimal
hydraulic gradient surface concept. MSc Thesis,
dept. of Civil and Environmental Engineering,
Universidad de los Andes, Bogotá, Col. (In
Spanish).
Perelman, L. and Ostfeld, A., 2007. An adaptive
heuristic cross entropy algorithm for optimal
design
of
water
distribution
systems.
Engineering Optimization, Vol.39, No.4, pp.
413-428.
Reca, J. and Martínez, J., 2006. Genetic algorithms
for the design of looped irrigation water
distribution
networks.
Water
Resources
Research, Vol.44, W05416.
Reca, J., Martínez, J., Gil, C. and Baños, R., 2007.
Application of several meta-heuristic techniques
to the optimization of real looped water
distribution
networks.
Water
Resources
Management, Vol.22, No.10, pp. 1367-1379.
Saldarriaga, J, Paez, D., Cuero, P., Leon, N., 2012.
Optimal power use surface for design of water
distribution systems, 14th Water Distribution
Systems Analysis Conference. Adelaide, South
Australia, pp. 468-480.
Savic, D. and Walters, G., 1997. Genetic algorithms
for least cost design of water distribution
networks. J. Water Resour. Plan. Manage., 67-
77.
Sung, Y.-H., Lin, M.-D., Lin, Y.-H. L., & Liu, Y.-
L., 2007. Tabu search solution of water
distribution network optimization. Journal of
Environmental Engineering and Management,
177-187.
Takahashi, S., Saldarriaga, S., Hernández, F., Díaz,
D. and Ochoa, S., 2010. An energy methodology
for the design of water distribution systems. In
Proceedings of the World Environmental and
Water Resources Congress 2010, ASCE.
Todini, E. (2000). “Looped water distribution
networks design using a resilience index based
heuristic approach”. Urban Water , 2 (3), pp. 115
- 122.
Tolson, B. A., 2009. Hybrid discrete dynamically
dimensioned search (HD-DDS) algorithm for
water distribution system design optimization.
Water Resources Research, 45 p.
Vairavamoorthy, K., 2005. Pipe index vector: A
method to improve genetic-algorithm-based pipe
optimization. J. Hydraul. Eng., 1117-1125.
Wu, I., 1975. Design of drip irrigation main lines.
Journal of Irrigation and Drainage Division 101,
265-278.
