
Recursos Hídricos
|
27
ct&i
Este artigo é parte integrante da
Revista Recursos Hídricos, Vol. 40, N.º 2, 27-38, dezembro de 2019.
© APRH, ISSN 0870-1741 | DOI 10.5894/rh40n2-cti3
Dimensión fractal e identificación de potenciales
sectores de servicio en redes de distribución de
agua potable utilizando criterios hidráulicos
Fractal Dimension Assessment and Identification of Potential
District-Metered Areas in Water Distribution Networks Using
Hydraulic Criteria
Kevin Vargas
1
, Camilo Salcedo
2
, Juan Saldarriaga
@, 3
@
Autor Correspondiente: jsaldarr@uniandes.edu.co
1
Investigador, Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA), Universidad de Los Andes, Colombia, Carrera 1 Este N° 19A – 40, Bogotá
2
Profesor Instructor, Departamento de Ingeniería Civil y Ambiental, Universidad de Los Andes, Colombia, Carrera 1 Este N° 19A – 40, Bogotá
3
Profesor Titular, Departamento de Ingeniería Civil y Ambiental, Universidad de Los Andes, Colombia, Carrera 1 Este N° 19A – 40, Bogotá
RESUMEN:
El algoritmo de Box Covering, utilizado para el cálculo de la dimensión fractal en Redes de Distribución
de Agua Potable (RDAPs), fue propuesto como una alternativa para identificar posibles sectores hidráulicos en
RDAPs. La calidad de posible sectorización de las redes se midió mediante el Índice de Modularidad (Q). A través del
uso de variables hidráulicas, como la Línea de Gradiente Hidráulico (LGH), se establecieron unos criterios (sumQ y
LGH*sumQ) para el cálculo de los pesos de las uniones (nudos, embalses, tanques, entre otros) en dicho método, se
realizaron pruebas para identificar sectores potenciales en las redes de Cazucá (sector de Bogotá, Colombia) Exnet y
Santa Marta, Colombia. La identificación de sectores obtenida con el algoritmo de Box Covering fue comparada con la
identificación de sectores obtenida mediante el algoritmo de Community Detection, así como con algunos resultados
de la Battle of Water Networks District-Metered Areas 2016 (BWNDMA). De esta manera, fue posible concluir que la
metodología propuesta es una alternativa viable para identificar posibles sectores hidráulicos en RDAPs de distintos
tamaños y complejidades.
Palabras clave: dimensión fractal; sectorización; criterios hidráulicos.
ABSTRACT:
Box-Covering Algorithm, used for the assessment of Fractal Dimension in Water Distribution Systems (WDS), was
proposed as an alternative for the identification of potential District Metered Areas (DMAs) within WDS. The performance of
the potential identified DMAs was measured through the Modularity Index (Q). Moreover, based in the hydraulic behavior
of the system including the Hydraulic Grade Line (HGL), some indexes (SumQ and HGL*sumQ) were proposed. Hence, these
hydraulic-based criteria were used for the assessment of the weight at the junctions of the system in the aforementioned
algorithm. Afterwards, several tests were developed for the potential identification of DMAs in 3 different networks: Cazucá
(a DMA in Bogota, Colombia), Exnet and Santa Marta, Colombia. The identification of DMAs obtained using Box Covering
Algorithm was compared with the results obtained through Community Detection Algorithm, as well as some results from
Battle of Water Networks District-Metered Areas (BWNDMA) 2016. Hence, it was possible to conclude that the proposed
methodology is a feasible alternative for the potential identification of DMA in WDS of different sizes and complexities.
Keywords: Fractal Dimension; DMA identification; Hydraulic Criteria; Box Covering Algorithm; Community Detection
Algorithm.
Kevin Vargas, Camilo Salcedo y Juan Saldarriaga

28
|
Recursos Hídricos
Kevin Vargas, Camilo Salcedo y Juan Saldarriaga
1. INTRODUCCIÓN
La fractalidad es una de las propiedades geométricas
encontradas de forma más recurrente en diferentes
sistemas naturales y artificiales, la cual se caracteriza
por la presencia de patrones similares a diferentes
escalas en estos. Aunque se han propuesto diversas
definiciones para un fractal, la que mejor se ajusta a
esta investigación corresponde a un arreglo, objeto
o sistema abstracto que presenta autosimilitud en
diferentes escalas, siendo esta última una propiedad
de un objeto en donde el todo es similar a una parte
de sí mismo.
Dentro de la propiedad de autosimilitud no
es necesario que en el sistema se presente
exactamente la misma estructura, pero sí el mismo
tipo de estructura geométrica en diferentes escalas.
Por su parte, la cuantificación de las propiedades
de un fractal se puede realizar a través de algunas
dimensiones: La dimensión topológica () o
dimensión “intuitiva” de cualquier objeto, arreglo
o sistema fractal, siempre es un número entero
(por ejemplo, un punto: , curva: , superficie: , etc.)
mientras que su dimensión fractal puede ser un
número decimal (fraccional) (Mandelbrot, 1983).
Ahora bien, en el caso de las Redes de Distribución
de Agua Potable – RDAP-, el concepto de
fractalidad se analiza desde una perspectiva menos
geométrica. Se considera una RDAP fractal como
aquella en la que sus uniones se conectan de
forma similar a diferentes escalas, lo cual implica
teóricamente un comportamiento similar de las
características relacionadas con la hidráulica de
la red a diferentes escalas. Para que esto último
se cumpla, no es necesario que la geometría del
sistema sea similar a diferentes escalas. Por lo tanto,
una RDAP fractal puede cambiar completamente su
geometría y seguir siendo igual de fractal siempre
que la conectividad entre sus nudos siga siendo la
misma. La autosimilitud en cuanto a conectividad
de las RDAP es causada por factores que pueden
ser atribuidos al ser humano, más que de origen
físico, debido a la forma en que son construidos los
sistemas de distribución de agua en general.
La identificación de estas características en las
redes de distribución de agua potable permite
realizar un análisis a gran escala con muy pocos
detalles, garantizando un alto nivel de confianza en
los resultados. Esto se puede hacer, antes de realizar
un análisis detallado a una escala más fina. Este
proceso ofrece una forma eficiente y confiable de
analizar y manejar información de sistemas de gran
tamaño (Diao, Butler e Ulanicky, 2017).
Debido a la identificación de propiedades de la
fractalidad en las redes de distribución de agua,
se ha propuesto su uso en la gestión operativa
de estos sistemas en actividades tales como la
identificación de sectores hidráulicos potenciales,
para posteriormente llevar a cabo la sectorización
de una red de distribución.
En relación con lo anterior, la sectorización consiste
en la división de una RDAP en zonas de menor
tamaño y complejidad, con el propósito de realizar
un manejo simplificado en aspectos inherentes
a una red de agua potable tales como su análisis,
planeación y su gestión (Laucelli et al., 2016). Sin
embargo, para que el proceso de sectorización sea
llevado a cabo en su totalidad, se debe abordar
toda su complejidad (Walski, Kaufman e Malos,
2001). Esto se desarrolla, en términos de los
aspectos técnicos relacionados con la instalación
de medidores y válvulas en sistemas reales, así
como sus costos asociados, lo cual resulta en un
proceso que requiere mucho énfasis por parte de
las compañías de servicios públicos para llevar a
cabo una sectorización efectiva.
En los últimos años, se han propuesto distintos tipos
de soluciones para abordar el problema operativo
de la sectorización de una RDAP, abordando la
identificación potencial de sectores de servicio
en una etapa del proceso, y determinando la
configuración y ubicación de los accesorios
necesarios en una fase posterior (Laucelli et al.
(2016), Gilbert et al. (2017), Martínez-Solano et al.
(2018) y Liu e Han (2018)).
Un espacio ideal para poner a prueba metodologías
como las descritas previamente fue el evento
científico The Battle of Water Networks District
Metered Areas (BWNDMA), el cual se desarrolló en
el marco de la versión 18 de la conferencia Water
Distribution System Analysis – WDSA 2016, llevada
a cabo en Cartagena, Colombia. Esta competencia
se centró en la identificación de nuevos sectores
hidráulicos en una red existente, en este caso
E-Town. La solución propuesta por cada equipo
debía garantizar el cumplimiento de restricciones
económicas, de calidad de agua y relacionadas con
la uniformidad de las presiones en el sistema en
dos escenarios distintos: Una época húmeda, y una
época de sequía con cortes de agua (Saldarriaga
et al., 2019).
Ahora bien, la presente investigación busca darle
al análisis de la fractalidad de una RDAP una
aplicación enfocada a la identificación de sectores
de servicio potenciales en este tipo de sistemas,
teniendo como ventaja una fuerte fundamentación
en el conocimiento de la conectividad del sistema
y su comportamiento hidráulico. Una vez estos
potenciales sectores de servicio se encuentran
definidos, se podrá proceder a realizar el análisis
Dimensión fractal e identificación de potenciales sectores de servicio en redes de distribución de agua potable utilizando criterios hidráulicos
Recursos Hídricos
|
29
ct&i
relacionado con la instalación de accesorios para
dividir efectivamente el sistema.
Debido a lo anterior, en la presente investigación se
propone el uso del algoritmo de “Box Covering” para
la identificación de posibles sectores hidráulicos.
La sectorización obtenida para las RDAPs fue
evaluada mediante el Índice de Modularidad (Q).
Cuando la división resultante no representa una
mejora significativa respecto a una simple división
aleatoria, este índice tiende a 0.0; por su parte,
entre más independiente sean los sectores entre
sí (existan menos interconexiones entre ellos) y
entre mayor sea la densidad de tuberías por nudo
en cada sector, este índice se acerca más a 1.0 (Zhu
et al., 2008). De manera general, una modularidad se
puede considerar alta cuando (Newman e Girvan,
2004). La metodología propuesta fue aplicada a tres
redes de distribución de agua potable distintas, en
donde se analizaron sistemas de diferentes tamaños
y configuraciones con el fin de determinar la validez
de la misma.
2. METODOLOGÍA
2.1 Cálculo de la Dimensión Fractal de una RDAP
Una red se considera fractal si existe una relación
potencial entre el número de grupos o “cajas” (
N
B
)
necesarias para cubrir todas las uniones de la red,
y el tamaño de cada caja en términos de uniones
(
l
B
) (Diao, Butler e Ulanicky, 2017). De esta forma,
una red se considera fractal si para todos los
l
B
posibles se obtienen valores de
N
B
de tal forma que
se cumpla la Ecuación 1.
N
B
= K
0
l
−
d
B B
(1)
En esta ecuación,
K
0
representa el número de cajas
para un
l
B
de 1 (es decir, el número total de uniones
de la red) y
d
B
es el factor de escala que especifica la
magnitud del cambio de las características en la red
con respecto a la escala a la cual es analizada; este
último se conoce como la dimensión fractal de la
red de distribución.
Ahora bien, si se toma el logaritmo en base 10 a
cada lado de la Ecuación 1, se obtiene la expresión
mostrada en la Ecuación 2. En otras palabras, una
red se considera fractal si existe una relación lineal
entre
Log(N
B
) y Log(l
B
) para todos los posibles l
B
.
Log
(N
b
) = −d
b
Log
(l
B
) + Log(K
0
)
(2)
Al realizar un ajuste lineal a los datos obtenidos, si el
coeficiente de determinación es lo suficientemente
alto, la red se considera fractal, y la dimensión
fractal se obtiene mediante el valor absoluto de
la pendiente de dicho ajuste. El procedimiento
seguido para escoger las cajas para cada tamaño de
caja y posteriormente calcular la dimensión fractal
para cada RDAP, fue el mismo que el procedimiento
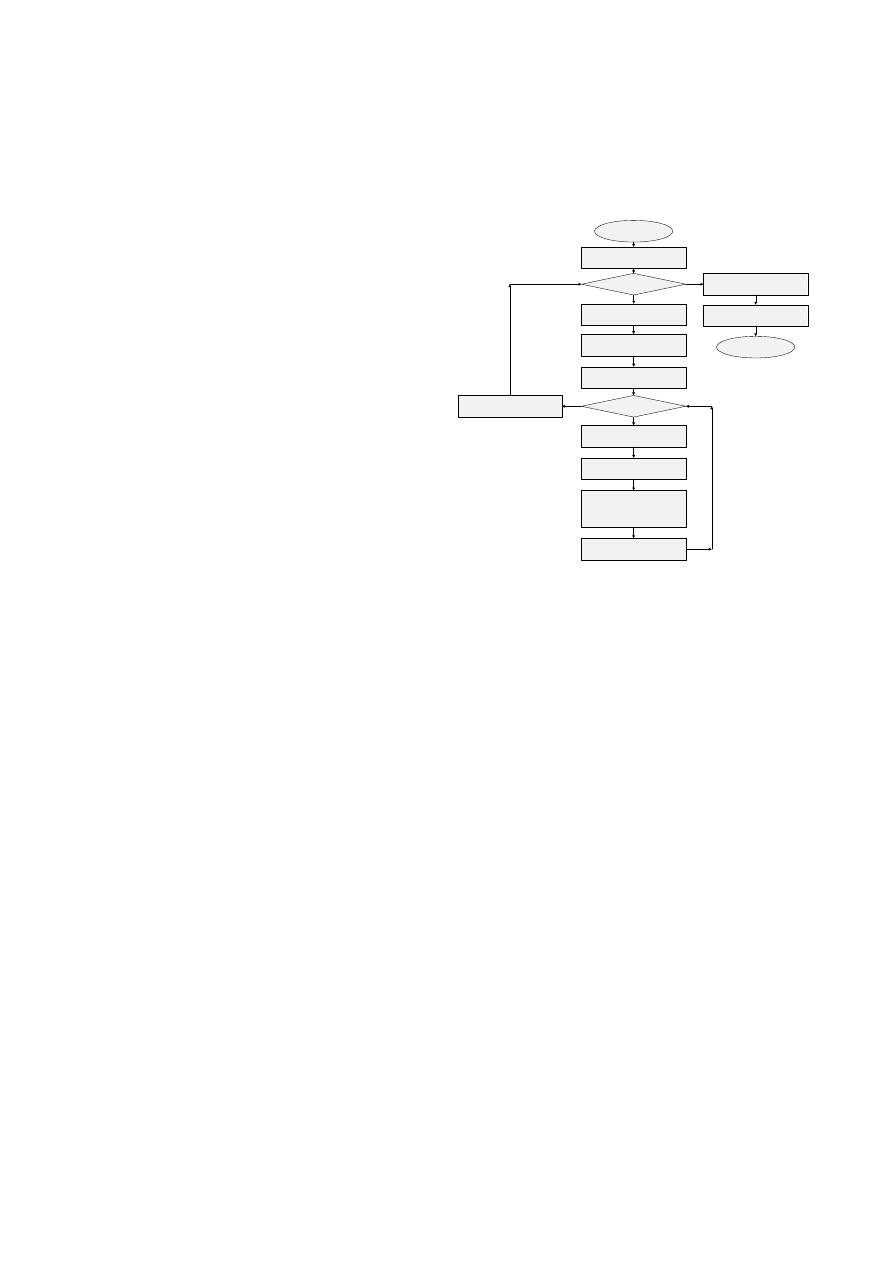
descrito por Song et al., (2007). Este algoritmo se
resume en la Figura 1.
INICIO
¿LB < LB_MÁX?
LB = LB + 2
Definir LB_MÁX
LB = 1; NB = Núm. Uniones
SÍ
“Liberar” todas las uniones
(NB = 0)
Paso = (LB-1)/2
Calcular el “peso” de cada unión
libre
¿Uniones Libres > 0?
Escoger la unión con mayor masa
como el centro de una nueva caja
Generar una nueva caja con las
uniones libres que rodean la
unión central con un paso igual al
definido anteriormente
NB = NB + 1
Guardar Log(NB) y Log(LB)
Hacer la regresión lineal de
Log(NB) vs Log(LB)
Imprimir la dimensión fractal:
d = -m
NO
FIN
SÍ
NO
Figura 1. Diagrama de flujo del algoritmo para el
cálculo de la dimensión fractal en redes.
En el método de Song et al., (2007), para el cálculo
del peso de cada unión de la red, se cuentan las
uniones que están conectadas a una distancia
menor o igual al tamaño del paso (en términos de
uniones) desde el centro que se esté considerando.
Esto equivale a asignarle a cada unión un peso
individual de una unidad. A este criterio se le asignó
el nombre de Criterio Topológico (
w
i
= 1) ya que
únicamente considera la topología de la red de
distribución.
Además del Criterio Topológico, en esta investigación
se incorporaron algunos criterios hidráulicos en
el cálculo de la dimensión fractal. Para esto, se
propusieron dos formas alternativas de asignarle el
peso individual a cada unión. En el caso de las RDAP,
una unión hace referencia a un nudo o conexión
entre dos o más tuberías.
El primer criterio hidráulico propuesto, denominado
como Criterio SumQ, consiste en la asignación del
peso mediante la sumatoria de todos los caudales que
entran a la unión i, representado por la Ecuación 3.
w
i
=
Q
ji
(3)
Por su parte, el segundo criterio hidráulico
propuesto, denominado como Criterio LGH*sumQ,
es igual al descrito previamente multiplicado por

30
|
Recursos Hídricos
Kevin Vargas, Camilo Salcedo y Juan Saldarriaga
la altura de la línea de gradiente hidráulico (LGH)
en la unión
i. Este criterio es calculado utilizando la
Ecuación 4.
w
i
= LGH
i
∗
Q
ji
(4)
Una vez se calculaban los pesos de cada unión con el
criterio seleccionado, se calculó el peso total de una
unión para determinar cuál debe ser el centro de la
siguiente caja de la forma descrita en el algoritmo
de Box Covering. Por su parte, el resto del algoritmo
se desarrolló sin ninguna modificación. Finalmente,
para todos los casos, si el
R
2
del ajuste resultaba
mayor o igual a 0.95, la red se consideró fractal.
A partir del procedimiento aquí descrito, se calculó
la dimensión fractal de un gran número de redes de
distribución de agua potable con cada criterio y se
compararon los resultados. Para analizar el efecto
del aumento de las demandas, se multiplicaron las
demandas base por factores arbitrarios y se calculó
la dimensión fractal incluyendo criterios hidráulicos
en estos casos.
2.2 Modularidad
Newman y Girvan (2004) definieron el concepto
de Modularidad como un indicador para evaluar
la división en comunidades o sectores de una red
en particular. Para definir este concepto, Zhu et al.,
(2008) definen el Índice de Modularidad
Q de una
red a través de la Ecuación 5.
Q
=
1
2m
µv
(A
µv
−
k
µ
k
v
2m
)δ(C
ω
C
v
)
(5)
en donde
μ, v representan dos vértices, o uniones,
cualquiera de la red,
m es el número total de
conexiones de la red (principalmente tuberías),
2m
es el número total de arcos,
A
uv
toma el valor de
1 si las uniones μ, v están conectadas, o 0 en caso
contrario, y
k
u
es el grado del vértice
μ representando
el número de tuberías conectadas a dicha unión.
Adicionalmente,
C
u
representa la comunidad – o
sector- al cual pertenece el vértice
μ, y δ(C
ω
C
v
)
toma el valor de 1 si
C
μ
=C
v
y
0 en caso contrario.
Al realizar modificaciones algebraicas, y en términos
de cada sector
i, se llega a la Ecuación 6 descrita a
continuación.
Q
=
j
(e
ii
− a
2
i
)
(6)
En la última ecuación,
e
ii
se puede interpretar y
calcular como la fracción del número de arcos
que conectan al sector
i con el j (en esa dirección
únicamente) respecto al número total de arcos. Por
lo tanto,
e
ii
es la fracción del número de arcos que
conectan las uniones del sector
i entre sí (en ambas
direcciones) respecto al total de arcos. Finalmente,
a
i
se puede definir como la fracción de la suma total
del número de conexiones, o vecinos, que tiene
cada unión perteneciente al sector
i.
El valor del índice de Modularidad
Q está definido
entre 0 y 1. Este puede ser utilizado para evaluar la
calidad de una determinada sectorización siendo
mejor entre más cercano se encuentre a 1.0, ya
que esto representa una mayor densidad de arcos
por unión en cada sector. Por su parte, este índice
será peor entre más cercano sea su valor a 0.0, pues
representa un menor número de conexiones entre
sectores. En adición, según algunos autores como
Diao et al. (2014)it is usually difficult to identify
the key features of the properties of the system,
and subsequently all the critical components
within the system for a given purpose of design
or control. One way is, however, to more explicitly
visualize the network structure and interactions
between components by dividing a WDS into a
number of clusters (subsystems, la modularidad
puede considerarse alta a partir de un valor de
aproximadamente 0.3.
Ahora bien, a partir de dos sectores
i y j dados,
el cambio en la modularidad
ΔQ
ii
resultante al
combinar ambos sectores para formar un nuevo
sector, se puede deducir fácilmente. Finalmente, el
cambio en la modularidad está dado finalmente
por la Ecuación 15 (Zhu, Wang, Ma, Pan, & Ding,
2008).
∆Q
ij
= 2(e
ij
− a
i
a
j
)
(7)
2.3 Identificación de Sectores Hidráulicos Usando el
Algoritmo Box Covering
El algoritmo de Box Covering, descrito por Song
et al. (2007), es ampliamente utilizado para el
cálculo de la dimensión fractal en redes reales.
Este algoritmo consiste en encontrar el número
de cajas
N
B
, definiendo una caja como un grupo
de uniones, necesarias para cubrir toda la red
para varias longitudes de caja
l
B
(en términos de
uniones). Posteriormente, se implementa el mismo
procedimiento descrito en la Sección 2.1 de este
artículo, determinando la dimensión fractal
d
B
de
la red, representado por el valor absoluto de la
pendiente del ajuste lineal realizado.
En esta investigación se propuso el uso de
únicamente una iteración del algoritmo en mención,
es decir, un solo valor de
l
B
y su correspondiente

Dimensión fractal e identificación de potenciales sectores de servicio en redes de distribución de agua potable utilizando criterios hidráulicos
Recursos Hídricos
|
31
ct&i
número de cajas
N
B
. De esta forma, los posibles
sectores finales resultantes del método se tomaron
simplemente como las cajas finales obtenidas
para una única longitud
l
B
. Los pasos principales
seguidos para la ejecución del algoritmo de Box
Covering para la sectorización de la red son descritos
a continuación. De igual manera, el procedimiento
que se debe seguir es el descrito en la Figura 1,
contemplando únicamente una sola longitud
l
B
.
1. Determinar cuál va a ser la longitud
l
B
de
las cajas, en términos de uniones, que será
empleada en el algoritmo. En la presente
investigación, se usaron varios
l
B
enteros e
impares y se escogieron las divisiones de la
RDAP que dieran los mejores resultados. Estas
últimas se caracterizan por tener los mayores
Índices de Modularidad
Q.
2. Definir el paso desde cada centro de las
cajas como (
l
B
- 1)/2 de forma que la máxima
distancia (en términos de uniones) entre
dos uniones cualquiera de una misma caja,
siguiendo la ruta más corta, resulte menor o
igual a
l
B
- 1.
3. De manera iterativa, se van a empezar a
generar las cajas hasta cubrir la totalidad
de la red. Para esto, en cada iteración se
calcula el “peso” individual de cada una de las
uniones libres, es decir que no pertenecen
aún a ninguna caja. Los criterios utilizados
para el cálculo de estos pesos corresponden a
los criterios hidráulicos SumQ y LGH*SumQ, y
el Criterio Topológico, definidos en la Sección
2.1.
4. Utilizando el paso dado por el en cuestión,
se suman todos los pesos encerrados por
la caja que se formaría alrededor de cada
unión contando únicamente con el peso
individual de las uniones libres (esta suma es
el peso total de cada unión). Una vez se tiene
el peso total de cada unión, se selecciona
aquella que tenga el mayor peso total cómo
el centro de la nueva caja y se cubren todas
las uniones libres a una distancia igual o
menor al paso siguiendo la ruta más corta en
todas las direcciones posibles desde el centro
seleccionado. Estas uniones cubiertas dejan
de estar libres para la siguiente iteración.
5. Este proceso iterativo continúa hasta que
no quede ninguna unión libre en la red de
distribución de agua potable.
6. Los posibles sectores finales corresponden a
las cajas generadas para el
l
B
seleccionado.
2.4 Identificación de Sectores Hidráulicos Usando el
Algoritmo Community Detection
El algoritmo de Community Detection es un
algoritmo utilizado para la identificación de
sectores, el cual maximiza el Índice de Modularidad
Q de la red al combinar sectores hasta que el
cambio en la modularidad (Ecuación 7) resultante
al combinar cualquier pareja de sectores en la
red, deje de ser positiva (Diao et al., 2014)it is
usually difficult to identify the key features of the
properties of the system, and subsequently all the
critical components within the system for a given
purpose of design or control. One way is, however,
to more explicitly visualize the network structure
and interactions between components by dividing
a WDS into a number of clusters (subsystems. Los
pasos para desarrollar este método se describen a
continuación:
1. Suponer que cada unión es un sector
independiente (
N
sectores
= ºN
uniones
).
2. Calcular la matriz (
N
sectores
x
N
sectores
) de cambio
de modularidad (
ΔQ
ii
) para cada pareja de
sectores
i, j con la Ecuación 7.
3. Combinar los sectores
i, j con el máximo
valor de
ΔQ
ii
. Para esto, se elimina la fila y la
columna , y se actualiza la fila y la columna
j*º de la nueva matriz de ΔQ
ii*º
para todos
los demás sectores conectados con el sector
i o el j ( j* hace referencia a la nueva fila y
columna
j que pudieron o no haberse movido
de posición).
4. Repetir los pasos 2 y 3 hasta que no exista
ningún
ΔQ
ij
> 0
Con el anterior algoritmo, se garantiza que la
Modularidad se maximice empezando con cada
unión como un sector; sin embargo, se debe tener
en cuenta que esto no garantiza que esta sea la
configuración de sectores que alcance la máxima
Modularidad posible en total para esa red.
De este modo, se puede afirmar que pueden existir
otras configuraciones de sectores que tengan una
Modularidad mayor a nivel global en la red. Sin
embargo, Diao, et al. (2014) [6] concluyeron que
al implementar la metodología de Community
Detection se encuentran valores muy altos de
Modularidad para la red en términos globales.
2.5 Combinación de Sectores Hidráulicos
Uno de los principales problemas relacionados con
el uso de las metodologías tales como Box Covering
y Community Detection para la identificación de
sectores en redes consiste en que el número de

32
|
Recursos Hídricos
Kevin Vargas, Camilo Salcedo y Juan Saldarriaga
sectores obtenido no es un número fijo, el cual es
ser determinado antes de aplicar cada algoritmo. De
este modo, este número podría diferir del número
de sectores deseado para una red real, como ocurre
en este caso con los sistemas de distribución de
agua potable. Por esta razón, en esta investigación
se propuso un método para reagrupar sectores
después de aplicar cada algoritmo hasta obtener
el número máximo deseado de sectores. En el caso
del algoritmo Community Detection, también se
establece un tamaño mínimo de sectores para que
el método se detenga luego de identificar un cierto
número de sectores, de acuerdo con los criterios
operativos deseados para el sistema.
Los criterios para combinar los sectores al llegar a
este punto del algoritmo propuesto consisten en
primer lugar, en maximizar la densidad de arcos por
unión dentro de cada sector, y, en segundo lugar,
minimizar el número de conexiones entre sectores
(los mismos criterios evaluados por el Índice de
Modularidad). Por lo tanto, el método busca la
pareja de sectores que cumpla de una mejor
manera los dos criterios propuestos mediante el uso
de la Ecuación 7. La actualización de las matrices
correspondientes a cada sector después de llevar
a cabo la combinación se hace de acuerdo con la
relación establecida por la Ecuación 6.
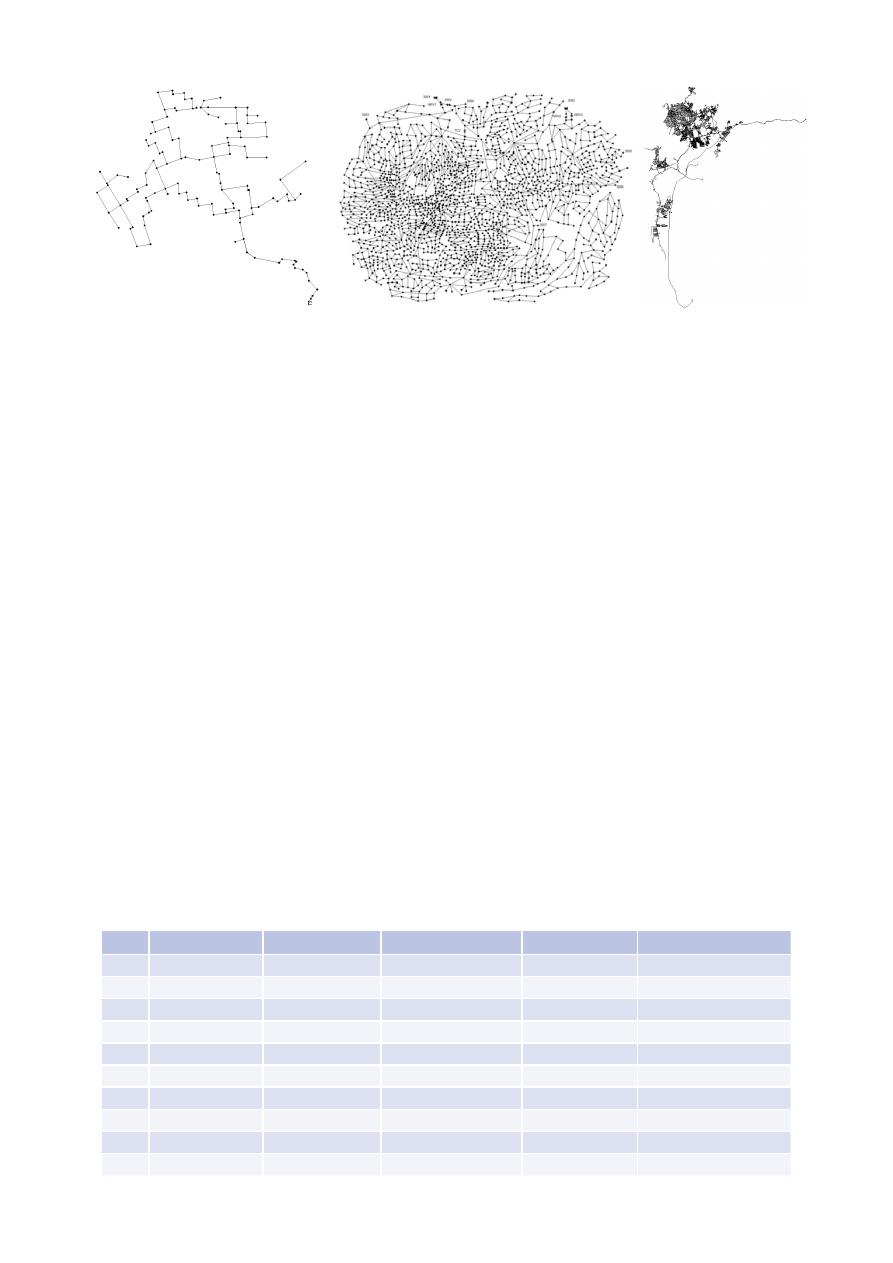
Figura 2. Esquema de RDAP en Colombia Usadas para el Cálculo de la Dimensión Fractal.
3. CASOS DE ESTUDIO
La metodología propuesta en esta investigación
fue probada utilizando distintos casos de estudio.
En primer lugar, para analizar el efecto de utilizar
criterios hidráulicos, además del topológico,
para determinar la dimensión fractal en RDAP se
consideraron 10 redes distintas pertenecientes a
ciudades de Colombia, cuyo tamaño oscilaba entre
666 y 4.813 nudos, y entre 761 y 5.621 tuberías. Estas
redes se muestran en la Figura 2.
En segundo lugar, las metodologías de identificación
de sectores hidráulicos en una RDAP fueron
implementadas utilizando las tres redes mostradas
en la Figura 3, las cuales tienen distintas topologías y
tamaños. La red de Cazucá, mostrada en la Figura 3a,
tiene un total de 150 tuberías y 146 uniones. La red
de Exnet (Farmani, Savic e Walters, 2005), mostrada
en la Figura 3b y ampliamente utilizada como una
red patrón en el ámbito de las redes de distribución,
cuenta con 2.467 conexiones, de las cuales 2.645
son tuberías, y 1.891 uniones. Finalmente, la tercera
red de estudio correspondió a la RDAP de Santa
Marta, Colombia, mostrada en la Figura 3c, la cual
cuenta con 13.976 conexiones (en donde 13.896 son
tuberías y 69 son accesorios tales como válvulas) y
11.063 uniones (Saldarriaga et al., 2019).
Dimensión fractal e identificación de potenciales sectores de servicio en redes de distribución de agua potable utilizando criterios hidráulicos
Recursos Hídricos
|
33
ct&i
4.
RESULTADOS
4.1 Cálculo de Dimensión Fractal en RDAP
En la Tabla 1 se muestra la dimensión fractal,
obtenida considerando los tres criterios propuestos
(Topológico, SumQ – ver Ecuación 3 y LGH*SumQ –
ver Ecuación 4) para el cálculo del peso para las 10
redes.
Como se puede ver en la Tabla 1, la dimensión fractal
obtenida con el criterio Topológico casi siempre
resultó mayor respecto a los valores obtenidos
con los otros dos criterios propuestos. Como se
observa, este comportamiento fue consistente
en todas las RDAP, exceptuando las redes 5 y 6, lo
cual probablemente ocurre ya que estas últimas
contaban con muchas concentraciones de nudos,
ubicadas de forma dispersa y poco interconectadas
en la red.
Por lo tanto, dado que en el criterio Topológico
siempre se empiezan a generar las cajas desde las
uniones que están rodeadas de un número mayor
a)
b)
c)
Figura 3. Esquema de las redes: a) Cazucá, b) Exnet y c) Santa Marta.
Red
No. de Nudos
No. de Tuberías Criterio Topológico Criterio SumQ
Criterio LGH*Sum(Q)
1
2.671
3.051
1,05
1,02
1,02
2
4.813
5.621
1,10
1,07
1,07
3
947
1.014
0,96
0,82
0,83
4
906
982
1,01
0,95
0,95
5
3.411
3.854
1,02
1,02
1,02
6
2.741
3.068
1,00
1,01
0,68
7
2.176
2.479
1,08
1,02
1,02
8
666
761
1,03
1,00
1,01
9
2.444
2.699
0,97
0,94
0,73
10
1.819
2.085
1,09
1,07
1,04
Tabla 1. Dimensión fractal utilizando los tres criterios propuestos para el cálculo del peso.
de uniones, en general, resultará en valores de
números de caja menores para mismos valores de .
De esta forma, se puede concluir que por lo general
esto resultará en mayores.
4.2 Identificación de Potenciales Sectores
Hidráulicos: Box Covering Y Community Detection
4.2.1 Red Cazucá
En el caso de la red de Cazucá, utilizando el
método de Box Covering, se calcularon los sectores
hidráulicos para distintos tamaños de caja posibles
utilizando las tres formas de calcular el peso de las
uniones variando los criterios utilizados. Para los
mismos tamaños de caja, también se identificaron
los potenciales sectores con un número máximo de
10. Por último, se identificaron los sectores con el
algoritmo de Community Detection para el número
de sectores que daba la máxima modularidad.
Posteriormente, se consideró un sector menos,
34
|
Recursos Hídricos
Kevin Vargas, Camilo Salcedo y Juan Saldarriaga
y luego con un sector más con el fin de verificar
que el resultado del medio efectivamente fuera el
de mayor modularidad. Además, se consideró un
número máximo de 20 y 10 sectores para comparar
con los resultados de Box Covering.
En la red de Cazucá, la Modularidad máxima con
el método de Community Detection se alcanza
cuando se tiene un número de 13 sectores. Por esta
razón, cuando se combinan los sectores hasta llegar
al número deseado de 10 sectores, la Modularidad
final es menor.
Los resultados obtenidos para números diferentes
de 13 sectores para Cazucá muestran que entre
más alejado esté la cantidad de sectores obtenida
respecto al número de sectores de la máxima
modularidad, menor es este indicador, tal como se
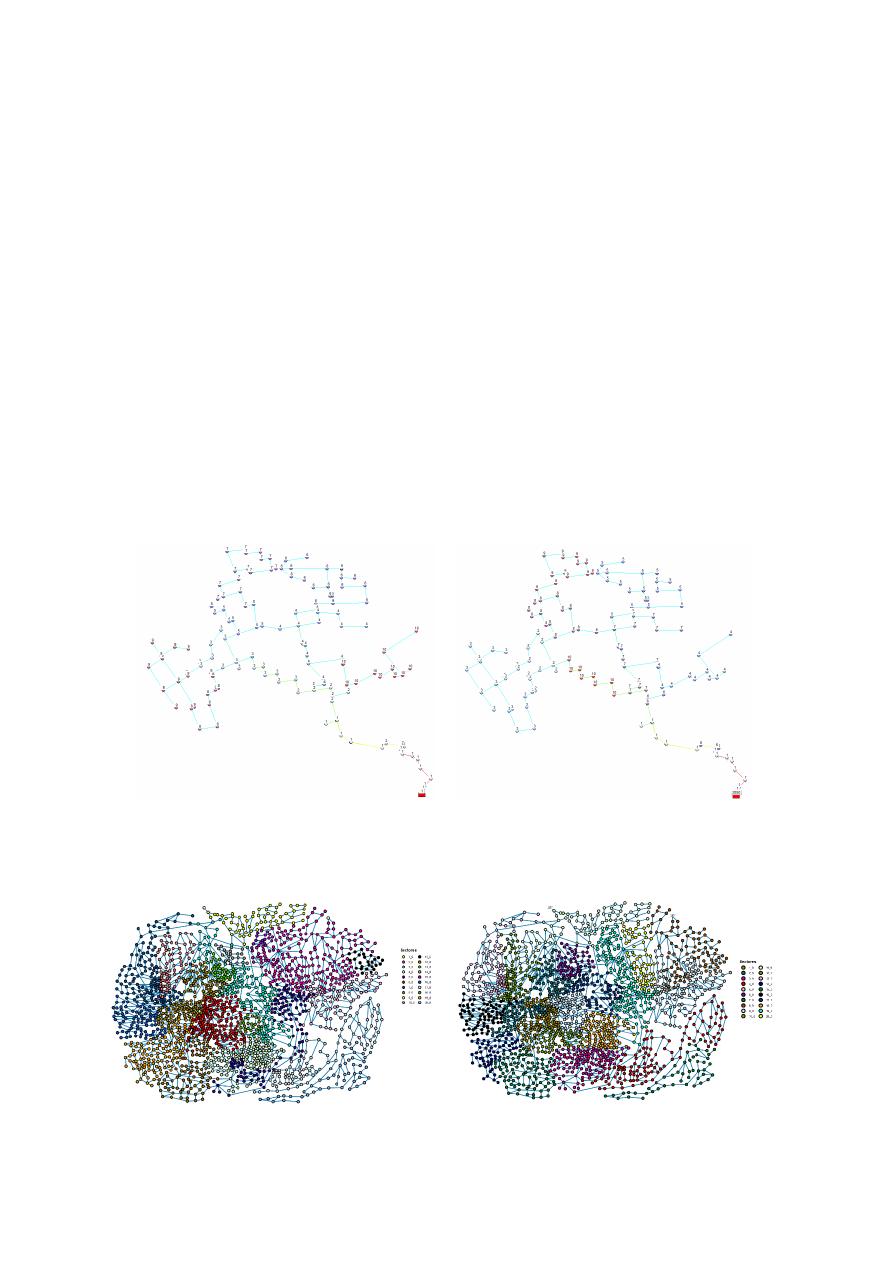
esperaba con este método. En la Figura 4 se compara
de forma visual el mejor resultado obtenido con
Box Covering (Figura 4a) con el mejor resultado
obtenido con Community Detection (Figura 4b)
después de combinar sectores hasta obtener un
número total de 10.
a)
b)
Figura 4. Posibles sectores en Cazucá (10 sectores) para: a) Box Covering con l_B=3 y criterio
sumQ y b) Community Detection..
4.2.2 Red Exnet
En el caso de Exnet, se probaron tamaños de caja de
11, 21, 31 y 41, mientras que con el método de Box
Covering, en primer lugar, no se limitó el número
máximo de sectores y posteriormente se asignó un
valor máximo de 20 sectores. En estos últimos casos,
se considerando los mismos tamaños, y se utilizaron
las tres formas de calcular el peso. Con el algoritmo
de Community Detection se hicieron las mismas
pruebas que en Cazucá, con el fin de verificar el
funcionamiento correcto del método, y se seleccionó
un número máximo de 20 sectores para comparar
los resultados con el método de Box Covering.
En esta red, la Modularidad máxima se obtuvo con
45 sectores; sin embargo, para disminuir el número
deseado a 20 sectores, la Modularidad continuó
siendo muy alta. En este caso, en la Figura 5a se
muestra la mejor división lograda con el método de
Box Covering, mientras en la Figura 5b se muestra un
esquema de los 20 sectores obtenidos finalmente al
aplicar el método completo.
a)
b)
Figura 5. Posibles sectores en Exnet (20 sectores) para:
a) Box Covering con l_B=11 y criterio LGH*sumQ y b) Community Detection.

Recursos Hídricos
|
35
ct&i
4.2.3 Red Santa Marta
Para el caso de Santa Marta, se probaron tamaños
de caja de 21, 31 y 41 calculando el peso usando
el criterio Topológico, y con número máximo de 15
y 59 sectores con el método de Box Covering con
el fin de comparar con los resultados reportados en
la Battle of Water Networks District Metered Areas
(BWNDMA 2016) (Saldarriaga et al., 2019). De igual
forma, para el método de Community Detection se
realizaron pruebas con número máximo de sectores
de 15, 59 y el de máxima Modularidad.
En este caso, la máxima Modularidad se obtuvo
con 91 sectores; sin embargo, para el número de
sectores deseado de 15 y 59 sectores esta medida
de desempeño continuó siendo muy alta (Figura 6a
y Figura 6b respectivamente). En esta red también
se obtuvo que entre más alejado se encuentre el
número de sectores del número de sectores de la
máxima Modularidad (91 en esta red), menor será la
Modularidad obtenida con este método.
Por su parte, al comparar los resultados obtenidos
mediante el método de Box Covering para tamaños
de caja de 21, se evidenció que el resultado
obtenido (ver Figura 7a) está compuesto por
a)
b)
Figura 6. Posibles sectores en Santa Marta (15 sectores) para: a) Box Covering con l_B=31 y criterio Topología y b)
Community Detection.
el mismo número de sectores que la solución
propuesta por Martínez-Solano et al. (2018) en la
BWNDMA 2016 (ver Figura 7b), la cual se alcanzó
mediante la combinación de criterios de ingeniería,
heurísticas y el Algoritmo METIS. De esta forma, se
valida el potencial del método propuesto para la
identificación de sectores hidráulicos en RDAP.
5. DISCUSIÓN DE RESULTADOS
En esta investigación se propuso una metodología
para identificar potenciales sectores hidráulicos
en una red de distribución de agua potable
fundamentado en el conocimiento de la
conectividad del sistema y su comportamiento
hidráulico, representado mediante la fractalidad
del sistema. La metodología propuesta se aplicó en
tres redes de distintas complejidades, obteniendo
resultados comparables con los disponibles en
literatura científica. No obstante, esta investigación
se centra únicamente en la identificación de
sectores potenciales.
Ahora bien, en la Figura 7 se muestra una
comparación entre los resultados obtenidos
mediante el algoritmo de Box-Covering utilizando

Kevin Vargas, Camilo Salcedo y Juan Saldarriaga et al.
36
|
Recursos Hídricos
un número de caja de 21 y el criterio topológico,
en relación con los resultados de Martínez-Solano
et al. (2018), la cual fue la mejor solución presentada
en la BWNDMA del 2016. Cómo se observa,
los potenciales sectores identificados son muy
similares en ambos casos, aun cuando en el caso de
esta investigación se emplea como fundamento la
conectividad de la RDAP, mientras Martínez-Solano
et al. (2018) utiliza la combinación de criterios de
ingeniería con heurísticas.
Este resultado demuestra la factibilidad de
implementación del algoritmo propuesto en
esta investigación para sistemas de distintas
complejidades, involucrando el comportamiento
hidráulico del sistema, permitiendo su aplicación
también en redes reales, siempre y cuando se
cuente con modelos hidráulicos robustos.
En términos operativos, se puede evidenciar que
la propuesta de Martínez-Solano et al. (2018) está
sujeta al cumplimiento de restricciones tales como la
uniformidad de presiones, la similitud en la demanda,
el costo de la solución, entre otros establecidos para
la participación en el evento científico BWNDMA
del 2016 (Saldarriaga et al., 2019). En este caso, el
algoritmo de Box Covering alcanza una distribución
y número similar de sectores únicamente basado
en el análisis de la fractalidad, y el cumplimiento de
restricciones hidráulicas tradicionales tales como
el cumplimiento de una presión mínima, evitando
también puntos de estancamiento. En este último
aspecto es importante mencionar que la presión de
servicio es una externalidad que cada sistema debe
cumplir de acuerdo a su normatividad vigente, por
lo cual no será una limitante para implementar el
algoritmo en cualquier sistema. En adición, cuando
se sectoriza una red, la capacidad de transporte de
agua en las tuberías disminuye. Debido a esto, se
debe tener en cuenta, también, que en el diseño
de los sectores definitivos se deben considerar las
alternativas de rehabilitación de los sectores en
cuanto a la capacidad de transporte de los tramos
de la red para que las presiones suministradas a los
nudos no sean inferiores a las mínimas establecidas
por norma.
De igual manera, en esta investigación no se
consideraron costos de instalación de medidores y
a)
b)
Figura 7. Posibles sectores en Santa Marta (59 sectores) para: a) Box Covering con l_B=21 y criterio Topológico y b)
Resultados de Martínez et al. en BWNDMA 2016 (Javier Martínez-Solano et al., 2018).

Dimensión fractal e identificación de potenciales sectores de servicio en redes de distribución de agua potable utilizando criterios hidráulicos
Recursos Hídricos
|
37
ct&i
válvulas, pues el alcance consistió únicamente en la
identificación de potenciales sectores hidráulicos
de servicio. Aun cuando esto ocurrió, los resultados
obtenidos fueron muy similares a los de Martínez-
Solano et al. (2018), el cual consideró costos de
instalación y operativos de acuerdo con las reglas
del BWNDMA (Saldarriaga et al., 2019). De esta
forma, se demuestra la factibilidad de implementar
esta metodología en un sistema tanto teórico como
real, pues sin tener un conocimiento de los costos
asociados con la instalación de accesorios para
sectorizar la red, se puede alcanzar un resultado
válido para la identificación preliminar y eficiente
de sectores hidráulicos. En una etapa posterior,
este resultado se podrá refinar más al considerar los
costos en mención.
CONCLUSIONES
La dimensión fractal de las redes siempre tenderá
a ser mayor si se calcula teniendo en cuenta el
Criterio Topológico únicamente, en comparación
con los métodos para el cálculo del peso que
involucran criterios hidráulicos tales como SumQ
y LGH*SumQ. Asimismo, se observó que la gran
mayoría de redes de distribución de agua potable
tienen características fractales de acuerdo con
el criterio del propuesto por Diao et al. (2014)it is
usually difficult to identify the key features of the
properties of the system, and subsequently all the
critical components within the system for a given
purpose of design or control. One way is, however,
to more explicitly visualize the network structure
and interactions between components by dividing
a WDS into a number of clusters (subsystems.
En relación con la identificación de sectores
potenciales, se evidenció que, para ninguna de
las redes estudiadas, ni para las pruebas que se
hicieron, fue posible conseguir una división con
Box Covering que superara la modularidad de
la máxima obtenida con Community Detection.
De esta forma, se evidenció que no parece haber
ninguna ventaja clara entre usar diferentes criterios
para calcular el peso de las uniones en el método de
Box Covering para identificar sectores. Por su parte,
la combinación de sectores utilizando los mismos
principios del método de Community Detection
probó ser una solución efectiva para obtener el
número de sectores deseado utilizando cualquiera
de los dos métodos estudiados, obteniendo
modularidades relativamente altas.
La metodología propuesta podría ser una alternativa
viable para identificar posibles sectores hidráulicos
en RDAPs grandes y complejas si el único criterio
es la modularidad de la división. Al comparar los
resultados obtenidos usando la metodología
propuesta respecto a otras aproximaciones
enfocadas a la sectorización de RDAP se evidencia
que se obtienen resultados comparables de manera
eficiente. Debido a esto, se evidencia la factibilidad
para implementar la metodología en sistemas
teóricos y reales.
Finalmente, la metodología propuesta es utilizada
para la identificación de sectores potenciales, como
una etapa previa a la sectorización, en donde sí
deben ser considerados costos de instalación de
accesorios, así como evaluar criterios operativos
al detalle. Sin embargo, a partir de los resultados
obtenidos se puede evidenciar el cumplimiento de
restricciones operativas mínimas que pueden dar
lugar a una primera aproximación al problema de
sectorización.
REFERENCIAS
Diao, K. et al. - Clustering analysis of water distribution
systems: Identifying critical components and
community impacts. Water Science and Technology.
ISSN 02731223. 2014). doi: 10.2166/wst.2014.268.
Diao, Kegong; BUTLER, David; ULANICKY, Bogumil -
Fractality in Water Distribution Networks. Em CCWI
2017 - Computing and Control for the Water Industry
Farmani, R.; Savic, D. A.; Walters, G. A. - Evolutionary multi-
objective optimization in water distribution network
design. Engineering Optimization. ISSN 0305215X.
2005). doi: 10.1080/03052150512331303436.
Gilbert, Denis et al. - Iterative Multistage Method for a
Large Water Network Sectorization into DMAs under
Multiple Design Objectives. Journal of Water Resources
Planning and Management. ISSN 0733-9496. 2017).
doi: 10.1061/(asce)wr.1943-5452.0000835.
Javier Martínez-Solano, F. et al. - Combining
Skeletonization, Setpoint Curves, and Heuristic
Algorithms to Define District Metering Areas in
the Battle of Water Networks District Metering
Areas. Journal of Water Resources Planning and
Management. ISSN 0733-9496. 2018). doi: 10.1061/
(asce)wr.1943-5452.0000938.
Laucelli, Daniele B. et al. - Optimal Design of District
Metering Areas. Em Procedia Engineering
Liu, Jun; Han, Rui - Spectral Clustering and Multicriteria
Decision for Design of District Metered Areas. Journal
of Water Resources Planning and Management.
ISSN 0733-9496. 2018). doi: 10.1061/(asce)wr.1943-
5452.0000916.

Kevin Vargas, Camilo Salcedo y Juan Saldarriaga et al.
38
|
Recursos Hídricos
Mandelbrot, Benoit B. - Fractals and the Geometey
of Nature. American Journal of Physics. ISSN 0002-
9505. 1983). doi: 10.1119/1.13295.
Newman, M. E. J.; Girvan, M. - Finding and evaluating
community structure in networks. Physical Review E
- Statistical, Nonlinear, and Soft Matter Physics. ISSN
1063651X. 2004). doi: 10.1103/PhysRevE.69.026113.
Saldarriaga, Juan et al. - Battle of the Water Networks
District Metered Areas. Journal of Water Resources
Planning and Management. ISSN 0733-9496. 2019).
doi: 10.1061/(asce)wr.1943-5452.0001035.
Song, Chaoming et al. - How to calculate the
fractal dimension of a complex network: The box
covering algorithm. Journal of Statistical Mechanics:
Theory and Experiment. ISSN 17425468. 2007). doi:
10.1088/1742-5468/2007/03/P03006.
Walski, T.; Kaufman, D.; Malos, W. - Establishing a
system submetering project. Em American Water Works
Association 2001 Conference, AWWA. Denver : [s.n.]
Zhu, Z. et al. - Scalable Community Discovery of Large
Networks. Em The Ninth International Conference on
Web-Age Information Management
