
PROYECTO DE GRADO
Ingeniería Civil
Ingeniería Ambiental
DETERMINACIÓN DEL ÁRBOL ÓPTIMO MULTICRITERIO DE UNA RED
DE DRENAJE URBANO QUE LLEVE AL DISEÑO DE MÍNIMO COSTO Y
MÁXIMA RESILIENCIA
Laura Lizzette Arroyo Cruzco
Asesor: Juan G. Saldarriaga Valderrama
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
BOGOTÁ D.C.
2021

AGRADECIMIENTOS
A Dios que siempre ilumina mi camino,
A mis padres y hermanos por su apoyo incondicional,
A mi asesor, Juan Saldarriaga por su brillante acompañamiento en este proceso,
A Juana Herrán por compartir sus conocimientos,
Y a todas las personas que de una u otra forma hicieron parte de este logro.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
i
TABLA DE CONTENIDO
1
Introducción ................................................................................................................................ 1
1.1
Objetivos ............................................................................................................................. 2
1.1.1
Objetivo General ......................................................................................................... 2
1.1.2
Objetivos Específicos ................................................................................................... 2
2
Antecedentes .............................................................................................................................. 3
3
Marco Teórico ............................................................................................................................. 5
3.1
Redes de Drenaje Urbano ................................................................................................... 5
3.2
Índices de resiliencia ........................................................................................................... 7
3.2.1
Índices de resiliencia de Haghighi & Bakshipour ......................................................... 7
3.2.2
Índices de resiliencia de Distancia ............................................................................... 8
3.2.3
Índices de resiliencia de Altura ................................................................................... 9
3.2.4
Índices de resiliencia de Distancia y Altura ............................................................... 10
3.2.5
Índices de resiliencia de Inicios ................................................................................. 11
3.2.6
Índices de resiliencia de Aguilar ................................................................................ 11
4
Metodología .............................................................................................................................. 13
4.1.
Metodología para el diseño optimizado de redes de drenaje urbano ............................. 13
4.1.1
Selección del trazado ................................................................................................ 14
4.1.2
Diseño Hidráulico ...................................................................................................... 14
4.1.3
Función de Costos ..................................................................................................... 15
4.2.
Optimización multiobjetivo de redes de drenaje urbano ................................................. 15
5
Resultados ................................................................................................................................. 22
5.1.
Red de Esmeralda .............................................................................................................. 23
5.2.
Red de Moeini ................................................................................................................... 30
6
Análisis de resultados ................................................................................................................ 34
6.1.
Red de Esmeralda .............................................................................................................. 34
6.2.
Red de Moeini ................................................................................................................... 35

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
ii
7
Conclusiones.............................................................................................................................. 36
8
Recomendaciones ..................................................................................................................... 37
9
Referencias ................................................................................................................................ 38

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
iii
ÍNDICE DE FIGURAS
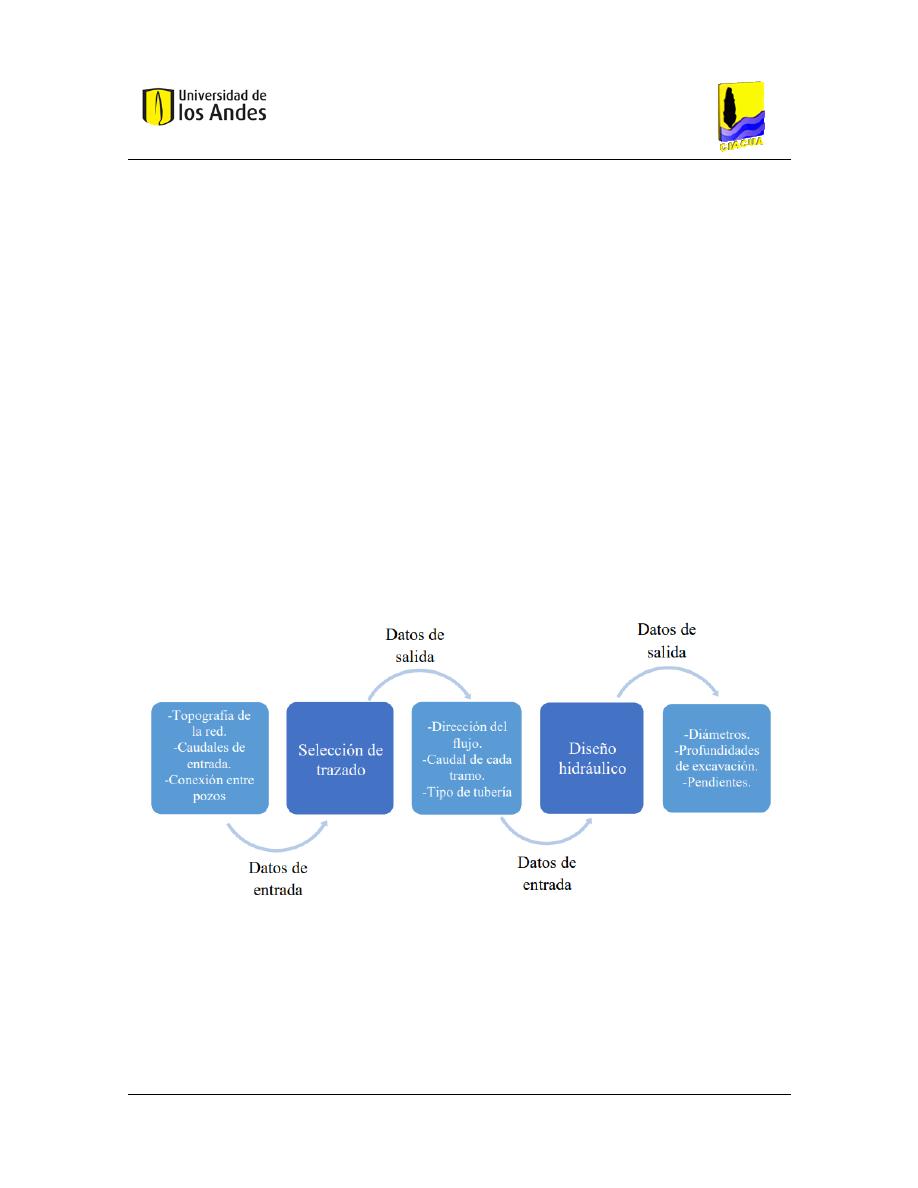
Figura 1 Proceso de diseño de una red de Drenaje Urbano Herrán (2020) ...................................... 13
Figura 2 Frontera de Pareto esperada para una red de drenaje urbano .......................................... 17
Figura 3 Optimización monoobjetivo del diseño de redes de drenaje urbano ................................. 18
Figura 4 Optimización multiobjetivo del diseño de redes de drenaje urbano .................................. 19
Figura 5 Cálculo de costos reales de trazados de una red de drenaje urbano ................................. 21

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
iv
ÍNDICE DE GRÁFICAS
Gráfica 1 Frontera de Pareto de costos aproximados -Haghighi & Bakshipour red de Esmeralda .. 23
Gráfica 2 Frontera de Pareto de costos reales- Haghighi & Bakshipour red de Esmeralda .............. 24
Gráfica 3 Frontera de Pareto de costos aproximados-Índice de Distancia red de Esmeralda .......... 24
Gráfica 4 Frontera de Pareto de costos reales del índice de Distancia para la red de Esmeralda .... 25
Gráfica 5 Frontera de Pareto de costos aproximados del índice de Altura red de Esmeralda ......... 25
Gráfica 6 Frontera de Pareto de costos reales del índice de Altura para la red de Esmeralda ........ 26
Gráfica 7 Frontera de Pareto de costos aproximados- Distancia y Altura red de Esmeralda ........... 26
Gráfica 8 Frontera de Pareto de costos reales - Distancia y Altura para la red de Esmeralda ........ 27
Gráfica 9 Frontera de Pareto de costos aproximados del índice de Inicios red de Esmeralda ........ 27
Gráfica 10 Frontera de Pareto de costos reales del índice de Inicios para la red de Esmeralda ...... 28
Gráfica 11 Frontera de Pareto de costos aproximados -Índice Aguilar red de Esmeralda ............... 28
Gráfica 12 Frontera de Pareto de costos reales del índice de Aguilar para la red de Esmeralda ..... 29
Gráfica 13 Frontera de Pareto definitiva de costos reales -Aguilar red de Esmeralda ..................... 29
Gráfica 14 Frontera de Pareto de costos aproximados - Haghighi & Bakshipour red de Moeini ..... 30
Gráfica 15 Frontera de Pareto de costos reales-Haghighi & Bakshipour red de Moeini .................. 31
Gráfica 16 Frontera de Pareto de costos aproximados - Distancia para la red de Moeini ............... 31
Gráfica 17 Frontera de Pareto de costos reales del índice de Distancia para la red de Moeini ....... 32
Gráfica 18 Frontera de Pareto de costos aproximados del índice de Aguilar para la red de Moeini 32
Gráfica 19 Frontera de Pareto de costos reales del índice de Aguilar para la red de Moeini .......... 33

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
v
ÍNDICE DE TABLAS
Tabla 1 Costos computaciones de la red de Esmeralda .................................................................... 30
Tabla 2 Costos computacionales de la red de Moeini ...................................................................... 33

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
vi
ÍNDICE DE ECUACIONES
Ecuación 1 Índice de resiliencia propuesto por Haghighi & Bakshipour (2016) ................................. 7
Ecuación 2 Resiliencia total de la red según el índice de Haghighi & Bakshipour (2016) ................... 8
Ecuación 3 Peso de cada tubería según el índice de Distancia propuesto por Herrán (2020) ........... 8
Ecuación 4 Distancia entre pozos según índice de Distancia propuesta por Herrán (2020) .............. 8
Ecuación 5 Índice de resiliencia de Distancia propuesto por Herrán (2020) ...................................... 9
Ecuación 6 Resiliencia total de la red según el índice de Distancia propuesto por Herrán (2020) ..... 9
Ecuación 7 Peso de cada tubería según el índice de Altura propuesto por Herrán (2020) ................ 9
Ecuación 8 Índice de resiliencia de Altura propuesto por Herrán (2020) ........................................ 10
Ecuación 9 Resiliencia total de la red según el índice de Altura propuesto por Herrán (2020) ....... 10
Ecuación 10 Distancia entre pozos según índice de Distancia y Altura de Herrán (2020) ................ 10
Ecuación 11 Índice de resiliencia de Distancia y Altura propuesto por Herrán (2020) ..................... 10
Ecuación 12 Resiliencia total de la red según el índice de Distancia y Altura de Herrán (2020) ...... 10
Ecuación 13 Resiliencia índice de Inicios propuesto por Herrán (2020) ........................................... 11
Ecuación 14 Resiliencia índice de Aguilar propuesto por Andrés Aguilar (2019) ............................. 11
Ecuación 15 Forma de una ecuación de costos ................................................................................ 15
Ecuación 16 Ecuación de costos de Maurer para un tramo de la red (2012) ................................... 16
Ecuación 17 Coeficiente alpha de la ecuación de Maurer (2012) ..................................................... 16
Ecuación 18 Coeficiente beta de la ecuación de Maurer (2012) ...................................................... 16
Ecuación 19 Ecuación de costos de Maurer para toda la red (2012) ................................................ 16
Ecuación 20 Función objetivo creada por el algoritmo NISE ............................................................ 20
Ecuación 21 Ponderador de la ecuación creada por la metodología NISE ....................................... 20

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
1
1 Introducción
Las redes de drenaje urbano son aquellas que permiten evacuar grandes cantidades de
agua provenientes de precipitaciones o de las viviendas y establecimientos de una ciudad.
Estas redes están compuestas por pozos de inspección, tuberías, sistema de bombeo y
diversos tipos de accesorios complementarios que permiten el correcto funcionamiento del
sistema (Duque, 2013). Por tanto, los sistemas de drenaje urbano son considerados un
servicio básico para una comunidad, ya que previenen enfermedades, contaminación y
malos olores al permitir evacuar aguas pluviales y residuales (Herrán, 2020). Ahora bien,
para diseñar una red de drenaje urbano se necesitan dos procesos importantes, en primer
lugar, es fundamental la escogencia de la topología de la red, es decir, decidir cuál es el
árbol que permite obtener el sistema que se desea construir. En este proceso, se obtiene
la dirección, tipo y caudal de cada una de las tuberías que conforman el sistema, para esto,
es necesario tener los caudales de entrada a cada uno de los pozos de inspección como
parámetro de entrada. Luego, se debe realizar el diseño hidráulico de la red, verificando
que se cumplan con las restricciones hidráulicas establecidas en la normativa (Duque,
2015). En este paso, debe tenerse como parámetro de entrada las variables encontradas
en la selección del trazado y se deben obtener las variables de diámetro, profundidad de
excavación y pendiente de cada una de las tuberías. En este sentido, el diseño de una red
de drenaje urbano es un procedimiento complejo, ya que implica múltiples variables que
describen el comportamiento de una misma red y el funcionamiento hidráulico del sistema
(Aguilar, 2019). En contraste al diseño de las redes de abastecimiento de agua potable, el
diseño de una red de drenaje urbano es un problema sin solución óptima encontrada, lo
cual genera preocupación en países como Colombia, que tienen un déficit en la cobertura
de saneamiento de su territorio (Zambrano, 2019).
Según el trabajo realizado por Aguilar en 2016 es posible encontrar el óptimo global de la
selección del trazado de una red de drenaje urbano a partir de una metodología que permite
optimizar los árboles posibles de la red con una función linealizada de costos, donde se
tiene en cuenta de forma indirecta variables del diseño hidráulico. Por tanto, a partir de la
revisión bibliográfica realizada, este documento, buscará verificar la metodología propuesta

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
2
por (Aguilar, 2019) donde se obtiene un conjunto de diseños óptimos teniendo en cuenta la
resiliencia y los costos del sistema. En este sentido, se tiene una metodología multiobjetivo
con dos funciones que se deben maximizar o minimizar según la variable analizada.
1.1 Objetivos
1.1.1 Objetivo General
Verificar la metodología que permite obtener el árbol óptimo multicriterio que lleve a una red
de drenaje urbano de máxima resiliencia y mínimo costo.
1.1.2 Objetivos Específicos
• Entender el programa de diseño de una red de drenaje urbano y sus características
principales.
• Realizar un estudio de los métodos de diseño tradicionales de una red de drenaje
urbano.
• Entender cómo es la escogencia de árboles de diseño de una red de drenaje urbano.
• Verificar los criterios para la escogencia del árbol de diseño de una red de drenaje
urbano y la determinación de la resiliencia del sistema.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
3
2 Antecedentes
En el Centro de Investigaciones de Acueductos y Alcantarillado de la Universidad de Los
Andes se han desarrollado diversos trabajos alrededor del tema de optimización del diseño
de una red de drenaje urbano. Lo anterior, teniendo en cuenta diversos aspectos como los
costos, la resiliencia del sistema, la selección óptima de trazados iniciales, entre otros.
Todos los trabajos anteriormente realizados, garantizan el cumplimiento de las restricciones
hidráulicas establecidas en el Reglamento Técnico del Sector de Agua Potable y
Saneamiento Básico (RAS 2000).
Entre las investigaciones realizadas en el CIACUA sobre el diseño óptimo de redes de
drenaje urbano se destacan la de Natalia Duque (2013) donde se desarrolló una
metodología para minimizar los costos de una red de drenaje urbano, en la que se
comprendía el diseño hidráulico como un problema de ruta más corta. Luego, en 2015
Natalia Duque continuó su investigación desarrollando una metodología que incluía la
selección del trazado en la cual se analizaba esta parte del diseño de la red como un
problema de tipo entero mixto. Asimismo, en esta investigación se desarrolló una
metodología iterativa que permitió unir la selección del trazado y el diseño hidráulico a partir
de un árbol óptimo aleatorio. Sin embargo, en esta metodología no se podía garantizar la
obtención de una selección óptima debido a que el primer trazado era aleatorio.
En 2016, Andrés Aguilar crea una metodología que permite conectar las dos partes del
diseño de redes de drenaje urbano de una forma más efectiva. Esta metodología, permite
tener variables del diseño hidráulico de forma indirecta en la selección del trazado. Lo
anterior, a partir de una transformación de la función de costos del diseño hidráulico para
que quede en variables de la selección del trazado, esto es posible al hacer uso de las
ecuaciones de Darcy-Weisbach y Manning. Luego, en 2019 Andrés Aguilar introduce la
optimización multiobjetivo a la investigación al agregar el objetivo de maximizar la resiliencia
de una red. Lo anterior, para garantizar que, si un tramo de la red deja de funcionar de
forma eficiente se afecte la menor cantidad de población aguas arriba del daño. Para esto,
Aguilar propuso un algoritmo Non-Inferior Set Estimation (NISE), el cual permite obtener
fronteras de Pareto donde se evidencien las soluciones óptimas de las dos variables que
se quieren optimizar, el costo de la red y su resiliencia. En esta metodología, se analiza el

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
4
índice de resiliencia de Haghighi y Bakshipour expuesto por ellos en una investigación
realizada en 2016. Además, Aguilar en 2019 crea su propio índice donde evalúa la
resiliencia de los trazados para obtener fronteras de Pareto para cada red analizada. Aguilar
muestra dos tipos de frontera de Pareto, la primera teniendo en cuenta los costos
aproximados y la segunda teniendo en cuenta los costos reales de la red. En 2020 Juana
Herrán añade cuatro índices de resiliencia a la investigación, los cuales nombra como índice
de Distancia, Altura, Distancia y Altura e Inicios para determinar las fronteras de Pareto
propuestas por Aguilar en 2019.
Por fuera del CIACUA, diversos autores alrededor del mundo han investigado sobre el
diseño optimizado de redes de drenaje urbano. Por ejemplo, en 1990 Li y Mathew hicieron
uso de modelos de programación no lineal (PLN) los factores topográficos óptimos del
diseño como lo son las pendientes de la tubería, su diámetro y su flujo. Estos autores
dividen la metodología en dos partes: En la primera se optimizan las pendientes y los
diámetros junto a las estaciones de bombeo y la segunda se dejan constantes todas las
variables del diseño para optimizar gradualmente el flujo de las tuberías a partir de un
algoritmo de ruta más corta (Aguilar, 2019). Sin embargo, la mayoría de los autores han
optado por desarrollar las investigaciones sobre el diseño de drenaje urbano a partir del
método de Algoritmos Genéticos (AG). Por ejemplo, en 2012 Haghighi & Bakshipour utilizan
esta metodología para determinar los diámetros y las cotas de excavación de una red de
drenaje urbano. Además, se han presentado variaciones y combinaciones de esta
metodología, como, por ejemplo, la alternativa desarrollada por Cisty que combina el
método AG con programación lineal o la alternativa que combina AG con programación
cuadrática desarrollada por Pan y Kao (Aguilar, 2019).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
5
3 Marco Teórico
3.1 Redes de Drenaje Urbano
Las redes de drenaje urbano son estructuras que permiten la evacuación del agua residual
y el agua lluvia directamente a plantas de tratamientos o a cuerpos receptores. Estas
estructuras tienen una gran importancia en la prevención de enfermedades para los seres
humanos y contaminación ambiental. Por lo anterior, se considera que el sistema de drenaje
urbano es un servicio básico con el que debería contar toda la población. Sin embargo, en
países como Colombia la cobertura nacional de estas redes para el año 2018 es del 82.84%
para el área urbana y del 14.36% para el área rural, con coberturas mínimas urbanas del
11.88% en departamentos como Guanía (Superservicios, 2018).
Existe una clasificación para las redes de drenaje urbano según la unión o no del transporte
de agua residual y agua lluvia. El primer tipo de sistema de drenaje es el combinado el cual
se diseña para transportar el agua proveniente de las precipitaciones y el agua residual en
las mismas tuberías. La gran ventaja de este sistema es su precio ya que, al necesitar una
misma tubería para los dos tipos de agua, los costos de todo el sistema disminuyen. Por
otra parte, el tipo de sistema de drenaje separado, como su nombre lo indica transporta el
agua residual y de lluvia en tuberías de forma independiente lo que aumenta el costo de
construcción de toda la red con respecto al sistema combinado (Butler, 2004).
Los sistemas de drenaje urbano son un conjunto de diversos tipos de elementos, es decir,
no solo están conformados por tuberías, sino que también necesitan otras estructuras para
funcionar, entre las más importantes encontramos: Los pozos de inspección, cámaras de
caída, sumideros, sumideros invertidos, estructuras de bombeo, aliviaderos, acometidas,
canales y bajantes, sistemas de almacenamiento temporal y canales abiertos
Pozos de inspección: Son estructuras encargadas de recibir el caudal de las tuberías
cercanas y permiten el acceso de personal especializado para el mantenimiento del
sistema. Además, los pozos de inspección permiten el cambio en la dirección del flujo y
cambios de diámetros.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
6
Cámaras de caída: Estas estructuras permiten disipar la energía del flujo una vez lleguen
al poso de inspección. Su importancia radica en proteger el sistema evitando que flujos
supercríticos causen daños en su infraestructura.
Sumideros: Son estructuras ubicadas en los bordes de los andenes y tienen como principal
objetivo recolectar el agua de escorrentía y conducirlas a estructuras de conexión o pozos
de inspección.
Sumideros invertidos: Son estructuras que se utilizan para sobrepasar obstáculos
inevitables (Aguilar, 2019).
Estructuras de bombeo: Son estructuras necesarias cuando el transporte de agua
residual o de lluvia no puede realizarse por gravedad. Debido a su alto costo, sólo deben
utilizarse si no hay otra alternativa a favor de la gravedad.
Aliviadero: Tienen como propósito separar los caudales que exceden la capacidad del
sistema y conducirlo a un sistema de drenaje de agua lluvia o a un almacenamiento
temporal (RAS, 2000).
Acometida: Son estructuras encargadas de recolectar y conducir el agua residual
proveniente de las casas.
Canales y Bajantes: Son estructuras complementarias utilizadas para recolectar el agua
lluvia de los techos (Herrán, 2020).
Sistema de almacenamiento temporal: Son estructuras que tienen como objetivo retener
el agua durante los picos de caudal o contaminación para que una vez pasado el evento de
lluvia que produjo el pico de caudal se pueda homogenizar el caudal y sus concentraciones
de contaminantes.
Canales abiertos: Son estructuras que tienen como objetivo conducir aguas lluvias hacia
un cuerpo receptor.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
7
3.2 Índices de resiliencia
En el diseño optimizado de redes de drenaje urbano no solo se busca que el sistema sea
lo más económico posible, sino que también se desea que la red sea resiliente. La
resiliencia es la capacidad que tiene el sistema de drenaje de afectar la menor población
aguas arriba de un daño en una tubería. Por lo tanto, para medir la resiliencia de una red
se han creado diversos índices de resiliencia. Existen dos criterios para medir la resiliencia
de una red: El porcentaje de caudal que pasa por una tubería y la estructura de la red. El
primer criterio es utilizado en el índice de Haghighi & Bakshipour, Distancia, Altura,
Distancia y Altura, el segundo criterio se utiliza en el índice de Inicios y el índice de Aguilar
utiliza una combinación de estos dos criterios. En este documento se evaluarán estos seis
índices de resiliencia que serán explicados a continuación:
3.2.1 Índices de resiliencia de Haghighi & Bakshipour
Este índice fue propuesto en 2016 por Haghighi y Bakshipour con el que indican que la
resiliencia de la red se mide como el complemento de la probabilidad de falla. Así, la
probabilidad de falla es el porcentaje del caudal de descarga que fluye por la tubería
analizada. Por lo tanto, la resiliencia es un porcentaje que se calcula como se muestra a
continuación:
𝑅
𝑖𝑗
= 1 −
𝑄
𝑖𝑗
𝑄
𝑜𝑢𝑡
Ecuación 1 Índice de resiliencia propuesto por Haghighi & Bakshipour (2016)
Donde:
𝑅
𝑖𝑗
es la resiliencia de la tubería que va del pozo
𝑖 al pozo 𝑗.
𝑄
𝑖𝑗
es el caudal que fluye por la tubería que va del pozo
𝑖 al pozo 𝑗.
𝑄
𝑜𝑢𝑡
es el caudal de salida de la red.
En este sentido, la resiliencia de toda la red será la suma de la resiliencia de todas las
tuberías que la componen, así:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
8
𝑅 = 1 −
∑
𝑄
𝑖𝑗
(𝑖,𝑗)∈𝐴
𝑛 ∗ 𝑄
𝑜𝑢𝑡
Ecuación 2 Resiliencia total de la red según el índice de Haghighi & Bakshipour (2016)
3.2.2 Índices de resiliencia de Distancia
En 2020 Juana Herrán planteó el índice de resiliencia de distancia, el cual mide la
confiabilidad de la red según su distancia al pozo de descarga. En este sentido, entre más
lejos esté una tubería averiada del pozo de descarga menor será su efecto en la población
aguas arriba de esta. Para esto, se le asigna un peso
𝑤 a cada tubería según su distancia
al pozo de descarga, así, los pozos que se encuentren más cerca al pozo de descarga
tendrán mayor peso y las tuberías distantes tendrán un menor valor de
𝑤. Para calcular el
valor
𝑤 se utilizará la siguiente ecuación:
𝑤
𝑖𝑗
= 1 −
𝑑
𝑖𝑀
𝑑
0𝑀
Ecuación 3 Peso de cada tubería según el índice de Distancia propuesto por Herrán (2020)
Además:
𝑑
𝑖𝑗
= √(𝑃𝑜𝑠𝑥
𝑖
− 𝑃𝑜𝑠𝑥
𝑗
)
2
+ (𝑃𝑜𝑠𝑦
𝑖
− 𝑃𝑜𝑠𝑦
𝑗
)
2
Ecuación 4 Distancia entre pozos según índice de Distancia propuesta por Herrán (2020)
Donde:
𝑤
𝑖𝑗
es el peso asignado a la tubería que va del pozo
𝑖 al 𝑗.
𝑑
𝑖𝑀
es la distancia entre el pozo
𝑖 que se encuentra aguas arriba de la tubería analizada y
𝑀 que es el punto de descarga.
𝑑
0𝑀
es la distancia entre el punto de descarga y el pozo de la red que se encuentra más
alejado de este.
𝑃𝑜𝑠𝑥
𝑖
es el valor de la coordenada
𝑥 del pozo aguas arriba de la tubería analizada.
𝑃𝑜𝑠𝑥
𝑗
es el valor de la coordenada
𝑥 del pozo aguas abajo de la tubería analizada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
9
𝑃𝑜𝑠𝑦
𝑖
es el valor de la coordenada
𝑦 del pozo aguas arriba de la tubería analizada.
𝑃𝑜𝑠𝑦
𝑗
es el valor de la coordenada
𝑦 del pozo aguas abajo de la tubería analizada.
Ahora bien, la resiliencia de cada tubería se calcula así:
𝑅
𝑖𝑗
= 1 −
𝑤
𝑖𝑗
∗ 𝑄
𝑖𝑗
𝑄
𝑜𝑢𝑡
Ecuación 5 Índice de resiliencia de Distancia propuesto por Herrán (2020)
Por lo tanto, la resiliencia de toda la red se calcula como la suma de la resiliencia de cada
tubería que compone la red, así:
𝑅 = 1 −
∑
𝑤
𝑖𝑗
∗ 𝑄
𝑖𝑗
(𝑖,𝑗)∈𝐴
𝑛 ∗ 𝑄
𝑜𝑢𝑡
Ecuación 6 Resiliencia total de la red según el índice de Distancia propuesto por Herrán (2020)
3.2.3 Índices de resiliencia de Altura
El índice de Altura creado por Juana Herrán es similar al índice de distancia, sólo que en
este índice se tiene en cuenta la diferencia de elevación de los pozos. Por esta razón, el
peso asignado a cada tubería se calcula así
:
𝑤
𝑖𝑗
= 1 −
|𝑃𝑜𝑠𝑧
𝑀
− 𝑃𝑜𝑠𝑧
𝑖
|
𝑃𝑜𝑠𝑧
𝑀
− 𝑃𝑜𝑠𝑧
0
Ecuación 7 Peso de cada tubería según el índice de Altura propuesto por Herrán (2020)
Donde:
𝑃𝑜𝑠𝑧
𝑀
es la elevación del pozo de descarga.
𝑃𝑜𝑠𝑧
𝑖
es la elevación del pozo aguas arriba de la tubería analizada.
𝑃𝑜𝑠𝑧
0
es la elevación del pozo más lejano del punto de descarga en cuanto a su altura.
Por lo tanto, al comparar la elevación de los pozos, se espera que aquellos que se
encuentren más distantes tengan un menor peso y por lo tanto un menor impacto en caso

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
10
de que se obstruya una tubería. Ahora bien, para calcular la resiliencia de una tubería de la
red según el índice de altura, se utiliza la siguiente ecuación:
𝑅
𝑖𝑗
= 1 −
𝑤
𝑖𝑗
∗ 𝑄
𝑖𝑗
𝑄
𝑜𝑢𝑡
Ecuación 8 Índice de resiliencia de Altura propuesto por Herrán (2020)
Para hallar la resiliencia de toda la red se hace uso de lo siguiente:
𝑅 = 1 −
∑
𝑤
𝑖𝑗
∗ 𝑄
𝑖𝑗
(𝑖,𝑗)∈𝐴
𝑛 ∗ 𝑄
𝑜𝑢𝑡
Ecuación 9 Resiliencia total de la red según el índice de Altura propuesto por Herrán (2020)
3.2.4 Índices de resiliencia de Distancia y Altura
Este índice surge de la combinación del índice de resiliencia de distancia y el índice de
resiliencia de altura. Por lo tanto, para calcular el peso asignado a cada tubería se tendrá
en cuenta las coordenadas
𝑥, 𝑦, 𝑧 de los pozos aguas arriba y aguas debajo de cada una
de las tuberías que conforman la red, así:
𝑑
𝑖𝑗
=
|𝑃𝑜𝑠𝑥
𝑖
− 𝑃𝑜𝑠𝑥
𝑗
|
|𝑃𝑜𝑠𝑥
0
− 𝑃𝑜𝑠𝑥
𝑀
|
+
|𝑃𝑜𝑠𝑦
𝑖
− 𝑃𝑜𝑠𝑦
𝑗
|
|𝑃𝑜𝑠𝑦
0
− 𝑃𝑜𝑠𝑦
𝑀
|
+
|𝑃𝑜𝑠𝑧
𝑖
− 𝑃𝑜𝑠𝑧
𝑗
|
|𝑃𝑜𝑠𝑧
0
− 𝑃𝑜𝑠𝑧
𝑀
|
Ecuación 10 Distancia entre pozos según índice de Distancia y Altura de Herrán (2020)
La confiabilidad de cada tubería y de toda la red se calcula de igual forma que en los índices
anteriores:
𝑅
𝑖𝑗
= 1 −
𝑤
𝑖𝑗
∗ 𝑄
𝑖𝑗
𝑄
𝑜𝑢𝑡
Ecuación 11 Índice de resiliencia de Distancia y Altura propuesto por Herrán (2020)
𝑅 = 1 −
∑
𝑤
𝑖𝑗
∗ 𝑄
𝑖𝑗
(𝑖,𝑗)∈𝐴
𝑛 ∗ 𝑄
𝑜𝑢𝑡
Ecuación 12 Resiliencia total de la red según el índice de Distancia y Altura de Herrán (2020)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
11
3.2.5 Índices de resiliencia de Inicios
El índice de resiliencia de Inicios fue creado por Herrán 2020 y busca medir la resiliencia
de la red según su grado de ramificación. En este sentido, se busca que la red sea lo más
ramificada posible, es decir, se maximicen el número de tuberías de tipo inicio. Lo anterior,
porque si una tubería de tipo inicio se obstruye no afecta ninguna tubería aguas arriba y si
una tubería de tipo continua se obstruye, se espera que esta no transporte un gran caudal
debido a que debe tener varias tuberías de inicio cerca (Herrán, 2020). Para calcular este
índice se utiliza la siguiente ecuación:
𝑅 =
∑
𝑥
𝑖𝑗𝐼𝑛𝑖𝑐𝑖𝑜
(𝑖,𝑗)∈𝐴
𝑛
Ecuación 13 Resiliencia índice de Inicios propuesto por Herrán (2020)
Donde:
𝑥
𝑖𝑗𝐼𝑛𝑖𝑐𝑖𝑜
es una variable binaria que indica si la tubería que va del pozo
𝑖 al 𝑗 existe y es de
tipo Inicio.
𝑛 es el número de tuberías totales de toda la red.
3.2.6 Índices de resiliencia de Aguilar
Este índice de resiliencia fue propuesto por Aguilar en 2019 y se mide la confiabilidad de la
red con la siguiente ecuación:
𝑅 = 1 −
∑
𝑒
𝑖𝑗𝑡
∗ 𝑥
𝑖𝑗𝑡
(𝑖,𝑗)∈𝐴
𝑛
Ecuación 14 Resiliencia índice de Aguilar propuesto por Andrés Aguilar (2019)
Donde:
𝑒
𝑖𝑗𝑡
es un cociente entre la suma de los caudales de entrada de todos los pozos que se
podrían ver afectados si se obstruye la tubería que va del pozo
𝑖 al pozo 𝑗 que es del tipo 𝑡
y el valor del caudal de descarga.
𝑥
𝑖𝑗𝑡
es una variable binaria que indica si la tubería que va del pozo
𝑖 al pozo 𝑗 que es del
tipo
𝑡 hace parte del trazado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
12
𝑛 es el número total de tramos.
Para encontrar la suma de los pozos que potencialmente se ven afectados por la
obstrucción de la tubería analizada se propone trazar una recta perpendicular a la tubería
y sumar los caudales de entrada de todos los pozos que se encuentren aguas arriba de
esta.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
13
4 Metodología
4.1. Metodología para el diseño optimizado de redes de drenaje urbano
Para diseñar redes de drenaje urbano se requiere ejecutar dos fases. La primera fase es la
selección del trazado, en esta se busca encontrar el caudal de diseño que fluye por cada
tubería de la red, el sentido del flujo y el tipo de tubería; es decir, si es de tipo inicio o
continua. Para encontrar estas variables de diseño, es necesario tener como parámetros
de entrada la topografía de la red, el caudal que entra a cada uno de los pozos de inspección
de la red y su conexión (Aguilar, 2019). Seguidamente, debe realizarse la segunda fase que
es el diseño hidráulico. En esta fase, se obtienen los diámetros de la tubería, las
profundidades de excavación y las pendientes de cada tramo de la red. Para llevar a cabo
esta fase, se deben tener como parámetros de entrada los datos de salida de la fase
anterior. Por esto, el diseño optimizado de redes de drenaje urbano es un proceso iterativo
y unificado que requiere la conexión de estas dos fases. En el diseño hidráulico se busca
optimizar los costos de la red a partir de una función de costos, además, se deben cumplir
todas las restricciones hidráulicas establecidas en la normativa del país donde se realiza el
diseño. En el siguiente esquema, se muestra el proceso secuencial del diseño de una red
de drenaje urbano:
Figura 1 Proceso de diseño de una red de Drenaje Urbano Herrán (2020)
En el Centro de Investigaciones en Acueductos y Alcantarillado (CIACUA) de la Universidad
de Los Andes, se ha desarrollado una metodología para las dos fases del proceso, las
cuales serán explicadas en las siguientes secciones.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
14
4.1.1 Selección del trazado
En esta fase, se deben recibir como parámetros de entrada la topografía de la red y el
caudal que entra a cada uno de los pozos de inspección. Una vez obtenidos los parámetros
de entrada, se procede a elegir un árbol de diseño que conecte todos los tramos de la red
teniendo en cuenta los supuestos planteados en el trabajo realizado por Natalia Duque en
el 2015, en el cual se indica que en cada calle del lugar que se desea construir la red de
drenaje debe ir una tubería y en la conexión de calles un pozo de inspección. La dirección
del flujo en todas las tuberías de la red puede ir en ambos sentidos a excepción del pozo
de descarga donde el flujo sólo puede ir en dirección al cuerpo receptor. El otro supuesto
de diseño es que la suma de los caudales de entradas es el caudal de salida, por lo tanto,
la única forma en la cual entra flujo en la red es a través de los pozos de inspección y la
única forma de salida es en el punto de descarga (Duque, 2015). Por último, se supone que
no puede haber recirculación en la red, es por esto por lo que deben diseñarse redes
abiertas a partir de dos tipos de tuberías, las tuberías de inicio y las continuas. Las tuberías
de inicio sólo transportan el caudal que reciben del pozo de inspección, mientras que las
tuberías de tipo continuo se encargan de transportar el caudal que reciben del pozo de
inspección y el caudal de todos los pozos ubicados aguas arriba de este.
Para modelar este problema, Natalia Duque en 2015 propuso modelarlo como un problema
de programación entera mixta (MIP por sus siglas en inglés). Duque propuso resolver este
problema a través de un grafo dirigido, en donde los pozos de inspección son los nodos del
grafo y las tuberías son los arcos (Herrán, 2020). Lo anterior, para definir las siguientes
variables:
𝑥
𝑖𝑗𝑡
que es una variable binaria que indica si la tubería que va del pozo
𝑖 al 𝑗 y es
de tipo
𝑡 existe y hace parte del trazado y la variable 𝑦
𝑖𝑗𝑡
que indica el caudal que fluye por
esa tubería.
4.1.2 Diseño Hidráulico
Una vez realizada la fase de selección del trazado se procede a realizar el diseño hidráulico
de la red. En esta fase se busca encontrar el diámetro de las tuberías que conforman la red,
la profundidad de excavación y la pendiente de cada uno de los tramos. Para seleccionar
estas variables, se utiliza una optimización monoobjetivo donde se busca optimizar la
función de costos cumpliendo con las restricciones hidráulicas. Para el caso de Colombia,
la normativa que estipula las restricciones que se deben cumplir es el Reglamento Técnico
para Sector de Agua Potable y Saneamiento Básico (RAS). En este trabajo, fueron
utilizadas las restricciones definidas en el RAS para un sistema de alcantarillado de alta
complejidad y se definen a continuación:
• Diámetro real mínimo: 200 𝑚𝑚 para alcantarillado sanitario convencional.
• Coeficiente 𝑛 de rugosidad de Manning: Entre 0.009 y 0.013 en tuberías de pared
lisas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
15
• Velocidad mínima: 0.45 𝑚/𝑠 para evitar el depósito de sólidos en las tuberías.
• Velocidad máxima: 5 𝑚/𝑠 en caso de velocidades mayores se debe justificar.
• Profundidad mínima de instalación: En vías peatonales o zonas verdes debe ser de
0.75 𝑚 mientras que para vías vehiculares debe ser mínimo 1.2 𝑚.
• Profundidad máxima de instalación: Debe ser de 5 𝑚 pero en caso de requerir mayor
profundidad se deben garantizar todas las restricciones hidráulicas.
• Pendiente máxima y mínima: Las pendientes deben cumplir con las profundidades
de instalación mencionadas.
• Profundidad hidráulica máxima: Debe ser entre el 70% y 85% para garantizar la
aireación de las aguas residuales.
Asimismo, Natalia Duque en su trabajo de 2015 indica que para que el diseño sea factible
las tuberías deben ir ubicadas a favor de la gravedad, las tuberías deben ir conectadas a la
altura de la cota de batea y el caudal que entra a las tuberías de tipo inicio deben tener ruta
para llegar al punto de descarga.
4.1.3 Función de Costos
En el diseño de redes de drenaje urbano la función de costos tiene un rol fundamental ya
que permitirá estimar los costos de construcción del sistema. Existen muchas funciones de
costos, la mayoría encontradas a partir de regresiones lineales o análisis estadísticos. Un
gran número de las funciones de costos sólo tienen en cuenta los costos de instalación de
las tuberías y los costos de excavación, ya que esto conforma el 70% del costo total de
construcción de una red de drenaje urbano (Aguilar, 2019). Es por esto, que las funciones
de costos se presentan principalmente de la siguiente forma:
𝑐
𝑖𝑗
= 𝑓(𝑑
𝑖𝑗
, ℎ
𝑖𝑗
)
Ecuación 15 Forma de una ecuación de costos
Donde:
𝑐
𝑖𝑗
son los costos de construcción de la red de drenaje urbano.
𝑑
𝑖𝑗
son los diámetros de las tuberías que conforman el sistema.
ℎ
𝑖𝑗
son las profundidades de excavación necesarias para instalar las tuberías.
4.2. Optimización multiobjetivo de redes de drenaje urbano
En la optimización multiobjetivo se busca maximizar o minimizar dos o más funciones
objetivo. Para el caso de este trabajo de redes de drenaje urbano se busca minimizar los
costos y maximizar la resiliencia. Por un lado, la función de costos utilizada es la ecuación
de Maurer, propuesta en el artículo
“Quantifying costs and lengths of urban drainage

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
16
systems wi
th a simple static sewer infrastructure model” por (Maurer, 2012) en el que busca
encontrar una ecuación para estimar los costos y las dimensiones de una red de drenaje
urbano teniendo en cuenta un análisis hidrológico, densidad poblacional y el área de la
zona. A continuación, se muestra la ecuación de costos de Maurer:
𝐶
𝑖𝑗
= 𝑎ℎ
𝑖𝑗
+ 𝛽
Ecuación 16 Ecuación de costos de Maurer para un tramo de la red (2012)
𝑎 = 𝑚
𝑎
𝑑
𝑖𝑗
+ 𝑛
𝑎
Ecuación 17 Coeficiente alpha de la ecuación de Maurer (2012)
𝛽 = 𝑚
𝛽
𝑑
𝑖𝑗
+ 𝑛
𝛽
Ecuación 18 Coeficiente beta de la ecuación de Maurer (2012)
𝐶
𝑖𝑗
= (𝑚
𝑎
𝑑
𝑖𝑗
+ 𝑛
𝑎
)ℎ
𝑖𝑗
+ 𝑚
𝛽
𝑑
𝑖𝑗
+ 𝑛
𝛽
Ecuación 19 Ecuación de costos de Maurer para toda la red (2012)
Donde:
𝐶
𝑖𝑗
es el costo de construcción del tramo en dólares por metro lineal de tubería.
ℎ
𝑖𝑗
es la profundidad promedio de excavación para instalar la tubería.
𝑑
𝑖𝑗
es el diámetro de la tubería en metros del tramo analizado.
𝑚
𝑎
, 𝑛
𝑎
, 𝑚
𝛽
, 𝑛
𝛽
son constantes de las regresiones lineales que explican la dependencia de
las variables frente al costo.
El valor de estas constantes se presenta a continuación:
𝑚
𝛼
= 1.02
𝑛
𝛼
= 127
𝑚
𝛽
= 0.11
𝑛
𝛽
= 37
En la optimización multiobjetivo no se obtiene una única solución óptima, sino que se
presentan múltiples alternativas óptimas que conforman una Frontera de Pareto. Las
Fronteras de Pareto son un conjunto de alternativas factibles que les permiten a los
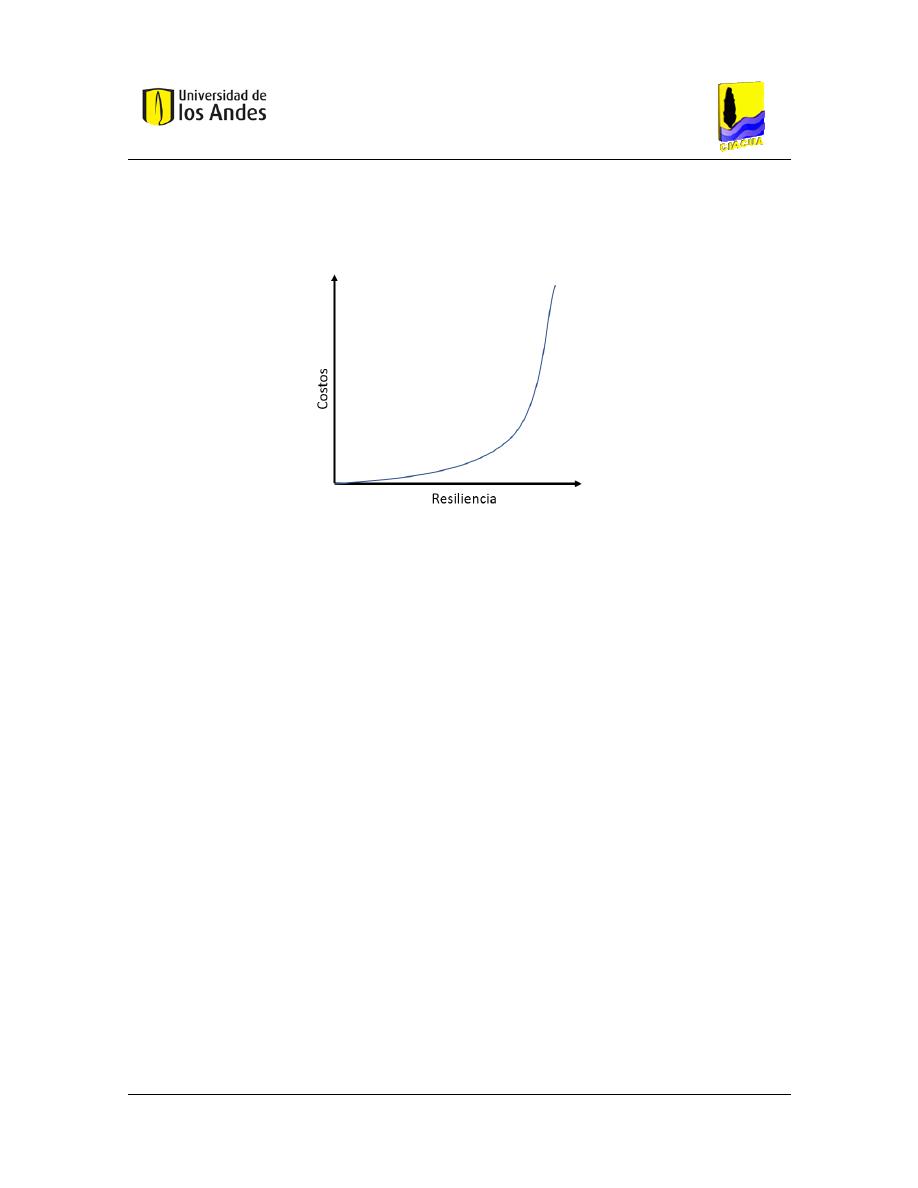
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
17
diseñadores analizar y escoger la solución que mejor represente sus intereses sin
necesidad de analizar todas las soluciones posibles. A continuación, se muestra la Frontera
de Pareto esperada en el diseño de redes de drenaje urbano.
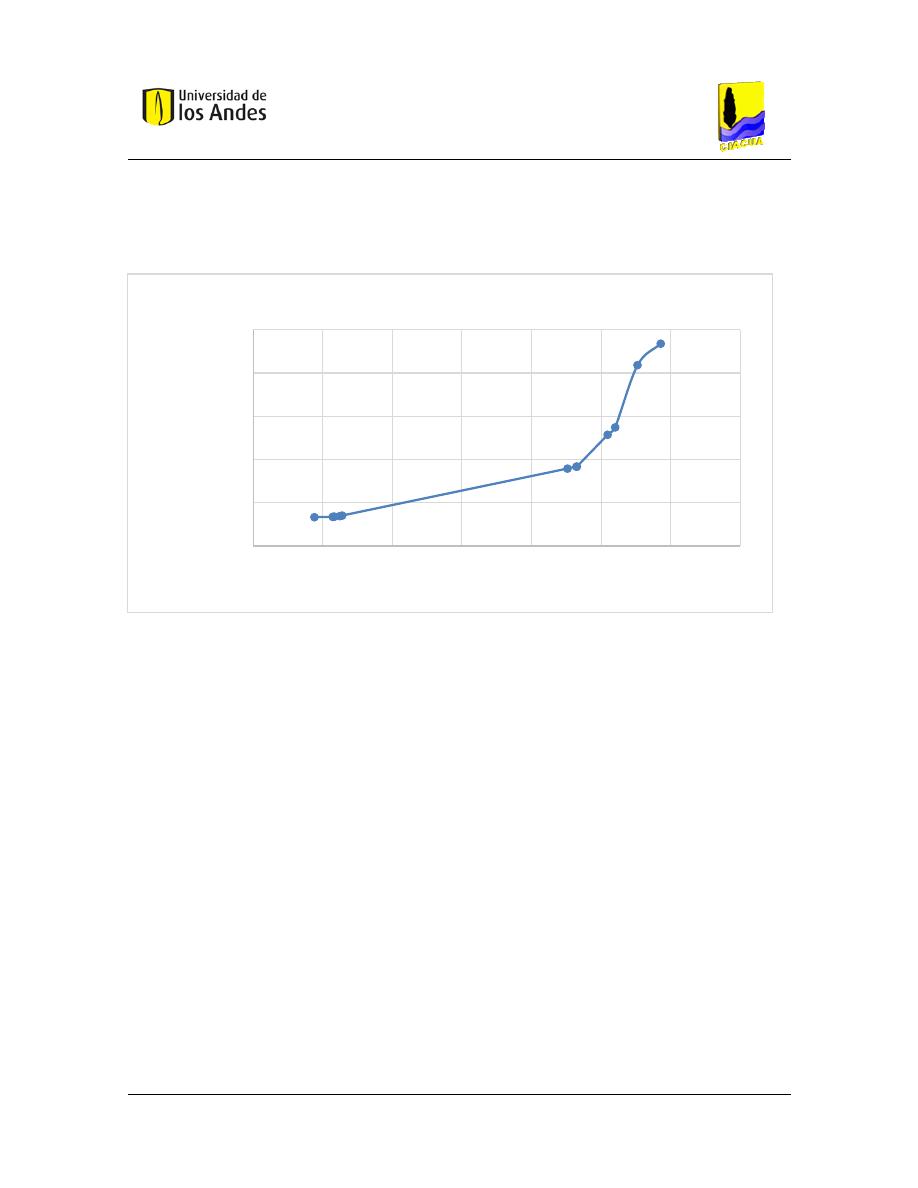
En la figura se observa que a medida que aumenta la resiliencia de la red debe aumentar
el costo de esta. En este trabajo, en la Frontera de Pareto inicial se presentan soluciones
dominantes y soluciones dominadas. Las soluciones dominadas se presentan si existe un
trazado que tenga una mayor resiliencia y un menor costo que esta. Por lo tanto, las
soluciones dominadas deben eliminarse de la Frontera de Pareto y sólo incluir las
soluciones dominantes.
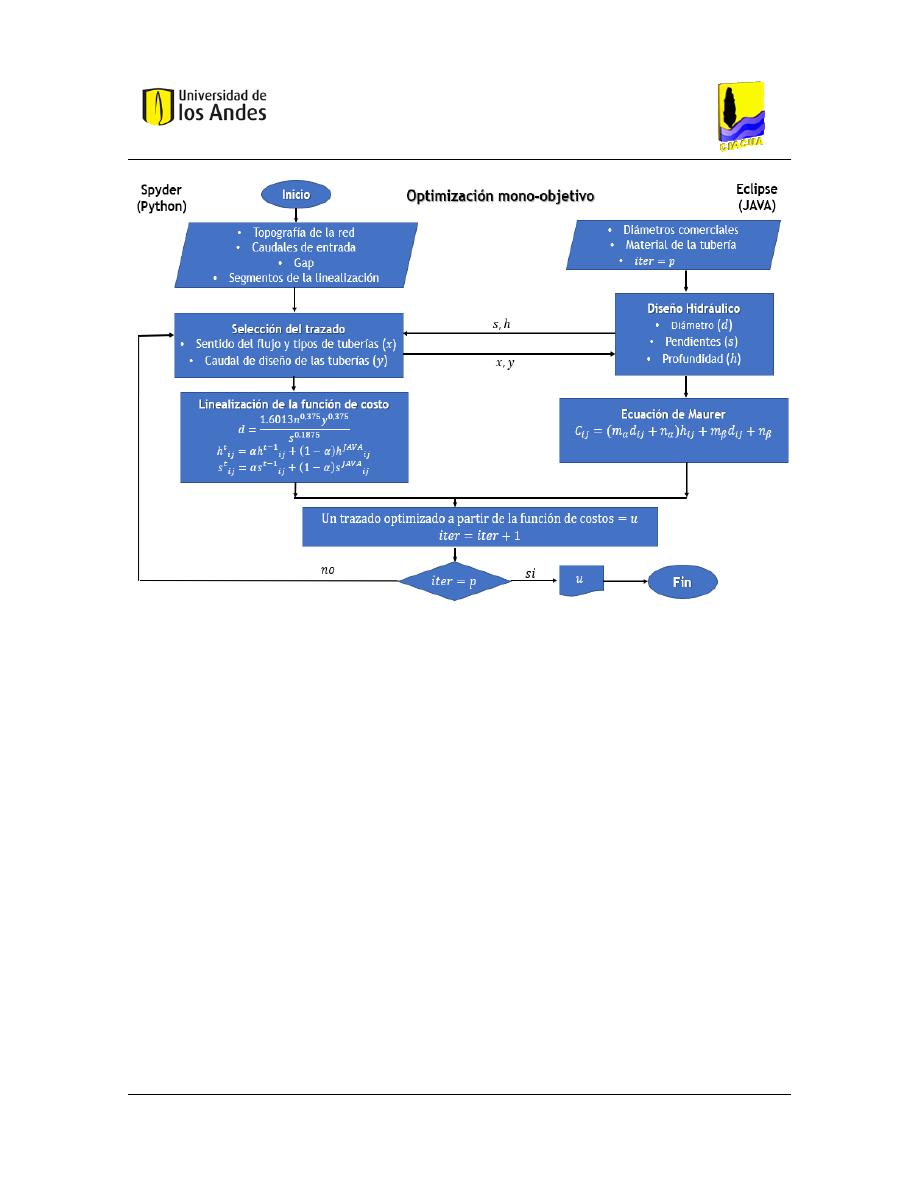
Ahora bien, para construir las Fronteras de Pareto de costos reales de las redes de drenaje
urbano se debe seguir el siguiente proceso: Primeramente, se debe realizar una
optimización monoobjetivo para seleccionar un primer trazado óptimo que sirva como
parámetro de entrada para la optimización multiobjetivo. A continuación, se muestra un
esquema que explica el procedimiento de la optimización monoobjetivo:
Figura 2 Frontera de Pareto esperada para una red de drenaje urbano
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
18
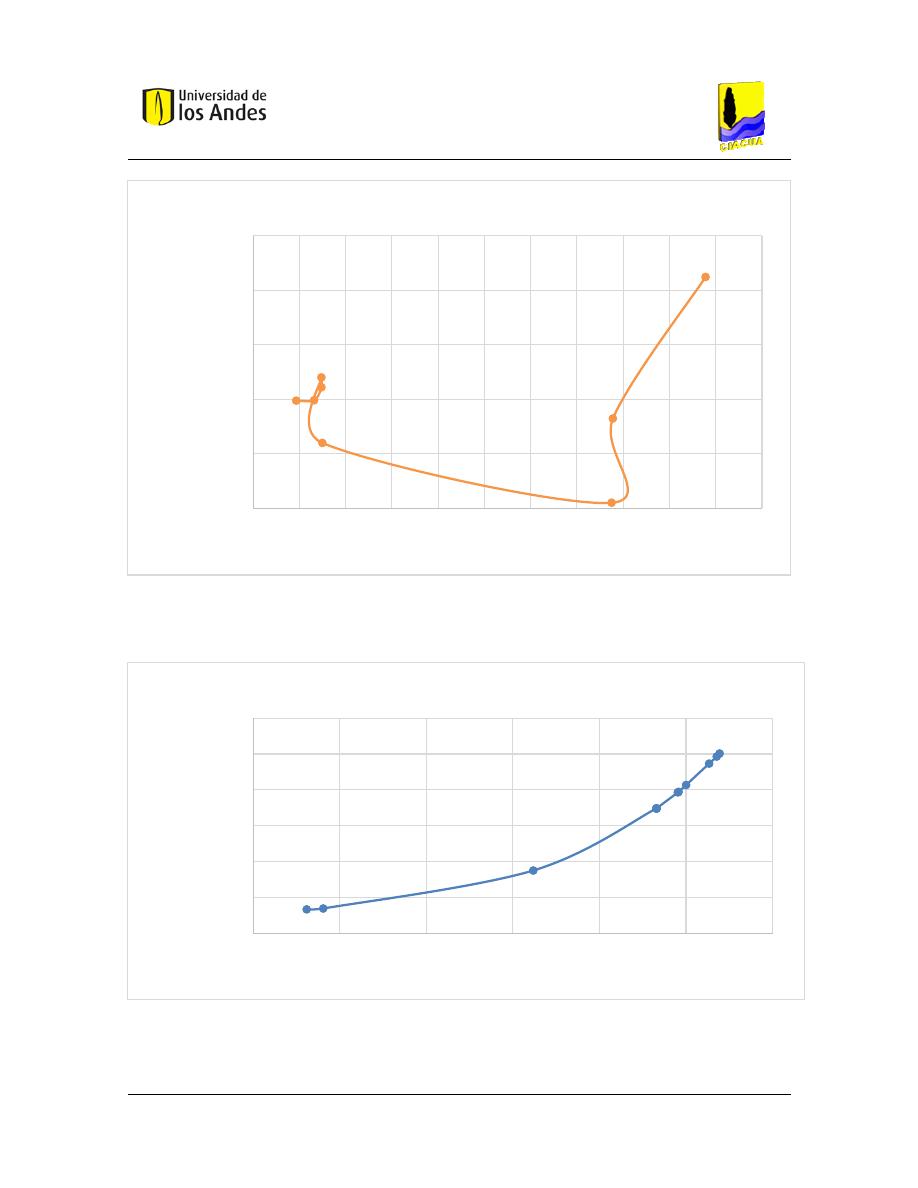
Figura 3 Optimización monoobjetivo del diseño de redes de drenaje urbano
En la figura anterior, la variable
𝑖𝑡𝑒𝑟 hace referencia al número de iteraciones que se desean
realizar entre la selección del trazado y el diseño hidráulico, en este trabajo, se utilizaron 10
iteraciones. La optimización monoobjetivo, empieza en la selección del trazado, es decir,
en el código de Python el cual recibe como parámetros de entrada la topografía de la red,
caudales de entrada a los pozos, el gap, que es un parámetro para minimizar costos
computacionales, y el número de segmentos en los cuales se quiere linealizar la función de
costos de Aguilar postulada en su trabajo de 2016. Una vez ejecutada esta parte del código,
se obtiene un trazado con las variables de caudales de diseño, sentido del flujo y tipos de
tuberías, a partir de la ecuación linealizada de costos de Aguilar. Luego, se ejecuta el diseño
hidráulico cuyo algoritmo se encuentra en JAVA donde se establecen los diámetros,
pendientes y profundidades de excavación a partir de la ecuación de costos de Maurer.
Este procedimiento se ejecuta el número de veces que se haya estipulado en la variable
𝑖𝑡𝑒𝑟, que para este trabajo fue de diez.
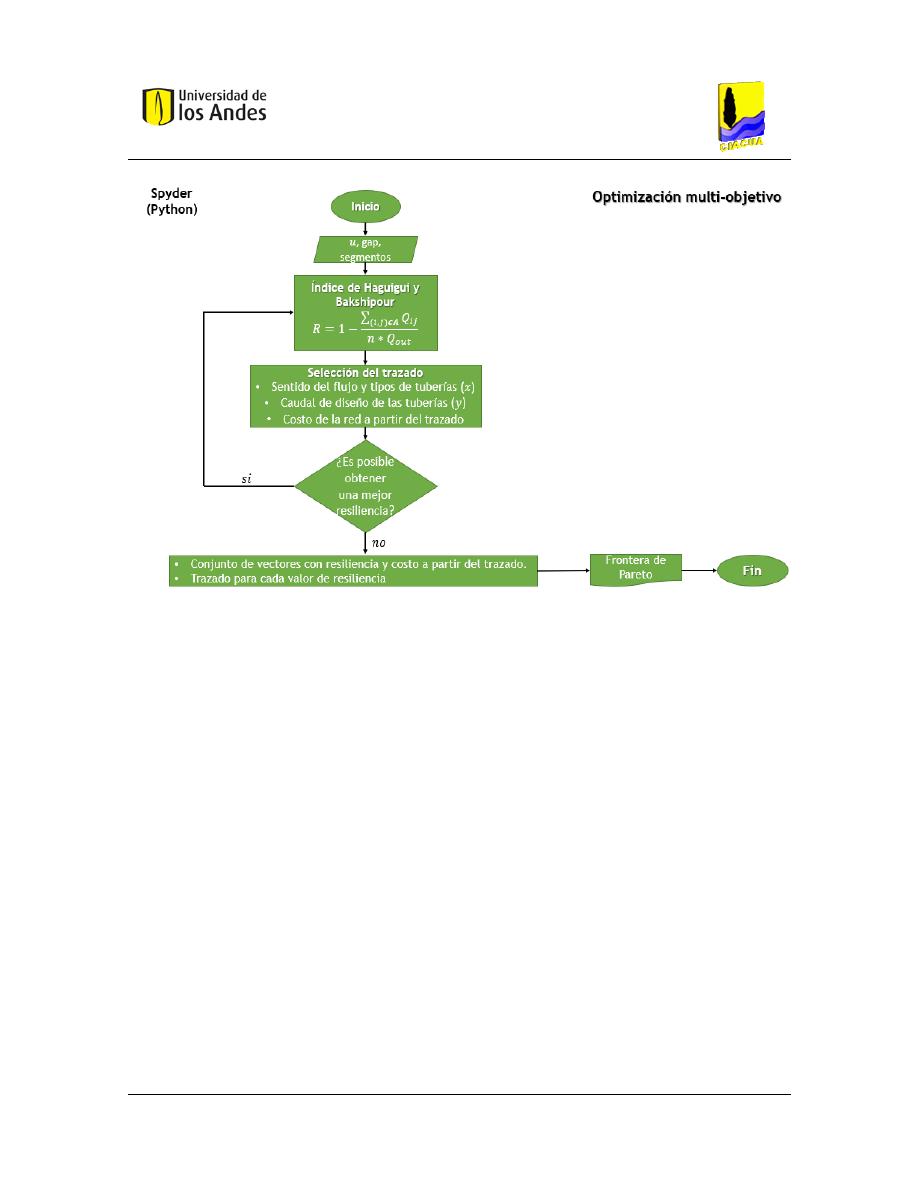
Seguidamente, se ejecuta la optimización multiobjetivo, la cual se muestra en el siguiente
diagrama de flujo específicamente para el índice de resiliencia de Haghighi & Bakshipour:
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
19
Figura 4 Optimización multiobjetivo del diseño de redes de drenaje urbano
Para la optimización multiobjetivo sólo se utiliza los algoritmos programados en Python.
Este proceso recibe como parámetro de entrada el trazado optimizado en la parte
monoobjetivo, el gap y el número de segmentos de la linealización. Seguidamente, se
calcula la resiliencia de la red con la ecuación del índice escogido, que puede ser el de
Haghighi & Bakshipour, Distancia, Altura, Distancia y Altura, Inicios o Aguilar, luego, se
determina si es posible escoger un trazado con una mayor resiliencia, de ser posible se
selecciona ese nuevo trazado aplicando el mismo procedimiento y si no es posible
encontrar una mejor resiliencia el algoritmo se detiene y se obtiene como resultado la
Frontera de Pareto de costos aproximados. Las dos funciones que se optimizan en este
paso es la función de costos y la función de resiliencia que se deben minimizar y maximizar
respectivamente. La ecuación de costos utilizada en la selección del trazado es la
establecida por Andrés Aguilar 2016, la cual fue desarrollada en función de las variables
del trazado a partir de las variables del diseño hidráulico, colocando por ejemplo, el diámetro
de las tuberías que es una variable del diseño hidráulico en función del caudal de diseño
que es una variable de la selección del trazado a partir de la ecuación de Darcy Weisbach
y la ecuación de Manning. Por otra parte, la otra función de resiliencia varía según los
índices explicados en la sección 3.2. Las Fronteras de Pareto son creadas a partir del
algoritmo Non-Inferior Set Estimation (NISE) desarrollado por Medrano y Church en 2015.
Este algoritmo construye una nueva función objetivo ponderando las dos funciones

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
20
objetivos planteadas, en este caso la función de costos y la función de resiliencia aplicando
la siguiente ecuación:
𝑧 = 𝑎 ∗ 𝑧
1
+ (1 − 𝑎) ∗ 𝑧
2
Ecuación 20 Función objetivo creada por el algoritmo NISE
Donde:
𝑧
1
indica minimizar los costos
𝑧
2
indica maximizar la resiliencia
𝑎 es el ponderador de las funciones objetivo
𝑧 es la nueva función objetivo creada por el algoritmo NISE.
El ponderador
𝑎 es una variable que oscila entre 0 y 1, el cual va cambiando en cada una
de las soluciones encontradas. El algoritmo NISE, comienza encontrado soluciones óptimas
con los extremos de los valores posibles de
𝑎, es decir, como si sólo si sólo se estuviera
minimizando los costos y como si sólo se estuviera maximizando la resiliencia. A partir de
estas dos soluciones, el ponderador empieza a oscilar entre 0 y 1 hasta obtener el conjunto
de soluciones óptimas que conformen la Frontera de Pareto (Herrán, 2020). A continuación,
se muestra la ecuación utilizada para generar un nuevo valor del ponderador:
𝑎 =
𝑧
2
(𝜎
𝑖
) − 𝑧
2
(𝜎
𝑗
)
(𝑧
2
(𝜎
𝑖
) − 𝑧
2
(𝜎
𝑗
) + 𝑧
1
(𝜎
𝑗
) − 𝑧
1
(𝜎
𝑖
))
Ecuación 21 Ponderador de la ecuación creada por la metodología NISE
Donde
𝜎
𝑖
y
𝜎
𝑗
son soluciones obtenidas de iteraciones previas. Como este algoritmo no
tiene criterio de parada, sólo se detendrá hasta encontrar todas las soluciones posibles que
conformen la Frontera de Pareto. Lo anterior, puede implicar un gran costo computacional,
por lo que en este trabajo se utilizó un gap propuesto por Aguilar 2019 de 0.03, es decir,
del 3% para disminuir el tiempo que requiere este algoritmo.
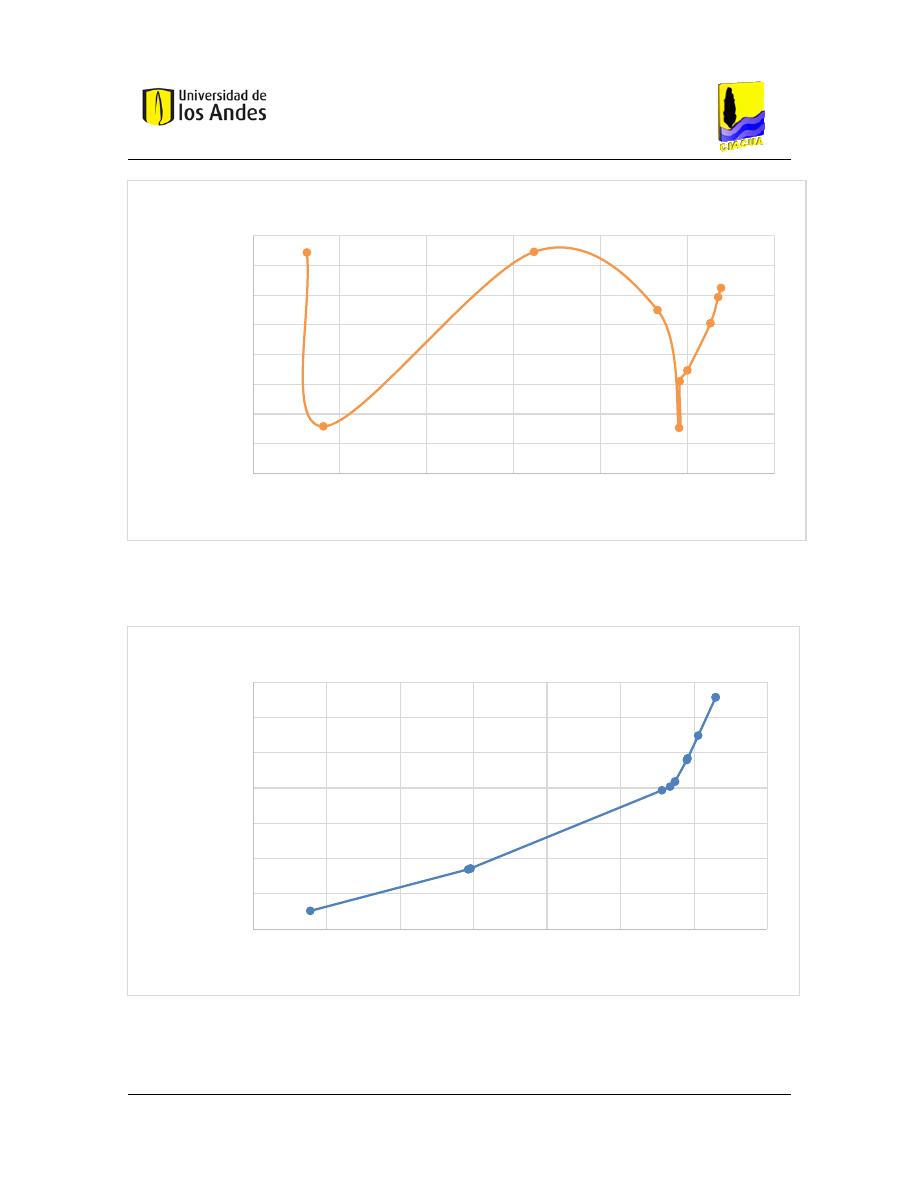
Por último, a cada trazado que pertenece a la frontera de Pareto obtenida en el paso
anterior, se le calcula el diseño hidráulico como se muestra a continuación:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
21
Figura 5 Cálculo de costos reales de trazados de una red de drenaje urbano
Una vez obtenidas las Fronteras de Pareto de costos aproximados, se procede a calcular
los costos reales de la red con el algoritmo de JAVA. Para esto, se utiliza la parte del diseño
hidráulico de la optimización monoobjetivo. Es posible que el número de soluciones que
conforman la frontera de Pareto de costos aproximados y de costos reales de una misma
red para un mismo índice de resiliencia no sean iguales. Lo anterior, indica que al pasar de
costos aproximados a costos reales algunos trazados tienen el mismo costo, por lo tanto,
en algunas Fronteras de Pareto de costos reales el número de soluciones disminuye.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
22
5 Resultados
La metodología propuesta en el apartado anterior se aplicó en dos redes de drenaje urbano:
la red de Moeini y la red de Esmeralda. Antes de aplicar la metodología NISE, se realizaron
10 iteraciones entre la selección del trazado y el diseño hidráulico para obtener un primer
trazado con un menor costo que sirva como input de la optimización multiobjetivo. Para esto
se tuvieron en cuenta las siguientes restricciones hidráulicas:
-
𝑛 de Manning: 0.009 (PVC)
-
𝑘
𝑠
:
1.5 𝑥10
−6
𝑚
-
Relación de llenado máxima: 85%
-
Velocidad mínima
5 𝑚/𝑠.
-
Velocidad máxima
10 𝑚/𝑠
-
Profundidad mínima de excavación:
1.2 𝑚
-
Profundidad máxima de excavación:
15 𝑚
-
Diámetros comerciales: {0.227, 0.284, 0.327, 0.362, 0.407, 0.452, 0.595, 0.670,
0.747, 0.824, 0.9, 0.9776, 1.054, 1.127}
Además, es importante resaltar que la ecuación de velocidad utilizada fue la ecuación de
Darcy Weisbach, el gap, número de segmentos y el alpha en la optimización multiobjetivo
es de 0.03, 7 y de 20 respectivamente.
Para la red de Esmeralda se evaluaron los índices de resiliencia de Haghighi & Bakshipour,
Aguilar, Distancia, Altura, Distancia y Altura e Inicios; para la red de Moeini sólo se
evaluaron los índices de de Haghighi & Bakshipour, Aguilar, Distancia e Inicios, esto, debido
a las características de cada una de estas redes. Para calcular el costo computacional de
la modelación de cada una de las redes se debe tener en cuenta el tiempo requerido en la
parte monoobjetivo que consta de las 10 iteraciones entre la selección del trazado y el
diseño hidráulico, la parte multiobjetivo y la parte final correspondiente al cálculo del diseño
hidráulico de los trazados encontrados en la parte multiobjetivo. A continuación, se
muestran las fronteras de Pareto encontradas para cada índice de resiliencia teniendo en
cuenta los costos aproximados, seguidamente se muestran las fronteras de Pareto que
representan los costos reales de la red y por último se presenta los costos computacionales
de la modelación de la red de Moeini y la red de Esmeralda.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
23
5.1. Red de Esmeralda
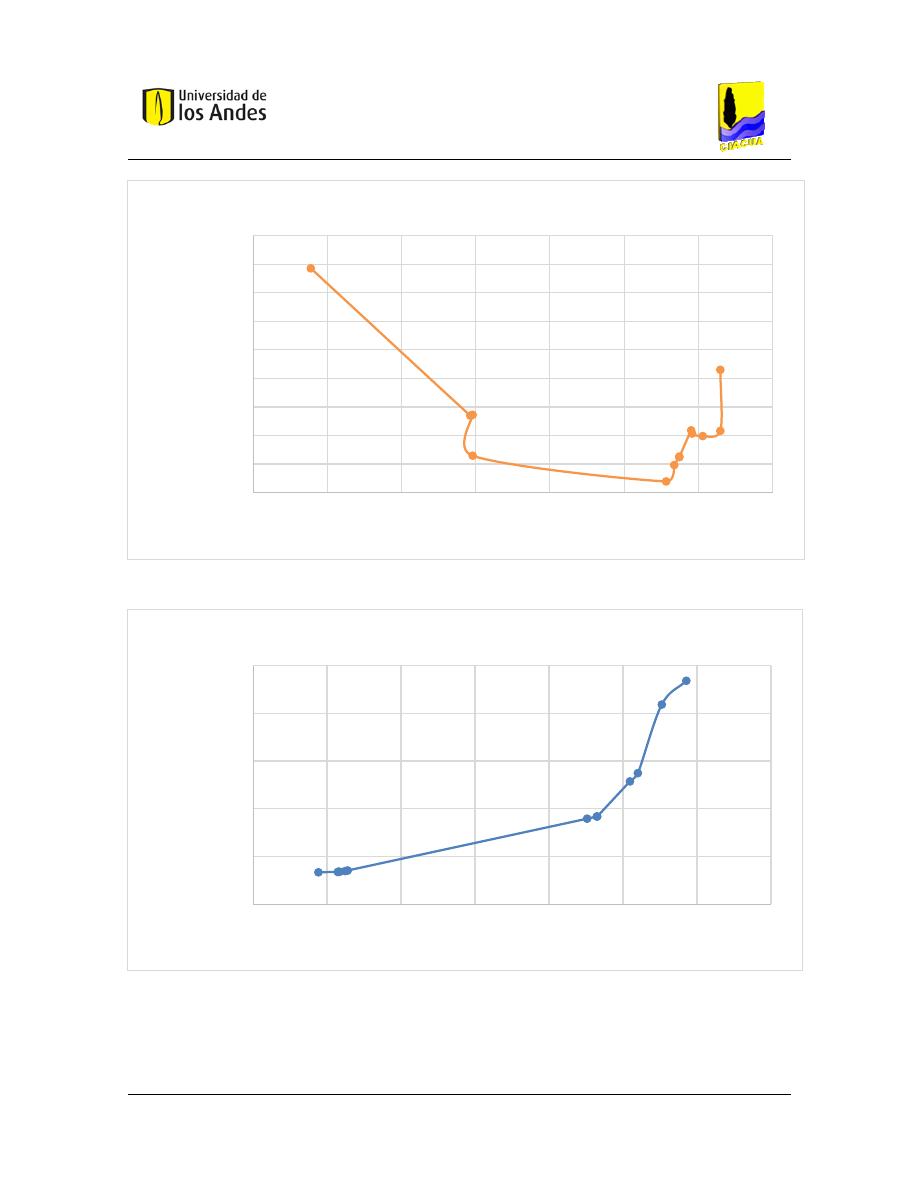
La frontera de Pareto del índice de resiliencia de Haghighi & Bakshipour teniendo en cuenta
los costos aproximados se presenta a continuación:
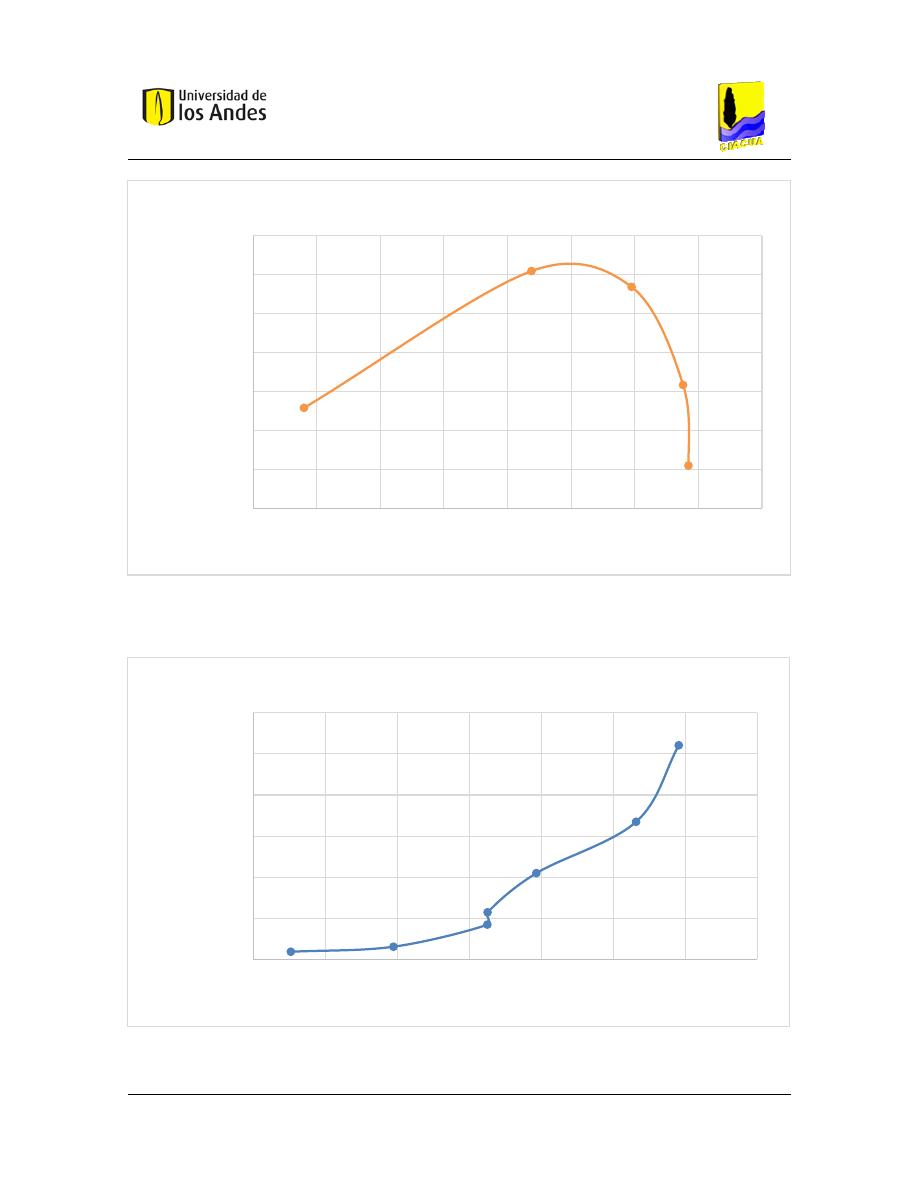
Gráfica 1 Frontera de Pareto de costos aproximados -Haghighi & Bakshipour red de Esmeralda
Luego de calcular el diseño hidráulico de cada uno de los trazados que se muestran en la
gráfica anterior se obtiene el siguiente resultado:
$ 14.500.000
$ 15.000.000
$ 15.500.000
$ 16.000.000
$ 16.500.000
$ 17.000.000
97,55
97,60
97,65
97,70
97,75
97,80
97,85
97,90
C
os
to
ap
roxim
ad
o
[U
SD
]
Resiliencia índice de Haghighi & Bakshipour[%]
Frontera de Pareto: Red de Esmeralda
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
24
Gráfica 2 Frontera de Pareto de costos reales- Haghighi & Bakshipour red de Esmeralda
Asimismo, se obtienen las fronteras de Pareto para los demás índices:
Gráfica 3 Frontera de Pareto de costos aproximados-Índice de Distancia red de Esmeralda
$ 25.500.000
$ 26.000.000
$ 26.500.000
$ 27.000.000
$ 27.500.000
$ 28.000.000
95,65
95,7
95,75
95,8
95,85
95,9
95,95
96
96,05
96,1
96,15
96,2
Cos
to
s
re
ale
s
[US
D]
Resiliencia índice de Haghighi & Bakshipour [%]
Frontera de Pareto: Red de Esmeralda
$ 14.700.000
$ 14.900.000
$ 15.100.000
$ 15.300.000
$ 15.500.000
$ 15.700.000
$ 15.900.000
97,50
97,55
97,60
97,65
97,70
97,75
97,80
C
os
to
ap
roxim
ad
o
[U
SD
]
Resiliencia índice de Distancia [%]
Frontera de Pareto: Red de Esmeralda
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
25
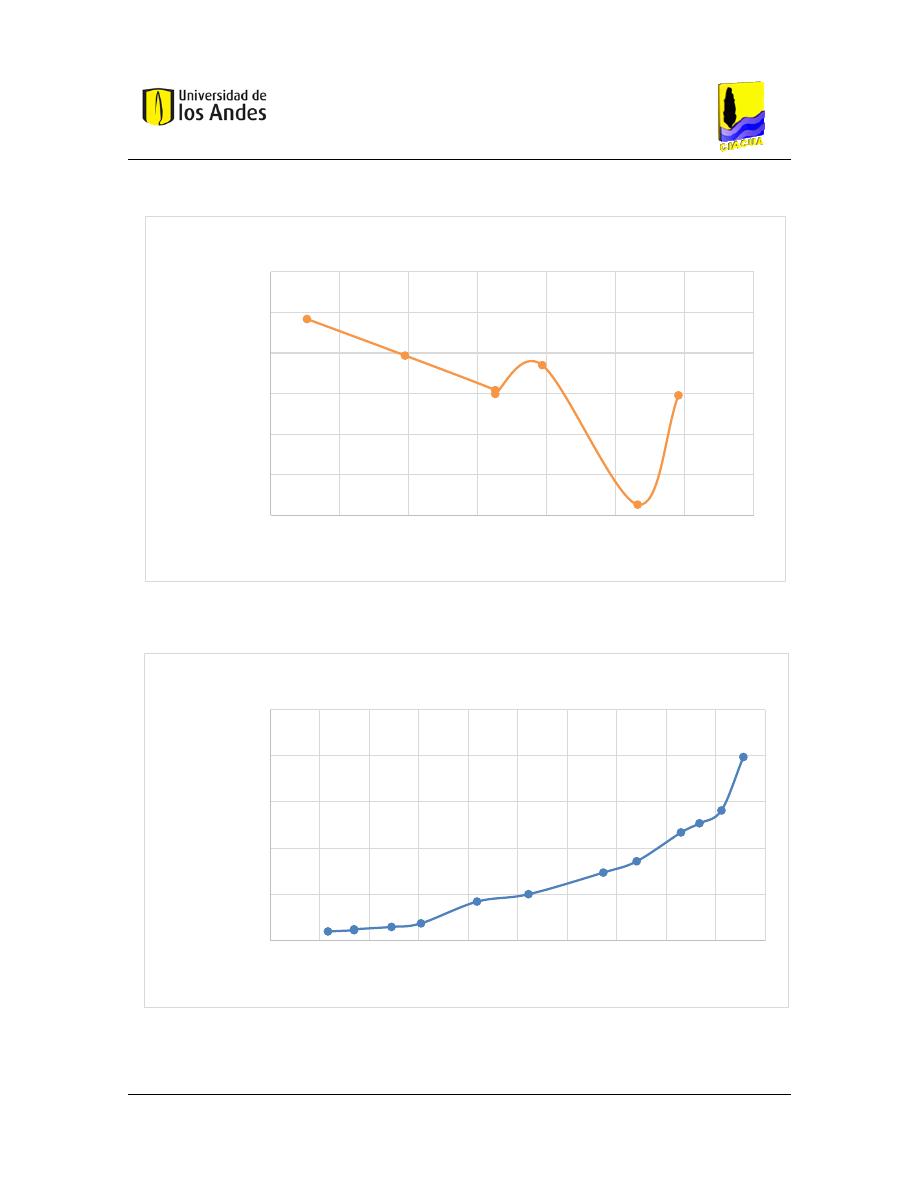
Gráfica 4 Frontera de Pareto de costos reales del índice de Distancia para la red de Esmeralda
Gráfica 5 Frontera de Pareto de costos aproximados del índice de Altura red de Esmeralda
$ 25.000.000
$ 25.200.000
$ 25.400.000
$ 25.600.000
$ 25.800.000
$ 26.000.000
$ 26.200.000
$ 26.400.000
$ 26.600.000
97,50
97,55
97,60
97,65
97,70
97,75
97,80
Cos
to
s
re
ale
s
[US
D]
Resiliencia índice de Distancia [%]
Frontera de Pareto: Red de Esmeralda
$ 15.800.000
$ 15.900.000
$ 16.000.000
$ 16.100.000
$ 16.200.000
$ 16.300.000
$ 16.400.000
$ 16.500.000
96,60
96,70
96,80
96,90
97,00
97,10
97,20
97,30
C
os
to
ap
roxim
ad
o
[U
SD
]
Resiliencia índice de Altura [%]
Frontera de Pareto: Red de Esmeralda
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
26
Gráfica 6 Frontera de Pareto de costos reales del índice de Altura para la red de Esmeralda
Gráfica 7 Frontera de Pareto de costos aproximados- Distancia y Altura red de Esmeralda
$ 26.000.000
$ 26.200.000
$ 26.400.000
$ 26.600.000
$ 26.800.000
$ 27.000.000
$ 27.200.000
$ 27.400.000
$ 27.600.000
$ 27.800.000
96,60
96,70
96,80
96,90
97,00
97,10
97,20
97,30
C
os
to
s
re
ale
s
[U
SD
]
Resiliencia índice de Altura [%]
Frontera de Pareto: Red de Esmeralda
$ 14.500.000
$ 15.000.000
$ 15.500.000
$ 16.000.000
$ 16.500.000
$ 17.000.000
97,55
97,60
97,65
97,70
97,75
97,80
97,85
97,90
C
os
to
ap
roxim
ad
o
[U
SD
]
Resiliencia índice de Distancia y Altura [%]
Frontera de Pareto: Red de Esmeralda
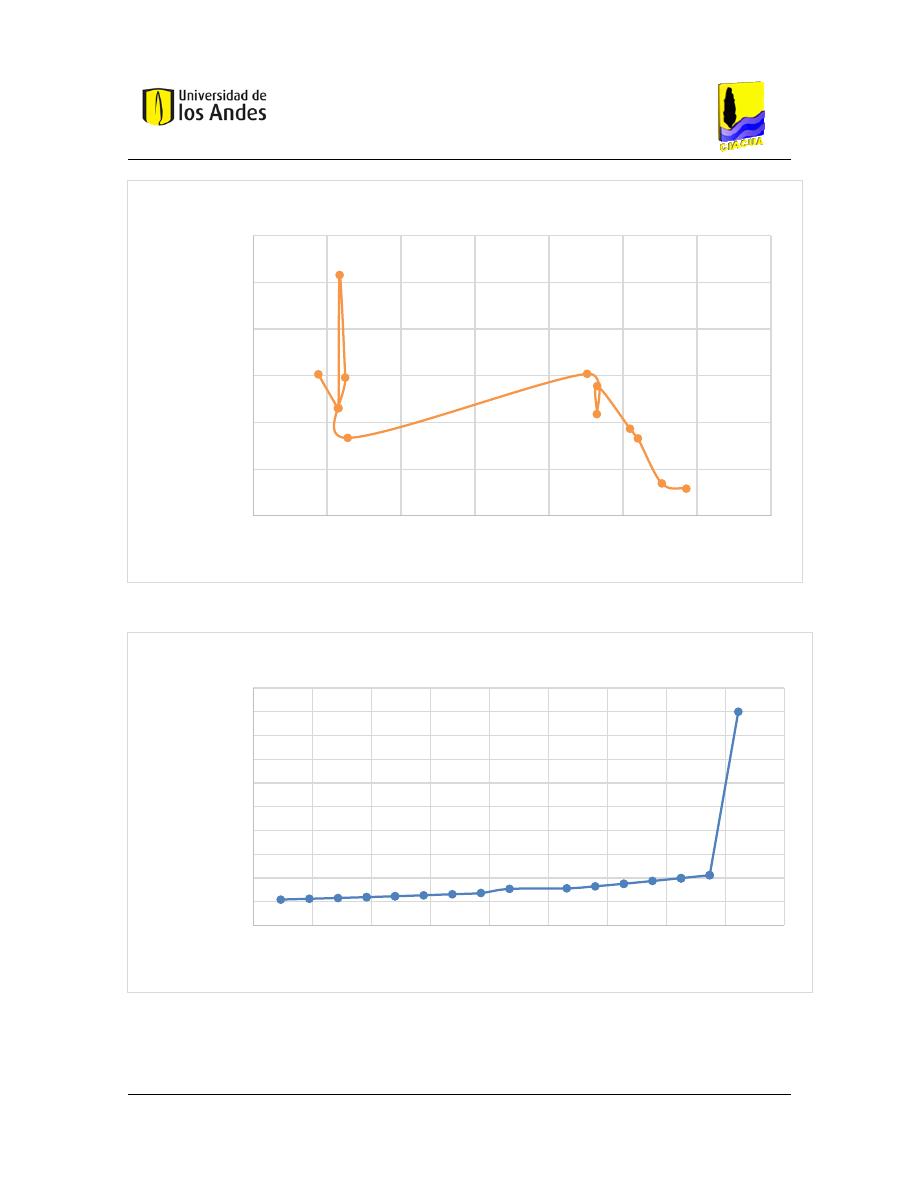
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
27
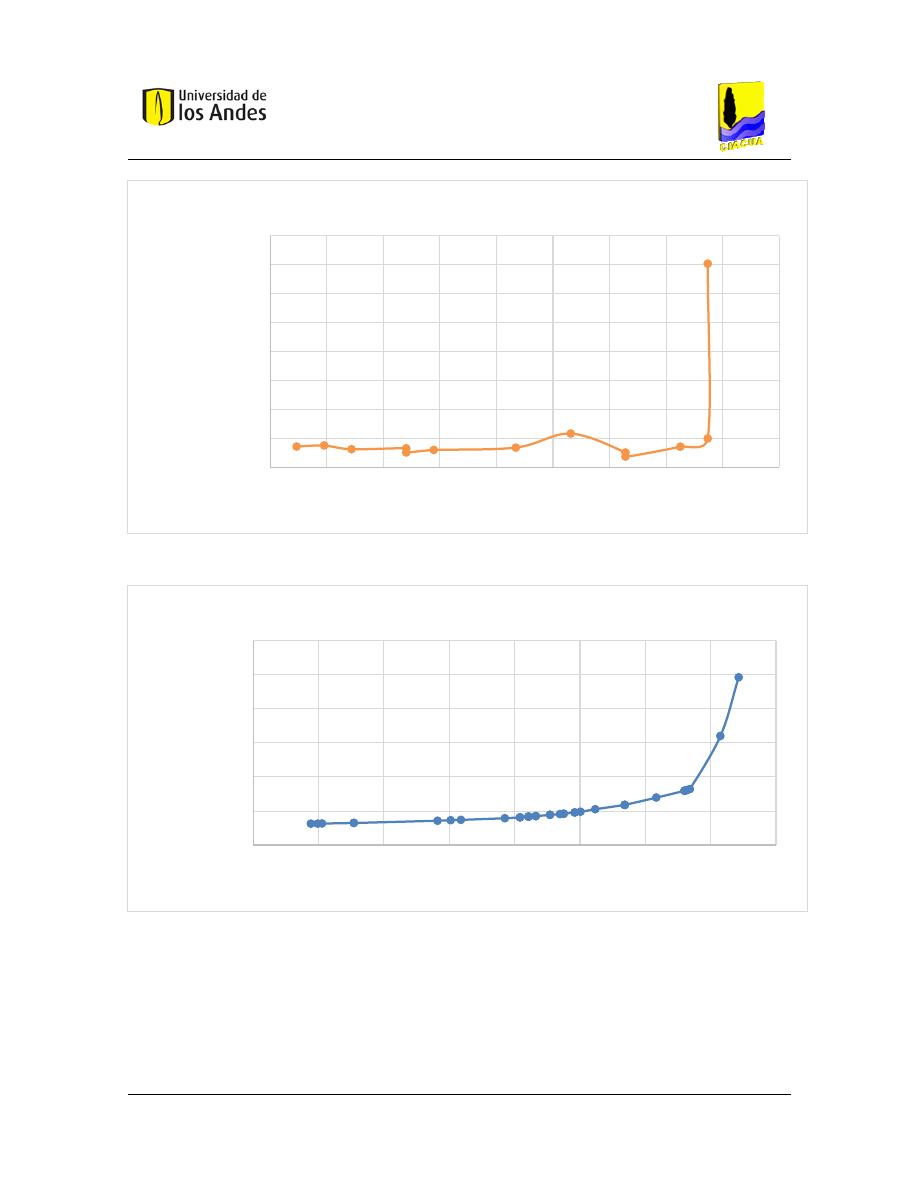
Gráfica 8 Frontera de Pareto de costos reales - Distancia y Altura para la red de Esmeralda
Gráfica 9 Frontera de Pareto de costos aproximados del índice de Inicios red de Esmeralda
$ 17.000.000
$ 19.000.000
$ 21.000.000
$ 23.000.000
$ 25.000.000
$ 27.000.000
$ 29.000.000
97,55
97,60
97,65
97,70
97,75
97,80
97,85
97,90
C
os
to
s
re
ale
s
[U
SD
]
Resiliencia índice de Distancia y Altura [%]
Frontera de Pareto: Red de Esmeralda
$ 14.600.000
$ 14.800.000
$ 15.000.000
$ 15.200.000
$ 15.400.000
$ 15.600.000
$ 15.800.000
$ 16.000.000
$ 16.200.000
$ 16.400.000
$ 16.600.000
31
31,5
32
32,5
33
33,5
34
34,5
35
35,5
C
os
to
s
ap
roxim
ad
os
[
U
SD
]
Resiliencia índice de Inicios [%]
Frontera de Pareto: Red de Esmeralda
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
28
Gráfica 10 Frontera de Pareto de costos reales del índice de Inicios para la red de Esmeralda
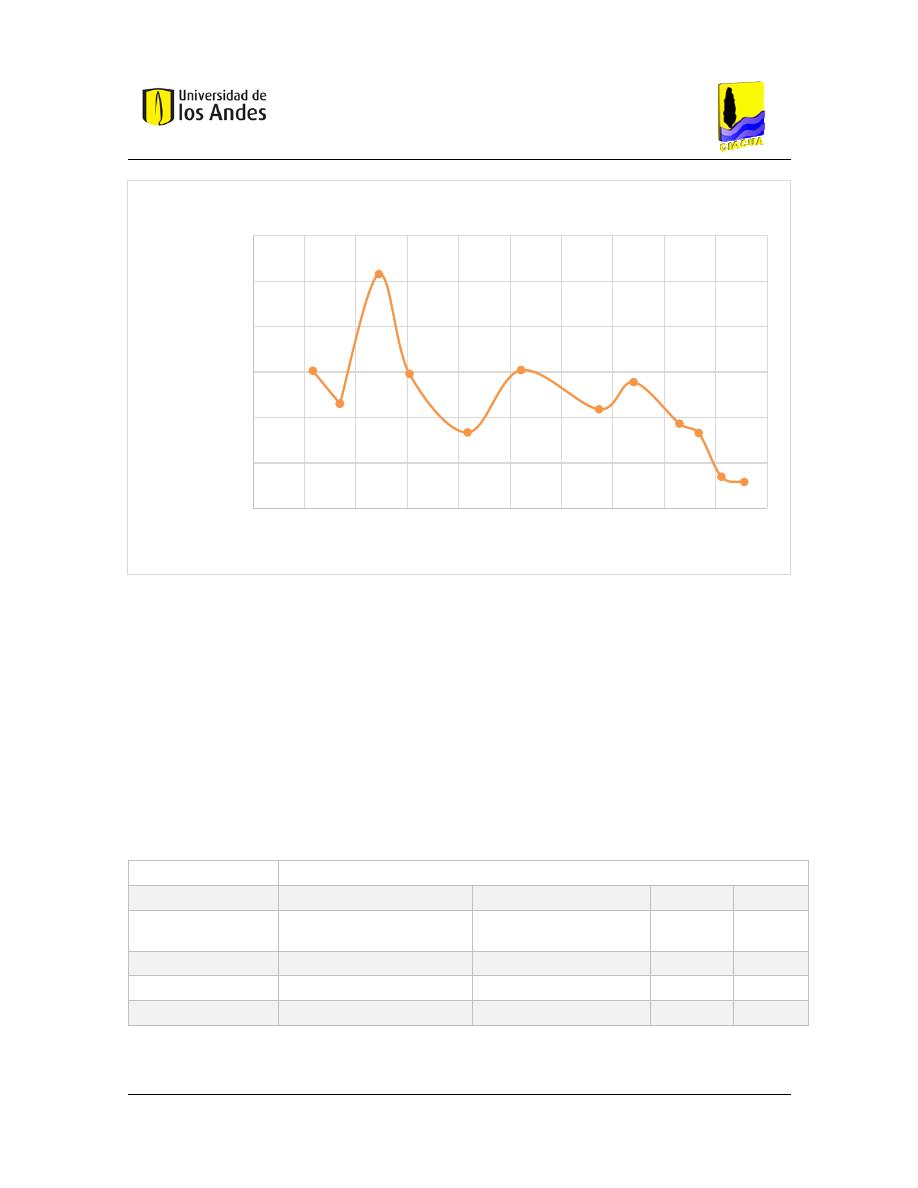
Gráfica 11 Frontera de Pareto de costos aproximados -Índice Aguilar red de Esmeralda
$ 26.000.000,00
$ 26.500.000,00
$ 27.000.000,00
$ 27.500.000,00
$ 28.000.000,00
$ 28.500.000,00
$ 29.000.000,00
$ 29.500.000,00
$ 30.000.000,00
31
31,5
32
32,5
33
33,5
34
34,5
35
35,5
C
os
to
s
Re
ale
s
[U
SD
]
Resiliencia índice de Inicios [%]
Frontera de Pareto: Red de Esmeralda
$ 14.500.000
$ 15.000.000
$ 15.500.000
$ 16.000.000
$ 16.500.000
$ 17.000.000
$ 17.500.000
52,00
53,00
54,00
55,00
56,00
57,00
58,00
59,00
60,00
C
os
to
ap
roxim
ad
o
[U
SD
]
Resiliencia índice de Aguilar [%]
Frontera de Pareto: Red de Esmeralda
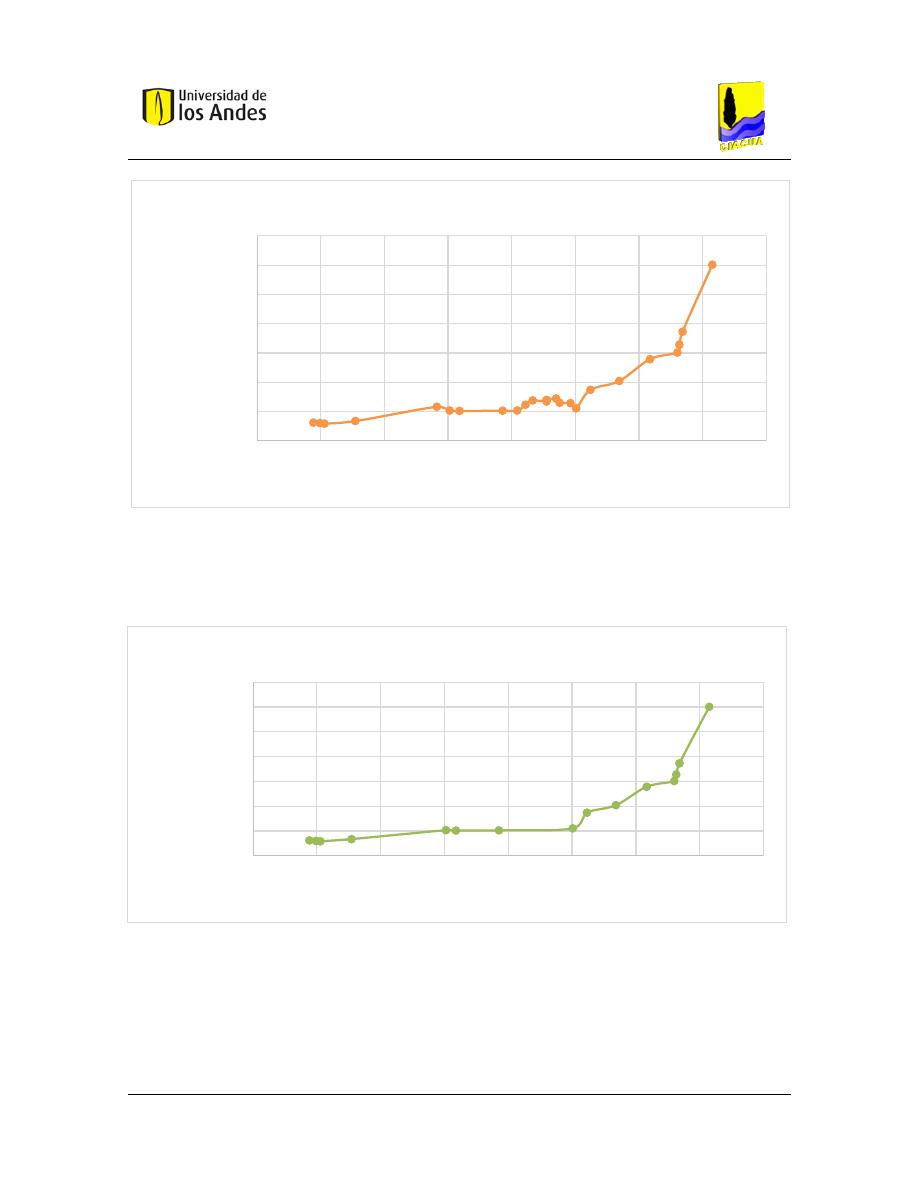
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
29
Para este índice de resiliencia en específico y para esta red fue posible construir la frontera
de Pareto real y coherente eliminando los trazados dominados y dejando exclusivamente
aquellos dominantes. A continuación, se presenta el resultado encontrado:
Gráfica 13 Frontera de Pareto definitiva de costos reales -Aguilar red de Esmeralda
Ahora bien, para conseguir los anteriores resultados, se tuvo un costo computacional en la
parte monoobjetivo de 5.17 horas ya que el tiempo requerido para la selección del trazado
de las 10 iteraciones es de 2.11 horas y el tiempo para el diseño hidráulico de estos trazados
es de 3.059 horas. A continuación, se muestran los tiempos requeridos para evaluar cada
$ 26.000.000
$ 26.500.000
$ 27.000.000
$ 27.500.000
$ 28.000.000
$ 28.500.000
$ 29.000.000
$ 29.500.000
52
53
54
55
56
57
58
59
60
C
os
to
s
re
ale
s
[U
SD
]
Resiliencia índice de Aguilar [%]
Frontera de Pareto: Red de Esmeralda
$ 26.000.000
$ 26.500.000
$ 27.000.000
$ 27.500.000
$ 28.000.000
$ 28.500.000
$ 29.000.000
$ 29.500.000
52
53
54
55
56
57
58
59
60
Cos
to
s
re
ales
[
U
SD]
Resiliencia índice de Aguilar [%]
Frontera de Pareto: Red de Esmeralda
Gráfica 12 Frontera de Pareto de costos reales del índice de Aguilar para la red de Esmeralda
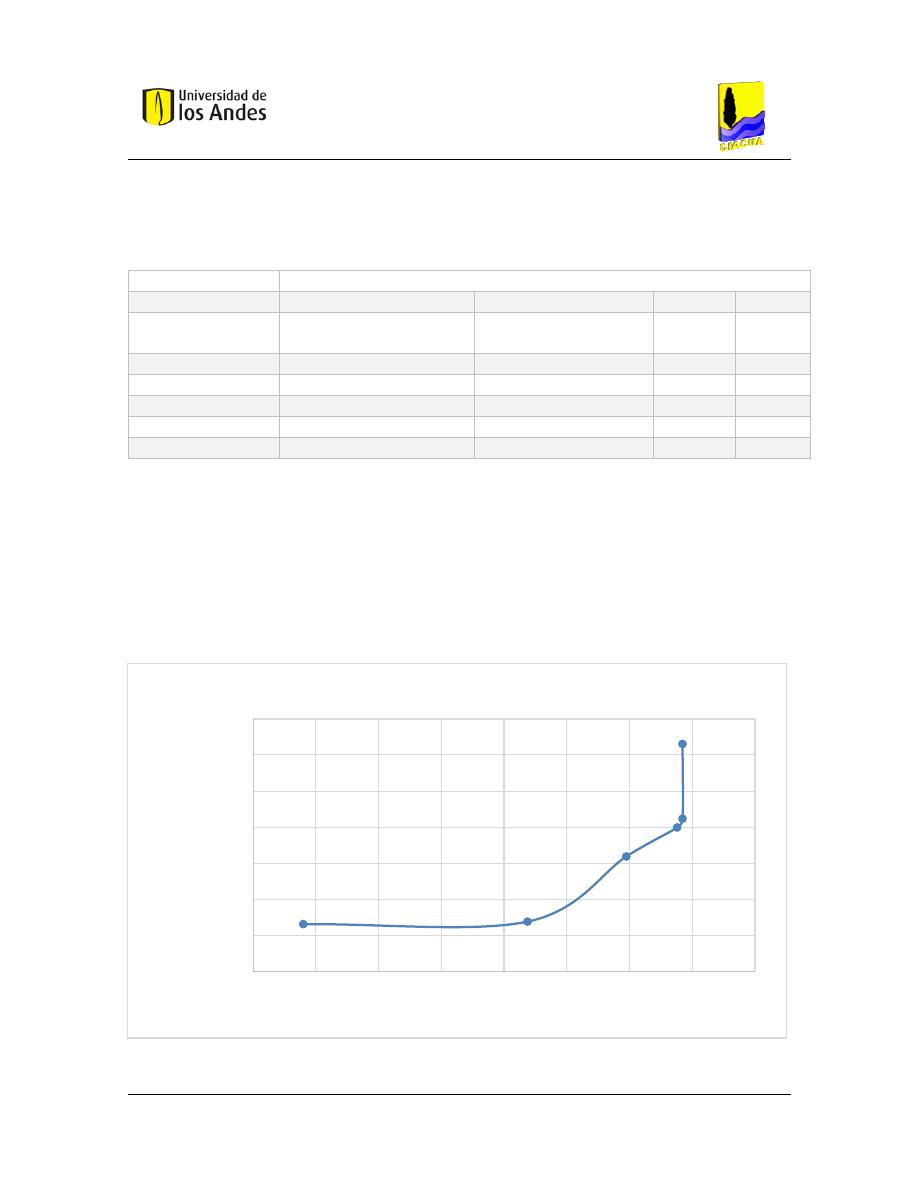
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
30
uno de los índices de resiliencia y el respectivo costo computacional para realizar el diseño
hidráulico de los trazados finales obtenidos:
Tabla 1 Costos computaciones de la red de Esmeralda
Costos Computacionales red de Esmeralda
Índice
Parte Multiobjetivo (s)
Diseño Hidráulico (s)
Total (s)
Total (h)
Haghighi
&
Bakshipour
10587,07
813,06
11400,12
3,17
Distancia
6298,06
1013,85
7311,91
2,03
Altura
20732,21
813,06
21545,27
5,98
Distancia y Altura
8501,63
813,06
9314,68
2,59
Inicios
17549,62
1404,84
18954,46
5,27
Aguilar
31173,34
2375,76
33549,10
9,32
5.2. Red de Moeini
Para la red de Moeini, se siguió el mismo procedimiento que para la red de Esmeralda, sin
embargo, en esta red no fue posible evaluar los índices de resiliencia de altura ni de
Distancia y Altura debido a las caracteríasticas de elevación de la red. A continuación, se
presentan las gráficas de las fronteras de Pareto de costos aproximados y costos reales
para cada uno de los índices de resiliencia posibles:
$ 9.000.000
$ 9.500.000
$ 10.000.000
$ 10.500.000
$ 11.000.000
$ 11.500.000
$ 12.000.000
$ 12.500.000
93,10
93,20
93,30
93,40
93,50
93,60
93,70
93,80
93,90
C
os
to
ap
roxim
ad
o
[U
SD
]
Resiliencia índice de Haghighi & Bakshipour [%]
Frontera de Pareto: Red de Moeini
Gráfica 14 Frontera de Pareto de costos aproximados - Haghighi & Bakshipour red de Moeini
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
31
Gráfica 15 Frontera de Pareto de costos reales-Haghighi & Bakshipour red de Moeini
Gráfica 16 Frontera de Pareto de costos aproximados - Distancia para la red de Moeini
$ 20.000.000
$ 21.000.000
$ 22.000.000
$ 23.000.000
$ 24.000.000
$ 25.000.000
$ 26.000.000
$ 27.000.000
93,1
93,2
93,3
93,4
93,5
93,6
93,7
93,8
93,9
Cos
to
s
re
ale
s
[US
D]
Resiliencia índice de Haghighi & Bakshipour[%]
Frontera de Pareto: Red de Moeini
$ 10.000.000
$ 10.500.000
$ 11.000.000
$ 11.500.000
$ 12.000.000
$ 12.500.000
$ 13.000.000
95,70
95,80
95,90
96,00
96,10
96,20
96,30
96,40
C
os
to
ap
roxim
ad
o
[U
SD
]
Resiliencia índice de Distancia [%]
Frontera de Pareto: Red de Moeini
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
32
$ 19.000.000
$ 20.000.000
$ 21.000.000
$ 22.000.000
$ 23.000.000
$ 24.000.000
$ 25.000.000
95,70
95,80
95,90
96,00
96,10
96,20
96,30
96,40
Cos
to
s
re
ales
[
U
SD]
Resiliencia índice de Distancia [%]
Frontera de Pareto: Red de Moeini
$ 10.000.000
$ 10.500.000
$ 11.000.000
$ 11.500.000
$ 12.000.000
$ 12.500.000
68
69
70
71
72
73
74
75
76
77
78
Cos
to
ap
ro
xim
ad
o
[U
SD]
Resiliencia índice de Aguilar [%]
Frontera de Pareto: Red de Moeini
Gráfica 17 Frontera de Pareto de costos reales del índice de Distancia para la red de Moeini
Gráfica 18 Frontera de Pareto de costos aproximados del índice de Aguilar para la red de Moeini
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
33
Gráfica 19 Frontera de Pareto de costos reales del índice de Aguilar para la red de Moeini
Con respecto a los costos computacionales de la red de Moeini, para la parte monoobjetivo fue
18,71 horas. Lo anterior, porque el tiempo requerido para la selección del trazado de las 10
iteraciones es de 3,93 horas y el tiempo para el diseño hidráulico de estos trazados es de 14,77
horas. A continuación, se presentan los tiempos requeridos para evaluar los índices de resiliencia y
su costo computacional para realizar el diseño hidráulico de los trazados obtenidos en las Fronteras
de Pareto de costos aproximados:
Tabla 2 Costos computacionales de la red de Moeini
$ 17.000.000
$ 19.000.000
$ 21.000.000
$ 23.000.000
$ 25.000.000
$ 27.000.000
$ 29.000.000
68
69
70
71
72
73
74
75
76
77
78
C
os
to
s
re
ale
s
[U
SD
]
Resiliencia índice de Aguilar [%]
Frontera de Pareto: Red de Moeini
Costos Computacionales red de Moeini
Índice
Parte Multiobjetivo (s)
Diseño Hidráulico (s)
Total (s)
Total (h)
Haghighi
&
Bakshipour
6996,53
532,84
7529,37
2,09
Distancia
2415,22
456,39
2871,61
0,80
Inicios
4117,35
550,42
4667,77
1,30
Aguilar
10738,99
813,06
11552,05
3,21

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
34
6 Análisis de resultados
En primer lugar, se observa que el comportamiento de cada una de las fronteras de Pareto
depende del índice evaluado. Además, se evidencia que al pasar los trazados encontrados
en la frontera de Pareto de costos aproximados a costos reales su comportamiento cambia
por completo, mostrando resultados que no conforman una Frontera de Pareto esperada.
Lo anterior, porque se espera que a medida que aumente la resiliencia de los trazados
aumente también su precio. Estos resultados son controversiales debido a que van en
desacuerdo con lo mostrado por Andrés Aguilar en su tesis de posgrado en 2019. Una vez
revisada la metodología, la programación de esta y su ejecución se evidencia que lo único
que puede estar fallando en el procedimiento es la ecuación de costos a partir del trazado.
Esto, ya que los resultados demuestran que esta ecuación no es una buena aproximación
a los costos reales de la red.
En segundo lugar, se muestra que no todos los índices pudieron ser evaluados en las dos
redes de drenaje urbano. Lo anterior, se debe porque la red de Moeini es una red
completamente plana y como el índice de Altura y el índice de Distancia y Altura dependen
de las diferencias en elevación de cada uno de los pozos que las componen no tiene sentido
evaluar estos índices en una red plana.
A continuación, se muestra un análisis más detallado de los resultados encontrados en la
red de Esmeralda y la red de Moeini.
6.1. Red de Esmeralda
En la red de Esmeralda la mayor resiliencia encontrada se obtuvo con el índice de Distancia
y Altura con un 97.84% y un costo real asociado de $18.158.761,93 este trazado también
corresponde al trazado más económico de todos los encontrados. El índice de resiliencia
con el que se encontraron los trazados de mayor valor con una menor resiliencia es con el
índice de Inicios con una resiliencia máxima de 35,10% y un costo real asociado de
$29.518.549,64. El índice de Aguilar evaluado en la red de Esmeralda es el que brinda
mayor número de soluciones para el diseñador, ya que brinda 23 trazados diferentes.
En la red de Esmeralda fue posible evaluar todos los índices de resiliencia propuestos en
la metodología, sin embargo, el costo computacional varió de un índice a otro. El índice que
más costo computacional tuvo fue el índice de Aguilar con 8,66 horas y el de menor costo
computacional fue el de Distancia con un tiempo requerido de 1,75 horas.
Para esta red, ocurre un caso excepcional en el índice de Aguilar, ya que al convertir los
costos aproximados en costos reales y eliminar los trazados no dominantes se puede
conseguir una muy buena frontera de Pareto. Lo anterior, puede presentarse debido a que
la red de Esmeralda es una red grande (385 pozos) y como el índice de Aguilar tiene en

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
35
cuenta el criterio de estructura de la red es más viable para el algoritmo encontrar trazados
adecuados en esta red debido a las múltiples alternativas posibles.
6.2. Red de Moeini
La red de Moeini por ser completamente plana, es decir, todos los pozos que la componen
tienen la misma elevación, por lo que no fue posible evaluar todos los índices de resiliencia.
Lo anterior, porque el índice de Distancia y Altura, índice de Altura necesitan un diferencial
de elevación de pozos para calcular la resiliencia de la red. En esta red, el trazado con
mayor resiliencia se obtuvo al evaluar el índice de Distancia, alcanzando una confiabilidad
del 96.29% asociado a un costo real de $21.960.063,42. El trazado más económico
encontrado se obtuvo al evaluar el índice de Aguilar con un costo real de $18.158.761,93 y
una resiliencia de 77.56%. El índice de resiliencia que mayor número de trazados produjo
fue el índice de Aguilar, con 12 trazados. Según los datos encontrados, para el índice de
Aguilar, el trazado con mayor resiliencia es el de menor costo. Lo anterior, va en contra de
lo resaltado por Andrés Aguilar en su trabajo de 2019 ya que indica que los trazados más
resilientes están asociados a un mayor costo.
Con respecto a los costos computacionales, la red de Moeini requirió menor tiempo que la
red de Esmeralda para evaluar los índices de resiliencia, para el índice de Haghighi &
Bakshipour se requirió un 51.67% menor costo computacional para evaluar la red, para el
índice de distancia la diferencia fue de un 153,75% menor tiempo, para el índice de Inicios
un 305.38% menos tiempo y para el índice de Aguilar un 190.34% menor tiempo
computacional. Lo anterior, se debe a que la red de Moeini solo tiene 82 pozos de
inspección mientras que la red de Esmeralda tiene 385 pozos, lo que la hace una red
pequeña que requiere poco costo computacional para evaluar los índices de resiliencia.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
36
7 Conclusiones
• Las Fronteras de Pareto de costos reales encontradas en este trabajo no coinciden
con los resultados encontrados por Aguilar 2019. Una vez revisada la metodología
empleada se asume que la ecuación que permite obtener los costos aproximados
de la red no es adecuada para estimar los costos reales.
• En las Fronteras de Pareto encontradas algunos trazados que presentan un alto
valor de resiliencia están asociados a bajos valores de costo. Lo anterior, es
controversial con los resultados encontrados por Aguilar, donde se afirma que a
medida que aumente la resiliencia de una red debe aumentar su precio.
• La red de Esmeralda requiere un mayor costo computacional que la red de Moeini
para evaluar los índices de resiliencia debido a su gran número de pozos de
inspección. Por lo tanto, el tiempo requerido para modelar una red depende
directamente del número de pozos que la compongan.
• El índice de Aguilar es el que provee un mayor número de trazados, esto permitirá
que el diseñador evalúe cual trazado desea escoger como diseño a ejecutar según
los criterios de precio y resiliencia que esté dispuesto a asumir.
• En las redes planas, como en el caso de la red de Moeini no es posible evaluar los
índices de Altura y Distancia y Altura debido a que estos requieren un diferencial de
elevación para calcular la resiliencia de la red.
• En algunos casos se puede presentar que el trazado con mayor resiliencia de la
frontera de Pareto sea el trazado con menor costo real, como sucede en el índice
de Distancia y Altura para la red de Esmeralda y en el índice de Aguilar y Haghighi
& Bakshipour para la red de Moeini.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
37
8 Recomendaciones
• Plantear otra ecuación de costos en la parte multiobjetivo de la metodología para
calcular los costos aproximados de las redes a evaluar ya que la utilizada no permite
estimar de forma adecuada los costos reales.
• Plantear nuevos índices de resiliencia teniendo en cuenta los criterios de porcentaje
de caudal de descarga que fluye en una tubería y la estructura de la red.
• Aplicar la metodología a más redes de drenaje urbano como a redes de alta
pendiente y redes con ángulos cercanos a los 90° para evaluar el comportamiento
de los índices de resiliencia.
• Utilizar las ventajas encontradas en este trabajo en cada índice de resiliencia para
plantear nuevas formas de evaluar la resiliencia de redes de drenaje urbano.
• Codificar de forma automática la metodología completa planteada en este trabajo.
En este sentido, se deberán unir la parte de selección del trazado y diseño hidráulico
para no realizar las iteraciones iniciales de forma manual. Además, deberá unirse el
diseño hidráulico de los trazados encontrados a partir de costos aproximados a la
parte inicial de la metodología estipulada.
• Modificar el código de selección de trazado para que una vez ejecutado muestre el
costo aproximado de cada uno de los tramos de la red, así como sucede en el diseño
hidráulico con los costos reales. Lo anterior, con el objetivo de comparar la diferencia
entre costos aproximados y reales por cada uno de los tramos de la red evaluada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
38
9 Referencias
Aguilar, A. (2016). Evaluación de funciones objetivo en la metodología exhaustiva
desarrollada por el CIACUA para el diseño optimizado de alcantarillados. (Tesis de
pregrado). Universidad de Los Andes, Bogotá.
Aguilar, A. (2019). Metodología para el Diseño Optimizado de Redes de Alcantarillado
Metodología para el Diseño Optimizado de Redes de Alcantarillado (Tesis de
mestría). Universidad de Los Andes, Bogotá.
Butler, D. &. (2004). Urban Drainage.
Duque, N. (2013). Metodología para la optimización del diseño de tuberías en serie en
sistemas de alcantarillado (Tesis de Pregrado). Universidad de los Andes, Bogotá.
Duque, N. (2015). Metodología para el Diseño Optimizado de Redes de Alcantarillado
(Tesis de Maestría). Universidad de los Andes, Bogotá. .
Haghighi, A. &. (2016). Reliability-based layout design of sewage collection systems in flat
areas. Urban Water Journal, 790
–802.
Herrán, J. (2020). Evaluación de índices de confiabilidad en modelo de optimización
multiobjetivo para el diseño de redes de drenaje urbano (Tesis de Pregrado).
Universidad de Los Andes, Bogotá.
Maurer, S. &. (2012). Quantifying costs and lengths of urban drainage systems with a simple
static sewer. Dubendorf, Suiza: Taylor & Francis.
Medrano, F. A. (2015). A Parallel Computing Framework for Finding the Supported Solutions
to a Biobjective Network Optimization Problem. Journal of Multi-Criteria Decision
Analysis.
RAS. (2000). Reglamento Técnico del Sector de Agua Potable y Saneamiento Basico RAS
- 2000. Ministerio de Desarrollo Económico. Bogotá, Colombia.
Superservicios. (2018). Estudio sectorial de los servicios públicos domiciliarios de
Acueducto
y
Alcantarillado
.
Obtenido
de
https://www.superservicios.gov.co/sites/default/archivos/Publicaciones/Publicacion
es/2020/Ene/informe_sectorial_aa_2018-20-12-2019.pdf
Zambrano, J. (2019). Diseño optimizado de redes de drenaje urbano. Casos de estudio
variando la topografía del terreno, la densidad de viviendas, los coeficientes de
impermeabilidad y la rugosidad de las tuberías (Tesis de Maestría). Universidad de
Los Andes, Bogotá.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Determinación del árbol óptimo multicriterio de una Red de Drenaje
Urbano que lleve al diseño de mínimo costo y máxima resiliencia
Laura Lizzette Arroyo Cruzco
Proyecto de grado
39
