
IAHR
CIC
XXV CONGRESO LATINOAMERICANO DE HIDRÁULICA
SAN JOSÉ, COSTA RICA, 9 AL 12 DE SETIEMBRE DE 2012
DETERMINACIÓN DE LAS ECUACIONES DE CAUDAL VS PRESIÓN DE
FUGAS POR FALLAS EN TUBERÍAS DE PVC BIORIENTADO
Diana Fonseca, Juan Ossa, Juan Saldarriaga
Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA), Departamento de Ingeniería Civil y Ambiental,
Universidad de los Andes, Bogotá, Colombia
dian-fon@uniandes.edu.co, js.ossa117@uniandes.edu.co
,
jsaldarr@uniandes.edu.co
,
RESUMEN:
Las pérdidas de agua constituyen uno de los mayores problemas, para el correcto funcionamiento de
Redes de Distribución de Agua Potable (RDAP), sin embargo, todavía existen muchas preguntas a
la hora de modelar su comportamiento. El presente artículo muestra los resultados de un trabajo en
el que se desarrolla, y se pone a prueba, una metodología para determinar ecuaciones, que
relacionen el caudal y la presión interna, en momentos en que se presentan fugas en tuberías de
PVC biorientado. Para llevar a cabo la investigación se construye un montaje de laboratorio, en el
que se experimenta con distintos tipos de falla en las paredes, tales como: orificios, ranuras
longitudinales y ranuras circunferenciales. Para cada una de estas, se genera un banco de datos que
relaciona la presión dentro del tubo y la descarga perdida. Usando esta información, y por medio de
un análisis estadístico, se genera una ecuación que relaciona ambas variables, para así simplificar el
problema y poder analizar las fugas como si fueran emisores.
ABSTRACT:
Understanding water loss behavior in Water Distribution Systems is very difficult, despite it being a
very common problem seen in water networks. This paper shows the results of a methodology
applied to bPVC pipes that experienced leakage. The methodology also determined equations that
related the water flow and its internal pressure. The elaboration of a laboratory simulation was
needed to complete the research. In the simulation, different types of failures—round holes,
longitudinal splits and circular cracks—presented themselves. Each failure was recorded and data
was collected so as to relate discharge and pressure. An equation was| obtains through the use of
this information and a statistical process. This equation related both variables. The problem was
therefore simplified, for it allowed the understanding of leakages as emitters.
PALABRAS CLAVES:
Redes de distribución; Tubos de PVC; Fugas de agua

INTRODUCCIÓN
En una red de distribución de agua potable (RDAP), una parte del caudal transportado es
consumido por los usuarios autorizados y otra se pierde de distintas formas. Esta fracción es medida
por medio del Índice de Agua No Contabilizada (IANC), e incluye el agua consumida que no se
factura, el caudal que no se mide, las conexiones ilegales y por supuesto las pérdidas de agua por
fugas. Estas últimas son uno de los problemas más graves en RDAP, no solo porque son bastante
frecuentes, sino también por la dificultad para rastrearlas. El Banco Mundial, ha definido que el
IANC para países con déficit de agua debe ser máximo del 15% (Ardakanian & Ghazali, 2003); sin
embargo, en muchos casos este valor es superado considerablemente, convirtiéndose en uno de los
mayores problemas para los operadores de los sistemas de distribución.
Existen muchas causas para que se generen fugas en una red; algunas de ellas son el
envejecimiento de la misma, la mala instalación de tuberías y accesorios, la mala calidad de los
materiales, los malos diseños, las conexiones ilegales y las presiones excesivas. Hay diferentes
estrategias para controlar las pérdidas, algunas de estas son: velocidad y calidad en las reparaciones,
control activo de pérdidas, gestión de redes y activos, y manejo de presiones de la red. Aunque
todas las opciones anteriores son válidas, el presente trabajo se centra en la última, y por ende se
cuestiona cómo reducir estos valores de forma efectiva. La importancia de esto, radica en el hecho
que se ha demostrado que los valores altos están fuertemente relacionados con las fugas (Walski, ,
Bezts, Posluszny, Weir, & Whitman, 2004) ); (Burnell & Race, 2000); (Farley & Trow, 2003);
(Martínez, Conejos & Vercher, 1999); (Stathis & Loganathan, 2000); y por ende, al evitar que
estas se encuentren por encima de ciertos límites, se logran disminuir las pérdidas.
El interrogante de cómo lograr esta reducción, está asociado con una buena calibración de la
red, que entre otras, debe contar dentro de sus variables de entrada, con una buena cuantificación
del caudal perdido. Lo anterior permite generar modelos, que detecten zonas donde se presenten
comportamientos anómalos, y que posiblemente estén asociados con fugas. Para evaluar esta
dependencia, es necesario conocer la relación que existe entre las dos variables; una opción es tratar
las fallas como emisores, es decir accesorios que dejan salir de la red una determinada descarga
como función de la altura piezométrica en el punto. Esta investigación está dedicada a establecer las
ecuaciones que relacionen las dos variables, en tuberías hechas de PVC molecularmente orientado.
Haciendo uso de la asociación mencionada anteriormente, y tomando como base estudios que han
demostrado su idoneidad (Greyvenstein & Van Zyl, 2005); (Ferrante, Massari, Brunone, &
Meniconi, 2010); (Van Zyl & Clayton, 2007); se define la siguiente ecuación para asociar las
características.
[1]
donde Q es el caudal perdido, h es la presión en la tubería, α (coeficiente de descarga) y β
(exponente) son variables que describen el tipo de falla. Estos parámetros varían según el tipo de
material del montaje, el tipo de falla que se esté poniendo a prueba y de algunas particularidades de
la investigación, que hacen variar los valores entre los distintos autores. Algunos ejemplos de esto
se muestran a continuación.
Tabla 1.-
Exponente β en función del material, características de la tubería y tipo de falla (Buckley, 2008).
Material
Tipo de
Falla
Tamaño
mm
Diámetro
mm
Espesor
de
pared
mm
β
Unplasticised
Poly
Vinyl
Chloride
(uPVC)
Orificio
6
110
3
0.511
8
110
3
0.524
10
110
3
0.514
12
110
3
0.509
uPVC
R.Long.
1.2 x 40 110
3
0.841
2 x 60
110
3
0.757
1.7 x 90 110
3
0.857
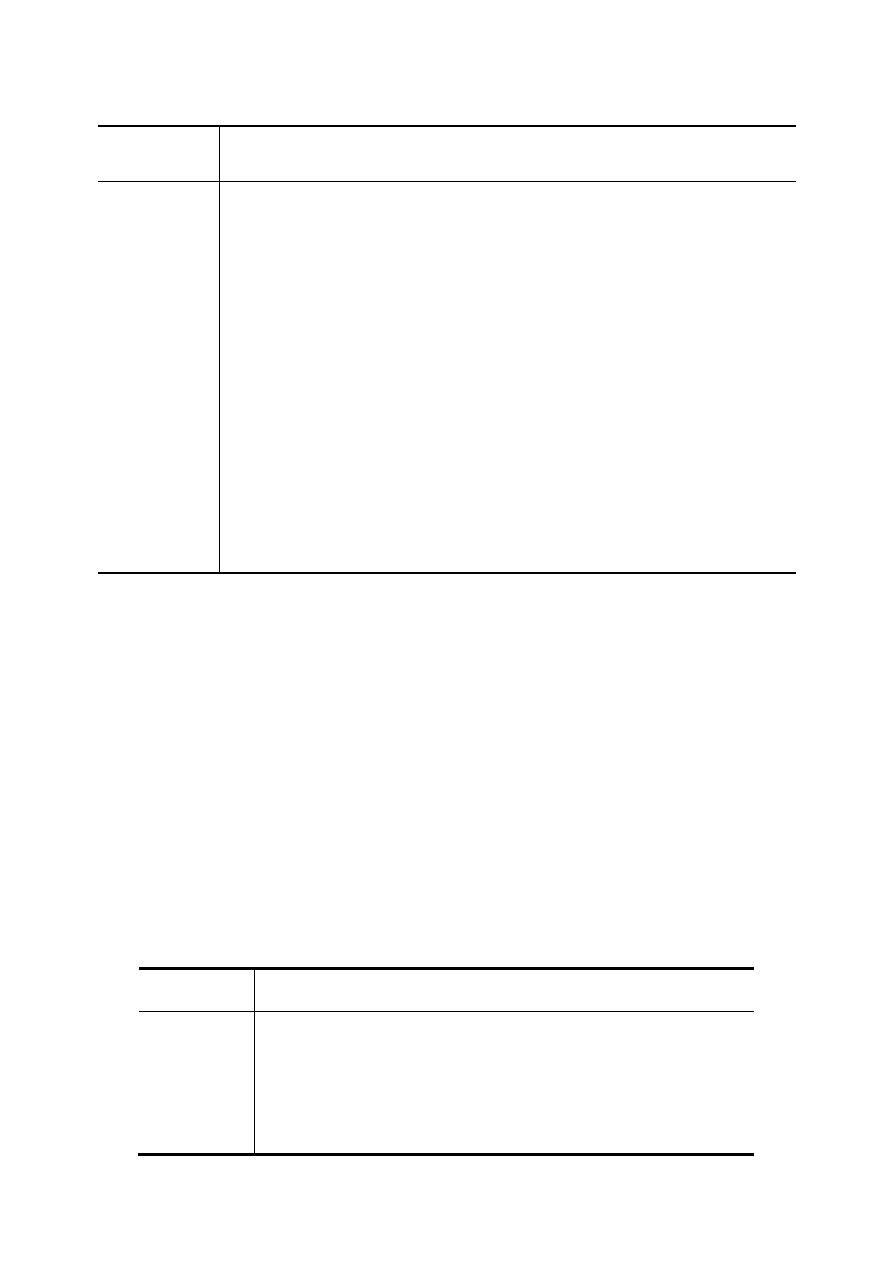
Tabla 2.-
Exponente β en función del material, características de la tubería y tipo de falla (Cassa, Van Zyl,
Laubscher, 2006).
Material
Tipo de Falla
Tamaño
mm
Diámetro
mm
Espesor
de
pared mm
β
uPVC
Orifico
6
110
3
0.508
8
110
3
0.507
10
110
3
0.507
12
110
3
0.508
Hierro fundido
Orifico
6
105.2
0.60
0.500
8
105.2
0.60
0.501
10
105.2
0.60
0.501
12
105.2
0.60
0.501
Acero
Orifico
6
104.6
0.31
0.501
8
104.6
0.31
0.501
10
104.6
0.31
0.501
12
104.6
0.31
0.502
uPVC
R.Long.
2 x 50
110
3
0.783
Hierro Fundido
R.Long.
0.5 x 50
105.2
0.60
0.661
Acero
R.Long.
1 x 50
104.6
0.31
0.723
uPVC
R.Circun
0.5 x40
110
3
0.557
2 x 150
110
3
1.154
Hierro Fundido
R.Circun
0.5 x40
105.2
0.60
0.513
1 x 150
105.2
0.60
0.946
Hierro Fundido
R.Circun
0.5 x40
104.6
0.31
0.519
1 x 150
104.6
0.31
1.017
Como se puede ver en la Tabla 1 y en la Tabla 2, los valores del exponente no varían mucho
como función de las características de la falla, excepto en las ranuras circunferenciales, pero sí lo
hacen en relación al tipo de fuga. Por lo general los orificios presentan valores cercanos a 0.5, para
las ranuras longitudinales es un poco mayor y para las circunferenciales está cercano a 1. Es
importante mencionar que el estudio de Cassa, además de ser bastante robusto en el número de
resultados, contó con una aproximación usando un análisis de elementos finitos aplicado a fallas en
tuberías; este tipo de acercamientos aumenta la confiabilidad de los datos y sienta una buena base
de comparación.
En el Centro de Investigaciones en Acueductos y Alcantarillados (CIACUA), de la
Universidad de los Andes, en Bogotá, Colombia, también se han hecho algunos análisis con
resultados similares. Uno de estos se muestra en la Tabla 3; en ella se puede evidenciar la
dependencia de los parámetros α y β respecto al tamaño de la falla y el diámetro de la tubería. El
parámetro α tiende a aumentar proporcionalmente con la longitud de la falla (Ranuras
longitudinales), y a disminuir a medida que crece el diámetro (orificios). El exponente β por su
parte, presenta una tendencia a incrementarse a medida que aumenta la longitud de la falla en las
ranuras, y a permanecer constante en el otro caso.
Tabla 3.-
Ecuaciones en función del tamaño de la tubería y el tipo de Falla (Ávila, 2003).
Diámetro
mm
Ecuación
Área
m
2
α
β
R
2
5.0
1.96x10
-5
52
0.5
0.986
7.7
4.65x10
-5
146.6
0.5
0.984
Longitud
mm
Ecuación
Área mm
2
α
β
R
2
12.25
12.25
26.90
0.48
0.976
37.20
37.20
52.92
0.64
0.998
60.0
60.0
82.82
0.758
0.996

OBJETIVOS
El objetivo principal de esta investigación es; determinar las ecuaciones que describen el
comportamiento hidráulico, de diferentes tipos de fallas en tuberías de PVC biorientado. Lo cual en
otras palabras, significa encontrar la relación existente entre caudal perdido y la presión en el punto
de fuga. Para esto se construyó un montaje de laboratorio, que permite la realización de distintas
pruebas en tuberías de PVC biorientado, sustituyendo el diámetro, el tipo de falla y sus
dimensiones. Se espera calibrar los parámetros de la ecuación de la falla (coeficiente de descarga y
exponente), para cada uno de los casos de prueba y con base en esto se espera determinar tendencias
de cada uno de los parámetros, como función de las distintas características. Finalmente, se espera
obtener un estimativo de la cantidad de agua que se podría perder en una red debido a las fugas.
DESCRIPCIÓN DEL MONTAJE
Para la realización de las pruebas se diseñó y construyó un montaje, en el Laboratorio de
Hidráulica de la Universidad de los Andes, Bogotá, Colombia, con la capacidad de probar dos tipos
de fallas simultáneamente, cada una en sección independiente. El modelo hace pasar el agua por un
circuito, que está constituido por las siguientes partes:
1. Bomba Tipo HY-FLO centrífuga con una capacidad para mover 6.3 L/s, a 75 m de altura
dinámica.
2. Dos canales independientes totalmente impermeabilizados. La división se hizo mediante
láminas de acrílico de 8 mm en la zona de prueba, con la finalidad de tener buena visibilidad
de las fugas, y con aglomerado de 12 mm para el resto de tramos.
3. Dos vertederos triangulares de 60° en acrílico, adaptados en cada una de las secciones de
prueba junto con un sensor para medir el nivel de agua.
El montaje se une al sistema de alimentación del laboratorio por medio de una válvula de
regulación de caudal; posteriormente una tubería de 3” llega hasta la bomba, donde se impulsara la
descarga. En este punto se ubica un cheque y una válvula de compuerta de 1 ½”, para evitar golpes
de ariete. Se sigue con un tubo del mismo tamaño hasta llegar un bypass, hecho con una Tee de 3x2
y otra válvula de compuerta, donde se regula la entrada de agua a los prototipos (Figura 2).
Finalmente se usa una tubería vertical de 3”, hasta llegar a una última válvula y una Tee, donde se
divide la descarga entre los dos canales (Figura 1). El equipo usado consta de un manómetro digital
marca Kobold, que se ubica antes de la división del modelo, y que mide la presión a la entrada del
mismo, y un sensor de nivel antes de los vertederos. Para usar estos dispositivos se desarrolló un
software, que lleva la información medida a un computador, y que procesa los datos de la lámina de
agua para entregar el valor del caudal que se está fugando de la tubería.
Figura 1.- Vista general del montaje.
Figura 2.- Vista lateral del sistema de
recirculación.
La última parte del montaje, son los prototipos de PVC biorientado (biaxial) que se ponen a
prueba. Esta tecnología se diferencia de los tubos comunes, pues durante el proceso de construcción
se estiran en línea las moléculas del polímero, obteniendo una orientación en sentido circunferencial
y longitudinal (Figura 3). Estos planos alineados incrementan la resistencia mecánica, la fortaleza
del material, la máxima tensión a la falla, que es la de resistencia a la rotura debido a la presión
interna, y la resistencia al impacto (PAVCO, 2008). Asimismo, al tener una estructura laminada,
disminuyen considerablemente la transmisión de fracturas a través de la pared de la tubería, y
reducen el riesgo ante ataques químicos y electroquímicos.
Figura 3.- Orientación molecular en tuberías de PVC biaxiales. Fuente (PAVCO, 2008).
METODOLOGÍA
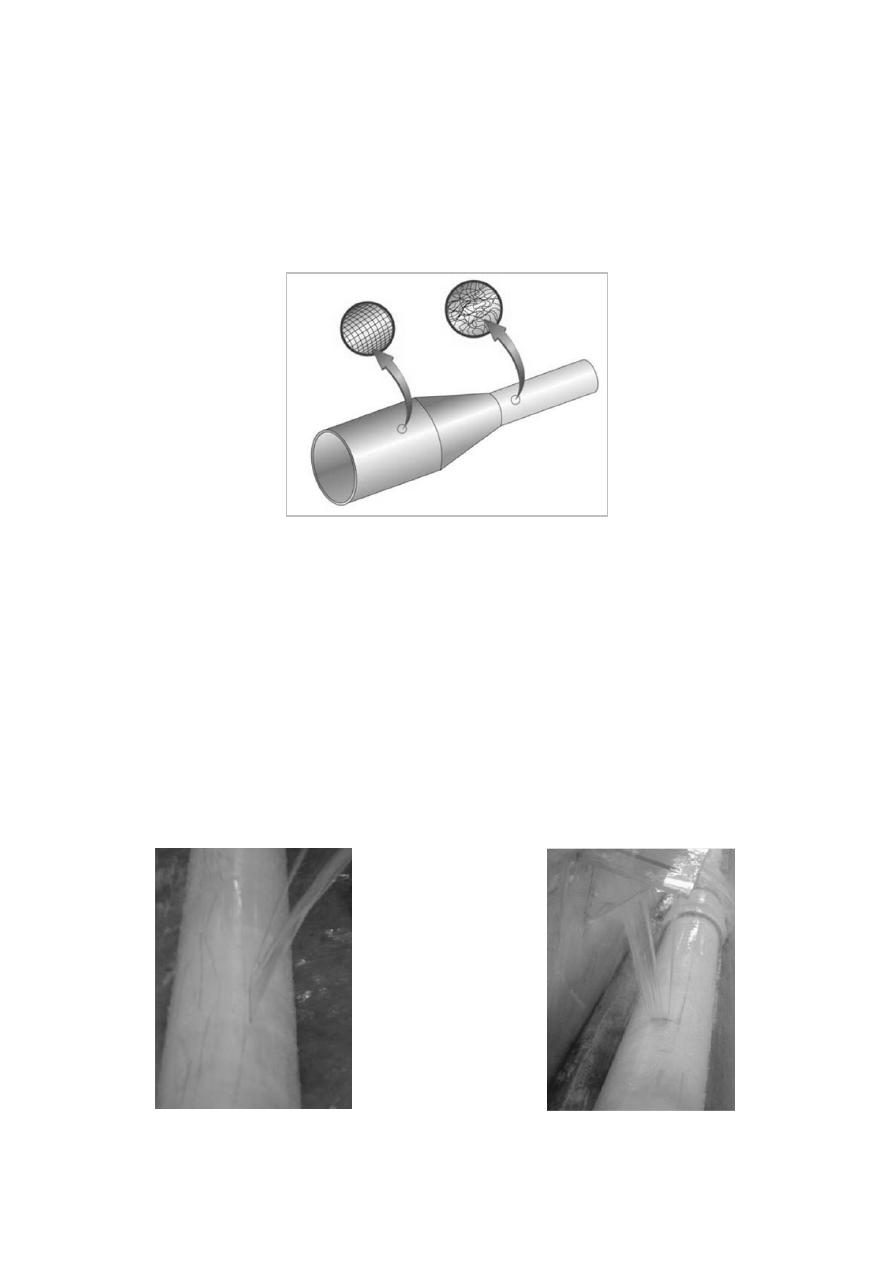
La preparación del modelo empieza generando la falla en los distintos tubos. Se representan
en total 3 tipos de fuga de diversos tamaños: ranuras longitudinales de 12, 37, 60 y 100 mm de largo
(Figura 4), ranuras transversales de 12 ,37 ,60 y 100 mm de largo (Figura 5), orificios de 3, 5, 7.7,
8.5 y 10 mm de diámetro (Figura 6), y collares de acometidas domiciliarias desfasados 50%, 100%,
o colocados correctamente pero sin empaque hermético (Figura 7). El objetivo de estos últimos, es
simular una inadecuada instalación de los accesorios, algo que es común en algunas edificaciones,
pero que nunca se ha estudiado. Una vez se le ha hecho la abertura a la tubería, se ubica en uno de
los canales y se conecta al sistema de abastecimiento. Se agrega un tapón en la parte final para
confinar el flujo, y se usa una abrazadera metálica para evitar que la fuerza del agua lo empuje. Se
hicieron pruebas en dos diámetros de tuberías de PVCO: 100 mm (4 pulgadas) y 150 mm (6
pulgadas).
Figura 4.- Representación de las ranuras
longitudinales.
Figura 5.- Representación de las ranuras
circunferenciales.
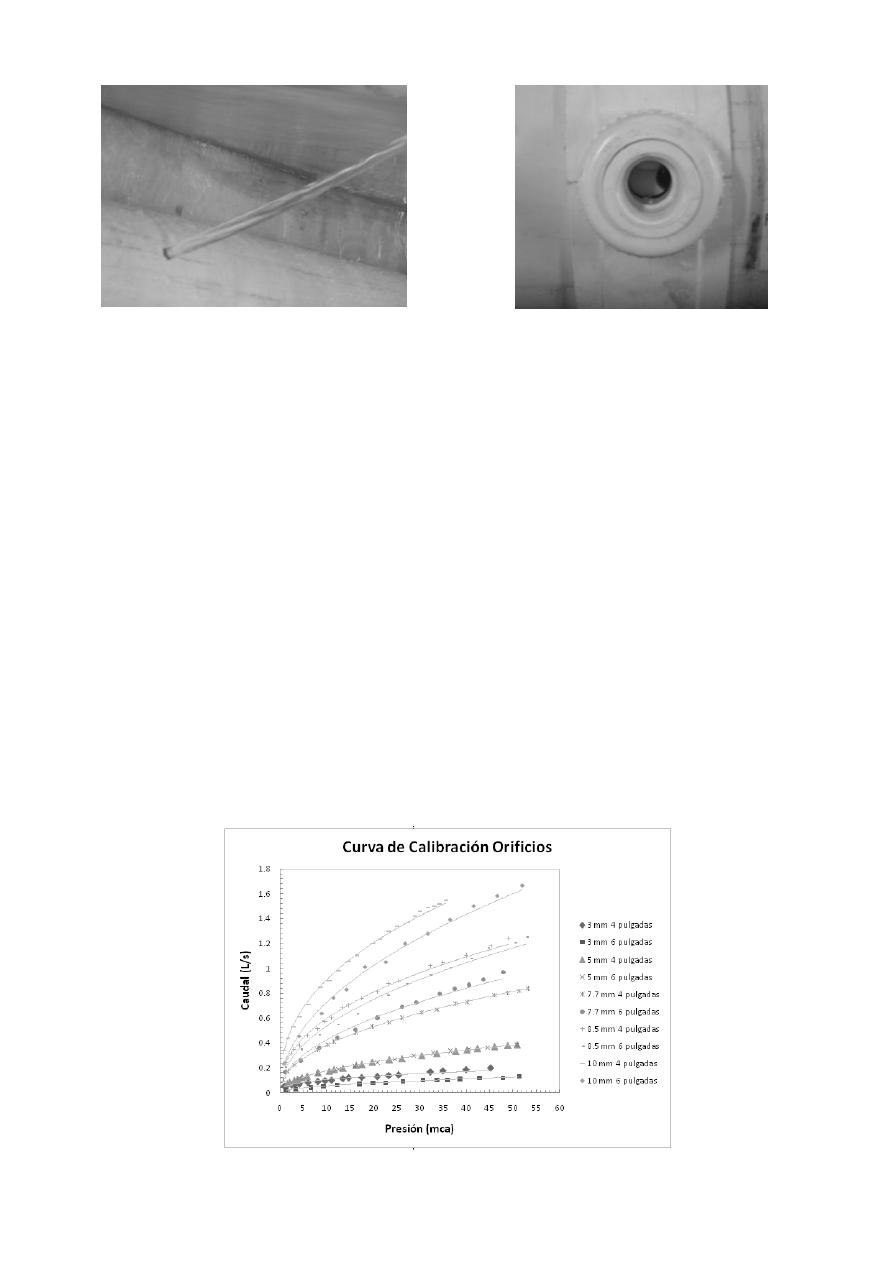
Figura 6.- Representación de los orificios.
Figura 7.- Representación de las fallas en
acometidas domiciliarias.
Cuando el montaje está listo, se comienza la toma de datos operando la válvula de entrada,
que varía la energía con la que ingresa el agua al sistema; estos cambios son medidos con el
manómetro digital. Se espera a que salga suficiente agua a través de la falla, para llenar el canal, y
para que la altura de flujo se estabilice aguas arriba del vertedero. Para la medición del nivel de la
lámina de agua, se usa el sensor electrónico junto con el software mencionado anteriormente. Una
vez se tiene la medida de la presión y el caudal, se abre o cierra la válvula de entrada y se repiten
todos los pasos. Para poder tener un banco de datos robusto, que permita un análisis estadístico
confiable, el proceso se repetía por lo menos para 20 combinaciones diferentes de variables.
RESULTADOS
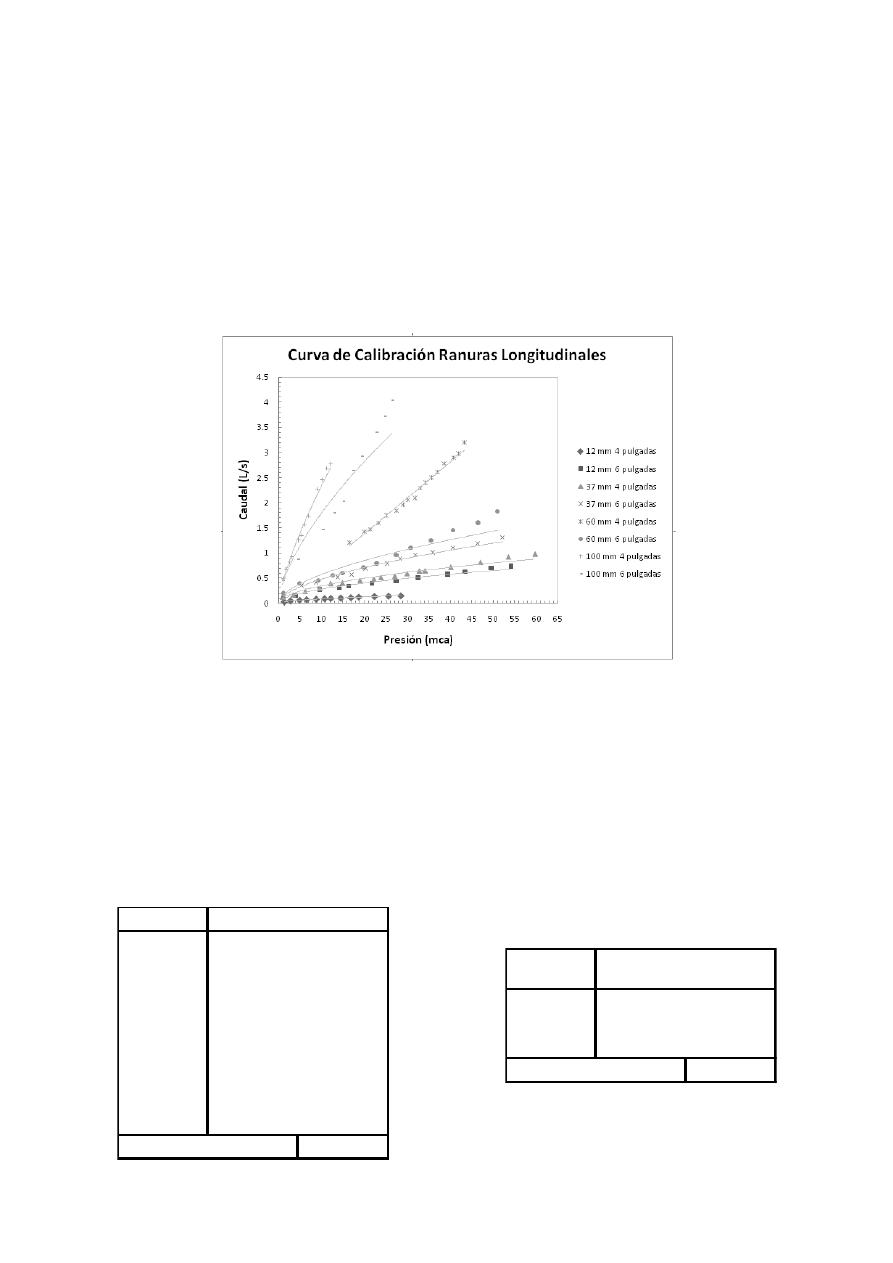
Luego de llevar a cabo las distintas pruebas, lo primero que se encuentra es que
efectivamente en la mayoría de los casos, el comportamiento de las distintas fallas puede ser
representado como un emisor. Como se puede apreciar en la Figura 8, los distintos puntos sea
ajustan de forma aceptable a las curvas, y los coeficientes de correlación casi siempre están por
encima del 90%. También se puede ver que en los orificios de 3, 8.5 y 10 mm, la curva de 4
pulgadas está por encima de la de 6 pulgadas; esto quiere decir que para estos casos, un mismo
valor de la presión produce mayores pérdidas en las tuberías pequeñas. Sin embargo, en el orifico
de 7.7 mm ocurre lo contrario, es decir que las pérdidas serían proporcionales al tamaño, para un
mismo valor de presión. Finalmente en el de 5 mm las dos curvas parecen sobreponerse, es decir
que no habría diferencia en el comportamiento dependiendo del tamaño.
Figura 8.- Curva de calibración de los orificios.
Un comportamiento similar se encuentra con las ranuras circunferenciales, y con los
collarines de derivación; sin embargo por la gran cantidad de datos, no se presentan todas las
gráficas. El caso contrario ocurrió con las ranuras longitudinales, cuyas curvas no parecen seguir
fielmente la misma dinámica. En la Figura 9 se puede ver que en los casos de 12 y 37 mm, existe
una tendencia similar entre ellas, que se puede asociar a los tipos de falla ya expuestos. Sin
embargo, para longitudes de 60 y 100 mm, las aproximaciones son bastante regulares, y en algunos
casos dejan dudas de la idoneidad de esta metodología para este tipo de fugas. La dispersión de los
datos es mucho mayor y por ende los coeficientes de correlación son mucho más bajos que los
anteriores. Es importante mencionar que los exponentes β para este caso, se encuentran entre 0.537
y 1.016, un rango bastante grande que explica el por qué de la diferencia de comportamiento entre
las distintas curvas y que deja muchas inquietudes sobre cómo representar estas pérdidas.
Figura 9.- Curva de calibración de las ranuras longitudinales.
En la Tabla 4 se pueden ver, para el caso de los orificios, los distintos valores de los
exponentes de la ecuación 1. Tal como se esperaba, la variación no es muy grande y el promedio
general se puede aproximar a 0.5. Esto quiere decir que sin importar el tamaño de la tubería, o las
características puntuales de la falla, las tendencias de las regresiones cuando estas son redondas,
tienden a ser similares. No se debe entender con esto que dada una presión y una geometría de la
fuga, se espera la misma descarga para cualquier tamaño; al contrario, dado que los coeficientes de
descarga no son los mismos la magnitud de la fuga varía según el caso. El punto es que las curvas
tienden a tener la misma forma para los orificios, independiente del resto de características.
Tabla 4.- Exponentes β para Orificios.
Tabla 5.- Exponentes β para collares de
derivación en conexiones domiciliarias.
Tubería
Orificio (mm)
β
5
0.4896
7,7
0.4679
8.5
0.4588
10
0.4279
3
0.5396
5
0.5007
7,7
0.5529
8.5
0.5365
10
0.5191
0.499
4 Pulgadas
6 Pulgadas
Promedio
Tubería
Collares
de
derivación
β
50%
0,5739
100%
0,574
Sin Empaque 0,73
0,623
4 Pulgadas
Promedio
En la Tabla 5 se puede observar el comportamiento de las fallas en conexiones
domiciliarias; en esta se evidencia principalmente que el porcentaje de desfase, no afecta
considerablemente el comportamiento de la fuga, y en cambio, la presencia o ausencia del empaque
si genera una variación importante. Los dos primeros valores se acercan un poco a los encontrados
con los orificios, lo que haría pensar que existen similitudes entre ambos fenómenos. En la Tabla 6
se encuentra la información para las ranuras longitudinales; como se mencionó anteriormente, la
variación encontrada es la más grande de todos los casos. El rango de valores se encuentra entre
0.537 y 1.016, es decir que para las longitudes mayores, este llega a ser casi el doble que para las
menores. Con base en esto, resulta muy complicado trabajar con un único exponente a la hora de
describir el caudal de fuga. Finalmente, en la Tabla 7 se encuentra la información de la última
prueba, las ranuras longitudinales. En ella se ve que el comportamiento es bastante similar al de los
orificios, y que exceptuando el caso de 12 mm en 6 pulgadas, la variación es mínima. Al respecto
de esta medición, se puede pensar que hubo un error procedimental que condujo a una diferencia
tan grande.
Tabla 6.- Exponentes β para Ranuras
longitudinales.
Tabla 7.- Exponentes β para Ranuras
circunferenciales.
CONCLUSIONES Y RECOMENDACIONES
Además de confirmar la relación existente entre la presión en la red, la geometría y el tipo de
la falla, con el caudal, se encuentra que vale la pena revisar algunos aspectos de la metodología, y
algunos de los rangos de los parámetros reportados en la literatura. Es evidente que para el caso de
los orificios no hay mucho por discutir; este tipo de acercamientos con exponentes cercanos a 0.5,
describen bastante bien este tipo de fugas. Sin embargo, para el caso de las ranuras
circunferenciales la variación de los exponentes es mucho mayor, y para pequeñas cambios en las
condiciones de entrada, los valores pueden diferenciarse considerablemente. Los resultados
encontrados en esta investigación (Tabla 7), y aquellos mencionados en los antecedentes (Tabla 2),
muestran heterogeneidad en el resultado que todavía no tiene una explicación clara. Es evidente que
a mayor tamaño las pérdidas aumentan, pero no se tiene una idea clara de cómo se da esta
asociación. Valdría la pena hacer un análisis de sensibilidad en las fallas, de esta forma se conocería
con mayor precisión, qué tanto afectan las características de la ranura a las variables de salida.
Teniendo en cuenta que de por sí, resulta bastante complejo definir qué tipos de falla se pueden
encontrar en una red, el hecho que existan nuevas incógnitas relacionadas con la geometría,
disminuirían bastante la aplicabilidad de esta metodología.
Para el caso de las ranuras longitudinales, los resultados muestran que el comportamiento
varía mucho más como función de las condiciones de entrada. En la Figura 9 se ve la poca precisión
que tuvieron algunas curvas al describir el comportamiento de la fuga; en algunos casos se puede
suponer que otro tipo de regresiones serían mucho más exactas. Además, si se comparan los
resultados de la Tabla 6 con los de la Tabla 2 y la Tabla 3, se puede ver que los rangos de variación
son mucho más grandes, y de nuevo, no se tiene una idea de cómo asociar las variables de entrada
Tubería
R. Longitudinal (mm) β
12
0.537
37
0.623
60
0.915
100
0.811
12
0.612
37
0.643
60
0.846
100
1.016
0.750
6 Pulgadas
Promedio
4 Pulgadas
Tubería
R.Circunferenciales (mm)
β
12
0.5581
37
0.4861
60
0.4296
100
0.4225
12
0.9828
37
0.4952
60
0.4888
100
0.4605
0.540
4 Pulgadas
6 Pulgadas
Promedio

con las de salida. En este caso ni siquiera se puede decir que hay proporcionalidad entre la geomtría
y el caudal fugado; en la figura mencionada se ve que en algunos casos es mayor en la tubería de
4”, y en otros es mayor en la de 6”. Un análisis de sensibilidad podría de nuevo ser una buena
opción, para dar una idea de la asociación entre las características y el resultado.
Por otro lado, teniendo en cuenta que se buscaba hacer un estimativo de la cantidad de agua
que se puede perder por fugas, se toma como presión de referencia en la red 25 mca, y se halla que:
para un orificio de 5 mm en una tubería de 4 pulgadas se está perdiendo 20.74 m
3
de agua al día. Si
se tiene en cambio, una ranura longitudinal o una circunferencial de 60 mm de longitud en una
tubería de 6 pulgadas, se estaría perdiendo entre 77.76 m
3
y 112.32 m
3
al día respectivamente. Estos
valores sin lugar a duda significan grandes pérdidas para los operadores, sobrecostos para los
usuarios y un pésimo uso de un recurso no renovable. Se podría pensar que esta presión es
exagerada para algunas zonas; sin embargo, en los puntos cercanos a los embalses, o zonas de
bombeo, resultaría antes muy bajo respecto al valor real.
En cuanto a los estudios de los collarines de derivación, se puede decir que este es un primer
acercamiento a unos accesorios que a pesar de su frecuente uso, no han sido asociados a las fugas o
al menos, no se ha estudiado su influencia en estas. Se pusieron a prueba dos casos fundamentados
en errores de instalación, para averiguar el comportamiento hidráulico de los mismos. A priori se
puede decir que este es bastante similar al encontrado con los orificios, y la variación dependiendo
del porcentaje de desfase es mínima. Por otro lado, el hecho de tener o no empaque hermético sí
constituye un factor que diferencia las situaciones, y por ende debe ser estudiado aparte. De todos
modos lo ideal es realizar más pruebas para corroborar lo encontrado en esta investigación,
haciendo variar porcentajes de desfase y diámetros de los tubos, y permitir así la generalización de
estas conclusiones.
Finalmente, a pesar que el presente trabajo no discute temas financieros de la gerencia de
redes, sí ayuda a confirmar que una metodología que busque manejar los excesos de presión en las
tuberías, puede reducir considerablemente los índices de fuga de caudales a través de distintas
fallas. El reto ahora consiste en cuantificar monetariamente la equivalencia de esta descarga, como
agua no facturada, para compararla con los costos de la reducción de las presiones, de
mantenimiento y otros, y averiguar qué tan factible resulta realizar estos cambios en las estrategias
de las compañías.
REFERENCIAS
Ardakanian, R., & Ghazali, A. (2003). “Pressure-Leakage relation in Urban Water distribution
system”. ASCE, 304-312.
Ávila, H. F. (2003). “Determinación de parámetros de fugas para fallas longitudinales y en
conexiones domiciliarias en tuberías de PVC”. Bogotá: Universidad de los Andes.
Buckley, R. S. (2006). “Theoretical investigation and experimentation into the expansion of round
holes and cracks within pressurised pipes”. Univerity of Johannesburg. Johannesburg.
Cassa, A., Van Zyl, J., & Laubscher, R. (2006). “A numerical investigation into the behaviour of
leak openings in uPVC pipes under pressure”. South African Biennial conferece and exhibition ,
WISA 2006.
Burnell, D., & Race, J. (2000). “Water distribution system analysis, patterns in water supply pipes
leakeage”. ASCE EWRI conference, Minneapolis.
Farley, M., & Trow, S. (2003). “Losses in water distribution networks”. IWA Publishing, London .
Ferrante, M., Massari, C., Brunone, B., & Meniconi, S. (2010). “Leakage and pipe materials”.
Water Distribution System Analysis , USA.
Greyvenstein, B., & Van Zyl, J. (2007). “An experimental investigation into the pressure- leakage
relationship of some failed water pipes”. Aqua- Journal of Water Supply: Research and
Technology, 56(2), 117-124.

Martínez, F., Conejos, P., & Vercher, J. (1999). “Developing an integrated model for water
distribution system considering both distribution leakage and presure-dependent demands”. ASCE
Water Resourse Conferene .
Mays, J. (1994). “Leakege, presure an Control”. BICS International conference on leakage control ,
London.
PAVCO. (2008). Manual Técnico: Tubosistemas Biaxial PVC Biorientado Dúctil. Recuperado el 1
de 12 de 2010, de http://www.pavco.com.co/files/data/20081216135146_s.pdf
Stathis, J. A., & Loganathan, G. V. (2000). “Analysis of pressure dependent leakeage in water
distribution system”. ASCE water resources conference.
Van Zyl, J. E., & Clayton, C. (2007). “The effect of pressure on leakage in water distribution
system”. Water Management 160 issue WM2 , 109-114.
Walski, T., Bezts, W., Posluszny, E., Weir, M., & Whitman, B. (2004). “Understanding the
hydraulics of water distribution system leaks” W. W. Congress, Ed. ASCE , 1-9.
