
IAHR
CIC
XX SEMINARIO NACIONAL DE HIDRÁULICA E HIDROLOGÍA
BARRANQUILLA, COLOMBIA, 8 AL 10 DE AGOSTO DE 2012
CRITERIOS DE DISEÑO DE TUBERÍAS FLUYENDO PARCIALMENTE
LLENAS: VELOCIDAD, ESFUERZO CORTANTE Y NÚMERO DE FROUDE
Freddy Ovalle, Juan Ossa, Andrés López, Juan Saldarriaga
Centro de Investigación en Acueductos y Alcantarillados de la Universidad de Los Andes –CIACUA–, Departamento
de Ingeniería Civil y Ambiental, Bogotá, Colombia, <f-
ovalle@uniandes.edu.co><da.lopez47@uniandes.edu.co><jsaldarr@uniandes.edu.co>
RESUMEN:
La metodología tradicional para el diseño de tuberías de alcantarillado se basa en dos requisitos: La
hidráulica y los factores ambientales. La hidráulica garantiza que dados ciertos parámetros de entra-
da (materiales, topografía y propiedades del fluido) se transporte el caudal demandado, evitando
ciertas condiciones no deseables como el incumplimiento de la restricción de máxima relación de
llenado; por otra parte, los factores ambientales deben ser tenidos en cuenta para evitar la sedimen-
tación de partículas y la formación de barreras que terminen por obstruir total o parcialmente el duc-
to, razón por la cual es importante diseñar bajo los criterios de velocidad y esfuerzo cortante míni-
mo, para facilitar la autolimpieza de la tubería. La concepción anterior se basaba en llevar a cabo un
diseño con los dos requisitos mencionados anteriormente, de tal manera que se garantizara el trans-
porte del caudal de diseño en la red para los parámetros previamente establecidos, sin implementar
métodos de optimización, razón por la cual se pueden obtener diseños sobredimensionados que au-
mentan innecesariamente el costo de los proyectos. Por lo tanto, es importante plantear un método
que permita encontrar el diseño óptimo, garantizando el cumplimiento de las restricciones construc-
tivas e hidráulicas por medio de la selección de la alternativa de costo mínimo. Partiendo de lo ante-
rior, en este trabajo se desarrolló un método de selección basado en una revisión exhaustiva de to-
das las alternativas posibles para un diseño dado, en el cual se evalúan todos los diseños factibles
(cumpliendo con las restricciones constructivas e hidráulicas), y se seleccionan solo aquellas alter-
nativas en las cuales la pendiente genera la máxima relación de llenado posible para un diámetro
determinado.
PALABRAS CLAVES: Pendientes propias; Diseño de alcantarillados; Optimización.

INTRODUCCIÓN
En la práctica de la Ingeniería, uno de los factores más importantes para la aprobación y eje-
cución de un proyecto es la valoración de costos globales de éste, razón por la cual la búsqueda de
la alternativa más económica que satisfaga a cabalidad todas las necesidades del proyecto, se con-
vierte en un proceso primordial dentro de su desarrollo.
El diseño de sistemas de drenaje urbano no debe ser la excepción al planteamiento anterior,
por el contrario, teniendo en cuenta el crecimiento evidente de las áreas urbanas y el aumento de
áreas impermeables que esto conlleva, es vital que estos sistemas sean diseñados de tal manera que
cumplan tanto con los requisitos hidráulicos como ambientales, enfocados en evitar problemas de
sanidad, inundaciones y contaminación en los cuerpos de agua, mediante la selección de la alterna-
tiva de mínimo costo.
Para satisfacer lo anterior, la concepción actual de los sistemas de drenaje urbano contrasta
con la que se tenia en el pasado, ya que contempla una visión integral de sus tres componentes: El
primero de ellos consiste en la red de drenaje, el segundo corresponde a la planta de tratamiento de
aguas residuales (PTAR) y el tercero se refiere al cuerpo receptor.
En el caso particular de este artículo, se presenta un método exhaustivo que cumple con las
restricciones constructivas y los parámetros hidráulicos, garantizando la selección del diseño óptimo
global al realizar una comparación de los costos constructivos de todas las alternativas posibles.
ANTECEDENTES
A finales del siglo XIX, las ecuaciones de Bazin y de Ganguillet y Kutter eran las más utili-
zadas para el cálculo de la velocidad en canales abiertos bajo la suposición de flujo uniforme; no
obstante, ésta última empleaba métodos tediosos para su solución y presentaba problemas dimen-
sionales. Debido a esto Robert Manning, partiendo de un ajuste realizado a 7 ecuaciones aproxima-
das para la velocidad en canales abiertos bajo la suposición de flujo uniforme (ecuaciones de Du
Buat (1786), Eytelwein (1814), Weisbach (1845), St. Venant (1851), Neville (1860), Darcy y Bazin
(1865) y Ganguillet y Kutter (1869)) llevó a cabo un cálculo de la velocidad para cada fórmula con
un rango del radio hidráulico entre 0.35 y 30 m para una pendiente dada. Con los resultados obteni-
dos, concluyó que la velocidad era proporcional a la pendiente elevada a la 1/2 y al radio hidráulico
elevado a la 4/7. Sin embargo, con el objetivo de obtener una ecuación más general, Manning anali-
zó los resultados de algunos experimentos seleccionados de Bazin en canales semicirculares reves-
tidos de cemento y con una mezcla de arena y cemento, a partir de los cuales concluyó que el expo-
nente para el radio hidráulico en ambos casos era muy cercano a 2/3, dando lugar a la siguiente
ecuación (Chie, 1991):
[1]
Es importante aclarar que el C
1
mostrado en la Ecuación [1] se refiere a un coeficiente pro-
puesto por Manning, el cual difiere del coeficiente propuesto por Chezy. Adicionalmente, el expo-
nente del radio hidráulico (2/3) fue sugerido en primera instancia por el Ingenierio Francés Gau-
ckler en 1867, el cual, al igual que Manning, basó su estudio en los experimentos desarrollados por
Darcy y por Bazin. Por esta razón la fórmula de Manning también es conocida como la fórmula de
Gauckler Manning.
Finalmente, Alfred Flamant sugirió que el C
1
propuesto por Manning podría expresarse como
el recíproco del n de Kutter en unidades simétricas, afirmación que fue presentada en textos subse-
cuentes y en 1918 el hidráulico americano King denominó éste coeficiente como el n de Manning;
resultando la ecuación que se conoce hoy en día como tal.
[2]
donde K
n
es igual a 1 en el Sistema Internacional y 1.49 para el Sistema Inglés.
A pesar de que la ecuación de Manning ha sido ampliamente utilizada en el diseño de tube-
rías fluyendo parcialmente llenas, diferentes estudios demuestran que debido a que es una formula-
ción empírica, ésta ecuación pierde validez para el diseño de alcantarillados que usan materiales
modernos, los cuales, debido a su baja rugosidad, presentan Flujo Turbulento Hidráulicamente Liso
(FTHL), y la ecuación de Manning solo funciona para FlujoTurbulento Hidráulicamente Rugoso
(FTHR). Por lo tanto, usar la ecuación de Manning con régimen de FTHL genera el sobredimensio-
namiento de la tubería en un 20% aproximadamente, lo cual incurre en un aumento de los costos del
diseño.
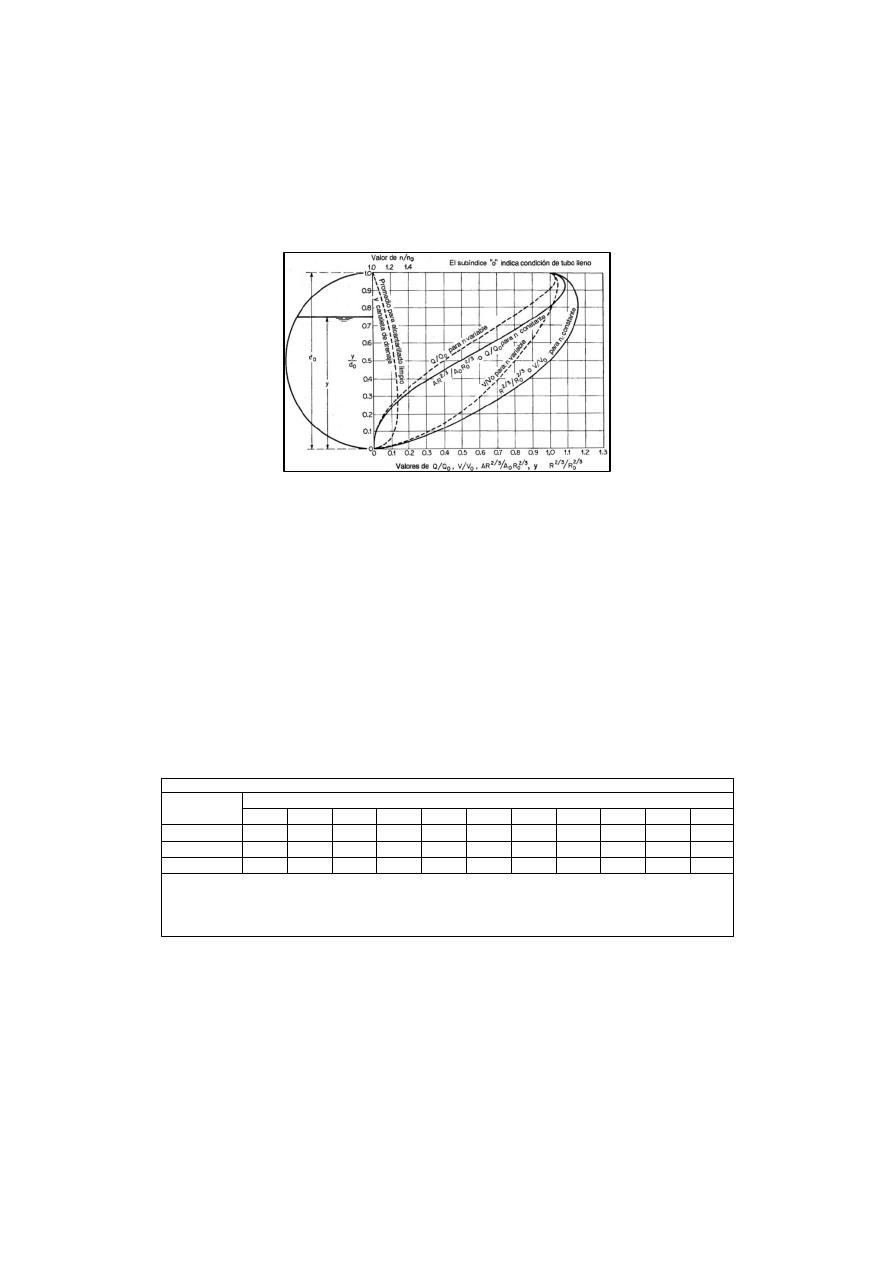
Figura 1.- Características del flujo para una sección circular con n de Manning constante y variable. (T.R.
Camp, s.f.)
En la Figura 1, se observa que para los diseños generados con valores del coeficiente de n de
Manning variable, el caudal máximo se encuentra para una profundidad ligeramente superior al
90% del diámetro interno y tiene una magnitud total de 1.07 veces el caudal a tubería llena. Mien-
tras que al utilizar el n de Manning constante el caudal máximo se encuentra a la misma profundi-
dad, pero su magnitud es de 1.18 veces el caudal de la tubería llena.
Por esta razón, la Sociedad Americana de Ingenieros Civiles (ASCE – American Society of
Civil Engineers) planteó una tabla en la cual, dependiendo del diámetro de la tubería, adopta un
rango válido para el coeficiente de Manning (mostrando 3 valores por cada diámetro, para diseños
conservadores, diseños menos conservadores, y los valores típicos).
Tabla 1. – Valores recomendados del n de Manning para cálculos en el diseño de alcantarillados
(ASCE , 2007)
BASE TEÓRICA
Las redes de drenaje urbano que están compuestas principalmente por tuberías, cámaras, sis-
temas de almacenamiento temporal, aliviaderos y estructuras de disipación de energía. Son las en-
cargadas de recolectar el agua residual y las aguas lluvias desde los sitios donde se generan hasta el
sitio final de disposición, que dependiendo de la capacidad de depuración del cuerpo receptor puede
ser éste o la PTAR.
El proceso de diseño de la red de drenaje urbano está obligado a cumplir con unas restric-
ciones de diseño y unos parámetros determinados por las características de la zona.
TABLE 5-2 Suggested Values of Manning for sewer Design Calculations
Condition
Pipe Diameters in inches
6
8
10
12
15
18
24
30
36
48
60
Extra Care
0.0092 0.0093 0.0095 0.0096 0.0097 0.0098 0.0100 0.0102 0.0103 0.0105 0.0107
Typical
0.0106 0.0107 0.0109 0.0110 0.0112 0.0113 0.0115 0.0117 0.0118 0.0121 0.0123
Substandard
0.0120 0.0121 0.0123 0.0125 0.0126 0.0127 0.0130 0.0133 0.0134 0.0137 0.0139
Note: Extra care values are calculated from the Darcy-Weisbach equation for 60 °F, 2 fps velocity, ε = 0.001 ft.
Typical values are 15% higer than Extra Care values; Substandard values are 30% higers thatn Extra Care values.
After Haestad, M. et al. (2004). Wastewater colletion system modeling and design, Haestad Press, Waterbury.
Conn, with permission

Restricciones de diseño
La normatividad está regulada por normas nacionales, en el caso de Colombia estas están
dadas por el Reglamento Técnico del Sector de Agua Potable y Saneamiento Básico – RAS. Las
restricciones se muestran en la Tabla 2.
Tabla 2.- Restricciones de diseño (Ministerio de Ambiente, vivienda y desarrollo, 2010)
El porcentaje de llenado se elige dependiendo del tipo de flujo, para flujos cuasicríticos en
los que el Número de Froude está entre 0.75 a 1.5 el porcentaje no puede exceder el 70%.
Diseño Hidráulico de redes de drenaje urbano
El proceso de diseño consiste en determinar cuáles son los diámetros de las tuberías que
transportan el caudal de diseño al igual que las pendientes más apropiadas para minimizar los cos-
tos. Para esto es necesario variar el diámetro de diseño al igual que la pendiente hasta que se cumpla
con el caudal de diseño, como se explicará en la metodología. Para esto es importante hacer uso de
la ecuación de conservación de la masa (ver Ecuación [6]).
[6]
donde Q es el caudal de diseño, v es la velocidad de flujo y A es el área mojada, la cual está
determinada geométricamente según el diámetro y el porcentaje de llenado. Existen diferentes for-
mas de calcular la velocidad de flujo; en este trabajo se utiliza la ecuación que resulta del cálculo de
las pérdidas por fricción haciendo uso de la ecuación de Darcy-Weisbach (Ecuación [7]) y la ecua-
ción de Colebrook-White (Ecuación [8]) para el cálculo del factor de fricción.
[7]
(
√
)
[8]
Obteniendo así una expresión de la velocidad que se cumple para todo tipo de flujo (ver
Ecuación [9]).
√
(
√
)
[9]
Restricción
Valor
unidad
Drenaje Sanitario
Drenaje Pluvial
Diámetro mínimo
200
250
mm
Velocidad mínima
0.45
0.75
m/s
Velocidad máxima
(Concreto-PVC)
5-10
5-10
m/s
Esfuerzo cortante mínimo
0.5
0.5
Pa
Relación de llenado máxima
70%-85%
70%-85%
-
Número de Froude cuasicrítico
0.75-1.5
0.75-1.5
-
Profundidad mínima cota clave
(Vías peatonales o zonas verdes)
0.7
0.7
m
Profundidad mínima cota clave
(Vías vehiculares)
1.2
1.2
m
Profundidad máxima cota clave
5
5
m

donde, h
f
es la pérdida de altura por fricción, f es el factor de fricción,
es la longitud del tu-
bería, d es el diámetro de la tubería, v es la velocidad de flujo, R es el radio hidráulico, k
s
es la ru-
gosidad y Re es el número de Reynolds.
METODOLOGÍA
Diseñar un tramo de un sistema de alcantarillado, entendido como la serie de tuberías que co-
nectan dos cámaras de inspección, consiste en encontrar un diámetro y una pendiente que permitan
el flujo de un caudal de diseño, a través de tuberías de un material determinado. Con el fin de sim-
plificar los cálculos y enmarcar el problema dentro de un contexto realista, se estableció una meto-
dología en la que la pendiente es una variable discreta, comprendida en el intervalo [0.001; 0.1] con
pasos de 1/1000, con el objetivo de no violar restricciones de velocidades mínimas y máximas. Las
pendientes candidatas para el diseño se denominan Pendientes Propias, concepto que se explica en
el siguiente apartado. Luego de esto, se expone una metodología para evaluar la viabilidad de dis-
poner una serie de tramos de alcantarillado, y encontrar de manera exhaustiva el conjunto que im-
plica los menores costos constructivos. Éstos se calculan haciendo uso de la expresión (Navarro,
2009):
(
)
[10]
donde C es el costo en pesos colombianos al año 2011, k es un factor de conversión que de-
pende de la inflación desde el año 2007, d es el diámetro de la tubería en metros y V es el volumen
de tierra excavado, en metros cúbicos. Nótese que sólo se incluyen los costos asociados a la compra
de la tubería, y a la excavación necesaria para su instalación, en donde entran a jugar la pendiente y
la longitud de ésta. Hay que tener en cuenta que este análisis no contempla los costos de las cámaras
de inspección, ni diseños que usen estaciones de bombeo. Todo el análisis se desarrolla suponiendo
que la pendiente del terreno es cero.
Pendiente Propia
La idea de pensar en la pendiente como una variable discreta tiene sentido si se observa el
problema desde la perspectiva del topógrafo. En el momento de instalar la tubería, éste va a tener
serias dificultades si la pendiente propuesta por el diseñador tiene una precisión mayor o igual a
3/1000. Es por esto que se limita la pendiente a los valores anteriormente descritos.
Es posible encontrar diseños que sean válidos para cualquier pendiente del intervalo [0.001;
0.1]. Sin embargo, no todos son apropiados ya que algunas de las pendientes harán que la profundi-
dad de agua sea más baja que el límite permitido, desaprovechando parte de la capacidad de la tube-
ría para dicho diámetro. Por lo tanto, la pendiente discreta que hace que por un diámetro determina-
do pase el caudal de diseño con la máxima relación de llenado posible, se denomina Pendiente Pro-
pia.
Algoritmo de Diseño de Tuberías de Alcantarillado
Los datos que se conocen para realizar cada diseño son: material del tubo, una pendiente que
pertenece al conjunto anteriormente definido y el caudal de diseño. El proceso que se sigue para
encontrar el diámetro comienza por tomar el menor valor de una lista de diámetros discretos dada
por los fabricantes. Para cada diámetro interno se establece el máximo porcentaje de llenado posible
según su valor, como se estipula en una versión preliminar del nuevo RAS: 70% si es menor a 0.5
metros; 85% si es mayor a 1 metro y 80% en los demás casos. Con esta relación de llenado es posi-
ble calcular la profundidad de flujo y el radio hidráulico resultante. Haciendo uso de las ecuaciones
[9] y [6] se encuentra el máximo caudal que puede transportar una tubería del material establecido
con el diámetro escogido y disponiendo la tubería con la pendiente que se conoce. En caso de que
este caudal máximo no sea mayor al caudal de diseño, se escoge un diámetro mas grande, reco-
rriendo la lista ordenada de diámetros de menor a mayor, y se repite el proceso hasta encontrar un
diámetro que tenga capacidad suficiente para transportar el caudal de diseño.
Habiendo encontrado el diámetro, se procede a calcular la profundidad normal de flujo que se
genera cuando, por esa tubería fluye el caudal de diseño. Ya que las ecuaciones son implícitas no es
posible hallar el valor de forma directa, razón por la cual se deben usar métodos numéricos. Se ha
diseñado un método basado en las ecuaciones hidráulicas, que mostró menor tiempo de convergen-
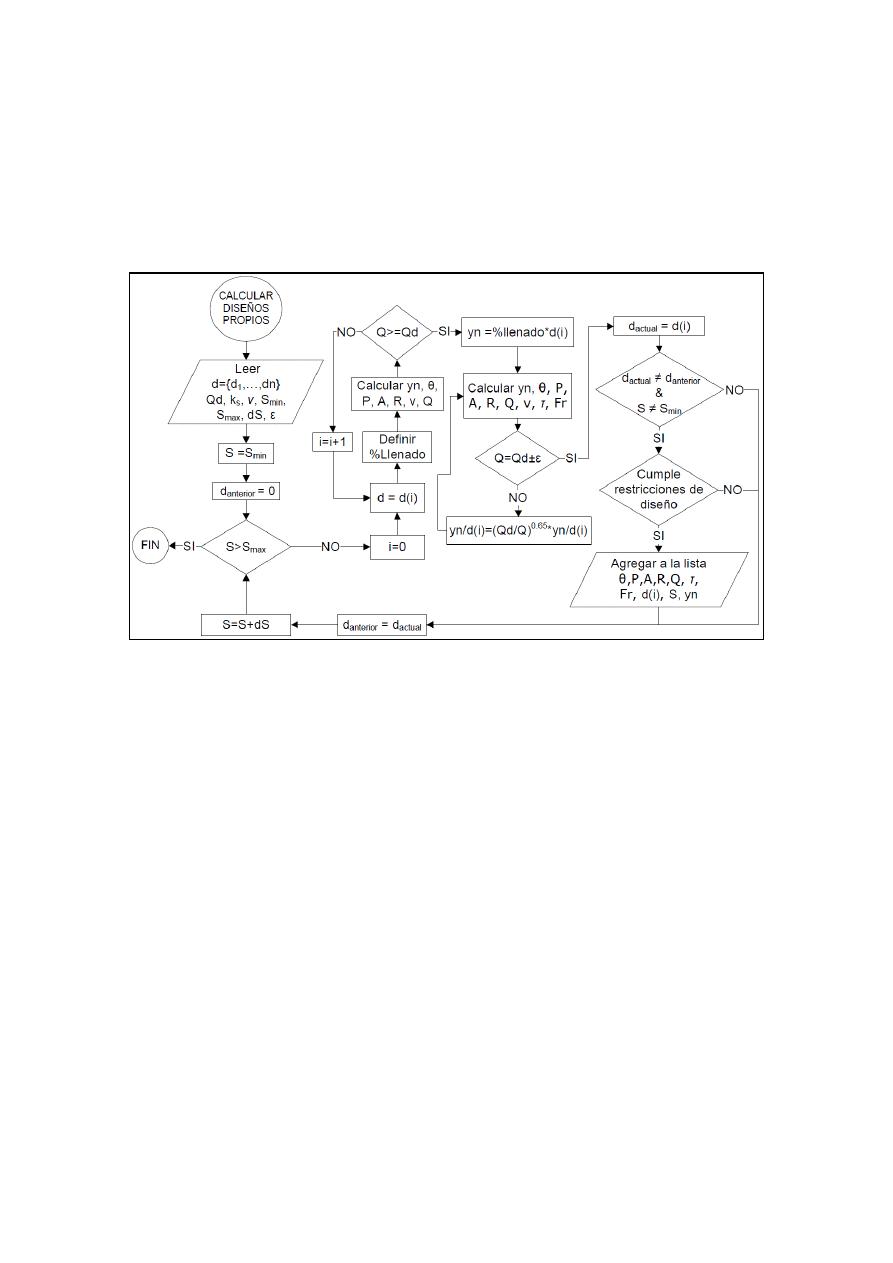
cia frente a los métodos numéricos de búsqueda de raíces tradicionales (ver Figura 2).
Figura 2.- Diagrama de flujo seguido para el proceso de diseño.
Si se observa con detenimiento el algoritmo, para encontrar los diseños propios (que corres-
ponden a aquellos diámetros calculados usando pendientes propias) basta con recorrer el intervalo
de pendientes de menor a mayor haciendo un diseño para cada valor. En el momento en el que el
diámetro resultante del diseño se vea disminuido con respecto al diseño anterior, se tiene una rela-
ción de llenado máxima para ese diámetro y, por lo tanto, un diseño propio. El diseño será tenido en
cuenta siempre y cuando cumpla con las restricciones hidráulicas establecidas en la norma.
Diseño de Sistemas de Alcantarillado
Cuando se diseña la línea principal de una red de alcantarillado, según la norma colombiana,
el diseñador tiene la responsabilidad de seleccionar la alternativa que implique los costos más bajos.
Para abordar el problema hay que pensar en la línea principal de una red de alcantarillado como la
serie de tramos más larga que recibe todos los flujos de una cuenca, llevándolos hasta el cuerpo
receptor. Se sabe que cada tramo tiene un conjunto de diseños propios posibles, que cumplen con
las restricciones hidráulicas. Una alternativa es aquella combinación de diseños propios hecha en
los tramos que conforman la línea principal de una red de alcantarillado. De esta manera se tiene
que el número total de alternativas es:
∏
[11]
donde n es el número de tramos y NPP
i
es el número de pendientes propias del tramo i-ésimo.
Dos de las restricciones adicionales que se establecen a la hora de diseñar sistemas de alcanta-
rillado corresponden a los límites de profundidad en los que deben disponerse los colectores; y el
hecho de que una tubería aguas abajo no puede tener un diámetro inferior al que tienen las tuberías
de aguas arriba. Buscando que el diseñador sea capaz de encontrar la alternativa de menor costo, se
propone una metodología de evaluación de alternativas de carácter exhaustivo, que verifica el cum-
plimiento de las restricciones establecidas para una línea de tramos de alcantarillado dispuestos en
serie. Esto se logró haciendo uso de herramientas computacionales, en las que se construyeron es-
tructuras de datos en forma de árbol, con tantas ramificaciones como alternativas se desprenden de
cada tramo. Al final de cada rama, se obtienen la misma cantidad de hojas como alternativas existan
en el problema, por lo que la ecuación [11] también es útil para calcular el número de rutas posibles
en la estructura de datos.
La evaluación de alternativas se lleva a cabo recorriendo la estructura de datos una única vez,
con el fin de optimizar el tiempo de ejecución. A medida que se encuentran alternativas válidas, se
construye otra estructura de datos, que contiene diseños enlazados linealmente. Al final de la ejecu-
ción, la estructura de datos contiene una lista de alternativas que cumplen con las restricciones. En
este punto, se calculan los costos de cada alternativa, con el fin de encontrar aquella que correspon-
de a la de costo constructivo menor, garantizando un mínimo global, puesto que el proceso se desa-
rrolla de manera exhaustiva.
RESULTADOS
Diseño de Tuberías de Alcantarillado
En el presente apartado se muestran los resultados de la ejecución del algoritmo que se mues-
tra en la Figura 2, y la forma como son identificadas las restricciones hidráulicas y las pendientes
propias de un tramo particular. Para un caudal de diseño de 82 L/s y un tramo de tuberías de PVC
de 75 metros de longitud, se obtienen los siguientes diseños.
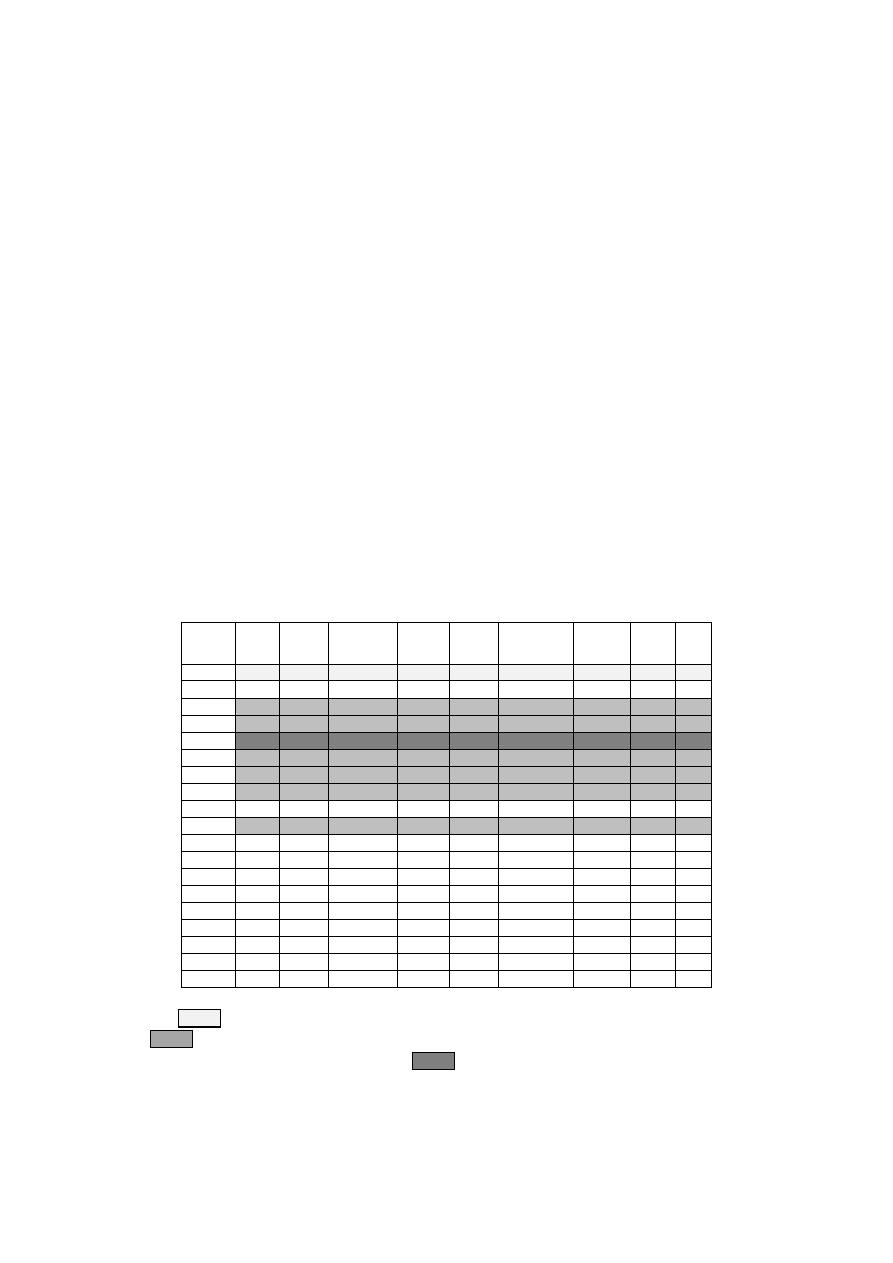
Tabla 3.- Diseños obtenidos con sus respectivas restricciones para el ejemplo.
Diseño
S
d
d interno
yn
yn/d Velocidad Caudal
T
Fr
[ - ]
[ - ] [pulg]
[m]
[m]
[ - ]
[m/s]
[m
3
/s]
[Pa] [ - ]
1
0.001
27
0.6858
0.5212 76.0%
0.996
0.3000 2.03 0.44
2
0.002
24
0.6096
0.4457 73.1%
1.312
0.3000 3.59 0.64
3
0.003
24
0.6096
0.3822 62.7%
1.558
0.3000 5.09 0.87
4
0.004
24
0.6096
0.3470 56.9%
1.749
0.3000 6.46 1.05
5
0.005
20
0.508
0.3752 73.9%
1.869
0.3000 7.49 1.00
6
0.006
20
0.508
0.3486 68.6%
2.023
0.3000 8.80 1.15
7
0.007
20
0.508
0.3293 64.8%
2.158
0.3000 10.04 1.29
8
0.008
20
0.508
0.3143 61.9%
2.278
0.3000 11.24 1.41
9
0.009
20
0.508
0.3020 59.4%
2.389
0.3000 12.39 1.52
10
0.01
18
0.4572
0.3180 69.6%
2.461
0.3000 13.26 1.46
11
0.011
18
0.4572
0.3067 67.1%
2.562
0.3000 14.40 1.57
12
0.012
18
0.4572
0.2971 65.0%
2.656
0.3000 15.51 1.67
13
0.013
18
0.4572
0.2888 63.2%
2.745
0.3000 16.59 1.76
14
0.014
18
0.4572
0.2815 61.6%
2.828
0.3000 17.66 1.85
15
0.015
18
0.4572
0.2750 60.2%
2.908
0.3000 18.70 1.93
16
0.016
18
0.4572
0.2692 58.9%
2.984
0.3000 19.73 2.01
17
0.017
18
0.4572
0.2639 57.7%
3.056
0.3000 20.75 2.09
18
0.018
18
0.4572
0.2591 56.7%
3.126
0.3000 21.75 2.17
19
0.019
16
0.4064
0.2794 68.7%
3.156
0.3000 22.30 2.01
donde corresponde a los diseños que incumplen con la restricción de esfuerzo cortante
mínimo; corresponde a los diseños que presentan un número de Froude entre 0.7 y 1.5, pero
que no incumplen con ninguna restricción; y corresponde a los diseños con número de Froude
entre 0.7 y 1.5 pero con una relación de llenado mayor al 70%. Los diseños propios son aquellos en
los que para un mismo diámetro se consigue la máxima relación de llenado. En la Tabla 3, los dise-
ños propios son: 2, 5, 10, 19.
El método numérico usado para encontrar la profundidad de flujo (yn) que se genera cuando
por una tubería conocida fluye el caudal de diseño, resultó ser muy eficiente. Esto se debe a que el
método está basado en un análisis hidráulico del problema a diferencia de otros métodos numéricos
tradicionales que mostraron un desempeño más bajo, como se muestra en la Tabla 4.
Tabla 4.- Iteraciones promedio para la convergencia de yn por diferentes métodos numéricos.
Método
Iteraciones Promedio
Hidráulico
3.07
Secante
3.45
Falsa posición
3.57
Bisección
8.20
Las iteraciones promedio se calcularon a partir de las iteraciones que presentaban cada uno de
los métodos cuando se usaban diferentes datos de entrada. Los datos de entrada que se usaron fue-
ron los mismos para todos los métodos y se probaron diferentes materiales. La precisión (ε) usada
en todos los métodos fue la misma.
Diseño de la rama principal de Alcantarillado
Se muestra el diseño de una línea principal de alcantarillado que consta de 10 tramos en serie,
hechos en PVC, con los datos que se muestran en la Tabla 5.
Tabla 5.- Datos usados para el diseño de una línea principal de alcantarillado.
Tramo N° Diseños Propios Caudal Longitud
[ - ]
[ - ]
[ m
3
/s ]
[ m ]
1
2
0.020
120
2
3
0.032
105
3
4
0.048
105
4
4
0.058
105
5
5
0.064
120
6
5
0.070
120
7
4
0.082
75
8
5
0.090
120
9
5
0.100
105
10
5
0.110
105
Se tiene que hay 1’200 000 alternativas posibles de combinar los diseños de los tramos. Lue-
go de ejecutar la evaluación exhaustiva, se llegó a que únicamente 152 alternativas cumplían con las
restricciones, y se estableció que la profundidad mínima de cota clave correspondía a la de una vía
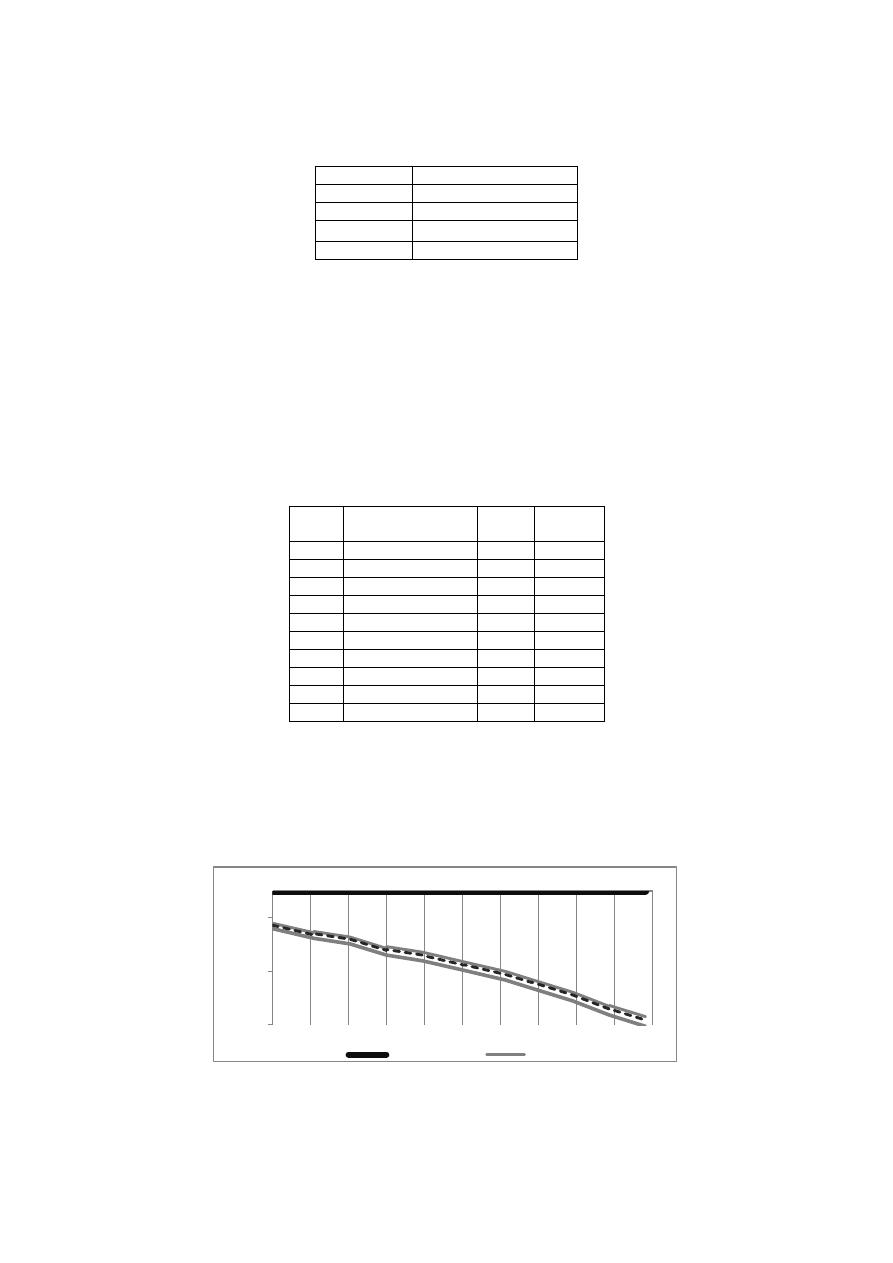
vehicular. Finalmente, los perfiles que forman los diseños de mayor y menor costo se muestran en
las Figuras 3 y 4 respectivamente.
Figura 3.- Perfil de la alternativa válida de costo mínimo.
-5,0
-3,0
-1,0 0
110
220
330
440
550
660
770
880
990 1100
D
istan
ci
a
Ver
tical
(m
)
Distancia Horizontal (m)
Perfil de la alternativa de menor costo
Terreno
Cota Clave

Figura 4.- Perfil de la alternativa válida de mayor costo.
La rutina que realizó la evaluación de 1’200 000 alternativas de forma exhaustiva, tardó 18
segundos en finalizar de manera exitosa la tarea. Esto se consiguió a través del uso de estructuras de
datos adecuadas para la búsqueda de caminos que cumplan con restricciones específicas.
ANÁLISIS DE RESULTADOS
El diseño de tuberías de alcantarillado es un problema especial, ya que involucra el cálculo de
dos variables que son discretas. La evaluación de un conjunto discreto de pendientes es una simpli-
ficación realista del problema, ya que se ajusta a las restricciones de diseño que están establecidas
en las normas. En el momento en el que se escogen pendientes propias para definir alternativas de
diseño para los tramos, se garantiza que al alcanzar el período de diseño, las tuberías van a ser utili-
zadas en su capacidad apropiada. Esta capacidad corresponde a la máxima posible que cumple con
todas las restricciones de diseño.
El uso de un método hidráulico para la convergencia de la profundidad normal de flujo permi-
te hacer diseños de una manera más eficiente, en comparación con el uso de otros métodos numéri-
cos. Esto ocurre ya que el método está basado en un análisis hidráulico del problema, la cual co-
rresponde a la filosofía que hay detrás de los métodos modernos de optimización en hidráulica, pues
hacen uso de funciones objetivo y restricciones que obedecen principios netamente hidráulicos.
El problema de diseño de líneas principales de alcantarillado se simplifica enormemente al es-
tablecer la pendiente como una variable discreta. Este planteamiento permite evaluar alternativas
finitas de diseño, lo que abre la posibilidad de hacer análisis exhaustivos en la evaluación de alter-
nativas. A partir de los resultados de este proceso, es posible encontrar un costo mínimo global que
resulta ser un diseño que cumple con todas las restricciones. El uso de estructuras de datos que per-
mitan evaluar el cumplimiento de restricciones a través de múltiples caminos, resulta fundamental a
la hora de establecer metodologías eficientes para realizar cálculos exhaustivos.
Se observa que de manera consistente, los diseños de menor costo tienen pendientes pequeñas
en los primeros tramos, y éstas van aumentando a medida que se avanza en la línea principal de
alcantarillado. De manera inversa ocurre con los diseños de mayor costo, pues estos presentan las
pendientes más altas en los primeros tramos las cuales van disminuyendo hacia el final de la línea
principal. Esto último es lo que ocurre generalmente en el drenaje natural, puesto que en una cuenca
el agua fluye en la dirección que presenta mayor gradiente de elevación. Esto hace que los perfiles
de elevación de los cursos de agua tengan, generalmente, pendientes empinadas al inicio y pendien-
tes bajas en su desembocadura.
CONCLUSIONES
La idea de realizar diseños exhaustivos cobra gran validez a través del uso de herramientas y
técnicas computacionales modernas, que al ser implementadas de manera adecuada, reducen
notoriamente los tiempos de cálculo.
-6,0
-4,0
-2,0
0,0
0
110 220 330 440 550 660 770 880 990 1100
D
istan
ci
a
Ver
tical
(m
)
Distancia Horizontal (m)
Perfil de la alternativa de mayor costo
Terreno
Cota Clave

En hidráulica, siempre que se planteen problemas de optimización, las restricciones, las fun-
ciones objetivo y los métodos numéricos usados, deben partir de análisis físicos e hidráuli-
cos que se enfoquen en el comportamiento de las variables en situaciones reales. De esta
manera se garantiza que la búsqueda de valores óptimos sea lo más eficiente posible.
Los procesos de optimización son muy importantes ya que por medio de éstos se puede rea-
lizar una valoración exhaustiva de alternativas en un tiempo corto, lo que se ve reflejado en
una reducción tanto de tiempos operacionales como de costos constructivos.
La metodología de diseño seleccionada es efectiva, ya que garantiza la valoración de todas
las alternativas posibles para un proyecto dado; de tal manera que después de realizar una
comparación entre éstas, se seleccione la mejor alternativa global.
El uso de estructuras de datos para llevar a cabo la evaluación de las alternativas a partir de
restricciones de diseño, alcanza niveles de eficiencia satisfactorios, teniendo en cuenta que
el problema de optimización se está solucionando de manera exhaustiva.
La pendiente es un parámetro fundamental a la hora de diseñar alcantarillados. Por tal moti-
vo, es importante discretizarla para poder hacer uso de ésta en la metodología de diseño.
Al hacer uso únicamente de pendientes propias para el diseño se logra aprovechar al máxi-
mo el diámetro de la tubería.
Las combinaciones de tramos que conforman una línea principal de alcantarillado, alcanzan
los menores costos cuando sus perfiles describen un aumento progresivo de la pendiente (y
un aumento progresivo en los cambios de ésta) a medida que se avanza en la serie.
REFERENCIAS
ASCE. (2007). Gravity Sanitary Sewer Design and Construction. Reston: American Society of Civ-
il Engineers.
Chie Yen, Ben. (1991). Channel Flow Resistance: Centennial of Manning´s Formula. Water Re-
sources Publications, LLC, 5-8. Colorado.
Ministerio de Ambiente, Vivienda y Desarrollo Territorial. (2010). Reglamento Técnico del Sector de
Agua Potable y Saneamiento Básico-RAS (versión preliminar). Bogotá.
Navarro, I. (2009). Diseño Optimizado de Redes de Drenaje Urbano. Bogotá: Universidad de los Andes.
