
TESIS II
CRITERIO DE ESFUERZO CORTANTE MÍNIMO VS
VELOCIDAD MÍNIMA PARA EL DISEÑO DE
ALCANTARILLADOS AUTOLIMPIANTES.
Presentado por:
Carlos Daniel Montes
Asesor: Juan G. Saldarriaga Valderrama
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
MAESTRÍA EN INGENIERÍA CIVIL
BOGOTÁ D.C.
2015

AGRADECIMIENTOS
A mi padre, que vive en mi corazón, en el de mi familia.
A mi madre, la persona a la que le debo cada momento de mi vida.
A Sergio, mi hermano.
A Laurita, mi compañera y confidente.
A Juan Saldarriaga, por permitirme el privilegio de trabajar en el CIACUA.
A todos ustedes, ¡Gracias!

“Ask not what your country can do for you, ask what you can do for your country”
John F. Kennedy

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
i
TABLA DE CONTENIDO
1 Introducción ............................................................................................................... 1
1.1
Antecedentes ...................................................................................................... 2
1.2
Justificación........................................................................................................ 4
1.3
Pregunta de Investigación ................................................................................. 5
1.4
Objetivos ............................................................................................................. 6
1.4.1
Objetivo General ......................................................................................... 6
1.4.2
Objetivos Específicos ................................................................................... 6
1.5
Metodología ........................................................................................................ 6
1.6
Resumen de Contenido ....................................................................................... 8
2 Marco Teórico ............................................................................................................ 9
2.1
Conceptos Generales .......................................................................................... 9
2.1.1
Sedimentos en Alcantarillados ................................................................... 9
2.1.2
Movimiento de Sedimentos en Alcantarillados ........................................ 10
2.1.3
Efectos Hidráulicos Debidos a la Sedimentación ..................................... 13
2.2
Autolimpieza en Sistemas de Alcantarillados ................................................. 13
2.3
Ecuaciones Básicas de Diseño .......................................................................... 14
2.4
Revisión de Metodologías Existentes ............................................................... 16
2.4.1
No – depósito de Sedimentos .................................................................... 16
2.4.2
Movimiento de Sedimentos Existentes en el Lecho de la Tubería ........... 40
2.4.3
Pendiente de Energía ................................................................................ 44
2.5
Parámetros de Diseño de Sistemas de Alcantarillado en el Mundo ............... 52
2.6
Resumen de Capítulo ....................................................................................... 54
3 Análisis Gráfico de Restricciones de Diseño ........................................................... 55
3.1
Análisis Gráfico de Restricciones de Diseño .................................................... 55
3.1.1
Criterios Tradicionales de Diseño ............................................................. 55
3.1.2
Metodología CIRIA .................................................................................... 59

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
ii
3.1.3
Metodología ASCE .................................................................................... 69
3.2
Otras metodologías ........................................................................................... 70
3.3
Comparación Multicriterio ............................................................................... 73
4 Análisis de Costos en el Diseño Optimizado de Sistemas de Alcantarillado ......... 75
4.1
Red Prototipo .................................................................................................... 75
4.2
Función de costos ............................................................................................. 77
4.3
Metodología para el diseño optimizado de sistemas de alcantarillado ........... 79
4.3.1
Planteamiento del problema ..................................................................... 80
4.4
Aplicación de la metodología ............................................................................ 84
4.4.1
CIE 7.0 ....................................................................................................... 84
4.4.2
Diseño optimizado por tramos .................................................................. 87
5 Análisis de Sensibilidad de los costos de diseño ..................................................... 91
5.1
Red de alcantarillado pluvial ........................................................................... 91
5.2
Red de alcantarillado sanitario ........................................................................ 95
5.3
Condiciones límite .......................................................................................... 100
5.4
Verificación de metodología ........................................................................... 105
6 Conclusiones y Recomendaciones ......................................................................... 112
7 Referencias Bibliográficas ..................................................................................... 115
8 Anexos ................................................................................................................... 123

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
iii
ÍNDICE DE FIGURAS
Figura 1. - Clasificación de criterios de autolimpieza de la literatura. Modificado de (Bong,
2014). .......................................................................................................................................... 3
Figura 2. – Metodología de Investigación ......................................................................................... 7
Figura 3. – Tubería fluyendo parcialmente llena. Tomado de (Salcedo, 2012). ........................... 14
Figura 4. – Comparación gráfica entre v = 0.6 m/s y el estándar GLUMRB. .............................. 18
Figura 5. – Variación del número de Froude en función del diámetro de la partícula y de la
concentración volumétrica de sedimentos. Tomado de (Ghani, 1993). ................................. 20
Figura 6. – Resultados obtenidos por Macke (1982). Tomado de (Ghani, 1993). ......................... 22
Figura 7. – Comparación de criterios. Tomado de (Mayerle, et al., 1991). .................................. 24
Figura 8. – Experimento realizado por Ghani (1993). Tomado de (Ghani, 1993). ....................... 25
Figura 9. – Validación de la Ecuación 27. Tomado de (Nalluri, et al., 1994). .............................. 27
Figura 10. - Montaje del experimento (Unidades en m). Tomado de (Vongvisessomjai, et al.,
2010). ........................................................................................................................................ 29
Figura 11. – Esquema unidimensional del modelo numérico. Tomado de (Ibro & Larsen, 2011).
................................................................................................................................................... 31
Figura 12. – Validación de la Ecuación 39 y Ecuación 40 con los experimentos realizados por
Ghani (1993). Tomado de (Ebtehaj, et al., 2013).................................................................... 33
Figura 13. – Comparación de las ecuaciones propuestas con distintas metodologías. ................ 33
Figura 14. – Clasificación de sedimentos en sistemas de alcantarillados. Tomado de (Alvarez,
1990) ......................................................................................................................................... 34
Figura 15. – Geometría de la sección transversal para tuberías con depósito de sedimentos en el
lecho de la tubería. Tomado de (Ghani, 1993) ........................................................................ 38
Figura 16. Validación de la Ecuación 53 y la Ecuación 54 con los experimentos realizados por
Ghani (1993). Tomado de (Ebtehaj, et al., 2013).................................................................... 40
Figura 17. – Validación de la Ecuación 53. Tomado de (Ebtehaj, et al., 2013). ........................... 40
Figura 18. – Criterio de movimiento incipiente para canales con fondo rígido. Tomado de
(Ghani, 1993). ........................................................................................................................... 42
Figura 19. – Relación entre Caudal, Pendiente y Diámetro. Tomado de (Bong, 2014). .............. 44
Figura 20. – Curva de esfuerzo cortante crítico en función de la velocidad. Tomado de (Enfinger
& Mitchell, 2010). ..................................................................................................................... 48
Figura 21. – Resultados del monitoreo. Tomado de (Enfinger & Mitchell, 2010)........................ 49

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
iv
Figura 22. – Porcentaje de material transportado en función del esfuerzo cortante para tuberías
de 200 mm con presencia de biopelículas. Tomado de (Rincón, et al., 2012). ...................... 50
Figura 23. – Valores de Manning para condiciones de flujo subcrítico con presencia de
biopelículas. Tomado de (Rincón, et al., 2012). ...................................................................... 51
Figura 24. – Metodología para criterios tradicionales. .................................................................. 56
Figura 25. – Comparación de criterios tradicionales [Velocidad Mínima]. .................................. 57
Figura 26. - Comparación de criterios tradicionales [Esfuerzo Cortante Mínimo]. ..................... 58
Figura 27. – Metodología propuesta por la CIRIA. Tomado de (Ackers, et al., 1996). ................ 60
Figura 28. – Comparación de Criterio I (CIRIA) ........................................................................... 61
Figura 29. – Variación de los resultados en función de la concentración de sedimentos. ........... 62
Figura 30. – Variación de los resultados en función de la densidad relativa del material ......... 62
Figura 31. – Variación de los resultados en función del diámetro de las partículas. .................. 63
Figura 32. – Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 100
μm. Criterio II de diseño. ........................................................................................................ 65
Figura 33. – Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 200
μm. Criterio II de diseño. ........................................................................................................ 65
Figura 34. – Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 300
μm. Criterio II de diseño. ........................................................................................................ 66
Figura 35. – Criterio III de diseño de alcantarillados. CIRIA ...................................................... 67
Figura 36. – Comparación 1 Criterios CIRIA. ............................................................................... 68
Figura 37. – Comparación 2 Criterios CIRIA. ............................................................................... 68
Figura 38. – Metodología de diseño recomendada por la ASCE (2007). ....................................... 69
Figura 39. – Variación del diámetro de la partícula para el diseño. ............................................ 70
Figura 40. – Metodología de diseño propuesta por Vongvisessomjai et al. (2010). ...................... 71
Figura 41. – Comparación de criterios Vongvisessomjai et al. (2010) y Ebtehaj et al. (2013). ... 72
Figura 42. – Variación de la concentración de sedimentos en el sistema. ................................... 72
Figura 43. – Variación del tamaño de la partícula en el sistema. ................................................ 73
Figura 44. – Comparación multicriterio de las metodologías estudiadas. ................................... 74
Figura 45. – Esquema de la red prototipo. ..................................................................................... 76
Figura 46. – Topografía del terreno para una ruta PMI92813 – PMP92951. .............................. 76
Figura 47. – Proyección del trapecio que produce el área excavada para una tubería de
alcantarillado. Tomado de (CIACUA, 2013). .......................................................................... 78

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
v
Figura 48. – Conjunto de nodos que pertenecen a un mismo pozo de inspección. Tomado de
(Duque, 2013). .......................................................................................................................... 81
Figura 49. – Representación de un arco (𝒗𝒊𝒌, 𝒗𝒋𝒌 + 𝟏). Tomado de (Duque, 2013). .................... 81
Figura 50. – Representación de un tramo de alcantarillado. Tomado de (Duque, 2013). ........... 82
Figura 51. – Metodología para el diseño optimizado de series de tramos de alcantarillado.
Tomado de (Duque, 2013). ....................................................................................................... 84
Figura 52. – Rutas red prototipo. Velocidad mínima = 0.6 m/s .................................................... 86
Figura 53. – Resultados del diseño optimizado para la red prototipo. ......................................... 90
Figura 54. – Resultados gráficos de diseños para cada caso de estudio. ...................................... 94
Figura 55. – Resultados gráficos de diseños para el Caso 1. ......................................................... 99
Figura 56. – Costos asociados a la Corrida 01. ............................................................................ 101
Figura 57. – Costos asociados a la Corrida 02. ............................................................................ 103
Figura 58. – Costos asociados a la corrida 05. ............................................................................. 104
Figura 59. – Límite de autolimpieza en alcantarillados. ............................................................ 105
Figura 60. – Red La Esmeralda. ................................................................................................... 106
Figura 61. – Subcuencas aferentes a cada pozo de la red y Lluvia de diseño. ........................... 107
Figura 62. – Rutas red La Esmeralda. ......................................................................................... 107
Figura 63. – Costos de la red La Esmeralda. ............................................................................... 108
Figura 64. – Localización de red pluvial en la gráfica de autolimpieza. .................................... 109
Figura 65. – Costos red La Esmeralda (Sanitario). ..................................................................... 110
Figura 66. – Localización de red pluvial en la gráfica de autolimpieza. .................................... 111

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
vi
ÍNDICE DE TABLAS
Tabla 1. – Características típicas de sedimentos aplicables en el Reino Unido. Modificado de
(Ackers, et al., 1996). ............................................................................................................... 10
Tabla 2. – Pendientes mínimas recomendadas en alcantarillados. Modificado de (Bizier, 2007).
................................................................................................................................................... 17
Tabla 3. – Características de los sedimentos. Modificado de Ghani (1993). ................................ 25
Tabla 4. – Parámetros característicos en el transporte de sedimentos aplicables en tuberías.
Tomado de (Ghani, 1993)......................................................................................................... 26
Tabla 5. – Valores de 𝜼. Tomado de Ghani (1993). ........................................................................ 36
Tabla 6. – Criterio de velocidad mínima. Tomado de Vongvisessomjai et al. (2010). ................. 52
Tabla 7. – Criterio de esfuerzo cortante mínimo. Tomado de Vongvisessomjai et al. (2010)...... 53
Tabla 8. – Valores recomendados en el continente Americano. .................................................... 53
Tabla 9. – Valores considerados para el análisis gráfico de los criterios tradicionales. .............. 55
Tabla 10. – Resultados de la metodología para cálculo de pendiente mínima. Valores
expresados en porcentaje. ........................................................................................................ 56
Tabla 11. - Resultados de la metodología [Esfuerzo Cortante Mínimo]. Valores expresados en
porcentaje. ................................................................................................................................ 58
Tabla 12. - Características de los Sedimentos ............................................................................... 61
Tabla 13. – Velocidades mínima requeridas para el Criterio III. Tomado de Ackers et al.,
(1996). ....................................................................................................................................... 67
Tabla 14. – Parámetros para comparación de Metodologías. ........................................................ 73
Tabla 15. – Valores de diseño para CIE 7.0. .................................................................................. 85
Tabla 16. – Criterios de autolimpieza considerados. ..................................................................... 86
Tabla 17. – Datos de entrada al modelo. Ruta principal. .............................................................. 87
Tabla 18. – Resultados diseño optimizado en la red prototipo. .................................................... 88
Tabla 19. – Variaciones consideradas para alcantarillado pluvial. .............................................. 91
Tabla 20. – Costos resultantes para cada caso de diseño. ............................................................. 92
Tabla 21. – Diferenciación de costos. .............................................................................................. 92
Tabla 22. – Resultados tabulares de diseños para cada caso de estudio. ..................................... 93
Tabla 23. – Variaciones consideradas para alcantarillado sanitario. .......................................... 95
Tabla 24. – Caso base para análisis de alcantarillado sanitario. ................................................. 96

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
vii
Tabla 25. – Restricciones de autolimpieza en alcantarillados sanitarios. ................................... 96
Tabla 26. – Costos resultantes para cada caso de diseño. Alcantarillado sanitario. ................... 96
Tabla 27. – Resultados de diseños para el Caso 1. ........................................................................ 98
Tabla 28. – Casos y corridas para análisis de condición límite................................................... 100
Tabla 29. – Resultados Corrida 01. ............................................................................................... 101
Tabla 30. – Resultados Corrida 02. ............................................................................................... 102
Tabla 31. – Resultados Corrida 05. ............................................................................................... 103
Tabla 32. – Costos de la red La Esmeralda. ................................................................................. 108
Tabla 33. – Costos red La Esmeralda (Sanitario). ....................................................................... 110

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
viii
ÍNDICE DE ECUACIONES
Ecuación 1. – Relación entre esfuerzo cortante mínimo y velocidad crítica de erosión. .............. 11
Ecuación 2. – Velocidad de corte. .................................................................................................... 12
Ecuación 3. – Ley de Stokes. ........................................................................................................... 12
Ecuación 4. – Profundidad de agua en una tubería. ...................................................................... 14
Ecuación 5. – Ángulo que forma la profundidad de agua. ............................................................. 14
Ecuación 6. – Área de la sección mojada. ....................................................................................... 15
Ecuación 7. – Perímetro mojado de la sección. ............................................................................... 15
Ecuación 8. – Radio hidráulico. ....................................................................................................... 15
Ecuación 9. – Ancho en la superficie. ............................................................................................. 15
Ecuación 10. – Profundidad hidráulica. ......................................................................................... 15
Ecuación 11. – Ecuación de Manning. ............................................................................................ 15
Ecuación 12. – Ecuación físicamente basada de velocidad. ........................................................... 15
Ecuación 13. – Diámetro requerido para transportar el caudal de diseño ................................... 16
Ecuación 14. – Planteamiento para la solución iterativa. ............................................................. 17
Ecuación 15. – Número de Froude modificado. .............................................................................. 19
Ecuación 16. – Ecuación de Robinson – Graf (1972). ..................................................................... 20
Ecuación 17. – Ecuación de Novak – Nalluri (1975) ...................................................................... 20
Ecuación 18. – Tasa de transporte de sedimentos. Macke (1982) ................................................ 21
Ecuación 19. – Ecuación de Macke (1982). ..................................................................................... 21
Ecuación 20. – Velocidad de sedimentación de las partículas. Macke (1982). ............................. 21
Ecuación 21. – Viscosidad cinemática del agua. Sakhuja (1987). ................................................. 22
Ecuación 22. – Ecuación de May (1982). ........................................................................................ 23
Ecuación 23. – Velocidad crítica. May (1982). ................................................................................ 23
Ecuación 24. – Ecuación de May et al. (1989) ................................................................................ 23
Ecuación 25. – Ecuación de Mayerle, Nalluri y Novak (1991). ..................................................... 24
Ecuación 26. – Ecuación de Ghani (1993). ..................................................................................... 26
Ecuación 27. – Ecuación de Nalluri et al (1994). ........................................................................... 27
Ecuación 28. – Ecuación de May et al. (1996). ............................................................................... 28

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
ix
Ecuación 29. – Velocidad límite. Tomado de May et al. (1996). .................................................... 28
Ecuación 30. – Velocidad de Camp. ................................................................................................ 29
Ecuación 31. – Esfuerzo cortante de Camp. ................................................................................... 29
Ecuación 32. – Ecuación de Vongvisessomjai et al. (2010) para carga en suspensión como
función del Radio Hidráulico. .................................................................................................. 30
Ecuación 33. – Ecuación Vongvisessomjai et al. (2010) para carga en suspensión como función
de la profundidad de agua. ...................................................................................................... 30
Ecuación 34. - Ecuación de Vongvisessomjai et al. (2010) para carga de lecho como función del
Radio Hidráulico. ..................................................................................................................... 30
Ecuación 35. - Ecuación de Vongvisessomjai et al. (2010) para carga de lecho como función de la
profundidad de agua. ............................................................................................................... 30
Ecuación 36. – Criterio RMSE evaluado por Ebtehaj et al. (2013). .............................................. 32
Ecuación 37. – Criterio MARE evaluado por Ebtehaj et al. (2013). .............................................. 32
Ecuación 38. – Criterio AIC evaluado por Ebtehaj et al. (2013). .................................................. 32
Ecuación 39. – Ecuación de Ebtehaj et al. (2013) como función del radio hidráulico. ................. 32
Ecuación 40. – Ecuación de Ebtehaj et al (2013) como función de la profundidad de agua. ....... 32
Ecuación 41. – Ecuación propuesta por May et al. (1989). ............................................................ 35
Ecuación 42. – Parámetro de transporte. Tomado de May (1993). ............................................... 35
Ecuación 43. – Parámetro de movilidad. Tomado de May (1993). ................................................ 35
Ecuación 44. – Factor de transición. Tomado de May (1993). ....................................................... 35
Ecuación 45. – Número de Reynolds de la partícula. Tomado de May (1993). ........................... 36
Ecuación 46. – Ecuación propuesta por Álvarez (1990). ................................................................ 36
Ecuación 47. – Parámetro de transporte de sedimentos. Tomado de Perrusquía (1991). ........... 37
Ecuación 48. – Ecuación propuesta por El – Zaemy (1991). ......................................................... 37
Ecuación 49. – Factor de fricción. Tomado de El – Zaemy (1991). ............................................... 37
Ecuación 50. – Ecuación propuesta por Nalluri y Alvarez (1992). ............................................... 38
Ecuación 51. – Ecuación propuesta por Ghani (1993). .................................................................. 39
Ecuación 52. – Factor de fricción compuesto. Tomado de Ghani (1993). ..................................... 39
Ecuación 53. – Ecuación propuesta por Ebtehaj et al. (2013) como función del radio hidráulico.
Depósito límite de sedimentos. ............................................................................................... 39
Ecuación 54. – Ecuación propuesta por Ebtehaj et al. (2013) como función de la profundidad de
agua. Depósito límite de sedimentos. ..................................................................................... 39

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
x
Ecuación 55. – Ecuación propuesta por Durand y Condolios (1956) ............................................ 41
Ecuación 56. – Ecuación propuesta por Laursen (1956)................................................................ 41
Ecuación 57. – Ecuación propuesta por Robinson y Graf (1972) .................................................. 41
Ecuación 58. – Ecuación propuesta por Novak y Nalluri (1975). ................................................. 41
Ecuación 59. – Ecuación propuesta por Novak y Nalluri (1984). ................................................. 42
Ecuación 60. – Velocidad de Camp ................................................................................................. 43
Ecuación 61. – Ecuación propuesta por Novak y Nalluri (1975). ................................................. 43
Ecuación 62. – Esfuerzo cortante de Camp. ................................................................................... 43
Ecuación 63. – Esfuerzo cortante en una tubería. ......................................................................... 46
Ecuación 64. – Esfuerzo cortante como función del diámetro de partícula. Tomado de Raths y
McCauley (1962). ..................................................................................................................... 46
Ecuación 65. – Velocidad crítica como función del esfuerzo cortante crítico. Tomado de Enfinger
et al. (2010). .............................................................................................................................. 48
Ecuación 66. – Ecuación propuesta por La Motta (1996). ............................................................. 49
Ecuación 67. – Modificación de la ecuación de Manning propuesta por Guzman et al. (2007)... 50
Ecuación 68. – Ecuación propuesta por Rincón et al. (2012). ........................................................ 51
Ecuación 69. – Ecuación de Ackers (1991). .................................................................................... 63
Ecuación 70. – Formulación ecuación de Ackers (1991). ............................................................... 64
Ecuación 71. – Costo de material por metro lineal de tubería. ..................................................... 77
Ecuación 72. – Costo de excavación por metro lineal de tubería. ................................................. 77
Ecuación 73. – Volumen excavado para instalar la tubería. ......................................................... 78
Ecuación 74. – Función de costos totales por metro lineal de tubería. ......................................... 78
Ecuación 75. – Planteamiento problema ruta crítica. ................................................................... 79
Ecuación 76. – Pendiente asociada al arco. Tomado de Duque (2013). ........................................ 82
Ecuación 77. – Variable de decisión. Tomado de Duque (2013). ................................................... 82
Ecuación 78. – Planteamiento de la función objetivo. Tomado de Duque (2013). ....................... 83
Ecuación 79. – Cálculo de Volumen. ............................................................................................... 83

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
xi
ÍNDICE DE ABREVIATURAS
𝐴
Área de la sección mojada
𝐵
Espacio lateral requerido para instalar la tubería
𝐵
𝑎
Constante adimensional para autolimpieza. Valor igual a 0.8
𝐶
𝑒
Costo de excavación por metro lineal de tubería
𝐶
𝑡
Costo de material por metro lineal de tubería
𝐶
𝑣
Concentración volumétrica de sedimentos
𝑑
50
Diámetro medio de partículas
𝐷
𝑔𝑟
Tamaño no dimensional de sedimentos
𝐷
Profundidad hidráulica
𝑑
Diámetro de la tubería
𝑑
𝑠
Diámetro de partícula
𝑒
Espesor de la pared de la tubería
𝐹
𝑟
Número de Froude
𝐹
𝑠
Parámetro de movilidad
𝑔
Aceleración de la gravedad
𝐻
Profundidad de excavación hasta la cota clave aguas arriba de la tubería
ℎ
Relleno que se debe disponer bajo la tubería
𝐻′
Profundidad de excavación hasta la cota clave aguas abajo de la tubería

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
xii
𝑘
Factor de conversión de pesos de diciembre de 2007 a mayo de 2009
𝑘
𝑐
Factor de conversión de unidades. 0.85 para Sistema Internacional de
Unidades
𝑘
𝑠
Rugosidad hidráulica del material de la tubería
𝐿
Longitud de la tubería
𝑛
Coeficiente de rugosidad de Manning
𝑃
Perímetro mojado de la sección
𝑄
Caudal de la tubería
𝑄
𝑑𝑤𝑓
Caudal en tiempo seco
𝑄
𝑤𝑤𝑓
Caudal en tiempo húmedo
𝑄
𝑚𝑖𝑛
Caudal mínimo en la tubería
𝑞
𝑠
Tasa de transporte de sedimentos por unidad de ancho
𝑄
𝑠
∗
Tasa de transporte de sedimentos
𝑅
Radio hidráulico de la sección
𝑅
∗𝑐
Número de Reynolds de la partícula
𝑅
𝑏
Radio hidráulico de la capa de sedimentos
𝑆
Pendiente de la tubería
𝑠
Densidad relativa sedimento - fluido
𝑇
Ancho de la superficie
𝑇°
Temperatura del agua

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
xiii
𝑈
∗
Velocidad de corte
𝑉
Volumen de excavación
𝑣
Velocidad del flujo
𝑣
𝑒
Velocidad crítica de erosión
𝑣
𝑐
Velocidad crítica para iniciar movimiento incipiente de partículas
𝑣
𝑐𝑎𝑚𝑝
Velocidad de Camp
𝑣
𝐿
Velocidad de autolimpieza
𝑣
𝑡
Velocidad límite
𝑊
𝑏
Ancho de sedimentos en la tubería
𝑊
𝑠
Velocidad de asentamiento de las partículas
𝑦
Profundidad de agua en la tubería
𝑦
𝑜
Profundidad de agua. Ghani (1993)
𝑦
𝑠
Profundidad de sedimentos en la tubería
𝛾
Peso específico del fluido
𝛾
𝑠
Peso específico de sedimentos
𝜂
Parámetro de transporte de sedimentos. May (1993)
𝜃
Ángulo que forma la profundidad de agua
𝜃
𝑏
Ángulo que forma la profundidad de sedimentos
𝜃
𝑚
Factor de transición
𝜆
Factor de fricción de Darcy - Weisbach

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
xiv
𝜆
𝑏
Factor de fricción del lecho de la tubería
𝜆
𝑐
Factor de fricción de Darcy - Weisbach compuesto entre la tubería y los
sedimentos
𝜈
Viscosidad cinemática del agua
𝜌
Densidad del fluido
𝜌
𝑠
Densidad del sedimento
𝜏
𝑏
Esfuerzo cortante límite de depósito de sedimentos
𝜏
𝑐
Esfuerzo cortante como función del diámetro de partícula. Raths y
McCauley (1962)
𝜏
𝑐𝑎𝑚𝑝
Esfuerzo cortante de Camp
𝜏
𝑚
Esfuerzo cortante como función del diámetro de partícula. La Motta
(1996)
𝜏
𝑜
Esfuerzo cortante crítico
𝛷′
𝑏
Parámetro de transporte de sedimentos. Perrusquía (1991)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
1
1 INTRODUCCIÓN
El suministro de agua a las poblaciones ha sido un tema de vital importancia para la
supervivencia. En un principio se pensó en el abastecimiento y el desalojo de las aguas
de la forma más rápida posible; esto sin considerar los impactos que se llegasen a tener
por dichas prácticas. Comúnmente se presentaban problemas de salud y malos olores
causados por el contacto directo con las aguas residuales que no se evacuaban
correctamente. Una de las primeras civilizaciones que pensó en el problema e intentó
resolverlo, fue la romana. Ellos construyeron una cloaca con el fin de drenar el agua del
Coliseo Romano. A partir de ese momento, nacieron los sistemas de drenaje conocidos
hoy en día y se dio la misma importancia al problema de suministro de agua para
consumo y a la evacuación de las aguas residuales (Butler & Davies, 2009).
El objetivo principal era evacuar lo más rápido posible las aguas residuales generadas
en la ciudad sin pensar en los daños potenciales que se podían generar por éstas
prácticas. Se empezaron a observar problemas en los cuerpos de agua receptores debido
a la contaminación proveniente de las aguas residuales de la población aguas arriba
(Saldarriaga, 2014). La problemática tomó mayor relevancia en la medida que las
poblaciones localizadas aguas abajo de la fuente de contaminación se empezaron a ver
perjudicadas. Esto invita a pensar, ¿Cuál es la mejor forma de evacuar las aguas
residuales de una ciudad sin afectar los cuerpos receptores y las poblaciones aguas
abajo?
Para responder la pregunta anterior, se deben considerar los sistemas de drenaje urbano
como una integralidad entre el sistema en sí, el nivel de tratamiento necesario de las
aguas evacuadas y el cuerpo receptor. El primer componente corresponde al sistema de
drenaje de la ciudad - el cual será el objeto de análisis de este proyecto – el cual es el
encargado de la evacuación de las aguas lluvia y residuales. El segundo componente
hace referencia al nivel de tratamiento necesario de las aguas evacuadas por el sistema
de drenaje para no afectar la calidad de agua del cuerpo receptor. En muchas ocasiones,
no es necesario realizar un tratamiento de las aguas residuales, puesto que, la masa de
agua del cuerpo receptor es mucho mayor a la carga de contaminante vertida.
Finalmente, según los usos del cuerpo receptor, se debe garantizar que el tratamiento
(o no tratamiento) realizado responda a cierta concentración de contaminante (e.g.
Coliformes Totales y Fecales, Compuestos nitrogenados, Materia Orgánica Carbonácea,
entre otros) en un punto de interés sobre el cuerpo receptor.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
2
Como se menciona anteriormente, el foco de investigación en éste trabajo es el diseño de
los sistemas de drenaje de las ciudades, específicamente lo relacionado a diseño de
alcantarillados autolimpiantes. Un correcto diseño que cumpla con las condiciones de
autolimpieza es fundamental para prevenir problemas de sedimentación, que generan
a su vez pérdida de capacidad hidráulica y contaminación del sistema debido a las
reacciones que se podrían presentar en la capa de sedimentos.
En el presente documento, se presenta una revisión bibliográfica de los diferentes
criterios de velocidad mínima y esfuerzo cortante mínimo para el diseño de
alcantarillados autolimpiantes, propuestos a lo largo del tiempo por diferentes autores.
Lo anterior se realiza con el fin de determinar qué criterio es el más adecuado (en
términos de aplicabilidad y costo) para plasmar en las normativas de diseño de
diferentes entidades. Igualmente, se realizan una serie de simulaciones para un
alcantarillado sanitario y uno pluvial, mediante las cuales se intenta concluir acerca de
la importancia (o no) de hacer uso de determinados criterios de autolimpieza en el diseño
optimizado de sistemas de alcantarillado.
1.1 Antecedentes
La sedimentación de partículas es un problema que afecta en gran medida los sistemas
de alcantarillados. El movimiento de éstos sedimentos genera un ciclo natural
compuesto por tres procesos principales: erosión, transporte y depósito (Ghani, 1993).
En largos periodos de tiempo, el depósito de los sólidos suspendidos incrementa el riesgo
de consolidación y posteriormente la cementación de los mismos. En particular, un
depósito permanente en las tuberías durante periodos secos genera cambios en la
sección transversal lo cual causa cambios en la rugosidad, que a su vez, afecta la
distribución de velocidades y consecuentemente la distribución de esfuerzos cortantes
en el fondo de la tubería (Ebtehaj, et al., 2013).
La Asociación de Investigación e Información de la Industria de la Construcción
(Construction Industry Research and Information Association, CIRIA) realizó estudios
enfocados en la presencia de sedimentos en sistemas de alcantarillados en el Reino
Unido (CIRIA, 1987). Las mayores problemáticas encontradas fueron el bloqueo,
sobrecarga, inundación y calidad del agua. La producción de sedimentos se ve afectada
por la localización geográfica, el tipo de alcantarillado, uso de tierra, época del año y el
régimen seco de lluvias anterior.
Con el fin de evitar estos problemas en los sistemas de alcantarillados, diferentes
autores han planteado metodologías para prevenir estos fenómenos. Bong (2014) realizó
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
3
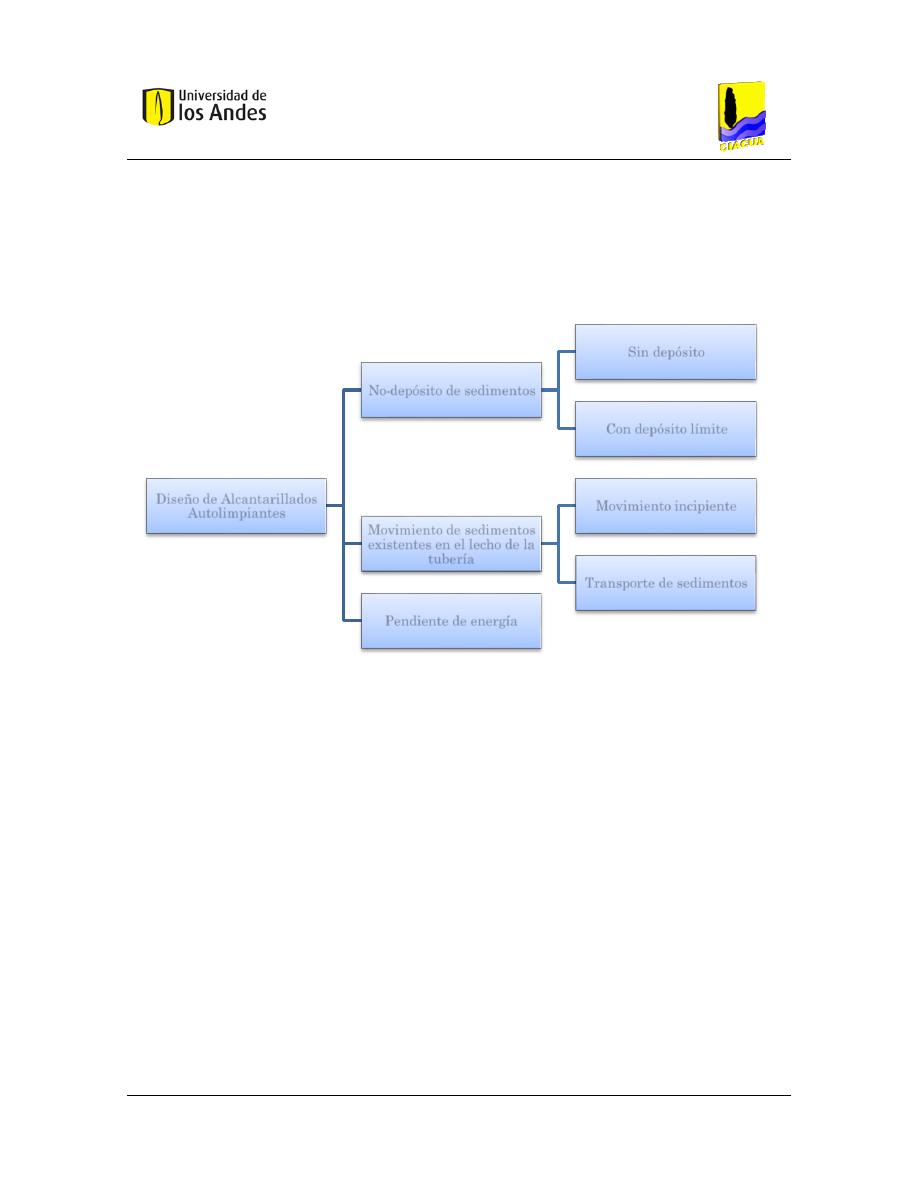
una revisión bibliográfica y clasificó los criterios y metodologías en tres grupos: 1)
Criterio de no-depósito de sedimentos; 2) Movimiento de sedimentos existentes en el
lecho de la tubería y 3) Pendiente de energía. Los criterios de diseño de cada grupo
pueden clasificarse, por lo tanto, en pequeños grupos como se muestra en la Figura 1.
En el primer grupo (No-depósito de sedimentos) se pueden incluir los criterios
tradicionales de diseño (velocidad mínima y esfuerzo cortante mínimo), los cuales se
encuentran en la mayoría de las Normas Técnicas de Diseño en el mundo. Usualmente
estos valores varían entre valores de velocidad de 0.6 y 0.9 m/s, según la condición del
flujo (tubería llena o parcialmente llena) y el tipo de alcantarillado (sanitario, pluvial o
combinado) y entre 1.3 y 12.6 N/m
2
para esfuerzo cortante mínimo. Ninguno de estos
criterios cuenta con una justificación teórica o investigación de fondo, por lo cual son
valores recomendados más por la experiencia de los diseñadores; lo anterior puede llevar
a diseños sobredimensionados y muy costosos en algunas ocasiones.
Diferentes estudios previos (Ebtehaj, et al., 2013) mostraron que un solo valor de
velocidad mínima o esfuerzo cortante mínimo no es adecuado para determinar las
condiciones de autolimpieza en tuberías de diferentes tamaño, rugosidades y gradientes
para todo el rango de sedimentos y condiciones de flujo encontrados en alcantarillados.
Dado lo anterior, el diseño de una velocidad de autolimpieza debe considerar diferentes
Diseño de Alcantarillados
Autolimpiantes
No-depósito de sedimentos
Sin depósito
Con depósito límite
Movimiento de sedimentos
existentes en el lecho de la
tubería
Movimiento incipiente
Transporte de sedimentos
Pendiente de energía
Figura 1. - Clasificación de criterios de autolimpieza de la literatura. Modificado de (Bong,
2014).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
4
parámetros como la concentración y el tamaño de los sedimentos, profundidad o radio
hidráulico, rugosidad y diámetro.
Este primer grupo se puede dividir en dos criterios de autolimpieza, no-depósito de
sedimentos y depósito límite. El primero de ellos, es un criterio de diseño conservativo
en el cual no se permite la sedimentación en el sistema. Se debe identificar el modo de
transporte de las partículas; ya sea como carga en suspensión o carga de lecho, esto con
el fin de hacer uso de alguna de las ecuaciones existentes de autolimpieza
(Vongvisessomjai, et al., 2010). El segundo de ellos es menos conservativo puesto que,
permite la presencia de una capa de sedimentos en el sistema lo cual reduce la pendiente
requerida de diseño (Bong, 2014). Este criterio permite eventualmente menores costos
de construcción; sin embargo, requiere de un mantenimiento más cuidadoso puesto que,
se estaría en presencia de condiciones cercanas a las críticas.
El segundo grupo de criterios de diseño, movimiento de sedimentos existentes en el lecho
de la tubería, asume que el sedimento ya se encuentra sedimentado en el lecho de la
tubería. Las ecuaciones desarrolladas bajo este criterio de diseño consideran algunos
aspectos de los sedimentos y características del sistema, con el fin de iniciar el
movimiento de los depósitos de sedimentos (Bong, 2014).
Finalmente, los criterios de diseño basados en la pendiente de energía, requieren
parámetros de entrada como condiciones del flujo, tasa de entrada de sedimentos,
características de las partículas como diámetro y densidad y características hidráulicas
de la tubería como su geometría y rugosidad hidráulica. Este tipo de criterios han sido
desarrollados en su mayoría por la Sociedad Estadounidense de Ingenieros Civiles
(American Society of Civil Engineers, ASCE) bajo el criterio de Tractive Force
1
propuesto
en el Manual de Diseño y Construcción de Alcantarillados Sanitario (Bizier, 2007). Cada
uno de los criterios presentados se estudiará en detalle.
1.2 Justificación
En la mayoría de las normativas de diseño del mundo los criterios tradicionales de
velocidad mínima y esfuerzo cortante mínimo se presentan como única restricción de
diseño. Usualmente no se consideran otros parámetros (material de la tubería,
características de los sedimentos, entre otros). Esto conlleva a realizar diseños en
muchos casos sobredimensionados y no optimizados de sistemas de alcantarillados tanto
pluviales, como combinados y sanitarios.
1
El concepto Tractive Force hace referencia a todos los esfuerzos actuantes sobre una partícula

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
5
El Reglamento Técnico del Sector de Agua Potable y Saneamiento Básico, RAS, propone
valores de 0.45 m/s y 1.5 N/m
2
para alcantarillados sanitarios y 0.75 m/s y 3 N/m
2
para
alcantarillados pluviales (RAS, 2000), los cuales son valores teóricos y sugeridos más
por la experiencia de los diseñadores que por una justificación teórica. Estos criterios
intentan calcular una pendiente a partir de un valor de velocidad y/o esfuerzo cortante
para condiciones de tubo lleno, lo cual conlleva a que si se presentan relaciones de
llenado menores a la de diseño, se aumente el riesgo de sedimentación de partículas
(Bizier, 2007).
Los criterios tradicionales han generado buenos resultados en términos de autolimpieza
en alcantarillados, pero resulta en diseños mucho mayores a los requeridos en casi la
totalidad de los casos (especialmente en diámetros pequeños cuya profundidad de agua
para caudales bajos es mayor al 20%) y en algunas ocasiones subestima la pendiente
real requerida (mayormente en tuberías con diámetros altos en los cuales la profundidad
sea menor al 30% y diámetros pequeños fluyendo con relaciones de llenado menores a
0.2) (Bizier, 2007).
El principal problema asociado con los criterios tradicionales se relaciona con el pobre
indicador de poder de autolimpieza que resulta al usar una velocidad mínima. Sin
embargo, esta práctica resulta ser conservativa, puesto que al generar mayores
pendientes se garantiza (en teoría) la autolimpieza para un alcantarillado.
Dado lo anterior, es fundamental revisar una serie de metodologías propuestas por
diferentes autores y normativas en el mundo para identificar las similitudes,
consideraciones, parámetros, resultados y validaciones. Así mismo, se debe hacer una
crítica a cada una de ellas y proponer la más adecuada para el diseño de alcantarillados.
Adicional a lo anterior mencionado, es fundamental entender la variabilidad en los
diseños optimizados de alcantarillados al hacer uso de un criterio u otro. Dado lo
anterior, la simulación de diferentes redes de alcantarillados bajo distintas condiciones
de caudal y topografía del terreno se antoja necesario para concluir acerca de lo anterior
mencionado.
1.3 Pregunta de Investigación
Diversos autores han propuesto criterios para el diseño de sistemas de alcantarillados
autolimpiantes bajo diferentes condiciones de flujo, características de los sedimentos,
material de la tubería y diámetro del sistema, por lo tanto, ¿Cuál resulta ser la
metodología más apropiada para diseñar sistemas de alcantarillados autolimpiantes y

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
6
qué tanta influencia tiene en el diseño optimizado de una red de alcantarillado el uso de
criterios de autolimpieza?
1.4 Objetivos
1.4.1 Objetivo General
Realizar una revisión del estado del arte de las metodologías y criterios de diseño de
alcantarillados autolimpiantes desarrolladas y propuestas por diferentes autores, con el
fin de establecer la influencia de éstas sobre el diseño optimizado de redes de
alcantarillado.
1.4.2 Objetivos Específicos
Realizar una revisión del estado del arte de las metodologías de diseño de
alcantarillados autolimpiantes existentes a nivel mundial.
Revisar los criterios de autolimpieza propuestos en las diferentes Normas
Técnicas de diseño de sistemas de alcantarillados en el mundo.
Realizar un análisis gráfico de las restricciones de diseño en el cual
simultáneamente se comparen las metodologías y valores encontrados en la
bibliografía.
Realizar un análisis comparativo de costos entre diseños de autolimpieza
aplicados al diseño optimizado de alcantarillados.
Realizar un análisis sensibilidad de los criterios de autolimpieza aplicados al
diseño optimizado de alcantarillados.
Concluir acerca de la influencia de los criterios de autolimpieza en el diseño
optimizado de redes de alcantarillado.
1.5 Metodología
La metodología de investigación se compone principalmente en tres pasos, los cuales se
resumen en la Figura 2. En primera instancia, se realizó una revisión bibliográfica de
los criterios de autolimpieza propuestos por diferentes autores. En este paso se
especifican las condiciones bajo las cuales se obtuvieron las ecuaciones y modelos, los

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
7
parámetros que afectan las velocidades y/o esfuerzos cortantes mínimos en tuberías, los
rangos de validez, las ecuaciones gobernantes y demás información de interés para
realizar los análisis posteriores. Igualmente, se identificó el tipo de transporte (e.g.
Carga de lecho y/o en suspensión) que corresponde el desarrollo de dicha ecuación y/o
metodología. Parte de esta primera etapa corresponde a la revisión de Normativas de
Diseño a nivel mundial para el diseño de alcantarillados. En este caso, se utiliza como
criterio de comparación la normativa colombiana y sus similitudes y diferencias en los
valores estipulados en cada una.
En segunda instancia es necesario realizar un análisis gráfico de las metodologías
consideradas en el paso anterior; esto con el fin de identificar los criterios más
restrictivos y los más holgados a la hora de diseñar un sistema de alcantarillado
autolimpiante. Esta comparación se realiza como función del diámetro de la tubería y
de la pendiente resultante de aplicar alguna ecuación de resistencia fluida (e.g Ecuación
de Manning).
Figura 2. – Metodología de Investigación.
Finalmente, se realiza una comparación de costos en el momento del diseño en sí, por lo
cual se deben asociar ecuaciones de análisis de costo (tubería en sí y excavación). Para
Revisión
Bibliográfica
•Metodologías y ecuaciones existentes
•Normas de Diseño a nivel mundial
Análisis Gráfico
de Restricciones
•Programación y comparación de criterios de
autolimpieza
Análisis de
Costo y
Sensibilidad de
Metodologías
•Comparación de costos en el diseño
optimizado.
•Sensibilidad de las metodologías de
autolimpieza

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
8
dicho propósito se emplea la metodología desarrollada por el Centro de Investigación
Estratégica para el Agua (CIE) mediante la estimación de la ruta más corta y el
algoritmo de Bellman-Ford (Duque, 2013). Igualmente, se realiza un análisis de
sensibilidad en el cual se simulan una serie de condiciones sobre una red de estudio y se
busca encontrar la afectación de las metodologías de autolimpieza en el costo final de un
diseño optimizado de un sistema de alcantarillado.
1.6 Resumen de Contenido
En el primer capítulo se presenta una introducción a la problemática estudiada, la
importancia de realizar dicha investigación, los objetivos propuestos y la metodología
que se plantea seguir para dar cumplimiento a dichos objetivos. Igualmente se da un
breve repaso de los tres grandes grupos de clasificación de criterios de autolimpieza en
sistemas de alcantarillados.
El segundo capítulo corresponde al foco de ésta investigación. Se presenta al lector de
forma detallada las metodologías de diseño existentes en las normas técnicas de
distintos países, las ecuaciones propuestas por diversos autores y entidades como la
ASCE y la CIRIA. Se muestran los experimentos realizados y los resultados de
investigación de cada autor, las consideraciones de cada modelo, entre otros.
El tercer capítulo corresponde al análisis comparativo de las metodologías consideradas
en el capítulo anterior. Para dicho análisis se evalúa la pendiente de autolimpieza
obtenida como función del diámetro de la tubería para una serie de criterios y
metodologías de autolimpieza consideradas.
El cuarto capítulo corresponde a la aplicación de las metodologías al diseño optimizado
de alcantarillados. En esta etapa se evalúa principalmente la variabilidad de los costos
producto de utilizar una restricción de velocidad mínima o esfuerzo cortante mínimo
como valor para garantizar autolimpieza en alcantarillados en una red prototipo de
estudio.
El quinto capítulo presenta el resultado de las simulaciones realizadas sobre la ruta
principal de la red prototipo. Se varían los caudales y la topografía del terreno y se
determina el límite de influencia (caudal vs pendiente del terreno) para el cual las
condiciones de autolimpieza dejan de ser una variable sensible del diseño optimizado de
sistemas de alcantarillado.
Finalmente, se presentan las conclusiones y recomendaciones, las referencias
bibliográficas consultadas y los anexos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
9
2 MARCO TEÓRICO
En este primer capítulo se presenta al lector una visión general de los conceptos básicos
relacionados al tema de autolimpieza en alcantarillados, una introducción al concepto
en sí, las ecuaciones básicas de diseño consideradas para los análisis y una revisión
detallada de las metodologías, criterios y ecuaciones existentes para el diseño. Se
consideran tres grandes grupos: 1) No – depósito de sedimentos; 2) Movimiento de
sedimentos existentes en el lecho de la tubería y 3) Pendientes de energía. Finalmente,
se presentan los valores recomendados en distintas normativas a nivel mundial para el
diseño de estos sistemas.
2.1 Conceptos Generales
La necesidad de diseñar sistemas de alcantarillados con capacidad de transportar
sedimentos ha sido reconocida por muchos años. Convencionalmente, se ha especificado
una velocidad mínima de autolimpieza la cual debe garantizarse para cierta
profundidad de flujo y con determinada frecuencia dentro del periodo de diseño y
operación del sistema. Esta consideración tradicional no contempla las características
propias del sedimento ni aspectos hidráulicos propios del sistema, por lo cual en muchas
ocasiones no se representa adecuadamente el fenómeno de transporte de sedimentos en
los sistemas de alcantarillado (Butler, et al., 2003). Lo anterior lleva a la necesidad de
entender qué son y cómo afectan los sedimentos los sistemas de alcantarillado.
2.1.1 Sedimentos en Alcantarillados
Los sedimentos en sistemas de alcantarillados se pueden definir como cualquier
partícula o material sedimentable existente en alcantarillados, tanto de agua lluvia
como sanitarios, que tienen la capacidad para formar depósitos en el lecho de las
tuberías (Butler, et al., 2003). Algunas partículas de poco tamaño o baja densidad,
pueden permanecer en suspensión durante las condiciones normales de flujo y operación
del sistema y por consiguiente serían transportadas en eventos de crecientes como carga
de lavado
2
. La presencia de partículas tiene un efecto importante en la capacidad
hidráulica del sistema de alcantarillado, pero, también puede tener una mayor
influencia en términos de contaminación ambiental (Ackers, et al., 1996) e inundaciones
debidas a la sobrecarga del sistema.
2
El término original es Washload (Ackers, et al., 1996).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
10
Sedimentos con bajas velocidades de asentamiento pueden formar únicamente depósitos
en el lecho en condiciones hidrológicas secas y pueden ser fácilmente resuspendidos
cuando se presentan eventos de crecientes generados por lluvias o variaciones diurnas.
En contraste, partículas grandes y densas pueden ser transportadas por caudales pico
(o máximos) que ocurren con muy baja frecuencia, por lo cual, en algunos casos se
pueden generar depósitos permanentes en los sistemas (Ackers, et al., 1996).
Generalmente los sedimentos se pueden clasificar en tres distintas formas: 1)
Sedimentos de origen sanitario; 2) Sedimentos de origen pluvial y 3) Arenas. La Tabla
1 presenta las características típicas de los sedimentos aplicables en el Reino Unido. De
esta tabla es importante resaltar que la mayor fuente de arenas resulta ser el agua
lluvia; sin embargo la diferencia radica en el tamaño de las partículas que generalmente
se encuentran en alcantarillados de éste tipo y las arenas.
Tabla 1. – Características típicas de sedimentos aplicables en el Reino Unido. Modificado de
(Ackers, et al., 1996).
Tipo
Modo de
Transporte
Concentración
[mg/L]
Tamaño medio de partícula
d
50
[μm]
Densidad Relativa
Bajo
Medio
Alto
Bajo
Medio
Alto
Bajo Medio Alto
Arenas
Lecho
10
50
200
300
750
1000
2,3
2,6
2,7
Pluvial
Suspensión
50
350
1000
20
60
100
1,1
2
2,5
Sanitario
Suspensión
100
350
500
10
40
60
1,01
1,4
1,6
Los tamaños que pueden ser transportados en suspensión o como carga de lecho pueden
variar acorde a las condiciones, sin embargo, se puede suponer que los sólidos menores
a 150 μm se encuentran en suspensión y las mayores como carga de lecho (Ackers, et
al., 1996). Es importante resaltar que los valores de concentración presentados en la
Tabla 1 son obtenidos de distintos estudios realizados en el Reino Unido (e.g. Sartor y
Boyd (1972), Ellis (1979), Mance y Harman (1978), entre otros) y por consiguiente estos
valores pueden variar en distintos países. Para dar un ejemplo de lo anterior, en Estados
Unidos, la concentración de sólidos suspendidos en alcantarillados sanitarios varía
entre 100 y 350 mg/L (Bizier, 2007), mientras que Brasil puede tener 390 mg/L en
promedio, Kenya 520 mg/L, Jordan 900 mg/L, Abu Dhabi 200 mg/L, entre otros (Metcalf
& Eddy, INC, 1991). Para el caso colombiano, se han encontrado concentraciones en
sistemas de alcantarillados entre 100 y 1000 mg/L para distintas estaciones de
monitoreo y diferentes sistemas (separado o combinado) (Rodríguez, et al., 2013).
2.1.2 Movimiento de Sedimentos en Alcantarillados
El movimiento de sedimentos en alcantarillados tiene tres fases: Arrastre, transporte y
depósito. A continuación se presenta cada una de las fases.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
11
2.1.2.1 Arrastre
Cuando el agua residual fluye sobre la capa de sedimentos del lecho de una tubería, las
fuerzas hidrodinámicas de levante y arrastre
3
son ejercidas sobre las partículas. Si la
combinación de estas dos fuerzas no excede el peso de la partícula y las fuerzas
cohesivas, entonces permanecen depositadas. Por el contrario, si se supera (se genera
desequilibrio) se da inicio al fenómeno de arrastre resultando en el movimiento de
partículas (Butler, et al., 2003). La condición límite en la cual el movimiento de
partículas es despreciable se encuentra usualmente definida en términos del esfuerzo
cortante mínimo y de la velocidad crítica de erosión. Estas se pueden relacionar de la
siguiente forma:
𝜏
0
=
𝜌𝜆𝑣
𝑒
2
8
Ecuación 1. – Relación entre esfuerzo cortante mínimo y velocidad crítica de erosión.
donde 𝜏
0
es el esfuerzo cortante crítico [Pa]; 𝜌 la densidad del fluído [kg/m
3
]; 𝜆 el factor
de fricción de Darcy – Weisbach y 𝑣
𝑒
la velocidad crítica de erosión [m/s]. En
alcantarillados pluviales, los sedimentos son en su mayoría inorgánicos y no-cohesivos;
sin embargo algunos depósitos pueden cementarse y generar depósitos permanentes por
largos periodos de tiempo. En alcantarillados sanitarios generalmente se presentan
sedimentos con características cohesivas, dada la naturaleza de las partículas y la
presencia de grasas y limos. Alcantarillados combinados presentan combinaciones de
sedimentos existentes en los anteriores mencionados.
La cohesión tiende a incrementar el valor del esfuerzo cortante que el flujo necesita
ejercer para iniciar el movimiento de partículas del lecho. En experimentos de
laboratorio, se ha observado que la erosión de partículas cohesivas se genera cuando el
esfuerzo cortante en el lecho está entre 2.5 N/m
2
y 7 N/m
2
para partículas granulares
(Butler, et al., 2003).
2.1.2.2 Transporte
Como se ha mencionado anteriormente, cuando el sedimento ingresa al sistema se puede
transportar como carga en suspensión o carga de lecho. Materiales finos tienden a
moverse como carga en suspensión y son influenciados en una primera instancia por las
fluctuaciones (turbulencia) existentes en el flujo. Materiales pesados se encuentran
como carga de lecho. El movimiento de estas partículas pesadas se ve afectado por la
3
Los términos originales son lift and drag forces (Butler, et al., 2003)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
12
distribución local de velocidades. En esta etapa es fundamental determinar el modo de
transporte de las partículas, el cual depende de la magnitud de la velocidad de corte y
la velocidad de sedimentación de las partículas (Butler, et al., 2003). Las ecuaciones
necesarias para el análisis son las siguientes:
𝑈
∗
= 𝑣√
𝜆
8
Ecuación 2. – Velocidad de corte.
𝑊
𝑠
= [
𝑔𝑑
2
18𝜈
] (
𝛾
𝑠
− 𝛾
𝛾
)
Ecuación 3. – Ley de Stokes.
donde 𝑈
∗
es la velocidad de corte [m/s]; 𝑣 la velocidad del flujo [m/s]; 𝜆 el factor de fricción;
𝑊
𝑠
la velocidad de asentamiento [m/s]; 𝑔 la aceleración de la gravedad [9.81 m/s
2
];
𝑑
𝑠
el diámetro de la partícula [m]; 𝜈 viscosidad cinemática del agua [m
2
/s]; 𝛾
𝑠
y 𝛾 los
pesos específicos de los sedimentos y el agua respectivamente [kg/m
3
]. La Ecuación 3
corresponde a la ley de Stokes. De acuerdo con May et al. (1996), si 𝑈
∗
> 0.75 𝑊
𝑠
, el
transporte de sedimentos se presentará como carga en suspensión; caso contrario se
presentaría como carga de lecho (Ebtehaj, et al., 2013).
Se han desarrollado grandes cantidades de ecuaciones para el transporte de sedimentos,
incluyendo ecuaciones predictivas basadas particularmente en canales altamente
erosionables como ríos. Estas ecuaciones se encuentran normalmente en términos de la
capacidad volumétrica de transporte de sedimentos del flujo, tanto para carga de lecho
como para carga en suspensión. Dichas ecuaciones no pueden ser aplicadas para el
diseño de sistemas de alcantarillados, puesto que, las condiciones en las tuberías son
diferentes que en los cauces naturales. Esto se debe básicamente a lo siguiente: Paredes
rígidas no erosionables en las tuberías, secciones transversales completamente
definidas y material transportado (Butler, et al., 2003).
2.1.2.3 Depósito
Si la velocidad de flujo o nivel de turbulencia decrecen, se presentará una reducción
significativa de la cantidad de sedimento presente como carga en suspensión. El
material acumulado como carga de lecho seguirá estando de ésta forma pero

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
13
eventualmente se puede acumular más sedimento debido a las bajas velocidades y por
consiguiente aumentar la profundidad del material presente en el fondo.
2.1.3 Efectos Hidráulicos Debidos a la Sedimentación
El depósito permanente de sedimentos durante épocas secas en la tubería puede causar
cambios en la sección transversal y rugosidad, lo cual afecta la distribución de
velocidades y consecuentemente la distribución del esfuerzo cortante del fondo de la
tubería (Ebtehaj, et al., 2013). Esto a su vez puede afectar el gradiente hidráulico
requerido para transportar el flujo (Ackers, et al., 1996). La presencia de sedimentos en
el sistema puede generar un pequeño incremento en las pérdidas de energía del sistema.
Experimentos de laboratorio sugieren que para tuberías lisas, con presencia de
sedimentos, el incremento en el gradiente hidráulico es alrededor del 7% en comparación
con tuberías limpias. Para tuberías rugosas, el incremento es sólo del 2% (Ackers, et al.,
1996).
2.2 Autolimpieza en Sistemas de Alcantarillados
El depósito de sedimentos en alcantarillados conlleva a efectos adversos en el desempeño
hidráulico de los sistemas y en el ambiente (Bong, 2013). Dado lo anterior, realizar un
diseño que garantice la autolimpieza en alcantarillados resulta fundamental. La
autolimpieza en sistemas de alcantarillados es un proceso que debe garantizar un
balance entre la cantidad de sedimento depositado y la tasa de erosión durante el
transporte de partículas en un periodo específico de tiempo, lo cual permita minimizar
los costos combinados de construcción, operación y mantenimiento del sistema (Butler,
et al., 2003). Dado lo anterior, no es necesario diseñar alcantarillados que operen en la
totalidad del tiempo sin ningún tipo de depósito de sedimentos, puesto que, se puede
permitir cierta profundidad de sedimentos. Lo anterior es una alternativa muy viable,
puesto que esta capa permite diseñar con pendientes menores; sin embargo se deberían
evaluar las condiciones adversas sobre la geometría y la rugosidad del sistema.
May et al. (1996) mostraron que la presencia de un depósito de sedimentos permite al
flujo mejorar la capacidad de transporte de sedimentos bajo condiciones de carga de
lecho. Dado lo anterior, se han desarrollado distintos estudios de los cuales se derivan
ecuaciones que representan el transporte de sedimentos y la capacidad de autolimpieza
en sistemas de alcantarillados. Estos criterios y ecuaciones se presentan de forma
detallada posteriormente.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
14
2.3 Ecuaciones Básicas de Diseño
Para el desarrollo de los diferentes criterios de autolimpieza en los sistemas de
alcantarillado, es necesario tener un conjunto de ecuaciones base que representen las
diferentes propiedades geométricas de la tubería. Usualmente en los sistemas reales no
se tienen condiciones de tubo lleno, por lo cual se deben emplear ecuaciones para
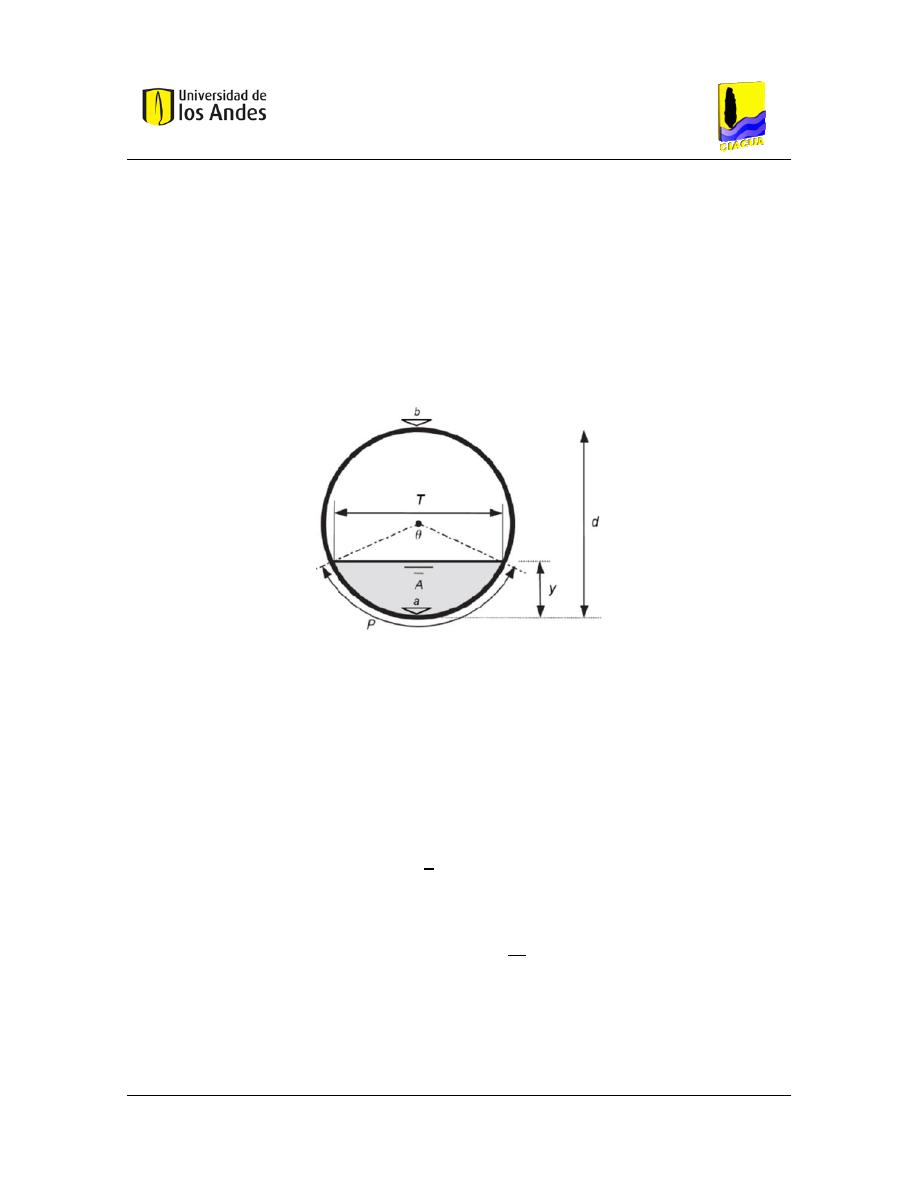
tuberías fluyendo parcialmente llenas. Una representación gráfica de las condiciones
existentes para esta condición de llenado se presenta en la Figura 3.
Figura 3. – Tubería fluyendo parcialmente llena. Tomado de Salcedo (2012).
donde 𝑇 es el ancho de la superficie; 𝑏 la cota clave de la tubería; 𝛳 el ángulo generado
por el ancho de la superficie; 𝐴 el área mojada de la sección transversal; 𝑎 la cota de
batea de la tubería; 𝑃 el perímetro mojado de la sección; 𝑦 la profundidad de agua en la
tubería y 𝑑 el diámetro de la sección. Cada una de las características geométricas
anteriores se puede describir mediante una ecuación:
𝑦 =
𝑑
2
(1 − cos (𝜃))
Ecuación 4. – Profundidad de agua en una tubería.
𝜃 = 2𝐶𝑜𝑠
−1
(1 −
2𝑦
𝑑
)
Ecuación 5. – Ángulo que forma la profundidad de agua.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
15
𝐴 =
𝑑
2
8
(𝜃 − sen (𝜃))
Ecuación 6. – Área de la sección mojada.
𝑃 =
𝑑
2
𝜃
Ecuación 7. – Perímetro mojado de la sección.
𝑅 =
𝑑
4
(
𝜃 − sen (𝜃)
𝜃
) =
𝐴
𝑃
Ecuación 8. – Radio hidráulico.
𝑇 = 𝑑 sin (
𝜃
2
)
Ecuación 9. – Ancho en la superficie.
𝐷 =
𝑑
8
(
𝜃 − sen (𝜃)
𝑠𝑒𝑛 (
𝜃
2)
) =
𝐴
𝑇
Ecuación 10. – Profundidad hidráulica.
Las ecuaciones anteriores permiten determinar las propiedades hidráulicas de una
tubería fluyendo parcial o totalmente llena. Con estas se pueden determinar algunas
propiedades propias de la tubería mediante la combinación con ecuaciones de resistencia
fluida. Entre las principales se encuentra la ecuación de Manning y de Darcy – Wiesbach
en conjunto con Colebrook – White (DW-CW):
𝑣 =
1
𝑛
𝑅
2/3
𝑆
1/2
Ecuación 11. – Ecuación de Manning.
𝑣 = −2√8𝑔𝑅𝑆 log
10
(
𝑘
𝑠
14.8𝑅
+
2.51𝜈
4𝑅√8𝑔𝑅𝑆
)
Ecuación 12. – Ecuación físicamente basada de velocidad.
La ecuación de Manning fue desarrollada originalmente y de forma empírica mediante
experimentos en canales rugosos en los cuales predominan condiciones de Flujo

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
16
Turbulento Hidráulicamente Rugoso. Dado lo anterior, para sistemas de alcantarillados
modernos en los cuales se pueden tener materiales lisos (e.g. PVC) la ecuación de
Manning no es válida, puesto que, se esperaría tener condiciones de Flujo Turbulento
Hidráulicamente Liso. Para estos casos, la ecuación físicamente basada de velocidad
(DW – CW) sería la indicada, ya que, ésta contempla los dos tipos de flujo.
2.4 Revisión de Metodologías Existentes
Como se mencionó anteriormente, existen tres grandes grupos para clasificar la
autolimpieza en sistemas de alcantarillados: 1) No-depósito de sedimentos; 2)
Movimiento de sedimentos existentes en el lecho de la tubería y 3) Pendiente de energía.
Cada uno de éstos se presenta a continuación, con sus respectivas ecuaciones,
consideraciones, limitaciones, entre otros.
2.4.1 No – depósito de Sedimentos
El primer criterio que se considera corresponde al no – depósito de sedimentos, el cual
corresponde a una velocidad mínima o esfuerzo cortante mínimo necesario para evitar
depósito de sedimentos en el sistema. En este grupo se pueden incluir los criterios
tradicionales de diseño, los cuales corresponden a valores de velocidad mínima entre 0.6
y 0.9 m/s y de esfuerzo cortante mínimo entre 1.3 y 12.6 N/m
2
. La idea en un principio
consistía en determinar la velocidad que se presentaría para el caudal máximo de diseño
y compararla con el valor estipulado en la normativa. El procedimiento general es el
siguiente (Bizier, 2007):
1) Estimar el diámetro para transportar el caudal máximo. Para condiciones de
tubo lleno se utiliza la siguiente ecuación:
𝑑 = 1.548 [
𝑛𝑄
𝑘
𝑐
𝑆
1/2
]
3/8
Ecuación 13. – Diámetro requerido para transportar el caudal de diseño
donde 𝑑 es el diámetro requerido para transportar el caudal máximo [m]; 𝑛 el
coeficiente de rugosidad de Manning; 𝑄 el caudal de diseño [m
3
/s]; 𝑘
𝑐
el factor de
conversión de unidades (0.85 en Sistema Internacional) y 𝑆 la pendiente de la
tubería [m/m].
2) Redondear el diámetro obtenido al siguiente diámetro comercial disponible.
3) Calcular la profundidad normal del flujo existente en el sistema. Esta se puede
obtener de la ecuación de Manning de forma iterativa.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
17
𝑛𝑄
𝑘
𝑐
𝑆
1/2
= 𝐴𝑅
1/3
Ecuación 14. – Planteamiento para la solución iterativa.
4) Para la profundidad normal obtenida en el paso anterior, se calcula la velocidad
(𝑣 = 𝑄/𝐴) y verificar que esta cumpla con el criterio establecido en la normativa.
En caso de que éste criterio no se cumpla, se debe aumentar la pendiente del
sistema hasta obtener una velocidad mayor o igual a la estipulada en la
normativa.
La Great Lakes Upper Mississippi River Board, GLUMRB, combinó el criterio
tradicional de 0.6 m/s con un coeficiente de rugosidad de Manning de 0.013 y creó un
estándar en el cual se establecen pendientes mínimas recomendadas para garantizar
autolimpieza en alcantarillados. Estos valores se presentan en la Tabla 2.
Tabla 2. – Pendientes mínimas recomendadas en alcantarillados. Modificado de (Bizier, 2007).
Diámetro de la Tubería
Pendiente [%]
In
mm Equivalente
Calculada GLUMRB
6
152
0.49
-
8
203
0.34
0.4
10
254
0.25
0.28
12
305
0.2
0.22
15
381
0.15
0.15
18
457
0.12
0.12
21
533
0.093
0.1
24
610
0.077
0.08
27
686
0.066
0.067
30
762
0.057
0.058
33
838
0.05
0.052
36
915
0.05
0.046
39
991
0.05
0.041
42
1067
0.05
0.037
De la Tabla 2, la columna “Calculada” corresponde al procedimiento descrito
anteriormente con un coeficiente de Manning de 0.013 y una velocidad mínima de 0.6
m/s. Igualmente, en las últimas cuatro filas de la columna tres, se tienen los mismos
valores de la pendiente; esto se debe a una recomendación de 0.05/100 como pendiente
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
18
mínima para diámetros grandes de tubería. Los valores igualmente se pueden graficar
para comparar los criterios.
Figura 4. – Comparación gráfica entre v = 0.6 m/s y el estándar GLUMRB.
Los valores propuestos por la GLUMRB han mostrado generar buenos resultados para
garantizar condiciones de autolimpieza; sin embargo éstos tienen un poder de
autolimpieza mayor al requerido en muchos casos (particularmente en tuberías con
diámetros pequeños donde la relación de llenado es superior al 20%) y menor en otros
(particularmente en tuberías con diámetros grandes fluyendo con una relación de
llenado menor al 30% y tuberías de diámetro pequeño fluyendo con relaciones de llenado
menores al 20%) (Bizier, 2007).
El problema existente con los criterios tradicionales es que la velocidad mínima resulta
ser un pobre indicador del verdadero potencial de autolimpieza en un sistema de
alcantarillado. Sin embargo, estos criterios resultan ser conservativos lo cual lleva a una
adecuada autolimpieza en la mayoría de los alcantarillados.
2.4.1.1 Sin Depósito de Sedimentos
El primero de los grupos existentes en el criterio de no-depósito de sedimentos
consiste en restringir completamente el fenómeno de sedimentación en los sistemas
de alcantarillados. Para hacer uso de este criterio de diseño, se debe identificar el
modelo de transporte de las partículas (Carga en suspensión o carga de lecho);

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
19
tamaño de los sedimentos, densidad y concentración; se debe contar con una ecuación
para predecir el transporte de sedimentos; datos o información del esfuerzo cortante
mínimo requerido para erosionar las partículas del lecho; y ecuaciones que
determinen la resistencia fluida en el sistema (Vongvisessomjai, et al., 2010).
Usualmente este criterio es el más empleado, puesto que es un criterio conservativo
en el cual se diseña la tubería con total restricción de depósito de sedimentos.
Durand (1953) llevó a cabo una serie de experimentos en tuberías lisas con diámetros
que oscilaban en un rango de 400 y 700 mm bajo condiciones de tubo lleno. Se usaron
arenas con diámetros de partículas entre 0.02 y 100 mm. Los resultados obtenidos
se expresaron en términos de un número de Froude, definido de la siguiente forma:
𝐹
𝑟
=
𝑣
√2𝑔(𝑠 − 1)𝑑
Ecuación 15. – Número de Froude modificado.
donde 𝐹
𝑟
es el número de Froude modificado [-]; 𝑣 la velocidad total del flujo [m/s]; 𝑔
la aceleración de la gravedad [m/s
2
]; 𝑠 el peso específico de las partículas y 𝑑 el
diámetro de la tubería [m]. Posteriormente diversos estudios (e.g Robinson – Graf
(1972), May (1982), CIRIA (1987), entre otros) confirmaron la importancia de éste
número de Froude en los estudios de transporte de sedimentos en tuberías. Durand
(1953) graficó el número de Froude obtenido como función de la concentración
volumétrica de sedimentos 𝐶
𝑣
, para diferentes diámetros de sedimentos. El resultado
se presenta en la Figura 5. Se muestra que 𝐹
𝑟
varía como función de 𝐶
𝑣
y el diámetro
de las partículas, 𝑑, con un rango entre 10 y 15% aproximadamente y permanece
constante posteriormente para partículas con diámetros mayores a 0.5 mm.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
20
Figura 5. – Variación del número de Froude como función del diámetro de la partícula y de
la concentración volumétrica de sedimentos. Tomado de (Ghani, 1993).
Robinson – Graf (1972) desarrollaron experimentos en dos tuberías lisas (102 mm y
152 mm) para condiciones de tubo lleno. Utilizaron dos tipos de arenas (𝑑
50
= 0.45
mm y 0.88 mm) transportadas como carga en suspensión para un rango de
velocidades entre 1.2 m/s y 2.5 m/s. Se realizó un análisis de regresión múltiple de
los datos obtenidos y se obtuvo la siguiente relación que presenta el mejor ajuste:
𝑣
√2𝑔(𝑠 − 1)𝑑
= 0.901𝐶
𝑣
0.106
(1 − 𝑆)
−1
Ecuación 16. – Ecuación de Robinson – Graf (1972).
donde 𝑆 es la pendiente de la tubería y los demás parámetros los descritos
anteriormente. El rango de concentración de sedimentos utilizado fue entre 10
3
ppm
y 7x10
4
ppm (Ghani, 1993).
Novak y Nalluri (1975) llevaron a cabo experimentos en tuberías lisas con diámetros
de 152 mm y 305 mm, las cuales fluían parcialmente llenas. Se utilizaron arenas con
diámetros entre 0.15 y 2 mm. Se realizaron análisis dimensionales y regresiones
múltiples y la ecuación que presentó mejor ajuste fue la siguiente:
𝐶
𝑣
= 4.1𝜆
𝑐
2.04
(
𝑑
𝑠
𝑅
)
−0.538
(
𝑣
𝐿
2
8𝑔(𝑠 − 1)𝑅
)
1.54
Ecuación 17. – Ecuación de Novak – Nalluri (1975)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
21
donde 𝜆
𝑐
es el factor de fricción de Darcy – Weisbach compuesto entre la tubería y
los sedimentos; 𝑣
𝐿
la velocidad límite para evitar el depósito de sedimentos en la
tubería [m/s] y 𝑅 el radio hidráulico [m]. El rango de la 𝐶
𝑣
considerado estaba entre
20 y 2400 ppm.
Macke (1982) realizó experimentos con tres tuberías lisas (192 mm, 290 mm y 445
mm) fluyendo parcialmente llenas y con presencia de arenas con tamaños (𝑑
50
) de
0.16 mm y 0.37 mm. Se derivó un modelo teórico y se verificó mediante análisis de
regresión lineal con datos observados. El resultado fue la siguiente ecuación:
𝑄
𝑠
∗
= 𝑄
𝑠
(𝜌
𝑠
− 𝜌)𝑔𝑊
𝑠
1.5
− 1.64𝑥10
−4
𝜏
𝑜
3
Ecuación 18. – Tasa de transporte de sedimentos. Macke (1982)
donde 𝑄
𝑠
∗
es la tasa de transporte de sedimentos [N·m
1.5
/s
2.5
]; 𝑊
𝑠
la velocidad de
sedimentación de las partículas [m/s] y 𝜌
𝑠
y 𝜌 las densidades del sedimento y el agua
respectivamente [kg/m
3
]. El rango estudiado de 𝑄
𝑠
∗
fue entre 10
-6
y 4x10
-3
N·m
1.5
/s
2.5
.
La Figura 6 muestra la zona de aplicación de Ecuación 18 (Región I); sin embargo
para la Región II, no se realizaron ajustes, puesto que, en ésta zona se presentan
curvas individuales que varían como función del tamaño de los sedimentos.
Mediante el uso de datos experimentales de estudios anteriores (Ambrose (1953) y
Robinson – Graf (1972)), Macke (1982) logró establecer la validez de la ecuación para
la Región I. La Ecuación 18 se reescribió y se originó la siguiente ecuación
dimensional, aplicable en el Sistema Internacional de Unidades (Ghani, 1993).
𝐶
𝑣
=
𝜆
𝐶
3
𝑣
𝐿
5
30.4(𝑆 − 1)𝑊
𝑆
1.5
𝐴
Ecuación 19. – Ecuación de Macke (1982).
Igualmente, para el cálculo de las velocidades de sedimentación de las partículas
May (1982) propuso la siguiente ecuación:
𝑊
𝑠
=
√9𝜈
2
+ 10
9
𝑑
2
𝑔(𝑠 − 1)(0.03869 + 0.0248𝑑
2
) − 3𝜈
10
−3
(0.11607 + 0.074405𝑑)
Ecuación 20. – Velocidad de sedimentación de las partículas. Macke (1982).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
22
La viscosidad cinemática del agua puede ser calculada como función de la
temperatura, 𝑇°, mediante la ecuación de Sakhuja (1987).
𝜈 =
1.79𝑥10
−6
1 + 0.03368𝑇° + 0.000221𝑇°
2
Ecuación 21. – Viscosidad cinemática del agua. Sakhuja (1987).
Figura 6. – Resultados obtenidos por Macke (1982). Tomado de (Ghani, 1993).
May (1982) estudió tuberías lisas con diámetros de 77 mm y 158 mm fluyendo parcial
y totalmente llenas. El tamaño de los sedimentos utilizados estuvo en un rango entre
0.64 y 7.9 mm. Se desarrolló un modelo teórico para transporte de carga de lecho el

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
23
cual está basado en las fuerzas actuantes a cada partícula. Dicho modelo se
simplificó mediante un análisis dimensional y resultó en la siguiente ecuación:
𝐶
𝑣
= 0.0205 (
𝑑
2
𝐴
) (
𝑑
𝑠
𝑅
)
0.6
(
𝑣
2
𝑔(𝑠 − 1)𝑑
)
3/2
(1 −
𝑣
𝑐
𝑣
)
4
Ecuación 22. – Ecuación de May (1982).
donde 𝑣
𝑐
es la velocidad crítica a la cual se inicia el movimiento incipiente de las
partículas [m/s]. Dicha velocidad se puede determinar de la siguiente forma:
𝑣
𝑐
= 0.61[𝑔(𝑠 − 1)𝑅]
0.5
(
𝑑
𝑠
𝑅
)
0.23
Ecuación 23. – Velocidad crítica. May (1982).
La ecuación anterior sólo es válida para tuberías lisas. Para materiales rugosos, el
valor debe ser 4/3 del resultado de aplicar la Ecuación 23. Los experimentos
realizados por May (1982) fueron para un rango de 𝐶
𝑣
entre 4.7 y 2100 ppm, 𝑣 entre
0.45 y 1.2 m/s y una densidad relativa (𝑠) de 2.65.
May et al. (1989) extendieron el estudio del año 1982 mediante la incorporación de
tuberías con diámetros mayores (300 mm) y rugosas (concreto), además con
partículas de 0.7 mm transportadas como carga de lecho. Los resultados obtenidos
en 1982 fueron analizados nuevamente para incluir el efecto de la relación de llenado
en la tubería (𝑦/𝑑). El resultado es una nueva ecuación:
𝐶
𝑣
= 0.0211 (
𝑦
𝑑
)
0.36
(
𝑑
2
𝐴
) (
𝑑
𝑠
𝑅
)
0.6
(
𝑣
𝐿
2
𝑔(𝑠 − 1)𝑑
)
3/2
(1 −
𝑣
𝑐
𝑣
𝐿
)
4
Ecuación 24. – Ecuación de May et al. (1989)
La ecuación anterior produce mejores resultados que la propuesta por May (1982).
Los estudios se realizaron cubriendo un rango de variación de 𝐶
𝑣
entre 0.3 y 443
ppm, velocidades entre 0.5 y 1.5 m/s, 𝑠 = 2.62 y relación de llenado entre 3/8 y 1.
Mayerle, Nalluri y Novak (1991) desarrollaron experimentos de laboratorio en una
tubería de 462 mm con fondo liso, arenas con diámetros entre 0.5 y 8.74 mm con peso
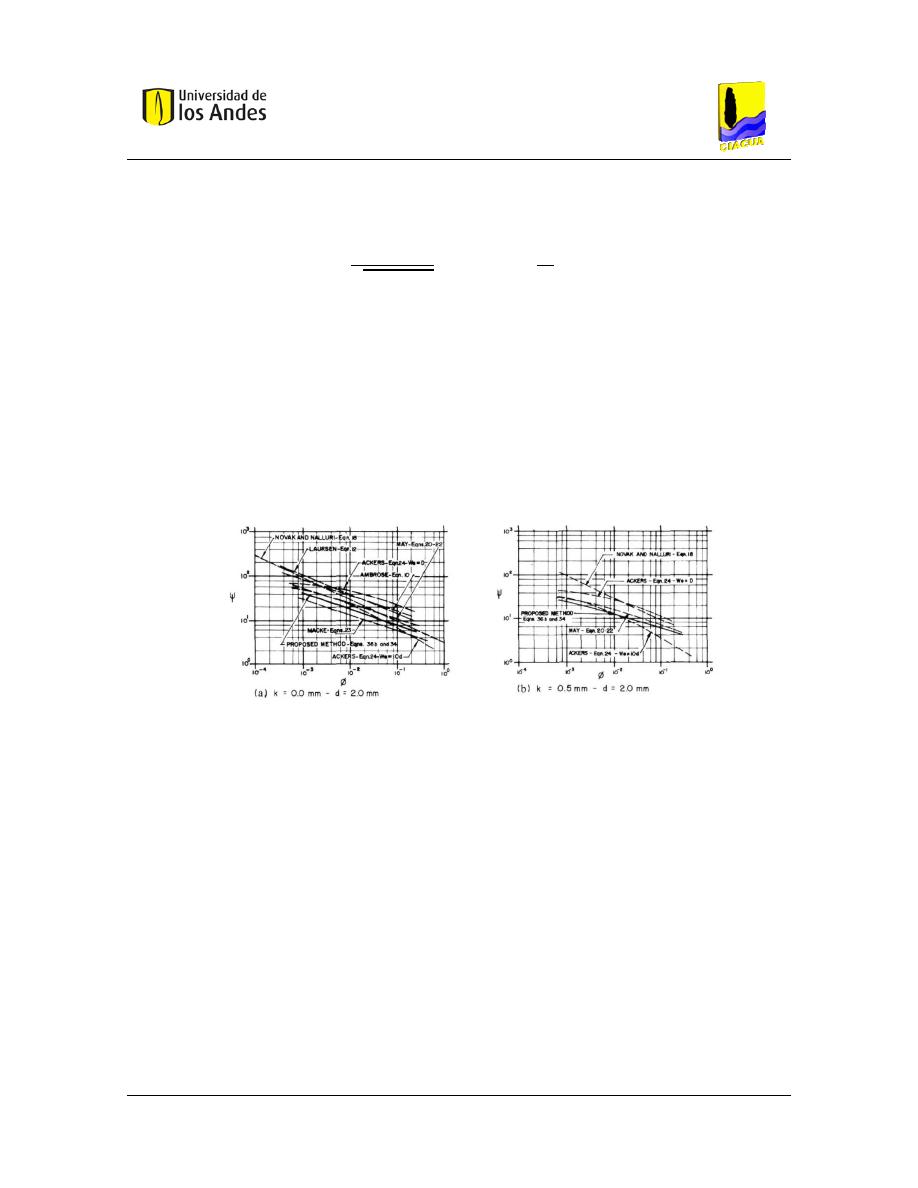
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
24
específico promedio de 2550 kg/m
3
. Realizaron análisis de regresión múltiple y
obtuvieron una ecuación para transporte de sedimentos en alcantarillados:
𝑣
𝑐
√𝑔𝑑(𝑠 − 1)
= 4.32𝐶
𝑣
0.23
(
𝑑
𝑠
𝑅
)
−0.68
Ecuación 25. – Ecuación de Mayerle, Nalluri y Novak (1991).
Concluyeron que la velocidad de autolimpieza decrece como función del tamaño de
la partícula y se incrementa con el radio hidráulico y la concentración de sedimentos.
Además de lo anterior, se realizó una comparación con otras metodologías
propuestas. Los resultados se muestran en la siguiente figura:
Figura 7. – Comparación de criterios. Tomado de (Mayerle, et al., 1991).
Ghani (1993) trabajó en tuberías de 154, 305 y 450 mm de diámetro, variando la
pendiente. La Figura 8 presenta el montaje realizado para la toma de datos. Los
sedimentos utilizados eran materiales no-cohesivos, y se intentó cubrir el rango de
tamaños encontrados normalmente en sistemas de alcantarillados (𝑑
50
= 0.5 – 10
mm). La Tabla 3 presenta los sedimentos utilizados para los experimentos, su
tamaño, densidad y peso específico.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
25
Tabla 3. – Características de los sedimentos. Modificado de Ghani (1993).
Tamaño d
50
[mm] Densidad [kg/m
3
] Peso Específico
0.46
2593
2.59
0.97
2577
2.58
2
2530
2.53
4.2
2569
2.57
5.7
2537
2.54
8.3
2550
2.55
Se concluyó que las variables básicas que gobiernan el proceso de transporte de
sedimentos en flujo uniforme para tuberías son: Profundidad del flujo, radio
hidráulico, velocidad media del flujo, esfuerzo cortante medio, viscosidad cinemática,
densidad del agua, tamaño de las partículas, densidad de las partículas,
concentración de los sedimentos, diámetro de la tubería, rugosidad de la tubería,
factor de fricción con presencia de sedimentos, pendiente del sistema y la aceleración
de la gravedad.
Figura 8. – Experimento realizado por Ghani (1993). Tomado de (Ghani, 1993).
Para las variables anteriormente mencionadas se aplicaron dos procedimientos; el
primero un análisis dimensional con el fin de obtener grupos de parámetros
dimensionales (Ver Tabla 4) y el segundo, la aplicación de ecuaciones semiempíricas
que consideran las fuerzas actuantes sobre cada una de las partículas. Igualmente
el análisis de regresión múltiple se empleó para obtener una ecuación que

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
26
representara correctamente el criterio de transporte de sedimentos en
alcantarillados.
Tabla 4. – Parámetros característicos en el transporte de sedimentos aplicables en
tuberías. Tomado de (Ghani, 1993).
La ecuación resultante (la que genera mejores resultados con los experimentos
realizados) se presenta en términos de la concentración volumétrica de sedimentos,
el tamaño de los sedimentos (tamaño no dimensional de sedimentos 𝐷
𝑔𝑟
) y el factor
de fricción:
𝑣
𝐿
√𝑔(𝑠 − 1)𝑑
50
= 3.08𝐶
𝑣
0.21
𝐷
𝑔𝑟
−0.09
(
𝑅
𝑑
50
)
0.53
𝜆
𝑐
−0.21
Ecuación 26. – Ecuación de Ghani (1993).
Nalluri et al. (1994) llevaron a cabo experimentos en tuberías con diámetros de 305
mm y fondo inmóvil (tanto liso como rugoso), sedimentos con tamaños entre 0.53 y
8.4 mm. El objetivo consistía en validar ecuaciones existentes (e.g. Alvarez (1990)) e
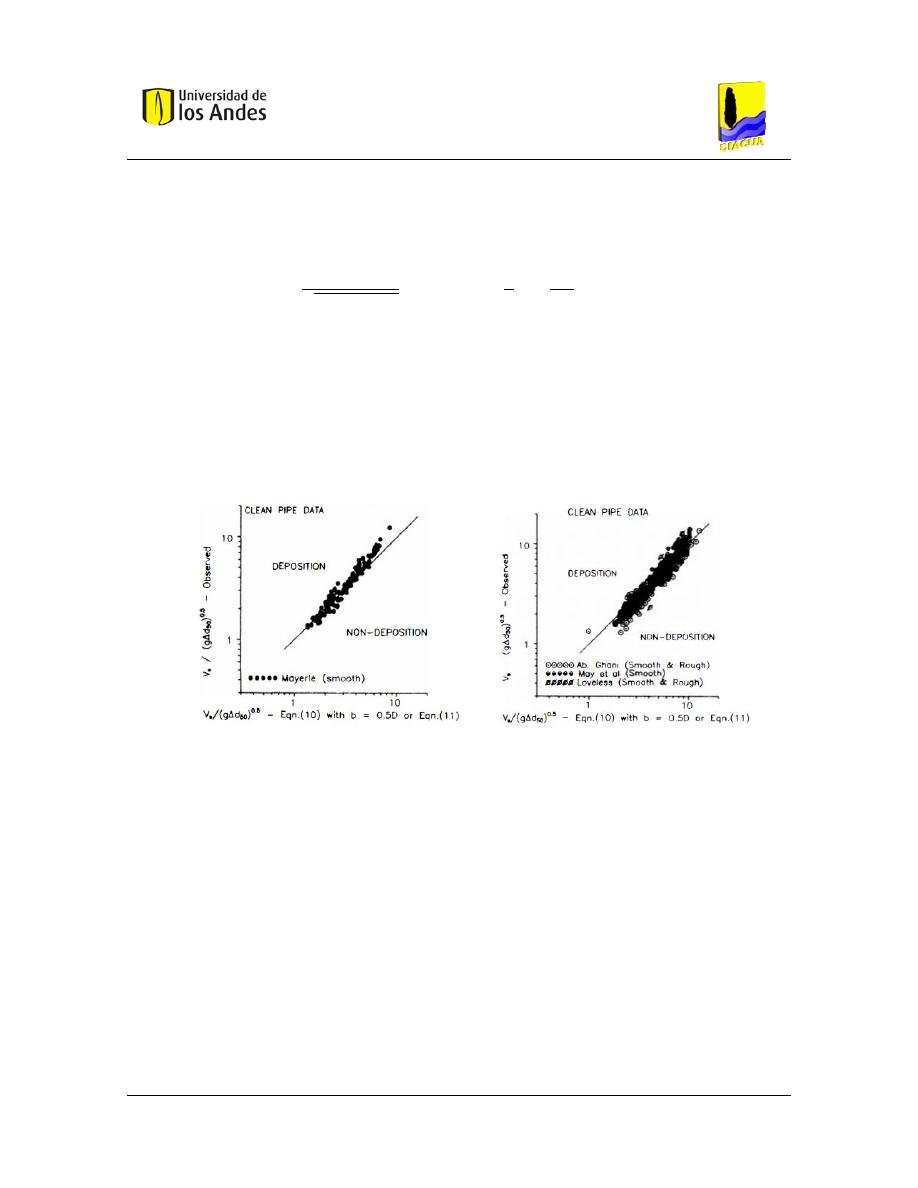
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
27
igualmente proponer una metodología o ecuación propia para representar la
autolimpieza en sistemas de alcantarillado. Se desarrollaron análisis de regresión
múltiple. La ecuación que representaba el mejor ajuste es la siguiente:
𝑣
𝐿
√𝑔(𝑠 − 1)𝑑
50
= 2.56𝐶
𝑣
0.165
(
𝑦
𝑑
)
0.4
(
𝑑
50
𝑑
)
−0.57
𝜆
𝑏
0.1
Ecuación 27. – Ecuación de Nalluri et al (1994).
donde 𝜆
𝑏
es el factor de fricción del lecho de la tubería. La ecuación anterior se validó
con datos experimentales y se observó un buen ajuste de los resultados.
Figura 9. – Validación de la Ecuación 27. Tomado de (Nalluri, et al., 1994).
Se pudo concluir que la ecuación presentada se ajusta a los valores observados en
los experimentos realizados anteriormente.
May et al. (1996) desarrollaron una ecuación a partir de 332 experimentos de
laboratorio. Estos experimentos incluían diámetros de tubería entre 77 y 450 mm,
tamaño de sedimentos entre 160 y 8300 μm, velocidades de flujo entre 0.24 y 1.5 m/s,
relación de llenado de la tubería entre 0.16 y 1 y concentraciones de sedimentos entre
2.3 y 2110 ppm. La ecuación es la siguiente:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
28
𝐶
𝑉
= 3.03𝑥10
−2
(
𝑑
2
𝐴
) (
𝑑
50
𝐷
)
0.6
(1 −
𝑣
𝑡
𝑣
𝐿
)
4
(
𝑣
𝐿
2
𝑔(𝑠 − 1)𝑑
)
1.5
Ecuación 28. – Ecuación de May et al. (1996).
De la ecuación anterior se debe calcular la velocidad límite
4
𝑣
𝑡
, la cual corresponde
a la siguiente expresión:
𝑣
𝑡
= 0.125√𝑔(𝑠 − 1)𝑑
50
(
𝑑
𝑑
50
)
0.47
Ecuación 29. – Velocidad límite. Tomado de May et al. (1996).
Recientemente Vongvisessomjai et al. (2010) realizaron experimentos en laboratorio
con tuberías de PVC cuyos diámetros se presentaban entre 100 y 150 mm, arenas
con diámetros de 0.2, 0.3 y 0.43 mm. Un montaje del experimento se presenta en la
Figura 10, en el cual se puede variar la pendiente como función de las velocidades y
profundidades del flujo. Las características propias del sedimento y las condiciones
del sistema permiten la presencia de sedimentos tanto suspendidos como en el lecho.
Los resultados son ecuaciones que relacionan el número de Froude, la concentración
volumétrica de sedimentos y el tamaño de las partículas. Se compararon los
resultados obtenidos de velocidad mínima con las obtenidas mediante la ecuación de
Camp (1942) y los criterios de Macke (1982) y May et al. (1996).
4
El término original es threshold velocity (May, et al., 1996).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
29
Figura 10. - Montaje del experimento (Unidades en m). Tomado de (Vongvisessomjai, et al.,
2010).
Durante los 21 experimentos realizados (Ver Anexo 1) se estableció que la carga en
suspensión se presenta para diámetros de 0.2 y 0.3 mm solamente. De esa tabla,
𝑉
𝐿𝑒𝑥𝑝𝑡
es la velocidad mínima, obtenida de los experimentos, para evitar depósito de
sedimentos mientras que 𝑉
𝐶𝑎𝑚𝑝
es la velocidad mínima para erosionar el lecho de
sedimentos. Igualmente, 𝜏
𝑏𝑒𝑑
es el esfuerzo cortante mínimo promedio cuando el
depósito de partículas se inicia. Este valor se comparó con el esfuerzo de Camp. Estos
valores se pueden determinar de la siguiente forma:
𝑣
𝑐𝑎𝑚𝑝
=
1
𝑛
𝑅
1/6
√𝐵
𝑎
(𝑠 − 1)𝑑
𝑠
Ecuación 30. – Velocidad de Camp.
𝜏
𝑐𝑎𝑚𝑝
= 𝐵
𝑎
𝜌𝑔(𝑠 − 1)𝑑
𝑠
Ecuación 31. – Esfuerzo cortante de Camp.
donde 𝐵
𝑎
es una constante adimensional igual a 0.8 para tener una adecuada
autolimpieza en alcantarillados. Dado que los criterios de Camp (1942) están
basados en el concepto de erosionar el depósito de sedimentos en el lecho, estos no
consideran la condición de no-depósito de sedimentos o el transporte de los mismos.
Dado lo anterior, estos no deberían utilizarse como criterios de autolimpieza. Con el

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
30
fin de desarrollar un criterio de autolimpieza, se realizó un análisis de regresión
mediante un software estadístico y se obtuvieron las siguientes ecuaciones:
𝑣
𝐿
√𝑔(𝑠 − 1)𝑑
50
= 1.03𝐶
𝑣
0.375
(
𝑑
50
𝑅
)
−1.08
Ecuación 32. – Ecuación de Vongvisessomjai et al. (2010) para carga en suspensión como
función del Radio Hidráulico.
𝑣
𝐿
√𝑔(𝑠 − 1)𝑑
50
= 2.69𝐶
𝑣
0.328
(
𝑑
50
𝑦
)
−0.717
Ecuación 33. – Ecuación Vongvisessomjai et al. (2010) para carga en suspensión como
función de la profundidad de agua.
Por otra parte, la carga de lecho se presenta para todos los diámetros de partículas
considerados. Se realizaron 28 experimentos para ésta condición (Ver Anexo 2). Al
igual que la carga de lecho se presentan los valores de la velocidad y esfuerzo
cortante de Camp y se comparan con los valores obtenidos experimentalmente.
Nuevamente se realiza el análisis de regresión y se obtienen las siguientes
ecuaciones de autolimpieza para carga de lecho:
𝑣
𝐿
√𝑔(𝑠 − 1)𝑑
50
= 4.31𝐶
𝑣
0.226
(
𝑑
50
𝑅
)
−0.616
Ecuación 34. - Ecuación de Vongvisessomjai et al. (2010) para carga de lecho como
función del Radio Hidráulico.
𝑣
𝐿
√𝑔(𝑠 − 1)𝑑
50
= 3.57𝐶
𝑣
0.21
(
𝑑
50
𝑦
)
−0.542
Ecuación 35. - Ecuación de Vongvisessomjai et al. (2010) para carga de lecho como
función de la profundidad de agua.
De las ecuaciones anteriores se puede plantear el siguiente procedimiento de diseño
(Vongvisessomjai, et al., 2010).
1) Determinar los parámetros de entrada al modelo: Concentración volumétrica de
sedimentos 𝐶
𝑣
, diámetro de las partículas 𝑑
𝑠
, densidad relativa 𝑠, coeficiente de
rugosidad de Manning 𝑛, caudal en tiempo seco 𝑄
𝑑𝑤𝑓
y tiempo húmedo 𝑄
𝑤𝑤𝑓
.
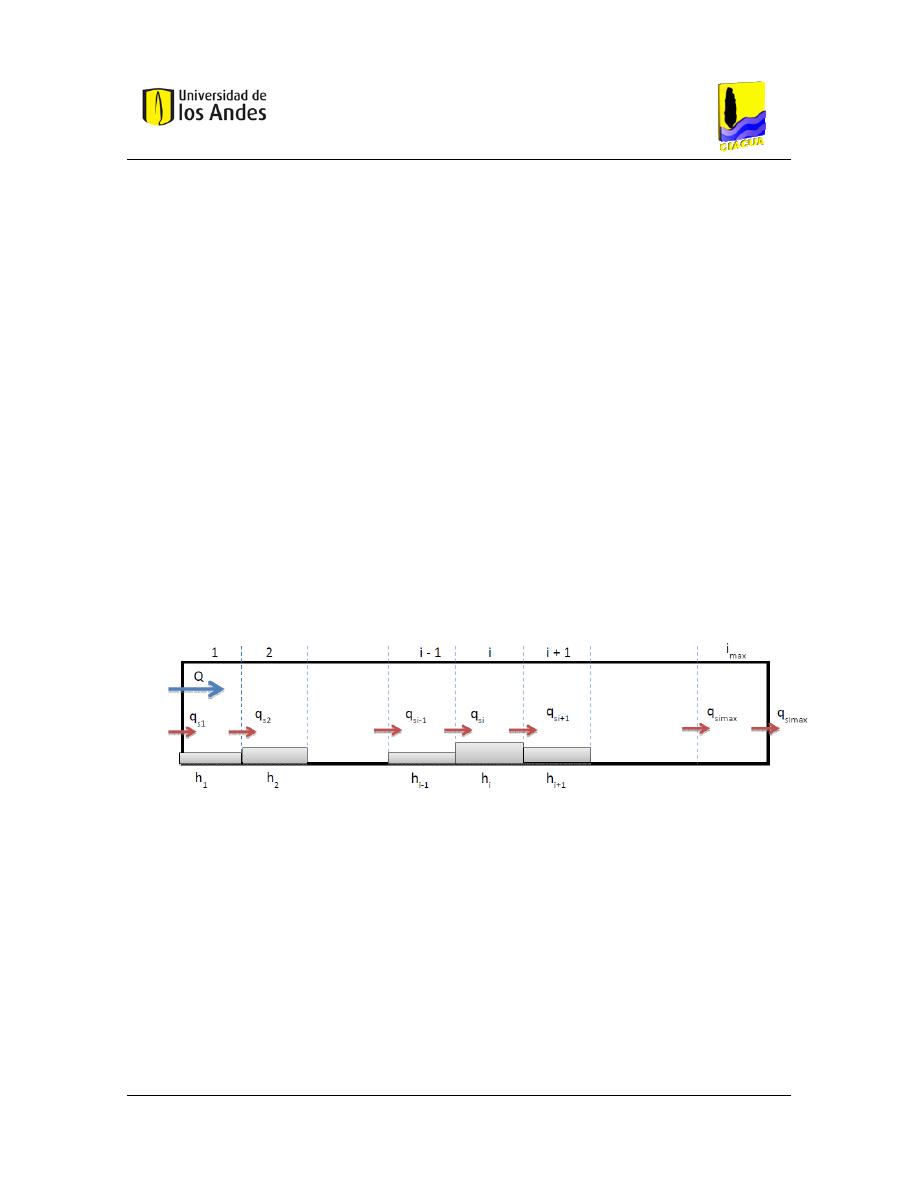
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
31
2) Para condiciones húmedas tomar la profundidad como 0.938𝑑, donde 𝑑 es el
diámetro es el diámetro de la tubería. Este diámetro se determina de la ecuación
de Manning.
3) Calcular la profundidad y velocidad para condiciones de tiempo seco.
4) Determinar el modo de transporte de las partículas: Carga de lecho o carga en
suspensión, ver Ecuación 20.
5) Si el modo de transporte de sedimentos se encuentra como carga en suspensión,
aplicar la Ecuación 32 o la Ecuación 33. Si se encuentra como carga de lecho
aplicar la Ecuación 34 o la Ecuación 35.
6) La velocidad 𝑣
𝐿
obtenida debe ser menor a la velocidad del flujo para condiciones
secas. En caso de no presentarse esta condición, se debe aumentar la pendiente
del sistema y repetir el procedimiento de cálculo.
Ibro y Larsen (2011) propusieron un método basado en diferencias finitas, para
modelar el transporte de sedimentos, haciendo especial énfasis en el problema de
autolimpieza. El esquema propuesto se muestra en la Figura 11. Igualmente se
realizaron experimentos de laboratorio en una tubería lisa de 240 mm de diámetro
con partículas de tamaño entre 0.075 mm y 0.25 mm.
Figura 11. – Esquema unidimensional del modelo numérico. Tomado de (Ibro & Larsen,
2011).
Por otra parte Ebtehaj et al. (2013) continúan la línea de investigación de estudios
anteriores, en la cual realizan regresiones lineales para obtener ecuaciones que
predicen la autolimpieza en sistemas de alcantarillados. Se usó una combinación de
los experimentos de laboratorio realizados por Ghani (1993) y Vongvisessomjai et al.
(2010). El método de comparación de resultado es el criterio de Error Cuadrático
Medio (RMSE) y el Error Medio Absoluto (MARE); sin embargo estos criterios no
permiten una comparación simultánea entre el promedio y la varianza de los
modelos; se propone el uso del Criterio de Información de Akaike (AIC) para verificar

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
32
los resultados generados por las ecuaciones propuestas y estudios anteriores (Ghani
(1993), May et al. (1996) y Vongvisessomjai et al. (2010)). Los anteriores criterios se
definen de la siguiente forma:
𝑅𝑀𝑆𝐸 = √
∑
(𝑥
𝑖
− 𝑦
𝑖
)
2
𝑛
𝑖=1
𝑛
Ecuación 36. – Criterio RMSE evaluado por Ebtehaj et al. (2013).
𝑀𝐴𝑅𝐸 =
1
𝑛
∑
|𝑥
𝑖
− 𝑦
𝑖
|
𝑥
𝑖
𝑛
𝑖=1
Ecuación 37. – Criterio MARE evaluado por Ebtehaj et al. (2013).
𝐴𝐼𝐶 = 𝑛 ∙ 𝑙𝑜𝑔 [
1
𝑛
∑(𝑥
𝑖
− 𝑦
𝑖
)
2
𝑛
𝑖=1
] + 2𝑘
Ecuación 38. – Criterio AIC evaluado por Ebtehaj et al. (2013).
Al realizar el análisis de regresión, se obtienen las siguientes ecuaciones aplicables
para carga en suspensión y de lecho:
𝑉
𝐿
√𝑔(𝑠 − 1)𝑑
50
= 4.49𝐶
𝑣
0.21
(
𝑑
50
𝑅
)
−0.54
Ecuación 39. – Ecuación de Ebtehaj et al. (2013) como función del radio hidráulico.
𝑉
𝐿
√𝑔(𝑠 − 1)𝑑
50
= 3.59𝐶
𝑣
0.22
(
𝑑
50
𝑦
)
−0.51
Ecuación 40. – Ecuación de Ebtehaj et al (2013) como función de la profundidad de agua.
Las ecuaciones anteriores se validaron con los datos obtenidos de forma
experimental por Ghani (1993). Los resultados se presentan en la Figura 12.
Igualmente, se realizó una comparación con las ecuaciones y metodologías
propuestas por May et al. (1996) y Vongvisessomjai et al (2010). Esta comparación
se presenta en la Figura 13.
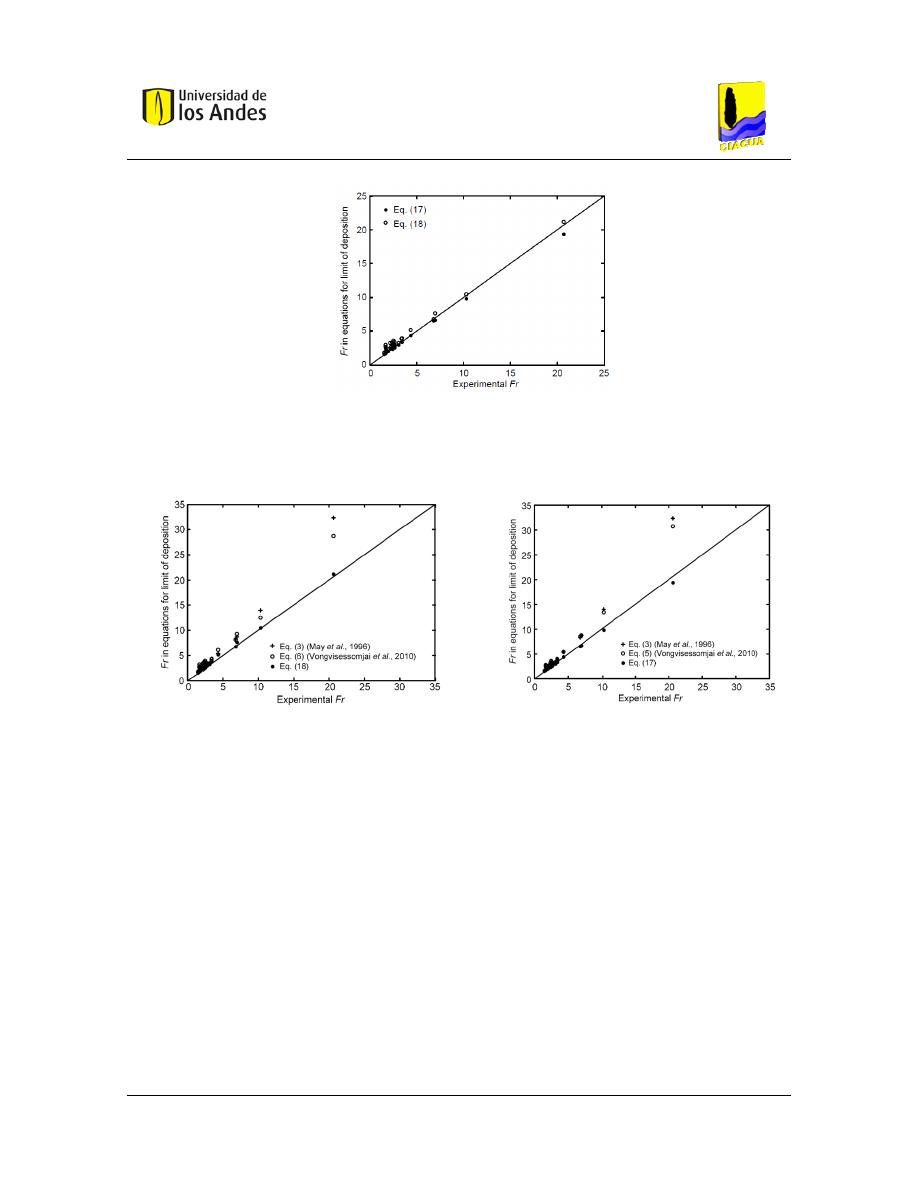
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
33
Figura 12. – Validación de la Ecuación 39 y Ecuación 40 con los experimentos realizados por
Ghani (1993). Tomado de (Ebtehaj, et al., 2013).
Figura 13. – Comparación de las ecuaciones propuestas con distintas metodologías.
En la Figura 13 se presentan las comparaciones de los resultados obtenidos por
distintos autores. A la izquierda se observa la comparación con la ecuación que se
encuentra como función de 𝑑
50
/𝑅 y a la derecha como función de 𝑑
50
/𝑦. Se concluye
por lo tanto que las ecuaciones obtenidas por Ebtehaj et al. (2013) resultan
representar de una mejor forma las condiciones reales de autolimpieza de una forma
más simple, además de requerir un menor número de parámetros para la estimación
de los resultados.
2.4.1.2 Con Depósito Límite de Sedimentos
El segundo grupo considerado corresponde al depósito límite de sedimentos. Este
criterio es menos conservativo que el anterior puesto que, se permite una pequeña
acumulación de sedimentos en el lecho de la tubería. Eventualmente esta
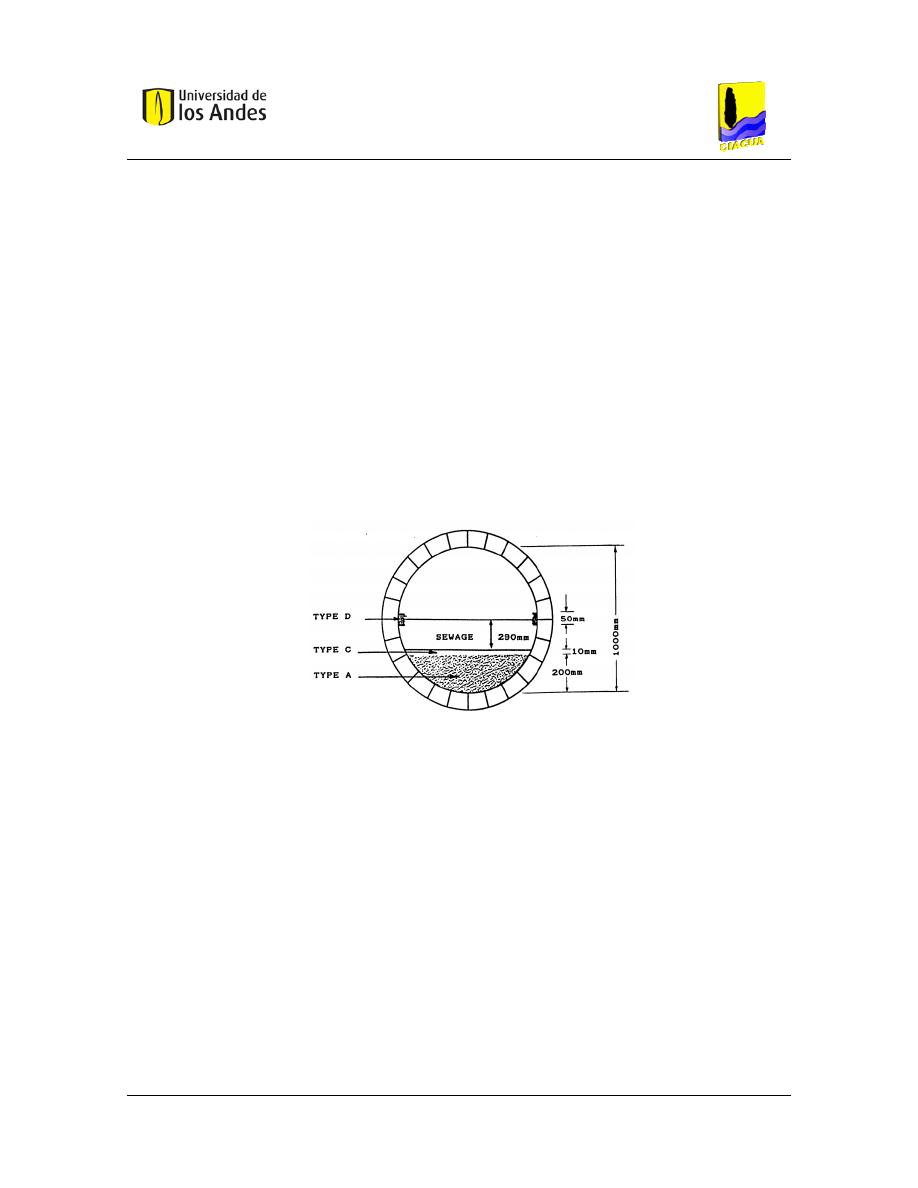
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
34
acumulación reduce la pendiente necesaria para garantizar autolimpieza; sin
embargo se requiere de mayor cuidado en el mantenimiento de los sistemas, dado
que, se encuentra en una condición muy cercana al límite (Vongvisessomjai, et al.,
2010). Si se realiza el diseño de forma incorrecta, la acumulación de sedimentos en
el fondo resultará ser un problema incontrolable y se aumentaría el riesgo de
presurización y sobrecarga en el sistema.
Los sedimentos se pueden clasificar en cinco clases: Tipo A, material grueso,
granular que se encuentra usualmente en el lecho de la tubería; Tipo B, igual al Tipo
A pero con adición de grasas, cemento, entre otros; Tipo C, material fijo móvil
encontrado en el límite de la capa superior de sedimentos Tipo A; Tipo D, biopelículas
y Tipo E, material fino y depósitos orgánicos encontrados en tanques de retención de
aguas lluvias.
Figura 14. – Clasificación de sedimentos en sistemas de alcantarillados. Tomado de
Álvarez (1990).
May et al. (1989) realizaron experimentos con pequeñas profundidades de depósito
en una tubería de 300 mm de diámetros y arenas de 0.72 mm con peso específico de
2.62 transportadas como carga de lecho. Los resultados obtenidos muestran un
incremento en la capacidad de transporte con la presencia de una pequeña capa de
sedimentos depositados. Con una profundidad relativa de sedimentos (𝑦
𝑠
/𝑑) del 1%,
se encontró que la capacidad de transporte se incrementa con un factor de dos, con
relación a condiciones sin presencia de éstos depósitos. Dado lo anterior, se propuso
una ecuación para esa profundidad relativa de sedimentos:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
35
𝐶
𝑣
= 0.04 (
𝑦
𝑑
)
0.36
(
𝑑
2
𝐴
) (
𝑑
𝑠
𝑅
)
0.6
(1 −
𝑣
𝑡
𝑣
𝐿
)
4
(
𝑣
𝐿
2
𝑔(𝑠 − 1)𝑑
)
1.5
Ecuación 41. – Ecuación propuesta por May et al. (1989).
La concentración volumétrica se presentó con un rango entre 6 y 1165 ppm,
velocidad entre 0.5 y 1.5 m/s, profundidad relativa de sedimentos entre 0.0008 y
0.1623 y la relación de llenado entre 0.5 y 1.
May (1993) extendió sus análisis e incluyó tuberías de concreto de 450 mm de
diámetro, arenas con tamaños de 0.47 y 0.73 mm con peso específico de 2.64. En este
estudio se derivó una relación semiempírica de transporte basada en el esfuerzo
cortante actuante en el lecho de sedimentos. Se definieron dos parámetros:
𝜂 = 𝐶
𝑣
(
𝑑
𝑊
𝑏
) (
𝐴
𝑑
2
) (
𝜃𝜆
𝑔
𝑣
𝐿
2
8𝑔(𝑠 − 1)𝑑
)
−1
Ecuación 42. – Parámetro de transporte. Tomado de May (1993).
𝐹
𝑠
= (
𝜃
𝑚
𝜆
𝑔
𝑣
𝐿
2
8𝑔(𝑠 − 1)𝑑
50
)
1/2
Ecuación 43. – Parámetro de movilidad. Tomado de May (1993).
Donde 𝜂 es un parámetro de transporte; 𝑊
𝑏
es el ancho del lecho de sedimentos en
la tubería [m]; 𝜃
𝑚
un factor de transición definido mediante la Ecuación 44 y 𝐹
𝑠
un
parámetro de movilidad de los sedimentos.
𝛳
𝑚
=
𝑒𝑥𝑝 (
𝑅
∗𝑐
12.5) − 1
𝑒𝑥𝑝 (
𝑅
∗𝑐
12.5) + 1
Ecuación 44. – Factor de transición. Tomado de May (1993).
donde 𝑅
∗𝑐
es el número de Reynolds de la partícula el cual está definido de la
siguiente forma:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
36
𝑅
∗𝑐
= √
𝜆
𝑠
8
(
𝑣𝑑
50
𝜈
)
Ecuación 45. – Número de Reynolds de la partícula. Tomado de May (1993).
Los valores de 𝜂 fueron definidos como función de 𝐹
𝑠
y se obtuvieron del análisis de
los datos experimentales en la tubería de 450 mm. Los resultados se presentan en la
Tabla 5.
Tabla 5. – Valores de 𝜼. Tomado de Ghani (1993).
Álvarez (1990) experimentó con sedimentos no-cohesivos en tuberías con diámetros
de 154 mm fluyendo parcialmente llenas. El tamaño de los sedimentos se encontraba
entre 0.5 y 4.1 mm con un peso específico promedio de 2.55. Se obtuvo una ecuación
mediante análisis de regresión múltiple que representa los resultados obtenidos
experimentalmente de forma adecuada:
𝜏
𝑏
𝜌(𝑠 − 1)𝑔𝑑
𝑠
= 1.6𝐶
𝑣
0.64
(
𝑑
𝑠
𝑅
𝑏
)
−1.27
𝜆
𝑏
0.62
Ecuación 46. – Ecuación propuesta por Álvarez (1990).
Los experimentos cubrieron un rango de concentración de sedimentos entre 2 y 131
ppm, profundidad relativa de sedimentos entre 0.105 y 0.392 y una relación de
llenado entre 0.3 y 0.8.
Perrusquía (1991) desarrolló experimentos en tuberías de 154, 225 y 450mm para
condiciones de flujo parcialmente lleno. Se utilizaron sedimentos con un rango entre

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
37
0.72 y 2.5 mm con peso específico entre 2.59 y 2.65. Los sedimentos se transportaron
como carga de lecho. Igualmente, se realizaron regresiones lineales múltiples para
derivar la ecuación que presenta la mejor medida de ajuste.
∅
𝑏
′
= 46137𝜃
𝑏
2.9
𝐷
𝑔𝑟
−1.2
(
𝑦
𝑑
𝑠
)
−0.7
(
𝑦
𝑑
)
0.7
(
𝑦
𝑠
𝑑
)
−0.62
Ecuación 47. – Parámetro de transporte de sedimentos. Tomado de Perrusquía (1991).
donde ∅
𝑏
′
es el parámetro de transporte de sedimentos definido como función de la
tasa de transporte por unidad de ancho, 𝑞
𝑠
, ∅
𝑏
′
= 𝑞
𝑠
/√𝑔(𝑠 − 1)𝑑
𝑠
3
. Se tomaron
valores entre 30 y 408 ppm para concentración de sedimentos, 0.294 y 0.668 m/s para
la velocidad de flujo, 0.2 y 0.4 para la profundidad relativa de sedimentos y 0.32 y
0.86 para la relación de llenado de la tubería.
El – Zaemy (1991) midió las tasas de transporte de sedimentos en tuberías de 305
mm de diámetro con fondo liso y rugoso fluyendo parcialmente llenas. Los
sedimentos considerados se encontraban en un rango entre 0.53 y 8.4 mm con un
peso específico de 2.59. Al igual que estudios anteriores, se realizó un análisis de
regresión múltiple y se propuso una ecuación para transporte de sedimentos en
alcantarillados:
𝜏
𝑜
𝜌(𝑠 − 1)𝑔𝑑
𝑠
= 0.55𝐶
𝑣
0.33
(
𝑊
𝑏
𝑦
)
−0.76
(
𝑑
𝑠
𝑑
)
−1.13
𝜆
𝑐
1.22
Ecuación 48. – Ecuación propuesta por El – Zaemy (1991).
donde 𝑏 es el ancho de la cama de sedimentos. Igualmente, se presenta una expresión
para el factor de fricción 𝜆
𝑠
:
𝜆
𝑐
= 0.88𝐶
𝑣
0.01
(
𝑊
𝑏
𝑦
)
0.03
𝜆
0.94
Ecuación 49. – Factor de fricción. Tomado de El – Zaemy (1991).
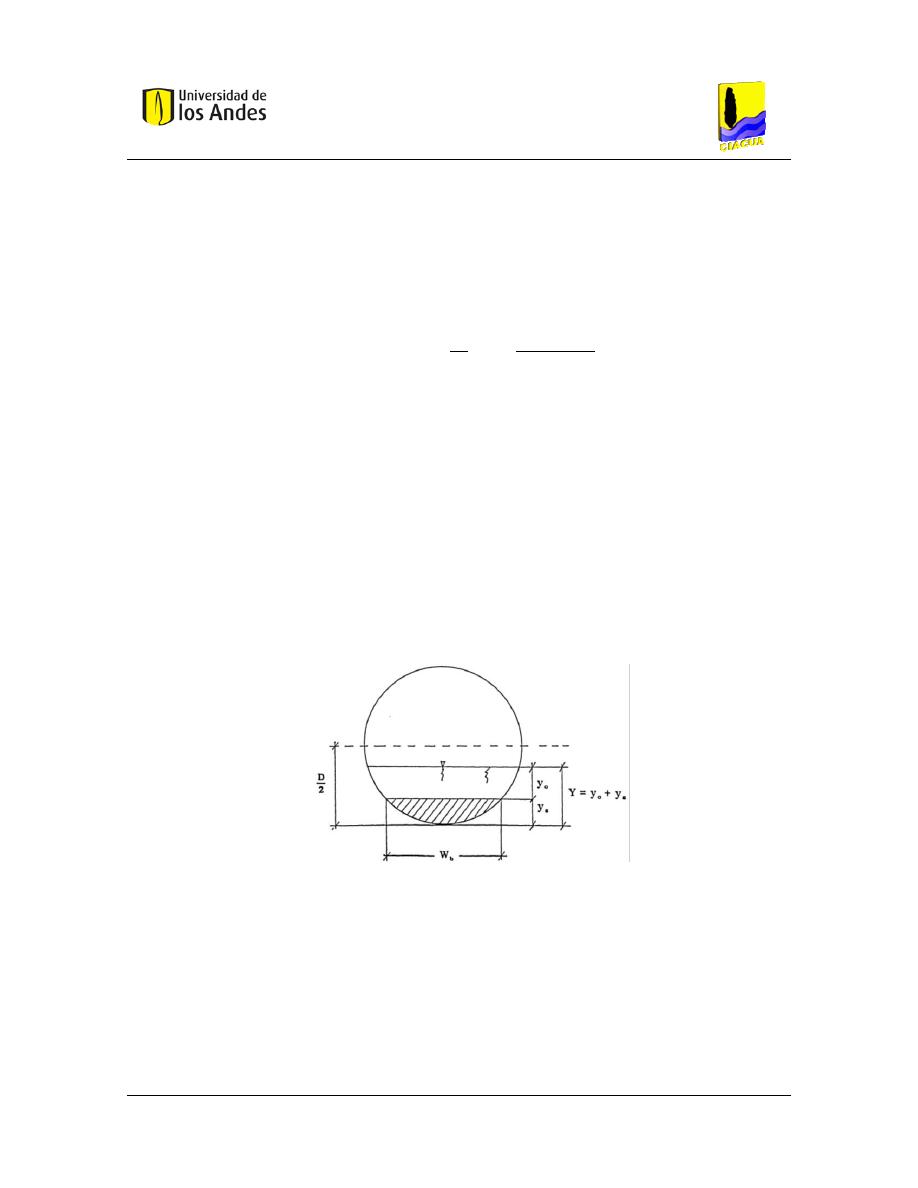
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
38
Estos experimentos se realizaron en un rango entre 11 y 512 ppm, 0.36 y 0.83 m/s
de velocidad, 1.1 y 7.4 𝑏/𝑦, 0.154 y 0.393 de profundidad relativa de sedimentos y
0.34 y 0.82 de relación de llenado.
Nalluri y Alvarez (1992) obtuvieron una ecuación aplicable para el caso de depósito
límite de sedimentos:
𝐶
𝑣
= 0.0185𝜆
0.59
(
𝑑
𝑠
𝑅
𝑏
)
0.419
[
𝑣
𝐿
2
𝑔(𝑠 − 1)𝑅
𝑏
]
1.56
Ecuación 50. – Ecuación propuesta por Nalluri y Alvarez (1992).
donde 𝑅
𝑏
corresponde a la porción del radio hidráulico que ocupa el lecho de
sedimentos en la tubería.
Ghani (1993) en su trabajo realizó estimaciones para no – depósito de sedimentos y
depósito límite. El primero se presentó previamente (Ver Ecuación 26), mientras que
en el segundo se considera una pequeña capa de sedimentos en el fondo de la tubería.
Una representación gráfica es la siguiente:
Figura 15. – Geometría de la sección transversal para tuberías con depósito de sedimentos
en el lecho de la tubería. Tomado de Ghani (1993).
La ecuación resultante para éste tipo de transporte es la siguiente:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
39
𝐶
𝑣
= 0.355𝜆
𝑐
1.94
(
𝑊
𝑏
𝑦
0
)
1.12
(
𝑑
𝑑
50
)
1.0
[
𝑣
𝐿
2
𝑔(𝑠 − 1)𝑑
]
3.12
Ecuación 51. – Ecuación propuesta por Ghani (1993).
donde 𝜆
𝑐
es el factor de fricción compuesto entre la capa de sedimentos y la tubería
y el cual se puede expresar de la siguiente forma:
𝜆
𝑐
= 0.0014𝐶
𝑣
−0.04
(
𝑊
𝑏
𝑦
0
)
0.34
(
𝑅
𝑑
50
)
0.24
𝐷
𝑔𝑟
0.54
Ecuación 52. – Factor de fricción compuesto. Tomado de Ghani (1993).
Ebtehaj et al. (2013) igualmente en su estudio derivaron ecuaciones basadas en datos
experimentales (Ghani (1993) y Vongvisessomjai et al. (2010). Las ecuaciones
resultantes del análisis de regresión múltiple son las siguientes:
𝑣
𝐿
√𝑔(𝑠 − 1)𝑑
50
= 2.5𝐶
𝑣
0.375
(
𝑑
50
𝑅
)
−0.766
(
𝑦
𝑠
𝑑
)
−0.258
Ecuación 53. – Ecuación propuesta por Ebtehaj et al. (2013) como función del radio hidráulico.
Depósito límite de sedimentos.
𝑣
𝐿
√𝑔(𝑠 − 1)𝑑
50
= 2.8𝐶
𝑣
0.335
(
𝑑
50
𝑦
)
−0.482
(
𝑦
𝑠
𝑑
)
−0.463
Ecuación 54. – Ecuación propuesta por Ebtehaj et al. (2013) como función de la profundidad de
agua. Depósito límite de sedimentos.
Estas ecuaciones se validan igualmente con los experimentos realizados por Ghani
(1993) y se comparar con los resultados del mismo autor. La Figura 16 y la Figura
17 presentan los resultados de dicha validación.
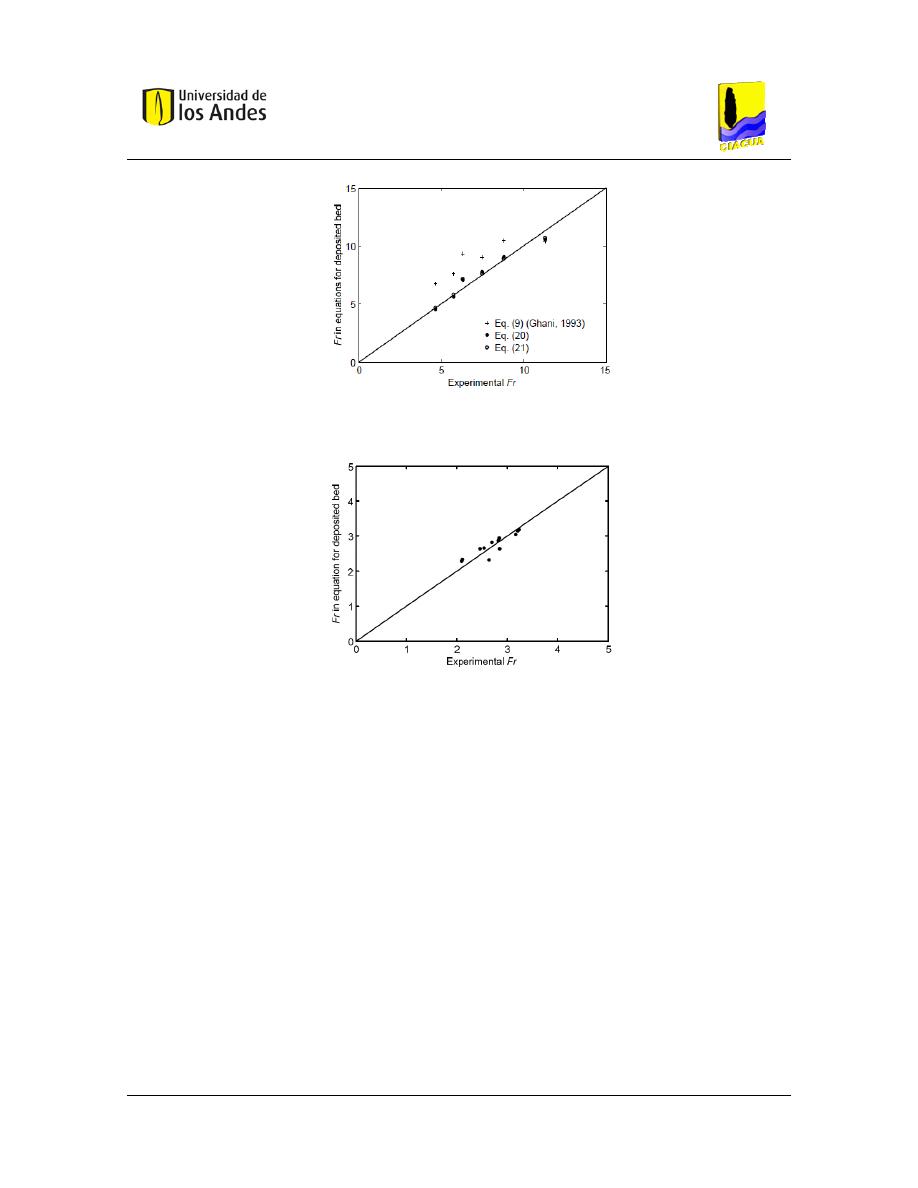
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
40
Figura 16. Validación de la Ecuación 53 y la Ecuación 54 con los experimentos realizados
por Ghani (1993). Tomado de Ebtehaj, et al., (2013).
Figura 17. – Validación de la Ecuación 53. Tomado de Ebtehaj, et al., (2013).
2.4.2 Movimiento de Sedimentos Existentes en el Lecho de la Tubería
El segundo gran grupo de criterios de autolimpieza en sistemas de alcantarillados,
corresponde al movimiento de sedimentos existentes en el lecho de la tubería. Este tipo
de diseño considera básicamente dos criterios: Velocidad y esfuerzo cortante.
2.4.2.1 Velocidad
El criterio de Velocidad se puede clasificar en dos grupos: Movimiento incipiente y
transporte de sedimentos. El trabajo realizado por Shields (1936) ha sido el estándar
para dar inicio a los estudios de movimiento incipiente y transporte de sedimentos.
Se definió un umbral entre transporte y no transporte y se construyó un diagrama
que permite observar cada una de las regiones (Ver Anexo 3). Existen pocos estudios
que han desarrollado conocimiento de éste tipo de transporte de sedimentos. Sin

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
41
embargo entre los más representativos se encuentran los realizados por Craven
(1953), Novak y Nalluri (1975, 1984) y Ojo (1978).
Craven (1953) desarrolló ecuaciones para transporte de carga de lecho en tuberías
fluyendo totalmente llenas. Dichas ecuaciones se obtienen de experimentos
realizados en laboratorio. Estos se llevaron a cabo en tuberías de 6 in de diámetro
con presencia de arenas de 0.25, 0.58 y 1.62 mm. Se graficó el gradiente de energía
como función de la tasa de descarga. Los resultados obtenidos se presentan en el
Anexo 4.
Durand y Condolios (1956), Laursen (1956), Robinson y Graf (1972) realizaron
experimentos y obtuvieron las siguientes ecuaciones:
𝑣
𝐿
√2𝑔𝑑(𝑠 − 1)
= 1.36𝐶
𝑣
0.136
Ecuación 55. – Ecuación propuesta por Durand y Condolios (1956)
𝑣
𝐿
√2𝑔𝑦
0
(𝑠 − 1)
= 7.0𝐶
𝑣
1/3
Ecuación 56. – Ecuación propuesta por Laursen (1956)
𝑣
𝐿
√2𝑔𝑑(𝑠 − 1)
=
1.4𝐶
𝑣
0.11
𝑑
𝑠
0.06
1 − 𝑡𝑎𝑛𝜃
Ecuación 57. – Ecuación propuesta por Robinson y Graf (1972)
Novak y Nalluri (1975) condujeron experimentos en tuberías circulares lisas con
diámetros de 152 y 305 mm. Se usaron sedimentos no – cohesivos con tamaños entre
0.6 y 50 mm y tuberías fluyendo parcialmente llenas. Los resultados experimentales
y el análisis teórico realizado llevaron a proponer la siguiente ecuación:
𝑣
𝑐
√𝑔𝑑
= 0.61(𝑆 − 1)
1/2
(
𝑑
𝑠
𝑅
)
−0.27
Ecuación 58. – Ecuación propuesta por Novak y Nalluri (1975).
Estos experimentos se llevaron a cabo para profundidades relativas de sedimentos,
𝑑
𝑠
/𝑅, entre 0.01 y 0.3. La Figura 18 presenta gráficamente los experimentos
realizados y la relación con la Ecuación 58.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
42
Figura 18. – Criterio de movimiento incipiente para canales con fondo rígido. Tomado de
Ghani (1993).
Ojo (1978) extendió el trabajo realizado por Novak y Nalluri (1975) en canales
rectangulares de 305 mm de ancho con el fin de incluir efectos de agrupamiento de
partículas. Se utilizaron arenas con un rango entre 0.3 y 4.2 mm. Las partículas
agrupadas se ubicaron de dos diferentes maneras: 1) Partículas espaciadas en todo
el ancho del canal y 2) Partículas espaciadas longitudinalmente a lo largo de la línea
central del canal.
Novak y Nalluri (1984) reanalizaron los datos de los experimentos realizados en el
año 1975 y combinaron sus análisis con los presentados por Ojo (1978). La ecuación
resultante es la siguiente:
𝑣
𝑐
√𝑔𝑑
= 0.50(𝑆 − 1)
1/2
(
𝑑
𝑠
𝑅
)
−0.40
Ecuación 59. – Ecuación propuesta por Novak y Nalluri (1984).
Para transporte de sedimentos o arrastre de sedimentos existentes en el lecho de la
tubería, Camp (1942) derivó una expresión para calcular la velocidad requerida para
erosionar el lecho de sedimentos existentes en una tubería:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
43
𝑉
𝑐𝑎𝑚𝑝
=
1
𝑛
𝑅
1/6
√𝐵
𝑎
(𝑠 − 1)𝑑
Ecuación 60. – Velocidad de Camp
donde 𝑛 es el coeficiente de rugosidad de Manning; 𝐵
𝑎
es una constante dimensional
igual a 0.8, la cual garantiza una adecuada autolimpieza en alcantarillados.
2.4.2.2 Esfuerzo Cortante
Lysne (1969) fue la primera persona en utilizar el diagrama de Shields para diseñar
tuberías con transporte de sedimentos y sugirió un valor de esfuerzo cortante
mínimo de 4 N/m
2
para garantizar autolimpieza en alcantarillados.
Yao (1974) extendió los estudios realizados por Lysne (1969) y midió la variación del
esfuerzo cortante a lo largo del perímetro de las tuberías fluyendo parcialmente
llenas. Encontró que el esfuerzo cortante en el fondo era siempre mayor que el valor
promedio y debería estar en el rango entre 1 y 4 N/m
2
para garantizar autolimpieza.
Igualmente concluyó que el problema de autolimpieza debe enfocarse en la región de
depósito de sedimentos, la cual ocurre alrededor del 10% del diámetro de la tubería.
Para tuberías fluyendo totalmente llenas y con partículas de diámetros entre 0.2 y 1
mm, el esfuerzo cortante mínimo en el fondo debe estar entre 1 y 2 N/m
2
.
Novak y Nalluri (1975) mostraron que el esfuerzo cortante crítico en el lecho de la
tubería para garantizar movimiento incipiente se puede definir por la siguiente
ecuación:
𝜏
𝑐
= 0.104(𝑠 − 1)𝑑
𝑠
0.4
Ecuación 61. – Ecuación propuesta por Novak y Nalluri (1975).
donde 𝜏
𝑐
es el esfuerzo cortante crítico para generar movimiento incipiente en la
tubería [N/m
2
]. El esfuerzo cortante mínimo en el lecho para transportar el material
sedimentado se puede expresar a partir de la Ecuación 62:
𝜏
𝐶𝑎𝑚𝑝
𝜌𝑔(𝑠 − 1)𝑑
𝑠
= 𝐵
𝑎
Ecuación 62. – Esfuerzo cortante de Camp.
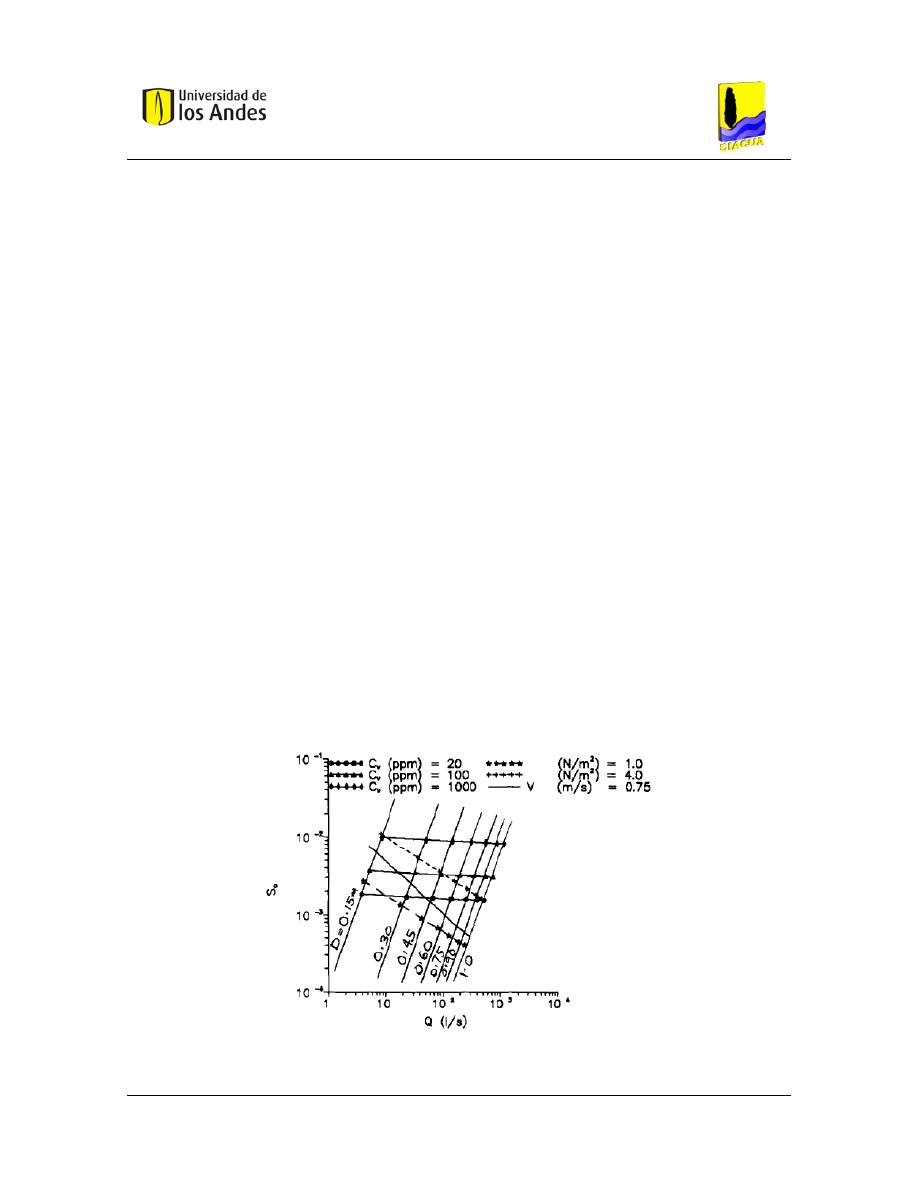
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
44
donde 𝜏
𝐶𝑎𝑚𝑝
es el esfuerzo cortante mínimo para erodar el depósito de sedimentos en
el lecho de la tubería [N/m
2
]. Este criterio no considera las características hidráulicas
del flujo. De la ecuación anterior, si se toma un valor de 𝐵
𝑎
= 0.8, que es el
recomendado para garantizar autolimpieza en alcantarillados y partículas con peso
específico de 2.6, el esfuerzo cortante requerido sería de 1.26 N/m
2
para tamaños de
partícula de 100 μm, mientras que para partículas con tamaños de 1 mm, el valor
requerido se incrementa a 12.6 N/m
2
.
2.4.3 Pendiente de Energía
Adicional a las ecuaciones de diseño presentadas anteriormente, existen otras prácticas
de diseño basadas en pendientes de energía y consideraciones geométricas para el diseño
de alcantarillados autolimpiantes. La pendiente mínima de la tubería es utilizada como
criterio para evitar depósito de sedimentos. Este criterio requiere parámetros de
entrada como condiciones típicas de caudal, tasa de transporte de sedimentos,
características de los sedimentos tales como tamaño y densidad, características
hidráulicas, geometría de la tubería, rugosidad hidráulica, entre otros. Si la
concentración volumétrica de sedimentos y la velocidad de sedimentación o
asentamiento de las partículas se fijan, entonces la pendiente mínima requerida para
mantener la autolimpieza en el sistema, se puede escribir en términos generales como
𝑆
𝑚𝑖𝑛
∝ 1/𝑅
1/3
.
Nalluri y Ghani (1996) desarrollaron curvas que relacionan la pendiente mínima del
sistema con el caudal y el diámetro de la tubería. El resultado se presenta en la siguiente
figura:
Figura 19. – Relación entre Caudal, Pendiente y Diámetro. Tomado de Bong (2014).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
45
Se han desarrollado curvas para calcular la pendiente mínima del sistema mediante el
método de Tractive Force sugerido por la Sociedad Estadounidense de Ingenieros
Civiles, ASCE.
2.4.3.1 Método Tractive Force [TF]
La Sociedad Estadounidense de Ingenieros Civiles (ASCE) recomienda realizar una
transición de los métodos tradicionales de diseño hacia éste nuevo método. Los
objetivos principales cuando se diseña un sistema de alcantarillado se pueden
enmarcar en dos grandes grupos: 1) Garantizar una capacidad de transporte del
caudal máximo de diseño y 2) Garantizar condiciones de autolimpieza en épocas de
caudales mínimos. Para cada tramo de la red, la pendiente de diseño debe ser la
mayor de las siguientes: 1) Pendiente necesaria para transportar el caudal máximo
de diseño; 2) La pendiente formada por las cámaras aguas arriba y aguas abajo y 3)
La pendiente requerida para garantizar autolimpieza (Merritt, 2009).
La razón por la cual se ha empezado a implementar este criterio de diseño, por
encima de los criterios tradicionales, se debe a los problemas que presentan esos
métodos: 1) La velocidad es un pobre indicador y predictor del poder de autolimpieza
en alcantarillados; 2) En algunos casos específicos estos criterios son adecuados; sin
embargo se generan pendientes mayores a las requeridas realmente y 3) El enfoque
de estos métodos se realiza en un rango de diámetros que difiere de los encontrados
normalmente en sistemas de alcantarillados.
Una aplicación correcta de ésta metodología requiere una adecuada selección de las
partículas de diseño, pero depende en mayor medida del caudal mínimo estimado.
Dado lo anterior, la pendiente mínima del sistema será una función del diámetro de
la tubería 𝑑, tamaño de la partícula (expresado en términos de su diámetro) 𝑑
𝑠
y del
caudal mínimo 𝑄
𝑚𝑖𝑛
(Merritt, 2009). Usualmente, el tamaño de la partícula no varía
entre tramos; sin embargo, para zonas en las cuales se presentan condiciones
inusuales o variables, se debe verificar este tamaño (se pueden presentar tamaños
mayores o menores).
Como se menciona anteriormente, el caudal mínimo de diseño es una variable
requerida para el cálculo. Este se define como “el mayor caudal con duración de 1
hora durante la semana de menor caudal existente en la vida útil del sistema”
5
. Este
caudal se debe estimar correctamente para cada tramo de la red. Si se observa, el
caudal mínimo real de la tubería es menor que el caudal mínimo requerido por el
Método Tractive Force (TF), esto se debe a la suposición a la cual está sometida este
5
El texto original es el siguiente: “Largest 1-h flowrate during the low flow week over the
system design life”. Tomado de (Merritt, 2009).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
46
método: Cuando ocurre sedimentación de partículas en el sistema, siempre ocurre
un caudal mínimo 𝑄
𝑚𝑖𝑛
, o mayor que mueve los depósitos de sedimentos antes de
que se aglomeren y formen una capa cohesiva (Merritt, 2009). Dado lo anterior, en
teoría el caudal mínimo 𝑄
𝑚𝑖𝑛
, ocurre con mayor frecuencia a una vez por semana
durante toda la vida útil del sistema, exceptuando la semana de menor caudal.
Igualmente, dado que el caudal aumenta con el tiempo, la autolimpieza ocurre más
frecuentemente (en algunas ocasiones de forma continua), puesto que, TF aumenta
con el incremento de caudal (Merritt, 2009).
TF se basa en el siguiente concepto: Si una tubería transporta adecuadamente los
sólidos que ingresan, entonces existe una partícula de arena de diseño que debe ser
transportada siempre y no se acumula de forma permanente en el lecho de la tubería.
Todos los demás sólidos son transportados con mayor facilidad que ésta partícula de
diseño. Para el caudal mínimo 𝑄
𝑚𝑖𝑛
, la partícula de diseño no se suspende por
turbulencia, pero es arrastrada a lo largo de la tubería como carga de lecho. En
algunas ocasiones se pueden encontrar partículas de mayor tamaño o peso en el
sistema; sin embargo, esto se presenta con poca frecuencia siempre y cuando se tenga
un mantenimiento adecuado del sistema. Igualmente, caudales pico, ayudarían a
prevenir crecimientos de películas y bloqueos en el sistema (Merritt, 2009). En
canales abiertos, el esfuerzo cortante medio se puede expresar mediante la siguiente
ecuación:
𝜏
0
= 𝛾𝑅𝑆
Ecuación 63. – Esfuerzo cortante en una tubería.
donde 𝜏
0
es el esfuerzo cortante promedio actuante sobre el canal (para éste caso
actuante en la tubería) [Pa]; 𝛾 el peso específico del agua [kg/m
3
]; 𝑅 el radio
hidráulico [m]y 𝑆 la pendiente de la tubería.
Raths y McCauley (1962) realizaron experimentos en tuberías e identificaron el TF
crítico necesario para mover partículas densas (arenas) como función del tamaño de
la partícula. Los resultados se pueden expresar mediante la siguiente ecuación:
𝜏
𝑐
= 𝑘
𝑐
𝑑
𝑠
0.277
Ecuación 64. – Esfuerzo cortante como función del diámetro de partícula. Tomado de Raths y
McCauley (1962).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
47
donde 𝑘
𝑐
= 0.867 para el Sistema Internacional de Unidades y 𝑑
𝑠
el diámetro en mm
de la partícula de diseño. Es importante resaltar que la ecuación anterior solo es
aplicable para partículas no cohesivas. Usualmente el diámetro de la partícula se
toma como 1 mm, puesto que es el valor típico asociado con alcantarillados sanitarios
(Merritt, 2009). Si se requiere diseñar para partículas con tamaños mayores, es
recomendable realizar un monitoreo de sedimentos y evaluar el tamaño de diseño de
las partículas.
El procedimiento general para diseñar alcantarillados mediante esta metodología
es el siguiente:
1. Determinar el caudal mínimo de diseño 𝑄
𝑚𝑖𝑛
, para el tramo. Un buen
estimativo de éste caudal es fundamental para garantizar la autolimpieza en
sistemas de alcantarillados.
2. Seleccionar un tamaño de partícula de diseño. Este valor normalmente se
encuentra entre 0.5 y 2 mm. Usar la Ecuación 64 para calcular el esfuerzo
cortante crítico necesario para el transporte de partículas.
3. Seleccionar un diámetro inicial de diseño de la tubería.
4. Seleccionar un valor adecuado del coeficiente de rugosidad de Manning.
Valores recomendados se encuentran en el Anexo 5.
5. Iterar la profundidad de flujo y resolver la Ecuación 4, Ecuación 5 y Ecuación
8. Ingresar el radio hidráulico obtenido en la Ecuación 63 y resolver para la
pendiente 𝑆, calcular el área de la sección con la Ecuación 6. Calcular el
caudal que transporta la tubería mediante alguna ecuación de resistencia
fluida. Continuar iterando la profundidad de flujo hasta que el caudal
calculado sea igual al mínimo de diseño 𝑄
𝑚𝑖𝑛
. La pendiente asociada con esa
condición es la pendiente mínima requerida para garantizar autolimpieza en
esa tubería.
Este procedimiento se desarrolló y verificó para partículas con diámetros de 1 mm y
peso específico de 2.7. El resultado fue una serie de ecuaciones que relacionan el
diámetro de la tubería con un coeficiente de rugosidad de Manning, el diámetro de
diseño de la partícula y el caudal mínimo de diseño. Estas ecuaciones presentaron
coeficiente de correlación del orden del 99.9% para relaciones de llenado entre 0.1 y
0.4. Estas se pueden extrapolar para valores entre 0.05 y 0.5 perdiendo algo de
precisión. En casos extraños donde el caudal mínimo de diseño resulte en relaciones
de llenado mayores a 0.5, se recomienda que se haga uso de una relación de 0.5 para
determinar la pendiente mínima de diseño. Las tablas y ecuaciones correspondientes
se presentan en los Anexos 6 y 7.
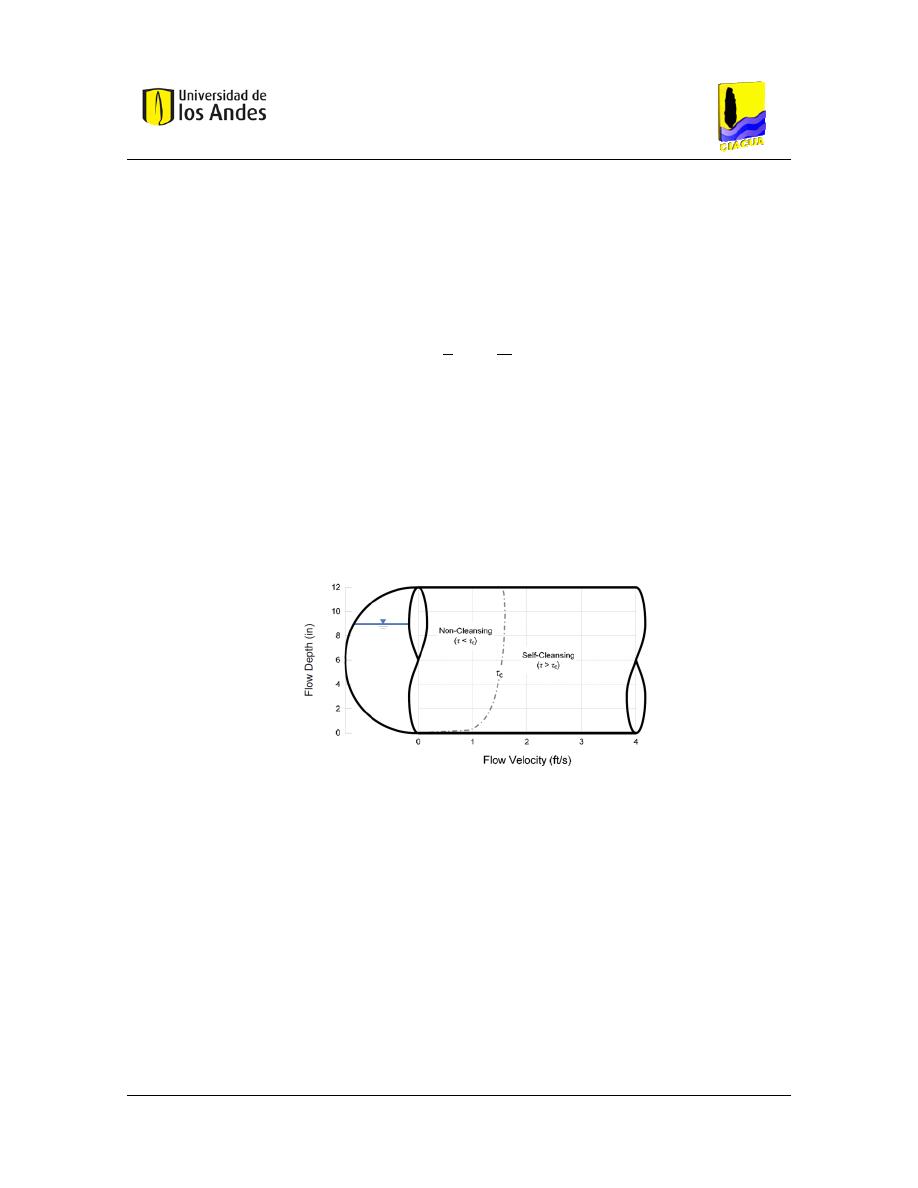
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
48
Recientemente Enfinger et al. (2010) evaluaron la capacidad de autolimpieza en
sistemas de alcantarillados mediante la aplicación del método TF. Esto se hizo
mediante diagramas de dispersión generados a partir de observaciones en campo.
La Ecuación 63 se puede reescribir e incorporar a la ecuación de Manning y se
obtiene una expresión que relaciona la velocidad de autolimpieza con el esfuerzo
cortante crítico:
𝑣
𝐿
=
1
𝑛
𝑅
1/6
(
𝜏
𝑐
𝛾
)
1/2
Ecuación 65. – Velocidad crítica como función del esfuerzo cortante crítico. Tomado de
Enfinger et al. (2010).
La ecuación anterior se resuelve para una lista de diámetros y el resultado es el
siguiente:
Figura 20. – Curva de esfuerzo cortante crítico como función de la velocidad. Tomado de
Enfinger & Mitchell (2010).
La figura anterior permite identificar las regiones en las cuales no se presenta
autolimpieza en alcantarillados. Lo anterior se aplicó en sistemas de alcantarillados
existentes en Estados Unidos y se revisó el esfuerzo cortante requerido para
transportar las partículas.
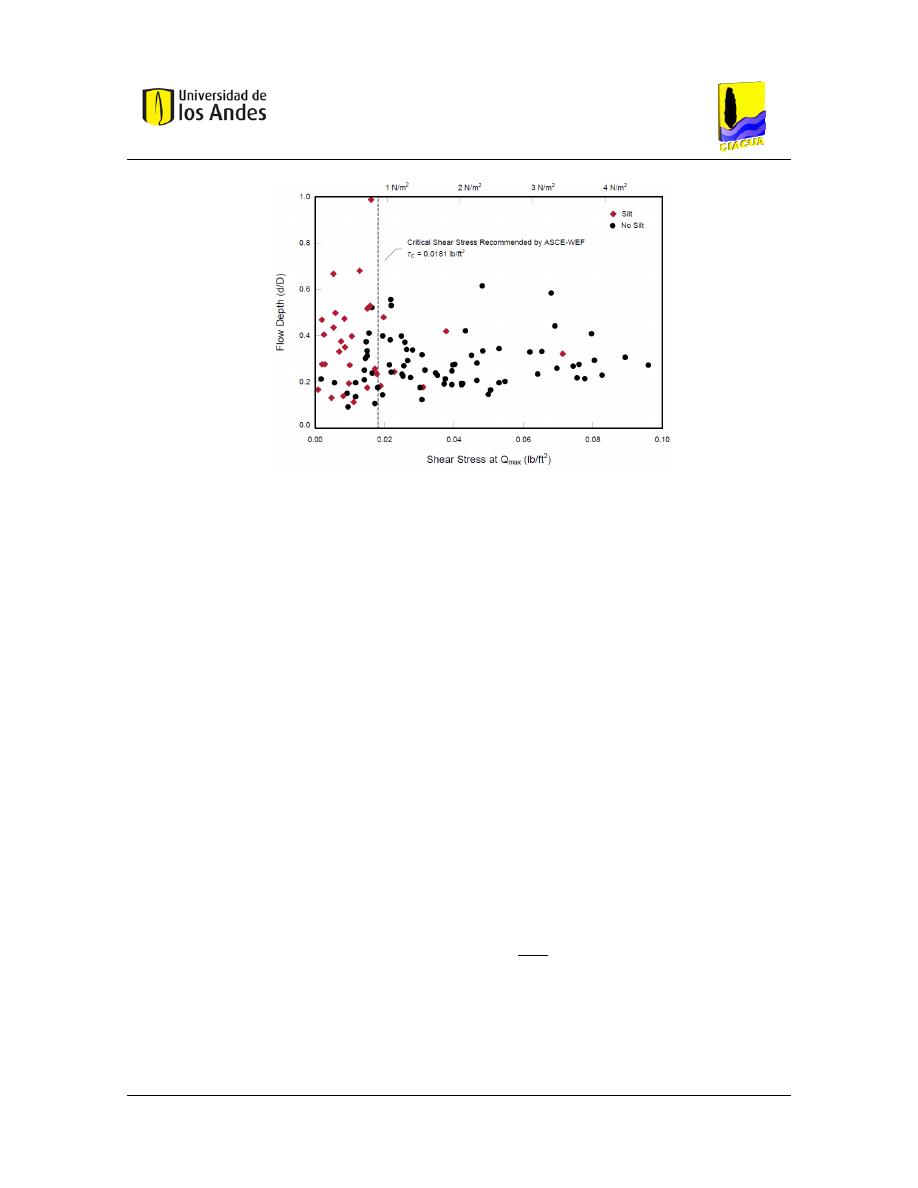
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
49
Figura 21. – Resultados del monitoreo. Tomado de Enfinger & Mitchell (2010).
La figura anterior muestra la relación existente entre el esfuerzo cortante y la
presencia o no de arenas en el sistema de alcantarillado. La línea punteada
corresponde al valor de 0.87 Pa recomendado por la ASCE para un tamaño de
partícula de 1 mm. Se observa que son mínimos los casos en los cuales existe
presencia de sedimentos en el alcantarillado para esfuerzos cortantes mayores a 0.87
Pa. Lo anterior se debe al periodo de tiempo sobre el cual tomaron los valores
(caudales menores al mínimo de diseño). Dada la validez de los resultados y la
muestra tomada (más de 100 alcantarillados en los Estados Unidos) Enfinger et al.
(2010) recomiendan la aplicación del método TF para el diseño de nuevos sistemas
de alcantarillado.
Rincón et al. (2012) argumentaron que el método TF fue desarrollado y propuesto
por Fair y Geyer (1954) quienes sugirieron que para garantizar condiciones de
autolimpieza, el esfuerzo debe ser igual o mayor al generado por un alcantarillado
fluyendo totalmente lleno con una velocidad de 0.6 m/s. En este caso, el esfuerzo se
puede calcular de la siguiente forma (La Motta, 1996):
𝜏
𝑚
= 0.571464𝛾
𝑛
2
𝑑
1/3
Ecuación 66. – Ecuación propuesta por La Motta (1996).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
50
Al realizar el cálculo para comparar los resultados entre métodos, se obtiene (𝑛 =
0.013; 𝑑 = 0.2 m y 𝛾 = 9,81 N/m
3
) un valor de 1.62 Pa, el cual es muy cercano al valor
experimental observado en la Universidad de New Orleans de 1.4 Pa (Rincón, et al.,
2012). Otra consideración discutida es la relacionada con el crecimiento de
biopelículas y su afectación con la hidráulica de los conductos, puesto que, estas
promueven la acumulación de partículas orgánicas e inorgánicas y dadas sus
propiedades cohesivas, se incrementa el crecimiento de la capa de sedimentos y
consecuentemente se eleva la rugosidad del medio (Guzman, et al., 2007). Para
diámetros de 200 mm, se demostró que se requiere de un esfuerzo mínimo de 1.4 Pa
para transportar el 90% de los sedimentos con diámetros de 0.25 mm. Esto se puede
observar en la Figura 22.
Figura 22. – Porcentaje de material transportado como función del esfuerzo cortante para
tuberías de 200 mm con presencia de biopelículas. Tomado de Rincón et al. (2012).
Lo anterior lleva a proponer una nueva metodología de cálculo de autolimpieza en
alcantarillados. Lo primero es determinar correctamente el coeficiente de Manning,
considerando la presencia de biopelículas en el medio. Guzman et al. (2007)
mostraron que el valor del coeficiente de Manning es función de la relación de llenado
y se ajusta a la siguiente ecuación:
𝑛 = 0.0186 (
𝑦
𝑑
)
−0.5415
Ecuación 67. – Modificación de la ecuación de Manning propuesta por Guzman et al. (2007)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
51
Figura 23. – Valores del coeficiente de Manning para condiciones de flujo subcrítico con
presencia de biopelículas. Tomado de Rincón et al. (2012).
Una vez determina el valor del coeficiente de Manning se debe solucionar la
siguiente ecuación para calcular el esfuerzo cortante crítico requerido para
garantizar autolimpieza en alcantarillados con presencia de biopelículas:
[
𝑑𝜏
𝑐
5/3
𝑐𝑜𝑠
−1
(1 −
𝑦
𝑑)
0.0186 (
𝑦
𝑑)
−0.5415
𝑄𝛾
5/3
]
6/7
=
4𝜏
𝑐
𝛾𝑑 {1 −
𝑠𝑖𝑛 [2𝑐𝑜𝑠
−1
(1 −
2𝑦
𝑑 )]
2𝑐𝑜𝑠
−1
(1 −
2𝑦
𝑑 )
}
Ecuación 68. – Ecuación propuesta por Rincón et al. (2012).
De lo anterior se puede concluir que el coeficiente de rugosidad de Manning se ve
afectado por la presencia de biopelículas y por lo tanto se debe calcular con la
Ecuación 67. Dado que el método de TF no considera las biopelículas que se forman
en las tuberías, se está subestimando las pendientes reales requeridas para
garantizar condiciones de autolimpieza en sistemas de alcantarillados. Igualmente,
se debe investigar el efecto de éstas biopelículas en tuberías con diámetros mayores
a 200 mm (Rincón, et al., 2012).
A lo anterior mencionado Merritt (2012), argumentó que las biopelículas
consideradas por Rincón et al. (2007) en sus experimentos no son acordes a las
encontradas usualmente en sistemas de alcantarillado. Adicionalmente, el valor
propuesto de 1.4 Pa resulta ser mucho mayor al realmente requerido, ya que, como
se menciona anteriormente, Enfinger et al. (2010) mostraron que el valor de 0.87 Pa,
propuesto por la ASCE para un tamaño de partícula de 1 mm, resulta ser adecuado

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
52
para el transporte de partículas. Esta validación se realizó para 214 alcantarillados
con diámetros entre 8 y 108 in (Merritt, 2012).
Cuando se presentan crecientes en el sistema, la formación eventual de biopelículas
desaparece, puesto que, esta condición de flujo es capaz de generar un esfuerzo
cortante mayor y turbulencia adicional que erosionan y limpian el lecho de la
tubería. Dado lo anterior, el esfuerzo cortante propuesto por la ASCE asegura un
cumplimiento de las condiciones de autolimpieza en alcantarillados.
2.5 Parámetros de Diseño de Sistemas de Alcantarillado en el
Mundo
Una vez revisadas las metodologías, ecuaciones y criterios desarrollados por diferentes
autores a lo largo de la historia, es necesario definir los valores adoptados por diferentes
normativas a nivel mundial y compararlas con el caso colombiano. Estas normativas
aplican el criterio de esfuerzo cortante mínimo o de velocidad mínima, según sea el caso.
Un resumen de los valores encontrados por (Vongvisessomjai, et al., 2010) se presenta
en las siguientes tablas:
Tabla 6. – Criterio de velocidad mínima. Tomado de Vongvisessomjai et al. (2010).
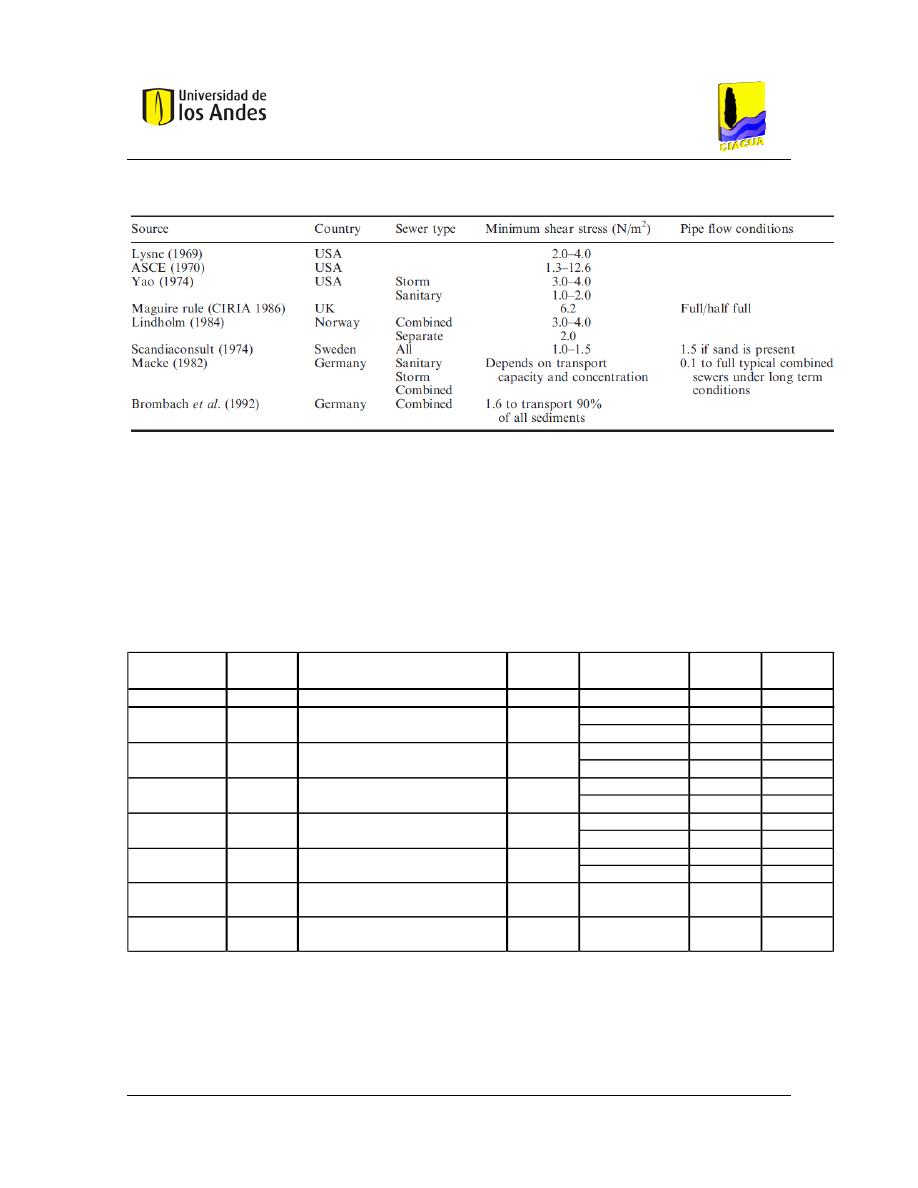
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
53
Tabla 7. – Criterio de esfuerzo cortante mínimo. Tomado de Vongvisessomjai et al. (2010).
Se observa que en algunos casos el valor de esfuerzo cortante mínimo varía
significativamente (Véase ASCE (1970)), lo cual lleva a desconocer realmente el valor
necesario para garantizar autolimpieza en alcantarillados. A nivel del continente
americano, algunas normas técnicas de diseño fueron consultadas, como se muestra a
continuación:
Tabla 8. – Valores recomendados en el continente Americano.
Entidad
País
Nombre de la Norma
Año
Tipo de
Alcantarillado
V min
Tao min
[-]
[-]
[-]
[-]
[-]
[m/s]
[Pa]
AR
0.45
1.5
AL y C
0.75
3
AR
0.45
1.5
AL y C
0.75
3
AR
-
1
AL y C
-
1.5
AR
0.45
-
AL
0.9
-
AL
0.6
-
AR
0.3
-
INAA
Nicaragüa
Normativa Alcantarillado
Sanitario Condominial
-
AR
0.6
1
Great Lakes
USA*
Recommended Standars for
Wastewater Facilities
2004
AR
0.6
-
EPM
Colombia
Guía para el Diseño Hidráulico
de Redes de Alcantarillado
2009
MinDesarrollo Colombia
RAS - 2000
2000
IBNORCA
Bolivia
NB 688
2007
INEN
Ecuador
CPE INEN 5
1992
CNA
Mexico
Manual de Agua Potable,
Alcantarillado y Saneamiento
2007

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
54
2.6 Resumen de Capítulo
El presente capítulo presentó una vista general de los criterios y metodologías para el
diseño de alcantarillados autolimpiantes. Se dio un primer vistazo de las ecuaciones
requeridas para cualquier cálculo de diseño y/o verificación en tuberías. Igualmente se
presentaron los métodos de diseño propuestos por diversos autores, los experimentos
realizados en laboratorio, las consideraciones de cada experimento y los resultados
obtenidos.
Se presentó en detalle el método de diseño mediante el concepto de Tractive Force,
recomendado por la ASCE en su manual de diseño de sistemas de alcantarillados. Este
método se debe evaluar con mayor detenimiento, puesto que, es el que presenta el menor
número de parámetros de entrada y el que se ha verificado y estudiado para diámetros
de tubería más acordes con la realidad.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
55
3 ANÁLISIS GRÁFICO DE RESTRICCIONES DE DISEÑO
El presente capítulo presenta la aplicación de las ecuaciones a una red prototipo de
estudio. Se evalúa cada una de las metodologías propuestas y consideradas con el fin de
compararlas gráficamente y mediante una evaluación de costos. Finalmente, se concluye
acerca de los resultados obtenidos.
3.1 Análisis Gráfico de Restricciones de Diseño
Para realizar el análisis gráfico de las restricciones de diseño, se utilizan cuatro
metodologías de diseño presentadas en el capítulo anterior: 1) Criterios tradicionales; 2)
Metodología CIRIA, 3) Metodología ASCE y 4) Otras metodologías.
3.1.1 Criterios Tradicionales de Diseño
La metodología para determinar la pendiente mínima requerida mediante la aplicación
de los criterios a nivel mundial se presenta en la Figura 24. Se busca comparar las
pendientes requeridas por cada criterio. La finalidad de este ejercicio es verificar qué
criterios son más restrictivos y cuáles más permisibles. Para realizar la comparación se
utilizan los siguientes valores establecidos en las normativas de diseño a nivel mundial:
Tabla 9. – Valores considerados para el análisis gráfico de los criterios tradicionales.
Entidad
País
Nombre de la Norma
Año
Tipo de
Alcantarillado
V min
Tao min
[-]
[-]
[-]
[-]
[-]
[m/s]
[Pa]
AR
0.45
1.5
AL y C
0.75
3
AR
0.45
1.5
AL y C
0.75
3
AR
-
1
AL y C
-
1.5
AR
0.45
-
AL
0.9
-
AL
0.6
-
AR
0.3
-
INAA
Nicaragüa
Normativa Alcantarillado
Sanitario Condominial
-
AR
0.6
1
Great Lakes
USA*
Recommended Standars for
Wastewater Facilities
2004
AR
0.6
-
AR
0.6
AL
0.9
AL
0.75
C
1
AR
0.3
C
0.6
EPM
Colombia
Guía para el Diseño Hidráulico
de Redes de Alcantarillado
2009
MinDesarrollo Colombia
RAS - 2000
2000
IBNORCA
Bolivia
NB 688
2007
INEN
Ecuador
CPE INEN 5
1992
CNA
Mexico
Manual de Agua Potable,
Alcantarillado y Saneamiento
2007
1.3
ASCE
USA
-
1970
-
UK
British Estándar BS 80001
1987
-
Ministerio del
Interior
Francia
-
1977
-
-
Europa
Estándar Europeo EN 752-4
1997
-
Todos
0.7

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
56
Figura 24. – Metodología para criterios tradicionales.
Al aplicar la metodología de la Figura 24 para un alcantarillado sanitario, se obtienen
valores de pendientes mínimas requeridas para garantizar autolimpieza mediante el
criterio tradicional de velocidad mínima. La Tabla 10 presenta los resultados obtenidos.
Tabla 10. – Resultados de la metodología para cálculo de pendiente mínima. Valores
expresados en porcentaje.
D [mm] EPM RAS INEN CNA INAA GLUMRB ASCE Francia EN 752-4
152
0.27 0.27
0.27
0.12
0.48
0.48
0.48
0.12
0.65
203
0.18 0.18
0.18
0.08
0.32
0.32
0.32
0.08
0.44
254
0.14 0.14
0.14
0.06
0.24
0.24
0.24
0.06
0.33
305
0.11 0.11
0.11
0.05
0.19
0.19
0.19
0.05
0.26
381
0.08 0.08
0.08
0.03
0.14
0.14
0.14
0.03
0.19
457
0.06 0.06
0.06
0.03
0.11
0.11
0.11
0.03
0.15
533
0.05 0.05
0.05
0.02
0.09
0.09
0.09
0.02
0.12
610
0.04 0.04
0.04
0.02
0.07
0.07
0.07
0.02
0.10
686
0.04 0.04
0.04
0.02
0.06
0.06
0.06
0.02
0.09
762
0.03 0.03
0.03
0.01
0.06
0.06
0.06
0.01
0.08
838
0.03 0.03
0.03
0.01
0.05
0.05
0.05
0.01
0.07
915
0.02 0.02
0.02
0.01
0.04
0.04
0.04
0.01
0.06
991
0.02 0.02
0.02
0.01
0.04
0.04
0.04
0.01
0.05
1067
0.02 0.02
0.02
0.01
0.04
0.04
0.04
0.01
0.05
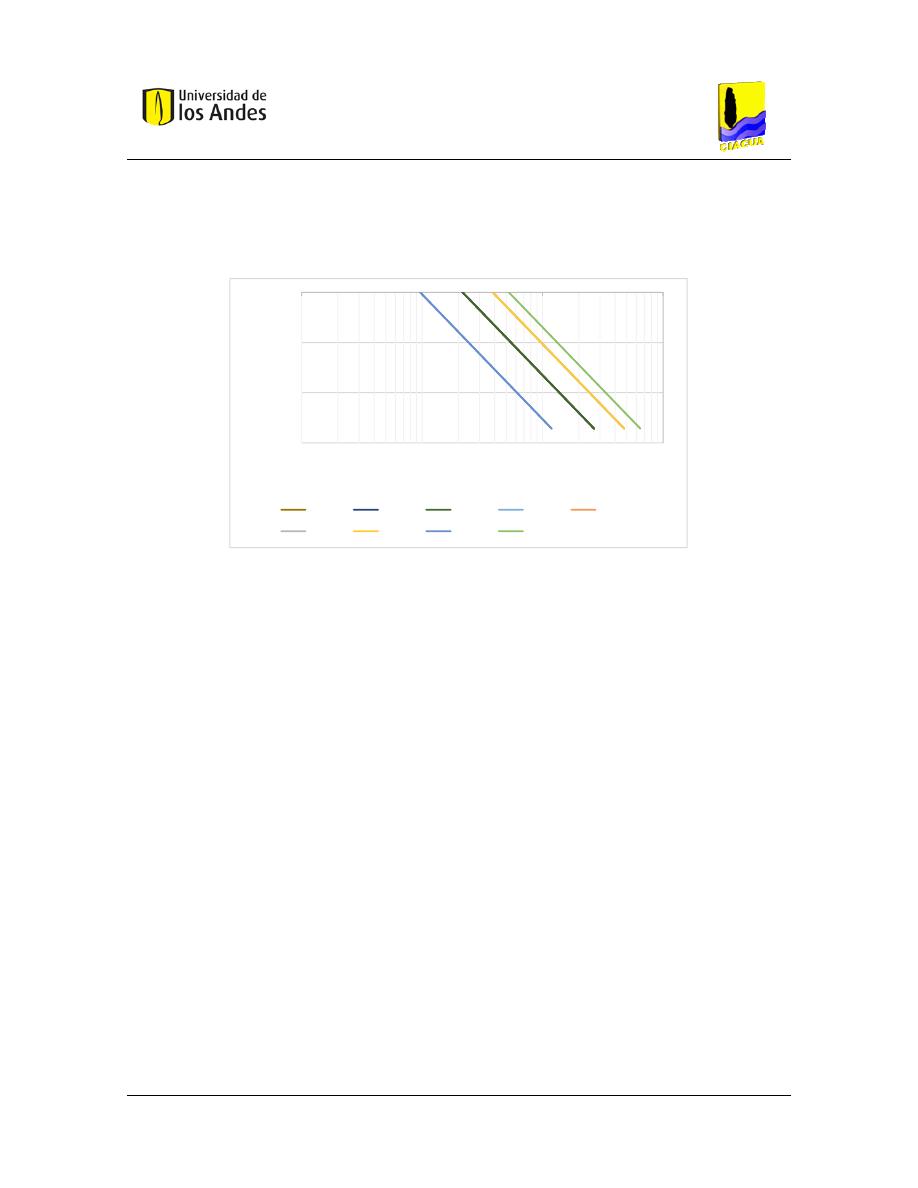
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
57
Los valores anteriores se pueden graficar y comparar entre sí, con el fin de evaluar qué
criterio resulta ser más restrictivo.
Figura 25. – Comparación de criterios tradicionales [Velocidad Mínima].
Se puede observar que la normativa más restrictiva corresponde al Estándar Europeo
EN 752 – 4, el cual corresponde a un valor de 0.7 m/s para criterio de velocidad mínima
en alcantarillado sanitario. Si el análisis se repite pero en un alcantarillado pluvial, se
encuentra que el más restrictivo sería el valor de 0.9 m/s correspondiente al valor
sugerido por la ASCE en el año 1970. El análisis anterior se repite para esfuerzo
cortante mínimo. La metodología a utilizar se presenta en la Figura 24 y los resultados
en la siguiente tabla:
0.125
0.25
0.5
1
0.00001
0.0001
0.001
0.01
Di
áme
tro
Tu
b
ería
[
m]
Pendiente Mínima [m/m]
EPM
RAS
INEN
CNA
INAA
GLUMRB
ASCE
Francia
EN 752-4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
58
Tabla 11. - Resultados de la metodología [Esfuerzo Cortante Mínimo]. Valores expresados en
porcentaje.
D [mm] EPM RAS INEN CNA INAA GLUMRB
152
0.40 0.40
0.27
0.27
0.35
3.38
203
0.30 0.30
0.20
0.20
0.26
2.53
254
0.24 0.24
0.16
0.16
0.21
2.02
305
0.20 0.20
0.13
0.13
0.17
1.68
381
0.16 0.16
0.11
0.11
0.14
1.35
457
0.13 0.13
0.09
0.09
0.12
1.12
533
0.11 0.11
0.08
0.08
0.10
0.96
610
0.10 0.10
0.07
0.07
0.09
0.84
686
0.09 0.09
0.06
0.06
0.08
0.75
762
0.08 0.08
0.05
0.05
0.07
0.67
838
0.07 0.07
0.05
0.05
0.06
0.61
915
0.07 0.07
0.04
0.04
0.06
0.56
991
0.06 0.06
0.04
0.04
0.05
0.52
1067
0.06 0.06
0.04
0.04
0.05
0.48
Estos valores se grafican y se comparan con las pendientes de la red prototipo. Los
resultados se presentan en la Figura 26.
Figura 26. - Comparación de criterios tradicionales [Esfuerzo Cortante Mínimo].
En la figura anterior se observa que el criterio de 12.6 Pa es muy restrictivo, lo cual
genera que las pendientes mínima requeridas para garantizar autolimpieza sean muy
0.125
0.25
0.5
1
0.0001
0.001
0.01
0.1
Di
ámet
ro
T
u
b
erí
a
[m]
Pendiente Mínima [m/m]
RAS
IBNORCA
INAA
ASCE [1.3 Pa]
EPM
ASCE [12.6 Pa]

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
59
elevadas lo cual puede llegar a afectar el diseño final de un sistema de alcantarillad.
Este criterio fue utilizado por la ASCE en la primera edición del libro Gravity Sanitary
Sewer Design and Construction (Bizier, 2007) en el año 1970; sin embargo, este valor
fue reemplazado por el método TF. La influencia de cada restricción en el diseño final
se evalúa posteriormente.
3.1.2 Metodología CIRIA
La metodología propuesta por la CIRIA en su Reporte 141 titulado “Design of Sewers to
Control Sediment Problems” (Ackers, et al., 1996) considera una serie de parámetros y
suposiciones para la correcta aplicación de las ecuaciones y diseño de sistemas de
alcantarillados autolimpiantes. El procedimiento general de diseño es el siguiente:
1. Identificar los componentes del procedimiento de diseño: En este paso
se deben definir los criterios de movilidad de los sedimentos adoptados para el
diseño, el tipo de sistema a diseñar, la capa de sedimentos permisible en el
alcantarillado y las condiciones y frecuencia de caudales.
2. Identificar las características y cargas de sedimentos: Disponibilidad de
datos e información, cambios en las cuencas aportantes al sistema y definir
valores apropiados de tamaño de partículas, peso específico y concentración.
3. Características hidráulicas de la tubería: En esta etapa se definen
características tales como la rugosidad de la tubería (y de la capa de sedimentos
si aplica), el efecto del depósito de sedimentos en el comportamiento hidráulico
del sistema, entre otros.
4. Definir el tipo de criterio a utilizar: En este paso se debe identificar las
condiciones para las cuales se van a diseñar. El método de la CIRIA considera
tres criterios básicos los cuales son:
a. Criterio I: Transporte de sedimentos en suspensión, el cual es aplicable
para alcantarillados de agua lluvia y en algunos casos agua residual.
b. Criterio II: Transporte de sedimentos
como carga de lecho, en el cual se
contemplan condiciones de depósito límite de sedimentos y de depósito
de sedimentos.
c. Criterio III: Se aplica en sedimentos con características cohesivas.
5. Determinación de la velocidad mínima: Se deben aplicar las ecuaciones propias
de cada criterio mencionado anteriormente, según sea el caso, y generar tablas
y gráficas de los resultados obtenidos.
6. Realizar un análisis de sensibilidad de parámetros: Se recomienda realizar
variaciones en las características iniciales del sistema y observar el efecto de
cada parámetro en la respuesta del modelo.
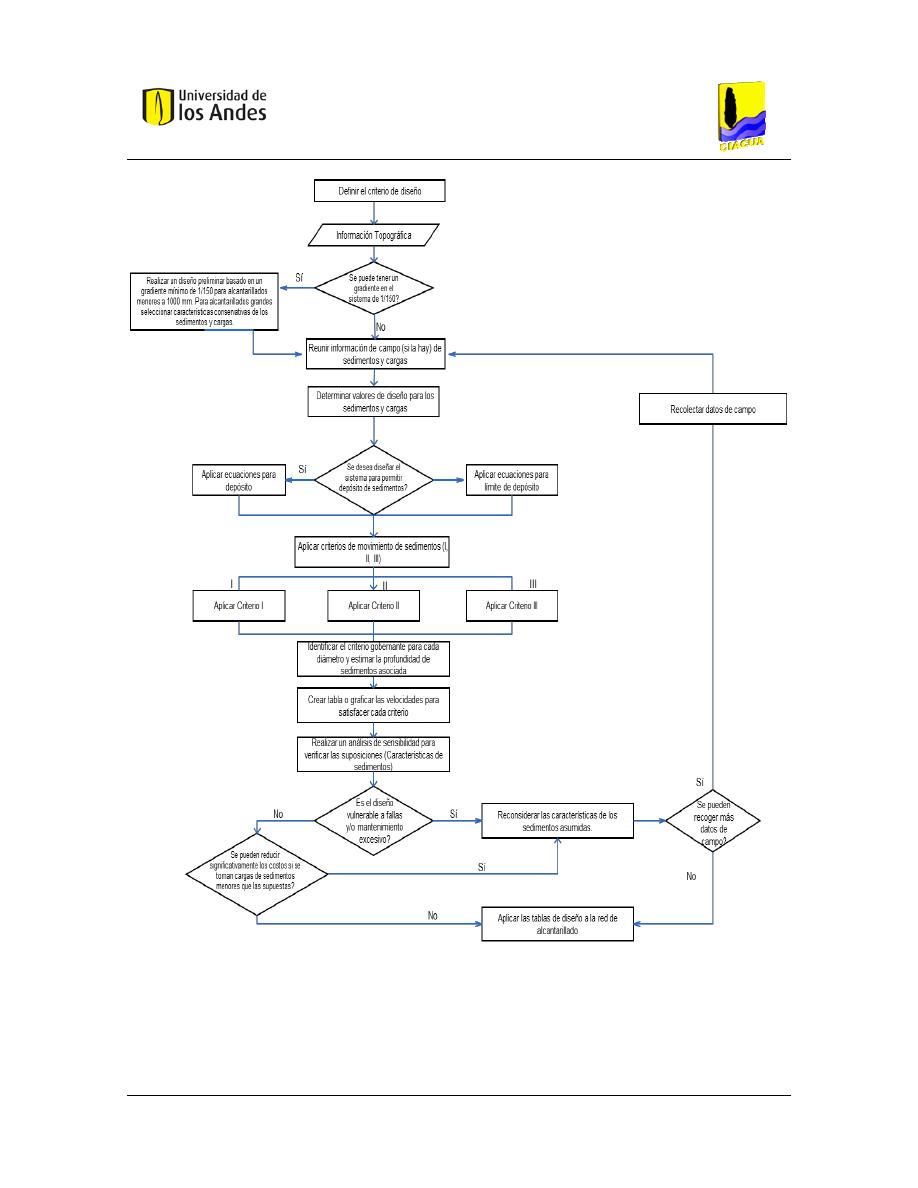
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
60
Figura 27. – Metodología propuesta por la CIRIA. Tomado de Ackers et al. (1996).
Una vez definido el procedimiento, se comparan las ecuaciones propias para cada
criterio. Para el Criterio I, Ackers et al. (1991) realizaron una verificación de las

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
61
ecuaciones propuestas en la literatura (Ver Capítulo II) y encontraron que la ecuación
de Macke (1982), es la que presenta mejores ajustes a los datos medidos
experimentalmente en laboratorio. Igualmente, otras ecuaciones como May et al. (1989),
Mayerle, Nalluri y Novak (1991) y May (1994) se consideran en la comparación gráfica.
Dada la naturaleza de las ecuaciones consideradas, es necesario ingresar algunos
parámetros propios de las características de sedimentos que ingresan al sistema. Para
este ejemplo se toman los siguientes valores:
Tabla 12. - Características de los Sedimentos
Nombre
Parámetro Unidad Valor
Concentración de Sedimentos
𝐶
𝑣
[mg/L]
50
Diámetro de Partícula
𝑑
[mm]
1
Peso Específico de los Sedimentos
𝑠
[-]
2.6
Los resultados al aplicar los modelos mencionados anteriormente son los siguientes:
Figura 28. – Comparación de Criterio I (CIRIA).
Se observa que de las ecuaciones consideradas, el modelo de May (1994) resulta ser el
más restrictivo, mientras que Mayerle, Nalluri & Novak (1991) es el menos restrictivo
(La curva no se alcanza a percibir en la figura). Las comparaciones anteriores se pueden
extender para análisis individuales de sensibilidad paramétrica. Para May et al. (1982)
0.0625
0.125
0.25
0.5
1
0.0005
0.005
Diáme
tro
T
u
b
ería
[m
]
Pendiente Mínima [m/m]
Macke (1982)
May et al. (1989)
Mayerle, Nalluri y Novak (1991)
May (1994)
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
62
se evalúa la influencia de la concentración de sedimentos 𝐶
𝑣
, la densidad relativa 𝑠 y el
diámetro de la partícula 𝑑. Los resultados obtenidos se presentan en las siguientes
figuras:
Figura 29. – Variación de los resultados como función de la concentración de sedimentos.
Figura 30. – Variación de los resultados como función de la densidad relativa del material.
0.0625
0.125
0.25
0.5
1
0.003
0.03
Diáme
tro
T
u
b
ería
[m
]
Pendiente Mínima [m/m]
Cv = 50 mg/L
Cv = 250 mg/L
Cv = 500 mg/L
0.0625
0.125
0.25
0.5
1
0.001
0.01
Diá
me
tro
Tu
b
ería
[
m]
Pendiente Mínima [m/m]
s = 2.6
s = 2
s = 1.5
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
63
Figura 31. – Variación de los resultados como función del diámetro de las partículas.
Las figuras anteriores permiten observar la variación de los resultados obtenidos
mediante la variación de los parámetros en la ecuación de May et al. (1989). Como es de
esperar, la pendiente mínima del sistema incrementa como función de la concentración
de sedimentos en el sistema, el diámetro de la partícula y la densidad relativa. Para
valores altos de éstas variables, las pendientes resultantes son altas; caso contrario,
para valores bajos, se obtienen pendientes bajas de autolimpieza.
El Criterio II se utiliza para sedimentos transportados como carga de lecho.
Investigaciones realizadas por Ackers et al. (1991) indican que este criterio se debería
aplicar en sistemas empinados (pendientes mayores al 1%) con diámetros mayores a 500
mm. Se realizó la verificación de las ecuaciones propuestas en el Capítulo II y se
encontró que la metodología de Ackers (1991) es la que genera mejores ajustes a los
datos medidos experimentalmente. La formulación de la metodología se expresa en
términos de una concentración de sedimentos de la siguiente forma:
𝐶
𝑣
= 𝐽 [𝑊
𝑒
𝑅
𝐴
]
𝛼
[
𝑑
𝑅
]
𝛽
𝜆
𝑐
𝛾
[
𝑉
[𝑔(𝑠 − 1)𝑅]
1/2
− 𝐾𝜆
𝑐
𝛿
(
𝑑
𝑅
)
𝜀
]
𝑚
Ecuación 69. – Ecuación de Ackers (1991).
donde 𝐶
𝑣
es la concentración volumétrica de sedimentos; 𝑊
𝑒
el ancho efectivo de la capa
de sedimentos. Los diferentes coeficientes considerados dependen en una gran medida
0.0625
0.125
0.25
0.5
1
0.003
Diáme
tro
T
u
b
ería
[m
]
Pendiente Mínima [m/m]
d = 5 mm
d = 2 mm
d = 1 mm

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
64
del tamaño de grano 𝐷
𝑔𝑟
. Cada uno de estos coeficientes se puede formular mediante las
siguientes expresiones:
𝐴
𝑔𝑟
= 0.14 +
0.23
√𝐷
𝑔𝑟
𝑛 = 1 − 0.56 log
10
𝐷
𝑔𝑟
𝑚 = 1.67 +
6.83
𝐷
𝑔𝑟
log
10
𝐻 = 2.79 log
10
𝐷
𝑔𝑟
− 0.98(log
10
𝐷
𝑔𝑟
)
2
− 3.46
𝐽 =
8
𝑛(𝑚−1)
2
𝐻
11.3
𝑚(1−𝑛)
𝐴
𝑔𝑟
𝑚
𝛼 = 1 − 𝑛
𝛽 = (10 − 4𝑚 − 𝑚𝑛) ÷ 10
𝛾 = 𝑛(𝑚 − 1) ÷ 2
𝐾 = 11.3
(1−𝑛)
𝑔
𝑛/2
𝐴
𝑔𝑟
𝛿 = −𝑛/2
𝜀 = (4 + 𝑛) ÷ 10
Ecuación 70. – Formulación ecuación de Ackers (1991).
Cuando se presenten sedimentos gruesos (𝐷
𝑔𝑟
> 60) se debe considerar 𝑚 = 1.78. Como
se puede observar, la aplicación de este criterio resulta ser muy complejo y en muchas
ocasiones, a falta de datos, lleva a realizar suposiciones que pueden no ser acordes con
la realidad. Usualmente los valores recomendados son aplicables en el Reino Unido, por
lo cual para el caso colombiano sería necesario realizar estudios propios y validar las
ecuaciones.
La CIRIA presenta tablas con valores de diseño aplicables a distintos tamaños de
partículas, concentración de sedimentos y profundidad de la cama de sedimentos en el
sistema. Dichas tablas se presentan en la sección de Anexos (8 – 11). Los resultados al
aplicar la metodología para una profundidad relativa de sedimentos de 1%, rugosidad
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
65
hidráulica de la tubería de 0.6 mm y partículas con peso específico de 2.6 se muestran
en las siguientes figuras:
Figura 32. – Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 100
μm. Criterio II de diseño.
Figura 33. – Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 200
μm. Criterio II de diseño.
0.125
0.25
0.5
1
2
4
0.00001
0.0001
0.001
0.01
Diáme
tro
T
u
b
ería
[m
]
Pendiente Mínima [m/m]
y
s
/D = 1%
k
o
= 0.6 mm
SG = 2.6
d = 0.1 mm
X = 50 mg/L
X = 350 mg/L
X = 1000 mg/L
0.125
0.25
0.5
1
2
4
0.0001
0.001
0.01
Diáme
tro
T
u
b
ería
[m
]
Pendiente Mínima [m/m]
y
s
/D = 1%
k
o
= 0.6 mm
SG = 2.6
d = 0.2 mm
X = 50 mg/L
X = 350 mg/L
X = 1000 mg/L
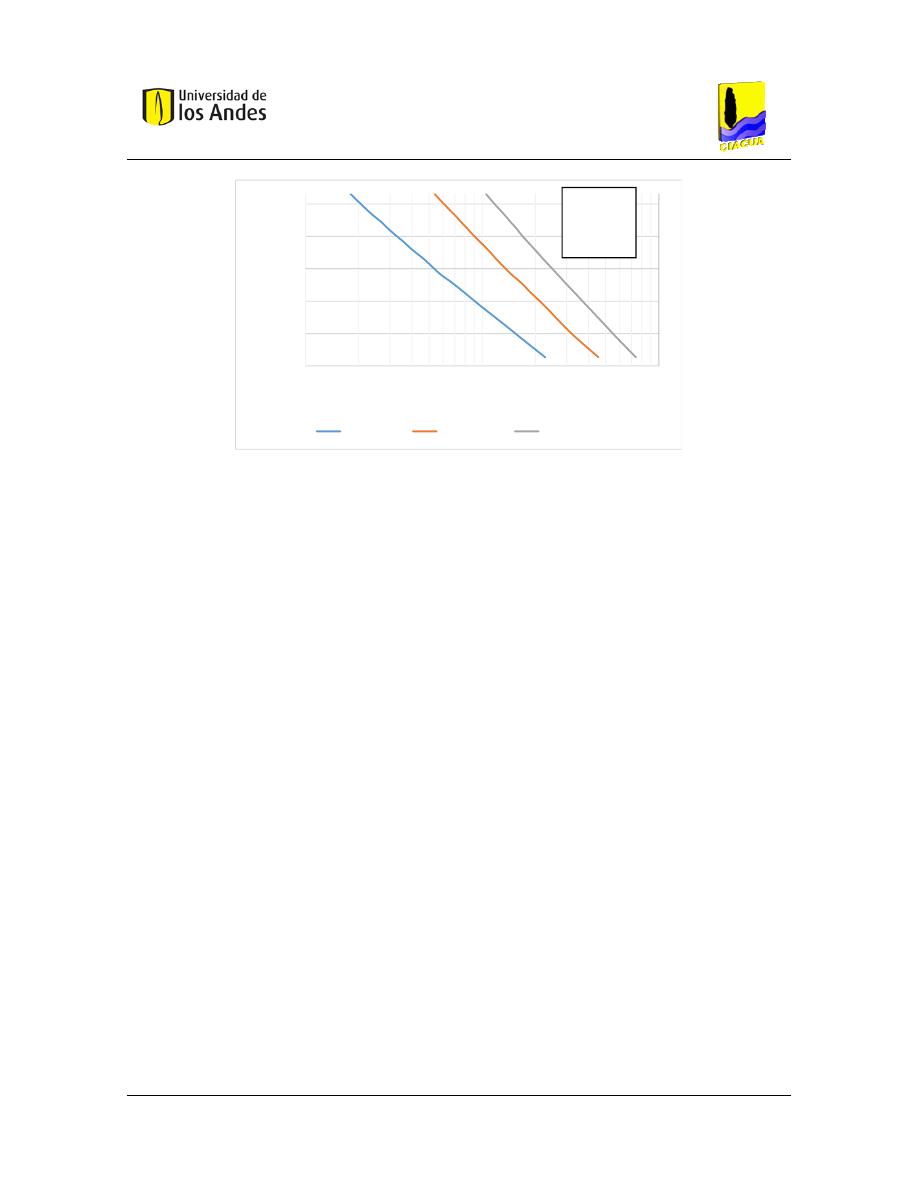
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
66
Figura 34. – Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 300
μm. Criterio II de diseño.
Las figuras anteriores permiten identificar la relación entre el diámetro de la tubería y
la pendiente mínima para el Criterio II propuesto por la CIRIA. Se observa que estas
ecuaciones se desarrollaron para tamaños de partículas máximos de 300 μm, por lo cual
no serían comparables con los demás criterios. Las otras figuras resultantes se
presentan en las Anexos 12 - 20.
Finalmente, el tercer Criterio se aplica para condiciones en las cuales hay presencia de
partículas cohesivas en el lecho de la tubería. La CIRIA recomienda los siguientes
valores para garantizar autolimpieza en alcantarillados con presencia de este tipo de
sedimentos:
0.125
0.25
0.5
1
2
4
0.0001
0.001
0.01
Diáme
tro
T
u
b
ería
[m
]
Pendiente Mínima [m/m]
y
s
/D = 1%
k
o
= 0.6 mm
SG = 2.6
d = 0.3 mm
X = 50 mg/L
X = 350 mg/L
X = 1000 mg/L

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
67
Tabla 13. – Velocidades mínima requeridas para el Criterio III. Tomado de Ackers et al., (1996).
D [mm] V
m
[m/s]
150
0.67
225
0.72
300
0.75
450
0.79
600
0.82
750
0.85
900
0.87
1000
0.88
1200
0.9
1500
0.92
1800
0.94
2100
0.96
2400
0.98
2700
0.99
3000
1
3400
1.01
4000
1.03
5000
1.06
Los valores anteriores se pueden expresar en términos de una pendiente mínima,
siguiendo el procedimiento descrito en el Numeral 3.1.1.
Figura 35. – Criterio III de diseño de alcantarillados. CIRIA.
0.125
0.25
0.5
1
2
4
0.0001
0.001
0.01
0.1
1
Diáme
tro
T
u
b
ería
[m
]
Pendiente Mínima [m/m]
CRITERIO III

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
68
La figura anterior muestra una variación de la pendiente como función del diámetro de
la tubería. Si se desean comparar los tres criterios propuestos por la CIRIA, aunque no
es posible dadas las características de cada método, se podrían generar figuras que
comparen cada criterio como función de algunos valores para cada parámetro.
Figura 36. – Comparación 1 Criterios CIRIA.
Figura 37. – Comparación 2 Criterios CIRIA.
Las figuras anteriores permiten identificar la variabilidad de cada criterio como función
de una serie de parámetros. Se observa que la ecuación de Macke (1982) es el criterio
menos restrictivo de los tres, lo cual se debe a la naturaleza de los sedimentos
(sedimentos en suspensión) que se consideran para hacer el análisis con esta ecuación.
D [m] CRITERIO I CRITERIO II CRITERIO III
0.15
0.00292
0.00366
0.00608
0.225
0.00195
0.00265
0.00409
0.3
0.00146
0.00207
0.00302
0.45
0.00097
0.00149
0.00195
0.6
0.00073
0.00117
0.00143
0.75
0.00058
0.00096
0.00114
0.9
0.00049
0.00084
0.00094
1.2
0.00037
0.00066
0.00069
1.5
0.00029
0.00054
0.00053
1.8
0.00024
0.00047
0.00044
2.1
0.00021
0.00041
0.00037
2.4
0.00018
0.00037
0.00032
2.7
0.00016
0.00033
0.00028
3
0.00015
0.00031
0.00025
3.4
0.00013
0.00027
0.00022
4
0.00011
0.00024
0.00018
5
0.00009
0.00020
0.00014
ys/D = 1%
Ko = 0.6 mm
SG = 2.6
d = 0.1 mm
Cv = 50 mg/L
COMPARACIÓN
0.15
0.3
0.6
1.2
2.4
4.8
0.00001
0.0001
0.001
0.01
0.1
1
Diáme
tro
T
u
b
ería
[m
]
Pendiente Mínima [m/m]
y
s
/D = 1%
k
o
= 0.6 mm
SG = 2.6
d = 0.3 mm
C
v
= 50 mg/L
CRITERIO I
CRITERIO II
CRITERIO III
D [m] CRITERIO I CRITERIO II CRITERIO III
0.15
0.00292
0.00504
0.00608
0.225
0.00195
0.00386
0.00409
0.3
0.00146
0.00319
0.00302
0.45
0.00097
0.00253
0.00195
0.6
0.00073
0.00213
0.00143
0.75
0.00058
0.00185
0.00114
0.9
0.00049
0.00167
0.00094
1.2
0.00037
0.00141
0.00069
1.5
0.00029
0.00125
0.00053
1.8
0.00024
0.00112
0.00044
2.1
0.00021
0.00103
0.00037
2.4
0.00018
0.00096
0.00032
2.7
0.00016
0.00090
0.00028
3
0.00015
0.00084
0.00025
3.4
0.00013
0.00081
0.00022
4
0.00011
0.00072
0.00018
5
0.00009
0.00064
0.00014
d = 0.3 mm
Cv = 1000 mg/L
COMPARACIÓN
ys/D = 5%
Ko = 0.6 mm
SG = 2.6
0.15
0.3
0.6
1.2
2.4
4.8
0.00001
0.0001
0.001
0.01
0.1
1
Di
áme
tro
Tu
b
ería
[
m]
Pendiente Mínima [m/m]
y
s
/D = 5%
k
o
= 0.6 mm
SG = 2.6
d = 0.3 mm
C
v
= 1000 mg/L
CRITERIO I
CRITERIO II
CRITERIO III

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
69
Igualmente, los Criterios II y III varían dependiendo de la concentración de entrada al
sistema y del tamaño de las partículas consideradas.
3.1.3 Metodología ASCE
La metodología propuesta por la ASCE en su último manual de diseño (Bizier, 2007),
recomienda utilizar el método TF para el diseño de alcantarillados que garanticen
condiciones de autolimpieza. El procedimiento básico de diseño se presenta en la Figura
38.
Figura 38. – Metodología de diseño recomendada por la ASCE (2007).
Se aplica el procedimiento para evaluar el efecto que tiene el diámetro de diseño de la
partícula. De la figura anterior, se observa que se debe seleccionar una profundidad de
agua menor al 50% del diámetro de la tubería (relación de llenado del 50%). Lo anterior
se debe realizar de esa manera, puesto que este criterio se desarrolla para caudales
mínimos, donde la profundidad del agua no supera ese valor. Para el caso donde se
presenten profundidades mayores, la autolimpieza se dará constantemente, puesto que
los esfuerzos cortantes serán mucho mayores a los mínimos requeridos por la
metodología de la ASCE. La Figura 39 presenta la variación que tiene el tamaño de la
partícula en el cálculo de las pendientes mínimas para garantizar autolimpieza. Se
observa, como es de esperar, que la relación entre el tamaño de la partícula y la

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
70
pendiente es proporcional y por consiguiente, a mayor tamaño de partícula, mayor
esfuerzo cortante requerido y mayor pendiente necesaria en el sistema.
Figura 39. – Variación del diámetro de la partícula para el diseño de la metodología de la
ASCE.
El coeficiente de rugosidad de Manning no sería en este caso una variable del modelo.
Esto se debe básicamente a que el esfuerzo crítico depende únicamente del valor
escogido para la partícula de diseño. Una vez evaluada la variación de los parámetros,
se verifica el cumplimiento o no, de la red prototipo, del criterio de autolimpieza.
3.2 Otras metodologías
Vongvisessomjai et al. (2010) proponen una metodología para el diseño de
alcantarillados aplicando las ecuaciones obtenidas en sus estudios. El diagrama de flujo
para aplicar la metodología es el siguiente:
0.125
0.25
0.5
1
0.00001
0.0001
0.001
0.01
0.1
1
Diáme
tro
T
u
b
ería
[m
]
Pendiente Mínima [m/m]
d = 1 mm
d = 0.5 mm
d = 2 mm
d = 5 mm
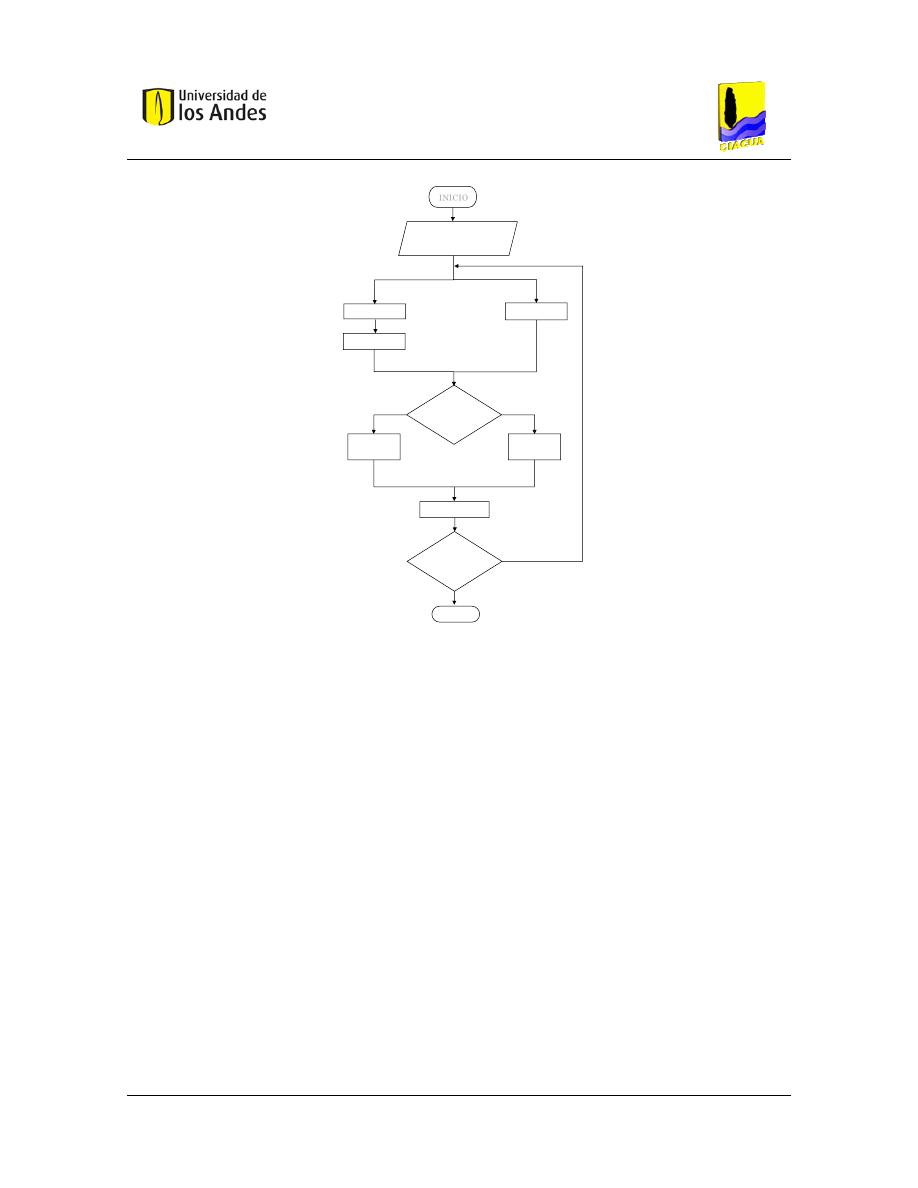
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
71
Figura 40. – Metodología de diseño propuesta por Vongvisessomjai et al. (2010).
Como se observa en la figura anterior, esta metodología igualmente requiere conocer
cargas de entrada de sedimentos en el sistema. Se observa que, a diferencia de la
propuesta por la ASCE, se diseña para dos condiciones de caudal (caudal en tiempo
húmedo y en tiempo seco). Con el fin de comparar qué tan restrictivos son los criterios,
se comparan las ecuaciones propuestas por Vongvisessomjai et al. (2010) y Ebtehaj et
al. (2013). Los resultados se presentan en la siguiente figura:
INICIO
Ingresar Cv, d, SG, S,
n, Q
dwf
y Q
wwf
dwf
Calcular y, V
Carga de
lecho o
suspensión?
FIN
Ecuación
32 o 33
Calcular V
L
Lecho
Calcular D
Condiciones Húmedas
Condiciones Secas
y = 0.938D
Ecuación
34 o 35
Suspensión
V > V
L
?
Sí
No
A
u
m
en
ta
r
la
P
en
dien
te
S
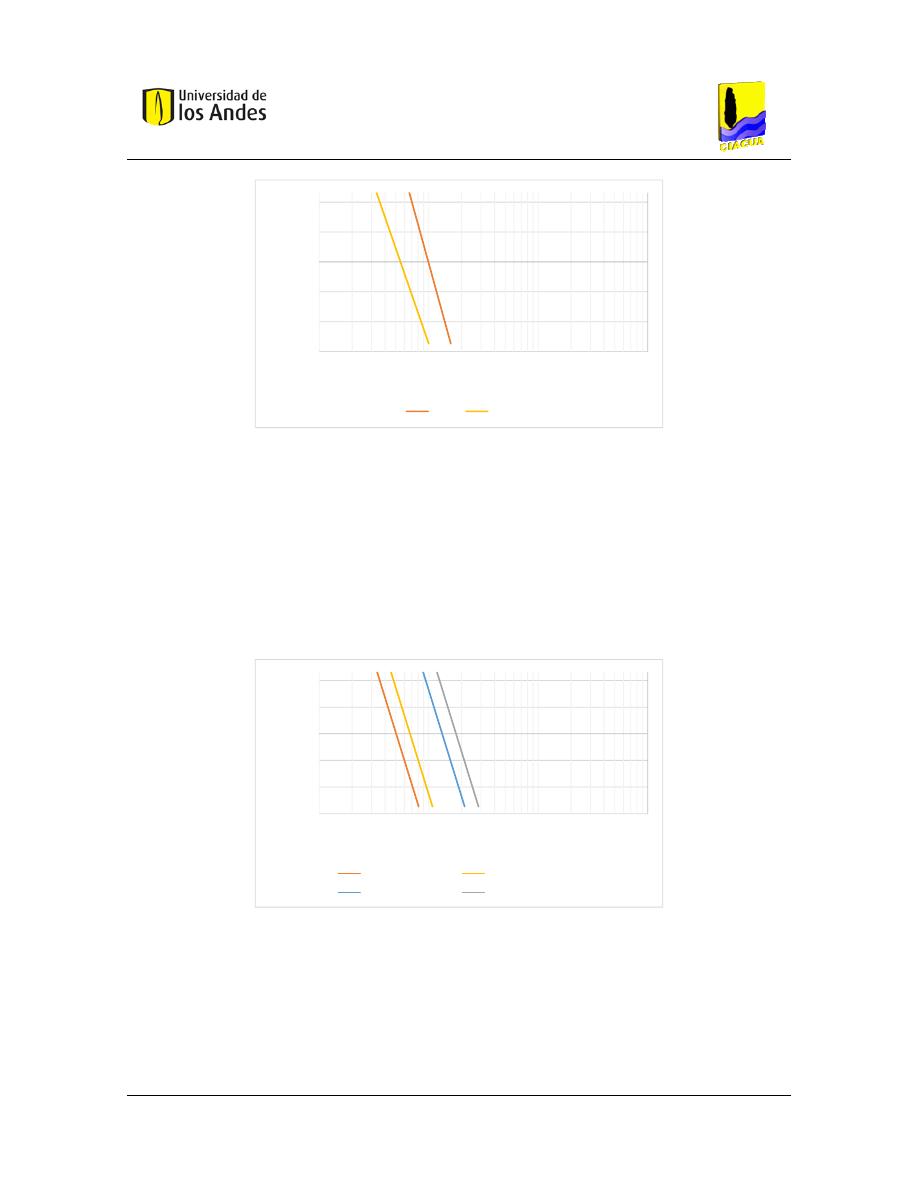
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
72
Figura 41. – Comparación de criterios Vongvisessomjai et al. (2010) y Ebtehaj et al. (2013).
La Figura 41 permite identificar y concluir que el criterio de Vongvisessomjai et al.
(2010) (Ecuación 35) es el más restrictivo. Igualmente, si se realiza un análisis de
sensibilidad para la Ecuación 35 mediante la variación de los parámetros de entrada, se
observaría el siguiente comportamiento:
Figura 42. – Variación de la concentración de sedimentos para el análisis de la metodología.
Al incrementar la carga de sedimentos en el sistema, se observa un aumento de la
pendiente requerida para garantizar autolimpieza. El procedimiento anterior se repite
0.125
0.25
0.5
1
2
4
0.001
0.01
0.1
1
Diá
me
tro
Tu
b
ería
[
m]
Pendiente Mínima [m/m]
Eq. 35
Eq. 40
0.125
0.25
0.5
1
2
4
0.001
0.01
0.1
1
Diáme
tro
T
u
b
ería
[m
]
Pendiente Mínima [m/m]
Eq. 35 - Cv = 50 mg/L
Eq. 35 - Cv = 100 mg/L
Eq. 35 - Cv = 500 mg/L
Eq. 35 - Cv = 1000 mg/L

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
73
con la variación del diámetro de la partícula. El resultado se presenta en la siguiente
figura:
Figura 43. – Variación del tamaño de la partícula para el análisis de la metodología.
Igualmente, se observa que a medida que se incrementa el diámetro de la partícula de
diseño, se genera una disminución de la pendiente requerida para garantizar
autolimpieza en el sistema. Esto es contrario a lo que se podría esperar en comparación
con los análisis presentados anteriormente de otras metodologías.
3.3 Comparación Multicriterio
Una vez determinadas e implementadas las metodologías estudiadas en este Capítulo,
resulta necesario realizar una comparación de todas en una misma figura, esto con el
fin de identificar globalmente cuál es la más restrictiva en el diseño de alcantarillados
autolimpiantes. Los parámetros a partir de los cuales se realiza la comparación son los
siguientes:
Tabla 14. – Parámetros para comparación de Metodologías.
Nombre
Parámetro Unidad Valor
Profundidad relativa Sedimento - Diámetro
𝑦
𝑠
𝐷
[%]
1
Rugosidad Hidráulica
𝐾
𝑜
[mm]
0.6
Peso Específico Sedimentos
𝑆𝐺
[-]
2.6
Diámetro de Partícula
𝑑
[mm]
0.1
Concentración de Sedimentos
𝐶
𝑣
[mg/L]
1000
0.125
0.25
0.5
1
2
4
0.001
0.01
0.1
1
Diáme
tro
T
u
b
ería
[m
]
Pendiente Mínima [m/m]
Eq. 35 - d = 1 mm
Eq. 35 - d = 0.5 mm
Eq. 35 - d = 2.5 mm
Eq. 35 - d = 5 mm

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
74
Al aplicar los parámetros anteriores en las principales metodologías contempladas en el
presente estudio, se obtiene una gráfica comparativa, en la cual se presenta el grado de
restricción de cada uno de ellos.
Figura 44. – Comparación multicriterio de las metodologías estudiadas.
La figura anterior permite identificar las metodologías que resultan ser más y menos
restrictivas. Como es de esperar, los criterios tradicionales de esfuerzo cortante mínimo
de 2 Pa y el Criterio III propuesto por la CIRIA, son los más restrictivos; esto se debe a
la naturaleza del desarrollo del método, en el cual se espera transportar partículas
cohesivas que se encuentran en el lecho de la tubería. Igualmente, los criterios de
velocidades mínimas tradicionales y de transporte de partículas propuestos por la
CIRIA resultan ser menos restrictivos que los anteriores mencionados; esto se debe
básicamente al tipo de partícula que son capaces de transportar y al modo de transporte.
Finalmente, el método propuesto por la ASCE resulta ser el menos conservativo y por
consiguiente el que permite pendientes menores en el sistema. La naturaleza del método
TF lleva a pendientes menores a las obtenidas con criterios tradicionales de diseño, lo
cual se refleja en la posibilidad de reducir costos de construcción de futuras redes.
0.125
0.25
0.5
1
2
4
0.00001
0.0001
0.001
0.01
0.1
1
Diáme
tro
T
u
b
ería
[m
]
Pendiente Mínima [m/m]
Vmin RAS
τmin RAS
CIRIA - I
CIRIA - II
CIRIA - III
Tractive Force
τmin ASCE

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
75
4 ANÁLISIS DE COSTOS EN EL DISEÑO OPTIMIZADO DE
SISTEMAS DE ALCANTARILLADO
Parte del objetivo del presente trabajo consiste en determinar qué tanta influencia
tienen los valores de velocidad y esfuerzo cortante mínimo propuestos en las diferentes
normativas y metodologías para el diseño de alcantarillados. Como se puede observar
en capítulos anteriores, existen distintos valores para los tipos de alcantarillados y bajo
diferentes condiciones, por lo cual es fundamental entender qué variación en términos
de costos resulta al utilizar, por ejemplo, un valor de velocidad mínima de 0.6 m/s o uno
de 0.9 m/s para el diseño optimizado de una red de alcantarillado. Dado lo anterior, en
el presente capítulo se presenta la red prototipo que se utiliza para los análisis, las
ecuaciones de costos consideradas y la metodología empleada para realizar el diseño
optimizado de una red de alcantarillado. Posterior a lo anterior, se presentan los
resultados obtenidos al diseñar un sistema de alcantarillados pluvial para diferentes
criterios de autolimpieza.
4.1 Red Prototipo
La red de estudio a partir de la cual se realizan todos los análisis, corresponde a una red
de agua lluvia localizada en el sector de Chicó en la ciudad de Bogotá. Cabe mencionar
que el objetivo de este ejercicio, es hacer uso de los pozos y la topografía del terreno
correspondiente a la red, puesto que, el diseño en sí busca obtener los diámetros y
pendientes respectivas de cada tubería que conforman la red. La Figura 45 presenta la
topología de la red.
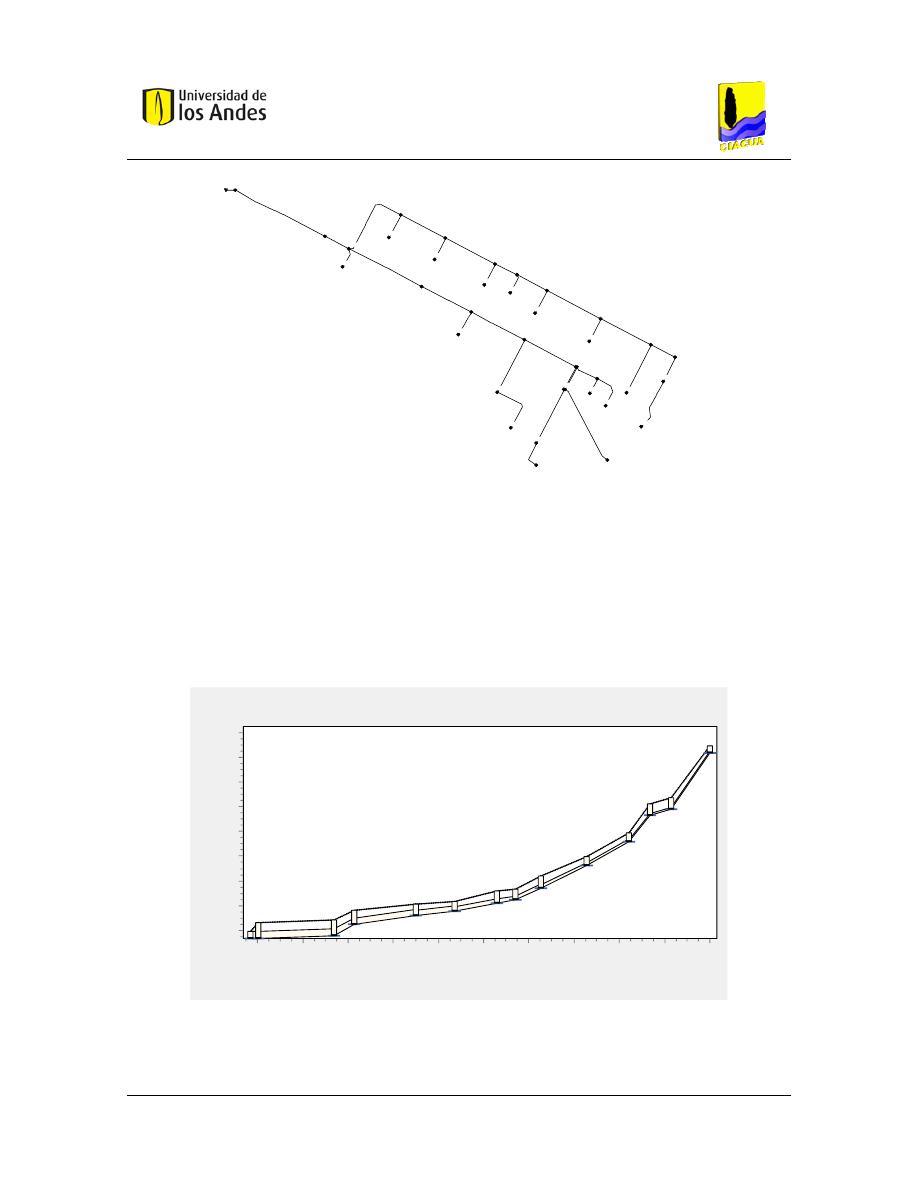
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
76
Figura 45. – Esquema de la red prototipo.
Esta red cuenta con un total de 37 nodos, 37 conductos y una descarga. Adicionalmente,
se cuenta con un evento de precipitación y áreas de drenaje a cada nodo. La topografía
del terreno original da como resultado una pendiente promedio del 1%
aproximadamente. Una vista transversal de la topografía del terreno se muestra en la
Figura 46.
Figura 46. – Topografía del terreno para una ruta PMI92813 – PMP92951.
PMI92748
PMP93182
PMP92903
PMI92766
PMI92813
PMI92774
PMI92775
PMI92764
PMP92827
PMP92828
PMP92901
PMP93107
PMP92934
PMP92900
PMP93198
PMP93004
PMP92933
PMI92735
PMP92864
PMP106155
PMP93000
PMI92786
PMP106384
PMI92792
PMP93036
PMP92896
PMI92734
PMP92876
PMI92736
PMP93099
PMI92754
PMP92926
PMP93031
PMI92782
PMP92925
PMP92990
PMP93024
PMP92951
Water Elevation Profile: Node PMI92813 - PMP92951
08/23/2013 00:05:00
Distancia [m]
2,000
1,800
1,600
1,400
1,200
1,000
800
600
400
200
0
E
le
va
ti
on
(
m
)
2,590
2,585
2,580
2,575
2,570
2,565
2,560
2,555
2,550

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
77
Al realizar la respectiva modelación hidrológica en la red de estudio, se obtienen los
caudales de diseño de cada tramo del sistema. Con estos valores y con las longitudes de
cada tubería y la topografía del terreno, se pueden iniciar los análisis para la red
prototipo.
4.2 Función de costos
Con el fin de representar mediante una expresión simple las variables que afectan los
costos en el diseño de un sistema de alcantarillado, Duque (2013) presenta el resultado
de un ajuste de ecuaciones conforme a la información de bases de datos del Ministerio
de Ambiente, Vivienda y Desarrollo Territorial (MAVDT), del Fondo Financiero de
Proyectos de Desarrollo (FONADE) y de empresas encargadas de prestar el servicio,
mediante un estudio de análisis de inversiones en acueducto y alcantarillado,
desarrollado por la Comisión de Agua Potable y Saneamiento Básico (CRA),
desarrolladas por Navarro (2009). Se encontró que los costos de las tuberías, son función
del diámetro de la misma y se pueden calcular mediante la siguiente expresión:
𝐶
𝑡
= 9579.31 ∙ 𝑘 ∙ 𝑑
0.5737
Ecuación 71. – Costo de material por metro lineal de tubería.
En la ecuación anterior, 𝐶
𝑡
es el costo por metro lineal de tubería a mayo de 2009
[COP/m]; 𝑑 el diámetro de la tubería [mm] y 𝑘 un factor de conversión de pesos de
diciembre de 2007 a mayo de 2009. Este factor 𝑘 se puede calcular como: (1 + 𝐼𝑃𝐶
2008
) ∙
(1 + 𝐼𝑃𝐶
2006/2009
) = 1.32. Igualmente, los costos de excavación son función del volumen
de excavación necesario para la instalación de la tubería. Estos se pueden representar
mediante la Ecuación 72.
𝐶
𝑒
= 1163.77 ∙ 𝑘 ∙ 𝑉
1.31
Ecuación 72. – Costo de excavación por metro lineal de tubería.
donde, 𝐶
𝑒
es el costo por metro lineal de tubería a mayo de 2009 [COP/m]; 𝑉 el volumen
de excavación por tubería [m
3
] y 𝑘 un factor de conversión de pesos de diciembre de 2007
a mayo de 2009 igual a 1.32. El volumen de excavación necesario para la instalación de
una tubería se puede determinar mediante el análisis de la Figura 47. El resultado se
muestra en la Ecuación 73.
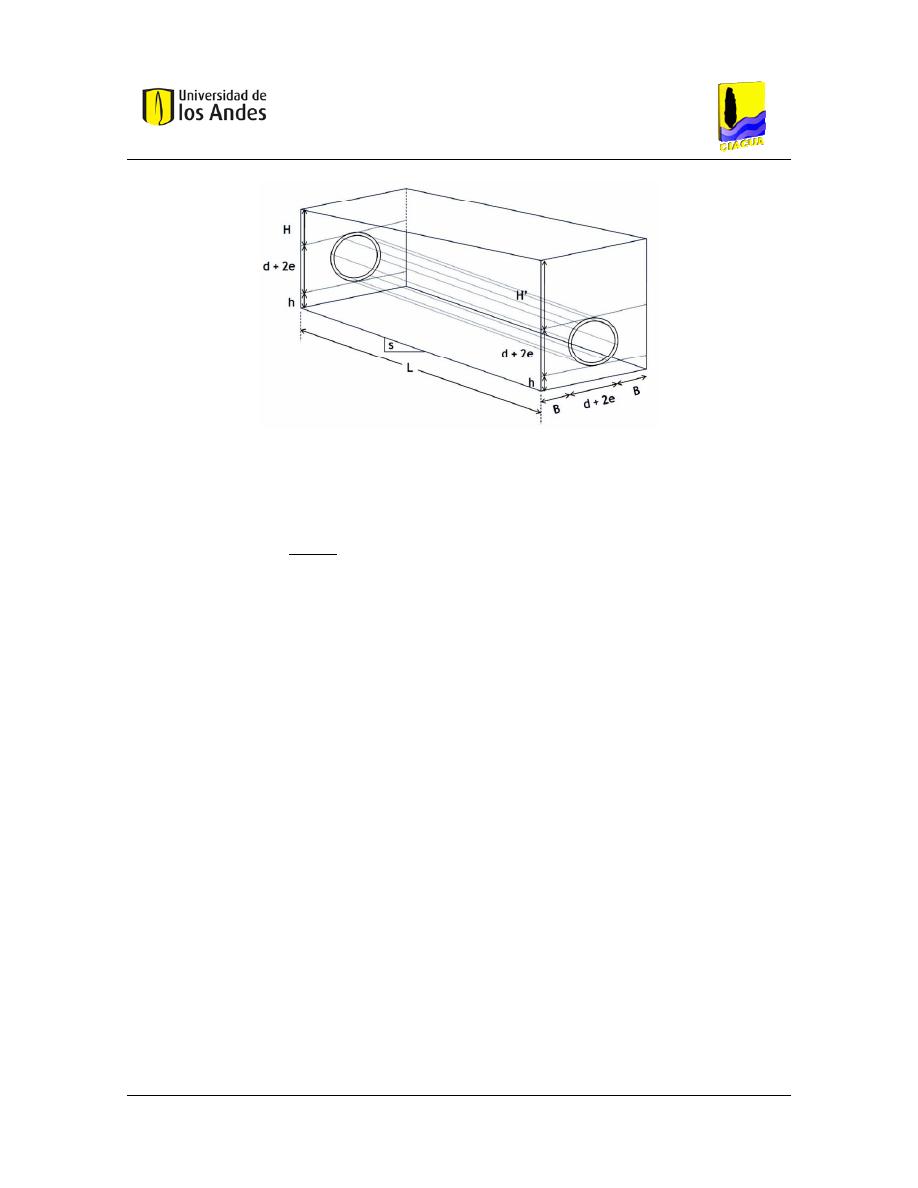
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
78
Figura 47. – Proyección del trapecio que produce el área excavada para una tubería de
alcantarillado. Tomado de (CIACUA, 2013).
𝑉 = ([
𝐻 + 𝐻′
2
] + 𝑑 + 2𝑒 + ℎ) ∙ (2𝐵 + 2𝑒 + 𝑑) ∙ (𝐿𝑐𝑜𝑠[tan
−1
𝑠])
Ecuación 73. – Volumen excavado para instalar la tubería.
En la ecuación anterior, 𝑉 es el volumen excavado para instalar la tubería [m
3
]; 𝐻 la
profundidad de excavación hasta la cota clave aguas arriba de la tubería [m]; 𝐻′ la
profundidad de excavación hasta la cota clave aguas abajo de la tubería; 𝑑 el diámetro
interno de la tubería; 𝑒 el espesor de la pared de la tubería; ℎ el relleno que se debe
disponer bajo la tubería; según el RAS 2000 se debe usar un valor de 15 cm; 𝐵 el espacio
lateral que debe dejarse a ambos lados de la tubería para su instalación [m]; 𝑠 la
pendiente de la tubería y 𝐿 la longitud de la misma. Dado lo anterior, los costos asociados
con la construcción de sistemas de alcantarillado se calculan como la suma entre los
costos de la tubería en sí y de excavación. El resultado es el siguiente:
𝐶 = 𝑘(9579.31 ∙ 𝑑
0.5737
+ 1163.77 ∙ 𝑉
1.31
)
Ecuación 74. – Función de costos totales por metro lineal de tubería.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
79
4.3 Metodología para el diseño optimizado de sistemas de
alcantarillado
La metodología considerada para la realización de los posteriores análisis está basada
en la tesis de Natalia Duque (Duque, 2013), en la cual se aborda el diseño optimizado
como un problema de optimización conocido como el problema de ruta más corta.
Básicamente existen cuatro componentes importantes para el modelaje y solución del
problema: los parámetros, las variables de decisión, las restricciones y la función
objetivo. Los parámetros proporcionan la información necesaria (o conocida) que se tiene
de los problemas. Las variables de decisiones son los aspectos del problema sobre los
cuales el decisor tiene injerencia. Las restricciones limitan el problema estableciendo
las reglas que se deben cumplir en una solución del mismo y finalmente, la función
objetivo guía la búsqueda de la solución que se quiere encontrar (Duque, 2013).
El problema de la ruta más corta pertenece a una rama de la optimización que estudia
los problemas de flujo en redes. Este problema busca encontrar el camino de mínimo
costo (distancia o tiempo de recorrido) desde un nodo específico inicial hasta un nodo
final. Matemáticamente el problema se define de la siguiente forma:
min ∑ 𝑐
𝑖𝑗
𝑥
𝑖𝑗
(𝑣
𝑖
,𝑣
𝑗
)∈𝐴
∑
𝑥
𝑖𝑗
{𝑗|(𝑣
𝑖
,𝑣
𝑗
)∈𝐴}
−
∑
𝑥
𝑗𝑖
{𝑗|(𝑣
𝑗
,𝑣
𝑖
)∈𝐴}
= {
1
𝑣
𝑖
= 𝑣
𝑠
0
𝑣
𝑖
≠ 𝑣
𝑠
, 𝑣
𝑡
∀𝑣
𝑖
∈ 𝑁
−1
𝑣
𝑖
= 𝑣
𝑡
𝑥
𝑖𝑗
∈ {0,1}∀𝑣
𝑖
∈ 𝑁, 𝑣
𝑗
∈ 𝑁
Ecuación 75. – Planteamiento problema ruta crítica.
donde, 𝑥
𝑖𝑗
es una variable binaria que toma el valor de uno si el arco (𝑖, 𝑗) ∈ 𝐴 está en la
solución del problema (el camino) o toma el valor de cero de lo contrario; 𝑐
𝑖𝑗
el costo de
utilizar el arco (𝑖, 𝑗) ∈ 𝐴 en el camino; 𝑣
𝑠
el nodo inicial del cual parte el camino y 𝑣
𝑡
el
nodo final del camino. De la Ecuación 75, la primera línea determina la función objetivo
del problema (en este caso la minimización de los costos); la segunda línea determina
las restricciones que garantizan que un camino parta del nodo 𝑣
𝑠
y llegue al nodo 𝑣
𝑡
y
finalmente la última línea establece la naturaleza binaria de las variables (Duque,
2013).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
80
La forma de solucionar el problema es mediante la aplicación de algún algoritmo que
permita resolverlo. Duque (2013) propone la resolución del problema mediante el
algoritmo de Bellman-Ford (Bellman, 1956). Este algoritmo fue desarrollado
inicialmente para conocer el camino que representa el mínimo tiempo de viaje entre dos
ciudades que hacen parte de un conjunto de 𝑁 ciudades, donde cada par de ciudades
están interconectadas entre sí por una vía que tiene un tiempo de viaje asociado. Estos
tiempos no son directamente proporcionales a las distancias, debido a la cantidad de
rutas que existen para viajar de una ciudad a otra y la variación del tráfico en cada una
de ellas.
4.3.1 Planteamiento del problema
La solución propuesta por Duque (2013) para el diseño optimizado de sistemas de
alcantarillados, se basa en el algoritmo de Bellman – Ford, descrito anteriormente. En
este se deben definir algunas etapas como: 1) Definición de los datos de entrada; 2)
Modelaje del grafo; 3) Definición de las variables de decisión y 4) Planteamiento de la
función objetivo. Estos pasos se describen detalladamente en el documento “Metodología
para la optimización del diseño de tuberías en serie en sistemas de alcantarillado”
(Duque, 2013).
Los datos de entrada son aquellos valores que representan el sistema inicial.
Básicamente se deben ingresar las características de las tuberías tales como, la
rugosidad absoluta, longitud de la tubería y los posibles diámetros que se podrían
utilizar en el diseño; igualmente la topografía del sitio donde se va a realizar el diseño,
el conjunto de pozos de inspección que conforman la serie de tramos y los caudales de
diseño de cada uno de los pozos.
El modelaje del grafo se realiza con el fin de representar una serie de tuberías, de tal
forma que hayan tantos arcos (tuberías que van desde un nodo inicial hasta uno
sucesivo) como tuberías posibles para cada tramo. Para esto, los pozos de inspección se
representan imaginariamente como grupo de nodos. Cada nodo representa una
profundidad a la cual se puede instalar la tubería a cota de batea y un diámetro. En
general se tiene un conjunto global de nodos:
𝒩: 𝐶𝑜𝑛𝑗𝑢𝑛𝑡𝑜 𝑑𝑒 𝑛𝑜𝑑𝑜𝑠
𝒩 = {𝑣
𝑜
, 𝑣
1
, 𝑣
2
, 𝑣
3
, … , 𝑣
𝑛
}
𝒩
𝑘
: 𝐶𝑜𝑛𝑗𝑢𝑛𝑡𝑜 𝑑𝑒 𝑛𝑜𝑑𝑜𝑠 𝑞𝑢𝑒 𝑝𝑒𝑟𝑡𝑒𝑛𝑒𝑐𝑒𝑛 𝑎𝑙 𝑝𝑜𝑧𝑜 𝑘 ∈ 𝑃
𝒩
𝑘
= {𝑣
1
𝑘
, 𝑣
2
𝑘
, 𝑣
3
𝑘
, … , 𝑣
𝑛𝑘
}
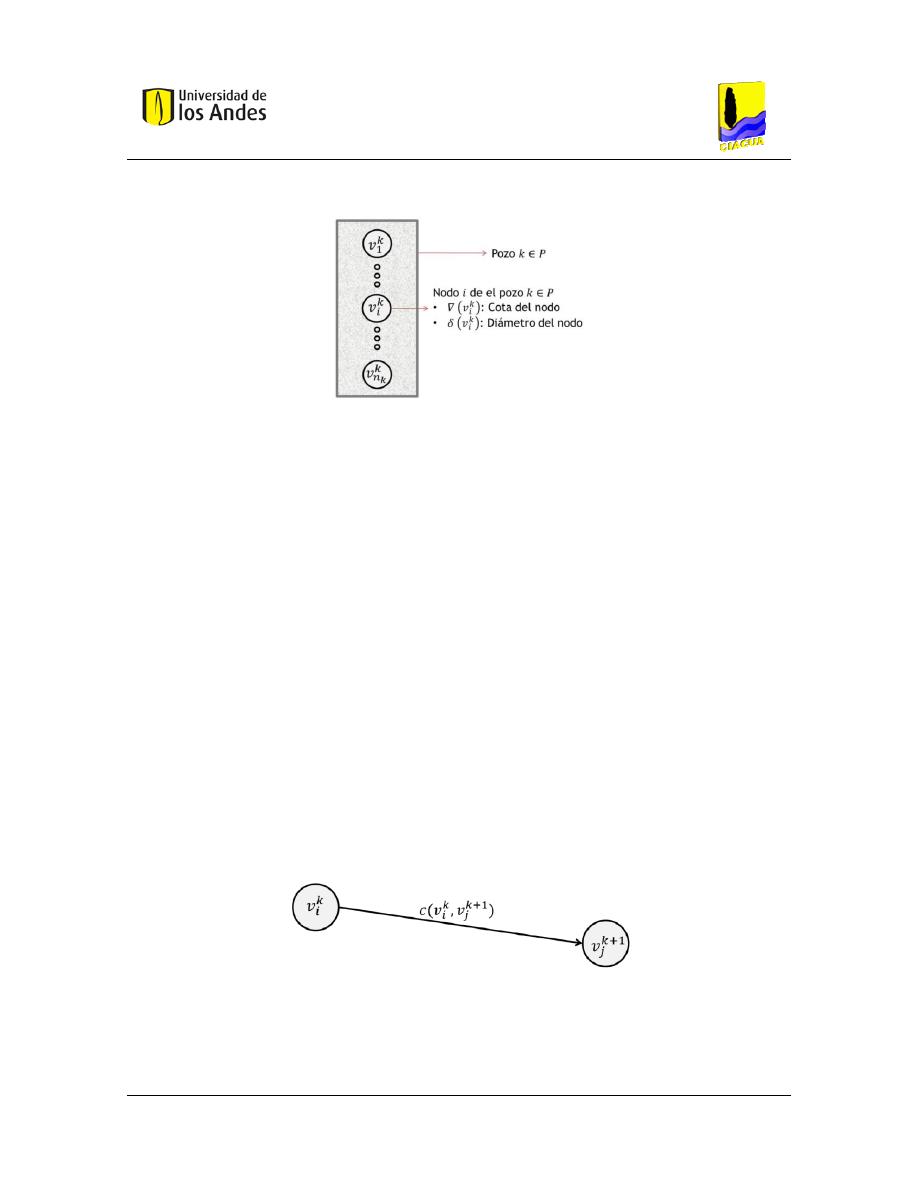
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
81
Figura 48. – Conjunto de nodos que pertenecen a un mismo pozo de inspección. Tomado de
Duque (2013).
Como se puede observar, cada nodo 𝑣
𝑖
𝑘
∈ 𝒩
𝑘
tiene dos atributos. El primero corresponde
a la cota en metros sobre el nivel de referencia ∇(𝑣
𝑖
𝑘
) y el segundo el diámetro 𝛿(𝑣
𝑖
𝑘
).
El primer atributo representa la cota batea de una tubería y el segundo el diámetro de
una tubería asociada con el tramo entre el pozo 𝑘 − 1 y 𝑘. Igualmente, el grafo también
lo conforman arcos (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) que se definen entre dos nodos 𝑣
𝑖
𝑘
∈ 𝒩
𝑘
y 𝑣
𝑗
𝑘+1
∈ 𝒩
𝑘+1
,
donde 𝑣
𝑖
𝑘
es el i-ésimo nodo del pozo 𝑘 ∈ 𝑃 y 𝑣
𝑗
𝑘+1
es el j-ésimo nodo del pozo
estrictamente siguiente 𝑘 + 1 ∈ 𝑃. Además. Cada arco tiene un costo asociado que
representa el costo total de construcción, es decir, la suma entre el costo de la tubería y
los costos de excavación, según la función de costos presentada (Ver Ecuación 74). La
notación y representación de un arco sería entonces:
𝒜: 𝐶𝑜𝑛𝑗𝑢𝑛𝑡𝑜 𝑑𝑒 𝑎𝑟𝑐𝑜𝑠
𝒜 = {(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
)|𝑣
𝑖
𝑘
∈ 𝒩
𝑘
, 𝑣
𝑗
𝑘+1
∈ 𝒩
𝑘+1
}
𝑐(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
): 𝐶𝑜𝑠𝑡𝑜 𝑑𝑒𝑙 𝑎𝑟𝑐𝑜 (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) ∈ 𝒜
Figura 49. – Representación de un arco (𝒗
𝒊
𝒌
, 𝒗
𝒋
𝒌+𝟏
). Tomado de Duque (2013).
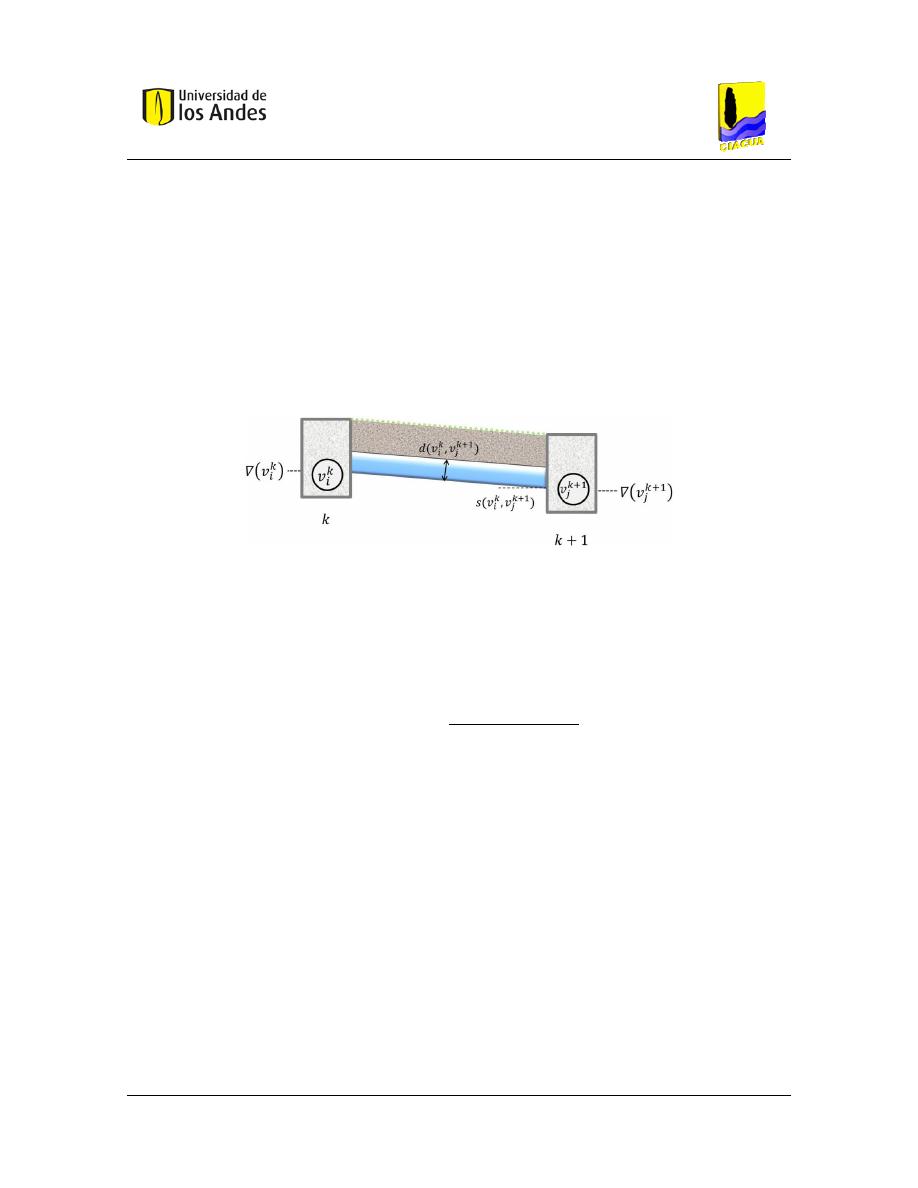
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
82
Anteriormente se menciona que el nodo carga la información del diámetro, por lo cual
el diámetro de un arco (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) adopta el valor del nodo 𝑣
𝑗
𝑘+1
∈ 𝒩
𝑘+1
. Asimismo, el
nodo carga la información de la cota batea donde se instalaría la tubería.
∇(𝑣
𝑖
𝑘
): 𝐶𝑜𝑡𝑎 𝑑𝑒 𝑐𝑎𝑑𝑎 𝑛𝑜𝑑𝑜 𝑖 𝑒𝑛 𝑒𝑙 𝑝𝑜𝑧𝑜 𝑘 ∈ 𝑃.
𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
): 𝐷𝑖á𝑚𝑒𝑡𝑟𝑜 𝑑𝑒𝑙 𝑎𝑟𝑐𝑜 (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
)
∈ 𝒜, 𝑟𝑒𝑝𝑟𝑒𝑠𝑒𝑛𝑡𝑎𝑑𝑜 𝑐𝑜𝑚𝑜 𝑢𝑛 𝑎𝑡𝑟𝑖𝑏𝑢𝑡𝑜 𝑑𝑒𝑙 𝑛𝑜𝑑𝑜 𝑣
𝑗
𝑘+1
∈ 𝒩
𝑘+1
𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) = 𝛿(𝑣
𝑗
𝑘+1
)
Figura 50. – Representación de un tramo de alcantarillado. Tomado de Duque (2013).
Igualmente, la pendiente asociada con el arco 𝑠(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
), es función de las cotas de los
nodos que lo componen. Esta se puede determinar mediante la siguiente expresión:
𝑠(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) =
∇(𝑣
𝑖
𝑘
) − ∇(𝑣
𝑗
𝑘+1
)
𝑙
Ecuación 76. – Pendiente asociada al arco. Tomado de Duque (2013).
En cuanto a las variables de decisión, estas serían fundamentalmente los arcos
(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) ∈ 𝒜. 𝑥
𝑖,𝑗
, es una variable binaria que toma el valor de uno (1) si el arco
(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) ∈ 𝒜 pertenece al camino que forma la ruta más corta o toma el valor de cero
(0) caso contrario. Lo anterior se plantea en la Ecuación 77.
𝑥
𝑖,𝑗
∈ {0,1}∀𝑣
𝑖
𝑘
∈ 𝒩, 𝑣
𝑗
𝑘+1
∈ 𝒩
Ecuación 77. – Variable de decisión. Tomado de Duque (2013).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
83
La escogencia de un arco (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) ∈ 𝒜 implica escoger un diámetro 𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) y una
pendiente de diseño 𝑠(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
).
Finalmente, con la función objetivo se busca minimizar los costos propios de la tubería
a diseñar y por consiguiente encontrar el diseño que, cumpliendo con todas las
restricciones, sea el más económico. La función objetivo sería entonces:
𝑚𝑖𝑛
∑ 𝑐(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
)𝑥
𝑖,𝑗
(𝑣
𝑖
,𝑣
𝑗
)∈𝒜
𝑐(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) = 𝑘 ∙ (9579.31 ∙ 𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
)
0.5737
+ 1163.77 ∙ 𝑉
1.31
)
Ecuación 78. – Planteamiento de la función objetivo. Tomado de Duque (2013).
El volumen se calcula entonces de la siguiente forma:
𝑉 = ([
𝐻 + 𝐻′
2
] + 𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) + 2𝑒 + ℎ)
∙ (2𝐵 + 2𝑒 + 𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) ∙ (𝑙 ∙ cos [tan
−1
𝑠(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
)]))
Ecuación 79. – Cálculo de Volumen.
donde 𝑉 es el volumen excavado para la instalación de la tubería [m
3
]; 𝐻 la profundidad
de excavación hasta la cota clave aguas arriba de la tubería [m]; 𝐻′ la profundidad de
excavación hasta la cota clave aguas abajo de la tubería [m]; 𝑑(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) el diámetro del
arco (𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) ∈ 𝒜 [m]; 𝑒 el espesor de la pared de la tubería [m]; ℎ el relleno que se
debe disponer bajo la tubería = 15 cm, según el RAS; 𝐵 el espacio lateral que debe dejarse
a ambos lados de la tubería para colocarla [m]; 𝑠(𝑣
𝑖
𝑘
, 𝑣
𝑗
𝑘+1
) la pendiente asociada al arco
y 𝑙 la longitud de la tubería [m].
Con el procedimiento mencionado anteriormente (representación de las tuberías como
grafos y proceso de selección del diseño óptimo) se puede describir la metodología de
diseño de una serie de tramos de alcantarillados, por medio de la siguiente figura:
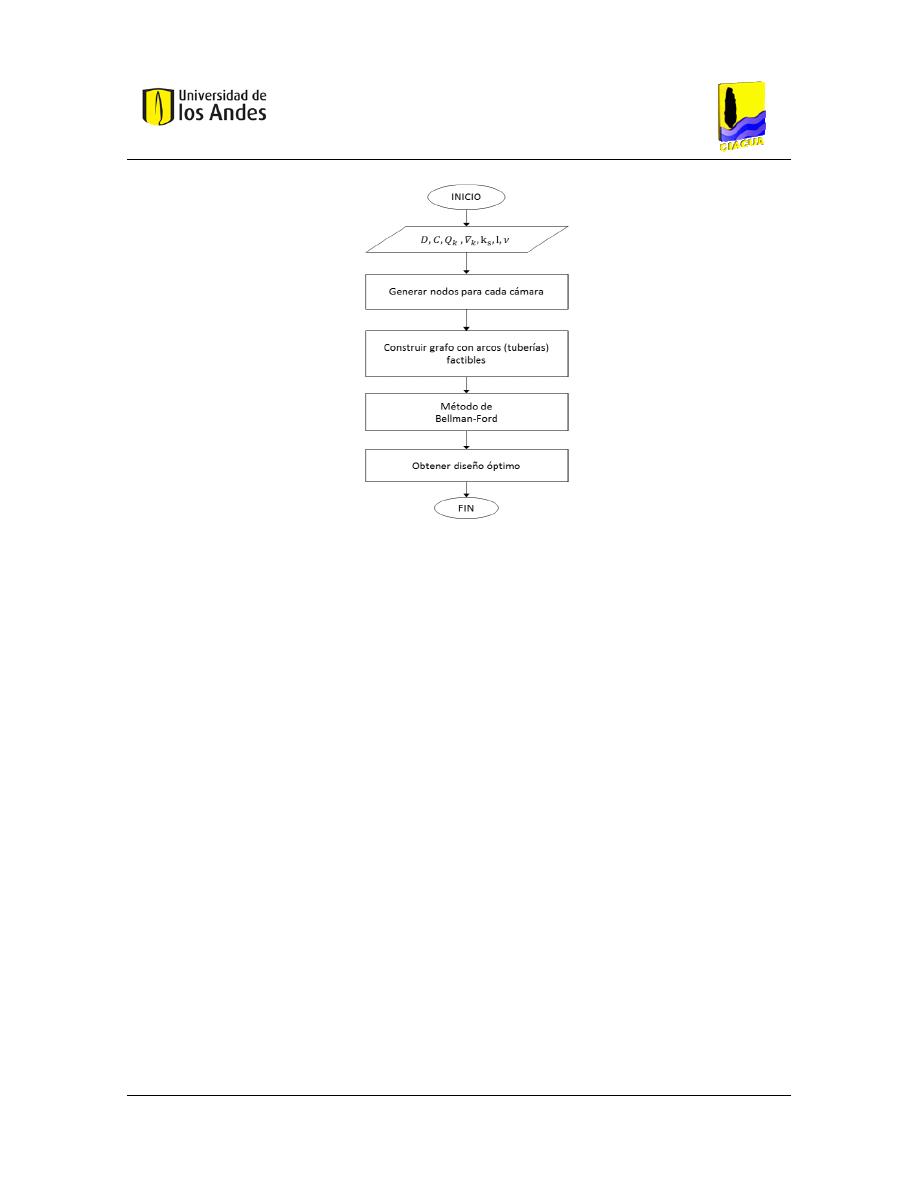
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
84
Figura 51. – Metodología para el diseño optimizado de series de tramos de alcantarillado.
Tomado de Duque (2013).
4.4 Aplicación de la metodología
La aplicación de la metodología se realiza en la red prototipo presentada anteriormente.
La finalidad de esta tarea es determinar qué tanta influencia tienen, en el diseño
optimizado, los diferentes valores y metodologías de autolimpieza propuestas en
diferentes normativas a nivel mundial. Para dicho fin se debe determinar primeramente
las rutas principales, secundarias y terciarias de la red y posteriormente la
configuración diámetro – pendiente de cada uno de los tubos pertenecientes a las rutas
encontradas. Para el primer paso se hace uso de la metodología propuesta por el Centro
de Investigación Estratégica del Agua (CIE) y en el segundo se aplica el algoritmo de
resolución del problema de ruta más corta, Bellman – Ford (Ver sección 4.3).
4.4.1 CIE 7.0
Como se menciona anteriormente, el uso del programa CIE 7.0 se realiza con el fin de
determinar, en la red prototipo, cuales son las rutas principales, secundarias y
terciarias. Cada una de ellas se puede definir de la siguiente manera:
1. Ruta principal: Aquella configuración de tuberías por la cual se mueve la mayor
cantidad de agua en el sistema.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
85
2. Ruta secundaria: Configuración de tuberías que desembocan en la ruta principal
obtenida anteriormente.
3. Ruta terciaria: Configuración de tuberías que desembocan en una ruta
secundaria.
Igualmente, esta configuración de rutas obtenidas puede verse afectada por los criterios
de autolimpieza que se consideren. En términos generales, el procedimiento que se lleva
a cabo para obtener las rutas es el siguiente: 1) Obtención de las coordenadas de los
pozos; 2) Obtención de la elevación (cota rasante) de cada pozo; 3) Determinación de los
caudales de diseño para cada tubería y 4) Obtención de las rutas en CIE 7.0. Un ejemplo
de la información requerida por el programa se presenta en la Tabla 15.
Tabla 15. – Valores de diseño para CIE 7.0.
ID
X (m)
Y (m)
RASANTE Hmin Hmax Descarga
1 1336443.971 1009812.393
2558.708
1.2
5
2 1336795.411 1009623.703
2566.121
1.2
5
3 1335969.251 1009872.803
2554.262
1.2
5
4 1336617.591 1009210.883
2573.461
1.2
5
5 1336277.691 1009898.903
2556.418
1.2
5
6 1336919.971 1009452.303 2577.320868
1.2
5
7 1336532.981 1009334.413
2570.744
1.2
5
8 1336850.911 1009408.123
2576.833
1.2
5
9 1336798.001 1009450.923
2573.967
1.2
5
10 1336125.351 1009972.543
2555.41
1.2
5
11 1336614.401 1009718.003
2561.97
1.2
5
12 1336531.761 1009786.683
2559.963
1.2
5
13 1336969.521 1009338.543
2587.335
1.2
5
14 1336357.771 1009646.933
2559.91
1.2
5
15 1336400.831 1009722.853
2559.98
1.2
5
16 1336487.291 1009453.683
2566.687
1.2
5
17 1336714.851 1009462.463
2570.318
1.2
5
18 1336578.731 1009629.103
2564.494
1.2
5
19 1336553.641 1009846.073
2558.328
1.2
5
20 1336234.211 1009807.983
2555.329
1.2
5
21 1336754.071 1009537.963
2569.258
1.2
5
22 1336711.681 1009463.213
2570.401
1.2
5
23 1336618.041 1009282.943
2573.801
1.2
5
24 1335910.571 1009974.783 2552.039038
1.2
5
25 1335990.841 1009933.243
2554.05
1.2
5
26 1337001.431 1009613.093
2569.69
1.2
5
27 1336821.631 1009498.263
2571.628
1.2
5
28 1336164.621 1010047.713
2555.31
1.2
5
29 1336834.651 1009699.723
2564.907
1.2
5
30 1337084.141 1009570.193
2575.501
1.2
5
31 1335611.631 1010130.963 2551.505005
1.2
5
32 1336314.671 1009969.823
2555.823
1.2
5
33 1336653.921 1009793.953
2561.064
1.2
5
34 1336480.881 1009883.463
2557.979
1.2
5
35 1337043.371 1009488.843
2576.787
1.2
5
36 1336856.191 1009226.113
2590.25
1.2
5
37 1336751.301 1009539.293
2567.198
1.2
5
38 1335578.461 1010129.913
2551.505
1.2
5
SI
NODOS
ID NODO_IN NODO_OUT Q [m3/s]
n
1
13
35
2.23416 0.013
2
35
30
0.37689 0.013
3
30
26
2.47572 0.013
4
26
29
0.2976
0.013
5
29
33
0.51705 0.013
6
33
19
0.53107 0.013
7
19
34
0.1782
0.013
8
34
32
0.399
0.013
9
32
28
0.35188 0.013
10
28
25
0.27279 0.013
11
25
24
0.36331 0.013
12
24
31
0.44062 0.013
13
31
38
0.21656 0.013
14
8
27
0.38266 0.013
15
27
21
0.29372 0.013
16
21
37
0.13406 0.013
17
37
18
0.14149 0.013
18
18
15
0.6495
0.013
19
15
20
0.41671 0.013
20
20
25
0.39034 0.013
21
36
17
4.82197 0.013
22
17
21
0.13619 0.013
23
4
23
0.36036 0.013
24
23
22
0.34659 0.013
25
22
37
0.62179 0.013
26
7
16
0.84453 0.013
27
16
18
0.75253 0.013
28
6
26
0.46247 0.013
29
2
29
0.38161 0.013
30
11
33
0.3488
0.013
31
12
19
0.25433 0.013
32
1
34
0.28235 0.013
33
5
32
0.29821 0.013
34
10
28
0.27478 0.013
35
9
27
0.18796 0.013
36
14
15
0.34921 0.013
37
3
25
0.12938 0.013
TUBOS
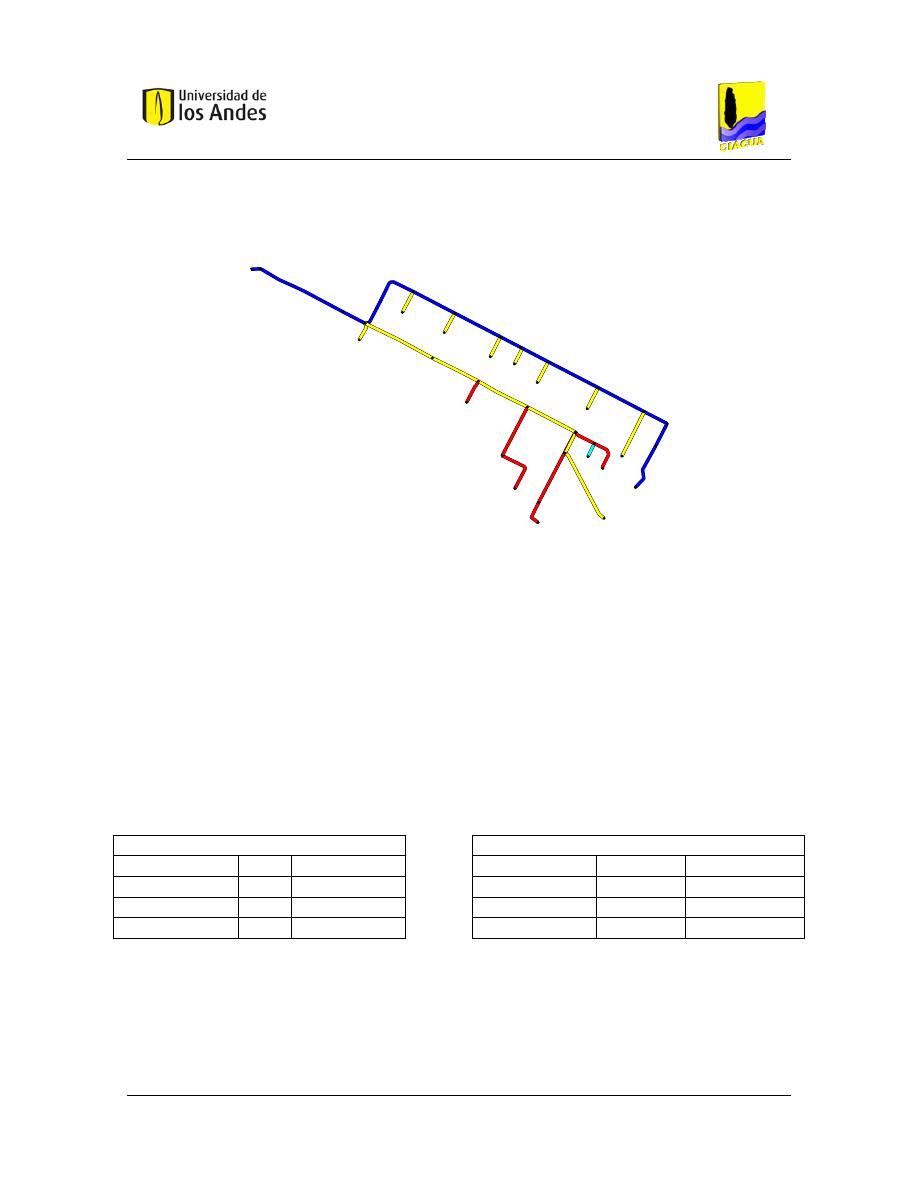
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
86
Con estos datos de entrada y modificando las restricciones de autolimpieza, se obtienen
las rutas en la red prototipo. La Figura 52 presenta los resultados de la metodología
aplicando una restricción de 0.6 m/s como velocidad mínima de autolimpieza.
Figura 52. – Rutas red prototipo. Velocidad mínima = 0.6 m/s
En la Figura 52 se puede observar la configuración de las rutas generadas en el
programa. En color azul oscuro se presenta la ruta principal, en color amarillo las
secundarias, en rojo las terciarias y en color azul claro las cuaternarias. El resultado
obtenido anteriormente se debe comparar con algún otro criterio de autolimpieza.
Inicialmente, se consideran los siguientes criterios de autolimpieza, aplicables al caso
de alcantarillado pluvial, para realizar la comparación:
Tabla 16. – Criterios de autolimpieza considerados.
Esfuerzo Cortante Mínimo
Velocidad Mínima
Fuente
País Valor [Pa]
Fuente
País
Valor [m/s]
Lysne (1969) USA
2
CNA (2007)
México
0.6
Yao (1974)
USA
4
RAS (2000)
Colombia
0.75
ASCE (1970) USA
12.6
INEN (1992)
Ecuador
0.9
Los resultados obtenidos al aplicar el mismo procedimiento se pueden consultar en los
Anexos 21-25. Como se puede observar, la restricción de autolimpieza no es una variable
sensible del modelo, por lo cual, cualquier restricción que se considere para la obtención
Línea
Caudal
0.01
150.00
192.00
256.00
LPS
08/23/2013 00:20:00

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
87
de las rutas en una red no afecta el resultado final. Una vez obtenidas las rutas de la
red, se procede a realizar el diseño optimizado por cada ruta de forma independiente.
4.4.2 Diseño optimizado por tramos
El diseño optimizado por tramos busca obtener un sistema con el menor costo posible
mediante la minimización de la función objetivo presentada anteriormente (Ver
Ecuación 78). Los datos de entrada al modelo serían entonces el caudal de diseño de
cada tramo de la ruta, la cota rasante de los pozos que conforman cada tramo y la
longitud de las tuberías. Un ejemplo de la información requerida se presenta en la Tabla
17.
Tabla 17. – Datos de entrada al modelo. Ruta principal.
Nodo Caudal [m
3
/s] Cota Rasante [m] Longitud [m]
0
0.22
2587.34
0.00
1
0.91
2576.79
172.65
2
1.88
2575.50
90.99
3
2.50
2569.69
93.17
4
2.64
2564.91
187.94
5
3.02
2561.06
203.82
6
3.26
2558.33
113.02
7
3.77
2557.98
81.80
8
4.42
2555.82
187.31
9
4.93
2555.31
169.06
10
10.28
2554.05
270.92
11
10.70
2552.04
90.38
12
10.94
2551.51
337.56
13
1000
2551.51
33.19
En la tabla anterior se tiene el conjunto de nodos que conforman la ruta que se va a
diseñar. Se observa que el Nodo 0 corresponde al nodo más aguas arriba, el Nodo 1 sería
el nodo inmediatamente aguas abajo del Nodo 0, el Nodo 2 el nodo aguas abajo del Nodo
1 y así sucesivamente hasta llegar al nodo más aguas abajo de la ruta (Nodo 13).
Igualmente, la columna de caudal, presenta el caudal de entrada a cada uno de los nodos
(y tuberías que conforman dos nodos consecutivos) y la longitud sería la respectiva de
cada tubería. Por ejemplo, el Nodo 0 y el Nodo 1 conforman el inicio y final del Tubo 1,
cuyo caudal de diseño es de 0.22 m
3
/s, longitud de 172.65 m y cuenta con una rasante
inicial de 2587.34 m y una rasante final de 2576.79 m. El Tubo 2 estaría conformado por
el nodo de inicio, Nodo 1, y el Nodo 2 como nodo final, tendría un caudal de diseño de
0.91 m
3
/s y una longitud de 90.99 m.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
88
Al aplicar la metodología para el diseño independiente por tramos, modificando las
restricciones de autolimpieza consideradas para el caso de un alcantarillado pluvial (Ver
Tabla 17) se obtiene el diseño optimizado de cada tubería que conforma la totalidad de
la red. Las tablas resultantes son las siguientes:
Tabla 18. – Resultados diseño optimizado en la red prototipo.
Tubo
Costo
Pendiente Diámetro
T01
6,453,557.95
$
0.06098
0.8
T02
2,971,064.40
$
0.014131
0.8
T03
3,056,985.85
$
0.062246
0.8
T04
7,156,314.14
$
0.025442
0.8
T05
9,894,386.06
$
0.019832
1
T06
5,006,556.53
$
0.024202
1
T07
4,310,017.41
$
0.010011
1.2
T08
14,280,600.82
$
0.010869
1.35
T09
13,944,217.96
$
0.003922
1.5
T10
25,924,138.33
$
0.004651
1.5
T11
6,569,827.86
$
0.022244
1.5
T12
57,286,426.63
$
0.003656
2.2
T13
3,435,002.04
$
0.047205
2.2
T14
3,860,653.08
$
0.042293
0.45
T15
16,536,861.57
$
0.066646
1
T16
5,046,049.37
$
0.036647
1
T17
106,520.48
$
0.064951
1.2
T18
26,939,520.45
$
0.019036
2.2
T19
33,389,503.22
$
0.022444
2.2
T20
30,470,486.75
$
0.024848
2.2
T21
49,467,821.44
$
0.004673
2.2
T22
1,759,155.12
$
0.014657
0.5
T23
2,478,511.56
$
0.041866
0.45
T24
1,820,862.46
$
0.03182
0.6
T25
748,710.91
$
0.044164
0.35
T26
1,797,121.34
$
0.012216
0.5
T27
2,560,375.42
$
0.004166
0.7
T28
7,525,020.68
$
0.015849
0.6
T29
2,620,865.68
$
0.032194
0.6
T30
1,113,326.08
$
0.023952
0.4
T31
5,074,080.04
$
0.0228
0.8
T32
7,733,932.39
$
0.012955
0.6
T33
1,599,795.31
$
0.014096
0.45
T34
2,437,574.49
$
0.016842
0.5
T35
1,651,312.64
$
0.008939
0.5
T36
1,927,236.62
$
0.007664
0.5
T37
1,090,759.69
$
0.011267
0.35
TOTAL
370,045,152.78
$
Velocidad = 0.6 m/s
Tubo
Costo
Pendiente Diámetro
T01
6,453,557.95
$
0.06098
0.8
T02
2,971,064.40
$
0.014131
0.8
T03
3,056,985.85
$
0.062246
0.8
T04
7,156,314.14
$
0.025442
0.8
T05
9,894,386.06
$
0.019832
1
T06
5,006,556.53
$
0.024202
1
T07
4,310,017.41
$
0.010011
1.2
T08
14,280,600.82
$
0.010869
1.35
T09
13,944,217.96
$
0.003922
1.5
T10
25,924,138.33
$
0.004651
1.5
T11
6,569,827.86
$
0.022244
1.5
T12
57,286,426.63
$
0.003656
2.2
T13
3,435,002.04
$
0.047205
2.2
T14
3,860,653.08
$
0.042293
0.45
T15
16,536,861.57
$
0.066646
1
T16
5,046,049.37
$
0.036647
1
T17
106,520.48
$
0.064951
1.2
T18
26,939,520.45
$
0.019036
2.2
T19
33,389,503.22
$
0.022444
2.2
T20
30,470,486.75
$
0.024848
2.2
T21
49,467,821.44
$
0.004673
2.2
T22
1,759,155.12
$
0.014657
0.5
T23
2,478,511.56
$
0.041866
0.45
T24
1,820,862.46
$
0.03182
0.6
T25
748,710.91
$
0.044164
0.35
T26
1,797,121.34
$
0.012216
0.5
T27
2,560,375.42
$
0.004166
0.7
T28
7,525,020.68
$
0.015849
0.6
T29
2,620,865.68
$
0.032194
0.6
T30
1,113,326.08
$
0.023952
0.4
T31
5,074,080.04
$
0.0228
0.8
T32
7,733,932.39
$
0.012955
0.6
T33
1,599,795.31
$
0.014096
0.45
T34
2,437,574.49
$
0.016842
0.5
T35
1,651,312.64
$
0.008939
0.5
T36
1,927,236.62
$
0.007664
0.5
T37
1,090,759.69
$
0.011267
0.35
TOTAL
370,045,152.78
$
Velocidad = 0.75 m/s
Tubo
Costo
Pendiente Diámetro
T01
6,453,557.95
$
0.06098
0.8
T02
2,971,064.40
$
0.014131
0.8
T03
3,056,985.85
$
0.062246
0.8
T04
7,156,314.14
$
0.025442
0.8
T05
9,894,386.06
$
0.019832
1
T06
5,006,556.53
$
0.024202
1
T07
4,310,017.41
$
0.010011
1.2
T08
14,280,600.82
$
0.010869
1.35
T09
13,944,217.96
$
0.003922
1.5
T10
25,924,138.33
$
0.004651
1.5
T11
6,569,827.86
$
0.022244
1.5
T12
57,286,426.63
$
0.003656
2.2
T13
3,435,002.04
$
0.047205
2.2
T14
3,860,653.08
$
0.042293
0.45
T15
16,536,861.57
$
0.066646
1
T16
5,046,049.37
$
0.036647
1
T17
106,520.48
$
0.064951
1.2
T18
26,939,520.45
$
0.019036
2.2
T19
33,389,503.22
$
0.022444
2.2
T20
30,470,486.75
$
0.024848
2.2
T21
49,467,821.44
$
0.004673
2.2
T22
1,759,155.12
$
0.014657
0.5
T23
2,478,511.56
$
0.041866
0.45
T24
1,820,862.46
$
0.03182
0.6
T25
748,710.91
$
0.044164
0.35
T26
1,797,121.34
$
0.012216
0.5
T27
2,560,375.42
$
0.004166
0.7
T28
7,525,020.68
$
0.015849
0.6
T29
2,620,865.68
$
0.032194
0.6
T30
1,113,326.08
$
0.023952
0.4
T31
5,074,080.04
$
0.0228
0.8
T32
7,733,932.39
$
0.012955
0.6
T33
1,599,795.31
$
0.014096
0.45
T34
2,437,574.49
$
0.016842
0.5
T35
1,651,312.64
$
0.008939
0.5
T36
1,927,236.62
$
0.007664
0.5
T37
1,090,759.69
$
0.011267
0.35
TOTAL
370,045,152.78
$
Velocidad = 0.9 m/s

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
89
La tabla anterior muestra los resultados obtenidos al aplicar el diseño optimizado por
tramos a la red prototipo de alcantarillado pluvial. Se observa que el criterio de
velocidad mínima o esfuerzo cortante mínimo no es representativo y no afecta el diseño
en sí. Solamente se evidencia una pequeña variación cuando se tiene como restricción
un esfuerzo cortante de 12 Pa, el cual fue un valor propuesto por la ASCE en el año 1970
y cuya validez ya no aplica para la norma actual de diseño. Dado lo anterior, se puede
concluir que para el caso de la red prototipo, los criterios de autolimpieza no juegan
ningún papel en el diseño optimizado de una red de alcantarillado pluvial. Lo anterior
se puede deber a dos factores: 1) El caudal que se transporta en el sistema de
alcantarillado conlleva a tener velocidades altas que se acercan más al límite de
velocidad máxima; 2) La topografía del terreno es favorable (topografía con altas
pendientes) lo cual lleva a obtener igualmente velocidades mayores.
Al realizar una gráfica (Ver Figura 53) de los resultados obtenidos para cada tubería
(pendiente vs diámetro) comparando las pendientes mínimas requeridas por cada uno
de los criterios de autolimpieza, se observa que efectivamente los diseños obtenidos se
encuentran más cerca de la restricción de velocidad máxima. Las velocidades mínimas
se encuentran muy por debajo de las existentes en la tubería. Dado lo anterior, se
plantean los siguientes interrogantes: ¿En alcantarillados sanitarios las restricciones de
Tubo
Costo
Pendiente Diámetro
T01
6,453,557.95
$
0.06098
0.8
T02
2,971,064.40
$
0.014131
0.8
T03
3,056,985.85
$
0.062246
0.8
T04
7,156,314.14
$
0.025442
0.8
T05
9,894,386.06
$
0.019832
1
T06
5,006,556.53
$
0.024202
1
T07
4,310,017.41
$
0.010011
1.2
T08
14,280,600.82
$
0.010869
1.35
T09
13,944,217.96
$
0.003922
1.5
T10
25,924,138.33
$
0.004651
1.5
T11
6,569,827.86
$
0.022244
1.5
T12
57,286,426.63
$
0.003656
2.2
T13
3,435,002.04
$
0.047205
2.2
T14
3,860,653.08
$
0.042293
0.45
T15
16,536,861.57
$
0.066646
1
T16
5,046,049.37
$
0.036647
1
T17
106,520.48
$
0.064951
1.2
T18
26,939,520.45
$
0.019036
2.2
T19
33,389,503.22
$
0.022444
2.2
T20
30,470,486.75
$
0.024848
2.2
T21
49,467,821.44
$
0.004673
2.2
T22
1,759,155.12
$
0.014657
0.5
T23
2,478,511.56
$
0.041866
0.45
T24
1,820,862.46
$
0.03182
0.6
T25
748,710.91
$
0.044164
0.35
T26
1,797,121.34
$
0.012216
0.5
T27
2,560,375.42
$
0.004166
0.7
T28
7,525,020.68
$
0.015849
0.6
T29
2,620,865.68
$
0.032194
0.6
T30
1,113,326.08
$
0.023952
0.4
T31
5,074,080.04
$
0.0228
0.8
T32
7,733,932.39
$
0.012955
0.6
T33
1,599,795.31
$
0.014096
0.45
T34
2,437,574.49
$
0.016842
0.5
T35
1,651,312.64
$
0.008939
0.5
T36
1,927,236.62
$
0.007664
0.5
T37
1,090,759.69
$
0.011267
0.35
TOTAL
370,045,152.78
$
Tao = 2 Pa
Tubo
Costo
Pendiente Diámetro
T01
6,453,557.95
$
0.06098
0.8
T02
2,971,064.40
$
0.014131
0.8
T03
3,056,985.85
$
0.062246
0.8
T04
7,156,314.14
$
0.025442
0.8
T05
9,894,386.06
$
0.019832
1
T06
5,006,556.53
$
0.024202
1
T07
4,310,017.41
$
0.010011
1.2
T08
14,280,600.82
$
0.010869
1.35
T09
13,944,217.96
$
0.003922
1.5
T10
25,924,138.33
$
0.004651
1.5
T11
6,569,827.86
$
0.022244
1.5
T12
57,286,426.63
$
0.003656
2.2
T13
3,435,002.04
$
0.047205
2.2
T14
3,860,653.08
$
0.042293
0.45
T15
16,536,861.57
$
0.066646
1
T16
5,046,049.37
$
0.036647
1
T17
106,520.48
$
0.064951
1.2
T18
26,939,520.45
$
0.019036
2.2
T19
33,389,503.22
$
0.022444
2.2
T20
30,470,486.75
$
0.024848
2.2
T21
49,467,821.44
$
0.004673
2.2
T22
1,759,155.12
$
0.014657
0.5
T23
2,478,511.56
$
0.041866
0.45
T24
1,820,862.46
$
0.03182
0.6
T25
748,710.91
$
0.044164
0.35
T26
1,797,121.34
$
0.012216
0.5
T27
2,560,375.42
$
0.004166
0.7
T28
7,525,020.68
$
0.015849
0.6
T29
2,620,865.68
$
0.032194
0.6
T30
1,113,326.08
$
0.023952
0.4
T31
5,074,080.04
$
0.0228
0.8
T32
7,733,932.39
$
0.012955
0.6
T33
1,599,795.31
$
0.014096
0.45
T34
2,437,574.49
$
0.016842
0.5
T35
1,651,312.64
$
0.008939
0.5
T36
1,927,236.62
$
0.007664
0.5
T37
1,090,759.69
$
0.011267
0.35
TOTAL
370,045,152.78
$
Tao = 4 Pa
Tubo
Costo
Pendiente Diámetro
T01
6,453,557.95
$
0.06098
0.8
T02
2,971,064.40
$
0.014131
0.8
T03
3,056,985.85
$
0.062246
0.8
T04
7,156,314.14
$
0.025442
0.8
T05
9,894,386.06
$
0.019832
1
T06
5,006,556.53
$
0.024202
1
T07
4,310,017.41
$
0.010011
1.2
T08
14,280,600.82
$
0.010869
1.35
T09
13,944,217.96
$
0.003922
1.5
T10
25,924,138.33
$
0.004651
1.5
T11
6,569,827.86
$
0.022244
1.5
T12
57,286,426.63
$
0.003656
2.2
T13
3,435,002.04
$
0.047205
2.2
T14
3,860,653.08
$
0.042293
0.45
T15
16,536,861.57
$
0.066646
1
T16
5,046,049.37
$
0.036647
1
T17
106,520.48
$
0.064951
1.2
T18
26,939,520.45
$
0.019036
2.2
T19
33,389,503.22
$
0.022444
2.2
T20
30,470,486.75
$
0.024848
2.2
T21
49,467,821.44
$
0.004673
2.2
T22
1,759,155.12
$
0.014657
0.5
T23
2,478,511.56
$
0.041866
0.45
T24
1,820,862.46
$
0.03182
0.6
T25
748,710.91
$
0.044164
0.35
T26
1,797,121.34
$
0.012216
0.5
T27
2,701,505.98
$
0.007345
0.7
T28
8,207,195.43
$
0.012257
0.7
T29
2,403,733.51
$
0.037314
0.6
T30
1,113,326.08
$
0.023952
0.4
T31
5,074,080.04
$
0.0228
0.8
T32
7,733,932.39
$
0.012955
0.6
T33
1,599,795.31
$
0.014096
0.45
T34
2,437,574.49
$
0.016842
0.5
T35
1,651,312.64
$
0.008939
0.5
T36
1,930,844.39
$
0.013323
0.45
T37
1,101,231.82
$
0.012017
0.35
TOTAL
370,665,405.81
$
Tao = 12 Pa
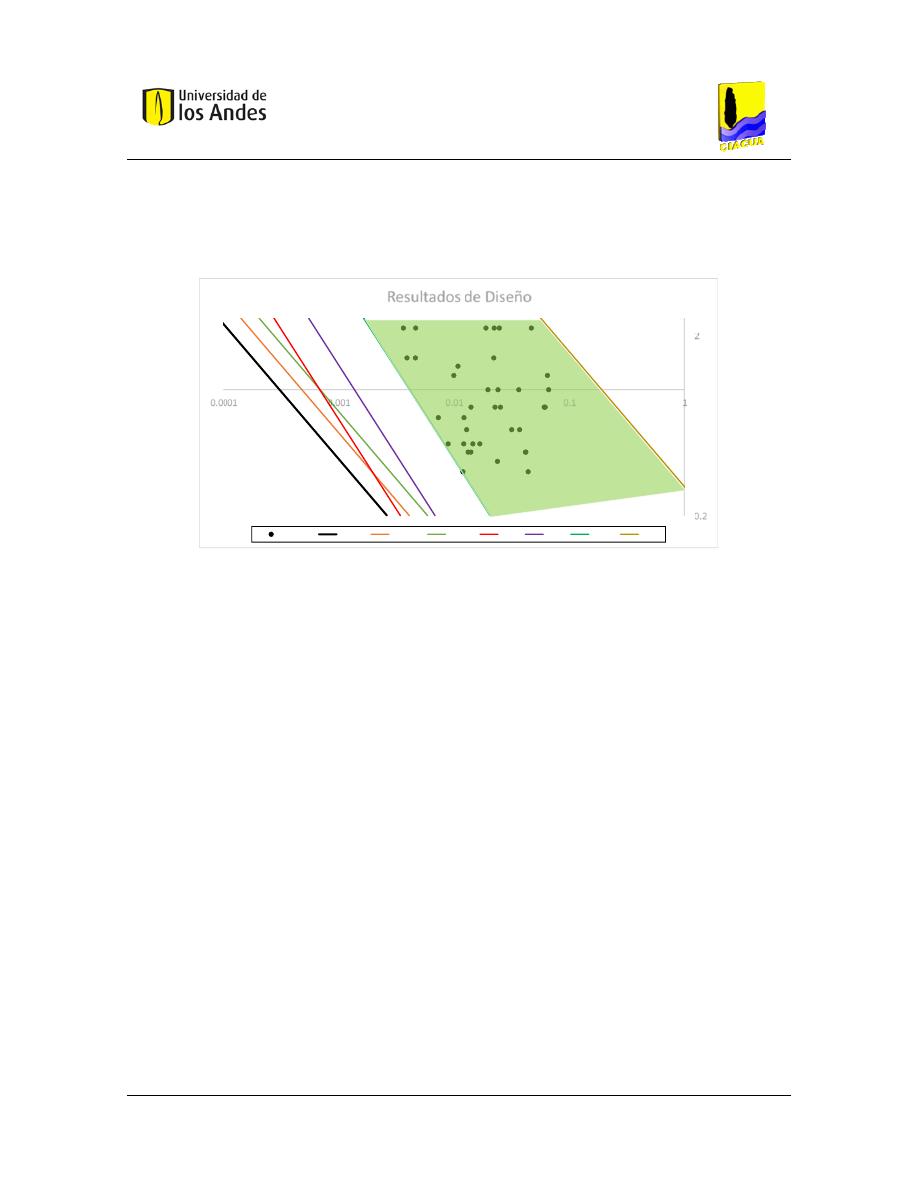
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
90
autolimpieza son importantes en el diseño optimizado? Y ¿Existe algún caudal límite
y/o pendiente límite en el cual las restricciones de autolimpieza pierdan importancia?
Figura 53. – Resultados del diseño optimizado para la red prototipo.
0.2
2
0.0001
0.001
0.01
0.1
1
Resultados de Diseño
Diseños
v = 0.6
v = 0.75
v = 0.9
τ = 2
τ = 4
τ = 12
vmax

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
91
5 ANÁLISIS DE SENSIBILIDAD DE LOS COSTOS DE
DISEÑO
El objetivo del presente capítulo es realizar diferentes variaciones a la red prototipo, con
el fin de encontrar los valores límites para los cuales las restricciones de autolimpieza
dejen de ser relevantes para el diseño. Se toma como base la ruta principal de la red
prototipo y se varían los caudales de diseño de cada tubería que conforma dicha ruta,
además de las cotas de terreno de cada pozo. Con lo anterior, se busca simular el
eventual comportamiento al diseñar redes de alcantarillados pluviales y sanitarios,
puesto que, se emplean caudales altos (pluviales) y caudales bajos (sanitarios) bajo
diferentes condiciones topográficas.
5.1 Red de alcantarillado pluvial
En este primer caso se toma la ruta principal de la red prototipo y se varían los caudales
de entrada y la topografía del terreno. En total se consideran nueve casos, los cuales se
resumen en la siguiente tabla:
Tabla 19. – Variaciones consideradas para alcantarillado pluvial.
Caso
Caudal
Topografía
1
Original
Original
2
50% Original
Original
3
10% Original
Original
4
Original
50% Original
5
Original
150% Original
6
Original
1% Original
7
150% Original
Original
8
150% Original
1% Original
9
150% Original 150% Original
Como se observa, se parte de un caso base (caso 1) y a partir de este se derivan los otros
8 casos. Los datos para el caso 1 se pueden observar en la Tabla 17; los otros 8 casos se
pueden consultar en los Anexos 26-33. Para cada uno de los casos de la Tabla 19, se
consideran los criterios de autolimpieza propios para un alcantarillado pluvial (Ver
Tabla 16). La finalidad de este ejercicio, es determinar qué importancia tiene el diseño
considerando restricciones de velocidad mínima y/o esfuerzo cortante mínimo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
92
Al aplicar la metodología de diseño optimizado presentada en la Figura 51, se obtienen
los costos totales resultantes para las diferentes variaciones de la ruta principal de la
red prototipo y bajo cada una de las restricciones de autolimpieza consideradas. Los
resultados se muestran en la Tabla 20.
Tabla 20. – Costos resultantes para cada caso de diseño.
Caso
v = 0.6 m/s
v = 0.75 m/s
v = 0.9 m/s
τ = 2 Pa
τ = 4 Pa
τ = 12 Pa
1
$ 140,234,251.07 $ 140,234,251.07 $ 140,234,251.07 $ 140,234,251.07 $ 140,234,251.07
$ 140,234,251.07
2
$ 103,615,791.36 $ 103,615,791.36 $ 103,615,791.36 $ 103,615,791.36 $ 103,615,791.36
$ 103,615,791.36
3
$ 56,199,756.41 $ 56,199,756.41 $ 56,199,756.41 $ 56,199,756.41 $ 56,199,756.41
$ 62,643,112.05
4
$ 181,137,494.58 $ 181,137,494.58 $ 181,137,494.58 $ 181,137,494.58 $ 181,137,494.58
$ 181,137,494.58
5
$ 127,847,610.51 $ 127,847,610.51 $ 127,847,610.51 $ 127,847,610.51 $ 127,847,610.51
$ 127,847,610.51
6
$ 595,272,014.83 $ 595,272,014.83 $ 595,272,014.83 $ 595,272,014.83 $ 595,272,014.83
$ 595,272,014.83
7
$ 177,227,642.59 $ 177,227,642.59 $ 177,227,642.59 $ 177,227,642.59 $ 177,227,642.59
$ 177,227,642.59
8
$ 677,584,811.00 $ 677,584,811.00 $ 677,584,811.00 $ 677,584,811.00 $ 677,584,811.00
$ 677,584,811.00
9
$ 156,486,461.31 $ 156,486,461.31 $ 156,486,461.31 $ 156,486,461.31 $ 156,486,461.31
$ 156,486,461.31
Los resultados anteriores permiten observar varias cosas. En primer lugar, se observa
que los resultados de diseño son indiferentes a las restricciones de autolimpieza; sin
embargo, para el caso 3, en el cual es caudal de diseño es sólo el 10% del original, se
presenta una pequeña variación para un criterio de esfuerzo cortante mínimo de 12 Pa.
Es importante recordar, que este valor de 12 Pa ya no es aplicable y que su consideración
en el análisis se realiza netamente de manera comparativa con valores actuales de las
normativas. En segundo lugar, para un mismo caso de caudal (1, 4, 5 y 6) a medida que
se aumenta la pendiente del terreno, se disminuyen los costos de las tuberías y
viceversa. Lo anterior se debe a la diferenciación que se hace entre los costos de
excavación y de las tuberías en sí con respecto al costo total; estos se presentan en la
Tabla 21.
Tabla 21. – Diferenciación de costos.
Caso Excavación [COP] Tubería [COP]
Total [COP]
% Excavación % Tubería
1
$ 112,644,643.49
$ 27,589,607.58 $ 140,177,808.77
80%
20%
2
$ 79,691,326.68
$ 23,924,464.68 $ 103,573,547.35
77%
23%
3
$ 45,467,797.62
$ 17,175,314.43 $ 62,617,555.27
73%
27%
4
$ 152,404,921.36
$ 28,732,573.22 $ 181,113,621.37
84%
16%
5
$ 101,346,653.56
$ 26,500,956.95 $ 127,760,631.72
79%
21%
6
$ 564,656,744.22
$ 30,615,270.61 $ 595,219,511.98
95%
5%
7
$ 148,131,340.15
$ 29,096,302.44 $ 177,166,030.26
84%
16%
8
$ 645,367,454.24
$ 32,217,356.76 $ 677,529,129.73
95%
5%
9
$ 127,258,501.38
$ 29,227,959.93 $ 156,379,585.03
81%
19%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
93
La tabla anterior muestra la diferenciación de costos y el respectivo porcentaje con
respecto a los costos totales. Por ejemplo, para el caso 1, el costo total es de
$140,177,808.77 COP de los cuales $112,644,643.49 COP [80% del total] corresponden
a los costos asociados a la excavación y $27,589,607.58 COP [20% del total] corresponden
a los costos asociados a la tubería en sí. Igualmente se observa que a medida que se
disminuye la pendiente para un mismo caso de caudal (1, 4, 5 y 6), el porcentaje del costo
asociado con la excavación se incrementa en comparación con una topografía más
inclinada. Se puede concluir entonces que a medida que se aumenta la pendiente del
terreno, el porcentaje asociado con el costo por excavación disminuye. Los diseños
resultantes para cada uno de los casos se presentan de forma tabular en la Tabla 22.
Tabla 22. – Resultados tabulares de diseños para cada caso de estudio.
Tubo
Pendiente
Diámetro
1
0.060993
0.7
2
0.014176
0.7
3
0.062238
0.7
4
0.025425
0.7
5
0.019867
0.9
6
0.024148
0.9
7
0.007946
1.05
8
0.010997
1.05
9
0.005383
1.35
10
0.00502
1.4
11
0.020023
1.4
12
0.005421
1.8
13
0.006026
1.8
CASO_01
Tubo
Pendiente
Diámetro
1
0.060993
0.5
2
0.014176
0.5
3
0.063305
0.53
4
0.025425
0.6
5
0.019376
0.7
6
0.024148
0.7
7
0.006724
0.9
8
0.011531
0.9
9
0.005383
1.05
10
0.005758
1.05
11
0.016705
1.05
12
0.005421
1.4
13
0.006026
1.4
CASO_02
Tubo
Pendiente
Diámetro
1
0.060993
0.3
2
0.014176
0.3
3
0.063305
0.35
4
0.025425
0.35
5
0.018886
0.38
6
0.024148
0.38
7
0.005501
0.5
8
0.011531
0.5
9
0.005383
0.6
10
0.00502
0.6
11
0.017811
0.6
12
0.005125
0.8
13
0.006026
0.8
CASO_03
Tubo
Pendiente
Diámetro
1
0.030568
0.8
2
0.007034
0.8
3
0.031111
0.8
4
0.012769
0.8
5
0.010401
1
6
0.012121
1
7
0.005746
1.2
8
0.0063
1.2
9
0.005028
1.35
10
0.005278
1.4
11
0.005643
1.8
12
0.005243
1.8
13
0.006026
1.8
CASO_04
Tubo
Pendiente
Diámetro
1
0.017811
0.6
2
0.021206
0.6
3
0.006026
0.8
4
0.038176
0.7
5
0.028739
0.8
6
0.036341
0.8
7
0.008802
1
8
0.017295
1
9
0.006861
1.2
10
0.007714
1.2
11
0.009072
1.8
12
0.005332
1.8
13
0.006026
1.8
CASO_05
Tubo
Pendiente
Diámetro
1
0.005502
1.05
2
0.005605
1.05
3
0.00601
1.2
4
0.005055
1.2
5
0.005102
1.2
6
0.005574
1.2
7
0.006112
1.2
8
0.005445
1.35
9
0.005383
1.35
10
0.005574
1.35
11
0.005753
1.8
12
0.005332
1.8
13
0.006026
1.8
CASO_06
Tubo
Pendiente
Diámetro
1
0.005028
1.35
2
0.014176
0.8
3
0.005643
1.8
4
0.026489
0.8
5
0.018886
1
6
0.024148
1
7
0.007946
1.2
8
0.010997
1.2
9
0.005974
1.5
10
0.006127
1.5
11
0.009072
1.8
12
0.008976
1.8
13
0.012051
1.8
CASO_07
Tubo
Pendiente
Diámetro
1
0.005213
1.2
2
0.005605
1.2
3
0.00601
1.35
4
0.005055
1.35
5
0.005102
1.35
6
0.005574
1.35
7
0.006112
1.35
8
0.005445
1.5
9
0.005974
1.5
10
0.005943
1.5
11
0.009072
1.8
12
0.008887
1.8
13
0.006026
2.2
CASO_08
Tubo
Pendiente
Diámetro
1
0.008802
1
2
0.021206
0.7
3
0.006861
1.2
4
0.038176
0.8
5
0.028739
0.9
6
0.036341
0.9
7
0.010024
1.2
8
0.017295
1.2
9
0.006861
1.4
10
0.006607
1.5
11
0.009072
1.8
12
0.005036
2.2
13
0.006026
2.2
CASO_09

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
94
Los diseños óptimos encontrados se presentan como función del diámetro y la pendiente
de la tubería para cada uno de los nueve casos considerados. Gráficamente estos diseños
se pueden comparar con las restricciones de autolimpieza de la siguiente forma:
Figura 54. – Resultados gráficos de diseños para cada caso de estudio.
Como es de esperar, la totalidad de los diseños cumplen para las restricciones de
autolimpieza consideradas. Igualmente, se observa que la mayoría de diseños óptimos
se acercan más al límite derecho de las gráficas, el cual corresponde al criterio de
velocidad máxima. Las velocidades y esfuerzos cortantes son mucho mayores a los
mínimos requeridos en las normativas de diseño de alcantarillados pluviales a nivel
mundial. Adicionalmente, el caso tres se observa que tiene cierta tendencia a tener
velocidades menores. Lo anterior se debe básicamente el caudal que está transportando
la tubería (90% menor al inicial), por lo cual se puede pensar que para sistemas de
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Diáme
tro
[
m]
Pendiente [m/m]
Caso 1
v = 0.6
v = 0.75
v = 0.9
Tao = 4
Tao = 12
v = 10
Diseños
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Di
áme
tro
[
m]
Pendiente [m/m]
Caso 2
v = 0.6
v = 0.75
v = 0.9
Tao = 4
Tao = 12
v = 10
Series3
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Diáme
tro
[
m
]
Pendiente [m/m]
Caso 3
v = 0.6
v = 0.75
v = 0.9
Tao = 4
Tao = 12
v = 10
Series3
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Diáme
tro
[
m
]
Pendiente [m/m]
Caso 4
v = 0.6
v = 0.75
v = 0.9
Tao = 4
Tao = 12
v = 10
Series3
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Diáme
tro
[
m
]
Pendiente [m/m]
Caso 5
v = 0.6
v = 0.75
v = 0.9
Tao = 4
Tao = 12
v = 10
Series3
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Diáme
tro
[
m
]
Pendiente [m/m]
Caso 6
v = 0.6
v = 0.75
v = 0.9
Tao = 4
Tao = 12
v = 10
Series3
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Diáme
tro
[
m
]
Pendiente [m/m]
Caso 7
v = 0.6
v = 0.75
v = 0.9
Tao = 4
Tao = 12
v = 10
Series3
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Diáme
tro
[
m]
Pendiente [m/m]
Caso 8
v = 0.6
v = 0.75
v = 0.9
Tao = 4
Tao = 12
v = 10
Series3
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Diáme
tro
[
m
]
Pendiente [m/m]
Caso 9
v = 0.6
v = 0.75
v = 0.9
Tao = 4
Tao = 12
v = 10
Series3

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
95
alcantarillado con bajos caudales de diseño (como es el caso de alcantarillados
sanitarios) las restricciones de autolimpieza sí pueden llegar a afectar el diseño final de
la red.
Dado lo anterior se puede concluir lo siguiente: En alcantarillados pluviales las
restricciones de autolimpieza no juegan un papel importante en el diseño optimizado,
puesto que, las velocidades y esfuerzos cortantes obtenidos son mucho mayores a los
mínimos requeridos por las normativas de diseño para garantizar condiciones de
autolimpieza al interior de una tubería. La naturaleza de un alcantarillado pluvial y
dado las condiciones a las cuales se ve sometido, llevan a condiciones de arrastre de
partículas sedimentables y sólidos existentes al interior de una tubería cuando se
presenten eventos de precipitación. En conclusión, un evento de precipitación “limpia”
el alcantarillado de partículas sedimentables, basuras, biopelículas, entre otros.
5.2 Red de alcantarillado sanitario
El segundo caso considerado simula una red de agua residual. Se toma la ruta principal
de la red prototipo y se parte del caso más crítico posible de caudal (1 L/s de ingreso a
cada nodo del sistema); se varía la topografía del terreno. En total se consideran cinco
casos, los cuales se resumen en la siguiente tabla:
Tabla 23. – Variaciones consideradas para alcantarillado sanitario.
Caso Caudal Topografía
1
Original
Original
2
Original 50% Original
3
Original 30% Original
4
Original 10% Original
5
Original 5% Original
Como se observa, se parte de un caso base (caso 1) y a partir de este se derivan los otros
4 casos. Los datos para el caso 1 se pueden observar en la Tabla 24. Para cada uno de
los casos se consideran los criterios de autolimpieza propios para un alcantarillado
sanitario (Ver Tabla 25). La finalidad de este ejercicio, es determinar qué importancia
tiene el diseño considerando restricciones de velocidad mínima y/o esfuerzo cortante
mínimo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
96
Tabla 24. – Caso base para análisis de alcantarillado sanitario.
Nodo Caudal [m
3
/s] Cota Rasante [m] Longitud [m]
0
0.001
2587.34
0.00
1
0.003
2576.79
172.65
2
0.005
2575.50
90.99
3
0.007
2569.69
93.17
4
0.009
2564.91
187.94
5
0.011
2561.06
203.82
6
0.013
2558.33
113.02
7
0.015
2557.98
81.80
8
0.017
2555.82
187.31
9
0.019
2555.31
169.06
10
0.021
2554.05
270.92
11
0.023
2552.04
90.38
12
0.025
2551.51
337.56
13
1000
2551.51
33.19
Al aplicar la metodología de diseño optimizado presentada en la Figura 51, se obtienen
los costos totales resultantes para las diferentes variaciones de la ruta principal de la
red prototipo y bajo cada una de las restricciones de autolimpieza consideradas. Los
resultados se muestran en la Tabla 26.
Tabla 25. – Restricciones de autolimpieza en alcantarillados sanitarios.
Tabla 26. – Costos resultantes para cada caso de diseño. Alcantarillado sanitario.
CASO
1
2
3
4
5
v = 0.3 m/s
$ 29,496,140.23 $ 36,519,243.18 $ 44,931,596.14 $ 78,035,209.11 $ 102,669,129.85
v = 0.45 m/s
$ 29,496,140.23 $ 36,519,243.18 $ 44,931,596.14 $ 86,652,566.93 $ 115,675,120.27
v = 0.6 m/s
$ 29,496,140.23 $ 36,563,855.43 $ 45,437,544.63 $ 129,345,212.41 $ 159,002,335.84
τ = 1 Pa
$ 29,496,140.23 $ 36,519,243.18 $ 44,931,596.14 $ 78,035,209.11 $ 106,353,537.14
τ = 1.5 Pa
$ 29,496,140.23 $ 36,519,243.18 $ 44,977,258.76 $ 91,962,353.81 $ 121,295,836.01
τ = 2 Pa
$ 29,496,140.23 $ 36,563,855.43 $ 45,069,795.02 $ 111,923,602.29 $ 142,550,253.41
Macke (1982)
$ 29,496,140.23 $ 36,519,243.18 $ 44,931,596.14 $ 78,035,209.11 $ 102,669,129.85
Tractive Force $ 29,496,140.23 $ 36,519,243.18 $ 44,931,596.14 $ 78,035,209.11 $ 102,669,129.85
Fuente
País
Valor [Pa]
RAS (2000)
Colombia
1.5
IBNORCA (2007) Bolivia
1
Yao (1974)
USA
2
Esfuerzo Cortante
Fuente
País
Valor [m/s]
RAS (2000) Colombia
0.45
CNA (2007)
México
0.3
ASCE (1970)
USA
0.6
Velocidad
Fuente
País
Valor
Macke (1982) Alemania 1.07 Pa
ASCE (2009)
USA
0.867 Pa
Nuevas Metodologías

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
97
Los resultados anteriores permiten observar varias cosas. En primer lugar, los
resultados de diseño son indiferentes a las restricciones de autolimpieza para
pendientes del terreno altas (> 1.8%), sin embargo, para los demás casos sí se presentan
variaciones entre criterios. Por ejemplo, para el caso 2 el costo total del sistema de
tuberías aumenta en $44,612.25 COP si se realiza un diseño basado en una velocidad
mínima de 0.6 m/s en reemplazo de una velocidad de 0.3 m/s. Igualmente, en la medida
que se disminuya la pendiente del terreno, la diferencia de costos entre un criterio muy
restrictivo (0.6 m/s) y uno no tan restrictivo (0.3 m/s) se incrementa. Otro fenómeno que
se puede identificar corresponde a la mayor variabilidad de costos generada por las
restricciones de autolimpieza. En pendientes de terreno altas la variación es mucho
menor que en topografías muy planas. Por ejemplo, para el caso 2 sólo se presenta
variación de costos con los criterios de v = 0.6 m/s y τ = 2 Pa, mientras que en el caso 5
los criterios de v = 0.45 m/s, v = 0.6 m/s, τ = 1 Pa, τ = 1.5 Pa y τ = 2 Pa generan costos
diferentes entre sí.
Los diseños resultantes, dado lo anterior, van a variar dependiendo del criterio de
autolimpieza con el cual se diseñe, por lo cual se deben presentar los resultados para
cada caso y bajo cada restricción de diseño. A continuación se presenta una serie de
tablas y gráficas con los resultados para el caso 1 de estudio. Los otros casos se presentan
en las Anexos 34-42.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
98
Tabla 27. – Resultados de diseños para el Caso 1.
Los diseños óptimos encontrados se presentan como función del diámetro y la pendiente
de la tubería para cada una de las restricciones de autolimpieza consideradas.
Gráficamente los resultados de la Tabla 27 se pueden ver de la siguiente forma:
Tubo Pendiente Diámetro
1
0.060993
0.2
2
0.014176
0.2
3
0.062238
0.2
4
0.025425
0.2
5
0.018886
0.2
6
0.024148
0.2
7
0.005501
0.2
8
0.010997
0.2
9
0.005383
0.25
10
0.00502
0.25
11
0.017811
0.25
12
0.005125
0.25
13
0.006026
0.25
V = 0.3 m/s
Tubo Pendiente Diámetro
1
0.060993
0.2
2
0.014176
0.2
3
0.062238
0.2
4
0.025425
0.2
5
0.018886
0.2
6
0.024148
0.2
7
0.005501
0.2
8
0.010997
0.2
9
0.005383
0.25
10
0.00502
0.25
11
0.017811
0.25
12
0.005125
0.25
13
0.006026
0.25
V = 0.45 m/s
Tubo Pendiente Diámetro
1
0.060993
0.2
2
0.014176
0.2
3
0.062238
0.2
4
0.025425
0.2
5
0.018886
0.2
6
0.024148
0.2
7
0.005501
0.2
8
0.010997
0.2
9
0.005383
0.25
10
0.00502
0.25
11
0.017811
0.25
12
0.005125
0.25
13
0.006026
0.25
V = 0.6 m/s
Tubo Pendiente Diámetro
1
0.060993
0.2
2
0.014176
0.2
3
0.062238
0.2
4
0.025425
0.2
5
0.018886
0.2
6
0.024148
0.2
7
0.005501
0.2
8
0.010997
0.2
9
0.005383
0.25
10
0.00502
0.25
11
0.017811
0.25
12
0.005125
0.25
13
0.006026
0.25
τ = 1 Pa
Tubo Pendiente Diámetro
1
0.060993
0.2
2
0.014176
0.2
3
0.062238
0.2
4
0.025425
0.2
5
0.018886
0.2
6
0.024148
0.2
7
0.005501
0.2
8
0.010997
0.2
9
0.005383
0.25
10
0.00502
0.25
11
0.017811
0.25
12
0.005125
0.25
13
0.006026
0.25
τ = 1.5 Pa
Tubo Pendiente Diámetro
1
0.060993
0.2
2
0.014176
0.2
3
0.062238
0.2
4
0.025425
0.2
5
0.018886
0.2
6
0.024148
0.2
7
0.005501
0.2
8
0.010997
0.2
9
0.005383
0.25
10
0.00502
0.25
11
0.017811
0.25
12
0.005125
0.25
13
0.006026
0.25
τ = 2 Pa
Tubo Pendiente Diámetro
1
0.060993
0.2
2
0.014176
0.2
3
0.062238
0.2
4
0.025425
0.2
5
0.018886
0.2
6
0.024148
0.2
7
0.005501
0.2
8
0.010997
0.2
9
0.005383
0.25
10
0.00502
0.25
11
0.017811
0.25
12
0.005125
0.25
13
0.006026
0.25
Macke (1982)
Tubo Pendiente Diámetro
1
0.060993
0.2
2
0.014176
0.2
3
0.062238
0.2
4
0.025425
0.2
5
0.018886
0.2
6
0.024148
0.2
7
0.005501
0.2
8
0.010997
0.2
9
0.005383
0.25
10
0.00502
0.25
11
0.017811
0.25
12
0.005125
0.25
13
0.006026
0.25
ASCE (2009)
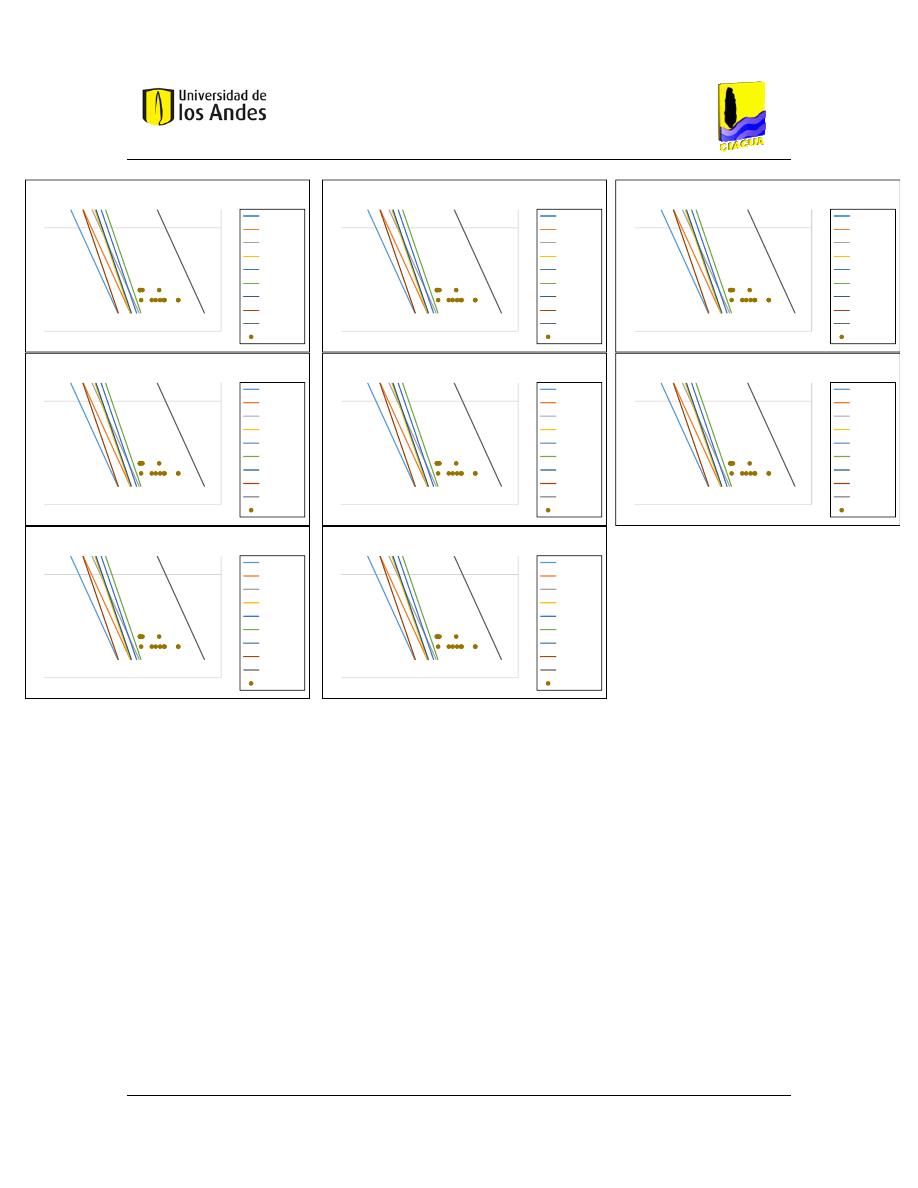
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
99
Figura 55. – Resultados gráficos de diseños para el Caso 1.
En la figura anterior se observa que para el caso de pendiente mayor (cercana a 1.8%)
los criterios de autolimpieza no afectan el diseño optimizado de una red de alcantarillado
sanitario, a pesar que el caudal de diseño es muy bajo. Caso contrario, y como se muestra
en la Tabla 26, a menores pendientes el diseño sí puede variar entre criterios de
autolimpieza. Dado lo anterior, resulta importante encontrar el punto de diseño en el
cual las restricciones de autolimpieza dejen de ser importantes en el diseño optimizado
de una red de alcantarillado. Se busca, por consiguiente, un valor de caudal y pendiente
límite.
Dado lo anterior se puede concluir lo siguiente: En alcantarillados sanitarios las
restricciones de autolimpieza sí juegan un papel importante en el diseño optimizado.
Sin embargo, estas consideraciones sólo resultan ser importantes para caudales bajos y
terrenos muy planos, en los cuales el drenaje de aguas lleva a generar costos muy
elevados. Para estos casos específicos se debería pensar en otras alternativas para el
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.3 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.45 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.6 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 1 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 1.5 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 2 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
Macke (1982)
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
TF (2009)
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
100
transporte de estas aguas. Igualmente, en casos en los cuales el caudal de diseño sea
menor a 1 L/s, no sería factible implementar un sistema de alcantarillado, puesto que,
se tendrían restricciones de diámetro mínimo y sería más costo/efectivo instalar otro
tipo de soluciones al drenaje de aguas residuales.
5.3 Condiciones límite
Como se menciona anteriormente, en caudales altos, el diseño optimizado de una red de
alcantarillado no se ve afectado por las restricciones de autolimpieza; caso contrario
para caudales bajos y condiciones topográficas poco favorables, sí se pueden presentar
variaciones en los costos finales si se diseña con un criterio u otro. Dado lo anterior, es
importante encontrar cuál resulta ser el límite de pendiente y caudal en el cual las
restricciones de autolimpieza dejen de ser importantes en el diseño optimizado de
alcantarillados. Para encontrar estos valores, se proponen cinco corridas y cada una de
ellas cuenta con seis casos de estudio. En total se simulan 30 diferentes combinaciones
de caudal pendiente y se maneja el diseño como una red de alcantarillado sanitario. Las
corridas y casos considerados se presentan en la Tabla 28.
Tabla 28. – Casos y corridas para análisis de condición límite.
Corrida
Caso 1
Caso 2
Caso 3
Caso 4
Caso 5
Caso 6
01 – Aumento
1 L/s en cada
nodo
Topografía
Original
50%
Topografía
Original
30%
Topografía
Original
10%
Topografía
Original
5%
Topografía
Original
Terreno
Plano
02 – Aumento
2 L/s en cada
nodo
Topografía
Original
50%
Topografía
Original
30%
Topografía
Original
10%
Topografía
Original
5%
Topografía
Original
Terreno
Plano
03 – Aumento
3 L/s en cada
nodo
Topografía
Original
50%
Topografía
Original
30%
Topografía
Original
10%
Topografía
Original
5%
Topografía
Original
Terreno
Plano
04 – Aumento
5 L/s en cada
nodo
Topografía
Original
50%
Topografía
Original
30%
Topografía
Original
10%
Topografía
Original
5%
Topografía
Original
Terreno
Plano
05 – Aumento
10 L/s en cada
nodo
Topografía
Original
50%
Topografía
Original
30%
Topografía
Original
10%
Topografía
Original
5%
Topografía
Original
Terreno
Plano
Las tablas de entrada para cada caso se presentan en los Anexos 43 – 72. Cada uno de
los casos anteriores, se simula para las diferentes condiciones de caudal (corridas) y se
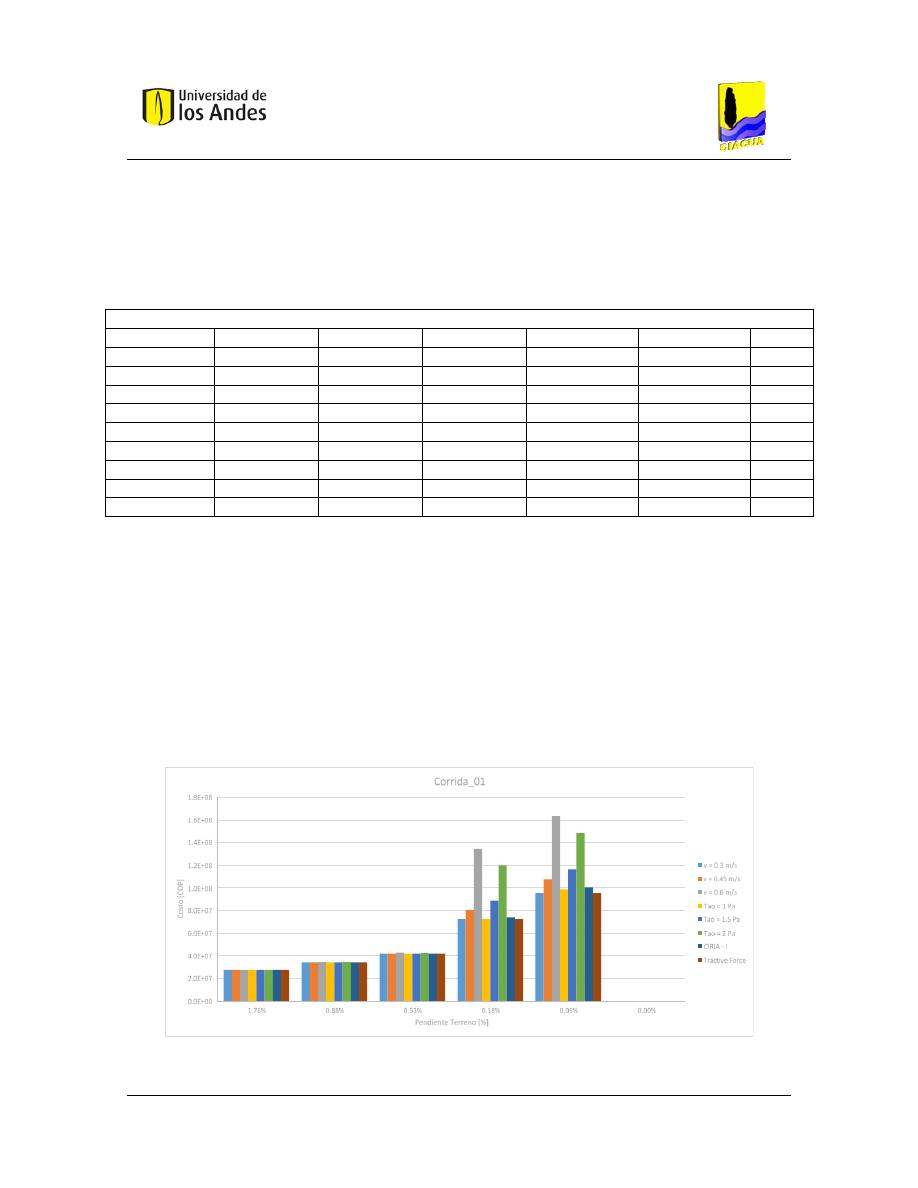
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
101
verifican las variaciones propias para cada restricción de autolimpieza. Los resultados
para la primera corrida se presentan en la Tabla 29.
Tabla 29. – Resultados Corrida 01.
Corrida 01. Aumento de caudal 1 L/s en cada nodo
Pendiente
1.76%
0.88%
0.53%
0.18%
0.09%
0.00%
Caso
1
2
3
4
5
6
v = 0.3 m/s
$ 27,466,804 $ 34,141,352 $ 41,777,958 $ 72,263,025 $ 95,195,163
-
v = 0.45 m/s $ 27,466,804 $ 34,141,352 $ 41,777,958 $ 80,374,687 $ 107,506,456
-
v = 0.6 m/s
$ 27,466,804 $ 34,322,331 $ 42,605,821 $ 134,355,829 $ 163,282,525
-
τ = 1 Pa
$ 27,466,804 $ 34,141,352 $ 41,777,958 $ 72,263,025 $ 98,664,563
-
τ = 1.5 Pa
$ 27,466,804 $ 34,141,352 $ 41,869,690 $ 88,548,885 $ 116,267,192
-
τ = 2 Pa
$ 27,466,804 $ 34,276,462 $ 42,196,689 $ 119,790,667 $ 148,265,165
-
Macke (1982) $ 27,466,804 $ 34,141,352 $ 41,777,958 $ 73,862,028 $ 100,413,983
-
ASCE (2009) $ 27,466,804 $ 34,141,352 $ 41,777,958 $ 72,263,025 $ 95,195,163
-
La tabla anterior permite determinar bajo qué condiciones de pendiente las restricciones
de autolimpieza afectan el diseño. Se observa que en una pendiente del 1.76% el costo
final es indiferente del criterio de autolimpieza empleado para ese incremento de caudal.
Es de esperar entonces, que si se aumenta la pendiente del terreno el diseño igualmente
va a tener los mismos costos entre criterios de autolimpieza. Adicional a lo anterior, se
observa que para pendientes menores y bajo ese caudal, sí se generan cambios.
Gráficamente lo anterior se puede presentar de la siguiente forma:
Figura 56. – Costos asociados a la Corrida 01.
0.0E+00
2.0E+07
4.0E+07
6.0E+07
8.0E+07
1.0E+08
1.2E+08
1.4E+08
1.6E+08
1.8E+08
1.76%
0.88%
0.53%
0.18%
0.09%
0.00%
Cos
to
[
COP]
Pendiente Terreno [%]
Corrida_01
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
Tao = 1 Pa
Tao = 1.5 Pa
Tao = 2 Pa
CIRIA - I
Tractive Force

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
102
La Figura 56 presenta las diferencias de costo asociadas con cada caso (pendiente de
terreno) bajo esa condición de caudal. Se observa que en la medida que se disminuya la
pendiente del terreno, la diferencia de costos entre criterios de autolimpieza aumenta.
Por ejemplo, la diferencia entre costos para la pendiente de 0.53% entre un criterio de
0.6 m/s y uno de 0.3 m/s es de $827,863.21 COP, mientras que para una pendiente
menor, de 0.09%, esa diferencia aumenta a $68,087,361.65 COP. Además de lo anterior,
se observa que el caso 6 (pendiente 0%) no tiene soluciones posibles de diseño, por lo
cual para esos caudales no es factible diseñar un sistema de alcantarillado en la zona.
Si este procedimiento se repite para la segunda corrida, se obtienen los siguientes
resultados:
Tabla 30. – Resultados Corrida 02.
Corrida 02. Aumento de caudal 2 L/s en cada nodo
Pendiente
1.76%
0.88%
0.53%
0.18%
0.09%
0.00%
Caso
1
2
3
4
5
6
v = 0.3 m/s
$ 29,496,140 $ 36,825,896 $ 48,193,688 $ 78,035,209 $ 102,669,130 $ 130,828,611
v = 0.45 m/s $ 29,496,140 $ 36,825,896
$ 48,193,688
$ 78,035,209 $ 102,669,130 $ 130,828,611
v = 0.6 m/s
$ 29,496,140 $ 36,825,896
$ 48,193,688
$ 95,476,449 $ 125,194,472 $ 154,862,941
τ = 1 Pa
$ 29,496,140 $ 36,825,896
$ 48,193,688
$ 78,035,209 $ 102,669,130 $ 130,828,611
τ = 1.5 Pa
$ 29,496,140
$ 36,825,896
$ 48,193,688
$ 81,446,009 $ 108,211,059 $ 136,745,209
τ = 2 Pa
$ 29,496,140
$ 36,825,896
$ 48,193,688
$ 93,543,044 $ 123,114,120 $ 154,629,324
Macke (1982) $ 29,496,140
$ 36,825,896
$ 48,193,688
$ 78,035,209 $ 102,669,130
$ 130,828,611
ASCE (2009) $ 29,496,140
$ 36,825,896
$ 48,193,688
$ 78,035,209 $ 102,669,130
$ 130,828,611
Consecuente a lo mencionado con anterioridad, se observa que si se incrementa el caudal
de diseño, la pendiente límite deja de ser la mayor (1.76%) y pasa a ser la de 0.53%. Para
esta pendiente, 0.53%, no es importante bajo qué condición de autolimpieza se haya
realizado el diseño, puesto que, el costo final de la red es igual para cualquier criterio de
autolimpieza. Gráficamente lo anterior se puede presentar de la siguiente forma:
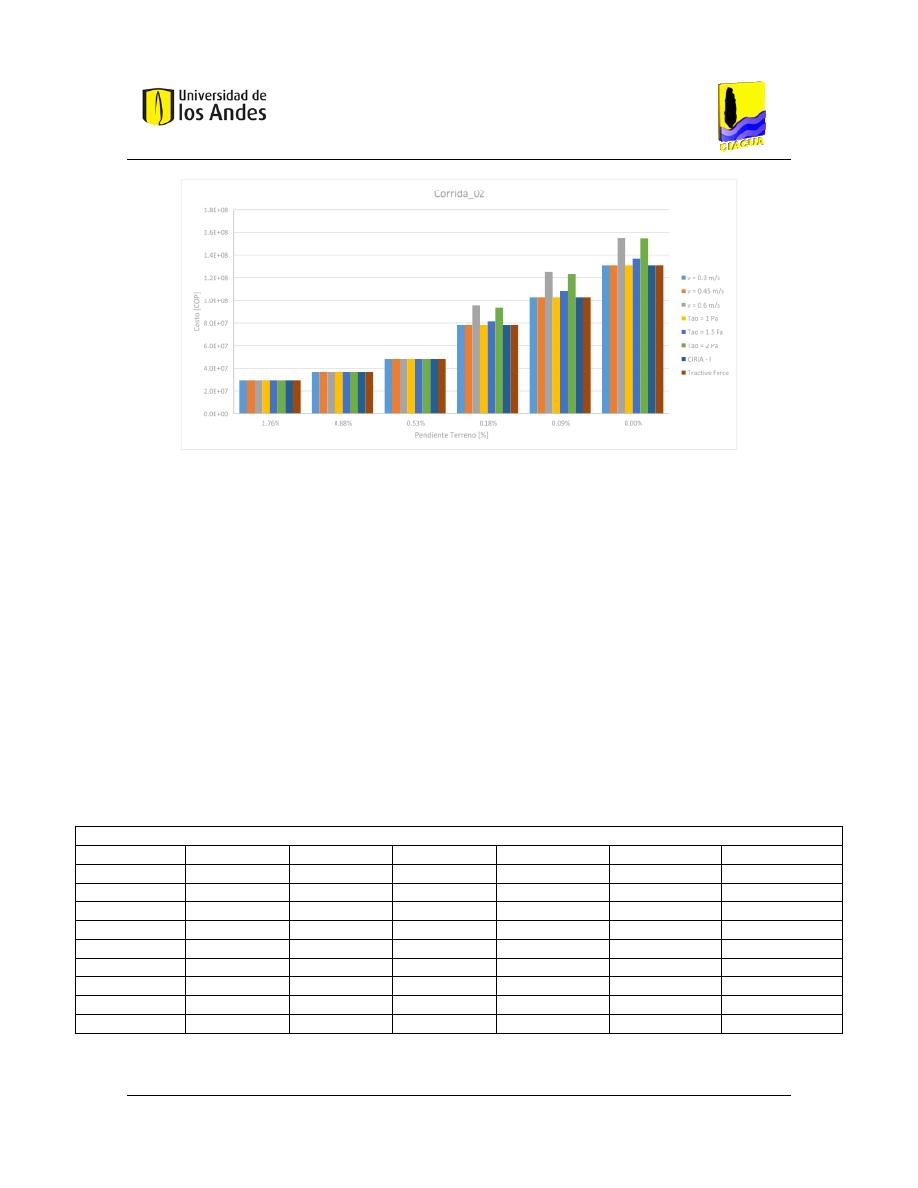
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
103
Figura 57. – Costos asociados a la Corrida 02.
La Figura 57 presenta las diferencias de costo asociadas con cada caso (pendiente de
terreno) bajo esa condición de caudal. Se observa que en la medida que se disminuya la
pendiente del terreno, la diferencia de costos entre criterios de autolimpieza aumenta.
Sin embargo, como se menciona con anterioridad, la pendiente límite disminuye en la
medida que se aumenta el caudal. Los casos intermedios 3 y 4 se presentan en los Anexos
75 y 76. Finalmente, el caso 5 muestra que para un caudal de ingreso de 10 L/s en cada
nodo de la red y bajo cualquier pendiente del terreno (incluso terreno plano) los criterios
de autolimpieza no son una variable que afecte el diseño de una red de alcantarillado.
Lo anterior mencionado se puede observar en la Tabla 31.
Tabla 31. – Resultados Corrida 05.
Corrida 05. Aumento de caudal 10 L/s en cada nodo
Pendiente
1.76%
0.88%
0.53%
0.18%
0.09%
0.00%
Caso
1
2
3
4
5
6
v = 0.3 m/s
$ 37,996,871 $ 47,047,295 $ 58,744,822 $ 100,594,048 $ 131,612,600 $ 168,650,186
v = 0.45 m/s $ 37,996,871 $ 47,047,295 $ 58,744,822 $ 100,594,048 $ 131,612,600 $ 168,650,186
v = 0.6 m/s
$ 37,996,871 $ 47,047,295 $ 58,744,822 $ 100,594,048 $ 131,612,600 $ 168,650,186
τ = 1 Pa
$ 37,996,871 $ 47,047,295 $ 58,744,822 $ 100,594,048 $ 131,612,600 $ 168,650,186
τ = 1.5 Pa
$ 37,996,871 $ 47,047,295 $ 58,744,822 $ 100,594,048 $ 131,612,600 $ 168,650,186
τ = 2 Pa
$ 37,996,871 $ 47,047,295 $ 58,744,822 $ 100,594,048 $ 131,612,600 $ 168,650,186
Macke (1982) $ 37,996,871 $ 47,047,295 $ 58,744,822 $ 100,594,048 $ 131,612,600 $ 168,650,186
ASCE (2009) $ 37,996,871 $ 47,047,295 $ 58,744,822 $ 100,594,048 $ 131,612,600 $ 168,650,186
0.0E+00
2.0E+07
4.0E+07
6.0E+07
8.0E+07
1.0E+08
1.2E+08
1.4E+08
1.6E+08
1.8E+08
1.76%
0.88%
0.53%
0.18%
0.09%
0.00%
Cos
to
[
COP]
Pendiente Terreno [%]
Corrida_02
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
Tao = 1 Pa
Tao = 1.5 Pa
Tao = 2 Pa
CIRIA - I
Tractive Force
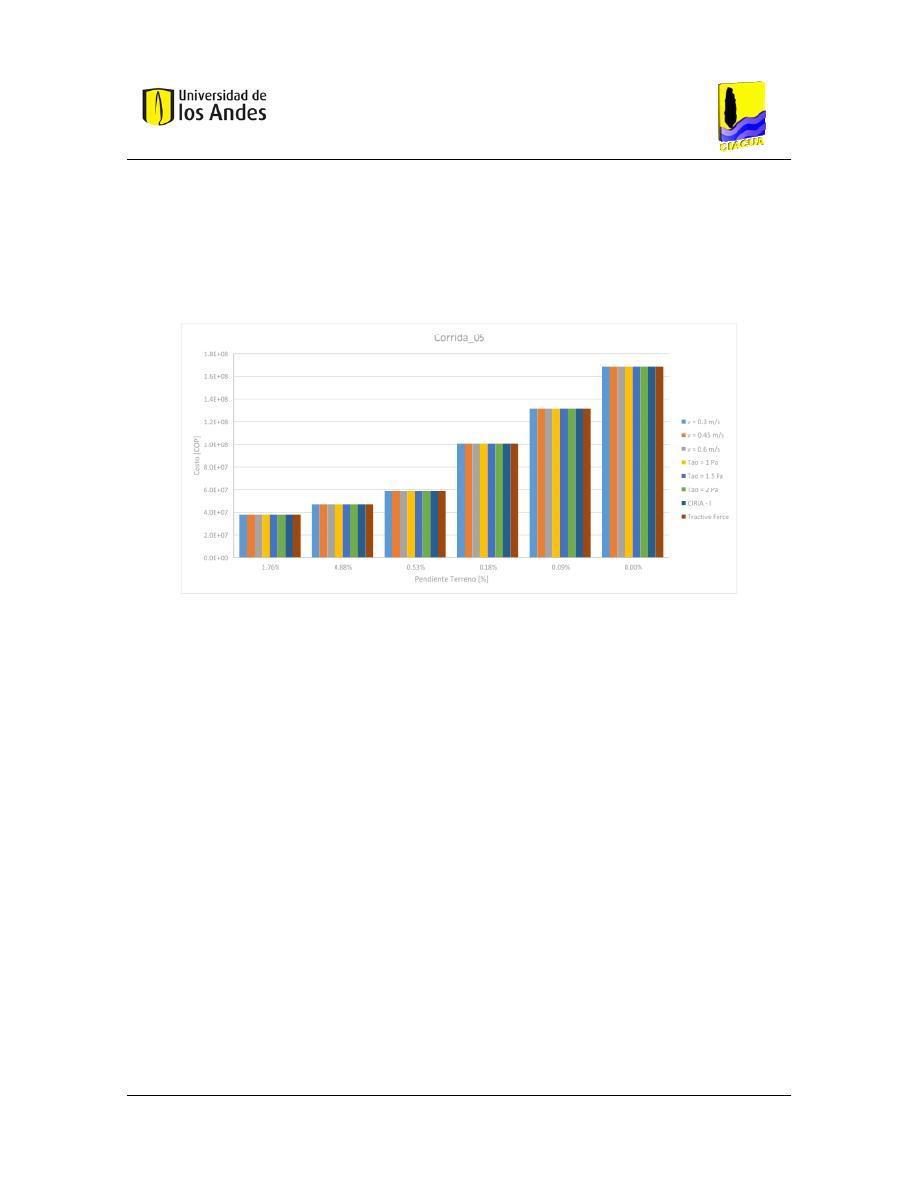
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
104
Como se menciona anteriormente, se observa que si el caudal de entrada a cada nodo
del sistema es superior o igual a 10 L/s, bajo cualquier condición topográfica, las
restricciones de autolimpieza dejan de ser un factor importante en el diseño optimizado
de un alcantarillado. Gráficamente lo anterior se puede presentar de la siguiente forma:
Figura 58. – Costos asociados a la corrida 05.
Al realizar una regresión potencial entre la pendiente del terreno y la diferencia de
caudales entre el nodo más alejado de la ruta y el nodo inicial, se obtiene lo siguiente:
0.0E+00
2.0E+07
4.0E+07
6.0E+07
8.0E+07
1.0E+08
1.2E+08
1.4E+08
1.6E+08
1.8E+08
1.76%
0.88%
0.53%
0.18%
0.09%
0.00%
Cos
to
[
COP]
Pendiente Terreno [%]
Corrida_05
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
Tao = 1 Pa
Tao = 1.5 Pa
Tao = 2 Pa
CIRIA - I
Tractive Force
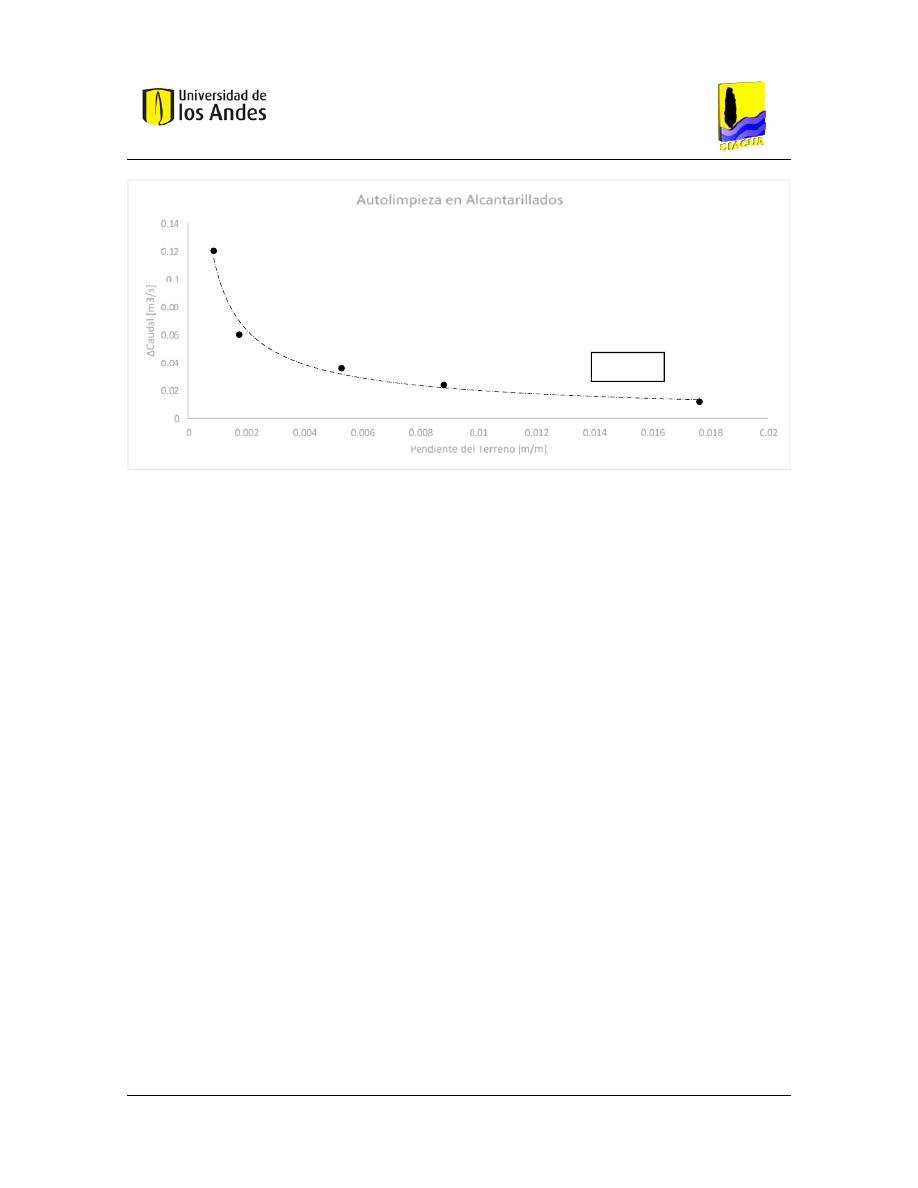
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
105
Figura 59. – Límite de autolimpieza en alcantarillados.
La Figura 59 presenta la relación existente entre el caudal de una red y la pendiente de
la misma. En las abscisas se tienen los datos de pendiente del terreno mientras que en
las ordenadas se presentan las diferencias de caudales entre el nodo de inicio y el nodo
final de la ruta principal de la red de alcantarillado. Por ejemplo, si la red cuenta con 10
nodos y en cada uno de ellos ingresa un caudal de 5 L/s, la diferencia de caudales
(ΔCaudal) será de 45 L/s.
La anterior figura muestra entonces la zona en la cual las restricciones de autolimpieza
no son representativas en el diseño optimizado de un sistema de alcantarillado. Si la red
a diseñar se encuentra por encima de la curva, los criterios de autolimpieza no juegan
un papel en el diseño por consiguiente se es indiferente un diseño con una velocidad de
0.6 m/s, un esfuerzo cortante de 1.5 Pa o con una metodología que se base en las
características de los sedimentos (CIRIA, ASCE).
5.4 Verificación de metodología
Con el fin de verificar los resultados obtenidos anteriormente, se procede a la aplicación
de un caso real de estudio en una red de alcantarillado. Esta se localiza en el sector de
La Esmeralda en la ciudad de Bogotá la cual cuenta con 28 pozos, 34 tuberías y 1 punto
de descarga. La finalidad de este ejercicio consiste en comprobar si bajo determinada
topografía del terreno y con dos configuraciones de caudal (pluvial y sanitario) se cumple
con las condiciones de autolimpieza mostradas en la Figura 59. Como se menciona
y = 0.0007x
-0.718
R² = 0.9804
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0
0.002
0.004
0.006
0.008
0.01
0.012
0.014
0.016
0.018
0.02
Δ
Cau
d
al
[m
3/s
]
Pendiente del Terreno [m/m]
Autolimpieza en Alcantarillados

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
106
anteriormente, esta red se localiza en el barrio La Esmeralda de la ciudad de Bogotá. El
sector se caracteriza por ser en su mayoría de uso residencial y tener una topografía con
pendientes muy bajas. Un esquema de la red se presenta en la Figura 60.
Figura 60. – Red La Esmeralda.
Esta red se va a tomar tanto para agua lluvia como para agua residual. Dado lo anterior,
el primer procedimiento a realizar es la determinación de los caudales de ingreso a cada
uno de los nodos en ambos casos. Para el caso de un alcantarillado pluvial, se deben
establecer las áreas de drenaje a cada nodo mediante un modelo de lluvia – escorrentía.
Se toma el modelo de Onda Cinemática empleado por EPASWMM complementado con
el modelo de infiltración de Número de Curva y se determinan los parámetros propios
de cada subcuenca. El cálculo de cada subcuenca se realiza mediante la aplicación de
Polígonos de Thiessen. El evento de precipitación y las áreas aferentes se muestran en
la Figura 61.
Nudo
Inundación
25.00
50.00
75.00
100.00
LPS
08/23/2013 00:01:00
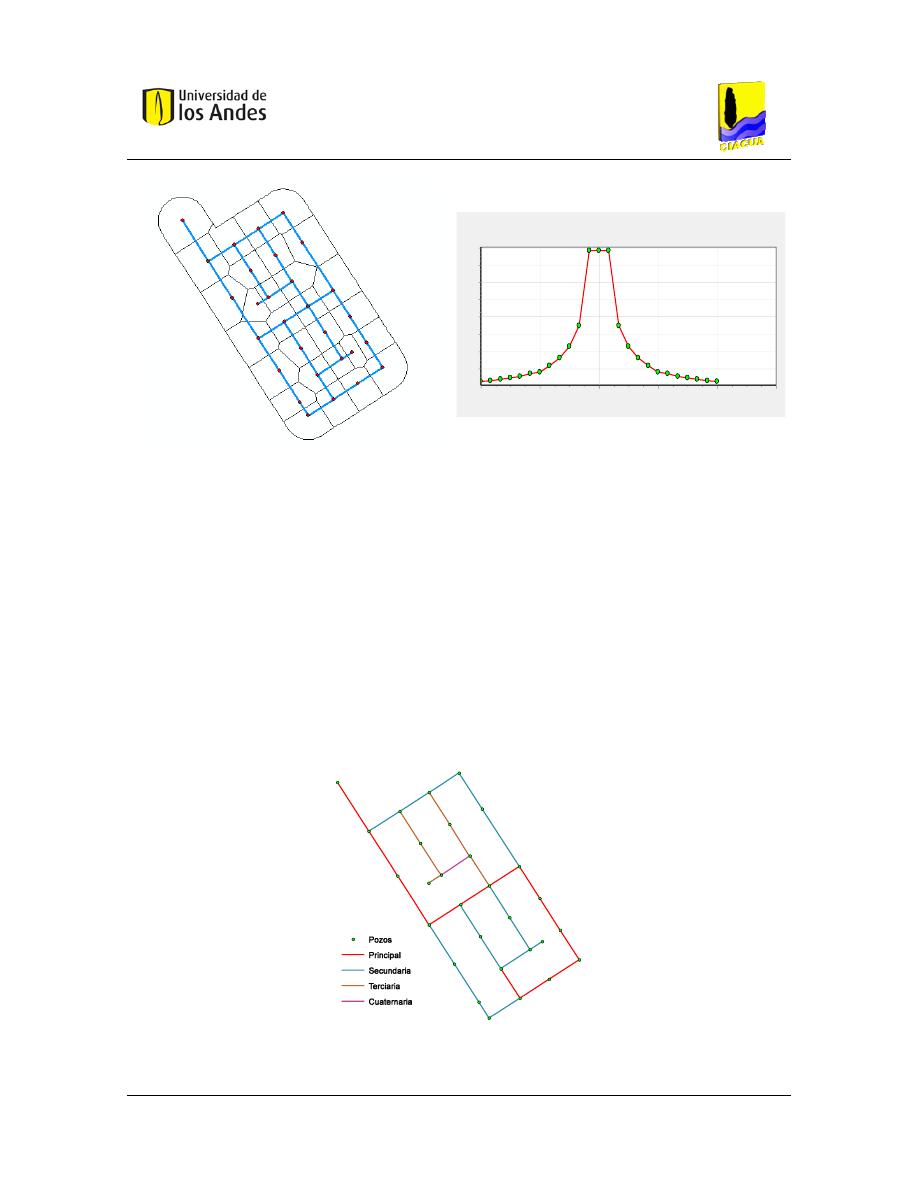
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
107
Figura 61. – Subcuencas aferentes a cada pozo de la red y Lluvia de diseño.
Una vez obtenidos los parámetros de las subcuencas y el evento de precipitación, se corre
el modelo de lluvia – escorrentía y se obtienen los hidrogramas de entrada a cada uno
de los pozos del sistema. Para el caso de simulación como alcantarillado sanitario, se
ingresa a cada uno de los nodos un caudal de 1 L/s. Con estos hidrogramas obtenidos, y
la topología de la red, se determinan las rutas mediante el programa CIE 7.0.
Para la determinación de las rutas en la red La Esmeralda se construyen las tablas con
los caudales de diseño propios de cada nodo del sistema. Estas se ingresan al programa
CIE 7.0 y se obtienen las rutas de la red. Estas se pueden ver en la siguiente figura:
Figura 62. – Rutas red La Esmeralda.
Series temporales CIACUA
Tiempo transcurrido (horas)
2.5
2
1.5
1
0.5
0
160
140
120
100
80
60
40
20
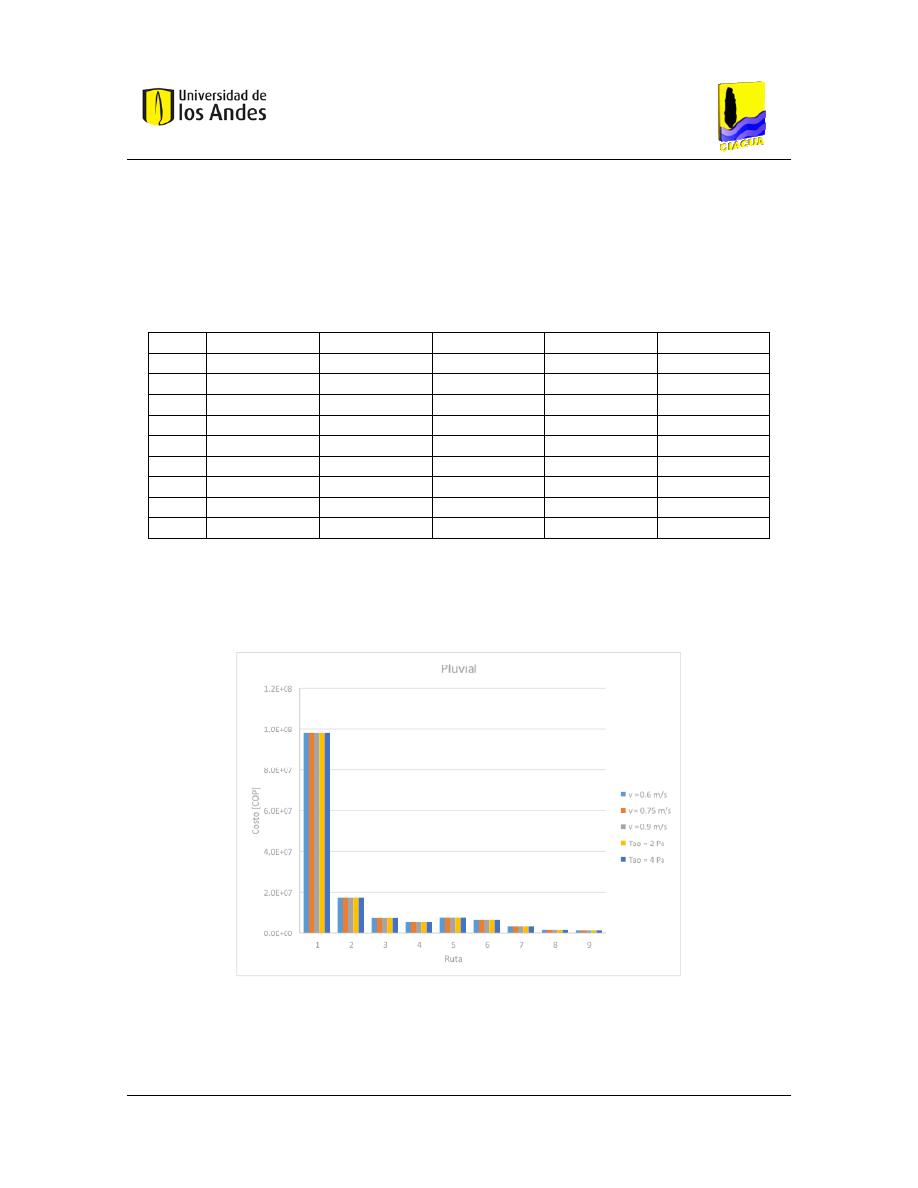
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
108
Una vez se obtienen las rutas, se procede a realizar el diseño independiente en cada una
de ellas. Para el caso en el cual se considera la red como un alcantarillado pluvial, se
obtiene la siguiente tabla con los resultados de diseño.
Tabla 32. – Costos de la red La Esmeralda.
Ruta v = 0.6 m/s v = 0.75 m/s v = 0.9 m/s
τ = 2 Pa
τ = 4 Pa
1
$ 98,129,014 $ 98,129,014 $ 98,129,014 $ 98,129,014 $ 98,129,014
2
$ 17,332,322 $ 17,332,322 $ 17,332,322 $ 17,332,322 $ 17,332,322
3
$ 7,436,627
$ 7,436,627
$ 7,436,627
$ 7,436,627
$ 7,436,627
4
$ 5,385,166
$ 5,385,166
$ 5,385,166
$ 5,385,166
$ 5,385,166
5
$ 7,475,462
$ 7,475,462
$ 7,475,462
$ 7,475,462
$ 7,475,462
6
$ 6,432,804
$ 6,432,804
$ 6,432,804
$ 6,432,804
$ 6,432,804
7
$ 3,284,050 $ 3,284,050 $ 3,284,050 $ 3,284,050 $ 3,284,050
8
$ 1,536,911 $ 1,536,911 $ 1,536,911 $ 1,536,911 $ 1,536,911
9
$ 1,247,101 $ 1,247,101 $ 1,247,101 $ 1,247,101 $ 1,247,101
Gráficamente estos resultados se pueden ver de la siguiente forma:
Figura 63. – Costos de la red La Esmeralda.
0.0E+00
2.0E+07
4.0E+07
6.0E+07
8.0E+07
1.0E+08
1.2E+08
1
2
3
4
5
6
7
8
9
Cos
to
[
COP]
Ruta
Pluvial
v = 0.6 m/s
v = 0.75 m/s
v = 0.9 m/s
Tao = 2 Pa
Tao = 4 Pa
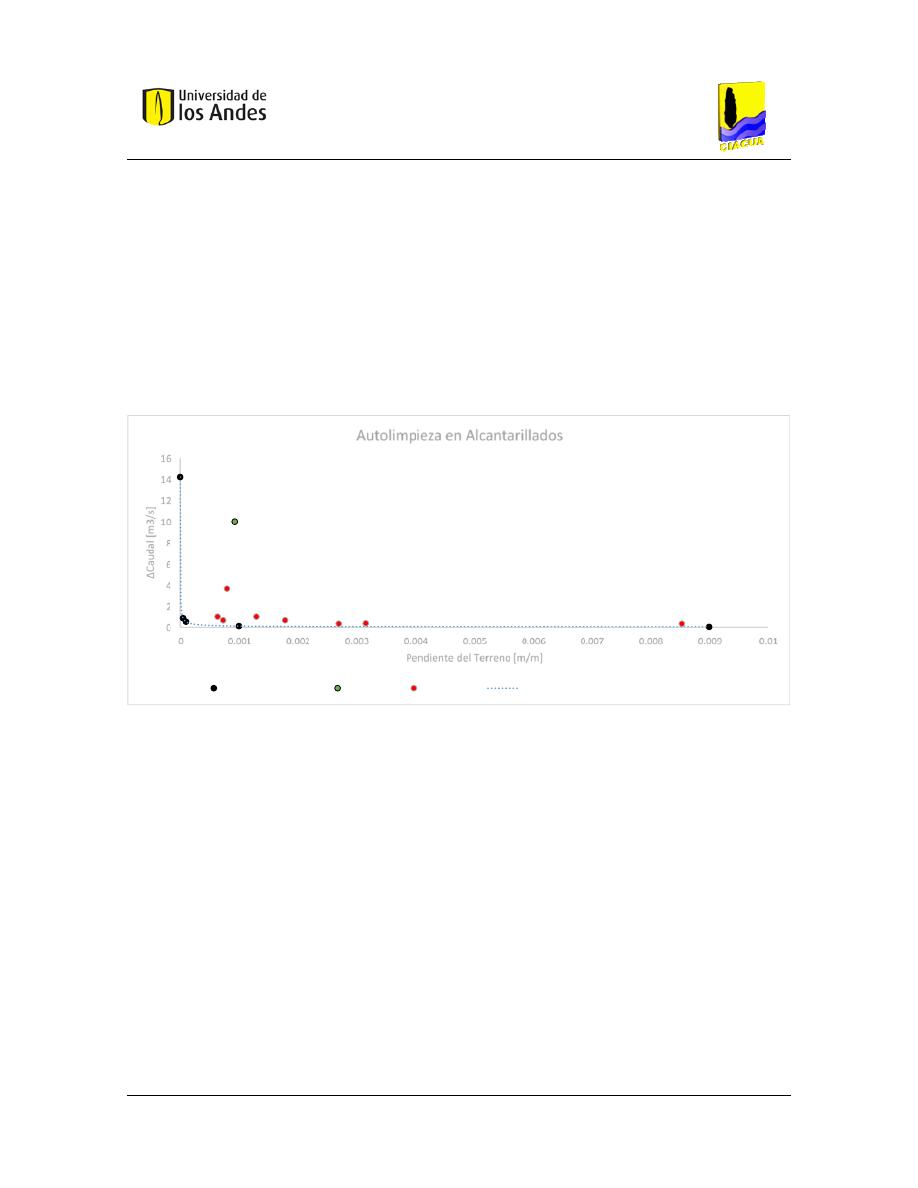
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
109
Se observa que los criterios de autolimpieza no afectan el diseño optimizado del sistema
de alcantarillado. Con el fin de comparar los resultados con la relación de autolimpieza
encontrada en la Figura 59, se debe establecer tanto la diferencia de caudales de diseño
entre el nodo de inicio y el nodo final de la ruta principal y la pendiente del terreno. Para
este primer caso de alcantarillado pluvial se tiene que la diferencia de caudales de diseño
entre el pozo de arranque y el pozo de descarga es de ∆𝑄 = 10 𝑚
3
/𝑠, para la ruta
principal, y la pendiente promedio de dicha ruta es de 0.093%. Con los valores anteriores
se puede comparar la ruta actual con la Figura 59 y se obtiene la siguiente figura:
Figura 64. – Localización de red pluvial en la gráfica de autolimpieza.
Como se puede observar, para la ruta principal de la red de La Esmeralda, se cumple la
autolimpieza. Esto se ve reflejado porque el punto verde, que representa a La
Esmeralda, se encuentra por encima de la curva de autolimpieza. Igualmente, como se
puede observar en la Figura 63, para todas las rutas que conforman la red de
alcantarillado de La Esmeralda, bajo cualquier criterio de autolimpieza da como
solución el mismo costo final de la red. Si este ejercicio se repite pero bajo condiciones
de alcantarillado sanitario, se obtienen los siguientes resultados:
0
2
4
6
8
10
12
14
16
0
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
0.009
0.01
Δ
Cau
d
al
[m
3/s
]
Pendiente del Terreno [m/m]
Autolimpieza en Alcantarillados
Límite Autolimpieza
Principal
Otras Rutas
Potencial (Límite Autolimpieza)
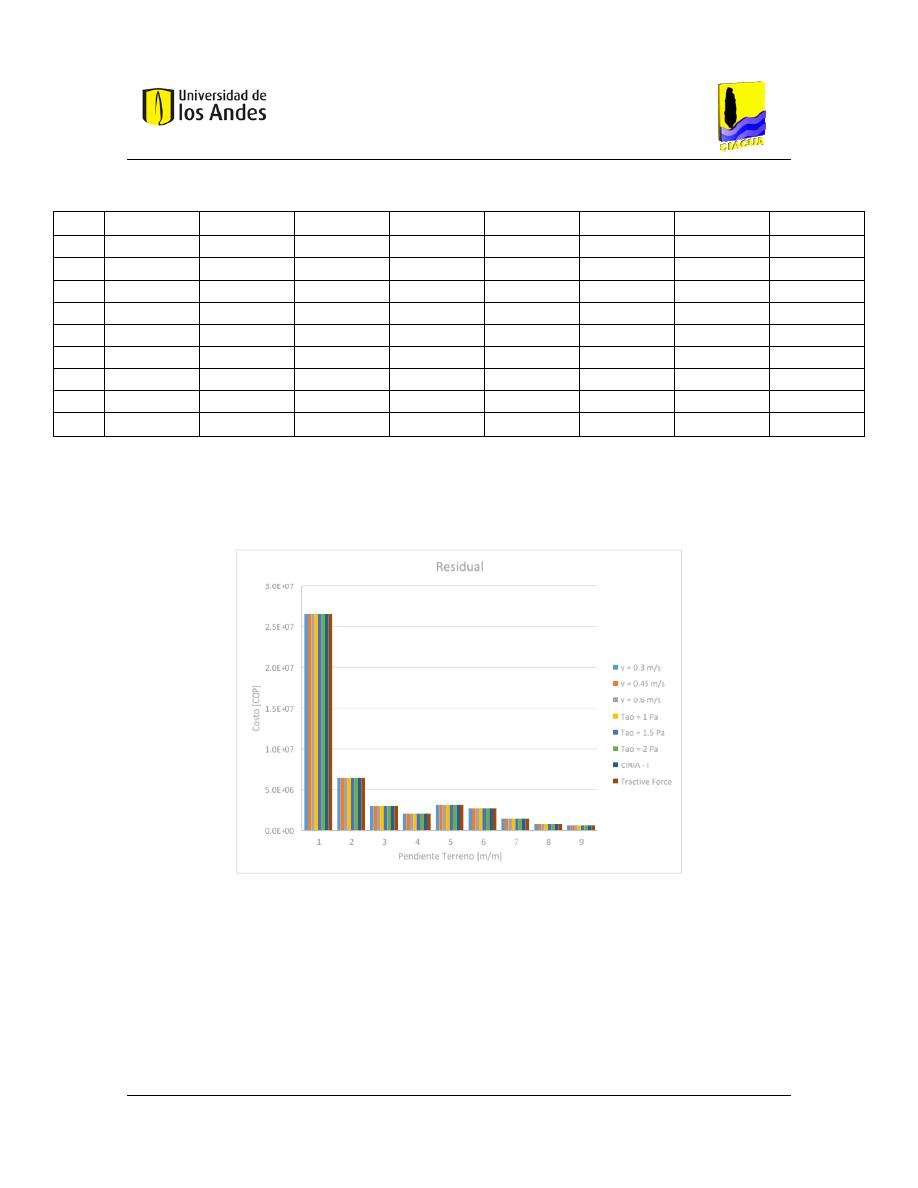
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
110
Tabla 33. – Costos red La Esmeralda (Sanitario).
Ruta
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
CIRIA
ASCE
1
$ 26,510,019 $ 26,510,019 $ 26,510,019 $ 26,510,019 $ 26,510,019 $ 26,510,019 $ 26,510,019 $ 26,510,019
2
$ 6,433,423
$ 6,433,423
$ 6,433,423
$ 6,433,423
$ 6,433,423
$ 6,433,423
$ 6,433,423
$ 6,433,423
3
$ 2,994,763
$ 2,994,763
$ 2,994,763
$ 2,994,763
$ 2,994,763
$ 2,994,763
$ 2,994,763
$ 2,994,763
4
$ 2,054,583
$ 2,054,583
$ 2,054,583
$ 2,054,583
$ 2,054,583
$ 2,054,583
$ 2,054,583
$ 2,054,583
5
$ 3,112,185
$ 3,112,185
$ 3,112,185
$ 3,112,185
$ 3,112,185
$ 3,112,185
$ 3,112,185
$ 3,112,185
6
$ 2,692,980
$ 2,692,980
$ 2,692,980
$ 2,692,980
$ 2,692,980
$ 2,692,980
$ 2,692,980
$ 2,692,980
7
$ 1,428,602
$ 1,428,602
$ 1,428,602
$ 1,428,602
$ 1,428,602
$ 1,428,602
$ 1,428,602
$ 1,428,602
8
$ 764,037
$ 764,037
$ 764,037
$ 764,037
$ 764,037
$ 764,037
$ 764,037
$ 764,037
9
$ 616,438
$ 616,438
$ 616,438
$ 616,438
$ 616,438
$ 616,438
$ 616,438
$ 616,438
Gráficamente los resultados se pueden ver de la siguiente forma:
Figura 65. – Costos red La Esmeralda (Sanitario).
Se observa que los criterios de autolimpieza no afectan el diseño optimizado del sistema
de alcantarillado. Con el fin de comparar los resultados con la relación de autolimpieza
encontrada en la Figura 59, se debe establecer tanto la diferencia de caudales de diseño
entre el nodo de inicio y el nodo final de la ruta principal y la pendiente del terreno. Para
este segundo caso de alcantarillado sanitario se tiene que la diferencia de caudales de
0.0E+00
5.0E+06
1.0E+07
1.5E+07
2.0E+07
2.5E+07
3.0E+07
1
2
3
4
5
6
7
8
9
Co
st
o
[
COP
]
Pendiente Terreno [m/m]
Residual
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
Tao = 1 Pa
Tao = 1.5 Pa
Tao = 2 Pa
CIRIA - I
Tractive Force
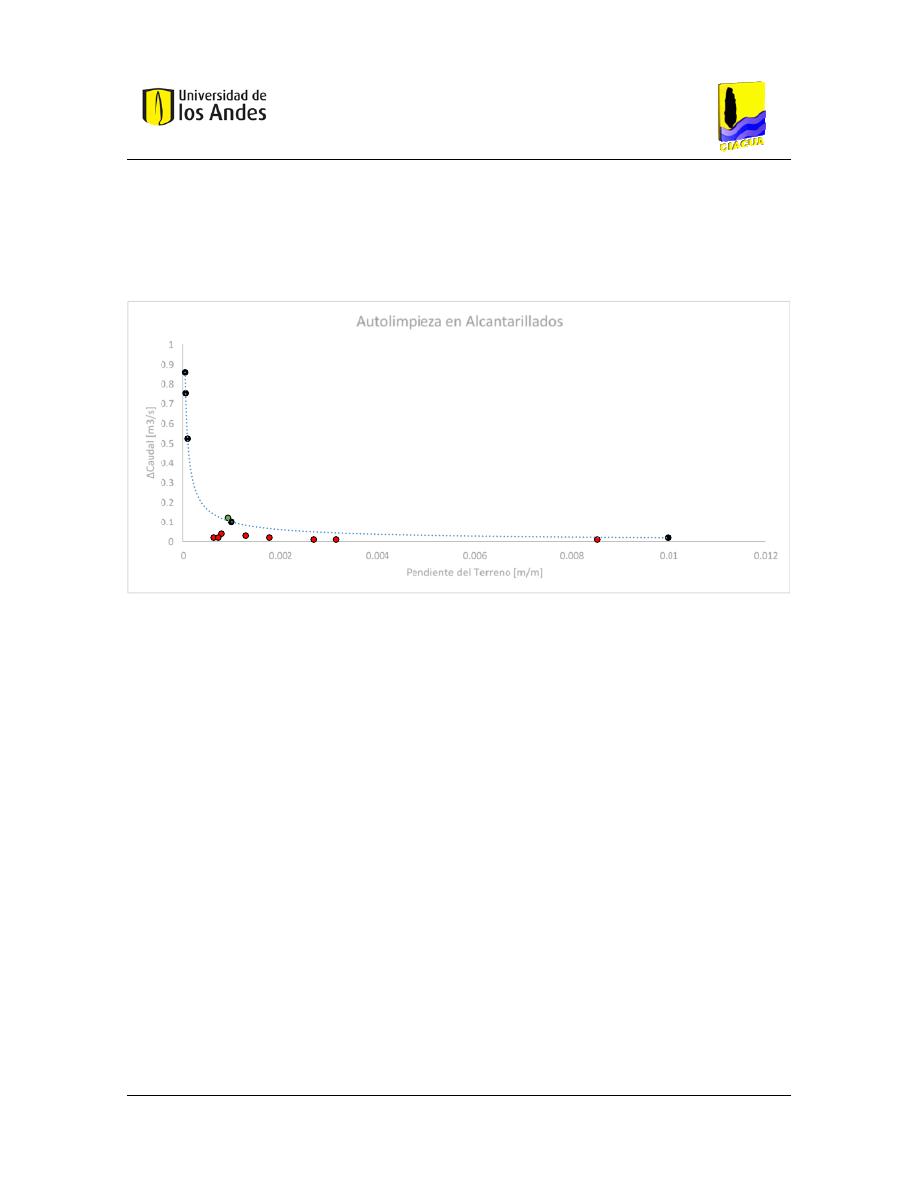
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
111
diseño entre el pozo de arranque y el pozo de descarga es de ∆𝑄 = 0.11 𝑚
3
/𝑠, para la ruta
principal, y la pendiente promedio de dicha ruta es de 0.093%. Con los valores anteriores
se puede comparar la ruta actual con la Figura 59 y se obtiene la siguiente figura:
Figura 66. – Localización de red sanitaria en la gráfica de autolimpieza.
Como se puede observar, para la ruta principal de la red de La Esmeralda, se cumple la
autolimpieza. Esto se ve reflejado porque el punto verde, que representa a La
Esmeralda, se encuentra por encima de la curva de autolimpieza. Igualmente, como se
puede observar en la Figura 65, para todas las rutas que conforman la red de
alcantarillado de La Esmeralda, bajo cualquier criterio de autolimpieza da como
solución el mismo costo final de la red. Se observa que las demás rutas de la red se
encuentran por debajo de la línea de autolimpieza, lo cual es de esperar para tuberías
con caudales muy bajos y pendientes muy planas. Adicional a lo anterior, como es de
esperar, dado que el caudal es menor y la pendiente es la misma, para el caso de
alcantarillado sanitario se está más cerca de la condición límite de autolimpieza, por lo
cual, para estos casos es importante realizar un estudio más detallado de los valores de
autolimpieza.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.002
0.004
0.006
0.008
0.01
0.012
Δ
Cau
d
al
[m
3/s
]
Pendiente del Terreno [m/m]
Autolimpieza en Alcantarillados

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
112
6 CONCLUSIONES Y RECOMENDACIONES
Los criterios tradicionales de autolimpieza han demostrado ser conservadores y
funcionales para el diseño de alcantarillados, tanto sanitarios como pluviales. Sin
embargo, el diseño con un criterio más restrictivo o uno más permisivo puede cambiar
el diseño final de una red de alcantarillado, dependiendo los caudales de diseño y la
topografía de la red.
La mayoría de los valores recomendados en las normativas de diseño a nivel mundial,
oscilan entre un valor de 0.6 m/s y 0.9 m/s como valor de velocidad mínima para un
alcantarillado pluvial y entre 0.3 m/s y 0.6 m/s en alcantarillados sanitarios. Estos
valores, como se puedo comprobar durante el desarrollo de la presente Tesis, son
indiferentes bajo ciertas condiciones del sistema. Principalmente, si se cuenta con un
alcantarillado pluvial, diseñar con un valor u otro es indiferente para el costo final del
sistema.
Existen varias metodologías que se han desarrollado recientemente, en las cuales se
busca obtener ecuaciones, en su mayoría análisis de regresión múltiple, que representen
la autolimpieza en alcantarillados como función de diversas variables que pueden
afectar el diseño en sí. Por ejemplo, para el caso de la ecuación de Nalluri, et al. (1994),
la proposición de un valor de velocidad mínima que garantice la autolimpieza en
sistemas de alcantarillado sanitarios, depende de variables como la aceleración de la
gravedad, el peso específico de las partículas de diseño, el diámetro de las partículas, la
concentración volumétrica de sedimentos que ingrese al sistema de alcantarillado, la
profundidad de agua, el diámetro de la tubería y el coeficiente de rugosidad hidráulico
de la capa de sedimentos del fondo de la tubería. Lo anterior, en la práctica, resulta ser
difícil de aplicar, puesto que, resulta casi imposible solicitarle al diseñador esa cantidad
de parámetros. Lo anterior lleva a suponer muchas variables y obtener estimativos
erróneos de la velocidad de autolimpieza real en un sistema de alcantarillado.
Las nuevas metodologías intentan reducir los valores de autolimpieza propuestos
tradicionalmente, sin embargo y como se menciona anteriormente, estas ecuaciones son
difíciles de aplicar en casos reales de diseño, especialmente para el caso colombiano en
el cual no existen grandes redes de monitoreo de sedimentos en sistemas de
alcantarillado. Lo anterior lleva a pensar en la necesidad de continuar diseñando con
los criterios tradicionales, que han demostrado tener una buena capacidad de
autolimpieza en alcantarillados a pesar de llevar en algunos casos a pendientes,
velocidades y/o esfuerzos cortantes mayores a los realmente requeridos en algunos casos
puntuales.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
113
El análisis gráfico de las restricciones de diseño mostró ser una herramienta poderosa
para predecir en una primera instancia cuáles deben ser las combinaciones de diámetro-
pendiente que se deben tener en el diseño final de un sistema de alcantarillado para su
cumplimiento de las restricciones de autolimpieza. Igualmente, las restricciones de
velocidad máxima se deben incluir como función del material de la tubería a diseñar.
Adicional a lo anterior mencionado, el criterio de velocidad máxima como restricción de
diseño es una variable que debe estudiarse con el mismo detalle que la restricción de
velocidad mínima y esfuerzo cortante mínimo.
En alcantarillados pluviales se demostró que las restricciones de autolimpieza no son
variables importantes e influyentes en el costo final del sistema de alcantarillado. Lo
anterior se debe fundamentalmente a los caudales que se manejan en este tipo de
alcantarillados (mucho mayores a los caudales generados en redes sanitarias) los cuales
llevan a velocidades mucho mayores a las requeridas para garantizar autolimpieza en
este tipo de sistemas. Dichas velocidades se acercan más a la restricción de velocidad
máxima, por lo cual, como se menciona con anterioridad, debe existir una verificación
más detallada de ésta restricción.
El caso de alcantarillados sanitarios es un poco distinto al caso pluvial, puesto que, los
caudales que se manejan son mucho menores. Sin embargo, y como se demostró en el
Capítulo 5, los casos que se verían influenciados son aquellos con topografía del terreno
muy plana y caudales muy bajos. Dichos casos resultan ser en muchas ocasiones escasos
y poco comunes; sin embargo se pueden presentar y generar variabilidad de diseños.
Complementario a lo anterior, se realizó un análisis de las condiciones límites a las
cuales las condiciones de autolimpieza dejan de ser relevantes en los diseños. Se observó
que existe una relación potencial entre la pendiente del terreno y la diferencia de
caudales en la red principal. La ecuación que describe la autolimpieza en alcantarillados
es ∆𝑄 = 0.0007𝑆
𝑇
−0.718
, donde ∆𝑄 es la diferencia de caudales [m
3
/s] entre el pozo inicial
y el pozo final de la ruta principal de la red de alcantarillado a diseñar y 𝑆
𝑇
la pendiente
del terreno correspondiente a la ruta principal. Si la red a diseñar se encuentra por
encima de esta curva, se podría afirmar que la restricción de autolimpieza no afecta el
diseño y por consiguiente es indiferente qué valor se utilice para dichos propósitos. Caso
contrario, si se encuentra por debajo de ésta ecuación, se deben considerar los criterios
de autolimpieza en el análisis.
Una primera recomendación acerca de los resultados obtenidos se enfoca al criterio de
velocidad máxima. No existen suficientes estudios que demuestren o sugieran qué valor
de velocidad máxima se debe restringir en el diseño. Este valor varía entre normativas
y no es muy claro exactamente qué valor se debe utilizar, dependiendo del material de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
114
la tubería a instalar. Dado lo anterior, se debería realizar un estudio en el cual se pruebe
la influencia de las altas velocidades y qué tanta afectación pueden tener en la tubería.
Igualmente, la ecuación de autolimpieza se obtuvo bajo determinadas condiciones de
pendiente y caudal, por lo cual, se recomienda ampliar el rango para encontrar una
ecuación un poco más confiable. Los casos de muy baja pendiente y altos caudales no
están muy bien definidos y tienden a converger a valores muy altos y pendientes muy
bajas.
Adicional a lo anterior surge la duda de ¿Qué criterio tradicional es más efectivo para
garantizar autolimpieza en alcantarillados tanto sanitarios como pluviales? Para
responder a lo anterior, se debería estudiar en un modelo físico de laboratorio la
capacidad de arrastre y transporte de sedimentos bajo distintos valores de velocidad y
esfuerzo cortante en una tubería. No se debería buscar una ecuación que incluya un
gran número de variables; por el contrario, bastaría con definir un límite de velocidad
para el cual cualquier tipo de partícula que pueda ingresar al sistema de alcantarillado
logre ser transportada. Lo anterior se debería igualmente validar mediante la
implementación de algún modelo de transporte de sedimentos en tuberías.
Finalmente, todos estos criterios y ecuaciones consideradas son resultado de años de
trabajo e investigación; sin embargo, si no se tiene un adecuado mantenimiento de los
sistemas y no se genera una conciencia a los ciudadanos de que arrojar basura y/o
desechos en las calles es perjudicial para el sistema de alcantarillado, da igual con qué
criterio se diseñe, puesto que, el sistema no va a tener la capacidad de transportar la
masa de agua para la cual fue diseñado y aparecerán los problemas que diariamente se
ven en las ciudades.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
115
7 REFERENCIAS BIBLIOGRÁFICAS
Ackers, J., Butler, D., Leggett, D. & May, R., 2001. Designing sewers to control sediment
problems. Urban Drainage Modeling, pp. 818-823.
Ackers, J., Butler, D. & May, R., 1996. Design of Sewers to Control Sediment Problems.
Londres: CIRIA.
Ackers, P., 1991. Sediment aspects of drainage and outfall design. Proceedings of the
International Symposium on Environmental Hydraulics.
Alvarez, E., 1990. The influence of cohesion on sediment movement in channels of
circular cross-section, s.l.: s.n.
Ambrose, H. H., 1953. 1953. The Transportation of Sand in Pipes; Free-Surface Flow,
Volumen 34, pp. 77-88.
Anon.,
2010.
[En
línea]
Available
at:
http://www.akitarescueoftulsa.com/sheilded-cat5-diagram-pdf/
[Último acceso: 05 06 2015].
Anon., 2012. Determinación de Caudales Máximos con el Método Racional. [En línea]
Available
at:
http://ingenieriacivil.tutorialesaldia.com/determinacion-de-caudales-
maximos-con-el-metodo-racional/
[Último acceso: 09 06 2015].
Bellman, R., 1956. On a routing problem, s.l.: s.n.
Bizier, P., 2007. Gravity Sanitary Sewer Design and Construction.
Bong, C., 2013. Self-cleansing urban drain using sediment flushing gate based on
incipient motion, Malaysia: Ph.D Thesis.
Bong, C. H., 2014. A review on the self-cleansing design criteria for sewer system.
UNIMAS e-Journal of Civil Engineering.
Butler, D. & Davies, J., 2009. Urban Drainage. Londres: SPON.
Butler, D., May, R. & Ackers, J., 2003. Self-Cleansing sewer design based on sediment
transport principles. Journal of Hydraulics Engineering, pp. 276-282.
Camp, T. R., 1942. Minimum velocities for sewers final report comm. to study limiting
velocities of flow in sewers.. Journal of Boston Society of Civil Engineers, 29(286).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
116
CIACUA, 2013. Diseño optimizado en redes de alcantarillado: Desarrollo de técnicas
computacionales exhaustivas para el diseño optimizado de redes de drenaje urbano.,
Bogotá: Universidad de los Andes.
CIRIA, 1987. Sediment movement in combined sewerage and stormwater drainage
systems.
Craven, J. P., 1953. The Transportation of Sand in Pipes; Free-Surface Flow. Hydraulics
Conference Proceedings, Iowa, Volumen 34, pp. 67-76.
Duque, N., 2013. Metodología para la Optimización del Diseño de Tuberías en Serie en
Sistemas de Alcantarillado, Bogotá: Universidad de los Andes.
Durand, R., 1953. Basic relationships of the transportation of solids in pipes. IAHR, pp.
89-103.
Durand, R. & Condolios, E., 1956. Donnees technique sur le refoulement hydralique des
materiaux solides en conduite. L'Industrie Minerals.
Ebtehaj, I., Bonakdari, H. & Sharifi, A., 2013. Design criteria for sediment transport in
sewers based on self-cleansing concept. Journal of Zhejiang University-SCIENCE A
(Applied Physics & Engineering), pp. 914-924.
El - Zaemy, A., 1991. Sediment transport over deposited beds in sewers. Ph.D Thesis.
Ellis, J. B. & Harrop, D. O., 1984. Variations in solids loadings to roadside gully pots.
Sci. Total Env., Volumen 33, pp. 203-211.
Enfinger, K. & Mitchell, P., 2010. Scattergraph Principles and Practice: Evaluating Self-
Cleansing in Existing Sewers Using the Tractive Force Method. World Environmental
and Water Resources Congress, pp. 4458-4467.
Fair, G. & Geyer, J., 1954. Water Supply and Wastewater Disposal. 1 ed. New York:
Wiley.
Ghani, A. A., 1993. Sediment Transport in Sewers. PhD Thesis. University of Newcastle
Upon Tyne.
Guzman, K. y otros, 2007. Effect of biofilm formation on roughness coefficient and solids
deposition in small-diameter PVC sewer pipes. Journal of Environmental Engineering,
133(4), pp. 364-371.
Ibro, I. & Larsen, T., 2011. Modeling of sediment transport and self-cleansing in sea
outfalls, s.l.: Aalborg Universitet.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
117
La Motta, E., 1996. Quick calculation of minimum slopes in sanitary sewer systems.
Technology Transfer Paper, 96(01).
Laursen, E., 1956. The hydraulic of a storm-drain system for sediment-transporting
flow. Iowa Highway Research Board.
Lysne, D., 1969. Hydraulic Design of Self-Cleaning Sewage Tunnels. Journal of the
Sanitary Engineering Division, 95(1), pp. 17-36.
Macke, E., 1982. About sedimentation at low concentrations in partly filled pipes,
Braunschweig: Ph.D Thesis.
Mance, G. & Harman, M. I., 1978. The quality of urban stormwater run-off. Urban
Storm Drainage, pp. 603-618.
Mayerle, R., Nalluri, C. & Novak, P., 1991. Sediment Transport in Rigid Bed
Conveyances. Journal of Hydraulic Research, 29(4), pp. 475-495.
May, R., 1982. Sediment transport in sewers. Hydraulic Research Station.
May, R., 1993. Sediment transport in pipes and sewers with deposited beds. Hydraulic
Research Ltd.
May, R., Ackers, J., Butler, D. & Jhon, S., 1996. Development of design methodology for
self-cleansing sewers. Water Science and Technology, 33(9), pp. 195-205.
Merritt, L., 2012. Closure to "Tractive Force Design For Sanitary Sewer Self-Cleansing".
Journal of Environmental Engineering, Volumen 138, pp. 525-528.
Merritt, L. B., 2009. Tractive Force Design for Sanitary Sewer Self-Cleansing. Journal
of Environmental Engineering, 135(12), pp. 1338-1347.
Metcalf & Eddy, INC, 1991. Wastewater engineering: Treatment, disposal and Reuse.
New York: McGraw-Hill.
Nalluri, C. & Alvarez, E., 1992. The influence of cohesion on sediment behaviour. Water
Science & Technology, 25(8), pp. 151-164.
Nalluri, C. & Ghani, A., 1996. Design options for self-cleansing storm sewers. Water
Science and Technology, Volumen 33, pp. 215-220.
Nalluri, C., Ghani, A. & El-Zaemey, A., 1994. Sediment transport over deposited beds
in sewers. Water Science Technology, 29(1-2), pp. 125-133.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
118
Navarro, I., 2009. Diseño Optimizado de Redes de Drenaje Urbano, Bogotá: Universidad
de los Andes.
Novak, P. & Nalluri, C., 1975. Sediment transport in smooth fixed bed channels.
Journal of the Hydraulic Division of the American Society of Civil Engineers, pp. 1139-
1154.
Novak, P. & Nalluri, C., 1984. Incipient Motion of Sediment Particles Over Fixed Beds.
Jpurnal of Hydraulic Research, 22(3), pp. 181-197.
Ojo, S., 1978. Study of incipient motion and sediment transport over fixed beds. Ph.D
Thesis.
Perez, C., 2014. Diseño hidráulico optimizado de redes de alcantarillados utilizando el
concepto de potencia específica, Bogotá: Universidad de los Andes.
Perrusquía, G., 1991. Bedload transport in storm sewers - stream traction in pipe
channels. Chalmers University of Technology.
RAS, 2000. Título D - Sistemas de Recolección y Evacuación de Aguas Residuales
Domésticas y Pluviales. Bogotá: s.n.
Raths, C. & McCauley, R., 1962. Deposition in a sanitary sewer. Water Sewer Works,
109(5), pp. 192-197.
Rincón, G., La Motta, E. & McCorquodale, A., 2012. Discussion of "Tractive Force Design
for Sanitary Sewer Self - Cleansing". Journal of Envorinmental Engineering, 135(12),
pp. 1338-1347.
Robinson, M. & Graf, W., 1972. Pipelines of low-concentration sand-water mixtures.
Journal of Hydraulics Division, Volumen 98, pp. 1221-1241.
Rodríguez, J. P., McIntyre, N., Díaz-Granados, M. & Achleitner, S., 2013. Generating
time-series of dry weather loads to sewers. En vironmental Modelling & Software, pp.
133-143.
Sakhuja|, V., 1987. A compilation of methods for predicting friction and sediment
transport in alluvial channels, s.l.: USEPA.
Salcedo, C., 2012. Diseño optimizado de sistemas de alcantarillado utilizando los
conceptos de resilencia y potencia unitaria, Bogotá: Universidad de los Andes.
Saldarriaga, J., 2014. Curso: Sistemas Integrados de Drenaje Urbano. Bogotá,
Universidad de los Andes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
119
Sartor, J. D. & Boyd, G. B., 1972. Water pollution aspects of street surface contaminants.
USEPA.
Shields,
A.,
1936.
Anwendundung der
ahnlichkeitsmechanik
und der
turbulenzforschung auf die geschiebeb ewegung.. Preuss Vers fur Waaerbau und
Shiffbau.
Universidad de los Andes, 2014. Drenaje Urbano y Cambio Climático: Hacia los
Sistemas de Alcantarillados del Futuro, Bogotá: Uniandes.
Vongvisessomjai, N., Tingsanchali, T. & Babel, M. S., 2010. Non-deposition design
criteria for sewers with part-full flow. Urban Water Journal, Volumen 7, pp. 61-77.
Wu, I. P., 1975. Design on Drip Irrigation Main Lines. Journal of the Irrigation and
Drainage Division, ASCE.
Yao, K., 1974. Sewer Line Design Based on Critical Shear Stress. Journal of the
Environmental Engineering Division, 100(2), pp. 507-520.
Young, P. C. & Wallis, S. G., 1993. Solute Transport and Dispersion in Channels.
Channel Network Hydrology, pp. 129-173.
Zou, R., Lung, W. S. & Guo, H., 2002. Neuronal Network Embedded Monte Carlo
Approach for Water Quality Modeling under Input Information Uncertainty. Journal of
Computing in Civil Engineering.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
120
LISTADO DE ANEXOS
Anexo 1. – Experimentos para carga en suspensión. Tomado de (Vongvisessomjai, et al., 2010).
................................................................................................................................................. 123
Anexo 2. – Experimentos para carga de lecho. Tomado de (Vongvisessomjai, et al., 2010). ..... 123
Anexo 3. – Diagrama de Shields. Tomado de (Anon., 2010) ........................................................ 124
Anexo 4. – Gradiente de energía en términos de la tasa de transporte de sedimentos. Tomado
de (Craven, 1953). .................................................................................................................. 125
Anexo 5. – Valores recomendados para el coeficiente de Manning. Tomado de (Bizier, 2007). 126
Anexo 6. – Ecuaciones de diseño para alcantarillados autolimpiantes mediante el método TF.
Tomado de (Merritt, 2009) ..................................................................................................... 127
Anexo 7. – Pendientes que garantizan autolimpieza en función del caudal mínimo. Tomado de
(Bizier, 2007). ......................................................................................................................... 128
Anexo 8. – Velocidades mínimas requeridas para el Criterio II [CIRIA]. Válidas para 𝒚𝒔𝑫 = 𝟏%.
Tomado de (Ackers, et al., 1996). .......................................................................................... 129
Anexo 9. - Velocidades mínimas requeridas para el Criterio II [CIRIA]. Válidas para 𝒚𝒔𝑫 = 𝟐%.
Tomado de (Ackers, et al., 1996). .......................................................................................... 129
Anexo 10. - Velocidades mínimas requeridas para el Criterio II [CIRIA]. Válidas para 𝒚𝒔𝑫 =
𝟓%. Tomado de (Ackers, et al., 1996). ................................................................................... 130
Anexo 11. - Velocidades mínimas requeridas para el Criterio II [CIRIA]. Válidas para 𝒚𝒔𝑫 =
𝟏𝟎%. Tomado de (Ackers, et al., 1996).................................................................................. 130
Anexo 12. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 100
μm. Criterio II de diseño........................................................................................................ 131
Anexo 13. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 200
μm. Criterio II de diseño........................................................................................................ 131
Anexo 14. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 300
μm. Criterio II de diseño........................................................................................................ 132
Anexo 15. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 100
μm. Criterio II de diseño........................................................................................................ 132
Anexo 16. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 200
μm. Criterio II de diseño........................................................................................................ 133
Anexo 17. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 300
μm. Criterio II de diseño........................................................................................................ 133
Anexo 18. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 100
μm. Criterio II de diseño........................................................................................................ 134

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
121
Anexo 19. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 200
μm. Criterio II de diseño........................................................................................................ 134
Anexo 20. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 300
μm. Criterio II de diseño........................................................................................................ 135
Anexo 21. – Rutas obtenidas en CIE 7.0. Velocidad mínima = 0.75 m/s .................................... 135
Anexo 22. - Rutas obtenidas en CIE 7.0. Velocidad mínima = 0.9 m/s ....................................... 136
Anexo 23. – Rutas obtenidas en CIE 7.0. Esfuerzo cortante mínimo = 2 Pa. ............................ 136
Anexo 24. - Rutas obtenidas en CIE 7.0. Esfuerzo cortante mínimo = 4 Pa. ............................. 137
Anexo 25. - Rutas obtenidas en CIE 7.0. Esfuerzo cortante mínimo = 12.6 Pa. ........................ 137
Anexo 26. – Datos de Entrada Alcantarillado Pluvial. Caso 2.................................................... 138
Anexo 27. – Datos de Entrada Alcantarillado Pluvial. Caso 3.................................................... 138
Anexo 28. – Datos de Entrada Alcantarillado Pluvial. Caso 3.................................................... 139
Anexo 29. – Datos de Entrada Alcantarillado Pluvial. Caso 4.................................................... 139
Anexo 30. – Datos de Entrada Alcantarillado Pluvial. Caso 5.................................................... 140
Anexo 31. – Datos de Entrada Alcantarillado Pluvial. Caso 6.................................................... 140
Anexo 32. – Datos de Entrada Alcantarillado Pluvial. Caso 7.................................................... 141
Anexo 33. – Datos de Entrada Alcantarillado Pluvial. Caso 8.................................................... 141
Anexo 34. – Resultados tabulares de diseños para el Caso 2. ..................................................... 142
Anexo 35. – Resultados tabulares de diseños para el Caso 3. ..................................................... 143
Anexo 36. – Resultados tabulares de diseños para el Caso 4. ..................................................... 144
Anexo 37. – Resultados tabulares de diseños para el Caso 5. ..................................................... 145
Anexo 38. – Resultados gráficos de diseño para el Caso 2. ......................................................... 146
Anexo 39. – Resultados gráficos de diseño para el Caso 3. ......................................................... 147
Anexo 40. – Resultados gráficos de diseño para el Caso 4. ......................................................... 148
Anexo 41. – Resultados gráficos de diseño para el Caso 5. ......................................................... 149
Anexo 42. – Resultados gráficos de diseño para el Caso 6. ......................................................... 150
Anexo 43. – Datos de entrada. Corrida 01_Caso 1. ...................................................................... 150
Anexo 44. – Datos de entrada. Corrida 01_Caso 2. ...................................................................... 151
Anexo 45. – Datos de entrada. Corrida 01_Caso 3. ...................................................................... 151
Anexo 46. – Datos de entrada. Corrida 01_Caso 4. ...................................................................... 152
Anexo 47. – Datos de entrada. Corrida 01_Caso 5. ...................................................................... 152

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
122
Anexo 48. – Datos de entrada. Corrida 01_Caso 6. ...................................................................... 153
Anexo 49. – Datos de entrada. Corrida 02_Caso 1. ...................................................................... 153
Anexo 50. – Datos de entrada. Corrida 02_Caso 2. ...................................................................... 154
Anexo 51. – Datos de entrada. Corrida 02_Caso 3. ...................................................................... 154
Anexo 52. – Datos de entrada. Corrida 02_Caso 4. ...................................................................... 155
Anexo 53. – Datos de entrada. Corrida 02_Caso 5. ...................................................................... 155
Anexo 54. – Datos de entrada. Corrida 02_Caso 6. ...................................................................... 156
Anexo 55. – Datos de entrada. Corrida 03_Caso 1. ...................................................................... 156
Anexo 56. – Datos de entrada. Corrida 03_Caso 2. ...................................................................... 157
Anexo 57. – Datos de entrada. Corrida 03_Caso 3. ...................................................................... 157
Anexo 58. – Datos de entrada. Corrida 03_Caso 4. ...................................................................... 158
Anexo 59. – Datos de entrada. Corrida 03_Caso 5. ...................................................................... 158
Anexo 60. – Datos de entrada. Corrida 03_Caso 6. ...................................................................... 159
Anexo 61. – Datos de entrada. Corrida 04_Caso 1. ...................................................................... 159
Anexo 62. – Datos de entrada. Corrida 04_Caso 2. ...................................................................... 160
Anexo 63. – Datos de entrada. Corrida 04_Caso 3. ...................................................................... 160
Anexo 64. – Datos de entrada. Corrida 04_Caso 4. ...................................................................... 161
Anexo 65. – Datos de entrada. Corrida 04_Caso 5. ...................................................................... 161
Anexo 66. – Datos de entrada. Corrida 04_Caso 6. ...................................................................... 162
Anexo 67. – Datos de entrada. Corrida 05_Caso 1. ...................................................................... 162
Anexo 68. – Datos de entrada. Corrida 05_Caso 2. ...................................................................... 163
Anexo 69. – Datos de entrada. Corrida 05_Caso 3. ...................................................................... 163
Anexo 70. – Datos de entrada. Corrida 05_Caso 4. ...................................................................... 164
Anexo 71. – Datos de entrada. Corrida 05_Caso 5. ...................................................................... 164
Anexo 72. – Datos de entrada. Corrida 05_Caso 6. ...................................................................... 165
Anexo 73. – Resultados Corrida 03. .............................................................................................. 165
Anexo 74. – Resultados Corrida 04. .............................................................................................. 166
Anexo 75. – Costos asociados a la Corrida 03. ............................................................................. 166
Anexo 76. – Costos asociados a la Corrida04. .............................................................................. 167
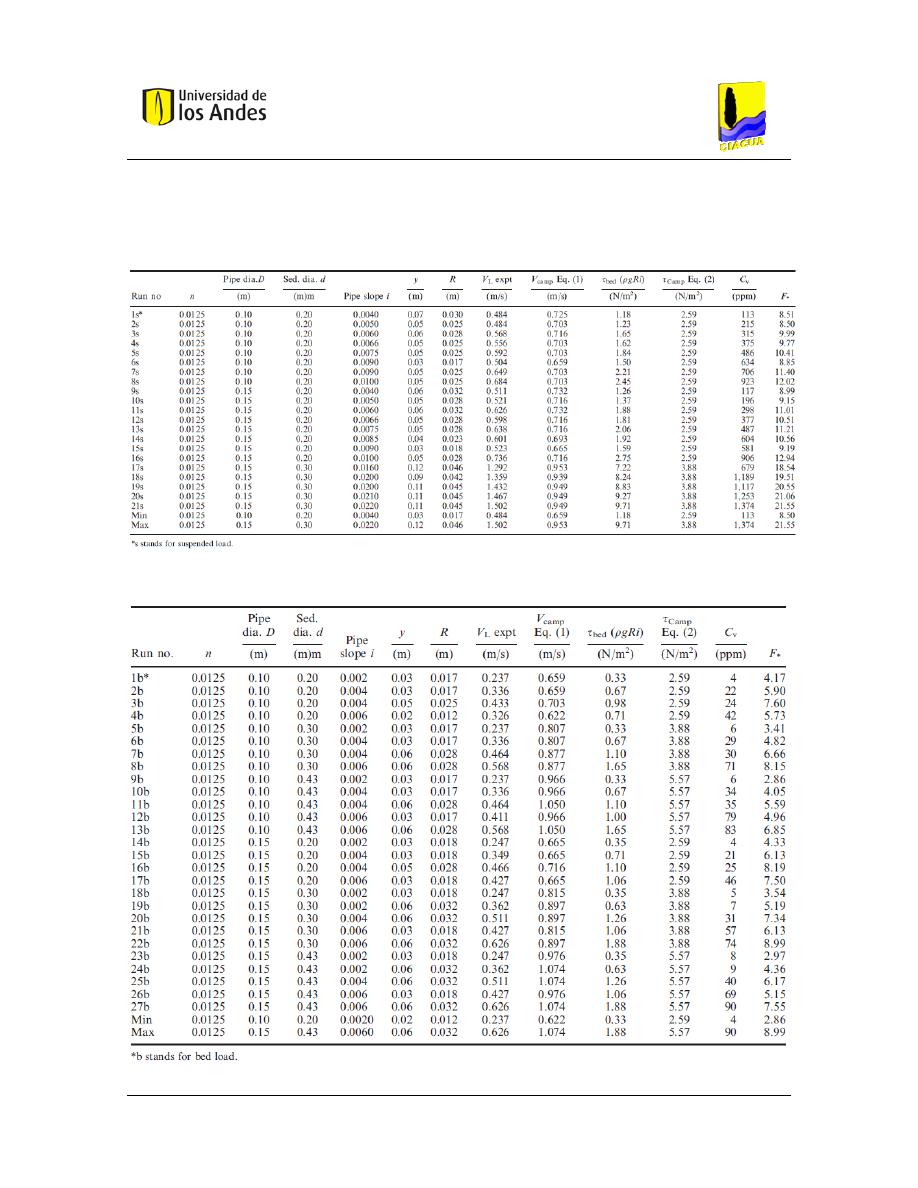
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
123
8 ANEXOS
Anexo 1. – Experimentos para carga en suspensión. Tomado de (Vongvisessomjai, et al., 2010).
Anexo 2. – Experimentos para carga de lecho. Tomado de (Vongvisessomjai, et al., 2010).
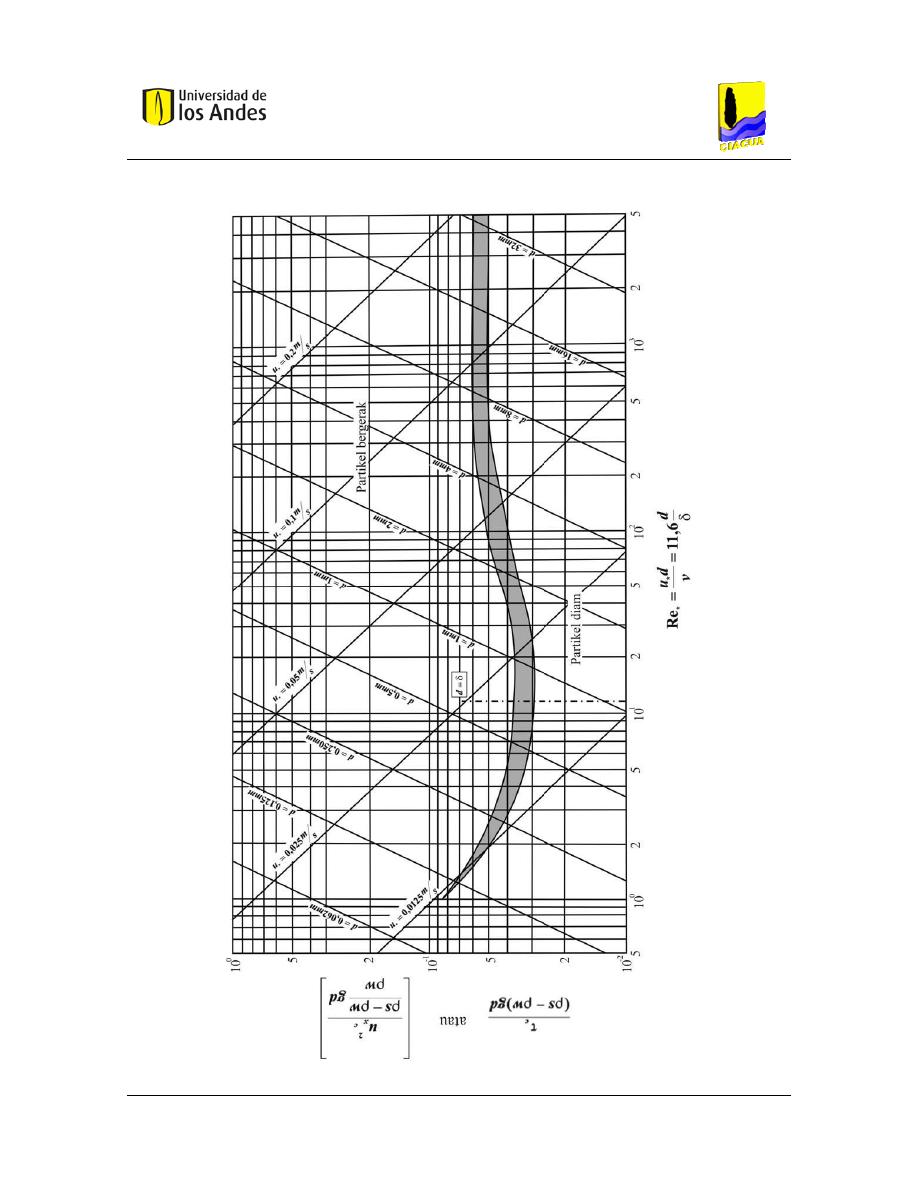
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
124
Anexo 3. – Diagrama de Shields. Tomado de (Anon., 2010)
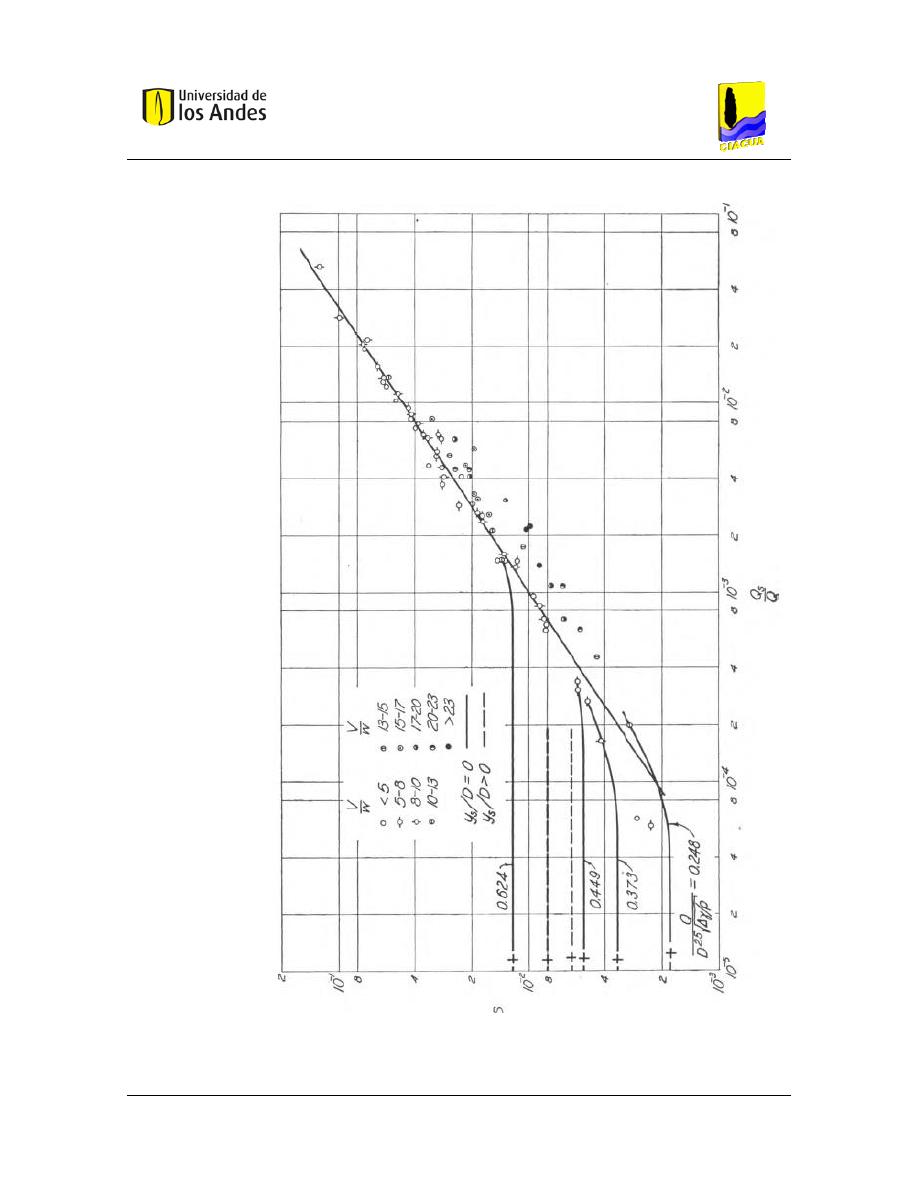
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
125
Anexo 4. – Gradiente de energía en términos de la tasa de transporte de sedimentos. Tomado
de (Craven, 1953).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
126
Anexo 5. – Valores recomendados para el coeficiente de Manning. Tomado de (Bizier, 2007).
6
8
10
12
15
18
24
30
36
48
60
C
on
se
rv
at
iv
o
0.
00
92
0.
00
93
0.
00
95
0.
00
96
0.
00
97
0.
00
98
0.
01
0.
01
02
0.
01
03
0.
01
05
0.
01
07
Tí
pi
co
0.
01
06
0.
01
07
0.
01
09
0.
01
1
0.
01
12
0.
01
13
0.
01
15
0.
01
17
0.
01
18
0.
01
21
0.
01
23
H
ol
ga
do
0.
01
2
0.
01
21
0.
01
23
0.
01
25
0.
01
26
0.
01
27
0.
01
3
0.
01
33
0.
01
34
0.
01
37
0.
01
39
C
on
di
ci
ón
D
iá
m
et
ro
d
e
la
T
ub
er
ía
D
[i
n]

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
127
Anexo 6. – Ecuaciones de diseño para alcantarillados autolimpiantes mediante el método TF.
Tomado de (Merritt, 2009)
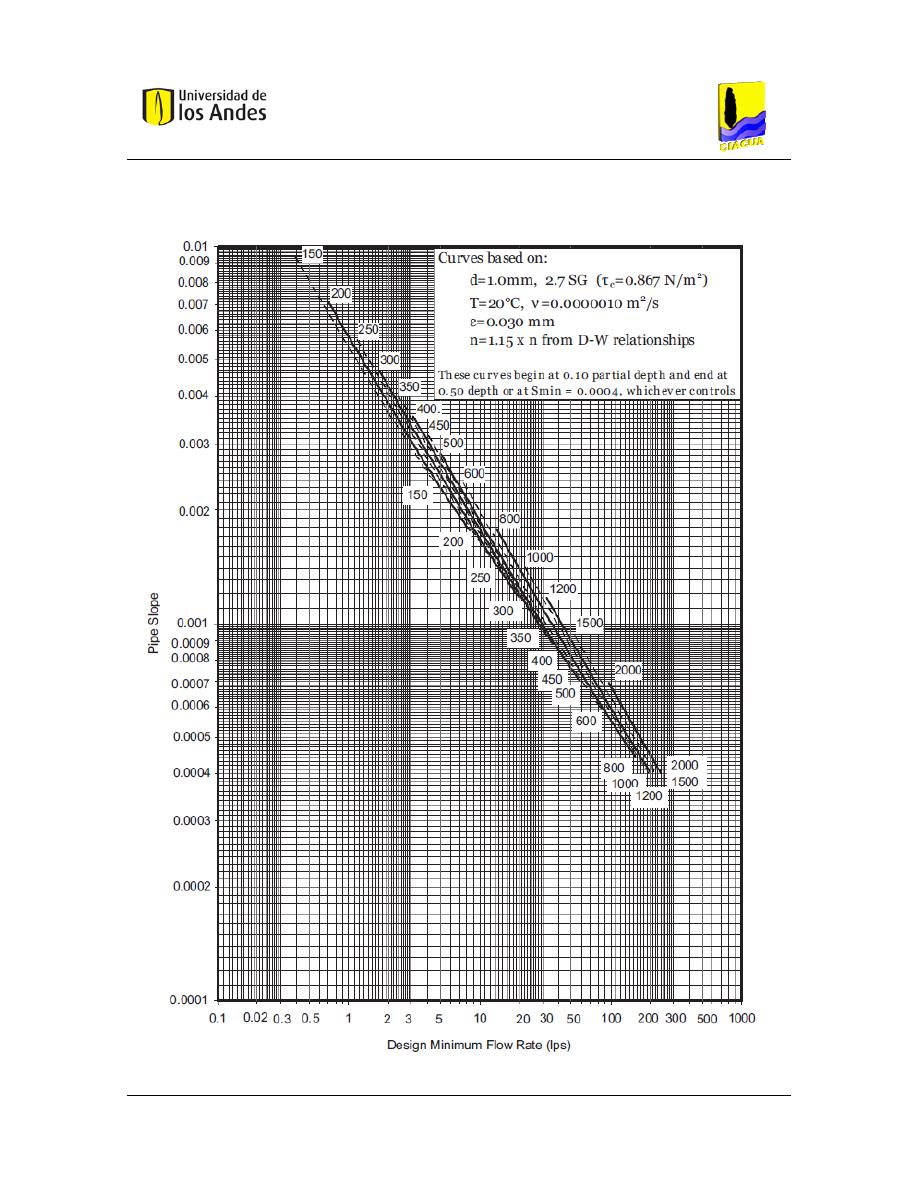
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
128
Anexo 7. – Pendientes que garantizan autolimpieza como función del caudal mínimo. Tomado
de (Bizier, 2007).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
129
Anexo 8. – Velocidades mínimas requeridas para el Criterio II [CIRIA]. Válidas para
𝒚
𝒔
𝑫
= 𝟏%.
Tomado de (Ackers, et al., 1996).
d
[mm]
d = 100 μm
d = 200 μm
d = 300 μm
X = 50
mg/L
X = 350
mg/L
X =
1000
mg/L
X = 50
mg/L
X = 350
mg/L
X =
1000
mg/L
X = 50
mg/L
X = 350
mg/L
X = 1000
mg/L
150
0.36
0.45
0.52
0.39
0.53
0.65
0.41
0.58
0.74
225
0.39
0.5
0.58
0.43
0.6
0.74
0.46
0.66
0.89
300
0.42
0.54
0.62
0.46
0.65
0.81
0.5
0.73
0.96
450
0.46
0.59
0.69
0.52
0.74
0.93
0.56
0.85
1.12
600
0.49
0.63
0.74
0.56
0.81
1.02
0.61
0.94
1.25
750
0.52
0.67
0.78
0.59
0.87
1.1
0.65
1.02
1.36
900
0.54
0.7
0.82
0.62
0.92
1.17
0.68
1.08
1.46
1200
0.57
0.75
0.88
0.68
1.01
1.29
0.75
1.2
1.63
1500
0.6
0.79
0.93
0.72
1.08
1.39
0.8
1.31
1.78
1800
0.63
0.83
0.98
0.76
1.15
1.48
0.85
1.4
1.91
2100
0.65
0.86
1.01
0.79
1.2
1.56
0.89
1.48
2.03
2400
0.67
0.89
1.05
0.82
1.26
1.63
0.93
1.56
2.15
2700
0.69
0.91
1.08
0.75
1.3
1.7
0.97
1.63
2.25
3000
0.7
0.94
1.11
0.87
1.35
1.76
1
1.7
2.35
3400
0.72
0.96
1.14
0.91
1.41
1.83
1.04
1.78
2.47
4000
0.75
1
1.19
0.95
1.48
1.94
1.1
1.89
2.63
5000
0.79
1.06
1.26
1.01
1.6
2.09
1.19
2.06
2.88
Anexo 9. - Velocidades mínimas requeridas para el Criterio II [CIRIA]. Válidas para
𝒚
𝒔
𝑫
= 𝟐%.
Tomado de (Ackers, et al., 1996).
D
[mm]
d = 100 μm
d = 200 μm
d = 300 μm
X =
50
mg/L
X = 350
mg/L
X = 1000
mg/L
X = 50
mg/L
X = 350
mg/L
X = 1000
mg/L
X = 50
mg/L
X = 350
mg/L
X = 1000
mg/L
150
0.35
0.43
0.5
0.37
0.5
0.61
0.39
0.54
0.68
225
0.38
0.48
0.55
0.41
0.56
0.7
0.43
0.62
0.79
300
0.41
0.52
0.6
0.44
0.62
0.76
0.47
0.68
0.88
450
0.44
0.57
0.66
0.49
0.7
0.87
0.52
0.78
1.03
600
0.47
0.61
0.71
0.53
0.76
0.96
0.57
0.87
1.15
750
0.5
0.64
0.75
0.56
0.82
1.03
0.61
0.94
1.25
900
0.52
0.67
0.79
0.59
0.86
1.1
0.64
1
1.34
1200
0.55
0.72
0.85
0.64
0.95
1.21
0.7
1.11
1.49
1500
0.58
0.76
0.89
0.68
1.01
1.3
0.75
1.2
1.63
1800
0.61
0.8
0.94
0.72
1.07
1.38
0.79
1.29
1.75
2100
0.63
0.82
0.97
0.75
1.13
1.46
0.83
1.36
1.86
2400
0.64
0.85
1
0.77
1.18
1.52
0.87
1.43
1.96
2700
0.66
0.88
1.03
0.8
1.22
1.58
0.9
1.5
2.05
3000
0.68
0.9
1.06
0.83
1.26
1.64
0.93
1.56
2.14
3400
0.7
0.93
1.1
0.85
1.32
1.71
0.97
1.63
2.25
4000
0.72
0.96
1.14
0.9
1.39
1.81
1.02
1.73
2.4
5000
0.76
1.01
1.2
0.95
1.49
1.95
1.1
1.89
2.62

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
130
Anexo 10. - Velocidades mínimas requeridas para el Criterio II [CIRIA]. Válidas para
𝒚
𝒔
𝑫
= 𝟓%.
Tomado de (Ackers, et al., 1996).
D
[mm]
d = 100 μm
d = 200 μm
d = 300 μm
X = 50
mg/L
X = 350
mg/L
X =
1000
mg/L
X = 50
mg/L
X = 350
mg/L
X =
1000
mg/L
X = 50
mg/L
X = 350
mg/L
X =
1000
mg/L
150
0.33
0.41
0.47
0.34
0.46
0.55
0.35
0.48
0.61
225
0.36
0.45
0.52
0.38
0.51
0.63
0.39
0.55
0.7
300
0.38
0.48
0.56
0.41
0.56
0.69
0.43
0.61
0.77
450
0.42
0.53
0.62
0.45
0.63
0.79
0.47
0.69
0.9
600
0.44
0.57
0.66
0.49
0.69
0.86
0.51
0.76
1
750
0.47
0.6
0.7
0.52
0.74
0.93
0.55
0.83
1.08
900
0.49
0.63
0.73
0.54
0.78
0.98
0.58
0.88
1.16
1200
0.52
0.67
0.79
0.58
0.85
1.08
0.63
0.97
1.29
1500
0.54
0.71
0.83
0.62
0.91
1.16
0.67
1.05
1.41
1800
0.57
0.74
0.87
0.65
0.97
1.24
0.7
1.15
1.51
2100
0.58
0.77
0.9
0.68
1.01
1.3
0.74
1.19
1.6
2400
0.6
0.79
0.93
0.7
1.06
1.36
0.77
1.25
1.69
2700
0.62
0.82
0.96
0.73
1.1
1.41
0.8
1.3
1.77
3000
0.63
0.84
0.99
0.75
1.13
1.46
0.82
1.35
1.84
3400
0.65
0.86
1.02
0.77
1.18
1.53
0.86
1.41
1.96
4000
0.67
0.89
1.06
0.81
1.24
1.61
0.9
1.5
2.06
5000
0.7
0.94
1.12
0.86
1.33
1.74
0.97
1.63
2.25
Anexo 11. - Velocidades mínimas requeridas para el Criterio II [CIRIA]. Válidas para
𝒚
𝒔
𝑫
= 𝟏𝟎%.
Tomado de (Ackers, et al., 1996).
D
[mm]
d = 100 μm
d = 200 μm
d = 300 μm
X = 50
mg/L
X = 350
mg/L
X =
1000
mg/L
X = 50
mg/L
X = 350
mg/L
X =
1000
mg/L
X = 50
mg/L
X = 350
mg/L
X =
1000
mg/L
150
0.31
0.38
0.44
0.32
0.42
0.5
0.33
0.44
0.54
225
0.34
0.42
0.49
0.35
0.47
0.57
0.36
0.5
0.62
300
0.36
0.45
0.52
0.38
0.51
0.63
0.39
0.54
0.69
450
0.39
0.5
0.58
0.42
0.58
0.71
0.43
0.62
0.79
600
0.42
0.53
0.62
0.45
0.63
0.78
0.47
0.68
0.88
750
0.44
0.56
0.65
0.47
0.67
0.84
0.5
0.73
0.95
900
0.46
0.59
0.68
0.5
0.71
0.89
0.52
0.78
1.02
1200
0.48
0.63
0.73
0.53
0.77
0.97
0.56
0.86
1.13
1500
0.51
0.66
0.78
0.57
0.82
1.05
0.6
0.93
1.23
1800
0.53
0.69
0.81
0.59
0.87
1.11
0.63
0.99
1.32
2100
0.55
0.72
0.84
0.62
0.91
1.17
0.66
1.04
1.4
2400
0.56
0.74
0.87
0.64
0.95
1.22
0.69
1.09
1.47
2700
0.58
0.76
0.89
0.66
0.99
1.27
0.71
1.14
1.54
3000
0.59
0.78
0.92
0.68
1.02
1.31
0.74
1.18
1.6
3400
0.61
0.8
0.95
0.7
1.06
1.37
0.76
1.24
1.68
4000
0.63
0.83
0.98
0.74
1.12
1.44
0.8
1.31
1.79
5000
0.66
0.88
1.04
0.78
1.2
1.55
0.86
1.42
1.95

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
131
Anexo 12. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 100 μm.
Criterio II de diseño.
Anexo 13. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 200 μm.
Criterio II de diseño.
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Pendiente
y
s
/D = 2%
k
o
= 0.6 mm
SG = 2.6
d = 0.1 mm
X = 50 mg/L
X = 350 mg/L
X = 1000 mg/L
0.1
1
0.0001
0.001
0.01
0.1
1
Pendiente
y
s
/D = 2%
k
o
= 0.6 mm
SG = 2.6
d = 0.2 mm
X = 50 mg/L
X = 350 mg/L
X = 1000 mg/L

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
132
Anexo 14. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 300 μm.
Criterio II de diseño.
Anexo 15. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 100
μm. Criterio II de diseño.
0.1
1
0.0001
0.001
0.01
0.1
1
Pendiente
y
s
/D = 2%
k
o
= 0.6 mm
SG = 2.6
d = 0.3 mm
X = 50 mg/L
X = 350 mg/L
X = 1000 mg/L
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Pendiente
y
s
/D = 5%
k
o
= 0.6 mm
SG = 2.6
d = 0.1 mm
X = 50 mg/L
X = 350 mg/L
X = 1000 mg/L
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
133
Anexo 16. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 200
μm. Criterio II de diseño.
Anexo 17. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 300 μm.
Criterio II de diseño.
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Pendiente
y
s
/D = 5%
k
o
= 0.6 mm
SG = 2.6
d = 0.2 mm
X = 50 mg/L
X = 350 mg/L
X = 1000 mg/L
0.1
1
0.0001
0.001
0.01
0.1
1
Pendiente
y
s
/D = 5%
k
o
= 0.6 mm
SG = 2.6
d = 0.3 mm
X = 50 mg/L
X = 350 mg/L
X = 1000 mg/L

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
134
Anexo 18. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 100 μm.
Criterio II de diseño.
Anexo 19. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 200 μm.
Criterio II de diseño.
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Pendiente
y
s
/D = 10%
k
o
= 0.6 mm
SG = 2.6
d = 0.1 mm
X = 50 mg/L
X = 350 mg/L
X = 1000 mg/L
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Pendiente
y
s
/D = 10%
k
o
= 0.6 mm
SG = 2.6
d = 0.2 mm
X = 50 mg/L
X = 350 mg/L
X = 1000 mg/L
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
135
Anexo 20. - Aplicación de la ecuación de Ackers (1982) para un diámetro de partícula de 300 μm.
Criterio II de diseño.
Anexo 21. – Rutas obtenidas en CIE 7.0. Velocidad mínima = 0.75 m/s
0.1
1
0.00001
0.0001
0.001
0.01
0.1
1
Pendiente
y
s
/D = 10%
k
o
= 0.6 mm
SG = 2.6
d = 0.3 mm
X = 50 mg/L
X = 350 mg/L
X = 1000 mg/L
Línea
Caudal
0.01
150.00
192.00
256.00
LPS
08/23/2013 00:20:00
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
136
Anexo 22. - Rutas obtenidas en CIE 7.0. Velocidad mínima = 0.9 m/s
Anexo 23. – Rutas obtenidas en CIE 7.0. Esfuerzo cortante mínimo = 2 Pa.
Línea
Caudal
0.01
150.00
192.00
256.00
LPS
08/23/2013 00:20:00
Línea
Caudal
0.01
150.00
192.00
256.00
LPS
08/23/2013 00:20:00
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
137
Anexo 24. - Rutas obtenidas en CIE 7.0. Esfuerzo cortante mínimo = 4 Pa.
Anexo 25. - Rutas obtenidas en CIE 7.0. Esfuerzo cortante mínimo = 12.6 Pa.
Línea
Caudal
0.01
150.00
192.00
256.00
LPS
08/23/2013 00:20:00
Línea
Caudal
0.01
150.00
192.00
256.00
LPS
08/23/2013 00:20:00

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
138
Anexo 26. – Datos de Entrada Alcantarillado Pluvial. Caso 2
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.11
2587.34
0.00
1
0.46
2576.79
172.65
2
0.94
2575.50
90.99
3
1.25
2569.69
93.17
4
1.32
2564.91
187.94
5
1.51
2561.06
203.82
6
1.63
2558.33
113.02
7
1.89
2557.98
81.80
8
2.21
2555.82
187.31
9
2.47
2555.31
169.06
10
5.14
2554.05
270.92
11
5.35
2552.04
90.38
12
5.47
2551.51
337.56
13
1000.00
2551.51
33.19
Anexo 27. – Datos de Entrada Alcantarillado Pluvial. Caso 3
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.02
2587.34
0.00
1
0.09
2576.79
172.65
2
0.19
2575.50
90.99
3
0.25
2569.69
93.17
4
0.26
2564.91
187.94
5
0.30
2561.06
203.82
6
0.33
2558.33
113.02
7
0.38
2557.98
81.80
8
0.44
2555.82
187.31
9
0.49
2555.31
169.06
10
1.03
2554.05
270.92
11
1.07
2552.04
90.38
12
1.09
2551.51
337.56
13
1000.00
2551.51
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
139
Anexo 28. – Datos de Entrada Alcantarillado Pluvial. Caso 3
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.22
1293.67
0.00
1
0.91
1288.40
172.65
2
1.88
1287.75
90.99
3
2.50
1284.85
93.17
4
2.64
1282.46
187.94
5
3.02
1280.53
203.82
6
3.26
1279.17
113.02
7
3.77
1278.99
81.80
8
4.42
1277.91
187.31
9
4.93
1277.66
169.06
10
10.28
1277.03
270.92
11
10.70
1276.02
90.38
12
10.94
1275.76
337.56
13
1000.00
1275.76
33.19
Anexo 29. – Datos de Entrada Alcantarillado Pluvial. Caso 4
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.22
3881.00
0.00
1
0.91
3865.18
172.65
2
1.88
3863.25
90.99
3
2.50
3854.54
93.17
4
2.64
3847.36
187.94
5
3.02
3841.60
203.82
6
3.26
3837.49
113.02
7
3.77
3836.97
81.80
8
4.42
3833.73
187.31
9
4.93
3832.97
169.06
10
10.28
3831.08
270.92
11
10.70
3828.06
90.38
12
10.94
3827.26
337.56
13
1000.00
3827.26
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
140
Anexo 30. – Datos de Entrada Alcantarillado Pluvial. Caso 5
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.22
25.87
0.00
1
0.91
25.77
172.65
2
1.88
25.76
90.99
3
2.50
25.70
93.17
4
2.64
25.65
187.94
5
3.02
25.61
203.82
6
3.26
25.58
113.02
7
3.77
25.58
81.80
8
4.42
25.56
187.31
9
4.93
25.55
169.06
10
10.28
25.54
270.92
11
10.70
25.52
90.38
12
10.94
25.52
337.56
13
1000.00
25.52
33.19
Anexo 31. – Datos de Entrada Alcantarillado Pluvial. Caso 6
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.33
2587.34
0.00
1
1.37
2576.79
172.65
2
2.82
2575.50
90.99
3
3.75
2569.69
93.17
4
3.96
2564.91
187.94
5
4.53
2561.06
203.82
6
4.89
2558.33
113.02
7
5.66
2557.98
81.80
8
6.63
2555.82
187.31
9
7.40
2555.31
169.06
10
15.42
2554.05
270.92
11
16.05
2552.04
90.38
12
16.41
2551.51
337.56
13
1000.00
2551.51
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
141
Anexo 32. – Datos de Entrada Alcantarillado Pluvial. Caso 7
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.33
25.87
0.00
1
1.37
25.77
172.65
2
2.82
25.76
90.99
3
3.75
25.70
93.17
4
3.96
25.65
187.94
5
4.53
25.61
203.82
6
4.89
25.58
113.02
7
5.66
25.58
81.80
8
6.63
25.56
187.31
9
7.40
25.55
169.06
10
15.42
25.54
270.92
11
16.05
25.52
90.38
12
16.41
25.52
337.56
13
1000.00
25.52
33.19
Anexo 33. – Datos de Entrada Alcantarillado Pluvial. Caso 8
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.33
3881.01
0.00
1
1.37
3865.19
172.65
2
2.82
3863.25
90.99
3
3.75
3854.54
93.17
4
3.96
3847.37
187.94
5
4.53
3841.59
203.82
6
4.89
3837.50
113.02
7
5.66
3836.97
81.80
8
6.63
3833.73
187.31
9
7.40
3832.97
169.06
10
15.42
3831.08
270.92
11
16.05
3828.06
90.38
12
16.41
3827.27
337.56
13
1000.00
3827.27
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
142
Anexo 34. – Resultados tabulares de diseños para el Caso 2.
Tubo Pendiente Diámetro
1
0.03051
0.2
2
0.007143
0.2
3
0.032183
0.2
4
0.012184
0.2
5
0.009959
0.2
6
0.011148
0.2
7
0.005868
0.2
8
0.005232
0.2
9
0.005028
0.25
10
0.005278
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
V = 0.3 m/s
Tubo Pendiente Diámetro
1
0.03051
0.2
2
0.007143
0.2
3
0.032183
0.2
4
0.012184
0.2
5
0.009959
0.2
6
0.011148
0.2
7
0.005868
0.2
8
0.005232
0.2
9
0.005028
0.25
10
0.005278
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
V = 0.45 m/s
Tubo Pendiente Diámetro
1
0.03051
0.2
2
0.008242
0.2
3
0.031111
0.2
4
0.012184
0.2
5
0.009959
0.2
6
0.011148
0.2
7
0.005868
0.2
8
0.005232
0.2
9
0.005028
0.25
10
0.005278
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
V = 0.6 m/s
Tubo Pendiente Diámetro
1
0.03051
0.2
2
0.007143
0.2
3
0.032183
0.2
4
0.012184
0.2
5
0.009959
0.2
6
0.011148
0.2
7
0.005868
0.2
8
0.005232
0.2
9
0.005028
0.25
10
0.005278
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
τ = 1 Pa
Tubo Pendiente Diámetro
1
0.03051
0.2
2
0.007143
0.2
3
0.032183
0.2
4
0.012184
0.2
5
0.009959
0.2
6
0.011148
0.2
7
0.005868
0.2
8
0.005232
0.2
9
0.005028
0.25
10
0.005278
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
τ = 1.5 Pa
Tubo Pendiente Diámetro
1
0.03051
0.2
2
0.008242
0.2
3
0.031111
0.2
4
0.012184
0.2
5
0.009959
0.2
6
0.011148
0.2
7
0.005868
0.2
8
0.005232
0.2
9
0.005028
0.25
10
0.005278
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
τ = 2 Pa
Tubo Pendiente Diámetro
1
0.03051
0.2
2
0.007143
0.2
3
0.032183
0.2
4
0.012184
0.2
5
0.009959
0.2
6
0.011148
0.2
7
0.005868
0.2
8
0.005232
0.2
9
0.005028
0.25
10
0.005278
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
Macke (1982)
Tubo Pendiente Diámetro
1
0.03051
0.2
2
0.007143
0.2
3
0.032183
0.2
4
0.012184
0.2
5
0.009959
0.2
6
0.011148
0.2
7
0.005868
0.2
8
0.005232
0.2
9
0.005028
0.25
10
0.005278
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
ASCE (2009)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
143
Anexo 35. – Resultados tabulares de diseños para el Caso 3.
Tubo Pendiente Diámetro
1
0.018879
0.2
2
0.005385
0.2
3
0.0176
0.2
4
0.007662
0.2
5
0.005152
0.2
6
0.00814
0.2
7
0.005012
0.2
8
0.005018
0.2
9
0.005087
0.25
10
0.005057
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
V = 0.3 m/s
Tubo Pendiente Diámetro
1
0.018879
0.2
2
0.005385
0.2
3
0.0176
0.2
4
0.007662
0.2
5
0.005152
0.2
6
0.00814
0.2
7
0.005012
0.2
8
0.005018
0.2
9
0.005087
0.25
10
0.005057
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
V = 0.45 m/s
Tubo Pendiente Diámetro
1
0.020615
0.2
2
0.008682
0.2
3
0.011162
0.2
4
0.007662
0.2
5
0.005152
0.2
6
0.00814
0.2
7
0.005012
0.2
8
0.005018
0.2
9
0.005087
0.25
10
0.005057
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
V = 0.6 m/s
Tubo Pendiente Diámetro
1
0.018879
0.2
2
0.005385
0.2
3
0.0176
0.2
4
0.007662
0.2
5
0.005152
0.2
6
0.00814
0.2
7
0.005012
0.2
8
0.005018
0.2
9
0.005087
0.25
10
0.005057
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
τ = 1 Pa
Tubo Pendiente Diámetro
1
0.018879
0.2
2
0.006484
0.2
3
0.016527
0.2
4
0.007662
0.2
5
0.005152
0.2
6
0.00814
0.2
7
0.005012
0.2
8
0.005018
0.2
9
0.005087
0.25
10
0.005057
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
τ = 1.5 Pa
Tubo Pendiente Diámetro
1
0.018879
0.2
2
0.008682
0.2
3
0.014381
0.2
4
0.007662
0.2
5
0.005152
0.2
6
0.00814
0.2
7
0.005012
0.2
8
0.005018
0.2
9
0.005087
0.25
10
0.005057
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
τ = 2 Pa
Tubo Pendiente Diámetro
1
0.018879
0.2
2
0.005385
0.2
3
0.0176
0.2
4
0.007662
0.2
5
0.005152
0.2
6
0.00814
0.2
7
0.005012
0.2
8
0.005018
0.2
9
0.005087
0.25
10
0.005057
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
Macke (1982)
Tubo Pendiente Diámetro
1
0.018879
0.2
2
0.005385
0.2
3
0.0176
0.2
4
0.007662
0.2
5
0.005152
0.2
6
0.00814
0.2
7
0.005012
0.2
8
0.005018
0.2
9
0.005087
0.25
10
0.005057
0.25
11
0.005643
0.25
12
0.005214
0.25
13
0.006026
0.25
ASCE (2009)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
144
Anexo 36. – Resultados tabulares de diseños para el Caso 4.
Tubo Pendiente Diámetro
1
0.006082
0.2
2
0.005825
0.2
3
0.005152
0.2
4
0.005214
0.2
5
0.005299
0.2
6
0.005132
0.2
7
0.005257
0.2
8
0.005445
0.2
9
0.005028
0.25
10
0.005241
0.25
11
0.005643
0.25
12
0.005184
0.25
13
0.006026
0.25
V = 0.3 m/s
Tubo Pendiente Diámetro
1
0.008977
0.2
2
0.005825
0.2
3
0.005152
0.2
4
0.005214
0.2
5
0.005299
0.2
6
0.005132
0.2
7
0.005257
0.2
8
0.005445
0.2
9
0.005028
0.25
10
0.005241
0.25
11
0.005643
0.25
12
0.005184
0.25
13
0.006026
0.25
V = 0.45 m/s
Tubo Pendiente Diámetro
1
0.020557
0.2
2
0.008023
0.2
3
0.006225
0.2
4
0.005214
0.2
5
0.005299
0.2
6
0.005132
0.2
7
0.005257
0.2
8
0.005445
0.2
9
0.005028
0.25
10
0.005241
0.25
11
0.005643
0.25
12
0.005184
0.25
13
0.006026
0.25
V = 0.6 m/s
Tubo Pendiente Diámetro
1
0.006082
0.2
2
0.005825
0.2
3
0.005152
0.2
4
0.005214
0.2
5
0.005299
0.2
6
0.005132
0.2
7
0.005257
0.2
8
0.005445
0.2
9
0.005028
0.25
10
0.005241
0.25
11
0.005643
0.25
12
0.005184
0.25
13
0.006026
0.25
τ = 1 Pa
Tubo Pendiente Diámetro
1
0.010715
0.2
2
0.005825
0.2
3
0.005152
0.2
4
0.005214
0.2
5
0.005299
0.2
6
0.005132
0.2
7
0.005257
0.2
8
0.005445
0.2
9
0.005028
0.25
10
0.005241
0.25
11
0.005643
0.25
12
0.005184
0.25
13
0.006026
0.25
τ = 1.5 Pa
Tubo Pendiente Diámetro
1
0.015347
0.2
2
0.008023
0.2
3
0.006225
0.2
4
0.005214
0.2
5
0.005299
0.2
6
0.005132
0.2
7
0.005257
0.2
8
0.005445
0.2
9
0.005028
0.25
10
0.005241
0.25
11
0.005643
0.25
12
0.005184
0.25
13
0.006026
0.25
τ = 2 Pa
Tubo Pendiente Diámetro
1
0.006082
0.2
2
0.005825
0.2
3
0.005152
0.2
4
0.005214
0.2
5
0.005299
0.2
6
0.005132
0.2
7
0.005257
0.2
8
0.005445
0.2
9
0.005028
0.25
10
0.005241
0.25
11
0.005643
0.25
12
0.005184
0.25
13
0.006026
0.25
Macke (1982)
Tubo Pendiente Diámetro
1
0.006082
0.2
2
0.005825
0.2
3
0.005152
0.2
4
0.005214
0.2
5
0.005299
0.2
6
0.005132
0.2
7
0.005257
0.2
8
0.005445
0.2
9
0.005028
0.25
10
0.005241
0.25
11
0.005643
0.25
12
0.005184
0.25
13
0.006026
0.25
ASCE (2009)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
145
Anexo 37. – Resultados tabulares de diseños para el Caso 5.
Tubo Pendiente Diámetro
1
0.005387
0.2
2
0.005055
0.2
3
0.005366
0.2
4
0.00548
0.2
5
0.005397
0.2
6
0.005574
0.2
7
0.005134
0.2
8
0.005392
0.2
9
0.005442
0.25
10
0.005057
0.25
11
0.005532
0.25
12
0.005095
0.25
13
0.006026
0.25
V = 0.3 m/s
Tubo Pendiente Diámetro
1
0.009441
0.2
2
0.005055
0.2
3
0.005366
0.2
4
0.00548
0.2
5
0.005397
0.2
6
0.005574
0.2
7
0.005134
0.2
8
0.005392
0.2
9
0.006033
0.2
10
0.005057
0.25
11
0.005532
0.25
12
0.005095
0.25
13
0.006026
0.25
V = 0.45 m/s
Tubo Pendiente Diámetro
1
0.020442
0.2
2
0.008352
0.2
3
0.005366
0.2
4
0.00548
0.2
5
0.005397
0.2
6
0.005574
0.2
7
0.005134
0.2
8
0.005392
0.2
9
0.006033
0.2
10
0.005057
0.25
11
0.005532
0.25
12
0.005095
0.25
13
0.006026
0.25
V = 0.6 m/s
Tubo Pendiente Diámetro
1
0.006545
0.2
2
0.005055
0.2
3
0.005366
0.2
4
0.00548
0.2
5
0.005397
0.2
6
0.005574
0.2
7
0.005134
0.2
8
0.005392
0.2
9
0.005442
0.25
10
0.005057
0.25
11
0.005532
0.25
12
0.005095
0.25
13
0.006026
0.25
τ = 1 Pa
Tubo Pendiente Diámetro
1
0.010599
0.2
2
0.006154
0.2
3
0.005366
0.2
4
0.00548
0.2
5
0.005397
0.2
6
0.005574
0.2
7
0.005134
0.2
8
0.005392
0.2
9
0.006033
0.2
10
0.005057
0.25
11
0.005532
0.25
12
0.005095
0.25
13
0.006026
0.25
τ = 1.5 Pa
Tubo Pendiente Diámetro
1
0.015231
0.2
2
0.008352
0.2
3
0.00644
0.2
4
0.00548
0.2
5
0.005397
0.2
6
0.005574
0.2
7
0.005134
0.2
8
0.005392
0.2
9
0.006033
0.2
10
0.005057
0.25
11
0.005532
0.25
12
0.005095
0.25
13
0.006026
0.25
τ = 2 Pa
Tubo Pendiente Diámetro
1
0.005387
0.2
2
0.005055
0.2
3
0.005366
0.2
4
0.00548
0.2
5
0.005397
0.2
6
0.005574
0.2
7
0.005134
0.2
8
0.005392
0.2
9
0.005442
0.25
10
0.005057
0.25
11
0.005532
0.25
12
0.005095
0.25
13
0.006026
0.25
Macke (1982)
Tubo Pendiente Diámetro
1
0.005387
0.2
2
0.005055
0.2
3
0.005366
0.2
4
0.00548
0.2
5
0.005397
0.2
6
0.005574
0.2
7
0.005134
0.2
8
0.005392
0.2
9
0.005442
0.25
10
0.005057
0.25
11
0.005532
0.25
12
0.005095
0.25
13
0.006026
0.25
ASCE (2009)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
146
Anexo 38. – Resultados gráficos de diseño para el Caso 2.
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.3 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.45 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.6 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 1 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 1.5 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 2 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
Macke (1982)
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
TF (2009)
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
147
Anexo 39. – Resultados gráficos de diseño para el Caso 3.
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.3 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.45 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.6 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 1 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 1.5 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 2 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
Macke (1982)
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
TF (2009)
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
148
Anexo 40. – Resultados gráficos de diseño para el Caso 4.
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.3 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.45 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.6 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 1 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 1.5 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 2 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
Macke (1982)
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
TF (2009)
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
149
Anexo 41. – Resultados gráficos de diseño para el Caso 5.
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.3 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.45 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.6 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 1 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 1.5 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 2 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
Macke (1982)
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
TF (2009)
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
150
Anexo 42. – Resultados gráficos de diseño para el Caso 6.
Anexo 43. – Datos de entrada. Corrida 01_Caso 1.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.001
2587.34
0.00
1
0.002
2576.79
172.65
2
0.003
2575.50
90.99
3
0.004
2569.69
93.17
4
0.005
2564.91
187.94
5
0.006
2561.06
203.82
6
0.007
2558.33
113.02
7
0.008
2557.98
81.80
8
0.009
2555.82
187.31
9
0.010
2555.31
169.06
10
0.011
2554.05
270.92
11
0.012
2552.04
90.38
12
0.013
2551.51
337.56
13
1000
2551.51
33.19
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.3 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.45 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
v = 0.6 m/s
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 1 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 1.5 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
τ = 2 Pa
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
Macke (1982)
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños
0.1
1
0.0000
0.0001
0.0010
0.0100
0.1000
1.0000
Pendiente
TF (2009)
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
τ = 1 Pa
τ = 1.5 Pa
τ = 2 Pa
Macke (1982)
Tractive Force
v = 5 m/s
Diseños

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
151
Anexo 44. – Datos de entrada. Corrida 01_Caso 2.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.001
1293.67
0.00
1
0.002
1288.40
172.65
2
0.003
1287.75
90.99
3
0.004
1284.85
93.17
4
0.005
1282.46
187.94
5
0.006
1280.53
203.82
6
0.007
1279.17
113.02
7
0.008
1278.99
81.80
8
0.009
1277.91
187.31
9
0.010
1277.66
169.06
10
0.011
1277.03
270.92
11
0.012
1276.02
90.38
12
0.013
1275.76
337.56
13
1000
1275.76
33.19
Anexo 45. – Datos de entrada. Corrida 01_Caso 3.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.001
776.20
0.00
1
0.002
773.04
172.65
2
0.003
772.65
90.99
3
0.004
770.91
93.17
4
0.005
769.47
187.94
5
0.006
768.32
203.82
6
0.007
767.50
113.02
7
0.008
767.39
81.80
8
0.009
766.75
187.31
9
0.010
766.59
169.06
10
0.011
766.22
270.92
11
0.012
765.61
90.38
12
0.013
765.45
337.56
13
1000
765.45
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
152
Anexo 46. – Datos de entrada. Corrida 01_Caso 4.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.001
258.73
0.00
1
0.002
257.68
172.65
2
0.003
257.55
90.99
3
0.004
256.97
93.17
4
0.005
256.49
187.94
5
0.006
256.11
203.82
6
0.007
255.83
113.02
7
0.008
255.80
81.80
8
0.009
255.58
187.31
9
0.010
255.53
169.06
10
0.011
255.41
270.92
11
0.012
255.20
90.38
12
0.013
255.15
337.56
13
1000
255.15
33.19
Anexo 47. – Datos de entrada. Corrida 01_Caso 5.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.001
129.37
0.00
1
0.002
128.84
172.65
2
0.003
128.78
90.99
3
0.004
128.48
93.17
4
0.005
128.25
187.94
5
0.006
128.05
203.82
6
0.007
127.92
113.02
7
0.008
127.90
81.80
8
0.009
127.79
187.31
9
0.010
127.77
169.06
10
0.011
127.70
270.92
11
0.012
127.60
90.38
12
0.013
127.58
337.56
13
1000
127.58
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
153
Anexo 48. – Datos de entrada. Corrida 01_Caso 6.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.001
100.00
0.00
1
0.002
100.00
172.65
2
0.003
100.00
90.99
3
0.004
100.00
93.17
4
0.005
100.00
187.94
5
0.006
100.00
203.82
6
0.007
100.00
113.02
7
0.008
100.00
81.80
8
0.009
100.00
187.31
9
0.010
100.00
169.06
10
0.011
100.00
270.92
11
0.012
100.00
90.38
12
0.013
100.00
337.56
13
1000
100.00
33.19
Anexo 49. – Datos de entrada. Corrida 02_Caso 1.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.002
2587.34
0.00
1
0.004
2576.79
172.65
2
0.006
2575.50
90.99
3
0.008
2569.69
93.17
4
0.010
2564.91
187.94
5
0.012
2561.06
203.82
6
0.014
2558.33
113.02
7
0.016
2557.98
81.80
8
0.018
2555.82
187.31
9
0.020
2555.31
169.06
10
0.022
2554.05
270.92
11
0.024
2552.04
90.38
12
0.026
2551.51
337.56
13
1000
2551.51
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
154
Anexo 50. – Datos de entrada. Corrida 02_Caso 2.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.002
1293.67
0.00
1
0.004
1288.40
172.65
2
0.006
1287.75
90.99
3
0.008
1284.85
93.17
4
0.010
1282.46
187.94
5
0.012
1280.53
203.82
6
0.014
1279.17
113.02
7
0.016
1278.99
81.80
8
0.018
1277.91
187.31
9
0.020
1277.66
169.06
10
0.022
1277.03
270.92
11
0.024
1276.02
90.38
12
0.026
1275.76
337.56
13
1000
1275.76
33.19
Anexo 51. – Datos de entrada. Corrida 02_Caso 3.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.002
776.20
0.00
1
0.004
773.04
172.65
2
0.006
772.65
90.99
3
0.008
770.91
93.17
4
0.010
769.47
187.94
5
0.012
768.32
203.82
6
0.014
767.50
113.02
7
0.016
767.39
81.80
8
0.018
766.75
187.31
9
0.020
766.59
169.06
10
0.022
766.22
270.92
11
0.024
765.61
90.38
12
0.026
765.45
337.56
13
1000
765.45
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
155
Anexo 52. – Datos de entrada. Corrida 02_Caso 4.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.002
258.73
0.00
1
0.004
257.68
172.65
2
0.006
257.55
90.99
3
0.008
256.97
93.17
4
0.010
256.49
187.94
5
0.012
256.11
203.82
6
0.014
255.83
113.02
7
0.016
255.80
81.80
8
0.018
255.58
187.31
9
0.020
255.53
169.06
10
0.022
255.41
270.92
11
0.024
255.20
90.38
12
0.026
255.15
337.56
13
1000
255.15
33.19
Anexo 53. – Datos de entrada. Corrida 02_Caso 5.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.002
129.37
0.00
1
0.004
128.84
172.65
2
0.006
128.78
90.99
3
0.008
128.48
93.17
4
0.010
128.25
187.94
5
0.012
128.05
203.82
6
0.014
127.92
113.02
7
0.016
127.90
81.80
8
0.018
127.79
187.31
9
0.020
127.77
169.06
10
0.022
127.70
270.92
11
0.024
127.60
90.38
12
0.026
127.58
337.56
13
1000
127.58
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
156
Anexo 54. – Datos de entrada. Corrida 02_Caso 6.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.002
100.00
0.00
1
0.004
100.00
172.65
2
0.006
100.00
90.99
3
0.008
100.00
93.17
4
0.010
100.00
187.94
5
0.012
100.00
203.82
6
0.014
100.00
113.02
7
0.016
100.00
81.80
8
0.018
100.00
187.31
9
0.020
100.00
169.06
10
0.022
100.00
270.92
11
0.024
100.00
90.38
12
0.026
100.00
337.56
13
1000
100.00
33.19
Anexo 55. – Datos de entrada. Corrida 03_Caso 1.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0030
2587.34
0.00
1
0.0060
2576.79
172.65
2
0.0090
2575.50
90.99
3
0.0120
2569.69
93.17
4
0.0150
2564.91
187.94
5
0.0180
2561.06
203.82
6
0.0210
2558.33
113.02
7
0.0240
2557.98
81.80
8
0.0270
2555.82
187.31
9
0.0300
2555.31
169.06
10
0.0330
2554.05
270.92
11
0.0360
2552.04
90.38
12
0.0390
2551.51
337.56
13
1000
2551.51
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
157
Anexo 56. – Datos de entrada. Corrida 03_Caso 2.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0030
1293.67
0.00
1
0.0060
1288.40
172.65
2
0.0090
1287.75
90.99
3
0.0120
1284.85
93.17
4
0.0150
1282.46
187.94
5
0.0180
1280.53
203.82
6
0.0210
1279.17
113.02
7
0.0240
1278.99
81.80
8
0.0270
1277.91
187.31
9
0.0300
1277.66
169.06
10
0.0330
1277.03
270.92
11
0.0360
1276.02
90.38
12
0.0390
1275.76
337.56
13
1000
1275.76
33.19
Anexo 57. – Datos de entrada. Corrida 03_Caso 3.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0030
776.20
0.00
1
0.0060
773.04
172.65
2
0.0090
772.65
90.99
3
0.0120
770.91
93.17
4
0.0150
769.47
187.94
5
0.0180
768.32
203.82
6
0.0210
767.50
113.02
7
0.0240
767.39
81.80
8
0.0270
766.75
187.31
9
0.0300
766.59
169.06
10
0.0330
766.22
270.92
11
0.0360
765.61
90.38
12
0.0390
765.45
337.56
13
1000
765.45
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
158
Anexo 58. – Datos de entrada. Corrida 03_Caso 4.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0030
258.73
0.00
1
0.0060
257.68
172.65
2
0.0090
257.55
90.99
3
0.0120
256.97
93.17
4
0.0150
256.49
187.94
5
0.0180
256.11
203.82
6
0.0210
255.83
113.02
7
0.0240
255.80
81.80
8
0.0270
255.58
187.31
9
0.0300
255.53
169.06
10
0.0330
255.41
270.92
11
0.0360
255.20
90.38
12
0.0390
255.15
337.56
13
1000
255.15
33.19
Anexo 59. – Datos de entrada. Corrida 03_Caso 5.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0030
129.37
0.00
1
0.0060
128.84
172.65
2
0.0090
128.78
90.99
3
0.0120
128.48
93.17
4
0.0150
128.25
187.94
5
0.0180
128.05
203.82
6
0.0210
127.92
113.02
7
0.0240
127.90
81.80
8
0.0270
127.79
187.31
9
0.0300
127.77
169.06
10
0.0330
127.70
270.92
11
0.0360
127.60
90.38
12
0.0390
127.58
337.56
13
1000
127.58
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
159
Anexo 60. – Datos de entrada. Corrida 03_Caso 6.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.003
100.00
0.00
1
0.006
100.00
172.65
2
0.009
100.00
90.99
3
0.012
100.00
93.17
4
0.015
100.00
187.94
5
0.018
100.00
203.82
6
0.021
100.00
113.02
7
0.024
100.00
81.80
8
0.027
100.00
187.31
9
0.030
100.00
169.06
10
0.033
100.00
270.92
11
0.036
100.00
90.38
12
0.039
100.00
337.56
13
1000
100.00
33.19
Anexo 61. – Datos de entrada. Corrida 04_Caso 1.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0050
2587.34
0.00
1
0.0100
2576.79
172.65
2
0.0150
2575.50
90.99
3
0.0200
2569.69
93.17
4
0.0250
2564.91
187.94
5
0.0300
2561.06
203.82
6
0.0350
2558.33
113.02
7
0.0400
2557.98
81.80
8
0.0450
2555.82
187.31
9
0.0500
2555.31
169.06
10
0.0550
2554.05
270.92
11
0.0600
2552.04
90.38
12
0.0650
2551.51
337.56
13
1000
2551.51
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
160
Anexo 62. – Datos de entrada. Corrida 04_Caso 2.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0050
1293.67
0.00
1
0.0100
1288.40
172.65
2
0.0150
1287.75
90.99
3
0.0200
1284.85
93.17
4
0.0250
1282.46
187.94
5
0.0300
1280.53
203.82
6
0.0350
1279.17
113.02
7
0.0400
1278.99
81.80
8
0.0450
1277.91
187.31
9
0.0500
1277.66
169.06
10
0.0550
1277.03
270.92
11
0.0600
1276.02
90.38
12
0.0650
1275.76
337.56
13
1000
1275.76
33.19
Anexo 63. – Datos de entrada. Corrida 04_Caso 3.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0050
776.20
0.00
1
0.0100
773.04
172.65
2
0.0150
772.65
90.99
3
0.0200
770.91
93.17
4
0.0250
769.47
187.94
5
0.0300
768.32
203.82
6
0.0350
767.50
113.02
7
0.0400
767.39
81.80
8
0.0450
766.75
187.31
9
0.0500
766.59
169.06
10
0.0550
766.22
270.92
11
0.0600
765.61
90.38
12
0.0650
765.45
337.56
13
1000
765.45
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
161
Anexo 64. – Datos de entrada. Corrida 04_Caso 4.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0050
258.73
0.00
1
0.0100
257.68
172.65
2
0.0150
257.55
90.99
3
0.0200
256.97
93.17
4
0.0250
256.49
187.94
5
0.0300
256.11
203.82
6
0.0350
255.83
113.02
7
0.0400
255.80
81.80
8
0.0450
255.58
187.31
9
0.0500
255.53
169.06
10
0.0550
255.41
270.92
11
0.0600
255.20
90.38
12
0.0650
255.15
337.56
13
1000
255.15
33.19
Anexo 65. – Datos de entrada. Corrida 04_Caso 5.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0050
129.37
0.00
1
0.0100
128.84
172.65
2
0.0150
128.78
90.99
3
0.0200
128.48
93.17
4
0.0250
128.25
187.94
5
0.0300
128.05
203.82
6
0.0350
127.92
113.02
7
0.0400
127.90
81.80
8
0.0450
127.79
187.31
9
0.0500
127.77
169.06
10
0.0550
127.70
270.92
11
0.0600
127.60
90.38
12
0.0650
127.58
337.56
13
1000
127.58
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
162
Anexo 66. – Datos de entrada. Corrida 04_Caso 6.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.005
100.00
0.00
1
0.010
100.00
172.65
2
0.015
100.00
90.99
3
0.020
100.00
93.17
4
0.025
100.00
187.94
5
0.030
100.00
203.82
6
0.035
100.00
113.02
7
0.040
100.00
81.80
8
0.045
100.00
187.31
9
0.050
100.00
169.06
10
0.055
100.00
270.92
11
0.060
100.00
90.38
12
0.065
100.00
337.56
13
1000
100.00
33.19
Anexo 67. – Datos de entrada. Corrida 05_Caso 1.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0100
2587.34
0.00
1
0.0200
2576.79
172.65
2
0.0300
2575.50
90.99
3
0.0400
2569.69
93.17
4
0.0500
2564.91
187.94
5
0.0600
2561.06
203.82
6
0.0700
2558.33
113.02
7
0.0800
2557.98
81.80
8
0.0900
2555.82
187.31
9
0.1000
2555.31
169.06
10
0.1100
2554.05
270.92
11
0.1200
2552.04
90.38
12
0.1300
2551.51
337.56
13
1000
2551.51
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
163
Anexo 68. – Datos de entrada. Corrida 05_Caso 2.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0100
1293.67
0.00
1
0.0200
1288.40
172.65
2
0.0300
1287.75
90.99
3
0.0400
1284.85
93.17
4
0.0500
1282.46
187.94
5
0.0600
1280.53
203.82
6
0.0700
1279.17
113.02
7
0.0800
1278.99
81.80
8
0.0900
1277.91
187.31
9
0.1000
1277.66
169.06
10
0.1100
1277.03
270.92
11
0.1200
1276.02
90.38
12
0.1300
1275.76
337.56
13
1000
1275.76
33.19
Anexo 69. – Datos de entrada. Corrida 05_Caso 3.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0100
776.20
0.00
1
0.0200
773.04
172.65
2
0.0300
772.65
90.99
3
0.0400
770.91
93.17
4
0.0500
769.47
187.94
5
0.0600
768.32
203.82
6
0.0700
767.50
113.02
7
0.0800
767.39
81.80
8
0.0900
766.75
187.31
9
0.1000
766.59
169.06
10
0.1100
766.22
270.92
11
0.1200
765.61
90.38
12
0.1300
765.45
337.56
13
1000
765.45
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
164
Anexo 70. – Datos de entrada. Corrida 05_Caso 4.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0100
258.73
0.00
1
0.0200
257.68
172.65
2
0.0300
257.55
90.99
3
0.0400
256.97
93.17
4
0.0500
256.49
187.94
5
0.0600
256.11
203.82
6
0.0700
255.83
113.02
7
0.0800
255.80
81.80
8
0.0900
255.58
187.31
9
0.1000
255.53
169.06
10
0.1100
255.41
270.92
11
0.1200
255.20
90.38
12
0.1300
255.15
337.56
13
1000
255.15
33.19
Anexo 71. – Datos de entrada. Corrida 05_Caso 5.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.0100
129.37
0.00
1
0.0200
128.84
172.65
2
0.0300
128.78
90.99
3
0.0400
128.48
93.17
4
0.0500
128.25
187.94
5
0.0600
128.05
203.82
6
0.0700
127.92
113.02
7
0.0800
127.90
81.80
8
0.0900
127.79
187.31
9
0.1000
127.77
169.06
10
0.1100
127.70
270.92
11
0.1200
127.60
90.38
12
0.1300
127.58
337.56
13
1000
127.58
33.19

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
165
Anexo 72. – Datos de entrada. Corrida 05_Caso 6.
NODO CAUDAL [m3/s] COTA_RASANTE_IN [m] LONGITUD [m]
0
0.010
100.00
0.00
1
0.020
100.00
172.65
2
0.030
100.00
90.99
3
0.040
100.00
93.17
4
0.050
100.00
187.94
5
0.060
100.00
203.82
6
0.070
100.00
113.02
7
0.080
100.00
81.80
8
0.090
100.00
187.31
9
0.100
100.00
169.06
10
0.110
100.00
270.92
11
0.120
100.00
90.38
12
0.130
100.00
337.56
13
1000
100.00
33.19
Anexo 73. – Resultados Corrida 03.
Corrida 03. Aumento de caudal 3 L/s en cada nodo
Pendiente
1.76%
0.88%
0.53%
0.18%
0.09%
0.00%
Caso
1
2
3
4
5
6
v = 0.3 m/s
$ 31,380,138 $ 38,910,201 $ 48,193,688 $ 84,111,722 $ 31,380,138 $ 38,910,201
v = 0.45 m/s $ 31,380,138 $ 38,910,201 $ 48,193,688 $ 84,111,722 $ 31,380,138 $ 38,910,201
v = 0.6 m/s
$ 31,380,138 $ 38,910,201 $ 48,193,688 $ 84,111,722 $ 31,380,138 $ 38,910,201
τ = 1 Pa
$ 31,380,138 $ 38,910,201 $ 48,193,688 $ 84,111,722 $ 31,380,138 $ 38,910,201
τ = 1.5 Pa
$ 31,380,138 $ 38,910,201 $ 48,193,688 $ 84,111,722 $ 31,380,138 $ 38,910,201
τ = 2 Pa
$ 31,380,138 $ 38,910,201 $ 48,193,688 $ 84,111,722 $ 31,380,138 $ 38,910,201
Macke (1982) $ 31,380,138 $ 38,910,201 $ 48,193,688 $ 84,111,722 $ 31,380,138 $ 38,910,201
ASCE (2009) $ 31,380,138 $ 38,910,201 $ 48,193,688 $ 84,111,722 $ 31,380,138 $ 38,910,201
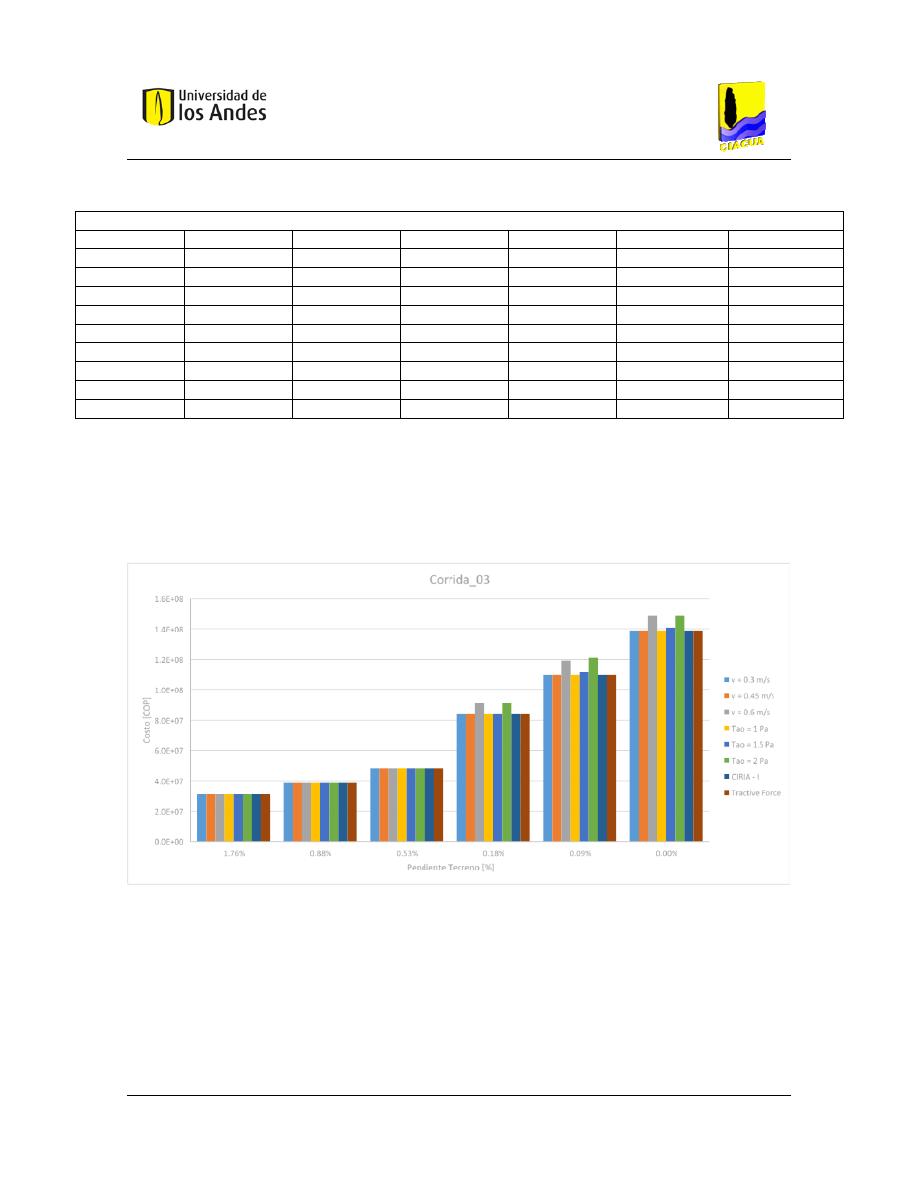
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
166
Anexo 74. – Resultados Corrida 04.
Corrida 04. Aumento de caudal 5 L/s en cada nodo
Pendiente
1.76%
0.88%
0.53%
0.18%
0.09%
0.00%
Caso
1
2
3
4
5
6
v = 0.3 m/s
$ 33,463,399 $ 43,418,178 $ 52,690,906 $ 92,191,076 $121,302,924 $153,685,208
v = 0.45 m/s $ 33,463,399 $ 43,418,178 $ 52,690,906 $ 92,191,076 $121,302,924 $153,685,208
v = 0.6 m/s
$ 33,463,399 $ 43,418,178 $ 52,690,906 $ 92,191,076 $121,302,924 $153,685,208
τ = 1 Pa
$ 33,463,399 $ 43,418,178 $ 52,690,906 $ 92,191,076 $121,302,924 $153,685,208
τ = 1.5 Pa
$ 33,463,399 $ 43,418,178 $ 52,690,906 $ 92,191,076 $121,302,924 $153,685,208
τ = 2 Pa
$ 33,463,399 $ 43,418,178 $ 52,690,906 $ 92,191,076 $121,302,924 $153,685,208
Macke (1982) $ 33,463,399 $ 43,418,178 $ 52,690,906 $ 92,191,076 $121,302,924 $153,685,208
ASCE (2009) $ 33,463,399 $ 43,418,178 $ 52,690,906 $ 92,191,076 $121,302,924 $153,685,208
Anexo 75. – Costos asociados a la Corrida 03.
0.0E+00
2.0E+07
4.0E+07
6.0E+07
8.0E+07
1.0E+08
1.2E+08
1.4E+08
1.6E+08
1.76%
0.88%
0.53%
0.18%
0.09%
0.00%
Cos
to
[
COP]
Pendiente Terreno [%]
Corrida_03
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
Tao = 1 Pa
Tao = 1.5 Pa
Tao = 2 Pa
CIRIA - I
Tractive Force
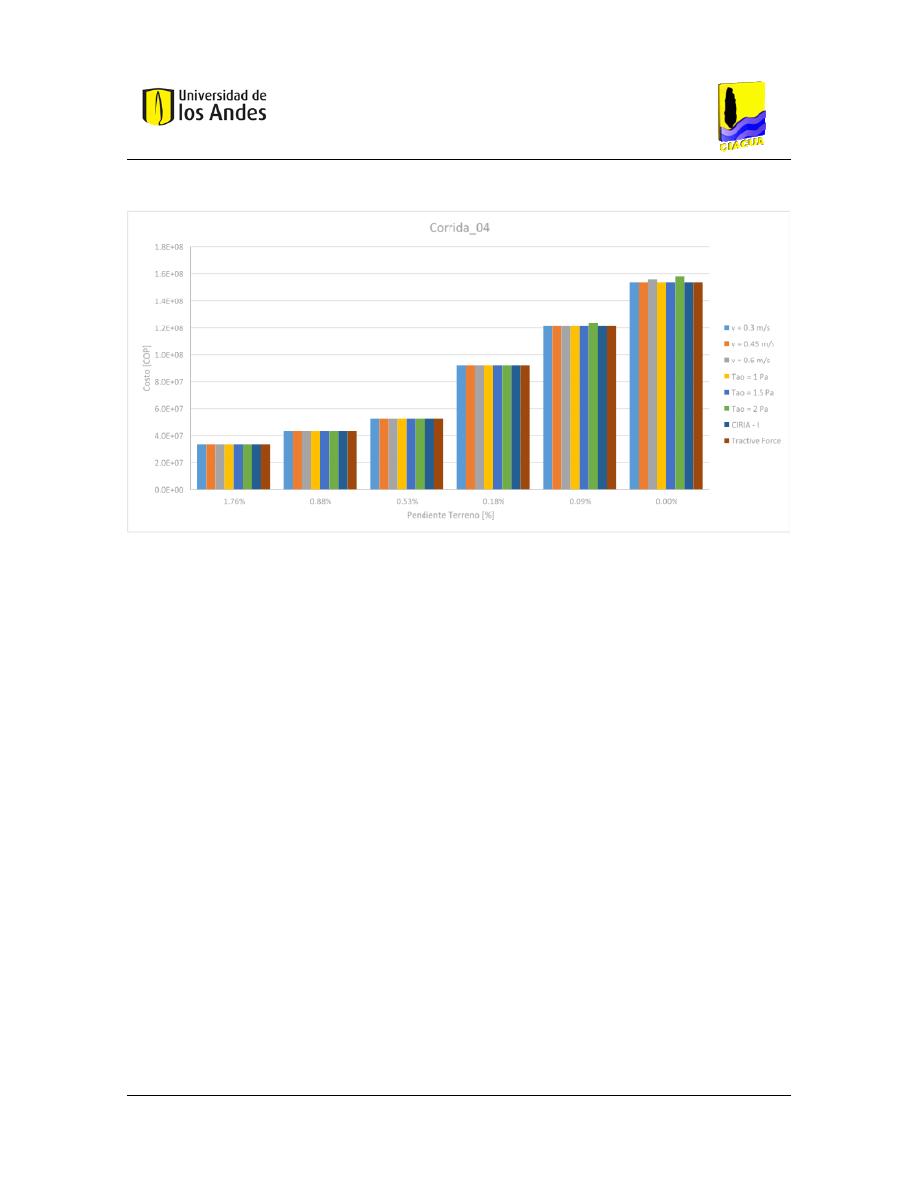
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Criterio de Esfuerzo Cortante Mínimo vs Velocidad Mínima para el Diseño
de Alcantarillados Autolimpiantes,
Carlos Daniel Montes
Tesis I
167
Anexo 76. – Costos asociados a la Corrida04.
0.0E+00
2.0E+07
4.0E+07
6.0E+07
8.0E+07
1.0E+08
1.2E+08
1.4E+08
1.6E+08
1.8E+08
1.76%
0.88%
0.53%
0.18%
0.09%
0.00%
Cos
to
[
COP]
Pendiente Terreno [%]
Corrida_04
v = 0.3 m/s
v = 0.45 m/s
v = 0.6 m/s
Tao = 1 Pa
Tao = 1.5 Pa
Tao = 2 Pa
CIRIA - I
Tractive Force
