
COMPORTAMIENTO HIDRÁULICO DE CÁMARAS DE UNIÓN BAJO
CONDICIONES DE FLUJO SUPERCRÍTICO
“XII Simposio Iberoamericano sobre planificación de sistemas de
abastecimiento y drenaje”
Juan Saldarriaga (1), Diego Páez (2), María Ximena Trujillo (3)
(1) Profesor Titular, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de
los Andes, Carrera 1 Este No. 19ª-40 Bogotá Colombia , 3394949 Ext: 2810 y
jsaldarr@uniandes..edu.co
(2) Profesor Instructor, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad
de los Andes, Carrera 1 Este No. 19ª-40 Bogotá Colombia, 3394949 Ext: 2810 y
da.paez27@uniandes.edu.co
(3) Investigadora, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de los
Andes,
Carrera
1
Este
No.
19ª-40
Bogotá
Colombia,
3394949
Ext:
2810y
mx.trujillo92@uniandes.edu.co
RESUMEN
Mediante un modelo de laboratorio de una cámara de unión se estudió el campo de flujo dominado por ondas
estacionarias. Probando diferentes escenarios y variando la relación de llenado de las tuberías de entrada
entre 20% y 85%, se identificó el patrón de flujo de acuerdo con las condiciones aguas arriba de la unión. Se
encontró que para mantener la capacidad de la cámara de unión, el diseño tradicional de la estructura debe
ser modificado. Por otro lado, se observó que cuando se forman curvas de remanso estas se desplazan hacia
la tubería de menor pendiente, favoreciendo la transición a flujo subcrítico.
Palabras claves: Cámaras de unión, modelo físico, drenaje urbano, interacciones estructura-ondas.
ABSTRACT
Hydraulics of supercritical flow across sewer junction manhole is explored using systematic
experimentation. Conduits’ filling ratios varied from 20% to 85% and flow scenarios were tested in order to
distinguish between diverse flow patterns, including shockwaves and hydraulic jumps. Different flow
regions were identified depending on the dynamic momentum components of the upstream flow. It was
found that, the common standard design of junction manhole with supercritical flow have to be revised.
Furthermore, when an inlet conduit has a hydraulic slope lower than 1%, backwater profile’s length expands
and prone the transition to subcritical flow.
Key words: Manholes, Laboratory study, sewer hydraulics, wave-structure interactions.
SOBRE EL AUTOR PRINCIPAL
Juan Saldarriaga: Profesor Titular de la Facultad de Ingeniería de la Universidad de los Andes. Área de
Recursos Hidráulicos, Departamento de Ingeniería Civil y Ambiental. Coordinador del Centro de Investigación
Estratégica del Agua (CIE-AGUA) de la Facultad de Ingeniería de la Universidad de los Andes. Director del
Centro de Investigaciones en Acueductos y Alcantarillados CIACUA del Departamento de Ingeniería Civil y
Ambiental de la Universidad de los Andes.
INTRODUCCIÓN
El flujo a la entrada de las cámaras de unión en
sistemas de alcantarillado puede ser subcrítico o
supercrítico. El flujo subcrítico puede ser tratado
como un flujo en una dimensión utilizando las
ecuaciones de energía con coeficientes de pérdida
apropiados. Pero el flujo supercrítico es no-uniforme
e inestable, por lo que necesita un tratamiento
bidimensional (2D) (Hager, 2010).
Ahora bien, la simulación adecuada de las
condiciones de unión es esencial para cualquier
modelo hidráulico de una red de alcantarillado, pues
si éstos no reflejan las condiciones físicas reales de
las uniones en la red, el efecto de utilizar ecuaciones
complejas para caracterizar el flujo no permanente a
través de las tuberías se anula (Bridge, 1984). La
descripción detallada de los patrones de ondas
estacionarias en los canales de unión fue presentada
por Schwalt y Hager en 1995. Más adelante, Del
Giudice & Hager (2001) y Hager (2002) estudiaron
la variación del campo de ondas de acuerdo con el
ángulo de entrada de las tuberías a la cámara de
unión. Encontraron que el comportamiento del
campo de flujo está dominado principalmente por el
número de Froude y la relación de llenado.
Gargano
&
Hager
(2001)
evaluaron
el
comportamiento de las cámaras de unión bajo flujo
supercrítico, obteniendo que la superficie libre está
dominada por la formación de ondas originadas por
el cambio de sección transversal de una tubería
circular a un canal en forma de U; También
concluyeron que las alturas relativas de la curva de
remanso menores a 0.25 no representaban un riesgo
de sobrecargar el sistema.
Hager (2010) llevó a cabo una serie de
experimentos para determinar el comportamiento
hidráulico de las cámaras de unión y de cambio de
dirección bajo flujo supercrítico. En este estudio se
propuso un diseño con extensiones en las uniones
laterales, para prevenir que la altura máxima de las
ondas
ocasionaran
daños
en
la
estructura.
Recientemente,
Saldarriaga
et
al.
(2011)
argumentaron que la complejidad del campo de flujo
ha impedido el desarrollo de ecuaciones analíticas y
a través de un estudio experimental estableció
información preliminar para encontrar ecuaciones de
diseño.
El propósito del estudio de este artículo es
identificar, en una cámara de unión simétrica, los
patrones de ondas de acuerdo con las condiciones
aguas
arriba
y
analizar
la
influencia
las
características de las ondas sobre la formación de
resaltos hidráulicos y curvas de remanso.
BASE TEÓRICA
El proceso de diseño de alcantarillados se basa en el
diseño de tuberías fluyendo parcialmente llenas, esto
suponiendo condiciones de flujo uniforme, es decir,
aquel flujo para el cual sus características
permanecen constantes en el espacio y en el tiempo.
Además, de acuerdo con el Título D del
Reglamento de Aguas y Saneamiento Básico del
Ministerio de Medio Ambiente de Colombia (RAS)
2011, cada uno de los tramos que forman parte del
sistema de alcantarillado debe diseñarse como un
conducto a flujo libre por gravedad, lo que implica
el uso de las ecuaciones de resistencia fluida para
una sección circular fluyendo parcialmente llena. La
ecuación más general para calcular las pérdidas por
fricción en ductos es la ecuación de Darcy-
Weisbach:
(1)
La ecuación anterior, describe la velocidad de flujo
(v) en función de la aceleración de la gravedad (g),
el radio hidráulico (R), la pendiente de la tubería (S),
la rugosidad del material del conducto (k
s
) y la
viscosidad cinemática del fluido (ν). En esta
investigación el número de Froude es definido
como:
(2)
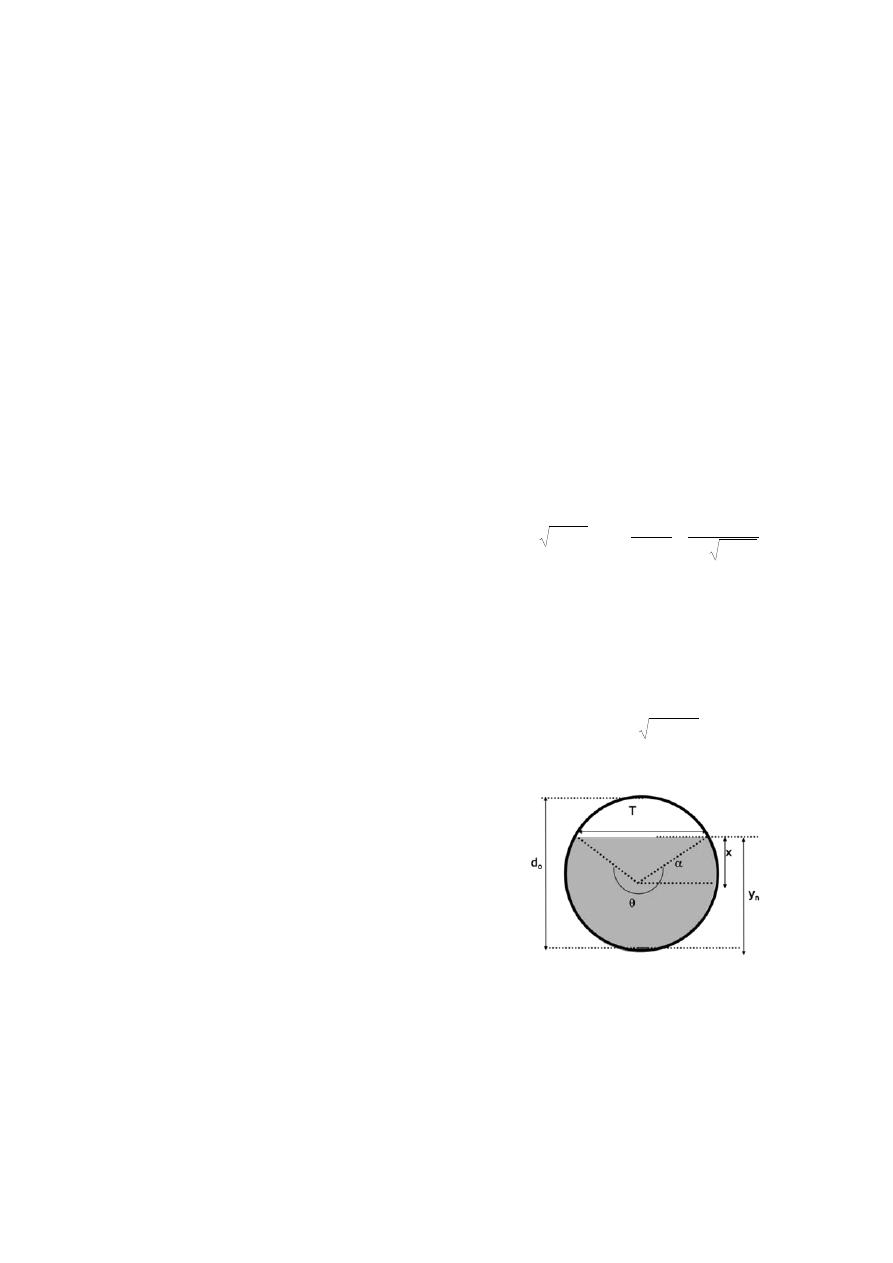
donde D = A/T es (Ver Figura 1).
Figura 1. Geometría de sección circular
fluyendo parcialmente llena.
Una vez definido el número de Froude para un
sección de escurrimiento circular, se adoptó la
caracterización del régimen de flujo supercrítico
adoptada por Hager & Gissoni (2005), donde se
especifican los límites entre un flujo subcrítico débil,
el flujo transicional, el flujo supercrítico y flujo
hipercrítico (ver Tabla 1).
gRS
R
R
k
gRS
v
s
8
4
51
.
2
8
.
14
log
8
2
10
)
/( gD
v
F

Tabla 1. Clasificación del flujo supercrítico a
partir del número de Froude.
Tomado de:
Gargano, R, Hager, W.H (2002).
Rango
Flujo
Características
0<F<0.7
Subcrítico
Débil
La superficie libre es casi
plana y hay efectos
dinámicos muy
pequeños; estos flujos
se comportan como flujo
a presión si F=0.
0.7<F<1.5
Transicional
Típicamente se
presentan ondas
superficiales y resaltos
hidráulicos.
1.5<F<3
Supercrítico
Flujo se comporta con
las características de
flujo dinámico.
F>3
Hipercrítico
Involucra dinámicas
fuertes de flujo, con un
alto potencial de daños
si el flujo es perturbado.
En la Tabla 1 se puede observar que una de las
características típicas del flujo transicional es la
presentación de ondas superficiales y resaltos
hidráulicos. El flujo supercrítico se caracteriza por
tener características de flujo dinámico, es decir, el
flujo se puede acelerar o desacelerar en cualquier
momento (Saldarriaga, 2011).
El modelo de onda dinámica normalmente es
utilizado para el cálculo hidráulico de los conductos
y canales que componen el sistema de alcantarillado
de zonas urbanas con pendientes de terreno muy
bajas. Sin embargo, hoy en día es evidente la
necesidad de implementar este modelo cuando el
flujo es supercrítico (Saldarriaga, 2011).
La formulación del problema requiere de dos
ecuaciones diferenciales que representan los
principios de continuidad y conservación de
momentum conocidas como ecuaciones de Saint-
Venant o ecuación de onda dinámica (Hager, 1994)
.
(3)
El primer y segundo término de la ecuación anterior,
representan la aceleración local y convectiva
respectivamente, por lo tanto su suma es el total de
fuerzas inerciales. El tercer término, es la suma de
las fuerzas de presión, fricción y pérdidas menores.
Por último se incluye una expresión para caudal
lateral por unidad de longitud, considerando el
coeficiente de Bousinesq ( ).
METODOLOGÍA
Los experimentos se realizaron en el Laboratorio de
Hidráulica de la Universidad de los Andes,
Colombia. Se probaron dos prototipos de modelos a
escala de las cámaras de unión. El primero,
fabricado en acrílico para observar fácilmente las
perturbaciones del flujo dado la unión (Figura 2a).
El segundo, un prototipo en polietileno utilizado
para la unión de tuberías de alcantarillado en PVC
(Figura 2b).
Figura 2. Modelos físicos probados a)
cámara de acrílico y b) cámara de
polietileno.
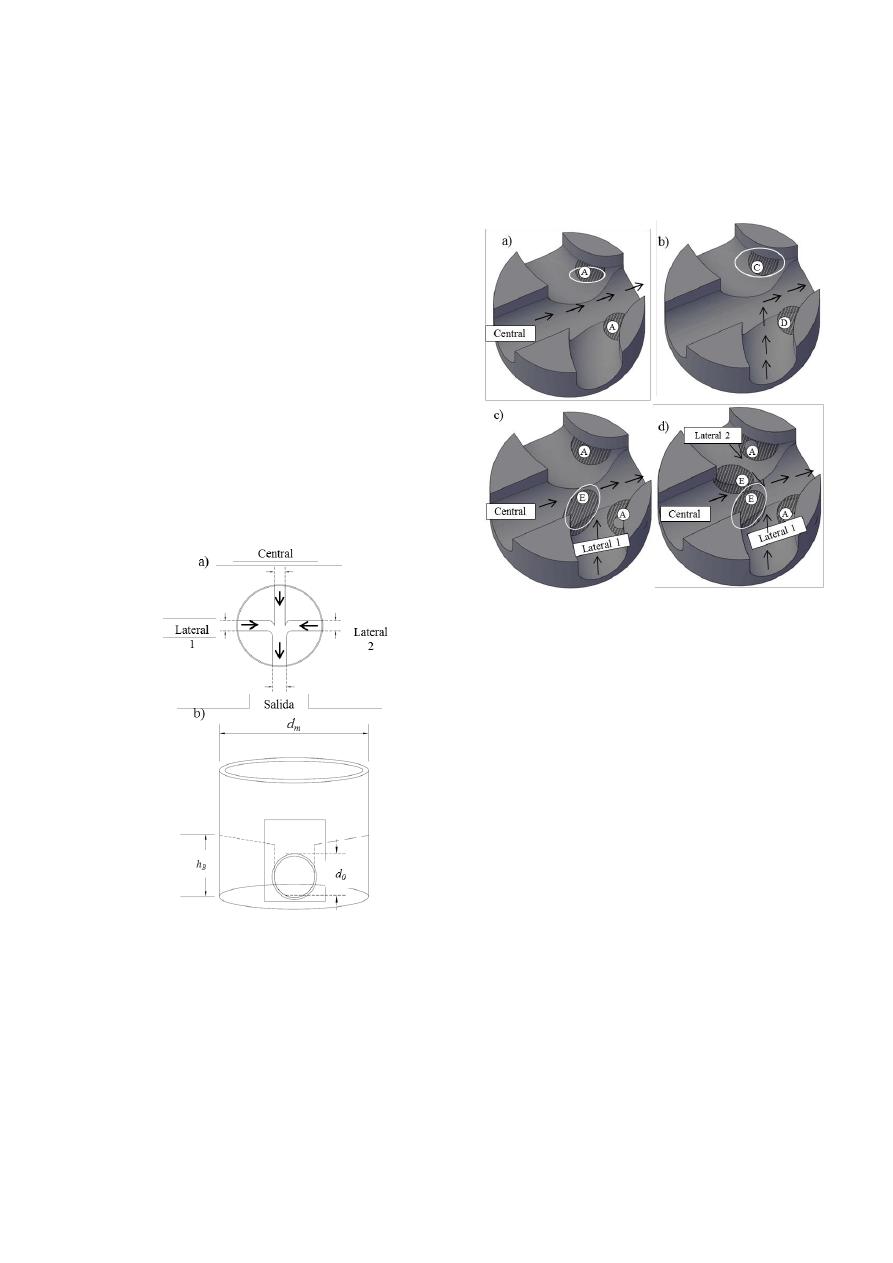
Las cámaras de unión eran simétricas, es decir,
tenían una central y dos laterales con un ángulo de
unión de 90° (Figura 3a). Las paredes de las
cañuelas (h
B
) cubrían completamente el diámetro de
las tuberías de entrada (d
0
) a lo que se le llama
cañuela completa. El diámetro de la cámara de unión
era 3.5d
0
, considerado como la proporción mínima
para que la unión tenga capacidad de recibir tres
entradas de caudal simultáneamente (Figura 3b). El
nivel del agua fue medido utilizando un sensor
ultrasónico con una precisión de ± 0.17mm.
Los parámetros independientes para cada tubería de
entrada (Subíndice Ax para Central, L1 para Lateral
1 y L2 para Lateral 2) eran: (1) Número de Froude
F
Ax
=Q
Ax
/(A
Ax
(gD
Ax
)
1/2
), F
L1
=Q
L1
/(A
L1
(gD
L1
)
1/2
) y
0
1
2
q
v
S
S
x
h
g
A
Q
x
A
t
Q
A
x
m
f
F
L2
=Q
L2
/(A
L2
(gD
L2
)
1/2
), (2) relación de llenado
Y=Y
n
/d
o
donde Y
n
= profundidad de flujo y d
o
=
diámetro de las tuberías de entrada y (3) las
pendientes de fondo de la tuberías de entrada S
Ax,
S
L1
y S
L2
.
Las relaciones de llenado de las tuberías de entrada
llegaron hasta 85% y los números de Froude
variaron entre 1.5 y 6.1; de esta forma se cubría todo
el espectro de número de Froude propuesto por
Gargano & Hager (2002). Las condiciones de flujo
variaban el número y dirección de los caudales de
entrada:
(1) Flujo Directo: se le denominó a probar caudales
por la tubería Central (Q
Ax
).
(2) Flujo Lateral 1: es enviar caudal por la tubería
Lateral 1 (Q
L1
).
(3) Unión de Flujos I: es la unión de flujos por la
tubería Lateral 1 y la tubería Central (Q
L1
-Q
Ax
).
(4)Unión de Flujos II: se le llama a la unión de flujos
por la tubería Lateral 1, Central y Lateral 2 (Q
L1
-Q
Ax
-Q
L2
).
Figura 3. Características geométricas de la
cámara a) simetría de las entradas, b)
parámetros de la cañuela.
RESULTADOS
En la cámara de unión se observaron cinco tipos de
ondas dependiendo del número y ángulo de los
caudales de entrada. La Onda A se presentaba
cuando las descargas laterales eran pequeñas y el
caudal central de entrada impactaba con las paredes
de la cañuela de salida (Figura 4a). La Onda B era la
confluencia a la salida de la cámara de las Ondas A.
La Onda C se formaba cuando el caudal lateral
impactaba el canal lateral opuesto (Figura 4b). La
Onda D se formaba como un reflejo de la Onda C en
la salida de la cámara. Finalmente, la Onda E era
característica de la unión de dos o más flujos en
diferente dirección (Figura 4c y 4d).
Figura 4. Clasificación de ondas generadas
en una cámara simétrica.
Flujo Directo
En la configuración de flujo más simple, donde el
flujo simplemente atraviesa la estructura de unión,
se formaron dos Ondas A (Figura 5a). Una en cada
uno de las paredes de la cañuela del canal central.
Además se formó una Onda B, la cual se desplazaba
hacia la salida de la cámara La altura máxima de las
Ondas A fue 0.38h
B
.
Flujo Lateral
El flujo lateral con un ángulo de entrada de 90°
representa una configuración típica de flujo en
alcantarillados, pues normalmente el trazado de la
red está bajo la malla vial. Se observaron dos tipos
de onda: C y D (Figura 5b).
La Onda C se formaba cuando el flujo lateral
impacta la cañuela del canal lateral opuesto.
Mientras que la Onda D, nunca se desarrollaba por sí
misma, sino que era un reflejo de la Onda C en la
salida de la cámara. A pesar de que la Onda C
siempre se desarrollaba en el mismo punto, el punto
de inicio se podía mover hacia aguas abajo si la
relación de llenado aumentaba. Por lo tanto, si la
onda se desarrollaba cerca de la tubería de salida, se
incrementaba el riesgo de sobrecarga. La altura
máxima de la Onda C fue 0.7h
B
.
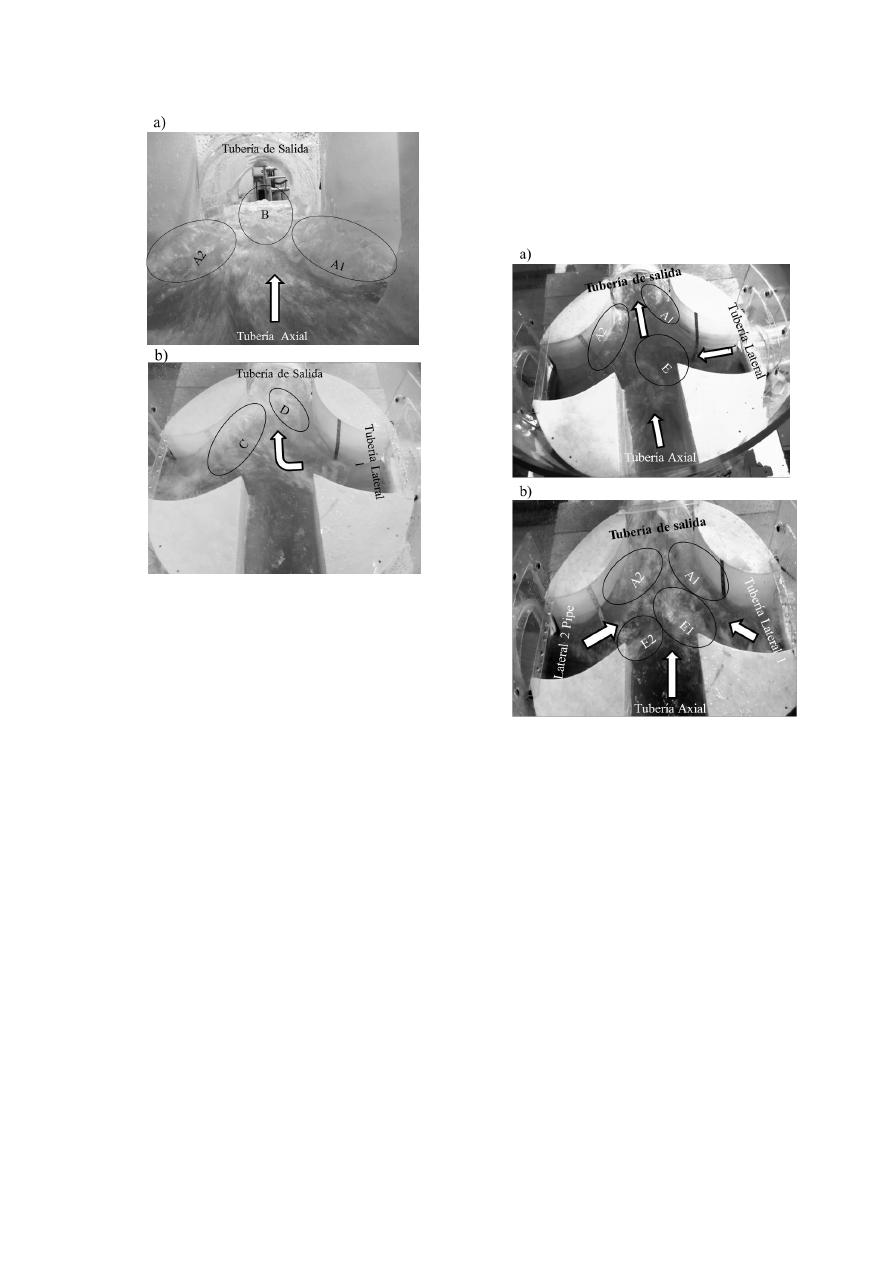
Figura 5. Campo de flujo a) Flujo Directo, b)
Flujo Lateral.
Unión de Flujos I
La coexistencia de un flujo lateral con el caudal que
entra por la tubería axial, recrea la situación en la
que la red de alcantarillado recolecta aguas
residuales o fluviales en diferentes puntos de un
centro urbano (Figura 6a).
Las Ondas A parecen ser dominantes en la tubería
central cuando Q
Ax
=0.9Q
L1
. Sin embargo, la onda
tipo E fue la que tuvo una altura máxima mayor,
pues la única manera de conservar el momentum en
la unión de dos flujos supercríticos en diferente
dirección es aumentar la profundidad. La Onda E
tuvo una altura máxima de 0.86h
B
y se localizaba el
centro de la cámara. Por lo tanto, podría llegar a
comprometer la capacidad la estructura de unión,
pues facilitaba la formación de una curva de
remanso cuya longitud se desplazaba hacia la tubería
de menor pendiente.
Unión de Flujos II
La unión de tres flujos representa una condición
crítica para la estructura de unión, pues ingresan tres
flujos supercríticos y ocurren dos cambios de
dirección simultáneamente. Se formaron cuatro
ondas: A1, A2, E1 y E2 (Figura 6b). La Onda A1 se
formaba cuando el caudal lateral 2 impactaba contra
el final del canal lateral 1. La Onda A2 se formaba
porque el caudal lateral 1 impactaba con el final del
canal lateral 2. Las ondas tipo E1 y E2 se
localizaban en los puntos de unión de los canales en
forma de U. La onda E1 fue la que obtuvo mayores
alturas máximas de onda cercanas a 0.73h
B.
La presencia de las ondas afectaba el régimen flujo
en la tubería central, pues se generaba un resalto
hidráulico a la entrada de la cámara que tendía a
desplazarse hace el conducto central.
Figura 6. Campo de flujo a) Unión de Flujos
I, b) Unión de Flujos II.
ANÁLISIS DE RESULTADOS
Análisis estadístico
Las ecuaciones preliminares de diseño describen la
altura máxima de las ondas en función de la relación
de llenado y el número de Froude de los conductos
de entrada. El ajuste estadístico se realizó mediante
un software estadístico y los resultados se
compararon con estudios anteriores realizados en la
Universidad de los Andes (Saldarriaga, 2011).
En la Tabla 2 se puede ver que la altura máxima de
la Onda E, característica de la unión de flujos en
diferente dirección, es inversamente proporcional al
número de Froude de la tubería Central (subíndice
Ax). Así mismo, se observa que los valores de los
coeficientes de determinación son altos, lo que
indica que las condiciones aguas arriba son
significativas para determinar la altura máxima de
las ondas.

Tabla 2. Altura máxima de las ondas en función
de la relación de las condiciones de aguas
arriba.
Ecuación
R
2
(1)
576
.
0
068
.
0
m ax
28
.
0
Ax
Ax
A
F
Y
h
0.73
(2)
438
.
0
1
671
.
0
1
m ax
18
.
2
L
L
C
F
Y
h
0.81
(3)
947
.
1
276
.
0
1
33
.
0
m ax
85
.
0
Ax
L
Ax
E
F
Y
Y
h
0.89
(4)
77
.
1
17
.
3
2
615
.
0
733
.
0
2
m ax
127
.
0
Ax
L
Ax
L
E
F
F
Y
Y
h
0.91
Análisis de la curva de remanso
Considerando que en la tubería de menor pendiente
se observaron resaltos hidráulicos (Figura 7a) y
curvas de remanso (Figura 7b), se analizaron los
perfiles axiales de flujo en la tubería a fin de
identificar cuando existiría un potencial riesgo de
sobrecarga.
Los resultados de los experimentos realizados
muestran
que
cuando
el
flujo
está
los
suficientemente aguas arriba de la cámara de unión
es supercrítico a profundidad normal. Sin embargo,
inmediatamente aguas arriba de la unión el flujo es
subcrítico (Figura 8).
Figura 7. Efectos de las ondas superficiales
en la tubería de menor pendiente a) resalto
hidráulico, b) curva de remanso.
En diferentes escenarios se observó la formación de
una curva de remanso que en el caso más crítico
alcanzaba a desplazarse hasta 4 m aguas arriba de la
entrada a la cámara de unión (Figura 8). Por lo tanto,
si el diámetro de la cámara aumentara, incrementaría
la longitud de las cañuelas y sería posible contener la
altura máxima de la curva de remanso. De esta
forma se podría prevenir la sobrecarga en la tubería
de menor pendiente.
Figura 8. Perfil axial de flujo en la tubería
central.
Por otro lado, se determinó la relación entre la altura
relativa de la propagación de la curva de remanso Y
i
= (h
i
-h
0
)/h
i
la y el número de Froude supercrítico de
la tubería central. En la Figura 9, se puede observar
que las alturas relativas para la Unión de Flujos I y
II, fueron mayores a 0.25, lo que indica que el riesgo
de sobrecarga en la tubería de central.
Figura 9. Altura relativa de la curva de
remanso en función de F
1
(
▲
) Q
L1
-Q
Ax
, (
■
)
Q
L1
-Q
Ax
- Q
L2.
CONCLUSIONES Y
RECOMENDACIONES
En conclusión, el patrón de ondas que se forma
dentro de las cámaras de unión de flujo depende de
las condiciones hidráulicas del conducto dominante.
Las ondas tipo A son características del Flujo
Directo y no representan ningún tipo de riesgo para
la sobrecarga de la tubería. Las ondas tipo C son
típicas de un cambio de dirección en el flujo de
entrada. Las ondas tipo E, se dan por la unión de

flujos en diferentes direcciones y estas son las que
representan un mayor reto para el diseño de la
estructura, pues al incrementar la profundidad del
agua en la cámara se desacelera el flujo, provocando
curvas de remanso, cuyas profundidades relativas
pueden llegar a sobrecargar la tubería de menor
pendiente.
Ahora bien, en lo que respecta a la metodología
utilizada en dos montajes diferentes, se puede decir
que es válida para probar la operación de las
estructuras de unión de flujo. Es importante resaltar
la importancia de probar modelos con geometrías
suaves que favorezcan un flujo continuo y poco
perturbado al ingresar a la estructura de unión.
Para continuar con los experimentos en este tema se
recomienda probar cámaras simétricas con diferentes
caídas para caracterizar el efecto sobre el campo de
flujo de un cambio de energía y un cambio de
sección transversal. Asimismo, se podría construir
una cámara de unión e tres entradas con un diámetro
sea superior a 3.5 veces el diámetro de las tuberías
de entrada para ver si es posible evitar la
propagación de la curva de remanso dentro de los
conductos.
Se recomienda que una vez se haya determinado de
forma empírica los diferentes patrones sería
interesante desarrollar modelos computacionales que
resuelvan el modelo de onda dinámica dentro de la
cámaras de unión, de manera que permitieran
insertar la modelación de la unión a la modelación
hidráulica detallada de la red de alcantarillado.
BIBLIOGRAFÍA
Bridge S, 1984. A study of unsteady flow wave
attenuation in partially filled pipe networks. A thesis
submitted for the degree of Doctor Philosophy.
Department of Mechanical Engineering, Brunel
University, 104-199.
Del Giudice, G., Hager, W.H. (2001). Supercritical flow
in 45° junction manhole. J. Irrig. Drain. Eng. 127(2),
100–108.
Gargano, R., Hager, W.H. (2002). Supercritical flow
across sewer manholes. J. Hydraulic Eng. 128(11),
1014–1017.
Gisonni, C., Hager, W.H. (2002). Supercritical flow in
manholes with a bend extension. Exp. Fluids 32(3),
357–365.
Gisonni, C., Hager, W.H. (2002). Supercritical flow in the
90° junction. Urban Water 4(4), 363–372.
Hager, W.H. (2010). Wastewater hydraulics: Theory and
practice, ed. 2. Springer, Berlin.
Krüger, S., Rutschmann, P. (2000). Numerical sensitivity
analysis of supercritical confluences to inaccuracy of
upstream
boundary
conditions.
Proc.
Hydroinformatics Iowa [CD-ROM].
Schwalt, M., Hager, W.H. (1995). Experiments to
supercritical junction flow. Exp. Fluids 18(6), 429–
437.
Sturm T.W., 2010. Open Channel Hydraulics. McGraw-
Hill. Second Edition. Singapure.
Saldarriaga J., Bermúdez N., Rubio D. (2011) Hydraulic
behavior of junction manholes under supercritical
flow conditions. J. Hydraulic Research. 50(6) 631-
636.
Saldarriaga J., (2011) Notas de Clase de Hidráulica de
Drenaje Urbano.
Ministerio de Vivienda y Desarrollo Territorial,
República de Colombia (MVDT). Reglamento de Agua y
Saneamiento Básico, Título D. (2011)
