
Universidad de los Andes
Facultad De Ingeniería
Departamento de Ingeniería Civil y Ambiental
TESIS DE ESPECIALIZACIÓN
INGENIERÍA DE SISTEMAS HÍDRICOS URBANOS
COMPARACIÓN ENTRE LOS SOFTWARES WATERGEMS Y REDES,
EN LA MODELACIÓN HIDRÁULICA DE REDES DE DISTRIBUCIÓN
DE AGUA POTABLE
Preparado por:
Ing. Juan Camilo Vergara Valderrama
Asesor:
Ing. Juan Guillermo Saldarriaga Valderrama
Informe Final Tesis
Bogotá, 17 de Febrero de 2012

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
2
Juan Camilo Vergara Valderrama
TABLA DE CONTENIDO
INTRODUCCIÓN ....................................................................................................................................................... 7
1
ANTECEDENTES Y OBJETIVOS .................................................................................................................. 8
1.1
ANTECEDENTES .......................................................................................................................................... 8
1.1.1
Objetivos Generales ............................................................................................................................... 8
1.1.2
Objetivos Específicos ............................................................................................................................. 8
2
ESTADO DEL ARTE ........................................................................................................................................ 9
3
METODOLOGÍA............................................................................................................................................. 28
3.1
METODOLOGÍA
PARA
LA
ELABORACIÓN
DE
MODELOS
HIDRÁULICOS
EN
WATERGEMS ..... 28
3.1.1
Construcción de la topología de los modelos hidráulicos.................................................................... 28
3.1.2
Procedimiento para la evaluación de la topología creada. ................................................................. 33
3.1.3
Asignación de elevaciones a los nodos de los modelos hidráulicos. .................................................... 34
3.1.4
Procedimiento para la asignación de demandas a los nodos del modelo. ........................................... 34
3.1.5
Visualización de la red en el software WaterGems. ............................................................................. 35
3.1.6
Ejecución del modelo. .......................................................................................................................... 35
3.1.7
Generación de reportes. ....................................................................................................................... 37
3.2
METODOLOGÍA
PARA
LA
ELABORACIÓN
DE
MODELOS
HIDRÁULICOS
EN
REDES .................. 37
DATOS Y ANÁLISIS DE DATOS ........................................................................................................................... 41
3.3
DATOS .......................................................................................................................................................... 41
3.3.1
Datos para el modelo de la red de distribución de agua potable “Olivos I” ...................................... 41
3.3.2
Datos para el modelo de la red de distribución de agua potable “Olivos II” ..................................... 44
3.3.3
Datos para el modelo de la red de distribución de agua potable “Olivos IV” .................................... 47
3.4
TABLAS ........................................................................................................................................................ 50
3.4.1
Tablas de resultados de la modelación de redes de distribución de agua potable mediante el software
WaterGems ......................................................................................................................................................... 50
3.4.2
Tablas de resultados de la modelación de redes de distribución de agua potable mediante el software
Redes
……………………………………………………………………………………………………………………..77
4
CONCLUSIONES ............................................................................................................................................ 91
5
BIBLIOGRAFÍA .............................................................................................................................................. 92

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
3
Juan Camilo Vergara Valderrama
ÍNDICE DE FIGURAS
F
IGURA
1.
C
UADRO DE DIALOGO PRINCIPAL SOFTWARE
W
ATER
G
EMS
. ........................................................................ 28
F
IGURA
2.
H
ERRAMIENTAS BÁSICAS DEL SOFTWARE
W
ATER
G
EMS
. ............................................................................. 29
F
IGURA
3.
C
UADRO DE PROPIEDADES PARA CADA ELEMENTO
. ..................................................................................... 30
F
IGURA
4.
P
ASOS
3
Y
4
DEL PROCESO DE CONSTRUCCIÓN TOPOLÓGICA DE MODELOS HIDRÁULICOS
(
NODOS
). ............. 30
F
IGURA
5.
P
ASO
5
DEL PROCESO DE CONSTRUCCIÓN TOPOLÓGICA DE MODELOS HIDRÁULICOS
(
NODOS
). ..................... 31
F
IGURA
6.
P
ASOS
7,
8
Y
9
DEL PROCESO DE CONSTRUCCIÓN TOPOLÓGICA DE MODELOS HIDRÁULICOS
(
NODOS
). ......... 32
F
IGURA
7.
P
ASOS
2,
3
Y
4
DEL PROCESO DE CONSTRUCCIÓN TOPOLÓGICA DE MODELOS HIDRÁULICOS
(
TUBOS
). .......... 33
F
IGURA
8.
C
REACIÓN DE LAS ÁREAS
(H
ERRAMIENTA
P
OLÍGONOS DE
T
HIESSEN
). ........................................................ 34
F
IGURA
9.
T
OPOLOGÍA DE LA RED
. ................................................................................................................................ 35
F
IGURA
10.
F
IN DE CÁLCULO DE LA RED
. ...................................................................................................................... 36
F
IGURA
11.
G
ENERACIÓN DE REPORTES DE RESULTADOS
. ............................................................................................ 37
F
IGURA
12.
E
XPORTAR ARCHIVO A
E
PANET
. ................................................................................................................. 38
F
IGURA
13.
A
RCHIVO DE
E
XCEL
E
PANET
. ..................................................................................................................... 38
F
IGURA
14.
M
ODELO DE DISTRIBUCIÓN DE DATOS
E
PANET
. ......................................................................................... 39
F
IGURA
15.
M
ODELO DE DISTRIBUCIÓN DE DATOS
R
EDES
. ........................................................................................... 39
F
IGURA
16.
C
IRCUITO
O
LIVOS
I
MODELADO EN EL SOFTWARE
R
EDES
. ......................................................................... 40
F
IGURA
17.
C
IRCUITO
O
LIVOS
IV
MODELADO EN EL SOFTWARE
R
EDES
. ...................................................................... 40
F
IGURA
18.
L
OCALIZACIÓN GENERAL
,
BARRIO
L
OS
O
LIVOS
I. ...................................................................................... 41
F
IGURA
19.
L
OCALIZACIÓN GENERAL
,
BARRIO
L
OS
O
LIVOS
II. .................................................................................... 44
F
IGURA
20.
L
OCALIZACIÓN GENERAL
,
BARRIO
L
OS
O
LIVOS
IV. ................................................................................... 47

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
4
Juan Camilo Vergara Valderrama
ÍNDICE DE TABLAS
T
ABLA
1.
L
OCALIZACIÓN GEOGRÁFICA BARRIO
L
OS
O
LIVOS
I ..................................................................................... 42
T
ABLA
2.
D
ATOS DE POBLACIÓN A ABASTECER
O
LIVOS
I. ............................................................................................ 42
T
ABLA
3.
C
URVA DE CONSUMO APLICADA A LA RED PROYECTADA
. ............................................................................. 43
T
ABLA
4.
C
URVA DE PRESIONES APLICADA AL PUNTO DE ALIMENTACIÓN RED PROYECTADA
. ...................................... 44
T
ABLA
5.
L
OCALIZACIÓN GEOGRÁFICA BARRIO
L
OS
O
LIVOS
II. ................................................................................... 45
T
ABLA
6.
D
ATOS DE POBLACIÓN A ABASTECER
O
LIVOS
II. ........................................................................................... 45
T
ABLA
7.
C
URVA DE CONSUMO APLICADA A LA RED PROYECTADA
. ............................................................................. 46
T
ABLA
8.
C
URVA DE PRESIONES APLICADA AL PUNTO DE ALIMENTACIÓN RED PROYECTADA
. ...................................... 46
T
ABLA
9.
L
OCALIZACIÓN GEOGRÁFICA BARRIO
L
OS
O
LIVOS
IV. ................................................................................. 47
T
ABLA
10.
D
ATOS DE POBLACIÓN A ABASTECER
O
LIVOS
IV. ....................................................................................... 48
T
ABLA
11.
C
URVA DE CONSUMO APLICADA A LA RED PROYECTADA
. ........................................................................... 48
T
ABLA
12.
C
URVA DE PRESIONES APLICADA AL PUNTO DE ALIMENTACIÓN RED PROYECTADA
. .................................... 49
T
ABLA
13.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA NODO DE LA RED
(R
EPORTE
1). ......................... 50
T
ABLA
14.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA NODO DE LA RED
(R
EPORTE
2). ......................... 51
T
ABLA
15.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA NODO DE LA RED
(R
EPORTE
3). ......................... 52
T
ABLA
16.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA TUBO DE LA RED
(R
EPORTE
1). .......................... 53
T
ABLA
17.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA TUBO DE LA RED
(R
EPORTE
2). .......................... 54
T
ABLA
18.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA TUBO DE LA RED
(R
EPORTE
3). .......................... 55
T
ABLA
19.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA TUBO DE LA RED
(R
EPORTE
4). .......................... 56
T
ABLA
20.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA TUBO DE LA RED
(R
EPORTE
5). .......................... 57
T
ABLA
21.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA TUBO DE LA RED
(R
EPORTE
6). .......................... 58
T
ABLA
22.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA VÁLVULA DE LA RED
(R
EPORTE
1). ................... 59
T
ABLA
23.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA VÁLVULA DE LA RED
(R
EPORTE
2). ................... 60
T
ABLA
24.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA NODO DE LA RED
(R
EPORTE
1). ......................... 61
T
ABLA
25.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA NODO DE LA RED
(R
EPORTE
2). ......................... 62
T
ABLA
26.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA NODO DE LA RED
(R
EPORTE
3). ......................... 63
T
ABLA
27.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA NODO DE LA RED
(R
EPORTE
4). ......................... 64
T
ABLA
28.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
II
PARA CADA TUBO DE LA RED
(R
EPORTE
1). ........................ 65
T
ABLA
29.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
II
PARA CADA TUBO DE LA RED
(R
EPORTE
2). ........................ 66
T
ABLA
30.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
II
PARA CADA TUBO DE LA RED
(R
EPORTE
3). ........................ 67
T
ABLA
31.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
II
PARA CADA TUBO DE LA RED
(R
EPORTE
4). ........................ 68
T
ABLA
32.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
II
PARA CADA TUBO DE LA RED
(R
EPORTE
5). ........................ 69
T
ABLA
33.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
II
PARA CADA TUBO DE LA RED
(R
EPORTE
6). ........................ 70
T
ABLA
34.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
II
PARA CADA VÁLVULA DE LA RED
(R
EPORTE
1). .................. 71
T
ABLA
35.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
II
PARA CADA VÁLVULA DE LA RED
(R
EPORTE
2). .................. 72
T
ABLA
36.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
IV
PARA CADA NODO DE LA RED
(R
EPORTE
1). ...................... 73
T
ABLA
37.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
IV
PARA CADA TUBO DE LA RED
(R
EPORTE
1). ....................... 74
T
ABLA
38.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
IV
PARA CADA TUBO DE LA RED
(R
EPORTE
2). ....................... 75
T
ABLA
39.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
IV
PARA CADA VÁLVULA DE LA RED
(R
EPORTE
1). ................ 76
T
ABLA
40.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
IV
PARA CADA NODO DE LA RED
(R
EPORTE
1). ...................... 77
T
ABLA
41.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
IV
PARA CADA TUBO DE LA RED
(R
EPORTE
1). ....................... 78
T
ABLA
42.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
IV
PARA CADA TUBO DE LA RED
(R
EPORTE
2). ....................... 79
T
ABLA
43.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA NODO DE LA RED
(R
EPORTE
1). ......................... 80
T
ABLA
44.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA NODO DE LA RED
(R
EPORTE
2). ......................... 81
T
ABLA
45.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA NODO DE LA RED
(R
EPORTE
3). ......................... 82
T
ABLA
46.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA TUBO DE LA RED
(R
EPORTE
1). .......................... 83
T
ABLA
47.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA TUBO DE LA RED
(R
EPORTE
2). .......................... 84
T
ABLA
48.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA TUBO DE LA RED
(R
EPORTE
3). .......................... 85

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
5
Juan Camilo Vergara Valderrama
T
ABLA
49.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA TUBO DE LA RED
(R
EPORTE
4). .......................... 86
T
ABLA
50.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA TUBO DE LA RED
(R
EPORTE
5). .......................... 87
T
ABLA
51.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA TUBO DE LA RED
(R
EPORTE
6). .......................... 88
T
ABLA
52.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA TUBO DE LA RED
(R
EPORTE
7). .......................... 89
T
ABLA
53.
R
ESULTADOS DE MODELACIÓN RED
O
LIVOS
I
PARA CADA TUBO DE LA RED
(R
EPORTE
8). .......................... 90

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
6
Juan Camilo Vergara Valderrama
ÍNDICE DE ECUACIONES
E
CUACIÓN
1.
P
ÉRDIDAS TOTALES CON UN ERROR
ΔQ
I
. ................................................................................................. 13
E
CUACIÓN
2.
A
LTURA PIEZOMÉTRICA CON PERDIDAS TOTALES
. ................................................................................... 13
E
CUACIÓN
3.
A
LTURA PIEZOMÉTRICA CON PERDIDAS TOTALES SIMPLIFICADA
. ............................................................ 13
E
CUACIÓN
4.
S
UMA PÉRDIDAS TOTALES EN UNA RED
. .................................................................................................. 14
E
CUACIÓN
5.
S
UMA PÉRDIDAS TOTALES EN UNA RED
. .................................................................................................. 14
E
CUACIÓN
6.
D
ELTA DE CAUDAL
H
ARDY
-C
ROSS
(
CORRECCIÓN DE CAUDAL
). ............................................................. 14
E
CUACIÓN
7.
D
ELTA DE CAUDAL
H
ARDY
-C
ROSS
(
CORRECCIÓN DE CAUDAL
)
SIMPLIFICADA
. ...................................... 14
E
CUACIÓN
8.
C
AUDAL EXPRESADO EN FUNCIÓN DE LA CARGA HIDRÁULICA
. ............................................................... 15
E
CUACIÓN
9.
C
AUDAL EXPRESADO EN FUNCIÓN DE LA CARGA HIDRÁULICA MENOS UN
ΔH
I
. ....................................... 15
E
CUACIÓN
10.
C
AUDAL EXPRESADO EN FUNCIÓN DE LA CARGA HIDRÁULICA MENOS UN
ΔH
I
. ..................................... 16
E
CUACIÓN
11.
T
EOREMA DEL
B
INOMIO
. ....................................................................................................................... 16
E
CUACIÓN
12.
T
EOREMA DEL
B
INOMIO SIMPLIFICADO
. ................................................................................................ 16
E
CUACIÓN
13.
C
AUDAL DE CADA ELEMENTO DE LA RED CON EL
T
EOREMA DEL
B
INOMIO SIMPLIFICADO
. ................... 16
E
CUACIÓN
14.
E
CUACIÓN DE CONTINUIDAD PARA UNA RED
. ........................................................................................ 16
E
CUACIÓN
15.
E
CUACIÓN DE CONTINUIDAD PARA UNA RED
......................................................................................... 17
E
CUACIÓN
16.
C
AUDALES IJ PARA CADA UNA DE LAS TUBERÍAS DE LA RED
. ................................................................ 17
E
CUACIÓN
17.
V
ARIACIÓN DE ALTURAS PIEZOMÉTRICAS
H
ARDY
-C
ROSS
..................................................................... 17
E
CUACIÓN
18.
E
CUACIÓN DE CONTINUIDAD PARA UNA RED
. ........................................................................................ 18
E
CUACIÓN
19.
C
AUDAL EXPRESADO EN FUNCIÓN DE LA CARGA HIDRÁULICA
. ............................................................. 18
E
CUACIÓN
20.
C
AUDAL EXPRESADO EN FUNCIÓN DE LA CARGA HIDRÁULICA
. ............................................................. 18
E
CUACIÓN
21.
C
AUDAL EXPRESADO EN FUNCIÓN DE LA CARGA HIDRÁULICA
. ............................................................. 18
E
CUACIÓN
22.
C
ONJUNTO DE ECUACIONES DIFERENCIALES
......................................................................................... 19
E
CUACIÓN
23.
E
CUACIÓN DIFERENCIAL EN FUNCIÓN DEL CAUDAL
............................................................................... 19
E
CUACIÓN
24.
C
ORRECCIÓN DE ALTURAS MEDIANTE EL MÉTODO DE
N
EWTON
-R
APSHON
. .......................................... 19
E
CUACIÓN
25.
E
CUACIÓN DE CONTINUIDAD MÉTODO DE LA TEORÍA LINEAL
. ............................................................... 20
E
CUACIÓN
26.
E
CUACIÓN DE CONSERVACIÓN DE LA ENERGÍA
. ..................................................................................... 20
E
CUACIÓN
27.
S
UMA DE CAUDALES PARA EL TRAMO IJ DE CADA CIRCUITO
. ................................................................. 20
E
CUACIÓN
28.
F
ACTOR K
IJ
. ........................................................................................................................................... 20
E
CUACIÓN
29.
P
ERDIDAS DE ENERGÍA TOTALES
. .......................................................................................................... 20
E
CUACIÓN
30.
F
ACTOR K
IJ
’. .......................................................................................................................................... 21
E
CUACIÓN
31.
F
ACTOR K
IJ
. ........................................................................................................................................... 21
E
CUACIÓN
32.
F
ACTOR K
IJ
’. .......................................................................................................................................... 21
E
CUACIÓN
33.
E
CUACIÓN DE CONTINUIDAD
M
ÉTODO DEL
G
RADIENTE
. ...................................................................... 22
E
CUACIÓN
34.
P
ÉRDIDAS DE ENERGÍA TOTALES
. .......................................................................................................... 22
E
CUACIÓN
35.
P
ERDIDAS DE ENERGÍA TOTAL POR UNA BOMBA U OTRO TIPO DE ACCESORIO
. ....................................... 22
E
CUACIÓN
36.
P
ARÁMETRO CARACTERÍSTICO DEL TUBO
. ............................................................................................. 23
E
CUACIÓN
37.
P
ÉRDIDAS DE ALTURA PIEZOMÉTRICA PARA CADA TRAMO
. ................................................................... 24
E
CUACIÓN
38.
S
ISTEMA MATRICIAL DE ECUACIONES PARA SOLUCIÓN
......................................................................... 25

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
7
Juan Camilo Vergara Valderrama
INTRODUCCIÓN
En el inicio de los tiempos el hombre tuvo la necesidad de suplir sus necesidades básicas; por
esto los grupos de personas se vieron en la necesidad ubicarse en zonas donde tuvieran un
cuerpo de agua cercano a su sitio de asentamiento.
A medida que el hombre fue evolucionando y el número de la población fue creciendo, se
vieron en la necesidad de expandir sus fronteras empezando por pequeñas aldeas hasta las
grandes ciudades que conocemos hoy en día.
Debido a lo anterior se tuvo que empezar a pensar en un sistema que pudiera tomar el agua de
los cuerpos de agua y conducirla hasta los lugares mas alejados de este, para así dar la
posibilidad de que cada una de las personas que hacen parte de una aldea, pueblo o ciudad,
tuvieran acceso a dicho fluido para poder suplir sus necesidades básicas y así mejorar su
calidad de vida.
A medida que las aldeas o pueblos se fueron expandiendo cada vez más, estas se estaban
convirtiendo paulatinamente en grandes ciudades las cuales requerían grandes sistemas de
distribución de agua, haciendo que estos cada vez fueran mucho más grandes y complejos de
calcular.
Debido a lo anterior se vio la necesidad de crear métodos de cálculo que fueran capaces de
dar una idea del comportamiento del agua al interior de la red de tubos, por lo que desde la
década de 1920 surgieron diferentes personajes que crearon y propusieron diferentes métodos
de cálculo como Hardy Cross, D.W. Martin y G. Peters (adaptación del método de Newton-
Raphson al caso de solución de redes de distribución de agua potable), D.J. Woody y C.O.A
Charles, E Todini, E.P.O´Conell entre otros.
Una vez fueron creados estos métodos de cálculo y la tecnología fue avanzando se fueron
creando softwares que lograran analizar las redes necesarias para satisfacer a las ciudades sin
necesidad de tomar tanto tiempo a la hora de hacer los cálculos pertinentes para dichas redes.
Hoy en día se puede encontrar muchos softwares especializados en hacer dichos cálculos para
redes de distribución de agua potable, por lo que el usuario tiene una gran variedad de
alternativas a escoger a excepción del costo que debe pagar para acceder a uno u otro
software.
En el presente documento se mostrará la comparación entre dos softwares que desarrollan los
cálculos pertinentes para redes de distribución de agua, con el fin de comparar los resultados
de uno y otro.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
8
Juan Camilo Vergara Valderrama
1 ANTECEDENTES Y OBJETIVOS
1.1 ANTECEDENTES
1.1.1 Objetivos Generales
Comparar los resultados obtenidos a la hora de realizar la modelación de diferentes redes
de distribución de agua, mediante la utilización de dos softwares de diseño el WaterGems
y el software Redes desarrollado por el CIACUA de la Universidad de los Andes.
1.1.2 Objetivos Específicos
Identificar las diferencias en cuanto al manejo de herramientas de modelación, facilidad
de construcción topológica de redes, claridad en la presentación de herramientas, para así
determinar que software es más sencillo de usar.
Observar los resultados en cuanto a parámetros hidráulicos y determinar si existe alguna
diferencia, entre uno y otro.
Determinar el grado de dificultad para realizar la modelación de una misma red en un
software y otro.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
9
Juan Camilo Vergara Valderrama
2 ESTADO DEL ARTE
En los últimos 70 años, diferentes métodos numéricos han sido usados (y siguen empleándose)
para estimar los caudales y presiones en redes de distribución de agua. Estos métodos van desde
aproximaciones gráficas basadas en analogías físicas, métodos numéricos iterativos simples hasta
complejas organizaciones matriciales para la resolución numérica de sistemas de ecuaciones no
lineales.
Es importante destacar que todos los métodos numéricos de análisis en redes de distribución se
basan en dos principios básicos como antiguos que se cumplen independientemente de la
configuración y elementos que componen el sistema, estos son: i) Ecuación de conservación de
masa en nodos y ii) Ecuación de conservación de energía aplicadas a un flujo incompresible a
través de un sistema a presión.
Las variables del modelo son entonces: a) los caudales internos que circulan por las líneas, b) los
caudales externos demandados por los nodos, c) la altura piezométrica y presión en los nodos del
sistema, y d) las pérdidas de carga en cada línea. En resumen, los métodos de análisis de redes de
distribución más significativos que abarcan un periodo de desarrollo de cerca de 6 décadas son
los siguientes:
- Método(s) de Hardy Cross, (corrección de caudales y corrección de alturas
piezométricas).
- Método de Newton-Raphson.
- Método de la Teoría Lineal.
- Método del Gradiente Hidráulico.
Es importante anotar que los métodos de la Teoría Lineal y Gradiente Hidráulico emplean
formulaciones matriciales aprovechando el gran poder de procesamiento numérico de los
computadores modernos.
Observando el desarrollo del tema a través de la historia, se puede identificar diferentes etapas
que son de gran aporte a lo que hoy se conoce como la modelación hidráulica por medio de
softwares.
En el siglo XVII se dieron los primeros desarrollos teóricos y experimentales sobre mecánica de
fluidos. De este siglo podemos destacar los aportes de Bernoulli (1738). En 1752 basado en las
formulaciones teóricas de Bernoulli, Leonard Euler planteo las ecuaciones de energía en la forma
que hoy conocemos y que sirven de base aún en los modelos hidráulicos actuales. En el mismo
siglo, Antoine Chézy (1770) encontró que en las pérdidas del agua en movimiento la relación
V
2
/RS permanecía razonablemente constante en ciertas condiciones. Relación que sirvió de base
en las ecuaciones de pérdidas por fricción desarrolladas posteriormente.
En 1839 los investigadores G. Hagen y J.L Poiseulle desarrollaron de manera independiente la
ecuación de pérdida de carga en pequeñas tuberías bajo regímenes de flujo laminar.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
10
Juan Camilo Vergara Valderrama
Para 1845 J. Weisbach publica tres volúmenes de ingeniería mecánica basados en los resultados
de sus experimentos. La famosa Ecuación Darcy-Weisbach surge de este trabajo como una
extensión a los trabajos previos de Chézy; de hecho existe una clara relación entre el coeficiente
C de Chézy con el factor de fricción de la ecuación de Darcy-Weisbach.
En 1883 los trabajos de experimentación O. Reynolds basados en observaciones previas de
Hagen, permitieron establecer una clara distinción entre los flujos laminar y turbulento. El
investigador identificó un número a dimensional para cuantificar la condición que permitía
clasificar estos tipos de regímenes de flujo.
Entre las décadas de 1900 - 1930 se presentaron también interesantes avances. Se debe destacar
el desarrollo de la teoría de capa límite que estudiaba la interacción entre los fluidos y las paredes
de las tuberías, estudio liderado por L.Prandtl y sus estudiantes T. Von Karman, J. Nikuradse, H.
Blasius y T. Stanton. Como resultado de años de investigación, se pudo demostrar experimental y
teóricamente el efecto de la pared de la tubería sobre el fluido y su perfil de velocidades. Cabe
destacar especialmente los experimentos de Nikuradse con partículas de arena normalizadas y
mediciones de pérdidas de carga que permitieron un mejor entendimiento para el cálculo del
factor de fricción en la fórmula de Darcy-Weisbach.
Mientras tanto en 1906, los investigadores A. Hazen y G.S. Williams desarrollaban una fórmula
empírica para el cálculo de pérdida de carga en tuberías. A pesar que no tenía la misma
rigurosidad teórica que la ecuación de Darcy-Weisbach, la fórmula hallada posteriormente
conocida como ecuación de Hazen-Williams permitió un fácil cálculo de las pérdidas y fue
ampliamente adoptada en Norte América.
Finalmente para este periodo, se debe destacar el trabajo realizado en 1938 por los investigadores
C. Colebrook y C. White quienes basándose en los trabajos de Prandtl y sus discípulos,
desarrollaron la ecuación de Colebrook-White para la determinación del factor de fricción/de la
formulación Darcy-Weisbach en tuberías comerciales.
Como consecuencia de este trabajo en 1944 L Moody de la Universidad de Princeton publica el
diagrama de Moody, el cual esencialmente es una representación gráfica de la Ecuación de
Colebrook-White para el rango flujo turbulento y la Ec. Hagen-Poiseulle en el rango de flujo
laminar.
Una vez se dieron estos grandes avances teóricos para el desarrollo de la hidráulica a presión,
fueron apareciendo personas que paulatinamente según las necesidades de cada uno de los
periodos de la época empezaron a desarrollar métodos de calculo de redes, a fin de poder lograr
conocer en detalle el comportamiento del agua en las redes de distribución de agua en las grandes
ciudades
En 1936 Hardy Cross un ingeniero estructural de la Universidad de Illinois, desarrolló un método
matemático para resolver un análisis de distribución de momentos en estructuras aporticadas.
Luego Cross entendió que el método desarrollado podría también ser usado para resolver

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
11
Juan Camilo Vergara Valderrama
caudales y presiones en redes malladas de distribución de agua y publicó un artículo técnico con
este método pionero de futuros desarrollos.
En los trabajos de Cross formulaban en esencia dos posibles metodologías: i) Corrección de
Caudales en las tuberías del sistema mediante un proceso iterativo incluyendo un factor de ajuste
de caudales en cada circuito, y ii) Corrección del Valor de Altura Piezométrica en cada nodo del
sistema bajo un proceso iterativo con un factor de ajuste para las alturas piezométricas o cargas
de los nodos. Para el cálculo de pérdidas por fricción se usaba la ecuación de Hazen-Williams.
Comparando ambos métodos, se observó que "la convergencia era lenta y no totalmente
satisfactoria" cuando se empleaba el método de corrección de alturas en nodos. Esto fue atribuido
a la dificultad en obtener buenas estimaciones iniciales de los valores de gradiente hidráulico en
los nodos. Como resultado el método de corrección de caudales por circuito tuvo la aceptación de
la comunidad de ingeniería y fue rápidamente conocido con el nombre exclusivo de "Método de
Hardy Cross".
Para 1950 se encuentra el analizador de redes de distribución desarrollado por Mcllroy. Este fue
un método análogo al modelo computacional eléctrico, desarrollado para simular el
comportamiento de un sistema de distribución de agua calculando los flujos como si fueran
corriente eléctrica en lugar de agua.
El comienzo de este periodo, se da a principios de los 50's con los primeros (básicos) modelos de
análisis de redes para computadores. Con la presentación de los primeros equipos de computo
(mainframes) y el establecimiento del lenguaje de programación FORTRAN, los investigadores
comenzaron con la implementación de las metodologías conocidas de análisis para su uso en los
primeros computadores digitales.
En 1957 los investigadores Hoag y Weinberg adaptaron el método de Hardy Cross para resolver
redes para computadores digitales. En la presentación de su implementación se discutieron
aspectos de velocidad, exactitud y la viabilidad económica de aplicar el método en un amplio
espectro de simulaciones de redes.
Subsecuentemente, dos firmas americanas de ingeniería como Rader & Associates y Brown &
Caldwell, emergieron como los pioneros en el uso del computador para analizar redes de
distribución de agua para sus clientes. En el mismo año, la firma de informática Datics
Corporation en Texas se convirtió en una de las primeras empresas en comercializar un programa
comercial.
Sin embargo, con la creciente sofisticación de los computadores a mediados de la década del 60,
más universidades e investigadores comenzaron a cuestionar el uso del método Hardy Cross para
analizar caudales y presiones en sistemas de distribución debido al reconocimiento de las
siguientes limitaciones del método: i) Dependiendo del tamaño y complejidad del sistema, el
método requería de muchas iteraciones para finalmente lograr la convergencia numérica y ii) el
método original estaba restringido a sistemas perfectamente simples y no simulaba
explícitamente el comportamiento de elementos singulares como válvulas, bombas, etc.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
12
Juan Camilo Vergara Valderrama
En respuesta a las limitaciones del Método de Cross, diferentes investigadores comenzaron a
analizar nuevas formulaciones y manejos matemáticos al análisis de redes los cuales pudieran
aprovechar de mejor manera las posibilidades aportadas por procesadores con cada vez mayores
velocidades de cálculo. Dentro de los métodos subsecuentemente desarrollados se encontraron: 1)
Método del Nodo Simultáneo, 2) Método del Circuito Simultáneo, 3) Método de Teoría Lineal y
4) Método Compuesto/Gradiente Conjugado.
En 1963 D.W. Martin y G. Peters fueron los primeros investigadores en publicar un algoritmo
que podía usarse para resolver simultáneamente el valor de gradiente hidráulico en cada nodo del
sistema de distribución. En la aplicación del algoritmo, las ecuaciones de pérdida de carga para
cada tubería estaban escritas en términos de los caudales en cada tubería expresados como una
función de los valores de gradiente en los nodos extremos de cada tramo. La sustitución de estas
ecuaciones dentro de la ecuación de conservación de masa en cada nodo traía consigo la
formación de un sistema de N Ecuaciones No-Lineales (siendo N el número de nodos).
En 1969 Alvin Fowler y su asistente Robert Epp de la Universidad de British Columbia (CA)
desarrollaron una nueva aproximación para el análisis de redes malladas que aplicaba el método
de Newton-Raphson para simultáneamente resolver los factores de ajuste de caudal asociados con
el método original de Cross (1936).
En 1972 los profesores Don J. Wood y Charles introdujeron una nueva formulación al problema
del análisis de redes malladas "El Método de Teoría Lineal" en el cual la conservación de masa
en los nodos y las ecuaciones de energía en cada circuito eran resueltas simultáneamente para
directamente hallar en caudal en cada una de las tuberías.
Posteriores investigaciones como las realizadas por Roland Jeppson de la Universidad de Utah en
colaboración con CH2M Hill trajeron consigo en 1976 el desarrollo de un nuevo software
comercial para el análisis de redes basado en el método del "Circuito Simultáneo". En el uso de
este algoritmo, las ecuaciones no-lineales de energía para cada circuito o ruta son escritas en
términos de los factores de ajuste de caudal. Así como en los métodos de "Nodo", las ecuaciones
los-linealizadas usando una expansión estándar de las Series de Taylor y luego son resueltas de
manera iterativa usando el método de Newton Raphson.
Finalmente este repaso por los métodos numéricos concluye con el Método del Gradiente el cual
fue propuesto en 1987 por Todini y Pilati. En esta formulación, las ecuaciones individuales de
energía en cada tubería se combinan con las ecuaciones individuales de conservación en cada
nodo para proveer una solución simultánea tanto de cargas en los nodos como caudales
individuales en las tuberías. Las ecuaciones no lineales de energía son linealizadas usando la
expansión en series de Taylor. Un aspecto por destacar del método es el trabajo con matrices de
manera dispersa, lo que permite a reducción de la memoria requerida y el tiempo de cálculo en
computadores.
Este método ha sido actualmente adoptado por la mayoría de programas de software comerciales
del mercado incluyendo EPANET, WaterCAD, WarterGems, H2OMap, InfoWater, etc.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
13
Juan Camilo Vergara Valderrama
A continuación se muestra el proceso matemático utilizado para llegar a desarrollar cada uno de
los métodos principales de cálculo para resolver redes de distribución de agua:
- Método de Hardy-Cross con corrección de caudales
En un principio este método fue desarrollado para el cálculo de estructuras en concreto y acero.
Pero más adelante Cross lo adapto al cálculo de redes cerradas de distribución de agua potable.
Para la adaptación del método al cálculo de redes de distribución de agua potable el profesor
Cross utilizó la ecuación de Hazen-Williams.
El método original se basa en suponer los caudales en cada uno de los tubos de la red e ir
corrigiendo esta suposición. Dado que se conocen todas las características de la tubería (d, k
s
,
Σk
m
, l), el método es un proceso de comprobación de diseño.
Para el cálculo de los caudales se debe primero suponer primero supone un error
en el
circuito i, por lo que las pérdidas para cada tubo son:
Ecuación 1. Pérdidas totales con un error ΔQ
i
.
Estableciendo una altura piezométrica donde se contemple las perdidas por fricción y menores, y
remplazando en la Ecuación 1 se tiene:
Ecuación 2. Altura piezométrica con perdidas totales.
El término
puede despreciarse en la parte derecha de esta última ecuación, ya que su orden
de magnitud es pequeño en comparación con los demás sumandos, luego:
Ecuación 3. Altura piezométrica con perdidas totales simplificada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
14
Juan Camilo Vergara Valderrama
Ahora, utilizando la siguiente ecuación:
Ecuación 4. Suma pérdidas totales en una red.
Se llega a la siguiente expresión:
Ecuación 5. Suma pérdidas totales en una red.
Despejando
se obtiene la siguiente ecuación para el cálculo del factor de corrección de
caudales en cada uno de los ciclos de cálculo:
Ecuación 6. Delta de caudal Hardy-Cross (corrección de caudal).
La anterior ecuación se puede rescribir de la siguiente forma:
Ecuación 7. Delta de caudal Hardy-Cross (corrección de caudal) simplificada.
- Método de Hardy-Cross con corrección de alturas piezométricas
Ya que para el método anteriormente mencionado es necesario balancear los caudales antes de
comenzar el proceso de cálculo, esto hace que el método se torne engorroso en el caso de que se
presenten redes de gran tamaño.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
15
Juan Camilo Vergara Valderrama
Debido a esto se tuvo la necesidad modificar el método. Esto fue planteado en 1938 por el
ingeniero R.J. Cornish, quien le dio el nombre de balance de cantidad, y se utilizó para resolver
las ecuaciones de altura.
El método de Hardy-Cross con corrección de alturas piezometricas se utiliza para resolver las
ecuaciones de altura piezométrica. De nuevo se utiliza la ecuación de Darcy-Weisbach para el
cálculo de las pérdidas por fricción, aunque se podría recurrir a cualquier ecuación de resistencia
fluida.
1
Ecuación 8. Caudal expresado en función de la carga hidráulica.
Este método propone suponer la altura piezométrica en vez de caudales en cada uno de los tubos
de la red, (la altura piezométrica en uno de los nodos es conocida o debe ser su defecto tiene que
ser superpuesta). Luego se ajustan las alturas piezométricas supuestas, nodo por nodo, hasta
completar todos los nodos de la red
Dichas alturas deben ser recalculadas mediante un proceso iterativo y este se detendrá hasta que
la diferencia de las alturas calculadas anteriormente y actuales sea muy pequeña.
El factor que se utiliza para corregir las alturas piezométricas en cada uno de los nodos se calcula
tal como se explica a continuación. Si se supone que la altura piezométrica
del nodo i esta
subestimada o sobrestimada:
2
Ecuación 9. Caudal expresado en función de la carga hidráulica menos un ΔH
i
.
1
Juan G Saldarriaga, (2007). Hidráulica de tuberías: Abastecimiento de agua, redes, riegos. (2da. Ed).
Bogotá, Colombia: Alfaomega-Uniandes.
2
Juan G Saldarriaga, (2007). Hidráulica de tuberías: Abastecimiento de agua, redes, riegos. (2da. Ed).
Bogotá, Colombia: Alfaomega-Uniandes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
16
Juan Camilo Vergara Valderrama
Rescribiendo la ecuación y dejándola en términos de altura se tendrá que:
Ecuación 10. Caudal expresado en función de la carga hidráulica menos un ΔH
i
.
Utilizando el Teorema del Binomio se tiene que el término de la derecha de la ecuación No. 10
queda:
Ecuación 11. Teorema del Binomio.
Eliminando los términos que tienen potencias altas se tiene que:
Ecuación 12. Teorema del Binomio simplificado.
Luego, al remplazar esta última ecuación en la Ecuación 10 se obtiene:
Ecuación 13. Caudal de cada elemento de la red con el Teorema del Binomio simplificado.
Por definición se puede decir que:
Ecuación 14. Ecuación de continuidad para una red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
17
Juan Camilo Vergara Valderrama
Si se remplazan los
se llega a:
Ecuación 15. Ecuación de continuidad para una red
expresado en función de alturas piezométricas.
En esta última ecuación se pueden identificar con facilidad los caudales
en cada una de las
tuberías. Luego:
3
Ecuación 16. Caudales ij para cada una de las tuberías de la red.
Finalmente al despejar el factor de corrección para las alturas piezométricas en los nodos de la
red se obtiene:
4
Ecuación 17. Variación de alturas piezométricas Hardy-Cross
(corrección de alturas piezométricas).
3
Juan G Saldarriaga, (2007). Hidráulica de tuberías: Abastecimiento de agua, redes, riegos. (2da. Ed).
Bogotá, Colombia: Alfaomega-Uniandes.
4
Juan G Saldarriaga, (2007). Hidráulica de tuberías: Abastecimiento de agua, redes, riegos. (2da. Ed).
Bogotá, Colombia: Alfaomega-Uniandes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
18
Juan Camilo Vergara Valderrama
- Método de Newton-Rhapson
Para el uso del Método de Newton –Rhapson en el caso de redes de distribución se tienen las
siguientes ecuaciones:
Ecuación 18. Ecuación de continuidad para una red.
= número de uniones (nodos)
= caudal demandado en la unión i
Utilizando la siguiente ecuación:
Ecuación 19. Caudal expresado en función de la carga hidráulica.
Se puede obtener que:
Ecuación 20. Caudal expresado en función de la carga hidráulica.
Es evidente que esta ecuación es de la forma siguiente:
Ecuación 21. Caudal expresado en función de la carga hidráulica.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
19
Juan Camilo Vergara Valderrama
Por lo que se obtiene un conjunto de ecuaciones que se pueden resolverse mediante el método
iterativo del Newton-Rapshon.
Ecuación 22. Conjunto de ecuaciones diferenciales
(solución mediante el método de Newton-Rapshon).
y
representan alturas piezométricas. Luego:
Ecuación 23. Ecuación diferencial en función del caudal
y la diferencia de altura piezométrica.
Después de acomodar, remplazar y hacer procesos de derivación se tiene que la expresión final
para la corrección de alturas será:
Ecuación 24. Corrección de alturas mediante el método de Newton-Rapshon.
En 1970 D.J. Woody y C.O.A. Charles. desarrollaron un nuevo método de cálculo el cual
consiste en resolver simultáneamente las ecuaciones de la conservación de la masa y la
conservación de la energía, con el fin de calcular el caudal. Uno de los aspectos más
característicos de este método es que el número de iteraciones que se tienen que realizar para
llegar a la respuesta es mucho menor.
- Método de la teoría lineal
El método de la teoría lineal se basa en las siguientes ecuaciones:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
20
Juan Camilo Vergara Valderrama
Para cada unión de la red se debe cumplir la ecuación de continuidad:
Ecuación 25. Ecuación de continuidad método de la teoría lineal.
Para cada circuito se debe cumplir la ecuación de conservación de la energía.
Ecuación 26. Ecuación de conservación de la energía.
La ecuación que existe para cada circuito es:
Ecuación 27. Suma de caudales para el tramo ij de cada circuito.
También se puede plantear que el factor
esta dado por:
Ecuación 28. Factor k
ij
.
Para lograr resolver el sistema de ecuaciones se propone el siguiente procedimiento:
Ecuación 29. Perdidas de energía totales.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
21
Juan Camilo Vergara Valderrama
En donde:
Ecuación 30. Factor k
ij
’.
A fin de que las ecuaciones anteriores sean válidas se debe hacer una suposición de caudal para
cada uno de los tubos. También a la hora de hacer la suposición de los caudales no hay necesidad
de hacer un previo cálculo de los mismos ya que no se debe cumplir la ecuación de continuidad
para cada uno de los nodos, el caudal supuesto puede ser igual para todos los tubos.
Para obtener los
en cada iteración se utilizan las siguientes ecuaciones:
Ecuación 31. Factor k
ij
.
Una vez obtenido dicho valor se puede calcular el coeficiente mediante la siguiente expresión:
Ecuación 32. Factor k
ij
’.
A la hora de empezar el cálculo de una determinada red se debe empezar en plantear las
ecuaciones de continuidad para cada uno de los nodos.
A continuación se deben plantear las ecuaciones de conservación de energía para cada circuito.
Una vez planteadas dichas ecuaciones se pueden organizar estas en forma matricial, por lo que la
resolución de este sistema matricial se puede expresar de la siguiente forma:
Las incógnitas de cada iteración son los
(matriz columna
), es decir, los caudales en cada
uno de los tubos que conforman la red; por lo que dicho sistema se puede resolver de la siguiente
forma:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
22
Juan Camilo Vergara Valderrama
De esta forma se obtendrán los valores de caudal para cada una de las tuberías.
- Método del gradiente
El método del Gradiente fue desarrollado por los profesores E. Todini y E.P.O’Conell en la
Universidad de Newcastle upon Tyne y or R. Salgado; en este método se planteó proponer
ecuaciones de energía individuales para cada tubo las cuales se combinan con las ecuaciones de
masa individuales en cada unión con el fin de obtener una solución simultánea tanto de los
caudales en las tuberías como de las alturas piezométricas en los nodos.
Para dicho método se debe cumplir que:
Ecuación 33. Ecuación de continuidad Método del Gradiente.
En cada tubo la energía total disponible se gasta en pérdidas por fricción y en pérdidas menores:
Ecuación 34. Pérdidas de energía totales.
Si se tienen en cuenta las pérdidas menores causadas por cualquier tipo de accesorio y la posible
existencia de bombas en algunos de los tubos de la red:
Ecuación 35. Perdidas de energía total por una bomba u otro tipo de accesorio.
Donde:
Exponente que depende de la ecuación de fricción utilizada (2.0 para el caso de la ecuación
de Darcy-Weisbach).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
23
Juan Camilo Vergara Valderrama
Parámetros características del tubo, las válvulas y las bombas.
5
Por consiguiente:
Ecuación 36. Parámetro característico del tubo.
El valor del parámetro incluye los factores de pérdidas por fricción y pérdidas menores. Para
algunos tipos de válvulas, el parámetro establece su relación
.
Para bombas colocadas en las tuberías se requieren los tres parámetros
y ya que la relación
entre la altura piezométrica suministrada por la bomba y el canal es polinomial.
Para el Método del Gradiente Hidráulico se hacen las siguientes definiciones adicionales, con el
fin de describir la topología de la red en forma matricial:
Matriz topológica tramo a nodo para los NS nodos de altura piezométrica fija. Su
dimensión es NT x NS con un valor igual a -1 en las filas correspondientes a los tramos
conectados a nodos de altura piezométrica fija.
NS = Número de nodos de altura piezométrica fija o conocida.
“Matriz de conectividad” asociada a cada uno de los nodos de la red. Su dimensión es
NT x NN con solo dos elementos diferentes de cero en la i-ésima fila:
-1 en la columna correspondiente al nodo inicial del tramo i.
1 en la columna correspondiente al nodo final del tramo i.
NN = Número de nodos con altura piezométrica desconocida.
NT = Número de tuberías de la red.
5
Juan G Saldarriaga, (2007). Hidráulica de tuberías: Abastecimiento de agua, redes, riegos. (2da. Ed).
Bogotá, Colombia: Alfaomega-Uniandes.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
24
Juan Camilo Vergara Valderrama
La pérdida de altura piezométrica en cada tramo de tubería es:
Ecuación 37. Pérdidas de altura piezométrica para cada tramo.
Matriz diagonal de NT x NT definida como sigue:
= Vector de caudales con dimensión NT x 1.
Vector de alturas piezométricas desconocidas con dimensiones NN x 1.
Vector de alturas piezométricas fijas con dimensión NS x 1.
donde:
Matriz transpuesta de
.
Vector de consumo en cada nodo de la red, con dimensión NN x 1.
Las anteriores ecuaciones se pueden expresar así:
Al realizar operaciones matemáticas la anterior ecuación queda:
=
Matriz diagonal
con dimensión NT x NT.
Matriz con dimensión NT x NT definida como:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
25
Juan Camilo Vergara Valderrama
representa el desbalance de energía por unidad de peso en cada tubo y
representa el
desbalance de caudal en cada nodo.
y
En el Método del Gradiente se soluciona el sistema descrito anteriormente, teniendo que para
cada iteración se tiene que:
y
Utilizando las propiedades y operaciones del algebra lineal y remplazando una ecuación en otra
se obtiene que:
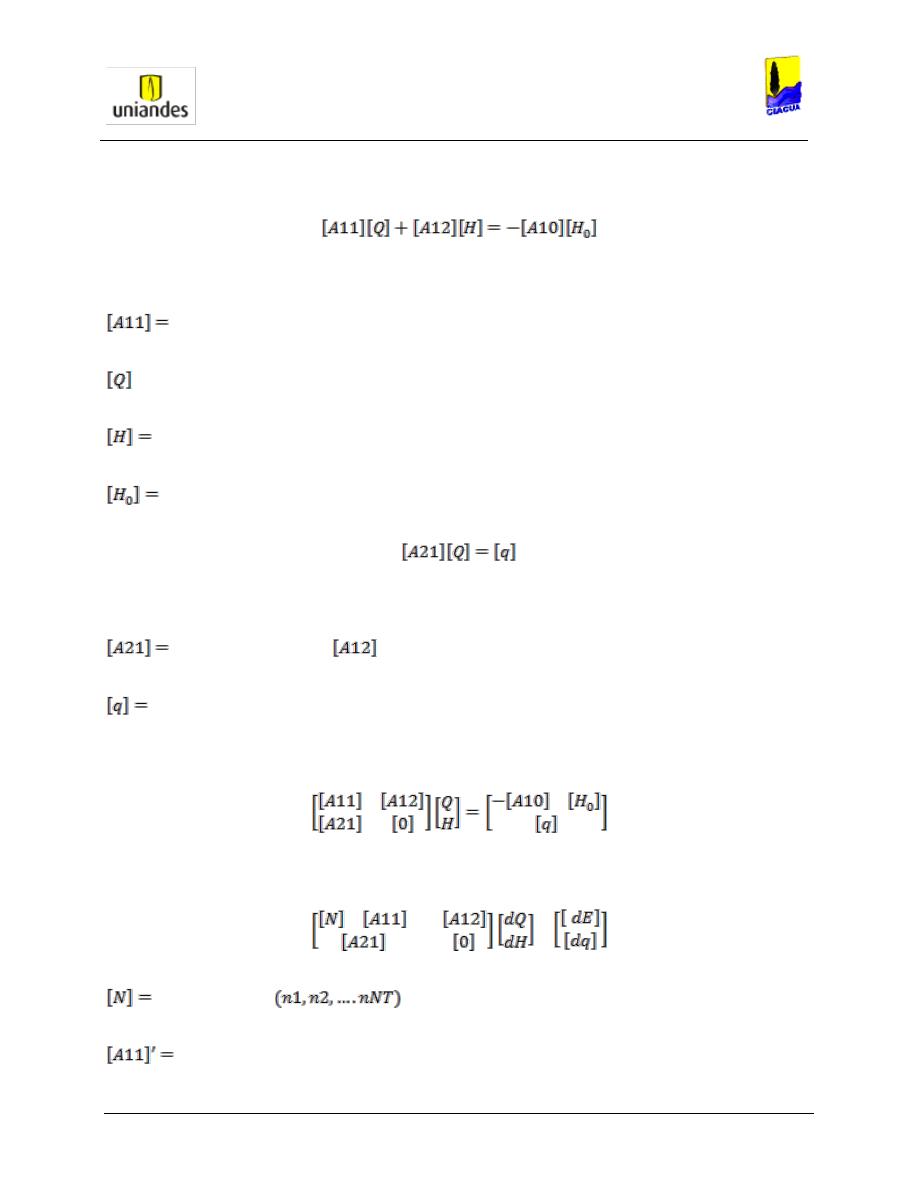
x
Se puede rescribir la ecuación anterior como un sistema de ecuaciones lineales para las alturas
piezométricas:
Ecuación 38. Sistema matricial de ecuaciones para solución
de redes mediante el método del gradiente.
Una vez se desarrollaron cada uno de los diferentes métodos y la capacidad tecnológica fue
desarrollándose, los investigadores fueron desarrollando pequeños programas donde tuvieran

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
26
Juan Camilo Vergara Valderrama
como base alguno de estos métodos para resolver dichas redes mediante herramientas
tecnológicas.
A principios de los 80's muchos de estos programas de "Investigación Académica" (ej: Fowler,
Jepsson, Sharmir y Howard, Wood, etc.) fueron paulatinamente convertidos en aplicaciones
comerciales de software que fueron promocionados y mercadeados a través de Universidades y/o
a través de empresa medianas e inclusive grandes corporaciones. Esto en paralelo con la
introducción del computador personal (PC) al público en general que a partir de 1981 surgió con
el éxito del IBM PC o compatible que hizo posible el llevar las metodologías de análisis a
equipos de escritorio.
Dentro de las primeras aplicaciones más importantes de la industria se destaca la entrada al
mercado a partir de 1982 de WATSIM desarrollado por Boeing Computer Services y de KYPIPE
por parte de la Universidad de Kentucky.
Paralelamente a principios de esta década se desarrolló el primer modelo de calidad de agua en
sistemas de distribución. En esencia se trataba de un modelo en periodo estático que empleaba las
formulaciones propuestas por D. Wood de la Universidad de Kentucky e investigadores de la
U.S. EPA.
A medida que avanzaban los 80's aparecieron las aplicaciones lanzadas por firmas
norteamericanas e internacionales como Expert Development Corporation (WATSYS), WRC
(WATNET), Charles Howard y Associates (SPP8), y SAFEGE Consulting Engineers (Piccolo)
emergieron como los proveedores de servicios integrales de modelación para varias empresas de
agua alrededor del mundo.
Los modelos entonces empezaron a extenderse a sistemas de mayor complejidad hidráulica y en
ese momento agencias gubernamentales como el USACE y la Agencia de Protección Ambiental
de EE.UU (U.S. EPA) también desarrollaron sus propias aplicaciones.
En el periodo que va de 1988 - 1990 aparecen ya implementaciones de modelos de calidad de
agua extendidos. Se puede destacar el modelo DWQM desarrollado por W. Graynman, R. Clark
y D. Males que permitía ejecutar simulaciones dinámicas de calidad a partir de los
caudales/velocidades generados por un modelo hidráulico y un esquema numérico alterno que
permitía rastrear sustancias conservativas o no-conservativas a lo largo de la red. En este modelo
cada tramo de tubería se representaba como una serie de sub-tramos y sub-nodos seleccionados
como una aproximación de la distancia que recorría la sustancia a ser analizada en un salto
(tiempo) de cálculo (Método de Elementos Discretos de Volumen).
Para mediados de 1992 sale al mercado la primera versión del software CyberNET. Este software
lanzado por la casa matriz Haestad Methods con base en Connecticut, incluyó como gran
novedad la integración del modelo hidráulico en un entorno CAD.
En 1993 se lanza la primera versión al público del Software EPANET desarrollado por un grupo
de trabajo de la U.S. EPA. La primera versión de EPANET se basó en dos modelos de uso

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
27
Juan Camilo Vergara Valderrama
público mencionados anteriormente: WADISO (Simulación Hidráulica) y DWQM (Modelación
Dinámica de Calidad). Es importante anotar que EPANET sufrió cambios significativos hasta el
lanzamiento de la versión EPANET 2.0 a finales de la década (1998 – 2000).
Si bien el algoritmo de Gradiente Hidráulico comenzó a ser una estándar de cálculo en la mayoría
de programas luego de su adopción por el EPANET, cada nueva versión los paquetes comerciales
traía consigo mejoras en el manejo de datos, reportes gráficos y tabulares, gestión de escenarios,
y la capacidad de interoperación con otros sistemas de información, especialmente con Bases de
Datos Comerciales y Sistemas de Información Geográfica (GIS).
A medida que se llega al final de la década del 90 y comienzos del siglo XXI, se encuentra que de
manera análoga que muchos desarrolladores de Software comercial lanzaron al mercado
diferentes paquetes de software o versiones más desarrolladas y en ambiente Windows de
programas comerciales previamente desarrollados para DOS.
Dentro esta lista, que fue actualizada se encontraban programas como: EPANET 2.0 (U.S. EPA),
WaterCAD 5.0 (Haestad Methods), WaterGems, Pipe 2000 (Civil Engineering Software Centre -
U.KY), H20Net/H20Map (MWH Soft, Inc.), MIKE NET (BOSS International, Inc.), AquaNet,
(Finite Technologies Inc.), ERACLITO y ARCHIMEDE (PROTEO s.r.l.), STANET
(Ingenieurbüro Fischer-Uhring), Wadiso SA (GLS Engineering Software Pty Ltd), entre otros.
En los últimos 10 años (después de 2002), el desarrollo y avance de los paquetes comerciales ha
sido tal que a pesar de compartir muchos la misma base del algoritmo de cálculo (Gradiente
Hidráulico) existe una marcada diferenciación entre los diferentes software especialmente en
conceptos de interoperabilidad, facilidad de uso, herramientas de productividad, procesos de
consulta multi-criterio, operaciones de análisis espacial, posibilidades gráficas, integración con
Sistemas de Información Geográfica (GIS), etc.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
28
Juan Camilo Vergara Valderrama
3 METODOLOGÍA
Para poder determinar si existe alguna diferencia en cuanto a los resultados hidráulicos que arroje
uno u otro software de modelación, se construirán y modelaran tres redes de distribución de agua
con un número de tuberías considerable.
Dichas redes que se presentaran a continuación son casos reales en los cuales se tuvo que
proyectar una solución de distribución del fluido, para tres zonas del Municipio de Soacha
ubicado en el Departamento de Cundinamarca por la salida al costado sur de la ciudad de Bogotá,
las cuales no contaban con un sistema confiable de distribución de agua potable.
3.1 METODOLOGÍA PARA LA ELABORACIÓN DE MODELOS
HIDRÁULICOS EN WATERGEMS
3.1.1 Construcción de la topología de los modelos hidráulicos.
Para la construcción de la topología de la red, el software WaterGems da la posibilidad de
construir manualmente la topología siguiendo el trazado de las calles y carreras o de importar un
archivo topográfico tipo shape existente.
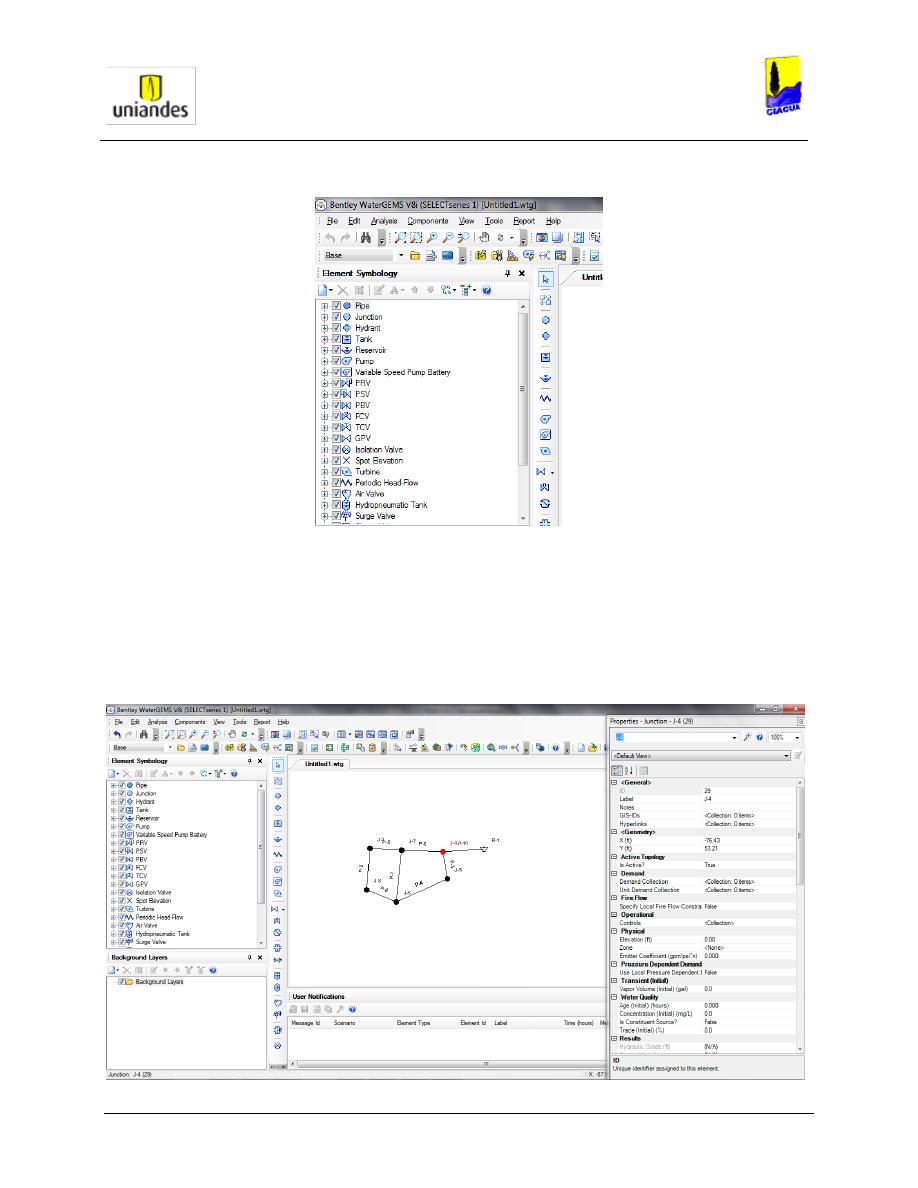
En el caso de que se requiera construir la topología de la red manualmente se debe utilizar las
herramientas básicas que ofrece este software, como los botones Junction, Pipe, Valve, Reservoir
y demás que se requieran para el desarrollo de un proyecto en específico.
Figura 1
. Cuadro de dialogo principal software WaterGems.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
29
Juan Camilo Vergara Valderrama
Figura 2
. Herramientas básicas del software WaterGems.
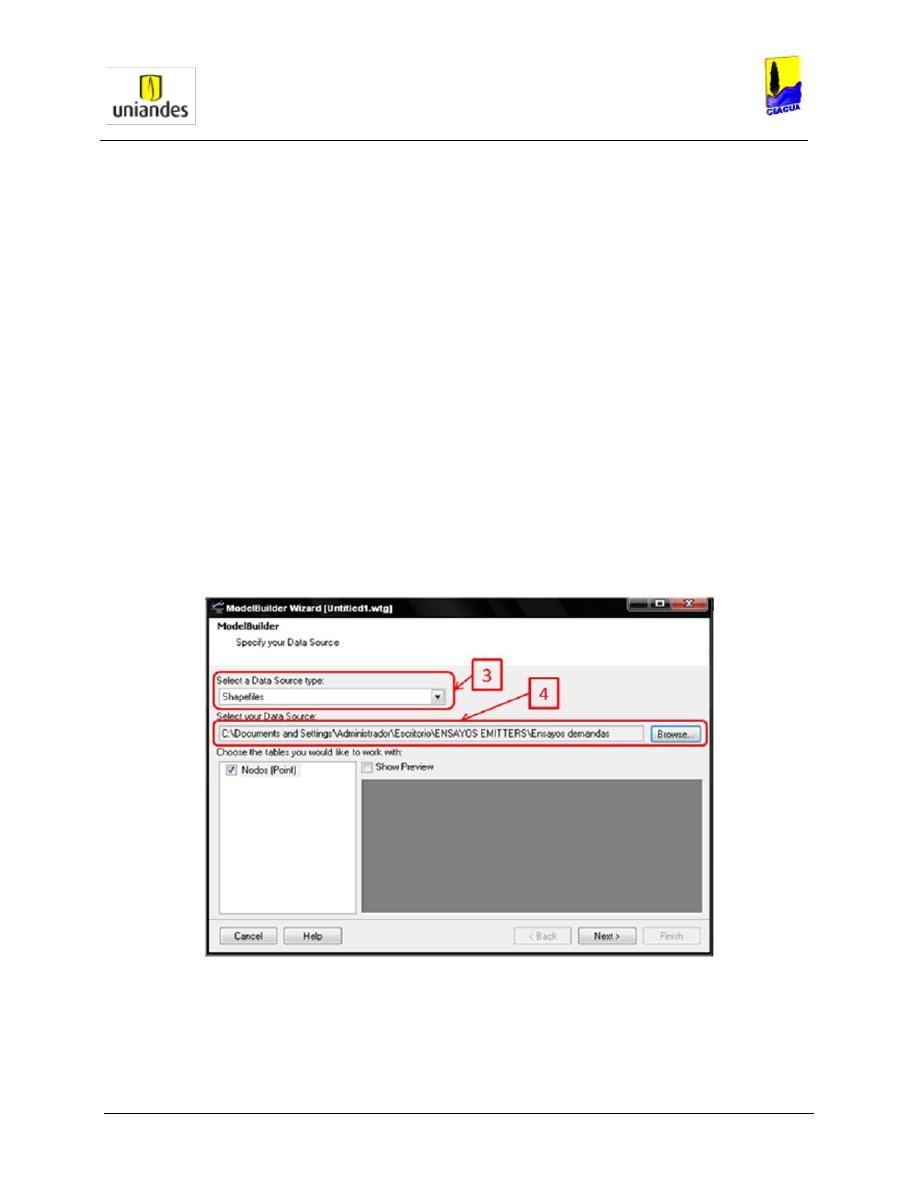
Al empezar a construir la red se debe elegir cada una de las herramientas básicas e insertarlas en
el cuadro de dialogo principal. Según sea el caso, cada uno de los elementos dibujados tienen la
propiedad de que sus características topográficas, hidráulicas y geométricas puedan ser
modificadas según las características del proyecto. Dichas propiedades de cada uno de los
elementos se muestran en el cuadro de propiedades del programa.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
30
Juan Camilo Vergara Valderrama
Figura 3
. Cuadro de propiedades para cada elemento.
Cuando se requiera construir la topología de una red existente se debe importar al software
WaterGems el archivo topográfico tipo shape correspondiente a la red en cuestión, y no se debe
hacer manualmente como se describió anteriormente, ya que la red existe y la información
topográfica tanto planimetrica como altimétrica está disponible. Cuando se presentan estos casos
el programa ofrece una herramienta llamada Modelbuilder la cual permite realizar lo
anteriormente enunciado.
Para la creación de nodos del modelo (Uniones, Válvulas, VRPs, Tanques, Reservorios, Bombas,
etc):
1. Abrir la herramienta Modelbuilder.
2. En el ModelBuilder, crear una nueva conexión.
3. Seleccionar como tipo de fuente de datos “Shapefiles”.
4. Seleccionar el archivo shape que se empleará como fuente.
5. Oprimir el botón Next> (siguiente).
Figura 4
. Pasos 3 y 4 del proceso de construcción topológica de modelos hidráulicos (nodos).
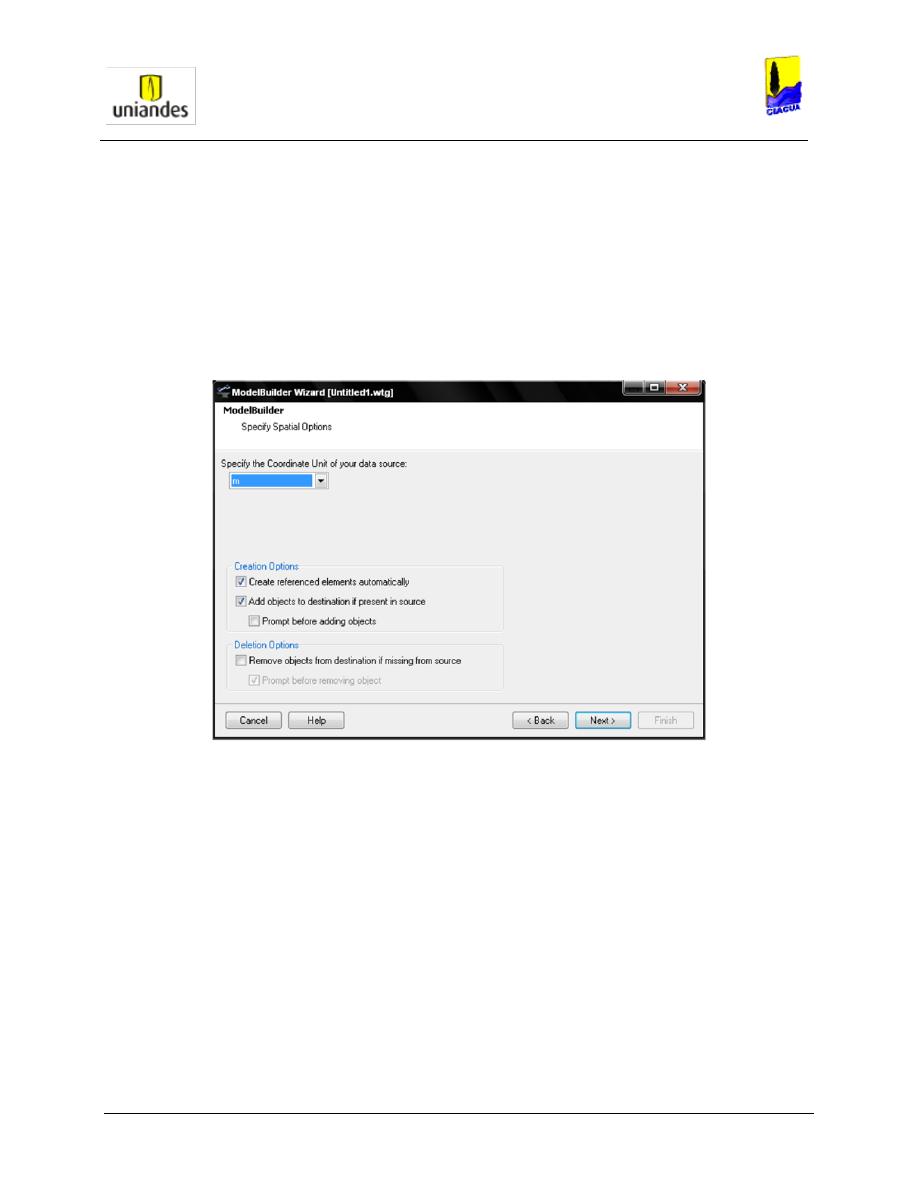
6. En la siguiente ventana, seleccionar la unidad para las coordenadas (metros) y las
opciones para la creación de los objetos en el modelo (en general se dejan las opciones
por defecto). Posteriormente, oprimir el botón Next> (siguiente).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
31
Juan Camilo Vergara Valderrama
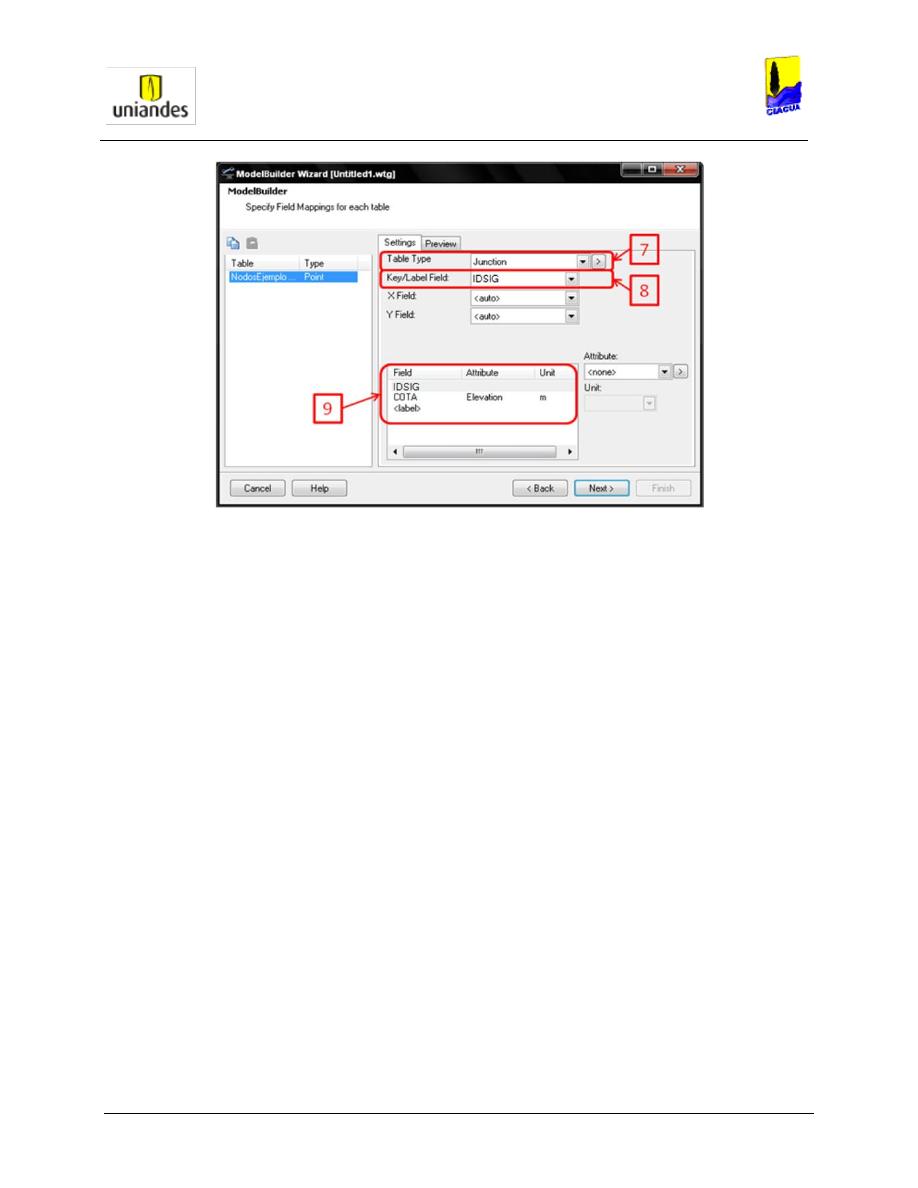
7. Seleccionar el tipo de tabla del modelo a sincronizar, según el tipo de datos que
contenga el archivo shape (Junction, PRV, Tank, etc.).
8. Seleccionar el campo clave de los datos contenidos en el archivo shape.
9. Correlacionar los datos del archivo shape con los datos de la tabla y asignar unidades
adecuadas. Oprimir el botón Next> (siguiente).
10. En el siguiente paso, señalar si se quiere construir el modelo de inmediato o no, y
oprimir el botón Finish.
Figura 5
. Paso 5 del proceso de construcción topológica de modelos hidráulicos (nodos).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
32
Juan Camilo Vergara Valderrama
Figura 6
. Pasos 7, 8 y 9 del proceso de construcción topológica de modelos hidráulicos (nodos).
Para la creación de tuberías del modelo:
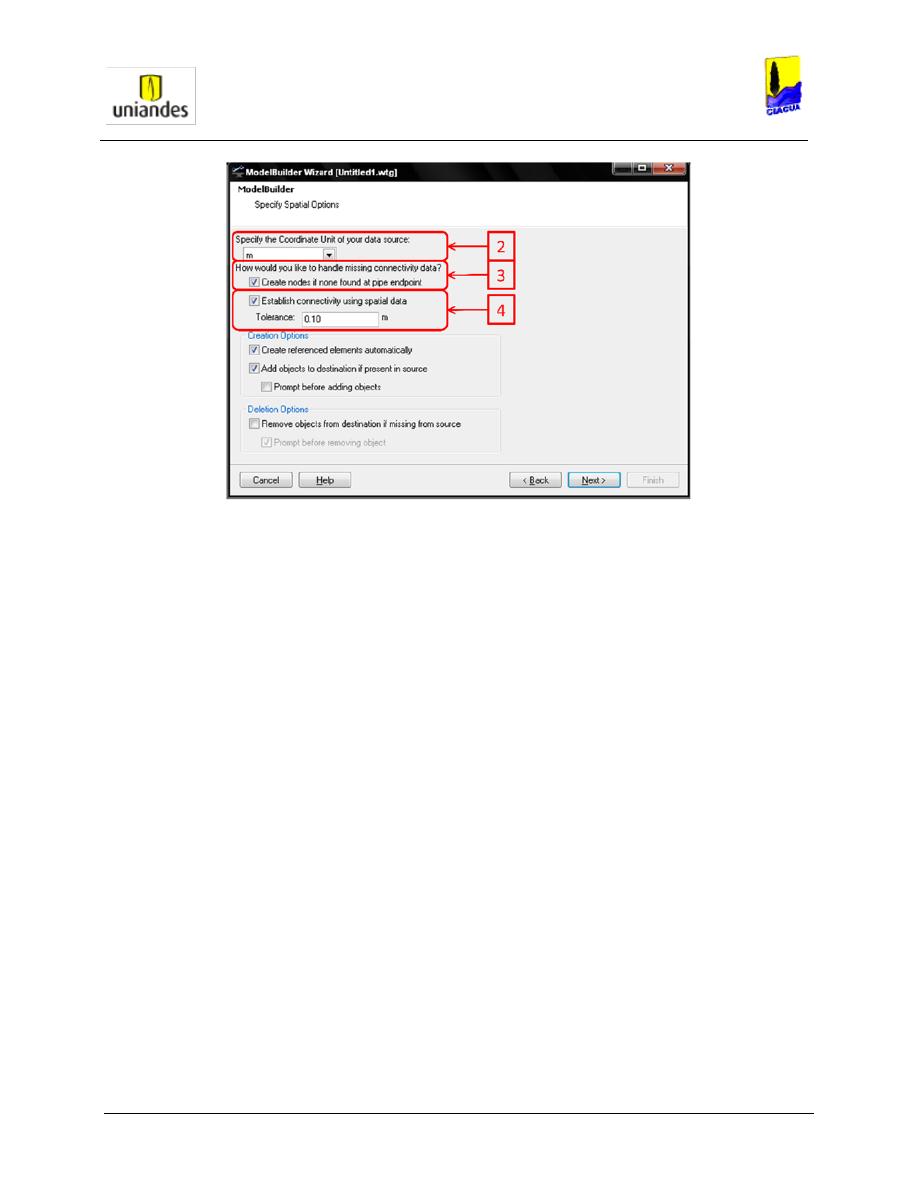
1. Se deben repetir los pasos 1 a 5 de la metodología para la creación de nodos.
2. Seleccionar la unidad para las coordenadas (en este caso metros).
3. El modelo de datos del programa WaterGEMS, y en general cualquier programa de
modelación hidráulica de redes, requieren una relación entre cada tubo y sus nodos inicial
y final. Por esto es necesario que al importar la información de la base de datos se cree la
relación entre cada tubo y sus nodos inicial y final empleando herramientas de análisis
topológico. Lo anterior se logra seleccionado la opción “Crear nodos si no se encuentra
alguno en el extremo del tubo”.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
33
Juan Camilo Vergara Valderrama
Figura 7
. Pasos 2, 3 y 4 del proceso de construcción topológica de modelos hidráulicos (tubos).
4. También se debe dejar señalada la opción “Establecer conectividad usando datos
espaciales”. Para esto se debe dar también una tolerancia para el análisis. Oprimir el
botón Next> (siguiente).
5. Seleccionar el tipo de tabla “Pipe” (tubería).
6. Seleccionar el campo clave de los datos contenidos en el archivo shape.
7. Correlacionar los datos del archivo shape con los datos de la tabla (por ejemplo
diámetro y material) y asignar unidades adecuadas. Oprimir el botón Next>
(siguiente).
8. En el siguiente paso, señalar si se quiere construir el modelo de inmediato o no, y
oprimir el botón Finish.
3.1.2 Procedimiento para la evaluación de la topología creada.
Una vez que se ha realizado la importación de la información para la construcción de la topología
de un modelo hidráulico, es necesario hacer una revisión general del modelo creado para detectar
posibles errores que se hubieran podido generar por diferentes causas, tales como:
Errores de dibujo en la información consignada.
Tuberías o nodos faltantes en la base de datos.
Tuberías o nodos redundantes en la base de datos.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
34
Juan Camilo Vergara Valderrama
3.1.3 Asignación de elevaciones a los nodos de los modelos hidráulicos.
El que un modelo hidráulico arroje buenos resultados depende en su mayor parte de que la
información empleada para la elaboración del mismo sea de buena calidad. Si no se cuenta con
buena información, no será posible alcanzar la precisión deseada. Uno de los puntos ante los
cuales es más susceptible la modelación hidráulica es la información altimétrica empleada para
asignar elevaciones a los nodos de modelo (uniones, válvulas, tanques, etc).
3.1.4 Procedimiento para la asignación de demandas a los nodos del
modelo.
La asignación de demandas a cada nodo del modelo de forma manual es una labor sumamente
dispendiosa. Por esto, el WaterGEMS ofrece una herramienta que permite hacer esta labor de
forma automática con base en la información digital que se dispone.
Se utilizó el método de áreas para la asignación de demandas a los nodos, del cual se crean los
polígonos de Thiessen desde el programa hidráulico y se distribuye el caudal según corresponda
al área aferente de cada nodo.
Figura 8
. Creación de las áreas (Herramienta Polígonos de Thiessen).
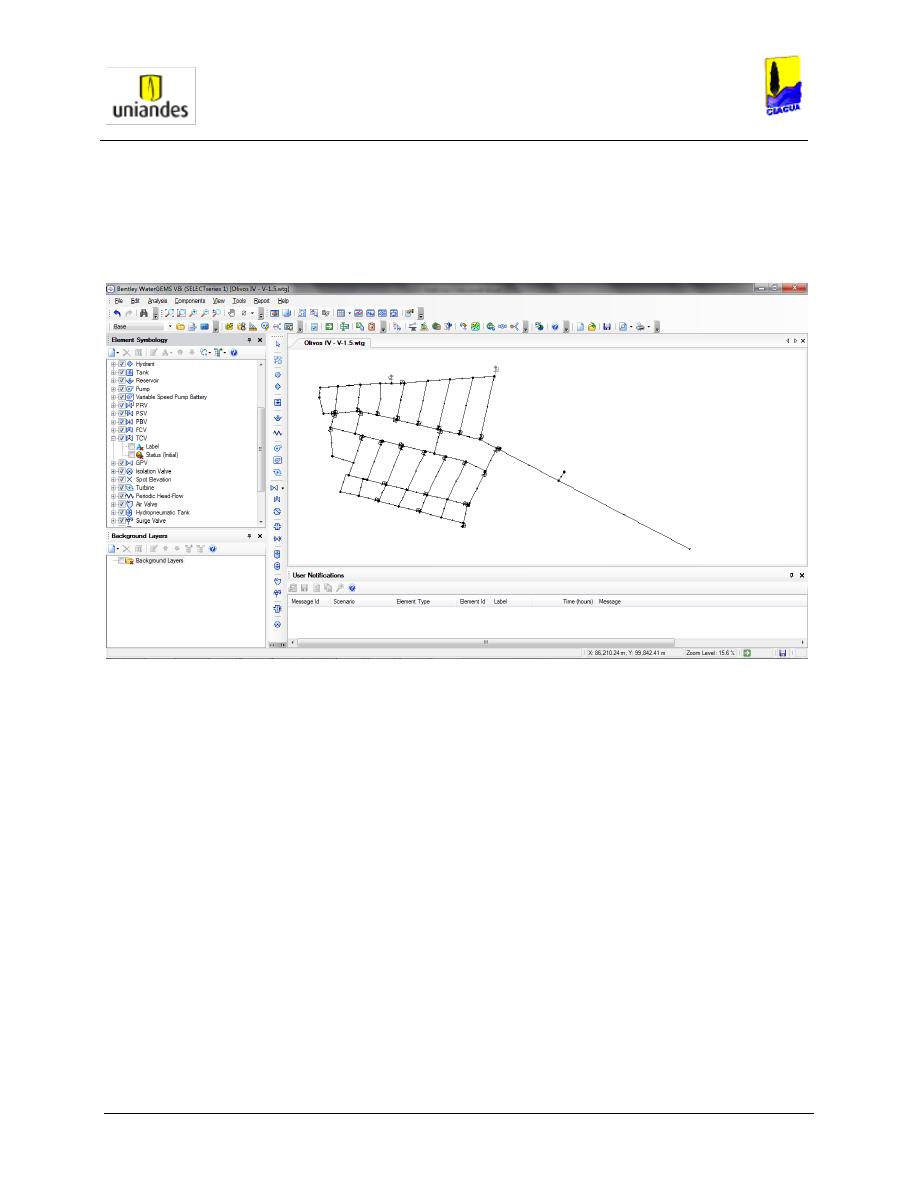
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
35
Juan Camilo Vergara Valderrama
3.1.5 Visualización de la red en el software WaterGems.
Una vez se haya construido la topología de la red, definiendo sus respectivos nodos, diámetros
materiales, coordenadas, elevaciones y demás características geométricas e hidráulicas, la red se
vera de la siguiente forma en el cuadro de diálogo:
Figura 9
. Topología de la red.
3.1.6 Ejecución del modelo.
Una vez se haya corroborado la información suministrada al modelo y se haya verificado que
todos los datos fueron ingresados correctamente, el paso a seguir es darle la orden al programa
para correr el modelo para esto se hace click en el botón “Run”.
Cuando el programa finalice el cálculo, se debe verificar que en el recuadro ubicado en la parte
inferior del cuadro de diálogo no se presente ningún error como se presenta a continuación:
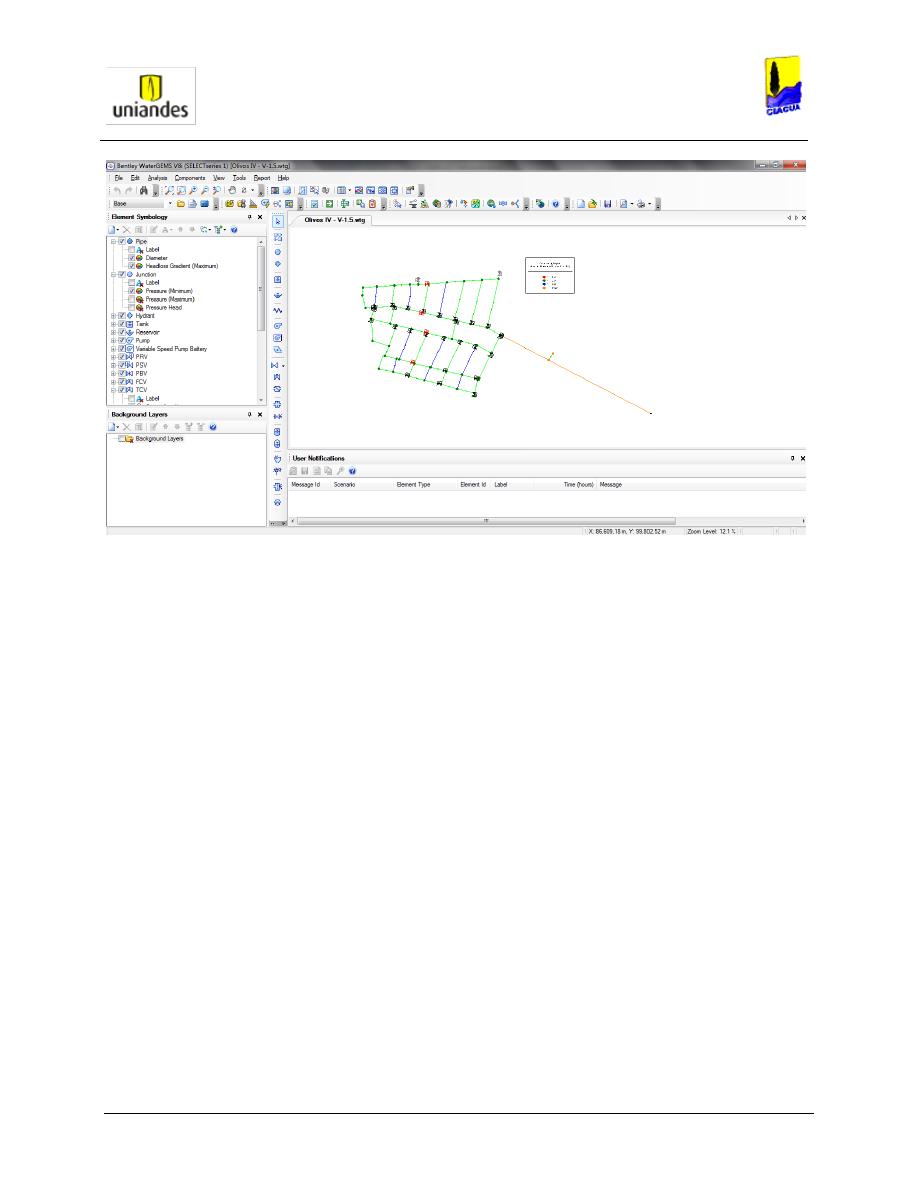
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
36
Juan Camilo Vergara Valderrama
Figura 10
. Fin de cálculo de la red.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
37
Juan Camilo Vergara Valderrama
3.1.7 Generación de reportes.
Para la generación de reportes, se debe seleccionar toda la red y hacer click derecho en cualquier
punto de la misma. Al realizar este proceso aparece una ventana de diálogo en la cual se
selecciona la opción “Edit Group…”.
Al hacer click en el botón “Edit Group” aparece una pantalla de diálogo en la cual muestra el
listado de cada uno de los elementos que conforman la red. Allí se debe elegir que tipo de reporte
se desea generar.
Figura 11
. Generación de reportes de resultados.
3.2 METODOLOGÍA PARA LA ELABORACIÓN DE MODELOS
HIDRÁULICOS EN REDES
Para este caso en particular, la construcción de la red de distribución de agua se realizó con en la
topología ya montada de la red, en el modelo realizado en el software WaterGems.
Para montar dicha red en el software Redes se debe primero exportar el archivo al software de
modelación “Epanet”. Para exportarlo se debe hacer click en “File”, “Export” y “Epanet”. Una
vez se den estas instrucciones se creara un archivo tipo “.inp”.
Dicho archivo se debe abrir con el software de Microsoft Office Excel. Una vez sea abierto este
archivo, se mostrarán todas las características de la red como nodos, tubos, coordenadas,
demandas, válvulas y otras más organizadas en columnas y filas.
Para poder abrir el archivo en el software Redes se debe ajustar dichos valores a la forma que por
defecto tiene el programa Redes; una vez hecha esta operación se podrá abrir sin generar error.
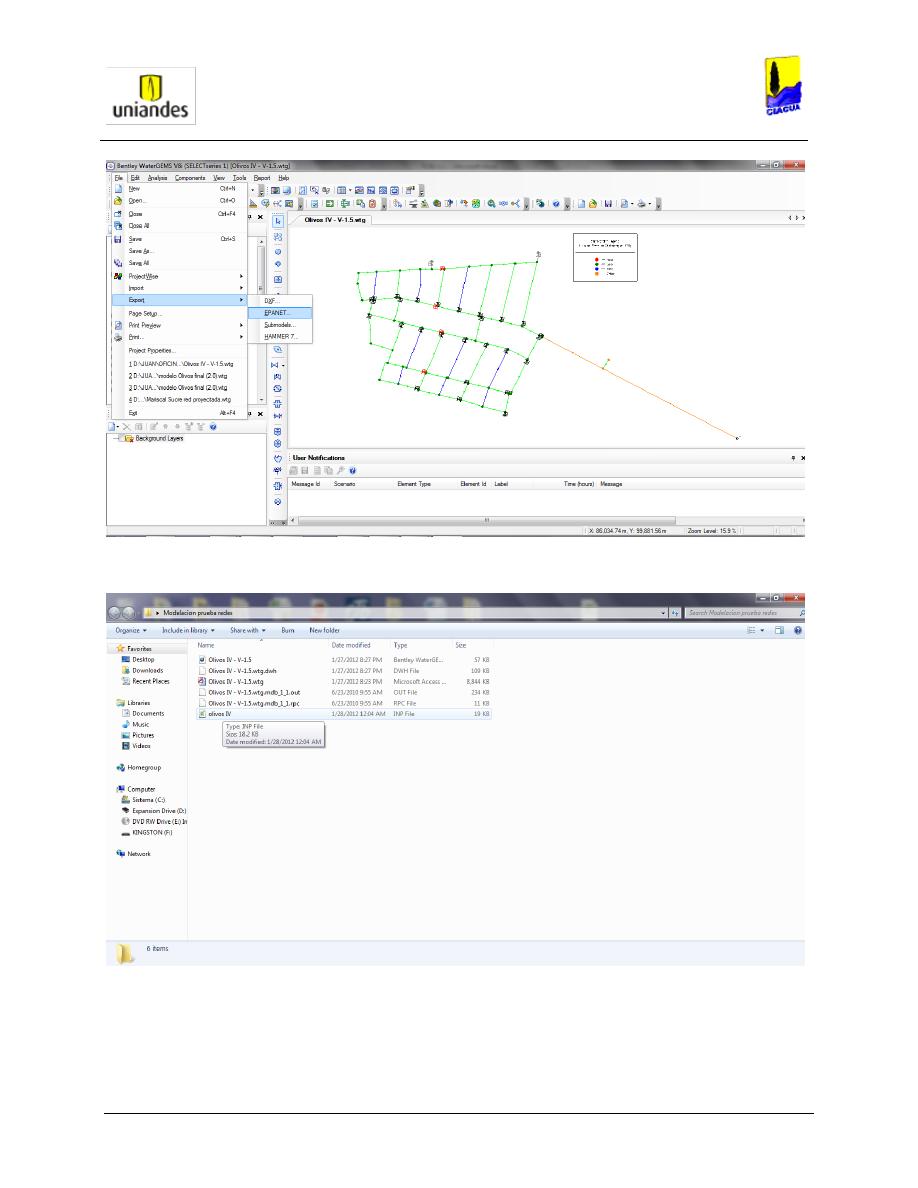
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
38
Juan Camilo Vergara Valderrama
Figura 12
. Exportar archivo a Epanet.
Figura 13
. Archivo de Excel Epanet.
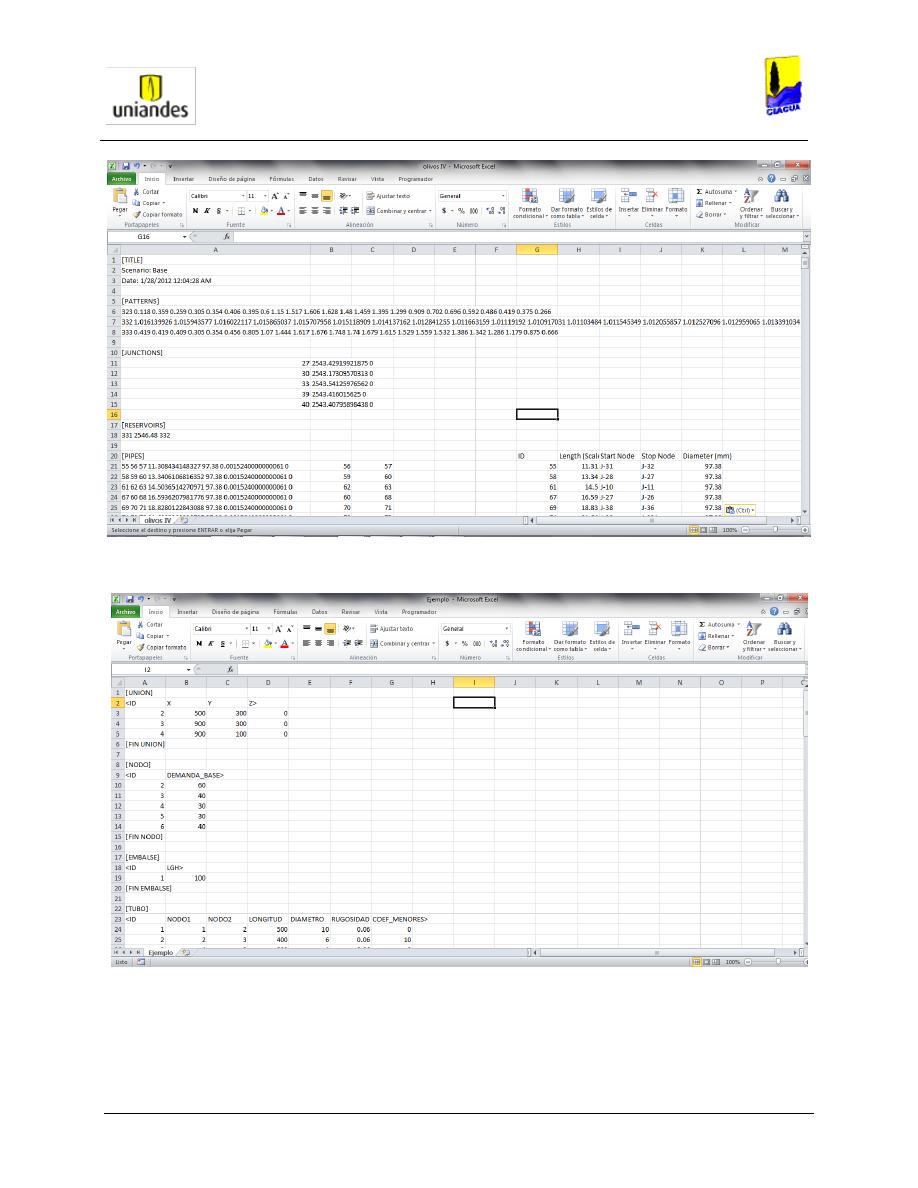
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
39
Juan Camilo Vergara Valderrama
Figura 14
. Modelo de distribución de datos Epanet.
Figura 15
. Modelo de distribución de datos Redes.
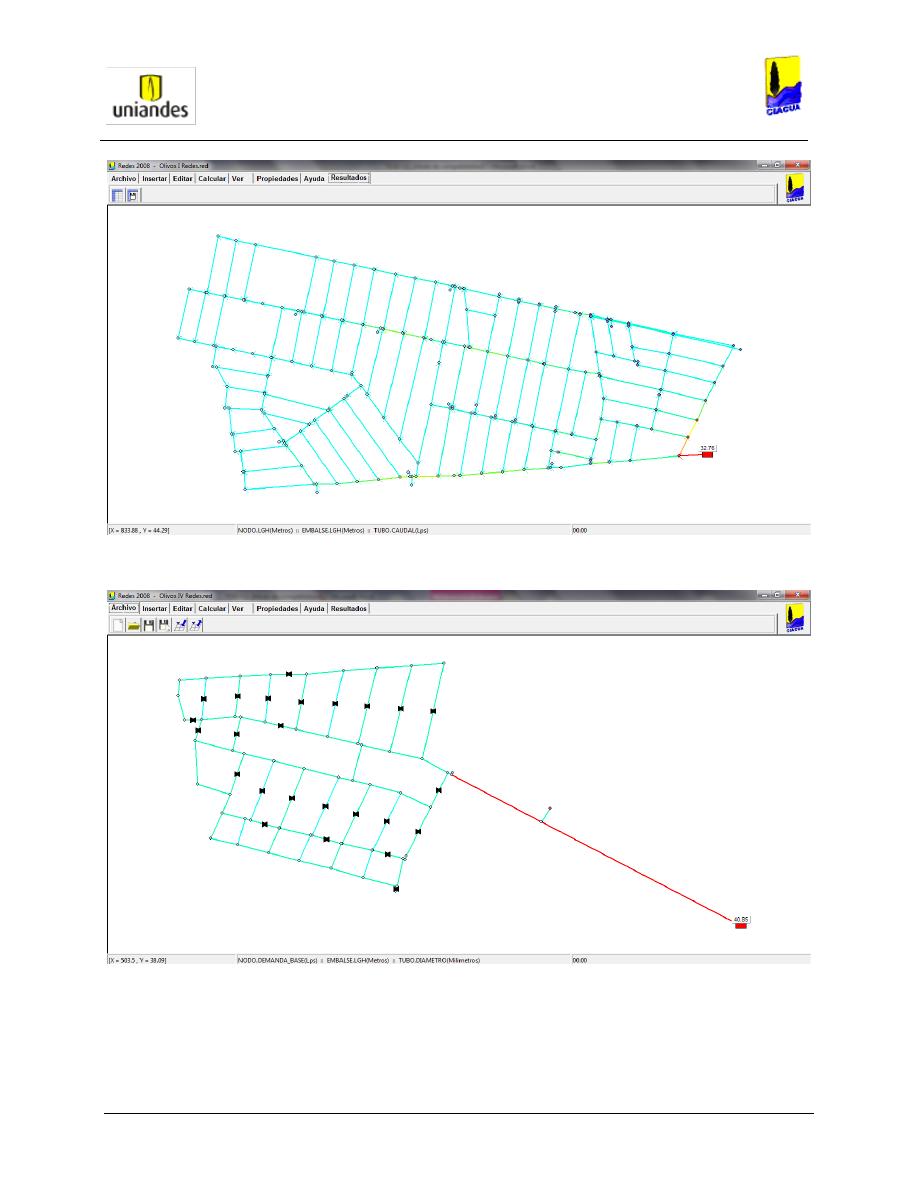
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
40
Juan Camilo Vergara Valderrama
Figura 16
. Circuito Olivos I modelado en el software Redes.
Figura 17
. Circuito Olivos IV modelado en el software Redes.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
41
Juan Camilo Vergara Valderrama
DATOS Y ANÁLISIS DE DATOS
3.3 DATOS
3.3.1 Datos para el modelo de la red de distribución de agua potable
“Olivos I”
El barrio Los Olivos I se encuentra ubicado en el Municipio de Soacha, en la Comuna 3. Limita
por el oriente con la calle 4 o con el barrio Juan Pablo I, por el occidente con la calle 1-Sur o con
el barrio Los Olivos II, por el sur con la Tv 13 o con el barrio Los Olivos III y por el norte con la
Tv 14ª o con la ciudad de Bogotá.
La localización descrita del barrio Los Olivos I, se presenta gráficamente en la figura que se
encuentra a continuación:
Figura 18. Localización general, barrio Los Olivos I.
Las coordenadas aproximadas en las cuales se enmarca el barrio son:
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
42
Juan Camilo Vergara Valderrama
NORTE
ESTE
100.422
86.853
100.100
86.360
Tabla 1.
Localización geográfica barrio Los Olivos I
Topográficamente el conjunto de los barrios de la parte baja de la Autopista Sur, en este caso
para el barrio Los Olivos I, corresponde a un desarrollo residencial de mejora progresiva y origen
subnormal completamente plano, con vías locales vehiculares con pendientes entre el 0.15% y el
0.5%, y vías peatonales muy estrechas, de pendientes longitudinales similares.
Concluyendo la estimación de la población del área servida, se resume esta en el siguiente
cuadro:
COMUNA 3
DENSIDAD DEMOGRÁFICA
(hab./ha)
ÁREA (ha)
POBLACIÓN DE DISEÑO
(habitantes)
Barrio Los Olivos I
615
10.21
6.279
Tabla 2.
Datos de población a abastecer Olivos I.
Se tomó el siguiente patrón de demanda el cual se relaciona a continuación:
TIME FROM START (HOURS)
MULTIPLIER
2
0.409
3
0.305
4
0.354
5
0.456
6
0.805
7
1.07
8
1.444
9
1.617
10
1.676
11
1.748
12
1.74
13
1.679
14
1.615
15
1.529
16
1.559

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
43
Juan Camilo Vergara Valderrama
TIME FROM START (HOURS)
MULTIPLIER
17
1.532
18
1.386
19
1.342
20
1.286
21
1.179
22
0.875
23
0.666
24
0.419
Tabla 3.
Curva de consumo aplicada a la red proyectada.
Los datos tomados para el nodo de alimentación de la red son:
Elevación = 2546.43 m.s.n.m
Presión media (m.c.a) = 31.02
Curva característica de presiones en el tiempo, asignada al punto de alimentación de la red
proyectada:
TIME FROM START (HOURS)
MULTIPLIER
1
1.0119029
2
1.0120286
3
1.0121739
4
1.0120247
5
1.0156101
6
1.0148522
7
1.0139725
8
1.0144123
9
1.013301
10
1.0129829
11
1.0127119
12
1.0130222
13
1.0130889
14
1.0135562
15
1.0139686
16
1.0145144
17
1.014915
18
1.0153352
19
1.0155983
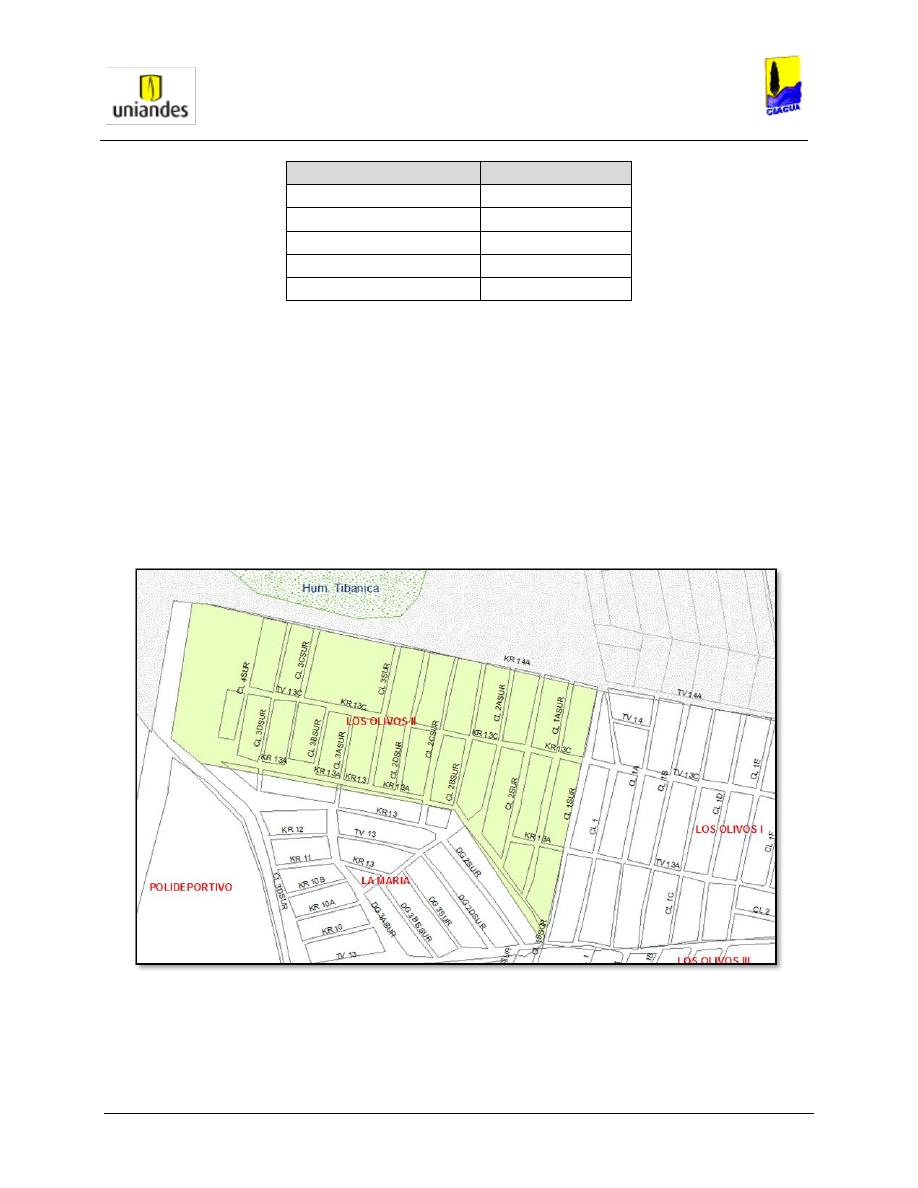
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
44
Juan Camilo Vergara Valderrama
TIME FROM START (HOURS)
MULTIPLIER
20
1.0136073
21
1.0139646
22
1.0147658
23
1.0115063
24
1.0121818
Tabla 4.
Curva de presiones aplicada al punto de alimentación red proyectada.
3.3.2 Datos para el modelo de la red de distribución de agua potable
“Olivos II”
El barrio Los Olivos II se encuentra ubicado en el Municipio de Soacha, en la Comuna 3. Limita
por el oriente con la calle 1-Sur o con el barrio Los Olivos I, por el occidente con la calle 4-Sur,
por el sur con la Cr 13ª o con el barrio La María y por el norte con la Tv 14ª o con la ciudad de
Bogotá. Al nor-occidente este barrio limita con el humedal Tibanica.
La localización descrita del barrio Los Olivos II, se presenta gráficamente en la figura que se
encuentra a continuación:
Figura 19.
Localización general, barrio Los Olivos II.
Las coordenadas aproximadas en las cuales se enmarca el barrio son:
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
45
Juan Camilo Vergara Valderrama
NORTE
ESTE
100.500
86.435
100.100
85.960
Tabla 5.
Localización geográfica barrio Los Olivos II.
La estimación de la población del área servida que se utilizó es:
COMUNA 3
DENSIDAD DEMOGRÁFICA
(hab./ha)
ÁREA (ha)
POBLACIÓN DE DISEÑO
(habitantes)
Barrio Los Olivos II
615
8.36
5.141
Tabla 6.
Datos de población a abastecer Olivos II.
Se tomó el siguiente patrón de demanda el cual se relaciona a continuación:
TIME FROM START (HOURS)
MULTIPLIER
2
0.409
3
0.305
4
0.354
5
0.456
6
0.805
7
1.07
8
1.444
9
1.617
10
1.676
11
1.748
12
1.74
13
1.679
14
1.615
15
1.529
16
1.559
17
1.532
18
1.386
19
1.342
20
1.286
21
1.179

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
46
Juan Camilo Vergara Valderrama
TIME FROM START (HOURS)
MULTIPLIER
22
0.875
23
0.666
24
0.419
Tabla 7.
Curva de consumo aplicada a la red proyectada.
Los datos tomados para el nodo de alimentación de la red son:
Elevación = 2546.43 m.s.n.m
Presión media (m.c.a) = 31.02
Curva característica de presiones en el tiempo, asignada al punto de alimentación de la red
proyectada:
TIME FROM START (HOURS)
MULTIPLIER
1
1.0119029
2
1.0120286
3
1.0121739
4
1.0120247
5
1.0156101
6
1.0148522
7
1.0139725
8
1.0144123
9
1.013301
10
1.0129829
11
1.0127119
12
1.0130222
13
1.0130889
14
1.0135562
15
1.0139686
16
1.0145144
17
1.014915
18
1.0153352
19
1.0155983
20
1.0136073
21
1.0139646
22
1.0147658
23
1.0115063
24
1.0121818
Tabla 8.
Curva de presiones aplicada al punto de alimentación red proyectada.
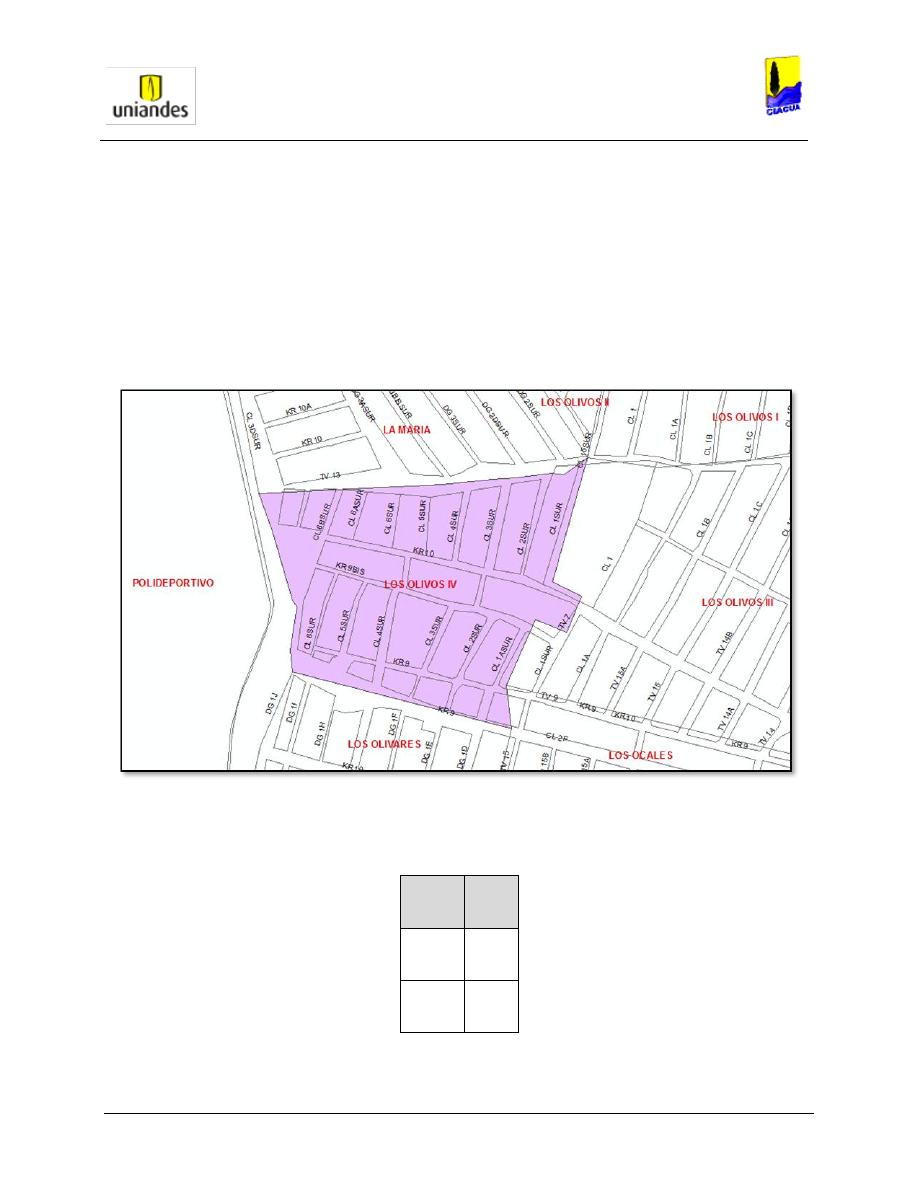
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
47
Juan Camilo Vergara Valderrama
3.3.3 Datos para el modelo de la red de distribución de agua potable
“Olivos IV”
El barrio Los Olivos IV se encuentra ubicado en el Municipio de Soacha, en la Comuna 3. Limita
por el oriente con las calles 1-Sur y calle 1 o con el barrio Los Olivos III, por el occidente con la
calle 6B-Sur, por el sur con la Cr 9 o con el barrio Los Olivares y por el norte con la Tv 13 o con
el barrio La María.
La localización descrita del barrio Los Olivos IV, se presenta gráficamente en la figura que se
encuentra a continuación:
Figura 20.
Localización general, barrio Los Olivos IV.
Las coordenadas aproximadas en las cuales se enmarca el barrio son:
NORTE
ESTE
100.100
86360
99900
86.100
Tabla 9.
Localización geográfica barrio Los Olivos IV.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
48
Juan Camilo Vergara Valderrama
La estimación de la población del área servida, se resume en el siguiente cuadro:
COMUNA 3
DENSIDAD DEMOGRÁFICA
(hab./ha)
ÁREA (ha)
POBLACIÓN DE DISEÑO
(habitantes)
Barrio Los Olivos IV
(Datos para
el modelo)
615
4.03
2.478
Tabla 10.
Datos de población a abastecer Olivos IV.
Se tomó el siguiente patrón de demanda el cual se relaciona a continuación:
TIME FROM START (HOURS)
MULTIPLIER
2
0.409
3
0.305
4
0.354
5
0.456
6
0.805
7
1.07
8
1.444
9
1.617
10
1.676
11
1.748
12
1.74
13
1.679
14
1.615
15
1.529
16
1.559
17
1.532
18
1.386
19
1.342
20
1.286
21
1.179
22
0.875
23
0.666
24
0.419
Tabla 11.
Curva de consumo aplicada a la red proyectada.
Elevación = 2546.48 m.s.n.m
Presión media (m.c.a) = 35.40

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
49
Juan Camilo Vergara Valderrama
Curva característica de presiones en el tiempo, asignada al punto de alimentación de la red
proyectada para el barrio Los Olivos IV:
Time from Start (hours)
Multiplier
1
1.01594358
2
1.01602212
3
1.01586504
4
1.01570796
5
1.01511891
6
1.01413716
7
1.01284126
8
1.01166316
9
1.01119192
10
1.01091703
11
1.01103484
12
1.01154535
13
1.01205586
14
1.0125271
15
1.01295907
16
1.01339103
17
1.01362665
18
1.013823
19
1.01413716
20
1.01433351
21
1.01476548
22
1.01547234
23
1.01613993
24
1.01613993
Tabla 12.
Curva de presiones aplicada al punto de alimentación red proyectada.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
50
Juan Camilo Vergara Valderrama
3.4 TABLAS
3.4.1 Tablas de resultados de la modelación de redes de distribución de
agua potable mediante el software WaterGems
3.4.1.1
Red de distribución los Olivos I (nodos)
Tabla 13.
Resultados de modelación red Olivos I para cada nodo de la red (Reporte 1).
ID
Elevation (m) Demand (L/s) Hydraulic Grade (m) Pressure (m H2O)
ID
Elevation (m)
Demand (L/s)
Hydraulic Grade (m) Pressure (m H2O)
27
2,544.29
0.03
2,559.89
15.6
156
2,543.31
0.2
2,559.94
16.6
29
2,544.27
0.04
2,559.89
15.6
158
2,543.34
0.2
2,559.89
16.5
31
2,544.10
0.04
2,559.89
15.8
160
2,543.30
0.2
2,559.88
16.6
33
2,543.55
0.04
2,559.89
16.3
162
2,543.17
0.2
2,559.87
16.7
35
2,543.69
0.04
2,559.88
16.2
164
2,543.07
0.21
2,559.87
16.8
39
2,543.50
0.05
2,559.88
16.4
166
2,542.75
0.21
2,559.87
17.1
41
2,543.38
0.05
2,559.87
16.5
168
2,542.77
0.21
2,559.87
17.1
43
2,543.14
0.05
2,559.86
16.7
170
2,543.00
0.21
2,559.83
16.8
45
2,543.08
0.06
2,559.85
16.8
172
2,543.02
0.22
2,559.81
16.8
47
2,542.93
0.06
2,559.80
16.9
174
2,542.99
0.22
2,559.79
16.8
49
2,542.90
0.06
2,559.79
16.9
176
2,543.00
0.22
2,559.78
16.8
51
2,543.08
0.06
2,559.78
16.7
178
2,543.01
0.22
2,559.71
16.7
53
2,542.79
0.07
2,559.75
17
213
2,544.05
0.27
2,565.97
21.9
56
2,543.79
0.07
2,559.89
16.1
215
2,544.05
0.27
2,565.90
21.9
58
2,543.77
0.07
2,559.89
16.1
217
2,544.05
0.27
2,565.92
21.9
60
2,543.39
0.08
2,559.89
16.5
221
2,543.84
0.28
2,565.20
21.4
62
2,543.37
0.08
2,559.89
16.5
223
2,543.56
0.28
2,564.55
21
64
2,543.02
0.08
2,559.89
16.9
225
2,543.67
0.28
2,563.83
20.2
66
2,543.01
0.08
2,559.89
16.9
227
2,543.57
0.29
2,562.98
19.4
68
2,542.88
0.09
2,559.88
17
229
2,543.55
0.29
2,562.68
19.1
70
2,542.89
0.09
2,559.88
17
231
2,543.47
0.29
2,561.78
18.3
72
2,543.08
0.09
2,559.87
16.8
233
2,543.28
0.29
2,560.92
17.6
76
2,543.08
0.1
2,559.87
16.8
235
2,543.41
0.3
2,560.83
17.4
78
2,543.12
0.1
2,559.87
16.8
237
2,543.44
0.3
2,560.79
17.4
80
2,543.12
0.1
2,559.87
16.8
239
2,543.29
0.3
2,560.62
17.3
82
2,543.01
0.1
2,559.87
16.9
241
2,543.29
0.3
2,560.36
17.1
84
2,543.00
0.11
2,559.87
16.9
243
2,543.15
0.31
2,560.21
17.1
86
2,542.99
0.11
2,559.86
16.9
245
2,543.17
0.31
2,560.11
16.9
88
2,542.97
0.11
2,559.86
16.9
247
2,543.00
0.31
2,560.04
17
90
2,542.96
0.11
2,559.83
16.9
249
2,543.00
0.31
2,560.04
17
92
2,542.88
0.12
2,559.80
16.9
251
2,543.27
0.32
2,559.96
16.7
94
2,542.87
0.12
2,559.80
16.9
253
2,542.94
0.32
2,559.95
17
96
2,542.80
0.12
2,559.78
17
255
2,542.98
0.32
2,559.94
17
98
2,542.80
0.12
2,559.78
17
257
2,542.83
0.32
2,559.93
17.1
101
2,542.80
0.13
2,559.75
17
259
2,542.92
0.33
2,559.92
17
103
2,543.05
0.13
2,559.72
16.7
261
2,542.82
0.33
2,559.91
17.1
105
2,543.10
5.36
2,559.64
16.5
263
2,542.85
0.33
2,559.91
17.1
119
2,544.55
0.15
2,566.01
21.5
265
2,542.81
0.33
2,559.89
17.1
121
2,544.21
0.15
2,565.74
21.5
267
2,542.82
0.34
2,559.89
17.1
123
2,544.19
0.15
2,565.73
21.5
269
2,543.08
0.34
2,559.87
16.8
125
2,544.01
0.16
2,565.26
21.2
271
2,542.69
0.34
2,559.91
17.2
127
2,544.01
0.16
2,565.25
21.2
273
2,542.68
0.34
2,559.92
17.2
129
2,543.93
0.16
2,564.90
21
275
2,542.67
0.35
2,559.93
17.3
131
2,543.91
0.16
2,564.82
20.9
277
2,542.72
0.35
2,559.94
17.2
133
2,543.77
0.17
2,564.54
20.8
279
2,542.70
0.35
2,559.96
17.3
135
2,543.75
0.17
2,564.46
20.7
281
2,542.69
0.35
2,559.96
17.3
137
2,543.69
0.17
2,564.28
20.6
283
2,542.68
0.36
2,559.97
17.3
139
2,543.68
0.17
2,564.21
20.5
285
2,543.17
0.36
2,560.00
16.8
141
2,543.62
0.18
2,561.59
18
288
2,543.17
0.36
2,559.83
16.7
143
2,543.64
0.18
2,561.60
18
290
2,543.19
0.36
2,559.82
16.6
145
2,543.83
0.18
2,560.38
16.5
293
2,542.69
0.37
2,559.89
17.2
147
2,543.32
0.18
2,560.56
17.2
296
2,543.46
0.37
2,559.98
16.5
150
2,543.46
0.19
2,560.14
16.7
298
2,543.49
0.37
2,560.01
16.5
152
2,543.40
0.19
2,559.99
16.6
300
2,543.19
0.38
2,560.01
16.8
154
2,543.26
0.19
2,559.94
16.7
302
2,543.18
0.38
2,560.01
16.8
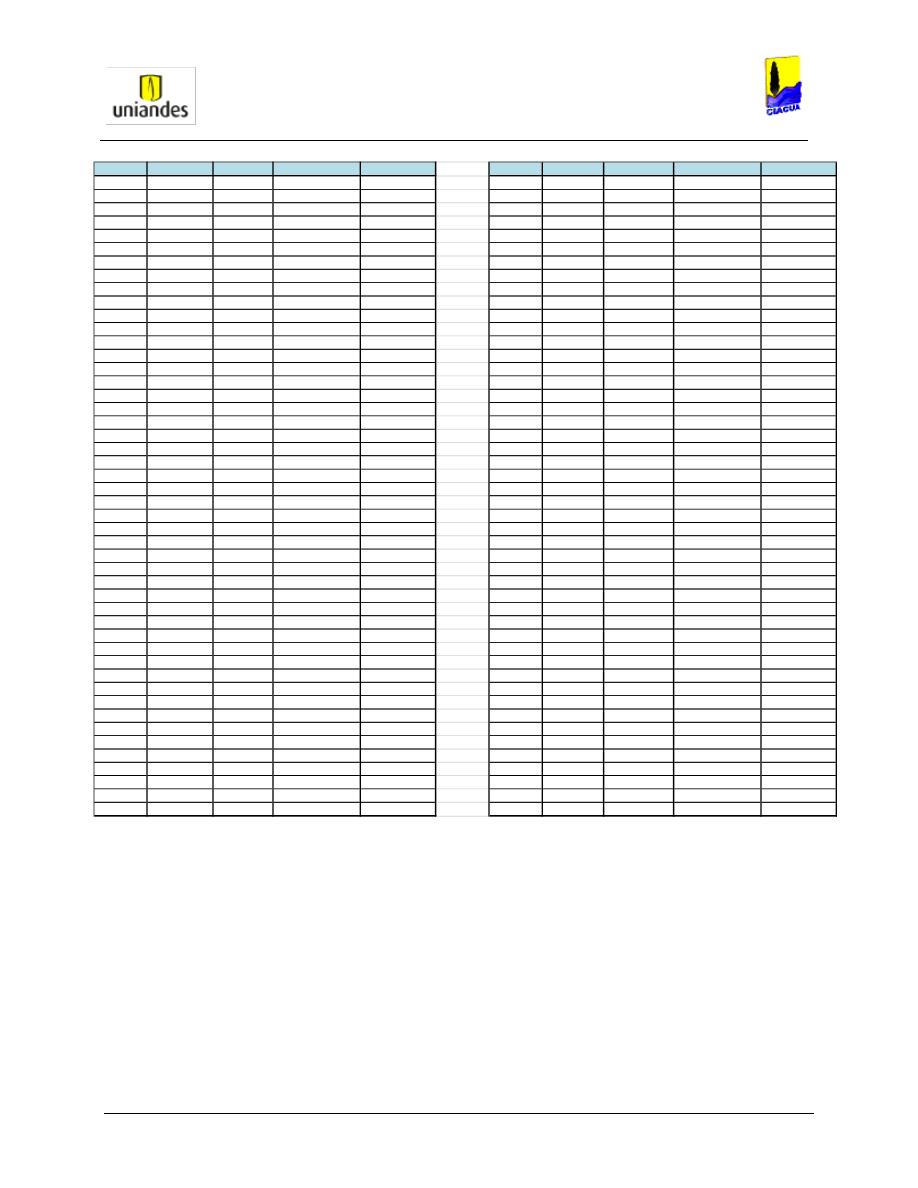
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
51
Juan Camilo Vergara Valderrama
Tabla 14.
Resultados de modelación red Olivos I para cada nodo de la red (Reporte 2).
ID
Elevation (m) Demand (L/s) Hydraulic Grade (m) Pressure (m H2O)
ID
Elevation (m)
Demand (L/s)
Hydraulic Grade (m) Pressure (m H2O)
304
2,543.06
0.38
2,559.99
16.9
682
2,546.12
0.86
2,565.93
19.8
306
2,543.14
0.38
2,559.99
16.8
683
2,546.09
0.86
2,565.91
19.8
310
2,542.69
0.39
2,559.91
17.2
684
2,546.04
0.86
2,565.80
19.8
314
2,542.69
0.39
2,559.89
17.2
685
2,546.04
0.86
2,565.81
19.8
323
2,543.02
0.41
2,560.01
17
686
2,546.02
0.86
2,565.69
19.7
351
2,542.98
0.44
2,559.89
16.9
687
2,545.97
0.86
2,566.01
20
356
2,542.98
0.45
2,559.88
16.9
688
2,546.09
0.86
2,566.01
19.9
359
2,543.66
0.45
2,561.59
17.9
689
2,546.31
0.87
2,566.16
19.9
363
2,543.68
0.46
2,561.59
17.9
690
2,546.46
0.87
2,566.17
19.7
365
2,544.05
0.46
2,565.97
21.9
692
2,544.52
0.87
2,561.45
16.9
368
2,544.28
0.46
2,559.88
15.6
693
2,544.98
0.87
2,565.20
20.2
370
2,543.00
0.46
2,559.86
16.9
694
2,544.27
0.87
2,561.47
17.2
372
2,543.30
0.47
2,560.79
17.5
695
2,546.79
0.87
2,568.42
21.6
374
2,542.71
0.47
2,559.96
17.2
696
2,547.10
0.87
2,567.29
20.2
604
2,544.42
0.76
2,561.44
17
697
2,546.34
0.88
2,566.19
19.9
605
2,543.87
0.76
2,559.89
16
698
2,546.31
0.88
2,566.24
19.9
608
2,543.95
0.76
2,560.00
16
699
2,546.08
0.88
2,566.28
20.2
609
2,543.74
0.76
2,564.35
20.6
701
2,546.35
0.88
2,566.21
19.9
610
2,543.81
0.77
2,564.56
20.8
702
2,546.38
0.88
2,566.09
19.7
611
2,543.96
0.77
2,564.91
21
703
2,546.08
0.88
2,565.91
19.8
616
2,544.29
0.77
2,566.05
21.8
704
2,546.04
0.88
2,565.81
19.8
617
2,544.04
0.77
2,566.28
22.2
705
2,545.95
0.89
2,565.65
19.7
619
2,543.76
0.78
2,560.83
17.1
706
2,545.73
0.89
2,565.48
19.8
624
2,543.04
0.78
2,560.04
17
707
2,545.34
0.89
2,565.35
20
653
2,544.52
0.82
2,561.45
16.9
709
2,545.25
0.89
2,565.36
20.1
656
2,546.40
0.82
2,572.03
25.6
711
2,546.54
0.89
2,567.44
20.9
657
2,546.39
0.83
2,568.92
22.5
713
2,545.41
0.9
2,566.86
21.5
658
2,545.84
0.83
2,567.83
22
716
2,546.01
0.9
2,565.69
19.7
660
2,545.30
0.83
2,566.97
21.7
717
2,544.53
0.9
2,561.45
16.9
661
2,545.37
0.83
2,566.81
21.4
728
2,547.10
0.91
2,566.12
19
662
2,545.48
0.83
2,566.59
21.1
729
2,546.12
0.92
2,565.93
19.8
663
2,544.56
0.83
2,566.00
21.4
730
2,545.08
0.92
2,565.35
20.3
664
2,544.00
0.83
2,559.89
15.9
732
2,545.37
0.92
2,565.36
20
666
2,544.33
0.84
2,561.47
17.1
733
2,545.61
0.92
2,565.42
19.8
667
2,545.70
0.84
2,565.95
20.2
734
2,545.69
0.92
2,565.50
19.8
668
2,546.02
0.84
2,566.16
20.1
737
2,544.21
0.93
2,565.73
21.5
669
2,546.09
0.84
2,566.30
20.2
738
2,545.76
0.93
2,565.50
19.7
670
2,545.85
0.84
2,566.58
20.7
739
2,545.35
0.93
2,565.36
20
671
2,545.77
0.84
2,566.65
20.9
740
2,545.59
0.93
2,565.42
19.8
672
2,546.06
0.84
2,567.52
21.5
741
2,545.06
0.93
2,565.35
20.3
673
2,546.33
0.85
2,568.21
21.9
742
2,546.37
0.93
2,566.09
19.7
674
2,546.43
0.85
2,568.31
21.9
743
2,545.34
0.93
2,565.70
20.4
675
2,546.69
0.85
2,570.46
23.8
744
2,545.25
0.93
2,565.36
20.1
676
2,546.76
0.85
2,569.35
22.6
745
2,545.11
0.94
2,565.22
20.1
677
2,546.98
0.85
2,567.91
20.9
746
2,544.96
0.94
2,565.11
20.1
678
2,547.10
0.85
2,567.57
20.5
747
2,544.60
0.94
2,565.06
20.5
680
2,546.35
0.85
2,566.59
20.2
748
2,546.47
0.94
2,567.85
21.4
681
2,546.37
0.86
2,566.09
19.7
749
2,546.56
0.94
2,567.34
20.8

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
52
Juan Camilo Vergara Valderrama
Tabla 15.
Resultados de modelación red Olivos I para cada nodo de la red (Reporte 3).
ID
Elevation (m) Demand (L/s) Hydraulic Grade (m) Pressure (m H2O)
750
2,546.68
0.94
2,566.85
20.2
751
2,546.71
0.94
2,566.56
19.9
752
2,546.37
0.94
2,566.21
19.8
759
2,546.09
0.95
2,565.91
19.8
903
2,544.02
1.13
2,559.89
15.9
967
2,544.34
1.21
2,561.47
17.1
1030
2,543.34
1.29
2,559.89
16.5
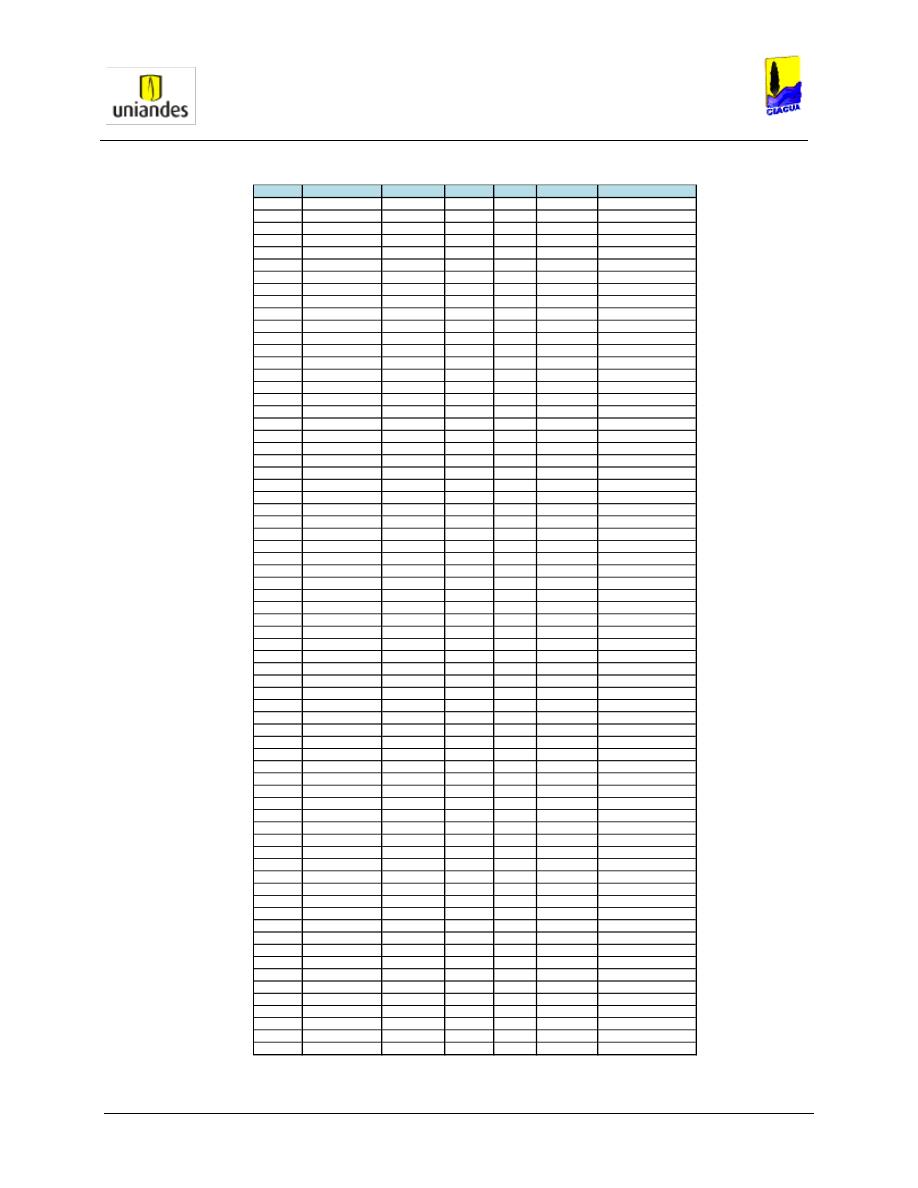
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
53
Juan Camilo Vergara Valderrama
3.4.1.2
Red de distribución los Olivos I (tubos)
Tabla 16.
Resultados de modelación red Olivos I para cada tubo de la red (Reporte 1).
ID
Length (Scaled) (m) Diameter (mm)
Material
Flow (L/s) Velocity (m/s) Headloss Gradient (m/m)
30
3.7
97.38
PVC
0.43
0.06
0.0001
32
27.58
97.38
PVC
-0.07
0.01
0
34
32.37
97.38
PVC
0.18
0.02
0
36
30.84
97.38
PVC
0.42
0.06
0.0001
42
31.73
97.38
PVC
0.82
0.11
0.0002
44
31.36
97.38
PVC
0.92
0.12
0.0003
46
28.88
97.38
PVC
1.11
0.15
0.0004
50
31.06
97.38
PVC
1.37
0.18
0.0005
52
28.71
97.38
PVC
1.03
0.14
0.0003
57
10.43
143.34
PVC
-1.23
0.08
0.0001
59
1.62
143.34
PVC
-1.59
0.1
0.0002
61
31.33
143.34
PVC
0.86
0.05
0
63
1.35
143.34
PVC
2.46
0.15
0.0004
65
30.32
143.34
PVC
2.11
0.13
0.0002
67
1.75
143.34
PVC
1.8
0.11
0.0002
71
1.32
143.34
PVC
1.82
0.11
0.0002
77
1.72
143.34
PVC
1.95
0.12
0.0002
79
30.4
143.34
PVC
2.03
0.13
0.0002
81
1.37
143.34
PVC
1.68
0.1
0.0002
83
27.5
143.34
PVC
1.73
0.11
0.0001
85
4.32
143.34
PVC
1.3
0.08
0.0001
87
5.68
143.34
PVC
1.44
0.09
0.0001
89
25.73
143.34
PVC
0.87
0.05
0
93
28.72
97.38
PVC
1.98
0.27
0.001
95
1.3
97.38
PVC
1.97
0.26
0.0009
97
29.31
97.38
PVC
1.81
0.24
0.0009
99
1.33
97.38
PVC
1.97
0.26
0.0009
100
27.26
97.38
PVC
1.91
0.26
0.0009
102
1.43
97.38
PVC
2.81
0.38
0.0019
104
26.55
97.38
PVC
2.06
0.28
0.0011
106
77.5
97.38
PVC
1.93
0.26
0.001
122
25.58
97.38
PVC
7.52
1.01
0.0106
124
1.01
97.38
PVC
5.85
0.78
0.0068
126
35.59
97.38
PVC
8.53
1.15
0.0132
128
1.06
97.38
PVC
7.51
1.01
0.0104
132
5.1
97.38
PVC
9.54
1.28
0.0162
134
27.2
97.38
PVC
7.34
0.99
0.0101
136
5.38
97.38
PVC
9.19
1.23
0.0151
138
26.44
97.38
PVC
5.96
0.8
0.007
140
5.1
97.38
PVC
8.44
1.13
0.0129
144
3.46
143.34
PVC
-7.36
0.46
0.0016
148
92.16
97.38
PVC
-2.91
0.39
0.002
153
41.62
97.38
PVC
4.09
0.55
0.0036
155
44.41
97.38
PVC
2.21
0.3
0.0012
157
16.37
97.38
PVC
0.68
0.09
0.0002
161
31.86
97.38
PVC
1.12
0.15
0.0004
163
31.74
97.38
PVC
0.74
0.1
0.0002
165
30.75
97.38
PVC
0.38
0.05
0
169
1.31
143.34
PVC
3.66
0.23
0.0005
173
30.71
97.38
PVC
1.9
0.25
0.0009
175
26.58
97.38
PVC
1.58
0.21
0.0007
177
4.1
97.38
PVC
3.32
0.45
0.0025
179
30.27
97.38
PVC
3.03
0.41
0.0021
180
26.07
97.38
PVC
3.43
0.46
0.0026
181
77.81
75.74
PVC
0.62
0.14
0.0004
182
78.24
75.74
PVC
0.07
0.01
0
183
78.69
75.74
PVC
-0.1
0.02
0
184
79.06
75.74
PVC
-0.08
0.02
0
194
65.96
75.74
PVC
-2.73
0.61
0.0058
199
12.9
75.74
PVC
2.65
0.59
0.0055
201
3.77
75.74
PVC
2.01
0.45
0.0034
203
3.97
75.74
PVC
1.24
0.28
0.0014
214
16.29
143.34
PVC
29.41
1.82
0.0191
216
3.6
143.34
PVC
28.68
1.78
0.0182
219
30.67
75.74
PVC
2.84
0.63
0.0063
220
11.55
75.74
PVC
-3.91
0.87
0.011
224
33.57
143.34
PVC
29.8
1.85
0.0196
226
32.88
143.34
PVC
31.56
1.96
0.0217
228
33.55
143.34
PVC
34.34
2.13
0.0253
230
8.22
143.34
PVC
42.32
2.62
0.0369
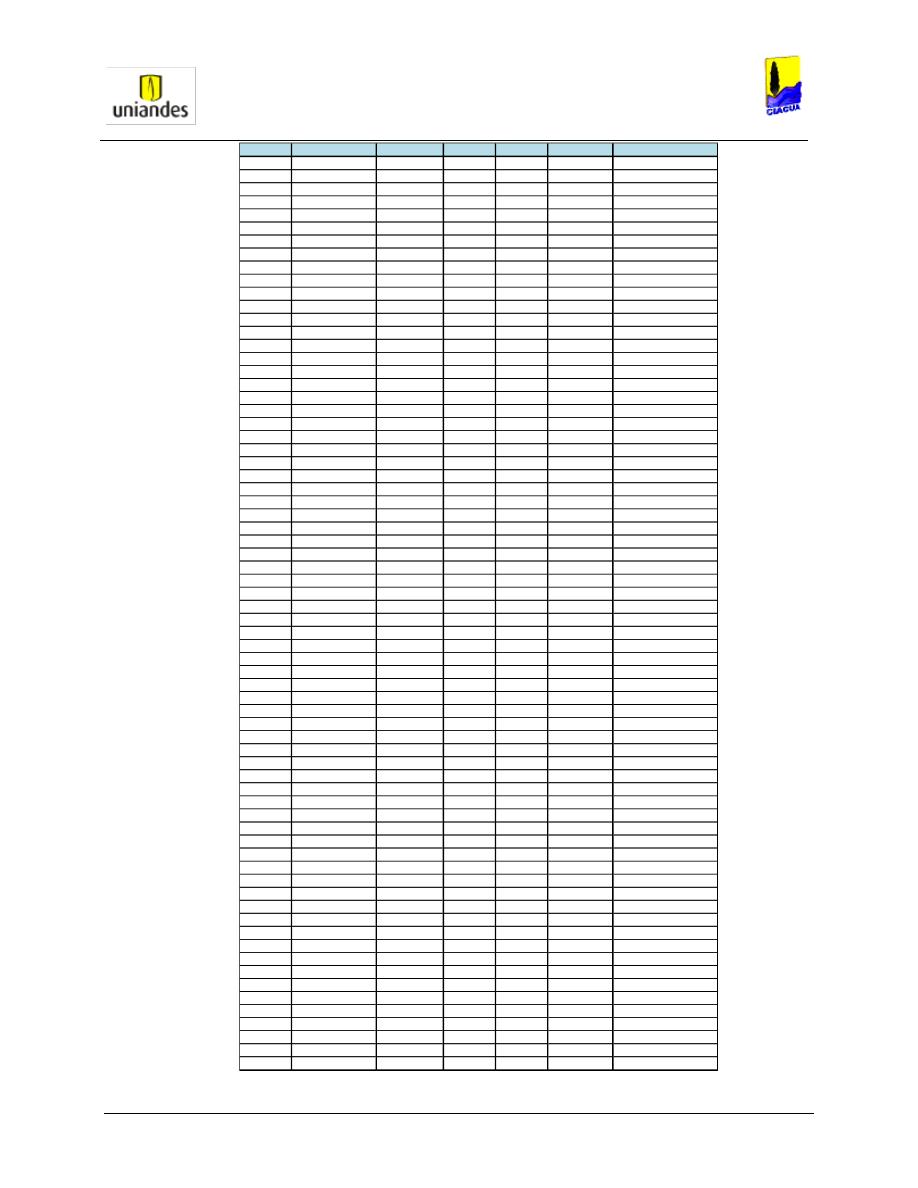
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
54
Juan Camilo Vergara Valderrama
Tabla 17.
Resultados de modelación red Olivos I para cada tubo de la red (Reporte 2).
ID
Length (Scaled) (m) Diameter (mm)
Material
Flow (L/s)
Velocity (m/s) Headloss Gradient (m/m)
232
24.83
143.34
PVC
42.03
2.6
0.0364
236
6.31
143.34
PVC
24.02
1.49
0.0132
238
3.49
143.34
PVC
22.95
1.42
0.0122
240
15.08
143.34
PVC
22.19
1.37
0.0115
242
33.96
143.34
PVC
17.49
1.08
0.0075
244
32.35
143.34
PVC
13.74
0.85
0.0049
246
31.91
143.34
PVC
10.75
0.67
0.0031
248
31.21
143.34
PVC
8.31
0.52
0.002
250
4.76
143.34
PVC
7.22
0.45
0.0016
254
27.78
75.74
PVC
0.54
0.12
0.0003
256
1.49
75.74
PVC
0.93
0.21
0.001
260
8.53
75.74
PVC
0.94
0.21
0.0009
262
27.59
75.74
PVC
0.61
0.14
0.0004
264
2.44
75.74
PVC
0.92
0.2
0.0009
266
39.83
75.74
PVC
0.59
0.13
0.0004
268
6.02
75.74
PVC
0.98
0.22
0.0009
276
6.43
143.34
PVC
-5.25
0.33
0.0009
278
28.44
143.34
PVC
-3.77
0.23
0.0005
280
24.17
143.34
PVC
-4.76
0.29
0.0007
282
3.42
143.34
PVC
-5.58
0.35
0.001
284
5.41
143.34
PVC
-3.98
0.25
0.0006
286
38.43
143.34
PVC
-4.99
0.31
0.0008
289
41.9
75.74
PVC
1.03
0.23
0.0011
292
6.14
97.38
PVC
-2.32
0.31
0.0014
295
28.89
143.34
PVC
3.94
0.24
0.0005
299
5.96
97.38
PVC
-4.62
0.62
0.0044
301
28.27
97.38
PVC
-0.6
0.08
0.0001
303
2.8
97.38
PVC
2.47
0.33
0.0015
307
17.39
97.38
PVC
0.21
0.03
0
311
1.37
143.34
PVC
-5.75
0.36
0.0011
316
1.02
143.34
PVC
-5.96
0.37
0.0012
317
25.93
143.34
PVC
-4.69
0.29
0.0007
325
10.09
97.38
PVC
2.42
0.32
0.0014
352
3.68
143.34
PVC
3.06
0.19
0.0003
353
27.07
143.34
PVC
2.17
0.13
0.0002
361
3.41
143.34
PVC
-7.18
0.44
0.0015
380
2.74
97.38
PVC
0
0
0
381
4.8
97.38
PVC
0
0
0
383
29.59
97.38
PVC
0.6
0.08
0.0001
384
3.75
97.38
PVC
0.6
0.08
0.0002
386
3.67
97.38
PVC
1.39
0.19
0.0005
387
91.23
97.38
PVC
1.39
0.19
0.0005
389
83.72
75.74
PVC
-0.29
0.06
0.0001
390
3.6
75.74
PVC
-0.29
0.06
0.0001
392
83.54
75.74
PVC
-0.28
0.06
0.0001
393
3.51
75.74
PVC
-0.28
0.06
0.0001
395
83.77
75.74
PVC
-0.22
0.05
0
396
3.24
75.74
PVC
-0.22
0.05
0
399
83.67
97.38
PVC
-0.27
0.04
0
400
3.31
97.38
PVC
-0.27
0.04
0
402
83.64
75.74
PVC
-0.15
0.03
0
403
3.41
75.74
PVC
-0.15
0.03
0
405
83.71
75.74
PVC
-0.25
0.06
0.0001
406
3.41
75.74
PVC
-0.25
0.06
0.0001
408
83.61
75.74
PVC
-0.33
0.07
0.0001
409
3.57
75.74
PVC
-0.33
0.07
0.0001
411
6.29
97.38
PVC
2.01
0.27
0.001
412
23.96
97.38
PVC
2.01
0.27
0.001
414
84.19
75.74
PVC
-0.04
0.01
0
415
3.5
75.74
PVC
-0.04
0.01
0
417
84.63
75.74
PVC
0.28
0.06
0.0001
418
3.43
75.74
PVC
0.28
0.06
0.0002
420
84.69
97.38
PVC
0.97
0.13
0.0003
421
3.74
97.38
PVC
0.97
0.13
0.0002
423
3.62
143.34
PVC
-1.26
0.08
0.0001
424
75.33
143.34
PVC
-1.26
0.08
0.0001
426
3.49
143.34
PVC
2.19
0.14
0.0002
427
26.96
143.34
PVC
2.19
0.14
0.0002
429
3.36
97.38
PVC
-0.46
0.06
0.0001
433
34.49
97.38
PVC
9.22
1.24
0.0152
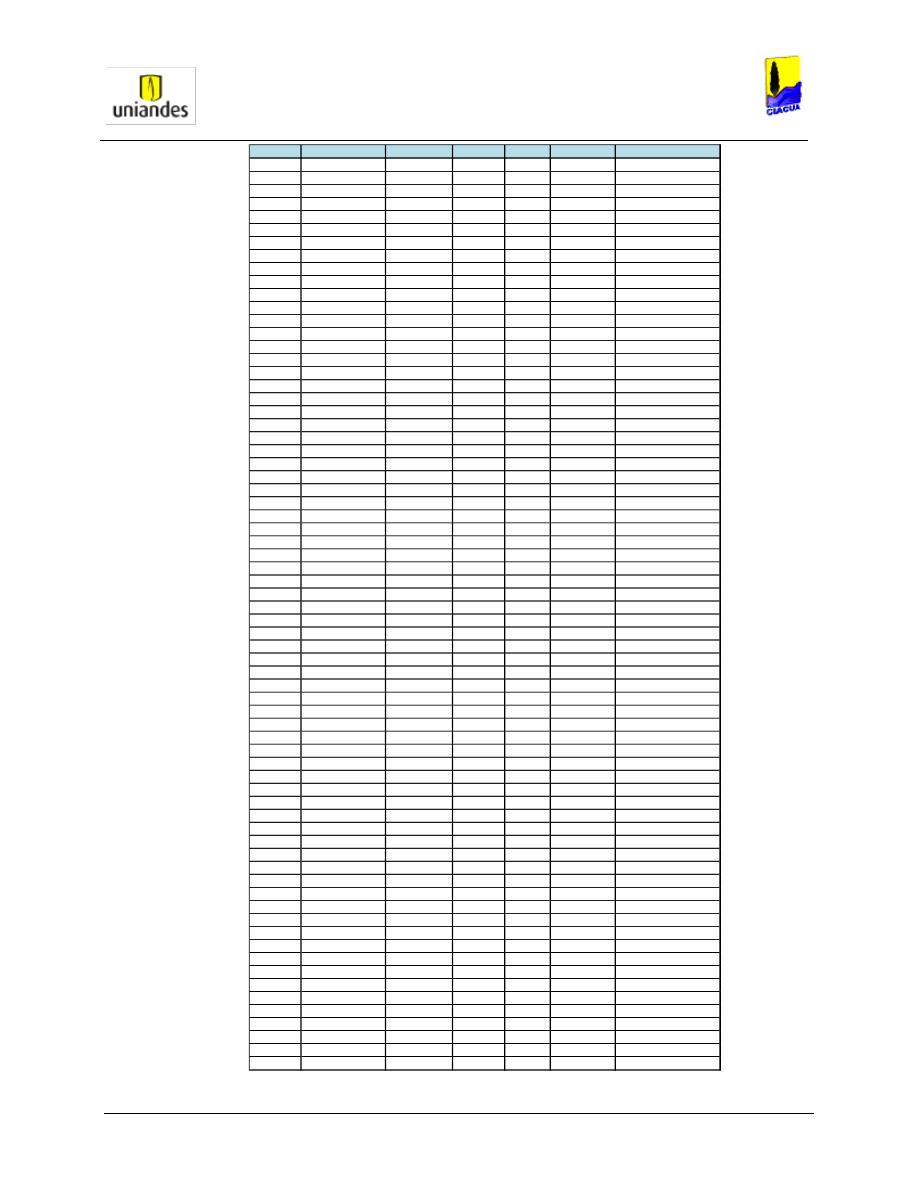
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
55
Juan Camilo Vergara Valderrama
Tabla 18.
Resultados de modelación red Olivos I para cada tubo de la red (Reporte 3).
ID
Length (Scaled) (m) Diameter (mm)
Material
Flow (L/s) Velocity (m/s) Headloss Gradient (m/m)
435
22.98
97.38
PVC
8.46
1.14
0.013
436
3.44
97.38
PVC
8.46
1.14
0.013
438
23.78
97.38
PVC
0
0
0
439
6.17
97.38
PVC
0
0
0
441
2.19
97.38
PVC
0
0
0
442
28.21
97.38
PVC
0
0
0
444
3.24
75.74
PVC
-0.8
0.18
0.0006
445
24.14
75.74
PVC
-0.8
0.18
0.0007
447
3.76
143.34
PVC
29.21
1.81
0.0189
448
33.27
143.34
PVC
29.21
1.81
0.0189
450
3.45
75.74
PVC
-0.87
0.19
0.0008
451
65.38
75.74
PVC
-0.87
0.19
0.0008
453
3.42
75.74
PVC
-2.04
0.45
0.0035
454
75.26
75.74
PVC
-2.04
0.45
0.0035
456
3.44
75.74
PVC
-3.06
0.68
0.0071
457
84.93
75.74
PVC
-3.06
0.68
0.0071
459
3.51
97.38
PVC
-8.26
1.11
0.0125
460
94.68
97.38
PVC
-8.26
1.11
0.0125
465
3.57
143.34
PVC
7.54
0.47
0.0017
466
102.28
143.34
PVC
7.53
0.47
0.0017
468
30.64
143.34
PVC
34.2
2.12
0.0251
469
3.53
143.34
PVC
34.2
2.12
0.0251
471
17.35
97.38
PVC
-9.89
1.33
0.0172
472
3.39
97.38
PVC
-9.89
1.33
0.0172
474
3.33
97.38
PVC
0.78
0.1
0.0002
475
10.59
97.38
PVC
0.78
0.1
0.0002
477
3.39
97.38
PVC
4.39
0.59
0.0041
478
146.91
97.38
PVC
4.39
0.59
0.0041
480
10.18
97.38
PVC
3.45
0.46
0.0027
481
122.81
97.38
PVC
3.45
0.46
0.0026
483
8.83
97.38
PVC
2.69
0.36
0.0017
484
107.52
97.38
PVC
2.69
0.36
0.0017
486
8.73
97.38
PVC
2.13
0.29
0.0011
487
91.39
97.38
PVC
2.13
0.29
0.0011
489
26.69
143.34
PVC
-6.06
0.38
0.0011
490
8.72
143.34
PVC
-6.06
0.38
0.0011
492
6.01
75.74
PVC
0.85
0.19
0.0007
493
100.53
75.74
PVC
0.85
0.19
0.0008
495
7
75.74
PVC
0.71
0.16
0.0006
496
83.67
75.74
PVC
0.71
0.16
0.0006
498
7.15
75.74
PVC
0.65
0.14
0.0005
499
65.05
75.74
PVC
0.65
0.14
0.0005
501
7.01
75.74
PVC
0.64
0.14
0.0005
502
57.49
75.74
PVC
0.64
0.14
0.0005
504
5.91
75.74
PVC
0.72
0.16
0.0006
505
44.72
75.74
PVC
0.72
0.16
0.0006
507
22
143.34
PVC
-4.19
0.26
0.0006
508
3.29
143.34
PVC
-4.19
0.26
0.0005
510
55.46
75.74
PVC
-0.73
0.16
0.0006
511
3.33
75.74
PVC
-0.73
0.16
0.0005
513
77.33
97.38
PVC
-1.65
0.22
0.0007
514
3.37
97.38
PVC
-1.65
0.22
0.0007
516
6
97.38
PVC
2.2
0.29
0.0012
517
23.74
97.38
PVC
2.2
0.29
0.0012
519
25.52
97.38
PVC
-0.07
0.01
0
520
5.85
97.38
PVC
-0.07
0.01
0
522
2.66
75.74
PVC
-0.25
0.05
0.0001
523
76.33
75.74
PVC
-0.25
0.05
0.0001
525
2.91
75.74
PVC
-0.15
0.03
0.0001
526
76.11
75.74
PVC
-0.15
0.03
0
528
3.06
75.74
PVC
-0.18
0.04
0
529
76.01
75.74
PVC
-0.18
0.04
0
531
72.29
97.38
PVC
-0.46
0.06
0.0001
532
3.45
97.38
PVC
-1.75
0.23
0.0008
534
16.49
97.38
PVC
3.07
0.41
0.0022
535
6.06
97.38
PVC
3.07
0.41
0.0022
537
102.04
97.38
PVC
1.34
0.18
0.0005
538
3.17
97.38
PVC
1.34
0.18
0.0006
540
3.41
97.38
PVC
-2.59
0.35
0.0016
541
23.64
97.38
PVC
-2.59
0.35
0.0016
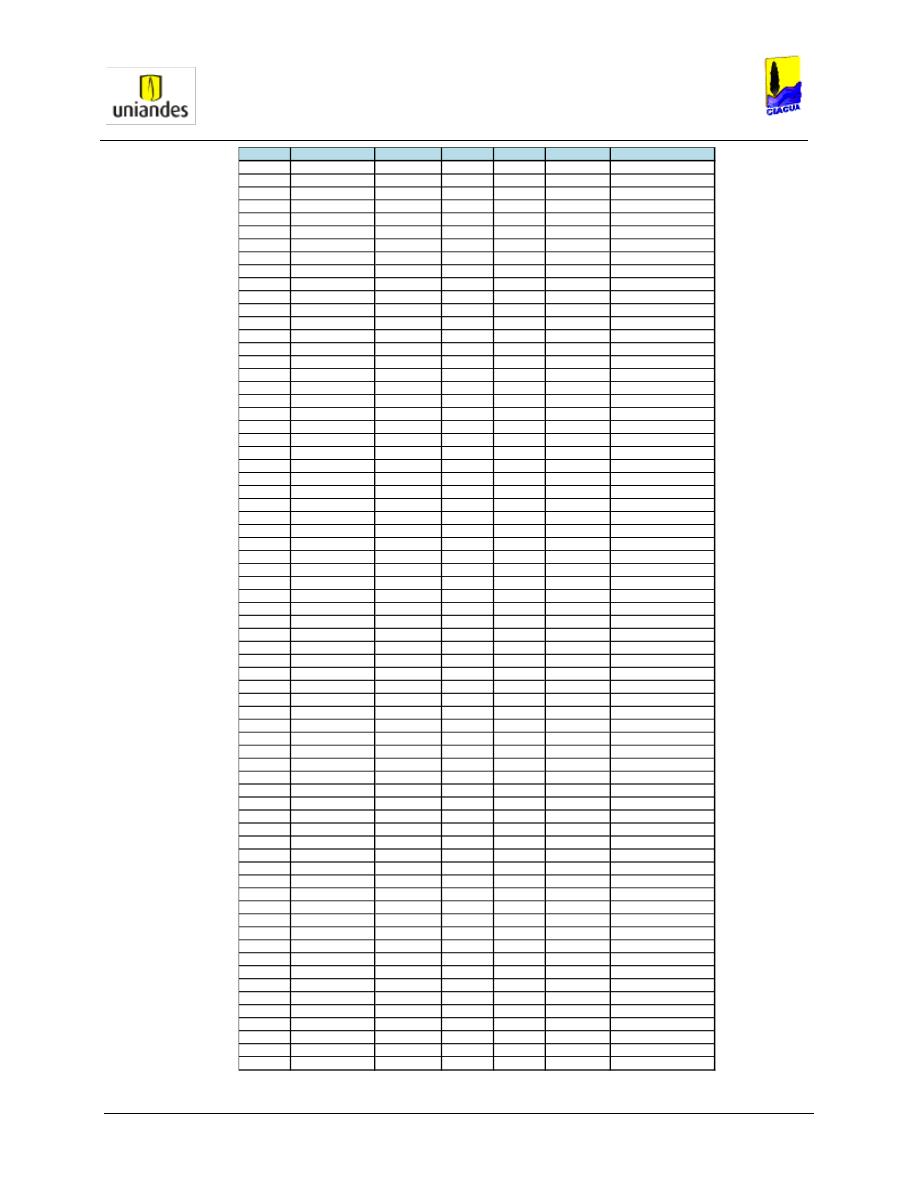
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
56
Juan Camilo Vergara Valderrama
Tabla 19.
Resultados de modelación red Olivos I para cada tubo de la red (Reporte 4).
ID
Length (Scaled) (m) Diameter (mm)
Material
Flow (L/s)
Velocity (m/s) Headloss Gradient (m/m)
543
131.33
97.38
PVC
1.68
0.23
0.0008
544
3.79
97.38
PVC
1.68
0.23
0.0007
546
159.76
97.38
PVC
2.52
0.34
0.0015
547
3.4
97.38
PVC
2.52
0.34
0.0015
549
2.33
97.38
PVC
6.79
0.91
0.0088
550
45.03
97.38
PVC
6.79
0.91
0.0088
555
124.45
97.38
PVC
1.66
0.22
0.0007
556
3.26
97.38
PVC
1.66
0.22
0.0007
558
99.43
97.38
PVC
1.95
0.26
0.001
559
3.26
97.38
PVC
1.95
0.26
0.001
561
72.29
97.38
PVC
1.83
0.25
0.0009
562
2.55
97.38
PVC
1.83
0.25
0.0009
564
26.9
97.38
PVC
1.95
0.26
0.001
565
3.43
97.38
PVC
1.95
0.26
0.001
567
3.45
75.74
PVC
0.47
0.1
0.0003
568
6.09
75.74
PVC
0.47
0.1
0.0003
570
28.64
75.74
PVC
0.61
0.14
0.0004
571
3.22
75.74
PVC
0.61
0.14
0.0005
573
30.13
75.74
PVC
0.64
0.14
0.0005
574
3.3
75.74
PVC
0.64
0.14
0.0005
576
3.34
97.38
PVC
-1.96
0.26
0.001
577
28.69
97.38
PVC
-1.96
0.26
0.001
580
3.47
75.74
PVC
0.45
0.1
0.0003
581
6.07
75.74
PVC
0.45
0.1
0.0002
583
3.54
75.74
PVC
0.46
0.1
0.0003
584
6
75.74
PVC
0.46
0.1
0.0003
587
3.42
75.74
PVC
0.47
0.1
0.0003
588
6.12
75.74
PVC
0.47
0.1
0.0003
590
3.41
75.74
PVC
0.46
0.1
0.0003
591
6.13
75.74
PVC
0.46
0.1
0.0002
593
3.4
75.74
PVC
0.47
0.1
0.0003
594
6.14
75.74
PVC
0.46
0.1
0.0002
597
91.48
143.34
PVC
-6.27
0.39
0.0012
599
3.46
97.38
PVC
0.78
0.11
0.0003
600
8.96
97.38
PVC
0.78
0.11
0.0002
753
0.48
101.6
PVC
15.09
1.86
0.0298
754
0.55
101.6
PVC
5.24
0.65
0.0049
755
0.59
76.2
PVC
-1.58
0.35
0.0025
756
0.64
101.6
PVC
6.74
0.83
0.007
757
1.07
76.2
PVC
0.88
0.19
0.0006
758
1.09
76.2
PVC
-0.4
0.09
0.0003
760
1.12
76.2
PVC
1.64
0.36
0.0024
761
1.18
76.2
PVC
0.79
0.17
0.0008
762
1.25
76.2
PVC
-1.23
0.27
0.0014
765
1.68
152.4
PVC
-1.21
0.07
0
766
1.74
76.2
PVC
-0.12
0.03
0
767
1.68
101.6
PVC
5.24
0.65
0.0044
768
1.73
76.2
PVC
-7.48
1.64
0.0338
769
1.91
101.6
PVC
-8.57
1.06
0.0109
770
1.91
76.2
PVC
-0.92
0.2
0.0008
771
2
76.2
PVC
-4.78
1.05
0.0153
773
2.03
152.4
PVC
-21.46
1.18
0.008
774
2.28
152.4
PVC
-5.4
0.3
0.0008
775
2.32
76.2
PVC
-0.92
0.2
0.0009
776
2.53
101.6
PVC
12.35
1.52
0.021
777
2.93
76.2
PVC
2.74
0.6
0.0057
778
3.09
152.4
PVC
58.55
3.21
0.0495
779
3.09
76.2
PVC
0.81
0.18
0.0007
780
3.22
76.2
PVC
2.54
0.56
0.0049
781
3.31
76.2
PVC
0.92
0.2
0.0008
782
3.37
76.2
PVC
0
0
0
783
3.38
76.2
PVC
0.55
0.12
0.0004
784
3.6
76.2
PVC
-0.92
0.2
0.0009
785
4.38
101.6
PVC
13.25
1.63
0.0238
786
4.48
101.6
PVC
14.21
1.75
0.027
787
4.59
76.2
PVC
-3.7
0.81
0.0097
788
4.64
76.2
PVC
2.49
0.55
0.0048
791
4.93
76.2
PVC
-2.82
0.62
0.006
792
5.08
76.2
PVC
2.14
0.47
0.0037
793
5.16
76.2
PVC
4.4
0.96
0.0131
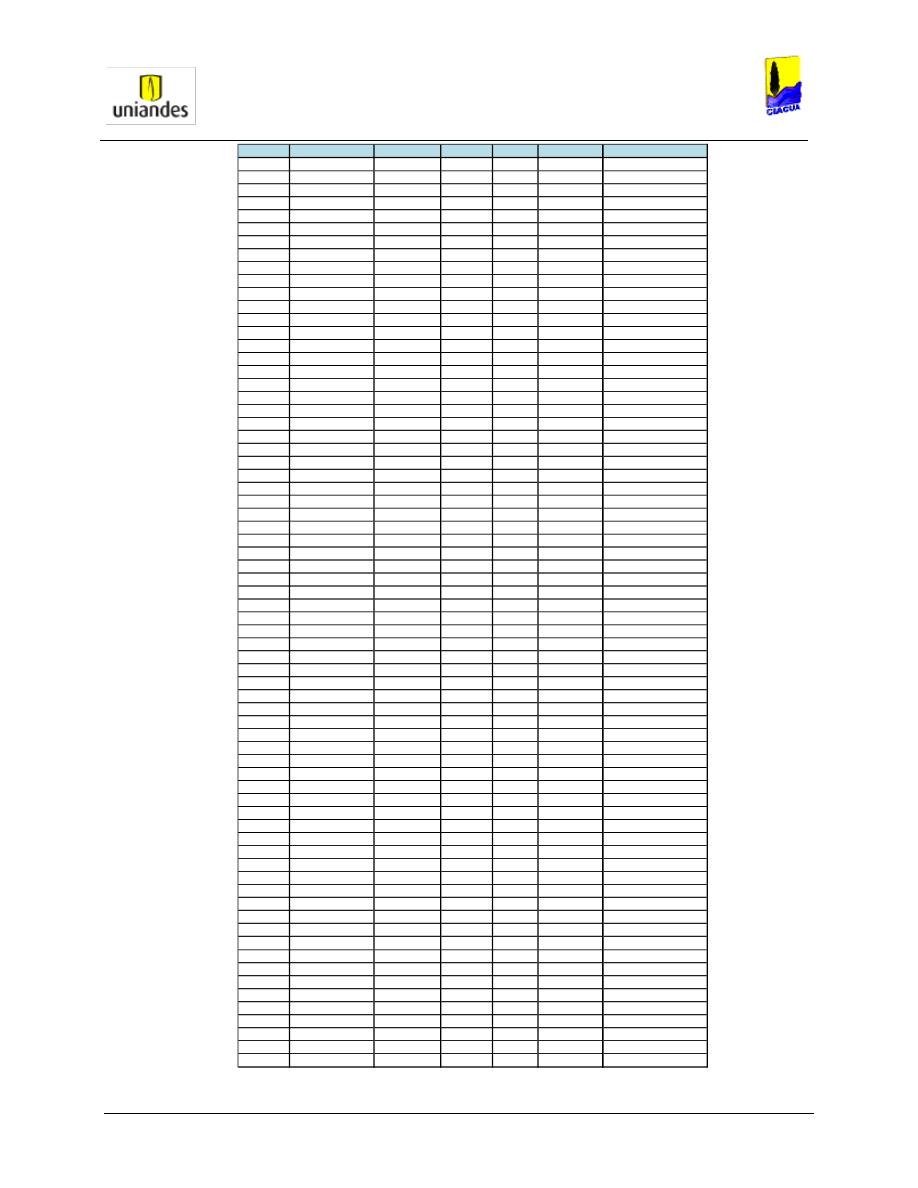
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
57
Juan Camilo Vergara Valderrama
Tabla 20.
Resultados de modelación red Olivos I para cada tubo de la red (Reporte 5).
ID
Length (Scaled) (m) Diameter (mm)
Material
Flow (L/s) Velocity (m/s) Headloss Gradient (m/m)
794
5.26
152.4
PVC
-15.87
0.87
0.0047
796
5.4
152.4
PVC
-5.4
0.3
0.0007
797
6.68
101.6
PVC
-10.28
1.27
0.0151
799
7.83
101.6
PVC
8.1
1
0.0098
800
7.92
76.2
PVC
-7.89
1.73
0.0373
801
7.91
152.4
PVC
-17.34
0.95
0.0055
803
8.15
76.2
PVC
-4.13
0.91
0.0118
805
8.99
76.2
PVC
-6.04
1.32
0.0231
808
10.77
76.2
PVC
-4.47
0.98
0.0135
809
10.89
152.4
PVC
0.92
0.05
0
810
13.86
76.2
PVC
0.91
0.2
0.0008
811
14.43
152.4
PVC
21.46
1.18
0.0081
812
13.68
101.6
PVC
8.11
1
0.0099
814
18.16
152.4
PVC
-21.46
1.18
0.0081
817
22.74
76.2
PVC
-0.46
0.1
0.0003
819
24
76.2
PVC
-7.48
1.64
0.0339
820
24.15
76.2
PVC
5.08
1.11
0.017
823
26.31
101.6
PVC
7.99
0.99
0.0096
825
26.1
76.2
PVC
-0.12
0.03
0
827
26.82
76.2
PVC
3.91
0.86
0.0107
828
26.87
76.2
PVC
2.78
0.61
0.0058
829
27.19
76.2
PVC
2.54
0.56
0.005
830
27.55
152.4
PVC
-17.64
0.97
0.0057
831
27.84
152.4
PVC
-44.26
2.43
0.0298
832
28.75
152.4
PVC
58.55
3.21
0.0495
833
28.88
152.4
PVC
26.44
1.45
0.0117
834
29.91
152.4
PVC
49.81
2.73
0.0369
835
30.08
76.2
PVC
4.75
1.04
0.0151
836
30.38
152.4
PVC
-16.45
0.9
0.005
839
30.63
76.2
PVC
4.09
0.9
0.0116
840
31.23
152.4
PVC
31.76
1.74
0.0163
842
31.28
152.4
PVC
-4.39
0.24
0.0005
843
32.93
101.6
PVC
-3.22
0.4
0.0019
844
31.58
76.2
PVC
-5.84
1.28
0.0218
845
31.74
101.6
PVC
4.54
0.56
0.0035
846
31.77
76.2
PVC
2.01
0.44
0.0033
847
32.61
101.6
PVC
3.42
0.42
0.0021
848
30.68
101.6
PVC
6.84
0.84
0.0073
849
32.2
101.6
PVC
2.68
0.33
0.0014
851
32.33
152.4
PVC
-47.58
2.61
0.034
852
32.34
152.4
PVC
-8.98
0.49
0.0017
853
32.72
76.2
PVC
1.69
0.37
0.0024
854
33.04
152.4
PVC
42.92
2.35
0.0282
856
33.64
152.4
PVC
-2.48
0.14
0.0002
857
34.24
76.2
PVC
-2.41
0.53
0.0045
858
34.43
101.6
PVC
7.36
0.91
0.0083
859
38.49
101.6
PVC
7.54
0.93
0.0087
860
41.59
76.2
PVC
0
0
0
862
44.06
152.4
PVC
-112.17
6.15
0.1625
863
46.23
152.4
PVC
-30.18
1.65
0.0149
865
49.01
76.2
PVC
4.4
0.96
0.0131
866
49.83
76.2
PVC
-7.89
1.73
0.0373
868
54.01
76.2
PVC
1.43
0.31
0.0018
870
55.93
76.2
PVC
-6.04
1.32
0.0231
871
56.32
101.6
PVC
4.52
0.56
0.0035
872
56.8
76.2
PVC
1.67
0.37
0.0024
873
58.36
152.4
PVC
-3.35
0.18
0.0003
875
58.22
76.2
PVC
2.49
0.55
0.0048
876
58.59
76.2
PVC
-2.46
0.54
0.0047
878
64.89
101.6
PVC
-10.28
1.27
0.0151
880
67.86
76.2
PVC
-4.47
0.98
0.0135
882
71.78
152.4
PVC
-19.73
1.08
0.0069
883
75.78
152.4
PVC
-52.8
2.89
0.041
884
77.8
76.2
PVC
-4.13
0.91
0.0118
885
81.42
76.2
PVC
-4.78
1.05
0.0152
886
82.32
76.2
PVC
1.25
0.27
0.0014
887
84.05
76.2
PVC
1.86
0.41
0.0029
889
85.83
76.2
PVC
-0.11
0.02
0
890
86.09
76.2
PVC
1.64
0.36
0.0023
891
92.75
76.2
PVC
0.91
0.2
0.0008

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
58
Juan Camilo Vergara Valderrama
Tabla 21.
Resultados de modelación red Olivos I para cada tubo de la red (Reporte 6).
ID
Length (Scaled) (m) Diameter (mm)
Material
Flow (L/s)
Velocity (m/s) Headloss Gradient (m/m)
892
94.28
152.4
PVC
-20.58
1.13
0.0075
893
94.28
101.6
PVC
-8.57
1.06
0.0109
901
5.77
152.4
PVC
-0.76
0.04
0.0001
905
2.11
152.4
PVC
-1.6
0.09
0
910
3.63
143.34
PVC
6.27
0.39
0.0012
912
0.79
75.74
PVC
1.52
0.34
0.0019
913
1.02
75.74
PVC
1.56
0.35
0.002
915
2.75
76.2
PVC
3.42
0.75
0.0084
916
81.97
76.2
PVC
3.42
0.75
0.0084
918
2.68
76.2
PVC
2.78
0.61
0.0058
919
64.5
76.2
PVC
2.78
0.61
0.0058
921
2.87
76.2
PVC
2.01
0.44
0.0033
922
59.09
76.2
PVC
2.01
0.44
0.0033
924
2.11
76.2
PVC
1.11
0.24
0.0011
925
95.5
76.2
PVC
1.11
0.24
0.0012
927
2.48
76.2
PVC
-0.59
0.13
0.0005
928
94.9
76.2
PVC
-0.59
0.13
0.0004
930
95.05
76.2
PVC
0.73
0.16
0.0006
931
2.85
76.2
PVC
0.73
0.16
0.0006
933
3.94
76.2
PVC
-1.96
0.43
0.0032
934
28.76
76.2
PVC
-1.96
0.43
0.0032
936
3.78
97.38
PVC
-9.22
1.24
0.0152
942
15.73
152.4
PVC
0.47
0.03
0
943
3.24
152.4
PVC
0.47
0.03
0
945
3.44
75.74
PVC
0.46
0.1
0.0003
946
6.11
75.74
PVC
0.46
0.1
0.0002
951
1.25
152.4
PVC
-12.47
0.68
0.0031
952
24.78
152.4
PVC
-12.47
0.68
0.0031
961
23.34
101.6
PVC
5.85
0.72
0.0055
962
1.82
101.6
PVC
5.85
0.72
0.0056
965
3.31
97.38
PVC
0.46
0.06
0.0001
966
84.56
97.38
PVC
0.46
0.06
0.0001
969
6.45
101.6
PVC
0
0
0
970
21.15
101.6
PVC
0
0
0
978
50.53
76.2
PVC
-4.69
1.03
0.0147
979
1.29
76.2
PVC
-4.69
1.03
0.0147
980
16.47
152.4
PVC
-18.99
1.04
0.0065
982
1.18
152.4
PVC
-14.61
0.8
0.004
983
25.55
152.4
PVC
-14.61
0.8
0.0041
990
1.59
76.2
PVC
4.96
1.09
0.0163
991
28.84
76.2
PVC
4.96
1.09
0.0163
993
6.03
76.2
PVC
4.19
0.92
0.012
994
2.19
76.2
PVC
4.19
0.92
0.0121
996
3.14
101.6
PVC
5.27
0.65
0.0045
997
30.05
101.6
PVC
5.27
0.65
0.0046
1000
20.93
76.2
PVC
-2.29
0.5
0.0041
1001
1.84
76.2
PVC
-2.29
0.5
0.0041
1003
4.57
76.2
PVC
-3.01
0.66
0.0067
1004
53.58
76.2
PVC
-3.01
0.66
0.0067
1006
41.26
76.2
PVC
-4.57
1
0.0141
1007
2.02
76.2
PVC
-4.57
1
0.014
1009
6.31
76.2
PVC
-1.35
0.3
0.0017
1010
65.46
76.2
PVC
-1.35
0.3
0.0017
1016
0.51
152.4
PVC
0.9
0.05
0
1017
0.95
152.4
PVC
44.26
2.43
0.0295
1020
1.22
152.4
PVC
0
0
0
1021
54.7
152.4
PVC
0
0
0
1023
2.04
152.4
PVC
0
0
0
1024
29.21
152.4
PVC
0
0
0
1026
2.36
97.38
PVC
0.13
0.02
0
1027
22.86
97.38
PVC
0.13
0.02
0

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
59
Juan Camilo Vergara Valderrama
3.4.1.3
Red de distribución los Olivos I (válvulas)
Tabla 22
. R
esultados de modelación red Olivos I para cada válvula de la red (Reporte 1).
ID
Elevation (m) Diameter (Valve) (mm) Headloss Coefficient Setting (Initial) Minor Loss Coefficient (Local) Flow (L/s) Hydraulic Grade (From) (m) Hydraulic Grade (To) (m) Headloss (m)
379
2,544.36
97.38
0
0.39
0
2,561.44
2,559.89
0
382
2,543.52
97.38
0
0.39
0.6
2,559.88
2,559.88
0
385
2,543.07
97.38
0
0.39
1.39
2,559.85
2,559.85
0
388
2,543.79
75.74
0
0.39
-0.29
2,559.89
2,559.89
0
391
2,543.37
75.74
0
0.39
-0.28
2,559.89
2,559.89
0
394
2,543.01
75.74
0
0.39
-0.22
2,559.89
2,559.89
0
398
2,542.88
97.38
0
0.39
-0.27
2,559.88
2,559.88
0
401
2,543.09
75.74
0
0.39
-0.15
2,559.87
2,559.87
0
404
2,543.12
75.74
0
0.39
-0.25
2,559.87
2,559.87
0
407
2,543.01
75.74
0
0.39
-0.33
2,559.87
2,559.87
0
410
2,542.97
97.38
0
0.39
2.01
2,559.86
2,559.86
0
413
2,542.89
75.74
0
0.39
-0.04
2,559.80
2,559.80
0
416
2,542.80
75.74
0
0.39
0.28
2,559.78
2,559.78
0
419
2,542.80
97.38
0
0.39
0.97
2,559.75
2,559.75
0
422
2,542.97
143.34
0
0.39
-1.26
2,559.86
2,559.86
0
425
2,542.91
143.34
0
0.39
2.19
2,559.88
2,559.88
0
428
2,542.89
97.38
0
0.39
-0.46
2,559.88
2,559.88
0
431
2,545.42
97.38
0
0.39
9.22
2,566.53
2,566.53
0
434
2,543.94
97.38
0
0.39
8.46
2,564.95
2,564.95
0
437
2,543.63
97.38
0
0.39
0
2,564.21
2,561.59
0
440
2,543.84
97.38
0
0.39
0
2,561.60
2,560.38
0
443
2,544.04
75.74
0
0.39
-0.8
2,565.90
2,565.90
0
446
2,544.02
143.34
0
0.39
29.21
2,565.83
2,565.83
0
449
2,543.85
75.74
0
0.39
-0.87
2,565.21
2,565.21
0
452
2,543.57
75.74
0
0.39
-2.04
2,564.56
2,564.56
0
455
2,543.66
75.74
0
0.39
-3.06
2,563.86
2,563.86
0
458
2,543.57
97.38
0
0.39
-8.26
2,563.03
2,563.03
0
464
2,543.45
143.34
0
0.39
7.53
2,561.77
2,561.77
0
467
2,543.25
143.34
0
0.39
34.2
2,561.01
2,561.01
0
470
2,543.16
97.38
0
0.39
-9.89
2,560.86
2,560.86
0
473
2,543.50
97.38
0
0.39
0.78
2,560.83
2,560.83
0
476
2,543.30
97.38
0
0.39
4.39
2,560.60
2,560.60
0
479
2,543.31
97.38
0
0.39
3.45
2,560.34
2,560.34
0
482
2,543.10
97.38
0
0.39
2.69
2,560.19
2,560.19
0
485
2,543.22
97.38
0
0.39
2.13
2,560.10
2,560.10
0
488
2,542.87
143.34
0
0.39
-6.06
2,560.03
2,560.03
0
491
2,543.00
75.74
0
0.39
0.85
2,560.03
2,560.03
0
494
2,543.13
75.74
0
0.39
0.71
2,559.99
2,559.99
0
497
2,542.70
75.74
0
0.39
0.65
2,559.96
2,559.96
0
500
2,542.73
75.74
0
0.39
0.64
2,559.94
2,559.94
0
503
2,542.70
75.74
0
0.39
0.72
2,559.92
2,559.92
0
506
2,542.68
143.34
0
0.39
-4.19
2,559.92
2,559.92
0
509
2,542.72
75.74
0
0.39
-0.73
2,559.90
2,559.90
0
512
2,542.72
97.38
0
0.39
-1.65
2,559.88
2,559.88
0
515
2,542.81
97.38
0
0.39
2.2
2,559.86
2,559.86
0
518
2,542.79
97.38
0
0.39
-0.07
2,559.87
2,559.87
0
521
2,543.00
75.74
0
0.39
-0.25
2,559.87
2,559.87
0
524
2,543.12
75.74
0
0.39
-0.15
2,559.87
2,559.87
0
527
2,543.08
75.74
0
0.39
-0.18
2,559.87
2,559.87
0
533
2,543.35
97.38
0
0.39
3.07
2,559.90
2,559.90
0
536
2,543.26
97.38
0
0.39
1.34
2,559.89
2,559.89
0
539
2,543.31
97.38
0
0.39
-2.59
2,559.94
2,559.94
0
542
2,543.40
97.38
0
0.39
1.68
2,559.90
2,559.90
0
545
2,543.45
97.38
0
0.39
2.52
2,559.90
2,559.90
0
548
2,543.33
97.38
0
0.39
6.79
2,560.54
2,560.54
0
554
2,543.41
97.38
0
0.39
1.66
2,559.89
2,559.89
0
557
2,543.18
97.38
0
0.39
1.95
2,559.91
2,559.91
0
560
2,543.05
97.38
0
0.39
1.83
2,559.93
2,559.93
0
563
2,542.71
97.38
0
0.39
1.95
2,559.97
2,559.97
0
566
2,542.70
75.74
0
0.39
0.47
2,559.96
2,559.96
0
569
2,542.83
75.74
0
0.39
0.61
2,559.93
2,559.93
0
572
2,543.06
75.74
0
0.39
0.64
2,559.87
2,559.87
0
575
2,543.02
97.38
0
0.39
-1.96
2,559.79
2,559.79
0
579
2,542.99
75.74
0
0.39
0.45
2,559.88
2,559.88
0
582
2,543.65
75.74
0
0.39
0.46
2,561.59
2,561.59
0

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
60
Juan Camilo Vergara Valderrama
Tabla 23.
Resultados de modelación red Olivos I para cada válvula de la red (Reporte 2).
ID
Elevation (m) Diameter (Valve) (mm) Headloss Coefficient Setting (Initial) Minor Loss Coefficient (Local) Flow (L/s) Hydraulic Grade (From) (m) Hydraulic Grade (To) (m) Headloss (m)
586
2,543.37
75.74
0
0.39
0.47
2,560.79
2,560.79
0
589
2,544.05
75.74
0
0.39
0.46
2,565.97
2,565.97
0
592
2,543.00
75.74
0
0.39
0.46
2,559.86
2,559.86
0
595
2,544.27
143.34
0
0.39
-6.27
2,561.48
2,561.48
0
598
2,543.01
97.38
0
0.39
0.78
2,560.04
2,560.04
0
627
2,545.98
76.2
0
0.39
-0.12
2,566.01
2,566.01
0
630
2,546.40
152.4
0
0.39
58.55
2,571.88
2,571.88
0
631
2,545.85
76.2
0
0.39
2.49
2,567.80
2,567.80
0
635
2,545.88
101.6
0
0.39
8.11
2,566.08
2,566.08
0
636
2,546.11
101.6
0
0.39
-8.57
2,566.32
2,566.32
0
637
2,545.87
76.2
0
0.39
-4.78
2,566.61
2,566.61
0
638
2,545.79
76.2
0
0.39
-7.48
2,566.71
2,566.71
0
639
2,546.69
76.2
0
0.39
-7.89
2,570.16
2,570.16
0
640
2,546.76
76.2
0
0.39
-6.04
2,569.15
2,569.15
0
641
2,547.10
152.4
0
0.39
-21.46
2,567.31
2,567.31
0
642
2,547.10
76.2
0
0.39
0.91
2,566.13
2,566.13
0
644
2,546.04
101.6
0
0.39
5.24
2,565.80
2,565.80
0
645
2,545.59
76.2
0
0.39
1.64
2,565.42
2,565.42
0
646
2,545.05
76.2
0
0.39
2.54
2,565.33
2,565.33
0
647
2,544.03
76.2
0
0.39
2.78
2,564.71
2,564.71
0
648
2,544.14
76.2
0
0.39
2.01
2,565.01
2,565.01
0
652
2,546.79
101.6
0
0.39
-10.28
2,568.32
2,568.32
0
914
2,544.60
76.2
0
0.39
3.42
2,565.04
2,565.04
0
917
2,544.96
76.2
0
0.39
2.78
2,565.09
2,565.09
0
920
2,545.11
76.2
0
0.39
2.01
2,565.21
2,565.21
0
923
2,545.25
76.2
0
0.39
1.11
2,565.36
2,565.36
0
926
2,545.34
76.2
0
0.39
-0.59
2,565.70
2,565.70
0
929
2,545.70
76.2
0
0.39
0.73
2,565.95
2,565.95
0
932
2,544.00
76.2
0
0.39
-1.96
2,559.91
2,559.91
0
941
2,543.98
152.4
0
0.39
0.47
2,559.89
2,559.89
0
944
2,544.28
75.74
0
0.39
0.46
2,559.88
2,559.88
0
950
2,545.60
152.4
0
0.39
-12.47
2,565.42
2,565.42
0
953
2,544.31
152.4
0
0.39
-5.4
2,561.47
2,561.47
0
956
2,547.10
152.4
0
0.39
21.46
2,567.46
2,567.46
0
959
2,545.40
152.4
0
0.39
-44.26
2,567.00
2,567.00
0
960
2,545.12
101.6
0
0.39
5.85
2,565.23
2,565.23
0
964
2,544.01
97.38
0
0.39
0.46
2,559.89
2,559.89
0
968
2,544.40
101.6
0
0.39
0
2,561.47
2,565.06
0
977
2,545.35
97.38
0
0.39
-4.69
2,566.79
2,566.79
0
981
2,546.04
97.38
0
0.39
-14.61
2,565.81
2,565.81
0
984
2,546.98
76.2
0
0.39
-4.47
2,567.77
2,567.77
0
985
2,547.10
76.2
0
0.39
-4.13
2,567.48
2,567.48
0
989
2,546.56
76.2
0
0.39
4.96
2,567.32
2,567.32
0
992
2,546.55
76.2
0
0.39
4.19
2,567.37
2,567.37
0
995
2,545.97
101.6
0
0.39
5.27
2,566.15
2,566.15
0
998
2,546.40
76.2
0
0.39
4.4
2,568.86
2,568.86
0
999
2,546.42
76.2
0
0.39
-2.29
2,568.30
2,568.30
0
1002
2,546.49
76.2
0
0.39
-3.01
2,566.20
2,566.20
0
1005
2,546.67
76.2
0
0.39
-4.57
2,566.82
2,566.82
0
1008
2,546.41
76.2
0
0.39
-1.35
2,566.10
2,566.10
0
1018
2,544.56
76.2
0
0.39
0
2,561.45
2,565.20
0
1019
2,544.53
152.4
0
0.39
0
2,561.45
2,565.35
0
1022
2,544.27
152.4
0
0.39
0
2,561.47
2,559.89
0
1025
2,543.18
97.38
0
0.39
0.13
2,560.01
2,560.01
0
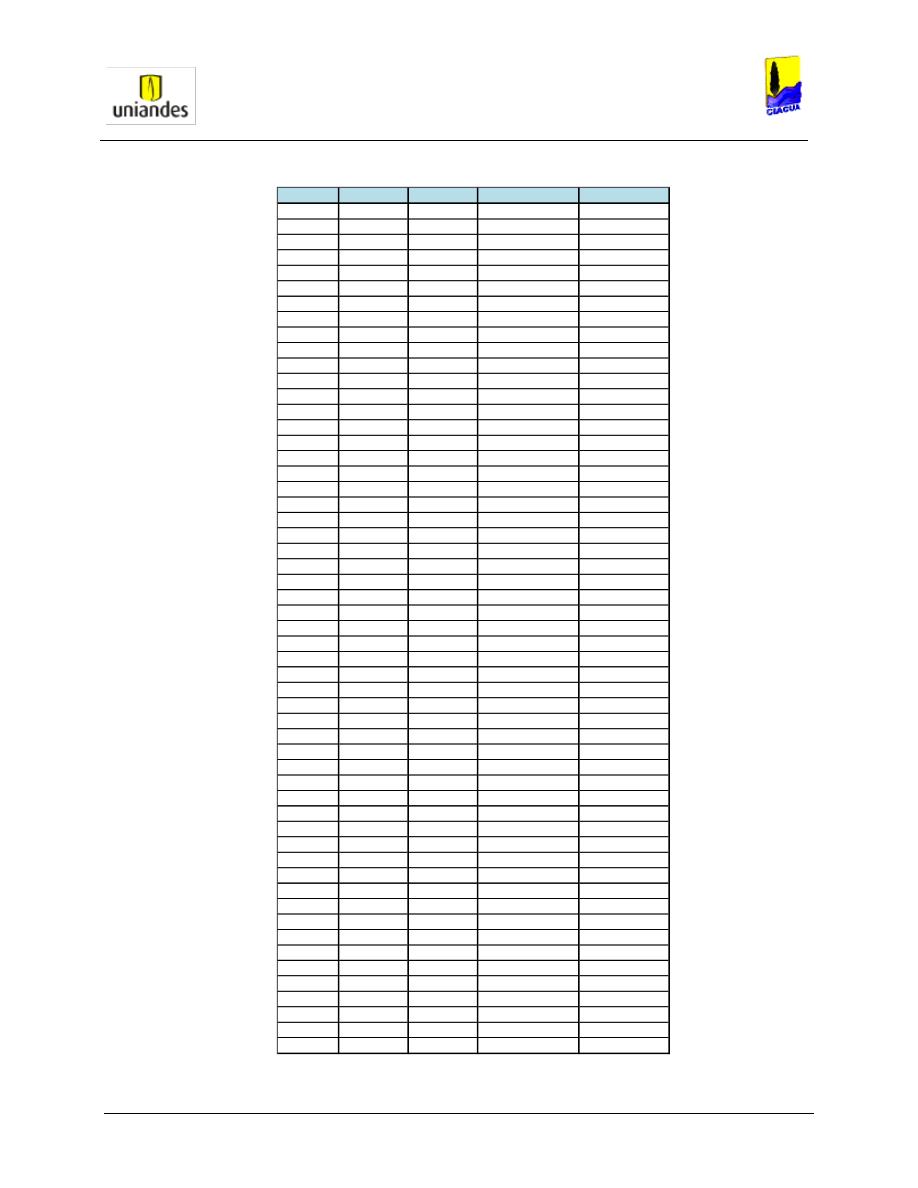
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
61
Juan Camilo Vergara Valderrama
3.4.1.4
Red de distribución los Olivos II (nodos)
Tabla 24.
Resultados de modelación red Olivos I para cada nodo de la red (Reporte 1).
ID
Elevation (m) Demand (L/s) Hydraulic Grade (m) Pressure (m H2O)
27
2,544.29
0.03
2,559.89
15.6
29
2,544.27
0.04
2,559.89
15.6
31
2,544.10
0.04
2,559.89
15.8
33
2,543.55
0.04
2,559.89
16.3
35
2,543.69
0.04
2,559.88
16.2
39
2,543.50
0.05
2,559.88
16.4
41
2,543.38
0.05
2,559.87
16.5
43
2,543.14
0.05
2,559.86
16.7
45
2,543.08
0.06
2,559.85
16.8
47
2,542.93
0.06
2,559.80
16.9
49
2,542.90
0.06
2,559.79
16.9
51
2,543.08
0.06
2,559.78
16.7
53
2,542.79
0.07
2,559.75
17
56
2,543.79
0.07
2,559.89
16.1
58
2,543.77
0.07
2,559.89
16.1
60
2,543.39
0.08
2,559.89
16.5
62
2,543.37
0.08
2,559.89
16.5
64
2,543.02
0.08
2,559.89
16.9
66
2,543.01
0.08
2,559.89
16.9
68
2,542.88
0.09
2,559.88
17
70
2,542.89
0.09
2,559.88
17
72
2,543.08
0.09
2,559.87
16.8
76
2,543.08
0.1
2,559.87
16.8
78
2,543.12
0.1
2,559.87
16.8
80
2,543.12
0.1
2,559.87
16.8
82
2,543.01
0.1
2,559.87
16.9
84
2,543.00
0.11
2,559.87
16.9
86
2,542.99
0.11
2,559.86
16.9
88
2,542.97
0.11
2,559.86
16.9
90
2,542.96
0.11
2,559.83
16.9
92
2,542.88
0.12
2,559.80
16.9
94
2,542.87
0.12
2,559.80
16.9
96
2,542.80
0.12
2,559.78
17
98
2,542.80
0.12
2,559.78
17
101
2,542.80
0.13
2,559.75
17
103
2,543.05
0.13
2,559.72
16.7
105
2,543.10
5.36
2,559.64
16.5
119
2,544.55
0.15
2,566.01
21.5
121
2,544.21
0.15
2,565.74
21.5
123
2,544.19
0.15
2,565.73
21.5
125
2,544.01
0.16
2,565.26
21.2
127
2,544.01
0.16
2,565.25
21.2
129
2,543.93
0.16
2,564.90
21
131
2,543.91
0.16
2,564.82
20.9
133
2,543.77
0.17
2,564.54
20.8
135
2,543.75
0.17
2,564.46
20.7
137
2,543.69
0.17
2,564.28
20.6
139
2,543.68
0.17
2,564.21
20.5
141
2,543.62
0.18
2,561.59
18
143
2,543.64
0.18
2,561.60
18
145
2,543.83
0.18
2,560.38
16.5
147
2,543.32
0.18
2,560.56
17.2
150
2,543.46
0.19
2,560.14
16.7
152
2,543.40
0.19
2,559.99
16.6
154
2,543.26
0.19
2,559.94
16.7

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
62
Juan Camilo Vergara Valderrama
Tabla 25
.
Resultados de modelación red Olivos I para cada nodo de la red (Reporte 2).
ID
Elevation (m) Demand (L/s) Hydraulic Grade (m) Pressure (m H2O)
156
2,543.31
0.2
2,559.94
16.6
158
2,543.34
0.2
2,559.89
16.5
160
2,543.30
0.2
2,559.88
16.6
162
2,543.17
0.2
2,559.87
16.7
164
2,543.07
0.21
2,559.87
16.8
166
2,542.75
0.21
2,559.87
17.1
168
2,542.77
0.21
2,559.87
17.1
170
2,543.00
0.21
2,559.83
16.8
172
2,543.02
0.22
2,559.81
16.8
174
2,542.99
0.22
2,559.79
16.8
176
2,543.00
0.22
2,559.78
16.8
178
2,543.01
0.22
2,559.71
16.7
213
2,544.05
0.27
2,565.97
21.9
215
2,544.05
0.27
2,565.90
21.9
217
2,544.05
0.27
2,565.92
21.9
221
2,543.84
0.28
2,565.20
21.4
223
2,543.56
0.28
2,564.55
21
225
2,543.67
0.28
2,563.83
20.2
227
2,543.57
0.29
2,562.98
19.4
229
2,543.55
0.29
2,562.68
19.1
231
2,543.47
0.29
2,561.78
18.3
233
2,543.28
0.29
2,560.92
17.6
235
2,543.41
0.3
2,560.83
17.4
237
2,543.44
0.3
2,560.79
17.4
239
2,543.29
0.3
2,560.62
17.3
241
2,543.29
0.3
2,560.36
17.1
243
2,543.15
0.31
2,560.21
17.1
245
2,543.17
0.31
2,560.11
16.9
247
2,543.00
0.31
2,560.04
17
249
2,543.00
0.31
2,560.04
17
251
2,543.27
0.32
2,559.96
16.7
253
2,542.94
0.32
2,559.95
17
255
2,542.98
0.32
2,559.94
17
257
2,542.83
0.32
2,559.93
17.1
259
2,542.92
0.33
2,559.92
17
261
2,542.82
0.33
2,559.91
17.1
263
2,542.85
0.33
2,559.91
17.1
265
2,542.81
0.33
2,559.89
17.1
267
2,542.82
0.34
2,559.89
17.1
269
2,543.08
0.34
2,559.87
16.8
271
2,542.69
0.34
2,559.91
17.2
273
2,542.68
0.34
2,559.92
17.2
275
2,542.67
0.35
2,559.93
17.3
277
2,542.72
0.35
2,559.94
17.2
279
2,542.70
0.35
2,559.96
17.3
281
2,542.69
0.35
2,559.96
17.3
283
2,542.68
0.36
2,559.97
17.3
285
2,543.17
0.36
2,560.00
16.8
288
2,543.17
0.36
2,559.83
16.7
290
2,543.19
0.36
2,559.82
16.6
293
2,542.69
0.37
2,559.89
17.2
296
2,543.46
0.37
2,559.98
16.5
298
2,543.49
0.37
2,560.01
16.5
300
2,543.19
0.38
2,560.01
16.8
302
2,543.18
0.38
2,560.01
16.8
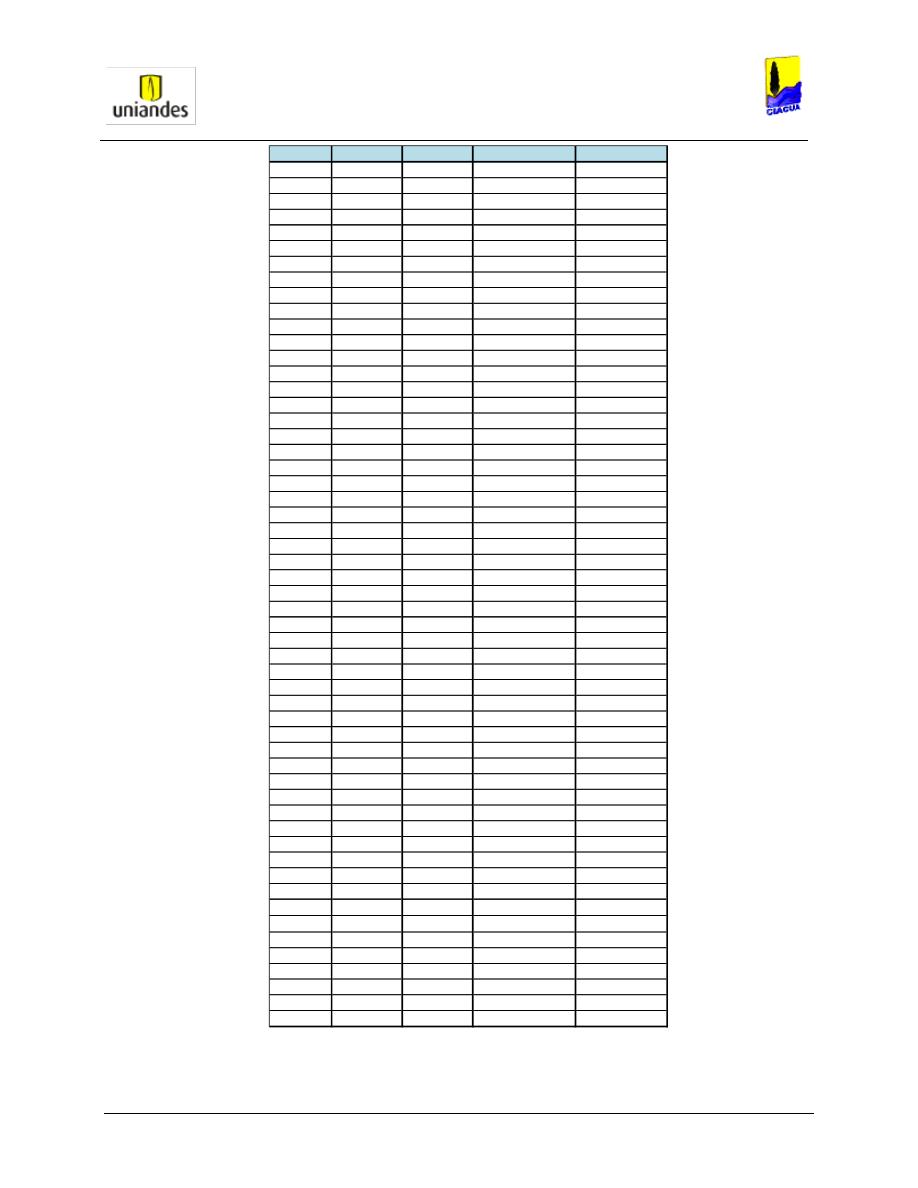
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
63
Juan Camilo Vergara Valderrama
Tabla 26.
Resultados de modelación red Olivos I para cada nodo de la red (Reporte 3).
ID
Elevation (m) Demand (L/s) Hydraulic Grade (m) Pressure (m H2O)
304
2,543.06
0.38
2,559.99
16.9
306
2,543.14
0.38
2,559.99
16.8
310
2,542.69
0.39
2,559.91
17.2
314
2,542.69
0.39
2,559.89
17.2
323
2,543.02
0.41
2,560.01
17
351
2,542.98
0.44
2,559.89
16.9
356
2,542.98
0.45
2,559.88
16.9
359
2,543.66
0.45
2,561.59
17.9
363
2,543.68
0.46
2,561.59
17.9
365
2,544.05
0.46
2,565.97
21.9
368
2,544.28
0.46
2,559.88
15.6
370
2,543.00
0.46
2,559.86
16.9
372
2,543.30
0.47
2,560.79
17.5
374
2,542.71
0.47
2,559.96
17.2
604
2,544.42
0.76
2,561.44
17
605
2,543.87
0.76
2,559.89
16
608
2,543.95
0.76
2,560.00
16
609
2,543.74
0.76
2,564.35
20.6
610
2,543.81
0.77
2,564.56
20.8
611
2,543.96
0.77
2,564.91
21
616
2,544.29
0.77
2,566.05
21.8
617
2,544.04
0.77
2,566.28
22.2
619
2,543.76
0.78
2,560.83
17.1
624
2,543.04
0.78
2,560.04
17
653
2,544.52
0.82
2,561.45
16.9
656
2,546.40
0.82
2,572.03
25.6
657
2,546.39
0.83
2,568.92
22.5
658
2,545.84
0.83
2,567.83
22
660
2,545.30
0.83
2,566.97
21.7
661
2,545.37
0.83
2,566.81
21.4
662
2,545.48
0.83
2,566.59
21.1
663
2,544.56
0.83
2,566.00
21.4
664
2,544.00
0.83
2,559.89
15.9
666
2,544.33
0.84
2,561.47
17.1
667
2,545.70
0.84
2,565.95
20.2
668
2,546.02
0.84
2,566.16
20.1
669
2,546.09
0.84
2,566.30
20.2
670
2,545.85
0.84
2,566.58
20.7
671
2,545.77
0.84
2,566.65
20.9
672
2,546.06
0.84
2,567.52
21.5
673
2,546.33
0.85
2,568.21
21.9
674
2,546.43
0.85
2,568.31
21.9
675
2,546.69
0.85
2,570.46
23.8
676
2,546.76
0.85
2,569.35
22.6
677
2,546.98
0.85
2,567.91
20.9
678
2,547.10
0.85
2,567.57
20.5
680
2,546.35
0.85
2,566.59
20.2
681
2,546.37
0.86
2,566.09
19.7
682
2,546.12
0.86
2,565.93
19.8
683
2,546.09
0.86
2,565.91
19.8
684
2,546.04
0.86
2,565.80
19.8
685
2,546.04
0.86
2,565.81
19.8
686
2,546.02
0.86
2,565.69
19.7
687
2,545.97
0.86
2,566.01
20
688
2,546.09
0.86
2,566.01
19.9
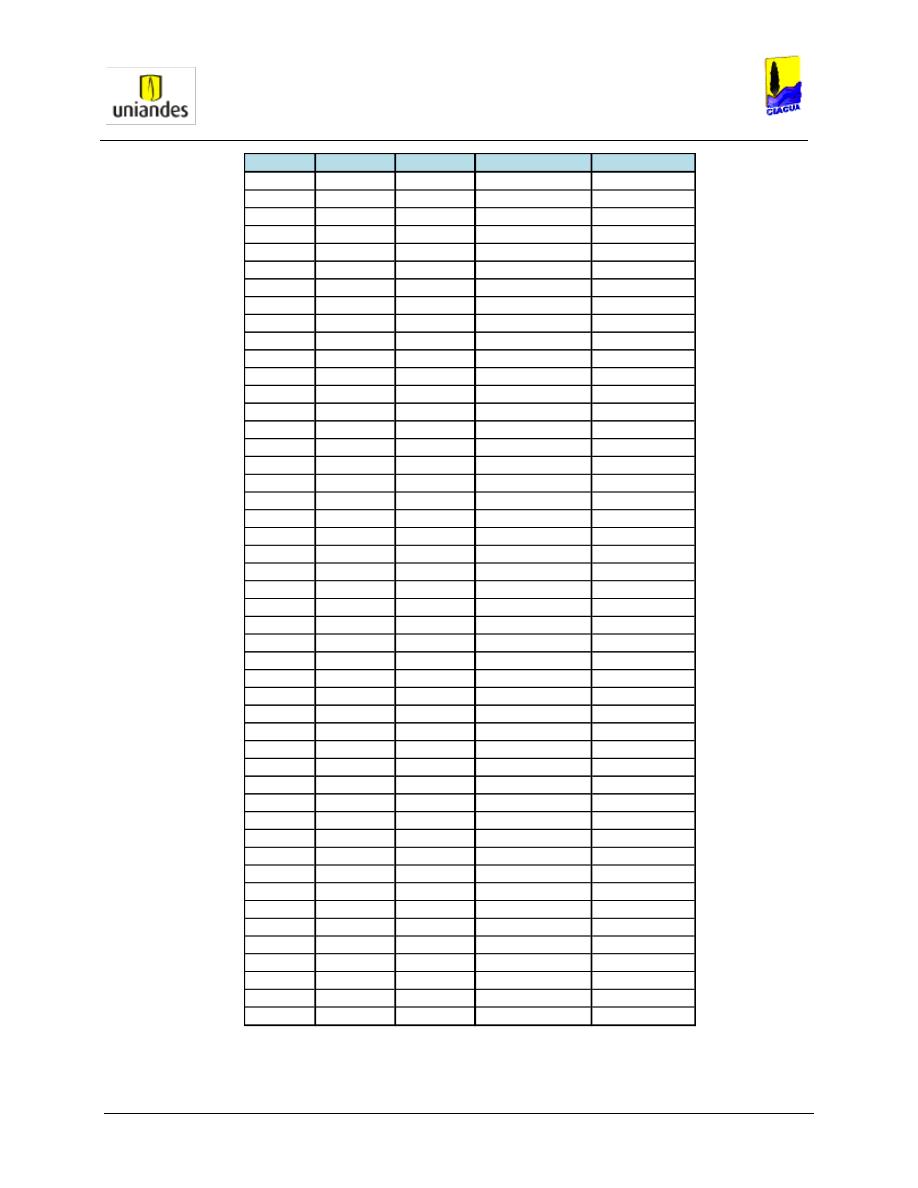
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
64
Juan Camilo Vergara Valderrama
Tabla 27.
Resultados de modelación red Olivos I para cada nodo de la red (Reporte 4).
ID
Elevation (m) Demand (L/s) Hydraulic Grade (m) Pressure (m H2O)
689
2,546.31
0.87
2,566.16
19.9
690
2,546.46
0.87
2,566.17
19.7
692
2,544.52
0.87
2,561.45
16.9
693
2,544.98
0.87
2,565.20
20.2
694
2,544.27
0.87
2,561.47
17.2
695
2,546.79
0.87
2,568.42
21.6
696
2,547.10
0.87
2,567.29
20.2
697
2,546.34
0.88
2,566.19
19.9
698
2,546.31
0.88
2,566.24
19.9
699
2,546.08
0.88
2,566.28
20.2
701
2,546.35
0.88
2,566.21
19.9
702
2,546.38
0.88
2,566.09
19.7
703
2,546.08
0.88
2,565.91
19.8
704
2,546.04
0.88
2,565.81
19.8
705
2,545.95
0.89
2,565.65
19.7
706
2,545.73
0.89
2,565.48
19.8
707
2,545.34
0.89
2,565.35
20
709
2,545.25
0.89
2,565.36
20.1
711
2,546.54
0.89
2,567.44
20.9
713
2,545.41
0.9
2,566.86
21.5
716
2,546.01
0.9
2,565.69
19.7
717
2,544.53
0.9
2,561.45
16.9
728
2,547.10
0.91
2,566.12
19
729
2,546.12
0.92
2,565.93
19.8
730
2,545.08
0.92
2,565.35
20.3
732
2,545.37
0.92
2,565.36
20
733
2,545.61
0.92
2,565.42
19.8
734
2,545.69
0.92
2,565.50
19.8
737
2,544.21
0.93
2,565.73
21.5
738
2,545.76
0.93
2,565.50
19.7
739
2,545.35
0.93
2,565.36
20
740
2,545.59
0.93
2,565.42
19.8
741
2,545.06
0.93
2,565.35
20.3
742
2,546.37
0.93
2,566.09
19.7
743
2,545.34
0.93
2,565.70
20.4
744
2,545.25
0.93
2,565.36
20.1
745
2,545.11
0.94
2,565.22
20.1
746
2,544.96
0.94
2,565.11
20.1
747
2,544.60
0.94
2,565.06
20.5
748
2,546.47
0.94
2,567.85
21.4
749
2,546.56
0.94
2,567.34
20.8
750
2,546.68
0.94
2,566.85
20.2
751
2,546.71
0.94
2,566.56
19.9
752
2,546.37
0.94
2,566.21
19.8
759
2,546.09
0.95
2,565.91
19.8
903
2,544.02
1.13
2,559.89
15.9
967
2,544.34
1.21
2,561.47
17.1
1030
2,543.34
1.29
2,559.89
16.5

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
65
Juan Camilo Vergara Valderrama
3.4.1.5
Red de distribución los Olivos II (tubos)
Tabla 28.
Resultados de modelación red Olivos II para cada tubo de la red (Reporte 1).
ID
Length (Scaled) (m) Diameter (mm)
Material
Flow (L/s) Velocity (m/s) Headloss Gradient (m/m)
30
3.7
97.38
PVC
0.43
0.06
0.0001
32
27.58
97.38
PVC
-0.07
0.01
0
34
32.37
97.38
PVC
0.18
0.02
0
36
30.84
97.38
PVC
0.42
0.06
0.0001
42
31.73
97.38
PVC
0.82
0.11
0.0002
44
31.36
97.38
PVC
0.92
0.12
0.0003
46
28.88
97.38
PVC
1.11
0.15
0.0004
50
31.06
97.38
PVC
1.37
0.18
0.0005
52
28.71
97.38
PVC
1.03
0.14
0.0003
57
10.43
143.34
PVC
-1.23
0.08
0.0001
59
1.62
143.34
PVC
-1.59
0.1
0.0002
61
31.33
143.34
PVC
0.86
0.05
0
63
1.35
143.34
PVC
2.46
0.15
0.0004
65
30.32
143.34
PVC
2.11
0.13
0.0002
67
1.75
143.34
PVC
1.8
0.11
0.0002
71
1.32
143.34
PVC
1.82
0.11
0.0002
77
1.72
143.34
PVC
1.95
0.12
0.0002
79
30.4
143.34
PVC
2.03
0.13
0.0002
81
1.37
143.34
PVC
1.68
0.1
0.0002
83
27.5
143.34
PVC
1.73
0.11
0.0001
85
4.32
143.34
PVC
1.3
0.08
0.0001
87
5.68
143.34
PVC
1.44
0.09
0.0001
89
25.73
143.34
PVC
0.87
0.05
0
93
28.72
97.38
PVC
1.98
0.27
0.001
95
1.3
97.38
PVC
1.97
0.26
0.0009
97
29.31
97.38
PVC
1.81
0.24
0.0009
99
1.33
97.38
PVC
1.97
0.26
0.0009
100
27.26
97.38
PVC
1.91
0.26
0.0009
102
1.43
97.38
PVC
2.81
0.38
0.0019
104
26.55
97.38
PVC
2.06
0.28
0.0011
106
77.5
97.38
PVC
1.93
0.26
0.001
122
25.58
97.38
PVC
7.52
1.01
0.0106
124
1.01
97.38
PVC
5.85
0.78
0.0068
126
35.59
97.38
PVC
8.53
1.15
0.0132
128
1.06
97.38
PVC
7.51
1.01
0.0104
132
5.1
97.38
PVC
9.54
1.28
0.0162
134
27.2
97.38
PVC
7.34
0.99
0.0101
136
5.38
97.38
PVC
9.19
1.23
0.0151
138
26.44
97.38
PVC
5.96
0.8
0.007
140
5.1
97.38
PVC
8.44
1.13
0.0129
144
3.46
143.34
PVC
-7.36
0.46
0.0016
148
92.16
97.38
PVC
-2.91
0.39
0.002
153
41.62
97.38
PVC
4.09
0.55
0.0036
155
44.41
97.38
PVC
2.21
0.3
0.0012
157
16.37
97.38
PVC
0.68
0.09
0.0002
161
31.86
97.38
PVC
1.12
0.15
0.0004
163
31.74
97.38
PVC
0.74
0.1
0.0002
165
30.75
97.38
PVC
0.38
0.05
0
169
1.31
143.34
PVC
3.66
0.23
0.0005
173
30.71
97.38
PVC
1.9
0.25
0.0009
175
26.58
97.38
PVC
1.58
0.21
0.0007
177
4.1
97.38
PVC
3.32
0.45
0.0025
179
30.27
97.38
PVC
3.03
0.41
0.0021
180
26.07
97.38
PVC
3.43
0.46
0.0026
181
77.81
75.74
PVC
0.62
0.14
0.0004
182
78.24
75.74
PVC
0.07
0.01
0
183
78.69
75.74
PVC
-0.1
0.02
0
184
79.06
75.74
PVC
-0.08
0.02
0
194
65.96
75.74
PVC
-2.73
0.61
0.0058
199
12.9
75.74
PVC
2.65
0.59
0.0055
201
3.77
75.74
PVC
2.01
0.45
0.0034
203
3.97
75.74
PVC
1.24
0.28
0.0014
214
16.29
143.34
PVC
29.41
1.82
0.0191
216
3.6
143.34
PVC
28.68
1.78
0.0182
219
30.67
75.74
PVC
2.84
0.63
0.0063
220
11.55
75.74
PVC
-3.91
0.87
0.011
224
33.57
143.34
PVC
29.8
1.85
0.0196
226
32.88
143.34
PVC
31.56
1.96
0.0217
228
33.55
143.34
PVC
34.34
2.13
0.0253
230
8.22
143.34
PVC
42.32
2.62
0.0369
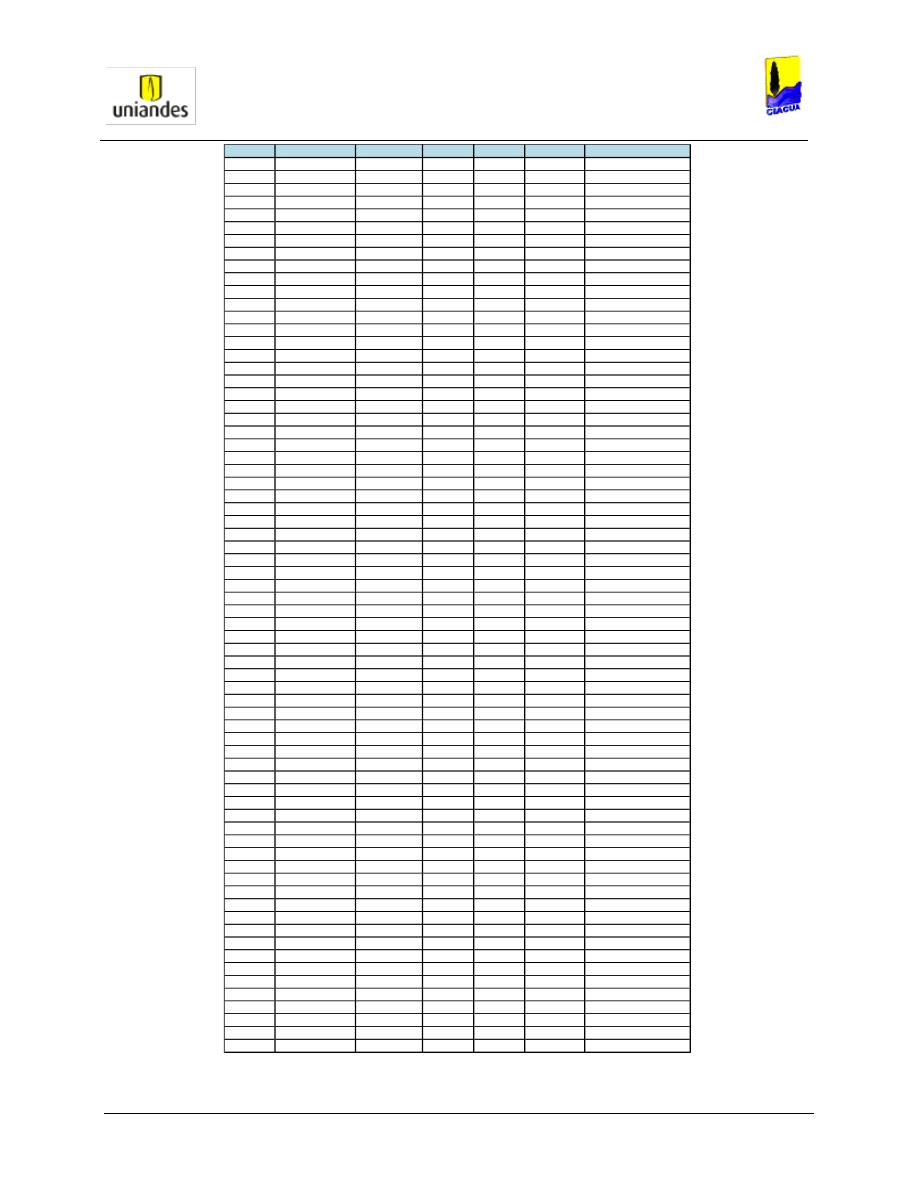
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
66
Juan Camilo Vergara Valderrama
Tabla 29.
Resultados de modelación red Olivos II para cada tubo de la red (Reporte 2).
ID
Length (Scaled) (m) Diameter (mm)
Material
Flow (L/s) Velocity (m/s) Headloss Gradient (m/m)
232
24.83
143.34
PVC
42.03
2.6
0.0364
236
6.31
143.34
PVC
24.02
1.49
0.0132
238
3.49
143.34
PVC
22.95
1.42
0.0122
240
15.08
143.34
PVC
22.19
1.37
0.0115
242
33.96
143.34
PVC
17.49
1.08
0.0075
244
32.35
143.34
PVC
13.74
0.85
0.0049
246
31.91
143.34
PVC
10.75
0.67
0.0031
248
31.21
143.34
PVC
8.31
0.52
0.002
250
4.76
143.34
PVC
7.22
0.45
0.0016
254
27.78
75.74
PVC
0.54
0.12
0.0003
256
1.49
75.74
PVC
0.93
0.21
0.001
260
8.53
75.74
PVC
0.94
0.21
0.0009
262
27.59
75.74
PVC
0.61
0.14
0.0004
264
2.44
75.74
PVC
0.92
0.2
0.0009
266
39.83
75.74
PVC
0.59
0.13
0.0004
268
6.02
75.74
PVC
0.98
0.22
0.0009
276
6.43
143.34
PVC
-5.25
0.33
0.0009
278
28.44
143.34
PVC
-3.77
0.23
0.0005
280
24.17
143.34
PVC
-4.76
0.29
0.0007
282
3.42
143.34
PVC
-5.58
0.35
0.001
284
5.41
143.34
PVC
-3.98
0.25
0.0006
286
38.43
143.34
PVC
-4.99
0.31
0.0008
289
41.9
75.74
PVC
1.03
0.23
0.0011
292
6.14
97.38
PVC
-2.32
0.31
0.0014
295
28.89
143.34
PVC
3.94
0.24
0.0005
299
5.96
97.38
PVC
-4.62
0.62
0.0044
301
28.27
97.38
PVC
-0.6
0.08
0.0001
303
2.8
97.38
PVC
2.47
0.33
0.0015
307
17.39
97.38
PVC
0.21
0.03
0
311
1.37
143.34
PVC
-5.75
0.36
0.0011
316
1.02
143.34
PVC
-5.96
0.37
0.0012
317
25.93
143.34
PVC
-4.69
0.29
0.0007
325
10.09
97.38
PVC
2.42
0.32
0.0014
352
3.68
143.34
PVC
3.06
0.19
0.0003
353
27.07
143.34
PVC
2.17
0.13
0.0002
361
3.41
143.34
PVC
-7.18
0.44
0.0015
380
2.74
97.38
PVC
0
0
0
381
4.8
97.38
PVC
0
0
0
383
29.59
97.38
PVC
0.6
0.08
0.0001
384
3.75
97.38
PVC
0.6
0.08
0.0002
386
3.67
97.38
PVC
1.39
0.19
0.0005
387
91.23
97.38
PVC
1.39
0.19
0.0005
389
83.72
75.74
PVC
-0.29
0.06
0.0001
390
3.6
75.74
PVC
-0.29
0.06
0.0001
392
83.54
75.74
PVC
-0.28
0.06
0.0001
393
3.51
75.74
PVC
-0.28
0.06
0.0001
395
83.77
75.74
PVC
-0.22
0.05
0
396
3.24
75.74
PVC
-0.22
0.05
0
399
83.67
97.38
PVC
-0.27
0.04
0
400
3.31
97.38
PVC
-0.27
0.04
0
402
83.64
75.74
PVC
-0.15
0.03
0
403
3.41
75.74
PVC
-0.15
0.03
0
405
83.71
75.74
PVC
-0.25
0.06
0.0001
406
3.41
75.74
PVC
-0.25
0.06
0.0001
408
83.61
75.74
PVC
-0.33
0.07
0.0001
409
3.57
75.74
PVC
-0.33
0.07
0.0001
411
6.29
97.38
PVC
2.01
0.27
0.001
412
23.96
97.38
PVC
2.01
0.27
0.001
414
84.19
75.74
PVC
-0.04
0.01
0
415
3.5
75.74
PVC
-0.04
0.01
0
417
84.63
75.74
PVC
0.28
0.06
0.0001
418
3.43
75.74
PVC
0.28
0.06
0.0002
420
84.69
97.38
PVC
0.97
0.13
0.0003
421
3.74
97.38
PVC
0.97
0.13
0.0002
423
3.62
143.34
PVC
-1.26
0.08
0.0001
424
75.33
143.34
PVC
-1.26
0.08
0.0001
426
3.49
143.34
PVC
2.19
0.14
0.0002
427
26.96
143.34
PVC
2.19
0.14
0.0002
429
3.36
97.38
PVC
-0.46
0.06
0.0001
433
34.49
97.38
PVC
9.22
1.24
0.0152
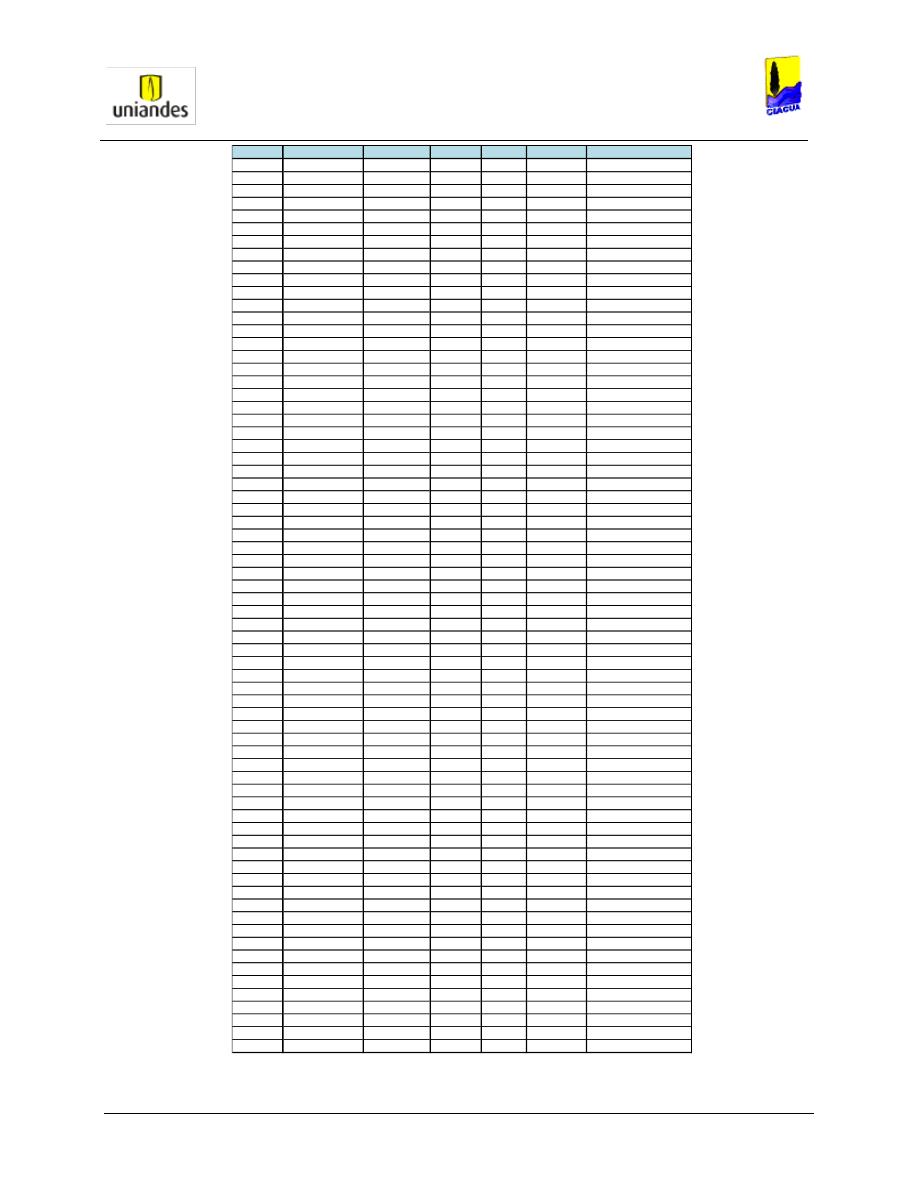
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
67
Juan Camilo Vergara Valderrama
Tabla 30.
Resultados de modelación red Olivos II para cada tubo de la red (Reporte 3).
ID
Length (Scaled) (m) Diameter (mm)
Material
Flow (L/s) Velocity (m/s) Headloss Gradient (m/m)
435
22.98
97.38
PVC
8.46
1.14
0.013
436
3.44
97.38
PVC
8.46
1.14
0.013
438
23.78
97.38
PVC
0
0
0
439
6.17
97.38
PVC
0
0
0
441
2.19
97.38
PVC
0
0
0
442
28.21
97.38
PVC
0
0
0
444
3.24
75.74
PVC
-0.8
0.18
0.0006
445
24.14
75.74
PVC
-0.8
0.18
0.0007
447
3.76
143.34
PVC
29.21
1.81
0.0189
448
33.27
143.34
PVC
29.21
1.81
0.0189
450
3.45
75.74
PVC
-0.87
0.19
0.0008
451
65.38
75.74
PVC
-0.87
0.19
0.0008
453
3.42
75.74
PVC
-2.04
0.45
0.0035
454
75.26
75.74
PVC
-2.04
0.45
0.0035
456
3.44
75.74
PVC
-3.06
0.68
0.0071
457
84.93
75.74
PVC
-3.06
0.68
0.0071
459
3.51
97.38
PVC
-8.26
1.11
0.0125
460
94.68
97.38
PVC
-8.26
1.11
0.0125
465
3.57
143.34
PVC
7.54
0.47
0.0017
466
102.28
143.34
PVC
7.53
0.47
0.0017
468
30.64
143.34
PVC
34.2
2.12
0.0251
469
3.53
143.34
PVC
34.2
2.12
0.0251
471
17.35
97.38
PVC
-9.89
1.33
0.0172
472
3.39
97.38
PVC
-9.89
1.33
0.0172
474
3.33
97.38
PVC
0.78
0.1
0.0002
475
10.59
97.38
PVC
0.78
0.1
0.0002
477
3.39
97.38
PVC
4.39
0.59
0.0041
478
146.91
97.38
PVC
4.39
0.59
0.0041
480
10.18
97.38
PVC
3.45
0.46
0.0027
481
122.81
97.38
PVC
3.45
0.46
0.0026
483
8.83
97.38
PVC
2.69
0.36
0.0017
484
107.52
97.38
PVC
2.69
0.36
0.0017
486
8.73
97.38
PVC
2.13
0.29
0.0011
487
91.39
97.38
PVC
2.13
0.29
0.0011
489
26.69
143.34
PVC
-6.06
0.38
0.0011
490
8.72
143.34
PVC
-6.06
0.38
0.0011
492
6.01
75.74
PVC
0.85
0.19
0.0007
493
100.53
75.74
PVC
0.85
0.19
0.0008
495
7
75.74
PVC
0.71
0.16
0.0006
496
83.67
75.74
PVC
0.71
0.16
0.0006
498
7.15
75.74
PVC
0.65
0.14
0.0005
499
65.05
75.74
PVC
0.65
0.14
0.0005
501
7.01
75.74
PVC
0.64
0.14
0.0005
502
57.49
75.74
PVC
0.64
0.14
0.0005
504
5.91
75.74
PVC
0.72
0.16
0.0006
505
44.72
75.74
PVC
0.72
0.16
0.0006
507
22
143.34
PVC
-4.19
0.26
0.0006
508
3.29
143.34
PVC
-4.19
0.26
0.0005
510
55.46
75.74
PVC
-0.73
0.16
0.0006
511
3.33
75.74
PVC
-0.73
0.16
0.0005
513
77.33
97.38
PVC
-1.65
0.22
0.0007
514
3.37
97.38
PVC
-1.65
0.22
0.0007
516
6
97.38
PVC
2.2
0.29
0.0012
517
23.74
97.38
PVC
2.2
0.29
0.0012
519
25.52
97.38
PVC
-0.07
0.01
0
520
5.85
97.38
PVC
-0.07
0.01
0
522
2.66
75.74
PVC
-0.25
0.05
0.0001
523
76.33
75.74
PVC
-0.25
0.05
0.0001
525
2.91
75.74
PVC
-0.15
0.03
0.0001
526
76.11
75.74
PVC
-0.15
0.03
0
528
3.06
75.74
PVC
-0.18
0.04
0
529
76.01
75.74
PVC
-0.18
0.04
0
531
72.29
97.38
PVC
-0.46
0.06
0.0001
532
3.45
97.38
PVC
-1.75
0.23
0.0008
534
16.49
97.38
PVC
3.07
0.41
0.0022
535
6.06
97.38
PVC
3.07
0.41
0.0022
537
102.04
97.38
PVC
1.34
0.18
0.0005
538
3.17
97.38
PVC
1.34
0.18
0.0006
540
3.41
97.38
PVC
-2.59
0.35
0.0016
541
23.64
97.38
PVC
-2.59
0.35
0.0016
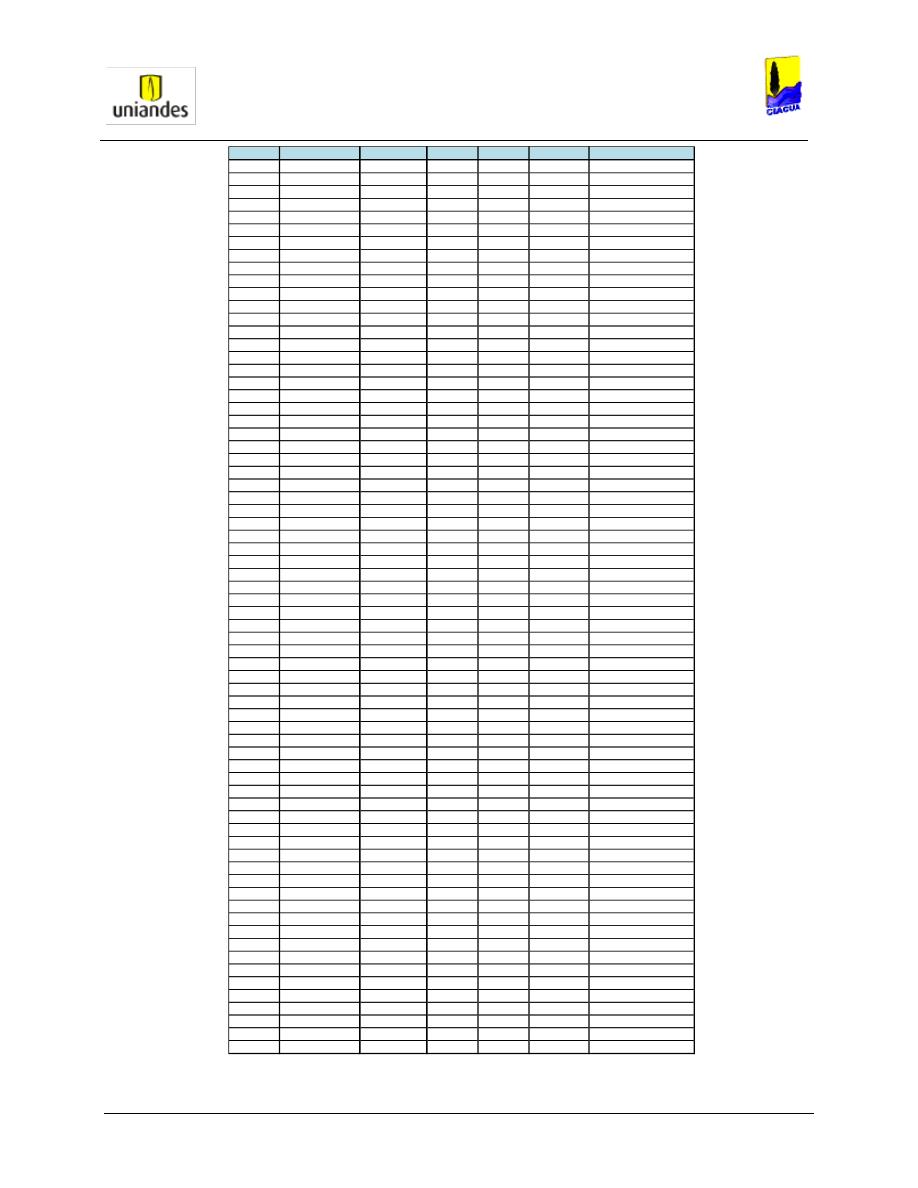
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
68
Juan Camilo Vergara Valderrama
Tabla 31.
Resultados de modelación red Olivos II para cada tubo de la red (Reporte 4).
ID
Length (Scaled) (m) Diameter (mm)
Material
Flow (L/s) Velocity (m/s) Headloss Gradient (m/m)
543
131.33
97.38
PVC
1.68
0.23
0.0008
544
3.79
97.38
PVC
1.68
0.23
0.0007
546
159.76
97.38
PVC
2.52
0.34
0.0015
547
3.4
97.38
PVC
2.52
0.34
0.0015
549
2.33
97.38
PVC
6.79
0.91
0.0088
550
45.03
97.38
PVC
6.79
0.91
0.0088
555
124.45
97.38
PVC
1.66
0.22
0.0007
556
3.26
97.38
PVC
1.66
0.22
0.0007
558
99.43
97.38
PVC
1.95
0.26
0.001
559
3.26
97.38
PVC
1.95
0.26
0.001
561
72.29
97.38
PVC
1.83
0.25
0.0009
562
2.55
97.38
PVC
1.83
0.25
0.0009
564
26.9
97.38
PVC
1.95
0.26
0.001
565
3.43
97.38
PVC
1.95
0.26
0.001
567
3.45
75.74
PVC
0.47
0.1
0.0003
568
6.09
75.74
PVC
0.47
0.1
0.0003
570
28.64
75.74
PVC
0.61
0.14
0.0004
571
3.22
75.74
PVC
0.61
0.14
0.0005
573
30.13
75.74
PVC
0.64
0.14
0.0005
574
3.3
75.74
PVC
0.64
0.14
0.0005
576
3.34
97.38
PVC
-1.96
0.26
0.001
577
28.69
97.38
PVC
-1.96
0.26
0.001
580
3.47
75.74
PVC
0.45
0.1
0.0003
581
6.07
75.74
PVC
0.45
0.1
0.0002
583
3.54
75.74
PVC
0.46
0.1
0.0003
584
6
75.74
PVC
0.46
0.1
0.0003
587
3.42
75.74
PVC
0.47
0.1
0.0003
588
6.12
75.74
PVC
0.47
0.1
0.0003
590
3.41
75.74
PVC
0.46
0.1
0.0003
591
6.13
75.74
PVC
0.46
0.1
0.0002
593
3.4
75.74
PVC
0.47
0.1
0.0003
594
6.14
75.74
PVC
0.46
0.1
0.0002
597
91.48
143.34
PVC
-6.27
0.39
0.0012
599
3.46
97.38
PVC
0.78
0.11
0.0003
600
8.96
97.38
PVC
0.78
0.11
0.0002
753
0.48
101.6
PVC
15.09
1.86
0.0298
754
0.55
101.6
PVC
5.24
0.65
0.0049
755
0.59
76.2
PVC
-1.58
0.35
0.0025
756
0.64
101.6
PVC
6.74
0.83
0.007
757
1.07
76.2
PVC
0.88
0.19
0.0006
758
1.09
76.2
PVC
-0.4
0.09
0.0003
760
1.12
76.2
PVC
1.64
0.36
0.0024
761
1.18
76.2
PVC
0.79
0.17
0.0008
762
1.25
76.2
PVC
-1.23
0.27
0.0014
765
1.68
152.4
PVC
-1.21
0.07
0
766
1.74
76.2
PVC
-0.12
0.03
0
767
1.68
101.6
PVC
5.24
0.65
0.0044
768
1.73
76.2
PVC
-7.48
1.64
0.0338
769
1.91
101.6
PVC
-8.57
1.06
0.0109
770
1.91
76.2
PVC
-0.92
0.2
0.0008
771
2
76.2
PVC
-4.78
1.05
0.0153
773
2.03
152.4
PVC
-21.46
1.18
0.008
774
2.28
152.4
PVC
-5.4
0.3
0.0008
775
2.32
76.2
PVC
-0.92
0.2
0.0009
776
2.53
101.6
PVC
12.35
1.52
0.021
777
2.93
76.2
PVC
2.74
0.6
0.0057
778
3.09
152.4
PVC
58.55
3.21
0.0495
779
3.09
76.2
PVC
0.81
0.18
0.0007
780
3.22
76.2
PVC
2.54
0.56
0.0049
781
3.31
76.2
PVC
0.92
0.2
0.0008
782
3.37
76.2
PVC
0
0
0
783
3.38
76.2
PVC
0.55
0.12
0.0004
784
3.6
76.2
PVC
-0.92
0.2
0.0009
785
4.38
101.6
PVC
13.25
1.63
0.0238
786
4.48
101.6
PVC
14.21
1.75
0.027
787
4.59
76.2
PVC
-3.7
0.81
0.0097
788
4.64
76.2
PVC
2.49
0.55
0.0048
791
4.93
76.2
PVC
-2.82
0.62
0.006
792
5.08
76.2
PVC
2.14
0.47
0.0037
793
5.16
76.2
PVC
4.4
0.96
0.0131
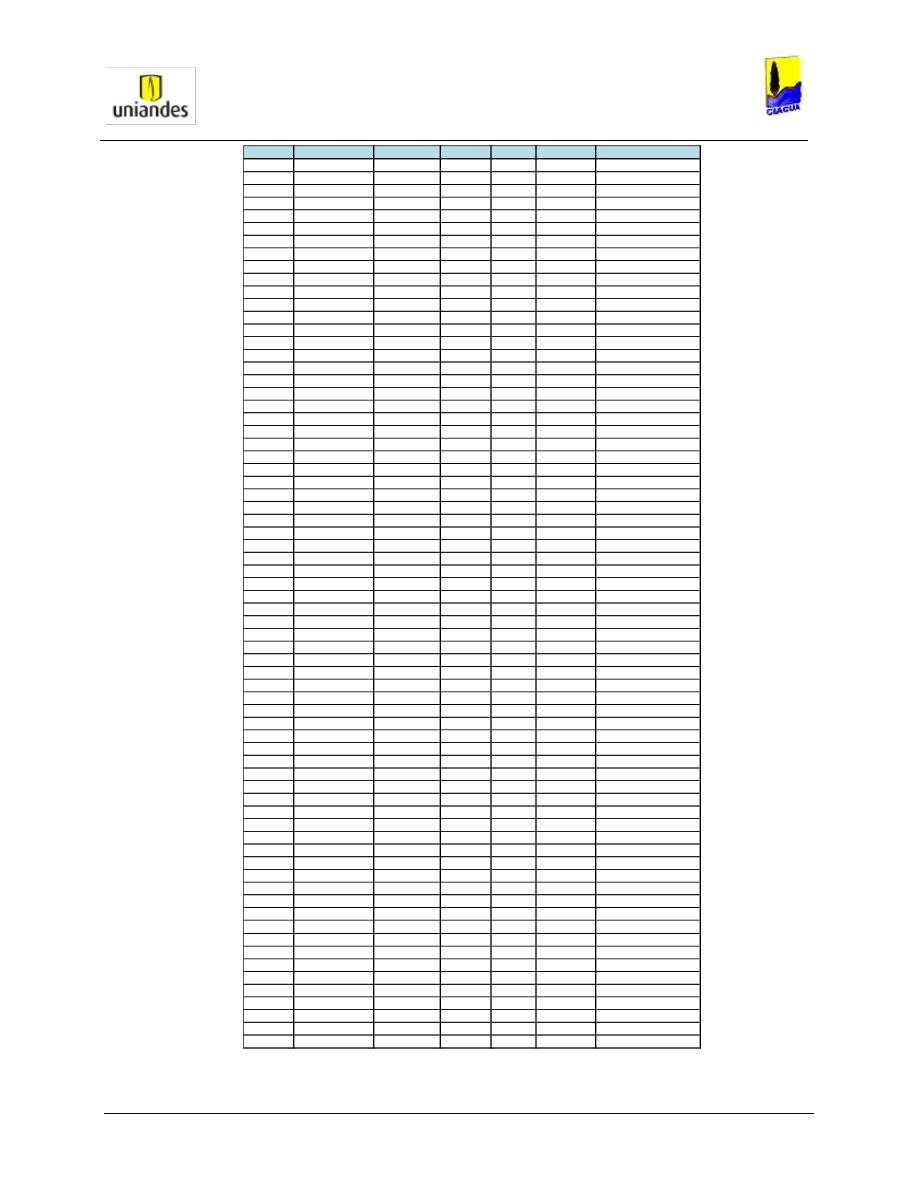
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
69
Juan Camilo Vergara Valderrama
Tabla 32.
Resultados de modelación red Olivos II para cada tubo de la red (Reporte 5).
ID
Length (Scaled) (m) Diameter (mm)
Material
Flow (L/s) Velocity (m/s) Headloss Gradient (m/m)
794
5.26
152.4
PVC
-15.87
0.87
0.0047
796
5.4
152.4
PVC
-5.4
0.3
0.0007
797
6.68
101.6
PVC
-10.28
1.27
0.0151
799
7.83
101.6
PVC
8.1
1
0.0098
800
7.92
76.2
PVC
-7.89
1.73
0.0373
801
7.91
152.4
PVC
-17.34
0.95
0.0055
803
8.15
76.2
PVC
-4.13
0.91
0.0118
805
8.99
76.2
PVC
-6.04
1.32
0.0231
808
10.77
76.2
PVC
-4.47
0.98
0.0135
809
10.89
152.4
PVC
0.92
0.05
0
810
13.86
76.2
PVC
0.91
0.2
0.0008
811
14.43
152.4
PVC
21.46
1.18
0.0081
812
13.68
101.6
PVC
8.11
1
0.0099
814
18.16
152.4
PVC
-21.46
1.18
0.0081
817
22.74
76.2
PVC
-0.46
0.1
0.0003
819
24
76.2
PVC
-7.48
1.64
0.0339
820
24.15
76.2
PVC
5.08
1.11
0.017
823
26.31
101.6
PVC
7.99
0.99
0.0096
825
26.1
76.2
PVC
-0.12
0.03
0
827
26.82
76.2
PVC
3.91
0.86
0.0107
828
26.87
76.2
PVC
2.78
0.61
0.0058
829
27.19
76.2
PVC
2.54
0.56
0.005
830
27.55
152.4
PVC
-17.64
0.97
0.0057
831
27.84
152.4
PVC
-44.26
2.43
0.0298
832
28.75
152.4
PVC
58.55
3.21
0.0495
833
28.88
152.4
PVC
26.44
1.45
0.0117
834
29.91
152.4
PVC
49.81
2.73
0.0369
835
30.08
76.2
PVC
4.75
1.04
0.0151
836
30.38
152.4
PVC
-16.45
0.9
0.005
839
30.63
76.2
PVC
4.09
0.9
0.0116
840
31.23
152.4
PVC
31.76
1.74
0.0163
842
31.28
152.4
PVC
-4.39
0.24
0.0005
843
32.93
101.6
PVC
-3.22
0.4
0.0019
844
31.58
76.2
PVC
-5.84
1.28
0.0218
845
31.74
101.6
PVC
4.54
0.56
0.0035
846
31.77
76.2
PVC
2.01
0.44
0.0033
847
32.61
101.6
PVC
3.42
0.42
0.0021
848
30.68
101.6
PVC
6.84
0.84
0.0073
849
32.2
101.6
PVC
2.68
0.33
0.0014
851
32.33
152.4
PVC
-47.58
2.61
0.034
852
32.34
152.4
PVC
-8.98
0.49
0.0017
853
32.72
76.2
PVC
1.69
0.37
0.0024
854
33.04
152.4
PVC
42.92
2.35
0.0282
856
33.64
152.4
PVC
-2.48
0.14
0.0002
857
34.24
76.2
PVC
-2.41
0.53
0.0045
858
34.43
101.6
PVC
7.36
0.91
0.0083
859
38.49
101.6
PVC
7.54
0.93
0.0087
860
41.59
76.2
PVC
0
0
0
862
44.06
152.4
PVC
-112.17
6.15
0.1625
863
46.23
152.4
PVC
-30.18
1.65
0.0149
865
49.01
76.2
PVC
4.4
0.96
0.0131
866
49.83
76.2
PVC
-7.89
1.73
0.0373
868
54.01
76.2
PVC
1.43
0.31
0.0018
870
55.93
76.2
PVC
-6.04
1.32
0.0231
871
56.32
101.6
PVC
4.52
0.56
0.0035
872
56.8
76.2
PVC
1.67
0.37
0.0024
873
58.36
152.4
PVC
-3.35
0.18
0.0003
875
58.22
76.2
PVC
2.49
0.55
0.0048
876
58.59
76.2
PVC
-2.46
0.54
0.0047
878
64.89
101.6
PVC
-10.28
1.27
0.0151
880
67.86
76.2
PVC
-4.47
0.98
0.0135
882
71.78
152.4
PVC
-19.73
1.08
0.0069
883
75.78
152.4
PVC
-52.8
2.89
0.041
884
77.8
76.2
PVC
-4.13
0.91
0.0118
885
81.42
76.2
PVC
-4.78
1.05
0.0152
886
82.32
76.2
PVC
1.25
0.27
0.0014
887
84.05
76.2
PVC
1.86
0.41
0.0029
889
85.83
76.2
PVC
-0.11
0.02
0
890
86.09
76.2
PVC
1.64
0.36
0.0023
891
92.75
76.2
PVC
0.91
0.2
0.0008
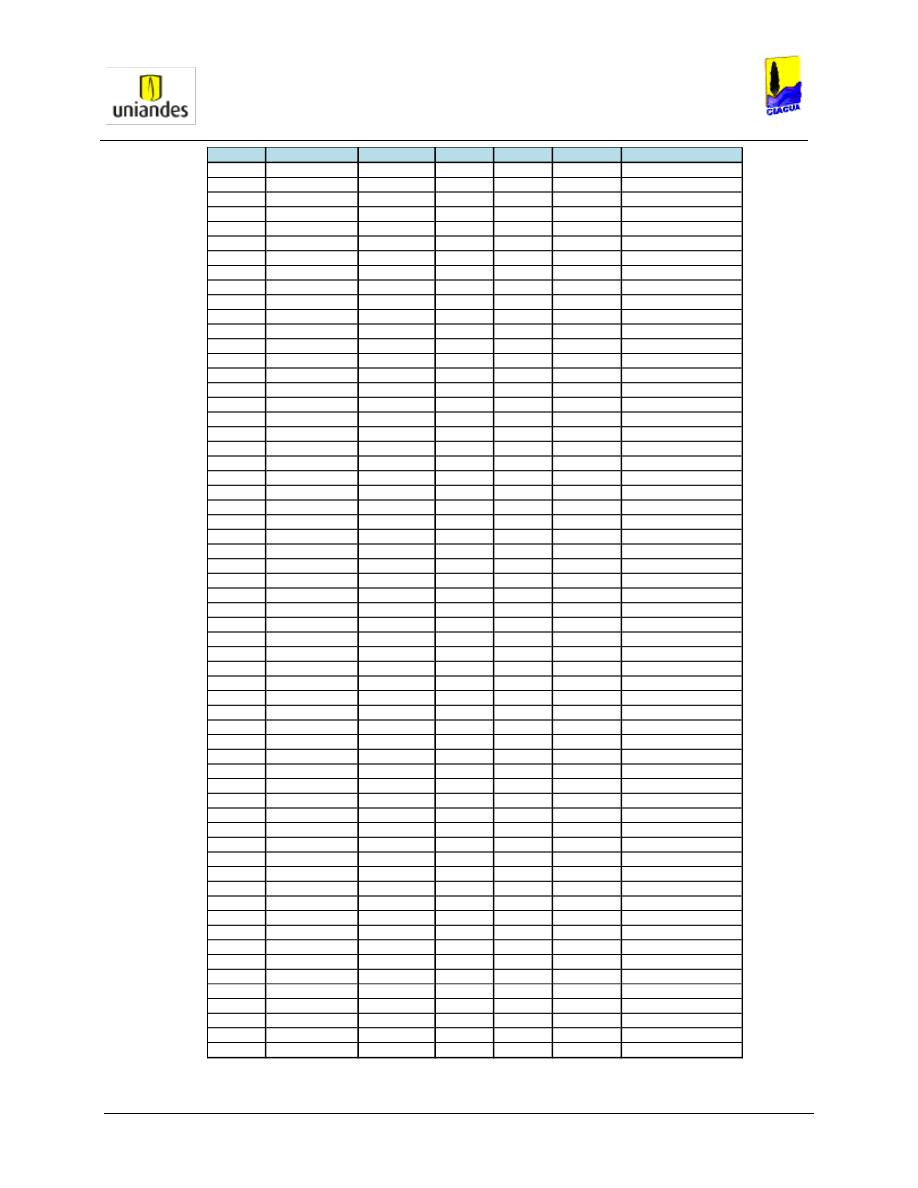
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
70
Juan Camilo Vergara Valderrama
Tabla 33.
Resultados de modelación red Olivos II para cada tubo de la red (Reporte 6).
ID
Length (Scaled) (m) Diameter (mm)
Material
Flow (L/s) Velocity (m/s) Headloss Gradient (m/m)
892
94.28
152.4
PVC
-20.58
1.13
0.0075
893
94.28
101.6
PVC
-8.57
1.06
0.0109
901
5.77
152.4
PVC
-0.76
0.04
0.0001
905
2.11
152.4
PVC
-1.6
0.09
0
910
3.63
143.34
PVC
6.27
0.39
0.0012
912
0.79
75.74
PVC
1.52
0.34
0.0019
913
1.02
75.74
PVC
1.56
0.35
0.002
915
2.75
76.2
PVC
3.42
0.75
0.0084
916
81.97
76.2
PVC
3.42
0.75
0.0084
918
2.68
76.2
PVC
2.78
0.61
0.0058
919
64.5
76.2
PVC
2.78
0.61
0.0058
921
2.87
76.2
PVC
2.01
0.44
0.0033
922
59.09
76.2
PVC
2.01
0.44
0.0033
924
2.11
76.2
PVC
1.11
0.24
0.0011
925
95.5
76.2
PVC
1.11
0.24
0.0012
927
2.48
76.2
PVC
-0.59
0.13
0.0005
928
94.9
76.2
PVC
-0.59
0.13
0.0004
930
95.05
76.2
PVC
0.73
0.16
0.0006
931
2.85
76.2
PVC
0.73
0.16
0.0006
933
3.94
76.2
PVC
-1.96
0.43
0.0032
934
28.76
76.2
PVC
-1.96
0.43
0.0032
936
3.78
97.38
PVC
-9.22
1.24
0.0152
942
15.73
152.4
PVC
0.47
0.03
0
943
3.24
152.4
PVC
0.47
0.03
0
945
3.44
75.74
PVC
0.46
0.1
0.0003
946
6.11
75.74
PVC
0.46
0.1
0.0002
951
1.25
152.4
PVC
-12.47
0.68
0.0031
952
24.78
152.4
PVC
-12.47
0.68
0.0031
961
23.34
101.6
PVC
5.85
0.72
0.0055
962
1.82
101.6
PVC
5.85
0.72
0.0056
965
3.31
97.38
PVC
0.46
0.06
0.0001
966
84.56
97.38
PVC
0.46
0.06
0.0001
969
6.45
101.6
PVC
0
0
0
970
21.15
101.6
PVC
0
0
0
978
50.53
76.2
PVC
-4.69
1.03
0.0147
979
1.29
76.2
PVC
-4.69
1.03
0.0147
980
16.47
152.4
PVC
-18.99
1.04
0.0065
982
1.18
152.4
PVC
-14.61
0.8
0.004
983
25.55
152.4
PVC
-14.61
0.8
0.0041
990
1.59
76.2
PVC
4.96
1.09
0.0163
991
28.84
76.2
PVC
4.96
1.09
0.0163
993
6.03
76.2
PVC
4.19
0.92
0.012
994
2.19
76.2
PVC
4.19
0.92
0.0121
996
3.14
101.6
PVC
5.27
0.65
0.0045
997
30.05
101.6
PVC
5.27
0.65
0.0046
1000
20.93
76.2
PVC
-2.29
0.5
0.0041
1001
1.84
76.2
PVC
-2.29
0.5
0.0041
1003
4.57
76.2
PVC
-3.01
0.66
0.0067
1004
53.58
76.2
PVC
-3.01
0.66
0.0067
1006
41.26
76.2
PVC
-4.57
1
0.0141
1007
2.02
76.2
PVC
-4.57
1
0.014
1009
6.31
76.2
PVC
-1.35
0.3
0.0017
1010
65.46
76.2
PVC
-1.35
0.3
0.0017
1016
0.51
152.4
PVC
0.9
0.05
0
1017
0.95
152.4
PVC
44.26
2.43
0.0295
1020
1.22
152.4
PVC
0
0
0
1021
54.7
152.4
PVC
0
0
0
1023
2.04
152.4
PVC
0
0
0
1024
29.21
152.4
PVC
0
0
0
1026
2.36
97.38
PVC
0.13
0.02
0
1027
22.86
97.38
PVC
0.13
0.02
0
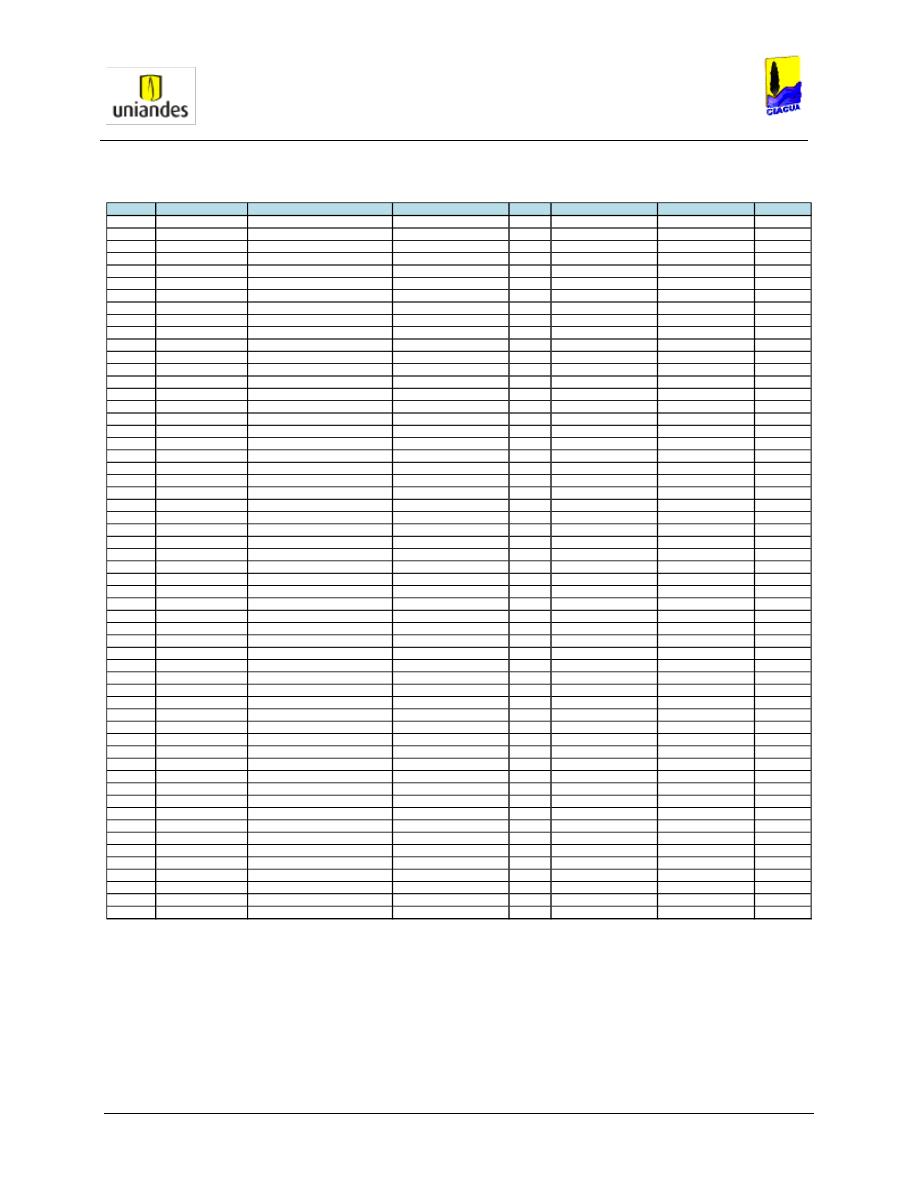
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
71
Juan Camilo Vergara Valderrama
3.4.1.6
Red de distribución los Olivos II (válvulas)
ID
Diameter (Valve) (mm) Headloss Coefficient Setting (Initial) Minor Loss Coefficient (Local) Flow (L/s) Hydraulic Grade (From) (m) Hydraulic Grade (To) (m) Headloss (m)
379
97.38
0
0.39
0
2,561.44
2,559.89
0
382
97.38
0
0.39
0.6
2,559.88
2,559.88
0
385
97.38
0
0.39
1.39
2,559.85
2,559.85
0
388
75.74
0
0.39
-0.29
2,559.89
2,559.89
0
391
75.74
0
0.39
-0.28
2,559.89
2,559.89
0
394
75.74
0
0.39
-0.22
2,559.89
2,559.89
0
398
97.38
0
0.39
-0.27
2,559.88
2,559.88
0
401
75.74
0
0.39
-0.15
2,559.87
2,559.87
0
404
75.74
0
0.39
-0.25
2,559.87
2,559.87
0
407
75.74
0
0.39
-0.33
2,559.87
2,559.87
0
410
97.38
0
0.39
2.01
2,559.86
2,559.86
0
413
75.74
0
0.39
-0.04
2,559.80
2,559.80
0
416
75.74
0
0.39
0.28
2,559.78
2,559.78
0
419
97.38
0
0.39
0.97
2,559.75
2,559.75
0
422
143.34
0
0.39
-1.26
2,559.86
2,559.86
0
425
143.34
0
0.39
2.19
2,559.88
2,559.88
0
428
97.38
0
0.39
-0.46
2,559.88
2,559.88
0
431
97.38
0
0.39
9.22
2,566.53
2,566.53
0
434
97.38
0
0.39
8.46
2,564.95
2,564.95
0
437
97.38
0
0.39
0
2,564.21
2,561.59
0
440
97.38
0
0.39
0
2,561.60
2,560.38
0
443
75.74
0
0.39
-0.8
2,565.90
2,565.90
0
446
143.34
0
0.39
29.21
2,565.83
2,565.83
0
449
75.74
0
0.39
-0.87
2,565.21
2,565.21
0
452
75.74
0
0.39
-2.04
2,564.56
2,564.56
0
455
75.74
0
0.39
-3.06
2,563.86
2,563.86
0
458
97.38
0
0.39
-8.26
2,563.03
2,563.03
0
464
143.34
0
0.39
7.53
2,561.77
2,561.77
0
467
143.34
0
0.39
34.2
2,561.01
2,561.01
0
470
97.38
0
0.39
-9.89
2,560.86
2,560.86
0
473
97.38
0
0.39
0.78
2,560.83
2,560.83
0
476
97.38
0
0.39
4.39
2,560.60
2,560.60
0
479
97.38
0
0.39
3.45
2,560.34
2,560.34
0
482
97.38
0
0.39
2.69
2,560.19
2,560.19
0
485
97.38
0
0.39
2.13
2,560.10
2,560.10
0
488
143.34
0
0.39
-6.06
2,560.03
2,560.03
0
491
75.74
0
0.39
0.85
2,560.03
2,560.03
0
494
75.74
0
0.39
0.71
2,559.99
2,559.99
0
497
75.74
0
0.39
0.65
2,559.96
2,559.96
0
500
75.74
0
0.39
0.64
2,559.94
2,559.94
0
503
75.74
0
0.39
0.72
2,559.92
2,559.92
0
506
143.34
0
0.39
-4.19
2,559.92
2,559.92
0
509
75.74
0
0.39
-0.73
2,559.90
2,559.90
0
512
97.38
0
0.39
-1.65
2,559.88
2,559.88
0
515
97.38
0
0.39
2.2
2,559.86
2,559.86
0
518
97.38
0
0.39
-0.07
2,559.87
2,559.87
0
521
75.74
0
0.39
-0.25
2,559.87
2,559.87
0
524
75.74
0
0.39
-0.15
2,559.87
2,559.87
0
527
75.74
0
0.39
-0.18
2,559.87
2,559.87
0
533
97.38
0
0.39
3.07
2,559.90
2,559.90
0
536
97.38
0
0.39
1.34
2,559.89
2,559.89
0
539
97.38
0
0.39
-2.59
2,559.94
2,559.94
0
542
97.38
0
0.39
1.68
2,559.90
2,559.90
0
545
97.38
0
0.39
2.52
2,559.90
2,559.90
0
548
97.38
0
0.39
6.79
2,560.54
2,560.54
0
554
97.38
0
0.39
1.66
2,559.89
2,559.89
0
557
97.38
0
0.39
1.95
2,559.91
2,559.91
0
Tabla 34.
Resultados de modelación red Olivos II para cada válvula de la red (Reporte 1).
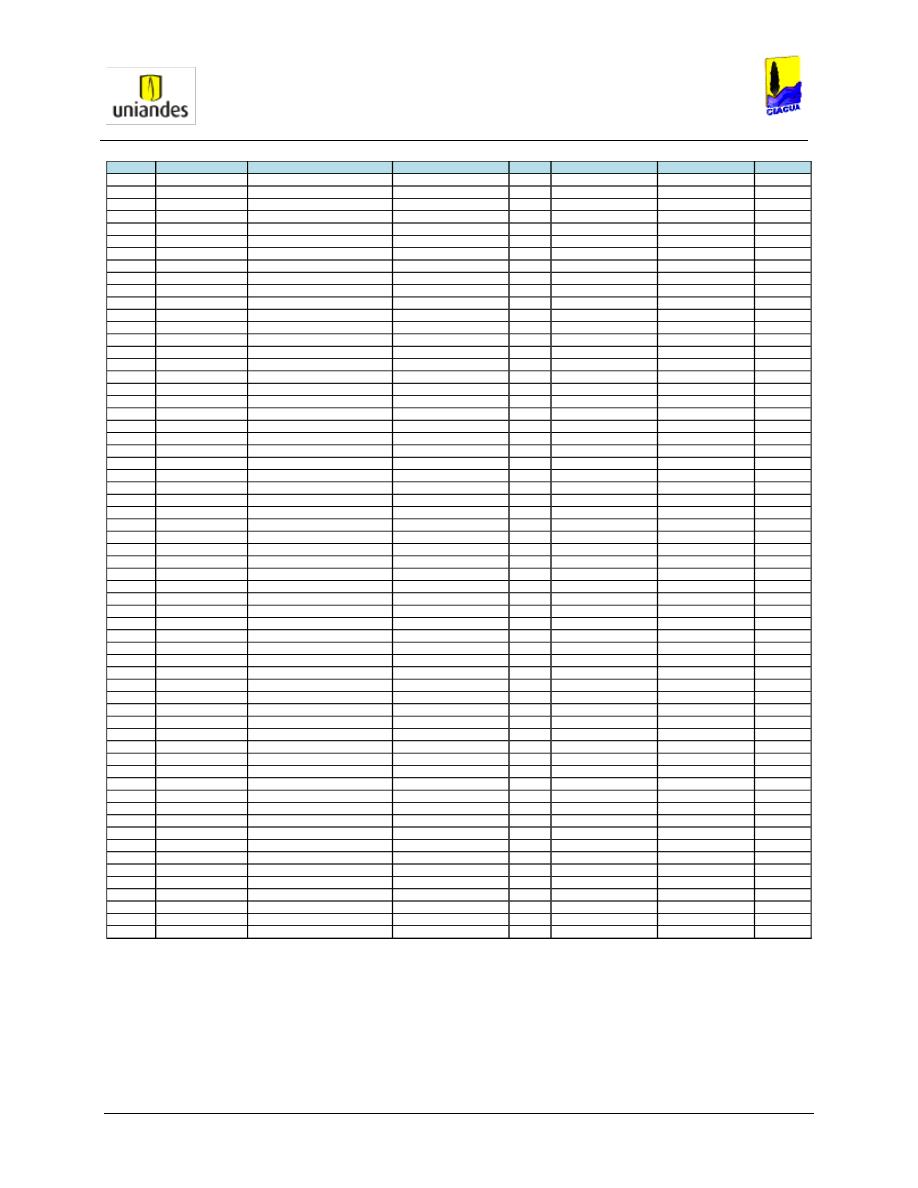
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
72
Juan Camilo Vergara Valderrama
ID
Diameter (Valve) (mm) Headloss Coefficient Setting (Initial) Minor Loss Coefficient (Local) Flow (L/s) Hydraulic Grade (From) (m) Hydraulic Grade (To) (m) Headloss (m)
560
97.38
0
0.39
1.83
2,559.93
2,559.93
0
563
97.38
0
0.39
1.95
2,559.97
2,559.97
0
566
75.74
0
0.39
0.47
2,559.96
2,559.96
0
569
75.74
0
0.39
0.61
2,559.93
2,559.93
0
572
75.74
0
0.39
0.64
2,559.87
2,559.87
0
575
97.38
0
0.39
-1.96
2,559.79
2,559.79
0
579
75.74
0
0.39
0.45
2,559.88
2,559.88
0
582
75.74
0
0.39
0.46
2,561.59
2,561.59
0
586
75.74
0
0.39
0.47
2,560.79
2,560.79
0
589
75.74
0
0.39
0.46
2,565.97
2,565.97
0
592
75.74
0
0.39
0.46
2,559.86
2,559.86
0
595
143.34
0
0.39
-6.27
2,561.48
2,561.48
0
598
97.38
0
0.39
0.78
2,560.04
2,560.04
0
627
76.2
0
0.39
-0.12
2,566.01
2,566.01
0
630
152.4
0
0.39
58.55
2,571.88
2,571.88
0
631
76.2
0
0.39
2.49
2,567.80
2,567.80
0
635
101.6
0
0.39
8.11
2,566.08
2,566.08
0
636
101.6
0
0.39
-8.57
2,566.32
2,566.32
0
637
76.2
0
0.39
-4.78
2,566.61
2,566.61
0
638
76.2
0
0.39
-7.48
2,566.71
2,566.71
0
639
76.2
0
0.39
-7.89
2,570.16
2,570.16
0
640
76.2
0
0.39
-6.04
2,569.15
2,569.15
0
641
152.4
0
0.39
-21.46
2,567.31
2,567.31
0
642
76.2
0
0.39
0.91
2,566.13
2,566.13
0
644
101.6
0
0.39
5.24
2,565.80
2,565.80
0
645
76.2
0
0.39
1.64
2,565.42
2,565.42
0
646
76.2
0
0.39
2.54
2,565.33
2,565.33
0
647
76.2
0
0.39
2.78
2,564.71
2,564.71
0
648
76.2
0
0.39
2.01
2,565.01
2,565.01
0
652
101.6
0
0.39
-10.28
2,568.32
2,568.32
0
914
76.2
0
0.39
3.42
2,565.04
2,565.04
0
917
76.2
0
0.39
2.78
2,565.09
2,565.09
0
920
76.2
0
0.39
2.01
2,565.21
2,565.21
0
923
76.2
0
0.39
1.11
2,565.36
2,565.36
0
926
76.2
0
0.39
-0.59
2,565.70
2,565.70
0
929
76.2
0
0.39
0.73
2,565.95
2,565.95
0
932
76.2
0
0.39
-1.96
2,559.91
2,559.91
0
941
152.4
0
0.39
0.47
2,559.89
2,559.89
0
944
75.74
0
0.39
0.46
2,559.88
2,559.88
0
950
152.4
0
0.39
-12.47
2,565.42
2,565.42
0
953
152.4
0
0.39
-5.4
2,561.47
2,561.47
0
956
152.4
0
0.39
21.46
2,567.46
2,567.46
0
959
152.4
0
0.39
-44.26
2,567.00
2,567.00
0
960
101.6
0
0.39
5.85
2,565.23
2,565.23
0
964
97.38
0
0.39
0.46
2,559.89
2,559.89
0
968
101.6
0
0.39
0
2,561.47
2,565.06
0
977
97.38
0
0.39
-4.69
2,566.79
2,566.79
0
981
97.38
0
0.39
-14.61
2,565.81
2,565.81
0
984
76.2
0
0.39
-4.47
2,567.77
2,567.77
0
985
76.2
0
0.39
-4.13
2,567.48
2,567.48
0
989
76.2
0
0.39
4.96
2,567.32
2,567.32
0
992
76.2
0
0.39
4.19
2,567.37
2,567.37
0
995
101.6
0
0.39
5.27
2,566.15
2,566.15
0
998
76.2
0
0.39
4.4
2,568.86
2,568.86
0
999
76.2
0
0.39
-2.29
2,568.30
2,568.30
0
1002
76.2
0
0.39
-3.01
2,566.20
2,566.20
0
1005
76.2
0
0.39
-4.57
2,566.82
2,566.82
0
1008
76.2
0
0.39
-1.35
2,566.10
2,566.10
0
1018
76.2
0
0.39
0
2,561.45
2,565.20
0
1019
152.4
0
0.39
0
2,561.45
2,565.35
0
1022
152.4
0
0.39
0
2,561.47
2,559.89
0
1025
97.38
0
0.39
0.13
2,560.01
2,560.01
0
Tabla 35.
Resultados de modelación red Olivos II para cada válvula de la red (Reporte 2).
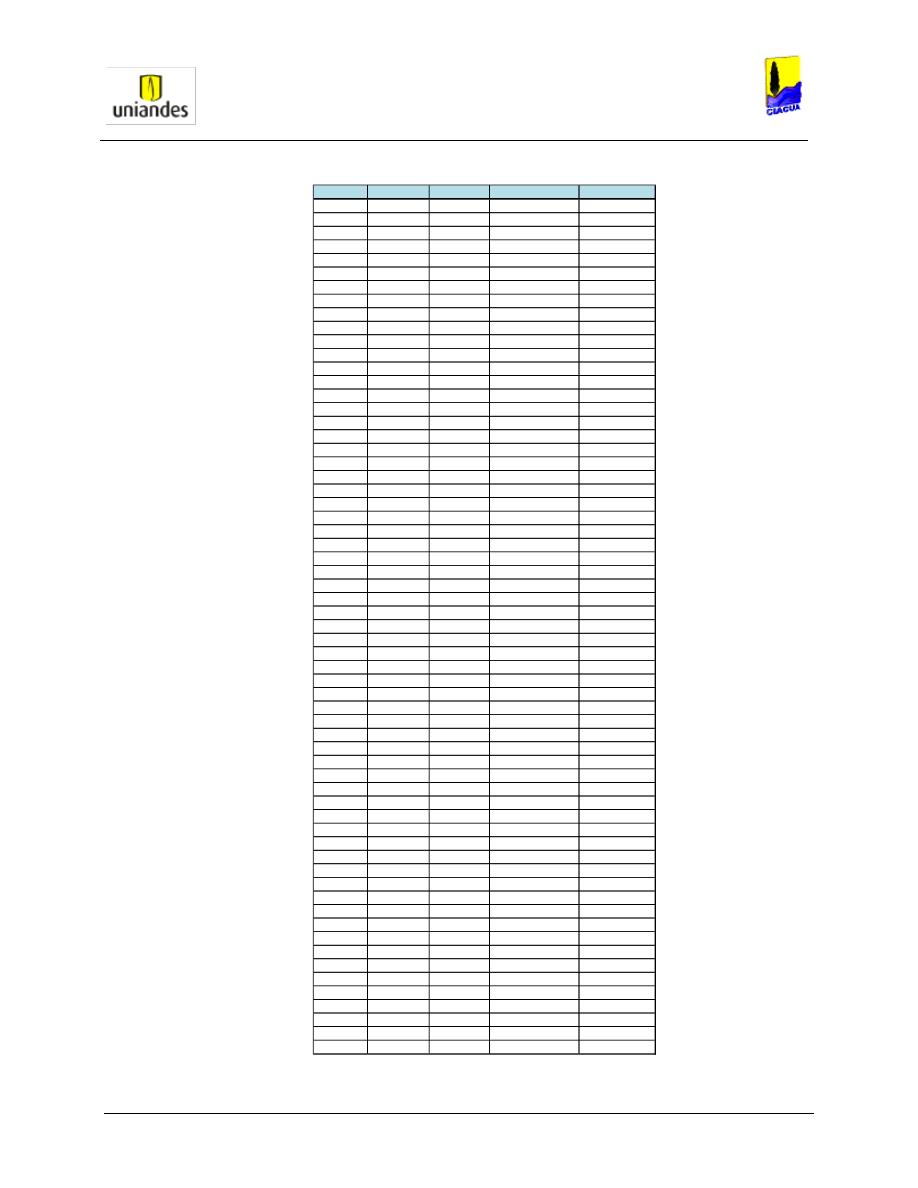
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
73
Juan Camilo Vergara Valderrama
3.4.1.7
Red de distribución los Olivos IV (nodos)
Tabla 36.
Resultados de modelación red Olivos IV para cada nodo de la red (Reporte 1).
ID
Elevation (m) Demand (L/s) Hydraulic Grade (m) Pressure (m H2O)
27
2,543.43
0.03
2,586.92
43.5
30
2,543.17
0.03
2,586.65
43.5
33
2,543.54
0.03
2,586.83
43.3
39
2,543.42
0.04
2,586.99
43.6
40
2,543.41
0.04
2,587.03
43.6
42
2,542.93
0.04
2,586.77
43.8
45
2,543.35
0.05
2,586.82
43.5
46
2,543.34
0.05
2,586.82
43.5
51
2,543.74
0.05
2,586.89
43.2
53
2,543.03
0.06
2,586.65
43.6
54
2,543.00
(N/A)
(N/A)
(N/A)
56
2,543.15
0.06
2,586.65
43.5
57
2,543.11
0.06
2,586.65
43.5
59
2,543.20
0.06
2,586.82
43.6
60
2,543.30
0.06
2,586.83
43.5
62
2,543.12
0.06
2,586.65
43.5
63
2,543.23
0.07
2,586.65
43.4
65
2,543.45
0.07
2,586.65
43.2
66
2,543.17
0.07
2,586.65
43.5
68
2,543.40
0.07
2,586.83
43.4
70
2,543.10
0.07
2,586.67
43.6
71
2,543.12
0.07
2,586.66
43.5
73
2,543.35
0.08
2,586.65
43.3
75
2,543.01
0.08
2,586.67
43.7
78
2,543.20
0.08
2,586.79
43.6
80
2,542.97
0.08
2,586.70
43.7
82
2,543.15
0.09
2,586.79
43.6
84
2,543.13
0.09
2,586.65
43.5
86
2,543.34
0.09
2,586.81
43.5
87
2,543.44
0.09
2,586.81
43.4
89
2,542.92
1.34
2,586.67
43.8
91
2,543.33
0.09
2,586.80
43.5
96
2,543.52
0.1
2,586.82
43.3
99
2,543.41
0.1
2,586.82
43.4
100
2,543.26
0.1
2,586.81
43.6
102
2,543.00
0.11
2,586.65
43.6
103
2,542.98
0.11
2,586.65
43.7
105
2,543.20
0.11
2,586.66
43.5
108
2,543.11
0.11
2,586.81
43.7
110
2,543.30
0.11
2,586.87
43.6
111
2,543.27
0.12
2,586.87
43.6
113
2,543.15
0.12
2,586.87
43.7
115
2,543.45
0.12
2,586.84
43.4
121
2,543.22
0.13
2,586.89
43.7
123
2,543.50
0.13
2,586.87
43.4
130
2,543.11
0.14
2,586.65
43.5
136
2,543.11
0.14
2,586.87
43.8
137
2,543.09
0.14
2,586.87
43.8
139
2,543.30
0.14
2,586.87
43.6
145
2,543.10
0.15
2,586.65
43.5
152
2,543.10
0.16
2,586.67
43.6
161
2,543.21
0.17
2,586.87
43.7
163
2,543.16
0.17
2,586.88
43.7
174
2,543.41
(N/A)
(N/A)
(N/A)
183
2,543.41
0.19
2,587.03
43.6
187
2,543.15
0.19
2,586.79
43.6
191
2,543.30
0.2
2,586.80
43.5
195
2,543.34
0.2
2,586.81
43.5
199
2,543.41
0.21
2,586.82
43.4
204
2,543.52
0.21
2,586.82
43.3
217
2,543.16
0.23
2,586.65
43.5
334
0
0
2,587.06
2,587.00
337
0
9.37
2,586.83
2,586.80
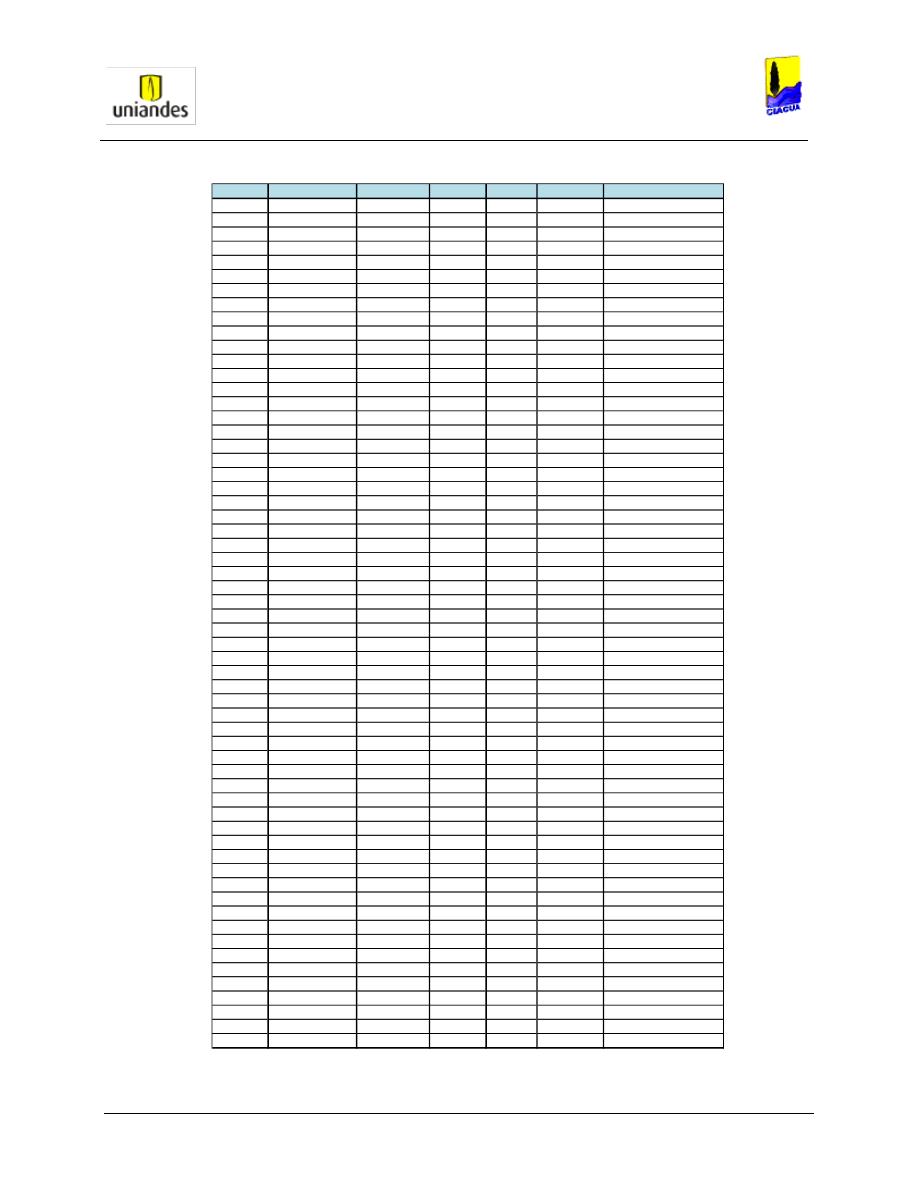
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
74
Juan Camilo Vergara Valderrama
3.4.1.8
Red de distribución los Olivos IV (tubos)
Tabla 37.
Resultados de modelación red Olivos IV para cada tubo de la red (Reporte 1).
ID
Length (Scaled) (m) Diameter (mm)
Material
Flow (L/s) Velocity (m/s) Headloss Gradient (m/km)
55
11.31
97.38
PVC
0.7
0.09
0.158
58
13.34
97.38
PVC
-1.77
0.24
0.826
61
14.5
97.38
PVC
-0.09
0.01
0
67
16.59
97.38
PVC
0.1
0.01
0.018
69
18.83
97.38
PVC
1.15
0.16
0.395
74
21.64
97.38
PVC
-0.52
0.07
0.096
76
23.57
97.38
PVC
-0.16
0.02
0.013
79
24.59
75.74
PVC
-1.14
0.25
1.271
81
24.91
97.38
PVC
1.68
0.23
0.753
83
25.02
97.38
PVC
0.03
0
0
85
25.11
97.38
PVC
0.56
0.08
0.107
88
29.03
97.38
PVC
-0.71
0.1
0.174
90
26.01
75.74
PVC
0.44
0.1
0.252
92
26.46
97.38
PVC
-2.05
0.28
1.069
95
26.32
97.38
PVC
-0.72
0.1
0.17
97
26.8
97.38
PVC
-3.24
0.44
2.377
98
27.03
75.74
PVC
0.3
0.07
0.11
101
28.16
97.38
PVC
0.1
0.01
0.011
104
28.41
97.38
PVC
-0.28
0.04
0.021
109
29.32
97.38
PVC
-0.04
0.01
0
114
29.43
97.38
PVC
-1.11
0.15
0.374
118
30.07
97.38
PVC
-0.04
0
0
120
30.64
97.38
PVC
-2.17
0.29
1.185
122
30.67
97.38
PVC
-1.86
0.25
0.902
125
30.78
97.38
PVC
-0.82
0.11
0.213
127
31.99
97.38
PVC
0.03
0
0
131
32.55
97.38
PVC
-0.62
0.08
0.137
135
34.01
97.38
PVC
0.3
0.04
0.026
143
36.25
97.38
PVC
0.19
0.03
0.016
171
15.69
97.38
PVC
-0.06
0.01
0
172
31.76
97.38
PVC
0.11
0.01
0.009
173
5.2
97.38
PVC
-0.22
0.03
0
176
30.08
97.38
PVC
0.99
0.13
0.307
177
32.49
97.38
PVC
1.16
0.16
0.394
178
31.31
97.38
PVC
0.56
0.07
0.114
180
23.15
97.38
PVC
0.1
0.01
0
181
3.49
97.38
PVC
0.36
0.05
0.085
182
27.19
97.38
PVC
-1.71
0.23
0.777
184
1.94
97.38
PVC
-0.19
0.03
0
185
5.37
97.38
PVC
0.55
0.07
0.111
188
0.74
97.38
PVC
-1.77
0.24
0.803
189
29.11
97.38
PVC
-0.94
0.13
0.276
192
1.49
97.38
PVC
-1.47
0.2
0.6
196
0.45
97.38
PVC
-1.75
0.23
0.669
197
28.96
97.38
PVC
-0.82
0.11
0.226
200
0.47
97.38
PVC
-1.22
0.16
0
205
3.02
97.38
PVC
1.82
0.24
0.886
207
2.4
97.38
PVC
-1.6
0.22
0.744
208
29.15
97.38
PVC
1.64
0.22
0.715
219
31.6
97.38
PVC
-0.6
0.08
0.122
221
3.3
97.38
PVC
(N/A)
(N/A)
(N/A)
222
10
97.38
PVC
(N/A)
(N/A)
(N/A)
224
7.72
97.38
PVC
(N/A)
(N/A)
(N/A)
225
3.48
97.38
PVC
(N/A)
(N/A)
(N/A)
227
15.48
97.38
PVC
0
0
0
228
2.46
97.38
PVC
0
0
0
230
2.2
97.38
PVC
-7.13
0.96
9.6
231
2.24
97.38
PVC
-7.13
0.96
9.548
233
2.42
97.38
PVC
3.84
0.52
3.204
234
33.5
97.38
PVC
3.84
0.52
3.207

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
75
Juan Camilo Vergara Valderrama
Tabla 38.
Resultados de modelación red Olivos IV para cada tubo de la red (Reporte 2).
ID
Length (Scaled) (m) Diameter (mm)
Material
Flow (L/s) Velocity (m/s) Headloss Gradient (m/km)
236
86.95
97.38
PVC
-1.04
0.14
0.329
237
4.16
97.38
PVC
-1.04
0.14
0.357
239
79.31
97.38
PVC
-0.34
0.05
0.038
240
3.06
97.38
PVC
-0.34
0.05
0
242
70.06
97.38
PVC
0.43
0.06
0.072
243
2.52
97.38
PVC
0.43
0.06
0
245
61.74
75.74
PVC
0.12
0.03
0.024
246
2.65
75.74
PVC
0.12
0.03
0
248
49.59
97.38
PVC
0.15
0.02
0.012
249
2.66
97.38
PVC
0.15
0.02
0
251
42.82
75.74
PVC
-0.07
0.01
0.014
252
2.35
75.74
PVC
-0.07
0.01
0
254
35.25
97.38
PVC
-0.18
0.02
0.008
255
2.41
97.38
PVC
-0.18
0.02
0
257
36.63
75.74
PVC
-0.09
0.02
0.016
258
2.06
75.74
PVC
-0.09
0.02
0
260
13.24
97.38
PVC
-0.22
0.03
0.022
261
2.47
97.38
PVC
-0.22
0.03
0
263
2.58
97.38
PVC
-0.49
0.07
0.115
264
18.09
97.38
PVC
-0.49
0.07
0.082
266
2.4
97.38
PVC
-0.45
0.06
0.124
267
29.89
97.38
PVC
-0.45
0.06
0.08
269
1.93
97.38
PVC
0
0
0
270
27.44
97.38
PVC
0
0
0
272
2.04
97.38
PVC
1.92
0.26
0.874
273
32.1
97.38
PVC
1.92
0.26
0.955
275
4.05
97.38
PVC
1.85
0.25
0.882
276
46.44
97.38
PVC
1.85
0.25
0.891
278
56.43
75.74
PVC
-0.63
0.14
0.464
279
3.32
75.74
PVC
-0.63
0.14
0.448
281
57.8
97.38
PVC
-1.13
0.15
0.386
282
2.98
97.38
PVC
-1.13
0.15
0.3
284
57.08
75.74
PVC
-0.57
0.13
0.381
285
2.79
75.74
PVC
-0.57
0.13
0.427
287
56.53
97.38
PVC
-1.02
0.14
0.316
288
3.36
97.38
PVC
-1.02
0.14
0.354
290
55.8
75.74
PVC
0.39
0.09
0.197
291
3.66
75.74
PVC
0.39
0.09
0.244
293
36.44
97.38
PVC
0.48
0.06
0.09
294
3.79
97.38
PVC
0.48
0.06
0.079
296
2.51
97.38
PVC
-0.37
0.05
0.119
297
38.31
97.38
PVC
-0.37
0.05
0.047
299
26.03
97.38
PVC
-0.79
0.11
0.206
300
3.29
97.38
PVC
-0.79
0.11
0.181
302
2.2
97.38
PVC
0.05
0.01
0
303
2.59
97.38
PVC
0.05
0.01
0
305
24.82
97.38
PVC
0
0
0
306
2.64
97.38
PVC
0
0
0
308
26.3
97.38
PVC
-3.28
0.44
2.422
309
3.24
97.38
PVC
-3.28
0.44
2.479
311
26.26
97.38
PVC
-1.1
0.15
0.363
312
2.22
97.38
PVC
-1.1
0.15
0.268
314
28.24
97.38
PVC
-1.28
0.17
0.474
315
2.76
97.38
PVC
-1.28
0.17
0.539
324
33.41
97.38
PVC
-1.14
0.15
0.383
326
27.03
97.38
PVC
0
0
0
327
2.12
97.38
PVC
0
0
0
335
94.28
203.2
PVC
-7.36
0.23
0.306
336
209.24
203.2
PVC
-16.73
0.52
1.3
338
14.67
97.38
PVC
9.37
1.26
15.659

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
76
Juan Camilo Vergara Valderrama
3.4.1.9
Red de distribución los Olivos IV (válvulas)
Tabla 39.
Resultados de modelación red Olivos IV para cada válvula de la red (Reporte 1).
ID
Elevation (m) Diameter (Valve) (mm) Headloss Coefficient Setting (Initial) Minor Loss Coefficient (Local) Flow (L/s) Hydraulic Grade (From) (m) Hydraulic Grade (To) (m) Headloss (m)
220
2,543.50
97.38
0
0.39
(N/A)
(N/A)
(N/A)
(N/A)
223
2,543.01
97.38
0
0.39
(N/A)
(N/A)
(N/A)
(N/A)
226
2,543.08
97.38
0
0.39
0
2,586.65
2,586.87
0
229
2,543.41
97.38
0
0.39
-7.13
2,587.01
2,587.01
0
232
2,543.41
97.38
0
0.39
3.84
2,586.98
2,586.98
0
235
2,543.45
97.38
0
0.39
-1.04
2,586.92
2,586.92
0
238
2,543.22
97.38
0
0.39
-0.34
2,586.89
2,586.89
0
241
2,543.29
97.38
0
0.39
0.43
2,586.87
2,586.87
0
244
2,543.27
75.74
0
0.39
0.12
2,586.87
2,586.87
0
247
2,543.14
97.38
0
0.39
0.15
2,586.87
2,586.87
0
250
2,543.16
75.74
0
0.39
-0.07
2,586.65
2,586.65
0
253
2,543.10
97.38
0
0.39
-0.18
2,586.65
2,586.65
0
256
2,543.17
75.74
0
0.39
-0.09
2,586.65
2,586.65
0
259
2,543.22
97.38
0
0.39
-0.22
2,586.65
2,586.65
0
262
2,543.20
97.38
0
0.39
-0.49
2,586.65
2,586.65
0
265
2,543.11
97.38
0
0.39
-0.45
2,586.65
2,586.65
0
268
2,543.15
97.38
0
0.39
0
2,586.87
2,586.65
0
271
2,543.30
97.38
0
0.39
1.92
2,586.86
2,586.86
0
274
2,543.50
97.38
0
0.39
1.85
2,586.87
2,586.87
0
277
2,543.44
75.74
0
0.39
-0.63
2,586.84
2,586.84
0
280
2,543.40
97.38
0
0.39
-1.13
2,586.83
2,586.83
0
283
2,543.20
75.74
0
0.39
-0.57
2,586.82
2,586.82
0
286
2,543.10
97.38
0
0.39
-1.02
2,586.81
2,586.81
0
289
2,543.18
75.74
0
0.39
0.39
2,586.66
2,586.66
0
292
2,543.14
97.38
0
0.39
0.48
2,586.65
2,586.65
0
295
2,543.35
97.38
0
0.39
-0.37
2,586.65
2,586.65
0
298
2,543.51
97.38
0
0.39
-0.79
2,586.82
2,586.82
0
301
2,543.35
97.38
0
0.39
0.05
2,586.82
2,586.82
0
304
2,543.15
97.38
0
0.39
0
2,586.67
2,586.79
0
307
2,542.93
97.38
0
0.39
-3.28
2,586.76
2,586.76
0
310
2,543.33
97.38
0
0.39
-1.1
2,586.81
2,586.81
0
313
2,543.42
97.38
0
0.39
-1.28
2,586.80
2,586.80
0
325
2,543.11
97.38
0
0.39
0
2,586.66
2,586.81
0
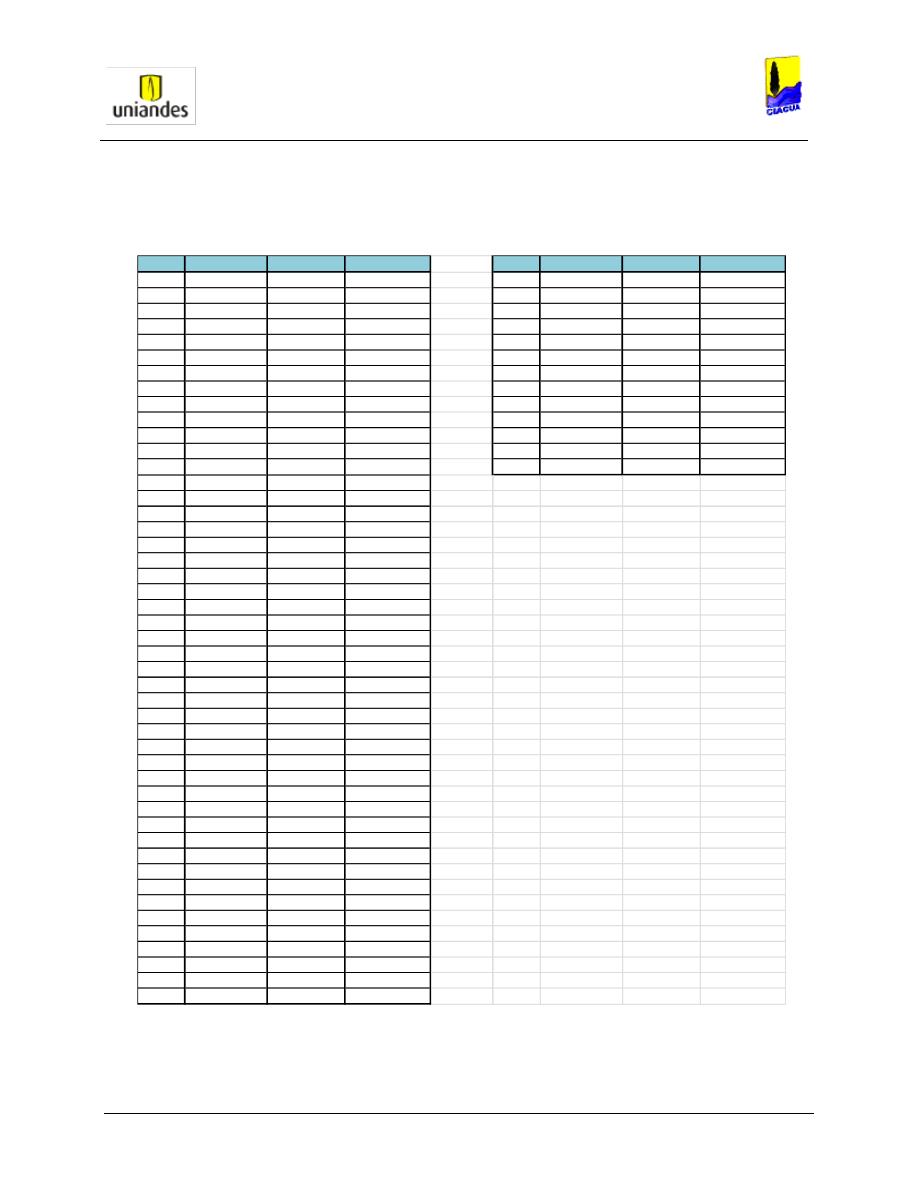
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
77
Juan Camilo Vergara Valderrama
3.4.2 Tablas de resultados de la modelación de redes de distribución de
agua potable mediante el software Redes
3.4.2.1
Red de distribución los Olivos IV (nodos)
Tabla 40.
Resultados de modelación red Olivos IV para cada nodo de la red (Reporte 1).
ID
Elevación (m)
Demanda (L/s) Presión (m.c.a)
ID
Elevación (m)
Demanda (L/s) Presión (m.c.a)
27
43.43
0.03
42.50029
145
43.1
0.15
42.97303
30
43.17
0.03
42.95407
152
43.1
0.16
43.01044
33
43.54
0.03
42.94465
161
43.21
0.17
43.12689
39
43.42
0.04
42.31356
163
43.16
0.17
43.13213
40
43.41
0.04
41.59259
183
43.41
0.19
41.59330
42
42.93
0.04
43.03270
187
43.15
0.19
43.03416
45
43.35
0.05
43.00924
191
43.3
0.2
43.04167
46
43.34
0.05
43.01568
195
43.34
0.2
43.04652
51
43.74
0.05
43.13701
199
43.41
0.21
43.04728
56
43.15
0.06
42.97333
204
43.52
0.21
42.95478
57
43.11
0.06
42.97472
217
43.16
0.23
43.00063
59
43.2
0.06
42.79163
334
0
0
40.83688
60
43.3
0.06
42.77577
337
0
9.37
32.98659
62
43.12
0.06
43.12388
63
43.23
0.07
43.12637
65
43.45
0.07
43.12836
66
43.17
0.07
42.97938
68
43.4
0.07
42.75055
70
43.1
0.07
43.00459
71
43.12
0.07
43.00400
73
43.35
0.08
42.98183
75
43.01
0.08
43.00862
78
43.2
0.08
43.03931
80
42.97
0.08
43.00601
82
43.15
0.09
43.03392
84
43.13
0.09
43.12073
86
43.34
0.09
43.04647
87
43.44
0.09
43.04315
89
42.92
1.34
42.99986
91
43.33
0.09
43.04142
96
43.52
0.1
42.96105
99
43.41
0.1
43.04725
100
43.26
0.1
43.03633
102
43
0.11
43.11663
103
42.98
0.11
43.11636
105
43.2
0.11
42.96562
108
43.11
0.11
42.89798
110
43.3
0.11
42.78279
111
43.27
0.12
42.84325
113
43.15
0.12
42.88778
115
43.45
0.12
42.68130
121
43.22
0.13
42.65972
123
43.5
0.13
42.57787
130
43.11
0.14
42.97150
136
43.11
0.14
43.12034
137
43.09
0.14
43.11636
139
43.3
0.14
42.77292

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
78
Juan Camilo Vergara Valderrama
3.4.2.2
Red de distribución los Olivos IV (tubos)
Tabla 41.
Resultados de modelación red Olivos IV para cada tubo de la red (Reporte 1).
ID
Longitud (m) Diametro (mm) Rugosidad (mm) Caudal (L/s) Velocidad (m/s) Fact. Friccion
55
11.31
97.38
0.0015
-0.6183
-0.083018
0.033917079
58
13.34
97.38
0.0015
2.2822
0.306425
0.024297428
61
14.5
97.38
0.0015
-0.7491
-0.100580
0.032191098
67
16.59
97.38
0.0015
2.6249
0.352438
0.023510701
69
18.83
97.38
0.0015
0.2978
0.039985
0.037646242
74
21.64
97.38
0.0015
-0.7868
-0.105642
0.031769255
76
23.57
97.38
0.0015
-0.4971
-0.066744
0.036045665
79
24.59
75.74
0.0015
0.2827
0.062746
0.039454744
81
24.91
97.38
0.0015
0.36
0.048336
0.03956171
83
25.02
97.38
0.0015
0.6267
0.084145
0.033791412
85
25.11
97.38
0.0015
0.6443
0.086508
0.033535571
88
29.03
97.38
0.0015
0.7279
0.097733
0.032441155
90
26.01
75.74
0.0015
0.2479
0.055022
0.039786112
92
26.46
97.38
0.0015
-0.8947
-0.120129
0.030703726
95
26.32
97.38
0.0015
2.9161
0.391537
0.022943461
97
26.8
97.38
0.0015
6.1884
0.830900
0.019418454
98
27.03
75.74
0.0015
0.6192
0.137433
0.031675988
101
28.16
97.38
0.0015
0.1815
0.024370
0.030867731
104
28.41
97.38
0.0015
0.9786
0.131394
0.029990801
109
29.32
97.38
0.0015
-3.1191
-0.418793
0.022591097
114
29.43
97.38
0.0015
3.3607
0.451232
0.022209711
118
30.07
97.38
0.0015
-2.5858
-0.347189
0.023593294
120
30.64
97.38
0.0015
5.2542
0.705468
0.020112915
122
30.67
97.38
0.0015
4.1175
0.552846
0.021218384
125
30.78
97.38
0.0015
0.8707
0.116907
0.030924828
127
31.99
97.38
0.0015
0.633
0.084991
0.033698693
131
32.55
97.38
0.0015
1.8629
0.250127
0.025509203
135
34.01
97.38
0.0015
0.6001
0.080574
0.03419772
143
36.25
97.38
0.0015
-0.8111
-0.108904
0.031512304
171
33.63
97.38
0.0015
-0.2977
-0.039971
0.03763412
172
31.76
97.38
0.0015
0.8199
0.110086
0.031421866
173
5.2
97.38
0.0015
1.0263
0.137799
0.029621942
176
30.08
97.38
0.0015
0.7265
0.097545
0.032458023
177
32.49
97.38
0.0015
0.7235
0.097142
0.032494323
178
31.31
97.38
0.0015
0.8418
0.113026
0.031202511
180
23.15
97.38
0.0015
1.7591
0.236190
0.025867387
181
3.49
97.38
0.0015
3.7283
0.500589
0.021694677
182
27.19
97.38
0.0015
4.6356
0.622410
0.020669923
184
1.94
97.38
0.0015
1.1579
0.155468
0.028716021
185
5.37
97.38
0.0015
-1.1124
-0.149359
0.029012876
188
0.74
97.38
0.0015
-1.0825
-0.145344
0.029216478
189
29.11
97.38
0.0015
-0.9321
-0.125151
0.03037501
192
1.49
97.38
0.0015
-0.7328
-0.098391
0.032382468
196
0.45
97.38
0.0015
-0.6171
-0.082856
0.033935226
197
28.96
97.38
0.0015
-0.2753
-0.036964
0.034697032
200
0.47
97.38
0.0015
-0.3923
-0.052673
0.038579099
205
3.02
97.38
0.0015
-4.1056
-0.551248
0.021232047
207
2.4
97.38
0.0015
3.5638
0.478502
0.021916379
208
29.15
97.38
0.0015
0.8822
0.118451
0.030817847
219
31.6
97.38
0.0015
-0.5684
-0.076318
0.03471609
230
4.44
97.38
0.0015
16.9952
2.281901
0.015842865
233
35.92
97.38
0.0015
-9.795
-1.315149
0.017652712
236
91.11
97.38
0.0015
0
0.000000
0
239
82.37
97.38
0.0015
0
0.000000
0
242
72.58
97.38
0.0015
0
0.000000
0
245
64.39
75.74
0.0015
0
0.000000
0
248
52.25
97.38
0.0015
0
0.000000
0
251
45.17
75.74
0.0015
0
0.000000
0
254
37.66
97.38
0.0015
0
0.000000
0
257
38.69
75.74
0.0015
0
0.000000
0
260
15.71
97.38
0.0015
0
0.000000
0
263
20.67
97.38
0.0015
-0.4533
-0.060863
0.037003447
266
32.29
97.38
0.0015
-0.5006
-0.067214
0.03597427
269
29.37
97.38
0.0015
-2.1937
-0.294542
0.024526821
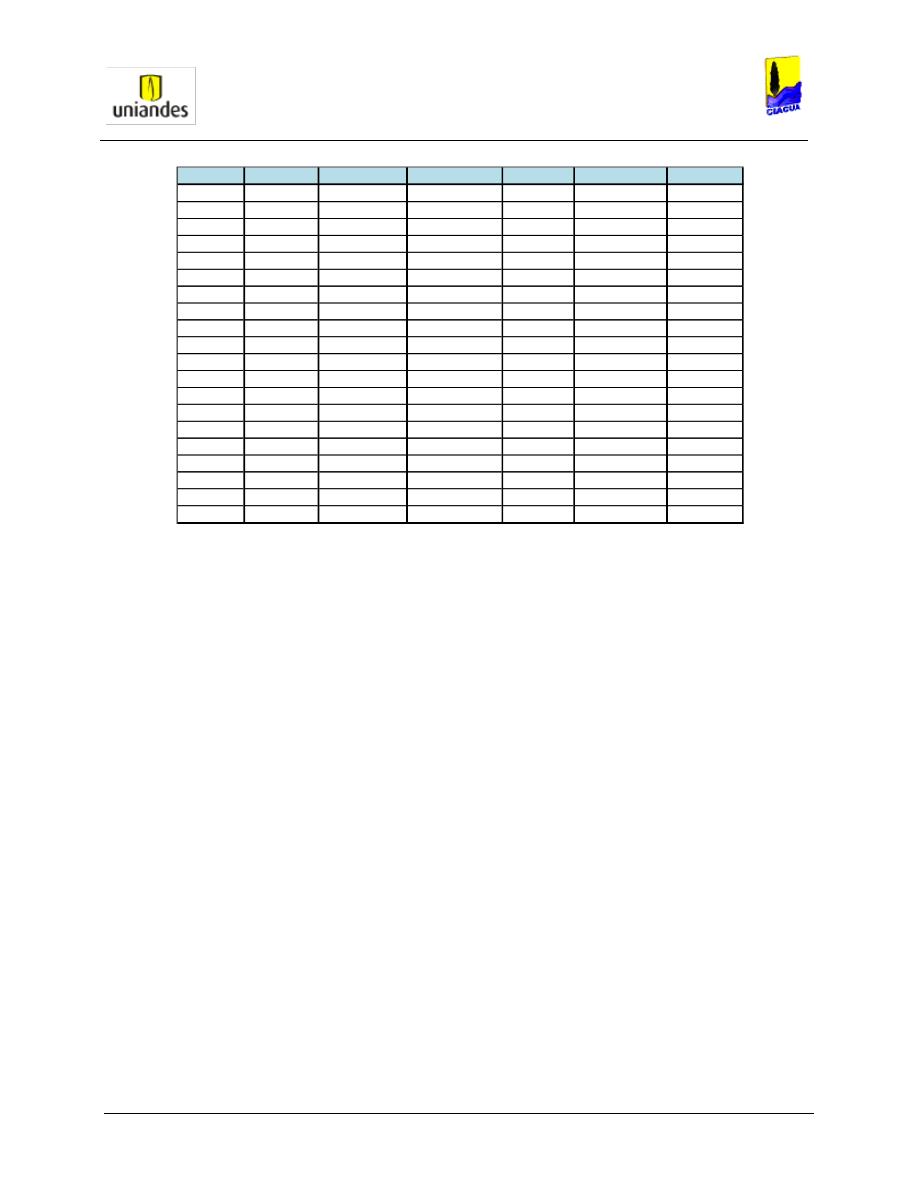
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
79
Juan Camilo Vergara Valderrama
Tabla 42.
Resultados de modelación red Olivos IV para cada tubo de la red (Reporte 2).
ID
Longitud (m) Diametro (mm) Rugosidad (mm) Caudal (L/s) Velocidad (m/s) Fact. Friccion
272
34.14
97.38
0.0015
-0.3214
-0.043154
0.039980021
275
50.49
97.38
0.0015
-4.8472
-0.650821
0.020468828
278
59.75
75.74
0.0015
0
0.000000
0
281
60.78
97.38
0.0015
0
0.000000
0
284
59.87
75.74
0.0015
0
0.000000
0
287
59.89
97.38
0.0015
0
0.000000
0
290
59.46
75.74
0.0015
0
0.000000
0
293
40.23
97.38
0.0015
0
0.000000
0
296
40.82
97.38
0.0015
-0.7377
-0.099049
0.032324323
299
29.32
97.38
0.0015
0
0.000000
0
302
4.79
97.38
0.0015
-0.5195
-0.069752
0.035600505
305
27.46
97.38
0.0015
-0.9732
-0.130669
0.030034116
308
29.54
97.38
0.0015
-0.8818
-0.118397
0.030821536
311
28.48
97.38
0.0015
-0.4246
-0.057010
0.037704876
314
31
97.38
0.0015
-0.3135
-0.042093
0.039337253
324
33.41
97.38
0.0015
1.7032
0.228684
0.026072373
326
29.15
97.38
0.0015
1.3527
0.181624
0.027605317
335
94.28
203.2
0.0015
19.4612
0.600112
0.017784392
336
209.24
203.2
0.0015
-2.0426
-0.062986
0.029975445
338
14.67
97.38
0.0015
15.1134
2.029237
0.01620284
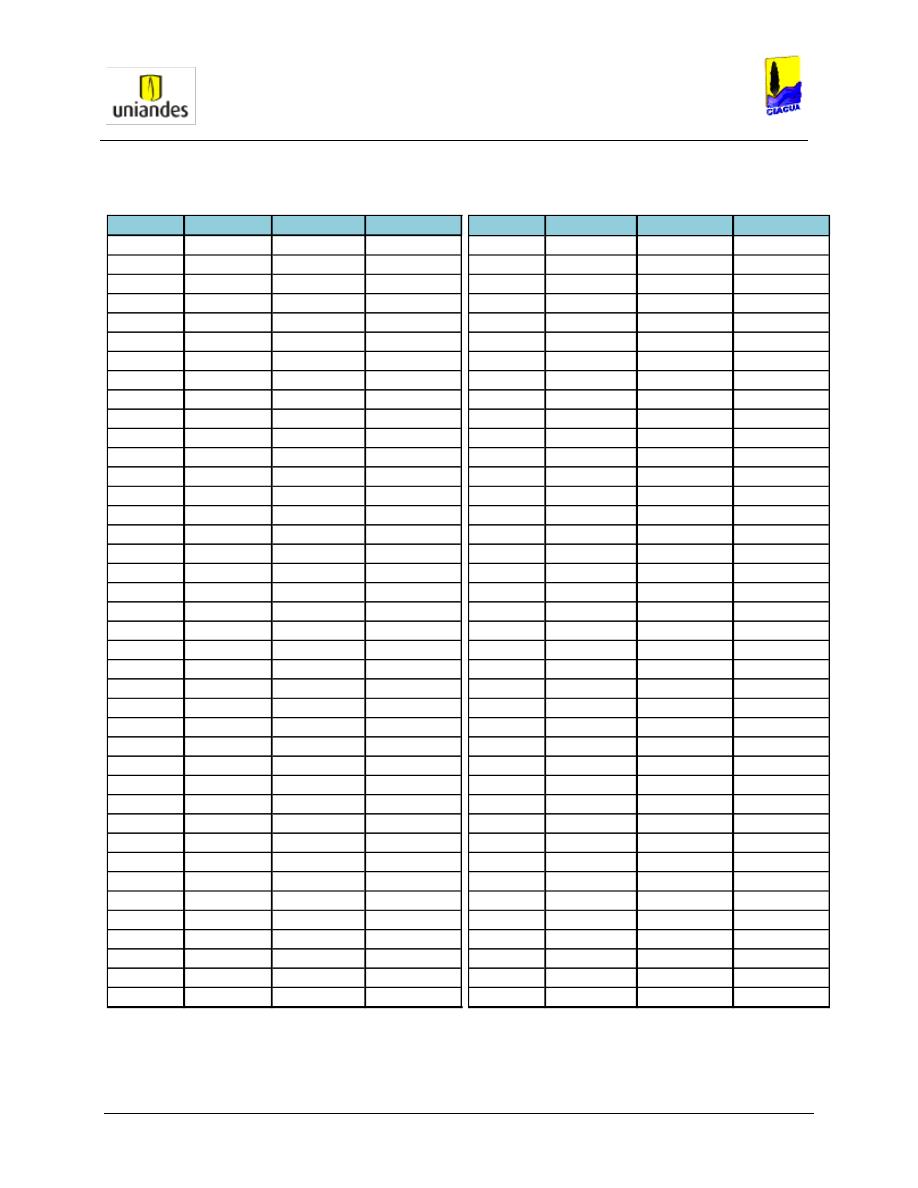
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
80
Juan Camilo Vergara Valderrama
3.4.2.3
Red de distribución los Olivos I (nodos)
Tabla 43.
Resultados de modelación red Olivos I para cada nodo de la red (Reporte 1).
ID
Elevación (m) Demanda (L/s) Presión (m.c.a)
27
4.291
0.13
2.899082661
29
4.27
0.13
2.883640289
31
4.103
1.29
3.147769928
33
3.55
5.36
2.823157549
35
3.686
0.15
4.516866207
39
3.495
0.15
4.285813332
41
3.383
0.15
4.280303478
43
3.142
0.16
4.041243553
45
3.078
0.16
4.037825108
47
2.932
0.16
3.89981389
49
2.898
0.16
3.869285107
51
3.075
0.17
3.7537148
53
2.787
0.17
3.733432531
56
3.788
0.17
3.655707121
58
3.769
0.17
3.638562202
60
3.386
0.18
3.573937893
62
3.371
0.18
3.569297552
64
3.019
0.18
3.500713825
66
3.008
0.18
3.37467885
68
2.88
0.19
3.346685886
70
2.887
0.19
3.292046309
72
3.083
0.19
3.208237171
76
3.083
0.2
3.172914028
78
3.117
0.2
3.148010492
80
3.116
0.2
3.11840415
82
3.014
0.2
3.090141535
84
3.001
0.21
3.058804989
86
2.994
0.21
2.944361687
88
2.969
0.21
2.944395304
90
2.963
0.21
2.935568571
92
2.876
0.22
2.925772905
94
2.872
0.22
2.916311026
96
2.801
0.22
2.912842989
98
2.799
0.22
2.874477625
101
2.79
0.27
3.962832928
103
3.05
0.27
3.960659981
105
3.1
0.27
4.314968109
119
4.55
0.28
3.883246422
121
4.2
0.28
3.7953794
123
4.19
0.28
3.705744028
ID
Elevación (m) Demanda (L/s) Presión (m.c.a)
125
4
0.29
3.613645554
127
4
0.29
3.589408636
129
3.93
0.29
3.522310734
131
3.9
0.29
3.372741938
133
3.77
0.3
3.345363617
135
3.75
0.3
3.330589056
137
3.69
0.3
3.272054911
139
3.68
0.3
3.174720287
141
3.61
0.31
3.103928328
143
3.63
0.31
3.050940275
145
3.83
0.31
3.00715661
147
3.32
0.31
3.002087593
150
3.45
0.32
2.95883131
152
3.4
0.32
2.939435244
154
3.25
0.32
2.937652826
156
3.3
0.32
2.928424597
158
3.34
0.33
2.922077179
160
3.29
0.33
2.914190531
162
3.17
0.33
2.913552046
164
3.07
0.33
2.914134502
166
2.75
0.34
2.914199591
168
2.76
0.34
2.931804657
170
3
0.03
3.603778601
172
3.01
0.34
2.938981295
174
2.99
0.34
2.939048767
176
3
0.35
2.939547062
178
3
0.35
2.940804005
213
4.04
0.35
2.945914268
215
4.04
0.35
2.947831392
217
4.05
0.36
2.949669361
221
3.84
0.36
2.97440815
223
3.55
0.36
2.932257414
225
3.66
0.04
3.592167377
227
3.56
0.36
2.931665897
229
3.54
0.37
2.939019203
231
3.46
0.37
3.162944555
233
3.28
0.37
3.160177946
235
3.41
0.38
3.096577406
237
3.43
0.38
3.084498167
239
3.28
0.38
3.041730165
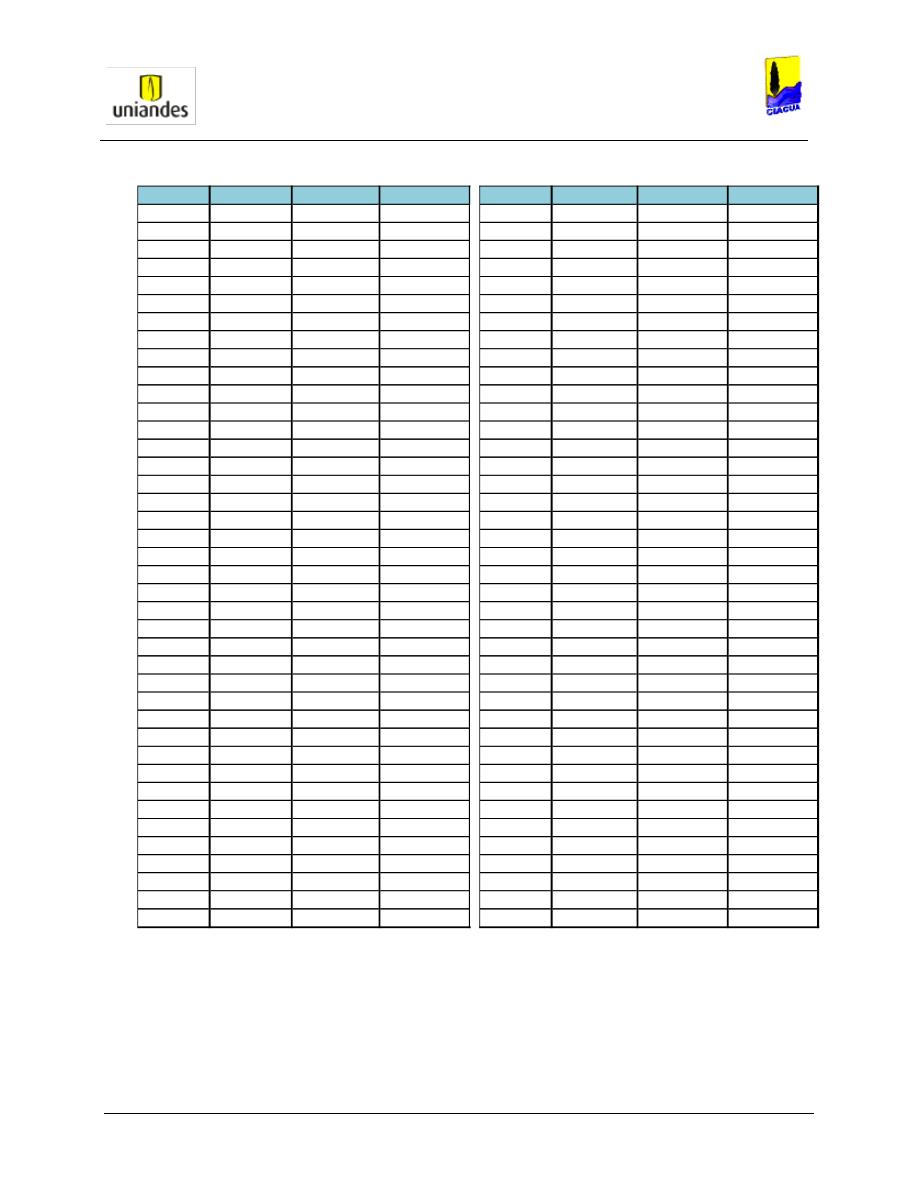
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
81
Juan Camilo Vergara Valderrama
Tabla 44.
Resultados de modelación red Olivos I para cada nodo de la red (Reporte 2).
ID
Elevación (m) Demanda (L/s) Presión (m.c.a)
241
3.29
0.38
3.03467536
243
3.15
0.04
3.456036091
245
3.16
0.39
2.939099312
247
3
0.39
2.938981295
249
3
0.41
3.058153629
251
3.26
0.04
3.355250835
253
2.94
0.04
3.276850939
255
2.97
0.44
3.199486732
257
2.82
0.45
3.191979885
259
2.92
0.45
3.575454712
261
2.81
0.46
3.575239182
263
2.85
0.46
3.962813377
265
2.8
0.46
3.592556715
267
2.82
0.46
3.056520462
269
3.07
0.47
3.326585293
271
2.69
0.47
2.937870502
273
2.68
0.05
3.203162432
275
2.67
0.05
3.143635511
277
2.72
0.05
3.103730679
279
2.69
0.06
3.071648598
281
2.69
0.06
2.983244658
283
2.68
0.06
2.965553045
285
3.16
0.06
2.962464571
288
3.16
0.07
2.901105165
290
3.19
0.07
3.378750324
293
2.69
0.07
3.374775887
296
3.45
0.08
3.300421
298
3.48
0.76
3.63405323
300
3.19
0.76
3.393870592
302
3.17
0.76
3.416252613
304
3.06
0.76
3.657068253
306
3.14
0.77
3.753371
310
2.69
0.77
3.900579453
314
2.69
0.77
4.597552776
323
3.02
0.77
3.973373413
351
2.98
0.78
3.345263958
356
2.98
0.08
3.297335863
359
3.65
0.78
3.005882502
363
3.67
0.08
3.213988781
365
4.04
0.82
3.637531757
ID
Elevación (m) Demanda (L/s) Presión (m.c.a)
243
3.15
0.04
3.456036091
245
3.16
0.39
2.939099312
247
3
0.39
2.938981295
249
3
0.41
3.058153629
251
3.26
0.04
3.355250835
253
2.94
0.04
3.276850939
255
2.97
0.44
3.199486732
257
2.82
0.45
3.191979885
259
2.92
0.45
3.575454712
261
2.81
0.46
3.575239182
263
2.85
0.46
3.962813377
265
2.8
0.46
3.592556715
267
2.82
0.46
3.056520462
269
3.07
0.47
3.326585293
271
2.69
0.47
2.937870502
273
2.68
0.05
3.203162432
275
2.67
0.05
3.143635511
277
2.72
0.05
3.103730679
279
2.69
0.06
3.071648598
281
2.69
0.06
2.983244658
283
2.68
0.06
2.965553045
285
3.16
0.06
2.962464571
288
3.16
0.07
2.901105165
290
3.19
0.07
3.378750324
293
2.69
0.07
3.374775887
296
3.45
0.08
3.300421
298
3.48
0.76
3.63405323
300
3.19
0.76
3.393870592
302
3.17
0.76
3.416252613
304
3.06
0.76
3.657068253
306
3.14
0.77
3.753371
310
2.69
0.77
3.900579453
314
2.69
0.77
4.597552776
323
3.02
0.77
3.973373413
351
2.98
0.78
3.345263958
356
2.98
0.08
3.297335863
359
3.65
0.78
3.005882502
363
3.67
0.08
3.213988781
365
4.04
0.82
3.637531757
368
4.27
0.82
8.037242889

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
82
Juan Camilo Vergara Valderrama
Tabla 45.
Resultados de modelación red Olivos I para cada nodo de la red (Reporte 3).
ID
Elevación (m) Demanda (L/s) Presión (m.c.a)
370
2.99
0.83
5.667331219
372
3.3
0.83
4.772284985
374
2.71
0.08
3.208901882
604
4.42
0.83
4.719043255
605
3.86
0.83
4.659923553
608
3.95
0.83
4.667431355
609
3.74
0.83
4.521884918
610
3.8
0.83
3.414788008
611
3.95
0.84
3.637677908
616
4.29
0.84
4.741034985
617
4.03
0.84
4.955907345
619
3.76
0.84
5.049920082
624
3.03
0.84
5.041266918
653
4.52
0.84
4.934097767
656
6.4
0.84
5.086681366
657
6.38
0.85
5.652588367
658
5.83
0.85
5.999148369
660
5.3
0.85
7.678449154
661
5.37
0.85
7.517098427
662
5.48
0.85
5.737196922
663
4.56
0.85
5.726681709
664
4
0.09
3.151120663
666
4.32
0.85
5.707221985
667
5.7
0.86
5.408730984
668
6.01
0.86
5.394342422
669
6.09
0.86
5.375868797
670
5.84
0.86
5.115609646
671
5.76
0.86
5.121063232
672
6.05
0.86
4.549880981
673
6.33
0.86
5.123127937
674
6.42
0.86
5.368219376
675
6.69
0.87
5.421534538
676
6.76
0.87
5.418813705
677
6.98
0.87
3.645850897
678
7.1
0.87
3.711127281
680
6.34
0.87
3.624613285
681
6.37
0.87
5.88829565
682
6.12
0.87
5.722289562
683
6.08
0.88
5.45624876
684
6.04
0.88
5.48760891
ID
Elevación (m) Demanda (L/s) Presión (m.c.a)
685
6.03
0.88
5.041180611
686
6.01
0.09
3.148679972
687
5.97
0.88
5.436768532
688
6.08
0.88
5.417468071
689
6.31
0.88
5.374700069
690
6.45
0.88
5.124121189
692
4.52
0.89
4.357926369
693
4.98
0.89
4.328316689
694
4.26
0.89
4.097063065
695
6.79
0.89
4.219011307
696
7.1
0.89
5.632154465
697
6.33
0.9
4.661126137
698
6.31
0.9
4.549778461
699
6.08
0.9
3.637666702
701
6.35
0.09
3.118103504
702
6.38
0.91
5.454322338
703
6.08
0.92
5.39433527
704
6.03
0.92
3.759482622
705
5.95
0.92
4.106857777
706
5.72
0.92
4.130945683
707
5.34
0.92
4.328491211
709
5.24
0.93
4.284655094
711
6.53
0.93
4.328442574
713
5.41
0.93
4.106761932
716
6.01
0.93
4.130940437
717
4.52
0.93
3.759274483
728
7.1
0.93
5.413537025
729
6.11
0.93
4.283051968
730
5.08
0.93
4.237792969
732
5.36
0.94
4.026374817
733
5.6
0.94
3.763719082
734
5.68
0.94
3.703780651
737
4.21
0.94
5.911432266
738
5.76
0.94
5.534812927
739
5.35
0.94
5.498295307
740
5.59
0.94
5.444543362
741
5.05
0.94
5.436757565
742
6.37
0.95
5.37514782
743
5.33
0.1
3.116710186
744
5.25
0.1
3.092216492
745
5.1
0.1
3.090964079
746
4.96
0.1
3.065969229
747
4.59
0.11
3.062169552
748
6.47
0.11
3.058037996
749
6.55
0.11
3.045959711
750
6.67
0.11
3.015125751
751
6.7
1.13
3.464118481
752
6.36
0.12
2.984913349
759
6.08
0.12
2.982274055
903
4.01
0.12
2.931063652
967
4.34
1.21
3.65633893
1030
3.34
0.12
2.928542852

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
83
Juan Camilo Vergara Valderrama
3.4.2.4
Red de distribución los Olivos I (nodos)
Tabla 46.
Resultados de modelación red Olivos I para cada tubo de la red (Reporte 1).
ID
Longitud (m) Diametro (mm) Rugosidad (mm) Caudal (L/s) Velocidad (m/s) Fact. Friccion
30
3.69814
97.38
0.0015
3.9549
0.531014139
0.021409765
32
27.5755
97.38
0.0015
5.1013
0.684938286
0.020242199
34
32.37
97.38
0.0015
3.9363
0.528516765
0.021432324
36
30.8376
97.38
0.0015
3.511
0.47141284
0.021990452
42
31.7297
97.38
0.0015
2.9567
0.396988421
0.022870409
44
31.3608
97.38
0.0015
2.3723
0.318522552
0.024075878
46
28.8816
97.38
0.0015
2.1959
0.294837783
0.024520968
50
31.0638
97.38
0.0015
1.4995
0.201333966
0.026904376
52
28.7122
97.38
0.0015
0.5714
0.076720392
0.034665318
57
10.4286
143.34
0.0015
7.2425
0.448811341
0.02038298
59
1.6157
143.34
0.0015
9.7416
0.603678365
0.019121386
61
31.3317
143.34
0.0015
9.5477
0.591662553
0.019203232
63
1.35035
143.34
0.0015
9.3471
0.579231547
0.019290242
65
30.3249
143.34
0.0015
10.365
0.642309913
0.018872123
67
1.74545
143.34
0.0015
10.7102
0.663701653
0.018742424
71
1.3174
143.34
0.0015
8.3109
0.515019147
0.019782478
77
1.71617
143.34
0.0015
5.2239
0.323720478
0.021921211
79
30.3963
143.34
0.0015
5.2022
0.322375748
0.021941896
81
1.37197
143.34
0.0015
5.5816
0.345886832
0.021595903
83
27.5045
143.34
0.0015
5.5674
0.34500687
0.021608283
85
4.31594
143.34
0.0015
5.4687
0.338890518
0.021695511
87
5.67516
143.34
0.0015
4.9121
0.304398507
0.022229973
89
25.7297
143.34
0.0015
3.8312
0.237416087
0.023543822
93
28.7162
97.38
0.0015
2.1291
0.285868721
0.024702291
95
1.30018
97.38
0.0015
3.0915
0.415087666
0.022637176
97
29.3079
97.38
0.0015
2.84
0.381319415
0.02308413
99
1.33492
97.38
0.0015
2.9676
0.398451935
0.022851025
100
27.2608
97.38
0.0015
2.076
0.278739122
0.02485199
102
1.43405
97.38
0.0015
2.515
0.33768251
0.023747204
104
26.5472
97.38
0.0015
1.5178
0.203791059
0.026823495
106
77.4988
97.38
0.0015
1.7956
0.241090543
0.025738245
122
25.5762
97.38
0.0015
7.1555
0.960750379
0.018832071
124
1.0111
97.38
0.0015
5.3921
0.723983246
0.020000516
126
35.5904
97.38
0.0015
6.0627
0.814022964
0.019503544
128
1.05818
97.38
0.0015
4.0191
0.539634106
0.021332971
132
5.10332
97.38
0.0015
5.6817
0.762867085
0.019776394
134
27.2016
97.38
0.0015
4.6889
0.62956641
0.020618138
136
5.3751
97.38
0.0015
4.3862
0.588923669
0.020923184

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
84
Juan Camilo Vergara Valderrama
ID
Longitud (m)Diametro (mm)
Rugosidad (mm)Caudal (L/s)Velocidad (m/s)
Fact. Friccion
138
26.4402
97.38
0.0015
3.8108
0.51166621 0.02158834
140
5.10492
97.38
0.0015
4.1079
0.55155705
0.0212294
144
3.46435
143.34
0.0015
6.9269
0.42925389
0.0205832
148
92.1627
97.38
0.0015
2.4714
0.33182845 0.02384491
153
41.6161
97.38
0.0015
2.4149
0.32424234 0.02397503
155
44.4082
97.38
0.0015
2.9667
0.39833109 0.02285262
157
16.373
97.38
0.0015
3.2
0.42965568 0.02245911
161
31.8621
97.38
0.0015
1.9836
0.26633281 0.02512522
163
31.7404
97.38
0.0015
1.936
0.25994169 0.02527278
165
30.7451
97.38
0.0015
2.0909
0.28073971 0.02480947
169
1.30719
143.34
0.0015
-0.7172
-0.04444425 0.03624485
173
30.7092
97.38
0.0015
1.0745
0.14427032 0.02927241
175
26.5787
97.38
0.0015
1.1447
0.15369589 0.02880047
177
4.1001
97.38
0.0015
1.88
0.25242271 0.02545278
179
30.2714
97.38
0.0015
2.3669
0.31779751 0.02408884
180
26.0722
97.38
0.0015
3.0382
0.40793121 0.02272774
181
77.8141
75.74
0.0015
0.537
0.11918835 0.03291494
182
78.238
75.74
0.0015
-0.4117
-0.09137773 0.03541897
183
78.6905
75.74
0.0015
-1.4125
-0.31350753 0.02567721
184
79.0621
75.74
0.0015
-1.4109
-0.3131524 0.02568428
194
65.9647
75.74
0.0015
-1.2041
-0.26725268 0.0267014
199
12.8961
75.74
0.0015
0.2819
0.06256833 0.03948762
201
3.76679
75.74
0.0015
-0.2602
-0.05775197 0.04063256
203
3.96739
75.74
0.0015
0.4023
0.08929138 0.03564945
214
16.2873
143.34
0.0015
4.5957
0.28479148 0.02257124
216
3.59515
143.34
0.0015
4.4214
0.27399026 0.02277294
219
30.6697
75.74
0.0015
1.1211
0.24883065 0.02717901
220
11.5514
75.74
0.0015
-6.366
-1.41294791 0.01833562
224
33.5705
143.34
0.0015
10.0856
0.62499574 0.01898133
226
32.8771
143.34
0.0015
10.3184
0.63942215 0.01889007
228
33.5462
143.34
0.0015
10.3586
0.64191331 0.01887458
230
8.2224
143.34
0.0015
10.7785
0.66793414 0.01871741
232
24.8348
143.34
0.0015
10.2662
0.63618736 0.01891029
236
6.31319
143.34
0.0015
13.3694
0.82848993 0.01789859
238
3.49158
143.34
0.0015
13.1877
0.81723014 0.01794899
240
15.0764
143.34
0.0015
12.5699
0.77894562 0.01812739
242
33.9572
143.34
0.0015
10.6113
0.65757291 0.01877902
244
32.3481
143.34
0.0015
9.1243
0.56542483 0.01938981
Tabla 47.
Resultados de modelación red Olivos I para cada tubo de la red (Reporte 2).
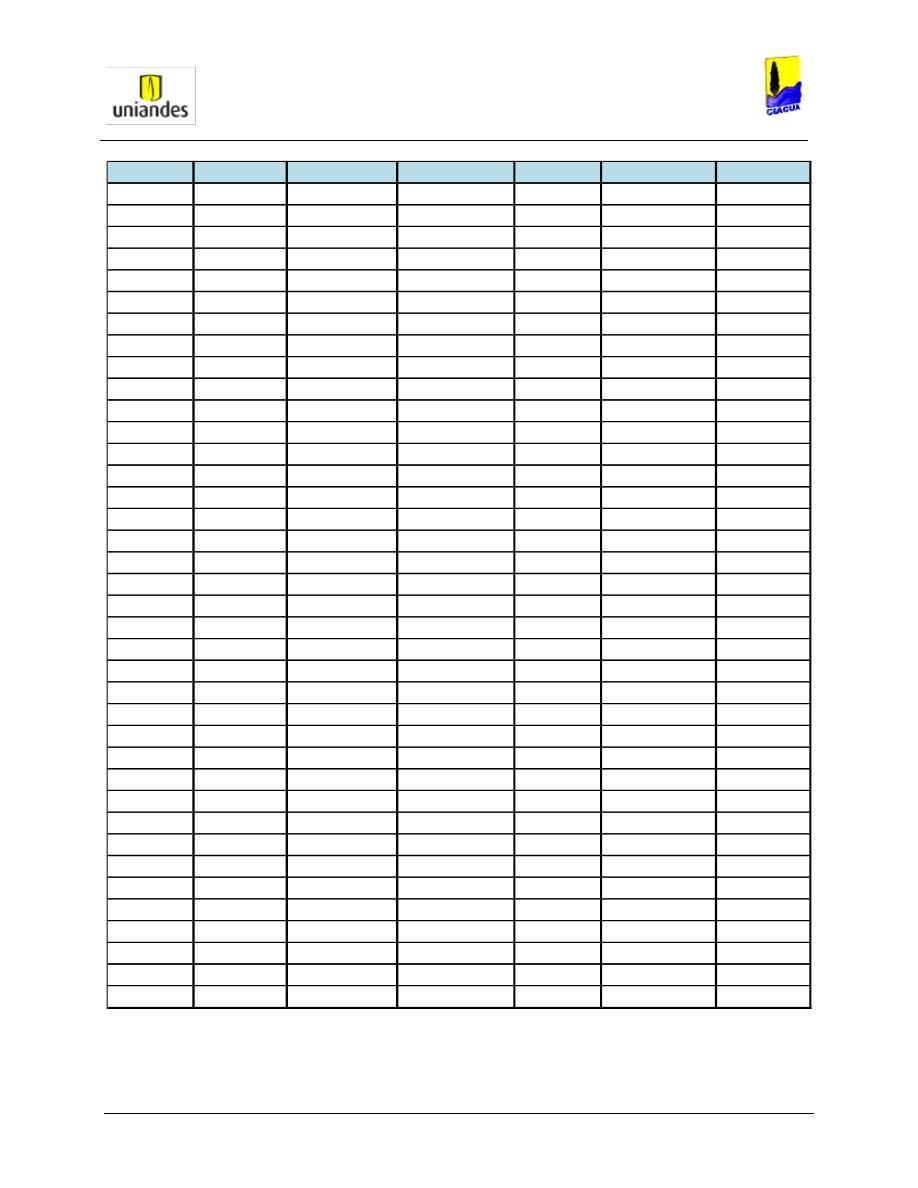
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
85
Juan Camilo Vergara Valderrama
ID
Longitud (m) Diametro (mm) Rugosidad (mm) Caudal (L/s) Velocidad (m/s) Fact. Friccion
246
31.9064
143.34
0.0015
7.8164
0.484375418
0.020046906
248
31.2078
143.34
0.0015
7.1099
0.440594236
0.020465668
250
4.75673
143.34
0.0015
6.0906
0.377429113
0.021177973
254
27.7827
75.74
0.0015
0.8498
0.188615007
0.029154266
256
1.49391
75.74
0.0015
1.1564
0.256665561
0.026970181
260
8.52598
75.74
0.0015
0.8819
0.195739674
0.02887852
262
27.5893
75.74
0.0015
0.5063
0.112374415
0.03344724
264
2.44349
75.74
0.0015
0.4804
0.106625852
0.033932565
266
39.8294
75.74
0.0015
-0.1017
-0.022572542
0.042712978
268
6.02338
75.74
0.0015
-0.0752
-0.016690808
0.057764758
276
6.4287
143.34
0.0015
-1.3652
-0.084600241
0.030406866
278
28.4355
143.34
0.0015
-0.9851
-0.061045779
0.033182516
280
24.1713
143.34
0.0015
-2.4319
-0.150702699
0.0262572
282
3.42208
143.34
0.0015
-4.2351
-0.262445414
0.02300064
284
5.4107
143.34
0.0015
-3.1876
-0.197532762
0.024590299
286
38.4314
143.34
0.0015
-4.5818
-0.283930107
0.022586944
289
41.9026
75.74
0.0015
-0.0751
-0.016668613
0.057841675
292
6.13861
97.38
0.0015
-0.5356
-0.071913619
0.035296856
295
28.8922
143.34
0.0015
-2.2523
-0.139573046
0.02675962
299
5.95912
97.38
0.0015
1.3336
0.179059004
0.02770428
301
28.2666
97.38
0.0015
3.2769
0.439980842
0.022337729
303
2.80015
97.38
0.0015
4.7291
0.63496396
0.020579594
307
17.3938
97.38
0.0015
1.234
0.165685971
0.0282542
311
1.36693
143.34
0.0015
-1.4535
-0.090072114
0.029912366
316
1.02058
143.34
0.0015
0.8897
0.055133925
0.034123473
317
25.9325
143.34
0.0015
0.0008
4.96E-05
10.27620863
325
10.0906
97.38
0.0015
2.728
0.366281466
0.023300612
352
3.67665
143.34
0.0015
9.9631
0.617404524
0.019030474
353
27.0676
143.34
0.0015
8.1442
0.504688895
0.019869244
361
3.408
143.34
0.0015
3.717
0.230339213
0.023711499
380
7.54308
97.38
0.0015
4.5412
0.609735116
0.020763609
383
33.34188
97.38
0.0015
3.2439
0.435550018
0.022389348
386
94.90367
97.38
0.0015
1.9864
0.266708763
0.025116688
389
87.31709
97.38
0.0015
1.9294
0.259055521
0.025293624
392
87.04693
75.74
0.0015
0.8266
0.183465715
0.029362946
395
87.01105
75.74
0.0015
0.8668
0.192388195
0.029006796
399
86.97786
75.74
0.0015
0.7774
0.172545665
0.029833363
402
87.04831
97.38
0.0015
1.0237
0.137449537
0.029641436
Tabla 48.
Resultados de modelación red Olivos I para cada tubo de la red (Reporte 3).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
86
Juan Camilo Vergara Valderrama
ID
Longitud (m)Diametro (mm)
Rugosidad (mm)Caudal (L/s)Velocidad (m/s)
Fact. Friccion
405
87.11494
75.74
0.0015
0.322
0.07146862 0.03798592
408
87.17934
75.74
0.0015
0.2292
0.05087145 0.03726647
411
30.25135
75.74
0.0015
1.0565
0.23449253 0.02758488
414
87.68539
97.38
0.0015
0.2006
0.02693404 0.02913158
417
88.05588
75.74
0.0015
0.6082
0.13499135 0.03182807
420
88.42999
75.74
0.0015
0.8468
0.18794915 0.02918081
423
78.94124
97.38
0.0015
2.3872
0.32052314 0.02404033
426
30.44827
143.34
0.0015
5.8901
0.3650043
0.02133686
429
113.592
143.34
0.0015
0.4084
0.02530819 0.03498529
433
38.2654
97.38
0.0015
4.4908
0.60296804 0.02081469
435
26.42056
97.38
0.0015
5.2657
0.70701185 0.02010339
438
29.95479
97.38
0.0015
3.2
0.42965568 0.02245911
441
30.40218
97.38
0.0015
3.2817
0.44062533 0.02233028
444
27.38138
75.74
0.0015
-4.4601
-0.98992915 0.01975573
447
37.03125
143.34
0.0015
8.8932
0.55110376 0.01949653
450
68.8252
75.74
0.0015
-1.6804
-0.37296853 0.02462688
453
78.68671
75.74
0.0015
-1.0081
-0.22375005 0.02791248
456
88.37565
75.74
0.0015
-0.5341
-0.11854469 0.03296339
459
98.18635
97.38
0.0015
-0.9415
-0.12641276 0.03029524
465
105.84574
143.34
0.0015
-3.7115
-0.22999838 0.02371975
468
34.17344
143.34
0.0015
13.4381
0.83274721 0.01787977
471
20.74627
97.38
0.0015
0.5259
0.07061123 0.03547824
474
13.91904
97.38
0.0015
0.136
0.01826037 0.04106637
477
150.29844
97.38
0.0015
1.7477
0.23465913 0.02590847
480
132.985
97.38
0.0015
1.5266
0.20497261 0.02678507
483
116.35047
97.38
0.0015
1.2125
0.16279922 0.02838014
486
100.12696
97.38
0.0015
0.7268
0.09758555
0.0324544
489
35.40696
143.34
0.0015
-5.1138
-0.31689768 0.02202737
492
106.54186
75.74
0.0015
0.621
0.13783234 0.03165146
495
90.67431
75.74
0.0015
0.6028
0.13379281 0.03190414
498
72.20057
75.74
0.0015
0.5149
0.1142832
0.03329368
501
64.50057
75.74
0.0015
0.6269
0.13914185 0.03157174
504
50.62797
75.74
0.0015
0.6943
0.15410143 0.03072897
507
25.29011
143.34
0.0015
0.1781
0.0110367
0.04615928
510
58.78862
97.38
0.0015
-0.6152
-0.0826013 0.03396406
513
80.69859
97.38
0.0015
-0.4935
-0.06626096 0.03611984
516
29.74228
97.38
0.0015
1.0306
0.13837598 0.02958985
519
31.37065
75.74
0.0015
2.1859
0.48516538 0.02315257
Tabla 49.
Resultados de modelación red Olivos I para cada tubo de la red (Reporte 4).
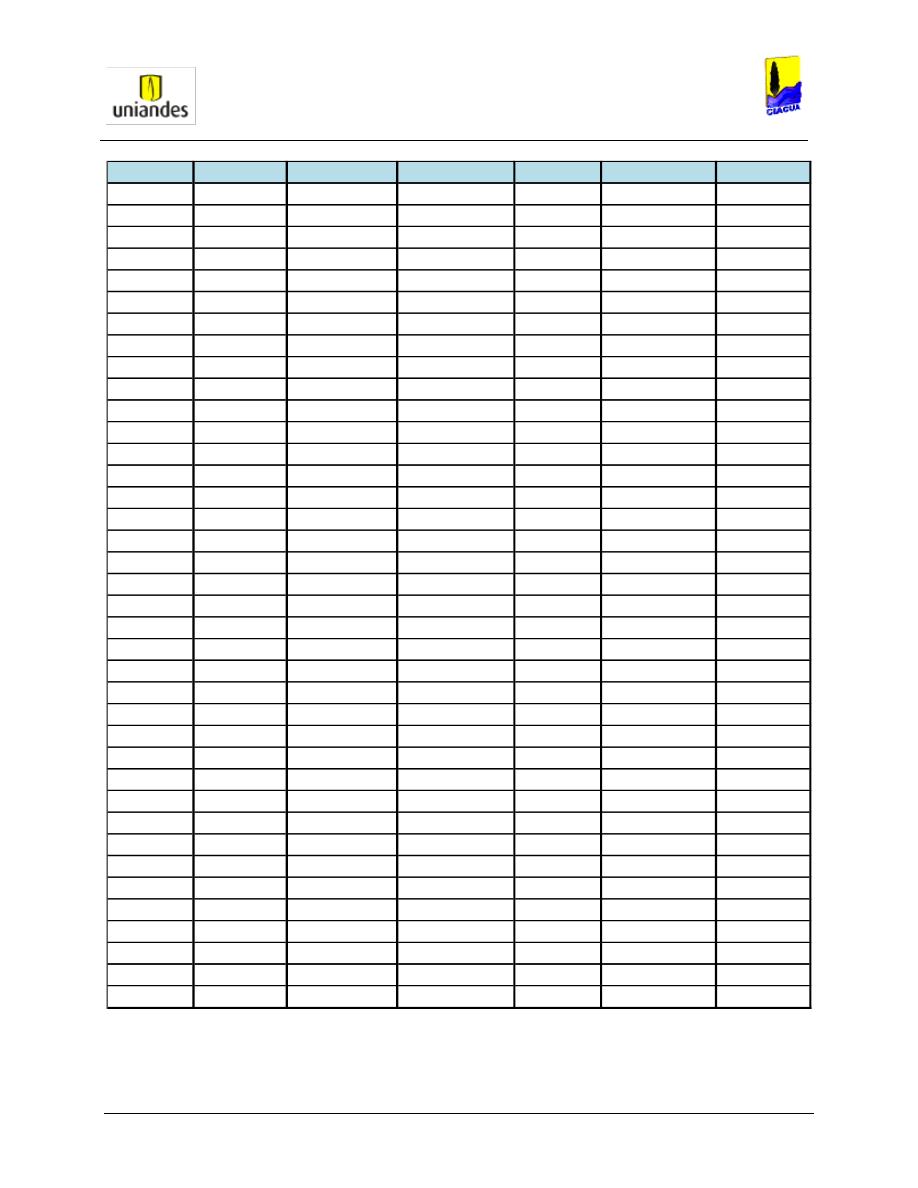
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
87
Juan Camilo Vergara Valderrama
ID
Longitud (m) Diametro (mm) Rugosidad (mm) Caudal (L/s) Velocidad (m/s) Fact. Friccion
522
78.99765
75.74
0.0015
0.1992
0.044212885
0.032188457
525
79.02273
75.74
0.0015
0.0724
0.016069342
0.059998754
528
79.06285
97.38
0.0015
-0.2619
-0.035164632
0.032913519
532
3.44742
97.38
0.0015
-0.4431
-0.059493885
0.037245377
534
22.55128
97.38
0.0015
2.1886
0.293857631
0.024540419
537
105.21142
97.38
0.0015
-0.12
-0.016112088
0.046541891
540
27.04662
97.38
0.0015
1.1679
0.156810896
0.028652917
543
135.12466
97.38
0.0015
-0.4132
-0.05547929
0.03800236
546
163.15803
97.38
0.0015
-0.7518
-0.100942231
0.032159956
549
47.36068
97.38
0.0015
1.5317
0.205657376
0.026762942
555
127.70498
97.38
0.0015
-0.0989
-0.013279046
0.056471455
558
102.69066
97.38
0.0015
2.5207
0.338447834
0.023734599
561
74.83986
75.74
0.0015
1.2493
0.277284924
0.026459737
564
30.33184
75.74
0.0015
1.9053
0.422885588
0.023906024
567
9.54113
75.74
0.0015
0.9474
0.210277545
0.028354985
570
31.86142
97.38
0.0015
1.0162
0.136442532
0.029698051
573
33.42869
75.74
0.0015
-0.7221
-0.160271707
0.0304136
576
32.02915
75.74
0.0015
-0.6839
-0.151793132
0.030851469
580
9.54136
75.74
0.0015
0.9104
0.202065312
0.028644433
583
9.5411
75.74
0.0015
0.1522
0.03378113
0.029401006
587
9.5411
75.74
0.0015
0.633
0.140495763
0.031490398
590
9.54112
143.34
0.0015
0.1822
0.011290773
0.045120565
593
9.54111
97.38
0.0015
0.7179
0.096390566
0.032562644
597
95.1101
143.34
0.0015
4.0462
0.250739447
0.023245628
599
12.41949
101.6
0.0015
0.6247
0.077053826
0.034218138
753
0.4801
76.2
0.0015
5.4866
1.203104843
0.018932674
754
2.2329
101.6
0.0015
3.8481
0.474645155
0.021745313
755
0.59033
76.2
0.0015
-2.7093
-0.594096882
0.022073584
756
0.6356
76.2
0.0015
7.1874
1.576057258
0.017908383
757
1.06733
76.2
0.0015
-0.0756
-0.016577612
0.057808097
758
1.09489
76.2
0.0015
-0.8352
-0.183143142
0.029330219
760
87.20834
76.2
0.0015
1.179
0.258531807
0.026881066
761
1.18359
152.4
0.0015
1.7205
0.09431806
0.029091381
762
1.24951
76.2
0.0015
2.2896
0.502064821
0.022937891
765
1.67506
101.6
0.0015
9.0102
1.111366071
0.01810836
766
27.84639
76.2
0.0015
-3.6519
-0.800790759
0.020655383
768
25.73311
76.2
0.0015
-2.9239
-0.641154495
0.021697978
769
96.18779
101.6
0.0015
-5.7843
-0.713466378
0.01987835
Tabla 50.
Resultados de modelación red Olivos I para cada tubo de la red (Reporte 5).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
88
Juan Camilo Vergara Valderrama
ID
Longitud (m)Diametro (mm)
Rugosidad (mm)Caudal (L/s)Velocidad (m/s)
Fact. Friccion
770
1.91049
152.4
0.0015
0.292
0.01600748 0.03021825
771
83.41692
76.2
0.0015
-4.0174
-0.88093781 0.02023099
773
34.62492
152.4
0.0015
-2.1438
-0.11752343 0.02750795
774
7.68573
152.4
0.0015
9.3351
0.51175154
0.0195474
775
2.31814
76.2
0.0015
0.1994
0.04372455 0.03203158
776
2.52723
152.4
0.0015
4.5559
0.2497551
0.02293649
777
2.92542
76.2
0.0015
2.1048
0.46154177 0.02338894
778
31.83306
152.4
0.0015
26.7473
1.46629088 0.01578145
779
3.09264
76.2
0.0015
1.219
0.26730303 0.02665998
780
30.40478
76.2
0.0015
1.3823
0.30311155 0.02585031
781
3.31475
76.2
0.0015
-0.2291
-0.05023718 0.03702572
782
44.9571
76.2
0.0015
-1.3154
-0.28844168 0.02616546
783
3.38354
101.6
0.0015
-0.7247
-0.08938836 0.03285419
784
3.59694
101.6
0.0015
0.2425
0.02991124 0.02978788
785
4.37655
76.2
0.0015
4.5905
1.00660751
0.0196594
786
4.47889
76.2
0.0015
5.6258
1.2336287
0.01883387
787
4.59492
76.2
0.0015
-3.165
-0.69402304 0.02131757
788
62.85802
76.2
0.0015
-2.6562
-0.58245308 0.0221727
791
4.93377
76.2
0.0015
-3.2198
-0.70603962 0.02123646
792
5.07666
152.4
0.0015
0.8322
0.04562133 0.03536137
793
54.17129
76.2
0.0015
0.5003
0.10970608
0.0336121
794
5.26202
101.6
0.0015
-4.7208
-0.58228862 0.02077788
799
21.50792
101.6
0.0015
8.4792
1.0458697
0.01833647
800
57.74978
76.2
0.0015
-7.1235
-1.56204523 0.01794087
801
7.90746
76.2
0.0015
-6.4422
-1.41264937
0.018313
803
85.9557
76.2
0.0015
-2.0929
-0.45893233 0.02341979
805
64.92232
76.2
0.0015
-6.5095
-1.42740695 0.01827398
808
78.6312
76.2
0.0015
-2.0031
-0.43924093 0.02366051
809
10.8876
152.4
0.0015
0.074
0.00405669
0.118116
810
106.6083
76.2
0.0015
-0.3728
-0.0817478 0.03648739
817
22.7386
76.2
0.0015
0.3087
0.06769192 0.03852083
820
24.1514
76.2
0.0015
4.2564
0.93334587 0.01998024
823
26.3117
76.2
0.0015
5.351
1.1733704
0.01903216
827
26.8202
76.2
0.0015
1.5811
0.34670453 0.02502401
828
94.0469
76.2
0.0015
0.2938
0.06442464 0.03908084
830
27.5477
152.4
0.0015
-4.803
-0.26330116 0.02265863
831
28.79145
152.4
0.0015
-9.7861
-0.53647543 0.01935092
833
28.875
152.4
0.0015
3.9147
0.21460442 0.02376266
Tabla 51.
Resultados de modelación red Olivos I para cada tubo de la red (Reporte 6).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
89
Juan Camilo Vergara Valderrama
ID
Longitud (m) Diametro (mm) Rugosidad (mm) Caudal (L/s) Velocidad (m/s) Fact. Friccion
834
29.9141
152.4
0.0015
17.7796
0.974680261
0.017099959
835
30.0802
76.2
0.0015
1.957
0.4291321
0.023789793
836
30.3791
152.4
0.0015
-6.814
-0.373544472
0.020937245
839
30.626
152.4
0.0015
3.1907
0.174914639
0.02494679
840
31.2258
101.6
0.0015
5.653
0.697271137
0.019977063
842
31.2849
76.2
0.0015
-4.1614
-0.912514216
0.02007762
843
32.9303
101.6
0.0015
-7.5414
-0.930196453
0.018789194
844
31.5813
76.2
0.0015
-5.4385
-1.192557447
0.018967589
845
31.7413
101.6
0.0015
7.633
0.941494885
0.018741781
846
152.82457
76.2
0.0015
0.95
0.208316553
0.028378558
847
32.6089
101.6
0.0015
-4.5487
-0.561060892
0.020948838
848
30.6837
152.4
0.0015
-3.122
-0.171148495
0.025077848
849
32.1982
152.4
0.0015
9.8226
0.538476362
0.019335546
851
32.3287
76.2
0.0015
-6.9315
-1.519943357
0.018040837
852
32.3436
152.4
0.0015
-5.8817
-0.32243565
0.021637228
853
32.7174
152.4
0.0015
1.1179
0.061283441
0.032599003
854
33.035
76.2
0.0015
9.55
2.094129562
0.016921021
856
33.6428
101.6
0.0015
-1.0416
-0.128476493
0.029834185
857
34.2368
101.6
0.0015
-2.9836
-0.368013119
0.023045455
858
34.4266
76.2
0.0015
-0.4776
-0.104728406
0.034043808
859
38.4939
152.4
0.0015
7.5904
0.416106833
0.020444862
862
44.0649
76.2
0.0015
-36.2644
-7.952078752
0.013306254
863
46.2339
76.2
0.0015
-5.1278
-1.12442697
0.019203396
868
54.0065
101.6
0.0015
-0.6846
-0.084442211
0.033367668
871
56.3227
152.4
0.0015
1.0454
0.05730898
0.033198675
872
56.8003
76.2
0.0015
0.3233
0.070893412
0.038008044
873
58.359
76.2
0.0015
0.3388
0.074292261
0.037498316
876
58.5899
76.2
0.0015
-2.6375
-0.578352536
0.022208234
878
136.54511
101.6
0.0015
-3.9765
-0.490482695
0.021585521
882
71.7769
76.2
0.0015
-2.393
-0.524738434
0.022706281
883
75.7814
76.2
0.0015
-7.4176
-1.626535648
0.017794432
886
82.317
76.2
0.0015
1.1219
0.246010885
0.02721499
887
84.0475
76.2
0.0015
2.3297
0.510857973
0.022846436
889
85.8345
76.2
0.0015
2.0289
0.444898374
0.023589887
892
94.275
152.4
0.0015
-2.4475
-0.134172306
0.026613992
901
5.77093
143.34
0.0015
-4.4146
-0.27356887
0.022781027
905
2.10827
75.74
0.0015
6.2101
1.378345557
0.018429411
912
0.79226
76.2
0.0015
1.3205
0.289560009
0.026140678
Tabla 52.
Resultados de modelación red Olivos I para cada tubo de la red (Reporte 7).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
90
Juan Camilo Vergara Valderrama
ID
Longitud (m)Diametro (mm)
Rugosidad (mm)Caudal (L/s)Velocidad (m/s)
Fact. Friccion
913
1.01931
76.2
0.0015
-2.6327
-0.57729999 0.02221741
915
84.72671
76.2
0.0015
0.7539
0.16531563 0.03012012
924
97.61195
76.2
0.0015
1.601
0.35106821 0.02494907
927
97.37445
76.2
0.0015
-0.1173
-0.02572161 0.03725739
930
97.89835
97.38
0.0015
-3.2675
-0.43871873 0.02235236
933
32.69875
152.4
0.0015
-1.1747
-0.06439723 0.03216572
942
18.9774
152.4
0.0015
-7.3198
-0.4012725 0.02060859
945
9.5411
101.6
0.0015
-0.3631
-0.04478669 0.04060421
951
26.02884
97.38
0.0015
-6.4907
-0.87148941 0.01922284
961
25.16628
101.6
0.0015
7.3078
0.90138298 0.01891362
965
87.86996
76.2
0.0015
-1.3852
-0.30374746 0.02583712
969
27.60087
152.4
0.0015
-9.3934
-0.51494756 0.01952131
978
51.8249
152.4
0.0015
-7.6906
-0.42159981 0.02038618
980
16.4713
76.2
0.0015
-7.8143
-1.71352425 0.0176086
982
26.73241
76.2
0.0015
-3.8647
-0.84745367 0.0204018
990
30.42948
101.6
0.0015
2.5737
0.31745387 0.02385367
993
8.21862
76.2
0.0015
4.314
0.94597643 0.01992259
996
33.19908
76.2
0.0015
-2.6667
-0.58475553 0.02215289
1000
22.76229
76.2
0.0015
-4.9652
-1.08877195 0.01933447
1003
58.15321
76.2
0.0015
-0.6637
-0.14553652 0.03114664
1006
43.27733
152.4
0.0015
-3.1382
-0.17203658 0.02504659
1009
71.77363
152.4
0.0015
-3.6601
-0.20064721 0.02414286
1016
0.51283
152.4
0.0015
-3.2536
-0.17836283 0.02483009
1020
55.92316
97.38
0.0015
-3.2143
-0.4315757 0.02243625
1023
31.24803
97.38
0.0015
5.216
0.70033876 0.02014474
1026
25.21009
97.38
0.0015
2.1209
0.28476773 0.02472508
Tabla 53.
Resultados de modelación red Olivos I para cada tubo de la red (Reporte 8).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
91
Juan Camilo Vergara Valderrama
4 CONCLUSIONES
Los dos softwares de diseño dan las mismas posibilidades de cálculo; sin embargo el
software WaterGems tiene un costo muy elevado respecto al software Redes, por lo que
esto hace que el costo del WaterGems se convierta en una limitante a la hora de su uso.
El cuadro de diálogo principal del software Redes es mucho más amigable que el cuadro
de dialogo del software WaterGems ya que allí las herramientas se encuentran mejor
indicadas y explicadas haciendo que el usuario no tenga problemas a la hora de construir
su modelo.
A la hora de importar la red existente del modelo de WaterGems al Software Redes, se
debe cumplir con varios pasos para que este se deje ejecutar en el software Redes. Una
vez importado al programa Epanet y generado el archivo en Excel, la transferencia de
datos puede llegar a ser engorrosa y demorada. Esto se debe a que la estructura de la base
de datos del programa Epanet no tiene la misma forma que la del programa Redes.
Los dos software de diseño indican mediante colores características tanto geométricas
como hidráulicas, lo cual hace que se puedan distinguir tramos con presiones y/o
velocidades críticas de una manera más fácil.
El software WaterGems da la facilidad de exportar un modelo hidráulico a otro programa
de modelación como el Epanet. Esto se logra directamente, ya que el WaterGems y el
Epanet son compatibles uno con el otro, haciendo que los tiempos de construcción del
modelo de un programa a otro sean prácticamente cero, y por lo tanto no se requiera
organizar los datos de entrada en hojas de Excel para que este se ejecute con éxito.
Al observar los resultados de modelación tanto para los modelos hechos mediante el
software WaterGems como en el programa Redes, se identifica que para el circuito Olivos
IV los valores de presión son muy parecidos siendo que la diferencia entre ellos es muy
pequeña. Para este mismo circuito se ve que la diferencia entre caudales es un poco mas
significativa
En el caso de la modelación del circuito Olivos I los resultados arrojados por los softwares
de modelación son drásticamente diferentes, esto se puede presentar debido a diversas
diferencias presentadas a la hora de desarrollar la construcción de la topología de la red
y/o de las elevaciones planteadas para cada uno de los modelos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados - CIACUA
Comparación entre los softwares WaterGems y Redes, en la modelación hidráulica
de redes de distribución de agua potable
92
Juan Camilo Vergara Valderrama
5
BIBLIOGRAFÍA
Lindell E. Ormsbee, (2006). The history of water distribution network analysis: The computer
age. Articulo por ASCE.
Universidad Politécnica de Valencia, (1996). Ingeniería hidráulica: Aplicada a los sistemas de
distribución de agua. (2da. Ed.). Valencia, España.
Juan G Saldarriaga, (2007). Hidráulica de tuberías: Abastecimiento de agua, redes, riegos. (2da.
Ed). Bogotá, Colombia: Alfaomega-Uniandes.
Haestad Methods Solution Center-Blentey Systems, Inc, (2006), Bentley Watergems V8i edition.
User Guide.
U.S. Environmental Protection Agency, Office of research and development, (2005), Water
distribution sistem analysis: Field studies, Modeling and management. Reference guide for
Utilities. Estados Unidos.
Mays L.W., (2000). Introduction, Water distribution system handbook. New York, NY, Estados
Unidos: McGraw Hill.
Haestad Methods, (2004), Advanced water distribution modeling and management. Waterbury,
Estados Unidos.
