
Universidad de los Andes
Facultad De Ingeniería
Departamento de Ingeniería Civil y Ambiental
TESIS DE ESPECIALIZACIÓN
INGENIERÍA DE SISTEMAS HÍDRICOS URBANOS
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
(HEC-RAS) y 2D (RIVER 2D)
Caso de Estudio:
Quebrada La Viga, Cali, Valle del Cauca.
Preparado por:
Ing. Oscar Darío Velásquez Mora
Asesor:
Ing. Diego Páez
Informe Final Tesis
Bogotá, Febrero 26 de 2014

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
2
Oscar Darío Velásquez Mora
TABLA DE CONTENIDO
INTRODUCCIÓN ....................................................................................................................................................... 6
1
OBJETIVOS ....................................................................................................................................................... 7
1.1
OBJETIVOS .................................................................................................................................................... 7
1.1.1
Objetivo General .................................................................................................................................... 7
1.1.2
Objetivos Específicos ............................................................................................................................. 7
2
MARCO TEORICO ........................................................................................................................................... 8
2.1
M
ODELOS
H
IDRÁULICOS
.................................................................................................................................. 8
2.1.1
HEC-RAS 4.0.......................................................................................................................................... 8
2.1.2
River 2D ............................................................................................................................................... 10
3
METODOLOGÍA............................................................................................................................................. 13
3.1
DESCRIPCION
DEL
AREA
DEL
PROYECTO ........................................................................................... 13
3.1.1
Quebrada La Viga ................................................................................................................................ 13
3.1.2
Climatología ......................................................................................................................................... 13
3.1.3
Caracterización Morfométrica de la Micro-cuenca ............................................................................. 13
3.2
HIDROLOGÍA .............................................................................................................................................. 14
3.2.1
Parámetros Básicos ............................................................................................................................. 14
3.2.2
Análisis de Frecuencias ....................................................................................................................... 14
3.2.3
Curvas Intensidad-Duración-Frecuencia ............................................................................................ 15
3.2.4
Hietograma de Diseño ......................................................................................................................... 16
3.2.5
Precipitación Efectiva .......................................................................................................................... 16
3.2.6
Número de Curva ................................................................................................................................. 17
3.2.7
Tiempo de Concentración .................................................................................................................... 17
3.3
CALCULO
DE
CAUDALES ........................................................................................................................ 19
3.3.1
Método del Hidrograma Triangular (Soil Conservation Service) ....................................................... 19
3.3.2
Resultados de los Caudales Método S.C.S 50 y 100 Años.................................................................... 20
4
RESULTADOS Y DISCUSION ...................................................................................................................... 22
4.1
M
ODELO
HEC-RAS
4.1.0 .............................................................................................................................. 22
4.2
M
ODELO
R
IVER
2D
0.95 ................................................................................................................................. 25
4.2.1
Modulo R2D_Bed ................................................................................................................................. 25
4.2.2
Modulo R2D_Mesh .............................................................................................................................. 26
4.2.3
Ejecución del Modelo River2D ............................................................................................................ 27
4.3
D
ISCUSIÓN DE
R
ESULTADOS
........................................................................................................................... 29
5
CONCLUSIONES ............................................................................................................................................ 30
6
RECOMENDACIONES .................................................................................................................................. 31
8
BIBLIOGRAFÍA .............................................................................................................................................. 32

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
3
Oscar Darío Velásquez Mora
ÍNDICE DE FIGURAS
F
IGURA
1.
E
SQUEMA DE MODELOS HIDRÁULICOS UNIDIMENSIONAL
(
X
),
BIDIMENSIONAL
(
X
,
Y
)
Y TRIDIMENSIONAL
(
X
,
Y
,
Z
). .................................................................................................................................................................. 6
F
IGURA
2.
E
STRUCTURA Y FUNCIONAMIENTO DE
R
IVER
2D. ....................................................................................... 11
F
IGURA
3.
C
URVA
I-F-D
PARA LA ZONA
S
UR
-
OCCIDENTE DE
C
ALI
. ........................................................................... 16
F
IGURA
4.
C
AUDAL PARA
T
R
=
100
AÑOS
.................................................................................................................... 21
F
IGURA
5.
M
ODELO
D
IGITAL DE
T
ERRENO
G
ENERADO
P
OR
A
UTO
CAD
C
IVIL
3D ..................................................... 22
F
IGURA
6.
S
ECCIONES
T
RANSVERSALES
I
MPORTADAS EN
HEC-RAS ......................................................................... 23
F
IGURA
7.
V
ISTA
E
VENTO DE
I
NUNDACIÓN EN
50
AÑOS Y
Q
=
1.48
M
3
/
S
.................................................................... 24
F
IGURA
8.
V
ISTA
E
VENTO DE
I
NUNDACIÓN EN
100
AÑOS Y
Q
=
1.84
M
3
/
S
................................................................... 24
F
IGURA
9.
A
RCHIVO
G
ENERADO
P
OR EL
M
ODULO
R2D_B
ED
..................................................................................... 26
F
IGURA
10.
T
OPOGRAFÍA Y
T
RIANGULACIÓN
G
ENERADA POR EL
M
ODULO
R2D_M
ESH
. ............................................ 27
F
IGURA
11.
M
ODELO
R
IVER
2D ................................................................................................................................... 28
F
IGURA
12.
V
ISTA
E
VENTO DE
I
NUNDACIÓN EN
50
AÑOS Y
Q
=
1.48
M
3
/
S
.................................................................. 28
F
IGURA
13.
V
ISTA
E
VENTO DE
I
NUNDACIÓN EN
100
AÑOS Y
Q
=
1.84
M
3
/
S
................................................................ 29

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
4
Oscar Darío Velásquez Mora
ÍNDICE DE TABLAS
T
ABLA
1.
F
ACTORES DE FRECUENCIA PARA DIFERENTES TIEMPOS DE RETORNO
. .......................................................... 15
T
ABLA
2.
P
RECIPITACIÓN TOTAL
.................................................................................................................................. 16
T
ABLA
3.
N
ÚMEROS DE CURVA DE ESCORRENTÍA PARA USOS DE TIERRA SUBURBANO Y URBANO
. ............................... 17
T
ABLA
4.
V
ALORES DE
CN,
C
OEFICIENTE DE ESCORRENTÍA
(C
)
Y N ADOPTADOS PARA LA QUEBRADA
L
A
V
IGA
. ....... 18
T
ABLA
5.
R
ESULTADOS DEL TIEMPO DE CONCENTRACIÓN
(
T
C
)
–
Q
UEBRADA
L
A
V
IGA
. ................................................ 19
T
ABLA
6.
C
AUDALES POR EL MÉTODO
S.C.S ................................................................................................................ 20
T
ABLA
7.
C
ONFIGURACIÓN DE
D
ATOS DE
E
NTRADA
T
OPOGRÁFICOS
P
ARA EL
M
ODULO
R2D_B
ED
............................ 25

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
5
Oscar Darío Velásquez Mora
ÍNDICE DE ECUACIONES
E
CUACIÓN
1.
E
CUACIONES DE
S
AINT
V
ENANT
. .............................................................................................................. 9
E
CUACIÓN
2.
E
CUACIONES DE ENERGÍA
. ......................................................................................................................... 9
E
CUACIÓN
3.
E
CUACIÓN DE PÉRDIDA DE ENERGÍA
. ....................................................................................................... 10
E
CUACIÓN
4.
L
ONGITUD DEL CAUCE PROMEDIO
. .......................................................................................................... 10
E
CUACIÓN
5.
C
ONTINUIDAD
. ....................................................................................................................................... 12
E
CUACIÓN
6.
M
OMENTUM PROMEDIADA EN LA VERTICAL EN LA DIRECCIÓN X
. ........................................................... 12
E
CUACIÓN
7.
M
OMENTUM PROMEDIADA EN LA VERTICAL EN LA DIRECCIÓN Y
. ........................................................... 12
E
CUACIÓN
8.
D
ISTRIBUCIÓN DE TIPO
1
DEL VALOR EXTREMO
. ..................................................................................... 14
E
CUACIÓN
9.
G
ENERACIÓN
C
URVAS
I.F.D
(F
ORERO Y
F
RANCO
,
2003). ....................................................................... 15
E
CUACIÓN
10.
T
IEMPO DE
C
ONCENTRACIÓN
-
O
NDA
C
INEMÁTICA
............................................................................. 17
E
CUACIÓN
11.
T
IEMPO DE
C
ONCENTRACIÓN
-
K
IRPICH
................................................................................................ 18
E
CUACIÓN
12.
T
IEMPO DE
C
ONCENTRACIÓN
–
F
EDERAL
A
VIATION
A
DMINISTRATION
. ............................................... 18
E
CUACIÓN
13.
C
AUDAL MÁX
.
–
S
OIL
C
ONSERVATION
S
ERVICE
. .................................................................................. 19
E
CUACIÓN
14.
T
IEMPO
P
ICO
HI
DROGRAMA
.
–
S
OIL
C
ONSERVATION
S
ERVICE
. ............................................................ 20

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
6
Oscar Darío Velásquez Mora
INTRODUCCIÓN
Un modelo hidrológico, busca representar los diferentes procesos involucrados en la distribución de la
lluvia y la generación de caudales en una determinada cuenca. En la actualidad se dispone de una amplia
variedad de modelos los cuales han sido planteados bajo ciertas hipótesis cuyo claro entendimiento
garantiza su correcto uso. En el presente trabajo se revisa y compara las metodologías de modelación de
inundaciones en 1D (Hec-RAS) y 2D (River 2D).
Al considerar el análisis de las bases de cada modelo, se puede determinar en qué situaciones resulta
conveniente utilizar uno u otro, como así también identificar sus principales potencialidades y
limitaciones, y en función de ellas establecer las necesidades a satisfacer en el desarrollo de nuevos
modelos compatibles con los datos disponibles de las cuencas locales.
Muchos estudios de mapeo de inundaciones se han realizado usando modelos hidrodinámicos
unidimensionales y bidimensionales (1D/2D). Algunos autores indican que los modelos hidráulicos 2D
son la tecnología de punta para la modelación de inundaciones.
Sin embargo, éstos modelos tienen la desventaja de que su aplicación está limitada por los altos
requerimientos de datos, hardware y software. A su vez, los modelos 1D son ampliamente usados y dan
resultados precisos en el cauce principal del río, pero son menos exactos para modelar el flujo de
desbordamiento sobre las márgenes hacia las planicies adyacentes.
Figura 1. Esquema de modelos hidráulicos unidimensional (x), bidimensional (x,y) y tridimensional (x,y,z).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
7
Oscar Darío Velásquez Mora
1 OBJETIVOS
1.1 OBJETIVOS
1.1.1 Objetivo General
Comparar dos metodologías de modelación de inundaciones fluviales: unidimensional (HEC-RAS)
y bidimensional (RIVER2D), teniendo en cuenta la información disponible de la cuenca,
hidrología y topografía.
1.1.2
Objetivos Específicos
Evaluar la aplicación de los modelos HEC RAS 4.1.0 y RIVER2D 0.95 en el análisis de un evento de
inundación para diferentes tiempos de retorno en la quebrada La Viga.
Comparar los resultados arrojados por los modelos en la modelación de un evento de inundación
en la quebrada La Viga, y encontrar posibles ventajas y desventajas en el proceso de elaboración
del modelo y el manejo que se debe hacer a los datos de entrada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
8
Oscar Darío Velásquez Mora
2 MARCO TEORICO
Alrededor del mundo hay un gran interés en la modelación de crecidas de ríos debido a los eventos de
inundación extremos ocurridos en la última década. Al ser las inundaciones uno de los riesgos naturales
más costosos, su análisis y prevención es un factor clave para las autoridades y organismos relacionados
a los recursos hídricos.
Los modelos de hidráulica de ríos usados para la modelación de inundaciones pueden clasificarse como
modelos hidrodinámicos 1D o 2D. Los modelos hidrodinámicos 1D son ampliamente usados, estos
modelos están basados en las ecuaciones de Saint Venant (leyes de conservación de la masa y momento)
para calcular la superficie libre del agua para flujo estacionario y no estacionario en canales abiertos.
Estas ecuaciones diferenciales parciales se resuelven mediante discretización numérica, usando
frecuentemente el método de diferencias finitas, y en algunos casos mediante elementos finitos o
volúmenes finitos, en un esquema implícito.
Por otra parte, en los modelos hidrodinámicos 2D, las ecuaciones de conservación de la masa y
momento son expresadas en dos dimensiones y los resultados se calculan en cada punto de la malla en
el dominio de solución. Los modelos 2D pueden resolverse usando el método de los elementos finitos.
Muchos estudios de mapeo de inundaciones han sido realizados usando modelos hidrodinámicos 1D y
2D. Algunos autores afirman que los modelos hidráulicos 2D son el estado del arte para la modelación de
inundaciones.
Aunque los modelos 1D son precisos en el cauce principal del río, éstos no son exactos para el flujo sobre
los bancos, por ejemplo para la modelación de la onda de propagación desde el río hacia la llanura de
inundación. Estos problemas no existen en los modelos 2D, sin embargo tienen la desventaja de requerir
un mayor tiempo de implementación, y una alta demanda de datos y tiempo computacional.
2.1 Modelos Hidráulicos
2.1.1 HEC-RAS 4.0
Este programa desarrollado para análisis de ríos es un modelo numérico para flujo unidimensional
permanente y no permanente, con transporte de sedimentos y con capacidad para trabajar con flujos
mixtos, subcríticos y supercrítico. Sus principales limitaciones son asumir lecho rígido y flujo
unidireccional, por lo que debe ser aplicado con cautela en ríos aluviales muy erosionables o muy
meandriformes; en estos casos puede ser recomendable recurrir a otro tipo de modelo más sofisticado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
9
Oscar Darío Velásquez Mora
El modelo permite realizar análisis de flujo unidimensional permanente, no permanente, cálculos
hidrodinámicos de lecho móvil y transporte de sedimentos. HEC RAS resuelve las ecuaciones completas
de Saint Venant para flujo no permanente unidimensional en canal abierto:
Donde Q es el caudal total por el cauce, A (Ac, A
f
) las secciones transversales del flujo (en el canal y la
llanura de inundación), Xc y X
f
son las distancias a lo largo del canal y la llanura de inundación, P es el
perímetro mojado, R es el radio hidráulico (A/P), n es el valor del coeficiente de Manning y S es la
pendiente de la línea de fricción. Φ como se reparte el flujo entre la llanura de inundación y el canal
principal de acuerdo a los coeficientes de transporte K
c
y K
f
.
Con el fin de obtener la solución, todas estas ecuaciones son discretizadas usando el método de
diferencias finitas y se resuelven usando el método implícito de los cuatro puntos.
Dentro de las bases teóricas para el cálculo de los perfiles de flujo unidimensionales, éstos son calculados
de una sección transversal a la otra resolviendo la ecuación de energía mediante un procedimiento
iterativo llamado el método del paso estándar.
Ecuación 1. Ecuaciones de Saint Venant.
Ecuación 2. Ecuaciones de energía.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
10
Oscar Darío Velásquez Mora
Donde he, es la pérdida de energía de una sección transversal a otra, la cual se calcula así:
Donde L es la longitud promedio ponderada del cauce, C es el coeficiente de expansión y contracción y
̅ es la pendiente de la línea de fricción.
La longitud del cauce promedio se calcula por medio de:
Donde Lob, Lch y Lrob son las longitudes entre secciones transversales en la llanura de inundación
izquierda, canal principal y llanura de inundación derecha, respectivamente;
̅̅̅̅̅,
̅̅̅̅̅,
̅̅̅̅̅̅ es el
promedio aritmético de los cauces entre secciones transversales para la llanura de inundación izquierda,
canal principal y llanura de inundación derecha, respectivamente.
2.1.2 River 2D
Es un modelo hidrodinámico bidimensional de elementos finitos (MEF) promediado en profundidad
desarrollado por la Universidad de Alberta en Canadá. Posee características únicas como su capacidad de
representar flujo sub- y supercrítico. Algoritmos especiales de agua subterránea permiten una transición
gradual entre agua superficial y subterránea en los bordes del río, que evitan quiebres bruscos en las
fronteras. El software consta de cuatro módulos complementarios, los cuales son R2D_Bed, R2D_Ice,
R2D_Mesh y el River 2D.
Ecuación 3. Ecuación de pérdida de energía.
Ecuación 4. Longitud del cauce promedio.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
11
Oscar Darío Velásquez Mora
Este modelo está basado en las ecuaciones de Saint Venant expresadas en forma conservativa, las cuales
son un sistema de tres ecuaciones: una conservación de masa y dos para componentes del vector
momentum. El modelo ha sido desarrollado para sistemas de ríos naturales con características especiales
tales como modelación de transiciones del flujo supercrítico a subcrítico, coberturas de hielo y área
mojadas variables.
Para la discretización espacial River 2D usa una malla no estructurada flexible compuesta por elementos
triangulares. Los métodos de elementos finitos usados en el modelo están basados en la formación
residual ponderada Streamline Upwind Petrov Galerking (SUPG). Mediante esta técnica se asegura la
estabilidad de la solución bajo todo el rango de condiciones de flujo, incluyendo subcrítico, supercrítico y
transicional. Es así como se hace uso de una discretización conservativa completa, lo cual asegura que no
se está perdiendo o ganando masa de fluido por encima del dominio modelado. Esto también permite la
implementación de las condiciones de frontera como flujo naturales o condiciones forzadas.
Las ecuaciones resueltas por el modelo River 2D son la ecuación de continuidad y las ecuaciones de
conservación de momentum en las direcciones X y Y. Estas ecuaciones no tienen una solución analítica
exacta, pero en condiciones iniciales y de frontera apropiadas pueden ser resueltas usando técnicas
numéricas, con el fin de encontrar el caudal y la altura de la lámina de agua en el tiempo y en el espacio.
Figura 2. Estructura y funcionamiento de River 2D.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
12
Oscar Darío Velásquez Mora
La ecuación de continuidad es:
La ecuación de momentum promediada en la vertical en la dirección x es:
La ecuación de momentum promediada en la vertical en la dirección y es:
Donde t = tiempo, h = profundidad del agua, (u,v) = velocidades promedio en las direcciones (x,y); qx
=uh= caudal en la dirección x por unidad de ancho; qy=vh=caudal en la dirección y por unidad de ancho;
(Sox, Soy) = pendiente del lecho en las direcciones τxx, τxy, τyx, τyy = componentes del esfuerzo cortante
turbulento horizontal; ρ = densidad del agua, g = aceleración de la gravedad.
Ecuación 5. Continuidad.
Ecuación 6. Momentum promediada en la vertical en la dirección x.
Ecuación 7.
Momentum promediada en la vertical en la dirección y.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
13
Oscar Darío Velásquez Mora
3 METODOLOGÍA
3.1 DESCRIPCION DEL AREA DEL PROYECTO
3.1.1 Quebrada La Viga
La quebrada se encuentra localizada al Sur occidente de la ciudad de Santiago de Cali (Colombia), y
tributa sus aguas al Río Pance, a través del canal del mismo nombre a la altura de la Carrera 158 Y
Avenida Cañas gordas. Se caracteriza por tener cauces cortos y áreas de drenaje con intermedia
intervención en la parte constructiva. En los alrededores la vegetación de sus zonas de protección es
media, solo se encuentra pastos, arvenses y algunos arbustos de mediano tamaño.
La quebrada Pancecito capta cerca de 34.44 ha, como parte de la cuenca de esta quebrada y continua
recogiendo el agua lluvia del sector de Pance en un área adicional de 56 ha, descargando finalmente en
el Río Pance a su paso por la Avenida Cañas gordas. La longitud aproximada de esta quebrada es de 340
m.
La pendiente de la cuenca hacia la parte media disminuye. Posteriormente, en la parte baja la pendiente
es moderada y en el cauce se encuentran depósitos de material aluvial.
3.1.2 Climatología
La cuenca de la Quebrada La Viga, presenta una precipitación de carácter bimodal teniendo dos
períodos secos y dos húmedos durante el año. Los períodos húmedos corresponden a los meses de Abril
– Junio y Octubre – Diciembre, y los secos a los meses de Enero – Marzo y Julio – Septiembre.
3.1.3 Caracterización Morfométrica de la Micro-cuenca
La caracterización fisiográfica de la micro-cuenca se realizó con base en la información del topográfico en
puntos específicos de la quebrada.
La Quebrada La Viga, posee una longitud total antes de entregar al río Pance de 368 m y un área de
34.994 ha, entregando al Río Pance en sentido norte - sur.
La zona objeto de este estudio se encuentra localizado en las coordenadas 111239.7448 E; 94174.1209 N
A 111 481.6199 E; 94338.3563 N, con cota 1006.00 msnm, en promedio.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
14
Oscar Darío Velásquez Mora
3.2 HIDROLOGÍA
Para el chequeo de altura de agua en las secciones y perfil hidráulico se utilizó el caudal de diseño con
una recurrencia media de 1 en 50 y 100 años. Para la aplicación de estos métodos es necesario conocer
los parámetros fisiográficos y climáticos de la cuenca.
3.2.1 Parámetros Básicos
La aplicación de los métodos requiere el cálculo de parámetro físicos de la cuenca y las características de
la lluvia como son la precipitación máxima en 24 horas, las curvas Intensidad – Frecuencia – Duración,
I.F.D., el patrón de distribución de la lluvia en el tiempo, el hietograma de precipitación y los valores de la
lluvia en exceso.
3.2.2 Análisis de Frecuencias
En el análisis de frecuencia se aplicó la distribución de Valor Extremo tipo (Gumbel ), en la cual se tomó
la estadística de los valores de cada periodo de duración de la serie de excedencias y se calculó el factor
de frecuencia mediante la fórmula:
1
ln
ln
5772
.
0
6
T
T
K
T
Ecuación 8. Distribución de tipo 1 del valor extremo.
Donde:
K
T
Factor de frecuencia.
T
periodo de retorno.
Las curvas I-F-D se calcularon para periodos de retorno de 5, 10, 20, 50 y 100 años, los factores de
frecuencia se consignan en la Tabla 1.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
15
Oscar Darío Velásquez Mora
Tabla 1. Factores
de frecuencia para diferentes tiempos de retorno.
Tiempo de Retorno
(Tr)
Factor de Frecuencia
(K
T
)
5
0.719
10
1.305
20
1.866
50
2.592
100
3.137
Fuente: Forero y Franco 2003
3.2.3 Curvas Intensidad-Duración-Frecuencia
Para la revisión y cálculo hidrológico de las cuencas del estudio se usó la ecuación I.F.D. propuesta por
(Forero y Franco 2003).
Esta ecuación general para la zona en Sur, se calculó haciendo un promedio ponderado entre las áreas
de influencia de cada estación en la zona.
827
.
0
134
.
0
)
782
.
11
(
1493
t
Tr
I
Ecuación 9. Generación Curvas I.F.D (Forero y Franco, 2003).
Donde:
I
Intensidad
Tr
Periodo de retorno
t
Tiempo de concentración
Las estaciones que se tuvieron en cuenta para la realización de la curva IFD de la zona sur occidental de
Cali fueron la estación Universidad del Valle, que constituyen una red meteorológica que cubre el área
urbana y suburbana. Esta estación presenta registros que en promedio alcanzan períodos de 32 años,
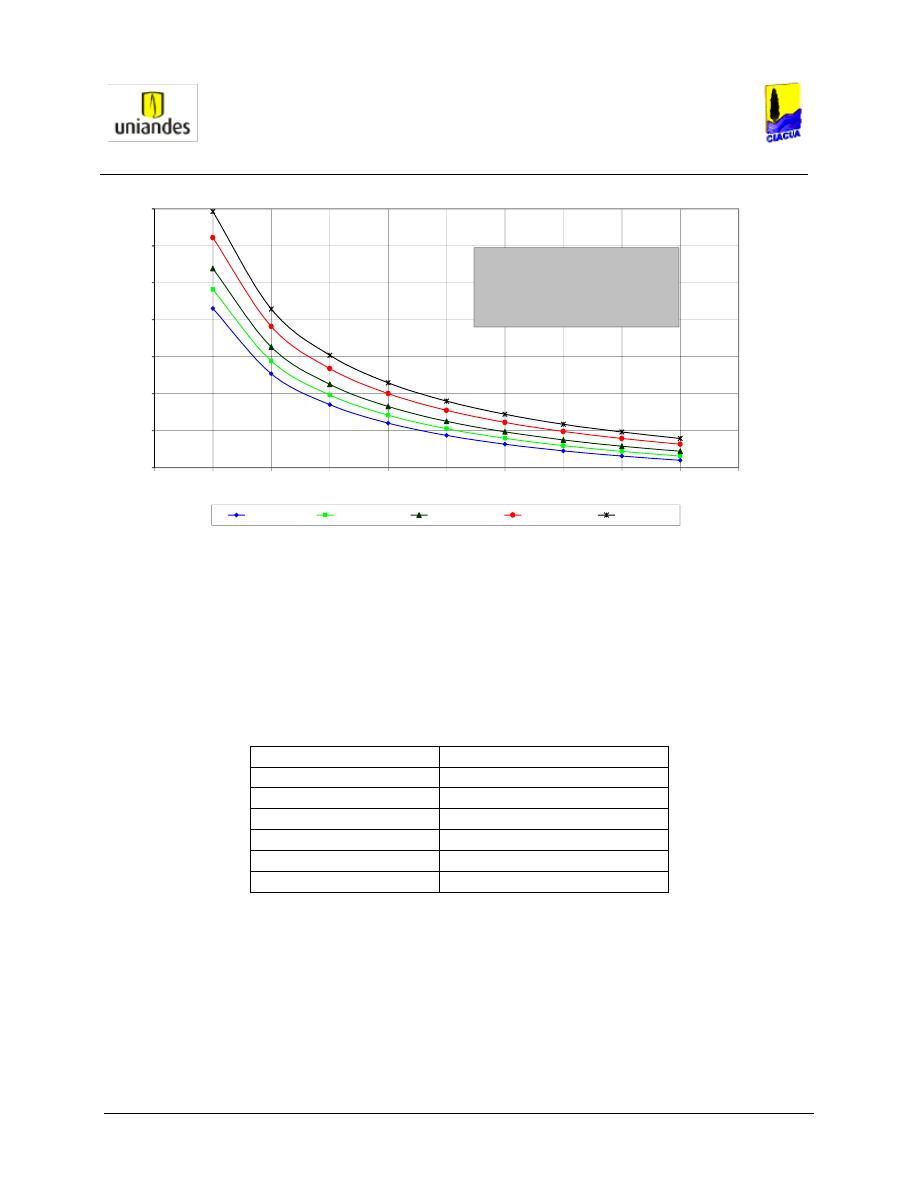
factor que implica suficiente representatividad de las muestras. La Figura 3. presenta la curva
Intensidad – Frecuencia – Duración para el Sur occidente de Cali. En ésta, la intensidad se presenta en
mm/hora y la duración en minutos, incluye los periodos de recurrencia 1: 5, 1: 10, 1: 20, 1: 50 y 1: 100.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
16
Oscar Darío Velásquez Mora
Figura 3. Curva
I-F-D para la zona Sur - occidente de Cali.
3.2.4 Hietograma de Diseño
Muestran los hietogramas de diseño de 1.5 horas utilizando del método de Keifer and Chu o hietrograma
de Chicago, para una tormenta con periodo de retorno (Tr) de 2, 5, 10 25 y 50 años, utilizando un
coeficiente de avance de tormenta de r = 0.3 típico para Cali.
Tabla 2. Precipitación total
Periodo de retorno
Precipitación total (mm)
2.33 años
68.33
5 años
76.54
10 años
84.16
25 años
95.6
50 años
105.1
100 años
115.1
3.2.5
Precipitación Efectiva
La determinación de la precipitación efectiva se realizó a partir del hietograma de precipitación de
diseño realizado por el método de la intensidad instantánea (Chicago) a partir de curvas I.F.D base para
la zona occidental de Cali realizado por Forero y Franco (2003) con la abstracción de perdidas utilizando
la metodología del SCS (USA).
FIGURA. 7. CURVAS IFD OBTENIDAS A PARTIR DE LA DISTRIBUCION DE GUMBEL I
ZONA SUROCCIDENTAL
20
40
60
80
100
120
140
160
0
20
40
60
80
100
120
140
160
180
200
DURACION DE LA LLUVIA (minutos)
IN
T
E
N
S
ID
A
D
(
mm
/h
o
ra
)
Tr=5 años
Tr=10 años
Tr=20 años
Tr=50 años
Tr=100 años
Nueva Ecuación
1493,51Tr
0,134
i(mm/h)= --------------------
(t+11,782)
0,827

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
17
Oscar Darío Velásquez Mora
3.2.6
Número de Curva
Para determinar el volumen de escurrimiento, es necesario estimar del valor del número adimensional
de curva CN, el cual depende de características de la cuenca tales como uso de la tierra, condiciones
permeabilidad del suelo y condiciones de humedad de la cuenca en el momento de ocurrir la
precipitación.
En las zonas objeto de estudio la cobertura vegetal varía sustancialmente de un área a otra, debido a la
alta tasa de intervención antrópica, es por esta razón, que para la cuencas de la Quebrada La Viga se
asume Grupo AMC II, Grupo Hidrológico del suelo B, y CN = 66 . Este dato se extrajo de la tabla creada
por el SCS de los EE.UU., (1964) donde se encuentran los números de curva de escorrentía para usos
selectos de tierra agrícola, suburbana y urbana ajustados a las cuencas. La Tabla 3
,
muestra algunos
valores de CN.
Tabla 3. Núm
eros de curva de escorrentía para usos de tierra suburbano y urbano.
Uso de la tierra
Grupo hidrológico de suelos
A
B
C
D
Áreas impermeables:
98
98
98
98
Parqueaderos pavimentados, techos,
Autopistas , etc.(Excluyendo derecho a vía)
98
98
98
98
Tierra Incluyendo derecho de vía
72
82
87
89
Calles y caminos pavimentados
98
98
98
98
Bosques, troncos delgados, cubierta pobre
45
66
77
83
3.2.7
Tiempo de Concentración
Se denomina como el tiempo requerido por una gota de agua para fluir desde el punto más remoto de la
cuenca hasta el punto de interés.
En este proyecto el tiempo de concentración (tc) se calculó utilizando diferentes ecuaciones, tales como:
-
Onda cinemática
3
.
0
4
.
0
6
.
0
6
.
0
93
.
0
S
i
n
L
t
C
Ecuación 10. Tiempo de Concentración - Onda Cinemática

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
18
Oscar Darío Velásquez Mora
Donde:
L
Longitud del flujo superficial (pie)
N
Coeficiente de rugosidad de Manning
I
Intensidad de lluvia (plg/h)
S
Pendiente promedio del terreno (pie/pie)
-
Kirpich
385
.
0
77
.
0
*
*
0078
.
0
S
L
T
c
Ecuación 11. Tiempo de Concentración - Kirpich
Donde:
L
Longitud del canal desde aguas arriba hasta la salida (pie)
S
Pendiente promedio de la cuenca (pie/pie)
- Federal Aviation Administration
33
.
0
5
.
0
1
.
1
8
.
1
S
L
C
t
C
Ecuación 12. Tiempo de Concentración – Federal Aviation Administration.
Donde:
t
C
Tiempo de concentración (min).
L
Longitud del flujo superficial = 1148 pie
S
Pendiente de la superficie = 1.71 %
C
Coeficiente de escorrentía del método racional = 0.60
Tabla 4.
Valores de CN, Coeficiente de escorrentía (C ) y n adoptados para la quebrada La Viga.
Descripción
Valor
CN
60
Coeficiente escorrentía (C )método Racional
0.6
Coeficiente de Manning (n)
0.015

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
19
Oscar Darío Velásquez Mora
En la Tabla 5, se presenta el cálculo de los tiempos de concentración por las diferentes metodologías.
Tabla 5. Resultados
del tiempo de concentración (t
c
) – Quebrada La Viga.
Método para estimar t
c
- Q. La Viga
Tr: 10 años
Tr: 100 años
F.A.A
6.6
41.6
KERBYS
15
55.6
KIRPICH
3.9
20.2
Se tomó como parámetro de diseño el tiempo de concentración (t
c
) calculado con el promedio de
KERBYS, KIRPICH, F.A.A; debido a que estas ecuaciones se desarrollan a partir del análisis de onda
cinemática de escorrentía superficial en superficies desarrolladas. En el modelo de onda cinemática la
cuenca se representa como un plano inclinado con una rugosidad promedio de las rugosidades que
conforman su superficie (techos, pavimentos, patios). En el caso de la Quebrada La Viga, se asume un
coeficiente de rugosidad de Manning igual a 0.04.
3.3 CALCULO DE CAUDALES
3.3.1 Método del Hidrograma Triangular (Soil Conservation Service)
El histograma de diseño se calcula una vez se conozcan la profundidad de la precipitación P, la duración
T
d
, la longitud de la base y la altura.
Para el cálculo del hidrograma como una representación triangular adaptada para Colombia.
p
T
PE
A
Q
*
*
191
.
0
max
Ecuación 13. Caudal máx. – Soil Conservation Service.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
20
Oscar Darío Velásquez Mora
Donde:
Q
máx
Caudal máximo
A
Área de la cuenca
PE
Precipitación efectiva
T
p
Tiempo pico del hidrograma.
6
.
0
*
2
c
r
p
T
T
T
Ecuación 14. Tiempo Pico HIdrograma. – Soil Conservation Service.
Donde:
T
r
Duración de la lluvia efectiva
T
c
Tiempo de concentración
En la Tabla 6, se resume los caudales para un área de 10 hectáreas aguas arriba de la zona de estudio, con
15 minutos de tiempo de concentración y las precipitaciones de la Tabla 2.
3.3.2 Resultados de los Caudales Método S.C.S 50 y 100 Años
El caudal máximo, se evaluó por los dos métodos mencionados anteriormente para una frecuencia
media de 1:50 y 1:100 años, aunque el área de ambas micro cuencas es menor a 1.0 Km
2
, se adoptó
como caudal de diseño el arrojado por el hidrograma unitario del SCS, debido a que este método tiene
en cuenta parámetros que el método racional omite; además el método racional arroja como resultado
caudales muy altos, lo cual implicaría estructuras demasiado grandes y costosas.
Los resultados obtenidos se presentan en la Tabla 6, para periodos de retorno de 50 y 100 años.
Tabla 6. Caudales por el método S.C.S
Área
Hectárea
Tc, min.
Tr, años
CN
Caudal, m
3
/s
0.3494
34.94
41.6
50
0.7
1.48
0.3494
34.94
41.6
100
0.7
1.84

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
21
Oscar Darío Velásquez Mora
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
5
10
15
20
Q
(m
³/
s
)
T (h)
Figura 4. Caudal para Tr = 100 años
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
22
Oscar Darío Velásquez Mora
4
RESULTADOS Y DISCUSION
4.1 Modelo HEC-RAS 4.1.0
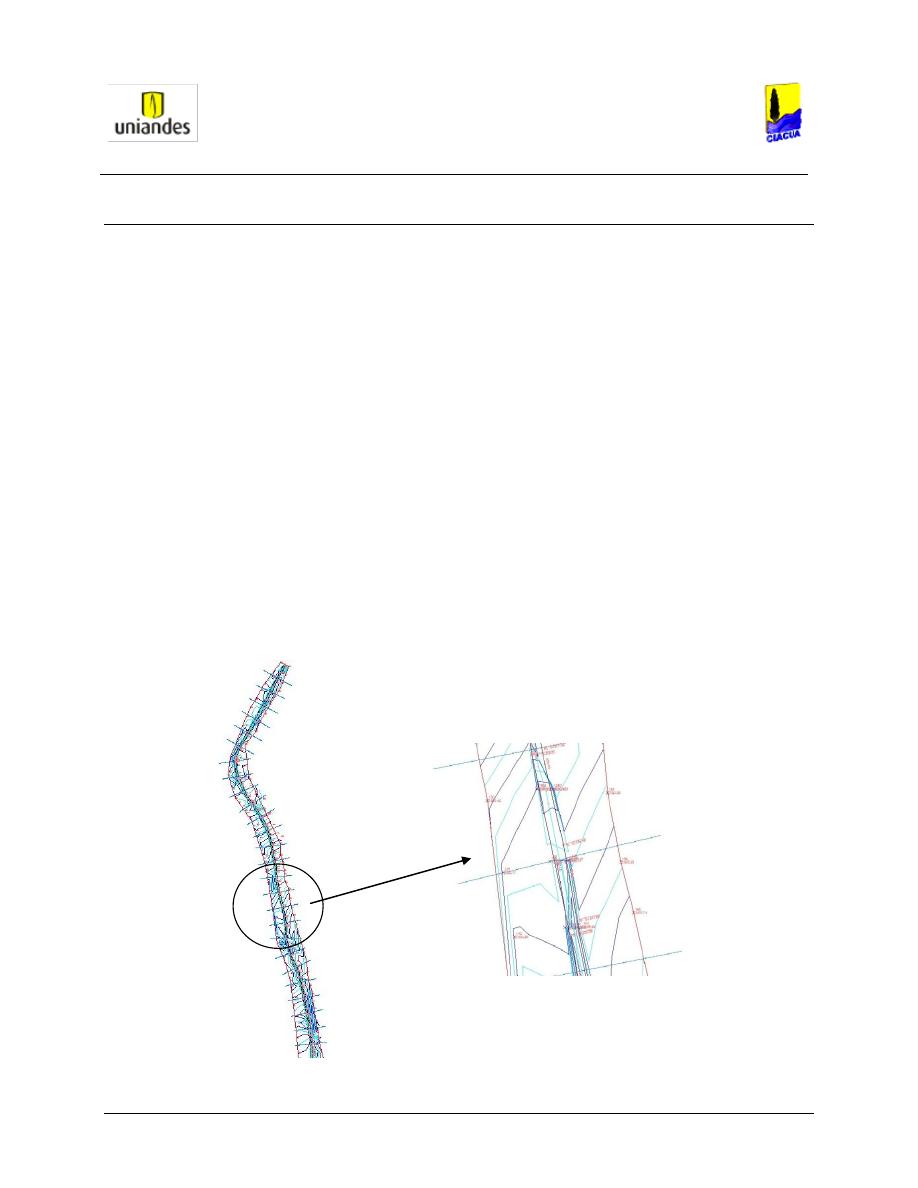
Para la generación del modelo en el programa HEC-RAS 4.1.0, se utilizó la información topográfica e
hidrológica de la zona de estudio a modelar.
El primer paso fue cargar las coordenadas X, Y, Z, en el programa Civil CAD 3D, el cual permite crear el
Modelo Digital de Terreno de la quebrada. Una vez generada la superficie, se procede a dibujar el eje de
alineamiento o eje principal del cauce de la quebrada, dicho eje se traza en sentido contrario al flujo.
Luego de generado dicho eje, se procede a crear las secciones trasversales, que para este caso se
trazaron cada 20 metros a lo largo del eje principal y con un ancho de 20 metros a la izquierda y derecha
de dicho eje.
Por último, se procede a dibujar el límite del canal principal, o sea el limite donde el flujo permanece
habitualmente en el canal, ésta información se puede obtener del levantamiento topográfico o de
imágenes satelitales.
Una vez realizado estos pasos, el programa AutoCAD Civil 3D, tiene un comando para exportar la
geometría de la quebrada a HEC-RAS, creando un archivo con extensión *.geo
Figura 5. Modelo Digital de Terreno
Generado Por AutoCAD Civil 3D
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
23
Oscar Darío Velásquez Mora
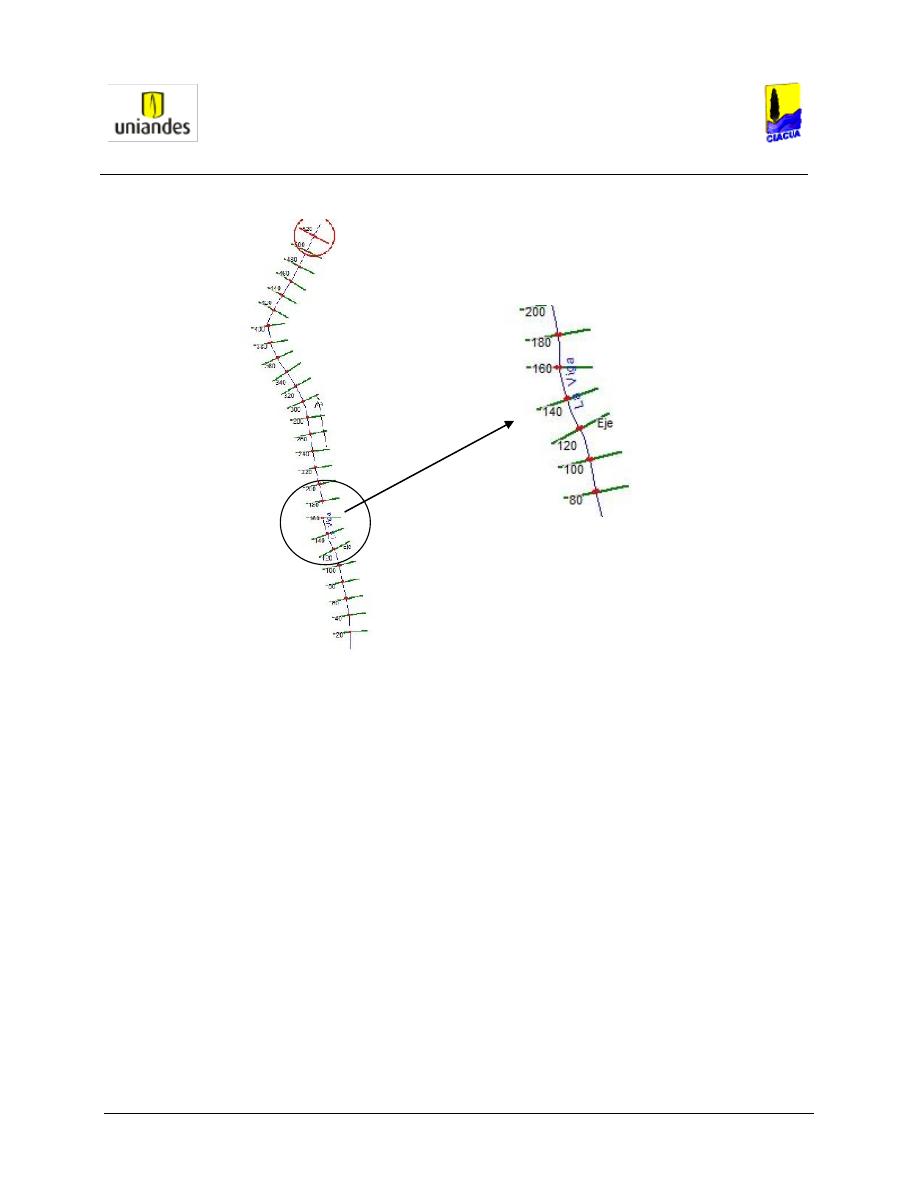
Luego de cargar la información de la geometría de la quebrada con sus respectivas secciones y rugosidad
de 0.015 para el fondo de la quebrada y 0.04 para el margen derecho e izquierdo, el paso siguiente es
cargar la información de caudales.
Para éste caso se asumió un estado de flujo permanente, y los caudales introducidos fueron los
obtenidos para una periodo de retorno de 50 y 100 años: 1.48 m
3
/s y 1.84 m
3
/s, respectivamente, y para
las condiciones de contorno, se utilizó en el campo de profundidad normal, la pendiente aguas arriba y
aguas debajo de la quebrada la cual es de 0.01.
El régimen de flujo utilizado para la simulación fue combinado, ya que se utilizaron datos aguas arriba y
aguas debajo de la pendiente de la quebrada.
Figura 6. Secciones Transversales Importadas en HEC-RAS
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
24
Oscar Darío Velásquez Mora
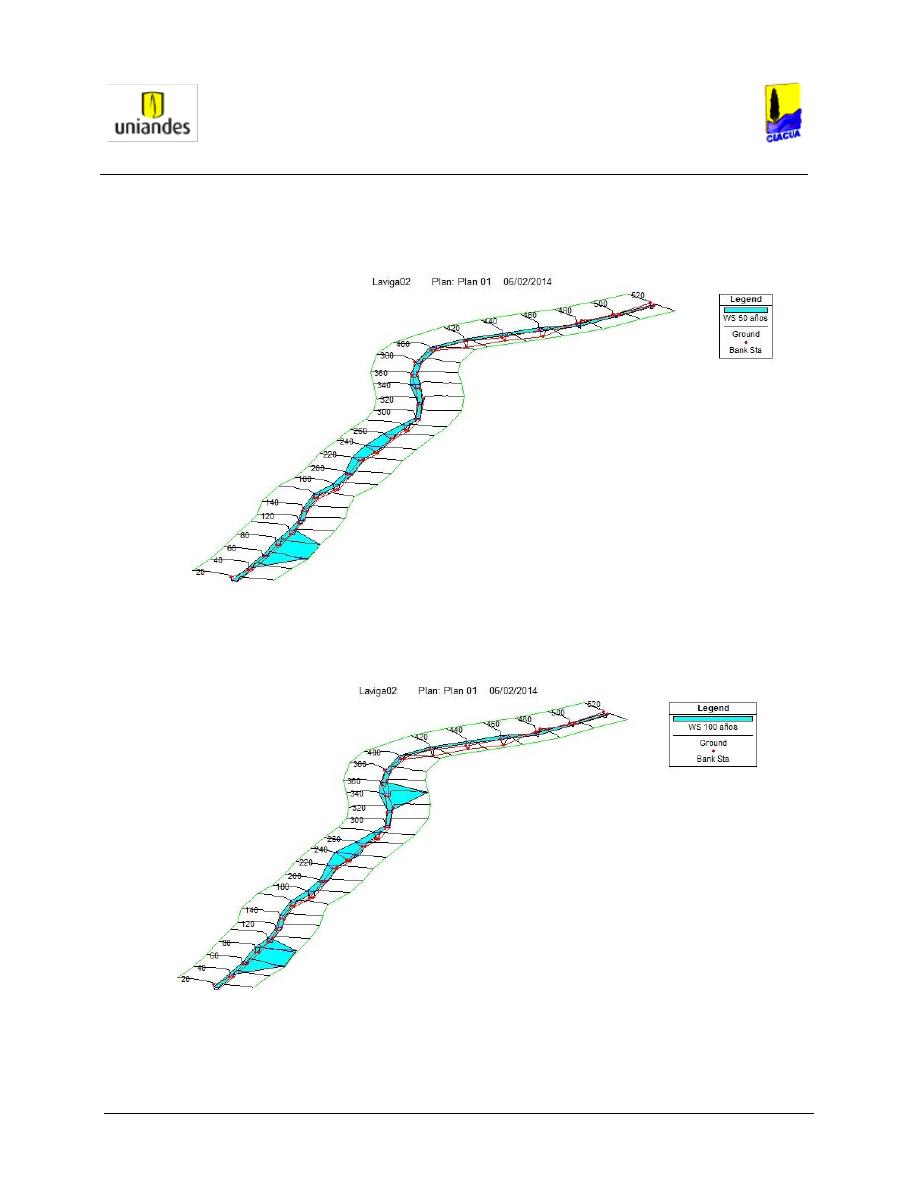
En la figura 7 y 8, se muestran los resultados arrojados para evento de precipitación con un tiempo de
retorno de 50 y 100 años, con unos caudales de 1.48 m
3
/s y 1.84 m
3
/s; respectivamente. Se asumió flujo
permanente.
Figura 8. Vista Evento de Inundación en 100 años y Q = 1.84 m
3
/s
Figura 7. Vista Evento de Inundación en 50 años y Q = 1.48 m
3
/s

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
25
Oscar Darío Velásquez Mora
4.2 Modelo River2D 0.95
El modelo hidráulico River2D, consta de cuatro módulos complementarios: R2D_Bed, R2D_Ice,
R2D_Mesh y el River 2D. Para la ejecución del modelo, dichos módulos deben ser ejecutados
secuencialmente.
4.2.1 Modulo R2D_Bed
Con ayuda del programa Autocad Civil 3D, se exportaron los puntos X, Y, Z del plano topográfico de la
quebrada a un archivo *txt, el cual debe estar ordenado como se muestra en la Tabla 7.
Tabla 7. Configuración de Datos de Entrada Topográficos Para el Modulo R2D_Bed
Se debe adicionar luego de la última línea de datos, el comando “No more nodes”, para que el modulo
R2D_Bed pueda cargar correctamente las coordenadas. Una vez realizado esto, se puede abrir el archivo
*.txt en el R2D_Bed generando la nube de puntos que conforman el canal y el terreno adyacente.
En este modulo, adicionalmente se debe configurar la rugosidad de fondo y también crear la frontera
computacional. Dicha frontera es la zona donde se han presentado inundaciones o donde se espera que
llegue la inundación con el caudal a modelar. El trazado de la frontera computacional se hace en sentido
contrario a las manecillas del reloj y a través de los nodos, terminando en el mismo nodo donde se
empezó el trazado.
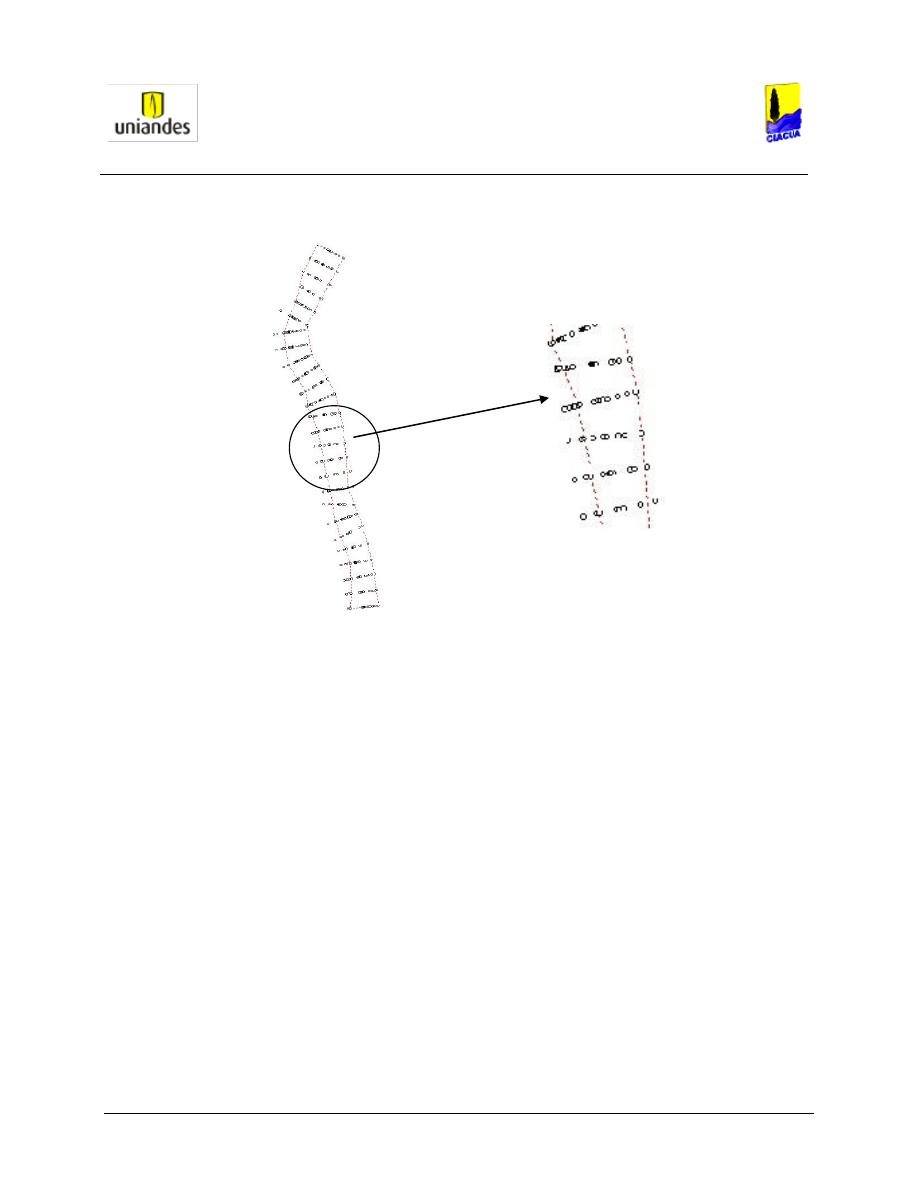
En la Figura 9, se muestra el archivo que se genera una vez terminado estos pasos en el modulo
R2D_Bed.
ID
X
Y
Z
Rugosidad
1
10911.685480 968987.989221 1001.692508 0.040000
2
10914.476234 968988.285408 1001.702493 0.040000
3
10914.992251 968988.340173 1001.700000 0.040000
4
10929.951815 968989.927854 1001.606254 0.040000
5
10931.114110 968990.051211 1000.801863 0.040000
6
10931.573784 968990.099996 1000.812106 0.040000
7
10932.475959 968990.195746 1000.832207 0.040000
No more nodes.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
26
Oscar Darío Velásquez Mora
4.2.2 Modulo R2D_Mesh
Este modulo permite la generación y edición de la malla computacional que finalmente servirá de
entrada al modelo hidráulico River2D. Este paso para algunos autores es considerado el “Arte Negro” de
la modelación bidimensional, ya que el objetivo es elaborar una malla suficientemente refinada en áreas
importantes manteniendo tiempos razonables de solución. (Arbeláez, J., 2010).
Los pasos a seguir son los siguientes:
Primero se carga el archivo *.bed, generado en el Modulo R2D_Bed, luego se discretiza la frontera
computacional que para este caso se escogió un valor de 5, después se especifican las condiciones de
frontera de entrada y salida. Para la frontera de entrada el programa pide el caudal para la frontera de
entrada y la cota de lámina de agua para la frontera de salida. Para el periodo de retorno de 50 años el
caudal de entrada es de 1.48 m
3
/s y la cota de lámina de agua a la salida de 1001.08 msnm. Para el
periodo de retorno de 100 años el caudal de entrada es de 1.84 m
3
/s y la cota de lámina de agua a la
salida de 1001.12 msnm.
Figura 9. Archivo Generado Por el Modulo R2D_Bed

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
27
Oscar Darío Velásquez Mora
Luego se llena el interior de la frontera computacional con nodos, el método escogido fue el “Uniform
Fill” con un valor de 3. Los nodos generados son triangulados las veces que se desee hasta obtener un
patrón de densidad de llenado que para éste caso, el valor de QI fue de 0.36. Los valores típicos
aceptados están entre 0.15 y 0.5 (Arbeláez, J. 2010).
Una vez obtenida una malla computacional aceptable, el archivo se graba en formato *.cdg. Al grabar el
archivo generado en este formato, el programa pregunta la cota de lamina de agua en la frontera de
entrada, dicho valor se obtuvo de los datos arrojados por el HEC-RAS, el cual fue de 1006.41 msnm, para
la condición de 50 años y 1006.45 msnm, para la condición de 100 años.
4.2.3 Ejecución del Modelo River2D
Para ejecutar el programa River2D, se debe abrir el archivo generado en el Modulo R2D_Mesh con
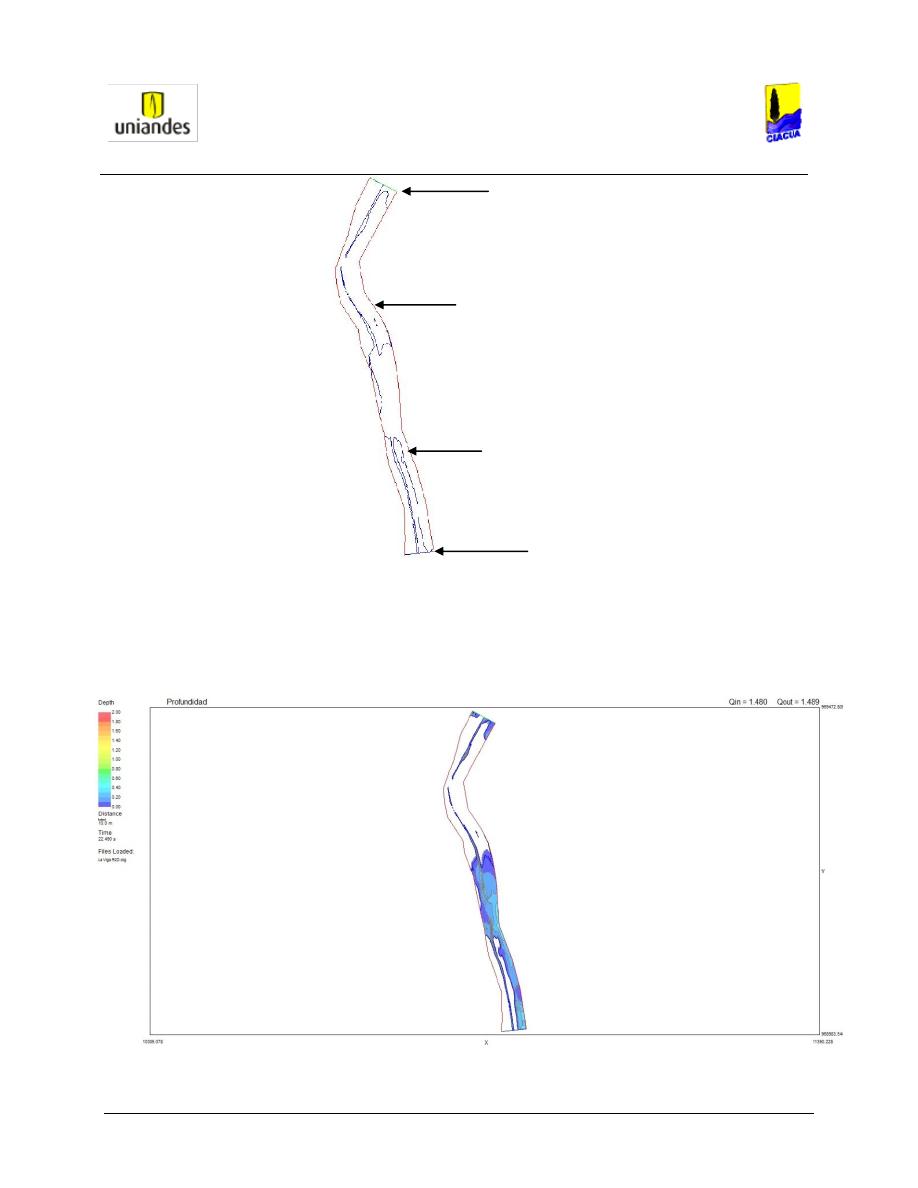
extensión *.cdg. En la Figura 11, se puede observar dos fronteras distintas: la frontera computacional
en rojo y el borde de agua en color azul, también se aprecia la frontera de entrada en color verde aguas
arriba del cauce y la frontera de salida aguas abajo en color azul.
Figura 10. Topografía y Triangulación Generada por el Modulo R2D_Mesh.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
28
Oscar Darío Velásquez Mora
El modelo fue ejecutado para flujo permanente, en la Figura 12 y 13, se muestran los resultados
arrojados para un evento de precipitación con un tiempo de retorno de 50 y 100 años, con unos caudales
de 1.48 m
3
/s y 1.84 m
3
/s; respectivamente.
Figura 12. Vista Evento de Inundación en 50 años y Q = 1.48 m
3
/s
Frontera de Entrada
Frontera Computacional
Borde de Agua
Frontera de Salida
Figura 11. Modelo River 2D

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
29
Oscar Darío Velásquez Mora
4.3 Discusión de Resultados
En el evento de inundación para 50 años, en el programa HEC-RAS muestra dos huellas de inundación;
una más marcada entre las secciones 40 a 100 y otra más leve entre las secciones 200 a la 280,
comparando este resultado con el arrojado por el programa River 2D, se puede observar que dicho
comportamiento se repite aproximadamente desde el mismo punto a ambos lados de la banca de la
Quebrada La Viga y con tendencia desbordarse sobre su margen derecha.
Para el evento de inundación de 100 años, en el programa HEC-RAS muestra ahora tres huellas de
inundación; las dos mencionadas anteriormente entre las secciones 40 a 100 y 200 a la 280, y la tercera
huella aparece entre las secciones 320 a 360, comparando este resultado con el arrojado por el
programa River 2D, se puede observar que dicho comportamiento se repite aproximadamente desde el
mismo punto a ambos lados de la banca de la Quebrada La Viga y con tendencia desbordarse sobre su
margen derecha al final del tramo de estudio.
Figura 13. Vista Evento de Inundación en 100 años y Q = 1.84 m
3
/s

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
30
Oscar Darío Velásquez Mora
5 CONCLUSIONES
Los resultados arrojados por este trabajo, concluyen que el modelo HEC RAS 4.0, resulto ser más
amigable y eficiente desde el punto de vista computacional, además permite varias maneras de
introducir la información topográfica de la zona de estudio, lo cual es muy importante a la hora de
modelar los datos de entrada hidrológicos.
Aunque, de acuerdo con varios autores, dicho modelo es limitado cuando se quiere representar
inundaciones, al no poder simular la difusión lateral de las ondas de crecida, y el manejo por secciones
de la topografía y no como una superficie. A pesar de esto, el modelo HEC-RAS, arrojó una aproximación
apropiada de las zonas de posible inundación de las zonas de estudio, la cual se pudo comparar con el
mostrado por River 2D.
El modelo River 2D, permite modelar con mayor precisión el comportamiento de flujo en la llanura de
inundación, pero computacionalmente, demanda más tiempo de cálculo y el manejo de los datos de
topografía se debe hacer lo más parecido posible a la realidad, ya que el módulo R2D_MESH, donde se
genera la malla computacional que sirve de entrada para el modelo hidráulico River 2D, en el caso de
este proyecto se debió hacer varios ensayos hasta llegar superficie lo más cercano a la realidad.
Con la adecuada información topográfica, hidrológica e hidráulica, los modelos hidráulicos son una
herramienta de alta confiabilidad para el análisis de eventos de inundación y que sus resultados estén
acordes con la realidad y sirvan para la correcta planificación y toma de decisiones a las autoridades de
cada región.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
31
Oscar Darío Velásquez Mora
6 RECOMENDACIONES
Para el proceso de obtención de una representación topográfica adecuada, en el modelo River 2D, se
recomienda el uso de batimetrías del cauce detalladas acompañadas de programas para la obtención de
un Modelo Digital del Terreno.
Al diseñar la malla computacional en el módulo R2D_Mesh, es necesario ser muy cuidadoso a la hora de
elaborar una malla suficientemente refinada en áreas importantes manteniendo tiempos razonables de
solución.
En el modelo HEC-RAS, se recomienda desarrollar técnicas apropiadas para el trazado e interpolación de
las secciones transversales, en casos de ríos de geometría compleja.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Comparación de Metodologías de Modelación de Inundaciones Fluviales en 1D
.
(HEC-RAS) y 2D (RIVER 2D). Caso de Estudio: Quebrada La Viga, Cali, Valle del
.
Cauca.
32
Oscar Darío Velásquez Mora
8 BIBLIOGRAFÍA
Ahmad, S., S.P. Simonovic, 1999. Comparison of one-dimensional and two-dimensional hydrodynamic
modeling approaches for Red river basin. Natural Resources Institute,. University of Manitoba, Canada.
Arbeláez, J., (2010). Evaluación de Herramientas Informáticas para el Análisis de Amenaza por
inundaciones, Tesis de Grado. Bogotá: Universidad de los Andes.
Castro, L,. & Willems, P., (2011).Desempeño de Modelos Hidráulicos 1D y 2D para la simulación de
inundaciones, Revista de la DIUC
Echeverry, J., (2012). Aproximaciones Metodológicas para el Análisis de Amenaza por Eventos de
Inundación, Tesis de Grado. Bogotá: Universidad de los Andes.
Forero, R., & Franco, D. (2003). Estudio Hidrológico E Hidrodinámico Del Sistema De Drenaje Pluvial De La
Zona Sur occidental En Santiago De Cali Mediante La Simulación numérica, Universidad del Valle.
Horrit, M., & Bates, P. (2002). Evaluatión of 1D and 2D numerical models for prediting river flood
inundation. Journal of Hydrology, 87-99.
Hydrologic Engineering Center. (2010) Hec RAS User´s Manual. Davis CA: US Army Corps of Engineers.
Steffler, P.M., & Blackburn, J. (2002). River 2D: Two-dimensional depth average model of river
hydrodynamicx and fish habitat. Introduction to depth averaged modeling and user´s manual.
Edmonton: Universidad de Alberta.
