
Universidad de los Andes
Facultad de Ingeniería
Departamento de Ingeniería Civil y Ambiental
Informe sujeto a revisión de Tesis II
Magíster en Ingeniería Civil
CAMBIO ÓPTIMO DE LA TOPOLOGÍA DE UNA RED CON EL FIN DE REDUCIR LOS
COSTOS OPERACIONALES DE REDES POR BOMBEO
Presentado por:
Ing. Sergio Andrés García Velandia
Asesor:
Ing. Juan Saldarriaga
Bogotá, Junio 2012

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
i
Tabla de contenido
Índice de Tablas ............................................................................................................................................. iii
Índice de Figuras ............................................................................................................................................ iv
Índice de Gráficas .......................................................................................................................................... vi
1
Introducción .......................................................................................................................................... 1
1.1
Objetivo General ........................................................................................................................... 2
1.1.1
Objetivos Específicos ............................................................................................................. 2
1.2
Descripción del sistema ................................................................................................................. 2
1.3
Contenido del informe .................................................................................................................. 3
2
Antecedentes ........................................................................................................................................ 5
2.1
Modelación hidráulica de RDAPs .................................................................................................. 5
2.1.1
Consideraciones iniciales ....................................................................................................... 5
2.1.2
Ecuaciones de conservación para RDAPs .............................................................................. 6
2.1.3
Método del gradiente hidráulico........................................................................................... 8
2.1.4
Resiliencia de la RDAP ......................................................................................................... 11
2.1.5
Potencia Unitaria de la red .................................................................................................. 13
2.1.6
Bombas ................................................................................................................................ 13
2.2
Optimización................................................................................................................................ 19
2.2.1
Programación lineal ............................................................................................................. 20
2.2.2
Método Simplex .................................................................................................................. 21
2.2.3
Teoría de Grafos .................................................................................................................. 22
2.3
Operación de los SB ..................................................................................................................... 25
2.3.1
Horarios de revisión y toma de decisiones (Richardson, 2011) .......................................... 25
2.3.2
Programación de los horarios de bombeo utilizando optimización ................................... 26
2.3.3
Programación de la operación de los SB utilizando Algoritmos Genéticos ......................... 28
3
Metodología general de análisis ......................................................................................................... 30
3.1
Información requerida para la modelación ................................................................................. 32
3.1.1
Información de Consumos................................................................................................... 32

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
ii
3.1.2
Cálculo hidráulico de la RDAP .............................................................................................. 33
3.1.3
Calibración de un modelo preliminar .................................................................................. 33
3.2
Ubicación del embalse secundario dentro de la RDAP ............................................................... 33
3.3
Determinación zona de influencia para el nuevo embalse ......................................................... 36
3.4
Definición red matriz asociada con el nuevo embalse ................................................................ 36
3.4.1
Solicitaciones generales para diseñar redes abiertas usando el algoritmo Árbol de
Expansión Mínima ............................................................................................................................... 37
3.5
Diseño optimizado de la red matriz ............................................................................................ 39
3.5.1
Definiciones iniciales ........................................................................................................... 40
3.5.2
Variables de Decisión .......................................................................................................... 40
3.5.3
Función Objetivo ................................................................................................................. 41
3.5.4
Restricciones ........................................................................................................................ 41
3.5.5
Conservación de la masa ..................................................................................................... 42
3.6
Evaluación del desempeño .......................................................................................................... 43
3.6.1
Desempeño hidráulico ........................................................................................................ 43
3.6.2
Desempeño económico ....................................................................................................... 44
4
Implementación de la metodología propuesta ................................................................................... 46
4.1
Software utilizado para la modelación ........................................................................................ 46
4.1.1
Redes ................................................................................................................................... 46
4.1.2
Xpress IVE ............................................................................................................................ 47
4.1.3
MS Excel............................................................................................................................... 49
4.1.4
ASIGNA V. 3.4 ..................................................................................................................... 50
5
Casos de Estudio .................................................................................................................................. 52
5.1
Información fundamental red Candelaria ................................................................................... 52
5.2
Información fundamental red Andalucía Alta ............................................................................. 55
5.3
Información fundamental red Bolívar ......................................................................................... 58
6
Resultados ........................................................................................................................................... 62
6.1
Aplicación de la metodología en los casos de estudio ................................................................ 62
6.1.1
Metodología aplicada a la red Candelaria ........................................................................... 62

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
iii
6.1.2
Metodología aplicada a la red Andalucía Alta ..................................................................... 77
6.1.3
Metodología aplicada a la red Bolívar ................................................................................. 87
7
Análisis de Resultados ......................................................................................................................... 94
7.1
Comparación hidráulica............................................................................................................... 94
7.2
Comparación económica ............................................................................................................. 96
8
Conclusiones generales ....................................................................................................................... 98
9
Recomendaciones para trabajos futuros .......................................................................................... 100
10
Bibliografía ..................................................................................................................................... 101

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
iii
Índice de Tablas
Tabla 2-1. Clasificación de las bombas de acuerdo con la velocidad específica (Saldarriaga, 2007). ......... 15
Tabla 5-1. Información principal red Candelaria. ........................................................................................ 52
Tabla 5-2. Información principal red Andalucía Alta. .................................................................................. 55
Tabla 5-3. Información principal red Bolívar. .............................................................................................. 58
Tabla 6-1. Información principal para la generación de la grilla de demanda. ........................................... 64
Tabla 6-2. Demanda acumulada (L/s) para cada celda de la grilla de densidad de demanda para la red de
Candelaria. ................................................................................................................................................... 66
Tabla 6-3. Ejemplo de estimación de los costos con formato Xpress-IVE para la formulación lineal del
diseño de la red matriz. ............................................................................................................................... 72
Tabla 6-4. Costos acumulados (L/s) para cada celda de la grilla de densidad de costo económico para la
red de Andalucía Alta. ................................................................................................................................. 79
Tabla 6-5. Costos acumulados (L/s) para cada celda de la grilla de densidad de demanda para la red de
Andalucía Alta.............................................................................................................................................. 89
Tabla 7-1. Análisis de sensibilidad para el número de tubos que conforman la red matriz respecto al
ahorro energético que producen. ............................................................................................................... 95
Tabla 7-2. Análisis de sensibilidad para el número de tubos que conforman la red matriz respecto al
ahorro económico que producen. ............................................................................................................... 97

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
iv
Índice de Figuras
Figura 2-1. Esquema de una RDAP. ............................................................................................................... 6
Figura 2-2. Definición del espacio de solución mediante restricciones lineales. ........................................ 22
Figura 3-1. Diagrama de flujo de la metodología general realizada. .......................................................... 31
Figura 3-2. Generación de la grilla de densidad para una RDAP ejemplo. .................................................. 35
Figura 4-1. Interfaz gráfica del software Redes (CIACUA, 2006). ................................................................ 47
Figura 4-2. Suite de optimización para el software Xpress –IVE. ................................................................ 48
Figura 4-3. Interfaz gráfica para el software Xpress –IVE............................................................................ 49
Figura 4-4. Interfaz gráfica para el software Microsoft Excel. .................................................................... 50
Figura 4-5. Interfaz gráfica para el software Microsoft Excel. .................................................................... 51
Figura 5-1. RDAP Candelaria, ubicada en el Departamento del Valle del Cauca. ....................................... 53
Figura 5-2. RDAP Andalucía Alta, ubicada en el Departamento del Valle del Cauca. ................................. 56
Figura 5-3. RDAP de Bolívar, ubicada en el Departamento del Valle del Cauca. ........................................ 59
Figura 6-1. (a) Red Candelaria graficada mediante el software REDES. (b) Generación de los nudos de
demanda de la RDAP mediante Excel. ........................................................................................................ 63
Figura 6-2. Grilla de densidad para la red Candelaria. ................................................................................ 65
Figura 6-3. Ubicación del embalse secundario en la celda seleccionada mediante la grilla de densidad. . 67
Figura 6-4. Potencia unitaria de la red Candelaria. ..................................................................................... 69
Figura 6-5. (a) Sector hidráulico de la red Candelaria graficada mediante el software REDES para el que el
nuevo embalse tiene influencia. (b) Generación de los nudos de demanda del sector hidráulico para el
cual el nuevo embalse tiene influencia mediante Excel. ............................................................................ 70
Figura 6-6. (a). Sector hidráulico de la red Candelaria. (b). Subconjunto perteneciente al sector hidráulico
definido como red matriz calculado mediante el algoritmo MST. .............................................................. 71
Figura 6-7. Declaración de conjuntos y parámetros de la formulación lineal en el software de
optimización Xpress – IVE. .......................................................................................................................... 73
Figura 6-8. Creación de las variables de decisión en Xpress – IVE. ............................................................. 74
Figura 6-9. (a) Red matriz diseñada. (b) Porcentaje de diámetro comercial presente en la red matriz. ... 75
Figura 6-10. Aplicación de la metodología a la red Candelaria. .................................................................. 76
Figura 6-11. (a) Red Andalucía Alta graficada mediante el software REDES. (b) Generación de los nudos
de demanda de la RDAP mediante Excel. ................................................................................................... 77
Figura 6-12. Grilla de densidad para la red Andalucía Alta. ........................................................................ 79
Figura 6-13. Ubicación del embalse secundario en la celda seleccionada mediante la grilla de densidad
para la red de Andalucía Alta. ..................................................................................................................... 80
Figura 6-14. Potencia unitaria de la red Andalucía Alta. ............................................................................. 82

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
v
Figura 6-15. (a) Sector hidráulico de la red Andalucía Alta graficada mediante el software REDES para el
que el nuevo embalse tiene influencia. (b) Generación de los nudos de demanda del sector hidráulico
para el cual el nuevo embalse tiene influencia mediante Excel. ................................................................ 83
Figura 6-16. (a). Sector hidráulico de la red Andalucía Alta. (b). Subconjunto perteneciente al sector
hidráulico definido como red matriz calculado mediante el algoritmo MST. ............................................. 84
Figura 6-17. Red matriz diseñada mediante el uso de programación lineal. La información presentada en
los tubos corresponde al diámetro en milímetros. ..................................................................................... 85
Figura 6-18. Red Andalucía Alta con el nuevo embalse y diámetros de la red matriz modificados. .......... 86
Figura 6-19. (a) Red Bolívar graficada mediante el software REDES. (b) Generación de los nudos de
demanda de la RDAP mediante Excel. ........................................................................................................ 87
Figura 6-20. Grilla de densidad para la red Bolívar. .................................................................................... 88
Figura 6-21. Ubicación del embalse secundario en la celda seleccionada mediante la grilla de densidad
para la red de Bolívar. ................................................................................................................................. 89
Figura 6-22. Potencia unitaria de la red de Bolívar. .................................................................................... 90
Figura 6-23. (a) Sector hidráulico de la red Bolívar graficada mediante el software REDES para el que el
nuevo embalse tiene influencia. (b) Generación de los nudos de demanda del sector hidráulico para el
cual el nuevo embalse tiene influencia mediante Excel. ............................................................................ 91
Figura 6-24. Red matriz para el nuevo embalse en la red Bolívar. .............................................................. 91
Figura 6-25. Red matriz diseñada utilizando programación lineal para el nuevo embalse en la red Bolívar.
..................................................................................................................................................................... 92
Figura 6-26. RDAP Bolívar, incluyendo el embalse agregado y los tubos cambiados dentro de la red matriz
definida. ....................................................................................................................................................... 93

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
vi
Índice de Gráficas
Gráfica 2-1. Curva de la bomba (Saldarriaga, 2007). ................................................................................... 16
Gráfica 2-2. Curva del sistema (Saldarriaga, 2007). .................................................................................... 17
Gráfica 2-3. Punto de operación de la bomba (Saldarriaga, 2007). ............................................................ 18
Gráfica 5-1. Demanda Base en los nudos en estado estable para la red de Candelaria. ............................ 54
Gráfica 5-2. Estado de presiones en los nudos en estado estable para la red de Candelaria. ................... 54
Gráfica 5-3. Estado de caudales en los tubos en estado estable para la red de Candelaria. ...................... 55
Gráfica 5-4. Estado de demandas en los nudos en estado estable para la red de Andalucía Alta. ............ 57
Gráfica 5-5. Estado de presiones en los nudos en estado estable para la red de Andalucía Alta. ............. 57
Gráfica 5-6. Estado de caudales en los tubos en estado estable para la red de Andalucía Alta. ................ 58
Gráfica 5-7. Estado de demandas en los nudos en estado estable para la red de Bolívar. ........................ 60
Gráfica 5-8. Estado de presiones en los nudos en estado estable para la red de Bolívar........................... 60
Gráfica 5-9. Estado de caudales en los tubos en estado estable para la red de Bolívar. ............................ 61
Gráfica 6-1. Potencia unitaria para los tubos pertenecientes a la red de Candelaria................................. 68
Gráfica 6-2. Estado de presiones en los nudos en estado estable para la red de Candelaria una vez se ha
aplicado la metodología. ............................................................................................................................. 75
Gráfica 6-3. Potencia unitaria para los tubos pertenecientes a la red de Andalucía Alta. ......................... 81
Gráfica 6-4. Potencia unitaria para los tubos pertenecientes a la red de Andalucía Alta. ......................... 87
Gráfica 6-5. Potencia unitaria para los tubos pertenecientes a la red de Bolívar. ...................................... 90
Gráfica 6-6. Estado de presiones en los nudos de la red Bolívar con el nuevo embalse. ........................... 92
Gráfica 7-1. Edad del agua en los nudos de la red Candelaria. ................................................................... 95
Gráfica 7-2. Comparación de costos entre a metodología y la operación tradicional. ............................... 96

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
1
1 Introducción
La operación de sistemas de bombeo (SB) en redes de distribución de agua potable (RDAP) pretende
satisfacer las condiciones hidráulicas requeridas por el sistema para dinámicas de operación particulares.
Se quiere cumplir con estas condiciones hidráulicas a un costo mínimo. Dentro de los costos asociados
con la operación de RDAP, los de bombeo resultan ser los más representativos (Richardson, 2011), por lo
que minimizar todos los costos asociados con los SB permite minimizar en gran medida los costos de las
RDAPs.
Particularmente en el caso de los SB, el costo más importante es el asociado con el consumo de energía
eléctrica, bien sea suministrada por combustibles fósiles, suministro local u otras fuentes. Se han
encontrado resultados considerables acerca de la cantidad de energía eléctrica consumida por las
bombas, como tener asociado el consumo del 20% de la electricidad mundial (Frenning, 2001).
Diferentes autores han realizado aproximaciones asociadas con la optimización de la operación de los SB
dentro de las RDAPs, por lo que podría considerarse resuelto el problema de la operación de una serie de
bombas para minimizar los costos de la energía. Se tiene entonces que para una estación de bombeo, de
la cual hacen parte diferentes bombas, no necesariamente iguales entre sí, la operación de estas bombas
de tal forma que el resultado genere el mínimo consumo eléctrico y se entregue suficiente altura
piezométrica al sistema.
Por este motivo, este trabajo de tesis no se enfoca en la operación de los diferentes SB pertenecientes a
las redes y supone de esta etapa un problema resuelto. Para el desarrollo de este trabajo, se utilizan
criterios adicionales a los ya considerados en la operación, y se busca encontrar el impacto sobre la red y
los costos económicos. En este sentido, se propone una metodología que considera cambios en la
topología de las RDAPs para disminuir mediante conceptos hidráulicos el uso de los SB y por ende, los
costos eléctricos asociados con su uso.
Para disminuir el uso de los SB, es necesario que la metodología propuesta en este documento considere
cambios en los diámetros de algunas tuberías pertenecientes a la red, así como la inclusión de nuevos
embalses y fuentes de almacenamiento y distribución. Se pretende entonces, mediante la ubicación de
nuevos embalses dentro de la red, disminuir la cantidad de agua que debe ser bombeada para satisfacer
la demanda presentada en la red en un instante de operación cualquiera. Particularmente se quiere que
bajo un escenario crítico el sistema esté en condiciones de otorgar la altura piezométrica suficiente para
distribuir agua a todos los nudos de consumo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
2
Para validar la metodología, se plantea una evaluación económica que cuantifique los resultados de ésta
sobre la operación de la RDAPs y se compara el beneficio económico que tiene la disminución de los SB
para un periodo de diseño dado.
1.1 Objetivo General
Proponer una metodología en la que se modifican condiciones hidráulicas de las RDAPs que permita
reducir la necesidad de bombeo del sistema, minimizando el costo eléctrico asociado con los SB en un
periodo de diseño específico y determinar su rentabilidad económica.
1.1.1 Objetivos Específicos
Determinar métodos que permitan cuantificar el desempeño hidráulico de los casos de estudio a
los cuales se les aplica la metodología propuesta.
Establecer los costos asociados con el mantenimiento y operación de las RDAPs para utilizarlos
Realizar un análisis de sensibilidad que permita determinar la influencia del periodo de diseño
dentro de la aplicación de la metodología propuesta.
Validar la metodología propuesta mediante una evaluación económica que reafirme o refute los
cambios que el método propone.
Determinar relaciones entre las variables hidráulicas y la evaluación económica de la inclusión de
embalses secundarios y cambios de diámetros como mecanismos para la disminuir el uso de SB.
Cuantificar el impacto hidráulico que tiene aplicar la metodología propuesta sobre la RDAP.
1.2 Descripción del sistema
Las RDAP se componen de series de tuberías, accesorios, válvulas, puntos de inspección y diferentes SB
que permiten llevar el agua hasta cualquier punto de la red. Este modelo está conectado a grandes
sistemas de captación y tratamiento de agua, y termina en la distribución del agua a los diferentes tipos
de edificaciones y usos que se pueden presentar. Una RDAP típica, tiene circuitos que permiten que el

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
3
sistema sea resiliente
1
y redundante para condiciones de operación y mantenimiento, así como de
posibles fallas que puedan presentarse. En este sentido, las RDAP se pueden considerar redes cerradas,
en las que el agua tiene más de un camino para llegar a cualquier punto.
Para modelar una RDAP, se supone una operación dinámica en la que deben ser consideradas las
variables de calidad de agua. Es decir, afectar la operación del sistema mediante el cierre o apertura de
válvulas, o el cambio en el uso de los SB afecta la concentración de cloro y este cambio debe ser
considerado en la operación general de la RDAP. En contraste, la condición energética de la red puede
considerarse constante, en cuyo caso el plano de alturas piezométricas resultante para el análisis de las
RDAP puede considerarse como la envolvente de todos los planos de altura piezométrica que puedan
presentarse.
Para los sistemas que conforman las RDAP, no es necesario considerar los micro - consumos propios de
los usuarios que acceden al servicio de agua potable. Esto se debe a que el nivel de agregación requerido
por las RDAP es lo suficientemente alto para considerar patrones fijos de demanda de agua. Bajo este
escenario, los SB conocen la cantidad de agua que debe ser bombeada en cada instante a la red, por lo
que la operación se limita únicamente al desarrollo de combinaciones en el uso de las bombas de tal
forma que se minimicen los costos económicos producto del uso de energía eléctrica.
Finalmente, la modelación física de la operación de RDAP, y por ende de los SB característicos, está
basada en ecuaciones físicamente basadas para el cálculo de las variables hidráulicas que caracterizan la
modelación. Se utiliza entonces la ecuación de Darcy-Weisbach en conjunto con la ecuación de
Colebrook-White para el desarrollo matemático de todas las variables.
1.3 Contenido del informe
Este informe presenta la metodología para suplir los objetivos planteados en Tesis I. En este sentido, se
realizó una recopilación de antecedentes sobre el tema de optimización en los SB de las RDAP.
Adicionalmente, se valida la metodología planteada con un caso de estudio de una red real colombiana.
Capítulo 1: Este capítulo presenta la introducción al problema planteado en este documento. Se dan los
conceptos generales, así como la definición de los objetivos.
1
Capacidad del sistema de responder a una falla.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
4
Capítulo 2: Presenta el marco conceptual que abarca el planteamiento del problema. Se introducen las
características principales de las RDAPs, así como de las bombas y se introducen algunas aproximaciones
al problema planteado.
Capítulo 3: Este capítulo explica la metodología desarrollada en el trabajo de tesis. Se muestra un
diagrama de flujo que resume la metodología y posteriormente cada paso es explicado en detalle.
Capítulo 4: Se desarrolla la implementación de la metodología en los diferentes paquetes de software
requeridos para su desarrollo.
Capítulo 5: Este capítulo presenta los casos de estudio trabajado en la investigación; contiene la
información básica de cada una de las redes.
Capítulo 6: Los resultados de aplicar la metodología son presentados en este capítulo. Se presentan
resultados hidráulicos y de calidad de agua para cada uno de los casos de estudio, así como resultados
económicos de implementar la metodología descrita en el Capítulo 3. Se presentan los pasos realizados
en cada uno de los casos de estudio para aplicar la metodología propuesta.
Capítulo 7: Una vez se tienen los resultados, este capítulo compara los resultados entre los diferentes
casos de estudio, así como una comparación entre la implementación de la metodología y no hacerlo.
Capítulo 8: Se presentan las conclusiones finales de esta investigación.
Capítulo 9: Se presentan algunas recomendaciones para trabajos futuros, así como posibles alternativas
a pasos específicos de la metodología propuesta.
Capítulo 10: Contiene la bibliografía utilizada en todo el desarrollo de este trabajo de tesis.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
5
2 Antecedentes
La operación de los SB supone un conocimiento adecuado del funcionamiento de las RDAPs, pues las
variables hidráulicas involucradas afectan directamente esta operación. Este capítulo introduce de
manera general los términos más relevantes en el estudio de los SB, abarcando los conceptos
hidráulicos, los conceptos de optimización utilizados a lo largo del trabajo y la interacción de éstos para
encontrar formas de operar los SB de tal forma que se cumplan las restricciones hidráulicas bajo un
costo económico mínimo.
2.1 Modelación hidráulica de RDAPs
Los métodos de modelación de redes de distribución de agua potable permiten calcular las variables
hidráulicas que son utilizadas, lo que permite un análisis profundo del funcionamiento de la misma. En la
actualidad, gracias a la capacidad computacional existente, es posible realizar operaciones que
demanden un gran espacio de memoria en un tiempo razonable, por lo que se presentará únicamente
los métodos más eficientes en términos de velocidad de convergencia, que tienen como limitante una
serie de operaciones matriciales. Dadas las condiciones computacionales actuales los cálculos pueden
realizarse de manera exitosa. De este hecho se sigue también el uso de las ecuaciones y métodos
físicamente basados, ya que su cálculo no resulta ser un problema.
2.1.1 Consideraciones iniciales
Como se mencionó en la descripción del sistema, las RDAP están conformadas por diferentes elementos,
como lo son las bombas, tanques de almacenamiento, embalses, válvulas, nudos de consumo y una red
de tuberías que conectan estos elementos. El propósito de las RDAP es suministrar agua bajo una
condición de presiones que satisfaga los requerimientos de cada uno de los usuarios del sistema (Mays,
Hydraulic Design Handbook, 1999).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
6
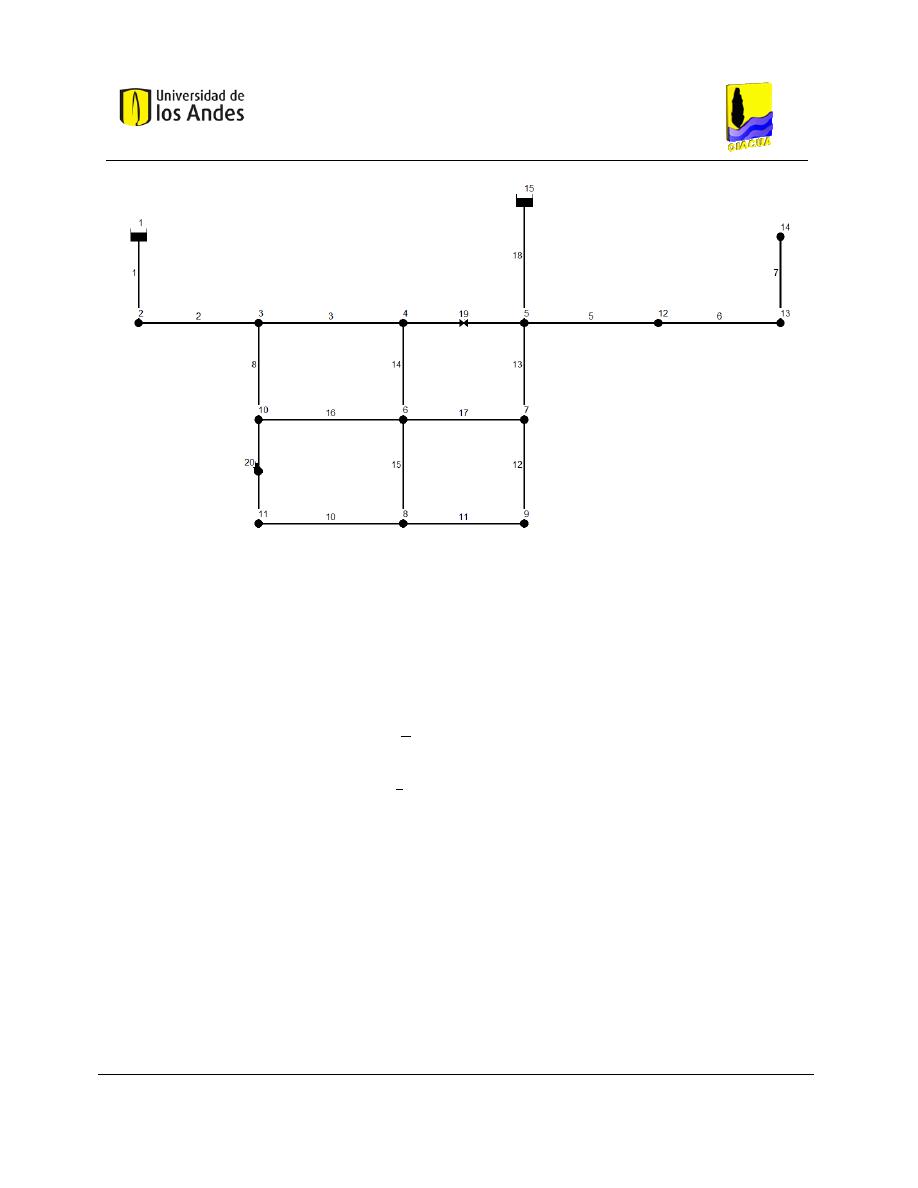
Figura 2-1. Esquema de una RDAP.
El caudal que pasa por cada uno de los tubos que conforman la RDAP depende de los consumos
particulares que se estén requiriendo dentro del sistema. Adicionalmente, la altura piezométrica en cada
uno de los nudos es la altura de presión más la elevación topográfica. La Ecuación 1 presenta esta
situación:
Ecuación 1
donde h representa la altura piezométrica,
la altura de presión y z la elevación topográfica.
2.1.2 Ecuaciones de conservación para RDAPs
Las ecuaciones que modelan adecuadamente las RDAPs están fundamentadas en las ecuaciones de
conservación de masa y conservación de energía. Para el primer caso, se tiene la situación en la que se
conoce el caudal que está siendo demando por el sistema, así como mediciones para establecer el caudal
que está entrando en la red para un periodo de tiempo dado. Por lo que cualquier diferencia puede estar
asociada con fugas o conexiones ilegales dentro de la red. Se supone además que todo es sistema se

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
7
encuentra presurizado, por lo que la situación de almacenamiento no es considerada para el balance de
masa dentro de las tuberías.
Se tiene entonces en términos generales para un nudo:
∑
∑
Ecuación 2
donde
representa el caudal que llega a ese nudo,
el caudal que continua al siguiente
tubo (o siguientes tubos) y
el caudal de consumo propio del nudo para ese instante de
tiempo.
Para el caso de la conservación de la energía, se supone que la diferencia de energía entre dos nudos
consecutivos de la red está constituida por las pérdidas de energía debidas a las pérdidas por fricción, y
aquellas asociadas con los accesorios y cambios de sección (pérdidas menores).
2.1.2.1 Modelación de las pérdidas por fricción
Se obtuvo la ecuación desarrollada por Darcy-Weisbach mediante el uso del análisis dimensional, que
tiene a las pérdidas de energía por fricción dentro de la tubería como función de la velocidad, rugosidad,
diámetro y fluido. En la Ecuación 3 se presenta la ecuación denominada Darcy-Weisbach (Saldarriaga,
2007).
Ecuación 3
en la que f corresponde al factor de fricción de Darcy, factor que es función del número de Reynolds y de
la rugosidad relativa, l es la longitud de la tubería, d el diámetro de la misma, v la velocidad del flujo y g
la gravedad.
Para poder obtener el factor de fricción de Darcy f, se utiliza la ecuación desarrollada por los
investigadores ingleses C.F. Colebrook y H. White (Saldarriaga, 2007).
√
(
√
)
Ecuación 4

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
8
2.1.2.2 Modelación de las pérdidas menores
En redes de distribución de agua potable existen accesorios que producen pérdidas de energía
adicionales a las contempladas anteriormente. Estas son producidas por válvulas, codos, o diferentes
dispositivos utilizados para la operación del sistema. Estas pérdidas de energía se calculan por medio de
la Ecuación 5 mostrada a continuación (Saldarriaga, 2007):
∑
Ecuación 5
donde Km es un coeficiente de pérdidas menores que depende del accesorio que se esté utilizando en la
red y generalmente es suministrado por el fabricante, v es la velocidad media del flujo y g es la
aceleración de la gravedad.
2.1.3 Método del gradiente hidráulico
Método matricial desarrollado por los profesores E.Todini y E.P.O Connell, planteando lo siguiente:
“las ecuaciones de energía individuales para cada tubo se combinan con las ecuaciones de masa
individuales en cada unión con el fin de obtener una solución simultánea tanto de los caudales en las
tuberías como de las alturas piezométricas en los nudos.” (Saldarriaga, 2007)
Para utilizar este método se requiere garantizar la conservación de masa en cada uno de los nudos, así
como el balance energético en cada circuito, para lo cual se supone una condición de flujo permanente.
El método supone la condición de flujo permanente, que garantiza que se cumplan las ecuaciones de
conservación de masa en cada uno de los nudos de la red y la ecuación de conservación de energía en
cada uno de sus circuitos.
De manera general se tiene que las pérdidas que afectan la red están expresadas en la Ecuación 6, en
donde se consideran efectos por accesorios y posibles bombas (Saldarriaga, 2007):
Ecuación 6
Para el caso particular de la ecuación de Darcy-Weisbach, el exponente n toma el valor de 2.0, mientras
que los coeficientes , y corresponden a parámetros característicos del tubo, las válvulas y las
bombas. Para poder definir el método del gradiente es necesario describir la topología de la red de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
9
distribución de agua potable en forma matricial, razón por la cual se introducen las siguientes
definiciones (Saldarriaga, 2007):
NT
:
Número total de tuberías en la red.
NN
:
Número de nudos con altura piezométrica definida.
[A12] :
Matriz de conectividad asociada a cada uno de los nudos de la red. Su
dimensión es NNxNT.
NS
:
Número de nudos de altura piezométrica fija o conocida.
[A10] :
Matriz topológica tubería a nudo para los NS nudos de cabeza fija. Su
dimensión es NT x NS.
De acuerdo con estas definiciones, es posible definir la pérdida de altura piezométrica entre dos nudos
conectados por una tubería como lo presenta la Ecuación 7:
[ ][ ] [ ][ ] [ ][
]
Ecuación 7
donde la matriz [A11] se define como sigue
[ ]
[
]
y los demás términos son
[Q]
:
Vector de caudales con dimensión NTx1.
[H]
:
Vector de alturas piezométricas desconocidas con dimensión NNx1.
[H
0
]
:
Vector de alturas piezométricas fijas con dimensión NSx1.
Para mantener la continuidad en todos los nudos de la red debe cumplirse la Ecuación 8 (Saldarriaga,
2007):

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
10
[ ][ ] [ ]
Ecuación 8
donde:
[A21] :
Transpuesta de la matriz [A12].
[q]
:
Vector de consumo (o demanda) en cada nudo de la red con dimensión
NNx1.
En términos matriciales las Ecuaciones 6 y 7 pueden escribirse como sigue:
[
[ ] [ ]
[ ]
[ ] ] [
[ ]
[ ]] [
[ ]
[
]
[ ]
]
Ecuación 9
La Ecuación 9 no es lineal, por lo que su desarrollo será una sucesión de valores lineales que permitan
una aproximación aceptable. Para esto se utilizará una expansión truncada de una serie de Taylor. Dada
esta restricción en la modelación del problema, se requiere hacer este procedimiento varias veces de
forma iterativa con el fin de mejorar en cada iteración los resultados a unos valores convergentes.
Aplicando el operador gradiente se obtiene (Saldarriaga, 2007):
[
[ ]
[ ]
[ ]
[ ] ] [
[ ]
[ ]] [
[ ]
[ ]]
Ecuación 10
donde:
[N]
:
Matriz diagonal (n1,n2,……,nNT) con dimensión NTxNT
[A11] :
Matriz con dimensión NTxNT definida como:
[ ]
[
]
Ecuación 11
Cada iteración tiene asociado un error producido por el truncamiento de la función original, por lo que
se tienen desbalances energéticos [dE] en los tubos y desbalances de masa [dq] en los nudos. Estos
desbalances pueden ser representados como sigue:
[ ] [ ][
] [ ][
] [ ][
]
Ecuación 12
y
[ ] [ ][
] [ ]
Ecuación 13

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
11
Para cada iteración de la Ecuación 13 se tiene que:
[ ] [
] [
]
Ecuación 14
y
[ ] [
] [
]
Ecuación 15
La solución es calculable mediante la siguiente ecuación:
[
[ ]
[ ]] [
[ ][ ] [ ]
[ ]
[ ]
]
[
[ ]
[ ]]
Ecuación 16
Los cálculos de caudales y presiones quedan entonces:
[
] {[ ]([ ][ ]
)
[ ]}
{[ ]([ ][ ]
)
[ ][
]
[ ][
] [ ][
] [ ] }
Ecuación 17
y
[
] { [ ] [ ][ ]
[ ] [ ]
(([ ][ ]
)
[ ][
] [ ][
] )}
Ecuación 18
2.1.4 Resiliencia de la RDAP
El concepto de Resiliencia de la RDAP fue introducido por Ezio Todini en el año 2000; lo definió como
“… la capacidad intrínseca que tiene una RDAP para superar fallas repentinas y se mide como la
proporción entre el excedente de potencia que es entregado a los usuarios y la máxima potencia que puede
ser disipada en la red cuando se cumplen exactamente los criterios y condiciones de diseño. El índice de
resiliencia proporciona una medida general de la redundancia del sistema: un mayor valor del índice de
resiliencia corresponde a una mayor redundancia.”

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
12
2.1.4.1 Índice de Resiliencia Ir
El Ir de una RDAP se define como una función que relaciona la potencia a disipar objetivo (
obj
dis
P
) con la
potencia real disipada (
real
dis
P
)
obj
dis
real
dis
r
P
P
I
1
Ecuación 19
donde:
r
I
: Índice de resiliencia.
real
dis
P
: Potencia disipada por la red real disipada.
obj
dis
P
: Potencia entregada característica de que en cada nodo la altura de presión sea mínima.
De forma general se tiene que el índice de resiliencia está dado por:
∑
[∑
∑
] ∑
Ecuación 20
donde:
: Demanda real del nodo i.
: Altura piezométrica requerida en los nodos de demanda.
: Altura mínima piezométrica requerida en los nodos de demanda.
: Caudal de entrada suministrado por el embalse i.
: Altura de entrada suministrado por el embalse i.
: Potencia por unidad de peso suministrada por la bomba i.
: Número de bombas propias de la red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
13
2.1.5 Potencia Unitaria de la red
La Potencia Unitaria PUTi se define como la altura piezométrica gastada en una tubería dada, es decir, la
diferencia de alturas piezométricas entre los nudos que conforman ese segmento de tubería, multiplicada
por el caudal que está pasando por ese tubo:
)
(
*
,
,
fin
i
inicio
i
i
UTi
q
h
q
P
Ecuación 21
Los pasos para aplicar la esqueletización con la Potencia Unitaria como costo hidráulico se presentan a
continuación:
2.1.6 Bombas
Las bombas hacen parte fundamental de las RDAP, pues permiten introducirle energía al sistema para
que este pueda funcionar en escenarios desfavorables en términos de altura piezométrica. Las bombas
son entonces los elementos principales de los SB, y en general existen varias tipos de bombas y
consideraciones que deben ser mencionadas.
2.1.6.1 Definiciones iniciales
De acuerdo con el Hydraulics Institute (HI), algunos de los términos necesarios para referirse a los SB son
los siguientes:
Bomba centrífuga: Máquina cinética capaz de convertir energía mecánica en energía hidráulica
mediante actividad centrífuga.
Rango de operación permitido: Rango de caudales definido por el fabricante de la bomba en el cual se
cumplen las restricciones de velocidad, cavitación, calentamiento mecánico, vibración, ruido, deflexión
de los ejes de la bomba, fatiga y en general cualquier limitación física para el adecuado funcionamiento
de la bomba.
Datum: Plano de referencia horizontal que permite tener una referencia para las diferentes mediciones y
alturas de presión que se dan en el manejo de bombas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
14
Altura: Para este documento, se considera la altura como una expresión de energía del líquido que
quiere ser bombeado respecto a un nivel de referencia dado (datum). Las unidades para la altura se
expresan en energía por unidad de peso del fluido.
Altura de presión atmosférica h
atm
: Presión atmosférica del sitio donde se encuentra ubicada la bomba
expresada en m del líquido de referencia.
Capacidad: Volumen total por unidad de tiempo en condiciones de succión por parte de la bomba.
Punto de mejor eficiencia (BEP
2
): Punto de operación de la bomba bajo la cual la eficiencia es máxima.
Altura de elevación: Energía potencial del líquido en relación con el datum escogido.
Altura de fricción: Energía hidráulica requerida para superar la resistencia debido a la fricción del
sistema de tuberías que conforman la RDAP y mover el líquido que se esté bombeando.
2.1.6.2 Bombas en sistemas de tuberías
De acuerdo con Saldarriaga (2007) las bombas pueden clasificarse como siguen:
Bombas centrífugas: Aquellas bombas en donde el agua entra de forma axial pero sale radialmente. Este
tipo de bombas puede manejar altas alturas piezométricas pero caudales bajos.
Bombas de flujo axial: Aquellas bombas en donde el agua entre y sale de forma axial. Para este tipo de
bombas, se tienen alturas piezométricas bajas pero caudales altos.
Bombas de flujo mixto: Aquellas bombas en donde el flujo entra axialmente pero la salida tiene
componentes tanto axiales como radiales.
Para establecer cuantitativamente el tipo de bomba que se tiene, se utiliza un parámetro dimensional
denominado velocidad específica (Saldarriaga, 2007):
Ecuación 22
donde:
2
BEP por sus siglas en inglés para Best Efficiency Point.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
15
Q = Caudal en galones americanos por minuto (gpm).
H= Altura piezométrica total de la bombas en pies.
N = Velocidad rotacional en revoluciones por minuto (rpm).
A manera general, es posible determinar aproximadamente el tipo de bomba con los rangos para la
velocidad específica presentados en la Tabla 2-1.
Tabla 2-1. Clasificación de las bombas de acuerdo con la velocidad específica (Saldarriaga, 2007).
Tipo de Bomba
Rango Ns
Centrífuga
500 a 2000
Flujo mixto
2000 a 7000
Flujo axial
7000 a 15000
Para la operación de la bomba es necesario ponderar dos factores. En primer lugar un aumento de la
velocidad específica supone un aumento en la eficiencia de las bombas. Sin embargo, los componentes
mecánicos de las bombas están expuestos a un desgaste mayor, por lo que el punto de operación debe
ser un punto intermedio.
En términos de la conservación de la energía, se puede definir la altura de la bomba como la suma de
todos los componentes energéticos presentes en el sistema. De manera general se tiene:
∑
∑
Ecuación 23
donde:
H
m
= Altura piezométrica total del sistema.
H
T
= Altura topográfica que debe ser vencida por la bomba.
h
f
= Pérdidas por fricción de las tuberías.
h
m
= Pérdidas menores en las tuberías por accesorios.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
16
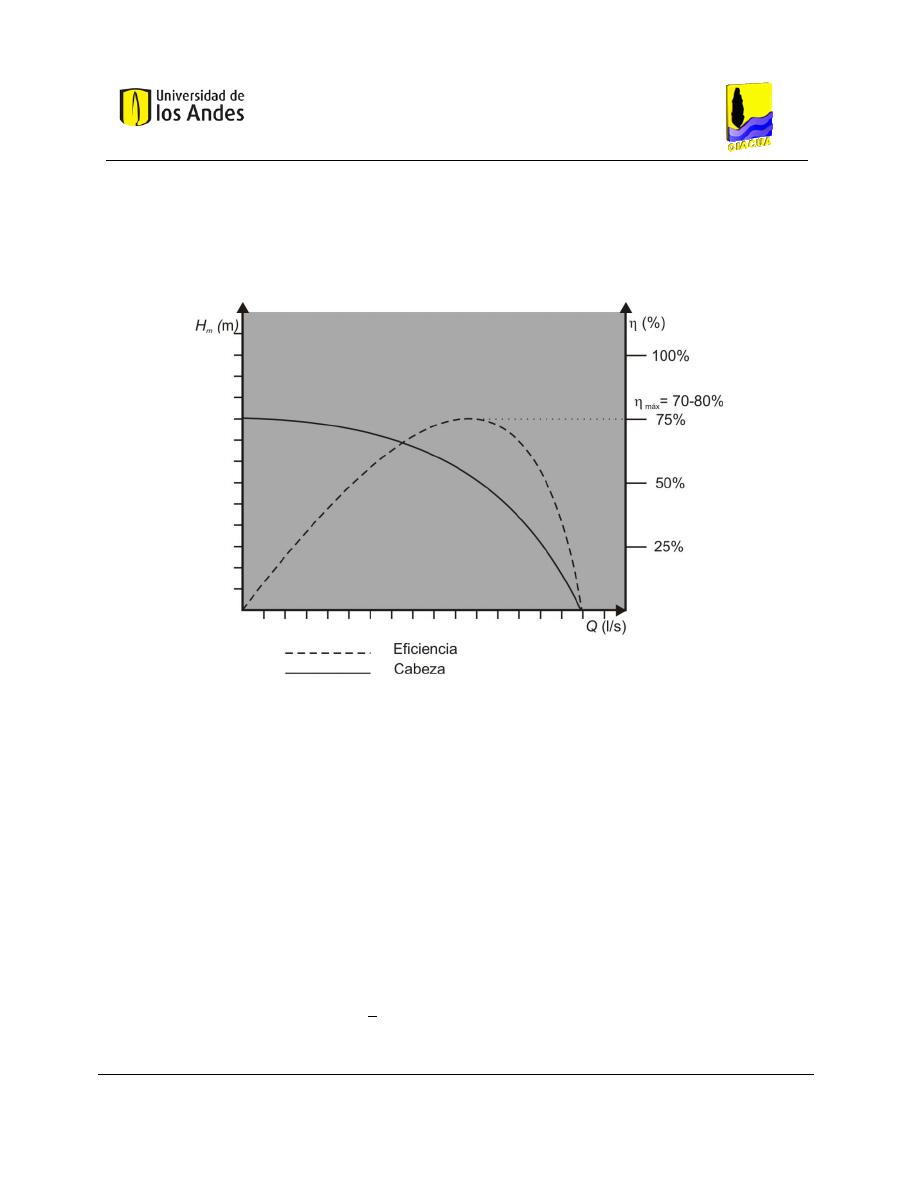
2.1.6.3 Curvas de la bomba
Las curvas de la bomba se caracterizan por graficar caudal contra altura piezométrica total y son propias
de cada bomba, motivo por el cual esta es información suministrada por el fabricante.
Gráfica 2-1. Curva de la bomba (Saldarriaga, 2007).
En términos generales, es posible aproximar la curva de la bomba a una ecuación cuadrática de la forma
(Saldarriaga, 2007):
Ecuación 24
Para obtener los parámetros desconocidos de la Ecuación 33 basta con reemplazar en tres puntos
diferentes la curva entregada por el fabricante, con lo que es sistema de ecuaciones tiene solución.
Para el cálculo de la potencia consumida por la bomba para un punto cualquiera de operación se tiene la
siguiente ecuación (Saldarriaga, 2007):
Ecuación 25
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
17
donde:
= Eficiencia conjunta bomba – motor.
Q = Caudal de operación de la bomba.
Hm = Altura piezométrica de operación de la bomba.
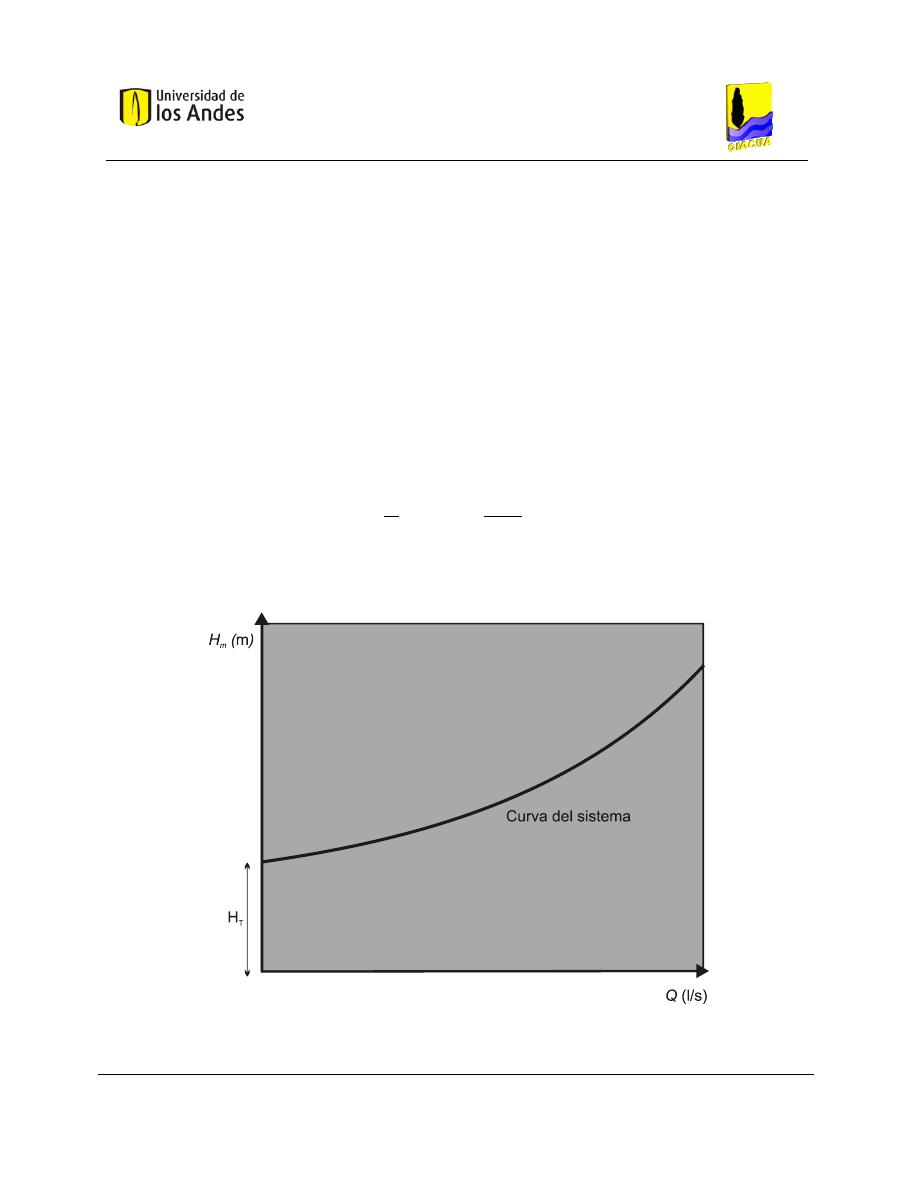
2.1.6.4 Curvas del sistema
La curva del sistema relaciona las condiciones de conservación de energía planteadas en la Ecuación 23,
obteniendo la siguiente ecuación (Saldarriaga, 2007):
(∑
∑
)
Ecuación 26
La forma general se presenta a continuación:
Gráfica 2-2. Curva del sistema (Saldarriaga, 2007).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
18
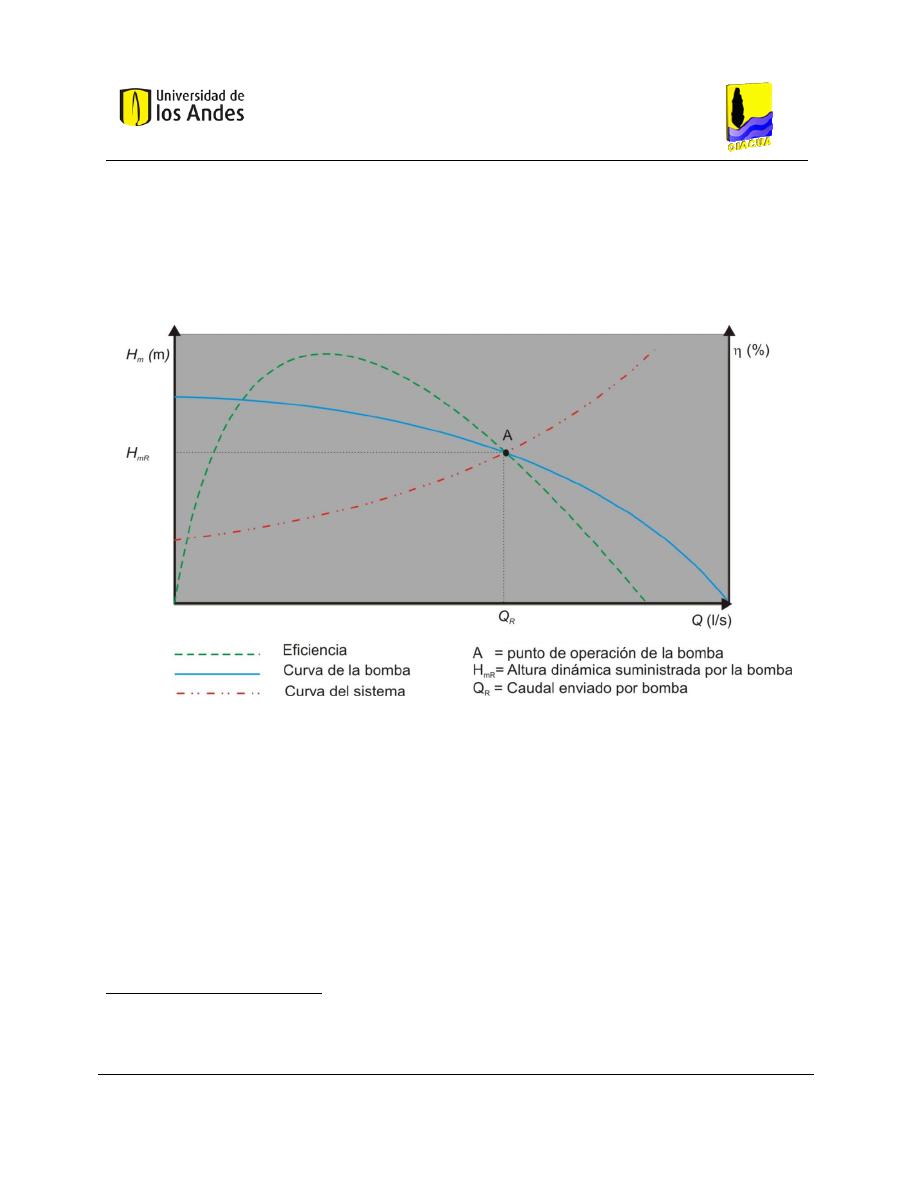
2.1.6.5 Punto de operación de la bomba
El punto de operación de la bomba se encuentra en el punto de intersección de la curva del sistema y la
curva de la bomba, pues es el momento en el que, para las condiciones inherentes al sistema, la bomba
puede suplir adecuadamente los requerimientos de energía.
Gráfica 2-3. Punto de operación de la bomba (Saldarriaga, 2007).
2.1.6.6 Altura de succión NPSH
3
Si la presión en la entrada o la salida de la bomba se encuentran por debajo de la presión atmosférica,
pueden presentarse eventos de cavitación
4
, fenómeno que afecta el desempeño de la bomba por
disminuir su capacidad.
La altura que se tiene por encima de la presión de vapor NPSH es (Saldarriaga, 2007):
3
Sigla en inglés para Net Positive Suction Head.
4
Fenómeno hidrodinámico que genera burbujas de vapor de agua (o cualquier otro fluido) por variaciones drásticas
en la presión.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
19
Ecuación 27
Rescribiendo los términos, la Ecuación 27 puede escribirse como:
Ecuación 28
donde:
Pa = Presión atmosférica absoluta.
Pv = Presión de vapor.
El término Hs se define de la siguiente forma:
Ecuación 29
donde:
h
s
= Altura del rotor de la bomba con respecto al nivel del agua en el tanque o embalse desde donde se
está succionando el caudal.
h
me
= Pérdidas menores causadas a la entrada de la tubería de succión.
h
fs
= Pérdidas por fricción en la tubería de succión.
= Altura de velocidad en la tubería de succión.
H
s
= Altura manométrica de succión.
2.2 Optimización
La optimización se refiere a la capacidad de encontrar la mejor solución posible para una formulación
dada. Se considera un espacio de solución claramente definido y finito, y una función objetivo
claramente identificable.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
20
Existen diferentes alternativas para optimizar una modelación particular. Por ejemplo, la optimización
multi-objetivo, que considera varias funciones objetivo para encontrar un punto en el cuál la interacción
de las mismas produzca la máxima eficiencia sobre el problema. Adicionalmente, existen optimizaciones
lineales y no lineales, que cambian su aproximación a la solución dependiendo de la naturaleza del
problema. Particularmente, se discute solamente el caso de optimización lineal, pues los problemas
abordados en este trabajo permiten una aproximación lineal.
2.2.1 Programación lineal
La programación lineal hace referencia a una rama de la optimización en la que se pueden solucionar
grandes problemas y ha hecho parte del proceso de decisión en la actualidad. La toma de decisiones en
el caso en el que se puede asegurar que la decisión tomada representa la mejor de todas las
posibilidades es un evento que permite la optimización. Este método, tuvo su mayor auge en 1947,
época posterior de la Segunda Guerra Mundial. En este periodo, la computación tuvo avances
considerables que permitían considerar elementos que anteriormente no podrían ser contemplados por
incapacidad computacional
(Dantzig, 2002).
2.2.1.1 Supuestos de la programación lineal
Para que un problema de optimización pueda ser considerado dentro de la categoría de solución
mediante la programación lineal, es necesario que una serie de supuestos se cumplan (Bazaraa, 2010):
Proporcionalidad: Si el valor de una variable de decisión, x
j
, se multiplica por una constante α, entonces
la contribución de dicha variable en la función objetivo (c
j
x
j
) y en las restricciones (a
ij
x
j
) también se
multiplica de acuerdo con α.
Aditividad: El valor de la función objetivo es la suma de las contribuciones individuales de las variables
de decisión. De igual forma, la actividad total dentro de una restricción es igual a la suma de las
actividades individuales de cada una de las variables de decisión.
Divisibilidad: Las variables de decisión pueden ser divididas en valores fraccionales (reales). En otras
palabras, los valores no enteros están permitidos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
21
Coeficientes determinísticos: Los coeficientes c
j
, a
ij
, b
i
son conocidos determinísticamente. En otras
palabras, ninguna distribución de probabilidad es asignada a dichos coeficientes, y se supone que se
conocen con certeza.
2.2.2 Método Simplex
El método Simplex es un algoritmo que permite solucionar problemas formulados mediante
programación lineal. Este método es iterativo y es conocido como algoritmo de punto exterior
(denominado así porque en cada iteración del método se encuentra en un vértice del espacio solución).
Como la formulación es lineal, en cada iteración la solución obtenida es mejor, hasta llegar a la mejor
solución posible del problema (un cambio de vértice en el espacio solución no lleva a una solución
mejor).
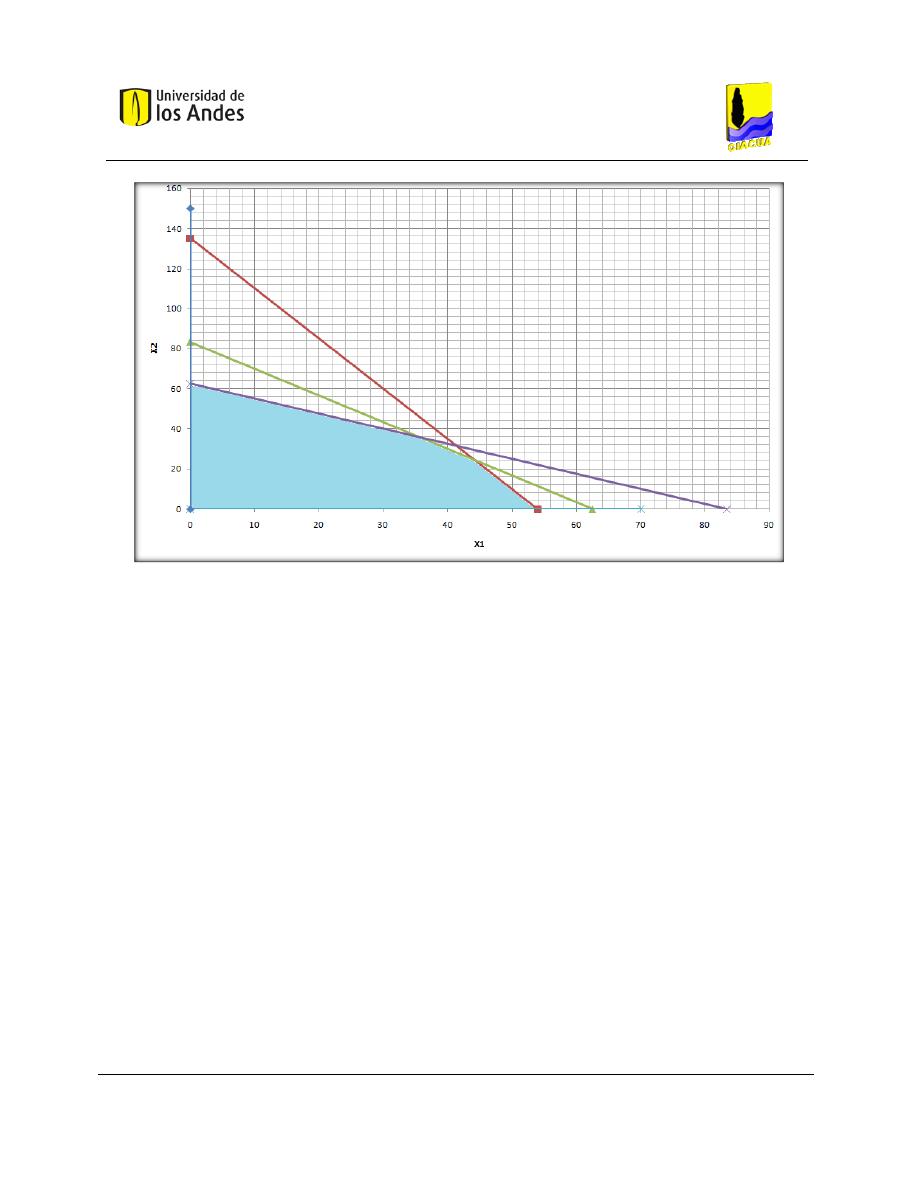
En cualquier caso se tiene una función objetivo que quiere ser minimizada o maximizada. Esta función
objetivo está sujeta a una serie de restricciones que configuran el problema. El polígono que se forma de
la intersección de todas las restricciones conforma el espacio solución. Como el espacio solución genera
un espacio finito, con un número finito de vértices, la solución es finita y cuantificable.
La Figura 2-2 presenta un ejemplo del espacio solución obtenido a partir de la interacción de tres
restricciones lineales. Para el caso de esta figura, las condiciones dominantes sobre las restricciones son
de menor o igual (<=), pues el área resaltada como espacio solución se encuentra por debajo de todas las
restricciones (a excepción de las restricciones de no negatividad).
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
22
Figura 2-2. Definición del espacio de solución mediante restricciones lineales.
2.2.3 Teoría de Grafos
Una de las aplicaciones del método Simplex está en los problemas de flujo en redes, pues éstos han sido
utilizados para modelar diversas situaciones cotidianas exitosamente, pues representan el manejo de
información en un contexto determinado. Particularmente, este tipo de modelaje permite el análisis de
un determinado flujo a lo largo de una red definida bajo unos supuestos establecidos.
2.2.3.1 Definiciones básicas de la teoría de grafos
A continuación se presentan los conceptos fundamentales para el desarrollo de problemas utilizando la
teoría de grafos como caso particular del método Simplex. Estos conceptos se utilizan de forma
específica y su uso en este documento (particularmente en el contexto de la teoría de grafos) implica
una rigurosidad matemática claramente definida.
Grafo: Consiste en un conjunto N de arcos y un conjunto A de arcos, se denota por G ( N , A )

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
23
Nodo: Consiste en una representación de puntos de ingreso y salida de información, se denota por N
Arco: Consiste en un apareamiento de los nodos i y j que, se denota por e = (i, j)
Red: Grafo con información sobre sus nodos y arcos, se denota por N= ( G , I )
2.2.3.2 Algoritmo de árbol de expansión mínima (MST)
Un Árbol de Expansión Mínima o MST por sus siglas en inglés (Minimum Spanning Tree) es un grafo en el
cual la suma de los costos de cada uno de los arcos que lo compone es mínima.
El escenario generado por un árbol de expansión mínima tendrá n – 1 arcos, donde n representa el
número de nodos, ya que la formulación del problema debe cumplir las siguientes restricciones:
∑
Ecuación 30
∑
| |
Ecuación 31
{ }
Ecuación 32
Se tiene además como supuestos generales de este tipo de problemas que la red no es dirigida, por lo
que resulta equivalente el costo unitario del nodo i al nodo j c ( i , j ), que el costo del nodo j al nodo i c ( j
, i ). Es decir, este método no considera un sentido en los flujos que se mueven por la red, ya que su
costo es indiferente de la dirección del mismo. Sin embargo, este costo sólo puede participar una vez en
la función objetivo, lo que indica que máximo, el costo puede estar asignado una única vez en la solución
final, lo que indica que no puede considerarse un cambio en el sentido del flujo para un determinado
arco.
Como última restricción al problema de MST, se tiene que el grafo generado no debe contener ciclos y
debe ser conecto, lo que implica que cada uno de los arcos de la red está conectado de manera única por
arcos pertenecientes a la solución de mínimo costo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
24
El de Árbol de Expansión Mínima, puede ser resuelto de forma iterativa y no requiere técnicas avanzadas
de solución, pues simplemente explora exhaustivamente la red y examina los costos de los arcos que
conectan a los nodos, para obtener el camino de costo mínimo incluyendo a todos los nodos en su
solución.
Este método tiene como limitantes el uso de variables reales y positivas, así como de linealidad en la
formulación general. Los problemas de Flujo en Redes utilizan como supuesto general rangos enteros,
por lo que en una primera lectura resultaría incompatible para utilizar Simplex. Sin embargo, una
propiedad característica de los problemas de Flujo en Redes es la unimodularidad, propiedad que
permite relajar la variable entera (que ésta tome valores enteros únicamente), obteniendo los mismos
resultados prácticos.
Para medir optimalidad en la solución de un árbol de expansión mínima en términos de minimizar la
suma total de los costos de cada uno de los arcos que lo compone, se pueden utilizar dos criterios, el
corte y la ruta. A continuación se explica cada uno de ellos.
Un árbol de expansión
es un árbol de expansión mínima si y sólo si satisface la siguiente condición de
optimalidad por corte:
Esta condición implica que al realizarse un corte cualquiera sobre la red, el arco que conecta el árbol de
expansión mínima es aquel que tenga menor costo sobre el corte, de lo contrario no se cumple la
condición.
La otra posibilidad de verificar que la solución obtenida es óptima, es utilizando el criterio de optimalidad
por ruta, la cual se presenta a continuación.
Un árbol de expansión
es un árbol de expansión mínima si y sólo si satisface la siguiente condición de
optimalidad por ruta:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
25
Cumpliendo con cualquier de las condiciones se garantiza la otra, por lo que basta verificar una de los
dos condiciones de optimalidad para asegurar que el grafo obtenido es un árbol de expansión mínima.
2.3 Operación de los SB
La operación de los SB se ha enfocado en encender y apagar bombas pertenecientes a SB de tal forma
que se puedan reducir los gastos operacionales debidos al elevado consumo de energía eléctrica o
energía fósil de las bombas manteniendo las condiciones mínimas de funcionamiento.
En este sentido, se han generado múltiples aproximaciones al problema. A continuación se presentan
algunas de estas:
2.3.1 Horarios de revisión y toma de decisiones (Richardson, 2011)
Richardson (2011) propone la generación de horarios para la revisión de las bombas, en donde la función
objetivo minimiza el costo del ciclo de vida de las bombas y el consumo de electricidad mediante
decisiones individuales en el tiempo respecto a la operación de las bombas. Los horarios también
permiten aumentar el desempeño de las bombas, pues un uso discontinuo contribuye a un menor
desgaste de los componentes mecánicos de las bombas.
Los supuestos principales para el desarrollo son:
-
Conservación de la masa en todo el modelo.
-
Funciones de costos lineales.
-
Costos de reparaciones fijos.
-
Existe independencia entre el funcionamiento de todas las bombas.
Como variables de decisión se proponen la edad de las bombas, las horas de operación, las condiciones
ambientales y de operación y finalmente la potencia consumida por unidad bombeada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
26
Para la descripción del modelo matemático se establece un plan de producción de bombeo de agua que
es revisado anualmente y considera incertidumbres asociadas con el proceso de cambio en la demanda
de agua requerida.
El objetivo de la programación de los horarios de encendido y apagado de las bombas es generar un
caudal igual al caudal requerido. Para hacer esto, la modelación tiene la limitación de caudales discretos
en cada estación de bombeo porque la velocidad de operación de cada una de las bombas es un valor
definido.
Para el proceso de toma de decisión se incluye también un modelo de deterioro mecánico que predice el
desempeño de las bombas y como cambia este a medida que aumenta el uso de una bomba particular.
Adicionalmente, el modelo utiliza información histórica para validar los resultados obtenidos.
Finalmente, los autores consideran el impacto económico de diferentes reparaciones del sistema con el
cálculo del periodo de retorno que recupera la inversión mediante análisis de incertidumbre y funciones
multi-objetivo que incluyen considerar emisiones de dióxido de carbono.
2.3.2 Programación de los horarios de bombeo utilizando optimización
La operación de las bombas dentro de los SB de tal forma que los costos energéticos se minimicen es el
objetivo fundamental de cualquier formulación. Dependiendo de las condiciones de cada sistema, o de
los requisitos particulares que cada investigador considere relevantes se han desarrollado diferentes
modelos que pretenden dar respuesta a esta situación. A continuación se presentan algunas
aproximaciones recurrentes dentro de este problema de la operación de los SB.
2.3.2.1 Programación lineal
La programación lineal (PL), como se explicó en este capítulo, utiliza funciones y restricciones lineales
para solucionar cualquier problema. Se necesita información de entrada al modelo, una función objetivo
que quiera optimizarse y una serie de restricciones que limiten las condiciones del problema.
Generalmente la función objetivo relaciona los costos de bombeo, los parámetros de entrada relacionan
información de simulaciones hidráulicas, como lo pueden ser la presión en los nudos de consumo y los
caudales en los tubos. Finalmente, las restricciones están relacionadas con las condiciones extremas de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
27
operación, como lo pueden ser presiones mínimas y máximas, tiempo continuo de operación de una
misma bomba o condiciones de mantenimiento del sistema.
Para abordar el problema que supone la operación de los sistemas de bombeo, Pasha (2009) considera
formulaciones que involucran el supuesto de linealidad en el modelo solución. Para esto, propone un
horario de operación de las bombas, manteniendo los requerimientos hidráulicos, que en su aplicación
reduce los costos económicos relacionados con la operación de los SB.
El autor considera que formulaciones demasiado complejas limitan el uso de los modelos en tiempo real,
por lo que limita las restricciones asociadas con el problema a las siguientes variables:
Energía requerida: Mediante cálculos hidráulicos se realizan simulaciones en periodos de un día
para establecer la pendiente de la curva de energía a lo largo del periodo de simulación.
Caudal bombeado: Dependiendo de las condiciones del sistema, no es necesario bombear
siempre la misma cantidad de agua
Demanda de consumo en los nudos: Componente aleatorio dentro del sistema, pues la
dinámica temporal de la demanda dentro del sistema puede considerarse como una variable
aleatoria.
Niveles en los tanques: Se consideran límites superiores e inferiores de niveles de agua en los
tanques para cualquier punto de operación del sistema.
Para Pasha (2009), la disminución en el consumo de energía en los SB mediante el uso de técnicas de
optimización puede alcanzar rendimientos entre un 10% a 20% superiores a los encontrados mediante la
experiencia o un ejercicio especulativo de prueba y error.
La formulación lineal considera un modelo diario, cuyas restricciones dependen de rangos de los niveles
de agua en los tanques y del caudal producido por las bombas. La metodología incluye una recolección
de la información física de la RDAP, la simulación hidráulica en periodos diarios para la obtención de las
ecuaciones de energía y finalmente la operación óptima de las bombas para producir el caudal
necesario.
2.3.2.2 Optimización dinámica
La optimización dinámica (DO
5
) es una técnica que permite modelar problemas de operación de SB
dentro de RDAPs a gran escala, mediante el uso de variables de decisión enteras. Se puede definir como
5
Por sus siglas en inglés Dynamic Optimization

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
28
el proceso para determinar las trayectorias de control de un sistema dinámico en un periodo de tiempo
finito de tal forma que se optimice una variable en particular (McCormick, 2003).
Este método converge rápidamente por la naturaleza de sus variables de decisión (enteras), pues se
quita complejidad el problema sin variables continuas. Mediante las trayectorias dinámicas es posible
establecer las condiciones que operación de las bombas que más afectan el desempeño del sistema.
Nuevamente, las condiciones topológicas del sistema son un parámetro de entrada y no una variable de
decisión.
2.3.3 Programación de la operación de los SB utilizando Algoritmos Genéticos
El uso de Algoritmos Genéticos (AG) en problemas asociados con las RDAPs ha sido ampliamente
desarrollado en los últimos años, pues la adaptabilidad de este tipo de métodos permite su uso en gran
variedad de áreas.
Los AG permiten utilizar situaciones de otro contexto para la solución de problemas específicos; hacen
uso de la teoría de la evolución y del concepto de la selección natural de Darwin para seleccionar las
mejores opciones de solución para un problema particular. Por ejemplo, se han utilizado métodos meta
– heurísticos de optimización que simulan el comportamiento de algunas colonias de hormigas, en
particular los movimientos de estas dentro de la colonia (López-Ibáñez & Prasad, 2008).
El objetivo de la formulación sigue siendo el mismo que en las demás aproximaciones, la minimización
del costo de la energía consumida por los SB dentro de las RDAPs. En relación con las aproximaciones de
optimización, el uso de AG presenta las siguientes ventajas:
Representar mediante la optimización a fidelidad un sistema de RDAPs implica un modelo
matemático complejo, que puede resultar difícil de aplicar en un contexto que no sea
académico.
Por la complejidad de algunos sistemas de distribución de agua, en ocasiones es necesario
realizar simplificaciones que pueden inducir a pérdida de información o deterioro de la misma.
En el desarrollo de modelos de alta complejidad que no pueden ser resueltos de manera
exhaustiva el uso de AG encuentra soluciones que si bien pueden no ser la de óptimo
desempeño, representan en términos generales muy buenas condiciones de operación.
El tiempo computacional empleado en la solución de un problema de operación de SB para
RDAPs puede llegar a ser sustancialmente menor en comparación con el mismo problema
resuelto mediante el uso de optimización, lo que puede ser un determinante para preferirlo. La

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
29
velocidad de cálculo es particularmente importante para la toma de decisiones en tiempo real y
la simulación de modificaciones al sistema para efectos de mantenimiento.
Si la formulación no es lineal, existe el problema de que la solución obtenida con un modelo de
optimización sea local. Este problema puede llevar a tomar decisiones equivocadas o sesgadas,
que funcionan solamente para un subconjunto del total de posibilidades que pueden
presentarse dentro del sistema.
Para caracterizar el problema, Sotelo, Basulado, & Doldán (2001) utilizan un simulador hidráulico
denominado H2ONET Scheduler, en donde es posible definir límites de presiones en los nudos,
velocidades máximas en las tuberías y rangos en los niveles de agua para los tanques.
En otro caso, el uso de AG permite generar simulaciones hidráulicas para la toma de decisiones en
tiempo real, en donde se plantean diferentes periodos de operación para los SB (Nitivattananon &
Sadowski, 1996):
Los autores tienen en cuenta los siguientes supuestos para su modelación:
Consideran cambios en la operación debido a cambios en la demanda del sistema, mediante el
uso de la descomposición de la RDAP en sub sistemas independientes.
Restricciones independientes para cada bomba.
Conservación de la masa para que sub sistema del modelo.
Tasas de cambio variables para el almacenamiento de agua en tanques.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
30
3 Metodología general de análisis
Se realizó una metodología que no tenga la aproximación tradicional al problema de la optimización de
la operación de los SB, pues este problema se considera resuelto. En contraste, se buscó incluir variables
que no han sido consideradas dentro de los enfoques tradicionales. Para esto, no se consideró la
operación de los sistemas de bombeo (por ser este un problema ampliamente estudiado en la
literatura); por el contrario, la metodología se enfocó en cambios hidráulicos para mejorar el desempeño
económico de la operación de la RDAP.
Se supone que la operación de los SB es óptima en cualquier momento de operación de la RDAP. Es
decir, este documento considera que la interacción de las diferentes bombas que pertenecen a un SB es
tal que la operación resultante es aquella de mínimo costo eléctrico. Esta decisión se tomó debido a los
avances significativos encontrados durante el proceso de búsqueda bibliográfica presentados en el
capítulo de Antecedentes del presente documento. De esta forma, esta metodología enfatiza cambios
topológicos y la inclusión de embalses adicionales dentro del sistema para amortiguar la carga que
inicialmente tienen los SB. Además de la ubicación de embalses adicionales, hay un cambio en el
diámetro de algunas de las tuberías cercas a estos embalses; esto con el ánimo de disminuir las pérdidas
por fricción debidas a diámetros bajos.
Por este motivo, aplicar esta metodología implica un costo inicial superior que las técnicas tradicionales
de disminución de costos (ya que hay que considerar cambios de diámetros para diferentes tuberías y los
costos asociados con la colocación, operación y mantenimiento de los nuevos embalses), pero para
distintos periodos de diseño, la metodología tiende a ser más rentable debido a los ahorros producidos
en la operación al largo plazo de los SB.
En este sentido, la metodología general consta de 8 pasos principales enunciados a continuación.
1. Recolección de información básica de la RDAP.
2. Ubicación del embalse secundario dentro de la RDAP.
3. Escogencia de la zona de influencia que tendrá el nuevo embalse.
4. Determinación de la zona de influencia del nuevo embalse.
5. Determinar la ruta desde el nuevo embalse hasta cada uno de los nudos de consumo
pertenecientes a la zona de influencia.
6. Cambio de diámetro de las tuberías pertenecientes a la zona de influencia y determinación de la
altura piezométrica disponible en el nuevo embalse.
7. Evaluación del desempeño del sistema (económico e hidráulico).
8. Repetición de los pasos 1 a 7 para colocar otro embalse en la red hasta encontrar una solución
de mínimo costo en un periodo de diseño dado.
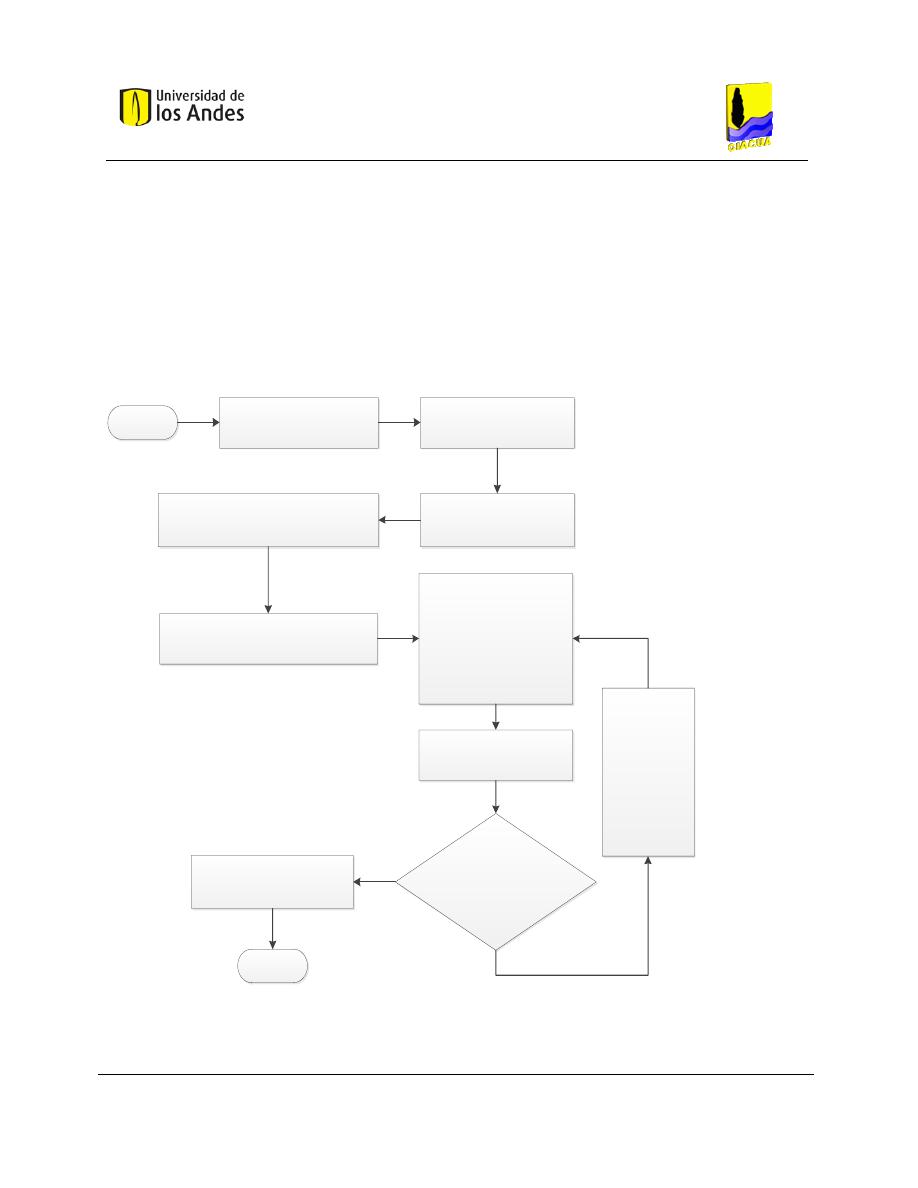
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
31
A continuación se presenta un diagrama de flujo en que se presentan esquemáticamente los pasos que
la metodología sigue para reducir los costos operacionales en redes que incluyen en su operación
bombeo. Es importante resaltar el componente iterativo que tiene la metodología, pues regula el
número de tuberías de la red que pueden ser modificadas de acuerdo con una tolerancia en el cambio de
la edad del agua. Se considera este concepto como medida de la calidad del agua dentro de todo el
sistema, de esta forma se asegura que no se están deteriorando las condiciones de calidad de agua una
vez se haya aplicado la metodología.
Inicio
Recolección de información básica
de la RDAP
Ubicación del embalse
secundario dentro de la RDAP
Escogencia de la zona de
influencia que tendrá el nuevo
embalse
Determinar los tubos que pueden ser
modificados para maximizar el efecto del nuevo
embalse mediante el uso del algoritmo MST
Definición grafo conexo inicial solamente con
arcos adyacentes al nuevo embalse
Diseño grafo con la metodología
descrita en el Capítulo 3.5,
obteniendo los valores para los
diámetros de las tuberías
pertenecientes al grafo, y la
altura del nuevo embalse para
satisfacer las condiciones
hidráulicas
Calcular la hidráulica del sistema
modificado, definir Ɛ
|Edad del agua original – Edad del
agua sistema modificado| < Ɛ Para
cualquier tubo de la re matriz
A cada nodo del
arco conexo se le
incluye su
adyacente,
generando un
nuevo modelo a
diseñar
Sí
Evaluación del desempaño del
sistema (Costos económicos e
hidráulicos)
Fin
No
Figura 3-1. Diagrama de flujo de la metodología general realizada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
32
A continuación se presentan cada uno de los pasos que conforman la metodología para minimizar el uso
de SB dentro de las RDAPs. En esta metodología, se pretende incluir embalses secundarios que reduzcan
la cantidad de agua que debe ser bombeada al sistema. De esta forma, para un periodo de diseño, es
posible reducir los costos eléctricos asociados con los SB.
3.1 Información requerida para la modelación
Se requiere conocer las características que conformarán la RDAP, para lo cual es necesario tener
información sobre los tanques, nudos de consumo, tuberías, accesorios y válvulas. Esta metodología está
planteada para evaluar el impacto que tiene aplicarla sobre redes existes. Sin embargo, la información
de entrada puede cambiar para aplicar la metodología a diseños que no han sido construidos.
En primer lugar es necesario tener la información de los consumos que se dan en la RDAP, para conocer
los requerimientos de agua que tiene la red. Adicionalmente, un cálculo hidráulico que permita tener
información de caudales en los tubos y presiones en los nudos.
3.1.1 Información de Consumos
Uno de los objetivos de la metodología propuesta es cuantificar el impacto económico e hidráulico que
tiene implementarla sobre una RDAP existente. Por este motivo, es importante conocer el estado de
demandas dentro del sistema, para poder representarlo adecuadamente y que los resultados obtenidos
luego de una simulación hidráulica sean acordes a las condiciones reales del sistema.
En el caso del cambio de diámetros que uno de los pasos de la metodología propuesta propone, la
información de los consumos debe estar enfocada a los posibles requerimientos que van a existir en la
nueva zona de influencia (también descrita en detalle dentro de la metodología). Si se está realizando un
diseño en un sector para riegos que mantendrán uniforme su demanda, el diseño será diferente a si se
diseña una red contra incendios para una población dinámica espacialmente. Para el caso del diseño de
RDAP, el nivel de agregación permite tener buenos estimativos para el diseño.
Para este paso es fundamental tener un completo estudio de demanda, conocer los usos que se
encuentran dentro del sistema y posibles cambios en los mismos. La topología de la red depende en gran
medida de la correcta información que se proyecte de los consumos, ya que de lo contrario podría
incurrirse en costos extras innecesarios o en fallas en el servicio por sub dimensionamiento en el diseño.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
33
3.1.2 Cálculo hidráulico de la RDAP
Una vez definido las características topológicas de la red y la información referente a las demandas de
consumo de toda la RDAP, es posible realizar algunos cálculos hidráulicos como lo pueden ser los
caudales en los tubos y las presiones en los nudos. Este cálculo permite tener las condiciones iniciales de
la red, lo que posteriormente permite analizar potenciales lugares críticos.
Los cálculos hidráulicos son la base de comparación hidráulica del sistema antes y después de aplicar la
metodología propuesta. En este sentido, la metodología pretende como mínimo mantener las
condiciones hidráulicas originales bajo un costo económico menor (disminuyendo los costos de
operación de los SB pertenecientes a la RDAP).
3.1.3 Calibración de un modelo preliminar
“La calibración consiste en el ajuste de un conjunto de 5 parámetros, los cuales gobiernan el
comportamiento hidráulico del modelo, buscando de estar forma lograr que este represente de la mejor
manera posible las mediciones en campo. La calibración final se logra encontrando la cantidad de agua
perdida, distribuyéndola espacialmente en el sistema como conexiones ilegales (demandas
desconocidas) y como fugas no detectables (emisores). Luego de hacer eso, es necesario determinar la
variación de los diámetros, rugosidades y pérdidas menores para que la energía del sistema represente
el comportamiento real de la red” (Rodríguez, 2007).
Tener un modelo calibrado, permite el seguimiento de cada una de las variables hidráulicas dentro del
sistema, así como la influencia que tendría algún cambio en la topología de la red en los valores de las
variables hidráulicas y el impacto en el servicio a los nudos de demanda y tanques de abastecimiento. Al
igual que con la información previa, el modelo calibrado será la base de la comparación hidráulica.
3.2 Ubicación del embalse secundario dentro de la RDAP
El segundo paso de la metodología implica considerar las posibilidades que existen para la ubicación de
un nuevo embalse dentro de la RDAP. En este sentido, se pretende encontrar un sector que maximice los
efectos de la inclusión de este elemento. Para lograrlo, se considera el criterio hidráulico de la densidad
de demanda en los nudos de consumo.
El criterio de densidad de demanda es un criterio geográfico en el que se buscan zonas de mayor
concentración de demanda de agua dentro de la RDAP. Como se tiene la información puntual del

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
34
consumo en cada uno de los nudos, es posible agregar espacialmente esta medida de tal forma que el
resultado sean zonas más densamente demandas que otras, y cuantificar estas diferencias.
La información necesaria de la red es aquella que caracteriza la topología de los nudos. En este caso, se
requieren las coordenadas x, y, z. Adicionalmente para cada nudo, existe una demanda asociada. Se
utilizó la demanda de consumo como criterio hidráulico porque esta puede medir el impacto que tiene la
ubicación geográfica del nuevo embalse. Adicionalmente, ubicar un embalse cerca a los sitios de mayor
consumo supone menores pérdidas acumuladas, por lo que se necesita menor energía disponible
(menor necesidad de bombeo, implicando menores costos energéticos en la operación de los SB) en el
embalse para el funcionamiento del sistema.
Se supone entonces que la demanda dentro de la RDAP es variable en el espacio, y los sitios con mayor
demanda son aquellos que necesitan mayor energía para poder transportar el agua en las cantidades
solicitadas. Por este motivo, una aproximación razonable resulta ubicar el embalse en sitios de alta
demanda. Para la aplicación de este criterio, se supone que las posibilidades de ubicación del nuevo
embalse dentro de la RDAP son discretas; es decir, existe un número finito de posibilidades de solución.
La división del espacio solución se hace entonces mediante una grilla de densidad, definida como la
división del sector geográfico, perteneciente al sector hidráulico de interés, en zonas discretas. La Figura
3-2 presenta un esquema de la grilla de densidad.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
35
Figura 3-2. Generación de la grilla de densidad para una RDAP ejemplo.
Una vez generada la grilla, es posible cuantificar el impacto que tiene cada una de las celdas sobre la
RDAP en función de la demanda de agua. En el caso particular de la demanda de agua, basta con sumar
todas las demandas que se encuentran dentro de la misma celda para encontrar la demanda de la celda.
La ubicación del embalse estará ubicada en la celda que pertenezca a la zona de influencia con mayor
consumo de agua en toda la grilla.
Es importante resaltar que se ha explicado el criterio de máxima densidad de demanda de agua como
factor para escoger la ubicación del nuevo embalse. Sin embargo, en forma análoga se utiliza el concepto
de densidad de grilla generalizado para probar otros factores críticos en la selección óptima de la
selección de la ubicación del embalse. Por ejemplo, se considera el caso en el que por razones
económicas es muy costoso ubicar el embalse en la zona de mayor consumo, por que no es viable
financiera ni económicamente. En estos casos, es necesario establecer criterios adicionales para la
ubicación del embalse.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
36
Por otra parte, es un criterio del diseñador determinar el tamaño de cada una de las celdas, pues
dependiendo del nivel de detalle que se quiera tener en la ubicación se pueden tener un mayor o menor
número de celdas para una misma RDAP. Dependiendo del criterio que se esté utilizando para
determinar la ubicación del embalse, es posible que se quiera un tamaño de grilla diferente.
Los casos de estudio desarrollados en este trabajo de tesis resaltan esta diferencia, utilizando diferentes
criterios para escoger la ubicación del embalse secundario en la RDAP, por lo que las diferencias de cada
caso de estudio se explican en detalle en el Capítulo de Análisis de Resultados.
3.3 Determinación zona de influencia para el nuevo embalse
Una vez se tiene definida la ubicación del nuevo embalse dentro de la RDAP, es necesario definir el
alcance que éste va a tener dentro del sistema en términos hidráulicos; es decir, hasta que nudos va a
suministrar prioritariamente el agua bajo un escenario de operación definido. Conocer esto es
importante para la posterior operación de toda la red y las posibles respuestas de la RDAP frente a algún
cambio. Adicionalmente, permite acotar pasos posteriores de la metodología.
Para hacer esto se realizan particiones de la red, de tal forma que se sub divide la red mediante algún
criterio hidráulico. En el caso de esta investigación, el criterio hidráulico utilizado es el de Potencia
Unitaria.
3.4 Definición red matriz asociada con el nuevo embalse
Para maximizar el efecto que tiene la inclusión de un nuevo embalse dentro de la RDAP, es necesario
modificar la geometría aledaña a la localización de este. Esto es necesario porque caudales muy altos en
comparación con el diámetro de la tubería, generan altas pérdidas por fricción, lo que reduce la
eficiencia del sistema, pues los SB requieren mayor energía para suplir las necesidades de la red. Por este
motivo, se supone que una sección de las tuberías cercanas al embalse, y representativas para el sector
hidráulico determinado en la zona de influencia del embalse debe ser modificada para mejorar las
condiciones hidráulicas de este nuevo sector.
Las condiciones de demanda se mantienen para todo el sector, y se pretende encontrar un subconjunto
de tuberías que sean modificadas para que sean modeladas como redes matrices. Inicialmente, se siguen
las recomendaciones dadas por Naranjo (2008) acerca de mantener secciones de tuberías en serie que

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
37
conformen tramos rectos y que recorran gran parte del sector hidráulico para la modelación de la red
matriz.
Una vez se ha definido el conjunto de tuberías que conformarán la red matriz, es necesario modificar las
demandas de los nudos pertenecientes para que la conservación de la masa se mantenga. En este
sentido, se utiliza un programa de asignación de demandas que asigna la demanda total del sector
hidráulico a aquellos nudos que pertenecen a la red matriz.
La forma en como se define el número de tuberías que pueden ser modificables en un paso posterior de
la metodología es mediante el uso del algoritmo de árbol de expansión mínima, definido en el Capítulo
de Antecedentes de este documento. Para aplicar dicho procedimiento, es necesario tener algunas
consideraciones básicas explicadas a continuación.
3.4.1 Solicitaciones generales para diseñar redes abiertas usando el algoritmo Árbol de
Expansión Mínima
En los diseños de una red abierta, como lo es la red que se quiere definir, se requiere una planificación
organizada de cada uno de los elementos que van a intervenir, con el fin de obtener resultados óptimos
en términos operativos y económicos. Realizar un estudio minucioso de las características hidráulicas de
la zona de estudio, así como de los requerimientos propios de un grupo de usuarios dado, permite
conocer a fondo las posibles complicaciones que pueden presentarse en el diseño, con lo cual es posible
priorizar algunos sectores de la red de acuerdo con su vulnerabilidad.
En el marco de un diseño completamente nuevo, encontrar algoritmos que permitan realizar los
procesos de cálculo y de conformación de la red en sí misma de maneras más eficientes en términos
operativos y económicos y menor tiempo de cálculo computacional debe ser una tarea superlativa. Es
importante resaltar la necesidad de análisis previos realizados para determinar las características de la
red, pues tener un algoritmo eficiente y óptimo para el diseño de una red de distribución carece de
sentido si la información con la que se está diseñando carece de veracidad.
El propósito general de este paso de la metodología es obtener un subconjunto de tuberías adyacentes
que en total resulten en la red matriz que alimentará al nuevo embalse dentro de la RDAP. Sin embargo,
como el objetivo fundamental de este trabajo de tesis es mejorar la operación de los SB, no se considera
únicamente el factor económico, sino factores en el cambio de la calidad de agua del sistema implícitos
en cualquier cambio topológico de la red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
38
A continuación se describen los elementos fundamentales que deben ser considerados para la
formulación del problema como un algoritmo MST.
3.4.1.1 Análisis de la Topología
Se requiere conocer las características que conformarán la nueva red abierta, para lo cual es necesario
tener información sobre los tanques, nodos de consumo, tuberías, accesorios y válvulas.
Es necesario establecer condiciones mínimas de diseño propias de cada caso particular que se esté
analizando, debido a que pueden existir condiciones externas a las consideraciones meramente
hidráulicas que influyan o limiten el problema. Por ejemplo, si hay un tubo que no puede ser incluido en
la solución porque físicamente no puede ser cambiado debido a las condiciones urbanas es necesario
conocerlo a priori. De esta forma, la solución obtenida es factible desde el punto de vista económico y
contribuye al mejoramiento del comportamiento hidráulico del sistema.
3.4.1.2 Información preliminar del caudal y la presión
Una vez definido las características topológicas de la red y la información referente a las demandas de
consumo en todo el territorio, es posible realizar algunos cálculos hidráulicos como lo pueden ser los
caudales en los tubos y las presiones en los nodos. Esto permite tener una idea general de las
condiciones iniciales del problema, lo que posteriormente permite analizar potenciales lugares críticos.
En caso de ser necesario, puede establecerse una ponderación especial a aquellos lugares a los cuales se
les quiera dar una importancia diferencial.
3.4.1.3 Calibración de un modelo preliminar
Tener un modelo calibrado, permite el seguimiento de cada una de las variables hidráulicas dentro del
sistema, así como la influencia que tendría algún cambio en la topología de la red en los valores de las
variables hidráulicas y el impacto en el servicio a los nodos de demanda y tanques de abastecimiento.
Bajo el modelo de la red redundante en número de tubos, contar con la posibilidad de generar
diferentes escenarios de prueba para correr el algoritmo permite tener un gran número de posibilidades.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
39
3.4.1.4 Modelación del algoritmo MST aplicado al caso del diseño de RDAP
Una vez se tiene la red redundante calibrada basada en los consumos potenciales obtenidos por el
análisis de información de usuarios, es posible aplicar el algoritmo MST, satisfaciendo cada una de las
demandas que tenga la red. Para poder aplicar el algoritmo los supuestos del problema deben estar
cumpliéndose, para lo cual es necesario realizar una modificación importante al grado asociado a la red
que quiera modelarse.
El grafo asociado con la red tendrá en los nodos la información referente a los nodos de consumo. Para
la modelación de las demandas salientes de la red en cada uno de los nodos de consumo, se utiliza otro
tipo de nodo ficticio denominado nodo de demanda, que estará conectado al nodo fin para que toda el
agua que ingresó a la red sea contabilizada al final, con lo que nuevamente se está garantizando el
balance.
La información que estará en cada uno de los arcos hace referencia a los costos unitarios que tiene
transportar el flujo por ese arco. Para el caso particular de este trabajo de tesis, se utilizará el cambio en
el Índice de Resiliencia que tiene el quitar ese tubo en el cálculo de la resiliencia de la red respecto al de
la red inicial. También se consideró la Potencia Unitaria como costo. Es importante resaltar que
solamente tendrán estos costos los arcos que estén definidos por aquellos nodos en el grafo que
representen un nodo de consumo en la red de distribución de agua potable. Para los arcos que definan la
conexión entre nodos de consumo y nodos ficticios, el costo asociado tendrá un valor de cero, ya que se
debe garantizar que estos arcos sean parte de la solución final, para cumplir las restricciones de balance
asociadas al problema.
3.5 Diseño optimizado de la red matriz
Una vez determinada la red matriz que quiere ser diseñada, es necesario diseñarla. Para realizar el
diseño de la red matriz que va a suponerse para zona de influencia del nuevo embalse, se utiliza una
formulación lineal. De acuerdo con este tipo de formulación, es necesario establecer una función
objetivo que desea ser optimizada (maximizada o minimizada), sujeta a una serie de restricciones que
definan un espacio solución finito.
Es importante resaltar que esta es sólo una de múltiples posibles formas de realizar el diseño
optimizado, se prefiere esta porque incluye la variable de decisión sobre los costos de bombeo. Sin
embargo, para el diseño tradicional de RDAPs hay aproximaciones ampliamente utilizadas en la literatura

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
40
como lo son el uso de Algoritmos Genéticos o cualquier otra heurística que si bien no aseguran una
condición óptima para el diseño, generan resultados económicamente factibles.
A continuación se presentan las condiciones generales que definen la formulación lineal que se propone
en esta metodología.
3.5.1 Definiciones iniciales
Para efectos de la formulación, es necesario definir los siguientes parámetros que pertenecen a la
formulación lineal propuesta (Mays & Tung, 1992).
Conjunto de tuberías que definen la red.
Conjunto de tuberías pertenecientes a la red que conforman la ruta desde el embalse hasta
el nudo n.
Conjunto de posibles diámetros de tubería para el tubo que conecta los nudos (i,j).
Costo por unidad de longitud de la tubería entre los nudos i, j de diámetro m.
Costo unitario de bombeo de la bomba w.
Gradiente hidráulico de la tubería de diámetro m conectando los nudos (i,j).
Elevación topográfica del embalse.
Altura piezométrica adicionada al sistema – Altura piezométrica del embalse.
Longitud de la tubería que conecta el tramo comprendido entre (i,j).
Mínima altura piezométrica requerida en el nudo n.
Máxima altura piezométrica requerida en el nudo n.
N
Número de nudos de consumo pertenecientes a la red.
3.5.2 Variables de Decisión
Las variables de decisión son aquellas variables que luego del proceso de optimización obtienen valores
tal que la función objetivo tiene su valor óptimo. Para esta formulación se tienen dos variables de
decisión, pues se considera el diámetro de las tuberías de la red matriz y la altura piezométrica requerida
para el SB requerido por el nuevo embalse. Cabe resaltar que la formulación propuesta considera
únicamente un embalse adicional, por lo que la variable de decisión es única. Si se tienen más sectores
hidráulicos, la formulación puede ser fácilmente modificable.
Longitud de la tubería entre los nudos i, j de diámetro m.
Altura piezométrica requerida para la bomba w.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
41
3.5.3 Función Objetivo
La función objetivo pretende minimizar los costos asociados con los SB. Para esta formulación en
particular, se tienen dos componentes a minimizar. El primer componente está relacionado con los
costos constructivos, mientras que el segundo componente incluye los costos por bombeo del SB
adicionado en esta metodología. Se tiene entonces:
∑ ∑
∑
3.5.4 Restricciones
Las restricciones permiten que el espacio solución de la formulación sea finito. En este sentido, las
restricciones definen el espacio solución. Como se explicó en el capítulo Método Simplex, las
restricciones generan un polígono, en donde en uno de los vértices se encuentra la solución óptima.
La primera restricción considerada es que la suma de tubos de diferente diámetro para un tramo que
conecta los nudos de consumo (i,j) debe ser igual a la longitud del tubo al que pertenecen.
∑
La segunda restricción considera la conservación de energía dentro de la RDAP. La restricción está
formulada para cada posible ruta que el agua puede tomar desde el embalse hasta cualquier nudo y
considera un rango de presiones admisibles para cada nudo. Esta formulación permite entonces tener
presiones diferentes para cada punto dependiendo del lugar en el que se encuentre dentro de la red.
∑
∑
∑

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
42
Finalmente, se consideran las restricciones de no negatividad, dado que no pueden existir distancias ni
energías negativas.
El conjunto de todas las restricciones anteriores define el espacio solución para el problema del diseño
de la red matriz. Es necesario entonces que este espacio sea factible (tenga alguna solución posible).
3.5.5 Conservación de la masa
En el caso de nuevos diseños de redes abiertas la información de los consumos debe estar enfocada a los
posibles requerimientos que van a existir en una determinada zona. Si se está realizando un diseño en un
sector para riegos que mantendrán uniforme su demanda, el diseño será diferente a si se diseña una red
contra incendios para una población dinámica espacialmente.
Para este paso es fundamental realizar un completo estudio de demanda, entender para qué se está
diseñando la nueva red con el fin de que el diseño propuesto sea acorde a las intenciones de las nuevas
poblaciones. La topología de la red depende en gran medida de la correcta información que se proyecte
de los consumos, ya que de lo contrario podría incurrirse en costos extras innecesarios o en fallas en el
servicio por sub dimensionamiento en el diseño.
3.5.5.1 Agregación de demandas
La agregación de demandas tiene como objetivo principal concentrar los nudos que tienen un bajo
consumo de agua potable en un solo nudo que agrupe todas las demandas de tal forma que la demanda
final sea representativa. El uso de la agregación de demandas simplifica el proceso de cálculo hidráulico
pues reduce el número de nudos con consumo, por lo que el cálculo de la presión debe ser realizado
para un menor número de nudos. Cabe aclarar que las demandas obtenidas en los nudos son siempre
una suposición.
La agregación de demandas se realiza utilizando el software Asigna, descrito en detalle en el Capítulo
Implementación de la metodología propuesta del presente documento.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
43
3.6 Evaluación del desempeño
El desempeño permite cuantificar el funcionamiento de la metodología propuesta sobre una RDAP en
comparación con la misma red sin aplicarle la metodología. Para la evaluación del desempeño que tiene
la metodología aplicada se consideran dos elementos, en primer lugar se considera el desempeño
hidráulico de la RDAP, y en segundo se considera el impacto económico que tiene sobre la operación de
la red. Se consideran independientes los desempeños económico e hidráulico, por lo que no se considera
ningún tipo de ponderación para tener una función única de desempeño.
No tener una función única de desempeño responde a la necesidad de caracterizar independientemente
cada uno de los factores que son afectados por la aplicación de la metodología propuesta.
3.6.1 Desempeño hidráulico
El desempeño hidráulico está relacionado con el uso eficiente de la energía para poder distribuir los
requerimientos de agua en toda la red. Se estudian variables hidráulicas como la presión en los nudos y
los caudales en los tubos. Asimismo, criterios energéticos explicados en el Capítulo de Antecedentes
como la Resiliencia de la Red y la Potencia Unitaria permiten analizar el desempeño.
Para el caso particular de esta metodología, se supone como condición mínima de funcionamiento un
estado de presiones que permita suplir cualquier estado de demandas que pueda presentarse dentro de
la operación de las RDAPs. Una vez se asegura este supuesto, es posible determinar relaciones que
midan el grado de uniformidad de presiones de la red, pues de acuerdo con Saldarriaga (2007), diseños
próximos a una línea recta se encuentran muy cercanos a un diseño económicamente óptimo, debido al
criterio descrito por Wu que describe una flecha en la Línea de Gradiente Hidráulico (LGH) respecto a
una línea recta.
Se pretende entonces que las condiciones hidráulicas dentro de la RDAP sean como mínimo iguales a las
presentadas originalmente en la red. En caso de que éstas cambien, los cambios deben implicar un mejor
desempeño hidráulico del sistema, en ningún caso un deterioro.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
44
3.6.2 Desempeño económico
El desempeño económico considera relaciones en los costos asociados con la construcción, operación y
mantenimiento de las RDAPs y determina los cambios que implica la metodología sobre estos. De
manera general, se tiene que los costos económicos están asociados con los costos constructivos, en
función del diámetro de las tuberías, a precios fijos de mantenimiento por periodo de tiempo, y a costos
variables de operación por periodo de tiempo.
3.6.2.1 Costos constructivos
Costos relacionados con la construcción de la RDAP. Se pueden considerar costos inherentes a las
tuberías y los demás elementos que conforman en su totalidad el sistema.
Para el caso de las tuberías, los costos constructivos son caracterizados usualmente por la siguiente
ecuación:
∑
Ecuación 33
donde:
: Costo constructivo de la red.
: Número de tubos en la red.
: Longitud del tubo .
: Diámetro del tubo .
, : Parámetros de la función de costos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
45
3.6.2.2 Costos de mantenimiento
Para los costos de mantenimiento de la red calibrada se suponen de valores constantes e independientes
de la modelación realizada en esta metodología. Para el caso de la metodología propuesta, es necesario
considerar aquellos costos inherentes al cambio de las tuberías que conforman la red matriz definida en
el Numeral 3.5. Adicionalmente es necesario considerar los costos de la construcción del tanque
secundario.
3.6.2.3 Costos de operación
Para los costos de operación se supone un valor fijo para cada SB perteneciente a la RDAP. Para su
estudio, se realiza un cálculo de Valor Presente Neto (VPN) para estimar los flujos futuros en un periodo
de estudio dado. El valor de energía eléctrica por unidad de bombeo será igual en el modelo calibrado
que en el modelo una vez se le haya aplicado la metodología propuesta en este capítulo. Sin embargo, la
metodología induce a reducir la cantidad de bombeo necesario para suministrar la energía suficiente al
sistema. Por este motivo, se tiene menos bombeo a lo largo del periodo de diseño de la operación de la
RDAP. Esta condición produce, al largo plazo, una disminución en los costos asociados con la operación
de los SB.
Para calcular el impacto, se utiliza el Valor Presente Neto (VPN), criterio que permite analizar y comparar
flujos que se dan en diferentes periodos de tiempo. En términos generales se tiene:
∑
Ecuación 34
donde:
F
j
: Flujos de caja en el periodo j.
i : Tasa de interés.
A
0
: Flujo de caja en el periodo presente.
n: Número de periodos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
46
4 Implementación de la metodología propuesta
La implementación de la metodología se realizó en diferentes programas computaciones dependiendo
de los requisitos que cada paso pretende. Como todo el trabajo se valida mediante la modelación de
RDAP y sus respectivos SB, es necesario utilizar software especializado que modele adecuadamente cada
uno de los pasos que han sido propuestos.
4.1 Software utilizado para la modelación
Le metodología descrita involucra diferentes pasos para el desarrollo de la misma, por este motivo,
diferentes software han sido utilizados para su desarrollo. Particularmente, es necesario un motor de
cálculo hidráulico, un optimizador que permita la solución de formulaciones lineales, y una hoja de
cálculo que permita determinar los sectores hidráulicos requeridos en la metodología.
A continuación se describen los programas particulares utilizados para cada uno de los pasos.
4.1.1 Redes
Programa de modelación hidráulica desarrollado por el Centro de Investigaciones en Acueductos y
Alcantarillados de la Universidad de los Andes – CIACUA. Particularmente en este trabajo se utilizará la
versión Redes 2006.02.16 Redes2006v1.0 que tiene incluido un módulo de Resiliencia, el cual permite
calcular la resiliencia de una red de distribución de agua potable.
Además, Redes permite el exportar información a hojas de cálculo y otros programas de modelación
hidráulica, lo que resulta muy conveniente para poder analizar los resultados encontrados.
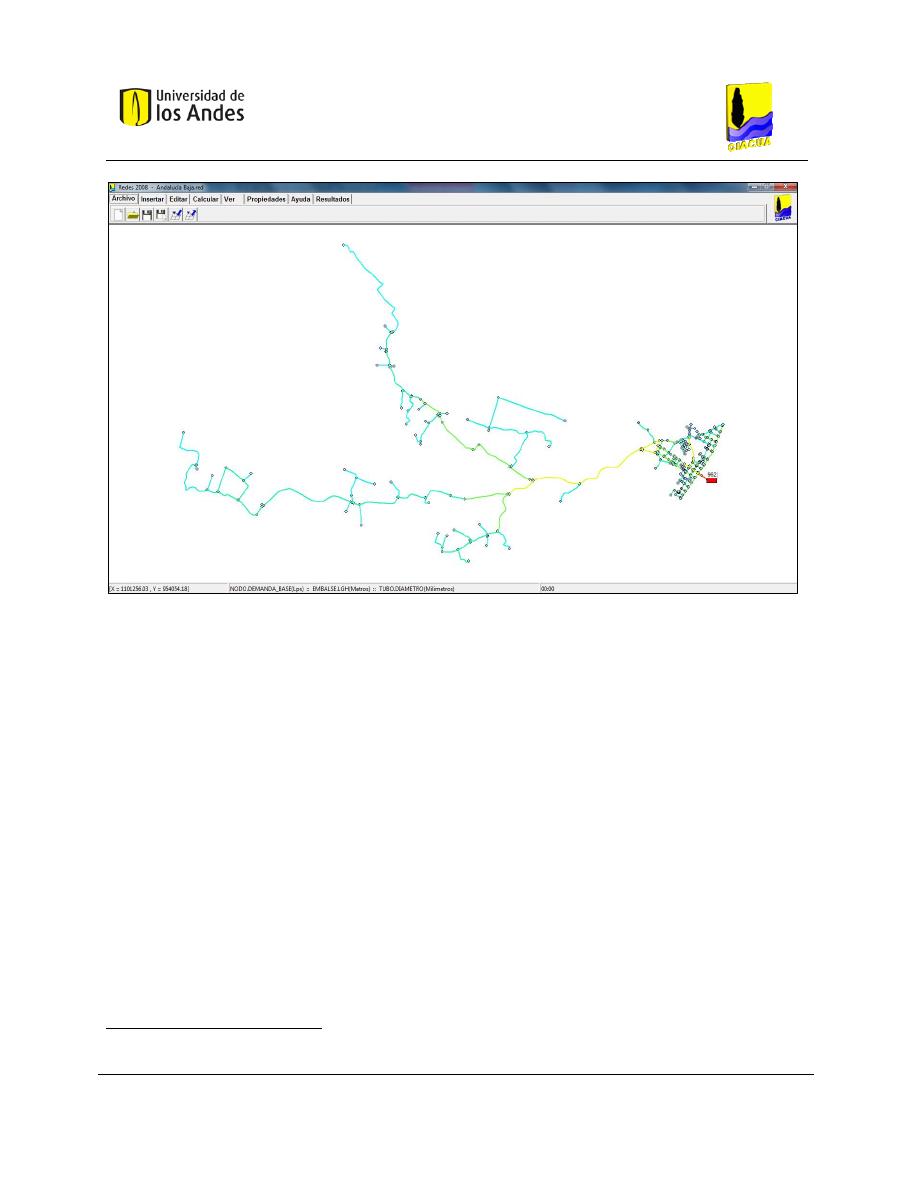
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
47
Figura 4-1. Interfaz gráfica del software Redes (CIACUA, 2006).
En este software se realizan todas las corridas hidráulicas necesarias para el desarrollo de la
metodología. Del mismo modo, mediante REDES es posible validar cada uno de los pasos de la
metodología y medir el desempeño hidráulico de la red y los costos constructivos.
4.1.2 Xpress IVE
El software Xpress IVE utiliza lenguaje Mosel, que es un lenguaje algebraico para programación
matemática (Medaglia, 2008a). Cuenta con un módulo de solución a problemas formulados mediante
programación lineal y permite considerar diferentes tipos de variables (p.e. variables tipo booleanas
6
,
enteras o reales).
A continuación se muestra la suite de optimización utilizado por el software.
6
Variables binarias que toman el valor de 0 o 1 para establecer si son falsas o verdaderas respectivamente.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
48
Figura 4-2. Suite de optimización para el software Xpress –IVE.
Permite resolver problemas lineales, además de la posibilidad de exportar los resultados para poder ser
utilizados en otros programas.
La formulación modelada en Xpress requiere como parámetros de inicio la conformación de la red en
términos de costos y arcos existentes. Este tipo de información se introduce de la red de distribución de
agua potable original. Es importante resaltar que no se requiere las condiciones geográficas de la red, ya
que cada costo es un ponderador que incluye todos los efectos de la misma.
A continuación, se presenta la interfaz característica de Xpress:
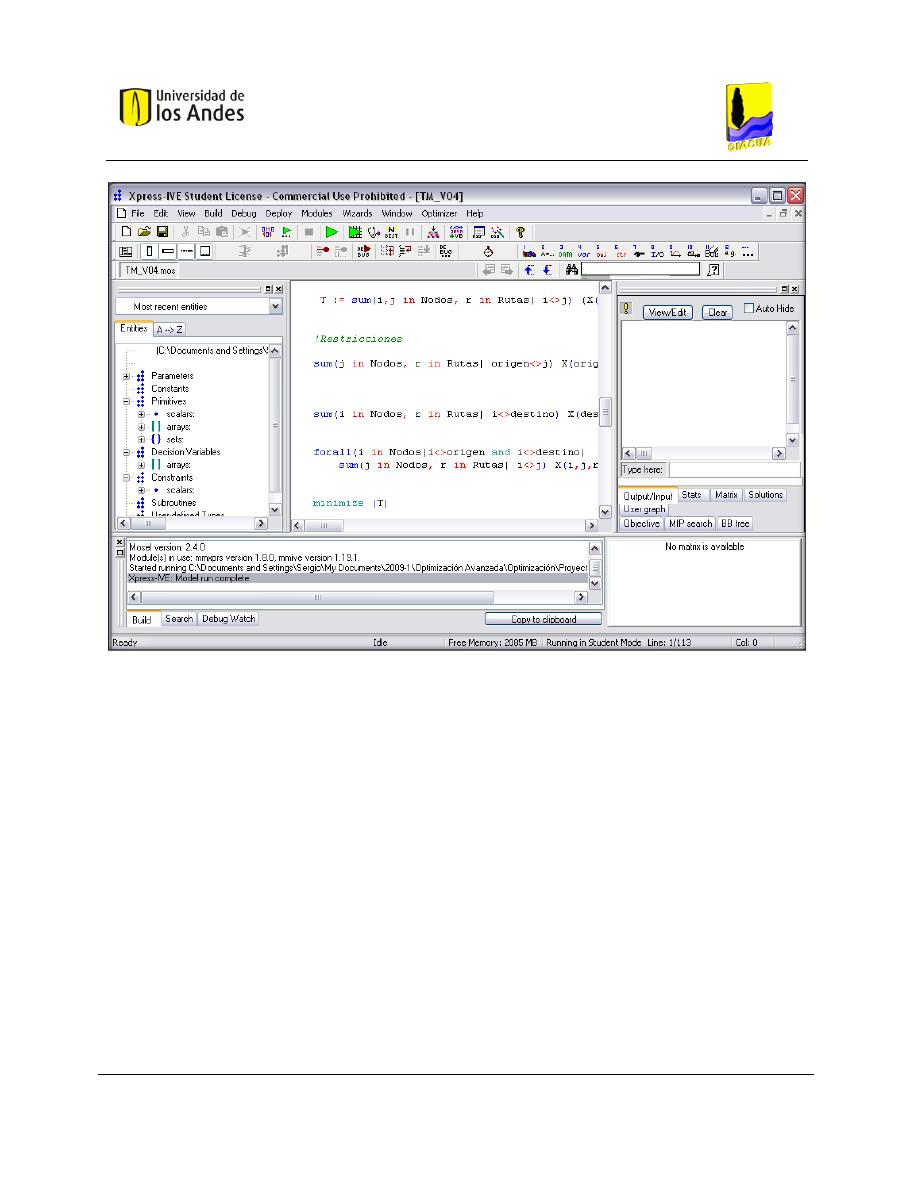
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
49
Figura 4-3. Interfaz gráfica para el software Xpress –IVE.
4.1.3 MS Excel
Para realizar los diferentes cálculos, se utilizó el software de cálculo Microsoft Excel, el cual permite
realizar múltiples cálculos y hacer programaciones mediante el uso de macros. Adicionalmente,
mediante el uso de este software es posible crear los archivos de entrada que necesita Xpress para
introducir los parámetros conocidos en la implementación.
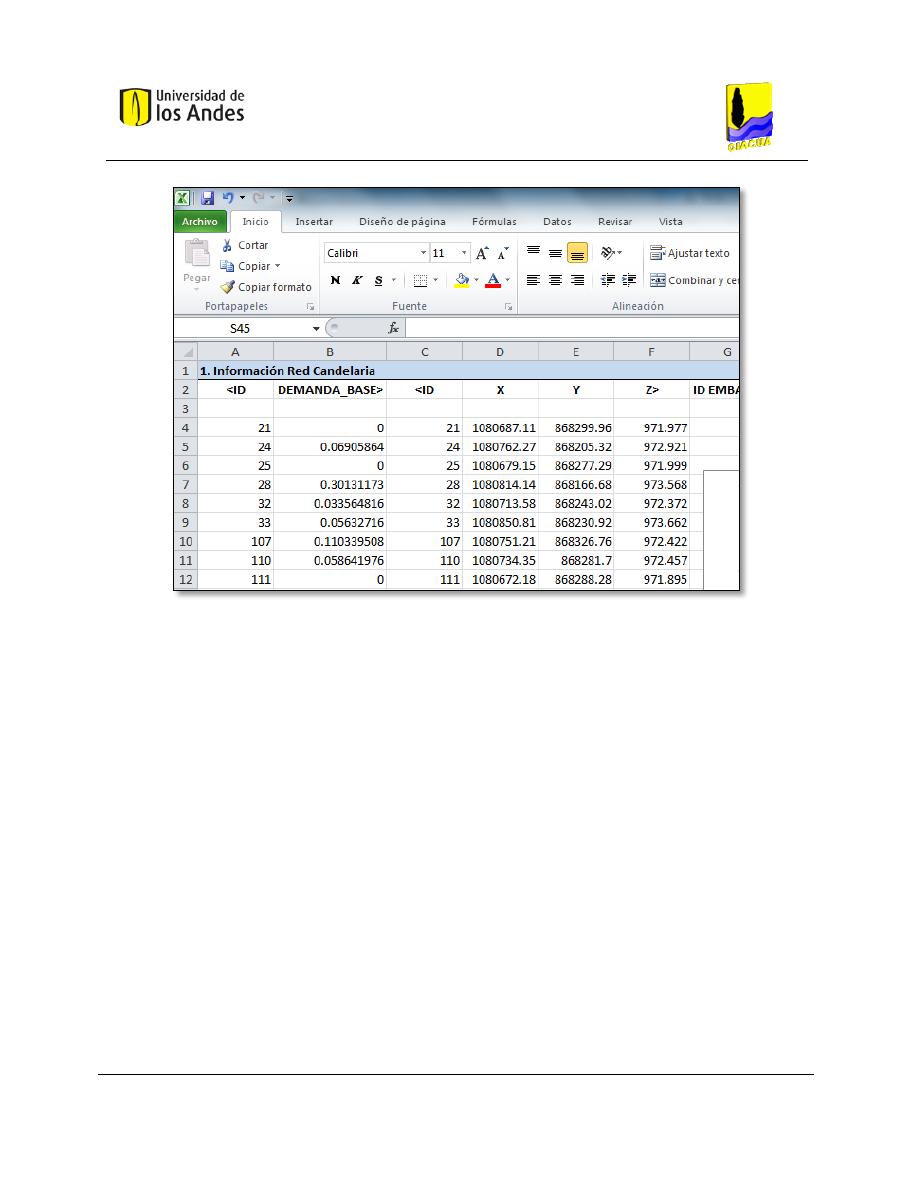
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
50
Figura 4-4. Interfaz gráfica para el software Microsoft Excel.
El software MS EXCEL se utiliza en la metodología para la generación de la grilla de densidad, la
generación de los parámetros de entrada a otros programas en el formato requerido por dicho software
y el cálculo de variables y relaciones hidráulicas (p.e. gradiente hidráulico desde el embalse hasta un
nudo de consumo particular), por lo que es fuente de entradas a diferentes pasos de la metodología.
4.1.4 ASIGNA V. 3.4
Asigna 3.4 es un programa desarrollado por el CIACUA que relaciona usuarios de una red de acueducto
con el nudo de la red del cual se alimentan. Las entradas del programa son archivos de texto que
contienen información sobre los nudos, las tuberías, los vértices y los usuarios. También una caja de
texto en la interfaz que permite escribir el diámetro máximo de tuberías conectables por los usuarios.
Esto es porque los usuarios generalmente solo se pueden conectar a la red a través de tuberías de cierto
diámetro o menor. Las salidas del programa son archivos de texto que contienen información acerca de
los usuarios y los nudos.
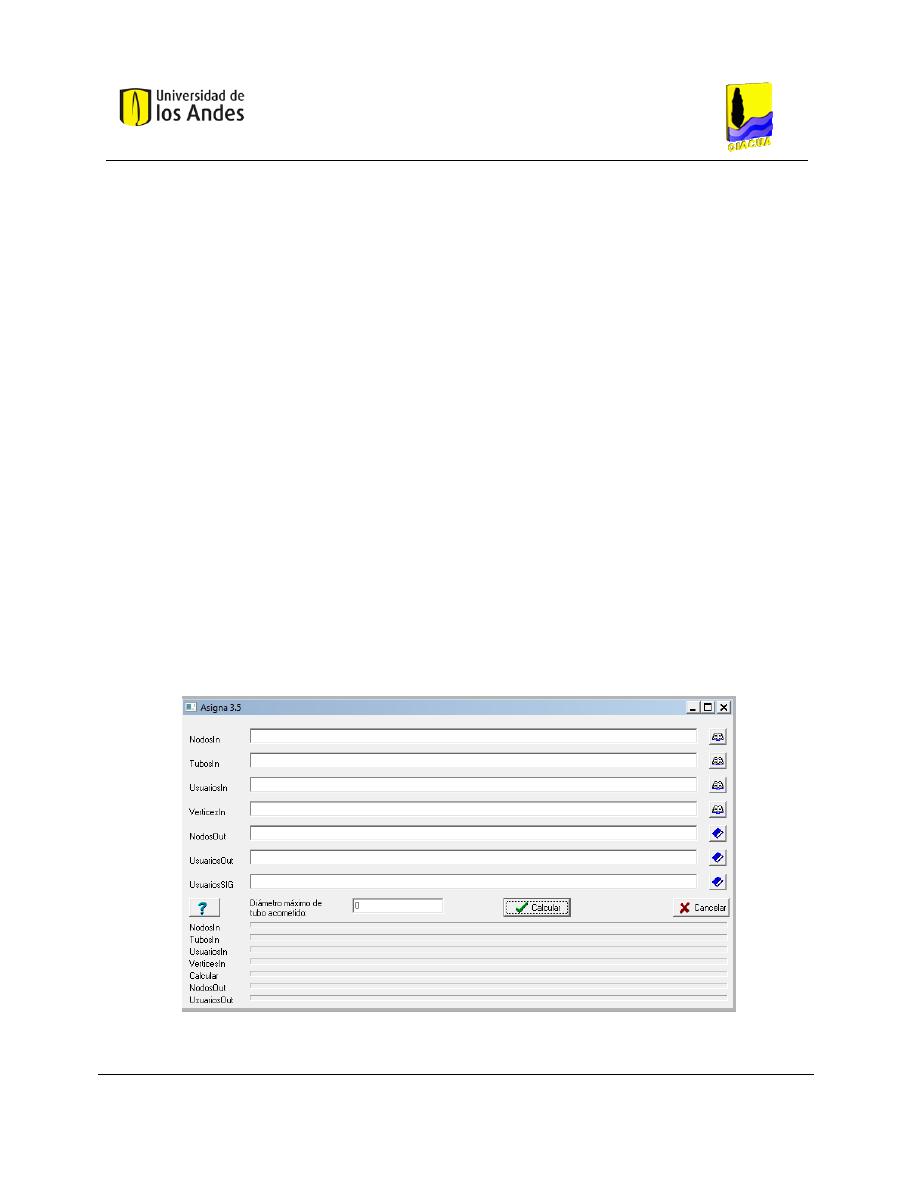
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
51
En las entradas, se especifica un identificador y las coordenadas para cada nudo. Para cada tubo se
especifica su identificador, dos identificadores de nudos, que son los nudos a los cuales se conecta el
tubo, y el diámetro. Para los usuarios se especifica su identificador, sus coordenadas y su consumo de
agua. Para los vértices se especifica el identificador del tubo al que se conecta, el orden del vértice en el
tubo y las coordenadas del tubo. En las salidas, los archivos muestran para cada usuario, su identificador,
el nudo al cual fue conectado por ASIGNA, y su consumo de agua. Para cada nudo, su identificador y su
demanda de agua a la red. Esta corresponde a la suma de las demandas de los usuarios que se le
conectaron.
De manera general, el procedimiento utilizado por ASIGNA para la asignación de demandas en un
determinado nudo en la RDAP es el siguiente:
1. Identificar qué nudo es cercano al punto de consumo.
2. Determinar si es aceptable la asignación al nudo escogido en el punto 1. Para esto se determina
que no existan cruces de calles.
3. Si el resultado del punto 2 es lógico; es decir, respeta el no cruce de calles, se realiza la
asignación. De lo contrario se busca un nuevo nudo candidato en el punto 1.
4. Repetir de forma iterativa hasta completar la asignación de todos los nudos
Este procedimiento permite establecer las demandas para cada punto de la RDAP de acuerdo con los
consumos reales medidos.
Figura 4-5. Interfaz gráfica para el software ASIGNA.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
52
5 Casos de Estudio
Para validar la metodología planteada, se utilizaron tres redes reales que han sido trabajadas
anteriormente en el CIACUA y corresponden a municipios colombianos. Para cada uno de los casos, la
metodología fue aplicada en su totalidad, permitiendo comparar los resultados de ésta respecto a los
costos operacionales. Cada una de las redes escogidas cuentas con toda la información necesaria para
poder aplicar la metodología, fundamentalmente la información necesaria por el software Asigna,
permitiendo realizar la agregación de demandas en el diseño de la red matriz adyacente al nuevo
embalse. Por este motivo, son idóneas para este trabajo de tesis. A continuación se presentan cada una
de las redes trabajadas.
De forma general, cada cado de estudio es presentado mediante la descripción topográfica del mismo,
su estado inicial de demandas, presiones y caudales. Esta información permite realizar toda la
metodología.
5.1 Información fundamental red Candelaria
Red que distribuye agua potable a la población de La Candelaria, ubicada en el suroccidente colombiano,
cuenta con dos sistemas de almacenamiento de agua ubicados muy cerca el uno del otro. Esta red,
abastece de agua a una población de aproximadamente 67.000 habitantes.
La información fundamental de la red se presenta en la Tabla 5-1.
Tabla 5-1. Información principal red Candelaria.
CARACTERÍSTICAS PRINCIPALES
DESCRIPCIÓN
Número de tuberías
559
Número de nudos
460
Número de tanques
2
Altura piezométrica del tanque
1005 msnm
Longitud total de las tuberías
23493 m
Demanda total
33 L/s
Material tuberías
PVC (ks = 0,0015 mm)
Diámetros comerciales
5.08 – 10.16 cm
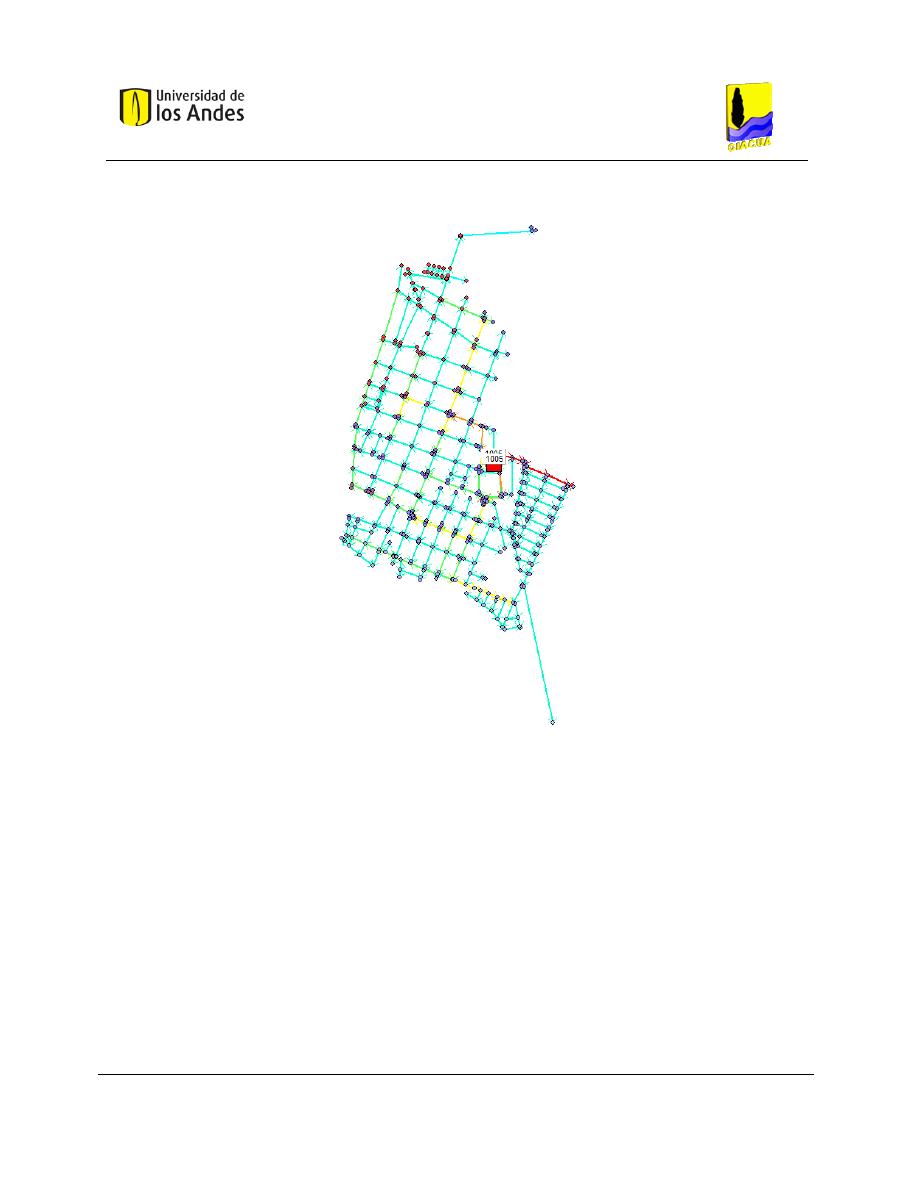
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
53
A continuación se presenta un esquema en donde se muestra la configuración topográfica de la red.
Figura 5-1. RDAP Candelaria, ubicada en el Departamento del Valle del Cauca.
Este modelo se encuentra calibrado por trabajos previos realizados en el CIACUA. Utilizando el software
REDES, se calcula la hidráulica en periodo estable para tener las variables hidráulicas principales, como lo
son las presiones en los nudos y los caudales en los tubos. La Gráfica 5-1 presenta la demanda de
consumo base en los nudos para la red de Candelaria, en donde se evidencian demandas cercanas a
cero, mientras que las máximas están en el orden de 0.36 L/s.
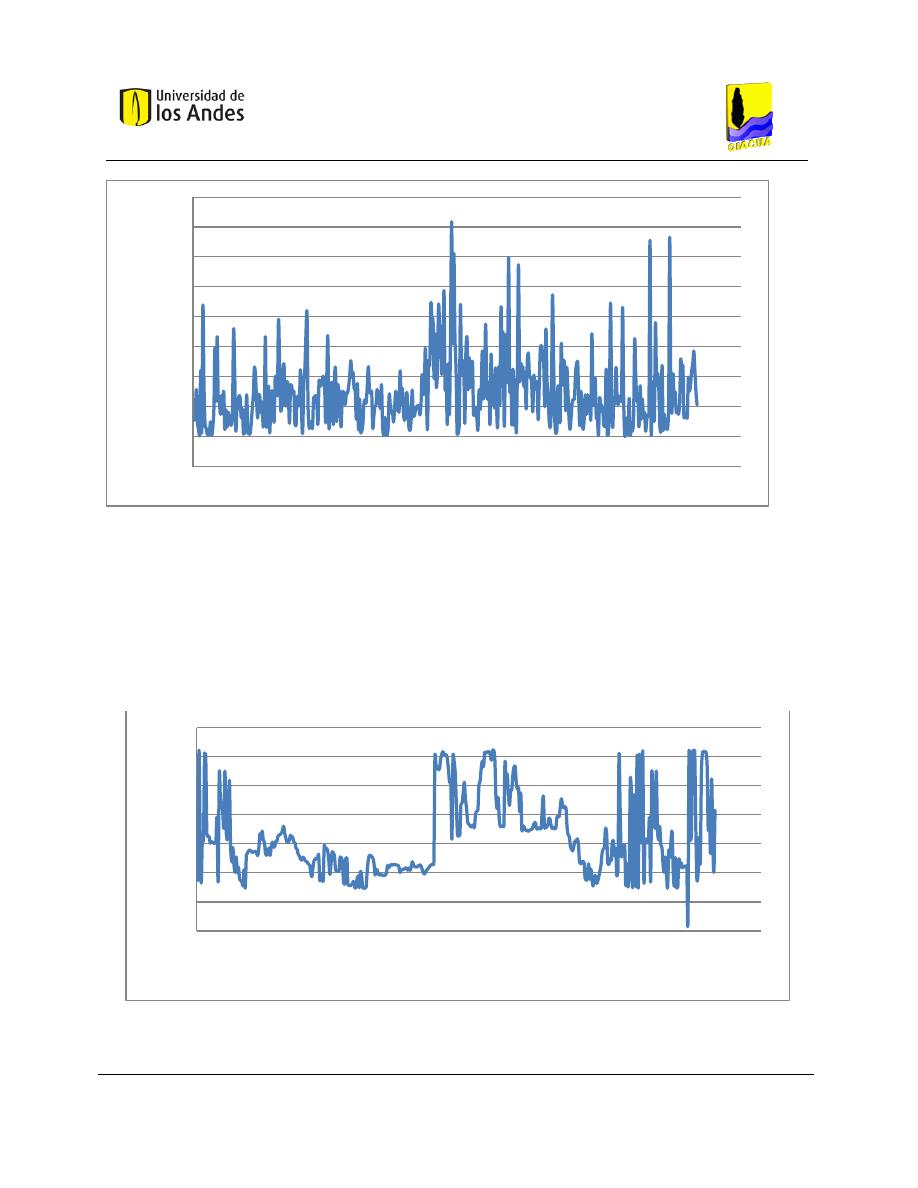
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
54
Gráfica 5-1. Demanda Base en los nudos en estado estable para la red de Candelaria.
Para el estado de demandas presentado en la Gráfica 5-1, se calcula la hidráulica de la red con el
software REDES, obteniendo la Gráfica 5-2 y la Gráfica 5-3 para las presiones en los nudos y los caudales
en los tubos respectivamente.
Gráfica 5-2. Estado de presiones en los nudos en estado estable para la red de Candelaria.
-0.05
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0
50
100
150
200
250
300
350
400
450
500
D
e
m
an
d
a B
ase
(Lp
s)
ID de los Nudos
28
29
30
31
32
33
34
35
0
50
100
150
200
250
300
350
400
450
500
Pr
e
si
ó
n
(
m
ca)
ID de los Nudos
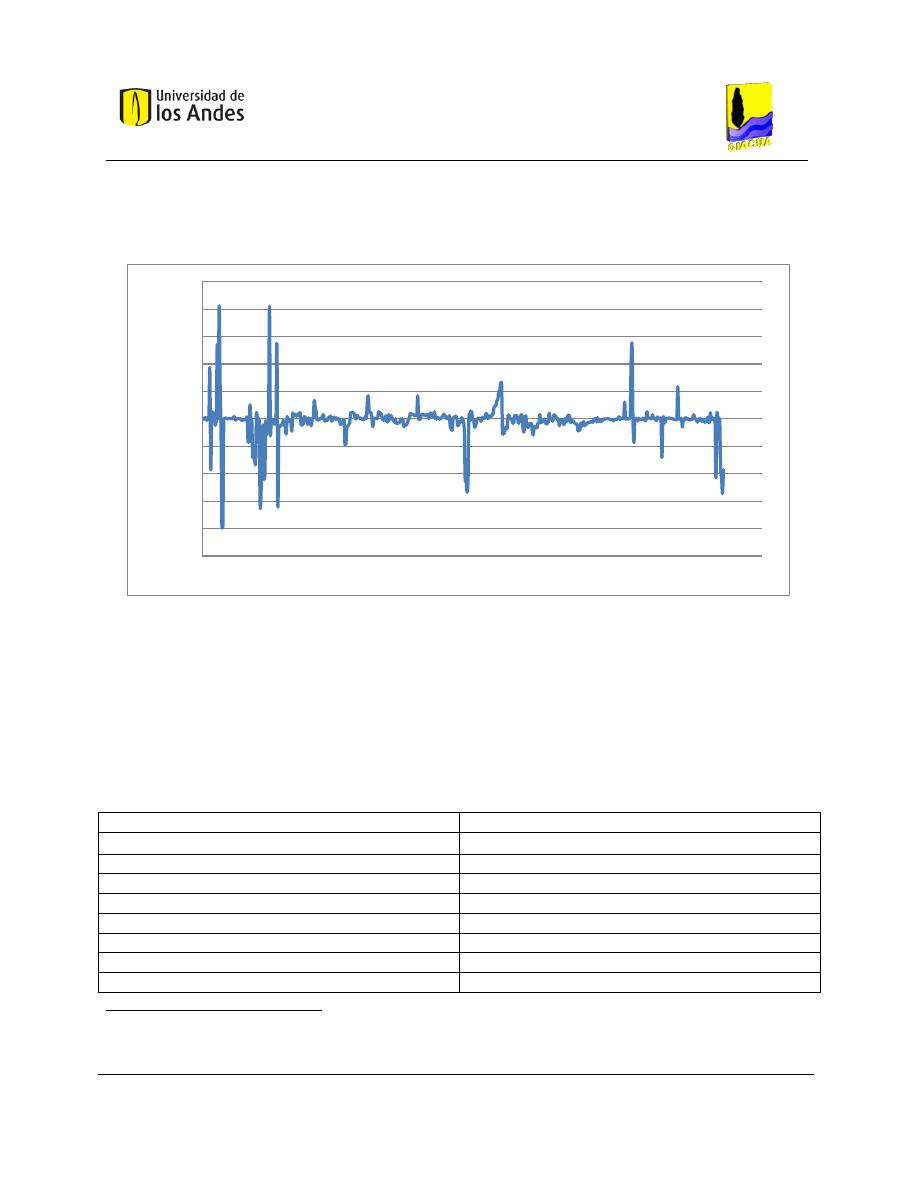
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
55
De forma análoga se presentan los caudales para las tuberías de la red. El signo negativo de algunos
caudales corresponde al sentido del flujo. Por ejemplo, si el tubo está definido como una conexión entre
el nudo i y el nudo j, y el caudal se mueve del nudo j al nudo i, el signo del caudal será negativo.
7
Gráfica 5-3. Estado de caudales en los tubos en estado estable para la red de Candelaria.
5.2 Información fundamental red Andalucía Alta
La red de Andalucía Alta se encuentra ubicada en el Departamento del Valle del Cauca, sus propiedades
fundamentales se presentan a continuación.
Tabla 5-2. Información principal red Andalucía Alta.
CARACTERÍSTICAS PRINCIPALES
DESCRIPCIÓN
Número de tuberías
360
Número de nudos
329
Número de tanques
1
Altura piezométrica del tanque
996 msnm
Longitud total de las tuberías
23587 m
Demanda total
20 L/s
Material tuberías
PVC (ks = 0,0015 mm)
Diámetros comerciales
5.08 – 10.16 cm
7
Esta nomenclatura es por defecto la utilizada por el software Redes, utilizado para realizar todos los cálculos
hidráulicos de este documento de tesis.
-25
-20
-15
-10
-5
0
5
10
15
20
25
0
100
200
300
400
500
600
Cau
d
al
(
Lp
s)
ID de las Tuberías
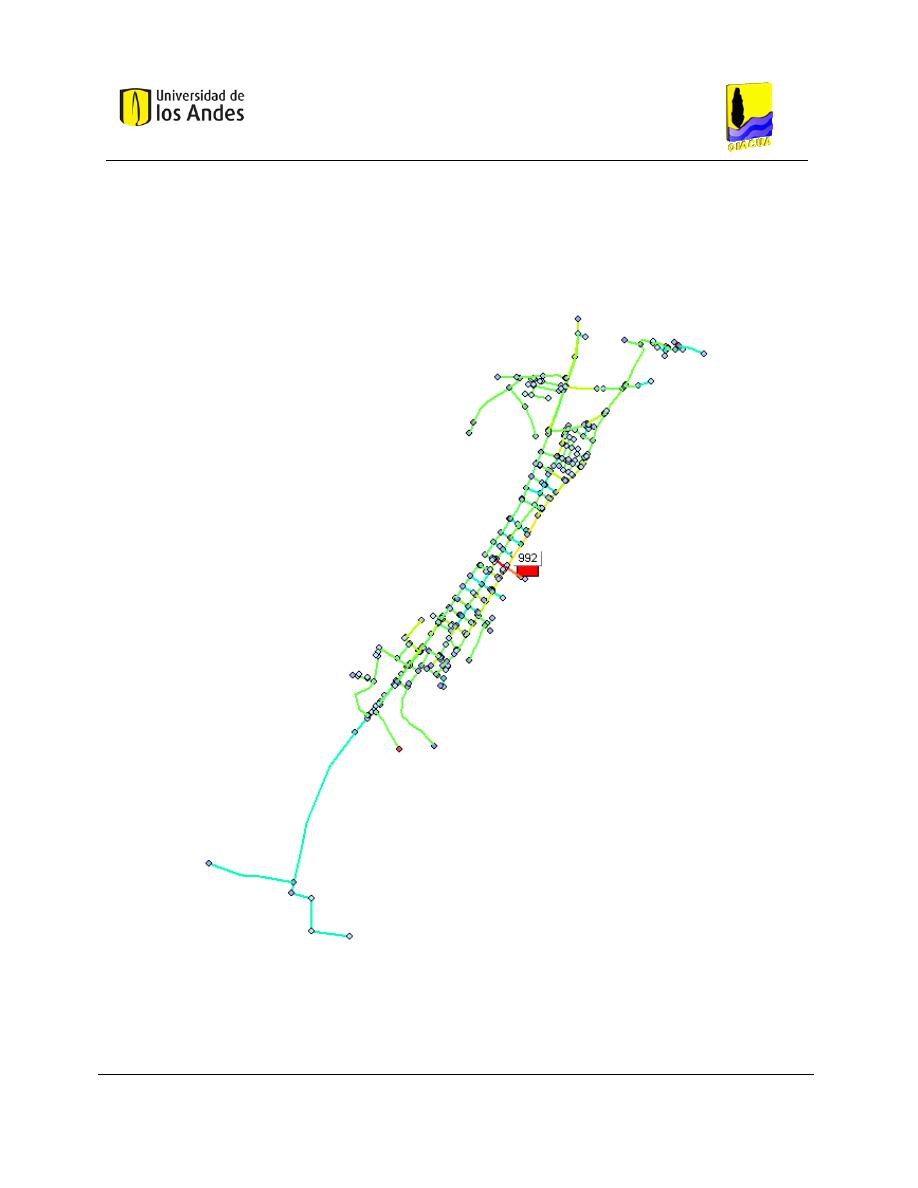
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
56
Igualmente, a continuación se presenta la red desde el software redes. Se puede observar que la
ubicación del embalse principal es similar a la ubicación encontrada en Candelaria, en el sentido en que
en ambos casos están en un extremo y geográficamente son centrales respecto a toda la red.
Figura 5-2. RDAP Andalucía Alta, ubicada en el Departamento del Valle del Cauca.
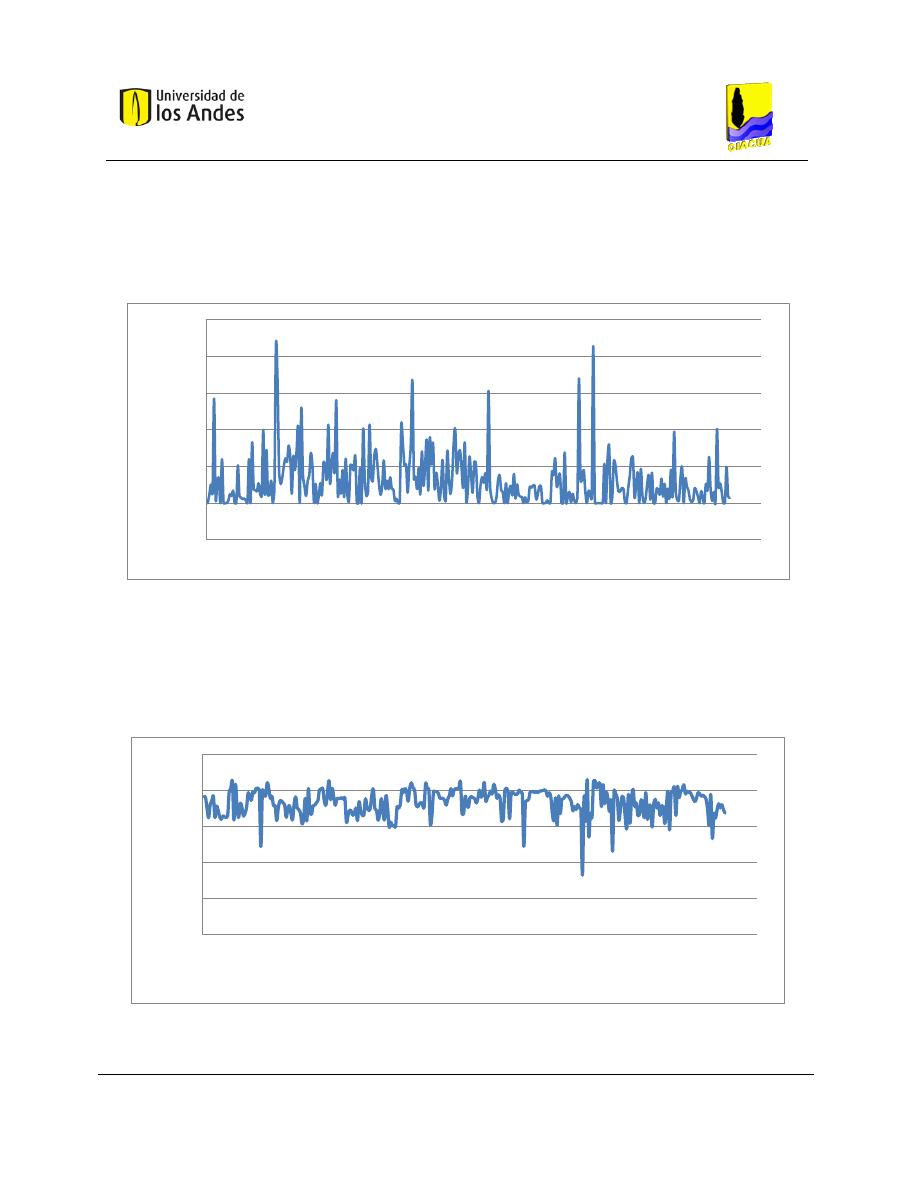
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
57
De forma análoga a lo presentado para la red de Candelaria, a continuación se muestran graficadas las
propiedades hidráulicas más relevantes de la red Andalucía Alta. En primer lugar se presentan las
demandas de cada uno de los nudos de la red.
Gráfica 5-4. Estado de demandas en los nudos en estado estable para la red de Andalucía Alta.
Las presiones obtenidas en los nudos se presentan a continuación.
Gráfica 5-5. Estado de presiones en los nudos en estado estable para la red de Andalucía Alta.
-0.1
0
0.1
0.2
0.3
0.4
0.5
0
50
100
150
200
250
300
350
D
e
m
an
d
a B
ase
(L/
s)
ID de los nudos
0
10
20
30
40
50
0
50
100
150
200
250
300
350
Pr
e
si
ó
n
(
m
ca)
ID de los nudos
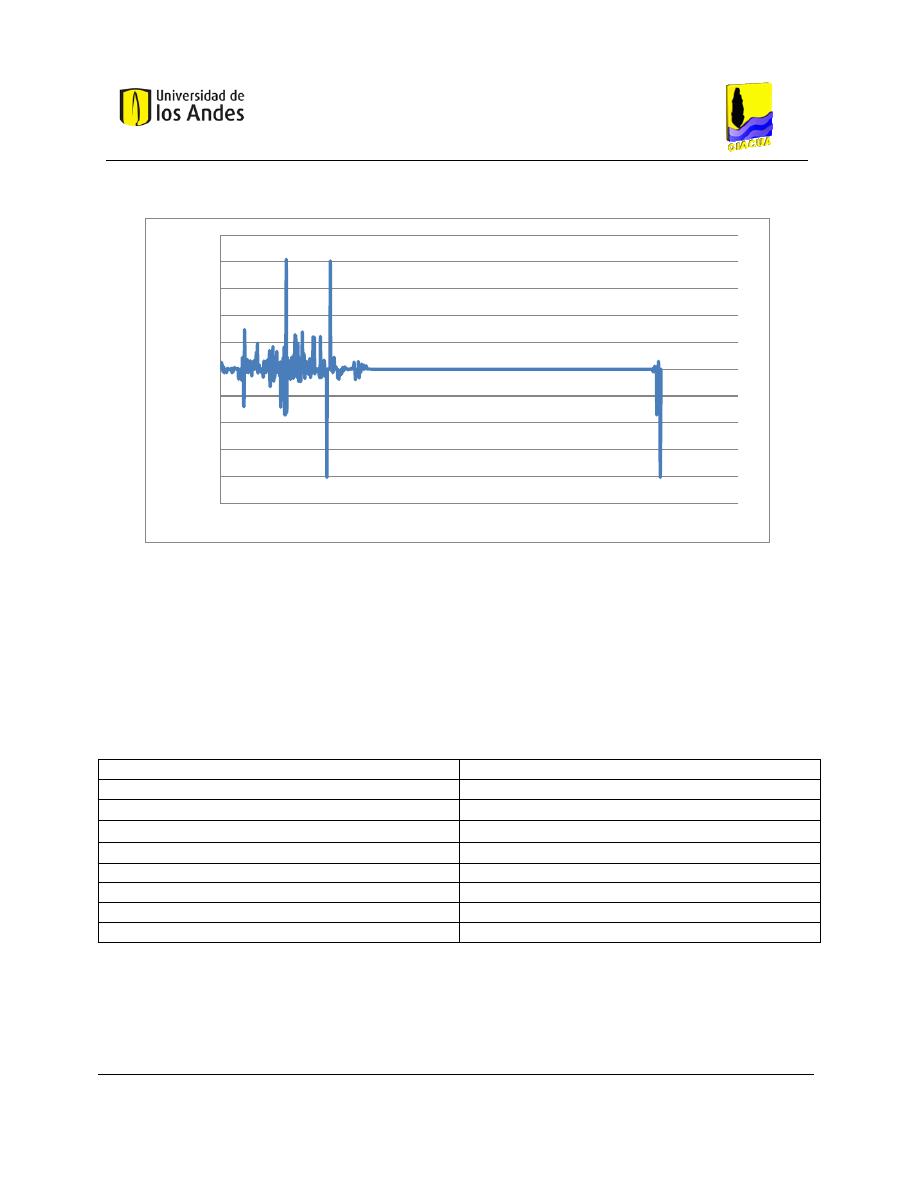
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
58
Finalmente, los caudales en los tubos se muestran en la Gráfica 5-6.
Gráfica 5-6. Estado de caudales en los tubos en estado estable para la red de Andalucía Alta.
5.3 Información fundamental red Bolívar
La red de Bolívar, al igual que los otros dos casos de estudio, también se encuentra localizada en el
Departamento del Valle del Cauca. Sus propiedades fundamentales se presentan a continuación.
Tabla 5-3. Información principal red Bolívar.
CARACTERÍSTICAS PRINCIPALES
DESCRIPCIÓN
Número de tuberías
333
Número de nudos
285
Número de tanques
1
Altura piezométrica del tanque
957 m
Longitud total de las tuberías
29450.16 m
Demanda total
11.97 L/s
Material tuberías
PVC (ks = 0,0015 mm)
Diámetros comerciales
5.08 – 10.16 cm
-25
-20
-15
-10
-5
0
5
10
15
20
25
0
200
400
600
800
1000
1200
Cau
d
al
(
L/s)
ID de los tubos
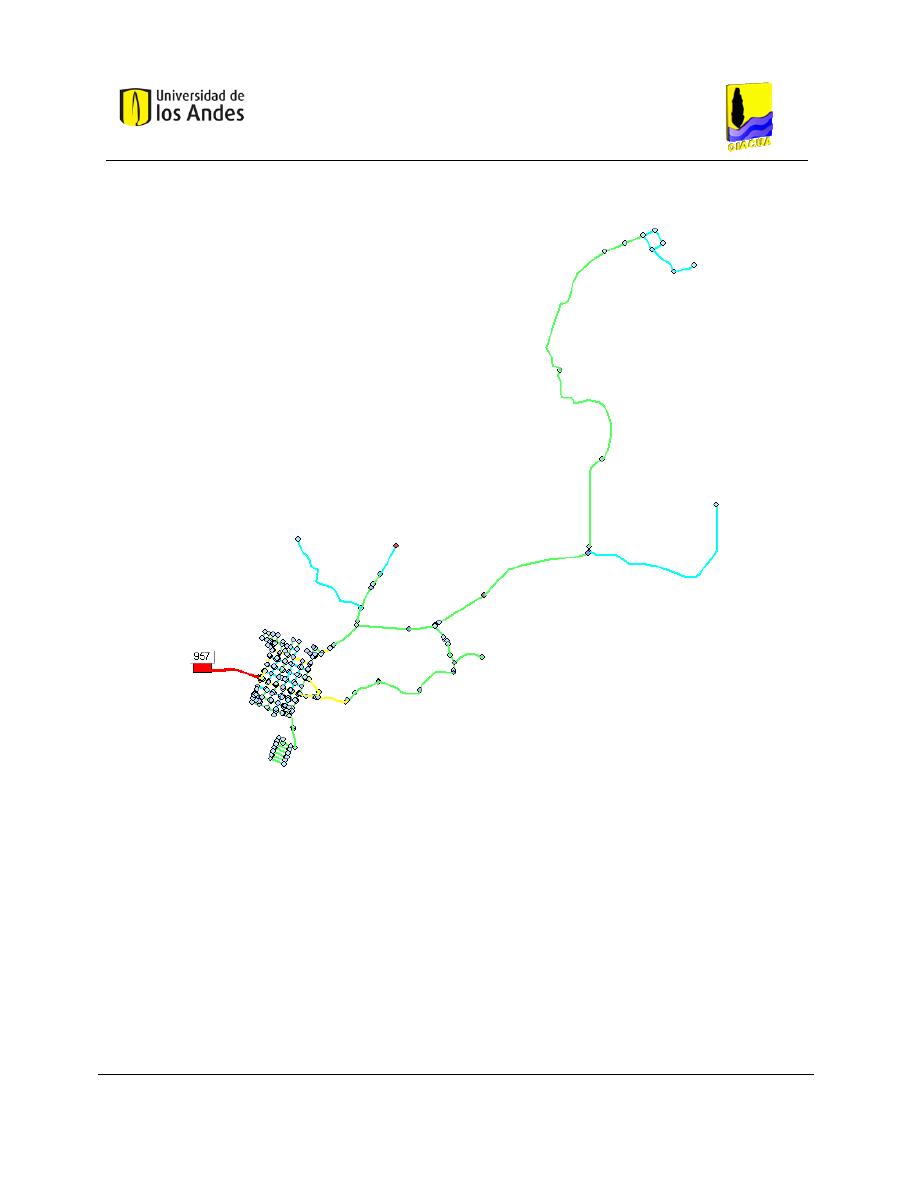
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
59
La distribución geográfica de la red se presenta a continuación.
Figura 5-3. RDAP de Bolívar, ubicada en el Departamento del Valle del Cauca.
A continuación se presenta la información correspondiente a la demanda base de la red, el estado de
presiones y los caudales en los tubos.
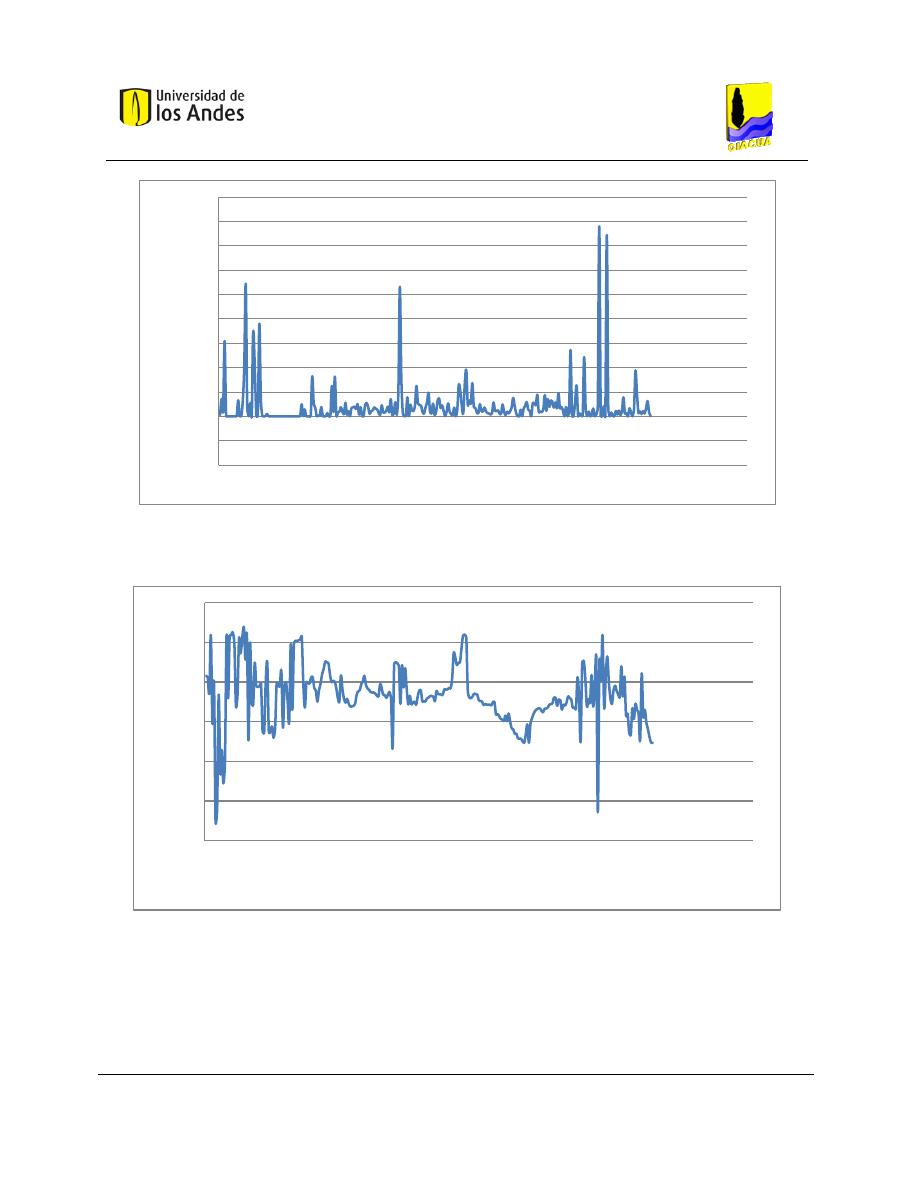
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
60
Gráfica 5-7. Estado de demandas en los nudos en estado estable para la red de Bolívar.
Gráfica 5-8. Estado de presiones en los nudos en estado estable para la red de Bolívar.
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
0
50
100
150
200
250
300
350
D
Em
an
d
a B
ase
(L/
s)
ID de los nudos
0
5
10
15
20
25
30
0
50
100
150
200
250
300
350
Pr
e
si
o
n
e
s (m
ca)
ID de los nudos
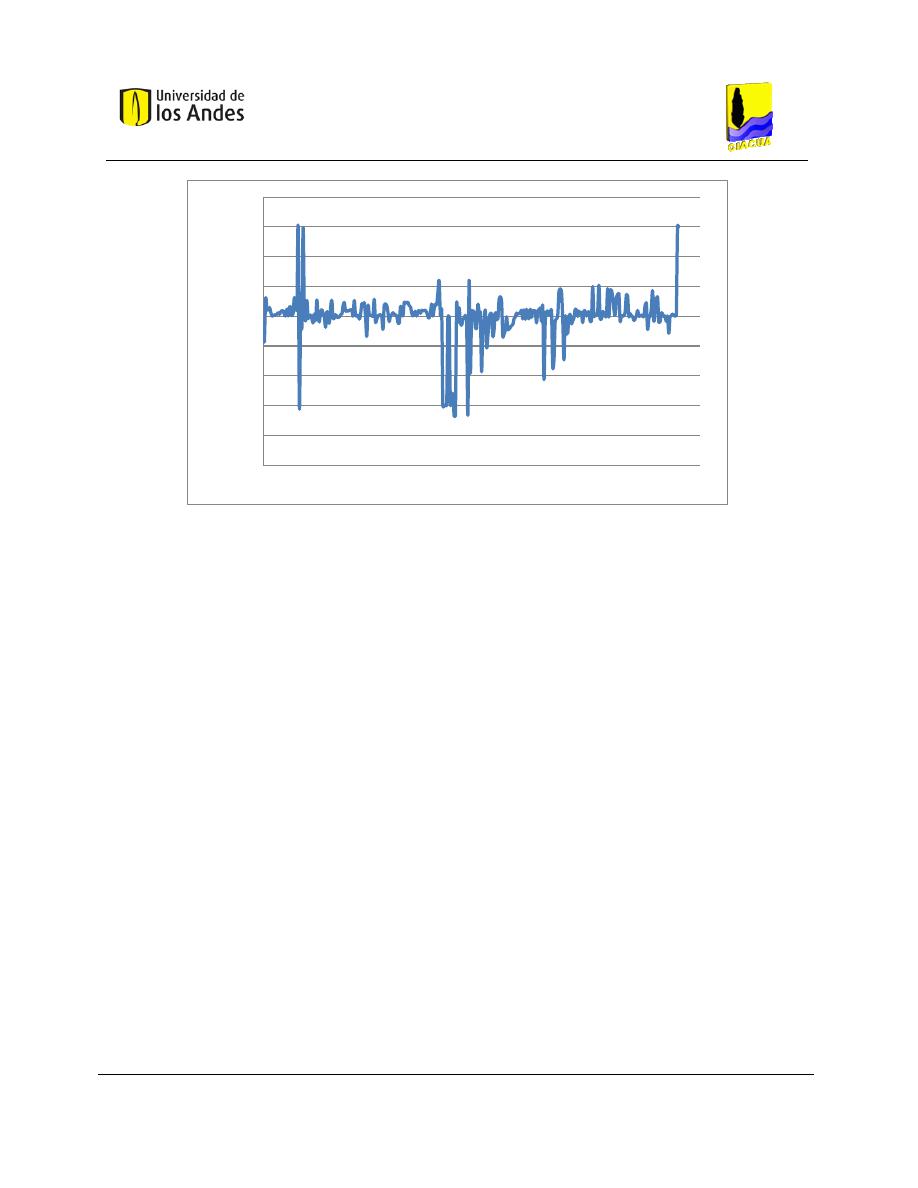
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
61
Gráfica 5-9. Estado de caudales en los tubos en estado estable para la red de Bolívar.
-25
-20
-15
-10
-5
0
5
10
15
20
0
50
100
150
200
250
300
350
Cau
d
al
(
L/s)
ID de los tubos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
62
6 Resultados
Aplicando la metodología descrita en el Capítulo 3, se obtuvieron los siguientes resultados para cada un
de los casos de estudio. En primer lugar, se describe la ejecución de la metodología como se muestra a
continuación.
6.1 Aplicación de la metodología en los casos de estudio
Para los diferentes casos de estudio descritos en el Capítulo 5 se aplicó la metodología descrita en el
Capítulo 3. A continuación se muestran nuevamente los pasos principales de la metodología.
1. Recolección de información básica de la RDAP.
2. Ubicación del embalse secundario dentro de la RDAP.
3. Escogencia de la zona de influencia que tendrá el nuevo embalse.
4. Determinación de la zona de influencia del nuevo embalse.
5. Determinar la ruta desde el nuevo embalse hasta cada uno de los nudos de consumo
pertenecientes a la zona de influencia.
6. Cambio de diámetro de las tuberías pertenecientes a la zona de influencia y determinación de la
altura piezométrica disponible en el nuevo embalse.
7. Evaluar el desempeño del sistema (económico e hidráulico).
Cada uno de estos pasos fue replicado en los casos de estudio obteniendo un modelo de cada red en el
que existe un embalse adicional a el (los) ya existente(s) y unas tuberías con diámetros diferentes.
Para la primera red, se explica en detalle cada uno de los pasos realizados para obtener los resultados.
Como el procedimiento es el mismo para todos los casos, las redes de Andalucía Alta y Bolívar solamente
presentan los resultados finales.
6.1.1 Metodología aplicada a la red Candelaria
Candelaria es la primera red a la que se la aplicó la metodología para reducir los costos operacionales en
redes que cuentan con SB. Se siguió el diagrama de flujo presentado en la Figura 3-1. El primer paso del
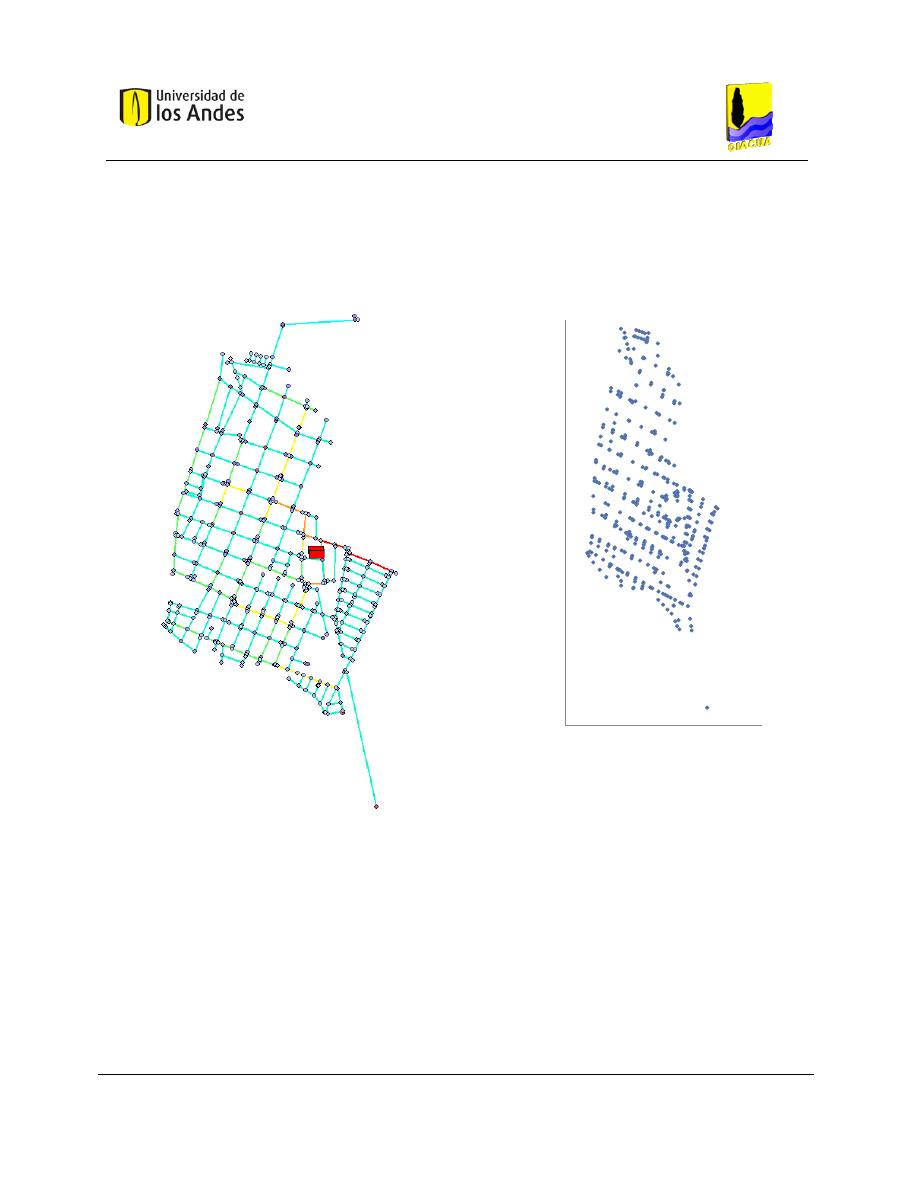
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
63
algoritmo, referente a la información requerida para poder comenzar a aplicar la metodología ya ha sido
presentado en el Capítulo 5.
Posteriormente es necesario establecer la ubicación del embalse secundario, para lo cual se utiliza la
grilla de densidad de consumo. A continuación se presenta un esquema de la red en Redes y MS Excel.
(a).
(b).
Figura 6-1. (a) Red Candelaria graficada mediante el software REDES. (b) Generación de los nudos de
demanda de la RDAP mediante Excel.
Una vez definido el sector hidráulico de influencia, es necesario establecer la ubicación del embalse
secundario que alimentará esta zona de la red. Para esto, es necesario ingresar algunos datos de la red
en Excel. En este sentido, la información requerida es: la ubicación en (x,y,z) de cada uno de los nudos de
consumo, la demanda asociada con cada uno de estos nudos y adicionalmente información propia del
diseñador sobre el tamaño de la grilla de densidad.
867400
867900
868400
868900
869400
1080500 1081000 1081500 1082000
Y
X

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
64
Para la generación de la grilla de densidad se necesita la siguiente información de entrada:
Tabla 6-1. Información principal para la generación de la grilla de demanda.
ID Nudos
Identificador para cada uno de los nudos de la RDAP
Demanda Base Consumo base que cada nudo de consumo tiene
Coordenada X
Ubicación geográfica en el eje X
Coordenada Y
Ubicación geográfica en el eje Y
Coordenada Z
Ubicación geográfica en el eje Z
ID Embalses
Identificador para los embalses de la RDAP
Con esta información el siguiente paso es determinar las propiedades de la grilla de densidad; es decir, el
tamaño de cada una de las celdas que la conforma. En este paso depende del diseñador y del grado de
detalle que se quiera tener acerca de la ubicación del embalse. Puede darse el caso en que se pierda
fidelidad de la información por tener un tamaño de celda muy pequeño. Esto se debe a que la grilla
supone una agregación de las demandas que se encuentran dentro de cada celda como valor para
escoger la ubicación. Si el grado de detalle es muy alto, no van a existir nudos para agregar en cada
celda, por lo que se pierde el objetivo principal de la generación de la grilla de demanda.
Para el caso de la red Candelaria, la grilla generada tiene 5 divisiones horizontalmente y 10 divisiones
verticalmente. En total, la red quedó dividida en 50 celdas diferentes.
Para los límites de la grilla, se consideran aquellos nudos externos de la red, por lo que los límites
siempre coinciden con la coordenada de alguno de los nudos del sistema. A continuación, la Figura 6-2
presenta la grilla para la red de Candelaria.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
65
Figura 6-2. Grilla de densidad para la red Candelaria
8
.
8
Esta figura presenta un esquema que conserva las condiciones topológicas de la red original, pero no se encuentra a
escala ni proporción respecto a la red original.
867000
867500
868000
868500
869000
869500
870000
10806001080800108100010812001081400 10816001081800
Y
X

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
66
De acuerdo con lo planteado en la metodología, el siguiente paso es sumar para cada celda la variable de
interés (en este caso la demanda de consumo).
Tabla 6-2. Demanda acumulada (L/s) para cada celda de la grilla de densidad de demanda para la red
de Candelaria.
0
1
2
3
4
9
0.0000
3.0312
3.1019
0.5650
0.0000
8
0.0000
2.3015
3.8058
1.3048
0.0000
7
0.3448
3.5948
2.8587
0.5809
0.0000
6
2.2811
1.8790
2.8586
0.0000
0.0000
5
1.4861
1.2234
1.3540
1.5673
0.4657
4
1.0908
1.5079
1.3850
1.2444
1.6024
3
1.2342
2.0438
1.7973
0.6194
0.7107
2
0.0000
0.3183
0.7188
1.6168
0.0000
1
0.0000
0.0000
0.0000
0.2184
0.0000
0
0.0000
0.0000
0.0000
0.0000
0.1129
De acuerdo con los resultados presentados en la Tabla 6-2, la celda con valor de demanda de consumo
máxima es la posición (1,7)
9
con un valor de 3.59481 L/s como consumo agregado. De forma gráfica, a
continuación se presenta una figura con la ubicación escogida resaltada en color amarillo.
9
Nomenclatura en relación con la Tabla 6-2 (posición X, posición Y).
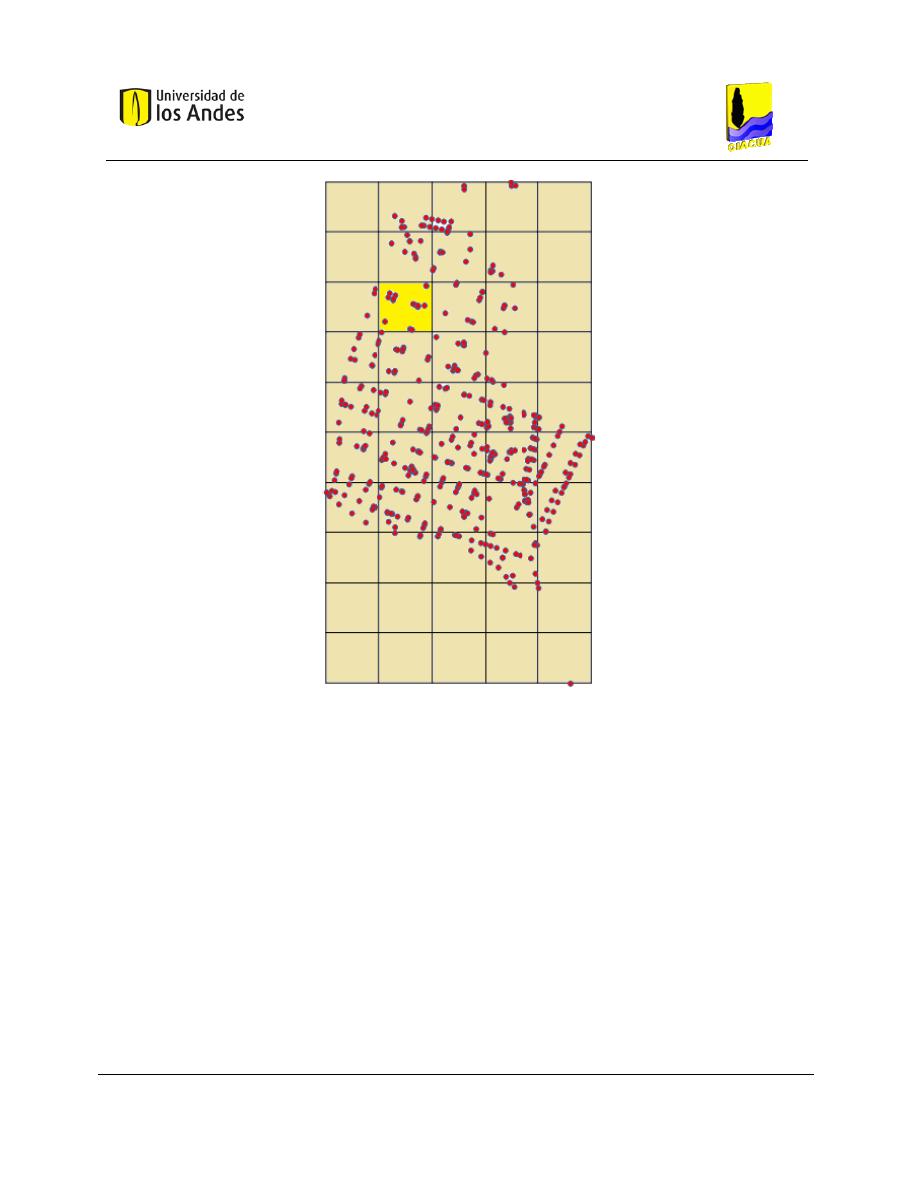
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
67
Figura 6-3. Selección de la zona en donde se ubicará el embalse secundario.
Siguiendo con la metodología, es necesario determinar la zona de influencia que puede tener la inclusión
de un nuevo embalse secundario dentro de la RDAP. Para este paso, es importante considerar aquellos
sectores del sistema en donde se presentan las peores condiciones hidráulicas, pues estos sectores
marcan posibilidades de división de la red.
Particularmente se utiliza el concepto de potencia unitaria para cada tubería, en donde se relaciona la
diferencia de energía entre el nudo aguas arriba y el nudo aguas abajo del tubo con el caudal que está
pasando en un momento dado. Como todos los cálculos se están realizando en periodo estable el caudal
es constante. La Gráfica 6-1 presenta los valores obtenidos para cada uno de los tubos.
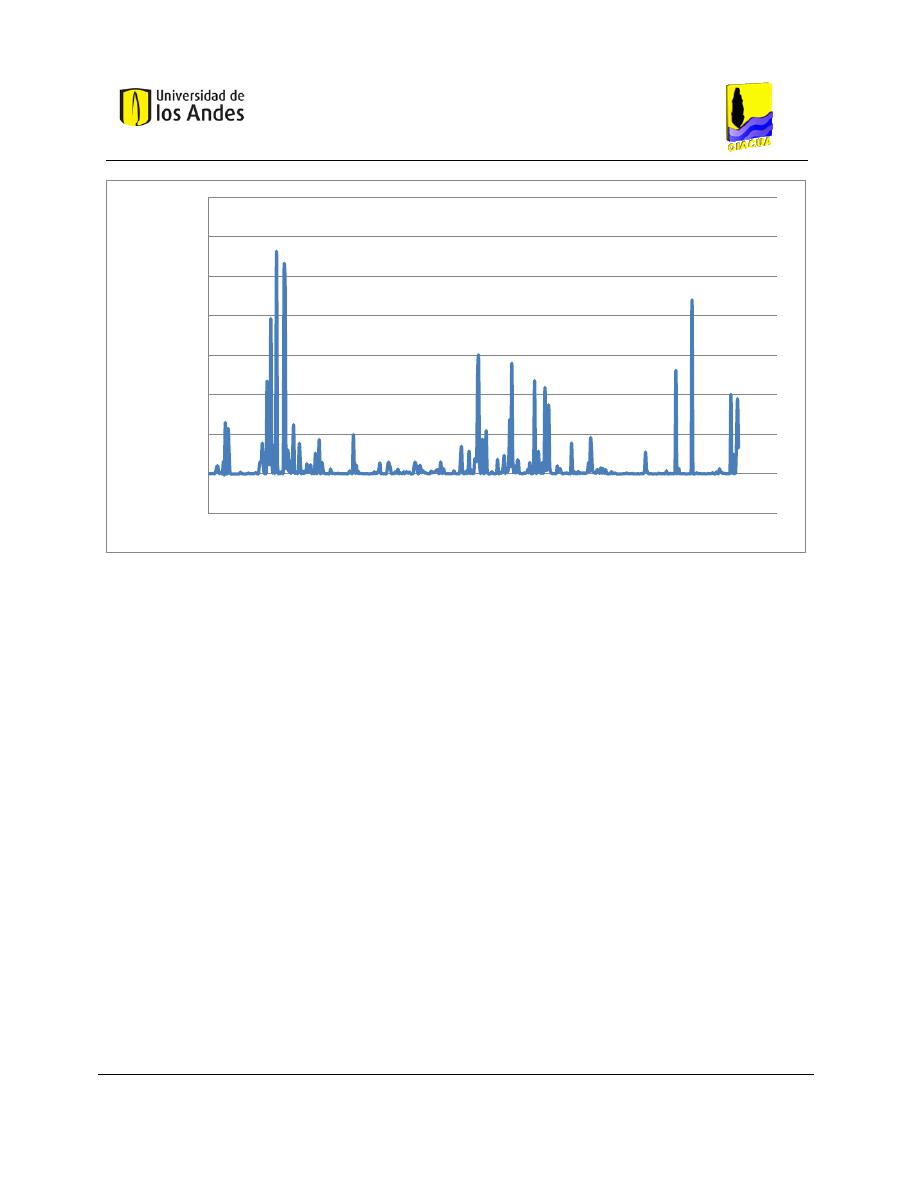
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
68
Gráfica 6-1. Potencia Unitaria para los tubos pertenecientes a la red de Candelaria.
Aquellos tubos con mayor Potencia Unitaria son lo que más están afectando la hidráulica de la RDAP, por
lo que son esas las tuberías que podrían definir un sector hidráulico independiente. La Figura 6-4
esquematiza la Potencia Unitaria para cada una de las tuberías que conforman la red.
-0.0002
0
0.0002
0.0004
0.0006
0.0008
0.001
0.0012
0.0014
0
100
200
300
400
500
600
Pot
e
n
ci
a Un
itar
ia
(m
4
/s)
ID de las Tuberías
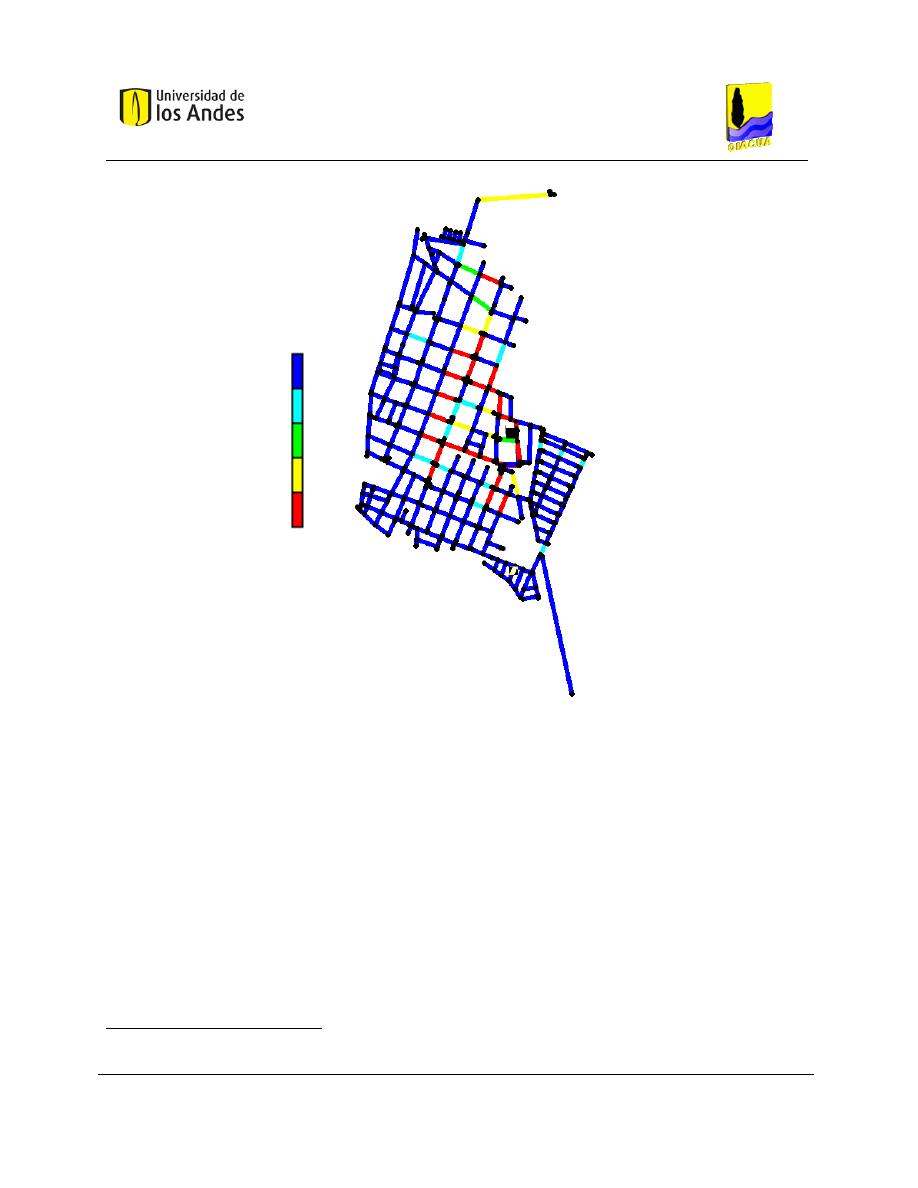
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
69
Figura 6-4. Potencia unitaria de la red Candelaria
10
.
La Figura 6-4 presenta posibles secciones de tuberías que pueden ser la referencia para la definición de
varios sectores hidráulicos independientes (para efectos de la modelación únicamente). En esta red la
mayor parte de tuberías con las mayores potencias unitarias permite dividir la red en dos grandes zonas.
Sin embargo, sólo una de las secciones tendría conexión con los embalses existentes, por lo que la
sección que quede sin embalses será la de interés para efectos de esta metodología. La Figura 6-5
presenta el sector hidráulico que será considerado para todo el desarrollo.
10
La escala de colores indica los colores más cálidos para las tuberías con mayor potencia unitaria.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
70
(a).
(b).
Figura 6-5. (a) Sector hidráulico de la red Candelaria graficada mediante el software REDES para el que
el nuevo embalse tiene influencia. (b) Generación de los nudos de demanda del sector hidráulico para
el cual el nuevo embalse tiene influencia mediante Excel.
Cuando la ubicación del embalse secundario ha sido definida y se tiene una partición de la red
especificando la zona de influencia de éste, es necesario establecer qué tuberías de ese sector hidráulico
van a ser modificadas para conectar adecuadamente el embalse de tal forma que se aproveche al
máximo su potencial. En este sentido, es necesario establecer la red matriz de este sector, que deberá
estar conectada con el embalse y deberá ser representativa en toda la red sin que el número de tuberías
que la conforme sea muy elevado, pues entre más tuberías hagan parte de la red matriz mayor será la
inversión en cambio de infraestructura.
Para esto se utiliza el algoritmo de árbol de expansión mínima, en el que se busca que todos los nudos de
interés queden conectados mediante un único camino. Sin embargo, es necesario un parámetro que
establezca el tamaño de la solución (p.e. considerar todos los nudos y tubos de la red o solamente una
fracción), por lo que se utilizaron criterios de calidad de agua como límites al tamaño de las posibles
soluciones. De esta forma, es necesario realizar un proceso iterativo que evalúe el impacto sobre la
868200
868400
868600
868800
869000
869200
869400
869600
869800
Y
X
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
71
calidad de agua cuando se aumenta el espacio solución. La Figura 6-6 presenta las tuberías seleccionadas
para conformar la red matriz.
(a).
(b).
Figura 6-6. (a). Sector hidráulico de la red Candelaria. (b). Subconjunto perteneciente al sector
hidráulico definido como red matriz calculado mediante el algoritmo MST
11
.
Una vez definido el conjunto de tubos que pueden ser modificables (red matriz) es necesario cuantificar
ese cambio. Para esto, un parámetro de entrada para el diseño de estas tuberías es el caudal de
consumo en cada nudo. Se supone que la agregación de demandas modela caracteriza adecuadamente
la demanda de cada nudo de la red matriz. Adicionalmente, el diseño puede modelar pérdidas objetivo
por cada tramo de tubería de forma independiente,
El diseño se traduce en conocer los parámetros iniciales requeridos en la formulación propuesta, por lo
que es necesario calcular la hidráulica en periodo estático para la red. Una vez se tienen las
11
Las figuras no se encuentran a escala.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
72
características hidráulicas, es posible generar la estructura de entrada para el software optimizador. Por
ejemplo, la tabla a continuación presenta la estructura de los costos constructivos para tres tuberías que
hacen parte de la red matriz. Para este caso, se utiliza la Ecuación 33 con un coeficiente k = 0.015 y con
exponente x = 1.46.
Tabla 6-3. Ejemplo de estimación de los costos con formato Xpress-IVE para la formulación lineal del
diseño de la red matriz.
t = Tubería NUDO1
NUDO2 Longitud (m) Diámetro (m)
Cijm
Xpress
1
252
20
69.488
0.0762 2430274 ("252","20","0.0762")2430274
2
1
390
970.518
0.0762 3394291 ("1","390","0.0762")33942913
34
29
20
86.733
0.0762 3033401 ("29","20","0.0762")3033401
La estructura de todos los parámetros es análoga, permitiendo correr el programa en Xpress IVE. Para
correr el programa, es necesario definir el nombre del archivo de entrada de los parámetros,
posteriormente declarar los conjuntos, parámetros y variables de decisión explicados en el Numeral 3.5
de este documento.
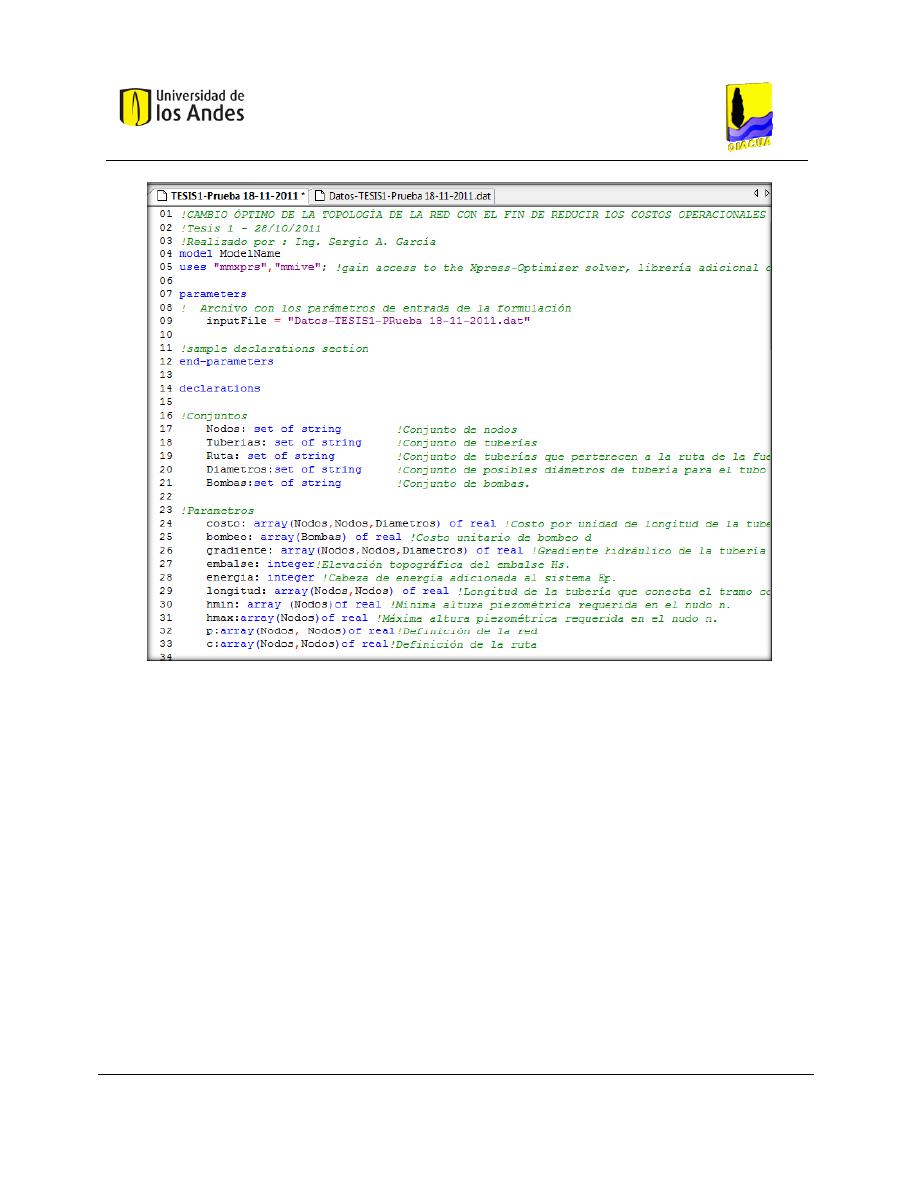
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
73
Figura 6-7. Declaración de conjuntos y parámetros de la formulación lineal en el software de
optimización Xpress – IVE.
Cuando todos los elementos se encuentran declarados, es necesario crear las variables de decisión que
van a ser consideradas dentro de la modelación. Particularmente, se suponen enteras; sin embargo, esta
condición puede ser fácilmente modificable.
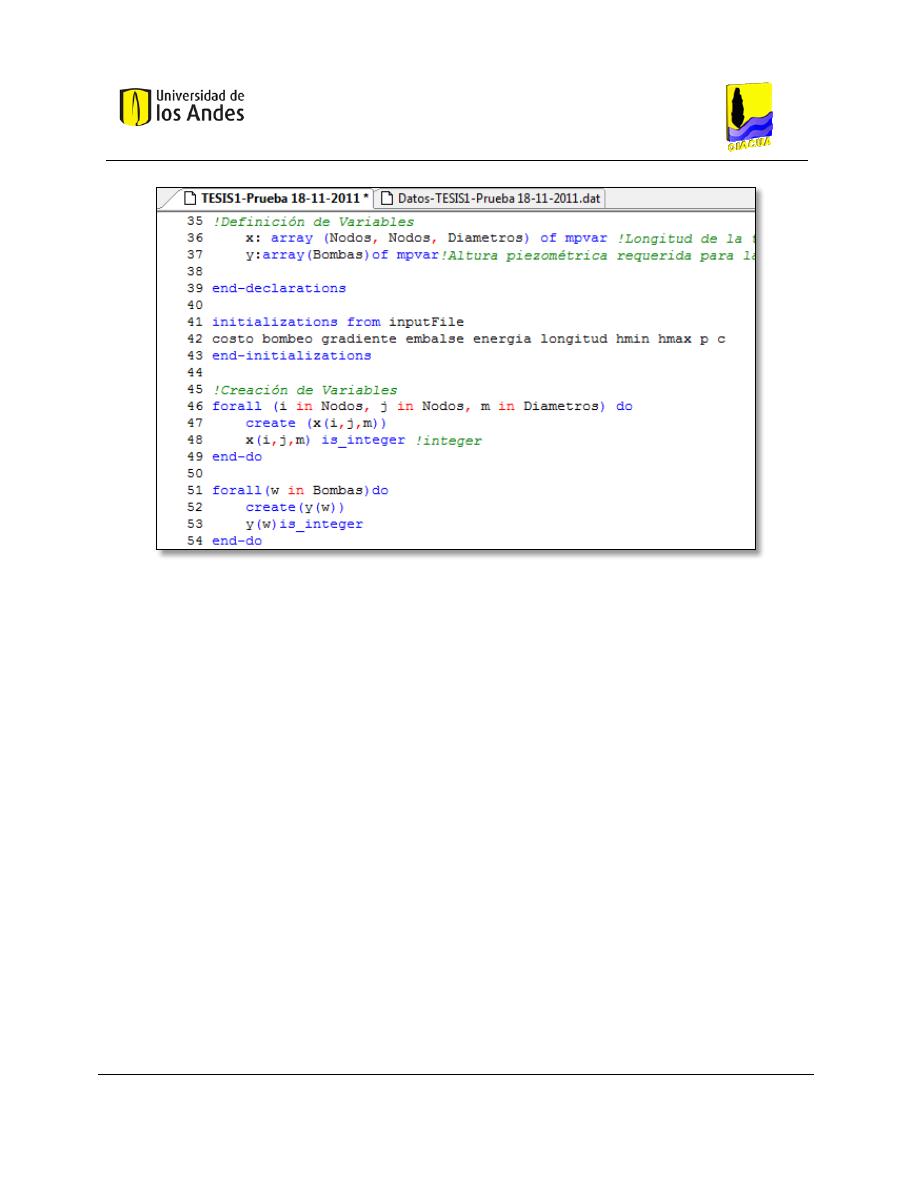
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
74
Figura 6-8. Creación de las variables de decisión en Xpress – IVE.
La solución de la formulación tiene un resultado que minimiza el costo planteado en la función objetivo.
Sin embargo, en la etapa actual del trabajo los costos todavía no corresponden a situaciones reales, por
lo que los resultados obtenidos permiten verificar que la formulación genera resultados, pero no se
puede validar la información todavía. Para que el proceso de validación pueda ser llevado a cabo es
necesario que los parámetros de entrada tengan una consistencia física. Por este motivo, al resultado
obtenido se le aplica una heurística del programa REDES para validarlo.
A continuación se presentan los diámetros obtenidos para la red matriz que considera toda la demanda
del sector hidráulico (para satisfacer el balance de masa), así como el estado de presiones de la red con
el embalse adicional y el cambio de tuberías de la red matriz.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
75
(a)
(b)
Figura 6-9. (a) Red matriz diseñada. (b) Porcentaje de diámetro comercial presente en la red matriz.
Gráfica 6-2. Estado de presiones en los nudos en estado estable para la red de Candelaria una vez se ha
aplicado la metodología.
0
2
4
6
8
10
12
14
16
18
20
0
50
100
150
200
250
300
350
400
450
500
Pr
e
si
ó
n
(
M
.C.A
)
ID de los Nudos
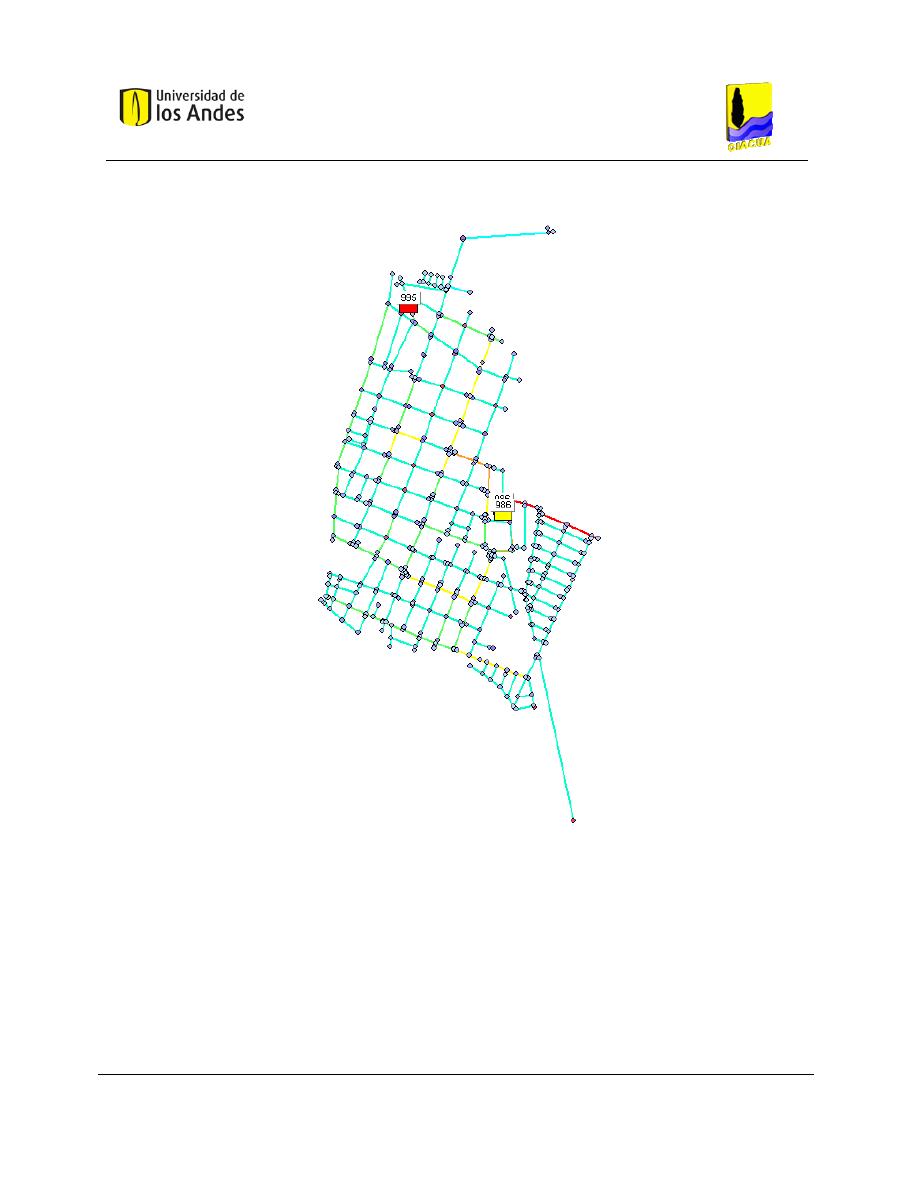
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
76
Figura 6-10. Aplicación de la metodología a la red Candelaria.
Finalmente, la Figura 6-10 presenta la red en su totalidad con el nuevo embalse de tal forma que se
minimizan los costos operacionales de la red. En el Capítulo Análisis de Resultados se presentan en
detalle los costos obtenidos.
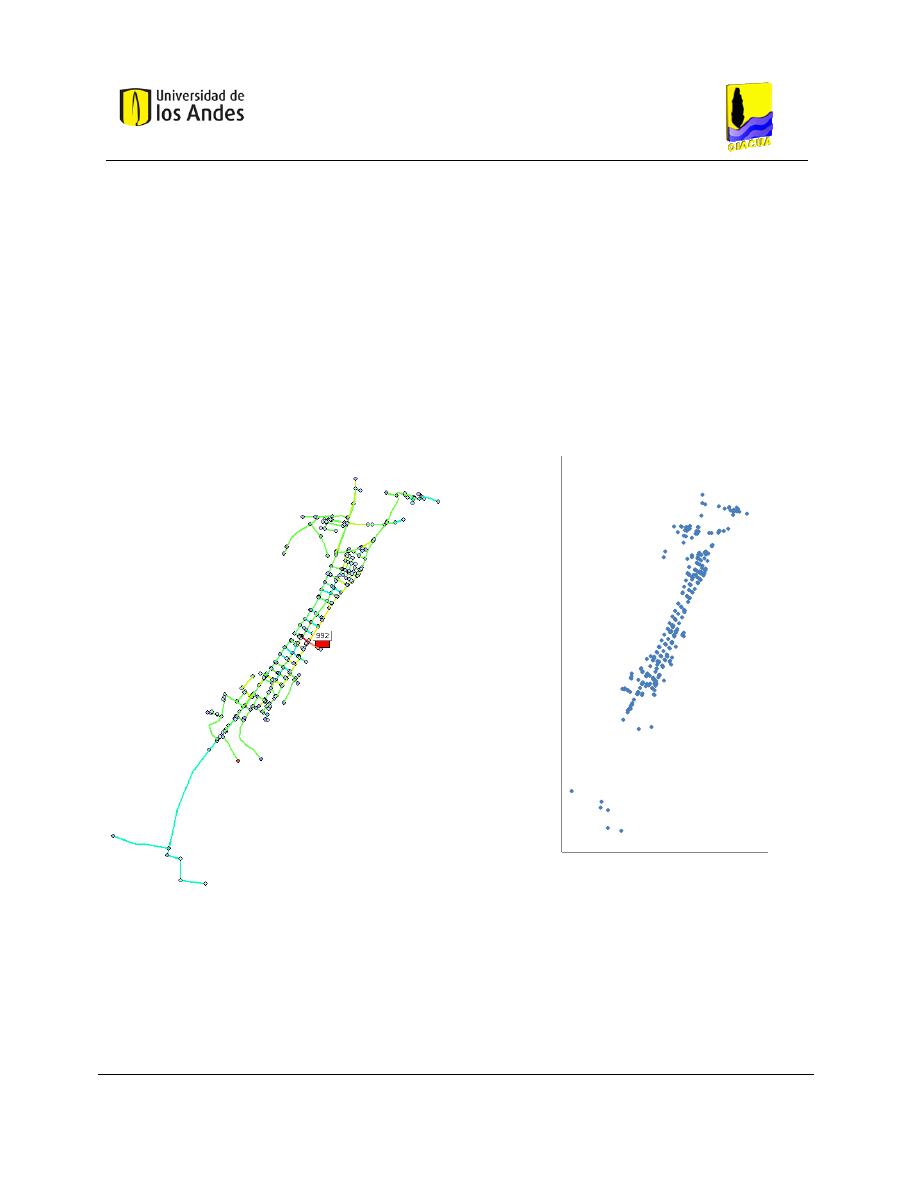
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
77
6.1.2 Metodología aplicada a la red Andalucía Alta
Para la red de Andalucía Alta se realizó el mismo procedimiento que con la red Candelaria. Cada uno de
los pasos se presenta a continuación.
En primera instancia, se utiliza un modelo geográfico de la red en formato MS Excel para la manipulación
de cálculos.
(a).
(b).
Figura 6-11. (a) Red Andalucía Alta graficada mediante el software REDES. (b) Generación de los nudos
de demanda de la RDAP mediante Excel.
950000
950500
951000
951500
952000
952500
953000
953500
954000
954500
955000
1099000
1101000
1103000
Y (m
)
X (m)
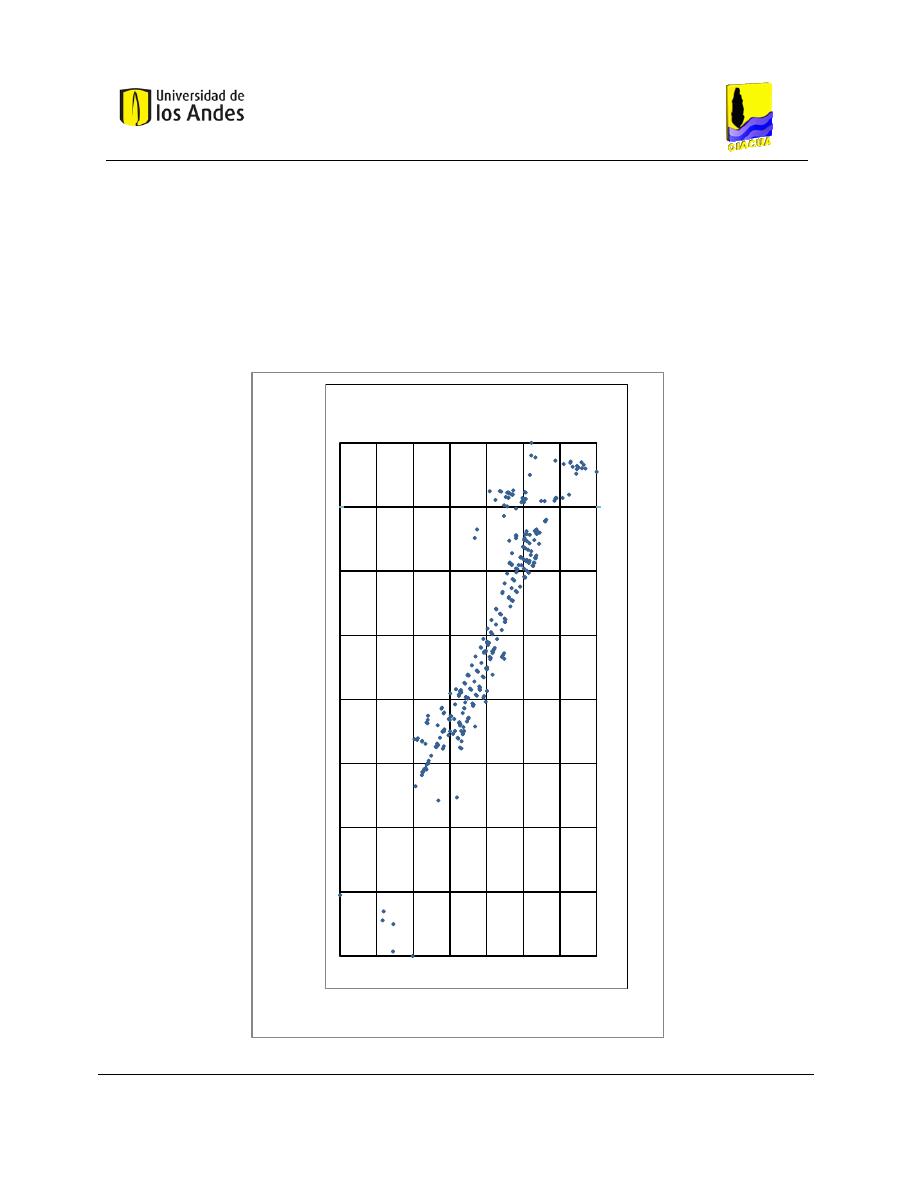
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
78
Una vez que se tiene el modelo en el formato adecuado, es posible realizar la grilla sobre la geografía de
la RDAP. En el caso de Andalucía Alta, el criterio utilizado para determinar la mejor ubicación del
embalse está asociado con costos económicos. Esta condición, simula escenarios en los que no es
factible construir el embalse considerando únicamente la condición hidráulica de densidad de demandas
de consumo. Los costos diferenciales de este escenario corresponden a los diferentes tipos de uso que
tiene el suelo. A continuación se presenta la grilla obtenida.
950000
950500
951000
951500
952000
952500
953000
953500
954000
954500
955000
1099000
1100000
1101000
1102000
1103000
Y (m
)
X (m)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
79
Figura 6-12. Grilla de densidad para la red Andalucía Alta
12
.
De acuerdo con lo expuesto anteriormente, se presentan los costos de cada una de las celdas de la grilla
simulando factores económicos. Estos costos han sido establecidos de forma aleatoria y se distribuyen
uniformemente.
Tabla 6-4. Costos acumulados (L/s) para cada celda de la grilla de densidad de costo económico para la
red de Andalucía Alta.
0
1
2
3
4
5
6
7
0
0
0
0
1274
670
787
6
0
0
0
143
1091 2199
0
5
0
0
0
0
1728
300
0
4
0
0
0
2496 1483
0
0
3
0
0
2046 1734
0
0
0
2
0
0
525
43
0
0
0
1
0
0
0
0
0
0
0
0
75
131
0
0
0
0
0
La Figura 6-13 presenta gráficamente el escenario expuesto en la Tabla 6-4.
12
Esta figura presenta un esquema que conserva las condiciones topológicas de la red original, pero no se encuentra
a escala ni proporción respecto a la red original.
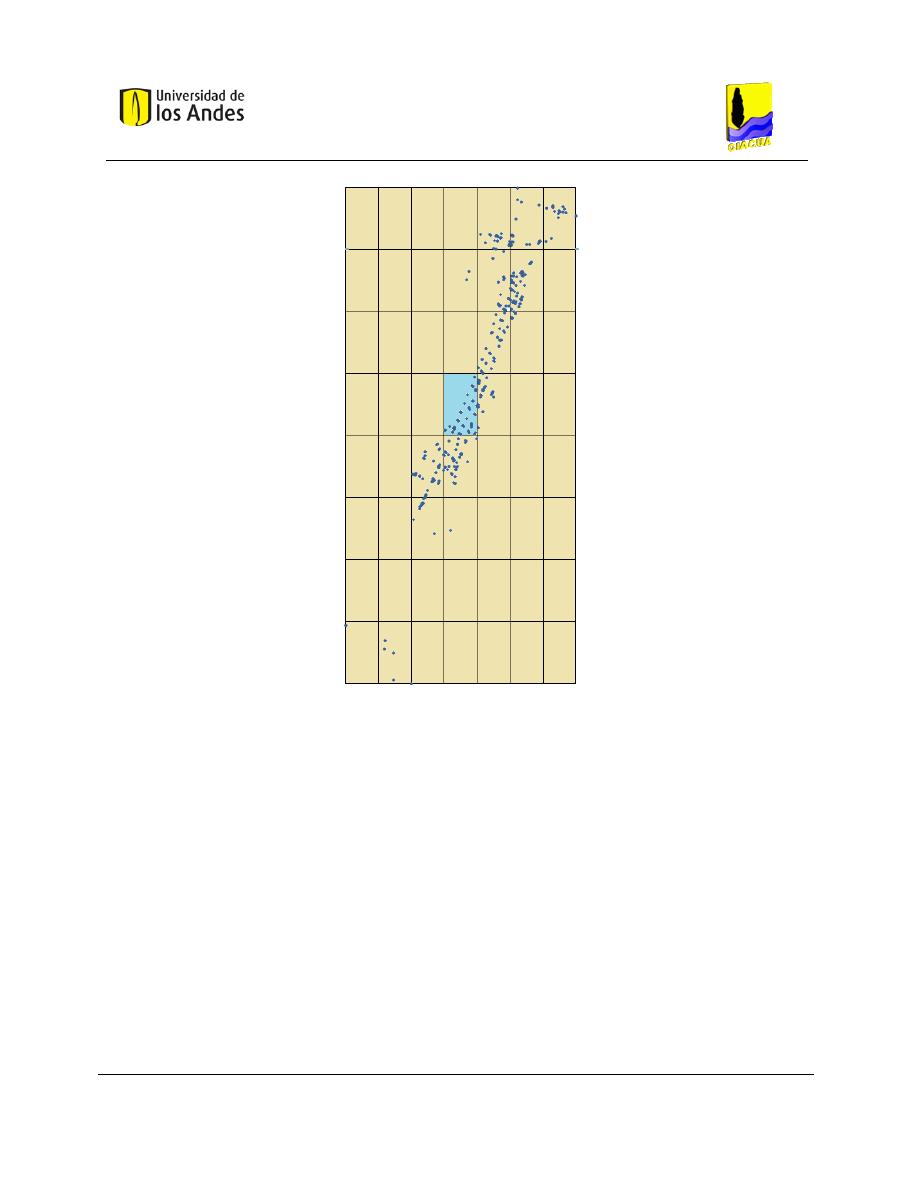
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
80
Figura 6-13. Ubicación del embalse secundario en la celda seleccionada mediante la grilla de densidad
para la red de Andalucía Alta.
En el cuadrante resaltado se encontrará el nuevo embalse. Particularmente para este caso, las
ubicaciones de los embalses (el embalse original y el que fue agregado) no se encuentran muy alejadas
una de la otra, debido a que el criterio considerado en este caso no tiene ningún significado en términos
hidráulicos.
Una vez que se estableció la ubicación del embalse, se procedió a realizar la partición de la RDAP en
diferentes sectores hidráulicos; la idea detrás de esta partición, es que cada embalse (tanto el original
como el que fue agregado) alimente prioritariamente un sector de la red, maximizando la eficiencia
hidráulica del sistema en su totalidad. Por este motivo, se calcula la Potencia Unitaria de cada uno de los
tubos de la red, con el ánimo de identificar aquellas tuberías que representan, en términos hidráulicos,
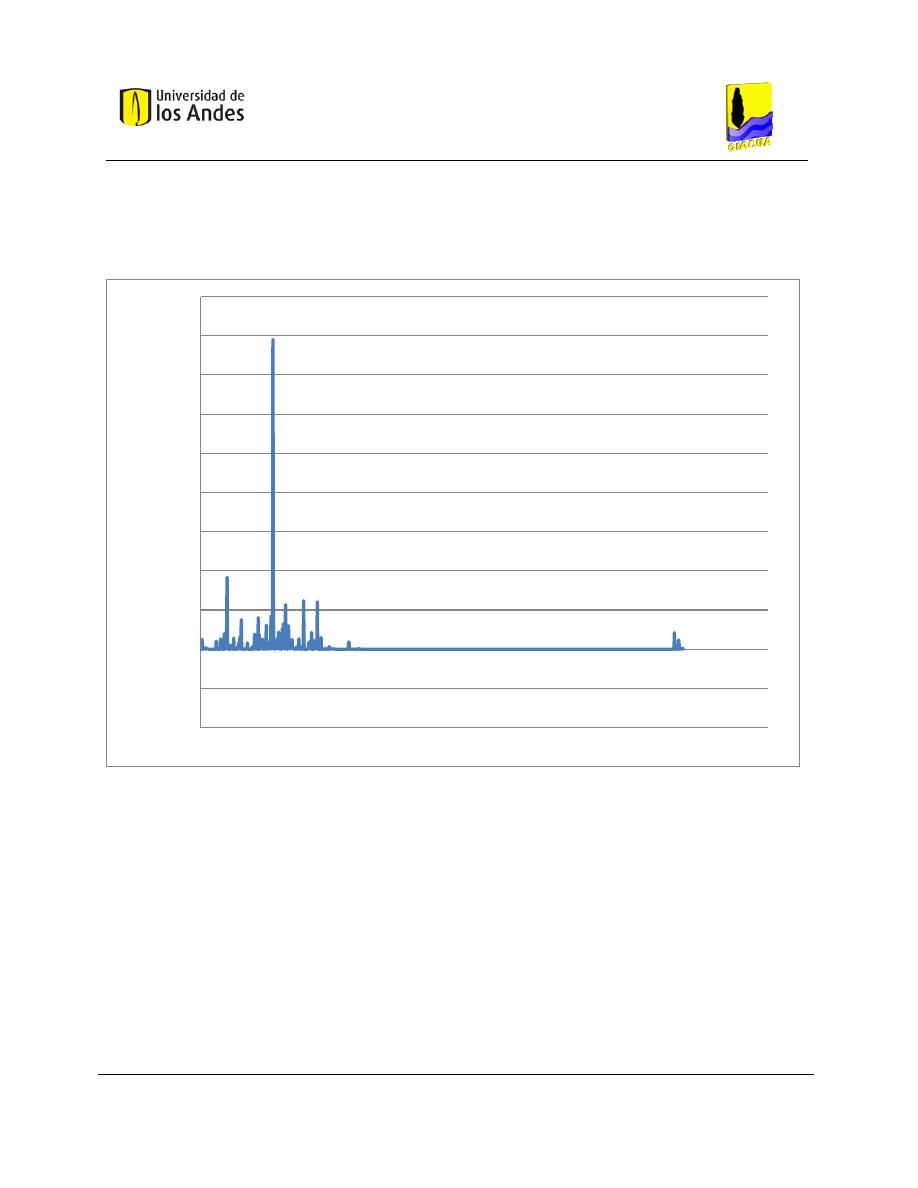
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
81
un punto clave dentro de la operación hidráulica de la red. A continuación, la Gráfica 6-3 presenta el
cálculo de la potencia unitaria para la red.
Gráfica 6-3. Potencia Unitaria para los tubos pertenecientes a la red de Andalucía Alta.
Con la información de la Potencia Unitaria para cada tubo, es posible realizar un mapa de tuberías
críticas dentro de la operación hidráulica del sistema. Mediante el uso de estos mapas gráficos, es
posible identificar posibles particiones de la red. La Figura 6-14 presenta este mapa en el que se muestra
la relevancia hidráulica, en términos de la Potencia Unitaria, de cada uno de los tubos de Andalucía Alta.
-0.004
-0.002
0
0.002
0.004
0.006
0.008
0.01
0.012
0.014
0.016
0.018
0
200
400
600
800
1000
1200
Pot
e
n
ci
a Un
itar
ia
(m
4
/s)
ID de los Tubos
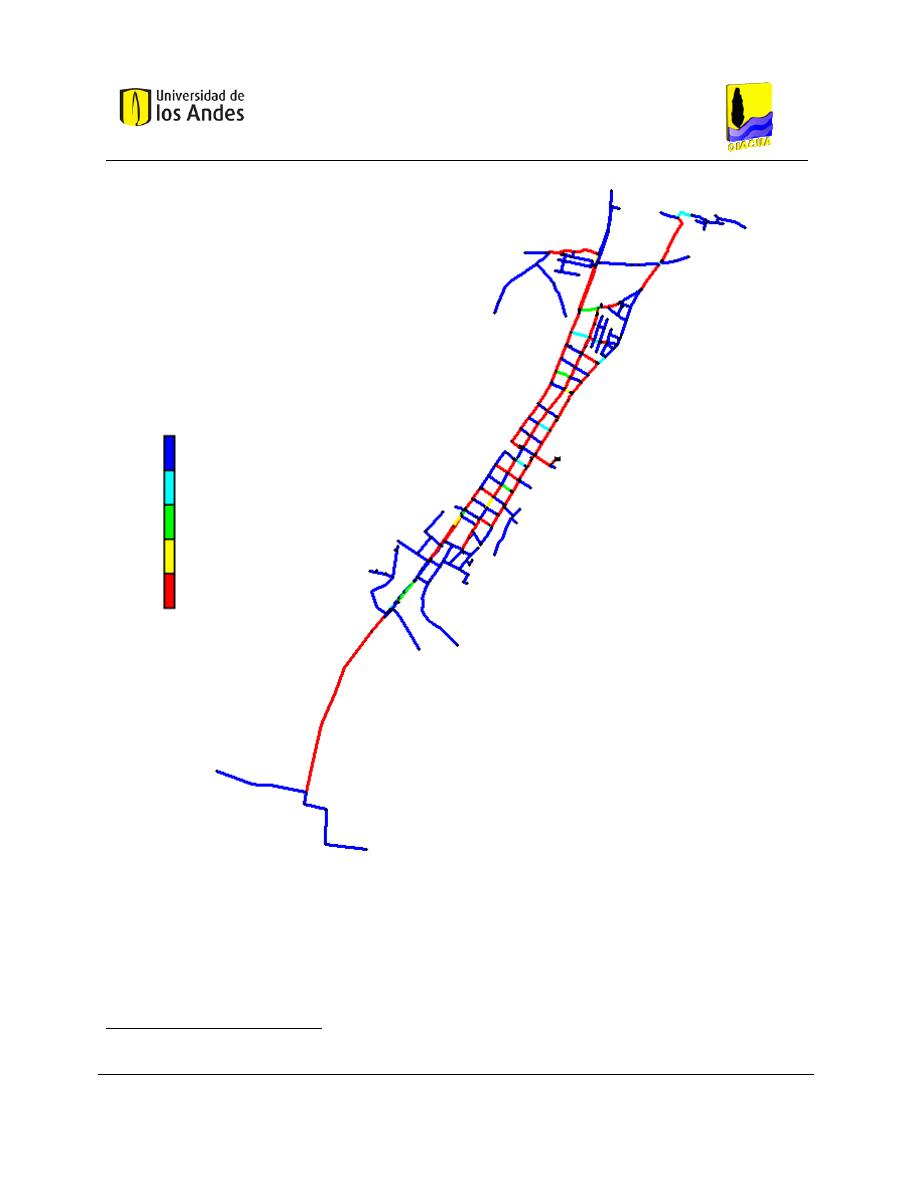
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
82
Figura 6-14. Potencia Unitaria de la red Andalucía Alta
13
.
De acuerdo con las tuberías críticas, se realizó una partición de la red en dos sectores hidráulicos. Cada
sector cuenta con una fuente de abastecimiento (embalse). A continuación se presenta el sector
hidráulico que tiene como fuente de abastecimiento el embalse agregado.
13
La escala de colores indica los colores más cálidos para las tuberías con mayor potencia unitaria.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
83
(a).
(b).
Figura 6-15. (a) Sector hidráulico de la red Andalucía Alta graficada mediante el software REDES para el
que el nuevo embalse tiene influencia. (b) Generación de los nudos de demanda del sector hidráulico
para el cual el nuevo embalse tiene influencia mediante Excel.
Una vez se tiene definido este sector hidráulico, se aplicó el algoritmo de árbol de expansión mínima
para encontrar el sub conjunto de tuberías que pueden cambiar su diámetro para efectos de maximizar
el impacto que tiene la agregación del nuevo embalse. Como en el caso de Candelaria, se establece una
tolerancia
14
en términos de cuánto puede deteriorarse la edad del agua y si la solución no cumple con la
tolerancia establecida es necesario reducir el número de tuberías modificables de la red. A continuación
14
Se utilizó en todos los casos una tolerancia del 3% en el cambio de la edad del agua de alguno de los tubos que
pretende ser modificable.
950000
950500
951000
951500
952000
952500
953000
1099000 1100000 1101000 1102000
Co
o
rd
e
n
ad
a
e
n
Y
(m
)
Coordenada en X (m)
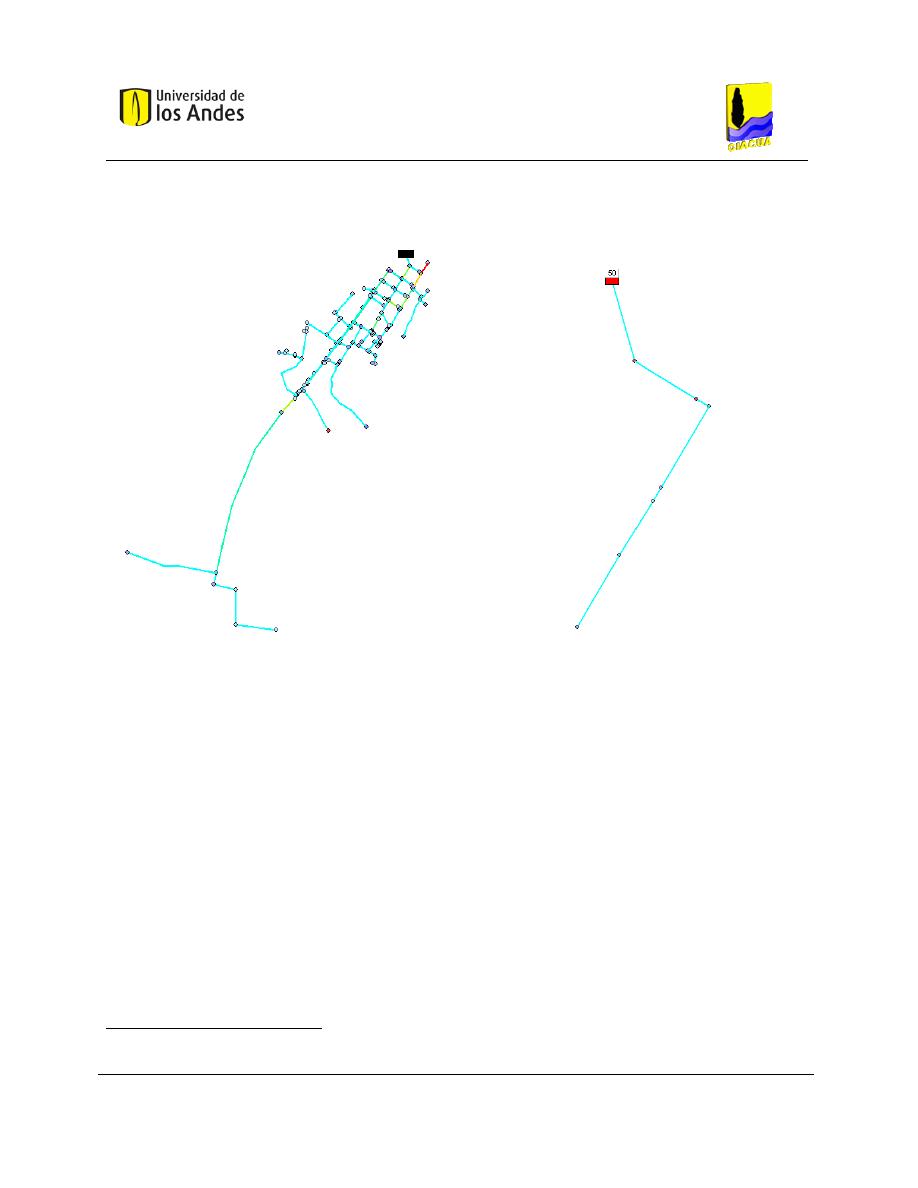
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
84
se presenta el sub conjunto de tuberías que en conjunto conforman la red matriz que se diseñó
posteriormente utilizando programación lineal.
(a).
(b).
Figura 6-16. (a). Sector hidráulico de la red Andalucía Alta. (b). Subconjunto perteneciente al sector
hidráulico definido como red matriz calculado mediante el algoritmo MST
15
.
Utilizando la misma implementación en Xpress IVE que para el caso de la red Candelaria, se aplicó el paso
descrito en el Capítulo 3.5 de la metodología y se obtuvo el siguiente resultado.
15
Las figuras no se encuentran a escala.
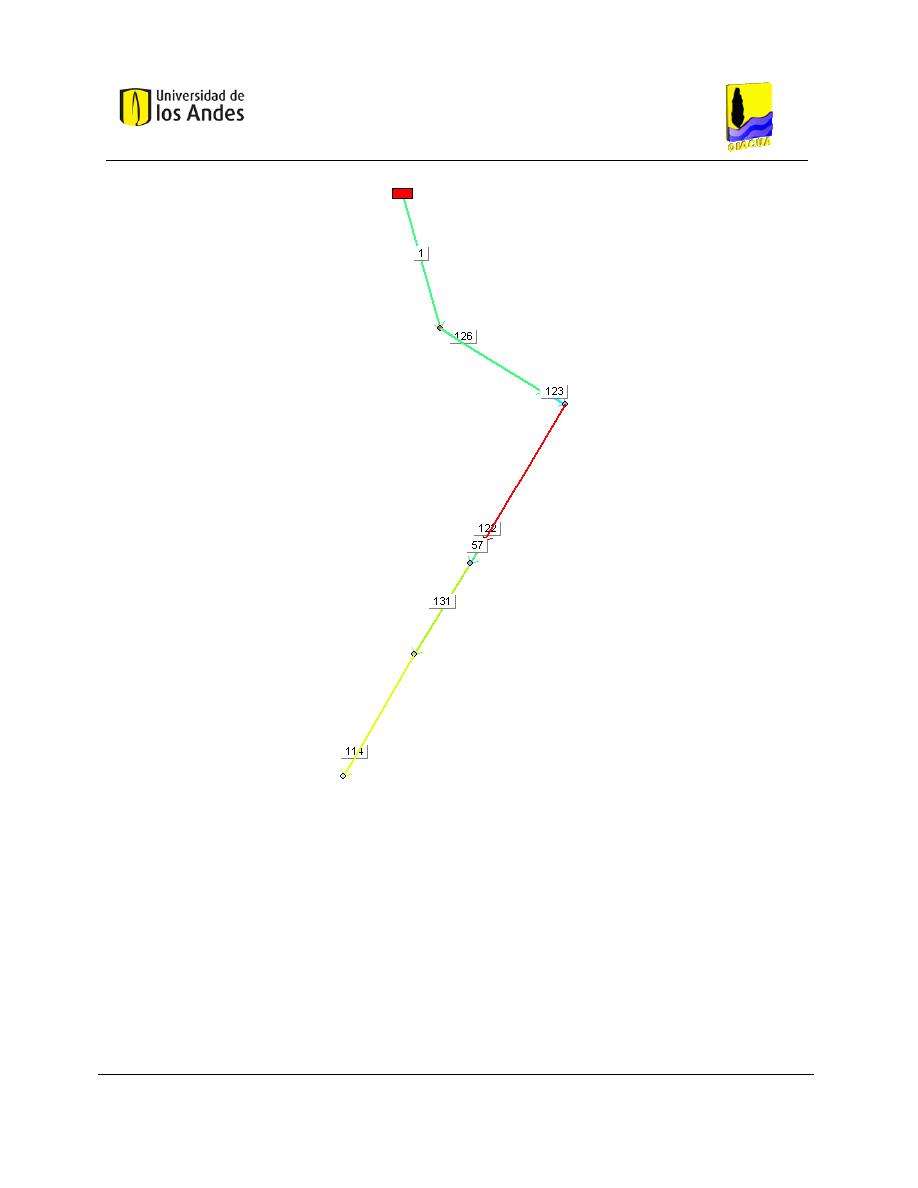
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
85
Figura 6-17. Red matriz diseñada mediante el uso de programación lineal. La información presentada
en los tubos corresponde al diámetro en milímetros.
La red Andalucía Alta completa, con el nuevo embalse integrado y con las modificaciones en los tubos de
la red matriz se presenta a continuación.
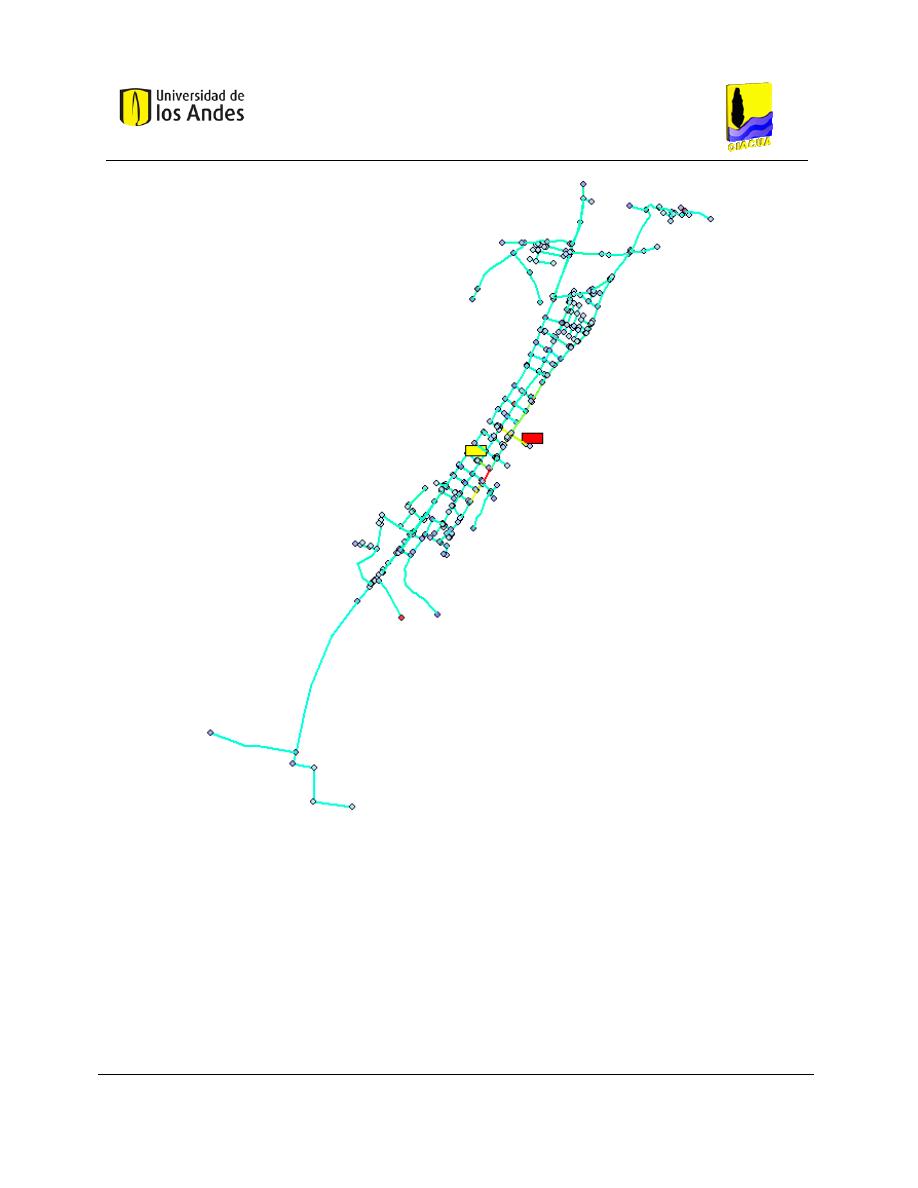
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
86
Figura 6-18. Red Andalucía Alta con el nuevo embalse y diámetros de la red matriz modificados.
El estado general de presión para cada uno de los nudos, luego de aplicar la metodología se presenta a
continuación.
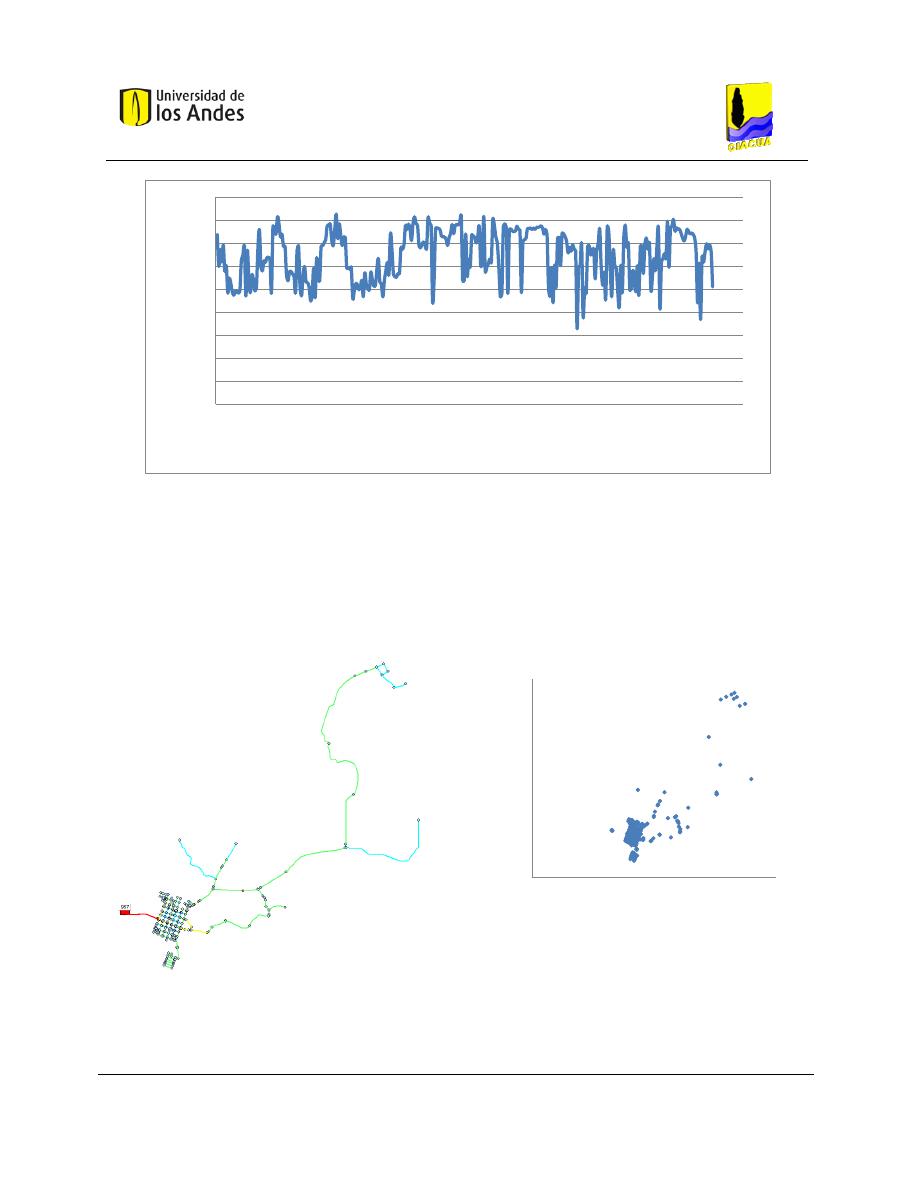
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
87
Gráfica 6-4. Presión de los nudos pertenecientes a la red de Andalucía Alta.
6.1.3 Metodología aplicada a la red Bolívar
Para Bolívar el procedimiento es análogo al realizado anteriormente. Se obtuvo lo siguiente:
(a).
(b).
Figura 6-19. (a) Red Bolívar graficada mediante el software REDES. (b) Generación de los nudos de
demanda de la RDAP mediante Excel.
0
5
10
15
20
25
30
35
40
45
0
50
100
150
200
250
300
350
Pr
e
si
ó
n
(
m
ca)
ID de los nudos
970000
971000
972000
973000
974000
975000
976000
977000
1095000
1100000
1105000
Co
o
rd
e
n
ad
a
e
n
Y
(m
)
Coordenada en X (m)
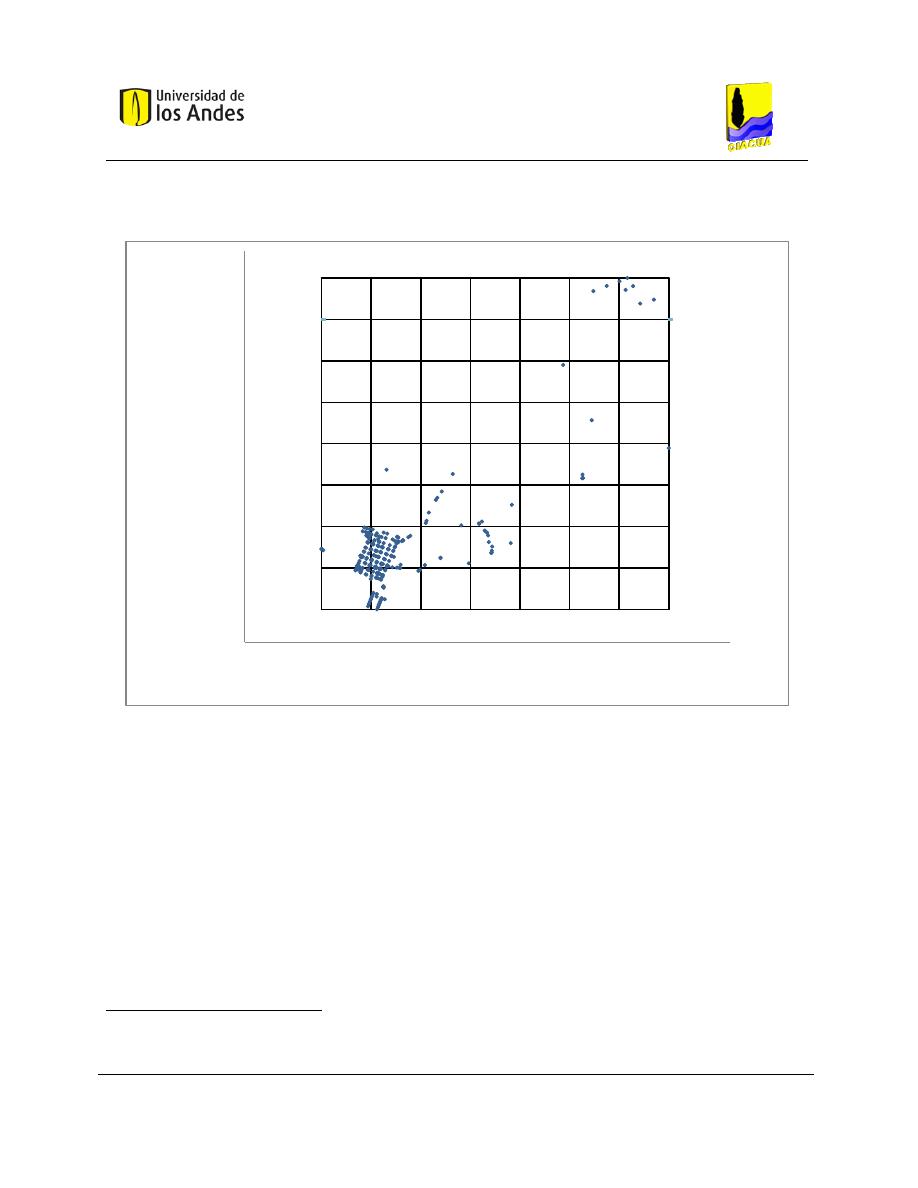
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
88
La grilla en este caso considera la elevación topográfica como criterio de densidad para la ubicación del
embalse.
Figura 6-20. Grilla de densidad para la red Bolívar
16
.
Para estimar la ubicación, se utiliza la siguiente tabla en donde está agregada la información de la
elevación topográfica.
16
Esta figura presenta un esquema que conserva las condiciones topológicas de la red original, pero no se encuentra
a escala ni proporción respecto a la red original.
970000
971000
972000
973000
974000
975000
976000
977000
1097000 1098000 1099000 1100000 1101000 1102000 1103000 1104000 1105000
Y (m
)
X (m)
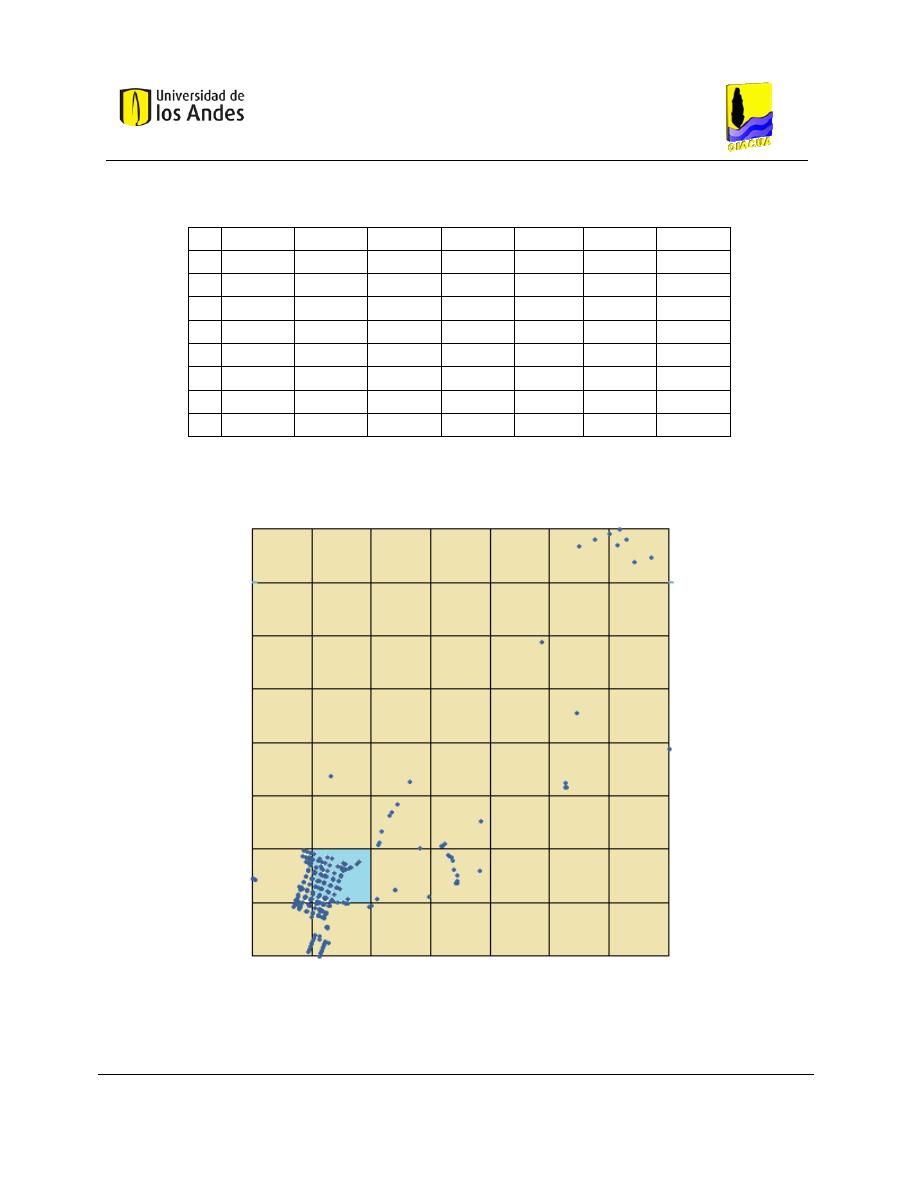
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
89
Tabla 6-5. Costos acumulados (L/s) para cada celda de la grilla de densidad de demanda para la red de
Bolívar.
0
1
2
3
4
5
6
7
0
0
0
0
0 1839.395 5522.585
6
0
0
0
0
0
0
0
5
0
0
0
0 926.311
0
0
4
0
0
0
0
0 925.284
0
3
0 939.298 919.645
0
0 3640.093 912.818
2
0
0 6458.05 3658.067
0
0
0
1 57813.01 100345.3 3679.632 10065.47
0
0
0
0 19511.1 48124.1
0
0
0
0
0
Se presenta gráficamente la información encontrada en la tabla anterior.
Figura 6-21. Ubicación del embalse secundario en la celda seleccionada mediante la grilla de densidad
para la red de Bolívar.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
90
Para calcular el sector hidráulico, se utiliza nuevamente el criterio de potencia unitaria de cada uno de
los tubos de toda la RDAP.
Gráfica 6-5. Potencia Unitaria para los tubos pertenecientes a la red de Bolívar.
Con esta información se puede realizar el mapa de tuberías, para establecer posibles sectores
hidráulicos.
Figura 6-22. Potencia Unitaria de la red de Bolívar
17
.
17
La escala de colores indica los colores más cálidos para las tuberías con mayor potencia unitaria.
-0.01
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0
200
400
600
800
1000
1200
1400
Pot
e
n
ci
a Un
itar
ia
(m
4
/s)
ID de los Tubos
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
91
Se presenta entonces el sector hidráulico que dependerá del nuevo embalse.
(a).
(b).
Figura 6-23. (a) Sector hidráulico de la red Bolívar graficada mediante el software REDES para el que el
nuevo embalse tiene influencia. (b) Generación de los nudos de demanda del sector hidráulico para el
cual el nuevo embalse tiene influencia mediante Excel.
Para definir las tuberías que van a conformar la red matriz, se utilizó el algoritmo MST para encontrar la
siguiente configuración de tuberías.
Figura 6-24. Red matriz para el nuevo embalse en la red Bolívar.
971000
972000
973000
974000
975000
976000
977000
1097500
1100000
1102500
1105000
Co
o
rd
e
n
ad
a
e
n
Y
(m
)
Coordenada en X (m)
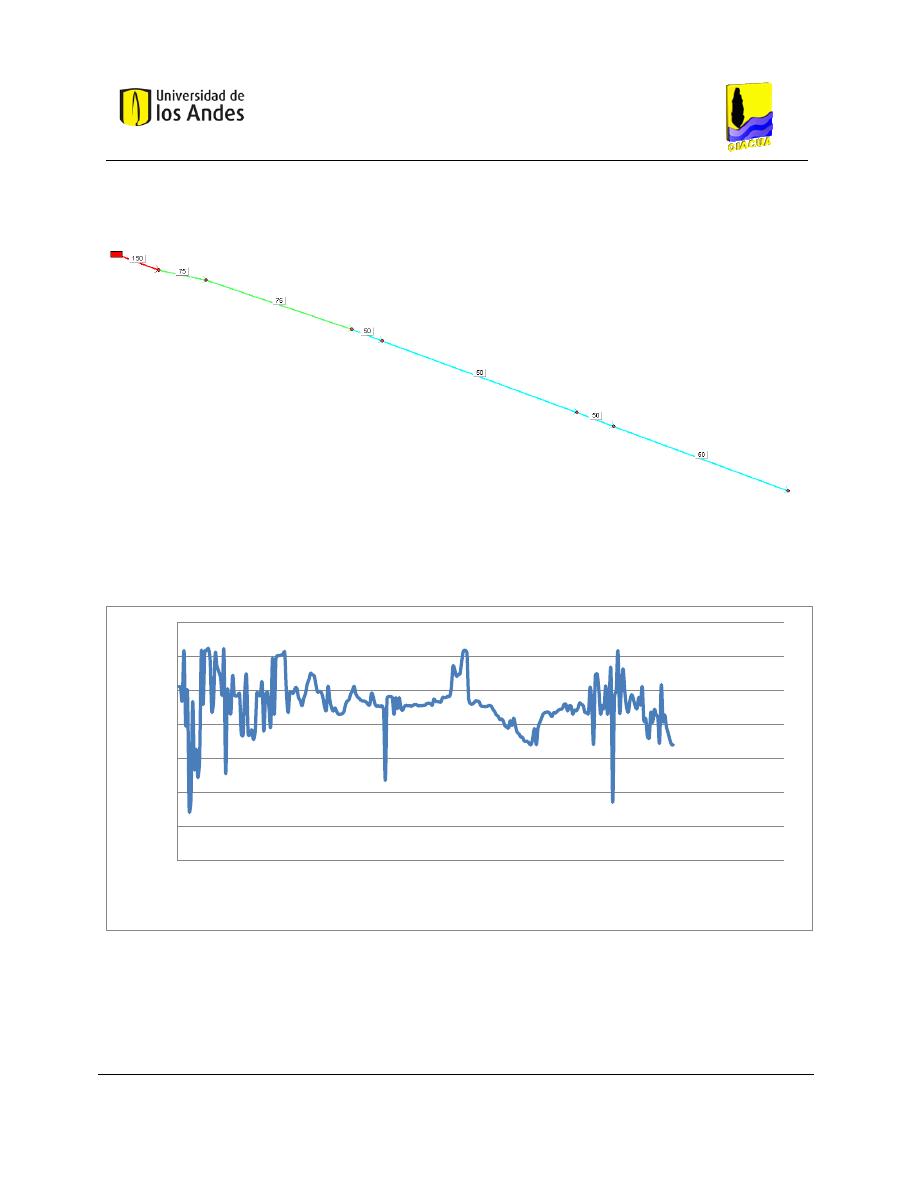
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
92
Una vez se definió la red matriz, se aplicó la formulación lineal descrita en la metodología para diseñar la
misma. Los resultados obtenidos fueron los siguientes:
Figura 6-25. Red matriz diseñada utilizando programación lineal para el nuevo embalse en la red
Bolívar.
Gráfica 6-6. Estado de presiones en los nudos de la red Bolívar con el nuevo embalse.
0
5
10
15
20
25
30
35
0
50
100
150
200
250
300
350
Pr
e
si
ó
n
(
m
ca)
ID de los nudos
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
93
Figura 6-26. RDAP Bolívar, incluyendo el embalse agregado y los tubos cambiados dentro de la red
matriz definida.
Una vez se aplicó la metodología a los tres casos de estudio, se obtuvo un modelo similar al original pero
con modificaciones topológicas y la inclusión de un nuevo embalse. Por esta misma razón, existen
implicaciones económicas que impactan la operación de las diferentes redes probadas. A continuación se
presentan los comentarios más relevantes para cada una de las redes analizadas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
94
7 Análisis de Resultados
La metodología descrita fue aplicada y replicada en diferentes casos de estudio para que se pudieran
establecer calificativos cuantitativos sobre la misma. En este sentido, los resultados pueden considerarse
en dos grandes bloques de análisis. En primer lugar, aquellos resultados que están asociados con las
variables hidráulicas, pues la metodología involucra numerables conceptos en este sentido y propone
cambios topológicos que afectan el desempeño hidráulico del sistema. En segundo lugar, se encuentran
los resultados de la operación hidráulica en un periodo de diseño factible, pues el objetivo principal de
este documento de tesis es proponer y validar una metodología que mejore los costos operaciones de
redes que utilizan SB en comparación con las aproximaciones tradicionales.
De acuerdo con esto, se analizan los resultados en estos dos grandes aspectos, reconociendo que la
interacción de ambos componentes está ligada con la operación real de cualquier RDAP que utilice SB
para satisfacer los requerimientos hidráulicos que deba suplir.
7.1 Comparación hidráulica
En términos de las variables hidráulicas, la metodología es conservadora en el sentido que aumenta
diámetros e incluye nuevos embalses. En este sentido, siempre se tiene como mínimo las condiciones
iniciales de la red sin haber realizado ningún cambio. Como se están incluyendo embalses, el estado de
presiones tiene a aumentar en toda la red, por este motivo la LGH del embalse original se modifica para
reducir este efecto. Si no se realizara esto, se tendría presiones comparativamente muy superiores y el
sistema tendría una redundancia innecesaria.
La metodología también considera el diseño de un subconjunto de tuberías denominado red matriz. Este
diseño, obtiene como variables de entrada los costos asociados (costos en términos de energía disipada
y altura piezométrica requerida) con mover el agua dentro de las tuberías y como variables de salida
genera una configuración de diámetros para las tuberías y una altura piezométrica para el embalse
nuevo. Estas condiciones de salida son válidas de forma exacta para la red matriz, puesto que fue esta la
información que recibió de entrada la formulación. Sin embargo, cuando esta solución se acopla con el
resto de la red la hidráulica de la red matriz interactúa con el resto del sistema, obligando a que cambien
las condiciones de optimalidad.
A continuación, la Tabla 7-1 resume las bondades que tiene implementar embalses secundarios para
reducir la LGH total del sistema.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
95
Tabla 7-1. Análisis de sensibilidad para el número de tubos que conforman la red matriz respecto al
ahorro energético que producen.
LGH total de
embalses
LGH total de embalses utilizando la
metodología
Diferencia Neta
Diferencia
porcentual
(m.c.a.)
(m.c.a.)
(m.c.a.)
%
12 tuberías
64
41
23
36%
10 tuberías
64
44
20
31%
7 tuberías
64
46
18
28%
5 tuberías
64
47
17
27%
3 tuberías
64
48
16
25%
Como se pudo observar en el Capítulo de Resultados, el estado de presiones de todas las redes bajo las
nuevas condiciones cumple condiciones mínimas de operación. En adición, las condiciones de calidad de
agua, en términos generales, han mejorado. Si bien hay tubos para los cuales la calidad de agua
empeoró, en total, la suma de la edad del agua de todos los tubos de la red resulta ser menor.
Gráfica 7-1. Edad del agua en los nudos de la red Candelaria.
La Gráfica 7-1 presenta el estado final de la red en términos de la Edad del Agua en los nudos. Como la
dinámica interna de la red ha sido modificada, es posible que se den casos en los que el agua que fluye
por una tubería cambie de sentido. Todas estas dinámicas cambian las condiciones de calidad de agua de
-10000
-8000
-6000
-4000
-2000
0
2000
4000
6000
8000
10000
1
17
33
49
65
81
97
11
3
12
9
14
5
16
1
17
7
19
3
20
9
22
5
24
1
25
7
27
3
28
9
30
5
32
1
33
7
35
3
36
9
38
5
40
1
41
7
43
3
44
9
Ed
ad
d
e
l Ag
u
a
(s)
ID de los nudos
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
96
todo el sistema. Sin embargo, el tiempo que toda el agua se encuentra dentro de la RDAP resulta ser
menor que el tiempo que permanecía sin aplicar la metodología. En este sentido, la metodología reduce
los tiempos de retención del agua y mejora la calidad de agua.
7.2 Comparación económica
En cuanto a la evaluación económica se encontró que la metodología cumple a cabalidad su objetivo
principal, pues mediante su aplicación, la operación de las RDAP que utilizan SB es más barata,
encontrando ahorros progresivos que pueden alcanzar más de la tercera parte de los costos totales de
operación. Es decir, con la implementación de esta metodología es posible reducir los costos
operacionales en una tercera parte.
Por ejemplo, la Gráfica 7-2 presenta una tendencia de los costos respecto al periodo de retorno con el
que se esté trabajando la operación de la RDAP. En este caso, es evidente que a medida que aumenta el
tiempo de retorno, el componente de costos operativos resulta ser más relevante. Este efecto, repercute
directamente sobre los costos totales, pues la metodología reduce los costos de operación, aumentando
unos costos iniciales por efecto de infraestructura
Gráfica 7-2. Comparación de costos entre a metodología y la operación tradicional.
$-
$1 000 000.00
$2 000 000.00
$3 000 000.00
$4 000 000.00
$5 000 000.00
$6 000 000.00
$7 000 000.00
$8 000 000.00
0
10
20
30
V
PN
(US
$
)
Periodo de Diseño (Años)
Operación
tradicional
Operación
aplicando
metodología
Tesis

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
97
La Tabla 7-2 presenta de manera general el impacto que tiene aumentar el número de tuberías de la red
matriz propuesta en la metodología respecto al ahorro que se obtiene luego de una operación de 25
años. El objeto de esta tabla es presentar las condiciones
Tabla 7-2. Análisis de sensibilidad para el número de tubos que conforman la red matriz respecto al
ahorro económico que produce para la red Candelaria.
Costo Inicial
$ 7 173 625.36
MODELO
COSTO TOTAL
Ahorro Neto
Ahorro porcentual
3
$ 5 402 961.96
$ 1 770 663.40
25%
5
$ 5 261 690.74
$ 1 911 934.62
27%
7
$ 5 203 453.41
$ 1 970 171.95
27%
10
$ 4 996 279.51
$ 2 177 345.85
30%
12
$ 4 652 545.64
$ 2 521 079.71
35%

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
98
8 Conclusiones generales
Este documento presenta los comentarios finales de un trabajo de investigación de un año académico,
en el que a partir de un fundamento teórico y un recuento académico de varias aproximaciones al
problema, se ha definido una metodología general que corresponde con el objetivo general planteado. A
partir del planteamiento de esta metodología, que involucra múltiples técnicas, conceptos e ideas de
diversos campos del conocimiento, se pudo aplicar sobre diferentes RDAP que existen y operan en la
realidad. En este sentido, los resultados de esta investigación permitirían a futuro tomar decisiones
prácticas y de gran valor para la sociedad.
En cuanto a la aproximación realizada en esta investigación, el aporte que ofrece esta propuesta es que
no considera independientes el problema de operación de las bombas dentro de la red y la hidráulica del
sistema. Tradicionalmente se tiene que parte de las restricciones que deben cumplir las estaciones de
bombeo radican en condiciones hidráulicas límites para el funcionamiento de la red. Sin embargo, las
variables de decisión nunca están ligadas con el desempeño hidráulico de la red. La propuesta
innovadora que tuvo este trabajo involucra un nuevo concepto en el que mediante cambios hidráulicos
en toda la red es posible disminuir la cantidad de bombeo requerido, y por ende, una disminución en los
costos de la operación y mantenimiento de las bombas.
En general, esta investigación buscó ser el punto de encuentro de múltiples técnicas de investigación
para el beneficio particular de los sistemas de RDAP y su operación en un contexto económico de
factibilidad y mejoramiento en cuanto a lo que su rentabilidad se refiere.
La hidráulica alrededor de los sistemas de distribución de agua potable, al igual que el manejo de las
estaciones de bombeo, son un marco ampliamente estudiado y entendido mediante el uso de
ecuaciones físicamente basadas. Sin embargo, incluir la variable de los costos asociados con la operación
ha introducido un nuevo elemento de análisis. En este sentido, se puede decir que el problema de la
operación de los SB para minimizar los costos inherentes al uso energético de las bombas es un
problema ampliamente estudiado y resuelto.
Todas las aproximaciones para la optimización de los SB consideran como parámetro de entrada la
cantidad de agua que debe ser bombeada al sistema. En ningún caso se consideran variaciones
topológicas a las RDAPs para disminuir este parámetro.
Las aproximaciones tradicionales incluyen variaciones sobre la demanda de agua que el sistema debe
suplir en un punto de operación determinado, pero no involucran en las modelaciones criterios
hidráulicos que permitan disminuir el uso de bombas.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
99
En la literatura existen amplios modelos de optimización en la operación puntual de SB (operación de las
bombas pertenecientes al SB para reducir los costos económicos). Sin embargo, es muy reducida la
información en donde se validen esto modelos con alternativas igualmente válidas, como lo son las
propuestas en este documento de tesis (metodología planteada).
La metodología propuesta en esta investigación resulta del encuentro de dos conceptos ampliamente
estudiados pero de forma independiente: la hidráulica de las RDAP y la optimización de recursos
económicos en los SB. Tradicionalmente, al ser estudiados de forma independiente, no resultaba clara la
interacción que estos dos elementos tienen en el funcionamiento general de los sistemas de acueducto,
motivo por el cual se utilizaron ambos conceptos como marco fundamental de la investigación.
La metodología prefiere el uso de algoritmos de solución exactos por encima de los heurísticos. Sin
embargo, utiliza formulaciones lineales sobre sub conjuntos pequeños del sistema, reduciendo el
tamaño del problema y evitando la situación de demoras en el cálculo computacional por efecto del
tamaño de la RDAP que esté siendo analizada.
Los análisis de resultados deben incluir un análisis de sensibilidad respecto a las condiciones de bombeo
mínimas con la que una RDAP puede operar. Sin importar el número de embalses, siempre existen
bombeos asociados con llevar el agua hasta estos puntos, por lo que siempre hay un factor coligado con
el bombeo. Es posible cuantificar la influencia sobre los costos y el número de embalses adicionales,
encontrando situaciones óptimas de funcionamiento.
La validación de los resultados debe realizarse en otras redes reales, de esta forma es posible analizar el
desempeño de la metodología frente a cambios en la topología de las RDAPs, cambios sustanciales en el
tipo de usuarios que conforman la red y su ubicación geográfica dentro de la misma y condiciones
hidráulicas particulares.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
100
9 Recomendaciones para trabajos futuros
La metodología desarrollada en este trabajo de tesis se enfocó en optimizar la operación hidráulica de
RDAP existentes a partir de un elemento que tradicionalmente no es considerado como variable de
decisión como lo es la inclusión de embalses secundarios dentro de sistemas previamente establecidos.
Sin embargo, un ejercicio análogo puede ser desarrollado para el caso del problema del diseño de RDAP,
pues comúnmente este problema está asociado con la configuración de diámetros que suplan las
condiciones hidráulicas bajo un mínimo costo. Entender el problema del diseño solamente como la
configuración de diámetros para satisfacer unas necesidades hidráulicas puede resultar incorrecta, pues
en el manejo integral de sistemas de distribución de agua existen otras variables que pueden
considerarse y enriquecer las soluciones definitivas.
En el caso de la aplicación de formulación lineal, las técnicas de solución implementadas son basadas en
algoritmos matemáticos que consideran las características de estructura del problema. Se modela una
situación particular y se le aplica un modelo matemático que pretende ajustar de manera óptima los
niveles de servicio de acuerdo a unas limitaciones dadas. Sin embargo, el problema modela una situación
hidráulica sin tener en cuenta ningún cálculo explícito en esta área. Si bien es cierto que las
ponderaciones de los arcos se realizan con el cambio en el Índice de Resiliencia o por la Potencia
Unitaria, hacer falta incluir otro tipo de variables hidráulicas que permitan una aproximación más afín. Es
por esto que los resultados obtenidos mediante esta metodología deben ser estudiados y analizados
desde una perspectiva hidráulica adecuada que regule las condiciones propias de cada red. En esta
medida, los resultados son una base para posibles diseños. No debe entonces tomarse como un único
camino y debe incluirse dentro de un conjunto de resultados.
Es posible considerar los resultados obtenidos como una ruta que muestra la ubicación de cada una de
las tuberías que conforma la red. Una vez se tiene esta ruta, es posible aplicar un diseño basado en AG o
Superficie Óptima de Presiones para obtener el diámetro de cada una de las tuberías.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
101
10 Bibliografía
Abbasi, E. &. (2010). An MILP-based formulation for minimizing pumping energy costs of oil pipelines:
Beneficial to both the environment and pipeline companies. Energy Systems, 393-416.
Araque, D. A. (2006). Optimización de Redes de Acueducto con el fin de Uniformizar el Estado de
Presiones. Tesis de maestría, Universidad de los Andes, Colombia, Bogota.
Araque, D. A. (2006). Optimización de Redes de Acueducto con el fin de Uniformizar el Estado de
Presiones. Tesis de Maestría, Universidad de los Andes, Bogotá.
Bazaraa, M. S. (2010). Linear programming and network flows.
Bernal, A. (2008). Diseño optimizado de ampliaciones de redes de distribución utilizando los conceptos de
Potencia y Resiliencia en la red. Tesis de Maestría, Universidad de los Andes, Bogotá.
Bernal, A. (2008). Diseño optimizado de ampliaciones de redes de distribución utilizando los conceptos de
Potencia y Resiliencia en la red. Tesis de Maestría, Universidad de los Andes, Bogotá.
Borzì, A., & Cutore, P. &. (2009). A methodology for the evaluation of optimal pumping system operation
through synthetic indices. Proceedings of the 10th Annual Water Distribution Systems Analysis
Conference, WDSA 2008, 532-542.
Boulos, P. F., Wu, Z., Orr, C. H., Moore, M., & Hsiung, P. &. (s.f.). Optimal pump operation of water
distribution systems using genetic algorithms.
CIACUA. (2006). Programa Redes. Bogotá: Universidad de los Andes.
Dantzig, G. B. (January de 2002). Linear Programming. Operations Research. Department of Management
Science and Engineering, 42-47.
Eiger, G., & Shamir, U. &.-T. (1994). Optimal design of water distribution networks. Water Resources
Research, 2637-2646.
Frenning, L. (2001). Pump life costs: A guife to LCC analysis for pumping systems. Hydraulic institute.
Hydraulics Institute, A. N. (1994). American Standard for Centrifugal Pumps for Nomenclature,
Definitions, Applications and Operation.
Jowitt, P. W. (1992). Optimal pump scheduling in water-supply networks. Journal of Water Resources
Planning and Management, 406-422.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
102
Lavric, V., & Iancu, P. &. (2005). Genetic algorithm optimisation of water consumption and wastewater
network topology. Journal of Cleaner Production, 13, 1395-1405.
López-Ibáñez, M., & Prasad, T. D. (2008). Ant colony optimization for optimal control of pumps in water
distribution networks. Journal of Water Resources Planning and Management, 337-346.
Mays, L. W. (1999). Hydraulic Design Handbook. New York: McGraw-Hill.
Mays, L. W., & Tung, Y.-K. (1992). Hydrosystems Engineering and Management. MC Graw Hill.
McCormick, G. &. (2003). Optimal pump scheduling in water supply systems with maximum demand
charges. Journal of Water Resources Planning and Management, 372-379.
Medaglia, A. (2008a). Introducción al Modelado. Presentación en clase, Universidad de los Andes,
Bogotá.
Naranjo Faccini, G. A. (2008). Metodología para la sectorización de redes existentes de distribución de
agua potable. Bogotá: Universidad de los Andes.
Naranjo, G. A., & Saldarriaga, J. G. (2007). Metodología para la sectorización de redes existentes de
distribución de agua potable. Artículo de Tesis, Centro de Investigación en Acueductos y
Alcantarillados de la Universidad de los Andes - CIACUA. Universidad de los Andes, Bogotá.
Nitivattananon, V., & Sadowski, E. C. (1996). Optimization of Water Supply System Operation. Journal of
water resources planning and management.
Ochoa Rodríguez, S. (2008). DISEÑO OPTIMIZADO DE REDES DE DISTRIBUCIÓN DE AGUA POTABLE CON
BASE EN EL CONCEPTO DE POTENCIA HIDRÁULICA. Bogotá.
Palumbo, G., & Pappalardo, D. &. (2002). Charge-pump circuits: Power-consumption optimization. IEEE
Transactions on Circuits and Systems I: Fundamental Theory and Applications, 1535-1542.
Pasha, M. F. (2009). Optimal pump scheduling by linear programming. Proceedings of World
Environmental and Water Resources Congress 2009 - World Environmental and Water Resources
Congress 2009: Great Rivers, 395-404.
Pezeshk, S. &. (1996). Adaptive search optimization in reducing pump operating costs. Journal of Water
Resources Planning and Management, 57-63.
Rao, Z. F., & Wicks, J. &. (2007). Optimising water supply and distribution operations. Proceedings of the
Institution of Civil Engineers: Water Management, 95-101.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Cambio óptimo de la topología de una red con el fin de reducir
los costos operacionales de redes por bombeo
MIC 201210 08
Sergio Andrés García Velandia
Proyecto de Grado de Magíster en Ingeniería Civil
103
Richardson, S. J. (2011). Modeling Tool to Support Budgeting and Planning Decisions for Pump Overhauls.
Journal of Water Resources Planning and Management, 327-334.
Rodríguez, D. (2007). Cómo afecta el Conocimiento del Catastro de la Res de Distribución de Agua Potable
el Comportamiento del Modelo Hidráulico y los Resultados de Calibración. Tesis de Maestría,
Universidad de los Andes, Bogotá.
Saldarriaga, J. G. (2007). HIDRÁULICA de TUBERÍAS ABASTECIMIENTO DE AGUA, REDES, RIEGOS. (L. J.
Buitragro, Ed.) Bogotá, D.C, Colombia: Alfaomega.
Sotelo, A., Basulado, J., & Doldán, P. &. (s.f.). Algoritmos evolutivos multiobjetivo combinados para la
optimización de la programación de bombeo en sistemas de suministro de agua .
Todini, E. (Septiembre de 2000). Looped water distribution networks design using a resilience index
based heuristic approach. UrbanWater.
Ulanicki, B., & Kahler, J. &. (2007). Dynamic optimization approach for solving an optimal scheduling
problem in water distribution systems. Journal of Water Resources Planning and Management,
23-32.
van Zyl, J. E., & Savic, D. A. (2004). Operational optimization of water distribution systems using a hybrid
genetic algorithm. Journal of Water Resources Planning and Management, 160-170.
Velasco, N. M. (2006b). Problema de flujo con costo mínimo. Presentación de la clase Flujo en Redes,
Departamento de Ingeniería industrial. Universidad de los Andes, Colombia, Bogotá.
Villalba, G. (2004). Algoritmos de optimización Combinatoria aplicados al diseño de redes de distribución
de agua potable. Tesis de Maestría, Universidad de los Andes, Bogotá.
Wu, Z. Y. (2009). Scalable parallel computing framework for pump scheduling optimization. Proceedings
of World Environmental and Water Resources Congress 2009 - World Environmental and Water
Resources Congress 2009: Great Rivers, 430-440.
Yu, G., & Powell, R. S. (1994). Optimized pump scheduling in water distribution systems. Journal of
Optimization Theory and Applications, 463-488.
